Автор: Кристиан Г.
Теги: аналитическая химия физическая химия химическая физика химия
ISBN: 978-5-94774-389-0
Год: 2009
Текст
ЛУЧШИЙ ЗАРУБЕЖНЫЙ УЧЕБНИК
АНАЛИТИЧЕСКАЯ
ХИМИЯ
ANALYTICAL CHEMISTRY
Sixth Edition
Gary D. Christian
University of Washington
JOHN WILEY I SONS. INC.
ЛУЧШИЙ ЗАРУБЕЖНЫЙ УЧЕБНИК
Г. КРИСТИАН
АНАЛИТИЧЕСКАЯ
ХИМИЯ
В двух томах
1
Перевод с английского
канд. хим. наук А. В. Гармаша,
канд. хим. наукН. В. Колычевой,
канд. хим. наук Г. В. Прохоровой
Вступительная статья
академика РАН Ю. А. Золотова
Москва
БИНОМ. Лаборатория знаний
2009
УДК 543
ББК 24.5я73
К82
Кристиан Г.
К82 Аналитическая химия : в 2 томах. / Г. Кристиан ; пер. с
англ. — М. : БИНОМ. Лаборатория знаний, 2009. — (Лучший
зарубежный учебник).
ISBN 978-5-94774-389-0 (БИНОМ. ЛЗ)
ISBN 0-471-21472-8 (англ.)
Т. 1. — 623 с.: ил.
ISBN 978-5-94774-390-6
В учебном издании, написанном американским ученым и талант-
ливым преподавателем, методически выдержанно изложен универси-
тетский учебный курс по аналитической химии, причем рассмотрены
новейшие методы анализа, а также анализ важнейших для современ-
ной аналитической практики объектов (клинический и экологический
анализ). В заключительном разделе приведено 40 лабораторных работ.
В русском издании выходит в двух томах. В т. 1 вошли гЛ. 1-15.
Для студентов вузов, изучающих аналитическую химию, аспирантов
и преподавателей.
УДК 543
ББК 24.5я73
Первый тираж издания осуществлен при финансовой поддержке
Российского фонда фундаментальных исследований по проекту № 06-03-46018
Учебное издание
Серия: «Лучший зарубежный учебник»
Кристиан Гэри
АНАЛИТИЧЕСКАЯ ХИМИЯ
В двух томах
Том 1
Ведущий редактор канд. хим. наук Т. И. Почкаева
Редактор канд. хим. наук Д. К. Новикова
Художник С. Инфантпэ, Н. А. Новак. Художественный редактор О. Г. Лапко
Компьютерная верстка: Л. В. Катуркина
Подписано в печать 01.12.08. Формат 70x100/16.
Усл. печ. л. 50.70. Тираж 1700 экз. Заказ3771.
Издательство «БИНОМ. Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3
Телефон: (499) 157-5272, e-mail: binom@Lbz.ru, http://www.Lbz.ru
ISBN 978-5-94774-390-6 (Т. 1)
ISBN 978-5-94774-389-0 (БИНОМ. ЛЗ)
ISBN 0-471-21472-8 (англ.)
Copyright © 2004 John Wiley & Sons, Inc.
All rights reserved.
Authorized Translation from
the English language edition
published by
John Wiley & Sons, Inc.
© Перевод, оформление,
БИНОМ, Лаборатория
знаний, 2008
Об авторе
Профессор Гэри Кристиан — известный американский ученый-аналитик и вы-
дающийся педагог. Он — автор многих научных публикаций по проточно-ин-
жекционному анализу, спектроскопическим и электрохимическим методам. Его
научные заслуги отмечены многими почетными наградами, в том числе высшей
наградой Американского химического общества (ACS) в области аналитиче-
ской химии — премией Фишера, премией отделения аналитической химии ACS
за выдающиеся достижения в области преподавания, золотой медалью журнала
Taianta и др. Кристиан избирался председателем отделения аналитической хи-
мии ACS, главным редактором международного журнала по аналитической хи-
мии Taianta, членом редколлегии многих других журналов.
Гэри Кристиан — автор нескольких учебников. Наибольшее признание из
них получил учебник «Аналитическая химия», который выдержал в США уже
шесть переизданий, начиная с 1971 г. В американских университетах этот учеб-
ник используют чаще, чем другие учебники по аналитической химии. Рецензии
на него были опубликованы в ряде журналов — все положительные.
Все это дало основание осуществить перевод книги на русский язык. Разу-
меется, было использовано последнее, шестое издание. Хотя после выхода аме-
риканского учебника прошло несколько лет, я уверен, что для хорошего
учебника по фундаментальной учебной дисциплине этот срок некритичен.
Содержание учебника, я думаю, смогут оценить сами читатели, прежде все-
го преподаватели. Конечно, как и в любом другом переводном учебнике приве-
денный в этой книге материал не вполне соответствует принятым в наших
высших учебных заведениях программам курса аналитической химии. Зато
учебник Кристиана чрезвычайно современен. В учебнике активно используются
компьютерные технологии, описаны методы работы в современной аналитиче-
ской лаборатории, приведены методики анализа важнейших объектов, включа-
ющих и биологические жидкости, и объекты экоанализа.
Переводные книги всегда способствуют повышению уровня преподавания
в нашей стране: они используются преподавателями для актуализации учебной
программы и методики преподавания, отдельные их разделы изучаются студен-
тами, аспирантами и молодыми учеными для знакомства с новыми методами и,
конечно же, они очень интересны для отечественных авторов учебных изданий
как путеводитель в их творческой работе. Опытные преподаватели вузов по-
мнят, что в 1970-е годы было переведено сразу несколько учебников и учебных
пособий. Наиболее известные из них — это двухтомник «Основы аналитиче-
ской химии» (авторы Скуг Д., Уэст Д. — М.: Мир, 1979) и «Количественный
6
ОБ АВТОРЕ
анализ» (авторы Фритц Дж., Шенк Г. — М.: Мир, 1978). Даже в наши трудные
времена удалось издать европейский учебник по аналитической химии (Пер. с
англ.; в 2-х т.; под ред. Р. Кельнера и др. — М.: Мир, 2005). Вероятно, подобным
образом будет «работать» и книга Г. Кристиана.
Я с большим удовольствием представляю этот перевод российским читате-
лям. Мне особенно приятно это сделать, поскольку я давно знаю автора лично,
выполнял с ним совместный проект по проточному анализу, бывал в его лабора-
тории в Сиэтле, да и в его доме; мы многократно встречались на международных
конференциях. Профессор Кристиан рад был узнать о подготовке русского изда-
ния его популярного учебника.
Мне также приятно осознавать, что перевод этой всеобъемлющей книги
был осуществлен большей частью сотрудниками моей кафедры: канд. хим. наук
А. В. Гармашом (введение, гл. 1-5, 9-11, 18, 23, практические работы, приложе-
ния), совместно канд. хим. наук Н. В. Колычевой и А. В. Гармашом (гл. 6-8),
канд. хим. наук Г. В. Прохоровой (гл. 12-15), канд. хим. наук А. В. Ивановым
(гл. 19-22). Другие главы перевели канд. хим. наук Е. Э. Григорьева (гл. 16-17) и
канд. хим. наук Т. П. Мосолова (гл. 24-26).
Я уверен, что эта книга, содержащая очень важный и современный матери-
ал по аналитической химии, методические качества которой проверены много-
кратными ее переизданиями за рубежом, обогатит библиотеку учебной
литературы университетов и высших специальных профессиональных заведе-
ний и будет востребована преподавателями и студентами.
академик Ю. А. Золотов
Сью — за десятилетия радости
и за поразительный талант быть бабушкой
Тане и Тэффи — за солнечный свет,
которым они освещают нашу жизнь
Предисловие
Учитель открывает дверь, но войдешь ли ты в нее, зависит от тебя.
Задача аналитической химии — охарактеризовать материю с химической точки
зрения, как качественно, так и количественно. Эта задача важна применительно
едва ли не к каждому аспекту нашей жизни, поскольку все, чем мы пользуемся,
представляет собой химические вещества. Чарльз Н. Рейли в конце своей жизни
сказал: «Аналитическая химия — это то, чем занимаются химики-аналитики».
Чем же они занимаются, мы и рассмотрим в данной книге.
Книга предназначена для студентов вузов, специализирующихся в химии и
областях, связанных с ней. В ней рассматриваются теоретические основы и мето-
ды количественного химического анализа, ознакомившись с которыми можно по-
добрать способ для определения количества того или иного вещества в пробе. Вы
научитесь разрабатывать методики анализа, узнаете, какая информация для этого
необходима, как отбирать лабораторную пробу, чтобы ее состав был представи-
тельным (т. е. соответствовал составу всего образца в целом), как подготовить
пробу для анализа, какие средства измерений есть в распоряжении химика-анали-
тика, как оценивать статистическую значимость результатов анализа. Гл. 24-26
иллюстрируют применение полученных вами знаний в сферах клинического ана-
лиза, геномики и протеомики, отбора проб и анализа объектов окружающей среды.
Рассмотренные в книге примеры применения методов аналитической хи-
мии не случайно относятся к наукам о живом, клинической химии, проблемам
загрязнения воды и воздуха, промышленному анализу. Значение аналитической
химии становится особенно понятным лишь тогда, когда приходит осознание
того, что неправильный анализ крови может угрожать жизни пациента, а ошибки
при контроле качества продукции могут обернуться серьезными финансовыми
потерями для производителя. Выполнение непрерывных автоматизированных
анализов позволяет химической промышленности экономить миллионы долла-
ров и обеспечивать максимальную эффективность производства.
Для кого предназначена данная книга?
Данная книга содержит общий курс количественного анализа. Объем приведен-
ного в ней материала заведомо больше того, что можно пройти за один семестр.
Поэтому преподаватель вправе самостоятельно выбирать те темы, которые он
8
предисловие
считает наиболее важными. Остальные разделы могут в этом случае рассматри-
ваться как дополнительный материал. Книгу можно использовать независимо от
того, в какой последовательности излагаются химические и инструментальные
методы анализа. В любом случае я надеюсь, что вы найдете время, чтобы прочи-
тать и те разделы, которые интересны сами по себе, хотя, возможно, и не являются
обязательными. Впоследствии их можно будет использовать в качестве спра-
вочной информации.
Что осталось неизменным?
Шестое издание книги существенно переработано и дополнено новыми источ-
никами (главным образом более поздними), но многие особенности предыду-
щих изданий сохранены. Каждой главе предшествует небольшой абзац,
раскрывающий общее содержание главы. Ключевые слова выделены жирным
шрифтом, а основные уравнения заключены в рамку . Это поможет читателю
при повторении материала. Чтобы обратить внимание на наиболее важные поня-
тия (и также помочь при повторении материала), некоторые предложения выде-
лены курсивом.
На протяжении всей книги внимание читателя постоянно обращается на
анализ размерностей физических величин. Это позволит лучше прочувствовать
постановку задачи. В книге используются размерности величин в системе СИ и
их общепринятые обозначения (л, мл, моль, сит. д.). Понятия «нормальность» и
«эквивалент» в книге также рассматриваются, однако основное внимание все же
уделено использованию понятий «молярность» и «моль». Вопросы, связанные с
«нормальностью», изложены таким образом, что преподаватель может не исполь-
зовать это понятие, если сочтет это не нужным.
Для облегчения работы задачи и рекомендуемая литература сгруппированы
по темам. Литературные источники значительно обновлены, добавлено много
новых задач. Всего в книге содержится 673 вопроса и задачи (а также руководст-
во по их решению).
В предыдущее издание было добавлено много новых тем, большинство из
которых сохранились в тексте данного издания, так как они важны для изучения
материала, например:
• статистика малых выборок;
• статистика пробоотбора;
• систематический подход к расчетам химических равновесий, основанный
на законах сохранения массы и заряда;
• гетерогенные равновесия;
• использование логарифмических диаграмм для представления сложных
равновесий (добавлен раздел по построению таких диаграмм при помощи
электронных таблиц);
• спектрометры с матрицами диодов;
• инфракрасная спектроскопия с преобразованием Фурье;
• ИК-спектроскопия в ближней области;
ПРВДИСЛОВИЕ
9
• оптоволоконные сенсоры;
• газовая хромато-масс-спектрометрия.
Что изменилось?
Изменено расположение некоторых глав для того, чтобы логически связать их
содержание с другими главами. По многочисленным просьбам читателей глава,
посвященная базовым средствам и операциям в аналитической химии, помещена
в начало книги (гл. 2). Возможно изучение отдельных разделов этой главы, необ-
ходимых для выполнения лабораторного практикума. Гл. 10, посвященная гра-
виметрическому методу анализа и равновесным процессам образования осадка,
в настоящем издании предшествует главе, описывающей реакции осаждения и
осадительное титрование. Такое расположение глав позволяет упорядочить из-
ложение близких по смыслу вопросов.
Основной метод анализа смесей веществ — хроматография — в последнее
время переживает бурное развитие, ее возможности непрерывно расширяются.
В связи с этим описание хроматографических методов расширено и дополнено:
целых три главы (19-21) посвящены основам хроматографии, газовой хроматог-
рафии и жидкостной хроматографии. Устаревшие методы, такие как бумажная
хроматография, не рассматриваются.
Что нового?
С момента выхода предыдущего, пятого, издания книги прошло почти десять
лет (вот результат моей слишком долгой работы в качестве декана!). За это вре-
мя многое изменилось. В шестом издании представлен ряд новых тем и глав, из-
менен характер изложения. Основные добавления состоят в следующем:
• для проведения вычислений, статистического анализа и построения графи-
ков на протяжении всей книги используются электронные таблицы Excel.
При помощи электронных таблиц построены многие кривые титрования,
рассчитаны значения молярных долей а и построены распределительные диа-
граммы а—pH, а также концентрационно-логарифмические диаграммы. Инст-
рукции по использованию электронных таблиц изложены в доступной форме,
так что можно легко понять их алгоритм. Обычно в таких инструкциях просто
указано, какую формулу необходимо ввести в определенную ячейку. Например,
если ячейка В11 должна содержать частное от деления чисел, находящихся в
ячейках А2 и АЗ, то в тексте приводится формула (=А2/А3). Результат появляет-
ся в ячейке Bl 1, в которую эта формула была введена. Номера ячеек, содержа-
щих формулы, в тексте выделены жирным шрифтом. Анализируя электронные
таблицы, часто приходится разбираться, что означает та или иная формула, на-
пример, значениями каких величин являются числа, частное которых вычисля-
ется в приведенном выше примере. Со сложными формулами и выражениями и
такая работа может быть весьма утомительной. Поэтому в инструкциях к элект-
ронным таблицам приведены не только формулы, непосредственно вводимые в
10
ПРВДИСЛОВИЕ
ячейки, но и исходные выражения. Читатель лучше оценит удобство такой фор-
мы представления инструкций, когда непосредственно начнет работать с приве-
денными в книге примерами для электронных таблиц.
• Добавлена новая глава «Хорошая лабораторная практика» — сборник нор-
мативных документов по обеспечению качества результатов химического
анализа.
Вопросы практического применения аналитической химии приобрели осо-
бую важность, когда административно были введены достаточно сложные и
строгие обязательные нормативы, призванные обеспечить правильность резуль-
татов химического анализа. Каждому аналитику, стремящемуся сделать карьеру,
известно, что знание этих нормативов будет весьма благоприятно воспринято ра-
ботодателем. Данная глава может служить введением к изучению этих вопро-
сов, а также кратким справочником. Она включает в себя следующие разделы:
• поверка (валидация) методики анализа;
• обеспечение качества результатов;
• аккредитация лабораторий;
• электронная документация и электронные подписи (новые нормы 21
CRF, часть 11).
• Еще одна новая глава посвящена геномике и протеомике.
Аналитическая химия сыграла решающую роль в успешном завершении ис-
торического проекта «Геном человека». Читатель, вероятно, знает об этом про-
екте. Разработанные для него методики стали рутинными для установления
последовательности ДНК сложных организмов, в судебной экспертизе и других
областях. В настоящее время начинается развитие протеомики, где аналитиче-
ская химия будет решать чрезвычайно важные и неосвоенные проблемы, связан-
ные с картированием белков; введение в эти методы также здесь описано. Глава
рассматривает следующие вопросы:
• проект «Геном человека»;
• секвенирование генов;
• полимеразная цепная реакция (ПЦР);
• ДНК-чипы;
• двумерный гель-электрофорез и времяпролетная масс-спектрометрия
с ионизацией методом лазерной десорбции из матрицы-мишени
(MALDI-TOF).
Кроме перечисленных выше книга содержит следующие новые темы:
• калибровка мерной посуды;
• ускоренная и микроволновая экстракция и вскрытие проб;
• ионселективные полевые транзисторы;
• спектральные базы данных в Интернете — коммерческие и бесплатные;
• твердофазная экстракция (сорбция) — раздел расширен; твердофазная мик-
роэкстракция;
ПРЕДИСЛОВИЕ
11
• номенклатура в хроматографии; рекомендованные ИЮПАК термины и
обозначения;
• теория эффективности хроматографических колонок — раздел расши-
рен;
• программное обеспечение для моделирования хроматографических про-
цессов и их использование для разработки методик;
• колонки для капиллярной газовой хроматографии — раздел расширен и об-
новлен;
• дискретный, непрерывный проточный пробоотбор и термодесорбция в га-
зовой хроматографии;
• быстрая газовая и жидкостная хроматография;
• жидкостная хромато-масс-спектрометрия (ЖХ-МС);
• масс-анализаторы для ГХ-МС и ЖХ-МС;
• неподвижные фазы для ВЭЖХ — раздел расширен; применение капилляр-
ных колонок малого диаметра для повышения чувствительности;
• капиллярный электрофорез — раздел расширен; капиллярная электрохро-
матография.
Практические работы
В книге описано 40 практических работ, иллюстрирующих большинство мето-
дов анализа. Работы сгруппированы по темам. Для каждой работы приведены
методика проведения эксперимента и соответствующие уравнения реакций, по-
этому читатель может сразу понять, что именно анализируется и каким образом.
Перечислены все реагенты и растворы, которые необходимо приготовить перед
выполнением работы, что позволяет выполнить работу быстро и эффективно.
Эксперименты, по возможности, продуманы таким образом, чтобы, в соответст-
вии с требованиями техники безопасности, избежать использования асбеста,
хлороформа, тетрахлорида углерода и бензола. Все работы, особенно связанные
с титрованием, спланированы так, чтобы уменьшить расход реагентов за счет
приготовления минимально возможных объемов реагентов (титрантов).
Исключены три работы, в которых используется ртуть. Удалена также
работа по бумажной хроматографии, поскольку в настоящее время бумажная
хроматография практически полностью вытеснена тонкослойной хроматогра-
фией. Для экономии места описание неферментативных кинетических методов
и соответствующая работа заменены работой по ферментативным методам. По
тем же причинам исключена работа по хроматографическому разделению коба-
льта и никеля на анионообменной колонке.
Добавлена новая работа (практическая работа 18) по определению жестко-
сти воды методом микротитрования (описание работы предоставил профессор
Джон Ричардсон из Шиппенсбургского университета). Аппаратура и техника
этой работы могут при желании быть использованы и в других работах по титри-
метрии. Если ваш преподаватель разработает и опробует такую работу вместе
12
ПРВДИСЛОВИЕ
с вами, я могу включить ее описание в следующее издание книги. Добавлены
две групповые работы (39 и 40), иллюстрирующие принципы статистической
поверки, которые описаны в гл. 4. Одна из них посвящена поверке методики и
контролю качества результатов; при этом отдельные члены рабочей группы вы-
полняют разные этапы поверки в рамках единого эксперимента. Вторая работа
моделирует межлабораторный эксперимент. В этой работе необходимо рассчи-
тать нормированные величины (z) для результатов, полученных каждым студен-
том в ходе одинакового для всех эксперимента (или нескольких таких
экспериментов). Зная z, студент может оценить качество своей работы.
Электронные таблицы. Мы настоятельно рекомендуем вам в ходе вы-
полнения практических работ использовать электронные таблицы для постро-
ения градуировочных графиков и статистического анализа результатов
эксперимента.
Компакт-диск
К книге прилагается компакт-диск, содержащий полезный материал, дополняю-
щий текст книги*. При чтении диска в первую очередь щелкните кнопкой мыши
на словах «Read те», чтобы увидеть подробное содержание диска. Файлы сгруп-
пированы в разделы («Вспомогательные данные», «Числовые таблицы», «Тексто-
вые таблицы», «Лабораторное оборудование», «Задачи для электронных таблиц»
и «Интернет-ссылки»). Там же содержатся примеры, которые могут служить хо-
рошим подспорьем при работе с электронными таблицами.
Несколько слов об Интернет-сайтах
В книге дано более 100 ссылок на Интернет-сайты, содержащие полезные до-
полнительные материалы. Чтобы не набирать адреса сайтов вручную, на ком-
пакт-диске приведены все имеющиеся в книге ссылки в порядке их появления,
глава за главой. Этот же список имеется и на сайте издательства John Wiley &
Sons, Inc. на странице, посвященной данной книге.
Чтобы открыть сайт, достаточно щелкнуть кнопкой мыши по соответствую-
щей ссылке. Если это не приводит к успеху, скопируйте ссылку, вставьте ее в
адресное окошко браузера и выполните команду Go (Перейти) или просто на-
жмите клавишу Enter (Ввод) на клавиатуре. Иногда страница может не откры-
ться. В этих случаях можно ввести адрес домашней страницы сайта и затем
перейти по ссылке к нужной странице. На сайтах фирм часто бывает необходи-
мо перейти к странице Product (Продукция). Можно воспользоваться и сред-
ствами поиска, имеющимися на многих сайтах. Адреса некоторых страниц со
временем могут быть изменены или вообще ликвидированы. При возникнове-
нии проблем с открытием сайтов пользуйтесь средствами поиска Интернета
(такими, как Google), осуществляя поиск по названию фирмы или ключевым
словам интересующей вас темы.
Имеется ввиду оригинальное издание на английском. В русской версии книги компакт-диск отсутствует.
Читатели могут обратиться на сайт J. Wiley & Sons, Inc.
ПРЕДИСЛОВИЕ
13
Домашняя страница книги в Интернете
У издательства John Wiley & Sons, Inc. есть страница в Интернете, посвященная
данной книге. Она содержит дополнительные материалы, которые могут время
от времени пополняться или обновляться. На этот сайт следует сообщать обо
всех ошибках, обнаруженных в книге. Дополнительные материалы к отдельным
главам книги представлены в виде краткого текста, если по нему щелкнуть кноп-
кой мыши, он развернется в полный текст. На сайте имеются также главы «Ме-
тодология поиска научной литературы» и «Решение аналитических проблем:
выбор метода анализа» из издания The Encyclopedia of Analytical Chemistry. Ин-
тернет-ссылки, приведенные в книге, также собраны на этом сайте; со временем
их адреса могут изменяться. Кроме того, на сайте имеются все рисунки и таб-
лицы, содержащиеся в книге; их можно скачивать и использовать для
подготовки демонстрационных материалов. Сайт находится по адресу:
www.wiley.com/college/christian.
Благодарности
При подготовке данной книги большую роль сыграли помощь и замечания
многих специалистов. Я особенно благодарен читателям предыдущих изданий
за их комментарии и предложения по доработке материала; я всегда приветст-
вую такие предложения. Мои коллеги оказали мне неоценимую помощь в ка-
честве критиков. Разумеется, иногда они высказывали противоположные
взгляды на содержание и расположение отдельных глав или разделов, но в ко-
нечном результате получился вариант, близкий к оптимальному, и который,
как я надеюсь, покажется читателям легким и приятным для чтения и изуче-
ния. Хочу особо поблагодарить профессоров Дениса Анджо (Университет
штата Калифорния, Лонг-Бич), Кевина Чемблисса (Университет Бейлор), Май-
кла Дегранпра (Университет Монтаны), Цзиньмо Хуана (Колледж Нью-Джер-
си), Айру Кралл (Северо-восточный университет), Гэри Лонга и Харольда
Макнейра (Технический университет Вирджинии), Джоди Редпеннинга (Уни-
верситет Небраски), Джона Ричардсона и Томаса Шредера (Шиппенсбургский
университет), Бенджамина Русилоски (Университет штата Делавэр), Джеймса
Рыбарчика (Болльский университет), Шерил Клейн Стивенс (Университет
Ксавье, Луизиана) и Филиппа Фегеля (Университет Среднего Запада). Профес-
сор Норманн Доричи (Университет штата Вашингтон) внес ценный вклад в
подготовку гл. 25, посвященной геномам и протеомике. Я благодарю также
Мэка Картера за его высококвалифицированную помощь, связанную с работой
на компьютере, и Шейлу Паркер за помощь в преодолении многих случайных
трудностей.
Высоким уровнем качества данное издание обязано профессионалам из из-
дательства John Wiley & Sons. Редакторы Дэвид Харрис и Дебора Бреннан контро-
лировали издательский процесс от начала до конца. Их ассистент Кэти Донован
осуществляла весь процесс редактирования и в связи с этим решала множество
вопросов. Производственный редактор Элизабет Суэйн отвечала за подготовку
14
предисловие
печатных форм текста. Сандра Ригби работала в качестве редактора иллюстра-
ций, ей вы обязаны рисунками, имеющимися в книге. Эрнестина Франко (Рет
Editorial Services) тщательно выполнила окончательную корректуру при подго-
товке книги к печати. Работать с этими людьми в ходе долгого, но приносящего
удовлетворение процесса создания книги было настоящим удовольствием.
На протяжении всех двух лет работы над книгой самой надежной опорой
была моя жена и лучший друг Сью. Она старательно расшифровывала и перепе-
чатывала рукописный текст. Спасибо, спасибо, спасибо!
Пособие по решению задач
В распоряжении преподавателей и студентов имеется всеобъемлющее пособие
по решению задач, в котором приведены полные решения всех задач и ответы на
все вопросы, содержащиеся в книге. Решения задач, требующих использования
электронных таблиц, приведены в виде таблиц на компакт-диске. Решения задач
с четными номерами приведены в Приложении F.
Гари Д. Кристиан
Январь 2003 г.
Сиэтл
Преподавать значит дважды учиться.
Жозеф Жубер
Список электронных таблиц, использованных в тексте
Во многих главах книги содержатся указания
к использованию электронных таблиц для по-
строения графиков и проведения вычислений.
Ниже приведен список приложений Microsoft
Excel, для удобства использования сгруппи-
рованных по темам. Все соответствующие
таблицы содержатся на компакт-диске (CD).
Таблицы, предназначенные для решения за-
дач, есть только на диске. Остальные таблицы
имеются и в тексте, и на диске. Прежде чем
обращаться к диску, всегда следует постарать-
ся составить необходимую таблицу самостоя-
тельно. Вы можете копировать таблицы с
компакт-диска на свой компьютер для их по-
следующего использования.
Работа с электронными таблицами
(разд. 3.8)
Заполнение ячеек: с. 127(1)
Сохранение таблицы: с. 128(1)
Печать таблицы: с. 129(1)
Абсолютные и относительные адреса ячеек:
с. 129(1)
Использование статистических функций Excel:
с. 131(1)
Полезные функции Excel: LOG 10, PRODUCT
(ПРОИЗВЕЛ), POWER (СТЕПЕНЬ), SQRT
(КОРЕНЬ), AVERAGE (СРЗНАЧ), MEDIAN
(МЕДИАНА), STDEV (СТАНДОТКЛОН),
TTEST (ТТЕСТ), VAR (ДИСПА) — с. 132(1)
Статистические расчеты
Стандартное отклонение: гл. 3, задачи 14, 15,
16, 20,21
Среднее (средневзвешенное) стандартное от-
клонение: гл. 3, задача 27
F-тест: гл. 3, задачи 25, 26, 28
/-Тест: гл. 3, задачи 29, 30
/-Тест для нескольких выборок: гл. 3, задача 42
Наложение погрешностей: гл. 3, задача 17 (сло-
жение-вычитание), 18 (умножение-деление)
Использование электронных таблиц
для построения градуировочных
графиков (разд. 3.18, рис. 3.9)
Мастер диаграмм
Линия тренда
Регрессионное уравнение по МНК, г2
Нахождение тангенса угла наклона, свободно-
го члена, коэффициента детерминации (без по-
строения графика): разд. 3.19, задачи 37,40,41
Программа ЛИНЕЙН (LINEST) для выполне-
ния дополнительных статистических вычисле-
ний (разд. 3.20, рис. 3.10, примеры 3.21, 3.22);
десять статистических функций: вычисление
углового коэффициента, его стандартного от-
клонения, г2, F-статистики, суммы квадратов
отклонений, свободного члена, его стандарт-
ного отклонения, стандартного отклонения
оценки (предсказания значений у), числа степе-
ней свободы, остаточной суммы квадратов.
Расчет неизвестной концентрации по градуиро-
вочной зависимости: с. 36(2); гл. 3, задача 38
Расчет стандартного отклонения неизвестного
содержания по градуировочной зависимости:
с. 37(2)
Расчет концентрации и ее стандартного откло-
нения методом добавок: с. 105(2)
Расчет концентрации и стандартного отклонения
методом внутреннего стандарта: с. 177(2);
гл. 20, задача 18
Построение распределительных
диаграмм а—pH (рис. 7.1, Н3РО4):
с. 345(1)
16
СПИСОК ЭЛЕКТРОННЫХ ТАБЛИЦ, ИСПОЛЬЗОВАННЫХ В ТЕКСТЕ
Построение концентрационно-лога-
рифмических диаграмм: с. 359(1);
гл. 7, задача 61 (СН3СООН)
Использование а-коэффициентов,
с. 365(1): гл. 7, задача 64 (яблочная кис-
лота, Н2А); гл. 7, задача 68 (рис. 7.4,
Н3РО4, Н3А)
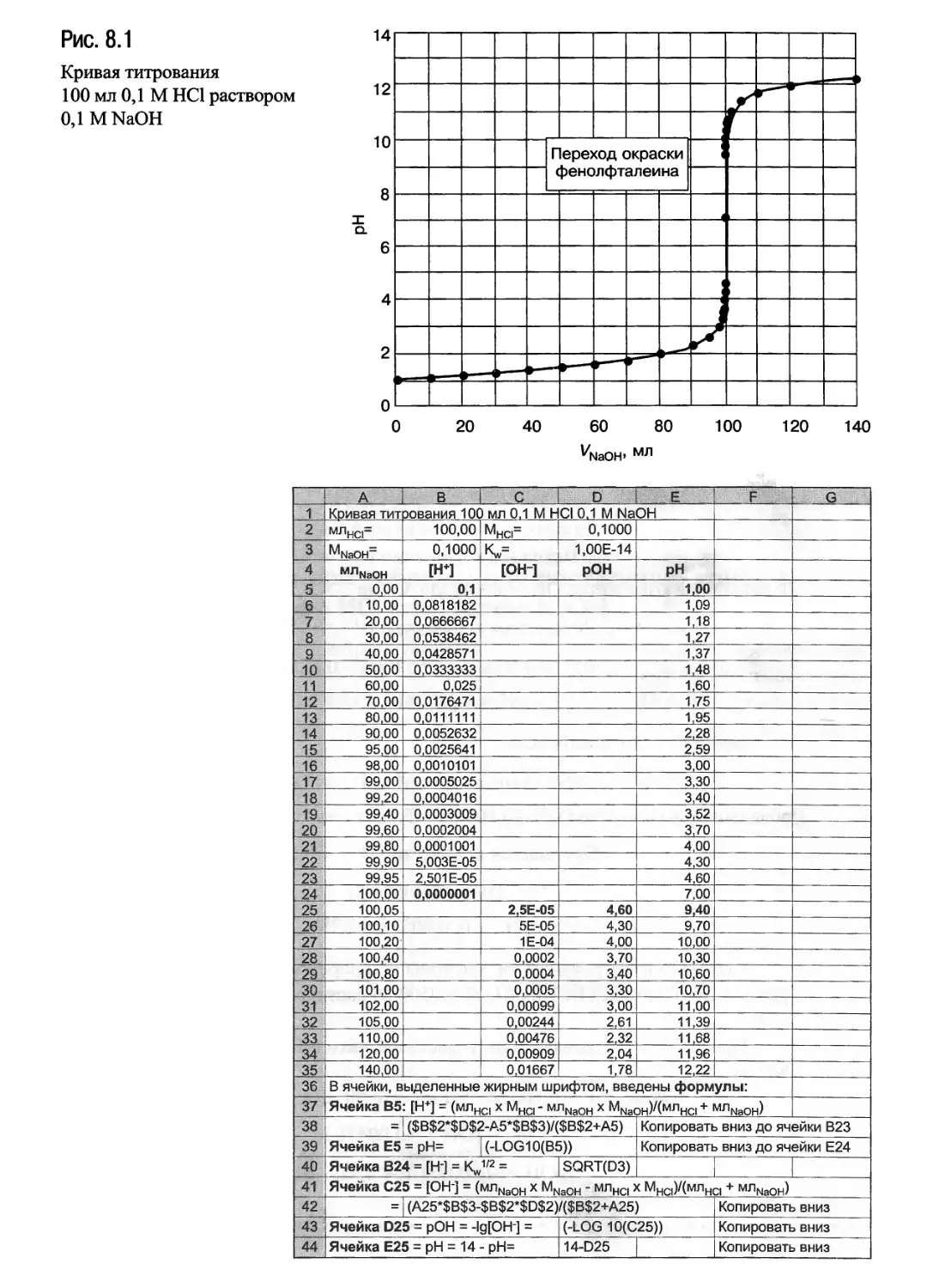
Построение кривых титрования
НС1 раствором NaOH (рис. 8.1): с. 375(1);
СН3СООН раствором NaOH: с. 377(1);
Н2СгО4 раствором NaOH (титрование двухос-
новной кислоты): CD, вспомогательные дан-
ные, гл. 8; с. 396(1);
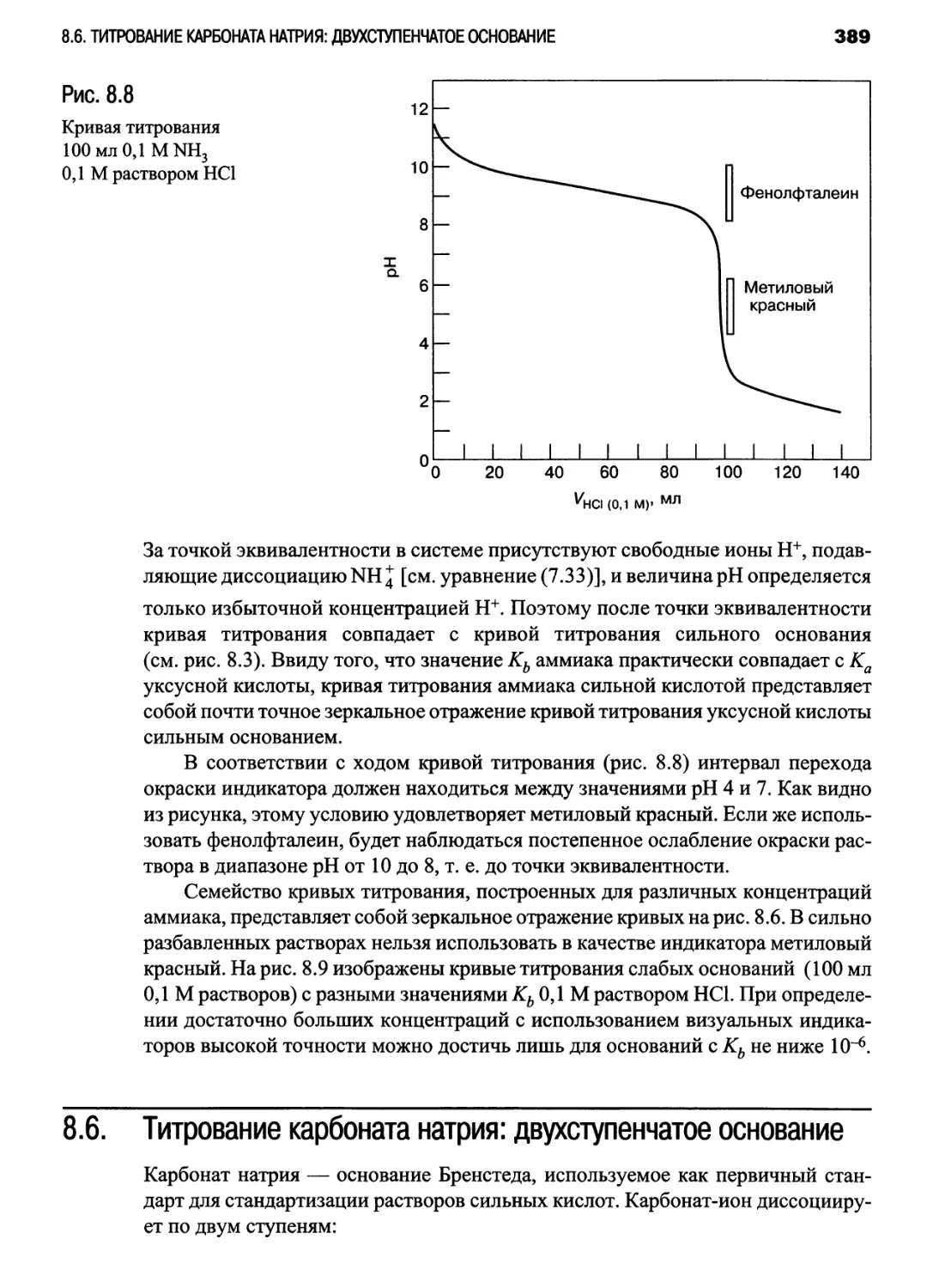
NH3 раствором НС1 (рис. 8.8): гл. 8, задача 35;
Са2+ раствором ЭДТА: гл. 9, задача 21;
СГ раствором AgNO3 (рис. 11.1): гл. 11, задача 12;
Fe2^ раствором Се4+ (рис. 14.1): гл. 14, задача 21
Построение первой и второй производных кри-
вой титрования (рис. 14.2 и 14.3): с. 589(1)
Построение зависимостей lg K'f от pH
(рис. 9.2): гл. 9, задача 20
Построение зависимостей
p-коэффициентов от концентрации
лиганда (зависимость р-коэффициентов
для системы Ад+— NH3: гл. 9, задача 22
Различные расчеты и построения
Калибровка мерной посуды (табл. 2.4): с. 72(1)
Приведение к весу в вакууме с учетом плотно-
сти образца (CD, гл. 2)
Расчеты активностей, коэффициентов активно-
сти: гл. 6, задачи 22, 23, 24, 26
Расчеты в гравиметрии: стр. 460(1); гл. 10, за-
дача 40 (пример 10.2, расчет массовой доли
р205)
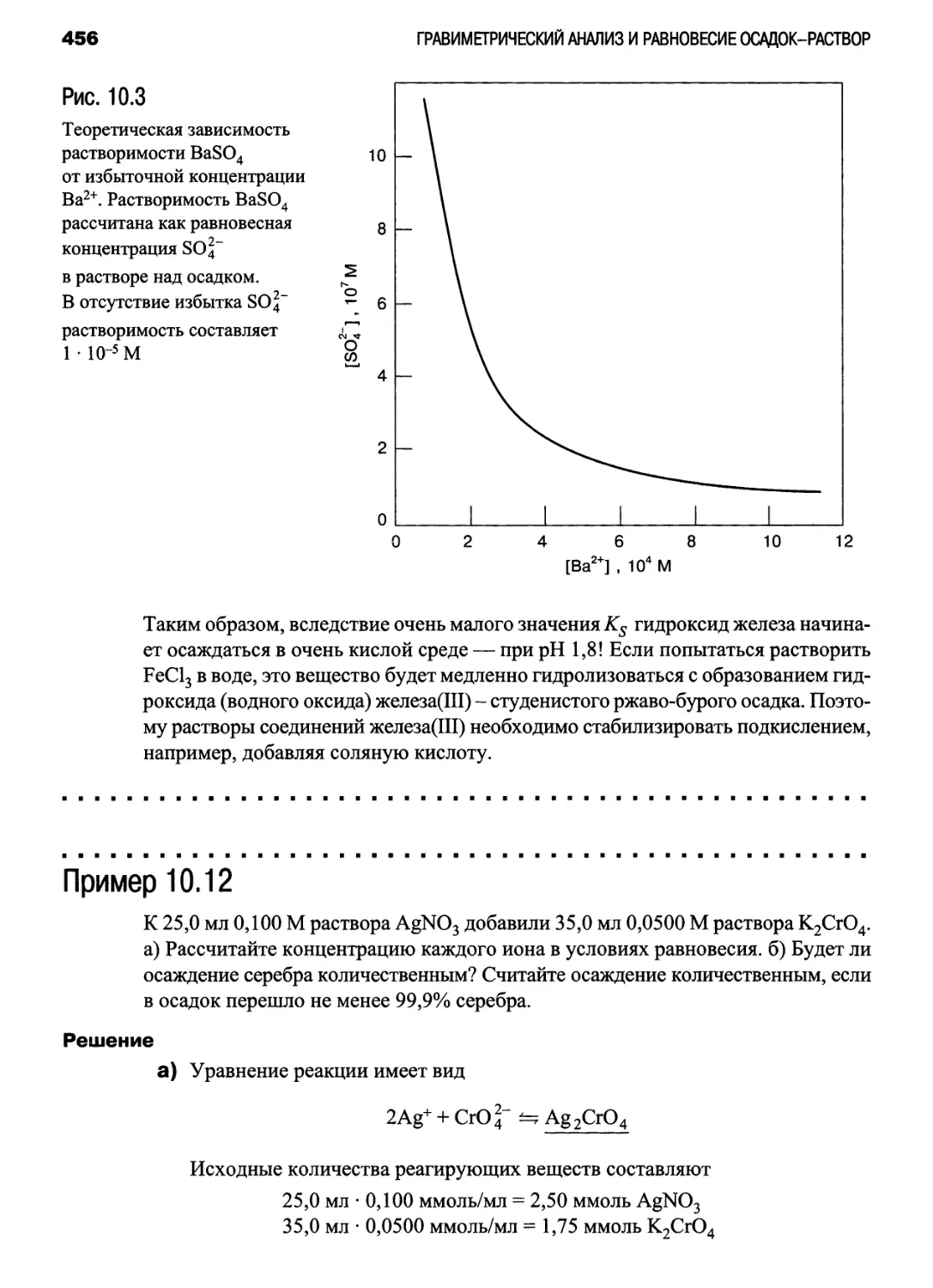
Зависимость растворимости BaSO4 от [Ва2+]
(рис. 10.5): гл. 10, задача 41
Зависимость растворимости от ионной силы
(рис. 10.6): гл. 10, задача 42
Зависимость Ван Деемтера: гл. 19, задача 11
Нахождение скорости реакции: гл. 22, пример 22.2
Построение зависимости Лайнуивера-Берка
(пример 22.1): гл. 22, задача 17
Стандартные вычисления в Excel
Решение квадратного уравнения при расчетах
равновесных концентраций (пример 6.1): гл. 6,
задача 25; гл. 7, пример 7.19 (CD)
Расчет растворимости из произведения раство-
римости: с. 460(1); гл. 10, задача 43 (пример
10.9)
Решение систем уравнений (пример 16.5, спек-
трофотометрический анализ смесей)
Глава 1
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ,
ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
Пока наше знание не измерено
и не выражено в цифрах,
оно немногого стоит.
Лорд Кельвин
Задача аналитической химии — охарактеризовать материю с химической точки
зрения и ответить на два важных вопроса: «что?» (качественный анализ) и
«сколько?» (количественный анализ). Все, что мы используем и потребляем, со-
стоит из химических веществ (химических соединений), и знание химического
состава многих веществ важно для повседневной жизни. Аналитическая химия
играет важную роль практически во всех областях химии, например в сельскохо-
зяйственной, клинической, судебной, фармацевтической химии, химии окружа-
ющей среды, химическом производстве и металлургии. Содержание азота в
удобрении определяет его ценность. Пищевые продукты необходимо анализиро-
вать на содержание как токсичных (в частности, остаточных количеств пестици-
дов), так и полезных веществ (витаминов). В воздухе больших городов необходимо
определять содержание монооксида углерода. Больным диабетом необходимо по-
стоянно контролировать содержание глюкозы в крови (в действительности боль-
шинство заболеваний диагностируется на основании результатов химических
анализов). Наличие на руке человека, защищавшегося от нападавшего, следов
элементов, содержащихся в порохе, доказывает, что из оружия был произведен
выстрел. Качество промышленной продукции часто зависит от соотношения в ней
химических веществ, поэтому определение их содержания — необходимая опера-
ция в ходе контроля качества. Так, содержание углерода в стали определяет ее
качество, а чистота лекарственных препаратов — их эффективность.
1.1. Что такое аналитическая наука?
Из приведенных примеров уже, в общем-то, понятно, что же представляет собой
дисциплина аналитическая химия. Было предпринято много попыток опреде-
лить ее содержание более строго и детально. В конце жизни Чарльз Н. Рейли ска-
зал: «Аналитическая химия — это то, чем занимаются химики-аналитики» [2].
Эта дисциплина расширила свои границы за пределы собственно химии, и мно-
гие ученые являются сторонниками использования более широкого понятия —
аналитическая наука. Этот термин используется в докладе Национального на-
учного фонда США, озаглавленном «Развитие курса аналитических наук». Но
18
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
даже этот термин не в полной мере отражает ту роль, которую в современной
аналитической химии играют развитие инструментальных методов и практиче-
ские приложения. В связи с этим одно из предложений состоит в том, чтобы ис-
пользовать термин аналитическая наука и технология [3].
В 1992 г. Федерация европейских химических обществ объявила конкурс на
лучшее определение аналитической химии. Было выбрано следующее определе-
ние, данное К. Камманом [Fresenius' J. Anal. Chem., 343 (1992) 812-813]:
Аналитическая химия предоставляет методы и средства, необходимые
для того, чтобы заглянуть в материальный мир... с целью ответа на
основные вопросы, касающиеся материала образца:
• Что?
• Где?
• Сколько?
• Каковы расположение, структура, форма?
Отделение аналитической химии Американского химического общества пред-
лагает всеобъемлющее определение аналитической химии, которое можно найти
на его сайте (www.acs-analytical.duq.edn/whatisanalyticalchem.html). Ниже приведе-
на его основная часть:
Аналитическая химия занимается поиском новых, улучшенных средств
определения химического состава природных и искусственных материа-
лов. Техника и методы этой науки используются для идентификации ве-
ществ, которые могут присутствовать в материале, и для определения
точных количеств идентифицированных веществ.
Химики-аналитики работают над повышением надежности существу-
ющих технологий, чтобы удовлетворять все возрастающим требованиям
к качеству измерений, постоянно возникающим в нашем обществе. Они
адаптируют проверенную методологию к новым типам материалов или к
тому, чтобы ответить на новые вопросы об их составе и реакционной спо-
собности. Они выполняют исследования, чтобы разработать совершенно
новые принципы измерений, и находятся на переднем крае использова-
ния в практических целях главных открытий и изобретений — таких, как
лазеры или микрочипы. Их усилия направлены на удовлетворение нужд
многих наук.
• В медицине аналитическая химия составляет основу клинических
лабораторных тестов, помогающих врачам диагностировать забо-
левания и добиваться успехов в их лечении.
• В промышленности аналитическая химия предоставляет средства
для испытаний сырья и гарантии качества готовой продукции, хи-
мический состав которой крайне важен. Многие продукты, исполь-
зуемые в быту, топливо, красители, лекарства и другие вещества
перед тем, как поступить в продажу, анализируют с помощью мето-
дик, разработанных химиками-аналитиками.
• Степень загрязнения окружающей среды часто оценивают при по-
мощи тестов на предполагаемые загрязнители, используя средства
и методы аналитической химии.
1.2. КАЧЕСТВЕННЫЙ И КОЛИЧЕСТВЕННЫЙ АНАЛИЗ
19
• Питательную ценность продуктов питания определяют при помощи
химических анализов на содержание основных компонентов — таких
как белки или углеводы, а также микрокомпонентов — таких, как
витамины или минеральные вещества. Даже калорийность пищи ча-
сто вычисляют на основании результатов химических анализов.
Кроме того, химики-аналитики вносят существенный вклад в самые раз-
нообразные области, например криминалистику, археологию и науку о
космосе.
1.2. Качественный и количественный анализ:
какую информацию сообщает нам каждый из них?
Дисциплина аналитическая химия состоит из качественного анализа и коли-
чественного анализа. Задача первого — идентификация элементов, ионов или
соединений, присутствующих в образце (при этом может представлять интерес
и наличие лишь одного определенного вещества), задача количественного ана-
лиза — определение того, сколько данного компонента (одного или нескольких)
содержится в образце. При этом образец может представлять собой твердое
тело, жидкость, газ или смесь. Наличие остатков пороха на руке человека обыч-
но представляет интерес лишь с качественной точки зрения (его количество не-
существенно), но цена угля определяется количественным содержанием в нем
примеси серы.
Количественный анализ
Качественный анализ
Печатается с любезного разрешения Merck KGaA.
20
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
Зарождение аналитической химии
Фактически, химические измерения и средства, необходимые для их проведения, упоми-
наются в самых ранних письменных источниках. Испытания золота огнем описаны в
библейской книге Пророка Захарии (13:9), а царь Вавилона жаловался египетскому фа-
раону Амменофису IV (1375-1350 гг. до н. э.) на то, что золото, которое тот ему послал,
«теряло в весе» после прокаливания в печи. Возможно, необходимость установления ис-
тинной ценности золота, возможно, была главным стимулом к получению знаний об ана-
лизе. Архимед (287-212 гг. до н. э.) выполнил неразрушающий анализ золотой короны
царя Герона. Он поместил корону, а также куски золота и серебра, равные ей по весу, в
сосуды с водой и измерил объемы воды, вытесненные каждым из трех объектов. Объем
воды, вытесненный короной, находился между объемами, вытесненными золотом и се-
ребром. Это доказывало, что корона состояла не из чистого золота!
Весы появились так давно, что в самых ранних из найденных документов это при-
писывается богам. Вавилоняне создали стандартные весы около 2600 г. до н. э. Они
считали весы настолько важным инструментом, что их использование контролировали
жрецы.
Алхимики собрали воедино химические познания, которые легли в основу качест-
венного анализа в его современном понимании. Роберт Бойль в книге «Химик-скеп-
тик» (1661 г.) использовал термин аналитик. Антуана Лавуазье считают «отцом
аналитической химии» благодаря тщательным количественным экспериментам, кото-
рые он провел (с использованием аналитических весов) для доказательства закона со-
хранения массы. По роду основной деятельности Лавуазье был сборщиком налогов, а
занятия наукой он рассматривал как хобби. Именно из-за своей деятельности по сбору
налогов он был казнен на гильотине 8 мая 1793 г. во время Великой французской рево-
люции.
Гравиметрия получила развитие в XVII веке, а титриметрия — в XVIII и XIX веках.
В 1829 г. Гей-Люссак при титриметрическом определении серебра достиг точности в
0,05% относительной погрешности!
Учебники по аналитической химии стали появляться в 1800-х гг. В 1845 г. в Герма-
нии Карл Фрезениус опубликовал «Руководство по количественному химическому ана-
лизу», а в 1894 г. вышла книга Вильгельма Оствальда «Научные основы аналитической
химии». Эта книга содержала теоретические объяснения многих явлений в аналитиче-
ской химии при помощи констант химических равновесий и оказала большое влияние на
развитие химии.
В XX веке наблюдалось развитие инструментальных средств анализа. Второе изда-
ние книги Стивена Попова «Количественный анализ», вышедшее в 1927 г., включало
электрохимические методы анализа, кондуктометрическое титрование, колориметриче-
ские методы. К настоящему времени был совершен большой прогресс в развитии техно-
логии химического анализа, которая включает сложные и высокопроизводительные
приборы, управляемые компьютерами и позволяющие проводить весьма сложные ана-
лизы и измерения при очень низких концентрациях веществ.
Данная книга научит читателя основам аналитической химии и вооружит средст-
вами для решения большинства аналитических задач. Более подробно об истории разви-
тия аналитической химии можно узнать из работы [7].
1.2. КАЧЕСТВЕННЫЙ И КОЛИЧЕСТВЕННЫЙ АНАЛИЗ
21
Качественный анализ можно проводить при помощи селективных химиче-
ских реакций или с использованием аппаратуры. Образование белого осадка при
добавлении раствора нитрата серебра к раствору пробы свидетельствует о нали-
чии хлорид-ионов. В результате некоторых химических реакций возникает ха-
рактерное окрашивание, свидетельствующее о наличии тех или иных классов
органических соединений, например, кетонов. Инфракрасные спектры позволя-
ют получить «отпечатки пальцев», уникальные для определенных органических
соединений или их функциональных групп.
Необходимо четко различать термины селективный и специфичный.
• Селективная реакция или тест протекает с несколькими или многими веще-
ствами, но предпочтительно — с одним определенным веществом.
• Специфичная реакция или тест протекает только с одним веществом.
К сожалению, очень мало реакций являются специфичными, но многие из них
обладают селективностью. Селективности можно достичь при помощи различ-
ных приемов, например:
• Специальная пробоподготовка (в частности, экстракция, осаждение).
• Использование селективных детекторов в измерительных приборах.
• Направленное химическое превращение (дериватизация) определяемого
компонента — например, дериватизация определенных функциональных
групп при помощи детектирующих реагентов.
• Использование хроматографии — высокопроизводительного метода разде-
ления.
Таким образом, лишь немногие методики анализа селективны сами по себе.
Обычно селективность достигается при помощи подходящей подготовки пробы
и выбора условий измерения.
Для количественного анализа данные о качественном составе образца часто
бывают известны заранее (например, известно, что кровь содержит глюкозу).
В противном случае аналитику необходимо выполнить качественные испыта-
ния прежде, чем заняться значительно более трудным количественным анализом.
Современные химические измерительные системы часто обладают достаточно
высокой селективностью, поэтому результаты количественных измерений од-
новременно являются и доказательствами качественного состава образца. Тем
не менее простые качественные тесты часто выполняются значительно быстрее,
чем процедуры количественного анализа. Качественный анализ делится на две
области: неорганический и органический. Неорганический анализ обычно пре-
подается во вводных курсах химических дисциплин, органический лучше пре-
подавать лишь после того, как студент освоит курс органической химии.
Для сравнения качественного и количественного анализа рассмотрим, на-
пример, последовательность аналитических процедур при тестировании проб на
запрещенные вещества во время Олимпийских игр. Список запрещенных препа-
ратов включает около 500 физиологически активных веществ различных классов:
стимуляторов, стероидов, бета-блокаторов, диуретиков, наркотиков, анальгети-
22
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИ МИКИ-АНАЛИТИКИ
ков, местных анестетиков и седативных средств. Некоторые из них можно обнару-
жить только по их метаболитам. Необходимо быстро протестировать множество
спортсменов, поэтому нерационально подвергать каждую пробу детальной про-
цедуре количественного анализа. Анализ включает в себя три стадии: стадия бы-
строго скрининга, стадия идентификации и, возможно, стадия количественного
анализа. На стадии быстрого скрининга пробы мочи в течение короткого време-
ни тестируют на наличие в них целых классов соединений, позволяющих отличить
их от «нормальных» проб. Для этого используют различные методы, включая
иммунный анализ, газовую и жидкостную хроматографию. Приблизительно в
5% случаев пробы показывают наличие веществ, которые могут быть или не
быть в числе запрещенных, однако нуждаются в идентификации. Пробы, вы-
звавшие подозрения в ходе скрининга, заново подвергают циклу пробоподготовки
(возможно, включающей гидролиз, экстракцию, дериватизацию) в зависимости от
природы соединений, которые надо идентифицировать. Для их идентификации
используют высокоселективный метод, сочетающий газовую хроматографию и
масс-спектрометрию (ГХ-МС). В этом методе сложные смеси разделяют при по-
мощи газовой хроматографии, а затем идентифицируют отдельные компоненты
при помощи масс-спектрометрии, позволяющей получать информацию о струк-
туре молекул веществ. Сочетание масс-спектрометрических и собственно хрома-
тографических (времена удерживания) данных позволяет с высокой вероятностью
сделать заключение о присутствии того или иного вещества. Анализ методом
ГХ-МС является длительным и дорогостоящим, поэтому его используют только
при крайней необходимости. После идентификации для некоторых веществ не-
обходимо точно определить их содержание, поскольку они могут присутство-
вать и в нормальных пробах (например, поступая из пищи, из лекарственных
средств или выделяясь в ходе жизнедеятельности организма — эндогенные стеро-
иды), но в низких концентрациях. Таким образом, необходимо подтвердить, что
их концентрации превышают норму. Для этого используют методы количественно-
го анализа — например, спектрофотометрию или ту же газовую хроматографию.
В данной книге рассматриваются главным образом методы количественно-
го анализа. При рассмотрении практического применения этих методов приве-
дены примеры из различных областей: наук о живом, клинической химии,
химии окружающей среды, техники безопасности и охраны здоровья, производ-
ственного анализа.
Давайте сначала кратко ознакомимся с процессом анализа в целом, а затем
перейдем к более подробному изучению методов (в последующих главах).
1.3. Мы начинаем процесс анализа
Общая схема процесса анализа приведена на рис. 1.1. Химик-аналитик должен
осуществлять все его стадии, он является ключевым звеном рабочей группы и
определяет, что, почему и как следует делать. Ниже подробно рассмотрены
стандартные операции химического анализа, общие для большинства типов ана-
лизов.
1.3. МЫ НАЧИНАЕМ ПРОЦЕСС АНАЛИЗА
23
Постановка задачи: что необходимо узнать (не обязательно все!)
Прежде чем планировать ход анализа, аналитик должен знать, какую информа-
цию требуется получить, для кого, с какой целью и какого рода пробу предстоит
проанализировать. Кроме того, он должен уметь устанавливать хорошие отно-
шения с заказчиком и это, возможно, окажется решающим моментом. В качестве
заказчика может выступать кто угодно — американское Агентство по охране окру-
жающей среды (Environmental Protection Agency, ЕРА), потребитель промышлен-
ной продукции, инженер, родственники — и у каждого будут свои критерии и
требования, свое понимание того, что включает в себя химический анализ и что
он означает. Поэтому важно, чтобы общение с заказчиком шло на языке, понят-
ном обеим сторонам. Если кто-нибудь поставит вам на стол бутылку с напитком и
спросит: «Что в ней находится?» или «Безопасно ли это в употреблении?», вам,
возможно, потребуется объяснить, что всего известно уже около 10 миллионов
различных химических соединений. Заказчик, который скажет: «Я хочу узнать,
какие элементы здесь содержатся», должен понять, что при средней стоимости
определения одного элемента порядка 20 долларов общая стоимость определения
85 элементов составит 1700 долларов, в то время как, возможно, содержание лишь
некоторых элементов представляет для него интерес.
Ко мне часто приходят дилетанты с образцами косметики, мечтающие вы-
пускать подделки и сделать состояние на их распространении. Но когда они узна-
ют, что определение необходимых ингредиентов в этой продукции при помощи
ряда сложных методов анализа может им обойтись очень дорого, они всегда
предпочитают заново обдумать свои намерения.
Такие понятия, как «безопасно», «отсутствует» или «нулевое содержание»,
не имеют ни строгого определения, ни смысла. Фразы типа «эта вода безопасна в
употреблении» — совсем не то, что должен говорить аналитик. Все, что он мо-
жет сделать, — это представить результаты анализа, охарактеризовав при этом
их точность, указав доверительные границы. Заказчик сам должен решить (воз-
можно, посоветовавшись с другими специалистами), можно ли эту воду исполь-
зовать для питья без угрозы для здоровья. Аналогично, не правильно указывать
в качестве результата «нуль», вместо этого должно быть: «ниже предела обнару-
жения» (который определяется характером измерений и типом измерительного
прибора). В подобных случаях необходимо говорить, что используемые методики
и средства измерений имеют ограниченные возможности. В то же время некото-
рые современные приборы позволяют измерять чрезвычайно малые содержа-
ния — например, на уровне нескольких частей на триллион (ppt), и это тоже
представляет собой проблему (по своей природе чаще всего политическую) при
разработке официальных нормативов. Например, может быть принят закон, тре-
бующий, чтобы в воде «отсутствовало» то или иное вещество. На практике в подоб-
ных случаях устанавливают предельно допустимые концентрации, определяемые
лишь возможностями анализа — тем, насколько низкие содержания можно об-
наружить. Но такие концентрации могут оказаться намного ниже природного
содержания этого вещества в воде или уровня, до которого его содержание мож-
но снизить. Химики-аналитики должны уметь эффективно доводить до сведе-
ния общественности, что представляют собой результаты анализов.
24
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
Постановка задачи
Необходимо учитывать:
• В чем состоит задача: что необходимо узнать? Нужен
качественный анализ или количественный?
• Для чего будет использована полученная информация?
Кто будет ее использовать?
• Когда она будет нужна?
• Насколько точными (правильными и воспроизводимыми)
должны быть результаты?
• Сколько средств отпущено на анализ?
• Аналитик должен посоветоваться с заказчиком, чтобы
составить осмысленный и эффективный план анализа,
включая получение пробы
Выбор метода и методики
Необходимо учитывать:
• Тип пробы
• Размер пробы
• Необходимую пробоподготовку
• Требуемую чувствительность (в зависимости от
диапазона концентраций определяемого вещества)
• Требуемую селективность, возможные мешающие
влияния
• Требуемую правильность и воспроизводимость
• Доступность аппаратуры
• Опыт работы, необходимость привлечения других
специалистов
• Стоимость анализа
• Быстроту выполнения анализа
• Должен ли анализ быть автоматизированным?
• Имеются ли в химической литературе необходимые
методики?
• Имеются ли стандартные методики?
Получение представительной пробы
Необходимо учитывать:
• Тип пробы, ее размер, степень гомогенности
• Погрешности пробоотбора
Рис. 1.1. Отдельные стадии химического анализа
Постановка задачи будет определять способ пробоподготовки, необходи-
мое количество пробы, требуемую чувствительность метода, его точностные ха-
рактеристики — правильность и воспроизводимость*, и то, какие операции
Правильность — это мера близости результата измерения к истинному значению измеряемой величины.
Воспроизводимость (прецизионность) — это мера близости результатов повторных измерений между со-
бой. Хорошая воспроизводимость не означает хорошую правильность. Более подробно эти понятия об-
суждаются в гл. 3.
1.3. МЫ НАЧИНАЕМ ПРОЦЕСС АНАЛИЗА
25
разделения могут потребоваться для устранения мешающих влияний. Как пра-
вило, определение микросодержания компонентов не требует такой высокой
точности, как определение основных компонентов, но в этом случае следует
уделять больше внимания предотвращению загрязнения пробы в ходе анализа.
Как только выбран метод анализа (принцип измерения), необходимо вы-
брать конкретную методику. При этом следует руководствоваться целым рядом
соображений, в том числе квалификацией аналитика, его опытом работы с теми
или иными приборами, доступностью необходимой аппаратуры, требуемой чув-
ствительностью и точностью, стоимость анализа и объемом средств, отпущен-
ных для его выполнения, временем выполнения анализа и тем, насколько быстро
должны быть получены результаты. Часто в справочниках описана одна или бо-
лее стандартные методики для определения данного аналита (компонента, ко-
торый необходимо определить) в пробе данного типа. Это вовсе не означает,
что методика может быть автоматически использована для проб другого типа.
Например, стандартная методика американского Агентства по охране окружаю-
щей среды для анализа почвенных вод может дать неверные результаты примени-
тельно к сточным водам. В химической литературе (журналах) содержится
множество описаний конкретных видов анализа. Целесообразно начать поиск ли-
тературы с реферативного журнала Chemical Abstracts (http://info.cas.org), изда-
ваемого Американским химическим обществом. Он содержит рефераты всех
статей, публикуемых в основных химических журналах мира. В журнале име-
ются годовые и сводные указатели, а многие библиотеки оснащены компьютер-
ными средствами поиска. Можно непосредственно изучать основные журналы
по аналитической химии, например, Analytica Chimica Acta, Analytical Chemistry,
Analytical Letters, Analyst, Applied Spectroscopy, Clinica Chimica Acta, Clinical
Chemistry, Journal of the Association of Official Analytical Chemists, Journal of
Chromatography, Spectrochimica Acta, Taianta. Если необходимая методика не
описана в литературе, аналитик часто может использовать данные литературы
об определяемом веществе, чтобы самостоятельно разработать подходящую
схему анализа. Наконец, аналитик может разработать свою собственную мето-
дику анализа данной пробы, опираясь на свои знания и опыт. Описания разнооб-
разных методик определения большого числа веществ содержатся в источниках,
приведенных в Приложении А.
Примеры описаний выполнения анализа разных типов проб содержатся в
гл. 24-26. В них рассмотрены некоторые широко используемые клинические,
биохимические и экологические анализы. Для выполнения отдельных анализов
применяют различные методы, разобранные в предыдущих главах. Поэтому
гл. 24-26, посвященные практическому применению аналитической химии, по-
лезно прочитать дважды: сейчас и после того, как будет изучена основная часть
книги. В этом случае можно в полной мере почувствовать, в чем состоит анализ
реальных проб и как выполняются такие анализы.
После того как задача поставлена, наступает очередь следующих этапов
анализа.
26
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
Получение представительной пробы:
невозможно анализировать объект целиком!
Обычно для химического анализа используют лишь небольшую часть того объ-
екта, который необходимо охарактеризовать. Но если размер объекта очень мал,
а его вещество не требуется использовать в дальнейшем, объект можно анализи-
ровать и целиком. Примером может служить определение следов пороха на
коже руки человека. Чаще всего исследуемый материал представляет собой
определенную ценность, и поэтому в результате отбора пробы он должен изме-
ниться как можно меньше.
Материал, от которого отбирается проба, может быть твердым, жидким или
газообразным. По своему строению он может быть гомогенным или гетероген-
ным. В первом случае для анализа может быть использована любая произвольно
отобранная проба. Во втором случае может представлять интерес пространст-
венное изменение состава пробы, тогда необходимо отобрать несколько проб.
Если же требуется установить среднее содержание компонента, используют
специальную технику пробоотбора, чтобы полученная проба была представите-
льной. Например, для определения среднего содержания белка в партии зерна
можно взять небольшую пробу из каждого мешка (для крупных партий — из
каждого десятого мешка), объединить их и тем самым получить генеральную
пробу. Технически отбор пробы легче всего осуществить, если исследуемый ма-
териал движется перед вами. Чем больше размер частиц материала, тем больше
должна быть и его генеральная проба. Генеральную пробу следует уменьшить,
чтобы получить лабораторную пробу массой несколько граммов или десятков
граммов. Из нее отбирают анализируемую пробу массой от нескольких мил-
лиграммов до нескольких граммов. При сокращении размера пробы может потре-
боваться многократный отбор порций (например, по две из четырех четвертей) и
их перемешивание, а также измельчение и просеивание для того, чтобы в конце
концов получить однородный порошок, пригодный для анализа. Таким образом,
генеральная проба имеет размер, достаточный для того, чтобы отобрать из нее
для анализа много порций. Лабораторная проба — это небольшая гомогенизи-
рованная порция генеральной пробы. Анализируемую пробу непосредственно
подвергают анализу. Отдельные способы отбора проб твердых, жидких и газо-
образных материалов рассмотрены в гл. 2.
При отборе проб биологических жидкостей могут играть роль условия, в ко-
торых они взяты, — например, принимал ли пациент перед этим пищу. Состав
крови до и после приема пищи значительно отличается, и для многих анализов
необходимо брать кровь натощак. После взятия образцов крови к ним бывает не-
обходимо добавить консерванты, например фторид натрия при определении
глюкозы, антикоагулянты. Их наличие может повлиять на результаты анализа.
Пробы крови можно, в зависимости от конкретных требований к анализу,
анализировать в виде цельной крови или предварительно разделить и анализи-
ровать плазму либо сыворотку. В большинстве случаев важным физиологиче-
ским показателем является концентрация вещества вне красных кровяных клеток,
поэтому для анализа используют сыворотку или плазму.
1.3. МЫ НАЧИНАЕМ ПРОЦЕСС АНАЛИЗА
27
Если порцию цельной крови оставить на несколько минут, то содержа-
щийся в ней растворимый белок фибриноген в результате сложной последова-
тельности химических реакций (с участием ионов кальция) превращается в
нерастворимый белок фибрин, составляющий основу геля — сгустка крови.
Поры пространственной сетки, образованной молекулами фибрина, захватыва-
ют красные и белые кровяные клетки. Таким образом, они входят в состав сгуст-
ка, хотя и не участвуют непосредственно в его образовании. Затем сгусток
сжимается и из него выделяется соломенно-желтая жидкость, сыворотка кро-
ви. Она не свертывается и остается в жидком состоянии неограниченно долго.
Процесс свертывания крови можно предотвратить при помощи добавок ве-
ществ-антикоагулянтов, например, гепарина или цитрат-ионов (образующих
комплексы с ионами кальция). После добавления антикоагулянтов для анализа
можно использовать аликвоту цельной крови либо отделить красные кровяные
клетки центрифугированием и анализировать оставшуюся розоватую жидкость,
называемую плазмой. То есть, сыворотка — это жидкость, получаемая путем
отделения от нее свернувшейся крови. Плазма — это жидкость, получаемая пу-
тем отделения несвернувшихся красных кровяных клеток. По своему химическо-
му составу плазма и сыворотка почти идентичны. Основное различие состоит в
том, что сыворотка не содержит фибриногена.
Подробности отбора проб различных материалов можно прочитать в спра-
вочниках по отдельным аспектам химического анализа. Можете посмотреть, в
частности, некоторые ссылки в конце данной главы.
Следует принимать специальные меры предосторожности при обработке и
хранении проб, чтобы предотвратить или минимизировать их загрязнение, по-
тери или изменение состава матрицы. Основными источниками загрязнений и
изменений пробы могут быть: 1) посуда, 2) атмосфера и 3) воздействие света.
Если результаты анализов предполагается использовать в качестве судебных до-
казательств, то необходимы специальные меры по охране проб. В ходе нашумев-
шего дела по обвинению известного американского спортсмена О. Дж. Симпсона
в убийстве в телевизионных новостях показывали кадры, на которых, в частно-
сти, люди помещали пробы, находящиеся без всякой охраны, в кузов автомоби-
ля, где температура воздуха была повышенной. Хотя это обстоятельство могло и
не повлиять на правильность результатов, оно дало защите повод дискредитиро-
вать результаты анализов.
Может потребоваться защита проб от действия атмосферы или света. На-
пример, если пробы представляют собой щелочные растворы, то они будут взаи-
модействовать с углекислым газом воздуха. При анализе образцов крови на
содержание СО2 их также следует защитить от действия атмосферы.
Необходимо принимать во внимание, что проба может быть неустойчивой.
В частности, растворы глюкозы неустойчивы, поэтому к пробам крови для опре-
деления глюкозы необходимо добавлять стабилизатор — фторид натрия. Разу-
меется, присутствие стабилизатора не должно искажать результаты анализа.
Белки и ферменты имеют склонность с течением времени денатурировать, поэ-
тому их надо определять немедленно. Следовые компоненты при хранении мо-
гут быть утрачены вследствие адсорбции на стенках сосуда.
28
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИ МИКИ-АНАЛИТИКИ
Пробы мочи неустойчивы, из них со временем осаждается фосфат кальция,
захватывая ионы металлов и другие вещества, которые могут представлять ин-
терес для анализа. Осаждение фосфата кальция можно предотвратить, подкис-
ляя пробу до pH 4,5 — обычно добавлением 1-2 мл ледяной уксусной кислоты
на 100 мл пробы. Пробы лучше хранить в холодильнике. Пробы мочи, а также
цельной крови, плазмы, сыворотки и тканей, можно хранить в замороженном
виде в течение долгого времени. Пробы крови, из которых удалены белки, более
устойчивы, чем пробы, не подвергшиеся обработке.
Пробы, которые содержат газы, вызывающие коррозию, часто взаимо-
действуют с материалом сосуда. Это касается, в частности, диоксида серы. Кро-
ме того, SO2, содержащийся в газах автомобильных выхлопов, часто теряется
из-за растворения в воде, образующейся в результате конденсации содержащей-
ся в пробе влаги. В подобных случаях предпочтительнее анализировать газ в по-
токе.
Подготовка пробы к анализу:
возможно, ее состав потребуется изменить
Первый шаг собственно анализа — измерение количества анализируемой пробы
(например, ее массы или объема). Это потребуется для расчета процентного со-
держания определяемого компонента. Количество анализируемой пробы дол-
жно быть измерено с той точностью, которая в данном случае необходима. Для
измерения массы обычно используют аналитические весы с погрешностью из-
мерения порядка 0,1 мг. В твердых пробах часто анализируют сухой остаток, по-
этому их следует предварительно высушить при температуре 110-120 °C (если
проба, разумеется, устойчива при этих температурах) и охладить в эксикаторе
перед взвешиванием. В некоторых случаях вследствие высокой гигроскопично-
сти проб могут потребоваться более высокие температуры и более продолжитель-
ное нагревание (например, в течение ночи). Требуемое количество анализируемой
пробы зависит от содержания в ней определяемого компонента и того, сколько
вещества необходимо для измерения сигнала. Для определения главных компо-
нентов может быть достаточно лишь 100-200 мг пробы, в то время, как для опре-
деления следовых компонентов может потребоваться несколько граммов. Как
правило, для анализа отбирают несколько параллельных проб, чтобы набрать
данные для статистической оценки точности анализа и получить более досто-
верные результаты.
По своей природе метод анализа может быть неразрушающим (недеструк-
тивным) — как например, при определении свинца в образцах красок рентге-
нофлуоресцентным методом, основанным на облучении пробы потоком
рентгеновских лучей и измерении интенсивности возникающего при этом ха-
рактеристического вторичного рентгеновского излучения. Однако гораздо
чаще твердые образцы перед анализом необходимо перевести в раствор. Неор-
ганические вещества можно растворить в различных кислотах и других средах,
обладающих окислительно-восстановительными или комплексообразующими
свойствами. Для растворения веществ, нерастворимых в кислотах, может потре-
1.3. МЫ НАЧИНАЕМ ПРОЦЕСС АНАЛИЗА
29
боваться сплавление с кислыми или щелочными плавнями, после чего эти веще-
ства становятся растворимыми в разбавленных кислотах или воде. Например,
сплавление с карбонатом натрия приводит к образованию карбонатов, раствори-
мых в кислотах.
Органические вещества, которые необходимо проанализировать на содер-
жание неорганических веществ, например, следов металлов, можно разрушить
посредством сухого озоления. Озолением называется разложение органических
веществ путем сжигания. В этом случае пробу медленно сжигают в печи при
температуре 400-700 °C, после чего получается неорганический остаток, рас-
творимый в разбавленных кислотах. С другой стороны, органические вещества
можно разрушить путем мокрого сожжения (минерализации) при нагревании с
кислотами-окислителями. Минерализация — это разложение органических ве-
ществ путем окисления в растворе. Обычно используют смесь серной и азотной
кислот. Биологические жидкости иногда можно анализировать непосредствен-
но. Однако часто определению мешают белки, поэтому их необходимо удалить.
Это можно сделать как посредством сухого озоления, так и мокрого сожжения.
Белки можно также осадить различными реагентами, после чего отфильтровать
или отцентрифугировать и получить безбелковый фильтрат.
Если определяемый компонент представляет собой органическое вещество,
методы пробоподготовки, использующие окисление, неприменимы. В этих слу-
чаях аналит можно отделить экстракцией или диализом, либо растворить пробу
в подходящем растворителе. Иногда и в этом случае возможно недеструктивное
определение. Примером может служить непосредственное определение белка в
пищевых продуктах при помощи ИК-спектроскопии в ближней области.
После перевода пробы в раствор следует создать определенные условия
среды, необходимые для осуществления следующего этапа анализа (разделения
или измерения). Например, часто необходимо установить определенное значе-
ние pH анализируемого раствора или добавить специальные реагенты, взаимо-
действующие с мешающими примесями и тем самым маскирующие их. Кроме
того, может потребоваться проведение реакции с участием самого аналита, чтобы
перевести его в форму, необходимую для разделения или измерения. Например, для
спектрофотометрического определения необходимо получить окрашенный про-
дукт реакции, а для определения методом газовой хроматографии — продукт,
обладающий летучестью. Для гравиметрического определения железа в виде
Fe2O3 требуется, чтобы все железо находилось в виде Fe(III) — обычной форме
существования этого элемента. Напротив, для титриметрического определения
с бихромат-ионами железо необходимо полностью перевести в Fe(II) до прове-
дения титрования. В этом случае необходимой стадией пробоподготовки явля-
ется восстановление.
Все растворители и реагенты, используемые для растворения пробы и дру-
гих операций пробоподготовки, должны иметь высокую чистоту (их квалифика-
ция должна быть не ниже ч. д. а.). Но даже такие реагенты могут содержать
следовые количества определяемого компонента. Поэтому необходимо подго-
товить и провести несколько параллельных контрольных опытов. Это особен-
но важно при определении следов веществ. Всегда проводите контрольные
30
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИ МИКИ-АНАЛИТИКИ
опыты\ В идеальном случае образец контрольного опыта содержит все компо-
ненты реальной пробы, кроме определяемого вещества. Его проводят через все
стадии анализа, используя такие же количества всех реагентов (включая воду).
Результат измерения, полученный в контрольном опыте, вычитают из результа-
тов, полученных для реальных проб. Тем самым находят чистое содержание ана-
лита в пробе. Если сигнал контрольного опыта имеет значительную величину,
это может привести к потере смысла результатов анализа. В то же время провес-
ти «идеальный» контрольный опыт часто оказывается невозможно.
Выполнение операций разделения
Чтобы устранить мешающие влияния и добиться требуемой селективности из-
мерения, а также чтобы сконцентрировать аналит для обеспечения более высо-
кой чувствительности или точности, часто бывает необходимо выполнить одну
или несколько последовательных операций разделения компонентов. Предпочти-
тельнее отделять аналит от матрицы, а не наоборот: в этом случае меньше вероят-
ность потерь аналита. Операции разделения могут представлять собой осаждение,
экстракцию несмешивающимся с водой растворителем, хроматографический
процесс, диализ или отгонку.
Измерение аналитического сигнала: вы выбираете метод!
Выбор метода измерения количества аналита зависит от множества факторов.
Не последнюю роль играет содержание аналита в пробе и требуемая точность
результатов. Множество существующих методов анализа различаются уровнем
селективности, чувствительности, точности (правильности и воспроизводимо-
сти), стоимости и скорости выполнения анализа. Гравиметрический метод
обычно включает в себя селективное отделение аналита в виде осадка с последу-
ющим крайне неселективным способом измерения — измерением его массы.
Титриметрический метод основан на взаимодействии аналита с измеренным
объемом раствора реагента известной концентрации в ходе процесса, называе-
мого титрованием. Свидетельством завершения реакции служит резкое изме-
нение какого-либо физического или химического свойства системы. Методы
гравиметрии и титриметрии обладают очень высокой точностью — относитель-
ная погрешность может составлять десятые доли процента и даже менее. Но они
позволяют определять только относительно большие количества аналита (поряд-
ка миллимолей или миллиграммов) и пригодны лишь для определения основных
компонентов. Титриметрический анализ выполняется быстрее гравиметриче-
ского и потому, при наличии выбора, он предпочтительнее.
Инструментальная техника используется во многих методах анализа. Ее
изучают в рамках отдельной дисциплины — инструментальных методах ана-
лиза. Инструментальные методы основаны на измерении физического свойства
пробы, например, электрических свойств или поглощения электромагнитного
излучения. Примерами инструментальных методов анализа могут служить спек-
трофотометрия (в ультрафиолетовой, видимой, инфракрасной области спектра),
флуориметрия, атомная спектроскопия (абсорбционная и эмиссионная), масс-спек-
1.3. МЫ НАЧИНАЕМ ПРОЦЕСС АНАЛИЗА
31
трометрия, спектрометрия ядерного магнитного резонанса (ЯМР), рентгенов-
ская спектроскопия (абсорбционная, флуоресцентная), электрохимические
методы анализа (потенциометрия, вольтамперометрия, кулонометрия), хрома-
тография (газовая, жидкостная) и радиохимические методы. В целом инструмента-
льные методы более чувствительны и селективны, чем классические (гравиметрия
и титриметрия), но они менее точны: относительная погрешность составляет
1-5% или более. Кроме того, инструментальные методы обычно более дорого-
стоящие, капиталоемкие. Однако с точки зрения стоимости одного определения
они могут быть дешевле, если учитывать и затраты рабочей силы. Инструмента-
льные анализы, как правило, выполняются быстрее, их можно автоматизиро-
вать, с их помощью можно определять содержание нескольких компонентов
одновременно. Особенно большими возможностями для анализа сложных сме-
сей обладают хроматографические методы. Они позволяют осуществлять разде-
ление и измерение одновременно. Разделение достигается за счет того, что
компоненты смеси имеют различное сродство к материалу хроматографической
колонки и при пропускании смеси через колонку выходят из нее (элюируются) в
течение разного времени. Для определения используется подходящий детектор,
реагирующий на каждое выходящее из колонки вещество. В результате форми-
руется сигнал в виде пика, площадь которого пропорциональна количеству ана-
лита.
В табл. 1.1. приведены характеристики различных методов анализа, описан-
ных в данной книге: чувствительность, воспроизводимость, селективность, ско-
рость и стоимость выполнения анализа. Данные, приведенные в этой таблице,
типичны для большинства приложений разных методов. Эти методы могут быть
использованы и для других целей, и в отдельных случаях характеристики могут
оказаться лучше указанных. Для титриметрического определения более низких
концентраций необходимо детектировать конец титрования инструментальны-
ми средствами. Если для решения задачи можно применить несколько методов,
то выбор определяется наличием необходимого оборудования и квалифициро-
ванного персонала, а также личными предпочтениями аналитика. Например, для
определения нитратов в речной воде на уровне 1 части на миллион (1 ppm или
1,6 • 10~5 М) можно использовать метод спектрофотометрии после проведения
реакции диазотирования с участием нитрат-ионов и образованием окрашенного
продукта. Фториды в зубной пасте можно определить потенциометрически при
помощи фторидселективного электрода. Сложные смеси углеводородов бензи-
на можно разделить и проанализировать при помощи газовой хроматографии.
Глюкозу в крови можно определить кинетическим методом по скорости фер-
ментативной реакции между глюкозой и кислородом, катализируемой фермен-
том глюкозооксидазой. При этом можно измерять как скорость расходования
кислорода, так и скорость образования продукта реакции — пероксида водоро-
да. Степень чистоты серебряного слитка можно определить гравиметрически,
растворив небольшую пробу объекта в азотной кислоте, осадив хлорид серебра
действием хлорид-ионов и измерив массу осадка.
Все методы анализа можно разделить на абсолютные и относительные.
В основе абсолютных методов лежит расчет содержания аналита с использова-
Таблица 1.1.
Сравнение различных методов анализа
Метод Ориентировоч- ный диапазон концентраций (моль/л) Ориентиро- вочная точ- ность (%) Селективность Скорость выполнения анализа Стоимость Объекты
Гравиметрия lO-'-lO-2 од низкая-средняя малая низкая неорг.
Титриметрия КН-ЦН 0,1-1 низкая-средняя средняя низкая неорг., орг.
Потенциометрия lO-’-lO-6 2 высокая высокая низкая неорг.
Электрогравиметрия, кулонометрия 0,01-2 средняя низкая-средняя средняя неорг., орг.
Вольтамперометрия 1о-мо-10 2-5 высокая средняя средняя неорг., орг.
Спектрофотометрия 10-3-10-6' 2 высокая-средняя высокая-средняя низкая-средняя неорг., орг.
Флуориметрия 10-6-10-9 2-5 средняя средняя средняя орг.
Атомная спектроскопия 10-3-10-9 2-10 высокая высокая средняя-высокая неорг. (многоэлементный)
Хроматография 10-3-10-9 2-5 высокая высокая-средняя средняя-высокая орг. (многокомпонентный)
Кинетические методы 10-2-10-10 2-10 высокая-средняя высокая-средняя средняя неорг., орг., ферменты
1.3. МЫ НАЧИНАЕМ ПРОЦЕСС АНАЛИЗА
33
нием фундаментальных констант, например, атомных масс. Так, в гравиметри-
ческом анализе аналит превращают в нерастворимое производное известного
химического состава и взвешивают его. Например, для определения хлорид-
ионов получают хлорид серебра AgCl. Массовая доля аналита в осадке известна,
в рассмотренном примере массовая доля хлорид-ионов составляет
оГ1_ = Мг п/Мг АаГ1 = 35,453/143,32 = 0,24737
СД Г к_/1 Г /\gVzi
(где Мг — относительная молекулярная масса). Таким образом легко рассчи-
тать содержание хлорид-ионов в полученном осадке. Однако большинство мето-
дов являются относительными, т. е. требуют сравнения результатов с данными,
полученными для раствора известной концентрации. Например, в титриметри-
ческом анализе используют знание стехиометрии реакции аналита с реаген-
том. Соляная кислота реагирует с гидроксидом натрия в соотношении 1 : 1
согласно уравнению
НС1 + NaOH -> NaCl + Н2О
Объем раствора гидроксида натрия, необходимый для полного протекания
этой реакции, можно измерить. Если молярная концентрация гидроксида натрия
в растворе известна, то можно рассчитать количество NaOH (в молях), добавлен-
ного к пробе (как произведение концентрации на объем). Так можно узнать и ко-
личество НС1 (в молях) в пробе. Но для этого необходимо в первую очередь
приготовить раствор реагента (гидроксида натрия) точно известной концентра-
ции. Таким образом, титриметричекий метод является относительным.
Большинство инструментальных методов анализа также являются относи-
тельными. Прибор регистрирует аналитический сигнал, обусловленный какими-
либо физическими свойствами пробы. Например, спектрофотометры измеряют
долю электромагнитного излучения источника света, поглощаемую раствором
пробы. Эту величину можно соотнести с концентрацией определяемого компо-
нента только посредством сравнения с такой же величиной, измеренной для рас-
твора с известной концентрацией аналита. Иными словами, в инструментальных
методах анализа требуется градуировка при помощи образцов сравнения.
Аналитический сигнал может быть связан с концентрацией определяемого
компонента линейно или нелинейно. Градуировка заключается в приготовлении
серии стандартных растворов аналита с известной концентрацией (как правило,
затем их подвергают той же обработке, что и анализируемую пробу), измерении
аналитического сигнала (величины отклика прибора) для каждого из них и по-
строении градуировочной кривой — зависимости аналитического сигнала от
концентрации аналита. При помощи этой зависимости определяют неизвестное
содержание аналита по величине его сигнала. Современные приборы, управляе-
мые компьютерами, часто позволяют проводить эту операцию автоматически и
выдают конечный результат в виде значения концентрации.
На величину аналитического сигнала может оказывать влияние состав мат-
рицы образца. В подобных случаях для того, чтобы устранить матричные эффек-
ты пробы, градуировку следует осуществлять по методу стандартных добавок.
34
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
При этом к отдельным порциям раствора пробы добавляют известные количест-
ва стандартного раствора аналита и измеряют увеличение сигнала, обусловленное
добавкой. При использовании метода добавок стандартный раствор находится в
той же среде, что и аналит. Этот способ градуировки будет обсуждаться подроб-
нее при рассмотрении отдельных методов анализа.
Вычисление результатов и предоставление отчета:
характеристика объекта в целом
После определения концентрации аналита в пробе полученные результаты ис-
пользуют для расчета количества аналита в исходном образце. Результат может
быть выражен как в абсолютных, так и в относительных величинах. Как прави-
ло, приводят относительное содержание, например, в виде массовой доли
(в процентах, частях на миллион или других величинах). Оно характеризует
правильность результатов. Можно выполнить серию параллельных определений
(три или более) и привести в отчете данные о воспроизводимости результатов —
например, величину стандартного отклонения. Данные о воспроизводимости пред-
ставляют важность, поскольку они позволяют охарактеризовать неопределен-
ность результата (см. гл. 3). Аналитик должен критически оценить, насколько
разумны полученные результаты в свете постановки исходной задачи. Помните,
что потребитель часто не имеет научной подготовки и может воспринимать
ваши цифры как истину в последней инстанции. Только вы, как аналитик, може-
те объяснить смысл этих цифр. Аналитик должен уметь дать квалифицирован-
ный совет по поводу всего, что касается смысла результата анализа. Поэтому
важно, чтобы вы нашли общий язык с «потребителем» ваших данных во всем,
что касается интерпретации результатов.
1.4. Поверка методики: вы должны доказать, что она работает!
Проблеме правильности результатов анализа необходимо уделять большое вни-
мание. Существуют два типа погрешностей измерений: случайные и система-
тические. Результат любого измерения содержит некоторую неопределенность.
Это приводит к тому, что результаты параллельных измерений распределены
случайным образом, например, в соответствии с законом нормального (гауссов-
ского) распределения. Эксперимент можно и нужно планировать таким образом,
чтобы уменьшить этот разброс, но его никогда нельзя устранить полностью. Сис-
тематическая погрешность приводит к смещению всех результатов измерений в
одном направлении. Это может происходить, например, вследствие того, что
матрица пробы уменьшает аналитический сигнал. Возможно, что аналитиче-
ские весы неправильно откалиброваны и все значения масс оказываются зани-
женными или завышенными. Из образца может быть не полностью удалена
влага — это тоже приводит к систематическим погрешностям.
1.4. ПОВЕРКА МЕТОДИКИ: ВЫ ДОЛЖНЫ ДОКАЗАТЬ, ЧТО ОНА РАБОТАЕТ!
35
Для обеспечения правильности результатов необходимо прежде всего пра-
вильно откалибровать измерительные приборы. Но это лишь первый шаг. В ходе
отработки методики следует проанализировать образцы, в которые добавлено
известное содержание аналита (в количествах как выше, так и ниже его пример-
ного содержания в пробе). Полученные результаты (после вычитания найденно-
го содержания аналита в самой пробе, проанализированной по той же методике)
должны находиться в пределах требуемой точности анализа. Для поверки новой
методики можно также сравнить результаты, полученные с ее помощью, с резу-
льтатами анализа той же пробы при помощи другой, общепринятой, методики.
Кроме того, существует множество стандартных образцов известного состава;
анализ стандартных образцов также позволяет убедиться в правильности испо-
льзуемой методики. Самый лучший способ проверить методику состоит в том,
чтобы проанализировать стандартный образец известного состава. В прода-
же имеются, например, стандартные образцы вод с известным содержанием
пестицидов или почв с известным содержанием приоритетных загрязнителей,
используемые для контроля окружающей среды. Американский Национальный
институт стандартов и технологий (National Institute of Standards and Technology,
NIST) изготавливает стандартные образцы объектов с матрицами различной
природы (сталей, опавших листьев и т. д.), содержание ряда аналитов в которых
тщательно определено, по крайней мере, двумя независимыми методами и офи-
циально удостоверено. Для всех содержаний указаны доверительные интервалы.
Различные агентства и промышленные концерны могут предоставить образцы
для межлабораторных экспериментов, в ходе которых образцы рассылают лабо-
раториям-участникам случайным образом. До выполнения анализов составы об-
разцов участникам не известны.
При использовании стандартных образцов их следует анализировать впере-
мешку с реальными пробами. Контрольный стандартный образец необходимо
анализировать хотя бы раз в день. Зависимость результатов его анализа от вре-
мени откладывают на карте контроля качества (контрольной карте). На ней же
откладывают известное значение стандартного отклонения методики. Если до-
пустить, что среднее значение измеряемой величины не изменяется со време-
нем, а ее распределение отвечает нормальному закону, то результат измерения
должен отличаться от истинного значения более чем на удвоенное стандартное
отклонение лишь в 1 случае из 20, а на 2,5 стандартных отклонения — в 1 случае
из 100. Если отклонения встречаются чаще, это указывает на наличие неском-
пенсированных погрешностей, которые могут быть вызваны нарушениями рабо-
ты аппаратуры, разрушением реагентов, неправильной градуировкой и другими
причинами.
Выполнение всех анализов, результаты которых предполагается использо-
вать в официальных целях (в том числе в суде), необходимо тщательно протоко-
лировать, а соответствующие методики — поверять в соответствии с нормами,
регламентируемыми государством. Для обеспечения поверки результатов ана-
лизов разработаны нормативные документы, называемые «Хорошей лаборатор-
ной практикой» (Good laboratory practice, GLP). Подробно эти правила
рассмотрены в гл. 4.
36
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
1.5. Как определить размер пробы?
Виды анализа часто классифицируют в зависимости от требуемого размера про-
бы. Такая классификация условна, а границы классов нечетки. В соответствии с
ней анализ можно разделить на следующие виды: мезо-, полумикро-, микро- и
ультрамикроанализ. Последние две категории часто объединяют под названи-
ем «анализ следовых количеств». В табл. 1.2 приведена приблизительная клас-
сификация методов в зависимости от массы или объема пробы. Классификация
по объему обычно применяется в клинических лабораториях. Для операций с
микро- и ультрамикроколичествами вещества необходима специальная аппара-
тура и микровесы.
Таблица 1.2
Классификация методов анализа по размеру пробы
Название Масса пробы (мг) Объем пробы (мкл)
Мезоанализ >100 >100
Полумикроанализ 10-100 50-100
Микроанализ 1-10 <50
Ультрамикроанализ <1
«Анализировать» и «определять» — различные понятия
Термины «анализировать» и «определять» различаются по значению. Говорит-
ся, что пробу анализируют на содержание в ней одного или нескольких компо-
нентов. Компоненты, содержание которых измеряют, называются аналитами.
Процесс измерения содержания аналита называется определением. Например,
в ходе анализа крови на содержание хлоридов мы определяем концентрацию
хлорид-ионов. Таким образом, пробу анализируют, чтобы определить в нем со-
держание компонента.
Компоненты пробы можно разделить на главные (содержание более 1%),
сопутствующие (0,1-1%) и следовые (менее 0,1%). Компоненты с содержани-
ем порядка частей на миллион и менее можно назвать ультраследовыми.
Анализ может быть полным или частичным в зависимости от того, опре-
деляют ли все компоненты пробы или только некоторые из них. Чаще всего в
ходе анализа необходимо определить содержание одного конкретного компо-
нента или класса веществ.
1.6. Некоторые полезные Интернет-сайты
Кроме многочисленных книг и других источников, отмеченных в основном тек-
сте и Приложении А (литература по аналитической химии), существует большое
1.6. НЕКОТОРЫЕ ПОЛЕЗНЫЕ ИНТЕРНЕТ-САЙТЫ
37
число Интернет-страниц, которые могут быть полезны химикам-аналитикам в
качестве дополнительных ресурсов. Разумеется, они часто претерпевают изме-
нения. Появляются и новые страницы. Однако те из них, что перечислены ниже,
в любом случае могут служить хорошей отправной точкой для получения мно-
гочисленной полезной информации.
Химия в целом
1. www.arc.org — домашняя страница Американского химического общества.
Имеется информация о журналах, конференциях, химические новости, по-
исковые базы данных (включая Chemical Abstracts) и многое другое.
2. www.chemweb.com — виртуальный клуб химиков. На сайте есть базы дан-
ных и сводные таблицы химического содержания. Действуют дискуссион-
ные форумы, ориентированные на различные химические дисциплины,
в частности, аналитическую химию. Для вступления в клуб необходимо за-
регистрироваться, регистрация бесплатная.
3- www.chemsoc.org — сеть сайтов химических обществ, поддерживаемая
британским Королевским химическим обществом. Информацию на сайт
предоставляют около 30 национальных химических обществ. Имеется вир-
туальная Периодическая таблица элементов, которую вы можете загрузить
в качестве экранной заставки компьютера.
4- http://micro.magnet.fsu.edu/primer/java/scienceopticsu/powersoflO/index.html
— посмотрите на это наглядное представление масштабов различных объек-
тов — начиная от протона и кончая Млечным путем, находящимся в
10 миллионах световых лет от Земли.
Аналитическая химия
1. www.acs-analytical.duq.edu — домашняя страница Отделения аналитиче-
ской химии Американского химического общества. На сайте имеется мно-
жество ссылок и других ресурсов, позволяющих переходить к различным
страницам, связанным с аналитической химией, по всему Интернету.
2. www.chem-uni.potsdam.de/linkcenter/analchem.html — коллекция ссылок
по аналитической химии, ведущих к университетским и другим сайтам все-
го мира.
3. www.cstl.nist.gov/nist839 — страница Отделения аналитической химии
Национального института стандартов и технологий США (NIST). Содер-
жит информацию о каждом из пяти своих направлений: спектрохимиче-
ских методов, методов органического анализа, газовой метрологии и
классических методов, молекулярной спектроскопии и микрожидкостных
методов, ядерно-физических методов анализа.
4. www.rsc.org/lap/rsccom/dab/analdiv.htm — сайт аналитического отделения
Королевского химического общества — британского аналога отделения
аналитической химии Американского химического общества.
38
ЗДЦАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИМИКИ-АНАЛИТИКИ
5. http://chemweb.chem.uconn.edu/Microchem/Index.html — сайт Американ-
ского микрохимического общества. Содержит ссылки на страницы науч-
ных сообществ по аналитической химии, конференций и личные страницы
отдельных ученых.
6. http://analytical.chemweb.com/home — форум по аналитической химии
сайта Chemweb, упомянутого выше.
7. www.asdlib.org — цифровая лаборатория по аналитическим наукам (Ana-
lytical Sciences Digital Laboratory, ASDL). Находится в начальной стадии
развития, но обещает стать ключевым источником ссылок на рецензируе-
мые сайты, посвященные преподаванию и технике аналитической химии.
Дополнительную информацию об этом сайте можно получить на тексто-
вом сайте, упомянутом ранее.
Что мы узнали из этой главы?
• Задача аналитической науки — охарактеризовать материю с химической
точки зрения: что и сколько? — стр. 17
• Аналитик должен знать, какого рода информацию о веществе ему надо по-
лучить, и уметь приготовить представительную пробу — стр. 23, 26
• Лишь в редких случаях химические измерения специфичны, поэтому для
обеспечения высокой селективности необходимы специальные дополните-
льные операции — стр. 28
• Вы должны уметь выбрать подходящий метод анализа — стр. 30
• Методики необходимо поверять — стр. 34
• Существует много Интернет-страниц, посвященных аналитической хи-
мии — стр. 36
Вопросы
1. Что такое аналитическая химия?
2. В чем разница между качественным и количественным анализом?
3. Перечислите основные этапы методики анализа. Кратко охарактеризуйте
каждый этап.
4. В чем разница между понятиями «анализировать» и «определять», «проба»
и «аналит»?
5. Что такое контрольный опыт?
6. Перечислите основные способы измерений, применяемые в химическом
анализе.
7 Перечислите основные методы разделения, применяемые в химическом
анализе.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
39
8. Дайте определение инструментальных методов анализа.
9. Что такое градуировочный график?
10. В чем различие между специфичной реакцией и селективной реакцией?
11. Пользуясь табл. 1.1, предложите методы для решения следующих задач:
а) определение степени чистоты NaCl в поваренной соли; б) определение
содержания уксусной кислоты в уксусе; в) определение pH воды плаватель-
ного бассейна.
Рекомендуемая литература
Общая
1. J. Tyson, Analysis. What Analytical Chemists Do. London: Royal Society of
Chemistry, 1988. Небольшая книга, в которой в весьма сжатой форме об-
суждается, чем и как занимаются химики-аналитики.
2. R. W. Murray, «Analytical Chemistry Is What Analytical Chemists Do», Edito-
rial, Anal. Chem., 66 (1994) 682A.
3. G. M. Hieftje, «But Is It Analytical Chemistry?», Am. Lab., October (1993) 53.
4. T. Kuwana, Chair, Curricular Developments in the Analytical Sciences. Отчет о со-
вещаниях 1996 и 1997 г., финансируемых национальным научным фондом
(National Science Foundation) (kuwana@sunglower.com).
5. R. A. DePalma and A. H. Ullman, «Professional Analytical Chemistry in Indust-
ry. A Short Course to Encourage Students to Attend Graduate School», J. Chem.
Ed., 68 (1991) 383. Описание краткого курса производственной аналитиче-
ской химии, преподаваемого по заявкам в университетах и колледжах спе-
циалистами компании Proctor & Gamble, с целью разъяснить, чем
занимаются химики-аналитики в промышленности. Основной акцент сде-
лан на тезисе: химик-аналитик — человек, решающий проблемы. С вопро-
сами обращаться по адресу parry. d@ pg.com.
6. С. A. Lucy, «How to Succeed in Analytical Chemistry: A Bibliography of Reso-
urces from the Literature», Taianta, 51 (2000) 1125. Обзор литературы на
темы: как приобрести оборудование, как написать рукопись и как получить
работу в области аналитической химии.
7. G. D. Christian, «Evolution and Revolution in Quantitative Analysis», Anal.
Chem., 67 (1995) 532А. История аналитической химии с момента возникно-
вения человечества.
Энциклопедии и справочники
8. R. A. Meyers, editor-in-chief, Encyclopedia of Analytical chemistry. Chichester:
Wiley, 2000. 15-томное издание, в котором 10 томов посвящены приложе-
ниям, а 5 томов — теории и аппаратуре.
40
ЗАДАЧИ АНАЛИТИЧЕСКОЙ ХИМИИ, ИЛИ ЧЕМ ЗАНИМАЮТСЯ ХИ МИКИ-АНАЛИТИКИ
9. A. Townsend, editor-in-chief, Encyclopedia of Analytical Science. London: Aca-
demic, 1995. 10-томное издание, охватывающее все практические аспекты
аналитических наук. Описаны все методы определения отдельных элемен-
тов, соединений и классов соединений в любых физических и биологиче-
ских матрицах.
10. J. A. Dean, Analytical Chemistry Handbook. New York: McGraw Hill, 1995.
Подробное описание классических и инструментальных методов анализа,
предварительных аналитических операций, включая методы разделения,
статистических методов в аналитической химии.
Пробоотбор
11. F. F. Pitard, Pierre Gy’s Sampling Theory and Sampling Practice. Vol. 1: Hete-
rogeneity and Sampling. Vol. II: Sampling Correctness and Sampling Practice.
Boca Raton, FL: CRC Press, 1989.
12. P. M. Gy and A. G. Boyle, Sampling for Analytical Purposes. Chichester: Wiley,
1998. Введение в теорию пробоотбора, написанное Пьером Ги и разъясня-
ющее выведенные им расчетные формулы — первоначально применитель-
но к отбору твердых проб, но справедливые и для жидких и многофазных
проб.
13. Р. М. Gy, Sampling of Heterogeneous and Dynamic Material Systems. Amster-
dam: Elsevier, 1992.
14. G. E. Baiulescu, P. Dumitrescu, and P. Gh. Zugravescu, Sampling. New York:
Ellis Horwood, 1991.
15. N. T. Crosby, ed., General Principles of Good Sampling Practice. London: Roy-
al Society of Chemistry, 1995.
16. P. M. Gy, «Introduction to Theory of Sampling I. Heterogeneity of a Population
of Uncorrelated Units», Trends Anal. Chem., 14(2) (1995) 67.
17. P. M. Gy, «Tutorial: Sampling or Gambling?». Process Control and Quality, 6
(1994) 97.
18. B. Kratochvil and J. K. Taylor, «Sampling for Chemical Analysic», Anal. Chem.,
53 (1981) 924A.
19. B. Kratochvil, «Sampling for Microanalysis: Theory and Strategies», Fresenius
J. Anal. Chem., 337 (1990) 808.
20. J. F. Vicard and D. Fraisse, «Sampling Issues», Fresenius’ J. Anal. Chem., 348
(1994) 101.
21. J. M. Hungerford and G. D. Christian, «Statistical Sampling Errors as Intrinsic
Limits on Detection in Dilute Solutions», Anal. Chem., 58 (1986) 2567.
Мешающие влияния
22. W. E. Van der Linden, «Definition and Classification of Interference in Analyti-
cal Procedures», Pure & Appl. Chem., 61 (1989) 91.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
41
Стандартные растворы
23. В. W. Smith and М. L. Parsons, «Preparation and Standard Solutions. Critically
Selected Compounds», J. Chem. Ed., 50 (1973) 679. Описано приготовление
стандартных растворов для 72 элементов — металлов и неметаллов.
24. М. Н. Gabb and W. Е. Latchem, A Handbook of Laboratory Solutions. New
York: Chemical Publishing, 1968.
25. http://pubs.acs.org/reagents/committee.html— страница комитета по ана-
литическим реагентам Американского химического общества.
Гоадуировка
26. Н. Mark, Principles and Practice of Spectroscopic Calibration. New York: Wi-
ley, 1991.
Стандартные образцы
27. H. Klich and R. Walker, «COMAR—The International Database for Certified
Reference Materials», Fresenius' J. Anal. Chem., 345 (1993) 104.
28. Office of Standard Reference Materials, Room B311, Chemistry Building, Nati-
onal Institute of Standards and Technology, Gaithersburg, Maryland 20899.
29. National Research Council of Canada, Division of Chemistry, Ottawa KIA OR6,
Canada.
30. R. Alverez, S. D. Rasberry and G. A. Uriano, «NBS Standard Reference Materi-
als: Update 1982», Anal. Chem., 54 (1982) 1239A.
31. R. W. Seward and R. Mavrodineanu, «Standard Reference Materials: Summary
of the Clinical Laboratory Standards Issued by the National Bureau of Stan-
dards», NBS (NIST) Special Publications 260-271, Washington, DC, 1981.
32. Стандартные образцы углей. Распространяются департаментом по энерге-
тике США (U.S. Department of Energy, Pittsburgh Mining Technology Center,
P. O. Box 10940, Pittsburgh, PA 15236). Образцы охарактеризованы по 14 па-
раметрам, включая содержание главных и следовых элементов.
Глава 2
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ
ХИМИЧЕСКОГО АНАЛИЗА
Сначала получи результат;
потом можешь делать с ним что угодно.
Марк Твен
Прежде, чем приступать к эксперименту, прочтите данную главу. В химическом
анализе для получения информации нужно провести измерения, порой специ-
фичные. Аналитическое оборудование и аппаратура, необходимые для этого,
рассматриваются в соответствующих главах книги. В то же время существует и
ряд общих для большинства методов положений, связанных с выполнением экс-
перимента. Эти вопросы обсуждаются в данной главе. К универсальному анали-
тическому оборудованию относятся аналитические весы, мерная посуда, а также
сушильные шкафы и фильтры. Некоторые тонкости, связанные с использовани-
ем этого оборудования, лучше всего объяснит ваш преподаватель непосредствен-
но в ходе выполнения лабораторных работ, тем более, что инструментальный
аппарат в различных лабораториях может несколько отличаться. Здесь же мы от-
метим лишь наиболее общие приемы при проведении анализа, которыми дол-
жен владеть квалифицированный аналитик.
Рисунки с изображением наиболее часто используемой лабораторной посу-
ды и другого оборудования приведены на компакт-диске.
2.1. Лабораторный журнал - самый главный документ
Прежде всего вам необходимо усвоить, что в аналитической лаборатории, более
чем где бы то ни было еще, имеют значение чистота и аккуратность. Это отно-
сится и к ведению лабораторного журнала. Все результаты необходимо записы-
вать в журнал чернилами непосредственно тогда, когда они получены. Работая в
аналитической лаборатории, вы быстро поймете, что выполнение этого требова-
ния — в ваших же интересах. Во-первых, вы сэкономите время на переписывании
данных. Кроме того, приучив себя записывать результаты сразу и в обязательном
порядке, вы станете более организованными и в самой работе. Это будет допол-
нительным выигрышем во времени. Во-вторых, если вы будете вести записи не-
посредственно в процессе эксперимента, то сможете обнаружить ошибки в
результатах измерений или расчетах. Наконец, записывая результаты сразу в
журнале (а не на черновиках), вы обезопасите себя от возможной потери или ис-
2.1. ЛАБОРАТОРНЫЙ ЖУРНАЛ - САМЫЙ ГЛАВНЫЙ ДОКУМЕНТ
43
кажения данных. Хорошее ведение лабораторного журнала — залог получения
достоверных результатов.
Для профессиональных химиков-аналитиков требование записывать на-
блюдения и результаты измерений непосредственно в журнал имеет особенно
большое значение. Полнота документации необходима в криминалистических,
производственных лабораториях, для совершения юридических действий, пода-
чи патентных заявок. В производственных исследовательских лабораториях,
страницы журнала должны быть подписаны (заверены) с указанием даты другим
лицом, знакомым с сутью работы. Это может понадобиться для установления
приоритета при подаче заявки на патент.
Приведенное ниже описание титриметрического определения карбоната
натрия в образце технической соды можно считать хорошим примером того, как
следует вести лабораторный журнал.
Дата: 7 сентября 2003 г.
Определение карбоната натрия в образце технической соды.
Суть анализа. Навеску соды растворяют в воде и титруют стандартным раствором соля-
ной кислоты с индикатором бромкрезоловым зеленым. Соляную кислоту предварите-
льно стандартизуют по первичному стандарту — карбонату натрия. Массы навесок
карбоната натрия и технической соды рассчитывают по разности.
Источник', описание практической работы 7.
Реакция титрования'. СО|~ + 2Н+ = Н2СО3
Стандартизация НС1
"гНа2С0/МГ)
| 105,99(мг/ммоль)- Инс1 (мл)
^а2СО3<МГ)
СНС1 (мг/ммоль) =
I WrNa2CO3 (МГ/ ММОЛЬ)- ИНС1 (мл)
Взятие навески Na2CO3 № опыта 1 2 3
Масса, г:
бюкса с веществом 24,2689 24,0522 23,8597
бюкса с остатками вещества 24,0522 23,8597 23,6269
Na^jCC^ 0,2167 0,1925 0,2328
Масса Na2CO3, мг Титрование Na2CO3 Показания бюретки, мл: 216,7 192,5 232,8
конечное 40,26 35,68 43,29
начальное 0,03 0,00 0,02
Объем НС1, мл 40,23 35,68 43,27
Концентрация НС1, М: 0,10164 О,1О18о 0,10152
Среднее: 0,10165М
Стандартное отклонение: 1,6 • 10~3
Размах: 2,8 • 10~3
(См. продолжение)
44
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Анализ образца соды (Продолжение)
сна (ммоль// мл) * ^нс1 (мл) ®№,со, - л/1навсски •1Ч-№,СО,(МГ/ММОЛЬ) (мг) •100% =
0,10165 (ммоль/ мл) • FHC1 (мл) • ~ • 105,99(мг/ ммоль) $
тнавески(МГ) Взятие навески технической соды
№ опыта Масса, г: 1 2 3
бюкса с веществом 25,6728 25,4673 25,2371
бюкса с остатками вещества 25,4673 25,2371 25,0027
навески 0,2055 0,2302 0,2344
Масса навески, мг Титрование технической соды Показания бюретки, мл: 205,5 230,2 234,4
конечное 35,67 40,00 40,70
начальное 0,00 0,01 0,05
Объем НС1, мл 35,67 39,99 40,65
Массовая доля Na2CO3, % Среднее: Стандартное отклонение: Размах: 93,50 93,50% 0,9 • 10“3 1,7 • 10~3 93,58 93,42
Приведенный пример — это лишь сокращенный вариант, в котором опуще-
ны все численные расчеты. В полной версии журнал должен содержать все вычис-
ления. В этом случае при необходимости ход вычислений можно впоследствии
проверить и найти ошибку.
Рекомендуется не заполнять все страницы журнала подряд, а оставлять сво-
бодные места: например, все левые страницы отводить под черновые вычисления,
а правые страницы—для обобщающих данных. Важно также, чтобы все данные
были записаны с правильным числом значащих цифр. Верное число значащих
цифр в результатах измерений и вычислений имеет решающее значение для
правильной интерпретации результатов анализа. Данная проблема обсуждает-
ся в гл. 3. Прежде, чем приступать к работе в лаборатории, этот материал следует
повторить.
2.2. ЛАБОРАТОРНЫЕ МАТЕРИАЛЫ И РЕАГЕНТЫ
45
Рекомендации по ведению лабораторного журнала
Лабораторный журнал — это хроника всей вашей работы как химика-аналитика. В нем
задокументировано все, что вы делаете. Это источник информации для отчетов, публи-
каций и официальных представлений. Успех или неудача деятельности вашей компании
может зависеть от того, насколько хорошо вы ведете эту документацию. Лабораторный
журнал является официальным документом при подаче заявки на патент, разработке
нормативных актов (при поверке методик, инспекциях и иных юридических действиях).
Запомните: то, что не записано, то не сделано! Именно ваш лабораторный журнал явля-
ется тем местом, где вы фиксируете новые идеи, которые в будущем могут стать основой
патента, поэтому важно записывать, в чем эти идеи заключаются и когда они появились.
Особенности ведения лабораторного журнала определяются личными предпочте-
ниями. Но существует ряд общих правил, выполнение которых необходимо для хороше-
го ведения журнала:
• Используйте тетрадь в твердом переплете (отсутствует угроза потери листов).
• Последовательно нумеруйте все страницы.
• Никогда не вырывайте листы. Если текст, написанный на странице, более не нужен,
просто перечеркните его.
• На каждой странице указывайте дату и подписывайте ее. Кроме того, пусть страницы
вашего журнала подписывает и датирует (возможно, спустя короткое время) кто-либо
еще, указывая: «С содержанием ознакомился такой-то».
• При описании экспериментов указывайте название работы и ее цели, ссылки на источ-
ники.
• Записывайте все данные в тот день, когда вы их получили.
Несколько слов об электронных журналах. Программное обеспечение со-
временных приборов часто позволяет собирать, хранить и обрабатывать данные,
поступающие непосредственно от прибора, используя в расчетах результаты
градуировки. В этом случае важно, чтобы программное обеспечение и градуи-
ровка прибора, так же, как и все стадии собственно методики анализа, были по-
верены. Это одно из требований «хорошей лабораторной практики» (гл. 4).
2.2. Лабораторные материалы и реагенты
В табл. 2.1 указаны свойства ряда материалов, часто применяемых в производст-
ве лабораторной аппаратуры. Для изготовления лабораторной посуды (стака-
нов, колб, пипеток, бюреток) чаще всего используется боросиликатное стекло
(торговых марок Pyrex, Kimax). Оно устойчиво к действию горячих растворов и
резким изменениям температуры. Для специальной посуды, используемой в
Таблица 2.1
Свойства некоторых материалов, используемых для изготовления лабораторной посуды
Материал Максимальная рабочая температура (°C) Устойчивость к резким изменениям температуры Химическая устойчивость Примечания
Боросиликатное стекло 200 Выдерживает резкое изменение на 150 °C Слабо подвергается действию горячих растворов щелочей Торговые марки: Pyrex (Coming Glass Works), Kimax (Owens-Illinois)
Мягкое стекло Низкая Разрушается растворами щелочей He содержит бора. Торговая марка Coming
Щелочеустойчивое стекло Более чувствительно, чем боросиликатное
Плавленый кварц 1050 Высокая Устойчив к действию большинства кислот, галогенов В кварцевых тиглях сплавляют различные вещества
Кварцевое стекло 1000 Высокая Более устойчиво к действию щелочей, чем боросиликатное стекло Используется так же, как плавленый кварц. Торговая марка Vycor (Coming)
Фарфор 1100 (глазированный) 1400 (неглазированный) Средняя Высокая
Материал Максимальная рабочая температура (°C) Устойчивость к резким изменениям температуры Химическая устойчивость Примечания
Платина Около 1500 Устойчива к действию большинства кислот и расплавов солей. Разрушается царской водкой, расплавами нитратов, цианидов, хлоридов при температуры >1000 °C. Используют также в виде сплавов с золотом, серебром и другими металлами Для повышения твердости обычно используют в виде сплавов с иридием или родием. В платиновых тиглях проводят сплавление и обработку фтористоводородной кислотой
Никель и железо При сплавлении пробы загрязняются материалом тигля Никелевые и железные тигли используют для проведения сплавления с пероксидами
Нержавеющая сталь 400-500 Высокая Не разрушается щелочами и кислотами, кроме конц. НС1, разб. H2SO4 и кипящей конц. HNO3
Полиэтилен 115 Не разрушается растворами щелочей и HF. Разрушается под действием многих органических растворителей (к действию ацетона и этанола устойчив) Пластичный материал
Полистирол 70 Не разрушается под действием HF. Разрушается многими органическими растворителями Достаточно хрупкий
Тефлон 250 Устойчив по отношению к большинству химических веществ Тефлоновая посуда используется для хранения растворов и реагентов при определении следов металлов
48
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
особых целях, могут применяться другие материалы, например, более устойчи-
вые к действию химических реактивов, высоких температур и т. д.
На форзаце одного из томов приведены различные квалификации чистоты
химических реактивов в соответствии с классификацией Американского хими-
ческого общества. В аналитической лаборатории следует использовать только
те реактивы, которые имеют квалификацию не ниже, чем «чистый для анализа»
(ч. д. a., A.C.S. reagent-grade) или «первичный стандарт» (primary standard). Для
выполнения анализов почти всегда используют реагенты квалификации ч. д. а.
Для приготовления стандартных растворов в титриметрии используют пер-
вичные стандарты.
Американское химическое общество публикует сводки критериев оценки
чистоты и качества основных лабораторных реактивов. Квалификация реакти-
вов, не указанных в этих списках, устанавливается непосредственно производи-
телями в соответствии с их собственными критериями.
Для реактивов квалификации ч. д. а., удовлетворяющих общим требовани-
ям чистоты, часто дополнительно указывают (на этикетке тары) результаты ана-
лизов на содержание отдельных примесей. Реактивы квалификации «первичный
стандарт», как правило, имеют содержание основного вещества не ниже 99,95%.
Они более дорогие, чем реактивы ч. д. а., и используются только для приготов-
ления стандартных растворов или для стандартизации растворов других ве-
ществ посредством проведения химических реакций (титрования). Не все
реактивы производятся в квалификации «первичный стандарт». Существуют
особые квалификации чистоты растворителей, применяемых для специальных
целей, например, «спектрально чистый» или «чистый для хроматографии». Та-
кие растворители подвергают специальной очистке, чтобы удалить примеси, ме-
шающие при выполнении конкретных задач. Аналогично этому, для определения
следовых количеств металлов выпускаются особо чистые кислоты. Их очищают
специальными приемами и более тщательно анализируют на содержание следов
различных элементов (обычно оно должно составлять не более нескольких час-
тей на миллиард).
Помимо коммерческих производителей, реактивы квалификации «первичный
стандарт» выпускает Национальный институт стандартов и технологий США.
В каталоге NIST Special Publication 260 перечислены выпускаемые институтом
стандартные образцы (см. страницу http://ts.nist.gov/ts/htdocs/230/232.htm, со-
держащую информацию о программе разработки стандартных образцов и их пе-
речень). Стандартный образец — это вещество сложного состава (например,
сплав), содержание компонентов которого точно установлено в результате ана-
лизов и официально удостоверено. Стандартные образцы используют для про-
верки и градуировки методик анализа.
На форзаце одного из томов приведены концентрации некоторых коммер-
ческих препаратов кислот и щелочей.
2.3. АНАЛИТИЧЕСКИЕ ВЕСЫ - НЕОБХОДИМЫЙ ИНСТРУМЕНТ
49
2.3. Аналитические весы - необходимый инструмент
Взвешивание — неотъемлемая операция почти любого анализа, которую испо-
льзуют для измерения массы пробы, для приготовления стандартных растворов.
В химическом анализе мы имеем дело с достаточно малыми массами, порядка
нескольких граммов, нескольких миллиграммов или даже меньше. Как правило,
массу необходимо измерять не менее чем с тремя или четырьмя значащими циф-
рами, поэтому лабораторные весы должны быть одновременно и чувствитель-
ными, и точными. Существует много сложных способов достижения этого
сочетания. Однако чаще всего для взвешивания используют полезный и универ-
сальный инструмент — аналитические весы.
Большинство аналитических весов, применяемых в настоящее время, явля-
ются электронными. В то же время до сих пор продолжают использовать меха-
нические одночашечные весы, поэтому мы опишем операции и с такими весами.
В основе действия весов обоих типов лежит сравнение веса одного тела с весом
другого (у электронных весов это осуществляется в ходе калибровки), на их ра-
боту оказывают влияние одни и те же факторы, например, дрейф нуля или вытал-
кивающая сила воздуха. Отметим, что на самом деле мы оперируем величинами
масс, а не весов. Вес тела — это сила тяжести, действующая на него. Она разная
в различных точках земного шара. Масса определяется только количеством ве-
щества, из которого состоит тело. Она не зависит от местоположения объекта.
Электронные весы — это очень удобно
Современные электронные весы удобны в работе, их показания более точны, а
устройство более надежно, чем у механических весов. При работе с ними не тре-
буется таких характерных для механических весов операций, как считывание
масс разновесов, вращение микрометрических винтов и считывание их показа-
ний, арретирование чашек. За счет этого измерения значительно ускоряются.
Общий вид электронных весов с цифровым табло показан на рис. 2.1, а принцип
их работы схематически представлен на рис. 2.2. В отличие от механических ве-
сов, в них отсутствуют разновесы и призмы. Чашка весов соединена с подвиж-
ным рычагом (рис. 2.2, 2), вся подвижная система уравновешена при помощи
электромагнита. Положение рычага контролируется специальным устройст-
вом — электрическим сканером (рис. 2.2, 7). Он также управляет электромагни-
том, поддерживая силу тока в его обмотке таким образом, чтобы чашка весов
при любой нагрузке находилась в исходном положении. Сила тока, протекаю-
щего через обмотку электромагнита, пропорциональна весу предмета, находя-
щегося на чашке весов. Эта величина преобразуется в цифровую форму и
передается микропроцессору, в свою очередь преобразующему сигнал в соот-
ветствующее значение веса. Оно отображается на цифровом табло. При этом
возможно автоматическое вычитание веса тары.
Таким образом, в основе действия электронных весов лежит принцип ком-
пенсации под действием электромагнитной силы, впервые описанный Ангстре-
мом в 1895 г. Но в процессе их работы происходит сравнение веса одного тела с
50
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.1
Общий вид электронных
аналитических весов. С любезного
разрешения Denver Instrument Со.
Denver Instrument Company —
собственник всех рисунков
весом другого. В начале работы весы необходимо «обнулить», т. е. откалибро-
вать при помощи тела известного веса. Когда на чашку весов помещают ка-
кой-либо предмет, его вес при помощи электронных устройств сравнивают с
известным весом. Это один из вариантов автоматической калибровки. Совре-
менные весы обладают целым рядом дополнительных возможностей, например,
позволяют осуществлять автоматическую компенсацию колебаний нулевого поло-
жения или флуктуаций результатов вследствие колебаний здания.
Электронные весы имеют единственную управляющую клавишу, при помо-
щи которой можно включать и выключать весы, обнулять табло и автоматически
вычитать вес тары. Поскольку результаты взвешивания являются электрическим
сигналом, их легко обрабатывать и хранить при помощи персонального компью-
тера. Можно автоматически рассчитывать статистические характеристики про-
цесса взвешивания.
Рис. 2.2
Принцип работы электронных весов:
1 — электронные разновесы; 2 — рычаг;
3 — обмотка электромагнита; 4 — датчик
температуры [К. М. Lang, American
Laboratory, March, 1983, p. 72]. Публикуется
с разрешения American Laboratory, Inc.
2.3. АНАЛИТИЧЕСКИЕ ВЕСЫ - НЕОБХОДИМЫЙ ИНСТРУМЕНТ
51
Электронные аналитические весы выпускаются для разных диапазонов масс
и с разной ценой деления. Макровесы позволяют взвешивать объекты массой до
160 г при цене деления 0,1 мг, а полумикровесы — до 30 г при цене деления
0,01 мг. Микровесы позволяют взвешивать с точностью до 1 мкг, а ультрамикро-
весы — от 0,1 мкг и ниже.
На пьезоэлектрических кварцевых весах можно взвешивать объекты массой
до 100 мкг. Они позволяют зафиксировать изменения массы порядка 1 нг (Г10-9 г)!
Чувствительным элементом весов является тонкий диск из кристаллического
кварца, на который посредством осаждения из пара нанесена тончайшая пленка
золота. Диск совершает колебания при строго определенной частоте, например,
10 МГц. Эта частота изменяется при малейшем изменении массы диска. Измене-
ние частоты колебаний измеряют и преобразуют в величину массы. Таким спосо-
бом можно зафиксировать очень малые изменения массы — порядка нескольких
процентов от массы моноатомнот^о или мономолекулярного слоя покрытия зо-
лотой подложки. Можно следить за изменением массы объекта во времени.
Одночашечные механические весы
Несмотря на то что механические весы постепенно вытесняются электронными,
они до сих пор находят широкое применение. Поэтому было бы неправильным
оставить механические весы без рассмотрения.
Взвешивание свиньи по методу Бернса:
1) Возьми совершенно прямую доску и уравновесь ее, положив на лесопильные
козлы.
2) Положи свинью на один конец доски.
3) Клади булыжники на другой конец доски до тех пор, пока она не придет в равно-
весие.
4) После этого тебе осталось узнать общий вес булыжников.
Механические аналитические весы представляют собой по существу рычаг
первого рода, используемый для сравнения двух масс. Рис. 2.3 иллюстрирует
принцип их действия. Точка опоры Л находится между точками приложения сил
В и С. Символом Мх обозначена неизвестная, а М2 — известная масса. Принцип
действия весов основан на том, что в условиях равновесия MXLX = М2Ь2. Если
сконструировать рычаг так, чтобы Lx = £2, то при равновесии Мх = М2. На коро-
мысле весов помещена указательная стрелка, позволяющая судить о наличии
равновесия. В ходе взвешивания подбирают значение М2 тех пор, пока стрел-
ка не возвратится в исходное положение, т. е. положение при отсутствии нагруз-
ки на чашке весов. На самом деле при помощи весов измеряют не массу, а вес.
Однако значения весов при заданных условиях взвешивания пропорциональны
значениям масс. Поэтому в обиходе термины «масса» и «вес» используют как
синонимы, а операцию измерения массы называют «взвешиванием». Гирьки из-
вестной массы называются разновесами.
52
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.3
Принцип действия механических
аналитических весов
В L2 С
В большинстве случаев механические аналитические весы являются одно-
чашечными. Типичная схема устройства таких весов изображена на рис. 2.4, а
внешний вид стандартных одночашечных весов — на рис. 2.5.
В отличие от рассмотренного выше случая, рычаг, используемый в одноча-
шечных весах, является несимметричным. Он опирается на ребро призмы, а вес
чашки весов, на которую помещают объект, действует на один из концов коро-
мысла рычага. Когда чашка весов не нагружена, к этому концу приложена сила
тяжести набора разновесов общей массой 160-200 г. На другом конце рычага
чашка отсутствует. Вместо нее там находится постоянный груз-противовес,
уравновешивающий чашку и разновесы. Он же является частью поршня-амор-
тизатора. Когда на чашку весов помещают взвешиваемый объект, часть разнове-
сов необходимо снять, чтобы восстановить равновесие. Это осуществляется
при помощи ручек, расположенных на передней панели весов. При их вращении
определенные разновесы (или их сочетания) поднимаются вверх и снимаются с
коромысла. Таким образом, манипуляции с разновесами никогда не производят-
Арретирование
и освобождение
чашки
Ручки управления
разновесами <
РИС. 2.4. Типичная схема устройства одночашечных весов
2.3. АНАЛИТИЧЕСКИЕ ВЕСЫ - НЕОБХОДИМЫЙ ИНСТРУМЕНТ
53
ся руками. Суммарный вес разновесов, снятых с коромысла, равен весу предме-
та, находящегося на чашке весов.
Обычно массы разновесов кратны 1 г или 0,1 г в зависимости от типа весов.
Поэтому нельзя добиться полного уравновешивания коромысла путем снятия
разновесов. Остаточный дисбаланс автоматически регистрируют при помощи
оптической системы. На один из концов коромысла нанесена оптическая шкала,
деления которой освещаются лампой и проецируются на экран со шкалой-нони-
усом. Последние десятичные цифры значения массы (до 0,1 мг) считывают с этой
шкалы и прибавляют к массе снятых разновесов. Величина остаточного дисбалан-
са может отображаться и на цифровом табло.
Исходное положение ненагруженной чашки весов и соответствующее ему
положение шкалы называются нулевой точкой весов, а положение под нагруз-
кой — точкой покоя. При взвешивании точку покоя устанавливают так, чтобы
она совпала с нулевой точкой. Обычно положение нулевой точки предваритель-
но устанавливают так, чтобы показание шкалы было нулевым. Для этого переме-
щают нониус при помощи специальной вращающейся ручки. Перед взвешиванием
всегда проверяйте положение нулевой точки.
В состоянии равновесия одночашечные весы находятся под постоянной на-
грузкой 160-200 г, независимо от массы взвешиваемого предмета. Однако поло-
жение центра тяжести коромысла изменяется в зависимости от веса предмета.
Соответственно, несколько изменяется и чувствительность весов.
Все разновесы одночашечных весов находятся внутри корпуса. Их положе-
ние управляется только ручками, расположенными на передней панели. Одна
ручка предназначена для манипуляций с разновесами массой в десятки граммов
(т. е. от 10 до 90 г), другая — единицы граммов (от 1 до 9 г), третья (если имеет-
ся) — сотни миллиграммов (от 0,1 до 0,9 г). Масса разновесов, снятых с коро-
мысла, отображается при помощи счетчиков, также расположенных на передней
панели. Равновесие коромысла устанавливается достаточно быстро благодаря
наличию воздушного поршневого демпфера.
С весами следует обращаться осторожно, чтобы не повредить ребра призм в
те моменты времени, когда весы не находятся в работе, а также когда объекты
помещают на чашку или снимают с нее. Для защиты призм и коромысла пред-
назначена рукоятка переключателя арретира, имеющая три положения. В сред-
нем положении как коромысло, так и чашка арретированы. В одном из двух
других положений чашка весов частично освобождается. Это положение исполь-
зуют тогда, когда приближенно определяют вес объекта. В последнем положе-
нии чашка полностью освобождается, чтобы весы могли прийти в равновесие.
При использовании одночашечных весов взвешивание может быть выполнено
менее чем за минуту.
Полумикро- и микровесы
В предыдущих разделах основное внимание уделялось обычным макровесам или
аналитическим весам. Они позволяют проводить измерения масс до 100-200 г с
точностью до 0,1 мг. Для решения большинства повседневных аналитических
54
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.5
Внешний вид стандартных одночашечных весов.
(С любезного разрешения Arthur Н. Thomas Company.)
задач этого достаточно. В то же время для весов всех рассмотренных типов су-
ществует возможность увеличения чувствительности посредством изменения
влияющих на нее параметров: уменьшения массы коромысла и чашки, увеличе-
ния длины коромысла и изменения положения его центра тяжести. Для изготов-
ления коромысла можно использовать более легкие материалы, поскольку
ввиду уменьшения общей нагрузки (по сравнению с обычными макровесами)
снижаются требования к прочности конструкционных материалов.
Полумикровесы позволяют взвешивать с точностью до 0,01 мг, ъ микровесы —
до 0,001 мг (1 мкг). Предельные нагрузки для таких весов соответственно ниже, чем
для обычных весов, а при работе с ними требуется повышенная аккуратность.
Дрейф нулевой точки
Нулевая точка весов не есть нечто постоянное, что может быть определено и
установлено раз и навсегда. Ее положение изменяется под воздействием множе-
ства факторов, в том числе изменений температуры и влажности окружающей
среды, а также статического электричества. Поэтому положение нулевой точки
следует проверять во время работы с весами, по крайней мере, каждые полчаса.
Вес в вакууме — наиболее точная величина
Результаты взвешиваний отражают, разумеется, вес тела в воздухе. Однако любое
тело теряет в весе столько, сколько весит вытесненный им воздух. В этом состоит
закон Архимеда (см. материал о возникновении аналитической химии, приведен-
ный в гл. 1). Плотность воздуха составляет 0,0012 г/см3 (1,2 мг/см3). То есть на
тело объемом 1 мл действует выталкивающая сила воздуха, равная 1,2 мг! Если
плотности объекта и разновесов равны, то одинаковы и их потери в весе, и изме-
ренное значение в точности соответствует весу объекта в вакууме, где выталкива-
ющая сила не действует. Но если эти плотности сильно различаются, различия в
2.3. АНАЛИТИЧЕСКИЕ ВЕСЫ - НЕОБХОДИМЫЙ ИНСТРУМЕНТ
55
величинах выталкивающих сил приведут к небольшой погрешности взвешива-
ния. Такая ситуация возникает при взвешивании объектов как с очень высокой
плотностью (например, платиновых сосудов — плотность платины составляет
21,4 г/см3, или ртути с плотностью 13,6 г/см3), так и с низкой плотностью (напри-
мер, воды, плотность ~1 г/см3). Для сравнения: плотность разновесов, обычно
применяемых для взвешивания, составляет около 8 г/см3. При очень тщательной
работе эту погрешность следует учитывать в виде соответствующей поправки.
Вычисление поправок на выталкивающую силу воздуха для одночашечных весов
описано в работе [14], а калибровка разновесов на одночашечных весах — в рабо-
те [10]. Выталкивающую силу, действующую натару для взвешивания, не следует
принимать во внимание, поскольку при вычислении массы объекта по разности
ее величина сокращается. Поправку на выталкивающую силу часто необходимо
учитывать при калибровке мерной посуды. Одни и те же поправки на выталкива-
ющую силу применимы как к механическим, так и к электронным весам (калибру-
емым при помощи разновесов из материала известной плотности).
В действительности в использовании поправок на выталкивающую силу,
как правило, нет необходимости, поскольку соответствующие погрешности час-
то сокращаются, например, при вычислении массовой доли определяемого ком-
понента. В этом случае одна и та же погрешность присутствует как в числителе
(концентрация стандартного раствора или масса гравиметрической формы), так
и в знаменателе (масса навески) алгебраического выражения. Разумеется, чтобы
эта погрешность оставалась действительно постоянной, все взвешивания необ-
ходимо производить в таре, изготовленной из одного и того же материала (оди-
наковой плотности).
Например, при калибровке мерной посуды вводить поправку на приведение
веса к значению в вакууме действительно необходимо. Для этого измеряют мас-
су воды или ртути, которая содержится в сосуде либо вытекает из него. Зная
плотность при соответствующей температуре, можно из массы рассчитать объ-
ем жидкости. Но даже в этом случае погрешность определения составляет по-
рядка одной десятой процента. В большинстве случаев такой погрешностью
можно пренебречь. Для точных расчетов существуют специальные таблицы пе-
ревода веса воды или ртути в воздухе к весу в вакууме при различных темпера-
турах.
Вес объекта в воздухе можно привести к весу в вакууме по следующей фор-
муле:
w =W- + W-
rr vac air "air
0,0012 0,0012
Do Dw
(2.1)
где FTvac — вес в вакууме, г; FTair — измеренный вес в воздухе, г; Do — плотность
объекта, г/см3; Dw — плотность материала разновесов, г/см3; 0,0012 (г/см3) —
плотность воздуха.
56
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Плотности наиболее распространенных материалов разновесов — латуни и не-
ржавеющей стали — составляют 8,4 и 7,8 г/см3 соответственно. Пример расчета
веса воды должен убедить вас в том, что даже в этом случае величина поправки
составляет порядка одной части на тысячу.
Пример 2.1
Удобный способ калибровки пипетки состоит во взвешивании воды, вытекшей
из нее. Объем воды может быть рассчитан из точных значений ее массы и плот-
ности при данной температуре. Предположим, что надо градуировать пипетку с
номинальным объемом 20 мл. Для взвешивания воды будем использовать колбу
с притертой пробкой. Пусть измеренное значение веса пустой колбы составляет
29,278 г, а колбы с водой — 49,272 г (используются разновесы из латуни). Како-
во значение веса содержащейся в колбе воды, приведенное к значению веса в ва-
кууме?
Решение
Вес воды на воздухе равен увеличению веса колбы и составляет
49,272-29,278 = 19,994 г
Плотность воды составляет 1,0 г/см3 (более точные значения в интервале темпе-
ратур от 10 до 30 °C см. в табл. 2.4). Отсюда
Wvac = 19,994 +19,994|
I 1,0
0,0012
8,4
= 20,015 г
Пример 2.2
Выполните расчеты с данными из примера 2.1 при условии, что разновесы изго-
товлены из нержавеющей стали (плотность 7,8 г/см3).
Решение
При расчетах избегайте округлений вплоть до получения конечного результата.
Вы получите ту же самую величину:
jyvac=19,994 + 19,994|^^-^^ | = 20,015 г
I 1,0 7,8 )
Таким образом, к весам любых типов можно применять одни и те же величины
поправок на выталкивающую силу (табл. 2.4 на стр. 72).
2.3. АНАЛИТИЧЕСКИЕ ВЕСЫ - НЕОБХОДИМЫЙ ИНСТРУМЕНТ
57
Источники погрешностей при взвешивании
Некоторые источники погрешностей при взвешивании — дрейф нулевой точки,
разновесы, выталкивающая сила воздуха — уже упоминались. Источником наибо-
лее серьезных погрешностей являются изменения температуры окружающей среды
или объекта. Они вызывают конвекционные потоки воздуха, которые обусловлива-
ют смещение нулевой точки или точки покоя. Горячие или слишком холодные
предметы перед взвешиванием необходимо привести к температуре окружающей
среды. Гигроскопичные материалы могут поглощать влагу, поэтому следует по
возможности избегать взвешивания в условиях высокой влажности или длитель-
ного нахождения образца на воздухе перед взвешиванием и в ходе его.
Общие правила взвешивания
Как мы видели, существует несколько типов весов. Порядок операций при рабо-
те с ними может быть различным для весов, изготовленных разными производите-
лями. Конкретный порядок работы с вашими весами вам объяснит преподаватель.
Но в любом случае важно: 1) предохранять призмы от повреждений; 2) предо-
хранять все детали весов от пыли и коррозии; 3) избегать загрязнений объекта
(как самой пробы, так и тары) или иных изменений его веса в ходе взвешивания
и 4) избегать грубых ошибок, вызванных конвекционными потоками воздуха.
Ниже приведены общие правила, которые вы должны усвоить до того, как при-
ступать к работе с любыми аналитическими весами. Выучите эти правила!
1 Никогда не берите взвешиваемый объект пальцами. Переносите объект,
обвернув его полоской чистой бумаги или при помощи щипцов.
2. Взвешивайте при комнатной температуре, чтобы избежать возникнове-
ния конвекционных потоков воздуха.
3- Никогда не кладите химические вещества непосредственно на чашку ве-
сов. Для взвешивания используйте тару (бюксы, стаканчики, часовые
стекла) или полоску кальки. Если вы все же просыпали вещество, немед-
ленно сметите его мягкой кисточкой.
4. Перед взвешиванием всегда закрывайте створки камеры весов. В про-
тивном случае вы можете получить неверные результаты, вызванные по-
токами воздуха.
5. При работе с механическими весами никогда не помещайте на чашку и
не убирайте с нее объект или разновесы, не убедившись, что коромысло
весов и чашка арретированы.
Взвешивание твердых веществ
Твердые вещества обычно взвешивают (а неметаллические — и высушивают) в
весовых бюксах (рис. 2.6). Они снабжены стандартными притертыми стеклян-
58
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.6. Бюксы для взвешивания
Рис. 2.7. Блюдечко для взвешивания
ными пробками. Гигроскопичные, поглощающие влагу из воздуха вещества не-
обходимо взвешивать в сосудах с хорошо притертой пробкой (крышкой). После-
довательное взятие нескольких навесок одного и того же объекта (а также
гигроскопичных веществ) удобнее всего выполнять по разности. В этом случае
время работы сокращается, особенно при использовании механических весов. Для
электронных весов экономия времени не столь велика. Идея такого взвешивания
состоит в том, что сначала взвешивают бюкс со всем содержащимся в нем вещест-
вом, затем порцию вещества отбирают (например, отсыпают), количественно
перенося ее в сосуд для растворения. Бюкс с оставшимся веществом снова взве-
шивают и рассчитывают массу отобранного вещества по разности. Затем точно
так же отбирают следующую порцию вещества и снова взвешивают бюкс, и так
далее. Например, см. записи в лабораторном журнале на с. 43-44 (определение
карбоната натрия в образце технической соды).
Очевидно, что при таком способе работы на каждую навеску приходится
одно взвешивание (и еще одно в самом начале). При этом масса каждой навески
представляет собой разность двух результатов взвешивания, а общая погреш-
ность значения массы складывается из погрешностей каждого из этих результатов.
В ходе взвешивания по разности необходимо держать бюкс плотно закрытым в
тех случаях, когда вещество гигроскопично или по каким-либо иным причинам
не может перед взвешиванием долго находиться в контакте с атмосферным воз-
духом. Если же опасность воздействия атмосферы отсутствует, бюкс закрывать
не обязательно.
Для непосредственного (прямого) взвешивания в качестве тары исполь-
зуют блюдечки (рис. 2.7) или лодочки для взвешивания, а также часовые стекла
и специальную бумагу (кальку). Сначала взвешивают пустую тару, а затем тару
с навеской. В этом случае для каждой навески необходимы два взвешивания.
После взвешивания навеску пересыпают в сосуд для растворения; остатки про-
бы со стенок тары переносят при помощи кисточки. Прямое взвешивание воз-
можно только в том случае, если проба не гигроскопична.
При очень точных (до десятых долей миллиграмма) взвешиваниях необхо-
димо предохранять тару от загрязнения посторонними веществами, которое мо-
жет вызвать изменение ее веса. В частности, не следует брать тару руками,
поскольку даже выделения пота могут исказить результат. Прежде чем брать
2.3. АНАЛИТИЧЕСКИЕ ВЕСЫ - НЕОБХОДИМЫЙ ИНСТРУМЕНТ
59
тару, ее следует обернуть полоской бумаги. Твердые пробы перед взятием наве-
ски часто бывает необходимо довести до постоянной массы. Во всех случаях
перед взвешиванием проба должна приобрести температуру окружающей среды
(весовой комнаты).
Взвешивание жидкостей
Жидкости обычно взвешивают методом прямого взвешивания. Жидкость поме-
щают в предварительно взвешенный сосуд (например, бюкс) и плотно закрывают,
чтобы предотвратить возможное испарение жидкости во время взвешивания, за-
тем взвешивают сосуд с жидкостью. Если массу жидкости определяют по разно-
сти, отбирая ее порцию пипеткой, необходимо несколько раз промыть пипетку,
собирая промывные воды в тот же сосуд, в который была перенесена основная
порция. При отборе порции необходимо следить, чтобы не потерять каплю жид-
кости из носика пипетки.
Взвешивание: какая точность вам необходима?
В химическом анализе существуют два типа взвешивания — ориентировочное
и точное. Ориентировочное взвешивание (с двумя или тремя значащими цифра-
ми) обычно проводят в тех случаях, когда достаточно знать массу вещества с
точностью, не превышающей нескольких процентов, например, при приготов-
лении растворов реагентов, которые предстоит стандартизовать при помощи
стандартных растворов точно известной концентрации, или при отборе проб ве-
ществ, которые необходимо высушить и впоследствии взвесить точно либо до-
бавить в раствор для создания определенной среды. Таким образом, для всех
веществ, количества которых не используются для расчета результата анализа,
достаточно ориентировочного взвешивания. Для ориентировочного взвешива-
ния не требуются аналитические весы, вполне достаточно технических весов
любой конструкции.
Точное взвешивание необходимо при взятии навески анализируемой про-
бы, взвешивании сухой гравиметрической формы в ходе гравиметрического
анализа или высушенного реагента, используемого для приготовления первич-
ного стандартного раствора. Во всех этих случаях значение массы объекта непо-
средственно используется для расчета результатов анализа. Это значение должно
быть известно не менее чем с четырьмя значащими цифрами. В этом случае
взвешивание осуществляется только на аналитических весах, как правило,
с точностью до 0,1 мг. Лишь в редких случаях берут навеску вещества, масса
которой точно известна заранее (например, 0,5000 г). Как правило, берут при-
мерное количество вещества (в данном случае около 0,5 г), но взвешивают его с
требуемой точностью (например, 0,5129 г). На аналитических весах необходимо
проводить лишь те взвешивания, результаты которых будут использоваться в
количественных расчетах. Некоторые вещества вообще никогда не взвешивают
на аналитических весах. Например, таблетированный гидроксид натрия столь
гигроскопичен, что непрерывно поглощает воду из атмосферы. Поэтому резуль-
таты взвешивания гидроксида натрия невоспроизводимы, а степень его чистоты
60
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
неизвестна. Чтобы приготовить раствор гидроксида натрия точно известной
концентрации, порцию вещества взвешивают ориентировочно на технических
весах, растворяют в воде, а затем полученный раствор стандартизуют при помо-
щи стандартного раствора кислоты.
2.4. Мерная посуда
Пожалуй, единственный метод анализа, где не требуются точные измерения
объема, — это гравиметрия. Во всех остальных методах, в которых используют-
ся растворы, такие измерения необходимы.
Мерные колбы
Мерные колбы используют для того, чтобы разбавить раствор
до точно известного объема. Вместимость мерных колб мо- ZX
жет изменяться в широких пределах — от 2 л и более до 1 мл. ( )
Стандартная мерная колба изображена на рис. 2.8. Мерные
колбы всегда отградуированы на заполнение (англ, «to conta-
in»). Это означает, что при определенной температуре (20 или
25 °C) объем жидкости, содержащейся в колбе, точно равен но-
минальному при условии, что нижний край мениска жидкости
(ее поверхности, искривленной вследствие капиллярного эф-
фекта — рис. 2.14) касается метки — горизонтальной линии, ) I
нанесенной на горлышко колбы. Температурный коэффици- / \
ент расширения стекла, из которого изготавливают мерные / \
колбы, достаточно мал, поэтому можно считать, что неболь- / \
шие колебания комнатной температуры не влияют на значе- у J
ние объема. Мерные колбы (как и другие мерные сосуды,
характеризующиеся меньшей точностью, например, мерные
цилиндры) часто маркируют ТС — «to contain». Кроме того, рИд 2.8
на стенке колбы, наряду с номинальным значением объема,
многие производители указывают и максимальную погреш-
ность этого значения. Например, на мерной колбе вместимостью 250 мл может
быть указано «±0,24 мл», что соответствует приблизительно 0,1% относитель-
ной погрешности. Вместимость мерных колб должна быть точно известна.
При работе с мерной колбой в нее сначала помещают небольшое количество
растворителя, обычно дистиллированной воды. Реактивы не следует помещать в
сухие колбы, поскольку поверхность стекла обладает сильным адсорбирующим
действием. Раствор в мерной колбе следует готовить поэтапно. Сначала в колбу
вносят тот реагент (твердый или жидкий), который необходимо растворить, а за-
тем добавляют растворитель в количестве не более двух третей объема колбы.
При этом все частицы реагента, прилипшие к стенкам горлышка колбы, следует
смыть на дно колбы. После этого реагент полностью растворяют и лишь затем
2.4. МЕРНАЯ ПОСУДА
61
добавляют остальную часть растворителя так, чтобы нижний край мениска ка-
сался метки колбы (метка при этом должна быть расположена на уровне глаз).
Если после этого на горлышке колбы выше метки остаются капельки воды, их
следует удалить фильтровальной бумагой. Необходимо протереть досуха шли-
фы колбы и притертой пробки.
Наконец, раствор в колбе перемешивают. Для этого колбу переворачивают,
плотно придерживая пробку, и интенсивно вращают или встряхивают ее в тече-
ние 5-10 с. После этого колбу снова переворачивают дном вниз и оставляют в та-
ком положении до тех пор, пока вся жидкость не стечет со стенок горлышка. Эту
процедуру повторяют 5-10 раз.
Примечание. Если в ходе разбавления вы перелили жидкость выше метки,
то и в этом случае имеется возможность сохранить и использовать раствор. Для
этого наклейте вдоль горлышка колбы тонкую полоску бумаги и отметьте на ней
остро заточенным карандашом, избегая перекосов, положение нижнего края ме-
ниска. Раствор тщательно перемешайте и перенесите в сухой сосуд. Затем запол-
ните колбу водой до фабричной метки. Наконец, при помощи бюретки (или
градуированной пипетки небольшого объема) добавляйте в колбу воду до тех
пор, пока нижний край мениска не коснется отметки, сделанной вами на бумаге.
Запишите значение объема воды, который вам пришлось для этого добавить,
прибавьте его к номинальному объему колбы и пересчитайте концентрацию рас-
твора, используя полученное значение объема.
Пипетки
Пипетки предназначены для того, чтобы отмерить и перенести определенный
объем жидкости. В частности, пипетки часто используют для отбора аликвоты
(определенной порции) раствора. Чтобы доля, которую составляет аликвота от
общего объема раствора, была известна, необходимо, чтобы был известен и об-
щий первоначальный объем раствора. Можно отобрать несколько последовате-
льных аликвот одного и того же раствора, но в этом случае важно, чтобы между
отборами раствор не испарялся и не разбавлялся. Существуют два основных
типа пипеток — мерные и градуированные (рис. 2.9 и 2.10). Некоторые разно-
видности градуированных пипеток называют клиническими или серологиче-
скими пипетками.
В отличие от мерных колб, пипетки отградуированы на вытекание (англ,
to deliver) определенного объема жидкости при заданной температуре и часто
помечаются TD. Как и в случае мерных колб, небольшие колебания температу-
ры не влияют на объем пипеток. При калибровке пипеток учитывают, что неко-
торая часть жидкости остается внутри в виде тонкой пленки на стенках, причем
толщина этой пленки в некоторой степени зависит от скорости опорожнения пи-
петки. Как правило, пипетки градуируют в расчете на свободное вытекание под
действием силы тяжести. При работе с пипетками необходимо следить, чтобы
скорость вытекания жидкости всегда была одной и той же.
Мерные пипетки отградуированы только на одно определенное значение
объема. Их используют в тех случаях, когда требуется отобрать объем жидкости
62
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
РИС. 2.9. Мерные пипетки
РИС. 2.10. Градуированные пипетки
с наибольшей точностью. Как правило, такими пипетками можно дозировать
объемы с точностью до четырех (в случае необходимости, при условии соответ-
ствующей градуировки — пяти) значащих цифр. Допустимые погрешности объ-
емов мерных пипеток класса А приведены в таблице на переднем форзаце
данного тома. Градуированные пипетки представляют собой цилиндрические
трубки, на поверхность которых нанесены значения объема с определенным ша-
гом. Они не настолько точны, как мерные пипетки, поскольку их внутренний
диаметр все же не вполне постоянен по высоте. В этом случае искажения формы
пипеток сильнее сказываются на величинах объемов, чем в случае мерных пипе-
ток с характерным утолщением по середине. Кроме того, толщина остаточной
пленки жидкости на стенках пипетки изменяется в зависимости от отмеренного
объема. При помощи градуированных пипеток можно достичь точности объема
в лучшем случае с тремя значащими цифрами, если только не откалибровать пи-
петку специально для определенного значения объема.
2.4. МЕРНАЯ ПОСУДА
63
Большинство градуированных пипеток калибруют на свободное вытекание,
т. е. с учетом того, что небольшой объем жидкости остается в носике. Его не сле-
дует вытряхивать или выдувать. Пипетку при опорожнении держат вертикаль-
но, касаясь кончиком стенки сосуда. Жидкость при этом вытекает плавно, без
разбрызгивания, а величина объема капли, остающейся в носике, хорошо вос-
производится. Жидкость из носика пипетки частично вытягивается под действи-
ем сил притяжения к стенкам сосуда.
Иногда пипетки (в том числе градуированные, если они отградуированы в
пределах всего внутреннего объема) калибруют на выдувание. При использова-
нии таких пипеток для того, чтобы отмерить номинальное значение объема, сле-
дует выдуть из носика остатки жидкости. Пипетки такого типа легко распознать,
поскольку в верхней части они всегда помечены одним или двумя кольцами
шероховатого стекла. Их не надо путать с цветными кольцами, используемыми
для маркировки объема пипетки. Из таких пипеток остаток жидкости следует
выдувать только после свободного вытекания основного объема под действием
силы тяжести. Преждевременное выдувание жидкости увеличивает скорость ее
истечения и приводит к изменению толщины остаточной пленки на стенках.
Мерные пипетки выпускают объемом от 100 до 0,5 мл и менее. Объемы гра-
дуированных и серологических пипеток могут составлять от 25 до 0,1 мл. Их
можно использовать и для высокоточной дозировки (особенно небольших объе-
мов), если специально откалибровать применительно к конкретному значению
объема. Мерные пипетки большого объема обычно характеризуются слишком бо-
льшой скоростью истечения — более высокой, чем скорость стекания пленки
жидкости со стенок. Кроме того, их диаметр слишком велик, из-за чего снижает-
ся точность считывания показаний.
Необходимо всегда обтирать наружную поверхность пипетки после заполне-
ния. При использовании неводных растворителей, а также растворов повышенной
вязкости пипетку следует заново откалибровать при помощи соответствующего
растворителя или раствора, чтобы учесть изменение скорости истекания.
Для заполнения пипетки жидкостью используют резиновые груши, по-
ршневые или иные пипетаторы. Прежде, чем ими пользоваться, поупражняйтесь
в заполнении пипетки водой с их помощью. Запрещается засасывать жидкости
ртом.
Шприцевые пипетки
Пипетки этого типа можно использовать для дозирования как больших, так и ма-
лых объемов. Положение метки на шприцевых пипетках может быть несколько
смещено относительно номинального объема, но воспроизводимость дозировки
может быть очень высокой — особенно если пипетка снабжена автоматическим
поршнем. При этом исключаются погрешности объема, обусловленные наличи-
ем пленки жидкости на внутренних стенках, поскольку вся жидкость выталкива-
ется поршнем. Значение объема вытекающей жидкости можно откалибровать с
высокой точностью. Шприцевые пипетки удобно использовать для дозирования
микролитровых объемов. Шприцевые пипетки объемом несколько микролитров
64
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.11
Микролитровая пипетка фирмы Hamilton
используют для ввода проб в газовые хроматографы. Пипетка такого типа, снаб-
женная иглой, изображена на рис. 2.11. Погрешности объемов таких пипеток не
выше, чем у других микропипеток. Дополнительным достоинством шприцевых
пипеток является возможность дозирования любого объема в пределах общего
объема пипетки.
Использование шприцевых пипеток очень удобно для точного дозирования
вязких или летучих жидкостей. При использовании обычных пипеток значения
объема будут искажены, поскольку для таких жидкостей толщина остаточной
пленки на стенках иная, чем для воды. Шприцевые пипетки удобно использо-
вать также для быстрого дозирования жидкостей. При последовательном дозиро-
вании нескольких жидкостей они хорошо перемешиваются, вследствие быстрого
вытекания.
Еще один тип шприцевых пипеток представлен на рис. 2.12. Такие пипетки
позволяют работать одной рукой, быстро отмерять постоянные объемы жидко-
Рис. 2.12
Одноканальная и
многоканальная пипетка
со съемными
наконечниками и
планшеты для
клинических анализов.
С любезного разрешения
Thermo Labsystems
2.4. МЕРНАЯ ПОСУДА
65
стей и широко применяются в клинических лабораториях. К пипеткам прилагается
набор сменных наконечников из пластмассы, например, на основе полипропилена.
Материал наконечников не смачивается водой. Поэтому искажения объемов,
обусловленные наличием пленки жидкости на стенках, отсутствуют. Кроме
того, поверхность таких материалов мало загрязняется. В пипетке содержится
распираемый пружиной поршень, который управляется кнопкой. Поршень име-
ет два положения упора: верхнее — дня набора жидкости, нижнее — для полно-
го опорожнения пипетки. В процессе работы жидкость никогда не контактирует
с самим поршнем, она наполняет только наконечник. Объемы пипеток могут со-
ставлять от 1 до 1000 мкл. Воспроизводимость дозирования зависит от величи-
ны объема и в лучшем случае составляет 1-2%.
Во многих случаях нет необходимости знать реальное значение объема, до-
зируемого микропипетками рассматриваемого и других типов, поскольку эти
пипетки используются для относительных измерений. Например, одну и ту же
пипетку — а следовательно, одно и то же значение объема — можно использо-
вать для дозирования аликвоты анализируемой пробы и стандартных растворов
с целью построения градуировочной зависимости. В подобных случаях воспро-
изводимость объема играет более важную роль, чем его абсолютное значение.
Стандартом для калибровки пипеток в Европе (где производится большая часть
пипеток такого типа) служит немецкий стандарт DIN 126650 (и соответствую-
щий ему международный стандарт ISO 8655). Калибровка пипеток производит-
ся гравиметрическим методом (путем взвешивания воды). В стандарте DIN не
указываются отдельные пределы для правильности и воспроизводимости, а ис-
пользуется значение суммарной погрешности, рассчитываемой как сумма пре-
дельно допустимой систематической погрешности и удвоенного стандартного
отклонения. Полученная величина представляет собой интервал, в котором с
95%-й вероятностью находится значение объема, дозируемого пипеткой (о стан-
дартных отклонениях и доверительных интервалах см. гл. 3). В табл. 2.2 приве-
дены предельно допустимые согласно стандарту DIN погрешности объемов для
одноканальных пипеток, а в табл. 2.3 — раздельные характеристики правильно-
сти и воспроизводимости для многоканальных пипеток.
Помимо шприцевых пипеток с ручным управлением, существуют механи-
зированные шприцевые пипетки, а также пипетки с электронным управлением и
перестраиваемым значением объема. С их помощью можно многократно дози-
ровать различные объемы жидкостей в автоматическом режиме. Выпускаются
также пипетки с несколькими каналами для одновременного дозирования не-
скольких, например, 12 или 16, аликвот. Их используют для добавления растворов в
ячейки специальных планшетов, применяемых в биотехнологии и клинических ла-
бораториях, где часто требуется обрабатывать тысячи проб (рис. 2.12). Дополните-
льную информацию о пипетках со сменными наконечниками можно получить
непосредственно у представителей их производителей, например, на сайтах
www.finnpipette.com и www.eppendorf.com.
66
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Таблица 2.2
Предельные погрешности для одноканальных шприцевых пипеток
согласно стандарту DIN 12650*
Номинальный объем, (мкл) Максимальная погрешность, (мкл) Относительная погрешность, (%)
1 ±0,15 ±15,0
2 ±0,20 ±10,0
5 ±0,30 ±6,0
10 ±0,30 ±3,0
20 ±0,40 ±2,0
50 ±0,80 ±1,6
100 ±1,50 ±1,5
200 ±2,00 ±1,0
500 ±5,00 ±1,0
1000 ±10,00 ±1,0
2000 ±20,00 ±1,0
5000 ±50,00 ±1,0
10000 ±100,00 ±1,0
* Указаны пределы в случае испытания пипеток производителем в строго контролируемых условиях. Если ис-
пытания проводит потребитель в обычных условиях, предельные величины погрешностей следует удвоить.
С любезного разрешения Thermo Labsystems Оу, Финляндия.
Таблица 2.3
Правильность и воспроизводимость одноканальных цифровых шприцевых пипеток
Finnpipettes
Диапазон (мкл) Шаг (мкл) Объем (мкл) Правильность Воспроизводимость*
(мкл) (%) ст. откл. (мкл) отн. ст. откл. (%)
0,2-2 0,01 2 ±0,050 ±2,5 0,040 2,0
0,2 ±0,024 ±12,0 0,020 10,0
0,5-10 0,1 10 ±0,100 ±1,0 0,050 0,5
1 ±0,025 ±2,5 0,020 2,0
0,5-10 0,1 10 ±0,100 ±1,0 0,080 0,8
1 ±0,035 ±3,5 0,030 3,0
2-20 0,1 20 ±0,200 ±1,0 0,080 0,4
2 ±0,060 ±3,0 0,030 1,5
5-40 0,5 40 ±0,240 ±0,6 0,120 0,3
5 ±0,100 ±2,0 0,100 2,0
10-100 1,0 100 ±0,80 ±0,8 0,20 0,2
10 ±0,30 ±3,0 0,10 1,0
20-200 1,0 200 ±1,20 ±0,6 0,40 0,2
20 ±0,36 ±1,8 0,14 0,7
200-1000 5,0 1000 ±6,00 ±0,6 2,00 0,2
200 ±1,80 ±0,9 0,60 0,3
100-1000 5,0 1000 ±6,00 ±0,6 2,00 0,2
100 ±1,00 ±1,0 0,60 0,6
* ст. откл. — стандартное отклонение, отн. ст. откл. — относительное стандартное отклонение.
С любезного разрешения Thermo Labsystems Оу, Финляндия.
2.4. МЕРНАЯ ПОСУДА
67
Бюретки
Бюретки применяются для точного дозирования переменных
объемов растворов. Их главная сфера применения — титрова-
ние, в ходе которого к раствору пробы непрерывно добавляют
стандартный раствор реагента до тех пор, пока не будет достиг-
нута конечная точка титрования, характеризующая заверше-
ние реакции. Обычные бюретки для титрования имеют шкалу
объемов, оцифрованную от 0 до 50 мл с ценой деления 0,1 мл.
Такая бюретка изображена на рис. 2.13. Пользуясь шкалой,
можно считывать показания до сотых миллилитра по положе-
нию мениска между делениями (с точностью ±0,02-0,03 мл).
Выпускаются также бюретки объемом 10,25 и 100 мл и микро-
бюретки объемом до 2 мл. Цена деления таких микробюреток
составляет 0,01 мл, что позволяет считывать показания до тысяч-
ных долей миллилитра. Ультрамикробюретки объемом 0,1 мл
имеют цену деления 0,001 мл (1 мкл); их используют для титро-
вания микролитровых объемов растворов.
Как и для пипеток, для бюреток обычных типов толщина
пленки жидкости на стенках влияет на точность дозировки.
Этот фактор может вносить существенные погрешности, если
скорость истечения жидкости не постоянна. Рекомендуется до-
бавлять жидкость по каплям с достаточно низкой скоростью,
15-20 мл в минуту, а по завершении титрования подождать не-
сколько секунд для полного стекания жидкости со стенок. На
практике вблизи конечной точки титрования скорость состав-
ляет всего несколько капель в минуту, поэтому специально
ждать, пока жидкость стечет, нет необходимости. В непосред-
ственной близости конечной точки можно добавлять жидкость
даже меньшими порциями, чем одна капля, если слегка открыть
и тут же закрыть дозирующий кран, после чего прикоснуться кончиком бюретки
к стенке сосуда. Порцию жидкости, приставшую к стенке, следует смыть в тит-
руемый раствор дистиллированной водой.
Работа с мерной посудой и уход за ней
Мы уже упоминали некоторые меры предосторожности при работе с мерными
колбами, пипетками и бюретками. Более подробно об этом расскажет ваш пре-
подаватель. В данном разделе обсуждим лишь общие правила работы с мерной
посудой.
Важнейшее значение имеет чистота внутренней поверхности посуды. Если
внутренняя поверхность покрыта слоем грязи или жира, жидкость не будет сте-
кать равномерно, в результате чего образуются отдельные капельки на стенках.
В этом случае калибровка посуды будет неправильной. Для начала следует не-
сколько раз промыть посуду изнутри водой. Затем можно промыть ее разбавлен-
ной азотной кислотой и снова несколько раз водой. Горлышки мерных колб
Рис. 2.13
Стандартная
бюретка
68
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
удобно мыть при помощи ершика, но при этом необходимо следить за тем, что-
бы не поцарапать внутренние стенки. Пипетки можно промывать небольшими
порциями раствора моющего средства, поворачивая их, чтобы омыть всю поверх-
ность. В продаже имеются специальные высокоэффективные моющие растворы.
Пипетки и бюретки следует как минимум дважды ополоснуть тем раство-
ром, которым они будут заполнены. Если пипетка или бюретка мокрая, ее следу-
ет сначала ополоснуть дистиллированной водой, а затем как минимум трижды
используемым раствором. Объем, идущий на каждое ополаскивание, должен со-
ставлять приблизительно одну пятую часть объема пипетки или бюретки. Не забы-
вайте предварительно ополаскивать пипетки и бюретки раствором, которым
будете их заполнять! Мерные колбы следует отмыть от следов предыдущего
раствора двумя-тремя порциями дистиллированной воды. Поскольку в дальней-
шем мерная колба будет заполнена водой до метки, высушивать ее нет необхо-
димости.
Обратите внимание, что с аналитической мерной посудой нельзя поступать
так, как часто обращаются с посудой в лабораториях по органическому синтезу:
высушивать в сушильном шкафу (это может привести к изменению ее объема),
при помощи полотенца, ополаскивать летучим органическим растворителем,
например, ацетоном (все это может вызвать загрязнение). Как правило, и не тре-
буется, чтобы мерная посуда была сухой. Вместо высушивания следует просто
ополоснуть посуду тем раствором, который будет в нее помещен.
При считывании показаний объемов следует избегать погрешностей парал-
лакса, связанных с неправильным взаимным расположением глаза, мениска и
шкалы. Это относится к считыванию показаний любой шкалы, в частности,
стрелочного указателя на аналитических весах. Правильное расположение гла-
за — на уровне мениска. Если глаз расположен выше мениска, считанное значе-
ние будет меньше истинного, и наоборот.
После работы с мерной посудой ее следует немедленно промыть дистилли-
рованной водой. Сухую посуду необходимо сначала промыть раствором моюще-
го средства. Мерные колбы при хранении закрывают пробками (рекомендуется
предварительно заполнить их дистиллированной водой). Бюретки перед хране-
нием заполняют дистиллированной водой и закрывают резиновыми пробками.
Как получить правильные и хорошо воспроизводимые
результаты титрования: общие указания
Если кран бюретки изготовлен из тефлона, смазывать его не нужно. Убедитесь,
что он вставлен достаточно плотно, для того чтобы раствор не подтекал, но не
настолько плотно, чтобы его было трудно поворачивать. Если кран изготовлен
из притертого стекла, его возможно придется смазать. Для этого поверхность
крана покрывают тонким слоем специальной смазки (не силиконовой). Вблизи
отверстия этот слой должен быть особенно тонким; необходимо следить, чтобы
смазка не попала в отверстие. После смазывания кран вставляют и вращают не-
сколько раз. Слой смазки должен быть прозрачным, а раствор не должен подте-
кать. Если слой смазки слишком толстый, смазка может попасть внутрь бюретки
2.4. МЕРНАЯ ПОСУДА
69
или закупорить отверстие крана. Из кончика бюретки или отверстия крана лиш-
нюю смазку удаляют при помощи тонкой проволоки. Повторим, что тефлоно-
вые краны не нуждаются в смазке. После того как кран подготовлен к работе,
бюретку заполняют выше нулевой отметки и открывают кран, чтобы заполнить
раствором носик. Проверьте, чтобы в носике бюретки не было пузырей воздуха.
В процессе титрования они могут выйти наружу и вызвать погрешность результа-
тов. Если пузыри есть, их надо выпустить под напором струи раствора, несколько
раз резко открывая и закрывая кран. Не должно быть пузырей и в самом объеме
бюретки. Если они все же есть, это означает, что бюретка скорее всего грязная.
Для установления начального уровня жидкости следует медленно спустить
раствор до нулевой отметки. Затем необходимо подождать и убедиться, что вся
жидкость стекла со стенок. Начальное показание, если оно отлично от нуля, сле-
дует считать с точностью до 0,02 мл (для бюреток объемом 50 мл). Для удобства
считывания показаний следует поместить темный предмет (можно даже палец)
за бюреткой на уровне мениска либо воспользоваться специальным осветителем
мениска (рис. 2.14). Осветитель мениска состоит из белого (сверху) и черного
(снизу) полей. Их границу необходимо расположить точно на уровне мениска.
При считывании показаний избегайте погрешностей параллакса.
Титруемый раствор помещают в коническую колбу. Колбу ставят на поверх-
ность белого цвета, а бюретку располагают над горлышком колбы. Раствор пе-
ремешивают, вращая колбу правой рукой, а краном управляют левой рукой
(рис. 2.15). При обхвате крана, показанном на рисунке, создается некоторое дав-
ление и предотвращается подтекание раствора. Для более эффективного переме-
шивания раствора можно использовать магнитную мешалку.
В ходе титрования индикатор сначала изменяет окраску в непосредствен-
ной близости от места падения капли титранта, поскольку там создается его ло-
кальная избыточная концентрация. При перемешивании титрант равномерно
РИС. 2.14. Осветитель мениска для бюреток Рис. 2.15. Правильное выполнение титрования
70
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
распределяется по всему объему колбы и взаимодействует с титруемым веще-
ством, поэтому исходная окраска индикатора быстро восстанавливается. По
мере приближения к конечной точке это восстановление окраски протекает все
медленнее, и раствор необходимо перемешивать все более тщательно. Перед
самой конечной точкой титрование прекращают и смывают раствор со стенок
колбы дистиллированной водой. Как уже говорилось, показания объема счи-
тывают с точностью до 0,02 мл, но объем капли может быть больше (от 0,02 до
0,05 мл). Поэтому перед самым концом титрования капли следует добавлять по
частям. Для этого кран очень медленно поворачивают до тех пор, пока из носи-
ка не появится часть капли, после чего кран закрывают. Затем прикасаются но-
сиком к стенке колбы и смывают титрант в колбу дистиллированной водой.
Можно также перенести часть капли из носика бюретки в колбу при помощи
стеклянной палочки с оттянутым концом. Признаком окончания титрования
является резкое и устойчивое (в течение по меньшей мере 30 с) изменение
окраски раствора.
Как правило, титрование повторяют три раза. Предварительно можно вы-
полнить ориентировочное титрования для приближенной оценки требуемого
объема титранта. Знание этой величины позволит ускорить процесс последую-
щего титрования.
По завершении титрования остатки титранта следует вылить. Возвращать
их обратно в сосуд с раствором титранта нельзя.
Если для индикации конечной точки титрования измеряют какое-либо фи-
зическое свойство, например, потенциал, то титруемый раствор перемешивают
магнитной мешалкой.
Точность и допустимые погрешности объема мерной посуды
Американским Национальным институтом стандартов и технологий (NIST)
установлены максимально допустимые абсолютные значения погрешностей
объемов для различных типов мерной посуды. Некоторые из них приведены на
переднем форзаце данного тома. Для посуды объемом около 25 мл относитель-
ные погрешности составляют порядка одной части на тысячу (0,1%), для посу-
ды меньшего объема погрешности выше. Буква «А» на мерной колбе, пипетке
или бюретке, свидетельствует о том, что посуда удовлетворяет классу точно-
сти А. Однако это ничего не говорит о реальной точности дозировки объема. В
продаже имеется специальная посуда, удовлетворяющая требованиям точности
NIST или сертифицированная NIST, но она значительно дороже, чем несертифи-
цированная. Более дешевая посуда может характеризоваться погрешностями
вдвое большими, чем установлено требованиями NIST. В то же время не со-
ставляет большого труда самостоятельно откалибровать такую посуду. При
этом будет достигнута точность дозировки объема, сопоставимая с требовани-
ями NIST или даже превышающая ее (см. практическую работу 2). Для боль-
шинства анализов достаточно использовать посуду класса точности А. Ее
можно дополнительно градуировать так, чтобы точность удовлетворяла
требованиям NIST.
2.4. МЕРНАЯ ПОСУДА
71
Для бюреток объемом 50 мл точность считывания показаний составляет
±0,02 мл. Поскольку показания бюретки всегда считывают дважды, общая абсо-
лютная неопределенность результата может достигать ±0,04 мл. Относительная
неопределенность (погрешность) в этом случае обратно пропорциональна вели-
чине объема. Очевидно, что при использовании 50-мл бюретки для снижения от-
носительной погрешности до 0,1% необходимо, чтобы объем титранта составил
не менее 40 мл. Если объем титранта меньше, следует использовать бюретки ме-
ньшего объема. Пипетки также характеризуются определенной погрешностью
считывания показаний. В отличие от бюреток, показания пипеток считывают то-
лько один раз. Погрешности, связанные с каждым считыванием показаний, на-
капливаются. См. гл. 3. «Наложение погрешностей».
Калибровка мерной посуды:
как достигнуть максимальной точности
Пример 2.1 иллюстрирует, как можно использовать уравнение (2.1) для калиб-
ровки мерной посуды, чтобы ввести поправку на выталкивающую силу воздуха,
т. е. привести массу воды, используемой для калибровки, к ее массе в вакууме.
Для нахождения объема посуды следует разделить массу содержащейся в ней
воды (в вакууме) на плотность воды при соответствующей температуре.
В табл. 2.4 приведены значения массы в вакууме для количества воды, масса
которой составляет один грамм в воздухе при атмосферном давлении и разных
температурах. Поправки рассчитаны для стальных разновесов плотностью
7,8 г/см3. Указанные значения используют для расчета объема мерной посуды
при ее калибровке из результатов взвешивания воды, содержащейся в ней или
вытекающей из нее. При использовании латунных разновесов плотностью
8,4 г/см3 значения мало отличаются от приведенных в таблице (см. пример 2.2).
В табл. 2.4 приведены также небольшие поправки на температурное расширение
или сжатие материала посуды — боросиликатного стекла (Pyrex или Kimax). Та-
кие стекла характеризуются объемным коэффициентом расширения порядка
0,000025 на градус Цельсия при температурах вблизи стандартной (20 °C). Это
приводит к изменению объема примерно на 0,0025% при изменении температу-
ры на один градус. Например, для объема 1 мл изменение составит 0,000025 мл.
Для воды изменение объема вблизи 20 °C составляет порядка 0,02% на один гра-
дус. Для пересчета значений объемов (и концентраций) с учетом расширения
(сжатия) воды можно использовать значения плотности воды при разных темпе-
ратурах, также приведенные в табл. 2.4.
Табл. 2.4 с введенными в нее формулами есть на прилагаемом к книге ком-
пакт-диске. Вы можете заменить значение в ячейке столбца В на реальный вес
воды (в колбе, пипетке или бюретке), который вы измерили при соответствую-
щей температуре, и автоматически рассчитать объем посуды при той же темпе-
ратуре и при 20 °C. Порядок работы с электронными таблицами описан в гл. 3.
На компакт-диске находятся также таблица и рисунок, изображающие зависи-
мость относительной погрешности взвешивания (по отношению к массе в ваку-
уме) от плотности объекта.
72
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Таблица 2.4
Данные для калибровки мерной посуды
А В _ С 0 Е F G н
1 Данные для калибровки мерной посуды
2 Вес в вакууме рассчитан применительно к стальным разновесам плотностью 7,8 г/см3.
3 Температурный коэффициент расширения боросиликатного стекла составляет 0,000025 мл/мл/°С.
4 I
5 Скопируйте эту таблицу, находящуюся на компакт-диске (глава 2), и используйте ее для расчетов объемов
6 мерной посуды по результатам калибровки. Для этого в ячейку столбца В, соответствующую заданной
7 температуре Т (столбец А), занесите вес воды, содержащейся в мерной посуде и измеренный на воздухе
8 при этой температуре. После этого в той же строке будут автоматически рассчитаны значения веса воды
9 в вакууме при температуре Т (столбец D) и при 20 °C (столбец F). Округлите рассчитанные значения до
10 необходимого числа значащих цифр (обычно четырех или пяти).
11
12 Т, °C Вес воды Вес в Объем Расширение стекла Объем при 20 °C, Плотность воды,
13 на воздухе, г вакууме, г при Т, мл по отн. к 20 °C, мл мл г/мл
14 10 1,0000 1,0010 1,0013 -0,000250 1,0016 0,9997026
15 11 1,0000 1,0010 1,0014 -0,000225 1,0017 0,9996081
16 12 1,0000 1,0010 1,0015 -0,000200 1,0017 0,9995004
17 13 1,0000 1,0010 1,0017 -0,000175 1,0018 0,9993801
18 14 1,0000 1,0010 1,0018 -0,000150 1,0020 0,9992474
19 15 1,0000 1,0010 1,0019 -0,000125 1,0021 0,9991026
20 16 1,0000 1,0010 1,0021 -0,000100 1,0022 0,9989460
21 17 1,0000 1,0010 1,0023 -0,000075 1,0023 0,9987779
22 18 1,0000 1,0010 1,0025 -0,000050 1,0025 0,9985896
23 19 1,0000 1,0010 1,0026 -0,000025 1,0027 0,9984082
24 20 1,0000 1,0010 1,0028 0,000000 1,0028 0,9982071
25 21 1,0000 1,0010 1,0031 0,000025 1,0030 0,9979955
26 22 1,0000 1,0010 1,0033 0,000050 1,0032 0,9977735
27 23 1,0000 1,0010 1,0035 0,000075 1,0034 0,9975415
28 24 1,0000 1,0010 1,0038 0,000100 1,0037 0,9972995
29 25 1,0000 1,0010 1,0040 0,000125 1,0039 0,9970479
30 26 1,0000 1,0010 1,0043 0,000150 1,0041 0,9967867
31 27 1,0000 1,0010 1,0045 0,000175 1,0044 0,9965162
32 28 1,0000 1,0010 1,0048 0,000200 1,0046 0,9962365
33 29 1,0000 1,0010 1,0051 0,000225 1,0049 0,9959478
34 30 1,0000 1,0010 1,0054 0,000250 1,0052 0,9956502
35
36 В ячейки, выделенные жирным шрифтом, введены формулы, приведенные ниже. Они скопированы вниз для
37 всех температур. Об установке таблицы см. главу 3.
38 Ячейка С14: Wvac = Wair + Wair(0,0012/Do - 0,0012/Dw) = Wair(0,0012/1,0 + 0,0012/7,8)
39 L = В14+В14*(0,0012/1,0-0,0012/7,8) скопирована вниз
40 Ячейка D14: \/т(мл) = WvacT(r)/DT(r/M л)
41 C14/G14 С скопирована вниз
42 Ячейка Е14: Расш. стекла = (Т - 20) (град.) • 0,000025 (мл/мл/град.) • Wajr(r)
43 1 | (А14-20)*0,000025*В14 скопирована вниз
44 Ячейка F14: V20rc=VT - Glassexp= D14-E14 скопирована вниз
2.4. МЕРНАЯ ПОСУДА
73
Пример 2.3
а) Пользуясь табл. 2.4, рассчитайте объем пипетки (номинальное значение
20 мл) по результатам взвешивания воды в воздухе из данных примера 2.1. При-
мите, что взвешивание проводили при 23 °C. б) Приведите полученный объем к
20 °C (изменения обусловлены сжатием стекла), в) Сравните значения объемов,
рассчитанные из величины веса на воздухе и из величин веса в вакууме и плот-
ности воды.
Решение
а) Из данных табл. 2.4 при 23 °C объем воды весом один грамм (на воздухе) со-
ставляет 1,0035 мл. Объем колбы составит
19,994 г • 1,0035 мл/г = 20,064 мл
б) Уменьшение объема за счет сжатия стекла при изменении температуры от
23 °C до 20 °C оставляет 0,0015 мл (0,000025 мл/мл/°С • 20 мл • 3 °C), поэтому
объем пипетки при 20 °C составит 20,062 мл.
в) Плотность воды при 23 °C равна 0,99754 г/мл, поэтому из величины веса в ва-
кууме
20,015 г / 0,99754 г/мл = 20,064 мл
получено то же значение, что и в пункте (а).
Пример 2.4
Вы приготовили раствор соляной кислоты и стандартизировали его титровани-
ем первичного стандарта — раствора карбоната натрия. В процессе титрования
температура воздуха в помещении составляла 23 °C. Найденное значение кон-
центрации — 0,11272 М. После этого в лаборатории вышла из строя отопитель-
ная система, и, когда вы использовали эту кислоту для титрования, температура
упала до 18 °C. Какой при этом стала концентрация титранта?
Решение
М 18 °с = м23 °с • (А8 °с /7?23 сс) = о,11272 • (0,99859/0,99754) = 0,11284 М
(о значащих цифрах и о том, что означает цифра нижнего индекса результата,
см. гл. 3).
74
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Техника калибровки мерной посуды
Как правило, результаты калибровки мерной посуды представляют с пятью зна-
чащими цифрами, что соответствует максимально возможной точности дози-
ровки объемов. Следовательно, чистая масса воды также должна быть измерена
не менее, чем с пятью значащими цифрами. Это означает, что, если объем посу-
ды превышает 10 мл, то достаточно взвешивания с точностью до 1 мг. Такое
взвешивание можно легко и быстро осуществить на технических весах, не при-
бегая к использованию более точных аналитических весов. Иногда бывает до-
статочно и четырех значащих цифр (о значащих цифрах см. гл. 3). Например,
калиброванный объем пипетки с номинальным объемом 10 мл может составлять
9,997 мл. Это значение столь же точное, как и 10,003 мл.
1. Калибровка мерных колб. Взвешивают чистую и сухую колбу вместе с
пробкой. Затем колбу заполняют до метки дистиллированной водой. На гор-
лышке колбы не должно быть капель. Если они есть, их удаляют фильтроваль-
ной бумагой. Температура колбы с водой должна равняться комнатной. После
этого взвешивают колбу с водой и измеряют температуру воды с точностью до
0,1 °C. Разность результатов взвешивания равна весу на воздухе воды, содержа-
щейся в колбе.
2. Калибровка пипеток. Взвешивают сухую коническую колбу, закрытую ре-
зиновой пробкой, или бюкс, закрытый стеклянной пробкой (выбор сосуда зави-
сит от объема воды, который предстоит взвесить). Пипетку заполняют водой
(температура которой известна), опорожняют в предварительно взвешенный со-
суд, используя стандартную технику пипетирования, и быстро закрывают сосуд,
чтобы избежать потерь воды вследствие испарения. Сосуд с водой взвешивают и
рассчитывают значение веса на воздухе воды, отмеренной пипеткой.
3. Калибровка бюреток. Бюретки калибруют аналогично пипеткам, но в этом
случае взвешивают несколько порций воды. Внутренняя поверхность бюретки
может не быть строго цилиндрической, поэтому дозируемый объем может отли-
чаться в ту или иную сторону от номинального. Это различие может быть раз-
ным для разных объемов. Поэтому рекомендуется откалибровать бюретку на
несколько значений объемов с шагом 20% от общего объема (например, 10 мл
для бюретки объемом 50 мл). Рекомендуется каждый раз заполнять бюретку во-
дой до нулевой отметки и отмерять очередную порцию воды в сухую колбу для
взвешивания. Это позволяет предотвратить потери воды вследствие испарения.
Можно заполнить бюретку один раз и отмерять последовательные порции в
одну и ту же колбу, но в этом случае все операции надо проводить быстро. Объ-
ем воды для взвешивания должен быть точно известен и близок к номинально-
му, но не обязательно в точности равен ему. Поэтому опорожнять бюретку
можно быстро, но после дозирования каждой порции следует подождать 10-20 с
для полного стекания воды со стенок и записать точное значение объема. По-
правки к значениям объема откладывают в виде зависимости от самого значения
2.4. МЕРНАЯ ПОСУДА
75
объема и соединяют полученные точки ломаной линией. Из полученного графи-
ка интерполяцией можно найти поправку для любого значения объема. Как пра-
вило, для пипеток объемом 50 мл поправки к номинальным значениям находятся
в пределах ±0,05 мл.
Пример 2.5
Бюретку объемом 50 мл калибруют, отбирая воду порциями по 10 мл. Бюретку
каждый раз заполняют водой до нулевой отметки. Результаты калибровки при-
ведены ниже.
Показания бюретки (мл) Вес порции воды (г)
10,02 10,03
20,08 20,03
29,99 29,85
40,06 39,90
49,98 49,86
Постройте зависимость поправки к объему от величины объема порции. Темпе-
ратура воды 20 °C, при взвешивании использованы стальные разновесы.
Решение
Из табл. 2.4 (или электронной таблицы 2.4 на компакт-диске) находим:
Wvac = 10,03 + 10,03 (0,00105) = 10,03 + 0,01 = 10,04 г
VT= 10,04 г / 0,9982 г/мл = 10,06 мл
Аналогично рассчитываем другие значения. Получаем данные для построения
требуемой зависимости:
Номинальный объем (мл) 10,02 20,08 29,99 40,06 49,98 Реальный объем (мл) Поправка (мл) 10,06 +0,04 20,09 +0,01 29,93 -0,04 40,01 -0,05 50,00 0,00
Эти данные откладывают в виде графика (по оси х — номинальные значения
объема, по оси у—поправки). Номинальные значения можно принять округлен-
но равными 10, 20, 30, 40 и 50 мл.
76
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Выбор мерной посуды: насколько точный объем должен быть?
Как и при взвешивании, при измерении объема возникают ситуации, когда его
значение должно быть известно точно, и ситуации, когда требуется лишь прибли-
женное значение. Например, приготовить стандартный раствор 0,1 М НС1 невоз-
можно путем разбавления до определенного значения точно отмеренного объема
концентрированной соляной кислоты, поскольку концентрация соляной кислоты
в исходном растворе не известна с требуемой точностью. Полученный разбавлен-
ный раствор все равно необходимо будет стандартизовать. Поэтому в данном слу-
чае объем концентрированной кислоты можно отмерить приближенно (и затем
провести стандартизацию разбавленного раствора). Из таблицы, приведенной на
переднем форзаце данного тома, видно, что концентрация коммерческих препара-
тов концентрированной соляной кислоты составляет около 12,4 М. Чтобы приго-
товить 1 л раствора с концентрацией около 0,1 М, необходимо отмерить примерно
8,1 мл концентрированной кислоты и разбавить до 1 л. Точное измерение объема
этой порции (а также объема воды, используемой для разбавления) было бы в
этом случае пустой тратой времени. Для измерения объема кислоты вполне доста-
точно использовать градуированный мерный цилиндр объемом 10 мл (или граду-
ированную пипетку того же объема), а разбавлять кислоту можно в любом, даже
неградуированном, сосуде объемом 1 л. С другой стороны, если требуется точно
разбавить исходный стандартный раствор, его объем необходимо отмерить мер-
ной пипеткой, а разбавление проводить в мерной колбе. Любые измерения объе-
мов, значения которых используются для расчетов содержаний веществ, следует
проводить с определенной для каждого конкретного случая точностью. Как пра-
вило, эта точность составляет четыре значащие цифры. Чтобы достичь такой
точности, необходимо использовать мерные пипетки и мерные колбы. Высокая
точность требуется и при взятии навесок (пробы и реактивов для приготовления
стандартных растворов), а также при разбавлении. Для точной дозировки пере-
менных объемов, как и при титровании, используют бюретки. Приготовление
растворов реактивов, необходимых лишь для создания определенных условий
(например, буферов для контроля pH), не требует высокой точности. Для этого
можно использовать мерную посуду меныпей точности, например, мерные ци-
линдры. С высокой точностью необходимо измерять только те значения объе-
мов, которые будут использованы для расчета содержания вещества.
2.5. Приготовление стандартных растворов щелочей
В качестве щелочного титранта обычно используют гидроксид натрия. Он все-
гда содержит значительные количества воды и карбоната натрия и, следователь-
но, не может являться первичным стандартом. Для выполнения точных работ
NaOH необходимо освободить от карбоната, поскольку в ходе титрования кар-
бонат натрия создает буферную систему. В результате этого переход окраски
индикатора в конечной точке становится менее четким. Кроме того, при исполь-
зовании индикатора фенолфталеина титрование раствором NaOH, содержащим
2.6. ПРИГОТОВЛЕНИЕ СТАНДАРТНЫХ РАСТВОРОВ КИСЛОТ
77
карбонат, приводит к систематической погрешности, поскольку в этих условиях
ионы СО3“ титруются только до НСО3 (поэтому NaOH предпочитают титровать
с метиловым оранжевым: при этом ионы СО3” титруются до СО2). Иными сло-
вами, кажущаяся молярная концентрация раствора щелочи увеличивается из-за
того, что образующиеся ионы НСО3 также способны титроваться.
Карбонат натрия практически нерастворим в концентрированных, близких
к насыщенным, растворах гидроксида натрия. Для удаления карбоната натрия
навеску NaOH растворяют в объеме воды, численно равном (в мл) массе NaOH в
граммах. Раствор оставляют на несколько дней для осаждения Na2CO3 и акку-
ратно декантируют* прозрачный маточный раствор. Маточный раствор можно
также отфильтровать через фильтрующий тигель Гуча с асбестовой прокладкой
(нельзя промывать фильтр после фильтрования). Однако асбест является канце-
рогенным материалом, поэтому первый способ предпочтительнее. Таким спосо-
бом нельзя освободить от карбонатов растворы КОН, так как К2СО3 растворим в
концентрированных растворах КОН.
Вода также содержит растворенный СО2, поглощенный из воздуха. Как пра-
вило, в ходе серийных анализов, не требующих высокой точности, погрешности,
вызываемые примесями карбонатов или СО2 в воде, можно считать пренебрежимо
малыми. Если же требуется высокая точность, СО2 необходимо удалить из всей
воды, используемой для приготовления растворов (особенно щелочных) для
кислотно-основного титрования. Это проще всего сделать при помощи кипяче-
ния с последующим охлаждением под струей воды.
Растворы гидроксида натрия обычно стандартизуют титрованием точных
навесок первичного стандарта — гидрофталата калия (КНР). Гидрофталат-ион
является слабой кислотой (Ка = 4 • 10-6), по силе сопоставимой с уксусной. Для
индикации конечной точки используют фенолфталеин. Растворы гидроксида
натрия хранят в закрытых пластмассовых сосудах для предотвращения погло-
щения СО2 из воздуха. Если же сосуд должен быть открытым (например, бу-
тыль, снабженная сифоном), ее предохраняют от контакта с воздухом при помо-
щи трубочки, заполненной аскаритом (асбестом, пропитанным NaOH). О приго-
товлении и стандартизации раствора NaOH см. практическую работу 6.
2.6. Приготовление стандартных растворов кислот
Для титрования оснований обычно применяют растворы соляной кислоты. Бо-
льшинство хлоридов растворимы в воде, при использовании этого титранта по-
бочные реакции протекают редко. С ним удобно работать. Как правило, соляная
кислота не может являться первичным стандартом (хотя иногда в качестве пер-
вичного стандарта используют азеотропную смесь НС1 и воды, кипящую при
* Раствор следует хранить в пробирке или другом подходящем сосуде, закрытой пробкой для предотвраще-
ния поглощения углекислоты воздуха. В противном случае углекислый газ будет продолжать реагировать
с гидроксидом натрия, образуя карбонат. Нельзя использовать стеклянные пробки: они «схватятся» кон-
центрированным раствором щелочи. Можно использовать резиновые пробки.
78
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
постоянной температуре). Поэтому готовят растворы соляной кислоты прибли-
зительной концентрации простым разбавлением концентрированной НС1. Для бо-
лее точных работ воду, используемую для разбавления, следует прокипятить,
хотя в данном случае это не имеет столь большого значения, как при приготов-
лении растворов NaOH. Кроме того, СО2 плохо растворим в сильнокислых рас-
творах и улетучивается из них при перемешивании.
Для стандартизации растворов НС1 обычно используют растворы первично-
го стандарта карбоната натрия. Его недостатком является нечеткий переход
окраски при использовании большинства индикаторов (метилового красного,
метилового пурпурного и т. д.). Чтобы переход стал более резким, вблизи конеч-
ной точки раствор нагревают до кипения. При использовании модифицированно-
го метилового оранжевого нагревания можно избежать, но переход недостаточно
резкий и в этом случае. Еще один недостаток карбоната натрия — малая моляр-
ная масса эквивалента Na2CO3. Другим первичным стандартом может служить
трис(гидроксиметил)аминометан (THAM) (HOCH2)3CNH2, он негигроскопичен
и более удобен в работе. Однако это вещество представляет собой достаточно
слабое основание (Кь =1,3-10-6) и также имеет малую молярную массу. При его
использовании индикация конечной точки не осложняется выделением СО2.
Этот первичный стандарт рекомендуется использовать всегда, кроме тех случа-
ев, когда раствор НС1 будет затем использован для титриметрического определе-
ния карбонатов. О приготовлении и стандартизации растворов соляной кислоты
см. практическую работу 7.
Если имеется стандартизованный раствор NaOH, можно стандартизировать
НС1 путем титрования ее аликвоты этим раствором. Переход окраски индикато-
ра в конечной точке очень резкий, титрование в этом случае можно выполнить
быстрее. Но раствор NaOH является вторичным стандартом. Концентрация
вторичных стандартов известна менее точно, чем первичных. Любая погреш-
ность, допущенная в ходе его стандартизации, скажется и на значении концент-
рации НС1. Следует титровать НС1 раствором щелочи, а не наоборот, для того,
чтобы уменьшить возможное поглощение СО2 раствором в колбе для титрова-
ния. При использовании NaOH индикаторами могут служить фенолфталеин или
бромтимоловый синий.
2.7. Другая аналитическая посуда и аппаратура:
подготовка и обработка проб
Помимо устройств и посуды для измерения массы и объема, при выполнении
анализов широко используют и другое оборудование.
Отбор проб крови
Для отбора проб крови используют шприцы.* Стеклянный или пластмассовый
шприц обычно снабжен иглой из нержавеющей стали или алюминия. При отбо-
* Вы не имеете права самостоятельно отбирать пробы крови, если не обучены этому. Этим занимается спе-
циально обученный персонал.
2.7. ДРУГАЯ АНАЛИТИЧЕСКАЯ ПОСУДА И АППАРАТУРА: ПОДГОТОВКА И ОБРАБОТКА ПРОБ
79
ре проб крови проблем, связанных с их загрязнением, как правило, не возникает.
Лишь в некоторых случаях при определении следовых количеств элементов не-
обходимо принимать специальные меры предосторожности. Вместо шприцов
часто используют специальные вакуумированные пробирки, закрытые резино-
вой пробкой. При их использовании один конец иглы погружают в вену, а другим
протыкают пробку. При этом порция крови втягивается в вакуумированное про-
странство. Если надо проанализировать цельную кровь или плазму крови, то в
пробирке может находиться антикоагулянт для предотвращения свертывания.
Если для анализа требуются небольшие количества крови, то кровь берут не
из вены, а из пальца. Из пальца можно выдавить до 0,5 мл крови или немного бо-
льше. Кровь собирают в маленькую пробирку, проколов палец стерилизован-
ным острым предметом.
Эксикаторы
Эксикаторы предназначены для хранения проб в сухой атмосфере в процессе
их охлаждения и перед взвешиванием. Иногда эксикаторы используют для вы-
сушивания влажных проб. В эксикаторах охлаждают образцы и посуду, которые
подвергались нагреванию (прокаливанию, высушиванию). Если анализируемые
пробы или реагенты подвергались нагреванию, то перед взвешиванием их необ-
ходимо охладить в эксикаторе. Стандартный вид стеклянного эксикатора изоб-
ражен на рис. 2.16. Эксикатор представляет собой герметично закрытый сосуд, в
котором поддерживается атмосфера с низкой влажностью. На дно эксикатора
помещают осушитель (например, хлорид кальция), поглощающий влагу. Осу-
шитель необходимо периодически менять, так как он со временем приходит в
негодность. Признаком этого служит видимое слеживание или расплывание
осушителя. Внутри эксикатора находится фарфоровая подставка с отверстиями,
в которые помещают бюксы, тигли и другую посуду перед взвешиванием. Герме-
тичность эксикатора обеспечивают при помощи стеклянной крышки с притертыми
краями, которые смазывают специальной смазкой. В вакуумных эксикаторах в
крышку вставлена трубка с краном для откачивания воздуха. В таких эксикато-
рах содержимое хранится в вакууме.
Крышку эксикатора следует открывать лишь на непродолжительное время
и только при необходимости. При каждом открывании крышки внутрь эксикато-
ра попадает атмосферный воздух, удаление влаги из которого происходит доста-
Рис. 2.16
Эксикатор и подставка
для него
80
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
точно медленно. Если эксикатор долго держать открытым, осушитель быстро
придет в негодность. Тигли и другую посуду, нагретую докрасна, перед помеще-
нием в эксикатор необходимо охладить на воздухе около 60 с. В противном слу-
чае воздух внутри эксикатора сильно нагреется еще до того, как крышка будет
закрыта, и при последующем его охлаждении внутри эксикатора образуется раз-
режение. Это, в свою очередь, приведет к тому, что при снятии крышки эксика-
тора атмосферный воздух резко проникнет внутрь, в результате чего частицы
пробы могут рассыпаться, потеряться. Нагретые бюксы следует хранить в экси-
каторе, не закрывая их крышками, иначе при охлаждении разрежение создастся
в бюксе, и крышку бюкса невозможно будет открыть. Крышку бюкса охлажда-
ют в эксикаторе рядом с самим бюксом.
В табл. 2.5 приведены наиболее распространенные осушители и их свойст-
ва. Отработанные оксид алюминия, перхлорат магния, оксид кальция, хлорид
кальция и силикагель можно регенерировать, нагревая их до 150,240, 500,275 и
150 °C соответственно.
Печи и сушильные шкафы
Муфельные печи (рис. 2.17) предназначены для прокаливания проб при высо-
ких температурах для перевода осаждаемых форм в гравиметрические и для
сжигания органической матрицы перед определением неорганических веществ.
Муфельные печи должны быть снабжены средствами регулирования температу-
ры, поскольку при температурах выше 500 °C возможны потери некоторых эле-
ментов. Муфельные печи позволяют создавать температуры до 1200 °C.
Сушильные шкафы используют для высушивания образцов перед взве-
шиванием. Стандартный вид сушильного шкафа показан на рис. 2.18. Для обес-
печения равномерного нагревания сушильные шкафы снабжены эффективной
Таблица 2.5
Некоторые распространенные осушители
Осушитель Емкость Расплывается* Торговое наименование
СаС12 (безводный) Высокая Да
CaSO4 Умеренная Нет Drierite (W. A. Hammond Drierite Со.)
СаО Умеренная Нет
MgClO4 (безводный) Высокая Да Anhydrone (J. Т. Baker Chemical Co.); Dehydrite (Arthur H. Thomas Co.)
Силикагель Низкая Нет
А12О3 Низкая Нет
р2о5 Низкая Да
При поглощении влаги превращается в жидкость
2.7. ДРУГАЯ АНАЛИТИЧЕСКАЯ ПОСУДА И АППАРАТУРА: ПОДГОТОВКА И ОБРАБОТКА ПРОБ
81
РИС. 2.17. Муфельная печь. С любезного разре-
шения Arthur Н. Thomas Company
РИС. 2.18. Сушильный шкаф. С любезного
разрешения Arthur Н. Thomas Company
системой вентиляции. Рабочая температура, как правило, составляет 110 °C, но
возможно повышение до 200-300 °C.
Вытяжные шкафы и камеры
В вытяжных шкафах проводят выпаривание растворов. Выпаривание хлорной
кислоты или кислых растворов, содержащих перхлораты, проводят в шкафах,
снабженных системой улавливания паров либо специально предназначенных
для работы с хлорной кислотой (т. е. элементы его конструкции должны быть
устойчивы к действию хлорной кислоты).
При определении следовых содержаний, например, следов металлов, необ-
ходимо принимать меры предосторожности во избежание загрязнения образцов.
Однако обычный вытяжной шкаф — это едва ли не самое «грязное» место лабо-
ратории, поскольку в него втягивается весь окружающий воздух, обтекая при
этом пробу. Для создания очень чистых рабочих зон служат ламинарные каме-
ры. Воздух в них подается после предварительной фильтрации, а внутри камеры
создается некоторое избыточное давление, чтобы в нее не проникал нефильтро-
ванный воздух извне. Схематическое устройство стандартной ламинарной каме-
ры изображено на рис. 2.19. В таких камерах используют высокоэффективные
фильтры, задерживающие все аэрозольные частицы размером более 0,3 мкм.
Если в ходе работы выделяются пары, то предпочтительнее работать в камерах с
вертикальным ламинарным потоком. В этом случае пары уносятся током возду-
82
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.19
Схема ламинарной камеры. С любезного
разрешения Dexion, Inc., 344 Beltine
Boulevard, Minneapolis, MN
Высокоэффективный
воздушный фильтр
П редварител ьн ы й
воздушный фильтр
ха и не попадают на оператора. Существуют специальные средства для поглоще-
ния ядовитых паров.
Промывал ки
Промывалки того или иного типа должны быть в любой аналитической лабора-
тории. Их используют для количественного перенесения твердых веществ или
растворов из сосуда в сосуд, для промывания осадков. В продаже имеются про-
мывалки, разнообразные по типу и размеру. Некоторые из них изображены на
рис. 2.20. Можно самостоятельно сделать промывалку из плоскодонной круглой
колбы и стеклянных трубок (рис. 2.20, б).
РИС. 2.20. Промывалки: а — полиэтиленовая (на сжатие); б — стеклянная (на выдувание)
2.7. ДРУГАЯ АНАЛИТИЧЕСКАЯ ПОСУДА И АППАРАТУРА: ПОДГОТОВКА И ОБРАБОТКА ПРОБ
83
Центрифуги и фильтры
Центрифуги находят множество разнообразных применений. В частности, в
клинических лабораториях с их помощью разделяют кровь на фракции (напри-
мер, отделяют сыворотку). Белки отделяют осаждением, а затем также центри-
фугируют.
Существуют различные типы фильтров для отделения осадков (например, в
гравиметрическом анализе). На рис. 2.21 изображены тигель Гуча, стеклянный и
фарфоровый фильтрующие тигли. Тигель Гуча изготовлен из фарфора; в его
донышке имеются отверстия. На дно такого тигля помещают фильтрующий
диск из пористого стекла. Ранее в тиглях Гуча чаще всего использовали асбесто-
вые фильтры. Но работа с ними была неудобной (такие фильтры прочно удержива-
ют мелкие частицы осадков) и потенциально опасной (сухие асбестовые волокна
обладают канцерогенными свойствами). Дно стеклянного фильтрующего тиг-
ля изготовлено из пористого стекла. Размер пор обозначают буквами F (англ,
fine, мелкопористый), М (англ, medium, среднепористый) или С (англ, coarse,
крупнопористый). Дно фарфорового фильтрующего тигля сделано из порис-
того неглазированного фарфора. Не рекомендуется использовать стеклянные
фильтры при работе с концентрированными щелочными растворами, поскольку
в такой среде они могут разрушаться. Максимальные рабочие температуры для
различных материалов тиглей приведены в табл. 2.1.
Студенистые осадки (такие, как водный оксид железа) нельзя фильтровать
через фильтрующие тигли, поскольку эти осадки забивают их поры. Фильтрова-
ние таких осадков идет медленно даже при использовании бумажных фильтров.
Для фильтрования тигли помещают в специальные держатели, которые
вставляют в горлышко колбы для фильтрования (рис. 2.22). Между колбой для
фильтрования и насосом помещают предохранительную колбу.
Беззольные бумажные фильтры широко используют для количественно-
го получения осадка во всех случаях, когда есть возможность полностью сжечь
фильтр, осадок при этом переходит в форму, пригодную для взвешивания
(см. гл. 10). Существует множество разновидностей фильтровальной бумаги для
работы с осадками разных типов. Виды бумаги, производимые фирмами Whatman
(http://www.whatman.plc.uk) и Schliecher and Schuell (www.s-und-s.de/english-
index.html), перечислены в табл. 2.6.
РИС. 2.21. Фильтрующие тигли: а — Гуча; б — стеклянный; в — фарфоровый
84
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Таблица 2.6
Виды фильтровальной бумаги
Частицы осадка Whatman Schliecher and Schnell
Очень мелкие (например, BaSO4) № 42 (2,5 мкм) № 589/2 или 5, синяя или красная лента (2-4 мкм)
Средние (например, AgCl) № 40 (8 мкм) № 589/2, белая лента (4-12 мкм)
Студенистые и крупнокристаллические осадки (например, Fe2O3 • хН2О) № 41 (20-25 мкм) № 589/1, черная лента (>12-25 мкм)
РИС. 2.22. Применение держателей для фильтрующих тиглей
Техника фильтрования
Скорость фильтрования можно увеличить за счет выбора подходящего типа фи-
льтровальной бумаги. На рис. 2.23 изображен правильно сложенный фильтр.
Фильтр складывают так, чтобы его дольки, составляющие по фильтра, налага-
лись друг на друга не полностью (зазор должен составлять приблизительно
3 мм). От фильтра с той стороны, которая будет прилегать к воронке, отрывают
уголок размером 5-6 мм. Это обеспечивает плотное прилегание фильтра без пу-
зырьков воздуха. Сложенный фильтр помещают в воронку, расправляют и сма-
чивают водой. Носик воронки заполняют водой и прижимают фильтр к стенкам.
Если все сделано правильно, носик воронки остается заполненным водой, пузы-
рьков не образуется. В этом случае давление столба воды обеспечивает высокую
скорость фильтрования. После подготовки фильтра необходимо немедленно
2.7. ДРУГАЯ АНАЛИТИЧЕСКАЯ ПОСУДА И АППАРАТУРА: ПОДГОТОВКА И ОБРАБОТКА ПРОБ
85
Рис. 2.23
Правильно сложенный бумажный фильтр
приступать к фильтрованию. В ходе фильтрования осадок должен заполнять по-
верхность фильтра не более чем на треть-половину, поскольку частицы осадка
часто имеют склонность «ползти» вверх по фильтру. Нельзя также допускать,
чтобы уровень жидкости поднимался над краем фильтра.
Перед фильтрованием осадок должен осесть на дно стакана. Дайте осадку
отстояться. В этом случае основную массу прозрачного раствора можно пере-
нести на фильтр декантированием. Эта порция отфильтруется очень быстро, по-
скольку поры фильтра еще не забиты частицами осадка.
В ходе декантации и особенно перенесения на фильтр основной массы осад-
ка следите за тем, чтобы не потерять часть осадка. Этого легко избежать, если
переносить осадок при помощи стеклянной палочки и промывалки, как показа-
но на рис. 2.24. В ходе декантации следует сливать раствор по палочке, которая
направляет его непосредственно в фильтр, предотвращая разбрызгивание. Оса-
док легче промывать, пока он еще находится в стакане. Для этого после деканта-
ции маточного раствора обмойте стенки стакана несколькими миллилитрами
промывной жидкости и снова дайте осадку отстояться. Затем декантируйте про-
мывную жидкость и повторите промывание еще два-три раза. После этого пере-
несите на фильтр основную массу осадка, держа стеклянную палочку и стакан
одной рукой, как показано на рис. 2.24, и смывая осадок на фильтр струей про-
мывной жидкости из промывалки.
Если осадок необходимо собрать количественно (например, в ходе грави-
метрического анализа), то последние порции осадка снимают со стенок стакана
при помощи резинового наконечника (рис. 2.25). Остатки осадка со стенок и с
наконечника смывают струей промывной жидкости. Вместо резинового нако-
нечника осадок можно собирать на фильтровальной бумаге. Для этого стенки
стакана протирают небольшим кусочком беззольной фильтровальной бумаги
(удерживая его пинцетом) и переносят его на фильтр.
После того, как весь осадок перенесен на фильтр, его промывают пятью-
шестью небольшими порциями промывной жидкости. Это значительно эффек-
тивнее, чем добавление одного большого объема сразу. Струю жидкости следу-
ет направлять вращательным движением, чтобы по возможности собрать осадок
в углу фильтра. Прежде, чем добавлять следующую порцию, дождитесь полного
стекания предыдущей. Не забудьте проверить полноту осаждения. Проверьте
осадок на полноту промывания при помощи качественной реакции на присутст-
вие осадителя в последних нескольких каплях фильтрата.
86
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
РИС. 2.24. Правильная техника переноса осадка на фильтр
Рис. 2.25. Палочка с резиновым наконечником
2.8. ПРОКАЛИВАНИЕ ОСАДКОВ В ГРАВИМЕТРИЧЕСКОМ АНАЛИЗЕ
87
2.8. Прокаливание осадков в гравиметрическом анализе
Если осадок прокаливают в фарфоровом фильтрующем тигле, из него сначала
следует удалить влагу на малом огне. Прокаливание можно проводить в муфель-
ной печи или на пламени горелки. При использовании горелки фильтрующий
тигель следует поместить в обычный тигель (фарфоровый или платиновый).
В противном случае восстановительные газы пламени будут проникать сквозь
поры фильтра.
Если фильтрование проводили через бумажный фильтр, фильтр с осадком
вынимают из воронки, аккуратно сворачивают и помещают в тигель так, чтобы
часть фильтра, содержащая основную массу осадка, была обращена ко дну
тигля. После этого фильтр необходимо высушить и озолить. Для этого тигель
устанавливают наклонно на угол фарфорового треугольника, слегка приоткрыв
крышку (рис. 2.26). Сначала на малом пламени горелки подсушивают содержи-
мое тигля, следя за тем, чтобы оно не рассыпалось. Затем интенсивность нагре-
вания постепенно увеличивают по мере того, как влага испаряется, а фильтр
обугливается. Следует избегать попадания пламени (обладающее восстанови-
тельными свойствами!) внутрь тигля. Если внезапно появляется большое коли-
чество дыма, это свидетельствует о том, что бумага может загореться. В этом
случае горелку необходимо убрать. Если возгорание все-таки произошло, пламя
следует немедленно погасить, накрыв тигель крышкой. Конечно, при этом на
крышке останутся частички угля, однако впоследствии они выгорят. Наконец,
когда выделение дыма прекратилось, обугленную бумагу полностью сжигают,
постепенно повышая температуру пламени. При этом частицы угля в тигле рас-
каляются, но они не должны давать пламени. Нагревание продолжают до тех
пор, пока полностью не сгорит весь уголь, а также частицы смолы на стенках и
крышке тигля. После этого тигель с осадком можно начинать прокаливать. Да-
льнейшее прокаливание можно также проводить на горелке (при максимально
высокой температуре пламени) либо в муфельной печи. Прокаливание тигля на-
чинайте постепенно.
Прежде чем помещать в тигель осадок или фильтр с осадком, тигель надо
довести до постоянной массы. Тигель высушивают (первый раз нагревая его в
течение часа, последующие разы — в течение получаса), если осадок нужно бу-
дет высушить, и прокаливают, если осадок нужно будет прокалить. Масса счи-
тается постоянной, если последовательные результаты взвешивания тигля на
учебных аналитических весах различаются не более чем на 0,3-0,4 мг. Таким же
образом доводят до постоянной массы тигель с осадком. В этом случае последу-
ющие нагревания также проводят в течение вдвое меньших промежутков време-
ни, чем первое. Перед каждым взвешиванием тигель необходимо охлаждать в
эксикаторе не менее получаса. Если тигель раскалился докрасна, то перед тем,
как помещать в эксикатор, его сначала следует охладить до отсутствия каления.
Тигель берут специальными тигельными щипцами — обычно из нержавеющей
стали или никелированными (во избежание загрязнений ржавчиной). Прежде
чем взвешивать тигель, на всякий случай поднесите к нему руку (не касаясь тиг-
ля!), чтобы убедиться, что от него не исходит тепло.
88
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.26
Тигель с крышкой на фарфоровом треугольнике
в процессе обугливания фильтра
2.9. Отбор пробы: твердой, жидкой, газообразной
Отбор представительной пробы — это аспект аналитической химии, с которым
начинающий студент часто не сталкивается, поскольку предполагается, что про-
бы, которые ему дают для практических занятий, являются гомогенными и пред-
ставительными. Однако именно эта операция может оказать решающее влияние
на весь ход анализа. Процесс пробоотбора может ограничивать точность и
важность результатов анализа в целом. Потенциально это самое слабое звено во
всей цепочке аналитических операций. От правильного обращения с пробой
крови во время ее отбора и после него иногда может зависеть жизнь пациента.
Если аналитик просто получил пробу, не участвуя сам в процессе ее отбора, то
результаты анализа могут быть квалифицированы лишь как результаты анализа
пробы «какой она была предоставлена». Если необходимо получить что-то бо-
льшее, то вся последовательность операций с пробой с самого начала должна
быть задокументирована.
Многие профессиональные сообщества разработали точные инструкции
для отбора проб различных веществ, в частности, Американское общество по те-
стированию и материалам (ASTM, http://www.astm.org), Международная ассоциа-
ция официальных химиков-аналитиков (АОAC International, http://www.aoac.org),
Американская ассоциация общественного здоровья (АРНА, http://www.apha.org).
При наличии необходимого опыта и применении статистических методов про-
боотбор можно выполнять с той же точностью, что и собственно определение.
О важных статистических аспектах пробоотбора см. гл. 3. К сожалению, ана-
литики часто оставляют эту проблему без должного внимания. В то же время,
степень простоты или сложности пробоотбора зависит от природы пробы.
В первую очередь нужно получить пробу, представительную по отношению
ко всему целому. Такая проба называется генеральной. В зависимости от харак-
тера исходного материала ее размер может варьироваться от нескольких граммов
(или даже менее) до килограммов. После того, как получена представительная ге-
неральная проба, может возникнуть необходимость ее уменьшения до таких раз-
меров, чтобы с ней было удобно работать. Такая уменьшенная проба и называется
собственно пробой (или лабораторной пробой). Для выполнения анализа из нее
берут отдельную порцию — аликвоту. Она называется анализируемой пробой.
2.9. ОТБОР ПРОБЫ: ТВЕРДОЙ, ЖИДКОЙ, ГАЗООБРАЗНОЙ
89
Отбирая отдельные аликвоты, можно выполнить несколько параллельных ана-
лизов одной и той же пробы.
В клинических лабораториях генеральные пробы можно, как правило, непо-
средственно использовать в качестве лабораторных, поскольку генеральные
пробы обычно невелики и однородны (например, пробы мочи или крови). Раз-
мер анализируемой пробы в этом случае составляет от нескольких миллилитров
до менее чем одной капли (нескольких микролитров).
Ниже мы рассмотрим некоторые проблемы, касающиеся отбора генераль-
ных проб твердых, жидких и газообразных веществ.
1. Твердые вещества. Отбор твердых проб — задача наиболее трудная из-за не-
однородностей вещества, различий в размерах его частиц и даже внутренних
различий в пределах одной частицы. Простейший, но, как правило, наименее на-
дежный способ отбора твердых проб — отбор наугад, когда случайным образом
берется проба и предполагается, что она представительна. Такой способ приво-
дит к удовлетворительным результатам только тогда, когда исходный материал
гомогенный. Для большей надежности в качестве генеральной пробы лучше
взять 1/100-1/50 часть вещества (если только оно не является однородным). Чем
больше размер частиц вещества, тем большей должна быть генеральная проба.
Очень простой и в то же время наиболее надежный способ отбора больших
проб твердых веществ — отбирать тогда, когда вещество находится в движении.
В этом случае в дело идет любая отобранная порция. Такой отбор можно
проводить систематически, отбирая отдельные «аликвоты», в сумме представ-
ляющие весь исходный материал. Приведем некоторые примеры.
В ходе погрузки или разгрузки мешков с цементом представительную про-
бу можно получить, отбирая, например, каждый пятидесятый мешок (или порцию
из каждого такого мешка). При транспортировке зерна на тачках можно отби-
рать по лопате зерна из каждой тачки. Все полученные таким путем порции объ-
единяют и получают генеральную пробу.
2. Жидкости. Жидкости, как правило, гомогенны, поэтому отбор жидких проб
проводить намного легче. В результате диффузии жидкость перемешивается
очень медленно. Поэтому, если жидкость негомогенна, перед отбором пробы ее
следует хорошо перемешать. Если жидкий объект гомогенен изначально, доста-
Отбор пробы. Из журнальной коллекции Chemical
Heritage Foundations' Othmer Library
90
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
точно лишь произвольным образом отобрать от него единственную пробу. При
отборе проб крови этот способ пригоден для решения любых практических за-
дач. В то же время перед отбором проб мочи рекомендуется собирать ее в течение
суток. В этом случае результаты будут более надежными, чем при однократном
взятии пробы.
Что действительно имеет очень важное значение при отборе проб биологи-
ческих жидкостей, так это момент отбора. Состав крови до и после еды значите-
льно различается. Во многих случаях кровь следует брать натощак. Иногда к
пробам крови добавляют консерванты, например, фторид натрия (для консерва-
ции глюкозы) или антикоагулянты.
Пробы крови можно, в зависимости от конкретных требований к анализу,
или анализировать в виде цельной крови, или предварительно разделять и анали-
зировать плазму или сыворотку. В большинстве случаев важным физиологиче-
ским показателем является концентрация вещества вне красных кровяных клеток,
поэтому для анализа используют сыворотку или плазму. Подробнее об отборе
проб биологических жидкостей см. гл. 24.
Если жидкие образцы негомогенны, а объемы достаточно малы, их следует
интенсивно перемешать и немедленно отобрать пробу. В частности, это касается
суспензий, частицы которых имеют склонность оседать. Из больших объемов
(например, из жидкости, текущей по трубам) пробы лучше всего отбирать после
пропускания жидкости через насос, поскольку при этом жидкость интенсивно
перемешивается. Пробы воды из больших резервуаров отбирают с помощью
специального заборника, позволяющего отбирать пробы с разных уровней. Про-
бы с разной глубины лучше отбирать по диагонали, а не по вертикали. Получен-
ные пробы жидкости можно проанализировать по отдельности и усреднить
результаты либо объединить пробы в одну генеральную пробу и выполнить не-
сколько параллельных анализов. Второй способ предпочтительнее, поскольку
он позволяет охарактеризовать точность результатов.
3. Газы. Наиболее распространенный способ отбора газов основан на вытесне-
нии газом жидкости. Жидкость выбирают так, чтобы газ был в ней малораство-
рим и не взаимодействовал с ней химически. Чаще всего используют ртуть. В
сосуд со ртутью газ подают сверху, ртуть при этом свободно вытекает снизу.
При таком способе на собирание средней пробы уходит много времени. В неко-
торых случаях достаточно отобрать одну произвольную пробу, например, пробу
выдыхаемого воздуха. Пациент при этом выдыхает в вакуумированный сосуд.
Выхлопные газы автомобильных двигателей также собирают в большие вакуу-
мированные сосуды из пластмассы. Подробнее об отборе проб объектов окружа-
ющей среды см. гл. 26.
Знание точного объема генеральной пробы газа не всегда бывает необходи-
мо. В пробах часто измеряют концентрации, а не количества тех или иных ком-
понентов. Если же знание объема газа необходимо, нужно учитывать, что на его
величину, а следовательно, и на величины концентраций оказывают влияние
температура и давление. Поэтому эти параметры имеют важное значение для
анализа газов.
2.10. ВЫСУШИВАНИЕ И РАСТВОРЕНИЕ ПРОБ
91
Все сказанное не относится к определению газообразных компонентов, рас-
творенных в жидкостях, например, СО2 или О2 в крови. В подобных случаях ру-
ководствуются правилами отбора жидких проб. Затем пробы соответствующим
образом обрабатывают, чтобы измерить содержание газа непосредственно в
жидкости либо выделить растворенный газ и затем проанализировать.
2.10. Высушивание и растворение проб
После отбора пробы для дальнейшего анализа ее, как правило, необходимо пере-
вести в раствор. Предварительно может потребоваться высушивание пробы,
взвешивание или измерение ее объема. Если проба уже представляет собой рас-
твор (пробы сыворотки крови, мочи, воды), могут потребоваться операции
осаждения, экстракции, концентрирования аналита. Разумеется, это может по-
требоваться и при анализе других проб.
В данном разделе описаны общие приемы перевода в раствор проб как неор-
< ганических, так и органических веществ. К таким приемам относятся растворе-
ние металлов и других неорганических веществ в кислотах или при помощи
сплавления со щелочными плавнями, разложение органических и биологиче-
ских материалов для определения неорганических компонентов при помощи
мокрого сжигания или сухого озоления, а также удаление из биологических
проб белков, мешающих определению неорганических или органических ком-
понентов.
Высушивание проб
Пробы твердых веществ часто содержат переменные количества адсорбирован-
ной воды. Неорганические вещества перед взвешиванием, как правило, высуши-
вают. Для этого пробу выдерживают 1-2 ч в сушильном шкафу при 105-110 °C.
Чтобы удалить более прочно связанную воду — например, кристаллизацион-
ную — может потребоваться более высокая температура.
Следует иметь в виду, что в ходе высушивания возможно разложение про-
бы или протекание побочных реакций. Вещества, которые неустойчивы при по-
вышенных температурах, высушивают в эксикаторе. Использование вакуумных
эксикаторов позволяет ускорить процесс высушивания. Если навеску берут без
предварительного высушивания, то результаты анализа можно отнести только к
пробе «как она есть»; это необходимо указать в отчете.
Образцы биологических тканей (растительных и животных) обычно высу-
шивают при повышенных температурах. Для таких образцов существуют раз-
ные формы представления результатов анализа — в расчете на массу влажного,
сухого образца или золы, см. гл. 1.
Растворение проб
Перед определением содержания аналита, как правило, необходимо провести
некоторые операции с пробой, чтобы перевести определяемое вещество в рас-
92
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
твор или, в случае биологических проб, избавиться от мешающих органических
веществ, например, белков. Способы пробоподготовки делятся на два основных
типаки: деструктивные (с полным разрушением матрицы) и недеструктивные
(либо частично деструктивные). Способы первого типа можно использовать
лишь тогда, когда аналит является неорганическим веществом либо в ходе анали-
за его переводят в неорганическое вещество (например, в ион аммония при опре-
делении органического азота по методу Кьельдаля — см. ниже). Если же аналит
представляет собой органическое вещество, применяют способы второго типа.
Растворение неорганических проб
Для многих неорганических веществ хорошими растворителями являются силь-
ные неорганические кислоты. Для растворения металлов, находящихся в ряду
напряжений левее водорода, чаще всего применяют соляную кислоту. Азотная
кислота, будучи сильным окислителем, растворяет большинство металлов, спла-
вы цветных металлов и сульфиды, нерастворимые в других кислотах.
Хлорная кислота в безводном состоянии (при нагревании до удаления вла-
ги) является очень сильным и высокоэффективным окислителем. Она растворя-
ет большинство металлов, а также разрушает примеси органических веществ.
Но ее следует применять с большой осторожностью, поскольку со многими лег-
ко окисляющимися веществами, в первую очередь органическими, она реагиру-
ет со взрывом.
Ряд неорганических веществ нерастворим в кислотах. Для перевода таких
веществ в раствор необходимо применить сплавление с плавнями — кислыми
или щелочными. Пробу смешивают с плавнем в соотношении 1:10-1:20 и нагре-
вают в тигле из подходящего материала до расплавления смеси. Сплавление за-
канчивают, когда плав станет прозрачным (обычно через 30 мин). Охлажденный
затвердевший плав растворяют в разбавленной кислоте или воде. В ходе сплав-
ления нерастворимые вещества взаимодействуют с плавнем, образуя раствори-
мые продукты. Один из наиболее распространенных щелочных плавней —
карбонат натрия, образующий растворимые в кислотах карбонаты.
Разложение органических веществ
для проведения неорганического анализа:
сжигание и растворение в кислотах-окислителях
Растительные и животные ткани, компоненты биологических жидкостей и дру-
гие органические вещества обычно разлагают посредством мокрого сожжения
под действием кипящих кислот-окислителей или смесей кислот либо путем
сухого озоления в муфельной печи при высоких температурах (400-700 °C).
В ходе мокрого сожжения органические вещества окисляются кислотами до ди-
оксида углерода, воды, других летучих продуктов и удаляются, а остаток содер-
жит лишь неорганические компоненты в виде солей или кислот. При сухом
озолении окислителем является атмосферный кислород. Органическое вещест-
во при этом сгорает, а остаток представляет собой неорганические вещества.
При сухом озолении можно использовать и дополнительные окислители.
2.10. ВЫСУШИВАНИЕ И РАСТВОРЕНИЕ ПРОБ
93
1. Сухое озоление. При анализе органических и биологических материалов час-
то используют различные виды сухого озоления, мокрого сжигания, а также их
сочетания. Но простое сухое озоление в отсутствие дополнительных реагентов
все же наиболее распространенный способ. В ходе сухого озоления органическое
вещество сгорает. При этом почти полностью извлекаются следы таких эле-
ментов, как свинец, цинк, кобальт, сурьма, хром, молибден, стронций и железо, а
их потери за счет улетучивания или связывания невелики. Обычно используют
фарфоровые тигли. Но если озоление проводится при температурах выше 500 °C,
в этом случае могут наблюдаться потери свинца за счет улетучивания (особенно
в присутствии хлоридов, как, например, в пробах крови или мочи). Потери свин-
ца за счет связывания меньше при использовании платиновых тиглей.
При добавлении окислителя к пробе эффективность озоления возрастает.
Один из лучших окислителей — нитрат магния. С его помощью можно количе-
ственно извлекать, кроме вышеперечисленных элементов, также мышьяк, медь
и серебро.
Биологические жидкости и влажные ткани перед помещением в муфельную
» печь выпаривают досуха на водяной бане или при осторожном нагревании.
В ходе озоления температуру печи следует повышать постепенно во избежание
слишком быстрого сгорания и задымления.
По завершении озоления остаток обычно смывают 1-2 мл горячей концент-
рированной или 6 М соляной кислотой и переносят в колбу или стакан для даль-
нейшей обработки.
Другой способ сухого озоления называется низкотемпературным. В этом
случае применяют радиочастотный разряд, вызывающий образование активиро-
ванных радикалов кислорода. Они очень реакционноспособны и разрушают ор-
ганическое вещество при низких температурах. Озоление можно проводить при
температурах ниже 100 °C, вследствие чего потери за счет улетучивания мини-
мальны. Кроме того, становится меньше загрязнений, поступающих из атмосферы
и со стенок тигля, а также уменьшаются потери на стенках тигля. Исследования с
использованием радионуклидов показали, что после полного окисления органи-
ческого вещества 17 представительных элементов извлекаются количественно.
Элементный анализ на содержание основных элементов органических ве-
ществ (например, углерода или водорода) обычно проводят путем сжигания
пробы в токе кислорода с последующим поглощением продуктов сгорания.
Пробу в платиновой лодочке помещают в трубку, нагревают и пропускают кис-
лород. Углерод при этом количественно окисляется до СО2, а водород —
до Н2О. Эти газы пропускают через систему предварительно взвешенных пат-
рончиков, заполненных соответствующими поглотителями. Например, для по-
глощения СО2 применяют аскарит (асбест, пропитанный гидроксидом натрия),
а для поглощения Н2О используют дегидрит (перхлорат магния). Привес погло-
тительного патрончика.равен массе, соответственно, СО2 и Н2О, выделившихся
из пробы. В этом методе анализа большое значение имеют конкретные детали,
поэтому, если вам придется его использовать, обратитесь к специальной литера-
туре по органическому элементному анализу.
94
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
2. Мокрое сожжение. В ходе мокрого сожжения органическое вещество окис-
ляется под действием кислот-окислителей. Распространенным способом окис-
ления органических веществ является мокрое сожжение под действием смеси
азотной и серной кислот. Серную кислоту обычно берут в небольшом объеме
(например, 5 мл), а азотную — в большем (20-30 мл). Мокрое сожжение, как
правило, проводят в колбе Кьельдаля (рис. 2.28). Азотная кислота разрушает
основную часть органического вещества, но не способна разрушить его остатки.
В ходе процесса азотная кислота испаряется, и остается одна серная кислота.
Об этом свидетельствует появление густого белого дыма SO3, циркулирующего
в колбе. К этому моменту раствор становится очень горячим. При такой темпе-
ратуре серная кислота растворяет остатки органического вещества. Если орга-
нического вещества слишком много или оно особо устойчиво к разложению, то
под действием серной кислоты может наблюдаться обугливание. В этом случае
следует добавить еще азотной кислоты. Сжигание продолжают до тех пор, пока
раствор не станет прозрачным. Всю процедуру следует проводит в вытяжном
шкафу. ,
Значительно большей эффективностью обладает смесь азотной, хлорной и
серной кислот в соотношении приблизительно 3:1:1 по объему. Десяти милли-
литров такой смеси обычно достаточно для полного разложения 10 г свежих
биологических тканей или крови. Горячая безводная хлорная кислота — очень
сильный окислитель. Она достаточно легко разлагает даже самые последние
остатки органического вещества. Нагревание ведут до тех пор, пока не испарит-
ся вся азотная кислота и не появятся пары хлорной кислоты. Они обладают ме-
ньшей плотностью, чем SO3, и поэтому заполняют весь объем колбы. Можно
вести нагревание и дальше, до полного испарения хлорной кислоты и появления
паров SO3, легко отличимых на глаз. Кислоты можно добавлять и постепенно.
В начале разложения в колбе должно быть достаточно много азотной кислоты
для разложения основной части органического вещества. Обязательно должна
присутствовать и серная кислота, чтобы проба не выпарилась досуха, а также во
избежание угрозы взрыва хлорной кислоты. Все работы, связанные с исполь-
зованием хлорной кислоты, следует проводить в вытяжном шкафу, специально
предназначенном для этого.
Указанная смесь становится еще более эффективной, если к ней добавить
небольшое количество Mo(VI), играющего роль катализатора. В этом случае по-
сле испарения воды и азотной кислоты окисление происходит очень бурно с силь-
ным выделением дыма и процесс завершается за считанные секунды. В результате
общее время разложения сильно сокращается.
Часто используют и смесь азотной и хлорной кислот. С хлорной кислотой
следует обращаться очень осторожно! Азотная кислота испаряется первой,,и
необходимо следить, чтобы хлорная кислота после этого не испарилась почти
досуха: в этом случае возможен сильный взрыв. Не рекомендуется применять
эту смесь до тех пор, пока вы не приобретете достаточный опыт в области мок-
рого сжигания. Хлорную кислоту нельзя добавлять непосредственно к орга-
ническим или биологическим материалам: всегда сначала добавляйте избыток
азотной кислоты. При использовании хлорной кислоты взрывы, как правило,
2.10. ВЫСУШИВАНИЕ И РАСТВОРЕНИЕ ПРОБ
95
вызваны образованием пероксидов, перед самым взрывом жидкость темнеет
(например, становится желто-коричневой). Некоторые органические вещест-
ва — такие как этанол, целлюлоза и многоатомные спирты — могут вызвать
внезапный взрыв горячей концентрированной хлорной кислоты, вероятно, из-за
образования этилперхлората.
При помощи смеси азотной, хлорной и серной кислот можно количественно
извлекать цинк, селен, мышьяк, медь, кобальт, серебро, кадмий, сурьму, хром,
молибден, стронций и железо. При использовании серной кислоты свинец часто
теряется. Для извлечения свинца следует использовать смесь азотной и хлорной
кислот; при этом извлекаются и все перечисленные элементы. Для предотвраще-
ния потерь селена в смеси должна присутствовать хлорная кислота. Она поддер-
живает сильно окислительную среду и предотвращает обугливание, в ходе
которого могут образоваться летучие соединения селена в низших степенях
окисления. Пробы, содержащие ртуть, нельзя разлагать методом сухого озоле-
ния, а мокрое сжигание следует проводить в приборе с обратным холодильни-
ком, поскольку ртуть и многие ее соединения летучи. Частичное разложение
органического вещества при этом часто предпочитают проводить при комнат-
ной температуре или'даже на холоду. Например, при анализе мочи, содержащей
существенно меньше органических веществ по сравнению с кровью, можно вос-
становить ртуть до металла при помощи Cu(I) и гидрохлорида гидроксиламина,
а органическое вещество разрушить перманганатом калия при комнатной тем-
пературе. Затем ртуть можно растворить и определить ее содержание.
Многие азотсодержащие соединения можно определять по методу Кьель-
даля, превращая азот в сульфат аммония. В ходе разложения по Къелъдалю азот
превращают в ион аммония, который затем отгоняют в виде аммиака и
оттитровывают. Смесь для разложения состоит из серной кислоты и сульфата ка-
лия (для повышения температуры кипения кислоты и, следовательно, эффектив-
ности разложения). Добавляют также катализатор, в качестве которого могут
выступать соединения меди или селена. После разложения органического веще-
ства смесь подщелачивают гидроксидом натрия и отгоняют аммиак в стандарт-
ный раствор соляной кислоты, взятый в избытке. Непрореагировавшую кислоту
оттитровывают стандартным раствором гидроксида натрия и по разности опре-
деляют количество поглощенного аммиака. Из найденного количества аммиака
и известного содержания азота в определяемом соединении можно рассчитать
содержание интересующего соединения. В частности, метод Кьельдаля является
самым точным методом определения белка. Более подробно об этом см. в гл. 8.
Как мокрое сожжение, так и сухое озоление имеют свои достоинства и огра-
ничения применения. Сравнительные достоинства различных методов разложе-
ния органических веществ подробно изучены. Тем не менее до сих пор нет
единого мнения о том, какому методу отдать предпочтение. Сухое озоление
привлекательно благодаря своей простоте и отсутствию серьезного завышения
результатов ввиду загрязнения пробы, поскольку в этом методе используют малые
количества реактивов (или вообще их не используют). Потенциальные источники
погрешностей при сухом озолении — потери элементов из-за улетучивания и
удерживания на стенках тигля. Эти адсорбированные элементы, в свою очередь,
96
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
могут загрязнять последующие пробы. Мокрое сожжение может быть предпоч-
тительнее благодаря быстроте (однако здесь требуется повышенное внимание со
стороны оператора), менее высоким рабочим температурам и отсутствию потерь
на стенках сосуда. Главный источник погрешностей при мокром сожжении —
загрязнения, вносимые реактивами. Остроту этой проблемы можно уменьшить,
используя особо чистые кислоты, которые сейчас широко доступны. Время, тре-
буемое для разложения одним или другим методом, зависит от состава пробы и
технических особенностей конкретного варианта метода. Обычно для сухого
разложения необходимо 2-4 ч, а для мокрого сожжения — 0,5-1 ч.
Микроволновая пробоподготовка
В настоящее время микроволновые печи широко используют для быстрого и эф-
фективного высушивания проб и их разложения кислотами. Сначала для этого
использовали бытовые печи, однако их использование было ограничено рядом
причин. Сейчас разработаны и используются специальные лабораторные печи;
именно они и будут рассмотрены ниже. Микроволновая пробоподготовка позво-
ляет уменьшить время, необходимое для разложения пробы, с нескольких часов
до нескольких минут, а также снизить фоновый сигнал благодаря использова-
нию меньших количеств реактивов.
1. Как происходит нагревание в микроволновых печах? Микроволновое из-
лучение занимает в электромагнитном спектре диапазон между инфракрасным
и радиочастотным излучением с длиной волны в области от 1000 мкм и выше
(300-300000 МГц или 3 • 108—3 • 1011 Гц, см. рис. 16.2). Оно состоит из двух со-
ставляющих — электрической и магнитной, векторы которых взаимно перпен-
дикулярны. Электрическая составляющая обусловливает перенос энергии от
источника излучения к облучаемому объекту. Воздействие микроволнового из-
лучения на частицы вещества проявляется в виде двух эффектов: вращения ди-
полей и ионной проводимости. Первый из них играет более значительную роль.
Когда микроволновое излучение проходит через вещество, молекулы, обладаю-
щие дипольным моментом, стремятся ориентироваться так, чтобы он был распо-
ложен по направлению вектора электрического поля. Чем полярнее молекула,
тем сильнее она взаимодействует с излучением. Это вызывает вращение моле-
кул и приводит к нагреванию вещества. Степень поглощения микроволновой
энергии зависит от величины дипольного момента и диэлектрической проницае-
мости вещества. Энергия поглощается сильнее всего, если время релаксации мо-
лекул совпадает с частотой микроволнового излучения. Для больших молекул,
например, молекул полимеров, время релаксации слишком велико, но по мере
нагревания вещества время релаксации уменьшается, а поглощение энергии воз-
растает. Наоборот, маленькие молекулы — такие как молекулы воды — релак-
сируют с частотой, более высокой, чем частота излучения. По мере нагревания
частота релаксации еще более увеличивается, а поглощение энергии в этом слу-
чае уменьшается.
Явление ионной проводимости состоит в том, что ионы, присутствующие в
веществе, под действием переменного электрического поля начинают попере-
2.10. ВЫСУШИВАНИЕ И РАСТВОРЕНИЕ ПРОБ
97
менно двигаться в противоположных направлениях. Это также приводит к на-
греванию объекта. По мере роста температуры ионная проводимость возрастает.
Поэтому вещества, содержащие ионы, с ростом температуры поглощают микро-
волновое излучение все сильнее. Деионизированная вода в микроволновом поле
нагревается медленно, но солевые растворы нагреваются очень быстро. Раство-
ры кислот тоже являются хорошими проводниками тока и нагреваются быстро.
Таким образом, нагревание вещества в микроволновом поле происходит за
счет вращения молекулярных диполей и движения ионов. Взаимодействие мик-
роволнового излучения с различными веществами может происходить по-раз-
ному. Материалы, хорошо отражающие микроволновое излучения — такие как
металлы — обладают высокой теплопроводностью. В микроволновом поле они
не нагреваются, а отражают падающее излучение. Вещества-изоляторы про-
зрачны для микроволнового излучение и также не нагреваются. Вещества, со-
стоящие из полярных молекул и ионов, хорошо поглощают микроволновое
излучения и нагреваются в микроволновом поле. Энергия микроволнового излу-
чения слишком мала для того, чтобы разорвать химические связи (хотя под дей-
ствием микроволнового излучения многие химические реакции ускоряются; это
обстоятельство вызвало повышенный интерес к использованию микроволново-
го излучения в химическом синтезе). Отмеченные свойства отражающих и изо-
лирующих материалов нашли применение при изготовлении микроволновых
устройств для разложения проб.
2. Конструкция лабораторной микроволновой печи. Для лабораторных це-
лей сначала использовали бытовые микроволновые печи. Однако быстро выяс-
нилось, что они нуждаются в модификации. Бытовые микроволновые печи
непригодны для нагревания проб малого размера. Лабораторные пробы обычно
значительно меньше по размерам, чем порции пищи, поэтому они поглощают
лишь незначительную часть энергии, генерируемой магнетроном. Непоглощен-
ное излучение возвращается к магнетрону, вызывая его перегрев и быстрый выход
из строя. Может возникнуть даже короткое замыкание. Поэтому лабораторные
печи конструируют так, чтобы защитить магнетрон от излучения. Основными
узлами таких печей (рис. 2.27) являются магнетрон, нагрузка, волновод, микро-
волновая камера и гомогенизатор микроволнового потока. Микроволновое из-
лучение, генерируемое магнетроном, по волноводу направляется в камеру.
Гомогенизатор перемешивает потоки микроволновой энергии и распространяет
ее в разных направлениях. Нагрузка изготавливается из ферромагнитного мате-
риала и размещается между магнетроном и волноводом. Она отклоняет микро-
волновое излучение, возвращающееся из камеры, к массивному керамическому
блоку, охлаждаемому вентилятором и, таким образом, защищает магнетрон.
Стандартная частота излучения 2450 МГц, используемая для приготовле-
ния пищи, оказалась удобной и для лабораторной работы. Мощность излучения
лабораторных печей обычно составляет 1200 Вт.
3. Кислотное разложение в микроволновых печах. Как правило, для предо-
хранения печи от паров кислот разложение проводят в автоклавах — закрытых
98
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.27. Схематическое устройство лабораторной микроволновой печи [G. Le Blanc, LC/GC
Suppl., 17(6S) (1999) S30]. С любезного разрешения LC/GCMagazine
пластмассовых сосудах из тефлона PFA (перфторалкоксиэтилена) или поликарбо-
ната. Кроме того, использование автоклавов имеет дополнительные преимущества.
Внутри сосуда создается повышенное давление, в результате чего температуры ки-
пения кислот повышаются. В этих условиях разложение происходит быстрее.
Нет и потерь летучих элементов. Современные печи снабжены устройствами
контроля давления и температуры (оптоволоконные температурные зонды из
материалов, прозрачных для микроволнового излучения). Использование тем-
пературного контроля позволяет осуществлять процессы экстракции, ускоряемые
под действием микроволнового поля: в этом случае необходимо поддерживать
относительно низкие температуры во избежание химического разложения ве-
ществ.
Пробоподготовка без разрушения или с частичным
разрушением матрицы
Очевидно, что для определения органических веществ можно использовать толь-
ко недеструктивные методы пробоподготовки. Иногда и при определении метал-
лов не возникает необходимости разрушать молекулярную структуру образца, в
частности, при анализе биологических жидкостей. Например, ряд металлов в
сыворотке крови или моче можно определять атомно-абсорбционным методом
путем прямого распыления пробы (при необходимости разбавленной) в пламя
горелки. Компоненты твердых веществ, в частности, почв, также иногда опреде-
ляют без разрушения матрицы, посредством экстракции подходящими реагента-
ми. Перед экстракцией образец необходимо тщательно измельчить и перемешать,
2.10. ВЫСУШИВАНИЕ И РАСТВОРЕНИЕ ПРОБ
99
а экстракцию проводить при кипячении с обратным холодильником. Следы
многих металлов можно экстрагировать из почв 1 М растворами хлорида аммо-
ния или уксусной кислоты. Некоторые элеме'нты отгоняют в виде летучих про-
изводных, например, селен в виде хлорида или бромида.
Безбелковые фильтраты
Белки, содержащиеся в биологических жидкостях, мешают при многих опреде-
лениях. Их следует предварительно отделить, не разрушая матрицу образца. Для
этого используют ряд реагентов, вызывающих коагуляцию и осаждение белков,
в частности, трихлоруксусную кислоту, вольфрамовую кислоту (смесь вольфра-
мата натрия и серной кислоты) или «нейтральную смесь» гидроксида бария и суль-
фата цинка. К отмеренному объему пробы (например, сыворотки крови) добавляют
отмеренный объем раствора реагента. После осаждения белка (приблизительно
через 10 мин) раствор фильтруют через сухой бумажный фильтр (не промывая
его) либо центрифугируют, после чего анализируют аликвоту полученного безбел-
кового фильтрата. Более подробно о приготовлении различных видов таких
фильтратов см. в гл. 24 (разд. «Отбор и хранение проб») и в описаниях соот-
ветствующих лабораторных работ.
Техника работы при высушивании й растворении проб
При высушивании и растворении проб следует соблюдать осторожность.
Если твердую пробу высушивают в бюксе, то бюкс следует открыть и поместить
вместе с крышкой в стакан во избежание распыления. Стакан подписывают и
прикрывают часовым стеклом.
Растворение навески проводят в стакане или конической колбе. Если при
этом возможно вспенивание, стакан прикрывают часовым стеклом. После пол-
ного растворения пробы стенки сосуда обмывают дистиллированной водой. Ча-
совое стекло также обмывают водой, собирая смывную жидкость в стакан.
После этого может потребоваться упарить раствор для уменьшения его объема.
Это удобнее всего делать в стакане, неплотно прикрытом часовым стеклом. Рас-
твор нагревают медленно, не доводя до кипения. Для нагревания используют во-
дяную баню или электроплитку с регулятором температуры.
Растворение в колбе Кьельдаля удобно тем, что при этом не происходит
разбрызгивания раствора. Колбы Кьельдаля (названные так потому, что перво-
начально их применяли только для определения азота по Кьельдалю) также
удобно использовать для всех видов мокрого сжигания органических проб и рас-
творения металлических образцов в кислотах. Колбы Кьельдаля выпускаются
различных объемов от 10 до 800 мл. Некоторые из них изображены на рис. 2.28.
Пробу и необходимую кислоту помещают на дно колбы. Колбу нагревают в на-
клонном положении. В этом случае даже при кипении раствора не происходит
его разбрызгивания, поскольку кислота конденсируется на стенках горлышка
колбы. Нагревать колбу можно на горелке или при помощи специального элект-
ронагреваемого держателя, позволяющего оперировать с несколькими колбами
одновременно.
100
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
Рис. 2.28
Колбы Кьельдаля
2.11. Безопасность в лаборатории
До того, как проводить эксперименты, вам необходимо ознакомиться с правила-
ми техники безопасности в лаборатории! Прочтите приложение D и материалы,
которые предоставит вам ваш преподаватель. Ваш преподаватель дополнитель-
но ознакомит вас со специфическими правилами и нормами работы в вашей ла-
боратории, а также с местонахождением реактивов. Более подробно вопросы
лабораторной техники безопасности обсуждаются в руководстве Safety in Acade-
mic Chemistry Laboratories, изданном Американским химическим обществом
[32]. В нем рассматриваются вопросы защиты персонала и ведения лаборатор-
ной документации, описаны рекомендованные приемы экспериментальной рабо-
ты, дана характеристика опасности различных химических веществ, приведены
рекомендации по изучению паспортов безопасности химических веществ и ма-
териалов (Material Safety Data Sheets, MSDS), описано защитное оборудование и
правила действий в чрезвычайных ситуациях. Приведены также правила утили-
зации отходов, терминология, касающаяся классификации отходов. В руковод-
стве содержатся также нормативы, регламентирующие контакт с опасными
химикатами, выработанные американским Управлением по технике безопасно-
сти и здоровью (Occupational Safety and Health Administration, OSHA) и требования
американского Агентства по защите окружающей среды. Подробно рассмотрены
правила обращения с неорганическими и органическими пероксидами, приве-
ден обширный список несовместимых химических веществ и нормы хранения
горючих и легковоспламеняющихся жидкостей. Этот буклет рекомендуется
прочитать всем студентам и преподавателям. Он бесплатно распространяется
(по одному экземпляру) Американским химическим обществом (The American
Chemical Society, Washington, DC, 1-800-227-5558).
Еще одно руководство, изданное Американским химическим обществом,
The Waste Management Manual for Laboratory Personnel [33] содержит обзор офи-
циальных нормативных актов по утилизации лабораторных отходов.
ВОПРОСЫ
101
Всегда носи в лаборатории защитные очки! Публикуется с любезного разрешения Merck KGaA
Что мы узнали из этой главы?
• Аккуратно заполняйте свой лабораторный журнал — стр. 42
• Используйте реактивы квалификации ч. д. а. — стр. 48
• Как пользоваться аналитическими весами — стр. 49
• Мерная посуда и правила обращения с ней — стр. 60, 67
• Как откалибровать мерную посуду — стр. 71
• Как приготовить стандартные растворы кислоты и щелочи — стр. 76, 77
• Распространенное лабораторное оборудование для подготовки и обработки
проб — стр. 78
• Как отфильтровать и подготовить осадок для гравиметрического определе-
ния — стр. 87
• Как отбирать пробы твердых, жидких и газообразных веществ — стр. 88
• Как приготовить раствор, содержащий определяемый компонент—стр. 91
Вопросы
1 - Опишите основные типы посуды, используемой для измерения объемов. Ука-
жите, какие из них отградуированы на заполнение, какие — на вытекание.
2. Опишите принцип действия и порядок работы с аналитическими весами.
102
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
3. Почему микровесы более чувствительны, чем обычные аналитические весы?
4. Что означает маркировка «TD» и «ТС» на мерной посуде?
5. Как проводится взятие навесок по разности?
6. В чем разница между нулевой точкой и точкой покоя весов?
7. Назовите основные правила работы с весами.
8. Опишите приготовление стандартных растворов НС1 и NaOH.
9. Опишите принципы, лежащие в основе сухого озоления и мокрого сжига-
ния органических и биологических материалов. Перечислите преимущест-
ва каждого метода.
10. Назовите два основных способа перевода в раствор неорганических веществ?
11. Что такое безбелковый фильтрат? Как его приготовить?
12. Какого рода ситуаций необходимо тщательно избегать, чтобы безопасно
использовать хлорную кислоту для разложения органических веществ?
13. Что такое генеральная, лабораторная, анализируемая проба? А что такое
случайная проба?
14. Какие процессы обусловливают нагревание вещества в микроволновом поле?
Задачи
Градуировка мерной посуды, температурные поправки
15. Вы калибруете мерную колбу номинального объема 25 мл, заполняя ее до
метки дистиллированной водой (температура 22 °C). Сухая закрытая проб-
кой колба весит 27,278 г, а заполненная закрытая колба — 52,127 г. Для
взвешивания использованы стальные разновесы. Чему равен объем колбы
при данной температуре? Чему он равен при 20 °C? Для самопроверки вве-
дите значение веса на воздухе при 22 °C в соответствующую ячейку элект-
ронной таблицы 2.4 (на компакт-диске) и сравните ответ с полученным
вами значением.
16. Вы калибруете пипетку номинального объема 25 мл при 25 °C, используя
стальные разновесы. Вес воды, вытекшей из пипетки, равен 24,971 г. Чему
равны объемы пипетки при 25 и 20 °C?
17. Вы откалибровали бюретку объемом 50 мл при 20 °C и получили следую-
щие величины поправок объемов:
Показания бюретки (мл) Поправка (мл)
10 +0,02
20 +0,03
30 0,00
40 -0,04
50 -0,02
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
103
После этого вы стали работать с бюреткой жарким летним днем при 30 °C.
Чему теперь равны значения поправок?
18. Вы приготовили стандартный раствор при 21 °C, а работаете с ним при
29 °C. Исходная концентрация раствора составляла 0,05129 М, а какой она
стала к моменту работы с ним?
Рекомендуемая литература
Реактивы и стандарты
1. Reagent Chemicals, American Chemical Society Specifications, 9th ed., Washin-
gton, DC: American Chemical Society, 2000.
2. Dictionary of Analytical Reagents, London: Chapman & Hall, 1993. Данные no
более чем 10000 реактивам.
3. J. R. Moody and E. S. Beary, «Purified Reagents for Trace Metal Analysis», Ta-
lanta, 29 (1982), 1003. Описано приготовление особо чистых кислот пере-
гонкой при пониженном давлении.
4. R. С. Richter, D. Link, and Н. М. Kingston, «On-Demand Production of High-
Purity Acids in the Analytical Laboratory», Spectroscopy, 15(1) (2000) 38. Опи-
сано приготовление особо чистых кислот при помощи коммерческой уста-
новки для перегонки при пониженном давлении.
5. www.thomsmithlabs.com — сайт компании «Thom Smith Laboratories», по-
ставляющей готовые комплекты реактивов (стандарты и образцы для ана-
лиза) для студенческих лабораторных работ по аналитической химии;
www.sigma-aldrich.com/analytical— сайт компании-поставщика стандарт-
ных растворов.
Аналитические весы
6. D. F. Rohrbach and М. Pickering, «А Comparison of Mechanical and Electronic
Balances», J. Chem. Ed., 59 (1982) 418.
7. R. M. Schoonover, «А Look at the Electronic Analytical Balance», Anal. Chem.,
54(1982) 973A.
8. К. M. Lang, «Time-Saving Applications of Electronic Analytical Balances», Am.
Lab., March (1983) 72.
Калибровка весов
9. W. D. Abele, «Laboratory Note: Time-Saving Applications of Electronic Balances»,
Am. Lab., 13 (1981) 154. Обсуждается калибровка весов при помощи стандар-
тов массы, откалиброванных Американским национальным институтом
стандартов и технологий.
104
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
10. D. F. Swinehart, «Calibration of Weights in a One-Pan Balance», Anal. Lett.,
10(1977) 1123.
Калибровка мерной посуды
11. G. D. Christian, «Coulometric Calibration of Micropipets», Microchem. J.,
9(1965) 16.
12. M. R. Masson, «Calibration of Plastic Laboratory Ware», Taianta, 28 (1981)
781. Таблицы для калибровки полипропиленовых сосудов.
13. W. Ryan, «Titrimetric and Gravimetric Calibration of Pipettors: A Survey»,
Am. J. Med. Technol., 48 (1982) 763. Калибровка пипетаторов объемом от 1
до 500 мкл.
14. М. R. Winward, Е. М. Woolley, and Е. A. Butler, «Air Buoyancy Corrections for
Single-Pan Balances», Anal. Chem., 49 (1977) 2126.
15. R. M. Schoonover and F. E. Jones, «Air Buoyancy Corrections in High-Accuracy
Weighing on Analytical Balances», Anal. Chem., 53 (1981) 900.
«Чистые» лаборатории
16. J. R. Moody, «The NBS Clean Laboratories for Trace Element Analysis», Anal.
Chem.,54(\<№!} 1358A.
Пробоотбор
17. J. A. Bishop, «An Experiment in Sampling», J. Chem. Ed., 35 (1958) 31.
18. J. R. Moody, «The Sampling, Handling and Storage of Materials for Trace Ana-
lysis», Phil. Trans. Roy. Soc. London, Ser. A, 305 (1982) 669.
19. G. E. Baiulescu, P. Dumitrescu, and P. Gh. Zugravescu, Sampling, Chichester:
Ellis Horwood, 1991.
Подготовка и растворение проб
20. G. D. Christian, «Medicine, Trace Elements, and Atomic Absorption Spectro-
scopy», Anal. Chem.,M\Y) (1969) 24A. Приготовление растворов биологиче-
ских жидкостей и тканей.
21. G. D. Christian, Е. С. Knoblock, and W. С. Purdy, «Polarographic Determinati-
on of Selenium in Biological Materials», J. Assoc. Ojfic. Agric. Chemists,
48 (1965) 877; R. K. Simon, G. D. Christian, and W. C. Purdy, «Coulometric De-
termination of Arsenic in Urine», Am. J. Clin. Pathol, 49 (1968) 207. Использо-
вание Mo(VI) в качестве катализатора при мокром сжигании.
22. Т. Т. Gorsuch, «Radiochemical Investigations on the Recovery for Analysis of
Trace Elements in Organic and Biological Materials», Analyst, 84 (1959) 135.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
105
23- S. Nobel and D. Nobel, «Determination of Mercury in Urine», Clin. Chem.,
4 (1958) 150. Мокрое сжигание при комнатной температуре.
24- G. Knapp, «Mechanical Techniques for Sample Decomposition and Element
Preconcentration», Mikrochim. Acta, II (1991) 445. Смеси кислот и их исполь-
зование для мокрого сжигания и других способов разложения.
Разложение в микроволновом поле
25- Н. М. Kingston and L. В. Jassie, eds., Introduction to Microwave Sample Prepa-
ration: Theory and Practice. Washington, D.C.: American Chemical Society,
1988.
26. H. M. Kingston and S. J. Haswell, eds., Microwave-Enhanced Chemistry: Fun-
damentals, Sample Preparation, and Applications, Washington, DC: American
Chemical Society, 1997.
27. H. M. Kingston and L. B. Jassie, «Microwave Energy for Acid Decomposition at
Elevated Temperatures and Pressures Using Biological and Botanical Samples»,
Anal. C/zem.,58(1986) 2534.
28. R. A. Nadkami, «Applications of Microwave Oven Sample Dissolution in Analy-
sis», Anal. Chem., 56 (1984) 2233.
29. B. D. Zehr, «Development of Inorganic Microwave Dissolutions», Am. Lab.,De-
cember (1992) 24. Также приведены свойства смесей кислот, используемых
для разложения.
30. J. К. Poudrier, «The Micro wave Oven as a Specialized Instrument», Today's
Chemist at Work (American Chemical Society), July/August (1995) 29.
31. www.cemx.com — сайт компании СЕМ — производителя лабораторных
микроволновых печей.
Безопасность в лаборатории
32. Safety in Academic Chemistry Laboratories, 6th ed., American Chemical Society,
Committee on Chemical Safety. Washington, D.C.: American Chemical Society,
1995.
33- The Waste Management Manual for Laboratory Personnel, Task Force on
RCRA, American Chemical Society, Department of Government Relations and
Science Policy. Washington, DC: American Chemical Society, 1990.
34. A. K. Furr, ed., CRC Handbook of Laboratory Safety, 4th ed. Boca Raton, FL:
CRC Press, 1993.
35- M.-A. Armour, Hazardous Laboratory Chemicals Disposal Guide, Boca Raton,
FL: CRC Press, 1990.
36. R. J. Alaimo, ed., Handbook of Chemical Health and Safety, Washington, DC:
American Chemical Society, 2001.
106
ОСНОВНЫЕ ИНСТРУМЕНТЫ И ОПЕРАЦИИ ХИМИЧЕСКОГО АНАЛИЗА
37. М. S. Lesny, «It's a Bad, Bad, Bad, Bad World», Today's Chemist at Work (Ame-
rican Chemical Society), December (2000) 26. Перечислены и обсуждаются
многочисленные правительственные, общественные и университетские
сайты, посвященные проблемам производственной безопасности и охраны
здоровья.
Паспорта безопасности химических веществ и материалов (MSDS)
38. http://siri.org/msds — поисковая база данных в режиме online, ссылки на
другие сайты, посвященные тем же проблемам.
39. www.env-sol.com — сайт Solutions Software Corporation. Перечни MSDS
доступны на DVD или CD-дисках.
Глава 3
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
В АНАЛИТИЧЕСКОЙ ХИМИИ
Факты упрямы, но статистика куда сговорчивее.
Марк Твен
43,8% всех статистических данных бесполезны.
Мудрость аналитика
Несмотря на то, что обработка данных производится после их получения, мы
считаем целесообразным обсудить вопросы обработки данных в начале книги,
поскольку знание основ статистического анализа важно при выполнении экс-
периментов. Оно необходимо для оценки значимости полученных данных, а
следовательно, для контроля каждой стадии анализа. Качество планирования
эксперимента (включая оценку требуемого размера пробы, необходимой точ-
ности измерений и числа параллельных определений) определяется тем, на-
сколько верно вы понимаете, что будут представлять собой получаемые вами
данные.
Применение электронных таблиц для обработки данных сильно облегчило
статистические и прочие вычисления. Сначала вы ознакомитесь со всеми дета-
лями вычислений на бумаге вручную, а затем с использованием электронных таб-
лиц, чтобы продемонстрировать преимущества таких расчетов при выполнении
рутинных вычислений. В этой главе мы узнаем, как можно пользоваться
таблицами Excel для решения задач аналитической химии.
3.1. Правильность и воспроизводимость - разные вещи
Понятие правильности характеризует степень близости измеренного значения
некоторой величины и ее истинного значения. Истинное значение в строгом
смысле слова, как правило, никогда не известно. Поэтому более реалистическим
определением правильности была бы близость между измеренным значением и
значением, принимаемым за истинное.
При условии хорошей техники эксперимента, например, при сравнении по-
лученных данных с результатами анализа стандартного образца сходного соста-
ва, можно сделать разумные предположения о правильности методики — в
пределах, ограниченных нашими знаниями о составе стандартного образца и
измерительной процедуре. Конечно, точность, с которой известен состав стан-
дартного образца, тоже не абсолютна, поскольку также определяется характе-
ристиками некоего измерительного процесса.
108
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
РИС. 3.1. Иллюстрация понятий «правильность» и «воспроизводимость».
Воспроизводимость по определению есть степень близости между резуль-
татами повторных измерений одной и той же величины. Мерой воспроизводимости
может служить стандартное отклонение, относительное стандартное отклонение,
размах данных или доверительный интервал (например, соответствующий 95%-й
доверительной вероятности) вокруг среднего. Хорошая воспроизводимость еще
не гарантирует высокой правильности: результаты анализа могут содержать си-
стематическую погрешность. Например, измеренные значения масс нескольких
одинаковых проб могут содержать одну и ту же погрешность. Эта погрешность
не влияет на воспроизводимость, но влияет на правильность. И наоборот, вос-
производимость может быть относительно низкой, а правильность, по крайней
мере, за счет случайных причин, оказаться высокой. Поскольку в реальной жиз-
ни истинные значения результатов анализа никогда не известны заранее, то чем
выше воспроизводимость, тем больше вероятность получить правильный резу-
льтат. Бесполезно надеяться, что результат случайно окажется правильным при
плохой воспроизводимости. Поэтому аналитик всегда стремится в первую оче-
редь добиться получения хорошо воспроизводимых результатов.
Если хочешь попасть в цель, стреляй куда угодно,
а потом то, во что ты попал, назови «целью».
Эшли Бриллиант
Понятия «правильность» и «воспроизводимость» можно проиллюстрировать
при помощи мишени (рис. 3.1). Предположим, в ходе упражнений по стрельбе
все пули попали в яблочко (мишень слева). В этом случае результаты правильны
и хорошо воспроизводимы. Мишень посередине демонстрирует результаты хо-
рошо воспроизводимые (рука твердая), но неправильные. Возможно, у оружия
сбит прицел. Результаты стрельбы по мишени справа плохо воспроизводимы, и
потому средний результат, скорее всего, неправильный. Таким образом, мы ви-
дим, что хорошая воспроизводимость необходима для достижения правильности,
но она отнюдь не гарантирует ее.
Как мы увидим вскоре, чем больше параллельных результатов имеется, тем
более надежным окажется средний результат. Число требуемых параллельных
измерений определяется требуемой правильностью и известной воспроизводи-
мостью методики.
3.2. ДЕТЕРМИНИРОВАННЫЕ (СИСТЕМАТИЧЕСКИЕ) ПОГРЕШНОСТИ
109
3.2. Детерминированные (систематические) погрешности
На показатели правильности и воспроизводимости влияют погрешности двух
типов. Детерминированные погрешности — это погрешности, величина кото-
рых может быть определена (как следует из их названия), которых в принципе
можно избежать или которые можно скорректировать. Они могут быть постоян-
ными по величине, например, если все взвешивания проводятся на одних и тех
же неоткалиброванных весах. Они могут быть и переменными по величине, од-
нако в силу их природы систематические погрешности можно вычислить и скор-
ректировать, как в случае бюретки, погрешности показаний которой составляют
разные значения для разных объемов.
Величина детерминированной погрешности может быть пропорциональна
размеру пробы или зависеть от нее более сложным образом. Чаще всего такие
погрешности имеют один и тот же знак, например, погрешности, обусловленные
потерями осадка за счет растворимости (отрицательные). Иногда их знак может
изменяться в зависимости от условий. Примером могут служить изменения объ-
ема раствора и его концентрации при изменении температуры. В этом случае их
можно скорректировать, если измерить температуру раствора. Такие детерми-
нированные погрешности, поддающиеся измерению, называются системати-
ческими. Детерминированные, или систематические, погрешности имеют не
случайный характер.
К наиболее распространенным систематическим погрешностям относятся:
1. Инструментальные погрешности. Возникают из-за неверных показа-
ний приборов, при использовании неоткалиброванных весов или мерной
посуды.
2. Субъективные погрешности. Это погрешности, обусловленные ошиб-
ками в работе аналитиков. Они уменьшаются с накоплением опыта рабо-
ты и при повышении внимания ко всем выполняемым руками операциям.
К типичным операциями, вызывающим такие погрешности, относятся
дозирование и перенос растворов, растворение пробы при нагревании
(за счет вспенивания, кипения раствора), высушивание пробы (если оно
проводится не до конца) и т. д. Такие погрешности трудно скорректиро-
вать. Другие источники субъективных погрешностей — арифметические
ошибки в ходе вычислений и предвзятость при считывании показаний
приборов.
3. Методические погрешности. Эти погрешности являются наиболее серь-
езными. Большинство погрешностей, упомянутых выше, можно миними-
зировать или скорректировать, но погрешностей, внутренне присущих
методике, избежать невозможно до тех пор, пока не будут изменены
условия определения. К источникам погрешностей методики относятся
110
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
соосаждение примесей и потери осадка за счет растворения, побочные
реакции, неполнота протекания реакций, загрязнения реактивов. Иногда
погрешности можно достаточно легко скомпенсировать, в частности,
путем проведения контрольного опыта. Контрольный опыт — это про-
ведение через все этапы методики пробы, не содержащей определяемого
компонента. Проведение контрольного опыта и последующее вычита-
ние полученных результатов из результатов анализа реального образца
является общепринятой практикой. Если, несмотря на все принятые
меры, погрешности методики остаются слишком большими, необходимо
выбрать другой подход к решению задачи. Впрочем, иногда приходится
пользоваться данной методикой за неимением лучшей...
Систематические погрешности могут быть аддитивными или мультипли-
кативными в зависимости от характера их влияния на результаты анализа. Для
обнаружения систематических погрешностей повсеместно принято добавлять к
пробе известное количество определяемого компонента и рассчитывать меру
правильности — отношение добавленного количества к найденному (см. гл. 1,
поверка методики). Анализ образцов известного состава (в первую очередь под-
ходящих стандартных образцов) также полезен для контроля погрешностей ме-
тодики и инструментальных погрешностей.
3.3. Недетерминированные (случайные) погрешности
Другой тип погрешностей — это недетерминированные погрешности, часто
называемые случайными. Они отражают неопределенность результата, прису-
щую любому измерению. Случайные погрешности проявляются в виде неболь-
ших различий между результатами последовательных измерений одной и той же
величины, проводимых одним и тем же аналитиком в одних и тех же условиях.
Конкретное значение каждой такой погрешности невозможно предсказать и
оценить заранее. Массив значений случайных погрешностей подчиняется неко-
торому закону случайного распределения. Поэтому для того, чтобы из серии экспе-
риментальных данных оценить наиболее вероятный результат, можно применять
методы теории вероятностей.
Детальное рассмотрение математических проблем теории вероятностей вы-
ходит за рамки данной книги. Отметим лишь, что случайные погрешности хими-
ческого анализа обычно подчиняются нормальному, или гауссовому, закону
распределения. График функции распределения Гаусса изображен на рис. 3.2.
Параметр о представляет собой стандартное отклонение для бесконечной се-
рии результатов (генеральной совокупности) и характеризует их воспроизводи-
мость, т. е. степень разброса данных. Из рис. 3.2. видно, что чем больше
3.4. ЗНАЧАЩИЕ ЦИФРЫ: СКОЛЬКО ТРЕБУЕТСЯ ЦИФР?
111
Рис. 3.2
Кривая нормального
распределения
погрешностей
Отклонения от среднего (в единицах стандартного отклонения)
погрешность по абсолютной величине, тем реже она встречается, а кроме того,
частоты появления положительных и отрицательных погрешностей одинаковы.
Погрешности, которые нами не замечены,
бесконечны и очень разнообразны.
В отличие от них, замеченные нами погрешности
конечны по определению.
Том Гибб
По сути недетерминированные погрешности обусловлены ограниченностью воз-
можностей аналитика контролировать или корректировать внешние условия
либо невозможностью распознать действие факторов, влияющих на результат
измерения. Некоторые случайные погрешности вызваны статистическим харак-
тером явлений, например, погрешности, связанные с подсчетом элементарных
частиц. Иногда при изменении условий некоторые погрешности неизвестной
природы исчезают. Но, разумеется, полностью исключить в ходе эксперимента
все мыслимые источники случайных погрешностей нельзя. Аналитик должен
лишь стремиться уменьшить их до допустимого или пренебрежимо малого
уровня. Недетерминированные погрешности имеют случайную природу. Избе-
жать их нельзя.
3.4. Значащие цифры: сколько требуется цифр?
Самое слабое звено во всей цепи операций любого анализа — то измерение, ко-
торое выполняется с наименьшей точностью. Бессмысленно стремиться прово-
дить другие измерения, с большей точностью, чем лимитирующее. Число
значащих цифр, необходимое для представления результата измерения с соот-
ветствующей точностью, называется числом значащих цифр. Поскольку неоп-
ределенность (неточность) любого измерения составляет по меньшей мере ±1 в
последней значащей цифре, следует оставлять все цифры, которые известны
точно, плюс одну недостоверную. Последняя цифра результата измерения имеет
неопределенное значение. Не следует писать после нее дополнительные цифры.
112
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Каждая цифра характеризует число единиц в том десятичном разряде, который
она представляет. Например, в числе 237 содержатся 2 сотни, 3 десятка и 7 еди-
ниц.
Цифра 0 может быть либо значащей, либо просто указывать на положение
запятой. Однако число значащих цифр результата измерения не зависит от поло-
жения запятой. Рассмотрим число 92067. Это число имеет пять значащих цифр
независимо от того, где стоит запятая. Например, это может быть 92067 мкм,
9,2067 см, 0,92067 дм или 0,092067 м — все эти величины имеют одно и то же
число значащих цифр. Они просто представляют разные способы выражения од-
ного и того же результата измерения (в разных единицах). В последнем случае
нуль между запятой и цифрой 9 лишь указывает место расположения запятой.
Если нуль расположен после запятой, то всегда понятно, является ли он знача-
щей цифрой или просто указывает на положение запятой. Например, в числе
727,0 нуль не является указателем положения запятой и представляет собой зна-
чащую часть числа. Но если нуль находится перед запятой, то интерпретация его
роли может быть неоднозначной. Нуль, предшествующий запятой, всегда знача-
щий, если он расположен между двумя ненулевыми цифрами (как в приведен-
ном примере с числом 92067). Однако для числа, записанного как 936600,
невозможно определить, является ли один из нулей, или оба, или ни один из них
простым указателем положения (предполагаемой) дробной части либо пред-
ставляет собой значащую составную часть результата измерения. Поэтому в по-
добных случаях лучше всего записывать число в экспоненциальной форме,
указывая перед показателем степени только значащие цифры. Например, число,
записанное как 9,3660 • 105 имеет пять значащих цифр. В этом случае число
936600 следует считать имеющим шесть значащих цифр.
Пример 3.1
Укажите, сколько значащих цифр содержат числа, записанные в приведенной
ниже форме. Укажите в них нули, являющиеся значащими.
0,216; 90,7; 800,0; 0,0670
Решение
0,216 три значащие цифры
90,7 три значащие цифры, нуль значащий
800,0 четыре значащие цифры, все нули значащие
0,0670 три значащие цифры, только последний нуль является значащим
Значимость последней цифры результата измерения можно проиллюстри-
ровать следующим образом. Предположим, каждый студент в группе измеряет
длину стержня, используя одну и ту же линейку. Линейка отградуирована с це-
3.4. ЗНАЧАЩИЕ ЦИФРЫ: СКОЛЬКО ТРЕБУЕТСЯ ЦИФР?
113
ной деления 1 мм. Можно выполнить измерение, округляя результат до 0,1 мм
(считывая показание по положению конца стержня между делениями), но по-
следняя цифра оценочная и потому неточная. Может быть получена, например,
следующая серия результатов:
36,4 мм; 36,8 мм; 36,0 мм; 37,0 мм; среднее — 36,6 мм.
Умножение и деление: мыслите относительными
категориями
Для многих измерений в запись результата включают одну цифру, которая явля-
ется оценочной и потому недостоверна (в последнем примере это десятые доли
миллиметра). Эта цифра представляет собой последнюю значащую цифру чис-
ла. Все цифры, следующие за ней, лишены смысла. При умножении и делении
неопределенность этой цифры переносится на конечный результат, ограничивая
тем самым число его достоверных цифр. Результат умножения или деления со-
держит, по крайней мере, такую же относительную неопределенность, как и тот
сомножитель (делимое, делитель), который обладает наибольшей относитель-
ной неопределенностью значения, т. е. одно из чисел с наименьшим числом знача-
щих цифр. Результат умножения или деления не может быть точнее наименее
точного числа участвующего в операции. Будем считать, что это число лимити-
рует точность результата. Если есть несколько чисел, участвующих в арифмети-
ческих действиях и имеющих одинаковое и наименьшее число значащих цифр,
то лимитирует точность то из них, у которого мантисса (число, состоящее из
всех выписанных подряд значащих цифр) является наименьшей по абсолютной
величине. Например, из двух чисел, имеющих по 3 значащих цифры — 0,0344 и
5,39, точность лимитирует первое (мантисса 344 меньше, чем 539).
Пример 3.2
В каждой следующей паре чисел найдите то, которое лимитирует точность при
операциях умножения и деления: а) 42,67 или 0,0967; б) 100,0 или 0,4570;
в) 0,10 или 0,0067.
Решение
а) 0,0967 (оно имеет три значащие цифры, а 42,67 — четыре).
б) 100,0. Оба числа имеют по четыре значащие цифры, но мантисса первого рав-
на 1000, а второго 4570. Соответственно, у первого числа неопределенность
значения — 1 часть на 1000, а у второго — 1 часть на 4570.
в) 0,10. Оба числа имеют по две значащие цифры, но неопределенность значе-
ния первого — 1 часть на 10 (10%), а второго — приблизительно 1 часть
на 70.
114
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Пример 3.3
Приведите результат следующих вычислений с наибольшим возможным чис-
лом значащих цифр и укажите, какой из участников арифметических действий
лимитирует точность результата.
35,63 -0,5481 -0,05300
1,1689
•100% = 88,5470578%
Решение
Точность лимитирует число 35,63. Поэтому результат надо представить как
88,55%, а производить вычисления более, чем с пятью значащими цифрами
(одну цифру оставляем в качестве запасной и затем округляем), смысла не име-
ет. Обратите внимание, что число 100% служит только для перемещения пози-
ции запятой и, следовательно, является точной величиной (можно сказать, что
оно содержит «бесконечно много» значащих цифр). Заметьте также, что число,
лимитирующее точность, характеризуется относительной неопределенностью
не менее чем 1 часть на 3600, поэтому и результат будет иметь относительную
неопределенность в лучшем случае 1 часть на 3600, или порядка 2,5 на 8900. Та-
ким образом, при выполнении вычислений следует не только правильно пред-
ставить результат (с точностью до последней значащей цифры), но и оценить ве-
личину его неопределенности. Конечный результат должен состоять только
из значащих цифр. При выполнении измерений следует стремиться к тому, чтобы
все результаты, используемые для расчетов, характеризовались приблизительно
одной и той же относительной неопределенностью значений.
Если мантисса конечного результата по абсолютной величине меньше ман-
тиссы числа, лимитирующего точность вычислений, то к результату вычислений
следует дописать еще одну цифру для того, чтобы не снизить неопределенность
его значения. Эту цифру пишут в виде нижнего индекса, чтобы подчеркнуть, что
она менее надежна.
Пример 3.4
Приведите результат следующих вычислений с максимальным числом знача-
щих цифр. Укажите число, лимитирующее точность вычислений.
_4W891 =
132,6-0,5247
Решение
Лимитирует точность число 891. Поскольку мантисса результата меньше, чем
мантисса этого числа, представим результат как 546,6. Последняя цифра записа-
ЗА ЗНАЧАЩИЕ ЦИФРЫ: СКОЛЬКО ТРЕБУЕТСЯ ЦИФР?
115
на в виде нижнего индекса, чтобы показать, что она менее надежна. Лимитирую-
щее точность число имеет относительную неопределенность порядка 1 части на
900, а результат — не менее 6 частей на 5500 (0,6 части на 550).
В ходе операций умножения и деления допускается округлять результат до
соответствующего числа значащих цифр на каждом этапе вычислений. Однако
для промежуточных результатов все же лучше сохранять по одной запасной
цифре и затем округлить конечный результат до нужного числа значащих цифр.
Сложение и вычитание: мыслите абсолютными категориями
При сложении и вычитании с цифрами обращаются иначе, чем при умножении и
делении. Здесь мы имеем дело не с относительными, а с абсолютными неопреде-
ленностями. В этом случае число значащих цифр результата зависит от того, где
расположены десятичные запятые в записи исходных величин. Число десяти-
чных знаков результата сложения или вычитания равно наименьшему их числу
среди участников этих арифметических действий. Предположим, мы рассчи-
тываем молярную массу вещества Ag2MoO4 из относительных атомных масс со-
ставляющих его элементов:
Ag 107,87 0
Ag 107,87 0
Mo 95,94
О 15,99 94
О 15,99 94
О 15,99 94
О 15,99 94
375,67 76
Атомная масса молибдена известна лишь с точностью до 0,01 а.е.м. Поэто-
му молярная масса любого соединения, содержащего молибден, не может быть
известна с более высокой точностью. Следовательно, максимальная точность, с
которой мы можем представить значение молярной массы Ag2MoO4, — 375,68.
Перед сложением или вычитанием все слагаемые (уменьшаемое, вычитаемое)
можно округлить в соответствии с числом десятичных знаков наименее точно
известной величины. Но, как и в случае умножения или деления, лучше оставить
по одной запасной цифре и по окончании вычислений округлить ее.
Подводя итог обсуждению значащих цифр, отметим два момента. Первый: с
какой точностью вам нужно знать конечный результат? Если, к примеру, вам не-
обходимо знать только, содержит проба: 12 или же 13% определяемого компо-
нента, то все требуемые измерения (и вычисления) достаточно проводить с
двумя значащими цифрами. Если масса навески составляет около 2 г, нет необ-
ходимости взвешивать ее точнее, чем до 0,1 г. И второй: с какой точностью вы
116
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
можете проводить измерения? Очевидно, что, если вы можете измерить значе-
ния оптической плотности окрашенного раствора лишь с тремя значащими циф-
рами (например, значение А = 0,447), то нет смысла измерять массу навески
точнее, чем до трех значащих цифр (например, 6,67 г).
Если мантисса какой-либо измеряемой величины меньше мантисс результа-
тов других измерений, то имеет смысл представлять результаты измерений с од-
ной дополнительной значащей цифрой. Поясним это на следующем примере.
Предположим, вы взвешиваете два объекта с весьма близкими массами (порядка
100 мг) и хотите получить значения их масс с одинаковой точностью, например,
до 0,1 мг или 1 части на тысячу. Масса первого объекта составляет 99,8 мг, а вто-
рого — 100,1 мг. Вы взвесили оба объекта с одинаковой точностью, но второе
значение приводите с одной дополнительной значащей цифрой. Здесь видна
аналогия с тем, как мы добавляем одну цифру к результату умножения или деле-
ния, если его мантисса меньше, чем мантисса числа, лимитирующего точность
вычислений.
Если известно, какая величина лимитирует точность в ходе расчетов, то при
необходимости точность результата можно повысить, либо сделав эту величину
больше (например, увеличив размер навески), либо повысив точность ее измере-
ния (например, проводя взвешивание на более точных весах с дополнительной
значащей цифрой). Кроме того, желательно увеличивать точность измерения
любых величин, мантисса которых мала по сравнению с мантиссами других ве-
личин, для того, чтобы неопределенности значений разных величин стали близ-
ки друг к другу.
В ходе анализа разные величины следует измерять с одинаковой абсолют-
ной неопределенностью, если их предстоит складывать или вычитать, и с одина-
ковой относительной неопределенностью, если их предстоит перемножать или
делить.
Прежде чем сообщить полученный тобою результат
кому бы то ни было, проверь его еще раз.
Эдмунд Ч. Беркли
Если вычисления включают в себя как операции сложения-вычитания, так и
умножения-деления, каждый этап необходимо контролировать отдельно. Реко-
мендуется на всякий случай сохранять одну дополнительную цифру в промежу-
точных результатах, а затем округлить ее в окончательном результате. При
использовании калькулятора можно сохранять все цифры промежуточных резу-
льтатов. Однако не следует думать, что все числа, выдаваемые калькулятором,
верны. Всегда старайтесь сначала оценить примерный порядок ожидаемого ре-
зультата. Если он должен быть около 2%, а калькулятор показывает 0,02, то, ве-
роятно, вы забыли умножить на 100. А если вы ожидаете получить результат
около 20%, а видите 4,3, то, скорее всего, вы допустили ошибку в расчетах, а воз-
можно, в измерениях.
3.4. ЗНАЧАЩИЕ ЦИФРЫ: СКОЛЬКО ТРЕБУЕТСЯ ЦИФР?
117
Пример 3.5
Приведите результат следующих вычислений с максимально возможным чис-
лом значащих цифр:
97 7
-100,0 + 36,04
32,42 )
687
Решение
301 36 +36,04 337 4
---= 0,0491!
687 687 1
В первой серии действий (деление и умножение) точность лимитирует число
97,7. Результат этих действий запишем как 301,36. Перед тем, как произвести
сложение, мы добавили к результату дополнительную (пятую) цифру. Результат
сложения мы округлим до четырех цифр, поскольку, при делении делитель бу-
дет иметь только три значащие цифры. В ходе заключительной операции деления
точность лимитирует делитель — число 687. Но результат по своей мантиссе мень-
ше, чем делитель, поэтому мы запишем его с одной дополнительной цифрой. От-
метим, что, если бы на первом этапе мы округлили результат до 301,4, то
числитель дроби стал бы равным 337,5, а конечный результат—0,4913 (впрочем,
он и в этом случае остается соизмеримым с экспериментальной погрешностью).
Логарифмирование: мыслите категориями мантисс
При переходе от логарифмов к антилогарифмам и наоборот логарифмируемое
число и мантисса логарифма имеют одно и то же число значащих цифр. Напом-
ним, что для логарифмической величины мантиссой называется его дробная
часть (см. приложение В, обзор правил действий с логарифмами). Все десяти-
чные знаки мантиссы логарифма, в том числе нули, являются значащими. Рас-
считаем значение pH 2,0 • 10-3 М раствора НС1, так как pH = -lg[H+]:
pH = -1g 2,0 • IO"3 = (-3 + 0,30) = 2,70
В этом примере -3 является характеристикой логарифма — точной величи-
ной, показателем степени 10 в числе 10-3; 0,30 является мантиссой, логарифмом
величины 2,0, имеющей две значащие цифры. Поэтому и мантисса представлена
с двумя значащими цифрами. Таким образом, здесь запись логарифмической ве-
личины содержит три цифры, несмотря на то, что величина концентрации приве-
дена с двумя значащими цифрами. В свою очередь, при взятии антилогарифмов
результат содержит столько значащих цифр, сколько десятичных знаков имеет
мантисса логарифма. Антилогарифм величины 0,072, мантисса которого содер-
жит три цифры, будет записан как 1,18, а логарифм 12,1 —как 1,083 (1 —харак-
теристика, 0,083 — мантисса, имеющая три значащие цифры).
118
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
3.5. Правила округления
Если цифра, следующая за последней значащей цифрой, больше 5, округление
ведут в большую сторону, а если меньше 5, то в меньшую сторону:
9,47 * 9,5
9,43 « 9,4
Если отбрасываемая цифра равна 5, последнюю значащую цифру округляют до
ближайшей четной:
8,65 « 8,6
8,75 « 8,8
8,55 « 8,6
Это правило основано на допущении, что последняя значащая цифра с равной
вероятностью может оказаться как нечетной, так и четной. Поэтому, если мас-
сив чисел достаточно велик, то в нем будет примерно одинаковое число четных
и нечетных цифр, предшествующих цифре 5. Отметим, что правило округления
до четного действует только тогда, когда необходимо отбросить только одну
цифру 5 (а не две цифры, например 51).
3.6. Способы выражения правильности
Для характеристики правильности результата можно использовать различные
численные величины. В любом случае для оценки правильности необходимо
иметь для сравнения значение измеряемой величины, принимаемое за истинное.
Абсолютная погрешность
Разность между измеренным и истинным значением с учетом знака называется
абсолютной погрешностью. Она имеет ту же размерность и выражена в тех же
единицах, что и измеряемая величина. Если проба содержит 2,62 г определяемо-
го вещества, а по результатам анализа найдено 2,52 г, то абсолютная погреш-
ность составляет-0,10 г. Если измеряемая величина представляет собой среднее
из нескольких значений, то погрешность называется средней. Среднюю по-
грешность можно вычислить и как среднее значение (с учетом знаков) индивиду-
альных погрешностей отдельных результатов.
Относительная погрешность
Отношение абсолютной или средней погрешности к истинному значению на-
зывается относительной погрешностью. Ее обычно выражают в процентах.
Так, в приведенном выше примере относительная погрешность составляет
(-0,10/2,62) • 100% = -3,8%. Относительной мерой правильности называется
отношение измеренного значения к истинному (также выраженное в процен-
3.7. СТАНДАРТНОЕ ОТКЛОНЕНИЕ - ВАЖНЕЙШАЯ СТАТИСТИЧЕСКАЯ ВЕЛИЧИНА
119
тах). В том же примере мера правильности составляет (2,52/2,62) • 100% = 96,2%.
Подчеркнем, что истинное значение никогда не бывает известно, поэтому для
вычисления как относительной погрешности, так и относительной меры правиль-
ности используют данные двух измерений.
Помимо процентов, относительную погрешность выражают и в других еди-
ницах. При очень точных измерениях относительная погрешность может со-
ставлять менее 1%, поэтому удобнее использовать более мелкие единицы. 1%
означает одну часть на 100, или 10 частей на 1000. Малые погрешности обычно
выражают в частях на тысячу (англ, part per thousand, ppt). Так, число 23 по от-
ношению к числу 6725 составляет 3,4 ppt. Воспроизводимость результатов изме-
рений также часто выражают в частях на тысячу.
Пример 3.6
Результат анализа составляет 36,97 г, а истинное значение принимается равным
37,06 г. Чему равна относительная погрешность (в частях на тысячу)?
Решение
Абсолютная погрешность = 36,97 г - 37,06 г = -0,09 г
Относительная погрешность = ‘ Ю00%о = -2,4 ppt
Для обозначения частей на тысячу используют символ %о подобно тому, как для
обозначения частей на сто — символ %.
3.7. Стандартное отклонение - важнейшая статистическая
величина
При проблемах с воспроизводимостью
проведи измерение только один раз.
Мудрость аналитика
Любой набор результатов анализа должен сопровождаться характеристикой их
воспроизводимости. Существуют различные способы выражения воспроизво-
димости.
Для воображаемого бесконечного набора результатов измерений введем ве-
личину, называемую стандартным отклонением и обозначаемую су:
-ц)2
НЧ- (ЗЛ)
120
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
где N — число измерений, х. — результат отдельного измерения, ар — среднее
из бесконечного набора результатов, т. е. предельное значение среднего при
7V —> оо. В действительности мы всегда располагаем лишь конечным набором ре-
зультатов. Среднее конечного набора данных обозначается х и вычисляется как
^(xf /7V), х —> ц с увеличением N.
Величину х можно использовать вместо ц при вычислении стандартного от-
клонения. Но в этом случае сумма квадратов отклонений единичных значений
от среднего [числитель дроби в выражении (3.1)] содержит не N, а только (N- 1)
независимых слагаемых (поскольку, зная (N- 1) единичных результатов и сред-
нее, всегда можно вычислить оставшийся единичный результат). Как говорят
статистики, в этом случае из исходных N степеней свободы одна степень свободы
использована для вычисления среднего, а для вычисления стандартного отклоне-
ния остается (N- 1) степеней свободы.
Можно показать, что для конечного числа данных (особенно при N < 30) бо-
лее точное приближение для о (оценка) получатся в случае, если в знаменателе
выражения (3.1) вместо общего числа данных N использовать число степеней
свободы (N- 1) (для компенсации возможных различий между х и ц). Тогда
стандартное отклонение, рассчитанное из конечного числа данных, будет выра-
жаться следующей формулой:
(3.2)
Величина s представляет собой лишь приближенную оценку и — тем более точ-
ную, чем больше число данных, из которых она рассчитана. Поскольку число ре-
зультатов, получаемых при химическом анализе, невелико, характеристикой
воспроизводимости всегда служит s. Для малого числа данных (четыре и менее)
существует другой способ оценки s — см. разд. 3.15 и уравнение (3.17).
Пример 3.7
Рассчитайте среднее и стандартное отклонение для следующей серии результа-
тов анализа: 15,67, 15,69 и 16,03 г.
Решение
xi х(-х (х,-х)2
15,67 0,13 0,0169
15,69 0,11 0,0121
16,03 0,23 0,0529
S 47,39 S 0,47 S 0,0819
3.7. СТАНДАРТНОЕ ОТКЛОНЕНИЕ - ВАЖНЕЙШАЯ СТАТИСТИЧЕСКАЯ ВЕЛИЧИНА
121
УX/ 47 39
х —2-—= 15,80
N 3
10,0819
V 3-1
= 0,20 г
Стандартное отклонение можно рассчитать и по следующей формуле, экви-
валентной выражению (3.2):
'IX2-(£*• )2Л
#-i
(3.3)
Эту формулу удобно использовать при вычислениях на калькуляторе. Отметим,
что многие калькуляторы снабжены встроенными программами для автомати-
ческого вычисления стандартного отклонения после ввода данных.
Пример 3.8
Рассчитайте стандартное отклонение для данных, приведенных в примере 3.7,
пользуясь уравнением (3.3).
Решение
X,- X,2
15,67 245,55
15,69 246,18
16,03 256,96
S 47,39 S 748,69
, (748,69-(47,39)г/3 =
\ 3-1
Различие в 0,01 г по сравнению с результатом расчета в примере 3.7 стати-
стически незначимо, поскольку колебания самих данных составляют по мень-
шей мере ±0,2 г. Пользуясь формулой (3.3), следует в промежуточных вычислениях
(х?) сохранять одну или даже две дополнительные цифры.
Стандартное отклонение, рассчитанное описанным выше способом, являет-
ся оценкой возможной погрешности результата единичного измерения. Сред-
ний результат из N измерений характеризуется меньшим возможным разбросом
значений по сравнению с единичными результатами. Чем больше N, тем меньше
этот разброс. При очень большом N среднее практически не отличается от ц, и
122
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
разброс его значений стремится к нулю. Можно показать, что среднее из /^резуль-
татов в W раз более достоверно, чем единичное значение. Так, случайная погреш-
ность среднего из четырех результатов измерений вдвое меньше, чем погрешность
результата единичного измерения. Воспроизводимость среднего значения возрас-
тает пропорционально корню квадратному из числа измерений.Таким образом,
Стандартное отклонение среднего = 5mean
(3.4)
Стандартное отклонение среднего иногда называют стандартной погрешно-
стью.
Часто стандартное отклонение выражают в относительной форме — в виде
относительного стандартного отклонения, представляющего собой отноше-
ние стандартного отклонения к среднему. Обычно его выражают в процентах и
в этом случае иногда называют коэффициентом вариации.
Пример 3.9
При выполнении параллельных взвешиваний получены четыре результата: 29,8,
30,2,28,6 и 29,7 мг. Рассчитайте стандартное отклонение единичного результата
и среднего значения. Выразите их в абсолютных единицах измерения и в отно-
сительных величинах (%).
Решение
xi xt-x (х,.-х)2
29,8 0,2 0,04
30,2 0,6 0,36
28,6 1,0 1,00
29,7 0,1 0,01
118,3 S 1,9 S 1,41
- 118’3 ЭОА
х =—— =29,6
4
141
s = Л —— = 0,69 мг (абсолютное стандартное отклонение)
V 4-1
• 100% = 2,3% (относительное стандартное отклонение)
0,69
5mean = ~~i=‘= ^34 мг (абсолютная стандартная погрешность)
л/4
034
• 100% = 1,1% (относительная стандартная погрешность)
3.7. СТАНДАРТНОЕ ОТКЛОНЕНИЕ - ВАЖНЕЙШАЯ СТАТИСТИЧЕСКАЯ ВЕЛИЧИНА
123
Воспроизводимость результатов измерений можно повысить, увеличив чис-
ло данных. Однако, как видно из уравнения (3.4), стандартное отклонение сред-
него обратно пропорционально не числу измерений, а лишь корню квадратному
из этого числа. Рано или поздно даже незначительное улучшение воспроизводи-
мости потребует слишком большого числа дополнительных данных. А чтобы
уменьшить стандартное отклонение, например, в 10 раз, число измерений необ-
ходимо увеличить в 100 раз.
Фактор случайности необходим для того,
чтобы результаты статистических расчетов
получились правильными.
Мудрость аналитика
Числом повторных измерений, достаточным для практических целей, мож-
но считать такое, при котором стандартное отклонение среднего, характеризую-
щее случайную погрешность, станет сравнимым по величине с систематической
погрешностью (если последнюю, разумеется, невозможно выявить и скорректи-
ровать). Это связано с тем, что систематические погрешности невозможно устра-
нить посредством повторных измерений.
Из величины стандартного отклонения можно рассчитать интервал, в кото-
рый результат измерения попадает с той или иной вероятностью. На рис. 3.2
изображены такие интервалы применительно к нормальному распределению.
Пользуясь уравнением кривой нормального распределения, можно показать ма-
тематически, что 68% всех величин отклонений единичных данных от среднего
попадает в интервал с полушириной s (точнее, а, поскольку этот вывод, строго
говоря, справедлив лишь для бесконечной серии данных). Аналогично, 95% от-
клонений попадают в интервал с полушириной 25, а 99% — в интервал с полуши-
риной 2,55. Таким образом, 68% результатов единичных измерений находятся в
интервале х ± 5, 95% — в интервале х ± 25, 99% — в интервале х ± 2,55 и т. д.
Повторим, что величины этих интервалов рассчитаны в предположении,
что серия результатов измерений бесконечна (см. ниже о понятии «доверитель-
ный интервал» а также пример 3.15). В действительности нельзя утверждать, что
истинное значение с вероятностью 95% попадает в интервал х ± 25. На то есть, по
крайней мере, две причины. Во-первых, это могло бы быть справедливо только
при отсутствии систематических погрешностей. Систематические погрешности
приводят к смещению всей кривой нормального распределения относительно
истинного значения. Во-вторых, число результатов всегда конечно. При этом,
чем оно меньше, тем менее достоверны значениях и 5. В то же время существует
способ расчета доверительных интервалов (см. далее) из величин х и 5, который
учитывает это обстоятельство.
Понятно, что данные по воспроизводимости результатов можно предста-
вить разными способами. Если результат представлен в виде х ± 8, всегда следу-
ет указывать, к каким условиям это относится и что именно означает 8.
В частности, это может быть 5,25, стандартное отклонение среднего или относи-
тельное стандартное отклонение.
124
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
В статистике часто используют величину, называемую дисперсией. Она
представляет собой квадрат стандартного отклонения s2. Мы будем пользовать-
ся величинами дисперсий при рассмотрении F-теста Фишера и наложения по-
грешностей (разд. 3.13).
3.8. Электронные таблицы
Электронные таблицы — это эффективные вычислительные программы, кото-
рые можно использовать в различных целях, в частности, для анализа данных и
построения графиков. Ими удобно пользоваться в ходе обработки данных, при
выполнении повторных измерений, отображении результатов в графической
или табличной форме. Электронные таблицы имеют встроенные функции, на-
пример, для вычисления стандартных отклонений и других статистических вели-
чин, выполнения расчетов по формулам и с данными, вводимыми пользователем.
К широко используемым электронным таблицам относятся Microsoft Excel, Lo-
tus 1-2-3 и Quattro Pro. В основе они все сходны, небольшие отличия есть в конк-
ретных командах и синтаксисе. В наших примерах мы будем использовать Excel
как наиболее распространенную и доступную программу.
Возможно, вы уже пользовались электронными таблицами ранее и знакомы
с их основными функциями. Здесь мы обобщенно рассмотрим те аспекты, кото-
рые представляют наибольший интерес для решения прикладных задач аналитиче-
ской химии. За более подробной информацией следует обратиться к руководствам
по работе с таблицами или справочной системе самой программы Excel Help, на-
жав соответствующую кнопку на панели инструментов.
На странице http://science.csustan.edu/titorial/Exel/index.htm находится пре-
восходное руководство по пользованию таблицами Excel, составленное препо-
давателями Университета штата Калифорния (округ Станислаус). В нем описа-
ны основные рабочие функции этих таблиц, включая ввод данных и формул,
форматирование ячеек, построение графиков и регрессионный анализ. Обязатель-
но прочтите его перед тем, как продолжать работу, — вы найдете это руководство
очень полезным. Сайт Университета западного Кентукки www.wku.edu/-conteed/
СНЕМЗЗО содержит сводку инструкций по построению графиков при помощи
таблиц Microsoft Excel и Lotus 1-2-3. Посетите также сайты, на которые ссыла-
ются страницы excelhandout.html и lotushandout.html.
Лист электронной таблицы состоит из ячеек, расположенных по столб-
цам (обозначенным А, В, С, ...) и строкам (1, 2, 3, ...). Отдельная ячейка обо-
значается комбинацией буквы столбца и номера строки, например, ВЗ. Это
обозначение ячейки называется также ее адресом или ссылкой. Для иллюстра-
ции на рис. 3.3 в некоторых ячейках приведены их обозначения-адреса. Если
навести указатель мыши (в форме крестика) на любую ячейку и щелкнуть левой
кнопкой мыши, то соответствующая ячейка становится активной (ее границы
выделяются жирными линиями), обозначение активной ячейки отображается в
верху экрана слева от окна формул, а ее содержимое — правее, в окне формул
после знака равенства.
3.8. ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
125
Заполнение ячеек
В каждую ячейку можно ввести текст, число или формулу. Именно благодаря
использованию формул электронные таблицы так удобны в работе. Они позво-
ляют проводить одни и те же вычисления с разными числами. Правила пользова-
ния формулами мы проиллюстрируем на примере расчета значений веса воды,
вытекающей из двух различных пипеток номинального объема 20 мл, по разно-
сти между весом мерной колбы, наполненной водой, и весом пустой колбы.
Каждый шаг вычислений сверяйте с рис. 3.4.
Откройте программу Excel, щелкнув кнопкой мыши по ее ярлыку (или вы-
звав ее из раздела Программы стартового меню). Чтобы ввести в ячейку текст,
число или формулу, дважды щелкните по ней. В перечисленные ниже ячейки вве-
дите следующее (по завершении ввода данных в ячейку нажимайте клавишу Enter):
Ячейка А1: Чистый вес
Ячейка АЗ: Пипетка
Ячейка А4: Колба + вода, г
Ячейка А5: Колба, г
Ячейка А6: Вода, г
Если вы хотите внести исправления в содержимое ячейки, дважды щелкни-
те по ней, после чего редактируйте текст. Текст можно редактировать и в окне
формул. Если вы щелкнете один раз, вводимый текст заменит прежний. Чтобы
полностью отобразить достаточно длинный текст в ячейках столбца А, увеличь-
те ширину этого столбца. Для этого установите указатель мыши точно на линию,
разделяющую столбцы А и В, в верхней части таблицы (в строке, содержащей
обозначения столбцов), и, оставляя кнопку мыши нажатой, перетаскивайте указа-
тель вправо до тех пор, пока ширина столбца не станет достаточной для отображе-
ния всего текста. При этом сместятся и все ячейки, расположенные правее.
Рис. 3.3
Ячейки электронной таблицы
А В С D Е
1 А1 В1 С1 ит. д.
2 А2 В2 С2 ит. д.
3 АЗ ВЗ СЗ ит. д.
4
5
Рис. 3.4
Заполнение ячеек
А В С D
1 Чистый вес
2
3 Пипетка 1 2
4 Колба+вода, г 47,702 49,239
5 Колба, г 27,687 29,199
6 Вода, г 20,015 20,040
7
8 ячейка В6=В4-В5
9 ячейка С6=С4-С5
10
126
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Продолжите ввод.
Ячейка ВЗ: 1
Ячейка СЗ: 2
Ячейка В4: 47,702
Ячейка С4: 49,239
Ячейка В5: 27,687
Ячейка С5: 29,199
Ячейка В6: =В4-В5
Формулу в ячейку В6 можно ввести и так: ввести символ «=», затем щелк-
нуть на ячейке В4, затем ввести символ «-», затем щелкнуть на ячейке В5. Все
ячейки, составляющие прямоугольный блок В4-С6, необходимо предваритель-
но отформатировать, чтобы числовые данные содержали три знака после запя-
той. Для этого сначала выделите этот блок (щелкните на ячейке в одном его углу
и перетащите указатель мыши к ячейке в противоположном углу). Затем в строке
Меню последовательно нажмите Формат: Ячейки: Число (Format:
Cells: Number). В появившееся окошко Число десятичных знаков
(Decimal places) введите 3 и нажмите клавишу ОК.
В ячейку С6 также необходимо ввести формулу. Вы, конечно, можете ее
просто набрать точно так же, как и при вводе в ячейку В6. Но можно поступить
проще, скопировав ее из ячейки В6. Подведите указатель мыши к правому ниж-
нему углу ячейки В6 и перетащите его в ячейку С6. При этом в ячейке С6 ока-
жется нужная формула. Точно так же можно поступить и при заполнении всех
ячеек, расположенных справа от С6, если вы калибруете еще другие пипетки.
Чтобы заполнить ячейку формулой, находящейся в соседней ячейке (сверху или
слева), можно поступить и так: выделить заполняемую ячейку, а затем последо-
вательно нажать Правка: Заполнить : Вниз (Edit: Fill: Down) (или
Вправо (Right), в зависимости от того, где расположена ячейка с копируемой
формулой).
Дважды щелкните на ячейке В6. При этом отобразится формула, содержа-
щаяся в этой ячейке, а также высветятся все другие ячейки, задействованные в
формуле. Эту же операцию проделайте и с ячейкой С6. Обратите внимание, что
каждый раз, когда вы щелкаете кнопкой мыши (один или два раза) на ячейке, со-
держащей формулу, то эта формула появляется в окне формул.
Сохранение электронной таблицы
Чтобы сохранить только что созданную вами электронную таблицу, последова-
тельно нажмите Файл: Сохранить как (File: Save As). Я предпочитаю
сначала сохранять все документы на рабочем столе. Оттуда их можно перемес-
тить в любую папку, например, Мои документы (Му Documents). В этом слу-
чае они не будут потеряны. Так что в верхнем из появившихся окон выберите
Рабочий стол (Desktop). В нижнее окно введите имя документа, например,
Pipet Calibration. После этого нажмите клавишу Сохранить (Save). Если вы за-
тем захотите переместить документ в какую-либо папку какого-либо диска, пе-
ретащите его ярлык с рабочего стола в соответствующую открытую папку.
3.8. ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
127
Печать электронной таблицы
Последовательно нажмите Файл: Параметры страницы (File: Page
Setup). По умолчанию лист печатается на бумаге книжного формата (Portrait),
т. е. 81 х 11 дюймов, ориентированного вертикально. Если вы выводите на пе-
чать большое число столбцов, может быть целесообразно ориентировать лист
бумаги горизонтально (Landscape). Если вы хотите, чтобы таблица была напеча-
тана с разделительными линиями сетки, нажмите Лист: Сетка (Sheet:
Gridlines). После этого все готово к печати. Нажмите Печать: ОК
(Print: ОК). На печать будет выведена только рабочая область листа, без
обозначений столбцов и строк.
Абсолютные и относительные адреса ячеек
В приведенном выше примере в ходе копирования формулы мы использовали
относительные адреса ячеек. Формула, введенная в ячейку В6, по существу,
означает следующее: «Из числа, расположенного на две ячейки выше (относите-
льно данной, т. е. В6), вычесть число, расположенное на одну ячейку выше».
Формула, скопированная в ячейку С6, содержит те же инструкции, но уже при-
менительно к ячейке С6.
Однако часто требуется, чтобы в каждом вычислении участвовала величи-
на, находящаяся в какой-то конкретной, одной и той же, ячейке — например, не-
кая константа. В этом случае мы должны задать в формуле адрес этой ячейки как
абсолютный адрес. Абсолютный адрес записывается при помощи знака «$», по-
мещаемого как перед обозначением столбца, так и перед номером строки, на-
пример, $В$2. В этом случае как бы мы ни перемещали формулу по строкам и
столбцам таблицы, адрес останется одним и тем же.
Проиллюстрируем сказанное на примере создания таблицы для расчета
средних значений из нескольких серий данных. Заполните лист таблицы следу-
ющим образом, сверяясь с рис. 3.5:
А1: Средний объем титранта
АЗ: Порядковый номер
ВЗ: Серия А, мл
СЗ: Серия В, мл
В4: 39,27
В5: 39,18
В6: 39,30
В7: 39,22
С4: 45,59
С5: 45,55
С6: 45,63
С7: 45,66
А4: 1
Порядковые номера титрований (1^1) можно ввести вручную. Однако су-
ществуют и автоматические способы ввода в соседние ячейки чисел, возраста-
ющих с определенным шагом. После ввода числа 1 в ячейку А4 нажмите
128
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Правка: Заполнить : Прогрессия (Edit: Fill: Series). В открыв-
шемся окне выберите опции По столбцам (Columns) и Арифметическая
(Linear), установите величину шага (Step Value) равной 1, Предельное
значение (Stop Value) равным 4 и нажмите ОК. Числа от 2 до 4 будут введе-
ны в ячейки А5-А7. Можно также предварительно выделить диапазон ячеек
(начиная с исходной А4), которые вы хотите заполнить. В этом случае нет не-
обходимости вводить предельное значение. Кроме того, вы можете осуществить
ввод при помощи формул. В ячейку А5 введите «=А4+1» (в этой формуле исполь-
зован относительный адрес}. Затем протяните эту формулу вниз, выделив ячей-
ку А5 и нажав Правка: Заполнить : Вниз (Edit: Fill: Down). Наконец,
после ввода формулы можно выделить ячейку А5, установить указатель мыши на ее
нижний правый угол и при нажатой кнопке мыши перетащить указатель до ячейки
А7. При этом формула автоматически скопируется во все ячейки диапазона.
Теперь в ячейку В8 введем формулу для расчета среднего. Оно равно сумме
значений, разделенной на число значений (оно находится в ячейке А7).
В8: =СУММ(В4:В7)/$А$7
Адрес делителя содержит символы «$», поскольку это абсолютный адрес
(далее мы скопируем эту формулу вправо, в ячейку С8, и при этом адрес делите-
ля не должен измениться). Помещая символ $ перед обозначением столбца и пе-
ред номером строки, мы гарантируем, что этот адрес останется неизменным при
копировании формулы как по горизонтали, так и по вертикали. Выражение
sum(B4:B7) — это синтаксическое выражение программы, предназначенное
для суммирования массива чисел — в данном случае начиная с ячейки В4 и за-
канчивая В7. При вводе этого выражения сами адреса ячеек набирать не обязатель-
но. Достаточно ввести «=СУММ(» , затем щелкнуть на ячейке В4, перетащить
указатель мыши до ячейки В7 и в заключение ввести «)».
Таким образом, мы рассчитали среднее для серии А и хотим сделать то же
самое для серии В. Для этого выделим ячейку В8, наведем курсор на ее правый
А I' В С D
1 Средний объем титранта
2
3 Порядковый номер Серия А, мл Серия В, мл
4 1 39,27 45,59
5 2 39,18 45,55
6 3 39,30 45,63
7 4 39,22 45,66
8 Среднее: 39,24 45,61
9 Ст. отклонение 0,053150729 0,047871355
10
11 Ячейка В8= СУММ(В4:В7)/$А$7 Скопировать вправо в ячейку С8
12 Ячейка В9= СТАНДОТКЛОН(В4:В7) Скопировать вправо в ячейку С9
13 Жирным шрифтом выделены те ячейки, в которые были введены формулы
Рис. 3.5. Относительные и абсолютные адреса ячеек
3.8. ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
129
нижний угол и при нажатой кнопке мыши перетащим его в ячейку С8. В ней не-
медленно появится значение среднего для второй серии! Щелкните дважды по
ячейке С8, и вы увидите содержащуюся в ней формулу. Обратите внимание, что
делитель имеет тот же адрес, что и в ячейке В8 (поскольку он абсолютный), а ад-
реса суммируемых значений изменились (они относительные). Если бы мы не
сопроводили адрес делителя символами «$», то программа считала бы его отно-
сительным, и в ячейке С8 он был бы не А7, а В7.
Использование статистических функций Excel
Программа Excel содержит множество математических и статистических функ-
ций. Их можно использовать в расчетах в готовом виде вместо того, чтобы писать
формулы. Попробуем использовать одну из таких функций для автоматического
вычисления среднего. Выделите пустую ячейку и щелкните мышкой на символе
«Д», расположенном на панели инструментов. При этом откроется окно Мас-
тер функций (Paste Function). В меню Категория (Function Cate-
gory) выберите Статистические (Statistical). После этого окно
приобретет следующий вид:
В меню Функция (Function Name) выберите СРЗНАЧ (AVERAGE) и нажмите
ОК. Далее в окне Число (Number) введите В4:В7 и снова нажмите ОК. Будет
вычислено то же самое значение среднего, которое вы получили при помощи соб-
ственной формулы. Можно также активировать ячейку и вручную ввести в нее
формулу =СРЗНАЧ(В4:В7) (=average(B4:B7)). Попробуйте и этот способ.
Рассчитаем теперь стандартное отклонение результатов. Выделите ячейку В9.
В меню Функция (Function Name)окна Статистические (Statisti-
cal Functions) выберите СТАНДОТКЛОН (STDEV) (или непосредственно
введите =СТАНДОТКЛОН(В4:В9) (=stdev(B4:B9)) в ячейку В9). Скопируйте
формулу из ячейки В9 в ячейку С9. Рассчитайте стандартные отклонения по
формуле (3.2) и сравните их с результатам расчетов программы Excel. Рассчи-
танные значения стандартных отклонений следует округлить, например, для се-
рии А до 0,05 мл.
130
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Полезные синтаксические выражения
Excel содержит множество математических и статистических функций (синтак-
сических выражений), использование которых упрощает ход вычислений. Вни-
мательно изучите списки функций [меню Вставка (Paste) Функция
(Function Name)] в категориях функций Математические (Math &
Trig) и Статистические (Statistical Function) окна Мастер фун-
кций (Paste Function) (открывается нажатием на кнопку с символом «£»
на панели инструментов). Ниже приведены некоторые функции, которые пона-
добятся при изучении этой книги:
Математические и тригонометрические функции
LOG 10 ПРОИЗВЕЛ (PRODUCT) СТЕПЕНЬ (POWER) КОРЕНЬ (SQRT) десятичный логарифм числа произведение массива данных возведение в степень квадратный корень
Статистические функции СРЗНАЧ (AVERAGE) МЕДИАНА (MEDIAN) СТАНДОТКЛОН (STDEV) ТТЕСТ (TTEST) среднее из серии данных медиана серии данных стандартное отклонение серии данных доверительная вероятность, соответствующая статистике теста Стьюдента
ДИСПА (VAR) дисперсия серии данных
Эти синтаксические выражения можно вводить вручную (как мы делали ра-
нее), указывая в скобках после имени функции диапазон ячеек, содержащих ар-
гументы.
Это краткое руководство послужит вам основой для более полного изуче-
ния возможностей электронных таблиц. Любую формулу, приведенную в книге,
вы можете ввести в активную ячейку и подставить в нее соответствующие дан-
ные для расчетов. Кроме того, электронные таблицы снабжены разнообразными
средствами для анализа данных. Вы можете строить графики и диаграммы, на-
пример, градуировочные зависимости (графики зависимости сигнала отклика
прибора от концентрации) и проводить статистический анализ полученных
данных. Некоторые примеры приведены далее в этой главе.
3.9. Наложение погрешностей: это не простое суммирование
При рассмотрении значащих цифр мы отметили, что для результата умножения
или деления относительная неопределенность не может быть выше, чем для
участвующей в операции величины, которая характеризуется наибольшей
относительной неопределенностью. Аналогично обстоит дело с абсолютными
неопределенностями значений при сложении или вычитании. До сих пор мы не
3.9. НАЛОЖЕНИЕ ПОГРЕШНОСТЕЙ: ЭТО НЕ ПРОСТОЕ СУММИРОВАНИЕ
131
рассматривали конкретные численные значения этих неопределенностей, а про-
сто предполагали, что неопределенность составляет по меньшей мере плюс-ми-
нус одну единицу в последней цифре каждого числа.
Если же неопределенность каждого значения известна, то существует воз-
можность оценить численное значение неопределенности результата вычислений.
В ходе последовательности вычислений неопределенность каждого исходного дан-
ного вносит свой вклад в общую неопределенность результата. Как говорят,
происходит наложение неопределенностей — относительных или абсолютных в
зависимости от характера арифметических действий (умножение-деление или
сложение-вычитание).
Сложение и вычитание:
мыслите категориями абсолютных дисперсий
Рассмотрим наложение неопределенностей при сложении и вычитании на сле-
дующем примере:
(65,06 ± 0,07) + (16,13 ± 0,01) - (22,68 ± 0,02) = 58,51 (±?)
Неопределенности, приведенные в этом примере, характеризуют случайные
(недетерминированные) погрешности, присущие соответствующим величинам и
выраженные в виде их стандартных отклонений. Максимально возможная по-
грешность суммы составила бы ±0,10. Это произошло бы в случае, если погрешно-
сти аргументов, во-первых, все одновременно приняли бы свои максимальные
значения, а, во-вторых, имели бы одинаковые знаки. Минимально возможная по-
грешность составила бы 0,00. Это возможно, если погрешности аргументов случай-
ным образом скомпенсируют друг друга. Оба эти крайних случая маловероятны;
наиболее вероятное значение погрешности находится где-то посередине. Мож-
но показать, что наиболее вероятное значение погрешности суммы или разности
равно квадратному корню из суммы абсолютных дисперсий аргументов (напо-
минаем, что при сложении и вычитании суммируются абсолютные неопреде-
ленности). Иными словами, абсолютная дисперсия суммы (разности) равна
сумме абсолютных дисперсий аргументов. Если а = b + с - то
= ^ь +S2C +s2d
sa = ^sb + Sc + sd
(3.5)
(3-6)
В приведенном примере
sa =7(±o>°7)2 +(±0,01)2 +(±0,02)2 =
= 7(±49-10“4) + (±1-10-4) + (±4-10“4) =
= V±54-10-4 =±7,3-IO-2
132
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Таким образом, результат составляет 58,51 ±0,07. Число ±0,07 характеризует
абсолютную неопределенность. Если мы хотим оценить относительную неопре-
деленность, то она составит
=2i2Z.ioo%=±од,%
58,51 2
Пример 3.10
Вы получили три равные по весу партии урановой руды. По данным анализа со-
держание урана в них составило 3,978 ± 0,004%, 2,536 ± 0,003% и 3,680 ± 0,003%
соответственно. Каково среднее содержание урана и чему равны абсолютная и
относительная неопределенности этой величины?
Решение
_ _ (3,978 ± 0,004%) + (2,536 ± 0,003%) + (3,680 ± 0,003%)
3
Неопределенность суммы равна
sa =7(±0,004)2 + (±0,003)2 +(±0,003)2 =
= 7(±16 • 10’6) + (±9 • 10’6) + (±9 • 10"6) =
= 7±34-1О~6 = ±5,8 • 10’3% U
Отсюда абсолютная неопределенность результата равна
10194
± 0,006% = 3,398 ± 0,006% U
3
Обратите внимание, что число 3 в знаменателе этой дроби точное и неопреде-
ленности не содержит. Поэтому относительная неопределенность содержания
урана составляет
5,8 10’3%U . 1П_3
----------= 2-10 или 0,2%
3,398% U
3.9. НАЛОЖЕНИЕ ПОГРЕШНОСТЕЙ: ЭТО НЕ ПРОСТОЕ СУММИРОВАНИЕ
133
Умножение и деление:
мыслите категориями относительных дисперсий
Рассмотрим следующую последовательность действий:
(13,67 ±0,02)-(120,4 ±0,2) = 356 0 (± ?)
4,623 ±0,006
В этом случае (при умножении и делении) складываются относительные неоп-
ределенности, а наиболее вероятная погрешность выражается корнем квадратным
из суммы относительных дисперсий. Таким образом, относительная дисперсия ре-
зультата равна сумме относительных дисперсий аргументов.
Если а = bc/d, то
(Sa ) rel (sb ) rel + (Sc ) rel (Sd ) rel
(3.7)
(Sa ) rel
) rel + (Sc ) rel + (Sd ) rel
(3.8)
В приведенном примере
(^)rei =^^ = ±0,0015
* rel 13,67
+02
fe)rel = —^— = ±0,0017
e 120,4
, . ±0,006 xnnniQ
(^)rel =---—--- = ±0,0013
d rel 4,623
±0,0015)2 +(±0,0017)2 +(±0,0013)2
) rel
= д/(±2,2 • 10-6 ) + (±2,9 • 10-6 ) + (±1,7 • 10-6 ) =
= д/(±6,8 • 10—6) = ±2,6 • 10“3
Абсолютная неопределенность рассчитывается как
sa = а • (sa ) rel = 356,0 • (±2,6 • 10’3) = ±0,93
Таким образом, результат следует представить как 356,0 ± 0,9.
Пример 3.11
Рассчитайте неопределенность величины количества хлорид-ионов (в миллимо-
лях), содержащихся в 250,0 мл анализируемого раствора, если на титрование
трех аликвот по 25,00 мл было израсходовано 36,78, 36,82 и 36,75 мл раствора
нитрата серебра. Концентрация раствора AgNO3 равна 0,1167 ± 0,0002 М.
134
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Решение
Среднее значение объема титранта равно
36,78+36,82 + 36,75
—----------------— = 36,78 мл
3
Неопределенность этой величины выразим в виде стандартного отклонения:
xi Xj-X (Х;-Х)2
36,78 0,00 0,0000
36,82 0,04 0,0016
36,75 0,03 0,0009
S 0,0025
/0,0025
V 3-1
= 0,035. С учетом неопределенности среднее значение объема
составляет 36,78 ± 0,04 мл.
Количество хлорид-ионов в аликвоте составляет
(0,1167 ± 0,0002 ммоль/мл) • (36,78 ± 0,04 мл) = 4,292 (±?)
_ ±0,0002
<Л+е1 - ОД167
= ±0,0017
_ ±0,035
Sc reI 36,78
= ±0,00095
(sa ) reI = д/ (±0,0017)2 + (±0,00095)2 =
= д/(±2,9 • 10’6 ) + (±0,90 • IO-6) =
= 7+3,8-IO"6 =±1,9-IO-3
Абсолютная неопределенность содержания Cl- (в миллимолях) составляет
4,292 • (±0,0019) = ±0,0082 ммоль
ммоль С1_ в 25 мл = 4,292 ± 0,0082 ммоль
ммоль С1~в 250 мл = 10(4,292 ± 0,0082) = 42,92 ± 0,08 ммоль
В ходе расчетов мы сохраняли по одной дополнительной цифре во всех проме-
жуточных результатах. Обратите внимание, что абсолютная неопределенность
содержания вещества пропорциональна размеру пробы. Она не остается посто-
янной, например, при увеличении в два раз массы или объема пробы.
Если расчетная формула содержит как операции умножения-деления, так и
сложения-вычитания, вычисление общей неопределенности следует проводить
поэтапно.
3.9. НАЛОЖЕНИЕ ПОГРЕШНОСТЕЙ: ЭТО НЕ ПРОСТОЕ СУММИРОВАНИЕ
135
Пример 3.12
Вы получили три партии железной руды весом 2852,1578 и 1877 фунтов (1b). Не-
определенности этих величин составляют ±5 1b. По результатам анализа содержа-
ние железа в этих партиях составляет 36,28 ± 0,04%, 22,68 ± 0,03% и 49,23 ± 0,06%
соответственно. Стоимость руды составляет 15 центов в расчете на один фунт
железа. Сколько вам предстоит заплатить за руду и какова неопределенность
этой величины?
Решение
Следует для каждой партии руды рассчитать массу железа и ее неопределен-
ность, а затем сложить значения масс и рассчитать неопределенность получен-
ного результата. Относительные неопределенности значений масс железа равны
= ±0,0017 — = ±0,0032 — = ±0,0027
2852 1578 1877
Относительные неопределенности результатов анализа равны
^^ = ±0,0011 =^ = ±0,0013 =^ = ±0,0012
36,28 22,68 49,23
Значения масс железа, содержащегося в партиях руды, равны
(2852±51b)-(36,28±0,04Q/o) ре
100
(sa ) ге1 - д/(±0,0017)2 +(±0,0011)2 = ±0,0020
sa =1034,7 • (±0,0020) = ±2,11b
lb Fe= 1034,7 ±2,1
(Везде сохраняем по одной дополнительной цифре!)
(1578±51ЬИ22,68±0,03°/о) ре
100
(sa ) ге1 = д/(±0,0032)2 + (±0,0013) 2 = ±0,0034
sa = 357,89 • (±0,0034) = ±1,2 1b
lb Fe= 357,9 ±1,2 lb
(1877±51b)-(49,23±0,06Q/o)= +
100
(sa ) rel = -J(±0,0027)2 + (±0,0012) 2 = ±0,0030
sa = 924,05 • (±0,0030) = ±2,8 lb
lb Fe = 924,0 ±2,8 lb
136
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Всего железа = (1034,7 ±2,11b) + (357,9 ± 1,21b) + (924,0 ± 2,81b) =
= 2316,6 (±?) 1Ь
sa = 7(±2,1)2 + (±1,2)2 +(±2,8)2 = ±3,71b
Общая масса железа = 2317 ± 41b
Стоимость составляет (2316,6 ±3,7 1b) ($0,15/1Ь) = $347,49 ± 0,56
Таким образом, вам предстоит заплатить 347,50 ± 0,60 долл.
Пример 3.13
Вы определяете содержание уксусной кислоты в уксусе путем титрования
стандартным раствором гидроксида натрия с индикатором фенолфталеином.
Порцию уксуса объемом около 5 мл взвесили в бюксе на аналитических весах.
Масса навески, рассчитанная по разности между массами заполненного и пустого
бюкса, составила 5,0268 г. Неопределенность результата отдельного взвешивания
составляет ±0,2 мг. Для определения точной концентрации раствора гидроксида на-
трия его стандартизовали, титруя точные навески особо чистого гидрофталата
калия. Концентрации, рассчитанные по результатам трех титрований, составили
0,1167, 0,1163 и 0,1164 М. На титрование пробы уксуса израсходовано 36,78 мл
стандартного раствора гидроксида натрия. Неопределенность результата считы-
вания показаний бюретки составляет ±0,02 мл. Какова массовая доля (%) уксус-
ной кислоты в уксусе и какова неопределенность этого значения?
Решение
Для нахождения массы навески необходимы два взвешивания — пустого и запол-
ненного бюкса. Каждый результат характеризуется неопределенностью ±0,2 мг,
поэтому неопределенность значения чистой массы навески (разности двух зна-
чений масс) составляет
5wt = (±0,2)2 + (±0,2)2 = ±0,3 мг
Среднее значение молярной концент-
рации раствора гидроксида натрия
равно 0,1165 М, а его стандартное от-
клонение (принимаемое в качестве
меры неопределенности) — 0,0002 М
(его можно рассчитать при помощи
Excel, см. фрагмент таблицы).
А В
1 N1 0,1167
2 N2 0,1163
3 N3 0,1164
4 Ст. отклон.: 0,000208
5
6 Ячейка В4 = СТАНДОТКЛОН(В1:ВЗ)
3.9. НАЛОЖЕНИЕ ПОГРЕШНОСТЕЙ: ЭТО НЕ ПРОСТОЕ СУММИРОВАНИЕ
137
Для нахождения объема раствора титранта необходимо двукратное считыва-
ние показаний бюретки (начального и конечного), поэтому неопределенность
объема титранта рассчитываем точно так же, как и неопределенность массы
навески:
svol = д/±0,022 + ±0,022 = ±0,03 мл
Число молей уксусной кислоты в пробе равно числу молей прореагировавшего с
ней гидроксида натрия. Поэтому массовая доля уксусной кислоты составляет
%НОАс=
(0,1165 ± 0,0002) ммоль/мл • (36,78 ± 0,03) мл • 60,05(мг/ммоль НО Ас)
=----------------------------------------------------------• 1U0/о
(5026,8 ±0,3)
= 5,119±?%
Неопределенность значения молярной массы уксусной кислоты будем считать
пренебрежимо малой (ее можно рассчитать с шестью значащими цифрами, об-
щий результат от этого не изменится).
(5м)ге1
±0,0002
0,1165
= ±0,0017
(*voi)rei = ^ = ±0,00082
эо, / о
+03
(5wt)rel = ^£- = ±0’00°060
d 5()26>8
Неопределенность результата анализа составляет
(stotal)rel = 7(±0,0017)2 +(±0,00082)2 +(±0,00060)2 = ±0,0020
5totai= 5,119- 0,0020 = ±0,010% уксусной кислоты
Таким образом, содержание уксусной кислоты составляет 5,119 ± 0,01%. Отно-
сительная неопределенность равна 0,2%.
Наибольший вклад в неопределенность результата внесла неопределен-
ность значения молярной концентрации раствора гидроксида натрия. Это еще
раз показывает, насколько важно тщательно стандартизовать растворы (а также
выполнять любые другие операции калибровки и градуировки, см. гл. 2).
138
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
3.10. Наложение погрешностей и значащие цифры
Ранее мы отмечали, что неопределенность результата вычислений характери-
зует, насколько точно известен этот результат. Иными словами, величина не-
определенности определяет число значащих цифр. Рассмотрим следующий
пример:
(73,1 ± 0,2) • (2,245 ± 0,008) = 164,1 ± 0,7
Значение неопределенности указывает нам, что результат следует привести с че-
тырьмя десятичными цифрами несмотря даже на то, что сомножитель, формаль-
но лимитирующий точность вычислений (73,1), имеет три значащие цифры
(здесь, кстати, нам не нужно приписывать к результату дополнительную цифру
в виде нижнего индекса, поскольку мы указываем реальное значение его неоп-
ределенности). Но это противоречие — кажущееся. Среди сомножителей наи-
большая величина относительной неопределенности составляет 0,0036, а
относительная неопределенность результата равна 0,0043. Таким образом, вслед-
ствие наложение погрешностей неопределенность несколько возросла. Если из-
вестны конкретные значения неопределенностей аргументов вычислений, то
точность не обязательно лимитирует тот из них, у которого наименьшее число
значащих цифр. Например, относительная неопределенность числа 78,1 ± 0,02
составляет 0,003, а числа 11,21 ± 0,08 — 0,007. Число значащих цифр результа-
та вычислений в общем случае определяется величиной его неопределенности,
обусловленной наложением погрешностей.
Рассмотрим еще один вычислительный пример:
(73,1 ± 0,9) • (2,245 ± 0,008) = 164,1 ± 2,1 = 164 ± 2
Неопределенность результата составляет несколько единиц, поэтому в его запи-
си все цифры, следующие после запятой, не имеют смысла. В этом примере отно-
сительные неопределенности аргумента, лимитирующего точность, и конечного
результата примерно одинаковы (±0,012), поскольку относительная неопреде-
ленность другого аргумента существенно меньше.
Пример 3.14
Приведите результаты следующих вычислений с необходимым числом знача-
щих цифр:
(а) (38,68 ± 0,07) - (6,16 ± 0,09) = 32,52
(12,18 ±0,08)-(23,04 ±0,07) = 8(_
1 ’ 3,247 ±0,006
3.11. КОНТРОЛЬНЫЕ КАРТЫ
139
Решение
(а) Рассчитанное значение абсолютной неопределенности результата равно ±0,11.
Поэтому результат следует представить как 32,5 ±0,1.
(б) Рассчитанное значение относительной неопределенности результата равно
0,0075, а абсолютной — 0,0075 • 86,43 = 0,65. Поэтому результат следует за-
писать как 86,4 ± 0,6, несмотря на то, что все числа, использованные в расче-
тах, содержат по четыре значащие цифры. Дело в том, что неопределенность
в четвертой цифре каждого из них достаточно велика (существенно превы-
шает одну единицу в соответствующем знаке); вследствие этого и неопреде-
ленность результата оказывается выше, чем это могло бы показаться на
первый взгляд. Относительная неопределенность результата вычислений со-
ставляет 0,0075, а наибольшая из относительных неопределенностей аргу-
ментов — 0,0066, очень близкое значение.
3.11. Контрольные карты
Контрольная карта качества — это график зависимости результата измерений
одной и той же величины от времени. Он строится в предположении, что измеря-
емая величина постоянна во времени и имеет гауссову функцию распределения.
Контрольные карты используют для проверки того, что результаты измерений
не выходят за рамки статистически допустимых отклонений. На контрольную
карту наносят среднюю горизонтальную прямую, представляющую истинное
(или принимаемое за таковое) значение измеряемой величины, а также одну или
две пары симметрично расположенных параллельных граничных линий — внут-
ренние и внешние контрольные границы. Положение этих границ рассчитыва-
ют из значения стандартного отклонения методики измерения, которое обычно
известно достаточно надежно и может считаться хорошим приближением для
величины о.
На контрольную карту периодически наносят результаты анализа одного
и того же образца с известным содержанием определяемого компонента. Пример
контрольной карты изображен на рис. 3.6. На ней отмечены результаты ежеднев-
ных определений общего содержания кальция в контрольных пробах сыворотки
крови. В ходе анализов эти контрольные пробы с известным содержанием каль-
ция случайным образом перемежают с реальными образцами. Внутренние конт-
рольные границы, как правило, проводят на расстоянии 2о от средней линии. При
этом вероятность выхода результата за границы, обусловленного чисто случайны-
ми факторами, составляет лишь 1 случай из 20. Внутренние границы называют еще
«границами предупреждения». Внешние контрольные границы откладывают на
расстоянии 2,5о либо Зег от средней линии. В этом случае вероятность случайно-
го (т. е. при отсутствии систематических погрешностей) выхода результата за
границы составляет 1 случай из 100 либо 500 соответственно. Обычно анализи-
руют одну контрольную пробу на одну партию реальных проб (например,
20 проб). Поэтому в течение дня можно получить несколько (7V) контрольных
140
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
+2,5ст 5 2
Контрольная карта результатов определения кальция за октябрь 2007
-2,5ст |__L J. J_ J_ J__l_l_l_l_L_L_L_L_L_L J_ J_ J_ J__l_l_l_L_L_L_L_L_L_L_L_l
ОКТ. 1 2 3 4 5 6 7 8 9 10 11 12 13141516171819202122232425262728293031
Дата
Рис. 3.6. Типичная контрольная карта
значений, а на карте откладывать среднее из них. Но в этом случае случайный
разброс данных должен быть в VjV раз меньше по сравнению с разбросом еди-
ничных результатов.
Если на карте обнаруживается систематический дрейф в одном направле-
нии (точек с одной стороны от средней линии становится существенно больше,
чем с другой), на это следует обратить особое внимание. Это может означать,
что либо эксперимент выходит из-под контроля, либо наблюдаются системати-
ческие погрешности анализа. Тенденция к выходу точек за контрольные границы
указывает на наличие одного или нескольких источников детерминированных
погрешностей. Аналитик должен проверить, не испортились ли реактивы, пра-
вильно ли работают приборы, нет ли помех за счет внешних условий и других
факторов. Появление дрейфов может также указывать на загрязнение реактивов,
ошибки в градуировке или приготовлении стандартов, а также на изменение со-
става контрольных образцов.
3.12. Доверительный интервал: насколько надежно значение?
Стандартное отклонение, рассчитанное из серии экспериментальных данных,
обобщенно характеризует воспроизводимость, присущую данной методике ана-
лиза. Но эта величина сама по себе еще не содержит информации о том, насколь-
ко близко может находиться среднее значение х от истинного значения. Здесь и
далее будем считать, что систематические погрешности отсутствуют; в этом
случае истинное значение равно ц. Однако теория статистики позволяет, исходя
из экспериментальных значений среднего и стандартного отклонения, рассчитать
интервал, внутри которого может с заданной вероятностью находиться величи-
на ц. Этот интервал называется доверительным интервалом, его границы —
доверительными границами, а соответствующая вероятность — доверитель-
ной вероятностью (ее обычно выражают в процентах).
3.12. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ: НАСКОЛЬКО НАДЕЖНО ЗНАЧЕНИЕ?
141
Положение доверительных границ для среднего значения рассчитывают по
формуле:
тт - , ts
Доверительные границы = х ± ——
(3.9)
Здесь t—статистический коэффициент, величина которого зависит от заданной
доверительной вероятности и числа степеней свободы (напомним, что оно равно
числу результатов измерений минус единица). Значения t для различных дове-
рительных вероятностей и значений числа степеней свободы v приведены в
табл. 3.1. Заметьте, что полуширина доверительного интервала — это произве-
дение коэффициента t на стандартное отклонение среднего (s/ Jn). Аналогично
можно рассчитать доверительный интервал и для единичного значения х (в этом
случае #= 1). Доверительный интервал для единичного значения равен х ± ts.
Он в V7V раз шире, чем для среднего. При этом число степеней свободы ко-
эффициента t должно быть равно числу степеней свободы стандартного от-
клонения з (число данных, из которых оно рассчитано, минус единица).
Таблица 3.1
Значения коэффициентов t для v степеней свободы
при различных доверительных вероятностях*
V Доверительная вероятность
90% 95% 99% 99,5%
1 6,314 12,706 63,657 127,32
2 2,920 4,303 9,925 4,089
3 2,353 3,182 5,841 7,453
4 2,132 2,776 4,604 5,598
5 2,015 2,571 4,032 4,773
6 1,943 2,447 3,707 4,317
7 1,895 2,365 3,500 4,029
8 1,860 2,306 3,355 3,832
9 1,833 2,262 3,250 3,690
10 1,812 2,228 3,169 3,581
15 1,753 2,131 2,947 3,252
20 1,725 2,086 2,845 3,153
25 1,708 2,060 2,787 3,078
00 1,645 1,960 2,576 2,807
* v = N- 1 — число степеней свободы.
142
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Пример 3.15
Образец технической соды проанализировали на содержание Na^C^ титрова-
нием стандартным раствором соляной кислоты. Для трех параллельных титро-
ваний получены значения 93,50, 93,58 и 93,43% Na2CO3. В каком интервале
значений с 95%-й вероятностью при отсутствии систематических погрешностей
находится истинное содержание Na2CO3?
Решение
При слишком большой доверительной вероятности доверительный интервал
оказывается слишком широким и может захватывать значения, содержащие сис-
тематическую погрешность. При слишком малой доверительной вероятности
доверительный интервал оказывается слишком узким, в него могут не попасть
значения, не содержащие систематической погрешности. Обычно оптимальны-
ми считаются доверительные вероятности 90-95%.
Среднее значение составляет 93,50%. Абсолютное стандартное отклонение
(рассчитайте его при помощи электронной таблицы!) составляет 0,075%. Для
95%-й доверительной вероятности и двух степеней свободы t = 4,303, и довери-
тельный интервал составляет
тт - - . ts 4,303-0,075 оасп,п1п0/
Доверительный интервал = х ± —— = 93,50 ±--—----= 93,50 ± 0,19%
4N V3
Таким образом, при отсутствии систематических погрешностей истинная вели-
чина с вероятностью 95% находится между 93,31 и 93,69%. Этот интервал явля-
ется доверительным интервалом для среднего результата измерений. В то же
время мы видели, что для единичного результата при бесконечном числе изме-
рений истинное значение в 95% случаев попадает в интервал шириной в два
стандартных отклонения (рис. 3.2). Действительно, для v = оо величины t равна
1,96 (табл. 3.1).
Вспомним также (разд. 3.7, рис. 3.2), что единичный результат измерения в
68% случаев попадает в интервал ±1о, в 95% случаев — в интервал ±2о и в 99%
случаев — в интервал ±2,5о. Поэтому возможно оценить величину стандартного
отклонения, зная величину доверительного интервала, и наоборот. Если для еди-
ничного значения для 95%-й доверительной вероятности доверительный интер-
вал составляет 27,37 ± 0,06 г, то стандартное отклонение примерно в два раза
меньше 0,06, т. е. 0,03 г. Эта величина одновременно является полушириной до-
верительного интервала для 68%-й доверительной вероятности. Строго говоря,
эти выводы справедливы лишь для бесконечной серии измерений. При малом
числе измерений значения коэффициентов t увеличиваются, и пропорционально
им увеличивается ширина доверительного интервала.
3.13. ТЕСТЫ СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ: ЕСТЬ ЛИ РАЗЛИЧИЕ МЕЖДУ ДАННЫМИ?
143
Для среднего значения ширина доверительного интервала непрерывно уме-
ньшается с ростом N, поскольку при этом уменьшаются t и s/VtV. Поэтому чем
больше измерений вы проведете, тем более уверенно можете гарантировать, что
истинное значение при отсутствии систематических погрешностей будет нахо-
диться в заданных границах или, наоборот, что эти границы будут более узкими
при заданной доверительной вероятности. В то же время с некоторого N значе-
ния t (как и s/Jn) начинают убывать очень медленно (табл. 3.1). Поэтому суще-
ствует разумный предел, выше которого нецелесообразно увеличивать число
параллельных измерений для увеличения точности.
3.13. Тесты статистической значимости:
есть ли различие между данными?
В ходе разработки новой методики анализа часто возникает необходимость
сравнить ее результаты с результатами общепринятой (возможно — стандарт-
ной) методики. Но как можно выяснить, есть ли значимое различие между резу-
льтатами, полученными при помощи двух методик? Здесь мы опять должны
прибегнуть к помощи статистики.
Решение вопроса о том, значимо ли один набор данных отличается от друго-
го, зависит не только от степени различия средних значений, но также от количе-
ства данных и степени их разброса. Существуют специальные статистические
таблицы, с помощью которых можно оценить, насколько велико должно быть
различие результатов, чтобы его нельзя было считать случайным. Для оценки
степени различия между разбросами серий данных используют F-тест, а для
оценки различия между средними значениями — Z-тест.
F-тест
F-тест показывает нам, имеется ли значимое различие между стандартными от-
клонениями двух серий данных. Для этого вычисляют величину F, представляю-
щую собой отношение дисперсий (т. е. квадратов стандартных отклонений)
сравниваемых серий:
(3.10)
При этом необходимо, чтобы sf было больше s|. Величина F характеризуется
двумя значениями числа степеней свободы Vj и v2, каждое из которых равно чис-
лу данных в соответствующей серии минус единица.
Если величина F, рассчитанная по уравнению (3.10), превосходит соответ-
ствующую табличную величину F для выбранной доверительной вероятности,
144
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Таблица 3.2
Коэффициенты F для 95%-й доверительной вероятности
\v' V2\ 2 3 4 5 6 7 8 9 10 15 20 30
2 19,0 19,2 19,2 19,3 19,3 19,4 19,4 19,4 19,4 19,4 19,4 19,5
3 9,55 9,28 9,12 9,01 8,94 8,89 8,85 8,81 8,79 8,70 8,66 8,62
4 6,94 6,59 6,39 6,26 6,16 6,09 6,04 6,00 5,96 5,86 5,80 5,75
5 5,79 5,41 5,19 5,05 4,95 4,88 4,82 4,77 4,74 4,62 4,56 4,50
6 5,14 4,76 4,53 4,39 4,28 4,21 4,15 4,10 4,06 3,94 3,87 3,81
7 4,74 4,35 4,12 3,97 3,87 3,79 3,73 3,68 3,64 3,51 3,44 3,38
8 4,46 4,07 3,84 3,69 3,58 3,50 3,44 3,39 3,35 3,22 3,15 3,08
9 4,26 3,86 3,63 3,48 3,37 3,29 3,23 3,18 3,14 3,01 2,94 2,86
ю 4,10 3,71 3,48 3,33 3,22 3,14 3,07 3,02 2,98 2,85 2,77 2,70
15 3,68 3,29 3,06 2,90 2,79 2,71 2,64 2,59 2,54 2,40 2,33 2,25
20 3,49 3,10 2,87 2,71 2,60 2,51 2,45 2,39 2,35 2,20 2,12 2,04
30 3,32 2,92 2,69 2,53 2,42 2,33 2,27 2,21 2,16 2,01 1,93 1,84
то различие между дисперсиями значимо. Табличные величины F для 95%-й до-
верительной вероятности приведены в табл. 3.2.
Пример 3.16
Вы разрабатываете новую фотометрическую методику определения глюкозы в сы-
воротке крови и используете для сравнения стандартную методику Фолинь—By.
Пользуясь приведенными ниже результатами параллельных анализов одной и
той же пробы, установите, существует ли значимое различие в воспроизводи-
мости двух методик.
Ваша методика (мг/дл) 127 125 123 130 131 126 129 среднее (xj) 127 Методика Фолинь—By (мг/дл) 130 128 131 129 127 125 среднее (х2) 128
3.13. ТЕСТЫ СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ: ЕСТЬ ЛИ РАЗЛИЧИЕ МЕЖДУ ДАННЫМИ?
145
Решение
2 _ E(x/i ~xi)2 _ 50
51 Nt-1 7-1
2_Z(x«-2-x2)2 _ 24 _
.Vo
2 W2-l 6-1
Отношение дисперсий рассчитывают таким образом, чтобы оно было больше
единицы. Табличное значение F для Vj = 6 и v2 = 5 составляет 4,95. Поскольку
рассчитанное значение меньше табличного, мы приходим к выводу, что значи-
мого различия в воспроизводимостях методик нет, т. е. их случайные погрешно-
сти — одного порядка.
t-Тест Стьюдента:
есть ли различие в результатах анализа по разным методикам?
Очень часто возникает необходимость установить, существует ли статистиче-
ски значимое различие между результатами, полученными при помощи двух
разных методик. Иными словами: можно ли считать результаты этих методик
одной и той же величиной? Для решения таких задач используют Z-тест Стью-
дента. Z-Тест используют для решения вопроса о том, является ли статистически
значимым различие между средними двух серий данных.
Будем называть одну из методик проверяемой, а другую — проверочной. Из
результатов этих методик специальным образом рассчитывают эксперимента-
льную величину t и сравнивают ее с табличным значением (табл. 3.1) для выбран-
ной доверительной вероятности и соответствующего числа степеней свободы.
Если рассчитанное значение t превосходит табличное, то при заданной довери-
тельной вероятности различие между результатами двух методик следует счи-
тать значимым. Если же оно не превосходит табличную величину, то у нас нет
никаких оснований считать различие данных значимым. Разумеется, это не
означает также, что полученные результаты идентичны.
Ниже описаны три различных варианта использования Л-теста. Один из них
применяют тогда, когда известно (из других результатов измерений) значение ц
с точностью, достаточной для того, чтобы его можно было считать истинным.
Если такое значение не известно, можно проанализировать одну и ту же пробу
по двум методикам несколько раз. Можно также проанализировать серию раз-
ных проб по двум методикам. При этом одна из используемых методик не дол-
жна содержать систематической погрешности.
146
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
1. Использование /-теста при известном значении измеряемой величины.
Заметьте, что уравнение (3.9) дает интервал значений измеряемой величины при
отсутствии систематических погрешностей. Поэтому можно записать, что
(3.11)
Из этого следует, что
±г = (х_ц)_
(3.12)
Если величина ц является достаточно надежной оценкой истинного результата
анализа, полученной по данным других измерений (например, она может быть
указана в паспорте стандартного образца, выпускаемого американским Нацио-
нальным институтом стандартов и технологий — NIST, либо представлять собой
значение атомной массы — основы химического анализа), то можно использовать
уравнение (3.12) для того, чтобы решить, являются ли результат измерений и его
истинное значение статистически эквивалентными.
Пример 3.17
Вы разрабатываете методику определения следов меди в биологических матери-
алах, основанную на мокром сжигании пробы с последующим атомно-абсорбцион-
ным определением. Для проверки правильности методики вы проанализировали
стандартный образец листьев яблони, предоставленный NIST. В результате от-
бора и анализа пяти проб получено среднее значение 10,8 ррш и стандартное от-
клонение 0,7 ppm. Паспортное значение содержания меди равно 11,7 ppm.
Можно ли считать результаты методики статистически правильными при 95%-й
доверительной вероятности?
Решение
д/ДГ д/5
+/= (х-ц)—_ = (10,8-11,7)^ =2,9
s 0,7
Поскольку произведено пять измерений, число степеней свободы (N-V) равно 4.
Соответствующее табличное значение t (табл. 3.1) для 95%-й доверительной ве-
роятности равно 2,776. Это меньше рассчитанного значения. Следовательно,
разработанная вами методика содержит систематическую погрешность. Иными
словами, с вероятностью не менее 95% различие между полученным результа-
том и паспортным значением не является случайным.
3.13. ТЕСТЫ СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ: ЕСТЬ ЛИ РАЗЛИЧИЕ МЕЖДУ ДАННЫМИ?
147
Из уравнения (3.12) следует, что чем выше воспроизводимость результатов,
т. е. чем меньше величина s, тем больше рассчитанное значение t. В этом случае
возрастает вероятность, что табличное значение t окажется меньше рассчитан-
ного. Таким образом, чем выше воспроизводимость результатов, тем легче выя-
вить неслучайные различия в данных. Кроме того, рассчитанные значения t
возрастают и с ростом числа измерений [множитель VV в формуле (3.12)]. Поэ-
тому результаты сравнения очень больших серий данных часто оказываются
статистически значимыми. Однако различия в данных, выявляемые в подобных
случаях, бывают очень тонкими и не имеют практического значения.
2. Сравнение средних двух серий данных. Z-Тест можно применять и для срав-
нения двух средних значений. В этом случае уравнение (3.12) несколько видоиз-
меняется: вместо ц в него подставляют среднее для второй серии, а вместо
величины, обратной стандартному отклонению среднего (VVIs), выражение:
N^2 Z
Nl+N2/ Р
где sp — средневзвешенное стандартное отклонение двух серий. Таким образом,
формула (3.12) преобразуется в
±f_*l ~Х2 N1N2
Sp \n1+n2
(3.13)
Средневзвешенное стандартное отклонение (его определение см. ниже) — это
величина, иногда используемая как улучшенная оценка воспроизводимости ме-
тодики. Она же используется для расчета воспроизводимости по двум сериям
данных в парном Z-тесте (см. ниже). Во всех подобных случаях воспроизводи-
мость оценивают из нескольких серий результатов анализов, например, данных,
полученных в разные дни или для образцов, несколько различающихся по соста-
ву. Это иногда бывает предпочтительнее, чем оценивать воспроизводимость из
единственной серии данных. Предпосылкой для таких оценок является допуще-
ние, что каждая серия данных характеризуется одной и той же величиной случай-
ной погрешности. В общем случае средневзвешенное стандартное отклонение
sp рассчитывают по формуле:
£(Л1 -*1) + £(*Z2-*2)2+- + £(x,* ~хк)2
N-k
(3.14)
где х!, х2, ..., хк — средние для 1 -й, 2-й, ..., £-й серии данных, axiX, xi2, ...,xik —
отдельные значения из соответствующих серий. N— общее число данных, рав-
148
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
ное сумме + N2 +...+ Nk. Например, если имеется 5 серий по 20 данных в каж-
дой (хотя в общем случае число данных в каждой серии может быть разным),
то к= 5, a N = 100. Число степеней свободы составляет (N - к), что равно
(N} - l) + (N2 -1) +...+ (Nk - 1). Таким образом, уравнение (3.14) представляет со-
бой комбинацию выражений для расчета стандартного отклонения каждой серии.
При использовании /-теста для сравнения двух средних предполагается, что
обе серии данных характеризуются приблизительно одинаковыми стандартны-
ми отклонениями, т. е. каждое значение s является приближенным значением
одной и той же величины и. Это предположение можно проверить при помощи
описанного выше F-теста.
Пример 3.18
Разработана новая методика гравиметрического определения Fe(III), в ходе ко-
торой железо осаждают в кристаллической форме в виде соединения включения с
борорганическим реагентом. Правильность методики проверили путем сравнения
результатов анализа железной руды с результатами, полученными при помощи
стандартной методики, включающей осаждение гидроксида железа аммиаком и
взвешивание Fe2O3. Результаты анализов (массовая доля железа, %) приведены
ниже.
Проверяемая методика
20,10%
20,50
18,65
19,25
19,40
19,99
х, = 19,65%
Стандартная методика
18,89%
19,20
19,00
19,70
19,40
х2 = 19,24%
Есть ли значимое различие между результатами двух методик?
Решение
х,-1 xn-xi (xn-Xi)2 х/2 хг2-х2 (Х,.2-Х2):
20,10 0,45 0,202 18,89 0,35 0,122
20,50 0,85 0,722 19,20 0,04 0,002
18,65 1,00 1,000 19,00 0,24 0,058
19,25 0,40 0,160 19,70 0,46 0,212
19,40 0,25 0,062 19,40 0,16 0,026
19,99 0,34 0,116 ~ ^г)2 = 0,420
SC^-Xj)2 = 2,262
3.13. ТЕСТЫ СТАТИСТИЧЕСКОЙ ЗНАЧИМОСТИ: ЕСТЬ ЛИ РАЗЛИЧИЕ МЕЖДУ ДАННЫМИ?
149
F _Д|2_ 0,262/5 _П1
-/ 0,420/4 ’
Эта величина меньше табличной (6,26). Поэтому серии данных имеют сопоста-
4 вимые величины стандартных отклонений, и мы можем применить /-тест для
сравнения средних:
'£(*,1 ~*1)2 +Z(x.-2 ~хг)2 _ 12,262 + 0,420
N{+N2-2 У 6 + 5-2
.19,65-19,24 6-5 _
ZL Г — л I — -э
0,546 V 6 + 5 3
Табличное значение t для девяти степеней свободы (N} + N2 - 2 = 6 + 5 - 2 = 9) при
95%-й доверительной вероятности равно 2,262. Таким образом, между результа-
тами, полученными при помощи двух методик, нет статистически значимого
различия.
Точно так же, как результаты анализа одной пробы по двум методикам,
можно сравнивать и результаты анализа двух проб при помощи одной мето-
дики.
3- Парный /-тест. В клинических лабораториях новую методику часто проверя-
ют при помощи стандартной методики, анализируя серию проб, несколько раз-
личающихся по составу (в пределах физиологических состояний). Для этого
случая экспериментальное значение t вычисляют несколько иначе. Сначала для
каждой z-й пробы рассчитывают разность D. между результатами анализа двух
методик (с учетом знака). Затем рассчитывают среднее значение разности, от-
клонения (Z) -D), и из них — стандартное отклонение sd. Значение t находят по
формуле:
(3.15)
(3.16)
150
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Пример 3.19
Вы разрабатываете новую методику определения азота мочевины крови и хоти-
те узнать, значимо ли отличаются ее результаты от результатов анализа при помо-
щи стандартной методики в диапазоне значений концентраций, которых можно
ожидать для большинства реальных проб. Предварительно было установлено,
что воспроизводимости обеих методик значимо не различаются. При анализе се-
рии проб получены следующие результаты:
Проба А Ваша методика (мг/дл) 10,2 Стандартная методика (мг/дл) 10,5 А -0,3 Di-D -0,6 (D-D? 0,36
В 12,7 11,9 0,8 0,5 0,25
С 8,6 8,7 -0,1 -0,4 0,16
D 17,5 16,9 0,6 0,3 0,09
Е 11,2 10,9 0,3 0,0 0,00
F 11,5 И,1 0,4 S 1,7 D = 0,28 0,1 0,01 S 0,87
Решение
Sd= ^1=0,42
d V6-1
0,28
0,42
•л/б =1,63
Табличное значение t для 95%-й доверительной вероятности и пяти степеней
свободы составляет 2,571. Рассчитанное значение t меньше табличного, следо-
вательно, при выбранной доверительной вероятности значимое различие между
результатами двух методик отсутствует.
Вывод о значимости различия двух величин, полученный при 95%-й дове-
рительной вероятности, обычно считается достаточно достоверным. Если такое
различие наблюдается даже при доверительной вероятности 99%, то этот вывод
еще более достоверный. Напротив, если выполнять Z-тест при слишком малой
доверительной вероятности (например, 80%), то можно ошибочно заключить,
что между значениями наблюдается различие, когда на самом деле его нет. Эта
ситуация называется ошибкой I рода. С другой стороны, при слишком высоких
доверительных вероятностях можно не заметить различия, когда оно есть
(ошибка II рода). В целом чем меньше рассчитанное значение /, тем более на-
дежным становится вывод об отсутствии значимого различия между сравнивае-
мыми значениями. Если при 95%-й доверительной вероятности рассчитанное и
3.14. ОТБРОС ПРОМАХОВ: Q-TECT
151
табличное значения t оказываются близки, то для окончательного решения во-
проса о различии величин обычно проводят дополнительные исследования.
3.14. Отброс промахов: Q-тест
Третий закон Финегла: в любом массиве данных величина, наиболее очевидным
образом представляющаяся правильной, ошибочна.
Часто в серии результатов параллельных анализов один из результатов за-
метно отличается от остальных. В таких случаях необходимо принять решение
исключить такой результат из серии или оставить его. К сожалению, критерия,
позволяющего однозначно решить, является ли результат грубым промахом или
обусловлен «обычной» случайной погрешностью, не существует. Разумеется,
всегда есть соблазн удалить вообще все крайние значения, поскольку они могут
существенно ухудшить общую статистику — увеличить значения стандартного
отклонения и дисперсии, а также значительно изменить величину среднего. Но
единственным надежным основанием для удаления результата может служить
установленный факт грубой ошибки, допущенной при его получении. Сохра-
нять такой результат в массиве данных нельзя.
На практике для решения вопроса о сохранении или удалении результата
следует руководствоваться опытом и здравым смыслом в не меньшей степени,
чем результатами каких-либо статистических тестов. Часто опытный аналитик
уже заранее примерно представляет себе, какую воспроизводимость следует
ожидать от методики, и легко распознает подозрительные данные. Если ожидае-
мое стандартное отклонение известно, то можно, например, удалять все резуль-
таты, отстоящие от среднего более чем на 2s или 2,5s: такие результаты могут
встретиться лишь в одном случае из 20 или 100 соответственно.
Тем не менее предложено множество тестов, позволяющих решать вопрос
об удалении результата чисто статистическими методами. Все они так или иначе
основаны на оценке величины некоторого интервала, внутри которого должны
находиться результаты, имеющие статистический смысл. Проблема состоит в
том, как же именно оценить такой интервал. Если он окажется слишком узким,
то вполне «хорошие» результаты могут быть отброшены. Если слишком широ-
ким — в серии слишком часто будут оставаться ошибочные данные. Среди ряда
тестов одним из наиболее статистически корректных (в применении к сериям
малого размера) является 0-тест. Именно его рекомендуется использовать для
выявления промахов. 0-тест состоит в следующем. Сначала все данные распо-
лагают в порядке возрастания или убывания. Затем вычисляют разность между
подозрительным значением и значением, ближайшим к нему, и делят эту раз-
ность (а) на размах всей серии (w) — разность между наибольшим и наимень-
шим значением: Q = a/w. Полученное отношение сравнивают с табличным
значением Q. Если рассчитанное значение Q равно табличному или превышает
его, подозрительное значение следует отбросить. Табличные значения Q для
90-, 95- и 99%-й доверительной вероятности и разного количества данных в се-
рии приведены в табл. 3.3.
152
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
2-тест используют для того, чтобы решить, обусловлено
ли выпадающее значение систематической
погрешностью. Если нет, то оно вызвано лишь обычной
случайной погрешностью и его надо оставить в серии
данных.
Таблица 3.3
Значения Q для разных значений доверительной вероятности*
Число данных в серии Доверительная вероятность
£?90 295 299
3 0,941 0,970 0,994
4 0,765 0,829 0,926
5 0,642 0,710 0,821
6 0,560 0,625 0,740
7 0,507 0,568 0,680
8 0,468 0,526 0,634
9 0,437 0,493 0,598
10 0,412 0,466 0,568
15 0,338 0,384 0,475
20 0,300 0,342 0,425
25 0,277 0,317 0,393
30 0,260 0,298 0,372
*По данным D. В. Rorabacher, Anal. Chem., 63 (1991) 139.
Пример 3.20
При определении хлоридов в отдельных аликвотах объединенной пробы сыво-
ротки крови получены следующие результаты (ммоль экв./л): 103, 106, 107 и
114. Одно из значений вызывает подозрения. Установите, можно ли при 95%-й
доверительной вероятности считать, что оно обусловлено лишь случайными по-
грешностями.
Решение
Подозрительным значением является 114 ммоль экв./л. Разность между ним и
ближайшим соседним значением (107 ммоль экв./л) составляет 7 ммоль экв./л.
Размах всей серии составляет 114-103 = 11 ммоль экв./л. Таким образом, рас-
считанное значение Q составляет 7/11 = 0,64. Табличное значение для серии из
четырех результатов составляет 0,829. Поскольку рассчитанное значение Q
меньше табличного, можно считать, что подозрительное значение обусловлено
лишь случайными погрешностями. Его не следует исключать из серии данных.
3.14. ОТБРОС ПРОМАХОВ: Q-TECT
153
Для малых серий данных (от трех до пяти значений) g-тест может выявить
промах только в том случае, если его отличие от остальных значений весьма ве-
лико. При этом вероятность, что промах останется в серии, высока, следовательно,
значение среднего арифметического окажется сильно искаженным. В подобных
случаях рекомендуется в качестве результата анализа указывать не среднее
арифметическое, а медиану. Для серии данных, упорядоченных по возрастанию,
медианой называется значение, находящееся в центре этой серии (если число
данных нечетное), либо полусумма двух центральных значений (если число дан-
ных четное). Перед средним арифметическим медиана имеет то преимущество,
что ее величина не подвержена столь сильному влиянию промахов. В приведен-
ном выше примере медиана составляет (округленно) 106 (среднее из двух центра-
льных значений, (106 + 107)/2), а среднее — 108. В данном случае эти величины
оказались близки.
Для интерпретации малых (три-пять значений) серий данных, когда одно из
значений заметно отличается от остальных, а оценка воспроизводимости суще-
ственно хуже ожидаемой, можно предложить следующий способ.
1 - Оцените случайную погрешность, которую разумно ожидать от исполь-
зуемой методики, и решите, действительно ли отклонение подозритель-
ного значения столь велико. Имейте в виду, что для серии из трех
значений, когда два из них очень близки, применение g-теста часто при-
водит к неверным выводам (см. ниже).
2- Проверьте все данные, на основании которых было рассчитано подозри-
тельное значение, и подумайте, не были ли допущены ошибки в ходе по-
лучения этих данных.
3. Если нет возможности получить дополнительные данные, примените
g-тест.
4. Если результат g-теста свидетельствует о том, что значение следует
оставить, то для малых наборов данных в качестве конечного результата
используйте медиану, а не среднее арифметическое.
5. В крайнем случае повторите анализ еще раз. Если новый результат хоро-
шо согласуется с теми данными, которые можно считать заведомо верны-
ми, то это дополнительный аргумент в пользу того, что подозрительное
значение следует отбросить. В то же время не следует повторять анали-
зы, добиваясь получения «верного», на ваш взгляд, результата.
g-тест бессмысленно применять к серии из трех значений, два из которых
совпадают: тест всегда укажет на необходимость исключения третьего значения,
как бы мало оно ни отличалось от двух других. Действительно, в этом случае
а = w, и рассчитанное значение g всегда равно 1. То же самое, очевидно, относит-
ся к серии из четырех результатов, три из которых совпадают, и так далее.
154
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
3.15. Статистика малых массивов данных
Статистические методы, разработанные для больших массивов данных, не все-
гда хорошо работают для малых. В предыдущих разделах мы обсудили возможные
способы оценки центрального значения (среднее арифметическое, х), разброса дан-
ных (стандартное отклонение, s) и границ доверительного интервала (при помощи
f-теста) для серии данных, имеющих нормальное распределение. Эти подходы хо-
рошо работают только в случае, когда массив данных достаточно велик. Но в хи-
мическом анализе мы, как правило, имеем дело с массивами данных малого
размера—менее 10, иногда всего 2-3. В этих случаях более подходящими могут
оказаться другие способы оценки.
Одним из методов, специально предназначенных для малых массивов дан-
ных, является рассмотренный выше 2-тест и основанные на нем правила интер-
претации подозрительных результатов.
Медиана может оказаться лучшей оценкой, чем среднее
В качестве оценки центрального значения серии данных может быть использо-
вана медиана М. Ее преимущество в том, что она не столь подвержена влиянию
экстремальных значений (выбросов), как среднее арифметическое х. Относите-
льную (по сравнению со средним арифметическим) эффективность использова-
ния медианы как оценки «истинного» среднего (т. е. среднего, рассчитанного
для бесконечной совокупности данных) можно охарактеризовать в виде показа-
теля эффективности Ем— отношения дисперсий медианы и среднего арифмети-
ческого при заданном размере серии. Величины Ем приведены в табл. 3.4. Они
изменяются от 1 для серии из двух значений (в этом случае медиана всегда сов-
падает со средним) до 0,64 для достаточно больших серий данных. Это означает,
что медиана, вычисленная из серии, содержащей 100 данных (в этом случае Ем
можно принять равным 0,64), является столь же надежной оценкой «истинного»
среднего значения, как и среднее арифметическое, рассчитанное из серии
100 • 0,64 = 64 данных. Аналогично медиана для 10 данных (Ем =0,71) содержит
столько же информации, как и среднее для 10 • 0,71 = 7 данных. При использова-
нии медианы отпадает необходимость решать вопрос о том, содержит ли серия
грубые промахи, и, следовательно, применять 2-тест. Показано, что для серии
из трех значений нормально распределенной величины медиана в любом случае
является лучшей оценкой, чем среднее из двух «лучших» (ближе всего располо-
женных друг к другу) значений.
Использование размаха вместо стандартного отклонения
Для небольших массивов данных величина размаха R является очень эффектив-
ной оценкой разброса результатов. Показатели эффективности для размаха ER,
приведенные в табл. 3.4, свидетельствуют о том, что для серий из четырех или
менее значений размах является практически столь же надежной оценкой, как и
стандартное отклонение. Причина заключается в том, что для малых серий дан-
ных стандартное отклонение само по себе является достаточно плохой оценкой
3.15. СТАТИСТИКА МАЛЫХ МАССИВОВ ДАННЫХ
155
Таблица 3.4
Показатели эффективности и коэффициенты пересчета
статистических характеристик для серий из 2-10 значений*
Число данных Показатель эффективности _ Коэффициент отклонения KR Коэффициент для расчета довери- тельного интервала по размаху
для медианы Ем для размаха ER {г, 0,95 {Г, 0,99
2 1,00 1,00 0,89 6,4 31,83
3 0,74 0,99 0,59 1,3 3,01
4 0,84 0,98 0,49 0,72 1,32
5 0,69 0,96 0,43 0,51 0,84
6 0,78 0,93 0,40 0,40 0,63
7 0,67 0,91 0,37 0,33 0,51
8 0,74 0,89 0,35 0,29 0,43
9 0,65 0,87 0,34 0,26 0,37
10 0,71 0,85 0,33 0,23 0,33
00 0,64 0,00 0,00 0,00 0,00
*По данным R. В. Dean, W. J. Dixon, Anal. Chem., 23 (1951) 636.
разброса (хотя и самой лучшей из всех возможных!). Из величины размаха для
серии данного размера можно оценить стандартное отклонение для бесконечной
совокупности данных, т. е. получить оценку величины о. Для этого значение
размаха необходимо умножить на коэффициент отклонения KR, значения ко-
торого также приведены в табл. 3.4.
s =RKr (3.17)
Для серии из четырех данных, приведенных в примере 3.9, стандартное от-
клонение составляет 0,69 мг, а размах — 1,6 мг. Умножив последнее значение на
величину KR для N= 4, получим s =1,6 мг • 0,49 = 0,78 мг, что близко к величине
стандартного отклонения. С ростом N эффективность размаха как оценки раз-
броса данных уменьшается по сравнению со стандартным отклонением.
При вычислении стандартного отклонения вместо среднего арифметиче-
ского можно использовать медиану. В этом случае влияние резко выделяющих-
ся данных также уменьшается. Еще раз воспользуемся данными примера 3.9:
для расчета стандартного отклонения по формуле (3.2) используем медиану
(29,8) вместо среднего. В этом случае стандартное отклонение окажется равным
0,73 вместо 0,69.
Расчет доверительных интервалов из величин размахов
Значения s, рассчитанные из величин размахов, можно использовать для расчета
границ доверительных интервалов. Эти расчеты производятся по аналогии с
обычной формулой (3.9), но значения коэффициентов пропорциональности надо
брать другие:
156
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Доверительный интервал = х ± Rtr
(3.18)
Вместо коэффициентов t из табл. 3.1 используют специальные коэффициенты tr,
приведенные в табл. 3.4 для 95- и 99%-й доверительной вероятности. Так, для
данных, приведенных в примере 3.15, доверительный интервал, рассчитанный
по уравнению (3.18) для 95%-й доверительной вероятности, составляет
93,50 ± 0,19 • 1,3 = 93,50 ± 0,25% Na2CO3.
3.16. Линейный метод наименьших квадратов:
как провести прямую?
Если требуется линейная зависимость, получи только два результата.
Мудрость аналитика
Аналитику часто приходится строить линейные зависимости, например, градуи-
ровочные прямые. Для обеспечения правильности результатов построение гра-
дуировочных зависимостей имеет решающее значение — ведь именно с их
помощью мы находим содержания веществ в неизвестных образцах! Однако все
результаты измерений характеризуются некоторой неопределенностью, и дан-
ные, используемые для построения градуировочных зависимостей, не составля-
ют исключения. Они неизбежно имеют разброс относительно прямой, и часто
прямую в таких случаях проводят интуитивно, на глаз, просто приложив линей-
ку так, чтобы точки были разбросаны относительно прямой более-менее равно-
мерно. Естественно, более надежным было бы использование статистических
методов, позволяющих определить наиболее вероятное расположение прямой.
Электронные таблицы содержат специальные статистические функции, позво-
ляющие без труда рассчитывать параметры линейных и даже нелинейных зави-
симостей, наилучшим образом соответствующих экспериментальным данным.
Но сначала мы рассмотрим, каким же образом программа рассчитывает эти па-
раметры и осуществляет их статистическую обработку.
Если предполагается, что зависимость между переменными х и у линейна,
то данные должны удовлетворять уравнению
у = тх + b (3.19)
Символом у обозначена зависимая переменная, символом х — независимая
переменная, а параметры т и b называются, соответственно, угловым коэффици-
ентом (тангенсом угла наклона) и свободным членом. Последний представляет
собой длину отрезка, отсекаемого прямой на оси ординату. Как правило, у явля-
ется результатом какого-либо измерения, соответствующего переменной вели-
чине х (рис. 3.7).Так, при построении градуировочного графика в спектро-
фотометрическом анализе у — это измеренное значение оптической плотности,
соответствующее концентрации стандартного раствора х. Нашей задачей явля-
ется нахождение параметров т и Ь.
3.16. ЛИНЕЙНЫЙ МЕТОД НАИМЕНЬШИХ КВДЦРАТОВ: КАК ПРОВЕСТИ ПРЯМУЮ?
157
х (независимая переменная)
РИС. 3.7. Прямая, построенная по методу наименьших квадратов
Метод наименьших квадратов
Статистическими методами можно показать, что экспериментальный набор дан-
ных наилучшим образом описывает та прямая, для которой сумма квадратов
отклонений экспериментальных значений от рассчитанных (эти отклонения
называются остатками) минимальна. Способ построения таких прямых назы-
вается методом наименьших квадратов. Если х — заданная величина (напри-
мер, концентрация), а у — измеряемая величина (оптическая плотность при
спектрофотометрических измерениях, площадь пика при хроматографических
измерениях и т. д.), то отклонения рассчитывают вдоль вертикальной оси у.
В этом случае предполагают, что значения независимой переменной xz не содер-
жат погрешностей. Обозначим экспериментальное значение у, соответствую-
щее заданному значению х-, как у., а рассчитанное значение у (т. е. лежащее на
прямой) — как j>z. Очевидно, величина^ в точности равна mxt + b. Тогда сумма
квадратов отклонений S равна:
s = Y(yi-yl)2=^yi-(mxi+b^2 (3.20)
Наилучшей прямой является та, для которой величина S минимальна. Для
нахождения соответствующих параметров следует продифференцировать выра-
жение для S по т и Ь, приравнять производные нулю и решить полученную сис-
тему из двух уравнений относительно т и Ь. Решениями являются:
£(*,- -х)(у,- - у)
£(*,• -к)2
Ъ- у — тх
(3.21)
(3.22)
где х — среднее из всех значений х/5 а у — среднее из всех значений у.. Выраже-
ние (3.21) можно преобразовать в форму, более удобную для вычислений (осо-
бенно на калькуляторе):
158
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
-[(Zx«)2 /"]
(3.23)
где п — общее число точек (пар значений х/5 уг).
Значения углового коэффициента и свободного члена, рассчитанные по ме-
тоду наименьших квадратов, характеризуют наиболее вероятное прохождение
прямолинейной зависимости.
Пример 3.21
В образце зерна определяли рибофлавин (витамин В2) путем измерения интен-
сивности флуоресценции вытяжки в 5%-й уксусной кислоте. Для построения
градуировочной зависимости были измерены интенсивности флуоресценции се-
рии стандартных растворов рибофлавина возрастающей концентрации. По по-
лученным данным при помощи метода наименьших квадратов рассчитайте
параметры наилучшей прямолинейной градуировочной зависимости и опреде-
лите концентрацию рибофлавина в анализируемом растворе (интенсивность его
флуоресценции равна 15,4).
Концентрация Интенсивность
рибофлавина, мкг/мл = ррт (х;) флуоресценции, усл. ед. (у,) X,2 Х1У,
0,000 0,00 0,0000 0,00
0,100 5,8 0,0100 0,58
0,200 12,2 0,0400 2,44
0,400 22,3 0,16Оо 8,92
0,800 43,3 О,64Оо 34,64
£х,- =1,500 Хл =83,6 £>• = О,85Оо =46>58
(£х,.)2 =2,250 п = 5 х = У х,- =0,3000 п y = S2± = 1б,72 п
Решение
При помощи уравнений (3.23) и (3.22) получаем:
46,5 8 - [(1,500 - 83,6)/5]
О,85Оо -2,250/5
= 53,75 (усл. ед./ррш)
b = 16,72 - (53,75 • О,ЗООо) = О,6о (усл. ед.)
3.16. ЛИНЕЙНЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ: КАК ПРОВЕСТИ ПРЯМУЮ?
159
РИС. 3.8. Градуировочный график, построенный методом наименьших квадратов по данным при-
мера 3.21
В ходе вычислений мы сохраняли максимальное число значащих цифр. Посколь-
ку экспериментальные данные (у) получены с точностью до одного знака после
запятой, величины т и b также округлим до одного знака после запятой. Таким
образом, уравнение градуировочной прямой имеет вид (ppm = мкг/мл):
у (усл. ед.) = 53,8 (усл. ед./ррт) • х (ррт) + 0,6 (усл. ед.)
Рассчитаем концентрацию в анализируемой пробе:
15,4 = 53,8х + 0,6
х = 0,275 мкг/мл
Для построения градуировочного графика достаточно взять два произвольных
значения х, отстоящих далеко друг от друга, рассчитать соответствующие им
значения у (или наоборот) и провести прямую через эти точки. На рис. 3.8
изображены экспериментальные точки и градуировочный график. Этот рису-
нок был построен при помощи программы Excel, позволяющей также вывести
уравнение прямой линии и значение квадрата коэффициента корреляции. Оно
является мерой близости экспериментальных и рассчитанных значений (см. да-
лее). Приведенные значения имеют дополнительные десятичные цифры, посколь-
ку их число определяется программой автоматически.
160
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Стандартные отклонения углового коэффициента и свободного
члена: они характеризуют неопределенность результата
Будем исходить из допущения, что для каждой точки градуировочного графика
значение ^-представляет собой случайную величину, распределенную по норма-
льному (гауссовому) закону. В соответствии с уравнением (3.20) отклонение ор-
динаты точки от градуировочной прямой равно угу1 = у - (тх + Ь). Из этих
значений можно рассчитать стандартное отклонение величин у. Расчет прово-
дится по аналогии с уравнением (3.2) за исключением того, что число степеней
свободы равно N - 2 (две степени свободы затрачены на нахождение двух пара-
метров — углового коэффициента и свободного члена):
/[£ У- - (Е У,- )2/N] - m2[^i - )2>]
N-2 N N-2
Эта величина называется стандартным отклонением относительно линии рег-
рессии. Неопределенности (стандартные отклонения) параметров т и b опреде-
ляются величиной s и могут быть из нее рассчитаны. Стандартное отклонение
углового коэффициента т равно
s2
s = _-У_
т Ш^)2
I
fc2-(&)2>
(3.25)
Здесь х, как и ранее, есть среднее из всех значений xz.
Стандартное отклонение свободного члена равно
Из стандартных отклонений, характеризующих неопределенности значений}/, т
и £, можно рассчитать стандартное отклонение содержания вещества в анализи-
руемой пробе х, пользуясь уравнением (3.19) и известным нам законом наложе-
ния (распространения) погрешностей*.
Указанный способ оценки неопределенности значения х достаточно приближенный. Закон наложения по-
грешностей в той его форме, которая приведена в книге, справедлив только в том случае, если все аргументы
взаимно некоррелированы. В то же время параметры градуировочной зависимости т и Ь, как правило, связа-
ны между собой отрицательной корреляцией. Это обстоятельство можно учесть и получить более реалистич-
ную оценку стандартного отклонения х. См., например, [Аналитическая химия. Проблемы и подходы. T. 2 /
Под ред. Р. Кельнера и др. М.: Мир, ООО «Издательство АСТ», 2004, с. 470]. — Прим, перев.
3.16. ЛИНЕЙНЫЙ МЕТОД НАИМЕНЬШИХ КВДЦРАТОВ: КАК ПРОВЕСТИ ПРЯМУЮ?
161
Пример 3.22
Оцените неопределенности значений углового коэффициента, свободного члена
и величину для данных из примера 3.21, а также неопределенность найденного
значения концентрации рибофлавина.
Решение
Чтобы рассчитать все требуемые величины неопределенностей, необходимы
значения ^yz2, (^yz2 )2, )2 и т2. Для данных, приведенных в при-
мере 3.21, (^у. )2 = (83,6)2 = 6989,0, (£х2)2 = O,85Oo, QV )2 = 2,250 и
т2 = (53,75)2 = 2,889 • 103. Значения (у,)2 равны 0,0, 33,6, 148,8, 497,3 и 1874,9.
Отсюда Ху- = 2554,6 (значение приводим с запасными цифрами). Из уравне-
ния (3.24):
_ /(2554,6-6989,0/5) - (53,75)2(О,85Оо -2,250/5) _+()б
sy А s ’ з Усл’ ед-
Из уравнения (3.25):
Sm
' (0,63)2
О,85Оо -2,250/5
= ±1,0 усл. ед./ррш
Из уравнения (3.26):
_ | 0,850о л А
sh =0,6 о --------------= ±0,4, усл. ед.
ь у 5(О,85Оо)-2,250 1
Отсюда т = 53,8 ± 1,0 и b = 0,6 ± 0,4.
Концентрацию рибофлавина в пробе рассчитаем как
(у ± sy)-(b ± sb )_ (15,4 ±0,6)-(0,6 + 0,4) _ПТ7 . 9
w±jm 53,8+1,0
Используя общие принципы наложения погрешностей (при сложении- вы-
читании суммируются абсолютные дисперсии, при умножении-делении — от-
носительные), получим оценку неопределенности величины х:
х = 0,215 ± 0,014 мкг/мл (ppm).
О расчетах стандартного отклонения относительно линии регрессии и стандарт-
ного отклонения х при помощи электронных таблиц см. в гл. 16.
162
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
3,17. Коэффициент корреляции и коэффициент детерминации
Коэффициент корреляции служит мерой корреляции (взаимной зависимости)
между двумя величинами.* Если связь между переменными х и у не является
строго функциональной, то нет смысла говорить о «наилучшем» значении у, со-
ответствующем данному х. Можно говорить лишь о «наиболее вероятном» зна-
чении у. Чем ближе экспериментальные значения к наиболее вероятным, тем
более определенной является зависимость между х и у. Это положение служит
основой для вычисления различных величин, характеризующих степень корре-
ляции между переменными.
Среди таких величин одна из самых простых по способу вычисления —
коэффициент корреляции Пирсона г. Он рассчитывается по формуле:
у (*,- -х)(^- - у)
nsxsy
(3.27)
где п — число данных (пар значений х,у), sx — стандартное отклонение х, sy —
стандартное отклонение у, хги — отдельные значения х и соответствующие им
значения у, х и у— средние значениях и у. Уравнение (3.27) можно записать в
другой форме:
^х^-пху
7(£Х2 ~ wx2xZ^2 -«х2)
^In^xf -(.^хУ ][n^yj ~(^уУ]
(3.28)
Несмотря на устрашающий внешний вид, формула (3.28) обычно оказывается
более удобной для вычисления г, чем формула (3.27), особенно при использова-
нии калькулятора.
Наибольшее возможное значение г равно 1. В этом случае между двумя пе-
ременными имеется строгая линейная зависимость. Если значение г равно нулю,
переменные можно считать полностью независимыми друг от друга. Наимень-
шее возможное значение г равно -1. В этом случае между переменными также
наблюдается строгая линейная зависимость. Отрицательное значение коэффи-
циента корреляции указывает на то, что с возрастанием одной переменной (напри-
мер, х) другая переменная (у) убывает. В этом случае коэффициент корреляции
между величинами х и -у по абсолютной величине тот же, что и между хи у, только
положительный.
Более строго — мерой близости этой зависимости к линейной. — Прим, перев.
3.17. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ И КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ
163
Пример 3.23
Рассчитайте коэффициент корреляции для данных из примера 3.19, приняв зах
результаты, полученные при помощи вашей методики, а за у — при помощи
стандартной методики.
Решение
Рассчитаем значения ^xz2 = 903,2, у? = 855,2, х = 12,0, у = 11,7и ]>\z- у{ - 878,5.
Отсюда по уравнению (3.28):
878,5 -6-12,0-11,7
________________________________= 0,991
7(903,2 - 6 • 12,02 )(855,2 - 6 • 11,72 )
Коэффициент корреляции можно рассчитать для данных градуировочного
графика. Он показывает, насколько близка к линейной связь между измеренны-
ми значениями аналитического сигнала и концентрациями стандартных растворов.
Как правило, если значение г находится в диапазоне 0,90-0,95, это свидетельствует
об удовлетворительном качестве градуировки, если в диапазоне 0,95-0,99 —
о хорошем, а если превышает 0,99 — об отличном качестве. При тщательной ра-
боте иногда можно получить значения г, превышающим 0,999.
При расчете коэффициента корреляции обе переменные рассматриваются
как равноправные. В действительности одна из них обычно является независи-
мой, а другая — зависимой. Численные значения г часто сбивают с толку. Вели-
чина коэффициента корреляции, равная 0,98, кажется весьма близкой к единице,
но соответствующий градуировочный график может быть довольно плохим.
Если значения г, меньше 0,9, это в любом случае свидетельствует о плохом каче-
стве градуировочной зависимости.
В этом отношении более наглядной оценкой соответствия двух серий дан-
ных служит квадрат коэффициента корреляции г2. Именно его вычисляет боль-
шинство стандартных статистических программ (включая Excel — см. рис. 3.8).
Величина г, равная 0,90, соответствует величине г2, равной лишь 0,81, а для
г = 0,95 г2 = 0,90. О близости серий данных можно судить по числу девяток в
значении г. Три девятки и более (г > 0,999) свидетельствуют об отличном соот-
ветствии. В дальнейшем в качестве меры близости серий данных мы будем ис-
пользовать величину г2. Ее часто называют коэффициентом детерминации.
Необходимо подчеркнуть, что коэффициент корреляции характеризует лишь
степень взаимозависимости между двумя массивами переменных в целом и со-
вершенно не свидетельствует о численной близости их значений. Вполне возмож-
на ситуация, когда между результатами анализов, полученными при помощи двух
методик, наблюдается высокая корреляция (значение г2 близко к единице), но
164
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
Z-тест показывает значимое различие между их средними значениями. Это мо-
жет быть, например, в случае, если одна из методик содержит постоянную сис-
тематическую погрешность. Если результаты анализов, полученные для разных
проб при помощи двух методик, представить в виде точек на плоскости (ось х —
данные одной методики, ось у — другой методики), то близость величины г2 к
единице говорит лишь о том, что точки хорошо ложатся на некоторую прямую
линию. Однако угловой коэффициент этой прямой может сколь угодно отличать-
ся от единицы, а свободный член — от нуля. В подобных случаях можно при по-
мощи эмпирических поправочных коэффициентов привести результаты обеих
методик в соответствие друг с другом во всем исследуемом диапазоне концент-
раций.
3.18. Использование электронных таблиц для построения
градуировочных графиков
Использование электронных таблиц позволяет избежать расчетов параметров
линейных зависимостей и их построения на листе миллиметровой бумаги вруч-
ную. Используем данные примера 3.21 для построения графика, изображенного
на рис. 3.8, при помощи Excel.
Откройте новый файл Excel и введите в указанные ячейки следующие дан-
ные.
Ячейка А1: Концентрация рибофлавина, мкг/мл (подберите необходимую
ширину столбца)
Ячейка В1: Интенсивность флуоресценции
Ячейка АЗ: 0,000
Ячейка А4: 0,100
Ячейка А5: 0,200
Ячейка А6: 0,400
Ячейка А7: 0,800
Ячейка ВЗ: 0,0
Ячейка В4: 5,8
Ячейка В5: 12,2
Ячейка В6: 22,3
Ячейка В7: 43,3
Отформатируйте ячейки так, чтобы числа в столбце А содержали три, а в столб-
це В — одну цифру после запятой.
Нажмите на кнопку Мастер диаграмм (Chart Wizard), расположен-
ную на панели инструментов. На экране появится окно Шаг 1 из 4 : тип
диаграммы (Step 1-Chart Type).
3.18. ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОННЫХ ТАБЛИЦ ДЛЯ ПОСТРОЕНИЯ ГРАДУИРОВОЧНЫХ ГРАФИКОВ
165
Выберите тип Точечная (Scatter) и далее Точечный (Scatter) (по
line), после чего нажмите клавишу Далее (Next).
В появившемся окне в строке Диапазон данных (Data Range) введите
АЗ:В7 [или откройте вкладку Ряд (Series), после чего введите диапазоны ад-
ресов переменных X и Y в отдельных строках и затем откройте вкладку Диапа-
зон данных (Data Range)].
Отметьте позицию В столбцах (Columns) и нажмите клавишу Далее
(Next).
В появившемся окне, содержащем несколько строк, введите текст:
• в строку Название диаграммы (Chart Title) — «Градуировочный
график»
• в строку Ось X (Value (X) axis) — «Концентрация рибофлавина»
• в строку Ось Y (Value (Y) axis) — «Интенсивность флуоресценции»
Откройте вкладку Линии сетки (Gridlines) и снимите отметку
Основные линии (Maj or gridlines).
Откройте вкладку Легенда (Legend) и снимите отметку Добавить ле-
генду (Show legend).
Откройте вкладку Подписи данных (Data labels) и отключите все
позиции (ради интереса можете попробовать проставлять отдельные галочки и
посмотреть, что получится).
Нажмите клавишу Далее (Next).
166
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
В появившемся окне отметьте позицию На отдельном листе (As New
sheet); в соответствующей строке при этом будет текст Диаграмма 1
(Chart 1).
Нажмите клавишу Готово (Finish). После этого градуировочный график
появится на отдельном листе файла Excel.
Теперь отобразим уравнение, полученное методом наименьших квадратов, и
величину г2. Выделите область диграммы. В строке Меню откройте меню Диа-
грамма (Chart) и выберите пункт Добавить линию тренда (Add Trend-
line). Откроется новое окно, в котором выберите пункт Линейная (Linear).
Далее откройте вкладку Параметры (Options) и отметьте позиции:
• Показывать уравнение на диаграмме (Display equation on
chart)
• Поместить на диаграмму величину достоверности аппрок-
симации (R2) (Display R-squared value on chart).
Нажмите клавишу OK.
Теперь взгляните на диаграмму. Щелкните по ней клавишей мыши, чтобы
убрать маркеры концов отрезка. Окошко с текстом, содержащим уравнение пря-
мой, можно переместить влево и увеличить. Для этого щелкните клавишей
мыши на уравнении. Оно окажется в прямоугольном окошке с небольшими
квадратиками по периметру. Щелкните по левому нижнему квадратику и пере-
тащите окошко влево вниз. Чтобы увеличить размер шрифта, в меню Формат
(Format) выберите Выделенные подписи данных ... : Шрифт (Se-
lect data labels : Font). Выберите размер шрифта 14 и нажмите ОК. Пе-
ретащите уравнение ближе к прямой. Вы можете увеличить и размер шрифта
подписей осей. Для этого щелкните по соответствующей подписи и далее посту-
пайте, как описано выше.
Область построения диаграммы имеет серый фон. Давайте от него избавим-
ся. Щелкните в произвольной точке фона, затем в меню Формат (Format) выбе-
рите Выделенная область построения ... (Select Plot Area).
Щелкните на квадратике, окрашенном в белый цвет, и нажмите ОК. После всего
этого ваша диаграмма будет иметь вид, подобный рис. 3.8.
При построении диаграммы вы можете в самом начале выделить ячейки, со-
держащие данные (АЗ:В7). В этом случае их адреса будут автоматически поме-
щены в соответствующую строку окна Диапазон данных (Data Range).
Кроме того, вы можете разместить диаграмму не на отдельном листе, а на том
же, куда вводили данные. Для этого вместо На отдельном листе (As New
sheet) вам следует отметить позицию На имеющемся (As object in); в соот-
ветствующей строке будет текст Лист 1 (Sheet 1). Рисунок, появившийся на ли-
сте с данными, вы можете переместить в любое место листа. Для этого щелкните
по рисунку и перетащите его за уголок. На рис. 3.9 изображен график, размещен-
ный на листе с данными. Попробуйте создать его. Если график размещен на листе
с данными, то при изменении данных в ячейках, использованных для построения,
график будет автоматически изменяться. Попробуйте проделать и это, пред-
варительно сохранив файл, а затем переименовав его. Если вы хотите вывести на
печать только график, то выделите его, щелкнув по нему кнопкой мыши.
3.19. РАСЧЕТ УГЛОВОГО КОЭФФИЦИЕНТА, СВОБОДНОГО ЧЛЕНА И КОЭФФИЦИЕНТА ДЕТЕРМИНАЦИИ
167
3.19. Расчет углового коэффициента,
свободного члена и коэффициента детерминации
при помощи электронных таблиц
Использование статистических функций Excel позволяет рассчитать величины
углового коэффициента, свободного члена и коэффициента детерминации ли-
нейной зависимости без построения графика. Откройте новый файл и введите
данные из примера 3.21 в ячейки АЗ:В7, как показано на рис. 3.9. В ячейку А9
введите текст «Свободный член», в ячейку А10 — «Угловой коэффициент», в
ячейку All — «R2». Выделите ячейку В9, нажмите fx: Статистические
(Statistical) и прокрутите меню с именами функций вниз до появления
строки ОТРЕЗОК (INTERCEPT). Выделите эту строку и нажмите ОК. В строке
Известные_значения_х (Known_x ’ s) введите диапазон адресов АЗ:А7, а в
строке Известные_значения_у (Known_y ’ s) — ВЗ:В7. Нажмите ОК, и ве-
личина свободного члена появится в ячейке В9. Аналогично поступите с ячей-
кой В10, выделив ее и выбрав в качестве имени функции SLOPE (НАКЛОН).
Значение углового коэффициента появится в ячейке В10. Наконец, выделите
ячейку Bl 1 и выберите имя функции КВ ПИРСОН (RSQ). В ячейке Bl 1 появится
значение г2. Сравните полученные значения с приведенными на рис. 3.9.
РИС. 3.9. Градуировочный график, вставленный в рабочий лист файла Excel (Лист 1)
168
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
3.20. Программа ЛИНЕЙН (UNEST) для выполнения различных
статистических расчетов
Электронные таблицы Excel снабжены программой ЛИНЕЙН (LINEST), позво-
ляющей быстро рассчитывать различные статистические характеристики для
наборов данных, — например, величины углового коэффициента, свободного
члена и их стандартные отклонения, коэффициент детерминации, стандартное
отклонение предсказания, а также многие другие, которые мы здесь обсуждать
не будем. Программа ЛИНЕЙН (LINEST) позволяет рассчитать одновременно 10
статистических величин, располагаемых в двух столбцах рабочего листа.
Откройте новый файл Excel и введите в ячейки АЗ : В7 данные градуировоч-
ного графика из примера 3.21 так же, как вы делали ранее (сверяйтесь с рис. 3.10).
Статистические характеристики будут помещены в’ 10 ячеек, поэтому давайте
сначала пометим каждое из них. Используем для рассчитанных величин ячейки
В9 : С13. Введите подписи:
Ячейка А9: угловой коэффициент
Ячейка А10: станд. откл. углового коэффициента
Ячейка All: R2
Ячейка А12: F
Ячейка А13: сумма квадратов отклонений
Ячейка D9: свободный член
Ячейка D10: станд. откл. свободного члена
Ячейка DI 1: станд. откл. оценки
Ячейка D12: число ст. своб.
Ячейка D13: остаточная сумма квадратов
А В С D Е
1 Концентрация рибофлавина, мкг/мл Интенсивность флуоресценции
2
3 0,000 0,0
4 0,100 5,8
5 0,200 12,2
6 0,400 22,3
1 0,800 43,3
8
9 угловой коэффициент 53,75 0,595 свободный член
10 станд. откл. углового коэффициента 1,017759 0,419633 станд. откл. свободного члена
11 R2 0,998926 0,643687 станд. откл. оценки
12 F 2789,119 3 число ст. своб.
РИС. 3.10. Использование программы ЛИНЕЙН (LINEST) для статистических расчетов
3.21. ПАКЕТЫ ПРИКЛАДНЫХ СТАТИСТИЧЕСКИХ ПРОГРАММ
169
Выделите ячейки В9:С13 и нажмите fx. В меню Статистические (Statis-
tical) выберите ЛИНЕЙН (LINEST) и нажмите ОК. В строке Изв_знач_у
(Known_y's) введите диапазон адресов ВЗ:В7, а в строке Изв_знач_х
(Known_x ’ s) — АЗ: А7. Затем в каждой из строк Константа (Const) и Ста-
тистика (Stats) наберите Истина («true»). Для продолжения вычислений
нажмите на клавиатуре комбинацию клавиш Shift, Ctrl и Enter и отпустите их.
Рассчитанные статистические величины появятся в выделенных ячейках. Ука-
занное сочетание клавиш необходимо нажимать всегда при использовании фун-
кций, возвращающих массив значений в диапазон ячеек. Значение углового
коэффициента появится в ячейке В9, а его стандартное отклонение — в ячейке
В10. Величина свободного члена и его стандартное отклонение появятся в ячей-
ках С9 и СЮ соответственно. Сравните величины стандартных отклонений с
рассчитанными в примере 3.22, а сами значения углового коэффициента, сво-
бодного члена, а также г2 — с рассчитанными в примере 3.22 или приведенными
на рис. 3.8.
Ячейка С11 содержит величину, названную «стандартное отклонение
оценки». Это синоним термина «стандартное отклонение относительно линии
регрессии» — уже известной нам величины, являющейся мерой погрешности
при расчете значений у. Чем эта величина меньше, тем ближе эксперименталь-
ные данные к рассчитанным. Ячейка В12 содержит экспериментальную величи-
ну F, ячейка С12 — число степеней свободы, использованное для ее расчета,
ячейка В13 — сумму квадратов, обусловленную регрессией, ячейка С13 — оста-
точную сумму квадратов.
Сколько значащих цифр необходимо указывать в записи статистических па-
раметров прямой? Ответ дают величины стандартных отклонений. Угловой коэф-
фициент характеризуется стандартным отклонением 1,0, поэтому его значение
лучше всего указать как 53,8 ± 1,0. Стандартное отклонение свободного члена
равно 0,42, поэтому значение свободного члена запишем в виде 0,6 ± 0,4.
См. также пример 3.22.
3.21. Пакеты прикладных статистических программ
Программа Excel содержит множество статистических функций, перечислен-
ных в меню Сервис (Tools). Для доступа к ним в меню Надстройки. . .
(Add-Ins) отметьте Analysis ToolPak, нажмите ОК и вернитесь к работе с
файлом. После этого в меню Сервис (Tools) появится пункт Анализ данных
(Data Analysis). В нем вы найдете 19 различных статистических программ.
Попробуйте поупражняться с ними: некоторые программы вы найдете очень по-
лезными. Одной из них, безусловно, является Поиск решения (Solver) —
программа для решения сложных уравнений. Как пользоваться этой программой,
описано в гл. 6. Посмотрите также список коммерческих программных продук-
тов для выполнения как простейших, так и более сложных статистических рас-
четов, приведенный на сайте www.wiley.com/college/christian.
170
ОБРАБОТКА ДАННЫХ И ЭЛЕКТРОННЫЕ ТАБЛИЦЫ
6 делений
Рис. 3.11. Один из способов оценки предела обнаружения. При непрерывной регистрации сигна-
ла видны как флуктуации фона, так и пик, обусловленный наличием аналита. Пик аналита можно
считать надежно детектируемым, если его высота вдвое превосходит размах колебаний фона (т. е.
в данном случае составляет 12 делений шкалы, считая от среднего уровня фона)
3.22. Предел обнаружения:
в аналитической химии нет понятия «нуль»!
До сих пор мы обсуждали применение статистических методов для вероя