ЭЛЕМЕНТАРНАЯ
МАТЕМАТИКА
ТЕОРИЯ И ПРАКТИКА
РЕШЕНИЯ ЗАДАЧ
В.В.Зайцев
В.В.Рыжков
М.И.Сканави
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
ПРЕДИСЛОВИЕ РЕДАКТОРА
Предлагаемое учебное пособие — это результат авторской пере-
работки известной книги «Элементарная математика», выдержавшей
целый ряд изданий, переведенной на английский язык и ставшей к
настоящему моменту библиографической редкостью. Удачное соче-
тание последовательного, методичного изложения теоретических ос-
нов курса элементарной математики с продуманным выбором целой
системы приемов решения задач позволило авторам создать пособие,
полезное как при начальном изучении математики в средней школе,
так и при повторном изучении с целью пополнить, укрепить и систе-
матизировать свои знания при подготовке к вступительным экзаме-
нам в ВУЗ. Помимо материалов программы вступительных экзаме-
нов в пособии приведены некоторые дополнительные разделы, спо-
собствующие углубленному пониманию курса элементарной матема-
тики.
Составной частью учебного пособия является изложение методов
решения задач по элементарной математике с приведением большого
числа решений типовых задач и задач для самостоятельного реше-
ния. Подбор задач проводился на основе «Сборника задач по матема-
тике для конкурсных экзаменов во ВТУЗы», изданного под редак-
цией М.И.Сканави и с участием авторов данной серии учебных посо-
бий.
Учебное пособие содержит весь необходимый материал и может
использоваться абсолютно автономно, без привлечения других учеб-
ников и задачников. Пособие разделено на серию отдельных выпу-
сков.
1.	Преобразования алгебраических выражений.
2.	Алгебраические уравнения и неравенства.
3.	Функции и графики. Логарифмические уравнения и неравенства.
4.	Тригонометрические функции.
5.	Тригонометрические уравнения и неравенства.
6.	Планиметрия.
7.	Стереометрия.
Издание всех выпусков серии планируется в 1992 году.
Все предложения, замечания и пожелания по содержанию настоя-
щего учебного пособия и заявки на последующие выпуски просим на-
правлять в адрес издательства: 119634, Москва, ул.Шолохова, дом 9,
«Международный научный центр ученых МГУ им. М.В.Ломоносова».
Н.Кислов
В.В.ЗАЙЦЕВ, В.В.РЫЖКОВ, М.И.СКАНАВИ
ЭЛЕМЕНТАРНАЯ
МАТЕМАТИКА
ТЕОРИЯ И ПРАКТИКА
РЕШЕНИЯ ЗАДАЧ
(в помощь поступающим в ВУЗы)
ВЫПУСК 4
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Редактор Н.В.КИСЛОВ
МЕЖДУНАРОДНЫЙ НАУЧНЫЙ ЦЕНТР УЧЕНЫХ МГУ
им. М.В.ЛОМОНОСОВА
Москва, 1 992 г.
51
3 177
УДК 510
ОТ АВТОРОВ
Настоящая серия учебных пособий явилась результатом пере-
работки книга «Элементарная математика», впервые вышедшей в
1967 году и переизданной в переработанном виде в 1974, 1976 гг. При
подготовке второго издания внезапно ушел из жизни инициатор и
один из авторов книги Марк Иванович Сканави, но его идеи и конкрет-
ные разработки вошли и в предлагаемое новое издание. Мы считаем
своим долгом включить М.И.Сканави в число авторов настоящего из-
дания.
3,.Зайцев, В.В,Рыжксв
Элементарная математика. Теория и практика решения задач
(в помощь поступающим в ВУЗы). Тригонометрические функции.
Зайцев В.В., Рыжков В.В., Сканави М.И. /Под рсд. Кислова Н.В. —
М.: Изд-во Международного научного центра ученых МГУ им.
М.В.Ломоносова, — 1992, — 104 с.
В пособии изложены теоретические основы курса элементарной математики, при-
ведены основные методы решения типовых задач и условия задач для самостоятельно-
го решения.
В настоящем выпуске рассмотрены свойства тригонометрических функций, мето-
ды тождественных преобразований тригонометрических выражений. Пособие пред-
назначено для учащихся старших классов школ с повышенной математической подго-
товкой, для слушателей подготовительных отделений ВУЗов и для поступающих в
ВУЗы.
Рецензенты:
Доктор физ.-мат. наук, профессор Ю.Г.Мартыненко
Канд. техн, наук доцент В.Е.Хроматов
„ 1602050000—001
J М56(03)—92
© Международный научный центр ученых МГУ им. М.В.Ломоносова, 1992 г.
Глава 1
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
§ 1. Векторы. Обобщение понятий угла и дуги
1. Вектор, проекция вектора. Вектором называется направлен-
ный отрезок в плоскости (в пространстве). При изучении тригоно-
метрических функций мы будем рассматривать векторы в плоскости.
С каждым вектором связывают понятия направления и длины (абсо-
лютной величины, модуля).
Для вектора (рис. 1) применяются следующие обозначения:
Рис. 1	Рис. 2
-
АВ=АВ=а, где А — начало вектора, В — его конец. Длина отрезка
АВ называется длиной вектора АВ (его абсотуотной величиной, мо-
дулем) и обозначается так: I АВ I, I а I или*1 АВ I. Для общности рас-
сматривается и случай нулевого отрезка АА, начало которого совпа-
дает с его концом. Такой отрезок называется нулевым вектором и
обозначается через 0. Нулевой вектор имеет длину, равную нулю;
ему не приписывается никакого направления.
Следует заметить, что всегда 13771 > 0, причем 13271 = 0 тогда и только тогда, ког-
да 377 — нулевой вектор.
Для векторов не имеют смысла понятия «больше» или «меньше». Можно только го-
ворить, что длина вектора АВ больше длины вектора CD, и писать: I АВ I > I CD I.
Два вектора а и b называются равными, если они:
1)	параллельны одной и той же прямой,
2)	одинаково направлены,
3)	имеют равные длины, т.е. lai = 1Ы (рис. 2).
Совокупность векторов с указанным выше определением равенства обычно назы-
вают системой свободных векторов. Термин «свободный вектор» связан с тем, что те-
перь один и тот же вектор может быть изображен направленным отрезком с началом в
любой точке: его можно свободно переносить из точки в точку.
4
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
Каждому вектору ~КВ можно поставить в соответствие лежащий на заданной оси
OL вектор AiВ\, где точки Ai и В| соответственно — проекции на ось OL точек АпВ
(рис. 3). Проекцией вектора~КБ на ось OL называется длина вектора АгВ;, взятая со
Рис. 3
Рис. 4
знаком плюс, если направление вектора A[Bi совпадает с положительным направле-
нием оси, и со знаком минус в противном случае. Итак, проекция вектора TlB на ось
есть по определению число (не вектор!). Условимся проекцию вектора на ось OL
Рис. 5
Рис. 6
обозначать так: про;уГВ. Возможны следующие случаи: а) прот7ГО = + 1 A| Bi 1>0 (рис. 3),
б) про/ДВ IAjBi КО (рис. 4), в) протДВ-О (рис. 5).
Рассмотрим теперь совокупность векторов, исходящих из одной
точки (начала). Такая совокупность векторов называется центриро-
ванной. Примем эту общую точку за начало О декартовой прямо-
угольной системы координат Оху.
Определение. Вектор ОМ, имеющий своим началом точку О
(начало координат) и своим концом произвольную точку М плоско-
сти, называется радиусом-вектором точки М или подвижным радиу-
сом (рис, 6). Радиус-вектор обозначается и так: г(М), т.е. ОМ -
=г(М). Через х и у обозначим соответственно абсциссу и-ординату
точки М, а через г — длину (модуль) вектора ОМ. Следовательно, г=
= 1OMI =1 r(M) I. Заметим, что координаты хиу точки М являются
§ I. ВЕКТОРЫ. ОБОБЩЕНИЕ ПОНЯТИЙ УГЛА И ДУГИ
5
вместе с тем проекциями ее радиуса-вектора г(м) на оси координат.
2.	Положительные углы и дуги, меньшие 360°. На координатной
плоскости Оху рассмотрим окружность радиуса R с центром в начале
координат (рис. 7).
Будем считать, что угол а =
= LAOE образован вращением не-
которого подвижного радиуса-век-
тора, абсолютная величина которо-
го равна R, в направлении, проти-
воположном движению часовой
стрелки, от начального положения
(Й, совпадающего с положитель-
ным направлением оси Ох, до ко-
нечного положения ОЕ. Такой угол
а считается положительным.
Обозначим через Г (один гра-
дус) угол, равный 1/360 части пол-
ного угла, т.е. угла, соответствую-
щего одному обороту радиус-векто-
ра. При вращении (в направлении
против движения часовой стрелки) подвижный радиус-вектор описы-
вает углы от 0° до 360°. Осями координат круг на рис. 7 делится на
четыре четверти: первая четверть АОВ, вторая ВОС, третья COD и
четвертая DO А. Если сторона ОЕ угла АОЕ расположена в первой,
второй, третьей или четвертой четверти, то угол АОЕ будем назы-
вать соответственно углом первой, второй, третьей или четвертой
четверти. В первой четверти угол а изменяется в пределах от 0° до
90°, во второй — от 90° до 180°, в третьей — от 180° до 270°, в четвер-
той — от 270° до 360°.
Если подвижный радиус-вектор описал угол АОЕ, равный а угло-
вым градусам, то его конец описал дугу окружности АЕ, равную а
дуговым градусам. Начало этой дуги находится в точке А, а конец —
в точке Е.
3.	Углы и дуги, большие 360°. В п. 2 мы ограничивались углами от
0° до 360°. Между тем в различных задачах приходится иметь дело
с вращениями, при которых совершается больше полного оборота,
например, с вращением маховика, с полетом спутника вокруг Земли
и т.д. Эти задачи приводят к необходимости обобщения понятия угла
(дуги), к необходимости введения углов (дуг), больших 360°. Рас-
смотрим угол АОЕ = а, где 0°< а <360° (рис. 7). Этот угол может
быть образован следующим образом: подвижный радиус-вектор из
своего первоначального положения О А сделал сначала п полных обо-
6
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
ротов в направлении против движения часовой стрелки, а потом еще
повернулся на угол а в том же направлении, и мы получили некото-
рый положительный угол /Зп, который связан с прежним углом а сле-
дующей формулой:
/3„ = 36О°ч+«,	(3.1)
где 0° с а < 360° и п — любое целое неотрицательное число. Угол [in
(при и а>0°) будем называть положительным углом, большим
360° (при п = 1 и а = 0 получаем угол, равный 360°). Существует бес-
конечное множество углов с начальной стороной ОА и конечной
стороной ОЕ, которые записываются при помощи формулы (3.1).
Например:
^0 = «, А = 360° + а, /32 = 720° + а ит.д.
Если подвижный радиус-вектор описал угол = 360°п + а, то его ко-
нец описал дугу, равную сумме целого числа п полных окружностей
и дуги АЕ. Существует бесконечное множество дуг, имеющих данное
начало А и данный конец Е. Все эти дуги также выражаются форму-
лой (3.1), но градусы, входящие в эту формулу, следует понимать
как дуговые.
4.	Отрицательные углы. Сложение и вычитание углов. Назовем
вращение подвижного радиуса-вектора в направлении против дви-
жения часовой стрелки положительным, а в противоположном на-
правлении (в направлении по движению часовой стрелки) — отри-
цательным. Угол, описанный при отрицательном вращении подвиж-
ного радиуса-вектора, назовем отрицательным углом.
При мер 1. На рис. 8 изображены два угла с общей начальной
стороной ОА и общей конечной стороной OD-. один равен +270°, дру-
гой - 90°.
Сумма двух углов. На координатной плоскости Оху рас-
смотрим окружность единичного радиуса с центром в начале коорди-
нат (рис. 9). Пусть произвольный угол а (на чертеже положитель-
ный) получен в результате вращения подвижного радиуса-вектора от
его начального положения О А, совпадающего с положительным на-
правлением оси Ох, до его конечного положения ОЕ. Примем теперь
положение радиуса-вектора ОЕ за начальное и отложим от него про-
извольный угол Р (на чертеже положительный), который получим в
результате вращения подвижного радиуса-вектора от его начального
положения ОЕ до его конечного положения ОС. В результате этих
действий мы получим угол, который будем называть суммой углов а
§ 1 ВЕКТОРЫ. ОБОБЩЕНИЕ ПОНЯТИЙ УГЛА И ДУГИ
7
Рис. 9
Рис. 8
и /3. (Начальное положение подвижного радиуса-вектора (5Z, конеч-
ное положение радиуса-вектора UU.)
Разность двух у гл о в. Под разностью двух углов а и/3, ко-
торую обозначим а - Д мы будем
понимать такой третий угол у, кото-
рый в сумме с углом @ дает угол а,
т. е. у = а — /3, если /3 + у = а. Раз-
ность двух углов аир можно трак-
товать как сумму углов а и -/3.
В самом деле, [а + (-/3) ] + ft = а
(рис. 10). Вообще, для любых углов
их сумма измеряется алгебраиче-
ской суммой действительных чи-
сел, измеряющих эти углы.
Пример 2. А АО В = +60°, а
Z.BOC = -909, тогда АЛОВ +АВОС =
=Z. АОС=60° + (-90°) = —30° (рис. 11).
Пример 3 . Угол /3 = +780°, а
угол fl’ = -1110°. Сумма их/3 + [}' =
= 780° +(-1110°) =-330°.
В формуле (3.1) предполагалось, что п — любое целое неотрица-
тельное число. Если же предположить, что п — любое целое число
(положительное, отрицательное или нуль), то при помощи формулы
;3И = 360°л +«,
(4.1)
8
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
Рис. 11
где 0° <«<360°, п = 0, ±1, ±2,
можно будет записать любой угол,
как положительный, так и отрица-
тельный.
Пример 4. Угол, равный
-1370°, можно записать так:
-1370° = 360° (-4) +70°.
Здесь п = -4; а = +70°.
Заметим, что все углы /Зп, запи-
санные при помощи формулы (4.1),
при разных значениях п, но одном
и том же а, имеют общие началь-
ную (ОА) и конечную (ОЁ) сторо-
ны (рис. 7). Поэтому построение
любого угла сводится к построе-
нию соответствующего неотрицательного угла а, меньшего 360°. На
рис. 7 углы Рп = а + 360°п между собой не отличаются, они различа-
ются лишь процессом вращения радиуса-вектора, который привел к
их образованию.
Упражнения
1.	Углом какой четверги является угол, равный:
а) 73°; б) 327°; в) 151°; г) 190°; д) 94°; е) 286°; ж) 359°?
2.	Углом какой четверти является угол, равный:
а) -30°; б) -260°; в) -98°; г) -300°; д) -89°; е) -272°?
3.	Представить угол Р в виде/Зп “360°п + а, где п — целое число, а а удовлетворяет
условию 0° <«<360°, если:
а) Р - -270°; б) р = 405°; в) р —960°; г) р = 1800°; д) Р - -1751°.
§ 2. Тригонометрические функции произвольного угла
5. Определение основных тригонометрических функций. Пусть
радиус-вектор г = ОМ точки М образует угол а с осью Ох (рис. 12),
причем х и у соответственно абсцисса и ордината конца М вектора, г —
его модуль, а величина угла а измеряется в градусах или в радианах.
1.	Синусом угла а (обозначение: sin а) называется отношение ор-
динаты у к длине г радиуса-вектора ОМ:
sina = ^.	(5.1)
Г
§ 2. ФУНКЦИИ ПРОИЗВОЛЬНОГО УГЛА
9
2.	Косинусом угла а (обозначение: cos а)
называется отношение абсциссы х к длине г
радиуса-вектора ОМ:
cos а-у.	(5.2)
3.	Тангенсом угла а (обозначение: tg а)
называется отношение синуса угла а к коси-
нусу этого угла:
4.	Котангенсом угла а (обозначение:
ctg ct) называется отношение косинуса угла а к синусу этого угла:
5.	Секансом угла а (обозначение: secrz) называется величина, об-
ратная cos а:
seca = —.	(5.5)
COS а
6.	Косекансом угла а (обозначение: cosec а) называется величи-
на, обратная sin а:
cosec а = -4—.	(5.6)
sin а
Замечание 1. Тригонометрические функции (5.1) — (5.6) яв-
ляются функциями только угла а, т.е. не зависят от длины подвиж-
ного радиуса-вектора. Для того, чтобы в этом убедиться, достаточно
доказать, что если подвижный радиус-вектор г образует с осью абс-
цисс данный угол а, то отношения х/r и у/г не зависят от длины ра-
диуса-вектора; читатель легко в этом убедится.
Замечание 2. Из определения tg а и ctg а следует, что
tg« = ^,	(5.7)
ctga=~.
У
(5.8)
Соотношения (5.7) и (5.8) можно было бы принять в качестве опре-
делений для tg а и ctg а.
10
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
Замечание 3. Аналогично получаем
sec а = -,
х
cosec а = -.
У
(5.9)
(5.10)
Соотношения (5.9) и (5.10) можно было бы также принять в качестве
определений для sec а и cosec а.
Замечание 4. Во всех определениях (5.1) — (5.6) мы предпо-
лагаем, что соответствующие отношения существуют (имеют
смысл). Например, tga имеет смысл, если cosa 0, ctg а имеет
смысл, если si па # 0, и т.д. Поскольку (замечание 1) тригонометри-
ческие функции (5.1—5.6) угла а не зависят от длины подвижного
радиуса-вектора, то в качестве радиуса-вектора можно брать вектор
с длиной, равной единице (I г I = г = 1). Такой вектор называют еди-
ничным радиусом-вектором. В случае единичного радиуса-вектора
движного единичного радиуса
диуса-вектора при изменении
ность, называемую единичной
формулы для основных тригономет-
рических функций запишутся так
(рис. 13):
.sina=y,	cosa=x,
tg«=^,	ctga=-. '	<5.11)
X	у
Формулы для tg а и ctg а оста-
лись прежними, а формулы для ос-
тальных основных тригонометриче-
ских функций приняли более про-
стой вид. Следовательно, синус и
косинус угла а равны соответствен-
но ординате и абсциссе конца по-
вектора. Конец этого единичного ра-
угла а от 0° до 360° опишет окруж-
окружностью (рис. 13). Для геомет-
рического истолкования тангенса и котангенса вводят понятия оси
тангенсов и оси котангенсов. Осью тангенсов называется перпен-
дикуляр, восставленный в точке А к неподвижному радиусу-вектору
О А. Положительное и отрицательное направления на оси тангенсов
выбирают так, чтобы они совпадали с соответствующими направле-
ниями оси ординат (рис. 14). Рассмотрим угол а = ААОМ и введем
понятие соответствующей точки оси тангенсов.
а)	Если точка М единичной окружности лежит справа от оси орди-
нат, то соответствующей ей точкой оси тангенсов назовем точку М\
(точку пересечения продолжения ОМ с осью тангенсов, рис. 14, а).
§ 2. ФУНКЦИИ ПРОИЗВОЛЬНОГО УГЛА
11
б)	Если точка М единичной окружности лежит слева от оси орди-
нат, то соответствующей ей точкой оси тангенсов назовем точку
(точку пересечения продолжения МО с осью тангенсов, ,рис. 14, б).
Заметим, что тангенс угла а численно равен ординате yi (рис. 14)
соответствующей точки оси тангенсов, т.е. всегда 1g а = у,.
Заметим еще следующее: если точка М лежит на оси ординат (на-
пример, а = 270°), то соответствующей ей точки оси тангенсов не су-
ществует, но при этом и tg а также не существует.
Осью котангенсов называется перпендикуляр, восставленный в точке В (конец
радиуса-вектора ОВ, образующего с осью Ох угол, равный 90°) к оси ординат. Поло-
жительное и отрицательное направления на оси котангенсов выбирают так, чтобы они
совпадали с соответствующими направлениями оси абсцисс (рис. 15). Введем понятие
Рис. 15
12
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
соответствующей точки оси котангенсов.
а)	Если точка М единичной окружности лежит над осью абсцисс, то соответствую-
щей ей точкой оси котангенсов назовем точку М\ (точку пересечения продолжения
ОМ с осью котангенсов, рис. 15, а).
б)	Если точка М единичной окружности лежит под осью абсцисс, то соответствую-
щей ей точкой оси котангенсов назовем точку Mi (точку пересечения продолжения
МО с осью котангенсов, рис. 15, б).
Аналогично предыдущему можно получить, что котангенс угла а равен абсциссе
Xi соответствующей точки оси котангенсов, т.е. ctg а = х\. Если точка М лежит на оси
абсцисс (например, а - 180°), то соответствующей ей точки оси котангенсов не суще-
ствует, но при этом и ctg а также не существует.
6. Изменение основных тригонометрических функций при изме-
нении угла от 0 до 2я. В дальнейшем мы будем использовать не толь-
ко градусную, но и радианную меру углов. Углом в один радиан на-
зывается угол, соответствующий дуге окружности, имеющей длину,
равную радиусу. В связи с этим напомним некоторые факты из гео-
метрии, относящиеся к градусной и радианной системам измерения
углов и дуг:
1)	при измерении углов и дуг в радианной системе наименование
единицы измерения — радиана обычно опускают и говорят, напри-
мер, «угол равен л/4» вместо «угол равен л/4 радиана»; «угол равен
1000» вместо «угол равен 1000 радиан»;
2)	при переходе от градусной меры (а градусов) к радианной мере
(а радиан) пользуются формулой
3)	при переходе от радианной меры (а радиан) к градусной мере
(а градусов) пользуются формулой
Полезно запомнить соответствующие значения в градусной и ра-
дианной мере некоторых наиболее часто встречающихся углов, при-
веденные в следующей таблице.
Градусы	0	30	45	60	90	180	270	360
Радианы	0	л/6	л/4	л/3	л/2	Л	Зл/2	2л
Рассмотрим теперь, как изменяется (по абсолютной величине и
знаку) каждая из основных тригонометрических функций при изме-
нении угла а от 0 до 2л. За их изменением проследим, пользуясь еди-
ничной окружностью (см. п. 5).
§ 2. ФУНКЦИИ ПРОИЗВОЛЬНОГО УГЛА
13
I. sin а. Согласно первой формуле (5.11) sin а = у, где у — ордина-
та конца подвижного единичного радиуса-вектора (см. рис. 13).
1)	0 < а <л/2 (первая четверть). Если углы и а2 удов-
летворяют неравенствам ^<а^<а2<л:/1 (рис. 16), то yi < у2, следова-
тельно, и sin «1 < sin «2- При возрастании угла а от 0 до л/2 sin сс мо-
нотонно возрастает от 0 до 1.
Рис. 18
У
Рис. 19
2)	л/2 < а <л (вторая четверть). Если углы и «2 удов-
летворяют неравенствам л/2<а^<а2<л (рис. 17), то yi > У2, следова-
тельно, и sin «] > sin «2- При возрастании угла а от л/2 до л sin а
монотонно убывает от 1 до 0.
14
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
3)	л < а «?Зл/2 (третья четверть). При возрастании угла
а («2 > «1) от л до Зл/2 sin а монотонно убывает (yi < yi) от 0 до -1
(рис. 18).
4)	Зл/2<а<2л (четвертая четверть). При возрастании уг-
ла а («2 > «1) от Зл/2 до 2л sin а монотонно возрастает (уг > yi) от -1
до 0 (рис. 19).
Вывод. При любом угле а абсолютная величина sin а не превос-
ходит 1, что записывается так:
Isinal < 1,	(6.3)
или в равносильной форме:
-1< sin а <1.	(6.4)
IL cos а. По второй формуле (5.11) cos а = х, где х — абсцисса
конца подвижного единичного радиуса-вектора (рис. 13).
1)	0 < а <л/2 (первая четверть). Для углов aj и аг, удов-
летворяющих неравенствам 0 < «| < «2 < л/2 (рис. 20, а), выполня-
ется неравенство %2<х1 (-Ч = ОМ'\ и хг = OM'i), следовательно,
cos «2 < cos ар При возрастании угла а от 0 до л 12 cos а монотонно
убывает от 1 до 0.
2)	л/2 с а <л (вторая четверть). При возрастании угла а
(«4 > аз) от л/2 до л cos а монотонно убывает (х$ < %з, где Х4 =
=-1 ОМ'41 и %з = -1 ОМ’з I) от 0 до -1 (рис. 20, а).
И	ff
Рис. 20
§ 2 ФУНКЦИИ ПРОИЗВОЛЬНОГО УГЛА
15
3)	л < а <Зл/2 (третья четверть). Для углов а$ и ag, удов-
летворяющих неравенствам л < а$ <	< Зл/2 (рис. 20, б), выпол-
няется неравенство х$ < Xf> (х$ = -1 ОМ'51 и х^ = -1 ОМ'ь I), следова-
тельно, cos «5 < cos ctf,. При возрастании угла а от л до Зл/2 cos а мо-
нотонно возрастает от -1 до 0.
4)	Зл/2<а<2л (четвертая четверть). При возрастании уг-
ла a (ag > «7) от Зл/2 до 2л cos а монотонно возрастает (xg > Х7, где
xg = ОМ'$ и Х7 = OM’-f) от 0 до 1 (рис. 20, б).
Вывод. При любом угле а абсолютная величина cos а не превос-
ходит 1, что записывается так:
I cos а I < 1,	(6.5)
или в равносильной форме:
-1 < cos а < 1.	(6.6.)
III. tg а. Тангенс угла а численно равен ординате соответствую-
щей точки оси тангенсов (см. п. 5).
1) 0 < а <л12 (первая четверть). Для углов а; и «2, удов-
летворяющих неравенствам 0 < а; <аз<л/2 (рис. 21), выполня-
ется неравенство У2>У1 (И = АМ; и У2 = AM 2), следовательно,
tg «2 > tg ар При возрастании угла а от 0 до л/2 tg а неограниченно
возрастает. Заметим, что tg^/2) не существует. Если угол а прибли-
жается к л/2, оставаясь меньше л/2, то tg а неограниченно возраста-
ет (tg а стремится к плюс бесконечности).
Рис. 21
Рис. 22
16
ГЛ- 1. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
Сходное положение встречается при изучении функции у = 1/х;
если х приближается к нулю, оставаясь больше нуля, то у = 1 /х стре-
мится к плюс бесконечности.
Это же условно записывают так:
tg а -*+оо пригде а < л/2.
2)л/2<а Сл: (вторая четверть). Для углов а\ и «2, удовлетво-
ряющих неравенствам л/2 < а\ < «2 < л (рис. 22), выполняется нера-
венство У2 > У1 <У1 = -1 АМ\ I и у2=- I АМъ I), следовательно, tg > tg a j.
При возрастании угла а от л/2 до л tg а возрастает до нуля.
Если а стремится к л/2, оставаясь больше я/2, то tg а неограни-
ченно возрастает по абсолютной величине, оставаясь отрицательным
(tg а стремится к минус бесконечности). Это записывается так:
tga -*—оо при а^л/2, где а>лЦ.
3) л с а < ЪлЦ (третья четверть). Тангенс ведет себя так
же, как и в первой четверти, т. е. возрастает от 0 до + оо. Рекомендуем
читателю сделать соответствующий рисунок, аналогичный рис. 21.
Если а стремится к Зтг/2, оставаясь меньше Зл/2, то tg а стремит-
ся к плюс бесконечности:
tga -»+оо при а -» Зл/2, а<Зтг/2.
4) Зя/2<а <2л (четвертая четверть). Тангенс ведет себя так
же, как и во второй четверти, т.е. возрастает от — оо до 0. Рекомендуем
читателю сделать соответствующий рисунок, аналогичный рис. 22.
Если а стремится к Зл/2, оставаясь больше Зл/2, то tg а стремит-
ся к минус бесконечности:
tga — оо при а -* Зл/2, а> Зл/2.
IV. ctg а. Котангенс угла а численно равен абсциссе соответствующей точки оси
котангенсов (см. п. 5).
1)0<а >»л/2 (первая четверть). Для углов/д и удовлетворяющих нера-
венствам 0 < «1 < «э < л/2 (рис. 23), выполняется неравенство л'2 < Xi (х, “ ВМ\ и Х2
- ВМг). следовательно, ctg a? < ciga,. При возрастании угла а от 0 до л72 ctg а убывает
до нуля. Если а стремится к нулю, оставаясь больше нуля, то ctg а стремится к плюс
бесконечности:
ctga-» + x при a О, где а > 0.
2)	т/2 с a < л (вторая четверть). Для углов «| и аз, удовлетворяющих не-
равенствам л/2 < «| < a > < л (рис. 24). выполняется неравенство хз < Xi (xi — I ВМ\ I
и лз “ _ I ВМ> I), следовательно, ctg aj < ctg ai. При возрастании угла а от л/2 до л
ctg а убывает 01 0 до - «. Если а стремится к л, оставаясь меньше я. то ctg а стремит-
ся i, минус бесконечное ।и:
§ 3. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
17
Рис. 23
Рис. 24
Разбор поведения ctg а в остальных четвертях предоставляется читателю. Приве-
дем только окончательные результаты:
3)	л < а < Зл/2 (третья четверть), ctg а убывает от + оо до 0; при а -» л,
где а > л, ctg а -» + оо ,
4)	Зл/2< а <2л (четвертаячетверть). ctg а убывает от 0 до -оо; при
а -» 2л, где а < 2л, ctg а — оо .
Упражнения
1.	Может ли синус угла бытьравным:
а) 3/5; б) -4/5; в) 10/9; г) V6/2; д) -<3/2; е) а+ 1/а, где а * О?
2.	Может ли косинус угла быть равным'
a) (V5 - 7з) / (<3 - 1); б) 0,835; в) -1 /sin 10°; г) VU / д) $7 /
3.	Углом какой четверти является угол а, у которого:
a) sin а < 0, cos а > 0; б) sin а > 0, cos с < 0: в) sin а > 0. cos а > 0; г) sin « < О,
cos а < 0; д) tg а < 0, cos а < 0; е) ctg а > 0, sin а < О?
§ 3. Соотношения между тригонометрическими функциями
одного и того же угла
7. Основные тригонометрические тождества. Между основными
тригонометрическими функциями произвольного угла а имеются
следующие тождественные соотношения:
1.	sin2a + cos2a = 1.	(7.1)
Доказательство. Принимая I г! = г = 1, получим (для произ-
вольного угла a) sin а = у, cos а = х, где хи у — проекции единичного
радиуса-вектора на оси координат (см. рис. 13). По теореме Пифаго-
18
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
ра 1x12 + 1 yl 2 = 1, так как IГ1 =1, откуда
sin2a + cos2« = 1.
где а л/2 + пл; п = 0, ±1, ±2,...
о	.	COS CL	(i-i
3.	ctga = -—,	(7.3)
° sin a
где a пл; n = 0, ±1, ±2, ...
Тождества (7.2) и (7.3) служат соответственно определениями
функций tga и ctg а (см. формулы (5.3) и (5.4).
4.	seca = ——,	(7.4)
cos а
где а * л/2 + пл; п = 0, ±1, ±2,...
5.	cosec «=^—,	(7.5)
sin а
где а пл; п = 0, ±1, ±2, ...
Тождества (7.4) и (7.5) служат соответственно определениями
функций sec а и cosec а (см. формулы (5.5) и (5.6).
Тождества (7.1) — (7.5) назовем основными. При помощи этих
основных тождеств выведем так называемые дополнительные тож-
дества.
6.	Перемножив почленно тождества (7.2) и (7.3), получим
tg«ctga = 1,	(7.6)
где а пл 12; п = 0, ±1, ±2, ...
7.	Разделив тождество (7.1) почленно на cos2a, при условии, что
cos «	0, получим
1+tg2a = sec2«,	(7.7)
где а л 12 + пл; п = 0, ±1, ±2,...
8.	Разделив тождество (7.1) почленно на sin2a, при условии, что
sin а -* 0, получим
1 + ctg2 а = cosec2 «,	(7.8)
§ 3. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
19
где а?* пл; п = 0, ±1, ±2,...
При помощи тождеств (7.1) — (7.8) можно производить преобра-
зования различных выражений, содержащих тригонометрические
функции, и получать новые тождества.
Пример 1. Доказать тождество
sin a cos2ot(l + tg2a) + cos a sin2 ot(l + ctg2 «) = sin a + cos a.
Решение. Заменив в левой части tg а и ctg а их выражениями
по формулам (7.2) и (7.3), получим
sin a cos2 а + sin3 а + cos a sin2 а + cos3 а =
= sin a (cos2 а + sin2 а) + cos a (sin2 а + cos2 a) = sin a + cos a.
После выполнения тождественных преобразований левая часть ра-
венства совпала с правой. Исходное тождество этим доказано.
Это же тождество можно доказать и по-другому, воспользовав-
шись формулами (7.7) и (7.8), а затем формулами (7.4) и (7.5). Ре-
комендуем это сделать читателю.
Пример 2. Упростить выражение
А = 2(sin6а + cos6a) -3(sin4a: + cos4a).	(*)
Решение. Используя тождество (7.1), получаем
(sin2 а + cos2 а)2 = 1,
откуда
sin4 a + cos4 at = 1-2sin2a cos2 a.	(7.9)
Аналогично находим
sin6 a + cos6 a = 1- 3sin4 a cos2 a - 3 sin2 a cos4 a =
= 1 -3sin2ar cos2 a: (sin2 a: + cos2 at) = l-3sin2 a cos2 at. (7.10)
Подставив (7.9) и (7.10) в (*), будем иметь
А = 2 - 6 sin2 a cos2 а - 3 + 6 sin2 a cos2 а = -1.
8. Вычисление значений тригонометрических функций по значе-
нию одной из них. При помощи формул (7.1) — (7.8) можно выра-
зить (с точностью до знака) через любую из шести тригонометриче-
ских функций угла а остальные пять функций. Мы ограничимся
только функциями sin a, cos а и tg a.
20
ГЛ I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
1.	Выражение ч е р е з sin а. Из тождества (7.1) находим
cos а = ±V1—sin^a .
(8.1)
Подставив найденное значение cos а в тождество (7.2), получим
sin а	/ о \
tg а = ±-т-•	(8.2)
V 1-sirra
где а * л/2 + ил; п = 0, ± 1, ± 2,...
2.	Выражение через cos «. Из тождества (7.1) находим	:
sin а = ±V 1 — cos2a .	(8.3) 'I
Подставив найденное значение sin а в тождество (7.2), получим	я
V1 -cos2a	„ , Я
tga= ±---------,	(8.4) я
°	cos а ’	Я
где а Ф л/2 + пл; n = 0, ± 1, ± 2,...	1
3.	Выражение через tg а. Из тождества (7.7) находим 1
sec а = ±Vl+tg^a . Подставив значение sec а в тождество (7.4),	1
получим из него	»
1
cos а = ±-л—,	(8.5)
V1 +tg'«
где а * л/2 + пл; п = 0, ± 1, ± 2, ...
Далее находим
sin a = tg a cos a = ±-т—°, ,	(8.6)
V)+ig*a
где a * л/2 + пл; n = 0, ± 1, ± 2, ...		|
При извлечении квадратного корня знак следует выбирать в зави- 1
симости от того, в какой четверти находится угол а.	I
Пример 1 . Известно, что cos а = -У5 и 180°< а < 270°. Вычис- s
лить sin a, tg а и ctg a.	j
Решение. Угол а принадлежит третьей четверти (рис. 25), в I
которой tg а > 0, ctg а > 0, sin а < 0.	I
С тгдовательно,	1
§ 3. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
21
tg« =
V1 -cos2«
cos а
~^5 = 4
-3/5	3’
ctga =
1 _ 3
tg a 4 ’
sin a = - V1 -cos2a - - V 1-^ = - |.
В дальнейшем мы будем использовать следующий факт:
Для того, чтобы два действительных числахиуможно было при-
нять за cos а и sin а одного и того же угла а, необходимо и достаточ-
ю, чтобы сумма их квадратов была равна единице: х2 + у2 = 1.
Доказательство. Необходимость. Если х = cos а и у = sin а,
то sin2 а + cos2 а = 1, т.е. х2 + у2 = 1.
Достаточность. Рассмотрим радиус-вектор ОМ (рис. 13) с про-
екциями х и у. Так как по условию х2 + у2 = 1 , то длина этого векто-
ра равна 1. Следовательно, ОМ —
единичный радиус-вектор. Согласно
первым двум формулам (5.11) sina=
= у и cos а = х, где а — угол, образо-
ванный подвижным единичным ра-
диусом-вектором ОМ и положи-
тельным направлением оси Ох.
Пример 2 . Могут ли' sin а и
cos а одного и того же угла а быть
равными соответственно:
а) 1У13 и -54з; б) Уз и -Уз?
Решение, а) Числа 12/13 и
-У13 обладают тем свойством, что
(>У13)2+(-5/1з)2=1. Следовательно,
по доказанному, существует такой
угол а, для которого sin а = 1У13 и
cos а = -54 з.	Рис. 25
б) Для чисел Уз и -Уз имеем
(Уз)2 + (-Уз)2 = У9 * 1. Следовательно, числа Уз и -Уз нельзя при-
нять за sin а и cos а одного и того же угла а.
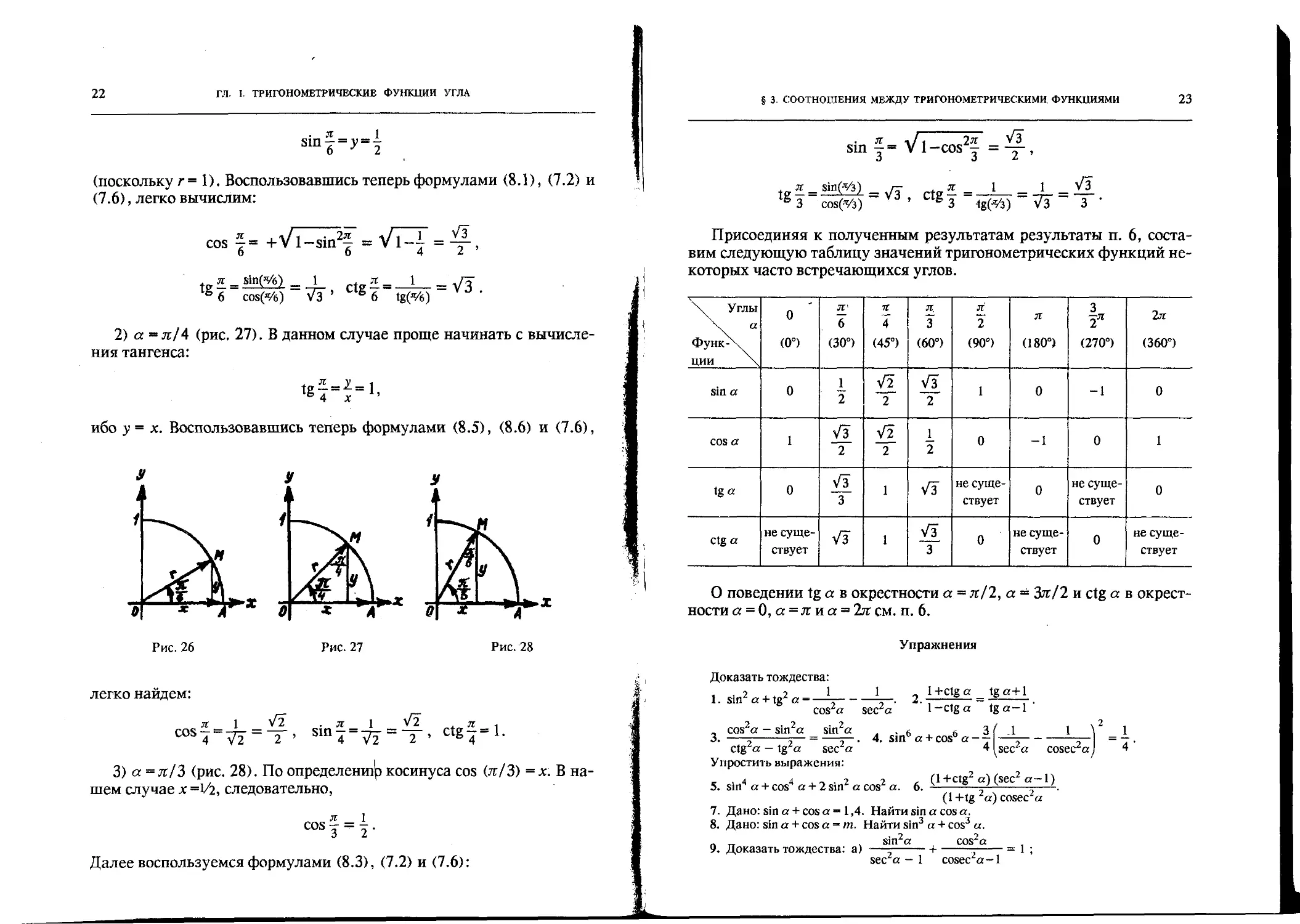
9. Значения тригонометрических функций некоторых углов.
Воспользовавшись сведениями из геометрии, найдем значения три-
гонометрических функций углов 30°, 45° и 60° (или соответственно в
радианной мере углов л/6, л/4 и л/3).
1) а = л/6 (рис. 26). На основании теоремы о том, что в прямо-
угольном треугольнике катет, лежащий против угла в 30°, равен по-
ловине гипотенузы, заключаем, что
22
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
(поскольку г = 1). Воспользовавшись теперь формулами (8.1), (7.2) и
(7.6), легко вычислим:
л . -I '	Г* ^з"
COS -7 = + V 1—Sin - = V 1—7 = -z- ,
6	6	4	2
л _ sin(V6) _ 1	. л _ 1	_
6 cos(Ve) 7з" ’	® 6 tg(%)
УЗ .
2) а = л/4 (рис. 27). В данном случае проще начинать с вычисле-
ния тангенса:
, л у .
tg_ = z= 1
° 4 х ’
ибо у = х. Воспользовавшись теперь формулами (8.5), (8.6) и (7.6),
легко найдем:
л 1 V2 . л 1 v2 л .
COS4=V2=^’ Sm4=V2=^"’ Ctg 4 = L
3) a = л/3 (рис. 28). По определений косинуса cos (л/3) =х. В на-
шем случае х =1/2, следовательно,
л 1
COS3 = 2
Далее воспользуемся формулами (8.3), (7.2) и (7.6):
§ 3. СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
23
. л \Г< 2л
sin -= V 1-cos - = -5- ,
о	о
л _ sin(-V3)
3 cos(V3)
= Уз, ctg| =
i 1 _У£
tg(V3) 7з” з
Присоединяя к полученным результатам результаты п. 6, соста-
вим следующую таблицу значений тригонометрических функций не-
которых часто встречающихся углов.
Углы ФуНК-^ч ЦИИ	\	0 (0°)	Л’ 6 (30°)	Л 4 (45°)	л 3 (60°)	л 2 (90°)	я (180°)	3 2Л (270°)	2л (360°)
sin a	0	J_ 2	У2 2	Уз 2	1	0	-1	0
cos a	1	Уз 2	У2 2	2	0	-1	0	1
tg a	0	Уз 3	1	Уз	не суще- ствует	0	не суще- ствует	0
ctg a	не суще- ствует	Уз	1	Уз 3	0	не суще- ствует	0	не суще- ствует
О поведении tg а в окрестности а = л/2, а = Зтг/2 и ctg а в окрест-
ности а = 0, а = л и а = 2л см. п. 6.
Упражнения
Доказать тождества:
, , 1 1
1. sin а + tgz а =--z-------
cos« seca
2 1 +ctg a _ tg «+1
' 1- ctg a tga-1 '
2	.2	.2
3 cos g ~ 5in Q _ sin a
ctg2a - tg2a sec2a
,•6.6 3f .1	1 V
4. sin0 a + cos0 a - — —5-—
4!sec« cosetra
x
4 ’
Упростить выражения:
e . 4	4,^.2	2	, (1+ctg2 a) (sec2 a-1)
5. sin a + cos a + 2 sin a cos a. 6. ------s—
(1+tg 2«) cosec2a
7.	Дано: sin a + cos a - 1,4. Найти sin a cos a.
8.	Дано: sin a + cos a = m. Найти sin3 a + cos3 a.
• 2	2
л TT	S Sirrct	COSXG
9.	Доказать тождества: а) —-------+-------------= 1 ;
sec2a - 1 cosec2cr~l
24
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
„ tga ctg2a—1	,	, . 2	.2	.2.2
б)	—-------:--= 1; в) tg а — stn a = tg a sin a.
1 — tg2a	a
10.	Получить формулы, выражающие тригонометрические функции sin a, cos a и
tg a через ctg a.
11.	Дано: sin a = 4/5 и л/2< a < л. Вычислить cos a, tg a и ctg a.
12.	Могут ли синус и косинус одного и того же угла а быть равными: а) 1/4 и -З/ч;
б) -4/V65 и7//б5?
§ 4. Четность, нечетность и периодичность
тригонометрических функций
10.	Четность и нечетность. Напомним, что функция у=/(х) назы-
вается четной, если для всех допустимых значений аргумента х зна-
чение аргумента (-х) является допустимым и
/(-х)=/(х).
Функция у=/(х) называется нечетной, если для всех допустимых
значений аргумента х значение аргумента (-х) является допустимым
и
/(-х) = —/(х).
Для тригонометрических функций справедлива следующая
Т е о р е м а . Функции cos а и sec а являются четными, т.е.
cos (-a) = cos а и sec (-«) = secct,
а функции sin a, tg a, ctg а и cosec а являются нечетными, т.е.
sin (-a) = - sin a, cosec (-a) =- cosec a,
tg(-a)=-tga, ctg (—a) =-ctg a.
Доказательство. Рассмотрим два угла, образованных еди-
ничным радиусом-вектором г: L АОЕ = а и L AOEi = -а (рис. 29). За-
метим, что абсцисса точек Е и Е\ одна и та же (х).
Согласно второй формуле (5.11) имеем cos a = х и cos (--а) = х, сле-
довательно,
cos (-а) - cos а.	(10.1)
Так как равенство (10.1) справедливо для любого угла а, то мы дока-
зали, что cos (-«) = cos а.
Четность sec а доказывается так:
§ 4. ЧЕТНОСТЬ, НЕЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ
25
sec (-а) = —т—- = —— = sec а.
cos(-a) cos а
Итак,
sec (-«) = sec«. (10.2)
Заметим, далее, что ординаты
точек Е и пртивоположны по
знаку (BE = у, ВЕ\ = -у). Согласно
первой формуле (5.11) имеем sin а=
=у и sin (-а) = -у, следовательно.
sin (-а) =-since. (10.3)
Используя формулу (7.2), а
также тождества (10.1) и (10.3),
получим
tg (-д) = sin(~Q) =
Ig (	' cost-а)
Рис. 29
-sin а
cos а
= -tg«.
Итак,
tg (-a) = —tga.
(10.4)
Для доказательства нечетности etga воспользуемся тождествами
(7.6) и (10.4).
ctg(-а) = ,	;— = - ctg а.
tg(-a) -tga
Итак,
ctg (-a) =-ctg a.	(10.5)
Рекомендуем читателю доказать, что справедливо и тождество
cosec (-а) = - cosec а.	(10.6)
Пример. Найти значения тригонометрических функций угла
а = -я/3.
Решение. Используя нечетность функций sin a, cosec a, tga и
ctg а, получим
sin (-я/3) =-sin (л/3) =-VJ/2,
26
ГЛ. 1. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
cosec (-я/3) =-cosec (л:/3) =
tg (-л/З) =-tg (л/3) = -<3,
ctg (-я/3) = -ctg(x/3) = -l/V3.
Используя четность функций cos а и sec а, получим
cos <—лг/3) = cos (лг/З) = 1/2, sec (-л/3) = sec (л/3) = 2.
11.	Понятие периодической функции. Тригонометрические фун-
кции обладают свойством периодичности, которое определяется в об-
щей форме следующим образом.
Определение. Функция fix) называется периодической с пе-
риодом Т(Т & 0), если для любого х выполнено условие: если функ-
ция определена в одной из точек х или х + Т, то она определена и во
второй точке, и ее значения в обеих точках равны между собой:
fix)=fix + T).	(11.1)
Докажем следующее предложение:
Если Т — период функции fix), mo и любое из чисел пТ, п =
= -1, ±2, ..., также является периодом fix).
Доказательство. Проведем сначала доказательство для —Т.
Для этого рассмотрим пару значений аргумента х и х + i-T) = х - Т. Из
записи
x=ix-T) + T
видно (в силу определения периодичности), что если функция опре-
делена в одной из точек х - Т, х, то она определена и во второй точке.
Далее устанавливаем равенство fix -Т) = fix):
fix) =fiix-T) + Т) =fix-T).
Доказательство того, что пТ при натуральном п является перио-
дом функции fix), проведем по индукции (случай отрицательного п
сводится к этому заменой Т на -Т). Итак, требуется установить, что
если fix) определена в одной из точек х, х + пТ, то она определена и
во второй точке, причем fix) =fix + пТ). Допустим, что утверждение
теоремы уже доказано для некоторого п = к (оно, например, очевидно
при п = 1). Докажем, что оно останется верным и для п = к + 1. Преж-
де всего, в силу того, что Т — период, замечаем, что если одно из
значений аргумента х + кТ и х + ik + 1)Т = (х + кТ) + Т принадлежит
области определения функции, то ей принадлежит и второе значе-
ние. Так как, по предположению индукции, такое же положение
§ 4. ЧЕТНОСТЬ, НЕЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ
27
справедливо и для пары точек х и х + кТ, то видно, что точки х и х +
+(Л + 1)Т принадлежат (или не принадлежат) области определения
/(х) одновременно. Далее устанавливаем равенство значений /(х) в
точках х и х + (к + 1) Т:
f(x+(k+l)T)=f(x + kT + T) = fix + кТ) =f(x)
(последнее — по предположению индукции).
Доказано, что пТ — период функции при любом целом п. Наи-
меньший положительный период функции (если он существует) на-
зывается основным периодом.
Пример 1. Функция /(х) = с (с — постоянная величина) имеет
своим периодом любое число. Основного периода здесь нет. График
этой функции изображен на рис. 30.
Пример 2. Напомним, что целой частью числа х (обозначе-
ние: [х ]) называется наибольшее целое число, не превосходящее х.
Целая часть х есть функция от х; ее график показан на рис. 31.
Дробной частью числа х (обозначение: (х)) называется разность
Рис. 31
Рис. 30
между х и его целой частью:
(х) = х - [х ].
Дробная часть х является периодической функцией с основным пе-
риодом Т = 1. Действительно,
(х + 1) = х+ 1 - [х+ 1 ],
и так как очевидно, что [х +1 ] = [х ] + 1, то
(х + 1) = х + 1 - [х + 1 ] = х + I - [х ] - 1 = х - [х ] = (х).
28
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
График дробной части х показан на рис. 32.
Пример 3. а) Рассмотрим сле-
?	дующую функцию / (х), опреде-
ленную для х, удовлетворяющих
неравенствам 0 < х < 2:
/(х) =
при 0< х <1,
при. 1 < х <2.
рис. 32	График функции изображен на
рис. 33.
б) С помощью этой функции /(х), приняв за основной период чис-
ло Т = 2, построим периодическую функцию F(x):
F(x) =
при 2п < х < 2п+1,
при 2п+1 < х < 2п+2,
п = 0, ±1, ±2,...
График функции F(x) изображен на рис. 34.
Рис. 33
Рис. 34
12.	Периодичность тригонометрических функций. Одним из
важных свойств тригонометрических функций является свойство пе-
риодичности, с которым мы в общем виде познакомились в п. 11. До-
кажем следующую теорему о периодичности тригонометрических
функций.
Теорема . Тригонометрические функции sin a, cos a, tg а,
ctg a, sec а и cosec а являются периодическими функциями, причем
основной период функций sin a, cos a, sec а и cosec а равен 2л (360°),
а основной период функций tg а и ctg а равен л (180°)
Доказательство. В пп. 3 и 4 мы ввели углы вида /3,; = 360°и + а,
где 0° < а < 360° ил — целое число (положительное, отрица-
" Пока мы рассматриваем тригонометрические функции угла, и период Т следует
рассматривать как угол; это замечание сохраняет силу вплоть до п. 15, где вводятся три-
гонометрические функции числового аргумента.
§ 4 ЧЕТНОСТЬ, НЕЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ
29
тельное или нуль). В радианной мере эти углы можно записать в ви-
де /Зп = 2лп +а, где 0< а< 2л и п — любое целое число (положитель-
ное, отрицательное или нуль). Напомним, что все углы при раз-
ных значениях п, но одном и том же а имеют общйе начальною
(СМ) и конечную (ОЕ) стороны (см. п. 4). Если воспользоваться пер-
вой из формул (5.11) для определения синуса, то получим
sin - sin ( 2лп + а) = у = sin а;
если воспользоваться второй из формул (5.11) для определения коси-
нуса, то получим
cos Рп = cos ( 2лп + а) = д- =с os а,
так как соответствующие значения
= 2л п + а одинаковы (рис. 35).
Аналогичный результат получается
и для других тригонометрических
функций. Мы приходим к следую-
щим формулам:
sin(2Trn+a) — sin а,
соз(2лтг+а) - cos а,
tg(2?rn+«) = tg«,	n
ctg(2.TH+«) = ctg а,
sec(2%n+«) = sec а,
созес(2лщ+а) = cosec а,
где п = 0,± 1, ±2, ...
Этим уже доказано, что Т = 2л
является периодом для всех основ-
ных тригонометрических функций.
Покажем, что для тангенса и котанге
щие формулы:
V и у для угла а и углов =
Рис. 35
справедливы также следую-
\&(лп+а) = tg«, 1
ctg(.7rn+a) = ctg a, |
где n = 0,± 1, ±2. ...
Рассмотрим два случая.
a)	n = 2Л, г. с. n — четное число (a =0, ±1, ±2, ...). В этом случае
имеем
30
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
ctg (лп + «) = ctg (2астг + а) = ctg а.
Здесь мы использовали полученные ранее формулы (12.1).
б)	и = 2k + 1, т. е. п — нечетное число (к = 0, ±1, ±2, ...). В этом
случае имеем
tg (лп + а) = tg (2кл + л + а) = tg (л + а),
ctg (лп + «) = ctg (2кл + л + а) = ctg (л + а).
Здесь мы использовали формулы (12.1).
Из геометрических соображений (рис.36) следует, что у = -yi
и .V = -Xi, где х и у — координаты конца подвижного единичного ра-
диуса-вектора г, образующего с осью абсцисс угол «, а х, и yj — ко-
ординаты конца подвижного единичного радиуса-вектора и, образу-
ющего с осью абсцисс угол л + а.
Мы имеем
tg (л + <:) = -- = — = tg а.
Л| -хх
Аналогично получаем с 1g (л + а) =
= ctg а. Следовательно, при любом
л = 0, ± 1, ±2,... имеем
tg (лп+а) = tg а,
cig (лт?+а) =ctg а.
Для углов в градусной мере ана-
Рис 36	логичные формулы получим, заме-
нив в формулах (12.1) 2лп на 360°//
и в формулах (12.2) лп на 180°//.
Этим доказано, что л (или 180°) — период для функций tg а и ctg а.
Остается доказать, что 2л — основной период для sin a, cos a, sec «
и cosec а, ал — основной период для tg а и ctg а. Докажем это только
для sin а, а для остальных основных пяти функций советуем это сде-
лать читателю.
Доказательство. Требуется доказать, что Т = 2л — наи-
меньший положительный угол такой, что для всех а выполняется
равенство sin( а+Т) = sin а. Проведем доказательство от противного.
Допустим, например, что существует угол А такой, что
sin (а+А) = sin а и 0 < А < 2л.
§ 4 ЧЕТНОСТЬ, НЕЧЕТНОСТЬ И ПЕРИОДИЧНОСТЬ
31
Так как в последнем равенстве а может быть любым (ведь это ра-
венство, по предположению, выполняется тождественно), то должно
выполняться, например, равенство
sin (у+А) = sin у = 1.
Но sin «=1 только для аргументов а вида а = л/2+2лп, где п = О,
±1, ±2, ... Следовательно, должно выполняться равенство л/2+А =
= л/2 + 2лп, откуда следует, что А = 2л н. Мы пришли к противоре-
чию, предположив, что 0 < А < 2л.
Для sin а наше утверждение доказано. Аналогично оно доказыва-
ется и для других тригонометрических функций.
Упражнения
1.	Угол а - —лг/6. Найти значения основных тригонометрических функций.
2.	Угол а - -45°. Найти значения основных тригонометрических функций.
3.	Показать, что следующие функции:
.	.4	2,. 4	, 1+2COSX , COS X Sin X
a	) y = sin х; б) y-x +tg х; в) у-т-; г) у =  -——;
J	хь	tg x+ctg х
.	sin х- tg х , Зх + 2sin х ч . , .	.	, . ,
д	) у =  -°—; е) у —-----;--------; ж) v = sin 1x1; 31 v = lsinxl, являются чет-
sin x+ctg х J ctg’ v
ными.
4.	Показать, что следующие функции:
a) y=ctg5x; б) y-x+lgx; Му =----------; г) y = -tg3x;
sm х
2
. X tg X . х + sin X
д) У =  --в— ; е) v = —~-----z—, являются нечетными,
l+secx - ctg-x+tg*x
5.	Указать, какие из следующих функций являются четными, нечетными и какие
не являются ни четными, ни нечетными:
.	,1 +sin X 4.2.
a) y“Smx + etgx; б) v=sinx + cosx; в)у = -—:; г) у-х +sm х+1;
'1 -sin х
д) у =x3+sin3x+l; е) у = iglsinxl.
6.	Указать периодические функции среди следующих функций:
a) y = cos2x; б) y-cosx2; в) y-xtgx; г) y = cos(l/x);
д) у - sinx + cosx; е) у - 2ctgx +3; ж) у —4; з) у - igeosx.
7.	Указать основной период (если он существует) следующих функций:
, sin х ,.	. ,	. х ,
а) у-—у—; o)y = sm2x; в) у-sin—; г) y = cosx+ctgx;
д) у = 2tgx + 3ctgx; е) y=5s'"v; ж) у-sinCr-—); з) v-sin(2x~);
о ’	о
и) y = sinx + sin^; к) у -sinx + sinj + siny; л) у-7; м) y = cosZ-rx,
32
ГЛ. I I РПГОЦОМГ 1 ГИЧКСКШ-Г ФУНКЦИИ УГЛА
§ 5. Формулы приведения
sin а.
(13.2)
13. Зависимость между тригонометрическими функциями до-
полнительных углов. Углы а и р назовем дополнительными до л/2,
если «+Д = л.72. Сходными (по названию) тригонометрическими фун-
кциями будем соответственно называть синус и косинус, тангенс и
котангенс, секанс и косеканс.
Теорема. Сходные тригонометрические функции дополни-
тельных углов равны между собой.
Доказательство. Докажем сначала, что
sin 1~«'| = cos а,	(13.1)
V )
cos
Предположим для определенности, что л/2< а <л\ тогда угол Д =
= л/2-а удовлетворяет неравенст-
вам -л/2< Д < 0. Построим теперь с
помощью подвижного единичного
радиуса-вектора г углы АОЕ = а и
АОЕ\ = ~р > 0 (рис. 37). Заметим,
что ДйгОЕ] = /ХВЕО (они прямо-
угольные, имеют равные гипотену-
зы I ОЕ I = I ОЁ\ I и равные острые
углы: А.ВЕО = «-л/2 - -Д = /_В\ОЕ\).
Из равенства треугольников имеем
-х = уч и X] = у. Следовательно,
sin (—jS) =sin(a-’r/2) = уч =-x = -cos«,
откуда sinta-T/2) =-cosa, но в силу
нечетности синуса sin(a-Tt/2) =
=—sinto/2-rz), и мы имеем sinU/2-or)=
= cosa.
Аналогично доказывается, что
соз(л/2-а) = sina.
Для остальных функций можно доказательство вести так:
ctg (f
sin(.T72-«) cos а
---Г'73----ч = -------~ Ctg «,
cos(.t/2-«) sin «-----°
cos(cr/2-a) __ sin a
sin(.rr/2-«J cosa
(13.3)
(13.4)
§ 5. ФОРМУЛЫ ПРИВЕДЕНИЯ
33
При выводе формул (13.3) и (13.4) мы пользовались только что дока-
занными формулами (13.1) и (13.2).
Замечание 1. При доказательстве теоремы мы считали, что
угол с? задан в радианах. Соответствующие формулы для угла а, из-
меренного в градусной мере, легко получить из формул (13.1) —
(13.4), заменив л/2 на 90°.
Замечание 2. При доказательстве теоремы мы предположили для
определенности, что угол а удовлетворяет неравенствам я/2 < а < л.
Можно показать, что теорема остается в силе и в случае любого угла
а (как положительного, так и отрицательного).
Пример. Заменить данные тригонометрические функции три-
гонометрическими функциями дополнительного угла:
ч	7Г 	/ 71 7t \	• 7t _ 1
1.	cos -Т = sin --- = sin - =
3	12	3 I	О 2
2.	tg 18° = ctg(90°-18°) =ctg72°.
3.	ctg 31°29'32" = tg(90°-31°29'32") =tg58°30'28".
14. Формулы приведения. Формулами приведения называются
формулы, выражающие тригонометрические функции углов -а,
л/2±а, л±а, Зл/2±а, 2л±а через тригонометрические функции уг-
ла а, где а — произвольный (допустимый) угол. Сами тригонометри-
ческие функции этих углов будем называть приводимыми тригоно-
метрическими функциями. Будем говорить для краткости, что углы
-а, л±а, 2л±а образованы откладыванием угла а от оси Ох (от гори-
зонтальной оси), а углы л/2±а и Зя/2±а образованы откладывани-
ем угла а от оси Оу (от вертикальной оси).
Пользуясь возможностью произвольного выбора угла а в форму-
лах (13.1)—(13.4), получим новые важные формулы (мы ограничи-
ваемся функциями sin a, cos a, tg a, ctg а.
а)	Заменив в формулах (13.1)-< 13.4) а на -а, получим
•sin (y+aj = cos(—а) = cosa,
cos у+а = sin(—а) = —sincr,
tg R-+a = ctg(-a) =-ctg a,
ctg [y+«] = tg(-«) = —tga.
(14.1)
б)	Заменив в формулах (14.1) a на л/2+а, а следовательно, л/2+а
на л+а, получим
34
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
•sin(%+a) = sin
л . л .
-+
= cos ly+a] =-sina,
12 I
со5(л+а) = cos
= -sin
= —cos a
(14.2)
(мы снова воспользовались тем, что формулы (14.1) справедливы для
любого угла а). Так как л является основным периодом для tg а и ctg
а, то
. tg^+а) = tga,
ctg(7r+a) = ctg a.
(14.3)
в)	Аналогично получим
•5ш[-|л+а1 = sin
= cos (л+а) = -cos а,
(3
cos -л
cos |-+(л+а) =-sin (л+а) = sin а.
Рекомендуем читателю доказать, что
' tg(’2-
/3	,
ctg —л+а = —tga.
= —ctg а,
г) Заменив в формулах (14.2) и
(14.3) а на -а, получим
(14.4)
(14.5)
. sin(r-a) = sin а,
соь(л—а) =— cos а,
д) Заменив в формулах (14.4)
• / З.т
sin ——а
(Зя ।
cos ——a = -sin a,
tg(tf-a) = —tga,
ctg(jT-a) = -ctg a.
(14.5) а на -а, получим
(14.6)
= —cos а,
tg —а = ctg а,
= tga.
(14.7)
и
e) В силу того, что 2л является
гонометрических функций, будем иметь
периодом для всех основных три-
.sin (2л—a) = sin(—a) =—sina,
cos (2л—a) = cos(—a) = cos a,
tg (2л—a) = tg(-a) = —tga,	I
ctg (2л-а) = ctg(-a) =-ctg a. I
(14.8)
§ 5. ФОРМУЛЫ ПРИВЕДЕНИЯ
35
ж) Аналогично е), будем иметь
. 5т(2л+а) — sin а,
cos(2n+a) = cos а,
1%(2л+а) = tg a,
ctg(2%+a) = ctg a.
(14.9)
Рекомендуем читателю написать формулы, аналогичные форму-
лам (14.1) — (14.9), для углов в градусной мере, заменив в послед-
них л/2 на 90°, л на 180°, Зл/2 на 270° и 2л на 360°.
Пример 1. Пользуясь формулами приведения, найти зна-
чения следующих тригонометрических функций (или выразить
их через значения тригонометрических функций острых углов):
a) sin(2jr/3); б) cos91°10'52"; в) ctgl82°12'46".
Решение, a) зп1(2л/3) = 51п(л/2+л/6) = cos (л/6) = V3 /2;
б) cos91°10'52" = cos(90°+l°10'52") =-sinl°10'52";
в) ctgl82°12'46" = ctg(180°+2°l2'46") = ctg2°12'46".
Пример 2. Найти tg(3%/2-a), если tga = 0,9.
Решение. tg^/2-a) = ctga = 1/tga = 10/9.
Сформулируем теперь общее правило приведения:
1) если угола откладывается от вертикальной оси {углы л/2±а,
Зл/2±а), то название приводимой функции меняется на сходное; ес-
ли же угол, а откладывается от горизонтальной оси (углы -а, л±а,
2л±а), то название приводимой функции сохраняется;
2) если приводимая функция имеет отрицательное значение,
то нужно соответствующую функцию угла а взять со знаком ми-
нус; если же приводимая функция имеет неотрицательное значе-
ние, то нужно соответствующую функцию угла а взять со знаком
плюс.
Проиллюстрируем это правило на примере угла = л+a. Заметим
еще раз, что правило приведения справедливо для любого угла а, но
для простоты запоминания и иллюстрации этого правила мы считаем
а острым положительным углом.
Итак, на рис.38 угол /3 = л+a =LAOE. Требуется выразить триго-
нометрические функции угла л+a через тригонометрические функ-
ции острого положительного угла а. Заметим, что угол а = /.ВОЕ =
— Z.AOE1. Согласно правилу приведения нужно выяснить:
1) соответствующие названия тригонометрических функций;
2) знаки приводимых тригонометрических фуйкций.
1) Так как угол а откладывается от горизонтальной оси (угол /3
имеет вид л+a), то названия приводимых функций сохраняются.
2) sin fl < 0, cos /3 < 0.
Учитывая 1) и 2), имеем
sin /3 = sin (л+a) = ~sin a, cos/3 = cos(л+a) =-cosa;
36
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
так как tg /3> 0 и ctg /? > 0, то
tg/5 = tg(;r+«) = tga,
ctg [i = ctgfrr+a) = ctg a.
Мы пришли к формулам (14.2) и (14.3). Рекомендуем читателю про-
иллюстрировать на чертеже типа рис.38 правило приведения для ос-
тальных углов (-а, л/2±а, л-а, Зл/2±а и 2л±а). Мы формулирова-
ли определения и правило для случаев, когда углы измерялись в ра-
дианах, но все остается в силе, если всюду заменить л/2.на 90°, л на
180°, Зл/2 на 270°, 2л на 360°, а угол а считать заданным в градусной
мере.
Объединим полученные для формул приведения результаты в
следующую таблицу.
\ Углы Функч ции \	—a	71 2~a (90°- —a )	71 2+“ (90°+ +a )	it—a (180°- ~a )	.t+« (180°+ +a)	3 ^-a (270°- —a)	3 (270°+ +a)	2.т —a (360°- —a)	2л+а (360°+ +a)
sin	-sin a	COS <2	cos а	sin a	-sin a	-cos Л	-cos а	-sin a	sin a
cos	cos a	sin а	-sin a	-coscr	-cos а	-sin a	sin a	cos a	cos а
tg	-tga	ctg a	-Ctg a	-tga	tga	ctg a	-ctg a	-tga	tga
cig	-ctg a	tga	-tga	-ctg a	ctg a	tga	-tga	-ctg a	ctg a
§ 5. ФОРМУЛЫ ПРИВЕДЕНИЯ
37
Для произвольного угла /3=^3(1=360°«+«, где 0°< а< 360°, или /? =
=/?н = 2лп+а, где 0< «<2 я; п = 0, ±1, ±2.если угол дан в радиа-
нах, задача отыскания sin/?, cos/?, tg/?, ctg/? с помощью формул
(12.1) и (12.2) сводится к отысканию тригонометрических функций
угла а.
Пример 3. Данугол/? = 13я/3. Найти sin/?, cos/? и tg/?.
Решение. Представим данный угол в виде /? = /?2 = 2 • 2я4-я/3.
Применив формулы (12.1) и (12.2), получим
• 13л	. /п П , Л\ -71
sin—j— = sin /2-2яЧ-	-\	=	sin— =	—	,
1Зл	/ л рч ,	Л \	ЛГ	1
cos— = cos (2 • 2я4-	-)	= cos- = -	,
•Э	\	и I	Q
. 1 3 Л	, ( » . Л \	.Л ЛлГ
tg— = tg (4я+	= tgj = V 3.
Пример 4. Найти sin fl, cos /? и tg /?, если fl = -1050°.
Решение. Представим данный угол в виде
/?=Дз = 360°(-3)+30°.
Применив формулу (12.1) получим
sin(-1050°) = sin[360°• (-3)4-30°] = sin30° - Д/г,
cos(-1050°) = cos [360°- (-3)+30о ] = cos30° = V3/2.
Тангенс найдем следующим образом:
1(КЛ°\ — sin(-1050°) _ 1/2	1
tg( 1050 * cos(-1050°) -7з72"7з-
Пример 5. Имеем угол /3 = -960°. Найти sin /?, cos /? и tg /?.
Решение. Представим данный угол в виде /3 = /?.з=360°х
х (-3)4-120°. Применив формулы (12.1) и (14.1), получим
sin (-960°) = sin [360° • (-3)4-120° ] = sin 120°=
= sin(90o4-30°) = cos30°« V3/2,
cos(-960°) = cos [360° • (-3)4-120° ] =
= cos 120° = cos(90°4-30°) = -sin30° = -1/2 ,
tg(-96o°) = stn(~960°) - yiZz _
igt > cos(-960°)	-1/2 VJ-
Пример 6. Найтиtg(21p/4).
Решение. tg--|^ = t g^5?r+^ = tg ^=1.
38
ГЛ. I. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА
Пример 7. Найтиctg1020°.
Решение, ctg 1020° = ctg (180° • 5+120°) = ctg 120° = ctg (90°+30°) =
= -tg(30°) =-l/V3.
Пример 8 . Доказать тождество
cos1 2 3 (л/2+a)	cos2(2rc-a) _ .
2	’	2	*
sec (л+а)-1 cosec (2л+а)-1
Решение. Применив формулы приведения, получим в левой
• 2	2
sin а , cos а . „
части предполагаемого тождества —z------------1-----х----= А. Далее,
sera - 1 cosec a - 1
.2	2
. sin a 2	. COS a . ?	2	,	 2 i
A =-------cos a 4----------y - sirra = cos a + singer = 1, т. e. левая
1 - cos a	1 - sin a
часть равна 1. Мы пришли к верному равенству, что и доказывает
наше тождество.
У пражнения
1. Заменить значения данных тригонометрических функций значениями тригоно-
метрических функций дополнительных углов: а) sin 54°; б) sin(^/4-3a); в) cos 53°;
г) cos (З.т/10); д) tg 51°; е) ctg (л/4~а/2); ж) ctg 36°28'46”.
2. Найти значения следующих тригонометрических функций (или выразить их
через значения тригонометрических функций острых углов): а) cos (2л/3);
б) sin 92°31в) ctg (5л/4); г) tg 330°.
3. Найти cig(3jr/2+a), если ctg a - 10/11.
4. Вычислить: а) 3sinOr/2)+4cos(27r/3)+6sin(13r/6); б) 2tgl80°— sin(-270°)+ cosl80°.
, ,,	С08(а-л/4) cos6r/4-a)
5. Упростить выражение —ь------------*------- .
sinz(a+?r/4)
6. Значения данных тригонометрических функций привести к значениям тригоно-
метрических функций неотрицательных острых углов: а) cos(32jt/3); б) sin2760°;
в) tg(-1845°);r) ctg2209°.
7. Вычислить выражение 2tgl095°+ctg975°+tg(—195°), зная, что tgl5o=2-V3^.
8. Доказать тождество 3 [sin4 5 (3^/2-a)+sin4(3ir+a)] -2 [sin6 7 8 (^/2+a)+sin6(5^-a)] =1.
Глава II
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО
АРГУМЕНТА И ИХ ГРАФИКИ
§ 1.	Тригонометрические функции числового аргумента
15.	Определение. В настоящей главе мы введем тригонометрические функции
числового аргумента. Многие вопросы математики, механики, физики и других наук
приводят к тригонометрическим функциям не только угла (дуги), но и аргументов со-
вершенно различной природы (длина, время, температура и т.д.). До сих пор под ар-
гументом тригонометрической функции понимался угол, измеренный в градусах или
радианах. Теперь мы обобщим понятия синуса, косинуса, тангенса, котангенса, секан-
са и косеканса, введя их как функции числового аргумента.
Определение. Тригонометрическими функциями числового аргумента х
называются одноименные тригонометрические функции угла, равного х радианам.
Поясним это определение на конкретных примерах.
Пример I . Вычислим значение sin(s/4) = sin 0,785... Здесь под л/4 - 0,785...
мы понимаем отвлеченное иррациональное число. Согласно определению sin (л/4) -
=8ш(л/4 радиан) =VT/2. Итак, sin(л/4) - sin 0,785... -уПп..
Пример 2. Вычислим значение sin 1,5. Здесь под 1,5 мы понимаем отвлеченное
число. Согласно определению sin 1,5 = sin(1,5 радиана) ” 0,9975 (см. приложение II).
Пример 3. Вычислим значение tg 1,3. Аналогично предыдущему получаем
tg 1,3 = tg(1,3 радиана) - 3,6021 (см. приложение II).
Итак, в дальнейшем под аргументом тригонометрических функций мы будем по-
нимать угол (дугу) или просто число в зависимости от той задачи, которую решаем.
Называя аргумент углом (дугой), мы можем подразумевать под ним число, с помощью
которого он измерен в радианах. Например, вместо слов «косинус числа 10» будем го-
ворить «косинус угла, равного 10 радианам».
16.	Области определения и области изменения значений тригонометрических
функций. Уточним области определения (существования) и области изменения значе-
ний тригонометрических функций, рассматриваемых как функции числового аргу-
мента (х—число). Здесь мы существенным образом воспользуемся результатами пп. 5
и 6.
1)	у = sinx. Так как соответствующая функция угла определена для всех углов х, то
и новая функция определена для всех действительных чисел х (-со < х < + оо). Синус
как функция угла изменяется в пределах от -1 до +1, следовательноб и новая функция
изменяется в пределах от -1 до +1, т.е. она удовлетворяет неравенствам -1 < sinx < 1.
(Область изменения значений функции sinx — отрезок [ — 1, 1 ] оси Оу.)
Для остальных функций сообщаем просто результаты. Рассуждения аналогичны
предыдущему.
2)	у = cosx. Область определения (существования): - с» < х < +<». Область измене-
ния функции: — 1 < cosx < +1.
40
ГЛ. II. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ГРАФИКИ
3)	у = tgx. Область определения (существования): х—любое действительное число,
кроме чисел видах = ^(2к+1), гдеЛ -0, ±1, ±2,...
Область изменения функции: - « < tg х < + “.
4)	у = ctgx. Область определения (существования): х — любое действительное чис-
ло, кроме чисел вида х = кл, где к = 0, ±1, ±2, ... Область изменения функции:
-00 < Ctg X < +«>.
Заметим, что все свойства тригонометрических функций угла (четность, нечет-
ность, периодичность) переносятся на тригонометрические функции числового аргу-
мента.
17.	Некоторые неравенства и их следствия. Выведем теперь некоторые неравенст-
ва и их следствия.
Неравенство 1. Для всех действительных значений х, удовлетворяющих
неравенствам 0 < х < л/2, справедливы следующие неравенства:
sin х «; х с tg х.	(17.1)
Доказательство. Пусть число х удовлетворяет неравенствам 0 < х < л/2.
Построим окружность радиуса 0.4=1 и в ней отложим от оси Ох центральный угол
АОМ, равный х радианам (рис.39). Из чертежа видно, что площадь А АОМ меньше
площади сектора АОМ, которая меньше площади А А0М\. Соответствующие площа-
1 1 -> 1
ди равны — ОАВМ, ~ОА~-х и	О А- АМ\. Следовательно,
1 1 ? 1
±ОА ВМ <±ОА1 2 х< ±ОААМ{.	(17.2)
Так как ОА= 1, то ЯМ = sinx, АМ\ = tgx, и неравенства (17.2) принимают вид
sin х < х < tg х.	(17.3)
Заметив, что sinO -tgO = 0, приходим к неравенствам (17.1).
Неравенство 2. Для всех действительных значений х справедливо неравен-
ство
I sin х I < 1x1.
(17.4)
(Абсолютная величина функции sinx не превосходит абсолютной величины ее аргу-
мента.)
Доказательство. 1) Если 0 < х < л/2, то неравенство (17.4) справедливо на
основании (17.1).
2) Если — л/2< х < 0, то, сделав замену переменной х на у по формуле у~—х, получим
siny = sin(-x) - -sinx, где у уже удовлетворяет неравенствам 0 <s у < л/2,и для него
справедливы неравенства 0 < siny < у. Вернувшись к переменной х, получим 0 <
< sin(—х) «; -х, или 0 < — sinx «; — х. Последние неравенства равносильны неравенст-
ву I sinx I с 1x1, ибо х «; 0.
3) Если же 1x1 > л/2, то и подавно IsinxK 1x1, так как IsinxI < 1.
Итак, мы доказали, что для всех действительных значений х- справедливо неравен-
ство (17.4).
Заметим, что только при х = 0 мы имеем равенство sinO = 0.
§1. ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
41
Неравенство 3. Для всех действи-
тельных значений х справедливы неравен-
ства
О <s l-cosx< х2/2	(17.5)
и, следовательно, неравенство
1 -х2/2 «; cosx.	(17.6)
Доказательство. По формуле 1 -
-cosa = 2sin2a/2 имеем
Рис. 39
О < }— cosx -2sin2^.
На основании неравенства (17.4) можем
писать sin2(x/2) < х2/4. Таким образом,
„ 	• 2 п х2 х2
О < 1 -cosx - 2snr— < 2 — = — , что и
2	4	2
требовалось доказать.
Из (17.5) получим
1 —— < cos х.
(17.6)
С помощью полученных неравенств изучим поведение cosx, sinx и tgx при ма-
лых х.
Следствие 1. При малых х
cosx = 1.
Доказательство. На основании (17.5) имеем 0 < 1 -cosx < х2/2, а это и зна-
чит, что cosx =» 1 при малых х, причем ошибка, которую мы допускаем при замене
cosx на 1, не превосходит х2/2.
Пример 1 . cos 0,1 = 1, причем 0 <l-cos 0,1 < 0,005.
Пример 2. cos 0,4 = 1, причем0 < 1-cos 0,4 с 0,08.
Следствие 2. При малыхх
sin х _
х
Доказательство. Пусть 0 < х < л /2; тогда на основании (17.3) имеем
sinx < х < tgx.
Разделим теперь sinx на каждый из членов последних неравенств; получим
, „ sinx
1 >-----> cos х.
(17.7)
42
ГЛ. II. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ГРАФИКИ
Умножим все члены неравенств (17.7) на -1; получим
sin х
х
Затем ко всем членам последних неравенств прибавим по единице, получим
а , sinx , ,
О < 1------< 1 -cos х.
(17.8)
(17.9)
Применив теперь одно из неравенств (17.5), получим
х 2
(17.10)
Мы вывели (17.10) в предположении, что 0 < х < л /2. Рекомендуем читателю дока-
зать самостоятельно, что (17.10) имеет место и при -л /2 < х < 0. Итак, при х , удов-
летворяющих условию 0 < 1x1 < л/2, справедливы неравенства (17.10). А это и зна-
чит, что (sinx)/x "» 1, т.е. sinx = х, причем ошибка, которую мы допускаем при замене
sinxHa х, не превосходит 1x13/2. Из (17.10) имеем lx- sinxГ < Iх!3/2.)
Пример 3 . sin 0,1 = 0,1, причем 0 < 0,1-sin 0,1 < 0,0005.
Пример 4. sin 0,2 = 0,2, причем 0 < 0,2-sin 0,2 < 0,004.
Упражнения
1. Указать области определения и области изменения следующих тригонометриче-
ских функций:
а) у - secx; б) у - cosecx.
2. Оценить ошибку, которую мы допустим, если приближенно положим:
a) cos 0,5 •» 1; б) cos 0,6 = 1; в) sin 0,3 «» 0,3; г) sin 0,4 = 0,4.
§ 2. Графики тригонометрических функций
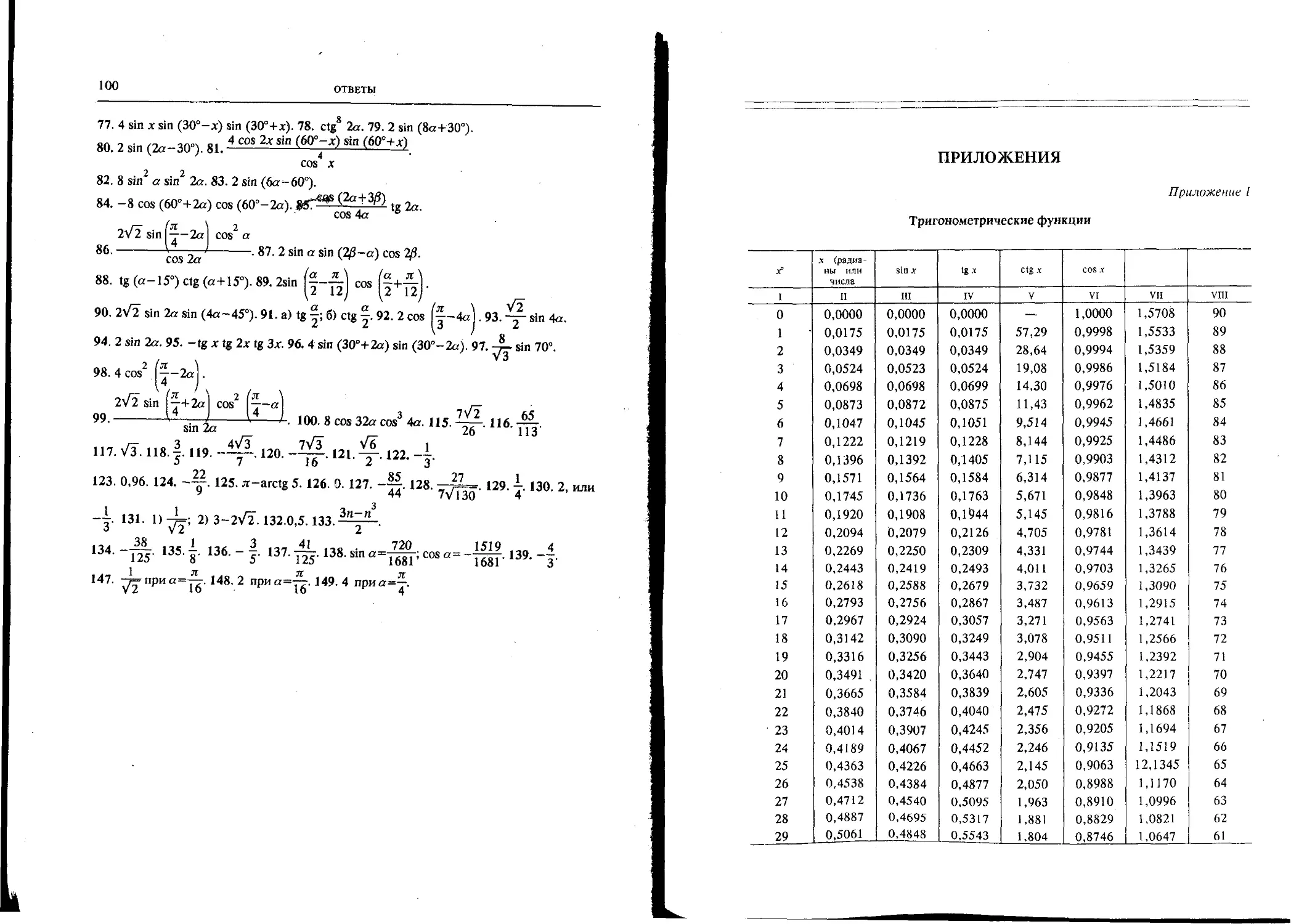
18. Первоначальные сведения о таблицах тригонометрических функций. В При-
ложениях к настоящей книге приведены таблицы, которые дают возможность полу-
чить значения основных тригонометрических функций с четырьмя значащими циф-
рами.
Приложение I. Таблица составлена для значений аргумента х в градусной
мере. В графе I даются значения аргумента х° с шагом в Г от 0° до 45°. В графе II дают-
ся соответствующие значения угла в радианной мере. Этой же графой можно пользо-
ваться для отыскания значений тригонометрических функций числового аргумента (см.
п.15). В графах III—VI даются соответственно значения тригонометрических функций
— значения sinx, tgx, ctgx и cosx, если 0° «; х° < 45°, и даются значения cosx, ctgx, tgx
и sinx, если 45° < х° < 90° (читай внизу!).Тригонометрические функции остальных
углов можно уже искать, используя всевозможные формулы приведения (см. п.14). В
графе VIII даются значения аргумента х° с шагом в 1° от 45° до 90° (читай снизу
вверх!). В графе VII даются соответствующие значения угла в радианной мере (или
просто числа!).
§ 2. ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
43
19. Основные графики.
1.	Синусоида (график функции у- sinx). 1) Область определения (су-
ществования) функции:
х — любое действительное число (—оо < х < + оо).
2)	Область изменения функции:
-1 < у < 1.
3)	Периодичность функции:
sinx — периодическая функция с основным периодом, равным 2л.
4)	Четность функции: sinx — нечетная функция, ибо sin(-x) - -sinx.
На основании пп. 3) и 4) достаточно построить график функции у - sinx на от-
резке [0, л], а затем продолжить его нечетно на отрезок [-я, 0] и, наконец, то, что
получится на отрезке [-л, л], продолжить периодически на всю числовую ось. Итак, в
дальнейшем будем изучать поведение нашей функции на отрезке [0, я].
5)	Точки пересечения с осями координат:
а)	с осью Оу (х - 0): у(0) - sinO = 0; график функции у - sinx проходит через нача-
ло координат;
б)	с осью Ох (у = 0) (нули функции).
Найдем те х, при которых у = sinx - 0. Такими значениями будут числа х* - кл(к - 0,
±1, ±2,...). Нас интересуют Хк из отрезка [0, л]. Такими х* будутхо -0 (уженайдено)
и Х|-л, а остальные нули функции расположены вне отрезка [0, я]. Следовательно,
нули sinx на отрезке [0, я] совпадают с концами этого отрезка.
6)	Наименьшие и наибольшие значения функции на отрезке [0, я].
Функция у - sinx на отрезке [0. я/2] монотонно возрастает от 0 до +1, а на отрезке
[я/2, я] монотонно убывает от +1 до 0 (см. п.6). Следовательно, наименьшими значе-
ниями будут у (0) - sinO = 0 и у (я) - бшл - 0; наибольшее значение достигается в одной
точке: у(я/2) " sin (я/2) - 1.
7)	Интервалы знакопостоянства функции.
На исследуемом отрезке [0, л] наша функция всюду неотрицательна, т.е. у =
= sinx > 0.
8)	На основании неравенств 0 < sinx < х для 0<х < я/2 (п.17) мы заключаем, что
наша синусоида на отрезке [0, л] должна распологаться ниже биссектрисы у - х пер-
вого координатного угла. Так как при этом x-sinx < х3/2, т.е. является при малых х
весьма малой величиной, то график у » sinx близок к графику у - х (касается биссект -
рисы I координатного угла).
После того, как функция исследована, приступаем к построению ее графика. Для
этого найдем некоторые «опорные» точки его, а затем соединим их плавной линией с
учетом свойств функции sinx.
Воспользуемся геометрическими соображениями. Рассмотрим первую четверть
единичной окружности (рис. 40) Разделим ее и соответствующий ей отрезок [0, я/2]
оси Ох, например, на 8 равных частей. Величина перпендикуляра, опущенного из
точки деления окружности на ось Ох, численно равна значению синуса соответствую-
щего угла и значению синуса соответствующего числового аргумента из отрезка [0,
я/2] оси Ох Во второй четверти (я/2 < х < л) синус убывает от 1 до 0. На основании
нашего геометрического построения можно заключить, что график синуса во второй
четверти (я/2 < х < л) симметричен его графику в первой четверти относительно
прямой х - я/2.
Соединив полученные «опорные» точки плавной линией, мы получим график
синуса (синусоиду) на отрезке [0, л]. При проведении линии (построении графика)
следует иметь в виду свойства 2), 6), 7) и 8). Затем продолжим график синуса на отре-
44
ГЛ. II. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ГРАФИКИ
зок [-л, 0], используя нечетность синуса, а именно построим на отрезке [-л, 0] гра-
фик, симметричный графику синуса на отрезке [0, л] относительно начала коорди-
нат. Имея график синуса, построенный на отрезке [-л, л], мы, используя его перио-
дичность, сможем продолжить его на всю числовую ось (рис.41).
Рис. 41
2. График функции у = cost. На основании формулы приведения мы имеем
у - cost = sin (л/2+т.).
Следовательно, график косинуса — это синусоида, сдвинутая по. оси Ох влево на
л/2. График косинуса построен на рис. 42.
3. Тангенсоида (график фу нк ции у =	) Область определения
функции:
х — любое действительное число, кроме чисел вида х„ - л/2 (2/г+1), где п - 0, ±1,
+ 2,...
2)	Область определения функции:
§ 2, ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
45
— 00 < у < +».
3)	Периодичность функции:
tgx — периодическая функция с основным периодом, равным л.
4)	Чётность функции:
tgx — нечетная функция, ибо tg(-x) = -tgx.
На основании 3) и 4) достаточно построить график функции у - tgx, на отрез-
ке [О, л/2], а далее продолжить его нечетно на отрезке [-л/2, 0] и, наконец, то, что
получится на отрезке [-л/2, л/2], продолжить периодически на всю числовую ось.
Итак, в дальнейшем будем изучать поведение нашей функции на отрезке [0, л/2].
5)	Точки пересечения с осями координат:
а) с осью Оу (х - 0) у (0) ” tgO ” 0; график функции у - tgx проходит через начало
координат;
б)	с осью Ох (у “ 0) (нули функции).
Найдем те значения х, при которых tg х - 0. Такими значениями будут х* ~ кл (к -
*0, ±1, ±2,...). Нас интересуют х* из отрезка [0, л/2]: хо -0 (уже найдено), а осталь-
ные нули функции расположены вне отрезка [0, л/2]. Следовательно, единственный
нуль tg х, находящийся на отрезке [0, л/2], совпадает с левым концом этого отрезка.
6)	Вертикальные асимптоты:
tg х определен всюду на отрезке [0, л/2], кроме точки х “ л/2.
Так как tg х -»+« при х -*л/2, х < л/2, то прямая х - л/2 является вертикальной
асимптотой для графика функции у = tgx.
7)	Наименьшие и наибольшие значения функции на отрезке [0, л/2].
На основании п.6 функция tg х на отрезке [0, л/2] монотонно возрастает от 0 до
+оо. Следовательно, наименьшее значение будет у (0) - tgO - 0, а наибольшего зна-
чения не будет, ибо tgx-»+co, когда х -»л/2, х < л/2.
8)	Интервалы знакопостоянства функции.
На исследуемом отрезке [0, л/2] функция tgx всюду неотрицательна, т.е. у = tgx > 0.
Следовательно, график функции лежит над осью Ох. На основании неравенств Ос
с sin х с х < tgx (см. 17.1) для 0< х <л/2
мы заключаем, что тангенсоида на отрезке
[0, л/2] должна располагаться в^ше биссек-
трисы у “х первого координатного угла.
После того, как функция исследована,
приступаем к построению ее графика. Для
этого найдем некоторые «опорные» точки
его, а затем соединим их плавной'линией с
учетом свойств функции tg х.
Воспользуемся геометрическими сообра-
жениями аналогично тому, как мы это дела-
ли в случае построения графика функции у -
sinx. Разделим опять первую четверть еди-
ничной окружности и соответствующий ей
отрезок [0, л/2] оси Ох, например, на 8 рав-
ных частей. На оси тангенсов получим от-
резки, численно равные тангенсам соответ-
ствующих углов. Далее, эти отрезки перене-
сем в соответствующие точки оси Ох. Концы
их соединим плавной линией и получим гра-
фик функции у - tgx (рис. 43). Вся тангенсо-
ида изображена на рис. 44.
Рис. 43
46
ГЛ. II. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ГРАФИКИ
Рис. 44
Рис. 45
4.	График функции у = ctgjt изображен на рис.45. Рекомендуем читателю
самостоятельно построить его. Для этого:
1)	построить график функции у == tgjc;
2)	сдвинуть построенный график влево по оси Ох на л/2 (получим график функ-
ции y = tg(.r+-jt/2));
3)	последний график зеркально отразить (перевернуть) относительно оси Ох (по-
сле выполнения последнего действия получим график функции у = ctg.v).
20.	Примеры построения графиков некоторых других тригонометрических фун-
кций. В дальнейшем мы будем коротко говорить: построить график функции у - f(x),
а понимать под этим следующее: провести исследование функции ytfix) и построить
ее график. Рассмотрим некоторые примеры.
Пример 1 . Построить график функции у - 2sin х.
Решение. Заметим, что график функции у - 2sin х получается из графика фун-
кции у = sin х, исследование которой проведено в Начале п.19, умножением каждой
его ординаты на 2. Нули же функции sin х совпадают с нулями функции 2sin х. Гра-
фик функции у - 2sin х изображен на рис. 46.
Рис. 46
Пример 2 . Построить график функции у = sin 2х.
Решение. Заметим, что график функции у - sin 2х получается из графика фун-
s 2. ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
47
кции .у = sin л сжатием по осп Ох в два раза. Основным периодом для функции у = sin 2.x
будет уже число л. График функции у = sin 2х изображен на рис.47.
Рис. 47
Пример 3 . Построить графики функций: а) у = sin i х I ; б) у - I sin х I .
Решение, а) Воспользуемся общим правилом построения графика функции у =
“/(1x1) по графику функции у “ fix): сохраняем часть графика у “ sin .г для х > 0 и
зеркально отражаем ее относительно оси Оу (часть графика у = sin х для х < О просто
отбрасываем). Получаем график, показанный на рис.48.
Рис. 48
б) Сохраняем часть синусоиды у - sin х, расположенную выше оси Ох; часть сину-
соиды, лежащая ниже оси Ох, зеркально отражается в оси Ох. Получаем график фун -
кции у “ I sin х I, показанный на рис.49.
21.	Дальнейшие примеры построения графиков функций.
iip и м е р 1 . Построить график функции у - 1g sin х.
Решение. 1) Область определения функции.
Функция определена дня тех значений аргумента х, для которых sin х > 0. Такие
значения аргумента заключены в пределах 2кя < х< (2Н1)я, где к =- 0, ± I, ±2,...
2)	Периодичность функции.
sin х — периодическая функция с основным периодом, равным ?т. Следо-
вательно, для тех х, для которых определена функция у - 1g sin х, мы будем иметь
48
ГЛ. II. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ГРАФИКИ
Ig sin (х+2л) = 1g sin а, т.е. исследуемая функция будет иметь периодом также число
2л. Исходя из соображений периодичности, достаточно исследовать нашу функцию на
любом отрезке длины 2л, например, на отрезке [0, 2л]. Но на отрезке [0, 2л] наша
функция определена не всюду — она определена только в интервале (0, л), поэтому в
дальнейшем будем изучать поведение данной функции в интервале (0, л).
3)	Область изменения функции.
В интервале (0, л) наибольшее значение, которое принимает sin .с, равно 1 (в точке
д' - л!2), а наименьшего значения нет, но при х -> 0, х > 0, и х-* л, х < л, sinx -»0, ос-
таваясь положительным. Функция Igsin х сначала возрастает от -оо до 0 (при
()< х < я/2), а затем убывает от 0 до - со (при л 12 с х < л). Итак, - оо < (g sin х «; 0.
4)	Четность функции.
Функция у = 1g sin х ни четная, ни нечетная.
5)	Точки пересечения с осями координат:
а)	с осью Оу (х = 0); наша функция определена только в интервале (0, л), а в
точке х=0 она не существует, поэтому точки пересечения с осью Оу не существуют;
б)	с осью Ох (у = 0) (нули функции); наша функция обращается в нуль в единст-
венной точке интервала (0, л) — в точке х“л/2, а в остальных точках этого интервала
она от лична от нуля.
6)	Вертикальные асимптоты.
Заметим, что прямые х — 0 и х = л являются вертикальными асимптотами для нашей
функции, ибо при х -*0, х> 0, у “1g sin х -»-оо и при х -* л, х< л, у - 1g sin х-»-<».
7)	Интервалы знакопостоянства функции. -
На исследуемом отрезке [0, л] наша функция всюду неположительна, т.е.
у= 1g sin х < 0, ибо 0 < sin х «» 1. Следовательно, график функции лежит под осью Ох.
8)	Наименьшие и наибольшие значения функции на отрезке [0, л].
Наибольшего значения функция достигает в единственной точке х = л/2, и это
значение равно 0 (у(л/2) = 1g sin(тг/2) - 0). Наименьшего значения функция не имеет,
ибо при х -»0, х > 0, и при х -> л, х < л, у = 1g sin х -*-оо. График функции у 4g sin х
изображен на рис.50.
Пример 2 . Построить график функции у = х sin2x.
Решение. 1) Область определения функции:
х — любое действительное число.
2)	Область расположения графика функции.
Заметим, что ixsin2xl с 1x1 (так как Isin2xI < 1), поэтому
-х «с х sin2x < х.
§ 2. ГРАФИКИ ТРИГОНОМЕТРИЧЕСКИХ. ФУНКЦИЙ
49
Рис. 50
Геометрически это означает, что график функции у = х sin2.x заключен между графи-
ками функций у - -х и у = х.
3)	Четность функции.
Данная функция, как произведение двух нечетных функций (х и sin2x), есть фун-
кция четная.
В дальнейшем будем исследовать функцию при х > 0.
4)	Точки пересечения с осями координат:
а)	с осью Оу (х = 0); при х = 0 мы имеем у = 0, следовательно, график функции
проходит через начало координат;
б)	с осью Ох (у = 0) (нули функции); функция обращается в нуль в точках, где
sin2x” 0, т.е. в точках вида х = лп/2 (п - 0, 1,2,...).
5)	Точки, в которых функция принимает значения, равные х или -х.
а)	х sin2x - х в точках, где sin2x = 1, т. е. в точках
х = .тп+л/4	(п-0,1,2,...);
б)	х sin2x = -х в точках, где sin2x = -1, т. е. в точках
х-лп+Зя/4	(л-0,1,2,...).
Построим график функции сначала для х > 0, а затем, используя четность нашей функ
ции, отразим его зеркально в оси Оу. График функции у-xsin2x изображен на рис. 51.
11 g X I
Пример 3 . Построить график функции v = х —в—.
Решение. 1) Область определения
функции.
Функция определена для тех значений
х, для которых существует и отлична от ну-
ля функция tg х, т. е. для всех х, кроме
71
Х = ЛП И х —— (2п+1),
где п - 0, ±1, ±2, ...
2)	Для всех х из области определения
функции имеем
= 11g х! _ [ х, если tg х > 0,
У х tg х | -х, если tg х < 0.
3)	Четность функции.
Функция—четная. Следовательно, доста-
Рис. 51
50
ГЛ И. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ГРАФИКИ
точно сначала построить ее график для х > 0.
4)	Заметим, что tg х > 0 при х > 0 в интервалах
лп< х<л/2+лп, где п-0,1,2,...,
т. е. в интервалах (0, л/2), (л, Зл/2) и т. д.;
tg х < 0 при х > 0 в интервалах
л/2+л п< х< я(п+1), где п-0,1,2,...,
т.е. в интервалах (л/2, я), (Зл/2, 2я) и т. д.
5)	Окончательно имеем (для х > 0)
Hgxl
tgx
J х, для лп< х< л/2+лп,
1-х, для л/2+лн < х < л(п+1),
где п = 0, 1,2, ...
Построим график функции сначала для х > 0, а затем,
функции, отразим его зеркально в оси Оу.
используя четность данной
I ts х I
График функции у = х —6—
tg X
изображен на рис. 52.
У пражнения
Провести исследование и построить графики следующих функций:
1)	у -see х; 2) у-cosec х; 3) у = 3 cosx; 4) у -cos3x; 5) у = cos Ixl; 6) у - Icos xl;
7) у = I cos I х I I, 8) y-lgcosx; 9) у =-cos(x/2); 10) у - х cos (х/2); 11) у- sinUx2);
12) у = 2lo«2cosr.
Глава III
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
§1. Формулы сложения и вычитания
22,	Расстояние между двумя точками на плоскости.
Задача. На плоскости даны две точки A(%i, У1) и В(%2> Най-
ти расстояние АВ между ними.
Решение. На рис.53 изображен случай, когда х2 >	> 0 и
у2 > yi >0. Мы же будем вести рас-
суждения, справедливые для
любого случая расположения
точек А и В. Заметим,
что АС = DE = I х2 - *1 1 и
ВС = IУ2 - Л । • По теореме Пифа-
гора из прямоугольного треуголь-
ника АС В имеем
АВ2 = АС2 + ВС2,
э	~	J	FWUJJ
или АВг = I х2 _ -И ।	। У2 ~ У1 । •
Так как I х2 - %i 12 = (х2 - хх)2 и 1у2 - И12 = (У2 ~ У1)2. т0
АВ2 = (х2 - -И)2 + (у2 - У1)2,
откуда имеем
АВ = V(х2 - хО2 + (у2 - У1)Т-	(22.1)
Пример. Найти расстояние между точками А(7 , -2) и В(4 . -6).
Решение. По формуле (22.1) имеем
АВ = V(4 - 7)2 + (-6 + 2)т = V25 = 5.
52	Гл. Ill ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
23.	Косинус суммы и разности двух аргументов.
а)	Косинус разности. Предположим, что углы а и р удов-
летворяют следующим двум услови- '•»
ям:
1)	0 < а < 2я, 0 < Р < 2л; 2) а > р. у
На рис.54 изображены углы a (LAOC)	il
и р (ААОВ). Точки А, В и С ле- 
жат на единичной окружности
(ОА = ОВ = ОС = 1). Заметим, что
А ВОС = а-р.
Кроме системы координат Оху бу-
дем рассматривать еще новую систему
координат Ох'у’, полученную из ста-
рой поворотом на угол р.
В дальнейшем будем использовать
тот факт, что расстояние ВС между
точками В и С, вычисленное в старой системе координат Оху и в но-
вой системе координат Ох'у', будет одинаково.
В системе координат Оху точка В имеет координаты (cos р, sin р),
а точка С — координаты (cos a, sin «). По формуле (22.1) имеем
ВС2 = (cos а - cos Р)2 + (sin а - sin /З)2 =
= cos2 а — 2 cos a cos Р + cos2 Р + sin2 а - 2 sin a sin р + sin2 р =	,
= 2 (1 - cos acos Р - sin a sin Р).	(23.1)
В системе координат Ох’у' точка В имеет координаты (1, 0), а точка
С — координаты (cos (а - /3), sin (а - РУ). По формуле (22.1) найдем	ъ
I
ВС2 = [cos (а - Р) - 1 ]2 + sin2 (а - Р) =	1
= cos2 (а — Р) - 2 cos (а - Р) + 1 + sin2 (а — Р) =
= 2 [1 — cos (а — )8)].	(23.2)
Приравняв правые части формул (23.1) и (23.2), получим выраже-
ние для косинуса разности двух углов:
cos (а — Р) = cos a cos Р + sin a sin р.	(23.3)
Заметим, что ограничения, наложенные на углы а и (5 условиями 1) и 2), можно	••
снять.	••
§ 1. ФОРМУЛЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
53
б)	косинус суммы. Так как формула (23.3) справедлива для
любых двух углов «иД то, заменив в ней р на -/3, получим
cos (а + р) = cos [а - (-/3) ] = cos a cos (-/?) + sin a sin (-/3).
Воспользовавшись четностью косинуса и нечетностью синуса, будем
иметь
cos (а + /3) = cos a cos /3 — sin a sin /3.
(23.4)
Пример. Вычислить cos (13л/12).
Решение.
13	3 л 3 я . 3	.	я
cos -т™- л = cos	(-Г я	+ -у)	= cos -т л	cos -у	- sin -г л sin =
12 М 3'	4	3	4	3
VI 1 VI Уз
2 ‘2	2'2
VI г-
-4-(1 4-VI) »-0,966.
Формулы (23.3) и (23.4), как и все выводимые в дальнейшем со-
отношения для тригонометрических функций, сохраняют свою силу
и для тригонометрических функций числового аргумента. Вообще, в
дальнейшем мы уже не будем всякий раз указывать, как понимается
аргумент тригонометрической функции (как угол или как число).
24.	Синус суммы и разности двух аргументов
а) Синус суммы. Воспользовавшись формулой приведения
(13.2), будем иметь
sin (а + р) = cos
= cos
- а - р
у-(«+/3)
К правой части последнего равенства применим формулу (23.3)
cos
= cos
cos р + sin
sin p -
= sin a cos P + cos a sin p.
Итак,
sin (a + P) = sin a cos P + cos a sin p.	(24.1)
б) Синус разности. Рекомендуем читателю вывести формулу
sin (а — Р) = sin а cos р — cos a sin /3.	(24.2)
54
Гл. Ill
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Пример. Вычислить sin 105°.
Р е ш е н и е . sin 105° = sin (60° + 45°) = sin 60° cos45° +
vy VT 1 V2 VT
+ cos 60° sin 45° = ----у + у ~y = “у + 1) ~ 0,966.
L L	Li it	1
25.	Тангенс суммы и разности двух аргументов
а) Тангенс суммы. При всех допустимых значениях аргу-
ментов а и р имеет место формула
+ / .	_ tg а + tg /3
tg(«+y3)	(25.1)
Доказательство. На основании формул (24.1) и (23 4) имеем
.	„ _ sin (а + /3) _ sin а cos /3 + cos a sin Д
8 I6' Р) - CQS +	_ cos cos Д _ sin а sin Д'	(25.2)
Разделив почленно числитель и знаменатель дроби, стоящей в пра-
вой части, на произведение cos a cos Д (мы предполагаем, что оно
отлично от нуля), получим (25.1).
б) Тангенс разности. Аналогично можно вывести формулу
. , пч _ tg а - tg ft
F) l+tgatg/3'	(25.3)
Рекомендуем читателю вывести ее самостоятельно.
Пример. Вычислить tg 105°.
Решение.
tg 105° = tg (60° 4-45°) =
tg 60° + tg 45° _ УЗ + 1
1 - tg 60° tg 45°	1 - V3
1)2 = “(2 + <3) = -3,732.
26. О формулах сложения для нескольких аргументов. Если возникает необходи-
мость найти тригонометрическую функцию трех (или более) слагаемых, то это можно
сделать, последовательно применив выведенные в пп.23—25 формулы. Например'
sin (а + /3 + у) = sin [(а + /3) + у] = sin (а + /3) cos у + cos (а + /3) sin у -
= (sin а cos /3 + cos a sin /3) cos у + ( os a cos /3 - sin а sin /3) sin у =
= sin a cos /3 cos у + cos a sin /3 cos у +
+ cos a cos ft sin у - sin a sin ft sin y.	(26 1)
Предлагаем читателю самостоятельно доказать, что
cos (а + ft + у) = cos a cos ft cos у - sin a sin ft cos у - sin a cos ft sin у -
- cos a sin ft sin у	(26.2
§ 2. ФОРМУЛЫ ДЛЯ ДВОЙНОГО И ПОЛОВИННОГО АРГУМЕНТА
55
и
tg (а + 0 + у)
tg а + tg 0 + tg у - tg а tg tg у
1 - tg a tg /? - tg /3 tg у - tg у tg a
(26.3)
У пражнения
Вычислить:
13	5
a) cos 105°; 6) sin — л; в) tg 15°; г) tg
§ 2. Формулы для двойного и половинного аргумента.
Выражение sin па и cos па через степени sin а и cos а
27. Тригонометрические функции двойного аргумента. Положив
в формулах (24.1), (23.4) и (25.1) а = /3, мы получаем следующие
формулы:
sin 2а = 2 sin a cos а.	(27.1)
cos 2а = cos2 а - sin2 а.	(27.2)
. -	2 tg а
tg 2а = ---.
1 - tg2 а	(27.3)
Пример. Упростить выражение
А = 2	(sin6 а + cos6 а) -	3 (sin4 а + cos4 а).	(27.4)
Решение.	Мы уже решали этот пример в п.7.	Используя фор-
мулы (7.9), (7.10) и (27.1), имеем
sin4 а + cos4 а = 1	- j sin2 2а,
sin6 а + cos6 а = 1	- 4 sin2 2а.
4
Подставив (27.5) и (27.6) в (27.4), получаем
Л = 2 — sin2 2а - 3 + -| sin2 2а = -1.
Формулы (27.1) — (27.3) можно использовать для любого аргумен-
та а считая его двойным для аргумента а/2. Например:
(27.5)
(27.6)
56
Гл. ш
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
. _ а\ п . а а
sin а = sin 2	= 2 sin -j cos ,
(а\ та . > а
cos а = cos 2 у = cos у - sin^ у ,
l Z I	£*	£t
tga = tg 2 к-
т 4 a
2 tg 2
!-tg 2
(27.7)
(27.8)
(27.9)
.a . _ a \	. a a
sin j = sin 2 Jq = 2 sin Jq cos jg
и т. д.
28. Выражение sin па и cos па через степени sin а и cos а при натуральном числе
п. Случай, когда п - 2, дан формулами (27.1), (27.2). Выразим теперь sin 3a, cos За,
sin 4а, cos 4а и вообще sin па, cos па через sin а и cos а. Укажем на два способа пол-
учения соответствующих формул. Покажем, например, как получаются формулы для
sin За и cos За.
Первый способ .Представляем sin За в виде sin (2а + а) и используем форму-
лу (24.1), а затем используем формулы (27.1) и (27.2):
sin За = sin (2а + а) = sin 2а cos а + cos 2а sin а =
= 2 sin a'cos2 а + cos2 a sin а — sin3a = 3 cos2 a sin а — sin3 а.
Итак,
Sin За = 3 cos2 a sin а - sin3 а.	(28.1)
2	2
В правую часть формулы входят sin а и cos а; заменив cos а на 1 — sin а, придем к
следующей формуле:
\f sin 3a = 3 sin a - 4 sin3 a,	(28.2)
которая содержит в правой части только степени sin а. Аналогичные формулы можно
получить для cos За (рекомендуем это сделать читателю):
Vcos За = cos3 а - 3 cos a sin2 а,	(28.3)
dos За = 4 cos3 а - 3 cos а.	(28.4)
Заметим, что формулы (28.1) и (28.2) являются частным случаем формулы (26.1),
когда в последней a = /1 = у. Формулы же (28.3) и (28.4) — частный случай формулы
(26.2).
Второй способ. Воспользуемся результатами, полученными в алгебре при
изучении комплексных чисел. На основании формулы Муавра
(cos а + / sin а)” = cos па + i sin па;	(28.5)
для случая, когда п - 3, имеем
(cos а + i sin a)3 = cos 3a + i sin 3a.	(28.6)
§ 2. ФОРМУЛЫ ДЛЯ ДВОЙНОГО И ПОЛОВИННОГО АРГУМЕНТА	57
Два комплексных числа равны тогда и только тогда, когда равны соответственно их
действительные и мнимые части. Теперь из равенства
3	2	2	3
cos а + 3 cos a sin a-i - 3 cos a sin а - sin a-i = cos За + i sin За, (28.7)
отделяя (и соответственно приравнивая) действительную и мнимую части, получим
формулы		.
cos За = cos3 а - 3 cos a sin2« у	(28.3)
И	2	3
sin За = 3 cos а sin а — sin' a.	(28.1)
В общем случае для получения sin па и cos па можно поступать также двумя спо-
собами: либо применять последовательно теоремы сложения (первый способ), либо
пользоваться формулой Муавра (второй способ).
29. Тригонометрические функции половинного аргумента.
Часто бывает необходимо, зная тригонометрические функции аргу-
мента а, найти тригонометрические функции аргумента а/2. Выве-
дем соответствующие формулы. Мы имеем
7 а . т а
cos у “ sin у ~ cos а-
(27.8)
Присоедини к этой формуле основное тригонометрическое тождество:
2 а , . 2 «	,
cosz у + sirr = 1.
Сложив почленно (27.8) и (29.1), получим
1 ,	п 2 а
1 + cos а - 2 cos^ у.
Вычитая (27.8) из (29.2), получим
1	п  т а
1	— cos а = 2 sin" 2’.
Из тождеств (29.2) и (29.3) соответственно имеем
э а	1	+	cos а	а-	1/	1	+	cos	а
cos -% =----2-----, или cos 2	=	± V	--------
. 7 а	1	—	cos в. .а	1/	1	—	cos	а
sinz у -----2-----> или sin 2	=	± V----2----
(29.1)
(29.2)
(29.3)
(29УЛ
(29.5)
Разделив почленно тождество<(29.3) на (29.2), приходим к тождеству
2	_ 1 ~ cos а
® 2	1 + cos а '
(29.6)
58
Гл. Ш
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Из последнего тождества имеем
tg2 =
1 + cos а
(29.7)
Применяя формулы (29.4), (29.5) и (29.7), следует всякий раз забо-
титься о знаке, который нужно взять перед радикалом.
Для вычисления tg (а/2) могут быть использованы и формулы,
выражающие tg (а/2) через cos а и sin а рационально. Выведем эти
формулы:
. а
sin -=
. , а 2
a) tg2=—г/
cos
- . а а
2s'"2c°S2 sing
2 cos2 2	1 + cosa'
(29.8)
(формула (29.8) имеет смысл только
а
2
Так как всегда 1 + cos а > О
при 1 + cos а > 0), то из (29.8) можно заключить, что знак tg во
всех случаях совпадает со знаком sin а.
б)
 а	О  2 а
8Ш тг	2 Sirr 2,
а _	2 _	2
7 ct	ct ct
cos 2^	2 cos у s*n 2"
1 - cos a
sin a
(29.9)
Из последней формулы также ясно, что знак tg'^ совпадает со зна-
ком sin а, ибо всегда 1 — cos а > 0.
П ри мер 1 . Найти sin 22°30’, cos 22°30' и tg 22°30/
Решение. Мы знаем, что cos 45° = sin 45° = V2/2. Следова-
тельно, применяя формулы (29.5), (29.4) и (29.9), получим
sin 22°30' - +
VT~Vf
2 ”
« 0,383;
-„о™,	. хГ +C0S 45°
cos 2z°30 - + V-----2"---
vT'+yf
2
= 0,924;
j cry? 4 5°
tg 22°30' = —« VI - 1 ~ 0,414.
sin 45°
Пример 2 . Дано: sin а = -4/>, где 3;т/2 < а < 2л. Найти
sin («/2) и cos (а/2).
§ г. ФОРМУЛЫ ДЛЯ ДВОЙНОГО И ПОЛОВИННОГО АРГУМЕНТА
59
Решение. Сначала находим

cos а = +V1 - sin2 а
16 _3
25 ~ 5'
Так как Зл/4 < а/2 < л, то sin (а/2) > 0, a cos (а/2) < 0.
Применяя формулы (29.5), (29.4) и беря в них радикалы с соот-
ветствующими знаками,получим
 а , 1/ I — cos а а/ 1 - У5
sm 2 - + V ?	- V 2
а _ а / 1 + cos а _ д/ 1 + У5
cos 2 " V 2	~	V 2
30. Выражение основных тригонометрических функций аргу-
мента а через tg (а/2). Иногда требуется основные тригонометриче-
ские функции (sin а, cos а, tg а и ctg а) выразить рационально че-
рез tg (а/2). Покажем, например, как это делается для sin а. Ис-
пользуя тождества
cos2 (а/2) + sin2 (а/2) = 1,
~ . а
sin а — 2 sin у сс
Разделив числитель и знаменатель дроби, стоящей в правой части
последнего равенства, почленно на cos2 (а/2), получим
sin а = z sin (а/ zj cos (а/L) и
можно писать
а _ 2 sin(a/2) cos (а/2)
2 cos2 (а/2) + sin2 (а/2)
sin а =
2 tg (а/2)
1 + tg2 (а/2)
(30.1)
Используя тождество cos а = cos2 (а/2) — sin2 (а/2), читатель мо-
жет доказать, что
cos a =
1 - tg2 (a/2)
1 + tg2 (a/2)
(30.2)
Соответствующая формула для tg a приводилась нами в п.27:
2 tg (a/2)
1 - tg2 (a/2)'
(30.3)
60
Гл. in
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Зная tg а, можно получить формулу
_ 1 - tg2 (ct/2)
Cg° 2 tg (а/2) •	(30.4)
Замечание. Формулы (30.1) —(30.4) имеют смысл для всех
значений аргумента а, кроме ап = (2п + 1) л, где п — целое число.
Пример 1. Дано tg (а/2) = 7/g. Найти sin a, cos а и tga.
Р е ш е и и е. На основании формулы (30.1) имеем
2-7/8	. 112
sin & —	т ”” 11 о •
1 + (7/8)2 ИЗ
.	1 ~ (7/Ю2	15
Аналогично cos а =-----5—%- =
1 + (7/8)2 ИЗ
sin« 112
tg а уже проще искать так: tg а -
п	~ _	2 + 3 cos а	а 2
Пример 2. Вычислить г:, если tg тт = — -л .
4-5 sin а ь 2	3
Решение. На основании формул (30.1) и (30.2) находим
2-(-Уз)	12	1-4/9	5
sin а =----1- , = -Тз, cos а = тт/ГД = ТУ-
1 + (-2'3)	13	1+4/9 13
2 + 3 cos а 2+15/13	41
Далее, 4 _ 5 sina - 4 + 60/13 - И2-
Упражнения
cos 2а cos а - sin а
1.	Доказать тождество ——-—г— =------——:------.
1 + sin 2а cos а + sin а
2.	Упростить выражение А = ?
Я з ।
2	У
, „	cos“«	1 . „
3.	Доказать тождество———-а----- -- -у sin 2а.
Cig (а/2) - tg (а/2;	4
4. Получить формулы, выражающие sin +z и cos 4а через степени sin а и cos а.
5. Упростить cos3 a cos За + sin3 a sin За.
6. Дано, sin а = — 3/5, где Зл < а < 7л/2. Вычислить sin (а/ 2), cos (а/2) и ig (а/2).
2
sin (х — л/4)	13л	)	2 cos (х - 5л74)
7.	Упростить -—)—:---гл ctg -----X-----, “Д 
*	sin (х + л/4)	(4	)	1 - sm 2х
2	2	2 G—В
8. Доказать тождество (cos а - cos /) + (sin а — sin — 4 sin
§ 3. ПРЕОБРАЗОВАНИЕ В СУММУ
61
„ „	,,	а, 1 - sin 2а	2 (л \
9.	Доказать, что sin а /1 + tg a tg — 1 +	in~2^ = tg а + tg — - а .
10.	Дано: tg («/2) = 6/5- Найти sin а и cos а.
3 sin а - 4 tg а	а	4
11.	Вычислить -z---—, если tg тт = —z-
5 ctg а + 6 cos а	2	3
12.	Получить выражение для tg За через tg а.
13.	Доказать тождество tg а + 2 tg 2а + 4 tg 4а + 8 tg 8а + 16 ctg 16<z = ctg а.
Л
14.	Найти ctg—.
О
§ 3.	Преобразование в сумму выражений вида
sin a cos /3, cos a cos (3 и sin a sin j3
31.	Основные формулы. Вернемся к формулам (24.1) и (24.2)
sin (а + /3) = sin a cos (3 + cos a sin /3,
sin (or — /3) = sin a cos (3 — cos a sin [3.
Сложив эти тождества почленно и разделив на 2, получим
,, sin (а + в) + sin (а - В)
sin a cos /3 =------------------ 	(311)
Выполнив аналогичные действия с формулами (23.3) и (23.4):
cos (а - /3) = cos a cos /3 + sin a sin /3,
cos (а + (3) = cos a cos (3 - sin a sin (3,
получим
o cos (a + B) + cos (a - (3)
cos a cos p ----x---------------2)
Вычтем из (23.3) почленно (23.4) и разделив на 2; получим
. ,, cos (а - /3) - cos (а + /3)
= —-------------------“ <3,.3)
32.	Примеры. Иногда при решении примеров, имея произведения
тригонометрических функций, например функций аргументов а и /3,
бывает полезно перейти к полусуммам или к-полуразностям соответ-
ствующих тригонометрических функций.
Пример 1 . У простить А =----------(feO + «)----------
4 sin (15° +у) sin (75° — у-)
Решение. Преобразовав произведение, стоящее в знаменате-
ле, получаем
62
Гл. Ш
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
__________sin (60° + а)__________________ sin (60° + ct)
2 [cos (60° - j) “ cos 90°]_____2 cos (60° -
Знаменатель преобразуем при помощи формулы приведения
cos (60° - |) = sin [90° - (60° - I)] = sin (30° +	.
Числитель же преобразуем так:
sin (60° + ct) = 2 sin (30° + I) cos (30° + |).
Тогда
2 sin (30° + y) cos (30° + y)
A =-------—--------------------— = cos (30° +	.
2 sin (30° +	v L’
Пример 2 . Вычислить A = sin 20° sin 40° sin 80°.
Решение. Заметим, что
sin 20° sin 40° = 1- (cos 20° - cos 60°) = cos 20° -
2	' 2	4
Далее,
A = i (2 cos 20° sin 80° - sin 80°) =
1	V3
- -7 (sin 100° + sin 60° - sin 80°) = -g-,
*T	*
так как sin 100° = sin 80°, a sin 60° = VJ/2.
Упражнения.
1.	He пользуясь формулами для sin 3« и cos За, упростить выражение
3	3	'
cos a cos За + sin a sin За.
2.	Доказать тождество 4 sin a sin (л/3 + «) sin (л/3 - а) = sin За.
3.	Вычислить А = cos 80° sin 50° cos 20°.
, „	,	(л а\ . (л а\ sin (За/2)
4.	Доказать тождество 4 cos — - — sin — - - = - .  —-стА
(6	2)	13	2/ sin («/2)
5.	Доказан., что cos 20° + 8 sin 70° sin 50° sin 10° ~ 2 sin2 80°.
§ 4. ПРЕОБРАЗОВАНИЕ СУММ В ПРОИЗВЕДЕНИЕ
63
6.	Вычислить 4 cos 10° cos 50° cos 70°.
_ _	л 2л
7.	Вычислить cos у cos —.
8.	Вычислить 16 sin 20° sin 40° sin 60° sin 80°.
9.	Вычислить tg 20° tg 40° tg 60° tg 80°.
§ 4.	Преобразование в произведение сумм вида
sin a±sin Д cos a±cos /? и tg a±tg /3
33.	Основные формулы. При вычислении различных выражений,
содержащих тригонометрические функции, с помощью таблиц лога-
рифмов и логарифмической линейки удобно иметь дело с произведе-
ниями, а не с суммами. Выведем ряд формул, которые позволяют от
сумм переходить к произведениям.
а)	Сумма с и н у с о в . Запишем формулу (31.1) в виде
sin (х + у) + sin (х - у) = 2 sin х cos у
и положим в ней х = (а+Д)/2 и у=(а-Д/2. Заметим, что
х + у = а и х - у = Д следовательно,
. „ а . а + В а - В
sin а + sin р - 2 sin —у1- cos —у'Ч
Пример 1. sin 14° + sin 28° = 2 sin 21° cos 7°.
Пример 2. sin 0,6 + sin 3,2 = 2 sin 1,9 cos 1,3.
б)	Разность синусов. Заменив в формуле (33.1) /3 на -Д
получим, учитывая нечетность синуса,
•	• о	Л • t*	Р w I
sin а - sin р = 2 sin —cos —2
(33.2)
Пример	3.	sin	16°	-	sin 13° =	2	sin 1 °30'	cos 14°30'.
j—г	л	.	лг	. л	лг	Зл
Пример	4	.	sin	-5-	—	sin -рг	=	2	sin -т^- cos
о 12	4о	46
в)	Сумма косинусов. Запишем формулу (31.2) в виде
cos (х + у) + cos (х - у) = 2 cos х cos у
и положим в ней х = (а + Д/2 и у = (а — Д)/2. Мы уже видели, что
х + у = а и х — у = /3', следовательно,
а о а + В а - В
cos а + cos р = 2 cos —у1- cos —у^.
4-	X	\OO.O/
64
Гл. Ш
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Пример 5.cos 52°30' + cos 16°30' = 2 cos 34°30' cos 18°.
Пример 6 . cos 0,8 + cos 2,8 = 2 cos 1,8 cos 1.
г)	Разность косинусов. Из формулы (31.3), аналогично
предыдущему, получается формула
cos а - cos /3 = 2 sin —sin у
(33.4)
Разность двух косинусов равна удвоенному произведению синуса
полусуммы на синус обратной полуразности их аргументов.
, л л л . 15л . л
Пример 7 . cos уд - cos у?,; = 2 sm sin
Пример 8 . cos 1,6 - cos 1,4 = -2sin 1,5 sin 0,1.
д)	Сумма тангенсов. Перейдя к синусам и косинусам, по-
лучим
х , о sin a, sin в sin a cos/3+cos a sin/3 sin (а+/3)	~
tg а+tg р =-+---5=-----------и--—=---*—(33.5)
cos а cos р cos a cos р	cos a cos р
Пример 9. tg 12° + tg 18° =-si" 30°	= 1 sec 12° sec 18°.
н к	е COS 12° COS 18	2
л л sin (л/3)	д/3 л
Пример 1 0.4 + * 12 - cos (л/4) cos (л/12) ~ V 2 sec 12'
е)	Разность тангенсов. Заменив в формуле (33.5) /3 на -/3,
будем иметь, учтя четность косинуса и нечетность тангенса,
,	. а sin (а - в)
tg а - tg р =----------54.
r cos a cos р
(33.6)
Пример 11. tgAjr_tg2L =---------.
16	16 _ 5л л
2 cos тт cos тт
16	16
Замечание. Последние две формулы (33.5) и (33.6) имеют
Л
смысл для аргументов « иД отличных от у (2п + 1), где n е Z.
34.	Примеры.
Пример 1 . Преобразовать в произведение tg а + ctg а.
Решение. Перейдя к sin а и cos а, получим
х	sin а , cos a sin2 а + cos2 а
tg а + ctg а =------+ —— =---------------------- ——?г-.
cos а sin a sin a cos a sin 2а
?
(34.1)
§ <1. преобразование сумм в произведение
65
Пример 2 . Преобразовать в произведение
А = ctg 60° + tg 40° + ctg 40° + ctg 30°.
Решение. Заменив ctg 60° по формуле приведения на tg 30° и
воспользовавшись формулой (34.1), получим
2	2
А = tg 30° + ctg 30° + tg 40° + ctg 40° =
° sin 60 sin 80
Далее, будем иметь
. _ 2 (sin 80° + sin 60°) _ 4 sin 70° cos 10°
sin 60° sin 80°	- sin 60° sin 80°
Последнее выражение можно упростить, если заметить, что
sin 60° = V3/2, a sin 80° = cos 10°. Теперь будем иметь
л 8 sin 70° cos 10°	8 .
А =-----ст---гдз— - sin 70°.
v3 cos 10 V3
Пример 3 . Преобразовать в произведение
А = cos На + 3 cos 9а + 3 cos la + cos 5а.
Р е ш е н и е . Воспользовавшись формулой (33.3), получим
Л = 2 cos 8а cos За + 6 cos 8а cos а = 2 cos 8а (cos За + 3 cos а).
Известно, что cos За = 4 cos3 а - 3 cos а, откуда
cos За + 3 cos а = 4 cos3 а, и мы имеем Л = 8 cos 8а cos3 а.
Пример 4 . Проверить, что tg 9° - tg 27° - tg 63° + tg 81 ° = 4.
Решение. Заменив по формуле приведения tg 81° на ctg 9°, а
tg 63° на ctg 27° и воспользовавшись формулой. (34.1), получим
tg 9° - tg 27° - tg 63° + tg 81° = tg 9° + ctg 9° - (tg 27° + ctg 27°) =
_	2	2 _ 2 (sin 54°—sin 18°) _ 4 sin 18° cos 36°_ 4 cos 36°
sin 18° sin 54°- sin 18° sin 54° ~ sin 18° sin 54° ~ sin 54°
Заметив, что cos 36° = sin 54°, мы приходим к равенству 4 = 4. Итак,
tg 9° - tg 27° - tg 63° + tg 81° = 4.
У и p а ж и e и и я
Преобразовать суммы функций в произведения:
1.	sin (тг/ЗО) + sin (.т/40). 2. sin 2,8 - sin 1,2. 3. cos 40° + cos 10°.
4. cos (л/10) - cos (л/20). 5. tg 3,2 + 1g 10,4. 6. ig 9Г45' - Ig 3°51 ’. 7. tg 2 + ctg 2.
66
Гл. Ill
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
8. Вычислить: tg 75° - tg 15°.
Преобразовать в произведение:
? 19 а) 9 /19
9.	sin Глл + тг - cos —л + — .
I о Z J	I о Z I
10.	sin 5а sin 4а + sin 4а sin За - sin 2а sin а.
11.-------------------5------------1- tg а + cos а + sin а.
2 tg (л/4 - a) sin2(.-r/4 + а)
12.	ctg 80° + tg 40° + ctg 40° + tg 80°.
4	1
13.	sin 7а - sin 5a - j sin 9а + — sin За.
Доказать тождества:
3	ci
14.	sin a - sin 2a + sin 3a = 4 cos ya cos a sin —.
1 - sin 2a
1 + sin 2a
3 tg a - tg' a_________2
„ 7 I©
1 - 3 tg2 a
3	1
—л + a + tg 3a.
16. cos a + cos 2a + cos 3a + cos 4a = 4 cos ~ cos a cos
5
21
Проверить равенства:
л 2л 5л л
17 tg — + tg-^~ + tg—+ tgy =
8 sin (7 л/18)
V3
18.	cos 80° + sin 20° + cos 60° + sin 40° + cos 40° = cos 65° cos 60° sec 85°.
19.	(sin 20° + sin 140°) (cos 50° + cos 70°) +
+ (sin 50° + cos 160°) (cos 40° - sin 70°) = 1.
20.	tg 10° tg 20° + tg 20° tg 60° + tg 60° tg 10° = 1.
21.	sin 50° sin 24° (tg 40° + ctg 24°) + cos 16° = 2 sin 74°.
22.	Вывести формулы для суммы и
ctg a + ctg /3 =
sin (a + /?) _
sin a sin /3'
ctg a - ctg /3 =
sin 0? - a)
sin a sin /?'
разности
двух
котангенсов:
§ 5. Преобразование некоторых выражений в произведения с
помощью введения вспомогательного аргумента
Некоторые суммы бывает возможно свести к произведениям, если соответствую-
щим образом ввести вспомогательный аргумент. Проиллюстрируем этот прием на от-
дельных примерах.
35. Преобразование в произведение выражения a sin а + b cos a.
Мы предполагаем, что а#0 и 6#0. Постараемся подобрать аргумент и положитель-
ный множитель/? так, чтобы было
а=р cos ч> и b = р sin <р.	(35.1)
Возведя в квадрат обе части равенств (35.1 )и сложив полученные равенства почленно,
2222	2	2	2	9
будем иметь a + b = р (cos + sin у?), откуда/? — а + Ь“ и
V~7---7"
а +Ь .	(35.2)
(В качестве р мы берем арифметическое значение корня.) После этого вспомогатель-
ный аргумент <р можно найти из соотношений
§ 5. ПРЕОБРАЗОВАНИЕ В ПРОИЗВЕДЕНИЯ
67
а а	. b b
cos <р = -= 7 и Sin yj = - =-7===.	(35.3)
Р Уа2 + Ь2	Р Vа2 + Ь2
Теперь будем иметь
a sin а + b cos а = р cos <р sin а + р sin <р cos а =
= р (sin a cos <р + cos a sin <р) = р sin (а + <р).
Итак,
a sin а + b cos а = р sin (« + <р).	(35.4)
Формулу (35 4) можно получить и так:
a sin а + b cos а = Va2 + 62 ( 1	„ sin а + > J2' cos а .
\Va2 + b2 Na2+b2
Положив теперь	'	'
V а2 + 62 = р > 0,.г ,а , = cos р и J2 . = sin р,
V а + Ь2	у а + Ь2
мы придем к форйуле (35.4).
Замечание. Тот факт, что такой аргумент существует, доказан в п. 8
/2	,2 Y
—°— + -Л—=1
2	,2 '	2	,2
а + b а + b
Пример 1 • Представить в виде произведения выражение А = ^3 sin а + cos а.
Решение. Здесь а = VJ, b = 1 и Va2 + b2 =2. Следовательно,
/— 1 )
А = V3 sin а + cos а = 2 sin а + — cos а .
Теперь полагаем
V3	1	.
- cos >р и 2 = sln <Р-
В качестве аргумента <р можно взять, например, р = л/6. Окончательно имеем
. /Т	.	_	1	Л	71\	- .	, Л.
А = V 3 sin а	+ cos а	=	2	(sin	a cos -7 +	cos a sin	—у	-	2 sin	(а + —).
\	о	о/	о
Пример 2	.	Представить	в виде	произведения выражение А = sin а +	cos а.
Решение. В этом примере а = 1 и b = 1, следовательно, Va2 + b2 = V2. Те-
г- (V2	V2"	)
перь поступаем, как в общем случае: А = V2 -у sin а + cos а . Положим
/2	•/З
~2~ = cos <р и “2" = sin р. В качестве аргумента р можно взять, например, р = л/4.
После этого получим
sin а + cos а = VT sin (а + —) .	(35.5)
36.	Преобразование в произведение выражений a sin а + b и a cos а + Ь при
О < 161 «: Iа!.
1)	Рассмотрим выражение a sin а + Ь. Запишем его следующим образом:
a sin а + b = a (sin а + b/d). Так как, по предположению, \b/a\ < 1, то можно поло-
жить b/a = sin <р. Теперь будем иметь
68
Гл. Ill
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Пример 1 . Преобразовать в произведение 2 sin а + 1.
Решение. 2 sin а + 1 = 2 (sin а + 1/2). Положим 1/2 = sin <р.
В качестве можно, например, взять л/6, и мы получим
2 sin а + 1 = 2 (sin а + у
, .	, . л,
sin а + sin —
/а л \
12 ~Т2 '
. . а л 1
= 4 sin - + — cos
2)	Рассмотрим выражение a cos а + Ь. Запишем его следующим образом:
</COS а + b = a (cos а + b/d). Так как, по предположению, Ib/a\ S 1, то можно поло-
жить b/a = cos if>. Теперь будем иметь
.	,	,	„ a + ф а — Ф
a cos с. + b = a (cos а + cos <р) = 2 a cos —cos —^-L.
Пример 2 • Преобразовать в произведение 2 cos a + ТУ.
Решение. 2 cos а + VT = 2 (cos а + '/2/2). Положим 72/2 = cos у>. В качестве
<р можно, например, взять л/4, и мы получим
Г-
2 cos а + V 2 = 2 (cos а +	) =
_ ,	л, „	(а я\ ।
= 2 (cos a + cos - =2 cos у + — cos
я
8
37.	Преобразование в произведение выражения a tg а + Ь.
Рассмотрим выражение a tg а + Ь, где <2*0. Запишем его следующим образом:
a tg а + b = a (tg а + b/d). Так как тангенс изменяется в пределах от -оо до +оо, то
при любых а и Ь можно положить b/a = tg <р, и мы получим
, ,	, b. ,	„ a sin (а + <р)
alga + b = а	(tgа	+ -)	= a (tgа	+ tgф)	=-—z-z.
\ а/ k ь 6 cos a cos
Пример. Преобразовать в произведение 3 tg a + Тз.
Рс ш е н и е . 3 tg а + V3 = 3 (tg а + ТУ/3). Положим 73/3 = tg р.
В качестве можно, например, взять л/6, и мы будем иметь
л. — 3 sin (g + л/6) _ 2 ТУ sin (a + л/6)
6/ cos a cos (л/6)	cos а
3 tgа + V3 =3 (tgа + tg
Упражнения
С помощью введения вспомогательного аргумента представить в виде произведе-
ний следующие выражения:
1. sin а — 'Г/ cos а. 2. sin а - cos а. 3. ТУ - 2 sin а. 4. 1 - 2 cos a. 5. 3 - 4 sin2 «.
6. <3tg 2a + 3. 7. 1 - 3 tg2 a. 8. 3 - 9 tg2 4a. 9.
1 + 7У sin 4a - 2 cos" 2a. 11.2 sin" a + ТУ sin 2a - 1.
1 - cos a + cos 2a. 10.
Глава IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
На протяжении многих лет в различных вузах на вступительных
экзаменах и в подготовительных отделениях широко используется
«Сборник задач по математике для поступающих во ВТУЗы» под ре-
дакцией М.И.Сканави. Начиная с 1969 года только в России в изда-
тельстве «Высшая школа» он издавался пять раз. Настоящее пособие
ориентировано на пятое издание (1988) этого задачника. При этом,
примеры не разделяются по группам сложности, ибо такое разделе-
ние всегда носит субъективный характер. В этом пособии разобраны
и приведены в качестве задач для самостоятельного решения наибо-
лее характерные примеры всех категорий сложности.
В настоящем выпуске пособия рассмотрены примеры тождествен-
ных преобразований тригонометрических выражений. Тождествен-
ное преобразование выражения — это преобразование, верное для
любых значений переменных, принадлежащих области определения
этого выражения. При этом всегда следует иметь в виду, что описа-
ние области определения выражения представляет отдельную зада-
чу, иногда достаточно сложную.
Для описания области определения различных выражений необ-
ходимо уметь решать соответствующие уравнения и неравенства. За-
дача нахождения области определения тригонометрических выраже-
ний будет рассмотрена в выпуске, посвященном тригонометрическим
уравнениям и неравенствам.
38. Образцы решений некоторых примеров
В этом пункте приводятся решения (не всегда самые простые и са-
мые красивые) отдельных примеров. Одни примеры разбираются
очень подробно со ссылками на соответствующие формулы, решения
же других примеров приводятся без этих ссылок, и читатель должен
сам установить соответствующие формулы, которые можно исполь-
зовать в ходе решения. Есть и примеры, к которым даются только
указания.
70
Гл IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ. ЗАДАЧ
Доказать тождества (1—9):
1. cos а + cos 2а + cos 6а + cos 7а - 4 cos (а/2) cos (5а/2) cos 4а.
А Применяя последовательно к левой части равенства формулу
(33.3), находим: А = (cos а 4- cos 2а) 4- (cos 6а 4- cos 7а) =
= 2 cos (За/2) cos (а/2) + 2 cos (13а/2) cos (а/2) =
=2cos(a/2)(cos(3a/2)4-cos(13a/2))=4cos(a/2) cos(5a/2) cos4a. V
sin ((201л/2) + За)	/Л , Q
1 - sin (За - 5л) ь v	7
sin ((201л/2) 4- За) _ cos За
1 - sin (За - 5л)	1 + sin За'
К левой части равенства мы применили формулы приведения.
Правую часть преобразуем по формуле ctg а/2 -	—. В нашем
1 ““ cos а
. /с /я , О /ох sin (5тг/2 4- 3a) cos За
случае ctg (5л/4 + За/2) =	, = -j—•—;Тож-
ь * 4	7	1 - cos (5л/2 4- За) 14- sin За
дество доказано. V
„ 1 4- ctg (2a - Зл/2) ctg (Зл/2 + a) _ 1
"1g (19л/2 4- a) 4- ctg (27л/2 + a) ~ 2 tg 2a'
А Применив в левой части равенства формулы приведе-
1 4- tg 2a tg a п
ния, получим	—-—s——-----. Далее имеем
ctg a 4- tg a
tga(l+T2^-)
I — a tB a 1	_
----5------=-----5—tg 2a
1 4- tg2 a 1 - tg2 a 2
. sin4 a 4- cos4 a — 1	2
4.---------------=
sin6 a 4- cos6 a — 1	3
А Используя тождество sin2 a 4- cos2 a
sin4 a 4- cos4 a = 1 - 1- sin2 2a и sin6 a
= 1, можно получить:
4- cos6 a = 1 - -r sin2 2a.
sin4 a 4- cos4 a — 1
sin6 a 4- cos6 a — 1
1  2 t
-y sin4 la ~
—2--------_ Л у/
з 2д 3'
-д- cos 2a
4
c . f. a f, a sin a — 4
5.	sin° tv - cos ’ x =-----------cos a.
2	2	4
ОБРАЗЦЫ РЕШЕНИЙ НЕКОТОРЫХ ПРИМЕРОВ
71
.	. t, а а а , . та га. . . ла . га ? а 4 л.
A sin0 j-cos0 2-=(smz y-cosz j) (sin4 y+smz у cosz y+cos4 -^)=
.. . 2 a ,	2 «,2	.2 a	Sin2 « - 4	„
= -cos a ((sinz 2 + cos -y) - sinz cos^ y) =-----------cos a . V
6.	ctg a - tg a - 2 tg la - 4 tg 4a = 8 ctg 8a.
* о	.	4 t 1	1 - tg2 a 2
А Заметим, что ctg a - tg a = tg a-— = —
Преобразуя левую часть тем же способом и далее, получим последо-
вательно
?	4	8
^-2tg2a-4tg4a = ^-4tg4a = ^ = 8ctg8a. V
7.	4 cos a cos р cos (а - р) - 2 cos2 (а - р) - cos 2р = cos 2a.
А 4 cos a cos p cos (a — y>) — 2 cos2 (a — %>) — cos 2p =
= 2 cos (a - p) (2 cos a cos p - cos (a - y?)) - cos 2p =
= 2 cos (a - p) (cos (a + p) + co^(a '-"/>) - созДо-^Ур)) - cos 2p =
= cos (a —.p + a ->yi) + cos(a- p -,a' + p) ~ cos ^P = cos 2a. V
Мы воспользовались формулой (31.2).
7 a
8.	8 cos4 a - 4 cos3 a - 8 cos2 a + 3 cos a 4- 1 = -2 sin j a sin y.
А Преобразуем правую часть по формуле (31.3)
— 2 sin —a sin — = cos 4a — cos 3a.
Используя формулы cos 4a = 8 cos4 a — 8 cos2 a + 1 и
cos 3a = 4 cos3 a — 3 cos a, мы докажем исходное тождество. V
П р и м е ч а н и е . Формулы для cos За (28.4) получены в § 2 гл.
III, а. формулу для cos 4a рекомендуем получить самостоятельно,
(см. Упражнение 4 из § 2 гл. III)
9.	Доказать, что для любого числа п слагаемых и любого
а 2лп (п G Z) справедливо равенство:
. па (п + I) a
sin	cos Л—2 —
cos a + cos 2a + cos 3a -I- ... + cos na =----------(♦)
sin у
A S„(a) = cos a + cos 2a + ... + cos na.
72
Гл. IV МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
сс
Умножив обе части этого равенства на 2 sin получим
2 Sn(a) sin у = 2 sm у cos а + 2 sin у cos Zee + ... 4- 2 sin у cos па .
Воспользуемся формулой (31.1). Получим:
т с , , . а . За . а . . 5а . За.
2 5/г(а) sin 2 = (sin - sin у) + (sin у - sin -у) + ...
. (2n + 1)	. (2п - 1)	. 2п + 1 .а
... + (sm —а ~ sin —2—а> = sin —2—а ~ Sin ~2'
(Первое слагаемое в каждой скобке взаимно уничтожается со вторым
слагаемым в следующей скобке). Применив формулу (33.2), по-
лучим
~	. . а па н+1
2 Sn(a) sin у = 2 siny cos —у-a.
Откуда следует, что что равенство (*) справедливо. V
Упростить выражения (10—18).
,,,	1 + sin 2а	7 , .п .
10.---------------------5— + cos2 (а - 40л)	(А)
cos (2а - 20л) ctg (а - ^л)
(1 + sin 2а) sin (а - ^л) sin (а - ~л)
А А =--------------------------------------h cos2 а =
cos (2а — 20л) cos (а — у) sin (а — -^л)
2(1 + sin 2а) sin2 (а - у)
=---------------------------1- cos2 а =
cos 2а sin (2а — у)
(1 + sin 2а) (1 - cos (2а - ~лУ)
Л ।	?
=-----------------z---------------1- cosz а-
-cos z 2а
(1+sin 2а) (1 —sin 2а)	9 cos2 2а ->	9	„
=-------------------------+cos а=-------j---hcosz а = -sinz а. Ч
cos 2а	cos 2а

т.РАЗЦЫ I’l.lllEIIHl'l НЕКОТОРЫХ nniyfFDII
7.3
Мы применяли формулы приведения. Формулы (29.5), (27.1) и (7.1)
[ । 1 ~ cos ~
tg 2а - ctg 2а
(А)
12. 2
1 + cos 8a
7 ~ tg 2a - ctg 2a
2 cos" 4a ,,	1 . _	„
------— cos 2a sin 2a = —=• sin 8a. V
cos 4a	2
— sin2 2z ~ sin2 3z - sin2 4z - sin2 5
(А)
_ I - cos 4z
1 — cos 8z 1 — cos 10z
A
А
2
= (cos 4z + cos 6z)+(cos 8z + cos 10z)=2 cos 5z cos z + 2 cos 9z cos z=
~ 2 cos z (cos 5z + cos 9z) = 4 tos z cos 2z cos 7z. V
jу 2 sin a — sin 2a
2 sin a + sin 2a
если: а) 0 < a < л; б) л < а < 2тг;
, 2 sin а — sin 2a 2 sin а (1 — cos a) > -<
----------------------— -----------s.------------- —-	.
2 sin a + sin 2a	2 sin a (I 4- cos a)	2
а) 0 < a < л б) л < a < 2л.
14. V(i^g2 |)(ctg2y - 1)
a	(! - (g2	(1 - tg2|)
A (1 - tg2 -y) (ctg2 у - 1) = 4-------------------=- 4 ctg2 a
2	2	2 tg-y 2 ig у
V (1 - tg2 y) (ctg2 - 1) = 2 1/ctgTa = 2 I ctg a ! V
tg2(2a 4) "" I
15.---------. ’	--	(A)
tg2(2a - |;i) + I
74
IT IV
MITO ihl РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
sin2 (2а - ^-) —cos2 (2а -
Л д —------------------------------==
•in2 (2а - ^j+cos2 (2а -
(1 - cos (4а - |))-(1 + cos (4а - -))
1 - cos (4а - у)+ 1 + cos (4а - у)
-2 cos (4а -
---------х---------- -sin 4а. V
Были применены формулы приведения и формулы (29.4) и (29.5)
37	39	41
sin (~ л — За) + sin ( ул + 4а) + sin (-у-л + 5а)
16 —_2-----------  у2..	---L--------- (А)
sin За + sin 4а + sin 5а
Л Применив формулы приведения и формулы (33.1), (33.3), по-
лучим
_ cos За	+ cos	4а	+ cos 5а	_	2	cos 4а	cos а	+	cos	4а _
sin За	+ sin	4а	+ sin 5а	2	sin 4а	cos а	+	sin	4а
cos 4а ( 2 cos а + 1) cos 4а .
— —:	1—----------;—П"	—	~-Л— —	Ctg 4а.	V
sin 4а (2 cos а + 1)	sin 4а	°
17.	sin3 3/3 cos 9/3 + cos3 3/3 sin 9/3	(A)
.	, ,2iO sin 12/3 - sin 6/3 ,	2 sin 12/3 + sin 6/3
A /1 = sin .3/3---------c_-------'- + cosi3p--------------------— =
I	3
= 2 (sin 12/3 4- cos 6/3 sin 6/3) = sin 12/3. V
18.	sin2 2а + sin2 3/3 + 2sin 2а sin 3/3 cos (2а 4- 3/3)	(A)
1 - cos 4а I - cos 6/3 n	э..
Л .1 =---------,~2----1-------- —c + 2 sin 2а sin 3/3 cos (2a + 3/3) =
2 cos (2a + 3/3) cos (?a — 3/3)	_ . „	. ... z_ „„
= I - — -------------' ---------------- + 2 sin 2а sin 3/3 cos (2а + 3/3) =
- 1 — cos (2a + 3/>; 1 os (2а — 3/3) — 2 sin 2а sin 3/3j =
- 1 -cos (2а + 3/7) Feos 2< os 3/3+sin 2а sin 3/3—2 sin 2a sin 3/31 =
ОБРАЗЦЫ РЕШЕНИЙ НЕКОТОРЫХ ПРИМЕРОВ
75
= 1 — cos (2а + 3/3) j^cos 2а cos 3/3 - sin 2а sin 3/3J =
-1—cos (2а + 3/3) (cos 2а cos 3/3 - sin 2а sin 3/3)= 1-cos2'(2a + 3/3; =
= sin2 (2a + 3/3)
Итак, A = sin2 (2a + 3/3) V
Преобразовать в произведение (19—25)
19.	1 + cos (2a + 630°) + sin (2a + 810°)
А Наше выражение обозначим для краткости буквой .1. Начнем,
как обычно, с формул приведения. /1=1 + sin 2a + cos 2a. Затем пе-
регруппируем и воспользуемся формулами (29.2), (27.1). Полечим.
/1 = (1 +cos 2a) + sin 2a = 2 cos2 a + 2 sin a cos a = 2 cos a (cos a + sin a).
Воспользовавшись приемом, изложенным в п. 35, получим
А = 2 VT cos a cos (45° — а), или /1 = 2 VT cos a sin (45° + a) V
20.	sin 5a — sin 6a — sin 7a + sin 8a (A)
A/l = (sin 5a-sin7a)4-(sin 8a —sin 6a)=-2sin a cos 6a+2sin a cos7a =
13 ct
= 2 sin a (cos 7a - cos 6a) = -4 sin a sin -ya sin у V
21.	sin a cos .v cos 2.r cos 8.v — -/ sin 12,v	(A)
4
А /!== sin 2а cos 2а cos 8a--sin 12a= = sin 4a cos 8a- = sin 1 2
2	4	4	4
sin 12x — sin 4 a
4
= g (-sin a — sin 12 a) =
О
—2 sin 8a cos 4.v = —t sin 8.v cos 4a. V
8	4
22.	.1 = tg3 a" - tg2 .v - 3 tg ,v + 3.
Л Разлож im /1 на множители, например, так:
-I) (tg.v—VI) (tg.v+v3) = (lgA-lg45o)(lg.v-1g 60°)(lg.v+ tg 60°)-
Воспользовавшись формулами (33.5) и (33.6), получим
76	Гл. IV МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
4 VT sin (х - 45°) sin (х - 60°) sin (x + 60°)
.4 =---------:---------------------------. V
cos-5 x
47	t
23.	A = 1 + cos (2a - -уя) + cos (2a - 9л) - ctg(~ + 2a).
А Сначала применим формулы приведения:
.4=1- sin 2а - cos 2а + tg 2а.
Далее преобразуем Л так:
_ cos 2а — cos 2а sin 2а — cos2 2а + sin 2а _
cos 2а	~
_ (1 -cos2a) cos 2a+sin2a (1 -cos2a) _ (i -cos 2a) (cos 2a+sin 2a) _
cos2a	cos 2a	~
2 VJ sin2 a cos (j - 2a)
=---------------1----1. v
cos 2a
24.	A = 4 cos x sin2 x - cos x + sin x.
A /l=4cos x -—y———cos x+sin x=2cos x-2cosx cos2x-cosx+sinx=
=cos x-cos Зх-cos x+sin x=sin x-cos 3x=sin x-sin (y-3x) =
л , 2	. л
x — =- + JX л + у — Зх
— 2 sin---2-----cos-----у----= 2 sin (2х — ^-) cos (-^ — х). V
25.	А = sin3 a cos За + cos3 а sin За.
.	.	. э sin 4а - sin 2а 7 sin 4а + sin 2а
А А = мп а----------------Ь cos а------2------“
1	113
= у (sin 4а + sin 2а cos 2а) = (sin 4а + у sin 4а) = у sin 4а. V
'	Z	4-
Л о к а з а т ь с п р а в е д л и в о с т ь р а в с н с т в (26—33)
26. (cos 34е) "1 + (tg 56°)-1 = ctg 28°.
ОБРАЗЦЫ РЕШЕНИЯ НЕКОТОРЫХ ПРИМЕРОВ
77
л 1	+	1	-	1	+	1
cos 34° tg 56° sin 56° tg 56°
_ 1 + tg2 28^	1 - tg2 28^ = —1— - ctg 28° V
" 2 tg 28°	2 tg 28°	tg 28° CTg ’
77 sin № cos 6° - sin 6° sin 66° _
’ sin 21° cos 39° - sin 39° cos 21° ~
A sin 24° cos 6° - sin 6° sin 66° = sin 24° cos 6° - cos 24° sin 6'
- sin (24° - 6°) = sin 18°.
sin 21° cos 39° - sin 39° cos 21° = sin (21° - 39°) = -sin 18°. V
28.	a) sin 15° = ——т
4
A sin 15° = sin (45° - 30°) = sin 45° cos 30° - cos 45° sin 30° =
72 7з _ 72 i 76-72
~ 2 2 " 2 2 -	4	' V
6)	cos 15° = ——----
А Это можно доказать, например, так:
1) cos 15'
2
V2 + 73
2
г- (73 + I)2
Заметим, что 2 + V3 =----j----> получим
cos15° = ^72
6 + V2
4 '
2)	cos 15° = V1 - sin2 15'
7б+72
4 V
29.	sin 20° sin 40° sin 60° sin 80° =
16
/3
A sin 20° sin 40° sin 60° sin 80° = sin 80° (cos 20° - cos 60°) =
78
Гл. IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
v3	1
= (cos 20° sin 80° - sin 80°) =
= -~Г (“I s0O° + -7 sin400° + | sin 60°) = ~ V
4	2 7 I 7	I	10
V? — 1	V51 +1.
30.	О sin 18° = —; 6) cos 36° = —;
a)	sin 1&° = ?
Заметим, что
cos 36° = cos (90° - 54°) = sin 54°
Угол a — 18° удовлетворяет уравнению sin 2a = cos 3« , т. e. уравне-
нию
2 sin a cos a = 4 cos3 a - 3 cos a
Обозначив sin a — z, получим квадратное уравнение (т. к. cos а Ф 0)
4 z1 + 2 z - 1 = 0,
корнями которого являются числа
-1+V5	-1-V5
zi -	4	; z2 -	4-	•
Среди этих чисел находится и sin 18°. Единственным числом, кото-
рое для этого подходит, является число Z]. Следовательно,
б)	cos 36° = ?
Зная sin 18°, найдем
cos 36° =1-2 sin2 18° = -—7—
4
31.8 cos cos cos = 1
ОБРАЗЦЫ РЕШЕНИЙ НЕКОТОРЫХ ПРИМЕРОВ
79
.	_	4л:	2л:	Л . л .	2 ,	2 ,
А	8 cos -Q-	cos -g- cos	-q	= 4	cos (cos -~л + cos	^л) =
У	J	7	У	3	У
г»	Л	. Л 2	—	Л	~	,	Л	Л,	.
=	“2 COS	-g +	4 COS -g COS дЛ = -2 COS -g + 2	(COS ~g + cos j) =	1
В процессе решения мы воспользовались формулами (31.2) и (33.3) V
„„	л	2л 4л 8л 16л	1
32.	cos 33 cos 22	cos ^3 СО5гзз COS~33~ =	32
А Домножим и разделим левую часть предполагаемого равенства
на 2 sin и воспользуемся формулой для синуса двойного угла.
Получим:
. 2л 2л: 4л 8л 16л
sm cos 2з cos 33 cos 33 cos -33-
2 sin 33
. 4л 4л 8л 16л
sm 22 cos 23 cos 33 cos _
. . л
4s,n33
8л	8л 16л	. 16л	16л
sm 23 cos	33	cos 33	_ sin 33 cos	33	_ t
-	o . л	ir  л:	32
8 sm 23	16 sm 23
33.	sin 10° + sin 20° + sin 30° + sin 40° + sin 50° =
= 0,5 sin 25° sin-1 5°
А В левой части предполагаемого равенства перегруппируем слага-
емые и сложим соответствующие синусы.
(sin 10° + sin 50°) + (sin 20° + sin 40°) + sin 30° =
= 2 sin 30° cos 20° + 2 sin 30° cos 10° + sin 30° =
= cos 20° + cos 10° + sin 30° = 2 cos 15° cos 5° + sin 30° =
= ,-Ц-о- (2 cos 15° cos 5° sin 5° + sin 30° sin5°) =
sm 5 v	7
=	--z0 (cos 15° sin 10° + Jr sin 5°) =
sin 5	2	'
1	f sin 25°	sin 5° sin 5°\ _
" sin 5° ( 2	2	+ 2 J-
= Jp sin 25° sin~1 5° V
so
Гл IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Вычислить, найти (34—44)
2 Z-I
8
3	. э Л о ^Л • 2 i
34.	sin2 у + COS2 -д- + sin2 -z- + cos
обо
А Обозначив, как обычно, все выражение через А и применив фор-
мулы (29.4) и (29.5), получим:
,	1	/,	л1,	3 \	1	/.	5 \
А =	( 1	-	cos -7| + Л 1	+	COS ~тЛ)	+	тг	(1	-	COS -дЛ	+
2	\	4/ 2 \	4 /	2	\	4/
+ 4(1 + cos 4л'j = 2 V
2 \	4 /
35.	sin /2а + ~лЛ , если 1g а = 7.
\	4 г	3
A sin /2а + 4л \ = sin 2а cos 4л + cos 2а sin 4л —
-	, 12\ _ _ Г7 ту
2 (13 13j ~ 26
Мы воспользовались формулами:
sin 2а =
2 tg а
1 + tg2 а
12
уу; cos 2а =
1 - tg2 а_____5_
1 4- tg2 а	13
36.	Вычислить без помощи таблиц sin4 15° + cos4 15°
A sin4 15° + cos4 15° = (sin2 15° + cos2 15°)2 - 2 sin2 15° cos2 15° =
1	->	7
= 1-4 sin2 30° = 4 V
Z	о
37.	sin4 15° - cos4 15° = ?
A sin4 15° - cos4 15° = (sin2 15° - cos2 15°) (sin2 15° + cos2 15°) =
V3
= -cos 30° = v
38.	Найти sin4 a + cos4 а, если известно, что sin a — cos a = —
1 = (cos2 a + sin2 a)2 = cos4 a + sin4 a + 2 cos2 a sin2 a
ОБРАЗЦЫ РЕШЕНИЙ НЕКОТОРЫХ ПРИМЕРУ)'
81
Теперь получаем
cos4 а + sin4 а - 1 - 2 cos2 a sin2 « = Г- 2 ~ = V
39.	Вычислить
, Л л Зл . 4 5л ,	4 2Л
А = sin4 g + cos4 у + sin4 у + cos у
.	. 7 a 1 - cos a
А	Воспользовавшись формулами sin4 у -----------2---- 11
7 a 1 + cos a
cos2 у =----2----,.получим:
sin
1 - COS -7
4
'	7	Л ,	1
1 - 2 cos у + у
cos
4 3 л
T
/. ,	Зл \	_ Зл 1
I + cos —r-	1 + 2 cos лг + +
4	4	2
. 4 5л
sin у =
1 -
5л' 2
cosy
'2
1 - 2 cos у + у
4
cos
4
7 \2
7л
cos —-
4
i,7 7л 1
i + 2 cos —r~ + x
4	2
4
Сложив последние равенства, будем иметь Л = у V
40. Найти
cos 70° cos 10° + cos 80° cos 20°
cos 69° cos 9° + cos 8 Г cos 2 Г
/А Применив формулу (31.2), получим:
cos 80° + cos 60° + cos 100° + cos 60°
cos 78° + cos 60° + cos 102° + cos 60°
82
Г,л IV МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
так как cos 100° = -cos 80°, cos 102° = -cos 78° V
., тт „	2 sin la - 3 cos 2a 4
41. Наити-j—:—,——=----v"> если tga = 3
4 sin 2a + 5 cos la
А Этот пример можно решить так:
. ~	2 tg а 6
Sin 2а =-------— = 77? =
1 + tg2 а Ю
3 о 1 - tg2 а 4
—; cos 2а =--------— = —р
5	1 + tg2 а 5
6 12
А 11
5
— = -1» = _9 v
20	8	4
5
„ sin 4а + sin 10а - sin 6а ...
42.	Наити------------------5---- (А), если sin а - cos а = т
cos 2а + 1 - 2 sin2 4а
А Заметим сразу же, что из равенства sin а — cos а = т следует:
sin 2а = 1 - т2. Преобразуем наше выражение:
X - ~2 sin а cos 5а + 2 sin 5а cos 5а _ 2 cos 5а (sin 5а - sin а) _
cos 2а + cos 8а	“	~
2 sin 2а cos За „ . „
= 2 sin 2а
2 cos 5а cos За
cos За
Откуда, А = 2 (1 - т2). V
43.	Найти sin а и cos а, если tg =
_2
3
Л .
2 tg у
, а 4
12
5 ’
2 tg 2
sin а =---------
1 ,	7 сс
!+tg22
120
169’
4 2 а
tg 2	119	„
cos а =------------ ———	V
l	+ lB2f	169
44.	Найти tg а, при котором справедливо равенство:
8 ctg а + 4 cos а - 0,5 sin а = 1
К
1
ОБРАЗЦЫ РЕШЕНИЙ НЕКОТОРЫХ ПРИМЕРОВ
83
л	л	/ч	1	8
А	4 cos а	(1—%—)	= 1	- —
\	8 / tg.
1	,о .	. tg а - 8
тг cos а (8 - tg а) =	-------
2	х 7 tg а
1. tg а = 8
2. tg а # 8
Ответ: tg а = 8.
Разные задачи (45—49)
1 1
у cos а = sin « = -2. Нет решения.
V
45.	Пусть А, В'и С — внутренние углы некоторого треугольника. До-
казать, что sin2 А + sin2 В + sin2 С - 2 cos A cos В cos С = 2
А А + В + С = л. С = л - (Л + В)
„	/ Л , m -2л	1 - cos 2А
cos С = -cos (А + В); sinz А =-~--
. о п 1 ~ COS 2В  2 п • 2 / л I
sinz В =-------2-----’> sin С = sinz (А + В);
2 cos A cos В cos (А 4- В) = cos (А + В) [cos (А + В) 4- cos (А - В) ]
cos (А 4- В) cos (А-В) = -^ cos 2 А 4- у cos 2В.
Используем полученные результаты:
sin2 А + sin2 В 4- sin2 С — 2 cos A cos В cos С =
= у - С°2 j	+ sin2 (А + В) 4- cos2 (А 4- В) 4-
cos 2А cos 2В _
+	2	+	2	- 2 v
46.	Если А 4- В 4- С = я, то
АВС
sin А 4- sin В 4- sin С = 4 cos у cos у cos у
Доказать
.	А 4- В л	С . А	4-	В . (л	С\ С
Л 2	“ 2	2 ’ sm	2 ~sin 2	2	”COS 2
84
Гл. IV МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
	+ В а-В , „ . С С
sin А + sin В + sin С - 2 sin —у - cos—-2 siny cos у -
О С
- 2 cos у
 Л - В . С\ 0 с
cos —— + sin у) = 2 cos у
cos
А — В А + В-,
___ + cos__>
, А В С „
= 4 cos у cos у cos у V
47.	Доказать следующее утверждение: для того, чтобы в треугольни-
ке АВС один из углов был равен 36° или 108°, необходимо чтобы вы-
полнялось равенство
sin 5А + sin 5В + sin 5С = 0.
А Известно, что
sin 5А + sin 5В + sin 5С = 4 cos т|л cos ^В cos
2	2	2
Пусть Л = 36. Тогда cos у 36° = cos 90° - 0 и мы получаем, что
sin 5Л + sin 5В + sin 5С = 0.
Если же А = 108°, то все равно cos у-108° = cos 270° = 0 V
48.	Найти наибольшее значение выражения
cos 2а + 1 л л
—"5------а при0<«<у.
ctg у - tg у
п 2	. а а
т . , п 2	2 cos a sin тг cos ,
. cos 2а + 1	2 cos а	2	2	1
А -------------- =------------=---------------------= .л-
. а а
Sin у COS у
Наибольшее значение достигается при а = ~ и равно у V
39. Текст примеров для самостоятельной работы
Доказать тождества (1 —39)
ТЕКСТ ПРИМЕРОВ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
85
1.	cos -ул: -9а + sin 10а 4- sin 1 la + sin 12a =
, a	21
= 4 cos у cos a cos -5-
2.	cos 2a + sin -- 3aj - cos 4a + cos 5a = -4sin sin a cos ya
3.	sin 2a (1 + tg 2a tg a) + * *	= tg 2a + tg2 (y + yj
sin у-л + 3a I /9	3
4'l-sin (3a^F)=Ctgi.4"M
5 tg 2g + tg 2A _ 1 = sin2 (a - fi)
2 tg (a 4- /3) cos 2a cos 2/3
. 15 , a\ , , ,	Э/3	3 .\	2 a
sin	2Д +	1	(1T|g	(7х ' 2Я))	C0S	4	= 1
°’	-/	yy	“773	3	\	8
tg (l*- 4J ~tg
-	2/	о /	• 2	/	।	13	V7	/71	-	\
7.	cos	(a —	3л)	—	sin	(	a + -ya j	=	-y- sin	у -	za
8.	cos 8a - sin 8a ctg 4a = cos 4a - 2 cos2 2a
9. ctg2 a - ctg2 /3 =
cos2 a — cos2 /3
sin2 a sin2 /3
a tg ba 1 ~ ctg2 ba _ ,	.. cos 8a + 1 _ £ s
U' tg2 6a - 1 ctg ba	' ctg 2a - tg 2a 2 '
12.	+	+ 2	2« = 2 cos"2 2a
tg (2a + /3) tg (2a - /3)
13.	cos4 .v + sin2 у + у sin2 2.v - 1 = sin (.v + y) sin (y - x)
86
Гл. IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
14.	cos ул + 4а + sin (33л - 8а) - sin (44л - 12а) =
= 4 cos 2а cos 4а sin 6а
sin2 (35л - 4а) + 4 cos2
15.----------------'-----------'
cos2 - 4а j - 4 cos2
cos 6a - cos 7a - cos 8a + cos 9a
sin 6a - sin 7a - sin 8a + sin 9a
45
2'
= ctg4 2а
t 15
= ctg-ya
1	fi3 И лТТ • (29	, \
2	cos -7-ТГ - 2a - V 3 sin ~л - 2a
{7------Ll——J-------------
9	\	25	)
cos -2a +2 cos -у-л + 2a
\	' 0	/
(83	\
18.	tg y-л - a - tga - 2 tg 2a = 4 ctg 4a
_ tg 2a
V3
19.	sin2 / - cos2 (х - 1) + 2 cos х cos t cos (х - t) = cos2 x
20.	cos2 t + cos2 (x — t) — 2 cos x cos t cos (x — t) = sin2 x
21.	sin a + sin /3 + sin у - sin (a + /3) cos / - cos (a + /3) sin у -
. . a + В . В + у . у + a
- 4 sin —у- sin £—~ sin ——
22.	cos» a - sin» a =
4
23.	1 - sin + 3aj cos 2a - cos (3a - sin 2a = 2 sin2 yx
24.	3 + 4 sin (4a +	+ sin ^8a +	— 8 sin4 2a
/cT|a - Vt|«_ _ . (л
' vctg a + /tg a ( 4
ТЕКСТ ПРИМЕРОВ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
87
.	/17	» \ . /л 0 ) sin 6а
26.	4 cos -т~я - 2а sin kj- ~ 2а = ——л—•
6	1	3 I sin la
27.	sin 1 4а sin 1 (60° - 4а) sin 1 (60° + 4а) = 4 sin 1 12а
28.	tg а -	(1 - sin 2а) = cos 2а
cos 8а tg 4а — sin 8а
' cos 8а ctg 4а + sin 2а
-tg2 4а
30.
2 cos2 2 а + СУ sin 4а — 1
2 sin2 2а + СУ sin 4а — 1
sin (4а -~\
\	6/
34. 1 — cos (2а — 21л) + cos (4а — 32л) =
= 4 cos 2а sin
/.т
[ 3 ~ а
 (л
МП 3
+ а |
/
35. 8 cos4 2а + 4 cos3 2а — 8 cos2 2а — 3 cos 2а. +1=2 cos 7а cos а
где п — число слагаемых и а^2лк.
88
Гл IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
37. cos а + cos За + cos 5а + ...+ cos (2м - 1)« =
sin 2па
2 sin а '
где п — число слагаемых и а^лп.
38. sin2 х + sin2 у - 2 sin х sin у cos (х - у) = sin2 (х - у)
,п 8 cos4 2а - 4 cos3 2а - 8 cos2 2а + 3 cos 2а + 1
оУ. -----т—-----------5-----------5--------------------= —tg 7а tg а
8 cos4 2а + 4 cos3 2а — 8 cos2 2а - 3 cos 2а + 1
Упростить выражение (40 - 68)
40 —
sin
sin (26л + ctg у - cos (28я +
Та \ ’ ~а~	77	аТ
cos Н- - 15л I ctg g- + cos I 2л ~ д' j
42. (1 — cos 1 а + tg а) (1 + cos а + tg а) cos а
sin 2а + 2 sin (4а - л) + sin 6а
cos 2а — 2 cos 4а + cos (6а - л)
1 + cos 4а + cos (4а —
44.-------------------------------L__
1 + cos (4а + я) + cos (4а + тгл)
\ Z !
sin 6а + cos (6а — Зл)
sin (л - 2а) cos 2а
46. - э ь
tg 2а — tg 4а
sin 8а sin (yr 4- 4а j
’ (1 + cos 4а) (1 + cos 8а)
Y 3 V
48. cos cos -у — sin х sin Зх - sin 2х sin Зх
ТЕКСТ ПРИМЕРОВ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
89
52 cos2 (а ~ 450°)	+ sin2 (а + 630°)
2' sin~2 (а + 270°) - 1 cos-2 (а - 90°) - 1
а х а tg 5 - ctg у 53 —		- а ,	а tg 2 + ctg 2	. . 1 +cos 2а + cos 4а + cos 6а 54.	X	 cos 2а + 2 cos 2а - 1
55. Vsin 2 (а — ~л) + cos 2 (а + ^л)
1 + sin а
I - sin а
1 — sin а
1 + sin а
если
а) 90°<а< 180°; б) 270°<а<360°
57. (cos 8а tg 4а - sin 8а) (cos 8а ctg 4а + sin 8а)
cos2 (4а — 53л) — 4 cos2 (2а — 61л) + 3
cos2 (4а + 53л) + 4 cos2 (2а + 61л) — 1
sin2 8а + 4 sin4 4а - 4 sin2 4а cos2 4а
60. ----------------х-----------~------------
4 — sin2 8а ~ 4 sin2 4а
61.
/	)4'’ ,
1 + cos /8а--------~-л \
90
Гл. IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
7 5
4 sin (5л —2x) sinz
1 + cos (60л + 8x)
cos2 4х
63.	(tg 255° - tg 555°) (tg 795° + tg 195°)
64.	cos 2 8а - tg2 (5л + 8а) - 2 cos2 2а - 73 cos - 4а
65. cos6
cos2
2
66.	3 sin la. cos 6а + 9 sin 2а cos 2а — sin 6а cos 6а — 3 sin 6а cos 2а
67.	4 (sin4 л' + cos4 х) - 4 (sin6x + cos6 х) - 1
68.------
sin"
Преобразовать в произведение (69—100)
69 i — cos (2а — 630°) + sin (2а + 630°)
70. cos За — cos 4а — cos 5а + cos 6а
71. sin 2а + sin 4а — sin 6а
72 a ~ CQS За ~ sin $a
’ cos а - 2 sin За — cos 5а
73. cos 2а + sin 4а — cos 6а
74 3 tg2 (« + 31л) - 1
1 - 3 tg2 (а + ~л)
75. sin 2а + cos 4а — sin 6а
76. sin х sin Зх + sin 4х sin 8х
77. sin Зх - 2 sin х
7§ ct84 ~ ctg2
tg4 2а — tg6 2а
79. 2 cos2 4а + 73 sin 8а — 1
80. 1 — 2 cos2 а + 73 sin 2а
81. tg4 х - 4 tg2 х + 3
ТЕКСТ ПРИМЕРОВ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
91
82. 4 cos2 (2a — улА + cos (2а - 7л) + sin |ул - 6а
\ Z /	\ Z
84. 6 sin2 2а - 1 - cos а
85 sin(2a-3^ + sin 3/5
cos 4a cos 2a
c,	2 cos2 2а - 1	. _ . т . а
86.------г-------г-------т~-------г— tg 2а + cos 2а - sm 2а
2 tg [7- - 2а I sin2 I—л - 2а j
4	14	/
87. cos2 (2/3 - а) - cos2 (« + j) - cos2 (2/3 - Зя)
89. cos ly - а
gg cos ~ s*n i,a ~ cos
' cos 2a + sin 4a — cos 6a
5 I2
cos(a + -^л)
cos a - sin a
90. sin 2а + cos 2а - cos 6а - sin 6а
9!	если а)0-<«<90-; 6)90°<а<180’
Vl+sma+Vl - sina
92: 2 cos2 (2а - л) - у/З sin (2% - 4а) - 1
93. cos2 (ул + 2а I - sin2 Ц-тг + 2а
I О	/	Io
n . sin 2a + cos 2a - cos 6a - sin 6a
у 4.----------— -------------------------
sin 4a + 2 sin2 2a — 1
96. cos2 2а - 3 sin2 2а
95. tgx + tg 2х - tg Зх
97. tg 390° + ctg 390° + tg 220° + ctg 220'
cos у - 8a
98. 2-------v—V-------J—
sin* 4 2a — cos4 2a
92
Гл, IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
100. cos 44а + 3 cos 36а + 3 cos 28а + cos 20а
Доказать справедливость равенств (101-114)
cos 28° cos 56°	cos 2° cos 4° _ V? sin 38°
sin 2°	sin 28°	~ 4 sin 2° sin 28°
102. 1 - 2 cos 40° = 0,5 cos'* 1 160°
I пт sin 20° cos 10° + cos 160° cos 100° _ .
sin 21° cos 9° + cos 159° cos 99° ~
104. sin2 * 4 70° sin2 50° sin2 10° =
cos ^2° cos 72° - cos 42° cos 18°
cos 63° cos 3° - cos 87° cos 27°
106. sin 10° sin 30° sin 50° sin 70° = 77-
16
107. ctg 60° + ig 60° + ctg 50° 4- tg 50° = X cos 20°
V
me л , 2л ,	4л, 6л 1
108. cos у + cos -у- + cos -у + cos = —J
109. cos 70° + 8 cos 20° cos 40° cos 80° = 2 cos2 35°
. ... 2л 4л 8л 16л	32л	1
I 10. cos yr cos ИТ cos ДТ cos 'ДТ' cos ~Д1Г = ДД
Hi. cos 410° + 8 cos 560° cos 220“ cos 440° = 2 cos2 25°
I i 2. sin 378° sin 774° - |
4
,., o . 2л , . 4л 6л 1 . 8л o . ч 2л э л
113. 3 sin у- + sinyy - sirijy - у sin"p7 = ° sin у? cos J?
1 14. cos 6° sin 24° cos 42 ° sin 12° = ~
ТЕКСТ ПРИМЕРОВ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
93
Вычислить, найти (115—139)
115. cos (2а + -д-л), если tg а = у
116. -7—г-т^-—, если ctg а = 5	117. 8 sin 80° cos 50° sin 20°
6 + 7 sin 2а
118.	cos у-, если sin а = и 450° < а <540°
4	ozo
cos4 75° - sin4 75°	8	. 8 _со
119.	з------------- 120. cos0 75 - sin’ 75°
cos4 75° + sin4 75°
12I-rHi™^(sin75O-sinl5O)
ex,	4	3
122.	ctg ту, если cos а = —= и л < а < y
123.	sin а, если sin тс + cos -х = 1,4
и,	, 'i . (9л	\	(11л _ \	9
124.	tg у + а - tg -д—а , если tg -у + 2а = у
125.	Число/3 тс < /3 <л , если известно, что tg (а + /3) = -гтг и
I Z	j	1 у
tg а — — 4
cos 427° cos 727° - cos 83° cos 743°
12 cos 128° cos 428° - cos 38° cos 22° tg 2
177 6 sin За - 7 cos За + 1
' 8 sin За + 9 cos За - Г
если tgy = 4
. _c	(а - /3)	.	. д 27 . а + в 7
128. cos л—у2-, если sin а + sin ? = -65’ g —2	= 9
у < а < Зл и —у < /3 < 0.
3	6	1
129. cos у cos у 130. ctg у, если известно, что sin х + cos х — v
О	О	Xi
94
Гл. IV
МЕТОДЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
131.	ctg если известно, что sin х — cos х =
1 + 2^2
3
э f 3	|	* и
132.	4 tgz I yr + а , если cosy = у
133.	sin3 а - cos3 а, если sin а — cos а = п
1Э, . х 5х	/ Злу 4 п л
134.	sin 2 cos -у, зная, что cos (х —у) = -у, и 0 < х <
135.	cos 440° sin 130° cos 340°
. ~ а	527 5
136.	cos-7, если cos а = -ттг? , х--
4	625 2
.. х . 5х . (9л
137. sin 2 sin у, если sin -у
= 3
5
138 sin а и cos а, если tg v =
4	4
139.	tg у если cos а = и 450° < а < 540'
Зная, что А, В и С — внутренние углы некоторого треугольника, до-
казать справедливость равенств (140—144)
3	3	3
140. sin 34 + sin 319 + sin ЗС = -4 cos у4 cos ^B cos yC
141. sin 4Л + sin 4B + sin 4C = -4 sin 2A sin IB sin 2C
, sin A + sin В + sin C .A ii
142.  -—-—:— ------—— = Ctg 37' Ctg 37
sin A + sin В - sin C 2	2
143. sin 2.4 + sin 2/3 + sin 2C - 4 sin A sin В sin C
144. sin 2«4 + sin 2nB + sin 2nC = (—1)"+! 4 sin nA sin nB sin tiC
145. Доказать следующее утверждение: для того, чтобы в треуголь-
нике ЛВС один из углов был равен 60°, необходимо и достаточно,
чтобы выполнялось равенство sin ЗА + sin ЗВ + sin ЗС = 0
ТЕКСТ ПРИМЕРОВ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
95
146.	Доказать следующее утверждение: для того, чтобы в треуголь-
нике АВС один из углов был равен 36° или 108°, достаточно, чтобы
выполнялось равенство sin 5/1 + sin 5В + sin 5С = 0.
147.	Найти наибольшее значение выражения
. т (23л	. \	.?	(33л	. । л л
sinz -----4а	— smz ------4а	при 0 < а	<
1 О	)	I О	)	о
148.	Найти наименьшее значение выражения
ctg 2а - tg 2а
при а е
149.	Найти наибольшее значение выражения
1	г- Гл Л"1
—---------т- при a G 0, тг
sin°a + cos°a	L ZJ
150.	Доказать, что если cos 2х = cos 2у cos 2z, то
1 + ctg (х + у) ctg (х - у) = sin~2 z
151.	Доказать, что выражение
4 cos 2a cos <f> cos (2a — <f>) + 2 sin2 (2a — <f>) — cos 2y
не зависит от <p
152.	Доказать, что если А и В — острые углы некоторого прямоуголь-
ного треугольника, то
sin 2А + sin 2В = 4 sin А • sin В
ОТВЕТЫ
Глава I
§ 1.	1. а) 1 четверть; б) IV четверть; в) II четверть; г) III четверть; д) II четверть; е)
IV четверть; ж) IV четверть. 2. а) IV четверть; б) II четверть; в) III четверть; г) I чет-
верть; д) IV четверть; е) I четверть. 3. а) п=-1,а=90°; б) п=1,а=45°; в)
п=-3, а=120°; г) п=5, а=0°; д) д=-5, а=49°.
§ 2.	1. а) Да; б) да; в) нет; г) нет; д) да; е) нет. 2. а) Да; б) да; в) нет; г) нет; д) да.
3. а) IV четверть; б) II четверть; в) I четверть; г) III четверть; д) II четверть; е) III чет-
верть.
§ 3.	5. 1. 6. sin2 а. 7. 0,48. 8.	\ 10. sin a=±l/Vl+ctg2 а ,
cos a=±ctg tz/Vi+ctg2 a, tg a=l/ctg a. 11. cos a=-3/5, tg a=-4/3, ctg a=-3/4. 12.
а) Нет; б) да.
§4.	1. sin (—л/6)=-1/2,	cos (-л/6)=^з"/2, tg (-л/6)=—VI/3,
ctg (-л/6) =-VI, sec (-л/6)=2/'У|1', cosec (-л/6)=-2. 2. sin (~45°)=-V2/2,
cos (-45°)=VI/2, tg (-45°)=-!, ctg (-45°)=-!, sec (-45°)=VI, cosec (-45°)=-V2.
5. а) Нечетная; б) ни четная, ни нечетная; в) ни четная, ни нечетная; г) четная; д) ни
четная, ни нечетная; е) четная. 6. а), д), е), ж), з). 7. а) 2л; б) л; в) 4л; г) 2л; д) л; е)
2л; ж) 2л; з) л; и) 6л; к) 30л; л) периодом является любое число (основного периода
нет); м) 1.
§ 5.	1. a) cos 36°; б) cos (л/4+За); в) sin 37°; г) sin (л/5); д) ctg 39°; е)
tg (л/4+а/2); ж) tg53°31’l4’'. 2. а) -1/2; б) cos2°31’; в) 1; г) -1/V3.3. -11/10. 4.
а) 4; б) -1.5. 1. 6. а) -1/2; б) -VI/2; в) — 1; г) ctg 49° или tg 41°. 7. 2(2-VI) == 0,54.
Рис. 55
ОТВЕТЫ
97
Глава II
§ 1. 1. а) Область определения функции: х — любое, кроме x=—(2n+i). Область
изменения функции I sec xl >1 ; б) область определения функции: х — любое, кроме
х=лп. Область изменения функции I cosec х I > 1. 2. а) 0 < 1—cos 0,5 < 0,125; б)
0 < 1 -cos 0,6 < 0,18; в) 0 < 0,3-sin 0,3 < 0,0135; г) 0 < 0,4-sin 0,4 < 0,032.
§ 2.1. 1) Рис. 55; 2) Рис. 56; 3) Рис. 57; 4) Рис. 58; 5) у = coslxl = cos х; 6) Рис.
59; 7) Рис.59, ибо у = I cos Ixl I = 1 cos xi; 8) Рис. 60; 9) Рис. 61; 10) Рис. 62; 11) Рис.
63; 12) Рис. 64.
Глава III
§ 1.1. а) -0,259; б) -0,259; в) 0,268; г) 3,73.
1	3	3
8 2.	2.	Л=-—-------.	4. sin 4а=4 sin a cos a-4sin a
®	5+4 sin х
,	4	, . 2	2.4	_	3 п ,.a
cos 4a=cos a—6 sm a cos a+sin a. 5. cos 2a. 6. sm y
cos a;
1
VTo’
3
VTo’
a
cos
a	„ _	4 sin 2x . „ .	60	II
tg 7.----------------. 10. sm а=тг, cos a= —77.
2	cos2 2x	61	61
3
11.	12. tg 3a=3-tg —~-y—й. 14. V2 + 1.
931	l-3tg a
§ 3.1. cos3 2a. 3. Л=1/8. 6. <3/2 = 0,87. 7. 1/4. 8. 3. 9. 3.
§ 4.1.2 sin ]-— cos 2. 2 sin 0,8 cos 2,0. 3. 2 cos 25° cos 15°.
240	240
Зтг . л sin 13,6	sin 87°54'	2 fi э /7 Q
4.-2 sin —	Sin —.	5.--r-T----77—.	6.------------^777- 7. ~—7-	8. 2 V3 ® 3,46.
40	40 cos 3,2 cos	10,4 cos 9145 cos 3 51 sin 4
V2
9. ~~2~ sin a. 10. 2 cos a sin 3a sin 5a.
A <77 (л \	2 a
2 V 2 cos ~a cos 77	v/7	o
14 J 2 ,V3 ~ 8 r . 3
-----------*----*-------- 12. .- Ano-----777. 13. •= cos 6a sm a.
cos a-----------sin 20 cos 50	3
10. 2 sin	11. 2 sin (2a-~r\.
\	0/	\	0/
98
ОТВЕТЫ
Рис. 59
Рис. 61
ОТВЕТЫ
99
Рис. 64
Глава IV
40. —. 41. -tg -7-. 42. 2 sin а. 43. tg 4а. 44. ctg 2а. 45. 2. 46. -cos 4а. 47. tg 2а .
О	о
48. cos cos у 49. sin у\ 50. cos 3 2х. 51. ctg4a. 52. 1.53. -cos а. 54. 2 cos 2а.
55.	21 sin ' 2сс 1.56. a) -2tga; 6) 2tg a. 57. -1.58. 1.59. tg4 2a. 60. tg4 4a .
(JT \	- 2
—+4a . 62. sin 4x cos 4x.
63.	8 V^. 64. 2 sin (4a-^ . 65. у 66. 2 sin3 4a. 67. -cos2 2x. 68.
r-	a	9a
69. 2 V 2 sin a cos (45°-a). 70. - 4 sin у sin a cos -y.
71. 4 sin a sin 2a sin 3a.72. ctg2 ctg ^a'
73. 4 sin 4a sin (a+15°) cos (a-15°). 74. tg	a'
75. 4 cos 4a sin (15°-a) cos (15°+a). 76. sin 5x sin lx.
100
ОТВЕТЫ
77. 4 sin x sin (30°-x) sin (30°+x). 78. ctg8 2a. 79. 2 sin (8a+30°).
80. 2 sin (2a—30°). 81.-4cos-^in (60°-x)sin (604x)
2V2 sin
86.------
4
COS X
82. 8 sin2 a sin2 2a. 83. 2 sin (6a-60°).
84.	-8 cos (60°+2a) cos (60°- 2a).	tg 2a.
(л \	2
I—-2a I cos a
*—r-J---------. 87. 2 sin a sin (2/3-a) cos 2&.
cos 2a	4	'
88. tg (a-15°) ctg (a+15°). 89. 2sin cos .
lx 1X J I *	/	—
90. 2^2 sin 2a sin (4a-45°). 91. a) tg y; 6) ctg y. 92. 2 cos (j~4a^  93. ~y- sin 4a.
' я
94. 2 sin 2a. 95. -tg x tg 2x tg 3x. 96. 4 sin (30°+2a) sin (30°-2a). 97.	sin 70°.
98. 4 cos2 2a.
14 I
2V2 sin fe-2a j cos2 (j-a'|	5
".----------U-X---------L—J-. 100. 8 cos 32a cos3 4a. 115. —. 116.
117. V3. 118.1.119.	120.	121.	122.
123. 0,96. 124.	125. Jt-arctg 5. 126. 0. 127. -77. 128. —Д=. 129- T- 130. 2, или
9	е	44	7V130	4
131. 1)4=; 2) 3-2V2.132.0,5.133. 3п~П .
3 V2	2
...	38	1	3 ni 41		720	1519	4
134. ---. 135. ? 136. - -. 137.	138. sm a=—; cos	139.
« AM 1	« АГ» Л	Л	A
148. 2 Прист-—. 149. 4 приа==—.
ПРИЛОЖЕНИЯ
Приложение I
Тригонометрические функции
х°	х (радиа- ны или числа	sin х	tg X	Ctg X	COS X		
I	II	Ш	IV	V	VI	VII	VIII
0	0,0000	0,0000	0,0000	—	1,0000	1,5708	90
1	0,0175	0,0175	0,0175	57,29	0,9998	1,5533	89
2	0,0349	0,0349	0,0349	28,64	0,9994	1,5359	88
3	0,0524	0,0523	0,0524	19,08	0,9986	1,5184	87
4	0,0698	0,0698	0,0699	14,30	0,9976	1,5010	86
5	0,0873	0,0872	0,0875	11,43	0,9962	1,4835	85
б	0,1047	0,1045	0,1051	9,514	0,9945	1,4661	84
7	0,1222	0,1219	0,1228	8,144	0,9925	1,4486	83
8	0,1396	0,1392	0,1405	7,115	0,9903	1,4312	82
9	0,1571	0,1564	0,1584	6,314	0,9877	1,4137	81
10	0,1745	0,1736	0,1763	5,671	0,9848	1,3963	80
11	0,1920	0,1908	0,1544	5,145	0,9816	1,3788	79
12	0,2094	0,2079	0,2126	4,705	0,9781	1,3614	78
13	0,2269	0,2250	0,2309	4,331	0,9744	1,3439	77
14	0,2443	0,2419	0,2493	4,011	0,9703	1,3265	76
15	0,2618	0,2588	0,2679	3,732	0,9659	1,3090	75
16	0,2793	0,2756	0,2867	3,487	0,9613	1,2915	74
17	0,2967	0,2924	0,3057	3,271	0,9563	1,2741	73
18	0,3142	0,3090	0,3249	3,078	0,9511	1,2566	72
19	0,3316	0,3256	0,3443	2,904	0,9455	1,2392	71
20	0,3491 .	0,3420	0,3640	2,747	0,9397	1,2217	70
21	0,3665	0,3584	0,3839	2,605	0,9336	1,2043	69
22	0,3840	0,3746	0,4040	2,475	0,9272	1,1868	68
23	0,4014	0,3907	0,4245	2,356	0,9205	1,1694	67
24	0,4189	0,4067	0,4452	2,246	0,9135	1,1519	66
25	0,4363	0,4226	0,4663	2,145	0,9063	12,1345	65
26	0,4538	0,4384	0,4877	2,050	0,8988	1,1170	64
27	0,4712	0,4540	0,5095	1,963	0,8910	1,0996	63
28	0,4887	0,4695	0,5317	1,881	0,8829	1,0821	62
29	0,5061	0,4848	0,5543	1,804	0,8746	1,0647	61
102
ПРИЛОЖЕНИЯ
	X (радиа- ны или числа	sin х	tgx	Ctg X	COS X		
I	II	III	IV	V	VI	VII	VIII
30	0,5236	0,5000	0,5774	1,732	0,8660	1,0472	60
31	0,5411	0,5150	0,6009	1,6643	0,8572	1,0297	59
32	0,5585	0,5299	0,6249	1,6003	0,8480	1,0123	58
33	0,5760	0,5446	0,6494	1,5399	0,8387	0,9948	57
34	0,5934	0,5592	0,6745	1,4826	0,8290	0,9774	56
35	0,6109	0,5736	0,7002	1,4281	0,8192	0,9599	55
36	0,6283	0,5878	0,7265	1,3764	0,8090	0,9425	54
37	0,6458	0,6018	0,7536	1,3270	0,7986	0,9250	53
38	0,6632	0,6157	0,7813	1,2799	0,7880	0,9076	52
39	0,6807	0,6293	0,8098	1,2349	0,7771	0,8901	51
40	0,6981	0,6428	0,8391	1,1918	0,7660	0,8727	50
41	0,7156	0,6561	0,8693	1,1504	0,7547	0,8552	49
42	0,7330	0,6691	0,9004	1,1106	0,7431	0,8378	48
43	0,7505	0,6820	0,9325	1,0724	0,7314	0,8203	47
44	0,7679	0,6947	0,9657	1,0355	0,7193	0,8029	46
45	0;7854	0,7071	1,0000	1,0000	0,7071	0,7854	45
		COS X	Ctg.Г	tgx	sin x	x (радиа- ны или числа)	Л*
Приложение II
Тригонометрические функции
х (радиа- ны или числа)	sin х	cos х	tgx	x (радиа- ны или числа)	sin х	cos х	tg X
I	П	III	IV	I	II	Ш	IV
0,0	0,0000	1,0000	0,0000	0,9	0,7833	0,6216	1,2602
0,1	0,0998	0,9950	0,1003	1,0	0,8415	0,5403	1,5574
0,2	0,1987	0,9801	0,2027	1,1	0,8912	0,4536	1,9648
0,3	0,2955	0,9553	0,3093	1,2	0,9320	0,3624	2,5722
0,4	0,3894	0,9211	0,4228	1,3	0,9636	0,2675	3,6021
0,5	0,4794	0,8776	0,5463	1,4	0,9854	0,1700	5,7979
0,6	0,5646	0,8253	0,6841	1,5	0,9975	0,0707	14,101
0,7	0,6442	0,7648	0,8423	1,6	0,9996	-0,0292	-34,233
0,8	0,7174	0,6967	1,0296				
ОГЛАВЛЕНИЕ
12.! Териодичиосг ь тригонометрических функций <28).
Упражнения.....................................................  31
§5. Формулы приведения ............................................... 32
13. Зависимость между тригонометрическими функциями дополнительных
углов (32). 14. Формулы приведения (33).
Упражнения.....................................................   38
Глава II. Тригонометрические функции числового аргумента и их графики. 39
§ 1. Тригонометрические функции числового аргумента ................... —
15. Определение (39). 16. Области определения и области изменения значе-
ний тригонометрических функций (39). 17. Некоторые неравенства и их
следствия (40).
Упражнения...................................................... 42
§2. Графики тригонометрических функций ............................... —
18. Первоначальные сведения о таблицах тригонометрических функций
(42). 19. Основные графики (43). 20. Примеры построения графиков некото-
рых других тригонометрических функций (46). 21. Дальнейшие примеры
построения графиков функций (47).
Упражнения ..................................................... 50
Глава Ш. Преобразование тригонометрических выражений ................ 51
§1.	Формулы сложения и вычитания..................................... —
22. Расстояние между двумя точками на плоскости (51). 23. Косинус суммы
и разности двух аргументов (52). 24. Синус суммы и разности двух аргумен-
тов (53). 25. Тангенс суммы и разности двух аргументов (54). 26. О форму-
лах сложения для нескольких аргументов (54).
Упражнения...................................................... 55
§ 2.	Формулы для двойного и половинного аргумента. Выражение sin па и cos па
через степени sin а и cos а.......................................... 55
104
ОГЛАВЛЕНИЕ
27. Тригонометрические функции двойного аргумента (55). 28. Выражение
sin па и cos па через степени sin а и cos а при натуральном числе п (56). 29.
Тригонометрические функции половинного аргумента (57). 30. Выражение
основных тригонометрических функций аргумента а через tg (а/2) (59).
Упражнения...................................................   60
§ 3.	Преобразование в сумму выражений вида sin a cos a, cos a cos fl и sin a sin /?... 61
31. Основные формулы (61). 32. Примеры (61).
Упражнения...................................................   62
§ 4.	Преобразование в произведение сумм вида sin a±sin fl, cos a±cos fl и tg a±tg fl 63
33. Основные формулы (63). 34. Примеры (64).
Упражнения...................................................   65
§ 5.	Преобразование некоторых выражений в произведения с помощью введения
вспомогательного аргумента.......................................    66
35.	Преобразование в произведение выражения a sin a + b cos а (66). 36.
Преобразование в произведение выражений a sin а 4- b и a cos а + b при
0< 161 < lai (67). 37. Преобразование в произведение выражения a tg а + b
(68).
Упражнения...................................................   68
Глава IV. Методы решения типовых задач.............................. 69
38.	Образцы решения некоторых примеров (69). 39. Примеры для самостоя-
тельной работы (84).
Ответы......................................................... 96
Приложение 1...................................................  101
Приложение 2...................................................102
ЛИТЕРАТУРА
1.	Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика (повтори-
тельный курс). — М: Наука, —1976.
2.	Zaitsev V. V., Ryzhkov V. V., Skanavi М. I. Elementary mathematics. — MIR, Pub-
lishers, Mockow, 1978.
3.	Сборник задач по математике для конкурсных экзаменов во ВТУЗы. /В. К. Еге-
рев, В. В. Зайцев, Б. А. Кордемский и др. Под ред. М. И. Сканави 1-ое изд. «Высшая
школа» 1969, 6-ое изд., М.: «Высшая школа», 1992.
Владимир Валентинович Зайцев
Валерий Витальевич Рыжков
Марк Иванович Сканави
ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА. ТЕОРИЯ И ПРАКТИКА РЕШЕНИЯ ЗАДАЧ
(в помощь поступающим в ВУЗы)
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Редактор издательства Н. В. Кислов. Ответственный редактор Л. Е. Пекарский.
Технический редактор Митрофанова Г. Г.
Корректоры Кагарова О., Собко М.
Сдано в набор 17.02.92. Подписано в печать 23.03.92 Формат 60 x 84/16.
Бумага офсетная. Гарнитура «Таймс». Печать офсетная. Усл. печ. л. 6,05
Усл. кр.-отт. 6,31 Зак. Тираж 20000 экз.
Цена договорная
Рукопись подготовлена при участии фирмы «Деловые консультации, Москва»
Отпечатано в типографии малого предприятия «ПРИНТ»,
119633, Москва, Приречная ул. 3 тел. 435-91-11