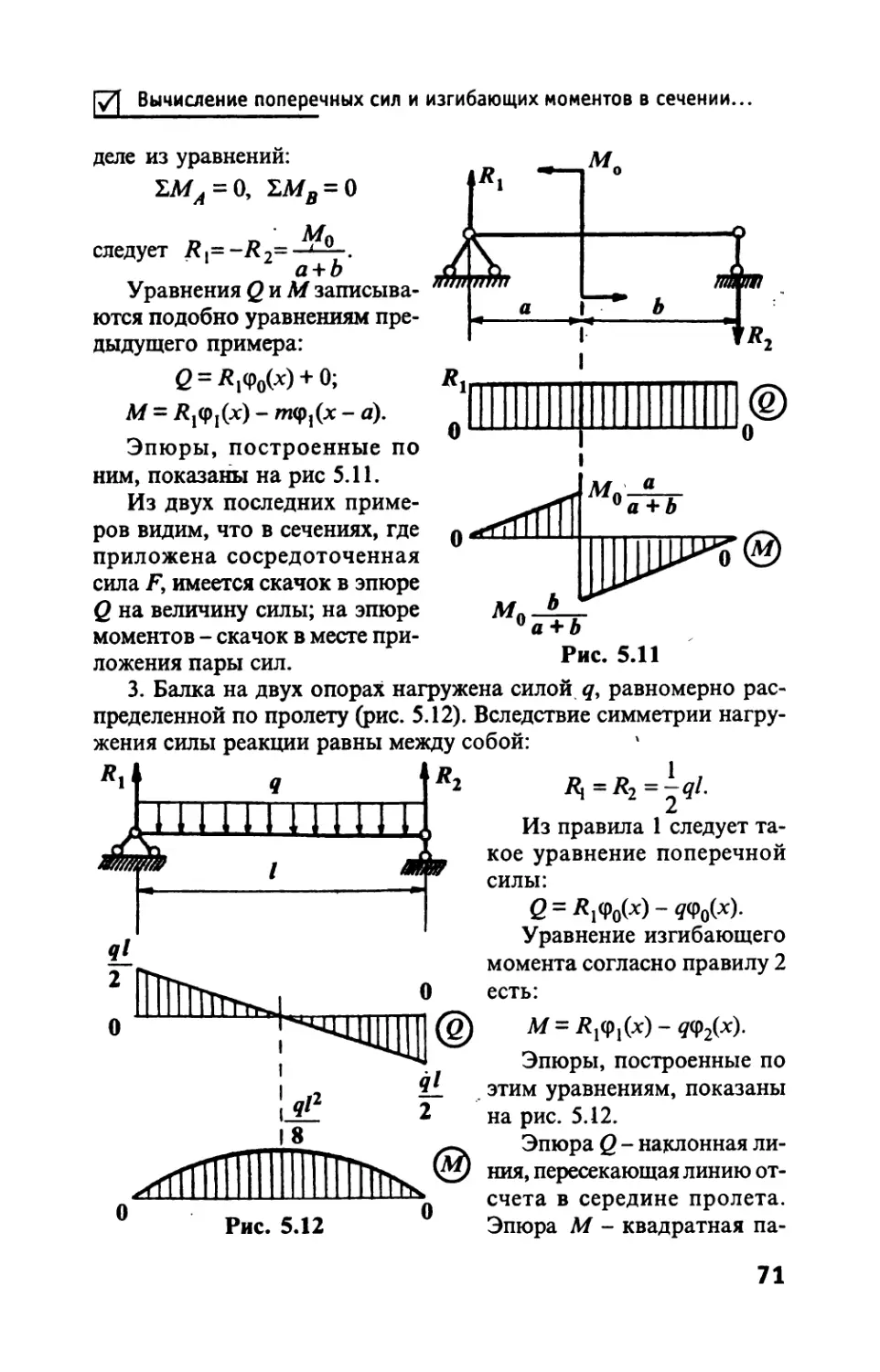
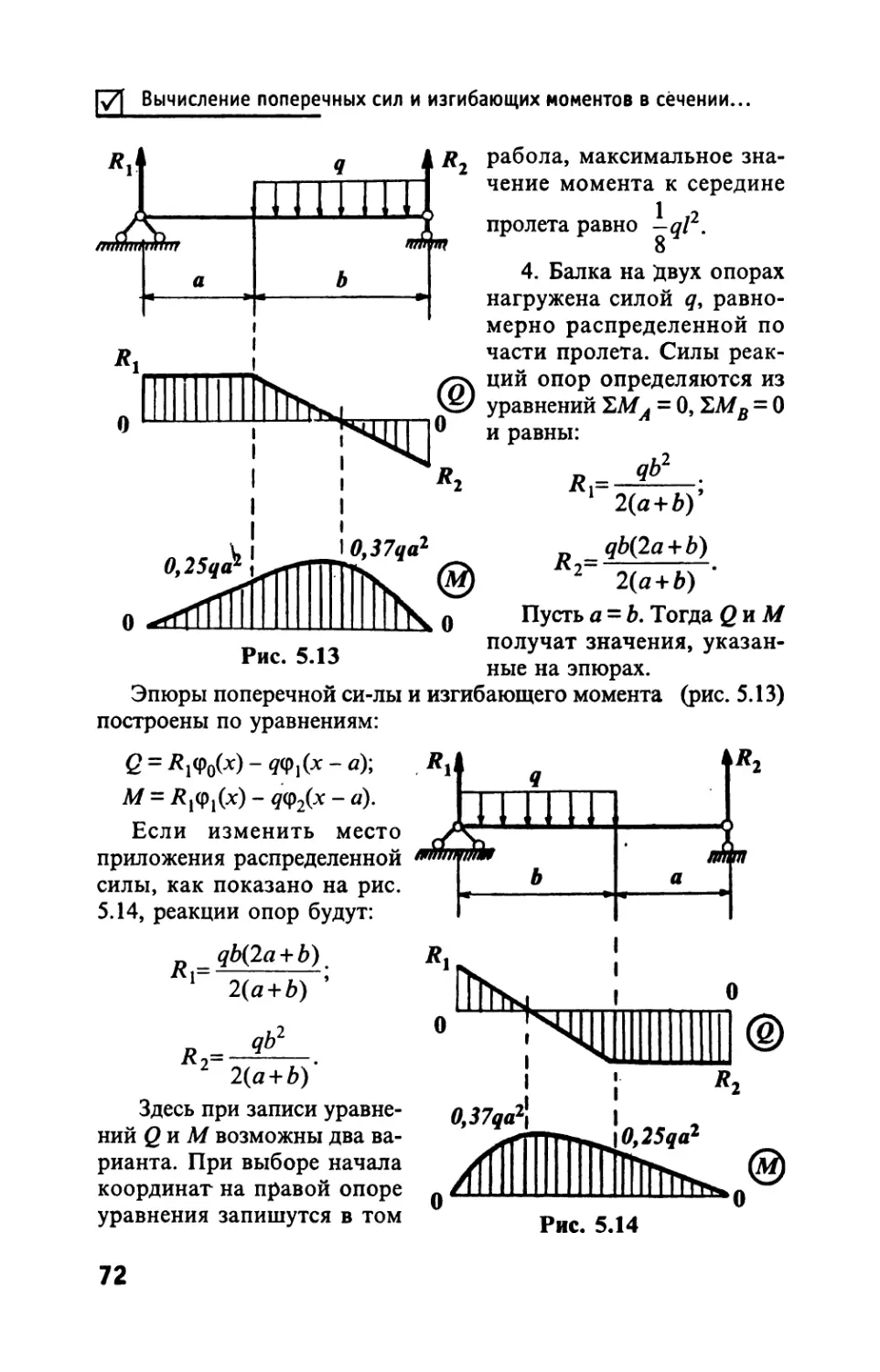
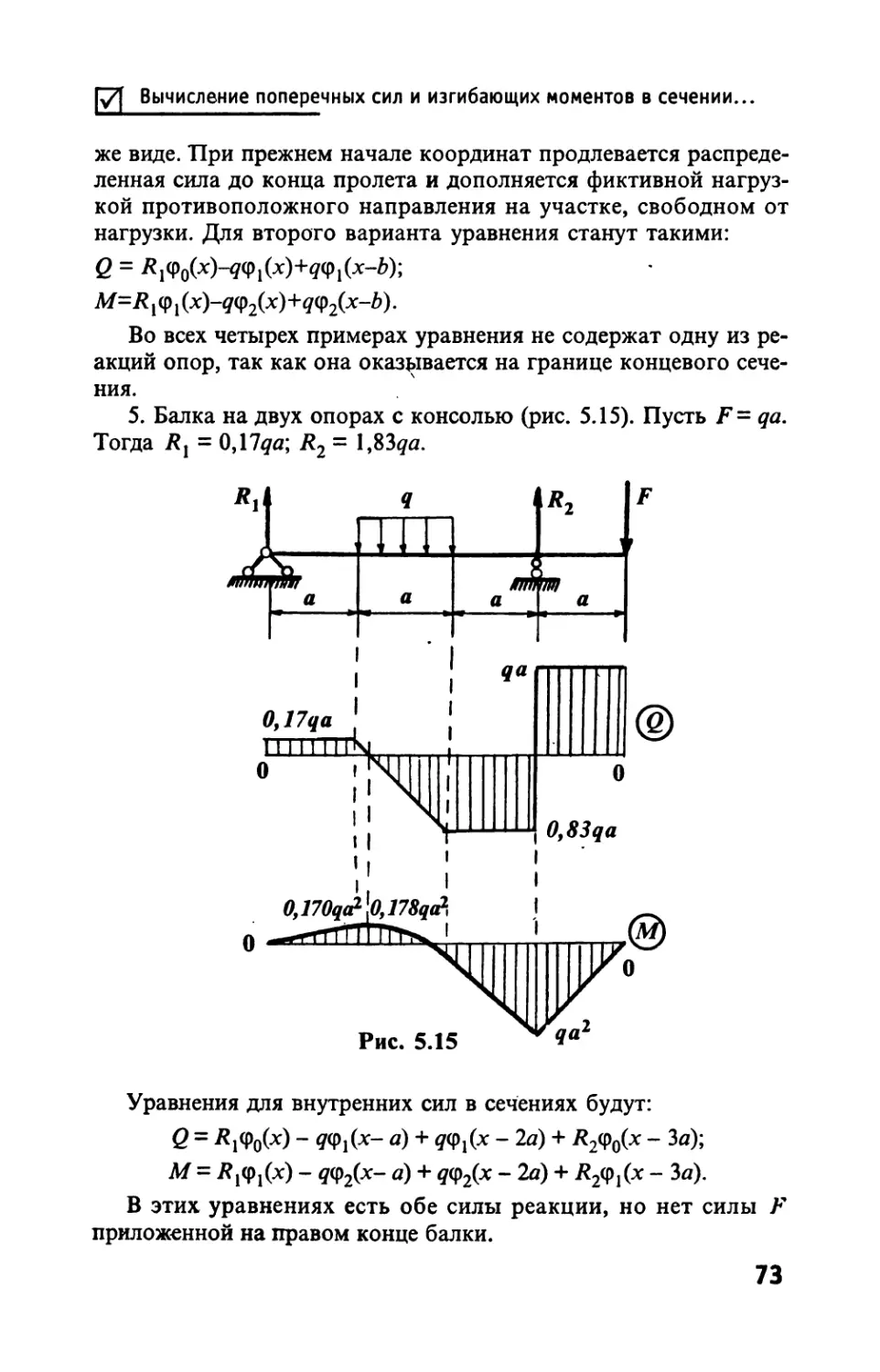
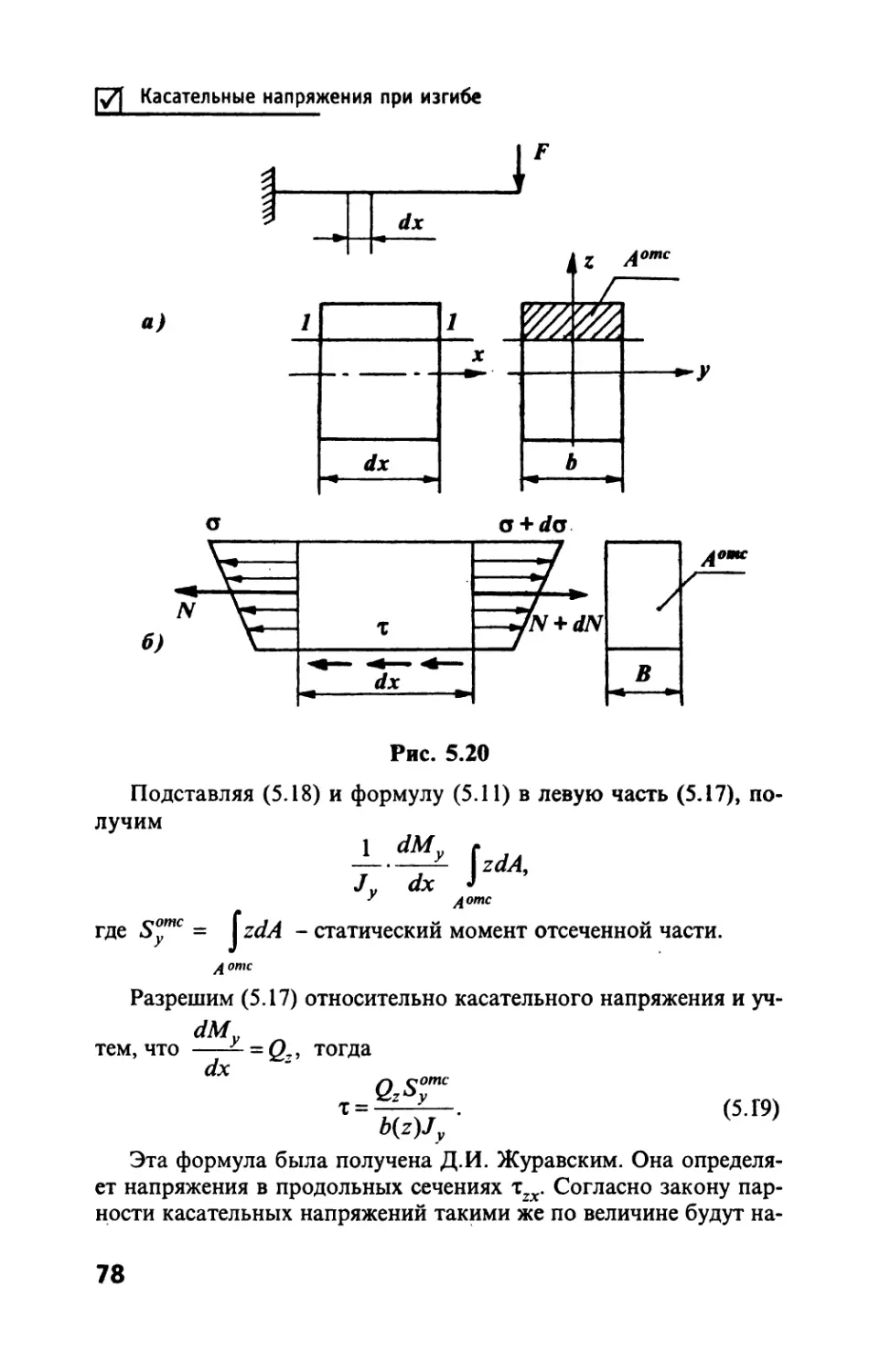
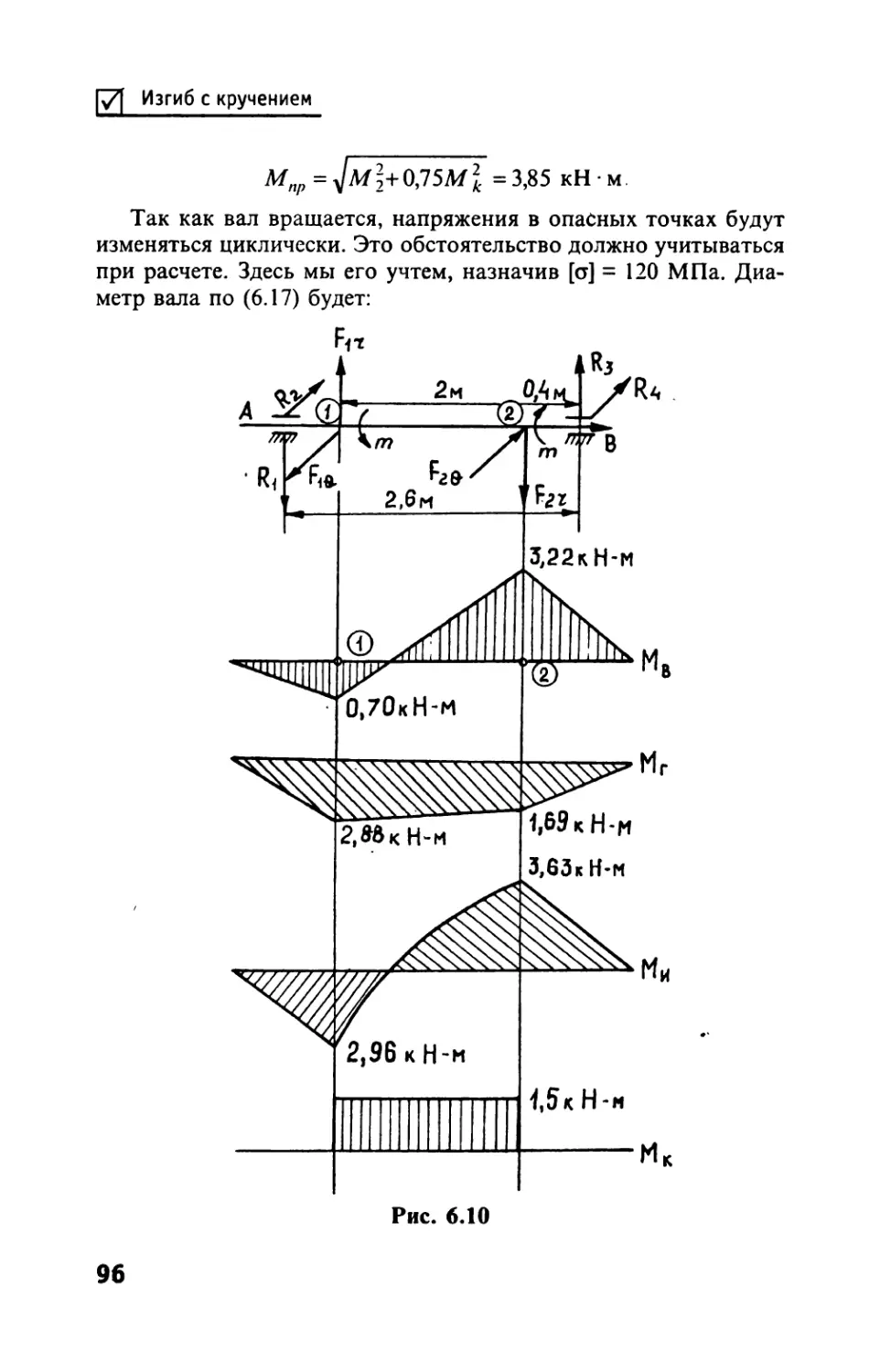
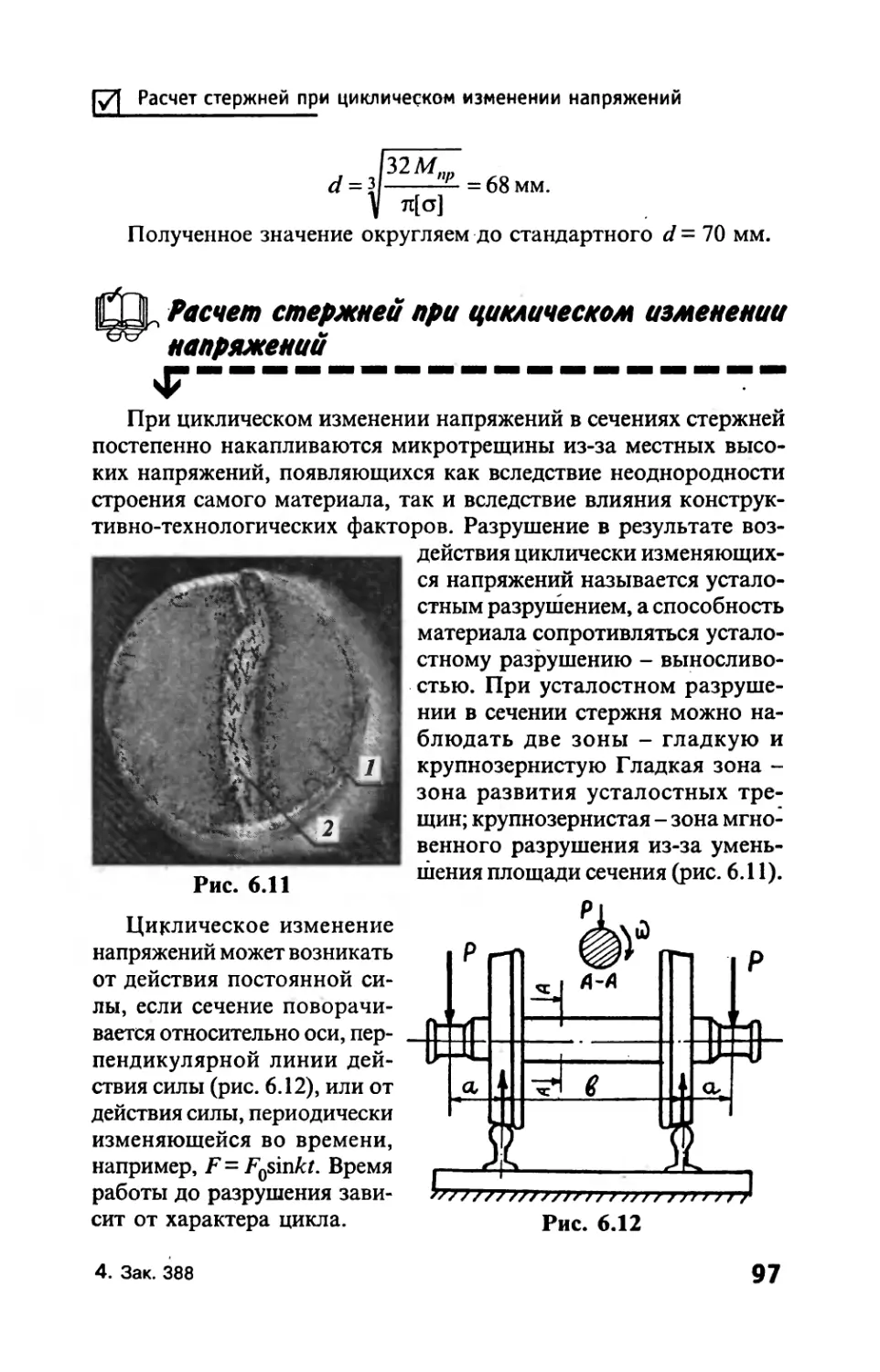
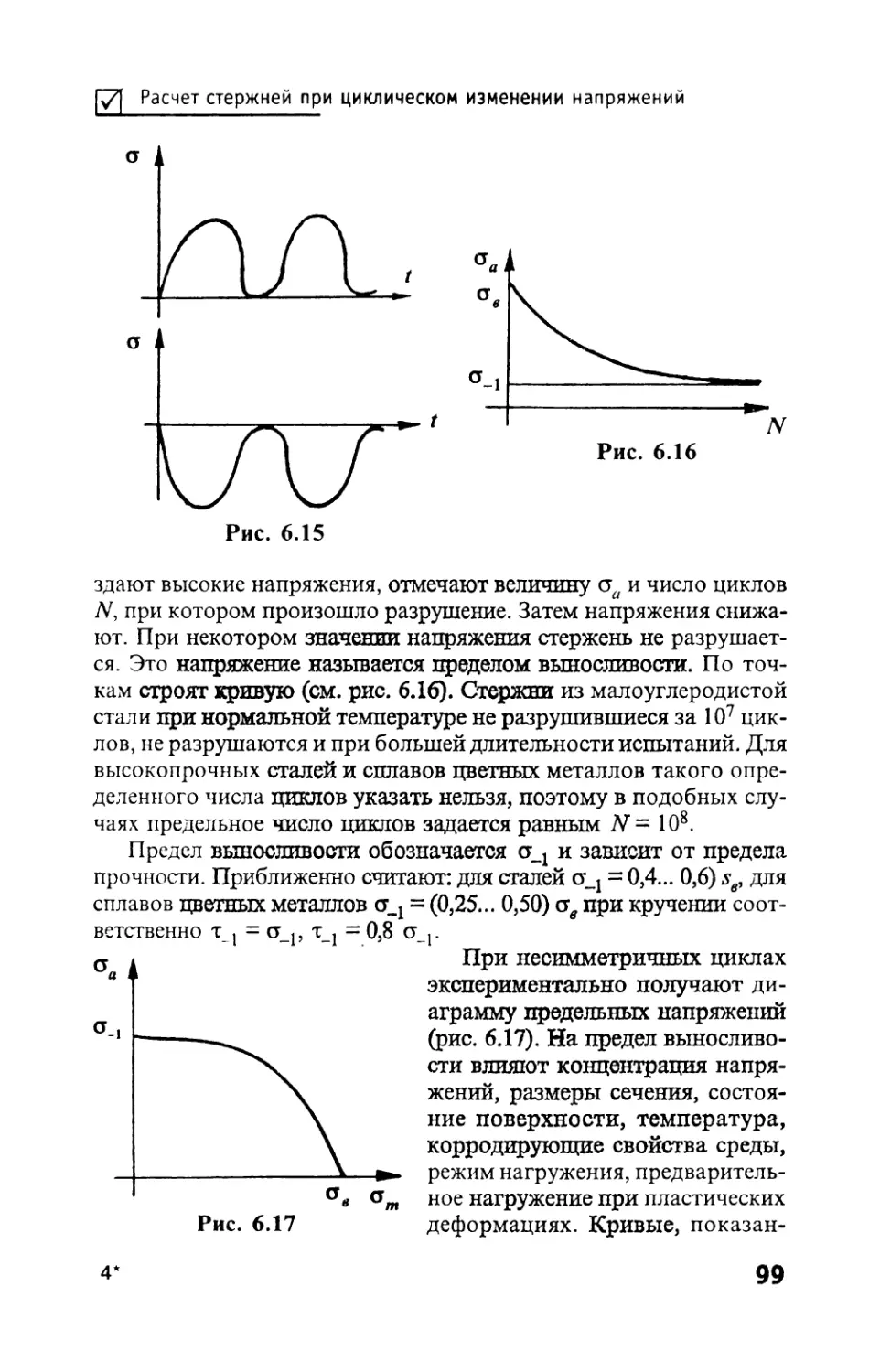
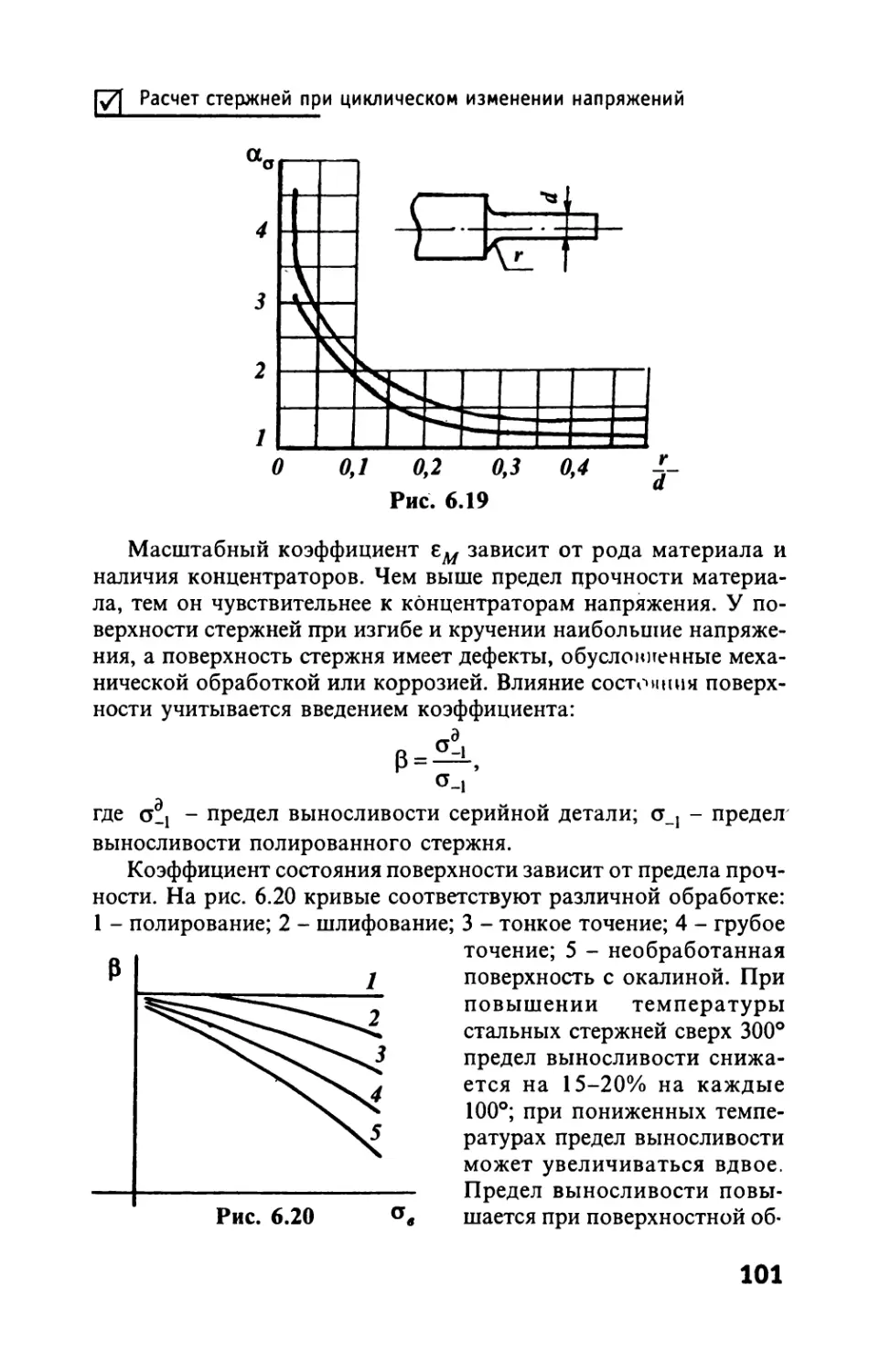
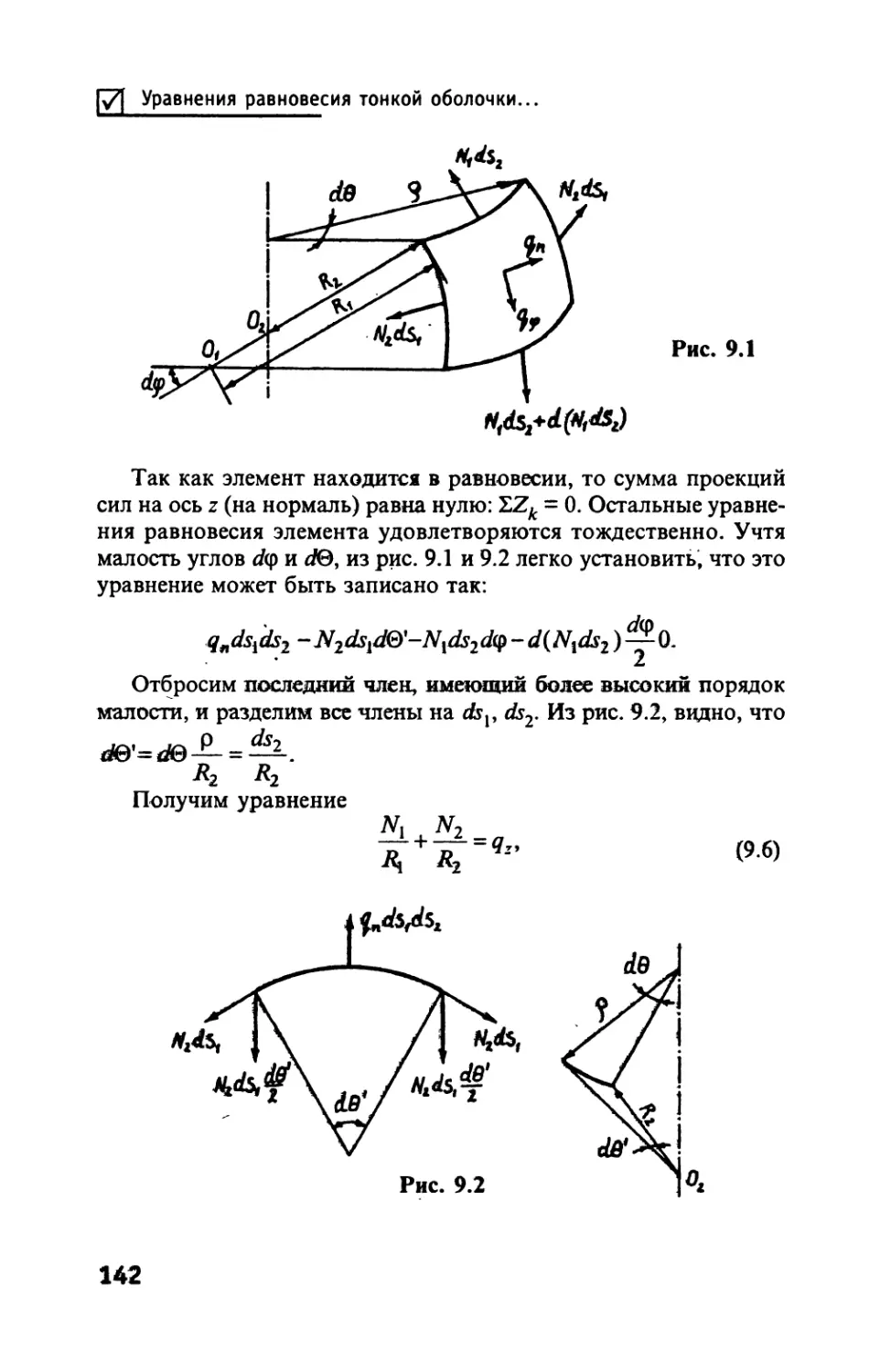
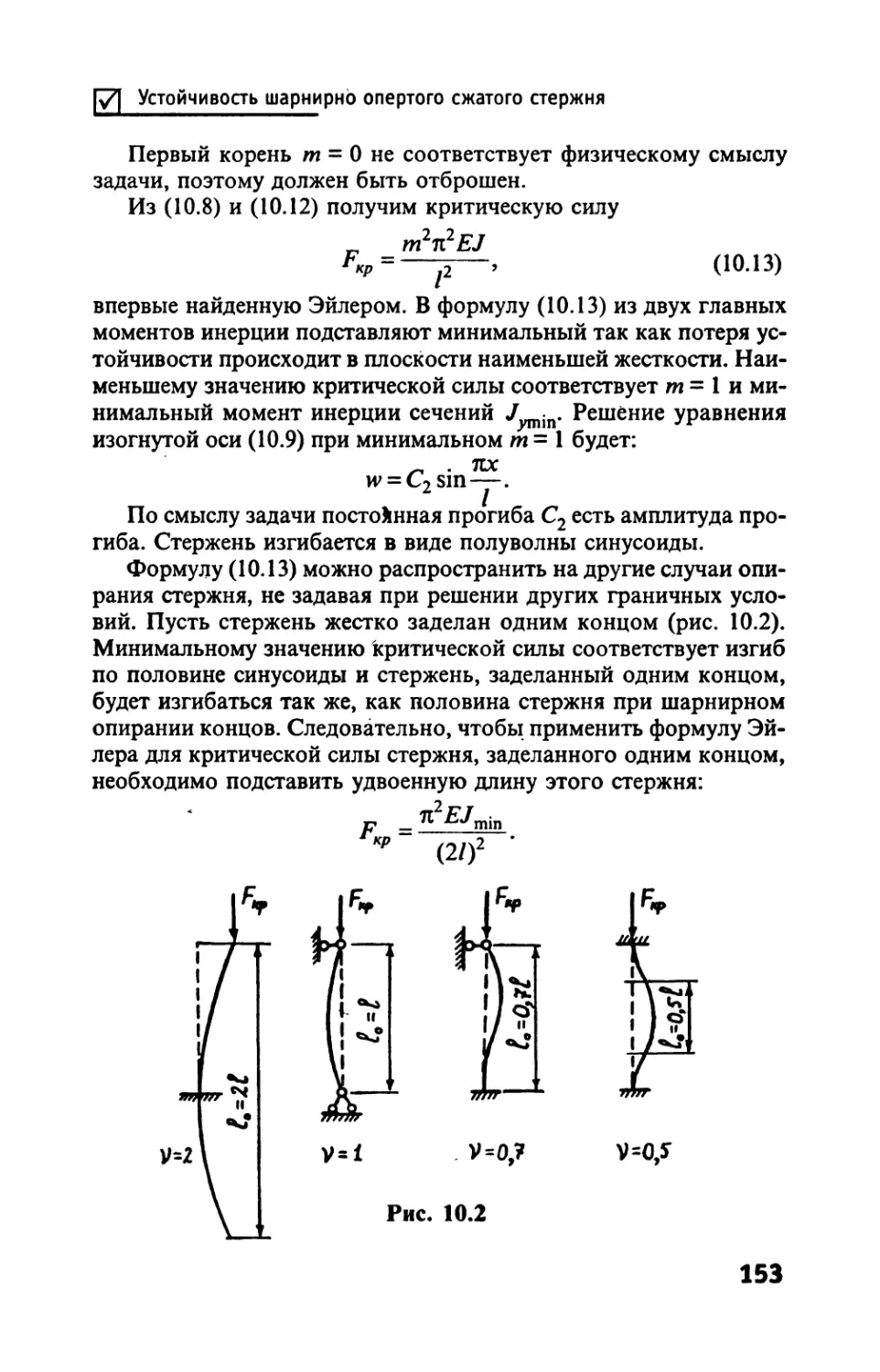
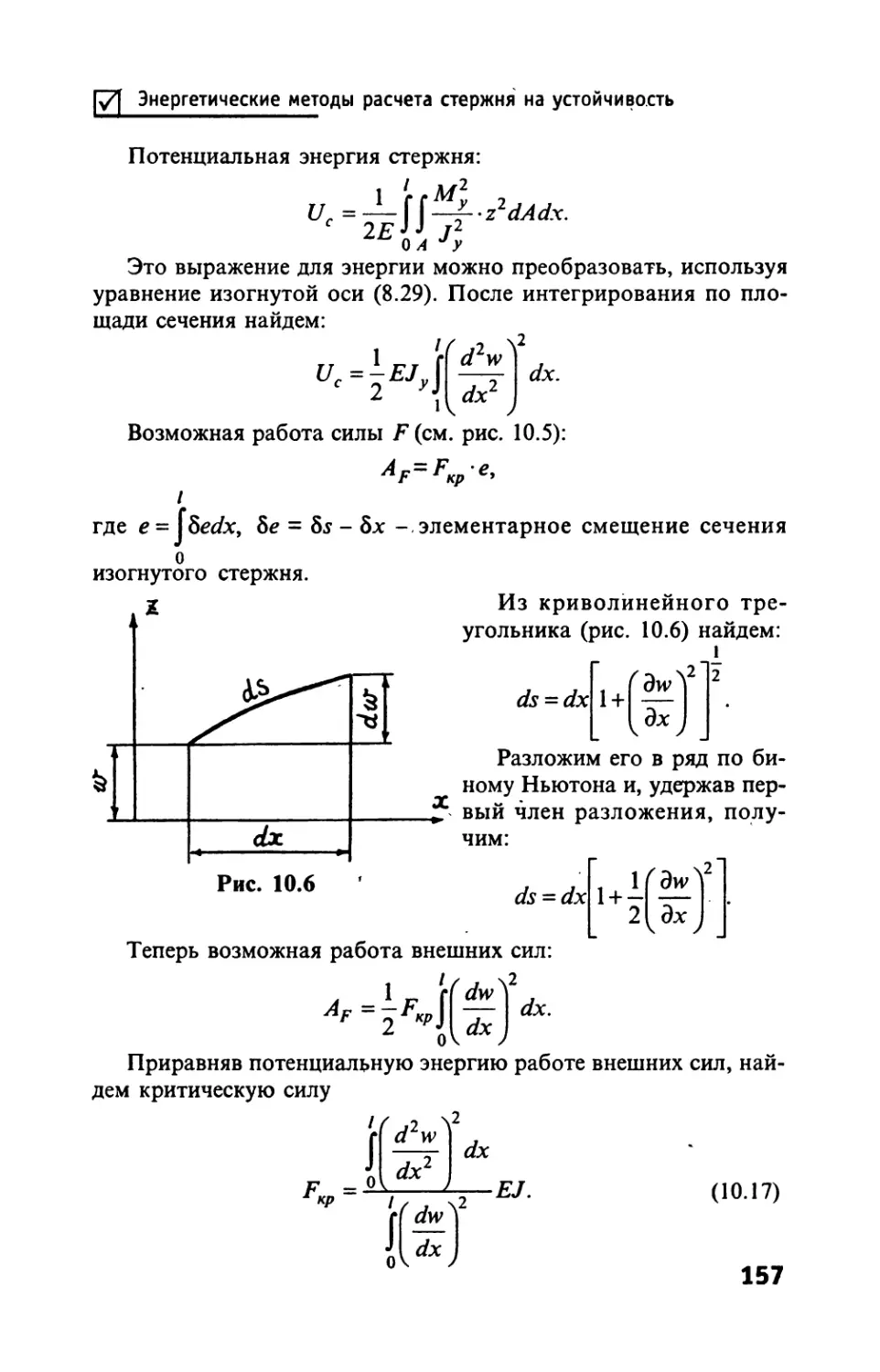
Сопротивление материалов - Тимофеев С.И.

Автор: Тимофеев С.И.

Теги: общетехнические дисциплины химия инженерия сопротивление материалов издательство феникс серия шпаргалки

ISBN: 5-222-04970-1

Год: 2004

Похожие

Ландшафтное проектирование. Дизайн сада

Справочник автомеханика

Взгляд в прошлое: воспоминания очевидца

Русская модель эффективного обогащения

Текст

СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
Для студентов
ВУЗов
Серия
«Шпаргалки»
С. И. Тимофеев
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ДЛЯ СТУДЕНТОВ ВУЗОВ
Ростов-на-Дону
«ФЕНИКС»
2004
ББК 30.1
Т41
Тимофеев С.И.
Т41 Сопротивление материалов. Серия «Шпаргалки».
Ростов н/Д: Феникс, 2004. — 192 с.
Эта книга универсальна: учебное пособие, справочник и подсказка
в нужный момент.
Изложенный в ней материал легко усваивается и быстро запоми-
нается.
Книга сэкономит вам время — подготовит к экзамену в предельно
короткий срок и поможет получить высший балл. В ней ответы на все
каверзные вопросы, поставленные самым строгим экзаменатором.
Для студентов вузов.
ISBN 5-222-04970-1 ББК 30.1
© Замысел и разработка серии
Баранчиковой Е.В., 2004
© Тимофеев С.И., 2004
© Оформление: изд-во «Феникс», 2004
Глава 1
внешние и внутренние силы
в деформированном теле,
нммжени* и деформации
47
Сила, как мера взаимодействия твердого тела с другими тела-
ми твердыми, жидкими или газообразными, введена Ньютоном.
Согласно третьему закону Ньютона силы, статические эквива-
ленты внешних сил, главный вектор Fe и главный момент Ме долж-
ны быть равны главному вектору F' главному моменту М' внут-
ренних сил В сечения стержня.
Существование внутренних сил легко проверить опытом, рас-
тягивая резиновый стержень, сгибая стальную линейку.
Существование твердого тела обусловлено силами взаимодей-
ствия между его частицами. При нагружении тела часть этих сил
противодействуют отделению частиц друг от друга. Эту часть в
«Сопротивлении материалов» называют внутренними силами.
Измерить эти силы в каждой точке мы не можем, измерению под-
даются только деформации в, окрестности некоторой точки. Ме-
тодами «Статики» мож-
но по известным вне-
шним силам найти ста-
тические эквиваленты в
некотором (любом) се-
чении, мысленно прове-
-1 денном через точку.
Пусть на тело дейст-
вует система самоурав-
новешенных внешних
сил (рис. 1.1, а). Рассе-
чем. тело плоскостью на
части А и В. Если тело
уравновешено, будут
уравновешены и его ча-
сти (рис 1.1, б). В соот-
3
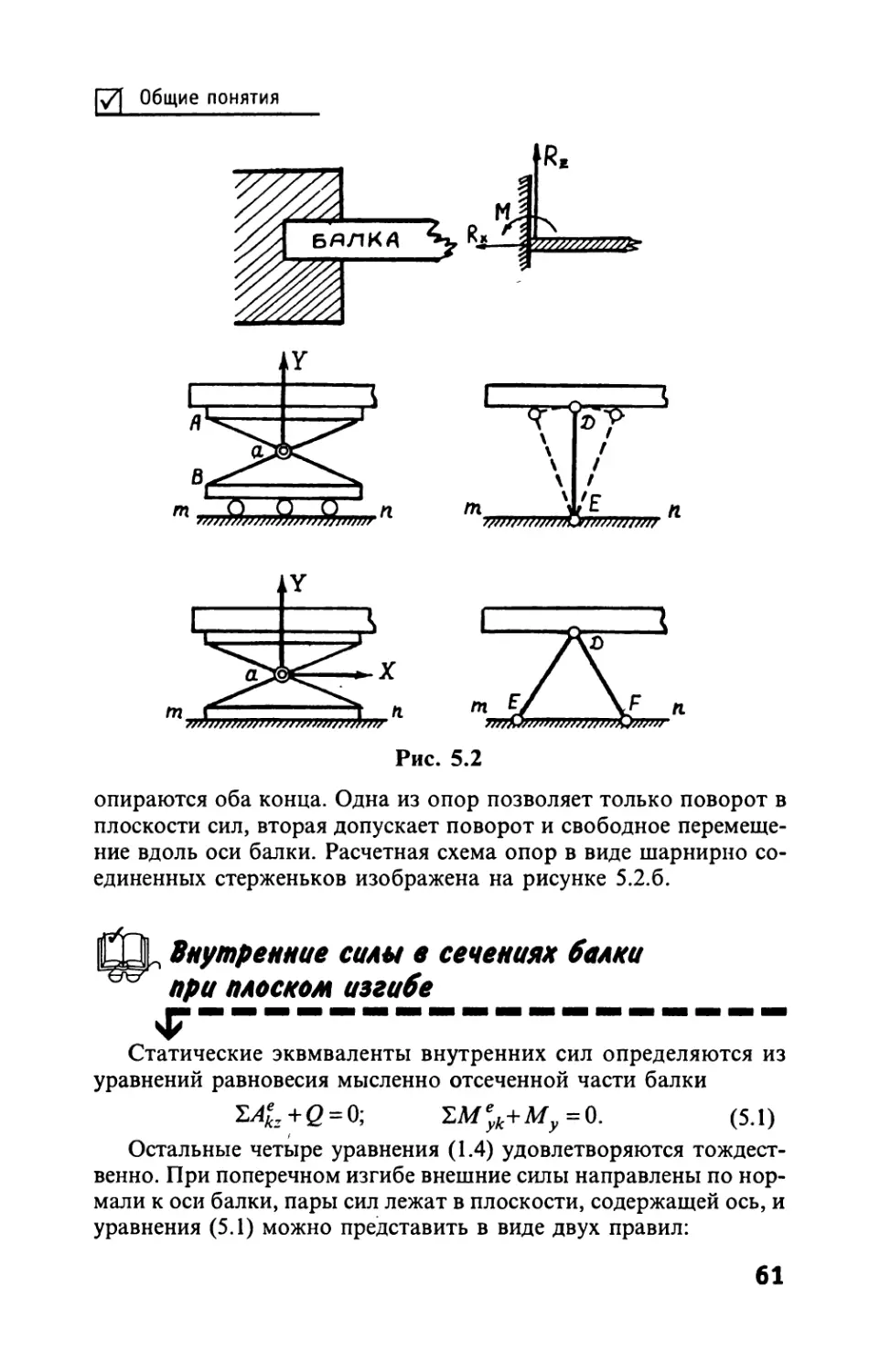
Статические эквиваленты внутренних сил...
ветствии с третьим законом Ньютона:
R^=-RiB-
Перенесем в центры сечений внешние и внутренние силы и за-
меним статическими эквивалентами - главными векторами R и
главными моментами М.
Необходимое и достаточное условия равновесия - равенство
нулю главного вектора и главного момента, т.е. для всего тела
Fo = O; Мо = О. (1.1)
Для частей (см. рис. 1.2)
^ + ^ = о;м^+м^ = о, (1.2)
FoB + F^=0;MoB + M'OB=°. (1.3)
где ей/- начальные буквы латинских слов внешний и внутрен-
ний.
Из (1.2) и (1.3) статические эк-
виваленты внутренних сил выра-
жаются через соответствующие
эквиваленты внешних сил.
Если сложить почленно уравне-
ния (1.2) и (1.3), получаются урав-
нения (1.1). Этот факт - свидетель-
ство зависимости уравнений (1.2)
Рис. 1.2
и (1.3),что делает возможным
определение главного векто-
ра F и главного’ момента М из
уравнений равновесия любой
мысленно отсеченной части.
Используется более простое.
Векторные уравнения в расче-
тах заменяются скалярными
(координатными).
Разложим векторы сил ча-
стей тела на оси координат
(рис. 1.3). Обозначим проек-
ции векторов внешних сил
^Fkx' ^Fky> ^Fkz> Z^kx’ ^^ky’
внутренних сил N, Q, Q,
My,M=,Mx = Mk.
Напряжения в точке
Проекции главного вектора и главного момента внутренних
сил на оси координат: N - нормальная сила (проекция на ось,
направленную по нормали к сечению), Q, Q - поперечные силы,
Мх = Мк - крутящий момент, Му, М_ - изгибающие моменты.
Суммы векторов (1.2) равны нулю, если равны нулю суммы их
проекций на оси координат, поэтому условия равновесия отсе-
ченной части тела запишутся в виде:
+ № 0; ЪРку + Qy = 0; + Qz = 0
ъмкх + Mk = Q; ЪМку + Му = Ъ, ZMkz + М. = 0. (1.4)
Из уравнения (1.4) определяются статические эквиваленты
внутренних сил.
Напряжения в тонне
Внутренние силы в каждой точке сечения заменя-
ются их эквивалентами в малой окрестности. Эта за-
мена возможна, если эта окрестность непрерывна
(первая гипотеза).
В малой окрестности некоторой точки сечения вы-
деляется бесконечно малая поверхность площадью
ДЛ. Все внутренние силы, приложенные на этой по-
верхности, приводятся к ее центру.
Ввиду малости плеч этих сил главным моментом
пренебрегают, (рис. 1.4), а некоторое среднее значе-
ние главного вектора Д7? Рис. 1.4
v ДЯ
р= lim-------
ДЛ—>0 ДЛ
(1.5)
называют вектором напряжения в точках этой малой площадки.
В расчетах пользуются проекциями вектора напряжения на оси
координат с началом в центре малой площадки (рис. 1.5). Ось х
направлена по нормали к сечению, оси у и z лежат (касаются) в
сечении. Проекцию вектора р на нормаль к сечению о называют
нормальным напряжением, проекции на оси у и z - тху и тхг - каса-
тельными напряжениями.
Перенося напряжения из всех точек сечения параллельно са-
мим себе в центр сечения, пользуясь леммой о параллельном пере-
5
Напряжения в точке
носе силы тела и аксиомой параллелограмма, получают статичес-
кие эквиваленты напряжений: нормальную N и поперечные силы
Qy, и Q. крутящий изгибающие моменты Му, (рис. 1.6).
Ввиду сплошности и однородности тела суммы можно заме-
нить интегралами по площади сечения, тогда
N = J <sdA-, Qy = J TxydA; Q: = J xxzdA-
A A A
Mv = ja zdA; Jo-ydA; Mk = f-t ijdA.
AAA
Здесь T = ^T2xy + T2xz, p = -Jy2+z2.
Способы вычисления интегралов основаны на гипотезах «Со-
противления материалов».
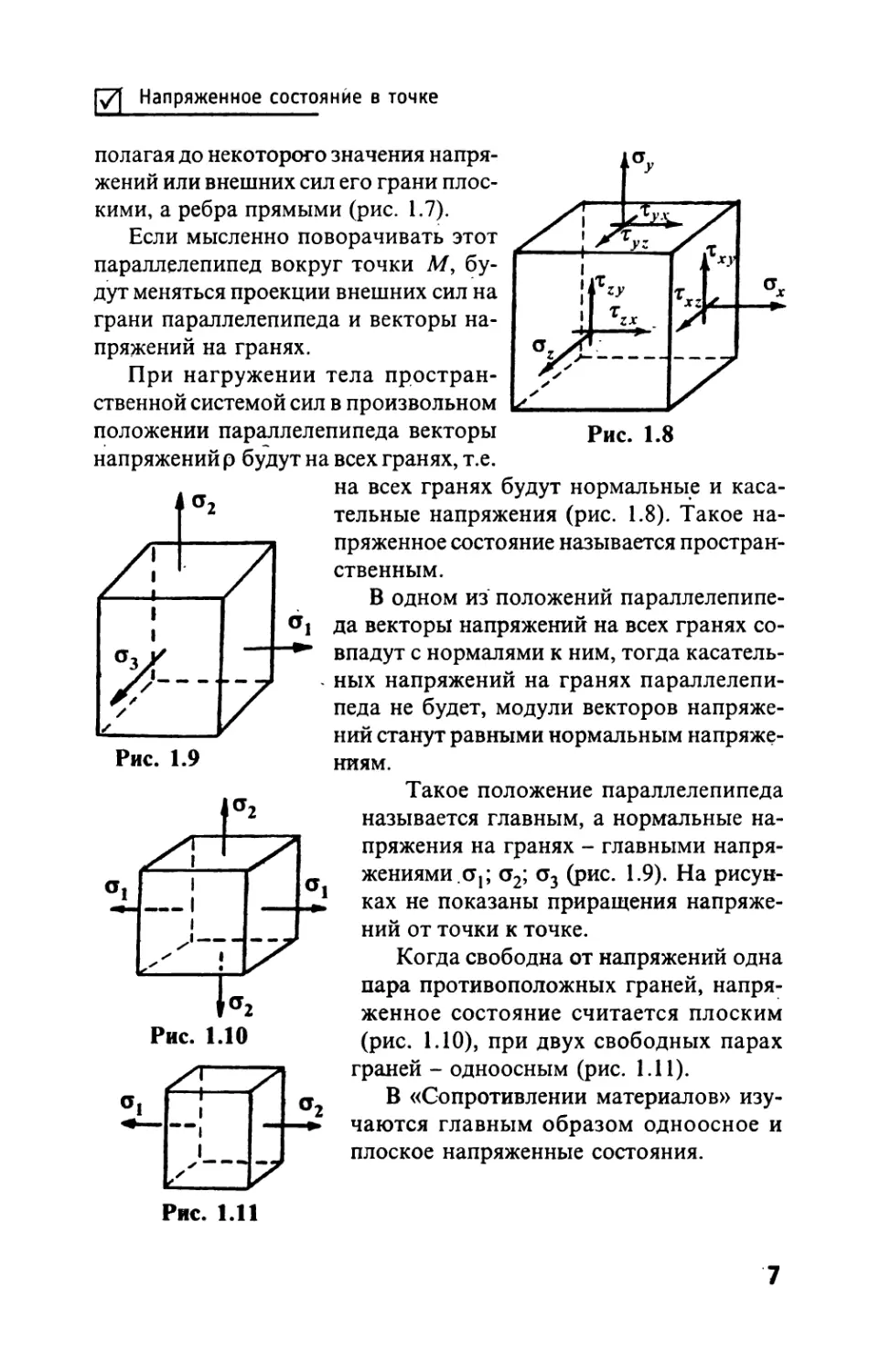
Напряженное состояние в точке
Через точку можно провести множество
плоских сечений, в каждом сечении получить
нормальные и касательные напряжения. Со-
вокупность этих напряжений принято назы-
вать напряженным состоянием в точке. На-
глядное представление о нем можно полу-
чить, выделив в малой окрестности точки М
бесконечно малый параллелепипед и пред-
Рис. 1.7
б
Напряженное состояние в точке
полагая до некоторого значения напря-
жений или внешних сил его грани плос-
кими, а ребра прямыми (рис. 1.7).
Если мысленно поворачивать этот
параллелепипед вокруг точки Л/, бу-
дут меняться проекции внешних сил на
грани параллелепипеда и векторы на-
пряжений на гранях.
При нагружении тела простран-
ственной системой сил в произвольном
положении параллелепипеда векторы рИс. 1.8
напряжений р будут на всех гранях, т.е.
на всех гранях будут нормальные и каса-
тельные напряжения (рис. 1.8). Такое на-
пряженное состояние называется простран-
ственным.
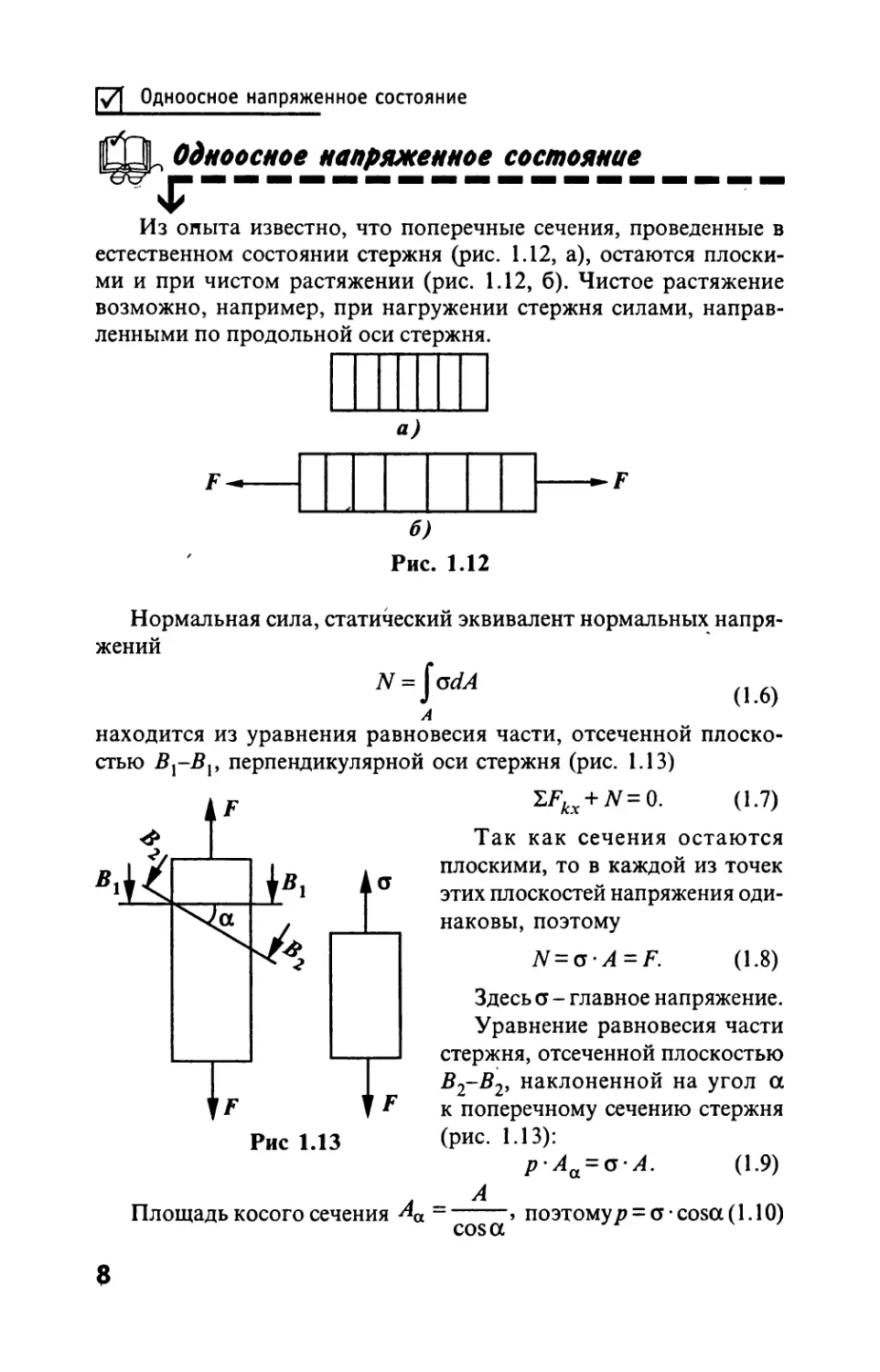
В одном из положений параллелепипе-
да векторы напряжений на всех гранях со-
впадут с нормалями к ним, тогда касатель-
ных напряжений на гранях параллелепи-
педа не будет, модули векторов напряже-
ний станут равными нормальным напряже-
ниям.
Рис. 1.9
Рис. 1.11
Такое положение параллелепипеда
называется главным, а нормальные на-
пряжения на гранях - главными напря-
жениями. Ор о2; а3 (рис. 1.9). На рисун-
ках не показаны приращения напряже-
ний от точки к точке.
Когда свободна от напряжений одна
пара противоположных граней, напря-
женное состояние считается плоским
(рис. 1.10), при двух свободных парах
граней - одноосным (рис. 1.11).
В «Сопротивлении материалов» изу-
чаются главным образом одноосное и
плоское напряженные состояния.
7
Одноосное напряженное состояние
Одноосное напряженное состояние
Из опыта известно, что поперечные сечения, проведенные в
естественном состоянии стержня (рис. 1.12, а), остаются плоски-
ми и при чистом растяжении (рис. 1.12, б). Чистое растяжение
возможно, например, при нагружении стержня силами, направ-
ленными по продольной оси стержня.
Рис. 1.12
Нормальная сила, статический эквивалент нормальных напря-
жений
(1-6)
плоско-
(1.7)
Площадь косого сечения
N = ^adA
А
находится из уравнения равновесия части, отсеченной
стью Bx-Bv перпендикулярной оси стержня (рис. 1.13)
E^X + JV=O.
Так как сечения остаются
плоскими, то в каждой из точек
этих плоскостей напряжения оди-
наковы, поэтому
N = aA=F. (1.8)
Здесь и - главное напряжение.
Уравнение равновесия части
стержня, отсеченной плоскостью
В2-В2, наклоненной на угол а
к поперечному сечению стержня
(рис. 1.13):
р-Аа = <зА.
А
------, поэтомур~(5* cosa (1.10)
COS Ct
(1.9)
8
Плоское напряженное состояние
Рис. 1.14
Разложив вектор р на ось нормальную к косому
сечению и на ось, лежащую в сечении, имеем нор-
мальное напряжение (рис. 1.14)
па-р • cosa = а • cos2a (111)
касательное
Из (1.12) следует, что наибольшее касательное
напряжение действует в сечении, наклоненном к по-
перечному сечению на угол a = 45°.
Плоское напряженное состояние
Очевидно существует такое положе-
ние бесконечно малого параллелепипе-
да, на гранях которого из уравнений
равновесия отсеченной части стержня
легко найти нормальные и касательные
напряжения на его гранях (рис. 1.15).
Если отсечь часть параллелепипеда
плоскостью, наклоненной к оси у на
угол а (см. рис. 1.15), то вместо парал-
лелепипеда получим трехгранную при-
зму (рис. 1.16). Действие отсеченной ча-
сти нужно заменить силами - про-
изведением нормальных напряже-
ний и (5^ и касательных тху, хух
на площадь граней. Напряжения
на наклонной грани можно найти
из уравнений равновесия в виде
суммы проекций плоской системы
сил на оси £ и Г| суммы их момен-
►' тов относительнд точки О:
Х = 0; Z0£= 0; ZHk = 0, (1.13)
где Hk, - проекции сил на оси
пЛ
Подставив в (1.13) значения моментов сил относительно точ-
ки О и проекций их на оси Г| и £, получим: .
Рис. 1.15
У
Рис. 1.16
9
Плоское напряженное состояние
т• dy • dz • — dx =т • dx • dz • — dy.
Л V •< 2 2 J
eadzds - axdydz • cos a - о vdxds • sin a +
+xxydydz • sin a - xyxdxdz • cos a = 0, (1.14)
x^dsdz - xxvdydz • cos a - xyxdxdz • sin a -
-<yx dydz • sin a + <sydxdz • cos a = 0.
Из первого уравнения следует хху = хух
закон парности касательных напряжений:
касательные напряжения на гранях па-
раллелепипеда направлены либо к обще-
му ребру соседних граней, либо от него
(рис. 1.17).
Второе и третье уравнения (1.13) пос-
ле деления на dsdz, при котором
dx . dy
— = sma, — = cosa, разрешаются от-
ds ds
носительно напряжений
= ’ cos2a + q • sin2a - т • sin2a;
л у лу
Ta = | ’ sin2a + Xxy ‘ cos2a- 0 •15)
Из (1.15) легко установить инвариант плоского напряженного
состояния
a<x+aa+90o=a^^ О’16)
постоянное значение суммы нормальных напряжений на двух вза-
имно перпендикулярных гранях бесконечно малого параллеле-
пипеда, выделенного в малой окрестности точки.

Главные напряжения в точке
при плоском напряженном состоянии

Из опыта известно, что разрушение силовых элементов кон-
струкции начинается в точках, где напряжения наибольшие. Сече-
ния, в которых лежат эти точки, называются опасными сечениями.
10
Главные напряжения в точке при плоском напряженном состоянии
В любой точке из всех напряжений в ней самое большое значе-
ние имеют главные напряжения. Их можно найти по напряжениям
на гранях бесконечно малого параллелепипеда oY, тху в неко-
тором удобном для их определения положении относительно ли-
ний действия внешних сил (см. рис. 1.16). Чтобы найти главное
положение бесконечно малого параллелепипеда относительно по-
ложения, показанного на рис. 1.16, воспользуемся известным в
математике способом определения значения аргумента функции,
при котором она экстремальна. В задачах о главных напряжени-
ях этот аргумент угол а в (1.15). Нормальные напряжения на не-
которой грани параллелепипеда экстремальны, если
^ = 0-’ (1.17)
оа
t Для решения (1.17) более удобен другой вид первого уравне-
ния (1.15). Его можно получить, представив квадраты синуса и
косинуса через функции углов 2а. Тогда
СТа = | <СТх + + | (<*х ~ ’cos2a " Хху' sin2a- 0 • 18)
После дифференцирования (1.18) вместо (1.17) получится
(ст, - ст ) • sin2a - 2т,„ • cos2a = 0. (1.19)
Л у лу
При сравнении (1.19) и второго уравнения (1.15) видно, что -
2тху = 0, т.е. угол а0, полученный из (1.19), определяет главное
положение параллелепипеда. После деления (1.19) на cos2a по-
лучается тангенс угла otg, определяющего главное положение па-
раллелепипеда
2txv
tg2ao =------(1.20)
Если подставить (1.20) в (1.18), вспомнив, что cos2a =
= ± .___L____, и представить sin2a = cos2a • tg2a, а потом вос-
71 + tg22a
пользоваться (1.19), то
cos2a = +-г-.: - =,
^Gx~<5y)2+^xy
• ~ 2t,v
sin2a = T-.- xy- (1.21)
11
Экстремальные значения касательных напряжений...
После подстановки (1.21) в (1.18) и приведения подобных чле-
нов получим наибольшее и наименьшее значения главных напря-
жений
mac = |ГСТХ + ± |- О,/ + 4т^. (1.22)
min
Сумма втах + о—л = &х + есть первый инвариант плоского
напряженного состояния.
Экстремальные значения касательный
напряжении при плоском напряженном
состоянии
ф—-------
Положение граней бесконечно малого параллелепипеда, при
котором касательные напряжения экстремальны, определяется
углом поворота ар относительно грани перпендикулярной оси х
(см. рис. 1.16) из уравнения
Из уравнений (1.12) и (1.23) следует
tg2a| = a^~q\ (1.24)
^ху
При сравнении (1.24) и (1.20) видно, что tg2aj = -ctg2a0, но
-ctg2a0 = tg(90° + 2a), т.е. 2a, = 90° + 2a0, поэтому
aj = a0 + 45° (1.25)
и максимальные касательные напряжения направлены под углом
45° к главным напряжениям, что подтверждается при растяжении
стержней с полированной поверхностью, на которой появляются
линии под углом 45° к оси стержня - следы плоскостей сдвига.
Если принять за исходное главное положение параллелепипе-
да и считать, что ах = птах, <зу = amin, ат^ = 0, из второго уравнения
(1.15) получается
^тах т(^тах ~~ ^min)’ (1.26)
min
а после подстановки главных напряжений (1.22) экстремальные
значения касательных напряжений
*тах = ±^(а^-СТ02+4Т^- (L27)
min
12
Экстремальные значения касательных напряжений...
Формулы (1.15) определяют плоское напряженное состояние в
точке.
О. Мор дал графическую связь между нормальными и каса-
тельными напряжениями в виде окружности (круга Мора), по-
строенного в координатах ст - т. Уравнение этой окружности по-
1 1
лучено из формул ста = — (стх + ст^) + — (стх - стг) • cos2a - тху • sin2a,
1
та = 2 (°* ~ ’ Sln2<X ’
cos2a возведением их в квадрат и
последующим сложением:
<\х-|(<*х + СМ +^ху=^Х + ^у)2+^Ху
(1.28)
Уравнение (1.28) по форме совпадает с уравнением окружно-
сти в декартовой системе координат (а - х)2 + by2 = R2, в котором
а и b — координаты центра.
В (1.28)a=i(ax + CTp,Z> = о, Я2=^(ах-о,)2+г2,. (1.29)
Порядок построения круга Мора по (1.29) нетрудно понять
(рис. 1.17.). Точки А и В на окружности построены по напряжени-
ям на двух взаимно перпендикулярных гранях параллелепипеда.
В графическом исследовании напряженного состояния в точке
теперь нет нужды, но круги Мора используются при определении
безопасного сочетания нормальных и касательных напряжений в
точках элементов конструкций, изготовленных из материалов с
разными пределами прочности при растяжении и сжатии.
13
Деформации в точке (геометрические уравнения)
Деформации в точке
(геометрические уравнения)
Под действием внешних сил, при нагреве и охлаждении части-
цы тела перемещаются, изменяются форма и размеры тела. Пусть
некоторая точка Л/ переместилась в положение Л/'. Отрезок ММ'
будем называть вектором полного перемещения точки. Его проек-
ции на оси х, у, z обозначим w, v, w соответственно (рис. 1.18).
В силу гипотезы о непрерывности и сплошности распределения ча-
стиц тела по объему проекции вектора перемещения будут функци-
ями координат, определяющими новые форму и размеры тела.
В качестве числовой меры изменения размеров и формы беско-
нечного малого параллелепипеда, выделенного в окрестности точки
с размерами dx, dy, dz в естественном состоянии тела, вводится
деформация, при этом предполагается, что- грани параллелепипе-
да остаются плоскими, а ребра прямыми. Это возможно, если пере-
мещения малы, а деформации исчезают при разгрузке тела.
Спроецируем грани параллелепипеда на координатные плос-
кости (рис. 1.18) и рассмотрим изменение длин ребер и прямых
углов между ними в плоскости хоу (рис 1.19).
Относительное изменение длины ребра АВ называют линей-
ной деформацией в направлении оси х:
14
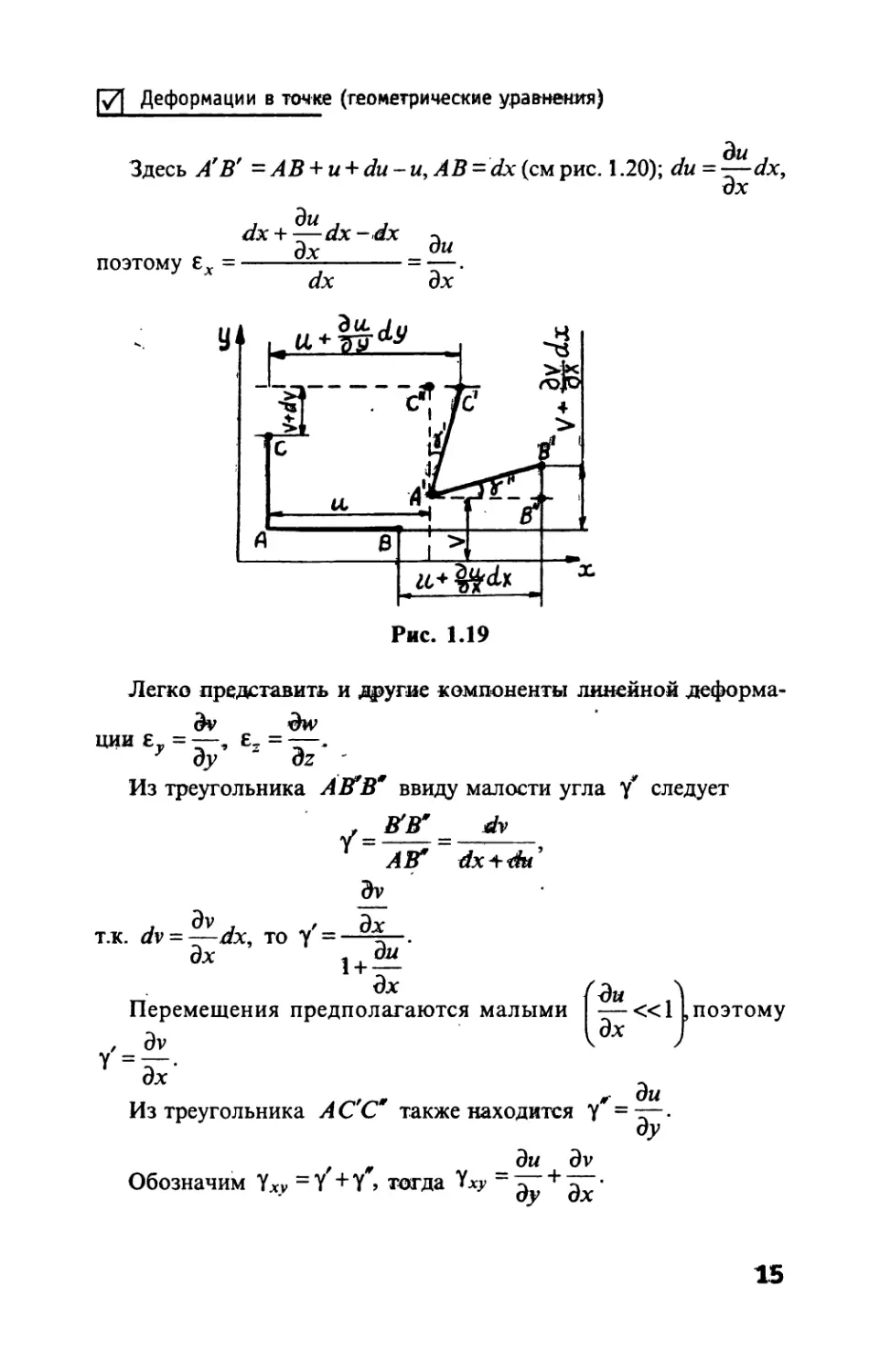
Деформации в точке (геометрические уравнения)
Здесь А'В' = АВ + u + du -и, АВ = dx (см рис. 1.20); du = —dx,
дх
Легко представить и другие компоненты линейной деформа-
dv dw
ОДИ £ = —, £2 = —.
7 Ъу dz '
Из треугольника A S'В* ввиду малости угла Y* следует
АВ* dx+du’
3v
т.к. dv = — dx, то у'= д* .
ах ]+а«
_ Эх .'I
Перемещения предполагаются малыми —«1 , поэтому
з I Эх
, dv \ /
Из треугольника АС С также находится у = — •
Эу
/ж _ ди dv
Обозначим УХу =У +У , тогда Уху +
15
[у?! Деформации в точке (геометрические уравнения)
Назовем Уху угловой деформацией (сдвигом). Рассматривая
две другие проекции параллелепипеда на координатные плоско-
сти, можно найти yxz, 4yz.
Итак, деформация в окрестности точки состоит из шести ком-
понентов:
Эм 3v 3w
ox z ду dz
ди dv ди дю dv дю
ду дх dz Эх dz ду
Уравнения (1.30) называют геометрическими, впервые их по-
лучил Коши. Матрица, составленная из компонент деформации,
называется тензором деформации
(1.31)
Геометрические уравнения получены из анализа деформации
одного параллелепипеда. Деформация множества таких парал-
лелепипедов должны быть такими, что при сложении из них тела
последнее не должно иметь пустот, т.е. деформации в окрестности
всех точек тела должны быть совместными. В соответствии с этим
между деформациями, зависящими от трех компонент перемеще-
ний, должны быть определенные соотношения. Шесть таких соот-
ношений, уравнений совместности деформаций, можно получать
двухкратным дифференцированием по х, у, z первых трех уравне-
ний (1.30), сложением вторых производных от уху, ухг, у и срав-
нением их со вторыми смешанными производными от ev, Еу, е_.
После этих операций получается три таких уравнения:
. , д2гу _ д2уху
Эу2 дх2 дхду ’
Э2е, _
dz2 + ду2 дхду ’
д2е, д2ех _ Э2уЛ.г
дх2 dz2 дхду
(1.32)
16

Деформации в точке (геометрические уравнения)
Еще три уравнения можно получить однократным дифферен-
цированием уху, yv_, Уу- сложением производных от первого и тре-
тьего и вычитанием производной от второго:
foxy дуА- _ Эух, _ Э2У
дх дх ду дхду
dv d2v Эе
Так как — = ev,to _ •••• = ——. Взяв производные от обоих
ду у дхду Эх
частей уравнении по у , получим
дД dz Эх ду J 2ЭхЭ/ (,33)
Аналогичные уравнения получаются из (1.33) кольцевой пере-
становкой индексов:
Э ( дуу- [ Эугл. Эу.у __ 2 э2е. .
Эг|^ Эх ду dz J дхду"
ду,л_2э2Ех
Эх ду dz дх dydz
(1.34)
Уравнения совместности деформаций получены Сен-Венаном.
Обобщенный закон Тука
V----------------------------------------------
Закон Гука и = е • Е установленный для одноосного напряжен-
ного состояния, можно распространить на пространственное и
плоское напряженные состояния, использовав принцип независи-
мости действия сил и известную из опыта связь между компонен-
тами линейной деформации: постоянное для данного изотропного
£у it
материала отношение ц = -Д- = —, называемое коэффициентом
Пуассона.
Подобно тому, как конечное ускорение точки, на которую
действует несколько сил, не зависит от порядка приложения сил,
при малых перемещениях деформация не зависит, от очередности
приложения сил. Здесь удобно оперировать не силами, а напряже-
ниями. Пусть известны главные напряжения ар о2, аз- Если растя-
жение происходит поочередно в направлении ор о2, аз> ДеФ°Рма"
ции станут соответственно такими:
17
Обобщенный закон Гука
еп=5-> £21 = е31=-Н£1Р
zs
Е22 = V ’ 612 = Е32 = - О ’35)
Jb
п3
£33 “ , £13 “ е23 Незз-
п,
В каждом из главных направлений деформации есть суммы:
е1 ~ Ен + е12 + Е33’
Е2 ~~ Е22 Е23 Е21’
£3 = £33 + £31 + 632’
если в них пол в. деформация? [ставить (1.35), получится обобщенный закон Гука с: -И(<^2 + с^з)!- Е 9 E2=^[tJ2-P'(<’3+Ol)]; <137) Е £з=^[аз-Н(О1+о2)]. Е
В произвол динат совпала ьном положении параллелепипеда, когда оси коор- ютс направлением ребер:
Е Л = к -+ о,)]; Уху = ZS (sr
£ , = 4k-H(°z+<*j]; Yjz = -^; (1.38) Е G
£ Для плоско _’=^к-д(Ох+^)]; Yxz=^- Е Cr то напряженного состояния: 1 / «i=y(®L-U®2); 1 (139) £2=-t;(<’2-UO|); Е
и 1 / = -(°х-ц<\); Е £у ~ (1.40) Е У =Х Y.v G
18
Потенциальная энергия деформации
При составлении уравнений равновесия удобен закон Гука в
напряжениях. Чтобы получить его, нужно в (1.39) первое уравне-
ние разрешить относительно Oj и подставить во второе, второе
разрешить относительно о2 и подставить в первое. После приве-
дения подобных членов
Е /
О!=-----г(Е!+ЦЕ2);
1-ц
Е (1-41)
а2 =----j-(E2+HEi);
1-й
можно записать такие же формулы для произвольного направле-
ния осей.
Потенциальная энергия деформации
При действии на тело внешних сил
изменяется его объем и форма, возни-
кают внутренние силы, накапливает-
ся энергия. Если деформации были уп-
ругими, после снятия внешних сил,
внутренние силы возвращают тело в
естественное состояние, совершая ра-
боту. Если не учитывать малые поте-
ри, работа внутренних сил А1 окажет-
ся равной потенциальной энергии UT
запасенной в теле: А1 = -UT.
Внутренние силы на гранях парал-
лелепипеда в главном положении
c^dydz; a2dxdz\ Q^dxdy совершают работу на перемещениях е^х;
e2dy; e3dz (рис. 1.20).
Ввиду линейной связи между напряжениями и деформациями
элементарная работа внутренних сил
dAl = dU = — dzdydzfaxtx + о2 e2 + °з езХ
Потенциальная энергия в единице объема
ГТ dU 1,
С/ = — = - (Q1E1 + О2Е2 + О3Е3 )
аУ 2
(1.42)
19
Потенциальная энергия деформации
может быть представлена или в напряжениях, или в деформациях.
Здесь представим полную удельную потенциальную энергию в на-
пряжениях, воспользовавшись обобщенным законом Гука (1.37).
После очевидных преобразований получим
и = + 02 + °з - + <*2<Ъ + ОзО,)]. (1.43)
2Е
Если меняется только объем параллелепипеда, все ребра удли-
няются (укорачиваются)* одинаково, и все напряжения равны, т.е.
а1 =а2=аз = ао
или
1,
°о = + °2 + <Ъ), (1.44)
тогда (1.43) примет вид
если учесть (1.44), станет
тт 1 “2ц,
U0 = -“(О!+о2+ °з) • (1.45)
2Е
Когда меняется только форма параллелепипеда, удельная по-
тенциальная энергия формоизменения 1/ф = U -
Подставив в правую часть этого равенства (1.43) и (1.45), по-
лучим
иФ = + а2 + °! - (<*1<*1 + <*2°3 + )]• (1.46)
5Е
При плоском напряженном состоянии
тт 1 + Ц z 2 2 \
(1.47)
jE
через напряжения в произвольном направлении
_ т 1+ LL z э о л 7 х
^^(Ox+^-^v + XP- (1.48)
jE
В теории пластин и оболочек полная удельная энергия дефор-
мации записывается в перемещениях.
20
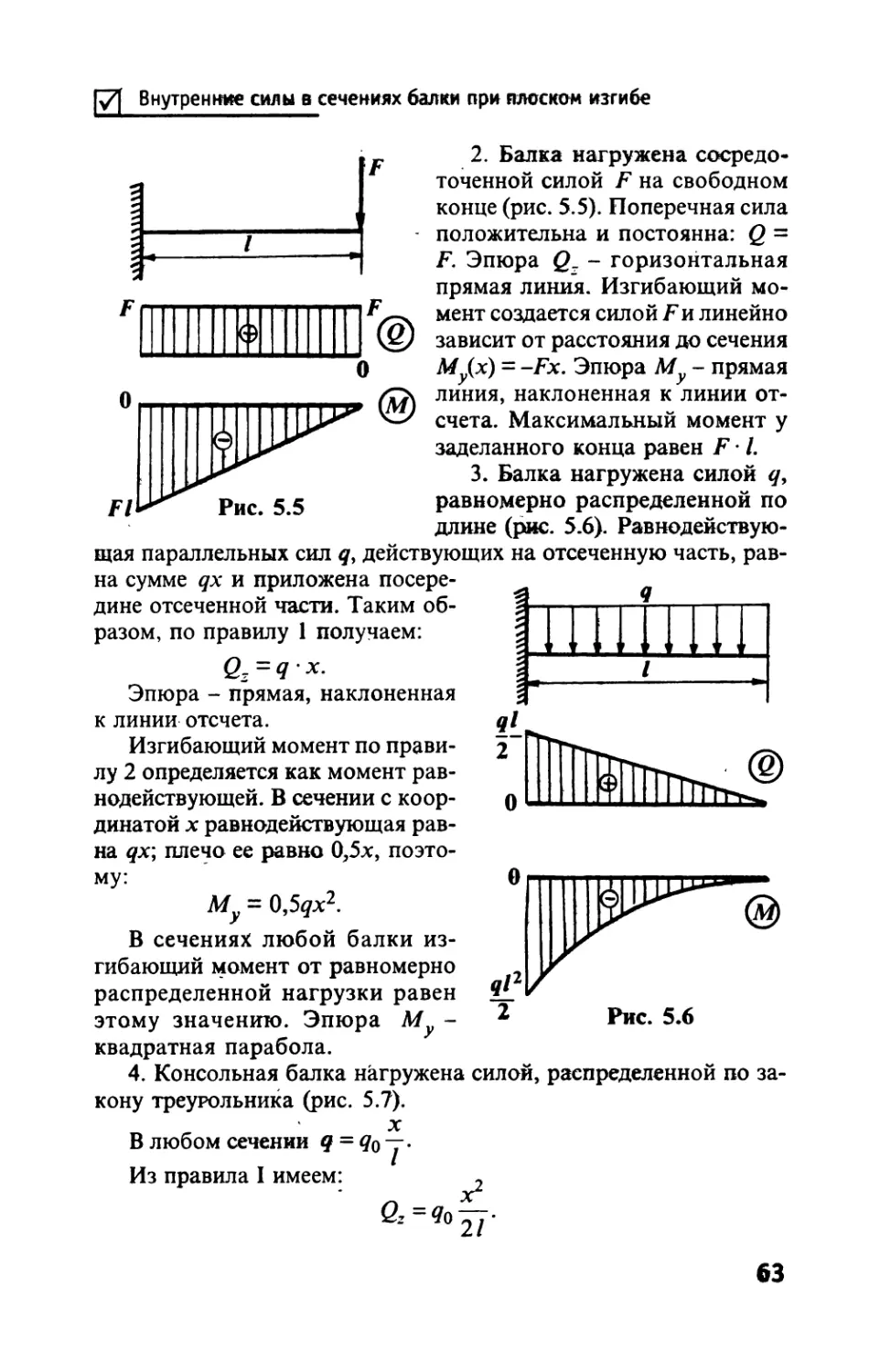
Нормальная сила
Главе 2
РАСТЯЖЕНИЕ (СЖАТИЕ) СТЕРЖНЕЙ
И СТЕРЖНЕВЫХ СИСТЕМ
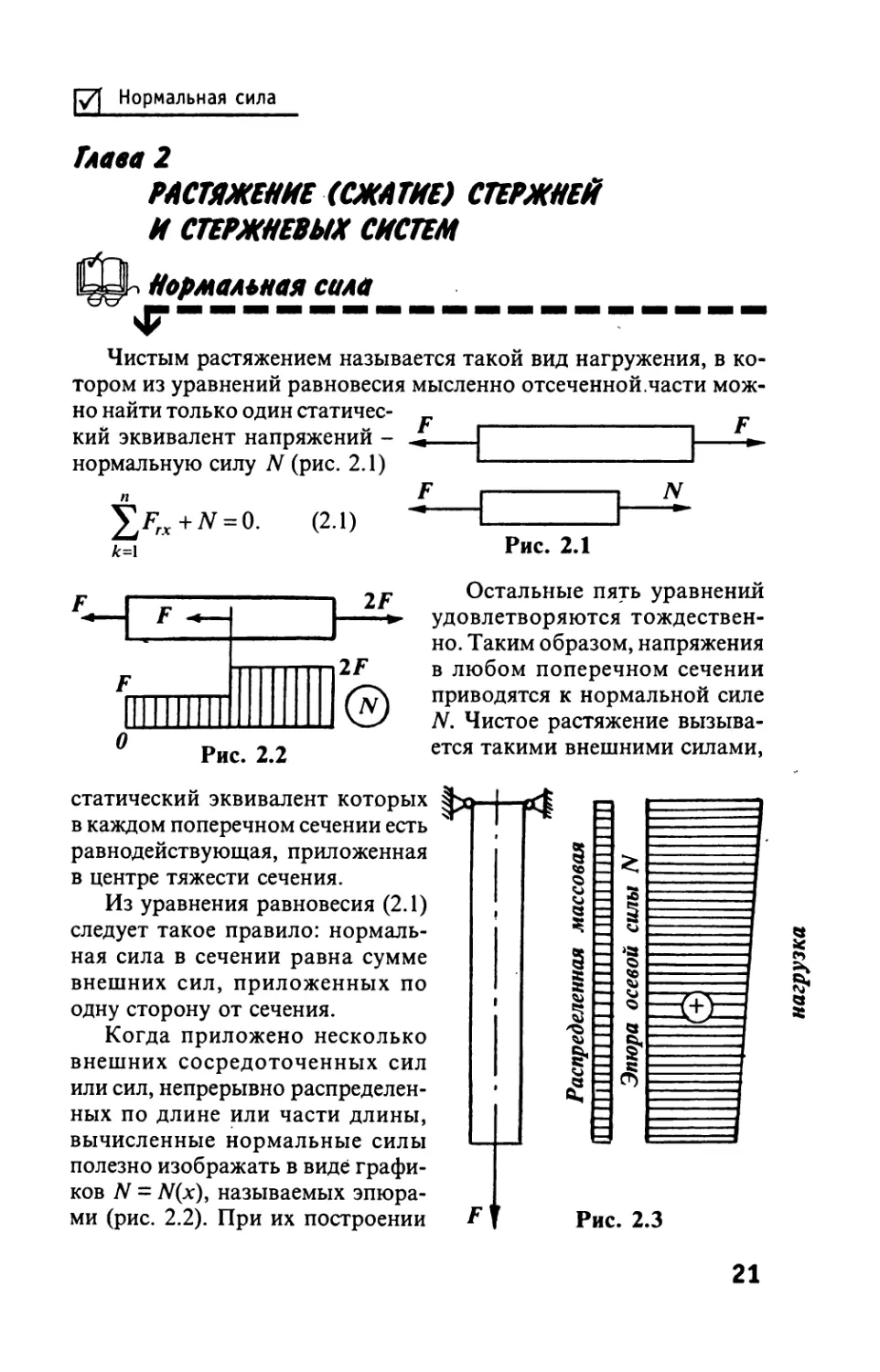
Нормальная сила
Чистым растяжением называется такой вид нагружения, в ко-
тором из уравнении равновесия мысленно отсеченной.части мож
но найти только один статичес-
кий эквивалент напряжений -
нормальную силу 7V (рис. 2.1)
p7x + tf = 0. (2.1)
к=\
Рис. 2.1
Рис. 2.2
Остальные пять уравнений
удовлетворяются тождествен-
но. Таким образом, напряжения
в любом поперечном сечении
приводятся к нормальной силе
N. Чистое растяжение вызыва-
ется такими внешними силами,
статический эквивалент которых
в каждом поперечном сечении есть
равнодействующая, приложенная
в центре тяжести сечения.
Из уравнения равновесия (2.1)
следует такое правило: нормаль-
ная сила в сечении равна сумме
внешних сил, приложенных по
одну сторону от сечения.
Когда приложено несколько
внешних сосредоточенных сил
или сил, непрерывно распределен-
ных по длине или части длины,
вычисленные нормальные силы
полезно изображать в виде графи-
ков N = N(x), называемых эпюра-
ми (рис. 2.2). При их построении
нагрузка
21
Нормальные напряжения и деформации
удобно пользоваться правилом вычисления N. В сечениях, где
приложены внешние силы, нормальная сила изменяется скачком
на величину внешней силы, функция N = N(x) в этих местах тер-
пит разрыв.
Заметим, что все внутренние силы, в общем случае есть кусоч-
но гладкие функции координаты х. При чистом растяжении обо-
лочки рассчитываются как стержни. На рисунке 2.3 показаны
эпюры нормальных сил в сечениях подвешенной цистерны.
Нормальная сила при растяжении считается положительной,
при сжатии - отрицательной.
IWL Нормальные напряжения и деформации
V--------------------------------------------------
В теории расчета силовых элементов конструкций, принима-
ются различные гипотезы, удовлетворительно согласующиеся с
результатами эксперимента:
— силовые элементы - тела с непрерывным и равномерным рас-
пределением массы (гипотеза сплошности);
— если не делается специальная оговорка, механические харак-
теристики одинаковы во всех направлениях, иными словами,
силовые элементы конструкций-изотропные тела;
— силовые элементы - абсолютно упругие тела (иные случаи ого-
вариваются);
— при нагружении несколькими силами, если перемещения точек
тела малы, напряжения в точках равны сумме напряжений,
вызванных каждой силой в отдельности - (принцип независи-
мости действия сил);
— напряжения в сечениях, удаленных от места приложения вне-
шних сил, не зависят от способа их приложения, а зависят толь-
ко от их статического эквивалента (рис. 2.4) (принцип Сен-
Венана);
— у стержня во всех случаях нагружения сечения, проведенные
плоскостью в естественном состоянии, остаются плоскими и
после приложения внешних сил (гипотеза плоских сечений).
К оболочкам и пластинам последняя гипотеза применима
только при чистом растяжении.
В теории расчета стержня (в сопротивлении материалов) гипо-
теза плоских сечений позволяет получить простые формулы для
напряжений. При чистом растяжении сечения, удаленные от мес-
та приложения сил на расстояниях не менее размера поперечного
22
[7[ Нормальные напряжения и деформации
сечения (принцип Сен-Венана), на самом деле остаются плоски-
ми. Это можно проверить, нагружая резиновый стержень (рис. 2.5)
с нанесенными на поверхности поперечными линиями. Каждое
сечение смещается параллельно самому себе. По определению
деформация в точке растянутого стержня
Arfx
ех =----------------------------.
dx
Во всех точках одного сечения они одинаковы.
(2.2)
— • — — —
Рис. 2.5
Нормальная сила - статический эквивалент нормальных на-
пряжений
N = jadA. (2.3)
А
23
Нормальные напряжения и деформации
Согласно закону Гука при растяжении
а = е£ (2.4)
у однородного изотропного тела модуль упругости Е в любом на-
правлении одинаков, одинаков и в каждой точке сечения. В силу
одинаковости деформаций и модуля упругости (2.3) можно запи-
сать так
N = EEjdA = eEA
В каждой точке одного сечения нормальное напряжение равно
отношению нормальной силы к площади сечения. Такое напря-
женное состояние называется однородным. Из опыта известно,
что при растяжении уменьшаются размеры поперечного сечения
(рис. 2.6). Для изотропного стержня их относительные изменения,
х Д6 Да
деформации е =— и =— одинаковы:
у b ~ а
Ey = Ez = -\^x, (2.6)
составляют часть продольной деформации, множитель при кото-
рой есть физическая константа материала и называется коэффици-
ентом Пуассона (1781-1840). Для большинства металлов и спла-
вов, применяемых в конструкциях машин и сооружений, ц = 0,3 и
не может быть больше 0,5. Заметим, что напряжения в направле-
нии осей у и z равны нулю, так как деформации гу и не стеснены.
1Z
Испытание материалов
на растяжение (сжатие)
Для расчета конструкций и их элементов на прочность и жест-
кость необходимо знать свойства материалов: предельное значе-
ние напряжений, модуль упругости, коэффициент Пуассона, спо-
24
Испытания материалов на растяжение (сжатие)
собность деформироваться при обработке, работать при перемен-
ных повышенных или пониженных температурах.
Наиболее важные характеристики материала определяются
при испытаниях на растяжение и сжатие.
Для этих испытаний из партии материала случайным образом
выбирается материал для изготовления стандартных образцов
материала. Стандартизация образцов облегчает сравнение резуль-
татов испытаний, проведенных в разных лабораториях. Образцы
вытачиваются из прутков или вырезаются из листа (рис 2.7).
Рис. 2.7
Рабочая длина образцов зависит от площади поперечного
сечения: 1р = 1 1,3>/Л.
Полная длина I (рис. 1.7.а) должна быть больше, чтобы при
измерении удлинения исключить части стержня, прилегающие к
головкам.
Рабочая длина нормальных круглых стержней равна 10 диа-
метрам, иногда применяются укороченные образцы с длиной I = 3d.
Для испытания на сжатие используются образцы длиной / = 2d. Ди-
аметр (площадь сечения) образцов зависит от максимального уси-
лия, развиваемого испытательной машиной. Обычно в лаборато-
риях для испытаний с целью определения предельных значений
напряжений металлических конструкционных материалов исполь-
зуются гидравлические испытательные машины (ГРМ) с макси-
мальным усилием 10-200 тонн. Силовой гидравлический цилиндр,
куда подается насосом масло, установлен на неподвижной раме
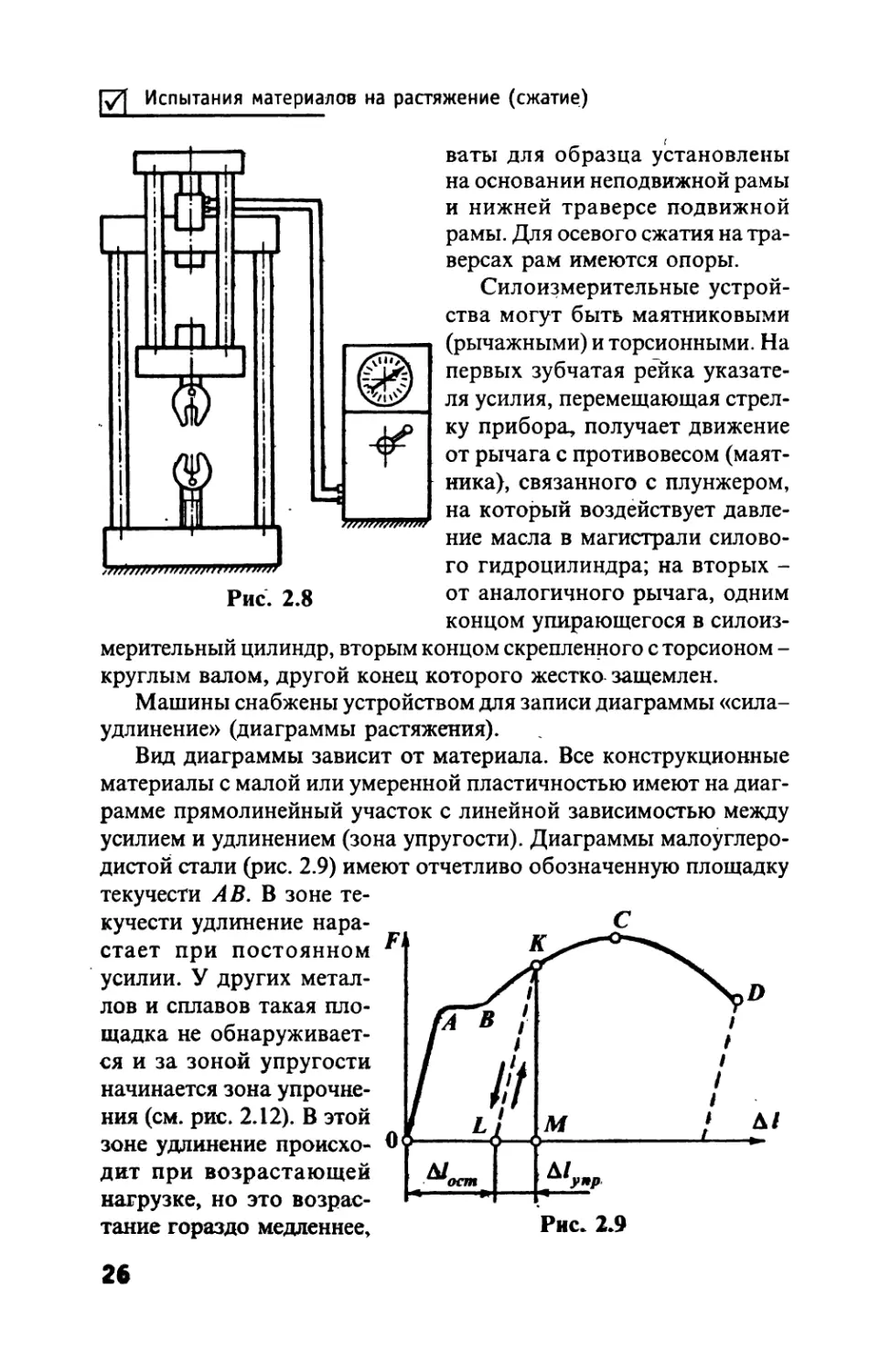
машины (рис. 2.8), состоящей из основания, двух колонн и непод-
вижной траверсы. Поршень гидроцилиндра связан с подвижной
рамой, две колонны которой соединены двумя траверсами. Зах-
25
Испытания материалов на растяжение (сжатие)
Рис. 2.8
ваты для образца установлены
на основании неподвижной рамы
и нижней траверсе подвижной
рамы. Для осевого сжатия на тра-
версах рам имеются опоры.
Силоизмерительные устрой-
ства могут быть маятниковыми
(рычажными) и торсионными. На
первых зубчатая рейка указате-
ля усилия, перемещающая стрел-
ку прибора, получает движение
от рычага с противовесом (маят-
ника), связанного с плунжером,
на который воздействует давле-
ние масла в магистрали силово-
го гидроцилиндра; на вторых -
от аналогичного рычага, одним
концом упирающегося в силоиз-
мерительный цилиндр, вторым концом скрепленного с торсионом -
круглым валом, другой конец которого жестко защемлен.
Машины снабжены устройством для записи диаграммы «сила-
удлинение» (диаграммы растяжения).
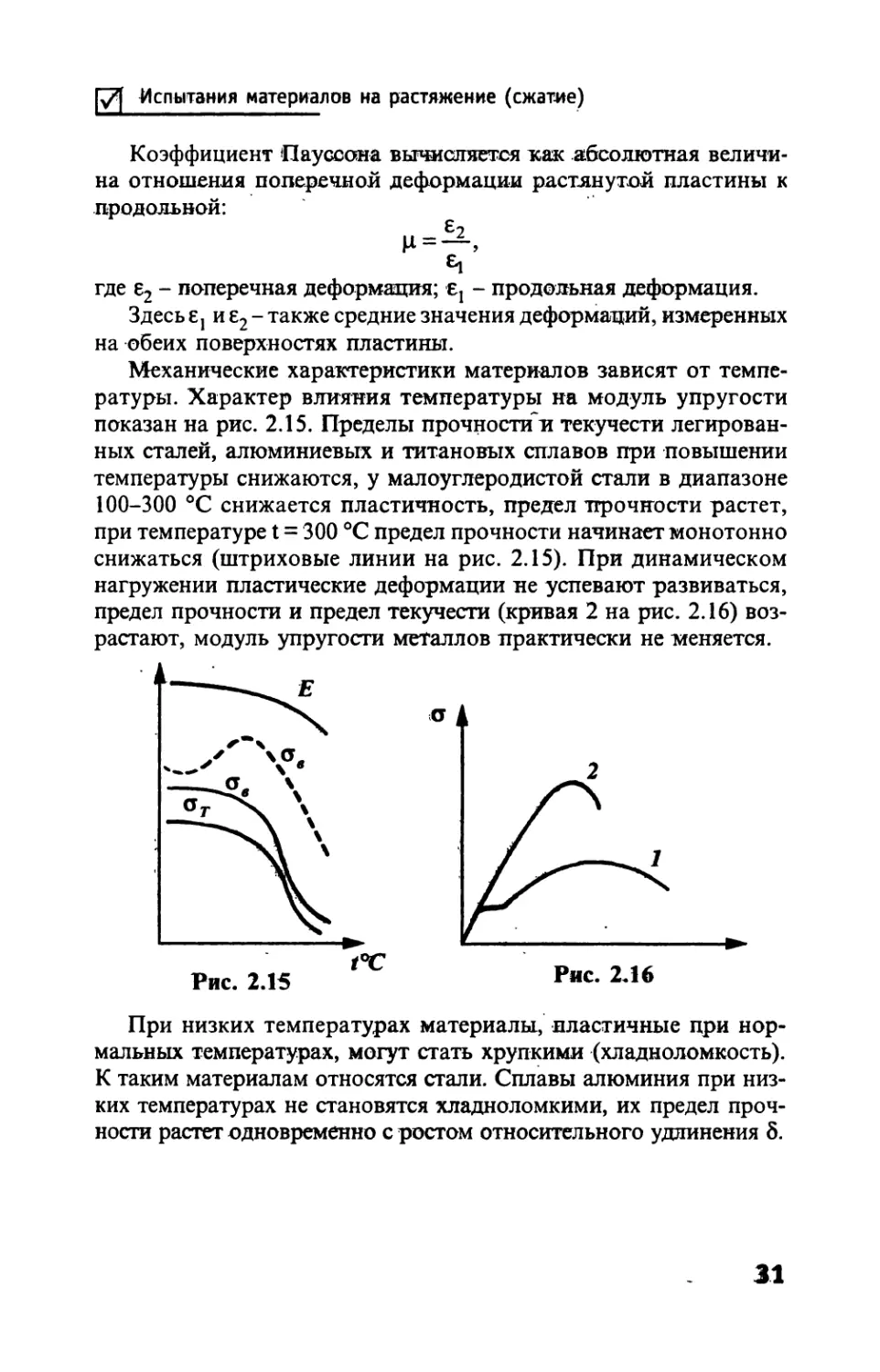
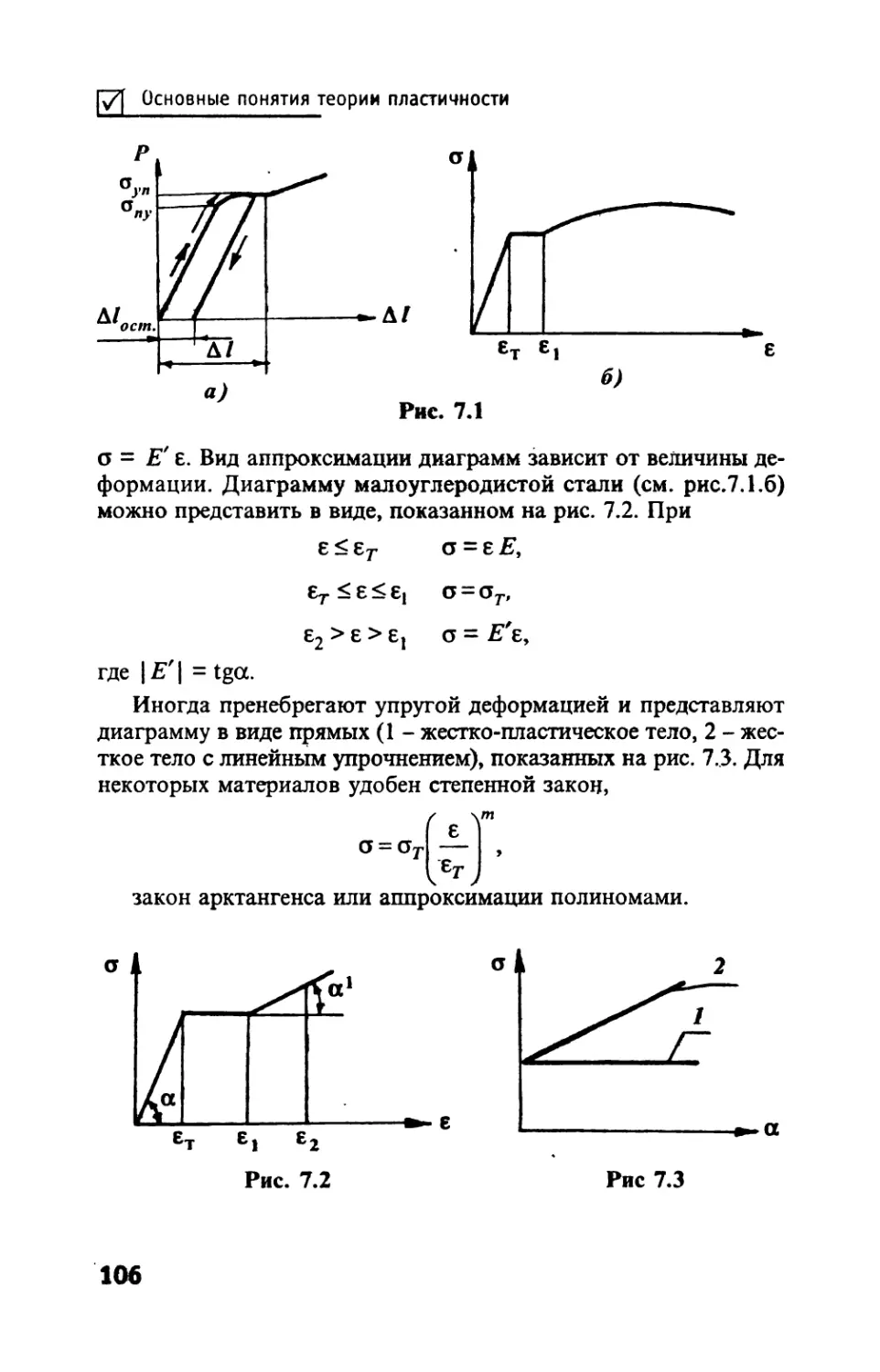
Вид диаграммы зависит от материала. Все конструкционные
материалы с малой или умеренной пластичностью имеют на диаг-
рамме прямолинейный участок с линейной зависимостью между
усилием и удлинением (зона упругости). Диаграммы малоуглеро-
дистой стали (рис. 2.9) имеют отчетливо обозначенную площадку
текучести АВ. В зоне те-
кучести удлинение нара-
стает при постоянном
усилии. У других метал-
лов и сплавов такая пло-
щадка не обнаруживает-
ся и за зоной упругости
начинается зона упрочне-
ния (см. рис. 2.12). В этой
зоне удлинение происхо-
дит при возрастающей
нагрузке, но это возрас-
тание гораздо медленнее,
Рис. 2.9
26
Испытания материалов на растяжение (сжатие)
чем в зоне упругости. В зоне упрочнения намечается место буду-
щего разрушения - на стержне образуется шейка (рис. 2.10), т.е.
местное сужение. Зона упрочнения кончается в точке С, где уси-
лие становится максимальным.

Рис. 2.10
Если разгрузить стержень в любой точке линии О А, деформа-
ции практически исчезают, остаточное удлинение будет очень
малым (только у идеально упругого материала останется перво-
начальная длина). Стержень, разгруженный на участках зон те-
кучести и упрочнения, сохранит часть удлинения Ыост (см. рис.
2.9). Линия повторного нагружения LK окажется длиннее О А .
Пластические деформации начинаются вследствие возникно-
вения необратимых сдвигов, атомы в кристаллической решетке
после прекращения действия внешней силы не возвращаются в
исходное положение, повышается температура образца, на его
полированной поверхности появляется густая сетка линий, на-
клоненных к оси на угол 45°, эти линии представляют собой мик-
роскопические неровности - следствие сдвигов в кристаллах.
Для оценки свойств матери-
алов диаграмма растяжения пе-
рестраивается в координатах
q-e (рис. 2.11). Она имеет тот
же вид, что и диаграмма, сня-
/ тая испытательной машиной.
/ Наибольшее напряжение апу9
/ для которого справедлив закон
/ Гука, называют пределом про-
!__ порциональности. Напряжение,
до которого не появляются ос-
Рис. 2.11 таточные деформации, называ-
ется пределом упругости. Для
определения пределов пропорциональности и упругости необ-
ходима тензометрическая аппаратура. Обычно за предел упруго-
сти принимают напряжение, при котором остаточная деформация
teocm ~ 0*5) • 10"5. В справочных пособиях пределы упругости и
пропорциональности указываются редко.
27
Испытания материалов на растяжение (сжатие)
На практике границей зоны про- . а
порциональности считается близ- j
кий к пределу упругости и более оп-
ределенный предел текучести. За /
предел текучести принимается на- 1 / __ 3
пряжение, при котором деформация /
растет без изменения внешней силы. / / 2\
J Площадка текучести на диаг- //
раммах растяжения большинства //
конструкционных материалов от- п/
сутствует (кривые на рис 2.12), где
изображены для сравнения диаграм- /г е
мы малоуглеродистой стали (1), дю- с-----------------►
ралюминия (2), титанового сплава рИс. 2.12
(3), высокоуглеродистой легиро-
ванной стали (4). Для таких материалов указываются условные
пределы текучести - напряжения, при которых остаточная де-
формация №ост - 0,002, что составляет 0,2% длины образца, иног-
да принимается teocm = 0,5%. Условный предел текучести обозна-
чается а02, индекс указывает соответствующую деформацию.
Если пределы текучести на растяжение и сжатие различны, ин-
декс 02 опускается, пределы текучести обозначаются соответ-
ственно ст п, ст.
т.р. т.с.
Предел прочности при испытании вычисляется как отноше-
ние максимальной нормальной растягивающей (сжимающей) силы
в сечении, которая равна силе, создаваемой испытательной ма-
N
шиной, к площади сечения ненагруженного образца ав =—
4)
Индекс в (время) указывает на кратковременность испытаний.
Предел прочности - это не напряжение, при котором происходит
разрушение образца, кроме того, он не равен напряжению в наи-
меньшем сечении (в шейке) растянутого образца в момент време-
ни, соответствующий максимальной силе. Предел прочности -
некоторое условное напряжение, просто определяемое и удобное
на практике для сравнения свойств материалов.
Значения предельных напряжений для некоторых материалов
указаны в табл. 2.1 в МПа.
При повышенных температурах в испытаниях на растяжение
наблюдается ползучесть, заключающаяся в медленном течении
материала при постоянном напряжении.
28
Испытания материалов на растяжение (сжатие)
Таблица 2.1
Материал Напряженность, в МПа 8, % Е, ГПа
(Утр (Уте Ов.р. вес.
Сталь 30 незака- ленная 330 330 530 - 28 200
Сталь 30 закален- ная 1030 900 1100 - 11 200
Сталь 45 незака-' ленная 370 _370 620 — 24 200
Сталь 45 закален- ная 1040 970 • 1080 - 13 200
Сталь 30ХГСА за- каленная 1400 1400 1620 - 10 210
Сталь 40ХНВ за- каленная 1720 2100 2050 - 10 215
Чугун серый СЧ28 140 310 150 640 0,6 70
Для сравнения материалов (не для расчетов) определяются пре-
делы ползучести - наибольшие напряжения, при которых дефор-
мация ползучести при данной температуре за определенный проме-
жуток времени не превы-
шает установленной вели-
чины (рис. 2.13). Предел
ползучести обозначается
буквой а с индексами, на-
пример, Оо2/200- Числи-
тель нижнего индекса -
допустимая деформация в
t(nac)%^ знаменатель - время в
часах, верхний индекс -
температура в °C.
Разрушение от ползу-
чести происходит при напряжениях, меньших, чем предел проч-
ности для данной температуры. Сравнительной характеристикой
длительной прочности различных материалов является предел дли-
тельной прочности.
Пределом длительной прочности называется напряжение, при
котором происходит разрушение образца после установленного
срока работы (действия этого напряжения) при заданной темпе-
ратуре. Обозначается предел длительной прочности буквой а с
29
Испытания материалов на растяжение (сжатие)
указанием времени работы в часах (нижний индекс) и температу-
ры (верхний индекс), например о1/00. Диаграмма испытаний строж-
ится в координатах а - г. При испытаниях на растяжение опреде-
ляется также относительное удлинение при разрыве:
4)
Для измерения удлинения по сечениям рабочая длина образца
разбивается на делительной машине рисками на десять участков,
для наглядности строится эпюра относительных удлинений. Ис-
пытанию на сжатие подвергаются только хрупкие материалы, уме-
ренно пластичные и пластичные- материалы при сжатии не разру-
шаются (рис. 2.14).
Модуль упругости Е и коэффициент Пуассона р также опреде-
ляются при растяжении. В опытах определяются деформации, по
которым вычисляются Е и ц. При растяжении стержней силой,
приложенной к концам, деформации в любой точке рабочей час-
N
ти стержня одинаковы и нормальные напряжения а = — во всех
' А
сечениях нормальная сила 'N = F , где F - усилие, создаваемое
машиной.
Сталь
Дуралюмин
Алюминий
Чугун
Рие. 2.14
ГГ г- Е' а Г7
По закону Гука Е = — или Е = —.
Деформации измеряются; тензометрическими приборами. Наи-
более удобными для этой цели являются измерители деформаций
с проволочными датчиками. Чтобы исключить влияние внецент-
ренного приложения растягивающей силы, датчики наклеивают-
е1
ся с двух противоположных сторон, тогда Е = —-—.
30
Испытания материалов на растяжение (сжатие)
Коэффициент Пауссона вычисляется как абсолютная величи-
на отношения поперечной деформации растянутой пластины к
продольной:
^2
м=—,
где е2 - поперечная деформация; Ej - продольная деформация.
Здесь £j и е2 - также средние значения деформаций, измеренных
на обеих поверхностях пластины.
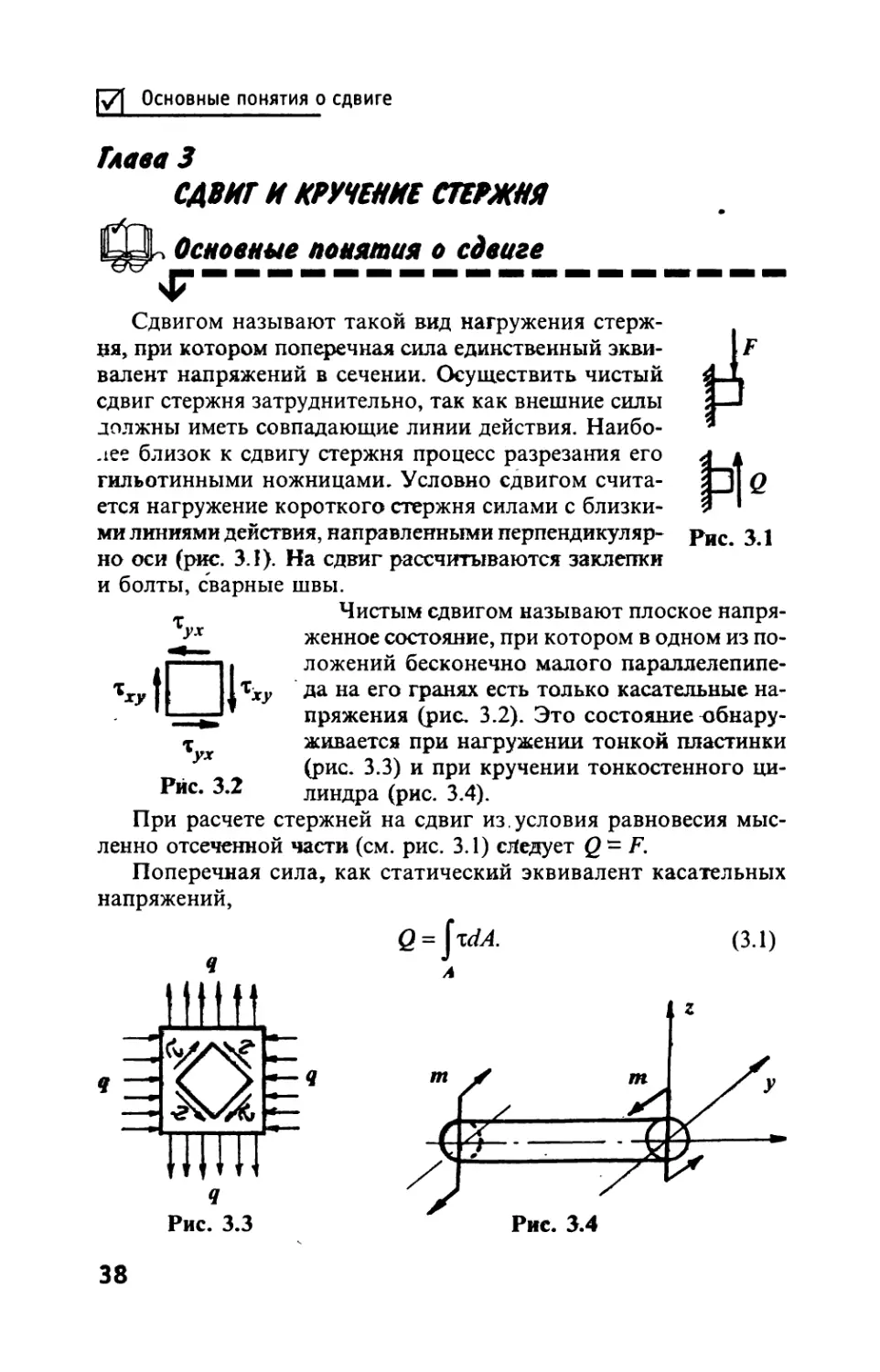
Механические характеристики материалов зависят от темпе-
ратуры. Характер влияния температуры на модуль упругости
показан на рис. 2.15. Пределы прочностей текучести легирован-
ных сталей, алюминиевых и титановых сплавов при повышении
температуры снижаются, у малоуглеродистой стали в диапазоне
100-300 °C снижается пластичность, предел прочности растет,
при температуре t = 300 °C предел прочности начинает монотонно
снижаться (штриховые линии на рис. 2.15). При динамическом
нагружении пластические деформации не успевают развиваться,
предел прочности и предел текучести (кривая 2 на рис. 2.16) воз-
растают, модуль упругости металлов практически не меняется.
При низких температурах материалы, пластичные при нор-
мальных температурах, могут стать хрупкими (хладноломкость).
К таким материалам относятся стали. Сплавы алюминия при низ-
ких температурах не становятся хладноломкими, их предел проч-
ности растет одновременно с ростом относительного удлинения 8.
31
Принципы расчета на прочность растянутых элементов конструкций
Принципы расчета на прочность
растянутых силовых элементов конструкций

Под прочностью силовых элементов конструкций (твердых тел
вообще) понимают способность сохранять свою целостность при
действии внешних сил.
Когда силы взаимодействия частиц тела становятся меньше
дополнительных внутренних сил в ней, вызванных внешними си-
лами, начинается разделение тела на части. Это разделение (раз-
рушение) начинается в некоторой точке, будем называть ее опас-
ной. Можно сказать, что в это время напряжение в точке достига-
ет своего предельного значения.
Существует два вида расчета:
— поверочный;
— проектный.
Поверочный расчет выполняется тогда, когда размеры попе-
речных сечений выбираются из конструктивных соображений.
При малых деформациях расчет ведется по напряжениям. Расчет
состоит в определении напряжений в опасных сечениях и сравне-
нии их с допускаемыми для выбранного материала. Допускае-
мые напряжения растяжения [а]^ и сжатия [а]с назначаются как
часть предельных для материала напряжений, называемых пре-
делом прочности и пределом текучести ат:
г 1 г л
[о] = — ИЛИ [о] = —
(2.7)
Коэффициенты запаса прочности находятся статистическими
методами по опыту эксплуатации аналогичных конструкций и
вводятся для компенсации неточного знания внешних сил и не-
стабильности механических характеристик материала, прежде
всего ств и стт, определяемых в лабораториях.
При поверочном расчете вычисляется напряжение в опасном
сечении, где сила N наибольшая, либо в сечении, ослабленном,
например, отверстиями или чем другим.
Наибольшее напряжение не должно превышать допустимое:
°тах^М-
Для летательных аппаратов применяются материалы со ста-
бильными свойствами, но внешние силы, прежде всего аэродина-
мические, могут изменяться в широких пределах, поэтому вво-
дится коэффициент безопасности/> 1 , по которому вычисляется
расчетная сила.
32
Принципы расчета на прочность растянутых элементов конструкций
Np=f -N3. (2.8)
Здесь N3 - нормальная сила, полученная для некоторых сред-
них условий эксплуатации.
За допустимое напряжение принимается либо предел прочнос-
ти, либо предел текучести, условие прочности:
А
если допустимы пластические деформации;
А т
когда деформации должны оставаться упругими.
При проектных расчетах находятся безопасные размеры сече-
л NP л N3
ния А = —А =--------, в некоторых случаях определяются допу-
°, [О]
стимые значения внешних сил.
Расчет стержневых систем
Стержневые системы со стержнями, работающими только на
растяжение или сжатие, называются фермами. В них стержни меж-
ду собою и с неподвижною опорою соединяются подвижно вра-
щательными или сферическими парами (шарнирами), силы при-
кладываются только в узлах соединения стержней.
Простейшая ферма состоит из двух стержней (рис. 2.17, а).
Ферма статически определима: в ней неизвестны две силы и
2. Зак. 388
33
Расчет стержневых систем
N2; системы внешних и внутренних сил сходятся в точке А, поэто-
му для нее можно составить два уравнения равновесия (рис. 2.17,6):
2^ = 0; 2^ = 0.
Из первого уравнения • sina + N2 • sina = 0 следует 7V| =
TV2.
Из второго находим их величину:
2N{ cosa- F=0; Nj =
2 cos a
0
Рис. 2.18
Если прибавить еще один стер-
жень (рис. 2.18), система становит-
ся статически неопределимой. Для
нее по-прежнему можно составить
лишь два уравнения равновесия
при трех неизвестных силах 7Vp N2,
Ny
A’j • since - N3 sina = 0;
• cosa + N2 + N3 • cosa - F= 0.
Недостающее уравнение можно
составить из условия совместнос-
ти деформаций стержней. Если при-
нять ввиду малости перемещений
Аа = 0 , то (рис. 2.19) A/j = А/2' cosa.
При растяжении силами, приложенными к концам стержня,
ввиду однородности деформированного состояния деформацию
вдоль оси можно определить как отношение приращения длины
стержня А/ к первоначальной длине
А/
е = —.
/
В силу (2.5) и закона Гука
AJ М
ЕА
поэтому (2.7) представляется в виде
A^i/i
—— = —— cosa. (2.10)
Д4 Е2А2
Из первого уравнения равно-
весия отсеченного узла А следует
N' = N2.
A
Рис. 2.19
34
Расчет стержневых систем
Положим жесткости стержней на растяжение одинаковыми,
тогда из (2.10) получим, учтя /3 = 1Х • cosa, Nx = N2 • cos2a.
Теперь из второго уравнения (2.11) найдется нормальная сила
в среднем стержне
2 l + 2cos3a (210
Нормальные силы в крайних, наклоненных к линии действия
внешней силы F на угол а,
Feos2 а
М = =-------z—
l + 2cos3a
(2.12)
Формулы (2.12) и (2.13) получены для фермы со стержнями
одинаковой жесткости на растяжение ЕА. Из (2.12) следует, что
при увеличении угла а между осями стержней доля внешней си-
лы, воспринимаемая наклоненными стержнями, уменьшается.
А-А
Рис. 2.20
Конструкция оказывается неравнопроч-
ной. При необходимости уменьшить вес и
расход материала сечения этих стержней
находят методом последовательных при-
ближений. На каждом этапе перемены
площади сечения вычисляются напряже-
ния по (3.5) и сравниваются с допускае-
мыми.
Рассмотрим еще два случая расчета
статически неопределимых систем.
На стальной болт надета медная труб-
ка. Трубка сжимается при навертывании
на болт гайки (рис. 2.20, а). Найдем по-
требный угол поворота гайки после ее ка-
сания о прокладку при заданном напря-
жении в сечениях болта. Составим урав-
нение равновесия части системы, отсечен-
ной плоскостью, перпендикулярной оси
стержня (рис. 2.20, б). В проекциях на ось
соединения Nx + N2 = 0.
При навертывании гайки трубка сжи-
мается, а болт растягивается. Ход гайки
5 = А?! + Д/2,
это и есть уравнение совместности дефор-
маций. Ход гайки равен числу оборотов
гайки л, умноженному на шаг резьбы р:
S-р • п.
2
35
Расчет стержневых систем
Из уравнения равновесия = -N2 = N.
Подставим это значение нормальной силы в уравнение совме-
стности деформаций
.J 1
рп = NI --+
1 1
£*2^2
(3.13)
к х N
Напряжение, заданное в сечениях болта а =—, подставим в
А
последнее уравнение
pn = Nl[— + ^-
Е, Е2А2
(3.13)
При известных площадях сечений, напряжении и шаге резьбы
легко находится угол поворота гайки.
Некоторые фрагменты сооружений и машин можно привести к
такой расчетной модели.
Абсолютно жесткий брус под-
вижно соединен одним концом с не-
подвижной опорой и поддерживает-
ся двумя стержнями (рис. 2.21). Если
не вводить в рассмотрение реакцию
опоры А, для системы можно соста-
вить лишь одно уравнение равнове-
сия, например, положить сумму мо-
ментов относительно точки А, рав-
ной нулю, = 0.
В этом уравнении будут две не-
известных силы в сечениях стержней
(1), (2). Причиной появления сил
и N2 могут быть, кроме веса бруса
(им можно и пренебречь), внешние
силы, нагрев стержней, разная их
длина (монтажный зазор).
Рассмотрим их поочередно.
Пусть в точке С йриложена сила
F(a + b)- Nx(a + b) - N2b = 0
Содержит две неизвестные силы и N2. Уравнение совмест-
ности деформаций стержней получим, полагая брус нерастяжи-
мым и несгибаемым. Из подобия треугольников (рис. 2.22) АСС'
и ЛЕВ'имеем ду а + ь
<2Л4>
36
[^1 Расчет стержневых систем
При одинаковых стержнях это уравнение примет вид
М _а + Ь
ТГ2~ ь
Задача легко разрешима.
При нагреве одного или обоих стержней вследствие абсолют-
ной жесткости бруса удлинению нагретого стержня
Д/ = al At,
где а - коэффициент линейного расширения; Д/ - разность темпе-
ратур, будет мешать другой. Вследствие этого в стержнях воз-
никнут нормальные силы 2V] и N2.
Из уравнения равновесия ЕЛ/А = 0 следует
^ = ЛГ2ТТТ- (215)
а + Ь
Уравнение совместности деформации останется прежним (2.15).
Пусть нагрет стержень /, тогда из (3.15) по известному Д/ полу-
чим N2 . При /j = 12
А7 «6ДС
ДГ2 =----------
Е2А2(а + Ь)
вычисляется из уравнения равновесия.
Допустим, что один из стержней, например, первый оказал-
ся короче, тогда при сборке обнаружится монтажный зазор (см.
рис. 2.22). После соединения второй стержень сожмется, а пер-
вый растянется. Из подобия треугольников АСС' и АВВ' полу-
чается такое уравнение (см. рис. 2.22) совместности деформаций:
Д-Д/. а + Ь
<216>
Уравнение равновесия ос-
танется в виде (2.16).
Для многостержневых ферм
составлять уравнения совмес-
тности деформаций сложно,
задача решается специальны-
ми методами - методом сил или
методом перемещений.
37
Основные понятия о сдвиге
Глава 3
СДВИГ И КРУЧЕНИЕ СТЕРЖНЯ
Основные понятия о сдвиге
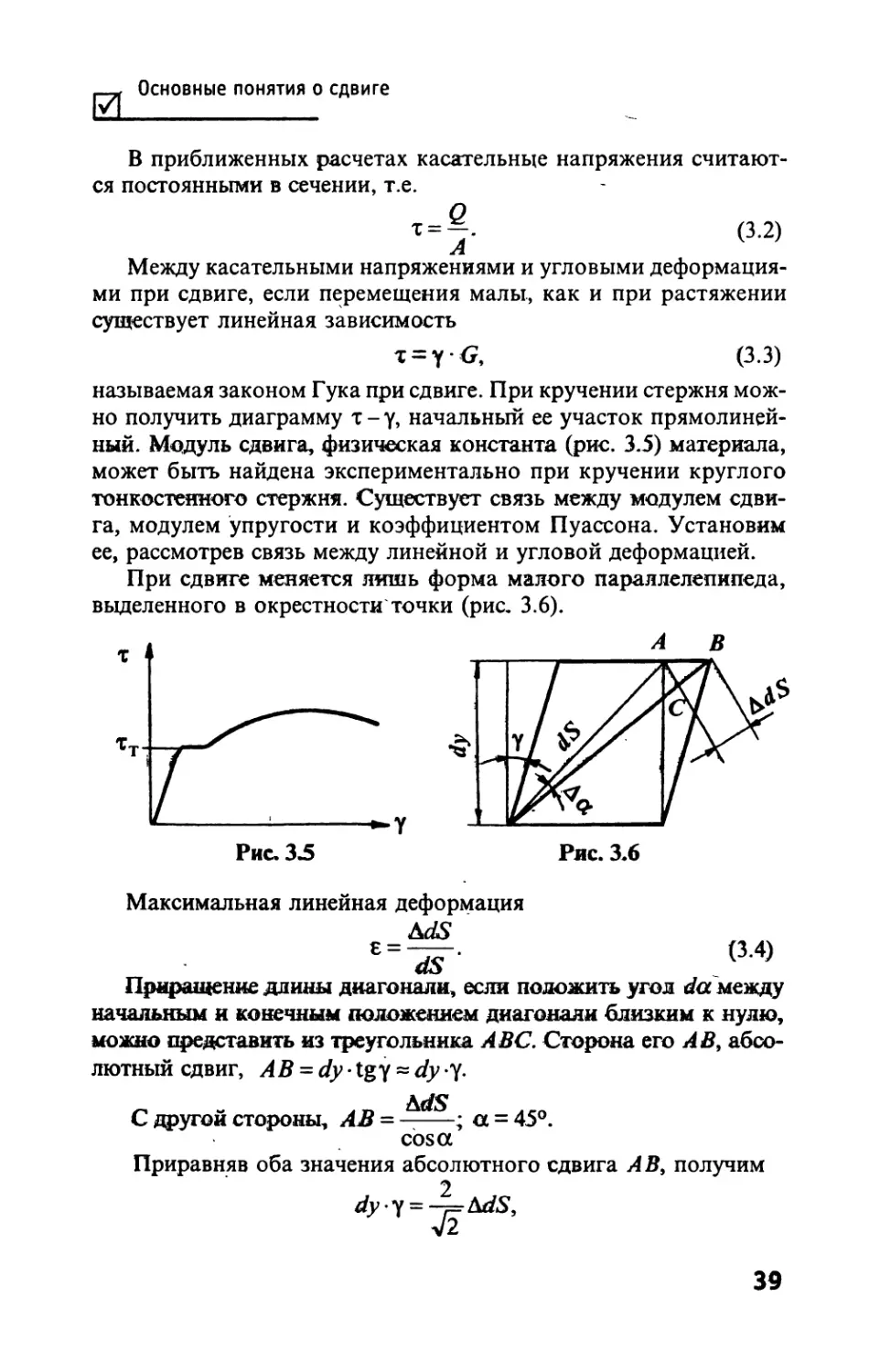
Сдвигом называют такой вид нагружения стерж-
ня, при котором поперечная сила единственный экви-
валент напряжений в сечении. Осуществить чистый
сдвиг стержня затруднительно, так как внешние силы
должны иметь совпадающие линии действия. Наибо-
й'
лее близок к сдвигу стержня процесс разрезания его
гильотинными ножницами. Условно сдвигом счита-
ется нагружение короткого стержня силами с близки-
ми линиями действия, направленными перпендикуляр-
но оси (рис. ЭЛ). На сдвиг рассчитываются заклепки
и болты, сварные швы.
Не
Рис. 3.1
Рйс. 3.2
Чистым сдвигом называют плоское напря-
женное состояние, при котором в одном из по-
ложений бесконечно малого параллелепипе-
да на его гранях есть только касательные на-
пряжения (рис. 3.2). Это состояние обнару-
живается при нагружении тонкой пластинки
(рис. 3.3) и при кручении тонкостенного ци-
линдра (рис. 3.4).
При расчете стержней на сдвиг из. условия равновесия мыс-
ленно отсеченной части (см. рис. 3.1) следует Q - F.
Поперечная сила, как статический эквивалент касательных
напряжений,
38
Основные понятия о сдвиге
В приближенных расчетах касательные напряжения считают-
ся постоянными в сечении, т.е.
Q
г = ^. (3.2)
А
Между касательными напряжениями и угловыми деформация-
ми при сдвиге, если перемещения малы, как и при растяжении
существует линейная зависимость
т = у <?, (3.3)
называемая законом Гука при сдвиге. При кручении стержня мож-
но получить диаграмму т - у, начальный ее участок прямолиней-
ный. Модуль сдвига, физическая константа (рис. 3.5) материала,
может быть найдена экспериментально при кручении круглого
тонкостенного стержня. Существует связь между модулем сдви-
га, модулем упругости и коэффициентом Пуассона. Установим
ее, рассмотрев связь между линейной и угловой деформацией.
При сдвиге меняется лишь форма малого параллелепипеда,
выделенного в окрестности точки (рис. 3.6).
Максимальная линейная деформация
AdS
(3.4)
Приращение длины диагонали, если положить угол da между
начальным и конечным положением диагонали близким к нулю,
можно представить из треугольника АВС. Сторона его АВ, абсо-
лютный сдвиг, AB = dy-tgy = dy у.
С другой стороны, А В =----; а = 45°.
cos а
Приравняв оба значения абсолютного сдвига АВ, получим
2
dyy = —=&dS,
V2
39
Основные понятия о сдвиге
т.е.
(3.5)
разделим на aS и учтем, что = sma = тогда
Л К
Y—= E|V2,
|e,l = |lY|.
При плоском деформированном состоянии
1 ,
е, = —(cfj
Е
В случае чистого сдвига Oj = -о2 это можно видеть и из рисун-
ка 3.3, следовательно, = —(1 + ц). Кроме того, согласно (1.26)
Е
Из закона Гука следует Y = — • Вместо (3.5) имеем
G
х 1т
-(1+ (!) = --,
Е 2Е
откуда получим
(3.6)
G =—-—
2(1+ ц)
К этой формуле можно прийти также из энергетических сооб-
ражений.
1Ш1п Расчет заклепочных соединений
V---------------------------------------------
На сдвиг (срез) рассчитывают болты, заклепки, шпонки, шли-
цы, сварные, паяные и клеевые швы при нагружении их силами,
перпендикулярными оси. При расчете определяются касательные
напряжения в поперечных сечениях и напряжения смятия. Болты и
заклепки, входящие в соединение, полагаются нагруженными
равномерно.
Касательные напряжения определяются по формуле (3.2). Пло-
щадь среза А вычисляется как произведение числа заклепок (бол-
тов) на площадь поперечного сечения одной заклепки и на число
плоскостей среза. Например, в соединении, показанном на ри-
сунке 3.7, заклепками соединены две полосы (1) через накладки
(2). На каждую полосу приходится по три заклепки, каждая из
40
Расчет заклепочных соединений
которых может одновременно срезаться в двух плоскостях. Об-
щая площадь среза и напряжение будут:
. nmnd1 4Q
А =-------; =-----тт-
4 птпсг
где d - диаметр заклепки.
Рис. 3.7
Условие прочности есть неравенство т < [т].
Допустимое касательное напряжение [т] задается как доля до-
пускаемого нормального напряжения, определяемая по критери-
ям прочности.
По критерию наибольших касательных напряжений эквива-
лентное напряжение
&экв ~~ ^max ~ ^min —
но при сдвиге
^тах —
поэтому
[т] = 0,5[о]. (3.7)
По энергетическому критерию сжв = д/сттах + o^in - omaxomin,
отсюда следует
[т] = 0,6[о]. (3.8)
Поверхности контакта соединяемых деталей и заклепок (бол-
тов) могут сминаться - на поверхности возникает пластическая
деформация. Контактные напряжения по цилиндрической повер-
хности распределяются неравномерно (рис. 3.8). В расчете на смя-
тие принимается равномерное распределение контактных напря-
жений, а площадью смятия считают проекцию поверхности кон-
такта - диаметральную плоскость. Напряжения смятия:
F
— А
^см
41
Расчет заклепочных соединений
Общая поверхность смятия в соединении
Асм
где п - число заклепок; h - толщина соединяемых деталей; d -
диаметр заклепки.
В соединении, показанном на рисунке 3.7, заЛ принимают мень-
шую из толщин - толщину соединяемой полосы или толщину
обеих накладок - 2Л2.
Условие прочности имеет вид:
^см —
Допускаемое напряжение смятия:
[aU = (1,3+2)Ц,.
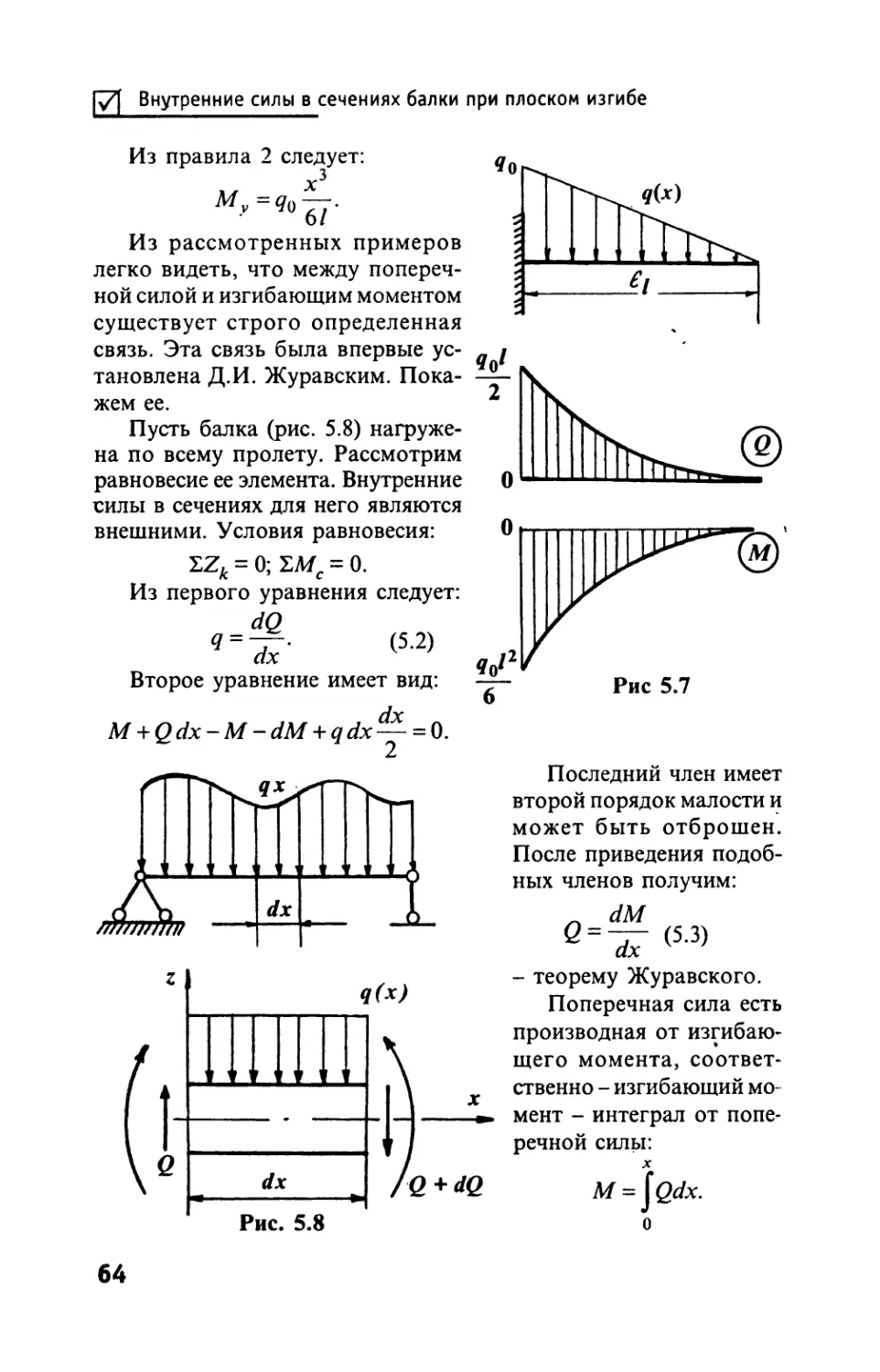
Кручение круглого стержня
Кручением будем называть такой вид нагружения, когда в
поперечных сечениях единственным статическим эквивалентом
является крутящий момент.
Крутящие моменты в сечении определяются по правилу: кру-
тящий момент равен сумме моментов внешних сил относитель-
но оси стержня, приложенных по одну сторону от сечения.
Правило вытекает из уравнения равновесия мысленно отсе-
ченной части. Для определенно-
сти вводится правило знаков:
крутящий момент положителен,
если направлен против хода ча-
совой стрелки при взгляде с кон-
ца внешней нормали (рис. 3.9).
Рис. 3.9
42
Кручение круглого стержня
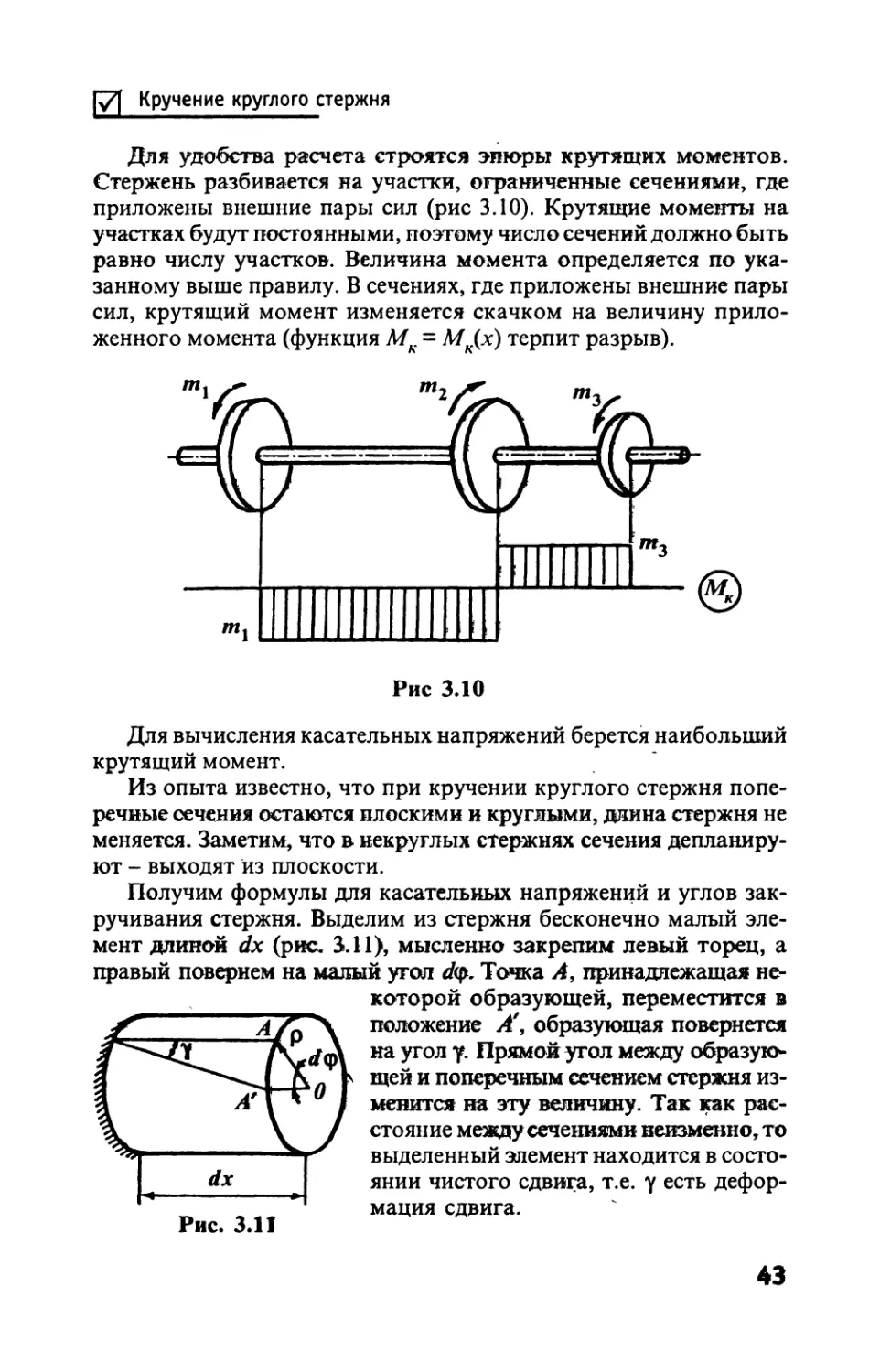
Для удобства расчета строятся эпюры крутящих моментов.
Стержень разбивается на участки, ограниченные сечениями, где
приложены внешние пары сил (рис 3.10). Крутящие моменты на
участках будут постоянными, поэтому число сечений должно быть
равно числу участков. Величина момента определяется по ука-
занному выше правилу. В сечениях, где приложены внешние пары
сил, крутящий момент изменяется скачком на величину прило-
женного момента (функция Мк = Мк(х) терпит разрыв).
Рис ЗЛО
Для вычисления касательных напряжений берется наибольший
крутящий момент.
Из опыта известно, что при кручении круглого стержня попе-
речные сечения остаются плоскими и круглыми, длина стержня не
меняется. Заметим, что в некрутлых стержнях сечения депланиру-
ют - выходят из плоскости.
Получим формулы для касательных напряжений и углов зак-
ручивания стержня. Выделим из стержня бесконечно малый эле-
мент длиной dx (рис. 3.11), мысленно закрепим левый торец, а
правый повернем на малый угол dty. Точка А, принадлежащая не-
которой образующей, переместится в
положение А', образующая повернется
на угол у. Прямой угол между образую-
щей и поперечным сечением стержня из-
менится на эту величину. Так как рас-
стояние между сечениями неизменно, то
выделенный элемент находится в состо-
янии чистого сдвига, т.е. у есть дефор-
мация сдвига.
43
[7J Кручение круглого стержня
Ввиду малости деформаций дугу А А ’ можно считать катетом
прямоугольного треугольника, a tgy = у. Дуга А А ’ = р^ф, следова-
тельно, ydx = pJ(p.
Таким образом, из геометрических соотношений установле-
на связь между угловой деформацией и полярной координатой
точки:
Y = P-T-
ах
(3.9)
(ЗЛО)
Обозначим 0 = — и назовем относительным углом закручи-
dx
вания. Воспользуемся законом Гука при сдвиге т = у G, тогда
т = Gp0.
Из уравнения равновесия отсеченной части стержня известен
крутящий момент Мк в сечениях. С касательным напряжением он
связан статическим уравнением
Мк =fxpdA.
а
Подставив т в (3.9), получим
Мк = G&jp2dA.
А
Интеграл по площади есть полярный момент инерции Jp, по-
этому м
0=ё< <311>
Заменим этим значением 0 в (3.8) и получим формулу для каса-
тельного напряжения в точках поперечного сечения стержня
Мк
т =—-р.
Jp
Из (3.12) следует, что касательные напря-
жения в центре сечения равны нулю и макси-
мальны у поверхности; В соответствии с зако-
ном парности также изменяются касательные
напряжения в продольном сечении (рис 3.12).
Для вычисления максимального касатель-
ного напряжения введем новую геометричес-
кую характеристику сечения
(3.12)
Рис. 3.12
wp=-^~
Ртах
и назовем ее полярным моментом сопротивления.
44
Кручение круглого стержня
Из (3.11) получим формулу:
Рис. 3.13
Из рисунка 3.12 видно, что внут-
ренняя часть сечения нагружена
мало, поэтому целесообразно разне-
сти материал от центра сечения. По-
лые стержни (валы) (рис. 3.13) при
одинаковом крутящем моменте лег-
че сплошных.
Полярные моменты сечений по-
лых валов определяются по формуле
И$ = ^(1-с4), (3-14)
п “ й
где D - наружный диаметр вала; с = —, а - внутрении диаметр
для сплошного стержня с = 0.
Угол закручивания стержня получим Из (3.11), разделив пере-
менные и проинтегрировав по длине стержня:
I М
<P={y^~dx- (3-15)
oGJp
Если крутящий момент не меняется по длине, а жесткость на
кручение GJp постоянна,
(3.16)
Итак, в поперечных и продольных сечениях стержня при кру-
чении возникают только касательные напряжения, т.е. грани бес-
конечно малого параллелепипеда, параллельные и перпендику-
лярные образующим, есть площадки сдвига. Под углом 45° к ним
находятся главные площадки. Таким характером напряженного
состояния объясняется различный вид разрушения стальных, чу-
гунных и деревянных стержней.
Рис. 3.14
45
Кручение круглого стержня
Стальной стержень разрушается от касательных напряжений
по поперечному сечению (рис. 3.14), в продольном сечении обра-
зование трещин затруднено из-за большей протяженности. Чугун-
ный стержень разрушается от растягивающих нормальных напря-
жений, направленных под углом 45° к образующей по винтовой
поверхности (рис. 3.15).
Рис. 3.15
Древесина легко скалывается вдоль волокон, поэтому разру-
шение деревянного стержня начинается с образования продоль-
ных трещин (рис. 3.16). Стержень вначале раскалывается, затем
отдельные части обрываются.
Рис. 3.16
Валы (круглые стержни) рассчитываются на прочность и жес-
ткость. При проверочном расчете действующее максимальное
касательное напряжение сравнивают с допускаемым, при проек-
тировочном - определяется диаметр вала в сечении. Для этого
(3.14) подставляется в (3.13):
п I 16Мк
£) = з/----Ц-.
V [т]л(1 - с4)
Величина с задается. Найденный диаметр проверяется по жес-
ткости подстановкой в (3.11). Допустимый относительный угол
закручивания зависит от вида машины (сооружения). В мостовых
кранах, например, при статическом нагружении [G] - 0,3°,при ди-
намическом [О] = 0,15°. Если при расчете задается передаваемая
мощность, крутящий момент определяется по формуле
М,. = —; =----,
со 30
где Р - мощность в ваттах; п - число оборотов в минуту.
В тех случаях, когда заметна разница в величине крутящего
момента по участкам, вал проектируется ступенчатым. Переход
46
[yl Кручение некруглых стержней
к новому диаметру должен быть плавным для уменьшения кон-
центрации напряжений, которая зависит от отношений диамет-
d
ров ступеней — и радиуса г закругления к меньшему диаметру d.
Концентрация напряжений возникает й при наличии отверстий.
Влияние концентрации напряжений особенно существенно при
циклическом изменении напряжений. Для высокопрочных мате-
риалов она должна учитываться и при постоянных значениях на-
пряжений. В расчетах концентрация напряжений учитывается
введением коэффициентов концентрации, определяемых теорети-
чески и экспериментально.
Кручение некруглых стержней
У некруглых стержней при кручении сечения депланируют
(рис. 3.17), поэтому нельзя получить простые формулы для вычис-
ления касательных напряже-
ний и углов закручивания.
Задача решается методами
теории упругости. Решение
приводится в виде формул для
максимальных касательных
напряжений и угла закручива-
ния стержней с сечениями раз-
личной формы.
Рис. 3.18
Формулы по структуре напоминают фор-
мулы круглого стержня. Эпюра касательных
напряжений в стержне прямоугольного сече-
ния показана на рисунке 3.18. Максимальное
напряжение:
Л/,.
T = Tmax ^
ab а
Угол закручивания:
Коэффициент а, Р, т| зависит от
соотношения длин сторон сечения.
47
Кручение некруглых стержней
Коэффициенты Значения коэффициентов при S/h
1 2 4 6 . 10
а 0,108 0,246 0,287 0,298 0,312 0,333
3 0,141 0,229 0,281 0,298 0,312 0,333
п 1,000 0,796 0,745 0,743 0,742 0,742
Максимальные напряжения у поверхности по середине длинной
стороны, по углам касательные напряжения равны нулю, закон
изменения их по сечению нелинейный.
В стержнях эллиптического сечения закон изменения по тол-
щине почти линейный (рис. 3.19). Максимальные напряжения раз-
виваются на концах малой оси,
оно вычисляется по формуле:
16ЛЛ
т =-------—
vmax . 7 •
natr
Угол закручивания:
256пМк1
Ф = —i------------•
Здесь приведены формулы
кручения некруглых стержней при
нестесненной депланации сече-
ний, т.е. стержней со свободными
в осевом направлении концами.
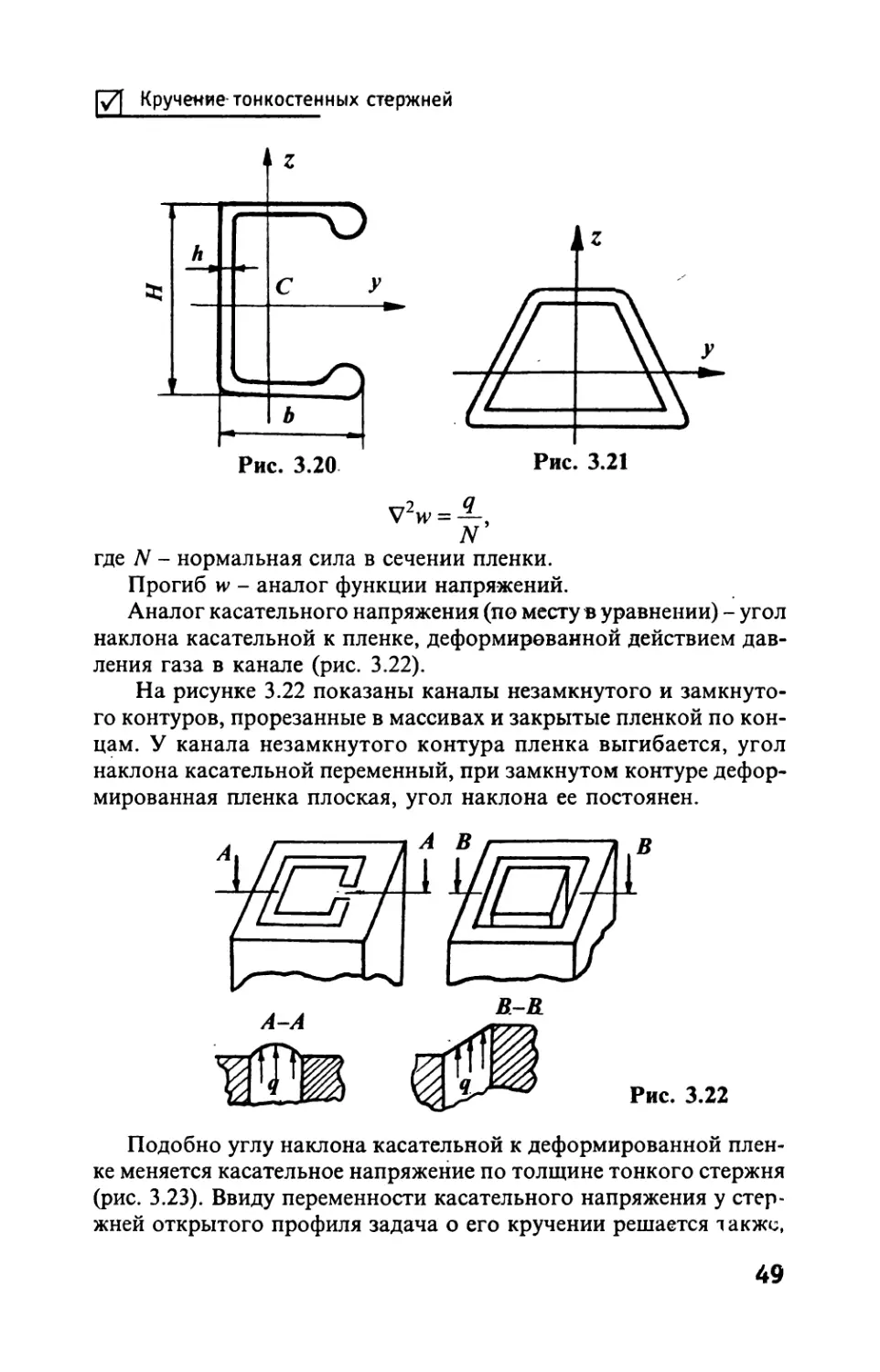
Кручение тонкостенных стержней
Тонкостенными называются стержни, толщина которых Л мала
в сравнении с другими размерами поперечного сечения (рис. 3.20).
Профиль сечения, средняя линия, равностоящая от наружных по-
верхностей, может быть открытым (см. рис. 3.20) или замкнутым
(рис. 3.21). У обоих этих видов стержней по-разному изменяются
касательные напряжения по толщине. Уравнение кручения тон-
ких стержней:
V2<£ = 2G0,
где Ф - функция напряжений,по структуре одинаково с уравнени-
ем изгиба мембраны, закрывающей канал с сечением, повторяю-
щим сечение стержня,
48
Кручение тонкостенных стержней
где N - нормальная сила в сечении пленки.
Прогиб w - аналог функции напряжений.
Аналог касательного напряжения (по месту в уравнении) - угол
наклона касательной к пленке, деформированной действием дав-
ления газа в канале (рис. 3.22).
На рисунке 3.22 показаны каналы незамкнутого и замкнуто-
го контуров, прорезанные в массивах и закрытые пленкой по кон-
цам. У канала незамкнутого контура пленка выгибается, угол
наклона касательной переменный, при замкнутом контуре дефор-
мированная пленка плоская, угол наклона ее постоянен.
Подобно углу наклона касательной к деформированной плен-
ке меняется касательное напряжение по толщине тонкого стержня
(рис. 3.23). Ввиду переменности касательного напряжения у стер-
жней открытого профиля задача о его кручении решается также,
49
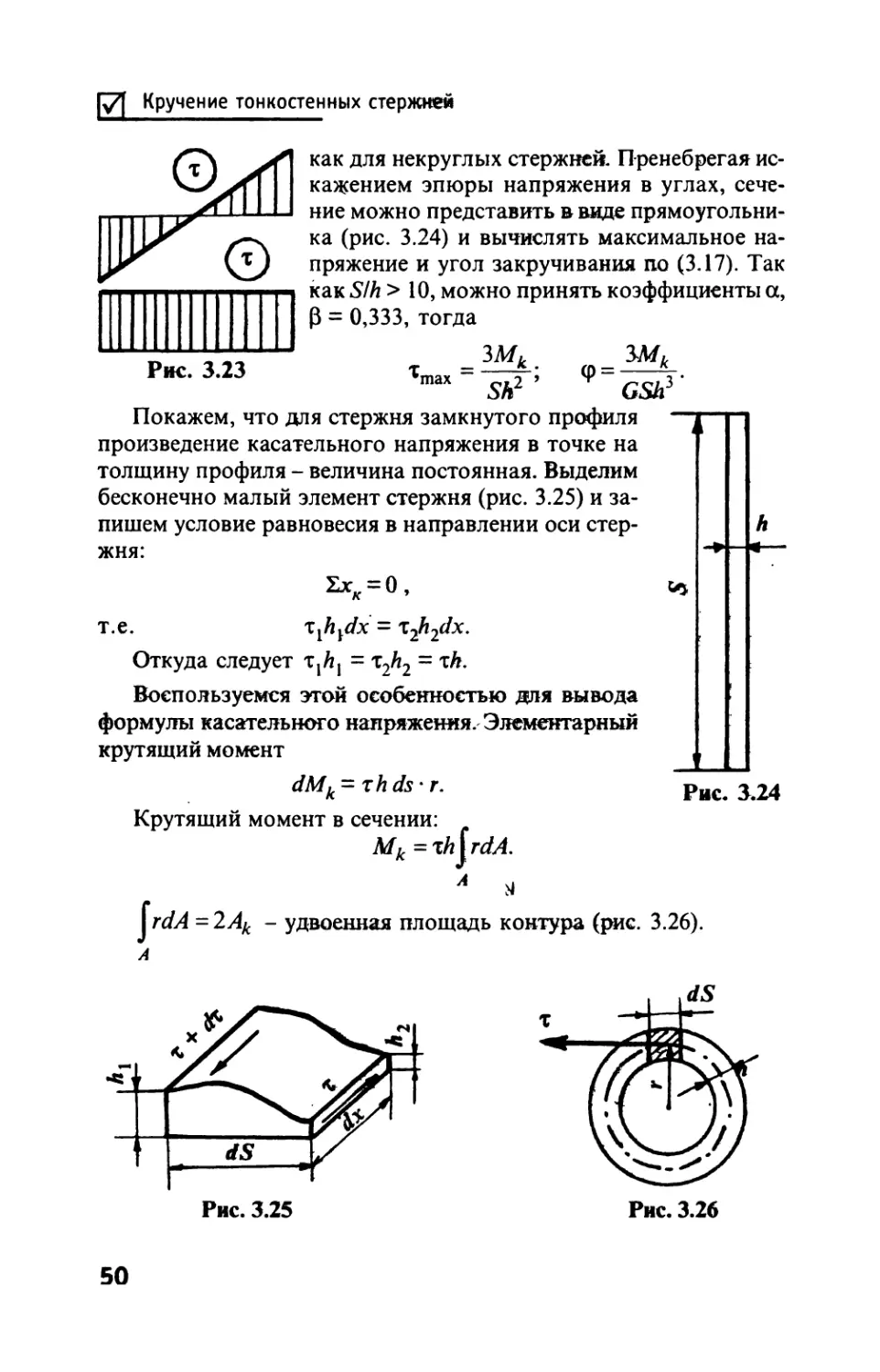
Кручение тонкостенных стержней
Рис. 3.23
как для некруглых стержней. Пренебрегая ис-
кажением эпюры напряжения в углах, сече-
ние можно представить в ваде прямоугольни-
ка (рис. 3.24) и вычислять максимальное на-
пряжение и угол закручивания по (3.17). Так
как S/h > 10, можно принять коэффициенты а,
Р = 0,333, тогда
змк змк
Ттах~5Л2’ Ф” GSh3
Покажем, что для стержня замкнутого профиля
произведение касательного напряжения в точке на
толщину профиля - величина постоянная. Выделим
бесконечно малый элемент стержня (рис. 3.25) и за-
пишем условие равновесия в направлении оси стер-
жня:
2хк = 0,
т.е. xfadx = xji2dx.
Откуда следует xxhx = т2А2 = xh.
Воспользуемся этой особенностью доя вывода
формулы касательного напряжения. Элементарный
крутящий момент
dMk -xhds' г.
Рис. 3.24
Крутящий момент в сечении:
Мк = xhjrdA.
А м
Jrt/J =2Ак - удвоенная площадь контура (рис. 3.26).
А
50
Кручение тонкостенных стержней
Таким образом, касательное напряжение
М.к
Т = 2ЙЛ <318>
равно отношению крутящего момента к удвоенному произве-
дению толщины в соответствующей точке на площадь, ограни-
ченную средней линией сечения.
Формулу для угла закручивания получим из принципа воз-
можных перемещений для деформируемого упругого тела:
Мkd(f> - U<ph dx ds = 0.
Здесь полагается, что в случае равновесия момент внешних т =
= Мк. Удельная потенциальная энергия при плоском напряжен-
ном состоянии:
1/ф= +С^-0^2 ).
ЗЕ
Прц чистом сдвиге Ст| = -о2 = Ъ поэтому
t/ф^т2.
Е
Вспомним (3.6) и получим:
Для всего стержня:
иФ= —
2G
Уф.С.
f{^—dxhds.
- величина постоянная, поэтому
Мк1 г ds
s.
Согласно (3.18) тЛ = ——
2^
h
Возможная работа внешних сил, приложенных к. стержню, есть
поэтому ф=
Когда толщина стержня всюду постоянна, Ф - ~ у
AGhAfr
При кручении стержни рассчитываются на прочность и прове-
ряются на жесткость - удельный угол закручивания сравнивает-
ся с допускаемым.
51
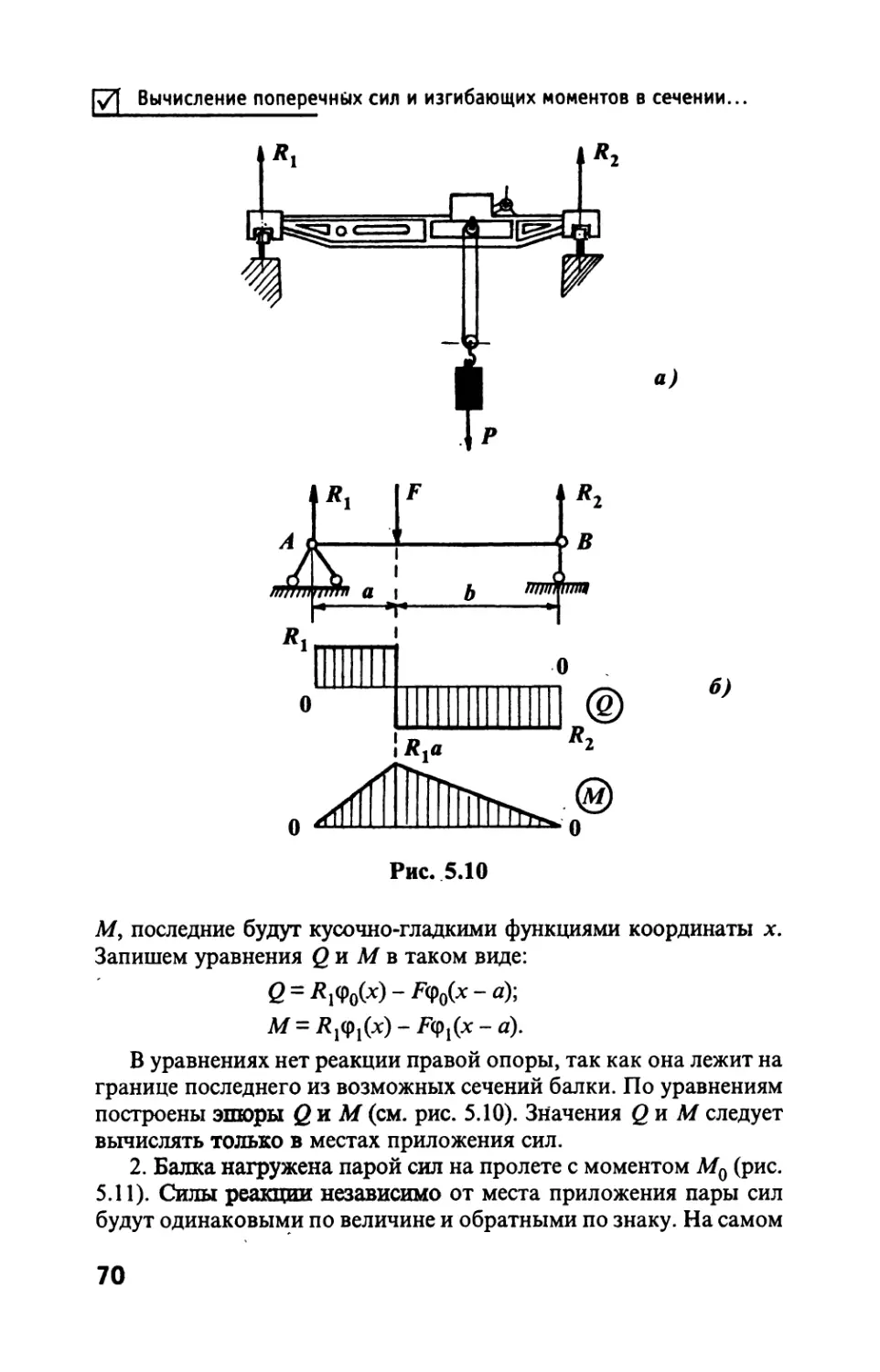
Моменты сечений
Глава 4
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
СЕЧЕНИИ СТЕРЖНЯ
Моменты сечений
При растяжении (сжатии) в формулу для напряжения в попе-
речном сечении входит площадь сечения. Это простейшая гео-
метрическая характеристика. В формулах для других случаев
нагружения появляются более сложные характеристики, называ-
емые моментами сечений, аналогичные моментам масс, применя-
емым в теоретической механике. В общем виде их можно предста-
вить как интегралы по площади:
J = ^P(y,z)dA,
А
в которых Р(у, z) - некоторые многочлены от координат попереч-
ного сечения. Среди моментов, необходимых для расчета стерж-
ней, рассмотрим статические моменты сечений:
Sy = ^zdA; Sz = J ydA; (4.1)
A A
полярный, момент инерции сечения:
Jp=jp2^, (4.2)
д
здесь р2 = у1 + z1.
Осевые моменты инерции сечения: х
JУ = Jz2dA-, J. = Jy2dA; (4.3)
А А
центробежный момент инерции сечения:
Jy,=^yzdA. (4.4)
А
Uh Основные теоремы о моментах сечений
V----------------------------------------------
Теорема 1. Моменты составного сечения равны сумме момен-
тов составляющих его частей.
Доказательство. Если сечение состоит из двух частей (рис. 4.1),
то по свойству интегралов:
52
Основные теоремы о моментах сечений
J P(y,z)dA = J P(y,z)dA + J P(y,z)dA.
A A\ A2
Следовательно, момент всего сечения:
J = Jj +
так как z)dA - момент всего се-
А
чения, интегралы в правой части такие же
моменты его частей Jx и J2. Итак, момент
сечения равен сумме моментов его частей.
Следствие. Моменты инерции много-
связных сечений, ограниченных не-
сколькими контурами (рис. 4.2), равны
разности моментов:
J ~ J\ ~ J1 ~
где J2 и J3 - моменты частей, ограни-
ченных соответствующими контурами.
Теорема 2. Осевые моменты инерции
двух равных сечений, симметрично рас-
положенных относительно оси, равны.
Каждому малому элементу одного
сечения можно поставить в соответ-
ствие равный элемент другого сечения.
Абсциссы их центров будут равны по
Рис. 4.2
величине и обратны по знаку (рис. 4.3):
-И = ~Уг
Моменты инерции этих сечений относительно оси симметрии
одинаковы:
Jl:=jyldA-, J2z=f(-y2)2dA.
А А
так как у? =(~№)2> Л -= ^2-*
Теорема 3. Центробежные момен-
ты инерции двух равных сечений, сим-
метрично расположенных относитель-
но оси, равны по величине и обратны
по знаку.
Воспользуемся рис. 4.3. По опреде-
лению
53
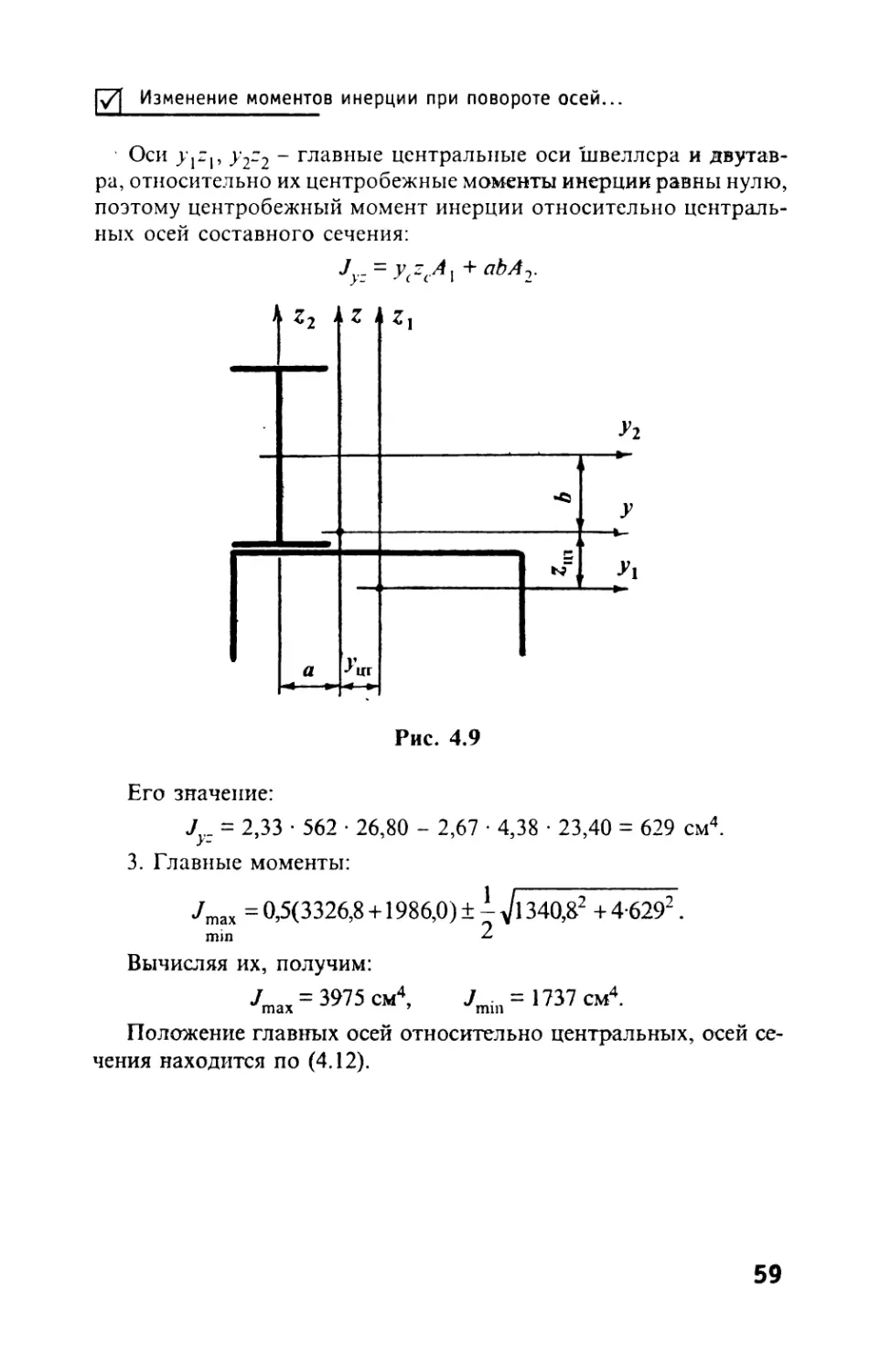
Изменение моментов сечений при параллельном переносе осей
J,,,. = jyzdA, J2y: = $(-y)zdA
А\
и A j = А 2 по условию, значит v2 = -/2r-.
Следствие. Центробежный момент инер-
ции сечения, одна из осей которого есть ось
симметрии, равен нулю.
Пусть ось z - ось симметрии (рис. 4.4).
Согласно первой теореме Jv_ = Jx v_ + но
по теореме 3 = -Дг_, т.е. Jv_ - 0.
Будем называть главными осями инер-
ции оси, относительно которых центробеж-
ный момент инерции равен нулю.
Изменение моментов сечений
при параллельном переносе осей
Пусть нам известны моменты относительно осей;; и z (рис. 4.5)
и необходимо найти моменты относительно параллельных им осей
ух и Обозначим расстояние между осями а и Ь. Тогда коорди-
наты точки сечения:
у1 = у + a; Zj = z + b.
По определению 5^] = jzxdA =J(- + b)dA.
А
Вычислив этот интеграл, име-
ем:
SyX = Sy + bA. (4.5)
Аналогично найдем
S2X = S. + aA. (4.6)
Статический момент сечения
изменяется на величину, равную
произведению площади на рас-
стояние между осями. Расстояние
между осями может быть любым
положительным и отрицатель-
ным. Можно подобрать их так,
чтобы
-ЬА = S : -аА =
у
54
Изменение моментов сечений при параллельном переносе осей
Эти значения а и b будут единственными, тогда можно найти
оси, относительно которых статичсскйе моменты равны нулю. Эти
оси будут проходить через центр тяжести сечения, поэтому их на-
зывают центральными. По формулам статических моментов мож-
но определить положение центра тяжести, если известны стати-
ческие моменты относительно каких-то осей, назовем их вспомо-
гательными и будем выбирать так, чтобы интегралы JydA и JzdA
вычислялись просто. а а
Координаты центра тяжести будут:
S. S
Ус=^ zc=~7-
А А
Координаты центра тяжести составного сечения в соответствии
с первой теоремой о моментах будут:
_ ZykAk . z _ ZzkAk
Ус ZAk ’ ‘ ’
где Ак - площади простых фигур, составляющих сечение; ук, zk -
координаты их центров тяжести относительно вспомогательных
осей.
Осевые моменты инерции сечения относительно параллельных
осей (см. рис. 4.5):
Jn = j(z + b)2 dA, = j(j> + a)2 zdA.
л2
Согласно (4.1) и (4.3) имеем:
Jyx = Jy +2bSy +b2A.
Аналогично относительно другой оси:
J— Л. + 2aS7 + а2 А.
Если оси у и z центральные,
= = 0 (4.8)
и Jn = Jy + b2A; J:i = J, + a2A.
Из последних формул следует, что момент инерции относи-
тельно центральной оси меньше, чем относительно любой другой
параллельной ей оси.
Центробежный момент инерции относительно новых парал-
лельных осей (см. рис. 4.5):
Л|.-| =}(>' + «)(- + b)dA,
А
55
Изменение моментов сечений при параллельном переносе осей
получим после интегрирования:
= Ат + а$у + bSz + abA.
Если оси у и z - центральные:
Jy^ =Jyz + abA. (4.9)
Полученные формулы используются при вычислении момен-
тов инерции простых и составных сечений.
Пример 4.1. Найти момент инерции прямоугольника относи-
тельно центральной оси (рис. 4.6).
Заменим переменную dA = bdz и вы-
числим:
п 1
J = b[z2dz = -bh3,
У I 3
тогда согласно (4.8)
J=~bh3--bh3=—bh3.
у 3 4 12
Пример 4.2. Найти момент инерции сечения, составленного
из пластины прямоугольного сечения 200 х 2 мм (стенка) и четы-
рех уголков 40 х 40 х 30, образующих полки составного стержня
(рис. 4.7), относительно оси у. Обозначим моменты инерции угол-
ка относительно собственной центральной оси J , площадь Alt
момент инерции стенки Jy2. Сечение
симметрично относительно оси z.
Момент инерции согласно (4.9):
Jy = Аг + Ai + •
Вычислим его. Площадь уголка
A j = 1,7 см2, Jyx = 2,35 см4,
г. =-Я-С; С = 1,09см находим из
2
ГОСТа и подставляем в формулу:
Jy = 133 + 4 • 2,35 + 4 • (10 - 1,09)2 =
= 682,24 см4.
-У
Рис. 4.7

56
р] Изменение моментов инерции при повороте осей...
Изменение моментов инерции
при повороте осей. Главные моменты инерции
Пусть даны моменты инерции
сечения относительно осей у. и z
(рис. 4.8) и нужно найти их отно-
сительно осей и и v, повернутых
на угол а. Координаты точки в
новой системе будут:
и = z sina + у cosa;
v= z cosa -у sina.
Моменты инерции относитель-
но повернутых осей:
Ju = J v2dA = J(z cos a - у sin a)rf4,
А А Рис. 4.8
Jv = ^u2dA = J(zsina + jcosa)rfJ,
A A
Juv = Jwv dA = J(zsina4-jcosa)(zcosa-jsina)JJ.
A A
После вычисления интегралов получим:
Ju = Jу cos2a + J7 sin2a - Jyr sin2a,
Jv = cos2a + Jy sin2a + Jyz sin2a,
JUv = “A)sin2a +Jyzcos2a. (410}
Почленное сложение двух первых уравнений показывает, что
Jy+Jz -Ju+Jv = J(j2 + z2)rfJ - сумма осевых моментов инер-
А
ции относительно перпендикулярных осей - величина постоянная.
и равная полярному моменту инерции Jp, так как у1 + z2 = р2, а
Jp=fp2dA.
А
Если сумма моментов инерции постоянна, то должны суще-
ствовать такие оси, относительно которых один момент максима-
лен, другой минимален. Назовем эти оси главными, оси симмет-
57
Изменение моментов инерции при повороте осей...
рии - всегда главные оси. Угод наклона этик осей к исходным
найдем из условия:
3J
-е=°- • (4.Н)
ОСС
Сравнение его с последним уравнением (4.10) показывает, что
относительно главных осей центробежный момент инерции равен
нулю. Из (4.11) определяется:
2J
tg2a=L-. (4.12)
Jy Jz
Используя процедуру, принятую при выводе формулы главных
напряжений, получим главные моменты инерции:
Лпах 4(^+A)±|j(Jy + A)2 +4J2..
min £
Рассмотрим на примере определение главных центральных
моментов инерции сечения, составленного из двух стандартных
профилей (рис. 4.'9): двутаврового № 20(2) и швеллера № 20(1); у
которых:
4, =26,6 см2; Jyi = 133 см4; Л, = 1520 см4;
А2 = 23,4 см2; Jyz = 2030 см4; = 155 см4.
1. Найдем положение центра тяжести. Примем за исходные
оси центральные оси швеллера:
_^АкУк.
Ус YAk ’ ' 2Л ’
Здесь ук и хк - расстояния от центров тяжести до исходных осей.
23,4 5 + 0 ... 23,4(2,07+10)+0 ...
ус =---------= 23,3 мм; =-------------•—----= 56,2 мм.
с 23,4+26,8 с 23,4+26,8
2. Вычислим Jy9
Л = Лг, + A\£ +J1I2 +л2Л2.
Здесь первый индекс обозначает номер составляющих сечений,
второй - номер оси.
Подставив значения, найдем:
Jy = 113 + 5,622 • 26,80 + 2,03 + 4,382 • 23,40 = 3326 см4;
Л = 1520 + 2,332 • 26,80 - 2,672 • 23,40 = 1986 см4.
58
Изменение моментов инерции при повороте осей...
Оси j jZj, >'2г2 - главные центральные оси швеллера и двутав-
ра, относительно их центробежные моменты инерции равны нулю,
поэтому центробежный момент инерции относительно централь-
ных осей составного сечения:
Jy- ~ y(zc^\ + abAj.
Его значение:
J = 2,33 • 562 • 26,80 - 2,67 • 4,38 • 23,40 = 629 см4.
>-
3. Главные моменты:
Jmax - 0,5(3326,8 +1986,0) ± - 71340,82 + 4-6292.
min 2
Вычисляя их, получим:
J = 3975 см4, J - = 1737 см4,
max ’ min
Положение главных осей относительно центральных, осей се-
чения находится по (4.12).
59
Общие понятия
Глава 5
ИЗГИЕ СТЕРЖНЕЙ
Общие понятия
F------------------------------------------------
Изгиб - вид нагружения силовых элементов машин и сооруже-
ний, при котором нормальные напряжения в поперечном сечении
сводятся к изгибающим моментам:
Mv =ja-zd4; Mz =joycL4,
A A
касательные - к поперечным силам:
Qy = j ^xydA\ Qz = J xX2dA.
A A
Все четыре статических эквивалента напряжений обнаружи-
ваются только при пространственном изгибе, когда изогнутая
ось - пространственная кривая. Пространственный изгиб вызы-
вается силами и парами сил, лежащими в разных плоскостях, со-
держащих продольную ось силового элемента.
Когда внешние силы лежат
в одной из главных плоскостей
инерции (рис. 5.1), происходит
изгиб в этой плоскости. При
плоском изгибе напряжения
приводятся к двум статическим
эквивалентам, например, к из-
гибающему моменту Му и по-
перечной силе 0Т'. Если вне-
шние силы составляют пары,
то во всех поперечных сечениях или в части их напряжения при-
водятся к изгибающим моментам. Такой изгиб называют чистым,
он может быть и плоским, и пространственным. Изгиб, при кото-
ром есть и поперечные силы Q, называется поперечным изгибом.
Здесь рассматривается плоский изгиб статически определимых
балок. Балками называют стержни, работающие главным обра-
зом на изгиб. Балки могут быть свободными и опертыми. При
действии на балку системы сил, лежащих в одной из главных плос-
костей инерции, опоры для обеспечения кинематической неизмен-
ности должны накладывать три связи. Для этого либо один конец
жестко закрепляется в неподвижной опоре (см. рис. 5.2, а), либо
60
Общие понятия
опираются оба конца. Одна из опор позволяет только поворот в
плоскости сил, вторая допускает поворот и свободное перемеще-
ние вдоль оси балки. Расчетная схема опор в виде шарнирно со-
единенных стерженьков изображена на рисунке 5.2.6.
IELL Внутренние силы в сечениях балки
при плоским изгибе
V----------------------------------------------
Статические эквмваленты внутренних сил определяются из
уравнений равновесия мысленно отсеченной части балки
ML + Q = 0; ХМ Му = 0. (5.1)
Остальные четыре уравнения (1.4) удовлетворяются тождест-
венно. При поперечном изгибе внешние силы направлены по нор-
мали к оси балки, пары сил лежат в плоскости, содержащей ось, и
уравнения (5.1) можно представить в виде двух правил:
61
Внутренние силы в сечениях балки при плоском изгибе
— поперечная сила равна сумме всех сил, приложенных по одну
сторону от сечения;
— изгибающий момент равен сумме моментов сил, приложенных
по одну сторону от сечения.
Введем также правила знаков. Будем считать силу Q положи-
тельной, если слева от сечения равнодействующая внешних сил
направлена вверх, а справа от сечение - вниз (рис. 5.3, а). Изги-
бающий момент М считаем положительным, если нижняя часть
балки растягивается, а верхняя сжимается; сумма моментов вне-
шних сил при этом направлена так, как показано на рис. 5.3, б.
с>о е<о
Рис. 5.3
Мо
О
Примечание, В строительстве приняты противоположные знаки
для Q и М.
Пользуясь приведенными правилами, рассмотрим вначале
наиболее простые примеры определения Q и М в балке,
защемленной одним концом.
1. Балка защемлена одним концом и нагружена парой сил с
моментом mQ (рис. 5.4). Нача-
ло координат удобно выбирать
на свободном конце. Сил, пер-
пендикулярных оси, нет; попе-
речная сила Qr всюду равна
нулю. Будем мысленно отсе-
кать правую часть балки. От-
носительно любого сечения х
= хк момент внешней пары оди-
наков, т.е. Му(х) = mQ. Это зна-
чение в некотором масштабе от-
кладывается вверх от линии
отсчета - строится эпюра мо-
мента. Штриховкой показыва-
ется направление отсчета.
е
Мо
.JJ0
Рис. 5.4
62
Внутренние силы в сечениях балки при плоском изгибе
Рис. 5.5
FI
2. Балка нагружена сосредо-
точенной силой F на свободном
конце (рис. 5.5). Поперечная сила
положительна и постоянна: Q =
F. Эпюра Q_ - горизонтальная
прямая линия. Изгибающий мо-
мент создается силой Ги линейно
зависит от расстояния до сечения
Л/ (х) = -Fx. Эпюра М - прямая
линия, наклоненная к линии от-
счета. Максимальный момент у
заделанного конца равен F • /.
3. Балка нагружена силой q,
равномерно распределенной по
длине (рис. 5.6). Равнодействую-
щая параллельных сил q, действующих на отсеченную часть, рав-
на сумме qx и приложена посере-
дине отсеченной части. Таким об-
разом, по правилу 1 получаем:
Qz = q х.
Эпюра - прямая, наклоненная
к линии отсчета.
Изгибающий момент по прави-
лу 2 определяется как момент рав-
нодействующей. В сечении с коор-
динатой х равнодействующая рав-
на qx; плечо ее равно 0,5х, поэто-
му:
Му = 0,5<ух2.
В сечениях любой балки из-
гибающий момент от равномерно
распределенной нагрузки равен
этому значению. Эпюра Му -
квадратная парабола.
4. Консольная балка нагружена силой, распределенной по за-
кону треугольника (рис. 5.7).
В любом сечении q - q0 —.
Из правила I имеем: ~
е-’=9о27‘
63
Внутренние силы в сечениях балки при плоском изгибе
Из правила 2 следует:
о/
Из рассмотренных примеров
легко видеть, что между попереч-
ной силой и изгибающим моментом
существует строго определенная
связь. Эта связь была впервые ус-
тановлена Д.И. Журавским. Пока-
жем ее.
Пусть балка (рис. 5.8) нагруже-
на по всему пролету. Рассмотрим
равновесие ее элемента. Внутренние О
силы в сечениях для него являются
внешними. Условия равновесия:
bZk = 0; ЪМС = 0.
Из первого уравнения следует:
dQ
(5-2)
Второе уравнение имеет вид:
Рис. 5.8
Последний член имеет
второй порядок малости и
может быть отброшен.
После приведения подоб-
ных членов получим:
_ dM
°‘17 <5”
- теорему Журавского.
Поперечная сила есть
производная от изгибаю-
щего момента, соответ-
ственно - изгибающий мо-
мент - интеграл от попе-
речной силы:
М = ^Qdx.
о
64
Внутренние силы в сечениях балки при плоском изгибе
При практических расчетах эпюры Q и М строят обычно для
отыскания опасного сечения - сечения, где внутренние силы имеют
наибольшие значения. В этих случаях находят значения Q и М в
характерных точках, в промежуточных сечениях эпюры строят
приближенно с учетом зависимостей (5.2) и (5.3). Из них следует:
— когда поперечная сила положительна, изгибающий момент воз-
растает, при отрицательном значении поперечной силы на уча-
стке момент убывает;
— в сечениях, где приложены сосредоточенные силы, поперечная
сила изменяется скачком (функция Q(x) терпит разрыв), эпюра
изгибающего момента не имеет общей касательной.
Поперечные силы и изгибающие моменты в сечениях балок,
нагруженных сосредоточенными силами, парами сил, силами, рас-
пределенными по части длины, есть кусочно-гладкие функции ко-
ординаты х. В силу указанных обстоятельств уравнения Q и М
удобно записывать через кусочно-гладкие функции вида фл(х - хД
где хк - координата внешней силы; п = 0, 1,2, 3, ...
Функции фл(х - таковы, что:
— прих<хА -ф„(х-хА.) = 0,
, ч (х-Хк)П
— при х > хА ф„(х-хА) =--------. (5.4)
л!
X
Легко видеть, что (х - хк )dx = ф,|+| (х - хк).
о
На самом деле, если х < хк при любом х, функция равна нулю,
равен нулю и интеграл от нее.
Если х > хк, то:
f , (х-хк)п+'
J <f>n(x-xk)dx = * = Ф„+1(х-хА). (5.5)
J (я+1)!
Ж Рекомендации по определению
поперечных сил и изгибающих моментов
в более сложных случаях нагружения
---------------------------------------------------------
Эпюры поперечных сил Q и изгибающих моментов М графи-
ки их изменения по длине балки, строятся для удобства расчетов.
В расчете обычно принимаются только наибольшие их значения в
3. Зак. 388 65
Рекомендации по определению поперечных сил...
балке или ее частях (при переменной жесткости EJ) Наибольшие
значения Q и М будут в следующих сечениях:
— где приложены сосредоточенные силы и пары сил;
— в начале или конце участков, распределенных по длине сил;
— где эпюра Q пересекает линию отсчета (в этих сечениях со-
гласно теореме Журавского изгибающий момент максимален);
где сечения балки меняются скачком.
Q и М необходимы для вычисления напряжений в граничных
сечениях.
При разнообразной нагрузке, а пока нет твердых навыков
вычислений, и в простых случаях нагружения, полезно записы-
вать уравнения для Q и М по правилам, изложенным выше.
* Таблица 5.1
Внутрен- няя сила Пара сил с . моментом /по Сосредот. сила F Равномерно распред, силаф Сила распред, по закону треугольн. 9 = у*
2(х) 0 F<po(x - Хк) F(pi(x - хк)
W) /Пофо(% - Хк) Fq\(x-xk) Гф2(х - Хк) уФзС*-**)
Допустимо составлять уравнения для каждого участка в от-
дельности в виде сумм сил или моментов. Для поперечной силы и
изгибающего момента будет столько уравнений, сколько участ-
ков между сосредоточенными силами (парами сил) и концами бал-
ки, свободных от нагрузки и участков распределенной силы. Эти
уравнения можно объединить в одно, обозначив границы между
участками вертикальными линиями. При такой записи уравнение
каждого участка включает и все предыдущие участки.
На рис.. 5.9 приведена схема балки, для которой необходимо
построить эпюры Q и М.
Разбиваем балку на участки по точкам приложения внешних
сил, при этом начало координат свяжем со свободным концом
балки (координату будем отсчитывать от левого конца). Напом-
ним, что выбор начала координат на свободном конце балки об-
легчает расчеты. Если бы мы выбрали начало координат в сече-
нии, примыкающем к заделке, то при построении эпюр необходи-
мо было бы предварительное определение реакций заделки. Эти
66
Рекомендации ло определению поперечных сил...
реакции будут поперечными силами и изгибающими моментами
на опоре.
На первом участке нет никаких сил, поэтому Q = 0. На втором
участке левее любого рассматриваемого сечения имеется толь-
ко одна сила направленная вниз, следовательно эпюра на
втором участке представляет собой прямую линию, параллель-
ную линии начала отсчета. Уравнение для Q на втором участке
(х<хк <2а)есть Q = F|n. На этом же участке изгибающий мо-
мент М = F(x - я)|п.
Подставляя в этом выражение значения х, соответствующие
границам участка, получим:
Л/|х=а = 0; Л/|х=2в = -Г-х.
В сечениях третьего участка (2а < х < 4а) добавляется сила
F2 = 2F, направленная вверх, следовательно,
Q = -F+2F=Flf
М = 0 - F,(x- d) + 2Fx(x - 2а).
Вычисляем значения М на границах участка:
— левая граница (х = 2а)М = -Fxa\
— правая граница (х = 4а): М = -Fx • За + 2FX 2а = Fxa.
3
67
Рекомендации по определению поперечных сил...
Общая запись уравнений для вычисления Q и М в любом
сечении балки, отстоящем на расстоянии х от начала координат,
имеет следующий вид:
2(х)= 0|j - FJjj + FJjjp (a)
M(x) = 0|T - Fx(x - a)|n + F2(x - 2a)|in. (b)
Здесь вертикальная черта с номером участка отделяет те сла-
гаемые, которые необходимо учитывать при вычислении попе-
речной силы Q и изгибающего момента М на соответствующих
участках (учитываются все слагаемые слева от черты).
Уравнения (а) и (Ь) могут быть записаны сразу в виде суммы
произведений внешних сил Fx и Г2, и функций фл(х - х^.
Поперечная сила
Q = -^(р0(х - а) + Г2(р0(х - 2а). (с)
х X
Так как М = jQdx, а|<р„(х-х,)</х = (ри+1(х-х0), то:
О о
М = -FjtpjCx - а) + F2tyx(x - 2а). (d)
Для построения эпюр обе силы вычисляются в сечениях (на
границах участков): х = 0; х = а; х = 2а; х = 4а.
При х < а из определения функций (рп(х - х0) следует, что Q и М
равны нулю. Если а < х < 2а (второй участок), то <р0(х - а) всюду,
а (рх(х - а) = х - а.
На границе этого участка имеем:
Qlx=a+dx = ~F\ ’ Q\x=2а = Л»
M\x=a+dx = ~F\dx = °; М^2а = Fr а-
Функции фл(х - х0) при х = хк терпят разрыв так же, как
поперечные силы в сечениях, где приложены сосредоточенные
силы F, т.е. при х = хк - dx - фл(х - х0); при х = хк + dx она скачком
возрастает до единицы, а функция ф^х- а) становится равной
аргументу.
На границах участка III из (с) и (d) имеем:
Q\x=2a+dx -~F\+ F2~ F> 6IX=4« = F\ ’
M\x=2a+dx = ~F\ (2a “ a + dx) = ~F\ ’ a'>
M\x^ = ~F\ (4a ~“) + F2 (4a ~d) = Fxd.
Эпюра, построенная по уравнениям (а), (b) или (с), (d) показана
на рис. 5.9.
68
Вычисление поперечных сил и изгибающих моментов в сечении...
Функции <рп(х - х0) предпочтительнее при неравномерном
распределении силы по длине балки. С увеличением порядка
функции внешней силы q(x) на единицу же увеличивается и номер
функции <рл(х -х0), например, при распределении силы q по закону
квадратной параболы поперечная сила:
Q(x) = ^q3(x-xk),
zo
а изгибающий момент:
М(х) = ^<р4(х-хк).
Данные вычисления при любой форме записи просты и могут
выполняться в уме. По приобретении твердых навыков в таких
задачах эпюры Q и М могут строиться без записи уравнений.
Особенно удобны функции <рл(х -хк) при интегрировании урав-
нений изгиба методом начальных параметров.
ДЦХ Вычисление поперечных сил и изгибающих
моментов в сечении билон ни двух опорах
V----------------------------------------------
Рассмотрим несколько примеров построения эпюр Q и М при
плоском изгибе балки на двух шарнирных опорах.
1. Балка нагружена сосредоточенной силой на пролете (рис.
5.10, а, б). К внешним силам для таких балок относятся и реакции
опор. При плоском изгибе к балке могут быть приложены сосре-
доточенные или распределенные по длине силы, образующие сис-
тему параллельных сил, и пары сил. Из возможных вариантов
уравнений равновесия плоской системы сил при вычислении ре-
акций предпочтительнее уравнения моментов относительно опор:
ХЛ^ = 0; ЕЛ/В = О.
Так как каждое из них содержит одну неизвестную реакцию, по-
лучаем:
Полезно проверить вычисление подстановкой Aj и R2 в третье
уравнение:
szt = o.
Полученные значения и R2 удовлетворяют уравнению. Сила F
делит балку на два участка с различными законами изменения Q и
69
Вычисление поперечных сил и изгибающих моментов в сечении...
М, последние будут кусочно-гладкими функциями координаты х.
Запишем уравнения Q и М в таком виде:
Q = W*) - *Р0(* -а);
М = RjCPj(х) - Fcpj(х - а).
В уравнениях нет реакции правой опоры, так как она лежит на
границе последнего из возможных сечений балки. По уравнениям
построены эпюры Q и М (см. рис. 5.10). Значения Q и М следует
вычислять только в местах приложения сил.
2. Балка нагружена парой сил на пролете с моментом Л/о (рис.
5.11). Силы реакции независимо от места приложения пары сил
будут одинаковыми по величине и обратными по знаку. На самом
70
Вычисление поперечных сил и изгибающих моментов в сечении...
деле из уравнений:
ЕМЛ=О, ЕЛ/Д = О
_ _ ' Мл
следует R^-R2- 4 -.
а + 6
Уравнения Q и М записыва-
ются подобно уравнениям пре-
дыдущего примера:
Q - Я1Ф0(*)+ °;
М = TfcjCpj(х) - тф,(х - а).
Эпюры, построенные по
ним, показаны на рис 5.11.
Из двух последних приме-
ров видим, что в сечениях, где
приложена сосредоточенная
сила F, имеется скачок в эпюре
Q на величину силы; на эпюре
моментов - скачок в месте при-
ложения пары сил.
3. Балка на двух опорах нагружена силой q, равномерно рас-
пределенной по пролету (рис. 5.12). Вследствие симметрии нагру-
жения силы реакции равны между собой:
Рис. 5.11
I
л, = л2 = 19/.
Из правила 1 следует та-
кое уравнение поперечной
силы:
2=а1ф0(х)-^ф0(х).
Уравнение изгибающего
момента согласно правилу 2
есть:
М = Я1Ф1(х) - ?ф2(*)-
Эпюры, построенные по
этим уравнениям, показаны
на рис. 5.12.
Эпюра Q - наклонная ли-
ния, пересекающая линию от-
счета в середине пролета.
Эпюра М - квадратная па-
71
Вычисление поперечных сил и изгибающих моментов в сечении...
t| ______
рабола, максимальное зна-
чение момента к середине
1 z2
пролета равно —qlz.
4. Балка на Двух опорах
нагружена силой q, равно-
мерно распределенной по
части пролета. Силы реак-
ций опор определяются из
уравнений = О, SA/в = О
и равны:
qb2 .
Л.=-------,
1 2(a+Z>)
qb(2a+b)
2 2(а + 6)
Пусть а = Ь. Тогда Q и М
получат значения, указан-
ные на эпюрах.
Эпюры поперечной си-лы и изгибающего момента (рис. 5.13)
построены по уравнениям:
о
Рис. 5.13
Q = Л]Ф0(х) - ^ф](х - а);
М = /?M(x) - <ЗФ2(х - а).
Если изменить место
приложения распределенной
силы, как показано на рис.
5.14, реакции опор будут:
R _qb(2a + b)
1 2(a + b) ’
R - qb2
2 2(a + Z>)
Здесь при записи уравне-
ний Q и М возможны два ва-
рианта. При выборе начала
координат на правой опоре
уравнения запишутся в том
72
Вычисление поперечных сил и изгибающих моментов в сечении...
же виде. При прежнем начале координат продлевается распреде-
ленная сила до конца пролета и дополняется фиктивной нагруз-
кой противоположного направления на участке, свободном от
нагрузки. Для второго варианта уравнения станут такими:
Q = ^1(p0(x)-^(p1(x)+w1(x-Z>);
Л/=Л,ф1(х)-9Ф2(х)+^ф2(х-6).
Во всех четырех примерах уравнения не содержат одну из ре-
акций опор, так как она оказывается на границе концевого сече-
ния.
5. Балка на двух опорах с консолью (рис. 5.15). Пусть F = qa.
Тогда Rx = 0,17#а; R2 = 1,83t?a.
Уравнения для внутренних сил в сечениях будут:
Q = Я1Ф0(х) - а) + яф/х - 2а) + Я2ф0(х - За);
М = /^ф/х) - <?ф2(х- а) + q<p2(x “ 2а) + Я2ф](х - За).
В этих уравнениях есть обе силы реакции, но нет силы F
приложенной на правом конце балки.
73
Нормальное напряжение при изгибе
Нормальное напряжение при изгибе
— - —

При чистом изгибе, когда по-
перечные силы равны нулю, се-
чения, проведенные в естествен-
ном состоянии балки плоско-
стью, перпендикулярной оси бал-
ки, остаются плоскими в натру- »
женном состоянии и поворачива-
ются относительно друг друга на
некоторый угол. Это можно уви-
деть, нагружая резиновый стер-
жень прямоугольного сечения
парами сил, приложенными по
концам (рис. 5.16) Изогнутая ось
балки - дуга окружности. При поперечном изгибе за счет сдвига
происходит депланация сечений, вызывающая дополнительные
нормальные напряжения. Их величина мала по сравнению с ос-
новными нормальными напряжениями, поэтому ими пренебрега-
ют,т.е. считают, что поперечные сечения остаются плоскими.
Одна часть балки (на рис. 5.16 верхняя) растягивается, дру-
гая сжимается, возникают нормальные напряжения. Получим фор-
мулу для их вычисления. Для этой цели воспользуемся известным
из второй главы статическим уравнением, полагая силы, лежа-
щими в плоскости xoz, тогда:
Му =jazdA,
А
а также законом Гука при одноосном напряженном состоянии
о = еЕ.
Для вычисления Интеграла нужно знать закон изменения де-
формаций в поперечном сечении. Очевидно, по ширине сечения
при плоском изгибе деформации будут одинаковыми, остается
узнать, как они изменяются по высоте сечения.
Выделим из балки бесконечно малый элемент длиной dx (рис.
5.17) и на расстоянии z от оси балки проведем линию АВ парал-
лельно оси х.
По определению деформация:
А'В'-АВ
--------
АВ
(5.6)
74
Нормальное напряжение при изгибе
Первоначальная длина АВ = dx, будем
полагать, что длина дуги радиуса р оста-
лась неизменной рб7ф = dx, тогда
е = (p + z)rf<p-prf<p = £ ' (5 7)
pjq> р’
т.е. деформация меняется по линейному
закону.
Теперь нормальное напряжение:
с = -Е, (5.8)
Р
подставим его в статическое уравнение:
М = — [z2dA. (5.9)
pi
Интеграл по площади от z2 есть осевой
момент инерции сечения Jy. Изгибающий
момент:
My=~Jy (5.10)
Р' д. р
Из (5.8) легко видеть, что — = —, исключим —, из (5.10) и
р z р
получим формулу для нормальных напряжений в поперечном се-
чении балки:
Mv
G = -^Z. (5.11)
Jy
Как и деформации нормальные напряжения изменяются по ли-
нейному закону. Остается узнать, откуда отсчитывать координа-
ту z. Ранее она отсчитывалась от центра сечения, через который
проходит ось неизогнутой балки. Легко проверить, что через центр
проходит и дуга радиусом р, т.е. что эта дуга и есть изогнутая ось
балки.
При изгибе нормальная сила:
W=j(jd4 = 0.
А
Подставим в интеграл а (5.11):

N
(5.12)
75
Нормальное напряжение при изгибе
Здесь может быть равен нулю только статический момент се-
чения = jzdA, но тогда ось х, от которой отсчитывается коор-
А
дината z, должна быть центральной,осью сечения.
Иногда в формуле
(5.11) индексы оси опуска-
ют, однако при этом пола-
гают, что момент инерции
должен вычисляться отно-
сительно нейтральной ли-
нии.
В однородной балке
жесткость на изгиб EJ по-
стоянна; ось изгибается по
дуге окружности, лежащей в силовой плоскости; напряжение а по
ширине сечения одинаково, поэтому эпюру напряжений можно изоб-
разить в виде линии, наклонной к плоскости сечения (рис. 5.18). »
Эпюра наглядно показывает, что напряжения в сечении рас-
пределены неравномерно: в центральной части сечения напряже-
ния малы, поэтому целесообразна такая форма сечения, у кото-
рой основная часть материала разнесена относительно нейтраль-
ной оси. Рациональную форму сечения имеют, например, двутав-
ровые стержни 1 и составленные из стенки и уголков 2; трехслой-
ные, состоящие из двух несущих слоев 4 и малопрочного легкого
заполнителя 3 (рис. 5.19).
Для расчета по напряжениям необходимо знать максимальные
напряжения. Введем новую геометрическую характеристику се-
чения - осевой момент сопротивления изгибу (5.13).
76
Касательные напряжения при изгибе
Jv J.
Wy=^- (5.13)
^max У max
Из (5.11) получим:
Mv
amax=-^- (5.14)
„У
wv
Критерием рациональности сечения можно принять —-,так
А
как допустимый изгибающий момент пропорционален моменту
сопротивления изгибу, а масса (вес стержня) - площади сечения.
LUL Касательные напряжения при изгибе
---------------------------------------------
При чистом изгибе поперечная сила Q = 0, следовательно, ка-
сательные напряжения равны нулю.
Для определения касательных, напряжений при попереч-
ном изгибе выделим из балки (рис. 5.20, а) элемент длиной dx
(рис. 5.20, б). Изгибающие моменты неодинаковы по длине, нео-
динаковыми будут и нормальные напряжения . Отсечем от эле-
мента по линии верхнюю часть и рассмотрим условие ее равнове-
сия. Нормальные напряжения, действующие на отсеченную часть,
заменим равнодействующими N и N + dN. Условие равновесия в
проекциях сил на ось х:
^ = 0 (5.15)
имеет Вид -N+N + dN + xb(z)dx = 0 • (5.16)
откуда dN i_/ ч — = tZ>(z), dx (5.17)
N= [adA.
доте
Так как N есть нормальная сила, действующая на отсеченную
часть, интеграл в статическом уравнении следует брать по пло-
щади отсеченной части Аотс;
dN (da ,
dx * dx
д omc
(5.18)
77
Касательные напряжения при изгибе
Рис. 5.20
Подставляя (5.18) и формулу (5.11) в левую часть (5.17), по-
лучим
1 dMy f АА
IzdA,
Jу dx J
Л--------доте
где S°mc = JzdA - статический момент отсеченной части.
д отс
Разрешим (5.17) относительно касательного напряжения и уч-
dMv
тем, что ---— = Q., тогда
Qomc
b(z)Jy
Эта формула была получена Д.И. Журавским. Она определя-
ет напряжения в продольных сечениях тТх. Согласно закону пар-
ности касательных напряжений такими же по величине будут на-
(5.Г9)
78
Касательные напряжения при изгибе
пряжения в поперечных сечениях (т_х). При выводе формулы в
(5.18) подставлялись нормальные напряжения, полученные без
учета влияния на них деформации сдвига, поэтому формулу Жу-
равского следует считать приближенной, но обеспечивающей
нужную точность.
Касательные напряжения в сечении меняются по закону Sy™ и
зависят от формы сечения. Можно показать, что в балках прямо-
угольного и двутаврового сечения касательное напряжение мак-
симально на нейтральной линии, где нормальные напряжения рав-
ны нулю. Эпюры касательных напряжений в балке прямоуголь-
ного и двутаврового сечений показаны
на рис. 5.21. По величине касательные
напряжения в длинных балках значи-
тельно меньше нормальных. Это легко
показать на примере консольной балки
прямоугольного сечения, нагруженной
силой на свободном конце (рис. 5.20).
Максимальное нормальное напряже-
ние:
CTmax w
„У
Для прямоугольного сечения:
где b - ширина сечения; h - высота.
Изгибающий момент в опасном сечении М = FI. Максималь-
ное касательное напряжение в балке прямоугольного сечения:
тта_ = 1,5—;
max г'
поперечная сила Q = F. Следовательно,
^шах _
Т___ h
В коротких балках изгибающий момент невелик, касательные
напряжения могут составлять значительную долю нормальных и
быть опасными для тонкостенных и деревянных балок. Балки с
тонкой стенкой рассчитывают на прочность по эквивалентным
напряжениям в точках, где одновременно велики нормальные и
касательные напряжения.
79
Перемещение при плоском изгибе
Перемещение при плоском изгибе
При выводе формулы (5.11) была получена зависимость кри-
визны от изгибающего момента и изгибной жесткости балки:
1 _ М
р" EJy'
Кривизна изогнутой оси в принятых обозначениях:
d2w
dx2
\2~|3/2 *
dw ]
L dx 1
1
р
При малых перемещениях, когда
жить:
' dw V
— «1, можно поло-
dx I
(5.20)
1 _ d2w
P dx2 ’
где iv - перемещение в плоскости изгиба (прогиб).
Уравнение изгиба балки постоянной жесткости можно запи-
сать в виде
dx2
Правая часть уравнения, изгибающий момент, есть кусочно-
гладкая функция координаты х. При большом числе участков в
эпюре уравнения (5.20) приходится интегрировать по участкам,
определяя при п участках 2п произвольных постоянных. Проще
эта задача решается методом начальных параметров. Первый
интеграл уравнения (5.20):
dw 1
— = — Mdx + Ч'.
dx
По смыслу постоянная 4х есть угол поворота сечения над опо-
рами балки.
Повторное интегрирование дает:
| XX
w = — f j М dx dx + Т • х + w0.
о о
где постоянная w0 есть прогиб в начале координат. Таким обра-
зом, необходимо вычислять лишь две постоянные интегрирова-
80
(5.21).
(5.22)
Перемещение при плоском изгибе
ния: 4х и и’о, их называют начальными параметрами.
Ранее было показано, что момент можно записать в виде произ-
ведения внешней силы на функцию фл = (х - х0), интеграл от кото-
рой х
J<pn (* - х„ )dx =ФЛ+, (х - х„ ),
О
т.е. интеграл от некоторой функции фл = (х - х0) равен функции со
следующим номером.
Постоянные 4х и и’о находятся из условий опирания:
х = 0; w = vv0;
х = 1; w = Wj.
Пример 5.1. Балка на двух опорах (см. рис. 5.14) нагружена
силой на пролете. Найдем уравнение прогибов. Для этой задачи
формула (5.22) примет следующий вид:
w = —f f[J?|фi(x) -F(pi(x - д)]dxdx + 4х • x + w0.
E 00
После интегрирования получим:
w = — [J? 1Ф1(х) - Гф ^x - fl)] + 4х • x + и’о. (5.23)
E
Находим начальные параметры:
При х = 0; w = vv0, значит w = 0.
При х = 1; w = wz, откуда 4х =-—[R{13 - F(l - fl)3].
6EJz
После подстановки 4х и и>0 в (5.23) вычисление прогибов балки в
любом сечении не представляет труда. Допускаемые значения про-
гибов устанавливают на основе эксплуатационных требований и
результатов эксперимента. При вычислении W из (5.23) необходимо
помнить о свойствах функции фл = (х - х0) (5.4). Следовательно,
слагаемое, содержащее F, следует учитывать только при х > а.
LJUL Критерии прочности ери плеском
и пространственном напряженных состояниях
47------------------------------------------------
При упругих деформациях расчет силовых элементов конст-
рукций на прочность ведется в напряжениях. При одноосном на-
пряженном состоянии, например, в растянутом стержне, предель-
81
Критерии прочности при плоском и пространственном ... состояниях
ную величину нормального напряжения находят эксперименталь-
но, доводя в лаборатории стержень из этого материала до разру-
шения.
При плоском и пространственном напряженных состояниях
возможно множество сочетаний значений главных напряжений,
получить это множество невозможно, кроме того, не все напря-
женные состояния реальных конструкций можно воспроизвести в
лаборатории.
Для оценки предельного напряженного состояния в опасных
(где напряжения наибольшие) точках на основе гипотез или ста-
тистических оценок известных экспериментальных данных вво-
дится некоторое эквивалентное напряжение. При оценке прочно-
сти это эквивалентное напряжение сравнивают с полученным для
выбранного материала предельными значениями напряжений в
опытах на растяжение (сжатие) или сдвиг, т.е. заменяют сложное
напряженное состояние одноосным, которое по какому-то при-
знаку, например, по напряжению и деформации, потенциальной
энергии эквивалентно реальному напряженному состоянию. Эк-
вивалентные напряжения выражаются аналитически через ком-
поненты действующих напряжений в виде равенства или нера-
венства, вид которых зависит от принятого критерия. Критерий
должен подтверждаться экспериментально.
Критерии прочности изотропных силовых элементов» Первы-
ми были критерии наибольших нормальных напряжений (за экви-
валентное принималось максимальное нормальное напряжение)
и наибольших деформаций (разрушение начинается при наиболь-
ших для материала деформациях). Эти критерии опытом подтвер-
ждаются для очень хрупких материалов (камень, стекло). В ма-
шиностроении из ранних критериев для материалов, одинаково
сопротивляющихся растяжению и сжатию, используются два :
— наибольших касательных напряжений;
— энергетический.
Согласно критерию наибольших касательных напряжений со-
стояние становится опасным, если касательное напряжение дос-
тигает предельного значения для материала, из которого изго-
товлен элемент конструкции. При этом значении касательного
напряжения материал переходит в пластическое состояние. При
испытании полированного круглого стержня на растяжение при
этом значении напряжения появляются на поверхности линии Лю-
дерса-Чернова, наклоненные к оси стержня под углом 45°. Под
этим углом действуют максимальные касательные напряжения.
82
Критерии прочности при плоском и пространственном ... состояниях
При пространственном
напряженном состоянии
максимальное касательное
напряжение по (1.26).
т _ ^max ~^min
max 2
В растянутом стержне
(112):
= j_
^max — 2 ®ор*
Здесь аор - опасное на-
пряжение при растяжении.
вор принимается за эквива-
лентное напряжение, т.е.
аэкв ” amax ” CTmin‘ (5.23)
Согласно энергетическому критерию предельным считается
состояние, при Котором потенциальная энергия формоизменения
становится равной потенциальной энергии формоизменения рас-
тянутого стержня в опасном состоянии:
и,=и;.
При одноосном напряженном состоянии ст2 = о3 = О согласно
(1.47)
ф ЗЕ
2
ор .
как и прежде считается cr = ст , т.е.
А jko ор
СТэкв = Jo? + + <^ - СТ1СТ2 - ст2о3 - 02^1. (5.24)
Оба критерия хорошо подтверждаются опытом для умеренно
пластичных материалов, эквивалентное напряжение по критерию
наибольших касательных напряжений больше, чем по энергети-
ческому на 12%.
В координатах о, т; о2, и3 можно построить предельные
поверхности. Область безопасных сочетаний главных' напряже-
ний по критерию наибольших касательных напряжений представ-
ляет собою поверхность шестигранной призмы с осью, равнонак-
лоненной по всем трем осям. Предельная поверхность энергети-
ческого критерия цилиндр, в который вписана шестигранная при-
зма, (рис. 5.23), при плоском напряженном состоянии - шести-
гранник и эллипс (рис. 5.24).
83
Критерии прочности при плоском и пространственном ... состояниях
Рис. 5.24
Рис.'5.23
Для материалов с разными пределами прочности на растяже-
ние и сжатие имеются аналоги рассмотренных здесь критериев:
— критерий О. Мора;
— критерий П.П. Баландина.
О. Мор в 1900 г. предложил предельную кривую в виде огиба-
ющей кругов Мора (рис. 5.25), построенных по известным экспе-
риментам, в качестве границы области безопасных сочетаний
напряжений в точке. По мере накопления экспериментальных
данных возможно уточнение границы. На практике используется
приближенная формула для эквивалентного напряжения, полу-
ченная при замене огибающей касательными к кругам Мора для
чистого растяжения и сжатия (рис. 5.26).
Уравнение касательной может быть записано так:
Oj = а + fc(T3,
где Gj и g3 - максимальное и минимальное напряжения.
Коэффициенты анк найдем, рассмотрев крайние случаи - ра-
стяжение и сжатие. При растяжении g3 = 0 = Gop, тогда а = аор-
опасное напряжение при растяжении. При’сжатии Gj = 0, g3 = GOf -
опасное напряжение сжатия. Теперь уравнение касательной при-
мет вид:
0 = (5.26)
Здесь напряжение сжатия считается отрицательным.
Из (5.26) следует к = —
<*ос
84
Критерии прочности при плоском и пространственном ... состояниях
За эквивалентное напряжение принимается опасное напряже-
ние растяжения, из (5.25) получаем:
°экв = О1-*аЗ- <5-27)
Критерий О. Мора, как и критерий наибольших касательных
напряжений, не учитывает среднего напряжения <т2, считается, что
это вносит погрешность порядка 17%.
Критерий П.П. Баландина построен на сравнении средней
удельной потенциальной энергии формоизменения с энергией фор-
моизменения одноосных напряженных состояний растяжения и
сжатия.
Средняя потенциальная энергия представляется как функция
среднего напряжения:
°ср = у(°1 +°2 + СТз)
U=a(Jrn + b. (5.28)
ср ср v '
Эта средняя энергия приравнивается к потенциальной энергии
формоизменения одноосных напряженных состояний, принимае-
мых за эквивалентные
иср=и™. (5.29)
Для определения коэффициентов а и ft в левую часть этого
равенства подставляются поочередно средние значения напряже-
ний растяжения = ~((а]р + 0 + 0) и сжатия <зсср = ^[а]с в опас-
ных до состояниях получается два уравнения:
14а],^ = ^[аП;
1 Г1 , 1 + LI г -2
--a[a]f+Z> = —
(530)
85
Расчет балок при изгибе
За опасные напряжения растяжения и сжатия приняты допус-
каемые напряжения.
Вычтя второе уравнение из первого, получим:
J
1+H/r т Г 1 \
откуда а = —— ([ст]р - [а]с),
ЗЕ
подставим его в (5.30) и получим:
ЗЕ
Условие прочности после внесения коэффициентов а и b в (5.50)
получается в виде неравенства:
[<т]Ор [а]с > о? + <522 + о} - о,а2 - о2а3 -о2О1~
-(а1+о2+о3)([о/,]-[о]с).
Существуют и иные условия прочности подобного типа. Вмес-
то главных напряжений в них могут вводиться напряжения в про-
извольных направлениях.
Расчет белек при изгибе
Расчет на прочность длинных балок при упругих деформаци-
ях ведется по напряжениям. В поверочном расчете максимальное
нормальное напряжение сравнивается с допускаемым
о = ^<
max w ~
В балках, принадлежащих летательным аппаратам, сравне-
ние ведется с пределом прочности, когда допустимы пластические
, ' ^МУ .
деформации птах =----— < или с пределом текучести.
Wy
Деревянные длинные балки, у которых мала прочность на скол,
проверяются на касательные напряжения. У балок прямоуголь-
ного сечения:
ттах =1,5-6-<[т],
Ьп
у круглых:
= 4_б_
3 то-2
86
Расчет балок при изгибе
Короткие балки с тонкими стенками рассчитываются по экви-
валентным напряжениям, так как в месте перехода полки в стен-
ку одновременно значительны и нормальные, и касательные на-
пряжения (рис. 5.33). Условие прочности по критерию максималь-
ных касательных напряжений примет вид:
°экв = отах -Отт = Vo2+4t2 <to].
По энергетическому критерию:
Оэкв =Vo^+3t^<[o].
Здесь нормальные напряжения определяются по формуле:
Му
а =—-z.
Jy
Для касательных напряжений применяют формулу Журавского:
hJy ’
где h - толщина стенки.
При резком изменении площади сечения балки за счет отвер-
стий, вырезов, сопряжения участков с различными размерами се-
чений, необходимо учитывать концентрацию напряжений в бал-
ках, изготовленных из высокопрочных сталей. Степень концент-
рации зависит от вида концентраторов и учитывается введением
в формулу для максимального нормального напряжения коэффи-
циента концентрации aG > 1:
Му
^тах “ и7 •
Момент сопротивления изгибу W вычисляется для ослаблен-
ного сечения. Коэффициент концентрации напряжений определя-
ется методами теории упругости, либо находится эксперименталь-
87
Расчет балок при изгибе
но. Величина коэффициента зависит от вида концентратора на-
пряжений. Наиболее частая необходимость учета концентрации
напряжений возникает при расчете валов.
Самые распространенные концентраторы круговые отверстия
и ступенчатые переходы сечения, они обычно скругляются. Кон-
центраторы напряжений особенно опасны при циклическом изме-
нении напряжений.
При непрерывном изменении жесткости балки за счет пере-
менной высоты Н, если угол наклона поверхности не более 20°,
нормальные напряжения а вычисляются по обычной формуле,
касательное напряжение находится по формуле:
= 6.57е + МЩх) Г _
Т” bJy + 4/ Jy dx'
из которой видно, что касательное напряжение зависит и от изги-
бающего момента.
Обычно балки переменной высоты бывают составными. Зак-
лепки или сварные швы рассчитываются на действие предельной
касательной силы, погонное значение которой:
" = QzS°ymc МНЬГ _ S°ymcH"IdH
1 Jy + 4/ I Jy \ dx ‘
Усилие, приходящееся на одну заклепку:
Т= 7^,
где 5 - шаг заклепок.
Допустимая сила [73 находится из условия среза:
tuZ2
4
где т - число возможных срезов, л - число заклепок, или из усло-
вия смятия
1Л =
из двух сил принимается меньшая.
Балки проверяются на жесткость, допустимый прогиб в строи-
тельных конструкциях wmax
---+---- Z. На летательных ап-
250 600 J
паратах допустимый прогиб задается нормами прочности, для ва-
।
лов механизмов и машин - стандартами.
as
Сложный изгиб
Глава 6
ПРОЧНОСТЬ СТЕРЖНЯ
ПРИ СЛОЖНОМ НАГРУЖЕНИИ
ИШь Сложный изгиб
V------------------------------------------
В общем случае нагружения статически определимых балок в
его сечениях из уравнений равновесия можно найти все шесть
статических эквивалентов нормальных и касательных напряже-
ний. После решения уравнений равновесия напряжения на осно-
ве принципа независимости действия сил есть суммы:
a=a(A9 + Q(A/J) + Q(A/z),
т = т(ер + т(е2) + т(Л/Д
Такой случай редок. Чаще встречаются изгиб с растяжением
(сжатием), сложный изгиб, изгиб с кручением, реже изгиб с растя-
жением (сжатием) и кручением.Сложный изгиб возникает от дей-
ствия сосредоточенных или распределенных вне-
шних сил, перпендикулярных оси и лежащих в
разных плоскостях, в том числе в обеих главных
плоскостях инерции, и пар сил. Разновидность
сложного изгиба, косой изгиб, вызывается сила-
ми, лежащими в одной плоскости, не совпадаю-
щей с главными плоскостями инерции.
В сечениях стержня в общем случае можно
выявить четыре силовых фактора - изгибающие
моментыи М2, поперечные силы Qy и Qz. Для
удобства их определения внешние силы, лежа-
щие в разных плоско-
стях, раскладываются на две составля-
ющие - проекции на главные плоско-
сти инерции.
Рассмотрим косой изгиб. Пусть на
балку (рис. 6.1) действует сила, лежа-
щая в плоскости, произвольно ориен-
тированной относительно главных
плоскостей инерции. Найдем изгибаю-
щий момент М и поперечную силу Q в
этой плоскости. В сечении будем рас-
кладывать момент силы по главным
осям инерции (рис. 6.2):
89
р] Сложный изгиб
Му = Л/sina; Mz = Л/cosa. (6.1)
Нормальное напряжение найдем как сумму напряжений от каж-
дого из моментов:
м м.
о =--~Z +—-у.
Jу J-.
Подставим (6.1), получим:
( .
zsina /сова
а = Л/ ---+------
(6.2)
(6.3)
гт Л . V у
Положив о = 0, найдем уравнение нейтральной линии
z = -y--tga. (6.4)
Нейтральная линия проходит через центр сечения, она не пер-
пендикулярна плоскости момента (плоскости внешних сил), так
как угловой коэффициент ее Л2 = - • ctga, а угловой коэффици-
ент силовой плоскости к2 = tga. Изгиб происходит не в плоскости
приложенных сил, а в другой плоскости, где жесткость меньшая.
Только при круглом и квадратном сечениях (Jy = J2) косой изгиб
невозможен. Угол наклона нейтральной линии к оси у одинаков
во всех сечениях, т.е. все сечения поворачиваются вокруг парал-
лельных линий, и изогнутая ось лежит в одной плоскости, перпен-
дикулярной нейтральной линии.
Опасной точкой сечения будет точка, наиболее удаленная от
нейтральной линии. В симметричном сечении эта точка находит-
ся просто, она является и наиболее удаленной от главных осей
инерции сечения. Максимальное напряжение в таких сечениях
находится по формуле:
(6.5)
max
sin a cos a
1^7+ W2
Если сечение имеет сложную форму, строится нейтральная
линия, находится графически наиболее удаленная от нее точка, и
координаты этой точки подставляются в формулу (6.3).
Проектировочный расчет при косом изгибе ведется методом
последовательных приближений. Вначале определяют потребный
момент сопротивления, полагая изгиб плоским:
w=—.
У [О]
90
р7! Изгиб с растяжением (сжатием)
Затем по этому значению Wy подбирают сечение с учетом со-
отношения моментов сопротивления W и W„.
Касательное напряжение также определяется в виде суммы:
Х = -^Н—+^Т7-- (6-6)
oJy oJz
Прогиб находится как геометрическая сумма перемещений в
плоскостях xoz и хоу: f = <jw2+v2. Перемещения w и v определя-
ются из решения уравнений изгиба в соответствующих плоскостях.
Изгиб с растяжением (сжатием)
Сложный изгиб с растяжением (сжатием) вызывается силами,
пересекающими ось стержня в разных плоскостях. Эквивалент-
ная система сил находится разложением внешних сил, приложен-
ных в некотором сечении по осям координат х, у, z. Статические
эквиваленты напряжений N, М? Mz, Q? Q„ находятся по извест-
ным правилам.
Нормальные напряжения вычисляются по формуле:
N М Mz
= + (6.7)
A Jz
Когда силы лежат в одной из главных плоскостей инерции,
например, в плоскости xoz, третье слагаемое исчезает:
N Му
сг = —+ —
(6.8)
Z.
У
Такое напряженное состояние
возникает в вертикально стоящей
цистерне при действии на нее вет-
рового потока, в плоских рамах,
состоящих из стержней, лежащих в
одной плоскости (рис. 6.3). В этой
же плоскости лежат внешние силы.
Частным случаем такого на-
гружения является внецентренное
растяжение (сжатие) силой F, при-
ложенной в точке j>0, z0 (рис. 6.4).
Рис. 6.3
91
Изгиб с растяжением (сжатием)
Относительно главных осей она со-
здает моменты:
ту = Fz0’ mz= рУ^
такими же будут изгибающие момен-
ты во всех сечениях.
Нормальное напряжение в сече-
нии определяется суммой
N М М.
о =— + —-z +—-
Л Jy Jz
Рис. 6.4
или
(6.9)
„ 1 ZZn УУа
= F — + —9-z + ^-y
J’ ..
Уравнение нейтральной линии сечения имеет вид:
z+?jry =0' (6.10)
z )
Из (6.10) видно, что нейт-
ральная линия при любых коор-
динатах точки приложения внеш-
ней силы не проходит через центр
сечения и может лежать как в се-
чении, так и за пределами его.
Расстояние от центра сечения до
нейтральной линии (рис. 6.5):
ос= 1 -.
I 2 2
№. №.
При проектировании стерж-
ней из материалов, плохо сопро-
тивляющихся растяжению (кирпич, бетон, серый чугун), желатель-
но не допускать растягивающих напряжений. Чтобы напряжения
в сечении имели один знак, т.е. нейтральная линия не пересекала
сечение, необходимо прикладывать силу в границах некоторой
области, называемой ядром (рис. 6.5). Когда сила приложена на
границе ядра сечения, нейтральная линия касается контура.
92
Изгиб с кручением
KLL Изгиб с кручением
---------------------------------------------------
Одновременному изгибу и кручению подвергаются валы раз-
личных механизмов, зубчатых, фрикционных, ременных от сил,
действующих в зацеплениях зубчатых колес, от натяжения рем-
ней, веса колес и шкивов.
Для расчета валов силы мысленно переносятся в центры их
сечений и согласно лемме о параллельном переносе силы прикла-
дываются пары сил с моментом, равным моменту силы относи-
тельно оси вала.
В зубчатых, цилиндрических,
ременных и фрикционных механиз-
мах силы перпендикулярны осям, в
механизмах с косозубыми и коничес-
кими колесами силы в зацеплении
имеют й осевые составляющие, при
их переносе на ось вала приклады-
ваются пары в плоскостях, содержа-
щих ось вала.
Таким образом, в сечениях вала
напряжения можно привести ко всем
шести эквивалентам, однако суще-
ственное значение для определения
безопасных размеров сечения имеют
напряжения от изгиба и кручения.
Покажем, что изгибающий и крутя-
щие моменты можно заменить экви-
валентным изгибающим моментом,
его называют также приведенным моментом.
Пусть коленообразный круглый стержень (рис. 6.6) нагружен
силой на свободном конце,, тогда участок АВ будет изгибаться и
закручиваться. Эпюры моментов показаны на рис. 6.7. Напря-
женное состояние в точке изображено на рис. 6.8. Оно относится к
типу плоских напряженных состояний
(Оу = 0) и по критерию наибольших ка-
сательных напряжений эквивалентное
напряжение 0ЭКВ = Qmax - Qmin, согласно
(см. стр. 87):
оэкв = 7сг2+4т2,
93
Изгиб с кручением
по энергетическому критерию:
аэк, = 777з7. (6.12)
Максимальное нормальное и касательное напряжения возни-
кают в точках у поверхности стержня, поэтому:
= 1^ 4
ЦТ)'
У круглых сечении Wp = 2Wy и
обозначим Мт = тогда условие прочности предста-
вится неравенством:
(6.13)
(6.W)
(6.15)
экв
wy
Если воспользоваться энергетическим критерием прочности:
A/=Ja/2+O,75A/£.
ЭКВ V У Л
Момент сопротивления изгибу сплошного вала:
у 32
Диаметр сплошного вала:
(6.16)
пустотелого:
'32МЯ,
rf = 3--------,
я[в]
(6.17)

(6.18)
Пример расчета на изгиб с кручением. Используем формулу
(6.15) для расчета промежуточного вала зубчатого редуктора с
цилиндрическими колесами радиусами начальных окружностей
= 100 мм; г2 = 150 мм, поперечный разрез которого показан на ри-
сунке 6.9, расчетная схема на рисунке 6.10. Усилия, действующие
на зубчатые колеса промежуточного вала, направлены по линии
зацепления колес, наклоненной к общей касательной начальных
94
Изгиб с кручением
Рис. 6.9
окружностей под углом а = 20°.
Разложим их на касательные (ок-
ружные) Fn, Fa и радикальные со-
ставляющие FrP Fr2, а затем пере-
несем на вал, приложив моменты
т{ = т2 = т (см* Рис- 6.Ю).
Пусть проекции усилий будут
FXr = 5,44 кН; F2r = 10,00кН;
Fa = 15,00 кН; Ft2 = 3,36 кН.
Определим реакции опор. В
вертикальной плоскости R} и R3
находим из уравнений:
0,2 Fj -2,2 • F^ + 2,6 • Я3 = 0;
2,6 • Fr2,4 • Flr + 0,4 • F2r + = 0,
Rx = 3,48 кН; R3 = 8,04 кН.
В горизонтальной плоскости R2 и R4 находим из уравнений:
0,2 • Flt-2,2 - F^ + 2,6 • Я4 = 0;
2,6 • Л2-2,4 • Flt + 0,4 • F2t = 0,
R2- 14,40 кН; F4 = 4,22kH.
Легко понять, что наибольшие изгибающие моменты будут в
сечениях 1 и 2 у колес, поэтому эпюры изгибающих моментов
можно строить приближенно, соединяя найденные значения пря-
мыми линиями. Эпюры изгибающих моментов даны на рисунке
6.10 в вертикальной и горизонтальной плоскостях. Сложим гео-
метрически моменты в опасных сечениях и М2.
= JmI+mI = 2,96 кН • м;
М2 = = 3,63. кН -м.
В сечениях между колесами эпюра М будет нелинейной, ха-
рактер ее приближенно показан на том же рисунке. Наиболее опас-
ным оказалось сечение 2.
Крутящий момент Mk между сечениями 1 и 2 одинаков: Мк-т
= Fu r= 1,5 кН м.
Ввиду малости моментов сил трения в подшипниках ими пре-
небрегаем.
Расчетный (приведенный) момент по теории удельной энергии
формоизменения в сечении 2:
95
Изгиб с кручением
Мпр = ^Мз+0,75М2к = 3,85 кН м
Так как вал вращается, напряжения в опасных точках будут
изменяться циклически. Это обстоятельство должно учитываться
при расчете. Здесь мы его учтем, назначив [а] = 120 МПа. Диа-
метр вала по (6.17) будет:
3,22кН-М
3,63кН-м
1,5к Н-м

Рис. 6.10
96
Расчет стержней при циклическом изменении напряжений
32Л/„р
л[а]
= 68 мм.
Полученное значение округляем до стандартного d = 70 мм.
||E-jJL Расчет стержней при циклическом изменении
напряжений
V-----------------------------------------“
При циклическом изменении напряжений в сечениях стержней
постепенно накапливаются микротрещины из-за местных высо-
ких напряжений, появляющихся как вследствие неоднородности
строения самого материала, так и вследствие влияния конструк-
тивно-технологических факторов. Разрушение в результате воз-
действия циклически изменяющих-
ся напряжений называется устало-
стным разрушением, а способность
материала сопротивляться устало-
стному разрушению - выносливо-
стью. При усталостном разруше-
нии в сечении стержня можно на-
блюдать две зоны - гладкую и
крупнозернистую Гладкая зона -
зона развития усталостных тре-
щин; крупнозернистая - зона мгно-
венного разрушения из-за умень-
шения площади сечения (рис. 6.11).
Рис. 6.11
Циклическое изменение
напряжений может возникать
от действия постоянной си-
лы, если сечение поворачи-
вается относительно оси, пер-
пендикулярной линии дей-
ствия силы (рис. 6.12), или от
действия силы, периодически
изменяющейся во времени,
например, F=FQsinkt. Время
работы до разрушения зави-
Рис. 6.12
сит от характера цикла.
4. Зак. 388
97
Расчет стержней при циклическом изменении напряжений
Циклом называют совокупность значений напряжений за вре-
мя одного периода. Различают симметричный (рис. 6.13) и несим-
метричный (рис. 6.14) циклы. Циклы характеризуются максималь-
ным и средним напряжениями, амплитудой напряжений, коэффи-
циентом асимметрии, формой и частотой. .
Среднее напряжение:
от = °Фах (6.20)
Амплитуда цикла:
^Pmax-Omin. (6,21)
Коэффициентом асимметрии цикла называется отношение ми-
нимального йапряжения цикла к максимальному напряжению:
г = -^. (6.22)
^шах
Циклы с одинаковыми значениями называются подобными.
Коэффициент асимметрии симметричного цикла г=-1, так как
^max ^min*
У пульсационных (отнулевых) циклов, показанных на рисун-
ке 6.15, г = 0 или г = -°°. Опыт показывает, что определяющими
характеристиками цикла являются amax, omin и г.
Наиболее опасным является симметричный цикл. При любом
циклическом изменении напряжений усталостное разрушение
становится возможным при определенном значении напряжений
цикла. Усталостные свойства материалов сравнивают по пре-
делу выносливости - наибольшему максимальному напряжению
симметричного цикла, при котором не происходит разрушение
(рис. 6.16). Предел выносливости определяют экспериментально
при чистом изгибе круглых полированных стержней диаметром
d- 7,5 мм на специальных машинах. При испытаниях сначала со-
98
Расчет стержней при циклическом изменении напряжений
Рис. 6.15
здают высокие напряжения, отмечают величину <за и число циклов
N, при котором произошло разрушение. Затем напряжения снижа-
ют. При некотором значении напряжения стержень не разрушает-
ся. Это напряжение называется пределом выносливости. По точ-
кам строят кривую (см. рис. 6.16). Стержни из малоуглеродистой
стали при нормальной температуре не разрушившиеся за 107 цик-
лов, не разрушаются и при большей длительности испытаний. Для
высокопрочных сталей и сплавов цветных металлов такого опре-
деленного числа циклов указать нельзя, поэтому в подобных слу-
чаях предельное число циклов задается равным N = 108.
Предел выносливости обозначается и зависит от предела
прочности. Приближенно считают: для сталей = 0,4... 0,6) se, для
сплавов цветных металлов о.! = (0,25... 0,50) при кручении соот-
ветственно т j = (У-р t_j = 0,8 О-р
а При несимметричных циклах
а экспериментально получают ди-
аграмму предельных напряжений
а-! -------- (рис. 6.17). На предел выносливо-
сти влияют концентрация напря-
жений, размеры сечения, состоя-
\ ние поверхности, температура,
\ корродирующие свойства среды,
_________________X—режим нагружения, предваритель-
на от ное нагружение при пластических
Рис. 6.17 деформациях. Кривые, показан-
4
99
Расчет стержней при циклическом изменении напряжений
ные на рисунках 6.16 и 6.17, строят при испытании полирован-
ных стандартных образцов диаметром d = 7,5 мм. Предельные
напряжения при испытаниях деталей машин и сооружений оказы-
ваются меньшими в результате действия перечисленных выше
факторов.
В местах резкого изменения поперечного сечения возникает
концентрация напряжений (рис. 6.18). Максимальное напряже-
ние может в 2-4 раза превышать номинальное, рассчитанное без
учета особенностей сечения. Влияние концентраторов напряже-
ний на предел выносливости учитываю! введением коэффициен-
тов концентрации напряжений:
(6-23)
определяемых теоретически или экспериментально (рис. 6.19). Дня
этого в (6.23) подставляют значения пределов выносливости глад-
кого стержня и стержня с концентратором
Предел выносливости снижается с увеличением поперечных раз-
меров стержня при растяжении, изгибе и кручении. Это снижение
объясняется уменьшением прочности за счет неоднородности за-
готовок больших размеров, меньшей чистоты поверхности, не-
стабильности, стабильности механических свойств материала в
объеме детали, большей вероятности появления опасных дефек-
тов. Поправка к предельным напряжениям вносится с помощью
масштабного коэффициента:
100
Расчет стержней при циклическом изменении напряжений
Масштабный коэффициент гм зависит от рода материала и
наличия концентраторов. Чем выше предел прочности материа-
ла, тем он чувствительнее к концентраторам напряжения. У по-
верхности стержней при изгибе и кручении наибольшие напряже-
ния, а поверхность стержня имеет дефекты, о бу слов) генные меха-
нической обработкой или коррозией. Влияние состонния поверх-
ности учитывается введением коэффициента:
0-1
где - предел выносливости серийной детали; ct_j - предел
выносливости полированного стержня.
Коэффициент состояния поверхности зависит от предела проч-
ности. На рис. 6.20 кривые соответствуют различной обработке:
1 - полирование; 2 - шлифование; 3 - тонкое точение; 4 - грубое
точение; 5 - необработанная
поверхность с окалиной. При
повышении температуры
стальных стержней сверх 300°
предел выносливости снижа-
ется на 15-20% на каждые
100°; при пониженных темпе-
ратурах предел выносливости
может увеличиваться вдвое.
Предел выносливости повы-
шается при поверхностной об-
101
р] Расчет стержней при циклическом изменении напряжений
работке деталей - закалке токами высокой частоты, цементации,
азотировании, обкатке роликами или обдуве дробью, увеличение
предела выносливости учитывают введением коэффициента kv.
Все перечисленные факторы учитываются введением одного
коэффициента:
(аа 1 И
к° = V (6'24)
ЕЛ/ Р JKv
Запас прочности при симметричном цикле изменения напряже-
ний растяжения и изгиба определяется по формуле:
S° = ~’ (6-25)
где (6.26)
При кручении запас прочности:
Sx = -^-. (6.27)
Запас прочности на изгиб с кручением обычно находится из
эллиптической зависимости, установленной опытом:
11 1
S2 ~ S2* S2‘ (6.28)
' В случае несимметричного цикла для вывода формулы коэф-
фициента запаса усталостной прочности используется известное
уравнение прямой, проходящей через две точки:
У~У1 _ У2~У1
X - Xj х2 - хх
Диаграмму предельных напряжений строят по трем точкам:
^-,^(0,св)(рис. 6.21).
(° „ 0);
В координатах и для лабораторного стержня уравнение
линии, ограничивающей область безопасных сочетаний аа и ош:
Og-g-l _ 2____
Яо-о ’
2

где о0 - амплитуда цикла с г = 0.
102
Расчет стержней при циклическом изменении напряжений
Для детали уравнение нижней прямой на рис. 6.21:
[« Я=1
L а* 1, о/, к
[стт]-0 _Оо._0 ‘
2ка
Рабочие участки этих линий ограничиваются линией, прове-
денной через точку под углом 45° к оси ow..
Обозначим: ~
2
Тогда амплитудное напряжение образца материала:
Заметим, что по опытным данным для углеродистых сталей
при из гибе и растяжении угловой коэффициент прямой Т = 0,1 ...
0,2 для легированных 4х = 0,2 ... 0,3.
Допустимое значение амплитудного напряжения детали:
[oj = 2-(<I-l
из подобия треугольников О АС и OBD имеем
теперь

103
Pl Расчет стержней при циклическом изменении напряжений
Это уравнение преобразуем к следующему виду:
О-1 - —(<*а Ат + <WP) = О-
Из подобия тех же треугольников Следует:
ОД=[^] = [Пд]
ОА ат аа ’
но отношение допускаемых напряжений [ow], [nJ к дейстую-
щим есть запас прочности по нормальным напряжениям Sa.
Следовательно, запас усталостной прочности по нормальным
напряжениям будет: <
с а-1
Аналогично можно получить и формулу коэффициента запаса
усталостной прочности по касательным напряжениям при круче-
нии:
Sx~ kaTa+'¥Tm' (631)
При кручении угловой коэффициент меньше, а именно:
— Т = 0,05...0,10 для углеродистых сталей;
— т = 0,10...0,15 для легированных статей.
При изгибе (растяжении) с кручением запас усталостной
прочности определяется из экспериментальной зависимости (6.28).
В ней Sa и Sx вычисляются по формулам (6.30), (6.31).
Формула (6.28) или
применима во всех случаях, как при одновременном достижении
максимальных значений нормальных о и касательных т напряже-
ний, так и при неодновременном их достижении.
104
Основные понятия теории пластичности
Глава 7
ПРОЧНОСТЬ СТЕРЖНЕЙ
ПРИ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ
EEL Основные понятая теории пластичности
V----------------------------------------------
Внешние силы в некоторых случаях могут стать выше допус-
каемых. Для сооружений и машин одноразового применения воз-
можны напряжения выше предела текучести. Закон Гука при рас-
четах на такие нагрузки применять нельзя: зависимость напряже-
ний от деформаций становится нелинейной. Часть энергии дефор-
мации превращается в тепловую и рассеивается.
Законы пластического деформирования и методы расчета при
напряжениях, превышающих предел упругости, изучаются в тео-
рии пластичности. Длительное нагружение силовых элементов
машин и сооружений при повышенной температуре приводит к
медленному течению материала под действием неизменных сил,
называемому ползучестью. Расчеты таких элементов конструк-
ции - предмет теории ползучести.
В теории пластичности различают активную и пассивную де-
формацию. Активной называют деформацию при непрерывном
нагружении и непрерывном росте напряжения. Деформации при
уменьшении силы называются пассивными. Нагружение называ-
ют простым, если все силы возрастают пропорционально некото-
рому параметру.
У идеально упругого материала деформации при нагружении
и разгружении пропорциональны напряжению, после снятия силы
деформации исчезают, правда у реальных упругих тел процесс
полного возвращения в недеформированное состояние очень мед-
ленный.
Когда напряжение при растяжении превышает предел упруго-
сти, деформации исчезают не полностью. Стержень после снятия
силы окажется длиннее (рис. 7.1). Линии нагружения и разгрузки
не совпадают.
Простейшие задачи теории пластичности, в которых боль-
шинство уравнений удовлетворяется тождественно, растяжение,
кручение, изгиб стержней, осесимметричная деформация толсто-
стенных цилиндрических и сферических оболочек решаются путем
аппроксимации (преобразования с упрощением) диаграмм о -
Связь между деформацией и напряжением устанавливается в виде
105
о = Ef г. Вид аппроксимации диаграмм зависит от величины де-
формации. Диаграмму малоуглеродистой стали (см. рис.7.1.6)
можно представить в виде, показанном на рис. 7.2. При
е < ег а = е £,
< е < о = аг,
е2 > е > Ej о = Е'е,
где |Е'| = tga.
Иногда пренебрегают упругой деформацией и представляют
диаграмму в виде прямых (1 - жестко-пластическое тело, 2 - жес-
ткое тело с линейным упрочнением), показанных на рис. 7.3. Для
некоторых материалов удобен степенной закон,
закон арктангенса или аппроксимации полиномами.
106
Чистый изгиб стержня
11Шк Чистый изгиб стержня
Как и при упругих деформациях при чистом изгибе сечения
остаются плоскими, поэтому деформация по высоте сечения меня-
ется по линейному закону:
Z
Е = —.
Р
Расчет сводится к определению предельного изгибающего мо-
мента:
My=^zdA.
А
Найдем предельный момент, полагая степенной закон зависи-
мости напряжений от деформаций (8.1) для балки, сечение кото-
рой имеет две оси симметрии.
Изгибающий момент:
М \z^xdz
у &ТГрт Jo
Zn
Представим Ег= —, где z0 - координата точек (рис. 7.4), в ко-
торой деформация Е > Ег, тогда предельный момент:
Рис. 7.4
107
Чистый изгиб стержня
При упругой диформации всюду в сече-
нии, кроме точек у поверхности, где а = ар
(рис. 7.5) т = 1, изгибающий момент балки
прямоугольного сечения:
По мере распространения зоны пластичес-
ких деформаций к нейтральной линии сечения
(оси у) изгибающий момент увеличивается. Состояние балки ста-
нет предельным, она превратится в мгновенный механизм за счет
образования пластического шарнира в сечении, где наибольший
изгибающий момент. В предельном состоянии z -» 0 (рис. 7.6)
предельный момент балки из идеально пластического материала
(ш = 0):
,z bh2
^упр -
Итак, для балки прямоугольного сечения из идеально пласти-
ческого материала Мпр увеличивается в 1,5 раза по сравнению с
моментом при упругих деформациях, у Двутавровых балок он
возрастает лишь в 1,18 раз. Читателю предлагается показать,
что в балках с одной осью симметрии сечения (рис. 7.7) нейтраль-
ная линия делит площадь сечения пополам, воспользовавшись
тем, что при изгибе:
# = |о4/Л = 0.
А
При поперечном изгибе задача определения предельного мо-
мента усложняется, но в первом приближении можно полагать
применимой гипотезу плоских сечений.
108
Чистое кручение круглого стержня
Чистое кручение круглого стержня
Рис. 7.8
Можно полагать, что и при пласти-
ческих деформациях сечения круглого
стержня остаются плоскими и сохраня-
ют свою форму, тогда из условия рав-
новесия элемента стержня длиной dx
(рис. 7.8) деформация сдвига:
у = 0р.
При степенном законе аппроксима-
ции диаграммы т - у:
z \т
I Y
т = тг — ,
Yr
крутящий момент:
Мк
Yri
заменой переменных у = р0, dA = 2лрф (рис. 7.9) приводится к
виду:
о
Если задать размеры упругой области радиусом г0 после ин-
тегрирования крутящий момент станет (рис. 7. ГО):
__ 2тТ гт+3
мк =------------.
rom т + 3
Эпюра касательных напряжений при идеальной пластичности
будет иметь вид, показанный на рис. 7.10.
109
Чистое кручение круглого стержня
Когда не допускается в опасных точках сечения напряжений
больше предела текучести и считается т = 1, а г0 = г, предельный
крутящийся момент:
яг
ЛГ = ----•
* т 2
В предельном состоянии стержня из идеального пластическо-
го материала (т = 0), когда по всему сечению деформации станут
пластическими (г0 -»0), предельный момент:
„ 2 з
Мклр=~1ПтГ ,
т.е. несущая способность увеличивается в 1,33 раза.
Предельное значение момента достигается при большом угле
закручивания, поэтому расчет по предельному моменту имеет
смысл только для пластических амортизаторов кручения.
Для статически неопределимых стер-
жней выигрыш в несущей способности
может быть выше. Пусть стержень за-
щемлен обеими концами и нагружен па-
рой сил с моментом (рис. 7.11). Уравне-
ние равновесия:
Л/о + = m
содержит два неизвестных. Условие со-
вместности деформаций - углы закру-
чивания левой I и правой II частей оди-
наковы:
Ф1=Фц-
Угол закручивания круглого стреж-
ня согласно (4.11): Рис. 7.11
Уравнение совместности деформаций однородного стрежня
Л/о • а= М{'Ь позволяет установить соотношения реактивных мо-
ментов
М0=М/—.
' а
Из уравнения равновесия найдется момент на правой опоре:
= m а ,
a + b
110
Чистое кручение круглого стержня
таким же будет и крутящий момент правой части стержня. В сече-
ниях левой части: . а
= m----7-
a + b
Из сравнения концевых моментов видно, что крутящий момент
больше в короткой части стержня. Когда в ней будет достигнуто
предельное состояние, длинная часть стержня будет сохранять
несущую способность. Для всего стержня из идеально пластиче-
ского материала предельное состояние наступит тогда, когда в
сечениях более длинной части пластические деформации разовь-
ются по всему сечению. Когда а = Ъ (см. рис. 7.11), предельное
состояние достигается сразу для всего стержня. Очевидно для это-
го случая выигрыш в несущей способности такой же, как и в ста-
тически определимом стержне.
Сравним несущую способность стержня, нагруженного парой
сил, приложенной ближе к одному из жестко защемленных концов
(а < Ь). Пусть b = па, и п = 2, 3, 4 ...
2
Примем b = 2а, тогда MKj =^m-
При расчете по допускаемым напряжениям при [т] = тг:
. _ ltd3
4 16
допускаемый момент пары сил, приложенной к стержню:
Г , 2nd3
[ли] =----тг.
3 16 т
При достижении предельного состояния в левой, более нагру-
женной части стержня:
М,
т.е.
nd3
ТГ’
г , 2nd3
[m ] =---тг.
3 12 Т -
В это время в правой части стержня крутящий момент вдвое
меньше:
1 ЛбР
Мк„ = ~МК, =тт—.
кп 2 1 1 24
Для стержня в целом состояние станет предельным при увели-
nd3
чении момента пары сил m на величину Дт = тг-^-, т.е. пре-
111
Растяжение статически неопределимой фермы
дельный момент этой пары:
липр = т + Дли = тг
3 1
24 + 24
nd3
~хг~6~'
Таким образом, для статически неопределимого стержня:
^=“=1,78,
[т) 36
т.е. несущая способность при расчете по Предельному состоянию
увеличивается больше, чем у статически определимого.
Заметим кстати, что дополнительные связи увеличивают несу-
щую способность.
Читателю предлагается повторить расчет при других значе-
ниях а и Ь.
ДХ Растяжение статически
неопределимых ферм
V-----------------------------------------------
В статически определимых фермах напряжения во всех стерж-
нях одинаковы и расчеты по допускаемым напряжениям не отлича-
ют ся от расчета по предельным нагрузкам.
Расчет статически неопределимой фермы
(рис. 7.12) по допускаемым напряжениям в п.
2.5. дал такие значения нормальных сил:
xr Feos2 а F
М=---------; n2 =---------
l + 2cosza l + 2cos а
Пусть стержни изготовлены из идеально
пластического материала, тогда предельным
можно считать состояние, в котором во всех
стержнях деформации станут пластическими.
Как только напряжения в среднем стержне
достигнут предела текучести, нормальная сила
в нем при дальнейшем нагружении останется постоянной:
7V2 о 'р * .
Внешняя сила в это время станет:
F=or4(l +2cos3a).
В крайних стержнях деформации будут еще упругими, система
станет статически определимой. Предельное состояние наступит,
Рис. 7.12
1 г F
112
Стержневые системы
когда в крайних стержнях напряжения станут равными пределу
текучести. Внешняя сила в этом состоянии:
F = aTA +2арЛ •cos3a=ar4(l +2cosa). r
Если для фермы a = 30° за допускаемое напряжение принять
F
предел текучести, то -^ = 1,19 (проверьте).
Примечание. Допущение об идеальной пластичности конст-
рукционных металлов и сплавов обеспечивают точность расче-
тов, принятую в инженерной практике.
Глава 8
СТЕРЖНЕВЫЕ КОНСТРУКЦИИ
И РАСЧЕТ ИХ НА ПРОЧНОСТЬ
Стержневые системы
•Г--------------------
В строительной механике стержневых систем обычно рассмат-
ривают только такие системы, перемещения и деформации кото-
рых суть линейные однородные функции внешних сил. Для них
справедлив принцип независимости действия сил и перемещение
от нескольких сил есть сумма:
A.r=8., Г, + 8.<Г> + ... + 8. F ,
iF /1 1 i2 2 И л’
где 8/jt - перемещения под действием силы Fk = 1.
Геометрически неизменяемой будем называть такую стержне-
вую систему, в которой невозможны относительные перемещения
частей без деформации.
В зависимости от связей меж-
ду стержнями и мест приложения
внешних сил стержневые системы
делятся на фермы и рамы. Фермой
называется геометрически неиз-
меняемая стержневая система, в
которой стержни между собой
соединяются шарнирно и работа-
ют преимущественно на растяжение и сжатие. Внешние силы при-
кладываются только в узлах (рис. 8.1).
113
Рис. 8.2
Геометрически неизменяемая стержневая система, в которой
элементы соединены между собой жестко и работают преимуще-
ственно на изгиб или кручение (сдвиг), называются рамами. Силы
к рамам могут прикладываться в любом сечении (рис. 8.2, а, б).
Различают плоские и пространственные рамы и фермы. Плос-
кой будем называть такую раму, у которой оси всех элементов
расположены в одной плоскости. В этой же плоскости лежат и
внешние силы.
В пространственных системах (рис. 8.2, в) оси элементов ле-
жат в разных плоскостях. Если нагрузки, действующие на плос-
кую раму, направлены перпендикулярно к плоскости рамы, та-
кую раму называют плоскопространственной (см. рис. 8.2, б).
Задача расчета при заданной геометрической схеме, известных
внешних силах (нагрузке) состоит в подборе сечений всех эле-
ментов с целью обеспечения достаточной надежности при мини-
мальных затратах материалов и стоимости. Основное содержа-
ние этой задачи заключается в определении перемещений систе-
мы, изгибающих моментов и поперечных сил.
Расчет стержневых систем основан на применении начала воз-
можных перемещений. Для упругих систем принцип возможных
перемещений можно сформулировать так: сумма работ внешних
и внутренних сил на любом возможном малом перемещении рав-
на нулю, если система находится в равновесии под действием
приложенных к ней внешних сил. Таким образом, в упругих сис-
темах к активным системам относят и внутренние силы.
За возможные перемещения принимают упругие перемещения,
вызываемые любыми видами нагрузки, т.е. наряду с заданным
нагружением вводится некоторое фиктивное нагружение при ус-
114
Стержневые системы
ловии, что смещения малы, граничите условия соответствуют
действительным, и выполняется условие совместности деформа-
ций (сплошности) конструкции.
Можно считать, что в упругих системах вся работа внутрен-
них и внешних сил затрачивается только на деформацию. При
таком допущении суммарная работа внешних и внутренних сил
на возможных перемещениях линейно деформируемой системы
зависит только от исходного и конечного состояний. Для неупру-
гих тел это допущение неправомерно, так как при пластических
деформациях часть работы превращается в тепловую и другие
виды энергии.
Для удобства анализа работы упругой системы пользуются
понятиями «обобщенная сила» и «обобщенное перемещение». Под
обобщенной силой понимают любое силовое воздействие на сис-
тему: пары сил, распределенные и сосредоточенные силы и т.п.
Перемещение, на котором обобщенная сила производит работу,
называют обобщенным перемещением. Каждой обобщенной силе
соответствует определенный тип обобщенного перемещения; со-
средоточенной силе - линейное перемещение; моменту - угловое
перемещение; распределенной нагрузке - площадь эпюры пере-
мещений на участке ее приложения. Далее для сокращения запи-
си слово «обобщенная» опускаем.
фбим
вннншхсил
Под действием нагрузки упругие тела (системы) деформиру-
ются. Нагрузка может прикладываться с различными скоростя-
ми. В этой главе изучается только статическое действие сил. Вне-
шние силы от начала и до конца нагружения уравновешиваются
внутренними аалами. Так как деформации тела растут постепен-
но, согласно закону Гука, также постепенно возрастает и воспри-
нимаемая упругим телом внешняя сила, так как в силу третьего
закона Ньютона силы существуют только в паре.
Пусть на упругую систему действует система внешних сил
F2,... Fn (рис. 8.3). Каждая из сил будет вызывать перемещение
точек системы. Для некоторой точки в направлении i эти переме-
щения будут следующими:
115
[у7[ Работа внешних сил
Д/F, = М
= \F2
=5Z F ,
8in - удельное пере-
мещение этой точки в
направлении i выз-
ванное силой Fn = 1 (пер-
вый индекс указывает направление; второй - причину перемеще-
ния). В соответствии с принципом независимости действия сил
полное перемещение в этом направлении будет равно сумме пере-
мещений, вызванных отдельными силами:
=AZTj +Л/г2 +--- + А/Г,,
или
Aif = 5,-iF] + 8,2F2 +... + 8inF„.
Перемещение системы в направлении действия всех заданных
сил можно записать так:
A1F -Зц^ +812F2 +8I3F3 +...+5|„F„;
.......................................... (8.1)
= ^nlF\+^n2F2+^n3F3+-- + ^nnFn-
Закон, выраженный (8.1), характеризует свойства материала
и свойства системы. Использовав свойства однородной линей-
ной функции его можно записать так:
д1г =^i[sn+5|2-^-+313-^- + ...+5ln-^- ,
I F> Fl Fl J
Д2Г =-/г2[зц-^- + 322 + 523 -^- + ...+52п-7- ,
I Г 2 Г2 г2
........................................... (8.2)
* т-( с Fl е F2 с F3 с
^nF~F\ 3„i-z;- + 8n2—+ 5п3—Ч-.-. + З^, .
Fn Fn Fn J
На основании принципа независимости действия сил можно
считать все силы приложенными одновременно и нарастающими
F F
пропорционально так, что отношения сил постоянны.
F\ Fn-\
116
Работа внешних сил
Тогда суммы в скобках тоже постоянны, поскольку 8ik харак-
теризуют только жесткость самой системы. Формулы можно пе-
реписать в другом виде:
&2F=B2F2> <8-3)
Д г=В F.
пг п п
Таким образом, перемещения си- р
стемы в направлении некоторой
силы линейно зависят от этой силы. 1
Уравнения (8.3) графически пред-
ставлены на рис. 8.4. >
Действительной работой внеш- 7л
ней силы называют работу, соверша- Л
емую силой на перемещениях, выз- 7Ц\ д
ванных всеми силами. Она равна 1>н] 11 I I I I I I I tF
площади фигуры под прямой: рис g 4
т.е.
Работа всех сил системы:
= (8-4)
Полная действительная работа внешних сил равна полусумме
произведений конечного значения каждой силы на конечное зна-
чение полного перемещения по напрвлению действия силы. Как
видно из (8.2) и (8.4), работа есть квадратичная функция сил, т.е.
работа не пропорциональна силе. Она не равна сумме работ ,
которые могли быть произведены каждой силой в отдельности,
кроме случаев, при которых перемещение в направлении одной
силы, вызванное другой силой, равно нулю.
Для определения возможной работы кроме заданного состоя-
ния системы будем рассматривать еще и некоторое возможное со-
стояние. Возможной работой заданных внешних сил будем назы-
вать их работу на возможных перемещениях, а возможными пере-
мещениями полагать перемещения,вызванные некоторой фиктив-
ной системой сил. Эти перемещения не существуют в действитель-
ности и не имеют физического смысла.
117
Работа внутренних сил
Представим их таким обра-
зом. Допустим, что к балке (рис.
8.5) приложены силы F{ и F2.
Под их действием балка про-
гнется и останется в состоянии
равновесия. Предположим, что
затем к балке приложены силы
F3 и F4, вызывающие в сечени-
ях, где приложены внешние
силы Fj и F2, возможные пере-
мещения Wj и И/'2. Тогда эти .
силы совершат возможную ра-
боту:
Al2 = FlWl + F2Wl
ЦХ Работа внутренних сил
47------------------------------------------
Во всех деформируемых силовых элементах конструкций воз-
никают внутренние силы. Пусть в сечениях А-А п В-В стержня,
отстоящих друг от друга на величину ds, действуют нормальная
сила N, поперечная сила Q и изгибающий момент М. Для элемен-
та, выделенного этими сечениями, они будут внешними силами
(рис. 8.6). Действитель-
ная работа их может
быть определена как
сумма работ статически
приложенных сил. Рабо-
та каждой из этих сил на
перемещениях, вызван-
ных другой силой, рав-
на нулю. Подумайте, почему?
Перемещение от действия нормальной силы равно удлинению
элемента:
tsds =
Nds
ЕА ’
Работа нормальной силы на этом перемещении:
dAN = --
N 2
N2ds
ЕА '
(fc.5)
118
Работа внутренних сил
Работу внешних сил принято считать отрицательной, так как
внутренние силы всегда направлены против перемещений от вне-
шних сил.
Для всего стержня:
л 1 f n2 а
<««
Под действием изгибающего момента край-
ние сечения элемента повернутся на угол rfcp
.ds 1 Afv
г 7 (рис. 8.7). Так как оф =— и — = —то
\ _____ / Р Р EJ
л mv
s\ / б/(р = —'—'ds.
EJy
Работа изгиба:
/\/Х i f m2v
V AM=--f-f-ds. (8.7)
Рис. 8.7 2sEJy
От действия поперечных сил концевые се-
чения элемента сдвигаются относительно друг друга на величину
А = yds, называемую абсолютным сдвигом. При равномерном рас-
пределении касательных напряжений, т.е. при т = —, абсолют-
ах А
ныи сдвиг:
GA
где G - модуль сдвига; А - площадь сечения.
Работа поперечной силы на этом перемещении:
1 г О2
(8-8)
На самом деле распределение касательных напряжений зави-
сит от формы сечения, влияние неравномерности учитывается пу-
тем введения в (8.8) коэффициента формы поперечного сечения rj.
Тогда:
1 г О2
AQ=~^}^ds- <8-9)
2 * Ст • А
Для прямоугольного сечения Г| = 1,20; для круглого сечения
А
Т] = 1,27; для двутаврового профиля т| = —, где Ас - площадь
119
Работа внутренних сил
сечения стенки. Во всех случаях интегрирование ведется в преде-
лах длины участка с одинаковой нагрузкой и одинаковой жест-
костью сечений.
Полная работа внутренних сил находится как сумма работ на
всех участках. Суммарная работа, взятая с обратным знаком,
называется потенциальной энергией U и выражает запас работы,
который можно получить при разгрузке упругого тела.
Для плоской стержневой системы:

<=1 $
М}
——as
EJ „
(8.10)
*=i s
В случае пространственной системы при произвольном нагру-
жении в сечениях возможны все шесть статических эквивалентов
напряжений. Тогда потенциальная энергия:
1 п жт2 п Л?- п
1 v"* (* , т-n е Qy , тЦ г Q~
—ds +
Л Л/2 п
<=1 S У «=1 S
(8.11)
i=^S JP
и =
Рис. 8.8
Правая часть (8.11) есть однородный алгебраический много-
член второй степени относительно внешних сил. Такие многочле-
ны называют квадратичными формами, поэтому говорят, что по-
тенциальная энергия может быть представлена в виде квадратич-
ной формы внешних сил. За независимые переменные принимали
внешние силы. Если принять за независимые переменные переме-
щения А/Т, соответствующие этим силам, потенциальную энер-
гию можно представить как функцию перемещений.
Потенциальная энергия (8.11) может
быть получена из (1.43) и формул для на-
пряжений растяжения, сдвига, кручения
и изгиба.
Возможной работой внутренних сил
будем называть работу внутренних сил
одного состояния на перемещениях дру-
гого состояния.
Пусть имеются два состояния: р и к
(рис. 8.8). Определим возможную работу
120
Работа внутренних сил
растягивающей силы Np на перемещениях к состояния, равных
AJ Nkds „
has —-----. Получим!
E A . tNp-Nk J
pk j EA dS'
Для остальных внутренних сил можно получить аналогичные
зависимости. Тогда возможная работа внутренних сил для про-
странственной системы может быть представлена в таком виде:
6 fOT* . ^СМУМУ^
(8.12)
мкмк J
——*-ds .
EJP
При вычислении работы внутренних сил линейно упругой си-
стемы (если в нее не входят стержни с большой кривизной) спра-
ведлив принцип независимости действия сил, так как работа каж-
дой из сил, N, Qz и Му на перемещениях, вызываемых другими
силами, равна нулю.
Теорема о взаимности работ
Теорема. Работа сил первого
состояния на перемещениях, выз-
ванных силами второго состоя-
ния, равна работе сил второго со-
стояния на перемещениях, вызван-
ных силами первого состояния.
Доказательство. Пусть даны
два различных состояния (рис. 8.9)
некоторой линейно деформируе-
мой системы, отвечающих двум
различным нагрузкам, и в обоих
Рис. 8.9
случаях система уравновешена.
121
Теорема о взаимности работ
Пусть вначале приложена сила Fv Обозначим ее работу Ап. Пос-
ле окончания этого процесса нагружения прикладывается сила F2,
совершающая работу А22. Сила F2 не только сама совершает ра-
боту, но и смещает точку приложения силы вторично вовле-
кая последнюю в работу. Обозначим эту работу Л12.
Полная работа:
А = Аи +
Рассмотрим полную работу при приложении сил в другом по-
рядке: сначала действует сила F2, затем Эта работа равна:
Л А22 2 Г
Работа внешних сил системы, находящейся в равновесии, рав-
на потенциальной энергии, которая зависит лишь от начального
и конечного состояний. Так как исходные и конечные состояния в
обоих случаях одинаковы, то:
^А22 + А\2~А22^А\1 +^21’
откуда
Л12 = Л21.
Эта теорема известна под названием теоремы Бетти, доказав-
шего ее в общем виде. Для случая стержня при растяжении теоре-
ма впервые доказана Максвеллом.
lUJL Теореме о взаимности перемещении
V-----------—----------------------------------
Теорема о взаимности перемещений вытекает из теоремы о вза-
имности работ.
Теорема. Перемещение точки приложения первой силы по ее
направлению от действия второй силы равно перемещению точки
приложения второй силы по направлению последней под действием
первой силы.
Доказательство. Рассмотрим два состояния упругой систе-
мы. В первом состоянии система нагружена единичной силой
Fx = 1, направленной по линии 1-1 ; во втором состоянии система
нагружена силой F2 =1, направленной по линии 2-2 (рис*. 8.10).
Пусть под действием силы F, точка В переместилась в положе-
ние В'. Проекцию ее перемещения на направление силы обозна-
чим 521. Первый индекс указывает направление перемещения;
122
Теорема о взаимности перемещений
второй индекс - причину, ее вызвавшую. Под действием силы F2
точка А переместится в положение А'. Обозначим 512проекцию ее
перемещения на направление силы Г2. На основании теоремы о
взаимности работы: _ _
Так как F} -F2, то
812=521. (8.14)
Эта теорема носит название теоремы Максвелла. В некото-
рых случаях ее выгодно применять для определения перемещений
непосредственно.
Аналогично из теоремы о
взаимности работ выводится
теорема о взаимности реак-
ций (рис. 8.11). Реакция, воз-
никающая в связи-1, когда
связь 2 переместится на еди-
ницу в своем направлении,
равна реакции в связи 2 при
перемещении связи 1 на еди-
ницу. В этом случае опреде-
ляется возможная работа от
сил реакций одной из опор на единичном перемещении второй
опоры. Теорема справедлива для реакции любого вида (силы и
момента силы).
123
Перемещения от внешних сил. Формула Мора
Перемещения от внешний сил. Формуле Мора
Г-------------------------------------------------
Перемещения точек стержневой системы определяются как для
оценки ее жесткости, так и для расчета статически неопредели-
мых систем.
Рассмотрим некоторую стержневую систему (рис. 8:12). Опре-
делим перемещение произвольной точки системы в произвольном
направлении i-i при действии заданной системы сил. Обозначим
его Д/г. Это действительное состояние системы 1 называют основ-
ным. Рассмотрим также возможное, т.е. воображаемое, состояние
2 этой же системы, в котором на систему действует только единич-
ная фиктивная сила, приложенная в точке искомого перемещения
по направлению i-i. В случае определения угла поворота прикла-
дывается сосредоточенный момент.
Обозначим эквивалентные внутренние усилия: .
— в состоянии 1, N, Му, Мк, Qy, Qz\
— в состоянии 2, N, Му, Mk,Qy, Сгде приложена сила
Г = 1.
Для состояния 2 за возможные перемещения примем перемеще-
ния под действием сил состояния 1. Примем направление силы
F = I за положительное. Ее работа на возможном перемещении
Д/7 (здесь «1» есть индекс сил основного состояния).
Я21 = F-AiF.
Индекс «2» при А означает, что это работа внешних сил вто-
рого состояния; индекс «1» означает, что эта работа выполняется
на перемещениях, вызванных внешними силами первого состоя-
ния. Согласно теореме о взаимности работ при F = 1.
124
Перемещения от внешних сил. Формула Мора
stQyQy , v }Q-Q-
i=\ 0 UA
:г , ^StMkMk
(8.15)
^12 “^21 ” 1 * Д/Г’
где А12 - возможная работа заданных внешних сил (состояния 1) на
перемещениях, вызванных фиктивной (единичной) силой F = I. Но
на основании принципа возможных перемещений для упругой
системы возможная работа внешних сил Л12 равна возможной
работе внутренних сил, взятой с обратным знаком. Последняя
определяется (8.12).
Таким образом, из теоремы о взаимности работ и принципа
возможных перемещений следует \F =|-А'\.
Подставив значение работы внутренних сил по (8.12), получим
искомое перемещение:
л X? f NN I (
/=1 О Jy <=1 0 - /=1 о к
Эта формула известна как формула Мора, входящие в нее ин-
тегралы называют интегралами Мора.
Формулу (8.15) можно применять и для криволинейных стерж-
ней, если радиус кривизны значительно превышает высоту сече-
ния (Я>5Н). В таких системах можно пренебречь изгибом от дей-
ствия нормальных сил и линейной деформацией за счет изгибаю-
щих моментов. Во многих случаях расчета формула (8.15) может
упрощаться. При расчете ферм, например, учитываются лишь
нормальные силы N и N при расчете рам пренебрегаем их нор-
мальными и поперечными силами, если не малы жесткость на ра-
стяжение и сдвиг, и т.п.
Перемещение точки приложения силы по направлению этой
силы можно найти также из теоремы Кастилиано: перемещение
некоторой точки по направлению действия заданной силы F- рав-
но частной производной от потенциальной энергии по этой силе:
^ = 0.
ал
Доказательство ее аналогично доказательству теоремы о вза-
имности работ.
Под интегральные функции в формуле (8.15) есть функции внут-
ренних сил. Интегралы Мора при известных функциях этих уси-
лий могут быть вычислены аналитически для участков стержней
(8.16)
125
Перемещения от внешних сил. Формула Мора
с одинаковыми законом изменения статических эквивалентов
напряжений и жесткости системы, полученные значения суммиру-
ются.
Перемещения точек системы определяют по формуле Мора в
такой последовательности:
1) вычисляют нормальные и поперечные силы, изгибающие и
крутящие моменты;
2) прикладывают единичную силу
по направлению искомого пе-
ремещения; при необходимос-
ти определения взаимных пере-
мещений отдельных точек (се-
чений) нужно приложить еди-
ничные силы, направленные в
разные стороны (точка А на рис. 8.13); _________
3) определяют статические эквиваленты напряжений 7V, М, Q
возможного состояния;
4) найденные значения сил подставляют в формулу (8.15) и вы-
числяют интегралы Мора.
Перемещения в статически неопределимых системах находят
после решения задачи методом сил. Знак перемещения зависит от
знаков эпюр сил. При одинаковых знаках эпюр перемещение на-
правлено по единичной силе. Эпюра единичных сил для прямоли-
нейного стержня постоянного сечения всегда прямолинейна. Если
эпюра имеет вид ломаной или жесткость стержня переменна, при
вычислении интегралов Мора ее разбивают на участки с одина-
ковым законом изменения внутреннего силового фактора или с
постоянной жесткостью. Полученные
значения интегралов складывают.
Пример 8.1. Определить прогиб
балки в точке, где приложена сила
F (рис. 8.14), если J= 6550 см4; А =
= 54,6 см2; Е = 200 ГПа; G= 160 ГПа.
Коэффициент неравномерности рас-
пределения касательных напряже-
ний т| - 2,6. Полное перемещение
Дг = Дм + Д^. Определим его состав-
ляющие. Перемещение от изгиба:
г А/ Л/у
S п J у

Рис. 8.14

126
Перемещения от внешних сил. Формула Мора
Эпюры М имеют два участка:
— от заданных сил на первом участке = 36х • 103 Н • м;
— на втором участке М2 = 24х • 103 Н • м;
— от единичной силы соответственно
М\ = 0,6х-103Н-м; Л/, = 0,4х- IO’H m.
Перемещение от изгиба:
103
2-Ю11-665-Ю’7

2 3
J36 • 0,6х2<?х+J24 0,4х2«/х
.0 о
= 11,7-10’3м.
Перемещение от сдвига:
где т| = 2,6.
Поперечные силы от заданной и единичной сил:
6] = 36 • 103 Н; Q2 = 24 • 103 Н;
е1=0,6Н; б2=0,4Н.
Перемещения от сдвига (за счет поперечной силы)

2,6-103
16-Ю10-54,6-Ю-4
2 3
j 36 • 0,6 dx+J (-24) • (-O,4)rfx
.о о
= 0,4-IO’3 м.
Полное перемещение:
А = +Де= 11,76 + 0,4 = 12,1 мм.
Др
Так как —— = 0,03, можно пренебречь влиянием поперечной
дл/
силы на прогиб балки. Решим эту задачу, вычисляя интегралы по
правилу Верещагина и пренебрегая прогибом от поперечной силы
Q. Перемещение:
д=-Д-(4Л1+я2л2),
EJ
где A j и А2 - площади эпюр моментов от заданной силы на участ-
ках; h} и h2 - ординаты единичных эпюр. Они равны:
Л1 = 72-103; Л2 = 1,5 • 72 • 103; Л^Л^О.8.
Вычисляем перемещение:
103
А =-----------------(72-0,8+1,5-72-0,8) = Ц7-1(Г3 м-
2-10 1-655-10”7
127
Перемещения от внешних сил. Формула Мора
Пример 8.2. Определить вертикальное и горизонтальное пере-
мещения свободного конца криволинейного стержня 1 сечения
(рис. 8.15), если Е = 70 ГПа; J= 1000 см4; Г= ЮкН; R = 1 м.
Полное перемещение находится как геометрическая сумма
вертикального и горизонтального перемещений.
Изгибающие моменты:
М = FR • sin(p; М\ = Я sin ср; Мг = /?(l-coscp).
Вертикальное перемещение:
. л-104-1 „.
Л п =----- sin ср лер =------------- = 22,4 мм.
В EJ J * * 4-7-10 °-10-5
Горизонтальное перемещение:
LuL Метод сил. Статическая неопределимости
Г"------------------------------------------
Теоремы об упругих системах составляют основу методов рас-
чета статически неопределимых систем. Наиболее широкое рас-
пространение получил метод сил. В строительной механике при-
меняется также метод перемещений.
Балки, рамы и фермы подразделяются на статически опреде-
лимые и статически неопределимые. Статически определимыми
называются такие системы, у которых реакции опор могут быть
определены из уравнений равновесия системы как жесткого тела,
а внутренние усилия - из уравнения равновесия мысленной отсе-
128
Метод сил. Статическая неопределимость
ченной части. Статически неопределимыми будем называть та-
кие системы, у которых реакции опор и напряжения не могут быть
найдены из уравнений равновесия.
Разность между числом неизвестных - реакций связей, внут-
ренних усилий - и числом уравнений статического равновесия,
которые могут быть составлены для системы, называют степенью
статической неопределимости. Число связей, обеспечивающих
^кинематическую неизменяемость системы, называется необходи-
мым. Связи, наложенные сверх необходимых, называются допол-
нительными или «лишними».
Связи делятся на внутренние и внешние. Внешние связи обес-
печиваются опорами.
д Если системы состоят из одно-
'Ятт тт го стержня (балка), для обеспече-
ния ее кинематической неизменя-
емости в плоскости нужно нало-
а жить три связи. По стержневой
I ? схеме необходимые для этого опо-
б) ры изображены на рис. 8.16, а. Те-
перь система состоит из четырех
стержней, соединенных пятью
,, у шарнирами, из которых один
даяг yfo тт? двойной. Для них в плоскости
можно составить двенадцать
уравнений равновесия, шарниры
гис. 3.10 накладывают столько же связей.
Цилиндрический шарнир в плоской раме накладывает две связи.
Введение двойного или многократного шарнира эквивалентно
к = п - 1 шарнирам, где п - число соединяемых звеньев. В про-
странственных рамах могут устанавливаться сферические шар-
ниры, накладывающие по три связи.
Поставим в середине пролета балки еще одну подвижную опо-
ру (см. рис. 8.16, в). Теперь для системы можно оставить пятнад-
цать уравнений, а шарниры накладывают шестнадцать связей.
Одна связь оказывается «лишней». Жесткая заделка или жесткое
соединение стержней в плоской системе накладывает на систему
три связи. Если на свободный конец жестко заделанной консоль-
ной балки установить подвижную шарнирную опору, одна связь
окажется «лишней» (см. рис. 8.16,6). Таким образом, число «лиш-
них» связей равно разности между числом наложенных связей и
числом уравнений равновесия для свободных стержней.
5. Зак. 389
129
Канонические уравнения метода сил
Из этих примеров нетрудно установить формулу для опреде-
ления общего числа «лишних» связей плоских систем:
Н = 2РХ + ЗР2 - Зл, (8.17)
а для пространственных систем формулу:
Н = 5РХ + 6Р2 + ЗР3 - 6л, (8.18)
где Н - число «лишних» связей (степень статической неопредели-
мости); Pj - число простых шарниров; Р2 - число жестких заде-
лок или жестких соединений стержней; Р3 - число сферических
шарниров; п - число стержней.
|h Канонические уравнения метода сил
Метод сил служит для расчета статически неопределимых си-
стем. В заданной системе удаляются «лишние» связи, в направле-
нии их действия прикладываются силы Хк, необходимые для со-
хранения кинематической неизменности системы. После преоб-
разования система должна стать статически определимой, в ней
не должно быть мгновенных механизмов.
Для определения неизвестных сил Хк составляют уравнения,
называемые каноническими. Число уравнений равно числу уда-
ленных связей. Суть каждого уравнения - перемещение в направ-
лении удаленной z-ой связи от всех активных и приложенных не-
известных сил Хк равно нулю.
С порядком составления уравнений познакомимся на примере
рамы, изображенной на рис. 8.17, а. Рама состоит из четырех же-
стко связанных друг с другом и неподвижным основанием стерж-
ней (п = 4).
Степень статической неопределимости:
Н = 3Pj + 2Р2 - Зл = 3 • 6 + 0 - 3 • 4 = 6.
Связи удаляют так, чтобы канонические уравнения были про-
ще. Здесь удалим правую опору и стержень (рис. 8.17, б).
130
Канонические уравнения метода сил
В точке А, где удалена жесткая опора, все три смещения точки
Л, линейные и угловые от заданных и неизвестных сил должны
быть равны нулю:
Д1(Х1,...,Х6,/0 = 0;
Д2(Хр...,Х6,Г) = 0;
Д3(Х1,...,Х6,Л = 0.
Первые индексы указывают направление перемещений. Вто-
рой индекс у перемещений указывает, что перемещение зависит
от всех шести неизвестных сил Хр ... , Х6 и заданной силы F. Ана-
логичное условие должно выполняться и в точке Е. В силу прин-
ципа независимости действия сил каждое из перемещений можно
записать в виде суммы:
^i(Xx...Xh,F)= ^iXx + \х2 +--- + Arf (8.19)
Так как перемещение пропорционально силе, то:
А,а = 8,г^. (8.20)
Коэффициенты 8ik есть перемещения по направлению i силы
под действием единичной силы. Под индексом F будем понимать
всю систему заданных сил.
В местах, где мысленно удалены связи, в заданной раме переме-
щений нет. Они должны быть равны нулю и в основной системе:
Д1(А'|...ЛГ6.£) = °; &2(Xl...X6,F) = $ &3(ХЪ..Х6.Г) =
Д4(Х|...Xb,F) =°; &5(Xt...X6,F) =°;Дб(А'1...Х6,£) = °-
Учтя (8.19) и (8.20), получим (8.21) в таком виде:
5цХ| +§12^2 + 813X3 + 814Х4 + 815Х5 + 816Х6 + Д1Г =0;
82|Х1 + 822^2 + $23^3 + §24^4 + $25^5 + $26^6 + Д2Г = Ф /о
§61+ $62^2 + $63^3 + $64^4 + $65^5 + ^66^6 + &6F “
Эти уравнения можно получить и энергетическим методом в
виде: ди
ЭХ,
Линейные уравнения (8.22) называются каноническими урав-
нениями метода сил, число их равно числу лишних связей. Такие
уравнения могут быть составлены для любой плоской или про-
странственной рамы. В краткой форме их можно записать так:
5
131
Канонические уравнения метода сил
8Л ^ + Д/Г=0.
В этой записи использовано правило суммирования по «не-
мым» индексам. «Немым индексом называется индекс, встречаю-
щийся в произведении дважды (к - в нашем случае). Наличие
«немого» индекса и означает, что по нему берется сумма, знак
которой для сокращения опускается. «Свободный» индекс i озна-
чает, что имеется не одно, а Н уравнений (f = 1, 2, 3, ... , Н), т.е.
число уравнений равно числу лишних связей.
В случае симметричной системы число уравнений можно умень-
шить правильным выбором основной системы. Кроме того, урав-
нения упростятся, так как согласно теореме о взаимности переме-
щений: о _ ~
°ik ”
При выводе уравнений причина возникновения перемещений
ничем не обусловлена, поэтому уравнения справедливы при дей-
ствии любой системы сил.
При малом числе лишних неизвестных Хк систему каноничес-
ких уравнений можно решить вручную, пользуясь алгоритмом Га-
усса, определяющим последовательность исключения неизвестных.
При большом числе уравнений используются машинные методы.
В матричной форме система (8.22) имеет следующий вид:
ЛУ=-Д.Г. (8.23)
Матрица единичных перемещений (матрица податливости)
симметрична и, квадратична:
<5н 8|2 813 81л
б2| 822 823 52л
А = 831 832 833 8з„
(8.24)
$п2 &пЗ &пп}
При статическом нагружении она вычисляется просто. Вслед-
ствие симметрии относительно главной диагонали определитель
такой матрицы det А > 0. Следовательно, решение канонических
уравнений не может быть неопределенным или равным бесконеч-
ности, если все 8Л определены и конечны и одновременно не рав-
ны нулю. Эти условия обеспечиваются геометрически неизменяе-
мой основной системой.
Матрица-столбец лишних неизвестных:
132
Канонические уравнения метода сил
Х =
(8.25)
матрица-столбец свободных членов (грузовых перемещений):
Д|Г
Д2£
(8.26)
Так как det Л ^Сосуществует обратная матрица А~1, решение
(8.23) записывается так:

Единичные перемещения 3/А. вычисляют по формуле Мора, в
интегралы Мора подставляют единичные изгибающие моменты
Мк Их эпюры строят для основной системы. При вычислении
перемещения от заданных сил подынтегральные функции интег-
ралов Мора произведения внутренних сил от заданной нагрузки
и от единичных сил. Грузовые и единичные перемещения могут
вычисляться матричным методом. После решения системы (8.22)
строят эпюры найденных сил Хк и х складывают с грузовой эпю-
рой. Сумма их есть эпюра изгибающих моментов заданной систе-
мы. Таким образом, метод сил состоит в одновременном преобра-
зовании сооружения и действующей на него системы сил.
Вместо расчета сложной системы с простой известной нагруз-
кой решают задачу расчета простой системы при сложной, час-
тью неизвестной нагрузке с помощью системы линейных уравне-
ний, содержащей все неизвестные.
Метод перемещение

Некоторые задачи расчета на прочность статически неопре-
делимых стержневых систем проще решаются методом перемеще-
ний. Так же, как и в методе сил, используется основная система.
При расчете по методу сил наиболее удобна статически опре-
делимая основная система, не содержащая простых и мгновен-
ных механизмов. Неизвестными становятся силы, приложенные
взамен удалённых связей.
133
Метод перемещений
Самая простая основная, система метода перемещений пред-
ставляет собой совокупность однопролетных балок с жестко за-
щемленными или шарнирно опертыми концами. При ее выборе
вводятся дополнительные связи, запрещающие поворот и линей-
ное смещение узлов соединения стержней.
Для сравнения основных систем
метода сил и метода перемещения
рассмотрим статически неопредели-
мую раму (рис. 8.18). Рама состоит
из двух стержней, жестко связанных
между собой и с неподвижной опо-
рой, степень статической неопреде-
лимости ее по формуле (8.17):
Я=3«3-2*3 = 3.
Наиболее простой основной сис-
темой метода сил, является система с
одной удаленной опорой (8.19, а).
Для определения неизвестных сил Хк составляются три кано-
нические уравнения (8.22).
Узел В рамы (см. рис. 8.18) при изгибе ригеля и стойки рамы
может поворачиваться в плоскости, смещению вверх и вниз, впра-
во и влево препятствуют стержни АВ и ВС, поэтому выбор основ-
ной системы метода перемещений однозначен - нужно запретить
Этот поворот устраняется введением дополнительной связи,
запрещающей только вращение узла В. На рис. 8.19,6 эта связь
показана условно в виде бал очки.
134
Метод перемещений
Введением новой связи вызовет появление реакции, не имею-
щей места в заданной системе. Обозначим ее индекс F указы-
вает причину появления реакции - приложенные к раме внешние
силы. Так как в заданной системе реакций от запрета поворота В
узла нет, то сумма реакций в узле, вызванных самим защемлени-
ем узла и заданными внешними силами вследствие запрета пово-
рота, должна быть равна нулю. В этом смысл канонических урав-
нений метода перемещений.
За неизвестные принимаются запрещенные перемещения zk. Так
как само z неизвестно, реакцию от него представляют в виде про-
изведения г^к, где - реакция в направлении /, вызванная зап-
ретом смещения на единицу. Единичная реакция играет роль,
аналогичную роли единичных перемещений в методе сил.
Итак, для рамы, изображенной на рис. 8.18, в которой запре-
щен только поворот одного узла, можно записать для определе-
ния величины этого поворота одно каноническое уравнение ме-
тода перемещения:
rnzi
(8.28)
Расчет рамы методом перемещений состоит в решении одного
канонического уравнения вместо трех в методе сил. Всегда ли
метод перемещений предпочтительнее метода сил?
Рис. 8.20
Ответим на этот вопрос, на приме-
ре другой трижды статически неопре-
делимой рамы (рис. 8.20). В ней возмож-
ны повороты узлов Ви С и их смеще-
ние по горизонтали, т.е. в основной
системе метода перемещений три допол-
нительных связи, показанные на том же
рис. 8.20. Для определения трех пере-
мещений придется, как и методе сил,
составлять три канонических уравне-
ния.
А

силу теоремы о
Заметим, что rik = rki в
взаимности реакций.
Как же найти число необходимых до-
полнительных связей? В методе силы чис-
ло неизвестных точно определялось по
формуле (8.17).
Число свободных узлов, а равно их по-
воротов, счесть просто. Иногда не ясно db»
число возможных поступательных движе- Рис*
135
Определение свободных членови коэффициентов...
ний этих узлов. Для их определения вводят взамен жестких узлов,
в том числе й опорных, простые шарниры (рис. 8.21), налагаю-
щие в плоскости две связи, если подвижность системы w, как раз-
ность'между числом степеней свободы всех стержней до их соеди-
нения и числом наложенных связей и* = ЗЯ - 2РХ > 0; у этой рамы
Wj = 1 и нужно ввести одну подвижную шарнирную опору, как
показано на рис. 8.20.
Определение свободных членов
и коэффициентов канонических уравнении
метода перемещении
Свободные члены уравнений (8.28) - реакции опор неопреде-
лимых балок. Их можно найти методом сил. Возможны три вари-
анта таких балок (рис. 8.22).
£
Л
*________1_
а)
Рис. 8.22
Если пренебрегать при расчетах рам нормальными силами в
сечениях, то для самой сложной схемы (см. рис. 8.22, а) степень
статической неопределимости можно считать равной двум.
Покажем последовательность вычисления опорных реакций
для самой простой балки (см. рис. 8.22, Ь), нагруженной равно-
мерно распределенной силой. Степень статической неопредели-
мости ее Я = 1 основную систему примем в виде, показанном на
рис. 8.23, а.
Каноническое уравнение метода сил:
5ц • 0
содержит только одну неизвестную. Коэффициент уравнения 5j j
и Д1/г свободный член найдем по формуле Мора:
Зц =—^Mi-Mvdx; Д|Г = — [MFMrdx.
EJ о EJ о
136
Определение свободных членови коэффициентов...
Интегралы Мора вычисляются аналитически или способом
Верещагина:
д1г=^у4Л1> 4 =|а=|^ а3, Aj=-a.
Так как
. 1 z. 2
А?= — a a, hi=—a,
2 2 1 3
то 2 1
6П=— а \
11 3EJ
Неизвестная реакция шарнирной опоры:
Оц 16
Реакции левой опоры равны поперечной силе и изгибающему
моменту на ней (см. рис. 8.23, d, е), т.е.
137
Определение свободных членови коэффициентов...
л 13 .. 5 2
Мл~-Ча.
Для других схем опорные реакции даются в справочных
пособиях.
Коэффициенты канонических уравнений
razk + RiF=0’
представляющие србою реакции от единичных перемещений опор,
можно найти из уравнения изгиба балки
= М9 (8.29)
dx
так как
то
dx
d2M
d4w
EJ—т- = в.
dx4
Мы ищем силы, возникающие от единичного поворота опоры,
поэтому примем q = 0, тогда уравнение получит вид:
Его общее решение, прогибы балки,
w = с{х3 + С2Х2 + с?х + с4, (8.30)
первую производную от него, угол поворота
dw „ 2
— = ЗфГ +2с2х + с3 (8.31)
можно рассматривать как единичное перемещение, от которого
потом с помощью уравнения изгиба (8.29) можно перейти к еди-
ничным реакциям rik.
Постоянные ci в (8.31) находятся из граничных условий. При
опирании обоих концов балки (см. рис. 8.22, а), х = 0 и х = /, примем
dw
А- (8.32)
Подставим (8.30) и (8.31) в граничные условия (8.32) и найдем
постоянные решения. Они будут:
с4 = wo! сз = Фо;
138
и.
Определение свободных членови коэффициентов...
(8.33)
1 / х 1 /
ci = ~а (Фо + Ф/) - -л (wi ~ X
г Г
1 3
с2 =-у(2ф0+Ф/) + ^(и’/-и>0).
Для отыскания опорных моментов по уравнению (8.29) най-
дем вторую производную от (8.30), для опорных сил - третью про-
изводную:
rf2‘V г . О £.
—г- = 6с1х + 2с2; —г = ос..
dx2 dx3
Изгибающий момент на опоре:
М = EJ(6c{x + 2с2)‘
Поперечная сила:
2 = EJ-6-cr
Если повернуть левую опору балки (х = 0) на угол (р Q и положить
ф ] = и’о = = 0 , получим:
1 2
С\ сЭ =---.
/2 2 I
Момент на левой опоре:
,, 4EL
А/о=----^-Фо-
4£J
Если Фо = 1, имеем единичный момент =-----; на другой
опоре (х = Z) момент:
2F Т
Mt = EJ(6cJ-2c2) = —j—(pQ.
Задавая поочередно все четыре граничных условия (8.32),
можно получить все опорные моменты и силы для любых условий
опирания балки.
Канонические уравнения метода перемещении.
Изгибающие моменты в сечениях рам
Канонические уравнения метода перемещений (8.28) можно
записать в матричной форме:
ЛZ+tf=0
(8.34)
139
Определение свободных членови коэффициентов...
Матрица коэффициентов
А,=
'll r12 " • r\n
r21 r22 ' " r2n
rnl rn2 rnn
(8.35)
называется матрицей жесткости системы, она симметрична отно-
сительно главной диагонали. Матрицы-столбц^! неизвестных пе-
ремещений и реакций:
(8.36)
Единичные реакции г^, возникающие за счет поворота узлов,
и узловые реакции от внешних сил берут из справочных таблиц,
либо вычисляют, как показано в п. 8.6.
Решение в матричном виде:
Z = A;'-R (8.37)
ищется так же, как и в методе сил.
Примечание. Сложные стержневые системы рассчитываюи
методом конечных элементов.
Глеев 9
НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ В ОБОЛОЧКАХ
Тонкие оболочки
Оболочки считаются тонкими, если отношение радиуса сред-
jR -R
ней поверхности а толщине — >100, у толстых оболочек — < 30.
п п
Если у тонкой оболочки нет резкого изменения кривизны и
жесткости, а внешние силы плавно изменяются по поверхности,
можно пренебречь напряжениями изгиба и кручения, считать на-
пряженные состояния плоскими.
140
р] Тонкие оболочки
Нормальные напряжения приводятся к двум статическим эк-
вивалентам - нормальным силам в меридиональном
п/
М = Jorfz (9.1)
_ п/
/2
и кольцевом
"А
N2 = jodz (92)
_«/
/2
направлениях, - касательным к сдвигающим силам
п/
^12=^21= /Т12^2> (9-3)
_л/
/2
касательные напряжения появляются при неравномерном распре-
делении силы по поверхности оболочки.
ДХ Уравнения равновесия тонкой оболочки
при осесимметричном нагружении
---------------------------------------------------
В сечениях тонких оболочек, нагруженных симметрично отно-
сительно оси, изгибаюими моментами и поперечными силами мож-
но пренебречь. Такое напряженное состояние называют безмо-
ментным.
Напряжения в сечениях оболочки определяются из уравнения
равновесия. Уравнения равновесия могут быть получены различ-
ными способами. Здесь мы воспользуемся условиями равновесия
бесконечно малого элемента оболочки и ее части.
Выделим мысленно из оболочки двумя меридиональными и дву-
мя кольцевыми нормальными сечениями бесконечно малый элемент
оболочки (рис. 9.1). Приложенную к нему распределенную по по-
верхности осесимметричную нагрузку интенсивностью q разложим
на две составляющие: нормальную qn и меридиональную (коль-
цевая составляющая qQ = 0). По граням элемента приложим нор-
мальные усилия, погонные значения которых равны Wj и TV2» ос"
тальные усилия при безмоментном напряженном состоянии сим-
метричной оболочки равны нулю.
141
Рис. 9.1
Так как элемент находится в равновесии, то сумма проекций
сил на ось z (на нормаль) равна нулю: XZk = 0. Остальные уравне-
ния равновесия элемента удовлетворяются тождественно. Учтя
малость углов Лр и из рис. 9.1 и 9.2 легко установить, что это
уравнение может быть записано так:
q^ds^lsz -Nids^'-N^dsidtf-d(Nids2 ) 'j'O.
Отбросим последний член, имеющий более высокий порядок
малости, и разделим все члены на ds{, ds2. Из рис. 9.2, видно, что
d0'=d©-2- = ^-.
Л2 &2
Получим уравнение
М N1
—+ —= ОТ,
Л R1
(9.6)
142
Уравнения равновесия тонкой оболочки...
ставим уравнение равновесия в
известное как уравнение Лапла-
са. В уравнении (9.6) два неизве-
стных. Второе уравнение легко
найти из условия равновесия ча-
сти оболочки, отсеченной по нор-
мали к срединной поверхности
(рис. 9.3).
Здесь и далее в главе за поло-
жительное направление распре-
деленных по поверхности сил
принято такое, как на рис. 9.3,
при ином направлении знаки уси-
лий меняются на обратные. Со-
проекциях сил на ось получим:
S1 5|
Так как d^coscp =Jp, то заменив переменную и сократив на 2п
имеем:
(9.7)
М = —Ц? Г («;-?<₽ tg ф)р </р,
rcosp^
где г - радиус сечения плоскостью, перпендикулярной оси, в ко-
тором определяется нормальная сила Nv
Если оболочка имеет круговой срез у вершины, нижний пре-
дел интегрирования будет г0 - радиус сечения среза.
Уравнения (9.6) и (9.7) можно записать в напряжениях.
Так как
то
(9.8)
М ^2
а1=Т-э а2 = -Г"
h h
R-2 h
При равномерном распределении давления по поверхности
(^ф = определение меридиональных усилий заметно упрощается:
2cos0
N2 = qr,
1 2/icosP
гг -Яг
а2--.
(9.9)
143
Напряжения и деформации в цилиндрическом баке...
Ю. Напряжения и деформации в цилиндрическом
баке с полусферическими днищами
при нагружении внутренним давлением
Ф"-----------------------------------------------
В цилиндрической оболочке (рис. 9.6) = °°, R2 = г в полу-
сферических оболочках = R2 - R3 = г. Из (9.6) и (9.8) при посто-
янном q, получим кольцевую силу и напряжение
N2 = 9r; о2=т-- (91°)
п
Из (9.9) имеем меридиональную силу и напряжение:
__ 1 1
N\=~qr, c^—qr. (911)
2 2п
Кольцевые напряжения вдвое больше меридиональных, поэто-
му разрушение цилиндрических оболочек от внутреннего давле-
ния происходит из-за трещин вдоль образующих. Деформации оп-
ределим из обобщенного закона Гука:
1 / ч 1 /
Е1=-(О1-ЦО2); e2=—(<j2-iui2).
Е Е
Подставив (9.10) в (9.11), получим:
Е,=ТТ(О’5'|Х); е2=-^(1-о,5ц). (9.12)
п ri Е П
В сферических оболочках (днищах) усилия и напряжения такие:
N{=N2=^qR, csx=<s2=^qr. (9.13)
деформации
qr л,
е1=е2=-^(1-Ц)- (9.14)
Е Л
При сравнении деформации цилиндрической и полусфериче-
ской оболочек видим, что не выполняется условие совместности
деформаций частей бака в месте соединения их между собой, хотя
напряжения одинаковы. Это несоответствие является недостат-
ком безмоментной теории, не учитывающей изгибающие момен-
ты и поперечные силы, которые возникают в местах изменения
кривизны оболочки. Вследствие разной жесткости цилиндричес-
кой и сферической оболочек условие неразрывности выполняет-
ся только путем изгиба частей сосуда в области, примыкающей к
сечению стыка.
Таким образом, в зоне, прилегающей к месту соединения обо-
лочек, должны действовать изгибающие моменты и поперечные
144
Напряжения и деформации в цилиндрическом баке...
силы. Напряжения в этой зоне, если радиус днища больше радиу-
са цилиндрической оболочки, могут достигать больших значе-
ний, быстро затухая по мере удаления от стыка. Если сосуд изго-
товлен из малопластичного материала (таковы многие сплавы с
высокой удельной прочностью и стеклопластики), принимаются
меры для их снижения.
Внутреннее давление может создаваться жидкостью и газом.
Тогда
Я=Ян+Яп (9-15)
где qH - давление газа (наддува); qr - гидростатическое давление.
Гидростатическое давление действует по нормали к поверх-
ности оболочки, величина его зависит от высоты столба жидко-
сти над данным сечением оболочки и не зависит от формы сосуда:
Яг = Чн>
где у - удельный вес жидкости; Н - высота столба жидкости.
ILUL Напряжения а толстостенных оболочная
•г---------------------------------------------
К толстостенным будем относить оболочки, у которых отно-
2^
шение радиуса к толщине оболочки — < 30. Напряженное состо-
h
яние таких оболочек нельзя считать плоским. Толстостенные обо-
лочки используются в баллонах высокого давления. Толстостен-
ными оболочками можно считать также втулки и полые валы ме-
ханизмов.
Рассмотрим наиболее общий случай оболочек - цилиндриче-
ский баллон со сферическими днищами. Будем считать цилиндри-
ческую оболочку достаточно длинной для того, чтобы напряже-
ния в поперечных сечениях полагать равномерно распределенны-
ми по толщине оболочки.
145
р’1 Напряжения в толстостенных оболочках
При осесимметричном нагружении
можно составить лишь два уравнения
равновесия: одно - из условий равно-
весия бесконечно малого элемента;
другое - из условий равновесия мыс-
ленно отсеченной части оболочки.
Двумя цилиндрическими поверхностя-
ми и парой плоскостей выделим бес-
конечно малый элемент цилиндричес-
кой оболочки (рис. 9.5). Спроецируем
силы на радиус оболочки:
в- + do
de
Рис. 9.5
(ор = 0.
Приведя подобные члены и разделив на JpJO, получим:
у(а p)-G0=O. (9.16)
Ф
///////

Второе уравнение равновесия со-
ставим, спроецировав-силы на ось
оболочки (рис. 9.6):
Л(Л2 - г2) - пг2я = 0 (9.1'7)
Два’уравнения содержат три неиз-
вестных напряжения. Недостающие
Рис. 9.6 уравнения найдем из условий совмес-
тности деформаций. Радиальная деформация малого элемента
толщиной ф (см. рис. 9.5):
А'В'-АВ
Ер АВ
Новая длина отрезка А"В' = w + dw - dp - w, следовательно
dw
е₽"ф
Кольцевая деформация цилиндрической оболочки при осесим-
метричном нагружении также зависит от w:
w
dw d
v Легко увидеть, что — = — (Е©р).
dp dp
(9.18)
(9.19)
146
Напряжения в толстостенных оболочках
Отсюда и из (9.19) следует такое уравнение совместности де-
формаций:
^ + ^2₽=о. (9.20)
Ф р
Уравнение (9.20) можно записать в напряжениях, использовав
обобщенный закон Гука:
Ер=77^р-М(<У0+Ох)1
Ев=^|?е-Ц(ар.+ ах)1 (9.21)
Е
Ex=T?k-H(Op+Oe)l
Е
Меридиональное напряжение ох = Еех + ц(ор + ав).
Исключим из первых двух уравнений (9.21) ох, подставим ер и
ее в (9.20) и получим два уравнения относительно неизвестных
напряжений ор и ое. Уравнения можно решить совместно. Проще
радиальное и кольцевое напряжения определить, если ввести фун-
кцию напряжений Ф, такую, что:
Ф </Ф
пр=-иа0=^. (9.22)
Р dp
Уравнение (9.16) подстановкой (9.22) удовлетворяется тожде-
ственно, а преобразованное с помощью (9.21) уравнение совмес-
тности деформаций (9.20), после подстановки (9.22) приведется к
следующему виду:
(9.23)
а2Ф 1 ф Л
Г +----------7=0.
dp2 р dp р2
Решение его можно найти в виде Ф = Cz p”.
После подстановки решения в (9.23), сокращения на Срп‘2 и
приведения подобных членов получается уравнение л2 - 1 = 0, т.е.
л = ± 1.
Следовательно, функция напряжений
Ф = С1Р+—,
Р
а напряжения
Л1’ С?
стр - С1 + ае = Q - (9.24)
Эти формулы получены Ламе, впервые решившим задачу.
147
[^1 Напряжения в толстостенных оболочках
Постоянные и С2 находятся из условий на поверхности ци-
линдрической оболочки. Если на наружной поверхности давле-
ние равно р, а на внутренней q, то при р = R напряжение ар = -р,
при р = г напряжение пр = -q.
Из первой формулы (9.24) следуют уравнения для определе-
ния Cj и С2:
С\^=-д-, с{+^=-р.
Их совместное решение дает:
г = дт2 - pR2 = {p-g)R2r2
* Л2-г2 ’ ~2 R2-r2 ’
При упругих деформациях в точке баллона высокого давле-
ния, не нагруженного по внешней поверхности (р = Я), главные
напряжения равны:
дг2
00 R2-г2
R1
Р2
дг2
°* = R^’
_ дг2
Р Л2-г2
(9.25)
Наибольшее из них и наименьшее <ур изменяются по толщи-
не оболочки (рис. 9.7); среднее по толщине постоянно. Наи-
большее эквивалентное напряжение - у внутренней поверхности,
по критерию максимальных касательных напряжений, например,
_ 24r2
®экв ^0 2 2 ’
К
Из (9.26) видно, что при большой тол-
щине R » г минимальное эквивалентное
напряжение <зэкв = 2q. Уже при R = 5г, &экв
= 2,Qlq. Учитывая погрешности измере-
ний, толщину оболочки можно считать
бесконечно большой, если R > 5г.
(9.26)
Рис. 9.7
148
|^| Основные понятия об устойчивости
Глава 10
УСТОЙЧИВОСТЬ СИЛОВЫХ ЭЛЕМЕНТОВ
КОНСТРУКЦИЙ
ДХ Основные понятия об устойчивости
----------------------------------------------
При расчетах на прочность предполагается, что между вне-
шними и внутренними силами существует устойчивое равнове-
сие. При сжатии стержней и оболочек вдоль продольной оси, кру-
чении и изгибе это равновесие остается устойчивым до опреде-
ленного значения внешних сил, равного критическим. Равнове-
сие может стать неустойчивым когда внешние силы достигнут
критического значения, а на систему действуют малые возмуще-
ния в виде случайных малых внешних или внутренних сил.
Незначительное повышение внешней силы сверх критической
приводит к недопустимому росту деформаций элемента конструк-
ции и последующему разрушению.
Способность нагруженной упругой системы (силового элемен-
та конструкции) сохранять состояние равновесия при действии
малых возмущений называется устойчивостью.
Теория устойчивости упругих систем исходит из основных
принципов механики, общей теории устойчивости равновесия или
движения систем.
Основные принципы механики доказаны для систем с конеч-
ным числом степеней свободы. Деформируемые тела состоят из
бесконечно большого числа материальных точек, непрерывно
распределенных по телу, но их перемещения связаны условиями
совместности деформаций. Иными словами, деформируемое тело
есть система несвободных точек, перемещения которых взаимо-
связаны и могут задаваться в виде тригонометрических рядов с
ограниченным числом членов. К этой системе применим принцип
возможных перемещений, если внешние силы консервативны.
В деформируемой системе к активным силам относятся не толь-
ко внешние F1, но и внутренние F' силы. Согласно принципу воз-
можных перемещений
Jjj^F/+Fj8r4/xJxcfe = °. (10.1)
Возможную работу внешних и внутренних сил называют ва-
риацией полной энергии системы.
149
Основные понятия об устойчивости
Полная энергия:
Э = U-А.
где U - потенциальная энергия; А - работа внешних сил.
В состоянии равновесия системы (внешние силы постоянны)
полная энергия есть функция перемещений:
Э = Э(и, v, w).
Зададим системе возможные перемещения и сохраним малые
(вариации) до второго порядка включительно, тогда
Э = Э0(м, v, и>) + 83 + 823. (10.2)
Согласно принципу возможных перемещений в состоянии рав-
новесия S3 = 0.
Так как потенциальная энергия определенно положительна,
вторая вариация энергии системы:
823>0. (10.3)
Вторая вариация энергии может быть равна нулю только тог-
да, когда все компоненты деформации на возможных перемеще-
ниях 8u, 8v, 8w равны нулю, но это возможно, если все точки сво-
бодны. В деформируемом теле все точки взаимосвязаны. Следо-
вательно, вторая вариация энергии уравновешенного тела при
идеальных связях всегда определенно положительна, т.е.:
823>0, (10.4)
и потенциальная энергия имеет строгий минимум, т.е. в положе-
нии устойчивого равновесия упругой системы:
8Э = 0. (10.5)
Если малые возмущения выведут ее из этого состояния равно-
весия, по прекращении действия возмущений она вернется в пре-
жнее положение.
Равновесие устойчиво, иными словами условие (10.5) выпол-
няется до тех пор, пока возможная работа внешней силы не ста-
нет больше работы внутренних сил (потенциальной энергии). Зна-
чение внешней силы в этом состоянии равно критической силе
элемента конструкции. Критическая сила есть функция жестко-
сти элемента конструкции. В критическом состоянии внешние воз-
мущения переведут систему в новое равновесное состояние с дру-
гим минимумом энергии.
Значение критической силы можно найти разными методами: пря-
мыми - (10.5) сразу приводится к алгебраическим уравнениям или
непрямыми - из (10.5) получают дифференциальные уравнения.
При статическом нагружении консервативными силами зада-
ча устойчивости решается как задача о равновесии. Ввд уравне-
150
Основные понятия об устойчивости
ний определяется выбором критерия устойчивости. Для этого слу-
чая нагружения их два - статический и энергетический.
При динамическом нагружении (силы меняются во времени так,
что их изменением за время, равное полупериоду свободных ко-
лебаний нельзя пренебречь), при неконсервативных силах следует
рассматривать устойчивость движения относительно невозмущен-
ного состояния и решать задачу устойчивости движения при пе-
реходе из невозмущенного состояния в возмущенное на основе
критерия устойчивости по форме совпадающего с критерием ус-
тойчивости движения А.М. Ляпунова.
Согласно теореме Ляпунова невозмущенное движение устой-
чиво, когда дифференциальные уравнения движения таковы, что
можно подобрать знакоопределенную функцию обобщенных ко-
dV
ординат Г(д), производная от которой —- знакопостоянная фун-
dt
кция противоположного знака или равна нулю.
Другими словами, невозмущенное движение устойчиво, если
можно подобрать такие величины отклонения обобщенных коор-
динат < 8j и обобщенных скоростей Л<7/0 < 82, что во все время
движения отклонение обобщенных координат меньше любого
наперед заданного числа е.
Неустойчивая система даже при самых малых отклонениях
начальных условий (8j и 82) скачком уходит в новое равновесное
состояние.
Отклонение обобщенных координат и обобщенных скоростей
элемента конструкций вызывается силами и условие устойчиво-
сти можно перефразировать так: состояние устойчиво, если ма-
лые приращения сил вызывают малые приращения перемещений
и скоростей.
Состояние системы критическое, если малые приращения внеш-
ней силы вызывают конечные приращения перемещений.
Уравнения устойчивости при нагружении консервативными
силами получают из вариационного уравнения (10.5), выбирая
критерий устойчивости.
Устойчивости шарнирно опертого
сжатого стержня
Воспользуемся статическим критерием и будем полагать пере-
мещения и деформации малыми, жесткость стержня EJy постоян-
ной; напряжения в стержне не выше предела пропорционально-
151
Устойчивость шарнирно опертого сжатого стержня
сти. Тогда для решения задачи можно использовать^ уравнения
изгиба стержня (5.20), полученное в п. 5.4:
EJy^ = Mv. (10.6)
ах
В нем знак изгибающего момента, определенный принятым ра-
нее правилом, совпадает со знаком кривизны стержня. В критиче-
ском состоянии сжатый стер-
жень изогнут, сила сохраняет
свое направление (рис. 10.1), из-
гибающий момент равен произ-
ведению силы на прогиб в се-
чении:
М — F • w.
у л кр
Знак изгибающего момента определяется знаком прогиба, а
d2w
знак кривизны —у оси сжатого стержня не совпадает со знаком
ах
момента, поэтому уравнение (10.6) следует записать так:
d2w
EJy^ = -FKpW. (Ю.7)
Обозначим:
к2 = —(10.8)
Тогда
^-^ + Л2и' = 0. (10.9)
dx
Известно, что решение такого линейного однородного урав-
нения (10.9) есть:
и’ = CjCOsZcx + C2sinfcx. (10.10)
Постоянные Cj и С2 должны удовлетворять граничным усло-
виям балки. Оба конца ее центра опираются на жесткие шарнир-
ные опоры, следовательно,
и> = 0 при х = 0,
и> = 0прих = /. (10.11)
Из первого уравнения следует С{ = 0; во втором условии нуж-
но положить sin kl = 0, чтобы условие не было тождественно рав-
но нулю; корень уравнения может принимать бесконечное множе-
ство значений:
где т = 0, 1, 2, 3, ...
152
к! = тп,
(10.12)
Устойчивость шарнирно опертого сжатого стержня
Первый корень т = 0 не соответствует физическому смыслу
задачи, поэтому должен быть отброшен.
Из (10.8) и (10.12) получим критическую силу
m2i?EJ
^=—[2-------’ (10.13)
впервые найденную Эйлером. В формулу (10.13) из двух главных
моментов инерции подставляют минимальный так как потеря ус-
тойчивости происходит в плоскости наименьшей жесткости. Наи-
меньшему значению критической силы соответствует т = 1 и ми-
нимальный момент инерции сечений Решение уравнения
изогнутой оси (10.9) при минимальном т = 1 будет:
. Ttx
w = C2sm—.
По смыслу задачи постоянная прогиба С2 есть амплитуда про-
гиба. Стержень изгибается в виде полуволны синусоиды.
Формулу (10.13) можно распространить на другие случаи опи-
рания стержня, не задавая при решении других граничных усло-
вий. Пусть стержень жестко заделан одним концом (рис. 10.2).
Минимальному значению критической силы соответствует изгиб
по половине синусоиды и стержень, заделанный одним концом,
будет изгибаться так же, как половина стержня при шарнирном
опирании концов. Следовательно, чтобы применить формулу Эй-
лера для критической силы стержня, заделанного одним концом,
необходимо подставить удвоенную длину этого стержня:
р _ 71 ^Лтнп
кр (21)2 ’
Рис. 10.2
У=0,7

153
Устойчивость шарнирно опертого сжатого стержня
При заделке обоих концов (см. рис. 10.2) образуются две полу-
волны синусоиды, средняя часть изгибается по одной полуволне,
концевые части оси образуют четверти синусоиды. Таким обра-
зом, в формулу F необходимо подставлять половину длины стер-
жня1 2
р _ 71 min
(0.5/)2 ‘
Аналогичными рассуждениями можно установить величину
коэффициента при длине стержня и в других случаях опирания,
обозначим его через v. Этот коэффициент называют коэффициен-
том приведения длины или коэффициентом опирания. На рис. 10.2
показаны наиболее распространенные случаи опирания и указа-
ны коэффициенты V. Их значения подставляют в формулу крити-
ческой силы:
р 71 ^min
Ркр~~(угГ' (1014)
Наиболее рациональными сечениями сжатых стержней явля-
ются кольцевые(трубчатые) и коробчатые сечения, имеющие оди-
наковые главные моменты инерции и наибольшее отношение же-
сткости к весу (рис. 10.3). Для стержней переменной жесткости и
в случае приложения
сил в сечениях между
опорами составляют
уравнения для каждого
участка. Более просто
подобные задачи реша-
ют энергетическим ме-
тодом.
Ш, Расчеты «а устойчивость
при пластических деформациях
V------------------------------------------------
Формула Эйлера получена при постоянном модуле упругости,
поэтому критическое напряжение должно быть:
(10.15)
Это неравенство ограничивает применение формулы. Введем
v/ J
гибкость стержня Л = —, где i = —- радиус инерции.
i А
154
Расчеты на устойчивость при пластических деформациях
Подставим (10.14) в (10.15), получим:
= (10.16)
Л z
Предельное (наименьшее) значение гибкости:
пример, формулу Ясинского:
При гибкости больше
предельной формулу Эйле-
ра применять нельзя. Как
видно из рис. 10.4, где кри-
вая 1 есть гипербола Эйле-
ра, при гибкостях меньше
предельных расходимость с
экспериментом становится
большой. Формула 10.14
дает завышенные значения
критического напряжения.
В этих случаях применяют
эмпирические формулы, на-
Рк.п = а- ЬК
кр ’
где а и b - коэффициенты, зависящие от материала; Л. - гибкость.
Хорошую сходимость обеспечивает также другая эксперимен-
тальная формула:
где = рэкр определяется по (10.14) .
•Ркр
На устойчивость сжатого стержня сильно влияют эксцентри-
цицет приложения силы, начальная кривизна и неоднородность
стержня, поэтому при расчете вводят коэффициенты запаса ус-
тойчивости. В некоторых случаях расчет на устойчивость при
пластической деформации заменяют расчетом на прочность по
сниженным допускаемым напряжениям на сжатие [crj. Критиче-
ское напряжение определяют как часть допускаемого напряже-
ния:
Лф = <р[°Д
155
Энергетические методы расчета стержня на устойчивость
Коэффициент снижения допускаемых напряжений ф задают для
каждого материала по гибкости ф = ф(Л) с увеличением гибкости ф
уменьшается.
При проверочных расчетах вычисляют гибкость и по ней из
таблицы находят ф. Проектировочный расчет выполняют мето-
дом последовательных приближений. В первом приближении
обычно принимают ф = 0,5. При этом значении находят площадь;
F
сечения А =----, по ней определяют гибкость, затем ф. Расчет
повторяют до получения нужной точности.
Энергетические методы расчета стержня
на устойчивость
Энергетический критерий устойчивости для стержня может
иметь такие два варианта:
— состояние стержня критическое, если потенциальная энергия
равна работе внешних сил (критерий С.П. Тимошенко) U=AF\
— вариация полной энергии 5Э = 0 в состоянии равновесия, близ-
ком к исходному, в которое стержень выведен малыми возму-
щениями, т.е. полная энергия сохраняет стационарное значе-
ние.
Рассмотрим устойчивость стержня, изображенного на рис. 10.5,
используя первый критерий. В критическом состоянии стержень
изогнут, напряженное состояние одноосное, поэтому удельная
потенциальная энергия (1.43):
156
[у] Энергетические методы расчета стержня на устойчивость
Потенциальная энергия стержня:
и с =-^-( \~z 2dAdx.
IF J J T2
0 A J у
Это выражение для энергии можно преобразовать, используя
уравнение изогнутой оси (8.29). После интегрирования по пло-
щади сечения найдем:
1 г
d2w
1 ч
Возможная работа силы Г(см. рис. 10.5):
FKp
dx.
/
где e = |8eJx, Зе = 8$ - 8х - элементарное смещение сечения
о
ds = dx
2
Из криволинейного тре-
угольника (рис. 10.6) найдем:
ЗиЛ2
дх J
Разложим его в ряд по би-
ному Ньютона и, удержав пер-
вый член разложения, полу-
чим:
ds = dx
. 1 ( Эи» Y
1+ik.
Теперь возможная работа внешних сил:
1 // _/ .\2
dx.
А>
ov J
Приравняв потенциальную энергию работе внешних сил, най-
дем критическую силу
П—
кр / / j
dx

(10.17)
о
157
Энергетические методы расчета стержня на устойчивость
функцию w(x) необходимо задать так, чтобы она удовлетворяла
условиям опирания стержня.
Используя вторую форму энергетического критерия, вариа-
цию энергии 8Э запишем в виде суммы частных вариаций. Функ-
п
цию w(x) представим в виде ряда удовлетворяющего
условиям опирания, где/,. - амплитуда периодических функции т),,.
/= 1, 2, 3,
Имеем
п.
5Э = —5/,
Э/
где i - «немой» индекс, по нему берут сумму.
Вариации 8/J произвольны и независимы, поэтому уравнение
удовлетворяется, если каждый из коэффициентов при них
»-0.
V,
Энергия Э есть квадратичная функция перемещений. Вычис-
лив производные, получаем систему п линейных однородных ал-
гебраических уравнений относительно амплитуд f.. Эта система
имеет решение, если определитель, составленный из коэффициен-
ЭЭ
тов при равен нулю: Det - 0. Уравнение — = 0 содержит неиз-
вестную критическую силу. При его решении находят п значений
F 9 за истинное значение принимают наименьшее.
Решение, полученное энергетическим методом, всегда выше
точного. Приближенное значение функции w накла-
дывает на стержень дополнительные связи, что рав-
носильно повышению его жесткости, однако ошиб-
ка определения критической силы может быть дос-
таточно малой.
Пример 10.1. Пусть стержень защемлен одним
концом, к свободному концу приложена сила/7(рис.
10.7) . Для изогнутой оси примем параболу w = fx2.
Подставив w в уравнение (10.17), получим:
2,47 EJ
Это значение отличается от точного FKn = ——--
КР
О
Рис. 10.7
158
Основные особенности устойчивости оболочек
на 20%. Если уточнить значение прогиба, приняв его в виде:
Н’ =^х2 +/3Х4,
критическая сила ~ ,
2,5£ Jmin
полученная из решения квадратного уравнения, будет отличать-
ся от точного значения на 1,2%. Так как модуль упругости опре-
деляется с меньшей точностью, эту ошибку можно считать допус-
тимой.
Основные особенности устойчивости оболочек
Тонкие оболочки обычно теряют устойчивость, т.е. переходят
из начального неискривленного (невозмущенного) равновесного
состояния в новое (возмущенное) равновесное состояние (выпу-
чиваются) при упругих деформациях. В конструкциях летатель-
ных аппаратов, в хранилищах жидкостей, в химических аппара-
тах обычно и применяются такие оболочки.
Оболочки могут терять устойчивость при нагружении осевой
сжимающей силой, равномерно или неравномерно распределен-
ным по поверхности внешним давлением, при изгибе и кручении
или при различных сочетаниях внешних сил. При стеснении пере-
мещений торцов замкнутые оболочки теряют устойчивость и от
действия сосредоточенных сил, приложенных нормально к сре-
динной поверхности.
Названные внешние силы могут прикладываться статически
159
Основные особенности устойчивости оболочек
В стержне и жесткой пластине после потери устойчивости на-
пряжения определяются изгибом. Переход к новому равновесно-
му состоянию идеальных стержней и пластин равновероятен в обе
стороны от срединной поверхности пластин или в любую сторону
от оси стержня (рис. 10.8, а). При потере устойчивости оболочки
вследствие кривизны поверхности, кроме изгибных напряжений,
возникают значительные растягивающие или сжимающие напря-
жения в срединной поверхности. Последние будут меньше при
смещении к центру кривизны, меньше будет и потенциальная энер-
гия. Согласно принципу возможных перемещений реализуют те
перемещения, при которых работа будет наименьшей, поэтому
точки оболочки в направлении нормали к срединной поверхнос-
ти смещаются преимущественно к центру кривизны.
Физическую картину поведения оболочки при нагружении
рассмотрим в случае осевого сжатия. Эта задача является наибо-
лее сложной в теории устойчивости цилиндрических оболочек.
При сжатии оболочки в осевом направлении силами, равно-
мерно распределенными по торцам, по мере роста нагрузки по-
тенциальная энергия оболочки увеличивается. Если оболочка
сохраняет цилиндрическую форму, вся потенциальная энергия
деформации есть энергия осевого сжатия. При некотором (крити-
ческом) значении нагрузки оболочка теряет устойчивость, про-
должая сжиматься вдоль образующей, деформируется в кольце-
вом направлении л изгибается. В момент потери устойчивости
потенциальная энергия становится равной работе внешних сил, в
закритическом состоянии она меньше.
Выпучивание оболочки может быть симметричным относитель-
но ее оси, но тонкие оболочки с ^->100 выпучиваются по асим-
метричной форме. Тщательно изготовленная оболочка по всей
поверхности покрывается вмятинами ромбовидной формы. Пере-,
ход к этому равновесному закритическому состоянию происхо-
дит с большой скоростью (0,006-0,010 с), сопровождается хлоп-
ком. В процессе хлопка форма выпучин (вмятин) изменяется до
тех пор, пока не будет достигнут наименьший уровень потенци-
альной энергии в новом равновесном состоянии. Прогибы смеще-
ния по нормали уже в начале потери устойчивости имеют порядок
толщины оболочки.
Существуют две теории упругой устойчивости оболочек и пла-
стин; линейная и нелинейная. В линейной теории предполагается,
что при достижении критической нагрузки малые возмущения при-
160
Устойчивость замкнутой цилиндрической оболочки...
водят к появлению новой устойчивой формы равновесия, беско-
нечно близкой к исходной.
Закритическое поведение оболочки линейная теория не опи-
сывает, так как она исходит из перемещений бесконечно малых
по сравнению с толщиной оболочки. По ней определяют только
критические напряжения или силы.
В нелинейной теории рассматриваются конечные перемеще-
ния, сравнимые с толщиной оболочки. Нелинейная теория уста-
навливает для оболочки интервал нагрузок от нижней критичес-
кой Р”р до верхней критической Р*р. Верхней критической на-
грузкой будем называть нагрузку, при которой происходит выпу-
чивание с образованием регулярных вмятин на поверхности. Ниж-
ней критической нагрузкой будем называть нагрузку, при которой
происходит обратный переход потерявшей устойчивость оболоч-
ки к начальному неискривленному состоянию (см. рис. 10.8, б).
Когда нагрузка меньше нижней критической единственным ус-
тойчивым равновесным состоянием является исходное.
Устойчивость замкнутой цилиндрической
оболочки, сжатой вдоль образующей
(линейная задача)
Сжатию в осевом направлении подвергаются
корпуса летательных аппаратов и некоторые ине-
нерные сооружения. Под действием осевой силы
отсеки корпусов (тонкостенные оболочки) могут
терять устойчивость.
Рассмотрим устойчивость идеальной изотропной
оболочки, шарнирно опертой по торцам и сжатой
силой, равномерно распределенной по концевым
сечениям, погонное значение которой обозначим FKp.
Будем полагать перемещения малыми и считать,
что произошла потеря устойчивости, если состоя-
ния оболочки, ближайшие к основному (невозму-
щенному) состоянию, становятся устойчивыми.
Предположим, что поверхность оболочки
при выпучивании симметрична относительно оси
(рис. 10.9). При этом поперечные сечения остают-
ся круговыми, а вдоль меридионального сечения
образуется несколько полуволн.
Р
Рис. 10.9
6. Зак. 388
161
Устойчивость замкнутой цилиндрической оболочки.:.
При симметричной деформации условие равновесия оболочки
описывается уравнением краевого эффекта:
.о4 q. Ni
—-+4(Ги> = -^--ц—,
dx4 D rD
где Nj - погонная меридиональная сила,
Л Eh3 - ,
D =-----------жесткость оболочки при изгибе.
12(1-ц2)
Пренебрегаем пуассоновым прогибом, т.е. полагаем ц = 0.
Тогда:
t/w .„4 <7,
dx* D
При осевом сжатии до потери устойчивости предположим со-
стояние оболочки безмоментным. Это упрощение возможно, так
как в большинстве случаев, встречающихся в практике, невоз-
мущенное состояние мало отличается от начального недеформи-
рованного состояния, перемещения нарастают при потере устой-
чивости. В критическом состоянии кроме меридиональных дефор-
маций возникают кольцевые де-
формации срединной поверхности
и изгиб. Чтобы воспользоваться
уравнением (10.18), введем фик-
тивную эквивалентную попереч-
ную силу q3, равную сумме проек-.
ций меридиональной силы на
нормаль к изогнутой поверхности
оболочки (см. рис. 10.10). Так как
в критическом состоянии F = N},
dw
а угол — мал и q3 = q_, то
(10.18)
(10.19)
(10.20)
__F d2w
^кр Л 2 *
дх
Теперь вместо (10.18) имеем:
Л А 4в,=0
dx4 D dx2
Условиям шарнирного опирания при осесимметричной форме
выпучивания удовлетворяет функция:
- . тих
w= f sin---------------------------,
Z
где f - неопределенный коэффициент.
(10.21)
162
Устойчивость замкнутой цилиндрической оболочки...
Подставив (10.21) в (10.20), имеем:
/ \4 >7 / \2
пт ] гкр [ пт
~Т +dI ~т
г /77TLJV _
+ 4(3 и/ sm —-— = 0,
откуда критическая сила:
' fkp=d
\2
W71
~Г
4Р4
пт
(10.22)
Формула (10.22) дает множество значений критической силы.
Z Ч2
_ I I Z- «V.
Обозначим а= -у- , будем считать т » 1 и найдем минималь-
dFk„
ную критическую силу из условия —— = 0.
Эа
Отсюда следует:
а = 2Р2; FKp = 4D&-.
Подставив значения D и Р, имеем:
Е h2
F*P
Критическое напряжение при ц = 0,3:
^KD h
Ркр=^- = 0,605Еу. (Ю.23)
Критическое напряжение, которое равно отношению крити-
ческой силы к толщине оболочки, во всех задачах устойчивости
здесь обозначается Ркр. Из (12.64) видно, что отношение крити-
ческого напряжения к модулю упругости имеет порядок отноше-
h
ния —.
Осесимметричная форма потери устойчивости свойственна
сравнительно толстым или нагретым оболочкам. Тонкие оболоч-
ки, у которых —>100, теряют устойчивость по асимметричной
h
форме, образуя волны не только вдоль оси, но и по кольцу. Обра-
зующая оболочки делится на т полуволн, окружность - на п волн
(рис. 10.11).
Решение линейных дифференциальных уравнений, в которых
учтена эта особенность критического состояния оболочки, при-
водит к тому же (10.23) значению критического напряжения.
6
163
[7[ Устойчивость замкнутой цилиндрической оболочки...
Рис. 10.11
При испытаниях оболочек на осевое сжатие потеря устойчи-
вости происходит хлопком. При упругих деформациях образуют-
ся вмятины ромбического типа (рис. 10.11); при пластических де-
формациях форма потери устойчивости осесимметричная.
Для равномерно нагруженных оболочек, изготовленных из ли-
стового материала, параметр критического, напряжения р* ока-
зывается равным 0,2-0,4. Эти результаты получены в последние
годы при тщательной обработке торцов оболочек. По данным
исследований различных авторов, полученным за последние 40-
50 лет, область экспериментальных значений р* имеет вид, пока-
занный на рис. 10.12. Кроме большого разброса значений (его
можно объяснить как различной величиной и характером началь-
ных погибей, так и степенью неравномерности нагружения), видна
тенденция к снижению критического напряжения по мере роста —,
h
которая не предсказывается известной линейной теорией. Для прак-
тических расчетов можно пользоваться кривой на рис. 10.12 - ма-
тематическим ожиданием функции:
р*=р* - .
и
Начальные неправильности определяются и технологией ме-
таллургического производства листовых материалов, и техноло-
гией изготовления оболочечных конструкций. Они могут быть
различными не только у разных изготовителей, но и у одного из-
164
Устойчивость замкнутой цилиндрической оболочки...
готовителя в разные годы. Причиной отклонений критической
нагрузки от расчетного значения, полученного по линейной тео-
рии, может быть существование у реальных оболочек начальных
неправильностей (погибей, разностенности, остаточных напряже-
ний), но -главным образом, несовершенство теории.
Наиболее сильное влияние, вероятно, оказывает начальная
погибь, амплитуда которой сравнима с толщиной оболочки. У
таких оболочек новое устойчивое состояние не будет бесконечно
близким к основному (докритическому), т.е. перемещения по нор-
мали к срединной поверхности нельзя считать бесконечно малы-
ми по сравнению с толщиной оболочки: происходят только те пе-
ремещения, при которых уровень энергии наименьший.
За нагрузку выпучивания следует принимать нагрузку, соот-
ветствующую наименьшему значению энергии Э, исследуя раз-
личные формы потери устойчивости.
Устойчивость цилиндрических оболочек
при действии внешнего давления
Оболочки, входящие в конструкцию корпусов летательных
аппаратов, резервуары для хранения жидкостей, подвергаются
действию равномерно распределенного по поверхности внешне-
го давления и могут терять устойчивость.
Рассмотрим задачу об упругой устойчивости круговой цилин-
дрической оболочки (рис. 10.13). Для решения ее три уравнения
авновесия оболочки в перемещениях и, v, w сводятся к одному:
D^w + ~^ + qr\74~ = 0. (10.24)
г2 дх4 ду2
Рис. 10.13
165
Устойчивость цилиндрических оболочек при действии ... давления
Как и при осевом сжатии q заменяется проекциями кольцевой
нормальной силы N2 на нормаль к срединной поверхности обо-
лочки, теряющей устойчивость
d2w
Яг Яэкв ^2 ~ 2 ’
дУ
докритическое состояние считается бемоментным, тогла в соот-
ветствии с (9.9) N2 = qr.
Решение (10.24) ищем в виде
w =/sinax sinPy,
_ rm n n
где обозначены a = —, p = —.
I r
Подставив решение, имеем:
Z)(a2 +p2)4 +^-a2 -£r(32(a2 +p2)2 =0,
rL
откуда
_ (а2 + Р2 )2 Eh а4
q = D----------1—-—-— ----z—-.
р2 г3 р2(а2 + Р2)2
Введем безразмерный параметр давления:
ЕЛ2
и приведем q к безразмерному виду. Из (10.25) видно, что мини-
мальному значению q соответствует т = 1. Тогда:
л4г5
л2 г2
л2/2
9
12(1-ц2)г
(
2 i ЯГ
п
л2/2
V > л/V 1 +
,2
f4 6
(10.25)
h
/ , [ЯГ
Если - >2 , и п > 4, то можно полагать —
Г {п!
для безразмерного давления q* упростится:
hn2 тс4г5
q* =---------------------------+--------.
12(1-ц2)г A/V
«1. Формула
(10.26)
Из условия —= 0 найдем число волн л, соответствующее
«*.. Э(и)
J min .—
п2 =Пт/б1/(1-ц2)!-,К.
I V h
166
[yj Устойчивость цилиндрических оболочек ори действии ... давления
Подставив это значение в (10.26), получим безразмерное кри-
тическое давление:
. Лд/б Г [7
^ 7/—ТТ7П' (10-27)
9^(1-И ) 7
При ц = 0,3 безразмерное давление:
<7* = 0,92^. (10.28)
/ V h
Критическое давление:
9^=О’92£7ГЛ- (10.29)
Эта формула впервые получена П.Ф. Папковичем и носит его
имя.
Можно показать, что формула Папковича применима для обо-
лочек средней длины, определяемой неравенствами:
0.92ЕЛ Г
‘’Чп
При безмоментном докритическом состоянии критическому
давлению соответствует критическое напряжение
Если напряжение больше предела пропорциональности
акр > > его истинное значение определяют по полуэмпириче-
ской формуле:
1 + £
П - ------—,
р 1+k+k2
(10.30)
Рис. 10.14
где к =----и соответственно полученному значению критиче-
ского напряжения уточняют критическое давление.
При внешнем давлении оболочка вдоль обра-
зующей выпучивается только по одной полувол-
не (рис. 10.14), поэтому условия опирания торцов
на критическую нагрузку влияют более заметно,
чем при осевом сжатии, при защемлении торцов
критическое давление в 1,5 раза выше, чем при
шарнирном опирании. Результаты эксперимен-
тальных исследований показывают, что линейная
теория дает завышение значения критических дав-
167
Р7[ Устойчивость цилиндрических оболочек при действии ... давления
лений, их верхнюю границу. Нижняя граница экспериментальных
значений получена из нелинейного решения энергетическим мето-
дом (рис. 10.15). При практических расчетах пользуются форму-
лой П.Ф. Папковича, умножая полученные qKp на некоторый коэф-
фициент V, значения которого ориентировочно могут быть взяты
г г г
такими: при — = 250 v = 0,7; при — = 500 v - 0,6; при — = 1000 v =
h h h
Продолно-поперечный изгиб балки
Такой изгиб может происхо-
дить либо при одновременном на-
гружении силами, лежащими в
плоскости наибольшей жесткос-
ти, и силой, направленной пер-
Рис. 10.17
двутаврового сечения, имеющего малый начальный изгиб w
Рис. 10.16
пендикулярно оси балки
(рис. 10.16), либо при вне-
центренном осевом сжа-
У тии (рис. 10.17).
Ограничимся случаем
внецентренного сжатия
(см. рис. 10.17) балки
о-
168

Продольно -поперечный изгиб балки
Уравнение изгиба:
d2w
EJy- + F(w-wQ) = My (10.31)
после двукратного дифференцирования с учетом теоремы Журав-
ского примет вид:
d4w d2 , ч
EJy —4- + F—(w - w0 ) = q
dx dx
или
(10.32)
(10.33)
9 -Г
Обозначим к =----, тогда общее решение неоднородного
EJ у
дифференциального уравнения (10.33) запишется в виде
w = CjCOsAjc + C2sin£x + С3х + С4 + w*. (10.34)
Общее решение однородного уравнения легко проверить под-
становкой. Частное решение неоднородного уравнения (10.33)
ю* при постоянном значении q и начального изгиба
- . 7LX
w0=/sm— , (10.35)
допустимо принять
w* = C5sin—+ С6х . (10.36)
Постоянные Ск найдем из граничных условий. При шарнирном
опирании концов балки:
х = 0, w = 0, =
у dx2
x=i, w = 0, — = 0.
dx2
q=-C4=-^ + e,
Fk2
C2 =-ectgkl—^(1-seckl),
Fk
3 I 2F
169
Свободные колебания стержней
с6 = здесь P=FFkp=±ZL (10.37)
Из (10.37) видно, что при F>FKp прогиб w быстро нарастает,
поэтому вводится запас прочности ц = 0,5+0,6, т.е. F< (0,5...0,6)/^.
Глввв 11
КОЛЕБАНИЯ СТЕРЖНЕВЫХ ЭЛЕМЕНТОВ
КОНСТРУКЦИЙ
njL Свободные колебания стержней
-------------------------------------------
Нарушение равновесия упругой системы под действием мгно-
венно приложенной или периодически прилагаемой силы, а так-
же при периодическом изменении параметров приводит к коле-
бательным движениям. Части системы (упругого тела) совершают
различные перемещения, поэтому при колебаниях возникают де-
формации. Величина этих деформаций может стать выше предель-
ной, полученной расчетом на статическое действие сил. Колеба-
ния также могут приводить к усталостному разрушению.
При конструировании и эксплуатации конструкций, работа-
ющих при быстро изменяющихся нагрузках, необходимо учиты-
вать возможность возникновения динамических напряжений и
деформаций, вызванных колебаниями. Напряжения и деформа-
ции при колебательных процессах могут определять несущую спо-
собность и эксплуатационные качества конструкций.
Сложность анализа колебаний зависит от числа степеней сво-
боды механической системы, под которыми понимают числа не-
зависимых координат, определяющих положение системы.
Жесткое тело, связанное с пружиной, массой которой можно
пренебречь, имеет одну степень свободы. Упругие тела (стержни,
пластины, оболочки) содержат бесконечно большое количество
материальных точек, но перемещения точек тела взаимосвязаны,
при решении практических задач выбирают расчетную модель с
конечным числом степеней свободы. Так, при поперечных коле-
баниях балки на двух опорах можно положить изогнутую ось в
виде синусоиды, тогда ее конфигурация в любой момент времени
определится прогибом средины /, т.е. балка будет системой с од-
ной степенью свободы.
170
и
Свободные колебания стержней
При исследовании упругих систем рассматриваются свобод-
ные (собственные), вынужденные и параметрические колебания.
Свободными (собственными) колебаниями называют колеба-
ния системы, выведенной из равновесия и представленной самой
себе: притока энергии извне при свободных колебаниях нет.
Под вынужденными колебаниями понимают движение упругой
системы под действием изменяющихся во времени внешних сил.
Параметрическими колебаниями называют колебания, вызы-
ваемые периодическими изменениями параметров системы (жест-
кости или массы) при действии внешних сил, направления пере-
мещений не совпадают с линией действия этих сил.
Внешние и внутренние силы, действующие на упругую систе-
му, по их роли в колебательных движениях подразделяются на
возмущающие, восстанавливающие и диссипативные.
Возмущающими силами называют внешние силы, изменяю-
щиеся во времени по различным законам.
Восстанавливающие силы - это силы упругости, возникаю-
щие из-за отклонения системы от положения равновесия, или силы
тяжести, стремящиеся вернуть систему в это положение. Восста-
навливающая сила может быть пропорциональна отклонению:
F-cu
(с - коэффициент жесткости системы) или связана с отклонением
нелинейной зависимостью.
Диссипативные силы - силы, вызывающие необратимую ра-
боту. К ним относятся силы сопротивления среды, силы трения в
опорах, силы внутреннего трения в'материале. Диссипативные
силы всегда противоположны скорости и связаны с ее величиной.
Свободные колебания вследствие действия диссипативных сил
затухают.
Период колебаний будем обозначать Т. Величину, обратную
периоду, - частоту колебаний (число колебаний в секунду) - обо-
значим р = —, а число колебании за 2л секунд - круговую часто-
2пТ „ с „
ту - (0 = —. Частота колебании упругих систем определяется
либо решением дифференциальных уравнений движения, либо
энергетическими методами.
Рассмотрим свободные колебания однородных стержней.
В однородном стержне со свободными концами возбудим продоль-
ные колебания ударом по одному из концов. Поперечные сечения
171
Свободные колебания стержней
будем считать плоскими и неперемещающимися в поперечном
направлении.
Вследствие кратковременного воздействия внешней силы на
один из концов по стержню со скоростью звука а = —, где Е -
модуль упругости; р - плотность, будут_распространяться дефор-
о 1Т_/ —
мации сжатия. За время —
они достигнут другого
конца стержня, отразившись от него, станут деформациями рас-
тяжения и за Время 0,5 Г достигнут конца, по которому был произ-
веден удар. Таким образом, за время Т деформации стержня бу-
дут такими же, что и в момент удара. Для составления уравнения
движения воспользуемся методом кинетостатики. Рассмотрим
элемент стержня длиной dx (рис. 11.1).
Пусть и(х, г) - перемещение сечения с координатой х, переме-
Эи ,
щение другого сечения элемента и + — dx.
дх
dx + u + -dx-u-dx з
Дх ди
Тогда деформация е =-----—-----------= —.
dx дх
В сечении х действует нормальная сила N; в сечении х + dx -
сила N + dN.
Масса элемента dm = рА dx.
. д2и 3N
Уравнение движения элемента рА—— = , но из закона
дг дх
du
Гука следует N = —ЕА.
dx
172
Свободные колебания стержней
(111)
(П.2)
Тогда уравнение движения (волновое уравнение):
d2u Е д2и 2 92и
dt2 Р дх2 дх2
Решение ищем в виде:
и = AV)sina)/.
После подстановки его в уравнение получаем:
^+4*=о.
dx2 а2
Это уравнение имеет следующее решение:
„ ~ . со ~ со
X = C1sin — x + C2cos —х,
а а
определяющее форму колебаний, т.е. закон амплитудных откло-
нений точек оси стержня от равновесного положения. Постоян-
ные Cj и С2 определяются из граничных условий.
На свободном конце N = 0, т.е. — = 0; на жестко защемлен-
ном конце и = 0 т.е. X = 0.
Пусть стержень (см. рис. 11.1) закреплен левым концом. Тогда
при х = 0 функция Х(х) - 0 следовательно С2 = 0. При х = /, — = 0,
дх
значит Q cos — / = 0. Очевидно, нужно принять cos — / = 0, так как
а а
при Cj = 0 имеем нулевое решение.
Корни трансцендентного уравнения cos—/ = 0:
а
со 2л _
— = —(2л-1); л = 1,2,3,
а I
отсюда собственная частота:
со =
(П.З)
В (11.3) стержень обладает п собственных частот колебаний.
Частота основного тона при п - 1 (низшая)
(0 =
обратно пропорциональна длине балки, растет с увеличением мо-
дуля упругости и уменьшается с ростом плотности.
173
Свободные колебания стержней
Перемещение точек стержня вдоль оси получим, подставив
значение частот и форм колебаний в (11.2):
и = G sin ——— sin cor. (11.4)
1 21
Формы колебаний с точностью до произвольной постоянной,
которая определяет масштаб, показаны на рис. 11.1.
При поперечных колебаниях нагрузкой для упругой балки
будут равномерно распределенные по длине силы инерции:
d2w
где т - масса единицы длины балки.
В случае равномерно распределенной по длине нагрузки урав-
нение изгиба: о z п \
d2 L гд2и>
—т EJ—г =?•
Эх2 Эх2
_ _ V ' «г-ж
Для балки .постоянного сечения, у которой EJ нт постоянны,
получим уравнение движения методом кинетостатики:
+ = (11.3)
т Эх4 Э/2
. Как и при продольных колебаниях, решение ищем в виде:
d2w
Эх2
w = Z(x)sincor.
После подстановки его в (11.5) имеем уравнение
^--k4z = 0, (11.6)
dx4
ГДе л 2
Л4 = рЛ(0 (
EJ
Решение уравнения (11.6), определяющего форму колебаний,
содержит четыре постоянных и имеет следующий вид:
z = CjSinAx + C2cosfcx + C3shkx + C4chkx. (11 -8)
Постоянные Cz определяются из граничных условий. Если бал-
ка закреплена по концам шарнирно, прогибы на опорах и изгиба-
ющие моменты равны нулю, имеем граничные условия:
j2 7
— при х = О, Z = 0 и —— = 0;
dx2
d2Z (1L9)
— при х = /, Z = 0 и —— = 0.
dx2
174
[^7[ Свободные колебания стержней
Первые два условия выполняются, если С2 = С4 = 0. Из двух
других имеем:
CjSinAV + C3shkl = 0,
-C2sinW + C2shkl =0. H 1.1 °)
Чтобы постоянные и С2 не были равными нулю, необходи-
мо приравнять к нулю определитель:
получим частотное уравнение:
sin kl
-sin А/
shW
shA:/
= 0, откуда
sinAcZ • shkl = 0.
Так как shfc/ 0, то частотное уравнение принимает вид:
sinkl = 0.
Корни уравнения есть kl = лтг, где п = 1, 2, 3, ...
Учитывая обозначение (11.7), получим:
л2л2 [ЁТ
= • (ПИ)
I2 У рЯ
В отличие от продольных колебаний частоты поперечных ко-
лебаний пропорциональны второй степени чисел натурального
ряда, обратно пропорциональны квадрату длины, пропорциональ-
ны корню квадратному из изгибной жесткости EJ и обратно про-
порциональны корню квадратному из погонной массы балки.
Определим собственные формы. Форма упругой линии балки
определяется (11.8). Так как shAzZ * 0, то из второго условия (11.9)
следует С3 = 0. Кроме того, к = Тогда форма упругой линии
~ ~ . ппх
определится из Z = ц sin——.
При колебаниях основного тона ось балки изгибается по од-
ной половине синусоида. Соответственно при п = 2 образуются
две полуволны; при п-3- три полуволны и т.д. ,
Для других концевых условий общее решение (11.8) удобно
выбрать в таком виде:
Z = C{S(kx) + С2Т(кх) + С3 U(kx) + С4 Г(Ах), (11.12)
где S(kx) = (cos Ах + ch Ах); Т = — (sinAx + shAx);
r r 1 \ 17 / 1Л ' 7 \ (11.13)
U = — (chAx - cosAx); V = — (shAx - sinAx) v 7
- балочные функции А.Н. Крылова.
175
Свободные колебания стержней
х = 0;
—7=0;
dx2
(И.14)
Перед дифферецированием (11.12) см. стр. 185.
Рассмотрим балку со свободными концами. Условия на концах:
х = I.
dx3
Если х = 0, они удовлетворяются при С2 = С4 = 0. При х = I
получим уравнения относительно и Су
CJchkl - cosZcZ) + CJshkl - sinkl) = 0;
Cj(sinA:Z + shZcZ) + CJchkl - cosZrZ) = 0.
Отличное от нуля решение для постоянных и С2 имеет при
равенстве нулю определителя уравнений (11.14). Из него следует
частотное уравнение:
coski • chkl = 0.
Первые четыре корня этого уравнения такие: kJ = 0; к; к21 =
= 4,730; kJ = 7,853; kJ = 10,996. Подставляя их в (11.7), определя-
ем частоты собственных колебаний. Первому корню, при котором
w = 0 соответствует плоское движение балки как твердого тела.
Форму изгибных колебаний можно получить из (11.12), пред-
варительно отыскав из (11.14) отношение CJC2, при соответству-
ющих значениях корней частотного уравнения kJ (i = 2, 3, 4).
В таком же порядке находят частоты и формы собственных
колебаний балок при других концевых условиях. Для определения
движение балки после начального возмущения нужно указать для
ее участков, к которым мгновенно прикладывается возмущающая
сила, начальные смещения и начальные скорости.
ЯШ1к Энергетические методы определения
частот собственных колебании стержней
Ф’---------------------------------------------
В инженерной практике приходится сталкиваться с изгибными
колебаниями балок переменного сечения, балок с присоединен-
ными массами, дисками и т.д. Простейшей расчетной моделью
будет система, состоящая из присоединенных масс и невесомой
упругой балки. Для такой системы можно составить п уравнений
движения (п - число присоединенных масс), аналогичных уравне-
ниям метода сил.
Расчетами установлено, что в большинстве случаев такая рас-
четная модель неприемлема, поскольку собственная масса балок
176
Энергетические методы определения частот собственных колебаний*.
соизмерима с присоединенными массами. Кроме того, жесткость
балок может меняться по длине. В таких случаях системы уравне-
ний движения становятся громоздкими. Более удобными будут
энергетические методы, например, метод Рэлея, основанный на
законе сохранения энергии, согласно которому сумма кинемати-
ческой и потенциальной энергии системы постоянна.
Рассмотрим этот способ для определения частоты собствен-
ных колебаний балки с присоединенными массами. Положим, что
колебания всех масс и самой балки синфазны. Тогда закон дви-
жения i массы можно записать так:
w- -fi sin(co/ + а),
а скорость будет:
Эи> г
— = /cocos((oz + а).
Когда балка и присоединенные массы проходят положения
равновесия, потенциальная энергия системы равна нулю, а кине-
тическая энергия максимальна, так как в этом положении макси-
мальна скорость. Максимум потенциальной энергии U достига-
ется в момент наибольшего отклонения системы от положения
равновесия.
Согласно закону сохранения энергии:
(11.15)
max max v 7
Кинетическая энергия системы:
T’max
Из (11.15) имеем формулу Рэлея:
(О2 = . (11.16)
Для определения потенциальной энергии нужно знать форму
оси балки, которую задают так, чтобы удовлетворить гранич-
ным условиям и приближенно дифференциальному уравнению
статического изгиба.
Истинное значение частоты всегда оказывается меньше вы
численной энергетическим методом, так как приближенный вы-
бор функции перемещений эквивалентен наложению на систему
дополнительных связей, увеличивающих жесткость системы. Луч-
шее приближение к истинному значению частот дает метод Рит-
ца. Потенциальную и кинетическую энергию записывают через
форму колебаний, которую выбирают в виде ряда, а частоту
(11.16) минимизируют по коэффициентам ряда.
177
Р7[ Энергетические методы определения частот собственных колебаний...
Рис. 11.2
Рассмотрим примеры определения частот по методу Рэлея.
Пример ILL Определить частоту собственных продольных
колебаний стержня, массой /л0, длиной /, жесткостью на растя-
жение ЕА, если к свободному концу подвешен
груз, массой т (рис. 11.2).
Примем продольные перемещения в виде,
удовлетворяющем граничным условиям:
и = /ysin((or+ а).
Здесь f - перемещения свободного конца.
Кинетическая энергия системы:
Ттах ~ 2® ^^ifi •
п Л у2
= j-г f\ ~Tdx + mft
/=1 О 1 1
определяется с учетом массы стержня.
Потенциальная энергия при растяжении:
U = - ---ах.
2{ЕА
Qmvb
Так как из закона Гука N = еЕА, а деформация
-1^/2
2 Г '
По формуле (11.16) находим:
2 ЕА
w Z1 Y
/ ~то + т
Эи f
е = —= ^-, то
дх I
(Н.17)
Коэффициент 1/3, стоящий перед массой стержня, называют
коэффициентом приведения. Он показывает, какую часть массы
стержня нужно добавить к массе груза , чтобы учесть инерцион-
ное действие самого стержня.
Пример 11.2. Определить частоту собственных колебаний
балки с присоединенным к середине пролета грузом. Масса бал-
ки аи0, масса груза т, жесткость балки на изгиб EJ постоянны
(рис. 11.3).
Прогиб зададим в виде:
, . гос
w = f sin—.
178
р] Энергетические методы определения частот собственных колебаний...
Эта функция удовлетворяет граничным условиям шарнирного
опирания. Потенциальная энергия балки:
dx2
Подставив в нее значение прогиба и проинтегрировав, для
.. 1гЛ/2 , Ej't(
U = - ---ах = —
2J FT 2 J
\2
dx.
определения частоты имеем:
I
sin2^rfx = (O,5rno + m)/2.
"hfi
2
Рис. 11.3
По (11.16) найдем часто-
ту колебаний:
to2 = nEJ----------. (11.18)
2/3(O,5?no + т)
Из (11.18) следует, что ко-
эффициент приведения массы
балки равен 0,5.
Вынужденные продольные колебания стержней
Рассмотрим колебания однородного стержня, один
конец которого закреплен, а к другому приложена
возмущающая сила F(t) (рис. 11.4). Воспользуемся
принципом Даламбера-Лагранжа.
Полная энергия системы:
3^U-ArAr
где U - потенциальная энергия; Aj - работа возмуща-
ющей силы; Aj - работа сил инерции, приложенных к
каждому элементу колеблющегося стержня.
Согласно принципу 8Э = St/ - 8А^~ 8Aj = 0.
Легко видеть, что потенциальную энергию растя-
fl
шшищц
F(t)
X
Рис. 11.4
жения можно определить в виде:
= dx.
2 JoW
179
Вынужденные продольные колебания стержней
Продольные перемещения представим в виде суммы переме-
щений, соответствующих формам колебаний:
K = £A.sin^p (11.19)
где амплитуды f = fm(t) - неизвестные функции времени. Теперь
потенциальная энергия:
п2 EJ 2 z2
U =------7 ™
1 а с 16/ ~ ”
где п = 1, 3, 5, ... т
Потенциальная энергия зависит от величин /т, амплитуд про-
дольных перемещений стержня. Зададим каждой из этих величин
возможное перемещение 8fm. Тогда возможное перемещение каж-
дой точки:
е . тих
ofm sin--,
Jm 21
а вариация потенциальной энергии:
х т 7 — ди _ 771 Л ЕА г
Для последующего анализа вынужденных колебаний целесо-
образно за возможные перемещения принять перемещения, задан-
ные формами колебаний:
. тюс
Ъит =Cmsm------.
771 т
При них вариация энергии:
8/
Найдем возможную работу возмущающей силыГ(/) приложен-
ной к концу стержня. Возможное перемещение конца стержня бу-
дет Ст sin^y^. Так как х = /, вариация возможной работы:
8Af =F(/)Cmsin^ = F(/)Cm(-l)^^j
Работа сил инерции на возможном перемещении (11.20):
А ^2
А у г д и -2 wrtx
---ЧтТС-"81П —7~dx-
8 о 1
' Подставим в интеграл ряд (11.19), получим:
g dt1
(11.20)
5Л,-
180
Вынужденные продольные колебания стержней
= 2g
(11.21)
Теперь уравнение 8Э = 0 запишется в таком виде:
d2fm t m2n2gE
dt2 4/\
откуда при известной функции F(f) можно получить все коэффи-
циенты ряда (11.19). Если сила F(t) имеет непериодический ха-
рактер, ее можно разложить в ряд:
НО = “о + flicoswz + a2cos2(OZ + Z>jSin(0/ + Z>2sin2(O/. (11.22)
Для определения коэффициента ряда ат и Ьт обе части равен-
ства (11.22) умножают на cos men Г и sin meat соответственно и интег-
рируют от t = 0 до t = т, где т - период возмущающей силы. Тогда:
2 т 2 т
я, = — jF(/)cosZ(0/rfr, = - |F(/)sin itotdt.
т о т о
Умножив обе части (11.22) на dt и проинтегрировав, получим
первый член ряда: т
ао -
Этот коэффициент представляет движение стержня как твер-
дого тела.
Если функция задана в аналитической форме, коэффициенты
ряда (11.22) могут быть вычислены по этим формулам- При гра-
фическом задании функций и невозможности записать их анали-
тически для интегрирования нужно использовать какой-либо чис-
ленный метод.
Уравнение (11.21) линейно, поэтому можно получить вынуж-
денные колебания как сумму вынужденных колебаний, определя-
емых каждым членом ряда.
Решение (11.21) имеет следующий вид:
г . тпа . . тпа
= Al cos------1 + sin--- " ‘
' 21 2 21
где a - скорость звука.
Рассмотрим случай гармонической вынуждающей силы F =
= Fosin&L Частное решение должно быть пропорционально sinfcr.
Примем его в виде fm = sinfcf, подставим в (11.21) и получим:
т-1
S 2(-l)~F0g
/И’
\2
тпа | . 2
---- -к
21
sin А?.
(11.23)
181
р7} Вынужденные продольные колебания стержней
Общее решение неоднородного уравнения представляет собой
свободные колебания, частное решение зависит от возмущающей
силы. Так как свободные колебания вследствие внутреннего тре-
ния быстро затухают, устанавливается процесс вынужденных ко-
лебаний. Первые циклы колебаний представляют собой переход-
ный процесс. Амплитуду свободных колебаний можно найти из об-
щего решения, задав начальные условия. Если до приложения воз-
мущающей силы стержень неподвижен, то при / = 0 можно принять:
f =0: = 0
Э/
откуда легко определить At и А2,
При установившемся режиме колебаний члены ряда (11.19)
определяются (11.22). Подставив (11.23) в (11.19), получим:
т-1
. “Г" . W71X
2FQgsinkt ) Sm 2/
»=—Хр—-Нтт‘1Д5-- (1|24>
т [ пгла ] ,2
I 2/ J
Из сравнения с (11.3) легко видеть, что
ггта
-^- = ^ 01-25)
- частота свободных продольных колебаний стержня, поэтому
можно записать:
т-1
2F0gsinkt -г, (-1) 2 . тпх
и =——--------> -Цг-—-sm-------;/п = 1,3,5,... (11.26)
У1А "<о2-*2 2Z
Совпадение частот сотл = к является условием резонанса, при
котором амплитуды колебаний могли бы неограниченно возрас-
ти при отсутствии диссипативных сил. Последние при колебани-
ях возникают вследствие внутреннего трения в материале стерж-
ня, поэтому амплитуды колебаний остаются конечными. Дисси-
пация (рассеяние) энергии может быть учтена добавлением к пол-
ной энергии работы силы сопротивления. Силу сопротивления
принимают пропорциональной скорости смещения сечений:
dt ’
где Н - постоянная материала.
Hg
Обозначим п = и назовем коэффициентом затухания ко-
лебаний. Уравнение (11.21) с учетом затухания колебаний вслед-
182
Вынужденные продольные колебания стержней
ствие внутренней диссипации энергии и (11.25) примет следую-
щий вид:
+ 2п + = F^~^~ •
dr dt Aly
После решения этого уравнения получим вместо (11.26):
т-1
2Fogsmkt5-, (-1) 2 • тпх
и = ——--------> --------sin-----; т = 1,3,5,...
т л/со2 - к2 + $п2к2 21
и при (о = к перемещения сечения остаются конечными. Расчеты
показывают, что силы внутреннего сопротивления оказывают на
перемещения заметное влияние лишь в области, близкой к резонан-
су, поэтому в областях, удаленных от резонанса, можно пользо-
ваться (11.24).
Подобные решения можно получить при других законах изме-
нения силы, а также при иных граничных условиях. Изменение
характера силы потребует лишь изменения f* - частного реше-
ния (11.21). При внезапном приложении постоянной силы F мак-
симальное перемещение свободного конца стержня (см. рис. 11.3)
легко находится из (11.24):
8FZ
и =;---Г z.----
EAir т т2
. тп
sin----
т 2 Е Eg
Так как квадрат скорости звука а - — = ——
Р Y
V 1 • W71 л2 2FI
и —5-sin—— = —, то ц =-----. т.е. вдвое больше, чем при ста-
2 4 ЕА
тическом нагружении.
Внезапное нагружение (разгрузка) стержня со свободными
концами вызывает такое же полное перемещение конца нагру-
женного стержня, что и постоянно действующая сила, растягива-
ющая стержень. Проверка формулы для и, предлагается читате-
лю методом, изложенным в этом параграфе. Продольные переме-
щения удобно применять в виде:
г г ЛИ7ГХ
«=/o+2y/mcos-p’ (11.27)
т 1
где т = 1, 2, 3,... Первый член ряда/0 - перемещение стержня как
абсолютно твердого тела определяется по второму закону Нью-
тона.
183
Вынужденные поперечные колебания однородной балки
Возможное перемещение удобно принять в виде:
5ww=Cwcos-y-.
Максимальное перемещение конца стержня при внезапном
нагружении постоянной силой наблюдается при достижении вол-
ной деформации ненагруженного конца, т.е. при t = —. Полное
а
перемещение находится по (11.27).
CLL Вынужденные поперечные колебания
однородной балки
Г-----------------------------------------
Вынужденные колебания возникают при действии периодичес-
кой силы. Рассмотрим вначале колебания, вызываемые силой
^(x)sin£/ распределенной по длине. Пусть балка постоянной жес-
ткости защемлена по концам. Воспользуемся принципом Далам-
бера-Лагранжа, тогда уравнение изгиба примет следующий вид:
d4w т 3vv2 q(x) . ,
дх4 EJ dt2 EJ
(11.28)
Его решение будем искать в виде w = Z(x)sin£/.
После подстановки реше-
ния, считая для упрощения пре-
образований интенсивность
силы постоянной q = qQ (рис.
11.5) и сократив на sin£/, из
(11.28) получим уравнение
форм колебаний, где
£^_a4z = -^-. (11.29)
dx4 EJ
Решение уравнения (11.29) - закон распределения амплитуд пе-
ремещений по длине балки - удобно искать в форме суммы балочных
функций А.Н. Крылова (11.13): 5 = S(dx),... V = V(dx), тогда
z = C15+C2r+C4l7+C4r.
(11.30)
184
Вынужденные поперечные колебания однородной балки
Частное решение неоднородного уравнения Z* = —— легко
EJ
устанавливается по виду правой части.
Постоянные С. найдем из условий на левом конце х = 0. Поло-
dZ
жим перемещение опоры Z = Zo, угол поворота ее = Фо, изги-
бающий момент и поперечную силу М = A/o; Q = Qo.
Производные от функций А.Н. Крылова опре-
деляются по схеме, изображенной на рис. 11.6. Они
будут такими:
dx dx
и т.д. Для вычислений Ct имеем:
— = + C2S + С3Т + C4U);
dx
Рис. 11.6
d^7
-^- = а2(С117 + С2И+С35+С4Т); (11.31)
dx
d^7
—=r = a3 (C,T + C2U + C3V + C4S).
dx5
При x = 0 все функции, кроме 5 равны нулю, а S=I. Из гранич-
ных условий на левом конце получаем:
С—z + 'С — • С — Л 1
1 • 2’V-C’C‘~a>EJ- <IL32)
После подстановки (11.32) решение (11.30) станет таким:
Z = z0S + -f5- (5 -1) + Т + и +
a4EJ a a2EJ a?EJ
По нему можно определить угол поворота сечения, а также
изгибающий момент и поперечную силу:
(11.33)
M = EJ^-~, Q = EJ^. (Ц.34)
dx dx
При нагружении балки сосредоточенными силами Fsinfcz или
распределенными по части длины, изгибающий момент MQ и по-
перечная сила Qq будут кусочно гладкими функциями координа-
ты х.
185
Ш. ОГЛАВЛЕНИЕ
ф-------------------------------------------------------
Глава 1. ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ
В ДЕФОРМИРОВАННОМ ТЕЛЕ.
НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ...............................3
Статические эквиваленты внутренних сил
в деформированном теле.............................3
Напряжения в точке.................................5
Напряженное состояние в точке......................6
Одноосное напряженное состояние....................8
Плоское напряженное состояние......................9
Главные напряжения в точке
при плоском напряженном состоянии.................10
Экстремальные значения касательных напряжений
при плоском напряженном состоянии.................12
Деформации в точке (геометрические уравнения).....14
Обобщенный закон Гука........................... 17
Потенциальная энергия деформации..................19
Глава 2. РАСТЯЖЕНИЕ (СЖАТИЕ) СТЕРЖНЕЙ
И СТЕРЖНЕВЫХ СИСТЕМ..................................21
Нормальная сила...................................21
Нормальные напряжения и деформации................22
Испытание материалов на растяжение (сжатие).......24
Принципы расчета на прочность
растянутых силовых элементов конструкций..........32
Расчет стержневых систем..........................33
Глава 3. СДВИГ И КРУЧЕНИЕ СТЕРЖНЯ....................38
Основные понятия о сдвиге.........................38
Расчет заклепочных соединений.....................40
Кручение круглого стержня.........................42
Кручение некруглых стержней.......................47
Кручение тонкостенных стержней....................48
Глава 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
СЕЧЕНИЙ СТЕРЖНЯ......................................52
Моменты сечений...................................52
Основные теоремы о моментах сечений...............52
Изменение моментов сечений
при параллельном переносе осей....................54
Изменение моментов инерции при повороте осей.
Главные моменты инерции...........................57
186
Оглавление
Глава 5. ИЗГИБ СТЕРЖНЕЙ..................................60
Общие понятия........................................60
Внутренние силы в сечениях балки при плоском изгибе...61
Рекомендации по определению
поперечных сил и изгибающих моментов
в более сложных случаях нагружения....................65
Вычисление поперечных сил и изгибающих моментов
в сечении балок на двух опорах........................69
Нормальное напряжение при изгибе......................74
Касательные напряжения при изгибе.....................77
Перемещение при плоском изгибе........................80
Критерии прочности при плоском
и пространственном напряженных состояниях.............81
Расчет балок при изгибе.....:.........................86
Глава 6. ПРОЧНОСТЬ СТЕРЖНЯ
ПРИ СЛОЖНОМ НАГРУЖЕНИИ...................................89
Сложный изгиб.........................................89
Изгиб с растяжением (сжатием).....j...................91
Изгиб с кручением.....................................93
Расчет стержней при циклическом изменении напряжений.97
Глава 7. ПРОЧНОСТЬ СТЕРЖНЕЙ
ПРИ ПЛАСТИЧЕСКИХ ДЕФОРМАЦИЯХ............................105
Основные понятия теории пластичности................105
Чистый изгиб стержня............................... 107
Чистое кручение круглого стержня.....................109
Растяжение статически неопределимых ферм.............112
Глава 8. СТЕРЖНЕВЫЕ КОНСТРУКЦИИ
И РАСЧЕТ ИХ НА ПРОЧНОСТЬ............................... 113
Стержневые системы.................................. 113
Работа внешних сил...................................115
Работа внутренних сил................................118
Теорема о взаимности работ...........................121
Теорема о взаимности перемещений.................... 122
Перемещения от внешних сил. Формула Мора.............124
Метод сил. Статическая неопределимость.............. 128
Канонические уравнения метода сил................... 130
Метод перемещений................................... 133
Определение свободных членов и коэффициентов
канонических уравнений метода перемещений............136
Канонические уравнения метода перемещений.
Изгибающие моменты в сечениях рам....................139
187
Оглавление
Глава 9. НАПРЯЖЕНИЕ И ДЕФОРМАЦИЯ В ОБОЛОЧКАХ.............140
Тонкие оболочки.......................................140
Уравнения равновесия тонкой оболочки
при осесимметричном нагружении.......................141
Напряжения и деформации в цилиндрическом баке
с полусферическими днищами при нагружении
внутренним давлением............................... 144
Напряжения в толстостенных оболочках................ 145
Глава 10. УСТОЙЧИВОСТЬ СИЛОВЫХ
ЭЛЕМЕНТОВ КОНСТРУКЦИЙ...................................149
Основные понятия об устойчивости.....................149
Устойчивость шарнирно опертого сжатого стержня.......151
Расчеты на устойчивость при пластических деформациях.154
Энергетические методы расчета стержня на устойчивость.156
Основные особенности устойчивости оболочек...........159
Устойчивость замкнутой цилиндрической оболочки,
сжатой вдоль образующей (линейная задача)............161
Устойчивость цилиндрических оболочек
при действии внешнего давления.......................165
Продолно-поперечный изгиб балки......................168
Глава 11. КОЛЕБАНИЯ СТЕРЖНЕВЫХ
ЭЛЕМЕНТОВ КОНСТРУКЦИЙ...................................170
Свободные колебания стержней.........................170
Энергетические методы определения частот
собственных колебаний стержней.......................176
Вынужденные продольные колебания стержней............179
Вынужденные поперечные колебания однородной балки.....184
Торговый дом
еникс
ПРЕДЛАГАЕТ:
0 Около 100 новых книг каждый месяц
0 Более 30.00 наименований книжной продукции собственного
производства
0 Более 1500 наименований обменной книжной продукции
от лучших издательств России
ОСУЩЕСТВЛЯЕМ:
0 Оптовую и розничную торговлю книжной продукцией
ГАРАНТИРУЕМ:
0 Своевременную доставку книг в любую точку страны,
ЗА СЧЕТ ИЗДАТЕЛЬСТВА, автотранспортом и ж/д контейнерами
0 МНОГОУРОВНЕВУЮ систему скидок
0 РЕАЛЬНЫЕ ЦЕНЫ
0 Надежный ДОХОД от реализации книг нашего издательства
НАШ АДРЕС:
344082, Ростов-на-Дону, пер. Халтуринский, 80.
ОТДЕЛ ОПТОВЫХ ПРОДАЖ - контактные телефоны:
8 (8632) 61-89-53, 61-89-54, 61-89-55, 61-89-56, 61-89-57, 61-89-58
Начальник отдела
Костенко Людмила Константиновна
тел.: 8 (8632) 61-89-52; e-mail: torg@phoenixrostov.ru
Менеджер по продажам на территории Москвы,
Центра европейской части России и Республики Казахстан
Чермантеева Татьяна Степановна e-mail: torg155@phoenixrostov.ru
Менеджер по продажам на территории Ставропольского,
Краснодарского краев
Сергиенко Сергей Николаевич e-mail: torg151@phoenixrostov.ru
Менеджер по продажам на территории Урала и Санкт-Петербурга
Литвинчук Елизавета Михайловна e-mail: torg153@phoenixrostov.ru
Менеджер по продажам на территории Восточной Сибири
Швечикова Ирина Владимировна e-mail: torg159@phoenixrostov.ru
Менеджер по продажам на территории Западной Сибири,
Украины, Республики Казахстан и других стран СНГ
Мезинов Антон Николаевич e-mail: torg154@phoenixrostov.ru
Менеджер по продажам на территории Дальнего Востока
и Республики Беларусь
Родионова Татьяна Александровна e-mail: torg152@phoenixrostov.ru
Менеджер по работе с каталогами
Яруга Игорь Игоревич e-mail: torg150@phoenixrostov.ru
Издательство
Приглашаем к сотрудничеству АВТОРОВ
для издания:
0 учебников для ПТУ, ссузов и вузов;
0 научной и научно-популярной литературы по МЕДИЦИНЕ и
ВЕТЕРИНАРИИ, ЮРИСПРУДЕНЦИИ и ЭКОНОМИКЕ,
СОЦИАЛЬНЫМ и ЕСТЕСТВЕННЫМ НАУКАМ;
0 литературы по ПРОГРАММИРОВАНИЮ и
ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ;
0 ПРИКЛАДНОЙ и ТЕХНИЧЕСКОЙ литературы;
0 литературы по СПОРТУ и БОЕВЫМ ИСКУССТВАМ;
0 ДЕТСКОЙ и ПЕДАГОГИЧЕСКОЙ литературы;
0 литературы по КУЛИНАРИИ и РУКОДЕЛИЮ.
ВЫСОКИЕ ГОНОРАРЫ!!! ВСЕ финансовые ЗАТРАТЫ БЕРЕМ НА СЕБЯ !!!
При принятии рукописи в производство. ВЫПЛАЧИВАЕМ гонорар на 10 %
ВЫШЕ ЛЮБОГО РОССИЙСКОГО ИЗДАТЕЛЬСТВА!!!
Рукописи не рецензируются и не возвращаются!
ПОЧТОВЫЙ АДРЕС:
344082, г. Ростов-на-Дону, пер. Халтуринский, 80
САЙТ http://www.phoenixrostovju
ДИРЕКТОР: Вальдман Леонид Ефимович
ПРИЕМНАЯ
тел.: 8 (8632) 61-89-50; e-mail: fenix@fiber.ru, fenix_office@mail.ru
ОТДЕЛ МАРКЕТИНГА
Начальник отдела Собко Сергей Дмитриевич
Тел, 8 (8632) 61-89-60; e-mail market@phoenixrostov.ru
РЕДАКЦИОННО-ИЗДАТЕЛЬСКИЕ ОТДЕЛЫ
Руководитель отдела
Баранчикова Елена Валентиновна
тел., 8 (8632) 61-89-78; e-mail: bev@phoenixrostov.ru
Руководитель отдела
Бузаева Елена Викторовна
тел., 8 (8632) 61-89-97; e-mail: buzaeva@phoenixrostov.ru
Руководитель отдела
Морозова Оксана Вячеславовна
тел., 8 (8632) 61-89-76; e-mail: morozova@phoenixrostov.ru
Руководитель отдела
Осташов Сергей Александрович
тел., 8 (8632) 61-89-75; e-mail: ostashov@phoenixrostov.ru
Руководитель отдела
Поргер Евгений Иванович
тел., 8 (8612) 743-139; e-mail: academpress@tsrv.ru
Торговый дом
еникс
В * Москве
книги издательства «Феникс» можно купить
для книготорговых организаций
В РЕГИОНАЛЬНЫХ ПРЕДСТАВИТЕЛЬСТВАХ,
РАСПОЛОЖЕННЫХ ПО АДРЕСУ:
1. ул. Космонавта Волкова, д. 25/2, 1-й этаж, м. «Войковское».
Тел./факс: (095) 156-05-68, тел.: 450-08-35 E-mail: fenix-m@ultranetru
Директор - Моисеенко Сергей Николаевич.
2. 111399, ул. Матеновская 9/13, р-н м. «Новогиреево»
Тел.: (095) 305-67-67, 517-32-95 E-mail: mosfen@bk.ru
Директор - Мячин Виталий Васильевич.
3. Издательский Торговый дом «КноРус»,
ул. Б. Переяславская, 46, метро «Рижская», «Проспект Мира»
Тел.: +7095-280-0207, 280-7254, 280-9106 E-mail: phoenix@korus.ru
В КРУПНЕЙШИХ МАГАЗИНАХ:
ТД «Библио-Глобус» ул. Мясницкая, 6 (тел. 925-24-57)
ТД «Москва» ул. Тверская, 8 (тел. 229-66-43)
«Московский Дом книги» ул. Новый Арбат, 8 (тел. 291-78-32)
«Молодая гвардия» ул. Большая Полянка, 28 (тел. 238-11-44)
«Дом педагогической книги» ул. Пушкинская, 7/5 (тел. 299-68-32)
«Медицинская книга» Комсомольский проспект, 25 (тел. 245-39-27)
В Санкт-Петербурге книги издательства «Феникс» можно купить:
«Дом книги» Невский проспект, 28
Тел. 318 65 04, факс 311 98 95. E-mail: noskova@hbook.spb.ru
ДЛЯ ОПТОВЫХ ПОКУПАТЕЛЕЙ
РЕГИОНАЛЬНОЕ ПРЕДСТАВИТЕЛЬСТВО:
198096, г. Санкт-Петербург, ул. Кронштадтская, 11, к. 42
тел.: (812) 183-24-56. E-mail: fenikc-peter@mail.ru
Нарзиева Анжела Рустамовна E-mail: anjeln@yandex.ru
Представительства в Ростове-на-Дону:
1. пер. Согласия, 3, тел. 8(8632) 999-339
2, пер Соборный, 17, тел. 8(8632) 624-707
3. ул. Большая Садовая, 70, тел. 8(8632) 620-673
4. ул. Немировича-Данченко, 78, тел. 8(8632) 446-934
5. ул. Пушкинская, 245/61 , тел. 8(8632) 665-832
E-mail: fenix21@inbox.ru
Книги издательства «Феникс» в Украине
ООО «Кредо», г. Донецк, пр. Ватутина, 2 (оф. 401),
тел. +38062-3456308, 3396085, e-mail: moiseenko@skif.net
г. Запорожье, ул. Глиссерная, 22, к. 19,
тел. +380612-134951, 145819, E-mail: vega@comint.net
г. Киев, ул. Вербовая, 17 (СПД Шкаран),
тел. +38044-4644946, 9084576 E-mail: kredok@i.com.ua
Серия
«Шпаргалки»
С.И. Тимофеев
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ДЛЯ СТУДЕНТОВ ВУЗОВ
Ответственный
за выпуск:
Редактор:
Корректор:
Художник:
Баранчикова Е.
Федоров И.
Петренко Н.
Тимофеева Е.
Лицензия ЛР № 065194 от 2 июня 1997 г.
Сдано в набор 18.05.2004 г. Подписано в печать 20.07.2004 г.
Формат 84x108 Бумага типографская.
Гарнитура Школьная.
Тираж 5000 экз. Заказ № 388.
Издательство «Феникс»
344082, г. Ростов-на-Дону,
пер. Халтуринский, 80
Отпечатано с готовых диапозитивов в ЗАО «Книга».
344019, г. Ростов-на-Дону, ул. Советская, 57
Качество печати соответствует предоставленным диапозитивам.