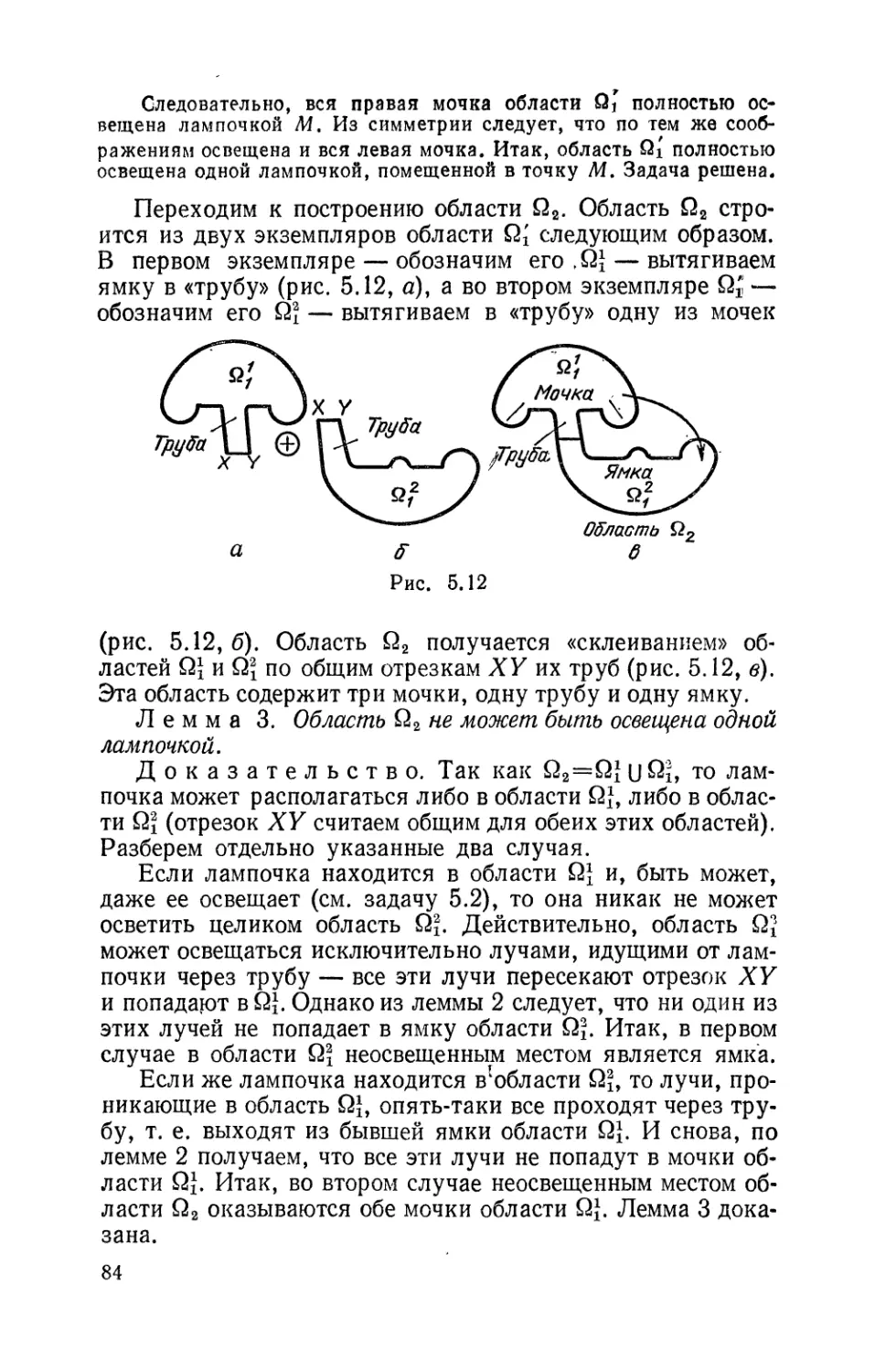
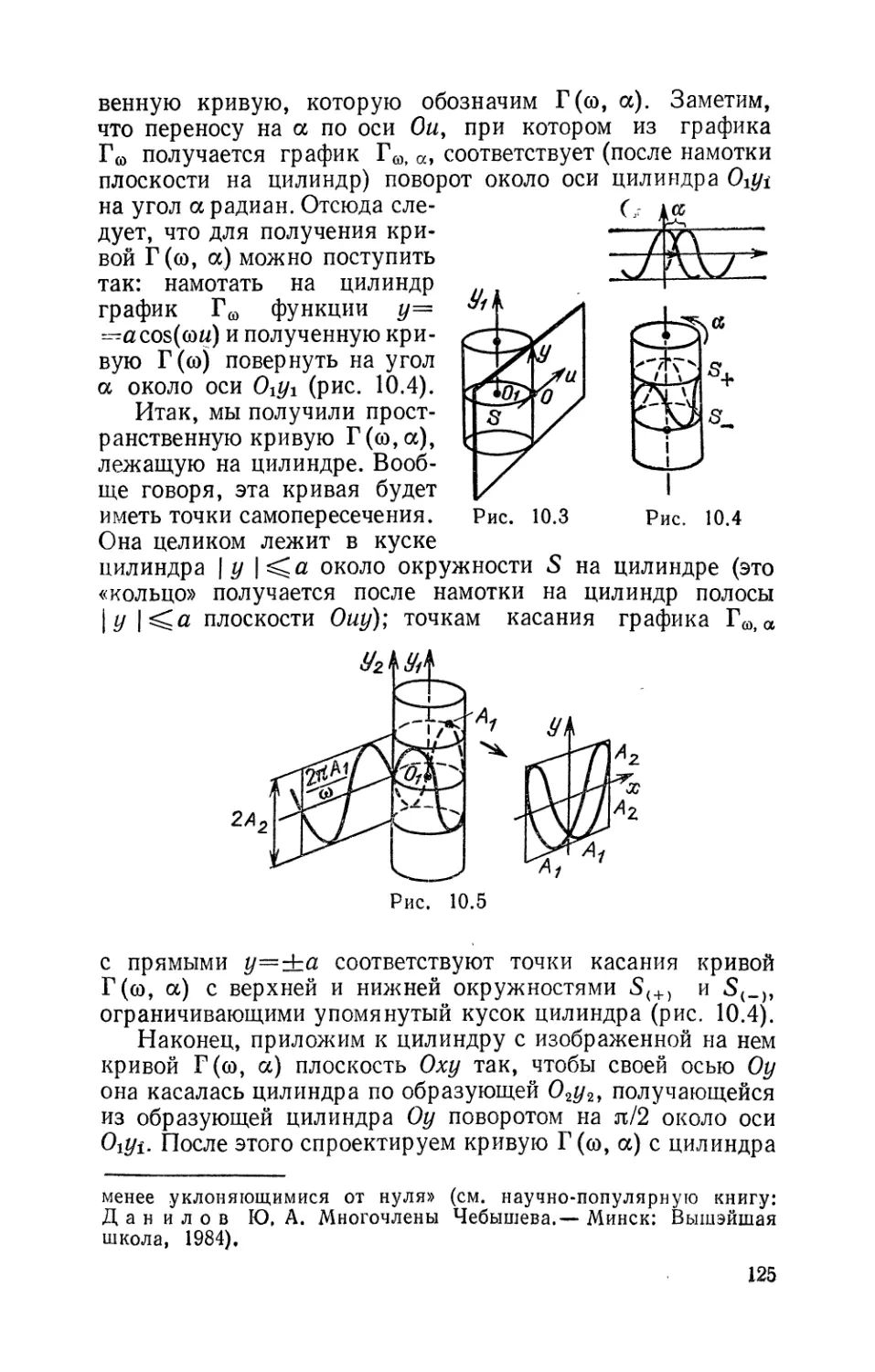
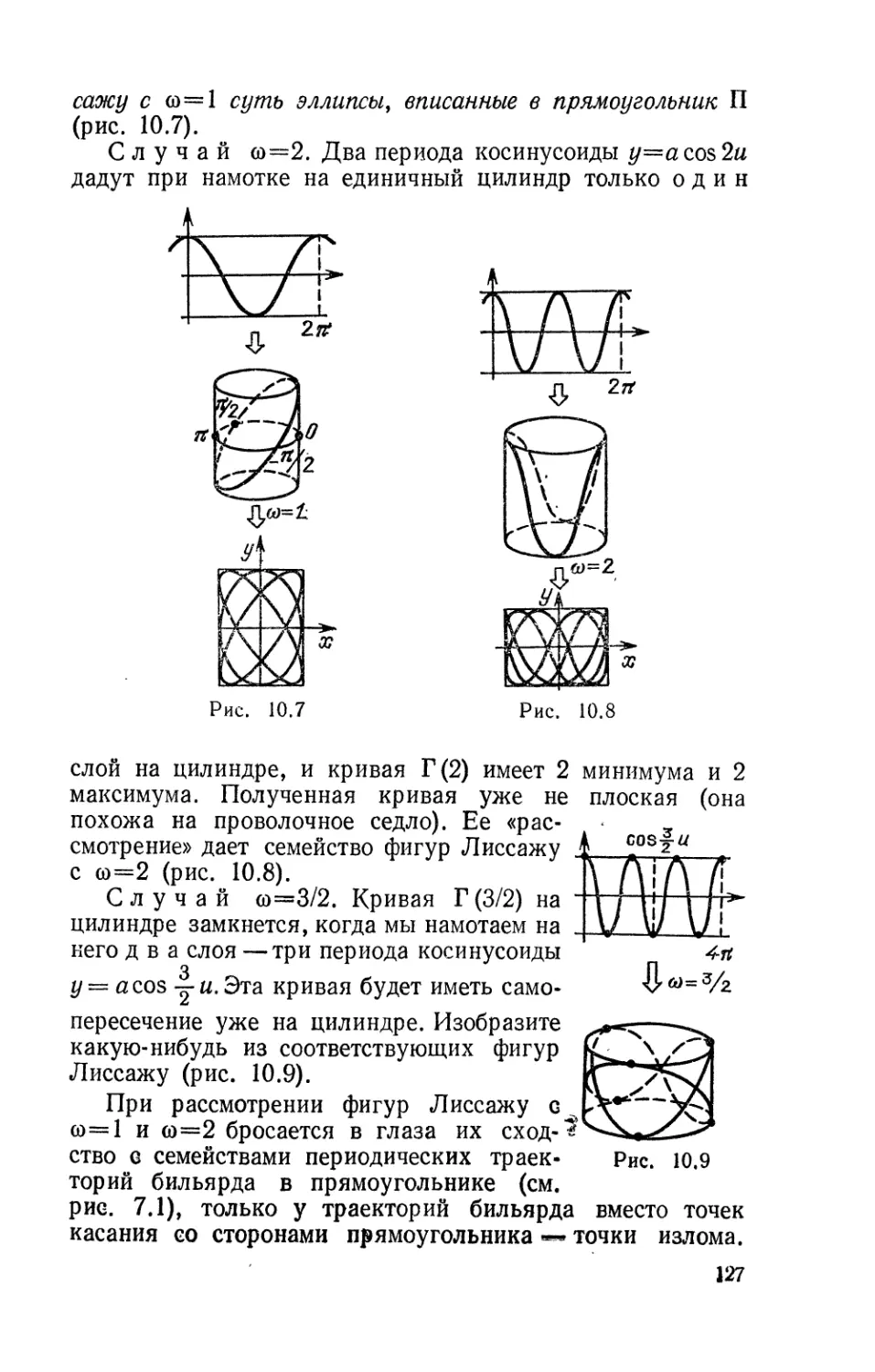
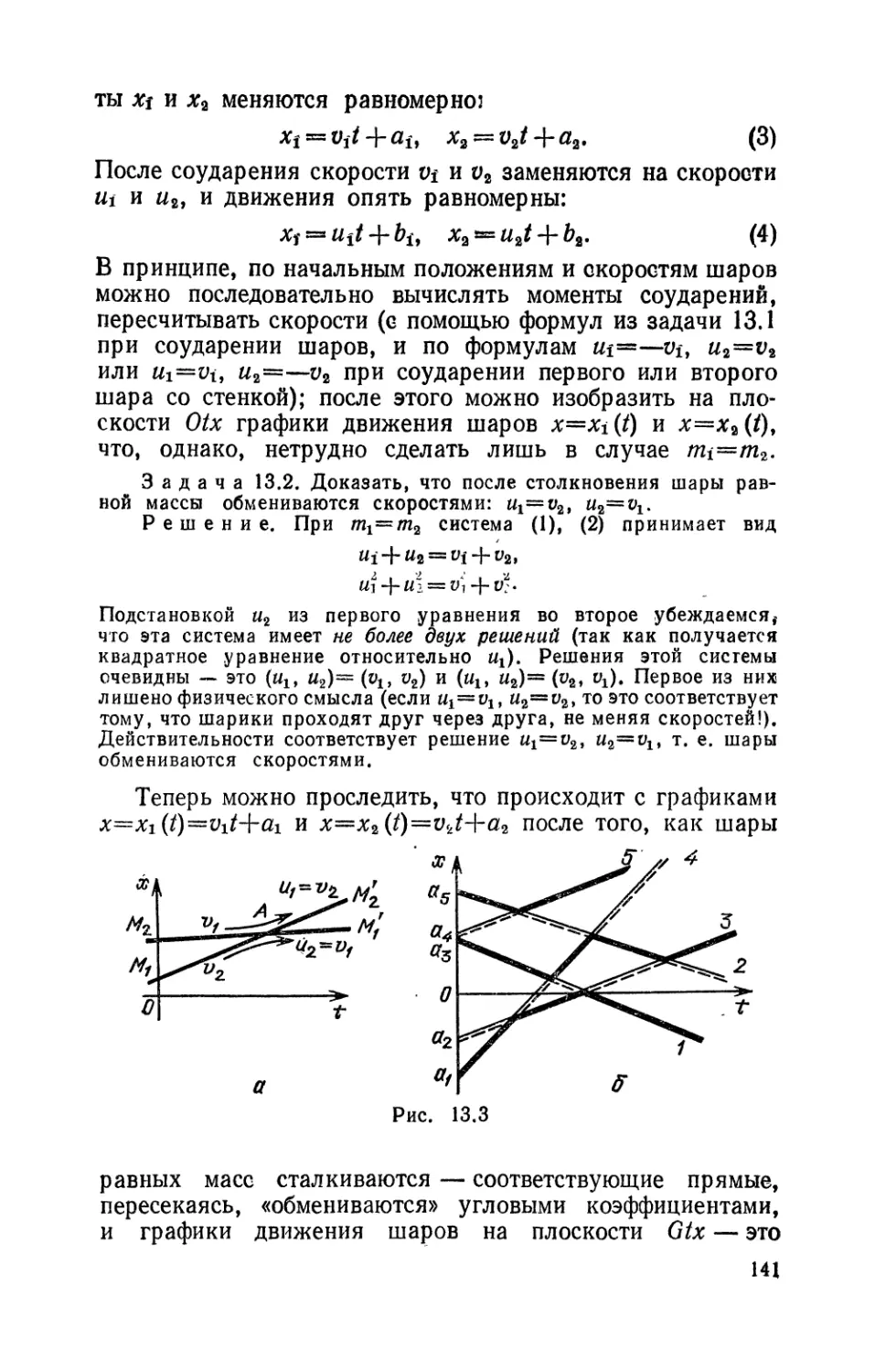
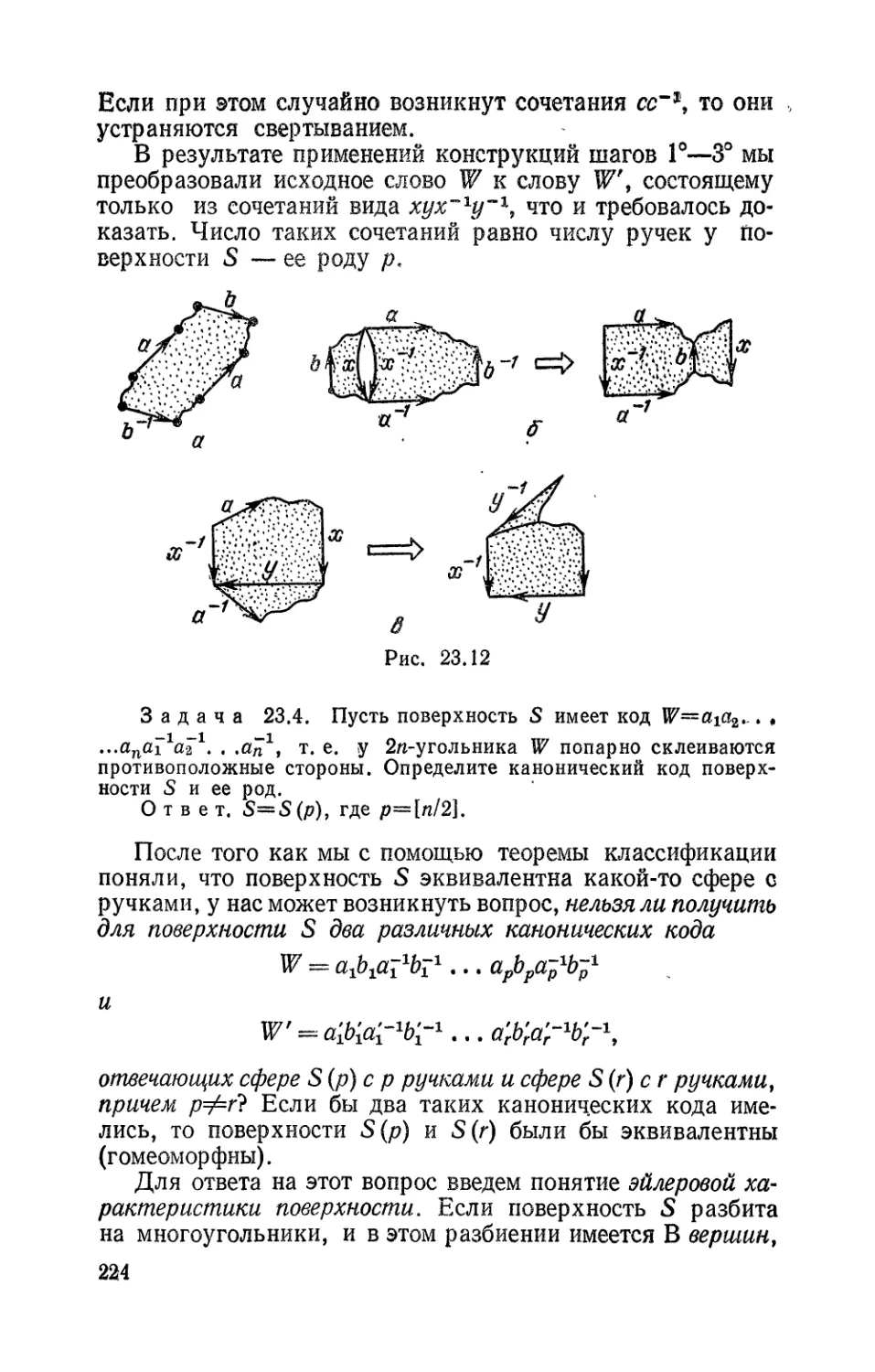
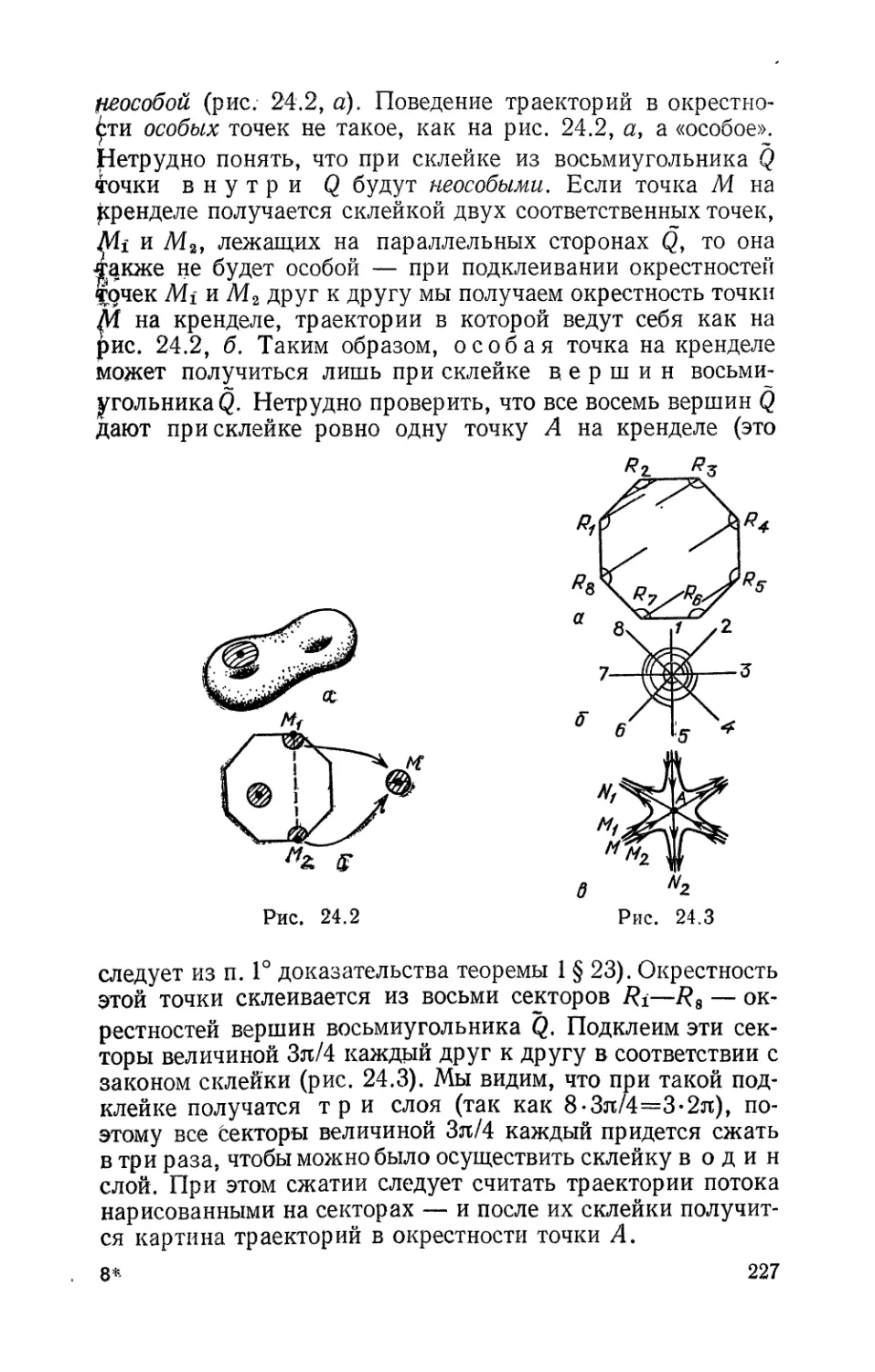
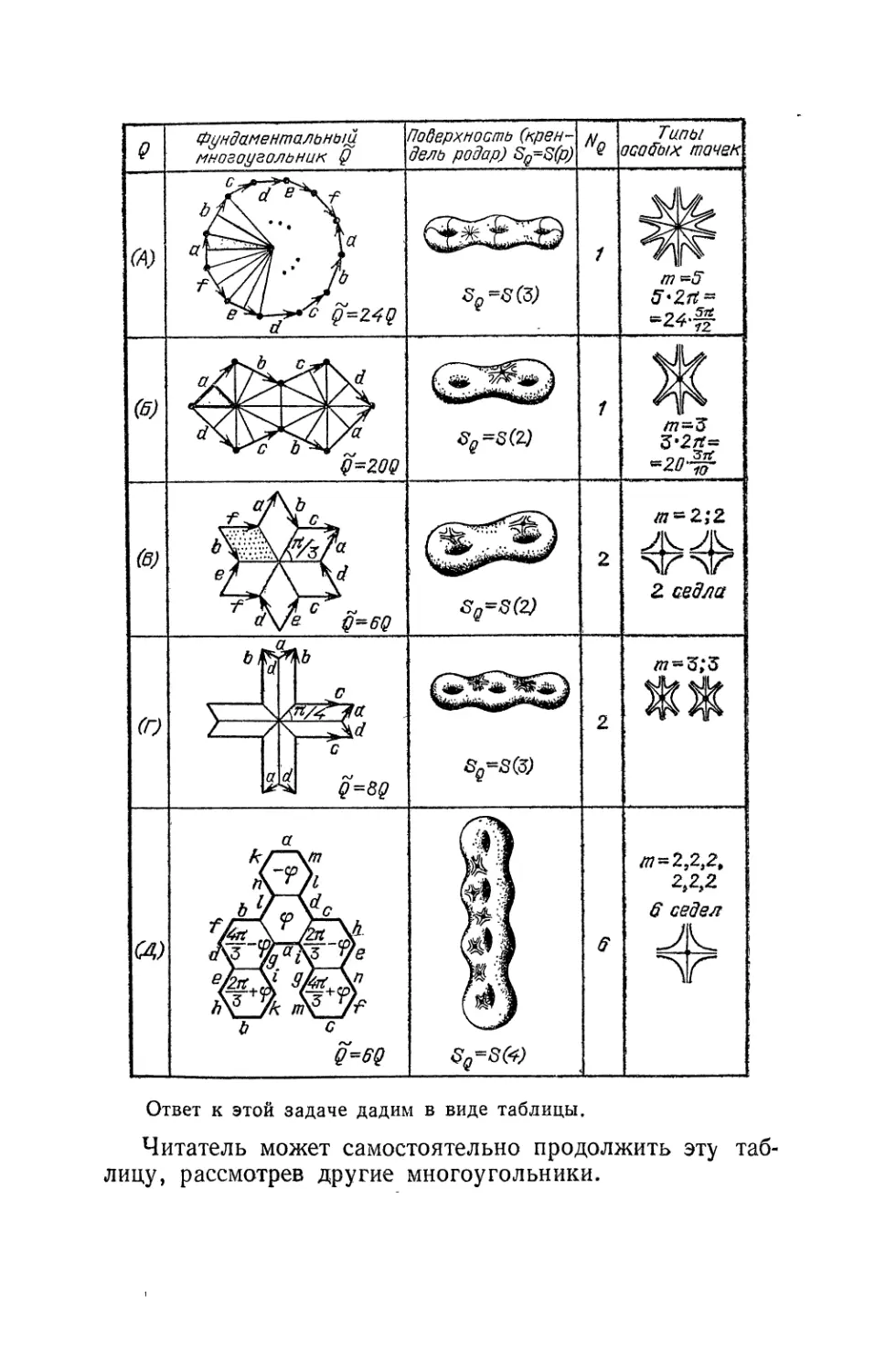
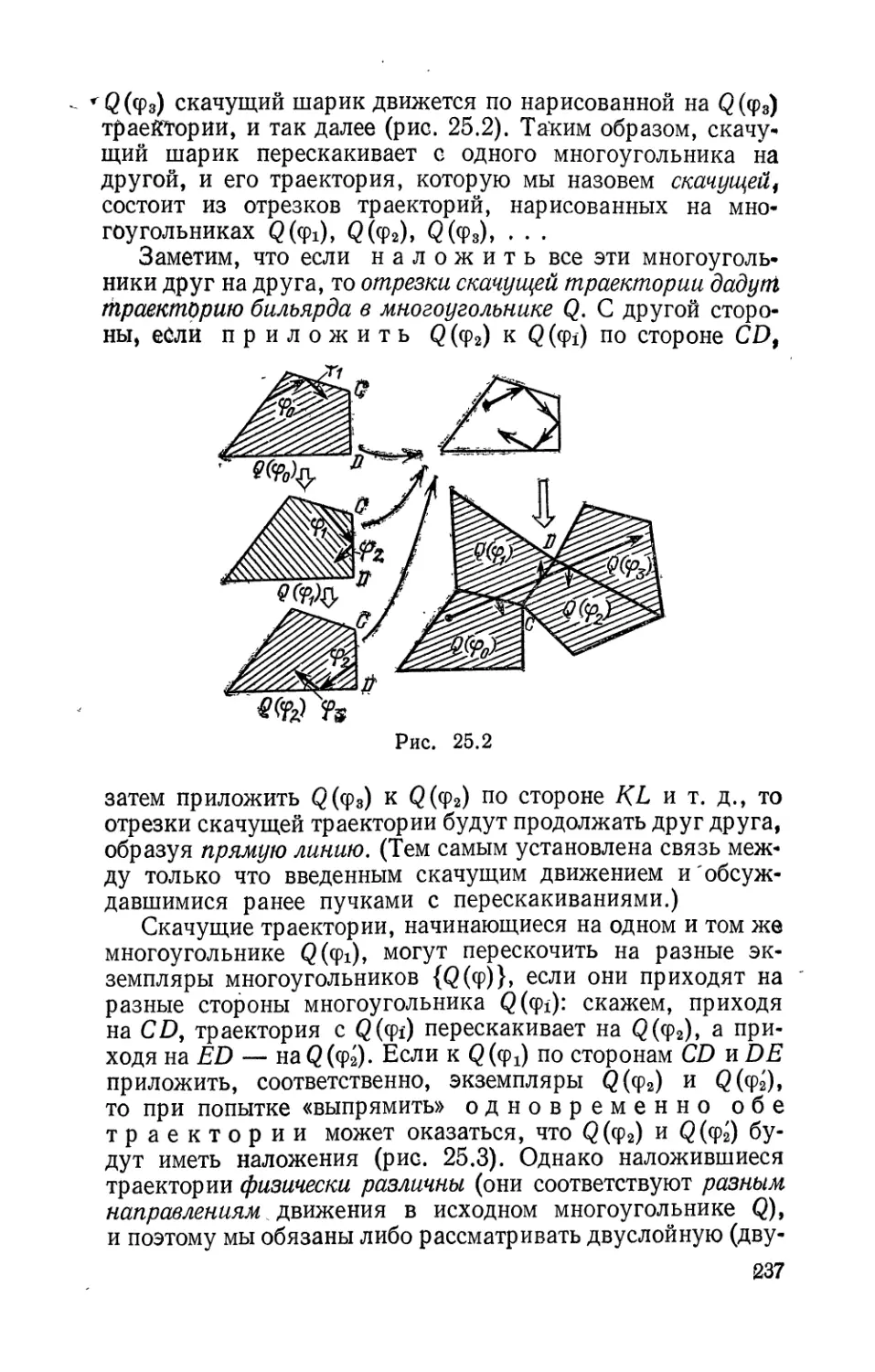
Текст
@
f [L
БИБЯИОТЕЧКА .КВАНТ-
ВЫПУОК 77
....... n 1>.. r .....4.
r. А. rАЛЬПЕРИН
А.Н. ЗЕМЛЯКОВ
МАТЕМАТИЧЕСКИЕ.
БИЛЬЯРДЫ
6ИЛЬЯРДНЫЕ ЗАДАЧИ
И СМЕЖНЫЕ ВОПРОСЫ
МАТЕМАТИКИ И МЕХАНИКИ
МОСКВА ,НАУКА»
r ЛАВНАЯ РЕДАКЦИЯ
ФИЗИКа-МАТЕМАТИЧЕСКОй ЛИТЕРАТУРЫ
1 9 9 а
ББК 22.18
[17
УДК 519.83(023)
Серия «Библиотечка «Квант»
основана в 1980 r.
РЕДАКUИОННАЯ КОЛЛЕrия
Академик ю. А. Осипьян (председатель), ДQКТОР физико-
математических наук А. и. Буздин (ученый секрета рь), ака..
демик А. А. Абрикосов, академик А. с. Боровик-Романов,
академик Б. 1(. Вайнштейн, заслуженный учитель РСФСР
Б. В. Воздвиженский, ак адемик В. л . rинзбурr, 81{адеМИI<
ю. В. fУJJяев, академик I А. п. Ершов 1, профессор с. п. I(а-
пица, академик А. Б. Миrдал, академик с. п. Новиков, ака-
демик АПН СССР В. f. Разумовский, академ ик Р.3. Саrдее в,
профессор я. А. Смородинекий , академик' С. л. Соболев 1,
член-корреспондент АН СССР I д. К. Фаддеев I
Реценвент
доктор фиэико-матеМ8тичеСКИ:l наук л. А. БУlluмовuч
fаJlьперин [. А., 3емJUlКОВ А. Н.
r 17 Математические бильярды (бильярдные задачи и
см жные вопросы математики и механики). М.:
Наука. rл. ред. физ.-мат. лит., 1990....... 288 c.
(Б чка «Квант». Вып. 77)
[SBN 5-02-014080 5
Рассказывается о поведении бильярдноrо шара на СТОле
произвольной формы без луз. Описание этоrо поведения
приводит к решению разнообразных вопросов математики
и механики: задач о переливании жидкости, об освещении
зеркальных комнат, об осциллоrрафе и фиrура Лиссажу и
др. На доступном школьникам языке вводятся понятия
конфиrурационноrо и фаЗОБоrо пространства, понятия rеоде-
8ических на простейших двумерных поверхностях, предла-
rаются (с решениями) мноrочисленные интересные задачи.
Для школьников 9......lO-х классов.
1604010000....012
r .. 053 (02)-90 1iJ2-89 ББК 22.18
ISBN 5-02-014080-5
@ Издательство «Н аука».
rлавная редакция физико-
математичеекой.литературы,
1990
оrЛАВЛЕНИЕ
Предисловие
Введение
Ч а о 'f ь 1. БИЛЬЯРДЫ В ВЫПУКЛЫХ ОБЛАСТЯХ а
КРИВОЛИНЕЙНОЙ rРАНИЦЕЙ
r л а в а 1. Бильярд в Kpyre
1. Шар в круrлом бильярде без луз
2. Теорема Якоби. Применение к теории чисел
3. Террема Пуанкаре о возвращении. Конфи-
rУ4эационное и фазовое пространства. Па-
радоко Цермело и модель ЭренфеаТОD
р л а в а 2. Бильярд в эллипсе
9 4. Эллипс и ero бильярдные овойотва. Кауа-
тик1i
5* .Задача об освещении невыпуклой области
6. Экстремальные свойотва бильярдных тра-
екторий. Принцип Ферма и теорема Бирк-
rофа
5
7
24
24
24
31
42
,
60
20
'/8
89
Ч а о т ь 11. rЕОМЕТРИЯ и ФИЗИКА прямоуrоль.
HOrO БИЛЬЯРДА 100
Р .п а в а 3. fеометрия прямоуrольноrо бильярда , 100
7. Бильярдный шар на прямоуrольном отоле
без луз 100
8. Тор и ero обмотки 108
9 9. Бильярд в прямоуrольнике и тор 117
Р л а в а 4. Физика прямоуrольноrо бильярда 122
10. Фиrуры Лиссажу 122
9 11 Бильярд в прямоуrолънике и осциллеrраф 129
12. Задача о пеленrе 133
Ч а о т ь 111. rЕОМЕТРИЯ и АРИФМЕТИКА СТОЛКНО-
ВЕНИЙ 1
r л а в а 5. Одномерный «rаз» из двух молекул 139
13. Два ynpyro оталкиваЮЩИХQЯ шара на ОТ-
резке 139
14. Два шара на отрезке: све.u.ение к бильярду
в треуrольнике 147
3
15. Два шара на полупрямой: сведение к би-
'льярду В уrле 153
r л а в а 6. Одномерный «rаз» из большоrо числа молекул 159
16. Три упруrих шара на прямой 159
17. п упруrих lиаров на прямой 165
18*. Число столкновений между молекулами
одномерноrо «rаэа» 178
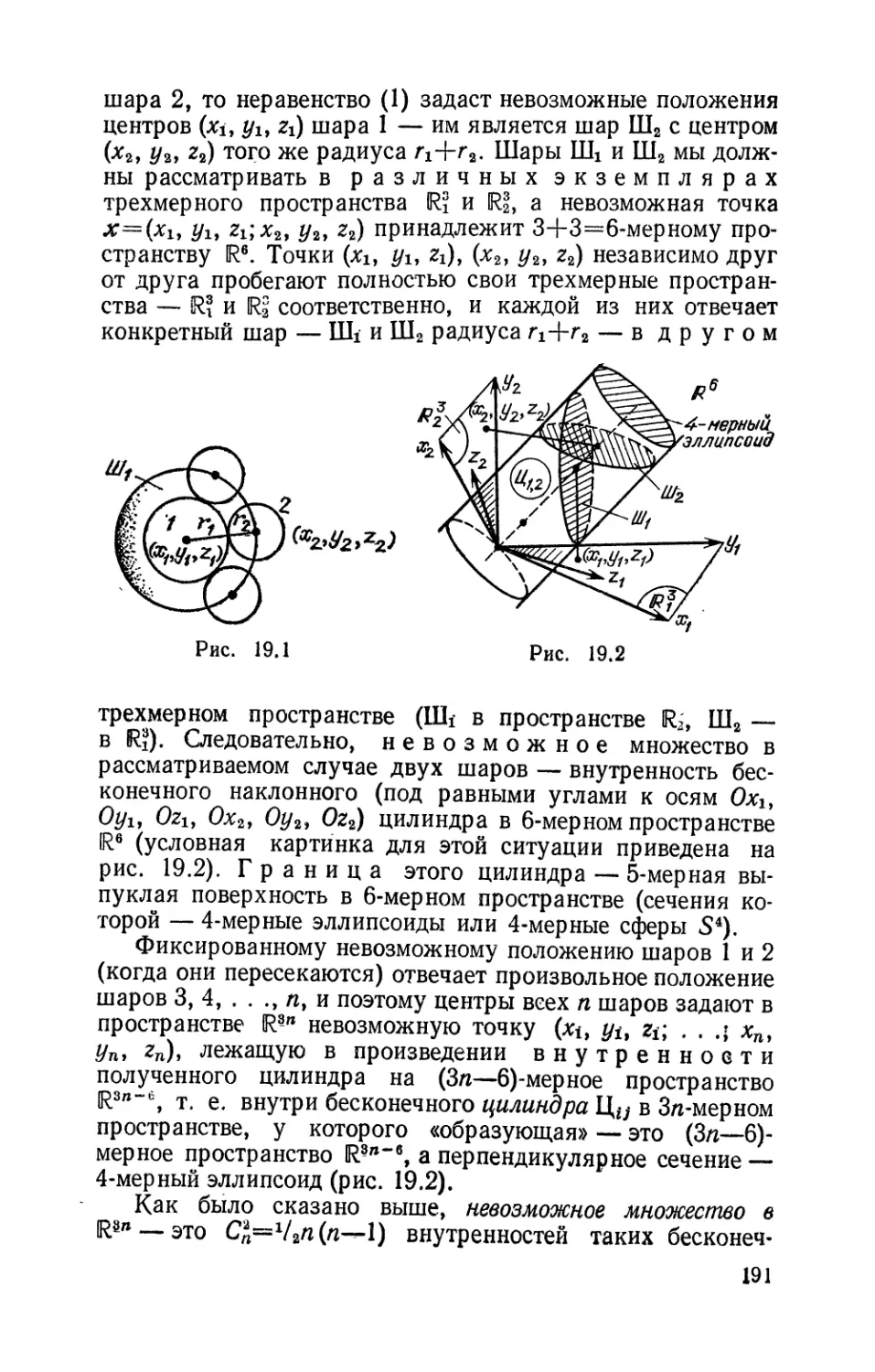
r л а в 3 7* *. tноrомерный: «rаз» 187
19. Конфиrурационное пространство «rаза» ИЭ
n молекул в пространстве и сосуде 190
20. Свед ние «rаза» В пространстве и сосу де
к бильярду 193
21. Рост числа столкновений мея<ду молеку-
лами «rаза» 197
ч -3 С Т Ь IV. БIdЛЬЯР ДЫ в мноrоуrОЛЬНИКАХ и
мноrоrРАННИКАХ 206
r 11 а в а 8. fеометрия мноrоуrольноrо бильярда 207
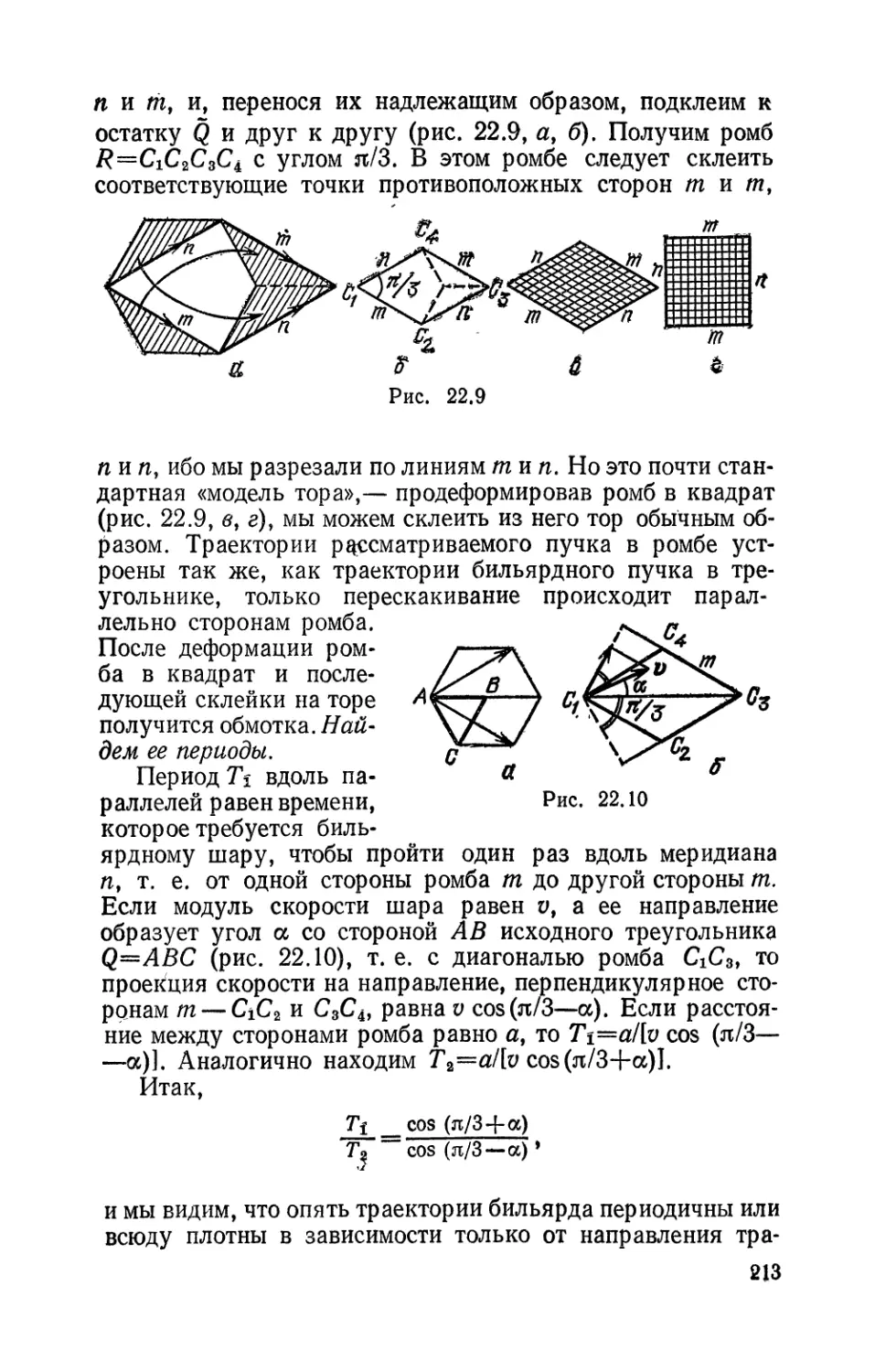
22. Бильярды в «торических» мноrоуrольниках 207
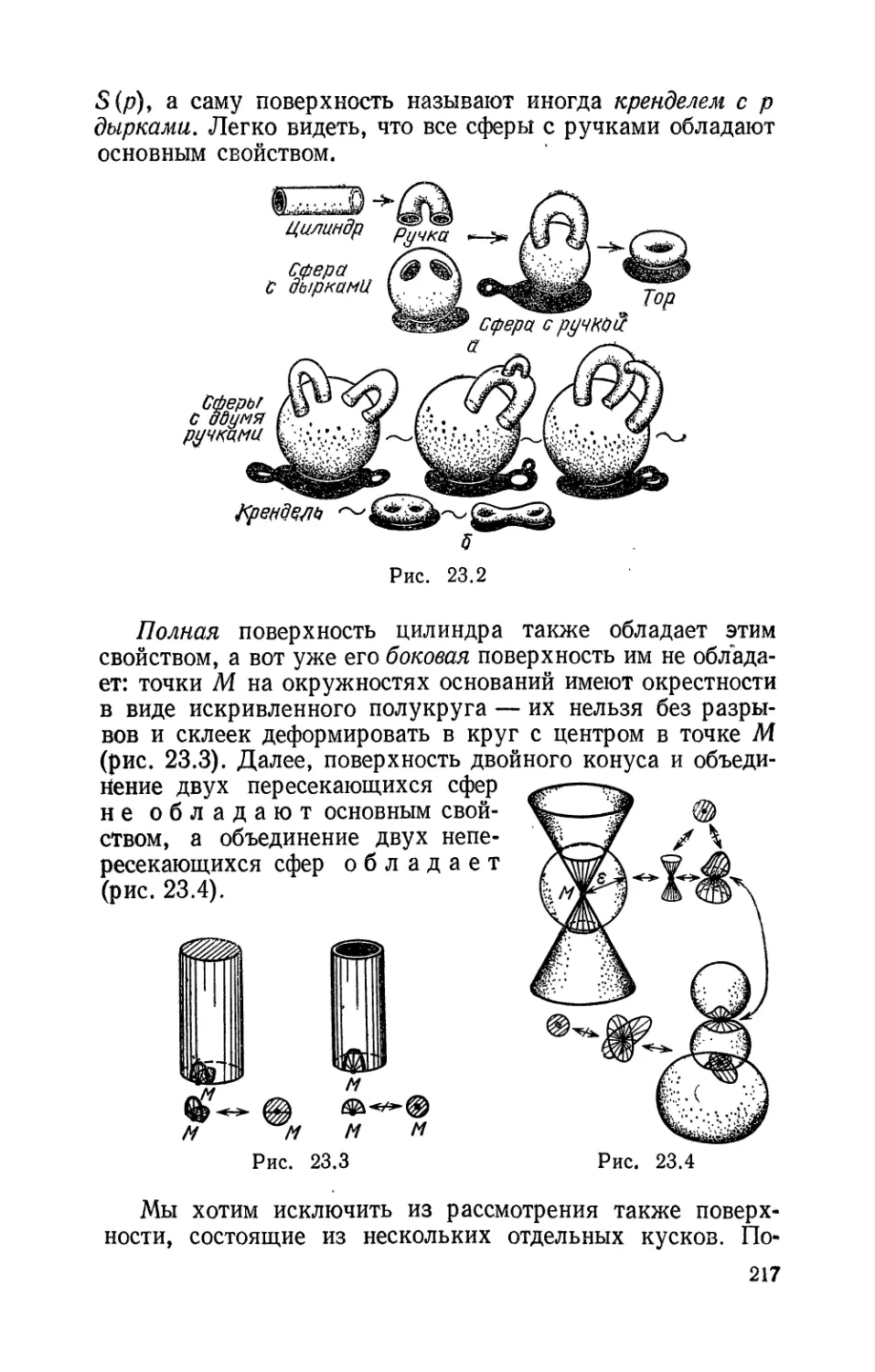
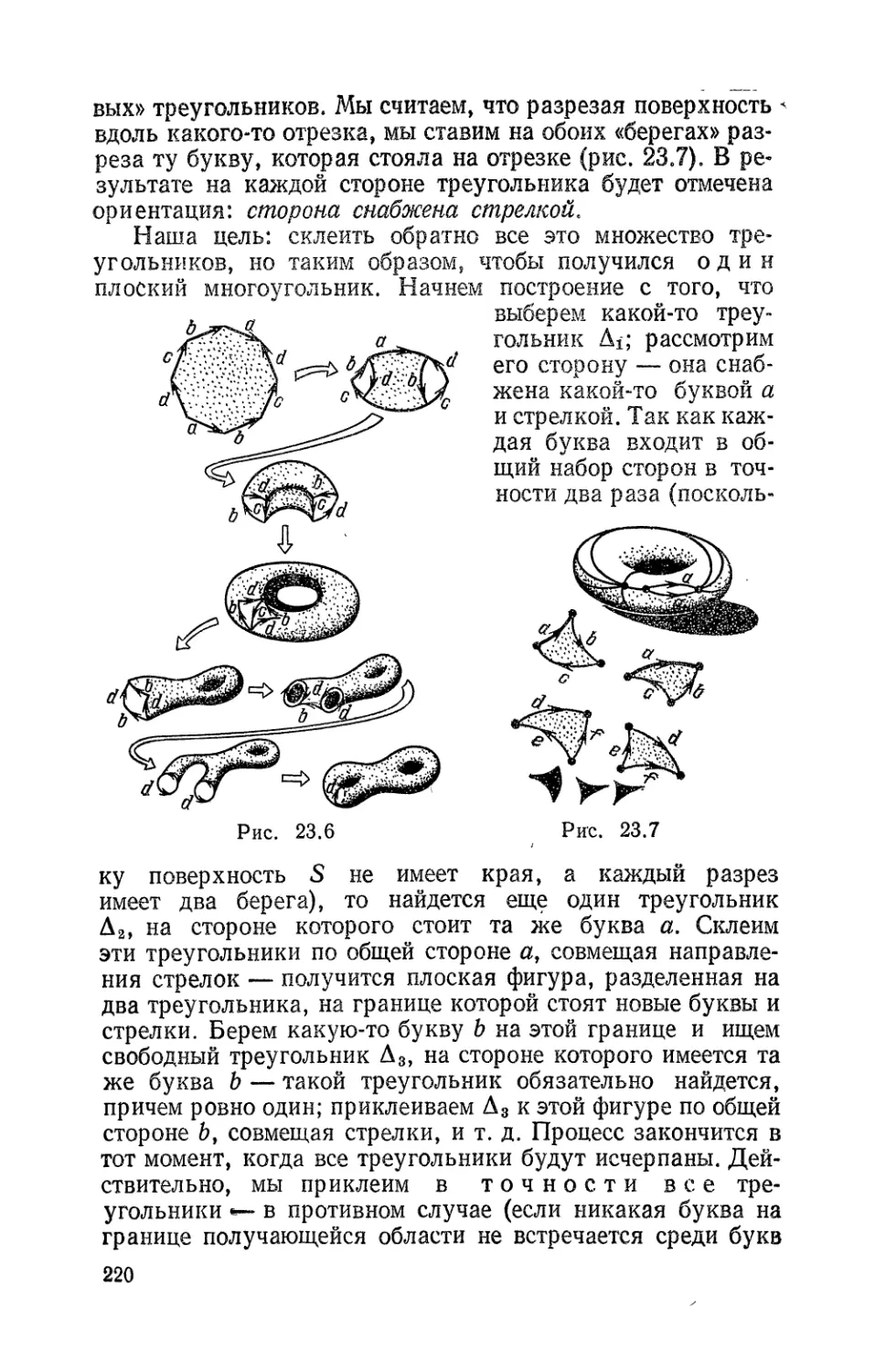
23. Склейка поверхностей из мноrоуrольников 216
24. Б ильярды в «рациональных» мноrоуrоль-
никах и поверхности 226
r л а в 3 9. Поведение бильярдных траекторий: в мноrоуrоль-
никах 235
25. Траектории в рациональных мноrоуrоль-
никах и обмотки кренделей 236
9 26. Может ли непериодическая траектория в
выпуклом мноrоуrольнике не быть всюду
плотной в нем? 246
27. Периодические траектории в мноrоуrоль-
никах и мноrоrранниках 255
Заключение 282
Список литературы 287
Посвящается
нашим JlчumеЛЯАt
ПРЕДИСЛОВИЕ
в данной книrе изучаются так называемые бильярд-
ные системы. К простейшим из ни относятся «бильярд в плоской
области» (точечный шар, движущийся внутри Kpyra, прямоуrольни-
ка, эллипса, мноrоуrольника и т. д.) И «одномерный бильярд» (ко-
нечное число точечны шаров, движущихся по отреЗI{У, лучу или
по всей бесконечной прямой). Общим свойством бильярдныХ! систем
является закон абсолютно упруrоrо отражения. О rеометрических,
«арифметических», физически СJIеДСТВИЯХ 9Toro закона и расска-
зывается в кн иrе.
Методы исследования бильярдных систем (например, анализ
поведения бильярдны траекторий), с одной стороны, примыкают
к традиционной rеометрии, а с друrой ..... лежат на стыке отраслей
современной математики ---- теории чисел, тополоrии, эрrодической
теории и теоретической механики. Будучи, как правило, вполне
элементарными, эти методы позволяют получить далеко не элемен-
тарные выводы.
Мноrие из излаrаемых в книrе результатов являются класси-
ческими и восходят к Кориолису, Больцману, Пуанкаре, Киркrофу.
Современная теория бильярдов является одним из актуальны на-
правлений математической физики. Ее основы были заложены со-
ветским математиком Я. r. Синаем и ero школой. Проблемы этой
теории непосредственно близки к переднему краю сеrодняшней ма-
1ематики. Поэтому книrа, возможно, будет интересна не только
школьникам, но и студентам, и специалистам ....... математикам, ме-
ханикам, физикам. В ней сформулировано немало вопросов, ос-
тающихся открытыми, и мы надеемся, что кому-нибудь из читателей
книrи удастся продвинуться в и исследовании. Учитывая элемен-
тарность методов (при неэлементарности результатов) и плодотвор-
ность свежеrо взrляда на рассматриваемые вопросы и проблемы, мы
особенно рассчитываем на читателей-старшеклассников.
Мноrие из решаемы в книrе задач разбирались на занятиях
кружков в физико-математической школе-интернате при Mry, в
летнем лаrере Малой академии наук Крыма «Искатель». Часть Ma
териала публиковалась в журнале «Квант» (см. список литературы
в конце книrи). Некоторые идеи и результаты, приводимые в кни-
re, неоднократно обсуждались с участниками семинара Mry по тео-
рии динамических систем и с ero руководителем Я. Р. Синаем *).
*) В течение долrоrо времени и до послеДНИ1Q дней своей жизни
этим семинаром вместе с я. r. Синаем руководил также замечатель-
ный математик и популяризатор науки В. М. Алексеев (1932 1980).
5
Этот семинар является ОДНИМ из наиболее известных мировых
центров по теории динамических сист м и, в частности, по теории
бильярдов; часть приводимых нами результатов принадлежит ero
частникам. Мноrолетнее участие авторов в работе этоrо семинара
в значительной мере способствовало 'написанию этой книrи.
Читателю не следует рассчитывать на леrкое 'чтение через
некоторые параrрафы, наверное, придется буквально продираться,
вооружившись карандашом и бумаrой, иноrда ножницами и
клеем, а мо}кет быть, микрокалькулятором и{.[и компьютером. Кни-
ry не обязательно читать подряд ---- напротив, проскочив (как
бильярдный шар) через параrраф или rлаву, читатель может найти
интересующий ero (и доступный ему) материал ---- потом можно и
возвратиться.
В книrе MHoro отступлений от чисто бильярдной тематики,
вызванных тем, что бильярды имеют отношение к большому числу
интересных и., на наш взrпяд, красивых вв;nач, и поэтому мы наде-
емея, что читатель сможет разнообразить свои впечатления, узнать
что-то новое R даже не сов-сем обычное.
НО стоит сразу предупредить любителей иrры в бильярд
в нашей книrе нет не только соответствующих полезных советов,
но даже и правил этой древней иrры. Эта книrа ---- по м а т е м а -
т и к е, а любителям ооычноrо БИJIЪИРJ:З мы можем порекомендовзть
публикации журнала «Наука И жизнь» (см. (О в списке литературы)
и книrу r. r. Кориолиса «Математическая теория явлений бильярд..
ной иеры» (М.: rостехиздат, 1956), а также посетить возродившие-
ся чемпионаты страны по бильярду.
Как известно, «иестроrо» не означает «неверно», ,равно как и
«CTpO не означает «уместно» или «интересно (это высказываевие
принадлежит современному американскому физику Дж. Лебови
цу ........ одному из ведущих специалистов по статистической механике).
Поэтому в большинстве важных математических ВОррОСОВ (при изло-
жении методов) мы старались придерживаться полной (насколько
это ВОЗМО)КНО при приня:том элементарном I10дходе) строrости, oд
нзко В ряде вопросов более общеrо (физическоrо) характера (коrда
касаnись общих принципов или идей) оrраничнлись интуитивным
уровнем описания. Это следует иметь в виду и читателю риrористу,
и читателю-«физику», при-выкmему больше доверять своей интуиции.
Представление о структуре книrи можно получить не только
из оrлавления в конце Введения, в котором сформулирована
основн ая часть рассматриваемых далее вопросов и nроблем, коротко
рассказано и о последовательности иэло ения.
Читатель, sаинтересовавшийсSl дальнейшими деталями «мате-
матики бильярдов» или друrими подходами к излаrаемым вопро-
сам, может обратиться к списку литературы в конце книrи.
Мы блаrодарны Я.. f. Синаю, внимательно прочитавшему всю
рукопись и сделавшему MHoro замечаний и предложений по улучше..
1-1 ию ее текста, а также Л. А. Бунимовичу, я. Б. Песипу, А. М. Сте-
п ину 'и ю. п. Соловьеву, своими эам.ечаниями способствовавшими
лучшению отдельных мест книrи.
ВВЕДЕНИЕ
Читатель, конечно имеет представление об
иrре в бил'Ьярд на прямоуrольном столе с JIузами (рис. В.l).
Появившись до нашей эры в Индии и Китае, бильярд через
MHoro веков перекочевал в европейские страны......... УПОМИ
нание о нем имеется в
анrлийских летописях
УI века. Более поздние
сведения о появлении
бильярда в Европе OT
НОСЯТСЯ К Х УI веку.
Так, французский ко-
роль Карл IX в Варфо
ломеевскую ночь, *) иr..
рал в БИЛЬЯРДt коrда раз Рис. Б.l
дался условный звон KO
локолов парижскоrо собора Ceh-ЖерменД'Акселеруа. ЗатеlVI
В.. Шекспир в «Антонии и Клеопатре» **) заставляет еrи
пеТСКУI{) царицу Клеопатру иrрать в бильярд со своей фрей
линой (акт l1t сцена 5; см. эпиrраф к части 111). В 1760 [.
анrлийский король reopr 11 издал указ, запрещающий
иrру в бильярд !3 общественных местах под страхом
штрафа в 10 фунтов.. В России бильярд стал известен и
распространился при Петре 1. Как правило, в бильярд
иrрали на прямоуrольном столе с шестью лузами, из KOTO
рых четыре располаrались в уrлах стола, а две в cepe
динах более длинных сторон; отличались эти иrры лишь
количеством шаров......... иноrда довольствовались тремя ша-
рами (как, например, анrлийский король rенрих VIII), а
иноrда ......... пятнадцатью или двадцатью.
*) Варфоломеевская ночь (известная также ПОД названием
«парижская кровавая баня»)...... историческое событие, происшедшее
в ночь на 24 aBrycTa 1572 r., коrда католики учинили избиение ryre'!
НОТОВ (французских протестантов)..
* *) Ш е к с пир В. Полное собрание сочинений: В 8 Т.
1.7......1\1.: Искусство, 1960. Траrедия написана в 1616 r.
7
Подобно тому как азартная иrра в кости вызвала к жиз-
ни «исчисление» вероятностей, иrра в бильярд послужила
u
предметом серьезных научных исследовании по механике
и математике. Описанию движения бильярдноrо llJapa
(с учетом трения) на прямоуrольном столе с лузами ПОСВЯа
щена книrа известноrо французскоrо физика r. r. Корио-
лиса, написанная им в 1835 r. за rод дq избрания ero ака..
демиком Парижской академии наук.
Известны различные варианты иrры на бильярде. На-
пример, так называемый французский бильярд вообще не
имеет луз (при иrре во французский бильярд HY:iKHO по
u
пасть в заданныи шар после нескольких столкновении
с друrими шарами......... см. литоrрафию известноrо худож-
ника XIX века А. Оберландера на второй странице об-
ложки). Французский бильярд и ПОСЛУ}l{ИЛ прообразом:
математическоrо бильярда, которому посвящена эта книrа.
Представьте себе rоризонтальный бильярдный стол
произвольной формы, но без луз. По этому столу без Tpe
иия ДВИ)I{ется точечный шар, абсолютно упруrо отраiкаЯСf}
ОТ бортов (рис. В. 2). Спрашивается, "акой может быть
траектория этО20 UlapUKa?
Математическая проблема бильярда, или проблема
траекторий, состоит в том, чтобы найти ответ на этот воп-
рос. Описанная механическая система точечный шар
в бильярдной области Q, оrраниченной бортом r (rраницеЙ
области Q), и называется матемаmическиА1- бuльярдОlll.
Траектория бильярда в области Q определяется начаЛЬНЫJ\,l
положением точки q (q Е Q) и начальным вектором ее CKO
рости 'V. Пренебрежение трением означает, что аБСОЛЮТНУIО
величину скорости 'V при движении точки мы считаем неИ2
u u u
меннои во времени, поэтому задаваемыи в начальныи MO
мент времени ,==о вектор 'V можно считать единичным,
характеризующимся лишь своим направлением. Направле-
ние вектора v(t), т. е. направление движения шара, Me
няется только при ero ударе о борт. Это происходит по зако-
ну абсолютно упруrоrо отражения: после удара шара
(ТОЧI{И q(t)) о борт r в точке Р шар движется так, что
ero «уrол падения равен уrлу отражения». Если борт r,
в окрестности точки Р криволинейный, то уrлы падения'
и отражения......... это уrлы, составленные «падающим» и «ОТ-
раженным» отрезками траектории Q касательной MN к крп"
вой r, проведени ой в точке Р (рис. В.2) *). Таким образом,
*) в физике обычно принято отсчитывать уrлы падения и от-
ражения от нормали к кривой r в точке Р. Нам удобнее отсчитывать
уrлы от касательной.
8
траектория бильярда......... это вписанная в кривую r ло.
маная, которая может быть о.цнозначно построена по сво-
ему начальному звену.
Борт r бильярда может иметь и точки излома.......... типа
точек Ai, А 2 , ... на рис. 8.2. Касательная к кривой r
в такой точке не определена. Поэтому бильярдную траек;,
ТОРИIО, попадающую в такую точку, мы будем считать oKarn-
чивающейся в ней. Такие «тупиковые» траектории B опре-
деленном смысле исключительны, и мы их, как правило,
N
tf2J&
00&
Рис. В.3
раССIvlатривать не будем. Сформулированная выше проб-
лема траекторий относится к поведению неособых, беско-
нечных во времени траекторий.
Общая математическая проблема бильярда заключается
в том, чтобы описать возможные типы бильярдных траек-
торий в данной области Q. Простейший принцип TaKoro
описания разделение траекторий на периодические, или
замкнуп2blе, и остальные непериодические. На рис. В.3
изображены некоторые периодические траектории бильяр-
дов в прямоуrольнике, в правильном треуrольнике, в
кр у re.
Траектория с «начальным условием» (q, 'V) будет перио-
дической (или замкнутой), если через некоторое время
(через период) точка возвращается в свое начальное поло-
жение q с первоначальной скоростью 'lJ. Периодические дви-
)I{ения воспринимаются как наиболее «правильные» ..........
такими мы привыкли представлять, например, движения
планет около Солнца и качания маятника. Рассматривае-
I\1ая проблема в отношении периодических траекторий сво-
дится, в частности, к вопросу о cyи eomвoвaHии: в любой ли
области Q существуют периодические (замкнутые) '(раек-
тории? Друrой вопрос........ о критерии периодичности: как
9
ПО данным начальным условиям (q, ) узнать, будет ЛИ СООТ-
ветствующая траектория периодической?
В первых двух частях книrи мы найдем критерии пеРИ<r
ДИЧНОСТИ для бильярдов в Kpyre и в прямоуrольиике. Во
второй r.лаве будет решен и вопрос о существовании перио-
дических траекторий бильярда в произво ьной выпуклой
области с rладкой (без изломов) rрани.цей. А вот этот же
во,прое для бильярдов в мноrоуroльниках (даже в тупо-
yroлЬНЫХ треуroльниках!) до настоящеro времени остается
открытым. Иначе rоворя, неизвестно, в J1юбом ли MHoro..
уrОЛhнике (или тупоуrольном треуrольнике) существуют
периодические траектории. А ведь этот вопрос, ПО сути,
относится к элементарной rеометрии Известные нам еве-
дения по данному ПОВОДУ приведены в rл. 9.
Интерес представляют и такие вопросы: Какое число
звеньев может иметь периодическая траектория? Какие
периоды имеют nерuoдuческие траектории в данной об..
.срсти (если принять минимальный период периодической
траектории, скажем, за единицу)?
ока3ыается,, это далеко не праздные вопросы........ Ha
пример, они имеют прямое отношение к исследованию спе.
циальных систем квантовой механики. Однако объяснение
u
этоrо выходит далеко за рлмки наших возможноатеи в дан-
u
иои книrе.
Взамен рассмотрим элемеmзрную задачу совсем из
друrой области, изящно решаемую G помощью бильярдов.
Речь пойдет о «переливаниях», которые, казалось бы, не
имеют уж ничеrо общеrо с биnьярдами.. Начнем е класси.
ческой rоловоломки.
И меются два оооуда ем.естu.мoc.тbЮ 7 u 11 литров и
ООJlьшая бачка, НQnO:llненlШЛ водой. Как, о noмощыо этих
двух сосудов oтJЦpитb ровно 2 Аитра воды? Всякие УЛQВКI1
запрещены, T е. на сосудах нельзя делать никаких OTMe
ТОК, их нельзя наклонять, чтобы отмерять доли литра,
н Т. Д.
Предложенная задача решается либо алrебраическим
метоДОМ, либо методом проб и ошибоК. При чем же здесь
б.ильярдные шары?
Как ии странно, НО, rоловоломки на переJlивание жид-
КОС'Iей можно оч.ень леrко решать,. вычерчивая бильярдную
траекторию шара,. отражающеrося от бортов ромбическоrо
стола! [рапиды таких CTOJIQB удрб нее вcero рисовать на бу-
мare. на которую нанесена сетка из одинаковыx равносто-
ронних треуrOOlЪНИКОВr В рассматриваемой задаче стороны
Cfола ДОЛЖНЫ иметь ДЛИН 7 Н 11 едИНИЦ {рис.- В.4). По
10
rОрИЗ0нтали отложено количество БОДЫ в 11-литровом со-
суде в любой l\10меит времени, а по вертикали........ та же ве-
личина для 7 литровоrо сосуда.
Как же пользоваться диаrрам ой? Представьте себе,
что шар находится в .левой нижней вершине в точке о.
Он будет перемещатъся ВДОЛЬ нижнею основания ромба ДО
тех пор, пока не достиrнет правой боковои стороны в точ-
ке 11. Это значает, что О t 2 :3 4 5 6' 7 В/}/I) Н
11 литровыи сосуд на- 7. 7-
полнен до краев, а. 7. Il /
литровЫЙ ПУСТ. Отразив- S '4
шись упруrо от правоrо о"'" 3
борта, шар покатится 2 2
вверх и влево и ударит- t - '0'/
ся о верхний борт в точ- O'f 1 2 4 5 -.6 7 8 1} fO 11 t
ке с координатами 4 по 1/. 4' 4- О 11 8 в f 1 О 11 5
, '"'" "'"
rОрИЗ0Нтали и 7 по верАО О 7 О 4- 4- .; О О 1 1 7
тикали. Это означает, f t
что В 11 литровом сосу- 5 О 11", () Э @
де осталось вcero 4,JlИТ- О 5 fj о 7
ра воды, а 7 литров из
Hero перелили в меньший Рис. В.4
сосуд.
Прослеживая дальнейший путЬ шара и ззписьmая все
этапы ero движения ДО тех пор, пока ОН не попадет в точку 2
BepxHero борта, вы получите -ответ и узнаете, в какой по-
следовательности необходимо производить переливавия,
чтобы отмерить 2 литра воды. Все 18 переливаний изобра-
,кены схематически на рис. В.4. Наклонные стрелки rOBO-
рят о ТОМ, что вода переливается из одноrо сосуда в друrой,
а вертикальные означают, что либо вода целиком ВЫЛИ
вается из менъшеro сосуда обратно в бочку, либо больший
сосуд надо наполнить водой до краев.
Является ли это решение самым коротким? Нет, су..
0(1
ществует второи путь, коrда воду сначала наливают в
7-литровый сосуд. Надиаrрамме (рис. В.4) это соответствует
тому, что шар из точки О ка-rится вверх вдоль левоro борта
до тех пор, пока не ударится в верхний борт. Нарисовав
траекторию бильярдноro шара, читатель убедится в том,
что точка 2 достиrается на этот раз за 14 отражений от
борта. Полученное решение G 14 переливаниями уже яв"
ляется самым коротким.
Требуется HeMHoro сообразительности, чтобы примени,?
метод бильярдноrо шара к JIЮбой задаче о переливанlUI
жидкости с ПОМОЩЬЮ не более чем трех СОСУДОВ. Поскольху
11
KpOM e как во введении об ЭТI-:Х задаqах мы rоворить больше
не будем, поrоворим об этом методе здесь более подробно.
Рассмотрим старую rоловоломку с тремя сосудами, вос-
ходящую еще к Никола Фонтана, итальянскому матема.
тику XVI века, KOToporo друзья называли Тартальей *).
Восьмилитровый сосуд до Kpa B наполнен водой. С помощью
двух -пустых сосудов объемом 3 и 5 литров воду надо по-
ровну раЗJIИТЬ в два больших сосуда. Диаrрамма д я этой
задачи ........ ромбический стол размером 3 х 5 ---- изображена
на рис. В.5. rлавная диаrо-
наль ромба, поделенная нак-
лонными прямыми на 8 частей,
относится к 8-литровому со-
суду.
Как и в предыдущей зада-
че, бильярдный шар начинает
свое движение из точки о.
Нарисовать ero траекторию
совсем несложно. С ее помо-
щью вы получите решение G минимальным числом перели-
ваНИЙ t равным 7.
Если объемы двух меньших сосудов не имеют общеrо
делителя (т. е. взаимно просты), а объем 'fpeTbero сосуда
больше или равен сумме объемов двух меньших; то G по-
мощью этих трех сосудов можно отмерить любое целое
число литров, начиная с 1 литра и кончая объемом среднеrо
сосуда.
Имея, например, сосуды вместимостью 15, lб и 31 литр,
вы сумеете отмерить любое количество воды от 1 до lб
литров. Такая процедура невозможна. если объемы двух
меньших сосудов имеют общий делитель (подумайте сами,
почему). Коrда объем большеrо еосуда меньше суммы
объемов двух друrих, возникают новые оrраничения. Если,
например, объемы сосудов равны 7, 9 и 12 литрам, то у РОМ-
бическоrо стола надо отсечь нижний правый уrол (рис.
В.б). Тоrда шар сможет попасть в любую точку от 1 до 9,
за исключением точки 6. Несмотря на то, что 7 и 9 взаимно
просты, отмерить б литров БОДЫ оказывается невозможным
IIз-за Toro, что самый большой сосуд имеет слишком ма..
ленький объем.
Q
1
.2 ":5
Рис, В,5
*) Тарталья по-итальянски означает «заика». Он рОДИЛСЯ в
1500 r. в цтал.ьянском rородс Брекчия. В 1512 f. во время взятия ro-
рода французами Тарталья был ранен в НИЖНЮIО часть лица, что
отразилось на ero речи; товарищи прозвали ero заикой.
12
Исследование раэличныIx возможностей, возникающих
при использовании GООУДОВ разных объемов, о ПОМОIЦЬЮ
метода «бильярдноrо шара» чрезвычайно увлекательно.
Однако заниматься этими вопросами мы в этой книrе Не
будем, оставив их на рассмотрение читателя. Отметим
только, что обобщение УК8эанноrо метода на случай четы-
рех сосудов сводится к дви- О 1 2 3 4.5
)I<ению бильярдноrо шара в 7 7
объемной (тетраэдрической) 5 б 6 5
области. 4 4
Предлаrаем читателю еще 3
одну задачу на переливания. / l' ,
3 а д а ч а. Имеется 10 лит- О (]\ \, '
ровое ведро, доверху заполнен- \ 1 \ \',8,1', \ , " \',
ное водой, и два пустых бидона \ \ , \ , , , \ ' '\ , XO
объемом 3 и 5 литров. Требуетtя , \ \ \ \ \ , \ , 1
часть БОДЫ (целое число литров) \ \ \ \ \ \ \ 4"3
вылить, а оставшуюся БОДУ раз- \ \ \ \, б .5
делить на три равные части. " \, 98 7
Рассмотрим друrой тип 121170
элементарных rеометрических
задач,ОТНОСЯЩИХСЯ к бильяр.. Рис. В.6
дам. В них либо требуется
найти замкнутую траекторию бильярдноrо шара в данном
I\tноrоуrольнике, либо найти путь бильярдноrо шара, по-
падаlощеrо через заданное число ударов из одной фиксиро-
uанной ТОЧКИ внутри мноrоуrольника в друrую.
Для решения таких задач существует очень удобный и
Ва1КНЫЙ метод «зеркальноrо отражения», или «ВЫПрЯМ-
ления» бильярдной траектории, принадлежащий немецкому
\
математику r. А. Шварцу *) (о применении этоrо метода
СМ. части 11 и IV). Метод этот является основным техни-
ческим пр иемом при решении бильярдных задач в MHoro-
уrольных областях Q и послужит нам в дальнейшем клю-
чом при нахождении и исследовании разнообразных биль-
ярдных траекторий. Опишем ero. ,.
Сложное, вообще rоворя, поведение бильярдной тра-
еl{ТОРИИ в мноrоуrольной области Q можно существенно
упростить, представив ero иначе. А именно, сядем на
бильярдный шар О, как барон Карл Фридрих Иероним фон
j\'юнхrаузен на пушечное ядро, и вооружимся системой
*) '.epAtaH А мандус Шварц (1843......1921) ..... известный немецкий
математик, специалист по математическому анализу и теории фун -
ций; имеет также крупные эаслуrи в областях, связанных с так на-
зываемой «изопериметрической проблемой».
13
координат, направив ось Оу по направлению движения,
а ось Ох....... вправо перпендикулярно оси Оу.. В этой сис
теме координат Hтna бильярдная траектория изобразится
осью Оу (т. е. прямой линией), а область Q будет представ-
ляться нам как последовательность копий Qi, Q2, Q3t . . .
этой области, «нанизанных» на ось Оу таким образом, что
соседние копии Qi и Qi+l зеркально СИfv1метричны относи..
тельно их общей стороны. В этом построении, связанном
с переходом к новой системе координат, и заКЛЮ'Iается
метод выпрямления бильярдной траектории.
Совокупность копий {Qi}, как бы нанизанных на «ко..
пье» Оу, образует «коридор» QQIQ2Qa t . . Возвращению из
системы координат Мюнхrаузе..
на в исходную, прикрепленную
к фиrуре Q, соответствует на-
ложению «rармошкоЙ» кор идо..
ра QQIQ2QS .. " . (который полез..
но считать прозрачным) на на-
ходную фиrуру Q; при этом ось
Оу переходит в рассматривае-
мую бильярдную траекторию.
Продемонстрируем метод
выпрямления на следующих
примерах.
А. Пусть на прямоуrОЛЬНО1\'I бильярдном столе нахо-
дится один шар; под каким уrлом ero следует направить
из точки А, чтобы он после заданноrо числа отражений оТ
бортов лопал в точку В (например, в лузу)?
Для решения отразим ПРЯ Iоуrольник (исходный би-
льярд) симметрично относительно всех ero сторон; все
полученные таким образом прямоуrольники вновь отразим
относительно всех их сторон, и так далее до бесконечности
(на рис. В.7 показаны также образы точки В при этих СИМ-
метриях). В результате всех сделанных отражений траек-
тория шарика «распрямляется» (например, на РИG. В.7
траектория АС 1 С 2 С з В последовательно переходит в
ACiD 1 D 2 B', ACID 1 E 1 B", ACiDiEiB'!!).
Если полученная «выпрямленная траектория» прохо-
дит через образ точки В в одном из прямоуrольников, ТО,
очевидно, траектория шара в исходном прямоуrольнике
пройдет через В. Поэтому, для Toro чтобы пустить шар из
точки А так, чтобы он после заданноrо числа отражений
о стенки прямоуrольноrо бильярда попал в точку В, нужно
провести такой отрезок с началом в точке А и концом в од-
ном из образов ТОЧКИ В, ч обы он пересек это же CalYl00
. .
. .
. .
. .
. .
. ,.
. .
. .
Рис. В.7
\ 14
число раз линии сетки «клетчатой плоскости». Проделав
обратную процедуру «свертывания» проведенноrо отрезка,
превратим ero в искомую траекторию в исходном бильярде
(рис. В.7). Общая «теория прямоуroльноrо бильярда» из-
ложена в части 11 книrи.
Б. Ра смотрим бильярд в равностороннем треуrольнике.
Поскольку одинаковыми равносторонними треуrольниками
можно без щелей и перекрытий замостить всю плоскость,
и здесь применима проде-
дура «ВЫПРЯЬfления биль-
u
ярднои траектории».
Оказывается, траекто-
рия бильярдноrо шара ре-
шает следующую известную
задачу: нлйти кратчайший
путь, по которому должна
ползти пчела из точки А
в пzочк-у В внутри равно-
стороннеео mреуеолыlкa,'
чтобы сначала наоладитЬСЯ Рис. В.В
.лtедом на одной стороне
пzpey , 20ЛЬnuкa потом сахаром......... на дРУ20Й стороне, и,
наконец, вареньем на третьей. (Предполаrается, что
каждая сторона полностью вымазана соответствующим
сладким веществом.)
Ответ приведен на рис. В .8. Нетрудно видеть, что любой
друrой путь, ведущий требуемым образом от А к В, после
зеркальных отражений превращается в путь из точки А
в точку BHI, длина KOToporo больше длины отреЗI{а А В'" ,
и поэтому не являетс кратчайшим.
В. Сразу же возникают два интересных вопроса, свя-
занные с обобщением плоскоrо бильярда на случай прост-
ранства: существуют ли зам/(,нутые бильярдные траекто--
рии 8Hyпlpu куба, Я8ляюще2ОСЯ пространственным анаЛО20Аt
квадрата, и тетраэдра nросmранственноео а/ШЛ02а рав-
носmоронне20 треуzольнuка?
Как и раньше, бильярдный шар считается идеальной
упруrой невесомой частицей, отражающейся от стенок по
закону «уrол падения равен уrлу отражения». Вместо шара
l\10ЖНО рассматривать луч света, отражающийся от зер
u
кальных стенок внутреннеи поверхности мноrоrранника и
не попадающий ни на ребра, ни в ero вершины (в противном
случае ответом на поставленный вопрос следовало бы счи-
тать любую из диаrоналей, по которой из конца в конец
двиrался бы шар).
15
в одной из мноrочисленных статей о Лыоисе I(эрролле *)
есть упоминание о бильярде внутри куба. Это одна из тех
задач, которые Не моrли не привлечь ВНИ!\1ания изобрета..
теля круrлоrо бильярдноrо стола. Идея об иrре в бильярд
внутри кубическоrо «стола» далеко не столь надуманна,
как это MO}l{eT показаться на первый взrляд. Дело в TOI\tI,
что реальные молекулы воздуха в кубической комнате
как раз и представляют собой «бильярд'ные шары», сталкис
вающиеся друr с друrом и со стенками комнаты по закону уп.
pyroro удара. Правда, онн находятся в поле тяжести и ис
пытывают сопротивление воздуха. Если отбросить эти orpa-
ничения, то получим настоящий бильярд с orpoMHbIM чис;.
лом (порядка 102 ) шаров. Этому бильярду мы посвятим
u
В нашеи книrе достаточно MHoro места....... практически всю
часть 111; (1 ним, кроме метода выпрямления бильярдной
траектории, связано MHoro разнообразных физических,
l'еометрических и алrебраических идей, часть которых бу-
дет OCBell eHa ни}ке.
Но верне 1СЯ к движению одноrо шара в кубе и приме-
ним к кубу тот же метод «выпрямления траектории», что
Рис. В.9
Рис. 8.10
и для квадрата. Произведя 5 отра}кений от rраней куба,
мы получим искомую замкнутую траекторию, изображен
ную H a рис.' В.9 жирной штриховой линией со стрелкой и
представляющу ю собой одну из четырех возможных тра-
*) Льюис Кэрролл (псевдоним Чарлза Доджсона) (1832.......1898),
автор знаменитых книr про Алису, математик по профессии, пре.
подаватель ОI{сфордскоrо университета (Анrлия), \Увлекалея и би..
льярдом. Он придумал I{руrлый бильярдный стол и сочинил пра-
вила иrры на этом столе (1890). О некоторы* изобретения* Кэр..
ролла рассказывает Niартин rарднер в свои попупярны книrа
«Математические досwrи», «Математические rоловоломки и развле-
чения», «Математические новеллы» и др.
16
екторий, каждая из которых является решением задачи.
Если «свернуть» кубы, проделав обратные отражения, по-
лучим замкнутую бильярдную траекторию из 6 звеньев
равной длины в исходном кубе. Представив себе куб разме w
ром: 1 х 1 х 1 , состоящим из 27 маленьких кубиков G ребром
1/8 кажДЫЙ, несложно ПОНЯ'I'Ь, что каждое звено этой траек-
тории является диаrональю TaKoro кубика (рис. В .10),
TaI{ что ero длина равна VI З /3 == 1/У З, а длина всей траекто-
рии составляет В/VЗ==2 V з.
Эта траектория известна химикам-орrаникам как «шее-
тиуrольник в форме кресла». Она чаото встречается в уrле w
родных соединениях, например в циклоrексане, rде шесть
уrлеродных атомов соединены одновалентными связями
в кольцо, а атомы водорода располаrаются вне этоrо кольца.
Интересно отметить также, что если эту бильярдную траек"
ТОрИIО спроектировать на любую rpaHb куба, то в проекции
получится прямоуrольник размером 1/8 Х 2/3, а если ее
с роектировать на три плоскости, параллельные трем диа..
rоналям, то получаются ромбьц еще в одной проекции (ка-
кой?) получается правильный шестиуrольник.
Обращаясь теперь ко второму вопросу........ о замкнутой
бильярдной траектории в тетраэдре'....... поступим точно
f
l: 1.10 А ,
,
Р2
А
ct
li'
Рис. В.l1
так же, как и в случае куба: отразив тетраэдр симметрично
относительно трех ero rраней (рис. В .11), мы получим замкw
нутую траекторию из четы,ех звеньев, которая по одному
разу касаеТGЯ каждой rрани. Существенно сложнее pe
шается задача о замкнутой бильярдной траектории, кото-
рая имеет все звенья равной длины. Одна такая траектория
изображена на рис. Б.l1 штриховой линией, а Bcero их
существует три, причем совершенно одинаковой формы.
11
Каждая И3 них имеет точки излома на rранях тетраэдра
в ОДНОЙ из вершин маленькоrо paBHQCTopOHHero треуrоль-
ника, расположенноrо в центре rрани. Стороны этоrо ма-
ленькоrо треуrольника равны' 1/10 ребра ИСХОДНQrо тет-
раэдра, а каждое звено траектории имеет длину l1V lO
0,3162777..., так что весь путь бильярдноrо шара внутри
тетраэдра составляет в этом случае- 4 · l/VТO 1,2649. . . .
Метод зеркальных отражений, который мы продемонст"
рировали на примерах А........ В, дает возможность не
только строить разнообразные периодические бильярдные
траектории в «хороших» мноrоуrольниках (или мноrоrрап..
никах), но и отыскать критерий периодичности траекторий
в таких областях, как прямоуrольник или правильный
треуrольник. Скажем, для бильярда в квадрате неособая
траектория, направленная под уrлом а к стороне квадрата,
окажется периодической в том и только в том случае, коrда
число k==tg а является рационаЛЫ-lblМ, T е. представимо
в виде обыкновенной дроби т/п (т........ целое, n нату-
ральное). А как же будут себя вести траектории, для ко-
торых исло k==tga uррацuонаЛЫ'lО? Например, если
tg а== У 2?
Примитивный ответ: эти траектории будут неnериоди-
чесКиМи,.......... rоворит нам только о том, что движение будет
каким-то «неправильным». Но «насколько неправильным»?
Это очень интересный вопрос, но ЛИШЬ в том случае, если
на Hero дается содержательный ответ! А таких ответов мо-
жет быть и несколько.
\
Во-первых, непериодическое движение может оказаться
«почти периодиче ким», или квазипериодическu.м, как при-
нято rоворить в классической механике. rрубо rоворя,
квазипериодичность движения означает, что хотя ero тра-
ектория и не замкнута, но через некоторое время (через
квазипериод) она идет близко к предыдущему отрезку
траектории. Характерные квазипериодические траектории
бильярдов в квадрате и Kpyre показаны на рис. В.12.
В о про с: обязана ли неперuодuческая rnраекmорuя
быть квазuперuодической? Оказывается, для бильярда в
l<pyre, в прямоуrольнике, в правильном треуrольнике и во
мноrих друrих мноrоуrольниках действительно обязана.
\
А вот в эллипсе существуют траектории, которые неперио-
дичны и не квззипериодичны, НО их, по сути, нем Horol
(См. ниже 4.) И опять-таI<И, в общем случае (ДЛЯ областей
произвольноrо вида и даже для мноrоуrОЛЬНИКQВ) ответ
u
на поставленныи вопрос неиэвестен.
18
Далее, если внимат .льно рассмотреть квазипериодиче-
ские траектории на РИСо В.12, становится понятным, что они
«стараются» все более плотно заполнить целую область:,
их близкие отрезки все сдвиrаются и сдвиrаются, так что
траектория на рис.. В.12, а заполняет «территорию» квад-
рата, а на рис. B.12, б ........ KpyroBoe кольцб. На сериях
рис. В .13, а, б (полученных с помощью компьютера) пока..
заи процесс постепенноrо распределения траекторий по
своим областям.
.а
5
Рис. В.12
Возникает следующий вопрос: не будут ли эти траекто-
рии всюду плотНыМи........ в квадрате, в кольце? Иначе ro
воря, оставит ли такая траектория хотя бы какое"нибудь
«пустое местечко» в области например, кружок (хотя бы
очень маленький), который она н и к о r Д а не пересечет?
Оказывается, в данных случаях н е о G т а в и Т! Указан..
ные непериодические траектории всюду плотно заполнят
соответствующую 'область: какой бы (сколь уrодно малый)
кружок мы ни взяли (в квадрате или в кольце), рано или
поздно траектория пересечет этот кружок. Если считать,
что бильярдный шар «чернильный» И оставляет после себя
след, то он со временем обязательно закрасит всю 06ласть
(квадрат или кольцо) целиком, каким бы тонким не был чер
нильныЙ след (но имеющим все таки ненулевую толщину).
Ясно, что периодическая траектория свойством всюду
плотности обладать не может......... она может заполнить об
пасть «очень плотно», но не всюду плотно. Обязана ли npo
извольная неnериодическая Аmраекmория в области Q быть
всюду плотной во всей этой области? Это будет верно (что
мы дальше докажем с помощью вполне элементарных рас-
суждений) для бильярда в прямоуrольнике, в правильном
треуrольнике и некоторых друrих областях. Это не так для
бильярда в Kpyre и эллипсе и даже в некоторых мноrоуrоль-
19
никах, что тоже будет нами ПОК8Э3НО (СМ. 26). rlаконец,
для мноrоуrольников (и просто для треуrольников) обп.(еrо
вида вопрос остается ОТКрЫТЫМ. Неизвестен пока ответ
да)f{е на более Пр1JСТОЙ (казалось бы!) вопрос: в любом ли
.ч....., ,;..<..Х'>, ,;,хХ, ,'. ,Х, "-
J; -' ' ," ., .xx;': ", ... ..
'.- ",, ,._)C'::" I '\ - '< ',''''v.
7>, 1 .y.!:', ",, . 'v x ...;:-..',)С,';
1 1 '=:' 1'>A ': '.A "1C, . , '\. "':"\'-.х)::>
<Л ' ' '''''; ' ;''' ''':''''.)I';*,\>l'\ ;)( ",' .'" '\'" '" 1f'/"J\.
:Ж*' ';:'''\ ':v,; )<.:-::
..: .,< ',':' \: "' У'<;<'(',
1 jt .
<. /;'(' ':.{';!: ' i/ ::-': : $f: ). :1
1r '. fll
а
5
Рис. B.13
9
AU-lО20У20ЛЬfluке Q существуепl всюду плотная (в Q) щраек-
тория?
(У СТрОЙGТБО всюду ПЛОТНЫХ множеств даже на числовой
прямой lR может быть довольно СЛО}КНЫМ. Простейшие
примеры таких множеств....... мно}кество всех рациональных
20
чисел О, или всех конечных десятичных дробей Qio, или
множество всех иррациональных чисел Q . Их всюду плот-
u u
ность почти очевидна: если взять на числовои пр ям о И лю-
бой интервал А сколь уrодно малой длины 8>0, то на нем
найдутся числа всех трех указанных типов. Действительно,
если взять число d положительное, но меньшее 8/2, то хотя
бы одна из точек :f:d, + 2d, + 3d, . . . попадет в интервал .
OCTaJIOCb выбрать число d в виде соответствующей дроби:
l/N, либо 10"'N, либо V 2 /N, rде N......... натуральное.)
ДальнеЙшим усилением. свойства всюду плотности
бильярдных траекторий является свойство их равномерной
распределеН1-l0сти в соответствующей области и более об
щее свойство ареодuчносmи, иrрающее важную роль в Ма-
тематике, механике, в статистической физике. Объясним,
в чем заключается общее свойство эрrодичности бильярда
в оБJIЗСТИ Q.
Если бильярдная траектория всюду плотна в области Q,
т. е. бильярдный шар рано или П0ЗДНО обязательно попа-
дает в любую заданную фиrуру Ф, лежащую в Q, то можно
заняться вопросом: какую долю времени шар nроводит
в фuеуре Ф? Имеется в виду, .что сначала мы вычисляем
долю вреl\tlени за фиксированный промежуток Т (т. е. вы-
числяем отношение (Т) == t/T, rде t........ вре /IЯ, в течение
KOToporo за промежуток Т шарик побывал в области Ф)"
а затем: устремляем Т к бесконечности и берем предел
л== Нт л(Т).
T-+rI'J
Если окажется, что указанная доля времени, которую
ПрОБQДИТ шарик в фиrуре Ф, nроnорциональна площади
ФUZУРbl Ф (или, что то же самое, пропорциональна отноше-
нию площади фиrуры Ф к площади области Q), и это верно
для «типичной» траектории, то rоворят, что данная бильярд-
ная система ареодична *). Отношение t/T (вернее, ero
предел при Т 00) называется «BpeMeHHbIM средним»,
а отношение площади фиrуры Ф к площади области Q
«пространственным средним». Поэтому эрrодичность сис-
темы формулируется еще и как возможность заменять вре-
*) CTporo rоворя, эр,юдuчносmь означает, что почти каждая
фазовая кривая проводит в измеримой области фазовоео пространства
(см. 3) ремя, пропорциональное объему этой области. Свойство,
о котором rоворится в тексте, можно называть «слабой вреодUЧflО-
стью». Термин «типичная траектория» эдесь не обсуждается, ero
следует понимать в интуитивном СМbIсле. (Для сравнения: «типич
иые» числа на отрезке [О, 1] иррациональные t а рациональные
числа........ «исключительные»,)
21
менные средние пространственными среДНИ!'9IИ. Траектория
в эрr.одической системе заполняет область всюду плотно и
paвHo pHO, т.е. «размазана» по области с равной «ПЛОТ-
ностью». Свойство 8р20дuчяоотu сильнее свойства всюду
плоmяocтu, поскольку подразумевает ero выполнение;
таким обрззом, И3 эрrодичности СИСТ 1Ы следует всюду
плотность типичной траектории, но не н оборот, хотя очень
часто оказывается, что если к.акая то траектория всюду
плотна,' то и БСЯ система эрrодична.
Изучению" эрrодических свойств динамических систем
посвящен целый раздел современной математики.......... так
называемая эрrодическая теория, изучающая «хаотические»
свойства динамических систем, в которую теория бильярдов
входит в качестве подраздела" Предмет настоящей книrи
также относится к этой теории..
С т р у к т у р а к н и r и. Изложение материала в КНИ
re ведется последовательньuми переходами от простых би
льярдных систем к более сложным. Трудные места в книrе
(иноrда ЭТО касается целых параrрафов и rлав) отмечены
одной или двумя (это зависит от сложности) звездочками;
при желании их можно пропустить.
В ч а с т и 1 книrи изучаются 6ыпljКЛЬLe бильgрдыI'
rраницы которых не содержат прямолинейных участков:
круrлый, эллиптический и ,произвольный бильярд с КрИВО
линейной rраницеи. Наряду с их исследованием дeMOHCT
рируются общие математические методы, позволяющие при
менять бильярд в этих областях к решению некоторых Teo
ретико числовых, rеометрических и физических задач
В ч а с т и 11 проведено полное исследование бильярда
8 прЯМОУ20льнuке, сводящееся к исследованию траекторий
равномерно движущейся по тору (поверхности бублика)
точки, и показана связь между бильярдными тра кториями
в прямоуrольнике и фиrурами Лиссажу на осциллоrрафе.
11сследованию «2аза шаров»......... упруrо сталкивающихся
твердых шаров в пространстве и сосуде посвящена
q а с-т ь 111. Интересными здесь являются rеометрические
методы решения задач о росте числа столкновений молекул,
расноложенных на прямой, плоскости, в пространстве и
в оrраниченных областях (<<сосудах»), сводящие paCCMOTpe
lIие системы шаров к бильярдам специальноrо вида.
Следующая часть книrи ........ q а с т ь 1 V ......... рассказывает
о бильярдах в мnоеоуеОЛЬ1iuках с произвольным числом
сторон. Оказывается, что, I<ЗК И В случае прямоуrольника,
бильярды .в мноrоуrО!Iьниках специальноrо вида (В «pa
циональных» мноrоуrОЛЬНИI<ах, все yr.1lbl которых соизме-
2
римы С п) сводятся к изучению непрерывных траеКТОРIП(>J
на замкнутых оrраниченных поверхностях Tal' Ha3ЫBae
мых «кренделях» ИЛИ «сферах С ручками» (СМ. рисунок на
третьей странице обложки). OTAeJIbHO изучаIОТСЯ некото-
u
рые классы периодических траектории в тупоуrольных
треуrольниках.
Наконец, в заключении читатель сможет «с высоты
птичьеrо полета» обозреть целые классы бильярдов, KOTO
рые в зависимости от области, в которой движется бильярд
вый шар, носят названия рассеивающих (бильярдов Синая),
фокусирующих и осциллирующих. В каждом классе бильяр-
ДОВ наблюдается свой тип поведения траекторий, но все
эти бильярды являются моделями реальных физических
систем, в которых движение неотличимо от случайноrо,
т. е. является хотя и однозначно определенным (детерми-
нированным), но крайне Ifереrулярным и непредсказуемым.
Модели, демонстрирующие подобное поведение, обнаружены
практически во всех разделах физики и число их непре-
рывно растет. Изложение этоrо материала книrи ведется
на обзор нам уровне.
ЧАСТЬ 1
БИЛЬЯРДЫ В ВЫПУКЛblХ ОБЛАСТЯХ
С КРИВОЛИНЕЙНОЙ fРАНИЦЕЙ
rлава 1
БИЛЬЯРД В KPYfE
Простейшая оrраниченная выпуклая область
с криволинейной rраницей на плоскости......... Kpyr. С иссле-
дования траекторий шара в круrлом бильярде мы и начнем
наш рассказ о бильярдах в выпуклых областях с криволи-
нейной !,раницей.
Во введении ставилась общая проблема бильярда в
произвольной области Q. Естественно ожидать, что для
простейшей области Q круеа точных ответов на по
ставленные во введении вопросы должно быть больше, че1УТ
для более сложных областей, а сами ответы должны быть
более простыми и окончательными, чем в друrих случаях.
1-1ными словами, естественно О}l(идать, что проблема биль
ярда в Kpyre поддается полному исследованию. Так оно и
оказывается. Более Toro, приводимые в этой rлаве рассуж
дения и теоремы являются фундаментом для всех послеДУIО.
щих рассуждений и результато.в.
t. Шар в Kpyr лом бильярде без луз
Рассмотрим шар в Kpyre Q, оrраниченно л
окружностью r. Ero траекториями являются вписанные
в r ломаные РОРIР2РЗР . . . , обладающие свойством pa
венства в.точках P 1 , Р 2 , Р з , . . . уrлов падения и отраже..
ния, отсчитываемых от касательных или от радиусов OPi,
ОР 2, . . . (рис. 1.1, а). Отметим, что из этоrо свойства сле-
дует, во-первых, что все звенья траектории равны ме)I{ДУ
собой:
р ОР i == Р J? 2 == Р 2 Р з == Р з р 4 == · · · ,
и во-вторых, что равны опирающиеся на них центральные
уrлы:
LP O OP 1 == LP 1 0P2 == LР 2 ОР з == ...
24
Действительно, для ЛJобоrо k== 1, 2, 3, . . . равны треуrоль-
ники Pk 10Pk И PkOPh+l, как равнобедренные с равными
уrлами при основаниях (рис. 1.1, б), откуда и вытекают
указанные равенства хорд и центральных уrлов.
Нетрудно видеть также, что середины {K i } всех звеньев
траеI{ТОРИИ удалены ОТ центра Kpyra на одинаковое расстоя
иие (почему?) и, таким образом, располо}кены на ОКРУЖ-
ности с тем )ие центром О. Следовательно, вСя бильярдная
траектория ,раСПОЛОiкена в KpyroBoM кольце (рис. 1.1, в)
Р3
РО
I (
/'1
а
N
Рк
Рис. 1.1
{j
Это позволяет очень просто строить все звенья бильярдноЙ
траектории по KaKOMY TO одному из них.......... для этоrо QOCTa-
точно провеети концентрическую с исходной окружность
'v радиуса ак, rде К середина данноrо звена, затем из
концов этоrо звена провести касательные к окружности l'
ДО пересечения с внешней окружностью r., затем из концов
построенных хорд........... опять касательные к ОКРУЖНОСТИ l'
до пересечения с r, и так далее это и будут звенья иско-
мой бильярдной траектории.
ТаI{ИМ образом, мы установили важное свойство:
любая бильярдная mраектория в l'русе ниКОсда не заходит
внутрь некоторосо концентрuческосо круса, ераницы кото-
рО20 касаются все ее звенья. Отсюда следует, что
бильярд в крусе не эрсодичен,
поскольку эрrодичность означает, как сформулировано во
введении, не только прохождение шара через любой Ma
ленький кружок внутри области Q в какой-то момент вре-
мени, но и, в частности, пребывание в нем за большой про
межуток времени т доли времени, равной в пределе (коrда
т устремляется к бесконечности) отношению площади этоrо
кружка к площади всей области Q; дЛЯ Kpyra же не выпол
иено даже первое из этих условий, которое носит название
25.
всюду плотности бильярдной траектории ПОЭТОl\JJУ
бильярдная траектория в крусе не всюду плотна в не},!.
Тем не менее мы можем выяснить не только УI{азаиные
факты отр ицатель Horo, так сказать, свойства, но и пол
ностью решить проблему бильярда в Kpyre: дать критерий,
позволяющий выделять периодические траектории и изу
чить характер поведения неперuодuческ.uх траекторий.
Для этоrо обозначим через а радианную меру уrлов
LPoOPf, LP 1 0P 2 , .... Ясно, что каждая вершина P h
траектории Р о Р 1 Р 2 Р з . . . получается из предыдущей Bep
шины. Pk f ПОВ9РОТОМ на уrол а относительно центра О
окружности r, откуда следует, что вершина Р п получается
из начальной вершины РО поворотом на уrол па. Докажем,
что вид бильярдной траектории в круее полностью oпpeдe
ляemся чuолом а. А именно:
(а) если число а ооизмерuмо с п, т. е. дробь а/л являепlСЯ
рациональным чиолом (равным некоторой дроби m/п с цe
лыми т и n), то бильярдная траектория периодична;
(б) еоли а и 1t несоизмерuмы, т. е. число rJ.j иррацuональ
НО, то отвечающая уелу а траектория непериодична.
Д о к а э а т е л ь с т в о. (а) Если а соизмеримо с п,
m
то ero можно представить в виде а == . 2л, rде т и n.........
n
целые числа. TorAa nа==2пт, и поэтому при повороте на
уrол па каждая точка окружности r переходит в себя.
В частности, все вершины рассматриваемой бильярдной
траектории Р о Р 1 Р 2 Р а .... обладают тем свойством, что
р n == Ро, Р "+l == P i , Р n+2 == р 2, ...,
Т. е. вершины, начиная с n й, повт,?ряются. Это и означает,
что бильярдная траектория периодична, и утверждение
пункта (а) доказано.
Сколько же звеньев будет содержать рассматриваемая
т а
траектория P o PiP 2 ... P ЕСЛИп-== 2п н е с о к р а т и.
м а я дробь, то отвечающая а периодическая траектория ........
это траектория PoPi. . .Pn f.Po, rде n ---- знаменатель ука.
занной дроби, и состоит она р о в н о из n звеньев. При m== 1
это будет правильный n-уrольник, вписанный в ,окруж-
ность r (рис. 1.2, а), а при т 2 бильярдная траектория
представляет собой правильную самопересекающуюся замк-
нутую (звездчатую) ломаную, вписанную в r (рис. 1.2, б).
Иными словами, бильярдный шар после n отражений от
борта r оказывается в ИСХОДНОЙ точке РО., сделав т оборо-
26
тов BOI<pyr центра О (Т. е. повернувшись BOKpyr центра
на уrол 2пm).
(6) Предположим, что бильярдная траектория и в этом
Селучае периодична. Докажем тоrД8, что а и 1t соизмеримы,
что противоречит условию пункта (б) и тем самым ДOKa3ЫBa
ет ero утверждение.
Из периодичности траектории вытекает, что, начиная с
HeI{OТOporo HO .fepa n, l3ерIПИНЫ траектории повторяются:
Рn==РО, Pn+1==Pt, Рn+2==Р2, И Т. Д. НО это означает, что
ри ПОБороте на па радиан точи"а Р о переходит сама в себя;
РО
Р4
m 3
21( == '1
РО
Р3
Рб
а ..1.
2ic 7
tJ
а
Рис. 1.2
следовательно, па есть целое кратное полноro уrла: nа===
О а 2fn
==2пт. ТСlода ==........................ р а ц и о н а л ь н о е число.
л п
1--1сI<омое противоречи получено.
Про периодические траектории в Kpyre мы уже выясни-
ли все досконально в пункте (а) приведенноrо доказатель-
ства. Доказательство же пункта (6) велось от противноrо и
ПОЭТОМУ качественное поведение непериодических TpaeKTO
рий нам пока неизвестно. Однако интуитивно ясно, что He
периодическая бильярдная траектория должна вести себя,
в отличие от периодической, неким «нереrулярным» спо
соБОМ.
Эту «нереrулярность» можно себе представить, например,
так. Будем считать, что бильярдный шар при движении oc
, тавляет «чеРНИиТIЬНЫЙ след) ненулевой «толщины». Если шар
описывает периодическую траекторию, то, хотя она может
быть очень «звездчатой» (см. п. (а)), и эаполнять кольцо К
между внешней и внутренней окружностями r и 'V «очень
плотно», но все-таки не «всюду плотно» ...... на кольце обяза
тельно ОС1анутся такие участки (например, маленькие
z1
кру}кки). которые периодичеСI<ая траектория никоrда не
пересечет (рис. 1.3).
3 а д а ч а. Укажите нетоцн,осmь на рис. 1.3.
у к а 8 а н и е. Траектория бильярдноrо шара не может пе
ресекать маленький кружок так, как на рис. 1.3'...... показанное
стреЛI<ОЙ звено не касается внутренней окружности кольца.
Иное дело, коrда шарик описывает н е пер и о Д и-
q е с к у ю траекторию. В этом случаQ он рано или поздно
побывает в л ю б о м кусочке кольца К. Друrими слова
ми, каким бы тонким ни был' чернильный
след, оставляемый бильярдным шаром (но
имеющим все-таки неuулеву!О толщину), он
со временем обязательно закрасит все КОЛЬ-
ЦО К целиком (рис. 1.4). Это и означает
нереrулярность, а на математическом язы-
ке «всюду nлотнооть» бильярдной тра-
ектории в кольце &(. (Вспомним, что в нача-
ле параrрафа мы выяснили, что никакая
бильярдная траектория в Kpyre Q не всюду
плотна в нем, т. е. чернильный след шара не может закра-
сить Bcero Kpyra; однако для кольца К такая возможность
лоrически ничему не противоречит.)
Оказывается, непериодическая траектория в Kpyre Q
действительно всюду плотна в кольце К G rраницей r u ,,1
Это утверждение мы еще раз сформули-
руем уже в виде математической теоремы
в 2 и там же полностью докажем.
А пока отметим, что утверждение о всю-
ду плотности бильярдной траектории в
кольце будет вытекать из Toro факта, что
точки отражения шара от борта Р о, Pi,
Р2, . . . расположены на окружности r
в G ю Д У п л о т н о, т. е. внутри лю-
бой дуеи L\ окружности r имеется хотя
бы одна точка Р к . Это последнее утверж-
дение носит название «теоремы Якоби» *).
Оно также будет доказано в 2. Отметим
здесь только, что теорема Якоби явля-
ется основным инструментом при дока-
зательстве почти всех дальнейших тео-
рем, связанных с «всюду плотностью»
бильярдных траекторий.
*) К. Т. Я. Якоби (1804 1851) ........ крупнейший немецкий ма..
T MaT K, известный своими исследованиями в теории чисел, в меха'!
нике Ц в друrих областях науки_ .
Рис. 1.3
Рис. 1.4
28
После Bcero скаэанноrо бильярд в Kpyre МОЖНО считать
полностью исследованнымо Резюмируем полученные резуль
таты в виде теоремы.
т е о р е м а 1. Траектория бильярда в круее являеm.ся
либо периодической, если число а'/'Л рационально, либо всюду
плотной в кольце К между бортом r и конценmрической о r
окружностью "(, если чuоло а/л иррационально.
3 а д а ч а 1.1. Бильярдный шар нахоДИТСЯ на круrлом столе
радиуса R== 1 На расстоянии 1 от ero центра. Установите характер
бильярдной траектории (периодическая она или нет, какую об
ласть;. всюду плотно заметает), если шарик выпущен под ;уrлом <р
к диаметру, на котором он находится (рис. 1.5).
О т в е Т. Периодична, если число arccos (1 sin ер) рацио
1t
нально, и всюду плотно заполняет кольцо с внутренним радиусом
1 sin <р в противном случае.
3 а д а ч а 1.2. Исследуйте бильярд а) в ПОЛУI<руrе (рис. 1.6);
б) в четвертькруrе (рис. 1.7). У!{ а 3 а н и е. Попробуйте свести
эти бильярды к бильярду в Kpyre.
Рис. 1.5
о
Рис. 1.6
Рис. 1.7
3 а Д а ч а 1.3. Исследуйте бильярд а) в KpyroBoM KOHцeH
'fрическом I(ольце; б) в KpyroBoM секторе уrловой величины а;
в) * в криволинейном четырехуrольнике t который высекается пз
кольца сектором уrловой велпчины а.
3 а д а ч а 1.4. а) Докаiките, что никакая непериодическая
бильярдная траектория в Kpyre не содержит двух параллельных
звеньев.
б) Мо)кет ли у периодической бильярдной траектории в Kpyre,
какие то два звена которой параллельны друr друrу, быть 1717
звеньев? 1718 звеньев? А если она самопересекающаяся? Если
может, укажите способ построения всех периодических траекторий
с таким числом звеньев и найдите максимаЛЬНУIО длину траектории
из этоrо класса (принимая радиус Kpyra за 1).
в) Обобп ите вопрос пу нкта б) на произвольное число звеньев
п (см. также задачу 6.6 из 6).
Реш е н и е. а) Если какие то два звена АВ и CD траектории
параллельны , то они центрально симметричны относительно центра
Kpyra о. Поэтому и вся траектория центрально симметрична OT
носительно О (рис. 1.8). Значит, если шар перешел со звена 'АВ
на звено CD после n отражений, то еще через n отражений он Bep
вется на звено А В, и вся траектория замкнется....... траектор ия
о кажется пер иодической.
Поэтому, если заранее выбрать радиус, внутренней окруж
ности l' КО.1JЫIЗ К (радиус внешней равен 1) и провести к 'V две
29
параллельиые касательные. '[о они заведомо н е б у Д. у т звень-
ями ОДНОЙ траектории, еСJIИ только число arccos , несоиэмеримо с п.
б), в). Есжи бильярдная траектория периодическая и coдep
жит два параллельных звена, то все звенья разбиваются на пары
nараллельных (рис... 1.8), так что число эвеньев п в этом случае
обязательно четно. Итак, 1717 звеньев быть н 8 М О Ж е т. 1718
звеньев у траектории быть может...... например, у пр-авильноrо
вписанноrо 1718 уrольника Р. Остальные бильярдные траектории
с изломами в вершинах мноrОУFольника р. получатся, если с()еди
нять эти вершины через одну, через две,. через три и т.. д. Однако
1718==2.859 (859...... простое число}, поэтому, соединяя вершины
через одну, получим два 859 уrольника без общих вершин. AHa
лоrична ситуации, коrда соединяются вершины через 3 (на чет
вертую), через 5 (на б ю) и Т. д........ получается несколько замкнутых
1
Рис. 1.8
12
11
4-
5
858
1
8
Рис. 1,9
1.10
ломаных. Если же соединять вершины через k.......l на k ю, rде k
взаимно просто с 1718 (т. е. вершину 1 соединить с (k+ l) й, 2 IO
С (k+2) й и Т. д.), то полученные замкнутые бильярдные ломаные
будут содержать ровно 1718 звеньев, причем все звенья будут раз
биты на 859 пар попарно параллельныx (СМ. рис. 1.9, на котором
изображена траектория из 14===2.7 звеньев). Наибольшей ДЛИНЫ
звенья' будут у траек1'ОрИИ, соеДИНЯlощей вершины 1 и 858, 2 и 859,
3 и 860 и т. д. Из треуrольника IMO на рис. 1.10 следует, что
длина звена (l 858) равна
l == 2 sin (а/2) == 2 sin (857п/3436).
Поскольку rОЛt стоящий ПОД знаком синуса. раве.н примерно
'Л/4. име.ем l::::= 2 sin (1&14)== поэтому максимальная ДЛИНа биль
ПРДВОЙ траектории из 1718 звеньев равна
L == 17181 == 3436 sin (857п/3436) 3436 У2 4851,632.
UПар при ее обходе сделает 857 оборотов.
3 а д а ч а 1.5.. В круrлом бильярде в некотором мес.те cдe
лава луза кружок радиуса &, не содержащий ц.ентра Kpyra..
Доказать, что точ.ечный бильярдный шар можно расположить
D такой точке Kpyra и запустить в таком направлении с единичной
скорос.тыо, что он а) не попадет в лузу никоrда; б) попадет в лузу 9
пройдя до поп.адания путь длины, большей заданной величины L.
0станется ли верным это утверждение, если шарик расположен
в заранее заданной 'rоч.ке Kpyra? А если 1'ОЧКУ ero р.асположения
можно выбирать. а направление вектора скорости фиксированно?
30
3 а Д а q а 1.6. В круrлом бильярде в заданных п т()чка
расположены точечные бильярдные шары. Доказать, что их можно
запустить в таких направлениях t что а) никакие два из них никоrда
не СТОJIКНУТСЯ, б) любые два из них столкнутся (-сталкнваtощиеся
шарики ПрОХОДЯТ друr сквозь друrа без отклонений).
3 а д а ч а 1.7. Докзаать, что два заданных шара радиуса
0,0001 можно запустить в круrлом бильярде радиуса 1 в такиХ!
напраВtlIеНИЯ j что они обязательно столкнутся друr с друrом,
но e раньше, чем каЖДЬ1Й из них пройдет путь заданной ДЛИНЫ L.
3 а д а ч а 1.8. Можно ли запустить два шара радиуса 10 ;t.o
в круrлом бильярде радиуеа 1 так, чтоБыI они никоrдз не СТОЛI(НУ
л иеь?
3 а д а ч а 1.9. Предположим, что бильярдная траектория
в Kpyre всюду плотно заполняет кольцо К. Верно ли, что любой
фиксированный кружок внутри кольца пересекают бесконечно
MHoro звеньев этой бильярдной траектории? А верно ли, что чер
какую то точку этоrо кружка не проходит ни одно звено TpaeK
тории?
3 а д а ч а 1.1 0*. Верно ли, что ДОЛЯ времени, ПрОБодимая
бильярдным шар.ом в кружке из ЭЭJl.ачи 1.9, равна (в пределе)
отношению площади этоrо KPYiKK3 к площади копьда К?
2. Теорема Якоби.
Применение к lеории чисел
В этом параrpафе мы докажем теорему, сфор-
мулированную в КОIЩе 1. Сформулируем ее здесь еще раз
(МЫ ПРИВОДИМ более -трудную часть теоремы).
т е о р е м а 1. Если ct и 3t неООUЗАtериМbl (Т. е. число
а/п иррационально), tпo любая mраекп10рия бильярда в кру-
се, отвечающая У2ЛУ а (т. е. каждое звено которой видно из
центра КРУ2а под уело м а; рис. 1.1, б), всюду плоп но запол
няеm КОЛЬЦО 11<.
Доказательство теоремы 1 опирается на следующую ос-
новную теорему этоrо параrрафа, в дальнейшем применяе-
м:ую в качест OCHOBHoro рабочеrо инструмента при доказа
тельстве утверждений, иноrда имеющих мало общеrо с
бильярдными задачами, например утверждений из теории
чисел (об этом СМ. ниже).
т е о р е м а Я к о б и. Пусть ct ----- несоизмеримое с 1t
Ч иоло, {Р О, Р f, Р 2, ... } == {Р k} ----- бесконечная nоследова
пlельносmь точек окружности r mакая, что каждая следу
ющая mочка nооледоваmеЛЬftостu Р k+i получается из преды-
дущей ,почки P k поворотом ОКОЛО центра на а радиан.
Тоеда для любой дуеu А окружности r хотя бы одна точк,а
пооледовательности {P k } lle:JЮuт на этой дуее.
3 а Д а ч 8. Докажите, Ч70 на дуre 1:1 находится бесконечно
MHora точек последовательности {Pk}.
31
Реш е w...и ...Если .бы 1l8. дуrе располаrалось тодько к о.
н е ч н о е число точеК' (например, как крайний случай, только
одна точка), то нашлась бы неI{оторая дуrа ', лежащая внутри
дуrи и не содержащая н и о Д н о й точки последоватеЛЬНОС1 н
{Pk}. Это противоречит теореме Якоби: по этой теореме на дуrе А'
имеется х о т я б ы о д н а точка последовательности.
Прежде чем доказывать теоремы Якоби, выведем из нее
теорему 1.
Д о к а з а т е л ь с т в о т е о р е м ы 1. Пусть а........
u
несоизмер имое G :rt число, 'У........ окружность, которои каса-
ются все звенья каждой отвечающей уrлу а бильярдной
траектории внутри окружности r. Пусть К кольцо
между 'V И r, а D ........ произвольный кружок внутри кольца
К. Проведем через центр кружка D хорду MN ОКРУЖНОСТИ
r, касающуюся окружности V (рис. 2.1). Если провести
касательные к кружку D, касающиеся окружности 1', то
ОНИ высекут на окружности r некоторую дуrу L\, в которой
расположена точка М. Очевидно, что для любой друrой
точки М' дуrи касательная, проведенная из нее к окруж-
Ности'V по ту же сторону, что и хорда MN, пер е с е ч е т
кружок D.
Рассмотрим теперь любую бильярдную н е пер и о Д и-
ч е с к у ю траекторию P O PiP 2 . . . , отвечающую уrлу сх.
Требуется доказать, что хотя бы одно из ее звеньев пересе-
кает кружок D.
Соrласно теореме Якоби, точки Р О , Pi, Р 2 , . . всюду
плотно заполняют окружность r. Следовательно, хотя бы
А одна из них, скажем Р п , лежит на пост
...,! м' роенной выше дуrе L\. В силу выбора этой
r.: .:;':,/:::': .:;. дуrи одно из двух звеньев траектории,
,: .':;'..: :':"": выходящей из точки Р п (а, тем самым, Ka
::" ':: сательных к окружности "(), пересекает
'.::':.:':' , r кружок D (в качестве точки М' на
: '.н:;.. .:-<.,: .:',:::', рис. 2.1 следует взять точку Р п ). Тем
'.-:.: :::(. .:;.:..:.: самым теорема 1 доказана.
· . д о к а з а т е л ь с т в о т е о р е..
Рис. 2.1 м ы я к о б и. Двиrаясь от точки .Ро
последовательными дуrовыми шаrами
величиной сх каждый (рис. 2.2) и попадая в точки Pt, Р 2 ,
Рз, . . " остановимся в точке Р n , как только в пер в ы е
перескочим точку Ро (дуrа PпPn 'f меньше 2л, а дуrа РОРn
больше 2л). Обозначим точку РО буквой А, а ближайшую
к ней из точек Р n f (до перескока) и Р n (после перескока) .........
буквой В. Тоrда ....... длина дуrи АВ......... не больше а)2:
<= сх/2.
32
Начав двиrаться от точки В прыжками величиной а,
мы через некоторое число шаrов попадем в точку, отстоя.
щую от точки В на , затем на 2р, потом на эр, и т. д.
(рис. 2.2).
Можно считать, что у нас сжался масштаб ДЛИНЫ и мы
движемся по окружности r дуrовыми шаrами уже величи
ной Р, по крайней мере вдвое мень- A P,
шими, чем величина шаrа а при на- 8 Pn 1 "O Р
чальном движении от точки А. с fЗ f:t
После определенноrо числа шаrов fJ O
величиной р каждый, мы впервые r
перескочим точку В и выберем пос- r а
ле этоrо ближайшую к ней (из двух
точек до перескока и после Hero) Pz
точку е. Пусть длина дуrи ве рав-
на ер, тоrда ер < /2 a/4. Как и выше, Рис. 2.2
получим, что можно опять изменить
масштаб длины и считать теперь величину прыlкаa рав-
и
нои ер.
Повторяя оцисанный процесс k раз, получим величину
прыжка, не большую чем r:x/2 k . НО при больших k величи-
на a/2 k стремится к нулю, т. е. становится меньшей про..
извольноrо числа 8 > О, так что мы попадем в любую, сколь
уrодно малую дуrу L.\, произвольно выбранную на окруж-
ности r. Теорема Якоби доказана.
Для любителей формальных доказательств описанное paCCY)K
дение проведем более техническим способом.
Пусть """,произвольная дуrа на окру}кности r, В.......ее радиан-
2п
ная мера. Выберем такое натуральное число N, что N < 8. Ра-
зобьем окружность r на N равных по длине дуr 1, 2, ..., N;
радианная мера каждой из них равна 2n/ N и меньше 8.
Рассмотрим теперь N + 1 первых точек последовательности
{Р/е}1 Т. е. точки Р О , Pi, ..., PN. Соrласно принципу Дирихле *),
ОТЯ бы на одной из N дуr f, (/.., N ле>кит по крайней мере Д в е
из ЭТИJQ точ@к; допустим, точки Р п И Р т лежат на дуrе i (счи-
таем m==n+l > п). Пусть длина J1уrи РпР т (в радианах) равна б,
2л
тоrда б < I i I == N < 8.
Рассмотрим далее точки ПОQледоватеЛЬНОQТИ {P k } е номерами
п, m==n+l, n+2l, п+3l, ...1 Т. е. точки Р n , Р n + х , P n + 2l ) ...,
каждая из которых получается из предыдущей поворотом на уrол
lа;......точно так же, как ТОЧl<З Рп+Е получается из ТОЧI{И Р п . Таким
*) Принциn Дuрихле состоит в следующем: если 8 k ящи/(аJO
лежит k+ 1 предмет, то хоmя бы в одном ящике больше одноео
nредлtета.
2 fi. А. rапьперин. А. Н. Земляков
83
образом, соседние точки выделенной последовательности отстояr
друr от Apyra на Ayry радианноА меры б. Так как б < е, то хотя
бы одна из точек Р П ' P п + z , Pп+tl' '.' обязана попвсть на дуrу L\.
Тем саМБ1М теорема ЯI<оби доказана.
Э а Д а ч а. rде в доказательстве теоремы Якоби испольэо--
валасъ несоизмеримость чисел а и п? (Если а и n соизмеримы,
то теорема, очевидно, неверна).
О т в е т. Из несоиsмеримости следует утверждение, что точки
А, В , С, ... различны (в доказательстве петитом....... различны
точки Р п И Рn+д. ·
Кроме теоремы 1, теорема Якоби имеет и MHOrO друrих
интересных следствий.
Одной из важных проблем теории чисел является зада-
ча о распределении дробных долей разных функций, в
частности мноrочленов. Задача о распределении дробных
u u
долеи мноrочленов связана с оценками числа решении дио-
фантовых уравнений (уравнений с целыми коэффициента-
ми, дЛЯ которых ищутся целочисленные решения) в алrеб-
раической теории чисел.
Рассмотрим мноrочлен у == a o x п +aix п .... 1 +. . .+an lX +
+а п . При каждом конкретном значении х можно вычислить
число у; при нецелых коэффициентах мноrочлена оно, как
правило, будет нецелым. Вычтя из Hero ero целую часть,
Т. е. н а и б о л ь ш е е целое число [у], не превосходящее у,
получим дробную часть числа у, которая обозначается фи-
rурными скобками: {у} ==у......... [у). Ясно, что всеrдаО {у}<l,
так что при каждом х число {у} принадлежит полуинтер-
валу [О, 1).
Как распределены числа {Yk} на nолуuнmервале [О, 1),
КО2да х nробе2аеm все целые чuола k ==. . ., .......2' .........1' О, 1,
2, . . . ?
Это и есть задача о распределении дробных долей мно-
rочленов. Теорема Якоби позволяет частично решить эту
задачу для л и н е й н ы х мноrочленов, т. е. мноrочленов
первой степени.
Утвер ж Д е н и е 1. Дробные части чисел Уп == ak+b,
коrда k пробеrает все целые значения от .......00 до + 00, либо
образуют к о н е ч н о е множество точек на полуинтер-
вале [Ot 1), либо в с ю Д у п л о т н о е множество ТQчек
на этом интервале. Первый случай реализуется при рацио-
нальном, а второй........ при иррациональном числе а (число Ь
при этом может быть произвольным).
Д о к а з а т е л ь с т в о. Искривим полуинтервал [О, 1),
на котором расположены дробные части {Yk}, TaK t чтобы
ero концы совпали, и t склеив их, получим окружность еди-
ничной длины 81 (рис. 2.3). Затем сделаем второй шаr: на-
34
бтае ВСЮ числовую ось fR па полученную окружность
так, чтобы точка Ь оси IR совпала со склеенными точками
О и 1 окружности (рис. 2.4). .
Тоrда все точки ak+b отпечатаются на окружности 81;
«выдямив»> эту окружность В исходный полуинтервал
[О, 1), мы получим на нем все дробные час- О
ти чисел Yk==ak+b. r
Однако на окружности 81 отпечатки всех
точек УЯ, получаются ИЗ отпечатка точки
уо==ь поворотом на уrлы ka радиан, rде
k==. е., .........2, ..........1' О, 1, 2, ... . Поэтому,
если число а рационально, то отпечатков на
81 будет конечное число; если же а ирраци-
онально, то их будет бесконечно MHoro и
располаrаться они на окружности будут, по теореме ЯКО
би, воюду плотно, а это и требовалось доказать. Утверж-
дение 1 доказано.
Для мноrочленов б6льших степеней, чем 1, решение
задачи о распределении дробных долей сущеGтвенно услож
u
няется, хотя с наrлядно-rеометрических позиции все дело
(рактически также сводится к применению теоремы Якоби,
. . .b 2C1. Ь--а Ь Ь+а Ь+2а bfOa...
--00 -< .. . @ . . . ")а +00
:g: : IR
, .
. :,....
Ь+а
д
Or
Рис, 2.3
..;. 00
0-- 60
.
.
"'й . о+6а"
Ь+50
Ь--2а
ь ....3 а.
Рис. 2.4
только не для окружности, а для тора (см. 8). НО об этом
мы поrоворим чуть позже........ в rл. 3, коrда речь пойдет
о бильярде в прямоуrольнике. Отметим пока только, Ha
сколько тесно взаимосвязаны разные разделы математики:
от rеометрических задач........ бильярдов в Kpyre ...... МЫ пере-
шли к задаче из совсем друrоrо раздела математики...... тео-
рии чисел, а позже перейдем к бильярдам в друrих обла-
стях, исследование которых поможет при решении совсем
новых задач из друrих областей математики. Собственно
u u u
rоворя, ОДНОИ из целеи нашеи книrи является попытка на
2* 35
конкретном наrлядном rеометрическом материале дать
почувствовать читателю мноrообразие математики и ее
единство.
Вернемся, однако, к вопросу о распределении дробных
долей мноrочленов. Полный ответ на Hero был получен в
виде теоремы выдающимся математиком ХХ века repMaHoM
Вейлем. Прежде чем сформулировать эту теорему, приведем
одно важное определение.
О п р е Д е л е н и е. Произвольная бесконечная пос-
ледовательность точек {Р п } на единичной окружности 81
(или на отрезке [О, 1]) называется равномерно распределен-
ной a 81 (на [О, 1]), если для любой ее дуrи (интервала)
t1 «доля» попавших на нее точек равна длине этой дуrи (ин-
тервала) 1(1\).
Иными словами, если оrраничиться лишь к о н е ч н ы м
числом n точек РО, Pi, . . . , Pn 1, то отношение числа k(n)
точек, попавших в дуrу 1\, к общему числу точек п, т. е.
их доля k(n)/n на окружности длины 1, будет мало отли-
чаться от длины дуrи 1(L\). Это отличие будет тем меньше,
чем большее число точеI{ мы рассматриваем, и в пределе при
n...-.+оо величины k(n)/n и l( ) совпадут. Сказанное можно
выразить формулой
Вт k(n) ==I(Ll).
п-+Ф п
(1)
Свойство равномерной распределенности асимптотиче..
CI{Oe.
Можно доказать следующее утверждение.
т е о р е м а о р а в н о м е р н о м р а с п р е Д е-
л е н и и т о ч е к н а о к р у ж н о с т и. Последователь..
ность точек РО, Р 1 , Р2, Р в , Р 4' . . . на окружности 81, по-
лученных каждая из предыдущей поворотом на иррацио-
нальный (несоизмеримый о 2л) уеол а, равномерно распреде..
лена на 81. '
Формально cTpororo доказательства этой теоремы мы
здесь не будем приводить; опишем лишь правдоподобные
рассуждения, которые при желании можно довести до стро-
roro доказательства. При доказательстве теоремы Якоби
мы пользовались тем обстоятельством, что сначала произво"
дились прыжки одинаковой величины сх, затем (после из..
менения масштаба длины)....... прыжки одной и той же
величины а/2, затем все прыжки становились равными,
'\' а/4, и Т. д. Итак, при каждой замене масштаба прыжки
имеют о Д н у и т у ж е в е л и ч и н у, которая меньше
величины прыжка при преДЫдущей замене масштаба в 2 или
36
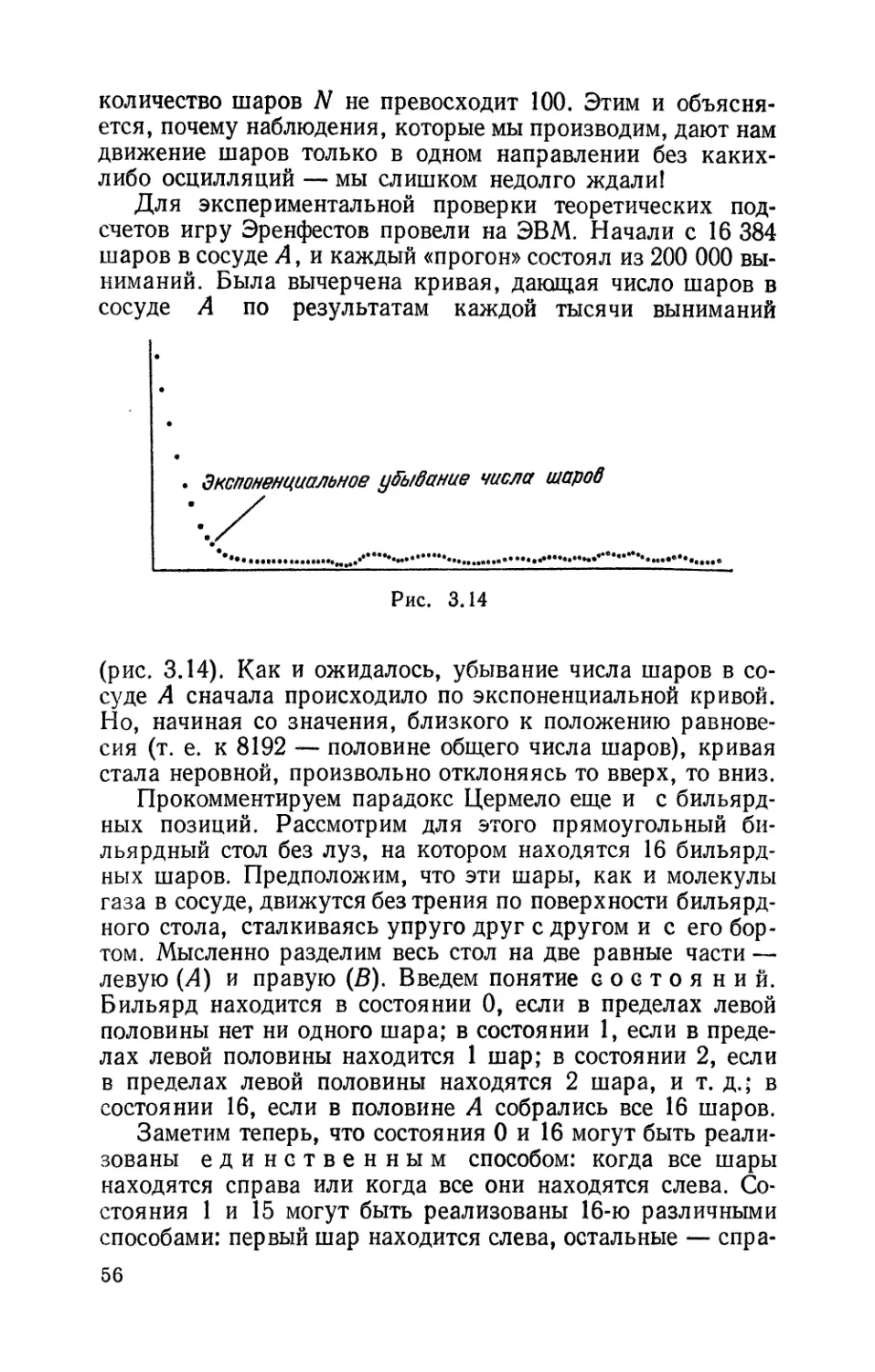
большее число раз. Равенство длин этих прыжков и их
экспоненциальное убывание *) при каждой замене масштаба
означает, что число точек, попавших в данный интервал L\,
пропорционально ero длине это выполнено тем точнее,
чем больше сделано замен масштабов длины. Но это и
означает равномерность распределения.
3 а д а ч а. / Доказать, что из равномерной Р аспределенносrи
последовательности точек {P k } на окружности S вытекает всюду
плотность их расположения на S .
Реш е н и е. Действительно, на любой дуrе L1 имеется хотя.
бы одна точка Р k.
Теорема r. Вейля о дробных долях мноrочленов форму-
лируется так.
т е о р е м а В е й л я. Если среди коэффициентов а о .
аl, а 2 , . . ., aп l мноеочлена у ==aoXn+aiX n -- 1 +. . .+а n __ 1 х +
+ а п хотя бы один число иррациональное, то последова
rпеЛЬflость {Yk}, еде Уп ==aok n + a 1 k n -- 1 +. . . + a n __ 1 k+a n , рав-
номерно распределена на полуинтервале [О, 1).
Теория paBHoMepHoro распределения была создана
[. Вейлем в 1916 rоду. Она появилась на стыке нескольких
математических дисциплин (действительный и комплекс-
ный анализ, теория чисел, теория вероятностей и др.)
и долrое время ее приложения оrраничивались различными
вопросами «чистой» математики и механики. ВычислитеJIЬ
ная математика заинтересовалась равномерно распределен-
ными последовательностями в 50-х rодах, после возникно-
вения методов Монте-Карло, коrда оказалось, что точки
таких последовательностеЙ MorYT в некоторых случаях иr..
рать роль квазислучайных чисел.
Классическое направление теории paBHoMepHoro распре-
деления связано с изучением дробных долей различных
функций (например, мноrочленов; см. выше), оценками
триrОНО1\1етрических сумм и следующим известным крите-
рием Вейля, связанным с эр rодичностью.
К р и т е р и й в е й л я. Для Toro чтобы последовательность
хо, Хl' х 2 , . . ., Х п , . . . была равномер но распределена на отрезке
[О, 1], необходимо и достаточно, чтобы для любой интеrрируемой
(по Риману) функции f (х) выполнялось соотношение: «среднее
временное равно среднему пространственному», Т. е.
n-- 1 1
lim ..!.. L f (Xk) == S f (х) dJC. (2)
n .... 00 n k= О О
*) Члены rеометрической проrрессии ak==aoqk со знаменателем
q, по модулю меньшим 1, образуют экспоненциально стремящуюся
к О последовательность.
87
На первый :взrляд требования (1) и (2) кажутся различными.
Чтобы показать связь между ними, выберем произвольный интер
вал !J.== (а, Ь) на отрезке [0,1] и рассмотрим функцию 'А(Х)' назЫ
ваемую обычно характеристической функцией, или индикатором
интервала А: она тождественно равна 1 на интервале t\ и тождест
венно равна О вне ero (рис. 2.5). Тоrда
n 1
f А (Xk) == f А (Хо) + f А (Xi) + ". + f А (Xn...j:)
k=O
есть число точек, попавших в интервал !J., Т. е. число k (n) из фор
мулы (1), а
1 а Ь 1 Ь
f А (х) dx== f А (х) dx+ f А (х) dx+ f А (х) dx , dx==b a==l Щ,
о о а ь а
поэтому при f ==! А (х) соотношения (2) и (1) совпадают.
1
ХО
а Т:со=.:с 1
а; ,
T2.;Cq=Xz
Рис. 2.6
Рис. 2.5
Совпадение BpeMeHHoro среднеrо и пространственноrо
среднеrо для простейшеrо случая равномерно распределен-
ной последовательности точек обобщается в теории дина-
мических систем на случай так называемых эрrодических
систем. В эрrодической системе действует преобразование Т,
не переводящее в себя никакоrо подмножества системы с
мерой, отличной от О или 1, т. е. из равенства Т(А)==А,
rде А подмножество системы, следует, что мера множест-
ва А (длина, площадь, объем А в одно-, двух- И трехмерном
случаях) равна либо О, либо 1. Примером эрrодической си-
стемы может служить окружность 81, на которой действует
преобразование поворота Т на иррациональный уrол а.
(рис. 2.6). Для этой системы выполнено равенство (2), по '
этому последовательность точек
Хо, ТХо == Xi, Т2 хо == Т (ТХо) == TXi == Х 2 , ...
(так называемая «орбита преобраэования Т») равномерно
распределена на окружности, а стало быть, всюду плотно
ее заполняет.
Именно равенство (2) и утверждает, что доля времени,
которую частица (скачущая по окружности точка) прово-
38
,ц T в' заданной обласrи (дуrе Д), равно мере (длине) этой
области.
Обсуждение вопросов, связанных с эрrодичностью, paB
номерной распределенностью и всюду плотностью, закон-
чим в этом параrрафе следующей замечательной арифмети
ческой задачей, решаемой бильярдным шаром в Kpyre.
3 а д а ч а. Рассмотрим последовательные степени двой
ки: 1, 2, 4, 8, 16, 32, 64, 128, 256, . . . и выпишем подряд
первые цифры полученных чисел:
1, 2, 4, 8, 1, З, 6, 1, 2, 5, 1, 2, 4, , . .
а) Встретится ли в этой последовательности цифра 7?
б) I{акая цифра встречается в последовательности чаще:
7 или 8? Во сколько раз?
в) Вообще, с любоrо ли набора цифр может начинаться
степень дв ойки? С к акой частотой появляется заданный Ha
бор цифр аl а 2. . .a r ?
Реш е н и е. Начнем решать задачу «с конца», т. е.
ответим сначала на вопрос в), который естественным обр а-
30М обобщает вопросы а) и б).
Пусть А==аlа2' . .a r ---- ,-з начно е число. Если 2 n Ha
чинается с набора А, то 2 n ==А. . . , а так как число А .
не меньше А. 10 k И cTporo меньше (А + 1) · 1 Ok, rде k .......... чис-
ло цифр, приписанных справа к А, то
А .10k 2 n < (А + 1).10 k .
Лоrарифмируя по основанию 10, получаем
k+lgA nlg2 <k+lg(A+I),
k п 192 lg А < k+ 19(A + l) lg А,== k+ 19 (1 + -}).
Отметим на числовой ОGИ все промежутки между числами k и
k + 19 ( 1 + ), т. е. окружим все целые точки k числовой
оси полуинтервалами одинаковой длины 19 ( 1 + ).
Возьмем теперь круrлый бильярд, длина окружности
KOToporo равна 1 (т. е. радиус бильярдноrо Kpyra равен
1/ (2л», и, как при доказательстве утверждения 1, намота-
ем числовую ось на rраницу этоrо бильярда ---- окруж-
ность 81 (рис. 2.7). Тоrда все целые точки О, 1, 2, . .. ,k,...
сольются в одну точку на окружности, а все промежутки
[k, k + 19 (1 + ) ] в одну дуrу L\ (о концомО, который
89
ей принадлежит) ДЛИНЫ l (А) == 19 ( 1 + ). Обозначим Ро
точку на окружности, в которую попадает при этой намотке
число (.....lg А).
А теперь задача сводится к моделированию первых цифр
последовательности 2 n следующим движение 1 бильярдноrо
шара в Kpyre: запускаем шар из точки РО В точку Р 1 на ок-
ружности такую, что PIP2==lg 2, и рассматриваем всю
последовательность РО, Pi,
Р2, Р з , . . 8 точек отраже-
ния шарика от борта; те п,
· для которых точки Р п при-
k+tg(t+ 1) надлежат дуrе д, являются
k ИСКОМЫl\1И показателями
двой ки ........ для них числа
2 п начин аются с набора
йl а 2. · .a r .
НО число а== 19 2 ........
иррациональное *), поэто-
му последовательность точек РО, Р1., Р2' . . 8 , получающихея
друr из друrа поворотом на уrол а, по теореме Я коби за-
полняет окружность всюду плотно. Следовательно, степень
дво йки может начинаться с произвольноrо набора цифр
А ==аlа28 . .a r . Более Toro, поскольку последовательность
точек Р О , Pi, Р 2 , . . . р а в н о м е р н о распределена на
окружности, доля тех чисел п, для которых 2 п начинается
с набора А, в пределе равна длине интервала , т . е. равна
tg ( 1 + ). Это и есть частота появления набора аlа2' . .а,
в качестве первых цифр чисел 2 n .
После сказанноrо ответить на вопросы а) и б) не пред-
ставляет труда. Цифра 7 в последовательности первых цифр
чисел 2 п обязательно встретится. Встречается она с часто-
той, равной Ig (1 + 1/7)==lg 8 lg 7. Цифра 8 в этой последо-
вательности встречается с частотой 19 (1 + 1/8) == 19 9........Ig 8.
Так как 8/7>9/8, то (как это ни странно на первый взrляд .....,..
особенно после рассмотрения начала последовательности,
указанной в уеловии задачи), семерки встречаютоя чаще
19 8 19 7
восьмерок, причем в 199....1g8 1,14 раз. А то, что вначале
восьмерки встречаются все же чаще еемерок, связано со
/R1
РО
k 1+tgQ+ 1)
K 1
Рис. 2.7
*) Если 19 2==т/п, rде т и п..... целые числа, то 2==10 m / n , и Tor..
да 2 п ==] от, чеI'О быть не может) та к как 2 n не мо}кет оканчиваться
нулем (п>О). .
40
следующим обстоятельством: иррациональное число Ig 2
примерно равно рациональному числу 3/10. Действительно,
сделав на окружности 10 прыжков длины 19 2" мы сдвинем
ся на дуrу 10 19 2 3, т. е. окажемся примерно в начальной
точке. Среди первых 10 степеней двойки нет ни одной, на-
чинающейся с 7 (это экспериментальный факт), а начинаю-
щиеся с 8 ........ есть, поэтому и среди следующих 10 степеней
двойки опять нет ни одной, начинающейся с 7 (а с 8 ........ есть)
и т. д.; это будет происходить до тех пор, пока 10п .lg 2
не станет уже существенно отличаться от целоrо числа .........
тоrда и появляется семерка.
В заключение отметим, что числа 3 n , 4 n ==2 2n , 5 n , Б В ,
7 В , 8 n , gn, 11 n, 12 n , 13 n и т. Д. (пропускаются степени, ос-
нования которых кратны 10) также чаще начинается с 7,
8 2 n '1 19 (8/7)
чем с ,причем, как и для , чаще в I'w == 19 (9/8) раз. Это
объясняется равномерностью распр'еделения точек на ок-
ружности длины 1 при отражении бильярдноrо шара с yr-
лами поворота a==lg 3, 194, Ig5, 196, . . ., являющимися
иррациональными числами.
3 а д а ч а 2.1. Промоделируйте бильярдом в Kpyre все степени
числа 3, начинающиеся с набора цифр 1989.
3 а д а ч а 2.2. Докажите, что если число р не является CTe
пенью 10, то среди чисел Р, р2, р3, р4, . . . найдутся такие, десятич
ная запись которых начинается с любой наперед заданной комби
нации цифр. С какой цифры чаще начинаются эти числа с 7
или 8 и ВО сколько раз? Сравните полученный ответ с ответом
для р== 2 и объясните полученный резуль-
тат.
3 а д а ч а 2.3. Существует ли такое
натуральное n, что sin n<10 100?
siп1
10"'1011
Рис. 2.8
Рис. 2.9
о т в е т. Существует. У R а в а н и 8. Промоделируйте по
следовательность sin О, sin 1, sin 2, sin 3, *. . бильярдом в Kpyre
радиуса 1 и учтите, что числа 1 и 2п несоизмеримы (рис. 2.8).
3 а Д а ч а 2.4. При качении одной окружности по друrой
lJlобая тОчка катящейся окружности описывает кривую с «острия
ми» ........ эпициклоиду (рис. 2.9). Докажите, что если радиусы этих
окружностей несоизмеримы, то «острия» эпициклоиды sаполняют
неподвижную окружность всюду плотно.
41
" 'з а Д а ч а 2.5. По окружности '81 ДЛИНЫ У2 катится снаружи
окружность 82 длины 1 (без проскальзывания). На окружности
S'}, красным цветом отмечена точка А касания двух окружностей.
При качении окружности 82 по 81 точка А делает на 81 в точках t
к?сания красные отпечати:и А1' А 2 ; Аз, . . . . в свою очередь, полу
чающиеся красные точки на окружности 81 делают отпечатки на I
окружности 82' которые, в свою очередь, делают отпечатки на OK ,
, ружности 81 И т. д. Сколько красных TO
S чек будет на окружности 81' J{оrда ок.
2. ружность 82 сделает n оборотов около
8 1 ? Иными словами, с какой скоростыо
растет число отпечатков на окружнос-
ти 8 1 ?
О т в е Т. На неnодвижной окружнос-
ти будет n точек. У к а s а н и е. После
первоrо оборота на 81' кроме точки А, бу-
дет только один красный отпечаток А 1 на
расстоянии 1 (по дуrе окружности 81) от
А (рис. 2.10), а на 82........ два отпечатка:
А' это бывшая точка А и отпечаток
от точки А. Точка А на 82 уже не даст HO
вых отпечатков на 81, а точка А' даст пос-
ле одноrо оборота один новый отпечаток
А 2 . Вообще, с кажДЫМ оборотом все, кро.
ме одной, красные точки на 82 пройдут
по своим старым слеДам на неподвижной
окружно ти и потому не дадут новых отпечатков, и лишь одна
новая точка будет давать отпечатки..... один за оборот. Таким
образом, отя красные отпечатки заполнят неподвижную окруж
ность всюду плотно, скорость их появления Bcero лишь линейная.
3 а д а ч а 2.6. Числа а и несоизмеримы между собой и с
числом п. Докажите, что ни при каком целом n сумма s== sin nа+
+sin n не равна 2, но существует бесконечно MHoro таких n, что
s отличается от 2 меньше чем на 0,000001. С какой частотой BCTp
чаются такие числа п?
Рис. 2.10
3. Теорема Пуанкаре о возвращении.
Конфиrурационное и фазовое пространства.
Парадокс Цермело и модель Эренфестов
1. В математике часто случается, что HeKOTO
рые утверждения или их следствия удается удачно обобщить
и получить при этом ряд новых, неизвестных ранее следст.
вий, иноrда далеко выходящих за рамки рассматриваемоrо
вопроса. Таким интересным во мноrих отношениях обобще-
нием следствия теоремы Якоби о попадании любой точки х
ОКРYJкности 81 В любую свою окрестность является теорема
Пуанкаре о возnращении, возникшая, впрочем, впервые из
потребностей механики. Мы позже расскажем, в связи (;
чем величайший математик нашеrо века Анри Пуанкаре
сформулировал эту теорему для механики, вначале же по-
42
rоворим о том, как естественным образом обобщается ука-
занное следствие теоремы Якоби.
В этой теореме фиrурирует окружность 81 И преобразо-
вание Т поворот окружности на некоторый уrол а.
Далее рассматривается произвольная точка х на 81 и ее
образы при поворотах на уrлы а, 2а, За, ........... точки
х, Т(х), Т2(х)==Т(Т(х», ТЗ(х)==Т(Т2(х» и т. д. (они В фор-
мулировке теоремы Якоби обозначались РО, Pi, Р 2 , . . .).
Все образы точки ее положения на окружности в пос-
ледовательные моменты времени........... в совокупности назы-
ваются орбитой преобразования Т. Про эту орбиту и УТ-
верждается, что при иррациональном а она всюду плотно
заполняет окружность, в частности некоторый образ точ-
ки х попадает в любую наперед заданную окрестность точ-
ки х (а при рациональном а орбита замкнется, Т. е. для не-
KOToporo n будет выполнено равенство Тn(х)==х).
,Окружность 81 будем считать расположенной на плос-
кости, а ее поворот представлять себе как преобразование
(поворот) всей плоскости, не меняющее площадей фиrур,
при котором окружность 81 переходит в себя: T(Sl)==Sl.
Анри Пуа каре заметил, что если плоскость........ двумерное
пространство........... заменить на пространство любоrо числа
измерений (трехмерное, четырехмерное и т. д.), окруж
ность на произвольную оrраниченную область *) D
в этом пространстве, а преобразование Т считать взаимно
однозначным (не «склеивающим» никакие две точки в одну),
сохраняющu.м, объемы и при этом nереводящuм область D
в себя, то указанное следствие из теоремы Якоби сразу же
обобщается, а ее доказательство упрощается. Приведем
формулировку теоремы Пуанкаре и ее доказательство.
т е о р е м а П у а н к а р е о в о 3 В Р а щ е н и и.
Пусть Т сохраняющее объемы взаимно однозначное nре-
образование nрос/пранства, переводящее осранuченную об-
ласть D пространства в себя: T(D)==D. ТОсда в любой сколь
уаодно малой OKpeCtпHOcmu U внутри D найдется точка х,
которая после неоколькuх nрuмененuй к ней nреобразования
т снова возвращается в область И: точка Тn (х) nринадле--
жит области Иnринекотором n>О (рис. 3.1). Более тоео,
почти все точки облаоти U возвращаю тоя снова в U объем
невозвращающuхся в U точек равен нулю * *).
*) 06ластыо в пространстве называется такая ero часть, KOTQ-
рая вместе с каждой точкой содержит целиком и некоторый шарик
с центром в ней.
**) Мы предполаrаем, что множество невозвращаlОЩИХСЯ точек
имеет объем.
43
3 а м е ч а н и е. Усилением теоремы Пуанкаре служит ут-
верждение. что почти все точки области и возвращаются 8 U бес--
конечfl,О МНО20 раз. На доказательстве этоrо усиления мы останав..
ливаться не будем.
Рис. 3.1
Рис. 3.2
Д о к а 3 а т е л ь с т в о Т е о р е м ы П у а н к аре.
Рассмотрим области И==ТО(И), т(и), Т2(И), ТЗ(И), . . . .
Их бесконечно MHoro, все они имеют одинаковый ненулевой
(по условию) объем и все содержатся внутри D.
Если бы никакие две из них не пересекались, то CYMMap
ный объем равнялся бы бесконечности и тоrда область D
не имела бы конечноrо объема. Однако область D оrраниче
на, и поэтому какие-то две (по крайней мере) области Tk .: И)
и ТЕ (И) (k> l О) пересекаются, т. е. имеют общие точки.
Но тоrда пересекаются и области т--е (Tk (U»===Tk l (И) И
T--l(Тl(U»===ТО(U)===U (рис. 3.2). Пусть у произволь
ная точка пересечения областей ТN (И) и и, rде n==k l.
Так как каждая точка области тn (И) получается из HeKO
торой точки области U в результате действия преобразова
ния ТN (по определению записи ТN (И», то и точка у, ле
)кащая в тn (И), получается из некоторой точки х области U
таким же способом: у== Тn (х). Но точка у одновреlVlенно ле
жит и в области и. Следовательно, точка х через п шаrов
вернулась опять в область и. Первая часть теоремы ДOKa
ззна.
Докажем вторую часть. Пусть V......... множество невоз
вращающихся в и точек. Тоrда множества V, T(V), Т2 (V),
T3(V), . . . попарно не пересекаются. Действительно, если
Tk (V) и Tl (V) пересекаются, то множество Tk l(V) пе
ресекается G V, а значит, некоторые точки из V вернулись
снова в V, а тем самым и в область и ......... противоречие. По..
скольку полученных множеств бесконечно MHoro и все они
имеют одинаковый объем v, то, в силу оrраниченности объе
ма области D, число v не может быть отличным от нуля.
Значит, объем мно)кества V равен О. Доказательство теоре-
мы завершено.
44
Из теоремы Пурнкаре о возвращении мы получим ниже
несколько интере !lЫХ следствий. А пока что отметим, что
из нее очень просто получается утверждение теоремы Яко-
би. Действительно, если Т....... поворот окружности 81 на
уrол а, то при ct == 2п!!!:.. (т и n целые) преобразование ТN ........
n
тождественное и любая точка х Е 81 через n шаrов возвраща-
ется в точности на свое место: ТN (х)==х. -Если же ct =1= 2п !!!:...
n
ни при каких целых т и n, то по теореме о возвращении
Z
т11(х)х
Т п-- l (х)
т п ....2(х)
81
Рис. 3.3
т2.(х)
для любоrо 8> О существует такое натуральное n, что
I тn (x) x 1<8 (рис. 3.3) следствие теоремы Якоби по-
лучено. Теперь остается лишь заметить, что все точки ок-
РУ}J{НОСТИ равноправны, и если у ........ ЛIобая точка из окрест-
ности и точки х, то она снова вернется в эту же окрест-
ность. Теорема Пуанкаре предсказывает также возвраще-
ние в окрестность исходноrо положения шарика, движуще-
rося без трения в несимметричной чашке (рис. 3.4).
Появление теоремы Пуанкаре о возвращении было сти-
u
мулировано развитием классическои механики, которая
на рубеже ХХ века приобрела практически завершенный ха-
рактер блаrодаря мноrочисленным выдающимся математи-
ческим работам как caMoro Анри Пуанкаре, так и друrих
математиков (Лаrранжа, rамильтона, Лиувилля, Якоби
И др.). Одним из освеiI{ающих моментов, внесенных этими
работами в классическую механику, было понятие КОНфU-
еурационноео и фаЭО80ео nрооmранств механической систе-
мы. Коснемся коротко этих понятий ....... они нам прпrодят"
ся и при изучении бильярдов (см. часть IV).
- 2. К о н Ф и r у р а Ц и о н н о е про с т р а н с т-
в о ........ это пространство конфuеурацuй, т. е. возможных
положений заданных объектов. Например, две точки Xi и
Х 2 , движущиеся по прямой IR:L, можно задать о Д н о й
45
изображающей или КОНфU2урацuонной точкой х, но уже рас-
положенной на плоскости 1R2; при этом первая координата
точки х определяет положение на прямой 1R1 первой точки
Xi, а вторая координата.......... положение второй точки Х 2
(рис. 3.5, а). Три точки Xi, Х 2 , Ха на прямой 1R. 1 заменяются
одной точкой х== (Xi, Х 2 , хз) TpeXMepHoro l\онфиrурационноrо
пространства IR. З (рис. 3.5, б); четыре точки Xf, Х 2 , Х з , Х 4
на прямой (Rl ----- одной точкой х== (Хl, X , ХЗ, Х 4 ) четырехмер-
Horo конфиrурационноrо пространства (R4 и Т. Д. (MHoro.
мерное пространство можно представлять себе как обычное
Х"5
@
( 1
t....A 1 I
,..., I 1/ {Cz.
.......J1
Х!
{cz
<XJ 1
СС2, ....f =-((C1i i) $з
I ,х2.
О Х! {С1
е
а.
5
Jj !/2 tfi4'
IJ 2 ,и 11, V
rJJZ ... I '... (:с 11\
I I"'"f .. -' ;t
31, и, I
9' 11 1 1 (f}z
i \!!.J 111
r 6 3:1
о
а
Рис. 3.5
трехмерное, но со мноrими независимыми осями коорди-
нат *); точка х== (Xi, . . ., Х n ) в нем имеет п координат, т. е.
столько, сколько имеетея независимых осей.) Увеличение
числа объектов увеличивает и число измерений конфиrур а..
ционноrо пространства, так называемую размерность про-
странства (число неэависимых координат), или иначе, число
степеней свободы;системы. Размерность онфиrурационноrо
пространства может быть увеличена и за счет увеличения
размерности исходноrо пространства, в котором распола
rаются сами объекты. Например, две точки х== (Х:(, Х 2 ),
у== (Yi, У2) на ПЛОСКОGТИ IRg задают одну точку z==(x, у)==
== (Хl, Х 2 , Yi, У2) в чеmырехмерном конфиrурационном
*) См. в журнале «Квант» Н9 6 за 1986 r. статью с. В. Дужина и
В. Н, Р бцова «Четырехмерный куб», в которой рассказывается о
четыре!Хмерном npoCrrpaHC(fBe. rиперплоскостя и .п.руrи MHorOMep-
Hbll1 объекта .
46
пространстве IR.' (рис. 3.5, в), а две точки JC == (Xi, X g , Ха)
И у== (Уl, У2, уз) в трехмерном пространстве (R8 задаются oд
ной конфиrурационной точкой z:;;: (х, )1) z::o: (Хl, Х 2 , Ха, Yi,
У2, Ув) в 6 AtepHOM пространстве (R6 (рис. З.5, е).
Часто на конфиrурацию объеI{ТОВ накладываются какие
либо оrраничения. Тоrда совокупность конфиrураций бу-
дет заполнять не все MHoroMepHoe пространство, а лишь
ero часть, и именно эта часть будет в этом случае называть...
ся конфиrурационным пространством. Например, если точ-
ка Х! на прямой 1R1 не может обrонять точку Х 2 , Т. е. если
. .
3)1 < сХ2
а
Рис. 3.6
всеrда Xi X2' то конфиrурационным пространством будет
множество точек плоскости {(Xi, Х 2 )}, удовлетворяющих
условию Х! Х 2 , т. е. полуплоскость в плоскости 1R 1
(рис. З.6, а). Е ли же две точки Х! и Х 2 , двиrаясь свободно
на отрезке [О, 1], не MorYT покинуть ero пределов, т. е.
O Xi 1 и 0 X2 1, то конфиrурационным пространством
будет множество точек {(Xj, Х 2 )}, заполняющих квадрат со
стороной 1 (рис. 3.6, б).
Еще пример: предположим, что две точки Xf. и Х 2 дви-
жутся по прямой 1R1 так, что всеrда Xi Х 2 , но расстояние
между точками не превосходит 1 ........ точки связаны нерастя
жимой (но rибкой) нитью длины 1. Тоrда координаты KOH
фиrурационной точки (Xft Х 2 ) удовлетворяют УСЛОВИЯlVl
Хl Х 2 Xf+ 1 и поэтому конфиrурационное пространство
этой системы....... наклоненная под уrлом 45<? полоса шири
ной 1/V 2.
Чтобы показать разнообразие конфиrурационных про-
странств, приведем более экзотические примеры. Конфи-
rурационное пространство системы, СОGтоящей из движу"
щихся по двум окружностям S} и Sk точек Х! и Х 2 ...... ЭТО мно-
жество точек х=== (Xf, Х 2 ) на двумерном торе..... поверхно-
сти «бублика». Тором является и конфиrурационное про-
u u
странство «двоиноrо маятника»..... механическои системы
из двух связанных вращающихся стержней, изображенной
на РИG. 8.10 (см. 8). Каждое положение двойноrо маят
ника задаеТGЯ парой уrлов '1'1, '1'2, меняющихся независимо
47
друr от друrа от О до 231. Более подробно о торе рассказы,:.
вается в 8.
Множество С упорядоченных пар точек (а, Ь), первая
из которых принадлежит множеству А, а вторая......... множест-
ву В, называется nрямы.JJl, произведением множеств А и В:
C A х В. Прямое произведение пространств (не являю-
щихся нульмерными .........точками) это пространство большей
размерности: [Rl Х [R2== fR3, [R2 Х fR2:::;: [R4. И т. д. Прямые
произведения друrих множеств устроены более сложно:
квадрат прямое произведение двух отрезков, тор
прямое произведение двух окружностей; бесконечный ци
линдр........ прямое произведение прямой на окружность
и т. д. *).
Иноrда только одно введение конфиrурационноrо про.
странства позволяет решить довольно трудную задачу (эта
популярная сейчас олимпиадная задача впервые была опуб-
ликована в 6 M выпуске серии «Матеl\латическое просвеще.
ние», 1961 r.).
3 а д а ч а (Н. Н. Константинов). Из 20рода А в 20род В
ведут две дОрО2и (рис. 3.7, а). Два велосипедиста, связанные
веревкой длины, меньшей 2а, моеут проехать из 20рода А
в еород В по разным дОрО2ам, не разорвав веревки. СМО2ут
ли разминуться, не столкнувшись дРУ2 о дРУ20М, два тол-
стяка радиуса а каждый, идя один из 20рода А в 20род В,
а дРУ20Й из еорода В в еород А?
Реш е н И . Введем вдоль первой дороrи координату
Xf, а вдоль второй дороrи......... координату Х 2 и рассмотрим
конфиrурационпую плоскость ОХIХ2' Одновременное поло-
жение велосипедистов или толстяков изображается конфи
rурационноЙ точкой :.;== (Xf, Х 2 ) ЭТОЙ плоскости. OДHOBpeMeH
НОМУ движению по обеим дороrам соответствует движение
конфиrурационной точки х. Если длина первой дороrи paB
на /i, а второй 12, то координата Х! меняется от О до /1,
а Х 2 ......... от О до l2 следовательно, конфиrурационная точка
обязана находиться в ПРSlмоуrольнике Ol(LM (рис. 3.7,6),
который и является конфиrураllИОННЫМ пространством.
Велосипедисты начинают двиrаться из rорода А (точка О
в конфиrурационном' простраJfстве), а заканчивают движе-
ние в rороде В (верIlIина прямоуrольника L). Значит, в
конфиrурационном пространстве движению велосипедистов
соответствует траектория (кривая) а, ИДУlцая из О в L.
*) Не следует думать, что конфиrурационное пространство .....
всеrда ПРЯМОt:} произведение. Тополоrичеси:и оно может быть уст..
роено сложнее: множество пар точек, наХОДНЩИХС51 на фиксиро"!
ванном расстоянии на сфере S J""'" это трехмерная сфера S .
48
Аналоrично, движению толстяков будет соответствовать
траектория , идущая из вершины М прямоуrольника в
вершину К. Очевидно, кривые а и , находясь внутри пря-
моуrольника OKLM, пересекутся в какой-то точке х===
== (Xi, Х 2 ) внутри Hero. В этой точке координаты велосипе-
дистов и толстяков одинаКО8Ы. Но это означает, что рас-
стояние между толстяками меньше 2а (ведь велосипедисты
I
А
cZ'2
М
5 1\ х,
'2.
а
о
Рис. 3.7
проехали это место, не разорвав веревки!), а следователь-
но, толстяки обязательно столкнутся. Задача решена.
Друrие, более eCTecTBeHHDIe примеры конфиrурацион-
ных пространств появятся в следующих частях этой книrи.
При движении конфиrурационной точки х. возникает ее
траектория х (t), называемая конфиаурационной траекто-
рией или орбитой.
3 а д а ч а. Что является конфиrурационным пространством
а) круrлоrо бильярда? б) Tpe точек прямой 1R1, из которых первые
две не обrоняют третьей? в) трех точек прямой 1R. 1 , из KOTOpЫ
первая всеrда левее второй, а вторая левее третьей? r) двух точеч-
ных П4анет, движущихся BOKpyr Солнца по окружностям? д) Ka
кова размерность конфиrурационноrо пространства девяти планет
Солнечной системы (планеты считать точками)?
О т в е т ы. а) Kpyr, в котором движется бильярдный шарик.
б) Пересечение полупространств Хl -<:хз и Х 2 -<:хз. в) Пересечение
полуп ростр анств Х1 -<:Х 2 и Х 2 -<:хз. r) Двум ер ный тор Т2=: 81 Х 81.
д) 1 + 1 +. . . + 1 == 9.
3. Фазовое пространство. Рассмотрим движение неко"
торой системы объектов частиц, тел и т. п. Добавим к
пространству конфиrураций {х} этих объектов простран-
ство их скоростей {'V} (векторов), Т. е. будем рассматривать
всевозможные пары {(х, 'V)}. Полученное множество пар
(х ......... положение, 'V ---- скорость) называется фазовым nрост-
ранством cuome/Jttbl, а изображающая систему точка (х, 'V) .......
фазовой точкой сиотемы. Иными словами, фазовым ПрОСТ"
ранством называется множество всевозможных состояний
движения системы. Например, если точка х на прямой (Rl
может двиrаться по ней с произвольной скоростью 'V, то
фазовым пространством будет nлоокооть 1R.2== { (х, о)}
49
(рис. 3.-8, а); фазовым JоростраПСТБQМ Д в у х точек .на
о р я м о й fRl будет четырехмерное пространство R'
(рис. 3.8, б), а д в у х точек на п л о с к о с т и ----- 8-мер-
ное пространство JR8 (поскольку У каждой точки по две коор-
динаты положения и по две координаты скорости, итоrо
4+4==8 координат; рис. 3.8 J в).
9
'О ..;
3J
(i) Vf Vz
.:.. )11
х, 3::2.
q
Q
(Vt,V2.) (w"w2J
I
(х"х )Q;,,// ZJ 1=$
O
6
Рис. 3.8
Процесс называется детерминироваWlЫМ, если весь ero
будущий ход и все ero прошлое о Д н о з н а q н о определя-
ются состоянием в настоящий момент. Такими процессами
являются, например, процессы радиоактивноrо распада
и размножения бактерий. Бывают инедетерминированные
u
процессы: таково ДВИ2Кение частиц Б квантовои механике
(ни прошлое, ни будущее не определены настоящим одно-
значно) или же распространения тепла (будущее определе-
но настоящим, а прошлое нет).
Классичеокая механика рассматривает движение систем,
будущее и прошлое которых однозначно определяются
начальными положениями и начальными скоростями всех
точек системы, т. е. рассматривает детерминированные про...
цессы. В каждый момент времени t o механическая система S
находится в положении х (t o ) и имеет КОНI{ретный вектор ско-
рости fJ (t o ); фазовая точка этой системы (x(t o ), 'V (t o )) пол-
ностью и однозначно (детерм:инированно) характеризует'
эволюцию системы как в прошлом, при всех t<t Ot TalK и в
будущем, при'всех [> t o . ,Зная одно-единственное состоя-
ние движения системы S (0)== (х (t o ), fJ (t o )) в l\iOMeHT [ о ,
u
можно однозначно определить состояния движения этон
системы сразу во все моменты времени: {S (t)}== {(х (t), f1 (t),
......оо</<оо}. Мно}кеатво состояний движения' {S(t)}
50
ЭТО множество в с е х фазовых точек {x(t), v(t)}, которое
носит название фазовой траектории. Таким образом, одна
точка фазовой траектории однозначно определяет в с ю фа
зовую траекторию (рис. 3.9). Если в
момент времени t o задать друrое на-
чальное состояние движения системы
S, т. е. взять друrую начальную фа-
зовую точку (х' (t o ), 'lJ' (t o »), то и вся
фазовая траектория {S' (t) }=={х' (t),
t{J' (t)} будет друrой. Никакие две раз-
личные фазовые траектории не мосут
nересекаmься, так как в противном
случае по фазовой точке их пересече-
ния (х (t 1 ), 'lJ (t 1 ) нельзя было бы однозначно восстано.
вить две раз н ы е фазовые точки (х (t o ), 'lJ (t » и (х' (t o ),
v' (t o »).
: , , {8 }
(Ха, vo)
i1J
Рис. 3.9
3 а Д а ч а. Может ли фазовая траектория механической си
стемы пересекать саму себя? Быть замкнутой?
О т в е т. Не может. Может.
Важно отличать состояние системы от состояния двuже.
ния: первое задается координатами, второе......... координаа
тами u скоростями. Зная одни лишь координаты {х}, мы
не мо}кем предсказать дальнейшее дви)кение системы, но
зная координаты {х} и скорости {'lJ} . можем. Предполо
жение о том, что замкнутую систему можно описать хоть
каким то фазовым пространством и системой кривых в нем
(иноrда все вместе называют фазовым портретом) ....... это Ma
тематическое содержание классическоrо принципа дeTep
минизма *).
Рассмотрим теперь механическую систему 8 в момеН1
t==O. Она может находиться в этот момент в различных co
стояниях 81(0), 82(0), 8з(0), о' ., которые задаются раз
личными фазовыми точками (Xf (О), 'lJ:i (О», (Х 2 (О), 'lJ 2 (О)),
(Ха (О), 'l18 (О», ... Каждое начальное состояние систеJ\tIЫ
8 i (О), Т. е. каждая начальная фазовая точка (Xl (О), 'l1i (О)),
В силу детерминированности, однозначно определяет в с ю
*) Известен знаменитый параДОI{С Зенона: летящая стрела и He
ПОДВИ}I{ная стрела находятся в одном и том же месте пространства;
чем же отличается полет от неподвижности? Ответ состоит в ТОМ)
что ВИДимое место стрелы ...... это Bcero ЛИIIIЬ проекция х на просто.
ранство положений ее «истинноrо места» в пространстве пар (х, v):
от фаЗОБоrо пространства остается только конфиrурационное. Па
радокс Зенона можно истолковать как первую JlOrSAKY о роли фа-
aOBoro пространства
51
фазовую траекторию {Si (t)} в фазовом пространстве, так
что для указанных начальных состоя ний системы S опреде
лено сразу бесконечно MHoro фазовых траекторий {Sl (t)},
{S2 (t)}, {Sз (t)}, ... (рис. 3.10). Преобразование, переводя-
щее любую начальную фазовую точку (х (О), 'lJ (О)) В точку
(х (t), 'lJ (t)), называется фазовым преобразованием за время t,
Tt, а множество всех преобразований {Tt}......... фазовым по-
током: каждая фазовая точка движеmся по своей фазовой
кривой.
В фазовом пространстве начальные состояния системы S
MorYT занимать некоторую область и ==и (О). в момент t
v
{S,(t)}
{S2(tJ}
(Sk(t)}
)
х
v
Рис. 3.10
ис. 3.11
все точки области U, двиrаясь каждая по своей фазовой
траектории, оказываются .В новых точках фазовоrо прост-
ранства и образуют новую область U (t) (рис. 3.11). I(aK свя-
заны между собой области U (О) и U (t)? Оказывается, на
этот счет для мноr'их механических систем (в частности, для
так называемых еамuльmоновых систем) справедлйва сле-
дующая замечательная теорема.
т е о р е м а Л и у в и л л я. Объемы облаСПlей и (О)
u и (t) одинаковы.
В дальнейшем будут рассматриваться системы, для KO
торых утверждение теоремы Лиувилля будет ВЫПОJIНЯТЬСЯ.
Исходя ИЗ этой теоремы, все фазовое пространство можно
представлять себе заполненной несжимаемой жидкостью,
которая движется в фазовом пространстве (несжимаемость
и означает сохранение объемов). Разберем два примера
движения такой «фазовой жидкости».
При м е р 1. Исследуем, как меняются состояния де-
вяти планет Солнечной системы. ДЛЯ ПРОСТQТЫ будем счи-
тать, что каждая из них представляет собой точку массы 1
и дви)кется BOKpyr Солнца по своей окружности" не влияя
на остальные планеты. Тоrда фазовым пространством этой
52
системы является 54 MepHoe пространство lR. \ поскольку
у ка}кдой планеты три пространственные координаты (они
выделяют 3 х 9===27 MepHoe конфиrурационное пространство
lR. 27 ) и три координаты вектора скорости (они выделяют 3 х
X9===27 MepHoe пространство скоростей). Однако поскольку
каждая планета с номером k (планеты нумеруются в порядке
удаления от Солнца) движется по окружности, то ее про
странственные координаты (X 1 , k' Х 2 , k' Х з , k) удовлетворяют
условию xi. k+X , k+X;, k==R:, rде Rh радиус орбиты k й
планеты, и поэтому конфиrурационная точка х, изображаю.
щая положение всех девяти планет, движется не по всему
27 MepHOMY пространству, а лишь по ero оrраниченной час
ти так называеl\10му9 мерномутору lr 9 ==SlxS 1 x... xS 1
-......... ......... ..........
9 раз
(о торе см. далее rлавы 3 и 8). Кроме Toro, абсолютная ве.
личина ( модуль) скорос ти каждой планеты постоянна:
I 'Оп 1== V V , 1 +v , +v , 2 == const, k === 1, 2, ..., 9. Каждое
из этих девяти равенств задает двумерную сферу, а все ра-
венства вместе выделяют в 27 MepHOM пространстве скоро-
стей оrраниченную часть 18 MepHoe «мноrообразие»
.мr 18 == S2 х 2 Х . . . х 52.
.......... ...................
9 раз
В итоrе в фазовом пространстве 1R54 выделяется HeKOTO
рое оrраниченное 9+ 18===27 MepHoe множество D== Т 9 Х
Х М18, переходящее под действием фазовоrо потока Т в
себя: т (D)===D. Если (х(О), '0(0)) ED фазовая точка
для обозначения состояния Солнечной системы в момент
t==O и U ее произвольная окрестность, т. е. множество
всех близких по координатам и скоростям положений ПЛа-
нет Солнечной системы, то U область в D, объем которой
под действием преобразования Т не меняется: объеАl
Т (U)===объем UпотеоремеЛиувилля. Мы пришли к услови
ям теоремы Пуанкаре о возвращении и можем заключить
из нее, что через некоторое время все планеты окажутся
вблизи своих начальных положений и будут илtеть nрuблu-
зительно начальные скорости: при некотором n точка
Тn (х (О), 'О (О)) будет лежать в той же окрестности и, что и
начальная фазовая точка (х (О), 'v (О)).
Друrим замечательным примером движения несжимае
мой фазовой жидкости, обсуждением KOToporo мы и заклю-
чим этот параrраф, служит слеДУЮlцая динамическая систе
ма, имеющая уже некоторое отношение к бильярдам.
При м е р 2*. Возьмем два сосуда, один (А), напол-
ненный rаэом, друrой (В) пустой. Что произойдет, если эти
53
сосуды соединить трубкой и открыть клапан соединитель-
ной трубк ?
В соответствии со вторым началом термодинамики rаз
устремится из сосуда А в сосуд В и будет перетекать из А
в В, пока давление в обоих сосудах не сравняется. Однако
мы сейчас рассмотрим эту же ситуацию совершенно с дру-
rой точки зрения, при этом привлечем теорему Пуанкаре
о возвращении и получим совершенно неожиданный ре-
зультатl ·
В статистической механике считается, что rаэ в сосуде
состоит из большоrо числа молекул, взаимодействующих
по законам классической механики. Такой rаз является
замкнутой (rамильтоновой) системой G большим числом
степеней свободы, и поэтому фа-
зовое пространство этой системы
имеет очень большую размерность
(как известно, в кубическом санти-
метре при нормальных условиях
содержится приблизительно 1023
молекул). Фазовый поток, опреде-
ляемый уравнениями движения мо-
лекул rаза, по теореме Лиувилля
Рис. 3.12 не меняет объемов областей фазо-
Boro пространства. А тоrда при-
менима теорема Пуанкаре: фазовая точка подходит с тече-
нием времени сколь уеодно близко к своему начальному
состоя НИIО, такому, при котором все молекулы rаза пе-
рейдут опять в сосуд А (рис. 3.12).
Итак, через некоторое время rаз снова соберется в сосу-
де А, а в сосуде В вновь будет вакуум. Возникает явное
противоречие со вторым начаЛ9М термодинамики: из Hero
следует, что rаз соберется снова в сосуде А с вероятностью
О, а теорема Пуанкаре утверждает, чТо.......... с вероятностью 11
Это противоречие носит название парадокса Цермело,
по имени математика, придумавшеrо ero в связи с дискус-
сией между физиками по обосноваНИIО термодинамики с по-
зиций молекулярно-кинетической теории. Разrадка пара-
докса состоит в том, что «некоторое время», через которое
повторится исходное (вернее, почти исходное) ПОЛО}J{ение
молекул rаза, больше времени существования Солнечной
системы.
Указанную разrадку наrлядно интерпретировали в
1907 rоду известные физики Пауль и Татьяна Эренфесты
на простой и красивой вероятностной модели. Сосуд А со-
держит большое количество пронумерованных Ш,аров (<<МО-
54
лекул rаза»), а сосуд В пуст. Из TpeTbero сосуда, наполнен-
Horo пронумерованными билетиками, вынимается науrад
один (скажем 17-й), и тоrда шар, отмеченный этим номером,
перекладывается из А в В. Билетик возвращается обратно
И возобновляется вынимание билетиков и перекладывание
шаров из сосуда в сосуд. Каждый раз, вынимая науrад
какой-то номер от 1 до N (N общее первоначальное чис
ло шаров в сосуде А), шар с этим номером перекладывают
из Toro сосуда, в котором он находится в этот момент, в дру-
rой (рис. 3.13).
,.. ..... .......
А 1/ " В
,
"..-....,
А / , В
/ I \
Рис. 3.13
Интуиция подсказывает нам, что до тех пор, пока в со-
суде А шаров HaMHoro больше, чем в сосуде В, вероятность
Toro, что мы вынем номер, принадлежащий шару из сосуда
А, будет заметно больше вероятности Toro, что мы вынем но-
мер, принадлежащий шару из сосуда В. Таким образом,
вначале будет наблюдаться сильный «переток» шаров из
сосуда А в сосуд В. Продолжая вынимать билетики, мы за
метим, что вероятность вытяrивания номера шара из сосу-
да А будет меняться в зависимости от предыдущих вынима
ний билетиков. (Эта форма зависимости вероятности от
предшествующих событий носит название цепи Маркова,
и в модели, которую мы рассматриваем, все имеющие к
этому отношение факты MorYT быть cTporo и точно выведе-
ны.) Оказывается, что в среднем число шаров в сосуде А
будет в действительности убывать с той скоростью, которую
и предсказывает термодинамическая теория, пока пример-
но п о л о в и н а шаров не окажется в сосуде В. Но вы-
числения показывают также, что если иrру продолжать
достаточно долrо, то с вероятностью 1 все шары попадут на-
зад в сосуд А, как и утверждает теорема Пуанкареl
Сколько же выниманий в среднем требуется, чтобы вер..
нуться снова к этому исходному положению?, Ответ rла..
сит........ 2 N , а это исключительно большое число, даже если
55
количество шаров N не превосходит 100. Этим и объясня-
ется, почему наблюдения, которые мы производим, дают нам
движение шаров только в одном направлении без каких-
либо осцилляций........ мы слишком недолrо ждалиl
Для экспериментальной проверки теоретических под-
счетов иrру Эренфестов провели на ЭВМ. Начали с 16 384
Lпаров в сосуде А, и каждый «проrон» состоял из 200 000 вы..
НИl\1аний. Была вычерчена кривая, даIOI.I.lая число шаров в
сосуде А по результатам каждой тысячи выниманий
.
.
.
.
. Эl<сnонеНl(lJольное !JObIDqHlJe ЧlJслlt шоро6
.../
.
..... . ...... ......... . .... ........ .... ................ ... ...............0............0....... о
Н.
Рис. 3.14
(рис. 3.14). Как и ожидалось, убывание числа шаров в со-
суде А сначала происходило по экспоненциальной кривой.
Но, начиная со значения, близкоrо к положению paBHOBe
сия (т. е. к 8192 .......... половине общеrо числа шаров), кривая
стала неровной, произвольно отклоняясь то вверх, то вниз.
Прокомментируем парадокс Цермело еще и с бильярд
ных позиций. Рассмотрим для этоrо прямоуrольный би-
льярдный стол без луз, на котором находятся 16 бильярд-
ных шаров. Предположим, что эти шары, как и молекулы
rаза в сосуде, движутся без трения по поверхности бильярд
Horo стола, сталкиваясь упруrо друr с друrом и с ero бор
ТОМ. Мысленно разделим весь стол на две равные части.........
левую (А) и правую (В). Введем понятие G о G Т О Я Н И й.
Бильярд находится в состоянии О, если в пределах левой
половины нет ни одноrо шара; в состоянии 1, если в преде-
лах левой половины находится 1 шар; в состоянии 2, если
в пределах левой половины находятся 2 шара, и Т. д.; В
состоянии 16, если в половине А собрались все 16 шаров.
Заметим теперь, что состояния О и 16 MorYT быть реали-
зованы е Д и н с т в е н н ы м способом: коrда все шары
находятся справа или коrда все они находятся слева. Со-
стояния 1 и 15 MorYT быть реализованы 16-ю различными
способами: первый шар находится слева, остальные.......... спра-
56
Ба; второй шар находится слева, остальные....... справа "
т. д. Для подсчета числа способов, которыми MorYT быть pea
лизованы состояния 2 и 14, будем рассуждать так. Имеется
15 способов, в которых участвует шар номер 1, а именно:
слева (справа) находятся шары 1 и 2, 1 и 3, . . ., 1 и 16;
14 способов, в которых участвует шар номер 2: это шары
2 и 3, 2 и 4, . N ., 2 и 16 (способ «2 и 1» уже учтен в предыду
щем случае); 13 способов с участием шара номер 3: это шары
3 и 4,3 и 5, . . .,3 и 16; и так далее. Bcero получаем 15+14+
+. . .+2+1==120 способов. Количество способов, KOTOPЫ
ми может быть реализовано каждое состояние, назовем
ero «весом». Сведем «веса» В табл иду.
Состояния Количество способов
реализации (свес»)
О И 16 1
О и 15 16
2 и 14 120
3 и 13 560
4 и 12 1820
5 и 11 4368
6 и 10 8008
7 и 9 11 440
8 12 870
Из таблицы видно, что наибольшим числом способов
MorYT быть реализованы состояния 7, 8 и 9, т. е. соСтояния,
коrда примерно половина шаров расположена на левой
половине бильярда, а друrая половина на правой. Для
- u
каждоrо отдельноrо шара нет никаких основании выделять
преимущественную область ero пребывания. С тем же yc
пехом мы можем утверждать, что нет никаких оснований
предпочесть одну какую либо конфиrураuию расположения
друrой. А тоrда, какова бы ни была эта конфиrурация,
рано или поздно она реализуется, а средний промеЖУТОI{
времени, в течение KOToporo на бильярдном столе имеет
место данная конфиrурация, одинаков для всех конфиrура
ций. Каждый из рассмотренных выше способов представля-
ет частный случай конфиrурации. Следовательно, средний
проме)l{УТОК времени, в течение KOToporo бильярд находит-
ся в данном состоянии, пропорционален количеству спо-
собов, которыми реаJlизуетея данное состояние. Поэтому
большую часть времени бильярдный стол проводит В coc
57
стаях 7, 8, 9 (примерно в 12 тысяч раз большую, чем в CO J
сtояниях О И 16).
Можно рассуждать и иначе. Если, бросив )Ззrляд на
бильярдный стол, мы застали ero в состоянии О или 1 (15
или 16), у нас есть все основания ожидать, что в скором вре-
мени на смену этому состоянию придет какое"нибудь более
часто встречающееся (аналоr выравнивания давления в при
мере с сосудами А и В с rазом). Наоборот, если мы застаем
стол в состоянии 7,8 или 9, у нас есть все основания считать,
что еще в течение достаточно долrоrо времени он будет пре-
бывать в этом состоянии. Можно сказать, что «состояние
бильярда стремится к состояниям 7, 8 или 9». Это верно в
том смысле, что действительно на смену редко встречаIО-
щимся состояниям быстро приходят часто встречающиеся
состояния.
Состояния, введенные выше, имеют и определенный фи
зический смысл. Заметим, что общая масса шаров, распо
ложенных, скажем, в левой половине бильярда, равна массе
одноrо шара, умноженной на номер состояния. 'С этих по
зиций можно сказать, что б6льшую часть времени бильярд-
ная система проводит в таком состоянии, коrда масса ша
ров, расположенных слева, примерно равна массе шаров
справа.
Мы специально потратили так MHoro времени, чтобы чи-
татель cMor до конца понять и как следует прочувствовать
следующее обстоятельство. Единственно реально наблю-
даемое на поверхности стола физическое явление......... это то,
что шары двиrаются, сталкиваются друr с друrом и с бортом
стола, и вследствие этоrо описывают весьма сложные траек-
тории. Все остальное есть лишь различные способы описа-
ния этоrо обстоятельства и, возможно, различные ero след-
ствия. Обнаруженные нами закономерности выполняются
тем точнее, чем больше имеется шаров (или молекул rаза в
сосуде). Например, для 16 шаров средний промежуток
времени, в течение KOToporo стол будет находиться в одном
из «средних» состояний, составляет примерно 0,328 от пол..
Horo времени наблюдения, для 50 шаров......... уже 0,8, для
100 шаров 0,94, ну а для 102 молекул rаза в сосуде оно
неотличимо от 1 (вспомним, что для rаза из TaKoro числа
молекул фазовое пространство 6.10 23 -мерноl).
Тем самым решение парадокса Цермело становится пол
ностью прозрачным: систеl\1а молекул стремится к состоя-
нию с наибольшим «весом», а состояние с наименьшим воз..
можным «весом», хотя обязательно и реализуется по
теореме ПуанКаре,...... НО в среднем это происходит ничтожно
58
редко. Как остроумно ответил великий физик л. Больцман
на возражения Цермело, связанные с теоремой Пуанкаре:
«Долrо же Вам придется ждать!»
3 а д а ч а*. Доказать, что если между бильярдными шарами
на прямоуrольном столе произошел хотя бы один удар, то за бес-
конечное время их произойдет бесконечно MHoro. У к а з а н и е.
Достаточно доказать, что в системе произойдет еще хотя бы один
удар (не обязательно между теми же шарами). Если состояние
системы «типичное», то по теореме Пуанкаре система вернется в
близкое к исходному состояние, и нужный нам удар произойдет .
Но да}l{е и в «исключительном» состоянии системы произойдет
второй УДар, так как рассматриваемую задачу можно свести к
движению точки на торе (см. части II IV), траектория которой .....
либо периодическая (и тоrда система возвращается в точности в
исходное состояние), либо всюду плотна (и тоrда система прихо
дит в близкое состояние).
rлава 2
БИЛЬЯРД В ЭЛЛИПСЕ
Нельзя отрицать. что буквально с nepBoro вэrЛЯДа крур при-
влекает нас своей простотой, однако даже самому консерва-
тивному астроному достаточно лишь мимолетноrо знакомства
С эллипсом, чтобы убедиться в том, что идеальная простота
Kpyra сродни бессмысленной улыбке ИДиота. По сравнению
со сведениями, которые несет эллипс, кру!' не дает н.ичеrо.
Возможно, рассчитывая на физическую простоту ВсеJlенной,
мы тоже мыслим окружностями, проецируя свое элементар-
ное мышление на бесконечно вапутанный окружающий мир...
Э. Белл.
Математика -- царица и служанка науки
Стол не выстлан сукном,
Кий изоrнут крюком,
И шары все на эллипс похожиl
Поэ. 1а «М икадо»
4. Эллипс и er'o бильярдные
снойства. Каустики
Хорошо известна задача о нахождении на за
данной прямой 1 такой точки М, дЛЯ которой сумма расстоя
ний до двух заданных точек А и В, лежащих по одну сторо"
ну от прямой l, наименьшая.
Искомой будет точка М пересече-
ния отрезка А 1 В с прямой 1, rде
A i точка, симметричная точке А
относительно прямой 1 (рис. 4.1).
Действительно, АМ+МВ==АIМ+
+МВ==АIВ, тоrда как для любой
J
/ друrой точки М' на прямой 1
имеем
АМ' + М'В == А 1 М' +М'В > А 1 В,
что вытекает из неравенства треуrольника (для А 1 М' В).
Следовательно, АМ'+М'В>АМ+МВ.
60
в
А
Lf:=L2
Рис. 4.1
И хотя эта задача настолько популярна, что без нее прак-
тически не обходится ни одно обсуждение задач на макси-
l\IYM и минимум *), мы приаели ее здесь потому, что она
послужит нам необходимым трамплином при нахождении
аналоrичной точки М на nроизвОЛЬ1iОЙ кривой; при исследо-
вании этой общей задачи мы сра-
зу же столкнемся с необходи-
1V10СТЬЮ использовать понятие
эллипса и ero бильярдные свой- С
ства.
Какое же отношение рассмот-
ренная задача имеет к эллипсу,
rиперболе или же друrой кри-
вой? И при чем здесь бильярд?
Впрочем, на последний вопрос ответить просто. Взrля-
нем еще раз на рис. 4.1: Ll==L3, а так как, кроме Toro,
L2== L3 (как вертикальные уrлы, ведь А 1 МВ ........ прямая!),
имеем Ll == L2. Следовательно, точка М на прямой 1 об
ладает тем свойоmвом, что АМ и ВМ являются звеньями
одной бильярдной траектории: эти звенья образуют равные
уеЛbl о «зеркалом» 1 (У20Л падения равен У2ЛУ отражения).
Вот теперь мы достаточно «вооружены» для рассмотрения
первоrо бильярдноrо, или оптическоrо, свойства эллипса.
НО прежде чем обсуждать ero, поrоворим о самом эллипсе
и ero простейших rеоме'!рических свойствах.
О п р е Д е л е н и е. Эллипсо.лt называется множество
точек М на плоскости, для которых сумма расстояний до
двух фиксированных точек F i И F 2 этой плоскости ........ вели-
чина постоянная (рис. 4.2):
р]м + Р 2 М == const.
Е
о
н
Рис. 4.2
3 а Д а ч а 4.1. Можно ли в эллипс вписать правильный MHoro-
уrольник? Если можно, то сколько сторон он может иметь?
О т в е т. Можно вписать только правильный треуrольник и
квадрат, поскольку вписанный правильный мноrоуrольник впи
сан одновременно и в окружность, пересекающуюся с эллипсом не
более чем в ч тырех точках.... вершинах мноrоуrольника.
На рис. 4.3 показано, как можно начертить эллипс на
бумаrе. Положим лист бумаrи на чертежную доску и прико-
лем к нему две кнопки или булавки. Напросив на них ни
тяное кольцо, длина KOToporo должна быть больше УДвоен..
Horo расстояния между кнопками, натянем нить острием
*) См., например, недавно вышеДШУIО в серии «Библиотечка
«Квант» книrу В. М. Тихомирова «Рассказы о максимумах и миниму-
мах» (М., 1986), а таК2ке книrу Н. Б. Васильева и В. л. rYTeHMa-
хера «Прямые и кривые» (М., 1978).
61
карандаша, чтобы получился треуrольник FiMF 2 . Если
вес.ти карандаш по бумаrе так, чтобы нить все время оста--.
валась натянутой, то треуrольник будет- деформироваться,
но ero периметр будет оставаться постоянным. Постоян-
ной будет и длина стороны F iF 2 следовательно F 1М + F 2М ==
==const и карандаш опишет эллипс. (Этот способ вычеРЧИ и
вания эллипса используют садовники при изrотовлении ЦBe
точных эллиптических клумб, только. они вместо кнопок
втыкают в землю два колышка, натяrивают кольцо из ве-
ревки, а сам эллипс вычерчивают на земле не карандашом,
а палкой о острым кон'
цом. Аналоrичным .спо
собом действовали древ-
ниеэтруски, рисуя слож-
ные овалы разrадку
способа рисования пред..
ложил великий физик
Максвелл, и с тех пор
они называются «овала о
ми Максвелла».)
Точки Р1. и Р 2 носят
Рис. 4.3 названия фокусов зллип.
Оа (от латинскоrо fo-
cus очаr *)) середина О отрезка FiF2 (линии фоку-
сов) центр аллипоа; отрезки CD и ЕН, первый из
которых ......... продолжение линии фокусов, а второй перпен-
дикулярен ему и проходит через пентр О эллипса (рис. 4.2),
называются ооями аллипоа, и если CD EH, то CD ........ боль-
шая ось, а ЕН ........ малая; половины этих осей, т. е. отрез-
ки OD, ОС и ОЕ, ОН называются полуосями, соответственно,
большой и малой; отношение расстояния от фокуса до цeHT
ра к большой полуоси, т. е. число ОР i/OC (или ОР 2/0D),
равное также отношению FiF 2 к большой оси CD, xapaKTe
ризует «сплюснутость» эллипса и называется ero экоцеНtrlрU-
оитетом. При совпадении фокусов эксцентриситет равен
нулю и эллипс превращается в окружность.
Обозначив большую полуось буквой а (OC===OD==a),
малую......... буквой Ь (ОЕ==ОН==Ь), половину длины отрезка
фокусов FiF 2 ....... буквой о (OFi==OF2==1/2FiF2==o) И эксцент-
риситет........ буквой е (OFi/OC==OF 2 /OD==e), найдем связь
между этими величинами. Соединив для этоrо точку Е с
фокусами, получим равнобедренный треуrОЛЬНИR FiEF 2
(рис. 4.2). Найдем ero стороны.
*) По причине, которая БУJliТ ясна .uальше.
62
Поскольку для любой точки М эллипса Ff.M+f'2M==
===const, то, взяв в качестве М точку D ........ правый конец
большой полуоси эллипса, получим
F 1 C==F 2 D, FID+F2D==const, F 1 D==F 1 0+a,
поэтому
F 1 D +F2D ==а + (Р 1 О + Р 1 С) == а+а == 2а.
Итак, const==2a. Тоrда для 6FiEF2 имеем FiE+EF2==2a, а
поскольку FiE===EF2' то F 1 E==EF 2 ==a. А теперь рассмотрим
прямоуrольный треуrольник Р 1 ОЕ с к атетам и ЕО==Ь , ОР 1 == С
и rипотенузой EFi==a. Из Hero с == уа 2 ..........Ь 2 , Ь == V a2 c2,
а эксцентриситет эллип а равен
с V а 2 ____Ь 2
e ·
a а '
отсюда с == ае и Ь == V a (ае)2 == а V 1..........e 2 .
3 а д а ч а 4.2. В эллипсе с большой полуосью 1 О см и эксцент
риситетом 0,1 вычислить, во сколько раз расстояние между фокусом
и центром превосходит разность полуосей.
О т в е т. В 20 раз (== 1 см: 0,5 мм).
3 а м е ч а н и е. Эллипс с нулевым эксцентриситетом
это окружность, а с малым (e O) ........ очень похож на окруж-
ность. Если расстояние фокуса от центра....... первоrо поряд-
ка мал ости, то различие полуосей......... BToporo порядка:
Ь == а V 1 e2 а (1......... 1 / 2 е 2 ) *). Известно, что орбиты планет
Солнечной системы являются эллипсами с очень малыми
эксцентриситетами (порядка 0,001),
в фокусе которых находится Сол нце.
Вернемся к первому бильярдному
(оптическому) свойству эллипса. Возь-
мем на эллипсе с фокусами F] и F 2
произвольную точку М (рис. 4.4).
Для любой точки N на эллипсе спра-
ведливо равенство
F 1 N + F 2 N == FiM + F 2 M,
а для точки N, лежащей внутри эллипса, сумма FiN+F 2 N
меньше, чем FiM+F2M. Построим прямую 1, проходящую
через точку М и образующую равные уrлы с отрезками
Р 1 М и Р 2 М: Ll==L2. Если теперь М'''''':' произвольная
точка прямой 1, отличная от М, то
Ff.M' + Р 2 М ! > FiM + Р2М'
*) При малы 1# Vl +х 1+"/2 '
Рис. 4.4
63
как это было выяснено в начале параrрафа. Следовательно,
точка М' лежит в н е эллипса.
Мы получили, что прямая 1 имеет т о л ь к о о Д н у
общую точку с эллипсом точку М; все же остальные точ
ки прямой 1 расположены в н е эллипса. Такую прямую
называют касательной. Таким образом, справедливо
у т в е р ж Д е н и е l! (первое бl:fльярдное свойство
эллипса). Касательная к эллипсу, nроведенная в еео nроuз-
вольной точке М, образует равные уелы с отрезками FfM
и F 2,М, ооединяющими оба фокуоа с этой точкой.
Из первоrо бильярдноrо свойства эллипса вытекает сра-
зу, что как бы мы ни выпустили бильярдный шар из одно..
ro фокуса, он после одноrо отражения от эллипса (от борта
стола) пройдет через второй фокус, после BToporo отраже
ния опять через первый фокус и так далее.
Знаменитый Льюис Кэрролл написал небольшую кни)i{
ку и об эллиптическом бильярдном столе. В одиннадцатом
издании Британской энциклопедии в примечании к CTaTЬ
о бильярде написано: «В 1907 r. в Анrлии для разнообразия
введен овальный стол». Однако ни у этоrо, ни у бильярдноrо
стола Льюиса Кэрролла луз не было. Только в 1964 r.
Эдвин Э. Робинсон получил патент на круrлый бильярдный
стол с четырьмя лузами. Тоrда же в США появилась при
думанная Артуром Фриrо иrра «Эллиптипул», В которой
луза располаrалась в одном из фокусов эллиптическоrо
стола. На таком столе, ударяя шары о борт, можно все вре-
мя выиrрывать.
Теперь мы можем дать иную интерпретацию решения за-
дачи о нахождении точки М на прямой l, реализующей мини-
мум суммы АiИ+ВМ для заданных
точек А и В (рис. 4.1): та точка М
на прямой 1 являетоя искомой, в ко/по.
рой один из эллипсов. о фокусами А u В
в касаетоя этой прямой (все такие, эл..
липсы называютоя софокусными).
В точности то же решение полу..
чится, если прямую 1 заменить про-
извольной кривой у. Сформулируем
точный вопрос.
В о про о. Дана кривая у и две п10чки А u В ПО одну сто..
РОНУ от нее (рис. 4.5). Как найти на кривой "( точnу М nza-
кую, чтобы сумма раостояний АМ+ВМ была (среди всех воз-
МОЖНblХ) минимальной... или Аtаксимальной?
Мы остаВJlяем читателю возможность самому Ilоразмыш-
Рис. 4,5
64
лять над этим вопросом, полный ответ на который отложим
до 6.
Остановимся HeMHoro на некоторых оптических интер-
претациях первоrо бильярдноrо свойства эллипса. Предпо..
ложим, что эллипс представляет собой «зеркальную» кри-
вую, от которой луч света отражается по закону «уrол па-
дения равен уrлу отражения». Если в .одном ИЗ фокусов
TaKoro зеркальноrо эллипса помещен точечный источник
света, то после отражения от стенок эллипса в с е лучи
пройдут через второй фокус. Описанное явление можно
а
Солнце
Земля
5
Рис. 4.6
наблюдать реально, в TpeXl\IepHOM пространстве. Для это-
ro HYjI{HO взять поверхность, получающуюся вращением эл-
липса BOKpyr прямой FIF2' соединяющей ero фокусы,
она называется эллипсоидо)}t ,враще1-lия, покрыть ее из-
нутри зеркальным слоем, а в ОД HOfitI из фокусов поrvrестить
точечный источник света (<<солнце»). Тоrда наблюдатель,
находящийся внутри эллипсоида, увидит Д в а «солнца».
В caMQM деле, обратив взrляд к первому фокусу, наблюда
тель непосредственно увидит раЗl\lещенное Tar.ti «солнце».
НО и, OCMOTpeB в направлении BToporo фокуса (I'де в дей
.ствительности ничеrо нет), ОН так)ке увидит «солнц »
(рис. 4.6, а). И как бы ни перемеIцался наблюдатель BHYT
ри зеркальноrо эллипсоида, на Hero почти везде будут CBe
тить два «сол нца».
Но вот наблюдатель, находящийся внутри зеркальноrо
эллипсоида, решил принять меры, которые избавят ero от
«мнимоrо солнца»; и поместил во втором фокусе небольшое
непрозрачное тело (<<экран»), преrраждающее путь OTpa
женным лучам. Результат оказывается несколько неожи
данным: теперь все лучи, исходящие от «солнца» Fi, после
отражения от стенок зеркальноrо ЭIl1Jлипсоида собираются
(<<фокусируются») на экране F 2, И это может вызвать ин-
тенсивный ero разоrрев. Например, поместив в СРОКУС Р 1
rорящую свечу, можно зажечь бумаж у, находящуюся во
втором фокусе. Заметьте, что для фокусировки не обяза-
8 r. А. fальпеrшн. А. Н. Земляков
65
u u
тельно иметь целыи зеРI<альныи эллипсоид, достаточно ис-
пользовать лишь часть ero поверхности *).
А что увидит «несrораемый» наблюдатель, оказавшийся
во втором фокусе F 2 эллипсоида, если в первый ero фокус Ff.
поместить источник света? Все лучи, выходящие И3 Fi
и отражающиеся от эллипсоида, попадают в точку Р 2 ; та-
ким образом, для наблюдателя в F 2 веоь fJллuпсоид будеrn све-
титься.
Если ИЗfОТОВИТЬ зеркальный эллиптический отража
тель, в одном ИЗ фокусов KOToporo находится Солнце (нас-
тоящееl), а в друrом ....... котел G водой, то можно добиться
кипения воды в котле за счет сфокусированноrо отража...
телем излучения Солнца. Удивительноrо в этом ничеrо
нет: ведь отражатель имеет большую площадь и со всей ero
поверхности сол ечная энерrия направляется на обоrрев
котла. Такие солнечные установки уже сейчас имеют не-
которое применение. А в будущем может быть удастся,
построив оrромный зеркаltьный отражатель (в форме час-
ти эллипсоида, рис. 4.6, б), использовать энерrию тех лу-
чей, которые проходят мимо Земли?
Отметим еще, что фокальное свойство эллипса использу-
ется для аттракционов. В CIIIA имеются знаменитые «щеп-
чущие rалереи», которые представляют собой помещения с
эллипсоидальными потолками. Наиболее известна шепчу-
щая rалерея в Скульптурном зале Капитолия, без посеще-
ния которой не обходится ни одна экскурсия. Прекрасная
комната шепотов, правда меньшеrо размера, имеется у
входа Б бар в нижнем этаже Центральноrо вокзала в Нью-
Йорке. Двое людей, стоящих там лицом к стене в диаrо-
нально противоположных уrлах квадратной площадки,
хорошо слышат друr друrа, даже коrда на площадке тол-
пятся люди **). Аналоrичный эффект наблюдается в Доме
композиторов в Дилижане (СССР). Впервые теория эффекта
«шепчущих rалерей» была предложена известным физиком
лордом о. Н. Рэлеем в ero статье 1910 r. «Проблема шеп-
(Iущей rалереи» и в ero классической книrе «Теория звука».
3 а д а ч а 4.3. Воэьмем вырезанный из бумаfИ Kpyr, поставим
на нем точку А в ЛIобом месте, отличном от центра, и сложим Kpyr
так, чтобы точка А совпала с какой либо точкой окру)кности. Pa
30fHeM листок и снова corHeid, совместив точку А уже с друrой
точкой ОI<РУЖНОС ТИ. Докажите, что если этот бумажный КРУI'
*) Поэтому фокус и называется фокусом...... по-латыни focus.......
это очае.
**) Отметим, что эффект «шепчущиХ! rалерей» был известен еще
в древнем Китае (свидетельством чему являются остатки стеИ t rле
этот эффеI{Т :хорошо проявляется) .
66
переrибать так, чтобы ero край все время ПРОХОДИЛ через точку А,
то оrибаlощая линия сrиба будет эллипсом (рис. 4.7).
Реш е н и е. Обозначим буквой О центр Kpyra. Пусть Kpyr
сrибается по прямой ХУ; на точку А попадает точка В края Kpyra i
при ЭТ9М ABl.xy и прямая ху делит отрезок АВ пополам. Обо-
значим буквой С точку пересечения прямых ХУ и ОВ (рис. 4.7,6).
Тоrда АС==ВС, поэтому OC+AC==OC+CB==R, rде R....... радиус
окружности. Следовательно, при любом сrибе Kpyra сумма ОС+АС
tt
а
Рис. 4.1
постоянна и равна ero радиусу. Следовательно, rеометрическое
место точек С, движущихся при перемещении точки В по окруж-
ности, является эллипсом Э с фокусами в точках: А и О. Из .биль
ярдноrо свойства эллипса следует, что все линии сrиба касательны
к эллипсу Э, поэтому он является оrибающей бесконечноrо множе--
ства линий сrиба ХУ.
3 а д а ч а 4.4. а) Докажите, что тень на столе, отбрасываемая
лежащим на нем круrлым мячом при ero освещении точечным
источником света S, является эллипсом. rде находится фокус
этоrо эллипса?
б) Наклоните !{руrлый цилиндрический стакан с водой под
некоторым уrлом. ДОI{ажите, что поверхность воды примет форму
эллипса.
Реш е н и е. Оба пункта задачи решаются одним приемом и
используют свойство равенства всех общих касательных к двум
заданным сферам. Приводимое доказательство предложено бель
rийским математиком Х 1 Х века ж. Данделеном в 1822 r.
а) Мяч вписан в конус с вершиной S, который пересекается с
плоскостью n (столом) по некоторой кривой '\'; А ---- точка касания
мяча с плоскостью л. Впишем в конус еще один шар, касающийся
плоскости п, но с друrой стороны (рис. 4.8, а) в точке В. Пусть
М произвольная точка кривой '\'. Через точку М и вершину
конуса S проведем прямую, касающуюся обоих шаров в точка1С
Х и У. Соединим точку М с точками А и В.
Отрезки М А и М Х ---- касательные к мячу, проведенные из
одной точки, значит, МА==МХ. По той же причине МВх:::МУ.
tледовательно,
МА+МВ==МХ +МУ==ХУ,
причем длина отрезка ХУ не зависит от положения точки М на
на кривой '\' ""'XY и есть общая касательная к двум шарам! Итак,
MA+MB==const, поэтому у ........ эллипс, что и требовалось доказать.
Фокусами эллипса '\' являются точки А и В в частности .мяч Ka
сается стола в фокусе отбрасываемой им тени.
1. 67
б) Решееие этой задачи почти дословно копирует решение
S3Д8ЧИ а. Действите..1JЬНО, если rраница поверхности воды есть
кривая V (рис. 4.8, б), то два вписанны в цилиндрический стакан
шара, касающиеся поверхности воды в точка А и В; обладают
тем свойством,; что для Лlобой точки М Е"? справедливо равенство
MA+MB==MX+MY==XY
rде ХУ --- общая касательная к 9ТИМ шарам, длина которой не
В8ВИСИТ от выбора точки М на 1'. СледоватеЛ6НО; поверхность воды
АН+ОН'#.ХУ
11
,g
Рис. 4.8
в cтa«afle дейстеUlпеЛЫ-lО имеет форму ЭЛ/luпса с фокусами в тОЧКйJD
А и В.
Используемые при доказательстве сфеРБI называются сферами
Данделена.
Теперь мы, основываясь на имеющихся знаниях reoMer-
рических свойств эллипса, получим некоторые друrие
бильярдные свойства эллипса.
у т в е р ж Д е н и е 2 (второе бильярдное свойство эл-
липса). Звенья траектории бильярдН020 шара, вblпущеННО20
из про uзволь н 020 фокуса эллипса,
асимптотичеоки (в пределе) отремят-
ся 1\, большой оси эллипса, т. е. nоолв
е некотороео чиола ударов о борт двuоюе-
ние шара будет проиоходиmь в с оль
уеодно малой полосе, оодеРЖJащей боль-
шую ось эллипса (рис. 4.9).
Д о к а з а т е л ь G Т В О можно
ПрОБОДИТЬ по-разному, например вы-
числить, как меняется расстояние от точеI{ ударов Ша-
ра об эллипс до ero большой оси и доказать затем, '4то
оно уменьшается быстрее, чем неКQторая убывающая reo..
метрическая проrреССИЯi или }ке доказать аналоrичное
Рис. 4.9
68
утверждение для уrлов, образуемых звеньями траекто-
рии с большой осью эллипса. Эти доказательства весьма
rромоздки и желающие r.1orYT попробовать свои силы на их
самостоятельном поиске. В качестве «подсказки» может
служить указание к задаче 4.5.
Мы же поступим по-друrому, не используя при доказа-
тельстве никаких формул, а используя только достаточно
простые, но одновременно изящные рассуждения.
Пусть Af, В 1 И А 2 три последовательные точки уда..
ров шара о борт, причем Af и А 2 лежат на верхней полови-
не эллипса, а В! на нижней (рис. 4.10). Тоrда, как леrко
А,
А 2
А/
3
Рис. 4.10
Рис. 4.11
видеть, точка А 2 лежит ниже точки Ai., т. е. ближе к боль- -
шой оси, поскольку LA 1 B 1 A 2 цел и KOJYl содержится в
LA 1 B 1 M (М левый конец большой оси эллипса).
Д,зльнейшие точки ударов об эллипс будеJVl обозначать
В 2'1 А 3, В 3, А 4' . . ., причем все точки В h располаrаются ниже
большой оси эллипса, а все Ah выше нее. При этом КЮК-
дая следующая точка А h будет находиться ниже предыду-
щей А п 1 (поскольку Ah лежит на дуrе эллипса АЛ 1М),
но выше точки М левоrо конца большой оси. Дока)кем,
что при k oo точка А,{ стремится к точке M, это и будет
доказывать утверждение 2.
Предположим, однако, что предельной точкой для пос-
ледовательности А 1, А 2, . . ., А л, . . . является не точка
М, анекоторая друrая точка, которую обознаЧИJVI А 00;
тоrда Аоо лежит выше большой оси (рис. 4.11). Это означа-
ет, что все звенья траектории В h i.Ah С достаточно больши
МИ номерами k сколь yzoaHO близко подходят к отрезку
ВооАоо, rде точка ВОО лежит на нижней половине эллипса
и является пересечением прямой Аоо Р 1 С эллипсом.
ЧпlО же произойдет, еоли бильярдныЙ [иар будет выпу-
щен из точки В 08 в точку А or?
Очевидно, если вся рассматриваемая нам:и траектория
сколь уrодно близко подходила к отрезку AooB , то теперь,
69
двиrаясь ИЗ Воа в Аоо, шар должен отразиться от эллипса
в точке А ое и пойти в т о ч н о с т и п о т о м у }I{ е
о т р е 3 к у АооВоо, но в о б Р а т н о м направлении
.от Асе к Вое! Однако при этом шар непременно должен прой-
ти опять через фокус Fi, поскольку он лежит на отрезке
А.Б оо , хотя по первому бильярдному свойству эллипса
шар после отражения в точке А 00 пойдет .по прямой А оор 2
через в т о рой фокус. Полученное противоречие дока-
зывает, что Аоо и М дОЛа/СНЫ совпадать: предельное движение
шара должно происходить В сколь уrодно малой окрест-
ности большой оси.
3 а м е ч а н и е. В математически рассужденияХ! часто ис
пользуется приведенный выше прием: для HeKoToporo множества
{Аn} состояний произвольной системы, имеющеrо предельное
состояние А 00, рассматривается Э,то предельное состояние системы
А. 00 и затем исследуются ero свойства, которые во мноrих случаяХ!
лизки к свойствам допредельных состояний системы Аn, А n+i, ...
?ная эти свойства, можно делать соотвеТСТВУlощие выводы о пове-
дении системы в целом.
в о про с. Обратим движение шара, выпущенноrо ИЗ
фокуса: звенья ero траектории, близкие к большой оси эл-
Р2 липса, начнут удаляться от большой
оси. Не противоречит ли это утверж-
дению 2?
1'4 3 а д а ч а 4.5. На rоризонтальном
диаметре окружности с центром О выб-
раны точки 01 и 02, равноудаленные ОТ О
(рис. 4.12). Для произвольной выбранной
точки Рl на окружности строятся точки
Р 2 , Ра, Р 4 , "" такие, что хорды Р 1 Р 2,
Рис. 4.12 Р 2 Р з, Р з Р 4 ,... попеременно проходят
через точки 01 и 02. Доказать, что поло-
жение !Хорды РпРn+1 при n-+оо стре-
мится к rоризонтальному диаметру.
у к а s а н и е. Можно провести рассуждения, аналоrич.
вые проводимым при доказательстве утверждения 2. Но можно,
введя обоз начения L. Р 1 001 == fP1, L. Р 2002== fP2; доказать, что
fP 1 ---е . fP"
tg 22 == 1 + е tg 21 , rде е== 010/ R, R ........ радиус окружности. Анапо..
rично вводятся уrлы fPs== L. Рз О0 1' fP4== L. Р 4002 И Т, д.; для ко-
ТОрЫХ! выполнены те же соотношения
t <Рз 1 ........ е t <Р2 t <р 4 1..... е t fPз
g "2 1 + е g2' g 2 1 +е g , и т. д
Таким образом, последовательность tg , tg 2 . tg B , ... образует
б . l e
есконеЧНУIО rеомеrрическую проrрессию со знаменателем r:t'в'
70
-
а потому ее общий член стремится к О. Следовательно. <1'п-'+О при
n OO, т. е. траектория стремится I{ I'ОРII онтальному отрезку.
Прея{де чем перейти к третьему бильярдному свойству
эллипса, введем в рассмотрение еще одну кривую, тесно
связанную с эллипсом. Эта кривая называется еиnерболоt1.
О п р е Д е л е н и е. ruперболой I
"
называется множество точек М на
плоскости, для которых модуль раз-
ности расстояний до двух фиксиро-
ванных точек F i И F 2 ....... фокусов rи.
перболы величина постоянная (рис.
4. 13):
f м F 1 ....... М F 21 == const.
rипербола состоит из двух «кус-
КОВ», называемых ее ветвями. Как и для эллипса, для rи-
перболы имеет место
О п т и ч е с 1\ О е с в о й с т в о. Касательная l в nро-
uзвольной точке М еиnерБОЛbt являетоя биосектрисой уела
LFiMF 2 : LI==L2 (рис. 4.13).
3 а д а ч а 4.6. Докажите справедливость оптическоrо свой
СIВ8 rиперболы.
у к а 8 а н и е. Решите задачу о нахождении на прямой 1
таI<:ОЙ точки, для которой р а 3 н О с т ь расстояний от двух за
данных точек А, В н а и б о л ь ш а я.
Рис. 4.13
Мы приведем еще один способ доказательства оптиче-
cKoro своЙства I"'иперболы. Возьмем на rиперболе две очень
Рис. 4.14
Рис. 4.15
близкие точки М и Mi (рис. 4.14), и пусть Р ..... точка пере-
сечения прямых FiM 1 и Р 2 М, а Q......... точка пересечения пря-
мых F 2 Mi И FiM. Посмотрим теперь «через лупу» на че-
тырехуrОЛЬНИI< M 1 PMQ (рис. 4.15). Мы можем считать (при-
близительно), что PM 1 ffMQ и PMIIM:iQ, так как точки Fi
И F 2 находятся очень далеко........... сравнительно с размерами
четырехуrольника M 1 PMQ. Итак, будем считать (прибли
71
}l-сенно), что M 1 PMQ ......... параллелоrрамм. Пр о ведем: теперь
ОI{РУЖНОСТИ с центрами Р, и Р 2 , проходящие через
точку Mi. Вблизи рассматриваемоrо параллелоrраl\1ма
(СМ. рис. 4.15) дуrи этих ОI{ружностей будут представлять-
ся ПрЯМБIМИ M'iL И M'IK, перпендикулярными сторонам
параллелоrраМ1\1а и поэтому
FiМ F2М==(F1L--t LМ) (F2К+КМ) ·
== (Р 1М} + LM)....... (Р 2 М ! + к М) == (Р f М i......... F 2М 1)+ (LM К М).
Но так как FIM F2M==F'iM1. F2Mi (М и М! лежат на
одной ветви rиперболы), то LM==KM. А тоrда прямоуrоль-
вые треуrольники LKMMi и 6LMMi равны (по rипотену-
зе и катету) И, следовательно, Ll== L2. Это и завершает до- '
казательство оптическоrо свойства rиперболы (для Toro
чтобы это «приближенное» рассуждение сделать ТОЧНЫМ,
нужно еще перейти к пределу при Mi---+M).
3 а lYl е ч а н и е. Для rиперболы оптическое свойство
можно сформулироват еще и так: лучи, выходящие из од- I
Il020 фокуса, отражаяоь от 2иперболы, будут раоходитЫJЯ
а
Рис. 4.16
таКИАt образом, что кажутся выходящими из втОрО20 ф
"уса.
у т в е р ж Д е н и е 3 (третье бильярдное свойство эл-
липса). Любая бильярдная траектория в эллипое касается
Jlибо эллипса, либо 2иперболы, софокусных (т. е. о теми оюе
фокусами) о данным эллипсом. Первый случай реализуется,
lWеда первое (а тем самым и nроизвольное) звено траектории
не пересекает отрезка фокусов, а второй случай.......... коеда
первое (а me/vt самым и nроизвольное) звено траектории от-
резок фокусов пересекает. При этом во втором случае соот-
ветствующие точки касания моеут лежать не на сами»
ввеньях ломаной, а на их продолжениях (рис. 4.16).
Д о к а э а т е л ь G Т В о. Пусть AIA и АА 2 ......... два пос-
ледовательных звена бильярдной траектории в. эллипсе,
причем отрезок AiA не пересекает отрезка фокусов FiFI
72
(рис. 4.17). Из первоrо бильярдноrо свойства эллипса следу"
ет, что LA 1 AFi== LA2AF2' поэтому отреЗОI{ АА 2 так)ке не
пересекает отрезка фокусов FiF 2 .
Возьмем ТОЧI{У Bf, симметричную Ff относительно AiA
и проведем отрезок BiF 2. Он пересечет AfA в точке C 1 ;
при этом uf==FiCi.-1- СfF2==ВiСf+СiF2==ВfF2' а для всякой
точки D на отрезке AiA, отличной от Cf, выполнено пера-
венство ui==FiCl+CiF2<FlD+DF2.
Отсюда следует, что эллипс, софокусный С ИСХОДНЫМ,
для KOToporo cYMl\1a расстояний дО Р! и Р 2 равна Uf, к а-
с а е т с я AfA И притом в точке C'f.. Аналоrичное построе-
ние проделаем с отрезком АА 2 (рис. 4.17), найдем ТОЧКУ
С 2 и величину U2==FIC2+C2F2. Таким образом, точка С,
лежит на СОфОКУСНОМ эллипсе с const===
== И 2 , касаfоще 1СЯ отрезка АА 2.
81
А 1
Рис. 4. 17
Рис. 4.18
Докажем, что точки С 1 И С 2 лежат н а о Д н о 1\1 И Т О М
Ж е эллипсе, т. е. докажем, что иl == и 2 . Для этоrо зам:етим,
что BIAF2== B2AFl (по двум: сторонам и уrлу между
ними с вершиной А), откуда BIF2===Br:.Fi, Т. е. Ul===U2'
что и требовалось. Итак, отрезки AIA и АА 2 касаются о д-
н о r о софокусноrо эллипса с константой и==В 1 Р 2==B 2 F i.
Случай rиперболы рассматривается аналоrично (раз-
берите ero самостоятельно) он возникает, коrда отреЗОI
AIA пересекается с отрезком FIF2 и LA 1 AA 2 лежит в н у т-
р И LF 1 AF 2 . Утверждение 3 доказано.
Третье бильярдное свойство эллипса позволяет ввести
понятие каустuческой кривой, сокращенно каустики.
О п р е Д е л е н и е. Пусть Q произвольная ВЫПУК-
лая область на плоскости, оrраниченная I{РИВОЙ r, в которой
бильярдный шар описывает траекторию ...Р lPoPl. . .
Кривая 1', ле)I{ащая внутри области Q, называется каусти-
кой, если выполнено следующее условие: из Toro, что хотя
бы одно звено PkP п+l траектории бильярда · . .Р iPoPf. . .
касается у, следует, что в с е остальные звенья этой тра-
ектории также касаются кривоЙ у (рис. 4.18). ИНЫ1iИ сло.
13
вами, траектория бильярдпоrо шара после каждоrо отра-
жения касается кривой V ....... каустики бильярда Q.
Простейшим примером каустики может служить ок-
ружность, которой касается траектория бильярдноrо шара
в Kpyre. В круrлом бильярде имеется только о Д н о с е-
м е й с т в о каустик........ конценmричеокие OKpY3IOHocmu.
Третье бильярдное свойство эллипса состоит в том, что
у эллиптическоrо бильярда Q существует д в а с е м е Й..
с т в а каустик: это ЭЛЛUnОbl r с И еunерболы Н с, соФокусные
с r ........ rраницей Q.
Оказывается, что все выпуклые области Q G достаточно
rладкой rраницей r (Т. е. такой, в кажДОЙ точке которой
можно провести касательную, причем в близких точках
.Q
а
о
Рис. 4.19
rраницы r эти касательные образуют друr с друrом малый
уrол) имеIОТ бесконечно MHoro каустик, накапливающихся
к rранице r (этот сложный результат установлен В. Ф. Ла-
зуткиным). Отсюда вытекает, что бильярд в области Q на
плоскости, оrраниченной rладкой выпуклой кривой r,
не эреодичен (напомним, что в случае эрrодичности шар про
водит в каждом кружочке внутри области Q время, пропор-
циональное ero площади в нашем же случае есть участки
области Q, куда шар вообще не попадает). Например, би-
льярдная траектория шара в эллипсе, не пересекающая
отрезка фокусов, может, самое большее, заполнить всюду
плотно кольцо между софокусными эллипсами r (внешняя
rраница кольца) и r с (внутренняя rраница кольца), но
никоrда не попадет внутрь области, оrраниченной эллип-
сом (рис. 4.19, а). Более Toro, если Q произвольная об-
ласть (а не только эллипс), r .......... ero rраница, а r с какая-
ТО каустика в Q, то почти любая непериодическая бильярдная
74
Пlраекторuя, касающаяся каустики r с, всюду плопzно за-
полняепz область между бортом бильярда r и этой каусти-
кой (<<кривое кольцо»; рис. 4.19, б) *).
Более прост такой факт, замеченный В. Б. Минасяном.
Оказывается, если задана в ы п у к л а я кривая 'V и тре-
буется найти все кривые r, для которых у является каусти-
кой, то их можно получить следующим образом. Обозна-
чим 1 (у) длину кривой у и зафиксируем число 8, превосходя-
щее 1 (у). Тоеда r==rs соспlоит из следуюu;eсо множества то-
чек А: если из А провести ка-
сательные отрезки к "(, найти Л. А
сумму длин этих оmрезков и S
части кривой "(, заключенной
между их концами, то эта
CY.AtMa будет постоянной и
равной 8 (рис. 4.20). Указан-
ный факт объясняется следую-
щим образом.
Если мы накинем на кри-
вую "( веревочную петлю дли-
ны 8, 8>1 ("(), и натянем ее в точке А, то две касательные
АХ и А У ИЗ точки А к кривой 'V вместе с оставшейся частью
веревки между ТОЧI{ами касания Х и У, плотно обтяrиваю-
щей у, в сумме дадут 8. Проведя через точку А прямую 1,
образующую равные уrлы с отреЗI{ами ХА и У А, ВИДИМ, что,
в силу выпуклости кривой "(, при малом перемещении вле-
во или вправо веревочной петли в натянутом состоянии точ-
ка А сходит с прямой 1 и оказывается в той же полуплоско-
сти относительно прямой 1, В которой расположена вся кри.'
вая 1'. Это и означает, что точка А перемещается также по
в ы п у к л о й кривой r, а поэтому прямая 1 является Ka i
сательной к r в точке А. Следовательно, ХА и А У два
последовательных звена б и л ь я р Д н о й траектории
внутри кривой r, касающиеся кривой 1'. Таким образом,
А"
a+b+u+z=c+d+z+x=S
Рис. 4.20
*) Доказательство этоrо факта довольно просто, но не совсем
элементарно. Достаточно доказать, что множество точен отражений
типичной бильярдной траектории всюду плотно на внешней rрани-
де r, а дальше действовать, как и в случае круrлоrо бильярда. OK(t..
sывается, кривую r можно отобразить взаимно однозначно и взаимно
непрерывно на окружность так, что последовательные точки отр а.
жения бильярдной траектории перейдут в равноотстоящие точки 11 [l
окружности (это утверждение носит в математике, в более общеj'[
формулировке, название «теорема Данжуа»). Если множество то..
чек на окружности всюду плотно ее заполняет, то и множеств']
прообразов ---- точек излома рассматриваемой бильярдной траеRТОрИlI
на кривой r ..... заполняет кривую r также всюду плотно,
75
действительно каустика для бильярда внутри области,
оrраниченной полученной кривой r.
Подведем итоr полученным сведениям о траекториях
эллиптическоrо бильярда (правда, не все факты нами дока-
заны). Бильярдная траектория в эллипсе либо периодиче-
ская (замкнутая......... к этим тр аектор иям относятся и две
оси эллипса), либо неперuодuческая. Во BTOpO:t\1 случае
выделяются траектории, звенья которых поочередно про-
ходят через фокусы ........ их поведение описывается вторым
бильярдным свойством. Остальные не-
периодические траектории всюду плот-
но заполняют либо кольцо между эл-
липса11И r и r с, либо область l\tIежду
двумя ветвями софокусной rиперболы
Н с (именно всюду плотность мы и не
f C O доказали).
В заключение параrрафа укажем на
интересную связь между бильярдом в
эллипсе и свободным движением MaTe
риальной точки на поверхности элли-
псоида. Движение частицы на эллипсои-
де происходит по кратчайшей кривой........
Рис. 4.21 так называемой ееодезuческой. Будем уст-
ремлять малую ось эллипсоида к нулю;
тоrда эллипсоид в пределе превратится в эллипс, а тра-
ектория частицы по rеодезической на эллипсоиде.......... в
бильярдную траекторию в этом эллипсе (рис. 4.21). При
этом разумно считать, что эллипс двусторонний и при каж-
дом отражении бильярдная траектория переходит с одной
стороны эллипса на друrую, двиrаясь прямолинейно (по
rеодезической) .
Эта идея сведения бильярдной задачи к задаче про reo-
дезические на «раздутом» бильярде, и обратно.......... задачи
про rеодезические к бильярдной ......... иrрает большую роль
при исследовании дина11ИКИ бильярда для областей, от-
личных от внутренности эллипса, и является l\10СТИКОМ,
связываIОЩИМ теорию динамиче ких систем G дифференци-
альной rеометрией.
Читателям, которым нравятся физико-математические
парадоксы, предлаrаем в завершение «эллиптической» темы
подумать над следующим парадокеом, на первый взrляд
опроверrающим второе начало терl\Iодинамики: в теплоизо-
лир ованной систеrvtе тел н е M о Ж е т происходить пере-
дачи тепла от тела более холодноrо (или той }ке температу-
ры) к телу более rорячему.
76
к парадоксу приводит построение такой теплоизолиро-
ванной системы, в которой, напротив, одно из тел с перво-
U u
начально одинаковом температурои начинает остывать, а
второе........ наrреваться. Рассмотрим конструкцию, показан-
ную на рис. 4.22 и состоящую из двух зеРI{альных половин
(Ее и AD) двух соФокусных ЭJ!ЛИПСОВ И соеДИНЯI-ОЩИХ их
прямолинейных зеркальных переrородок АВ и CD (А и
D концы малой полуоси внешнеrо эллипса, В и а........
BHYTpeHHero)..B фокусах Ff, Р 2 ПО 1ещены два точечных иа-
точника тепла, первоначально имеющие р а в н ы е тем-
пературы; зеркальные стенки конструк- ""......"
ции отражают все лучи (без KaKoro- 1/ "
либо поrлощения). Соrласно первому I F, \
бильярдному свойству эллипса, все теп. I \
ловые лучи, выходящие из источника Р у , I / 1
частью отразившись от стенки Ее, час- I / \11 '
тью .......... от стенки AD, попадают в точку А . . 'о. С. I
F 2' Если бы в о е тепловые лучи, исхо- ':i'\ . .:.) 11
дящие из BToporo источника F 2, попа- " .;:
дали бы в точку Fr., то тоrда оба источ-
ника не" меняли бы со временем свою
температуру.
Однако н е в с е лучи из F 2 попада-
ют в Fi. На рис. 4.22 изображена одна из Рис. 4.22
траекторий луча F 2 MNF 2 , который ПОG-
ле отражения в точке М внешнеrо эллипса попадает в пе-
реrородку De (двиrаясь при этом в направлении фокуса
Fi), отражается от нее в точке N и ... попадает снова в
F 2! То же самое происходит и с лучами, попадающими ана-
, чала в переrородку, отражающимися от нее и после BToporo
отражения от внешнеrо эллипса снова попадаlОЩИМИ в
F 2 (на рис. 4.22 изображена одна из траекторий, отражаю-
щаяся от переrородки АВ).
В результате тело Р 2 получает, кроме лучей от тела Р1.,
часть своих собственных лучей, и поэтому наЧИIlает Harpe-
ваться; тело же Fj остывает. Налицо явное нарушение вто-
poro начала термодинамики. В чем же дело? (В качестве
указания к разrадке парадокса предлаrаем читателю за-
менить точечные источники Р! и Р 2 маленькими кружками
и посмотреть, как проходят отраженные лучи вблизи фо-
кусов) .
77
5*. Задача об освещении
невыпуклой области
Простые rеометрические свойства эллипса,
описанные в предыдущем параrрафе, MorYT быть использо-
ваны при исследовании следующеrо вопроса: каким наи-
меньшим количеством tnочечных источников света (лампо-
чек) МОЖНО осветить BflympeHHocmb оера"fluчеНflОЙ обласпlU Q
на плоскости? rранида aQ области Q представляет собой
Рис. 5.1
Рис. 5.2
замкнутую несамопересекающуюся кривую L на плоскости:
таким образом, двиrаясь по кривой [, мы будем оставлять
область Q все время по одну GTOPOHY от [.
Конечно же, если область Q является выпуклой (т. е.
с каждымИ ДВУl\1Я ее точками А, В весь отрезок АВ принад-
ле.я{ит области), то достаточно о Д н о й лампочки, которую
можно поместить в произвольном месте (рис. 5.1). Действи-
тельно, если О........ лампочка, а А ........ произвольная точка об-
ласти Q, то луч ОА освещает точку А; таким образом, в G е
точки области Q освещены лампочкой о.
А если область Q н е в ы п у к л а? Тоrда одной лампоч"
ки для освещения области может уже не хватить: на рис. 5.2
L Рис. 5.3
Рис. 5.4
лампочка О не освещает ни одной точки А, лежащей в за-
· штрихованной области. Впрочем, на РИG. 5.2 мы просто не-
удачно выбрали местоположение для лампочки: точка на
рис. 5.3 уже выбрана более удачно, и лампочка О освещает
всю область Q.
Если область Q содержит такую точку О, и которой
«видны» все остальные ее точки (как, например, области
78
на рис. 5.3 и 5.4) , то область Q наэьmают звездчаmой, а
точку О «точкой видимости». К звездчатым областям
относятся, в частности, все выпуклые фиrуры. Ясно, что
л ю б у ю звездчатую область можно осветить одной лам-
почкой (rде ее следует поместить?).
Предполо}ким теперь, что Q НtLэвездчатая область:
никакая ее точка О не является «точкой видимости». Тоrда \
одна лампочка, в какое бы место области мы ее не помести-
ли, полностью ее н е о с в е т и т: для освещения Q нужно
больше одной лампочки. Можно предположить, что для
освещения хватит к о н е ч н о l' О числа лампочек, как
,бы сложно ни была устроена область Q, лишь бы только ее
rраница L==aQ не имела точек излома, или, каи rоворят,
была достаточно rладкой. Это подтверждается строrой тео-
ремой, которую мы приведем в конце этоrо параrрафа в
ней даются необходимые и достаточные условия на струк-
туру rраницы. Эти условия в математике коротко называ-
ются условиями еладкостu ераницы.
Пока что нами ничеrо не было сказано о бильярдных
свойствах области Q и о связи сформулированноrо вопроса
об освещении с бильярдами.
Мы уже знаем, что движение луча света при отражении
от rраницы области осуществляется по бильярдному закону
«уrлы падения и отражения равны». Поэтому, чтобы пос-
тавленный вопрос об освещении приобрел новое звучание,
будем считать, что ераница области Q ........ зеркальная, и лю-
бой луч света при попадании на ераницу оmраЖJаеmоя от нее
по бильярдному закону. При такой постановке рассматри-
ваемая задача, о одной стороны, должна, по-видимому, уп-
роститься, поскольку мноrие невыпуклые области, rрани-
цы которых раньше «поrлощали» свет и которые не моrли
быть освещены одной лампочкой, теперь, обладая зеркаль-
u u
нои rраницеи, позволяют лучам проникать в «запретные»
зоны и освещать их; а, с друrой стороны, задача должна
усложниться, так как теперь мы вынуждены следить за всем
бесконечным ходом каждоrо луча, исходящеrо из точечноrо
источника.
Итак, считая G этоrо момента и до KOHЦ параrрафа об-
ласть Q зеркальной, попробуем дать предварительный, rи-
u u
потетическии ответ на исходныи вопрос.
Ответ 1. Для освещения любой оеранuченной области Q
дОСfпаточно одной лампочки.
Обсудим этот ответ. Мы дали ero в надежде на то, что
u U
некоторым луч, выпущенныи из лампочки, рано или позд-
но, после MHoroKpaTHbIX отражений от rраницы, попадет
79
в наперед 33Д3IIПУIО точку об. !асти. r1.зпр!It t':р еСЛJ:l Q - .....
невыпуклый МIIоrоуrольннк (рис. 5.5), то лучи, выпур ен"
ные из произвольноrо то ечноrо источника О внутри Hero,
полностью осветят этот мноrоуrольник, как бы «хитро»
ни была устроена ero rраница. Это утверждение про MHoro-
уrольник все специаЛИОТБI-математики, занимающиеся
бильярдными проблемами, считают справедливым, хотя
CTporo оно до СИХ нор не доказано. (H KOTopыe вопросы,
связанные (3 бильярдами в мноrоуrольниках, приводят
порой к неО}I{иданным результатам.......... об
этом подробнее рассказано в четвертой
чаети книrи.)
Мы же будем считать теперь, что
rраница aQ не имеет изломов, т. е. в
u
каждои точке rраницы можно провести
касательную. Казалось бы, если для ос-
вещения невыпуклоrо мноrоуrольника,
как было сказано (но не доказано), хва-
Р 5 5 тит одной лампочки , то для области Q, \
ис. .
u
получающеися из мноrоуrольника
«скруrлением» ero вершин, одной лампочки хватит тем бо...
JI ее.
Однако rипотетический ответ 1, являясь (с большой Bepo
ятностью) верным для мноrоуrольников, неверен в общем слу-
чае....... для областей о rладкой rраницей. В замечательном
а /
о
Рис. 5.6
примере области, для освещения которой нужно MHoro лам-
почек, используется только знание Toro, что выпущенный
из одноrо фокуса эллипса луч света после отражения прой..
дет через второй ero фокуо, а луч, выпущенный не из фа..
yca, никоrда не пройдет ни через один фОКУО (рио. 5.6, а, б).
Сформулируем существование такой области в виде утверж-
дения.
у т в е р ж Д е н и е 1. Для любоео наmуральн.оео n
существуепl область с еладкой ераницей, для освещения Ко-
торой необходимо более n точечных источников (ламnо-
Ч . .
80
r;остроим ЛЕНО эту область 'j и докаж l\tl для нее утверж-
дение 1. Построение производится в нескодько этапов *).
Этап 1 о Рассмотрим верхнюю половину ЭЛJlипса с боль-
шой осыо 118, дополненную двумя «мочками», оrраниченны-
ми полуокружностями, соеДИНЯIОЩИМИ фокусы Р! и 1;2 с
точками А и В (рис. 5.7). Полу-
ченной области Qf Д::lДИМ назва.
ние «телефон».
Л е )\1 м а 1. Нuкакпй луч, А
выходящий из левой мочки те..
лефона Qi, НИКОёда не попадет . ЛеОаR
на оmрезок FiF 2 . ночка
Д о к а 3 а т е л ь с т в о. Рис. 5.7
Действительно, рассмотрим пер-
вое отражение луча, выпущенноrо из левой мочки (рис.
5.8, а). Как падающий, так и отраженный лучи лежат
в н е 6 FfXF 2 , поэтому отраженный луч не пересечет
отрезок FfF 2 . Если У ....... вторая точка отражения
f1
о
Рис. 5.8
(рис. 5.8, б), то падающий и отраженный лучи в точке У
лежат в н е 6FfYF2 и опять-таки не пересекают отрезок
фокусов FfF2. Вообще, если первоначально выпущенный
Из мочки луч отражается от точки Z rраницы iJQ17 лежащей
на эллипсе (т. е. выше прямой Р 1 ,Р 2 ), то он и отраженный
луч обязательно расположены вне 6.FIZF2' Следовательно,
u u
выпущенныи из левои мочки луч в конце концов попадет в
правую мочку, ни разу не пересекая отрезка фокусов FiF 2 ;
после одноrо или нескольких отражений в правой мочке
луч до вторичноrо попадания в левую мочку также ни разу
не пересечет отрезка FfF2, что следует из приведенноrо
выше расоуждения И полной равноправности обеих 10чек.
Это и доказывает лемму 1.
Приведем еще одно столь же простое, но более изящное, дo
казательство леммы 1. Отбросим мысленно нижнюю fраницу об
*) На каждом 9тапе строится область, rраница которой в мес-
тах! соединения криволинейныХ! и прямолинейных частей эатем
«сrлаживается» (91'0 особо не оrоваривается в дальнеЙlпем).
81
пасти а1 (обе полуокружности мочек и отреэоо фокусов), и допол..
ним телефон нижней половиной эллипса. Мы не знаем, как луч
света ведет себя в мочке, но как только он выходит из нее в верх..
нюю половину эллипса, будем считать, что он отразился от нижней
(фиктивной) половины эллипса в соотвеТСТВУlощей точке С (рис. 5.9).
Но, как МЫ знаем из 4, любая бильярдная траектория в эллипсе,
одно ввено которой не пересекает РIР2' обладает тем СВОЙСТВОМ,
ЧТО И В С е ее звенья не пересекают отрезка фокусов Р 1 Р 2 (поскольку
все звенья касаются софокусноrо эллипса, содержащеrо отрезок
Р 1 Р 2 внутри себя). В частности, этим свойством оБЛ3Д310Т звенья
в верхней части эллипса, которые в действительности являются
звеньями траектории луча света, выпущенноrо из левой мочки;
этим доказательство леммы 1 и завершается.
о'
1
Рис. 5.9
ЛеВая ЛраlJая
ноч/(а НОЧКQ
Рис. 5.10
Этап 2. От телефона О! леrко перейти к зеркальной об-
ласти Q2, которая не может быть освещена одной лампочкой.
Построим сначала область Q , изображенную на
рис. 5.10; она отличается от области Qi тем, что середина
отрезка FiF 2 заменена неrлуБОI<ОЙ «ямкой» в виде полуок
ружности.
Л е м м а 2. Еоли лампочка находится в/одной из моче1\,
или же в ямке, п10 она не ocвeи aeт область Q полностью.
Д о к а 3 а т е л ь G Т В о. Если лампочка расположена
в одной из мочек, то ни один луч, исходящий из нее, не пе
p ceKaeT отрезка Р 1 Р 2 по лемме 1 и тем самым не попадает
в ямку. Следовательно, в этом случае ямка вообще не ос-
вещена.
Пусть теперь лампочка О находится в ямке. Предполо-
жим, что какой-то луч 'У, исходящий из лампочки, после
HeKoToporo числа отра>кений от rраницы aQ попал в мочку,
для определенности в левую. Есл точка Р мочки освещена
этим лучом, то перенесем лампочку О из ямки в ТОЧКУ Р.
Тоrда один из лучей, выходящих из лампочки Р, rеометри.
ческая траектория KOToporo совпадает с траекторией луча у
(изменено только направление движения), попадет в
ямку, и освет ит точку О В ней. Это противоречит лемме
1 ......... никакой л уч, исходящий из точки Р, не может .попасть
в ямку. Лемма 2 доказана.
82
I ,
3 а Д а ч а 5. '. Можно ли область Оl осветить тремя лампоч-
ками?
О т в е т, Можно, и даже напрямую (т. е. без отражениА от
,
rраницы) ...... ПОСКОЛЬКУ О1 можно представить в виде объединения
трех звездчатых областей (каких?).
3 а д 8 Ч а 5.2. l\\ожно ли область Q; осветить о Д н о й лам-
почкой?
О т в е т. lИ о О/СН, О . У к а з а н и е, Поместите лампочку в
точку М ...... середину дуrи эллипса (рис, 5.11 t а),
М М
fj
Рис. 5.11
Реш е н и е. Для доказательства Toro, что лампочка; поме-
,
щенная в середину М дуrи эллипса, осветит всю область Оl, ДО-
статочно доказать, что полностью будут освещены обе мочки те-
,
лефона (вся остальная часть области Ql освещается лампочкой
напрямую),
Рассмотрим для доказательства набор специально выбран-
HЫ лучей, выходящиJC: из М. Первый ЛУЧ выберем выходящим из
М в сторону центра 01 левой мочки (рис. 5.11; б). Проходя через
центр полуокружности 01' луч МО 1 отражается от нее в точке К 1
и движется в противоположном направлении К1М' попадает в
точку М, отражается от дуrи эллипса в этой точке, проходит затем
через центр 02 правой мочки (полуокружности) и, отразившись
от правой ПОЛУОКРУЖНОСТИ в точке К2' движется опять в обратном
направлении К2М' чтобы после отражения в точке М начать снова
двиrаться по МК 1 . Таким образом, МК 1 МК 2 М........ периодическая
бильярдная траектория.
В качестве BToporo луча, выпущенноrо из лампочки М, BЫ
берем такой, который после отражения в точке N 1 левой мочки
пройдет через левый фокус эллипса Р 1 . Такой луч у найдется,
поскольку луч, идущий из М в А .... левый конец большой оси
(рис. 5.11), после отражения попадет в некоторую точку левой
мочки, а луч, идущий из М в К 1 ; отражается в К 1 в обратном Ha
правлении; таким образом, некоторый луч у== М N 1 лежащий
между лучами МА и МК 1; после отражения пройдет через Р 1 .
Далее, луч V отразится от дуrи эллипса (в точке N 2) и попадет
во второй фокус эллипса F 2.
Наконец, рассмотрим все лучи, расположенные м е ж Д у
лучом V==MN 1 И лучом МК 1 . Поскольку лучи у и МК 1 определяют
на правой мочке точки Р 2 и К2' то все лучи между ними заполняют
целиком всю дуrу Р 2 К 2 полуокружности. Соединив Р 2 и К 2 отрез
ком, находим, что все рассмотренные лучи освещают полностью
cer'MeHT Kpyra Р 2 К 2 (он заштрихован на рис, 5.11, б),
83
.,
Следоват льно, вся правая мочка области О1 полностью ос-
ветцена лампочкой М. Из симметрии следует, что по тем же сооб--
,
ражениям осnещена и вся левая мочка. Итак, область аl полностыо
освещена одной лампочкой, помещенной в точку М. Задача решена.
Переходим к построению области Q2' Область Q2 стро-
ится из двух экземпляров области Q слеДУIОЩИМ обраЗ0М.
В первом экземпляре ----- обозначим ero. Q ----- вытяrиваем
ямку в «трубу» (рис. 5.12, а), а во втором ЭI{земпляре Q ..........
обозначим ero Q ----- вытяrиваем в «трубу» одну из l\10чеI{
а
о
Рис. 5.12
(рис. 5.12, б). Область Q2 получается «склеиванием» об..
ластей Q и Qi по общим отрезкам ХУ их труб (рис. 5.12, в).
Эта область содержит три мочки, одну трубу и одну ямку.
Л е м м 8 3. Область Q2 не .А1-0жет быпzь освещена одной
лампочкой.
Д о I{ а з а т е л ь с т в о. Так как Q2===Qi U Qi, то лам-
почка может располаrаться либо в области QI, либо в облас-
ти Q (отрезок ХУ считаем общим для обеих этих областей).
Разберем отдельно указанные два случая.
Если лампочка находится в области Q и, быть может,
даже ее освещает (см. задачу 5.2), то она никаI{ не MO}I{eT
осветить целиком область Q . Действительно, область Qi
может освещаться исключительно лучами, идущими от лам
почки через трубу ----- все эти лучи пересекают отреЗОI{ ХУ
и попадаJQТ в Q . Однако из леммы 2 следует, что ни ОДИН из
этих лучей не попадает в ямку области Qi. Итак, в первом
случае в области Qi неосвещенным местом является ямк"а.
Если же лампочка находится вIобласти Qi, то лучи, про
никающие в область Q , опять-таки все проходят через тру-
бу, т. е. выходят из бывшей ямки области Q}. И снова, по
лемме 2 получаем, что все эти лучи не попадут в мочки об-
ласти Qt. Итак, во BTOpOl\'1 случае неосвещенным местом об-
ласти Q2 оказываются обе мочки области Qt. Лемма 3 дока-
зана.
84
Этап 3. Сейчас l\1bI rvl0дернпзируем область Q2 и постро-
им область Q, о котороЙ rоворится в утв р)кдении 1.
Для этоrо не будеrvI оrраничивать количество областей
Q , из которых будет построена область Q. Не будем также
подробно описывать построение области Q, а отошлем чита-
теля сразу к рис. 5.13, на котором изображена структура
области Q.
Область Q содержит большое число :мочек и труб, а так_
же одну ямку. Она состоит из объединения областей Qf
,
. . .
ОолаСll1lJ. Q
Рис. 5.13
в каЯ{ДУlО из которых включается часть трубы, оrраничен-
ная обрезком ХУ с соответствующими индексами. Поэтому
если лаl\lпочка О находится в области Qf, то она не может
осветить целиком ни область QI-- 1 (при i> 1), ни область Qi11
(при i<2N), так как лучи, проникающие в эти области из
Qt через соединяющие их трубы, либо не осветят мочек, либо
не осветят ямки. (Подробное доказательство аналоrично
приведеНН011У в лемме 3.)
Следовательно, на каждую область Qf, [==1, 2, . . ., 2N,
нужно для ее освещения н е м е н е е о Д н о й лампочки,
которая должна располаrаться в этой области. Значит, для
полноrо освещения всей области Q HY)I{HO не менее 2N лам-
почек. Поэтому, если 2N>n, то область Q не может быть ос-
вещена n лампочками. Утвер)кдение 1, таКИl\f образом, пол-
ностью доказано.
После сказанноrо мы rvIO}l\eM дать второй rипотетический
ответ на поставленныЙ вопрос о числе лампочек.
Ответ 2. Для освеtцения любой оераfluчеflНОЙ области Q
всееда достаточно КОflечноео числа лампочек.
Построенный пример показывает, что это конечное число
лампочек мо}кет оказаться сколь уrодно большим.
Однако и ответ 2 оказывается HeBepHbIl\11 В действитель-
ности справедливо
у т в е р ж Д е н и е 2. Существует mакая оераflичеН,-
flая область Q*, для освеtцения копzорой необходимо беско-
нечно }Лflоео лампочек.
85
Докажем это утверждение. Рассмотрим рис. 5.13 и от-
бросим в нем всю правую часть, идущую после мноrОТQЧИЯ.
N\ноrоточие на возникшей картинке будет означать тепеРr,
что «телефоны» Q , Q , Qr, . . . продолжаются одинаковым
образом вправо до бесконечности. Как следует из утверж
дения 1, полученную бесконечную неоrраниченную
область н е л ь з я осветить конечным числом лампочеI{.
Однако в утверждении 2 rоворится об оераflичеНflОй области
Q*.
Получить ее из построенной неоrраниченноЙ области
несложно, если применить известный в математике прием
* =:.
Рис. 5.14
«сжатия»: он состоит В том, что вместо одинаковых (кон-
rруэнтных) областей Qf рассматриваются области, убываю-
щие в своих размерах по rеометрической проrрессии, на-
пример, со знаменателем 2. Итак, считаем область 1/ 2Q
вдвое меньшей области Qt, область 1/ 4Q вдвое меньшей
области 1/ 2 Qi и так далее (рис. 5.14).
Полученная в результате область Q* ИI\1еет конечные раз..
меры (по rоризонтали размер примерно вдвое больший, чем
rоризонтальный размер области Q}) и обладает тем свой-
ством, что для ее освещения нужно бесконечно MHoro лам-
почек. Утверждение 2 доказано.
Отметим, что область Q* имеет на rранице о с о б у ю
точку Р; в неи, как rоворят математики, нарушается елад-
кость ераницы. Нетрудно видеть, что никакой луч, выпущен-
ный из произвольной точки области Q*, не достиrает точки
р (объясните, почему).
Для каких 02раничеННblХ областей Q ответ 2 все же
справедлив?
Здесь мы вынуждены вер нуться:к началу этоrо параrрафа
и дать ответ на поставленный вопрос об устройстве rраницы
aQ области Q, которую i'ложно осветить конечным числом
лампочек н а п р я м у ю (т. е. без отражений от rраницы).
Ясно, что ответ на этот вопрос будет одновременно ответом
и на/поставленныЙ вопрос про зеркальную область, посколь-
ку если зеркальную область нельзя осветить конечным ЧИС 4
86
лом лампочек (как, например, область Q* на рис. 5.14),
то и наПРЯI\1УЮ ее осветить нельзя; если }ке область Q мож-
но осветить конечным числом лампочек напрямую, то и
зеркальная область Q освещается тем же (конечным) на-
БОрО1\1 лампочек (а может быть, и меньшим набороr-л).
Выше мы ОТl\fечали, что звездчатая область освещается
ОДНОЙ лампочкой, помещенной в«точку видимости». Любая
оБJlасть, которан может быть разбита на конечное число
звездчатых областей, освещается конечным числом лампочек
напрямую........ по числу звездчатых областей разбиения.
lp
· c f apllHI.J.I1,Q
о
Рис. 5.15
о
ОТСlода следует, что область Q* на рио. 5.14 не может быть
разбита на к о н е ч н о е число звездчатых областей
(объясните, почему). Все дело в том, что rраница aQ*
имеет особую точку Р ....... в ней нарушается rлаДI<ОСТЬ rpa-
ницы. Оказывается, что если в с е точки rраницы области
Q ........ неособые (точное определение см. ниже), то Q может
быть покрыта к о н е ч н ы м числом звездчатых областей,
и тем самым, освещена конечным числом лампочек.
L{адим точное определение неособой точки и приведем
формулировку утверждения о разбиении области на звезд-
чатые множества.
О п р е Д е л е н и е. Точка Р rраницы aQ называется
н е о с о б о й, если, во-первых, через Р можно провести
касательную lp (прямую, имеющую G rраницей aQ только
одну общую точку........ Р), вo втopыx, через близкие к Р точ-
ки rраницы Q также можно провести касательные IQ, и,
B-'!lретьuх, уrол a==IQ lp между касательными lQ и lp ЯВ-
ляется н е п р еры в н о й функцией длины дуrи '-"'QP,
проходящей от точки Q к точке Р по rранице aQ (рис.
5.15, а). Если все точки rраницы неособые, то rОБОрЯТ, что
rраница aQ имеет rладкость С 1 и называют ее С1-rладкой
.,
ераницеu.
rеометрический смысл С 1 -rладкой rраницы aQ состоит
в том, что на малой дуrе .........АВ rраницы все касательные ма-
ло отличаются друr от друrа, т. е. все попарные уrлы меж-
ду ними малы и тем меньше, чем ближе друr к друrу точки
87
А и В (рис. 5.15, б). Это означает, что пересечение Kpyra Dp
с центром Р Е aQ с областью Q мало отличается от пересече-
ния Kpyra D р с полуплоскостью, оrраниченной касательной
в ТОЧI{е Р (рис. 5.15, в).
у т в е р ,И Д е н и е 3. Любая оераниченная оБЛQСfпь Q
с С 1 -еладкой ераницей дQ является объединением конечноzо
числа звездчатых множеств.
Д о I{ а 3 а т е л ь с т в о. Для каждой точки Р области
Q выберем о т к рыт ы й Kpyr *) Dp с центром Р, ц е-
л и к о м лежащий в области Q, если Р ......... ее внутренняя
точка, и пересекающий Q по 3 В е 3 Д Ч а т о м у множест-
ву, если Р лежит на rранице. Последнее можно сделать,
поскольку Р ........... н е о с о б а я точка rраницы и пересече-
ние D n Q мало отличается от пересечения Kpyra D р с по-
луплоскостью, оrраниченной касательной в точке Р
(рис. 5.15, в).
Таким образом, вся область Q оказывается ПОI{РЫТОЙ
бесконечным числом открытых KpyroB D р, центры которых
лежат в Q или на rранице aQ. Из математическоrо анализа
известно, что из этоео nокрып1UЯ можно выбрать конечное ЧИС-
ло элементов (Kpyzoe), также полностью nокрывоющuх вСl0
облаоть Q (поскольку Q......... замкнутое * *) и оrраниченное
множество на плоскости). Рассматривая пересечения этих
KpyroB с областью Q, мы видим, что они являются з в е э д-
ч а т ы м и множествами. Таким образом, получаем покры-
тие области Q конечным числом звездчатых множеств, что и
требовалось доказать.
Сформулируем окончательный результат в виде тео-
ремы.
Т е о р е м а. Зеркальная область Q, оzраниченная зам-
кнутой кривой L без изломов (т. е. lпакой, в каждой точке
которой можно npoeeCfпu единственную касатеЛЬНУ10) , мо-
оюет 6ыть освещена (и даже напрямую) конечным наборо.м
лампочек, если L является кривой еладкости С 1 . Если же хо-
тя бы одна точка кривой L являетоя особой, КонеЧflоео на-
бора лампочек для освещения области Q может не хва-
титh.
*) То есть Kpyr без rраницы.
**) Множество называется за,Attкнуmbl.Аt, если все ero предельные
точки принэдлежат самому множеству. Таким множеством являет-
ся, в частности, область с rраницей. (Напомним, что предельная
точка множества S это такая точка, в любой окрестнос'f.И которой
расположено бесконечно MHoro точек множества S.)
88
6. эI{стремалыIеe свойства
бильярдных траекторий.
ПРИНЦJfП Ферl\fа и теорема БИРI(rофа
Начнем параrраф о ответа на следуюшиЙ воп-
рос, уже поставленный в 4.
В о про о. Ь'слu 'У......... проuзвольная l(,рuвая на J'lЛОСКD-
оти, А u В ......... nZOS1.1(,U, лежаu uе по одну сп10РОnУ 0111 , то
еде оледует вblбра;nь ,почку М на кривой '\', чтобы сумма
АМ+ВМ длин О.mреЗКО8 АМ и ВМ была .iНUflllмаЛЫiОЙ . . .
или максимальной?
Поясним предварительно, почему в вопросе фиrурирует
как .минимум суммы АМ+ВМ, так и ее максимум.
z-
м l
/у '-'8 y
/ °6
А '
Рис. 6.2
Рис. 6.1
Если кривая "r обращена своей выпуклостью в сторону
точек А и В (рис. 6.1), то для траектории АМВ нетрудно
опять вывести «принцип наименьшеrо пути» (справедливый
в случае, коrда "r прямая): путь АМВ кратчайший, если
отрезки АМ и ВМ образуют с касательной к кривой у
в точке М равные уrлы. Действительно, вся кривая l' ле-
жит по одну сторону от своей касательной 1, а ТОЧI{И А И
В ......... по друrую, стало быть, для произвольной точки М' Е '\',
отличной от М, имеем
АМ' + М'В > АМ +МВ.
Однако, если "r обращена к точкам А и В не выпуклостью,
а воrнутостью (рис. 6.2), то приведенное рассуждение не
проходит: кривая "r вместе с точками А и В лежит по одну
сторону от касательной 1 и выписанное выше неравенство
становится неверным. Сейчас вы увидите, что от суммы
АМ+МВ нельзя требовать только ее минимальности, а
правильно rоворить об экстремальности, подразумевая так-
же друrой крайний случай......... максимальность суммы АМ +
+МВ.
Итак, мы ищем на кривой т таI{УЮ точку (или точки) kl,
чтобы сумма расстояний от двух заданных точек А и В,
лежащих п о о Д н у сторону от 1', была Э J{ с т р е м а л Ь-
Н О Й (минимальной или макси:мальной).
89
Если l' ........ эллипс С фокусами А и В, то в качестве точки 1\1
МОЖНО взять любую ТОЧКУ эллипса: сумма АМ +МВ здесь
всеrда одна и та .iKe. Если же V ...... не эллипс с фокусами А
и В, то рассмотрим для каждоrо числа s, большеrо длины
отрезка АВ, множество rs таких точек М, дЛЯ которых
AM+MB==s. Тоrда rs........ эллипс с фокусами А и В, а
fHq}l{eCTBO всех таких эллипсов {rs} .образует семейство
С о Ф о к у с н ы х эллипсов: чем больше s, тем больше
размеры этих эллипсов и меньше их эксцентрисите ы.
В прямоуrольной системе координат Оху софокусные эллипсы
с центром О записываются единой формулой, вависящей от одноrо
параметра t:
х2 у2
а 2 + t + Ь 2 + t == 1 ,
rде а и Ь фиксированные числа. То, что ДЛЯ разных t эти эл..
липсы имеют одинаковые фокусы, следует из рис, 4.2 и из постоян..
ства разностей квадратов полуосей:
а 2 --Ь 2 == (а 2 + t) -- (Ь 2 + t),
поскольку все эти разности pa Hы 02....... квадрату расстояния от
центра до фокуса эллипса (докажите это); при t==O получаем эллипс
с полуосями а и Ь и эксцентриситетом е==с/а. у эллипса, внутри кото..
poro расположен софокусный эллипс, эксцентриситет меньше, так
как величина с У них один акова, а 'у BHYTpe HHero эллипса большая
полуось меньше (e2==c/Ya 2 +t 2 > ef== с/У a 2 +tf при t 2 < ti).
Докажем, что искомой экстремальной точкой М (если
она существует) на у лоляе/пея mакая точка, в которой один
из эллипсов r $0 укаЗQflНО20 семеЙСfпва касается кривой у.
а
,
6
в самом деле, если кривая l' по обе стороны от точки
касания М лежит в н е касающеrося ее эллипса r $0
(рис. 6.3, а), то сумма АМ+ВМ МllflUМйЛЬНй, поскольку лю-
бая друrая точка М' на l' лежит одновременно на софокус-
ном эллипсе r $1 CSf >80, т. е. sl==AM' +М' B>so==AM +МВ.
Если же кривая r вблизи точки М лежит в. н У т р и
касающеrося ее в М эллипса r $0 (рис. 6.3, б), то длина ло-
90
маной АМВ, равная 50, больше чем длина любой друrой ло
маной AJ\lI' В, так как точка М' лежит на софокусном эл
липсе rs с Si<So.
«Смеш 1 анный случай», изображенный на рис. 6.3, 8,
не дает ни минимума, ни максимума. Экстремум следует
понимать, как сказано выше....... по сравнению с б л и з к и-
м и к М точками (такой экстремум называют локальным).
Если предположить, что мы умеем строить семейство
софокусных эллипсов и находить точки касания эллипсов
u u
этоrо семеиства с кривои 1', то утверждение можно считать
доказанным.
Для наших целей вполне достаточно TaKoro (принци-
пиально возможноrо, но с трудом осуществимоrо на прак-
тике) способа отыскания локальных минимумов и максиму-
мов длины ломаной АМВ, и мы сейчас извлечем из этоrо
способа замечательные следствия.
Из первоrо бильярдноrо свойства эллипса следует
Общий принцип ЭКGтремальности
б и л ь я р Д н о й т р а е к т о р и и. Если ломаная А МВ
о данными концами А и В и точкой излома М, принадлежа-
щей данной кривой 'V, имеет наименьшую или наибольшую
(Т. е. экстремальную) длину среди всех б л и з к и х к
u u
неи двузвенных ломаных с точками излома на кривои у
И Т е м и ж е концами А и В, то эта ломаная является тра-
екторией бильярдноrо шара (бильярдной траекторией),
ведущей из точки А в точку В после отражения от борта,
имеющеrо форму кривой 1'.
Д о к а э а т е л ь с т в о. Кривая l' в точке М касается
kakoro-то эллипса r s с фокусами А и В. Следовательно, ка-
сательная 1 к кривой Оу в точке )\,1 является одновременно и
ка(!ательной к эллипсу r s . Но уrлы, образованные звенья-
ми АМ и ВМ ломаной AM G касательной 1 к эллипсу, рав-
ны между совой. Это и означает, что АМВ бильярдная
траектория G бортом 'V, что и требовалось доказать.
3 а Д 8 Ч а 6.1. Привести пример кривой "У, показывающиЙ,
что обраrцение принципа экстремальности бильярдной траектории
неверно: может случиться TaK j что б и л ь я р Д н а я траектория
АМВ не является ни локально минимальной, ни локально MaK
симальной.
3 а д а ч а 6.2. Доказать, что если кривая l' в ы п у к л З,
Т. е. целиком лежит по одну сторону от своей касательной, то об
раrцение принципа экстремальности бильярдной траектории спра
ведливо: любая бильярдная траектория А М В в этом случае имеет
или локально минимальную, или локально максимальную длину.
Приведем пример, поI<а3ыающий,' что для в ы п у К-
u u
Л О И кривом l' MorYT реализовываться о Д н о в р е м е Н-
91
н о и минимальные, и лаксимальные бильярдные двухзвен-
вые ломаные АЛ1В. Пусть у ......... окружность, А и В ....... фикси-
рованные точки внутри этой окружности. Тоrда из семей-
ства {l"s} софокусных эллипсов с фокусами А и В выделя-
ются четыре эллипса r SI ' r S2' r SЗ' r s,' два из которых
касаются окружности 'V вНУlпреННИА! образом пусть это
эллипсы r s и r s , а два эллипсы r s и r s внеш-
1 2 . 3
ним образом. Возникшие четыре точки касания M:i, М 2,
lVl з , Л1 4 (рис. 6.4) являются точками столкновения с бортом
'\' бильярдноrо шара, который из точки А после одноrо удара
М (тах) О борт попадает в точку В,
3 И доставляющие: точки M 1 И
М 2 локальный IИНИМУМ
длины ломаной АМВ, точки
М з и М 4. локальный мак-
симум этой длины.
Принцип экстремальности
бильярдной траектории яв-
ляется частным (и простей-
шим) случаем одноrо из основ-
ных принципов классической
механики и оптики nринцu-
па наUнlеньшесо действия, или ЭКСlпреАtаЛЬНО20 nринципа Фер-
ма (в оптике он носит название nринцuпа Мопертюи). В оп..
тике принцип Ферма (Мопертюи) состоит в том, что свет вы-
бирает из всех возможных путеЙ, соединяющих две данные
точки, тот путь, который требует н а и м е н ь ш е r о вре-
мени для ero прохо}кдения. Применительно к бильярду
этот принцип мол{но сформулировать так: бильярдный шар
«умный» И выбирает самый короткий из всех возможных
путей ( 1Ы считаем раз и навсеrда скорость бильярдноrо ша-
ра постоянной, поэтому минимальность длины ero тра-
ектории эквивалентна минимальности времени ero дви}ке-
ния по этой траектории). Фактически этот принцип для
бильярдноrо шара нами обоснован выше чисто математи-
чески. Оказывается, всю классичеСКУI-G механику можно
строить как rеометрическую оптику MHoroMepHoro прост-
ранства, основываясь именно на принципе Ферма, носяще-
ro в механике название «принцип rамильтона» (подробнее
об этом см., например, книrу В. и. Арнольда «Математи-
ческие методы классической rvlеханики» (М.: Наука, 1979,
с. 217 и далее)). Но эта аналоrия оптики и механики не-
элем нтарна (она требует развитой техники дифференци-
альноrо исчисления) и останавливаться на ней мы не будем,
а обратимся к более простой и наrлядной аналоrии.
92
r
114 (таоо)
Рис. 6.4
3 а Д а q а 6.3. Докажите nранцип обратимости: если биль-
ЯрДНЫЙ шар попал из точки А в точку В после нескольки OTpa
}J{ений ОТ борта l' бильярдноrо стола. то при ero движении из точки
В с противоположной начальной скоростью ша р попадет в точку А j
двиrаясь точно по тому же пути, но в обратном направлении.
Принцип обратимости мы уже использовали в рассуждения 5.
Прпнцип Ферl\iа позволяет чисто математически доказать
закон Снеллиуса ...... Декарта о преломлении луча света на
rранице двух оптических сред Q разной плотностью (<<си-
нус уrла падения луча света в первой среде и синус уrла
преломления во второй среде относятся как оптические
плотности этих сред»; рис. 6.5), а также ДОI<аэать, что от-
u
ношение оптических плотностен 1
двух сред равно отношению скорос- О,
тей движения света в них. На этих I
доказательствах мы также не будем : : : : : : : : : : 1 :::::::::
. . . . . . 8.. . . . . . . . . . . . .
эдесь останавливаться, они увели . . . . . . . .
бы нас далеко от бильярдной те:мы.
Отметим лишь, что принцип Фер-
ма, в отличие от nринципа причин-
ности в физике (суть KOToporo сос-
тоит в том, что свет последователь-
u
но идет из однон точки простран-
ства в друrую, затем в следующую и
Т. д.) совсем иначе объясняет причину явлений в природе.
Вместо причинной обусловленности, коrда из одноrо на-
шеrо действия вытекает друrое, из Toro........ третье и т. д.,
u
этот принцип rоворит следующее: в даннои ситуации свет
выбирает путь G наименьшим, или, правильнее, с экстре-
мальным временем прохождения. Но к а к удается свету
выбирать такой путь? Р а э в е Д ы в а е т он что ли сосед-
ние пути и сравнивает их потом друr с друrом? в некотором
смысле т а к и про и с х о Д н т. Эта способность света
связана с понятием длины волны и поэтому ее нельзя по-
нять в рамках rеометрической ОПТИI{И; длина волны, rрубо
u
rоворя, есть тот отрезок впереди ле)кащеrо пути, которым
свет может «почувствовать» И сравнить G соседними путя-
ми *). Бильярдный шар является как бы математической
... ........... .....
8tn 01 п !
sin 92. П2. v 2
Рис. 6.5
*) Ответ на поставленный вопрос о свете дает квантовая меха-
ника, а ответ на вопрос, почему при отражении луча света от зерка-
ла время ero движения от источника А до детектора В также экстре-
мально (иными словами, почему при отражении от зеркала уrол
падения равен уrлу отражения) дает КЭД...... квантовая электродина-
мика (см. недавно вышедшую в «Библиотечке «Квант» книrу извест-
Horo американскоrо физика Ричарда ФеЙнмана «КЭД. Странная те-
ория света и вещества» (вып. 66. М.: HaYI{a. 1988).
93
абстракцией CBeroBoro луча, во внутреннее состояние. кото-
рой заложена «длина ВОЛНЫ», позволяющая шару выбирать
кратчайший (экстремальный) путь среди всех близких
(<<виртуальных», т. е. возможных) путей.
Принцип Ферма приводит также к так называемому
принципу Fюйееflса, который, в свою очередь, объясняет,
почему кратчайшими путями распространения света явля-
ются л учи. Обсудим HeMHoro этот момент с математиче-
ских позиций.
Пусть в точке А расположен источник света. Рассмот-
рим множество всех.точек Х, дО которых свет из точки А
ФА (t +1')
А х
а
Q
Рис. 6.6
l\10жет дойти З3 время, не большее заданноrо t. rраница
ФА (t) этоrо множества называется волновым фронтом точ-
ки А через время t и состоит из точек, до которых свет может
дойти за время t и не может дойти быстрее. Мы не предпо-
лаrаем, что среда, в которой распространяется свет, одно-
родная, поэтому волновой фронт ФА (t) не обязательно яв-
ляется окружностью. Между волновыми фронтами, сооТ-
ветствующими разным значениям t, имеется замечательное
соотношение, открытое rюйrенсом, которое и носит назва-
ние принципа rюйrенса. Этот принцип мы сформулируем
в виде теоремы.
т е о р е м а r ю й r е н с а. Рассмотрим волновой
qJpOHm ФА (t) lпочкu А через время t. Построим для ка3ltдой
1почки Х этоео фронта, считая их источниками света, вол-
новой фрОН1n Фх('t) через время Т. Тоеда волновой фронт
Ф A(t+T) I1l0чки А через время t+T будет оеuбать все построен-
ные фронты Фх(Т) (Х Е ФА (t); рис. 6.6, а).
Д о к а 3 а т е л ь с т в о. Рассмотрим точку У на фрон-
теФ А (t+T) точки А через время t+T. Тоrда существует tfYTb
из А в У, по которому время распространения света p B1io
{+Т, и нет более KopOTKoro пути. Рассмотрим на этом ути
точку Х, дО которой свет идет время t. Никакоrо б о JI е е
к о р о т к о r о пути из А в Х не может быть, так как в
противном случае путь из А в У не был бы кратчайшим (ero
94
можно было бы укоротить). Значит, точка Х лежит на фронте
ФА (t). Точно так же, путь ХУ свет ПРОХОДИТ за время т,
и из точки Х в точку У нет более KopoTKoro пути. Следова-
тельно, точка У лежит на фронте Фх('t) точки Х за
время t'.
Докажем, что фронты ФА (t+'t) И Фх(-r) к а G а ю т с я
друr друrа в точке У, а не пересекаются. Если бы они пере.
секались (рис. 6.6, 8), то В некоторые точки фронта Ф А (t+'t)
луч Mor бы из точки Х добраться за время, меньшее 't, а
значит, из точки А ....... за время, меньшее t+'t. Это проти-
воречит определению фронта Ф А (t+'t). Итак, фронты
Фх('t) И ФА (t+'t) К а G а ю т G Я друr друrа в точке У,
что и требовалось доказать.
Принцип rюйrенса приводит к двум описаниям процессэ
распространения света. Во первых, из Hero следует, что дос-
u
таточно следить за лучами, т. е. кратчаишими путями рас-
пространения света. В этом случае локальный характер
распространения света задается ero вектором скорости. Ес-
ли направление луча известно, то величина вектора СКо-
рости задается свойствами среды. А а друrой стороны, мож-
но следить за волновым фронтом и исследовать ero пове-
дение.
Бильярдный шар как бы сочетает в себе оба принципа
u u
rеометрическои оптики........ прямолинеиность ДВИ)l{ения луча
света в однородной среде и осyuцествление выбора среди
всех возможных близких друr к друrу траекторий экстре-
мальной, определяемой касанием волновоrо фронта........ в
данном случае это один из софокусных эллипсов С бор-
том бильярда.
Это сочетание двух принципов rеометрической оптики
позволяет доказать одну важпую и сложную теорему о пе-
риодических бильярдных траекториях в в ы п у к л ы х
о б л а с т я х с достаточно rладкой rраницей (см. о. 97).
. К ее обсуждению мы и перейдем.
Рассмотрим бильярдный стол в виде в ы n у к л о й
области Q (1 rладкой rраницей r. Диаметр этоrо стола, Т. е.
отреЗОI{ с концами на rранице r н а и б о л ь шей воз-
можной длины обладает следующим замечательным свойст-
вом: он перпендuкулярен еранице r 8 своих концах.
Действительно, если наибольшая хорда MN не перпен-
дикулярна к касательной 1 к rранице r в точке М, то сдви-
нув HeMHoro точку М по кривой r в точку /11' так, чтобы
уrол М' MN был тупым (РИG. 6.7), ПОЛУЧИ 1 треуrольник
Ml'I1'N, в котором сторона M'N больше стороны lИN (как
лежаШ,ая против тупоrо уrла). Следовательно, хорда Л1N
95
имеет не максимаЛЬНУIО длину, что противоречит предпо
ло}кеНИfО.
ОТСlода вытекает, что если запустить бильярдный шар
ПО aUaAtempy стола Q, то он будет сталкиваться с бортом r
под прямым уrлом и отражаясь, двиrаться по диаметру.
Итак, длиннейшая хорда бильярдноrо выпуклоrо стола,
проЙденная шаром в обоих направлениях, дает одно из
r простейших nер.иодических движе-
ний дви}кение периода 2, т. е. по
двузвенной траектории (звенья кото-
Н рой отличаются направлениями). Ес-
ли мы начнем теперь непрерывно вра-
щать эту хорду, уменьшая ее длину
настолько мало, насколько это возмож-
но, так, чтобы в конце этоrо преобра-
зования оба ее конца поменялись местами, мы будем иметь
промежуточное положение наименьшей длины, которое бу-
дет хордой, пересекающей r в месте наименыней ширины
стола Q (см. задачу 6.4). Эта хорда дает второе периодиче-
ское движение, также периода 2.
3 а д а ч а 6.4. Докажите, что эта вторая хорда имеет длину,
равную наименьшей ширине полосы, оrраниченной двумя парал
лельными прямыми, в которую полностыо f!омещается вся область Q.
Детальное изучение небольших возмущений обоих этих
периодических движений показывает, что движение вдоль
наибольшей хорды неустойчиво (т. е. малое отклонение
вектора скорости приводит к большим изменениям траек-
тории шара), в то время как второе движение может быть
устойчивым или неустойчивым.
Далее, будем искать периодическое движение бильярд-
Horo шара периода 3, т. е. «rармонический» треуrольник
с вершинами на кривой r, являющийся бильярдной тра-
екторией. Ero, как и периодическую траекторию перио-
да 2, следует искать среди всевозможных вписанных в Q
треуrольников, и выбрать среди них треуrольник макси..
маЛЬНОёО параметра. CTporoe доказательство этоrо (и более
общеrо) факта мы приведем чуть позже, а сейчас обратим
внимание на два обстоятельства: во-первых, rармониче-
скому треуrольнику отвечают Д в а периодических дви-
жения.......... по и против часовой стрелки; во-вторых, при
непрерывном изменении этоrо треуrольника, не меняя
порядка ero вершин и стараясь уменьшать ero периметр
настолько мало, насколько это возможно, так, чтобы в
конце этоrо преобразования получить тот же треуrольник.
96
но с циклически переставленными вершинами, мы прой
, t u
eM через треуrольник наименьшеrо периметра, которыи
также будет rармоническим и также будет COOTBeTCT OBaTЬ
двум (по и против часовой стрелки) периодическим дви
'жениям периода 3.
Таким же путем может быть установлено существование
двух rармонических п уrольников, делающих k п/2 обо
ротов вдоль кривой r, rде k число, взаимно простое с п
(точное утверждение содержится в формулировке зада
чи 6.6). Два периодических движения, соответствующих
п-уrольнику типа маКСИ.А1ума, будут неустойчивы, в то Bpe
мя как два периодических движения, соответствующих
п-уrольнику типа минимакса, MorYT быть устойчивыми
или неустойчивыми.
Поняв принципиально картину поведения указанных
периодических бильярдных траекторий в выпуклых об
JIастях, сформулируем и докажем точную математическую
теорему о периодических дви)кениях бильярдноrо шара в
выпуклой области Q. Теорема и ее доказательство, которое
мы здесь приведем, принадлежит известному американ
скому математику Дж. Биркrофу (1884 1944).
т е о р е м а Б и р к r о Ф а. J1 бильярда в любоЙ вы
пуклой облаоти Q на плоскости, Оёраниченной замкнупiой
еладкой кривой r, сущеотвуют периодичеокие бильярдные
I траектории с любым числом звеньев п 3.
Д о к а з а т е л ь с т в о. Пусть число п фиксировано.
I Построим конкретную периодическую бильярдную Tpa
екторию из п звеньев.
Рассмотрим всевозможные вписанные в Q замкнутые
ломаные у, число сторон у которых не превосходит п (в
рассмотрение входят вписанные трехзвенные, четырех-
звенные, ..., п звенные ломаные). Выберем среди них
ту ломаную 1'0, у которой периметр м а к с и м а л е н.
(Мы не будем вдаваться здесь в подробности, связанные
с доказательством существования такой ломаной.)
Мы утверждаем, что тоrда ломаная Уо имеет ровно п
звеньев.
Действительно, если бы число звеньев у нее было MeHЬ
ше п, то ее периметр можно было бы увеличить, заменив
произвольное ее звено PiP 2 на ломаную Р 1 Р ОР2 С верши
ной РО на дуrе между Р! и Р2'
Докажем теперь, что Уо бильярдная траектория (1
области Q, т. е. при всех k последовательные зве ья ло
маной Pk iPk и PkPh+i образуют равные уrлы о Kaca
тельной к r в точке P1l, (рис. 6.8).
4 17. А. [альпеРIlН. А. Н. Земляков
9J
Из максимальности периметра ломаной rоследует, что
сумма Ph iP+PPk+i для всех точек Р на дуrе Pk iPkPk+f.
кривой r максимальна I1MeHHo при Р==Р п , иначе периметр
ломаной ro можно было бы увеличить.
Рассматривая семейство эллипсов rs с фокусами в
точках Pп ! и Pk+i, найдеТVf тот эллипс r s' который к а-
с а е т с я кривоц r в.о некоторой точ-
ке Р такой эллипс обязательно най-
дется, так как наша кривая rладкая
и выпуклая. Но тоrда ясно, что
сумма Pk iP+PPk+l максимальна по
всем точкаI\-1 Р, лежащим на дуrе r
ме)I{ДУ Pп ! и Р п + 1 : для любой дру-
rой точки М Е r соответствующий ей
эллипс из семейства rs пер е с е-
к а е т кривую r и лежит cTporo
внутри эллипса r so ' поэтому Pk lM+
+МР h+l<Ph iP+PPh+l. ОТСlода вы-
текает, что касание эллипса r $0 с кривой r цроисходит
именно в точке Р==Р п . А тоrда из первоrо бильярдноrо
свойства эллипса следует, что звенья Ph iPk и РпРп+l
образуют р а в н ы е уrлы с прямой 1, являющейся OДHO
временно касательной как к эллипсу r $0' так и к кривой
r в точке Р п и поэтому Ph 'iP h И PkPk+I два звена биль-
ярдной ломаной в области Q. Теорема полностью доказана.
t
3 а Д а ч а 6.5. I{акой из вписанных в окружность п уrоль
ников имеет наибольший периметр?
Реш е н и е. Правильный п уrольник. Действительно, замк
нутаи бильярдная траектория из п звеньев в окружности является
ломаной максимальной длины (по теореме Биркrофа), а с друrой
стороны,....... это обязательно правильный п уrол ь ник (если только
шар делает один оборот BOKpyr центра; СМ. Э 1).
3 а д а ч а 6.6. Пусть фиксировано натуральное число п 3.
Обозначим через <р (п) количество чисел k, меньших п и взаимно
простых с п *). Докажите, что существует не менее ер (п)/2 перио
дических п звенных бильярдных ломаных на плоскости, вписанны)(:
в данную выпуклую область Q с rладкой rраницей r (рис. 6.9).
Реш е н и е. При доказательстве теоремы Биркrофа можно
было оrраничитьси доказательством существования бильярдной
*) Функция <р (п) называется функцией Эйлера и вычисляется
по формуле
<р(п) == п ( 1....J.... ) ( l....J.. ) f,t ( l J.. ) ,
Pi Р2 Р k
rде п== p 1p:l. . .P " ...... каноническое разложение n на простые мно-
ители.
98
траекторпи, при движении по которой бильярдный шар обойдет
кривую r р о в н о о Д и н раз; то же доказательство остается
fJIраведливым в классе всех ломаных, обходящих кривую F ровно
раз а, ровно 3 раз а и так далее. При этом следует заметить,
что 1) число обходов k достаточно брать только взаимно простым
с n, и что 2) обходу шарика вдоль ломаной, делающей k оборотов
2.
5 2
5 2
б'
7
7
7
({
о
Рис. 6.9
в
ПО часовой стрелке, отвечает та же ломаная, но делаrощая k обо--
p TOB против часовой стрелки. Поэтому rеометрически различных
поманых лишь <р (n)/2, что и требовалось доказать.
3 а д а ч а 6.7. (Задача ФаflЬЯflО.) Докажите, что в области Q.
имеющей форму остРОУ20ЛЬflО20 треуrольника, существует замit
нутая бильярдная траектория из трех звеньев. У к а з а н и е.
Точки излома этой траектории..... основания высот треуrольника
(см. 27).
3 а д а ч а 6.8. Верно ли, что в любом треуrольном бильярде
существует периодическая бильярдная траектория из а) 6 звеньев?
б) из меньшеrо, чем заданное п, числа звеньев?
О т в е т. а) В остроуrольном существует всеrда; в тупоуrОЛIr
ном, как правило, не существует б) в тупоуrольном треуrольнике
с очень тупым уrлом число звеньев у любой периодической траек'"
тории может быть сколь wrодно большим (т. е. для заданноrо п
число звеньев может превосходить п). Это связано с тем, что если
бильярдный шар попал в острый уrол, то вылететь из этоrо уrла
он сможет только после очень большоrо числа отражений (под-
робнее об этом см. rл. 6 и 27 rл. 8).
Задача 6.8 показывает, что теорема Биркrофа для мноrоуrоль
ников неверна, Причина этоrо будет прояснена в Э 27.
4.r.
ЧАСТЬ 11
""\
rЕОМЕТРИЯ и ФИЗИКА
прямоуrольноrо БИЛЬЯРДА
rлава 3
rЕОМЕТРИЯ прямоуrольноrо БИЛЬЯРДА
в этой rлаве сформулированная во введении
общая проблема бильярдных траекторий исследуется для
бильярда в прямоуrольнике. Прямоуrольник, как и Kpyr,
имеет во всех своих rраничных точках (кроме вершин)
п о с т о я н н у ю кривизну......... только не положитель-
ную, как у Kpyra, а нулевую. Кроме Toro, одинаковыми
прямоуrольниками можно замостить всю плоскость, как
это было объяснено во введении. Именно поэтому для биль-
ярда в прямоуrольнике, так же как и для бильярда в
Kpyre, естественно ожидать полноrо решения проблемы
поведения бильярдных траекторий. Оказывается, методы,
использованные в rл. 1, работают и в случае прямоуrоль-
ника, позволяя не только провести полное исследование
рассматриваемоrо прямоуrольноrо бильярда, но и свести
ero, в некотором смысле, к уже изученному бильярду в
Kpyre.
7. Бильярдный шар на прямоуrОJIЬНОМ
столе без луз
Напомним, что бильярдом в прямоуrольнике
называется такая система: один точечный бильярдный
шар на прямоуrольном бильярдном столе ABCD без луз,
ДВИiКУЩИЙСЯ по нему без трения и отражающийся от ero
сторон (<<бортов») по бильярдному закону «усол падения
равен уелу ompa'J/ceHия » .
Простейшие бильярдные траектории в ПРЯ 10уrоль
нике......... периодические. Они MorYT быть нескольких типов:
состоять из дважды проходимых отрезков между противо-
положными сторонаl\1И (рис. 7.1, а); образовывать семей
ства параллелоrраммов со сторонами, параллельными
диаrона.лям прямоуrольника (рис. 7.1, б); образовьтвать
100
амопересекающиеся замкнутые ломаные (р ис. 7.1, в)
и т. д.
Бывают и такие траектории, которые попадают в вер-
шины прямоуrольника (рис. 7.1, е). В таком случае не-
ронятно, как шару следует двиrаться после выхода «из
уrла»: закон упруrоrо отрв}кения на этот счет никаких
указаний не дает. Все такие траектории мы будем назы-
вать оообымu И, как правило, рассматривать не будем,
.lJ
с D
с D
I .....
J
r: lJ
С?
А
ц
lJ А
()
в А
Рис. 7.1
{j
е А
а
в
т. е. если траектория попала в вершину, оборвем ее, и 01'
траектории останется только ее часть (полутр аектор ия).
(Впрочем, из дальнейших рассмотрений будет понятно,
что в случае прямоуrольноrо бильярда шар можно считать
вылетающим после попадания в вершину в точности в
противоположном направлении; TaKoro
рывода нельзя делать для бильярда в Pj'
произвольном мноrоуrольнике. Объясне-
ние этому вы сможете найти, решив
задачу 7.3, или же обратившись к
rл. 8). Аз
«Сходу» нарисовать хотя бы одну не- Р,
'!ерuодuческую траекторию бильярда в
hрямоуrольнике уже значительно слож- 'fU.44-
нее. Задачу о распознавании периоди-
ческих и непериодических траекторий
бильярда мы сейчас решим с помощью
упоминавшейся во введе...нии процедуры «выпрямления тра.
кТорий». Опишем ее в общем случае......... для бильярда
в произвольном мноrоуrольнике.
Пусть РiР 2 Р з . . . произвольная не особая (т. е. не
попадающая в уrлы) траектория бильярда в мноrоуrоль.
нике Q==AfA2A8. . .А п (рис. 7.2). Построим по этой ло-
маной специальную прямую. А именно, отразим наш мно"
rоуrольник Q вместе с ломаной Р 2 Р эр 4. . . относительно
той стороны мноrоуrольника, на котороЙ лежит точка Р.
(первое звено ломаной Pi P 2 мы не TporaeM). Соrласно
закону отражения, отрезок P2P , симметричный отрезку
\
101
Р2РЗ, является продолжением отрезка PiP 2 , и первый
I\УСОК ломаной PiP 2 Р з Р 4. . · ........... Р 1 Р 2 Р з ........... нами выпрям-
лен. Теперь отразим второй (полученный из Q при первом
отражении) мноrоуrольник Qi. относительно той ero сто-
роны, на которой лежит следующая точка излома Рае
Получим следующий мноrоуrольник Q2' и образ звена р;р:
при новом отражении будет, опять,:,таки, продолжением
отрезка PiP 2 P'. Продолжая так и далее, мы можем любой
/(
А'
J1 Jj
,А В А
а
H
.
,
;f \ I
в
кусок ломаной PiP 2Р эР 4. .. «выпрямить», т. е. последо-
ватеЛЬНЫl\1И отражениями превратить в отрезок прямой
PIP2P P . · · ·
Конечно, для разных траекторий придется делать раз-
личные последовательности выпрямляющих отражений.
Однако если мы рассматриваем бильярд в прямоуrоль..
нике, lЫ можем с caMoro начала с помощью отражений
замостить в с 10 П Л О G К О С Т Ь прямоуrольникаrvlИ, рав-
ными данному, получив решетку из прямоуrольников.
Нарисовав на этой ПЛОСКОСТИ произвольный луч, не про-
ходящий ни через одну из вершин получившихся прямо-
уrольников, мы можем G помощью процедуры, обратной
описанной, «сложить» этот луч в траекторию бильярда
в исходном прямоуrольнике ABCD (рис. 7.3, а). Заметим,
что при таком «складывании» решетки прямоуrольников
в исходный прямоуrольник ABCD в каХ{ДУIО точку М
прямоуrольника ABCD попадает бесконечно MHoro точек
Мт,n плоскости........ именно, все те точки, которые полу-
чаются из М описанными выше отражениями (риа. 7.3, б).
Если траектория, выходящая из точки М под уrлом ct
к стороне АВ, периодична, то это означает, что после вы..,
прямления из этой траектории ПОЛУЧИТGЯ прямая, прохо-
дящая через М и через одну из точек Mтn,пo. Если нуме-
ровать ТОЧI{И Мт,п индеI{сами т и n, как указано на рис.
7.3, б, то точка М то . nо олжна быть такой, что то и по-.........
102
четные числа. 11менно (и только) в этом случае бильярд-
ный шар проходит через ту же точку М под прежним
уrлом а: цомера то и по показывают, сколько нужно сде-
лать отражений относительно вертикальных и rоризон-
тальных сторон прямоуrольников, чтобы получить из
точки Мто,nо точку М; при этом нечетное число отра-
жений меняет направление, четное же не меняет (см.
рис. 7.3, в).
Докажем, что неособая траекп'l-ОрИЯ, выходящая из точки
М nрямоуеОЛЫiика ABCD под уелом а к стороне АВ, пе-
риодична в том и только в том случае, коеда mанеенс ее
уела наклона k== tg а соизмерим о отношением сторон
а2/а! nрямоуеольника ABCD.
Действительно, только что было выяснено, что перио-
дичны те и только те траектории, которые (после выпрям-
ления) соответствуют прямым, идущим ИЗ т<?чки М В одну
к
а
б
Рис. 7.4
из точек вида M2тt2n. Заметим теперь, ч ТОЧК 2mt2n
получается из М сдвиrом на вектор 2т. АВ+2n · AD (до-
кажите это: рис. 7.4, а), так что MM 2mt 2 n K имеет ка-
теты с длинами МК ==2та! и М 2тt2nK ==2па 2 . Таким
образом,
k == t а == 2 та2 .!!::!...
g 2nа! n ai'
Т. е. k соизмеримо с a 2 /af. Обратно, если число k соизме-
римо с a 2 /ai, Т. е. k ==.!!!:... a , то любая ПрЯl\1;ЗЯ, выходящая
n аl I
из точки М с TaHreHcoM уrла наклона k, проходит чер ез
точку, получающуюся из М СДВИI'ОМ на вектор 2т.АВ+
2п.АD, т. е. через точку M2mt2n (проверьтеl). Если эт
прямая не проходит через вершины прямоуrольнико ,
то ей соответствует неособая периодичеСI{ая траектория,
что и требовалось доказать.
103
Заметим, что в рассматриваемом случае мы bce-такИ
можем ПРОДОЛ:tI{ИТЬ и любую оообую, т. е. заканчиваю
щуюся в одной из вершин прямоуrольника, траеКТОРИIQ
за эту вершину: ничто не 'мешает на плоскости, замощенной
нашими прямоуrольниками, продолжить, например, мс
за вершину С (рис. 7.4, б), и считать тем самым, ЧТО t
попав в, вершину С, бильярдный шаR вылетает из нее по
ТОМУ же пути, по I{aKoMY он туда залетел......... после соот-
ветствующих отражений луч СМ' совмещается с лучом
СМ. Таким образом, в случае бильярда в прямоуrОЛЬНИI<е
можно считать, что движение по любой траектории про-
должается неоrраниченно во времени (например, дважды
проходимая диаrональ АС прямоуrольника......... это перио-
дическая траектория).
Из доказанноrо утверждения следует
т е о р е м а 1. Если maHzeHC У2ла наклона k трае1\,-
пzopuu ооизмеРИ.Аt о число},! k O ==a 2 /ai, то независuмо от на-
чальноео положения бильярдНО20 шара еео движ:ение будет
периодическu.А1,; в противном случае траектория неперио-
дична.
Итак, с помощью теоремы 1 мы научились по началь-
ному звену траектории шара определять, является ли эта
траектория периодической или непериодической. Для этоrо
надо найти отношение длин сторон прямоуrольника или,
что то же самое, TaHreHc уrла наклона диаrонали прямо-
уrОЛЬНИI{а и TaHreHc уrла, под КОТОрЫI\1 запущен IIlарик,
и поделить первое число на второе: если в результате
получится рациональное число, то траектория периодична,
если же....... иррациональное, то непериодична. I<стати,
отсюда сразу следует также и то обстоятельство, что для
фиксированноrо начальноrо вектора скорости шара тра-
ектория будет периодической или непериодическоЙ н е-
3 а в и Q И М О от ero начальноrо положения на ПрЯ1\10-
уrольном столе. Поэтому, если запустить параллельно
ppyr друrу сразу несколы{о бильярдных шаров, они либо
одновременно опишут периодические траектории, либо
НИJ{оrда не пройдут по своему старому следу. Последова-
тельность отрал{ений этих шаров от бортов бильярда будет
различной, если они находятся достаточно далеко друr
от друrа. Если )ке шары находятся достаточно близко, то
последовательн()сть бортов, от которых они отра)каются,
будет одной и тоЙ я{е (рис. 7.5, а). Если первое звено тра-
ектории одноrо бильярдноrо шара ОКРУ>КИТЬ параллель-
ными звеНЬЯl\1fИ целоrо семеЙства траекторий друrих ПНlрОВ,
ТО полученные траеI{ТОрИП, в случае, коrда они периоди-
104
ческие, заполнят самопересекающийся «коридор» (рис.
7.5, б). Таким образом, зная одну периодическую траек.
торию, мы параллельным сдвиrом ее звеньев получаем
друrую перио дическ ую траекторию.
- I'W
а
о
Рис. 7.5
3 а Д а ч а 7.1. а) Доказать, что у всех неособых «параллель--
ных» периодических траекторий в прямоуrольнике равное число
звеньев и равные длины. б)* Доказать, что в прямоуrольнике
существуют сколь уrодно длинные периодические траектории.
Реш е н и е. Это следует из рассмотрения выпрямлеННЫ)Q
траекторий, изображающихся на решетке прямоуrольников paB
ныии параллельными отрезками.
3 а д а ч а 7.2. У края бильярда, имеющеrо форму правильноrо
2n уrольника, стоит шар. Как надо запустить шар от борта, чтобы ОН.
отразившись по разу от всех бортов, вернулся в ту же точку? д
казать, что при этом длина пути шара не зависит от выбора начаJJЬ--
ной точки.
Как же ведет себя на прямоуrольном столе н е п е-
р и о Д и ч е с к а я бильярдная траектория? В !<pyre и
эллипсе, как мы помним, непериодическая траектория не
заходила в некоторые участки......... в концентрический Kpyr
" и, соответственно, в софокусный эллипс (или В криволи-
нейные cerMeHTbI софокусной rиперболы), однако запол-
няла всюду плотно кольцо между их rраницами. В прямо-
уrольнике она уже заходит во все ero участки и заполняет
ero всюду плотно. В этом и состоит основной результат
о непериодических траекториях в прямЬуrольном бильярде.
Т е о р е м а 2. Еоли k/k o ....... иррациональное число, то
любая траектория с уеловым коэффициентом k всюду плотно
запОЛflяеlп весь nрямоуеольнuк, т. е. пересекает любой
(сколь уеодно Аtалый) КРУ2, лежащий внутри Неео.
Таким образом, если точечный бильярдный шар за-
пустить из любоrо положения М в любом направлении CXI
таком, что число tg a/tg <р иррационально, rде ч' ........ уrол
наклона диаrонали к rоризонтальной стороне, то он рано
или поздно столкнется G друrИl\1, уже неточечным бильярд-
ным шаром (диском) N, куда бы мы ero ни поставили и
сколь бы мал он ни былl Следовательно, иrрокам (в:случае
отсутствия трения) не нужно особенно стараться, чтобы
попасть в друrой шар (или лузуl), надо лишь И1\леть терпе-
ние и время, чтобы дождаться нужноrо столкновения.
105
Доказательство теоремы 2 будет дано в 9 9 и будет
опираться, как и в случае Kpyra, на теорему Якоби.
Наметим здесь лишь краткую схему ее доказательства.
По прямоуrольнику ABCD будет построен «фундаменталь-
ный» прямоуrольник вчетверо болыпих размеров, в ко-
TOpOI\1 исходная бильярдная траектория превратится в
«скаЧУЩУIО» со стороны на сторону траекторию; для из
бавления от этих «скачков» rранип:а фундаментальноrо
прямоуrольника будет специальным образом склеена, и в
результате склейки получится замечательная поверх-
/ ность тор (<<бублик»), на котором «скачущая» траек-
тория превратится уже в непрерывную кривую'. Иссле-
дование этоЙ крипой и приведет к доказательству теоремы 2.
Примечательно, что для прямоуrольноrо бильярда спра-
ведлива следующая а л ь т е р н а т и в а: либо траек-
rпорuя бильярда периодична, либо всюду плотно запОЛНЯРlп
прЯАiоуеОЛЬfiUК. В rл. 9 выяснится, что это верно не для
всякоrо выпуклоrо 1VIноrоуrольника (при выяснении опять
будет использована теорема Якоби!).
3 а д а ч а 7.3*. Найдите критерий периодичности бильярдных
траекториЙ в равностороннем TpeyrOJ1bHIIKe.
3 а д а ч а 7.4*. Укажите все мноrоуrольники Q, которыми
с помощью описанных выше последовательных отра)кений можно
вамостить ПЛОСКОСТЬ без перекрытий и так, чтобы Лlобая цепочка
последовательны1\. отра}кений, при КОТОРОЙ из Q получается какой то
мноrоуrольник Q', давала один и тот же результат. (Например,
правильными шестиуrольниками можно замостить плоскость, oд
нако последнее требование здесь не выполнено...... от шестиуrоль
ннка Q к соседней ячейке Q' можно прийти двумя способами
с помощЬЮ одноrо отра)кения относительно А F и с помощью KOM
позиции двух отражений........ относительно АВ и затем относительно
х Е
n
с
"С
t1
Рис. 1.7
Рис. 7.6
АР' (рис. 7.6). Результаты будут разные....... скажем, в вершину,
обозначенную буквой Х, в первом случае переходит вершина Е,
во втором ........ вершина С.
3 а м е ч а н и е. Задача 7.4 и друrие близкие вопросы обсуж
даIОТСЯ в статье А. Н. В иленкина « Калейдоскопы» (Квант. 1972.
N'Q 8. с. 41 49), правда в друrой связи.
3 а д а ч а 7.5. Пусть бильярдная траектория М А попадает
в вершину А iYfла ВАС величины а. С помощью п'оследователь
106
ных отра)кений замостим часть плоскости уrлами той же величины
(рис. 7.7), продолжим МА за вершину А и Qбратными отражениями
построим луч А М". Казалось бы, тем самым мы можем опредеЛИТЬj
как выходит бильярдный шар из вершины уrла (ПОД направлением
АМ"). Однако здесь может возникнуть неоднозначность, ибо после-
довательные отражения исходноrо уrла можно начать со стороны
АВ или со стороны АС, и может оказаться, что от этоrо sаВИСILТ
ваправление АМ". Рассмотрите случай уrла а==2'Л/З. Выясните,
для каких уrлов а упомянутая неоднозначность не возникает.
3 а д а ч а 7.6. В прямоуrольном бильярде из точки А посы...
ается шар параллельно диаrонали. Найти множество таI{И)Q точек
М в бильярде, что второй шар, посланный из точки М Qдновре--
iyIeHHo с первым и с тоЙ же скоростью (как по величине, так и по
направлению), столкнется с ним.
3 а д а ч а 7.7. В точечное отверстие rраницы прямоуrольноrо
бильярда влетает бильярдный шар. Может ли шар с HeKoToporo
момента начать двиrаться внутри бильярда по замкнутой TpaeK
тории? А если бильярд не прямоуrольный? (Указание: поменяйте
скорость шара на противоположную.)
3 а д а ч а 7.8. В прямоуrольном бильярде шар движется ПQ
sамкнутой траектории. Уrол между какими то двумя соседнимй
ввеньями равен 90 Q . а) Может ли у траектории быть 4 звена? Если
да, то при каком соотношении сторон? б) А может ли быть 5 звеньев?
6 звеньев? 17 звеньев? 18 звеньев?
3 а д а ч а 7.9. В прямоуrольном бильярде произвольным
образом запущены два неточечных шара под уrлами а и к ОДН9МУ
борту, причем tg ct и tg иррациональны. Обязательно ли они
коrда либо столкнутся?
3 а д а ч а 7.10. Из вершины прямоуrольноrо бильярда раз
мером тХ 2п, rде т и п ....... целые нечетные числа, ПОД уrЛОl\1 45 Q
к стороне послан шар. Попадет ли он после нескольких отражений
от бортов: а) в ПРОТИВОПОЛО)l{НУЮ вершину; б) в соседнюю верши ну
(рассмотреть два случая соседней вершины);- в) в середину какой...
либо стороны? r) Сможет ли шар побывать в середине двух про...
тивоположных сторон?
3 а д а ч а 7.11. Как будет вести себя шар в прямоуrольном
бильярде из задачи 7.10, если ero выпустить из вершины под уrлом
зоо? 60 0 ?
3 а д а ч а 7.12. а) Занумеруем стороны прямоуrольноrо биль
ярда числами 1, 2, 3, 4. Пусть в нем движется шар, траектория
KOToporo непериодическая. Выпишем подряд номера Bce сторон,
о которые отражался шар: пl' п 2 , nВ; . . . . Может ли полученная
последовательность оказаться периодической?
б)* Решите ту же задачу для непериодической траектории у
в ПРОИЗВОЛЬНОМ выпуклом k...уrольнике; стороны KOToporo зануме
рованы числами от 1 до k.
Реш е н и е. Докажем, что последовательность flt. j п2; . . ! ......
непериодическая, от противноrо. I
Пусть период последовательности 1Zt.; n2У . . .. равен Т i причем
т четно (в противном случае рассмотрим удвоенный период). Вы..
прямим траекторию у шарика, сделав последовательные отражения
мноrоуrольника относительно сторон nl, n 2 , п з _ ... . Получим
коридор из одинаковы мноrоуrольников Мl' М 2' М З, t . ., содер"
)кащий прямую l...... выпрямленную траекторию "(.
Рассмотрим в этом коридоре мноrоуrольники М 1 и М T+t.
МноrоуrОJ1ЬНИI{ М Т+l MOllteT быть получен из М 1 либо параплель..
107
БЫМ переносом на некоторый вектор й, либо параллельным перено
сом и поворотом. Во втором случае А1 т + 1 получается из М 1 одним
поворотом с центром в некоторой точке О на некоторый уrол а.
А тоrда в цепочке мноrоуrольников Ml' MT+f, M2T+f, . . . каж
дый из них получается из предыдущеrо либо параллельным пере
носом на один и тот же вектор й, либо поворотом на один и тот же
rол а с центром о. Во втором случае весь коридор располаrался
бы в оrраниченной части плоскости и поэтому не Mor бы содержать
ПрЯМУIО 1. Следовательно, возможен только первыЙ случай: MH020
У20ЛЬНUКU в указанной цепочке получаюпzся' последовательно друа
из друеа параллеЛЬflblМ переносом на вектор а. А тоrда все звенья
траектории у с номерами 1, Т+ 1, 2Т+ 1, . . . в исходном MHoro
уrольнике М 1 параллельны друr друrу. Если они начинаIОТСЯ в
раз л и ч н ы х точках Аl' А2' Аз, А4' . . . одной и той же CTO
роны мноrоуrольника Мl' то нетрудно видеть, что А 1 А 2 ==А 2 А з ==
== А з А 4 ==. . . . Это противоречит тому, что все эти точки лежат на
одной стороне мноrоуrольника, поскольку сумма' А 1 А 2 + А 2 А з +
+А з А 4 +. . . бесконечна. Таким образом, все точки А 1 , А 2 , . . .
совпадают, а потому совпадаIОТ и звен:ья траектории,\, с номерами 1,
T+l, 2T+l, 3T+l, ..., т. е. '\' периодическая траектория,
что противоречит условию задачи.
3 а м е ч а н и е. В пространственном мноrоrраннике после
ДОВ8'тельность n 1 , n 2 , n з , ... номеров rраней, от которых OTpa}Ka
ется бильярдны.й шар, может быть периодической, несмотря на
то, что траектория шара,\, непериодическая. Это связано с тем, что
в пространстве кроме параллельных переносов и поворотов BOKpyr
осей имеются еще и винтовые движения: повороты BOKpyr осей
со сдвиrами вдоль них. В этом случае множество точек отражения
шара от любой из rраней пk заполняет всюду плотно некоторыЙ
эллипс на этой rрани.
8. Тор и ero обмотки
Временно оставим бильярды в прямоуrоль
нике и обратимся к весьма важным поверхностям, часто
встречающимся в механике.......... к торам. Тором называется'ПО
верхность, получающаяся при вращении окру)!{ности 81 OT
носительно непересекающей эту окружность прямой MN,
Н
А
T(Jjl
IN
Рвс. 8.1
ле>кащей в плоскости окружности (РИ0. 8.1). Форму
тира имеют надувноЙ епасательный Kpyr, автомобильная
камера, поверхность бублика. На торе, как и' на сфере,
108
можно провести МеридиаНы......... линии пересечения тора СО
всевозможными плоскостями, проходящими через ось вра.
щения MN, и параллели окружности, получающиеся
u I
ИЗ точек исходнои окружности при вращении относительно"
MN (рис. 8.2). Выбрав на торе «rринвичский меридиан»
и «экватор», т. е. зафиксировав меридиан и параллель,
«rринDц..ЧСJ<UU' »
нериilиан
st'2 .
sь. " t}J 211 а
о '/Jf ь
о а
6 6
lJ
"
Рис. 8.3
можно ввести на нем долrоту "1'1, отсчитываемую по парап-
лелям от выбранноrо меридиана, и широту '1'2, отсчитыва-
емую по меридианам от экватора (рис. 8.3, а). Более точно,
точка А тора Т имеет координаты ('Фi, '1'2), если она полу-
чается из точки О пересечения выбранных линий поворо-
том на уrол 'Ф2 вдоль меридиана и последующим поворотом
на уrол '1'1 относительно оси MN (оба поворота осуществ-
ляются в выбранных направлениях; рис. 18.3, б). Уrлы
'Фj и '1'2 будем измерять в радианаХj плоская (как в reor
рафии) карта тора представляет собой квадрат на плоскости
а
l;
d
h t:::> (b o t=:>
1...
...
CI.
Рис. 8.4
0'1']11'2: О 'Фl 2л, О 'Ф2 2л. Точки ЭI{ватора (Ф2 ==0 или 21&)
И «rринвичскоrо l\fеридиана» ('Фf==О или 2л) представ-
лены на этой карте дважды....... точки нижней и верхней
стороны квадрата, лежащие на одной вертикали (т. е.
точки вида (фj, о) и ('1'1, 2л)) изобрая{ают одну и п1У же пzочку
u u
на торе; аналоrично, точки левои и правои сторон квад-
рата, ле}кащие на одной rОРИЗ0нтали, изображаfОТ также
одну u rпy же точку. Будем считать карту резиновой и
склеим упомянутые точки; на рис. 8.4 склеиваемые стороны
обозначены одинаковыми букваI\1И (а, Ь) со стрелкзl'ЛИ, пока-
зывающими, как НУlI{НО склеивать эти стороны (стрелку
109
со стрелкой......... в т о м ж е направлении). Как и сле-
довало ожидать, в результате получим тор, а сетка rори-
u u
З0нталеи и вертикалеи на карте превратится в сетку па-
раллелей и меридианов на торе. Иноrда тор и определяют,
как поверхность, получающуюся из «резиновоrо» кв ад"
рата указанной склейкой.
Рассмотрим теперь простейшее движение точки по тору:
пусть точка А ДВИ)J{ется так, что ее широта и долrота ме-
няются pa8HOMepflO......... с постоянными скоростями ffii И (02.
2
и ф CfiJ 1SJ
Q
2"
Рис. 8.5
в этом случае можно написать формулы для зависимости
Wi и '1'2 от времени [:
Wi == а + юft, 11'2 == + <02 t .
Здесь имеется в виду, что, как и в триrонометрии, мы по-
зволяем координатам 'Фi и 11'2 принимать произвольные
(большие 21& и отрицательные) значения, однако не забы-
ваем, что для любых целых т и n точка о координатами
(Фi+2пm, 'Ф2+2пп) совпадает G точкой G координатами
(фf, 11'2). На всей плоскости 0'фl\)'2 написанные уравнения
задают прямую 'ф2 == :; 'Фf + '\'. Учтем теперь, что в дейст-
вительности мы должны считать, что 'Фf И '1'2 меняются
лишь от О ДО 2п, так что как только точка, движущаяся
u u u
ПО этои прямои, доходит до однои ИЗ сторон квадрата,
являющеrОGЯ картой тора, эта точка «перескакивает» в
u
соответствующую точку противоположнои стороны квад-
рата и продолжает ДВИfаться по квадрату в том же направ"
JIении, что и раньше........ до следующеrо перескакивания
(РИG. 8.5). Таким образом, на карте соответствующиЙ «марш..
рут» траектория движения....... состоит из отрезков, па..
u
раллельных друr друrу; после склеики квадрата в тор эти
отрезки склеиваются к непрерывную кривую на торе........
она обматывает тор G «уrловыми» скоростями Ф:{ по эква..
тору и (02 по меридиану (на промежуточном этапе склейки
мы получаем движение по винтовой линии на. цилиндре G
соответствующим перескакиванием а одноrо ero основания
110
I на друrое). Эта кривая называется траекторией обмотка
тора с частотами (01, (2)'
Выясним, коrда траектория обмотки тора с частотами
(Фl, (2) является з а м к н у т о й (п е р и о Д и ч е с-
к ой).
Если Фl==О, то траектория это меридиан, и дви)ке-
иие по нему периодично с периодом Т 2 ==2п/0 2 . Если O 2 ===-
==0, то происходит периодическое движение по параллели.
Пусть обе частоты 01 и Ф2 отличны от о. Тоrда через
промежутки вреrvfени, кратные Тi==2n/Фi, движущаяся
,точка оказывается на одном и том ЖJе меридиане, а через
промежутки вре:м:ени, кратные Т 2 ==2п/0 2 , точка оказы-
вается на одной u той же nараллеЛll. ,...71вижение перио-
дично тоrда и только Tor-
да, коrда через некоторое
время Т точка окажется в
своем первоначаЛЬНОl\1 мес-
те, т. е. на тех же парал-
лели и меридиане. Для а
этоrо нужно, чтобы этот
промежуток времени Т был
кратен как Ti, TaI{ и Т 2 ,
Т. е. T==mTi и Т==nТ 2 G целыми т и n. Таким образом,
необходимое и достаточное условие
пер и о Д и ч н о с т и ДВИ)I{ения ........ это существование на-
туральных т и п таких, что mTi==nT2, т. е. т.2Л/Фi=:::4
==n.2Л/0 2 ; последнее означает, что число (t)2/ Ф i Р а ц и о-
н а Л ь н о (Ф2/UJl==m/п).
Итак, если 0i и Ф2' скажем, поло)кительны и СОНЗl\1е-
римы друr с друrом, то любая траектория обмотки с ча-
стотами 01, Ф2 периодична. На торе это будет замкнутая
кривая, причем если (J)2/юi......... несократимая дробь, то эта
кривая n раз обходит тор ВДОЛЬ параллели и т раз......... ВДОЛЬ
меридиана. Такая кривая называется цихлом типа (т, п).
На рис. 8.6, а изображен цикл типа (3,1), а на рио.
8.6, б ......... ЦИКЛ типа (3,2).
Из полученных рассуждений БытеI<ает, что в случае
н е с о и з м е р и м ы х частот О>! и 0>2 траектория об-
мотки будет неперuодuческой.
Как же она будет обматывать тор? Ответ на этот БОПрОG
дает
т е о р е м а. Еолu чuoло Ю==ОО2/00i иррационально, то
любая mраекпzорuя соответотвующей обмотки тора воюду
плотна на торе, т. е. проходит через любую (сколь уеодно
малую) область на торе.
Тип (3..1) ,
Рис. 8.6
111
д о к а 3 а т е л ь с Т В о. Пусть и .........произвольНая область
на Торе; проведем меридиан S тора, пересекаIQЩИЙ область
и по дуrе 8. (рис. 8.7), и рассмотрим последовательные
точки пересечения траектории обмотки тора с этим мери-
дианом........... Р О , Pf, Р2' . . . . Точка, двиrаясь вдоль траек-
тории, возвращается на меридиан S через промежутки
времени, равные Тi==2'Л/(J)f. За каждый такой промежуток
вре:мени долrота точки '1'2 меняется на одну и ту же вес,ТIИ
чину qJ == (J)2 Т i == :: · 2n: == (i) · 2n:. Это означает, что точка Р n
пересечения траектории с меридианом S получается из
предыдущей точки пе-
ресечения Pп T поворо-
том на уrол СР== (J). 2'Л
вдоль этоrо меридиана.
В случае и р р а Ц и о-
н а л ь н О с т и (1) из
теоремы Якоби вытека-
ет, что хотя бы одна
из точек Р п попадет на
дуrу L1. Следовательно, траектория пересечет область lJ,
что и требовалось доказать.
Отметим также, что, поскольку последовательность
точек Р п на меридиане S не только всюду плотна, а еще
и р а в н о м е р н о распределена (т. е. точка Р п попадает
в произвольную дуrу 8. меридиана S с вероятностью, равной
отношению ее длины к длине меридиана) и аналоrичное
утвер)кдение имеет место и для произвольной параллели
на торе, траектория обмотки тора G иррационаЛЬНЫl\1 (u
заполняет тор р а в н о м е р н о, т. е. движущаяся рав-
номерно вдоль этой траектории точка ПрОБОДИТ в наперед
заданной области и тора время, пропорциональное ее
площади.
Зафиксировав частоты обмотки (О{ и (02' мы можеfii
через к а ж Д у ю точку тора провести траекторию этой
об!\fОТКИ И рассмотреть все эти траектории сразу. Они
образуют так называемый п о т о к траекторий, или иначе,
о б I\1 О Т К У т о р а (до сих пор речь шла только о тра м
ектор иях оБМОТI{И). Если число (j) == (J) 2/ (О! рационально,
то обrv10тка называется рациональной, в противном случае
rоворят об иррациональной обмотке тора. Bc€ траектории
рациональной обмотки тора nерuодиЧ; bl (g одним и тем же
i1ериодом) 9 любая траеI ТОрИЯ иррациональной 06rv1 ':Tr H
60юду плотно заполняет тор.
112
сэ
Рис. 8. 7
1\'\ожно интерпретировать упомянутые потоки так: на
торической планете lror дует ветер так, что на квад-
рате (карте тора) направление ветра одинаково во всех
точках под уrлом а к оси О'фl (рис. 8.8, й). Сев на воз-
душныЙ шар, мы полеТИl\tl по ветру., Если нам повезет с
поrодой tg а окажется uрраЦUО1iаЛЬrlbt/JI[,, то наше пу-
тешествие будет веСЬ1\1Ц познавательным, ибо мы побывае!vl
(б.паrодаря только ветру, который, по преДПGло}кеf:iИЮ,
не 11еняется) над всеJl'tu уzолка.МU tпuрической ,1JlQNembt!
cfz
2'1t
Joc
b
,/
2" ер.,
о
Ветер
На планете Tor
(!
Ва/пер
#а Земле
"
Рис. 8.8
Если же tg c't будет раtiuонаЛЬflЫJrl, мы соверШИl\1 { Q{\ ЧЦt)е
...
кру[о(ветное путешествие», вернувшись в ту же точку.
(На сферической Земле TaKoro ветра не бывает - это
весьма сложная теорема. Более простой, но нетривиаль,fIЫЙ
факт зак.пlочается в том, что в любой момент времени на
Земле найдется хотя бы одна точка, в котороЙ нет ветра!
(рис. 8.8, б). Существование таких «ветров» на торе и
является причиной Toro, что эта IIоверхность чаете iIояв
ляется в задачах м:еханики. Объяснение )ке такой исклю
чительности тора состоит в том, что ero так называеман
эйл рова характеристика равна НУЛIО. Об ЭЙJIеровои xa
рактеристике повеРХНQстей см. 23; более подробно об
этuм и о связи эйлеровой характеристики со свойствами
{(ветров» на поверхности теоремой Пуанкаре о СУММё
индексов BeKTopHoro поля MO)I{HO прочитать в книI
В, r< Болтянскоrо и В. А. Ефремовича «Наrлядная rono
лоrия» (<<Библиотечка «Квант», 1982. Вып. 21).
3 а м е ч а н и е о б о б м о т к а х т о р а. Кроме
KOHKpeTHoro представления тора в виде поверхности буб
лика, ero МО)l{НО представить и абстрактно, как множе-
ство пар точек ('Фi '1'2), rде 'Фi и 'Ф2 независимо друr от друrа
ПрИНИl\1ают произвольные значения ОТ О до 2л, Т. е. МО)КНО
считать, что точки Фi И \)12 движутся каждая равномерно
по своеЙ окружности, а тор {('Ф17 '2)} ....... это конфuеураtfUОН-
!13
ное nрОСl11ранство этих точек. Именно поэтому rоварят,
что «тор есть прямое произведение окружностей» и запи-
сывают это в виде Т2===8 1 Х 81. Если при этом отношение
уrловых скоростей ю 2 /ш! движущихся по окружностям
точек иррационально, то это означает, что конфиrурацион-
ная траектория точки 11'== ('1'1, '1'2) на торе всюду плотно
ero заполняет, и следовательно, точки ! и 'Ф2 на своих
окружностях в некоторый момент времени будут нахо-
диться почти в первоначальном (Т. е. в сколь уrодно близ-
ком к нему) положении. Аналоrично, если имеется n>2
окружностей, по которым равномерно движутся точки Р1.,
Р2' · . ., Рn, то их конфиrурационным пространством будет
поверхность n MepHoro тора lr n ==8 1 х 81 х. . . х 81 (п раз),
расположенноrо в 2п MepHOM пространстве 1R.2n=::(R2X
х. . . х 1R.2 (п раз) (абстрактный двумерныЙ тор 1"2 можно
считать вложенным в 4-мерное пространство (R4), по ко-
торому движется одна конфиrураnионная точка '1'== ('Фi,
'1'2". .,'Фn), rде О<'Фi 2n, i==l,..., n. Если (И1, 02,...
. . . ,0n ......... уrловые скорости движения точек Pi, . . ., Рn ПО
окружностям, т. е. 'Фi==0it+'Р!, . . ., 'Ч'n=:0 n t+'Рn, rде 'Рl,...
. . ., срп........ фазы (начальные положения точек на окруж-
ностях), то точка 'Ф (t)== (0it+<fJt, . . ., (unt+CPn) описывает
на торе ТN траекторию обмотки. Оказывается, эта траек-
тория, как и в случае двумерноrо тора, либо заА1кнута,
либо всюду плотно заполняет некоторый тор Tk, k<.п.
(В механике торы ТN наэываIОТСЯ лиувиллевскими то-
рами, а равномерное движение ТОЧI{И по тору........ «условно-
периодическим» движением.) Заl'vlКНУТОЙ траектория будет,
если k 1 Юi+.. w+kn0n==O при некоторых целых kj, ...
. . . , k n , а всюду плотной........ если аJ{ИХ целых чисел нет.
Это замечание дает возможность быстро решить не-
простые задачи 8.7 8.10.
3 а д а ч а 8.1. Какая поверхность получится, если у прямо
rольника (рис. 8.4) склеить сначала стороны Ь, а потом стороны а?
Ь 3 а д а ч а 8.2. Рассмотрим «резиновый»
шестиуrольник и склеим попарно ero проти-
воположные СТОРОНЫ. Какая поверхность при
этом получится?
3 а д а ч а 8.3. Какая поверхность полу-
Ь чится после попарной склейки противополо-
ЖНЫ2С сторон правильноrо восьмиуrолъника?
3 а д а q а 8.4. Какая повер ность по-
ЛУЧИТСЯ, если склеить стороны восьмиуrоль-
ника так, как указано на рис. 8.9?
Рис. 8.9 3 а д- а ч а 8.5. Резиновый мяч (или rло-
бус) МОЖНО вывернуть наизнанку, проделав в нем Д PKY. Можно
ли подобным образом вывер НУТЬ наизнанку тор? Что в ЭТОМ слу-
чае произойдет с параЛJIеJIЯМИ и меридианами?
ь
ь
114
3 а Д а ч а 8.6. Нарисуем на торе цикл типа (rn, п)., затем по-
ло)ким веревочку на эту кривую и свяжем ее концы, и, наконец,
берем (уничтоя{им) тор, оставив веревочку. В каких случая
на веревочке после распут.ывания не будет узлов? (Рассмотрите
для наttала цикл типа (3,2) ........ см. рис. 8.6,6.)
3 а д а ч а 8.7*. а) Доказать, что существует такое натураль-
ное n, что числа 2 n и ЗN начинаются с цифры 7 одновремеnн'о.
б) Верно ли то же самое для чисел 2 n и 5 п ?
Реш е н и е. а) Мы должны найти такие натуральные числа n и
k 1 , k 2 , чтобы одновременно выполнялись равенства 7 .lOkl 2n < 8 .IOk l
И 7 .lOk 2 З п < 8.10 k 2, или, иначе,
ki n Ig 2 .....lg 7 < kf + 19 (8/7),
k'}. < п Ig 3 ......lg 7 < ki + 19 (8/7).
Если вспомнить решение задачи про первые цифры чисел 2 n в
конце 2, то мы приходим К следующей ситуации: на одно й и
той же ОIСРУЖНОСТИ 8J. длины 1 отмечена дуrа 1:1 длина 19 (8/7) 11
точка Ро.......отпечатоК числа (.....lg 7) при намотке числовой оси R],
, "
на эту окружность; точка ро «раздваивается» на две Ро и Ро (обе
они сливаются с РО) и каждая из них начинает «прыrать» по ок-
ружности в одну CTOpOH прыжками величиной Ig2 и 193 соот-
, , ,
ветственно; в результате возникают их «СJlеды» Рl' Р 2 , p . .. и
" " "
Рl, Р 2 , P , "11 Надо доказать, что через некоторое равное число
п прыжков обе эти точки окажутся на указанном интервале L\ ......э1'О
n и будет искомым.
Рассматривая конфиrурационное пространство пар точек (p ,
p ), получаем двумерный тор T ::::8:tXS1, причем уrловая скорость
движения конфиrурационной точки Р == (p , p ) по меридиану тора
(по первому экземпляру окружности 81) равна 0)1 == 19 2, а уrЛОВQЯ
скорость движения по параллели тора (второму экземпляру 81)
равна 0)2 == 19 3. Если бы движение конфиrурационной точки Р по
тору Т 2 было непрерывным, то ее траектория заполнила бы этот
тор всюду плотно. Однако движение точки Р дискретно....... она
«ска чет», меняя свое положение на торе только в целочисленные
моменты времени t == 1, 2, 3, ..., n, .. i, И поэтому теорему об
обмотках тора применить здесь нельзя. Доказать, что множество
«следов» точки Р всюду плотно на торе T , можно, если каким-
то образом удастся дискретное движение точки Р превратить в
непрерывное TaK чтобы пол чилась некоторая обмотка тора, но,
разумеется, wже не двумерноrо.
lV10ЖНО поступить следующим образом. Введем формально еще
одну окружность, по которой запустим третью точку, p ", кото-
рая будет двиrатьея непрерывно с постоянной r овой скоростью
0)з== 1. Рассмотрим конфиr;урационное пространство трех точек
(Р') Р", pta), каждая из которых движется по своей окружности
ДЛИН1,I 1...... первые две движутся равномерно в wrловыми скорос.
тями O)i и 0)2, а третья движется равномерно с frловой ско-
ростью юз. Им является трехмерный тор T3==8 1 X8:tX8 1 и по нему
конфиrурационная точка Р == (Р'-" Р") pf.U) движется уже непре-
рывно, sадавая обмотку тора T . Исходный тор Tg можно пред-
Gтавлять себе располо}кенным в трехмерном торе T так же, как
окруя{ность 81 В торе T g ...... в виде параллеJJИ (рис. 8.2); тоrда
раасматриваемая обмотка тора Т 3 перевекает тор T через р а В-
н ы е (единичные) промежутки времени II оставляет на этой «дву-
115
мерной параллели» следы точки пересечения Р п ==(Р;, p ), KQ
торые ЯВЛЯIОТСЯ конфиrурационными точками на торе Т 2 . Полу.
ченная обмотка тора ТЗ, по сделанному B конце 8 замечанию,
бу дет всюду плотной в ТЗ, если л J k (()i + k 2 (J)2 + kз(J)з ::j.::. О при
в с е х целых k 1 , k 2 , k3. В нашем случае выражение для л имеет
вид л==k 1 1g 2+k21g3+k3, и если бы оно принимало значение О
при некоторых целых ki, k 2 , k з , ТО 10 Л === 2 k 13 k 210 k з == 1, откуда
k 1 == k 2 == k3 == О В силу взаимной ПРОСТQТЫ чисел 2, 3, 5. Значит,
А ::j.::. О при всех целых k 1 , k 2 , k з , поэтому 'обмотка всюду плотна
на ТЗ и, следовательно, точки ее пересечения с lr g заполняют
тор Т 2 всюду плотно, что и требовалось доказать.
б) Если первая цифра у чисел 2 п и 5 n равна х, то, представнв
эти числа в виде 2 п ==сх.l0 п , 5 п == .10п (О < СХ, < 1), видим, что
при х < 3 a < 1 и поэтому произведение самих чисел меньше
1012 противоречие; при х > 3 a > 1 и тоrда произведение самиXl
qисел больше 10 n опять противоречие. Поэтому остается только
возможность х == 3: при перемножении а на «в столбик» проис-
ходит перенос единицы в разряд единиц, Т. е. (О,З...).(О,З.i ]
"рев ращается в 1,000... О.
Итак, oafloBpeMeflflO числа 2 п и 5 n ocym flачиflаться только (J
mройки (например, при n == 5). И это несмотря на то, что каждое
из этих чисел может начинаться с произвольной цифрыl
rеометрически возникшее явление объясняется тем, что по.
строенная в пункте а) обмотка TpexMepHoro тора уже не будет
всюду плотной в нем; в силу равенства 2.5== 10 число л==ki 192+
+k21g5+k3 может стать равным нулю при некоторых целых kf,
k 2 , k з (каких?); поэтому эта обмотка будет пересекать двумерный
тор Т 2 по множеству точек, не всюду плотному на Т 2 (так как
сама обмотка тора ТЗ в рассматриваемом случае всюду плотно
заполняет лишь некоторый двумерный тор, расположенный в T3
но не совпадающий с T ).
Задача пункта б) предлаrалась первым из авторов для реше-
ния в журнале «Квант» (1988, М2 4). Предлаrаем решить анало-
........... rичную задачу для троек чисел 2 n , З h ,
81 ","', 7 n и 2 n , з n , 5 n .
I' «,./l,llоuной', 3 а д а ч а 8.8. BOKpyr Солнца вра-
I наятН/.Jk» \ щается планета с радиусом орбиты R.;
I О \ а BOKpyr нее в той же плоскости......
\ I ' спутник с радиусом орбиты " причем
\ I ---, 1 rловые скорости И 13ращения несо-
" : / ,82. измеримы. ДО!{ёэать, что спутник аа-
.л ',..... \ --" полнит всюду плотно кольцо с центром
9' 2 h1 "'"..1_: в Солнце, внутренний радиус KOToporo
2" а @ равен (R '), а внешний...... (R+r).
..... bIb1 ф 3 а м е ч а н и е. Указанная систе-
I t.;.Т ма «Солнце планета...... спутник» но-
21f 1} а То." сит еще название «двойной маятник»;
Р ero конфиrурационное пространстВо......
ис. 8.10 тор Т 2 (рис. 8.1 О).
3 а д а ч а 8.9. Рассмотрим систе-
му, СОСТОЯЩУIО из ДBY планет одинаКОБоrо радиуса в>О, враща..
ющихся по окру}кностям различны радиусов с общим пентром
О и расположенных в различных ПЛОСI{ОСТЯ:Х (более БЛИSI{ая к О
планета А видна под большим уrлом из ТОЧI{И О, че 1 планета В),
Доказать, что если отношение yr ловы:х Сl{оростеЙ вращения пла..
116
нет иррационаJIЬНО, то затмение более далекой планеты близкой
рланетой (с точки зрения наблюдателя, находящеrося в центре О
системы) будет происходить бесконеч ное число раз.
Реш е н и е. Затмение _ ПРОИСХОДИТ, если в данный момент
времени t планеты А и В оказываются близко к одному из двух
лучей, на которые точка О разбивает прямую пересечения пло
скостей орбит (рис. 8.11). Если (еро, 'Фо) точка тора, COOTBeTCTBY
{ощая поло}кению планет на таком луче А М, то затмение произой
eT, если точка тора (ер, 'Ф), соответствующая : поло}кению планет в
момент времени t, удовлетворяет условию I ep epo 1+ I 'Ф 'Фо I <
<1'1 1'2' rде 1'1 и 1'2 уrлы, под которыми видны планеты из
точки о. Такие точки (ер, '1') образуют квадрат с центром в точке
(СРо, 'Фо) и диаrональю 2(1'1 1'2). Если в момент времени t==O поло
}кения центров планет А, В характеРИЗУIОТСЯ уrлами а и , то в
произвольный момент t соответствующие им уrлы будут равны
'ф ь 0)2 0)2
CP==O)l t + a , 'Ф==0)2t+ , откуда === и 'Ф== ер+л, rде
ер ........ а о) 1 0)1
(О.") А.
Л== а+ р. Координаты ер, Ф связаны, таким образом, линей-
СОl
ным соотношением, задающ м на плоскости Оер'Ф прямую с уrловым
коэффициентом 0)21 Ы1. В силу иррацио-
нальности 0)21 Ыl на торе возникает и р- \ А
р а Ц и о н а л ь н а я обмотка, и поэтому
конфиrурационная точка (ер,'Ф) рано или д
поздно подойдет к точке (еро, 'Фо), что и дo
казывает требуемое: найдется бесконечное
множество точек (ер, 'Ф), для которых бу-
дет происходить затмение. Задача ре-
!
шена.
З а Д а ч а 8.10. Из некоторой точки
сферической планеты одновременно отпра-
вились в бесконечное путешествие два
путешественника, каждый по своему большому Kpyry и со своей
ростоянной скоростью. Доказать, что путешествеНН!1КИ вновь B Tp
тятся, т. е. расстояние между ними в некоторыи момент станет
меньше 1 м. r-
3 а д а ч а 8.11. Двое IЧасов со стрелками идут равномерно,
но одни ИЗ них HeMHoro отстают. а) Доказать, что в какой то мо"
мент показания часов будут отличаться менее чем на 1 с. б)* P
шить ту же задачу для п равномерно идущих часов со стрелками:
доказать, что найдется момент времени, коrда показания любой
пары часов будут отличаться менее чем на 1 С.
9. БИJIЬЯрД В прямоуrольнике и тор
Напомним, что в 9 7 для изучения траекторий
бильярда в прямоуrольнике Q==ABCD была предложена
следующая конструкция.
Прежде Bcero с помощью отражений относительно
сторон прямоуrольника ABCD, а также относительно
сторон у}ке отра>кенных ПРЯ1\10уrольников замостим BCIO
плоскость ПРЯl\10уrольниками QтJn' равными ABCD==.
117
==QOt О. Прямоуrольник Qт, n получается из прямоуrоль
ника -' ABCD с помощью ln последовательных отрюкений
относительно вертикальных сторон и n последовательных
отражений относительно rоризонтальных осей (рис. 9.1,а).
Проведя на замощенной описанным образом плоскости
прямую MN, мы можем с помощью обратных отражений
ее куски, ле}кащие в прямоуrольниках Qm n' перевести
. '
в исходный прямоуrольник QO, о. Тем самым из прямой
lJ
"т,п
С fl 1 f
:' t;. 0'0' '.: 1)10
: Ol}'"::::'
.." ....
А В
а
о'
Рис. 9.1
MN МЫ получим траекторию бильярда в пря:моуrольнике
QO, о (рис. 9.1 t 6).
Удобно изучать не одну бильярдную траекторию от-
дельно, а целый пучок траекторий. Для этоrо на замощен-
ной плоскости проведем семейство nараллеЛЬНblХ друа
друсу nрЯА"-blХ с уrлом наклона а к оси АВ. Теперь заме-
тим, что нет необходимости рассматривать этот пучок пря-
мых на в с е й плоскости, а достаточно оrраничиться
четырьмя пряМоуrольНикаМи........... QO,Ot Qi,Ot Qo,i И Ql,lt
образующими один большой прямоуrольник П===ААiА Аl
(рис. 9.1 t в). ДОПУСТИ 1, траектория MN нашеrо пучка в
точке Mi покидает прямоуrОЛЬНИI) п. Двумя отражениями
относительно прямых АIА} и DDi мы возвращаеJvL луч M 1 N
внутри прямоуrольника п. I(омпозиция упомянутых ОТ-
ражений есть параллельный переНОG на вектор А lА t и
луч М lN при этом переносе переходит в луч М N'. В свою
очередь, коrда луч M N' в точке М 2 выходит ОПЯТЬ из
прямоуrольника П, мы G помощью параллельноrо пере-
носа, задаваемоrо вектором AiA, переносим луч M 2 N'
внутрь П, и так далее. Вместо Toro, чтобы рассматривать
движение шара по прямой MN, мы можем (и, как мы сей-
чао увидим, это более удобно) считать, что доходя ДО rpa-
НИЦЫ прямоуrольника П, шар перескакивает в €OOTBeT-
GТВУЮЩУЮ точку противополо}кной GTOpOHbI И Движется
в том же направлении ДО следующеrо перескакиваНИЯi
таким образом, траектория шара СОGТОИТ ИЗ последова-
118
тельности параллельных отрезков на прямоуrольнике П.
Чтобы получить из этой траектории траекторию бильярда,
достаточно переrнуть прямоуrольник П по средним ли-
ниям (рис. 9.2). Прямоуrольн?к П назовем «фундамен
тальным прямоуrольником» для исходноrо прямоуrоль..
Horo бильярда.
Конечно, более удобно рассматривать движение по
непрерывным траекториям. Для этоrо достаточно склеить
соотвеТСТВУlощие точки противоположных сторон: склеить
ь
lJ
t
-&
МN
\1
IOOO
а
· brJO 1i() b
I
Рис. 9.2
Рис. 9.3
верХНЮIО и нижнюю стороны а в прямоуrольнике П, по
лучив цилиндр, а затем боковые стороны Ь (рис. 9.3).
Ясно, что после склейки оснований цилиндра получится
тор, а рассмотренные выше траектории станут непрерыв-
ными ........ это и будут траектории оБJvtоmкu тора!
Найдем ч а с т о т ы этой обмотки. Если считать,
что бильярдный шар движется со скоростью 1, то при
движении под уrлом а к стороне АВ прямоуrольника
ABCD проекции скорости на rоризонтаЛЬНУIО и верти-
кальную оси равны Vi===COS а и v 2 ==sin (Х. В терминах
координат на торе Vi и V 2 ........ это скорости движения кон-
фиrурационной точки вдоль параллелей и вдоль мерИдиа-
нов. В нашем случае тор склеен из прямоуrольника П со
сторонами 2ai и 2а 2 (здесь ai==AB, a 2 ==AD ......... стороны исход-
Horo прямоуrольника ABCD) и периоды движения по эква-
2aj 2ai 2а? 2а2
тору и по меридиану равны Т 1 == == , T2== == .
Vj COS а. V2 Sln а.
Соrласно определению, соответствующие частоты равны
2л COS а siп а.
(()1 == Т 1 ==л ' (()2 == Л аа
119
Вспомнив результаты Э 8, получаем:
w a
(1) если число w==.......!..==......!..tga рационально, пlO опи-
(й! а2
санная об.Аtотка тора рациональна, и все ее траектории
периодичны;
а-
(2) случаю иррациональности ro ==.......!. tg а соответствует
а2
иррациональная обмоП!ка тора, и тО2да любая траеКlnория
обмотки всюду плотно заполняет тор.
Поскольку бильярдный поток на прямоуrольнике Q
==ABCD получается из обмотки тора (или, что то же самое,
«потока С пере скаки вани ем» на прямоуrольнике П) скла-
дыванием тора вчетверо, соответствующим складыванию
прямоуrольника П по средним линиям, мы получаем из
р а ц, и о н а л ь н ы х обмоток тора пучки пер и о-
Д и ч е с к и х бильярдных траекторий на прямоуrоль-
нике Q, а из и р р а ц и о н а л ь ы ы х обмоток.......... пучки
н е пер и о Д и ч е с к и х и в с ю Д у п л о т н ы х на
прямоуrольнике Q траекторий бильярда. Тем самым тео-
рема 2 из Э 7 о всюду плотности бильярдных траекторий
доказана.
Резюмируем проделанное в 7 9.
Б ильярд в nрямоуеольнике удается свести к обмоткам
тора, при атом траектории бильярда оказываются либо
периодическими, либо всюду плотными в nрямоусольнuке,'
периодичность (или всюду плотность) траектории опреде-
ляется только начальным направлением двuжения, но не
зависит 'CJm начальноео положения шара.
К изучению бильярдов в мноrоуrольниках МЫ вернемся
позже, в rл. 8 и 9, а сейчас в виде задач затронем несколько
интересных вопросов, связанных с обмотками тора.
3 а д а ч а 9.1 (СМ. 22). Доказать, что для бильярда в равно-
бедренном прямоуrольном треуrольнике любая неособая траек-
тория либо периодична, либо ВСIОДУ плотно заполняет треуrоль..
ник. Показать, что особые траектории этоrо бильярда (т. е. те тра..
ектории, которые попадают в вершины) можно естественным об
разом продолжить за вершины (см. задачу 7.5) так, что они оказы..
ваются опять либо периодическими, либо всюду плотными.
3 а Д а ч а 9.2 (см. 9 22). Доказать утвер)кдение задачи 9.1 для
бильярда в равностороннем треуrольнике. (Для 9Toro попытайтесь
обобщить рассмотрения этоrо параrрафа на случай плоскости,
замощенной равносторонними треуrольннками попробуЙте or..
раничиться несколькими треуrольниками, как выше мы оrрани
чились четырьмя прямоуrольниками; постройте затем «поток С
переска кива нием».)
3 а д а ч а 9.3 (см. Э 15 и rл. 7). При изучении бпльярдов в
мноrоуrольниках (например в треуrольниках) возникяет следую
щий Вопрос....... не может ли бильярдная траектория «застрять»
120
в уrле (не попасть точно в вершину уrла, а «запутаться» около
вершины конечно, если так бывает, то эти траектории не MorYT
быть всюду плотными!)? Ответьте на 9ТОТ вопрос. Сформулируем
задачу более точно.
Дан уrол А радианной величины сх. Бильярдный шарик за
летает внутрь этоrо уrла. Сколько может произойти столкновений
шара со сторонами уrла, прежде чем шар вы-
летит из уrла и полетит без столкновений?
(Стороны уrла бесконечные лучи; рис. 9.4).
Может ли быть бесконечно MHoro столкно-
вений? (Рассмотрите сначала случаи а==
==п/2, п/4, п/з, 231/5.) ДОI{ажите, что шар вы-
летит из уrла в направлении, параллельном А
направлению влета, тоrда и только тоrда,
коrДа а==п/п, rде п натуральное число.
При доказательстве теоремы 2 из 7
можно было воспользоваться следующей лем-
мой.
3 а д а ч а 9.4 (ле.А1ма о заЙцах). В He
котором узле О квадратной решетки Haxo
дится охотник, а в остальных узлах сидят
одинаковые и одинаково расположенные 8ай
цы кружки радиуса в с центрами в этих узлах. Охотник нау-
rад стреляет (траектория пули луч 1, выходящий из точки О).
Вернется ли он домой с добычей?
Реш е н и е. Если траектория пули проходит через узел, OT
личный от точки О, то заяц, сидящий в этом узле, будет убит «в
самое сердце» (в центр кружка).
l Поэтому интересен только тот слу-
чай, коrда узел О....... единственный
на траектории пули, т. е. TaHreHc
уrла наклона луча 1 к оси Ох и р-
р а Ц и о н а л е н. Оказывается, что
и в этом СJlучае какой нибудь заяц
будет убит. Обозначим точки пер
сечения луча 1 с вертикальными пря-
мыми сетки через Ао==О, А 1 , А 2 ,
Аз, . .., Аn, . .. (рис. 9.5). COB
местим все квадраты решетки, кото-
рые пересеI{ ает луч 1, с !{вадратом
OMN К, тоrда ка}кдая точка А п пе
u А '
реидет в некоторую точку ri на CTO
роне М N. Найдутся такие точки
r ,
А т и Aт+/i't расстояние между KOTO
рыми будет меньшо е (почему?).
Дока)ките самостоятельно, что тоrда
расстояние от точки А k до одноrо
из узлов решетки меньше 8 (в частности, если A и А:п+k сов-
падают, то Ak будет узлом решеткп).
Решение этой задачи почти Воспроизводит доказательство
теоремы Якоби, и то обстоятеЛЬСТDО, что если из точек прямоЙ,
заполняющих ее ВСIОДУ плотно, выпустить пучок параЛJIельных
прямых, то они ваПОЛНЯIОТ всюду плотно ВСЮ ПЛОСI{ОСТЬ.
к
О=-А о
N
А'5
A
А4
Az
А'
! 5
Рис. 9.5
А
Рис. 9.4
rлава 4
ФИЗИКА прямоуrольноrо БИЛЬЯРДА
Эта rлава посвящена как фиrурам Лиссажу ,
так и их изображениям на экране осциллоrрафа, XOpOllIO
известным физикам-элекtронщикам. Мы приведем мате-
матическое определение этих понятий И свяжем их (с
помощью осциллоrрафа) с бильярдом в прямоуrольнике
и обмотками тора, а также решим с помощью обмоток тора
одну rеометричеСКУIО задачу об обнаружении неподвиж-
Horo объекта на плоскости.
Основной материал этой rлавы мы будем «разбавлять»
задачами, решения KOTOpHIX (иноrда приводимые в тексте)
используются для получения последующих реЗУЛЬ1атов,
поэтому желательно, чтобы читатель принял активное
участие в решении этих задач.
10. Фиrуры Лиссажу *)
Фиrурами Лиссажу называются кривые на
плоскости Оху, описываемые во времени t точкой с коор-
динатами х {t), У (t), rде
х (t) == а 1 cos (OOi t + CPi),
у (t) == а 2 cos (OO2 t + СР2)'
коrда t меняется 01'........00 до +00. Здесь аl>О, а 2 >0
постоянные, называемые амплитудами фиrуры Лисса-
)КУ; OOi>O, 002>0......... постоянные, называемые часпzотами
фиrуры Лиссажу; CPi и ср2.......... постоянные, называе1Vlые
начальными фазами. Друrими словами, фиеурой Лиссажу
называется траекmория точки, коmорая дВU:JlCется по
(1)
*) Лиссажу Жюль Антуан (1822......1880) ....... французский физик.
Фиrуры, названные ero именем, он применил п;ля оптическоrо нс'!
следования сложения колебаний.
122
плоскости Оху так, что ее координаты х и у соверша/{)т
еармонические колебания, Т. е. меняются по rармониче-
скому закону (1). Фиrуры Лиссажу можно наблюдать на
экране осциллоrрафа, подавая соответствующие наПРЯ)I{ения
на rоризонтальную и вертикальную оси.
Поскольку при любом t выполнены неравенства
Ix(t)l ai, ly(t)l a2'
фиrура Лиссажу целиком лежит в прямоуrольнике Q
размерами 2af на 2а 2 с центром в начале координат. Да-
пее, если cos (<Oit+<Pl)==:f: 1, то при этих значениях t фи-
rypa Лиссажу соприкасается с в е р т и к а л ь н ы м и
сторонами прямоуrольника Q, а при t таких, что cos (w 2 t+
+ <P2)==:f:1, фиrура Лиссажу касается r о риз о н т а л ь-
н ы х сторон Q.
Заметим, что координата x(t) меняется периодически
с периодом Тi==2Л/Wf и координата у (t) тоже периоди-
чески, но с друrим периодом........ Т 2==2л/w 2 . Дви)кение
точки (x(t), y(t)) будет периодическим в TOl\l И
только том случае, коrда для некоторых целых т и п mТ 1 ==
==пТ 2 , т. е. коrда Tf и Т 2 соизмеримы (продумайте это).
T 00
Поскольку Т 1 ===.....2., условие периодичности состоит в
2 001
Р аци ональности числ а ffi == 002 .
, 001
Сейчас мы укажем удобный способ изображения фи
ryp Лиссажу, а заодно получим информацию о поведении
непериодических фиrур Лиссажу. Прежде Bcero, введем
вместо t новую переменную
и == ffi 1 t + ЧJi;
коrда t меняется от oo до +00, и тол{е меняется от ..........00
до + 00, и наоборот. Выразим t через и:
1 1
t == OOf и OOi CPi
И подставим полученное выражение в формулу для у (t);
в результате возникнет еледующая зависимость у от и:
у (и) == а 2 cos (wu + ) == а 2 cos ro (и.......а) ,
rде W==W2/Wf., a==........ /<o, ==cp2......<OqJi. Наконец, выберем
за единицу масштаба af., Т. е. заменим ai на 1, а 2 на а==
==a2/ a i. Теперь формулы, задаЮЩИе фиrуру Лиссажу ,
принимают совсем простой вид:
х (и) ;:;:::: воз и, у (и) == а cos (00 (и...... а».
123
f1a рис. 10.1 нарисованы вырожденные фиrуры Лиссажу
с фазой а==О, ш== 1 (рис. 10.1, а) и ш==2 (рис. 10.1, б):
рри ш== 1 и а==О у==а cos и==ах и мы получаем дважды
проходимый отрезок прямой; если ю==2 и а==О, то у==
11 ==а cos 2и==а (2cos 2 и 1)==2ax2 a и
соответствующая фиrура Лиссажу ........
дважды проходимая дуrа параболы.
3 а Д а ч а 10.1. Докажите, чт,р при
а==О и ю==п (п натуральное чисдо) фи-
rypa Лиссажу представляет собою часть
rрафика мноrочлена степени п: у== Т п (х).
(Мноrочлены, получающиеся таким обра-
зом, называЮ1СЯ ,М,НО20члена,М,u чеБыlе--
ва *).)
в общем случае (при а =1=0) у нель-
зя разумным образом выразить через
х, и мы поступим иначе. Чтобы нари-
совать на плоскости Оху заданную
уравнениями (2) фиrуру Лиссажу,
которую мы I обозначим L (ю, а), нарисуем сначала на
вспомоrательной плоскости Оиу rрафик функции
у == а cos roи,
который обозначим r 0). Чтобы получить rрафик r (о, а
функции у==а cos w (и a), достаточно перенести rрафик
r ffi на а вдоль оси Ои (рис. 10.2). - ,
Рассмотрим бесконечный прямой /1
круrовой цилиндр радиуса 1, на кото-
ром выделена одна образующая........ ось
Оу . и одна направляющая окруж-
ность s. Приложим плоскость Оиу К
цилиндру, совместив оси Оу на плоскости
и на цилиндре так, чтобы ось Ои каса-
лась окружности s. Теперь намотаем
всю плоскость Оиу на цилиндр (рис.
10.3). Конечно, процедура намотки лишь
воображаемая; плоскость считается «бес-
конечно тонкой», прозрачной на ней
лишь отмечена кривая r ш, (у, (указанная
u
намотка аналоrична намотке прямои
1R.1 на ОI{РУЖНОСТЬ при решении числовой задачи в Э 2).
Эта кривая, намотанная на цилиндр, дает пространст-
х
«,=0
(А:) = 1
!I
LC
а=О
bl=Z
Рис. 10.1
q
II
и
*) п. Л. Чебышев (1821 1894) крупнейший русский мате'!
матик, основоположник петербурrской математич'еской школЦ!.
Мноrочлены. названные ero именем. ЯВJIЯЮТСЯ мноrочленами. на.ш,
124
венную кривую, которую обозначим r «(О, а). Заметим,
что переносу на ct по оси Ои, при котором из rрафика
r u) получается rрафик r (о, сх, соответствует (после намотки
плоскости на цилиндр) поворот около оси цилиндра 01У!
на уrол а радиан. Отсюда сле (J; ai
дует, что для получения кри-
вой r «(О, а) IОЖНО поступить
так: намотать на цилиндр
rрафик r 00 функции у==
асоs((Оц) и полученную кри
вую r «(О) повернуть на уrол
а около оси 01Уl (рис. 10.4).
Итак, 1\1Ы получили прост В...
ранственную кривую r «(О, а),
лежащую на цилиндре. Вооб
ще rоворя, эта кривая будет
и леть точки самопересечения. Рис. 10.3 Рис. 10.4
Она целиком лежит в куске
пилиндра 'У I а около окружности S на цилиндре (это
«кольцо» получается после намотки на цилиндр полосы
I у , а плоскости Оиу); точкам касания rрафика r 00, а.
112
2А 2
Рис. 10.5
А 1
с пряrJЫМИ у== + а соответствуют ТОЧКИ касания кривой
r «(О, а) с верхней и нил<ней окружностями S(+) И S( )'
оrраничивающими УПОI\1ЯНУТЫЙ кусок цилиндра (рис. 10.4).
Наконец, ПРИЛО)J{ИМ к цилиндру С изображенной на неl\Л
кривой r «(О, а) плоскость Оху так, чтобы своей осью Оу
она касалась цилиндра по образующей 02У2, получающейся
ИЗ образующей цилиндра Оу поворотом на л/2 ОКОЛО оси
01Yi. После эrоrо спроектируем КРИВУIО I' «(О, а) с цилиндра
менее УКЛОНЯIОЩИМИСЯ от нуля» (СМ. научно-популярную книrу:
Д а н и л о в Ю, А. МНОI'очлены ЧеБЫПlева. Минск: выllэйшаяя
школа, 1984).
125
на плоскость Оху так сказать, посмотрим на кривую
r (ш, а) сбоку так, чтобы ось цилиндра OiYf слиласЪ с
образующей 02У2 цилиндра и осью Оу на плоскости, а
образующая цилиндра Оу спроектировал ась в прямую
х==1 (рис. 10.5).
3 а д а ч а 10.2. Доказать, что проекция кривой r (00, а) на
плоскость Оху есть фиrура Лиссажу L (00, сх).
Реш е н и е. Точка (и, а cos 00 (и........сх)) rрафика r 00, а ПОС.1!6
намотки плоскости Оuу на цилиндр перейдет в точку цилиндра и,
высота которой над окружностью S по Ha -
Х равляющей цилиндра равна h==a cos 00 (u......ct),
и при проекции на плоскость Оху TotlKa U
перейдет в точку и' с ординатЫ! !/=h==
==cos 00 (и a). Чтобы найти абсциссу точки И',
рассмотрим точку М, в которой проходящая
через U направляющая цилиндра пер с j{аёт
окружность S (рис. 10.6). Уrол L0102M,
соrласно определению намотки; раВен U, II
координата по оси Ох проекции М HB Ох
равна 02M'==COS и. Таким образом, проек-
ция точки U на плоскость Оху имеет к60Р"
динаты (х, у)== (cos и, cos 00 (и.......а», что и требовалось ДOKa aTЬ
Итак, для построения фиrур Лиссажу L(oo, а) доста-
точно намотать к о с и н у с о и Д у у==а cos шu на цилиндр
и затем спроектировать ее на соответствующую плоскость
(повернув перед этим на уrол а кривую или плоскость
Oxyl). Таким образом, чтобы нарисовать G е м е й G Т В О
фиrур Лиссажу L (ш, а) с фиксированным 00 и разными <х,
достаточно построить Bcero лишь о Д н у Кривую......... ци-
линдрическую косинусоиду r (00). РаСС 10ТРИМ несколько
частных случаев.
С л у чай ro== 1. При намотке косинусоиды У==а cos u
на единичныЙ цилиндр один период (О и<2л) косину-
соиды наложится на цилиндр ровно один раз, и r (1) будет
замкнутой кривой с одним минимумом и одним максимумом
(самой высокой и самой низкой точкой, если высоту из-
мерять пр образующим цилиндра).
3 а д а ч а 10.3. Доказать, что кривая r (1) ...... n л о с к а я,
Т. е. целиком лежит в одной плоскости. (Эта кривая есть сечение
цилиндра плоскостыо .)
3 а д а ч а 10.4. Доказать, что сечение цилиндра плоскосты,,
наклонной к ero оси, есть эллипс (определение эллипса см. в 4).
(Решение 'этой вадачи с помощью сфер Данделена приведено в
4 ...... см. задачу 4.4.)
«Рассматриваи» полученную кривую с разных сторон,
нетрудно изобразить семейство фиrур Лиссажу с 00== 1
(Т. е. о 001==002). ПОСКОЛЬКУ перпендикулярная проекция
эллипса есть либо Kpyr, либо опять эллипс,' фиеуры Лис-
о
8
Рис. 10.6
126
сажу с ro== 1 суть эллипсы, вписанные в пРЯМОУ20ЛЫ-lИК П
(рис. 10.7).
С л у чай ro==2. Два периода косинусоиды у==а cos 2и
дадут при намотке на единичный цилиндр только о Д и н
{>
Рис. 10.7
Рис. 10.8
слой на цилиндре, и кривая r (2) имеет 2 минимума и 2
маI{симума. Полученная кривая уже не плоская (она
похожа на проволочное седло). Ее «рас-
смотрение» дает семейство фиrур Лиссажу
с ф ==2 (рис. 10.8).
С л у чай ro==3/2. Кривая r (3/2) на
цилиндре заМI{нется, коrда мы нам:отаем на
Hero Д в а слоя......... тр И пер иода коси нусоиды
3
У == а cos 2" и. Эта кривая будет иметь само-
пересечение уже на цилиндре. Изобразите
какую-нибудь И3 соответствующих фиrур
Лиссажу (рис. 10.9).
При рассмотрении фиrур Лиссажу G
ф== 1 и ro==2 бросается в rлаза их сход-
ство G семействами периодических траек-
торий бильярда в прямоуrольнике (см.
рис. 7.1), только У траекторий бильярда вместо точек
касания ео сторонами прямоуrольника точки И3..'Iома.
4-п
(д= 3/2
Рис. 10.9
127
Это сходство отнюдь не случайно, и мы ero обсудим в сле-
дующем параrрафе (подумайте над этим вопросом caMO
-стоятельно) .
Займемся теперь непериодическими фиrурами Лиссажу .
т е о р е м а. Лl0бая неперuодuческая фuсура Лиссажу
всюду плотно заполняет nРЯМОУсОЛЬНUК п== { I х I 1,
'YI a}.
Д о к а з а т е л ь с т в о. Посколнку фиrура Лиссажу
L«(j), а) получается в результате проекции цилиндриче-
ской косинусоиды r (ю, а) на плоскость Оху, причем ПрО
- екция части цилиндра Ц == { I у I а}, лежащеrо между
окружностями S(+) и S( ) (см. выше) есть в точности
прямоуrольник П, достаточно доказать, что при иppaциo
нальном (j) кривая r (ю, сх) всюду плотно заполняет ци
линдр ц. Для этоrо рассмотрим точки касания кривой
r«(j), а) с верхней окружностью S(+). Они получаются
при намотке на окружность S(+) из точек касания rрафика
у==а COS (j) (и cx) с пря:мой у==а, т. е. из таких точек ,ип,
что ffi (иn а)==2пп. Отсюда находим:
П2n
и == cx + n .
n о)
После намотки эти точки дадут последовательность точек
М п на окружности S(+>, причем, поскольку и п ариф-
метическая проrрессия с разностью ер==2п/ю , точки М п
получаются каждая из предыдущей поворотом по окруж-
ности S(+> на уrол ер. Соrласно теореме Якоби ( 2),
если числа ер и n н е с о и з м е р и м ы' точки М п
всюду плотно заполняют окружность S(+). Несоизмери-
мость ер с n означает иррациональность отношения ср/п==
==2/ю , т. е. иррациональность ю. Из всюду плотности
мно}кества точек М п по окру}кности S(+) уже несложно
вывести всюду плотность кривой r«(j), сх) на цилиндре (про..
ведите подробный вывод сами). Теорема доказана.
Эта теорема тоже весьма напоминает соответствующие
свойства бильярдных траекторий. Из нее следует, что
самый лучший способ нарисовать фиrуру Лиссажу с ир-
рациональным ffi зарисовать сплошь весь прямоуrоль..
ник П I Если наблюдать такую фиrуру ЛиссЮ!{у на эк..
ране осциллоrрафа, то можно заметить, что она плывет
за экраном как бы поворачивается невидимый цилиндр
(; нарисованной на нем цилиндрической косинусоидой.
На Cal\10M деле это не плывущая, а о Д н а и т а ж е фи-
rypa Лиссажу (если только не меняются фазы ер1 и СР2)'
но ранее начерченная ее часть потухла на э'кране. Если
128
бы не было TaKoro затухания, то мы увидели бы всюду
плотную на экране фиrуру Лиссажу , если только отно-
шение 00== Ю2/Юl «подобрать иррациональным». (<<Всюду
плотность» на экране соответствовала бы тому, что весь
экран светился бы; более Toro, экран светился бы все
равномернее и равНомернее'........... но это довольно сложное
утверждение.) Заметим, что «иррациональных чисел боль..
ше, чем рациональных»: рациональные числа моя{но за-
нумеровать, а иррациональные нельзя. В теории вероят-
ностей часто используется следующий факт: «если науrад
ткнуть пальцем (точечным!) в какую-либо точку на чис-
ловой прямой, то с вероятностью 1 J.\tIbI попадем в точку с
иррациональной координатой». Поэтому подобрать 00 ир-
рациональным мо)кно, выбрав ero «науrад».
Задачи физики, в которых появляются фиrуры Лиссажу ,
довольно подробно рассмотрены в ряде статей из «Кванта»: Минц
Н. А. Странный маятник (1971. М2 6. С. 30 32); Коткин r. л.
Опыты с маятниками (1972..NQ 1. с. 26 31); Сипаева Н. А. Фиrуры
Лиссажу (1972..NQ 7. с. 23 28). Там же описаны соотвеТСТВУIощие
опыты.
3 а Д а ч а 10.5. Придумать способ рисования кривых на пло
скости Оху, задаваемых уравнениями: а) х== sin t, у== f (t); б) х==! (t),
y==cos '. (Здесь f (t) заданная функция; мы имеем в виду способ,
аналоrичный описанному способу построения фиrур Лиссажу .)
З а Д а ч а 10.6. Докажите, что фиrуры Лиссажу L (1/ <о, сх.)
с амплитудами аl ==а 2 == 1 равны соотвеТСТВУIОЩИМ фиrурам Лис
сажу L (ю, ) с тем же <о и каким то . (Рассмотрите сначала случаи
(о"" 2 ( == ) j (0== n ( == ). rде n натуральное.)
3 а Д а ч а 10.7. Какое наибольшее число точек самопересе
чения может иметь фиrура Лиссажу , если а) ю==п, б) 00== 1/n,
в) OO==fll/n (т и п натуральные)?
11. Бильярд в прямоуrольнике
и осциллоrраф
В 9 было показано, что траектории биль..
ярда в прямоуrольнике получаются из траекторий обмоток
тора т «складыванием тора вчетверо». Рисунок 11.1 Ha
поминает, в чем состоит это складывание. С точки зрения
u
математики с помощью этоrо складывания мы каждом
точке М тора 1" ставим в соответствие некоторую вполне
определенную точку М' прямоуrольника Q. Такое соот-
ветствие, как хорошо известно (см., например, раздел I1
книrи А. Н. Колмоrорова «Математика....... наука и профес-
сия», «Библиотечка «Квант», 1988. Вып. 64), называется
отображенuем тора Т fla nряМ,оуzольнu1\, Q. Обозначим
5 r. А. fапьперин, А. Н. 3eMJI;IK08
129
ero f б:
f б : i ). Q, f б (Nl) :== J\t1' ·
Для точки N внутри Q имеется ровно 4 прообраЗG точки
MIt М 2! М Зt М4 тора, для KOTOPIJIX fб (Mh)==N (рис. 11.2).
Если на торе рассмотреть кривую r, ЯВДЯI-ОЩУЮСЯ траек-
торией обмотки тора (см. 8), то образ этой кривоЙ при
отображе'Нии fб кривая fб(f)
1'. c-) ЕЕ3 11 в прямоуrОЛЬИИI\е, ЯВЛЯЮШ,аяся
lпраекпzорuей бильярда.
.{l, в 10 мы обратили виима..
О ине на сходство между траекто'"
риями бильярда и фиrурами
п Лиссажу (рис. 11.3). Оказывает-,
v ся, причины этоrо сходства coc
Q'O о fJ тоя т В том, что фиеуры Jlacca
жу также являются образами
траекторий обмоток тора при
1lекотором отображении 10 тора
т в прямоуrольник П, в который вписаны фиrуры Лисса-
жу ........ п== {(х, у): I х I ai, I у I а 2 }, если фиrуры Лис-
сажу задаются формулами
х (t) == aj COS (ю 1 t + 1)' у (t) == а 2 cos (ю 2 t + {J)2)'
Отображение ' : 1" --+П мы сейчас опишем. Оно оказы-
вается весьма похожим на отображение fб; если отобра-
Рис. 11.1
п
. М 2 M .
.М , М4.
/ТБ
ф ф j
.
e \8N
Рис. 11.2
Рис. 11.3
жение f б назвать «бильярдом», то отображение f о естест-
венно назвать «свободным осциллоерафом» (осциллоерафом,
показывающим фиrуры Лиссажу).
Итак, в целом ситуация такова. Имеются два «почти
одинаковых» отображения fб и 10 тора т в прямоуrольник.
При этом траектория r обмотки тора при отображении
«бильярд» переходит в траекторию бильярд fб (f), при
отображении «осциллоrраф» переходит в фиrуру Лиссажу
130
{о (r). в этом смысле «бильярд» и «осциллоrраф» устроены.
одинаково, или, как часто rоворят в таких случаях, и з о-
м о р Ф н ы.
Опишем теперь отображение «свободный осциллоrраф»
'о. РаСС1\10ТрИМ тор Т с коорд.инатами ('Фf, '1'2) на нем (дол.
rотой и широтой........ см. 8). Точке тора М G координатами
('\ f, 'Ч'2) поставим в соответствие точку М' плоскости Оху
с координатами x==aicos 'l'f, y==a 2 cos '1'2 и положим м' ==
==:fo(M). Тем самым отображение 10 полностью определе-
но ....... оно задается формулой
f о ( 'f, 2) == (ai cos '1'1, а 2 cos '1(2).
Траектория r обмотки тора о частотами (O)i, 0)2) зада.
ется формулами
'Pi (t) == O)l t + CPi, '1'2 (t) == 0)2 t + СР2.
Образ траектории r этой обмотки при отображении 'О
на плоскости есть кривая
f о (f) == {fo ('1'1 (t), '1'2 (t»: 00 < t < + оо} ==
== {(а! COS 'I'i (t), а 2 os '1'2 (t»! ....... 00 < t < + оо}.
Подставляя сюда выражения для 'Фi (t) и '1'2 (t), ПОЛУЧИl\1,
как и ожидалось, формулы фи )tРЫ Лиссажу:
10 (r)== {(а 1 cos (O)lt+CPl), а 2 cos (0)2t+CV2)3 00 < t < + оо}.
Таким образом, действительно, фиrуры Лиссажу являются
образами траекторий обмоток тора при отображении 10.
Посмотрим теперь, как «устроено»
ЭТО отображение. Разобьем тор на Ф2
четыре квадрата, как указано на рис. 2"
11.4. Пусть М == ('i'1, '1'2)........ точка
внутри квадрата Qoo, т. е. 0<'1'1<1&,
0<'Ф2<n; рассмотрим еще три точки
Mfo== (2Л: 'i'1, '1'2), М oi== (фi, 2л: Ф2),
Mii== (2n Фf, 2Л: 'Ф2)' Нетрудно ви-
деть, что эти точки получаются из М
симметриями относительно средних
линий квадрата; с друrой стороны, соrласно известным
формулам триrонометрии
10 (M io ) == 10 (M oi ) ==/0 (M ii ) == 'О (М)
(проверьтеf), Т. е. эти четыре точки при отображении {о
переходят в одну.......... точно так же, как и пр и соответст-
вующем отображении fб. Наконец, поскольку функция
z==cos'I' осуществляет взаимно однозначное отображение
5* 131
1&
'
. .
М О' M II 9ft
.М 1'110
.
....
,.
(100 1f 910 2" 'Р1
Рис. 11.4
отрезка О <'Ф <:л на отрезок .........1 <z 1, отобра}кение (х, у)==
r=: (a1cos 'Фi, a 2 cos '1'2) отображает взаимно однозначно квад-
рат Qoo на прямоуrольник П == {.........а1 <.х <.аl, .........а 2 <.у <.а2}
(проверьте!).
Итак, отображение «осциллоrраф» " действует так:
сначала тор -П- «складывается», как и при отображении
«бильярд» fб, вчетверо соответствующий квадрат пере-
rибается по средним линиям и превращается в свою чет-
верть Qoo. При этом траектории обмотки превращаются
в траектории бильярда в квадрате Qoo. После этоrо к ]{вад-
рату Q применяется взаимно. однозначное отображение f *
ero на прямоуrольник П, при котором траектории биль-
ярда «сrлаживаются» И превращаются в фиrуры Лиссажу!
(Последнее отображение при ai==a 2 == 1 есть с}катие, но не
равномерное; блаrодаря неравномерности и сrлаживаются
уrлы.) Приведенное описание показывает, что «бильярд»
и «осциллоrраф» действительно «изоморфны» «отлича-
ются на взаимно однозначное преобразование». Изоморфизм
мех{ду фиrурами Лиссажу и траекториями бильярда можно
пояснить довольно просто и по-друrому. При дви)кении
точки (х (t), У (t)), описываемом уравнениями фиrуры Лис-
сажу
х (t) == а 1 cos (Юi t + С{)1), у (t) == а 2 cos (ro 2 t + С{)2),
координаты х и у (или проекции точки (х, у) на оси Ох
и Оу) совершают сармонuческие колебания. При движении
же бильярдноrо шара (х, у) по ПрЯМОУI'ОЛЬНИКУ {О <.х <.аl,
О <.у <.а 2 } координаты х и у также совершают колебания,
только не rармонические, а соответствующие закону уп..
pyroro отражения. Можно написать формулы, по которым
меНЯI{)ТСЯ х и у в этом случае:
x(t)==a l I 2 { ; 1 t + bl} 11, у (t)==a 2 /2 { ;:2 t+b 2 } 11.
Здесь {и} обозначение для дробной части числа и. rpa-
фиk зависимости х от t, задаваемой выписанной формулоi"'!,
схематически изображен на рис.
11.5. Таки yf образом, траектории
бильярда задаются формулами,
аналоrичными формулам для фи-
ryp Лиссажу с той разницеЙ,
что вместо функции cos u в этих
формулах фиrурирует функция
с(и) == 12 {и} 11.
3 а д а ч а 11.1. Полученное описание фиrур Лиссажу K8I{
образов траекторий обмотки тора при указанном' отображений
.х
Рис. 11.5
132
дает возможность сразу доказать ВСIОДУ плотность фиrур Лиссажу
с иррациональным отношением (f)2/rot. Проnедите точное рассуж
дение.
3 а д а ч 8 11.2. Отображение f о есть композиция проекций
тора убедитесь в ЭТОМ t показав, что при описанном ниже по..
строении (по шаrам) получаются фиrуры Лиссажу .
1 ш а r, На плоскости О'Фl '1'2 рисуем ПрЯМУIО и наматываем
эту плоскость на еОрUЗ0нтальный цилиндр радиуса 1.
2 ш а r. Проектируем получеННУIО на цилиндре КРИВУIО на
пло кость ОФIУ.
3 Ш а r. Наматываем плоскость О'ФIУ на вертикальныЙ цилиндр
радиуса 1.
4 ш а r. Проектируем получеННУIО на цилиндре КРИВУIО на
плоскость Оху дол}кны получиться фиrуры Лиссажу с ампли"
тудами а 1 ==а 2 == 1.
12. Задача о пеленrе
Пусть на плоскости даны две различные точки
А! И А 2 . Около этих точек вращаются прямые II и l2 С
постоянными уrловыми скоростями (йl и 002. Пусть М (t)
точка пересечения прямых II и 12 В мо- "
мент времени t. Задача о пеленее заклrQ-
чается в описании «кривой пеленr'а» М
траектории движения точки М (t) (рис.
12.1). В некоторые моменты времени
прямые II и l2 параллельны тоrда мы (iJ1
считаем (как и происходит на самом
деле), что точка М «отлучил ась на бес-
конечность».
Если периоды вращения Т 1 ===2п/I 001 , И Т 2 ===2л/1 002 I
С о и з fvl е р и м ы, то, очевидно, движение точки М (t)
будет периодическим повторяющимся через некоторый
промежуток времени. Однако нарисовать соответствующие
кривые не так уж .просто, и мы, в качестве разминки, or
раничимся рассмотрением случая Фi==Ю2.
Если Юi==Ю2==Ю, т. е. движение прямых 11 и 12 про...
исходит с одинаковыми уrловыми скоростями и в одном
направлении, то из рис. 12.2 видно, что уrлы CXi и СХ 2 равны
(оба эти уrла равны ю.Llt) и поэтому уrлы LAiMA 2 и
LA 1 M' А 2 равны. Следовательно, в этом случае точка
М (t) движется по дуrе окружности, проходящей через
точки Af И А 2 *).. Какая именно это дуrа, зависит от на...
чальных положений прямых li и 12 (если в на9альный
момент 1i и l2 параллельны, то они будут такими и всеrда).
A
, *) Как известно, множество точек М, лежащиХ! по одну сторону
ОТ прямой AiA2 И таких, что LA 1 MA 2 ==a==const, представляет со-
бой дуrу окружности с хордой А 1 А 2.
133
Нетрудно ПQК8зать, что после перехода прямой 12 через
положение А 2 А! точка М продолжает двиrаться по дуrе
той же окружности, что и раньше. Таким образом, «пе-
лене» с частота.А1-U <Ui== (1)2 пpoucxoauпz по окружностЯ.Аt,
nроходящuм через точ/{и А i И А 2.
В случае юi===----(й2 кривые пеленrа будут rиперболами,
проходящими через точки А! И А 2 (рис. 12.3), доказатель-
/1'
А2.
Рис. 12.2
ство чеrо мы не приводим. Попробуйте нарисовать какие-
нибудь кривые пеленrа с 001== + 2(02-
Т е о р е м а. Если (й) и 002 несоuзмерUМbl, то любая
кривая пелеflеа всюду плотно заполняет всю плоскость,
. т. е. пересекает любой круе на nлос-
, М кости (еде бы он ни лежал u сколь
',о н' бы мал он ни был).
Нетрудно вывести эту теорему из
теоремы Якоби. Мы поступим, одна..
ко, чуть изящнее....... построим отобра..
жение 'П тора 1r в плоскость [(2, при
котором траектории обмотки тора G
u
частотами <U:t, 002 переидут в соответст-
Рис. 12.3 вующие кривые пеленrа.
Это отображение fп: 1r [(2 (ес-
тественно ero назвать « пелене ом ») чрезвычайно просто----
точке тора М с координатами 'Фi, '1'2 мы ставим в соот-
ветствие точку М' пересечения прямых 1i И 12' проходящих
через наши две точки А! И А? И образующих о ПрЯl\fОЙ
А 1 А 2 уrлы 'i'i и 'Ф2 соответственно (рис. 12.4). Таким об..
разом, тор lr.......... конфиrурационное пространство точек М.
При этом мы считаем, что на каждой из прямых li И 19
выбраны направления, и уrлы '1'1, '1'2 отсчитываются ОТ
направления луча AiA? до этих выбранных направлений.
Если оказывается, что прямые 11 ('1']) И 12 (1.Р2) параллель-
ны, то соответствующая ТОЧI{а тора переходит «в бесконеч..
ность» (так будет на «диаrонали» тора 'Фi ==\1'2 и на парал-
134
лельной «кривой» 'Ф2=='Фi::r:;л). Отображение fп выбрано име1/,. .
но так, чтобы при aBU{)fCeHUU КОн'фU2урационн'ОЙ точки
тора по траектории оБАtоткu:
'Фl === ю l t + (Рl' '1'2 == (fJ2 t + (])2
образ этой точки на плоскости двиёался по кривой пелеНёаf
(ОбдумаЙте это] утверждение.) Отображение fn будет ото-
бражением тора на всю пЛОСКОС/rlЬ, приче:м даже ч е т ы-
р е х к р а т н ы м точки ('1'1, \}'2), ("1'1+1&, '1'2), ('1'1, 'Ф2+П),
z
"M
I
J
rt
"' rf,,, ::' '<\,}.1\ :
Т, '.::: ..' '.. ' .':.. 7'
, , ....'. ,. .. ' . .... '. .
М'" М 'О.. .' ......'
'.:'::: '. :. .: ::.:.: :.:: :
,.:.: -. : .:.\.... ..".. .. :-..;
СР1
Рис. 12.4
о 1f Zif"'1 .
Рис. 12.5
Т"
А
в
Ф1
Рис. 12.6
(Фl+п, 'Ф2+п) при \}'1*'Ф2 и 0<'1'1<1&, 0<'Ф2<п переходят
в одну и ту же точку плоскости. Сетка параллелей и ме-
ридианов на торе при таком отображении переходит в сет-
ку, образованную пересечениями прямых, проходящих
через точки А 1 и А 2 (рис. 12.5).
135
Если roi и 0>2 несоuэ.меРUМbl, то на торе траектория l'
ero обмотки всюду плотна, и отсюда немедленно следует
всюду плотность кривой пеленrа 'П (r). Д е й с т в и ·
т е л ь н о, чтобы показать, что кривая пеленrа заденет
кружок К (рис. 12.6), рассмотрим прямоуrольник (или
I{вадрат) и на торе Т, переходящий при отображении
fn внутрь Kpyra К. Поскольку траектория r пересекает и
(что следует из всюду ПЛОТНОGТИ r. на торе), кривая "е.
ленrа f п (r) переаекает КI ,
На этом мы закончим раасмотрение вопросов, связан.
ных с обмотками торов, и вновь возвратимся к бильярдам.
ЧАСТЬ 1I1
rЕОМЕТРИЯ И АРИФМЕТИКА
СТОЛКНОВЕНИЙ
.............
При Д в о 1) в & й)
Эй, музыкантыl
Входит Мардиан.
К л е о n а т р а:
Нет, не надо их,"
Давай, в шары сыrраем, Хармиана.
В. Шекспир. «Антоний н Клеопатра)
в этой части книrи будет ИСGледована ме-
ханическая система «еа8 абсолютно упруеих шарО8»........
система шаров, упруrо сталкивающихся друr с друrом,
а также со стенками сосуда, в который эта система поме-
щена. В физике часто пользуются такой моделью при опи-
сании поведения реальноrо rаза, Т. е. считают молекулы
. rаза/ твердыми шарами, а столкновения между ними......
упруrими. В дальнейшем мы часто для удобства шары
будем называть молекулами. В нормальных условиях
число содержащихся в 1 см 3 молекул воздуха очень ве-
лико их порядка 1023, и от MHoroKpaTHbIx столкнове-
ний молекул друr с друrом возникает «хаос»......... равно.-
мерное распределение молекул.
Изучение движения молекул rаза относится к области
физики, называемой статистической механикой. Основы
этой науки были заложены в трудах Максвелла, Больц..
мана, rиббса. Людвиr Больцман *) выдвинул так назы-
ваемую «эрrодическую rипотезу», в настоящее время но-
сящую ero имя и состоящую в том, что система «rаз шаров»)
эрrодична * *). На этой rипотезе основан вывод известных
из школьноrо курса физики законов Бойля lv1ариотта,
rеЙ Лlоссака, уравнения Клапейрона ....... Менделеева и др у-
rих уравнений молекулярно кинетической теории rаза.
Однако сама rипотеза Больцмана до сих пор доказана
только для частных случаев.
*) ЛюдвU2 Больцман, (1844......1906) выдаIОЩИЙСЯ австрийский
ченый, работы KOToporo оказали orpoMHoe влияние на развитие
фундаментальной физики в силу их пуинципиальной новизны и I'ЛУ"
бины. Относящаяся к статистическои механике эрrодическая rИDО'"
q'еза отражает лишь небольшую часть чрезвычайно разносторонней
научной деятельности л. Больцмана.
I * *) О понятии эрrодичности см. конец введения.
137
Выдающийся вклад в решение этой проблемы и в обо-
снование статистической механики внесли советские уче-
ные Н. С. I(рылов И Я. r. 'Синай. Важной идеей в их ис-
следованиях явилось то, что rаз можно заменить бильяр-
дом, правда, в очень мноrомерной и криволинейной об..
ласти специальноrо вида. Возникновение MHoroMepHoro
пространства rоворит о сложности рассматриваемой задачи.
Сведение системы абсолютно упруrих шаров к системе
бильярдноrо типа впервые появилось в книrе Н. с. Крыло-
ва «Работы по обоснованию статистической физики»
(М.: Изд-во АН СССР, 1950), а последовательная матема-
тическая теория была развита я. r. Синаем, который в
1970 r. в работе «Динамические системы с упруrими от-
ражениями» (см. [17]) доказал, что уже система из двух
твердых дисков в прямоуrольнике является эрrодичной.
В этой части мы остановимся TOJIbKO на простейших
rеометрических и «арифметических» свойствах «rаза ша-
ров». rеометрию столкновений отражает описание конфи-
rурационноrо пространства системы, сведение ее к биль-
ярду и описание поведения полученной бильярдной ча..
стицы; а арифметику подсчет числа столкновений между
шарами.
Изучение rеометрии и арифrvlетики столкновений в си-
стеме Д в у м е р н ы х дисков ИЛИ т р е х м е р н ы х (а
тем более MHoroMepHbIX) шаров довольно сложно для на-
чинающеrо читателя. Поэтому эту центральную тему мы
поставили в конец части 111 и отметили ее двумя звездоч-
ками rл. 7 при первом чтении можно пропустить. Вза-
мен этоrо в rл. 5 и 6 МЫ подробно рассматриваем модель
о Д н о м е р н о r о «rаза» систему упруrо сталкиваю-
щихся частиц на прямой или ее части (ПОЛУПрЯ1\10Й или
отрезке). Эта модель существенно проще и вполне до-
ступна школьникам. При ее изучении сначала возникает
рассматривавшийся ранее бильярд в прямоуrольнике, и
мы можем применять уже известные из части 11 резуль-
таты. Попутно обнаружатся и новые эффекты, которые
частично будут исследованы сразу же, а частично сведутся
к изучению бильярдов в мноrоуrольниках.......... эти биль-
ярды рассматриваются в части IV.
В rл. 5 разобран простейший случай одномерноrо «ra-
за» .......... системы Д в у х частиц на прямой. Для Hero про-
водится относительно полное исследование.
Уже для одномерноrо «rаза» ИЗ Т Р е х молекул полное
исследование системы может быть осуществлено до конца,
лишь коrда молекулы не заключены в какой-либо «сосуд» ..........
138
отрезок, а свободно движутся по бесконечной прямой.
сталкиваясь только друr с друrом. Изучение поведения
систеl\fЫ из трех молекул на отрезке сразу приводит к
системе из большоrо числа молекул на прямой, и оно
мо}кет быть исследовано только качественно (т. е. MorYT
быть получены лишь некоторые оценки на различные
u
параметры Системы......... число столкновении между моле-
кулами и т. п.). Некоторые результаты этоrо исследования
приведены в rл. 6. Трудным в этой rлаве является 18,
u u u
которыи отмечен однои звездочкои.
rлава 5
ОДНОМЕРНЫЙ «rдз» ИЗ ДВУХ МОЛЕКУЛ
в этой rлаве исследуется одномерный «rаэ»
из Д в у х молекул....... двух шаров на отрезке, упруrо
сталкивающихся друr G друrом и упруrо отражающихся
от концов этоrо отрезка. Доказывается, что указанная
система эквивалентна бильярду в прямоуrольном треуrоль-
нике; исследование возможных бильярдных траекторий
дает возможность предсказъ вать поведение шаров на
отрезке.
13. Два упруrо сталкивающихея шара
на отрезке
Пусть на отрезке -ОА длины а движутся без
трения два точечных шара, имеющих массы тl и т 2 (рис.
13.1). Считается, что шары сталкиваются между собой
абсолютно упруво, т. е. если до соу-
дарен:ия их скорости были равны Vf
и V 2 , то их скорости после соударе- 0 1
иия Ui И и 2 вычисляются из закона
сохранения импульса 0 1
m 1 u i + m 2 и 2 == m 1 v i + m 2 v 2
(1) 0 1
т, v, Vz т2. ")
I A
т
1 т .2
.. ' А
. т 2
I A
J
и закона сохранения энерrии
1/2mlи + 1/2m2и == 1/2mlVi + 1/2m2V -, (2)
Формулы (1) и (2) составляют систему уравнений, из ко-
торой, зная Vf и V2, можно найти Uf и и 2 (рис. 13.1).
3 а д а ч а 13.1. а) Найти из системы (1), (2) и 1 и и21 б) Найти
изменения импульсов Pl И P2 шаров после удара.
139
рис. 13.1
о т в е т.
mi...... т2 2 т э
8) "r ...... + Vi + " + 02,
, т! т! пZl тi
ma тi
"1 == . ".. Vi + ,' 1 L' V2.
i тi т! + тg
тiт2 )
б) Рi==тiUi--пliVi== ' + (Vэ..... v l'
тl т2 ·
тi т '/.
P2 -=.... P! == + ' (Vi'" V2)'
тl т2
, ' I
"МП JIЬС каждоrо шара меняется на пОЛО:JlCtlf1fRЛЬflУЮ величину
\ .
Ар... т т 2 1 V2 Vi I! 1/ пeBoro шара он у м е н ь ш а е т с я на
Ар, npaBoro .......На dp у в е JI и Ч и в а е т с я *).
.явные формулы для иi И И2 нам не потребуются, важно
ишь знать, что законы сохранения (1) и (2) позволяют
однозначно определить иi и И 2 по Vi И V 2 0 Далее, мы счи-
таем, что шары абсолютно упруrо
V f I A отскакивают от rраниц отрезка то.
(J I и v чек О и А. Это означает, что при соу-
O l f I A дарении, скажем, первоrо шара с точ-
кой О, шар отскакивает от О и дви-
Рис. 13.2 жется с первоначальной скоростью,
но в противоположном направле-
нии: иl == Vf (рис. 13.2).
Физическим прототипом этой математической модели
служит система двух жестких (упруrих) маленьких шаров
acc т! и т 2 , катающихся без трения в тяж лом желобе
f1A со стенками О и А. Иноrда эту систему мы будем на..
8ывать «одномерным вазом двух молекул».
Сформулируем интересующие нас вопросы.
1. При каких начальных скоростях и положениях шаров
движение cucmeMbt двух шаров периодично?
2. Какие бывают непериодическuе режимы движения
шаров?
Введем на отрезке ОА систему координат Ох, выбрав
точку О за начало отсчета, и обозначим Х! и Х 2 координаты
apOB. В промежутке времени между соударениями (ша-
u
ров друr с друrом или одноrо из них с соответствующеи
стенкой) скорости шаров Vi и V2 не меняются, а координа-
*) Заметим, что при столкновении скорость правоrо шара
fдожет только увеличиться (хотя ее модуль может и rменьшиться,
если, например, шар двиrался влево и ero скорость была отри-
цательной) о
140
ты Xf и Х2 меняются равномерно]
Xj == vft + af, Х 2 === v 2 t + а 2 . (3)
После соударения скорости Vi И v 2 заменяются на СКОРООТИ
Ui И и 2 , И движения опять равномерны:
Xf == uft + b j , Х 2 == u 2 t + b g . (4)
Б принципе, по начальным положениям и ОКОРОGТЯМ шаров
можно последовательно вычислять моменты соударений,
пересчитывать скорости (е помощью формул из задачи 13.1
при соударении шаров, и по формулам Uf , ==........Vf U 2 ==V 2
или иl ==Vi, U 2 ==.........V 2 при соударении nepBoro или BToporo
шара со стенкой); после этоrо можно изобразить на пло
скости Otx rрафики движения шаров X==Xi (t) и Х==Х 2 (t),
что, однако, нетрудно сделать лишь в случае тi==т 2 .
3 а д а ч а 13.2. Доказать, что после столкновения шары paB
ной массы обмениваются скоростями: иl==и 2 , U 2 ==V 1 .
Реш е н и е. При тl == т 2 система (1), (2) принимает вид
I
Ui+ и2== и! + и2,
) -) , :;!,
из + и3, == v; + и.'.
ПодстаНОВI\ОЙ и 2 из первоrо равнения во второе беждаеМСЯi
ЧТО эта система имеет не более двух решенuй (так как получается
квадратное уравнение относительно иl). Решения этой системы
очевидны...... это (и 1 , и 2 )== (V 1 , V 2 ) И (иl, и 2 )== (v 2 , ( 1 ). Первое из ни
лишено физическоrо смысла (если иl==иl, и 2 ==и 2 , то это соответствует
тому, что шарики проходят друr через друrа, не меняя скоростей!).
Действительности соответствует решение иl==и 2 , и 2 ==и 1 , т. е. шары
обмениваются скоростями.
Теперь можно проследить, что происходит с rрафИI<ами
Х==Хl (t)==v 1 t+al и Х==Х 2 (t)==v t+a2 после Toro, как шары
3J 5' 4
05
о
1;
о
.Т
Q
6'
Рис. 13.3
равных масс сталкиваются......... соответствующие прямые,
пересекаясь, «обмениваются» уrловыми коэффициентами,
и rрафики движения шаров на плоскости Gtx......... это
141
симметричные друr к друrу ломаные MiAM и M2AM
(рис. 13.3,а).
3 а д а ч а 13.3. На оси Ох движутся n шаров одинаковой массы.
Как выrлядят rрафики движения всех эти.х щаров на плоскости
Otx, если шары сталкиваются между собой абсолютно упруrо и
только попарно (тройные столкновения исключаются)? (PaCCMOT
рите сначала случаи п==3 и 4.) Каково максимальное число столк
новений эти шаров (после KOToporo шаРаI разлетаются без столк..
новений)? Может ли произойти бесконечное число соударений?
(Напомним, что в этой задаче на оси Ох нет никаки.х «стенок».)
Реш е н и е. Совокупность rрафиков движения п шаров paB
ны.х масс представляет собой объединение n лучей на плоскости
Otx, проведенны из начальны положений шаров х==а; (при '==О)
с уrловыми коэффициентами Vi (рис. 13.3,6);' по такой картинке
леrко проследить rрафик движения X==Xi(t). (Из РИСУНI{а видно,
что первый шар после разлета имеет скорость V8, второй....... Vб,
третий V 2 ; четвертый....... Vl И пятый V4.) Видно, что MaKcи
мальное число N mах соударений п шаров равных масс равно макси..
мальному числу точе!( попарных пересечений п лучей Н,а плоскости.
Поскольку каждые два луча MorYT пересекаться только в одной
точке, N max равно числу пар из n лу ей, т. е, N max ==C ==п (п 1)/2.
Физически N тах достиrается, например, так: шары движутся
слева направо, причем начальная скорость каждоrо шара больше
скорости ero правоrо соседа.
Чтобы уяснить, как ведут себя rрафики движения
системы двух шаров н а о т рез к е, осталось рассмот-
реть, что происходит, например, G rрафиком Х==Х 2 (t)==
==v 2 t+a 2 после Toro, как второй шар сталкивается со
(J
IJ)
it
(J \$1. (t) Q'
Рис. 13.4
1:
стенкой А. Этот rрафик заменяется на Х==Х 2 (t)==u 2 t+b 2 ,
rде U 2 ==.........V 2 i таким образом, уrловой коэффициент rрафика
меняет знак, как только Х==Х 2 (t) становится равным а
(т. е. второй шар налетает на стенку), и rрафик как бы
«отражается» от прямой х==а. Аналоrично, rрафик Х==Х! (t)
при столкновении первоrо шара со сreнкой О отражается
от прямой х==о (рис. 13.4,а).
Сейчас мы уже можем нарисовать rрафики X==Xi (t)
и Х==Х 2 (t) движения двух шаров р а в н о. й массы на
отрезке (см. рис. 13.4,б). Для этоrо достаточно знать
14
лишь нач\ iiЪньrе пБJП5жеliия й nачаJi ьныI в скорости ша.
ров.
а а Д а ч а 13.4. Доказать с помощью описанны:м rрафиков,
что движение двух шаров равной массы на отрезке ОА периодично
тоrда и только тоrД8j коrда начальные скорости шаров V 1 и V 2 со-
измеримы.
3 а м е ч а н и е. Мы не обсуждаем здесь вопроса о том, что
происходит, коrДа оба шара одновременно налетают на одну и
ту же стенку. Эти особые движения анализируются ниже.
В общем случае тl=1=т 2 рисовать rрафики X::Z%Xi (t)
и Х==Х 2 (t) довольно трудоеlViкое занятие, ибо закон из-
менения скоростей при столкновении не есть просто обмен
скоростями. Налетая на тяжелый шар, леrкий отскаки-
вает, чуть изменяя ero CKOp CTЬ (рис.
13.5; для наrлядности мы рисуем шары
толстыми, по предположению же они TO
чечные). Как же быть? Выход из положе-
ния таков.
Будем следить за, движением шаров
о Д н о в р е м е н н о, т. е. рассмотрим
КОНфU2ураЦUОН1iое пространство, опреде-
ленное в общем виде в 3. Именно, если
шары находятся в точках Х==Х! и Х==Х 2 ,
этому положению системы поставим в
соответствие точку М на плоскости ОХIХе, имеющую
координаты (Xi, Х2). Плоскость OXiX 2 конфиrураци-
онное пространство нашей системы. При движении ша-
ров на отрезке их координаты Xi и Х2 меняются во
времени; таким образом, изменяются во времени и
координаты (Xi, Х 2 ) точки м плоскости OXiX 2 , т. е. эта
(однаl) точка движется по плоскости OXiX2' Напомним,
что точка М называется изображающей или КОНфU2урацu-
ОННОЙ точкой (отметим, что TO не есть реальная мате-
риальная ......... точка; это лишь «абстрактная», вспомоrатель-
ная точкаl). Таким обрц..зом, одновременному движению
двух шаров соответствует движение конфиrурационной
точки М на плоскости OXiX 2 . Поскольку В промежутках
времени между столкновениями Xi и Х2 меняются по ли-
нейному закону (Xi==Vit+aj, X 2 ==v 2 t+a 2 ), от столкно-
вения до столкновения точка М движется по прямой на
плоскости ОХIХ2, причем с постоянной скоростью v== (Vi, v 2 )J
Эта «воображаемая» скорость изображающей точки назы-
вается КОНфU2ураЦUOНIlОЙ скоростью точки М.
При движении шаров по отрезку ОА координаты шаров
подчиняются неравенствам О Xf <Х 2 -<.а. Эти неравенства
задают на плоскости OXiX2 равнобедренный прямоуrоль-
143
э
Рис. ]3.5
ный треуrольник Q, оrраниqенный прямыми Xi==O, Хl ==Х Я
И Х2==а, и конфиrурационная точка движется в пределах
Toro треуrольника (рис. 13.6,а). Если точка М попадает
на ero 2uпоmенузу ОВ (Xi==X2) , то это соответствует столк-
новению шаров между .собой. Соударению же шаров со
стенками О и А соответствует «столкновение» конфиrу-
рационной точки М с катетами ОА (x1 ==O ) и АВ (Х 2 ==а)
треуrольника Q.
w2 :&2. a'z.
!
О СС1 О 311 О -+8 Х,
...
'а О 6
Рис. 13.6
Итак, от столкновения до столкновения (т. е. при дви-
жении внутри треуrольника Q) конфиrурационная точка
движется по прямой со скоростью f}== (Vi, V 2 ). После «со-
ударения» точки М с rраницей треуrольника скорости и!
И V 2 заменяются на и! и и 2, точка М «отскакивает» от rpa
ницы и снова движется, но уже по новой прямой с новой
скоростью и== (Ui, и 2 ). Посмотрим теперь, как точка "'1
отскакивает от rраниц. (Еще раз отметим, что точка "'1,
ее движение по треуrольнику и отскакивание от rраницы
воображаемые, однако они описывают реальное движение
двух шаров по отрезку ОА.)
При соударении точки М с катетом ОА (Xi.==O) конфи-
rурационная скорость f}== (Vf t V 2 ) заменяется на и== (Ul,
и!)== ( Vi., V 2 ), т. е. меняется ее компонента по оси OXi.
Очевидно, это соответствует тому, что М отражается от ОА
по закону упруrоrо удара (У20Л падения равен увлу оmра-
OJCeния). При столкновении М а катетом АВ (х 2 ==а) ско-
рость 'l1== (Vf, V 2 ) заменяется на и== (Uf, и 2 )== (Vf, .........V 2 ) ,
Т. е. меняется ее компонента по оси OX2 это соответствует
упруrому отражению точки М от катета АВ (рис. 13.6,б).
К сожалению, «закон отскакивания» точки М от rипоте-
нузы АВ, определяемый из законов сохранения (1) и (2),
вовсе не совпадает с законом упруrоrо отражения, если
mi=l=m 2 . Проще Bcero в TOM убедиться, изобразив траек-
1"
торию,точки М для соударения леrкоrо и тяжелото шаров
(см. рис. 13.6,в). Поэтому при тl=1=т'А траектории точки М
в треуrОЛЫIИI\.е Q рисовать не так уж просто. Однако
ПОЛО)l{ение можно исправить, и это мы сделаем в следующем
параrрафе.
3 а Д а ч а 13.5. Доказать, что при тl == т 2 з кон отскаки
ванин конфиrурационной точки А1 от rипотенузы есть закон п
pyroro отражения.
Реш е н и е. В случае т 1 == rn 2 при столкновении шаров про..
исходит обмен скоростями: U 2 ==V 1 ' U 1 ==V 2 (СМ. задачу 13.2). Следо
вательно, при соударении конфиrурационной
точки М с rипотенузой QB происходит замена
'0== (V 1 , V 2 ) на l/'== (и 1 , и 2 )== (V 2 , V 1 ), Т. е. вектор
и конфиrурационной скорости после соударения
получается из вектора 'lJ пер е с Т а н о В..
к о й к о о р Д и н а т. Отсюда очевидно (рис.
13.7), что вектор и симметричен вектору 'D от-
носительно биссектрисы OL координатноrо yrJIa
L-I02 (если отло:ж:ить fJ и и от одной точки О).
Но это и означает, что уrлы, образуемые rpa.
екторией точки А1 до и после отскакивания от
rипотенузы, равны.
Из задачи 13.5 вытекает MHoro заме.
чательных следствий. Например, нетруд-
НО видеть, что траектории бильярда в треуrольнике Q по-
лучаются из траекторий бильярда в квадрате ОА1ЗС (рис.
А 8 13.8) «складыванием» квадрата по диа
rонали ОБ. Отсюда следует, что движе-
ние двух шаров равной массы на отрезке
ОА периодично тоеда и только тоеда,
коеда танеенс уела наклона, cooтвem
ствующий бильярдной траектории,
с: т. е. V2/Vf, рациональное число. Если
же число V 2 /Vi иррационально, то cooт
веmcтвующая траектория бильярда в
квадрате ОАБе всюду плотно заполняет квадрат (см.
9 9). Отсюда следует, что получающаяся из этой TpaeK
тории складыванием вдоль ОБ траектория бильярда в
треуrольнике Q тоже всюду плотно заполняет треуrольник
(проверьтеl). Для системы двух шаров на отрезке полу-
чаем такое следствие.
т е о р е м а. ЕСАИ два шара равной массы тl ==m 2
движу/пся по отрезку ОА так, что их начальные скорости
Vl и V'A несоизмерuмы, то для любых двух сколь уеодно малых
интервалов отрезка ОА в некоторый момент времени t
первый шар будет находиться в первом интервале, а втo
рой ......... во втором.
о
Рис. 13.8
2
и
IJ
О 1
А ):)' и.:;):':" 6
' ::и.:: .::
о
Рис. 13.7
145
Действительно, таким положениям шаров соответст-
вует прямоуrОЛЬНИI{ П со сторонами I1х! и AX j в треуrоль..
нике ОАВ (рис. 13.9), а всюду плотная траектория обяза..
телЬНО пересекает Пf
Траектории шаров, обладающих описанным в теореме
свойством, являются, таким образом, всюду плотными.
Можно сказать поэтому, что для lpapOB равной массы
движение на отрезке либо перио..
диц'н'О, либо всюду плоmно. Такие
свойства движений уже обсужда..
лись нами ранее. К ним мы еще
вернемся в части IV.
Подведем итоrи этоrо naparpa..
фа. Вместо Toro, чтобы следить
за движением Д в у х шаров на
отрезке, можно следитЬ за движе..
нием о Д н о й изображающей ТОЧ"
ки М В треуrольнике Q. Точки
этоrо' треуrольника изображают
положение обоих шаров системы;
этот 1 еуrольник Q является конфuеураЦUОflНblМ простран..
cmвOM системы двух шаров на отрезке. Траектории точки М
на Q (так называемые к,онфuеураЦUО1-lflые траектории сис..
тeJUbl) суть ломаные внутри Q. Дальнейший анализ «rаза»
из двух молекул ПрОБОДИТСЯ в следующем параrрафе.
I(онечно, конфиrурационное пространство можно оп-
ределить и для нескольких шаров на прямой. Например,
для трех шаров на прямой нужно взять три оси OXi, Ох 2 ,
ОХЗ В пространстве, и по ЭТИМ осям откладывать коорди-
наты nepBoro, BToporo и TpeTbero шаров. Тем еамым по-
u u u
ложение трех шаров на прямои задается однои точком в
трехмерном пространстве ОХIХ2ХЗ, и конфиrурационное
пространство Q такой системы будет уже подмножеством
трехмер Horo простр а нства [RЗ.
3 а д а ч а 13.6. Указать в трехмерном пространстве fRЗ КОН-
фиrурационное пространство системы трех шаров на прямой Ох.
3 а д а ч а 13.7. Нарисовать на плоскости fR2 конфиrурадион
ное пространство системы двух шаров на полупрямой x o (в точке
О прямой поставлена упруrо отражающая стенка).
3 а Д а ч а 13.8. Найти конфиrурационное пространство си..
стемы трех шаров на отрезке О-<:х <.а. Как ведут себя конфиrу
рационные траектории этой системы, если массы шаров одина-
ковы (и шары сталкиваются абсолютно ;упруrо друr с друrом и
со стенками х==о и х==а)?
о
3},
0 1 (1) (I} I a.
AJJI Axz..
Рис. 13.9
При рассмотрении системы ч е т ы р е х шаров на пря-
мой конфиrурационное пространство будет уже ч е т ы-
146
р е х м е р н ы м ...... положение всех четырех шаров зада.
ется четырьмя числами (Xf, Х2, Ха, Х 4 ). Если рассматривать
систему Д в у х шаров на плоскости Оху, ТО дЛЯ описания
их положения нужно тоже четыре числа...... координаты пер-
Boro шара (Xi, Уl) и координаты BToporo шара (Х 2 , у2)'........
и конфиrурационное пространство снова четырехмерно.
Таким образом, при анализе адач механики возникает
необходимость рассматривать пространство четырех и более
измерений. Но об этом мы подробно rоворили уже в 9 3.
В'9 14 будет произведено специальное линейное преоб- -
разование конфиrурационноrо пространства системы двух
шаров на отрезке, в результате чеrо-задача о поведении этой
системы сведется к бильярдной задаче в треуrольнике.
14. Два шара на отрезке: сведение
к бильярду в треуrольнике
Прежде чем сводить систему двух шаров на
отрезке к бильярдной системе *), напомним необходимые
сведения из rеометрии, касающиеся векторов. Для опреде-
ленности будем rОБОрИТЬ о векторах в пространстве.
Скалярным произведением (k, х) ненулевых векторов k и хна-
зывается ч и G Л о, равное произведению длин этих векторов I k I и
1 х I на косинуо rла между ними:
(k, х) == I k 1.1 х 1. соэ <р.
Из этоrо определения следует, что для любоr@ числа л
(лk, х) == л (k, х)
(k, х) == (х, k).
Кроме Toro, поскольку f k 1 соэ <р есть численная величина проек-
и
а
k
А
р t1: (k)
>-
i»
о
I 1. -:.{J]
p (k +1) =P (k) +P{JIJ(I)
14.1
Рис.
ции вектора k на направление вектора Х, которую мы обозначим
Р х (k), то (рис. 14.1,а)
;(k, х) == f х t. p х (k).
Нетру дно видеть, что ДJJЯ любых ДBY векторов k и 1 проекция
их суммы на напр авление вектора х равна сумме проекций век-
*) В изложении способа сведения рассматриваемой механичеoii
ской системы к бильярду мы придерживаемся лекции 10 кни.
rи 110].
147
торов k и 1 Н8 ЭТО направление (рие. 14.1,6):1
р ох (k + 1) == Р JC (k) + р х (/),
..1
Подставив эту формулу в преДЫДУЩУIО, получим основное свой-
ство скалярноrо произведения .... л и н е й н о с т ь:
(k+l, x)==(k, x)+tl, x).
Пусть теперь в пространстве выбрана ортоrональная система
к<Уординат ОХIХ2ХЗ, и еl, е2, е3...... едuниЧl-lblе 8 векторы, направленные
по осям координат; пусть координаты
векторов k и х в этой системе равны
(ki, k 2 , k з ) И (Хl, Х2, хз). Это означает,
что k == klеl+k2е2+kзе8 и х == Xlei +
+Х2е2 + хsез (рис. 14.2). ПОДСТЭВИМ
эти выражения вместо k и х в ска-
лярное произведение (k, х); восполь-
зовавшись выписанными выше фор-
мулами, а также тем, что (еl, еl)==
с:: (е2, ез) == (ез, ез) == 1, а (еl, е2) ==
==(еl, ез)==(е2' ез)==О (так как
соэ 0==1, а соэ (л/2) == О), получим
формулу для скалярноrо произведения в координатах:
(k, х) == k1Xi + k2X2 + k3XS.
k'd --....... ..... .....h :::'(k 1, k 2., /с: "3)
I
I
I
в случае плоскости соответственно получим
(k, х) == k1Xi + k2X2.
Вернемся теперь к результатам Э 13, касающимся си
стемы двух шаров масс ml и m 2 на отрезке О X a. Напом
ним эти результаты. Пусть Xj и Х 2 координаты шаров;
тоrда О Xl X2 a. Эти неравенства задают на плоскости
ОХIХ2 треуrольник Q, и положение обоих шаров определяет
конфиrурационную точку М == (Хl, Х 2 ) в этом треуrольнике.
При движении шаров по отрезку координаты Хl и Х 2 меня
ются, а конфиrурационная точка М движется по треуrоль
нику Q. Между двумя столкновениями скорости Vl и V 2
шаров и конфиrурационная скорость 'V== (Vl, V 2 ) изобра..
)кающей точки не меняются, и конфиrурационная .ТОЧI{а М
движется по отрезку внутри треуrОЛЬНИI{а. «Соударению»
точки М С катетами треуrольника ОА и ОБ соответствует
столкновение первоrо или BToporo шара на отрезке ОА
с соответствующей стенкой (О или А), и после столкновения
конфиrурационная скорость становится равной и== ( Vl,
и 2 ) или и== (Vl, V2), что соответствует lпруrому отражению
точки М от катетов. Если ml=1=m 2 , то соударение точки М
с rипотенузой, соответствующее столкновению шаров друr
с друrом, ведет к замене конфиrурационной скорости
v== (Vl,V 2 ) на скорость и== (иl, и 2 ), вычисляеМУIQ из законов
сохранения импульса и энерrии (см. формулы (1), (2) 13),
148
и точка Л1 отскакивает от rипотенузы вовсе н е п о закону
ynpyroro отрал(ения. Задача, которую мы сейчас решим,
заКЛiочается в том, чтобы изменить координаты Xi и Х2
так, чтобы и последнее из описанных соударений точки М
происходило как в бильярде «уrол падения равен .уrлу
отражения)"
Законы сохранения импульса и энерrии нам удобнее
записать в виде
m 1 V 1 + т 2 V 2 === const,
mlV + fп2V == const.
(1 )
(2)
Введем вместо Х! и Х з координаты Xi и Х 2 по формулам
Х 1 == V m 1 Х 1 , Х 2 == V т 2 Х 2 ,
Т. е. «растянем» плоскость ОХIХ2 по осям ОХ! И ОХ 2 В V т 1
и V m 2 раз соответственно. По"!.ожение nepBoro шара будет
определять теперь координата Xf, а BToporo координата
;2; положению lпаро! сопоставим изоб- .1:2
ражающую точку М с координатами
(Xi, Х2) на плоскости ОХIХ2. Посколь-
ку
....
xi
Х 1 == У ml '
....
Х2
Х 2 == V m2 '
'"
IJ
о
rv
CXf
Рис. 14.3
а Х! и Х 2 удовлетворяют неравенствам О <Хl <Х 2 <а, числа Xi
и ;2 удовлеТВОРЯIОТ неравенствам О x 1 /v т 1 x 2 /v т 2
a, и изображающие точки М заполняют на плоскости
OX X2 треуrольник Q==oA.B, оrраниченный прямыми
Х 1 == О (оА), Х 2 == V т 2 а (Ав), x 1 /v т 1 == x 2 /v т 2 (аВ)
(РИG. 14.3). Нетрудно вычислить координаты точки В:
Ь 1 :::: а vт;, Ь 2 === а V т 2 , откуда следует, что ОВ==а. т, rде
т== (v mi , V т 2 ).
Движению шаров по отрезку ОА соответствует движение
изображающей ТОЧКI1 iЙ в треуrольнике Q, причем, как
и раньше, конфиrурационная скорость ii н е м е н я е т с я
в течение ,промежутка времени между столкновениями,
Т. е. при движении точки М внутри треуrольника Q. Новая
конфиrурационная скорость есть
f, == (v 1 , ( 2 ) == (v т 1 V 1 , V т ! V 2 ).
149
Дейотвительно, так как X1t == Y Xkf
Ао dx k V ........... dx k V ............
Vk== == mk dt == mkv , k== 1, 2.
ДОI<ажем, что uзображаЮlцая точка М при соударении
с любой из сторон пzреуеольника Q отражаепzся по закону
упРУ20ео соударения.
Действительно, леrко видеть, что при соударении М с
катетами ОА и 08 конфиrурационная скорость v== (V1",
V 2 ), как и раньше, становится равной и== ( v, V 2 ) или и==
== (Vi, .........v 2 ) , что соответствует упруrому соударению с ка-
тетами. Соударение М с rипотеНУЗ0Й ОБ подчиняется
законам сохранения (1) и (2). Перепишем их в новых обоз-
начениях Vf == V m! Vi, V 2 == V т 2 V 2 . Закон сохранен я
энерrии (2) примет вид
+ V == const,
. е. дри соударении с rипотенузой квадрат длины вектора
v не меняепzся, откуда
I v I == const. (3)
Закон сохранения импульса (1) дает
V т 1 (;! + V т 2 V 2 == const,
или (см. выше формулу для скалярноrо произведения)
.....
(v, т) == const,
rде m == (V т 1 , V т 2 ). Поскольку m ........ постоянный вектор,
а (v, т)== I .v I · I т I · cos ер, rде ер уrол 1ежду векто-
рами v и т, то ИЗ Toro, что I , не меняется (см. (3»), сле..
дует, что косинус УI'ла lVlежду v и m при соударении изобра-
жающей точки с rипотенуsой, ОБ также не меняется. Бспом-
нив, что ОВ===а.m, т. е. rипотенуза имеет то же направле-
ние, что и вектор т, мы получаем, что при этом соударении
не меняется косинус уrла между конфиrурационной ско-
ростью v и rипотенузой. Таким образом, если <pi....... уrол
падения конфиrур ационной точки М, <р2....... уrол ее отраже-
ния, то cos ер1 ==cos <Р2' откуда следует, что epi==<P2, что И
требовалось доказать! (Возможность CP2==1t CP1 исключается
из физических соображений....... почему?)
150
Итак, доказана
т е о р е м а 1. Замена координат Xk с::: ут; X k (k=== 1 ,2)
сводит систему двух шаров массы mf u т 2 на отрезке
длины а к бильярду в прямоуеольном треуеольнике Qa==
==оАв с Kaпretпaмu АВ == а V mi u ОА == а V rn 2 , т. е.
с острым уелом LAoB, равным
r ..............
, lп'
(х == а rc tg У .......!...
m2
Теперь естественно попытаться решить для системы ша-
ров с массами mi, т 2 на отрезке [О, а], т. е. для бильярда
в треуr'ольнике Qси общую проблему бильярдных траекто-
рий. Эта проблема исследована нами для бильярда в пря-
м:оуr ольнике свед ением I\ обмоткам тора. К сожалению,
.
'" fJ
А
)
ромооца РОНа
Рис. 14.4
rеометрическое сведение бильярда в Qa при rx=l=n/4 к биль-
ярду в прямоуrольнике невозможно: отражениями относи-
тельно сторон треуrольника можно получить бильярд
в ромбоиде или ромбе) '" но не в прямоуrольнике
(рис. 14.4).
Конечно, можно попытаться свести этот бильярд н е-
п о с р е Д с т в е н н о к тору (мы так «стремимся» К тору
потому, что при удаче можно будет применить теорему Яко-
би). Это можно сделать, кроме а==n/4, увы, еще только в
случае а==n/6 (или а==n/З). Справедливо следующее утвер-
ждение, которое мы докажем позже, в 22 rл. 8.
т е о р е м а 2. Бильярд в пРЯМОУZОЛЬflОМ mреуzольнике
Qa с острым уzлом а сводится к обмоткам тора mozaa u
{полько тоzда, КО2да а==n/4 u n/6 (или n/З), т. е. коеда тl===
==т 2 и тi==Зт 2 (или т 2 ===З т l).
Отметим, что н е Б л ю б о м прямоуrольном треуrоль-
нике каждая бильярдная траектория либо периодична,
либо всюду плотна: при малых величинах остроео уела а
бильярдная траекпzория в nрямоуеольном треуеольнике
Qa может заполнять всюду плотно лишь некоторую подоб-
ласпzь атоео mреуеольника. Пример построения такой
151
траектории в мноrоуrольниках с числом сторон п 4 б
лее прост и единообразен, чем для треуrольника Qa(n==3):
он приводится В 25. На языке «rаэа» из двух моле-
кул ситуация может быть сформулирована следующим об
разом:
т е о р е м а 3. Можно подобрать такое соотношение
масс Jrtежду шарами и выбрать такие их начальные состоя-
ния (координаты и _ скорости), что множесn-юо точек
столкновения этих шаров на отрезке [Ь, а] будет либо
а) конеЧНblht, либо б) всюду плотно заполнять весь отрезок
[О, а], либо в) всюду плотно заполнять конечное ЧU ЛО
н'еllересекаЮЩUХGЯ опlрезков на отрезке [О, а].
Этой теоремоЙ резюме мы и закончим параrраф о систе-
ме из двух молекул на отрезке.
3 а Д а ч а 14.1 *. а) .Доказать, что система трех шаров р а B
н О Й массы на отрезке сводится к бильярду в некотором т е т р з--
э Д р е. б)* Доказать, что при подходящем выборе координат си--
стема трех ша ров раз н ы х масс -т1, т 2 , тз также сводится к
бильярду в некотором тетраэдре.
3 а д а ч а 14.2. Рассмотрим систему двух шаров масс т1 и т 2
на полупрямой х>О, причем в точке х==о на этой прямой постав--
лена упруrо отражаlощая стенка. Пусть в момент времени t==O
правый шар движется по направлению к стенке. Всеrда ли левый
шар после к о н е ч н о r о числа соударениЙ оттолкнет правый?
(Рассмотрите ситуаЦИIО, коrда т 2 rораздо больше т 1 .) Верно ли,
что в этой системе произойдет лишь к о н е ч н о е число столк
новений N? Если верно, то мо)кет ли N быть СКОЛЬ усодно большu.М
(при данных т 1 и п1 2 )? Можно ли написать, что N <.N o , rде число
N o зависит т о л ь к о от масс Iпаров?
3 а д а ч а 14.3* (сы. 15). Рассмотрим систему трех шаров
масс пz 1 , rfl 2 , тз на бесконечной прямой без стенок, и пусть в Ha
чальный момент времени первый и третий шары движутся Ha
встречу друr друrу. Сможет ли второЙ шар растолкать первый
и третий шары? (Представьте, что m 2 очень леrкий пинr..понrо
вый шарик, а m 1 и тз массивные стальные шары.) 0тветь-
те так}ке в этом случае на три последние вопроса предыдущей
задачи.
3 а д а ч а 14.4. Луч света попал в зеркало, пмеlощее форму
бесконечноrо а) двуrранноrо уrла, б)* TpexrpaHHoI'o (или mhoro--
rpaHHoro) уrла. В случае б) будеl'Л считать, что луч никоrД8 не
попадает точно в ребра двуrранных уrлов. Мо)кет ли быть так,
что луч «запутывается» внутри зеркала и никоrда не вылетает
оттуда?
3 а д а ч а 14.5. а) Дано зеркало, имеющее форму двуrранноrо
уrла величины (Х. Бы рассматриваете в нем изображение свечи_
Сколько Bcero изображениЙ свечи можно увидеть? б)* * Ответить
на тот )ке вопрос для зеркала, имеющеl'О форму TpexrpaHHoro
уrлв, двуrранные уrлы KOToporo равны А, В, С.
152
А 15. Два шара на ПОJlупрямоА
сведение к бильярду в уrле
В этом параrрафе мы ответим на некоторые
u
важные для дальнеишеrо исследования системы одномер-
Horo rаэа вопросы, связанные с двумя молекулами на оря-
v u
мои. и полупрямои.
А. В качестве nepBoro шаrа решим задачу И3 9: может
ли бильярдная траектория «запутаться» внутри уела и
остаться там навсееда?
Поставим задачу более точно. Рассмотрим бильярд в бес-
конечной области Qi, оrраниченной двумя сторонами уrла
AoAAi величины а. Траектории бильярда в такой области
А,
L
А Ав
Рис.' 15.1
А 1
н
А Р2 Ао .
Рис. 15.2
определяются как обычно.......... это ломаные, по которым дви-
)кется шар, УПРУI О отра)каясь от сторон уrла. Отличие этоrо
бильярда от бильярда в оrраниченной области состоит в том,
что в данном случае траектория может «уходить в бесконеч-
ность», т. е. после одноrо из соударений шар будет двиrать-
ся по лучу, никоrда более не соударяясь GO сторонами уrла.
Так будет в том случае, коrда направление движения шара
лежит между направлениями лучей ААо и АА 1 (рис. 15.1).
Вопрос заключается в следующем: всякая ли траектория
бильярда внутри уела АоААl после некотороео конечноео
числа N отражений Ofll сторон уела УХОдUп-l на бесконеч
ность?
Ответ оказывается утвердительным. Для Toro чтобы ЭТО
доказать, рассмотрим про,Извольную траекторию М Р I Р 2> . .
И примеНИl\1 к ней проuедуру выпрямления G помощью после-
довательных отражений относительно сторон уrла AoAAi
(рис. 15.2).
Если первая точка соударения Pi лежит на луче AAi,
то мы отражаем уrол Ql==LA o AA 1 относительно луча AA i
и получаем уrол Q2=== LA 1 AA 2 . Затем мы отражаем уrол Q2
относительно луча АА 2 и получаем уrол Qз==LА 2 АА s
и т. д. (рис. 15.3). Применяя к отрезку РI Р 2 рассматривае-
мой траектории МРI Р 2 Р З". одно из упомянутых отраже-
153
ний, К следующему отрезку Р2 Р З ........... два отражения (отно..
сительно AAi и АА 2 ) и Т. Д., мы переместим эти отрезки в
уrлы Q2' Qз и т. д.; из закона «уrол падения равен уrлу
отражения» следует, что отраженные отрезки составляют
луч продолжение луча МРl за точку Рl на плоскости.
Обратно, мы можем замостить с помощью описанных
отражений часть плоскости уrлами Ql, Q2,... Начертивпроиз
вольный лу ч МР 1 , идущий из очки М внутри уrла Q
в сторону точки Pi на луче AAi, теми же отражениями,
А,
А4
А
Рис. 15.3
Ао
15.4
НО проводимыми В противоположном порядке, мы можем
построить по лучу МР 1 бильярдную траекторию МР 1 Р 2 ...
внутри уrла Ql. Из сказанноrо выше вытекает, что указан-
ным образом получается л ю б а я бильярдная траектория
MPiP 2 ..., первая точка излома которой лежит на луче
AAi. Точкам пересечения луча MPi с лучами AAi, АА 2 ,. . .,
делящими плоскость на уrлы Qi, Q2' . .., при обратных
отражениях соответствуют точки соударения Рl, Р 2 , . . .
траектории со сторонами уrла Qi. Очевидно, всевозможные
лучи МР 1 (при различных положениях точек М внутри
Qi И точек Pi на луче АА 1 ) заполняют заштрихованную
на рис. 15.4 область Q между лучом ААо и лучом AA .........
продолжением: луча AAi за точку А. В этой области Q с по-
мощью отражений можно поместить лишь к о н е ч н о е
число N o рассматриваемых уrлов Ql, Q2,. . . так как все
эти уrлы равны по величине (Х, а уrол Q (больший развер
иутоrо) измеряется величиной n+(Х, то No(x n+(X, откуда
N o «n/(X)+l. Иначе r воря, число уrлов Ql' Q2,...,
помещающихся внутри Q, равно
N o ==[ : J+l;
эдесь [и] ....... обозначение для целой части числа u (наиболь
шеrо целоrо числа, не превосходящеrо и). Если сторона
AAN o последнеrо из этих уrлов QN(\==ANo l.AANo не COB
падает с лучом АА 1, то луч МР 1 может проходить еще по
154
одному уrлу...... уrлу QN(J+'f., получаrощемуся из QN" отра-
жением относительно луча AAN o ' однако луч MPj уже не
может пересечь луч AAN n +l' ибо этот луч лежит вне обла-
сти Q. В э ом случае (AA No *AA ) луч MPi может пере-
сечь C3l\10e большее N o лучей.......... AAi, АА 2 ,..., AAN.
Это означает, что число N соударений бильярдной траекто-
рии со сторонами уrла не превосходит N o :
N::;;No==[ : ]+l.
Заметим, что N может принимать любое значение от 1 до
N o ......... это зависит от направления луча MP t .
В случае, коrда луч AAN o совпадает с лучом AA , нет
необходимости раССJ\1атривать еще один уrол QN,,+f.' ибо
луч М Рl не может пересечь луча АА N o . Этот случай (АА НО ===
==AA ) соответствует тому, что n есть целое кратное числа
а, и максимальное число соударений тоrда равно No l
(луч мр! мо)кет пересекать лучи AAi, АА 2 ,. . ., AAN o --l).
Подведем итоrи. Для числа а, О<а<п, положим
{ No==[ : ]+l,
N(a)== [ 1t ]
N o 1 ==
а '
1t
если ...... не целое,
сх.
п
если ...... uелое.
а
т е о р е м а. При движении бильярдноео шара внутри
уела величины а траектория шара имеет не более чем N (а)
точек соударения со сторонами уела, u после некоrnорОёО
числа N <.N (а) .соударений эта траектория уходит на
бесконечность.
Нетрудно видеть, что введенное выше число N (а) можно
при любых а записать одной формулой:
N (сх) == [ : J
(проверьте этоl).
Б. Доказанная в п... А теорема дает возможность найти
I\1аксимальное число столкновений шаров масс тl и т 2 , дви-
rающихся по полупрямой x o, В точке х==о которой
поставлена отражающая стенка (задача 14.2). Координаты
Хl и Х 2 этих шаров удовлетворяют неравенствам О Xi <Х 2 .
После введения координат Xi == V т 1 Хl и Х 2 == V т 2 х 2 , как в
14, мы:можем свести систему этих шаров к движению КОН-
фиrурационной точки М == (;1, Х 2 ) внутри уrла Q на плоско-
155
....
.... Х 1 Х
сти OXiX 2 . задаваемоrо неравенствами 0< у':'" < y ' :
т} пZ2
точка М движется внутри этоrо уrла (LA ОВ на рис. 15.5)
по бильярдной траектории, а точкам соударения траектории
со сторонами уrла (ОВ или ОА) соответствуют столкнове
ния исходных шаров (друr с друrом или левоrо шара со
стенкой в точке х==о COOTBeTCTBeHHO . Прямая ОВ задается
"" '"
х х (y
уравнением у':'" == ,y . и точка с координатами т 1 .
тl т2
V m 2 ) лежит на ней. Отсюда следует, что величина а yr-
ла А 08 равна
сх. == arctg .. /" ml .
V т2
Таким образом, максимальное число столкновений рас-
сматриваемых шаров равно
( rm ) [ :rt ]
N(a)==N arctg У == у' ·
т2 arctg тl/ т2
Тем самым решена задача 14.2: первыЙ шар столкнется со
вторым шаром и со стенкой не более чем N (а) раз, после чеrо
(&1 Xz
0 1 . .
Xz 1",::", в
: :Y' '.
. . .
..,
:':.:'::: arc tg I:i:
2.
::с
=-
J)
. ""-1
Х1
2 4-
Рис. 15.6
r
Рис. 15.5
шары разлетятся и больше столкновений не будет. В част-
ности, получаем следующее.
1) Если тl==m 2 , то a==arctg 1==п/4 и
N(cx.)== I п74 ] == [ 4J==4;
ответ этот можно получить и из соображений обмена ско-
ростями при упруrих соударениях шаров масс тi.==т 2 .
Картинка столкновений (рис. 15.6) на плоскости OtXf вы-
rлядит в данном случае, как на рис. 13.3,6 (столкновения
пронумерованы цифрами 1, 2, 3, 4).
156
2) Если тi ,М,ноео,М,еньше т 2 . ТО "11 j' И a:::arctg "1I/ iiii
V т2 V m2
«довольно малые» числа. Из формулы для N (а) следует, что
.,
число столкновении в этом случае «довольно велико», как
u
и следовало ожидать: леrкии шарик т} «мечется» между
стенкой и тяжелым шариком т2 достаточно долrо, прея{де
чем «отпихнет» (но «отпихнет» обязательно!) шарик m 2 от
стенки.
В. Приложим теперь доказанную в п. А теорему к за-
даче о числе отражений луча света в зеркале, имеющем
А
..; ,.."
а
6
в'
8
Рис. 15.7
форму бесконечноrо двуrранноrо уrла величины ct (задача
14.4а). Прежде Bcero следует точно сформулировать за
кон отражения луча света от плоскоrо зеркала или закон
отражения летающеrо в пространстве точечноrо бильярд-
Horo шара от плоскости (уместнее было бы rоворить о ша-
рике для иrры в пинr"понr). Пусть ломаная АР В ......... это
траектория луча света (или шарика), отражающаяся от
плоскости:? в точке Р. Известный из физики закон отра-
}кения rласит: лучи РА и РВ и перпендикуляр PN к пло
скости :? в точке Р лежат в одной плоскости off, причем
лучи' Р А и Р В оБРЗЗУIОТ С лучом Р N одина.КОБые уr,ЛЫ
\57
(рис. 15.7, а). Отсюда следует, что при отражении относи-
тельно плоскости луч Р В переходит в луч Р В', являю-
щийся продолжением луча АР за точку Р (рис. 15.7, б).
Таким образом, к траектории луча света внутри зеркала,
имеющеrо форму бесконечноrо двуrранноrо уrла Qf с rpa-
нями f/)o И fPi И ребром АВ (рис. 15.7, в), можно применить
процедуру отражения в rранях этоrо уrла, аналоrичную
описанной в п. А; при этом последовательными отражения-
ми можно выпрямить траекторию MPiP2.......... превра-
тить ее в луч MPi, который пересекает двуrранные уrлы
Q2' Qs,. . ., получающиеся из Qf последовательными отра-
жеНИЯ1\1И в rранях уrла. Точки пересечения луча MPi о
полуплоскостями :Pt, :?2,. .. соответствуют точкам отра-
жения луча света от rраней :J o и fJi исходноrо уrла. Если
рассмотреть плоскость 5l, перпендикулярную общему реб-
ру АВ всех двуrранных уrлов Qi, Q2,. . ., И луч МР! спроек-
тировать на эту плоскость в луч м' P , то, рассматривая
точ!{и пересечения луча М' P с лучами AAi, АА 2 ,. . .,
получающимися в пересечении плоскости 51, с полуплоско..
стями fiЭ о , fj3i,' ' ., как и при доказательстве теоремы п. А,
получим: максимальное число отражений луча света в ера..
нях зеркала, имеющеео фОр.АtУ двуеранноео уела величины а,
равно N (а)== [ зt/а]. Задача решена. Друrой путь к ее
решению вытекает из утверждения следующей задачи.
3 а д а ч а. Доказать, что если уrол АР В в пространстве IR
спроектировать на плоскость 5/" параллельную биссектрисе PL
этоrо уrла, то п ро кция Р' L' биссектрисы на эту плоскость 51,
является биссектрисой проекции А' Р' В' рассматриваемоrо уrла.
Вывести ОТСlода, что проекция траектории луча света внутри
зеркала, имеющеrо форму двуrранноrо уrла Q о ребром АВ, на
плоскость 5t, перпендикулярную АВ, является бильярдной траек-
торией внутри плоскоrо УI'ла AoAAt, получающеrося в сечении
двуrранноrо уrла Q плоскостью .
Теперь мы полностью rOToBbI к исследованию одномер-
. Horo «rаза» из трех и большеrо числа молекул.
"
rЛ8В86
ОДНОМЕРН ЫЙ «fАЗ»
ИЗ БОЛЬШОfО ЧИСЛА МОЛЕКУЛ
в этой rлаве мы послед.овательно пере}lдем от
двух к трем и большему числу молекул одномерноrо «rаза».
При этом мы исследуем сначала систему п шаров (упруrих
частиц) произвольной массы на прямой. В 16 мы получим
т о ч н у ю оценку числа столкновений r р е х шаров на
прямой, зависящую только от соотношений между их мас-
сами (но не зависящую от их начальных положений и ско-
ростей); затем ответим на вопрос о том, может ли в системе
из п упруrих шаров на прямой ПРОИЗ0ЙТИ бесконечно /I1,HOeO
столкновении (в 17 даIОТСЯ два разных подхода к ответу на
этот вопрос....... аналитический и изящный rеометрический);
наконец, в 18 ответ 17 подкрепляется р а в н о м е р-
н о й (т. е. не зависящей от начальных условий) оценкой
числа столкновений в системе из п упруrих шаров на пря-
мой и с ее помощью оценивается рост числа столкновений n
молекул «rаза» в одномерном сосуде........... на отрезке прямой.
16. Три упруrих шара на ПРЯl\fОЙ
Рассмотрим систему трех шаров масс тl, т 2 ,
тз, движущихся по оси Ох. Предположим, что шары точеч-
ные, сталкиваются друr с друrом абсолютно упруrо, причем
происходят только поп а р н ы е столкновения: левоrо ша-
рика (mi) со средним (т 2 ) и среднеrо с правым (тз).
Всееда ли в такой системе происходит конечное число
столкновений на всем бесконечном проме;}/сутке времени, или
же существуют такие начальныle условия (положения, ско-
рости u массы шаров в момент t==O) , что число столкно-
вений бесконечно?
Нетривиальность этоrо вопроса наrлядно демонстриру-
ется на таком примере. Пусть два очень больших «сталь-
159
ных» шара движутся с очень малыми скоростями навстречу
друr друrу, а между ними летает с очень БОJlЬШОЙ CKO
ростью очень леrкий пинr понrовый шарик, отскакивая от
u
стальных шаров как от стенок со все возрастающем скоро-
стью по l\лере приближения этих шаров друr к друrу.
Совершенно неясно, «растолкает» ли леrкий пинr понrовый
шарик массивные шары, а если да.){{е и растолкает, то не
может ли он до этоrо момента (заметьте, на к о н е ч н о !\/I
?Iромежутке времени!), увеличивая частоту своих колебаний
'1 скорость, уже столкнуться с ними бесконечно MHoro
раз? Мы докажем в ЭТОl\f параrрафе, что такоео не пpoucxo
оuт: число столкновений между тремя шарами на прямой
всеrда конечно и зависит только от соотношений их масс
(но не зависит от их начальных положений и скоростей).
Точная оценка ЭТОI'О числа прнводится в формулируемоЙ
в конце параrрафа теореме.
l(оординаты трех шаров обозначим Хl, Х 2 , ХЗ И будем
ОТ!\1ечать положение шаров конфиrурационной точкой М ==
==л(Хl t Х9" Хз) TpeXMepHoro пространства [R3 с системой КООР"
3)1 < Х 2 сХ3' динат ОХI Х 2 Х З. Всевозможr ые по-
. .. ложения конфиrурационнои точки
з'z М подчиняются неравенствам Хl<
X2 ХЗ. Первое из НИХ, Хl X2'
задает в пространстве ОХIХ2ХЗ полу-
пространство, лежащее по одну
сторону ОТ плоскости 1,2' задан
Х2. ной уравнением Хl==Х 2 ; второе,
Х 2 X3, задает полупространство,
оrран иченное плоскостью ?2,з С
Рис. 16.1 уравнением Х 2 == з. Оба неравенства
в м е с т е задают пер е с е ч e
н и е этих полупространств один из двуrранных уrлов
Q, образованный плоскостями 1,2 и 2,з (рис. 16.1). Ребро
этоrо двуrранноrо уrла прямая OL, задаваемая paBeHCT
вами Хl ==Х 2 ==хз. Положению конфиrурационной точки
М == (Хl, Х 2 , Хз) на rранях Q плоскостях fP 1,2 И 2,3 .........
соответствуют попарные столкновения между шарикаlVIИ
Хl==Х 2 и х 2 ==хз; если же М лежит на ребре уrла OL, то это
соответствует т рой н о м у столкновению шаров Х1 ==
==х 2 ==х з , которое мы не будем рассматривать. При ДВИ}J{е
нии шаров по прям ой Ох в течение промежутка времени от
столкновения до столкнрвения скорости шаров Vi, V 2 , V З
сохраняются; это означает, что при соответствующем дви-
жении точки М == (Хl' Х 2, Хз) в конфиrурационном прост-
ранстве ОХIХ2ХЗ эта точка М движется с постоянной КQНфИ-
160
'rурационной CKOpOCTbJQ fJ== (Vi, V 2 , VЗ) по некоторой прямой.
.ПОСtllе столкновения М Qтскакивает от соответств'укiщей
траки уrла Q с новой скоростью и== (Ui., и 2 , из); СОстав..
U '
JIяющие новои скорости иl, и2, из вычисляются из соответ"
ствующих законов сохранения. Например, при СТОЛkно"
вении шаров ml и m 2 (при 'отскакивании М от плоскости
fP 1 . 2 ) из==vз, а скорости иl и и 2 определяются законами
сохранения (1), (2) из 13. Вообще rоворя, этот закон отска..
кивания вовсе не есть закон упруrоrо отражения точки 'М
от соответствующей плоскости. Напомним, что при у п..
р у r о м отражении точки М, налетающей со скоростью'
fJ== (Vl, V 2 , Vз) на плоскость :Р, скорость w== (WjJ W 2 , w )'
ТОЧКИ М после отражения определяется следую ими уело..
вними: .
(А) длины векторов fJ и w равны: r fJ f == , w 1;
r (Б) если I n ....... вектор, nерnендикулярныu плоскости ,
т.о - векторы fJ, W и n компла.нарнbt, т. е. лежат в одной
плоскости; , ;
(В) уелы, образуемыевекmорамu fJ u wcoeKтopoM n, paвHbl
(но w=l= fJ); это условие удобно записать с помощью С1ЩЛЯР-
н,оео nроuзведенuя: .
('W t n) == ...... (о, п) .
3 а м е ч а н и е, о т н о с я Щ е е с я к э л е м е н т а р н о й
r е о м е т р и и. Если плоскость fP в пространстве ОХ 1 Х 2 Ха задает-
ся уравнением
aiXi + а2 Х 2 + азхs == С,
то это уравнение можно переписать с помощью скалярноrо произ--
ведении в виде
(а, х) == с,
rде а ...... вектор с координатами (аl' а2, аз), ах...... вектор с началом
в начале координат 0== (О, О, О) и концом в точке М с координа
там'и (Хl' Х 2 , Ха). Вспоминая rеометричее-кий смысл скаJlярноrо
произведения (см. начало 14), запишем наше уравнение в виде
I а 1. р а (х) == С,
r де Р а (х) ..... численная величина проекции вектора х на направ--
Jlение вектора а. Таким образом, плоскость fP, заданная уравне--
мнем (а., х)::::;с аlХl+а2Х2+а8ХЗ==С состоит из тех и только тех
............
точек. Af, для которых численная величина проекции вектора ОА1
на вектор а равна данной величине, .
Р ' о
а (х) == I а 1 .
О сюда ясно, ч о ПЛОСКОСТЬ fP перпендикулярна вектору а. Таким
образом, в качестве вектора n, перпендикулярноrо к плоскости ,
заданной уравнением аlХl +а2х2+азхз==с, можно взять вектор
n=== а=== «(11' а 2 , аз).
6 r. А. rальперин. А. Н. Земляков
161
Введем вместо Xi, Х 2 , Ха друrие координаты Xi, Х 2 , Хз,
аналоrичные рассмотренным в 14, так, чтобы движение
новой изображающей точки М == (Xf, Х 2 , Хз) подчинялось
закону упруrоro отражения при соударениях с плоскостями
отражений 1,2 и ffi 2 ,a В пространстве ОХIХ2ХЗ. Именно, по-
ложим
Х 1 == V m 1 х 1 , Х 2 == V т 2 х 2 , .Ха== V тз х з ..
Движение точки М == (Х:(, Х2, Хз) происходит в двуrранном
уrле Q, задаваемом неравенствами
"'" -- .....
Х 1 Х 2 .........- Х 3
y 1I у....... ·
1п1 т2 тз
Этот уrол оrраничен плоскостями столкновений 53 i ,2 и 2,З,
заданными соответственно уравнениями
-- ....
Х1 Х2 х2 .......... ХЗ .
V тl .......... V m2 ' 11 m'J V тз '
ребро ero........ прямая ol, заданная уравнением
--
Хl Х2 Ха
11 т! ут; ....... V тз L
Скорость (,== (Vi, -О 2, vз) изображающей точки М по-преж-
нему не меняется в промежуток времени между сто.лкнове
ниями и связана со СI{ОРОСТЬЮ 'V== (Vl, V 2t v з ) формулами
V 1 == V т] V 1 , и 2 === v т 2 V 2 , V S == V тз v s .
Докажем, что соударение изображающей точки М с nло
скосmямu столкновений 1, 2 И 2, 8 (отвечающее попарным
спzолкн.О8еНUЯМ шаров тl, т!, тз) ,!poи xoдит по закону
уnруеоео отражения, T е. скорости 'v и 11, ДО И после соу...
ударения удовлетворяют условиям (А), (Б), (8), сформули-
рованным выше. Доказательство этоrо такое же, как и в
14.
Рассмотрим, например, соударение точки М с плоскостью
столкновения f, 2. В старых координатах OXi, ОХ2, ОХЗ I{ОрОСТИ
V И и до и после столкновения связаны соотношениями
из == V8'
т1 и l + т2 и 2 == ml V ! + m2 V 2,
2 2 2 2
тl и l + т2и2 == тi V l + пZ2V2.
Перейдем в этих равнениях к величинам == у пZk vk
162
....
и Uk ==
== у mk Uk. Получим
ИЗ == vз,
у т1 и1 + у т2 и2 == V т1 и! f-- У m2 V2,
....2 2 .....2 2
Иl + И2 == иl + и2.
(l)
(2)
(3)
Возводя обе части равенства (1) в квадрат и складывая с равен..
ством (3), получим
....2 2 2 2 2 2
Иl + И2+ из == иl + и2 +Vз,
откуда следует, что 1 ii 1 == I i 1. Тем самым условие (А) проверено.
Чтобы проверить условие (Б), т. е. компланарность векторов
== (Vlt из, vз), ii == СИi, и2, из) и вектора n, перпендику лярноrо
плоскости столкновения 1, 2, достаточно представить n в виде
Л;V+Л2 U (тоrда n лежит в плоскости векторов V, и). Так как
Nравнение плоскости :?i, 2 имеет вид
Х! Х2
У тl ....... У т2 '
или
1... 1.... ...
..r Xi...... y Х2 + О. хз == О,
r m1 m2
то соrласно замечанию, сделанному выше, в качестве вектора n
можно взять вектор
n==( y1iiii ' yk; . о).
...... ..... .........
Вычтем из вектора со вектор и; так как vз == Из, мы получим вектор
v ....... и == (и1 ....... и1 , V2 ..... и 2, О).
Перепишем уравнение (2) в виде
у т1 (V1 ...... и1) ==........ -v т2 (v2..... 'И2) == л,
(2 е )
rде 'A число, которому равны обе части этоrо равенства. Отсюда
л --... л
иl ....... и! == ..r ' и2...... и2 ===...... ...r ·
r ml r m2
....
Сравнивая теперь формулы для n и для ".......и, получаем
cV...... и == лn,
1.. 1...
откуда 1t ==т 'О....... Т а. Таким образом, вектор n выражен через
v и ii B явном виде, и условие (Б), таким образом, доказано..
Наконец, проверим, что и условие (В), т. е. соотношение
(и, n) == (v, n)
(4)
тоже выполнено. Запишем обе части докззываемоrо соотношения
(4) в координатах, учитывая, что n == ( / . y ' О ) :
т! тз
Ul
У ml
... ....
и2 ( и1 и2 )
У тз == ........ у m"! У m2 I
6
163
Чтобы доказать (4'), перепишем (2) и (3) в виде
V т1 (V1 ....... il 1 ) == V т2 (и2 ),
"'2 2 ....2.
Vl ....... и 1. == U V2'
Разделив почленно последнее равенство на предпоследнее получим
требуемое соотношение (4'). 3aI{OH упруrоrо столкновения' BЫ
полнен.
'TaK, система трех шаров масс тl, т 2 , тз H оси Ох
сводится к бильярду внутри двуrранноrо уrла Q. Чтобы
нзйти м а к с и м а л ь н о е возможное
число столкновений между I1] ар.ам и , до
ИХ разлета, достаточно знать величину,а
двуrранноrо уrла Q, выра)кенную'через
массы т], m 2 , тз- Найдем ее. :':
Уrол между rранями двуrранноrо yr..
ла равен уrлу между векторами, пер,лен",
дикулярными rраням этоrо уrла и соот"
ветственно направле»ными (рис.' li6 2;
\ Рис. 16.2 поясните это). В данном случае rрани
уrла плоскости 1, 2 И 1, 3' а нужным
образом направленные векторы, перпендикулярные к этим
ПЛОСI{ОСТЯМ .......... это
п12==( V 1 ' Vlm2 ' о) и п 2з ( o, y ' /т; )
(см. rеометрическое замечание). Рассмотрим скалярное
произведение этих векторов; если а .......... уrол между BeKTO
рами,\ то мы имеем .
I п 12 1. I п 2з l cos а == (п 12 , п 2з ) ==
== ]- . о + ( .......... 1 ) ( .......... ) + О. 1 ==
v ml У т2 V т2 V тз /т2.
УЧИТЬJвая, что
...! I 1 ,r 1 1
I п 12 1 == V тl + т2 ' I п 2з l == V т2 + тз '
находим
. 1 /rп2 . ... / m)fп
CQS а --:--- ... / I 1... / 1 1 == V (т1+m2) (т2+т'з) ! :
V тl + пZ2 V т2 + тз . ' ,
, '
Т. е.
164
иl + Vl
У т 1
'" '"
U2+ V 2
У т2 ·
(4')
I Итак,
а == arccos V m 1 m з /[(тt + т 2 ) (т J + тз)] .
Учитывая результаты, полученные в 15, получаем еле..
дующее утверждение.
т е о р е м а. Каковы бы ни были начальные положения
uскороститрех шаров масс тl, т 2 , mзнаnря.мой, эmи шары
разлетятся после не более чем N (тl, т 2 , тз) попарных
сmолкновении (и будуm затем дви аmься уже без столкно-
.вений); здесь
I [ n ]
N (т 1 , т 2 , тз) == ........ . (5)
, arccos у mlmз/[(ml+m2)(та+тз») .
Заметьте, что из «чисто физических» соображений полу-
чить такую оценку было бы весьма трудно (напомним, что
оценка т о ч н а я ......... может быть р 6 в н о N (ml' т 2 , тз)
столкновений 1). Более Toro, вовсе не очевидно, что
шары разлетятся после HeKoToporo числа столкновений!
(Заметим, что при тl===т 2 ==т з ==т эта оценка дает
N (т) == [ n (1/2) ] == 3, что равно C , как и должно'
- > arccos
быть для трех шаров равных масс.)
Только что решенную задачу о числе столкновений трех
шаров можно поставить и в случае n шаров на прямой с
асса и mi, т 2 ,. . ., т n . Однако уже при n==4 придется
рассматривать' изображающую точку М== (Хl, Х 2 , Ха, Х 4 )
в четырехмерном конфиrурационном пространстве R'.
Конечно, при определенных навыках и некоторой смелости
можно разобраться и G бильярдом в четырехмерном прост"
ранстве. Мы, прежде чем читатель перейдет к 9 17, оставим
ему этот случай в качестве задачи; укажем только, что
задачу о числе столкновений ч е т ы р е х шаров различ--
ной массы можно свести к задаче о числе отражений луча
света, попавшеrо в зеркало, имеющее форму TpexrpaHHo"
ro уrла (в обычном трехмерном пространстве; см. задачу
14.4б»). Последняя задача и сама по себе весьма сложна;
она будет решена также в 17. Что касается n>4 шаров,
то можно пойти и по друrому пути, указанному в 9 17 и 18.
17. n уоруrих шаров на прямой
Для n>З шаров о массами mt', т2,. . ., т n ,
движущихся по ОСИ Ох, так же как и для трех шаров, мож-
но ввести конфиrурационное пространство......... (п l )-rраи-
иый уrол Q в n-мерном координатном пространстве lR.п==
165
==ОХ 1 Х 2 Х з ... Х n , выделяемый неравенствами
Х 1 Х 2 Х З · · · Х п
(каждое неравенство Xk -<:Xk+i задает полупростраНСТБО в
(Rn) .
Все рассуждения предыдущеrо параrрафа, сводящие
систему из n шаров к бильярду в (п l)-rранном уrле
Q ...... { Хl Х2 Х N }
== v тl У т2 ::::::::: · · · v т n '
rде Xi, Х 2 ,. . ., х n новые координаты в конфиrурацион"
ном пространстве (Rn, связанные со старыми координатами
Xi, Х 2 ,. . ., Х п равенствами
Х 1 == V т ! Xit Х 2 ==у т 2 Х 2 , ..., Х n === V тп х п ,
переносятся дословно и на этот общий случай, но посколь-
ку при п > 3 число n l больше 2, задача уже не сводится
к плоскому случаю отражения бильярдной конфиrураци..
онной точки М происходят н е в Д в у r р а н н о м у r л е,
т. е. происходят не"от двух, а от большеrо числа стенок.
С MHororpaHHbIM (даже трехrрзнным) yrJIOM все становится
rораздо сложнее уже в трехмерном пространстве (RЗ. По-
этому мы временно отойдем от TaKoro раССМQтрения, сводя-
щеrо всю задачу к м HoroMep ной' rеометрин, и попробуем
применить аналитические методы при исследовании сист
мы из n молекул на прямой. В конце параrр.афа мы вновь
вернемся к конфиrурационному пространству и предложим
читателю красивое rеометрическое решение.
Сформулируем еще раз задачу о «rазе» молекул на пря-
мой, решаемую в этом параrрафе *).
Для п шаров на прямой с массами mt, . . ., m п , началь-
нЬ/,ми положениями Xt, . . '" Х п и скор()стями V t , . . ., V N
выяснить, всееда ли конечно число столкновений между
ними на бес.кон,ечном промежутке времени, считая все проис-
ходЯl.цuе столкновения парными и уnруеими (т. е. подчu
няющuмucя законам сохранения импульса u энер2иu; СМ.
формулы (1) и (2) 13).
В случае шаров р а в н ы х масс, тl==. . .==т n , ответ на
u
этот вопрос утвердительныи: полное ero решение приведено
в задаче 13.3. Максимальное число столкновений между
*) Впервые эту вадачу (и даже более общую...... о вылете
бильярдной частицы из MHororpaHHoro уrла) чисто .rеометрически
решил я. r. Синай (СМ. [7]); аналитическое решение предложили
неззвисимо А. Авдеев и пер.ВЫЙ из авторов этой I{ниrи.
I
166
шарами в этом случае равно ч и с л у пар шаров C ==
==n (n 1)/2 и связано это, напомним, с тем, что при столк
новении двух одинаковых шаров они просто обмениваются
скоростями, или, rОБОрЯ иначе, один шар как бы проходит
сквозь друrой, поменявшись с ним на ходу номерами (по-
этому-то кюкдый шар может «пройти сквозь друrой» лишь
не более n 1 раз).
Для п> 3 шаров произвольных масс ответ на поставлен-
ный вопрос также у т в е р Д и т е л ь н ы Й, хотя полу-
чить верхнюю оценку числа N столкновений между ними
существенно труднее, чем для шаров равных масс или для
трех шаров разных масс. Эту оценку мы получим в 18,
а сейчас приведем самое короткое из известных нам ана-
литических решений задачи.
А. Аналитическое решение.
т е о р е м а 1. Ч иСАО столкновений в системе из n упру-
еих шаров на прЯА!ОЙ конечно на бесконечном промежутке
времени.
Д о к а 3 а т е л ь G Т В О будем вести индукцией по чиа
лу шаров. В Э 16 было доказано, что при n == 3 число
столкновении конечно.
Д о п у с т и м (это будет предположением индукции),
что при любых начальных условиях в ерупne из люБО20 числа
k < n шаров за время от О до Т (еде Т MOJ/cem быть равно
+ 00) происходит только конечное число столкновений.
Д о к а ж е м, что конечным будет и число столкновений в
системе из k==n шаров (шаr индукции).
Доказательство поведем о т про т и в н о r о. Предпо-
ложим, что при каких-то начальных условиях п шаров за
время от О до Т сталкиваются б е с к о н е ч н о м н о r о
раз, и получим противоречие.
10. Перенумеруем шары в порядке их следования по
оси Х, но с п р а в а н а л е в о (рис. 17.1). В каждыЙ
п · · · к+1 k .. · 3 2 1
:808r .l...
УВеличение импульса Pk
Рис. 17.1
I момент времени будем рассматривать суммарный импульс k
п Р а в ы х шаров:
Pk === m 1 V i + m 2 v 2 + ... 'r- mkVk,
rде k принимает все значения от 1 до n. Докажем, что при
167
каждом nарном столкновении импульс Pk .может только
увеличиться.
Действительно, Рл не меняется, если сталкиваются шары
левее (k+ 1 )-ro или правее k-ro....... в первом случае шары
с номерами k+2, . . ., n никак не влияют на сумму тlVj +
+. . .+mh,vk, а во втором не меняется скорость '{)h и суммар-
ный импульс Ph j==тlVl+. . .+тh lV1t l (рис. 17..]). Если
же k-й шар сталкивается с (k+ l)-M, то Рл увеличивается,
ибо (k+ l) й шар толкает k-й вправо, увеличивая скорость
Vh, а тем самым и сумму ml V l+. . .+mkVk.
, Занумеруем теперь подряд натуральными числами
1, 2, . .. , S, ... все происходящие столкновения в системе
шаров. Пусть V S) ....... скорость i-ro шара после s-ro по поряд-
ку столкновения в системе (в котором i-й шар Mor и не
участвовать), а PkS) ......... импульс Рл после s-ro столкновения.
Из скаэанноrо выше следует, что для каждоrо k == 1, 2,. . .
. . ., n последовательность {Pk S >} н е у б ы в а ю Щ а я, т. е.
(1 \ С') (8)
Pk Pk' ... P ...
с друrой стороны, при всех столкновениях суммарная кине-
тическая энерrия всех n шаров сохраняется:
1 ( + i + + . ) Е t
12 m t V 1 m 2 v'}. · . · mnV n == == cons ·
Отсюда следует, что скорость каждоrо шара i в каждый
момент времени оrраничена с в е р х у:
тjVi 2Е и I Vj I V 2 т .. / т 2 ,
1 V тln
rде т tn il1 ......... наименьшая из масс тi, . . ., т n . А тоrда для
любоrо k и Лlобоrо s получаем
r
PkS} mllv s>l+ ... +mklvkS)I (m1+...+пlk) 11 2 ,
r т m1n
т. е. после каждоrо столкновения двух шаров исходной
системы суммарный импульс п р а в о й k-точечной:системы
шаров с номерами 1, 2, . . ., k оrраничен сверху числом
(ml + ... +m k ) V2E/m min .
Итак, при каждом k == 1, 2, . . ., п последовательность
{P<k)}, s== 1, 2, . . . t является монотОflflОЙ и оераfluчеН1iОЙ.
Поэтому, соrласно теореме Вейерштрасса *), все последо-
вательности {p( )}, {p( )}, . . ., {p )} имеIОТ пределы при
*) Которая утверждает, что оrраниченная монотонная (воз-
раСТ810щая или \у БЫВ 3Iощая) после.llовательность {х n } имеет предел
при n... 00.
168
:s--+oo. Но p(i)===fпlV( ), следовательно, существует предел
I lim v S) == Ш 1 .
' <х>
Далее, P( )==mlV( )+т2V( ), поэтому существует и предел
lim v S) == Ш 2 (объясните подробно, почему). Точно так же,
' CIC
из равенства p( )==тlv(i)+т2V( )+тsv( ) и существования
пределов Нт p S), Нт v1 8 ) == Wi, Нт v S) == Ш 2 следует су-
s ф S*(Ю S CIC
ществование предела liт v S) == Ш в . Продолжая это рассуж-
s ф
дение, выводим существование пределов скоростей в с е х
шаров *):
Нm Vk S ) == Wk'
в*<х>
k == 1, 2, ..., n.
20. Теперь мы покажем, что все предельные скорости lt.J 1&
равны между собой: Wl == W 2 == . . . == Ш п == W.
Рассмотрим два соседних шара: k-й и (k+ 1 )-й. За время
от О до Т, в течение KOToporo по нашему предположению 8
системе из n шаров произошло б е с к о н е ч н о е число
столкновений, k-й и (k+ l)-й шары также должны были
столкнуться б е (! к о н е ч н о MHoro раз.
Действительно, если бы они столкнулись лишь К О Н е ч-
н о е - число раз, то с HeKoToporo момента t o , rде 0< t o < Т,
они перестали бы сталк.uватЬС!f- и тоrда вся система из п
шаров с момента t(j разделилась бы на две: п р а в у Ю, в
которую входят шары G номерами от 1 до k, и л е в у ю........
с номерами от k+ 1 до n. В каждой из этих систем ЧИCJ10
шаров cTporo меньше n, а тоrда по предположению индук"
ции число столкновений в каждой из них конечно как на
промежутке времени от О до t o , так и на промежутке времени
оТ /0 дО Т. В результате получаем, что и во всей системе из п
щаров число столкновений на промежутке времени (О, Т)
к о н е ч н о, что противоречит нашему исходному пред-
ПОЛО)l{ению.
Рассмотрим некоторое столкновение между шарами k
и k + 1; пусть оно имеет номер s в серии всех столкновений
системы из n шаров. Из закона сохранения импульса
имеем равенство
(<:) + (8) т V (S--l) + V (S--l)
mkv/ l пZk+iVk+l...... k kJ m k + 1 k+l
*) л. Н. Васерштейн и Р. А. I'альперин доказали общее T"!
верждение о том, ЧТО в JIюбой (даже мноrомерной) система из конеч"!
Horo ЧИСJlа центрально отталкивающихся частиц все частицы имею'!'
предельные скорости. Это тверждение используется при llоказа..
тельстве теоремы в rл. 7.
169
(при этом (s.........!)-e столкновение мо}кет произойти и между
шарами, отличными от k и k+l), а из закона сохранения
энерrии ......... равенство
т (v (S» + т (и (В) ) 2 т (V (S 1» ) 2 + 1"tl.S 1» 2
k k k+l k+l ......... k k - mk+i ""k+l .
Переносами слаrаемых в разные части равенств получаем
m ( v(S) V(S l» fn ( V(S--11 и(В»
k k k ......... k+l k+l k+l ,
mk «VkS») (t'kS 1»)2) == тk+l «V<':+f»)2 (VkSJl) 2) ,
и после почленноrо дел ния последнеrо равенства на пред-
последнее (такое деление возможно: v( )=I= VkS l) и V l=1= V( + ) ,
поскольку s-й удар произошел именно между k-M и (k+ l)-M
шаром!) получаем соотношение
V (S) + V (S l) V (S l) + V (S)
k k ......... k+l k+l.
Оно справедливо для б е с к о н е ч н о r о числа столкно-
вениЙ s между k-M и (k+ l)-м шаром, поэтому в нем можно
перейти к пределу при S OO. ДЛЯ предельных скоростей
получим 2Wh,==2wk+l' откуда Wh,==Wk+l0 Итак, все предель-
Hbte скорости равны метсду собой:
Ш 1 ==Ш 2 == ... == W N ==ш,
что мы и хотели доказать в этом пункте.
3 0 П (О) (О) r ·
. усть v 1, . . .., V п: ......... начальные скорости шаров,
из закона сохранения импульса следует, что для каждоrо
столкновения s выполнено равенство
и (О) + + т V (O) (8) + + V (S)
т 1 1 · · · n п ........ т 1 и 1 · · · т n п ·
Поэтому, переходя к пределу при s: oo, находим
m 1 t1°) + ... + mnvh,O> == (m 1 + ... + т n ) ш,
отку да
(0) + ! (О)
тl V l ... тnVn
ш== + .
ml + '.. т n
Но величина справа ----- скорость центра масс всей системы
из п шаров. Итак, скорость каждо о шара стремится к
скорости центра масс всей системы (если число соударений
бесконечно).
Перейдем в связи с этим в систему центра масс, Т. е. в
систему отсчета координат, которая движется относительно
u
исходнои системы отсчета равномерно со скоростью w.
В пей все предельные скорости равны о; следовательно, и
п р е Д е л ь н а я э н е р ,r и я в системе центра масс
170
равна о. Однако в силу инерциальности системы отсчета,
v v u
связаннои G центром масс, в неи, как и в исходнои системе,
выполнен закон сохранения энерrии; а раз п р е Д е JI Ь--
Н а я энерrия равна о, то и н а ч а л ь н а я энерrия
шаров в системе центра масс также равна о.
Это может быть лишь тоrда, коrда все начальные скорости
шаров в системе центра масс были равны о, т. е. коrда в ис-
ходной системе отсчета все начальные скорости шаров были
равны w.
Но при одинаковых начальных скоростях шаров столк-
новений между ними вообще не может nроисходить! Это
противоречит исходному предположению о том, что в систе-
ме происходит б е с к о н е ч н о MHoro столкновении.
Следовательно, исходное предположение неверно..........
число столкновений может быть только конечным, что и
требовалось доказать.
Повторим кратко схему доказательства нашеrо утвер>к-
дения. Мы предположили, что в л ю б о й системе с .меньшим
че-м п числом шаров количество столкновений конечно (8
для п==3 это предположение мы доказали в 16), и пред-
положили затем, что в н е к о т о рой системе из п шаров
I{оличество столкновений б е о к о н е ч н о. Отсюда мы
вывели, что любые два соседних шара ДОЛЖНЫ сталкиваться
друr с друrом также бесконечно MHoro раз, а тоrда их СКО-
рости должны С Т Р е м и т ь с я к одному и тому же пре.
делу, равному скорости центра маса системы. Но, поскольку
выполнен закон сохранения энерrии, эти скорости уже с
начаЛЬНО20 МОМЕнта равнялись скорости центра масс. Од-
нако шары с равными скоростями вообще не MorYT сталки
ватьсяl Итак, если предположить бесконечность количества
ударов в «rазе» из п молекул, то из этоrо выводится, что это
количество равно НУЛIО явный абсурдl Поэтому число
ударов и в системе из n шаров конечно на всем бесконеч-
ном интервале времени. Это число мы оценим явно в 18.
Б rеометричеСК9е решение *). К рассмотренному краси-
вому аналитическому рассуждению добавим теперь reoMeT-
рическое, пожалуй еще бол е красивое и прозрачное рас-
суждение, использующее, как мы обещали в начале пара-
rрафа, конфиrурационное пространство....... мноrоrранный
уrол Q. Заодно обобщим ситуацию и сформулируем сле-
дующую задачу.
*) Это решение существенно отличается от впервые предложен.
Horo Я. v. Синаем решения в статье (7). Оно было получено неЗ8'!!
висимо А, М. Степиным В первым из авторов этой книrи.
111
в ,М,ноео,М,ерно,М, пространстве расположен произвольный
n 2ранный уеол Q с вершиной в начале координат о. Внутри
эmоео ,М,н,оеовранноео уела движется бильярдная частица,
отражаясь уnруео (по бильярдНОАtУ закону) от еео ераней.
Перестанет ли коеда-нибудь бильярдная частица сталки-
ваться с еранями уела Q? Конечно или бесконечно число ее
оmраженuй от ераней за бесконечное "время?
Для двуrранноrо уrла величиной а ответ мы знаем: иско-
мое число отражений конечно и не превосходит N (а)==
== [ л/аl (СМ. 15, п. В). Число N (а) было получено
с помощью выпрямления траектории....... превращения ее в
прямую. Так же, но несколько хитрее, мы поступим и
сейчас.
т е о р е м а 2. Бильярдная частица в мноеоеранном
уеле Q с некотороео ,М,омента движется по лучу, не пересе..
IШЮt.Цe,М,У еео ераней. До этоео момента частица сделает не
более N (Q) отражений от ераней Q, приче'м' число N (Q) за-
висит только от еео.меmрических характеристик уела
Q, но не от начаЛЬНО20 положения и направления скорости
частицы.
,Д о к а 3 а т е л ь С Т В о. Для наrлядности докажем тео-
рему 2 в случае MHororpaHHoro уrла в т р е х м е р н о м
пространстве R3. Пусть (1.,1, а 2 , . . ., (1.,п ........ двуеранны.е
уrлы MHororpaHHoro уrла Q. Опишем сферу 82 радиуса 1 о
центром в вершине О уrла Q. Тоrда п-rранный уrол Q вы-
сечет на сфере S2сферическuй ,М,НО20уеольник u'l==A 1 A 2 . . .А п ,
вершины KOToporo А , точки пересечения ребер уrла Q
со сферой, а стороны At A 2' А2 А з, . . ., А п А 1 ......... дуrи боль-
ших окружностей, высекаемые на сфере ero rранями
(рис. 17.2, а). Длины сторон AtAi+l мноrоуrольника равны
плоским уrлам A i OA ' + 1 (так как радиус сферы равен 1),
а уrлы At, . . ., А п мноrоуrольника л........ ByrpaHHbIM
уrлам аl, a 2' . . ., a n MHororpaHHoro уrла Q.
Рассмотрим теперь бильярдную траекторию внутри Q.
Она представляет собой мноrозвенную ломаную. не обяза-
тельно лежащую в одной плоскости, число изломов которой
нам неизвестно оно может быть как конечным, так и бес-
конечным (пока мы ничеrо не знаем), а также может Л,ибо
содержать бесконечный луч (тоrда бильярдная частица,
летящая по нему, уже не сталкивается со стенками MHoro..
rрзнноrо уrла Q), либо не содержать TaKoro бесконечноrо
луча (в ЭТОМ случае MHOJКeCTBO соударений со стенками
172
заведомо бес!{онечно; но и в первом случае число соударе-
!lИQ может быть априори бесконечным ......... только звенья
ТR ектории в этом случае становятся сколь уrодно малыми.
Н. частица как бы «застревает» в уrле Q).
ПримеFIИМ к бильярдной траектории уже использовав-
ШУJOся ранее процедуру «выпрямления», состоящую в 'том,
что мы каждый раз производим симметричное отражение
уrла Q и бильярдной траектории относительно очередной
DЬ/flрянленная
траектОРIJН
q
а
6
Рис. 17.2 , ,
ero rрани, от которой отражается частица (подробнее о
процедуре выпрямления см. во ведении и в пп. А и\ В
,15). В результате таких отражений (которых может быть
и ($есконечно MHoro, по неизвестному пока числу точек изло.
ма траектории) получим последовательность MHororpa HbIX
уrлов Q, Qi, Q2' Qз, . . ., каждые два из которых симмет-
ри'чны друr друrу относител,ьно общей rрани, и прямую 1,
пересекающую эти мноrоrранные уrлы,........ выпрямленную
quльярдную mраекторию. Мноrоrранные уrлы {Qi} высе-
кают на сфере 82 р а в н ы е сферические мноrоуrольники,
имеющие общие CTOpOHЫ, все они получаются симм т-
ричными отражениями на сфере из мноrоуrольника t!l==:l
1 А 1 А 2 . . .А п .
Рассмотрим центральную проекцию бильярдной тра-
е'КТОрИИ в уrле Q на сферу с центром о. На сфере получится
мноrозвенная ломаная, расположенная в сферическом мно-
tоуrольнике Л и состоящая из дуr больших окружностей
сферы 82. Звенья этой ломаной отра аются от сторон сфери-
чеС'коrо мноrоуrольника АI . . . А п .по закону «уrол паде-
ния равен уrлу отражения». Действительно, пусть отра-
жение происходит, например, от стороны A:iA2' т. е. про-
екция бильярдной частицы на сферу 82 движется по зве-
ньям М 1 М 2 и м 2 м 3' rде ТОЧК а М 2 лежит на стороне A:iA
173
(рис. 17.3). Следовательно, сама частица отражается от
rрани OAfA 2 MHororpaHHoro уrла Q. Отразив Q симметрич-
но относительно этой rрани (переведя ero в мноrоrранный
уrол Ql) мы «выпрямим)} два соседних звена бильярдной
траектории.......... проекция на сферу отрезка, симметричноrо
второму звену траектории, будет дуrой M2M , являющейся
продолжением дуrи М 1 М 2 . Следовательно, LA 1 M 2 Mi==
== LA 2 M 2 M;, а так как LA 2 M 2 M;== LA2M2Mз, то
LA 1 M 2 Mf== LА 2 М 2 М з звенья М 1 М 2 и М2М3 Ha
клонены к стороне AfA 2 под равными уrлами, что и требо
валось.
Итак, nроекция на сферу бильярдной траектории в
уеле Q является бильярдной траекторией в сферичес/(,ом
мно оу ольнике cIl. После выпрямления бильярдной траек-
тории в Q, что в проекции на сферу отвечает выпрямлеНИIО
бильярдной траектории в сфе
рическом мноrоуrольнике Л, по
лучим, как уже rоворилось, пря
мую 1 и ее центральную проек-
цню на сферу с центром О .......... дy
ry 1'. Но дуrа l' .......... это в точности
половина большой окружности!
Это хорошо ВИДНО из рис. 17.2, б
Рис. 17.3 (концы дуrи l' не включаются в
нее). Следовательно, длина дуrи
'\' равна л, и, тем самым, бильярдная кривая в уrле Q
(имеющая бесконечную длину) превращается в ломаную
внутри мноrоуrольника Jl конечной длины зt (начало и
конец этой ломаной MorYT лежать cTporo внутри' еЛ).
Еще раз внимательно исследуем звенья бильярдной ло-
маной в мноrоуrольнике CIl. Проекция М бильярдной
частицы движется по сферической ломаной внутри MHoro
уrольника Л и проходит суммарный путь длины зt. Если
точка М движется по тем звеньям сферической ломаной,
которые отражаются от двух с о с е Д н и х сторон MHoro-
уrольника eIl, например от сторон Ai lAi И AiAi+l' то она
отражается от этих сторон (не являющихся сторонами
уrла A i мноrоуrольника еЛ) не более N (аi)== [ л/аi]
раз (таково число отражений бильярдной частицы от
двуrранноrо уrла с ребром OA i и rранями OAi iAi и
OAiAi+i; СМ. также рис. 17.2, в). Но не может ли возник-
нуть такая ситуация: точка М попадает в уrол A i б е с к о-
н е ч н о м н о r о раз, пр-ичем каждый раз в с е б л " & е
174
и б л и ж е к вершине А,....... это не будет противоречить
u
конечности суммарном длины всех проходимых ею звеньев
внутр и tIl!
Чтобы oTBeprHYTb такую возможность, поступим сле-
дующим образом: окружим каждую вершину А i кружком
K i фиксированноrо радиуса так, чтобы кружки не пересе-
кались, а оставшуюся часть мноrоуrольника tIl (за исклю-
чением всех этих кружков) обозначим :УЗ (рис. 17.4). Пусть
d м н н и м а л ь н о е расстояние между точками сто-
рон AiA 2 , А 2 А з , . . ., AnAi, принадлежащих части 93 мно-
rоуrольника (т. е. между точ- К
ками сторон ai, . . ., а n , не ле- А 2. K
жащими в кружках {K i }). Тоrда 2-
точка М, выйдя из кружка Kt,
вновь попадет в этот кружок,
u
лишь проидя расстояние, не
меньшее d. Сколько же раз точка
М может попасть в кружок K i ?
Вне этоrо кружка она прохо- Рис. 17.4
дит путь, меньший CYMMapHoro
u
пути по в с е м звеньям, Т. е. меньшии п: значит,
количество ее заходов в кружок K i не может превос-
ходить m==[nld]+l. Внутри же каждоrо кружка К , точка
м сталкивается только со сторонами уела А i И испы-
тьшает, по сказанному выше, не более N (ai) столкновений.
Bcero столкновений точки М со сторонами мноroуrольника
Jl в н у т р и всех кружков поэтому не более т (N (аl)+
+N(a 2 )+. . .+N(a n ». К этому числу следует добавить
количество столкновений точки М G частями сторон ai, . . .
. . ., а n мноroуroльника ,л, лежащими в н е кружков {K i }.
Но от одноrо TaKoro столкновения до друrоrо точка М
проходит путь, не меньший d, поэтому число этих GТОЛКНО-
вений не больше указзнноrо выше числа т. Следовательно,
общее число столкновений точки М со сторонами МН020-
У2 ОЛЬfluка eIl, равное чuслу стОЛКн'овенuй бильярдной ча-
стицы с 2ранями У2ла Q, не npeвocxoдutп
N N(Q}==m(N(Clwi)+N(rJva)+ ... + N(a п )+l)==
;= ([ J + 1 ) ( 1 [ :J [ ] .. · [ :п 1) ,
еде ai, . . .11 (Жn........ двУ2ранные уалbt МНО20еранноео уела Q.
МЫ, таким образом, не только доказали, что число N
столкновений частицы G rранями уrла Q в трехмерном про-
странстве конечно, но и оценили ero числом N (Q), завися-
175
щим Т О Л Ь к о от rеометрии MHororpaHHoro уrла Q
T ero плоских уrлов (они неявно I входят В величину d) и
ДBy paHHЫX уrлов cti, а 2 , . . ., (х n . , "
Аналоrичное рассуждение, по существу индукционное,
ороводится и для MHororpaHHoro уrла Q в MHoroMepHOM
пространстве IR. k (k>3). Случай TpeXMepHoro пространства
R8 мы свели к случаю двумерноrо, но уже сфери ескоrо
пространства 82 (правда, с оrраниченным мноrqуrольни-
К()М, а не с бесконечным уrлом); точно так же, случай четы..
.peXMepHoro пространства IR. k сводится к рассмотрению
ссферическоrо» мноrоrранника на Т р е Х м е р н о й еди-
.ничной сфере 8 З == {x +x +x:+x == l}, и т. д. В резульrате
получается р а в н о м е р н а я (Т. е. зависящая только от
rеометрии уrла Q) оценка числа ударов о rранями. ' . ,\
, Остановимся коротко на доказательстве для' iобщеrо
'случая k MepHoro пространства fR4, в котором наХ9Д ТСЯ
k-мерный n-rранный уrол Qk с вершиной в начале: I\ООРДИ-
нат О, и сведем ,ero к случаю размерности k l.. Опишем
единичную (k........l)-МерНую сферу Sk--J, с центром в 0'; rр ни
уrла Qk высекут на сфере 8 ft -- 1 некоторый сферический
(k........l ) мер ный м Hororp аннн к
сА. Бильярдная траектория
вместе с бильярдной части-
цей проектируется на сферу
8 ft -- l в виде «сферической
бильярдной ломаной» в ,;1" по
которой движется точка М.
После выпрямления бильярд-
ной траектории получаем пря-
мую 1, центральная проекция
которой на сферу 8 k -- 1 дает по-
ловину дуrи большой окруж-
ности длины 1t (рис. 17.2, б). Следовательно, сумма длин
звеньев сферической бильярдной ломаной в сферическом
мноrоrраннике rJt равна п. Точки пересечения ребер МНО-
rorpaHHoro уrла Q со сферой 8 k -- l ........ вершины At, А 2 . . . .
! · ., А п окружим непересекающимися шарами Kt, .. . ., l(n
размерности k........l; ДВУl\iерные, трехмерные, ..., (k........2)..
мерные rрани мноrранника rJt окружим попарно непересе-
кающимися окрестностями (k l) мерными цилин,цра и
(схематически эrо изображено на рис. 17.5). Внутри каж-
oro шар,8 K i точка м отражается только от (k 2).MepHbIx
rраней (k l)-мерНbIХ мноrоrраиных уrлов Q:--l, Q:7"l... " .
'116
Рис. 17.5
. . . t Q l; поэтому число столкновений точки - М с этими-
1: rранями не превосходит' некоторой константы, зависящей,
по предположению индукции, только от rеометрии уtлов
Q l,. . ., Q "'l. Аналоrичные равномерные оценки имеют
место и для отражений точки М от rраней сферическоrо
мноrоrранника Л, находящихся внутри построенных ци-
линдров. Как и в случае пространства [Rs и сферы 82, в слу
чае пространства Rk и сферы 8 k ..... 1 мы должны учесть KO
личество заходов точки М в построенные шары и цилиндры;
по аналоrичным соображениям, они не превосходят H KO-
Toporo числа т=== [n!d] + 1, rде d rеометрическая харак-
теристика оставшейся после выкидывания шаров и цил'инД-
ров из мно!оrранника rIl части 93. В- резу ьтате ожно
ПOllучить верхнюю р.а в н о м е р н у ю оценку числа GТОЛ-
кновений точки М с rранями сферическоrо мноrоrранника
-cIl, которая оценивает сверху также и число столкновений
исходной бильярдной частицы. Теорема 2, таким обра'ЗQМ,
доказана. \ \ . ,
Заодно получено второе решение задачи .про -Л" шаров' на
прямой; для этоrо в качестве мноrоrраииOiО уrла Q M дyeT
брать (n l) rранный уrол Q == { ' (Хl. .... Х n ) Е IRn: .: .
_ тl
< . .. ;-k. }. в отличие от приведенноrо аналитичес-
Koro решения, rде утверждается ишь, что число столt{но-
венин между шарами не может быть бесконечным, в re6Me
1'Р' иче с ком решении получен ,rораздо более СИJIЬНЫЙ
результат, rоворящий о наличии единой (р а в н о 1\1 е р-
н о й) оценки числа столкновений .для всех систем шаров
с данными массами.
т е о р е 1\1 а 3. Число столкновепий 'за бескопечпый про-
межуmоf\, вре/vlени между п шарами па прямой меньше пeKO
'торой копстанты N (ml, ..., т ), зависящей только otп
соотношений масс эmих шаров ml, . . ., т п (эти cooтHO
шенuя определяются ееометрией мпоеоерапноео уела
Q(тt, . . ., пz n ), т. е. плоскими, двуераппыми, трехер'аи.
. пы.ма, . . ., уелами Q) и -пе зависящей от начальных поло..
eltu(J,' х 1, . . ., Х п tl скоростей Vl', · . ., V N шаров. .;'
!' Исходя из некоторых друrи , более физических сообра-
; жений. получим оценку константы N (mi., . . ., m n ) в '18.
: 1 3 а д а ч а*. В прямой круrовой конус влетае.т бильярдная
часmil.а. а) Перестанет ли она коrда нибудь сталкиваться с' ним?
б) Конечно ли число ее столкновений, с поверхностью конуса?
L'l7
в) Если да, то зависит ли это число от начальны положения и
скорости частицы?
О т в е т. а) ПереСТ8нет. б) Кснечно. в) Зависит. У к а з а н и е
к реш е н и ю. Рассмотрим центральную проекцию бильярдной
траек'тории у на сферу с центром в вершине конуса. Вся спроек-
тированная траектория у' будет располаrаться в круrлой «шапоч
ке», высекаемой a сфере конусом, причем ломаная у' будет вести
себя в «шапочке», как бильярд в обычном Kpxre, т. е. будет распо
лаrаrься полностью в KpyroBoM кольце и иметь равные звенья.
Рассуждая, как и раньше, нетрудно показать, что длина ломаной
у' равна n, поэтому число звеньев у у', а тем самым и у у конечно.
Но чем «касательнее» частица будет запущена в конус, тем звенья
лом.аной ')" будут меньше, и поэтому их количество будет зависеть
от начальноrо состояния влетающей частицы.
18*. Число столкновений между
МОJlекулами одномерноrо «rаза»
В этом параrрафе мы сначала оценим число
столкновений между n молекулами «rазз» на прямой, а за-
тем решим аналоrичную задачу в «сосуде»......... на отрезке
прямой. rеометрическое решение задачи о числе столкно-
веций между n шарами с массами т1., . . ., т п , упруrо
u
сталкивающимися на прямои, дает возможность получить
верхнюю оценку этоrо числа, но выписать ее явно на основе
соображений 9 17 довольно затруднительно. Мы приведем
новые соображения, которые позволят получить искомую
оценку аналитически и выписать ее явно. Эта оценка будет
зависеть только от числа n шаров и от отношения макси-
мальной массы mтах в системе к минимальной массе mmin.
При ее выводе мы будем использовать полученные в 17
знания о том, что число столкновений в рассматриваемой
системе конечно на бесконечном промежутке времени (и
некоторые следствия, например о том, ,QTO моменты столкно-
вений t1, t 2 , . . . не MorYT скапливаться на оси времени, и
Т. д.). Будет доказана
т е о р е м а 1. Ч UC(lO столкновений в систеА1,е из п
шаров на nрЯ1rLОЙ с Аtасса.iИU trll, . . ., ,п п не nревосхадиm
2 ( 8n (n.......l) т max ) 11-- 2 t rде т тах u тml n ........МйКсuмалЬная u
тmin
Аtuнuмальная масса шара.
Д о к а э а т е л ь G Т В О *). Перейдем к системе коор-
д инат а начало м в центре масс системы шаров. В этой
*) Прежде чем читать 110казатеJIЬСТВО, читателю полезно озна-
комиться с принципом Лаrранжа. которому посвящен «Рассказ
двенадцатый» поминавшейся в 4 книrи B И. Ти!Хомирова «Расска.
вы о максимума и минимумах». Впрочем кратко Э'fОТ принцип иs-
ложен нами на с. 180.
178
системе отсчета
m 1 x 1 + ... +тпхп===О, m 1 v 1 + ... +тnVn===O.
Энерrию всей системы молекул в рассматриваемой системе
отсчета обозначим Е:
n 2
Vi
тiT==E.
i= 1
Занумеруем подряд моменты столкновений частиц: t 1 <
<t 2 <t 3 <. . . Соrласно закону сохранения импульса в MO
мент t k импульс каждой.из столкнувшихся частиц изменя-
ется на одну и ту же п о л о ж и т е л ь н у ю величину,
которую обозначим I1pk (мы считаем скорость частицы поло
жительной при ее движении вправо по прямой и отрица
тельной при ее движении влево): импульс левой столкнув-
шейся частицы уменьшается на I1pk>O, а правой уве-
личивается на I1pk (см. задачу 13.1). Пусть pi==mivi
импульс частицы i, а N ==N (ml, . . ., т n )......... общее число
столкновений в рассматриваемой системе шаров за беско-
нечный промежуток времени. Оценку числа N проведем в
несколько этапов.
Этап 1. Оценим сумму I1pi+l1p2+. . .+I1PN. ДЛЯ этоrо
умножим импульс каждоrо шара на ero номер и сложим по-
лученные величины, т. е. рассмотрим функцию времени t
rl
с? (t) === 1 · Рl (t) + 2. Р2 (t) + ... + n. Рп (t) == i. Pi (t).
i::::: 1
Функция fJ (t) постоянна между двумя столкновениями и
меняется только в момент столкновения t k на некоторую
величину l1 k. Вычислим l1 k, считая, что в момент t h
столкнулись шары r и ,+1:
с? (t k О) === 1 · Рl + ... +,. Р r + (, + 1) Р r+ i + ... + n · Р n'
с? (t k + О) == 1 · Рl + ... +, (Pr........ Llpk) + (, + 1) (Pr+l+ I1 Pk) + ...
...+n.Рn,
I1fP k == (t k + О)........ fj'J (t k........ O ) == I1Pk.
Итак, (t) в момент удара t k меняется на Pk' Если мы
найдем верхнюю и нижнюю оценки шах И с? min функ-
ции с? (t), то мы тем самым сможем получить и верхнюю
оценку для суммы Pk' поскольку
k
N
I1Рk шах min'
k=J
179
Как будет следовать из дальнейшеrо, достаточно полу ить
только верхнюю оцеИI<У '") тах (мы УВИДИМ, что fJ min :::::
=== fJ тах).
Рассмотрим ФУнкцию *)
!l' == ( i. m.v. + 'А. m.t'. + 11.. ,п. v; " II.E
1 1 1 1 &' 1. 2 / &"
t =]
rде л и f.t неоriред ленные коэффициенты. .Б искомой
экстремальной точке 'lJ== (Vl, ..., V п ) все производные
этой функции по переменным Vi, i== 1,.. . ., n, обращаются
в нуль: .
,
2 v.::::;' (i + 'А) тi + f.tmiV, == о.
1
Отсюда получаем n равенств:
i+л
Vi ==...... fJ. ' i == 1, 2,' ..., n.
n
Подставив найденное значение Vi в равенство т;Vi' '':'' \O',
i= ]
найдем
n
i. т;
11 i = I
I'.
п
mj'
i = 1
М 1
................ м '
rl
rде М == тj........ суммар ная масса всей системы шаров, а
i = 1
п
М 1 == i. т; первый момент (этот термин взят из теории
{= j
вероятностей) .
.+л
Подставив теперь Vi == l В -равенство
J-t
п '2
" т 2 i V i
k.. === Е ,
i= 1
,*) Функция .z называется функцией ЛаераН'J/са (см. об этом
уже УIJоминаВШУIОСЯ книrу В. М. Тихомирова «Рассказы о макси-
MYMa и минимумах»), а применяемый здесь метод носит название
«правило множителеЙ Лаrранжа» и состоит в том, что, до-бавляя
к оцениваемой ФУНКЦИI:I f}(t) все имеющиеся оrраничения, YMHO)KeH .
ные на неопределенные коэффициенты (в данном СЛУflае TP
л ( t mjЩ ) и 11 ( t m и E ) , дифференциров нием, по ,
t=l t=l
ченнои функции .z находят экстремальные точки.
180
u
наидем
==:1:: V 21 · t т, (i + л) .
i= 1
n
ИЛИ, введя обозначение М з == i . т[ (второй момент)
i= I
И подставляя найденное значение л,
-. / 1 ( M )
J.t==:i: V 2Е М з M ·
Зная л и J.t, можно вычислить экстремальные значения
ФУНКЦИИ (t):
:?extr== t iтiVi== =F V 2В( Ma ,:} ).
l= I
Отсюда следует. ЧТО
:? тах == !Р mln == V 2В ( М а ) I
следовательно.
fAPIl fj3max :?mln==2 ax ==2 -v 2В( Ма л;J ). (1)
k== I
3 а м е ч а' н и е. Читатели, знакомые с теорией вероятно
М м 2 /м
С1'ей, заметят, что число O == 2----М 1 есть дисперсия случай-
ной величины , ПРИНИМ810щей значение i с вероятностыо mi/ М.
По этому вып олнено нерзвеНС180
VMaM M M.V 'l;+ .n2 ( 'l+ .nу==:
==М. n....l
2
которое превращается в равенство, если положить крайние массы
т 1 11 т п равными М/2, а все прочие массы нулю (это неравеи
ство можно доказать и чисто 8лrебраически).
Этап 2. Всю ось времени t разобьем на «быстрые про-
межутки», на каждом из которых какие-то два соседних
шара имеют большую относительную скорость и не сталки-
ваются друr с друrом. Напомним, что начало системы
координат находится в центре масс системы п шаров.
Промежуток времени [t 1 . [ 2 ] (rде t 2 может, вообще rOBO'"
ря, принять значение +00, тоrда отрезок превратится в
181
полуинтервал [t 1 , +00» будем называть бblстрым, если
какие то два соседних шара i l и i ни разу не сталкиваются
в течение этоrо промежутка, причем их относительная
скорость превышает некоторую положительную постоян-
ную Ci>O: I Vi (t) Vi i (t) I Ci при всех t Е [ti, t 2 ].
Конечно, л ю б о й промежуток времени, в течение
KOToporo в системе не было вообще стdлкновений,......... быст-
рый (поскольку положительную константу Ci можно опре-
делить уже после выбора этоrо промежутка как модуль
разности скоростей частиц i.........} и i). Это верно, но только в
этом случае Ci будет зависеть от положений и скоростей
шаров, а этоrо мы хотим избежать, чтобы получить оценку
числа столкновений. Наша цель......... с н а ч а л а подобрать
константы Ct, не зависящие от положений и скоростей ша-
ров, а з а т е м уже получить соотв етс твующие быстрые
промежутки. Заодно мы хотим, чтобы каждый момент вре-
мени t попадал хотя бы в один из таких быстрых проме-
жутков.
У т в е р ж Д е н и е. Существуеm такой набор кон-
стант С2, С8, . . ., Сп, зависящих только от .масС частиц u
полной кинетической 8нереии Е, что объ.единение быстрых
промежутков времени по всем парам (i.........l, i) покрывает всю
ось времени.
Д о к а 3 а т е л ь с т в о. Введем число
с==
Y 2 I
,
mi
i= ]
1
(2)
rде М==тl+. . .+т n . Положим теперь для каждоrо i==2,
3, 4, . . .
тi l+тi
С.==() .
1 mi 1mi
Утверждается, что для каждоrо момента времени t су..
ществует такое i, что I Vt (t).........Vi...l (t) I C! ........ ЭТО И озна-
чает, что все быстрые промежутки покрывают полностью
ось времени..
Предположим, однако, противное: пусть внекоторый
момент t для всех i==2, 3, . . ., n
IVl(t)........Vl..i(t)1 <с mi 'i i .
т ' ...l т ,
с учетом этоrо предположения справедливы такие пера-
182
венства (для определенности считаем, например, что i < j):
tVi Vj I I Vi Vi+11 + I Vi+l Vi+21 + · · · + I Vj...i Vj 1<
< с ( тi+тi+1 + . . . + т/ l +т/ ) == с [ ( + ......!..... ) +
mi т i+l тj lmj mi mi+l
+ ( + ) + . . . + ( 1 + 1 ) +
mi+1 mi+2 mj 2 mj 1
+ ( т) l + / ) J === о [2 ( i + тi l + · .. + ;/ )
] < 2с ( +... + ) .
т, mj mi mj
Так как начало координат находится в центре масс системы,
то в каждый момент для каждоrо шара i существует шар j
такой, что скорости Vi И Vj имеют противоположные на-
правления, а тоrда, учитывая (2),
(,; 1) 2 уЕ(
fv,1 <IVi Vjl < 20 l т, J === (L. *) 2М 1: j )==
=== y
для всех i == 1, 2, . . ., п.
Оценим кинетическую энерrию всей системы шаров
сверху:
2Е
п 2 п mi Е n
Е === 1: т щ < 1: 2М ==м 1: m, ==Е.
i=l i=1 i=l
Полученное противоречивое неравенство Е<Е доказывает
неправомерность сделанноrо нами предположения. Утверж-
дение доказано. l
Этап 3. Оценим количество быстрых промежутков.
Каждому 1аксимальному по длине быстрому промежутку
[t 1 , t 2 ] соответствует «сильный» удар некоторых шаров
i l и i, происходящий или в момент t 1 , или в момент t 2 ,
при этом ДЛЯ всех t Е [t 1 , t 2 ]
I (t) (t)l ........... mi i+mi
Vi Vi--1 C . . .
т , 1т,
Изменение импульса при этом ударе paBHO (см. зада-
чу 13.1Y
А I I т, 1т,
L1 Р (i -- 'i. t i) == V 1 .......... V i -- i + -;:::::; с.
mi i т,
С друrой стороны, P<i--it i> равно какому-то PA, -rде k ......
номер момента t h В последовательности всех моментов
183
столкновений шаров, и поэтому изменение импульса при
каждом сильном ударе не меньше С: p k C. Следова-
тельно, количество сильных ударов н е б о л ь ш е чем
( 1 I1Pk )/ с. Оценим это число. учитывая формулы (1) и
(2):
I APk 2 V 2Е ( М 2 ) (n 1) 2
( ) 1 ===4 , I VM2M Ml.
с I I .. / Е li: 1 m l J
l т, J v 2М
t= 1
Осталось теперь заметить, что каждый момент сильноrо
удара конеи отрезка [t 1 , t 2 ]....... принадлежит не более
чем д в у м быстрым промежуткам, стало быть, число бы-
стрых промежутков не болы е YABoeHIioro числа сильных
ударов, т. е. не превосходит величины
(n 1)
К === 8 I mj I V М 2 М M .
i= 1 J
(3)
,
Этап 4. Оценим число столкновений N (тj, . . ., т n ).
Итак, существует разбиение оси времени, состоящее не
более чем из К отрезков, причем на каждом отрезке (бы-
стром промежутке) всю систему шаров можно считать раз.,
битой на две невзаимодеиствующие системы. Поэтому мож-
но воспользоваться индукцией и написать:
N (пZ 1t ..., т n ) K. шах (N (mj, .". т т )+
I<r<п
+ N (тт+1' '.', т n » + число сильных ударов,
rде N (тl, . . ., т т ) ......... число столкновений в системе ,
шаров с массами тl, . . ., m r . Мы будем далее делать rpy-
'бые оценки, заменяя, например К/2 на К и Т. п........ нас ин-
тересует лишь возможность получить я в н у ю фор м у-
л у для оценки.
Так как число сильных ударов не больше К (даже не
больше К/2), то
N (т 1, ..., т n ) К. шах (N (т 1, ... t m т ) +
1<,.<11
+N (m'+it "', т n ) +-1).
Пусть Т r ......... максимальное из чисел N (т{ " . . .-, т ; ,), r де
mi \' . . ., т; r ........ произвольные r MaCG из ml, . . .» т п , Т. е.
184
т r равно максимальному числу столкновений в системе из
r шаров, 'выбранных из данных п шаров. Тоrда
ТТ <: к (2Tr__l + 1)
(МЫ опять выписали заведом:о rрубую оценку).
Наконец, введя Ur==Tr+1, получаем
U r == Тт+ 1 K (2(Ur__l 1) + 1) + 1 2ки т __ ж .
Из этоrо неравенства уже леrко получить оценку для и п :
и n 2ки n--l (2К)2 U п--2 ... (2К)n-- ё U 2 2 (2K)n"'
(между двумя шарами на прямой может произойти макси-
мум один удар, так что T 2 ==1, а и 2 ==2).
Следовательно, учитывая равенство (3), получаем
[ (n ') ] п 9
N (т 1 . ..., т n ) :::;; 2 16l i J V М 2 М M
(4)
n 1 1
Т ак как ...!!.... и V м 2М M < ........ 2 М (п......... 1)
тi mmin
i= 1
1
2 п (п........ 1) т тах (см. замечание в конце пер Boro этапа),
то окончательно получаем верхнюю OneHI{y числа столкно-
вений в исходной системе п шаров:
N (m 1t ... t т n ) 2 ( 16 2 1 п (п........l) т шах ) n-- ===
тmln
== 2 ( Вп 2 (n........l) ттах ) n-- а . (5)
тmln
Конечно, оценка (5) rрубее оценки (4), но одновременно
наrляднее ее. Теорема 1 доказана.
'Выведем теперь из теоремы 1 общий результат о росте
числа столкновений между молекулами rаза в одномерном
«сосуде» отрезке ХУ с упруrо отражающими краями
Х и У (при столкновении шарика с краем концом от-
резка....... ero скорость меняется на противоположную).
т е о р е м а 2. Число столкновений в системе из п
шаров в одномерном «сосуде» ХУ растет не более чем С лu
нейной скоростью по времени t. Иными словами, существуЮtп
такие константы Ci и С2. не зависящие от начальных поло.
женuй u скоростей шаров, а зависящие только от масс u
полной энер2ии системы, что число столкновений в сосуде
ХУ за время t не превосходuт N (t) <C 1 t+C2.
185
д о к а з а т е' л ь с'т В о. Отразим симметрично отре"
зок ХУ вместе со всей системой шаров (поменяв при этом
скорости всех шаров 'на противоположные) относительно
концов Х и У. Получим отрезок Х'У', на котором уже
движутся 3n шаров (рис. 18.1). Столкновению шара с кон-
цом отрезка ХУ отвечает в новой системе на отрезке Х' У'
столкновение двух шаров равной массы (рассматриваемоrо
и симметричноrо ему), движущихся навстречу друr друrу с
yr "х у х'
, ..... I ..
I 1
Рис. 18..1
равными, но противополо}кными скоростями; после столк-
новения эти шары разлетятся, поменявшись скоростями.
Можно считать поэтому, что они просто прошли друr сквозь
друrа. Положим длину отрезка ХУ равной 1. За время 8t==
"
1 1 11 / тшiп u
;:::: == ..r == JI 2Е ни один шарик, начавшии
V max у 2Е / тmin
двиrаться из точки Х' или У', не может долететь до концов
отрезка ХУ. Поэтому за время 8t сиСlпема шаров в «сосуде»
ХУ не чувствует краев Х' u У' «сосуда» Х' У'. С.т.tедователь
но, за время 8t число столкновений шаров в сосуде ХУ
между собой и об края Х и У не превосходит числа N Зп
столкновении 3n шаров на всей бесконечной прямой (так,
будто концы Х' и у, отсутствуют все это время). По TeQpe
ме 1
N 3п < 2 ( 72n 2 (3n 1) тт x ) 3n.... .
т'nln
За промежуток времени 't, который можно покрыть отрез...
ками t1.t в количестве k == [ ;t ] + 1 ([.] целая часть) про
изойдет, следовательно, не более N(t)<.k.N зn столкнове-
ний:
N(t) ([ ;t ]+l) Nзп Nзп V п t+NЗn==Сlt+С2'
что и требовалось доказать.
rлава 7**
мноrОМЕРНЫЙ «rA3»
Уже исследование системы из n упруrих ша-
рОБ н а п р я м о й представляет собой весьма непростую
задачу, отчасти решенную нами в rл. 6. Исследование
двумерноrо и TpeXMepHoro «rаза» молекул вносит новые
особенности: меняется характер столкновений и качествен..
но сложнее становится конфиrурационное пространство
системы. Тем не менее систему из n молекул удается свести
к бильярдной (правда, мноrомерной) системе (т. е. к дви-
жению бильярдноrо шара в некоторой области) и доказать
утверждения, аналоrичные теоремам 17 и 18. Мы предпо-
u
лаrаем, что в системе происходят 'только Д в о и н ы е
столкновения.
Опишем, как происходит упруrое столкновение Д в у х
шаров. Отметим, что, в отличие от шаров на ПрЯl\10Й из
rл. 6, которые мы считали точечными, в этой rлаве будут
рассматриваться шары ненулевоrо радиуса. Разложим
скорость каждоrо шара на
две составляющие нап-
равленную вдоль линии
центров шаров и перпенди-
кулярную к ней. В момент
столкновения шаров, коrда
расстояние между их цент-
рами равно сумме радиу-
сов и они имеют общую ка-
сательную плоскость !Р, происходит перераспределение
н о р м а л ь н ы х с о с т а в л я ю Щ и х скоростей «при-
лета» fJ.L, направленных по линии центров шаров (перпен-
дикулярно плоскости fr), соrласно формулам (13.1) и
(13.2) законам сохранения импульса и энерrии (это дает
два алrебраических уравнения с двумя однозначно опреде-
ляемыми неизвестными ....... новыми составляющими СКОРО-
Ю7
3u
Рис. А
стей ВДОЛЬ линии их центров). Параллельные же плоскости
fP (танrенциальные) составляющие скоростей fJlI остаются
без изменения (рис. А). Сложив новые составляющие ско-
ростей каждоrо шара, получим скорости их «отлета» (на
рис. А fJотлета=== 'lJ!\ + и .L). Отметим, что в нашей модели
шары при ударе не закручиваются.
Уже одно знание правила обмена скоростей при столк"
новении двух шаров позволяет решать разнообразные зада..
чи. Приведем две такие задачи.
3 а Д а ч а 1. Под каким уrлом MorYT разлетаться два одина 40
ковык упруrих шара, один из которых покоится?
, Реш е н и е. Случай Ц е н т р а л ь н о r о удара исследо..
вался в задаче 13.2: налетаIОЩИЙ шар после удара останавлива..
ется, а покоящийся приобретает скорость налетающеrо, как будто
Н8ле'rевший шар прошел «сквозь» Hero. Уrол разлета здесь равен о.
Если же удар н е Ц е н т р а л ь н ы й, то движущийся шар
полностью передает неподвижному свою центраЛЬНУIО составляю-
щую, оставляя себе ортоrональную составляющую. Следовательно.
уroл разлета шаров в этом случае в с е r Д а равен 90 О .
3 а д а ч а 2. Плоскость разделена вертикальной прямой 1
на две полуплоскости. В левой полуплоскости раСПОЛОiкен один
шар, в правой....... п шаров, все шары одинаковы. Шар из левой
полуплоскости посылается снекоторой скоростыо в opaBY и
между шарами начинают происходить упруrие столкновения.
Какое наибольшее число шаров может оказаться в левой полупло..
скости в результате всех столкновений?
Реш е н и е. Слева от прямой 1 н е м о r у т оказаться все
n+ 1 шаров, так как полный импу льс всей системы постоянен и
равен импульсу оервоначально дв ижущеrося шара, т. е. направлен
вправо. Н е м о r у т слева окаа аться и п шаров, так как в этом
случае справа от 1 двиrался бы о Д и н шар, и из закона сохранения
импульса ero скорость превосходила бы скорость исходноrо шара
(чтобы скомпенсировать отр ицатеЛЬНУIО вдоль rоризонтальной
оси Ох составляющую импул ьса п левых шаров), а тоrда ero ки
нетическая 9нерrия превзошла бы исходную, что противоречит
закону сохранения энерrии.
- Докажем, что слева Olп tlрЯАtОЙ 1 м'оеут оказаться n 1 шаров.
у т в е р ж Д 8 Н И е 1. Можно "laK поставить неподвU:JIСНЫЙ
Ulap на пути движущеzося. Чfпо двuжущийся шар после удара от..
клонится на проuзвольный наперед эаданный малый увол. Это ясно
из Toro, что шар можно поставить так, что налетающий шар только
HeMHoro ero коснется. а, значит, и отклонится несильно, При этом
уrол разлета этих двух шаров будет равен 90 Q соrласно решению
предыдущей задачи.
у т в е р ж Д е н и е 2, НеподВU:JlСНЫЙ luap MO:JICHO поставить
ma , что если налетающий шар имеет отрицательную составЛЯIО"
щую С1Wрости вдоль оси Ох t "tO после сtпОЛКltове н I./,Я скорости обоих
шаров будут иметь Оfприцательные составляющие вдоль этой же
оси. Это утверждение...... следствие предыдущеrо: если скорость (1
налетающеrо шара составляет rол а <900 с отрицательным наорав"
лением оси Ох, то неподвижный шар можно постав,ИТЬ так. ЧI0
скорость первоrо шара "1 после СТОJlкновения буде1 составлять с 'о
уrол ==1/2(900......cx), а с ОТрИЦ8'lельным направлением оси Ох ......
188
уrол a+ ==1/2(a+900)<90°. CKOp CTЬ BToporo шара 11'2' направ
Ji нная под 900 к скорости "1 первоrо шара, составит с отрицатель
ным направлением оси Ох уrол 1/2 (900 a) <900, т. е. обе скорости
"1 и "2 имеют отрицательные составляющие вдоль оси Ох.
Перейдем к доказательству OCHoBHoro утверждения задачи.
Присвоим шару слева от прямой 1 номер О, а шары справа от, l
занумеруем числами 1, 2, 3, . . ., n. Шар 1 поставим на пути шара О
так, чтобы шар О после СТОЛI{нове-
ния отклонился на 100 (это можно
сделать соrласно утверждению 1);
шар 1 полетит под уrлом 80 Q
к положительному направлению
оси Ох. На пути шара 1 поставим
шар 2 Так, чтобы шар 1 откло-
нился на уrол ] 00, тоrда шар 2 по..
летит под уrлом 200 к отрицатель-
ному направлению оси Ох (рис. Б).
Шар 3 поставим так, чтобы после
столкновения с ним шара 2 оба
они полетели в отрицательном направлении оси Ох (утверждеНН,е 2).
На пути шаров 2 и 3 поставим шары 4 и 5 соответственно так, чтобы'
все шары: 2, 3, 4 и 5 после столкновений продолжаЛI:I двиrа J:> S:
влево. Эта процедура продолжается до полноrо исчерпания запаса
шаров. Задача решена.
2'
200
3)
о
Рис. Б
В' этой rлаве будет последовательно приведено:
А. Описание конфиrурационноrо пространства системы n
упруrо сталкивающихся шаров в пространстве и в сосуде
специальной формы (к ним относятся ( 19) мноrоуrольАИ
ки и мноrоrраниики).
Б. Сведение рассматриваемой системы из п шзров., к
бильярду в мноrомерной области сложной формы, описан
ной довольно просто в 20.
В. Доказательство Д и с к р е т н о с т и м ножеСТf3а
моментов столкновений в системе п шаров (т. е. Toro, что
удары не накапливаются: число ударов между шарами и C
стенками сосуда в любой конечный промежуток времени ко-
нечно; см. Э 21). Фактически это доказательство сводится к
решению такой задачи: может ли бильярдная частица, ,пo
павшая в криволинейный увол, стороны котОрОёО направле-
ны выпуклосmями навсmречу друв дРУёУ, «застрять» в не.м?
Ответ на этот вопрос отрицателен; он решается здесь вполне
школьными методами.
\ , r. Доказательство Toro, что шары произвольных масс
Н8'" плоскости или В пространстве разлетаются после К,О-
н \е ч н о r о числа ударов, и оценка роста числа ударов в
«r'ззе» из п молекул в сосуде (например, в параллелепипе-
де, или любом друrом мноrоrраннике, а также в сосудах с
выпуклыми внутрь стенками; см. конец 21).
189
19. Конфиrурационное IIространство
«rаза» ИЗ n молекул в пространстве и сосуде
Пусть в пространстве IR (случай плоскости
1R.2 аналоrичен) расположены n «твердых» шаров с радиусами
'i, '2, . . . 'n (об их массах речь пойдет позже). «Твердость»)
означает здесь, что ни один шар не может зайти внутрь
друrоrо, т. е. расстояние между центрами любых двух ша-
ров i и j не меньше суммы их радиусов.
Каково КОНфИ2ураЦИОНflое пространство этих n шаров?
Конфиrурационное пространство о Д н о r о шара
то самое трехмерное пространство, в котором он находит-
ся, поскольку ero центр может находиться в л ю б о й точ-
ке этоrо пространства (х, у, z).
Положения центров всех п шаров определяют, таким об-
разом, п трехмерных пространств, т. е. 3п-мерное изобра-
жающее пространство !R 3n , любая точка х Koтoporo имеет
3п координат .......... последовательно выписанных координат
центров п шаров: х== (Хl, Уl, ZI; Х2, У2, Z2; . . . Х n , Уп, Zn).
Однако н е л ю б а я точка пространства IR.зn задает
какое-то расположение твердых шаров, т. е. не любая точка
lR;}n является конфиrурационной. Действительно, расстоя
ние между центрами (Xi, Yi, Zi), (Xj, Yj, Zj) шаров i и j долж-
но быть больше или равно сумме их радиусов 'i+rj; поэто-
му неравенство
(Xi Xj) +(Yi Yj) +(Zi Zj) < ('i+'j) (1)
задает н е в о з м о ж н о е расположение этих шаров
(коrда один шар «залез» внутрь BToporo).
Для каждой пары (i, j) мы должны написать неравенство
(1) получим C ==1/2n(п.........1) неравенств, в совокупности
задающих то множество в изобра,каlощем пространстве 1R 3n ,
rде конфиrурационная точка располаrаться н е м о }К е т.
Это множество назовем невоз.моаICНbtМ, а любую ее точку
Не80З.можной точкой. Дополнение к невозможному множест-
ву в IRзи ......... это и есть та область Q, rде располаrается кон-
фиrурационная точка, т. е. Q......... конфиrурационное про-
странство системы n твердых шаров. Опише .1 ero более де-
тально.
Возьмем шары с номерами 1 и 2 (радиусов '1 и (2) и за-
будем на время об остальных п.........2 шарах. Если центр (Хl'
Уl, Zl) шара 1 зафиксировать, то неравенство (1) для i==l,
j==2 задаст множество н.евОЗМОЖН,blХ центров (х 2 , У2' Z2)
шара 2. Им является шар Ш 1 « центром (Хl' Yl,Zl) радиуса
'1+'2 (рис. 19.1). Если Же. зафиксировать центр (Х2, Yz, Z2)
190
шара 2, то неравенство (1) задаст невозможные положения
центров (Xi, Уl, ZI) шара 1 .......... им является шар Ш 2 с центром
(Х 2 , У2' Z2) TOI:O же радиуса '1+'2. Шары Ш 1 и Ш 2 мы долж-
ны рассматривать в р а 3 л и ч н ы х э к 3 е м п л я р а х
TpeXMepHoro пространства IR и IR , а невозможная точка
х==(хl' YI, ZI; Х 2 , У2, Z2) принадлежит 3+3==б мерному про-
странству 1R6. Точки (Хl' Уl, ZI)' (х 2 , У2' Z2) независимо друr
от друrа пробеrают полностью свои трехмерные простран-
ства !R и IRg соответственно, и каждой из них отвечает
конкретный шар........ Ш:i и Ш 2 радиуса '1 +'2 .......... в Д р у r о м
2
(ЩZ'!/2) Z2)
1<6
v
4 HepHыи
эллиnсоиjJ
Ilt
Рис. 19.1
Рис. 19.2
трехмерном пространстве (Ш:i в пространстве IR z , ш 2 ..........
В fR ). Следовательно, н е в о э м о ж н о е множество в
рассматриваемом случае двух шаров........ внутренность бес
конечноrо наклонноrо (под равными уrлами к осям OXI,
ОУ1, OZI, ОХ2' ОУ2' OZ2) цилиндра в б-мерном пространстве
[R6 (условная картинка для этой ситуации приведена на
рис. 19.2). r р а н и Ц а этоrо цилиндра........ Б-мерная BЫ
пуклая поверхность в б-мерном пространстве (сечения ко-
торой 4 MepHыe эллипсоиды или 4-мерные сферы S4).
Фиксированному невозможному положению шаров 1 и 2
(коrда они пересекаются) отвечает произвольное положение
шаров 3, 4, . . ., п, и поэтому центры всех п шаров задают в
пространстве lR:J n невозможную точку (Xi, Yi, Zi; . . .; Х n ,
Уп, Zn), лежащую в произведении в н у т р е н н о G Т И
полученноrо цилиндра на (3п 6)-MepHoe пространство
IRЗn"'б, т. е. внутри бесконечноrо цилиндра ЦiJ в 3п-мерном
пространстве, у KOToporo «образующая»........ это (3п.......6)-
мерное пространство lR. n--6, а перпеНдикулярное сечение.......
4-мерный эллипсоид (рис. 19.2).
Как бьiло сказано выше, невозможное множество в
lR. n ...... это C ==1/2n (n l) внутренностей таких бесконеч-
191
ных цилиндров Цij, а конфиrурационное пространство Q ..........
область в н е этих цилиндров. Заметим, что все C ЦИЛИНД-
ров пересекаются по некоторой области в R3n ,......... она СООТ-
ветствует одновременному пересечению всех n шаров в ис-
ХОДНОf\Л трехмерном пространстве. ,
Из Bcero сказанноrо важно усвоить следующее: конФuzу-
рационное пространство п свободных упруеих твердых трех-
мерных шаров Q это JrtHOeoMepHoe (3n MepHoe) простран-
ство, из котОрО20 выкинуто C выпУ'(ЛblХ множеств ЦiJ
(читатель может представлять себе ЦiJ в виде обычных
трехмерных цилиндров), так что само Q невыпуклое
множесmво. \
Иным"и словами, конфиrурационным простраНСТВQМ Q
можно считать бесконечный сосуд с выпуклыми внутрь
стенками (rраницами цилиндров), ВНУТРИ KOToporo летает
конфиrурационная точка х, KaI{ TO отражаясь от ero стенок
(рис. 19.3) Если точка. к попадает на цилиндр ЦiJ' то' это
значит, что в этот момент столк.
нулись шары i и j, а, остальные
шары не столкнулись.
" ...
: ' . .
.. .' ; :.
. . " ,.'. . .
'.: (.:. ;". :.,::. ":. '.;' ;' . . ::-: ::.: . . :.: .::;:':
Рис. 19.3
COC!JiJ(J/ с «ВI1ЗОН»
Рис. 19.4
Перейдем l{ «rазу» молекул в сосуде. Мы оrраничимся
специал ным, но ШИРОКИМ классом сосудов, похожих на
конфиrурационное пространство «rаза» молекул. Сосуд
это часть TpexMepHoro пространства, оrраниченная или не-
оrраниченная, которая получается, если ИЗ пространства вы-
кинуть конечное число выпуклых тел (как выше в 3n Mep"
НОМ пространстве были выкинуты выпуклые пересекающиеся
цилиндры Цij). Стенки сосуда, таким образом, считаются
выпуклыми внутрь сосуда (среди них MorYT встречаться и
плоские стенки) (рис. 19.4). Например, сосудом может быть
мноrоrранный уrол с плоскими или выпуклыми внутрь
стенками. ,Рассуждениями, аналоrичными приведеНН IМ ВР!-
ше, можно показать, что справедливо
, ' у т в е р ж Д е н и е. КонфиеураЦИОflflЫМ npocmpaftqm-
вом с исme,М,ы n твердых упруеuх шаров в трехмерном сосуде
192 ' < ,
с выпуклыми внутрь стенками является сосуд Q в 3п-мерном
пространстве также с выпуклыми внутрь (3n 1)-MepHЫMи
стеНl,ами.
В следующем параrрафе мы сведем движение конфиrу-
рационной точки S'B указанном сосуде Q к дв жению би-
JIЬЯРДНОЙ частицы в некотором друrом сосуде Q, имеющем
также выпуклые внутрь стенки.
20. Сведение «rаза» В пространстве
и сосуде к бильярду
Итак, мы выяснили устройство конфиrура..
ционноrо пространства Q системы n твердых шаров в про-
странстве и в сосуде с выпуклыми внутрь стенками: Q пред-
ставляет собой сосуд в 3n-мерном пространстве 1R 3n С вы-
пуклыми внутрь (3п 1)-мерными стенками Wf, . . ., W k.
пространстве 1R 3n имеется 3п осей: OXi, Оу, OZi; ОХ2'
ОУ2, OZ2; . . .; ОХ n , ОУn, OZn, а конфиrурационная точка
х Е Q имеет 3п координат: х== (Xi, Yi, Zl; · . .; х n , Уn, Zn).
Конфиrурационная точка х движется в сосуде Q следующим
образом: между ее столкновениями со стенками {W i } она
движется равномерно и прямолинейно (это соответствует
тому, что в исходной системе трехмерных шаров в сосуде
также нет столкновений, т. е. шары движутся равномерно и
прямолинейно); столкновению шара с друrим шаром или со
стенкой сосуда соответствует попадание конфиrурационной
точки х на одну из стенок W i сосуда Q (если точка х попала
на пересечение двух или нескольких стенок, то это соот-
u
ветствует троиному или MHoroKpaTHoMY столкновению ша-
ров, а такие столкновения мы исключили из р.ассмотрения).
Таким образом, конфиrурационная траектория является
u u
ломанои, состоящеи из прямых звеньев.
Как и: в rл. 5 и 6, произведем преобразование простран-
ства IR зп , выполнив следующие растяжения по осям:
Х 1 ::= V т! х 1 ,
х 2 ==У т 2 х 2 ,
Уl == V т! Yf,
У2 == V т 2 У2'
Zl == V т 1 Zl;
Z2 == V т 2 Z2;
. . . . . .
. . . . . .
...... .
хп==У тn х n , уn==У тn уn, zn==V mn z n .
При таком преобразовании область Q перейдет в область Q
также с выпуклыми внутрь стенками Wf, . . ., w lн а тра-
ектория конфиrурационной точки x в траекторию новой
7. r. А. rальперин, А. Н. Земляков 193
точки
JC === (х 1 , Уl, Zl, · · ., Х n , Уn' Zn),
которая такж€ является ломаной. Будем обозначать пере..
ход от JC К Х символически равенством х == v т х, rде Уm
символизирует указанные растяж€ния
по осям. Докажем следующее
у т в е р ж Д е н и е. Точка х яв.
ляется бильярдной частицей в сосуде
Q, т. е. .модуль ее скорости равен 1 u
каждые два соседние звена ее траекто-
рии образуют равные уелы с внутрен-
ней нормалью п к стенке W в точке llЗ-
лома траектории (РИGо 20.1).
3 а м е ч а н и е. Прежде чем читать
дальше, советуем читателю вновь обра
титься к Э 16, rде аналоrичное утверждение для трех шаров на
прямой доказано с ПОМОЩЬЮ понятия скалярноrо произведения
векторов.
Рис. 20.1
д о к а 3 а т е л ь с т в о. Замене координат х === v m х
соотвеТСТВJЛет точно такая же замена скорости точки Х,
т. е. если V=={Vi, ..., 'V п ) 'CKOpOCTЬ конфиrурационной
точки х, а i......... скорость точки Х, то == v m 'lJ!
.v === ( f, ..., .v n ) ==.(У 11li (11' V m 2 fJ 2 , ..., v т п fJ n ),
rде Vi треХ Iерная скорость i-ro шара в рассматриваемый
момент времени. Пусть Е полная энерrия всей системы п
шаров:
.n п
Е 1: 1 I 1 2 1: т; ('О;, 'О;)
2 т (1. ·
. 1 2'
i= 1 i= 1
по закону сохранения энерrии E==const. Положим (выбо-
ром соответствующей единиды измерения энерrии) 2Е== 1.
Тоrда .
n n
I v I === (v, v) == (У тi Vi, V тi 'lJi) == т,. (Vi' V;):::::
i==l i=l
n
== т; I Vi I == 2Е == 1.
i ::.: 1
Итак, проверено, что модуль скорости точки х в каждый
момент равен 1. Осталось проверить свойство «уrол П8де-
194
НИЯ равен уrлу отражения». Для этоrо достаточно доказаl Ь 9
что веКtпор равный разности CKoPOCпzeu 01плеmа u прuлеп!а
в точке столкновения со стенкой, перпендuкудярен к Эlпой
стенке (пzочнее, к касапlеЛЬ1tой 1\, этой Сlпенке пЛОСКОСlпu).
Пусть fJп скорость при,пета точки Х., а V o ........... скорость
ее отлета (р НС. 20 о 1). Если точка ; попала на стенку W СО 8
суда Q, то это означает , что либо какой то шар в ИСХОДНОМ
COCy дe сто,пкну лея с ero стенкой ......... будем считать, что это
шар 1, либо столкнулись какие-то два шара в сосуде.........
будеlVi считать что это шары 1 и 2. Тоrда
:V П === (У m! Vfп) )/ lп z 'lJ 2п ; V тз (1з, V пZ 4 fJ 4' ....
о . ., v тп, V n) Е [Rsn .,
ilo == (У пZ 1 't'io, V ln 2 112-0; V m з 'l1 з , V т", 'v 4, ...
· · .., v т п 'V n ) Е 1R3n,
rде Viп, 'Oio .......... скорости прилета и отлета i-ro шара в трех...
мерном сосуде, i== 1, 2 (скорости шаров 3, 4, . . ., п, разу...
меется, не меняются в момент удара). В случае, коrда шар 1
сталкивается со стенкой, V 2n == '020 == V 2 .
Обозначим через Р (двумерную) плоскость касания столк...
нувшихся шар,оВ 11 и 2 или шара 1 со стенкой в трехмерном
сосуде; ей отвечает (3п.........l}-Мерная касательная плоскость
fP к рассматриваемой стенке W сосуда Q (рис. 20.2).
RO
:r =5'" :J11 t
Рис. 20.2
Разберем сначала случай столк-новения Ulapo8. Напом",
ним, что в момент упруrоrо столкновения шаров их TaHreH-
циальные составляющие сохраняются, а нормальные пе-
рераспределяются по законам сохранения импульса и
энерrии.
Пусть шары 1 и 2 столкнулись друr с друrом и коснулись
плоскости Р в точке, являющеЙся концом TpeXMepHoro
вектора а, а шары 3, 4, . . ., n в этот МО1\1ент расположены
произвольным образом......... их центрами ЯВJIЯЮТСЯ произволь-
1* 195
ные (допустимые) векторы rз, r't . . .,rr r n TpeXMepHoro про-
странства. Тоrда 3n-мерный вектор
r==(V a, vm;a; r 8 , rijt "" r n ) е IRзп
отвечает столкновению шаров 1 и 2 и ле)l{ИТ в плоскости
9J, причем если вектор а пробеrает все пространство (R
(или всю область внутри сосуда в fR.3, еСЛИ1Jассматривается
«rаз» в сосуде), то плоскость fP состоит только из таких век-
торов. Следовательно, нам надо доказать, что (V o v п ) У;
этоrо достаточно, чтобы «уrол падения» был равен «уrлу
отражения». Вычислим скалярное произведение этих век-
торов и получим о, что u дока{лсет их взаиМflУl0 перпенди-
1Сулярность. Напомним, что скалярное произведение двух
векторов одноrо евклидова пространства IRN (любой раз..
мерности N) равно сумме произведений их одноименных ко..
ординат:
«Xi, Х 2 , ..., XN), (Yi, У2, ..., Уn» ==
== XiYi + Х 2 У2 + · · · + ХnУn.
Скалярное произведение в IR.зn, В отличие от скалярноrо
произведения (', .) в IR. , будем обозначать (', ') .
Вычисляем:
tiо f,п == (у т} «(1iо fJiп); ут; (fJ 20 ........fJ 2п ); о; о; о; ...; о);
.... ...
< "'0 .......... 11 п , r> ==
==«V тi ( iо iП); V т2 (fJ20 112П); о; ...; О),
(у т} а; V т 2 а; r 8; ...; r n» == (у mi (fJio.......... iп),
V тl а)+(V т2 (1120 'fJ2П)' У т 2 а)+0+... +о==:
== mi ( io fJiп, а) + т 2 (1120 2П' а) ::=-::
== (pi+) Pl >, а) + (p +> .......p -->, а) == (I1р} + Ilp2' а) == о.
Здесь введены следующие обозначения: P(1)==mi 10,
P ( > т I P (+) т I P ( > т I A p . p (+) P ( > Д п
1 l"iп' 2 2"2o, 2 2"2П'L.1 1 1........ l' 'Y2
p (!>""""P(2> ........ импульсы, приобретенные соответственно ша..
рами 1 и 2 после удара. При этом по закону сохранения Иfd-
пульса L\Pi+ L\p2 ==0; действительно, p(l>+p("2) ==p(i>+p <t> .
Мы доказали тем самым, что точка ; отражается по
бильярдному закону, коrда она попадает на стенку пr, яв-
.пяющуюся каким-то цилиндром Цi, 2, Т. е. коrда стенка W
отвечает за столкн овение шар в 1 и 2.
196
Если же стенка W сосуда Q отвечает за СТОЛI{новение
шара 1 с какой"то стенкой исходноrо TpeXMepHoro сосуда,
то надо доказать, что
(Vo" i1 п ) 1. k,
rде
k ==- (У ПZ 1 Ь; r 2; r з; ...; r n) Е [R3'
Ь Е ПZ 3 ......... вектор, принадле}И.ащий двумерной плоскости
касания шара 1 со стенкой исходноrо сосуда; r 2 , rз, .. . .
. . ., r n Е 1R3.........допустимьre центры шаров 2, 3, . . ., n, а/ (120==
== fJ 20 == "'2. Опять вычисляем скаляр ное произведение и
получаем о:
«;z,o....... v п ), k> ==
::= < (У т! ( "'10 t'fo); о; ...; о) t (ViЩ Ь; r 2; r з; ...; r n) > ==
===(V ml ("'10 "'in), V ml b)==(mi(lfo mlVln, Ь)==
== (р<+>........Р<..), Ь) == ( P, Ь) == о,
поскольку р<+>==р(--) при абсолютно упруrом ударе шара
о стенку. Утверждение доказано.
21. Рост числа столкновений между
молекулами «rаза»
в предыдущих двух параrрафах движение аб-
солютно упруrих шаров в трехмерном пространстве или
сосуде с выпуклыми внутрь стенками было сведено к дви-
жению бильярдной частицы х в области Q 3n-мерноrо про-
странства (RЗn, представляющей
собой сосуд с выпуклыми внутрь
стенками Wi, ..., Wh,. СосудQ
обобщает рассмотренные в rл. 6
мноrоrрапны уrлы с плоскими
v
стенками....... Q может быть мно" Ннова.ераННЫI1 увал
rоrранным уrлом или оrрани- · G ЬО8н!/тымu стенками
ченной областью с выпуклыми Р пс. 21.1
'lHympb стенками (рис. 21.1).
Возникает вопрос, аналоrичный поставленному в rл..
5 и 6:
.....
MoeYln ли точки столкновения частицы х со стенками
сосуда Q бесконечно накапливаться? Например, I ;иожеtn ли
бильярдная частица х «застрять» в уеле с выпуклыми внутрь
cтeHKaAtU? (I--Ia плоскости леrко нарисовать две касающиесп
197
крИВЫе, образующие нулевой уrол вылетит ли из пеео
бильярдная частица или застрянет?) Более точно:
Конечuо ли число столкuовений бильярдной частицы ;
в Q со спlенками {W i }/ за конеЧfiЫU пРО.klежуtпок вреЛ1енu
Т<+оо?
Положительный ответ на этот вопрос дается Teope v'10Ii 1
и означает Д и с 1{ р е т н о с т ь (т.. е. .. отсутствие точек
8' ... .. . о. .88" ts-i8i" >-
t", t 2 t" $ 't k Т t', Т2 ... t- oo . t'
Дискретное и неОI1СlфетНОе
множестllа
Рис. 21.2
накопления) множества {t k } моментов столкновений
(рис. 21.2).
Т е о р е I\1 а 1. Мuожество моментов стОЛl(!-lовенuu
бильярдной частицы ic в оосуде Q с еео стенкаАtИ дискретно.
е л е Д с т в и е. ii1ножество всех AtOMeurпoe столкнове-
ний в системе абсолютно уnруеих шаров, движущuхся в
сосуде с выпУКЛbllJttи внутрь стенками, дискретно: на любом
конечном интервале времени число столкновений шаров друе
с друео.м u со стеН/ЮйJ.tU конечно.
Д о к а 3 а т е л ь с т в о т е о р е м.ы проведем от про-
тивноrо. Предположим, что существует точка накопления
to=#=+OO моментов tf, t 2 , tfJ, . . . столкновений частицы i о
стенки сосуда Q. Раз th--+tо.цри k oo, то в сосуде Q есть точ-
ка А, являющаяся ееометрuческой точкой накопления то-
чек столкновения, т. е. x(th) A при th to. Точка А при-
надлежит сразу нескольким стенкам W it , . . ., W 1 . S сосуда ",
образующим «кривой мноrоrранный уrол с ВЫПУКЛЫl\fИ на-
встречу друr друrу стенками». Мы будем считать, что рас-
сматриваемые моменты столкновения находятся на таком
маленьком интервале BOKpyr точки t o , что точка х сталки-
Еается т о л ь к о с указанными стенками сосуда Q, и уже
не сталкивается с остальными ero стенками (с которыми
моrла сталкиваться до этоrо). Кроме Toro, частица х ни-
коrда не попадает в А ........ удар в А запрещен.
Пусть р (х (t), А) расстояние от частицы х до точки А
в момент t. Из Toro, что x(t) A, следует, что
p( (t), А) О при t t o . (1)
Мы же докажем сейчас, что при всех t, С1WЛЬ уеодно близких
I
198
к t o , р (x(t), А) больше неи:оторой положительной KOHcтaH
ты, т. е. не стремится 1\, О, и тем самым получим нужное
противоречие.
Для этоrо мы введем следующую функцию времени
r (t) расстояние от точки А до л у ч а УХ (t) с началом в
точке х (t) и направленным в сторону движения частицы х
(рис. 21.3).
.:. А r r(t) .
l. (t) «(Т)
t1i а
1((
}' (t)
A
c(t)
о
Рис. 21.3
л е м м а. Функция r (t) «расстояние от точки А до
луча Ух (t)>> ....... положительная неубывающая функция пe
ременной t.
Д о к а 3 а т е л ь с т в Q этой леммы разобьем на две
части: докажем ее сначала на промежутке (tk i, t k ) между
двумя ударами,. а затем в сам момент удара t k (вернее,
на маленьком промежутке (tk B, th+B), охватывающем MO
мент удара).
1. Между двумя последовательными ударами частu:цы
о стенки сосуда луч УХ (t) передвиrается по себе перехо-
дит в свою часть, т. е. 1'х (t) содержит луч ух (t') при t'>t,
поэтому расстояние от точки А до луча ух (t') может толь-
ко увеличиться (как на рис. 21.3, б, коrда это расстояние
равно длине отрезка с концами А и х) либо остаться тем же
(как на рис. 21.3, а, коrда расстояние от А до луча равно
длине перпендикуляра, опущенноrо из А на этот луч).
Итак, если t<t' моменты времени между двумя после
довательными ударами, то r(t) <.r(t').
2. Пусть теперь t k момент столкновения' частицы со
стенкой W, (tk 8, t k +8) .......... маленький временной интер
вал BOKpyr этоrо момента.
Обозначим у(")==Ух (th 8) луч, по KOTOP01iY частица
п о Д л е т е л а к стенке W, а 1'<+)==1'; (t h )......... луч, по кото-
рому она о т л е т е л а от этой стенки. Пусть :Р .......... Kaca
тельная плоскость KCJ:eHKe W в точке удара x(t h ), причем:
в с я стенка лежит по одну сторону от Нее, как оrраничиваю
щая выпуклое множество (рис. 21.4). Если отразить луч
199
1'(+) симметрично относительно плоскости SJ, то он перейдет
в луч 1' ) (t h ) ......... продолжение луча 1'(--> (см. рис. 21.4), и
поэтому луч '\'1......) (t h ) с началом в точке х (t h ) Е W лежит с
той же стороны от плоскости fJ, что и точка А 7 а луч ,,<+)
С друеой стороны от плоскости fJ. Следовательно, расстоя-
ние АВ дО луча 1'{....) меньше рас-
стояния АС дО луча 1'<+), что и
означает, что r(tk 8)<rk(tk+8).
Лемма доказана.
Из нее следует, что частица х
не может сколь уrодно близко
приблизиться к точке А, т. е. не-
верна формула (1). Действитель-
но, в противном случае сколь
уrодно :м:алым стало бы и рас..
стояние r (t) при t---+-t o , хотя в
_ лемме было доказано, что рас-
стояние r (t) от точки А до луча,
'по которому движется частица,
не меньше расстояния r (О) ОТ
ТОЧI{И А до первоначальноrо луча "/Х (О), по которому летела
астица. Можно даже оценить, сколько времени частица х (О)
будет приближаться к точке А........ оно не больше (в предпо-
ложении, что модуль скорости частицы равен 1) расстояния
d (О) от точки Х (О) ДО точки В ......... основания перпендикуляра
w
t'
'Z' t-=d(o)
5
21.5
АВ, опущенноrо из А на луч 1'х (О) (рис. 21.5, а). Действи-
тельно, если бы на пути частицы не было стенки W, она
приближалась бы к точке А по лучу "(х (О) вплоть до совпа-
дения с точкой В, т. е. время d(O), а потом CTaJla бы удалять-
ся от точки А. Но из-за Toro, что в результате столкновений
со стенками расстояние r (t) от точки А до луча движения
200
'чаСТlfЦЫ р а G т е т , расстояние d(t) от точки x(t) до осно-
вания перпендикуляра В (t)p опущенноrо ИЗ А на луч.')'; (t),
У м е н ь ш а е т с Я, и общее время приБЛИ}I{ения части..
ЦЫ i к точке А поэтому меньше d (О) (rрафик изменения d (t)
приведен на рис 21.5, б).
Теорема 1, таким образом, ДОI{азана.
Сделаем простое, :но очень важное замечание. Теорема
в иеI{ОТОРОМ смысле обобIl ает rеометрические теоремы 15
о «незастреваемости» бильярдноrо шара в уrле с прямоли..
нейными сторонами на плоскости и в MHororpaHHoM уrле с
плоскими стенками в пространстве. Однако есть и сущест-
венное отличие. В Э 15 мы фактически во всех случаях ука-
зали число столкновений со стенками уrла, больше KOToporo
не мо)кет быть на всем бескон чном интервале времени.
В нашей же теореме 1 мы этоrо не только не утверждали,
но и н е м о ж е м утверждать существования такой оцен"
ки числа ударов.
В самом деле, если взять на плоскости «нулевой» уrол,
образованный двумя касающимися выпуклыми кривыми,
смотрящими друr навстречу друrу (например, двумя пара-
болами у==.........10... 1О х 2 и у== lO--lООх 2 ), то чем ближе к их общей
касательной мы запустим бильярдную частицу, тем боль-
шее число столкновений произойдет, прежде чем она выле-
тит из этоrо уrла, и это число может быть сделано больше
любоrо наперед заданноrо N O . Однако если рассматриваемый
кривой уrол «ненулевой», т. е. в Hero можно поместить обыч-
ный мноrоrранный уrол с плоскими стенками так, что ero
вершина принадлежит пересечению стенок кривоrо уrла,
то верхняя оценка числа ударов, по-видимому (пока это
недоказанная rипотеза) , существует. Сообщим без доказа-
тельства, что для системы шаров в трехмерном пространст-
....
ве в отвечающем ей бильярде Q все кривые MHororpaHHbIe
уrлы между соседними стенками сосуда {W i } н е н у л е-
вые. Это позволит нам доказать конечность числа столк-
новении между шарами в пространстве на всем бесконечном
интервале времени, а не только на любом конечном, прав-
да, уже не rеометрическим, а аналитическим способом,
похожим на доказательство 17. На основе этоrо будет
затем объяснено, почему число столкновений ме)кду моле-
кулами «I'аза», помещенноrо в сосуд с плоскими и выпуклы-
МИ внутрь стенками, растет л и н е й н о со временем.
т е о р е м а 2. В системе из п упруеих шаров с проuз-
вОЛЬНЫАl,и массаЛ1U mi, . . е, ,п п , двuжущuхся в трехмерно),!'
201
npOCfnpaflCfnee, за беСf\,ОfletlflЬtй npOAle{)fCY"l0K времени .JUожепz
v и
nроuзоuтu лишь конечное число СfпОЛК1iовеnuu.
Д о к а з а т е л ь с т в о. Разобье 1 сначала всю систе
f\ЛУ шаров на а в т о н о м н ы е rруппы, т. е. такие rруппы,
что никакие два шара из разных rрупп начиная с HeKOTO
poro момента То уже НИI(оrда не сталкиваются друr с дpy
rOM (таких rрупп может быть и одна......... вся система шаров).
Мы хотим доказать, что таких ерупп будет ровно n'; по oд
ному tuapy в еруппе это и означает,
'2 что шары с момента То не сталкиваются.
Если в каКОЙ ТQ rруппе больше OДHO
2 ro шара, то в ней происходит бесконеч
ное ЧИ О столкновений (иначе rрупца
распалась бы на более мелкие aBTOHOM
ные подrруппы), причем для Лlобыхдвух
шаров А и В ИЗ этой rруппы найдутся
такие шары С 1 , С 2 , . . ., C h из той же
rруппы, что А сталкивается с С! бескоо
нечно MHoro раз, Ci и C2 сталкиваются
бесконечно MHoro раз, . . ., Ся, и В сталкиваются бесконеч-
но MHoro раз: можно представлять себе связный rраф G
конечным числом вершин, символизирующих шары в rруппе,
причем ребром соединены те вершины, для которых соот-
ветствующие шары сталкиваются бесконечно MHoro раз
(рис. 21.6)..
Предположим, что имеются автономные rруппы, в KO
торых больше одноrо шара. Рассмотрим одну из них и обоз
начим ее 1 (в качестве примера можно иметь в виду rруппу,
изображенную на рис. 21.6). Выберем в этой rрупnе какие
то два шара, сталкивающихся между собой бесконечное
число раз. Выше уже доказано, что все эти столкновения
между ними не MorYT произойти на к о н е ч н о м проме
жутке времени (столкновения не скапливаются по Teope
ме 1), так что эти моменты столкновений стремятся к + 00.
Точно так же, как и в 17 при аналитическом доказательст
ве конечности числа столкновений между п шарами н а
п р Я м о й (см. п. А Э 17), можно доказать, что у э!пuх
шаров существуют предельные скорости при t--+oo, равные
между собой как век!поры (мы не останавливаемся на под.
робном доказательстве, полученном л. Н. ВасерштеЙНОIvl
и r. А. rальпериным и использующем существенную Ma
тематическую технику, связанную с системами центрально
отталкивающихся частиц). А так как любые два шар/а из aB
тономной rруппы 1 соединяются в rрафе некоторой цепочкой
шаров, сталкивающихся попарно бесконечно MHoro раз,
202
11
10
3
8 7
АfJтОНGМНlJЯ
арулпа шарад
8
Рис. 21.6
то и у всех ш ров существуют предельныIe скорости при
t---+oo, причем все они равны между собой (как векторы) и
равны векторной скорости ценпzра .масс рассматриваемой
автономной rруппы [.
Перейдем поэтому в инерциальную систему координат,
связанную с центром масс rруппы [ в ней центр масс
труппы [ имеет нулевую скорость. Тоrда скорости всех ша
ров rруппы [ в выбранной системе координат стреrvIЯТСЯ к
О при t oo (к скорости центра масс rруппы), и, следова
тельно, полная кинетическая энерrия Е] (t) этой aBTOHOM
ной rруппы стремится к О при t oo.
Однако в силу автономности rруппы [ при t>T o (Ha
ПОI\1НИМ, что в момент То произошеJI распад всей системы п
шаров на автономные rруппы эти rруппы перестали
взаимодействовать друr с друrом) в ней выполнен закон cox
ранения полной энерrии (в нашем случае он совпадает с
законом сохранения полной энерrии поступательноrо дви
жения): E[(t)==cQnst при t>To. Но поскольку E](t) o
при t oo, имеем const==O; значит, с момента То все шары
rруппы [ имеют т о ж Д е с т в е н н о нулевую скорость
в системе центра масс.
Поэтому с момента Т о в rруnпе [ не происходит н и
о Д н о r о с т о л к н о в е н и я, QTO противоречит тому,
что их в rруппе [ бесконечно MHoro при t >ТО.
Следовательно, предположение, что в автономной rруп
пе может быть б о л ь ш е о Д н o.r о шара, противоречи-
во, откуда вытекает, что автономных rрупn с момента То
ровно п по одному шару в каждой. Это означает, что с
момента То все шары движутся равномерно и прямолиней-
но. Теорема 2 доказана.
Итак, шары в пространетве после конечноrо числа yдa
ров перестают сталкиваться.
3 а Д а ч а 21.1. Мо}кет ли система шаров в каком либо сосуде
вести себя следующим образом: с HeKoToporo момента шары пере--
cTaIoT сталкиваться со стенками сосуда (а сталкиваются т о л 'Ь К О
между собой)?
Имеется 2uпоmеза (ее доказательство интенсивно раз-
рабатывается математиками в последнее время), что это
число ударов меньше некоторой величины N o , не зависящей
от начальных положений и скоростей шаров (при фиксиро
ванной полной энерrии системы); т. е. имеет место р а B
н о М е р н а я по начальным условиям оценка числа yдa
ров. Более общая rипотеза: в MHororpaHHoM «ненулевом»
уrле с выпуклыми внутрь стенками (т. е. во внешности к
выпуклым телам пространства, имеющим общее непустое
203
uересечение) также имеет место равномерная оценка: би...
lJья'рдная частица испытывает от стенок уrла отражения,
ftисло которых не превышает числа N о, не зависящеrо от
начальноrо состояния частицы (из второй rипотезы не-
трудно вывести rипотезу о шарах).
Из этих rипотез можно получить, что если rаз из n моле-
кул (шаров) находится в сосуде, имеющем вид параллеле-
пипеда или друrоrо мноrоrранника, или в сосуде с выпук-
лыми внутрь стенками (среди которых MorYT быть и плос...
кие стенки), то число столкновений молекул rаза друr с
друrом и со стенками за время t не превосходит C 1 t+C2'
а
о-
Рис. 21.7
rде Ci и С2 некоторые постоянные, зависящие только от
кинетической энерrии Е системы и rеометрии сосуда.
Например, для параллелепипеда надо поступить точно
так же, как и при доказательстве теоремы 2 Э 17: отразить
параллелепипед П симметрично относительно всех своих
rраней, ребер и вершин вместе с содержащимся внутри
Hero «rазом», получив новый параллелепипед П' с объемом
и числом молекул в 27 раз б ольшим ( рис. 21.7, а). За l\1алый
промежуток времени Ilt == V т min /(2E) влияние краев парал-
лелепипеда П' не будет чувствоваться внутри П, и поэтому
число столкновений n молекул внутри П за этот промежу-
ток не будет превосходить константы N 27n , которой оце...
нивается число столкновений 27п молекул во всем про-
странстве (R3. За время t число столкновений поэтому
не больше
N(t) ([ ;t ] +1 )N27п N27п V ,; n t+N 27п == C 1 t+C 2 ,
что и требовалось доказать.
В общем. }ке случае сосуда с выпуклыми внутрь стенка-
ми (некоторые стенки MorYT быть и плоскими) следует по-
204
ступить TaK: 'в конфиrурационном пространстве Gистемы .......
сосуде Q с БЫПУКЛЫl\llИ внутрь стенками окруя{ить ero
вершины, ребра и rрани всех размерностей окрестностями
(рис. 21 а7, б), внутри которых число столкновений меньше
фиксированных универсальных KOHCTaHTi перелет же из
одной окрестности в друrую длится промежуток времени,
больший HeKOToporo to>O, и поэтому число ударов при этом
перелете не больше числа столкновений в системе свобод-
ных шаров в пространстве, Т. е. не больше некоторой дру-
rой константы. Поэтому число ударов эдесь также не пре-
восходит Cit+C2.
ЧАСТЬ IV
.... '" ...#...... .. ... ...'"
ИЛЬЯРДЫ В мноrоуrОЛЬНИКАХ
и MHOrOfPAHHJtKAX
Во второй части книrи подробно рассматри
вался бильярд в прямоуrольнике, и ero исследование СВО"
дилось к изучению траекторий точки, движущейся по TO
py, двумерной замкнутой поверхности «с одной дыркой»
(поверхности бублика). Оказывается, во мноrих случаях
изучение бильярда в мноrоуrольниках сводится к изучению
траекторий точки, движущейся по кренделю, двумерной
замкнутой поверхности с двумя или большим числом «ды-
рок». Такие поверхности возникают в классической меха-
нике при рассмотрении вопросов, связанных с так назы..
ваемыми интеrрируемыми и почти интеrрируемыми дина-
мическими системами, и являются rеометрическими след-
ствиями законов сохранения в системе (или, как rоворят
механики, первых интеrралов системы: на этих поверхно-
стях некоторая функция принимает постоянное значение).
у нас они естественным образом возникнут при рассмотре..
нии динамических систем «бильярд в мноеОУ20ЛЬflике» и «ша-
ры на оmрезке». Эти поверхности переходят в себя под дейст-
вием фазовоrо потока (см. 3) и поэтому называются ИН-
вариантными (т. е. «сохраняющимися»).
Часть IV состоит из двух rлав 8 и 9. В rл. 8 дается
подробное описание поверхностей, отвечающих бильярдам
в конкретных мноrоуrольниках, объясняется, как такие
поверхности склеиваются из нескольких экземпляров
мноrоуrольника, и решается вопрос о поведении mипиЧНЫJa
бильярдных траекторий в рассматриваемых мноrоуrоль-
никах.
В rл. 9 изучаются бильярды в мноrоуrольниках,
уrлы которых соизмеримы с л в так называемых ра-
циональных мноrоуrольниках: исследуется поведение ти-
пичных и индивидуальных (выбранных специальным обра-
зом) бильярдных траекторий. В этой же rлаве изучаются
периодические траектории в мноrоуrольниках и мноrоrраи-
никах.
206
Рлава 8
rЕОМЕТРИЯ MHOrOYfOillbHOrO БИЛЬЯРДА
в этой rлаве исследуются бильярды в так на-
зываемых торических мноrоуrольниках, отличных от пря..
моуrольника, но сводящихся К изучению торических об..
I\10TOK ( 22), а также бильярды в мноrоуrольниках, СВОДЯ
щихся к обмоткам более сложных поверхностей ( 24). Опи
сание и классификация этих поверхностей приводится в
23.
22. Бильярды в «торических»
мноrоуrОЛЬНИI(ах
Пусть Q мноrоуrольник на плоскости. За-
дача, которую мы решаем, KaK можно qолее подробно
исследовать поведение траекторий бильярда в мноrоyrоль-
нике Q. Траектории бильярда, ран-о или поздно попадающие
в одну из вершин мноrоyroльника Q, мы называем особыми
и считаем закончившимися в со-
ответствующей вершине. В 7 была
указана проце ура выпрямления
любоrо куска особой или неособой
траектории: превращение ero с по-
мощью последовательных отраже-
ний в отрезок прямой линии (см.
рис 7.2). В 9 для исследования
траекторий бильярда в прямоу-
rольнике было проведено изобра-
женное на рис. 22.1 построение,
которое СОСТOJIт в частичном вы-
прямлении траектории с помощью
отражений. При этом мы оrрани-
чиваемся ч е т ы р ь м я прямо..
уrольниками .......... исходным прямоуrольником Q и тремя пря-
моуrольниками Qfo, Qof, Qfi, получающимися из Q отраже-
ниями относительно двух ero сторон и их общей вершины.
Как только вьmрямленный кусок траектории ММ' пере-
секает rраницу большоrо четырехуrольника Q == AAiA 2 А 3,
выходящий из Q луч PiM' мы переносим параллельно.........
так, чтобы сторона AiA 2 совместил ась со стороной АА з ;
иначе rоворя, из полученной (переносом из точки Pi) на
отрезке АА з точки P МЫ проводим луч P P2 В том же нап-
равлении, что и исходный луч MM . Далее, переносим
точку Р2 со стороны А з А 2 В соответствующую точку p
207
А
A f
p; k ?1
P 'tl
Рис. 22.1
на стороне АА! и ПрОБОДИМ через p следующий отрезок
траектории........ в T01vI же направлении.
С одной стороны, если с помощью отражений наложить
прямоуrольники QI0' Qof, QfI на прямоуrольник Q, то OT
резки MPi, P P2' Р Рз И Т. д. дадут на Q траекторию
бильярда.
С друrой TOpOHЫ, чтобы траектория на большом пря
моуrольнике Q стала непрерывной, достаточно склеить CO
ответствующие точки сторон А з А 2 И AAi, а затем сторон
А 1 А 2 И АА з . После склейки отрезки MPf, P P2' Р Рз, . . .
составят непрерывную кривую на торе, получающемся из
Q в результате склейки (см. Э 8). Эта кривая является тpa
екторией соответствующей обмотки тора.
О т с т у п л е н и е. В дальнейшем нам придется
с клеивать п ове рхности из разных мноrоуrольников; Bcer
t t - } да при этом склеиваемые сто-
' t1... c j c .... ....:...c РОНЫ будем обозначать одина-
ковыми буквами со стрелка..
ми, показывающими, в каком
направлении приклеиваются
{: $ стороны друr кдруrу. В прин-
ципе, можно пару сторон с и
с приклеить друr к друrу в
а II двух направлениях (рис.
Рис. 22.2 22.2,а и 22.2,6): в первом
случае из прямо)"rольника
получается поверхность цилиндра, во втором так назы
ваемый лист Мё6иуса. Это совсем разные поверхности: край
цилиндра состоит из двух замкнутых кривых «верхней»
S<+) и «нижней» s<....); край же листа Мёбиуса одна кри-
вая s.
3 а д а ч а 22.1. Что получится из листа Мёбиуса, если ero
разрезать вдоль средней линии (она помечена штриховой линией
на рис. 22.2, б)?
При склейке поверхности из мноrоуrольника полезно
считать мноrоуrольник эластичным, а траектории нари
сованными на нем. Эластичность мноrоуrольника нужна,
чтобы ero сжимать или вытяrивать для осуществления
склейки. При этом склеиваемые друr с друrом стрелки мож-
но сжимать и вытяrивать одновременно, но вытяrивать со-
вершенно одинаково (чтобы обозначенные одной буквой точ-
ки на стрелках совпали после склейки).
Вернемся после сделанноrо отступления к обсуждению
бильярда в прямоуrо.льнике. Вместо Toro чтобы рассматри-
208
вать одну индивидуальную траекторию на большом пря-
моуrольнике Q, состоящую ив параллельных друr друrу
отр,езков, удобнее сразу рассмотреть в с е траектории од-
Horo и Toro же направления......... в 9 они назывались пуч-
КОМ параллеЛЬНblХ траекторий. Разным исходным направле-
I ниям соотве!.ствуют разные пучки. После склейки прямо-
уrольника Q в тор указанным выше способом те отрезки
u
данноrо направления, которые лежат на однои траектории,
автоматически подклеятся друr к друrу. В этом и состоит
некоторое преимущество рассмотрения целоrо пучка тра..
екторий. После склейкц разные пучки параллельных тра-
екторий дадут разные обмотки тора ( 9). Напомним
полученные в 8 сведения об обмотках торов. Обмоткой
тора называется пучок траекторий ----- кривых на торе'........
по которым движется точка, если ее движение складывает
ся из paBHoMepHoro вращения вдоль параллелей и равно-
MepHoro вращения вдоль меридианов, характеризуемых
соответствующими периодами обмотки Т! и Т 2 (Т! вре-
мя, за которое точка возвращается на те же меридианы,
т 2 .......... время возвращения на те же параллели) . Если пе-
риоды 1'! и Т 2 обмотки соизмеримы, т. е. Ti/T 2==т/п ......... ра-
циональное число, то движение точки периодично с периодом
T==nTi==mT 2 и происходит по замкнутым кривым на торе.
В случае коrда Ti и Т 2 несоизмерUМbl, движение неперио-
дUЧflО, и каждая траектория этой (иррациональной) об-
мотки всюду плотно заполняет тор.
Найдем периоды обмоток, получающихся из COOTBeTCT
вующих потоков бильярдных траекторий в Q. Если Vf и
V 2 ........ составляющие скорости движении бильярдноrd шара
по rоризонтальному и вертикальному направлениям, .йl
и а2......... длины соответствующих сторон исходноrо прямо
уrольника Q, то леrко видеть, что соответствующие перио-
ды равны
Т 2а! Т 2а2
1 ........ ' 2 v;-- ·
т f V2 ! а2 af t
Их отношение есть T == == g (х, rде (х ........ уrол
2 Vl а! а2
траекторий пучка с rоризонтальным направлением AAi.
а'
Если ...2. tg (Х иррационально, то траектории бильярда
а2
всюду плотно заполняют прямоуrольник; в противном
случае траектории бильярда периодичны (это следует из
сформулированноrо свойства обмоток тора и из спосо а
получения бильярдных траекторий из траекторий на Q).
209
в э 13 было дано решение задачи о бильярде в прямо-
уrольном треyrольнике с острым уrлом ср==л/4. Именно рас..
сматривался пучок параллельных траекторий в квадрате Q,
составленном из восьми экземпляров треуrольника Q
ИЗ Q:::;=Q8 И Qi+Q7' получающихея из Q отражениями
(рис. 22.3). Если траектория мр! выходит из квадрата Q,
то ее продолжение Pi M ', лежащее, например, в треуrоль-
нике Q (см. рис. 22.3), следует пере-
нести в треуrольник Q6: треуrольmrк
Q получается из Q6 параллельным
переносом, и нет необходимости рас-
сматривать ПРОДОЛLКение Р 1 м' траек-
тории бильярда в этот треуrольник,
ибо иа соответствующей точКи Р уже
проведен кусок траектории P P2 дан-
Horo пучка, который при соответст-
вующих симметриях дает тот же кусок
траектории БИRьярда в треуrольнике
Q, что и PiM'. Точно так же убеж..
даемся, что и все прочие треуrоль-
ники Qk, полученные из Qh отражениями относительно
сторон квадрата Q, получаются из каких-то треyrоль-
ников набора Qi, Q2, . .., Qs параллельным переносом
(например, Q ......... ИЗ Q4, Q ИЗ Q7 И Т.. д.). Поэтому
при выходе траектории за пределы Q нет необходимости ри-
совать продолжение траектории в соответствующем тре-
уrольнике Qk можно перенести ТОЧКУ выхода Р в соот-
етствующую точку. Р' противоположной стороны квадрата
Q и двиrать.ся по уже нарисованной траектории пучка па-
раллельных траекторий. Таким образом, траектории биль-
ярда в Q получаются из описанных траекторий потока с
перескаки анием с одной стороны на противоположную в
квадрате Q отражениями, при которых все треуrОЛЬНИI{И
Ql, . . . Q7 накладываются на Q; чтобы сделать траектории
непрерывными, нужно склеить противоположные стороны
квадрата, как указано на рис. 22.4. Отметим, что правило
клейки выбирается не произвольным образоrvl, а в соот-
ветствии с естественной процедурой выпрямления траекто-
рии бильярда. На торе получаем обмотку; если (Vi, V 2 ) ..........
составляющие скорости бильярдноr? шара вдоль rоризон-
тальноrо и вертикальноrо катетов треуrольника, а длины
катетов равны а, то периоды обмотки равны Ti==2a/Vl'
Т 2 ==2а/и 2 , Ti/T 2 ==V 2 /Vi и ИЗ свойств обмотки тора получаем:
р.'
1
Рис. 22.3
210
Если OmHOlUJ HUe V 2 !Vf рационально, ,по пlраеКПlОрUЯ
бильярда периодична в п реусольнuке Q, в пpomU8HOht случпе
траектория всюду пЛОfпно заполняепl весь mреУсОЛЫ-ltlК Q.
За летим, ЧТО t как и в случае бильярда в прямоуrольни-
ке , в рЗССl\10треННQМ случае особые траектории, попадаю-
щие в вершины треуrольника, можно естественным обра-
+ +[7 ь_ь
[S[2J или ...
0SJ.. [Z[SJ+rzj · [7
Рис. 22.4
ЗОМ продолжить за вершины на рис. 22.5 показано, как
продолжить траекторИю, попадающую в точку А вер-
шину уrла п!4. Будучи таким образом продолжены, особые
траектории ничем не отличаются от неособых после склеи-
вания квадрата в тор.
Исследуем теперь бильярд в равностороннем mреуеоль-
нике Q. Рассмотрим в нем пучок параллельных траекторий.
q
М
Р п
:2 fi ч
Рис. 22.5
Рис. 22.6
Построим с помощью отражений еще пять таких же тре-
уrольников ........ Ql +QБ; они вме.сте с Q==Qв обраЗУIОТ Пр l-
вильный шестиуrольник Q (рис. 22.6). Распространим пу-
чок параллельных траекторий на весь TOT шестиуrОЛЬНИIС
При выходе траектории из пределов Q продолжение тра-
екторий следовало бы рисовать в симметричных треуrоль
никах Qk, но, они получаются из Qi Qв параллельными пе-
реноса АИ (например, ........ из Qб' Q ......... из Qв и т. д.), и
поэтому вместо отрезка траектории Р М, выходящеrо из
Q, достаточно рассмотреть уже нарисованный отрезок pf К
211
\
внутри Q, rде точк.з Р'....... соответствующая точке Р точ-
ка противоположной стороны шестиуrольника Q. Таким
образом, если считать, что вижущаяся точка, доходя ДО
стороны s шестиуrольника Q, MrHoBeHHo перескакивает в
такую же точку на противоположной стороне s' шести..
а уrольника и продолжает
C 00 Двиrаться в том же направ-
,.J ф лении, то получающиеся
lJ....1 С I ,траектории (последователь.
а ности параллельных отрез-
\l::::L А v\ А ков MPf, P P2' Р Рз, · · .)
<> 'у v при наложении G помощью
симметрий всех составляю-
щих шестиуrольник Q тре-
уrольников на треуrОЛЬНИR
Q==Qв (рис. 22.7) в треуrольнике Q дают траектории
бильярда. С друrой стороны, «закон перескакивания»
дает правило попарной склейки стЩJон шестиуrольника
Q; произведя эти склейки ----- см. рис. 22.8........ получим
т о р (что не было очевидно с caMoro начала!). Для
в а А
Ь fJ
(/ 11 r'f) ,
Рис. 22.7
А
Ь
fj q А
«
А A A
I;Jl1 b b
, 'Р IJ fJ
с
р
Рис. 22.8
D
8
удобства на склеиваемом шестиуrольнике нанесены rори..
З0нтальные линии, а склеиваемые друr с друrом вер-
шины помечены одинаковыми буквами А и В. При склей-
ке получае1\1ЫЙ «по дороrе» цилиндр (рис. 22.8,в) прихо-
дится «подкручивать», чтобы произвести склейку сто-
рон Ь и с. rОРИЗ0нтальные линии в конце концов дадут на
торе не параллели, а линии обмотки типа (2,1), т. е. замк-
нутые кривые, делающие два оборота вдоль rtaраллелей и
один вдоль меридианов. Пучок параллельных траекторий
дает на торе семейство кривых, но получится ли обмотка
тора еще вопрос!
Здесь ПО1\10rает друrой способ склейки тора из шести-
УI ольника Q. Именно, склеим пары сторон й, Ь, с еще на
плоскости, отрезав от Q треуrольники Lli и Ll 2 по отрезкам
212
n и т, и, перенося их надлежащим образом, подклеим R
остатку Q и друr к друrу (рис. 22.9, а, б). Получим ромб
R==С 1 С 2 С з С4, с уrлом 'Я/з. В этом ромбе следует склеить
соответствующие точки противоположных сторон m и т,
а
:п.
т
4 о
Рис. 22.9
n и n, ибо мы разрезали по линиям m и n. Но это почти стан-
дартная «модель Topa», продеформировав ромб в квадрат
(рис. 22.9, 8, е), мы можем склеить из Hero тор обычным об-
разом. Траектории РЦ:ссматриваемоrо пучка в ромбе уст-
роены так же, как траектории бильярдноrо пучка в тре-
уrольнике, только перескакивание происходит парал-
лельно сторонам ромба. С
После деформации ром.. 4- т
ба в кuвадра: И после- lli V
дующеи склеики на торе А n'/ ОЗ
получится обмотка. Най-
дем ее периоды. 112
Период Т} вдоль па. а 6
раллелей равен времени, Рис. 22.10
которое требуется биль-
ярдному шару, чтобы пройти один раз вдоль меридиана
n, Т. е. от одной стороны ромба т до друrой стороны т.
Если модуль скорости шара равен v, а ее направление
образует уrол сх со стороной АВ исходноrо треуrОЛЬНИК8
Q==ABC (рис. 22.10), т. е. с диаrональю ромба С 1 С з , то
(
проекция скорости на направление, перпендикулярное сто-
Р9нам т........ C i C 2 и С з С 4 , равна v cos (1t/З сх). Если расстоя-
ние между сторонами ромба равно а, то Ti==a/[v cos (л/3
.......сх)]. Аналоrично находим T 2 ===a/[v cos (л/З+сх)J.
Итак,
Tf соэ (л/3+а)
== cos (n /3 ..... а) t
и мы видим, что опять траектории бильярда периодичны или
всюду плотны в зависимости только от направления тра-
213
еJ{ТОрИИ. ПОСJ{ОЛЫ{У eos ( :+- r.t ) == COS r.t + v;,з sin а,
7'! cos a VЗ sin а 1....... VЗ tg а
1'2 == соsа+V3Sinа I t--У3tg'а;
== 1 2 УЗ.!..g а == 1 ,
1+УЗ tga l+СVЗ tga) l
а это число рационально или иррационально в зависимости
от Toro, рационально или иррационально число k === V 3 tg а.
Подведем итоrи. Если описаНflЫJl;lИ вьuuе построеflИЯll1,и
бильярд в МНО20УсОЛЬflике Q можно свести к обмопIкаj14 Пlора,
пl0 Jvtносоусольник Q будеhlназывать торическим. Для биль-
ярда в торическом !\1ноrоуrольнике Q выполнена следую-
щая альтернатива:
либо траектория периодична;
либо траектория всюду плотно заполняет весь MHOZO-
усольник Q. ..:1
В рассмотренных примерах тот факт, какая часть аль-
тернативы имеет место, зависит лишь от направления движе-
ния бильярдноrо шара, но не от ero начальноrо положе-
ния.
Для любоrо торическоrо мноrоуrольника проблема
бильярда может быть разрешена (т. е. все траектории мо-
rYT быть классифицированы в указанном смысле).
Какие -еще мноrоуrольники, кроме рассмотренных трех
типов; являются торическими? ОК8зывае-тся, торическим
является лишь еще прямоуrольный треyrольник с остры-
ми уrлами 'Л/б и 'Л/3 (половина равносторонпеrо треуrоль-
ника). Справедлива
т е о р ,е м а 1. Бильярды в МНО20У20льн;иках, отличных
от указанных 'четырех типов (nрямоуеольник u mреуеольни-
ки с У2лами 'Л/2, n/4, п/4; 'Л/3, 'Л/3, л/3; 'Л/2, 'Л/б, п/3) нельзя
свести к обмоткам торов.
Мы приведем доказательство этой теоремы в конце еле-
дующеrо параrрафа.
З а Д а ч а 22.2. Свести бильярд в прямоуrольном треуrоль
нике с уrлами 'Л/б и 'Л/3 к обмоткам торов (осуществив построения,
аналоrичные проводившимся выше).
З а Д а ч а 22.3 (см. 24). Провести построения, аналоrичные
nроводившимся выше, для случая прямоуrольноrо треуrольнпка
с уrлами 'Л/8 и 3'Л/8: свести бильярд к .пучкам параллельных Tpa
екторий с перескакиваниями. Затем осуществить склейку сторон,
соответствующую получающимся перескаl{иваниям и убедиться,
что полученная поверхность н е я в л я е т с я тором, т. е. Tpe
уrольник с yr лами 'Л/2, 'Л/В, 3л/8 н е т о р и ч е с к и й.
214
в заключение рассмо рим еще одну занимательную
картинку относящуюся к бильярду в-равностороннем тре..
уrольнике Q==ABC. Именно рассмотрим в Q пучок траекто-
рий, параллельньrx стороне АВ. Чтобы нарисовать продол..
жение этих траекторий, не НУ}КНО производить отражения
относительно стороны АВ (ибо траектории ee He пересекают),
а достаточно продолжить траектории в два треуrольника
Qf и Q2, образующих вместе с Q трапецию Q==ACA'C'
(рис. 22.11). Траекторию МР,
выходящую из трапеции в точ-
ке Р, следовало бы продолжить
в треуrольник Q , но после пос..
ледовательных отражений отре...
З0К РМ' дает в исходном тре-
уrольнике уже нарисованный там
отрезок р' N; соrласно нашим
правилам мы будем считать, что
движущаяся по Nl Р точка, дойдя ДО Р, перескакивает в точку
Р' и продолжает двиrаться по трапеции в том же направле-
нии. Иначе rоворя, параллельный пучок на трапеции следует
интерпретировать как пуч.ок с перескакиванием со стрелки а
в соответствующую точку стрелки а' (рис. 22.12). Чтобы
траектории стали непрерывными, стрелки нужно склеить
f!
((.f \11 4 . -- .;.:; .:-.:-
t .... ....... .....д ........... . . ........ \ ). I
...... .,.......... j\ 8
.... n 11'
(J1
Рис.
Рис. 22.12
(в указанном направлении!). После склейки мы получим
лист l\1ёбиуса (1), а на нем......... пучок траекторий, параллель
ных средней линии листа Мёбиуса. На исходном треуrоль..
нике Q==ABC этот ПУЧ0К дает траекторию KLM, составлен
ную из средних линий треуrольника АВС (она соответствует
средней линии листа Мёбиуса), и семейство «двойных» Tpa
екторий, окружающих KLM. Оказывается, при анализе
задач механики MorYT появляться даже такие «странные»
поверхности, как лист Мёбиуса. rлавные }ке ({странности»
нас ждут в Э 24.
Для понимания Э 2{! опишем предварительно (в 23)
построение двумерных поверхностей Q помощью склейки
мноrоуrольников и докажем теорему классификации дву-
мерных поверхностей
215
23. Склейка поверхностей
из мноrоуrольников
Замкнутая мноrоrранная поверхность опре..
деляется в школьном учебнике rеометрии как 1\1ножество
точек в пространстве, составленное из мноrоуrОJIЬНИКОВ и
удовлеТВОРЯЮlцее некоторым УСЛОВИЯJ\I.
О с Н о в н о е с в о й с т в о такой поверхности за..
1
ключается в T01\tI, что каждая ее точка iVl обладает OKpectп"!'
.j
н'остью, которая может быть непрерывно прео.бразована в
обычный Kpyr с центром в точке 1\11 (рис. 23.1). О к р е с Т-
Н О С Т Ь Ю точки М будем называть множество точек по-
верхности, удаленных оТ М не более чет ,л на некоторое рас-
стояние 8>0. При наших непрерывных преобразованиях
м
> . @
> @
M @
Окрестность точки М
Рис. 23. 1
окрестность можно изrибать, местаl\fИ сжимать или рас-
тяrивать, но запрещается «склеивать» между собой ее точки
и «разрывать» окрестность. Если представить себе окрест-
ность точки М сделанной из резины, то нужное преобразо-
вание можно получить, если положить окрестность ПОД
пресс и, медленно растяrивая (так, чтобы не получилось
складок и разрывов), расплющить ее. УказаННЫlVI основ-
ным свойством обладают не только замкнутые MHororpaH-
вые, но и искривленные поверхности, например сфера или
тор. Если в сфере вырезать две дырки и заклеить их под-
ходящим образом изоrнутой «ручкой»........ боковой поверх-
ностью цилиндра, то получится сфера с ручкой (поверх-
ность rири), которая может быть преобразована в тор сжа-
тиями и растяжениями (рис. 23.2, а). Приклеив к сфере
аналоrичным образом д в е ручки, мы получим так назы-
ваемый креН,дель, или сферу с двумя ручками; на рис 23.2, б
эта поверхность представлена в пяти видах. Можно тем
же способом построить сферу S (р) с люБЬiМ числом прикле-
енных ручек p o; число р называется родо/и поверхности
216
s (р), а саму поверхность называют иноrда кренделелl, с р
ablpKaAtU. Леrко видеть, что все сферы с ручками обладают
основным свойством. .
1:::] (N '" .
. . . . . ," ) 1 .
I ," .. J .. .
.;:) .
ЦиЛIlНdР Р!JЧКCl
С:ферf.1
(; оырканц
--
Тор
СферQ с Р/JЧКtJ!l
tl
Сшеры
с fJtJумя
Р.1'1ка.I1Ц
/(peflf/qllb
Рис. 23.2
Полная поверхность цилиндра также обладает этим
свойством, а вот Y:ZKe ero боковая поверхность им не обл"ада-
ет: точки М на окружностях оснований имеют окрестности
в виде искривленноrо полукруrа их нельзя без разры..
вов и склеек деформировать в Kpyr с центром в точке А1
(рис. 23.3). Далее, поверхность двойноrо конуса и объеди-
нение двух пересекающихся сфер
н е о б л а Д а ю т основным свой-
ством, а объединение двух непе-
ресекающихся сфер о б л а Д а е т
(рис. 23.4).
11 11
fi
11 11 f1 М
Рис. 23.3
@ r
Рис. 23.4
Мы хотим исключить из рассмотрения также поверх-
ности, состоящие из нескольких отдельных кусков. По-
211
требуеIv1 поэтому, чтобы любые две точки пq ерхности можно
было соедИНИТЬ проходящей по поверхности непрерывной
линией. Это свойство называется связностью поверхности.
Итак, рассматриваемые в дальнеЙШем поверхности
связные.
Не будем мы рассматривать и бесконечно протяженные
поверхности такие, как плоскость или бесконечная ци
линдрическая поверхность, а также поверхности типа KPy
ra без rраницы (открытоео круеа) о Поэтому наложим еще
условие конечности. Потребуем, чтобы поверхность мож
но было разбить (разрезать) на к о н е ч н о е число «кри
волинейных мноrоуrольников», каждый из которых без
разрывов и склеек можно преобразовать в плоский выпук
лый мноrоуrольник (с rраницами). Например, сфера по
экватору и четырем меридианам разрезается на 8 криволи
нейных треуrольников, а плоскость на конечное число MHO
rоуrольников разбить нельзя. Если поверхность разбита
на треуrольники, любые два из которых либо имеют общую
сторону, либо общую вершину, либо вообще не пересе
каются, то это разбиение называется трианеуляцией ПО
верхности.
Итак, далее мы рассматриваем только такие поверх
насти (множества точек пространства), которые обладают
тремя перечисленными свойствами: основным свойством,
свойством конечности и С8язностью. Эти поверхности бу
дем коротко называть двУЛtерными компактными пoвepx
ностями без края (иноrда .слова «без края» будем опускат ).
Заметим, что любая рассматриваемая поверхность делит
пространство на две части........... внешнюю (неоrранич.енную)
и внутреннюю (оrраниченную) и поэтому являет я ДBYCTO
раннеЙ, а также является ориентируеhlОЙ: любую малень
кую окружность с нанесенной на ней ориентацией (стрелкой)
н е л ь з я так подвинуть по поверхности, чтобы она Bep
нулась на старое место, но ориентация на ней изменилась.
Следуе1' отметить, что имеются также неориентируемые
поверхности, например лист Мёбиуса (см. рис. 22.12),
имеющий о Д Н У сторону (на нем ориентацию окружности
МО)КНО изменить специальным ее движением по листу
вдоль средней линии), но такие поверхности имеют к рай
и здесь не рассматриваются.
L{Be компактные поверхности считаются эквивалентны
ми (матем атики rоворят mополоеuчески эквиваленmными),
если существует о б р а т и м о е отображение одной из
них на друrую, при котором нет ни разрывов, ни склеек,
но допускаются растяжения и сжатия, изrибания и разrи
218
бания (для таких отображений в математике также есть
специальное слово еомеоморфизм). ,Например, поверх-
ность тетраэдра эквивалентна (rомеоморфна) сфере, Две
последние поверхности на рис. 23.2, а эквивалентны тору,
а все пять поверхностей на рис. 23.2, б ЭI{вивалентны дpyr
ДРУI'У.
3 а д а ч а 23.1. ПокаЛПIте, что сфера 1 тор и:рендель и вообще
сфера с любым числом ручек S (р) обладают своЙством конечности,
Т. е. ука)ките их разбиеНIIЯ на ко-
нечное число !(РИЕолине'Йных MHoro-
уrоль инков.
3'3 Д а ч а 23.2. Ука2ките, сфере
с каким числом ручек эквивалентна:
а) поверхность чашки (рис. 23.5, а);
б) поверхность стула (рис. 23.5, б);
в) поверхность oKoHHoro переплета
(рис. 23.5, в); r) поверхность «плас
тилиновоrо человечка», у KOToporo
пальцы рук образуют два сцеплен-
ных кольца (рис. 23.5, е).
3 а д а ч а 23.3*. Покажите, что
тор и сфера не эквивалентны.
у к а з а н и е. Придумайте та-
кое свойство, которое сохра яется
при рассматриваемых преобразовани-
ях (rомеоморфизмах) и которым одна
из этих поверхностей обладает, а
друrая нет.
а
1]1]
J}
е
и
Лластl1ЛIJ нодь//.(
челоlJечек
Рис. 23.5
Поверхность, обладающая свойством конечности, ,раз-
резается на мноrоуrольники и поэтому может быть СКi1Iееиа
из мноrоуrольников. Каким наименьшим числом МНО20-
У20льнuков можно при этом обойтись? Мы уже видели, что
тор может быть получен склейкой противоположных сто-
рон квадрата (или прямоуrольника), т. е. для тора доста-
точно иметь о Д и и мноrоуrольник. Для кренделя ,8,(2)
(т.. е. для сферы с двумя ручками) достаточно также о д-
н о r о мноrоуrольника 8 уrольника (рис. 23.6). Ока-
зывается, любая компактная поверхность S может 6blпZb
склеена из одНО20 МflО20уеольника W, который называется
разверткой поверхности S. Собственно rоворя, это почти
очевидно, и вот почему.
Трианrулируем поверхность S и каждую сторону К3Ж-
доrо треуrольника отметим какой-либо буквой, причем раз-
ные отрезки отметим разными буквами. Кроме Toro, каж-
ДУJО сторону треуrольника о р и е н т и р у е м, т. е. по-
ставим на ней произвольным образом стрелку. Разрежем
поверхность S вдоль всех полученных отрезков (сторон
треуrольников) ........ S рассыпется на конечное число «кря-
219
вых» треуrольников Мы считаеМ t что разрезая поверхность
ВДОЛЬ и:акоrо"то отрезка, мы ставим на обоих «береrах» раз-
реза ту букву, которая стояла на отрезке (рис. 2307)0 В ре...
зультаrе на кажДОЙ стороне треуrольиика будет отмечена
ориентация: сторона снабжена стрел!,ой.
Наша цель: склеить обратно все это множество Tpe
уrОЛЬНИКОВ t но таким обраЗ0М чтобы получился о д и н
плоскиЙ м:ноrоуrОI11ЬНИК. Начнем построение с Toro, что
выберем какой-то Tpey
rо.пьник llf; рассмотрим
ero сторону она снаб-
жена какой то буквой а
и стрелкоЙ. Так как каж-
дая буква входит в об-
щий набор сторон в точ-
ности два раза (посколь..
.,:: Q .... ::.: ''.'''' ...'
.t,"',':
..... .' . ,."
. ....... . .... .;,
(;' . . .'...,
с' :::::""
';':"\:.\ '1" J tf v
<: 6'
)o--r"
Ри'с. 23.7
ку поверхность S не имеет края, а каждый разрез
имеет два береrа) t то найдется ещ один треуrольник
d 2 , на стороне KOToporo стоит та же буква а. Склеим
эти треуrольники по общей стороне а, совмещая направле-
ния стрелок....... ПОJIУЧИТСЯ плоская фиrура, разделенная на
два треуrольника, на rранице КОТОРОЙ стоят новые буквы и
стрелки. Берем какую-то букву Ь на этой rранице и ищем:
свободный треуrольник 8з, на стороне KOToporo имеется та
же буква Ь......... такой треуrольник обязательно найдется,
причем ровно один; приклеиваем 8з к этой фиrуре по общей
стороне Ь, совмещая стрелки, и т. д. Процесс закончится в
тот момент, коrда все треуrольники будут исчерпаны.. Дей-
ствительно, мы приклеим в т о ч н о с т и в с е тре-
уrольники в противном случае (если никакая буква на
rранице получающейся области не встречается среди букв
220
./
!la оставшихся еще неприсоединенных треуrольниках),
:склеив все попарные буквы, вернемся к. ИСХОДНОЙ поверх-
ности S, и она окажется несвязной (состоящей больше чем из
одноrо куска) противоречие со свойством связности.
Итак, при указанном склеивании мы исчерпаем в с е
треуrольники и получим плоский мноrоуrольник W с
буквами и стрелками на сторонах ero rраницы, причем
каждая буква будет встречаться ровно два раза, так что
число сторон у W будет четным. Зафиксируем на MHoro-
уrольнике u7 ориентацию, а затем, начав с произвольной
веРIПИНЫ и совершая обход rраницы, последовательно вы-
пишем все буквы на сторонах W, причем, если направление
обхода с о в п а Д а е т со стрелкой на стороне, будем пи-
сать букву в степени (+ 1); если же н е с о в п а Д а е т ........
пишем в показателе (.......1). В результате получится слово W
W :1: 1 :1: 1 :1: 1 ( 23 8)
вида ===ai 1 ai 2 о . .aik рис. ., однозначно задающее
мноrоуrольник W (мы специально мноrоуrольник и слово
обозначаем одной буквой W).
Мы сопоставили каждой поверхности S мноrоуrольник
и слово W, правда, неоднозначно (слово зависит от триан-
rуляции поверхности). Слово W
можно рассматривать как код
поверхности S, и это кодирова-
ние неоднозначно: одной и той
же поверхности отвечает беско-
нечное число кОДОв......... по числу
трианrуляций на S. Если про-
извести требуемые склейки на
rранице мноrоуrольника п7
(склеивая CTOpOHЫ с одинаковы-
ми буквами по стрелке), то по-
лучим исходную поверхность.
Оказывается, однако, что
поверхность S может быть
склеена из TaKoro мноrоуrольника W, дЛЯ KOToporo совер-
шенно ясно, что после склейки поверхность S будет пред-
ставлять собой S (р) ........ сферу с р ручками. Этим мноrоуrоль-
ником является 4р..уrольник с кодом W==albla'ilb'ila2bg
а;lЬ;l. . .а р Ь р а р 1 Ь;1: слово аlы1l1ьl11 отвечает тору сфере
с одной ручкой S (1), слово аlы1l1ьl1а2ь2а;:lь;11 дает склей.
ку двух ручек, Т. е. крендель S (2); . . . вообще, каждая
новая четверка букв akbkaf1b--"J.отвечает приклейке од ой
новой ручки к уже имеющейся сфере с ручками (reoMeT"
рически это несложно представить, производя указан ые
а t1 з
f
1 ....1 ...1
W=O,U 5 Q2" 0404 0,02 аз
коа мноаОУ80ЛЬНI1ка
Рис. 23.8
221.
в слове последовательные склейки). СЛОБО W==aibfa;lb;l. .. "
, . .а р Ь р а,/Ь р 1 называется канонuчесf"UМ, а отвечающий
erviy мноrоуrольник W канонической разверткой поверх
ности s. Сформуди:руеNI точную теорему.
т е о р е м а 1 (теорема к..тrасеифи-кации двумерных ком..
пактных поверхностей оез края). ЛНJбая КОJrlпакmная ориеп..
тuруеАtfая пoeepXHocпlb S в lпрех 'uе!Хf.tОЛt npOCt1lpaliCпlee ЭК
8UfJале1-unна (еомеоморфна) сфер:! с Р!Jчка ФlU S (р).
д о к а 3 а т е л ь с т в О. iДо таточно доказать; что у
поверхности S имеется канонический код аlы1l1ьl\\ ot .
. . .а р Ь р ар l Ь;l.
мыI уже знаем, что поверхность S имеет как{)й..то КОД
W, оrrвечающий неко'FОРОЙ три:анrуляuйи. l\1ноrОУI'ОЛЬНИК
W представляет собой плоский ttеmНОУсОЛЬflUК с числом сто..
А рои 2п (п не обязательно четно), все старо..
1; .... с ры KOTOpOI'O разбиты на пары с одинаКОВЬП:1И
В :: (:':'::"':'\:- ' '.: ::": fj буквами, и каждая пара зате:м склеивается
а : \')/:";}:. /. ct так, чтобы стрелки на них совпали.-При Э'f.ОМ
А "::'::.:/ /:\/.:':;:: склеиваются и ершины, KOTor:bIe разбива..
с ." fJ ются на rpуппы, внутри каждои из которых
В они склеиваются в одну точку (напр И1\1ер,
,д,де аруппы на рис. 23.9 все вершины шестиуrольника
Вершин разбиваются на две rруппы......... черные и
Рис. 23.9 белые).
Доказательство теоремы будет ПрОВО
диться следующим образом: будем перестраивать MHoro
уrольник W с помощью операций (разрезаний и приклеива
ний), выполнение КОТОРЫХ приводит к друrому коду той же
повеРХ!lОСТИ S или эквивалентной (rомеоморфной) ей; про
делав все эти операции придем в конце концов к иска...
мому коду аlы1l1ьl1... .а р Ь р а р 1 Ь;1, отвечающему сфере
с р ручками, откуда и сделаем вывод, что S rомеоморфна
S (р). Нужные нам перестройки таковы.
1 . Слово W можно перестроить так, чтобы все верши...
ны МНО20уеОЛЬflика W склеuлись 8 одну точку.
Предположим, что количество rрупп склеивающихся
точек больше одной. ОбознаЧИl\1 одну из этих rрупп {Р},
друrую rруппу {Q}. Тоrда имеется такое ребро а, что ero
начало принадлежит rруппе {Р}, а конец rруппе {Q}.
Выполним разрезание и последующую склейку мноrоуrоль
ника W/ указанные на рис. 23.10. ,Напомним, что каждая
буква на rранице мноrоуrольника встречается дважды;
нас сейчас интересуют две буквы с на рисунке, которые
склеим по стрелке. Результат перестройки (разрезания и
склейки) мноrоуrольник W', у KOToporo вершин в МНО"
222
жестве {Р} 'стало на одну меньше, а Б множ.естве {Q}.........
на одну больше. Взяв еще одну Бер:ШlIНУ ИЗ {Р}, мы тоже
можем УНИЧТОЖИTh ее с ПОМОЩЬЮ какой-нибудь rруппы (не
обязательно с ПОМОЩЬЮ {Q}). Так будем уменьшать число
вершин в rруппе {Р}, пока
в {Р} не останется р о в н о
о Д н а вершина. Последний
шаr: так как в {Р} ОД Н а
вершина, соседние ребра име
ют вид а и a l. Тоrда делаем
перестройку , указанную на
рис. 23.11 (склеиваем ребра а
и a-- 1 ) и уничтожаем послед-
нюю вершину в rруппе {Р}. Рис.
ТаКИl\.1И операциями уничто-
жаем постепенно все rруппы вершин, кроме одноЙ, вер-
шины которой составляют полный набор вершин возник
шеrо мноrоуrОЛЬffiIка и склеивают поэтому в одну точку.
20. Если W==Aaa-- 1 В, еде А и В ....... слова, а ....... буква, то
W можно перестроить в слово W'==AB. Эта операция,
называемая свертыванием, показана на рис. 23.11.
Рис. 23. 11
в дальнеЙШем считаем, что в СЛОЕе W нет сочетаний ви-
да aa --l. З,8метим акже, что в слове W нет 'н ДВУХ одинах&
выхбуквв одинаковых степеНЯХ,Т.е. 'W=F.. .0,...
W --1 --1 u
. . .а . . . и ....,....... ra .. д ..., поскольку при склеике
таких ДВУХ противоположно ориентированных сторон по-
верхность S становится неориенmируемой ----- существует
путь, вдоль KOToporo у окружности меняется ориентация
(эта склейка эквивалентна добавлению листа Мебиуса, KO
торый мы исключили из рассмотрения). Таким образом,
если в слове W встретилась буква а, то буква а встретится в
W вновь лишь в степени ( 1).
30. Если буквы а и a-- 1 не стоят рядом в слове W (что мы
предположили выше), то найдутся буквы Ь и Ь.... а такие,
что пары а, a--1u Ь, b-- 1 разделяют друе друеа (рис. 23.12, а).
Тоеда ату четверку .можно заменить на сочетание вида
xyx"'ly"'l, сохраняя условия шаеО8 1'? и 20 (рис. 23.12, б и в).
223
ЕСJlИ при этом случайно возникнут сочетания сс ж, ТО они
устраняются свертыванием.
В результате применений КОНСТРУI{ЦИЙ шаrов 10........30 мы
преобразовали исходное слово W к слову W', состоящему
только из сочетаний вида хух.... 1 у--l, что И требовалось до-
казать. Число таких сочетаний равно числу ручек у По-
верхности S ....... ее роду р
lJ
с::;'>
--1
f1
а
tJ
w с:=::;>
о !J
Рис. 23. 12
3 а Д а ч а 23.4. Пусть поверхность S имеет код W==ala2." .
1 1 1 2 W
...а п аl а2 . . .ап , т. е. n уrольника попарно склеиваются
противоположные стороны. Определите канонический код поверх..
ности S и ее род. .
О т в е т. S==S(p), rде p==[nI2].
После Toro как мы с помощью теоремы классификации
поняли, что поверхность S эквивалентна какой-то сфере с
ручками, у нас может возникнуть вопрос, нельзя ли получить
для поверхности S два различных канонических кода
W ::=: аlы1l1ьl11 . . . а р Ь р а р 1 Ь;1
и
W / ' Ь ' ' l b ' l ' Ь ' ' l b ' l
а 1 1 а 1 1 ... а r ,й r r ,
отвечающих сфере S (р) с р ручками и сфере S (r) с r ручками,
причем p=l=r? Если бы два таких каНОНИt{еских кода име-
лись, то поверхности S (р) и S (r) были бы эквивалентны
(rомеОlV10рфНЫ) .
Для ответа на этот вопрос введем понятие айлеровой ха-
рактеристики поверхности. Если поверхность S разбита
на мноrоуrольники, и в этом разбиении имеется В вершин,
224
р ребер и r ераней (мноrоуrольников), то число
Х (5) == B P + r
JIазывается эйлеровой характеристикой поверхности 8.Если
W произвольная развертка поверхности 8, то с помо
J:дью элементарных операций 1° 3° она преобразуется в
, Rаноническую развертку. Леrко заметить, что эти элемен
apHыe операции не меняют числа Х (8). В самом деле, коrда
f
tI bI в мноrоуrольнике проводим диаrональ, числа Р и r
f в е л и ч и в а ю т с я на 1, а В н е м е н я е т с я;
коrда производим разрезание вдоль проведенной диаrона
\ЛИ с последующим склеиванием, числа Р и r у м е н ь ш a
ю т с я на 1 при н е и з м е н н о м В; при свертывании
'(отбрасывании сочетания aa-- 1 ) числа В и Р у м е н ь ш a
Ю т с я на 1, а r не меняется. Поэтому величина B P+ r
во всех случаях не меняется.
Пусть тепер ь w......... к а н о н и ч е с к а я развертка
albiallbl1. . .а р Ь р а;lЬ р 1 . Для нее В == 1 (все вершины склее-
ны в одну; см. п. 10 доказательства теоремы 1), Р==2р (та-
ково число сторон у канонической развертки) и r== 1 (МНО-
rоуrольник w......... о Д и н). Получаем
Х (8) == 1.........2 р + 1 == 2.........2 р .
Поэтому, если бы существовали д в а р а 3 л и Ч н ы х
канонических кода W и W!, указанных выше, то мы полу-
чили бы
х (8) == 2.......2р == 2 2r,
откуда р==' И, следовательно, слова W и W' совпадают.
Следовательно, справедлива
'т е о р е м а 2. Никакие две сферы с разНЫJJtl числом ру-
чек не эквивалентны (не 80мео.морфны).
3 а д а ч а 23.5. а) Докажите, что у всякоrо выпуклоrо MHorG-
rранника сумма числа вершин -Н rраней больше числа ребер на 29
б) Вычислите эйлерову арактеристику тора и кренделя S (2).
в) Докажите, что для любой трианrуляции любой поверхности
В+ Р+ r ...... четное число.
Друrое доказательство теорем 1 и 2 приведено в книrе:
Б о л т я н с к и й В. r., Е фре м о в и ч В. А. Наrляд-
ная тополоrия........ М.: Наука, 1982 (<<Б иблиотечка «Квант»,
вып. 21).
Теперь, зная, как двумерные поверхности склеиваются
из мноrоуrольника, ВНОВЬ вернемся к бильярдам в MHoro-
уrольниках.
8 r. А. [альперин, А. Н. 3еМJIЯКОВ
225
24. Бильярды в «рациональных»
мноrоуrольниках и поверхности
Рассмотрим билья.рд в прямоуrольном тре-
уrольнике Q с острыми уrлами 'Л/8 и Зп/8. ,Пучок параллель..
ных траекторий в этом треуrольник продолжим до пучка
в правильном восьмиуrольник Q, соста.вленном из 16
треуrольников, равных Q и получающихся из Q последова
тельнымИ отражениями относительно катета и rипотенузы,
уrол 'ме}кду которыми равен 'Л/8 (рис. 24.1, а). Как и в 22,
711 7(0
Рис. 24.1
d
ь
нетрудно проверить, Ч'f<О траектории БИVIьярда в исходном
треуrольнике 'Q получаются при наложении всех упомяну..
тых треуrольников на треуrольник Q из траекторий точки,
u u
движущеися по нарисованным отрез ам и перескакивающеи
с одной стороны восьмиуrольника Q на соответствующую
точку противоположной (параллельнод) ,стороны. Т,аким
образом, бильярд задает склейку сторон ,восьмиу,rольника
.Q., указанную на рис. 24.1, б).
Осуществим эту склейку. Внимательно проследите за
ее этапами (рис. 23.6). В результате мы получим крендель
описанную в 23 поверхность, как бы склеенную из двух
торов. При склеЙке отрезки траектории указаыноrо выше
пучка с перескакиванием подклеятся друr к ;друrу и обра-
зуют непрерывную траекторию на кренделе. Все траекто-
рии данноrо пучка параллельных траекторий после склей...
ки дадут пучок траекториЙ на ренделе, который мы будем
называть оБАl,откой кренделя.
В отличие от обмоток тора, обмотки кренделя имеют
особые точки; в данном случае на кренделе будет ровно одна
особая точка А, к описанию которой мы и переходим. [ру-
бо rоворя, если в окрестности точки А1 траектории ведут
себя «примерно параллельно», то такая точка М называется
226
fl,eособой (рис; 24'.2, а). Поведение траекторий в окрестно..
ти особых точек не такое, как на рис. 24.2, а, а «особое>
t!етрудно понять, что при СКJIейке из восьr.лиуrольника Q
q-очки в Н У т р и Q будут flеособыJИU. Если точка М на
ренделе получается склейкой двух cooTBeTcTBeHH IX точек,
! и М 2 , лежащих на параллельных сторонах Q, то она
ij<!кже Ije будет особой при подклеивании окрестностеЙ
Qчек М! и М 2 друr к друrу мы получаем окрестность точки
{и на кренделе, траектории в которой ведут себя как на
РИС. 24.2, б. Таким образом, о с о б а я точка на кренделе
может получиться лишь при склейке :а ерш и н восьми..
уrольника Q. Нетрудно проверить, что все восемь вершин Q
дают при склейке ровно одну точку А на кренделе (это
R2. R3
Р 1
R4
R8
а
R5
7
3
Рис. 24.2
(j Н2.
Рис. 24.3
следует из п. 10 доказательства теоремы 19 23). Окрестность
этой точки склеивается из восьми секторов Ri R8 ок-
рестностей вершин восьмиуrольника Q. Подклеим эти сек-
торы величиной 3n/4 каЖДрlЙ друr к друrу в соответствии с
законом склепки (рис. 24.3). Мы видим, что при такой под-
клейке получатся т р и слоя (так как 8.3n/4==3.2n), по..
этому все секторыI величиной 3n/4 каждый придется сжать
в три раза, чтобы можно было осуществить склейку в о Д и н
слой. При этом сжатии следует считать траектории потока
нарисованными на секторах......... и после ИХ склейки получит-
ся картина траекторий в окрестности точки А.
8 227
Мы увидим после осуществления подклейки (соответст",
вующие рассуждения приведены ниже), что в точку А
в х о Д я т р о в н о Т р И траектории, и в ы х о Д я т
р о в н о т р и траектории. Эти траектории соответствую'l'
особым траекториям бильярда в треуrольнике Q, заканчива-
Зл
ющимся или выходящим из вершин уrлов величины 8'
именно из э т и х вершин получаются восемь вершин вось-
миуrольника Q. В три вершины Аз, А4' А5 траектории
пучка параллельных линий входят, а из трех Ai, А 7,
А А выходят. После склейки входящие и выходящие
траектории дают входящие в особую точку А и выходя-
щие из нее траектории; эти особые траектории, кончающие-
ся и начинающиеся в А t называют сепаратриса.АtИ, Т. е.
)l
,r:=2 c o
Н;
R2.
R4 ct (t
/(,
*( <==:> ',;; '\ '.
::,
t ", .
,:,
n==-3
« Обезьянье»
се8ло
Ж <==:> l1ультIJсеиl.
п=4
Рис. 24.4
R$
о
*
11
tJ
Рис. 24.5
«разделяющими». Сепаратрисы действительно как бы раз.
деляют остальные траектории две близкие к сепаратри.
се МА траектории M 1 N1. и M 2 N 2 , лежащие по разные сто.
роны от МА после Toro, как сепаратриса заканчивается, t
точке А, уходят друr от друrа.
Итак, бильярд в треуеольнике Q с уелами t F tJ
Зл
""8 сводится к обмоткам кренделя. Эти обмотки имеют
ровно одну особую точку А, поведение траекторий в окрест-
ности которой описано выше.
228
В общем случае особые точки с таким поведением траек-
торий называются мульmuседла.мu., Мультиседла MorYT
MeTЬ Лlобое четное число 2п сепаратрис ........... п входящих и
h выходящих; единственное оrраничение состоит в том, что
п 2. Такое мультиседло будет называться мульmuседлоМ,
типа n. Мультиседло типа п==2 принято называть просто
седЛОJl1 (рис. 24.4).
Оказывается, мультиседла появляются всякий раз при
псследовании поведения пучка параллельных траекторий
БИ!JТIьярда в мноrоуrольнике Q, близких к особым траекто-
рияl\tl бильярда, заходящим в вершины уrлов мноrоуrоль-
lIика Q. Прежде чем дать некоторую общую конструкцию,
приведем еще один способ построения мультиседла типа 3,
появляющеrося на' кренделе, склеенном из правильноrо
восьмиуrольника.
Будем приклеивать друr к друrу введенные выше секто-
u 3п Ф
ры величинои 4' н е Д е о р м и р у я их при этом,
3п
как делалось ранее. Уrлы секторов равны 4' и у)ке после
приклеивания сектора R2 к сектору Rl следующий подклеи-
ваемый к R2 сектор Rз перекроется . с Rl (рис. 24.5, а).
Мы будем считать, что перекрывающаяся с Rl часть сек-
тора Rз образует новый слой, или лист, идущий с в е р х у
над Rl (рис. 24.5, б); секторы R4 и R5' приклеиваемые далее,
тоже лежат на втором листе над первым листом
(рис. 24.5, в). Сектор R6 дает уже тройное наложение (вмес-
те с Rl и Rз), и мы будем считать, что секторы R6' R" R8
идут уже по третьему листу. Сделав полный (тройной)
оборот BOKpyr особой точки, мы вновь попадаем в сектор Rl,
поэтому свободный край Rs следовало бы приклеить к сво-
бодному краю Ri, но для этоrо ero нужно «продеть» через
два нижних листа (рис. 26.6, ё); если сделать так, то полу-
чится поверхность с самопересечением, как на рис. 24.5, д.
Состоящую из трех листов окрестность точки А называют
трехлистной ветвящейся окрестностью А, а саму точку А ........
точкой ветвления порядка 3. Чтобы получить из ветвящей-
ся окрестности точки А обычную окрестность точки А
на кренделе, нужно сжать ветвящуюся окрестность в три
раза так, чтобы каждЫЙ из трех листов превратился в КРУ-
u 2п
rовои сектор с уrлом 3' а после этоrо подклеить ДРуr к
друrу свободные края первоrо и последнеrо листов, прев-
ратившихея в секторы. Эта процедура была выполнена
выше.
229
Поскольку при склейке секторов Rl RB в ветвящуюся
поверхность бильярдные траектории подклеивались друr
к друrу и образовывали на !<аждом листе семейство парал-
лельных линий одноrо и Toro же направления, то на каж-
дом листе р о в н о о Д н а траектория входит в точку ветв-
ления А и р о в н о о Д н а траектория выходит из А,
причем траектории, лежащие по одну сторону от входящей
в А сепаратрисы остаются на том же листе, а лежащие по
друrУIО сторону переходят на друrой лист. При указан
HOl\1 трехкратном сжатии ветвящейся окрестности сепарат
рисы останутся входящими в А и выходящими из А луча
ми, а остальные траектории превратятся в идущие вдоль
соответствующих сепаратрис кривые. Таким образом, пос
ле сжатия пучка параллельных траекторий на 3 листной
ветвящейся окрестности точки ветвления А получитс.я муль-
тиседло типа 3.
Сепаратрисы, входящие в особую точку А, следует счи
тать заканчивающимся в этой точке, ибо при выборе пути
выхода бильярдноrо шара, движущеrося по сепаратрисе,
возникает несколько возможностей каждая из выходя
щих из А сепаратрис ничем не хуже друrих. (Эту неодно-
значность мы и обходим, считая, что сепаратрисы закан
чuваются в А; образно rоворя, бильярдный шар, попав в А,
сидит там и думает, по какому же пути ему пойти, и ни-
как не MO)l{eT найти ответа. Мы бессильны помочь «думаю
щему» шару, ибо ни из каких разумных соображений вы-
брать один путь из трех нельзя, и поэтому мы считаем, что
шар останется в А. Обдумайте и вы эту ситуацию.)
Рассмотрим теперь общую задачу о поведении пучка
параллельных траекторий бильярда в каком-то мноrоуrоль-
нике Q, близких к траектории МА, заходящей в вершину
А мноrоуrольника Q. Пусть и== LBAC ........ уrол MHoro
уrольника Q при вершине А, а......... величина этоrо уrла.
Попробуем, как раньше, продолжить пучок параллельных
траекторий в уrле и== иf на уrлы и 2 , ИЗ, и 4 , ..., полу-
чающиеся из U последовательными отражениями (эти от-
ражения нужны для выпрямления бильярдной траектории
(рис. 24.6)). Строя уrлы] {Ил}, на каждом из них нарисуем
пучок параллельных траекторий в TOlVI же направлении, что
и в уrле и. Последовательно «обкладывая» вершину А yr-
лами и п , мы видим, что, вообще rоворя, после одноrо «обо...
рота» BOKpyr А свободная сторона АС исходноrо уrла и
вовсе не обязана совместиться с соответствующей стороной
AC z I{aKOrO TO из уrлов ИЛ ....... возможно, поверх Иf, и 2 , . . .
придется наложить второй слой уrлов U л: поверх BTOpO
230
f<? слоя можеТ'a[Iечь третий и т. д. РаССМОТРИ!\1 тот случай,
15 0r да после m-кратноrо обкладывания около вершины А
tIекоторая сторона АС п все-таки совместится с АС. Тоrда
J!аша процедура обрывается, и мы получаем т листную BeT
вящуюся окрестность точки А, а также пучок параллельных
'
, - I
tф ,
Рис. 24.6
траекторий одноrо и Toro же направления на каждом из т
листов. При этом следует считать, что траектория со CTO
роны АС исходноrо уrла И переходит на- сторону АС п пас-
леднеrо из уrлов U k . После m-краТНоrо сжатия ветвящейся
окрестности все т листов превратятся в т секторов вели-
чины 2'Л/т каждый; подклеив после сжатия АС п к АС, мы
получим обычную окрестность точки А. Пучок параллель-
ных траекторий на т-листной окрестности дает мультисед
ло типа т на обычной окрестности.
Заметим, что если АС п действительно совпадет с АС
и мы получим т-листную окрестность точки А, то последний
из уrлов U k имеет ч е т н ы й номер, ибо при последова-
тельных отражениях стороны AC k и ABl чередуются
(рис. 24.6). Следовательно, на т листах, составляющих
вместе уrол величины 2'Лт, укладывается четное число 2п
уrлов {U k } величины а. Отсюда 2nа==2:n:т и а==( ; ):n:.
Обратно, если величина сх исходноrо уrла и представляет-
ся в виде а==( )1'&, rде т и n взаимно просты, то леrко про-
верить, что после 2п последовательных отражений сторона
АС п впервые совпадет с АС, а уrлы Ui, и 2 , . . ., и 2n да-
дут m-листную "ветвящуюся окрестность точки А. Таким
образом, конечнолuсmная веmвящаяся окрестность верши-
ны А у ла величины а может быть построена в 'том и толь-
ко в том случае, коеда а имеет вид ( : )1'&, т. е. а соuзмерu-
231
JrlO С n. В противно л случае (коrда отношение а/л иррацио-
нально) окрестность описанноrо выше типа построить не
удается, и случай несоизмеримых с л уrлов не дает таких
«простых» особых точек, как точки ветвления конечноrо
порядка.
:n;
ЗаметиI'Л, что если а имеет вид a== , т. е. т== 1, опи-
п
санное построение сразу дает однолuстную окрестность, и
особая траектория, попадающая в точку А, может быть
естественным (и однозначным) образом продолжена за точ-
ку А. В этом случае точку А не имеет смысла считать осо-
бой. Сказанное позволяет доказать теорему 1 из 22.
Предварительно предлаrаем читателям решить неслож-
ную задачу.
3 а д а ч а 24.1. Найти все мноrоуrольники Q, все уrлы KO
торых имеют вид п/п (бильярд в таких мноrоуrольниках не будет
иметь особых точек и особых траекторий).
Решение задачи 24.1 показывает, что к указанному виду
«неособых» мноrоуrольников относятся торические MHoro-
уrольники четырех указанных в теореме 1 Э 22 видов
и т о л ь к о они. Значит, во всех остальных мноrоуrоль-
никах бильярдные пучки либо имеют особые точки типа муль-
тиседел (коrда все уrлы мноrоуrольника соизмеримы с
n), либо, если хотя бы один/ уrол мноrоуrольника несоиз:ме-
рим с л, более сложные особенности. Это и доказывает тео-
рему 1 из Э 22.
При м е р 1. Пусть и уrол величины а==2л/3. Tor-
да ero вершина А имеет 2"листную окрестность, что дает
особую точку типа седла (m===2). Такими являются все уrлы
правильноrо шесmuу ольнuка. Отсюда вытекает, что даже
бильярд в правильном шестиуrольнике имеет особенности
(см. ниже задачу 24.3).
Вернемся теперь к построению обмоток кренделей, от-
вечающих бильярдам и разберем несколько примеров их
построения.
При м е р 2. Пусть Q прямоуrольный треуrольник
с острыми уrлами аl ==л/l0 и а 2 ==2л/5. Рассмотрим пучок
параллельных траекторий в правильном 10..уrольнике Q,
составленном из 20 треуrольников, равных Q, «обложенных»
с помощью последовательных отражений BOKpyr вершин
уrла ai. Нетрудно проверить, ....что бильярд задает склейку
пар противоположных сторон Q (траектории бильярда по..
лучаются из траекторий параллельноrо пучка именно с та..
КИ viи перескакиваниями).
232
3 а Д а ч а 24.2. Произвести указанную склейку и выяснить,
к обмотке какоЙ поверхности сводится этот бильярд. Выяснить;
сколько и каких особых точек будет иметь получающаяся обмотка.
Реш е н и е. После склейки получится такой )ке, как и paHЬ
ше, крендель с двумя дырками (нарисуйте картинки самостоятель
но; СМ. также теорему Э 23). Особые точки будут получаться из
вершины уrлов сх 2 ==2л/5 это будут седла (мультиседла типа 2).
Bcero таких уrлов столько же, сколько треуrольников в 10 уrоль
нике, Т. е. 20; так как 2 .2n== 10 .2л/5, одно мультиседло полуqа
ется склейкой 10 экземпляров уrла величины СХ 2 . Следовательно,
на кренделе будет ровно 20/10==2 седла. (Друrой способ это уви
деть показать, что вершины 10 уrольника Q при склеЙке дают
на кренделе две точки А и В; каждая из них будет особой с
двумя входящими и двумя выходящими сепаратрисаМII.)
Итак, бильярд в mреУ20льнике с уелами 'Л/2, 'Л/IО, 2л/5
сводиmся к обмоmке кренделя, имеющей две особые mочки
типа седла.
Во всех разобранных ПРИIVlерах торы и крендели полу-
чались склейкоЙ сторон HeKOToporo мноrоуrольника Q, по-
лучающеrося из исходноrо мноrоуrольника Q ero уклады-
ванием на плоскость с помощью симметрий. В мноrоуrоль-
нике Q, который мы будем теперь называть фундаменталь-
ным МНО20У20ЛЬНИКОМ, рассматривался пучок параллельных
траекторий с перескакиванием с одной стороны Q на дру-
rую. Перескакивание определялось так, чтобы траектории
«скачущеrо» пучка, представляющие собой последователь-
ности пар ллельных отрезков на Q, после обратноrо «скла-
дывания» Q на исходный мноrоуrольник Q давали бы траек-
тории бильярда в Q. С друrой стороны, закон перескакива..
ния определял склейку фундаментальноrо мноrоуrольника
Q, после которой из Q получалась некоторая поверхность
. SQ (тор или крендель). Траектории пучка с перескакива-
нием после склеЙКJI давали уже непрерывные траектории на
S Q. Движение по этим траекториям называется обмоmкой
поверхности SQ. Эта обмотка может иметь некоторое число
N ==N Q о с о б ы х точек, типы мультиседел которых рав-
ны mf, т 2 , " . ., mN.
3 а Д а ч а 24.3. Исследовать бильярды в перечисленных: НИ)J(е
мноrоуrольника:х: Q (построить для них фундаментальные MHoro
уrольники Q; указать вакон склейки сторон Q; выяснить (проделав
склейку), какой вид имеет поверхность S Q найти число особыXi
точек N==NQ и их! типы ml' . . " m1v):
А) Q...... треуrольник с уrлами 'Л,/2, л/12, 5л/12;
Б) Q ......... треуrольник с уrлами n/2, 'Л/б, 3л/lО;
В) Q параллелоrрамм с уrлами 'Л/З и 2л/З
r) Q......... пара.ллелоrрамм с уrлами л/4 и 3л/4;.
Д) Q......... правильный шестиуrольник
233
Ф!lНdС1t1ентальнь;,й f!O/}epXflOCтb (KpeH N Типы
f) I1ноаоувольник (J авль роВар) Sr;=:S(P) е осооых тачех
с
*
f1 '" .. '" ,. \
" .
(А) 1
т ;::.5
8e 8(3) 5-2п =
=24- S7t
d 12
G;S *
'.. ;7, -t'
t",. ..... J . '.' : _, L",
(б) 1
де =8(2) т=о
B'2ft=
rv 3т(
t;=20fl с;; 20.ю
т= 2.;2
фф
(IЗ) . .'" с..... ". .. 1. . .,' 2
"',.. ,,.t
SQ=S(2) 2 се8да
т=5;3
**
(1) 2
8 е "=В(3)
Q =8f2
а
т=2,2 2.
2,2,2
8 се8ел
(4) fi +
V=8fi $e a(4)
Ответ к этой задаче даДИМ в виде таблицы.
Читатель может самостоятельно продолжить эту таб-
лицу, рассмотрев друrие мноrоуrольники.
rлава 9
ПОВЕДЕНИЕ БИЛЬЯРДНЫХ ТРАЕКТОРИЙ
В мноrоуrОЛЬНИКАХ
Здесь рассматриваются, в основном, бильярды
в мноrоуrольниках с соизмеримыми Q л уrлами рацио-
нальных мноrоуrольниках.
Бильярд в любом рациональном мноrоуrольнике, как и
бильярд в прямоуrольнике, сводится к обмоткам, но уже
не тора, а кренделя сферы с ручками, который полу-
чается в результате склеек нескольких экземпляров МНО-
rоуrольника. Однако обмотки кренделя, в отличие от об-
моток тора, имеют особенности......... так называемые точки
ветвления, отвечающие, rрубо rоворя, склеиваемым вер-
шинам мноrоуrольника; бильярдные же траектории, ис-
КРИВИВШИСЬ после склеек, имеют в окрестностях точек вет-
вления вид rипербол (см. 24).
Оказывается, что для обмоток кренделей справедлива
почти та же теорема, что и для обмоток тора: «типичная» об-
мотка кренделя заполняет еео ес/оду nлотюо. Эта те.орема
формулируется в 25. Результаты 25 получены Н. Н. ЗеJ..i-
ляковым и А. Б. Катком (СМ. [19] в спис е литеР'8ТУРЫ).
В отличие от обмоток тора, делящихС'я в 'точности на два
класса: периодические и всюду плотные на всем торе, на
кренделе бывают непериодические траектории, получаю-
щиеся после склеек из бильярдных траекторий и заполня-
ющие всюду плотно лишь ч а с 'т ь кренделя. Построение
такой траектории приведено в Э 26, а доказательство Toro,
что она заполняет часть кренделя, основано на теореме
Якоби. (В механике появление кренделей возникает в тех
случаях, коrда функции, выражающие законы сохранения,
«не перестановочны», или, как rоворят, «не находятся в ин-
волюции».) Наконец, в 27 доказывается, что в любом
рациональном мноrоуrольнике существует периодическая
траектория и исследуются периодические траектории в не..
которых тупоутольных треуrольниках.
235
25. Траектории
в раЦlIональных мноrоуrольниках
и оБМОl кв кренделей
в этом параrрафе мы ответим на два вопроса,
которые, возможно, уже возникли и у читателя.
В любом ли мносоусольнике Q бильярд можно свести к
обмотке некоторой поверхности SQ?
Что aaelп сведение бильярдов к обмоткам кренделей SQ?
Пре}кде Bcero опишем еще один подход к бильярдам,
дающий возможность строить пучки с перескакиванием.
Пусть Q фиксированный" мноrоуrоль-
ник. Выберем на плоскости направле-
ние отсчета уrлов скажем, будем за-
давать направление fJ на Q уrлом <р,
отсчитываемым от направления сторо-
ны АВ мноrоуrольника Q про т и в
часовой стрелки до направления 'V. Уrол
<р будем измерять в радианах, причем
так, что O <p<2n (рис. 25.1). 4t
Для каждоrо числа <р между О и 2n заrотовим свой эк-
земпляр мноrоуrольника Q, на KOTOpOlVI нарисуеlVI пучок
параллельных траекторий с направлением <р. Этот MHoro-
уrольник Q с нарисованными на нем траекториями обозна-
чим Q(<p). Таким образом, мы «запасли» бесконечный набор
экземпляров Q (<р) мноrоуrольника Q. Наложив их друr на
друrа в порядке возрастания <р, получим приз лу высоты
2л;, в основании которой лежит мноrоуrольник Q.
Рассмотрим шар, «скачущий» С одноrо мноrоуrольника
на друrие мноrоуrольники по следующему правилу. Если
в начальный момент времени шар находился на мноrоуrоль-
нике Q(<Pl), то он движется по своей траектории до тех пор,
пока не попадет на одну из сторон, скажем CD. Если бы
шар был бильярдный, то он отскочил бы от стороны CD
по закону упруrоrо отражения и стал бы двиrаться под
новым направлением <Р2. Наш же скачущий шарик переска-
кивает со стороны CD мноrоуrольника Q(<Pl) в ту же точку
той же стороны CD д Р У r о r о мноrоуrольника Q (<Р2) ,
rде <Р2 было определено выше (из закона упруrоrо отраже
ния), и движется по нарисованной на Q(<P2) траектории.
Дойдя до стороны К L мноrоуrольника Q (<Р2) , шар ик пере-
скакивает в ту же точку на той же стороне KL с л е Д y
ю Щ е r о мноrоуrольника Q (<Рз), rде <рз........ направление,
под которым движется бильярдный шар после соударения
со стороной KL, налетев на нее под направлением <Р2. На
2 6
А
в
Рис. 25. 1
уQ{срз) скачущий шарик движется по нарисованной на Q«(f)з)
траей-Тории, и так далее (рис. 25.2). Таким образом, скачv
щий шарик перескакивает с одноrо мноrоуrольника на
друrой, и ero траектория, которую мы назовем скачущей,
состоит из отрезков траекторий, нарисованных на МНО-
rоуrольниках Q (СР1) , Q (СР2), Q (СРз), . · .
Заметим, что если н а л о ж и т ь все эти мноrоуrоль-
ики друr на друrа, то отрезки скачущей траектории дадуni
траеt<т9РUЮ бильярда в МНОсОУ20льнике Q. С друrой сторо-
ны t если при л о ж и т ь Q(CP2) к Q(cpf) по стороне CD,
, ';f" 1
т';% r:
TO ;
t
Рис. 25.2
затем приложить Q(срз) К Q(CP2) по стороне KL и т. Д., то
отрезки скачущей траектории будут продолжать друr друrа,
образуя прямую линию. (Тем самым установлена связь меж.
ду только что введенным скачущим движением и' обсуж-
давшимися ранее пучками с перескакиваниями.)
Скачущие траектории, начинающиеся на одном и том же
мноrоуrольнике Q (ер1)' MorYT перескочить на разные эк..
земпляры мноrоуrольников { Q (ер) }, если они пр иходят на
разные стороны мноrоуrольника Q (cpf): скажем, приходя
на CD, траектория с Q(epi) перескакивает на Q(CP2), а при..
ходя на ED ....... на Q (cp ). Если к Q (СР1) по сторонам CD и D Е
приложить, соответственно, экземпляры Q(ep2) и Q(ep ),
то при попытке «выпрямить» О Д н о в р е м е н н о о б е
т р а е к т о р и и может оказаться, что Q «(Р2) и Q (cp ) бу..
дут иметь наложения (рис. 25.3). Однако наложившиеся
траектории физически различны (они соответствуют разным
направлениям, движения в исходном мноrоуrольнике Q),
и поэтому мы обязаны либо рассматривать двуслойную (дву-
231
л,истную) поверхность, наложенную на плоскость (это ири.. ..
водит к точкам ветвления из 24), либо считать, что экзеrvr..
пляры Q'( <Р2) и Q (ep ) «изrотовлены из эластичноrо материа
ла», и деформировать их так, чтобы при приложении (т. е.
при подклейке) их к Q(Cf)1) они не перекрывались. Дефор.
мацию экземпляров {Q(cp)} следует
делать (и это очень существенно!)
в м е с т е с FIарисованным на них
траекториями; вторая из указанных
точек зрения приводит к склейкам
e(5'?z) из мноrоуrольников {Q(cp)} различ-
Horo рода вспомоrательных поверх-
ностей, что и делалось нами ранее.
Заметим, что если Q невыпуклый
мноrоуrольник, то даже прикладыва-
иие к Q(CP1) одноrо экземпляра приводит к nерекрытuям
(и к рассмотрению мноrолистных поверхностей).
З а Д а ч а 25.1. Для каких мноrоуrольников Q ска-
чущие траектории, начинающиеея в каком-то из экземпля-
ров Q (СР1) , после всевозможных перескакиваний побываIОТ
только в к о н е ч н о м наборе мноrоуrольников Q (ер1)'
Q(CP2), . · ., Q(CPN) и не попадут ни на один из друrих экзем-
пляров Q(cp)? (Такие мноrоутольники для краткости будем
называть имеющими конечный тип. В этом и только в этом
случае можно надеяться, что после указанных выше склеек
получится какая-нибудь «конечная» поверхность, а скачу-
щий поток приведет к обмотке этой
поверхности.)
r.p' Чтобы решить сформулированную
задачу, напишем формулу для закона
перескакивания (или закона склеЙ..
ки),
. 3 а д а ч а 25.2. Пусть скачущая
тра€ктория из экземпляра Q(ep) пере
скакивает в экземпляр Q (ер') через
сторону KL, образующую с выбран-
Hым направлением АВ (от KOToporo
отсчитываются уrлы ср) уrол а. Выразить ер' через ер и а.
Реш е н и е. Соrласно определению скачущих TpaeK
торий, задачу можно сформулировать так: бильярдный шар,
двиrаясь под уrлом ер к направлению АВ, ударяется О CTO
р'ОНУ KL, образующую с АВ уrол а; найти yrOJI ср' l\fежду
направлением движения шара после удара и стороной АВ.
Из рис. 25.4 ясно, что ср'+у==сх, <p== +a Из закона уп..
pyroro отражения ==y, поэтому cp'==a........1'==cx ==cx
238
Рис. 25.3
1<
А
8
Рис. 25.4
({p a)==2a;.........q>. Нужная формула. 'получена:
ер' == 2a <p. (1)
3 а д а ч а 25.3 Обозначим стороны мнотоуrОJ1Ыlика Q
буквами ai==AB, а 2 , аз, . . ., а п ; пусть ап уrол между
стороной ап и направлением АВ (в ч:астности, cti=={)). До-
пустим, что все числа СХl, . . ., сх. п соизмеримы сп, т. е. имеют
вид ап== (m я ,!пh)1t. Доказать, что в этом ,случае мноrоуroль..
. ник Q имеет конечный тип (cм задачу 25.1).
Реш е н и е. Приведем дроби mh,/п'h, к наименьшему
общему знаменателю N запишем СХп в виде аk==(rk/N)'Л.
Докажеl'vl, что скачущие траектории, начинающиеся в мно-
rоуrольнике Q (СРО), после л ю б о r о числа перескакива..
ний оказываются в одном из мноrоуrолъников Q ( ер), rде
ер имеет вид
:1: + пZ 2
ер ::;::= <Рт === + СРо N л,
т==О, 1,2, ..., N I.
(2)
Очевидно, <Р==СРО имеет такой вид. Поэтому достаточно OKa-
зать, что если ср имеет указанный вид и из мноrоуrольника
Q(<p) траектория перескакивает в Q(q>'), то и <р' имеет такой
же вид. Допустим, что перескакивание происходит через
сторону ап. Соrлзсно формуле (1)
' 2 2 'k
<р :=:: СХ k fP == · N л......... ер ·
Если (f) == <p == :f:fPo + ; 2л, то
, '-k 2 ( + т 2 ) ........ + 7kт---.т 2 =F
tp == N л ......... =1:: <р () N 3't ':С: + (j) о N п == <р,. в'" т ,
Т. е. tp' имеет опять такой Ж'е БИД. Утверждение доказано.
3 а д а ч а 25.4. Доказать, что предположение задачи 5 З
(все rл,ы fXk соизмеримы с п) выполнено тоrда и толькО тоrдаi
коrда все rлы мноrоуrольника Q соизмеримы с п.
Мноrоуrольники Q, вее уrлы к:оторых соизмеримы с 31,
;для краткости мы называе 1 рациональными. Эти MHoro-
уrольники, как доказано, относятся к конечному типу, и
только для них бильярд может быть сведен к обмотке соот-
ветствующей поверхности. Построение этой поверхности мы
сейчас и опишем.
Приведем все числа ап из задачи 25.3 к наименьшему об..
щему знаменателю N, как в решении этой задачи, и ,раа-
смотрим 2N экзе пляров п-уrольника Q===Q (cp ), rде cp оп-
ределены формулами (2). Соrласно .задаче 25.3, мноrоуrоль-
239
НИ » этоrо Ha QR p определенной ч ярдqм' MHoro-
уr Jtьнике Q с леf;jке приклеиваются друr к друру: n.2N
CT6 OH этих мноrоуrОJlЬНИКОВ разбиваются на пары в OOT-
ветСтвии с законом склейки, и эти пары сторон подклеи-
ваются друr к друrу. Конечно, частично склейку можно
произвести, riриkладывая (без перекрытий) мноrоуrоль-
ники Q (cp ) друr к друrу на плоскости при этом получает-
ся большой мноrоуrольник Q на плоскости, который мы
ранее называли фундаментальным. Для окончательной
скЛейки следует считать фундаментальный мноrоуrольник
и мноrоуrольники Q (cp ) эластичными.
т е о р е м а 1. В результате описанной склейки MflOZO-
уzольников {Q(cp )} получится замкнутая ориентируемая
поверхность SQ, вид которой однозначно определяется на-
бором уzлов CX:i, . , ., СХ n , или же набором уzлов мноzоуzоль-
ника Q.
На доказательстве этой теоремы мы останавливаться не
будем; оно вытекает из общей теоремы 23 о склейке
поверхностей из мноrоуrольников и рассуждений 24.
Из определения склеек следует, что скачущие траекто-
рии на поверхности SQ будут непрерывными, и поток этих
траекторий дает обмотку SQ (возможно, с особыми точками).
Поверхность SQ является кренделем S (р) HeKoToporo рода р,
Т. е. сферой с р ручками (см. 23).
Можно показать, что поверхности S Q из теоремы 1 не MorYT
быть сферами (т. е. SQ=FS (О)), а торами (SQ==S (1» они являются
лишь тоrда, коrда Q принадлежит к одному из перечисленных в тео-
реме 1 из 22 торических типов. (Это следует из поминавшейся
в 8 теоремы Пуанкаре «о ветрах» на поверхностях.) Отсюда Bыl
текает, что для системы двух упруrих шаров на отрезке (см. 9 13)
их движение сводится к потокам на инвариантных торах только при
соотношениях ма сс т 1 ==т 2 , m 2 ==3т 1 и т 1 ==3т 2 , в случае же коrда
frол сх== arctg у mf/m2 с о и 3 М е р и м с n (см. 14), система шаров "
имеет две не меняющиеся со временем функции, два так называеМЫ)Q :
первых инmеерала: интеrрал энерrии Н == 1/ 2т1 vi+ '-/ 2m2v и ин-
теrрал F (ер)== I ер I mod (2л/ N) (определенный в решении задачи
25.3), и сводится к потокам на инвариантных кренделях рода р;;З::2
Итак, мы установили, что для рациональных MHoro-
уrольников изучение бильярда можно свести к изучению
обмоток кренделей.
При м еры. Проделаем описанную процедуру для
некоторых рациональных мноrоуrольников, частью уже
исследованных ранее. (
А. Q nрямоуzольник. Тоrда СХl==аз==О, СХ 2 , ===CXL[==n/2
общий знаменатель дробей N==2, и для склейки SQ нужно
24()
взять 2М ==.4 эк емпляра Q (cp) с cp:r= + cp И cp=:;:::1t::l=cpo.. «Но-
вая» склейка, конечно, дает то же; что и раньше, в 9 9,
тор.
Б. Q r-образный 6-У20льник (рис. 25.5). Здесь аl==
==аз==а 5 ==О, а 2 ==а 4 ==а 6 ==п/2, !у ==2, и SQ получается из
2N==4 экземпляров Q(cp) с ср== + сро и ср==зt + сро. На плос-
кости сразу нарисуем фундаментальный мноrоуrольник Q,
имеющий форму рамы; склеиваемые стороны обозна9ены
. r1LJ 17
114ua2. t:ф
а:5'
fJ
€В .. hr
.,'......., +
;:;:::::; . '\ 11' '
I ;: ''О .
.а" :. ..
Рис. 25.5
I одинаковыми буквами. После склейки сторон внешнеrо кон-
T pa получается тор с прямоуrольным Bыpe3 M; «оттянув»
этот вырез, отрежем кусок тора по кривом т и склеим
пары сторон с и d ........ получим тор с дыркой т, края которой
ужно приклеить к краям такой же дырки на исходном торе.
:в итоrе получим крендель S (2). Соответствующая обмотка
имеет ровно одну особую точку мультиседло типа 3,
получающееся при склейке вер-
:HQ HYTPeHHero контура рам- n Illi BiY ! т
р а Д а ч а 25.5. Постройте по- j, :X ?\::;.: :./ ': :? J;
ерхности s Q для мноrоуrольников
Q, имеющих форму букв П, О, т Рис. 25.6
(рис. 25.6).
В. Q равносторонний mреуеольник,. Для пеrо ai==O,
а 2 ==2п/3, аз==п/3; N ==3 и SQ склеивается из 2N ==6 эк-
земпляров Q(cp) дЛЯ <p==::I:<POJ 211:/3::1:сро, 4п/3::!:сро. I
241
r. Q nравильuый 6-уеольнuк. Здесь «i a4==O, a.2
ct 5==1t/3, аз==а6 2:n;/3; N==3, SQ склеивается из '2М==6
шестиуrольников Q (ер), rде ep::z= + epo, 2л/3 + еро, 4л/3 + еро.
д. Q .......... nрямоусольный треусольнuк с услами :п;/s и 3 :rt/8.
Для Hero СХl==О, сх 2 ==л/2, схз==n/s; N==8 и SQ склеи-вается
из 2N==16 треуrольников Q(ep), с ({)== + СРО+ (т/S)2л, [де
т==О, 1,2, . . .,7.
Е. Q nРЯМОУ20ЛЬНЫЙ /nреуеольник с уелами n/5 и
Зл/10. Для Hero СХl==О, CG 2 ==л/2; сх з ==л/5; N==10 и SQ склеи-
вается из 20 экземпляров Q (ер), с ер== + еро+ (т/10)2л, [де
т==О, 1, 2, . . ., 9.
Перейдем теперь к ответу 'на в т о рой вопрос: какие
выводы позволяет сделать сведение бильярдов в рациональ-
ных мносоусольниках к обмоткам кренделей? В отличие от
обl\10ТОК торов, обмотки кренделей.......... значительно более
сложный объект, и если обмотки тора были полностью ис-
следованы в S с помощью теоремы Якоби о поворотах ОК-
ружности, то аналоrичный анализ обмоток кренделей дале-
ко не так прост. Мы лишь сформулируем теорему о бильяр-
дах в рациональных мноrоуrольниках, доказываемую с
помощью рассмотрения обмоток кренделей.
Направления траекторий бильярда в любом рациональ-
ном мноrоуrольнике Q можно разделить на два класса, ко-
торые мы назовем «плохими» И «хорошими». (Определение
этих классов направлений приведено ниже.)
т е о р е м а 2. Любая траектория, идущая в «хорошем})
направлении, всюду плотно заполняет мноеоусольник Q
(либо попадет в вершину Q, u тОсда ее продолжение в обрат-
ную сторону всюду плотно заполняет Q) .......... это свойство
не зависит от начальносо положения'бuльярдносо шара. Сре-
ди траекторий, идущих в «плохих» направлениях, мосут
вСlпречаться периодические траектории. Наконец, хороших
направлений «значительно больше», чем «плохих» (множество
«плохих» направлений можно занумеровать натуральными
числаЛiU) .
Приведем построение, с помощью KOToporo определяют-
ся «плохие» направления.
Зафиксируем пол жение AiA 2 . . .А п мноrоуrольника Q
на плоскости, и разрешим «перекатывать» мноrоуrольник Q
из cBoero первоначальноrо положения последовательными
отражениями (переворачиваниями) относительно ero сто-
рон (в произвольной последовательности), и отметим на
плоскости в с е точки В1, В 2 , . . ., в которые JMorYT попасть
вершины мноrоуrольника Q. (Множество этих точек 93==
== {Bi, В2, . . .}, разумеется, бесконечно, однако счетно.)
242
«Плохими» направлениями называются направления Bce
возможных лучей вида AkBk, rде Ak любая вершина
мноrоуrольника Q в исходном положении, В l произ..
вольная точка множества :в. Остальные направления Ha
зываются «хорошими». В следующем параrрафе будет при..
веден пример бильярдной траектории, идущей в «плохом»
направлении, но не периодической.
3 а Д а ч а 25.6. Доказать, что для произвольноrо мноrоуrоль
ника Q (даже иррациональноrо) есть хотя бы одно «хорошее» Ha
правление.
3 а д а ч а 25.7. Построить множество &l для торических MHO
rоуrольников и проверить, что теорема 2 для них выполнена.
3 а д а ч а 25.8. Построить множество CffJ для правильноrо
Q уrольника; для ромба с уrлом n/з (и для параллелоrрамма с Ta
КИМ же уrлом).
3 а д а ч а 25.9*. Доказать, что для правильных n уrольников
при п*3, 4 и 6 множество dlJ всюду плотно на nлоскостu, т. е. в
любом Kpyre произвольноrо радиуса в найдется хотя бы одна точка
&TOrO множества. \
Реш е н и е. Достаточно доказать, что множество cvft Ц е н T
Р О В мноrоуrольников всюду плотно. Е.сли правильный n уrоль-
ник Q перекатить через свои стороны ч е т н о е число р'аз, то
стороны полученноrо n уrольника Q' будут параллельны сторонам
исходноrо, так что Q' получается из Q параллельным переносом.
Докажем две леммы.
Л е м м а 1. Если 1nри вершины А, В, С nараллелоерамма
прuнадлежат множеству aJ/;, та и четвертая еео вершuна D ,nак{ясе
принадлежuт множеству 0.;#.
Д о к а з а т е л ь е т в о следует из Toro, что мы сможем
пройти из точки С в точку D, осуществляя те же параллельные
перевосы мноrоyrольника, что и при переходе из точки В в точку А.
Л е м м а 2. Множество &f{; переходит в себя nри повороте на
уеол 2n/ n вокруе любой из еео точек.
Д о к а з а т е л ь с т в о. Построим цепочку n уrольников, при
мыкающих друr к друrу по стороне и «соединяющих» наш n уrоль
ник Q с центром в точке О с n уrольником с центром в любой дpy
rой точке А множества GJt. При повороте на уrол 2n/ n BOKpyr точки
О эта цепочка мноrоуrольников переходит в друrую цепочку, coe
диняющую исходный мноrоуrольник с мноrоуrольником, центром
KOToporo является точка А', полученная из А тем же поворотом.
Следовательно, точка А' также принадлежит множеству C>/It и лемма 2
доказана.
Мы хотим доказать, что множество rYft всюду плотно на
плоскости, в 'частности, что в нем найдутся сколь уеодно близкие
точки.
Предположим, что это не так, т. е. предположим, что все pac
стояния между точками множества GIIt больше HeKoToporo положи
тельноrо числа d. Отсюда и из леммы 1 следует, что' a1t ...... реш е T
к а, т. е. точки множества GJft ---- ЭТО точка пересечения двух се..-
мейств параллельных прямых разрезающи1С плоскость на оди
наковые параллелоrраммы (докажите это сами). Но из леммы 2
следует, что эта решетка переходит в себя при повороте на утол 2n/ n.
ИЗ ЭТОl"'О немедленно- следует, что суи{ествует nравиЛЬRЫЙ n уеоль
243
I I
ник с вершинами в ее узлах. Докажем, что тоrда п может быть paBHQ
только 3, 4 и 6 это будет противоречить условию задачи и тем
самым опроверrать наше предположение, что множество G.Jt не всюду
плотно.
Числа п==3, 4 и 6 подходят. Если n==5, то, проведя в правиль--
ном 5 уrольнике с вершинами в узлах решетки Q//t в с е диаrо--
нали, получим, что 5 иXl точек пересечения так)ке принадлежат
решетке (как четвертые вершины параллелоrраммов, три из ко--
торых узлы решетки). В полученном меньшем 5 уrольнике',
подобном исходному, опять проведем все диаrонали........ получим
меньший подобный 5 уrольник с вершинами в узлах и т. д. В конце
концов сторона пятиуrольника станет меньше минимальноrо рас--
стояния между узлами решетки, и в этот момент возникнет пр<r
тиворечие.
Если )ке n 7, то все отрезки, соеДИНЯlощие центр О n уrоль--
ника с ero вершинами, параллельна перенесем в узел решетки,
чтобы точка О I совпала с этим узлом. Вторые концы этиXl отрезков
будут также лежать в узлах решетки rYft по лемме 1. Проделав это
построение нужное число раз, придем к тому, что возникнет n--
уrольник с вершинами в узлаXl. все стороны KOToporo меньше ми--
нимальноrо расстояния между узлами реПlетки OJIt ---- противо-
речие. Задача 25.9 решена.
Оказывается, множество :УЗ, построенное выше по МНО-
rоуrольнику Q, «почти для всех» мноrоуrольников Q (на-
пример, для иррациональных мноrоуrольников) всюду плот-
но на плоскостиl Попробуйте это доказать.
3 а д а ч а 25.10. Докажите, что для почти всех начальныl
положений двух упруrих точечных шаров на отрезке [О, а}, массы
которых относятся как 1 : (3+ 2 У 2) , множество точек их столк--
новений друr с друrом всюду плотно на отрезке [О, а].
Реш е н и е. Движение шаров эквивалентно бильярду
прямоуrольном треуrольнике Q с уrлом л/8, поскольку (см! 14)
тl ==
m2
1 == 3...... 2 У2 == (У2 ..... 1)2 ==
3+2 У2
::::: ( 1..... cos (Л/4» ) 2 == ( 2 sin 2 (л/8) ) ==t 2"::
sin (л/4) 2 sin (л/В) cos (л/В) g 8 11
"'
Выбрав для бильярдной частицы в треуrольнике Q «хорошее»
направление, получим в нем, по теореме 2, всюду плотную биль--
ярдную траекторию. Точки излома траектории, лежащие на rи--
потенузе, всюду плотно ее заполняют. Но эти точки и отвечают
точкам столкновений шаров на отрезке [О, а], что и требовалось
доказать.
Теорема 2 для торических мноrоуrольников была дока-
зана в части 11; для остальных рациональных мноrоуrоль-
ников (даже для правильноrо 6 уrольника) элементарное
ее доказательство в настоящее время неизвестно.
Про бильярды в мноrоуrольниках, хотя бы одиН уrол
которых несоuзмерuм с Л, известно совсем HeMHoro. Как фи-
244
зики, так и математики уверены в справедливости следую..
щих утверждений. .
r и п о т е з а 1. Если хотя бы один уеол мноеоуеоль-
ника Q несоизмерим с n, то «типичная» траектория би-
льярда в Q всюду плотно заполняет мноеоуеольник Q.
r и п о т е з а 11. Более тоео, типичная траектория
бильярда проходит (<<рано или поздно») сколь уеодно близ-
ко к любой наперед заданной точке мноеоуеольника Q под
направлением, сколь уеодно близким к любому наперед за-
данному направлению в этой точке. (Как следует из задачи
Рис. 25.7
25.3, утверждение rипотезы 11 в случае рациональных МНО"
rоуrольников несправедливо. С друrой стороны, теорема 2........
TO утвер}кдение rипотезы 1 для рациональных мноrоуrоль..
ников. Слова «типичная траектория» имеют смысл выбран-
ная наУ2ад траектория).
Недавно математики С. Кирчкоф, r. Мазур и Дж. Смай-
ли доказали, что для бесконеЧНО20 множества «иррациональ-
ных» мноеоуеольников еиnотеза 11 справедлива *). Однако
для nроизвОЛЬН020 иррациональноrо мноrоуrольника Q она
пока не доказана. (Здесь уместно отметить, что rипотеза 11
доказана для бильярда в так называемых «BorHYTbIX» МНО"
rоуrольниках ....... в области Q, оrраниченных дуrами кри-
вых, выпуклыми внутрь Q (эти бильярды носят названия
«бильярдов Синая»; см. Заключение); она также доказана
для бильярда в прямоуrольнике с вырезанным из Hero кру-
rOM (рис. 25.7). Обе упомянутые теоремы очень сложны и не
элементарны.) Для бильярдов в иррациональных MHoro-
*) Эти авторы доказали также, что для «почти всех» поверх-
ностей S Q' rде Q ...... рациональный мноrоуrольник, бильярдный по-
OK на них эрrодичен. Используя их результат, А. М. Степин и
Ф. Эрдман доказали, что для «массивноrо» множества прямоуrоль-
HDlXi «'реуrольников (так называемоrо «всюду плотноrо множества
второй катеrории») бильярд эрrодичен; тем самым для механической
системы «два упруrи шара на отрезке» эрrодичность является «ти-
iIичным свойством.
245
уrольниках пока что неизвестно доказательство даже тако-
ro «ослабления» rипотезы 1:
r и п о т е 3 а о. В nроизвОЛЬflОМ МflО20У20ЛЬfluке Q су-
ществует хотя бы одна траектория, всюду плотно запод-
няющая Q.
Доказано пока только следующее утверждение, при-
надлежащее К. Болдриrини, Ф. Маркетти и М. Кину: ти-
пичная бильярдная траектория в nроизвольном МНО20уеоль-
нике сколь У20дно близко подходит хотя бы к одной из е20
вершин (причем это доказательство опять-таки не эле-
ментарно).
В пользу этих rипотез, выдвинутых на основе «общих
физических соображений», rоворят. только результаты чис..
ленных экспериментов на ЭВМ. (В этих экспериментах для
простоты р сематриваются бильярды в прямоуrольных тре..
уrольниках, отвечающих системе двух шаров на отрезке.)
В заключение отметим два весьма интересных икраеи..
вых направления, в которых можно развивать изложенные
здесь методы и идеи. Первое.......... это бильярды в MHororpaH"
никах, второе.......... бильярды в сферических мноrоуrольни"
ках (т. е. в мноrоуrольниках на сфере, оrраниченных ду..
rами больших KpyroB; бильярдный шар в этом случае ДВИ--
жетея по дуrам больших KpyroB и отра2f{ается от сторон по
закону «уrол падения равен уrлу отражения». СМ. reOMeT"
рическое доказательство утверждения в 9 17).
3 а д а ч а 25.11 *. Пусть Q....... мноrоrранник. Ввести (опре.-
делить) «скачущие траектории» и решить задачу 25.1 для этоrо
случая.
26. Может ли непериодическая траектория
в выпуклом мноrоуrольнике
не быть всюду плотной в нем?
П о л о ж и т е л ь н о М у ответу на выне-
сенный в заrоловок вопрос будет посвящен весь настоящий
параrраф. Более тото, оказывается, что непериодические и
не всюду плотные траектории бывают уже в рациональных
мноrоуrольниках. Из теоремы 2 25 немедленно следует,
что все такие траектории идут в «плохих» направлениях,
и поэтому не являются типичными. Однако сама возмож"
насть существования этих траекторий rОБОрИТ о rораздо
большей сложности структуры обмоток инвариантных
кренделей, чем обмоток торов, которые либо периодические,
либо всюду плотны.
Точный ответ на поставленнЫЙ ВОПРОС заключен в сле-
ДУlощей теореме.
246
Т е о 'р е м а 1. Для люБО20 п на ,плоскости сущесmвуеПl
qыnуклый n УсОЛЬНUК Q, в котором найдется неnерuодuче
екая и не всюду nлопUiая бильярдная траектория у.
Докажем мы эту теорему конструктивно для каждоrо
r:t предъявим n уrольник и бильярдную траекторию в нем,
оторая будет обладать указанным свойством. Опишем план
доказательства. Мы рассмотрим только случай n 4, а
'rлучай треуrольника (п==3), как существенно более СЛО2Коа
ВЫЙ, затронем в конце параrрафа.
А
,l
l
;
.. .;/ :i!
', .-. ;< ,
с
о"
n=В
Рис. 26.1
Сначала будет построен специальный выпуклый шестu
уеольник АВСА' В' С', в котором мы укажем бильярдную
траекторию, всюду плотно ero заполняющую, причем би
льярдный шар н и раз у не отраз.ится от сторон АВ и
А'В'. Затем, продолжая пары сторон АС', ВС и В'С',
А ' С до их пересечения в точках L и L', получим четblрех
уеОЛЬflUК LCL' С', в котором указанная бильярдная траек"
тория ни разу не попадет в окрестности ABL и А' В' L' Bep
шин L и L' (рис. 26 1, а). Тем самым теорема будет доказана
для n ==4. Для n===5, 6, 7, . . ., . . . доказательство получа
ется просто из случая n==4: достаточно обрезать светлые
уrолки у четырехуrольника LCL' С', как мы получим MHO
rоуrольник с нужным числом сторон, а бильярдная TpaeK
тория в нем (например в 9-уrольнике на рис. 25.1, б) по-
прежнему будет всюду плотно заполнять шестиуrольник
АВСА' В'С' и не будет заходить в обрезанные окрестности
вершин L и L'.
Приступим К построению искомоrо шестиуrольника
АВСА'В'С' и нужной нам бильярдной траектории. Шести...
уrольник АВСА'В'С' будет удовлетворять следующим ус-
ловиям:
1 . Он цеflmрально сuммеmричен: ABIIA'B', AC'[IA'C и
BCIIB'C' (рис. 26.2; стороны АВ и А' В' считаем верти
кальными); ,
20. УсОЛ при вершине А равен n/2+a, усол при вершине
В равен Jt/2+ , еде О<а, р<л/2, причем
ctg 2а > tg , ctg 2 > tg (Х (1)
247
(условия (1) возникнут сами собой, коrда мы в дальнейшем
станем исследовать бильярдную траекторию);
30. Перпендикуляр кстороне АС' в точке А является одно-
временно биссектрисой У2ла LBAC, а перпендикуляр к сто-
роне ЕС является одновременно биссектрисой У2ла LABC!
(рис. 26.2).
Приведем rеометрическое построение шестиуrольника G
такими свойствами. Зафиксируем острые уrлы а и .
а) Проведем через конец А отрезка АВ прямую АС ПОД
уrлом 2а, а через конец В прямую ВС' под уrлом 2
(рис. 26.2). Обе прямые АС и ВС' пе-
ресекутся в некоторой точке, посколь-
IЗ' ку 2а+2 <л.
б) Проведем биссектрисы уrлов
LBAC и LABC'.
А' в) К первой биссектрисе проведем
· через точку А перпендикуляр АС' и
ко второЙ биссектрисе.......... перпенди-
куляр ВС. Точки С' и С получаются
как точки пересечения проведенных
перпендикуляров к биссектрисам с
ПРЯIv1ЫМИ ВС' И АС. В результате по.
лучится фиrура, затемненная на рис. 26.2.
r) Осталось провести прямые С' В' 11 ве и СА' 11 АС'
и отложить на них отрезки С' В' ==ВС и СА' == 4C', а затем
соединить отрезком точки А' и В'.
Нетрудно видеть, что построенный шестиуrольник
АВСА' В 'С' будет центрально симl\;lетричныltII (требование 1 О)
и удовлетворять требованиям 20 и 30.
Объясним «бильярдный» смысл условия 300 Допустим,
что мы послали точечный бильярдный шар из точки В в
точку А вдоль стороны БА, забыв на время, что А и В
вершины. Тоrда шар отразится от прямой АС' и пойдет по
прямой АС в вершину С. Точно так же, если шар движется
из вершины А в вершину В, то он, отразившись от прямой
ЕС, попадет в вершину С'. Таким образом, ВАС и АВС'
двухзвенные «предельные» бильярдные траектории, вооб..
ще то исключаемые нами из рассмотрения (мы доrоворились
в прошлых параrрафах считать попавший в вершину уrла
шар застрявшим в ней), но иrрающие важную роль при до-
казательстве. Тем же свойством обладают двухзвенные би-
льярдные траектории А'В'С и В'А'С' (рис. 26.3), коrда шар
движется из вершины в вершину вдоль стороны А'В'..
Пусть теперь бильярдны шар расположен в не которой
точке Х внутри шестиуrольника АВСА' В' С'. Запустим ero
248
о'
А
с
. Построение
шестUI/В ОЛЫllJК[(
Рис. 26.2
со скоростью, по модулю равной 1, параллельно стороне
АВ вверх. Дока)кем, что при некотором выборе услов а и
вся бильярдная траектория движения шара вс/оду плотно
заполнит шестиусольник АВСА' В' С' .
Рассмотрим для доказательства пучок отрезков внутри
шестиуrольника, параллельных стороне АВ, концы кото-
рых принадлежат rранице шестиуrольника. Наш шар дви-
жется вверх вдоль одноrо из этих отрезков MN. После пер-
Boro отражения от стороны шестиуrольника (АС' на
рис. 26.3) он движется по отрезку N М' параллельно диа-
rонали АС и, отразившись в точке , .
М/ от противоположной стороны СА', с
начинает двиrаться вверх по друrому
отрезку из пучка параллельных:
М/ N' "АВ (это происходит вследст-
вие свойства 3° шестиуrольника
АВСА' В'С'). Следовательно, можно
рассмотреть бильярдное преобразова-
ние пучка параллельных отрезков,
переводящее отрезок MN в отрезок
М/ N/, т. е. одно вертикальное звено
бильярдной траектории в следующее вертикальное звено
этой же траектории, а сам пучок в себя (рис. 26.3). А как
ведут себя наклонные звенья траектории, параллельные
либо диаrонали АС, либо диаrонали ВС'? Очень просто: если
шар отразился от одной из сторон АС' или СА /, то наклонное
звено будет идти параллельно диаrонали АС; если же шар
отразился от стороны ВС или симметричной еЙ В'С/
то параллельно диаrонали ВС'.
Это дает нам возможность по абсциссе х точки Х, в ко-
торой находится шар, движущийся вертикально вверх, оп-
ределить абсциссу t(x) точки, в которой окажется шар, Kor-
да будет двиrаться по следующему вертикально лу звену
своей траектории. Поместим непосредственно под шести-
уrольником rОРИЗ0нтальный отрезок [О, 1], отметив ero
концы числами О и 1 (О это проекция стороны АВ, 1
проекция А' В' на отрезок), и спроектируем весь пучок вер-
тикальных отрезков на этот отрезок. В результате проек-
ции каждое звено пучка перейдет в о Д н у точку, а весь
пучок целиком в отрезок [О, 1]. Под действиеlVl бильярд-
Horo преобразования каждое вертикальное звено бильярд-
ной траектории переходит в следующее вертикальное звено,
следовательно проекция х этоrо звена перейдет в проекцию
f (х) BToporo вертикальноrо звена. Как по числу х вычислить
число '(х)?
,.,r
С
v
Пучок траектор/)ц
Рис. 26.3
249
Для ответа на этот вопрос естественно весь пучок парал
лельных отрезков разделить на два: левый от стороны АВ
дО вертикальной прямой 1, проходящей через вершину С'
шестиуrольника, и правый от прямой 1 до стороны А' В'
(рис. 26.4). Левый пучок спроектируется на отрезок [О, а],
а правый на отрезок [а, 1].
Точка О левый конец отрезка [О, 1] под действием
t переходит в точку f(О), которая есть проекция на [О, 1]
вертикальноrо звена, прохо-
дящеrо через вершину С (в это
звено переходит сторона АВ
под действием бильярдноrо
с/'
IJ
1
с l
.о х !J (1. 9 {Q+(t a) ,
Рис. 26.4
.;t
JS
.....
Q)
о ........"...... ;=2а , f
Д
{ "ffc)=X+b b= a
t::)
. O !
r(r(3J»== + 2.0
.
T(T(Tr;r;)))= + lJ
Рис. 26.5
о х а
1
преобразования), а точка а проекция вертикальноrо
звена C'D' (рис. 26.4) в точку {(а)==1 (в проекцию сто-
роны А'В' на отрезок [О, 1], т. е. в ero правый конец). He
трудно сообразить, используя равенство противоположных
сторон параллелоrрамма, что, поскольку точка а смести-
лась вправо на 1 а, то и в с е точки отрезка [О, а] под дей-
ствием преобразования f сместятся вправо на l a, т. е.
{(0)===1 a, и вообще f(x)==x + (1 a) при О x a.
Если же вертикальное звено принадлежит правому пуч-
ку и проектируется в точку у на отрезке [а, 1], то аналоrич
ные рассуждения показывают, что под действием бильярд-
Horo преобразования оно перейдет в звено, проектирую-
щееся вточкуу аЕ[О, 1], т. е. f(y)==y a при a y l.
Наrлядно действие преобразования f отрезка [О, 1] co
стоит в перемене местами отрезков 10, а] и [а, 1], или, по
друrому, в nерекладblваflUU этих отрезков (рис. 26.5). BBe
дем обозначение Ь== 1 а. Мы получили, что
t х+Ь при хЕ[О, а];
,(х)==\ x a при хЕ[а, 1]. (1)
Если свернуть отрезок [О, 1] в ОКРУЖНОСТЬ 81 единичной
250
длины, то выписанная двойная формула для t превратится
в одинарную:
f(x)===x+b при xES 1 . (2)
Действительно, при О x a эта формула совпадает с ис-
ходной, а при x a точка f(x)==x a==:(x+b) 1 на
окружности 81 совпадает с точкой х+Ь (так как длина
окружности равна 1).
Таким образом, перекладblваfluе 1 двух отрезков эквива
лентно повороту окружноспzи 81 на уrол Ь== l a. Поэтому
можно воспользоваться теоремой Якоби из 2 и сформули
ровать следующее
у т в е р ж Д е н и е. Перекладblванuе f двух опzрезков
[О, а] u [а, 1} является либо периодическим при рациональ
ном а, либо всюду плотНblllt при иррационально.М а: тpa
ектория любой точки' х Е [О, 11 (последовательность f(x),
I(t(x)), I(t (1 (х))), · · .) либо пери- 01
одическая, либо всюду плотно
заполняет оmрезок [О, 1].
Из этоrо утверждения выте- А
кает, что пр и рациональном а
бильярдная траектория в шее-
тиуrольнике АВСА' В' С' перио-
дическая (замкнутая), а при ир-
рациональном а всюду плотно
заполняет весь шестиУ20ЛЬНИК.
Нам осталось поэтому лишь по-
добрать такой шестиуrольник,
чтобы для Hero число а было иррациональным. Зафикси-
руем длину стороны АВ (с фиксирования отрезка АВ мы
начали построение шестиуrольника АВСА' В' С') и выразим
числа а и Ь== 1 а через АВ и уrлы а и р. Обратимся к
рис. 26.6.
Из прямоуrольноrо 6 АМС ' получаем С'М==АМх
xtg а ==atg сх, а из прямоуrольноrо 6.Bc'N......... C'N==
==BN. tg (л/2 2 )==а ctg 2 . Поскольку, с одной стороны,
MN==C' N.........C' М==а (ctg 2 .........tg а), а с друrой MN ==АВ,
находим АВ==а (ctg 2 tg а) и
АВ
а == ctg 2 tg а ·
Аналоrичным образом можно получить формулу дЛЯ Ь:
АВ
Ь :::z: ctg 2(;(..... tg · (4)
Положительность чисел а и Ь эквивалентна выполнению ус-
ловия 2<?, накладываемому на шестиуrольник.
1
1
(3)
Q51
Поскольку отрезок АВ фиксирован, а функции ctg 2
и tg непрерывны, мо)кно непрерывным изменением уrлов
а И добиться Toro, чтобы отношение AB/(ctg 2 tg а)
стало иррациональным (это отношение иррационально
для почти всех сх и из интервала (О, п/2)). Итак, для по-
чти всех шестиуrольников число а == а (сх, ) иррацио-
нально.
Следовательно, для почти всех шесmиУ20льников, yдoв
леmворяющих условиям 1 о, 20, 30, указанная бильярдная тpa
ектория всюду nлопzна в них, что u требовалось доказать.
Таким образом, для n == 4 и для n> 4 теорема доказана.
Для п == 3 теорему доказывать не будем; отметим только,
что существует равнобедренный треуrольник с очень тупым
уrлом при вершине, в котором специальным образом (очень
хитрым!) построенная бильярдная траектория всюду плот
но заполняет лишь некоторую ero часть. Доказательство в
случае n==3 опять сводится к рассмотрению перекладывания
двух отрезков, возникающеrо при специальных симметрич
ных отражениях треуrольника относительно ero сторон.
Следствием теоремы 1 для n == 3 служит теорема 3 из
14. Действительно, для «rаза» из двух точечных молекул
на отрезке конфиrурационным пространством является пря-
моуrольный треуrольник, а если отношение l\laCC молекул
очень велико, то острый уrол этоrо треуrольника очень мал.
Отражая треуrольник относительно катета, лежащеrо про-
тив этоrо уrла, получаем равнобедренный треуrольник с
очень тупым уrлом (близким к л) при вершине. Неперио-
дическая, но и не всюду плотная траектория в этом Tpe
уrольнике заполняет всюду плотно конечное число отрезков
на 2иnоmенузе исходноrо треуrольника, что и доказывает
теорему 3 из 14.
Формулы (3) и (4) для вычисления а позволяют постро"
ить К О Н К Р е т н ы е n уrольники, в которых указанная
бильярдная траектория всюду плотно заполняет лишь не..
которую часть. Можно даже построить р а Ц и о н а л ь-
н ы е мноrоуrольники с этим свойством. Построим сначала
шестиуrольник АВСА'В'С', дЛЯ KOToporo а==л/12, ==
==п/6........ уrлы при ero вершинах А, В, С равны 7п/12, 2п/3
и 3:n:/4 соответственно. Заметим, что нам в действительности
достаточно рроверить, что отношение h (сх, )==a/b==a/ (1 а)
иррационально (объясните сами, почему); ЧИС"lIО а/Ь уже не
зависит от длины отрезка АВ. Вычисляем:
( п 3Т ) а (Y 1 ) ' ( 1 1 ) Y
h 12' 6' ==-ь== 3 уз I уз 2+УЗ ==2+ 3,
252
т. е. а/Ь иррационально и, значит, указрнная выше бильярд-
ная траектория в таком шестиуrольнике всюду плотна.
Продлевая ero стороны до взаимных пересечениЙ, как на
рис. 26.1, а, получаем параллелоrрамм с уrлами л/4 и
Зл/4, а обрезая специальныl'л образом эти уrлы, как на
рис. 26.1, б, получаем друrие мноrоуrольники с уrлами,
соизмеримыми с Л, т. е. рациональные мноrоуrольники,
обладающие требуемой бильярдной траекторией.
мыI знаем (см. Э 25), что бильярд в рациональных МНО-
rоуrольниках сводится к обмоткам кренделей. В случае
параллелоrрамма с уrлами л/4 и
Зл/4 бильярд в нем сводится к об
моткам кренделя рода р==З (сферы
с тремя ручками), имеющеrо два
мул ьтиседл а одинаковых типов
тl==т 2 ==3 (см. таблицу к задаче
24.3). Проследим, как на этой по-
верхности сфере с тремя ручка-
ми ведет себя построенный пу-
чок параллельных отрезков.
Мы знаем, что бильярдное пре-
образование пучка параллельных
отрезков, описанное выше, являет-
ся перекладыванием двух отрезков,
что наrлядно можно изобразить в
виде потока кривых на двойной
«ленте» (р ис. 26.7).
Эта двойная лента тополоrически эквивалентна (roMeo-
морфна) тору 1r с дыркой, так}ке показанному на рис. 26.7.
Бильярдная траектория в шестиуrольнике на торе lr всюду
плотно заполняет ero, Оl\1ывая оба береrа дырки (смыкаю-
щихся в особых точках А и В, причем из первой во вторую
идут две сепаратрисы): левый пучок параллельных отрез-
ков в шестиуrольнике омывает дырку на торе слева, а пра-
вый справа. К этоЙ дырке подклеивается сфера с двумя
ручками, в которой также имеется дырка: обе поверхности
подклеиваются краями своих дырок по их rраницам. Итак,
nосmроенная бильярдная траектория всюду плотно запол-
няет одну ручку поверхности S (3) и не заходит на осталь-
ные две ручки.
Такая же тополоrическая ситуация имеет место и в об-
щем случае для построенноrо р а Ц и о н а л ь н о r о
n*уrольника: бильярдная траекпzория заполняет всюду плот-
но одну из ручек поверхности S (р), отвечающей эmому n-
уеодьнику (число ручек р зависит от типов мулыrшседел,
253
clA/J
Рис. 26.7
т. е. oпz услов при вершинах п-усольника), u не заходит на
остальные ручки. Это следует опять-таки из Toro, что в
пучке параллельных отрезков происходит перекладыва-
ине двух отрезков, т. е. имеет место картина, изображен..
ная на рис. 26.7
Сформудируем в заключение две интересных, но труд-
но доказываемых теоремы о периодических бильярдных
ТР,аекториях в рассматриваемом п-уrольнике Q и о неперио..
дических, но и не всюду плотных траекториях в трехмерных
мноrоrранниках.
т е о р е м а 2. Пусть Q п-У20льник из теоремы 1.
Тоеда для любой наперед заданной точки в шестиУ20льнике
АВСА' В' С' внутри Q сколь У20дно близко к этой точке про..
ходит периодическая бильярдная траектория, направле..
ние которой сколь yzoaHO мало отличается от вертикаль-
НО20 (параллеЛЬНО20 отрезку АВ).
Можно сказать и по-друrому:
Пусть Q п-уrольник из теоремы 1, Х произволь..
ная точка в шестиуrольнике АВСА'В'С' внутри Q. Тоrда
бильярдный шар можно поместить в точку М, сколь уrод..
но близкую к точке Х, и запу ст ить ero под таким малым yr..
лом к вертикали (т. е. почти параллельно стороне АВ),
что шарик опишет периодическую бильярдную траекторию.
Отметим, что при доказательстве теоремы 2 существен-
ным образом используются свойства цепных дробей. И,
наконец,
т е о р е м а 3. В пространстве существует выпуклый
МНО202ранник, в котором найдется непериодическая бильяр
дная mраектория, заполняющая всюду плотно трехмерную
область внутри не20.
Таким мноrоrранником является прямая призма Q, в
основании которой лежит n-уrолъник Q из теоремы 1. Ока-
зывается, бильярдному шару можно придать такую началь-
но/ю скорость 'V, что проекция шара на основании призмы
Q будет описывать всюду плотную траекторию в шести-
уrольнике АВСА' В'С' внутри Q, а ero проекция на образую-
щую призмы заполняет ее всюду плотно; таким образом,
траектория шара всrоду плотно з-аполнит призму Q' С осно-
ванием АВСА' В'С' и той же высотой, что и призма Q. Дока-
зательство этой теоремы также не элементарно.
Прямая треуrольная призма служит конфиrурационным
пространством «rаз.а из двух молекул» шаров масс тl и
т 2 одинаковоrо диаметра D, и:rvrеющих одинаковую верти
кальную состаВЛЯЮЩУIО сКорости'....... расположенноrо в
квадрате размером 1 х 1 с упруrо отражающими стен-ками.
254
-
\
r ... ,
I 1
1, \
I l'
I 1 i(
l (
..
I ....
\( I
1) Nи Q
'11
,,? I
Рис. 26.8
Точки столкновения этих шаров всюду плотно заполняют
несколько прямоуеОЛЬflИКОВ. внутри этоео Keai}pama
I
(рис. 26.8). Это утверждение вытекает из теоремы 3 Э 1'4 и
теоремы 3 настоящеrо параrрафа.
27. Периодические траектории
в мноrоуrольниках и мноrоrранниках
1. Мы уже MHoro узнали о свойствах биль'яр
дов в разнообразных мноrоуrольниках. Мы узнали, что в
торических мноrоуrольниках каждая бильярдная TpaeKTO
рия либо периодична, либо всюду плотна (э 22); что дви
жение бильярдноrо шара в рациональном мноrоуrольнике
эквивалентно движению фазовой точки по некоторой по
верхности обмотке сферы с ручками (э 24); что типичные
траектории в рациональных мноrоуrольниках заполняют
их всюду плотно (э 25), но что не всякая траектория 'ЯВilI'Я
ется либо периодической, либо всюду плотной (э 26), как
это имеет место для торических мноrоуrОJIЬНИКОВ.
Однако мы еще не задавали такой «п'ростейший» вопрос:
а в каждом ли МНО20уеОЛЬfluке существует периодическая
бильярдная траектория?
До сих пор полноrо ответа на Hero нет даже для Tpe
уrольников. В этом параrрафе будет дан ответ лишь для pa
ционаЛЬНblХ мноrоуrольников и приведены известные в Ha
стоящее время и просто описываемые конструкции периоди
ческих траекторий в довольно большом классе треуrоль
ников.
Читателям, внимательно изучившим 6 rл. 2, может
показаться, что теорема Биркrофа о наличии периодической
бильярдной траектории с любым ЧИСJIОМ звеньев в любой
выпуклой области с rладкой rраницей переносится и на слу-
чай выпуклых I\lноrоуrольников. Однако это не так чуть
позже мы докажем, что у периодических траекторий в HeKO
торых треуrольниках число звеньев не может быть MeHЬ
шим заранее заданной величины, и укажем на то «препятст
Вие», из за KOToporo доказательство TeopeMы БИРI{rофа для
255
мпоrоуrольников «не ПРОХОДИТ» (см. в связи с этим задачу
6.8) .
Доказательство существования периодических бильяр-
дныIx траекторий в рациональных мноrоуrольниках, приве
денное в этом параrрафе, интересно тем, что в нем неожидан
ным образом используется абстрактная теорема Пуанкаре
о возвращении из 3, которая будет применена к инвари
антной поверхности, описанной в 24. Кроме Toro, теорема
Пуанкаре позволит сделать некоторые интересные выводы
и Для случая произвольной (не обязательно MHoroyro b
ной) области, в которой движется бильярдный шар. При
написании этоrо параrрафа нами частично использована
статья [14].
2. Прежде чем переходить к конкретным утверждениям
о периодических траекториях в мноrоуrольниках и их до-
казательствам, сформулируем справедливую, на наш взrляд,
rипотезу о периодических бильярдных траекториях в лю-
бой области на плоскости, до сих пор не доказанную и не
опроверrнутую.
r и п о т е з а. В Лf{)бой оеранuченной области Q на
плоскости с кусочно zладкой 2раницей существует nepиo
дическая бильярдная траектория.
(То же утверждение о периодических траекториях, По-
видимому, справедливо и в пространстве любоrо числа изме-
рений. Аналоrичная rипотеза о существовании в любой
оrраниченной области хотя бы одной всюду плотной траек"
тории уже неверно например, всюду плотных траекто-
рий нет в Kpyre и в «телефоне» Q2 из 5 rл. 2.)
3. Начнем исследование периодических траекторий в
мноrоуrольниках с решения задачи 6.7 задачи Фаньяно.
Т е о р е м а 1" В любом осmроуеольном треУ20льнике
АВС существует периодическая траектория. А именно она
cOCmOuпl из трех звеньев, образующих вписанный треУ20ЛЬ-
ник миНU; lаЛЬНО20 пери.метра; верtUИНbl этоа.о треуеольника
явля/опzся основаНИЯJiU высот исходflО20 остРОУ20ЛЬНО20
треУ20льнuка АВС *).
Д о к а 3 а т е л ь с т в о. Мы докажем сначала, что СТО-
ронь! треуrольн ика, вершины KOToporo Р, а, Е оспа-
*) Дадим механическую интерпретацию трехзвенной периоди-
ческой траектории в остроуrольном треуrольнике АВС. Пусть на
каждой из ero сторон надето по колечку, которые свободно MorYT
скользить по сторонам. Колечки попарно соединим натянутыми ре-
зинками и отпустим. При этом колечки и резинки образуют верши..
ны и стороны треуrольника наименьшеrо периметра, вписанноrо
в АВС, который одновременно является периодической бильярдной
траекторией в нем,
256
в ния высот АЕ, вр и са треуrольника АВС, образуют
периодическую бильярдную траекторию. Для этоrо доста-
точно доказать, что все «уrлы падения}) равны соответст-
вующим «уrлам отражения»: LAFG == LEFC, LAGF
== LBGE, LBEG == LCEF.
Докажем, например, что LAFG == LEFC (остальные
равенства получаются аналоrично). Пусть высоты АЕ, вр
и са пересекаются в точке Н. В
Построим на отрезках АН и
СВ, как на диаметрах, две ок-
ружности (рис. 27.1).
Первая окружность пройдет
через точки G и р, поскольку
LAGH == LАFН=='Л/2, а вторая
по аналоrичной причине че-
рез точки Е и Р. По теореме
о вписанных уrлах имеем:
LAFG== LAHG (оба ВПИGанных
уrла опираются на одну и ту же дуrу окружности ........АО)
и LEFC== LEHC (как опирающиеся на дуrу ........Ес). Но
уrлы LAHG и LEHG вертикальные; из их равенства
следует, что LAFG== LEFC, что и требовалось доказать.
Таким образом, мы доказали, что ОЕра ----- периодиче-
СI<ая бильярдная траектория в 6.АВС.
Докажем теперь, что 6,ОЕР имеет минимальный пери-
метр среди всех треуrольников, вписанных в 6ABC, это
свойство является эксmремальным (в данном случае ........ МИ-
НU/YlаЛЬНbtМ) свойством периодической траектории ОЕра.
А'
А
в"
и"
е"
" I
" с "
а
Рис. 27.2
Рис. 27.1
А
Е'
ё
е"
с' G С" {J
о
Для этоrо будем выпрямлять траекторию ОЕРй: 6.АВС
отраЗИi\tl от стороны ВС; полученный таким путем ,6А 'ВС
отразим от стороны СА'; результат этоrо BToporo отражения
отразим от стороны А' В' и после этоrо произведем еще три
отражения последовательно от сторон в' С', С' А" и
А 11 В" (рис. 27.2, а).
9 r. А. rальперин, А. Н. Земляков
257
Обратим прежде Бсеrо внимание на то, что конечное
А " В " С " б
положение может ыть получено ИЗ начальноrо
положения АВС простым nараллеЛЬflbtМ nереносо.м. Чтобы в
этом убедиться, посмотрим, что происходит G треуrольни-
ком после двух первых отражений. Очевидно, что эти два
отражения эквивалентны одному повороту. ABC по ча
совой стрелке BOKpyr неподвижной вершины С на уrол 2С
(буквами А, В, С обозначены и величины уrлов при вер-
шинах А, В, С). Точно так же мы моrли бы перевести ero
из этоrо положения в пятое вращением по часовой CTpeJII<e
около неподвижной точки В' на уrол 2В и, наконец, вра-
щением на уrол 2А BOKpyr неподвижной точки А" мы при-
вели бы ero в положение седьмое, Т. е. в конечное. В итоrе
ABC повернулся по часовой стрелке на уrол 2А+2В+
+2С==2(А+В+С)==2п.- в результате ABC совершает
полный оборот и принимает то же положение, что и вначале,
оказываясь лишь передвинутым по плоскости параллельно
себе. В частности, АВ 11 А"В", АС 11 А"С" и ЕС 11 В"С".
Нетрудно видеть, что 6,ОРЕ после всех 'указанных отра-
жений перейдет в 6О"Р"Е", причем длина отрезка ЕЕ" будет
равна удвоенному периметру OPE -----это следует из Toro,
что по доказанному ОР Еа ....... бильярдная траектория, и
u
поэтому она после указанных отражении «выпрямится»
именно в отрезок ЕЕ" (рис. 27.2, а). Стороны любоrо дру- .
roro 6ИVW, вписанноrо в 6АВС, после Toro же набора
отражений перейдут в ломаную И. . .И", причем, как HeT
РУДНО показать (докажитеl), отрезок ИИ" будет параллелен
отрезку ЕЕ" и равен ему по длине (используйте то, что ВС 11
"В"С"). Значит, длина этой ломаной будет б о л ь ш е длиныI
отрезка ии"==ЕЕ", т. е. периметр 6UVW будет больше
периметра 6ОЕР. Значит, периметр 6ОЕР минимально
возможный, что и требовалось доказать.
З а м е ч а н и е. Кроме периодической траектории
ОРЕа в остроуrольном 6АВС существует бесконечно мноео
друrих периодических траекторий. Действительно, если
МБI пошлем шар не по отрезку РЕ, а по близкому и паРЗJ1.
лельному ему отрезку Р' Е', который мы можем выбрать
бесконечным числом способов, то шар опишет «параллель-
ную» ОРЕа периодическую траекторию F'E'G'F"E"G"f"
вдвое большей длины, чем аРЕа (рис. 27.2, б). Докажите
это утверждение самостоятельно. Таким образом, траек-
тория орЕО....... это как бы «сдвоенная» траектория
р' Е'О' Р" Е"а" Р'.
Вообще, если r периодическая бильярдная траекто-
Р!1 Я внекотором мноrоуrольнике Q, то любая близкая ей
2F8
«пар аллельная» (в указанном выш смысле) траектория r"
таюке будет периодической, так как шар отражается от тех
}ке самых сторон и в той же последовательности. Значит,
построив одну периодическую траекторию, мы одновре-
менно получаем бесконечно MHoro друrих периодических
траекторий той же длины. Это множество траекторий
носит название «пучок параллельных траекторий».
4. Для тупОУсОЛЬflО20 треуrольника дело обстоит rораз..
до сложней. Во-первых, в нем только основание одной из
высот поп дает на сторону, а не на ее предложение; осталь.
ные два основания лежат вне треуrольника, поэтому дока-
зательство теоремы 1 «не работает». Нельзя получить в
тупоуrольном треуrольнике периодическую траекторию из
u
трех звеньев еще и потому, что вписанныи в Hero треуrоль-
ник минимальноrо периметра вырождается в высоту ВН,
опущенную на максимальную сторону АС. Более Toro, в
конкретном тупоуrольном треуrольнике периодическая
траеI{ТОРИЯ из минимально возможноrо количества звеньев
может быть очень длинной. А именно справедлива
т е о р е м а 2. Для любосо натураЛЬНО20 числа псу-
ществует тупоусольный треУ20ЛЬНИК Аве, в котором лю-
бая периодическая бильярдная траектория имеет. больше
чем n звеньев.
Д о к а з а т е л ь с т в о. Выберем такие малые числа
а и , чтобы число N (а, )==min {......[......п/а], .......[ n/ ]}
превосходило заданное число n (N (а)== [.........п/а]\........ мак-
симальное число отражений шара в уrле величиной а).
Кроме Toro, потребуем, чтобы числа сх, и 3t были рацио-
нально независимыми, Т. е. чтобы если хотя бы одно из
ц е л ы х чисел k, т, 1 отлично от О, то сумма k(X+m +
+lл=FО. Возьмем числа а и в качестве острых уrлов ту-
поуrольноrо f::.:. АВС (выраженных в радианах). Если в
6 АБС нет ни одной периодической бильярдной траектории
(мы считаем........ см. rипотезу, что TaKoro никоrда не
бывает), то теорема 2 доказана. (Это чисто лоrическое вы-
сказывание: если kakoro-то объекта не существует, то для
Hero выполнено л ю б о е свойство, в частности то, что
звеньев у несуществующей периодической траектории боль-
ше п.)
Пусть теперь r ........ некоторая периодическая траектория
в 6.АВС. Докажем, что у нее имеется хотя бы одно звено
ХУ, концы KOToporo лежат на боковых сторонах АВ и ве
(р ис. 27.3, а).
Предположим противное: пусть бильярдный шар после
каждоrо удара от боковой GTOpOНbI попадает на основание
j* 9
АС" Т. е. отражается от еторон треуrольника так: боковая
сторона оенование .... боковая сторона основание .....
. . .
Тоrда из рис. 27.3, б можно определить, как связаны
уrлы Q' и Q" двух соседних отражений шара от основания:
либо Q" ==ср.......2а, либо Q" ==Q'+2 (см. по этому поводу зада-
Л чу 25.2, rде для друrоrо
уrла приводится похожая
. . фОРМУJIа). Следова ельно,
C если сро........ начальныи уrол,
А а fi под которым шар был запу-
щен к основанию АС, то
после HeKoToporo очередно-
ro отражения он равен
Ф==сро+т ......kа, rде т и
k .......... целые числа. Посколь-
ку траектория r периоди-
ческая, при некоторых т
и k уrол Ф должен отли-
чаться от уrла СРО на полное число оборотов:
Ф == СРо + 2ns ::::;> <Ро + m ka == СРо + 2ns
/ (.......... k) а + т + ( s) 2л == о.
Мы получили, что а, и 3t рационально вйвисимы, а это
противоречит выбору уrлов а и . Следовательно, наше
предположение о том, что шар после каждоrо отражения от
боковой стороны попадает на основание АС, неверно, Т. е.
u
В последовательности ero отражении от сторон треуrоль..
ника обязательно встретится пара
. . . боковая сторона боковая спl0рона . . .
Итак, периодическая траектория r действительно содержит
такое звено ХУ, что Х Е АВ, У Е ВС.
Посмотрим, как движется шар после пролета по звену
ХУ (допустим, от Х к У). В силу малости уrлов а и
отрезок ХУ либо параллелен основанию АС, либо наклонен
к АС под малым уrлом. «Выпрямляя» бильярдную траек-
торию, видим, что шар будет после пролета по отрезку ХУ
ДБиrаться в LBCA дО тех пор, пока не столкнется с ero
сторонами ве и СА максимальное возможное число раз
N ( )== [........n/ ] (см. Э 15, п. А); лишь после всех этих от-
ражений шар «вылетит» из LBCA, т. е. начнет отражаться
только от сторон АВ и АС. Обратив движение шара во
времени, аналоrичным образом исследуем ero движение
в LBAC после пролета по звену ХУ от У к X Шар будет
260
. /P a. IЗ
" I W Р
А , trJ т" С
VJ 9' 5 r т
Рис. 27.3
двиrаться в LBAC дО тех пор, 'пока не совершит в нем
максимальное возможное число отражений N (cx)== [ п/a].
Итак, траектория r содержит не менее N (сх, )==min {N (сх),
N ( )} звеньев, что соrласно выбору уrлов сх и превосхо"
дит исходное число n. Теорема 2 доказана.
5. Теорема 2 показывает, ЧТQ для мноrоуrольника тео-
реl'ла Биркrофа «Не работает». Это объясняется тем, что в
теореме Биркrофа рассматриваются cTporo выпуклые об-
ласти, rраницы которых являются 2ладкимu кривыми, т. е.
не имеют изломов, как у мноrоуrольников. Если начать
проводить доказательство этой теоремы для мноrоуrольни
ков, то сразу видно «препятствие», не позволяющее ее дока-
зать. Оно состоит в том, что нужная периодическая траек"
тория из даННОI'О числа n звеньев имеет часть своих точек
излома в в ерш и н а х мноrоуrольника, а такие траекто-
рии нами не рассматриваются. Если rраницу мноrоуrоль
ника у всех вершин «сrладить», то для. полученной обласrи
теорема Биркrофа уже будет верна, при этом все точки
излома у периодической n"звенной траектории (rде п<
<N (сх, ) из теоремы 2) будут сосредоточены на «сrла-
женных» участках, и только при n>N (сх, ) шар начнет
отражаться от прямолинейных участков rраницы.
6*. Рассмотрим одно общее свойство БИJIЬЯРДНЫХ тра-
екторий в произвольной области Q. Имеет Me TO важная
Т е о р е м а 3. Почти любая бильярдная траектория
r в облtEти Q либо является периодической, либо проходит
СКОЛЬ У80дно близко и под СКОЛЬ усодно малым услом к любоЙ
своей точке.
3 а м е ч а н и . Теорема 3 отнюдь не утверждает, что
если бильярдная траектория в Q не периодична, то она всюду
плотна в Q. Напомним, что в конце 26 указан пример об
ласти Q, в которой построенная траектория не периодична
и не всюду плотна в Q. Друrой пример Q Kpyr.
Д о к а з а т е л ь с т в о этой теоремы основывается на
рассмотрении Ф а 3 о в О r о пространства системы. (Чи-
тателю мы рекомендуем здесь еще раз просмотреть 3.)
А" Фаз о в о е про с т р а н с т в о. Множество на...
правлений, под которыми бильярдный шар может двиrать..
ся с единичной скоростью, образует
а) окружность 81 В случае плоской области Q;
б) двумерную сферу s в случае пространственной об...
ласти Q (а если Q ........ n"мерная область, то (n l) мерную
сферу Sп--l).
Точками фазовоrо пространства Q являются пары
(q, (1), rде q поло}кение шара в области Q (точка), а
261
t{J направление движения шара, I{оrда он находится в
точке q; можно считать, что v ......... это точка (конец вектора)
на окружности 81 в двумерном случае, и точка на сфере
Sn--1 для больших размерностей.
Мы оrраничимся здесь п л о с к о й областью Q; в общем
случае доказательство повторяется почти дословно, с за...
меной «окружности» на «сферу». Окружность 81 можно
представлять себе в виде отрезка [О, 211:], У KOToporo «скле-
ены» КОНЦЫ О и 211,. Фазовое пространство Q получается из
прямоrо произведения Q на 81, Т. е. из множества пар (q, v),
rде q Е Q, fI Е 81, некоторыми склейками. Ero можно пред-
ставить наrлядно в ВИде призмы, в основании которой
(rp'J
!l
J
расположена область Q, а образующей является полуинтер-
вал [О, 211:). Надо помнить только, что мноrие точки rрани-
цы этоrо цилиндра Q «склеены» ........ представляют совпадаю-
щие точки (например склеены оба основания призмы ..........
нижнее и верхнее). Далее, вся призма «расслоена» на бес-
конечное число слоев........ областей Q «(1), причем Q ('lJ) .....-..
это исходная область Q, но снабженная пучком параллель-
ных отрезков в направлении v: шар на слое Q ('lJ) движется в
направлении (1, в какую бы точку ero ни поместить. Можно
на плоскости, содержащей область Q, выбрать некоторую
ориентированную ось 1 и направление (1 заменить уrлом <р,
образованным этим направлением с осью 1(O ep<211:).
Тоrда шар после отражения от rраницы Q начнет ДБиrаться
в направлении f}', образующем некоторый новый уrол ер' (}
осью 1 (рис. 27.4). В цилиндре Q это будет отвечать тому,
что фазовая точка, двиrаясь по слою Q ('lJ)==Q (ер) и дойдя до
ero rраницы, «перескочит» на слой Q «(I')==Q (ер'), соответ-
ствующие ТОЧI{И (А, ер) и (А, ср') rраниц Q(cp) и Q(q/) при
этом склеятся друr с друrом. (Эта ситуация в точности соот-
ветствует описанию «скачущей» траектории из 25, поэтому
советуем читателю еще раз перечитать начало 25.)
262
Б. Ф а 3 о в Ы е т р а е к т о р и и. Итак, фазовая тра-
ектория это скачущие в цилиндре Q со слоя на слой OT
резки; если осуществить все склейки точек rраницы ци-
линдра типа (А, ep) (A, ер'), то получится непрерывная
кривая в трехмерном фазовом пространстве Q. В 25 в ка-
честве областей Q подробно рассматривались рациональ-
ные мноrоуrольники, и в результате всех склеек возникал()
непрерывная фазовая траектория, целиком расположенная
на некоторой двумерной поверхности сфере с ручками
S (р). Этот важный факт нам приrодится позже. В общем
случае фазовая кривая не лежит ни на какой поверхности,
а каким-то сложным образом располаrается в трехмерном
мноrообразии Q.
В. Т е о р е м а Л и у в и л л я. Теорема состоит в
том, что бильярдный фазовый поток, т. е. совокупность
бильярдных преобразований St в фазовом пространстве Q,
сохраняет объем в Q. Это означает, что если в Q выделИТЬ
некоторую область fЛ, то под действием бильярдноrо пре..
образования S t эта область перейдет за время t в область
fД' ===St (51,) Toro же объема.
Докажем теорему Лиувилля в случае, коrда выделение
области 5lc:Q это одновременное выделение какой-то
площадки Р в бильярде Q и kakoro-то отрезка 8. на обра-
зующей цилиндра [О, 2л). Затем одновременно из в с е х
точек {q} площадки Р мы выпускаем с единичной скоростью
бесконечное число бильярдных шаров, каждый под своим
уrлом ер, отвечающим некоторой точке отрезка Д. Через
время t все шары займут новое положение {q'} и образуют
площадку Р'; при этом они будут двиrаться под уrла-
ми {ер'} из HeKoToporo HOBoro отрезка 8.' образующей ци-
линдра.
Пока шары движутся внутри бильярда Q, отрезок 8. на-
правлений их движения не меняется: 8.'===8., при этом пло-
щадь р' равна площади Р, а значит и объемы трехмерных
областей 51, и f/t' одинаковы (они равны произведению пло-
щади Р на длину отрезка Д). Коrда же происходит отраже
ние относительно rраницы Q, то, разбивая rраницу бильяр
да Q на мелкие дуrи и заменяя каждую такую дуrу l\1алым
отрезком, получаем после процедуры «выпрямления» близ-
ких траекторий через этот малый отрезок, что площадь пло
щадки р' не изменилась и длина отрезка 8.' новых направ-
лений движения шаров также не изменилось; стало быть,
не изменился и объем области f/t' в цилиндре Q ----- он остал
ся равным объему исходной области f/t. Теорема Лиувилля
для бильярдов доказана.
'263
[. т е о р е м а П у а н к а р е о в о з в р а Щ е н и и.
Таким образом, отображение 8t удовлетворяет условиям
теоремы Пуанкаре о возвращении: St(Q)==Q и St сохраняет
меру (объем) в Q. А тоrда из этой теоремы следуеТ t что
n о ч т и в с е точки из л ю б о й окрестности и ТОЧI{И
(q, tJ) Е Q снова возвращаются в ту же окрестность и. Это и
означает, что бильярдный шар вновь (притом бесконечное
ЧИGЛО раз!) возвращается как в сколь уrодно малую окрест-
ность своей исходной точки q бильярда Qt так и в сколь уrод-,
но малую окрестность исходноrо направления ер. Если би-
льярдная траектория в Q пер и о Д и ч н а, то фазовая
точка приходит в точности в исходное положение (q, <р)
бесконечно MHoro раЗj если же бильярдная траектория в Q
н е пер и о Д и ч н а, то можно показать, что в общем
случае она заполнит всюду плотно некоторую подобласть
фаЗОБоrо пространства Q.
Все сказанное выше верно в случае, коrда число слоев
{Q(ep)} бесконечно. Для этоrо случая теорема 3 доказа-
на. Однако не всеrда множество слоев {Q (ер)} бесконечно.
7*. Остановимся особо на случае, коrда Q рациональ-
ный МflоzоуеОЛЬflИК. Тоrда множество {Q(ep)} состоит ИЗ
к о н е ч н о r о числа слоев: бильярд-
ный шар в мноrоуrольнике, выпущен-
ный под произвольным уrлом СРО К
одной из своих сторон, после всевоз-
u
можных отражении от rраницы MHoro-
уrольника может двиrаться лишь в ко-
u
нечном количестве направлении СРО, CPit
ер2,. . ., ер N (рис. 27.5). в 24 было дока-
зано, что после соответствующей склейки
слоев Q (еро), Q (СР1), Q (ер2),. .., Q (ср N)
Рис. 27.5 возникает поверхность G!t....... сфера с
ручками, инвариантная (т. е. переходя-
ll\8Я в себя) относительно действия фазовоrо (бильярдноrо)
нотока St. При этом фазовый поток St сохраняет, как было
уже сказано, фазовый объем, и опять применима теорема
Пуанкаре о возвращении. Из нее, в частности, следует, что
фазовая точка бесконечно MHoro раз попадает в сколь уrодно
малую OKpeCT OCTЬ точки (q, еро), т. е. попадает в точки (q '
' ) 1 " '
q> , rде q q 1<8 И Icp........ep I < 8 (8 произвольное,
заранее выбранное малое положительное число). Но если
число 8 очень мало, Т. е. меньше всех величин IcpO.......epi 1,
, cpi.......ep j 1, r де [, j == 1 ,. · . t N, j=l= i, то I сро.........ер" <8 пр И
())' Е {СРо, ср!, . . ., ср N} будет выполняться лишь для <р' ==
2ft
1} (r:'N)
". . .
Q (St'
I)(rp.,)
Il(f!'q)
64
==fPo, Следовательно, для рациональноrо мноrоуrольника Q
мы доказали более сильное утвер}кдение.
т е о р е м а 4. Любая бильярдная траектория r в
рациОflаЛЬflОht МflО20У20ЛЬflике пересекает любую окрест..
НОСП1Ь любой своей точки под одни,М, и тем же flаправленuе.Аl,
(а не под сколь У20дно близким).
Иными словами, бильярдный шар в рациональном мно"
rоуrольнике Q может быть запущен под проиэвольным
фиксированным уrлом СРо К выбранному направлению 1
отсчета уrлов так, что он будет бесконечно MHoro раз под-
ходить сколь уrодно близко I{ своему начальному положе-
нию под т е м ж е с а м ы м уrлом <Ро К прямой 1.
Заметим, что о наличии периодической траектории в Q
теорема 4 ничеrо не rоворит. Более Toro 26 дает примеры
траекторий, удовлетворяющих теореме 1, но не периоди-
ческих.
8. И тем не менее остается сделать еще один только ма-
ленький шаr, чтобы получить периодическую траекторию в
л ю б о м рациональном мноrоуrольнике.
т е о р е м а 5. В любом рациОflальном МНО20У20ЛЬflU1re
Q СУlцествует периодическая траектория.
Д о к а 3 а т е л ь с т в о *). Выберем в качестве оси 1
И п. 6А произвольную сторону АВ мн6rоуrольника Q.
Положим в теореме 4 сро==п/2. Это означает, что шар послан
перпендикулярно стороне АВ.
Докажем, что в этом случае шар можно выпустить из
такой точки стороны АВ, что ero движение будет периоди"
ческим.
Действительно, соrласно утверждению теоремы 4, шар
может быть запущен по прямой р AB из точки С стороны
АВ так, что через некоторое время он снова будет двиrаться
по некоторой прямой р', перпендикулярной АВ и проходя..
щей вблизи от р. Если прямая р' совпадает G р, то все дока-
зано: шар отражается перпендикулярно от стороны АВ и
движется по первоначальной траектории. Не менее очевиден
*) Приводимое доказательство предложено А. М. Степ иным.
Недавно американский математик f. Мазур. используя мощные
современные аналитические методы, доказал, что множество на-
правлений звеньев периодических траекторий всюду плотно на
окружности 81 , Т. е. звенья периодической траектории в рациональ-
ном мноrоуrольнике MorYT образовывatfЬ сколь уrодно малый уrол
с любой наперед выбранной прямой. Таким образом. узки пучков
паr.Jаллельны периодически:м траекторий в рациональном MHoro-
rольнике в действительности бесконечно MHoro. Преимущества
теометрическоrо доказательства состоит в том, что оно обобrцается
и на рациональные мноrоrранники (см, п. 10).
265
и случай различных прямых р и р': если шар движется по
прямоЙ р' о т с т о р о н ы АВ, то следовательно, перед
. ,
этим он двиrался по прям:ой р к с т о р о н е АВ. Значит,
после отражения от стороны АВ шар пойдет в т о ч н о с т и
по тому же пути, по которому он двиrался до отражения, но
в обратном направлении. А это и означает, что траектория
ero движения периодическая. Теорема 5 доказана.
С л е Д с т в и е. В любом рациональном п уеольнике Q
СУLl{eспюует не менее 11,/2 несовпадающих периодических lпра-
eKlпopuu, U.ktеющих разНЫЕ наборы сторон, с которыми
происходят столкновения шара.
Д о к а з а т е л ь с т в о. По теореме 5 периодическую
траеКТОРИIО можно направить перпендикулярно к а ж Д о й
из п сторон мноrоуrольника. Однако эти траектории' MorYT
иметь один и тот же набор сторон. Поскольку никакая
траектория не может иметь звенья, перпендикулярные
б о л е е ч е м двум сторонам f\1ноrоуrольника, получаем,
что не менее п/2 из этих траекторий имеют разные наборы
отра}I{ений. Следствие доказано.
Нетрудно построить n-уrольник, в котором р о в н о
п/2 различных периодических траекторий со звеньями,
перпендикулярными сторонам: это любой 2k уrольник (п==
==2k) с попарно параллельными сторонами (например,
правильный 2k-уrольник).
11з теоремы 5 получается очень красивая rеом:етричесlЦtЯ
картина на тои инвариантной поверхности, которая склеи-
вается из нескольких экземпляров данноrо мноrоуrольника.
Эта поверхность в общем случае является сферой с р руч-
ками S (р) и некоторым !{оличеством особых точек........ муль-
ТIIседел разных типов (см. 25). На этой поверхности
«перпендикулярная» периодическая траектория r, пост-
роенная в доказатеtlIьстве теоремы 5, замкнута и, разумеется,
не попадает ни в одну особую точку. Начав двиrать по сто-
роне АВ точку С, из которой перпендикулярно АВ запу-
скается шар, ВИДИМ, что траектория r будет периодической
тоrда и только тоrда, коrда она не попадает ни в одну особую
точку на повеРХНОС1И S(p). Это соответствует тому, что
перпендикуляр р, восстановленный в точке С на основании
АВ, не проходит ни через одну из вершин мноrQуrольников,
полученных отражениями из исходноrо мноrоуrольника Q
при выпрямлении траектории r (при этих отражениях
траектория r переходит в перпендикуляр р; рис. 27.6).
Как только перпендикуляр р пройдет через какую-то вер-
шину одноrо из отраженных мноrоуrольнпков, так сразу
траектория r попадет в особую точку на поверхности S (р).
66
Из рис. 27.6 видно, что д л я в с е х т о ч е к С, ле>кащих
на интервале С 1 С 2 сАВ, rде Ci, С 2 основания перпен
дикуляров Р! и Р2 К прямой АВ, проходящих через две
вершины отраженных мноrоуrольников, запущенный из
точки С шар опишет периодическую траекторию одной и
той же длины. Перпендикуляры
Р! и Р2 задают «коридор» перио ,.......,,"/
u u" ..... 1/ '. "
дических траектории равнои ".: '/ .; , .....,. .'
длины. Можно доказать (этоrо . ..... , ( \. ': ....
мы делать здесь не будем), что
весь отрезок АВ разбивается на
к' о н е ч н о е число отрезков,
каждый из которых задает се-
мейство периодических «перпен-
u
дикулярных» траектории одина-
ковой длины (траектории в воз-
никающих «коридорах» имеют
одинаковую последовательность
отражений). Отсюда следует,
что длины «перпендикулярных»
u
траектории оrраничены.
9. Вернемся вновь к периодическим траекториям в тре-
уrольниках. Пусть а и ....... величины острых уrлов А и С
ABC: О<а, <п/2. Проведем на плоскости две взаимно
перпендикулярные оси и будем отмечать на rоризонталь-
ной оси величину уrла а, а на вертикальной......... величину
уrла . Пара (а, ) характеризует (с точностью до подобия)
треуrольник АВС, которому поставим в соответствие одну
точку М с координатами (а, ) на плоскости Oa . Напри..
мер, точке М== (n/З, n/З) соответствует равносторонний
треуrольник, а точке М == (n/4, п/4) ......... равнобедренный
прямоуrольный треуrольник.
3 а д а ч а 27.1. а) Какие треуrольники соответствуют точкам
(л/б, л/З); (л./l00, л/lОО); (а, ), rде а+ >л/2; а+ <л/2? б) Ka
ким треуrольникам отвечают точки на плоскости Oa , отстоящие
от начала координат (О, О) на расстояние, меньшее л/lОО?
О т в е т. а) Прямоуrольный; равнобедренный тупоуrольныЙ;
остроуrОЛЬНЫЙi тупоуrольный. б) Тупоуrольные треуrольники с
тупым уrлом 1'>(100...... V 2 )л/l00.
Множество точек (а, ) на плоскости Oa заполняет
в первой четверти квадрат OXYZ без rраницы со стороной
п/2: О<а<:n;/2, O< <п/2. Этот квадрат назовем «диаrрам
мой треуrольников» D.
Отметим на диаrрамме D те точки (а, ), для которых в
отвечающих им треуrольниках с острыми уrлами а и
существует периодичеСI<ая траектория. I
(JQ2
Рис. 27.6
fj
'267
Из теоремы 1, ДОI<азанной выше, следует, что на диаrрам-
ме отмечены в с е точки, идущие выше диаrонали XZ квад-
рата OXYZ, соединяющей вершины Х== (О, п/2) и z==
== (п/2, О) (рис. 27.7, а). Действительно, верхний (закра
шенный) 6XYZ на рис. 27.7, а отвечает в с е м остроуrоль..
ным треуrольникам, поскольку для этих точек cx+ >
>п/2, а тоrда третий уrол треуrольника у==п....... «(X+ )<
<л: /2 ......... остр рIЙ .
Всем точкам XOZ на диаrрамме D п о Д Д и а r о н a
JI ь Ю XZ квадрата отвечают туnоуеОЛЬНblе АВС, посколь"
ку при (Х+Р<n/2 тре..
тий уrол треуrольника
у==л:....... (а+ »п/2 ........ ту-
пой (все nрямоуеОЛЬНЬte
тре..уrольники отмечены
u
l-' точками самои диаrона-
ли XZ). Если каждый
из yr лов (х и соизме
рим с Л, т. е. если а==
== (р/q)л:, == (т/п)л, р,
q, т, п целые числа,
то 6.А8С ........ рациональный (третий уrол '\' тоже соизмерим
с п); отсюда по теореме 5 в 6 А ВС существует периоди
ческая траектория. Следовательно, на диаrрамме D OTMe
чены все рациональные точки в треуrольнике OXZ, запол
няющие ero всюду плотно (рис. 27.7, б). Множество таких
точек счетно, а ero мера (площадь) равна О.
, Однако можно указать в l:::::. OXZ более «массивное» МНО-
>I\ество отмеченных точе , имеющее ненулевую площадь.
Оно возникает при рассмотрении следующих трех конст-
рукций, ул<е не связанных с соизмеримостью' уrлов а и
С Л.
;s
х (iJ, )
"
z (f ,o)
а
Рис. 27.7
{}
oQJ,OJ
КОНСТРУКЦИЯ 1.
Т е о р е м а 6. Пусть острые У2Лbl а и ABC связаны
соотношением k(X==m <1t/2, еде k и т..... некоторые Hamy
раЛЬН,blе числа. Тоеда в дАВС существует периодическая
Illравкmорuя.
Д о к а з а т е л ь с т в о. Отразим ABO зеркально k........}
раз относительно своих сторон, начиная (3 отражения OTHO
сительно стороны АВ и двиrаясь против часовой стрелки
(при каждом таком зеркальном отражении вершина А
неподвижна) и т раз относительно своих сторон, начиная с
отражения относительно стороны АС и двиrаясь также
против часовой стрелки (при этих ОТРClli{ениях неподвижна
268
вершина В ..... ем. рве. 27.8). «Конечные» стороны отражен-
ных треуrольников АВ' в ЭА' в силу равенотва ka==mp бу.
дут параллеЛЬНБI ДРУl' друrУJ АВ' 11 ОА', а в GИЛУ условий
ka<n/2, тр<п/2, и еторонам АВ' и СА' можно провеоти
общий перпендикуЛЯр Hf.H 2t целиком лежащий в «коридо-
ре» отраженных треуrольников (рис. /3'
27.8). Если запустить бильярдный
шар по отрезку НЖН2' Gчитая АВ' и
СА I отражающими Gтенками, ТО он
будет еовершать периодическое движе-
н и е Н i........ Н 2........ Н 1........ Н '}/_.... Н i........ Н 'А......... · .
между АВ' и СА'. Следовательно,
сделав обратные отражения треу-
rольников (k отражений по часовой
стрелке Q неподвижной вершиной А
и т+ 1 отражений по часовой стрел-
ке\с неподвижной вершиной С), «свер-
нем» отрезок Н iH 2 в бильярдную тр а-
екторию в 6АВС, которая, очевид-
Но, будет периодической, что и тре-
бовалось доказать.
3 а д а ч 8 27.2. Из KaKoro числа звеньев состоит построенная
периодическая траектория?
.4в1 I СА'
А'
Рис. 27.8
3 а м е ч а н и е 1. Из теоремы 6 следует, что в любом
равнобедренном треуrольнике оуществует периодическая
lIt . ntt. 8
се
А
{JJ
А с
#2.
Q
8 Hz.
1-1.'
А . ... Ла 1f
(д Hz. "
/l
Рис. 27.9
бильярдная траектория из Д в y x звеньев (рис. 27.9, а).
Однако если острый уrол при основании АС таков, что
nа<'Л/2 при некотором n, то существуют периодические
траектории из четырех, шести, . . ., 2п звеньев (рис. 27.9,6).
Вообще, если обе части равенства krx==тP можно умно-
жить на такое число n, что будет по-прежнему п. ka==п. т <:::
<п/2, то ИЗ равенств 2. krx:::;:2. т , 3. ka==3. т , . . .
269
. . . t n .ka==п.пzP и приведенных выпеe рассуждений сле-
дует, что в 6,АВС существуют периодические траектории
из k+т, 2 (k+rn) , 3 (k+т), . . ., n (k+т) звеньев. «Парал..
лельные» им периодические траектории состоят из Toro
же числа звеньев.
3 а.м е ч а н и е 2. В равнобедренном рациональном
треуrольнике есть еще один замечательный тип периоди-
ческих траекторий: если у траектории r одно звено V па-
раллельно основанию АС, то r ---- периодическая TpaeI{TO
рия. Это следует из теоремы 4.
Действительно, по теореме 4 сколь уrодно близко к зве-
ну у проходит друrое звено у' траектории r, параллельное
(быть может, ,,' и V СОВ-
(d падают). Запустим из точки
7t М пересечения высоты ВН
2 и звена в противопо-
ложных направлениях од-
новременно два одинако-
rt вых бильярдных шара с
4- ... равными скоростями. Через
некоторое время они одно-
временно окажутся в точке
М' пересечения высоты ВВ
", и звена у', двиrаясь на-
встречу друr друrу, ОТ-
толкнутся друr от друrа и
начнут двиrаться симмет-
рично в обратных направлениях по уже пройденному пу-
ТИ. Следовательно, через какое-то время шары вновь ока-
}f(УТСЯ в точке М на звене V, столкнутся, и процесо начнет
повторяться. Это и доказывает, что траеI{ТОРИЯ r........ пе-
РIlодическая. (Более Toro, отсюда вытекает, что у r имеется
не более двух звеньев, параллельных АС.)
Аналоrичное утверждение справедливо для любоrо
рациональноrо мноrоуrольника Q, имеющеео ОСЬ симметрии:
u
послав шар перпендикулярно этои оси, получаем периоди-
ч скую траекторию. Удовольствие повторить приведенное
рассуждение для этоrо случая мы предоставляем читателям.
Конструкция 1 (теорема 6) дает на треуrОЛЬнике OXZ
диаrраммы D «веер» отрезков, лежащих на прямых { ==
=== (k/m)cx}, начинающихся в начале координат (О, О) и кон-
чающихся в точках {(л:/(2k), п/(2m))}, rде k и т...... BceB03
можные натуральные числа (РИG. 27.10). «Веер» состоит ИЗ
(QeTHOrO множества отрезков и имеет нулевую плоскую
rv:epy.
t270
I(онструкuия 11.
Два друrих «веера» отрезков, ВЫХОДЯIЦИХ на диаrрамме D
из точек (n/2, О) и (О, п/2), дает следующая Teoperv18.
Т е о р е м а 7. Если острые У2ЛЫ rl tl 6АВС связаны
равенством rl+k ==:rt/2, еде k ........ натуральное число, приЧЕМ
2a+ >n/2, то в 6АВС существуеrfl периодическая пzpaeK.
тория. То rнce имеет место для треУ20ЛЬНUКО8, у которых
+kct==1t/2, 2 +a>п/2.
с л е Д с т в и е. В любом nрямоуеольном треуеольнuке
сущеСlrlвует периодическая траектория (для доказаfпельст-
ва в ,пеореме 7 доспzатОЧflО с 1
положипzь k== 1 ). .
Докаэате л ь с т-
в о. Сделав k симметрич-
ных отражений ABC п о
u
И про т и в часовом стрел-
ки, при которых вершина
С, отвечающая уrлу , не-
подвижна, получим симмет-
ричный относительно пря-
мой АС «веер» АВ... Рис. 27.11
, n . РСР'. . .В' А треуrоль-
ников на плоскости (рис. 27.11). Рассмотрим «ромбоид»
АВСВ' и в нем отрезок ММ', параллельный диаrонали ром-
боида ВВ' и близкий к ней (ММ' l.AC). Выпустим по от-
резку М' М бильярдный шар. В силу неравенства 2rl+
+ >n/2 шар после отражения от стороны АВ пойдет
по прямой MN, пересекающей все стороны треуrоль.
u U
ников, лежащих в левои полуплоскости, . оrраниченнои
прямой АС (проверьте это!). Затем он отразится по
бильярдному закону от стороны СР последнеrо треуrоль-
ника в точке N, и, в силу равенства rl+k ==n/2, пойдет по
отрезку NN', параллельному ММ' (NN' AC; проверьте
это). Оказавшись в правой полуплоскости, шар отразится
от стороны сР' соответствующеrо треуrольника в точке N'
U
и опишет симметричную полутраекторию в правои полупло-
скости.
\ В результате шар опишет периодическую, симметрич-
ную относительно прямой АС, четырехзвенную траекторию
M'MNN' в «веере» треуrольников АВ.. .РСР'. . .В'А.
Сложив этот веер «rармошкой», свернем траекторию
M'MNN' в периодическую траекторию r в исходном Tp -
уrОJIьнике АВС. Теорема 7 доказана. ,
«(Веерная» конструкция из треуrольников АВ. . .РСР'...
.. .В'А дает «веер» на диаrр.амме D: он образован отрезками,
271
выходящими ИЗ точки Z диаrраммы в направлении точек
(О, п/2), (О, п/4), (О, n/б), . .., (О, n/(2k»,...; вторые
КОНЦЫ этих отрезков лежат на ПрЯl\1:0Й 2cx+ ==п/2, соеди.
р няющей точку Х диаrраммы с
точкой (п/4, О) (РИG. 27.12).
Аналоrичный «веер» выхо-
дит из точки х. Отрезки пер.
Boro «веера» лежат на прямых
{j} == cz + }. «сrущаю-
щихся» к оси Осх, а BToporo
на ПрЯМЫХ { :== kcz + } .
z «сrущающихся» К оси O .
" 3 а м е ч а н и е. Приве-
денная здесь конструкция в
точности повторяет идею тео-
ремы 5, но не использует «ра"
циональности» уrлов треуrольника. А именно, периодичес-
кой является любая траектория в рассматриваемом треу-
rоЛЬнике, два звена которой перпендикулярны основанию
АС.
КОНСТРУКЦИЯ 111 (устойчивые траектории).
В этой конструкции будут фиrурировать неравенства,
связывающие уrлы rx и , которые дадут сразу целые о б-
JI а с т и отмеченных на диаrрамме D точек.
I Р, р 2.'
I А' с' I
I I
I I
I 1/' I I
.II/Ь I l' Н2
I Н, I I k н,
2.
С А Н3
о
Рис. 27.13
Рассмотрим для тупоуrольноrо 6АВС с острыми уrлами
а и такие натуральные числа k и т, что kr:x<1t/2 и т <
<л/2, но (k+ 1)(X 1t/2 и (т+ 1) зt/2. Сделаем k........l зеркаль-
ных отражений LBAC и т.......1 зеркальных отражений LACB
так, чтобы «крайние» лучи АА' и СС' образовывали с пря-
272
мой АС уrлы LA 'AC==kct и LC'CA==тp, лежащие в
верхней полуплоскости (рис. 27.13, а). Эти крайние лучи
ле}кат в «коридоре» между перпендикулярами pf, Р2 К отрез-
ку АС, восставленнымИ в ero концах А и С. Следователь-
но, лучи АА! И сс' пересекаются; точку их пересече;ния
обозначим В'.
3 а д а ч а 27.3. Доказать, что 6.АВ'й остРОУ20ЛЬНЫЙ.
В остроуrольном 6.АВ'С построим, соrласно теореме 1,
периодическую бильярдную траекторию Н iH 2 Н 9, точки
излома которой основания высот CHi, АН 2 И B'H s
(рис. 27.13,6). Если отрезок HiH 2 будет пересекать исход-
ный 6АВС, т. е. этот отрезок будет лежать н и ж е вер-
шины В, то сделав (k I)+ (т l) «обратных» зеркальных
отражений образов уrлов LBAC и LBCA вместе с кусками
траектории HiH2H8' мы переведем бильярдную траекторию
НiН2НЗВ AB'C в периодическую бильярдную траекторию
в исходном тупоуrольном 6.АВС, содержащую 2 (k.........l)+
+2 (т I)+3==2 (k+т) 1 звеньев.
Итак, необходимым и достаточным условиеl\1 (крите-
pUeAt) существования в тупоуrольном 6АВС периодической
траектории рассматриваемоrо вида является прохождение
отрезка HfH2 ниже вершины тупоrо уrла В. Очевидно, что
если острые уrлы (х и в ABC HeMHoro «пошевелить» произ
вольным образом, т. е. заменить 6АВС на 6.AfBfCi с остры-
1\1И уrлами CXi и i, мало отличающимися от СХ и соответст-
венно, то в нем также будет существовать периодическая
траектория рассматриваемоrо вида. Отсюда вытекает, что
на диаrрамм D отмеченные точки для данных k и т
заЙlVlУТ целую область. Следующее неравенство является
критерием Toro, что отрезок НIН2, пересекает 6. АВС .
У т в е р ж Д е н и е 1. Отрезок Н lН? npoXoaufrf ниже
вершины В (пересекает ABC) mozaa и только 'mozaa,
коеда выполнено н ер авенс тв о
tg ( krx ) ctg + tg ( т ) ctg rx <
< 1 + tg ( krx ) tg ( т ) (1 )
или эквuвалентное еJll,У HepaвeHcmвo
(1 ctg kcx. tg а) (1 ctg m ' tg ) > 1 tg ct tg . (1')
Утверждение 1 мы предоставляем доказать читателю
самостоятельно, оставляя ero в качестве не очень сложной,
u u u
но довольно rромоздкои элементарнои rеометрическои
задачи.
273
Неравенствз (1), (1') задают бесконечное (счетное) число
областей На диаrрамме D, которые нумеруются парами
натуральных чисел (k, nz). Приведем несколько более удоб-
НЫХ последовательных ослаблений точноrо неравенства (1),
которые также rарантируют прохождение отрезка HiH,
ниже вершины В:
tg ( ka ) tg ( т )
tg 6 + tg а 1 t (2)
1- kct .;....... т
+ а < 1 , (3)
ka< t т <y. (4)
Эти неравенства задают все меньшtIе и меньшие области по
сравнению с областью, задаваемой неравенством (1). На их
доказательстве останавливаться мы также не будем. Приве-
дем множество точек на диаrрамме D, задающееся неравен-
ством (1) (на рис. 27.14, а изображены посл довательно
1i 7t 7i 1f 11 1t
2п 14 12 10 8 6
f (ff, :)
., . ,
, ., t
х-т=2
, . . ,
1t ".' .
8
(,l
о-
.!1....
6
п
8 ri
1t 10
[2 1t
.!.[ 14-
: 15
f(
2п
тt
4
Рис. 27.14
вложенные области (1)=:>(2)=:>(3):)(4) для k==m==2, а на
рис. 27.14, б ......... б6льшая часть MHo eCTBa (1)). Это множест-
во состоит ИЗ объединения бесконечноrо числа серий ча-
стично пересекающихся криволинейных «равнобедренных»
«прямоуrольных» треуrольников, идущих вниз и влево от
«базовоrо» треуrольника с вершиной ( ;n ' ). rде n==2.
3, 4, . .. Кривые rраницы задаются выра ением (1), в
274
котором знак неравенства заменен знаком равенства, и
очень похожи на куски эллипсов (неравенство (3), заменен-
ное на равенство, дает в точности уравнение эллипса).
Таким образом, доказана
т е о р е м а 8. Если 8 туnоуеОЛЬ1l0М ABC острые
уелы rt u удовлетворяют неравенствам
k З't А 3t 1t 3t
а<2. mfJ<2' (k+l)a 2t (т+l) 2
с целыми k и т и одному из неравенств (1), (2), (3) или
(4), то в нем существует периодическая траектория из
2 (k+т)........1 звеньев и пучок «параллельных» ей периодиче-
ских траекторий из вдвое большеео числа звеньев.
р ;з
х х
а
о'
_:\ :. .' ... .. ': ?t::,:,iJ:y,:'
it\. ...... . "".'"'''>'''
[ . ""> ,:;э.(
1 :I . i . !J . l . . \ )Jj . . "" K "';' . " . "
!1!IIM.Mt.., :.--. . .
/'
' .
' ;: . . -
z
Z"
Рис. 27.15
Завершающий этап в исследовании периодических биль-
ярдных траекторий в треуrольниках состоит в одновремен-
ном изображении всех отмеченных ранее точек на диаrрам-
ме D. Это изображение получ тся, если мы наложим :все
диаrраммы рис. 27.7, б, 27.10, 27.12 и 27.14, б друr на друrа
с изображенными на них множествами точек. В результате
получим диаrрамму D, которая изображена на рис. 27.15, а.
На рис. 27.15, б изображено rипотетическое множество
точек, отвечающих высказанной в начале этоrо параrрафа
rипотезе,......... полностью зачерненный квадрат OXYZ.
Вообще следует сказать, что периодические траектории
весьма чувствительны к форме треуrольника. Причина
u
, разрушения или рождения периодическои траектории......
прохождение через уrло:Вую точку rраницы. Этим обстоя-
тельством объясняется замысловатый характер фиrуры
рис. 27.14, б, изображающей множество тупоуrольных
треуrольников G периодическими траекториями, построен-
ными в конструкции 111.
10*. Завершим этот параrраф пространственным анало-
rOM теоремы 5. Проведем через произвольную точку О
276
пространства плоскости. параллельныIe Всем rраням некото-
poro мноrоrранника Q, и начнем совершать относительно
них зеркальные отражения. После каждоrо отражения будут
u
получаться, кроме исходных плоскостеи, новые плоско-
сти, относительно которых также будем производить отра-
жен ия.
Будем рассматривать мноrоrранники Q со следующим
u
своиством: в результате всех возможных отражении отно-
сительно исходных и вновь возникающих плоскос/пей полу-
чится лишь конечное число направлений, перпенд,UКУЛЯР-
НЫХ этим плоскостям,. Мноrоуrольник Q на плоскости,
обладающий таким свойством, является р а Ц и о н а л ь-
н ы м ....... все ero уrлы соизмеримы с п. По аналоrии MHoro-
rранник Q мы будем также называть рациональНыМ........ все
двуrранные уrлы между любыми двумя ero rранями, также
соизмеримы ос п (докажите!). (Правда, в отличие от плоскоrо
случая одной только рациональности уrлов нам будет не-
достаточно.)
Все рациональные мноrоrранники классифицированы
для всех раз:м:ерностей пространства. Среди них имеются
мноrоrранники, которые в научной литературе носят, в
честь знаменитоrо математика repMaHa Вейля, название
«камера Вейля» и появляются при изучении cOBpeMeHHoro
алrебро-rеометрическоrо раздела математики ....... теории
rрупп и алrебр Ли. Из камер Вейля составляются рацио-
нальные мноrоrранники. (Камеры Вейля возникают и в
современных исследованиях по механике и физике.)
Как и для рациональных мноrоуrольников, для рацио-
нальных мноrоrранников справедливо следующее утверж-
дение.
у т в е р ж Д е н и е 2. В рационаЛЬНОАt МНО202раннике
при движении по бильярдНЫА-t траеКlпориям из даННО20
началЬНО20 направления М,ожет получиться только конеч-
ный набор направлений движения.
Д о к а 3 а т е л ь с т в о. «Выпрямляя» бильярдную
траекторию, т. е. производя зеркальные отражения относи-
тельно тех rраней мноrоrранника, на которых расположены
u
точки излома траектории, в силу рациональности MHororpaH-
ника получаем, что в какой-то мрмент будет произведено
отражение относительно плоскости, параллельной уже
ранее рассмотренной rрани. Это означает, что направление
движения бильярдноrо шара в этот момент совпадает G
одним из предыдущих ero направлений движения. Следова-
тельно, общее !{оличество направлений движения бильярд-
Horo шара конечно, что и требовалось доказать.
276
Из этоrо утверждения вытекает .
т е о р е м а 8. В любом рациональном мноеО2раннике Q
существует бесконечно мноео периодических бильярдных
траекторий.
Д о к а s а т е л ь с т в о почти дословно повторяет дока-
зательство теорем 3, 4 и 5. Действительно, фазовое прост
ранство Q бильярдной системы в Q получается из прямоrо
произведения Q х Sn--l (Sn"'l (п.......1 )-мерная сфера на-
правлений движения шара, если Q.........п мерный MHororpaH-
НИК) некоторыми склейками (отождеСТВJlениями точек), а в
силу рациональности мноrоrранника Q и утверждения 2
фазовая траектория в Q располаrается лишь в к о н е ч
н о м числе «слоев»....... В мноrоrранниках Q(cpo), Q(CP1), . . .
. . . , Q (СРт): в них шар движется в направлениях СРо, cpi,. . .
. . . , СРт. По теореме Пуанкаре о возвращении получаем, что
фазовая точка вернется в"сколь уrодно близкую к начальной
точку, причем под тем же направлением, под каким начала
двиrаться (см. теорему 4).
Если исходный уrол вылета шара равен сро==л/2, то шар
может быть выпущен из такой точки фиксированной rрани
мноrоrранника перпендикулярно ей (этих точек бесконечно
MHoro), что через некоторое время он столкнется с этой же
rранью опять под прямым уrлом (см. теорему 5). После от-
ра}кения шар начнет двиrаться в обратном направлении по
той же траектории. Следовательно, указанная траектория
движения является периодической. Если число rраней у Q
равно N, то аналоrичных «ортоrональных» бильярдных
траекторий не менее N/2........ по одной для каждоЙ rрани
(с учетом Toro, что для каких-то двух rраней может полу-
читься та же самая траектория). BOKpyr каждой периоди-
U U
ческои траектории имеется целыи пучок «параллельных»
u u
"еи периодических траектории, поэтому множество периоди
ческих траекторий в рациональном мноrоrраннике Q бес.
конечно. Теорема 8 доказана.
Доказательство существования периодической траек-
тории в любом мноrоrраннике до сих пор не известно. На-
помним только, что почти любая бильярдная траектория r
в любой области Q подходит к любой своей точке q Е r
сколь уrодно близко и поД сколь уrодно малым уrлом (Teope
ма 3).
3 а Д а ч 8 27.4.. В правильном треуrольнике, как и в Лlобом
ОСТРОУVОЛЬНОМ; с ществуют периодические траектории из трех и
из шести 8веньев (рис, 27.2). Оуществуют ли в правильном тре.
уrольнике периодические траектории из ббльwеrо ЧИСJ18 звеньев?
Иа сколь rrодно большоrо числа 8ввньев?
277
3 а Д а ч а 27.5. Бильярдный шар, отражаясь от сторон пра--
вильноrо треуrольника, прошел через некоторую точку 7 раз.
Доказать, что он пройдет через эту же точку еще хотя бы один раз.
Останется ли верным это утверждение, если заменить число 7 на 6?
3 а д а ч а 27.6. Дан рациональный мноrоуrольник Q. ДOKa
жите, что существует число n==n (Q), обладающее следующим свой
ством: если бильярдный шар в Q прошел через некоторую точку п
раз, то он пройдет через нее еще хотя бы раз, а если шар прошел че-
рез эту точку меньше п раз, то, вообще rОБОрЯ, через нее он может
больше и не пройти.
З а Д а ч а 27.7. Докажите утверждение задачи 26.6 для pa
циональных мноrоrранников (мноrоrранников Вейля). У к а з a
н и е. Воспользуйтесь утверждением 2 из п. 27.10.
3 а д а ч а 27.8* (r. А. rальперин, А. М. Степин). а) Докажите,
что ни в каком треуrольнике с попарно различными сторонами
нет четырехзвенной периодической траектории. б) Существует ли
остроуrольный треуrольник, имеющий периодическую траекторию
из 5 звеньев? Из 7? Ответьте на этот вопрос для любоrо нечетноrо
ч сла 2k+ 1, k>3. в)** -Постройте периодическую траекторию из
15 звеньев в тупоуrольном треуrольниkе с уrлами а и р, удовле.-
творяющими условиям
1 n
8..... 1000 < а < 8" t
n
3" < < За.
Реш е н и е. а) Предположим, что в некотором треуrольнике
имеется четырехзвенная периодическая траектория. Тоrда какие то
Д в е из четырех ее точек излома А, В, С, D находятся на одной
стороне треуrольника, а две друrие на этой стороне не лежат.
Пусть, например, на стороне MN треуrольника лежат точки В
и D. Однако хорошо известно, что на прямой MN существует
т о л ь к о о Д н а точка Х, дЛЯ которой LAXM== L,CXN (см.
рис. 4.1). Следовательно, точки В и D совпадают, и наша траек-
тория оказывается двухзвенной, что противоречит сделанному
предположению. .
б) Искомый треуrольник существует в обоих случаях. Строится
он так, как об этом рассказано в конструкции 111.
Если остроуrольный 6АВС таков, что L"B <n/4, то, отразив ero
симметрично относительно стороны ВС, продлим сторону БА'
полученноrо .6А' ВС дО пересечения в точке С' с продолжением
стороны АС исходноrо треуrольника. Леrко видеть, что возникаю
щий 6ABCI,....... остроуrольный (L-АВС'==2LВ<n/2, C'<L.BCA<
<n/2) и поэтому в нем существует трехзвенная периодическая
траектория, точки излома Н 1 , Н 2 , Нз которой основания высот
6.АВС'. Заметим, что высота ВН З является одновременно высотой
и в 6,АВС, поэтому точка Нз лежит внутри отрезка АС, а не на ero
продолжении СС' (как моrло бы случайно оказаться). Кроме
Toro, н 2 еВА'. Отразив теперь симмеtрично относительно прямой
ВС часть трехзвенной траектории Н 1 Н 2 Н з , лежащей вне 6АБС,
получаем 5 звенную периодическую траекторию в 6,АВС. Друrая
5 звенная периодическая траектория получается тем же способом,
если сделать вначале зеркальное отражение 6.А ВС относительно
стороны АС.
Аналоrично строится остроуrольный 6.АВС, содержащий
7 звенную периодическую траеКТОРИIО: если LB<n/6, 10 надо
сделать Д в а зеркальных отражения ABC BOKpyr вершины В
278
против часовой стрелки, продлить сторону БА" у получившейся
фиrуры Ф==ВАА' А" дО пересечения в точке С' с продолжением
стороны АС, и построить трехзвенную периодическую траекторию
Н 1 Н 2 Н В в остроуrольном,6АВС', целиком располо}кенную в фиrуре
Ф. (Принадлежность траектории Н 1 Н 2 Н З фиrуре Ф можно доказать
непосредственно оставляем это читателю, а мо}кно, проверив
выполнение неравенства (1') из конструкции 111, справедливое
для' рассматриваемоrо треуrольника.) Сворачивая затем фиrуру Ф
в трехслойную «rармошку», т. е. делая последовательно .обратные
отражения 8еркально симметричных треуrольников вместе с pac
положенными в них частями траектории Н 1 Н 2 Н З , получим 7 звен
ную периодическую траекторию в 6.АВС. Друrая 7 звенная Tpa
ектория получится, если делать отражения 6.АВС BOKpyr вершины
Б по часовой стреЛI{е. Заметим, кстати, что в ,6АВС одновременно
имеются и две 5 звенных периодических траектории (почему?).
Вообще, если L.B <n/2k (при этом rлы А и С превосходят
n л, А u
"2 2k ' поскольку 6. 8С q,cтроуrольныи), то BOKpyr вершины В
(1
мо}кно сделать k 1 зеркальных отражений 6.АВС, а затем, получив
«коридор» Ф для частично выпрямленной траектории, по указан
ному выше рецепту построить остроуrольный 6.А ВС' и трехзвен
ную (частично выпрямленную) траекторию в нем, которая при
сворачивании «коридора» Ф в rармошку даст 3+2(k 1)==2k+l..
авенную периодическую траекторию в ,6АБС. В этом же треуrоль
нике имеются также и периодические траектории из 2k 1, 2k З, . . .
. . ., 5 и З звеньев это следует из Toro, что описанную проце
дуру отражений можно проделать k 2, k 3, ... раз. Таких
траекторий довольно MHoro ведь кроме «большоrо» остроуrоль
Horo 6,АВС' можно строить и друrие остроуrольные треуrольники
с вершиной В, вмещающие в себя «коридор» Ф, а затем чертить в
них соответствующие периодические траектории.
в) Построим периодическую траекторию в 6,АВС, уелы Koтo
раео а== L,BAC и == L.BCA удовлетворяют неравенствам
31 1 л п
8 1000 < а < 8 ' 3 < < За.
Пусть точка А' симметрична точке А относительно прямой ВС,
В' ......... точке В относительно А' С, С' ..... точке С относительно А' В' ,
F ......... точке С относительно АВ, р'........ точке С относительно АР
(рис. 27.16). Поскольку >л/З, точка Б' лежит ниже прямой АС:
L.АСВ'==3 >л. Пусть Е точка пересечения отрезка А' Б' с
прямой АС. Так как в 6,.А' ЕС уrол А' ЕС равен л.........(а+ (п 2 »==
==2 а>2n/З а>2л;/З.........л/8>n/2, точка С', как симметричная
точке С относительно А' В', лежит ниже прямой АС. Оказывается,
что прямая А'С' наклонена в л е в о, т. е. L-A'DC острый:
LA'DC==п (2a+ (п......2 »==2( .........a)<4a<4 .л/8==п/2. Из сло
вий на а и следует, что L,f' АС и LA' DA ...... острые.
Докажем, что в остроуrольном 6.AND, образованном прямыми
AD, AF' и DA' основание высоты Нl' опущенной на AD, принад
лежит отрезку АС. Действительно, LA'DA==2 .......2a<4a== LF' AD
(здесь ИСПОЛЬЗQвано неравенство <За) и поэтому достаточно
ваметить, что CD <АС. Последнее неравевство выполнено, по
скольку сторона CD в 6A'CD лежит против уrла CA'D, paBHoro 2а
и меньшеrо уrла A'DC, противолежащеrо стороне А'С и paBHoro
2p 2a (2сх <n/4 <n13 <р),
219
Пусть Н 2 И НЗ....... основания высот; опущенны На боковые
СТОр'оны 6AND. Каждый из уrлов6.АND при вершинах А и D
отличается ОТ п/2 меньше, чем на 0,004 (проверьте!), поэтому от-
резок Н 2 Н З пройдет ниже точки В. Фиrуру Ф, составлеННУIО из
7 треуrольников, равных.6.АВС (см. рис. 27.16), наложим «rармош
/ A N
,/ "
/ "
/ "
/ '"
/ '-
/
/ \
/ \
/ \
/ \
/ \
I \
I \
I ,
" < 0,004 < 0, 004 \ I
- < )!i\ 1<
, ,
'F' t
,
,
A,t
I
'>1
I
I
I
1/3
I
J
J
I
I
J
la
)
Н 2
Н 1 fJ
с'
Рис. 27.16
кой» на 6АБС. При этом периодическая траектория Н 1 Н 2 Н з Нi
в Ф перейдет в периодическую траекторию в 6АВС, остоящую
из 15 звеньев. Задача в) полностью решена.
Заметим, что'построенная траектория '\' B ABC из задачи
27.8 в) у с т о й ч и в а: это означает, что при небольшой
деформации 6,АВС (т. е. небольшими изменениями уrлов 'z
и при ero основании) она переходит в близкую к rф.r 15-
звенную периодическую траекторию.
О б щ и й с п о с о б построения тупоуrольных тре-
"
уrольников с усmоuчuвымu периодическими траеКТОрИЯl\1И
таков (ч а G т Н Ы Й случай изло)кен выше в конструкции 111).
280
Пусть для треуrольника !:lo G вершинами А, В; С и
острыми уrлами а, при основании АС построена цепочка,
треуrольников
--21' ..., 6.--1.9 CH 6.'1., ..., 2k' ,
пересекающихся с rоризонтальной прямой АС и верхней
полуплоскостью, причем соседние треуrольники цепочки
имеют общую сторону и симметричны относительно нее.
Поскольку результат применения двух последовательных
u u
отражении относительно непараллельных осеи есть пово-
рот, то треуrольник 6--21 повернут относительно 60 на
некоторый уrол пlа+n2 +nзп; аналоrично, треуrольник
6.2k повернут относительно треуrольника60 На уrол тlа+
+т2 +mS:n;. Предположим, что пары целых чисел (пi, п 2 )
и (тi, т 2 ) непропорциональны, а треуrольники 6--21 и
62k имеют стороны, перпендикулярные прямой АС. Если к
тому же на прямой АС нет друrих вершин треуrольников
цепочки, кроме А и С, то оказывается, что сколь уrодно
малым изменением уrлов а и можно получить треуrоль-
ники, имеющие устойчивые периодические, траектории.
Остается только заметить, что построенная в решении
задачи в) 15-звенная периодическая траектория получается
применением этой общей конструкции к пря оуrольному
треуrольнику с уrлом 'Я/В.
ЗАКЛЮЧЕНИЕ
Изложенные в книrе результаты о поведении
бильярдных траекторий в специальных областях Kpyre,
эллипсе, прямоуrольнике, «рациональных» мноrоуrоль-
никах дают лишь первые, начальные сведения о теории
бильярдов. Хотя эти результаты красивы и интересны,
но они, по сути дела, составляют лишь небольшой «остро-
вок» в теории бильярдов.
Начало современной теории бильярдов было положено в
трудах Я. r. Синая. В 1970 r. им была опубликована фун-
5uльярiJ CUHlIп
Рис. 3.1
Рис. 3.2
даментальная работа [17], в которой введен и изучен боль-
шой класс бильярдных систем...... так называемых рассе-
ивающих бильярдов, которые впоследствии стали называть-
ся «бильярдами Синая».
Б ильярдbl Синая устроены так: их rраница состоит из
кусков выпуклых кривых (в пространстве кусков выпук-
лых поверхностей), обращенных своими выпуклостями
внутрь бильярдной области (рис. 3.1). Эти бильярды явля-
ются рассеива/ощимu: любой (не обязательно узкий) пучок
бильярдных частиц, летящих параллельно, после отраже-
ния от ВЫПУI{ЛОЙ стенки разлетается расходящимся веером
(рио, 3.2) и остается расходящимся при всех последующих
отражениях от rраницы бильярдной области. Эта ситуация
v
({ардинально отличается от тои, которая имеет место, ска.
282
жем, для бильярда в мноrоуrольнике, rде параллельный
пучок после столкновения с прямолинейной стенкой оста-
ется по прежнему параллельным, если только не попадает в
вершину. В бильярде Синая близкие вначале бильярдные
траектории с течением времени достаточно быстро расхо-
дятся и уrол между соседними траекториями первоначально
параллельноrо пучка возрастает после каждоrо отражения
от rраницы. Поскольку площадь области Q конечна, траек-
тории бесконечной длины начинают со временем перепуты
ваться, что приводит к хаосу.
На cTporoM математическом языке это обстоятельство
находит свое выражение в следующем важном свойстве
бильярдных траекторий (см. [17]): 8 рассеивающих бильяр-
дах имеет место эреодиЧflость, т. е. типичная траектория
бильярдноrо шара проходит сколь уrодно близко от любой
точки q бильярда Q, причем во всевозможных направле-
ниях, и приводит В любой окрестности точки q долю време-
ни, пропорциональную площади этой окрестности. Отметим
также, что бильярды Синая обладают сильной неусmойчи-
востью, которая характеризуется тем, что даже небольшое
изменение начальноrо состояния (положения q или скорости
(1) бильярдной частицы в области Q ПРИВОДИТ к «сильным»
изменениям ero траектории, которая очень быстро перестает
быть похожей на исходную.
Теория рассеивающих бильярдов применяется при ис-
следовании мноrих важных моделей статистической физи-
ки при доказательстве эрrодичности rаза твердых стал-
кивающихся молекул, исследовании rаза Лоренца (см.
[18]) и друrих.
Впоследствии л. А. Бунимович исследовал друrой класс
бильярдов....... так называемые фокусирующие бильярды
(или, как теперь принято их называть, бильярды Буни-
мовuча) , в которых, несмотря на отсутствие рассеива
ющих участков rраницы, также обнаруживается явление
рассеивания И, как следствие, хаотичность поведения
траекторий.
Наиболее известным и популярным примером TaKoro
бильярда является «стадион», который получится, если
раздвинуть две половинки круrлоrо бильярда и вставить
между ними одинаковые параллельные отрезки (Т. е. rpa-
u
ница «стадиона» состоит из двух дуr окружностеи и двух
касательных к ним отреЗI{ОВ) ....... рис. 3.3, а. Несмотря на то,
что два прямолинейных участка rраницы «стадиона» MorYT
быть сколь уrодно малыми, а carv1 стадион почти не отличать-
ся от Kpyra, бильярд в «стадионе» будет уже хаотическимl
283
(Напомним, что бильярдная траектория в KpYI"e не всюду..
плотна в нем.)
Хаотичность имеет место и ,для друrих примеров биль.
ярдов Бунимовича, изображенных на рис. 3.3, б 8.
Бильярды на рис. 3.3, б, в являются модификациями
стандарТНоrо «стадиона», поскольку имеют только круrлые
u
И прямолинеиные куски rраницы, и поэтому их также можно
называть «стадцонами» (нестандартными). rраницы «цветоч"
нообразных» областей на рис. 3.3, 2, д состоят только и
а
о
«СтаиЦОНI1/ »
6
8D
1I
«ЦОеh1fJЧI/QоOjJu.ЭНЬlё» ОоАасmи
@
ж
е
«ru.брцQtJl»
Рис. 3.3
дуr окружностей. Наконец, из рассмотренных уже областей
можно вырезать разнообразные дыры (рис. 3.3, е, ж) или
же создавать «rибриды» соединять специальным образом
куски рассеивающих и фокусирующих бильярдов, как на
рис. 3.3, з.
Отметим, что круrлые куски rраниц стадионов и цветоч-
нообразных областей (дуrи окружностей) обладают следую'"
щим важным свойством: дополнение к любой дуrе до целоЙ
окружности расположено внутри области......... только в ЭТО11
случае бильярд в соответствующей области будет хаотич.
ным. Например если рассмотреть бильярд, состоящиi"'1
из двух одинаковых круrлых Cer!\1eHTOB, то, в случае коrда
cerMeHT вмещает в себя острый уrол (т. е. содержит полу
Kpyr), бильярд будет хаотичным, а коrда вписанный уrол
прямоЙ или тупой....... хаотичностИ нет (рис. 3.4, а, б). Во
втором случае у бильярда имеется у с т о й q и в а я пери..
4
..одическая траектория АВ периода 2....... €сли эту траекторию
немното «пошевелить», то возникшая новая траектория будет
по-прежнему располаrаться вблизи отрезка АВ. В cerMeHTe
же рис. 3.4, а емещенная траектория уйдет от исходноrо
положения и заполнит со временем всю область.
Весьма интересным является ВОПРОG очиеле rеометри-
u
чески различных периодических траектории в произвольном
оrраниченном бильярде. Можно .-.- ,
доказать, что для cтporo выпукло- < /' 8 "
ro бильярда е rладкой rраницей на { Ш '
плоскости число N (п) периодичеG- I
ких траекторий, имеющих не более \'
чем' n . звеньев, при больших п не \ А /}
меньше 3п 2 /n 2 . Эта оценка была 0".........../
фактически известна еще Биркrо- Рис. 3.4
фу, который определял число k-
звенных траекторий для каждоrо k от 3 до п (см. 6).
Совсем недавно И. К. Бабенко, используя средства
u
современном тополоrии, доказал, что для cTporo выпуклоrо
бильярда с rладкой rраницей в трехмерном пространстве
число N (п) при больших п не меньше п 2 /2 In n.
Вообще rоворя, такая оценка является довольно rрубой
и во мноrих случаях может быть улучшена. В случае рас-
сеивающеrо бильярда я. r. Синаем, Н. И. Черновым и
Л. А. Бунимовичем недавно получена асимптотически точ-
ная оценка числа N (п): 2 c l n <.N (п) -<:2 С l n , rде С:[ и С2 ......
некоторые тополоrические характеристики р ассматр и вае..
Moro бильярда. Таким образом" в бильярдах Синая число
периодических траекторий растет экспоненциально с ростом
числа звеньев п. Кроме Toro, можно показать, что периоди-
ческие траектории рассеивающеrо бильярда всюду плотны в
фазовом пространстве. Имеются также сообрйжения в поль-
зу Toro, что и в выпуклом бильярде с rладкой rраницей
общеrо ВИда число периодических траекторий растет экспо
ненциально с ростом п.
Напоследок упомянем о так называемых осциллирую-
щих бильярдах на бесконечных бильярдных столах. Биль-
ярд называется осцuллuрующuJ.l" если у Hero существуют
ОСЦИЛЛИРУlощие траектории........ временами уходящие сколь
уrодно далеко, а временами возвращающиеся. Поведение
бильярдноrо шара на столе, уходящем в бесконечность,
является моделью движения частицы в электромаrнитных
полях, определенных конфиrурацией (<<ловушках»).
Следующий специальный класс осциллирующих биль-
ярдов исследовал А. М. Леонтович (1962 r.). Рассмотрим
285
стол, оrраниченный осью абсцисс и «колоколообразной)}...
кривой...... rрафиком положительной непрерывной четной
rладкой функции f (х), стремящейся при Ixl---+ oo к некото-
рой прямой y==A O (рис. 3.5). Бильярдная ,траектория
будет н е о r р а н и ч е н н о Й, если она не заключается -В
полосу Х! <.х <Х 2 ни при каких Xi и Х 2 , И О С Ц И Л Л И Р У ю-
щей, если она пересекает ось Оу бесконечно MHoro раз.
А. 1\1. Леонтович доказал, что при А>О с у щ е с т в у ю т
осциллирующие траектории (но существует и бесконечно
!/ MHoro неосциллирующих, ухо-
1 дящих на бесконечность без
возвращения к оси Оу), а при
А а. А ==0 л ю б а я траектория
9' )O""' ""''''''' осциллирующая (среди них есть
J] как оrраниченные, так и иеоr.
1 й =- раниченные траектории).
При изучении бильярдов в
неоrраниченных областях ес-
тественно возникает постановка
О tf J1 задачи о рассеянии в области
Рис. 3.5 параллельноrо пучка частиц
(или волновоrо фронта). Рас-
сматривая эту задачу, А. Ю. Плахов и А. М. Степин
описали области, для которых рассеянный (уходящий)
пучок параллелен исходному (входящему). Такое поведение
пучка является аналоrом KBaHTOBoro эффекта аномальноrо
рассеяния, впервые экспериментально обнаруженноrо в
1986 r. Б. я. Зельдовичем и ero коллеrами по Физическому
институту АН СССР.
В действительности современная теория бильярдов не
оrраничивается только упомянутыми выше системами:
имеется MHoro друrих классов бильярдов, которые сейчас
исследуются математиками и физиками. Долrое время при
изучении таких бильярдов основное внимание уделялось
u
вопросам о хаотичности траеКТОРИИi в этом направлении в
последнее время были получены весьма общие результаты.
Однако наряду с этим никоrда не ослабевал интерес и к
таким задачам, которые рассматривались в нашей книrе.
Для их решения, по-видимому, нельзя предложить столь
же общие методы, и поэтому решение конкретных задач
всеrда представляет известный интерес, тем более что, как
мы у)ке отмечали, оно иноrда достиrается применением эле..
ментарных приемов.
Тех читателей, которые захотят попробовать здесь свои
сиды, ждет широкое поле деятельности.
СПИСОК ЛИТЕРАТУРЫ
J. Кориолuс F. F. Математическая теория явлений бильярдной
иrры.......... М.: rостехиздат, 1956.
2. Борахвос/пов В. Бильярд // Наука и жизнь. 1966. .NI N2 2.....4 t 6, 11.
3. FальnерU/-l F. А. Бильярд // Квант. 1981. Н24.
4. Земляков А. Н. Математика бильярда // Квант. 1976. Н25.
5. Зе.ll1,ляков А. Н. Арифметика и rеометрия столкновений // Квант.
1978. М2 4.
6. Земляков А. Н. Бильярды и поверхности // Квант. 1979. Н29.
7. Синай я. Т. Бильярдные траектории в MHororpaHHOM уrле // Ус-
пехи математических наук. 1978. Т. 33, вып. 1.
8. Fальnерин F. А. Упруrие столкновения частиц на прямой // Ус-
пехи математических наук. 1978. Т. 33, вып. 1.
9. Fальnерин F. А. О системах абсолютно упруrих шаров, движу-
щихся в пространстве или сосуде // Доклады АН СССР. 1979.
Т. 245, М2 2.
10. Синай Я. r. Введение в эрrодическую теорию (лекция 10).......
Ереван: Изд-во EpeBaHcKoro университета, 1973.
11. Корнфельд и. п., Синай я. F., Фомин с. В. Эрrодическая тео-
рия. М.: Наука, 1980. rл. 6.
12. БирК20ф r. Динамические систеМы...... М.; Л.: оrиз, 1941.
13. Арнольд В. И. Математические методы классической механи-
ки. М.: Наука, 1979.
14. Fальnериft F. А., CтenufL А. М. Периодические движения
бильярдноrо шара // Квант. 1989. Н2 3. '
15. Тихомиров В. М. Рассказы о максимума:х и минимумах. М.:
Наука, 1986 (Библиотечка «I<BaHT». Вып. 56).
16. Берже М. rеометрия: в 2-х тоМах...... М.: Мир, 1984. rл. 9 и
17.
17. Синай я. F. Динамические системы с упруrими отражениями.
Эрrодические свойства рассеивающих бильярдов // Успехи ма-
тематических 'наук. 1970. Т. 25, вып. 2.
18. Синай я. F. Эрrодические свойства rаза Лоренца // Функцио-
нальный анализ и ero приложения. 1979. Т. 13, вып. 3.
19. Земляков А. Н., Каток А. Б. Тополоrическая транзитивность
бильярдов в мноrоуrольниках // Математические заметки. 1975.
Т. 18, М2 2.
Научно поп у JIЯ рное И3Дд ине
rАЛЬПЕР!1Н rРИ20РUЙ Александрович.
ЗЕМЛЯКОВ Александр Николаевич
МАТЕМАТИЧЕСКИЕ БИЛЬЯРДЫ
(бильярдные вэдачи и смежные вопросы матема-
ТИКИ и механики)
Библиоrеч а «Квант»: выпуск 77
8аведующий реДакцией r. о. Куликов
Редактор А. 1'. М ордвинцев
Художественный редактор Т. Н. КольчеН1(О
Технический редактор Е. В. Мороэова
Корректоры о. М. Карпова, л. О. Сомова
ИВ N!! 32724
СДt1НО В набор 20.06.89. Подписано к печати 23.01.90. Т-06432. Формат
84Х 108/32. Бумаrа офс. IN 2. rарнитура литературная. Печать высокая.
УСЛ. печ. л. 15.12. Уел. кр.-отт. 15,96. Уч.-изд. л. 16,92. Тираж 130000 ЭК8.
6акаэ N2 9 325. Цена 65 КОП.
Ордена ТрУДовоrо KpacHoro Знамени издательство «Наука»
fлавная редакция физико математической литературы
11 7071 Москва В-71, Ленинский проспект. 15
Ордена Октябрьской Революции и ордена Трудовоrо KpaCHoro 3HaMeHJf
МПО «Первая Образцовая типоrрафия» rосударственноrо комитета СССР
по печати. 113054 MOCI{Ba, Валовая, 28
Отпечатано на полиrрафкомбинате ЦК ЛКСМ УкраИНБJ «Молодь ордена Тру-
довоrо l(pacHoro Знамени издательско-полиrрафическоrо объединения ЦК ВЛКСМ
1(!\t\ОЛОД8Я rвардия ; 252119, r. Киев-119, УЛ,...Пархоменко, 38 44.