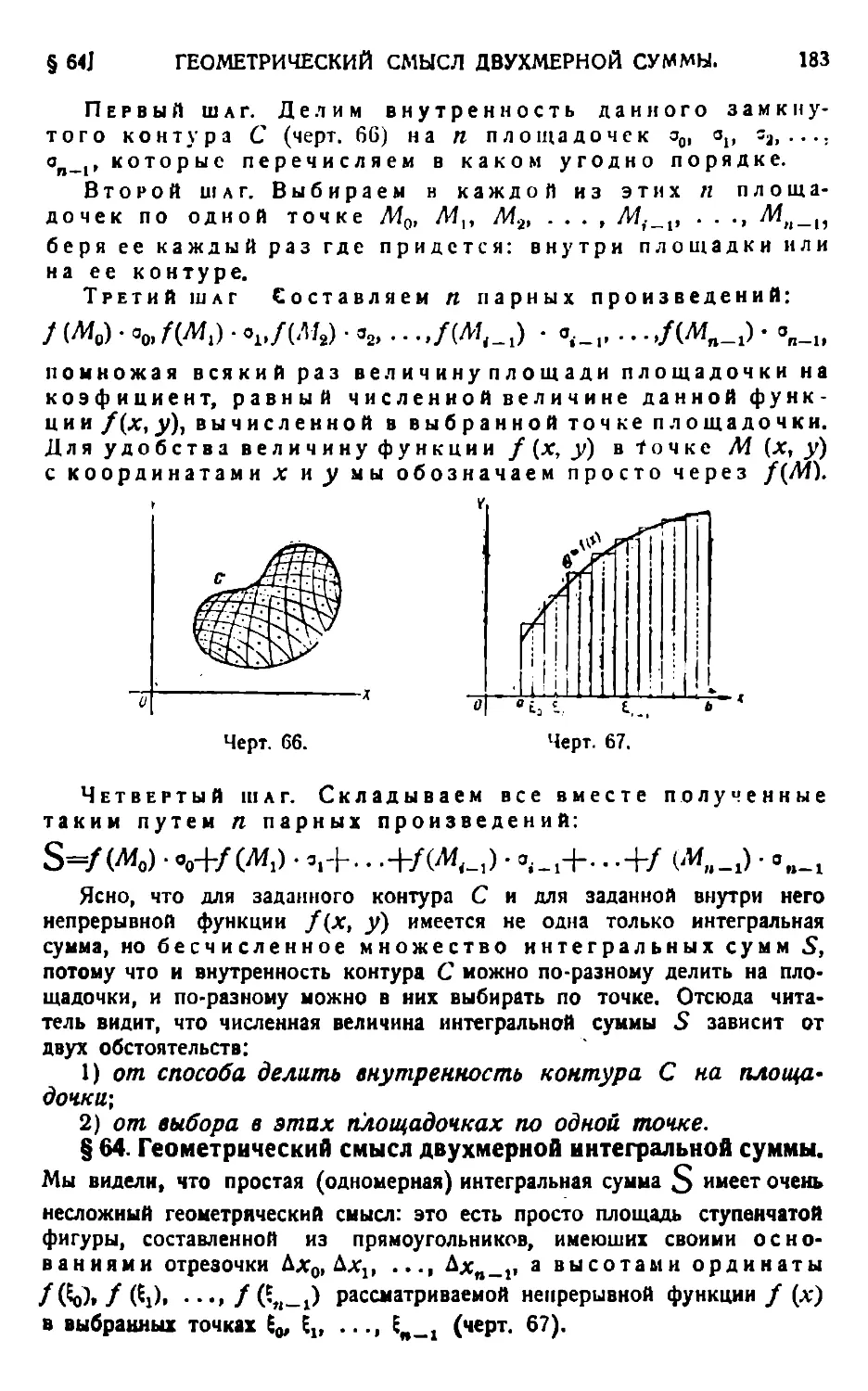
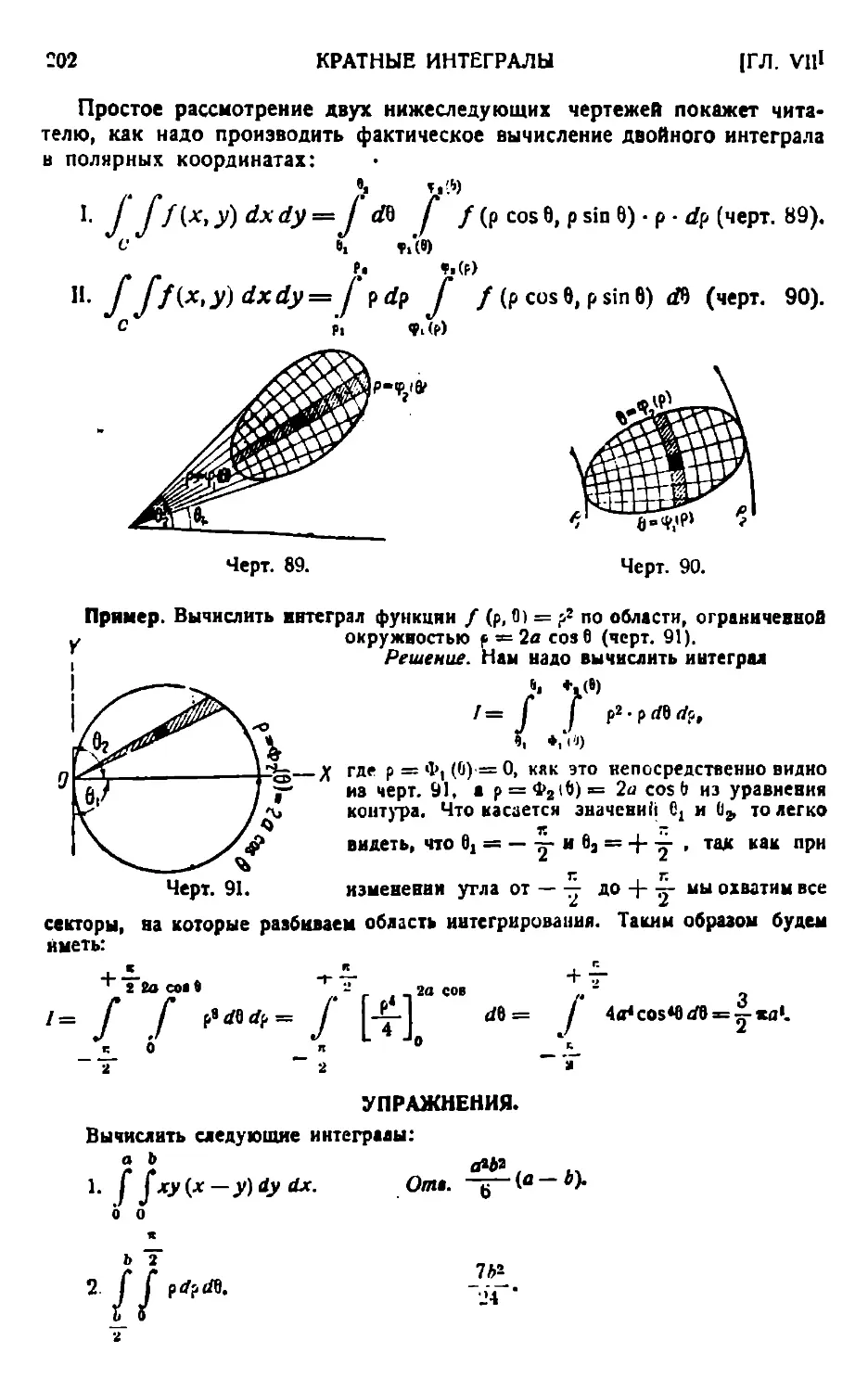
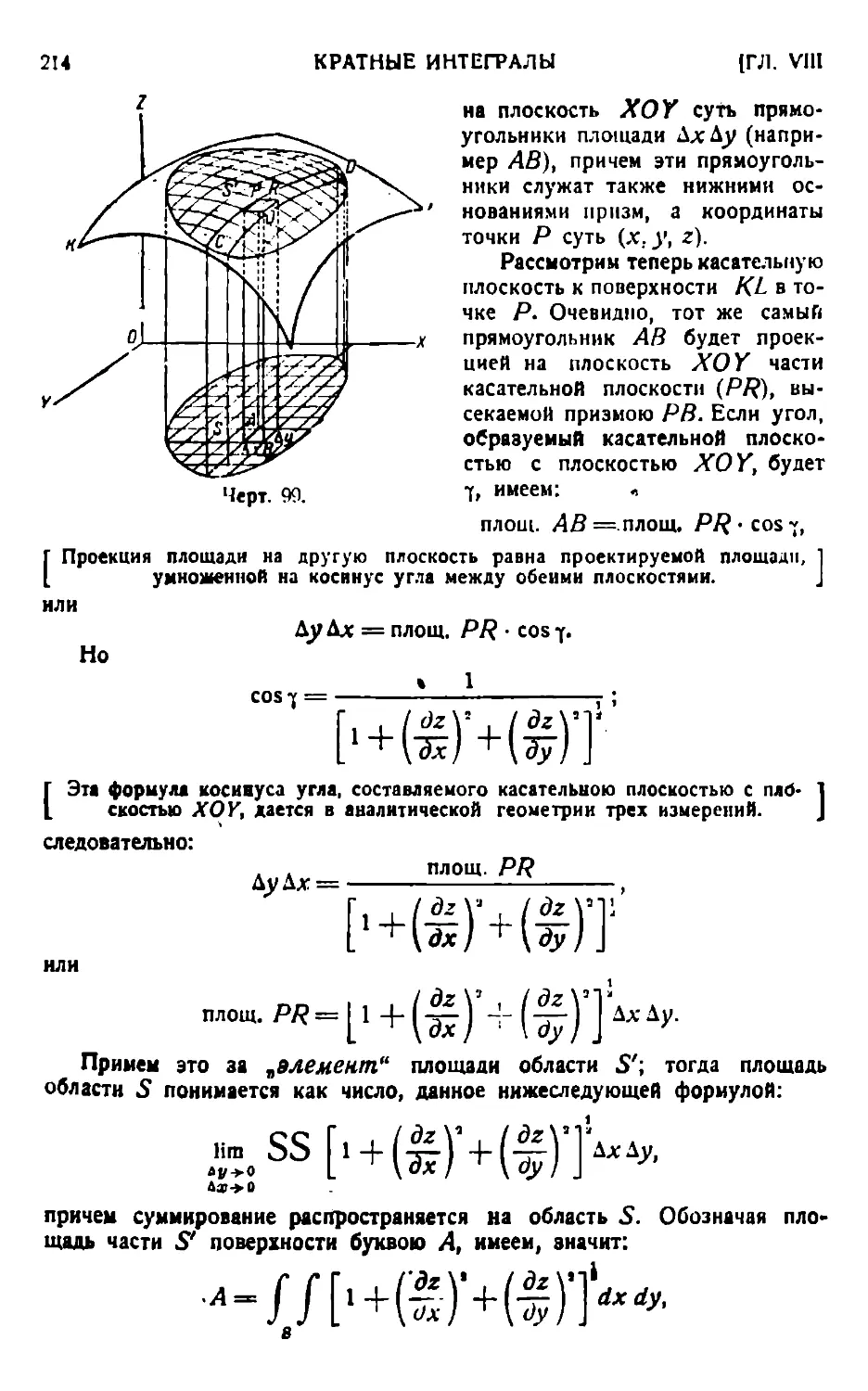
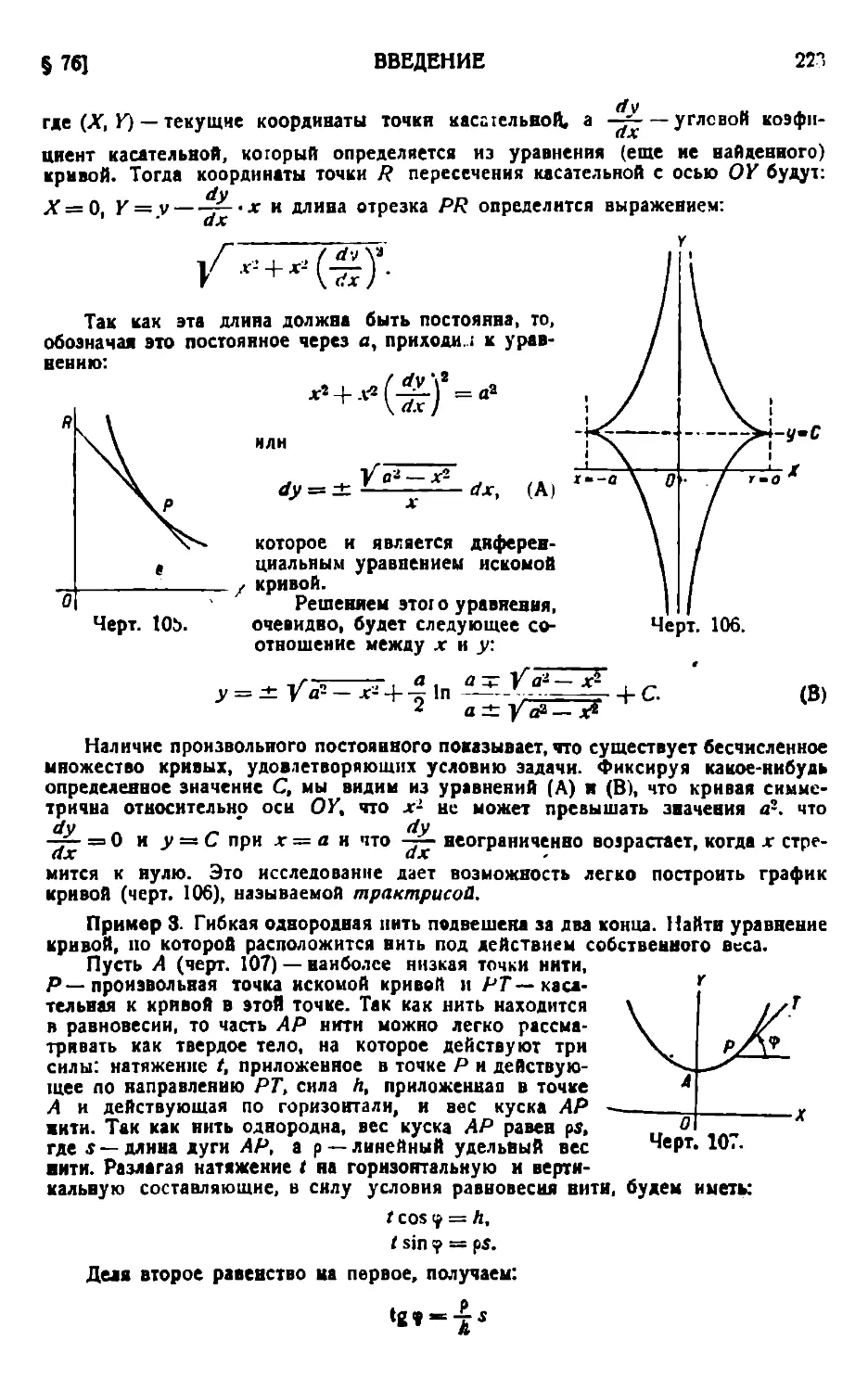
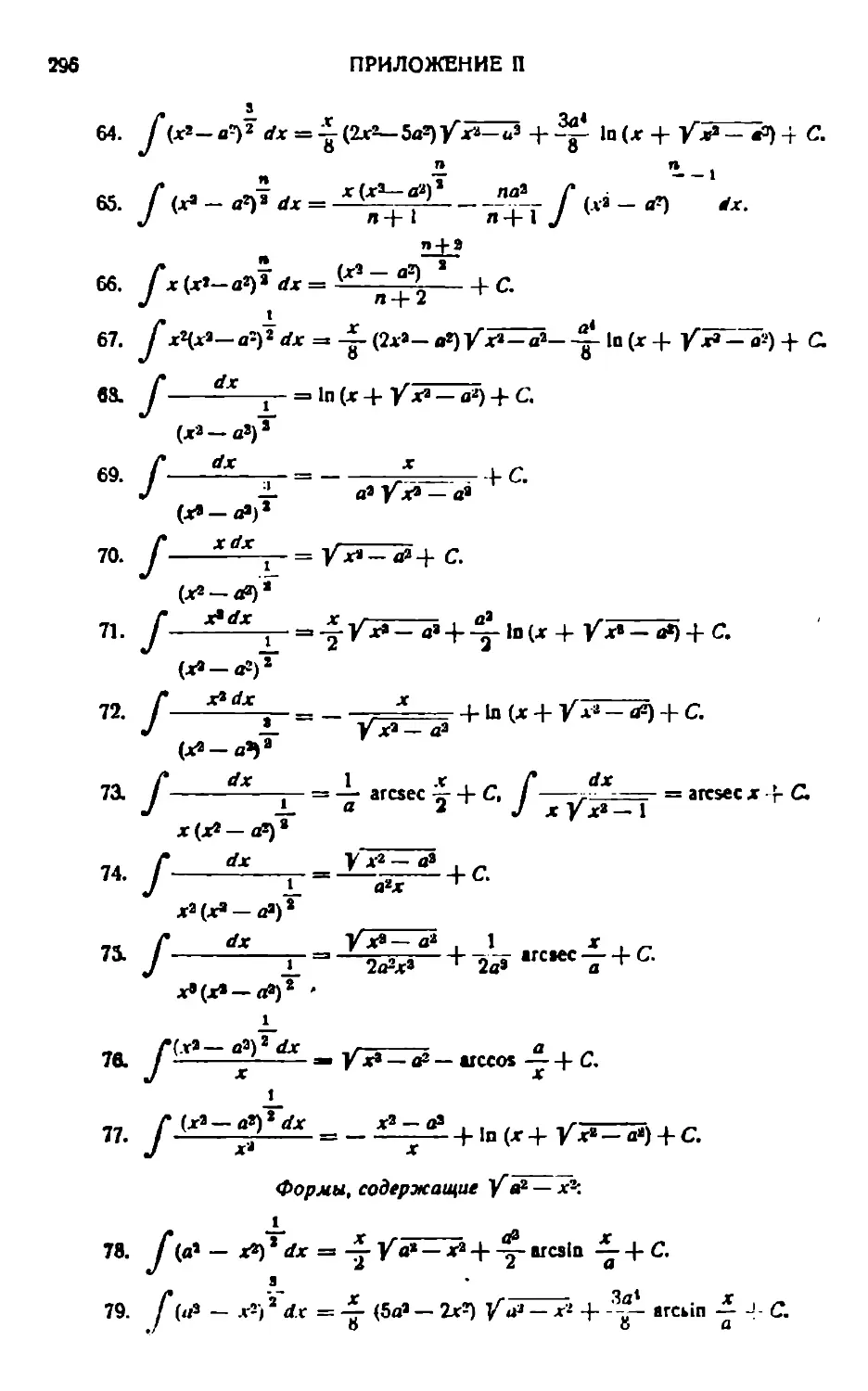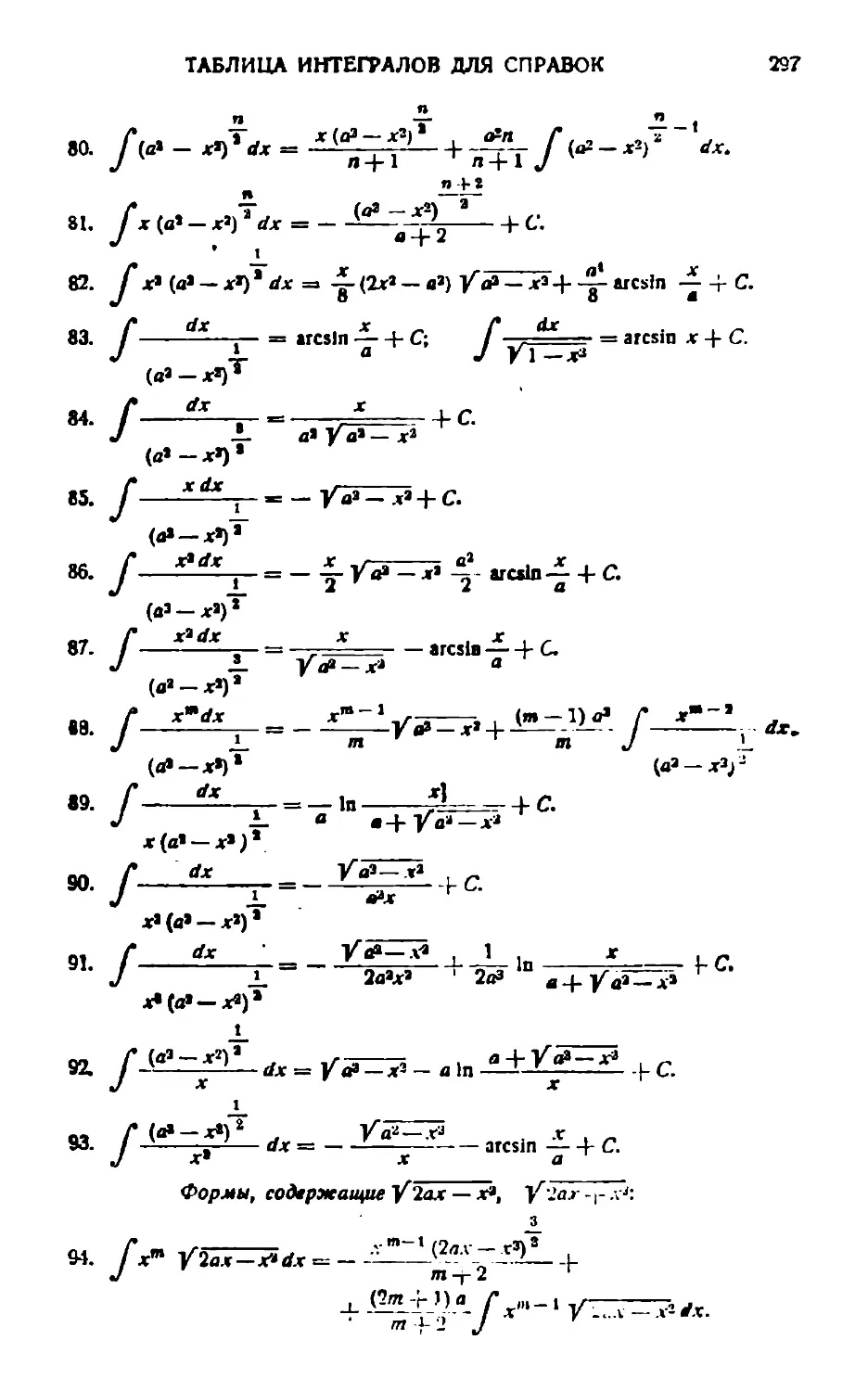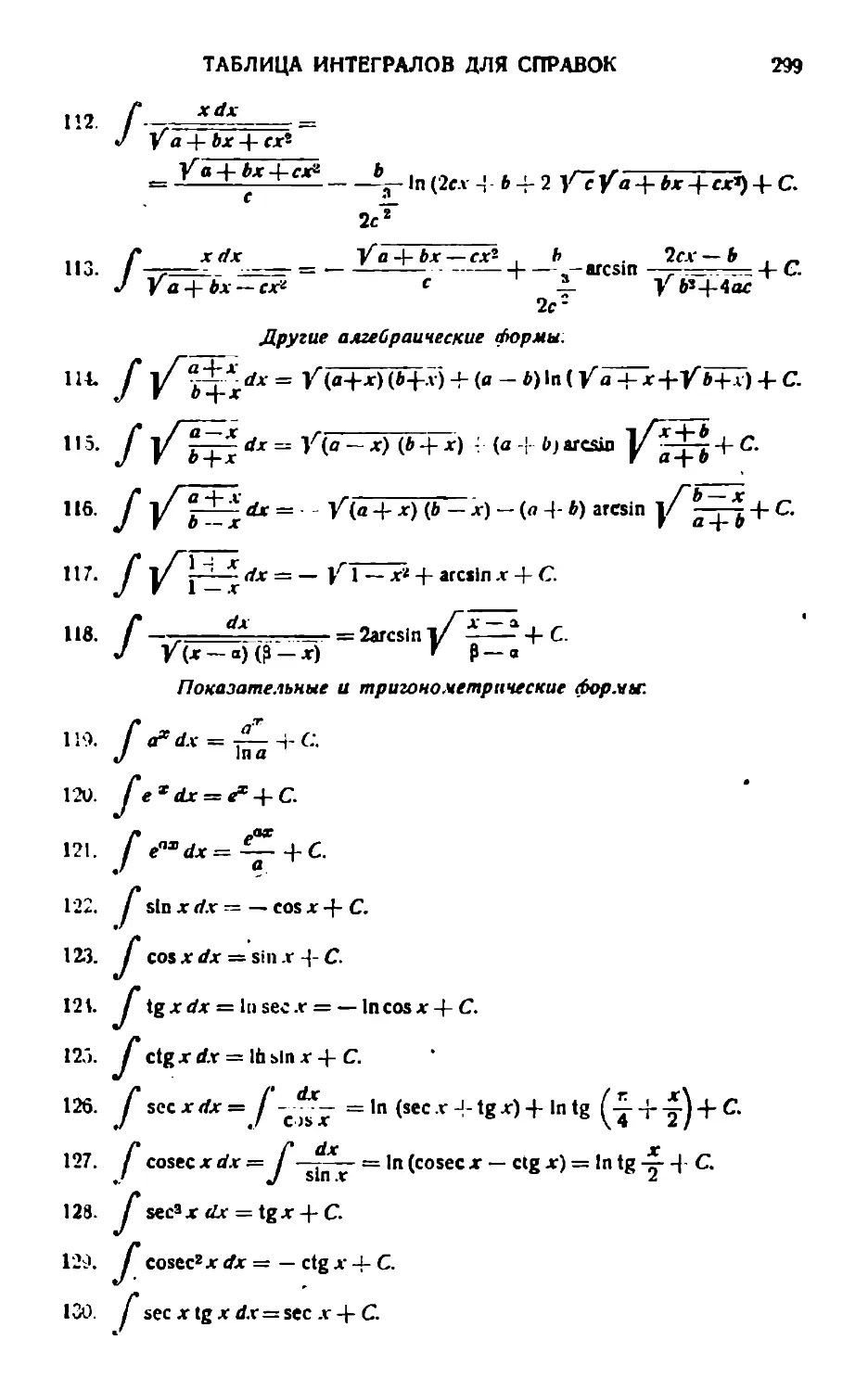Текст
В. ГРЭНВИЛЬ и Н. ЛУЗИН
X 5 ' • "7 **
КУРС ДИФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
ЧАСТЬ I!
ИНТЕГРАЛЬНОЕ
ИСЧИСЛЕНИЕ
< / •
i Допущено в HO'. femee учебника е 19U г. Всесоюзным Комитетом по енсшеиу техническому образоеанаю пря ЦИК СССР
онти
ГОСУДАРСТВЕННОЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО МОСКВА 1934 ЛЕНИНГРАД
Глава I.
Суммирование бесконечно малых.
О суммах ограниченного числа бесконечно малых 5. — О том, что надо понимать под суммою возрастающего числа бесконечно малых 6.—О важности сумм бесконечно малых: площадь кривой в прямоугольных координатах 9; площадь кривой в полярных координатах 11; объем тела вращения 12; длина дуги плоской кривой 14; поверхность тела вращения 15. — Интегральные суммы 16. — Обозначения интегральной суммы 19. — Обозначение предела интегральной суммы. Определенный интеграл 21Г — Предел интегральной суммы не зависит от Выбора точек на отрезочках 25. — Первообразная функция 27.—Предел интегральной суммы не зависит от способа деления основного отрезка 31. — Фактическое вычисление предела интегральной суммы 33. — Решение пяти основных задач геометрии 35. — О взаимоотношении диференциального и интегрального исчислений 45. — Настоящее и кажущееся переменные 46. — Определенный интеграл как функция своих пределов 43.
Глава П.
Неопределенный интеграл. Непосредственное интегрирование.
Интегрирование как действие обратное диференцированвю — 52. Основные свойства неопределенных интегоалов 54. — О вычисляемости и невычисляемости неопределенных интегралов 56. —Таблица и непосредственное интегрирование 57. — Тригонометрические диференциалы 73. — Интегрирование выражений, содержащих — tun V jfl-^ а* 78. — О множественности ответов при интегрировании 81.
Глава 111.
Постоянное интегрирования.
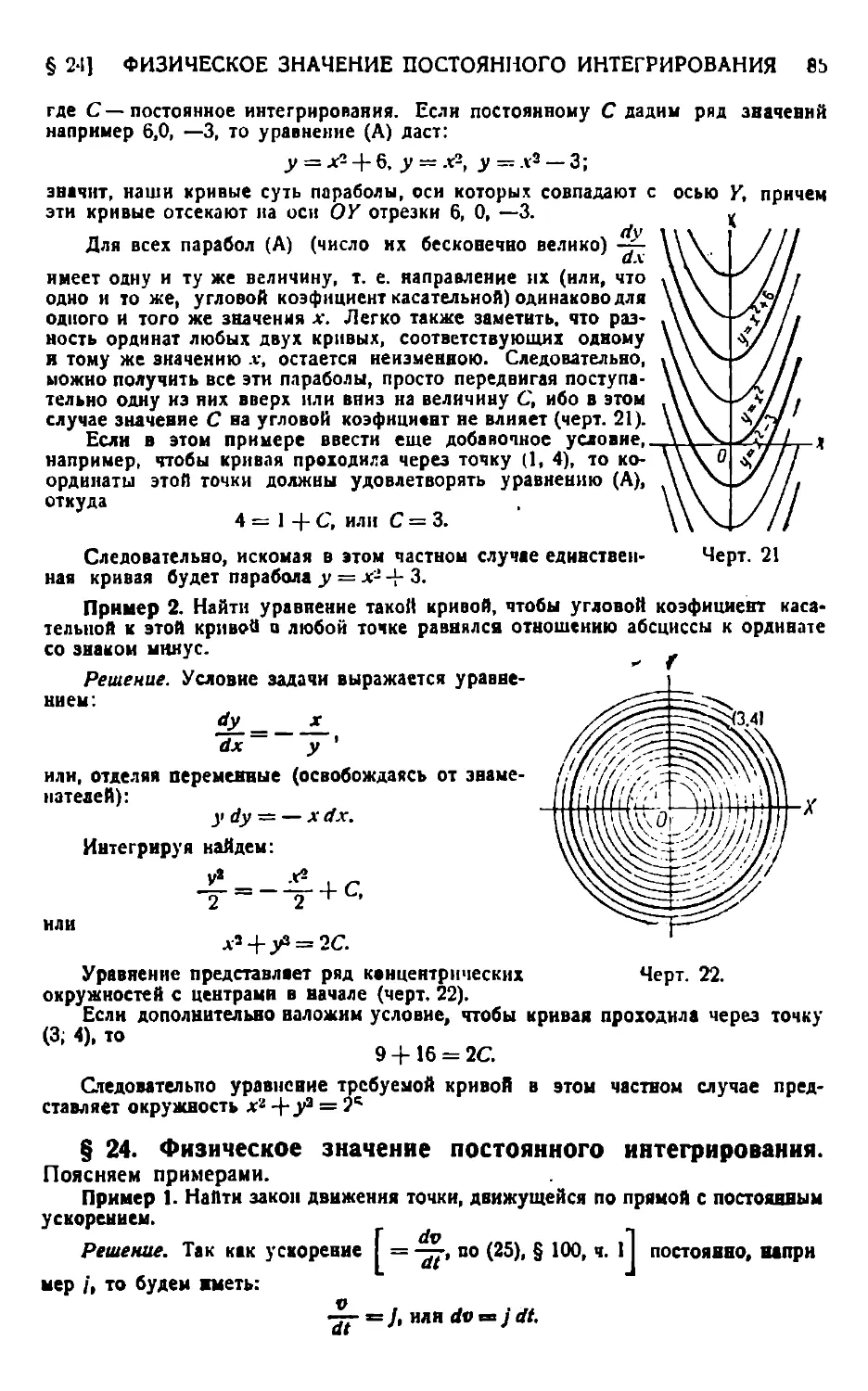
Определение постоянного интегрирования ^14. — Геометрическое значение постоянного интегрирования 84. — Физическое значение постоянного интегрирования 85.
Глава IV.
Интегрирование рациональных дробей.
Введение 91. — Случай I 91. — Случай II 93. — Случай III 94. — Случай IV 96. Глава V.
Интегрирование посредством подстановки нового переменного. Рационализация. Биномиальные диференциалы. Тригонометрические диференциалы. Интегрирование по частям.
Введение 101- — Диференциалы, содержащие дробные степени одного х 101. — Диференциалы, содержащие дробные степени одного a -j- bx 102. — Диференциалы, не содержащие иных радикалов кроме Уа -f- bx Ю4. — Диферен-
циалы, не содержащие иных радикалов кроме V a -f- bx — 105. — Биномиальные диференциалы 107. — Условия интегрируемости биномиального диферен-циала 108.—Преобразование тригонометрических диференциалов 111.— Формула интегрирования по частям 113. — Интегралы вида J*e',rsln or dx и
cos пх dx 116.— Разные подстановки 117.
* Глава VI.
Определенный интеграл.
Способ суммировать бесконечно малые 119. — Определенный интеграл 121. — Свойства определенного интеграла 123. — Бесконечные пределы 136. — Случай, когда ф (х) разрывна 13|7, .
Глава VII.
Приложения интегрального исчисления.
Равномерные бесконечно малые 141. — Равномерно-равносильные бесконечно чалые 142. — Бесконечно малые равномерно-высшего порядка 142. — Абсолютно ограниченные суммы бесконечно малых 144. — Второй принцип анализа бесконечно малых 145. — Общая схема применения интегрального исчисления 146. — Плошадь кривой в декартовых координатах 147. — Плошадь, когда кривая задана уравнениями в параметрической форме 150. — Площадь кривой в полярных координатах 153, —Объем тела вращения 155.— Длина дуги плоской кривой в декартовых координатах 158.— Длина дуги кривой в полярных координатах 160.— Поверхность тела вращения 162. — Определение объема тела по площади поперечного сечения 165. — Центр тяжести 167. — Давление жидкости 175.— Работа 177.
Глава VIII.
Кратные интегралы.
Двухмерная интегральная сумма 182. — Геометрический смысл двухмерной интегральной суммы 183.— Двойной (определенный) интеграл ^. — Геометрический смысл двойного интеграла 188. — Вычисление двойного интеграла. Случай прямоугольного контура 190.—Общий случай криволинейного контура 195. — Двойной интеграл в полярных координатах 201. — Приложения двойного интеграла. Объем цилиндрического тела 204.— Площади, ограниченные плоскими кривыми 205. — Центр тяжести площади плоской фигуры 207. — Момент инерции площади плоской фигуры 210. — Общий метод вычисления площади поверхности 213. — Нахождение объемов посредством тройного интегрирования 218.
Глава IX.
Обыкновенные днференциальные уравнения.
Введение 222. — Порядок и степень днференцнальяого уравнения 224.— Решение диференциальных уравнений. Постоянные интегрирования 225. — Поверка решений днференциального уравнения 226. — Днференциальные уравнения первого порядка и первой степени227.— Уравнение Бернулли 234. — Некоторые виды диферен.шальных уравнений второго порядка 235. — Линейные днференциальные уравнения второго порядка с постоянными коэфнциектами. Простейшие механические колебания 241. — Однородное линейное уравнение второго порядка с постоянными коэфициеятами. Формальное решение 242. — Физическая интерпретация решения. Свободное колебание 248. — Неоднородные линейные днференциальные уравнения второго порядка с постоянными коэфи-циентами 251. — Некоторые другие частные виды правой части неоднородного линейного уравнения 2-го порядка 255. — Линейные днференциальные уравнения с постоянными коэфипиентами порядка выше второго 260. — Основные теоремы 261. —Вид общего интеграла линейного днференциального уравнения л-го порядка, правая часть которого равна нулю 262. — Решение линейного однородного уравнения с постоянными коэфицнентами л-го порядка 263. Неоднородные линейные уравнения высших порядков 267.
Глава X.
Приближенное интегрирование.
Задача приближенного интегрирования 277. — Правило трапеции 277. — Правило Симпсона 278.
Приложение I. Доказательство основной теоремы интегрального исчисления. Приложение II. Таблица интегралов для справок.
ГЛАВА Т.
СУММИРОВАНИЕ БЕСКОНЕЧНО МАЛЫХ.
(К сведению читателей. Читатель может отложить чтение этой главы, начав прямо с главы 11 и переходя к следующим по порядку главам, сделанным независимыми от главы I.)
§ I. О суммах ограниченного числа бесконечно малых. Понятие суммы кажется столь простым, что сначала не возникает и подозрения, что здесь могут быть вообще какие-нибудь разговоры: составить сумму нескольких чисел — это значит сложить их вместе, т. е. соединить их в одно число; вот и все.
Однако когда дело идет не о сумме постоянных чисел, а о сумме переменных величин, тогда дело коренным образом изменяется, и здесь требуется большое внимание, потому что здесь говорить о полном слиянии слагаемых величин в одну на первых порах представляется весьма затрудниГельным. И в частности это относится к суммам бесконечно малых.
Напомним читателю, что бесконечно малым называется всякая переменная величина а, имеющая нуль своим пределом:
lima = 0. .
Это значит, что величина а ведет себя так, что какое бы заранее мы ни выбрали положительное число е, обязательно наступит такой момент времени, начиная с которого абсолютная величина | а | сделается и впредь будет оставаться меньше, чем в, т. е. | а | < е.
Напомним, наконец, читателю основное предложение о сумме бесконечно малых:
Сумма ограниченного числа бесконечно малых есть опять бесконечно малое.
Например, чтобы убедиться в том, что сумма а пяти бесконечно малых а, ?, 7, 8, т(:
e = a +
есть бесконечно малое, нам следует, взяв какое-нибудь положительное число е, просто подождать того момента времени, когда все пять абсолютных величин |a|, |£|, |f], |8|, И| станут одновременно
меньше и будут впредь все время оставаться такими же. Ясно, что
О
с этого момента сама сумма o = a-]~p Т+3 + Ч будет в свою очередь
все дальнейшее время оставаться по абсолютной величине меньше, чем
е । в е е е . .
5- + -5--Г-5 + = т-е-,а,<е-
А так как такое рассуждение можно применить для любого е, то это значит, что сумма о пяти бесконечно малых есть бесконечно малое.
§ 2. О том, что надо понимать под суммою возрастающего числа бесконечно малых. Мы только что указали, что сумма ограниченного числа бесконечно малых непременно есть бесконечно малое. Ничего подобного не будет, если мы станем брать .суммы неограниченного числа бесконечно малых**, которые иногда называют еще менее удачным термином, говоря о „суммах бесконечно большого числа бесконечно малых слагаемых".
Ведь на деле совсем нет никакого „неограниченного числа** или, еще хуже, „бесконечно большого числа*: всякое целое число, например число 5, по самой своей сути всегда и во всех случаях есть неизменной и конечное. А раз оно, будучи постоянным, остается всегда самим собою 1), то оно тем самым является и ограниченным.
Спрашивается, в каком же тогда смысле отваживаются говорит/ о „неограниченном числе бесконечно малых*, или, еще хуже, о „бесконечно большом числе бесконечно малых*? Читатель должен быть заранее предупрежден, что эти слова являются лишь очень кратким, но совершенно неправильным способом выражения и что самый выигрыш краткости получается вдесь за счет н в ущерб ясности и правильности мышления.
На самом деле под указанными смутными, хотя и краткими, словами подразумевается очень сложное явление. Вот в чем оно состоит.
Представим себе, что в определенный момент времени у нас имеется т количеств а, р, -у,...и, сумму величин которых мы обозначим через -з: *
° = а+£~Н+ •••-(-<
В рассматриваемый момент времени/и есть целое вполне определенное число; что же касается а, р, 7,..., р, то в этот момент времени они имеют также строго определенные числовые значения.
Пусть теперь время станет течь, и пусть с течением времени все количества о, р, 7, .., р будут стремиться к нулю как к пределу, в то время как их число т будет неограниченно возрастать. Это значит, что теперь с течением времени все числовые величины рассмотренных раньше количеств а, 0, 7,...,р придут в движение и начнут все по абсолютной величине безгранично умаляться, но одновременно с этим в сумме a-f-P~|-7~b-'-~bl*’ будут безгранично возникать все новые и новые слагаемые, которых раньше в ней не было
*) Читатель не должен смешивать числа и величины. Всякое число, если оно есть истинное число, а не замаскированная переменная величина, всегда неизменно и конечно. Например, число 5, относительно которого даже нелепо спрашивать, конечно ли и постоянно ли оно. Иное дело — величина, которая может изменяться каждое мгновение.
и которые, едва появившись, будут уже все дальнейшее время в ней оставаться и начнут в свою очередь сами стремиться к нулю.
Вот только в этих условиях про сумму о и говорят, что а есть .сумма неограниченного числа бесконечно малых". Мы же будем помнить, что лишь ради краткости речи мы будем допускать — теперь уже совершенно сознательно — этот весьма неправильный способ выражения, потому что про сумму а в сущности следовало бы говорить так:
о есть сумма безгранично увеличивающегося числа безгранично умаляющихся слагаемых.
Из всего сказанного читатель должен заключить," что сумма а возрастающего числа бесконечно малых есть математическое понятие, собственно, очень сложное, н что поэтому нет никаких оснований дожидаться от этой суммы о всех тех свойств, которые раньше были установлены для сумм двух, трех пяти и вообще невозрастающего числа бесконечно малых.
В частности, нет ничего удивительного, что
сумма возрастающего числа бесконечно малых во обще не есть величина бесконечно малая.
Чтобы убедиться в этом, достаточно просто рассмотреть следующий пример.
Пусть т есть какое-нибудь целое положительное число. Фор-1 , 1
мула т • — = 1 нам говорит о том, что если мы возьмем за слагаемое — т т
и повторим его в точности т раз, то в сумме а мы получим единицу, т. е.
Обозначим первое слагаемое через а, второе слагаемое—через р, третье— через f,..., и, наконец, последнее слагаемое — через у., т. е. положим
1 о 1 1 1
<Х = -, р= -------, У=--------,..., }1=—.
т Г т т т
Ясно, что мы получим равенство.
о = а-|-Р + тЧ- • •+и-= к
Пусть теперь целое число т начнет безгранично возрастать. Ясно что каждое из т слагаемых а, р, у,. . .,и явится тогда бесконечно малым, потому что дробь — становится в этих условиях переменной вели-чиной, имеющей своим пределом нуль, а число слагаемых суммы будет неограниченно увеличиваться. И однако сумма a = a-|-P4-'f4-----|-H вовсе не есть бесконечно малое, потому что а=1.
Читатель не должен считать все эти вещи бесполезными тонкостями, а должен прямо иметь в виду, что все интегральное исчисление посвящено, в сущности, рассмотрению сумм возрастающего числа бесконечно малых.
Поэтому является крайне важным, чтобы читатель не торопился с изучением основ и как можно яснее представил себе свойства таких сумм.
Всякий шаг вперед в смысле приобретения ясности в основах есть крупнейший выигрыш в отношении даже и приложений, которые предстанут для ума читателя не как нечто совершенно новое и неожиданное, а лишь как простые упражнения, в уже известном ему материале.
В частности, пусть читатель попробует для проверки ясности своего понимания выяснить себе, почему данное выше доказательство б е с к о н е ч н о й малости суммы с = a-f- р • -+р» составленной из т бесконечно малых слагаемых а, р, т,...,р., верное, когда т есть неизменное число, становится ложным, когда т безгранично возрастает.
Отв. Когда число слагаемых а, р, р. не изменяется, мы можем, взяв какое-нибудь положительное число с, разделить его на т. Полученная дробь —- есть положительное нензменяющееся количество. И так как сла-т
гаемые а, р, ?,..., р суть величины бесконечно малые, то дли первой из них, а, наступит такое время /]( начиная с которого мы будем иметь |а|< —; для второй из них, S, тоже наступит такое время L, начиная с которого мы будем иметь р|< А;...; и для последней из них, р, также в свою очередь наступит такое время /от, начиная с которого мы будем иметь |р|<-^. Ясно, что когда время перейдет за все эти моменты tt, I,,..., tm, мы будем уже одновременно иметь сразу все т неравенств;
откуда и следует окончательное неравенство:
. , , t , I , , е е
1 1 т ' т ' т т
т. е. |«|<«, что и обнаруживает бесконечную малость суммы с.
Если жес = <>4-Р-|-..,-|-|л есть сумма возрастающего числа бесконечно малых, то, разумеется, мы можем рассмотреть ее в определенный момент времени, когда число ее слагаемых равно еще т, и, разумеется, можем ваять дробь . Но когда время начнет течь, то т начнет безгранично расти, и, значит, взятая вами дробь — начнет.сама в свою очередь бесконечно умаляться. А тогда просто может никогда не наступить такой момент времени когда первое слагаемое, а, станет ио абсолютной величине меньше, чем потому что и а и обе теперь бесконечно малые, и еще неизвестно, какое из них будет обгонять другое в своем стремлении к нулю.
Это как раз и происходит в вышеприведенном примере, где а = ₽ = j . .= 1
= р = — и где, таким образом, никогда не может случиться, чтобы мы имели Л1
неравенство Iе! <~ Уже *»я *<1, вапрнмер для «= -у.
§ 3. О важности сумм бесконечно малых. Для ясного понимания этой важности надо иметь в виду, что только благодаря суммам бесконечно малых было получено, наконец, полное решение множества математических и физических задач, перед которыми в бессилии останавливались предшественники Ньютона и Лейбница. Только благодаря суммам бесконечно малых стало возможным изучение движения тел, а вместе с ним осуществилось развитие механики и астрономии. Только благодаря суммам бесконечно малых физики и естественники получили в свои руки могущественнейшее средство для изучения законов природы. Только благодаря суммам бесконечно малых геометрия получила беспрепятственную возможность дальнейшего развития, так как благодаря им впервые были полностью решены труднейшие задачи о площадях, длинах дуг, объемах и поверхностях. И только благодаря сумкам бесконечно малых сама матема-
тика была поднята на высшую ступень, завоевав новую область, называемую .высшей математикой*.
Полное понимание существенной важности сумм бесконечно малых придет к читателю само собою, по мере изучения им интегрального исчисления. Но уже и сейчас читатель может почувствовать эту важность, ознакомившись со следующими задачами и способом их решения интегральным исчислением.
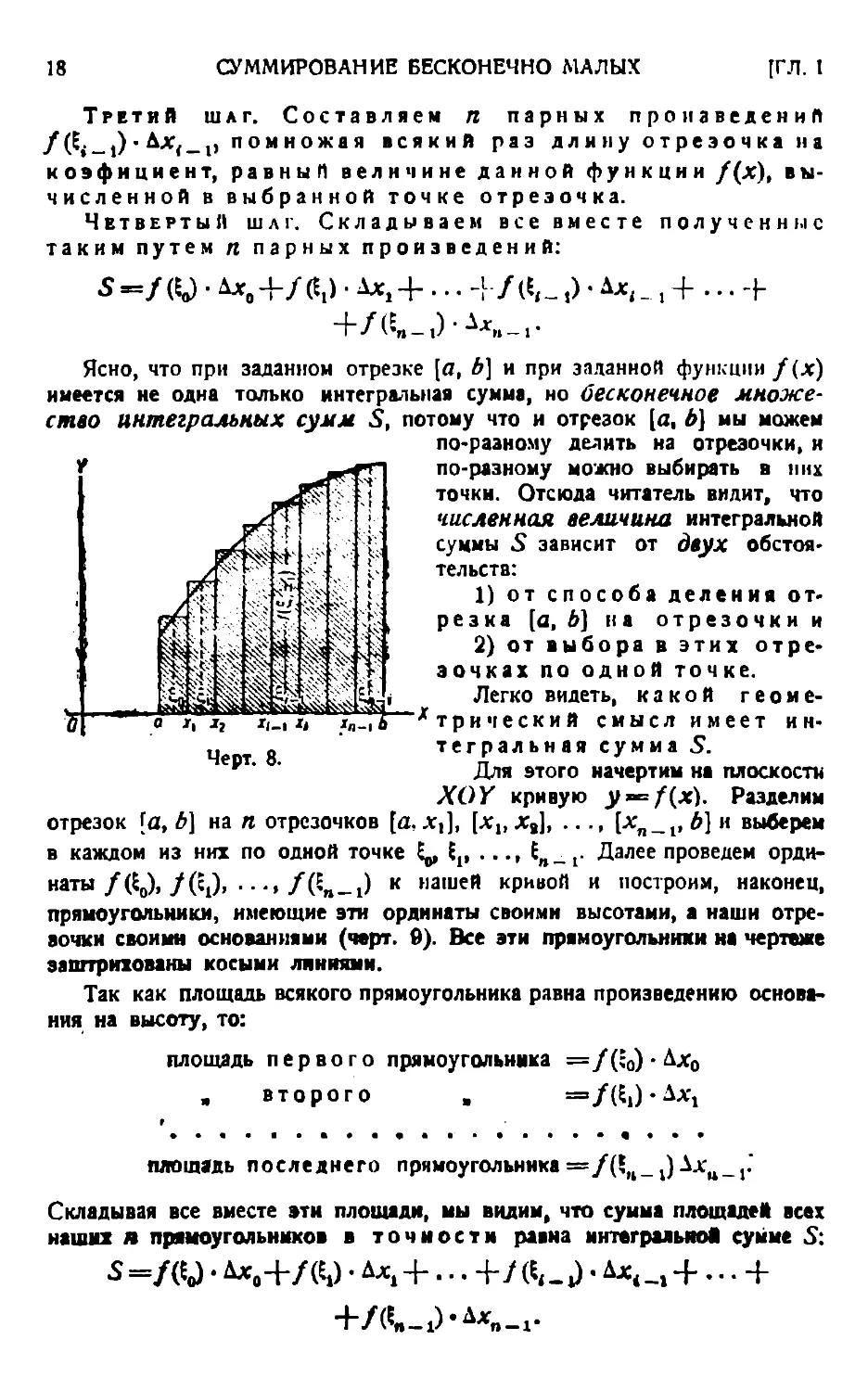
I. П Л О Щ А Д Ь* К Р И В О й В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ.
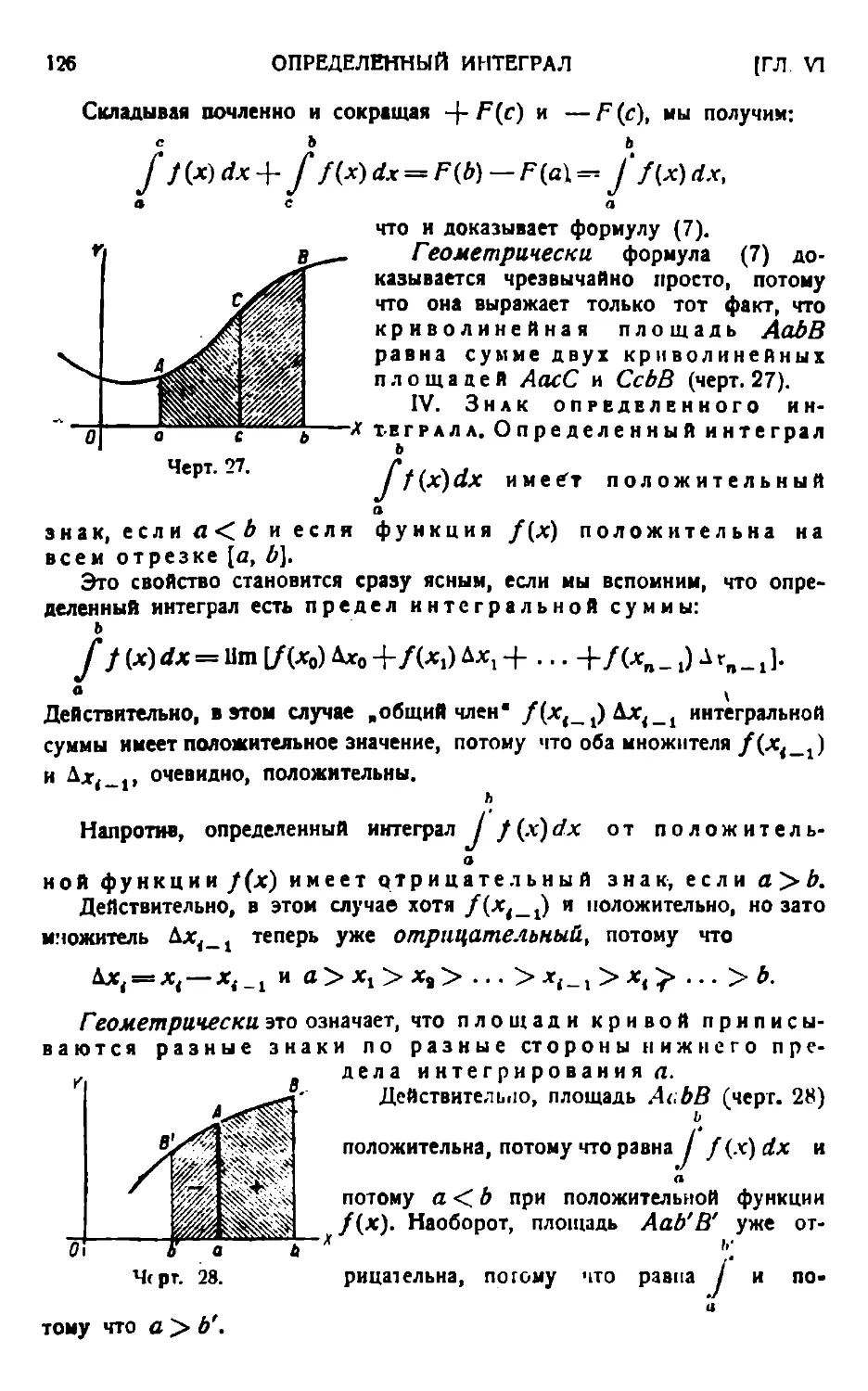
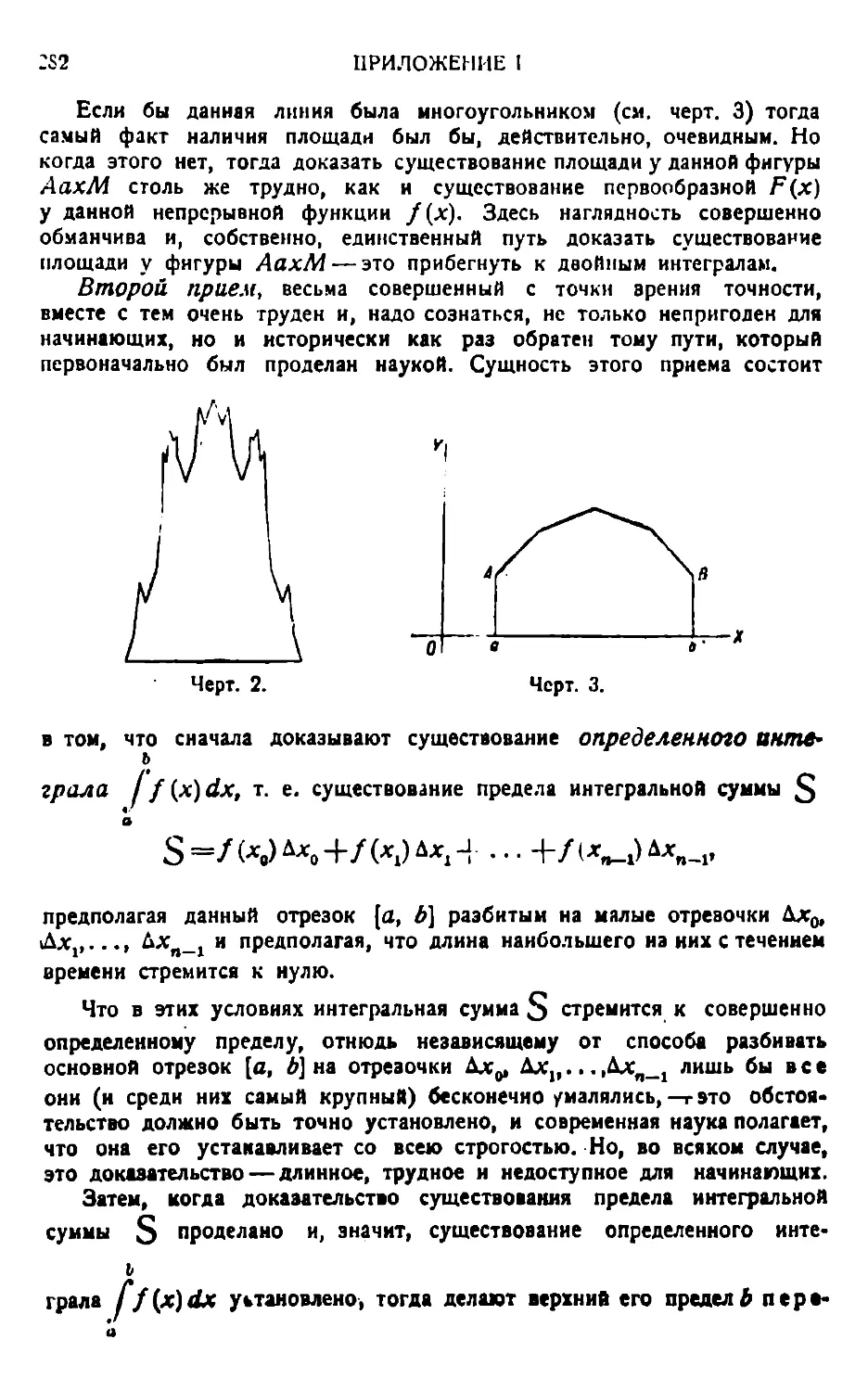
Речь идет о точном определении площади так называемой .криволинейной трапеции*, т. е. фигуры АаЬВ, ограниченной осью абсцисс, двумя ординатами и кривой дугой АВ (черт. 1). За образец подражания берем элементарную геометрию.
Читатель знает, что элементарная геометрия рассматривает площадь круга как промежуточную между площадями двух правильных многоугольников: одного — вписанного в этот круг, а другого — описанного. И так как разность площадей двух этих многоугольников безгранично умаляется, когда число сторон обоих правильных многоугольников неограниченно увеличивается, то элементарная геометрия
отсюда заключает, что площадь круга есть предел площади правильного многоугольника (вписанного или описанного —безразлично), когда число его сторонбезграничновозрастает.
Точно так же и здесь. Площадь криволинейной трапеции АаЬВ прямым образом — т. е. непосредственно и с абсолютной точностью— мы измерить, разумеется, не можем. Поэтому мы употребим обходный путь. Для этого разделим сначала всю данную нам криволинейную трапецию АаЬВ на весьма большое число чрезвычайно узких криволинейных т р а п е ц и й, как указано на левом рисунке черт. 1, прямыми, параллельными оси OY. Назовем для простоты каждую из этих узких криволинейных трапеций „элементарной трапецией*.
Истинную величину площади элементарной трапеции найти столь же трудно, как и величину площади всей криволинейной трапеции АаЬВ. Но мы можем вписать в элементарную трапецию и описать около нее два прямоугольника, имеющих то же самое основание, как рассматриваемая элементарная трапеция, и имеющих высотами минимальную и максимальную ординату того кусочка данной непрерывной кривой АВ, который ограничивает сверху нашу элементарную трапецию. На среднем рисунке черт. 1 изображены две элементарные трапеции с вписанными и описанными прямоугольниками, причем для левой трапеции максимальная и минимальная ординаты соответствующего кусочка кривой являются просто боковыми ее сторонами, а для правой трапеции эти ординаты суть некоторые внутренние.
Если мы это построение вписанного и описанного прямоугольников проделаем для всех наших элементарных трапеций, то получим две ступенчатые фигуры, изображенные на правом рисунке того же чертежа, одна из которых вписана в данную криволинейную трапецию АаЬВ, а другая описана около нее. Естественно поэтому рассматривать истинную площадь данной криволинейной трапеции АаЬВ как величину промежуточную между площадями вписанной и описанной ступенчатой фигуры
Разность этих двух площадей представлена, очевидно, суммою тех прямоугольничков, которые содержаг кусочки нашей кривой; эти прямоугольнички изображены белыми на правом рисунке. Если мы переместим их все, двигая параллельно оси OY так, чтобы их верхние основания поместились на одной прямой, то видим, что вся их сумма помещается в узкой горизонтальной ленте, основанием которой служит данный отрезок [а, 6], а высотой е. Здесь в Можно рассматривать как величину сколь угодно малую. Действительно, функция y=f(x), соответствующая заданной кривой АВ, предполагается непрерывной на отрезке [а, 6]. А это означает, что разность двух каких-нибудь ее ординат делается бесконечно умаляющейся, когда разность двух соответствующих абсцисс бесконечно умаляется. Поэтому, если мы сделаем наши элементарные трапеции достаточно узкими, разность между максимальной и минимальной ординатами у каждой из них будет меньше в, где в есть сколь угодно малая величина. Поэтому все прямоугольнички, составляющие разность обеих ступенчатых фигур, имеют высоты меньшие, чем е.
Таким образом разность площадей вписанной и описанной ступенчатой фигуры становится меньше площади указанной узкой горизонтальной ленты, следовательно, меньше чем а • (д— а). Так как в можно взять сколь угодно малым, то отсюда и следует, что когда все элементарные трапеции бесконечно утончаются, разность площадей вписанной и описанной ступенчатой фигуры безгранично умаляется. Отсюда, как и в случае площади круга, естественно заключить, что площадь криволинейной трапеции АаЬВ есть предел площади ступенчатой фигуры (вписанной или описанной — безразлично), когда все элементарные трапеции бесконечно утончаются.
Так как площадь а ступенчатой фигуры (например вписанной) равна сумме площадей составляющих ее прямоугольников, то, обозначая их площади (вычисляющиеся, понятно, без всякого труда) соответственно через а, Р. мы получим для площади а рассматриваемой ступенчатой
(приближенной) фигуры равенство:
° = аН-Р + т-Ь---+1х-
Когда• все элементарные трапеции бесконечно утончаются, причем число их, понятно, безгранично возрастает, тогда площади прямоугольников a, [i, у,...,р бесконечно умаляются, а их сумма о становится перемен-ной величиной, имеющей своим преде- «ХаА
ЛОМ *) истинную площадь заданной кри-волинейной трапеции АаЬВ, т. е.
площадь4aM?=lim(a-|-p-|-7-|-...-|-|*) ----Н-ь-
Мы видим, что искомая кри Черт. 2.
волинейная площадь есть предел суммы возрастающего числа бесконечно малых.
II. Площадь кривой в полярных координатах.
Для читателя, который со вниманием прочел разъяснения к рреды-дущей задаче, здесь не нужны длинйые объяснения.
Криволинейный сектор АОВ (черт. 2), площадь которого ищется, мы делим на весьма большое число чрезвычайно тонких криволинейных секторов, которые называем элементарными секторами.
Площадь элементарного сектора определить, разумеется, столь же трудно, как и площадь самого данного криволинейного сектора АОВ. Поэтому мы заключаем всяк>^А^фрментарный сектор между двумя круговыми секторами, один игдоддоых вписан, а другой описан.
Вследствие этого искомая площадь криволинейного сектора АОВ
*) С геометрической точки зрения нам нет ни малейшей надобности доказывать, что переменная величина а в действительности имеет предел (и, стало быть, не будет безгранично колебаться), потому что криволинейная трапеция АаЬВ в действительности имеет площадь, к которой я безгранично приближается. Однако в дальнейшем мы, исходя уже из аналитических соображений, попутно увидим, что переменная величина о в самом деле имеет предел, так как мы его тут же и вычислим с абсолютной точностью. Это замечание относятся и ко всем остальным аадачам.
окажется заключенной между площадями двух ступенчатых фигур, одна из которых составлена из вписанных круговых секторов, другая же—из описанных.
Разность площадей обеих ступенчатых фигур представлена, очевидно, суммою криволинейных прямоугольничков (на рисунке: белых), которые содержат кусочки дуги АВ, ограничивающие элементарные секторы. „Высотами* этих криволинейных прямоугольничков мы будем считать разности радиусов их круговых „оснований*.
Так как данная дуга АВ непрерывна, то можно предложенный криволинейный сектор АОВ разделить на столь тонкие элементарные секторы, что „высоты* указанных прямоугольников окажутся все меньше, чем е; здесь s есть положительное число, сколь угодно малое.
Чтобы оценить сумму площадей этих прямоугольничков, проведем дугу CD круга, радиус которого ОС есть постоянный и больше всякого радиуса-вектора данной кривой дуги АВ. Отложим на радиусах этой дуги CD, внутрь, отрезок в. Мы получим таким образом тонкую полоску CDFE, „основанием* которой служит дуга CD, а „высотой* — отрезок в. Когда в безгранично умаляется, площадь полоски CDFE также, очевидно, безгранично умаляется. Ясно, что радиусы, служащие сторонами элементарных секторов, будучи продолжены, разделят полоску CDFE на криволинейные прямоугольники, соответственно большие указанных прямоугольников. Отсюда и следует, что с у м м а площадей этих прямоугольничков бесконечно умаляется вместе с числом а.
Таким образом разность площадей вписанной и описанной ступенчатой фигуры бесконечно умаляется, когда все элементарные секторы бесконечно утончаются. Отсюда, как и для площади круга, естественно заключить, что площадь криволинейного сектора АОВ есть предел площади ступенчатой фигуры (вписанной или описанной — безразлично), когда все элементарные секторы бесконечно утончаются.
Так как площадь о ступенчатой фигуры (например вписанной) равна сумме площадей составляющих ее круговых секторов, то, обозначив площади их (вычисляющиеся, понятно, без всякого труда) соответственно через а, 0, 7,мы получим для площади о рассматриваемой (приближенной) фигуры равенство:
в = «+₽4т г-••Не-
когда все элементарные секторы бесконечно утончаются, причем число т их, понятно, безгранично возрастает, тогда а, 3. I.!А беско-
нечно умаляются, а их сумма о становится переменной величиной, имеющей своим пределом истинную площадб заданного криволинейного сектора АОВ, т. е.
площадь АОВ = lim (а -ф- p-pf -I-... -Ни-).
Мы видим, что искомая криволинейная площадь есть предел суммы возрастающего числа бесконечно малых.
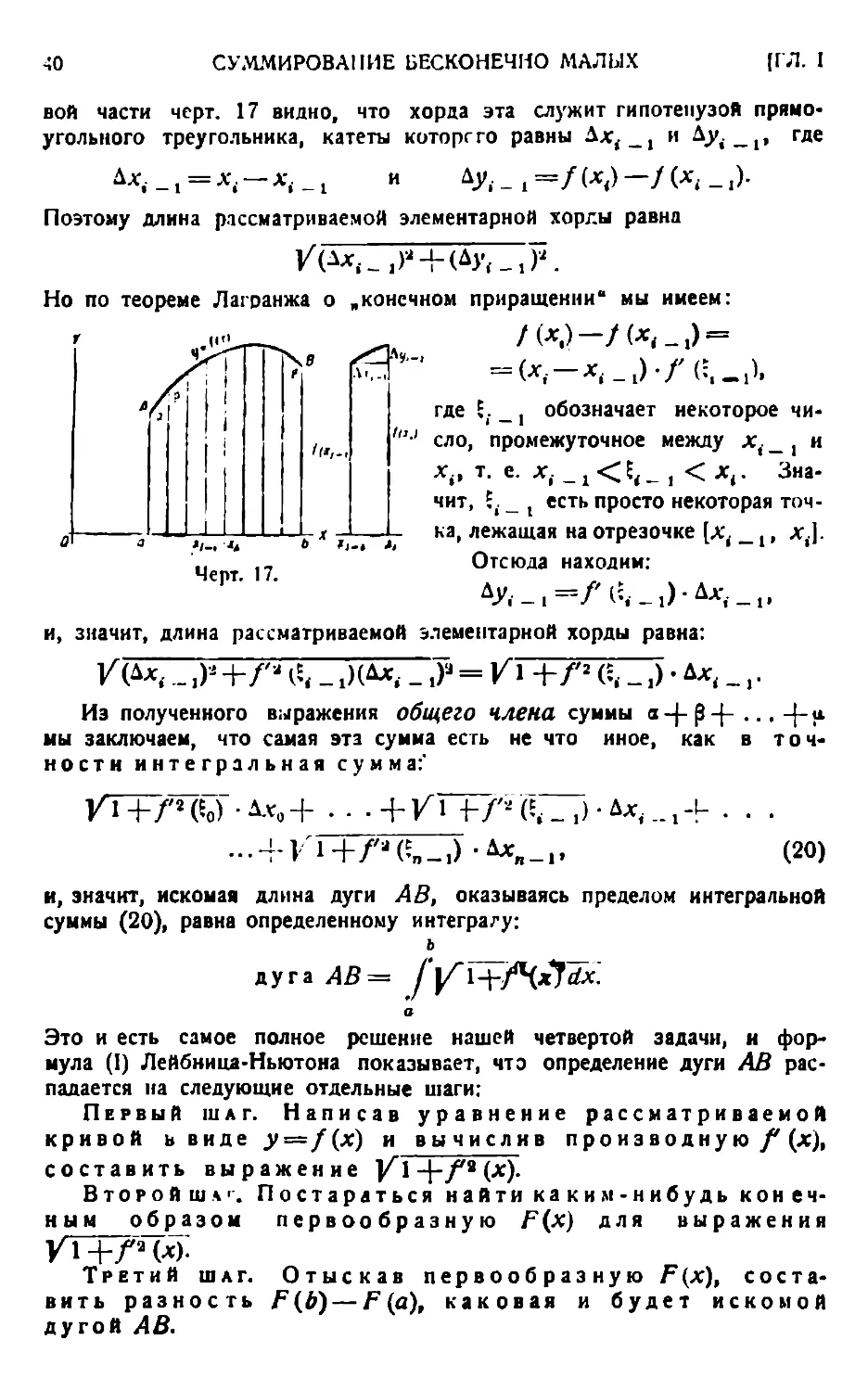
Ш. ОБЪЕМ ТЕЛА ВРАЩЕНИЯ.
Требуется найти точную величину объема тела вращения AiABBu образованного вращением дуги АВ пло-
бъема правильной призмы (вписан-
Черт. 3. обоими объемами вписанного и описанного
ской непрерывной кривой около некоторой оси вращения (черт. 3).
За образец для подражания берем элементарную геометрию и вспоминаем, что объем круглого цилиндра рассматривается там как величина промежуточная между объемами двух правильных призм: одной — вписанной в этот цилиндр, а другой — описанной. И так как разность объемов двух этих призм безгранично умаляется, когда число граней обеих правильных призм неограниченно увеличивается, то элементарная геометрия отсюда заключает, что объем круглого цилиндра есть предел о ной или описанной — безразлично), когда число ее граней безгранично возрастает.
Точно так же поступаем п мы: рассекаем данное тело вращения на тонкие диски, которые назовем элементарными дисками, плоскостями, перпендикулярными оси вращения, вписывая и описывая около каждого из них круглый цилиндрик, как показано на чертеже. Таким образом мы получаем два зубчатых тела, составленных из вписанных и описанных цилиндриков, и естественно рассматривать объем данного тела вращения AiABBl как промежуточный между зубчатого тела.
Разность объемов этих
суммы объемов тонких колец, получающихся от вращения прямоугольничков, содержащих дужки кривой АВ. Когда элементарные диски, на которые рассечено данное тело вращения АхАВВи становятся достаточно тонкими, высоты наших вращающихся прямоугольничков в силу непрерывности кривой АВ делаются меньше, чем е, где в — сколь угодно малое положительное число. А отсюда следует, что сумма объемов указанных колец будет меньше объема только одного кольца, которое мы получаем, вращая узкий прямоугольник CDEF, имеющий а своею высотою и основание которого CD, параллельное и равное отрезку ab, удалено от оси вращения Х'Х на постоянное расстояние аС. большее всякой ординаты данной дуги АВ. Ясно, что когда в бесконечно умаляется, рассматриваемое кольцо делается все более и более тонким, и, значит, его объем также бесконечно умаляется.
Таким образом разность объемов вписанного и описанного зубчатого тела бесконечно умаляется, когда все элементарные диски бесконечно
тел. очевидно, состоит из
утончаются. Отсюда, как я в случае объема круглого цилиндра, естественно заключить, что объем тела вращения А1АВВ1 есть предел объема ступенчатого тела (вписанного или описанного — безразлично), когда все элементарные диски бесконечно утончаются.
Так как объем в ступенчатого тела (например вписанного) равен сумме объемов составляющих его цилиндриков, то, обозначая объемы их (вычисляющиеся, понятно, б^з всякого труда) соответственно через а, 0, 7....р., мы получим для объема а рассматриваемого (приближенного)
зубчатого тела равенство:
Когда все диски бесконечно утончаются, причем число т их, понятно, безгранично возрастает, тогда а, 0, 7,..., р. бесконечно умаляются, а их сумма а становится переменной величиной, имеющей своим пределом истинный объем заданного тела вращения АхАВВи т. е.
объем AtABBt = lim (<х0 7-j- • •. +«*)•
Мы видим, что искомый об-ъем тела вращения есть предел суммы возрастающего-числа бесконечно малых.
IV. Длина дуги плоской кривой.
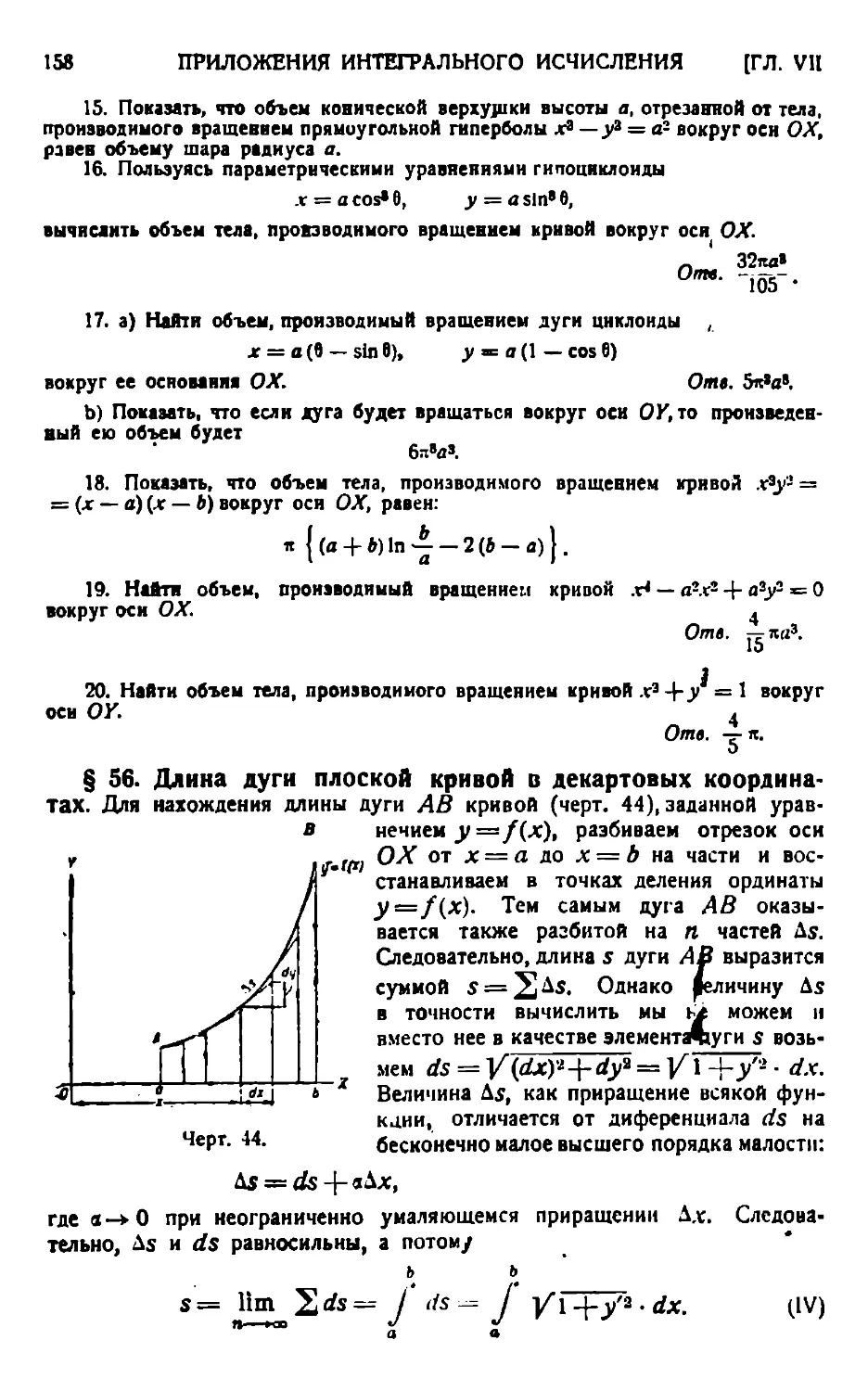
Требуется найти точную длину дуги АВ плоской кривой, имеющей непрерывно изменяющуюся касательную.
Здесь также мы за образец для подражания берем элементарную геометрию.
Вспомнив, что в элементарной геометрии длина окружности рассматривается как предел периметра правильного вписанного многоугольника, когда число его сторон безгранично возрастает, мы разделим данную нам
8 кривую дугу Л В на весьма большое число /о чрезвычайно маленьких дужек и соединим
* Черт. 4. оба конца каждой из них хордою. Назо-
вем ради ясности каждую из этих хорд элементарною хордою. Таким образом мы получим некоторую ломаную, вписанную в нашу кривую дугу ЛВ и имеющую своими звеньями элементарные хорды (черт. 4).
Обозначим длины элементарных Хорд через а, 0, 7, . . .,р. Тогда длина <з построенной вписанной (приближенной) ломаной будет составлена из длин наших элементарных хорд, т. е.
о = а-|-р4-7 }-... -J-р
Когда все элементарные хорды бесконечно умаляются, причем число т их, понятно, безгранично возрастает, тогда а, 0, 7, ...,р бесконечно умаляются, а их сумма о становится переменной величиной, предел
которой рассматривается как истинная длина данной кривой дуги АВ, т. е.
дуга Л2? = Пт (а-|~₽ 4-Т*г • • • + (*•)•
Здесь опять истинная длина кривой дуги есть предел сумм возрастающего числа бесконечно малых.
V. Поверхность тела вращения.
Требуется найти точную величину поверхности тела вращения АХАВВХ (черт. 5), образованного вращением дуги АВ плоской кривой с непрерывно изменяющейся касательной.
Элементарная геометрия для отыскания точной величины поверхности шара прибегает к следующему приему: сначала берут поло-
вину окружности с вписанной в нее половиной правильного многоугольника и потом всю эту фигуру вращают около диаметра, стягивающего концы вращаемой полуокружности. При этом вращении полуокружность опишет в пространстве полную поверхность шара, -а описанный многоугольник опишет сложное тело вращения, состоящее из ряда усеченных круглых конусов, примыкающих один к другому. Искомая поверхность шара рассматривается как предел поверхности этого сложного тела вращения, когда число сторон указанного правильного многоугольника
безгранично возрастает.
Аналогично мы поступаем и в нашем случае: сначала мы вписываем в данную вращающуюся дугу АВ какую-нибудь ломаную с весьма большим числом чрезвычайно малых звеньев. Вращение этой ломаной около оси вращения ОХ даст сложное тело вращения, состоящее из
т тонких усеченных круглых конусов, примыкающих друг к другу и' называемых нами элементарными конусами (черт. 5). Обозначая боковые поверхности этих элементарных конусов через а, р, ц, мы для поверхности о сложного (приближенного) тела вращения имеем очевидное равенство:
Когда все элементарные конусы бесконечно утончаются, причем число т их, понятно, безгранично возрастает, тогда а, р, р бесконечно умаляются, а их сумма а становится переменной величиной, предел которой рассматривается как истинная величина поверхности данного тела вращения AXABBV т. е. *
поверхность АХАВВХ — lim (а -|- р-}"7 4* • • •
Здесь опять истинная величина поверхности вращения есть предел суммы возрастающего числа бесконечно малых.
Указанные пять задач являются самыми основными для геометрии. Мы ограничимся ими, хотя можно было бы привести еще множество других задач, основных для механики и физики: во всех них неизвестная истинная величина является всегда пределом, суммы возрастающего числа бесконечно малых.
Теперь читатель должен дать себе отчет в том, что, хотя решение всех этих задач и сводится к отысканию предела суммы возрастающего числа бесконечно малых, однако отыскивать на деле пределы этих сумм он еще не умеет. Читатель должен понять, что сейчас речь идет о приобретении дополнительного умения находить точные пределы этих сумм на деле, т. е. конечным образом. Без такого умения все предыдущие рассуждения обращаются в пустые разговоры и не стоили бы решительно ничего, потому что здесь дело идет об умении отыскивать точные пределы конечным образом, не прибегая ни к какому бесконечному процессу, не кончающемуся никогда.
Великая заслуга основателей анализа бесконечно малых — Ньютона и Лейбница — заключается вовсе не в том, что они указали путь решения многочисленнейших и важнейших задач помощью суммирования бесконечно малых, но она состоит в том, что они открыли прием, позволяющий фактически выполнять такое суммирование, доводя его до самого ко'нца, как это ни кажется невероятным с первого взгляда. Без такого приема все предыдущие рассуждения были бы праздными разговорами; без такого умения фактически суммировать бесконечно малые анализ бесконечно малых был бы давно забыт.
Первый шаг, сделанный Ньютоном и Лейбницем при открытии ими анализа бесконечно малых, состоял в установлении того важного обстоя-х.__________ ________ тельства, что отыскание преде-
о а г, >, 2. ' >,].,» лов всяких сумм бесконечно
Черт. 6. малых, как бы разнообразны они
ни были и из каких бы задач они ни исходили, всегда сводится на отыскание предела так называемой интегральной суммы.
Интегральная сумма является на ипро с тейшим видом суммы бесконечно малых.
§ 4. Интегральные суммы. Возьмем какой-нибудь отрезок [л, ft], лежащий на оси Х'Х, и разделим его на п каких-нибудь частей, поместив на него п — 1 точек деления, которые мы обозначим по порядк а через jc, хг, ..., xn t (черт. 6). Для стройности обозначений мы и начальную точку а отрезка [a, ft] обозначим через х0, и его конечную точку ft обозначим через хп, т. е. положим
х0 = а, х„ = ft.
Отрезочек [х<_1, Jcj называется общим отрезочком; здесь буква i обозначает номер отрезочка и пробегает одно за другим все числа 1, 2,
3, ...,n—1. Длина общего отрезочка [xt._(, xj, очевидно, равна разности xf — х4_,; согласно обычаю диференциального исчисления эта разность рассматривается как приращение ^xt_t начальной абсциссы х<_1, сообразно чему там пишут:
,xi xi-i ^xt_f
Поэтому все наши п отрезочков будут иметь своими длинами соответственно количества
Дх„, Дх„ Дл2, Дх,_1............Дхг(_,
До сих пор мы имели дело только с отрезком [а, 6]; сделаем теперь новый важный шаг и допустим, что на отрезке [а, д] нам задана некоторая непрерывная функция /(х).
Выберем в каждом из наших п отрезочков по одной точке, беря ее произвольным образом, где захочется, внутри или на конце. Таким образом пусть в первом отрезочке [а, х,] (черт. 7) х-_г , &>-,» д
выбрана некоторая точка Eq, во 0 Z| z‘ ' 11 '-1’ втором отрезочке [х,, х,] выбра- _ ^Р1- 7-
на точка Е,..в общем отрезочке [х4_, х<] выбрана точка и, наконец, в последнем
отрезочке [xn_l,Z>] выбрана точка EZ|_,.
Возьмем теперь длину Дх4-1 общего отрезоч ка[Х1._р х4] и помножим ее на коэфициент / (?<_]), равный значению заданной функции f (х) в выбранной точке этого отрезочка. Таким образом мы получим произведение двух множителей:
/(=._.)-Ч-г
То, что мы сейчас сделали с .общим* отрезочком [xf _р xj, проделаем теперь с каждым отрезочком в отдельности и возьмем сумму S всех п составленных таким образом парных произведений:
S=/(E0) • • Ах, + ... -]-/ i) • Дх1_1-|- • • • +
+/«._,)-Ч
Вот эта-то сумма S и называется интегральной суммой, и рассмотрение таких сумм имеет для. всего анализа бес
конечно малых совершенно исключительное значение.
Из сказанного ясно, что для составления интегральной суммы 5 должны быть выполнены следующие четыре шага:
Первый шаг. Делим данный отрезок [а, А] на п отрезочков.
Второй шаг. Выбираем в каждом из них по одной
точке, где придется: внутри отрезочка или на его конце.
2 Зав. 2853. — Гранвиль а Лувил, ч. II, Интегральное вочиолепжв
Третий шаг. Составляем п парных произведений помножая всякий раз длину отрезочка на коэфнциент, равный величине данной функции f(x), вычисленной в выбранной точке отрезочка.
Четвертый шаг. Складываем все вместе полученные таким путем п парных произведений:
s-/(U • Ч+/(М i) • Ч - > + • • • +
+/(ЕП_.) • Ч,-Г
Ясно, что при заданном отрезке [а, Ь} и при заданной функции f (х) имеется не одна только интегральная сумма, но бесконечное множество интегральных сумм S, потому что и отрезок [а, Ь\ мы можем по-разному делить на отрезочки, и
по-разному можно выбирать в них точки. Отсюда читатель видит, что численная величина интегральной суммы S зависит от двух обстоятельств:
1) от способа деления отрезка [а, Ь} на отрезочки и
2) от выбора в этих отрезочках по одной точке.
Легко видеть, какой геометрический смысл имеет интегральная сумма S.
Для этого начертим на плоскости
XOY кривую jz = /(x). Разделим отрезок [а, Ь\ на п отрезочков [a, xj, [х„ ха], ..., (хя1, b] и выберем
в каждом из них по одной точке ..., £„_г Далее проведем ординаты /(£0),/(ч), к нашей кривой и построим, наконец,
прямоугольники, имеющие эти ординаты своими высотами, а наши отрезочки своими основаниями (черт. 9). Все эти прямоугольники на чертеже заштрихованы косыми линиями.
Так как площадь всякого прямоугольника равна произведению основания на высоту, то:
площадь первого прямоугольника = /(;0) • Ах0 „ второго „ =/(£,). Ax'j
площадь последнего прямоугольника =/($п_ J Лхи_,
Складывая все вместе эти площади, мы видим, что сумма площадей всех наши л прямоугольников в точности равна интегральной сумме S: s =/<у • Дх,+/(У • Ах,J _,+ •• +
Таким образом интегральная сумма 5 численно равна площади ступенчатой фигуры, составленной из прямоугольников, построенных на отрезочках Дл'(_, как основаниях и на ординатах /(£,_,) как высотах.
§ 5. Обозначения интегральной суммы. Интегральная сумма была нами написана в строчку в виде >):
/(*о) Д*о +/(•*,) Ч + • • • +f(X{ _ ,) Ч _,+ •••+/ (Хп _ ,) • Длгп_ ! .
Легко видеть, что это обозначение интегральной суммы есть неполное, иначе говоря, сокращенное.
Действительно, написать полностью сумму каких-либо количеств — это значит: выписать яге эти количества одно за другим подряд, не опуская ни одного.
Однако для интегральной суммы мы этого не можем сделать, потому что не знаем, чему равно целое число п. Поэтому мы вынуждены доволь* ствоваться неполным ее выписыванием, т. е. сокращенным, написав сперва первый член, потом второй член, далее „общий" член и, наконец, последний член. Три точки ..., предшествующие общему члену, и три точки ..., следующие за общим членом, как раз и свидетельствуют о том, что интегральная сумма написана неполно, сокращеннр, иначе говоря, обозначена символически.
К подобному символическому обозначению прибегают не только тогда, когда не могут фактически выписать всех членов суммы, но и тогда, когда число слагаемых слишком велико, чтобы трудиться писать их все. Например, чтобы написать сумму всех целых чисел первой сотни, мы не станем выписывать их все, а пишем сокращенно:
1-|-24-...-ь/+... + 100.
Но такая символическая запись нс очень удобна, и поэтому ее часто заменяют другим более удобным символическим обозначением.
Для этого очень часто записывают предыдущую сумму символом:
4 = 100 i, 4 = 1
который расшифровывается следующим образом.
Латинская3) буква S указывает на то, что надо взять
1) Мы полагаем здесь 50 = .ve> ^=*1. .... 5»-i= rr»-r Иначе говоря, выбираем точку 6<_1 постоянно в левом конце отрезочка [л,.гД Мы дальше увидим, что всегда можво ограничиться рассмотрением только такого выбора точек С(_ а н, значит, только таких интегральных сумм.
г) В теории рядов суммирование обозначается не латинскою буквою Si а греческою буквою 2, так что бесконечный ряд
"1 + «Ч+ ••• +«„-]- ... записывается символом
, сумму', за знаком суммы S выписан ,общий* член этой суммы, обозначенный просто буквою /; внизу знака суммы S написано равенство 1=1, показывающее, с чего следует начать изменять общий член i нашей суммы; вверху знака суммы S написано равенство i = 100, показывающее, чем следует окончить изменение общего члена/ нашей суммы.
Если мы теперь применим этот способ обозначения к интегральной сумме:
/Ч) Ч +/ Ч) Ч + • • • + /Ч _,) Ч -1 + • • • +
+ /(*„-!) Ч-1> (1)
то получим символ:
। -- м
,5 /4-1) Ч-п (?)
обозначающий:
1) что надо взять сумму парных произведений вида f(xi_l)^xi_i\
2) что при суммировании значок i начинает изменяться с единицы; ' 3) что при суммировании значок i кончает свое изменение на числе п.
С течением времени к только что указанному символу (2) так привыкли, что стали его выписывать все небрежнее и небрежнее, стараясь еще более его упростить и совершенно не боясь при этом утратить истинный смысл этого символа и его первоначальное понимание. Для этого стали сначала опускать внизу и вверху буквы S равенства i— 1 и 1 = п, довольствуясь лишь постановкой внизу и вверху буквы S самих чисел 1 и п, теперь уже без всякого знака равенства:
S/4
Потом заметили, что обозначает побщу1о“ точку 1 деления отрезка [а, А], и начали ее обозначать просто самой буквой х, не боясь никаких недоразумений; при этом вышеуказанный символ стал выглядеть так; -5/(х)Дх.
Но .здесь уже сильно начал чувствоваться недостаток этого символа, преднаэнаненндго обозначать интегральную сумму (1); в интегральной сумме (1) ведь очень хорошо видно, между какими границами изменяется „общая0 точка деления х,_,: свое изменение х(_, начинает от х0, причем х0 = а, и кончает х^, свое изменение, придя в х р причем величина хп-1 является непосредственно соседней с величиной х,„ где уже х„=Ъ.
Учитывая это обстоятельство и необходимость записывать, между какими границами изменяется общая точка х в предыдущей записи интегральной суммы, начали обозначать интегральную сумму ч
/ Ч) Лхо 4-/Ч) Ч + • - * +/Ч -1) Ч-1 + • • • +/ Ч-1) Ч-i
та:;:
ь
S/(x)Ax. (3)
а
Этот самый символ и принимается окончательно, потому что несмотря на его краткость в нем сказано все:
1) и то, что берется конечная сумма парных произведений вида /(х)-Дх, причем весь отрезок [a, ft] разделен точками х на конечное число отрезочков Ах, где точ) а де юния х служит всякий раз левым концом,.
2) и то, что общая точка деления х начинает свое изменение, отправляясь от начала а данного отрезка, и, заканчивая свое изменение, приходит в его конец Ь.
§ 6. Обозначение предела интегральной суммы. Определенный интеграл. Вообразим теперь бесконечный, никогда не прекращающийся процесс, состоящий в том, что рассматриваются с течением времени все разные и разные способы деления данного отрезка [а, Ь} на отрезочки все более и более мелкие так, что при этом длина наибольшего отрезочка—в рассматриваемом каждый раз способе деления — с течением времени стремится к нулю.
Это значит, что в какой-нибудь момент времени t рассматривается определенный сносов деления отрезка [а, Ь], дающий отрезочки
[a, xj [хр х,], ..., [х._,, х,.], ..., [x„_pft],
и что ..о мере того, как время t безгранично возрастает, t —► -}- ею, указанные отрезочки все делаются все более н более мелкими, потому что даже самый большой из них и тот по своей длине стремится к нулю. А отсюда следует, что число п указанных отрезочков должно безгранично возрастать с течением времени, п ->•-{- ос, потому что раз все отрезочки делаются все более и более мелкими, то, чтобы из них составился нензменяющийся отрезок [a, ft], их число п непременно должно безгранично увеличиваться.
Таким образом с течением времени отрезочки
[«, Xj], [Хр Xj,..., [л-,._рХ(],,.., [хя_р ft]
безгранично умаляются, в то время как их число п безгранично увеличивается.
Выберем теперь в каждом из указанных, отрезочков по одной точкр
ЕЕ Е Е
и составим при помощи этих отрезочков и этих точек интегральную сумму
• •• •• • +7(^)4»-!. (4)
Здесь нам нужно обратить внимание читателя на следующее важное предложение:
Лемма. Если заданная функция /(х) непрерывна на отрезке [a, ft], интегральная сумма в указанномпроцессе
становится суммою возрастающего числа бесконечно малых.
Доказательство. Раз функция/(х) непрерывна на отрезке [а, А], она должна на нем быть ограниченной ‘). Это значит, что имеется такое постоянное положительное число М, которое превосходит абсолютную величину функции /(х) во всякой точке х отрезка [а, Ь], т. е.
|/(х)|<М
С другой стороны, наступит такой момент времени, когда даже наибольший из отрезочков [a, xj, [xr хо], ..., [хя_р А] сделается и будет впредь оставаться сколь угодно малым. Пусть « есть произвольно взятое положительное число. Из сказанного ясно, что в частности наи* больший из указанных отрезочков, а, стало быть, и всякий из них, по своей длине будет меньше, чем начиная с некоторого момента времени. Отсюда же следует, что абсолютная величина всякого члена /(’,•-1) ^xi-1 интегральной суммы сделается и останется меньше, чем е, потому что
А это и означает, что все члены интегральной суммы (4) с течением времени безгранично умаляются, тогда как их число безгранично возрастает.
Читатель хорошо сделает, если заметит себе, что для неограниченных функций f(x) доказанная лемма ложна.
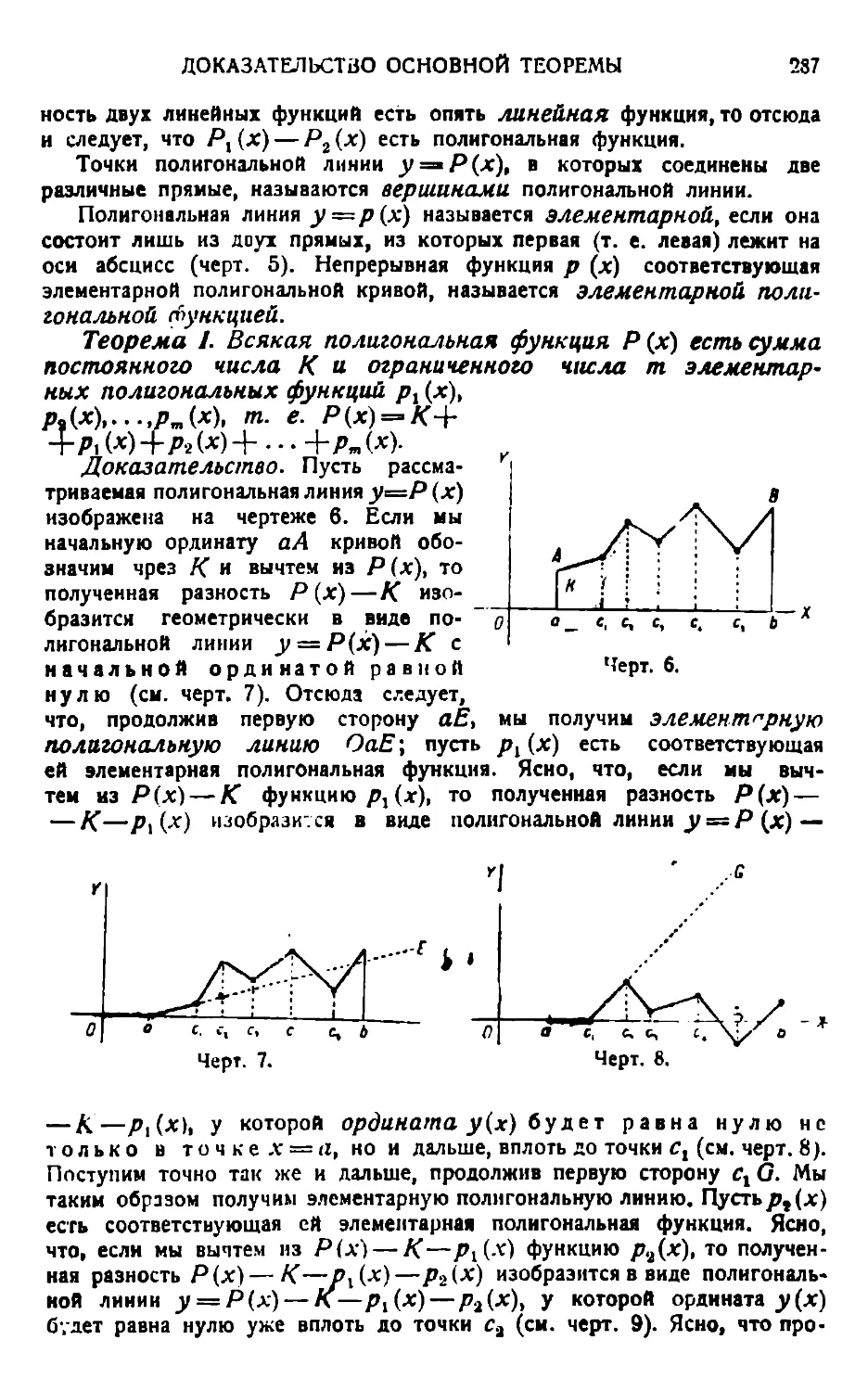
Для примера возьмем функцию /(х), определенную равенством /(х) = — для всякого х, отличного от нуля, и согласимся считать, что /(0) = 0. При приближении аргумента х к нулю функция неограниченно возрастает н при х = 0 обращается в бесконечность, т. е. при х = 0 не имеет никакого значения. Чтобы избежать этого, мы и полагаем ее значение / (0) в левом конце отрезка [0,1] равным нулю. Таким образом те-(, , (л перь функция определена во всех точ-
'--- ках отрезка [0,1] но она не является
непрерывной на этом отрезке. За основной отрезок [а, 4] возьмем отрезок [0,1]. Разделим же отрезок[0,1] нал равных отрезочков и возьмем в каждом из них, в средине, по одной точке.
Как показывает черт. 9, мы имеем: _ 1 _ 2 _ л-.
•Ч--7Г- х2- „ • •••• хп-1~ п >
» - 1 = _ JL Е - 5 Е ?П~1
2я • ~ 2л ’ 2 ~"2л ‘ ‘ -1 “ 2л •
Д, Л(., Л,
Черт. 9.
Но в силу самого свойства взятой нами функция /(х) мы имеем/(;<) =-1-.
Jl Смп например, Грэввиль-Луэнн, часть 1, глава IV (Теория пределов), 42, налагающий свойства непрерывных функций.
Поэтому интегральная сумма
/(?0) Ьх0 4 /(4) 4- • • • -!-/(;„ _х) АЧ» _.
в вашем саучае будет такой:
млн, иначе:
2л 1 . 2/i 1 . ( 2л 1
1 /Г + 3 ’ ~ + “И 2л — 1 7Г *
т. е. окончательно
2 2 2
2+4+^-+-'-+^Аг-О О 4П — 1
Мы видим, что эту сумму никак не приходится назвать .суммой возрастающего числа бесконечно малых*, потому что ее члены вовсе не стремятся к нулю с течением времени (например, первый член постоянно равен двойке).
Возвратимся теперь к нашей интегральной сумме
/G0)A*0+/(«i) ^14-... ,) Ах,^хп_г. (4)
В предыдущем параграфе мы уже обращали внимание читателя на то чрезвычайно важное соображение, что численная величина интегральной суммы существенно зависит от двух обстоятельств:
1) от того, на какие отрезочки [а,xj, ..., [х „Ь\ разбит основной отрезок [а, Ь\\
2) от того, какие точки с0, .... ? выбраны по одной в каждом из этих и отреаочков.
Напротив, как увидит на дальнейшего читатель, численная величина предела интегральной суммы в описанном выше бесконечном процессе совершенно не зависит:
1) ни от способа разбивать основной отрезок [а, д] на отрезочки;
2) ни от выбора по одной точке в каждом из этих отрезочков.
Иначе говоря, какие бы способы раздробления отрезка [а, на, отрезочки все более и более мелкие мы ни рассматривали и каким бы образом мы ни выбирали в этих отрезочках по одной точке, предел интегральной суммы всегда будет один и тот же, лишь бы наибольший из втнх отрезочков без1ранично умалялся стечением времени.
В следующих параграфах эта независимость предела инте-тральных сумм от способа разбиения на отрезочки и от выбора в них по одной точке будет строго доказана для непрерывных функций /(х). Пока же мы примем этот факт на веру и познакомимся сейчас лишь с чрезвычайно важным обозначением этого предела.
Раз предел интегральной суммы не зависит от расположения точек Ео, • • •» £„-1, выбираемых но одной на отрезочках [a, xj, ..., [хп_р Ь], то мы их там можем брать где угодно. Возьмем же их в левых концах рассматриваемых отрезочков, т. е. положим:
£0 = *о> \ = •••> ^1-1=Хп-Г
Тогда интегральная сумма будет:
/(*о) д-*о+/’ (*i) Д*1+ • • • +/(*,• _ ,) д*< _ х+ • • +/(*„ -1) д*„- г (1)
Мы видели, что при более сжатой записи эта интегральная сумма обозначается так:
Ь/(х)Дх. (3)
а
Отсюда ясно, что предел этой интегральной суммы в сущности следовало бы писать полностью так:
ь
lini S / (х) Ах. (5)
(I
Вместо же этого найдено более удобным пользоваться для обозначения предела интегральной суммы следующим стилизованным обозначением*
ь
f f(x)dx. (6)
а
Этим обозначением, введенным еще Лейбницем, мы и будем отныне пользоваться.
Сообразно такому особенному обозначению предела интегральной суммы преде.: этот получил вместе с тем и особенное название: „определенный. интеграл*. Символ (6) при его записывании произносится так: „определенный интеграл от а до Ь эф икс дэ икс*. При этом буквы а и Ь, стоящие внизу и вверху знака J* определенного интеграла, называются (в сущности неправильно) „пределами* определенного интеграла, причем:
буква а называется „нижним пределом* определенного интеграла; буква b называется „верхним пределом* определенного интеграла. Основной отрезок [а, Ь] называется „областью определенного интегрирования* или чаще всего (но менее правильно) „интервалом интегрирования*.
По поводу этого в высшей степени важного для всего математического анализа обозначения (6) определенного интеграла читатель заранее должен быть предупрежденным в нескольких отношениях и должен обратить на эти предупреждения самое серьезное внимание.
Во-первых, обозначение (6) определенного интеграла имеет совершенно исключительную важность для всего дальнейшего. Все дальнейшее течение интегрального исчисления является лишь ознакомлением со свойствами этого обозначения и является, собственно, только углубленным его изучением. Этот символ (6) определенного интеграла как бы уже предопределяет самое содержание интегрального исчисления и в чрезвычайно сжаток виде содержит огромное число ценных правил для геометрии, механики и физики.
Во-вторых, читатель должен понять, что определенный интеграл ь
/ f(x)dx и
отнюдь не есть никакая „сумма**, хотя бы и „бесконечно малых", но лишь предел такой суммы. Значит, собственно, мы имеем равенство:
ь ь
lii’i S /(х) Дх = f(x)dx, (7)
,l (t
где налево стоит явным образом предел интегральной суммы, т. е. н а-стоящей суммы в каждый момент времени конечного числа конечных количеств, которые лишь с течением времени безгранично умаляются, тогда как их число безгранично увеличивается. Направо же в равенстве (7) стоит символ, лишь обозначающий этот предел. Длинный знак J, напоминающий знак S истинной суммы, указывает на то, что переход к пределу интегральной суммы считается уже завершенным. Выражение f(x)dx, стоящее за знаком интеграла, должно напоминать нам о том, что был выполнен переход к пределу интегральной суммы, составленной при помощи непрерывной заданной функции /(х). Выражение /(х) Ах, стоящее налево за знаком S интегральной суммы, есть настоящее слагаемое, составленное из произведения /(х) на Ах, а выражение /(х) dx, стоящее направо за знакам определенного интеграла, считать составленным из двух .множителей* /(х) и dx пока нельзя. Таким образом в символе
ъ
J f(x)dx а
все части должны рассматриваться как прочно связанные вместе; значит, это есть цельный, хотя и сложный, символ с неотделимыми друг от друга частями, обозначающий собою лишь одно число: предел интегральной суммы; самое начертание этого символа сохраняет, так сказать, отпечаток той интегральной суммы, переходом к пределу которой получено численное значение этого символа.
Лишь впоследствии, когда свойства этого символа будут достаточно изучены, читатель будет в праве передвигать известные части этого символа и даже преобразовывать их согласно строжайшим правилам.
§ 7. Предел интегральной суммы не зависит от выбора точек на отрезочках. Чтобы убедиться в этом, возьмем две различные интегральные суммы:
s'=/(0 ч>+М) ч+... t) . .+м_х) ч.-/ и
s"=/<) ч 4- /•(<> д*,+.. ,) ч - -+Ж _,) ч,-,
происходящие от двух разных выборов точек в одних и тех же отрезочках [a, xj, [хр х„], . .., й]. Пусть в первом случае за
выбранные точки взяты Е^, Ер ..., Ея_1( а во втором случае выбраны точки Е" Е"...E''_t (черт. 16).
E-g. . Составим теперь разность
• * л S' — S’
1ерт. 10. и покажем, что она бесконечно
умаляется, когда наибольший из отрезочков [a, xj, ..., [хя_р стремится по длине к нулю, т. е. что
lim (S' — S ) = 0.
Для этого вспомним, что заданная функция /(х) непрерывна на основном отрезке [а, 6]. Это значит, что разность /(Ez) —/(Е') двух значений функции безгранично умаляется по абсолютной величине, когда обе точки Е' и Е" безгранично сближаются между собою, причем совершенно неважно, где они находятся на отрезке и как они в нем движутся. Говоря более точным языком, это значит, что для любого положительного постоянного числа е всегда будет верным неравенство:
!/(;•- НГ)|<е,
лишь бы предварительно были удовлетворено неравенство:
I'- - Г1 <TJ,
где число т], выражающее меру близости между собою точек Е' и Е", зависит только от взятого числа в и вовсе не зависит от положения точек Е' и Е". |
Вспомнив это, вычтем почленно из интегральной суммы S интегральную сумму О ; мы получим:
S' - S". [/ (0 дх,- /О') +...
выписывая ради краткости лишь разности двух первых и двух последних членов обеих интегральных сумм. Общим членим этой разности, очевидно, будет квадратная скобка:
за которую можно вывести множителем Дх< — 1; это нам даст*.
i/lQT/Ob ' ОТ
Но так как даже наибольший из отрезочков [a, xj, ..[хп_р />] с течением времени безгранично умалязтся, то наступит такой момент, когда всякий из этих п отрезочков будет оставаться но длине меньше, чем ц
А тогдт для всякого номера i обе выбранные точки и t окажутся одна к другой ближе, чем на т„ и, значит, мы будем иметь:
1/(С,)-/(('_ ,)1<е.
Из выражения (8) видно, что общий член разности S — S по абсолютной величине будет меньше, чем «• | 1, и, следовательно, и са-
мая разность S'-S" по абсолютной величине будет меньше, чем сумма
6 I I ’ Г е I I 4“ • • I ‘ S I ^Xi - 1 I + • • • I ' 8 I ^ХП — 11 = .„Ч
= .||Ax0|-r|AxJ+ - - • ------4-14,-J} < }
Но количество |Дх1_1| является длиной отрезочка (х,.^, х4]; поэтому сумма количеств | Лх, | равна просто длине основного отрезка [а, Ь\, т. е. равна |д— а|. Поэтому все выражение (9) просто равно:
е . \Ь — а
Итак, мы заключаем, что
[S'-S"| <е • \Ь —а|. (10)
Так как число е можно взять сколь угодно малым, а основной отрезок [а, £] остается неизменным, то поэтому следует, что разность интегральных сумм S' — S' с течением времени бесконечно умаляется. Отсюда и следует, что пределы интегральных сумм S' И S" никогда не могут быть различными.
§ 8. Первообразная функция. Произвол в первообразных функциях. Сейчас мы введем чрезвычайно важное для всего дальнейшего понятие: понятие первообразной. • функции. На первый взгляд может показаться, что, оторвавшись от предыдущего изложения, мы делаем скачок в сторону. Однако читатель должен знать, что введение этого понятия в высшей степени важно не только для обещанного ранее доказательства независимости предела интегральной суммы от способа деления основного отрезка [а, б] на отрезочки, но—что важнее всего— для самого вычисления этого предела интегральной суммы.
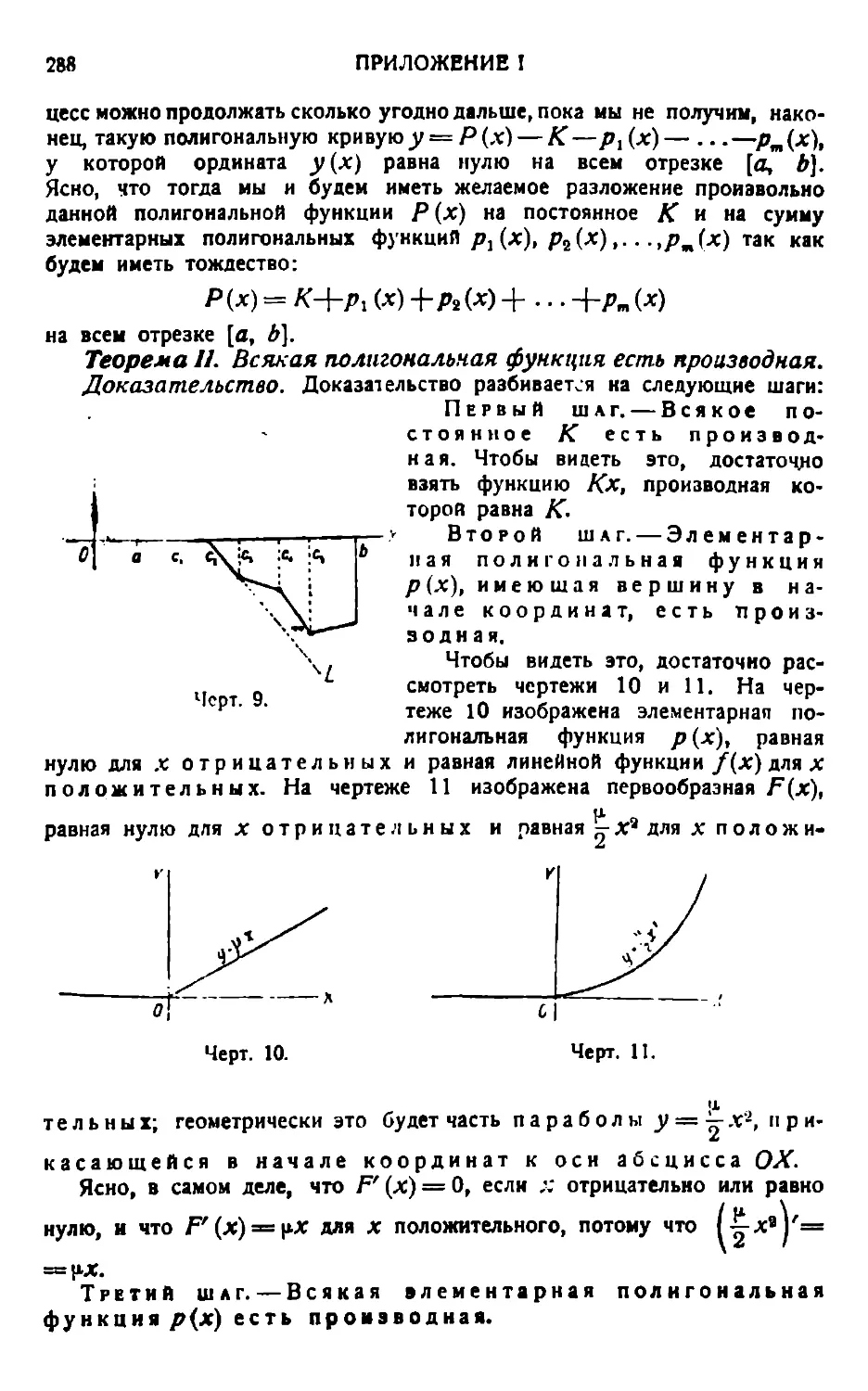
Пусть на отрезке [л, Ь] нам дана какая-нибудь функция /(х). Первообразной функцией для нее называется просто всякая непрерывная функция Л(х), имеющая /(х)своею производною всюду на отрезке [а, Ь] ').
Следовательно, если непрерывная функция F(x) есть первообразная для /(х) на отрезке [а, 6], то это значит, что мы имеем равенство:
*) .Всюду на отрезке [а, 6]* это значит, что данная функция /(х) является производною от непрерывной функции Г (х) во всякой точке х отрезка (в, ft] беа всякого исключения. Чтобы не было каких-либо сомнений относительно самих граничных точек а и Ь отрезка [a, ft], читатель должен себе представить, что непрерывная Функция Л'(х) определена вне основного отрезка [о, ft], хотя бы на самом небольшом пространстве, перед точкою а и за точкою Ь, Здесь мы предполагаем, понятно, что a<ft.
". е.
F'(x) =f(x)
всюду на отрезке [а, Ь], включая его концы.
Читатель, прочтя это определение, в праве спросить:
„Всегда ли имеется первообразная у заданной функции /(х)?“ Здесь читатель должен быть заранее предупрежден,, что для всякой непрерывной на отрезке [а, Ь] функции/(х) действительно имеется первообразная F(x).
Это значит, что
всякая непрерывная на отрезке [а, функция /(х) может быть рассматриваема как производная от некоторой другой непрерывной функции F(x), F' (х)=/(х).
Эта важная теорема математического анализа не допускает никаких исключений: безусловно, у всякой непрерывной функции /(х) имеется первообразная F(x) ‘).
Совсем другой вопрос: как отыскать для заданной непрерывной функции /(X) ее первообразную F(x)?
Этот вопрос уже совсем иной природы, так как математический анализ, доказывая существование первообразной F(x) для всякой непрерывной /(х), вовсе не утверждает, что ее можно фактически (т. е. конечным образом) отыскать. Но читатель должен быть предупрежден в истинности этой важной теоремы математического анализа, совсем независимо от того, умеет ли он отыскать первообразную для данной непрерывной/(х) и можно ли ее вообще отыскать конечным образом.
Пример 1. Отыскать первообразную для тп.
Решение. Иэ диференинального'исчислення мы знаем, что производная от хт равна тх"-1. А нам надо получить в качестве производной не пи^*~*, а только л”. Поэтому естественно сперва приравнять m — 1 = л я затем уменьшить в т
раз функцию Xм, чтобы и производная, уменьшившись в т раз, лишилась ненужного нам множителя т. Эти косвенные рассуждения заставляют нас
Но такие догадки не должны приниматься за серьезное доказательство, и поэтому здесь необходима точная проверка:
d лп + 1 _ 1 d п +1 _ /Lt! гя +1 ~1 = г*1
dx п + 1 ” л + 1 ’ dx п + 1
Читатель видит, что догадка оказалась верной и что ——есть первообраэ-
3 а меча н не. Данное решениене годится, если л = — 1, потому что тогда знаменатель п + 1 обращается в нуль. Но раз л = — 1, то, значит, тре
*) Как показы Лебег, для доказательства этой важной теоремы математического анализа вовсе Нет ни необходимости прибегать к понятию определенного напирала, ни надобности вообще иметь дело с суммированием бесконечно малых. Мы не можем в рамках настоящей книги дать доказательство Лебега, собственно очень простое.
буется отыскать первообразную для х~ *= каковая есть, очевидно, In .с.
Таким образом первообразная для х”, когда л =— 1, есть 1пх.
Пример 2. Отыскать первообразную для sinx.
Решение. Вспомним из дифереицнального исчисления, что производная от cosx равна — sinx. Значит, мы догадываемся, что, переменив знак у созх, мы получим как производную уже не — sinx, а просто sinx. Проверим:
—— (— cos х) =-— cos х = — (— sin x) = sin x.
dx dx
Итак, первообразная для sinx есть — cosx.
t При отыскании первообразных очень важен вопрос:
Сколько имеется у данной непрерывной функции /(х) всех возможных первообразных?
Легко видеть, что их имеется всегда бесконечное множество. Действительно, если F(х) есть какая-нибудь найденная для /(х) первообразная, то первообразной же для нее явится, очевидно, всякая функция
’ Г(х)4-с,
полученная прибавлением к найденной первообразной F{x) произвольной постоянной. С.
В самом деле, помня из днференциального исчисления, что производная постоянной равна нулю, мы имеем:
^х)+а = агм 0
dx dx 1 dx J 1 J '
откуда и следует, что F(x)4-G также является первообразной для /(х), каково бы ни было постоянное С.
Таким образом:
прибавляя произвольную постоянную С к какой-нибудь найденной первообразной F(x) для /(х), мы получаем бесконечное семейство, F(x) -J-С, других первообразных для той же самой /(х).
Существенную важность представляет обратный вопрос:
Какова степень произвола среди всех первообразных для данной f (х)? Другими словами: найденное семейство первообразны х, F(x)-j- С, содержит ли вдействи-те л ь н ост и в с е в о зм ож н ы е первое бразные для/(х), или имеются еще и такие другие первообразные для /(х), которые не содержатся в семействе F (х) 4- С?
Легко доказать, что семейство первообразных F(x)-{-C соаержит действительно все возможные первообразные для /(х). Для этого достаточно доказать лишь предложение:
Теорема. Непрерывная функция, имеющая производную, равную нулю, может быть только величиной постоянной.
Доказательство. Пусть функция Ф (х) непрерывна на отрезке [а, Ь\ и имеет производную, равную нулю, всюду на этом отрезке. Это значит, что
Ф' (х) = О
какова бы ни была точка х на отрезке [а, 6].
Теперь, если рассматриваемая функция Ф (х) не есть постоянная на отрезке [а, 6], то это значит, что имеются на этом отрезке такие две величины X] и ха, в которых значения функции Ф (х) существенно различны, т. е.
Ф (х,) ф Ф (х9). (11)
С другой стороны, прилагая теорему Лагранжа о конечном приращении, мы имеем:
Ф (х2) — Ф (х,) = (х2 — хЭ Ф7 (Е), (12)
tie величина Е содержится между х, и х2. Поэтому Е содержится на отрезке [а, 6], и, значит, Ф7(Е) = 0. Отсюда равенство (12) приводит к равенству:
Ф(ха)-Ф(х1) = 0,
явно противоречащему неравенству (11). Итак, функция Ф (х) с нулевой производной может быть только постоянной, величиной.
Следствие. Две непрерывных функции, производные которых равны, разнятся одна от другой лишь на постоянную.
Для доказательства возьмем какие-нибудь две непрерывные функции Fi (х) и Г9 (х), имеющие на отрезке [а, Ь\ во всякой точке одну и ту же производную. Значит, мы имеем равенство:
= <13)
во всякой точке отрезка [а, А].
Обозначив разность обеих наших функций (х) и F9 (л) через Ф(х):
Ф(х) = Г9(х)-51(х), (14)
мы из равенства (13) немедленно выводим, что непрерывная функция Ф(х) равна постоянной величине С всюду па отрезке [а, А], т. е. Ф(х) = С. Отсюда равенство (14) дает окончательно тождество:
Г2(х) = Л(х)фС, справедливое на отрезке [а, Ь], что и доказывает наше предложение.
Следствие. Так как первообразной функцией для данной /(х) на отрезке [а, 6] называется всякая непрерывная функция, имеющая всюду /(х) своею производною, то отсюда следует, что две разли тые перво-образные F(x) я F1(x) для данной f (х) могут разниться одна от другой лишь на постоянную величину С, т. е.
F1(x)=F(x)4-C.
Из всего сказанного вытекает следующая окончательная теорема.
Теорема. Ф о р м у л a F (х) -j- С, где F (х) есть какая-нибудь одна найденная первообразная для заданной функции /(X) И где Сесть произвольное постоянное, охватывает все возможные первообразные для /(х). Всякая отдельная первообразная для данной/(х) получаете я, если давать
постоянной С какое-нибудь определенное частное численное значение.
Из этой теоремы как следствие вытекает предложение, важность и самый смысл которого на первый раз будет не совсем ясен для читателя, но значение которого раскроется ему в следующем параграфе.
Следствие. Разность F(а)—F(b) двух значений первообразной для /(х) в концах отрезка [а, Ь] есть количество, зависящее только от заданной функции /(х) и от основного отрезка [а, д] а отнюдь не зависящее о т выбранной первообразной F (х).
Доказательство. Пусть Fo (х) есть некоторая найденная первообразная для /(X), заданной на отрезке [а, 6]. Пусть F (х) есть какая-нибудь другая первообразная для / (х). На основании предыдущей теоремы имеем тождество:
F(x) = F0 (х) -’ -С0, (15)
где Со есть численное значение произвольной постоянной С. Подставляя в тождество (15) вместо х сначала Ь, а потом а, имеем:
F(^) = F0(^) + C0 и F(a) = F0(a)4-C0.
Отсюда, вычитая второе равенство из первого, находим равенство:
F (b) — F (а) = FQ (b) — Fo (а), как раз и выражающее то, что нам надо, а именно, что разность двух значений какой-нибудь первообразной в концах отрезка [а, д] численно остается всегда той же самой, независимо от того, какая именно первообразная берется для этого.
Важность н смысл этого следствия станут немного более ясными читателю, если, забегая вперед, сказать, что разность F (Ь) — F (а) двух значений первообразной в концах отрезка [а. Л] для f (х) как раз равна пределу интегральных сумм для функции /(х) в основном отрезке [а, 6], т. е. определенному интегралу' ь J f^xjdx. а
§ 9. Предел интегральной суммы не зависит от способа деления основного отрезка [а, д] на отрезочки. Чтобы убедиться в этом, возьмем непрерывную функцию f (х) и произвольный способ деления основного отрезка [а, Л] на отрезочки
la. JC1L [*!, -*я]. (Х4-1, Л,],..., [X,,-!, Л].
Пусть F (х) есть какая-нибудь первообразная для / (х) на отрезке [а, А]. Ясно, что имеем точное равенство:
F(b)-F (а) => [F (х,) - F(a)]+(F(xJ-F (х,)] + ... +
.• • • +[F(x,)-F(x,_1)]+... + [FW-F(xn_I)].
В этом убеждаемся простым раскрытием скобок и делая уничтожение равных членов с противоположными знаками.
Применим теперь теорему Лагранжа оконечном приращении к «общему* члену F (х4)— F(xi_l) написанной суммы:
F (х() — F (xf _,) = (х( — х( _ t) • F' _ ,), (16)
где число , есть промежуточное между х{ _ х и х(, т. е. есть
точка, лежащая на отрезочке [х. _,, xj.
Так как F (х) есть первообразная для / (х), то имеем тождество F' (х) = f (х) всюду на отрезке [а, Д]. В частности же мы имеем равенство:
Что же касается разности х( — *<_(» то эт0> очевидно, просто — есть длина отрезочка [xt_ ,, xj, т. е. количество Дх(_х. Поэтому формула (16) перепишется в виде:
F(x(} — F(x,. _Х)=/(Е<_Х) Дх._1, и, значит, предыдущая сумма примет вид
F (b) — F(a) =/ (В,) Ах0 +/ (ч) Л+ • • •
...+/(*<_,) ^_i+ •••+/(;„_,) (17)
Это есть точное равенство. Вообразим теперь бесконечный процесс, состоящий в делении основного отрезка [a, Д] на все более и более мелкие отрезочки [д, хх], [х,, х3],..., [х,,^, Ь\ так, что длина наибольшего из них с течением времени безгранично умаляется. Так как равенство (17) есть точное равенство, то оно, будучи верным до перехода к пределу, остается верным и в пределе. Значит, мы будем иметь:
F (Д) - F (а) = lim [/ (Ео) Дх0 (Е.) Дхх +•.•+/ (Е„ _,) Дх„ _
Таким образом предел интегральной суммы при произвольном способе деления основного отрезка [а, Д] на бесконечно умаляющиеся отрезочки [«, xj, [х1( х2],. .., [хп_1(Д]и при некотором специальном в*ы б о р е в них точек Eq, продиктованном теоремой Лагранжа, ока-
зывается равным разности F(b) — F(a) п.ъух. значений первообразной для f (х) в концах отрезка [а, Ь\.
Но в § 7 мы видели, что предел интегральной суммы совершенно не зависит от выбора точек Eq, Elt..., Е„_, на отрезочках.
Отсюда мы заключаем о справедливости чрезвычайно важной теоремы:
Теорема. Предел интегральной суммы для непрерывной функции /(х) на отрезке [а, Д] не зависит ни от способа дробления его на бесконечно умаляющиеся отрезочки ни от выбора в них точек и численно равен
разности двух значений первообразной для /(х)вксн-ц а х отрезка [а, А].
§ 10. Фактическое вычисление предела интегральной суммы. Основная формула Лейбница-Ньютона. Только что доказанная теорема в конце предыдущего параграфа как раз дает могущественный способ вычислять до конца пределы сумм возрастающего числа бесконечно малых.
Мы увидим дальше, что вычисление предела таких сумм сводится к вычислению предела интегральных сумм, являющихся самыми простыми из сумм бесконечно умаляющихся.
Пусть нам нужно вычислить предел интегральной суммы
/(х0)дМ-/(*1) д*1+- ••+/(*< - 1)Дл',_! -Ь • •+/(*„-!) д*„-г (О
Прямо это сделать невозможно, потому что рассматриваемый процесс умаления отрезочков никогда не прекращается, т. е. бесконечен, и исчерпать его до конца нельзя.
Но вот обходный путь, указанный Лейбницем и Ньютоном: хотя мы и не можем исчерпать до конца наш бесконечный процесс, однако мы очень часто можем при помощи алгебраических или иных конечных манипуляций отыскать первообразную F(x) для данной непрерывной функции f(x). А раз — тем или иным способом — первообразная F (х) для /(х) отыскана, мы просто составляем разность значений
F(b) — F(a)
этой первообразной для концов отрезка [а, />]: эта разность и будет в точности пределом интегральной суммы (1).
Мы уже знаем (см. § 5), что интегральная сумма (1) обозначается символом:
5/(х)дх, О)
а
а предел этой интегральной суммы, называемый „определенным интегралом*, обозначается символом:
ь
J'f(.x)dx. (6)
а
С другой стороны, мы видели, что предел интегральной суммы (1) в точности равен разности значений первообразной F (х) для f (х):
F{b} — F(a)
в концах основного отрезка [а, />].
Сопоставляя это, мы приходим к основной формуле Лейбница-Ньютона: ь ।
[’f(x)dx = F(b}-F(a), (1)
(I
читающейся так: „определенный интеграл от f (х) на каком-нибудь отрезке равен разности численных значений первообразной для /(х) в концах этого отрезка*.
3 Зак. 2833. — Грэпвндь н Лузин, ч. II, интегральное нсчнслемжв
При этом читатель должен хорошо помнить, что функции / (х) непременно предполагается непрерывной на всем основном отрезке [а, />].
Примечание. Формула (1) Лейбница-Ныотоняможет оказаться ложной, когда функция f (х) перестает быть непрерывной на отрезке [а, 6|. Читатель должен иметь в виду это важное обстоятельство, так как, упустив его из вида, он может прийти к грубейшим численным ошибкам в чисто технических задачах.
Пример такой ошибки. Читатель хочет вычислить определенный интеграл от функции на отрезке — -у, 1 j • Ясно, что он никак уж не может получить отрицательного ответа потому, что заданная функция /(х) = ^положительна везде. Но если, читатель позабудет предварительно проверить, непрерывна ли его функция /(.г) на отрезке и пРименит Ф°Р*
мулу Лейбница-Ньютона, то получит следующие выкладки:
. 1
первообразная для —есть
1
Значит, он получит невозможный отрицательный ответ: — 3.
Эта ошибка произошла по той причине, что функция f (х) = — имеет разрыв внутри отрезка y.lj, именио ° точке а=0-
Из формулы ([) Лейбница-Ньютона следует, что для отыскания предела интегральной суммы:
f(x0) АХо+/Ю Д*1-Ь • •+/ • • +/ (1)
при заданной непрерывной функции f (х) на отрезке [а, Ь\ должны быть проделаны следующие шаги:
Первый шаг. Постараться, путем догадки или применением какого-нибудь конечного при ем а, отыскать первообразную F (х) для заданной / (х).
Второй шаг. Отыскав п е р в о об ра з н у ю F (х), со с т а в и т ь разность F(b)-—F (а) ее значений в концах отрезка [а, Ь\. Эта разность и будет искомый предел.
Здесь нам нужно сделать следующее практическое допо.пнение:
Найдено целесообразным разность F (Ь) — Л'(а) обозначать символом:
выражающим, что надо сначала в квадратной скобке заменить переменное х ч и с л о м Ь, потом там же заменить
переменное х числом а и, наконец, вычесть из первого численного результата второй численный результат. Понятно, таким образом мы получим нужную нам разность:
F(*)-F(a).
Указанное обозначение особенно удобно в случае, когда формула F(x), содержащая букву х, очень сложна или очень длинна.
Г т312
Пример. Вычислить! -у I
1
Решение.
Заменяя х на 2, имеем:
23 _ 8_ з “ з •
Заменяя .г на 1, имеем:
13
3 ’
Вычитая из первого результата второй, находим:
Z з з ~ з ’
Формула Лейбница-Ньютона является величайшим открытием в математике для всех времен. Величайшая сила его заключается в том, что здесь бесконечный по существу процесс точного вычисления предела суммы возрастающего числа бесконечно умаляющихся слагаемых сразу заменяется конечным процессом отыскания первообразной, причем окончательный результат получается сабсолютною точностью.
В этом смысле формулу (I) Лейбница-Ньютона можно назвать методом суммирования бесконечно малых ’).
Величайшая мощь этого открытия состоит в чрезвычайно легкой применимости этого способа суммировать бесконечно малые для решения большого количества задач геометрии, механики, физики и естествознания. Мы сейчас увидим это на примере геометрии.
§ II. Решение пяти основных задач геометрии. Эти пять задач были перечислены в § 3, и там же был подробно намечен путь их решения. Сейчас, опираясь на основную формулу (I) Лейбница-Ньютона мы дадим полное их решение. Мы просим читателя отнестись к пол.
*) В этом смысле .суммирование бесконечно малых* опередило на несколько столетий .суммирование бесконечных рядов*. В самом деле, для бесконечных чясловых рядов мы не имеем до настоящего момента никакого способа находить их точную сумму (предполагая ряд даже с положительными
СЮ
членами и сходящимся). Например, мы знаем достоверно, что ряд схо-
П = 1
дится, но незнаем его суммы. У нас нет здесь ничего подобного формуле Лейбница-Ньютона, и в этом смысле теория бесконечных рядов еще дожидается своего Лейбница.
ним рисункам 1, 2, 3, 4 и 5 в § 3, так как здесь мы даем лишь наиболее существенную деталь этих рисунков.
I. Решение задачи о площади кривой в прямоугольных КООРДИНАТАХ.
Мы видели в § 3, что искомая площадь аАВЬ определяется так: площадь аАВЬ = lim (а -J- £ -I- ... -|- а), т. е. как предел суммы возрастающего числа бесконечно умаляющихся.
я0бщш1 член1* этой суммы, как показывает прилагаемый чертеж, (черт. 11), есть площадь заштрихованного прямоугольника, основанием которого служит х{ — х( _ = Дх(. _ ,, а высотой — ордината f(xt _ i)- Поэтому „общий член** суммы равен
/ (Х1 _ i) _ 1,
и, значит, самая сумма я р ' И !* есть в точности интегральная сумма
f(x0) Дхо-Шх,) Дх,4-.. • Дх(_,4-.. •+/(*„_,) Дхп_г (I)
Поэтому искомая площадь аАВЬ, оказываясь пределом интегральной суммы (1), равна определенному интегралу: ь
площадь аАВЬ = J'f (х) dx. (П)
а
Это и есть самое полное решение первой важнейшей задачи геометрии, так как формула (I) Лейбница-Ньютона показывает, что определение площади аАВЬ распадается на следующие отдельные шаги.
Первый шаг. Постараться, догадкой или применением какого-нибудь конечного процесса, отыскать первообразную F(x) для f(x).
Второй шаг. Отыскав первообразную F (х), составить разность/7 (£) — F (а), каковая ибудет искомою площадью аАВЬ.
Пример. Найти площадь одной волны синусоиды j = sin.r (черт. 12).
Решение. Первый шаг. Первообразная для sin х есть — cos х 4- С, как показывает непосредственная проверка.
Второй шаг. Составляем разность:
[ — cos х + C]J =[ — cos я Ц- С) — [ — cos 0 + CJ = = [-(-1)+С]-[-1+С] = [1 + С)-(-1 + С]=+2.
Оте. Искомая площадь равна 2.
II. Решение за дач и о и лошади кривой в полярных координатах.
Мы видели в § 3, что искомая площадь АО В определяется так: площадь /ЮТ? = lim (a-f-р~|~ .. .-(-ц), '
т. е. как предел суммы возрастающего числа бесконечно умаляющихся.
Мы предполагаем, что уравнение данной кривой в полярных координатах есть p = /‘('j) и что угол ЛОВ (черт. 13) разделен на п, частей прямыми, наклоненными к полярной оси ОФ под углами о, < <р9 < 93 <. .. < ?„_,, причем наклон радиуса-вектора ОА к полярной Z'Z'y
оси равен ?0 = а, и соответствующий на- //zjZ-
клон радиуса-вектора ОВ есть = Ь.
В этих условиях общий член ука- ‘
занной суммы есть площадь заштри-хованного кругового сектора, обе стороны которого наклонены к оси ОФ ♦
под углами , и to. и радиус которого Черт. 13.
равен /(?,_,). Отсюда следует, что угол между сторонами заштрихованного кр/Рового сектора равен разности ? < - 1 = - 1 ‘
Но из элементарной геометрии известно, что площадь всякого кругового сектора равна половине произведения угла между его сторонами на квадрат радиуса.
Отсюда следует, что общий член указанной суммы равен
-и
и, значит, самая сумма j J-3-j-... ч есть не что иное, как в точности интегральная сумма:
. . . +±/?(?п_1)Д?я_1. (18)
Поэтому искомая площадь АОВ, оказываясь пределом интегральной суммы (18), равна определенному интегралу:
ь
площадь АОВ= Г4-/2 (?) </? (П1)
f
Это и есть самое полное решение нашей второй задачи, так как формула (I) Лейбница-Ньютона показывает, что определение площади АОВ распадается на следующие отдельные шаги.
Первый шаг. Постараться отыскать каким-нибудь конечным образом первообразную F(?) для выражения
Второй шаг. Отыскав первообразную F (?), составить разность F(Ь) — F(а), каковая и будет искомою площадью АОВ.
Пример. ЬРа fl т и плот
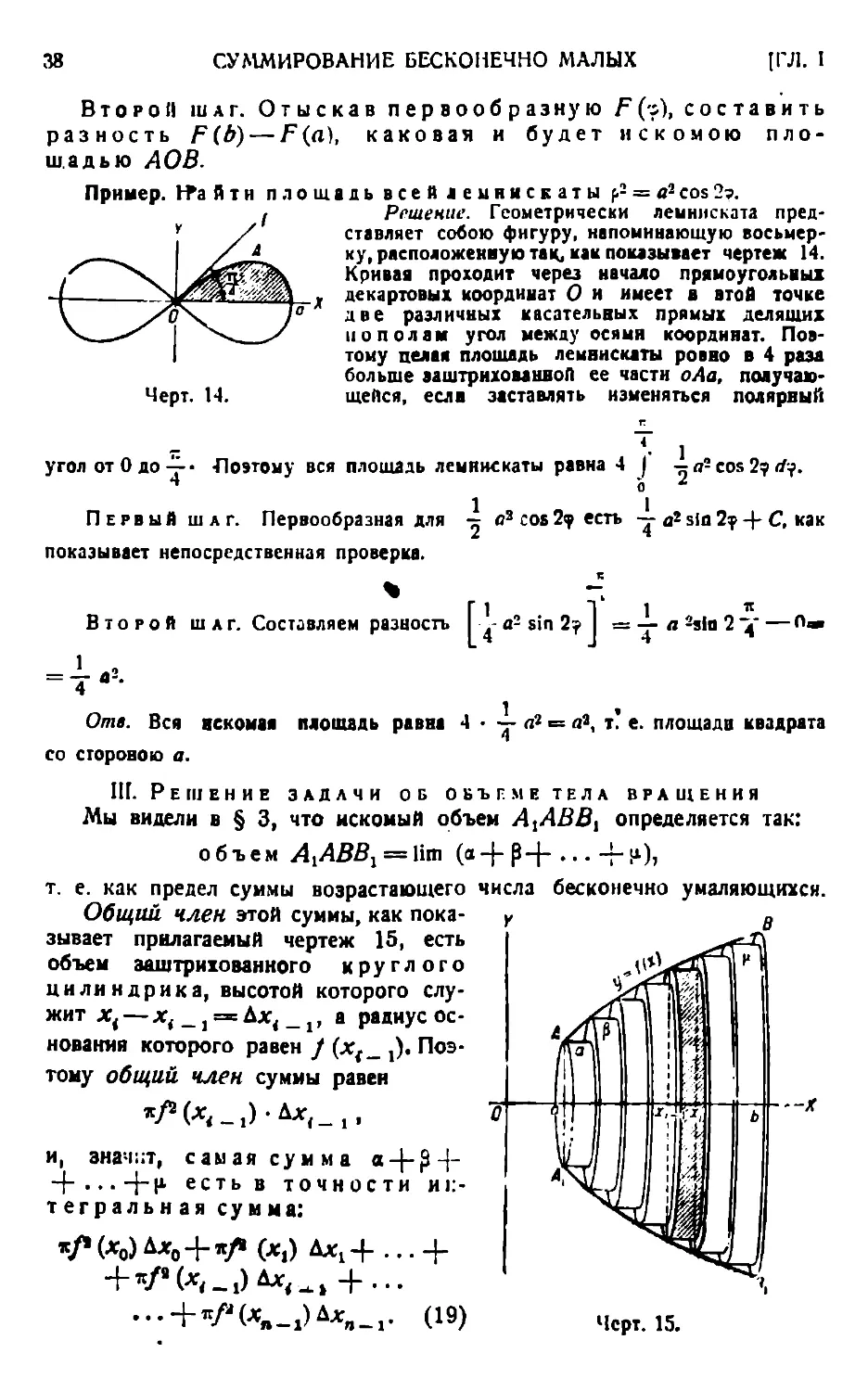
адь всей лемнискаты р2 = a2 cos 2?.
Решение. Геометрически лемниската представляет собою фигуру, напоминающую восьмерку, расположенную так, «ан показывает чертеж 14. Кривая проходит через начало прямоугольных декартовых координат О и имеет в этой точке две различных касательных прямых делящих пополам угол между осями координат. Пов-тому целая площадь лемнискаты ровно в 4 раза больше заштрихованной ее части оАа, получающейся, если заставлять изменяться полярный
a2 cos 2? rf?.
угол от 0 до ~ Поэтому вся площадь лемнискаты равна 4 | ** о
Первый шаг. Первообразная для о3 cos 2? есть — a2 sin 2? 4- С как показывает непосредственная проверка.
Второй шаг. Составляем разность a2 sin 2?
1 21
— a 2sin 2 Т — 4 л
Отв. Вся искомая со стороною а.
плошадь равна 4 • у <i! = aa, г е. площади квадрата
П1. Решение задачи об объеме тела вращения
Мы видели в § 3, что искомый объем AiABBt определяется так: объем AiABB1 = lim (а-|- p-f-... -рн),
т. е. как предел суммы возрастающего Общий член этой суммы, как показывает прилагаемый чертеж 15, есть объем заштрихованного круглого цилиндрика, высотой которого служит х( — х( _, = bxt _ j, а радиус основания которого равен / (х{_ ,). Поэтому общий член суммы равен
и, значит, самая сумма а-|-р-}_ ~Ь...+н есть в точности интегральная сумма:
1С/' (^о) Ч” (-*1) AXj Ч- • • • “Н + + •••
(19)
Поэтому искомый объем АХАВВХ, оказываясь пределом интегральной суммы (19), равен определенному интегралу: ь
объем АХАВВХ = f (х) dx. (IV)
<1
Это и есть самое полное решение нашей третьей задачи, так как формула (I) Лейбница-Ньютона показывает, что определение объема АХАВВХ распадается на следующие отдельные шаги:
Первый шаг. Постараться найти каким-нибудь конечным образом первообразную F (X) для выражения (х).
Второй шаг. Отыскав первообразную F (х), составить разность F ф) — F(a), к а к о в а я и будет искомым объемом.
Пример. Найти объем, производимый вращением эллипса около его оси (черт. 16).
Решение. Пусть уравнение эллипса есть 4- ’ = 1. Мы находим от-а* 0-
сюда у- = (а- — Х-). И так как уравнение вращаемой кривой предпола-
гается в виде.у = /(х), то поэтому мы заклю-
чаем, что в нашем случае У2(.г) = (гР-х-У. а-
Так как ясно, что объем всего данного тела вдвое больше объема того тела, которое получается вращением дуги аАЬ эллипс'., то искомый объем всего тела равен
и
Черт. 10.
“ 63 f •>
Первый шаг. Первообразная для п — (в- — х2)есть ~ — ^а-х
С.
как показывает непосредственная проверка. Второй шаг. Составляем разность
[«г(л-^+с]’-[«5(л-^)+с]-к>+с|~£4“’
Оте. Весь искомый объем равен 4- г.аЬ2. Если а = Ь, тогда ясно, что вра-
4
шлется круг радиуса а. Объем же шара радиуса а равен у кл*. Это как раз и выходит из полученной формулы, если сделать а = Ь.
IV. Решение задачи о длине плоской кривой.
Мы видели в § 3, что искомая длина дуги АВ определяется так: дуга АВ = lira (а-}-₽ + • • • + Р)«
т. е. опять как предел суммы возрастающего числа бесконечно-ума-ляюшихся.
Общим членом этой суммы является, очевидно, длина элементарной хорды, концы которой имеют своими абсциссами: Х;_х и х(. Из пра-
вой части черт. 17 видно, что хорда эта служит гипотенузой прямоугольного треугольника, катеты которсго равны и Ду,-_р где
д*. _i = a;—и дл_ 1 =/(•*?— /Ч -1)-
Поэтому длина рассматриваемой элементарной хорды равна
Но по теореме Лагранжа о .конечном приращении** мы имеем:
/ (*.) — t _,) =
= (х,— х( _)/'
где , обозначает некоторое число, промежуточное между xt_x и xit т. е. х, _ J ( < х(. Значит, -, _ t есть просто некоторая точка, лежащая на отрезочке [х( _ ,, xj.
Отсюда находим:
- 1 =/' -1) • Ч
и, значит, длина рассматриваемой элементарной хорды равна:
/(Дх,.._1Г4-Л^_1)(Ч_1Р = /1+/'2 • Ч - > •
Из полученного выражения общего члена суммы а-|- |3-|- ... -f-u мы заключаем, что самая эта сумма есть не что иное, как в точности интегральная сумма:'
уТТ/'Чи -4 + • • -+/1 №(1_1)-Дх<..1-^ . . .
-4-1. (20)
и, значит, искомая длина дуги АВ, оказываясь пределом интегральной суммы (20), равна определенному интегралу:
ъ дуга АВ — I yi-\-f\x^dx. а
Это и есть самое полное решение нашей четвертой задачи, и формула (I) Лейбница-Ньютона показывает, что определение дуги АВ распадается на следующие отдельные шаги:
Первый шаг. Написав уравнение рассматриваемой кривой ь в и д е у=f (х) и вычислив производную/' (х), составить выражение 1 -\-f2 (х).
В тор о й ш а . Постараться найти каким-нибудь конечным образом первообразную F (х) для выражения
Третий шаг. Отыскав первообразную F(х), составить разность F(b)— F (а), каковая и будет искомой дугой АВ.
Пример. Найт:, длину дуги цепной линии
а ( Т t
у - ? \е 4 е ) от х - 0 до х = а.
Решение. Первый шаг:
/1+/'"(*) =
Второй шаг. Первообразная для
X
2
есть
как показывает непосредственная проверка. Третий шаг. Составляем разность:
V. Решение задачи о поверхности тела вращения.
Мы видели из § 3, что искомая поверхность АХАВВХ определяется так:
поверхность АХАВВХ = lim (а “ЬР)»
т. е. как предел суммы возрастающего числа бесконечно умаляющихся.
Общим членом этой суммы является, очевидно, боковая поверхность усеченного круглого конуса, радиусы обоих оснований которого равны и / (a\), а образующая которого равна, как показывает
правая часть черт. 18:
V (Дх,_ЛЧ-(4У,_1)2“
Поэтому боковая поверхность рассматриваемого элементарного усеченного конуса равна
2r.f(x, )4-2ir/(*<) <-----------------
, 12 • /(Ч-.Р+Зд-,)’
(так как боковая поверхность усеченного круглого конуса равна полусумме окружностей обоих его оснований, умноженной х>фсо9рзэующую).
Преобразуем немного это выражение. Согласно сказанному в предыдущей задаче, квадратный корень перепишется в виде:
так что все наше выражение будет равно:
2к. J Дх,-,.
Здесь число есть промежуточное между числами х{и х(, так что Ef_j есть просто некоторая точка отрезочка , xj.
К сожалению, это выражение еще не есть общий член интегральной суммы; поэтому здесь необходимы дальнейшие преобразования.
Для стого заметим, что полусумма
/(x<_i )+/(*,)
2
бесконечно приближаете» просто к / (;,_!)• Действительно, составляя разность этой полусуммы и / (£<_,), мы имеем:
--------2----------f (с< =--------------------2------------------
И так как точка |<_1 лежит на отрезочке [х<_1 , х,], а функция/ (х) непрерывна, то отсюда следует, что обе квадратные скобки [/(х1_1)— — /(£<_,)] ы [/ (х<)—/(&<_!)] бесконечно умаляются, когда все отрезочки [a, xj, [х1( xj......[x„_i, бесконечно умаляются. А отсюда
следует, что и вся правая часть предыдущего равенства бесконечно умаляется, т. е. что мы имеем неравенство:
когда все отрезочки [a, х,].[х„_,, Ь] становятся достаточно ма-
лыми; здесь число е есть положительное и малое по желанидо.
Предыдущее неравенство, разумеется, всегда можно переписать в виде равенства:
где число
по абсолютной величине меньше единицы, т. е.
Из этого равенства мы выводим:
2
откуда и следует, что найденное нами выше выражение для .общего члена** суммы а -|~ р -J- ... 4- И разбивается на два слагаемых:
2V(4_t) Ю+ЛО,-.)-Ах,.!
и
2^_, - г ГН/'Чй’Ч-г
Поэтому и самая сумма а 4* ° 4~ • • • I1 оказывается составленной из двух сумм:
<=1 и
е X s" 2«е<_1 /14- р (E4_t) . Дх4 _1.
Первая сумма есть, очевидно, в точности интегральная сумма, пределом которой является, понятно, определенный интеграл
ь
J2V(X) /14-Л (x)-dx. о
Вторая сумма, к сожалению, не есть интегральная сумма; аато сразу можно доказать, что эта сумма ограничена.
Действительно, раз мы предполагаем, что касательная к данной кривой у = f (х) непрерывно изменяется, то это означает, что производная f (х) есть также непрерывная функция. А отсюда следует, что и функция
2z /1 4- Л (х)
также будет непрерывной и, значит, о гр а н и ч ей н о й. Следовательно, существует такое постоянное положительное Af, М > О, что для всякого х на отрезке [а, А] мы имеем:
|2« /1+Л(х)| < М.
Но так как
| 2кё< _ ж /П-/'-’ Дх<_11 = | О,..., I • |' 2z /1 ,) | • |Ax,._J
и так как все числа 0(. _х имеют абсолютную величину меньше чем единица, < 1, то отсюда заключаем, что мы просто имеем:
i2A_! /1Т/'2О
Поэтому для всей нашей второй суммы находим неравенство:
1=Я S
<=1
2^6^,/1Дх(1, <SM <—п
Дх.
= М S px,-i | = М X длину отрезка (а, 6]. « 1
Отсюда и следует, что вся наша вторая сумма ограничена, и так как, когда наибольший из отрезочков [а, х,].., [х/1( xj,..., бесконечно умаляется, величина е может быть сделана сколь угодно малой, то вся вторая составная часть суммы а 4~ ?-j- . . . + !*• бесконечно умаляется.
Из сказанного следует, что предел суммы а ? 4" • • • ~Ь Р будет в точности равен пределу первой суммы (интегральной), и, значит:
ь
поверхность АХАВВ^ = J 2к/ (х) 1 -f- /'2(х) • dx. (VI)
Cl
Это и есть самое полное решение нашей последней задачи, и формула (1) Лейбница-Ньютона показывает, что определение поверхности А1АВВ1 распадается на следующие отдельные шаги:
Первый шаг. Вычислить производную /' (х) данной функции /(х) и составить выражение:
Второй шаг. Постараться найти каким-нибудь конечным образом первообразную F(x) для выражения
2«/(х) V 1+/'2(х).
Третий шаг. Отыскав первообразную F(x), составить разность F(b)— F(a), каковая и будет искомой поверхностью AtABBi.
Пример. Найта площадь поверхности шара, образуемого вращением окружности х’+дйзг* около оси ОХ.
Решение. Первый шаг:
/'«----
,________Г га V г2 4- и»
2к/(х) /1 +//а (х) = 2к-у 1 + = 2г.у • г = 2кг.
Второй шаг. Первообразная для 2кг есть 2пгх4-С.
Третий шаг. Так как для получения шара надо вращать окружность от х = — г до х = г, то
F (6) - F (а) = F(r) — F(— г)«=[2wx + С)*' = 2w« — (- 2w«)« 4w«.
§ 12. О взаимоотношении днференциального и интегрального исчислений. Читатель видит, что важнейшие и труднейшие задачи геометрии сводятся к суммированию бесконечно малых и что могущественный способ выполнять до конца это суммирование, открытый Лейбницем и Ньютоном, состоит в разыскивании конечным образом пердообразных функций.
Таким образом ближайшее внимание должно быть всецело сосредоточено на выработке ряда целесообразных приемов разыскания конечным образом первообразной функции, т. е. функции F(x), имеющей данную f (х) своею производною:
F' (х)=/(х).
Здесь знание даже всякой отдельной первообразной функции F (х) является драгоценным, потому что тотчас же дает возможность получить при ее помощи решение ряда трудных задач. Например, знание того, x»+i
что --j—— есть первообразная для хч, немедленно позволяет получить
п -j~ 1
площади всех таких кривых у = Р(х), для которых Р(х) есть многочлен от х любой степени.
Диференциальное исчисление учит нас, каким образом, имея данной функцию F (х), найти ее производную F' (х) =/ (х). Иначе говоря, в диференциальном исчислении мы спускаемся от заданной F (х) к ее производной F' (х) = / (х):
F(x)^/(x).
Для этого диференциальное исчисление дает ряд твердых правил, позволяющих от всякой фактически написанной (т. е. в конечном виде) функции F (х) спуститься до ее производной f(x) = F(x). Правила эти совершенно достаточны для этой цели, потому что читатель знает, что, поступая согласно этим правилам, можно найти производную /(х) = = F'(x) от любой фактически написанной функции.
Одной из важных задач интегрального исчисления является задача отыскания первообразной F (х) для данной /(х). Иначе говоря, интегральное исчисление учит нас, каким образом нам подняться от заданной производной f (х) до ее первообразной F(x):
Г(х)<-/(х).
Таким образом среди важных задач, составляющих предмет интегрального исчисления, одной из первых *) является задача обращения диферен-цирования, т.е. отыскание по заданному диференциалу /(x)dx первообразной функции F (х).
Для этого интегральное исчисление предлагает ряд целесообразных приемов, достаточных для довольно многих случаев. Но читатель не должен заблуждаться относительно силы этих приемов: приемы эти лишь систематизируют и приводят в некоторый порядок первоначальный подход при помощи непосредственного нащупывания и догадки. Современное состояние науки еще не позволяет дать общее правило, каким
*) Но отнюдь не единственной.
образом от заданной функции f(x) подняться до ее первообразной F(x), притом в некоторых, и к тому же весьма простых, случаях получение первообразной в конечном виде даже и невозможно.
§ 13. Настоящее переменное и кажущееся переменное Переменное интеграции. Для более ясного понимания тех приемов, при помощи которых поднимаются отданной функции /(х) к ее первообразной F (х), необходимо различать настоящее переменное от кажу ще гося.
Для пояснения берем самый простой случай.
Пусть, например, дело идет о целых числах первой сотни:
1, 2, 3, 4, 5, 6, 7..100.
Мы знаем, что переменной величиной математический анализ называет букву, например х, которая с течением времени изменяет свое численное значение.
Переменное, определенное таким образом, есть настоящее переменное. ,
В нашем частном случае мы можем условиться рассматривать какую-нибудь букву, например букву i, как обозначающую в разные моменты времени различные целые числа из первой сотни. То число из первой сотни, которое обозначает буква i в данный момент, называется значением переменной величины i в данный момент. Это значение вообще изменяется от момента к моменту.
Буква i, рассматриваемая так, есть настоящее перемен н о е.
Но бывают случаи, когда та же самая буква i рассматривается совсем иначе.
Пусть, например, речь идет о сумме всех чисел первой сотни, которая, как легко вычислить, равна 5050.
Эту сумму мы можем написать в виде:
пю
S '•
1
Здесь роль буквы i совсем иная, так как во всякий момент времени буква i предполагается уже пробежавшей последовательно все числа первой сотни при их суммировании. Здесь буква i выполняет лишь служебную вспомогательную роль в процессе суммирования чисел первой сотни, и после того, как этот процесс суммирования закончен и получен численный результат 5050, о букве i забывают, потому что она сама по себе не оказывает ни малейшего влияния на окончательный численный (5050) результат.
Буква /, рассматриваемая так, есть кажущееся переменное. В нашем случае буква i (кажущееся переменное) называется еще переменным суммирования.
Так как кажущееся переменное не оказывает само по себе ни малейшего влияния на окончательный численный результат, то, не будучи важным само по себе, оно всегда может быть обозначено всякой другой буквой, которая еще свободна, т. е. еще не занята ни в каком другом обозначении.
Например, сумму первой сотни целых чисел можно обозначить как 100 Sk, 1
если буква k еще не была ранее употреблена ни в каком другом обозначении.
Смешивать настоящее переменное с кажущимся переменным нельзя, так как это смешение нередко ведет к прямым ошибкам.
Обращаясь к интегральной сумме:
/(Ло)Дхо+/(-Ч)Ч + • • • • • • +/(*я-1)Ч-1. (О
которая, как мы знаем (см. § 5) обозначается так:
ь
S /(х)Ч (3)
а
мы видим, что буква х есть кажущееся переменное или переменное суммирования, так как она не входит в окончательный результат и не оказывает сама по себе ни малейшего влияния на численную величину интегральной суммы.
Поэтому рассматриваемую интегральную сумму (3) вполне можно, не сделав никакой ошибки, написать в любом виде:
ь h ь
S / (С М, S / (нр «, S f(y) ±у И т. д., а а а
если только буквы t, и, у и т. д. не были уже употреблены в качестве настоящих переменных.
Поэтому и самый определенный ин те гр ал ь
J f(x)dx а
может быть без всякого ущерба написан в любом виде: Ь b Ь
I" f(t)dt, у* f(u)du, I f\y)dy и т. д. а и <1
Здесь буквы х, t, у и т. д. суть опять кажущиеся переменные или переменные интеграции. Эти переменные имеют чисто служебное значение и совсем не входят в окончательную численную величину определенного интеграла, которая по формуле (I) Лейбница-Ньютона всегда равна разности F(ft) — F (а), так что можно писать безразлично как:
ь ь
F(b)-F(a) = F(b) — F(a) = J‘f(u)du\
о ц
Ъ
F(b)—F(a)=j‘f(y)dy.
Таким образом переменное интеграции может быть обозначено безразлично какою буквою и не оказывает ни малейшего влияния на численную величину определенного интеграла.
Напротив, буквы b и а, стоящие вверху и внизу определенного интеграла, суть уже настоящие переменные, и малейшее изменение их влечет существенное изменение самой численной величины определенного интеграла.
§ 14. Определенный интеграл как функция своих пределов. Неопределенный интеграл. Рассмотрим определенный интеграл
ь
J f(x)dx. (6)
По формуле (I) Лейбница-Ньютона его численная величина дается равенством:
ь
F(b) — F (а) = ff (-*) dx, (I)
а
где F есть какая-нибудь первообразная для данной /.
В формуле (I) Лейбница-Ньютона буква х есть переменно е интеграции (т. е. „кажущееся** переменное), от которого нисколько не зависит численная величина определенного интеграла, тогда как буквы а и b суть настоящие переменные, и от изменения их, как показывает левая часть F (Ь) — F(а) формулы (I), очень существенно зависит самая численная величина определенного интеграла.
Чтобы легче было проследить изменение численной величины определенного интеграла, происходящее от изменения пределов, мы сначала обозначим переменное интеграции не буквой х, а какой-нибудь другой буквой, например t, менее связанной с обычным представлением независимого (и, значит, настоящего) переменного; затем, рассматривая верхний предел Ь определенного интеграла как независимое переменное, естественно его в обеих частях равенства (1) обозначить через букву х. Указанные изменения нам дадут равенство:
X
F(x)-F(a) = f f{t)dt. (Г)
и
Что же касается нижнего предела а, то мы его оставляем неизменным, т. е. сохраняющим всегда одну и ту же численную величину а.
Равенство (Г) сразу приводит нас к ряду важных заключений:
Во-первых, определенный интеграл J f (t) dt есть не-(4
прерывная функция своего верхнего предела; функция эта бесконечно умаляется, когда верхний предел приближается к нижнему, предполагаемому постоянным.
Чтобы убедиться в этом, достаточно рассмотреть левую часть F(x)— F(a) формулы (Г): эта часть, очевидно, есть непрерывная функция аргумента х, потому что F(x) непрерывна и когда х безгранично приближается к a, F (х) стремится к F(a) как к пределу. Значит, разность F (х) — F (и) стремится к нулю.
Во-вторых, определенный интеграл / f (t)dt есть перво-а 1 образная функция для /(х), т. е. производная от него по х равна в точности / (х).
Чтобы убедиться в этом, достаточно взять производную от определенного интеграла по х:
X
A J/(0Л = A [F(x)-F(a)] = F(x)=/(x), а
потому что F (х) есть первообразная для /(х) и, значит,
Г(х) = /(х).
Как важное следствие мы получаем:
Следствие. Выражение
j' fit) dt \-С, (VII)
где С — постоянная величина, есть всегда первообразная функция для заданной f (х). Всякая первообразная функция F (х) для / (х) получается из формулы (VII) при надлежащем выборе числовой величины постоянной С.
Действительно, во-первых:
d dx
X
ff(t)dt + C а
а
и, значит, выражение (VII) при всяком постоянном С есть первообразная для /(х). Во-вторых, всякая наперед заданная первообразная F (х) для f (х) получается по формуле (VII), так как для этого, как показывает формула (!'), достаточно сделать C — F(a).
Дадим теперь одно из важнейших понятий интегрального исчисления — понятие неопределенного интеграла.
Для этого заметим сначала, что выражение
X
J" f (t) dtС (VII)
а
при неизменном а и при постоянном С, получившем определенное численное значение, обозначает, понятно, совершенно определенную функцию аргумента х, именно ту самую единственную первообразную для /(х), которая равна величине постоянной С при х = а.
4 Зак. 2853. — Гронвнд* м Лузин, ч. II, Интегральное нсчпсиохшо
Если же мы, оставляя всегда неизменным а, будем всячески изменять постоянное С, то разумеется, выражение (VII) будет давать всевозможные первообразные для /(х). Значит, при пробеге буквою С всех постоянных чисел выражение (VII) даст семейство всех возможных первообразных для данной /(х).
Теперь, для того чтобы прийти к понятию неопределенного интеграла, поступают так:
I Во-первых, вместо буквы t переменного интеграции пишут снова букву х, что дает:
X f f(x)dx-\C. (VII')
а
Для объяснения скажем, что такое переписывание выражения (VII) еще не представляет слишком большой опасности, если только читатель будет знать, что буквах, стоящая в верхнем пределе, и буквах, стоящая под знаком интеграл а, имеют совершенно различный смысл: первая х обозначает настоящее переменное, могущее принимать какие угодно величины; вторая х есть кажущееся переменное, предназначенное последовательно пробегать числа от а до настоящего переменного х.
Во-вторых, в выражении (VII') опускают оба предела интегрирования и также постоянное С. Полученный таким образом усеченный сим.вол
f f(x)dx (VIII)
и есть неопределенный интеграл.
Для этого мы заметим, что в символе (VIII) опущенные пределы а и х интегрирования воображаются написанными, но постоянное С рассматривается теперь уже не как определенное постоянное, а как произвольное постоянное, и считается входящим в состав неопределенного интеграла.
У f(x)dx.
Таким образом неопределенный интеграл J f(x)dx представляет собою любую первообразную функцию F(x)-\-C для заданной f (х).
Иначе говоря, этот символ есть просто «общий член* F(x)-L-C, семейства всех первообразных для /(х)
Итак согласно самому смыслу неопределенного интеграла имеем равенство:
f f(x)dx=F(x}-'r-C, (IX)
где F(x) есть какая-нибудь определенная первообразная для /(х). а С есть произвольное постоянное.
Из равенства (IX) следуют два замечательных соотношения. Возьмем
§ 14] ОПРЕДЕЛЕНИЙ ИНТЕГРАЛ КАК ФУНКЦИЯ СВОИХ ПРЕДЕЛОВ 51 какую-нибудь совершенно определенную первообразную F(x) для заданной /(х). По определению первообразной имеем:
Г(х)=/(х), откуда *
dF (х) = Г (х) dx =f (х) dx.
Поэтому, с одной стороны, диференцируя равенство (IX), мы получим:
d fdx =/(x) dx. (X)
С другой стороны, равенство (IX) прости переписывается в виде: f dF(x) = F(x) + C. (XI)
Равенства (X) н (XI) показывают, что оба знака: d и J', поставленные рядом вместе, безразлично в какой комбинации d или Jd, взаимно уничтожают друг друга, если не считаться с прибавлением произвольного постоянного.
Поэтому символ ^неопределенного интеграла обозначает вместе с тем действие, обратное действию d дифе-ренцнрования.
Для сравнения напомним, что символ У квадратного корня обозначает действие, обратное действие ()* возведения в квадрат.
Ближайшей целью читателя должно явиться умение находить неопределенные интегралы ff(x)dx.»)
') К сведению читателей. Читатель, начавший изучение интегрального исчисления с первой главы, может теперь перейти к чтению § 16, свойство 3.
ГЛАВА П.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. НЕПОСРЕДСТВЕННОЕ ИНТЕГРИРОВАНИЕ.
(К сведению читателей. Читатель может начинать изучение интегрального исчисления с этой главы, не справляясь с содержанием главы 1.)
§ 15. Интегрирование как действие обратное диференциро-ванию. Читатель еще в арифметике освоился с взаимной обратностыо действий сложения и вычитания, умножения и деления. В алгебре же читатель познакомился с тем, что извлечение корня есть действие, обратное возвышению в степень, рассматриваемому там как действие прямое, причем для этого обратного действия вводится даже особый знак радикала: Y-
Совершенно также в диференциальном исчислении рассматривается прямое действие: диференцирование, имеющее целью: для заданной F(x) находить ее диференциал f(x) dx. Иначе говоря, диференциальное исчисление учит нас тому, каким образом от заданной функции F (х) спуститься к ее диференциалу dF = = f(x)dx, т. е.
F(x)-/(x)dx.
В интегральном исчислении изучается обратное действие — интегрирование, ставящее целью:
по заданному диференциалу /(х)dx разыскивать его первообразную функцию F(x).
Первообразной, же функцией для заданного выражения f(x)dx называется всякая такая функция F(x), которая имеет его своим диференциалом, т. t. dF(x)= f(x)dx, или — что то же самое—которая имеет функцию/(х) своею производною: F'(x)=/(x).
Другими словами, интегральное исчисление учит нас тому, каким образом от заданного диференциала f(x)dx подняться к его первообразной F(x), т. е.
f(x)-/(x)dx.
Диференциальное исчисление употребляет для прямого действия дифе-ренцирования знак d, так что символ dF(x) обозначает диференциал функции F{x).
Интегральное исчисление употребляет для обратного действия интегрирования знак J , так что символ
f fMdx
обозначает любую первообразную F(x) для /(.v).
Этот символ
f f(x)dx
называется неопределенным интегралом от функции /(х) и произносится следующим образом:
^неопределенный интеграл от эф икс дэ икс".
Чтобы объяснить читателю, почему знак J называется знаком неопределенного интеграла, будет полезно продолжить далее нашу аналогию между обоими знаками обратных действий: радикала Y и интеграла J*.
Квадратный радикал обозначает действие, обратное действию ()9 возвышения в квадрат и всегда сопровождается многозначностью, т. е. неопределенностью. Так, например, выражение У 4 обозначает любое из двух чисел —2 и —2, потому что оба эти числа, будучи возведены в квадрат, дадут 4.
Подобно этому интеграл J" f(x)dx, обозначающий действие, обратное диференцированию, всегда сопровождается неопределенностью* Ясно в самом деле, что если F (х) есть некоторая определенная первообразная для / (х), т. е. такая, что F' (х)=/(х), то и всякая сумма F(x) С, где С есть постоянная величина, явится тоже первообразной для / (х), потому что производная постоянного есть нуль, и, значит:
rf(F(x) + C] _ dF(x) _ dx dx J 1 Л
Поэтому-то символ неопределенного интеграла J f(x)dx, обозначая любую первообразную для /(х), изображает всякую функцию F(x)-|-C, где С есть постоянная величина
т) Читатель должен быть предупрежден, что выражение F(х) -|- С действительно охватывает семейство всех первообразных для /(х), не опуская ни одной из них. Чтобы в этом убедиться, допустим, что Ф (х) есть тоже какая-то первообразная для /(х), т. е. Ф'(х) = /(х). Но тогда разность Ф(х) —F(x) имеет производную, тождественно равную нулю, так как
)Ф (х) - F (х)Г = Ф' (х) - F' (х) = /(х) -/(х) = О, и значит, эта разность есть некоторая постоянная величина Со, т. е. имеем тождественно Ф(х) — Г(х) = С0, откуда имеем тождество Ф (х) = F(x)+Со, что и надо было обнаружить.
Строгое изложение этого дано в § 8 главы I.
Следовательно, по самому смыслу символа неопределенного интеграла мы имеем следующее основное равенство;
f /(x)dx = F(x)4 С, (1)
где F(x) есть некоторая определенная — впрочем, безразлично какая — первообразная функция для /(х), а С есть так называемое произвольное постоянное.
Иногда называют выражение F(x) функциональной частью неопределенного интеграла, а С—постоянным интегрирования.
Таким образом на символ J J\x)dx неопределенного интеграла читатель должен смотреть как на знак, выражающий любую первообразную для / (х), подобно тому как в алгебре буквы а, Ь, ... обозначают любые числа. Сообразно этому, С обозначает произвольное постоянное, и употребление его столь своеобразно, что наверное будет вызывать у читателя первое время некоторое недоумение; например, мы, складывая С-\-С, будем всегда писать в результате не 2С, а просто С, потому что если С есть „произвольное постоянное", то и 2С есть тоже .произвольное постоянное* и, значит, его можно обозначить просто через С.
Читатель, делая выкладки с неопределенными инте
гралами J f(x)dx, всегда должен, имея в виду равенство (I), представлять произвольное постоянное С входящим в состав неопределенного интеграла.
Сумма скольких угодно произвольных постоянных и каких угодии численных постоянных пишется в виде только одного произвольного постоянного С.
Пример 1. Если Г(х) = лЗ, то Р' (х) = /(х) — Зх*. Поэтому по основной формуле (I) имеем:
J Зх^х=х» + С. *
Пример 2. Если /’(х) = sinx, то F' (х) = /(х) = cosx; поэтому
J cos х dx = sin х + С.
Пример 3. Если F (х) = arctg х, то F' (х) = /(х) = * —, поэтому
1 X*
dx
1-f-x®
arctg х + С.
§ 16. Основные свойства неопределенных интегралов. Этих свойств всего четыре и все они вытекают из самого смысла неопределенного интеграла, содержащегося в основной формуле (I);
y’/(x)rfx = F(x)4-C.
(О
Свойство 1. Диференцируем основное равенство (IX). Налево мы имеем d [" f(x)dx. Направо мы получим:
d [F(x) 4- С] = dF(х) = F' (х) dx=f (х) dx.
Значит, окончательно
d j'f(x)dx = f(x) dx. (II)
Словесно свойство первое выражается так: знаки d и J' взаимно уничтожаются.
Свойство 2. Так как dF (х) = f (x)dx, то основную формулу (I) можно просто переписать так:
fdF(x)=F(x)±C. <Ш)
Словесно свойство второе читается так:
знаки у* и d взаимно уничтожаются, если не обращать внимания на произвольное'постоянное.
Замечание. Мы видим, что действие f интегрирования и действие d диферевцирования взаимно обратны, потому что парализуют друг друга, будучи поставлены рядом вместе, безразлично в какой комбинации: dj или J" d, так что их можно просто зачеркнуть оба вместе, если не считаться с прибавлением произвольной постоянной С.
Свойство 3. Оно читается так:
постоянный множитель можно выносить из-под знака интеграла
И выражается формулой:
Jaf (x)dx = a J* f(x)dx, (IV)
в которой а есть постоянный множитель, не содержащий переменного х. Эта формула доказывается непосредственной проверкой дифе-ренцированием. Действительно, по формуле (II) диференциал левой части равен:
d J af(x)dx = af(x)dx ;
диференциал же правой части равен:
da J f(x)dx = ad J’ f(x)dx = af(x)dx, так как постоянное а можно выносить из-под знака d диференциала. А раз диференцналы обеих частей, левой и правой, равны друг другу, то и самые эти части разнятся друг от друга лишь на постоянное слагаемое, которое считается всегда включенным в знак J* неопределенного интеграла.
Свойство 4. Оно читается так:
интеграл алгебраической суммы равен алгебраической сумме интегралов
и выражается формулой:
J (и. -|- v — dx = у"и dx / vdx — f wdx (V)
в которой буквы и, v, w, ... обозначают какие-нибудь функции переменного х и имеются лишь в конечном числе.
Формула эта опять доказывается непосредственной проверкой дифе-ренцированием. Действительно, диференциал левой части равен:
d J (и4-г> — w— ...) dx = (и 4-v — w +••• )dx;
диференциал правой части равен:
d ( [udx -I’vdx — I tc dx-\-...) = d J'и dx •-
d I vdx — d w dx~'r ... = и dxv dx — wdx-\- ...
по формуле диференциала алгебраической суммы. И раз диференциалы обеих частей равны друг другу, самые эти части разнятся лишь на постоянное слагаемое, которое считается всегда входящим в состав неопределенного интеграла.
§ 17. О вычисляемости и невычисляемости неопределенных интегралов. Читатель уже знает, что одною из важных задач интегрального исчисления является: для заданной производной f(x) отыскать ее первообразную F(x).
Здесь читатель вправе спросить:
всегда лн имеется первообразная у заданной функции /(х)? Читатель должен быть заранее предупрежден, что у всякой непрерывной на отрезке [а, Ь\ функций /(х) действительно имеется первообразная F (х).
Это значит, что:
всякая непрерывная на отрезке [а, Ь] функция /(х) может быть рассматриваема как производная от некоторой другой непрерывной функции F (х), т. е. F' (х)=/(х).
Эта важная теорема математического анализа не допускает никаких исключений: безусловно у всякой непрерывной /(х) имеется первообразная F(x) *). Совсем иной вопрос:
как отыскать для заданной непрерывной функции /(х) ее первообразную F(x)?
Этот вопрос уже совсем иной природы, потому что математический анализ, утверждая, что у всякой непрерывной /(х) имеется первообразная F(x), вовсе не собирается утверждать, что ее можно фактически (т. е. конечным образом) отыскать.
Читатель должен знать, что алгебраические и всякие иные конечные
1) Более подробно об этом сказано в § 8 и в § 12 главы I.
манипуляции необходимо приводят к весьма ограниченному кругу неопределенных интегралов
которые можно фактически (г. с. конечным образом) .взять*. И здесь наблюдаются на первых порах многие неожиданности, которые можно приписать как бы капризу случая.
Рассмотрим, например, четыре интеграла:
гл
J 1g -V J X
и
/dx Г sin x ,
sinx’’ J x X'
Интегралы нижней строчки очень похожи на интегралы верхней строчки, так как все их различие состоит только в том, что в них вместо 1g написано sin. И, однако, между ними имеется громадная разница. Первый интеграл верхней строчки не берется (в конечном виде), второй же берется очень легко:
/4^-=^+с-
Наоборот, первый интеграл нижней строчки берется
Г dx , х .
I -— = igtg т + С,
J sin х 2
второй же интеграл не берется (в конечном виде).
Интегральное исчисление предлагает ряд целесообразных приемов, достаточных для довольно многих случаев. Но читатель не должен заблуждаться относительно силы этих приемов: приемы эти лишь систематизируют и приводят в некоторый порядок первоначальный подход при помощи непосредственного нащупывания и догадки, и ничего более. Современное состояние науки еще не позволяет дать общее правило получения в конечном виде первообразной. Притом, как мы видели, в некоторых случаях первообразная J" f(x)dx и .невычислима*, не может быть выражена в конечном виде.
§ 18. Таблица и непосредственное интегрирование,
современном состоянии пауки интегрирование в сущности есть
цесс целесообразно направленных гаданий и попыток, и поэтому для облегчения дела составлена таблица так называемых основных интегралов.
Способ непосредственного интегрирования, о котором здесь идет речь, состоит в том, что мы сравниваем данный диферен-циал f(x)dx, который надо проинтегрировать, с формулами этой таблицы, и если окажется, что он там содержится, то интеграл найден.
Если же его там нет, тогда все-таки пробуют его привести к ним
т. е.
При про-
употребляя те или иные приемы, из которых некоторые требуют большого искусства или даже удачи, и достигнуть этого искусства можно только практикой.
Большая часть нашей книжки по интегральному исчислению будет посвящена интегрированию таких функций, которые часто встречаются при решении практических задач.
Из каждого результата диференцировани я всегда выводится путем обращения одна формула для интегрирования.
Таблица основных интегралов
II.
III.
У*а/(гт) = f(v) dv.
J №)+»«-<(«’)) Л>—
‘ л-4-l
IV.
V.
VI.
VIII.
a” dv = ~—
Ina 1 ? dv = e°-}C.
sin v dv = — cos v -|- C. .
x.
J cos’v
Г dv
XI. I -T-T---
J sin-v
XIII. ctg vdv = In sin v -f- C.
, I dv , , v i
xiv. I——=intg-3r4-c.
J sin v w
;dv . . fv , г ------— Intg (-П- + -Г cosv ь \ 2 1 4
XVI. У = arc tg v -{- С = — arc etg v-\-C.
XVII. Г-^Ц = 1|П1±^4-С.^:>
J 1 — v2 2 1 — ’ •
Г dv * ~1
XVIII. J у-- = аге sin v-^-C— —аге cos v + C,
С dv / -------\
XIX- J F£7T7"=ln V + у =1 )+
Так как формулы (I), (II) и (111) представляют собой лишь свойства 2, 3 и 4 неопределенного интеграла, изложенные и доказанные в § 16, то переходим сразу к дальнейшим формулам.
Доказательство формулы (IV). Из
d , - C]=vndv \ п-\-1 1 /
диференциального исчисления находим:
/„n+i 7J 1 "•‘,’ = 7тг+с
Это имеет место для всех значений п, за исключением п = — 1. В самом деле, при п = — 1 формула (4) дает:
Л-^=^гтг+с=|+^ что не имеет никакого смысла.
Случай п = — 1 дается формулой (V).
Доказательство формулы (V). Из формулы
' d (In v 4- С) = ~
диференциального исчисления тотчас имеем:
f — = 1по4-С.
Этот результат можно представить в более сжатой форме, если постоянное интегрирования обозначить через In с. Таким образом будет:
С dv , , . ,
| — = In v -4- In с = In cv.
J v 1
Формула (V) показывает, что если выражение под внаком интеграла есть дробь, числитель которой есть диференциал знаменателя, то интеграл есть натуральный логарифм знаменателя.
УПРАЖНЕНИЯ.
На формулы от (I) до (V).
Проверить следующие интегрирования.
/х’
xtdx = -у С, по формуле (IV), где v = л л п = б. з
2. / Yxdx = / х-(1л= — С — у .г- 4- С, по формуле (4). где
"2
1
V = X II Л = — .
X
3. J' = j' x~3dx = С= — 4- С, по формуле (IV), где
v = х и л = — 3.
по (II)
x2dx - 3
х* 5x3 Зхз
““"З----Г + 4х + С.
по (IV).
Примечание. Хотя каждое отдельное интегрирование и вносят свое собственное произвольное постоянное, однако мы ставим лишь одно постоянное, обозначавшее их алгебраическую сумму.
по (I) 2 _ 1 2
4- j* 3cx*dx = 2a J* х 2 dx—b J x~2dx3c J* x* dx =
по (I!) 1 5
x 2 1 r3
= 2a-^--ft- -^--|-3C.^- + C = 1 1 о
~2" ~3
по (IV)
= 4a Vx + у- + у ex ’ + C.
/X10 3v7
(2x® — 3x* + 12x3 _ 3) dx = ~ + 3x‘ — Зх + C.
D l
Указание. Раскрыть сперва скобки.
з
24. /* (а= - j’-p Vydy = ^(4- - 4- - £-) + С.
J \ V I II Ю /
3 э — —
25. f (У~а - /7)3 dt = aTt -2at2 + 3<>' Р + С. л) “ О
/г 10 Зх®
(Х2 _ 2)3 x3rfx = _ 2±_ + 2х« - 2х< + С.
3
27. Г (а2 4- b-x-y^xrtx = (д2 +Л1А— + С. J *ЛО“
Указание. Можно этот интеграл прнвест^к формуле (IV). В самом деле, положив v = а3 + b'-x- и R —*у> имеем: dv = 2b-xdx. Если теперь ввести постоянный множитель 2ft2, поставив его перед xdx, а обратное ему значение1) — перед знаком интеграла (чтобы величина выражения не изменилась), то можно интегрировать выражение, обращаясь к (IV), именно к формуле: /. wn + i
/ v"dv = —— + С.
J "+1
Найдем:
1 1 j
(аг-Ьft»x»)2 xdx=^j (а2-|-ft2x’)2 262xrfxg^5 J (e»+ ft’x2)3d(a3 + ft2x2) = 3 3
1 (fl2+t2x2) 2 , (a’+ftSx2)2 ,
2ft2’ 3 T"G — 3J3 “rG-
_____________ 2 О Если А есть какое-нибудь число, тогда называется ему обратным
Л
числом.
э
2Я. [ Vа* - xixdx=-\- (а3 — х3)г С. J о
г - 1 -
. 29. / (Зал? + 46x3)8 (2пх + 46x8)dx = у (Зал8 + 46л8)8 -|- С.
4
Указание. Обращаемся к (IV), положив о = Заха + 4^** нп = -г и
г - ь -
30. j b Сбах3 + 86л8)8 (2ах + 46л8) dx = (бал8 + йбл8)8 -}- С.
3). у* ХЧХ1.± = 2 (fl3+ лЗ)Т + с.
(в8Ч-хЗ)Т
Указание. Написав в форме J* (а8 4-х8) * л8dx, применяем (TVL
32. /* -=-2/1^14-С.
«/ у 1 — л
1 э
33. У* 2ку(^ + 1)2 <У=^(^ + Р8)3 +С, 1_ 8
34. У*(1 + И 3>rfx = у(1 + Н8 + С.
* 35. f sin8xcoaxrfx = f (sin x)8 cos xdx = —4- С. J J 3
Указание. Положить v = sinх, dv = cosхdx, п~2 и применить формулу (IV).
36. /*cos5 х sin х dx = — COg х + J D
37. f sin8 ax cos ax dx = -J- sin4 аж -|- C,
J W
38. f cos43x sleSxrfx = —-2-cos*3x-(-G,
J
39. f xrf<—=-Va8-^ + G
J У a8 — X*
.rt /* 5a dt _ a , _
J (b-ф “ (б-/)8 +G
4L J /1 + жвх^ = у(14^)а +Л
42. f 3 sds =- |.(l_s8)T + C.
. лл Г un~lda (a + bun)l~m J (.a + bff bn^-m)
§ 18]
44 Г 2asas.= ________g_______ с
J (*2 _ С2 (/,! _ eV) Т
., (* 3axdx За , , , _ , ~
45’ J ~ 2еа П + е~л^ +
_ /* Зах dx л Г х dx , _
Решение. J =3а / ^ + Лг3- + С. по (II).
Этот интеграл аналогичен (V). В самом деле, положив v = b2 + е®х2, имеем dv = 2e2xdx. Если под знак интеграла ввести множитель 2г2 и перед знаком интеграла поставить то величина выражения не изменится, но числитель будет теперь диференциалом знаменателя. Следовательно:
fxdx_______Г Z^xdx _ За /^(Ь2 + е2х2) _ Зя,_^., , .
3 J b2+&x2 2<? J ~Ь2 '+d'-х? 2е2 J Ь2^&х2 - 2ез,п (^+ ***)+ с-
* 46- f = yln(.v2-1)4-1пс = 1псК^з^Т.
« f =|п е(л’ - 3‘",'|Т
« /тйтт5=,"'<2*,+”т-
._ /* bbxdx с
49. / ----= In-------------
J 8а — 6t>xa _5_
(8в — 6*х»)12
5°/7ТГ = -'-т + т-,"('+”+С-
Указание. Предварительно делим числитель на знаменатель.
5L /f^Errfx = x-ln(2x + 3)2+C?
*/ "Т"
52. С- 1 — 1 dx = — In (xn — лх) + С.
J хп — пх п
53. Г 2 S +4-lnZ+c.
/ уо yi yi I' 2 J
/in~ irfi 1
-----— = -i- In (a + */") + c.
a-\-btn *
55. (InoF -|"(lna)1+ C.
d/’ = -y + r + 2,n(r-1)+C. ’
ет Г Iddx
57‘ J -?Tpr=2In(^ + l)+C.
58. /* —— = — -i- Id (a b cos x) + C.
J a-\ dcosx b
59-/т?зМт“4|п(1+3,8,,+с
60. /* + ев + In (е* - I) + С.
J ев — 1 *
—-----dr = In (er + 1)з - г + С.
62. Произвести следующие интегрирования и проверить результат днферен-цированием:
a) J* (4х2 dx.
Решение. J ^4 х2 Ч) dx = 4 Cx'-dx - 2 /* = J J X 4л® 2±__2!пх+С.
_ . / 4x3 Проверка, d I -у- -21пх+с) = (|. 3x3-2.1)rfx = (4x®-^-)rfx.
b) J"*- j) j P a di ‘ ~W r) /•(л-3 + 1) dx J x + 2 •
«) /* 5/xdx, k) У r t~’M- S)
d) e) 3 f у*dy' ° J tn) j Г ь y^-dx. () P Me У7^ u> J V&-c4i f ^Ц-^Ц-dx. P 9s2 ds J S-З’
0 2 f 76 7 d6. n)J P axn~'dx ‘ (b-cxn)’"' V) У Уа — bxdx.
g) w) ' b-cy- P cosec2? d^ J d — e ctg у'
h) C s’B + "ds. p) J r m.4 %) n|e
1) J a?3 <*?• ” J ^‘_(x_-l)dr ' хз-2х + 5 y’ f °" °’'T-
Доказательство формул (VI) и. (VII). Оно тотчас же следует из соответствующих формул диференцирования.
УПРАЖНЕНИЯ.
На формулы (VI) и (VII).
Проверить следующие интегрирования.
1 ‘ f ba2*dx = д + С. J 2 in а
Решение. I ba^dx = b /
aixdx.
по (II).
Этот интеграл аналогичен (VI). Пусть v = 2х; тогда dv = 2dx. Поставив множитель 2 перед dx, а множитель -i- перед знаком интеграла, имеем:
l.bf а**<1х = ±J' a-^2dx = ^J' a^d(2x) = ^±С. по (VI).
2. у 3e’dx = Зе* + С.
3. j‘ е*‘“ xcos x dx = е“и х+с.
4. /‘ (е51 + а“) dx = i (eix + V С. J о \ in a j
/• eos x
eiewx s\nxdx = - -----ЬС.
6. у e n dx = ле ” + C.
8. J' e~ Xdx = - e~ x + C.
9. /V + <* Ь" (у i-2) dx = -1 e®*+<*+« 4. c. r anz bni
10. / (enx - bmr) dx = —:--------u + C.
J ' ' n In a m In b
Г aTe*
11. / a?e*dx = г-;-.-----|-C.
J 1 4- Ina
13. f + e-vr dy = ^(e-«-е-'Ъ + Ъ + С.
17. Произвести следующие интегрирования и проверить результат диферен-
пированием:
а) у* e^ds. f) У 2*'tdt. k) J* ae-^dx.
/. у ,. /* 3dt
b) / b dx. в) / tferdx. 0 / 1Z-r-
J J и V e
с) / e^dx. h) Г —у- m) /*a*'xdx.
i)/«r. П)/’ДЛ.
»X J
e) /* e~9xdx. j) ('.eadx. 0) /" (t^Pdx.
5 Зак. 2853. — Гранвиль а Лузин, ч II, И>гг<*гралькое иочнслена»
Р) f W* s) f «“"“sin в rffl. v) /
Ч) f a2Bin’’cosTrf?. t) f ^-ixdx^
. — x xa 17
r) /\e“ +* ajdx. u) J' etg<sec2f dt.
Доказательство формул (VIII)—(XI). Эти формулы прямо следуют из соответствующих формул диференцирования.
Доказательство формулы (XII).
sin у dv ____ f —sin vrfv frf(cosv)________
cosv J cos v J cosv no(V).
= — In cosv -J- C = In sec у C
[Ибо — 1ncosv = — In—-— = — In 1 4- In sec v = in seer.
1 sec у 1
Доказательство формулы (XIII).
/ fcosvrfv Г d(sinv) . , . _
etg У dy = I --:----= I -----:----- = In Sin V -4- С ПО (V).
* J sinv J sinv 1 ’
ig у dy —
Доказательство формулы (XIV).
в (14), получаем:
Но так как sin I у-}--^- j =cosv, то
УПРАЖНЕНИЯ.
На формулы (VIII)—(XV).
Проверить следующие интегрирования.
У’ , „ cos2ax . „
sin 2<urdx=---------1- C.
Решение. Формула аналогична с (VIII). В самом деле, положив v = Чах, имеем dv = Ча dx. Поставив множитель Ча перед dx, а множитель перед знаком интеграла, найдем:
f sin 4axdx = /*sin Чах -4adx = /*sin Чах d (Чах) =
J Ча J Ча J ' '
= ± (- сов Чах) + C = - —4 C no (Vlil)
2. / cos mxdx s= — sin/n.c+ C.
J m
3. y*tg bxdx =-j- In cos bx 4- C.
,У-ггы-“т'п,8(-2- + т) + с
5.y_^_ = o,„tsi+c. sin — a
v 6. /*sec 3/ tg 3/ dt = sec 3/ 4 C. J 3
v 7. у cosec ay ctg ay dy =-cosec ay 4 C,
'•/ТИ7 = —f‘,«lr + C
9- /* ctg -7- dx = 2 In sin + C.
10. y*sec2 x3 • -v2 dx = -y tg x3 4 C.
‘di. у (tg64ctg6)*d0 = tgв — ctg0 4 C.
H2. У (sec a — tg a)3 da = 2 (tg a — sec o) — « 4 C.
/13. /* (tg 4s— 1)« 4s = 4 tg 2s 4 In cos 2s 4 C.
<z *
И. у (cos — — sin 36^48 = 3 sin у 4 у cos 38 4 C.
15. J (sin ax 4 sin ~) dx = —cos ax — a cos 4 G
16. У k cos (a 4 ty) dy = -y sin (a 4 by) 4 C.
17. I cosec• x3dx = —^-ctgx3-l-C. •/ &
18. У cos (In x) = sin (In x) 4 C.
v !9. f ~ ctg v * * * * x +cosec < 4 c - <g 4 G
V “ |r
Указание. Умножить числитель и знаменатель на 1— cosxf
/dr . ’’ *•
-j—r-,---— tgx — secx4C.
1 4 sin ж 6
21. Произвести нижеследующие интегрирования и проверить результат днфе-ренцировааием:
a) J sin -у- dx, Vb) / ctge***1^.
*^с) J* cos [b + ax i dx.
Г dx J sin2 2ax ' /• dx e) J cosa3x'
/ (tgf + sec
b> УЛ-
J tgw о /* tg4rfx-.. г dx___
" J sin2 (a — bx)'
”/«&•
. Г dx
n) / -.---------.
,/ 1 — cosx
') j (tg4s — ctg|jrfs.
j (ctgx- ip dx.
*r) /‘ rix
'J 1 — sin X
/" 2a dt
J sin bt * Г 5b db ’J cos 30 *
Доказательство формулы (XVI). Эта формула следует непосредственно из соответствующей формулы диференцирования.
Доказательство формулы (XVII). Так как
1 - 1 ( 1
1 —V2 2 \ 1 — v
то имеем:
= 1[-1п(1-г/)4-1п(1Н-г/)] :-С=”’ ~ S' е
_ 1 ч » , с
-Т"’ТТТ7--С
Доказательство формулы (XVIII). Эта формула следует непосредственно из соответствующей формулы диференцирования.
Доказательство формулы (XIX). Положим tr = tgz, где г — новое dz
переменное. Диференцируя, получаем: dv = с~-г- . Делая подстановку,
находим:
dz_________
cos9 z J/4!-j- tgJz
==,п^(т+т) + с
По известным формулам тригонометрии будем иметь:
7 2 2. 2 2 2
sin—+ cos — Sin2— -4-2sin—- cos — 4-COS2-2-
Л» i I it b Л»
----------------- r, z । . , z cos г
cos" "2" “Г sin2 —
1 -sin г 1 , ,
=-----------—------------(- tg z.
cos z cos z
Но так как tg z = v, to
следовательно:
Для случая
1 cosz
1
cos z
tgz='y-H/t's-T 1
положим:
1 v =--------
cos z
откуда
Тогда будем иметь:
. sin z dz du =-----------.
cos2 z
sin zdz _ f* sin zdz
1 , „ V" 1—cos2z • cosz
----——l-cos®z cos2z
= f-^- = intg(/-4-^-) + c = ln (——Ftgz) + c =
J cos z \ 2 1 4 / 1 \ cos z / 1
= ln(—-----1-1/ —L------/ + C=ln(T/ + /^2^T)4-C =
\cos z 1 У cos2z / 1 1 ' 1
= In (v 4- У — i -f- v’) + C.
Весьма часто приходится интегрировать дробные функции, имеющие в числителе только один член, в то время как знаменатель дроби представляет собой многочлен второй степени или радикал второй степени из квадратичного многочлена. Нижеследующая таблица поможет читателю в выборе формулы, которую следует применить для интегрирования.
На формулы (XVI)—(XIX).
Проверить следующие интегрирования.
Решение. Интеграл приводится к формуле 1XVI).
Вынесем в знаменателе за скобку 9:
3
Положим -g- = v, откуда dx = — du. Следовательно: О J
dx __ 4 — 9x2 —
___dx___ /16—
151а
~ з
2 — Зл ‘ *
I Зх . arcsln 4 G.
4. f . dX = arcsln -£ + С.
J /9-х« 3
5. Г -~=£ = In (x 4- /^9) 4- C.
J y.r» —9
6. f = In (x+ r^+9) + C.
J у x*4-9
- Г 3dx 5 , x . „
K —з arct«y + c
8. /•^L_e_L |n "^£. + c
J 2ac ax-}-c
’ 10^+£j_+c.
J b-x* 6 V$ Xs — b
10. Г 5х dx 5 , , . _ /7г^ = 2- г + с- >
11. Г ах dx а х3 . „ / л*4-е4- 2е3 ак‘8^ + С
12. Г eat _ е bt-\-a / а? - bifl 2ab bt - а + u
13. /*—-е — arcsln ef 4~ С.
14. Г Ids 7 , ,/Т , „ /fa-» уз’"’"‘И з'К
15. Г dv 1 ,
16. /* COS a da 1 f Sin а \ , _ / а^+^а а ) + С-
17. / - , — = "cs,n (1п х) + с-' х У 1 — 1п2х
18. Ау₽+АЗ -« '“(“+ ’,‘Ч-^Ч+С.
19. «=> + с.
20. Г du . и + b , / —/ - - = arcsin —1 к С. ' Vdt-(u + b) а
21. f ad^ а . г — е , „ 1 (г-е)24-б» b “rCtg Ь
22. Г dx * 1 . х 4-1 . „ ‘ х*4-2х4-5 ~ 2 “rctC 2 1 С'
Указание. Дополнив в знаменателе до полного квадрата, это выражение можно привести к форме, подобной примеру 7. Именно:
dx /* dx _ Г dx
х* + 2х + 5 ” J (х®+2х+1)4-4 “ J (х-)-1)»4-4 “
1 . х+1।
= У arctg —+ с.
tio (XVI).
Здесь v = х -|- 1 и а = 2. ______ Г dx
2х___1
= arcsln ———- 4- С. 4
Указание. Дополнив подкоренное выражение до полного квадрата, приводим к примеру 14:
dx
Xs
у2-(ха-х)
arcsln 5-Ж о
по (XVIII).
____
9 7
Здесь v = x — 4 и а = 4.
2 2
24.
Г dx 2
J Ч+х + х* = ^TarctS
2х+ 1 /3
1 , 8х +
— a resin — - /41
27. /* tfX. — = arcsin (2х - 3)Ч С. J /зх —х2- 2
/Л» 1 , V — 5 _
vi- 6v-h5 - 4 П 'v — 1 С‘
29 Г________= _ J= 2У-1-3- /Т с
J у^+Зу + 1 /5 2J + 3+/5 '
3»/-гяЧт?-+ 4 ь ’л?+7+1) + с
31* J* 2^ _ 2Jr + 1 = arct® (2г — 11 +
32. /’ dS---= In (s + а Ч /2аУ+^) + С.
J V Ъаз + *’•
Г (Ь Ч- ex) dx Ь . х , е „
33- J ' = — arctg - + — In («® + х2) + С.
Указание. Дробь, числитель которой содержит несколько членов, может быть часто проинтегрирована при помощи разбиения ее на сумму дробей, числителями которых являются отдельные члены числителя данной дроби, а знаменатели которых есть один и тот же знаменатель данной дроби, и сведения таким обравом интеграла втой дроби к сумме интегралов более простых дробей. Так, для последнего примера будем иметь:
/' (Ь + ex) dx _ /* b dx /* ex dx __ , Г______________________________dx_____ /* х dx
J d- -f- ха J а2 + х2 ,/ а: х2 ~ J а* л* е J а- Ч- х2 ’
и теперь каждый из интегралов легко вычисляется.
/(Зх— 1) dx 3 , , , , 1 , х , „
xt + 9 = у In (х2 Ч; 9)-3- arctg -3 -I- С.
/2х —5 1 , _ 5.x /V-/T .
dx = — In (Зх® — 2)-In --7=- 4- " • 3x®—2-------------------------------3 2/6 x / 3 4-/-'
36. /* =_3 /эТГ^_2 arcsin — +C.
J /9-s® 3
37. У rfx=/^+44-31n (x4-/I»+4) + C.
38. f = _5_ y-3/1_e-1. у-— /3/2_9 j _|_ C#
J / 3P —9 3 /Т
39. Произвести нижеследующие интегрирования и проверить результаты дифе-ренцированием:
dx
У 4 - 25х= a dx
3- 12л1 ‘
2dt 3/2 _ 5/ + 2 ’
»/d) f
sin 0 tfO
У9 — 4cos- 6
Г (2г — 3) dx
L J х~ Н- 4
✓d l'-yJ2^.dV.
/dx -----------. Х- + 6Л-НЗ
г 2dx J У 25x2 — 4'
i) Г btty . J 12y3 + 3
J J Узу--2" f(£+2)4( 4^-3 n /' <ar — dx J У 1 + 9x2 /’ dx Ш) / r------------.
./ У 8 + 4л- - 4№ /' 3dx
n> J У5Т=+Т'
dw
12w2 — 3 340
УУ^зв-dt
У7/-4Г3 + о * eaxdx
e'ax’ (35 — 5) ds У Г-^9?
(2x + 3) dx
У 42x2 — b- ’ dt
У (2 —4T+2
§ 19. Тригонометрические диференциалы. Рассмотри^ теперь некоторые тригонометрические диференциалы, часто встречающиеся и легко интегрируемые приведением к основным формулам путем простых тригонометрических преобразований.
Пример 1. Найти J*sin"* х cos" х dx.
Если одно из чисел т и п есть положительное нечетное число, причем все равно, каково будет другое, то легко выполнить интегрирование посредством формулы (IV):
Cvndv = ^-.
J «4-1 .
В самом деле, интеграл приводится к форме:
j (члены, содержащие только cosx) sin xdx, если у sinx показатель нечетный, и к форме
У™ (члены, содержащие только sinх) cosxdx, если у cos х показатель нечетный. Поясним это примерами.
Пример 1. Найти sir3 .: zosfixdx.
Решение. J sin-'х cos3 xdx = sin2х cos4х • cosх dx =
= j' sin2x (1 — sitfx)2 coSxdx =
= J* (sin2x — 2 sin4x + sln’x) cosx4x =
= J' (sin x)2 cos x dx — 2 J' (sin x)4 cos x dx + J* (sin x)6 cos x dx = sinsx 2sin6x . sin7x . _
= —3-------5— + -7-+C ПО (IV).
Здесь v = sin x, dv «= cos x dx и n = 2, 4 и 6 соответственно.
1.
4.
*5.
V 6.
12.
cos5 .г dx.
cos> xdx = / cos2 х cos x dx =
•In8 х) cos х dx =
/sln^ X sin3 x cos x dx = sin x-л-1 C.
УПРАЖНЕНИЯ.
sin5xdx = 4-cos3x — cosx -f- C. О . « j sin3x . sin3 x cos x dx = —4-----1- C.
О , . , 2 , cosbx
sin5 xdx = — COS X + TJ- cos5 X-------=—
о О
- . . 2 • я I sinbx .
cos5xdx = sin x ••—г?- sin®x-|--o
। sin2
sin s cos = —2--------г
cos4 x sin3 x dx = —1- cos5 x + 4- cos’ x + C. 0 /
> 1 cos3e I Z'
COS2 a sin a da =-----—T + C.
о cos3 x dx 1 . , -
——--------= cosec x — cosec5x -|- C.
sin* x 3
sin5 a da , , -
-----;— = sec a + COS a + C.
COS5 a 1
5
7 ’° 7 "
_ slnT Sin’ , + C.
sin’ 6 COSse<rt = 4- sin3 0-----Sin’ 0-|--4rSln’ 6 + C.
V 11 1 I
1 -- у COS3JI + у cos*_y) + C.
~L=<= dy= — 2 У cos /cosjl
cos'* tdt 3 . 1 . /, —-------= -o SinJ * ( 1-
Vsin t
sin5 68 cos 68 M = 4- C.
cos’ 26 sin 20 db = - -+ c. 0
16. Произвести следующие интегрирования и проверить результат дмферен-цированием:
sin31 cos31 dt.
. , 2x 2x
sin- — cos —-□ 3
/, 6 „ cos5 -y <76.
e) / cos — sin — dx. h) / cos3 3x sin 3x dx. J a a J
iff) J' cos5 ex sin ax dx. |/i) j sin5 bs cos bs ds
Пример 2. Найти J' \g*xdxwm J cig* xdx.
Эти выражения легко интегрируются при п целом, почти по тому же плану, как и предыдущие примеры.
Пример. Найти J* tg4 х dx. ,
Решение. J tg'xdx = tg2x (sec2.г — 1) dx — „ ;
= J' tgxssz-xdx — j* tg2xdx =
= У* (tgx)2 d (tgx) — j' (sec*x — l)dx =
= -3— ~<g x-l-x + C.
Пример 3. Найти J зес"хйлилн J cosec"xdx.
Эти примеры интегрируются легко, когда п есть целое положительное четное число.
Пример. Найти / sec® xdx.
J* secc х dx =
Решение.
Itg- -г + l)2 sec2 x dx =
У (tg v)4 sc ’ x dx4-2 У (tgx)2 sec2xdx 4 j"sec2xdx = _ !fc+s-!£.+(,,+c.
Пример 4. Найти j tg” x sec" x dx или J ctg" x cosec" x dx.
Когда n есть положительное четное число, поступаем, как в примереJ3.
Пример 1. Найти J" tg’x sec4 xdx.
Решение. J tg® x sec4 xdx = Jtg® x (tg2 x 4- 1) sec2 x dx =
= J (tg x)8 sec2 x dx 4- J tg® x sec2 x dx = —4-+ C.
Здесь o = tgx, do = sec2 xdx и т. д. - • -
Когда m нечетное, можем поступать, как в следующей примере.
Пример 2. Найти / tg6 х
sec®xdx = j tg4x sec2x secx tgxdxsa
У (sec2 x — I)2 sec2 x sec x tg x dx =
(sec® x - 2 sec1 x 4- sec2 x) see x tg x dx
___ sec7 x 2 sec® x sec3 x u ’
- — -= $ - 3 - G
: по (IV).
Здесь v a sec x, dv *= sec x tg x dx и т. д.
УПРАЖНЕНИЯ.
V/ 1- J* tg3 х dx = -у Х- + In cos х + Ct
2. J* ctg3 x dx = —-- In sin x + C.
v3- J ctg< T ax = -ctfi3 у+3 ctg у+x+ c
/» 11
5. / Gtg^ di = — -• ctg4 a + -л- Ctg- a + In sin a -f- C.
6 J tg»2.rfy = tg*Z_2 tg3 +4 In sec^ + C.
7. y*sec®xrfx = + —|^4- tg’x+ tgx + G
/2 1
cosec6 x dx = — ctg x —- ctg3 x — — ctgJ x 4- C. О 0
9- f tg4 <9 sec* ?rf? = + —s— + C
10. J* tg3 в sec6 в dd = у sec7 0 —sec5 0 C.
/. r . . ctg«x cte8x , „ ctg5 x cosec* x dx =-f---f.—[- C
О о
3 - A
/з . j 2tg2 x , 2 tg2 x . _ tg xsec*xrfx =—у-----1--y-[- C.
A A
/, . a „2 Zsec*y 2see2y . 1 \ , _ tg5y вес у dy — 2 sec у -----4- g-J 4- C.
-VT- = ts“-2cle“--3 +6-
* 15. /* (tg3 z 4- tg* z) dz = \ tg»z 4-€.
</ r * 1
16. J (tg 14- ctg O’ dt = у (tg31 - ctg3 n 4- In tg21 + c.
17. Произвестй'нйжеследулщие интегрировании #4' и проверить результат лифе-
реицированнем: g) h) !* sec3 6 tg2 6 rf6. / cosec3 ? ctg3 ? J?.
a) b) J t^2ldt. f ctg3 у di. ш) п) Г JL^^dx. J COS- X 2^ J »ln»x
c) J’ tg3 ax dx. i) Гtg3 / secs tdt. о) J* sec*x«/x.
d) f ct**£ dx‘ V j) / ctg5y cosec3y//y. Р) У cosec* xdx.
e) Г J tg*/ • V k) Г tg31 sec31 dt. ч) У tg x sec3 x dx.
f) ’/• 3d6 J ctg* 46 ‘ i) Г bdB f ctg’6 ’ г) J*ctg x cosec3 x dx.
Пример 5. Найти J sin" х cos* х dx посредством кратных углов.
Когда или т или п суть нечетные положительные целые числа, кратчайший способ указан в примере I этого параграфа. Когда /пи л-оба четные положительные целые числа, данное диференциальное выражение можно преобразовать посредством надлежащих тригонометрических подстановок в выражение, содержащее синусы и косинусы кратных углов, и затем интегрировать. Для этого служат формулы:
sinucosu = — sin2u по 43, § 199, ч. I, л»
sinsM = y----у cos 2м по 46, § 199, ч. I,
At At
cos‘-m= —- -i- cos2u по 46, § 199, ч. I,
I
Пример 1. Найти J cos-xdx.
Решение, j' cos2 х dx = J ( у -|- 4 cos ) =
= уУ dx + у у cos 2x dx = у + у sin 2x + C.
sin2 x cos2 -v dx.
sin2 .v cos2 .v dx —
2xdx
£ 4
(4 т со54л) ax=
sin4x+C.
Примерз. Найти J sin1 л cos2 xdx.
Решение.
x cos x)2 sin2 x dx =
1 1 о \ w
у - - у cos 2x j dx =
sin2 2x cos 2x dx =
dx -
2x.cos 2.r dx =
x sin 4x sin8 2x
“Тб ~ 64 “48~
Пример 4. Найти J sinmxcosnx
sin mx sin nx dx
или
J cos mx cos nx dx, если и ± л.
По формуле 47, § 199, ч. 1, sin тх cos пх = -1 sin (я 4- п) х + + -у sin (я — л) х. Следовательно,
sin тх cos пх dx = J sin (я + л) х dx + J* sin (я — л) х </х = _ _ cos (я + л)х _ cos (я — п)х . _ ~ 2 (я + л) 2 (я — л) '
Подобно этому, найдем:
J* sin ях sin пх dx =
/ cos тх cos пх dx =
sin (я л) х sin (я — л) х _
2 (я + л) ' 2 (я — л) '
sin (я + л) х , sin (я — л) х , .
2 (я + л) + 2 (in-л) ' .
УПРАЖНЕНИЯ.
v 1. /* cos8 х dx = + 4- sill 2х + С.
J 2 4
V „ Г . . , Зх sin 2х . sin 4х , „ Lt,
2- / sin1xrfx = -y------------h—32~+с-
*3. J cos*xdx = — + -^- + -32~ + C-
¥ . Г • j 1 /- . , _ , sins2x .3 , . \ ,
4. / sin*x dx -T£- (5x — 4 sin 2x -----5---— sin 4x) + C.
•/ ID \ J 4 /
. 1 /- । . , „ sln82x .3 , . \
cos* xdx = -Гт- I 5x + 4 sin 2x-------h ~r sin 4x ) - -
10 \ J 4 /
„ /• , . , . sin8 2a . a sin 4a
6. J sin*acos*arfe =------5g- + -jg — -64“+ C-
* 7. J" sin* t cos* t dt = ~ ( 3/ -’sin U + ) ! C.
8. /* cos*x sin® x dx = -Дг. ( 5x-|- sih82x — sin 4x — J 120 \ О о /
u , e J cos8y cos2y . _
* 9. / cos3ys!n5y dy =----------------+ C.
/, - 'r c . sin llz slnz sin 5z s^p6z dz =-------22— H---------h C.
/fi -j sin Ils . sln3.s
cos 4s cos 7s ds = —----1----g----1- C.
V 12. / cos 4- x sin 4- x dx = — 4- cos x f- c°8 4- * -f- C.
J 4 4 2 i
V13. f cos3x cos ^xdx sin -Ц- x + sin 4 x + C.
J v ZD О 1U о
§ 20. Интегрирование выражений, содержащих / иля V хР+ау ПрИ помощи тригонометрических подстановок. В большом числе случаев при интегрировании выражений этого типа весьма быстро приводят к цели следующие подстановки:
J для выражений, содержащих У а9 — х9 подстановка х с= a sin z,
п • * У а9 -|- х9 я х = a tg z.
У/х9 — а9 „
Пример 1. 1 g . COS Z
(аа —х2)2
Решение. Положим х = a sin г; тогда
dx = a cos z dz
dx (* a cos z dz
Z = I Z ~
(e2 - x2)2 J (л2 — ehln2 z)2
a cos zdz 1*
a3 cos2 z e2
dz cos®z
,82+c=.-77fey+c
Так как sin z = — , то, построив прямоугольный треугольник с противо-
лежащим углу z катетом х и гипотенузою а, катет будет равен У а2 — х3 в tg z = = Х- - (черт. 19).
у в® — х2
Пример 2.
будем иметь: прилежащий к углу г
Решение. Положим х = tg z 2); тогда . dz dx =----------------—
cos-г
dx _ Р _______________dz___________ /* __________dz_______
х I cos2г tgz /tg2z + 1 / cos2 z tgz-- —-
V v *• cos z
dZ X Z . _ i 1 — cos Z
---- = In tg -77 C = In ;----- in z 6 2 slnz
1 sfn z
. V *3 + 1 - 1 , z-= In -------—------C.
. 1 1 secz Vx2-4-l .
Так как tg z = x, ctg : = - и ----------- (черт. 20).
УПРАЖНЕНИЯ.
1. f ~.дй. dx — У x2 — a2 — a arccos — -} C. J X X '
2. С У a2 — x2 dx= у У а2-х2У arcsin -j- + C.
’) Можно воспользоваться также соответственно подстановками: x = ncosz, . а
х — a ctg Z, X = —;—. ь sinz
®) В этом примере а = 1.
3. f </х = 1п (х +
4. Г -^= = 4 arcsln x-^ZEZ 4 /
J /1-х2 2 2
/• dx _ (2x2-1) , г
J х* УТз+Т 3x3 + С-
6. /• Хл^+С.
J х- У х2 4- а2 а2х
/• у Х1_аг (хэ-дз)» 1
1 J-----х^ = За2х> ' С- j
Дополнительные упражнения.
Произвести нижеследующие интегрирования и проворить результат диферен-
пированием: 1 Г ds
’j г : v 17.
sin1 X •' у 1 4- 3s - s3
f ( х=-ПИх 18.
V2J x + 2 У cos6 dx.
V 3. 1 C (ax + fe)tfx 19. /' dX
y~jfi — a8 J х®4-2х4-Г
* *'J г tg« 4<й- 20. Г ifidx J 7^3 *
''‘J f (4xX. i)rf.y Q1 /' rfO
~V 1 -5.V- J sin 20 '
6. 1 /* dx 22. Г dt
J cos 3# ’
V 2 4- 2x - x -
7. j r -4~3^ dt. У1 - a2 fl 23.
J v x-3
8U f 24. Г dy
' 2^-? 4-1 ’ J y-yi _ 6> 4-10
9. , Г 4x*dx 25. /• ax dx
' 1 — 4x‘ ‘
J b — ex2
’°'J f (tg 3x — I)2 dx. *, 26. Г xdx J (14-xS)8'
V lk ) r tg8в sec80<fli. 27. /* dx
V 12‘ J ( sin1 dx. J («+М"
2 28. r l+gsr? M-
"'J /• d6 J i + tg о
cos* в 29. r
14. j C J X* У x’ - 1
P4-&4-5'
m J /* 3 cos 6 40 30. J (a — 3x2)M 2x dx.
5 —7 sin в . । .е.+ч’ V 31 /* 2x2 dx
i16. ] 1 / — " J (o’-х8)2
V'J /а-
32.
33.
34.
35.
1 — 2х
9х- — п2
dx.
cos3 ах sin axdx.
sin26xrfx.
40. Нижеследующие функции являются производными неизвестных функций найти эти функции и проверить результаты диференцированием:
a) 5x34-sin2x.
Решение. Чтобы найти искомую функцию, надо проинтегрировать выражение
(5х3 + sin 2х) dx.
Таким образом получим:
У^(5х3 -|- sin 2.v) dx = -cos 2г 4- С.
Проверка:
-г- - -г cos 2х 4- С') = 5х3 4- sin 2г.
dx \ 4 I J
Ь) 5х3 — 6х. k) . av.J~ s) 1
с) 2х2 — Зх — 4. d) cos2 ах 4- sin— . а ’ У 3 4*4 x'-n + c x2 4- 4x — 1 ’ . a* sec4 —. b
t)
V a2f2 - b2
е) V а 4- Ъх. п ах + ь Ьх 4- а , 5 —fc m) . 9 — 4s3 г3 П) 5-2z‘ til I
V 4 — x2 4- 2x
ь> 5 4- 2х V) U“-e a)
h)l±*L. ,) ' 4х2 — 7 mx4-n’ p) cos24p.v. 4) tg’-f w) X) 1 л-3 (14-x2)2. 1
r) x3 Ух-' —1
" Vp-Wx1 V У У) x2 fl’-p3.
§ 21. О множественности ответов при интегрировании. Читатель в первое время бывает не мало смущен, видя, что самые разнообразные ответы на один и тот же неопределенный интеграл оказываются все одинаково верными, т. с. как будто мы имеем здесь множественность верных ответов. Легко, однако, понять причину этого кажущегося парадокса.
Возьмем самый простой пример.
Мы знаем, что
d , , 1 d 1
— arcsinх = -4-. и -----arccosx= _ .
dx /1—х3 dx —/1—
5 Эжж. Ш8. — Ггвняипь ж Луажя, ч. ТТ, Пггтегральжов жожжежожж»
Отсюда мы заключаем, что одновременно
resin х-}-С и | -----= — arccos х — С.
J 4-/1—х»
Ответы как будто различные.
На самом деле ответы всегда тождественны между собою, и кажущееся различие ответов всегда вызывается различием произвольных постоянных в этих случаях, обозначенных тем не менее одною и тою же буквою С.
Это легко обнаружить на приведенном случае. Действительно, из тригонометрии читатель знает, что cos ---------------------------j^ = siny.
Обозначив их общую величину через х, имеем:
cos —у^ = х и sin у = д'. Поэтому
---------------------у = arccos х и у = arcsin д', л и, значит, к у = arcsm х = —----------------------arccos х,
л» откуда (1Г
-у -|-С
Таким образом мы видим, что произвольное постоянное С второго ответа
равно произвольному постоянному первого ответа, увеличенному на — .
Различие произвольных постоянных и создало здесь кажущееся различие самих ответов.
Пример. Имеем право писать:
У* = arctg х-arctg 1 + С И
У* = arctg х +arctg I + С,
так как формулы эти, очевидно, дают один и тот же ответ, но при разним обозначении произвольной постоянной.
С другой стороны, читатель из тригонометрии знает, что
tg (а - Ь)
tg (а + ft)
___tg а — tg b 1 + tg я • tg ft
и
= tga + tgft 1 — tg а • tg ft ‘
Значит: и
Полагая в этих равенствах а = arctg 1х и b = arctg I и, значит, х = tg а и 1 = tg b, находим:
. , , х — 1
arctgх — arctg 1 = arctg * и
arctg х + arctg 1 = arctg .
Поэтому / dx . x — 1 . _ /* dx . x +1 , _
l^ = arctg T+7+C " J T+^ = arCtg — rC
Ответы кажутся разными. На самом деле только С различно в пер в ом и втором случаях.
ГЛАВА III.
ПОСТОЯННОЕ ИНТЕГРИРОВАНИЯ.
§ 22. Определение постоянного интегрирования из начальных условий. Как было выяснено в главах I и II, результат интегрирования содержит произвольное постоянное, т. е. задача нахождения первообразной функции по данной функции дает бесчисленное множество ответов. Однако многие задачи, решающиеся при помощи интегрирования, требуют нахождения одной определенной первообразной функции; а так как все первообразные функции отличаются друг от друга только значением произвольного постоянного, то, значит, нахождение определенной первообразной функции сводится к нахождению определенного значения произвольного постоянного. Очевидно, в таком случае нам должно быть известно значение интеграла для некоторого значения переменного. Поэтому условия задач такого рода, помимо днференциального выражения, содержат еще и некоторые дополнительные данные. Поясним это примером.
Пример. Найти функцию, первая производная которой есть За2 — 2х + 5 и которая должна равняться 12 при х = 1.
Решение. (Зх2 — 2х 4- 5) dx есть данное диференциальное выражение, которое нужно интегрировать. Имеем:
J (Зх2 - 2г + 5) dx = х2 - х2 + 5х ; с, где С—постоянное интегрирования. По условию задачи, этот результат должеп равняться 12 при х = I, т. е.
12 = 1 — 1 + 5 + С. или С=7.
Искомая функция будет, следовательно, х» — х2 + 5х + 7.
§ 23. Геометрическое значение постоянного интегрирования.
Поясним примерами.
Пример 1. Найти уравнение кривой, в каждой точке которой угловой коэфипиент касательной равен 2х.
Решение. Так как угловой коэфициент касательной к кривой в любой точке du
равен то по условию задачи имеем:
•— = 2х, или dy = 2х dv.
dx
Интегрируя, находим у = 2 J* xdx, или
У = х2+С (А
где С—постоянное интегрирования. Если постоянному Сдадим ряд значений например 6,0, —3, то уравнение (А) даст:
у = л- + 6, у = х2, у = х3 — 3;
значит, наши кривые суть параболы, оси которых совпадают с осью У, причем эти кривые отсекают на оси ОУ отрезки 6, 0, —3.
_ л . , , . dv
Для всех парабол (А) (число их бесконечно велико)
имеет одну и ту же величину, т. е. направление их (или, что одно и то же, угловой коэфициент касательной) одинаково для одного и того же значения х. Легко также заметить, что разность ординат любых двух кривых, соответствующих одному и тому же значению х, остается неизменною. Следовательно, можно получить все эти параболы, просто передвигая поступательно одну из них вверх или вниз на величину С, ибо в этом случае значение С на угловой коэфициент не влияет (черт. 21).
Если в этом примере ввести еще добавочное условие, например, чтобы кривая проходила через точку (1, 4), то координаты этой точки должны удовлетворять уравнению (А), откуда
4 — 1 С, или С = 3.
Следовательно, искомая в этом частном случае единственная кривая будет парабола у = х- + 3.
Пример 2. Найти уравнение такой кривой, чтобы угловой коэфициент касательной к этой кривой о любой точке равнялся отношению абсциссы к ординате со знаком минус.
Решение. Условие задачи выражается уравнением:
dx у 1
или, отделяя переменные (освобождаясь от знаменателей):
у dy= — х dx.
Интегрируя найдем:
V3 с2
1 = -22- + С
или
Черт. 22.
Уравнение представляет ряд концентрических окружностей с центрами в начале (черт. 22).
Если дополнительно наложим условие, чтобы кривая проходила через точку (3; 4), то
9 + 16 = 2С.
Следовательно уравнение требуемой кривой в этом частном случае представляет окружность х'г -f-y3 = 2s
§ 24. Физическое значение постоянного интегрирования.
Поясняем примерами.
Пример 1. Найти закон движения точки, движущейся по прямой с постоянным ускорением.
[dv 1
= по (25), § 100, ч. 1 постоянно, напри
мер /, то будем иметь: р — = ], или dv^j dt.
Интегрируя, найдем: v=jt-\-C. (А)
Для определения С положим, что начальная скорость равна vu. т. е. пусть
v — г’ц при t = 0.
Подстановка в (А) дает:
= 0 -|- С, или С - т'о.
Следовательно, уравнение (А) примет вид:
= (В)
Так как v= [(18), § 97, ч. I), то пт (В) найдем:
5Г = " + ^ или ds = jt dt vodt. Интегрируя, получаем:
5= 4 + + с. (С)
Для определения С положим, что начальный путь ( = расстоянию при t — 0) будет s0, т. е. пусть
s = sd при / = U.
Подстановка этих значений в (С) дает:
Sj = 0 + 0 + С, или С --
Следовательно, уравнение (С) примет вид:
л =“7 + + (О)
Положив j = g, v9 = 0, s0 = 0, s = It в (В) и (D), найдем закон движения падающего тела в пустоте, когда оно выходит из состояния покоя, именно:
v = gt, (BJ
К
А = (DJ
Исключая t из (Ва) и (DJ, найдем:
»=
Пример 2. Исследовать движение тела, брошенного с начальной скоростью v0 образующей угол а с горизонтом, пренебрегая сопротивлением воздуха. .
Решение. Пусть движение происходит в плоскости XOY (черт. 23).; ОХ — горизонтальная линия, а ОУ—вертикальная, и пусть тело брошено из начала.
у Пусть на тело действует только тяжесть. Тогда
ускорение в горизонтальном, направлении будо Жуль, в вертикальном оно будет — g. Из уравнения (26) § 101, ч. 1, имеем:
dvt dvt
~dF=0 " =
Интегрируя, найдем:
ЧеР’-23. и v, = -£t+C,.
по v0 соз = горизонтальной проекция начальное скорости, г0 11п а = вертикальной проекции начальной скорости.
Следовательно:
Q = о0 cos a, C2 = vl) sin а.
откуда
о, — t’oссз а< vy — — £7 ' Vg'sir. з. (Е)
Из (20) н (21), § 98, ч. I, имеем: v. = 4^, vu = следовательно, (Е) даст: at • at dx dy , .
— = о0 cos а, = — gt Ч v0 sin а, или dx = о0 cos a dt, dy = — gtdt-\- v0 sin a dt. Интегрируя, найдем:
л= pocos a-Z -j- Cj, y =-gP 4- v0 sin a • t + C4. (F)
Для определения C3 и Ct замечаем, что при t = О х = 0 и у = 0.
Подстановка в (F) даст С3 = 0 и С4 = 0. Отсюда х = р0 cos a t . (О
и
V ----gt- + v0 sin a • t. (H)
'сключение t из (G) в (H) даст:
<tv2
> = xtga-_/l—, (I)
2i>0 COS'a
т. e. уравнение траектории, показывающее, что тело опишет параболу.
УПРАЖНЕНИЯ.
1. Найти функцию, первая производная которой равна:
а) х— 3, зная, что при х = 2 функция равна 9.
Отв. -у--3х+ 13.
Ь) 34-х — 5х2, зная, что при л =б функция равна —200.
Отв. 124 + ЗхЧ-4-Z о
с) уа — №у, зная, что при у = 2 функция равна нулю.
Отв. -J-y4- -у 62У + 2*2-4-
d) sin a + cos а, зная, что при а = функция равна 2.
Отв. sin a — cos a + 1.
e) 4---д 2. зная> что ПРН * = l функция равна нулю
Отв. In (2t — fl).
f) sec10 4- tg в, зная, что при 0=0 функция равна 5.
Оли. tg 0 — In соз 0 + 5. . 1 . « g) •«, что при х = а функция «= .
Отв. — arctg-----к «г-,
а ‘ а 1 4а
h) Ьх3 + ах 4- 4. зная, что при х = Ъ функция равна 10.
1) У / -]--, зная, что при t = 4 функция равна нулю.
У t
j) ctg ? — cosec'-’ зная, что при о = 4J- функция = 3.
к) Зе24’/, зная, что при Т=0 функция —
2. Найти уравнение семейства таких кривых, чтобы угловой коэфициент в любой точке кривой семейства был равен:
а) х. b) 2с - 2. с) у . d)-£. е)^, . I) Зх2. g) х2-!-5х. h) у .1)
.. v ,.62х .. а-х , 1 ~Г х
П “ IT-k}d^- П " Ь^-ш) ху- п)з'0' т- Р) Т-у •
Отв. а) Параболы у = -у -j- С. Ь) Параболы у = х3 — 2д С. с) Параболы
V" 1*3
у2 = 2х + С. d) Полукубическис параболы у = -у 4- С. е) Полукубические па-
уЗ j-2
раболы = 4т-+ С. f) Кубические параболы у = х3 С. g) Кубические пара-О А
д-з 5 уз
болы у = -5- -(- -х-х2 + С. Ь) Кубические параболы-^- = х 4 С. i) Равносто-О 2, 0
ронние гиперболы у3—х2 = С. j) Равносторонние гиперболы ху =- С. к) Гипер-
V3
болы <Ру — tPx — С. 1) Эллипсы Ь3у3 + а3х* = С. т) 1пу = -у 4- С или у = а»
= Се г. п) )пу = х 4- С или у = Се*. о) Прямые у = тх 4- С. р) Окружности х24-у24-2х-2^+ С=0.
3. Найти уравнения кривых, определенных в примере 2 (а), (с), (d), (I) 0), (m), которые проходят через точцу (2,-1).
X5—4
Отв. (а)х- — 2у — 6 = 0; (т)у =- — е 2
и т. д.
4. Найти уравнения кривых, определенных в примере 2 (b), (е), (g), (h), (о), (р), которые проходят через начало координат.
Отв. (Ь) у3 = х2 — 2х; (о) у = тх и т. д.
5. Найти уравнение кривой, поднормаль которой постоянна и равна 2а.
Отв. Парабола у3 = 4ох 4- С.
dv
Указание. По (4), § 92, ч. I, поднормаль равна у .
6. Найти кривую, у которой подкасательная постоянна и равна а [см. (3),
§ 92, li. I]. Отв. а \ау = х^-с.
7. Найти кривую, у которой поднормаль равна абсциссе точки касания. Отв. у3 — х*=С, равносторонняя гипербола.
8. Найти кривую, у которой нормаль постоянна (= R), полагая, что у = R при х = 0. Отв. Окружность ж3 4-у2 = R2-
У казан не. По (6), §92, ч. I, длина нормали равна у у 14- > или
_ 1
dx = ±(R2 — у') 2 у dy.
9. Найти кривую, подкасательная которой втрое больше абсциссы точки касаиия- Отв. х = су*.
10. Показать, что кривая, у которой полярная подкасательная [см. (13) § 95, ч. 1] имеет постоянную величину, есть обратная спираль.
11. Покавать, что кривая, у которой полярная поднормаль [см. (14), §95, ч. I] постоянна, есть архимедова спираль.
12. Найти кривую, у которой полярная поднормаль пропорциональна длине радиуса вектора. Отв р =
13. Найти кривую, у которой полярная поднормаль пропорциональна синусу полярного угла. О/па. р = с - a cos 0.
14. Найти кривую, у которой полярная подкасательная пропорциональна длине радиуса-вектора. Отв = се<л.
15. Определить кривую, у которой полярная подкасательная находится в постоянном отношении к полярной поднормали. дтв р _ ее<а
16. Найти уравнение кривой, у которой угол между радиусом-вектором и касательной составляет половину полярного угла.
Отв. р = с (1 — cos 6).
« Полагая, что при 1 = 0 скорость v = v0, найти соотношение между v п I зная, что ускорение равно;
17. Нулю.
18. Постоянному j.
19. а + bt.
Отв. v = va.
Отв. v = о0 jt.
Отв. v = t>0 + at + у ЬР.
Полагая, что s = 0 при t = 0, найти соотношение между s и 1, зная, что скорость равна:
20. Постоянному (= t’u).
21. т nt.
Отв. s = VqI.
Отв. s — mt + 1 nt2.
22. 3 + 21 - ЗА Отв. s = 3/ + Р - Р.
23. Скорость тела, выходящего из состояния покоя, равна 5Р м/сек по истечении t секунд, а) Как далеко будет оно отстоять от точки выхода спустя 3 секунды? Ь) Во сколько времени пройдет оно 360 м, считая от точки выхода?
Отв. а) 45 м, Ь) 6 сек.
24. Полагая, что s = 2 при 1 = 1, найти соотношение между s и I, зная, что скорость равна:
а) 3. Ь) 2/— 3. с)Р+2/-1. d)~. е) 4/»-4. f) ~.
rt 5
Отв. a)s = 3/-l. b)s = /5-3/-[-4. с) s = V -|- Р - t + -i. d) s = b
= m / 4-2. e)s = /‘-4/4-5. f) S= - -t+* + 2.
25. Полагая, что v = 3 при 1 = 2, найти соотношение между v и г, зная, что ускорение равно:
а) 2. Ь)ЗГ+1. c)fl — 2t. d)J- + t
fl f
Отв. a)t> = 2f —1. b) v = fl -J-1 — 7. c) v = -- — fl 3. d) v = InF
26. Скорость тела, выходящего из состояния покоя, равна 5Р м)сек по истечении t секунд. 1) Как далеко будет оно отстоять от точки выхода спустя 3 секунды? Ь) Во сколько времени пройдет оно 360 м, считая от точки выхода?
Отв. а) 45 м\ Ъ) 6 сек.
27. Тело выходит из точки О, и спустя t секунд скорость его в направлении осн ОХ равна 12/, а в направлении О Иравна At- — 9. Найти: а) расстояния, пройденные параллельно каждой оси; Ь) уравнение траектории.
Отв. а) х = б/2; у = fl — 9/;
Ыу^(|х-9> /-*-•
28. Тело движется таким образом, что скорости его по направлениям осей ОХ" и OY равны соответственно Ах и Ау. Показать, что траекторией его служит равносторонняя гипербола.
29. Тело, выходя из начала координат, по истечении t секунд движется со скоростью 6/ по направлению оси ОХ и скоростью ЗР — 3 по направлению оси OY. Найти:
а) расстояние, проходимое за t секунд по направлению каждой из осей;
Ь) уравнение траектории движения.
Отв. а) х = ЗА, у = fl — 3/; *
b) 27у- = х (х - 9)«.
ГЛАВА IV.
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ.
§ 25. Введение. Рациональная дробь есть такая дробь, у которой числитель и знаменатель суть многочлены, т. е. целые рациональные функции 1). Если степень числителя равна или больше степени знаменателя, то дробь может быть обращена в смешанное количество делением числителя на знаменатель. Например:
x’-j-2x-H JW' x»+2*J Г’
Последнее слагаемоег’е<Аъ дробь,- приведенная к простейшему виду, так как степень числителя меньше степени знаменателя. Очевидно, что целые члены интегрируются прямо, и, следовательно, остается рассмотреть эту дробь.
Для интегрирования такой дроби часто бывает необходимо разложить ее на так называемые простые элементы, т. е. заменить алгебраическою суммою таких новых дробей, интегрирование которых можно бы было выполнить. В алгебре доказывается, что это всегда возможно, если мы умеем знаменатель разложить на действительные, первоначальные множители.
§ 26. Случай 1. Множители знаменателя все первой степени и не повторяются.
В алгебре доказывается, что всякому не повторяющемуся множителю первой степени, каков, например, х — а, соответствует элемент вида:
А х — а '
Такую дробь можно тотчас же интегрировать следующим образом:
/А dx . f dx ... . . „
-------=t А I--------= А 1п (х — а) 4- С.
х — a J х — а 4 ‘
п и « Г (2x-f-3)rfx
Пример. Найти J •
Решение. Множители знаменателя суть х, х — 1, х + 2; полагаем
2х + 3 _А В С
х(х — 1)(х-|-2) х^х- 1тх + 2’ w
где А, В, С—подлежащие определению постоянные.
*) Г. е. переменное не входит с отрицательным показателем (см. § 28, ч. 1)
Освободив (А) от дробей, имеем:
2х + 3 = А (.V - 1)(яс -Ь 2) + В(х + 2)х 4- С(л - 1).г =
= (A+B^G)jc? НИ4-2В-С)х-2Л. (В)
Так как это равенство есть тождество, то, следуя методу неопределенных коэфициентов, приравниваем коэфициенты одинаковых степеней х в обеих частях и получаем три совместных уравнения;
' А + В + С = 0, |
А4-2В-С=2, I (С)
— 2А = 3. |
Решив эти уравнения, найдем:
Подстановка в (А) этих значений дает; 2x4-3 3 5 1
х(х-1)(.с4-2) “ 2х+3(х-1) 6(х-|-2)'
Отсюда
/* 2х 4- 3 _ 3 Г dx 5 /• dx 1 Г dx _
/ х(х-1)(*4-2) Х ~ ij x+3jx-l bj x-f-2 Б
= — ~ In X 4- In (X - 1) - 1 In (x 4- 2) 4- In c = In C8(X~ f .
x= (X4-2)6
Более краткий способ нахождения значений А, В и С из (В) таков: Положив в равенстве (В) множитель х = 0, имеем: 3 = — 2А, или А = — •?.
Положив множитель х — 1 = 0, или х = 1, имеем: 5 = ЗВ, или В = .
О
Положив множитель х 2 = О, или х = — 2, имеем: — 1 = 6С, или С= —.
о
УПРАЖНЕНИЯ.
1.
2.
(2х - 1) dx (х—1)(х —2)
= 1п
^+с.
Xdx = 1, (х4-3)«
(х4-1(х + 3)(х + 5) 8 (х4-5)Ь(х4-1)
4- С.
3.
(х —1)</х с(х4-4)2
х»4-6х4-8 П ± (х4-2)2
4- f =,п Iе + 3>’ <х - 2)1 •
5- f = *П + + с-Г (2х»4-1)Лс , ,1(х4-2)<» ,
б- J x» + 3x + 2=^~fa + ln х+1 +С
х5 4- х» — 8 лэ xs х2 (х — 2)5
- ЖЗ-4Х— dx= з + з+^ + Ш -А-__ + С.
x*dx _х» , 1 Х-1 , 16 ,
(X2 - 1) (х + 2) 2 2л + t* " (х+ 1)3 + 3' п
(a-b)ydy _ (у — а)“ _|_ С.
^-{a + b)y + ab ,п (у—Ь)ъ
(P + pq)dt = (t-p) (t + q) _j_ с
Ш-р)и + ч) t ' '
(2г*-5)^ = 1 1п
z‘-5«3+6 2/2
2 . 1 .
J-С.
§ 27. Случай II. Множители знаменателя все первой степени и некоторые повторяются.
Каждому n-кратному множителю первой степени, каков, например, (х — а)", отвечает п элементов:
—-------1-----~-------h... н——.
(х —а)"~ (х —‘ х—а
Последняя дробь интегрируется, как в случае I. Все остальные интегрируются по формуле степени. Так:
/* dX » С , Ч— 71 • ^4 1 ✓"»
I -------- = Л | (х — a) dx =------------^-4-С.
J (х — а) J (1—п) (х—а) 1
/х3 -4-1 —-----——,</Х .
X (X — 1 )3
Решение. Так как х — 1 входит множителем трижды, полагаем хЗ-М А , В , С , D x(x-iy х г (х-I)1 т(х-1)'-тх-Г
По освобождении от дробей получаем:
х3 + 1 = А (х - I)3 4- Вх + Сх (х - 1) + Dx (х - I)2 =
= (А + D) хз + ( - 3 А + С - 2D) х* + (ЗА + В - С + D) х - А.
Уравняв коэфнциенты при одинаковых степенях х, находим систему четырех уравнений:
A-|-D = l,
- ЗА 4- С-W = О,
ЗА + В-С+ D = 0.
-А= 1.
Решая их, находим: А = — 1, В = 2, С = 1, D = 2 и
х® + 1 _ 'l J 2 I 1 2
х(х-1у>- X (Х-1)3“Г (х-1)2^х-1 •
Отсюда
/ +2<' -1 > + с -
(X- 1)»
УПРАЖНЕНИЯ.
/* 1 > 1 х — 2 1 (х - 1)» (х - 2) " х - 1 1 ,п х - 1 + С‘
*2. р х^ dx 4 / (х + 2)3 (х + 1) " х + 2 + ,п + ’> + С-
v3. - -Ч+'" +с- f Xе — 4х2 + 4х х — 2 ха /• х®+1 1 2
4. / , A dx=f- . .... —г--Ь In (х — 1)+С. / (х— 1)3 (х— 1)3 X — 1 ' 71
/4x»-x»+l)rfx_x« , 1 , 1 , „ х-1 , г / хз-хз - 2ЬЖ + Ьх |1п х"|С
6. Г (lr+2)rfx _ 4лг+3 хз u / Х(х+1)3 2 (X4- I)2 1 (Х~-1)2
7. Г x>dx _ _ 5х+12 / х+_4 у / (х; + 2)3(х + 4)з - хз + бх+8 1 ш 1 x + 2J
8. f >, + 5>a-|-8y-J-4 - у+2 +|п(-> +1> + С-
J (Т* — 2F 4 (Р - 2) 8у 2 t — У
/as1 ds . , 2а3 о®
ТГРоГ — '"<*+«>+ J+-S— 2-<7+^г
1 '• - т£тр >=>"+»>- -
12.
(i+ax)dr .8, л Г+гх’ + хв 5'5'
§ 28. Случай 111. Знаменатель содержит множители второй степени1) но неповторяющиеся.
Каждому неповторяющемуся квадратному множителю, каков ха^-рх-[-д, соответствует одна элементарная дробь вида:
Ах-\-В
Х* + рх+д '
Эту дробь можно интегрировать в общем виде следующим образом:
Г (Ax-\~B)dx _ Г ( Лх+~2 2~+Д) dx _
j xn-+px + q I + =
Г Ар 1
I придав к числителю и вычтя из вето I
I) Коэфициенты этих множителей действительны, но корни мнимые, т. е.
— иначе они могли бы быть оазложены на множители пеовой степени.
[пополнив знаменатель второго интеграла до полного квадрата]
=41п (хз+^+»)+(1Я=^)агс,е v2r+f.+c-
2 — pi j у ^Ч—Р*
Так как дс® -}-рх -j- q = 0 имеет мнимые корни, то 4q—/>•>(),так что никаких мнимостей в окончательном результате уже не будет. >
/* 4z/v
Пример. Найти /
„ „ .4 А , Вх + С
Решение. Полагаем —7-гт~Т\ =------5-7—
х (х® + 4) х Xs + 4
Освободив от дробей, имеем: _Л
4 = А (х® + 4) + х (Вх + С) = (Л + В) х® + Сх + 4Л.
Приравнивая коэфициенты при одинаковых степенях х, получим:
А + В = О, С = О, 4А = 4, откуда
А - 1, В = — 1, С=0, так что 4 _ 1 х
х (х® + 4) - Т х® + 4 ‘
__4dx
х(х®4-4)
Следовательно:
— =1пх - — In (.г® + 4) + In с = In
-4 2 /х®-4-4
УПРАЖНЕНИЯ.
dx , -------= In
X(*» + D xdx
FTl)(^r+‘4)
; + С.
2 x
+ _ arctg-J + C. £ r (2x3 —3x —3)rfx _ (x3-2x4-5)*
./ (X - 1) (Л-3 - 2x + 5) x — 1
• Г x3 dx I . 1 -r x , , _
V 4. / ;-----z = -г- In-,--!-- arctgx + C.
J 1- r* 4 1 — x 6
5 f_________dx_________1 x*_____________________
• J (X® + 1) (хз + X) “ 4 ,n(x + 1)3 (x® +D 2
»/ , Г (x« - 6) dx , x« 4 4 . 3 . x 3 _ x ,
* 6. / --------f---= In - + -x- «ctg -s- — arctg 4- C.
J x« + 6x®4-8 /x’4-2 2 2 /Г /2
1 , 10 п
+• у «ctg 4- c.
1 arctgx+C.
Г (5л;—l)rfx г=-2х + 5 . 5 t х-1
J (х2 + 3) (х* - 2л г >) ~ ,П х2 + 3 + 2 *rctg ~2
_Л"',гй+с
§ 29. Случай IV. Знаменатель содержит множители второй степени, причем некоторые" из них повторяются.
Каждому n-кратному множителю вида (ха-|-рх-!-<7)" соответствуете элементов (п > 1):
Ах-\-В____, СхН-Р__________ . , /.x + Af
(х’4-рх-1-д)я "Г (x’H-px-f-0"-* т ’ “ х'^\-рх-\-д’
Для вывода формулы интегрирования первого слагаемого поступаем так:
(х? + рх + Ч)
в числителе и вычтя
-4/(x.+px + ?)-"(2x+rt dx+ (?^Л)
Интефируя первый член, имеем:
/ (х’+А’С-Н)" — 2(1— л)(х2+^х + ^)’‘-1
, (ЪВ-АрХ Г dx
•Ц 2 )J (x"4-/>x-W)M’ 1
Днференцируем функцию
л( х+* V 1 2<л - > (*+£)’
Лг\(лЧ-м+«)”"7 (х’+м+v?-1 •
ИЛИ
— (2л —3) .(^4-^+v)""'
Так н
как х2 + рх 4- q = ( х + + ( ? —
( х+-03 = (ла + рх + ?)-( 7~4*)-
Интегрируя обе части равенства (С), найдем;
---------„ , = — (2/д—З) / ——- ——. 4-J (xa^pX_L^-*
4-2 (п — 1) (?-£) I-------—-----г,
V 4 IJ {хг+рх + ду
откуда, решая относительно последнего интеграла, получаем:
г ' Р-
Г__________________________________________+
J (x’+^x4-v)n 2(л —1)(<7 — у-)(ха+/’х + ?)Л-1
4------------------f-------— ,D)
Подставляя этот результат во вторую часть равенства (В), находим '):
Г Ах + В Д(р»-4у)4-(2В-Л/>)(2л4-р)
J (*Я4-М + ?)П 2(л-1)(4у-р’)(л«4-рх4-^)п-1‘Г
(2В-Д//)(2л-3) С dx
(Л—1)(4?—/7а) J 1 f
1) 4^_рЭ^>о, ибо корни уравнения х«4-рх + д=0 мнимы.
7 Зак. £853. — Гравии в Луакв, ч. II, Ижтегральаое ксчппленже
Отсюда видно, что наш интеграл зависит от нахождения интеграла рациональной дроби того же тнпа, но в ней квадратный множитель повторяется только п—1 раз. Прилагая формулу (Е) последовательно п—1 раз, очевидно, мы в конце концов приведем наш интеграл к
dx x*+px-\-q'
а этот интеграл легко найти, дополнив квадрат, как указано в § 28, случай III; стоит лишь положить Л=0 и В=1.
Таким же образом можно интегрировать все дроби в (А), кроме последней. А эту последнюю, именно:
Lx-j-M
х^+рх + д’
можно интегрировать способом, указанным в § 28, случай III.
Пример 1. Найти
(х3 4-ха 4-2j//х (Х2 4-2)2
Решение. Так как х3 4- 2 встречается множителем дважды, полагаем
x3j-x2-}-2 Ах + В Cx + D (х*4-2)а (ха4-2)а + л-«+2 ’
г
По освобождении от дробей имеем:
л» 4- Х2 + 2 = Ах 4- в 4- (Cv 4- О) (х* 4- 2) =
= Сха 4- Dx'14- (А 4- 2С) X 4- В 4- 2D.
Приравнивая коэфициенты при одинаковых степенях х, найдем: С= 1, D = 1, А 4- 2С = О, В 4- 2D = 2.
Отсюда
А= -2, В = 0, С= 1, D= 1.
Следовательно: х* 4-х* 4-2 _ 2х , х4-1 (х2-|-2)а “ (ха 4- 2Я + X* 4- 2
/• (л14-х24-2)dx f 2xdx , /* xdx /* dx
J (x«4-2p “ J (x»4-2)2 J x2 + J x2'-p,=
= —— 4- -7= arctg -4-- -- i 1D ( "2 + 2) + c-
X«4-2 Y 2 Y2 2 ' т /т
Пример 2. Найти
2х»4-х-|-3 (x*+lF
dx.
Решение. Так к .кх3 + 1 встречается множителем дважды, имеем:
2лг»4-х4-3 Ах + В Cx + D (x» + ip = (х*-|-1)» + х»4-1 •
Освобождая от дробей, найдем:
2х» -|-х + 3 = Ал4-В + (Сх + О)(л»+1).
Приравнивая коафициеиты одинаковых степеней х и решая, найдем:
А = -1, В = 3, С = 2, 0 = 0.
Следовательно:
2xs4-x + 3 f — х + 3 J , 2xrfx , Г—x + 3.
(x’+ip dx~ J (x’+l)3 * +x^+ 1“ ln<x‘ + 1) +/ (Sa'+ip dx‘
Прилагаем теперь формулу (В) к последнему интегралу; имеем:
А = - 1, В = 3, р - 0, q = 1, п = 2.
Подстановка дает:
-хЦ-3^„_ 1+Зх 3 Л dx 14-ас , 3
(х34- 1)3 2(х24" 1)+ 2 J xs-hl 2(хЗ-|- 1) + 2 arctgЛ
Следовательно:
/* 2x3 4-х 4-3 1-|-Зх .3
J (.^Т)— = 1,1 {л + + 2(.t3+ 1) + -о arctgx4- С.
УПРАЖНЕНИЯ.
1 Г х’ + х — 1 2 —х । „Та 1 . х . _
' J (хэ + 2)» * ~ 4(л3 + 2) + А 4/2 ЯГ в /? +
1 f -------1|,,(Л' + ,> + т,”<‘+'!>+2-$тт) + й
/• х7 4- X5 4- дЗ 4- X 5 10 | 19. . л .
3‘ J (л2 + 2)» (хз 4- З)3 dx ~ Ч (хЗ + 2) + дЗ - 3 + 2 1П + 2)
- 9 In (хЗ 4- 3) 4- С.
л /• (4хг —8x)rfx Зхз —х (х-1)з
4’ J (х — 1)> (ха4- 1)3 - (х-1) (ха 4-1) +1п х--[-1 +arct8x + £-
. Г (a*4-2)rfx = iac-24_ arctg2-^3 + C.
J (хЗ-8х 4-3)’ 3(л«-3x4-3) 3/3 /Т
Так как нетрудно убедиться, что всякую рациональную функцию всегда можно привести :: частному двух целых рациональных функций, т. е. к рациональной дроби, то из предыдущих параграфов этой главы следует, что любую рациональную функцию, знаменатель которой мы умеем разложить на действительные множители первой и второй степе* ней, можно представить в виде алгебраической суммы целых рациональных функций и элементов — дробей. Члены этой суммы все имеют такой вид, интегрирование которого нами выполнено выше. Отсюда:
Teope.ua. Можно найти интеграл каждой рациональной функции, знаменатель которой разлагается на действительные множители первой и второй степеней; этот интеграл выражается через алгебраические, логарифмические и обратные тригонометрические (круговые) функции, т. е. в итоге через элементарные функции.
ГЛАВА V.
ИНТЕГРИРОВАНИЕ ПОСРЕДСТВОМ ПОДСТАНОВКИ НОВОГО ПЕРЕМЕННОГО. РАЦИОНАЛИЗАЦИЯ. БИНОМИАЛЬНЫЕ ДИ-ФЕРЕНЦИАЛЫ. ТРИГОНОМЕТРИЧЕСКИЕ ДИФЕРЕНЦИАЛЫ.
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ.
§ 30. Введение. В последней главе было показано, что все рациональные функции, знаменатели которых разлагаются на действительные множители первой и второй степеней, можно интегрировать. Из алгебраических функций не рациональных, т. е. содержащих радикалы, только сравнительно немногие можно прямо интегрировать, находя интегралы в виде элементарных функций. Однако посредством подстановки нового переменного иногда можно эти функции преобразовать в такие функции, которые либо находятся в списке основных формул (§ 18), либо рациональны. Способ интегрирования функции подстановкою вместо старого переменного такой функции нового переменного, чтобы результат оказался рациональною функцией, иногда называется интегрированием посредством рационализации. Это очень важный прием интегрирования, и мы рассмотрим некоторые из более важных случаев, входящих в эту группу.
§ 31. Дчференциалы, содержащие дробные степени одного х. Такое выражение можно преобразовать в рациональную форму посредством подстановки
x = z",
где п есть наименьший общий знаменатель дробных показателей х.
Ибо таким путем х, dx и каждый радикал (т. е. всякую дробную степень) можно выразить рационально в функции г.
Пример. Найти
г д /•л-3 —х4 / -dx-
Решение. Так как общее наименьшее кратное знаменателей дробных пок.'.за-телей равно 12, полагаем:
х =
Здесь
2 1 1
</x = 12z”rfa, х3=дв х4«=л», х’=Л
Следовательно:
2s — 2я
12с” rfz = 12 /* и13 - г") dz =
= А 2ц _ А г9 + с А л.«_ х 4 _ь с /О / о
1
[Подставив обратно значение г в функции х, именно z = х12 J. Общая форма рассмотренного здесь интеграла есть
(1 X х" j dx, i_
где R означает рациональную функцию от х"
§ 32. Диференциалы, содержащие дробные степени одного а-\-Ьх. Такое выражение можно преобразовать в рациональную форму посредством подстановки
аН- bx = zn, где п есть наименьший общий знаменатель дробных показателей выражения а-{- Ьх.
Ибо таким образом х, dx и каждый радикал (т. е. всякую дробн/ю степень) можно выразить рационально в функции z.
Пример. Найти
/(fX
А Г’ (14-х)2 + (14-х)2
Решение. Пусть
1 4-х = г2; тогда
s _t_
dx = 2z dz, (1 4- х)2 = zB и (14-х)2 — z.
Следовательно:
t
= 2 arctg z 4- С = 2 arctg (1 + х)2 4 С»
если подставить обратно значение z в функции х.
Следовательно, рассмотренный здесь общий интеграл имеет вид:
dx
где R означает рациональную функцию.
УПРАЖНЕНИЯ.
13.
dx г
Г=3
6 -1
з
и
3
2
£
3
dx
. --------г____ = 2 arctg 2 — .
J (24-х) /14-х 8 2
§ 33. Диференциалы, не содержащие иных радикалов, кроме
Такое выражение можно преобразовать в рационам-чую форму посредством подстановки:
В самом деле, возвысив в квадрат и решив относительно х, имеем:
г3 — а
следовательно:
dx —
и
Следовательно, выражения х, dx и У а-}-Ьх-\-л? как функции z рациональны.
Пример. Найти
dx
Решение. Положим
’) Если радикал имеет вид: Уп + рх qх*, где ?>0, то можно написать:
— — х-Ь следовательно, он подходит под вышенаписавный вид,
Я Я п . р где а = —, Ь = —. Я Я
Воввышая квадрат и решая относительно х, имеем;
2z + Г
отсюдг
_ 2(z2_+_z + l)rfz
’ (2z + Ip
я
Следовательно,
Х) - 2z + 1 •
dx
2(z= + z+ \}dz (2z+l?
^T = ln[(2z+l)cl-
2z+1
= In [(2х Ц- 2 /Г+ х + х2) с], после подстановки обратно значения г в функции х.
§ 34. Днференцигпы, не содержащие иных радикалов, кроме )/ а-\ Ьх — х21). Такое выражение можно преобразовать в рациональную форму посредством подстановки:
У а Ьх — х2 = У(х — а) (3 — х) = (х — a) z, где х—а и р — х суть действительные2) делители трехчлена a -j- Ьх—х2. ____________
В самом деле, если Уа-\-Ьх— х* * = У(х — а)(?- -х) = (х — a)z, то, возвысив в квадрат, сократив на (х — а) и решив относительно х. имеем:
.. «** + ?
Х~ г24-1 ’ откуда
. 2(<i — ^zdz (z®+l)a
и
Va + ^x-x2 [ = (х - a) z] = (?~3)^.
i) Если радикал будет иметь вид: Уп-\-рх — дх\ где ^>0, то его можно написать так-. У q 1/ — -I- — х — х-, и он, следовательно, подходит под за-r q q
п . р данное выражение, в котором а = —, 6 = i-,
*) Если делители трехчлена а + Ьх — хг мнимы, тогда раяикал Уа-f-bx — x3 есть мнимый для всех значений х, В самом деле, если один из множителей равен х — т -|- in, другой должен быть — (х — т — in), и, следовательно:
а + Ьх — х2 = — (х — т + in)(x — т — in) = — [(х — т)2 + л2],
что отрицательно для всех значений х. Поэтому мы рассмотрим только те случаи, когда множители действительны. _________
Следовательно, х, dx и Уа-\-Ьх— ха, рассматриваемые как функции переменного z, рациональны.
/dx
У 2 + х-х2
Решение. Так как 2 х — х2 = (х +1) (2 — х), полагаем
/(х+ 1)(2-х) = (х + 1) г.
Возвысив в квадрат и решив относительно х, найдем:
2-z2
Х- z2.Li •
Отсюда . — bzdz
dX- (Л2+ 1)2
И V 2 + X — Ха [ = (X + 1) zl =
Следовательно: dx
У 2 + х — х2
—2 У = - 2 arctg z + С = - 2 arctg |/ +
С.
подставив обратно значение z в функции х.
УПРАЖНЕНИЯ.
1.
dx 1 .
----д——In
= 2 arctg (х + V х2 + 2х - 1) + С.
J in
dx
= arctg
2
l/5. Г Vx»j-4x<iv =-8+ ln(x + 2+ rx2-r4x) + C.
J ** x + /x»+4x
6 Г xdx - 8+ 6x__c
I 1 25/2“+3x^2x2
J (2+Зх —2X1)1
v 7. f--——r= XJLg= + C
I 1 а* У2дх-хг
(Чах — Х^-
J Р£±^=|п(ж+^1 + ^гга2__^_+а
9. f ,+ -.-«^r+rg+m
J x Ух»+х + 1 x + l + /x« + x + l
,0. r_ £„ = _/’,,cte/'SH3+c.
УхУЗх-б-х» г 3 3(x-2)
Ясно, что общий интеграл, рассмотренный в двух последних параграфах, имеет вн_;
J' R (х, \га + Ьх г ex* 2 * * *) dx
где R означает рациональную функцию.
Соединив результаты этой главы с общею теоремою на стр. 100, можем установить следующую теорему:
Теорема. Можно интегрировать всякую рациональную функцию от х и квадратного корня полинома не выше второй степени и выразить результат через элементарные функции1)-
§ 35. Биномиальные диференциалы. Диференциал вида х"'(a-\-bxn)pdx,
где а и b какие угодно постоянные, а показатели т, п, р — числа рациональные, называется биномиальным диференциалом.
Пусть
X = z\ откуда dx = аг’-1 dz и
хт (а 4- bx”)p dx = ,гш’ + а-‘ (а 4-^'" У dz.
Если целое а выбрать так, чтобы та и па были также числами, целыми 2), то замечаем, что данный диференциал эквивалентен другому того же вида, где т и п заменены целыми числами. Так же
хт (а 4- />х’У dx = хп+пр (ах~п Л-bfdx есть преобразование данного диференцнала в другой того же вида, где показатель п при х заменен числом —п. Следовательно, каков бы ни был знак при п, в одном из обоих диференциалов показатель при х в скобках может быть принят положительным.
Когда р — число целое, бином можно раскрыть по формуле бинома Ньютона и диференциал интегрировать почленно. В нижеследующем .р , * г
принимается дробным числом; мы заменяем его дробью —, где ги$ — числа целые 8).
Из сказанного заключаем:
Всякий биномиальный диференциал можно привести к виду:
лм (а 4- bx”)1 dx, где т, п, г, s — числа цел ые и п — положительное число.
*) Однако, как и прежде, предполагается, что в каждом случае знаменатель рациональной функции мы умеем разложить на действительные множителя первой и второй степени.
2) Всегда можно выбрать а так, чтобы /па н ла были целыми, ибо можио„а
принять за наименьшее кратное знаменателей у т и л.
*) Случай целого р этим не исключается, во является частным случаем,
где г = р, s = 1.
§ 36. Условия интегрируемости биномиального диференциала.
х” dx.
(А)
Случай 1. Пусть
а 4~ bx* = z‘. Следовательно,
далее
откуда
Подставляя в (А), находи» «+1 , £. _ / а \ " хт (a-\-bxn)a dx = г’ +»-* — dz.
4 1 bn ~ \ b /
Вторая часть этого выражения будет рациональна, если т -f-1 п
будет целым числом или нулем.
Случай II. Положим
а -j- bx* = z’x”. Отсюда
а 4- bx* = z’x" = -г-.
1 z — о
Поэто_:у
(а 4- Ьх*)в =a7(zl — b)~ 7 zr;
далее
x^an(z* — b) п, хте=ап (? — Ь) ”
и^
dx = —-п г? 2е ~1 (2* — b)~ V dz.
Годставив в (А), получим:
xn{a-\-bxny = а п я (z'- Ь)У п 8 z dz.
Вторая часть этого выражения будет рациональна, если
м-Н . г
п S
есть целое число или нуль.
Итак, биномиальный диференциал
xn(a-\-6xn)edx
можно интегрировать посредством рационализации в сле-дующих случаях *):
_ . , „ тп4-1
Случаи 1. Если —±— равно целому числу или нулю; тогда интегрирование производится посредством подстановки:
аН bxn = z‘.
О * ГТ гч I 1 I Г
Случаи 11. Если —---(-—равно целому числу или
нулю; тогда интегрирование производится п осре дч-ством подстановки:
а bx” = z'x”.
УПРАЖНЕНИЯ.
1 2л + *д! - ах = -гт • - . ---
х3 dx
_®
(в + bx2) »
Решение, т = 3, л = 2, г = — 3, s — 1, так что 1 = 2, числу целому.
1.
л 3 (а -J-
Следовательно, пример относится к случаю 1; полагаем а + ftx2 = л3, откуда
1 я
fz2—a\s . zdz . . ..у2 .
х = j- J , dx =---------j------j и (а + bxi) = А
Ь 3(2г—в)®
Итак,
з
z dz “V i b г(^ — а)г
i) Предполагая, как и всюду прежде, что знаменатель получаюше1ся при этом рациональной функции можно разложить на действительные множители первой и второй степеней.
2 Г (2хЗ-1)(1+жЗ) 2 ,
' J x*V 1 +x’J Эл»
_ . п r 1 т +1 , г » „
Решение, т = — 4, п = 2, -- = —-и ----1- = — 2, числу целому.
Следовательно, пример относится ж случаю II; полагаем
1
1 + х3 = z = ^+х3)а,
X
откуда
(*а-1)а
далее, 1 . 1 . 2 dz
Г = —----. Л'4 =-= --И (ТХ = —------------—
.V- jj .< (Z3—1)3
(л»-1)3 (**-1)
Итак,
zdz з~ (л2-!)3 1 z
(zs-ip* J. (*-1)а
= - f Р-1)*-
3.
4.
5.
6.
7.
dx
ID
1-G
= (1 4-*3) a (x2 2) + c.
-In a
_______ex_______ /в» —хз 4-rt
— а(1 + x*)
2
3
X3(l 4-л«)’
«. f-----_Lta OL
•> в у дз+у1 a
j(^+>a)a
— i
9. J /»(! 4-20) *Л = (1 4-20)* 4-C.
10. [и (1 + и)2 du = (1 + и)2 (5а — 2) + С.
di ___ 1 а3 ,
£ ~ За £ + С'
(а + 6а2)1 (а + btfl) 8 2 118 5
12. f^(\+^Tdb = 3(1 + в2)’ —А(103)J + 3 (1+в2)3 +с. J -t о 1U
13. /----=------------^+2fl-£ + С.
х3 (а + х3) 8 2а2х (а + х3)8
§ 37. Преобразование тригонометрических днференциалов.
Из тригонометрии известно, что
х X
(A) sin х = 2 sin — cos ~,
л» &
X X
(Bl cos x = cos* --sin9 —.
Л» it
Ho tg-. x 1 1 * 2
sin — =-------=------f = r
cosec у у ctg»y-]-l у i+te’y
x 1 1
cos 2 — x -------------—•
secT I/ V ~
Положив tg —= z, или x = 2 arctg z, & имеем:
x z x 1
2 /14-z9 2 /1-1-Z*
Подставляя в (А) и (В), имеем: 2z 1 — z9
s'"* = -npy “SX = T+^-
Диференцируя x = 2 arctg z, имеем:
rfx =
2rfz l-H9’
Так как sinx, cosx и dx выражены здесь рационально в функции z, то:
Тригонометрический диференциал, в который входят sinx
112 ИНТЕГРИРОВАНИЕ ПОСРЕДСТВОМ ПОДСТАНОВКИ [ГЛ. V и cosх только рационально, можно преобразовать подстановкою:
, х
tgT = Z>
или, что то же, подстановкою:
. 2г 1 —z3 , 2dz
sinx“T+z“’ “SX = T+^’ dx = T+^
в другое днференциальное выражение, уже рациональное относительно г.
Очевидно, что, если тригонометрический диференциал содержит tgx, ctgx, secx, cosec х только рационально, то он подходит под вышеприведенную теорему, ибо эти четыре функции можно выразить рационально либо через slnx, либо через cosx, либо одновременно через slnx и cos х. Отсюда следует, что можно интегрировать любой рацио нальный тригонометрический диференциал.
УПРАЖНЕНИЯ.
У* (1 + sin х) dx 1 . х . . х , 1 . , л- , _
sin х (1 + cos х) “ 4 2 + g 2'2 1,1 tg 2 + С
Решение. Так как этот диференциал рационален относительно slnx и cosx, то, совершив указанную подстановку, тотчас имеем:
/fl
\ 1 + z'2/ 1 + л'- /' (1 + z- + 2г) dz _
2г (1 । 1 ~г' । “ J г(1+А24-1 —'#) — i + z2V^i4-2-;
= у J(г |- 24-z- l)dz - — \ ~- -|- 2z + In з ) + С =
= J-tg2y + ‘g4+ 2 ln(tB-2-) + C-
Г ---------JlizlYa
J 4 — 5 slnx 3 j
'3- -4««8(2ttf)+C.
*5- /s=^K-Ta"«<3t'x>+c
. ! d. 1 18T + 2
6- /^+таг; =т'"^++с-
v 7- /T+linx^ Цг + 2 "c,g(,gy) + C----Цг + Х+С-
J 14-sinx J + t X k 2/ l + t x
„ /’cosxdr „ . f Х\ , X . _ . X . „
8- J ГТ cos х = 2 irc,8 (‘8 2) -tg 2 + С = Х - tg 2 + С-
9. Вывести по способу втого параграфа формулы (XIV) и (XV) § 18.
§ 38. Формула интегрирования по частям. Если а и v суть функции одного независимого переменного, то из формулы диферснци-рования 5, § 123, ч. I:
d (uv) = и dv v du по перенесении имеем:
udv = d (uv) — v du.
Интегрируя, имеем обратную формулу:
Jи dv = uv — j*vdu, (А)
называемую формулою интегрирования по частям. Помощью этой формулы интегрирование произведения udv, которого мы не могли бы иногда выполнить непосредственно, приводится ,в зависимость от интегрирования vdu, которое иногда может быть выполнено без труда. Этот способ интегрирования по частям — один из наиболее употребительных в интегральном исчислении.
Чтобы эту формулу можно было приложить к какому-либо данному случаю, нужно, чтобы данный диференциал разлагался на два множителя: и и dv. Для выбора этих множителей нельзя дать никаких общих указаний, за исключением того, что
a) dx должно быть частью множителя dv и
Ь) чтобы можно было найти интегрированием V. Следующие примеры укажут нам детали приложения формулы.
Пример 1. Найти cos х dr.
Решение. Пусть и х и dv = cos х dx, откуда
du=dx и v = Jcosxdx = sin x.
Подставляя в (А), имеем: и dv и v v du
J x coax dx = x sinx — j" sinx dx = xsinx + cosx-4-C.
Пример 2. Найти
f x In x dx.
Решение. Пусть
и = In x я dv = x dx, откуда
. dx f jfl
du = — и v= / x dx = -д-.
x J 2
Подставляя в (А), имеем:
/* . . . x3 Г x3 dx x® . x3 - _
/ xlnxdx = lnx —— I Inx — — 4-C
Пример 3. Найти
/xenr dx.
8 3»к. 2853. — Граважоь Луаая, ч II, Иктегрюъноо жочжодвж»
Решение. Пусть и = е“* и dv = х dx, откуда /г* л dx = — .
Подставляя в (А), имеем:
f xe^dx^e^^- f ~ eaaadx = ^^-£ Г^e^dx.
J 2 J 2 2 2 J
Ho j^cnx dx интегрируется уже гораздо сложнее, чем хеа* dx, а это показывает, что мы выбрали наши множители не надлежащим образом. Положим вместо этого
и = х К dv = dx, •тжуда
e°*dr =---.
а
Подставляя в (А), находим:
Может случиться, что формулу интегрирования по частям придется применять несколько раз, как в нижеследующем примере.
Пример 4. Найти
Решение. Пусть
и = х2 и dv = е09 dx, откуда
du = 2xdx и У= /* dx - -—.
J а
Подставляя в (А), имеем:
x*eaxdx = з?-----(^—2xdx - / xe^dx. (В)
a J a a a J
Интеграл в последнем члене был уже найден в предыдущем примере:
/»а® xeaa’rfx= — а
Подставляя этот результат в (В), имеем:
К числу наиболее важных приложений способа интегрирования по частям относится интегрирование:
а) диференциалов, содержащих произведения,
Ь) диференциалов, содержащих логарифмы,
с) диференциалов, содержащих круговые функции, (т. е. обратные тригонометрическим).
§ 38] УПРАЖНЕНИЯ 115 УПРАЖНЕНИЯ.
1- J х3 Inxdx = (in х — у ) С.
2. J a sin а da = — а COS a 4" Sin а С.
3. / arcsln xdx = х arcsln х -j- И — хг + С.
Указание. Полагаем: и = arcsln х и dv = dx и т. д.
4. J Inxdx = x(lnх — 1) + С.
5. J arctgxdx = arctgx — In (1 4* x-) 2 -j- C. /• _ Xn + » f j x
6. / x" In xdx = ——r (In x —- ) + C. J n +1 \ я_|_ i ; r
7. /' jfi 4-1 X 1 x arctg xdx = —— arctg x — v + C.
8. f arcctgy dy = y arcctgy + у In (1 -j-y3) + C.
9. [to. u.]+c
10. /•«л.ЛЛ » + !] + c. J |_lna In3 a In8 a]
И. j*cos fl In sin 0 d!) = sin 0 (In sin в — 1) + C.
12. J' xVr dx = ex (x2 — 2x + 2) 4- C.
13. />e“dx = -^(x8-^+^-AW. . J a \ a ' a3 дЗ ) r /
*’'14. Г x sin x cos xdx = sin 2x — 4- x cos 2x + C. */ о 4
✓15. J x3e~x dx = e-®(2 - 2x - x8) + C.
»П6. J' arctg Yxdx = xarctg Y* — Vx + arctg Yx 4- C.
✓ 17. 1 x3 In x dx = (in x — 4- C.
✓18. f sin1? d<? = 2 cos ? 4- 2? sin <? — y1 cos ? ]- C.
19. y’fn xP dx = x [ln3x - 2 lnx4- 2] 4- C.
20. J*a tg3 a da = a tg a — — 4- In COS а 4- C.
21. /• Inxdx x , . . । „ J (x4- ip x4-l nx ln(x + 1) + ^-
Указание. Полагаем
, . dx и = In x a do = .——Гт;- и t. * > (•» HP
v22. / .V» arcslnxdx = ~ arcsln х -J- ~ — х? С.
./ J 9
23. J' sec2 6 In tg 6 rf8 = tg 6(ln tg в — 1) -J- C.
24. j* In (In x) = In x • In (In x) — In x -|- C.
25. Г+-1)— = 2 /х+Т[1п(х + 1)-2] + C.
J Ух+1
Г - 1 - 2 -
26. / x2(a-x»)2 dx = - ~x»(a - x2)2 (a-x2) 2 + C. J О 10
1
Указание. Полагаем и = х2 и dv = (л — х2) 2 х dx т. д.
27. ---------------^[jnSx + linx + lj + C.
х 2 Зх2 \
28. У* Уд2—х2 dx =у /аг _ Л2* ц-arcsin+ С.
= - у (х2 + 2) (1 - х2)2 + С. У 1 — х2 d
v30. у* У«2 + х2 dx = -J У а2 4-х2 + -£in (х 4- y'rf+TS’) + С.
^/31. ( х'ах-— ?r+^arCslnA + c.
J /д2 —2 2 а
§ 39. Интегралы вида J* еах sin nxdx и у* еах cos nxdx.
Интегрируя по частям е“ sin nxdx, полагаем
и = еах и dv = sinnxdx,
откуда
du = aeaa>dx и v =
cosnx n
Подставляя в формулу (A), § 38, именно:
vdn,
найдем:
;a® , j eMcosnx . а Г nx . ...
e sin nxdx =--------------1- —- I e cos nx dx. (A)
Интегрируя e°* sin nxdx опять по частям, полагаем теперь
u = slnnx и dv = ea“dxt
откуда
e°* du = n cosnxdx и v = — .
a
Подставляя в (А), § 38, находим:
/лг • с sin fix fl (* ах j
e sxnnxdx —---------------— I e cosnxdx. (B)
Исключая [ e"T cosnxdx из (А) и (В), имее»
(а‘2 п‘~) J епх sin пх dx = (a sin пх — п cos пх), или
/ОХ . . с01 (a sin пх — п cos пх) . _
е sin пх dx =--------т-—т----------- -4- С.
а2 л 2
Подобно этому найдем:
/ог . (п sin пх-г-a cosnx) . _
е cos пх dx =----------, -----4- С.
а2 4- па 1
Читателю, который будет проделывать нижеследующие упражнения, рекомендуем не пользоваться данными выше результатами как готовыми формулами, а следовать методу, какими они были найдены, чтобы приобрести уверенность в интегрировании.
УПРАЖНЕНИЯ.
. /* е1
v< 1. / esinxrfx = -%- (sin х — cos х) 4 С.
Г
2. / e®cosxrfx = (sin х + cos л) + С.
^З. f е2* cos 3 х dx = (3 sin ЗХ + 2 cos Зх) + С.
J 10
fslnxdx _ sinx-f-cosx „
J ё* 2ех
/‘cosZrdx 1 , п _ _ . । „
--з = — (2 sin 2х — 3 cos 2х) 4- С. в8®---------1с?®
И 6. y>sln>xdX-g(l- +
7. f ё со*.* = + 5?s-?°) + С.
V 8. / е а cos у dx = в я (sin у + cos у j + С.
9. J* еа* (sin аа + cos <и) da = е-—^1^1. _|-/Здр
eu (sin 2х — cos 2л) dx = (sin 2л — 5 cos 2л) + С.
1 о
§ 40. Разные подстановки. Рассмотренные до сих пор подстановки приводили данное диференциальное выражение к рациональному виду. Однако в большом числе случаев можно выполнять интеграции посредством подстановок, не приводящих данного диференциала к ра
циональному виду, но здесь нельзя дать никакого общего правила, а можно руководствоваться только опытностью, приобретенною упраж* нениями.
Вот одна из весьма употребительных подстановок:
1 Лг
х =—, ах =---а ,
Z Z2
называемая подстановкою обратного количества.
Приведем пример на эту подстановку.
Пример. Найти
Решение. Сделав подстановку
dx = —
dz гг '
вайдем:
1 — — I)1.*- (“'8e,,>+C- + C УПРАЖНЕНИЯ.
’ Г dx = 1 In х8 4- С J л^Н-л») 3«3 дз + лз Т
, /• xSrfx 18x» + 27x+ll , . . .
1 /(-7^йй= —6(x+l)» +l°(x + D + C-
4. /* ~J = ------rX + C.
J - в® V a* + x®
(в* + х«)2
, Г dx 1 ex
5. /---,. = — In-----,
J xyat^n? а xn-•
Полагаем x! = z.
Полагаем x — 2 = z.
Полагаем x 1 = z.
Полагаем x = у.
„ a
Полагаем x = у
6. f—= |(x’-3)(x^+ip +a (x2+l)8
Полагаем jfl + 1 = z.
/*---Г Лх - — in-----------f ------r. Полагаем x = .
J x Vl+x + x* 2 + x + 21<l+x+x® *
8. / У1^~1ПХdx = |(1 Ц-InxP + C. Полагаем 1 + In x= z.
9. f—^v = (3fX ~ + a Полагаем e1 + 1 ~ z'
(^4-1)4 .
10. f — — + — ln(«x_ 21+C J e^-2^ 2^ 4+4 Полагаем = z.
11 /* x?dx 1 x V1 — x® Полагаем x « cos z.
J У1—x» 2 arc,lnx 2 1 C'
12, Г у a®—x® dx = у arcsin y+ у V «s — ** +C. Полагаем x = a sin z.
ГЛАВА VL
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
[К сведению читателей. Читатель, начавший изучение интегрального исчисления с гл. I, может перейти к чтению § 4, рубрики II, VIII, X и далее до конца главы.]
§ 41. Способ суммирования бесконечно малых. Читатель уже знает, что у всякой непрерывной функции fix) имеется первообразная Fix), т. е. такая непрерывная функция Fix), что
Г(х)=/(л).
И далее читатель знает, что первообразных для данной /(х) имеется не одна только, но бесчисленное множество, и что все они разнятся друг от друга лишь п р и б а в о ч н ы м постоянным слагаемым. Наконец, читатель научился отыскивать конечными выкладками во многих случаях первообразную для заданной fix}, причем для этой цели он пользовался знаком неопределенного интеграла
f f(x)dx,
обозначающим просто произвольную первообразную для заданной fix), и где произвольное постоянное С считается включенным в знак неопределенного интеграла.
Разыскание первообразных является чрезвычайно важным. Читатель вскоре увидит, что первообразные функции позволяют решать до конца многочисленные и труднейшие задачи геометрии, механики и физики. В этом смысле знание всякой первообразной является весьма ценным.
Эта важность отыскивания первообразных происходит от того, что они являются самым могуществен ным средством суммирова- 0 ния бесконечно малых. '--j I,'I, j, ‘‘д.-,& *
Зададимся непрерывной на от- „ 24
резке [а, Ь] функцией fix), и Р • •
пусть F(x) есть какая-нибудь ее первообразная (причем совершенно неважно, какая именно).
Разобьем данный отрезок [а, А] на п частей, равных или неравных, и составим разность
Fib)-Fia)
значений первообразной F(x) в концах заданного- отрезка [а, 6].
Ясно, что эта разность в точности равна сумме таких же разностей, составленных для тех отрезков,
на которые мы разбили весь данный отрезок [а, £],
F(b)-F(a) = [F(x1)-F(a)]-J-[F(xa)-F(xI)]+... ...-I- [F(x<) — F(x,_j)] + - • • + [F^-Ffx^,)].
потому что, раскрыв квадратные скобки и делая сокращения членов с противоположными знаками, мы и получим снова нашу разность F(*)-F(a).
Но теорема Лагранжа о .конечном приращении* нам дает равенство:
F(x4) - Flx.-J = (xf— х(_,)F' (Е<_ ,), (16)
где число (черт. 24) есть промежуточное иежлу х(1 и х., т. е. 6<_1 есть просто некоторая точка, находящаяся на отрезочке [x^j.xJ.
Так как разность х, — x,-i есть, очевидно, длина отрезочка [х,_х(], то ее естественно обозначить просто через Axf_t, положив
xi — Xi-l
Вспомнив же, что F(х) есть первообразная длн /(х), мы имеем тожде* ство F'(x)-—/(х) для всякого х и, следовательно, в частности имеем:
/?'(Н<_1)=/(^_1)-
Поэтому разность F(d) — (F(a) теперь можно написать в виде:
F(^)-F(a) =/(В0)Дх0-Ь/(Е1)ДхгЬ.. .+/(Е(_,)Ч-i + • •
••• О
Написанное равенство (1) есть равенство совершенно точное при любом** разбиении отрезка [а, Д) на малые отрезочки [а, х,], [ХрХ,],..., [хп-1 Д]; но оно справедливо лишь при том совершенно специальном выборе в этих малых отрезочках соответственных точек Ео, Ер..., Еп_р который предписывается упомянутой теоремой Лагранжа.
Представим себе теперь, что с течением времени все отре-зочки [a, xj, [хр х.,],..., [х„_р Ь] начинают безгранично умаляться, так что даже наибольший из них имеет длину, стремящуюся к нулю. Тогда предыдущая сумма является суммою возрастающего числа бесконечно умаляющихся слагаемых.
Так как равенство (1) верно всегда, т. е. до перехода к пределу, то оно вёрно и в пределе, потому что .две величины, всегда равные друг другу, имеют равными и их пределы*, и, значит:
lim (/Go) Дх0 Н-/(У Ах, + ... +/(«<_i) Ч-1 + • • •
•. • 4-№_1)Ч.-1] = F(b)-FW- (2)
Полученное равенство (2) замечательно тем, что оно справедливо не только при каком-то частном выборе точек Е^ Вр..., Е х по одной на отрезочках [a, xj, [х,, xt],[хп_р Ь] как эго предписывается
теоремой Лагранжа, но при всяком решительно выборе точек Ео, .., En_j по одной на отрезочках [a, xj, (хр xj,..., [х^, Ь] »). Ввилу этого формула (2) является замечательнейшим средством суммирования бесконечно малых, открытым Лейбницем и Ньютоном и словесно выражающимся так:
для отыскания предела суммы бесконечно малых
/(Ео) Дх0 4-/(Е,) Дх,+... +Д'<_ J Ч-,4-... +/(Е„_,) Дх„ _ „ когда все отрезочки, на которые разбит отрезок [а, Ь\, безгранично умаляются, нужно выполнить лишь следующие два шага:
Первый шаг. Постараться отыскать конечным образом какую-нибудь первообразную F(x) для /(х).
Второй шаг. Найдя первообразную F(x), составить разность F(b) — F(a) ее значений в концах основного отрезка [л, Ь]. Эта разность и есть искомый предел.
§ 42. Определенный интеграл. Сумма
/(U4-t7G1)4+- • Ч-.+- • -+/(^_x)4-i (2)
называется интегральной суммой. Так как предел ее совершенно не зависит от выбора точек Ео, Ер..., Еп_х, по одной в отрезочках [a, xj, [хр xj,..., [хп_р £], то обычно их берут все в левых концах этих отрезочков. Вследствие такого выбора точек Е<—1 интегральная сумма (4) принимает вид:
f (Хо) Ч +/(*1) Ч + • • • +/Ч _ х) Ч- х + • • +/(*„ _ х) Ч _ р (2*)
где ради стройности обозначения мы полагаем х0 = а и та^же хп = Ь, Интегральная сумма (2*) сокращенно пишется в виде:
ь
S/W4 (3)
а где буква х при составлении суммы последовательно пробегает все точки деления х0, хр х,,..., х<,..., хп_1 — начиная с начальной точки х0-=аи кончая точкой хп_р соседней с концевой хп = д (и только точки деления, а не все вообще точки отрезка [а, д]).
Вследствие такого обозначения интегральной суммы (2*) и предел ее обозначают также похожим знаком и пишут:
f /(*) (4)
u
и называют этот предел определенным интегралом.
Здесь в высшей степени важно читателю помнить, что сумма (3) есть настоящая сумма с настоящими слагаемыми /(х)Дх, являю-
Об этом читатель может справиться в § 7 главы L
щимися просто парными произведениями f(x{i) • Дх1_1 для I, пробегающего числа 1, 2, 3,..., п.
Что же касается определенного интеграла (4), то сам он не является суммой и не содержит никаких слагаемых, потому что определенный интеграл (4) есть только предел интегральной суммы (3), а не самая сумма. Поэтому, правильно говоря, следовало бы вместо знака (4) определенного интеграла, собственно, писать:
ь lira S f{x) Ьх.
в
Однако, исключительно ради облегчения нашей памяти, иногда говорят об определенном интеграле (6) как о некоторой фиктивной сумме, ,общим членом* которой является в ы р аж е н ие /(х) dx 1).
Введя понятие об определенном интеграле как о пределе интегральной суммы и введя его знак (4), мы можем теперь переписать равенство (2) в виде:
ъ
f f(x)dx = F(b)-F(a). (I)
u
Это и есть знаменитая формула Лейбница-Ньютона, связывающая в одно оба исчисления: диференциальное и интегральное и лежащая в основании всего современного математического анализа.
Так как F(x) есть любая первообразная для /(х), то, вспоминая, что неопределенный интеграл I f (х) dx как раз и есть произвольная первообразная для /(х), мы можем формулу (I) Лейбница-Ньютона переписать в виде:
ь ъ
J /W dx = [У* / (х) dx\ . (1*)
а а
Здесь в левой части стоит определенный интеграл, т. е. предел интегральной суммы (3); направо же. в квадратной скобке, стоит неопределенный интеграл, т. е. произвольная первообразная для /(х). Значки же а и Ь, поставленные внизу и вверх}' квадратной скобки, показывают, что, отыскав конечным образом неопределенный интеграл, надо в него сначала вместо буквы х подставить число Ь, потом подставить в него же вместо буквы х число а и, наконец, вычесть из первого численного результата второй.
Тогда произвольная постоянная С, входящая в знак неопределенного интеграла, выпадет сама собою.
Значки же а и Ь, поставленные внизу и вверху определенного интеграла, называются пределами интегрирования 2); причем а
1) Более подробно об этом скаэаво в § 6 главы I.
х) Название неправильное и несколько опасное, потому что слово .предел" уже употреблялось раньше в совершенно другом смысле, когда говорилось
есть нижний предел и b есть верхний предел. Здесь значки эти просто указывают то обстоятельство, что в интегральной сумме (3) буква X пробегала деления отрезка [а, Ь] от точки а и до точки Ь.
Заметим, наконец, что буква х, стоящая направо в квадратной скобке под знаком неопределенного интеграла, ecjb настоящее независимое переменное. Но буква х, стоящая налево под знаком определенного интеграла, есть только кажущееся переменное, потому что она в свое время была нужна только для пробегания по всем слагаемым /(х)Дх интегральной суммы (3), так что численная величина этой интегральной суммы (3), а стало быть, и ее пределы — определенного интеграла (4) — нисколько не зависят от этой буквы х. Поэтому в этом случае буква х называется переменным интеграции, и это переменное интеграции так же хорошо может быть обрзна-чено и всякой иной буквой, например буквою t, так что мы всегда имеем: ь ь
J'f(x) dx = f a a
§ 43. Свойства определенного интеграла. Важнейшие свойства определенного интеграла такие:
I. Определенный интеграл есть мерэ площади. В самом деле, интегральная сумма
/(•*<,) Дхо + Ж) Дх1 4- • • • +/(*< _ 1) -Ч _, + • • • +/(х„ _,) Дх„_ J2*) состоит из суммы парных произведений вида:
Дх(_г
Это же парное произведение изображает площадь прямоугольничка (черного), основанием которого служит разность xt — х<_, = Дх4_,, а высотой ордина1а /(x,_j) кривой в точке х(_г Поэтому вся интегральная сумма (1) есть сумма площадей таких прямоугольников, или, иначе говоря, есть площадь ступенчатой фигуры, вписанной в криволинейную трапецию АаЬВ, ограниченную сверху кривой у =f(x) (черт. 25). Вследствие этого площадь криволинейной трапеции АаЬВ несколько больше интегральной суммы (2*).
Но если бы вместо интегральной суммы (2*) взяли более общую интегральную сумму:
/(и^0+/(удх14-...+Ле<_1)^_1+’--+/(ч-1)д*м-1 (б) и выбрали точки Ео, Е,,..., Е„_ , в правых концах отрезочков [а,xj [хр xj,..., [хп_м д], то получили бы, очевидно, зубчатую фигуру,
о пределе «переменной величины*. Было бы лучше в дивом случае называть он b .границами интегрированна*.
уже описанную около криволинейной трапеции АаЬВ. Поэтому площадь криволинейной трапеции АаЬВ была бы несколько меньше интегральной суммы (5) при таком выборе точек £0,
А так как предел интегральной суммы (5), когда все отрезочки [a, xj, [х1( ха],... , [х„_ р £], стремятся к нулю, при всяком выборе точек Ео, есть всегда один и тот же, равный определен-
ному интегралу
t>
J'f(x)dx, (4)
а
то отсюда заключаем, что этот определенный интеграл (4) как раз в точности и равен площади криволинейной трапеции АаЬВ.
При этом выводе мы предполагали данную функцию /(л) непрерывной на отрезке [а, д], т. е. не допускающей на нем никаких разрывов (и, следовательно, уходов в бесконечность), а самый этот отрезок [а, д] конечным.
П. Средняя величина функции. Если имеется какая-нибудь переменная величина у, принимающая численные значения yit то „средними значением переменной у* называется в этих условиях, как известно, среднее арифметическое чисел ylt y2t..уп, т. е. выражение:
У1 +je + - • .
п
Подобно этому, „средней величиной непрерывной функции" /(л) на отрезке [а, 6] называется выражение:
ь
f f(x)dx а________
Ь — а
Докажем, что это выражение в самом деле равно величине данной функции /(л) в некоторой внутренней точке с, т. е. равно/(с).
Действительно, в силу формулы (Г) Лейбница-Ньютона мы имеем*.
ь
f f{x)dx = F{b-)-F(a), (I)
а
где F(x) есть первообразная для /(л). В силу же теоремы Лагранжа о конечном приращении мы имеем:
F(*) -F(a) = (b - a) F' (с) = (Ь - а)/(с),
где с есть число промежуточное между числами а и Ь, т. е. точка, лежащая внутри отрезка [а, Ь].
Поэтому, опираясь на формулу (I) Лейбница-Ньютона, мы получаем,
во-первых, теорему о среднем значении для определенного интеграла, выражаемую равенством:
ь
f f(x)dx=f(c)(b-a), (6)
а
и, во-вторых, доказательство того, что предыдущее выражение .сред-ней величины непрерывной функции** в самом деле равно f(c), т. е. действительной величине функции / (х) в некоторой внутреннеГ точке с.
»
/ f(x)dx (4—а)/(г)
4^- = —^—/И-
Геометрически теорема о среднем (6) доказывается чрезвычайно просто. Депствигельно,площадь АаЬВ криволинейной трапеции больше площади вписанного четырехугольника AabQ и меньше площади описанного четырехугольника РаЬВ (черт. 26). Значит, она в точности равна площади некоторого промежуточно го четырехугольника RabT, основанием которого служит тот же самый отрезок [а, Ь} и высота которого равна отрезку сС, служащему ординатой / (с) кривой у= f(x) в некоторой внутренней точке С отрезка [а, А].
Иными словами, криволинейная площадь АаЬВ равна (Ь — a)f(c), что и доказывает нашу „теорему о среднем значении", ъ
j f (х) dx = f (с) (b — а), и
П1. Деление отрезка интегрирования. Пусть на отрезке [а, Ь] лежит какая-нибудь промежуточная точка с так, что отрезок (а, разделен на два отрезка: [а, с] и [с, Ь]. В этих условиях мы имеем такое предложение:
Ь е Ь
f /(х) dx = f /(х) dx + У'/(х) dx. (7)
о а с
Чтобы доказать его, возьмем какую-нибудь первообразную для /(х). Тогда по формуле (I) Лейбница-Ньютона мы имеем:
е
f f(x)dx = F(c) — F(a), а
b
J‘f(x)dx = F(b)-F(c).
Складывая почленно и сокращая F(c) и — F (с), мы получим:
У/(х) dx 4-у*У(х) dx = F(b) -F(a\=-- J f(x) dx, at a
Черт. 27.
знак, если a<b и если всем отрезке [а, А].
что и доказывает формулу (7).
Геометрически формула (7) доказывается чрезвычайно просто, потому что она выражает только тот факт, что криволинейная площадь АаЬВ равна сумме двух криволинейных площадей АасС и СсЬВ (черт. 27).
IV. Знак определенного интеграла. Определенный интеграл ъ
Jf(x)dx имеет положительный а функция у (х) положительна на
Это свойство становится сразу ясным, если мы вспомним,
что опре-
деленный интеграл есть предел интегральной суммы: ь
У*у (х) dx = Um [У(х0) Дх0 +У(*1) Д*1 + • • • +/(*„ _ J д r„_ J.
° \
Действительно, в этом случае .общий член* f(x{_i)^x{_i интегральной
суммы имеет положительное значение, потому что оба множителя У(х<_1)
и &х, .. очевидно, положительны.
h
Напротив, определенный интеграл J f(x)dx от п о л о ж и т е л ь-а
ной функции у(х) имеет отрицательный знак, если а > £.
Действительно, в этом случае хотя У(х<_1) и положительно, но зато множитель Ьх<_1 теперь уже отрицательный, потому что
Дх( = х( —xtl и a>Xj>x9> ... >х,_1>х1^ ... > Ь.
Геометрически это означает, что площади кривой приписываются разные знаки по разные стороны нижнего предела интегрированиям.
Действительно, площадь АсЬВ (черт. 28) ъ положительна, потому что равна у f(x)dx и <1
потому а<,Ь при положительной функции У(х). Наоборот, площадь АаЬ'В' уже от-!>
Черт. 28. рицательна, потому что равна / и по-
а
тому что а > Ь'.
Примем теперь а < Ь и предположим функцию /(х) отрицательной, ъ
Определенный интеграл j* / (х) dx имеет отрицательный знак, если а < Ь а
и если функция f (х) отрицательна на всем отрезке [а, 6].
Это свойство сразу вытекает из рассмотрения интегральной суммы, потому что в „общем члене" /(х<_1)Дх1_1 первый множитель /(х<_1) отрицательный, а второй множитель Дх<_1, очевидно, положительный, так как а < Ь.
Геометрически это означает, что площади кривых расположенных над осью абсцисс, считаются положительными, а площади кривых, рас-
положенных под осью абсцисс, — отри- Черт. 29.
Нательными (черт. 29).
Примечание. Читатель, желающий вычислить сумму площадей двух соседних волн синусоиды у = sinх и прибегнувший с этой целью к интегральному исчислению, не у должен быть изумленным, когда в ответе д
получит нуль. Это просто означает, что площадь одной волны (находящейся выше осн ОХ) положительна и площадь другой волны (находящейся ниже оси ОХ) отрицатель-н а (черт. 30).
Действительно, сумма искомых площадей
равна Черт. 30.
f sin xdx = [ — cos хГ = — cos 2л + cos 0 = — 1 4- 1 = 0
□ о
V. Перестановка пределов интегрирования. Переставить пределы интегрирования это значит переменить знак интеграла на обратный.
Действительно, приняв, что а < b и что а < хх < х, <... . ..<х , < Ь, мы имеем:
/ /(•*) dx = lira \f (x0)(xt — x0) 4-/(xx) (x3 — х,) -I- ...
• • • +/(х<+1) (X, —x4_,) 4-... +/(xn_J)(x„-Xn_1)].
Если же мы переставим пределы интегрирования а и д,то нам придется рассматривать уже нс положительный отрезок [а, А], а отрицательный отрезок [6, а]. Беря те же самые точки деления, мы имеем теперь:
> хп — 1 >Хп-з > • • х1'^> а,
и, значит, „общим членом" интегральной суммы теперь будет не (х< —х<_1),апроизведение/(х<_1) (x(_t—х^потом^ что теперь мы рассматриваем уже не положительный отрезочек [х4_р х(], а отрица
тельный отрезочек х<_1] с начальною точкою и с конечною точкою х(1' Таким образом мы имеем:
ь
f /(*) dx = Hm [/(хя _ t) (xn _, — xn) 4- ... a
• • • 4-7(*< _ № _ t—*<)+•• • -r/(^o) (X0 — *ll-
Так как новая интегральная сумма имеет те же самые члены, что и прежняя, только они идут в другом порядке с обратным знаком, то ясно, что а b
f f{x)dx = — f f{x)dx. b a
Это предложение можно доказать еще проще, сославшись на формулу Лейбница-Ньютона:
ь f f{x)dx = F(b) — F (а}, а
где F(x) есть какая-нибудь первообразная для /(х).
Мы знаем, что формула эта справедлива для любых а я Ь. В частности, она будет справедлива, если число а заменить числом Ь, и число b заменить числом а. Поэтому
Я
j' f(x)dx = F(a)-F(b).
Отсюда сразу видно, что
/*/(х) dx = — У f{x>dx.
Как следствие подучаем: интеграл между равными пределами всегда равен нулю, т. е. а
J f(x)dx = 0. а
Действительно, полагая в формуле Лейбница-Ньютона Ь = а, мы сразу получаем: а
f/ (x')dx = F(a) — F(a) = O.
VI. Определенный интеграл от суммы функций. Предположим, что данная нам непрерывная функция /(х), определенный
§ 431 ь интеграл j* f(x) dx которой мы ищем, разбивается на алгебраическую а сумму нескольких функций, например трех:
f (*) = « (х) -h v (х) — w (х).
В этом случае искомый определенный интеграл от функции / (х) сам, в свою очередь, разбивается на алгебраическую сумму трех определенных интегралов: л ь в л
j f(x)dx = у u(x)dx-j- j v(x)dx~ / w(x)dx. a a a a
Чтобы доказать это, достаточно заметить, что интегральная сумма ь
3/(х)Дх разбивается на алгебраическую сумму трех интегральных a сумм: ь ь ь в
s f(x) Дх = S и(х) Ах 4- S у (х) Ах — S w (х) Ах, а а а а
потому что .общий член* /(х4_х) А (х4_х) разбивается, очевидно, на сумму трех „общих членов14:
/ (х4 _Дх4 _ х = u (х4 _ J Дх4 _, 4~ ? (х4 _,) Дх4 _ х — w (х4 _ х) Дх4 _ х.
Поэтому, совершая переход к пределу, мы можем писать: ь ъ Ь h
lim 3 /(х) Ах = lim 3 и (х) Дх 4- lim 3 V (х) \х — lim 3 ® (х) Дх, a a a ; a
Т. е. 6 ft ft b
J f(x}dx = J a(x)t/x4- j v(x)dx— J w(x)dx. a a a a
VII. Вынос ПОСТОЯННОГО МНОЖИТЕЛЯ ЗА ЗНАК ОПРЕДЕЛЕННОГО интеграла. Пусть нам нужно найти определенный инте-ь
грал K-f(x)dx, где К есть постоянный множитель. Согласно самому a смыслу определенного интеграла мы имеем: ь ъ
I К •/(*) dx — lim S К • /(х) Дх. а а
Но в интегральной сумме мы имеем право ваять за знак суммы общий к
9 Зак. 2853. — Гранапла н Лг«пв, ч. II, Интаграаьжоа ксчкслапа
множитель всех слагаемых, т. е. написать: t> ь
SK-/(x)bx = K-Sf(X)bX. а о
Поэтому, совершая переход к пределу, мы имеем: ь ь
Иш S К • /(х) Ах = К • Пт S/(х) Ах, а а
и, следовательно: ь 6
f K-f(x)dx = K- [ f(x)dx, а а
что и показывает, что постоянный множитель можно выносить за знак определенного интеграла.
VIII. Интегрирование по частям при опредвлвнном интегрировании. Вспомним из диференциального исчисления, что (uv)' = u'v -f- Uv'.
Отсюда, в силу правила (VI) определенного интегрирования суммы, мы имеем: ь ь ь
У (uv)' dx = j" и' v dx-\- f v' и dx. a a a
Но в силу основной формулы Лейбница-Ньютона мы имеем: ь
f f(x) dx —F(b) —F (а), а
где F(x) есть какая-нибудь первообразная для /(х). И так как первообразной для (uv)', очевидно, является uv, то
> г 7
/ (uv)' dx = [uvl , '
и, следовательно, формула определенного интегрирования по частям напишется так:
/ uv' dx = [itd] — / u'v dx.
J a J
a a
Лучше всего эту формулу писать в виде: ь й ”
I и dv = [uv]— / vdu.
IX. Определенный интеграл как функция верхнего предела. Возьмем какую-нибудь непрерывную функцию / (х), заданную
на основном отрезке [Л, В], и рассмотрим на этом основном отрезке произвольный отрезок [я, д]. Пусть
ь //(x)rfx а
определенный интеграл, взятый от заданной функции /(х) по отрезку [а, Л]. Ясно, что если этот отрезок [а, 3] будет изменяться, по длине или по положению, перемещаясь все время внутри основного отрезка [Л, В], то и численная величина определенного интеграла ъ
J f (х) dx а
будет также изменяться. Напротив, если отрезок интегрирования [а, Ь] остается неизменным, т. е. если пределы а и 6 интегрирования постоянны, то и численная величина рассматриваемого определенного интеграла останется также неизменной.
Отсюда й следует, что численная величина определенного ь
интеграла j*f(x)dx есть функция его пределов а и Ь. а
Спрашивается теперь; какая же это будет пункция? Так как определенный интеграл сохраняет свою абсолютную величину и только меняет свой знак на обратный при перестановке пределов а и Ь, то можно ограничиться рассмотрением зависимости определенного интеграла лишь от своего верхнего предела Ь, считая нижний предел а неизменным.
Применим для этого формулу Лейбница-Ньютона;
ь
f f (х) dx = F (ф) — F (а), а
Из этой формулы непосредственно выявляются следующие основные свойства определенного интеграла, рассматриваемого как функция своего верхнего предела Ь:
1. Определенный интеграл есть непрерывная функция своего верхнего предела.
Действительно, изменяя в формуле Лейбница-Ньютона
ь
J‘f (х) dx = F (b) — F (а) а
непрерывным образом верхний предел Ь и оставляя а неизменным, мы получаем непрерывное изменение численной величины определенного интеграла, потому что первообразная функция F(x) есть непрерывная функция своего аргумента х.
2. Определенный интеграл есть дифференцируемая функция своего верхнего предела, и производная его по верхнему
пределу численно равна подинтегральной функции, вычисленной для верхнего предела.
Действительно, делая в формуле Лейбница-Ньютона верхний предел b переменным, а нижний предел а постоянным, мы можем написать:
ъ
рр(^=Л-1Г(6)-Г(ап.
Но так как число а есть постоянное, то постоянной величиной будет и F (а). Поэтому & = 0. А, с другой стороны, так как F(x) есть
аЬ
первообразная для /(х), то имеем для всякого численного значения аргумента х равенство:
Поэтому в частности для х = b имеем:
Сопоставляя все сказанное, мы получаем: ь fWdx=f(b).
а X. Замена переменного в определенном интеграле. Эта замена требует от читателя чрезвычайного внимания, потому что иначе легко получить грубейшие численные «ошибки.
Самое правило замены в определенном интеграле выражается формулой: ь л
f f(x)dx = f /[?(/)]• о'(0^, а а
где замена старого переменного интеграции х на новое переменное интеграции t производится равенством:
* = ?(/) и где старые пределы интеграции а и Ь выражаются чёрез новые пределы интеграции аир равенствами:
a = s(a) и 6 = <р(Р).
Данное правило замены переменного в определенном интеграле верно не всегда, а только при определенных условиях, нарушая которые мы рискуем получить грубые численные ошибки.
Dot те условия, при которых данное правило верно:
1) Функция f (х) старого аргумента х должна быть
непрерПйпогона некотором основном отрезке [Л^х-^5], содержащем отрезок старой интеграции
2) Должны иметь место равенства: a = o(aj и А = о(р), означающие, что в концах « и р отрезка [а-С/<;р] новой интеграции функция «(t) принимает соответственно численные значения а и b старых пределов интеграции.
3) Функция <s (/) и ее производная с' (7) обе должны быть непрерывными на отрезке [а-С/-СР] новой интеграции.
4) Должно все время соблюдаться неравенство: Л <<?(/) <5 при пробеге аргументом /отрезка [а <;/-Ср] новой интеграции. Это неравенство запрещает при новой интеграции численным значениям функции <р (/) выходить из того основного отрезка [Л<^х^Д], в котором заранее была обеспечена непрерывность данной функции /(х).
При этих условиях данное выше правило замены старого переменного интеграции новым — верно. Для доказательства рассмотрим сначала ь
одну левую часть j f(x}dx рассматриваемого правила. По формуле а
Лейбница-Ньютона имеем:
h
f f(x)dx = F(b) — F(a). а
Рассматривая число а как постоянное, верхний же предел b как переменный и зависящий от аргумента р по формуле А = мы имеем:
ь
' /7(x)rfx = F[o(P)]-F(a). А
О
Отсюда мы заключаем, что определенный интеграл J*/(х) rfx зави-а
сит от р и что производная его по р вычисляется так: ь
|(f |,(Я1 - Г(.) 1 -1 f |,Й1-
= П?(?)1 •<(?)=/[?(?)] *
потому что F(a) есть постоянное, и его производная по р равна нулю, и потому что F(x) есть первообразная для /(х), и значит, для всякого численного х имеем F' (х)=/(х). В частности для х = <р(Р):
• [<?(?)] =/[?(₽)]•
§
С другой стороны, правая часть / /[<?(/)]• ?'(/) dt рассматривав-
мого правила является также функцией аргумента р, причем нижний предел новой интеграции а рассматривается как постоянная величина. Поэтому в силу свойства IX определенных интегралов мы имеем:
3
“р j а
Из этого мы заключаем, что производные по р от левой и от правой частей равенства, выражающего доказываемое правило, равны друг другу; а это значит, что самые эти левая и правая части разнятся друг от друга лишь на величину постоянную, совершенно не зависящую от р. Поэтому мы можем написать
/[?«)] =
где К есть константа, не зависящая от р. Отсюда следует, что мы можем аргумент р полагать равным любой величине, и величина константы К от этого не изменится. Положим же р = а. Тогда а (а) = <? (р), и, значит, а = Ь. Поэтому константа К будет разностью двух интегралов с равными пределами, т. е. К=0— 0 = 0, потому что интеграл с равными пределами равен нулю. Но если К= 0, то предыдущее равенство дает:
ь ₽
f f{x)dx = f /[?(/))• ?'(*)#. а о
что и требовалось доказать.
а
Пример. Найти / Уаа — х2 dx, принимая х = а 81п 0. о
Решение.
V ifi — x*dx = о2 У1 — sin* 6 • cos 6 dO = в2 cos2 6 dO.
Когда
x = a, a = a sin 0, т. e. 6 = у, а 'когда
x = 0, 0 = a sin в, т. e, в = 0.
Следовательно: к
* «
У Vai-x^dx= j' e2cos26d6= в о .o
При этой перемене пределов разумеется, что, когда б воарастает от 0 *
до у, то х возрастает от 0 до а.
УПРАЖНЕНИЯ.
Вычислить нижеследующие интегралы, применяя указанные подстановки.
1.
= 4- 21пЗ.
Полагаем Ух — г.
Полагаем x = az.
_ 1
Полагаем * = —. z
Полагаем У1 — л’ = z.
4
/* (sin 0 -|- cos 0) rfO _ In 3
J 3 4- sin 20 ~V о
la &______
10. /* - Лх = 4 — a.
/ ^ + 3
/ ydy 3/2
U- J УГ+ 4у ~ 2 •
Полагаем sin 0 — cos 0 = z.
Полагаем e® = z.
Полагаем x = asln2z.
Полагаем x — 2 = z3.
Полагаем e® — 1 = z2.
Полагаем 2 + 4y — z.
12.
cos/
Полагаем tg у = z.
ins
13. Г y^ZTldx^^=^. J Jf
Полагаем a® — 1 = &
d
Полагаем у = a sin г.
о
t
15. у Г27Т7-Л = ГЗ-11П(2+/3). о
Полагаем <4-1 = z.
§ 44. Бесконечные пределы. До сих пор пределы интегрирования мы считали конечными. Но даже в элементарных вопросах иногда при* холится отказаться от этого ограничения и рассматривать интегралы с бесконечными пределами. В некоторых случаях это бывает возможно, если пользоваться следующими определениями. Я
Если верхнйй предел бесконечен, то полагаем (по определению) • +» ъ
а когда бесконечен нижний предел, то полагаем (по определению)
предполагая заранее, что эти пределы существуют.
“f- Hu b
_ /• вдзлг /• 8а2 dx ,, Г. , , х 1»
Решение. I 1,т / ~1|т 4л'arctg -к- =
J л2 — 4а3 j>+oo./ л2 + 4а2 2а Jo
О о
= lim [4а2 arctg | = 4а2 • = 2г.аг.
Истолкуем этот результат геометрически (черт. 31). Кривая, выражаемая данной функцией, есть локон, уравнение которого и есть
8дэ
= х- -f- 4а2
Значит,
ь
/' 8a’rfx , „ , Ь
а
§ 45] СЛУЧАЙ, КОГДА Ч (х) ЕСТЬ ФУНКЦИЯ ПРЕРЫВНАЯ 137
По мере того как ордината Qb будет неограниченно удаляться вправо, выражение
4аг arctg -Д-
6 2а
всегда будет оставаться величиною конечною, и, переходя к пределу, мы подучаем
lim
2nd*;
эта величина, как мы видим, является также конечною величиною. Во всех аналогичных случаях условимся называть этот результат перехода к пределу попрежне-му величиной площади кривой, хотя, строго говоря, вта площадь и не вполне замкнута.
Пример 3. Найти f -х-.
Решение.
lim (In b).
Ъ JU
Но при возрастании Ь до бесконечности предел In Ь не существует, следовательно, в этом случае интеграл не имеет смысла.
§ 45. Случай, когда 7 (х) есть функция прерывная. Рассмотрим теперь случаи, когда интегрируемая функция для отдельных значений переменного, лежащих внутри пределов интегрирования, претерпевает разрыв непрерывности.
Сначала рассмотрим случай, когда подинтегральная функция непрерывна для всех значений х, лежащих между пределами а и Ь, кроме значения х = а.
Если а <С Ь и в положительно, берем такое определение интеграла:
ь
I <f(x)dx = lim у*<?(x)dx; а а + •
(А)
если же ? (х) непрерывна при всех значениях х, кроме х = Ь, берем такое определение интеграла:
ь-ч.
(В)
предполагая, что пределы при в -► 0 существуют.
Пример 1. Найти
Решение. Здесь обращается
/аа_ха
тельно, по формуле (В)
в бесконечность при х = а. Следова-
dx
Пример2. Найти
Решение. Здесь — обращается в бесконечность при х = 0. Следовательно, по формуле (А)
1 1
Г dx /‘ dx ( 1 \
/ —= 11m / = lim In— 1.
,/ -t ,->o J x i+o \ 1 J ' 0 «
В этом случае никакого предела не существует, а следовательно, не суще* ствует и интеграла.
Если с лежит между а и Ь и функция <р(х) непрерывна для всех значений х в этих пределах, за исключением значения х = с, то, полагая, что вне' — числа положительные, интеграл между а и b определяем, формулою-.
Ъ с —• Ь
f<f(x)dx = lim /*'$(x)dx-\- lim Гy(x)dx, (С)
a a c-H'
предполагая, что каждый предел в отдельности существует.
la
fQxdx ------р
Решение. Здесь подиитегральнав функция обращается в бесконечность при х = а, т. е. при аначении х, лежащем между пределами интеграции 0 и За. Следовательно, нужно обратиться к определению (С). Итак,
sa
Г Ixdx
[1 3(x» — a3)1
a—* Sa
„ f 2xdx . [* 2xdx
lhn I J ,,m / -2
• «0 I — i'-H) I —
J (^-aS)» (js-a»)»
рЫ - 3^(а+ •')«—*
площ. OPR = Г ———у = 3 ^(а — е)2 — д2 За 3 о °2) ’
По мере перемещения РЕ вправо к асимптоте, т. е. по мере приближения • к нулю, _________________________________________2
3 (а - 02 - а2 + За 8
остается конечным количеством, и lim I 3 у (а — с)-' — а2 + За 8 1 = За3 также • ->о L J
»
• тть конечное количество. Как в примере 2, § 44, За8 называется величинойпло-щ |дн, ограниченной кривой ОЕ, асимптотой и осью ОХ. Подобным же образом
За
площ. E’QRG= Г — ——— = 3{/8^2-Зу/(а-Н')2-а*
а %,’ (х2 —а2)8
остается конечною, когда Qi' двигается влево к асимптоте, и, когда s' прнбли-2 2
жается к нулю, результат ба8 есть также количество конечное. Поэтому 6а 8 называется величиной площади между QR, асимптотою, ординатою для х = 3а 2
и ОХ. Сложив результаты, получаем 9а* , и это называется площадью вправо от OY между кривою, ординатою для х = За и ОХ.
2а
Пример 2. Найти
а
Реиинш. Эта функция также обращается в бесконечность между пределами интегрирования. Следовательно, прилагая (С), получим
2а а—• 2а
/rfx .. /• dx . /* dx
(x — dp (x — а)2 +Дто/ (x — а)2 —
о о+«'
= lim Г------—]““*+ Нт Г-------—
,>о1 х — а Jo .>oL х—а
d (х—а
В этом случае пределы не существуют, и интеграл нс имеет смысла.
Начертив кривую, изображающую данную функцию (черт. 33), и заметив пределы/ найдем, что, повидимому, существует большое сходство с предыдущим примером. Однако на деле затененную часть нельзя рассматривать, строго говоря, как площадь, и знак интеграла в данном случае не имеет смысла.
Насколько важно исследоиать, обращается или нет данная функция в бесконечность внутри пределов интегрирования, обнаруживается тотчас же, если приложить к нашему примеру формулу интегрирования без всякого ния. Так,
исследова-
Черт. 33.
Результат ввиду вышеприведенного исследования явно абсурдный, ибо подинтегральная функция положительна.
ГЛАВА VH.
ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ.
АЛГЕБРА БЕСКОНЕЧНО МАЛЫХ.
[К сведению читателей. Так как читатель, начавший изучение интегрального исчисления с гл. I, уже знаком с принципами приложения интегрального исчисления к геометрии и знает соответствующие формулы, то он может, просмотр» примеры, решенные в тексте § 52, обратиться к чтению § 53, затем к решению примеров §§ 53, 54, 55, 56, затем замечание к § 57 и примеры к этому параграф}*; далее примеры к § 58 и с § 59 все подряд до конца книги].
§ 46. Равномерные бесконечно малые. Мы уже знаем, что бесконечно малой называется такая переменная величина а, для которой с некоторого момента имеется и впредь сохраняется неравенство j а | < е, где е есть произвольно выбранное положительное число.
Пусть теперь у нас имеется не одна только переменная величина а, но безгранично увеличивающееся число т переменных величин:
а, 9, 7,..., и.
Если все эти переменные величины таковы, что для них с некоторого момента одновременно имеются и впредь сохраняются неравенства:
|в|<е, 1?|<е, |т|<в,..., |р|<в, ;
где е есть произвольно выбранное положительное число, то тогда 'а называются равномерными беско-
нечно малыми.
Пример!. Количества а = — ,₽ = —, т =— , ...,р =—.когдачисло /и тп /п т
их т безгранично возрастает, являются равномерными бесконечно малыми, потому что мы имеем одновременно | а] < с, |?К«,..., |р | < », если т сделается достаточно большим.
_ „ v 1-23 т
Пример 2. Количества а = — . ? = — , 1 — —..... р = —.когдачисло r г т т т т
их т безгранично возрастает, будут просто бесконечно малыми, но не будут равномерными бесконечно малыми. Действительно, на месте, имеющем своим номером k, считая слево направо, находится количество —, которое, очевидно, бесконечно умаляется, когда т безгранично возрастает, потому что место k, занимаемое им, задано и, значит, неизменно. Но количества, a, 7,. . ., р не могут быть равномерными бесконечно малыми, потому что при всякем т имеем р = 1, и значит, хотя каждое нз этих количеств, взятое на определенном месте, и стремится к нулю, но все одновременяо они не могут безгрвничьо умаляться.
Читатель должен обратить внимание на то, что буква р не обозначает в рассматриваемом процессе определенного количества, потому что место т буквы р все время изменяется, будучи безгранично возрастающим.
§ 47. Равномерно-равносильные бесконечно малые. Мы знаем, что два бесконечно малые а и а' называются равносильными, если их а' отношение — имеет пределом единицу, т. е. если разность а
-—1 \ а
есть бесконечно малое.
Пусть у нас теперь имеется не одна только пара (а, а') бесконечно малых, но безгранично увеличивающееся число т пар бесконечно малых
(а, а'), (Р,И, (Т.П..., W),
которые мы для ясности просто подпишем друг под другом: “> 7. •• •»
7'.- Р',
так что бесконечно малые всякой пары подписаны одно под другим.
Бесконечно малые а, 0, у,..., и называются равномерноравносильными бесконечно малыми а', 0', 7',..., ц', когда разности
суть равномерные бесконечно малые.
Это определение выражает только то, что бесконечно малые а и а', . . а' В7
0 и 0, т и 7,..., Риц таковы, что их отношения —, -у, t' V-'
-— одновременно стремятся к единице как к пределу, потому что мы имеем в некоторый момент времени удовлетворенными для них сразу все неравенства:
которые в дальнейшем сохраняются уже все время.
§ 48. Бесконечно малые равномерно*высшего порядка. Мы знаем, что бесконечно малое а" называется бесконечно малым высшего . а"
порядка, чем а, если отношение — есть бесконечно малое, т. е. если начиная с некоторого момента имеется и впредь сохраняется неравенство;
а."
а
< е.
Пусть теперь у нас имеется не одна только пара (а, а') бесконечно малых, но безгранично увеличивающееся число пар бесконечно малых:
(«. «"). (₽. Г). (7, 7'),..., (И, И.
которые мы для ясности опять подпишем друг под другом:
«, Р, I,--, Р. а', р", 7",..., и" так что бесконечно малые всякой пэры подписаны одно под другим. Бесконечно малые а", р", 1",..., р" называются бесконечно малыми равномерно-высшего порядка, чем бесконечно малые а, р, .....р, если соответственные отношения
Г Г £
а ’ р ’ т и
суть равномерные бесконечно малые. Это важное определение выражает только то, что бесконечно малые а", р", т",..., р" таковы, что начиная с некоторого момента одновременно имеются и впредь сохраняются неравенства:
где в есть произвольно выбранное положительное число.
Следовательно, это определение учитывает не что иное, как просто лишь одновременную малость сразу всех а, р, 7,..., р по отношению ко всем а", р", 7",..., р", в остальном же это определение совершенно такое же, какое было дано раньше для одного бесконечно малого высшего порядка.
Читатель уже знает, что бесконечно малые а и а' тогда и только . тогда равносильны одно другому, когда их разность а' — а есть бесконечно малое высшего порядка, чем а. После только что сделанного замечания читатель примет как естественное следующее предложение:
Теорема. Бесконечно малые а', р', 7',..., р' тогда и только тогда равномерно-равносильны бесконечно малым а, р, 7,.... р, когда их соответственные разности а'— а, Р' — р, 7' — 7,..., р'— Н суть бесконечно малые равномерно-высшего порядка, чем а, р, 7,..., р.
Для доказательства достаточно заметить, что неравенства
— — 1 а < е, L-i < е, li- 1 1 1 < в,. .. 1 £-1 1* < в,
характеризующие равномерную равносильность бесконечно малых
<* > ₽, !,- а и Р. Т, ..., р, переписываются в виде:
а' — а- 1<е р'-р ! 7' — 7 р' —р
а 1 е- 1 ’ 1 Т и
характеризующем равномерно-высший порядок разностей а'—о, р' — р, Y—7,..., V-'—р сравнительно с данными бесконечно малыми а, р, 7,..., р.
Если мы теперь обозначим разности а — а', р — р', 7 — 7', ...,р —р' соответственно через а", р*, 7",..., р’ и напишем:
а — а' = а", р —р/ = ;Л 7 —7' = f,.--, Н—=
144 ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ [ГЛ. VII то имеем:
a = a'-J-a', 0 = 0'Ц-0’, 7 = 7'4" 7"»-• Р = и'-г11'
Здесь а', 0', 7',..., и' суть бесконечно малые, равномерно-равносильные данным бесконечно малым а, 0 у,..., р; с другой стороны, бесконечно малые а", 0", 7",.. ., и." суть равномерно-высшего порядка, чем данные бесконечно малые в, 0, 7,..., р. И так как количества а', 0', 7',..., р' получаются, очевидно, из а, 0, 7,..., р зачеркиванием у них слагаемых а", 0", т",. • р", то отсюда вытекает такое следствие:
Бесконечно малые а', 0', р' равномерно-равносильные данным бесконечно малым а, 0, 7,..., р, получаются из а, 0, 7,...,р отбрасыванием (зачеркиванием или опу* сканием) у них частей равномерно-высшего порядка.
Это следствие очень важно, так как имеет уже практическое значение: имея данными суммы
a = 0 = 0'4-0", 7 = /4-р = р'-|_р"
бесконечно малых, мы просто зачеркиваем в них бесконечно малые а", 0", ’{",, р" равномерно-высшего порядка; полученные новые бесконечно малые
а7, 07, у7,. . .. р7 оказываются равномерно-равносильными данным а, 0, р.
§ 49. Абсолютно-ограниченные суммы бесконечно малых. Сумма «-|-0-{-7-|-...-|-р возрастающего числа бесконечно малых называется абсолютно-ограниченной, когда сумма их абсолютных величин |вЦ-|0Ц-|71_г • • • г1р1 ограничена, т. е. если имеем сохраняющимся все время неравенство:
|a| + l₽l + lTH-...
где К есть положительная постоянная величина.
Ill 1
Пример 1. Полагая о = — , В =—, у =—р = — , мы имеем от т т т
сумму бесконечно малых а -г 0 + Т 4* + Р абсолютно-ограниченной,
потому что все они положительны и так как их сумма а р -|- у -|- ... —р- есть
величина ограниченная, ибо она, очевидно, равна--1--h -.-H-=
от от от т
= — Хя=1. Здесь число бесконечно малых а, р, у,..., р предполагается т
равным т и безгранично возрастающим вместе с т.
„ п п 1 1 о 1 , 1 11
Пример 2. Полагая a —----- =, р =------------F , у --7=,...,
тут тут тут
1 1 ц = — ± —7=, мы имеем: т /т
“ + ₽ + 7 + •. т Р = ~Х w == 1>
потому что бесконечно малые, содержащие в знаменателе У~т, взаимно уничтожатся, когда т есть число четное, что мы и будем предполагать для простоты. Но, с другой стороны, имеем, очевидно:
откуда
1»1 + 131 + 1т1+••• + Ы> \Xm = -?L-l = /т- 1.
\ У т т / у т
Мы видим, что при безгранично возрастающем т число /т — 1 само безгранично возрастает, и значит, сумма бесконечно малых 7 Ч- ... —|- н не есть абсолютно-ограниченная, хотя ее численная величина для всякого четного т равна единице.
§ 50. Второй принцип анализа бесконечно малых. Предыдущие рассмотрения были необходимы для установления важнейшего в математическом анализе принципа, так называемого второго принципа бесконечно малых,, благодаря которому делаются возможными многочисленные приложения интегрального исчисления к геометрии, механике, физике, химии, биологии и вообще к естествознанию. Поэтому второй принцип нередко называют принципом интегрального исчисления.
Второй принцип бесконечно малых (принцип интегрального исчисления). При отыскании точного предела абсолютноограниченной суммы бесконечно малых всех их можно заменить равномерно-равносильными, не изменив тем самым величины этого предела.
Доказательство. Пусть o = a4-p-j-f4_-- - J1 — абсолютноограниченная сумма бесконечно малых, точный предел lim о которой нам нужно найти. Так как а есть, по условию, абсолютно-ограниченная сумма бесконечно малых, то мы должны все время иметь неравенство:
М + 131 + И1 + • • • + Н < к,
где К есть положительная постоянная величина.
Пусть новые бесконечно малые д', р', р' равномерно-равносильны данным бесконечно малым а, р, 7,..., р; обозначим через о' сумму новых бесконечно малых:
°' = а' + У +1' "Г • • • + н'-
Вычитая из прежней суммы о новую сумму з', имеем:
’ —’' = (« —«') + (? —₽') + (! —Г) + + (Н —И-
Введя обозначение
а — а' = а", р —р' = рл, 7 —7'= 7">- Р-~ р' = 1<
мы видим, что бесконечно малые а", Р", 7’,..., р" суть равномерновысшего порядка, чем бесконечно малые а, р, 7,...,р. Это значит, что каково бы ни было произвольно выбранное положительное число е, наступит такой момент, начиная с которого мы будем постоянно иметь неравенство:
или |a"|<e-|a|, | ₽" | < е • | р |, 17" I < • ' 171....... 1И < « • |н|-
Ю Э&в. 2868. г- Грвявиь Луви, ч. II, Интегральное ночжолекжа
Отсюда следует, что
|а',|+|Г1 + 1Г1+--- + 1И<
< 8 ’ I а I “Ь е • | р |-|-е • 17 е • | [а | =
= е(|а| |-|Р1 + |-Г|+.. • +|р|) < •• К. И так как
К + ₽'-Н" + . + р'КИ-Ч₽"Ц-|Г| + .. .+1^1,
то поэтому мы, начиная с некоторого момента времени, будем иметь:
|a’4-r + f+---+l'’l<s-Ar.
Но так как К есть постоянная величина, а « можно взять сколь угодно малым, то отсюда следует, что сумма
а’ + Р’ + У’+.-.+н’
есть бесконечно малая величина, и, значит:
11т(а" + р" + <+...+И = 0.
С другой стороны, мы имеем, очевидно:
а-о'=а’ + Р’+-Г+..-+и'Т.
Поэтому
11m (а — </) = О,
и, следовательно, пределы Пт а и lima7 переменных величин а и о' не могут быть разными:
11m а = 11m а'.
Проще всего второй принцип бесконечно малых применяется в виде практического правила.
При вычислении предела абсолютно-ограниченной суммы бесконечно малых всегда можно пренебрегать бесконечно малыми равномерно-высшего порядка.
Действительно, пренебрегая бесконечно малыми равномерно-высшего порядка, мы просто заменяем данные бесконечно малые другими, им равномерно-равносильными. Но второй принцип бесконечно малых именно и позволяет делать такую замену, когда дело идет о пределах абсолютно-ограниченных сумм бесконечно малых.
ПРИЛОЖЕНИЯ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ.
§ 51. Общая схема применения интегрального исчисления. Интегральное исчисление применяется к самым разнообразным вопросам геометрии, механики, физики, химии, биологии и вообще естествознания, следуя всегда одной и той же схеме. Вот эта схема:
Если нам необходимо определить какую-нибудь величину V, то мы разбиваем ее на большое число малых часТИЦ У=а-Н + 7+-..+^
и стараемся представить общий член этой суммы в виде парного произведения:
Обычно сделать это в точности не удается, но зато часто удается это сделать, пренебрегая бесконечно малыми равномерно-высшего порядка сравнительно с численными величинами членов а, р, Т,..., р, так что искомая величина V предстанет в виде интегральной суммы:
/(*0) Д^о+/(^) +/(*2) Д*2 -Н • • • +/(•*„-!)
но не со всею точностью, а лишь с погрешностью, равной сумме отброшенных бесконечно малых высшего порядка.
Однако, когда частицы а, {3, ., у. делаются бесконечно малыми,
отброшенные бесконечно малые высшего порядка дают в сумме погрешность, также бесконечно умаляющуюся1), так что полученное равенство для V и для интегральной суммы S/(x)Ax в пределе восстанавливается, и мы имеем совершенно точное равенство уже без малейшей погрешности:
ь
А тогда, если мы сможем отыскать конечным образом первообразную для /(х), мы вычисляем искомую величину V по формуле Лейбница-Ньютона: ь
V=[f
Заметим, что когда удается „общий член“ суммы У==а-|-?-|-
,-J-и, отбросив бесконечно малое высшего порядка, предста-
вить в виде парного произведения:
f[x) • Дх или /(х) • dx,
тогда это выражение называется элементом величины V.
§ 52. Площадь кривой в декартовых координатах. Площадь, ограниченную дугой кривой, заданной уравнением у =f (х), двумя ординатами х — а, х = Ь и отрезком оси абсцисс от а до Ь, мы рассматриваем как предел 11m (а 4- ? + 7 4" • • • + i1) суммы площадей прямоугольников, когда все длины оснований этих прямоугольников бесконечно умаляются
*) Эго следует вэ второго принципа бесконечно малых, который здесь имеет полную силу, если функция /(л) есть непрерывная и если отрезок интегрирования [а, Ь] конечен. Действительно, в этом случае интегральная сумма есть, очевидно, абсолютно-ограниченная сумма бесконечно малых, потому что
<Л4 при всяком х, и, значит, ь ь
S|/(x).Ax|<SA(.|lc|<.W.|6-e|. а а
(черт. 34). Следовательно, за элемент площади U мы принимаем площадь прямоугольника укх —ydx *). Покажем, что мы вправе это сделать.
Для этого надо показать, что площадь криволинейной полоски, обозначенной на чертеже через Д67, и площадь у dx прямоугольника отличаются друг от друга на бесконечно малое высшего порядка сравнительно со взятым элементом.
Обозначим через у' наибольшую ординату и через у" — наименьшую ординату на отрезочке dx. Тогда можем написать:
|ДС/—ydx\< \y'dx—y"dx\ = \y/ —ya\dx,
как это очевидно само по себе и наглядно видно на черт. 35, изображающем площадь Д(/ и все необходимые построения. В силу непрерывности функции у =/(х) разность у'—jf при неограниченном умалении dx является величиной бесконечно малой. Обозначим ее через л. Следовательно, будем иметь:
| Д^/ —ydx | < | а [ dx, или
Д£/—ydx = 3 dx, где
|₽| < |а|.
Рассматривая теперь отношение
3 dx _ р
~У^х~~у'
Черт. 35.
заключаем, что разность Д£7—ydx — действительно величина высшего порядка малости, потому что р стремится к нулю при а неограниченно умаляющемся, а у есть величина неограниченная.
Итак, мы показали, что Д£/ и ydx равносильны. А так как интегральная сумма в данном случае абсолютно-ограниченная (см. сноску на стр. 147), то искомая площадь определится формулой:
ь ь
U = У* ydx = J J (x)dx. (I)
a a
Можно совершенно аналогичным образом показать, что элемент интегральной суммы, выбираемый для определения искомой величины, отличается от части само**величины, соответствующей этому элементу, на бесконечно малое высшего порядка и для других приложений интегрального исчисления. Поэтому вследствие ясности этого положения мы не будем приводить подробного исследования этого вопроса, предоставляя читателю в каждом отдельном случае провести соответствующее доказательство самостоятельно.
1) Нам безразлично, писать ли Ах или dx, потому что раз буква х обозначает независимое переменное , то Дх = dx.
За высоту прямоугольника мы приняли значение у в левом конце интервала Дх, но так как интегральная сумма не зависит от выбора точки на отрезочке Дх, то можно было бы за высоту принять любую ординату на втом отрезочке.
Пример 1. Найти «лошадь, заключенную между полукубическою параболою у2 = х8 и прямою х = 4 (черт. 36).
Решение. Найдем сначала площадь ОМР, половину искомой площади ОРР' для верхней ветви кривой у= Ух2; применяя формулу (1) и b = 4, находим:
и
замечая, что а = О
* 3
/' т . 64 4
/ х2 dx = -z- = 12— ,/ 5 5
о
и
Следовательно: г i ч площ. ОРР' = 2 • = 25-^-.
а
Если единицею длины служит сантиметр, то площадь
ОРР' « 2^4 смХ э
а
Примечание. Для нижней ветви у = —Xs, откуда
4 <Л=-124.
знаку отрица-
площ. ОМР" = 6
Эта площадь лежит под осью ОХ и по те ль на, ибо ординаты отрицательны.
При нахождении площади ОМР мы получили положительный результат, ибо площадь находилась выше оси ОХ и потому ординаты были положительны.
3
Результат 25у представляет величину полной площади, причем знак во внимание не принимается. В тех случаях, когда кривая в пределах интегрирования пересекает ось ОХ, необходимо обращать внимание на знак площади.
Пример 2. Найти площадь, заключенную между параболой х® — 4ау и локоном Аньези v= 8аЭ х2-|-4аа "
Решение. Для определения пределов интегрирования решаем уравнения данных кривых совместно, чтобы найти точки, в которых кривые пересекаются. Найдем, что координаты точки А суть (— 2а, а), а точки С (2а, а).
Из черт. 37 видно, что площ. АОСВ = площ. DECBA—площ. DECOA. Но
О -2а О
га f
Черт. 37.
X
площ. DECBA = 2 X площ.
плот. DECOA = 2 X площ.
2а
/• 8а3 dx _ J х2 -I- 4а2 “ 7:3 о
2а
/х® 4
^-Лх = Д-а«. 4а 3
о
Следовательно:
площ. АОСВ = 2яа® — у а® = 2а® (it — у).
Можно решить вопрос другим способом, рассматривая подоску Ро как мемент площади. Если ордината, соответствующая локону, будет а ордн-
ната, соответствующая параболе, — /*, то диференциальное выражение площади полоски PS будет (у — у") dx. Подставив значения /а/» функции х из данных уравнений, получим:
площ. АОСВ = 2 X площ. ОСВ = 2 / (У —у")dx^= б
2а п /' / 8а3 ал- \ . „ q ( 2 >
= 2 / —, . . , — — ) rfx = 2u- г —7 I.
J \ xl -j- 4a2 4a / \ 3)
и
x2
Пример 3. Найти площадь эллипс»-^- =^- = 1.
Решение. Ищем площадь квадранта, т. е. четверти ОАВ (черт. 38), причем
Следовательно, площадь всего эллипса равна nab.
§ 53. Площадь, когда кривая задана уравнениями в параметрической форме. Если кривая задается уравнениями в параметрической форме:
* = ?(0. у = ^(0, ТО( по формуле подстановки в определенном интеграле (см. свойство X, стр. 132), площадь, ограниченная кривой, выразится следующим образом:
\ f (I*)
t. где пределы и t* определяются из равенств: в = ?(0> * = Так, при вычислении площади вллипса в примере 3, § 52, проще было бы обратиться к параметрическим уравнениям эллипса:
х = a cos ?, у = Ъ sin y, где параметром (§ 93, ч. I) служит эксцентрический угол <?. Имеем:
у = b sin f, dx = — a sin f dy.
Когда x = 0, f = у, а когда х = а, у = 0.
Подставляя в (I) § 52, найдем: а О
площ. О АВ = J у dx = — J" ab sin8 ? df = .
О «
3
Следовательно, вся площадь равна nab.
УПРАЖНЕНИЯ
1. Вычислить площадь, ограниченную прямою у = 5х, осью ОХ и ординатою = 2- Отв. 10.
2. Вычислить площадь, ограниченную параболой у2 = 4х, осью ОХ и прямыми х — 4 и х = 9. ]
Отв. 25-5-. О
3. Найти площадь круга х2 + = г®. Omg ггЯ
4. Найти площадь фигуры, ограниченной линиями у2 = 9х и у = Зх.
Отв. у У
5. Найти площадь, заключенную между равнобочною гиперболой ху = а2, осью ОХ и ординатами х = а и х = 2а. ^me д2 1п 2
b. Найти площадь, заключенную между кривою у = 4 — х2 и осью ОХ.
Отв. Ю-j-.
О
7. Найти площадь, заключенную между полукубической параболой у2 = х3, осью OY и прямою у = 4.
Отв. -I/ 2 .
8. Найти площадь фигуры, ограниченной гипоциклоидой
1 г L
<•+/ = а3.
3 Отв. „па2.
Q
(х а? \
е° 4-е ° I, осью OY и
прямою х = a. .
Отв. [с8 - 1].
10. Найти площадь фигуры, ограниченной кривой у = х3, прямой у = 8 и осью OY. Отв 12
11. Найти площадь, ограниченную кривою у = In х, осью ОХ и ординатами х = 1их = а. Ота. а(1па-1)4-1.
£ -
12. Найти всю площадь фигуры, ограниченной кривой (у) 4~ (yj == 1-_ Зга5
Отв. .
4
13. Найти всп площадь фигуры, огравиченной кривой агуг = х* (2а — х).
Отв. ка>.
14. Найти площадь, ограниченную кривыми х(у — ех) = sin х и 2ху = = 2sinx + x’, осью OY и ординатою х = L
t
Отв. x«)rfx = <?-£-= 1,55+ ...
о
. 8в3
15. Наити площадь, содержащуюся между локоном Аньези у =
и осью ОХ, асимптотою кривой. Qme ^ка3
хз
16. Найти площадь, заключенную между циссоидою У* = 2а — х и W асимп* ютой х = 2а. Ome.Zr.aX
17. Нлйти площадь, содержащуюся между параболами у* = 2рх и х2 = 2ру.
п 4 . Отв. рХ
18. Найти площадь, содержащуюся между параболою у2 = 2х и кругом
V2 = 4* ~ XX Отв Q g-Q
19. Найти всю площадь фигуры, ограниченной линиями у = х*, у = 2х
ч У = х. 7
Отв.
О
20. Найти выражение площади, ограниченной равнобочной гиперболой к9 — /=*а2, осью ОХ и диаметром, проходящим через любую точку (х, j).
Отв. In .
2 а
21. Найти путем интегрирования площадь треугольника, ограниченного осью OY и прямыми 2х +_у + 8 = 0 и у = — 4.
/ Отв. 4.
22. Найти площадь круга
х = г соз 6, | у = г sin 8, / где 0 — параметр.
Отв. кг-.
23. Найти площадь, ограниченную одной дугой циклоиды
х = а (8 — sin 8), 1
у = а (1 — cos 6), / где 6 — параметр.
i Казание. Так как х изменяется от 0 до 2ка, 8 изменяется от о до 2л.
Отв. Зла3, т. е. утроенная площадь производящего круга.
24. Найти площадь, ограниченную кардиоидой
х = а (2 cos t — cos 20, ) - 3 .
I Отв. -угкаХ
у = а (2 sin t — sin 20. J 2
25. Найти площадь гипоциклоиды
х = a cos’ 8, | j = aatn*О, )
где в — параметр. 3 3
Отв. -т- на2, т. е. площади описанного круга, о о
26. НаЛти площадь, образуемую петлею декартова листа х3 + у3 = Заху (черт. 39).
Указание. Пусть у = tx\ тогда За.’. ЗдР . 1 - 2Г3 „ .4
' = !+£’ и dx = (1+7.7ZadL
Пределы для t суть 0 и со. ‘ 3
i Отз. у а3.
X
27. Найти площади фигур, ограниченных следующими линиями:
а) (у — х)3 = х3, у = 0.
Ь) (х -у*')- = у5, х = 0.
с) а3у = х (х2 — в2), у = 0.
d) x(1+j2)=1, х = 0.
е) у = х (1 - х2), у = 0.
f) х=у3(у-1), х = 0.
g) у3 = х* (2х + 1).
11) у2 = X2 (2х + 1).
1) у = х + 4, у = 2х + 4, у = 0.
j) у = х3 + 5, у = 0, х = 0, х — 3.
к) у = 2хя, х = 0, у = 1, у = 4.
1) х3=у + 9, у = 0.
Оша.
1
21 •
1 , Та’
1
2 ' 1
12 '
4 105*
2
15 ' ш) у2 — 4 + х = 0, х = 0.
п) ху = х®, у = 0, х = -i’, х = 1.
о) ху = 4, у = 1, у = 5.
р) х = 10у, y = , у = 2.
§ 54. Площадь кривой в полярных координатах. Разность площадей кривого сектора и вписанного в него многоугольника есть бесконечно 1алое высшего порядка. Следовательно, за элемент dU
* 1
площади ЛС9 (черт. 40) мы принимаем площадь — p’rfO
ного кривого сектора. Поэтому, площадь U всег'' криволинейного сектора АОВ дается формулой:
ь ь
1/саПЛОЩ. АОВ =
Здесь р=/(<р) есть уравнение заданной кривой. Пример. Найти всю площадь лемнискаты
заштрихован-
Черт. 40.
f3 = н3 соя 29.
Решение. Так как кривая симметрична и относительно ОХ, и относительно ОУ, то вся площадь равна учетверенной площади ОАВ (черт. 41).
г Так как р обращается в нуль при 6 =
' к _ к
= —, то при изменении 0 от 0 до радиус-
В^р1р.01 вектор опишет площадь ОАВ. Отсюда подстановка в (II) даст:
полная площадь = 4 X площ. ЗАВ
!
А
Черт. 41.
i/
о
т. е. площадь обеих петель равна площади квадрата, построенного на стороне ОА.
УПРАЖНЕНИЯ.
1. Вычислить площадь, описываемую радиусом-вектором спирали Архимеда р = аО, при одном ei о обороте, при начале движения от 0 = 0.
j Отв. 4г ifia* 1.
О
2. Вычислить площадь одной петли кривой р = a cos 2В.
Отв. -1 по».
О
3. Показать, что вся площадь кривой р = a sin 26 равна половине площади описанного круга.
4. Вычислить полную площадь кардиоиды р = а (1 — cos 0). „ 3 „
Отв. у па» т. е. ушестеренной площади производящего круга.
5. Найти площадь круга р = a cos 6. Отв. па».
6. Доказать, что площадь трех петель кривой t> = a sin 30 равна четверти площади описанного круга.
7. Доказать, что площадь, описанная при одном обороте радиуса-вектора спирали р = е*, соответствующем 6 = 2г., равна четверти площади квадрата, построенного на радиусе-векторе без кв. ед.
ч '
8. Найти площадь, ограниченную параболой р = a sec2 и х. рдой, перпен-днкулсрной к ее оси и проведенной через фокус
8а» Отв.
О
9. Показать, что площадь, ограниченная любыми двумя радиусами-векторами гиперболической спирали рб = а, пропорциональна разности этих радиусов.
о»б»
10. Найти площадь эллипса р* = е + cos2 6 * Omt- *ab'
И. Найти всю площадь кривой р = a (sin 26 + cos 20). Отв. г.а-.
12. Найти площадь, ограниченную одной петлей кривой р2 cos 0a2 sin .30.
Отв. j а» — у а11п 2.
13. Найти площадь кривой p = asins-=-, лежащую ниже ОХ.
О
Отв. (Юг.+ 27 f 3)-g-.
14. Найти площадь, ограниченную кривой p2 = oasin40.' Отв. а2.
15. Найти площади, ограниченные следующими кривыми и радиксами-векторами, соответствующими указанным значениям полярного угла:
а) р = tg 0, 0 = 0, 0 = .
ie
Ь) р= е-, 6 - j, 6=у.
с) р--- я2 зесЦ. 6 = -£, 0_-^.
& О О
d)‘ р = sec 0 + tg 0, 6 = 0, 6 = y>
s) р = sin у + cosy, 6 = 0, 6 = у.
f) р = a sin 6 + b cos 6, 6 = 0, 6 = у.
16. Найти площади фигур, ограниченных
каждой из нижеследующих кривых:
а) р2 = 4 sin 26.
b) р — a cos 30.
с) р =8 sin 40.
d) р = 1 + 2 cos 6.
е) р — 3 + cos 0.
1) р = 2 — sin 0.
g) р2 = я2 (I — cos 6).
h) p = a (1 +sln6).
I) p = a cos 50.
§ 55. Объем
ного в него круглого цилиндрика есть бесконечно малое высшего порядка. Следовательно, за элемент dV объема (черт. 42) тела вращения
мы принимаем объем ty^dx заштрихованного круглого цилиндрика. Поэ-
тела вращения. Разность объемов диска и вписан-
тому искомый объем V всего тела вращения AiABBi дается формулой:
V— объем A}AHBt —
tt a
Здесь y = f (х)— уравнение вращающейся плоской кривой.
Пример. Вычислить объем, производимый вращением эллипса
Л-
— + -А_ = 1
а2 г б2
вокруг оси О?;,
Решение. Так как у3 комый объем вдвое больше объема производимого вращением ОАВ (черт. 43), то подстановкой в (111) найдем:
a
ь*
(o’-х») и ne-
V__ '2
и
9 r.ab3, О
(Ш)
X
Черт 42.
Черт. 43.
о
откуда
V=~r.ab2. О
Для проверки результата положим h = а. Найдем:
V = 4- ядз, О *
объем шара, представляющего лишь частный случай эллипсоида. Когда эллипс вращается вокруг большой оси, тело называется удлиненным сфероидом; когда — около малой Ося, тело называется сжатым сфероидом.
УПРАЖНЕНИЯ
1. Найти объем шара, производимого вращением круга хг+_у2 = г® вокруг своего диаметра. 4
Отв. пгя.
2. Посредством интегрирования найти объем прямого конуса, производимого вращением вокруг оси ОХ прямой, соединяющей начало с точкою (а, Ь).
Отв. -i-rtaM. и
3. Найти объем конуса, производимого вращением прямой примера 2 вокруг оси ОУ. j
Отв. у па2Ь.
4. Найти объем кольца (т^>а), производимого вращением круга х8-|-+ - ЬУ = а2 вокруг ОХ. Отв 2_2д^
5. Найти при помощи интегрирования объем цилиндра, образуемого вращением прямоугольника, ограниченного прямыми х = 0, у = 0, х = 6, у = 4: а) вокруг оси ОХ', Ь) вокруг оси ОУ.
6. Найти объем параболоида вращения, производимого вращением дуги параболы д2 =' 4ах между началом и точкою (Xj, yt) вокруг ее оси.
Отв. 2ках* = у пу’ xj, т. е. половина объема описанного цилиндра Найти объем, производимый вращением дуги примера 6 вокруг оси ОУ.
п ^'1 1 ’ 1
Отв. —- - =— пх у , т.е. — цилиндра.
80а’ 5 51
высота которого равнЯ yt, а радиус основания pafiH хР Посредством интегрирования найти объем конуса, произви^1мого враще-вокруг ОХ части прямой <х — 5у -f- 3 = 0, содержащейся между осями „ 9 10 ! Отв. —п.
9. Найти объем, производимый вращением вокруг оси ОХ кривой (х— 4а) у2 = = ах (х — За) между пределами х = 0 и х = За.
Отв. -у па8 (15 — 16 In 2).
10. Найти объем тела, образуемого вращением вокруг осн ОХ каждой из площадей, ограниченных нижеследующими линиями: а _а £ и) Гипоциклоидой х* =а8,
7.
8. йием координат.
л 32 it д’
°"*- Тй-
1 - • 1
Ь) Дугой параболы х3 -|-у3 = аг; х = 0; y = Q.
с) Одной дугой синусоиды у = sin х.
d) Параболой у1 = 4х и пряхой х = 4.
с) Кривой у = хе* и прямыми х = 1, у = 0. Отв.
f) Кривой у2 = Эх и прямой у = Зх.
g) Кривой у = х* и прямыми у = 0, х = 1.
h) Кривой у2 (6 — х) = х2 и прямыми у = 0, х = 0, х = 4.
1) 4у* = х3, х = 4.
Отв.
яд*
ТУ-
Отв.
Отв. 32я.
7 («•-!). Отв.
j) У(1+хЗ) = Х, У = 0, х = 0, х = 8.
к) у(х —2р= 1, у = о, х = 3, У = 4.
1>у= = (х + 2)з, > = о, х = —1, х = 0.
щ) (X — \)у = 2, У = 0, х = 2, х = 5.
И. Найти объемы тел, образуемых вращением площадей, ограниченных следующими линиями:
Вокруг оси ОХ Вокруг ocJOY
а) у = е*, х = 0, у = 0. Отв. к ~2 2я
Ь) у = х», х = 2, у = 0. 128к 7 64к
с) ау- = х3, у — 0, х = а. 1 . — по® 4 •у яд’
d) 5^"'- 48к 64я
е) (7)'+©!-Ь 32 35™*2 4-О
f) у2 = 9х, у = 0, х = 9.
g) _уа = 4 —х, х = 0.
h) у2 = х-|-9, х = 0.
j) хЗ=16-у, у = 0.
к) x* + 9y» = 36.
1) у = 2х, у = 0, х = 3.
х® = 1 -ку, у = 0.
ш)
12. Найт! объем, производимый вращением цепной линии у = вокруг оси (КС от х =. 0 до х = Ь.
аЬ _
_ яд* I а а\ . кагЬ
Отв.^^е — е J+-J-.
13. Найти объем тела, производимого вращением циссоиды 3^ = 2а—х во* круг ее асимптоты х = 2а,
Отв. 2я>д>.
dv v
14. Дан угловой коэфнциент касательной к трактриссе, ~ ~ ;
найти тело, производимое вращением трактриссы вокруг ОХ.
2 Отв. тир.
3
15. Показать, что объем конической верхушки высоты а, отрезанной от тела, производимого вращением прямоугольной гиперболы х3 — _уа = а2 вокруг оси ОХ, равен объему шара радиуса а.
16. Пользуясь параметрическими уравнениями гипоциклоиды
х = a cos* 0, у = a sin* 6, вычислить объем тела, производимого вращением кривой вокруг оси ОХ.
17. а) Найти объем, производимый вращением дуги циклоиды , х = а(в — sin 6), у = а (1 — cos в)
вокруг ее основания ОХ. Отв. 5к*а*.
Ъ) Показать, что если луга будет вращаться вокруг оси ОУ, то произведенный ею объем будет
6п*а*.
18. Показать, что объем тела, производимого вращением кривой х3у-‘ = = (х — а) (х — Ь) вокруг оси ОХ, равен:
« {(а + *)1п 2(6 - о)).
19. Найти объем, производимый вращением кривой х* — а2х2 + а2у2 *= О вокруг оси ОХ. 4
Отв. гу ла3.
10
1
20. Найти объем тела, производимого вращением кривой ха+у =1 вокруг оси ОУ. 4
Отв. -г-д.
О
§ 56. Длина дуги плоской кривой в декартовых координатах. Для нахождения длины дуги АВ кривой (черт. 44), заданной уравнением у = f(x), разбиваем отрезок оси ОХ от х = а до х = Ь на части и восстанавливаем в точках деления ординаты y=f(x). Тем самым дуга АВ оказывается также разбитой на п частей As. Следовательно, длина s дуги АВ выразится суммой s = 2^S. Однако реличину As в точности вычислить мы можем и вместо нее в качестве элементАуги s возьмем ds = У (dx)*-\-dy* = У1 +/9 dx. Величина As, как приращение всякой функции, отличается от диференциала ds на бесконечно малое высшего порядка малости:
As = ds-[-aAx, где а->0 при неограниченно умаляющемся приращении Ах. Следовательно, As и ds равносильны, а потом/ ь ь
s= lim I ds — j у1 д_ ya. dx. (1V)
bod «/
a a
Пример. Найти длину окружности круга, х3 + у3 = г4 (черт. 45).
Решение. Диференцнруя, находим: w
[Подставляя у3 = г® — х3 из уравнения круга дяя исключения у.] Отсюда т
/dx Г . xlr пг
Vfi-x* L do 2
Значит, для всей окружности дуга равна 2пг.
УПРАЖНЕНИЯ.
1. Вычислить длину ординаты х = 5а.
2. Найти всю длину
3. Спрямить цепную
дуги полукубической параболы ау3 = х® от начала до
’ 1 Z
гипоциклоиды х3+у3=а3.
X X
линию у = -^ео-[-е °) отх = 0
п 335
Оте. -^-а.
Отв. 6а.
до точки (х, у).
4. Спрямить кривую Эау3 = х (х — За)3 от х = 0 до х = За.
Отв. 2а/3.
2
5. Найти
2 з 1
= 1 в одном квадранте.
Отв.
6. Найти длину
кривой е?
от х = а до х = Ь.
7. Найти длину
ветви циклоиды
ег6-1 Отв. In -----
е3*-! г,
х=^а(1 — sin /), у = а(1 — cost).
8. Уравнения эволюты круга суть: х = a (cos 6 + в sin 6), у = a(sln 0 — б cos 6);
Отв. 8a.
найти длину дуги от в = 0 до в = вР
9. Найти длину дуги кривой х = е* sin О, v = е' cos в от 6 = 0 до ’ 6 = у .
Ота. —-ав’
10. Найти длины дуг следующих кривых:
I
b) _у = 1п(1—хi) 2); х = 0, х=А.
х3 * * 1
с) у=±._±1пх; х=1. х = 2.
d) _у = 1пх; х = 1, х = 4,
е) V = In see х; х = 0, х = •
3
0 у = In sec х; х= , х = у .
§ 57. Длина дуги кривой в полярных координатах. За элемент ds дуги АВ (черт. 46) мы принимаем гипотенузу прямоугольного треугольника, один катет которого равен pd6, г другой равен dp, т. е. выражение:
ЛВ _____________ г----------
Л. . у(р<*>)’+№)’=j/ ра+(^)
Поэтому искомая длина 5 кривой дуги АВ дается формулой:
ь _____________
s = Ayra АВ- J Р’ + (^)’Л о a
Черт. 46. Здесь уравнение заданной кривой пред-
полагается написанным в виде:
Р=/(6)-
Замечание. Легко вывести формулу длины дуги кривой, заданной уравнением ₽ =/(?). у
также следующим образом. Так как *
ь I
s =fds. * (IV)
a
то, переходя к полярным координатам, получим:
(dy)3 = (dx)2 + «у)3; х = р cos у = р sin ?.
Значит:
dx = cos f dp — p sin ? df, dy = sin dp -J- p сов <p d<p.
i) Треугольник, отмеченный на чертеже, криволинейный, потому что две его
стороны — кривые линии. Но если соединить прямыми все три его вершины, то
получится обыкновенный треугольник, стороны которого будут отличаться от pdf,
dp и У(р dtf + (df J2 лишь на бесконечно малое высшего порядка сравнитель-
но с df.
Значит:
(ds)2 = (cos ? dp — р Sin tp dp)3 4- (sin P dp j- p COS ? iff}2 =
xscos2 <p (dp)3—2p sin f cos p dp dy + p3 sin3 <p (dp)2 + sin p(dp)2 + 2? sin p cos p d? dp 4~
+ p3 cos3 p (dp)3 = (dp)3 4- (p dp)2.
Следовательно ь ®
s = j ds = fV (d?)- 4- (p dp)3 о Pi
или
r.
s=J'V ™
Pl
Пример. Найти длину кардиоиды р = л(1 4- cos6).
Решение. Здесь ~ = — я sin fl.
Изменяя 0 от 0 до я, мы заставим точку Р (черт. 47) описать половину кривой. Подставляя в (V), найдем:
J [а3 (1 4-cos Г)3 4-л3 sin3 flfdfl = лу (2 4- - cos 0) d()=2a cosydfl = 4a. о o' 6 .
Отсюда
s = 8л.
1
УПРАЖНЕНИЯ.
I. Найти длину спирали Архимеда, р = вО, от начала до конца первого завитка.
Отв. г.а угГ+4^34-4 In (2- 4- /1 + 4*2).
2. Спрямить спираль р = е"' от начала до точки
Отв.
• а
3. Найти всю длину кривой p = esin;i -. Ошв. 4у-л.
о Л
4. Найти длину окружности круга p = 2rsinfl. Отв. 2кг.
5. Найти мину гиперболической спирали рв = а от (р(| 0t) до (р№ в.,).
Отв. V&+И - р? + в I" -р--(а+ .
* h(e 4' а~ + ₽••)"
6. Найти длину дуги циссоиды р —2atgflsln0 от 0 = 0 до 0 = -^-«
Отв. 2а / У 5 - 2 - V 3 In —? .-3^--1
I / 2(2 r /3)1 •
7. Найти дайну дуги параболы р = л sec3 от 0 = — у до в = -у.
/ 7; 3 \
Отв. 2л ^scc у 4- inig - xj’
Н Зав. SI5S. — Граовль ж Луша, ч. II, Ижтвгральвос всяжслеша
8. Показать, что вся длина эпициклоиды 4(р2 — о2)3 = 27a4p2sin26, вычерчи
ваемой точкою круга радиуса у, катящегося по неподвижному кругу радиуса а, равна 12а.
9. Показать, что длина всей кривой р = а sin3-я-равна -у- н что длины отрезков ОА, АВ, ВС образуют арифметическую прогрессию (черт. 48).
§ 58. Поверхность тела вращения. За элемент dS поверхности АВВ^А^ тела вращения мы
принимаем боковую поверхность усеченного круглого конуса, образую-
щая которого равна элементу ds дуги, а радиусы оснований равны у. Следовательно, по теореме
боковая поверхность усеченного круглого конуса равна полусумме окружностей обоих оснований, умноженной на образующую мы имеем для элемента dS выражение:
2nydS или
2-_у /1 -|-yatfx.
Отсюда следует, что искомая поверхность S тела вращения А1АВВ1 дается формулой:
S = поверхность AvABBt = ь
=2к У* J У1+У’</х. (VI)
а
Здесь уравнение вращающейся кривой предполагается написанным
Черт. 50.
в виде:
J =/(•«)•
Пример. Найти площадь поверхности вращения, производимой вращением гипо-» > ?
циклоиды х =а вокруг оси ОХ.
Решение. Здесь
dx
Подставляя в (VI) н замечая, что дуга ВА произведет только половину искомой поверхности (черт. 50), имеем:
£
2
= 2к
о
1 л/ 2 2.V 1 л
•= 2кд* J —ха/ах ,з rfx = — яда. о
Следовательно:
S = ¥*a
О
УПРАЖНЕНИЯ.
1. Найти поверхность шара, производимого вращением круга хг + у2 = тч вокруг диаметра. Qme
2. Найти площадь поверхности, производимой вращением параболы у2 4дх вокруг ОХ, от начала до точки, в которой х = За.
Отв.
3. Найти интегрированием площадь поверхности конуса, производимого вращением вокруг оси ОХ прямой, соединяющей начало с точкою (д, Ь).
4. Найти интегрированием площадь боковой поверхности конуса, образуемого вращением отрезка прямой у = 2х от х = 0 до х — 2: а) вокруг оси ОХ\ Ь) вокруг оси ОУ.
5. Найти интегрированием площадь боковой поверхности цилиндра, образуемого вращением отреака прямой х = 4 оту = 0 до у = 6 вокруг оси ОУ.
6. Найти интегрированием площадь боковой поверхности усеченного конуса, образуемого вращением вокруг оси ОХ отрезка прямой 2у = х-~ 4отх = 0 до х = 3.
7. Параболические зеркала и рефлекторы имеют форму поверхности параболоида вращения. Найти площадь поверхности такого зеркала, если известно, что диаметр его наибольшего поперечного сечения (перпендикулярного оси вращения) равен 6 м, а отрезок оси от вершины до этого поперечного сечения 2 м. 4g
Отв. — к кв. м.
4
8. Найти поверхность тора, производимого вращением круга х3 4- (у — б)2 = а3 вокруг оси ОХ. Отв 4K.ab
Указание. Положительное значение У д'- — х3 дает внешнюю поверхность, а отрицательное — внутреннюю.
9. Вычислить поверхность, производимую вращением цепной линии
а 2
а . «
е 4-е
вокруг оси ОХ от х = 0 до х = а.
Отв. ?— (е2 — с~- -1- 4).
10. Найти поверхность, производимую вращением кардиоиды ' х = а (2 cos в — cos 20), 1
' у = а (2 sin в. — sta 20), J
вокруг осн ОХ
Отв. 125 шД О
11. Показать, что поверхность, производимая вращением циклоиды
х = а (0 — sin 0), у = а (1 — cos Ь)
64
вокруг оси ОХравна -х-г.а-, а вокруг оси ОУ равна 16г.2я2. О
12. Показать, что поверхность, производимая вращением крисой х* + 3 = 6х\) вокруг оси ОУ от х = 1 до х = 2, равна п^+,п2)« а вокруг оси ОХ 47 равна я.
10
13. Показать, что поверхность, производимая вращением кубической параболы у = х3 вокруг оси ОХ от х = 0 до х = 1, есть
1
2к У* V 1+9x<-.’rfx = ^(/ПЮО—1). о
14. Показать, что если криву ю уг 4- 4х = 21пу вращать вокруг осн ОХ от у = 1 до у = 2, то произведенная поверхность равна п.
«5
15. Найти площадь поверхности, образуемой вращением вокруг оси ОХ дуги каждой из следующих кривых:
а) у = е ®, от х = 0 до х = со.
Ь) Петли кривой 9ду2 = х (Зе — х)'-.
с) 6я2х> = х* Ц- За*, от х = а до х = 2а.
d) Петли кривой Яя2^2 = а-х- — х*.
е) у = ех, от х = — оо до х = 0. () у 2х = 4, от х = 0 до х = 2.
g) Зу — 6х = 6, от х = 0 до х = 2. h) х2 +4^ = 16.
Отв z । / 2-|-In (1 + /2)]. 3-я2.
47 16 ™2 4 ‘
«I / 24 In (1 /2)].
i) Ox-'4-/= 36.
j) у- = 9x, от x = 0 до х = 1.
16. Найти площадь поверхности, образуемой жеследующих кривых вокруг оси О У:
вращением дуги каждой из ни-
а) х 4- ty = 6, от у = 0 до у = 3.
Ь) Зх 4- 2у = 12, от у = 0 до у = 4. с) х2 = 4у, от у = 0 до у = 3.
Ъ) х2416у2=16.
е) 4х2-Ьу-’ = 100.
f) Зх = у’, от у = 0 до у = 1.
g) х = у8, от у = 0 до у = 3.
Отв.
J(730)2 -l
h) 6а2ху = х4 — За*, от х = а до х = Зя.
1) 4у = х2 — 21пх, от х = 1 до х — 4.
j) 2у = х /х« — 1 4- In (х — /х- — 1), от
(20 4- In 3) г.я».
24 z.
х = 2 до х = 5. 78-.
17. Найти площадь поверхности, образуемой вращением дуги каждой из нижеследующих кривых: 1) вокруг оси ОХ\ 2) вокруг оси ОУ:
Вокруг оси ОХ Вокруг оси ОУ
_у2 у2 2гдЛ 1 -I- с
а) эллипс —4-75= !• Отв. 2кЬ24----------------arcsine 2пд24--------In
(1 € С \ €
У дз —£4
Указание. е =---------------(эксцентриситет эллипса).
Ь) л = е’sin 0, х 2 - 4г .
у = е® cos О, от 0 = 0 до 0 = у . | 5 (е у (2« + 1)
с) Зх-’ + 4уг = ЗА + (1 + 3 Щ 3)
<1) х 'Ну — 4. от х — 0 до х — 4.
е) у = 2.V + 4, от у = 4 до у <= 8.
I) х24-2у2=16.
§ 59. Определение объема тела по площади поперечного сечения, заданной как функция расстояния от неподвижной точки. В § 55 было показано, каким образом вычисляется объем тела вращения посредством простого интегрирования. Очевидно, тело вращения можно рассматривать как образованное движущимся кругом, центр которого лежи’ на оси вращения, а плоскость круга к ней перпенди
кулярна, причем радиус круга изменяется. Так, на черт. 51 можно предположить, что круг ACBD, плоскость которого перпендикулярна ОХ, производит тело вращения OEGFH, в, то время как центр его движется от О к JV, а радиус МС (= _у) непрерывно изменяется с изменением ОМ (= х) по закону, определяемому уравнением плоской кривой, вращением которой можно произвести это тело.
Покажем теперь, каким образом можно приложить эту мысль к вычислению объемов тел, не представляющих собою тел вращения, когда возможно площади параллельных плоских сечений тела представить функциями их расстояний от неподвижной точки.
Разобьем тело, изображенное на черт. 52, на п слоев плоскостями, перпендикулярными оси ОХ, и примем начало координат за упомянутую выше неподвижную точку. Пусть FDE есть одно из сечений тела. Построим на этом сечении прямую призму, второе основание которой лежит на следующем сечении тела.
Так как по предположению площадь сечения FDE есть функция ON, т. е. х, обозначим эту площадь через / (х), и пусть Ах есть высота призмы.
Следовательно, /(х)Дх есть элемент объема V призмы, и искомый объем V есть предел суммы объемов призм при неограниченном возрастании числа делений п при условии, что все Дх стремятся к нулю. Таким образом получаем:
п к
V= lim S /(х.)Дх,= / /(x)dx. (VII)
Очевидно, что тело ОАВС (черт. 52) можно рассматривать как тело, образованное сечением DEF, перемещающимся непрерывно при изменении х от 0 до ОМ. Нижеследующие примеры служат иллюстрацией этой идеи.
Пример 1. Вычислить объем эллипсоида
- 4- — Ч - — = 1 v а1'Ьг'с- *
посредством одного интегрирования.
Решение. Рассмотрим сечение эллипсоида, перпендикулярное к ОХ, например ABCD (черт. 53), имеющее полуоси Ь' и с’. Уравнение эллипса НЕЮ в плоскости XOY есть - 2
- 4- — = 1.
Решая его относительно у (= 6') в функции х ( = ОМ), имеем: b' = — V а- — х-. а
Подобным образом уравнение эллипса EFGI в плоскости XOZ дает:
а
Отсюда площадь сечения по эллипсу ABCD будет:
т.Ъс
r.b'c' = -^(.a2-x*)=f(x).
Подставив в (VII), имеем:
V
л
:2) dx = — r.abc,
«э
—а
Итак, на эллипсоид можно смотреть так, как будто он произведен переменным эллипсом ABCD, движущимся от О к Е, причем центр его все время находится на ОХ, а плоскость его остается перпендикулярной к этой оси.
Пример 2. Найти объем прямого коноида ]) с круглым основанием, если радиус основания есть г, а высота а.
Решение. Расположив оси коордйнат, как показано на черт. 54, рассмотрим сечение PQR, Перпендикулярное ОХ. Это сечение есть равнобедренный треугольник, а так как
RM=V2rx — л ’ (что находим, решая относительно у уравнение х2 +у- = 2гх круга ORAQ) и
МР<=а, то площадь этого сечения будет: a V2rxх2 = f (х). Подстановка в (VII) даст: тг
V = а / у 2rx — x2dx = -^ r.r2a. о
Это — как раз половина объема цилиндра с теми же основанием и высотою.
1) Рассматривая приложенное решение этрй задачи, читатель легко поймет,
каково определение коноида
УПРАЖНЕНИЯ.
1. Точка пересечения диагоналей квадрата перемещается вдоль диаметра круга радиуса а; при этом плоское .. в которой лежит квадрат, все время остается перпендикулярной плоскости круга, а две противоположные вершины квадрата перемещаются по окружности. Найти объем тела, образуемого этим движущимся квадратом. g
Отв. — а*.
О
2. Равносторонний треугольник перемещается так, что плоскость, в которой он лежит, все время остается перпендикулярной оси ОХ, а вершины основания движутся соответственно вдоль ветвей парабол у2 = 16лх и у2 = 4a.v, расположенных над осью ОХ. Найти объем тела, образующегося движущимся треугольником, если он перемещается от начала координат до точки, абсцисса которой равна а. .—
Отв. а8.
3. Прямоугольник перемешается от некоторой точки по направлению, перпендикулярному плоскости, в которой он лежит, таким образом, что одна из непараллельных сторон прямоугольника все время остается равной {расстоянию от этой точки, а другая — квадрату этого расстояния. Найти объем тела, образуемого движущимся прямоугольником, при перемещении его на 2 м.
I Отв. 4 ж3.
4. Равнобедренный прямоугольный треугольник перемещается от одного конца большой оси эллипса — 4-^=1 до другого, так что концы гипотенузы движутся по этому эллипсу; плоскость, в которой лежит прямоугольник, все время остается перпендикулярной оси эллипса. Найти объем тела, образуемого движущимся треугольником.
Отв. -3-.
5. На двойной ординате гипоциклоиды
2 2 г_
х® ya = а8
как на основании построен равнобедренный треугольник, высота которого равна ординате и который лежит в плоскости, перпендикулярной плоскости гипоциклоиды. Найти объем тела, образуемого этим треугольником, при перемещении его от х = — а, до х = а. о»
Опта. ^л8.
6. Окружность перемещается таким образом, что одна из его точек остается АС®
все время на оси OY, центр описывает эллипс — 4-р = 1. а плоскость, в которой лежит окружность, все время перпендикулярнз осЛОК. Найти объем тела, описываемого окружностью. «
Отв. -= пдяб.
О
§ 60. Центр тяжести. Напомним сперва несколько основных положений механики.
1. Равнодействующая нескольких параллельных сил равна сумме этих сил.
2. Моментом силы относительно оси, перпендикулярной направлению силы, называется произведение силы на расстояние от оси до линии действия силы.
3. Момент равнодействующей нескольких сил равен сумме моментов отдельных сил.
Рассмотрим систему п материальных точек:
Л(х„ J,). j2)......Р„(х„, у„),
расположенных в плоскости XOY (черт. 55).
Пусть т{, т2, ..., тп— массы этих точек. Веса этих точек образуют систему параллельных сил mxg, m.,g, ..., m,.g, где g—ускорение силы тяжести. Согласно вышеуказанному положению механики равнодей-
ствующая этих сил
Черт. 55.
t п
№=™£-\-"г£-г . . . +mng=g2i mt. i=l
Действие этой равнодействующей силы будет направлено по прямой, параллельной силе тяжести, которая пройдет через точку с абсциссой, определяемой из условия, что момент силы UZ относительно оси, проходящей через начало координат О перпендикулярно плоскости XOY, равен сумме
моментов составляющих сил т£{.
Предположим сперва, что сила тяжести направлена параллельно оси О Y. Обозначим абсциссу точки пересечения прямой, по которой направлена равнодействующая 1Г, с осью ОХ через х. Тогда момент силы U7 относительно упомянутой оси есть gx S mt, а силы — произведение Следовательно:
gxSm, = gSmlXi.
Аналогично, если сила тяжести имеет направление, параллельное оси ОХ, и если у есть ордината точки пересечения прямой, по которой направлена равнодействующая, то
gyS
Эти две прямые пересекаются в точке О, координаты которой, следовательно, определяются формулами:
- - S
Sm, ’ Smt
Более того, если направление силы тяжести лежит в плоскости ХО Y, но не совпадает ни с направлением оси ОХ, ни оси OY, то равнодействующая направлена по прямой, проходящей через точку G. Это можно доказать, раскладывая силу Тяжести каждой точки на две силы, параллельные соответственно оси ОХ и оси OY, находя равнодействующую каждой из этих двух систем сил и складывая, наконец, эти две равнодействующие.
Точка G называется центром тяжести системы п материальных точек.
Нахождение центра тяжести линии, поверхности или тала основано на следующем методе.
Представим себе фигуру, центр тяжести которой мы ищем, разбитой на п малых элементарных частей, вес каждой из которых считаем приложенным в некоторой точке этой части. Если т—масса всей фигуры,
то масса элементарной части может быть обозначена через Лот. Тогда, если (х„ yt) — координаты точки, в которой сосредоточена масса /-го элемента, то координаты центра тяжести определятся, очевидно, переходом к пределу:
- S хЛт, - SуДпч
х — lim , V = Inn -ь-4--- ,
S дш S Л/н
Т. Г.
_ / xdni /у dm
- = , у = =4— • (VIII)
J dm у dm
v
Чтобы вычислить интегралы, входящие в полученные формулы, подинтегральные выражения должны быть выражены через одно переменное. Пределы интегрирования определяются конкретными условиями задачи.
Пример 1. Найти центр тяжести четверти окружности х--~у2 = а2, расположенной в первом квадранте.
Решение. Разбиваем дугу окружности на п частей ds (черт. 56); обозначив через р линейную плотность кривой, получим: dm = р ds. Следовательно: _ f'.xds _ fpvds Х=-—----------------------, у — • .
- j р ds J ь ds
Считая плотность постоянной, выносим р за знаки интегралов н сокращаем. Тогда знамеватедь каждой дроби становится равным просто г. Чтобы вычислить числители, применяем известную формулу:
ds = V [dxY + (tfy)' = у dx = - у dy, причем за начало отсчета длины дуги s принимаем точку А; личина положительная, a dy — отрицательная.
Следовательно: с п
j .V as = —f ady — a2. j"yds - j a dx = a-a b
и ( Ча J^=T‘ Таким образом получаем:
Черт. 5G.
тогда dx есть ье-
Пример 2. Найти центр тяжести четверти окружности примера 1 при условии, что линейная плотность дуги изменяется пропорционально длине дуги.
Решение. В этом случае.
dт — xs ds.
Для того чтобы легче выполнить интегрирование, воспользуемся уравнениями окружности в параметрической форме:
х = a cos f, у = а Яп ф.
J) Под линейной плотностью подразумевается Отношение массы точек, по-крььающиж дугу, к длине ее.
Тогда получим: а 7 f в»? cos ? rf?
- I^ds „ 4-_ 8
х = ' ----------------•-= —5— а,
J ** у | a2pd<f и о г . ( а»? sin? <7?
_ _ | sv ds _ __ 8д
} I s ds — г--
J 2,
J eflydy о
Пример 3. Найти центр тяжести плошали, ограниченной параболой у* “ Арх, осью ОХ и ординатой точки (Л, k) кривой (черт. 57).
Решение. Обозначая поверхностную плотность площади через р, будем иметь*.
dm — ру dx, и эту массу можно рассматривать сосредоточенной в точке ^х, элементарной < пдошадн.
Тогда
а о
Считая плотность р постоянной и выражая у через х, из уравнения кривой получаем:
* 2 h‘ А. . £ з
J ху dx *=Чр - ! х * dx = -ур * Л 2 = уЛ5А, о и
h h
у J’уг dx = Ip J x dx = р№= у AA2 u c
и
Г -Г - 4 2
I ydx = 1p'1 / xl dx= —p^ k1 =-^hk, и Q
Следовательно:
-3.-3.
Л=-5Л( У=ьк jpS у*
Пример 4. Найти центр тяжести сегмента эллипса + = 1. ограничен*
ного хордой, проходящей черев.концы полуосей эллипса (черт. 58).
Решение. Разбиваем сегмент прамыми, параллельными оси ОУ, на п элементов. Если уг — ордината точки эллипса, уг — ордината точки хорды, то элемент площади будет равен произведению (уг — yt)dx. и поэтому
</л1 = р(у2-Л)</х.
Положим поверхностную плотность равной р = const. Масса этого элемента может быть представлена сосредоточенной в точке
Следовательно:
а
f (У1~У1)*4х
Г (Л-Л)Лг о
Из уравнения эллипса имеем:
* = 1 и из уравнения хорды:
<*
Знаменатель J есть величина площади четверти эллипса без
о
I nab ab
площади треугольника, т. е. ---
Следовательно: а / х[/а» —х« — (а — x)]dx - _ о_________________________________________2а
А аб(«—!Л 7 3(я—2)’
к 4 2?
Пример 5. Найти центр тяжести сферического сегмента, образованного вращением площади BDE (черт. 59) вокруг оси ОУ, причем известно, что ОВ — а и ОЕ = с.
Решение. Разобьем сегмент плоскостями, перпендикулярными оси ОУ, на л элементарных объемов. Объем элемента равен ях* dy, и поэтому
dm » рях* dy (р = const.).
Массу этого элемента можно представить себе сосредоточенной в точке (0, у/), т. е. в центре основания элементе. Следовательно, абсцисса центра тяжести сегмента х = О, а ордината
а а
f У ((•"хг dy) I (о2У — у3) dy
о_____________ = е__________________з (а 4- с>=
“ — <» ~ 4 2а 4- с
j'p-.xdy J(a3 — y!)dy
о с
Пример 6. Найти центр тяжести поверхности сферического сегмента примера 5.
Решение. Разбиваем поверхность на элементы плоскостями, перпендикулярными осн OY. Тогда площадь элемента поверхности будет равна 2кх ds, и
dm = 2rpx ds (р = const.).
Массу этого элемента мои.по считать сосредоточенной в точке (0, у); из . , a d •
уравнения окружности найдем: ds = - , и, следовательно:
с
УПРАЖНЕНИЯ 1).
1. Найти центр тяжести полуокружности х24-уг = а3, расположенной над ОСЬЮ ОХ. , г)п .
Ота. 10,-^).
2 2 2
2. Найти центр тяжести дуги гипоциклоиды х 3 +j’J = а а , расположенной вад осью ОХ. , .
о~. (о. £).
3. Найти центр тяжести площади параболического сегмента.
3 Отв. На осн параболы, на расстоянии -т- высоты сегмента, считая и
от вершины параболы.
4. Найти центр тяжести площади треугольника.
Отв. Точка пересечения медиан.
5. Найти центр тяжести площади четверти эллипса.
О- (£. £)•
6. Найти центр тяжести площади, ограниченной полукубической параболой оу2==х3 и двойной произвольной ординатой.
Отв. , о), где * = й — уравнение ординаты.
1) в задачах, в которых ничего не говорится о плотности, предполагается, что плотность постоянна.
7. Найти центр тяжести площади, ограниченной параболой х* -|- 4у — 16 - о и осью ОХ. „
Отв. (О. А).
8. Найти центр тяжести полушара.
Отв. Центр тяжести лежит на радиусе, перпендикулярном осно-3 ванию, на высоте — расстэя-
• о
вия от основания.
9. Найти центр тяжести тела, образованного вращением вокруг оси ОУ V- у-
фигуры, ограниченной гиперболой — фг = 1 и прямыми у = 0, у = Ь.
Отв. у = £-к.
10
10. Найти центр тяжести поверхности половины шара.
Отв. В середине оси.
11. Найти центр тяжести поверхности прямого кругового конуса.
Отв. На оси, на высоте расстояния от основания.
12. Найти центр тяжести площади, ограниченной дугой синусоиды н отрезком оси ОХ от х = 0 до х = к.
Отв.
13. Найти центр тяжести площади, заключенной между параболой 1 1 1
.г 2 + у 2 =а 3 и осями координат.
Отв. :.
\ о О J
14. Найти центр тяжести дуги цепной линии “)от точки
имеющей абсциссу х = 0, до точки, абсцисса которой х = а.
Отв. +
\ е + 1 (е- — 1) )
15. Найти центр тяжести тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболой у2 = Арх, осью ОХ и прямой х = а.
Отв. х = ~. и
16. Найти центр тяжести площади, ограниченной параболами у- = 20/ и х5 = 20у. Отв (9>
17. Найти центр тяжести площади, ограниченной параболой у3 = 4х, осью ОУ и прямой у = 4.
Отв.
18. Найти центр тяжести тела, образованного вращением вокруг оси OY фигуры, ограниченной параболой уг = Арх, осью ОУ и прямой у = к.
п - 5 ь
Отв. у = — к.
О
4-.’
19, Найти центр тяжести поверхности полушара, если плотность в точке поверхности пропорциональна расстоянию точки от основания полушара.
2 Отв. На осн, на высоте — расстояния от основания.
О
20. Найти центр тяжести площади гипоциклоиды х = а cos’ij, у = а sin3?, содержащейся в первом квадранте.
_ / 256а 256а \
Отв. ,1С -, '
\ 315- 315п 7
• X2 Iй
21. Найти центр тяжести площади, ограниченной эллипсом = 1.
окружностью лг» + >а = а» и осью OY. . 4а 4 (d _|_
‘ \ Зт: ’ Зк / ’
22. Найти центр тяжести площади, общей для параболы х- — 8у = 0 и окружности х3-J-v*—128 = 0. , .
Отв' (°* 5(2 + Зп))-
23. Найти центр тяжести площади, ограниченной одной дугой циклоиды х = a (t — sin /), У = о (1 — cos Q и осью ОХ. . с .
24. Найти центр тяжести дуги циклоиды х = a (t — sin t),,у = а (1 — cos/) между первыми двумя точками циклоиды, лежащими нс оси ОХ.
Отв. ^ка, у а .
25. Найти центр тяжести тела, образованного вращением вокруг оси ОХ фигуры, ограниченной параболой у- = 4х и прямой х = й, если плотность тела в точке (х, у) равна —.
Х z, - й
Отв. х = -7J-.
26. Найти центр тяжести площади, ограниченной окружностями х3+у! = а; x3+j^ — 2ах = 0 и осью ОХ. . д 5д .
Отв. _ 3 /3) / ’
27. Показать, что центр тяжести кругового сектора лежит на биссектрисе
2 “ПТ центрального угла а, на расстоянии —а-------от вершины (а — радиус круга).
У
28. Найти центр тяжести плошали, ограниченной параболами х3 — Др (у — й)=0,’ л-,— 4ру = 0, осью OY и прямой х = а. fab а3 \
(Т’ I +12?)’
29. :Найти центр тяжести дуги кривой Эау3 — х (х — За)2 = 0, заключенной между ординатами х = 0 и х = 8а. , -
30. Найти центр тяжести поверхности шарового слоя, заключенного между параллельными плоскостями, проходящими на расстояниях й( и й, от центра шара.
Отв. На диаметре шара, перпендикулярном основаниям слоя, на середине расстояния между основаниями.
31. Найти центр тяжести тела, образованного вращением вокруг оси ОУ фигуры, ограниченной параболой x* = 4ру и произвольной прямой, проходящей через вершину параболы. Qmi На середжне отрезка оси вращения.
32. Найти центр тяжести поверхности, образованной вращением вокруг полярной оси одной петли лемнискаты г* = 2а2 cos 26.
Отв. (V”3+ 1).
О
33. Показать, что площадь поверхности, образуемой вращением дуги плоской кривой вокруг оси, лежащей в плоскости кривой, равна проивведению длины дуги кривой на длину окружности, описываемой центром тяжести дуги вращающейся кривой.
34. Показать, что объем тела, образуемого вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры, равен произведению площади фигуры на длину окружности, описываемой центром тяжести площади фигуры.
§ 61. Давление ЖИДКОСТИ. Перейдем теперь к рассмотрению во-
проса о вычислении величины давления жидкости на вертикальную пла-
стинку, погруженную в жидкость.
Предположим, что ABCD (черт. 60) представляет часть вертикальной пластинки, например часть вертикальной стенки резервуара, наполненного жидкостью. Требуется вычислить величину давления жидкости на эту площадку. Расположим оси координат, как указано на черт. 60, где ось OY выбрана совпадающей с уровнем жидкости. Разделим отрезок АВ на п небольших интервалов и построим п прямоугольников, как это сделано на черт. 60. Площадь одного прямоугольника (например прямоугольника ЕР) равна у • &х. ^сли бы этот прямоугольник был расположен на глубине X, считая от уровня жидкости
ния жидкости на прямоугольник была бы равна
в горизонтальной плоскости в сосуде, то величина давле-
* wxy Ьх >),
где w — вес единицы объема жидкости. Так как давление жидкости во вс» стороны одинаково, то отсюда следует, что wxy&x есть элементарное давление на пластинку. Следовательно, величин давления Р на пластинку ABCD будет равна:
п
Ъ
Р = lim S = w
j xydx. а
(IX)
Для фактического вычисления по формуле .(IX) следует выразить у как функцию х из уравнения кривой CD, ограничивающей пластинку.
В дальнейшем вес кубического метра воды будем считать равным 1000 кг {=w).
>) Давление жидкости на горизонтальную площадку равно весу столба жидкости, имеющего эту площадку своим основанием и высотой — расстояние площадки от свободной поверхности жидкости.
Пример. Труба лежащая горизонтально, поперечным сечением которой яв ляется круг диаметра 6 м, наполовину наполнена водой. Найти величину давле* ния воды на вертикальную заслонку, закрывающую трубу.
Решение. Уравнение окружности есть
Л* + =; 9.
Следовательно, v = 1^9 — ла; IF = 1000, и пределы интегрирования суть л = 0 и b = 3.
Подставляя эти значения в формулу (IX), получим величину давления па вертикальную часть заслонки, расположенную ^вправо от оси ОХ (черт. 61).
Черт. 61. Р = 2 9000 = 18 000 кг,
УПРАЖНЕНИЯ.
1. Найти давление, испытываемое прямоугольником, вертикально по груженным в воду, если известно, что основание его равно 8 .и, высота 12 м верхнее основание параллельно свободной поверхности воды и находится на глубине 5 м. Отв 105б т
2. Равносторонний треугольник, сторона которого равна 4 м, вертикально погружен в воду, так что одна из его сторон лежит на поверхности воды. Определить величину давления воды на площадь этого треугольника.
Отв. 8000 кг.
& Найти величину давления на площадь треугольника, основание которого равно 10 м, высота 4.к, погруженного вводу таким образом, что основание его параллельно свободной поверхности воды, высота расположена вертикально, и вершина лежит на поверхности воды. ।
Отв. 53 — т.
О
4. Найти величину давления, на площадь треугольника, основание которого равно 8 м, высота — 6 м, погруженного в воду таким образом, что основание его лежит ниже вершины и параллельно свободной поверхности воды, высота расположена вертикально, и вершина находится на глубине 3 м.
Отв. 168 т.
5. Верхний край шлюза, имеющего форму квадрата со стороной, равной 8 м лежит на поверхности воды. Определить величину давления на каждую нз частей шлюза, образуемую делением квадрата одной из его диагоналей.
Отв. 85 333,33 кг и 170666,67 кг.
6. Плотина имеет форму трапеции, две горизонтальные стороны которой имеют соответственно 400 м и 100 м, а высота равна 20 м Верхнее, более длинное, основание лежит на^ровне свободной поверхности воды. Найти величину давления на плотину. ,
Отв. 4233 — т.
О
7. Цилиндрический бак, лежащий горизонтально на земле, наполовину наполнен маслом. Вертикальная плоская стенка бака имеет диаметр, равный 4 м. Удельный вес масла равен 0,9. Определить величину давления на каждую из плоских вертикальных стенок бака.
Отв. 4800 кг.
8. Металлический щит, имеющий форму параболического сегмента, ограниченного хордой, перпендикулярной оси параболы, погружен в воду. Вершина сегмента лежит на поверхности воды. Высота сегмента равна 20 м и ширина 12 ж. Найти величину давления на щит.
9. На какую глубину надо опустеть щит примера 8, чтобы величина давления удвоилась? Отв 12 м
10. Резервуар, поперечное сечёфяе которого имеет форму половины эллипса, глубнной 2 м и шириной 2 м доверху наполнен водой. Найти величину давления, производимого водой на одет из плоских вертикальных стенок резервуара.
? Отв. 2666,27 кг.
11. Найти величину давления taa пластинку, ограниченную дугой синусоиды и прямой, соединяющей концы дуги, если пластинка вертикально погружена в жидкость, так что прямая, ограничивающая пластинку, лежит на поверхности воды.
Л 1
Отв. юв, где ш — удельный вес жидкости.
12. Найти величину давления на поверхность шара, имеющего диаметр, равный 6 м, если шар погружен в воду так, что его центр находится на Шубине 10 м относительно свободной поверхности воды.
Отв. 360 000ч кг.
Указание. Величина давления равна
+»
• 2kw | _y(10-rx)rfs
— з
§ 62. Работа. Если величина силы, действующей по направлению движения, постоянна, то под работой, произведенной силой, подразумевают произведение силы на путь —s0, пройденный материальной точкой, где обозначает конечную, a s0—начальную точку движения. Если сила переменная, то работа может быть определена только с помощью предельного перехода. Мы разбиваем весь отрезок пути от £0 до 5, на п частей и предполагаем, что в каждом частичном небольшом интервале сила имеет постоянное значение, например то значение, какое она принимает в некоторой произвольно взятой точке 5 этого интервала. Тогда произведение f (s) ds дает нам элементарную работу, а полная работа W, произведенная силой, выразится так:
* .?
IF= lim S f (?) ds = / f(s)ds. (X)
Если направление действующей силы совпадает с направлением движения, то произведенная работа положительна (положительно затраченная работа); в противоположном случае работа отрицательна (приобретенная работа).
Пример. Вычислить работу, производимую при растягивании пружины на 5 см, если известно, что сила, которая требуется для растяжения пружины, пропорциональна удлинению х пружины и что для удлинения пружины на 1 см требуется сила, равная 1 кг.
Решение. Действующая сила в настоящем примере равна, очевидно, kx. Так как для удлинения пружины на 1 см требуется сила в 1 кг, то при х = 1
12 3®к. 2ЯЬЗ. — ГрФппиль и Лузин, я. П, Пыгегрвльвое исчжспенпо
сила kx = k • 0,01 = 1, откуда k =100. Пружина растягивается от положения равновесия х0 = 0 до конечного положения xt = 0,05. Следовательно, по фор* муле (X) будем иметь:
0,ОБ
W= f 100х rfx = 50 [x2J*’°5 = 0,125кг-я. О
Рассмотрим в частности работу, производимую весом жидкости при выливании жидкости из сосуда, представляющего собой тело вращения.
Возьмем какой-нибудь сосуд, наполненный жидкостью, например такой, как изображено па черт. 62; в рассматриваемом случае оси координат удобно расположить так, как указано на этом чертеже, причем ось OY лежит в плоскости, ограничивающей сосуд сверху. Вычислим работу, производимую весом жидкости при опускании ее уровня от глубины а до глубины b (черт. 62).
Рассмотрим сечение резервуара плоскостью, перпендикулярной оси вращения, на расстоянии х от свободной поверхности жидкости. Площадь этого сечения равна ту*. На площадь рассматриваемой площадки действует вес столба жидкости, имеющего у площадку своим основанием и координату х высотой, т. е. сила wity^x, где w — вес единицы объема жидкости. Эта сила может быть представлена приложенной к центру тяжести площадки и действующей .по направлению оси вращения, т. е. оси ОХ. Поэтому сила f (х), фигурирующая в формуле (X), выразится теперь в виде куЧх, и искомая работа IF выразится формулой:
ь
(X*)
а
Для фактического вычисления интегралу надо у выразить в функции от х из уравнения кривой, образующей тело вращения.
Пример. Вычислить работу, необходимую для того, чтобы выкачать воду из полусферического сосуда, диаметр котороср равен 10 м (черт. 63).
Решение. Уравнение окружности есть
I, что
откуда у2 = 100 — х2. Вес кубического метра воды ш= 1000 кг, и пределы интеграла суть: в = 0, Ь = 10. Подставляя в формулу (X*), получаем:
ю
UZ = 1000л у (100 - x-i X dx = 2,5 • 10«я кг • м. о
УПРАЖНЕНИЯ.
работа, необходимая для того, чтобы растянуть металлическую проволоку длины а до длины а + х, пропорциональна ~ н что сила,
равная 4543,6 г, удлиняет проволоку длиною 90 см на 0,1 см. Найти работу* силы, которую необходимо произвести, чтобы растянут в проволоку длиною 90 см до длины 90,5 см. Ота 141 75 2. см>
2. Тело движется прямолинейно по закону х = efl, где х — длина пути, проходимого за время t. Сопротивление среды пропорционально квадрату скорости. Найти работу, производимую сопротивлением при передвижении тела от точки л- = 0 до точки х = о.
27 ’/----
Отв. — k у с-а1, где k — коэфициеит сопротивления.
3. Предполагая, что сила притяжения центром земли тела, находящегося ниже поверхности земли, пропорциональна расстоянию тела от центра, найти работу, которую необходимо произвести, чтобы перевести тело массы т от точки, находящейся на расстоянии а ниже поверхности земли, до поверхности.
/илг
Отв. (2аг — а-), где г—радиус земли g — ускорение силы тяжести.
4. Предполагая, что над землей сила притяжения обратно пропорциональна квадрату расстояния от центра земли, найти работу, которую необходимо произвести, чтобы поднять тело массы т с поверхности земли на расстояние а.
_ mgar
Отв. —, где г — радиус земли.
5. Резервуар, имеющий форму конуса, высота которого равна 12 м, наполнен жидкостью; удельный вес жидкости 1,3. Основание конуса представляет собой круг, имеющий 8 м в диаметре. Найти работу, производимую весом жидкости при опорожнении резервуара. Qmg 24g 60Q_ м
6. Найти работу, затрачиваемую при выкачивании воды из резервуара, имеющего форму половины эллипсоида вращения, наполненного водой. Верхнее основание резервуара представляет собой круг, диаметр которого равен 6 м. Глубина резервуара равна 5 м. Qmg 56250 м
Рассмотрим еще несколько примеров, характеризующих методы приложения интегрального исчисления.
Пример 1. С какою силою тонкий прямой однородный стержень всюду одинаковой толщины, имеющий длину / и массу М, притягивает материальную точку Р массы т (черт. 64), лежащую на продолжении линии стержня в ^расстоянии а от т ----
одного из концов стержня? р j ,. / Zj
Решение. Положим, что, стержень разделен на равные бесконечно малые части (эле- Черт. 64.
менты) длины dx.
М
-j- = массе единицы длины стержня; следовательно:
AJ
—j~ dx = массе одного элемента.
По ньютонову закону притяжения между любыми двумя массами const X произведение масс г (расстояние между ними)2
следовательно, сила притяжения между частицею Р и элементом стержня равна
-у- mdx
dx
. Мт о —-•
(х + а)-
где о = const, что и дает элемент искомой силы притяжения. Полное же притяжение между частицею Р и стержнем, будучи пределом суммы всех таких элементарных притяжений от х = 0 до х = /, будет:
/ . М 1
I В / т dx _ . Мт
J (х + ар I о о
Полагая в примере 1, что точка Р находится на перпендикуляре, восставленном к стержню, на расстоянии а от него, найти силу, с которой стержень притягивает точку. 2тМ I
Отв. J -—-— arctg -х— • al ° 2а
Пример 2. Сосуд, имеющий вид прямого круглого конуса (черт. 65), наполнен водою. Если высота его h, а радиус основания г, то сколько времени нужно будет, чтобы он сам собою опорожнился через отверстие площади а при его вершине?
Решение. Известно, что если пренебречь всеми осложняющими явление сопротивлениями, то скорость истечения через отверстие равна скорости, приобретаемой свободно падающим телом с высоты, равной глубине воды в сосуде. Следовательно, обозначая эту глубину буквою х, имеем:
V = Y 2gx.
Пусть в элемент времени dt вытекает объем dQ воды, Черт. 65. а соответствующее понижение поверхности назовем dx. В единицу времени вытекает из отверстия объем воды
а /2^, измеряемый прямым цилиндром, площадь основания которого есть а, а высота v( = Y2gx). Следовательно, в течение времени dt вытекает
dQ = а V2gx dt. (А)
Если обозначить буквою 5 площадь поверхности воды, когда глубина равна х, то по известной геометрической теореме
S xs с г.г2х2
пГ- Л- Л2
Но объем воды, вытекшей за время dt, можно также рассматривать как объем цилиндра АВ, у которого площадь основания равна S, а высота равна dx-, отсюда
nr^x^ dx dQ = Sdx<= • (В)
Приравнивая (А) и (В) и решая относительно dt, имеем* *
.. T.fix- dx dt =------,—u—,
ah2 К2gx
а потому
nr»x2 dx ah2 Y 2gx
2кг2 Y h
5a Y?g
Пример 3. Идеальный газ, заключенный в цилиндрический сосуд, закрытый подвижным поршнем, расширяясь, увеличивается в объеме, передвигая при этом поршень. Найти работу, совершаемую силой давления газа на поршень, если
известно, что объём газа увеличивается от величины Уп до Ц. Температуру предполагаем иеизменяюшейся.
Решение. Пусть с — площадь поперечного сечении сосуда. Если обозначим . , dv’
через dv приращение объема газа, то выражение --- даст соответствующую
приращению dv величину перемещения поршня. k
На основании закона Бойля-Мариотта имеем: pv = k = const, откуда Р= — kc
равно силе давления газа на единицу площади поршня, и Р = равно силе давления на всю площадь поршня. Следовательно, работа, соответствующая приращению объема dv, равна kc dx , .. .
—— • (сила давления X перемещение поршня),
откуда
/?**1 = *1п-^. J v vQ
к
ГЛАВА VIII.
КРАТНЫЕ ИНТЕГРАЛЫ.
ДВОЙНЫЕ ИНТЕГРАЛЫ. '
§ 63. Двухмерная интегральная сумма. Мы уже знаем, что интегральной суммой называется сумма
s -Ж) Ал-0Ч-/(М Да-! 4- • • • -!-/(£._,) 4- • • •
• • • +/('„_,) Да;,-!.
составляемая по следующему правилу:
Первый шаг. Делим данный отрезок [а, Ь} на п отрезочков:
(а, х,], [хр х2],..„ [х,..,, х,.].[хп_р Ь].
Второй шаг. Выбираем в каждом из этих п отрезочков произвольным образом по одной точке:
£Oi ^п- • • < S-p • • • ’ £»-i •
Третий шаг. Составляем п парных произведений /(Е (-1) • Дх<_р помножая длину отрезочка на коэфициент, равный величине данной непрерывной функции f(xj в выбранной точке этого отрезочка.
Четвертый шаг, Складываем полученные парные произведения все вместе.
Такие интегральны^ суммы мы будем теперь называть простыми или одномерными.
Совершенно по такому же правилу составляются двухмерные интегральные суммы, к рассмотрению которых нам и следует перейти.
Представим себе, что на плоскости XOY у нас имеется замкнутая кривая С, не пересекающая самое себя. Пусть внутри кривой С и на ней самой нам задана непрерывная функция /(х, у) двух независимых переменных х и у. Это значит, что всякой точке М (х, у), лежащей внутри С или на ней самой, отвечает вполне определенная численная величина рассматриваемой непрерывной функции / (х, у).
Определение. Двухмерной интегральной суммой называется сумма
Oo-HW . ох+ .. . -ЕН/И^) . ai_1 4- .. . +/(Ч.-!) • %-п составляемая по следующему правилу:
Первый шаг. Делим внутренность данного замкнутого контура С (черт. 66) на п площадочек а0, ар за, .... о„_,, которые перечисляем в каком угодно порядке.
Второй шаг. Выбираем в каждой из этих п площадочек по одной точке Мо, /И„ М2> - • • , Л),._р .... беря ее каждый раз где придется: внутри площадки или на ее контуре.
Третий шаг Составляем п парных произведений: / (Ч) • °о>W • • *2. • • ../(4-1) • °.-Р • • • -М-1) • %-1.
помножая всякий раз величинуплощади площадочки на коэфициент, равный ч и с л е н н о й в е л и ч и н е данной функции /(х, у), вычисленной в выбранной точке площадочки. Для удобства величину функции f (х, у) в Точке М (х, у) с координатами х ну мы обозначаем просто через
Четвертый шаг. Складываем все вместе полученные таким путем п парных произведений:
S=/(4) • »о+/(Ч) • vh • -+/(4-,) • °1_1+- • •+/ (4-1) •
Ясно, что для заданного контура С и для заданной внутри него непрерывной функции /(х, у) имеется не одна только интегральная сумма, но бесчисленное множество интегральных сумм S, потому что и внутренность контура С можно по-разному делить на площадочки, и по-разному можно в них выбирать по точке. Отсюда читатель видит, что численная величина интегральной суммы S зависит от двух обстоятельств:
1) от способа делить внутренность контура С на площадочки;
2) от выбора в этих площадочках по одной точке.
§ 64. Геометрический смысл двухмерной интегральной суммы. Мы видели, что простая (одномерная) интегральная сумма S имеет очень несложный геометрический смысл: это есть просто площадь ступенчатой фигуры, составленной из прямоугольников, имеющих своими основаниями отрезочки Дх0, ДХ].....Axn_P а высотами ординаты
• • •» / (’я-1) рассматриваемой непрерывной функции / (х) в выбранных точках Ео, Ер ..., (черт. 67).
ванне которого плоское
Черт. 68.
Совершенно аналогичное геометрическое истолкование имеет двухмерная интегральная сумма 3 -
Для этой цели мы проводим в трехмерном пространстве OXYZ (черт. 68) непрерывную поверхность, имеющую своим уравнением z=f(x,y),
где f (х, _у) как раз и есть заданная нам непрерывная функция внутри замкнутого контура С.
Этот последний лежит на плоскости XOY. Если мы через его точки проведем перпендикуляры к плоскости ХО Y, доводя их лишь до пересечения с нашею поверхностью и обрывая их на ней, мы получим большой цилиндр, образующие которого параллельны оси OZ, нижнее осно->енно вся внутренность плоского замкнутого контура С) н верхнее основание которого кривое (именно кусок нашей поверхности, ограниченной кривым замкнутым контуром СУ).
Но внутренность плоского контура С была нами ранее разделена на п малых площадочек о,, а„, Если мы
теперь в граничных точках каждой площадочки восстановим точно так же перпендикуляры к плоскости ХОY, доводя их лишь до пересечения с нашей поверхностью, мы будем иметь п тонких цилиндриков, образующие которых параллельны оси OZ. Нижними основаниями этих цилиндриков служат плоские площадочки а верхними основаниями— кривые кусочки нашей поверхно-эго контура С', начерченного, как сказано
выше, на поверхности. Ясно, что объем всего цилиндра в точности равен сумме п этих тонких цилиндриков.
Но раньше мы выбрали в каждой из плоских малых площадочек °о> °р °й. • • •» по одной точке Af0, Mlf М.„ ..., Af„_r Если мы теперь восставим в каждой из этих точек /И_, перпендикуляр к плоскости XOY, доводя его попрежнему лишь до пересечения с поверхностью, и если мы проведем через его конец, лежащий на этой поверхности, плоскость, параллельную горизонтальной плоскости XOY, мы получим цилиндрик, имеющий теперь уже оба своих основания плоскими и параллельными. Нижнее основание этого цилиндрика есть малая площадочка верхнее основание его по размерам и форме тождественно с площадочкой о,._ , только поднято на высоту, равную величине функции f (х, у) в выбранной точке Ж. ,, т. е. равную Образующие же нашего цилиндрика, разумеется, параллельны оси OZ, т. е. вертикальны.
Мы для удобства называем этот цилиндрик с плоскими основаниями столбиком. Ясно, что столбик, опирающийся на площадочку о<_1, есть либо вписанный в цилиндрик, с кривым верхним основанием, опи-
сти, лежащие внутри
рающийся тоже на либо описанный около него, либо промежуточный. Все дело в том, как выбрана точка Л1._1 в площадочке о4_ : выбрана ли точка /И,, так, что величина f есть
наименьшая из всех величин функции f(x,y) в площадочке з._р или величина /есть наибольшая, или промежуточная между наименьшей и наибольшей.
Итак, над каждой малой площадочкой о4 возвышается тонкий вертикальный столбик с параллельными (горизонтальными) основаниями. Из элементарной же геометрии известно, что объем прямого цилиндра равен произведению площади основания на высоту. Следовательно, объем рассматриваемого столбика в точности равен парному произведению:
МмН-р
потому что площадь основания столбика равна я , а высота его равна } (7И ._ ().
Если мы теперь построим указанный тонкий столбик над каждою площадочкой о,._р мы получим ступенчатое тело, составленное из п столбиков, объемом которого будет служить наша интегральная сумма: S=/W • .+ • • •+/
Таким образом двухмерная интегральная сумма 3 численно равна объему ступенчатого тела, составленного из вертикальных столбиков, имеющих площадочки oj_1 своими основаниями и аппликаты ’) f (Л1<_1) поверхности своими высотами.
§ 65. Двойной (определенный) интеграл. Мы знаем, что простая (одномерная) интегральная сумма
S=/('o) Дхо+/01)Дл1+ • • • +/(L.)4-rF • • • 1 х)ДЧ.-1
стремится к совершенно определенному пределу, когда наибольший из отрезочков Дх0, Axt.д*,_1> • Да’(1-1> на которые мы разделили
данный отрезок [а, б], бесконечно умаляется. При этом функция /(х) предполагается непрерывной на*всем отрезке [а, Ь\. Далее, мы знаем, что этот предел интегральной суммы 3 называется определенным интегралом от функции / (х), взятым по отрезку [а, 6] и обозначается знаком
ъ
J f(x)dx.
!) Если х, у, z суть коордияаты точки М в трехмерйом пространстве, то х — абсцисса, у — ордината и л — аппликата.
Затем, мы знаем, что определенный интеграл фактически вычисляется по формуле Лейбница-Ньютона:
ь
У / (х) dx = F(b) — F (а), и
где F(x) обозначает первообразную для /(х), т. е. F' (х)=/(х).
И, наконец, мы знаем, каков геометрический смысл определенного интеграла: простой (однократный) определенный интеграл геометрически обозначает величину площади АаЬВ (черт. 69), ограниченной отрезком [а, Ь], ординатами в его концах и данной кривой y=f(x).
Перейдем теперь к рассмотрению двухмерной интегральной суммы; S=/W • v!-/W • М- • • +m_,) • • .+/(/W„_t) •
Предположим, что площадочки а0, а)( о2, ..., ап_р на которые мы разделили внутренность заданного контура С (черт. 70), изменяются с тече-
нием времени и начинают безгранично умаляться (и не в смысле одной только величины площади площадочек, но и в смысле размера их диаметров), так что даже самый большой из их диаметров *) и тот безгранично умаляется. Это значит, что площадочки о0, ор а2, ..., о делаются все более и более мелкими. И так как они должны заполнять постоянную площадь внутри контура С, то их число неизбежно должно безгранично увеличиваться. С другой стороны, непрерывная функция /(х, у) есть ограниченная; поэтому для всех точек М (х, у) мы имеем неравенство:
I/MICK,
где К есть постоянная величина. Отсюда следует, что „общий член*
1) Диаметром D какой-либо плоской фигуры Р называется наибольшая из хорд этой фигуры. На прилагаемом черт. 71 диаметром, очевидно, является _ хорда D. Если фигура с течением времени изменяется /________________\ так, что ее диаметр безгранично умаляется, то это зна-
[. n Л чит, что она стягивается в точку. Если же толь-
\ ’ * у ко плошадь фигуры безграиично умаляется, то отсюда
еще не следует, что она должна стягиваться в точку, । , так как фигура может оставаться весьма длинной и
Черт 71 только безгранично утончаться.
f(Mt_,) • двухмерной интегральной суммы 5 имеет абсолютную величину меньше чем
•
и, значит, безгранично умаляете:!.
Таким образом, когда наибольший из диаметров площадочек э0, о)( а„, ..., о j безгранично умаляется, тогда двухмерная интегральная суммаЗ становится суммой безгранично увеличивающегося числа бесконечно умаляющихся слагаемых.
В этих условиях двухмерная интегральная сумма S стремится к определенному пределу, всегда одному и тому же, какую бы форму ни имели бесконечно умаляющиеся площадочки %, °„_i « каким бы образом ни выбирали в них точки
м0, м;, м2,..., ж„_,.
Мы не можем в рамках настоящей книги входить в доказательство этого чрезвычайно важного предложения математического анализа. Мы ограничимся тем, что просто предупредим читателя об его истинности, отсылая к более полным курсам анализа. При этом в §§ 67—68 мы дадим способ фактического вычисления этого предела, что будет служить достаточно сильным основанием для суждения о его существовании.
Предел двухмерной интегральной суммы S называется двойным (определенным) интегралом и обозначается знаком, аналогичным знаку простого (однократного) интеграла, именно:
J J f{x,y)dxdy.
Читается этот знак так: „двойной интеграл по внутренности кон-,лура С зф икс игрек де икс де игрек*.
Постановка значка контура С под знак эм двойного интеграла j' J" есть указание на то, что „интегрирование* (т. е. суммирование в сопровождении затем перехода к пределу) ведется по всей внутренности контура С. Постановка значка контура С совершенно аналогична постановке ь
пределов а и Ь в определенном интеграле J' f(x)dx. а
Примечание. Как и простой (однократный) определенный интеграл ь
| / (х) dx, двойной (определенный) интеграл получил такое символическое обозначение, которое всегда бы нам'напоминало, пределом какого именно выражения он служит. Именно, двухмерная интегральная сумма
/(м0) • =0+/(Л11) • ч +... +/(лт<_ х) +/(/И„_1) •
может быть составлена в предположении, что площадочки з0, cv ..., съ_х являются прямоугольничками, происходящими разрезыванием внутренности контура С прямыми линиями, параллельными осям координат ОХ я OY (черт. 72). Предположить это мы всегда вправе, так как предел интегральной суммы не зависит от формы
площадочек о](..., зи лишь бы они все безгранично умалялись (диаметром). Но есяи мы дадим площадочкам з0, зг..t прямоугольную форму, как было
указано, то .общий член* ишегральной суммы напишется в виде тройного произведения:
/(х(,у7)- bxf&yj,
потому что .общей площадочкой* будет теперь та, которая составлена из точек М (х,у), абсциссы которых х удовлетворяют неравенствам и ор-
динаты которых удовлетворяют неравенствам у <у^ +,. Поэтому п л о ща д ь ю такой площадочки будет произведение • Ду^. Выбирая же точку М на этой „общей* площадочке с координатами xit yj, мы и имеем общий член интегральной суммы написанным в виде f(xt, у^) bxithyj, и, значит, сама интегральная сумма напишется в виде:
SS/(r,, yj)bx{- byj, i j
где первое [суммирование делается по значку J, что дает вертикальную полоску, содержащуюся внутри контура С, а второе суммирование по значку I
заставляет эту полоску двигаться слева направо, описывая таким образом внутренность всего контура С.
Если теперь общее приращение абсциссы bxt написать просто в виде Ьх, а „общее* приращение byj ординаты написать просто в виде Ду, то интегральная сумма напишется в виде:
SS/(x,y) Ах Ду.
Естественно поэтому и предел интегральной суммы, т. е. двойной (определенный) ингеграл, написать так, чтобы некоторые следы интегральной суммы были
сохранены в обозначении предела. Отсюда и получилось обозначение двойного
определенного) интеграла в виде:
[ f f\x,y)dxdy.
§ 66. Геометрический смысл двойного интеграла. В силу изложенного ранее о'геометрическом смысле двухмерной интегральной суммы, геометрический смысл двойного (определенного) интеграла очень прост. Мы видели, что двухмерная интегральная сумма обозначает объем ступенчатого тела, составленного из вертикальных столбиков, имеющих площадо-
Черт. 73.
чки о.своими основаниями и аппликаты поверхности своими высота-
ми.
Обозначим через V объем вертикального цилиндрического тела (черт. 73),
—X образующие которого параллельны оси OZ нижним основанием которого служит внутренность плоского контура С, лежащего на плоскости ЛО У, а верхнее основание которого кривое, представляющее собою кусок поверхности z=f(x, у), прикрывающий
сверху рассматриваемое цилиндрическое тело. Если, приняв какое-нибудь деление внутренности контура С на площадочки а0, ар а2, . .а
мы выберем точки Л70, МХ,М„ Mn_i в них так, чтобы соответствующие аппликаты f _ f) всегда были минимальнымив этих площадочках, тогда столбики, имеющие а<_1 своими основаниями и своими высотами, понятно, будут вписанными в вертикальные цилиндрики, имеющие а. своим нижним основанием и кусочек поверхности z = f(x, _у) своим верхним основанием. Значит, раз столбик является частью цилиндрика, в который он вписан, то объем столбика будет меньше объема этого цилиндрика. И так как объем столбика равен ,) • о. _ р то отсюда следует, что сумма объемов всех п столбиков, равная, очевидно, интегральной сумме:
S=/W • ’o+/W • от-
будет меньше суммы объемов всех п цилиндриков; эта же последняя, очевидно, равна объему V всего цилиндрического тела. Итак, мы находим, что при выборе точек Л40, Л1Р ..., Mn_v дающих минимальные аппликаты, S < И. Поэтому и предел интегральной суммы $ не может быть больше, чем V. Следовательно:
/* J f(x,y)dxdy^V. (!
Если теперь мы сделаем другой выбор точек Af0, Afr .. ., ЛГ„ _ (, выбирая их так, чтобы аппликаты были максимальными
в площадочках тогда рассматриваемые столбики, имеющие основаниями и высотами будут, очевидно, уже описанными
около соответствующих цилиндриков, и, значит, ступенчатое тело, составленное из столбиков, будет содержать все цилиндрическое тело. Так как объем ступенчатого тела есть интегральная сумма, то поэтому при таком выборе точек Л!и, Л/р Л/.„ ..., Мп1 мы получим § > V, и,
значит:
///(x,j)dxrfy>V.
Сопоставление двух предыдущих неравенств дает: , у) dx dy = V.
с
Следовательно, двойной (определенный) интегр-йл от непрерывной функции f(x,y) по внутренности контураС численно равен объему вертикального цилиндрического тела, имеющего в н у т ре н и о ст ь к о н ту р а С одн»(м своим основанием, и кусок поверхности z=f(xyy) другим своим основанием.
Заметим, что если Поверхность z = f(x, у) расположена под плоскостью XOY, то двойной интеграл, а стало быть, и объем V тела
отрицательны, потому что в этом случае функция f(x,у) отрицательна.
§ 67. Вычисление двойного интеграла. Случай прямоугольного контура. Случай этот самый простой, и с него естественно начать вычисление двойного интеграла.
Возьмем прямоугольник PQTR (черт. 74), все точки М (х, у) площади которого имеют абсциссу х заключенной между а и b и ординатур содержащейся между с и d, т. е. а х Л и с ^у ^d.
Пусть функция /(х,у) есть непрерывная внутри этого прямоугольника, включая контур.
Чтобы вычислить двойной интеграл f f f(.x,y)dxdy, гдтк
естественно разбить прямоугольник PQ TR на маленькие прямоугольнички,
проводя прямые, параллельные осям координат. Разделим для этого отре-
зок [а, Ь], лежащий на оси ОХ, на k малых отрезочков, при помощи точек деления а <Xj< х2<...<xfc_j <ипро ведем через эти точки деления прямые, параллельные оси OY. Аналогично, разделим отрезок [с, d], лежащий на оси OY, на т малых отрезочков при помощи точек деления с < ух < у. < ... < ут_, < d и проведем через эти точки деления прямые, параллельные оси ОХ.
Ясно, что вследствие этого данный прямоугольник PQTR разобьется
на k X нг прямоугольников, для которых и следует составить интегральную сумму; при этом для удобства мы выбираем точки М в нижнем левом углу каждого из этих четырехугольников. Таким образом в прямо
угольничке
< х < х{, yj _ , <у <_yj,
заштрихованном на чертеже, нами будет выбрана точка (х,._„ у}_,}.
Этот прямоугольничек мы будем рассматривать как „общий**. Его площадь, очевидно, равна Дх1 X ДУ,.
Поэтому „общий" член интегральной суммы будет
Следовательно, вся интегральная сумма будет
i~k — 1 J=m — 1 s s ж-ржьч-х-ч-х-<=0 1=0
Оба указанных суммирования здесь производятся одновременно. Но рассматриваемая интегральная сумма есть конечная, а во всякой конечной сумме можно изменять как угодно порядок суммирова
ния. Естественно поэтому в целях удобнейшего вычисления предлагаемой интегральной суммы попробовать вычислить ее двумя следующими способами.
Первый способ.
Сначала суммирование, ведется по букве у и уже затем по букве к.
Так как буква у снабжена значком у, а буква х— значком г, то нужно сначала суммировать по значку j и уже затем — по i. Значит, мы имеем:
i = k — \ J=m-1
S -Ч-1Х S /(•*.-> —0 j—0
Заметим при этом, что. просуммировав по значку у, мы сразу же у полученной частной суммы выносим за знак суммирования общий множитель так как он один и тот же у всех членов частной суммы.
Напишем эту двухмерную интегральную сумму для простоты иначе, именно: уничтожим значки у букв х и у, предполагая, что значения этих букв изменяются не непрерывно, а скачками, причем буква х пробегает числа а, хр х2, ..., хъ_1, и буква у пробегает числа с, yt уг, ..., ym_r Тогда наша двухмерная интегральная сумма напишется так: ь d
S Ах х S / (х, у) • Ду.
„ а с
Геометрически такой порядок расположения слагаемых в двухмерной интегральной сумме означает, что сначала набираются слагаемые
по вертикальной полоске, так как при у первом (внутреннем) суммировании буква х предполагается постоянной (черт. 75).
И уже затем, набрав слагаемые по всем вертикальным полоскам, мы производим второе (наружное) суммирование, складывая все вертикальные суммы, для чего теперь уже нужно изменять х. __
Будем теперь безгранично умалять диа- 0 метры одновременно всех прямоугольников, на которые был разбит данный прямоугольник PQTR. Мы знаем, что тогда
двухмерная интегральная
сумма стремится к совершенно определенному пределу, который есть двойной интеграл
f f f(x,y)dxdy PQTR по площади прямоугольника PQTR.
Так как бесконечное умаление прямоугольничков мы вольны производить, как нам вздумается, то мы можем сначала бесконечно умалять высоты Ду этих прямоугольничков ’)> оставляя неприкосновенными их
1) Кажущаяся рискованность этого рассуждения не дает места даже формально каким-либо сомнениям, так как ведь мы с самого начала пред-
основания Дх. Но вследствие того, что первая (внутренняя) сумма есть, очевидно, простая (одномерная) интегральная сумма, то ее пределом при этом приближении высот Ду прямоугольников к нулю будет простой (однократный) определенный интеграл
d J у) dy.
взятый между постоянными пределами с и d по буквеу в предположении буквы х постоянной.
Значит, подводя все Ду к нулю, мы имеем как промежуточный этап вычисления двойного интеграла количество
ь г
S X f f(x, у) dy. а с
Наконец, подводя к нулю Дх, мы находим уже окончательный результат:
В й f f dx • f PQTR a c
Итак, вычисление двойного интеграла по прямоугольнику требует
таких действий:
Первый шаг . Предполагая букву х постоянным числом, проинтегрировать функцию / (х, у) по букве у между пределами с и rf, определяющими се изменение, у Второй шаг. Полученный после
Черт. 76.
первого шага результат проинтегрировать по букве х между пределами а и Ь, определяющими ее изменение.
Прилагаемый черт. 76 служит читателю для напоминания о том, что интегрирование сначала идет по вертикальным полоскам (значит, х постоянно) и уже после этого интегрирование ведется по х от а до Ь.
Второй способ.
Сначала суммирование ведется по букве х, а уже затем по букве у.
Все, что было сказано выше о первом способе, приложимо и ко второму, потому что свойства переменных х и у совершенно одинаковы. Только здесь все идет наоборот, так как буквы х иу здесь меняются ролями.
Прежде всего мы еще раз изменяем порядок слагаемых в двухмерной интегральной сумме, производя сначала суммирование по значку i, и
полагаем существование предела двухмерной интеграль-вой суммы.
уже потом — по значку у. Это дает право написать двухмерную интегральную сумму в виде:
j т — 1 i — к — 1
S 4y./_iX S Ж-рУ,-!) • Ч-!-
J=0 i=0
Здесь мы, производя частное суммирование по значку i, выносим количество Д^-_, как постоянный множитель за знак этого частного суммирования.
Полученную формулу мы пишем в виде: d ь
зО-ч
с и
сделав прежнее соглашение о том, что буквы х и у пробегают не все возможные величины, но лишь а, хр хг, ..хк_1 и с, yv yt, . .., J к Геометрически такой порядок расположения слагаемых в двухмерной интегральной сумме означает, что сначала набираются слагаемые по горизонтальной полоске, потому что при первом (внутреннем) суммировании буква у предполагается постоянной. И уже затем, набрав слагаемые по всем горизонтальным полоскам, мы производим второе (наружное) суммирование, складывая все горизонтальные суммы, для чего теперь уже нужно изменять у.
Для полного вычисления двойного интеграла
///<*•»
PQTR
мы должны одновременно бесконечно умалять
стороны Дх и Ьу наших прямоугольников в выражении двухмерной интегральной суммы. Производя сначала бесконечное умаление сторон Дх, мы имеем в качестве промежуточного этапа вычисления предела двухмерной интегральной суммы количество
а ь
Sty* ff(x,y)&x. с а
Наконец, приближая к нулю Ду, мы находим уже окончательный результат:
a h
Правило: Первый шаг. Предполагая бу к ву у постоянным числом, проинтегрировать функцию f{x, у) по букве х между пределами а и Ь, определяющими ее изменение.
Второй шаг. Полученный после первого шага резуль-
13 Зак. 2853. — Гранвиль и Луаия, ч. II, Интегральное исчисление
тат проинтегрировать по буквеуг между пределами сия', определяющими ее изменение.
Прилагаемый черт. 78 послужит читателю напоминанием того, что интегрирование сначала идет по горизонтальной полоске (у постоянно) и уже затем по букве у от с до d.
Пример 1. Вычислить интеграл
f (xydxdy
p'qrt
по прямоугольнику PQRT, вершины (10, F), (10,7), (2,7) (черт. 79).
которого лежат соответственно в точках
Черт. 78.
Черт. 79.
Первый
СПОСОБ.
Первый шаг. Предполагая букву х постоянной, интегрируем функцию ху по букве у между пределами 1 и 7, определяющими ее изменения:
xdx / у dy = х dx
2 -1 х dx
Второй шаг. Полученный после первого шага результат интегрируем по букве х между пределами 2 и 10, определяющими ее изменение:'
10 ю
24y’xrfx=24^j =24-48= 1152.
2 ’
Короче вычисление следует записывать так: 10 7 10 7
( /* ху dx dy = I f xy dx dy= У dx • /.
J i
ю
dx =
PQRT
10
или
10 7
10 7
10 dx — (
7 dx =
PQBT
10
24ж<Гх = 1 152.
Второй способ.
Меняя порядок интегрирования, т. е. интегрируя сперва по х, а затем по у получим:
= 48 Нг]7= 48,24 = 1 152-
Пример 2. Вычислить объем прямоугольного параллелепипеда (черт. 80), основанием которого служит прямоугольник примера 1, а высота равна 5 * *).
Положим f (х, у) = 5. Тогда двойной интеграл
J" f 5dx dy. PQRT
согласно его геометрическому смыслу (§ 66) даст искомый объем параллелепипеда
10 7
f [ 5dx dy = f f 5dx dy = r'QRT 2 i
10 7 10 7 10
= 5 f Jdx dy = 5j" dx j" dy = 5 J" [y]’dx =
2 1' 2 3 2
io
= 5 f 6dx = 5 • 6 • 8 = 240.
Пример 3. Вычислить объем прямого параллелепипеда, срезанного сверху параболоидом х = 4--ха — у2 и стоящего над квадратом, который образуется в плоскости XOY прямыми х = ± 1, у = ± 1 (черт. 81).
В данном случае f(x,y) = z — 4 — ха — у-, и мы
Черт. 80.
будем иметь:
§ 68. Общий случай криволинейного контура. Мы сначала предполагаем криволинейный контур С таким, что всякая вертикальная прямая встречает его не более как в двух точках (черт. 82). Случай этот мы рассматриваем по аналогии с предыдущим -).
1) Разумеется, для вычисления объема параллелепипеда нет нужды пользо-' ваться интегральным исчислением, и рассматриваемый пример служит только иллюстрацией исследуемого вопроса.
*) Мы отсылаем для строгого рассмотрения зтого случая к более полным курсам математического анализа.
Если абсцисса точки Р есть х, то длины обоих отрезков: РМХ и РМг, где Mt и Л4а суть две точки встречи криволинейного контура С с вертикальной прямой, проведенной через точку Р, понятно, зависят от х. Следовательно, длины отрезков PMt и Р/Й2 будут две функции аргумента х.
Мы вводим обозначения:
РМХ = ?! (х) и РМг — о., (х) и предполагаем, что наш контур С таков, что функции (х) и (х) непрерывные.
Пусть /(х, у) есть данная нам непрерывная функция внутри кон* тура С, включая и самый контур.
Чтобы иметь двухмерную интегральную сумму, мы делим внутренность контура С на весьма малые прямоугольнички, проводя прямые, параллельные осям координат ОХ и OY. Образующиеся при этом прямоугольнички будут двух сортов: полные и обрезанные криволинейным контуром С. Первые будут лежать внутри контура С, вторые будут прорезаны контуром С. Этими последними мы будем всегда пренебрегать, потому что тот добавок, который «они вносят в двухмерную интегральную сумму, будет безгранично умаляться с бесконечным умалением диаметров всех прямоугольничков. Действительно, обо
значая площади этих обрезанных контуром С прямоугольников через
®1, ®2, ...,
и выбрав в них как-нибудь по одной точке М'. М", ..М(р\ мы видим, что этими неполными прямоугольничками будут внесены в двухмерную интегральную сумму слагаемые:
/си')-®,,/т-®2, ...,/(.и(/”).®р.
Но функция f(x,y), будучи непрерывной, есть функция ограниченная. Это значит, что им^.м всегда
1/(х,^)|</С,
где К—положительная постоянная.
Поэтому слагаемые, внесенные в двухмерную интегральную сумму обрезанными прямоугольничками, все вместе составят количество, по абсолютной величине меньшее, чем
К • ®1 + К • ®а 4" ... + К • ®р или
K(®j-;-®a4-...4-®р).
Но ®j 4~ “а 4" • 4“ есть вся площадь этих обрезанных контуром С прямоугольничков. Читатель должен рассматривать как очевидный тог факт, что сумма ®, 4~®э 4" • • • 4“®j> площадей обрезанных контуром С прямоугольничков стремится к нулю вместе
Черт. 82.
с бесконечным умалением диаметров этих прямоугольничков. Итак, имеем lim (а^ -|- ш3 -|- ... -|- — 0, что доказывает,
что неполными прямоугольничками всегда можно пренебрегать.
Что же касается полных, то мы берем их все и для, того чтобы иметь двухмерную интегральную сумму, выбираем в каждом из них точку М в нижнем левом углу его. Поэтому, если прямоугольничек
есть „общий" полный четырехугольничек, то он внесет в двухмерную интегральную сумму слагаемые:
и, значит, вся двухмерная интегральная сумма (кроме слагаемых, происходящих от неполных четырехугольничков) будет:
SS№-г
< J
где значки i и j должны браться лишь такими, чтобы соответствующий прямоугольничек (х. _, х х{, yj_l^.y ^У<) непременно попал внутрь контура С и не был ни обрезанным, ни совсем внешним для контура С.
Написав эту двухмерную интегральную сумму сокращенно в виде:
х у
ftie х и у пробегают отнюдь не все возможные числа, а лишь те числа xt, у,, которые послужили для покрытия внутренности контура С сетью четырехугольничков и притом с тем ограничением, чтобы соответствующие четырехугольнички попадали полностью внутрь контура С, мы производим перегруппировку слагаемых.
Именно, мы сначала набираем слагаемые для прямоугольничков, составляющих вертикальную полоску. Значит, набирая вертикальную полоску, мы обязаны рассматривать букву х как постоянное число; поэтому у всех этих слагаемых множитель Ах будет одинаковым, и его, следовательно, можно вынести за знак этого частного (по вертикальной полоске) суммирования. И уже затем, набрав слагаемые по вертикальным полоскам, мы должны будем сложить все эти вертикальные суммы, для чего теперь нужно изменять букву х.
Если мы выполним указанную перегруппировку, двухмерная интегральная сумма примет вид:
х V
Для вычисления двойного интеграла
f f fi*,y}dxdy
мы должны одновременно бесконечно умалять стороны Дх и ду наших прямоугольничков в выражении двухмерной интегральной суммы. Произведем сначала бесконечное умаление сторон Ду, как было объяснено в случае прямоугольного контура интеграции. Мы будем иметь в качестве промежуточного этапа вычисления предела двухмерной интегральной суммы количество:
$ДхХ У f(x,y)dy, х Ъ (л)
потому что при х постоянном точки М (х, у), выбранные в прямоугольничках рассматриваемой вертикальной полоски, находятся только на отрезке ЛТ( Л1а, деля его на бесконечно умаляющиеся части. Поэтому при X постоянном переменное интеграции у пробегает лишь отрезок и, значит, при интегрировании по у мы имеем:
где X в этот момент рассматривается лишь как постоянная величина. Наконец, приближая к нулю Дх, мы имеем уже окончательный результат.
ь
f f f(x,y) dxdy = J' dX‘ f f(x,y)dyt
JCJ a Ju*'
где а и b — это те два крайние значения абсциссы х, которые вообще только возможны для абсцисс вершин прямоугольничков, лежащих внутри контура С. Значит, а и Ь суть такие два числа, что вертикальные прямые х = а и х = Ь прикасаются к контуру С слева и справа, содержа его между ними.
Таким образом имеем правило:
Первый шаг. Предполагая контур С (черт. 83) пересекающимся не более чем в двух точках всякой вертикаль
ной прямой, найти уравнение у = в?1(*) его нижней линии и уравнение у = <р2(*) его верхней линии.
Второй шаг. Предполагая букву X постоянным числом, проинтегрировать функцию /(х,у) по букве у между пределами о((х) и ®2(х), определяющими изменение величин этсй буквы при х постоянном.
Третий шаг. Полученный .после
второго шага результат проинтегрировать по букве х между двумя постоянными числами а и Ь, находимыми из того соображения, чтобы контур С содержался между прямыми х = а иу = Ь, прикасаясь к ним.
Так как роли букв х и у одинаковые, то читатель без всяких новых рассуждений видит справедливость следующего дополнительного правила:
Первый шаг. Предполагая контур С пересекающимся не более чем в двух точках всякой горизонтальной пр я
мой, найти уравнение х = ?| (j,) его левой линии и уравнение х = ?2(у) его правой линии (черт. 84).
Второй шаг. Предполагая буквуj постоянным числом, проинтегрировать функцию f(x,y) по букве х между пределами -Э] (у) и гоСу), определяющими изменение величин этой буквы при х постоянном.
Третий шаг. Полученный после второго шага результат проинтегрировать по букве у между двумя постоянными числами с и d, находимыми из того соображения, чтобы контур С содержался между прямыми у = с п y = d, прикасаясь к ним.
Если контур С пересекается и прямыми вертикальными и прямыми горизонтальными не более чем в двух точках, то к нему приложимы сразу оба предыдущих правила, и тогда надо поступать, как удобнее.
Черт. 84. Черт. 85.
Если контур С пересекается параллелями осям координат более чем в двух точках, тогда площадь, содержащуюся внутри контура С, разбивают на такие части, к которым можно уже применить предыдущие правила.
Например, достаточно рассечь фигуру, представленную на черт. 85 по пунктирным линиям, чтобы предыдущие правила оказались применимыми к каждой из трех частных фигур в отдельности. Ясно, что двойной интеграл по внутренности контура С будет равен сумме трех двойных интегралов по внутренности частных фигур.
Пример. Проинтегрировать функцию /(х.у) — х + 2у, если рассматриваются значения ее в области, ограниченной линиями у- — 4 х и х = 5 (черт. 86).
Решение. Искомый интеграл есть: d ♦,(!/)
/= f f (x + 2y)dydx, с ♦.(!/)
причем первое интегрирование мы будем производить по х.
Первый шаг. Находим уравнения _ х = <I>j (у) и х = Фа (у) левой и правой * линии контура, ограничивающего рассматриваемую область. Левой линией является парабола. Поэтому из уравнепия ее находим: х=у*—4; правая линия есть прямая х = 5. Следовательно, х = (у) = у1 — С
и х = Ф,(у) = 5.
Второй шаг. Предполагая букву у постоянным числом, интегрируем функцию х~Ь~2у по букве х между найденными пределами х=уг —4 и х = 5:
/’ Г г- I6 Q v1
у (х -J- 2.v) rfv = [— 4 5v' J ( = у ?У + 4 V2 + 2У + .
Третий шаг. Полученный результат надо теперь проинтегрировать по букве у между двумя постоянными пределами с и d, которые определяются из того соображения, чтобы контур С содержался между прямыми у = с и у = d. Очевидно, в этом случае такими прямыми являются прямые, параллельные оси ОХ и проходящие через точки пересечения прямой х = 5 с параболой. Для определения координат точек В и С решаем совместно уравнения параболы и прямой и находим: В (5,3); С (5, —3). Следовательно, уравнения искомых прямых.будут: у = — 3,у = 4- 3. Итак, искомыми пределами являются с = — 3, d = -|- 3. Поэтому пишем: '
4-3
1=,/ (4н 2у++2у3 4)dy=501-— з
Когда у читателя приобретается навык в решении такого рода задач, можно вычисление интегралов производить короче, сразу найдя значения пределов внутреннего и внешнего интегралов. Таким образом будем иметь:
' + 3 5 +3
/ = /” /(х + 2у) dy dx = /’ [£ + 2->’ ‘
-3 k -3
=J (4+2у+~ У )dy=з<4-— 3
Решим теперь этот же пример, изменив порядок интегрирования: Ь *,(х)
/ = f J {х 4- 2jz) dx dy. a
Первый шаг. Находим уравнения у = Ф. (xj и у = Ф2(х) нижней и верхней линий, ограничивающих рассматриваемую область (черт. 67). Нижней линией является нижняя ветвь параболы у1 = 4 + х, а верхней — верхняя ее ветвь. Поэтому получим:
у = Ф1 (х) = - /Г+7 И
у = Ф2 (х) = + У4Т7.
Второй шаг. Предполагая букву х постоянным числом, интегрируем функцию х4-2у по букве у между найденными в первом шаге пределами:
f (л + 2у)<у = 2х/ГТТ — l'4-f-X
Третий шаг. Полученный результат надо теперь проинтегрировать по букве х между двумя постоянными пределами а я Ъ, которые определяются из того соображения, чтобы контур С содержался между прямыми х = а и х = Ь. Очевидно, что таковыми прямыми являются в нашем случае — слева прямая,
проходящая через вершину параболы параллельво оси OY, а справа — прямая л = 5. Уравнение левой прямой есть х=— 4, ибо точка А имеет координаты (— 4, 0). Таким образом а = — 4, Ь = 5. Поэтому будем иметь:
+? ' 9
1= j Зл-/1 + хЛс = 50у.
-4
Заметим, что при интегрирования вторым способом мы пришли к необходимости вычислить более трудный интеграл, чем при первом способе. Поэтому при выборе порядка интегрирования следует руководствоваться соображением о сложности получающихся после первого интегрирования функций. В примере 1 § 71 мы покажем, что при выборе порядка интегрирования следует принимать в соображение также и характер контура, ограничивающего область интегрирования.
§ 69. Двойной интеграл в полярных координатах. Мы знаем} что при вычислении двойного интеграла
J /'f(x,y)dxdy с'
вовсе необязательно пользоваться непременно бесконечно умаляющимися прямоугольничками, имеющими стороны, параллельные осям координат ОХ и ОУ: здесь возможен бесконечный произвол, так как бесконечно умаляющиеся площадочки з0, зи о2, ..., зв1, служащие для составления двухмерной интегральной суммы, могут быть самой прихотливой формы. Мы ведь знаем, что всегда будем иметь:
f f f(x,y) dxdy=\im . 3l+.. .-L/GW,,-,). %_t),
где oo, ap ..., зп1 — бесконечно умаляющиеся площадочки, на которые разбивается внутренность контура С, и соответственно выбранные в них точки. Иногда оказывается чрезвычайно удобным пользоваться при вычислении двойного интеграла полярными координатами.
В этом случае площадочки з0, о,, ..., оп1 образуются двумя семействами линий: прямыми, исходящими из полюса О, и окружностями, имеющими полюс О своим центром (чертеж 88).
В этих условиях ясно, что, пренебрегая бесконечно малыми высших порядков (что делается на основании второго принципа бесконечно малых, приложимого ко всяким абсолютно-ограниченным суммам бесконечно умаляющихся и, в частности, к двухмерным интегральным суммам), величина „общей1* площадочки будет:
Р • dp db, и, значит, двойной интеграл напишется в
виде: / f F(p, 6)p.rfp.dft.
Простое рассмотрение двух нижеследующих чертежей покажет читателю, как надо производить фактическое вычисление двойного интеграла в полярных координатах:
П. У* Jf{xty) dxdy = I р dp у* / (p cos 6, p sin в) (й (черт. 90). c pi
Черт. 89.
Черт. 90.
Пример. Вычислить интеграл функции / (р, 0) = р2 по области, ограниченной окружностью р = 2fl cos в (черт. 91).
Решение. Нам надо вычислить интеграл
*.(»)
/= [ Г p2-prferfp,
5,
где р = Ф, (0) = 0, как это непосредственно видно из черт. 91, а р = Ф2(Ь) = 2u cos b из уравнения контура. Что касается значений Ct и (Jj, то легко видеть, что flj = — у и в, = + у , так как при изменении угла от — у до 4* у мы охватим все
секторы, на которые разбиваем область интегрирования. Таким образом будем иметь:
УПРАЖНЕНИЯ.
Вычислить следующие интегралы:
1. f j*xy (х — у) dy dx. Оте. -jj~(fl_ ^)-
о о
ъ 2
2 //
а 2у
3. J* J* xydydx.
О у — а
ко (1^-со»6)
р2 sin О rfO df.
11в«
Отв. —24~
ч .
О I
b 10t
4а»
3 ’
ta
Pdt ds.
6*з.
v, dv dw.
143flS
30
J j ev dvdwt и о
3
1 a x f Г xy'dxdy.
О 2® а х /' Г х dx dy
— fl5 3
в aa 13
о а сое 6
2 t соя I
-^-In2.
□ 0
2
о
г а
11.
с о 2
12. Проинтегрировать функцию f (x, y) = 1 no киями у2 = x и x = a.
13. Проинтегрировать функцию /(p, 6) = sin6 окружностью p = a cos 0,
области, ограниченной ли-s л 2 Т Отв. -%-а . и
по области, ограниченной
Отв. . О
1
по области, ограни-
14. Проинтегрировать функцию fix, у}
чениой осью OY и параболой у2 = а2 — ах. gmt
15. Проинтегрировать функцию f (х, у) — у2 по области, ограниченной
осью ОХ и прямыми у = х и х = 2а. 16л1
Отв. — .
U
16. Проинтегрировать функцию / (о, 6) = р по области, ограниченной одной петлей кривой р = а • sin 2G. 2
Отв. — а3.
17. Проинтегрировать функцию / (р, 0) = р по области, ограпич иной полярной осью и линиями р = а и о = а (1 -j- cos в). ,
Отв. -^-(14 +9с).
ПРИЛОЖЕНИЯ ДВОЙНОГО ИНТЕГРАЛА. .
§ 70. Объем цилиндрического тела. В § 66 было уже показано, что если функция z = f(x, у) представляет собой уравнение поверхности, ограничивающей цилиндрическое тело, образующие которого параллельны оси OZ, а направляющая лежит на плоскости XOY, то двойной интеграл этой функции по области, ограниченной контуром С, выражает объем этого цилиндрического тела:
V=f f f(x,y)dxdy. --------------
В § 67 нами был рассмотрен пример (см. пример 3) на вычисление объема цилиндрического тела.
УПРАЖНЕНИЯ.
1. Найти объем тела, ограниченного цилиндрическими поверхностями у = № х- — у и поверхностью z — 12 г у — л-. q
Omt- 4 nd’
2. Найти объем тела, ограниченного плоскостью XOY, цилиндром хг 4-у2 = 1 ч плоскостью х 4-у + z = 3.
Отв. Зя.
, 3. Найти объем тела, расположенного в первом октанте и ограниченного цилиндром (х — I)2 4- (у — 1)2 = 1 н параболоидом ху = г.
Отв. я.
4. Вычислить объем тела, ограниченного плоскостью XOY, цилиндром х«4-уа —2дх = 0 и поверхностью прямого кругового конуса, вершина которого расположена в начале координат, ось совпадает с осью 02, и угол осевого сечения при вершине равен 90°. g
Отв. у а3.
5. Найти объем тела, ограниченного поверхностью шара радиуса а и поверхностью прямого кругового цилиндра, радиус поперечного сечения которого а ,
равен у н одна из образующих которого проходит через центр шара.
7 Отв. -г-яд3.
о
в. Вычислить объем тела, которое снизу ограничено площадью лемнискаты р* = д® ctefO, расположенной в плоскости XOY, сверху поверхностью шара х3 -(-у2 4- zl — <Р, а с боков цилиндрической поверхностью, направляющей для которой служит лемниската.
Отв. у а3 (Зя 4-20-16 /2).
6. Найти объем тела, ограниченного плоскостью XOY, параболоидом az =xJ 4-у3 и цилиндром х- 4- у2 = 2а х.
Отв. -% яд3.
§71]
ПЛОЩАДИ, ОГРАНИЧЕННЫЕ ПЛОСКИМИ КРИВЫМИ
205
§ 71. Площади, ограниченные плоскими кривыми. Как известно, двойной интеграл функции / (х, у) по области, ограниченной контуром С, выражает собой объем цилиндрического тела, образующие которого параллельны оси OZ и которое ограничено поверхностью г=/(х,у). Положим f (х, у) = I. Тогда, очевидно, интеграл
или
У У pdpd6
будет выражать объем прямой призмы, построенной на основании, ограниченном контуром С, и имеющей высоту, равную единице. Численно этот объем равен величине площади фигуры, ограниченной, контуром С. Отсюда следует, что площади плоских фигур могут быть вычислены при помощи двойных интегралов
У J dx dy (в прямоугольных координатах) и
У У pdpdb (в полярных координатах). с
Пример 1. Найти площадь фигуры, ограниченной параболой у1 = 4х + 4 и примой у = 2 — .г (черт. 92).
Решение. Решая уравнения данных линий совместно, найдем точки Пересе* чения параболы и прямой: А (0,2) и В (8, —6). Интегрируем сперва по х. Тогда уравнение левой ограничивающей кривой х = Ф; (у)
, v3 — 4 Y
найдем из уравнения параболы: х = '—— , а уравнение правой, х = Ф2СУ) — из уравнения прямой: х=2—у. Постоянные пределы с и d равны, очевидно, —6 и -|- 2. Таким образом будем иметь: /|т\
2 2-[/ 2 Т j х ————— х
S= J j dydX=J С2--»'-—
—в 1/--4 -6 X<
4
Замечание. Если бы мы сперва стали интегри-ровать по у, то все вычисление было бы более слож- Черт. 92. ным: слева от оси OY надо было бы интегрировать между пределами у = — У4х -|- 4 , у == + У4х -|- 4, а справа — между пределами у = — 1/Г4х + 4 и у = 2 — х. Следовательно, искомая площадь S выразилась бы суммой двух двойных интегралов:
О + 1’4х+4 а 2—х
S = У У dxdy 4 j у dxdy -4 _ т о _ vii+V
Пример 2. Вычислить площадь круга р = 2а cos 6 (черт. 91 стр. 202), пользуясь двойным интегралом.
Решение. Как в примере на стр. 202, найдем пределы интегрирования: по р, от 6 до 2а соз в и по в от — -j до + у . Следовательно, будем иметь:
S — j j , '0 rfp = по3. Я
~ т
УПРАЖНЕНИЯ.
1. Посредством двойного интегрирования найти площадь прямоугольника образуемого осями координат и двумя прямыми, проведенными через точку (а, Ь) параллельно осям координат. дтв
2. Посредством двойного интегрирования найти площадь треугольника, образуемого осью ОХ и прямыми х = а и у = — х.
, а 1 О' me. ab.
3. Вычислить посредством двойного интегрирования площадь круга = Л Отв. г.г\
4. Посредством двойного интегрирования найти площадь, ограниченную прямой ОА и параболой, вершина которой лежит в точке О, осью которой служит ОХ и которая, как и прямая ОА, проходит через точку А {а, Ь).
Отв. —. . о
5. Посредством двойного интегрирования найти площадь, содержащуюся между двумя параболами Зу2 = 25х и bx*=,3y. Qmt
6. Посредством двойного интегриревания найти площадь, ограниченную кривыми у = х2иу = 2 — х2. , л
Отв. 2
7. Посредством двойного интегрирования найти площадь, заключенную между гиперболой ху = 4 и прямой х+у — 5 = 0. ,
Отв. (15 —8 In 4).
8. Найти посредством двойного интегрирования площадь, содержащуюся между параболами у/1= 4ах + 4а2 и у2 = — 4Ьх + 4Ь-.
Отв. (а + Ь) Уab. и
9. Вычислить площадь в первом квадранте, лежащую между параболой у2 = ах И ОКРУЖНОСТЬЮ у2 = 2вХ — X2. 19
Отв. 1™»-4а2. 4 3
X® у®
10. Найти площадь эллипса-^- + -р- = 1 посредством двойного интегрирования. Отв. т.аЬ.
11. Посредством двойного интегрирования найти площади фигур, ограниченных следующими линиями:
1,1 п &
а) хг +у- = д ; х+у = о. 3
b) у2 = 9 х; у2 = 9 — З.г. 48.
с) у = sinx; у = свах; х = 0. —1.
«в3 л
- , 2у = X, X = 0.
л • Н- 4а-
2_ 2 2
е) ха + у3 = , х + у = а.
d) у
Отв. а3 (я — 1).
f) у2 = х + 4, у2 = 4 — 2х.
g) у2 = 4а2 — х2, у1 = 4а* — 4ах.
а2__ Зла2
~3 32'
I) 4у2 = Xе, у = х.
к) х2 — у2 = 14, Xs
12. Двойным интегрированием найти всю площадь кардиоиды р = а (1 — cosO) Отв. каа.
13. Двойным интегрированием вычислить всю площадь лемнискаты p2 = a3cos20. Qma ai
14. Двойным интегрированием вычислить площадь, ограниченную параболой р = a sec2 н прямой, проходящей через фокус параболы перпендикулярно полярной оси. 8 &
3
15. Посредством двойного интегрирования найти площадь, содержащуюся между кругами р = я cos 6, р = Ь соя 6 интегрируя сперва по р.
Отв. 27г..
Отв. Д-(М-й«).
О
16. При помощи двойного интегрирования найти площади, ограниченные следующими линиями:
а) р = 6 sin 0, р = 12 sin 6.
b) р cos 0 = 4, р = S.
с) р = a secs Л. ( р = 2я.
о а адЭ
2а2к------=- .
и па2 ~2 ’
d) р = а (1 + cos 0), р = 2а cos 6
е) р sin 6 = 5, р = 10.
f) р = 8 cos 0, р cos 0 = 2.
g) р = 2а cos 6, р = 8 cos 0.
§ 72. Центр тяжести площади плоской фигуры. Если обозначим через хну координаты центра тяжести площади плоской фигуры, то, как было показано в § 60,
т.
т
dm = wdxdy
где хну — координаты точки, в которой сосредоточена масса dm элемента площади. Следовательно, мы можем положить
или dm = шр dp d<),
плотность рассматриваемой площади.
где ш есть поверхностная
Благодаря этому в качестве пределов суммы слагаемых вила mxdxdy.
nydxdy и <s>dxdy получим теперь двойные интегралы. Таким образом будем иметь:
_ У* у* vxdxdy _ у J'vydxdy
J Jл dx dy У J j'vdx dy
причем интегралы должны быть вычисляемы по площади, центр тяжести которой мы ищем.
Для случая полярных координат х = р cos 6, у = р sin 0, и поэтому вышеприведенные формулы принимают вид:
_ /* /*®РЯ cos ® - /* /" ®Ра s*n ® ^Р
X — — ’ --------- , у = -—-________________,
J* у <np dp d6 у у ®р dp dO
Если плотность ш постоянна, то, вынося о> за знак интегралов, получим формулы в более простом виде. В дальнейшем всюду мы ограничимся рассмотрением именно этого простейшего случая, а потому в нижеследующих примерах будем подразумевать ш постоянной, не оговаривая этого.
V- у-
Пример 1. Найти центр тяжести сегмента эллипса — + >1, ограни-
ченного прямой, проходящей через концы осей эллипса в первом квадранте (черт. 93).
Решение. Первое интегрирование производим по у. Для нахождения поеделов интегрирования надо знать уравнение прямой, ограничивающей сегмент эллипса. Легко видеть, что это уравнение имеет вид:
Ьх + ау = аЬ.
\ Тогда нижний предел (х) находим из уравнения пря-J____у „ _ . . аЬ — Ьх
д * мой: Ф, (х) = —-— ; из уравнения эллипса имеем:
93- ф„ (х) = — Ya- — х*.
' а
Пределами внешнего интегрирования являются а = 0 и Ь = а. Вычисляем теперь интегралы, входящие в формулы, которые определяют координаты центра тяжести: па а
J J1 х tlx dy = j ( — х Yа2 — х'- - Ьх 4- ^-^rfx =«= Ьа\ О аЪ — Ъх U
о — /а1—®’ .
а а * а
У у ydxdy=^J(— Ьхг 4- а62х) dx = Ьга, О аЬ — bs о
— Уа*—хг а а
I J dx dy = ab(it — 2). 6 аЬ — bs
Следовательно:
7 = -^--. у = - 7Ь 1) 3(я-2) 3(л-2) }'
Пример 2. Найти центр тяжести площади, ограниченной окружностями р = a cos 0, р = Ь cos 6 (черт. 94).
Решение. Из симметрии фигуры непосредственно заключаем, что у = 0.
Вычисляем интегралы, входящие в формулу, определяющую абсциссу х:
2 В сов »
УПРАЖНЕНИЯ.
1. Найти центры тяжести площадей, ограниченных следующими линиями:
а) Четверть круга.
Ь) Четверть эллипса.
с) у2 = 4х, х = 4, у — 0.
Отв. х = у = .
J Зп
4а
Зк
- 1“
“ 5
'Ь
>’ = з7’
3
У = 2 •
d) у = sin х, у = 0, от х = 0 до х — г..
— т:
>= У
2
е) Четверть площади, ограниченной гипоциклоидой х 8 -J-у3 = а8
f) у2 = 4ах, х = h.
g)y = 2x, у = 0, х = 3.
h) у® = 8х, у = 0, у + х = 6.
I) (2а — х) уа = х’, х = 2а.
j) («2 ~ = "* х = 0.
L 1 1
к) х 2 +у 2 = а 2 , х = 0, у
- — лооа
Отв- Х=> = -315Г-
х = — , у = 0.
х-=у=2._
7 = 2,48, у = 1,4.
- 5а — п л=-з-’ у = °-
х = —, у = 0. п — -
-0. Х = у=у.
*) Этот же пример был решен нами на стр. 172. Читателю полезно сравнить оба решени^.
14 Зак. 28ЬЗ. — rpjtdflBVffyaBK, ч II, Интегральное всчаеаекжо
1) Циклоиды х = a (t — sin t), у = а (1 — cos t). п ~ — 5а
О:пв. х = ап, у *= — .
О
2. Найти центры тяжести площадей фигур, ограниченных линиями:
„ - г. Via
Oms. х «---------
о
« - 108л -
Отв- Х=105к =J
— 5а — х = у=0.
р cos fl = 2.
р = 8 cos 0.
фигуры. Момен-
а) Петлей р- = в2 cos 20.
Ь) Петлей кривой р = a sin в.
с) Кардиоидой р = а (1 + cos 0).
От».
I) р = 8 cos О, g) р = 2 cos в,
-0.
d) р = 6 sin 0, р = 12 sin 0.
е) р cos 0 = 4, р = 8.
§ 73. Моменты инерции площади плоской
том инерции, относительно оси материальной точки называется этой точки на квадрат расстояния от оси. Моментом инерции относительно оси системы п материальных точек называется сумма моментов инерции отдельных точек. Пользуясь этим определением, можем следующим образом распространить понятие момента инерции на площадь плоской фигуры.
Разобьем площадь фигуры на элементарные площадочки так, как указано на чертеже 95.
таких площадочек. Обозначим координаты
произведение массы
Пусть PG — одна из
точки Р через (х, у). Площадь элемента равна dx dy. Положим раз навсегда плотность фигуры равной единице во всех точках. Тогда масса элемента будет равна dx dy. Если требуется найти момент инерции относительно оси ОХ, то за момент инерции площадочки PG можно приближенно принять произведение y^dxdy. Тогда, следуя общему методу, за момент инерции относительно ОХ всей площади фигуры примем г ,.
lim 00 y-dxdy— / / yPdxdy.
Д>->0 v «/
°
Обозначая момент инерции площади относительно оси ОХ через /х, получаем: л »
4= / Jy2dxdy.
Аналогичным образом найдем:
4 — У* J x*dxdy.
Если осью, относительно которой ищется момент инерции, является прямая, отличная от оси координат, то, обозначая через R расстояние
точки Р от этой оси (черт. 96), для момента инерции I всей площади фигуры таким же образом получим выражение:
/=У* J R-dx dy, с''
где R теперь уже является функцией аргументов х и у.
Будем обозначать момент инерции площади относительно начала координат О через /0. Тогда, очевидно, R = У х--J- у3, и мы получаем:
4 =//(я8+J2) dy.
Последняя формула дает:
k=ff(*+P)dxdy =
c • c
Итак, получаем теорему:
Момент инерции площади плоской фигура относительно начала координат равен сумме моментов инерции площади относительно двух взаимно перпендикулярных осей, проходящих через эту Точку.
Принимая во внимание, что элементарная площадочка в полярных координатах выражается произведением pd6dp, что х = р cos в, у «= р sin в, X2 -|-_у2 = р2, получим формулы моментов инерции в полярных координатах;
lx= J y*p8sin20d0 dp,
Iv — J ps cos2 0 dO dp,
1= f f R2pd4dp, = f fp'dbdp.
Пример 1. Найти /0 площади, ограниченной параболой у2=4ах, прямой у = 2а и осью ОУ (черт. 97).
Решение. Интегрируем сперва по х. Тогда, применяя формулу полярного момента инерции, подучаем:
Черт. 97.
(х3 4- у3) dy dx =
Пример 2. Найти 1у площади примера 1 (черт. 97), Решение. Соответствующая формула дает:
На 4а 2а
О и О
S' Пример 3. Найти /0 площади петли кривой
/ ] р = a sin 26 (черт. 98).
/ л? I Решение. Применяя соответствующую формулу, по-
/ Zz Z лучаем:
/ zZ yZ — —
/ xZ 'i 4 Bln 29 2
/ Г Г 1 Г T
I/——/0= / / p3rfOdp = — a* I sin426dti = —• >ta4.
О --------J J 4 J 64
oo о
Черт. 98.
УПРАЖНЕНИЯ.
1. Найти /0 площади, ограниченной прямыми х = а, у = 0, у = — х.
Оте. ab (-£ + ±-).
2. Вычислить /у площади прямоугольника, ограниченного прямыми х = а, у = Ь и координатными осями. *
Отв. W + V «5
3. Найти /0 площади прямоугольного треугольника, составляемого осями координат с прямою, соединяющею точки (а, 0), (О, Ь).
От.. “£<^+25.
4. Найти /_ площади круга х2+у2 = г2.
Отв. -г- . 4
х2 у2
5. Найти площади эллипса — 4--=гг = 1.
Отв.
4
6. Найти /0 площади круга х2 4- у2 = п 1 Отв. — г.г*.
X2 у2
7. Найти /0 площади эллипса 4- -^-= 1. Сравнить результат с предыдущей задачей; .
Отв. Zj— (а2 4- &).
8. Найти /0 площади, заключенной между прямою и параболой, осью которой является ось ОХ, если каждая из них соединяет начало с точкою (а, 6).
ab / а2 , Ь2\ Отв. - (—+ з-).
9. Найти 70 площади, ограниченной параболою у2 = 4ах, прямою х 4- у — За = О и осью ОХ. 314а4
о™.
10. Найти /0 площади круга р = 2а cos 0. 3 .
Отв. -у па4.
0
11. Найти /0 площади, ограниченной параболой р = a sec2 -j-, ординатой, проходящей через фокус параболы, и полярной осью. ^«4
Отв.
12. Найти /„ для площади лемнискаты s'- = a2 cos 20.
Отв. 4- -а*.
О
13. Найти /ц для всей площади кардиоиды о = а (1 — cos 0). „ 35пб'
о™. —.
14. Найти 1Х и 1у площади, ограниченной линиями у2 = lav, у = 0 и х = xt
Отв. Г = —, х 15 ’
. _?тЛ
Т •
15. Найти момент инерции площади прямоугольного треугольника, катеты которого равны а и Ь, относительно вершины прямого угла.
....
О/па. -jy (ц2 -I- Ь2).
16. Найти площади, ограниченной линиями у2 = 4а..-. x-|-j> = 3a, у— О л г 46 Отв. 1у = — я'.
г е г
17. Найти /. площади, ограниченной гипоциклоидой .г3 3 = а'' .
л 21 Отв. зр- -ц‘.
18. Найти /х площади, ограниченной петлей кривой p = acos20.
Отв. тйо(45*-128)-
19. Найти момент инерции полукруга радиуса а относительно касательной параллельной диаметру, ограничивающему полукруг.
Отв. -^-(15я- 32).
20. Вычислить момент инерции площади ограниченной параболой у1 = ах и прямой х = а, относительно прямой у
л 8 , Отв. ---а*.
О
§ 74. Общий метод вычисления площади поверхности. Метод нахождения площади поверхности, данный в § 58, приложим только к поверхности вращения. Далим теперь общий метод. Пусть уравнение поверхности АТ. на черт. 99 будет:
z=f(x,y), и пусть требуется вычислить площадь S' этой поверхности.
Обозначим ортогональную проекцию площади S' на плоскость XOY буквою 5. Проведем плоскости, параллельные YOZ и XOZf в расстояниях друг от друга, равных соответственно Дх и Ду. Эти пло* скости дадут усеченные призмы (например РВ), ограниченные сверху частями (например PQ) данной поверхности, проекции которых
на плоскость XOY суть прямоугольники площади ДхДу (например АВ), причем эти прямоугольники служат также нижними основаниями призм, а координаты точки Р суть (х. z).
Рассмотрим теперь касательную плоскость к поверхности KL в точке Р. Очевидно, тот же самый прямоугольник АВ будет проекцией на плоскость XOY части касательной плоскости (Рр), высекаемой призмою РВ. Если угол, образуемый касательной плоскостью с плоскостью XOY, будет 7, имеем: «
площ. ДВ —площ. PP-cos-,
Проекция площади на другую плоскость равна проектируемой площади, умноженной на косинус угла между обеими плоскостями.
или
Но
Sy Дх = площ. РР • cos 7.
[Эта формула косинуса угла, составляемого скостыо XOY, дается в аналитической
следовательно:
касательною плоскостью с плб-геометрии трех измерений.
ДуДх =
ПЛОЩ.
РР
ИЛИ
площ.
Дх Ду.
Примем области S
это за „элемент" площади области 5'; тогда площадь понимается как число, данное нижеследующей формулой:
v СС Г. । / V । / даЛ’Гл *
Дф->0
причем суммирование распространяется на область S. Обозначая площадь части S' поверхности буквою А, имеем, значит:
f 74] ОБЩИЙ МЕТОД ВЫЧИСЛЕНИЯ ПЛОЩАДИ ПОВЕРХНОСТИ 215 причем пределы интегрирования зависят от проекции на плоскость XOY области, площадь которой вычисляем. Следовательно, пределы интегрирования даст нам кривая или кривые, ограничивающие область S в плоскости XOY, совершенно таким же образом, как мы находили их в предыдущих параграфах.
Если было бы удобнее проектировать рассматриваемую площадь на плоскость XOZ, то мы имели бы формулу:
. Г Г Г. । / dv \* / ду VTj j А= I 1 -И — I + “Л dxdz, J J L \ох I \dz ] ] s
причем пределы даст ограничивающая область S кривая [теперь £ есть проекция требуемой площади на плоскость XOZ].
Подобным же образом имеем:
s
а пределы находим, проектируя рассматриваемую площадь на пло-скость YOZ.
В некоторых задачах требуется вычислить площадь некоторой части одной поверхности, отсекаемую другою поверхностью. В таких случаях частные производные, фигурирующие в формулах, надо вычислять, разумеется, из уравнения той поверхности, часть площади которой мы ищем.
Так как границы области интеграции находят проектированием искомой площади на одну из координатных плоскостей, то нужно помнить, что:
для нахождения проекции искомой площади на плоскость XOY нужно из уравнений поверхностей, пересечение которых дает замыкающую эту площадь кривую, исключить z.
Подобным же образом для нахождения границы проекции на плоскость XOZ надо исключить у, а для нахождения проекции на плоскость YOZ, надо исключить х.
Эта площадь поверхности иллюстрирует также интегрирование функции, распространенное на данную площадь. Так, в первой формуле мы интегрируем функцию
распространяя интегрирование на проекцию искомой криволинейной площади поверхности на плоскость XOY.
Пример 1. Посредством двойного интегрирования найти поверхность шара x2 4->,2 + zl = r2.
Решение. Пусть восьмая часть искомой поверхности будет АВС. Имеем: dz _ х dz _ у
dx z ' <fy ~ z '
и
1 -L ‘ _ — 1 - L _Z_ L Х__ — I X---LJ— = ------:-----
' \ дх } т \ dy ) г- ' z- z- г' — х- — у-
Проекция вычисляемой площади на пл. XOY есть АОВ, область, ограниченная ---- ,---- 1 ллч. г = о [QBу = 0 (А Оу. х3 + у1 = г- (ВА).
ливнями (черт. 100): х
Интегрируя сперва по у, мы суммируем все элементы полосы (например DEFG), проектируемой на пл. XOY в форме также полосы (MNEG), т. е. пределы у суть нуль и MP (= Vг®—х3). Затем, интегрируя по х, суммируем все полосы, образующие поверхность АВС, т. е. пределы суть шую
нуль и ОА(=г). Подставляя в соответствую-формулу, находим:
гг*
2
или
г dx dy
А
о
А = 4-г3.
на поверхности прямого ця-поверхность цилиндра высе-
г находится
Вычислить
шара радиуса
Пример 2. Центр линдра, радиус основания которого у. ченную шаром.
Решение. Взяв начало координат ось Z, а диаметр прямого сечения цилиндра за ось X.HaiixeMi что уравнение шара будет х- у- + z3 = г3, а цилиндра х3 + у3 = гх. Очевидно, ODAPB
в центре шара, образующую цилиндра за
(черт. 101) есть четверть искомой цилиндрической поверхности. Так как эта поверхность проектируется на плоскость XOY в виде дуги ODA полукруга, то на этой плоскости нет области S, по которой можно было бы определить пределы интегрирования в этой плоскости; поэтому проектируем нашу поверхность, например, на плоскость XOZ. Область S, на которую распространяется интегрирование, будет ОАСВ, ограниченная линиями: а = 0(ОА); х = 0(ОВ);
+ гх = Xs (АСВ), причем последнее уравнение найдем, исключив у из уравнений обеих поверхностей. Интегрируя спераа по z, — что означает суммирование всех элементов вертикальной полоски (напри мер PD), — будем иметь пределами для г пуль и Y г* — гх. Затем интегрируем по х, пределами будут нуль и г.
на цилиндре, то частные производные.
Y
—X
Черт. 101.
т. е. суммируем все эти полоски, причем Так как искомая поверхность лежит требуемые соответствующею формулою настоящего параграфа, должны быть най< дены из уравнения цилиндра.
Имеем:
ду _ • — Ъс ду
дх ~ п- 1
Таким образом имеем:
2у
dz
1
Г - 2х \2] 2 . .
—л------I Л dx.
о
о
Подставляя значение у в функции х из уравнения цилиндра, найдем:
о о
УПРАЖНЕНИЯ.
1. В последнем примере вычислить часть шаровой поверхности, высекаемой цилиндром.
Г > ГД?—X*
Отв. 4r f С —r dX_= 2(г — 2)г2.
J J У г2 - х- - у-и О
2. Оси двух равных прямых круглых цилиндров, у которых основания имеют радиус г, пересекаются под прямым углом; найти часть поверхности одного, высекаемую другим.
Указание. Уравнения цилиндров пусть будут х* -j- z- = г* и х2 -*-у* = г2.
г I Г«— Xs
Отв. 8г f f =
J J У г2 — х2 о о
3. Найти часть площади поверхности сферы х- -f- у- z2 = 100, заключенной между плоскостями х = — 8 и х = 6.
4. Найти часть площади поверхности цилиндра х2 4-у2 = г2, содержащейся между плоскостью г — тх и плоскостью XOY. q
5. Найти площадь поверхности z2 + (xcos з -j-ysina)2 = г-, содержащейся в первом октанте. г.
Отв.-----------.
sin a cos а
6. Найти часть площади плоскости ~ + т — = 1, заключенную между координатными плоскостями. .
Отв. у У Ь*с2 + с'-'Д- + a212.
7. Найти часть площади поверхности параболоида у2 + z- = 4ах, отсекаемого цилиндром у2 = ах н плоскостью х = За.
Отв. — -а2.
О
8. Найти часть площади поверхности цилиндра уа = ах, отсекаемой параболоидом у2 -|- z3 = 4ах н плоскостью х = За. _ ,
Отв. (13 V 3—1)
/3
2 2 X
9. Найти часть площади цилиндрической поверхности у3 4-z 3 —а3, отсекаемой поверхностью, проектирующейся на плоскость ХОУ в виде кривой 2 2 а
г 9 _1_ ® - п 2 - ~
= а
~ 12 .
Олта. -г-д*.
э
10. Найти площадь части поверхности шара х2 + у2 + z2 = 2ау, отсекаемой конусом хг + z2 = у*.
Отв. 2паа.
§ 76. Нахождение объемов посредством тройного интегрирования. Иногда объем тела, ограничиваемого поверхностями, уравнения которых даны, можно вычислить посредством трех последовательных интегрирований, — процессом, который просто есть расширение метода, изложенного в предыдущих параграфах этой главы.
Представим себе, что рассматриваемое тело разделено на прямоугольные параллелепипеды с измерениями Az, Ay, Ах плоскостями, параллельными плоскостям координат. Объем одного из таких параллелепипедов буде::
Дх • Ду • Az и мы примем его за элемент объема.
Будем теперь суммировать все такие элементы внутри области /?, ограниченной данными поверхностями, суммируя сперва все элементы столбца, параллельного одной из координатных осей; затем, суммируем все такие столбцы, заполняющие слой, параллельный одной из координатных плоскостей, содержащих эту ось; наконец, суммируем все такие слои, распространяя это суммирование на всю рассматриваемую область. Объем V тела будет, следовательно, пределом этой тройной суммы, по мере того как Az, Ду и Дх, каждое, приближается к пределу нуль, т. е.
И = lim S S S Дх Ay Az,
Д.т->0 н
Д|/->0
Лг ->0
причем суммирование распространяется на всю область R, ограниченную данными поверхностями, или, что то же:
V= / f' J' dxdydz,
я
причем пределы интегрирования зависят от уравнений ограничивающих поверхностей.
Таким образом, обобщая начало § 51, мы рассматриваем объем как результат интегрирования постоянной функции /(х,у, z)=l, распространенной на всю данную область. Но часто некоторые задачи требуют интегрирования уже переменной функции от х, у, z, распространяя ее на всю область, что обозначается символом:
f [ f f(x,y, z)dxdy
dz,
каковой, разумеется, есть предел некоторой тройной суммы, аналогичной уже исследованной нами двойной сумме. Метод вычисления такого тройного интеграла совершенно аналогичен уже рассмотренному в § 68 методу вычисления двойного интеграла.
Пример 1. Найти объем части эллипсоида
г® V® 2®
— 4--А-Д- — хз 1.
лежащей в первом октанте.
Решение. Пусть часть эллипсоида, объем которой требуется вычислить, будет ОАВС (черт. 102); уравнения ограничивающих поверхностей будут:
п$+4+4=1(Лб°-
2) z = 0(OABi,
3) у —О (CMC),
4) х = 0(ОВС).
PQ есть элемент, т.е. один из прямоугольных параллелепипедов с ребрами Дг, Ду, Дх, на которые область разделяется плоскостями, параллельными координатным плоскостям.
Интегрируя сперва по z, мы составляем сумму всех таких элементов в столбце (например RS), причем пределами интегрирования будут нуль [из (2)] и
[из (I), решая относительно г].
Интегрируя затер по у, мы суммируем все такие столбцы в слое (например DEMNQF), причем пределы у будут нуль [из (3)[ и MG = b 1 — £из уравнения кривой АОВ, а именно + решенного относительно у^.
Наконец, интегрируя по х, мы составляем сумму всех таких слоев в целой области ОАВС, при ем пределами для х будут пуль [из (4)| и ОА = а.
Итак,
п *сЬ Г r.abc
= mj (a2-x2)dr = —. о
Следовательно, объем всего эллипсоида раве.п
4 ~аЬс- >
О
Пример 2. Найти объем тела, заключенного между параболоидом вращения x^4-y2=az, цилиндром Лз -f-jja = 2ах и плоскостью z = 0 (черт. 103).
Решение. Пределы для z суть нуль и NP ( х2 + уа
( -----£*—, найденное решением уравнения парабо-
лоида относительно z).
Пределы для у суть нуль и MN(= V 2пх —х-, найденное решением уравнения цилиндра относительно у).
Пределы для х суть нуль в ОА(=2а).
Эти пределы относятся к Следовательво:
телу ONAB, составляющему половину требуемого-
Отсюда
УПРАЖНЕНИЯ.
1. Тройным интегрированием найти объем шара .v- и ^4-2=-А
_ 4 ,
Отв. -5-кг3.
«5
2. Найти объем одного из клиньев, вырезаемых из цилиндра ха + у'1 — плоскостями z = 0* и z = тх.
г 1 г—аг1 тх
Отв. 2 J ! I dxdydz = у а3т.
об б
3. Найти объем прямого эллиптического цилиндра, ось которого совпадает с о^ью ОХ, а высота равна 2а, если уравнение основания есть с2_у2 4~ Ь^г1 — Ь‘*с-.
с Ем-И abb
Отв. 2J*J" J* dxdydz = 2r.abc.
00 о
4. Найти весь объем, ограниченный поверхностью
Omf.
abc 90 ’
2 2 Я 2
5. Найти весь объем, ограниченный поверхностью х 3 '' -j- zs = а*.
Отв.
Аг.а3 ‘ЗУ’
6. Найти объем, вырезаемый в шаре радиуса а прямым круговым цилиндром, у которого радиус основания есть Ь, а ось проходит через центр шара.
2
7. Тройным интегрированием найти объем тела, ограниченного плоскостями х = а, у = bt z = тх и координатными плоскостями XOY и XOZ.
Отв. mbd*.
8. Центр шара радиуса г лежит на поверхности прямого кругового цилиндра, у которого радиус основания есть —. Найти объем части цилиндра, вырезаемой шаром.
9. Найти объем, ограниченный гиперболическим параболоидом сг = ху, плоскостью ХОУ н плоскостями х = alt х = а* у = б,, у = Ь*
(я* в?) *1)
Оте.----------<с-------.
10. Найти объем, общий двум цилиндрам х3 + J'2 = г® и х2 4- z® = А л 16 . Отв. — г®.
О
11. Найти объем тетраедра, образованного координатными плоскостями и пло-
+ т=1* Отв. ,'аЬе.
О
12. Найти объем, общий параболоиду + А = 4ах и цилиндру х3 + у* = 2ох.
Отв. 2ла®4-4Да*. О
13. Найти объем тела, ограниченного параболоидом x3-[-y3 — z = 1 и плоскостью ХОУ.
Отв. ~.
14. Найти объем тела, ограниченного параболоидом у3 + z2 = 4ах, цилиндром и2 = ах и плоскостью х = За. _ ,„
л Отв. (6z + 9 1^3) а3.
15. Найти объем, ограниченный плоскостью z = 0, цилиндром (х—а)2-|-+ — Ь)3 = г3 и гиперболическим параболоидом ху = cz. -abr-
Отв. ------..
с
16. Найти объем тела, ограниченного поверхностями z = 0, х2-|-у! = 4az х2 + у2 = 2сх. _ , .
17. Найти объем, замыкаемый поверхностями у3 4- л2 = lax и х — z = 2.
Отв. 8na®.
18. Найти объем тела в первом октанте, ограниченного посредством поверхностей ху = аг и х + г = а. _
Отв. — In4ja3.
19. Найти объем, содержащийся между плоскостью г = 0, цилиндром _у®= — х2 и параболоидом ах2 -4- by3 = 2z. 4 . , .
От‘- -г(-*+т)-
20. Найти полные объемы тел, ограниченных следующими поверхностями:
X® V® 2^
Ь) "5»+^ = 1-
с) (X2 + р z2j2 = 27a2 хуг.
d) (х2 + j2 + г3 + с2 - a2)2 = lc2 (х2 + у2).
е) (х2 + у1 + г3)3 = схуг.
\ о2 Ь3 + с2 ) а3 + Ь3 с3'
Отв.
8каЬс ~5~ *
2Аса3. с3
360 • n3abc 4 /2‘
ГЛАВА IX.
ОБЫКНОВЕННЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
§ 76. Введение. Многие задачи механики, физики и техники приводятся к уравнениям, содержащим производные или диференциалы. Такие уравнения называются диференциальными уравнениями.
Рассмотрим несколько задач, приводящих к составлению и решению диференциальных уравнений.
Пример 1. Найти уравнение кривой, угловой коэфициент касательной к которой в каждой точке в два раза больше абсциссы точки касания.
Согласно условию задачи имеем:
-f - = 2л-dx
у
Черт. 104.
ил..
dy — 'ixdx. (А)
Чтобы решить полученное д.ференциальное уравнение, проинтегрируем каждую часть его:
У = + С.
Таким образом, отправляясь от уравнения (А), мы получили в качестве его решения семейство кривых (черт. 104), зависящих от произвольного постоянного С; каждая кривая этого семейства удовлетворяет условию задачи.
Есл1?мы потребуем еще, чтобы искомая кривая проходила через точку (2,3), то, подставляя эти координаты в уравнение семейства, получим:
3 = 4 -|- С, откуда С = — 1,
т. е. введение этого дополнительного условия требует, чтобы С имело вполне определенное значение; другими словами, введение дополнительного условия определяет только одну кривую из всех кривых семейства1 и уравнение (А) имеет в качестве решения одну определенную функцию.
Если бы мы потребовали, чтобы кривая проходила не через точку (2, 3), а черев точку (—3, 10), то тогда получили бы:
10 = 9 - С. откуда С — 1, и уравнение искомой кривой было бы:
у = х2 4-1.
Пример 2. Hart,и уравнение кривой, длина отрезка касательной которой от точки касания до пересечения с осью ОУ была бы постоянна.
Пусть Р(х,у) (черт. 105) — произвольная точка искомой кривой. Уравнение касательной к кривой в точке Р есть:
где {X, Y) — текущие координаты точки касательной, а -^-—углевой коэфи-циент касательной, который определяется из уравнения (еще ие найденного) кривой. Тогда координаты точки R пересечения касательной с осью OY будут: Х=0, Y=v--------т-'Х и длина отрезка PR определится выражением:
ах
Так как эта длина должна быть постоянна, то, обозначая это постоянное через а, приходи.: к урав-
нению:
млн
dy = zt ------------dx, (к)
которое и является днферен-циальным уравнением искомой J, кривой.
Решением этот о уравнения, очевидно, будет следующее соотношение между х и у:
у = ± Va'--x- + ^\n
(В)
Наличие произвольного постоянного показывает, что существует бесчисленное множество кривых, удовлетворяющих условию задачи. Фиксируя какое-нибудь определенное значение С, мы видим из уравнений (А) и (В), что кривая симметрична относительно оси OY, что х- не может превышать значения а2. что dy . ' dy
=0 и у = С при х — а н что неограниченно возрастает, когда х стремится к нулю. Это исследование дает возможность легко построить график кривой (черт. 106), называемой трактрисой.
веса.
Пример 3- Гибкая однородная нить подвешена за два конца. Найти уравнение кривой, по которой расположится вить под действием собственного
Пусть А (черт. 107) — наиболее низкая точки нити, Р—произвольная точка искомой кривой и РТ — касательная к кривой в этой точке. Так как нить находится в равновесии, то часть АР нити можно легко рассматривать как твердое тело, на которое действуют три силы: натяжение t, приложенное в точке Р и действующее по направлению РТ, сила h, приложенная в точке А и действующая по горизонтали, и вес куска АР — нити. Так как нить однородна, вес куска АР равен рз, -
где л—длина дуги АР, а р — линейный удельный вес Черт. 10.. нити. Разлагая натяжение t на горизонтальную и вертикальную составляющие, в силу условия равновесия нити, будем иметь:
t cos ip -: h, t sin ? = ps.
Деля второе равенство на первое, получаем:
‘«’-J4
или
где а =-----постоянная величина.
Р
Полученное диференциальное уравнение содержит три переменных: х, v и л; но, диферениируя его по х, получим только два переменных:
[см. ч. I, § 121, формула (7)].
,, , rfv fPv dp
Чтобы решить уравнение (С), положим = р, тогда , и урав-
ьение (С) преобразуется в уравнение:
e^ = /И?
или dp dx
/1 + р- а
откуда имеем:
1П(Р 4- /1+/Я) = -i т С. (D)
В самой низкой точке А кривой х = 0, и угловой ко^фициент касательной dv
= р = 0;"Подставляя эти значения в уравнение (Dj, находим, что С=*0. Следовательно, можем написать:
X
р I- Уха-У-= еп
Поэтому
у=^(е*А-' “)+С'.
Значение С' зависит от положения оси ОХ, потому что у = а 4- С' при х = 0, Так как положение осн ОХ мы можем выбрать по нашему желанию, то, взяв расстояние ОА = а, получим О' = 0, и окончательно приходим к уравнению:
представляющему собой уравнение цепной линии.
§ 77. Порядок и степень диференциального уравнения. С диференциальными уравнениями мы встречались уже в первой части, таковы, например, уравнения:
1) = Пр. 23, стр. 221
' dxa ' dx 1
2) + Пр. 4, стр. 280
’ \ dx 1 / \ dx2 / \ dx 1 J dx dx*
3>^= 4) = ' dx* 5) dy — a sin 0. = 12 (2х — 1). Ь*Х J -x-rfX. а*у a9 sin 26 .. Пр. 1, стр. 199 Пр. 1, стр. 221 Пр. 2, стр. 263
6) dp — - — -—‘—dd Р Пр. 3, стр. 263
7) d*y = (20х8 — 12х) dx9. Пр. 1, стр. 264
л ди ди
х дх 4- у-д- = 5и. 1 J ду Пр. 7, стр. 327
. д*и , &и „ ди
У) Х дх* । У дхду 2 дх ‘ Пр. 8, стр. 342
10) аг()уя = <1+3^г + х'-у’г!)“ Пр. 7, стр. 341
Вся глава ' XI в диференциальном исчислении и вся глава III в инте-
тральном исчислении занимаются в сущности диференциальными уравнениями.
Обыкновенное диференциальное уравнение содержит только одно независимое переменное. Первые 7 из вышеприведенных примеров суть обыкновенные днференциальные уравнения.
Диференциальное уравнение с частными производными содержит более одного независимого переменного: таковы примеры 8, 9 и 10.
В этой главе рассматриваются только обыкновенные диференциаль-ные уравнения.
Порядок диференциального уравнения есть порядок высшей производной (или диференциала) в нем. Так, 3, 5, 6 и 8 суть уравнения первого порядка-, 1, 4 и 7 суть уравнения второго порядка-, а 2 и 10 — третьего порядка.
Степень диференциального удранення, алгебраического относительно производных (или диференциалов), есть степень высшей в нем производной (или диференциала), когда уравнение освобождено от радикалов и от дробей. Так, все вышеприведетные примеры диференциальных уравнений суть уравнения первой степени.
§ 78. Решение диференциальных уравнений. Постоянные интегрирования. Решение или интеграл данного диференциального уравнения есть такое соотношение между переменными, при котором данное диференциальное уравнение тождественно удовлетворяется. Так,
y = CjSinjc •' (1)
есть решение диференциального уравнения:
15 Зав. 3858. — Гр»жжжль а Луввв, ч II, Ихтвграаьвов жочжспвнж»
В самом деле, диференцируя (1), найдем:
^ = -c1Slnx. (3)
Подставляя (1) и (3) в (2), получаем;
— с, sin х -L сх sin х = О,
показывающее, что (1) удовлетворяет (2) тождественно. Здесь с, есть произвольное постоянное. Таким же точно образом
y = c2cosx, (4)
как легко убедиться, есть решение уравнения (2) для любого значения с2 Соотношение у _ sin х _|_ cos х
есть еще более общее решение уравнения (2). В самом деле, давая частные значения количествам сх и г8, легко видеть, что (5) чключает в себя как частный случай решения (1) и (4) *).
Произвольные постоянные г, и с2, входящие в эти решения, называются постоянными интегрирования. Решение вроде решения (5), содержащее несколько произвольных постоянных количеств, число которых равно порядку уравнения (в данном случае двум), называется общим решением или интегралом а). Получаемые из него решения, если этим постоянным давать частные значения, называются частными решениями или частными интегралами.
Считается, что диференциальное уравнение решено, если удалось найти для искомого переменного выражения, содержащие неопределенные интегралы, все равно, могут ли быть эти неопределенные интегралы взяты, или нет.
§ 79. Поверка решений днференциального уравнения. Проблеме решения диференциальных уравнений полезно предпослать указания, которые позволили бы читателю лучше освоиться с тем, что разумеют под именем решения днференциального уравнения, а для этого лучше всего будет проверить несколько данных решений.
Пример. Показать, что
у = Cj.v cos In х -|- CjX sin In x x In x (A)
сть решение диференцвального уравнения:
x* 2 * * — x 4- 2_y — x In x. B)
dx9 dx 1 J '
Решение. Диференцируя (А), находим:
== (c2 — c,) sin In x 4- (ca 4- c,) cos In x 4- In x 4- 1. (C)
day . , . sin In x , . . cos In x , 2 _4
4. C,)-_— +(C3-C,)—4-J. (D)
Подставив (А), (С) и (D) в (В), убедимся, что это уравнение тождественно удовлетворяется.
1) Достаточно положить либо ct = 0, либо с.: = 0.
2) В теории диференциальных уравнений доказывается, что общее решение
содержит п произвольных постоянных, если порядок днференциального уравне-
ния есть п.
УПРАЖНЕНИЯ.
Проверить следующие решения соответственных днференииальных уравнений:
Диференциальные уравнения. Решения.
1. fdyVdyd^ \dx J dx dx 1 „ ( dv \a . „ dv л 2y{dx)+2xdx y~Q- 4. Ф.+2_ ^r_0. dx* t x dx* 5 2A dy Aav = e® X dX* dx ‘ я>'=<г- 6^_4^ + 6^_4| + v=0. dx* dx3 1 dx1 dx _ о r rfv . - 1 7. xa — 5x —— + 5y = —. dx* dx x 8. x -^—y + xVjfl-ya = Q . dy . sin lx 9-?T+>'C0SX= 2 • 10- u.-ЙH-2-^ = o. dx* 1 x dx у = cx + c — c2. y2 = 2cx + c3. /Л/* yi_fxa 4-^=0. y = Cix + -^-+ c3. y-(cl + cix^+{F-w. У = (<a + V +«»»* + <•**•) «Р. 4у=3^ + с1х*4-с,х V arcsln — = с — г. X у = slnx — 1 4-ce~,inT. у = fle“ « -j- сге~ ° “C81n x. У = -у т сг.
§ 80. Диференциальные уравнения первого порядка и первой степени. Подобное уравнение всегда можно привести к виду
М dx -|- N dy = О, где М и W суть функции хну. Диференциальные уравнения, относящиеся к этому виду, можно разделить на следующие типы.
Тип I. Уравнения с отделимыми переменными. Когда члены диференциального уравнения можно распределить так, чтобы оно приняло вид:
f(x)dx + F(y)dy = O, (1)
где /(х) есть функция одного х, a F(y) есть функция одного у, то процесс приведения уравнения к написанной форме называется отделением переменных', решение такого уравнения получается прямым интегрированием. Так, интегрируя (I), получаем общее решение:
f f(x)dx + f F(y)dy = c, (II)
где с — произвольное постоянное.
Уравнения, заданные не в такой простой форме, как (I), часто можно бывает привести к этому виду, следуя нижеследующему правилу onide-ления переменных.
Первый шаг. Освобождаем от дробей и, если уравне-
ние содержит производные, умножаем его на диферен-
циал независимого переменного.
Второй шаг. Соединяем в один член все члены, содержащие один и тот же диференциал. Если после этого уравнение примет вид:
ХГЛс-Ь А"Г<у = 0,
Пример 1. Решить уравнение -- .
Решение.
Первый шаг.
(1 4-хЗ) ху dy = (\+ у») dx.
Второй шаг.
(1 + Я dx - х (1 + хЗ)у dy = 0.
Чтобы отделить переменные, делим теперь уравнение на
х(1+х=)(1+Я и находим:
Sx-_____УаУ_ — п
Х(1+Х*) 1+у2
Третий шаг.
/• __ Г = г
J х(1 + хЗ) J
dx _ Г xdx /* у dy = ,/ х J 1 4- Д'2 J 1 +У’ ’
1пх - 1 In (1 + х2)-1 In(1 +я = с.
In (1-|-Xе) (1+у2) = 2 In х — 2С.
Этот результат можно представить в более сжатой форме, если - 2С заменить ерез 1п с, другими словами — если дать произвольному переменному другой вид. Решение примет вид:
In (1 + х2) (1 +Я « 1п х» + 1п с,
In (Н-хг) (1 +Уг) = 1псх«,
(I + х2) (1 +Я = ехг.
Пример 2. Решить уравнение:
«(^^+2y) = -vyg.
Решение.
Первый шаг.
ах dy + lay dx = ху dy.
Второй шаг.
2оуdx4-х (а—у) dy = 0.
Для отделения переменных делим на ху.
ЧаЛх (я—y)rfy = 0 л "Г У
Третий шаг.
2а In х -j- а 1л у —у = С, a Inx^y = С
In jfly = — + — -а ' а
Перехода от логарифмов к показательным функциям, можем этот результат написать в форме:
- + - — х?у — еа ° или хгу = еа-ва.
с
Наконец, обозначив постоянное еа буквою с, имеем решение в виде:
у_ хгу = се °.
Пример 3. Решить уравнение:
rfx-i- /Г=^4у = 0.
Решение.
Первый шаг.
У1 —y'-dx + У I -х« dy = 0.
Второй шаг.
+
У 1-х2 yi— у*
Т РЕТНЙ ШАГ
Г dx 4- /* —'-У— = С
J J ут-у- ’
arcsln л -|- arcsin_y -= С.
Этот результат можпо представить в другой форме. Обозначим arcsln х через у и arcslnу через ф. Тогда полученное решение перепишется в виде: у -у ф = С, от ;уда sin (у -|- ф) = sin С или sin у cos ф Ц- cosy sin ф = sin С. Но так как sin у = х, 51пф=_у, cos y = У1 — х\ сэ5ф= У1 — у2, то получим:
X УТ=у*+у где sin С = А.
УПРАЖНЕНИЯ.
Диференциальные уравнения Решения
1. у dx — х dy = 0. y = cx. J
2. (1 + y)dx—(\-х) dy = 0. (14-y) (1—x) = c.
3. (1+x)>rfx+(l — у) x dy = 0. In xy + X — у = c.
4. (x2 — a2) dy —y dx = 0. га x — a У =C x + «-
5. (x*-yx*) ^+^ + xy = 0. ^i^ + In ^- = c. xy x 1
6. ifi dv + (v — a) du = 0. v — a = ce “.
-du 1 + u1 v+e
dv ^14- o»’ U = ; • 1 — tv
8. (Is?) dt — t - ds = 0.
9. dp р tg в db = 0.
10. sin в cos ? М — cos 0 sin <fdf = O.
11. sec2 * * * 8 tg f di -I- sec2 <p tg 6 df — 0.
12. sec2 6 tg f df 4* sec2 f tg 0 d9 = 0.
13. xy dx — (a -|- x) (b 4- y) dy = 0.
14. (1 + x2) dy — V\— y- dx = 0.
15. /Г^х2 dy — V\— y- = 0.
16. 3e* tgy dx 4- (1 — e*) sec1у dy = 0.
17. 2x'ydy = (14-x2)dx
18. (x — j»*x) dx 4- (y — x2y) dy = 0.
19. {jfly + x) dy + (xy1 - v) dx = 0.
2t2 — arctg s - - c.
p = c cos 0.
cos f = c cos 6.
tg в tg ? = c.
sin2 8 + sin2 f = c.
X — у — C + In (a + х)ау*. arcsin j — arctg x = г.
у VЬ^х2 — x Y = с. tgy = с (1 — е*)\
У---J-4-х + с.
х24-у = л-у-Ч с-
ху 4- In — = с.
Тип II. Однородные уравнения. Диференциальное уравнение
М dx-\- Ndy = 0
называется однородным, когда Л1 и W суть однородные функции от х и у одинаковой степени ’)• Такие диференциальные уравнения можно интегрировать посредством подстановки
у = vx.
Эта подстановка приводит к диференциальному уравнению относительно v и х, в котором переменные отделимы и которое, следовательно, можно интегрировать по правилу, формулированному на стр. 227.
Пример. Решить уравнение:
у 4-у- £L = xa^..
' dx У dx Решение. у2 dx 4-(х2 — ху) dy = 0. Так как ато — однородное уравнение, мы преобразовываем его подстановкою: у = ох, откуда dy = v dx 4- х dv, и уравнение обращается в
v2x*dx 4- Qr2 — рх2) (о dx 4- х dv) = 0,
x4>dx4-х* (1 — v) dv = 0.
Для отделения переменных делим на vx8. Имеем:
dx । (1 —v)dv _р
2) Функция от х и у называется однородною относительно переменных, если
результат замены х и у количествами кх и Ху (где к произвольно) приводит
к первоначальной функции, умноженной на некоторую степень К. Эта степень К
называется степенью однородной функции.
h. х In v — v = С, In vx = С + v, vx = ес+в = ef - e", vx = cev.
Ho v = Следовательно, решение будет: у, у =сёс .
УПРАЖНЕНИЯ.
Диференциальные уравнения.
1- (х + >) <br + xdy = 0.
2. (x+>)rfx + O--x)<y = 0.
3. х dy —у dtx = V х*4* J*2 dx.
4. (By + 10x) dx + (5y + 7x) dy = 0.
t. (2 У st — s) dt +1 ds = 0.
G. (< — s) dt 4-1 ds = 0.
Я te* = .-.
7. x cos — • ~ = v cos -----x.
x dx x
8. xy* dy = (x® + У3) dx.
9. (x»~2y®) dx + 2xydy = V.
10. (x3 4-j13) dx = xy dy.
Решения.
(x3 + 2xy) - c. i
In (x» — arctg — = c.
x
1 + ley — c=xa = 0.
(x+^p (2x+>)> = <:.
= 3xs In ex. y* = — x3 In ex. y* = x*-\-cx.
11. x cos -=£- (y dx 4- x dy) = у sta (x dy — у dx).
Отв. xy cos — = c.
Тип ill. Линейные уравнения. Диференциальное уравнение называется линейным, если оно первой степени относительно зависимого переменного (обыкновенно у) и его производных (или диференциа-лов). Линейное диференциальное уравнение первого порядка имеет виц -^+^=Q. (»0
ИЛ
гдеРи Q суть функции одного х (или некоторые заданные постоянные числа).
Чтобы найти интеграл уравнения (А), положим у = ttz, (G)
где и и z суть две подлежащие определению функции от х. Диферен-цнруя (III), имеем: d dz , du
dx dx' dx v '
Подставив (7) и (6) в (III), находим: dz . du . п _
и -з—Н 2 ~г~ + Puz = Q> dx 1 dx 1
или
и + + z=Q. (8)
dx 1 \ dx 1 / '
Постараемся теперь определить, если это возможно, функцию и так, чтобы член* с z исчезал. Это значит, что мы требуем, чтобы коэфи-циент при z обратился в нуль, т. е.
Отсюда
du „ j — =— Pdx, и
или
1п и = — J* Pdx,
откуда
= (9)
Уравнение (8) превратится, следовательно, в уравнение: dz л “^ = Q-
Чтобы найти z из последнего уравнения, подставим в него значение для и из (9) и интегрируем. Имеем;
f ~=Q
' dx
Cidz^Qel?*” dx
(\z = J Qe^rdx dx^-C.
Решение уравнения (III) найдем, подставив значения для и и z в (6). Таким образом окончательно получим:
y = e~SPdx(J Qefpix dx-J-C). (HI*)
Для проверки правильности (III*) нужно прямо найденный интеграл подставить в (III). При решении следующих за сим примеров советуем
Ч Произвольное постоянное с, можно было бы положить сразу равным единице, так как функция и может быть какой угодно, лишь бы только скобка в уравнении (8) обращалась в нуль; а вто будет и при сх = 1. Из дальнейшего решения читатель увидит, что с, все равно исчезает в окончательном результате, чего и следоваао ожидать заранее, так как общий интеграл днференциального уравнения перього порядка может содержать только одно произвольное постоянное, которое возникает необходимо при нахождении функции а.
учащемуся отыскивать решения, следуя вышеуказанному методу, а не прямо пользоваться формулою (III*). При подстановке значений и и в (6) постоянное интегрирования q сокращается [см. (Ш*)].
Пример. Решить уравнение.-rfy_______________________2у
dx х +
Решение. Очевидно, это — линейное уравнение (III), где 5 2 2
р= а <?“(* + !) .
(х+1)2.
(А)
„ dy dz . du „
Пусть у = uz; следовательно, -— = и —- 4-z —. Подставляя в данное ура в-
- , ах ах ах
нение находим:
dt | du lux dx 1 Z dx 1 + j
или
ь
du 2u
(В)
Для определения и приравниваем нулю коэфициент при z. Находим: du 2и dx Т+7 “ °’
du 2dx
In и — 2 In (1 + х), и = (1+л)-’. (С)
Так как член при z обращен в нуль, уравнение (В) будет иметь вид: ,5 2
Заменив и его значением ив (С), находим:
= U + 1) ' . dz — (х -j-1)* dx.
+c
Подставляя значении It н г в у = иг, имеем искомое решение;
^_2(£±!>1+С(ж + 1), О
УПРАЖНЕНИЯ.
Диференциальные уравнения
1. ir—- <А‘ + V-
dx х 4- 1
Решения.
2j' = (x + l)«4-c(x + l)«.
3. х (1 — хг) dy -f- (2х» — l)_yrfx = ajfldx. у = ex + ex У1 — x’.
, . xydx a dx *" 4,.-!+.> r ds . , ... 5. cos t + s sin 1. 1 6. -ТГ + 5 COS t =5 — sin al 1 _ dy n , - 7 -xy = e x • 8 rf4- v - - 8- dx+ x > - xn‘ „ dy , 1 9. -A+y = — 7-dx e* dy . 1 — 2x , 10-——-v~l- j = ax+e (1 + x2)8. s = sin t + c cos t. s = sin t — 1 + ce~ 1 j'-x'f^ + r). = ex + e. e*y =x + e. > у =x»(l +<-ex).
§ 81. Уравнение Бернулли. Уравнением Бернулли называется уравнение вида:
^+^=0/, (iv)
где Р и Q суть функции от х. Это уравнение решается тем же методом, что и линейное уравнение.
Пример.
Полагая y = uv, будем иметь: 1 (du и\ , dv _ . .
+ = (А)
Приравняв нулю скобг /, найдем и: . v
du и —----— = 0, откуда и = х.
Подставив в уравнение (А), получим: rfv . . dv , , 1 х* .
= — = ^dx;^ = — -K,
и окончательно, так как v = -^—\ х
1_______Xs . с
у3 ~ 2 • х5
УПРАЖНЕНИЯ.
Дифференциальные уравнения.
1. Q + xy^xty3. dx J
2. (J-x*) ^. — ху = ах)Ф.
Решения. у-г = лх4-1 + сгу. у~(с УТ^-Н)"1.
3. Зу2 г/х
4. (*• v*+ •*>) = !•
5. (у In х — 1) у dx = х dy.
6. V — COSX -г- — yi cosx (1 dx
7. x inx.
vs = ceaT - -£±2----L .
a a2
Г и ] x 1(2-У2) ei +d = <’*•
> = (ex 4-Inx + I)-1.
. tgx4-secx
9,n rl
y~1 = In X -|- 1 -|- ex.
§ 82. Некоторые виды дяференцнальных уравнений второго порядка.
Тип I.
Непосредственное интегрирование этого уравнения дает:
> = / [/ f(x)dxj dx 4- ctx + Ct.
. Этот метод приложим также к диференциальным уравнениям порядка выше второго, имеющим аналогичный вид:
Пример. Диференциальные уравнения этого типа встречаются в теории изгибания бахок. Каждая сила, действующая на балку (каковы, например, нагрузки балки и реакции опор), имеет момент относительно какого-нибудь поперечного сечения балки, равпый произведению силы на расстояние точки приложения силы от сечения. Сумма М моментов всех сил, расположенных по одну сторону от данного сечения, носит наименование изгибающего момента балки относительно сечения. С другой стороны, в сопротивлении материалов доказывается, что изгибающий момент балки равен где Е — модуль упру-К
гости вещества балки и /--момент инерции площади поперечного сечения относительно горизонтальной линии, проходящей через центр тяжести площади поперечного сечения1)! и R—радиус кривизны кривой нагиба балки. По формуле 3, ч. I, § 131.
1 _ /Г-
(Ру г/л-’
, т , dr
где х считается изменяющимся вдоль балки. Та;: как в обычных случаях -J dx
есть велччи«1 весьма малая вследствие малой искривленности балки, мы мржем
бев чув^вительной ошибки положить — = . Поэтому нагибающий момент
*) E и I— величии постоянные.
принимается равным EI — . Таким образом получаем диференциальное уравнение изогнутой оси балки:
Е1 = М. dxi
причем под осью балки понимают линию, проходящую через центры тяжести поперечных сечений балки.
Применим эти понятия к нахождению формы оси балки (изгибание балки), равномерно нагруженной, концы которой расположены на опорах.
Пусть / —расстояние между опорами и ш — нагрузка, приходящаяся на погонный метр балки. Расположим начало координат в середине балки. Возьмем поперечное сечение балки на расстоянии х от начала и рассмотрим силы, приложенные вправо or него. Этими силами являются: нагрузка на правую часть и реакция опоры. Нагрузка, приходящаяся на правую часть равна w ----,
и так как нагрузка предположена равномерной, то ее действие можно заменить действием силы той же величины, приложенной к центру тяжести правой части, отстоящему на расстоянии — — д• ) от поперечного оечения. Момент этой силы есть j z 2
~ "2 W (Т ~ Х ) •
Реакция опоры равна —, так как полная нагрузка есть то/. Следовательно момент этой реакции относительно поперечного сечения равен wl (I \ 2 G Х)'
Таким образом получаем уравнение:
(т-'Н(-НЧ (’Ч
Первое интегрирование дает:
Так как в середине направление осн балки горизонтально, то = 0 прв х = О, откуда Ci = 0. Интегрируя вторично, получаем: w /Рх* х»\ ,
Е у~ 2 \ 8 12 / + C l>
причем tg с= 0, так как у = 0 при х = 0.
Следовательно, искомое уравнение изогнутой осн балки есть: w fPx* jr*\ £{у = ^Г\Гь---------------------------ТГ?
Тип П.
Существенный здесь является то, что уравнение этого типа не содержит явным образом у.
dy &у dp
Для решения этого уравнения положим тогда № =
и уравнение преобразуется к виду: = f (х, р), т. е. к уравнению
rfy
первого порядка. Определив из него р, из уравнения —£~=р найдем у.
В § 76, пример 3, мы видели, что к решению уравнения этого типа приводится решение задачи нахождения формы равновесия гибкой нити, подвешенной за два конца.
Тип III.
Характерным для уравнений этого типа является отсутствие явным образом х. Если мы применим тот же способ решения, что и для урав-,, dp , ,
нений типа П, то придем к уравнению: (у, р), содержащему
п dy
три переменные х, у, р. Поэтому, положив =р, вторую производную у
по х представим следующим образом:
= 1). rfx2 dy ’ dx р dy
Благодаря этому данное уравнение преобразуется в уравнение первого порядка:
Найдя из него р, определим далее у из уравнения: iL=p. dx р
Пример 1. Найти закон движеввя маятника, состоящего нз небольшого тела массы т, привешенного к нити длины I.
Пусть 0 — угол отклонения маятника от вертикального положения и пусть соответствующая ему дуга равна s. Весом инти и сопротивлением среды пренебрегаем. Тогда будем иметь единственную силу — силу тяжести mg тела массы т. Маятник будет стремиться вернуться к вертикальному положению под действием составляющей веса mg Эта составляющая равна — mg sin 6. Согласно
<Ps „
закону Ньютона эта же сила определяется выражением Следовательно, уравнение движения будет следующее:
А т = — mg sin 0.
1) Это равносильно тому, что мы считаем р функцией не от х, а от у. В самом деле, в таком случае по теореме производной функция от функции (§ 70, ч. 1) будем иметь:
dp _ dp ay dx ~ dy dx'
Предположим, что маятник отклоняется лишь на малые углы в. Тогда без существенной ошибки можем положить sin 0 = в. Так к^к 0 = -J-, то уравнение движения перепишется в виде: A? g
=----- 3.
uf- I
„ ds <Ps dp
По агая — =p, откуда = p --£, получаем; al aP tfs
„ dp _ g p~dl = - T s-
Разделяя переменные и интегрируя, находим:
2
£ Ji
l 2
g
Полагая q = в’, имеем:
или
откуда
что дает:
Предположим, что маятник проходит через ввртлкальное положение в момент времени Тогда, при t = /0 дуга № 0 и са = — ]/~~ 10. Следовательно* последнее уравнение примет вид:
arc tin -у = |/ -у (t — Г,),
откуда
з = a sin у у (1 — Zo).
/ £
Дуга з достигает максимального значения при sin у у (/ — /oj = ]. Cie-довятельно, постоянное а представляет собой амплитуду колебания маятника.
Пример 2. Найти уравнение кривой, радиус кривизны которой в каждой точке (х, у) равен длине нормали (отрезок нормали между точкой кривой и осью ОХ).
Радиус кривизны равен
3
,.нж
d^y' йх» .
(§ 134. ч. 1); длина нормали определяется выражением:
(§ 92, ч. 1). Следовательно, условию задачи соответствуют два уравнения: а
Л)
и
dx*
3 rfy\q2'
(В)
« ,.. n d\' d*y dp
Решаем уравнение (А). Положив = p и =p , получаем:
или
dy р dp
что дает:
откуда
Заменяя р через приходим к уравнению:
dx
или
dy .
J = dx.
Интегрируя последнее уравнение, находим:
1
откуда
' 2 4 '
Следовательно, искомая кривая есть цепная линия с вершиной в точке (о, с,) (см. § 76).
Решая тем же методом уравнение (В), последовательно получим:
что дает:
У
-лкуда
V С\~У*
Р = -----у----.
_ dy
Заменив далее р через получим уравнение:
ydy j — = dx,
решая которое найдем уравнение: 1/” 2 2*
-И е1~У = Х“С2
или
Это есть уравнение окружности, центр которой лежит на оси ОХ.
УПРАЖНЕНИЯ.
Диференциальные уравнения Решения
1. — 2cosx. dx* 2-^=2- 3. -2- = s,nS0-dv9 хь У = би + 2sinx + ctx3 + CjX + ct и = V3 In О + С,»» 4- CgO + ca. cos86 . 7cost) , r. , p- -27 + 9 +c*62 + 4- е2в -j- c3.
4. "У = х-. dx" rn\xm + n , , У~ '(m + n)! +c,A +••• • • • 4" cn—ix 4" rn‘
5. = а*у. rfX2 dy а ь-¥=7* 7 = 1 . dfl Уел В _ 1 dx"- V1—ха 9 X^y-^L = X^ s- х dx* dx -+Ш- ax = In(y 4- Vyr+ q) 4- tj или у = с^е03* 4 c^03. + е2у = — a. 1 1 11 ЗТ = 2а<(л2-2С1)(з¥4-<ч)34-<3- у = X arc sin X 4- У 1 — X8 4- ctx 4- c.^ y = ex(x-l)-i Cix-4- c2. i *a i y = c,1nx —— 4-ca. 4y4- = qx-4- -^-Inx. 4 у = q sec cx (x — ej.
II.
V + et In у = х -L Сг.
^-У dx*
-|- tgx = sin 2x. 1 dx b
у = с3 + Cj sin х — х-----sin2x.
У —
^(а-е.)
_|_ е— Мя—е,)]_
<Г-'<
Х dX-
= 0.
- , . Зх
6y+f1 = c1x’ ——.
*1
§ 83. Линейные днференциальные уравнения второго порядка с постоянными коэфициентами. Простейшие механические колебания. Вопросы колебания связаны с исследованием уравнения вида:
^+,.£-Л,=Х, (V)
тип Ш.
4
Черт. 108.
где X есть функция одного х или постоянное число, а и р3— постоянные ьеличины.
Уравнение (V) является частным случаем линейных диференциальных уравнений, общее определение которых дано в § 80, К , уравнениям этого вида мы приходим, решая, например, следующую простую задачу.
Рассмотрим вертикальные колебания тела массы т, подвешенного на пружине, около положения равновесия; в положении равновесия вес тела точно уравновешивается упругой силой пружины.
Обозначим через х расстояние тела по вертикальному направлению, считая от положения равновесия (черт. 108), и предположим, что движение происходит в среде, сопротивление которой пропорционально скорости.
На тело, во-первых, будет действовать сила, стремящаяся вернуть его в положение равновесия, —так называемая восстанавливающая сила пружины; допустим, что величина этой силы пропорциональна отклонению тела от положения равновесия, и положим ее равной — сх, где коэфициент с служит мерой прочности упругой связи. Так как с предполагается положительным, то сила, направленная всегда к точке х = 0, имеет отрицательное значение при положительных значениях х и поло
жительное значение, когда х принимает значения отрицательные.
Во-вторых, на тело действует сила сопротивления, пропорциональная
скорости —тт- и направленная противоположно скорости; поэтому она ас
. dx . численно выражается в виде — о—гг, где Ь— положительная постоянная. dt
По основному закону Ньютона произведение массы т на ускорение d*x ‘
-ту равно восстанавливающей силе пружины, сложенной с силой сопро-
16 Зав. И53. — Гравввта Луавв, в. II, Ивтегральвоо вовжввавжа
тивления.
будет:
Следовательно, диференциальное уравнение движения тела
т
<?х dt*
bS-cx
или
<v')
и х h
Если это уравнение разделим на т и обозначим — через л., с т
а — через ра, то получим уравнение вида: /я . dx .
лг+а-^+лх’О,
которое является частным случаем уравнения (VI).
Если предположим еще, что точка подвеса сама совершает вертикальные колебания, причем се вертикальную координату будем считать функцией F (/), зависящей от времени, то фактическое удлинение пружины будет теперь не х, а х — F (?) и поэтому восстанавливающая сила пружины станет равной —с[х — F(t)]. В таком случае вместо уравнения (VI) мы получим уравнение:
b~dt+cx = F^' <vn)
t. e. опять-таки уравнение вида (V).
Если F(£) = 0, то колебание называют свободным, и диференциальное уравнение движения — однородным. Если F(t) не равно нулю для всех значений t, то говорят о вынужденном колебании, и диференциальное уравнение движения называют неоднородным. Член F(t} именуют возмущающим членом.
Это исследогание простого случая колебательного движения приводит нас к необходимости обратиться к рассмотрению вопроса о решении уравнения (V). Начнем исследование с решения однородного уравнения.
§ 84. Однородное линейное уравнение второго порядка С постоянными коэфициентами. Формальное решение. Для уравнения
g+A-^+M-0 (V)
мы не можем найти общего интеграла способами, подобными тем, какие применялись для решения всех ранее рассмотренных диференциальных уравнений. Этот способ состоял в том, что путем различных преобразований мы сводили дело к вычислению интегралов. Теперь мы пойдем совершенно иным путем. Именно мы покажем, что общее решение. уравнения (V*) может быть найдено при помощи его постных решений.
Допустим, что мы каким-нибудь образом нашли два частных решения У1 и У* уравнения (V*) и допустим, что эти функции ух и уа линейно независимые, т. е. что нельзя подобрать такого постоянного числа k, чтобы функции ух и yt были связаны между собою равенством у, = AjJi-
Например, функции y^slnx, у, = cosx, очевидно, линейно независимые Напротив, функции _У1 — и Уя = е3+Ях линейно зависимые, потому что у, = е8 + 21 = е8 е2® = iyt, где А = е8.
Тогда общим интегралом уравнения (V*) будет являться функция
У = + (VIII)
Чтобы доказать это предложение, покажем что функция (VIII) удовлетворяет уравнению (V*). Для этого подставляем ее вместо у в левую часть уравнения (V*), Будем иметь:
+л +„ о,, +,,) =
=^(^г+^$+Р'л) +с« (^’ Ч-а^Ч-лл) • Первая скобка полученного выражения представляет собою результат подстановки частного решения _у, в левую часть уравнения (V*) вместо у; поэтому эта скобка равна нулю. Аналогично — вторая скобка тоже равна нулю. Следовательно подстановка суммы ciy1-j-ciya обращает левую часть уравнения (V*) в нуль. [Это [показывает, что функция (VIII) есть решение нашего днференциального уравнения. Но вместе с тем эта функция является и общим интегралом уравнения (V*), так как содержит два произвольных постоянных с, и са (см. сноску на стр. 225 ).
Если бы функции jZj и у2 не были линейно независимыми, т. е. если бы ya = kylt то образовать из этих решений общий интеграл было бы невозможно. В самом деле, мы в таком случае имели бы:
У = G Л -г c^ky, = (сх + cik)yl = суи
т. е. функция у содержала бы только одно произвольное постоянное с. Следовательно, теперь задача сводится к нахождению вида линейнонезависимых частных решений ух и уй.
Для этого предположим, что частное решение имеет вид у = егя, где г ^сть постоянное количество. Будем иметь:
Подставляя эти значения в левую часть уравнения (V*), получим;
ег’(га+Р1''4-Л)-
Таким образом, для того чтобы функция eTI была решением диференци-ального уравнения, необходимо и достаточно, чтобы многочлен г9 обратился в нуль, т. е. чтобы постоянное г было корнем уравнения:
'а+А'-+А = 0. (IX)
Будем называть это уравнение характеристическим.
При его решении возможны три случая.
1. Корни rt и га характеристического уравнения мо-
244 ОБЫКНОВЕННЫЕ ДИФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ [ГЛ. IX гут оказаться действительными различными. Мы получим тогда два частных решения:
= и Уч = ег'х
диференциального уравнения (V*). Функции еТ'х и линейно неза-висимые, потому что их отношение = е'Г| Tt}x есть величина переменная, между тем как, согласно определению, отношение функций линейно зависимых есть величина постоянная
Л
= k.
Следовательно, согласно вышеуказанному, в случае различных действительных корней характеристического уравнения общим интегралом уравнения (V*) будет являться функция
у = схег'х-\-с.гег,х. (X)
2. Корни Г| и га характеристического уравнения могут оказаться комплексными сопряженными. Это будет в том
Pi
случае, если разность —-р2 окажется меньше нуля. Обозначим в этом
случае
корни
короче в виде:
Следовательно:
fj = а р/ и га = а — {?i.
Тогда общий интеграл (X) напишется в виде:
у = схеь+™х 4- с/’ -30х = е*1 (c1e'tx4- с2е~?,х).
Чтобы не иметь дела с мнимыми выражениями, применим формулу Эйлера:
ё1* = cos г 4" i sin z ’)•
Полагая z = |Эх и затем z = — [Ьс, получим:
у — е'* [с, cos ([be 4" * s,n ₽*) + % (cos ?x — *sin ?•*)] =
= e’x [(^i + %)cos ₽* -Н<ч — ca)1 sln •
i) Формулу Эблера можно вывести следующим образом. Из примера 17 стр. 373, ч. 1 нам известно, что
X X® X® X® —
^ = 1+т+^г+1г+7г+^ + -;
Постоянные q и са суть произвольные постоянные. Поэтому ыы можем давать им значения, какие нам заблагорассудится, в частности можем считать их мнимыми. Обозначим теперь через А и В два каких-нибудь действительных числа. В силу того, что с, и с2 — произвольные величины, мы всегда сможем их подобрать так, чтобы
ci + с2 = А и (ci — са)* 1 =
В самом деле, для этого нужно, чтобы
что возможно при любых А и В в силу произвольности сх и с Следовательно, общий интеграл может быть написан в вид?:
у — ’т (Д cos^x-j-Bsin рх),
где А и В — какие угодно действительные постоянные числа, т. е. действительные произвольные постоянные.
Итак, в случае комплексных сопряженных корней гх = а -|-г2 = а — рг характеристического уравнения общий интеграл может быть представлен в действительной форме, именно в виде:
у = в11 (A cos рх -|- В sin Зх),
где А и В — действительные произвольные постоянные.
' 3. Корни характеристического уравнения могут оказаться равными. В таком случае частные решения .у, и у3 будут одинаковыми и тем самым не линейно независимыми, а потому образовать из них общий интеграл диференциального уравнения нельзя. Поэтому, если функцию ух = ег'х примем за одно частное решение> второе частное решение будем искать в виде такой функции, которая была бы линейно независимой относительно функции ух = еТ'х.
J^ih этого, очевидно, достаточно, чтобы второе частное решение имело вид: у* = иег'х, где и есть какая-нибудь покамест неизвестная функция от х.
заменяя х через й, получим:
1 i • г *2 * * t । । : & *
* ~ 1 * 1 2! 1 3! + 4! 1 51 6! '' * —
Г. z2 z‘ z« . \ . . / z zs z* \
21 + 41 61 + 1 31 +,51
Но из I-ой части, стр. 372 известно, что ряды, стоящие в скобках, представляют собой разложения cos л и alnz. Следовательно, получаем:
еи = cos г -|-1 sin г.
Примечание. Этот вывод, разумеется, не является строгим, так как мы пользуемся рядом Маклорепа, который был выведен нами для действительного аргумента, а здесь мы применяем ряд^для комплексного аргумента, не доказывая справедливости такого применения.
Чтобы определить вид функции и, подставим предполагаемое решение
у2 = иег,х в левую часть уравнения (V*). Будем иметь:
dyz du r<x . Г131
er,x -j- r\ uel, dx dx ii'
d~u r x . du x । д x e + 2r, -7- 4- r\ ue',
dx3 1 « 1 dx 11 ’
и подстановка в (А*) дает:
&У Г.Х I г» r,X t 2 ri® I / *ЛХ I r.x\ I Г.Х
ZFe + 2r>sf + r‘“e +p‘ {^e +r‘"e )+^ue =
= «'' [+<2ri + w jr+“1 +- p,)
Так как г, есть корень характеристического уравнения, то r\-\-plri +А = 0' Сумма 2r\-\~Pi тоже равна нулю, ибо, в силу известного свойства корней квадратного уравнения, 2г\ = —pv Следовательно, чтобы ueTiX было решением уравнения (V*), необходимо и достаточно, чтобы dau
—— = 0. Отсюда имеем: dx* du . —г- <=k,= const. dx 1
В силу того, что мы ищем только частное решение, можем положить
Aj = 1. Тогда из уравнения = 1 найдем:
где Аг—постоянное, которое мы можем положить равным нулю, ибо мы ищем частное решение. Итак, мы приходим к заключению, что второе частное решение, когда г\ = г2, есть:
у2 = хег,х.
Следовательно, для случая г\ = гг общим интегралом уравнения (V*) является функция
у = схеТ'х Д-с2хег'х.
Итак, резюмируя все три случая, получаем следующее правило решения уравнения:
g+A^+^-0- (V)
Первый шаг. Составляем характеристическое уравнение:
И 4-4-Рг = 0.
Второй шаг. Решая его, находим корни гх и га.
Третий шаг. Составляем общий интеграл уравнения согласно следующей таблице:
Корни rt и rt Общий интеграл
Действительные различные у = cteTlX 4-
Комплексные: Г1 = а -4 К гг = з — pi у = a’® (A cos р* 4- в lJn ?*) (А и С—действительные произвольные постоянные)
Равные: г, = г3 y = Cler^ + Caxe^x
Пример 1. — 4 — 5у = 0.
r r dx* dx '
Решение.
Первый ШАГ. г2 — 4г — 5 = 0.
Второй ШАГ.
П = 24- у 44-5 = 5.
га = 2 — у44-5 = — 1.
Третий ШАГ. > = c1eSit + с*~я.
Пример 2. -^>4-6 «У dx* 1 dx + 13у = 0.
Решение.
Первый Второй ШАГ. г* 4- 6г 4- 13 = 0.
ШАГ.
Г1 = -34- у 9_ 13 = -34-21,
Г,в= -3- У9 — 13 = —3 —2/.
Третий ШАГ.
е ~ (A cos 2х 4- в ata 2*Ъ
Пример 8. &У in rfjr« "* dx 4-38> = 0.
Решение. Первый ПА Г. г* 4- 12г 4- 38 = 0.
Второй Третий ШАГ. rx=*i—С.
ШАГ.
у = rke *" 4- е,хе *®.
§ 85. Физическая интерпретация решения одного уравнения второго порядка. Свободное колебание. Применим полученные результаты к исследованию уравнения колебания (VI), § 83.
Для этого уравнения характеристическое уравнение имеет вид:
. А = о
т ' т
и _______
__—Ь-\~УЬ2— 4 тс __________ —Ь— УЬ2—Ате
Г1~~ 2т ’ Г~~~ 2т
Заметим, что если корни действительны, то оба они оказываются отрицательными.
Случаи 1 и 3 имеют место соответственно при Ь2 > Ате и Ь- = Ате. Общее решение диференциального уравнения движения выражается в этих --ь-«
случаях через показательные функции и функцию te т . Это показывает, что мы имеем дело с апериодическими затухающими движениями, т. е. такими явлениями, когда отклонение х от положения х = 0 с возрастанием t асимптотически приближается к нулю и колебаний около значения х = 0 никаких нет. Объясняется это тем, что влияние сопротивления (коэфициент сопротивлении Ь) настолько велико, что упругие силы не могут вызвать колебательных движений.
Совершенно иную картину мы имеем для случая 2, т. е. для случая, когда Ь2 < 4/пс, или когда сопротивление настолько мало (й2 < 4/пг), что корни и г2 оказываются мнимыми.
Обозначая их попрежнему через г1 = а-{-р* и га = а — р/, где
Ь . У Ате — Ь2 .
а = — -— и 3 =---------------, имеем общее решение в виде:
2т г 2т
х = е 2”‘ (4 cos р/ В sin 3/).
Весьма часто этому решению в приложениях придают другую форму. Именно, положим
А = а cos ро, В = а sin ро,
где а и 8 — два новых постоянных. Зная А и В, мы определяем а и >3: а = УА^У~В\ S=larctg^.
ji И
Тогда общий интеграл примет вид:
_ -Lt _ ь-
х = е Яп (a cos ро cos р£ -|- a sin ро sin f') = е 2м ta cos р (t — о), или, написав вместо р букву v:
—— t
х = a cos v (t — о) е *“* .
В частном случае, при Ь = 0, мы получаем простейшие колебания, мкон которых выражается уравнением:
х = a cos v (t — 8). /
Эти колебания представляют собой периодические движения. Так как косинус есть функция периодическая, то всякое положение точки повторяется снова через определенный промежуток времени Т, называемый периодом колебания. Период колебания определяется весьма просто.
Обозначим через и t2 последовательные моменты времени, в которые точка занимает одно и то же положение. Тогда будем иметь:
v {t2 — 3) —v (/( — 3) = 2тг,
откуда
Наибольшее значение х = а. Поэтому величина а называется максимальным значением или амплитудой колебания. Число v называется частотой колебания; оно измеряет быстроту, с которой движение пе-
риодически повторяется. Величина v3 носит наименование сдвига фазы колебания.
В рассматриваемом нами простейшем случае амплитуда а остается все время величиной постоянной; поэтому этот вид. колебания называют незатухающим колебанием.
Если b ф 0» то выражение
-
х = ае 2т cos v (/ — 3)
Черт. 109.
дает нам затухающие гармонические колебания-, амплитуда их не -4-‘
остается постоянной, а определяется выражением: ае ~ , т. е. убывает по закону изменения показательной функции и тем быстрее, чем больше
множитель затухания Этот множитель называют логарифмическим декрементом. На черт. 109 изображен ход таких затухающих коле-21:
баний. Как и в случае простейших колебаний, величина Т = — назы-v
вается периодом колебания, а >3 — сдвигом фазы.
Значения постоянных а и 3 определяются из начальных условий (см. гл. Ill); таковыми обычно являются начальное положение х0 и скорость ф0.
Пример 1. Материальная точка массы т движется прямолинейно, приближаясь к центру, отталкивающему ее с силой k2mx, где х—расстояние точки от центра. Движение начинается с расстояния а от центра с начальной скоростью ka. Показать, что точка, неограниченно приближаясь к центру, никогда его не достигнет.
Решение. Принимая центр за начало координат, имеем:
d2x at»
Характеристическое уравнение есть
откуда гх'= к, г, —— к. Следовательно:
_ - Jet । у, JW x = Cir +с^ .
Для определения q и с, по начальным условиям продиференцируем полученное уравнение по I:
^ = v=cik^t — ctke~M.
Так как при t — 0 задано: х = а и v = — ка, то получаем: а = q + q, — а = q - q, •
откуда имеем:
с, = 0, ct = а.
Следовательно, закон движения выражается уравнением: х = ae~kt, откуда и видим, что х = 0 при t = со.
Пример 2. Маятник, состоящий из небольшого тела массы т, привешенного к нити длины I, качается в среде, сопротивление которой пропорционально скорости. Найти период колебания.
Решение. Следуя методу решения примера 1, § 82, рассматривая опять лишь незначительные отклонения маятника от положения равновесия и заменяя поэтому sin в через 6, получаем диференциальное уравнение движения маятника:
(Ps . . ds , mg _
Составляем характеристическое уравнение:
mr^ + кг 4- “ 0.
Решая, находим его корни:
откуда
Решение уравнения имеет вид:
-м _________
a-oe-cos/f—
Следовательно, период Г колебания равен:
2я
1/~g__ *а
Г I 4т»
Диференцаамные уравнения
1 -^=9у.
2 . 4-у » 0.
dx* •
УПРАЖНЕНИЯ.
Решения
У = qese 4-с,е_Жг.
у = Асов -r-[-S sinx.
— —
3. =о ах* ах У = Cl + f2t®-
у = cte3x -J- c.jeix-
У = (q + Cjx) c2*.
6-S-6?7+13-" = °- у = e31 (A cos 2.v + В sin 2л).
7- S+3SH10>'=0- У = + V5® •
« +”•>’=°- у = e~x (Л cos 3.t -|- В sin 3x).
9. + 3 - 2у = 0. dx* dx -3 + V17 -3-117 a ' , 2 x y = c{e 4- c*
w-4s-'2fi-+9>=a a a 7 A 2 x у = c,e 4- c^xe ‘
L < » . ’’3 y = e [_/lcos — X 4-В sin —
12. Сила, натягивающая пружину, пропорциональна увеличению ее длины и равна 1 кг, когда длина увеличивается на 4 см. К пружине подвешен груз весом 2 кг. Найти период колебательного движения, которое получит этот груз, если его слегка оттяиуть книзу и затем отпустить.
Отв. Г = —-1/ — сек.
5 г I
13. Два одинаковых груза подвешены к концу пружины. Найти движение, которое получит один груз, если другой оборвется.
Отв. x = acos^j/r где а—увеличение длины пружины
под действием одного груза в состоянии покоя.
14. Материальная точка массы т притягивается каждым из двух центров с силой, пропорциональной расстоянию. Множитель пропорциональности равен k. Расстояние между центрами равно 2с. В начальный момент точка находится на линии соединения центров, на расстоянии а от ее середины. Начальная скорость равна нулю. Найти закон движения точки.
Отв. х = д cos (1/ — f |,
§ 86. Неоднородные линейные диференциальные уравнения второго порядка с постоянными коэфнциентами. Как было указано в § 83, эти уравнения имеют вид:
$+л£+Л,-ЛГ. (V)
где X есть функция одного х или постоянное, a a, pt и р*— постоянные величины.
Докажем следующую теорему: если и есть частное решение уравнения (У) uv — общее решаше того же уравнения, но без при
вой части, то общий интеграл уравнения (V) имеет вид-.у = v -J- и.
Действительно, подставляя функцию v-y-u вместо у в левую часть уравнения (V), получаем:
<Z2(u-|-u) . d(v-±u} , । . / d-v . dv \
+A—+A •zr+W’) +
так как первая скобка равна нулю, а вторая по условию дает X. Решение у = v -|-и является общим, так, как часть его v содержит два произвольных постоянных. Так как функция v есть общий интеграл однородного уравнения, решать которое мы уже умеем, следовательно, задача решения уравнения (V) сводится к нахождению его частного решения и.
Часть v общего решения будем называть дополнительной функцией, а и — частным интегралом.
Для практики наибольший интерес представляет случай, когда X = т sin а>х -|- п cos шх, где т, п и ®— постоянные числа.
Чтобы найти частный интеграл и, допустим, что он имеет вид:
И = М sin шх N cos ®х,
где М и N — неизвестные нам пока коэфициенты. Мы определим их путем нижеследующих соображений.
Так, как по нашему предположению М sin ®х 4* N cos ®х есть частное решение уравнения (V), то подстановка его в уравнение (V) должна дать тождество:
(Р(Мsin <охAfcos®х) , d(ЛТsin ®х -j- Ncos ®х) , Лс® I" ~dx ‘
4- рг (Л4 sin ®х 4- Afcos ®х) = т sin ®х 4- п cos ®х или
(— Л4®2—PiNa-}- р^М) sin ®х4~( — Na? рхМ<ь-\-p^N) cos ®х = = т sin ®х 4- л cos ®х.
Так как полученное равенство должно быть тождеством, то коэфициенты при sin®x и cosux в левой и правой частях его должны быть равны:
— Mvfi — PtNu -J- р2М = т
— М®’ 4- ргМ<а 4- p^N = п.
Таким образом мы получаем два уравнения относительно М и N, из которых и сможем определить числовые значения искомых коэфини-ентов М и N.
Пример.
4л£“4лН3-увСО92г-
Решение. Найдем сперва дополнительную функцию v. Для «того решаем уравнение*.
~ 4
Составляем характеристическое уравнение:
4г* — 4г-3 = С -
3 1
откуда G = у и г, = — у.
Следовательно: в 1
— я —т*
v = схе * 4- сге 1 ,
Положим теперь u= М sin 2х +A'cos 2г. Диференцируя два раза, получаем! -^И- = 2 М cos 2х — IN sin 2х, dx ’
= — 4Л4 sin 2х — 4N сов 2х. dx*
Подставляя в данное уравнение, приходим к тождеству:
4 ( — 4Л4 sin 2х — 4.7 cos 2х) — 4 (2Л1 cos 2х — 27 sin2x) — — 3(Afsin2x -f- 7cos2x) = cos2x, или
( — 19Af 4- 8AQsln2r 4~ (— 197 — BAf) cos2x = cos2x, откуда
— 19Л4 4-87 = 0, — 197—851=1.
Решая эту систему уравнений, получаем:
м--Л- и- 21 М~ 425’ N~ 425'
Поэтому 8 . „ 19
“ = “ 125 Sin ~ 425 C0S 2V*
Следовательно, общий интеграл есть:
— — — т
у = с{е~ 4 2 — (8sin2x4-19cos2х).
Однако, если рх — 0, т. е. диференциальное уравнение, имеет вид:
^1 + РъУ = /я sin шх -j- л cos (V**)
и если дополнительная часть v, т. е. общий интеграл уравнения без правой части:
^+« = 0.
окажется равным:
v = A sin ®х 4* В cos ®х, ч
то искать частный интеграл и в виде:
и = М sin сох 4- N cos ®х
уже нельзя, так как подстановка ивлевую часть уравнения (V**) обращает ее в нуль. Тогда частный интеграл следует брать в форме:
и = х(М sin ®х4“Л^ cos ®х).
Пример.
4т- 4- 4у = 2 ata 2х — 3 сов 2г.
dx*
Решение. Находим дополнительную функцию v, решая уравнение:
* ^+^ = 0,
что дает:
v = A sin 2.с + В cos 2с.
Следовательно, правая часть данного уравнения является частным интегралом уравнения без правой части. Поэтому полагаем
и = х(М sin 2с -|- Ncos 2x1.
Будем иметь:
= М sin 2х + N cos 2х + х (2М cos 2х — 2N sin 2л), ах
= 2Afcos2r—2Nsin2r + 2Afccs2r—2Nsln2r + х(—4Afsln2r — 4Ncos2c).
Подставляя в данное нам уравнение, получаем:
4М cot 2x — ANsin 2.с + х ( — 4ЛГ sin 2с — 4Ncos 2с) 4л (М sin 2с + Ncos 2r) =
= 2 sin 2с — 3 cos 2v, откуда получаем:
4.И = —3, - 4N = 2 и
Следовательно: 3 , „ 1
и = — sin 2с —cos 2с
н
3 1
у = A sin 2х + В cos 2с — — sin 2с — — cos 2с.
Резюмируем правило решения уравнения вида:
+ А « sin + п cos тх- (V***)
Общий интеграл имеет вид:
у = v -j- и,
где тг есть общее решение этого же уравнения, но без правой части (дополнительная функция), и и —частное решение уравнения (V***) (частный интеграл). Частный интеграл и щем в форме:
и = М sin <dx Л/ cos <dx,
где ЛТи W—неизвестные коэфициенты, которые мы определяем, подставляя и в уравнение (V***) и приравнивая коэфициенты при sin v>x и cos а>х.
Если правая часть есть частный интеграл этого уравнения без правой части (это возможно, если уравнение d*y । , I ч
имеет вил: = /« sin шх-f-rtcos ®ЛС)| т0 частный инте-
грал уравнения (V**) ищем в форме:
и = х 'М sin a>x-\-N cos ®х).
Пример. Пусть дано жифереипиальное уравнение движения:
+ 9х = 2 соа 31. (А)
Решив его, получим закон движения:
х = A sin 3/ + В cos 3t -}- sin 3t. О
Поступая, как в § 85, представим это решение в форме:
х = a cos 3 (t — 8) + — sin 3f, (В)
О
где постоянные а=Ул*4-В3 и I = 4-arctgопределяют из начальных О о
условий.
Полученное решение (В) показывает, что рассматриваемое движение является сложным колебательным движением, складывающимся из собственного колебания и колебания -=- sin 3/, обусловленного наличием возбуждающей силы 4;- cos 3f. Амплитуда собственного колебания есть постоянная величина, равная а, а амплитуда колебания -^- sin 3t — переменная и равная -у. Следовательно, с течением времени общая амплитуда колебания (В) неограниченно возрастает. Это объясняется тем, что периоды собственного колебания и колебания, обусловленного внешней силой 2 cos 3/, совпадают Т = ~ , см. § 85^ . Полученный результат представляет собой простейший случай сложного явлейия, называемого резонансом. Более подробное рассмотрение этого явления не входит в аадачу нашего курса.
§ 87. Некоторые другие частные виды правой части неоднородного линейного уравнения второго порядка. В этом параграфе рассмотрим кратко еще несколько видов правой части уравнения:
(V)
и способы решения уравнения соответственно каждому виду.
Так как на основании теоремы, доказанной в § 86, общее решение уравнения для всякой формы правой части X уравнения (V) представляет собой сумму у = v -|- а, где v есть общее решение уравнения (V), если положить в нем X = 0, а и — частный интеграл полного уравнения (V), то наша задача сводится тем самым к нахождению и для каждого частного вида X.
I. Если Х== bxn~l -f- ... -\-р, то с ле ду ет по л ожить и = Дх”4-Вд:"“,4-...4-Р,
где неизвестные коэфициенты А, В,..., Р определяются таким же способом, как это мы делали в предшествующем параграфе (метод неопределенных коэфициентов). Если, однако, р9 = 0, то надо положить
zr = 4xn+1-r-Bxn+--- + ^.
2. Если Х=теа*, то следует положить и = Me".
Однако, если а есть простой корень характеристического уравнения, то следует положить
и = Мхе”, а если кратный, то
и = Мх*еЛ1.
3. Если
X = ear (т sin ® х -|- п cos ®х), то следует положить
и = еа* (/И sin <вх -j- N cos ®х).
Если же члены eeicos®x и e**sin®x являются частными интегралами уравнения без правой части, то следует поло* жить
а = хе"* (М sin ®х -J- TV cos ®х).
Пример 1.
- ~~ - бу = 6 - 7х - Зх’.
rf.c2 dx
Решение. Решаем уравнение:
v = Cjeto -|- х .
Полагаем «
и = Ах2 + Вх 4- С, откуда имеем:
-= 2Ах - В, -j-r = 2А. dx dxJ
Подставляем в данное уравнение:
2А — 2Ах - В - бАх2 - 6Вх - 6С = 6 — 7х - Зх2.
Приравнивая коэфициенты при одинаковых степенях х, получим: — 6А = —3; —2A-6fi = —7; 2А — В-6С=6.
Решая эту систему, находим:
А = 1; Bal; С=-1.
Следовательно,
у = + -~ + х — 1.
Пример 2.
<Pv , dy
dx^r dx
Решение. Решаем уравнение:
v = ®-
Если мы положим
и == Ах2 + Вх + С,
то после подстановки и в левую часть данного нам уравнения получим многочлен только первой степени.
Поэтому полегаем
откуда имеем: tin Их
и = Ал* '5^4- Сх,
= ЗАд2 Н -Lix • С, 44 - 'Ах -I- 2В. dx- 1
Подставляя в уравнение, получим:
6Ах + 2S + ЗА№ + 2Вх + С = №.
Приравнивая коэфициеиты при одипзковыд степенях х, будем иметь: 3/8 = 1; 64 + 2В = 0; 2В4-С=0.
Решая эту систему уравнения, найдем:
Л —Д=-1; С—2. О
Следовательно:
Пример 3.
у = q + с* х + - *3 + 2х.
<ру I dy dx3 "Г dx
- бу = е*х.
Решение. Общее решение уравнения без правой части да:т: v = 4-
Положим
н = Me*9.
Будем иметь:
= AMetT; = 16Afe4x. dx dxi
Подставляя в данное уравнение, получим:
14Af?s = eu, откуда находим:
-4
Следовательно:
У= +
Пример 4. rf- . dv . .
—4 ; ±4> = г -
dx3 dx 9
Решение. Решая уравнение без правой части, получим:
v = с{е2х 4- с^хе3*.
Так как 2 есть кратный корень характеристического уравнения, т* полагаем:
и = Мх2е1лл откуда имеем:
= 2Мхе3х 4- 2Мх~е3х -, = 2Ме^ + ЪМхе21 4 АМхге931.
ах аХ”
Подстановка в полное уравнение дает:
2Meix + ШхеР1 — 4 (ЧМхе3* + 2Mj№) + 4Мж2е2х = г9,
17 Звх. 28SB. — Грапжяь в Пуажж, ч. П, Ивпгряяьаое вствелевх*
откуда получаем:
М -
£ 2 ‘
Следовательно:
4 О -
Хе 1 1
у = + с^хе21 -|-------•
4. Если X = A'j -j- Х2 -. 4~ Хк и е с л и и, — частное решение уравнение:
гРу , dy .
— частное решение ура внени я: £+л£+л,=х, и т. д., то
и = «! 4- и2 ••• 4- и„.
В справедливости этого предложения легко убедиться непосредственной подстановкой и в полное уравнение.
Поэтому, если правая часть представляет собой суммы функций тех частных видов, которые мы рассмотрели, то решение уравнения разбивается на решение ряда более простых уравнений.
Пример 5.
«Ру _ 4 dy e 4*2 _ is соя 3
dx- dx 1
Решение. Решаем сперва уравнение:
^ 4^- + 8у = 0-.
rfxJ dx J
v = е2х (A sin 2х -|- В cos 2х).
Находим теперь частный интеграл и( уравнения:
_44>+8у=4х2. dx* dx J
Для этого полагаем ик = Ах2 + Bx -|- С и находим:
И1 = у(14-4х + 4х2).
Находим теперь частный интеграл иа уравнения:
— 4 ^Г~ + 8у = — 15 cos Зх.
dx1 dx J
Полагая для этого ил = Л4в1пЗх-|- ТУсоаЗх, найдем:
и2 — (3 соа Зх + 36 sin Зх).
Следовательно, общий интеграл первоначально данного уравнения будет:
у = в2® (Л sin 2х + В cos 2х)+4-(14-4х4-4лЛ4 О
+ (3 cos Зх 4- 36 sin Зх).
§ *1 УПРАЖНЕНИЯ 259
УПРАЖНЕНИЯ.
Найти общий интеграл :<а хдэго из уравнений:
1. <Г-у 7 2 Отв. у = с/' 4- с/® 4- 12f47 1
п <Рз dfl - (PS = i 4-1. s = 4- с2е-а‘ — -+-1.
3. <Ру а.^ 4- 2у = 8 sin 2х. 1 dx J . у = схеТ с^~ 2® —
— — (6 sin 2х 4- 2 сое 2х).
4. ач dP — la^r 4- a2s = e1. at
5. (Ру ~dl? + 2 -^-+y = ^. У=^ е~х (qx-i-сг) 4-у е2’.
6. (Ру -> = 5x4-2. У = tie* 4- е^е~ ® — 5х — 2
7. (Ру dx* — 4 4- 3> = x dx 1 J У = + с/® т у х + 4- О У
& <Ру dxfl 4-6-^- + 5> = e2®. > = C1,-®4-V-to+4-*to-
as + 4s+4'>' = 4x2 -8х +2-у = (С1Х + Cs) е~ ** + (х -2)<
10. + 9у = бе8®. у = et cos Зх 4- е, sin Зх 4- 4- е’®.
ах* • ~ ' О
" -г? ~5 £+/ - «/• +
Отв. у = ея I С] cos -х V 3 + с, sin —— ) 4- х8 4- Зх8.
13- S +8 £ + в 2в"“ Отв- У =(х + с1)в~31 + е'~'я-
14, S“ 3S = 2“6x‘ J^i+c/J’ + *2-
15. ™ «*® sin 2х.
dx8 v
Отв. у = qe_ *® + с^е2® — (sin 2х 4- 2 cos 2х).
1& S+4S+5-y=20cos3x-
Отв. у = e~ta (Л cos х 4- В sin х) + -^-(3sin Зх — cos Зх).
17. 4 -^4 — 4 — 3v = 2 sin х 4- cos 2.v.
dx2 dx
to .г
Отв. y=cte 2 -- c^e 2 -b -gy (8 cos x — 14 slnx)-
— (8 sin 2x + 19 cos lx}.
18. ~ — 2 + 3y = e~ x cos x.
dx3 dx ,
e~x
Отв. у = e® (A cos У 2x 4- В sin 2x) + - (5 cos .v — 4 sin x).
19. -y4 + 9y = 2sin3x. dx2
20. + 2 + 4y = 2.v ’г Зе2®.
Отв. у = e~x (A cos У Зх В sin У Зх) 4- -у (2x — 1 4- e‘~c).
, 21. Груз весом 4 кг привешен к пружине и увеличивает ее длину на 1 см. Определить, по какому закону будет двигаться груз, если верхнему концу пружины придать периодическое движение, совершающееся по закону:
у = sin УlOUg/, где у измеряется по вертикали.
Отв. х = у sin У iCQe" < — / cos У lOOgt— —z COJ у foog t 4- /- где / — длина пружины в естественном состоянии,
§ 88. Линейные диференциальные уравнения с постоянными коэфициентами порядка выше второго. Диференциальное уравнение порядка п называется линейным, если оно содержит искомую функцию и ее производные в первой степени. Следовательно, линейное уравнение должно иметь вид:
<?'У , dn~iy , dy
dxn ' Pi dxn~l 1 ” ' Pn~l dx ' РпУ X’ (X)
где pv pit..., pnt X суть функции от х. Если plt pv.. .рЛ— постоянные числа, то уравнение называется линейным с постоянными коэфициентами.
Метод решения таких уравнений совершенно аналогичен методу решения, примененному нами для линейных уравнений с постоянными коэфициентами второго порядка.
Чтобы упростить запись, в дальнейшем левую часть уравнения (XI) будем обозначать через <р(_у):
dn~'y
dxn~l
• ±Pny-
I т
§ £9. Основные теоремы. Прежде всего докажем несколько простых теорем, которые дадут возможность обосновать способ образования общего интеграла линейного уравнения п-го порядка с постоянными коэфициентами. Нижеследующие три теоремы служат для изучения свойств функции o(j), причем эти теоремы справедливы как для слу* чая, когда коэфициенты pt, р2,..., рп являются постоянными числами, так и для случая, когда они представляют собой функции от х.
Теорема I. Пусть и есть некоторая функция от х и С — постоянное количество; тогда имеем тождественно:
г (Си) = С? (и).
Доказательство.
? (с«)=с -i-АС +... + -
ах ах
„((Ги . dn~lu , . \ п .
= с (~туг -гPi + • • • 4"А« I = СФ («)
\их ах /
Теорема II. Если и, и и, — какие-нибудь функции от х, то имеем тождественно:
’ тМ «2) = ? («О+ ?(««)•
Доказате. '.ьство.
. г/” 4-г rf”-1 (“i 4-«») > । , .
? («1 + “а) = — - -г А----------; ~ + • • • + А =
** их их
( dnUi . dn~\ . \ .
“Vd?-+A’d?=i'+- ,лл)+
* + ("7^+А ' +/,а) =т W+tW-
\ d:: dx I
Совершенно таким же образом можно показать, что если и1, и2>..ик — какие-нибудь функции от х, то
ф (Ц14- “а + • • + А) = ф (А) 4" ? (а) 4- • • • 4- ф (а)-
Теорема III. Если а^, и9, ик — какие-ниб’удь функции от х, a ct, с3, ..., ск — произвольные постоянные числа, то ? (^i“i 4- 6ан2 4- • • • 4" **“*) = (И1) 4- (иг) 4- ... 4- (ик\
Доказательство. По теореме И имеем:
? (^i«i 4-^2“з 4- • • • 4- <\«а) = ? 4- ф 4- • • • 4- ф (^»«*)>
а из теоремы I следует, что
ф(С1«1) = С1ф(И1), ф(^«я) = с2о(«й).
что и доказывает теорему.
§ 90. Вид общего интеграла линейного диференциального уравнения, правая часть которого равна нулю. Пусть дано уравнение:
+...+AV-0. <ХГ)
где ри р9, р„ суть функции от х. Докажем следующую теорему:
Теорема. Если и,, ы2..............ик суть решения уравнении
(XI*), т. е. такие функции, что
с(и1) = 0, <р(ца) = О.... с(пл) = 0,
то функция
4- с2Ца + • • • "г с,и„ (XII)
где Ср с2, ..., ск — произвольные постоянные числа, также является решением этого уравнения.
Доказательство. На основании теоремы III предыдущего параграфа имеем:
<? (Ci«i + ^«2 -г • • • -г </."*) = (“1) + с& (“а) + • • -I-G? («*) = 0.
а это и показывает, что функция (XII) есть решение уравнения (XI*).
Мы будем различать два типа решений диференциального уравнения.
Если и, и «2—решения уравнения и если решение и2 не может быть представлено в форме и.3 = kuv где k—определенное постоянное число, то будем говорить, что и^ есть решение, отличное от ut. Если ц, и и.2— два решения, отличные друг от друга, то третье решение называете' отличным от первых двух, если оно не может быть представлено в виде:
A1W, 4"Ааи2,
где и Аа—два определенных постоянных числа, и т. д.
Например, очевидно, что если u, = $in х и ua = cos х суть решения диференциального уравнения, то эти решения отличны друг от друга.
X х •
Если a1 = cps2 —, u2 = sin2 — и u8 = cosx, то решение cosx не \ Z 2
отлично от первых двух, ибо
X X
cos х = с os2 — sin2 ,
т. е.
un = klul-\-k9tti,
где Aj = 1 и k.3 = — 1.
В случае, если и1( и2.ик суть все отличные решения, то гово-
рят еще также, что эти функции линейно независимы.
Пусть каким-нибудь способом мы нашли п отличных решений ик, И2, ..., и„ уравнения (XI*). В таком случае общий интеграл этого уравнения имеет вид:
> = (Х1Н)
где cv са...сп— произвольные постоянные числа.
Действительно, во-первых, по теореме этого параграфа функция (XIII) есть решение уравнения.
Во-вторых, в силу линейной независимости функций «.•>........ип
функция (XIII) содержит п продольных постоянных.
В самом деле, если бы функции их, и.,, .... ип не были линейно независимыми, то функция (XIII) не содержала бы п существенно различных произвольных постоянных. Если бы, например, un=AJu,-|-+ Л3м3 1 _ 1, то функция (XIII) могла бы быть пре-
образована к виду:
+ + ••• и.;и
У = <"1 + ^«2 .
откуда видно, что произвольных постоянных только п—1.
Таким образом функция (XIII) удовлетворяет двум условиям, характеризующим общее решение днференциального уравнения.
Все рассуждения настоящего параграфа остаются, разумеется, справедливыми и по отношению к линейному уравнению без правой части с постоянными коэфициептами как к частному случаю уравнения (3). Поэтому мы приходим к заключению, что вопрос решения уравнения с постоянными коэфициентами сводится к умению отыскать п различных частных его решений.
§ 91. Решение линейного однородного уравнения с постоянными коэфициентами Л-ГО порядка. Рассмотрим уравнение:
НРЛ = °. (xiv) ах ах
где рр р2.....р„ — постоянные числа.
Для решения его ищем сперва частное решение вида: и = егх,
где г — постоянное количество. Будем иметь: du _ „ da« dx ’ dX*
d и ___ _n rx
dx' ~r e '
Подставляя значения производных в левую часть уравнения (XIV), получим.
<Р (е") = erx (rn+Plrn~l -j- ... = етх* (г). (XV)
Для того чтобы функция е" была решением днференциального уравнения, необходимо и достаточно, чтобы функция <? (?п) обращалась в нуль, т. е. чтобы г было корнем многочлена ф(г). Для нахождения корней многочлена <{^г) надо, следовательно, решить уравнение:
+ (r) = r’*4.p/‘-1 + ...4-pn = o, которое будем называть характеристическим уравнением диферен-циального уравнения (XIV).
При peiuc.-ци характеристического уравнения возможны следующие случаи:
1. Корни характеристического уравнения ...,/• всеразличные. • "
В этом случае каждому корню будет соответствовать одно частное решение диференциального уравнения; таким образом будем иметь п частных решений:
= ег‘х, и2 = с 'х, .ип = ег*х.
Так как все функции и„ и.,....и„ линейно независимы, то согласно
§ 90, общий интеграл уравнения (XIV) будет иметь вид:
У = с/'х -ь с„ег*х + ... -{ спег*х.
Пример 1. Решить уравневие
Решение. Составляем характеристическое уравнение:
г‘ - Н- 27 = 0. Решая его, находим корни:
ri = + 3, /5 = — 3, г, = 4- Y 3, rt — — У 3.
Пишем общий интеграл данного уравнения:
у = qe3* + c,z-te + е,с''*х +
Если среди корней характеристического уравнегтя окажется комплексный корень г, = а -{- 0<, то по известной теореме алгебры найдется другой корень, ему сопряженный = — (3Z. Этим двум корням будут соответствовать частные решения вида:
а общий интеграл будет содержать сумму:
с/’+™х-\-се'' ~?i>х = еах (c,eiix 4-с^е’ {'х).
Чтобы решение не содержало мнимых выражений, воспользуемся формулой Эйлера (см. § 84) и приведем полученное выражение к виду:
е,х [с, (cos i sin 0х) 4~ (cos 0х — i sin 0x)l =
= е* КА 4- <у) cos ₽* 4-1 A— sin 3хЬ
Положим <\4-<>вА — Су) = В, где А и В — произвольные
постоянные действительные числа. В силу того, что су и — произвольные величины, мы всегда можем так подобрать их значения, чтобы написанные равенства были справедливы для любых значений А и В *). Благодаря этому общий интегрел может быть представлен в виде суммы
J) Более подробив вто преобразование изложено в § 84.
показательных функций, умноженных на постоянные произвольные числа, и выражений вида:
е™ (Я cos рх -|- В sin Зх).
Пример 2. Решить уравнение:
Решение. Составляем характеристическое уравнение:
г» 4- 2г2 - 8 = 0; решая его, находим корни:
И = + У 2, 'а = — /2, г3 = И, ri = — %.
Пишем общий интеграл:
у = cte ’ 2 с с,е~ 1 'ix 4- A cos 2х 4- В sin 2х
(в этом случае а = 0, р = 2).
2. Среди корней характеристического уравнения имеются кратные корни.
В этом случае для нахождения общего интеграла нельзя применить способ, данный в рубрике 1, так как еперь уже не все п частных решений вида eri будут отличными: например, если rL = га, то реше* ние ет* булет тождественно с решением ег'г.
В этом случае для нахождения общего интеграла следует руковод ствоваться следующим правилом:
Если Г) есть двухкратный корень характеристического уравнения, то диференциальное уравнение имеет два частных отличных решения:
ег>х и xervT.
Если г. есть трехкратный корень характеристического уравнения, то диференциальное уравнение имеет три частных линейно независимых решения:
Т' Т Т\Х 2 Г' X
е ' , хе * , хе'
и т. д.
Проверим это правило на примере диференциального уравнения третьего порядка:
*+Л£+Л-*>-0
Пусть корни уравнения
'•84-/va+/v+A=°
будут: rt = га и гя. Покажем, что хет* есть решение диференциального уравнения.
Действительно, подстановка функции хет* вместо у в левую часть диференциального уравнения дает:
хег,х (г’ 4- pj\ -f- р3\ + pj + ег'х (Зг3,4- 2pirl + д-).
Так как есть корень характеристического уравнения, то
* (G) = ri + Pj\ + pj\ + pt = 0.
Выражение во второй скобке есть производная 6(гх) по г,:
~5'“‘> =3'’М'2/’Лт л'-
Так как гх есть кратный корень многочлена 6 (г), то он является также корнем и производной этого многочлена (см. ч. I, § 96). Поэтому
3ri 4~2p1riH- Р* — °-
Это и доказывает, что функция хет* есть частное решение днференциального уравнения.
Если гх есть кратный мнимый корень гх = а4~?*> то обязательно найдется корень г =а— р/ той же кратности, что и гх. Пусть, например, корни гх и гл кратности 2. Тогда в состав общего интеграла войдет сумма вида:
с^г 4- с[хе'хх 4- 4- /хА® =
= Скг+М« + * + Х [с'/' i ™ ’4- Ч =
= (Л cos 4" 5 8ln ?*) + И' cos рх 4- В' sin рх), где А, В, А' и В' — действительные произвольные постоянные.
Таким образом в случае кратных корней характеристического уравнения общий интеграл выразится в виде суммы выражений:
clerx, с2хег'х, сах'ег,х, ... и е°х (Лх cos рх 4- В> sin рх), хе™ (i48cospx4-Basin рх), х2е’х (Д8 cos рх 4~ si" Рх), ...
Пример 3. Решить уравнение
*Z + 2^ + v = 0.
dx4 dx*
Решение. Составляем характеристическое уравнение: г* + 2г«+ 1=0.
Решив его, найдем корни:
fj = i, гг = i, r3 = — i, rt = /.
Следовательно, общий интеграл имеет вид:
у = A cos х В sin х -|- х (уЦ cos х + sin х).
Резюмируем все рассмотренные случаи решения уравнения (3).
а) Каждый действительный простой корень гх характеристического уравнения
.••4-Рп = 0
дает частное решение вида: А*.
Ь) Каждая пара простых мнимых корней а±р» характеристического уравнения дает два частных решения вида: cos Зх и е4* sin Зх.
с) Каждый кратный корень кратности s дает $ частных решений, получаемых умножением частных решений а и b на 1, х, х2, х®-1.
Общий интеграл диференциального уравнения является суммой п частных решений, причем каждое частное решение предварительно множится на произвольную постоянную величину.
УПРАЖНЕНИЯ.
Найти обшиб интеграл каждого из уравнений !• Й-4'Й'=0- Отв- У = + + _ iPs tPs с rfs . л , _2t .
<i*y
3. -H Л 4 zHy = 0. у = (t! 4- qx) cos nx 4- (q 4- q) sin nx.
4. -^=s. O/ne. s = с/4-* 2 cos 4-Я «In
S-+3-S--^ = 0- + +
^S-3S+2S+2>=o.
Отв. у = qe 2 4" ** И cos x -|- fl sin x). § 92. Неоднородные линейные уравнения высших порядков. Рассмотрим теперь уравнение с правой частью n-го порядка:
(?(У)=-^-+А^т+--- +РаУ = ^. (XV)
ах ах
где pit...,pa — постоянные числа, а X — функция от х. Решение такого уравнения основывается на следующей теЬреме.
Теорема. Пусть v есть общее решение уравнения:
? О') = о,
и и — частное решение полного уравнения (XV), т. е. такая функция, что
?(«) = *
Тогда общим интегралом уравнения (XV) является фу и кция v-\-u.
Доказательство. Покажем прежде всего, что функция v-j-u есть решение уравнения (XV).
В самом деле, на основании теоремы II, § 89, имеем:
о (v -f- а) = <? (v) 4- ? (и).
А так как о (v) = 0, a ? (н) = X, то
с (г) 4- <? (//) = X, что н дсказывает наше утверждение.
Это решение v-\-u содержат 'п произвольных постоянных, так как v есть общее решение уравнения ф (у) = 0. Следовательно, функция v-L-u является вместе с тем и общим решением уравнения (XV) 1).
Так как однородное уравнение о (у) = 0 решать мы уже умеем, то решение уравнения (XV) сводится таким образом к нахождению частного решения и.
Слагаемое v будем называть дополнительной функцией, а слагаемое и — частным интегралом.
Как и для случая линейнЛс уравнений второго порядка, ограничимся рассмотрением только нескольких частных видов функции X.
1. X = ахп-\-bxn~l... ±р.
Для нахождения частного интеграла и положим
и = Ахп + Вхп~1+ ... 4-Р,
где А, В, ..., Р — неизвестные коэфициенты. Для нахождения этих ко^фициентов подставим и в левую часть уравнения (XV). Приравнивая затем коэфициенты при одинаковых степенях х в левой и правой частях уравнения, получим систему уравнений, позволяющую определить коэфициенты А, В.....Р (метод неопределенных коэфициентов).
, Однако, если рп = 0, то следует положить
и = Дхп+14-5хп4- ... 4-Рх.
w Если Рп = 0и =0. то следует положить
и = Ахп+2 4- Вхп+* 4- ... А-Рх\ и т. д.
Пример 1. Решить уравнение:
Д. *У v., dx3 ' dx
Легко видеть, что, подставив в левую часть вместо у многочлен четвертой степени, мы в результате получим многочлен только третьей степени. Поэтому-то и следует положить
и = Ах».4- Вх* + Сх* + Dx2 4- Er.
Будем иметь:
= 5Ах« 4- 4Вх8 4- ЗСх2 4- 2Dx 4- Е,
££ = 20Ах3 4- 12Вх2 4- 6Сх 4- 2D,
~ = 60Ах2 4- 24Вх 4- 6С.
*) Заметим, что теорема остается справедливой и для уравнения, в котором коэфициенты рь р* ..., р являются функциями от х.
Подставляя вычисленные производные в левую часть данного вам уравнения и приравнивая коэфициенты при одинаковых степенях х левой и правой частей, придем к системе уравнений:
54 = 1; В = 0; 60/1 + ЗС = О, 24В-}-20 = 0; 6С+Е = 0, откуда получим;
Л = -Ь В = 0; С= - 4; D = 0; Е= ’4. О
. Таким образом найдем частный интеграл:
и = ^-х* — 4х3 -j- 24х.
О
rf’v . dy п „
Решая теперь уравнение = 0, найдем дополнительную функцию о:
v = ct + A cosх 4- Bsln х.
Следовательно, уравнение, данное в примере, имеет общий интеграл:
у =. v и = г, 4- A cosx -|- Bsln х -}- -'-х5 — 4х3-}- 24х. О
2. Если Х = те", то следует положить
и = Me".
Однако, если а есть s-кратный корень характеристического уравнения, то следует положить
v = Мх’е".
Неизвестный коэфициент М найдем подстановкой и в левую часть Уравнения.
Пример 2. Решить уравнение:
' * Й~8Й+16У = 8с-х-
dx1 dx*
Решение. Решая сперва уравнение:
rf.v4 dx* J
найдем дополнительную функцию:
v = qe2® 4- с^хе3*4- с^-21 4- ctxe~Z£ •
Так как в этом случае а = 2 есть двойной корень характеристического уравнения, то полагаем
и = .'Лх2е2х •
Подставляя и в данное нам уравнение, получим:
ЗглГе2® = 8с2®, откуда
м-1.
V- 9 С^едоватеяыго, и = — е, я общий интеграл 4
V = е2® + е~ ** (с3 + с*х).
3. Если X = тcosрх л sin рх, то следует положить и = М cos рх -I" N sin рх.
Однако, если cospx и sinpx встречаются в числе членов дополнительной функции, то следует положить
и = х [/И cos рх -р N sin рх].
Неизвестные коэфициенты М и N определяются методом неопределенных коэфнциентов.
Пример 3. Решить уравнение:
(Ру . (Ру . „
-Л + ~г1 = sin 2х.
djfi 1 dx1
Решение. Находим сперва дополнительную функцию:
© = q + Сгх + све~® .
Полагая далее и = Мsin2x-|-Wcos2х и подставляя эту функцию в уравнение, получим:
(&N — 4Л1) sin 2х — (4N+ 8Af) cos 2х = sin 2х, откуда имеем:
8N-444 = 1,
4ЛГ4-8Л4 =0.
Решая эту систему, находим:
Л1 = ~20’N= io’
Следовательно, и = — sin 2х cos 2х, и общий интеграл
у = q + qx + сге~ х — sin 2х + cos 2х.
4. Если Х = евх (т cos px-}-«sin рх), то следует положить а = еы (М cos рх - j- N sin рх).
Если же члены еах cos рх и епх sin рх входят в дополнительную функцию, то следует положить
и = хеах (ЛГ cos рх—]—Л/ sin рх).
Пример 4. Решить уравнение:
^ + 3^ + 3^O = 5^sinx.
dx3 1 dx’ 1 dx ' '
Решение. Находим сперва дополнительную функцию:
v = (q+cjx + сзх»). Полагаем
и = (Л1 sin х + N cos х) *
Подставляя в данное нам уравнение, получим:
е* [(2Л4 — 11Л0 sinх 4- (11Л4 4- 27V) cosxj » Se'atax,
откуда имеем:
2Af—1^ = 5,
11.W4- 2W = 0.
Решая ату систему, находим:
Следовательно:
v = 4_ е* (2 sin х — 11 cos х).
и общий интеграл имеет вид:
у = е~ х (с, + м 4- Cjx2) -|- ех (2 sin х — 11 со' •)
5. Ес л и Х = Ху +-Ya-|- • • •+<¥, несли Uy есть частный интеграл уравнения «p(j) = Ar1, U3 — частный интеграл уравнения ? СУ) = Xit..., и,— частный интеграл уравнения <р (у) = X,, то
“=«14-02 4- ••• +«,•
В справедливости этого предложения легко убедиться непосредственной подстановкой и в уравнение (XV).
Поэтому, если правая часть представляет собой сумму функций тех частных видов, которые мы только что рассмотрели, то решение полного уравнения разбивается на решение ряда более простых уравнений.
УПРАЖНЕНИЯ.
Найти общие интегралы каждого из уравнений:
lS3+j'"jc, + jc-
х __
Отв. у = Сув~х -|- в 2 ^4 cos 4- Д sin 4- х» 4- х — 6.
2-S+3B^-^=3xa+10sin3x-
Отв. у = + с^~х 4- с*~ *® — 4. (20 — 6х + 9х») +
+ -4 (cos Зх — sin Зх).
3. Jy_^+4g-4y = cos2r.
dx3 dX3 ах
Отв. у = с1еж + f с3 - cos 2х + ( св - sin2х.
От«.у = ^’( е,--£)~1-г,в( »• + j)+
Отв. у = (q + с»х) cos х 4 (г3 4 с4х) sin х — 4 4- * 4- х».
6. 4- 5 - 36у = 20г2® cos3x.
dx* 1 dx»
Ств. у = Ci»3* 4- es* 2® 4- с» cos Зх 4- c3 sin Зх-(sin 3x 4- ? cos3x\
7. ^ + 2^ = 2v + 25e~®sin2x. dx* 1 dx3
Отв. у = ct 4 м4 Сзcosx Уз 4 ctsin хУ2 + —
e~x
yj~ (13 sin2x 4 16 cos 2x).
8.
S + 4S = 4cOs4x-
Отв. y = ct + v + c3x2 -t- c^~ *® 4 (cos 4x — sin 1x).
Дополнительные упражнения к главе IX z
Решить следующие днференциальные уравнения:
1. х (1 -у)Лг4у(1 — x)dy = 0. Отв. х 4 у 4 In (х — 1) (у — 1) = С. •
2. sec2 ydx + cos®хdy = 0. Отв. 4 tg х 4 2у 4sin2у = С.
3. у® dx — (х® 4 2ху) dy — 0. Отв. у (х 4- у) = Сх.
4. (х Ух*4у® — y^dx + xydy = 0*
Отв Ух3 4 у® 4 x inx = сх. • y
Отв. х (е® 4 1) = с. е'^®
Отв. у = -д- (Зх® — х) 4 сх.
Отв. х —у — 1 4 се~ v .
Отв. у —______еЯ .
с — (х— 1) е® .
Отв. х® — d* — 2су.
j rfy= 0. Отв. у = ех.
у У
5. [ (х — у) ес -4 х] dx 4 хе® dy = 0.
6. х dy — <y 4 х®ег’) dx = 0.
7. rfx+ (х —у) dy = 0.
8. (х4 Wydx + (х4- \?dy = dx.
9. (у 4- <J*) dx — dy = 0.
10. (у — Ух®4У-’)dx ~ х dy = 0.
12. х®У1 - y-dx—у УТ^
Отв. arcsinx —x
13. 2xy dx — (4x® 4- 5*1dy = 0-
14. xdx+(y— Ух3+У) dy = 0.
1S> SHI’
is diy - 1 -
I0-dx®_(l 4-x)*
17. = sec® ax .
dx3
1
18. Решить уравнение , dv то y = 0 и -i=O.
jfl dy = 0.
V1 — х® 4 5' У1 — У2 arcsln у = с.
Отв. у* = е (у® 4 2х®).
Отв. х- =₽ с® 4 2су.
Отв. у = х (in х 4 с,) 4 са.
Отв. у = с,х 4 с4 — In (1 4 Jf).
Отв. у = qx 4 с2 — j-. In cos ar.
У у, если известно, что - когда х «= — 1
Отв. 1 296 у = (л 4 1)*.
~ л • . • к
19. Решить уравнение = 2.У1 + ®У» если известно, что когда x = —t то у = 0 и = 3. Отв. у = V3tg Vз(х - у).
20. Решить уравнение «tgay + *g У> если У = ° и = 1 при х = •
аЛ1 Л* 2
Отв. в1пу»х — у.
21. Решить уравнение = tgj'+tg’j'. если у = у и = 1 при х = 0. Отв. х = In (1^2 sin у).
Решить следующие диференциальные уравнения:
22. dx* dx2 29. dx 2 f dx
23. (Ру _ а dxs ~~ х 30. । -х dl+' = e '
24. ^+^ = 3х>/ dx 1 х 31.
25. 3^+-^-=^ dx X + 1 у* 32.
26. (4у+ Зх)^+у = 2х. 33. х2у dx — (Xs + у®) dy = 0.
27. 2—-4-5—— 12х = 0. dP dt 34. S-3 £,+*=«•
28. <Pv е । с ^.-5^ + 6у = е . 35. g+ytgx = L
36. Показать, что кривая, обладающая тем свойством, что угловой коэфи циент касательной в каждой ее точке пропорционален абсциссе этой точки, есть парабола.
37. Найти уравиевие кривой, проходящей через точку (0, —2) и обладающей тем свойством, что угловой коэфицнент касательной в каждой ее точке равен ординате втой точки, увеличенной на 3 единицы.
z Отв. х — In (у + 3).
38. Найти уравнение кривой, угловой ковфициент касательвой к которой в каждой точке кривой пропорционален квадрату ординаты этой точки и которая проходит через точку (1, 1).
Отв. k(x — 1)у—у + 1 =0. где А — коэфициент пропорциональности.
39. Найти уравнение кривой, угловой коэфициент касательвой к которой в любой точке кривой в п раз больше углового тоэфициента прямой, соединяющей начало координат с втой точкой. . _
Отв. у = сх".
40. Найти уравнение кривой в полярных координатах, обладающей тем свойством, что тангенс угла, который образует радиус-вектор каждой ее точки с касательной к кривой в этой точке, равен обратной величине радиуса-вектора с противоположным знаком. 0me г (6 -|- с) = 1
41. Найти уравнение кривой в полярных координатах, обладающей тем свойством, что тангенс угла, образуемого радиусом-вектором каждой ее точки с кривой, равен квадрату величины радиуса-вектора втой точки.
Отв. fl = 2 (в 4- с)
42. Найти уравнение кривой в полярных координатах, обладающей тем
18 Зав. МП. — Грьжяжжь ж Лувиж, ч. II, Ижтетрьжьжов жочжогепе
свойством, что угол, образуемый радиусом-вектором каждой ее точки и касательной к кривой в этой точке, в л раз больше полярного угла.
Отв. г” = с sin в.
43. Найти уравнение кривой, обладающей тем свойством, что касательная в каждой ее точке и прямая, соединяющая эту точку с началом координат, образуют с осью ОХ дополнительные углы. Qmf xi_yi=.e
44. Показать, что если все нормали к крнвой проходят через одну и ту же определенную точку, то эта кривая есть окружность.
45. Найти уравнение кривой, обладающей тем свойством, что длина перпендикуляра, опущенного из начала координат на касательную в любой точке кривой, равна абсциссе этой точки. &тв & _|_ у3 = (Х
46. Найти уравнение крнвой, обладающей тем свойством, что длина перпендикуляра, опущенного из точки пересечения ординаты каждой точки с осью ОХ на касательную в этой точке, есть постоянная величина, равная а.
Отв. у = у\е ° е “ ).
47. Найти уравнение крнвой, обладающей тем свойством, что длина части нормали, заключенной между кривой и осью ОХ, для каждой точки кривой пропорциональна квадрату ординаты этой точки.
Отв. (е*(в“в) + е— где коэфициент пропорциональности.
48. Найти уравнение крнвой в полярных координатах, обладающей тем свойством, что длина перпендикуляра, опущенного из полюса на касательную в любой точке кривой, пропорциональна длине радиуса-вектора этой точки.
Отв. г = се к . где k — коэфициент пропорциональности.
49. Найти уравнение каната подвесного моста, предполагая, что нагрузка на дугу каната пропорциональна ее проекции на горизонтальную прямую.
Отв. у = ах* Ч- Ь.
Указание. Весом самого каната можно пренебречь.
50. Найти кривую, обладающую тем свойством, что величина площади, ограниченной этой кривой, осью ОХ, неподвижной фиксированной ординатой х — а и движущейся переменной ординатой, пропорциональна разности длин неподвижной и переменной ординаты.
х — п
Отв. у = се к , где А — коэфициент пропорциональности.
51. Найти уравнение кривой, обладающей тем свойством, что величина площади, ограниченная этой кривой, осью ОХ, фиксированной ординатой и движущейся ординатой, пропорциональна длине дуги, ограничивающей площадь.
k I ~~k k \
Отв, у *= уI * + е ) где А — коэфициент пропорциональности.
52. Точка движется со скоростью, пропорциональной проходимому расстоянию. Известно, что в течение 10 сек. точка проходит 100 жив течение 15 сек.— 200 м. Найта аакон движения. (
Они. в — 25 • 2*.
53. Предполагается, что скорость понижения уровня воды, вытекающей из отверстия на дне цилиндрического сосуда, пропорциональна корню квадратному ив высоты уровня над дном сосуда. Если в течение 20 мин. уровень воды понижается на половину высоты над дном сосуда, то в течение какого времени вода вытечет из сосуда? Опв мин
54. Найти уравнение кривой, радиус кривизны которой есть постоянная величина, равная а. Отв _ с^г
55. Найти уравнение кривой, радиус кривизны которой в каждой точке равен кубу длины нормали к кривой в этой точке.
Отв. cty2 — с’ (х + с,)’ = 1.
56. Материальная точка массы т движется по прямой линии к центру, кото-рым притягивается с силой, равной , где г — расстояние точки от центра, а р. — постоянная величина. В начальный момент движения точка натодится на расстоянии а от центра, и скорость ее равна нулю. Во сколько времени точка достигнет центра?
Отв.
VI*
57. Материальная точка массы т движется по прямой линии к центру, при-а
тягнвающему ее с силой, равной т?г , где г — расстояние точки от центра, а — постоянная величина. В начальный момент движения точка находится на расстоянии а от центра и имеет скорость, равную нулю. Во сколько времени точка достигнет центра? 4
2д
58. Материальная точка массы т движется по пр мой линии к центру, который притягивает ее с силой, величина которой изменяется прямо пропорционально расстоянию точки от центра. Движение начинается на расстоянии а от центра с начальной скоростью, равной нулю. Определить скорость движения точки в момент, когда точка пройдет половину расстояния, отделяющего ее от центра. ___
„ а . .
Отв. у у —, где к — коэфициент пропорциональности.
59) Материальная точка массы 1 движется прямолинейно, приближаясь к центру, притягивающему ее с силой, равной , где г—расстояние точки от центра. Движение начинается на расстоянии а от центра с начальной скоростью, равной —^=.. Во сколько времени точка пройдет половину расстояния, уд отделяющего ее от центра? , _
Отв. (1 - У1) /дз.
60. Материальная точка массы 1 под действием постоянной силы проходит расстояние d. Начальная скорость равна и,, и конечная vt. Найти время, в течение которого точка проходит расстояние d.
Отв. , .
61. Материальная Уочка движется прямолинейно к центру, притягивающему ее с силой, равной где г—расстояние точки от центра. Начальная ско
63. трения равной
рость равна нулю. Показать, что средняя скорость на первой половине пути относится к средней скорости на второй половине, как (я — 2): (л -|- 2).
62. Найти скорость, которую приобретает при падении на землю тело, падающее с бесконечно большой высоты под действием притяжения землн, обратно пропорционального квадрату расстояния от центра землн (радиус землн считаем равным 6350 км).
Отв. Приблизительно 11,15 км]сек. Найти скорость, приобретаемую материальной точкой, скользящей без по кривой у =f (х) под действием силы тяжести, с начальной скоростью, нулю.
Отв. YУ)> где Уо~ ордината начальной точки движения.
Указание. Диференциальное уравнение движения есть
tfls dy
d(* 6 ds
Умножая обе его части на —, получаем: d*s ds _ dy ds или
1 d fds^ _ dy ~2 dt \dt) edt
и т. д.
64. Материальная точка массы m брошена вверх с начальной скоростью Допуская, что сопротивление воздуха пропорционально квадрату Скорости (коэ-фнцнент пропорциональности k) и что скорость, с которой точка упадает обратно на землю, равна v2, выразить о, как функцию и массы точки.
Отв. v3 = vv 1 /---——-
у mg+ kvy’
65. Найти изгибание балки, горизонтально укрепленной одним концом и нагруженной ьа другом.
Отв. Efy = -w(^-£y Указание. См. пример на стр. 234.
66. Найти изгибание балки, горизонтально укрепленной одним концом н равномерно нагруженной.
О„„
67. Балка лежит горизонтально, и концы ее укреплены на подпорках. К середине балки подвешен груз. Найти изгиб: ние балки.
n w //х2 х2\
Отв. =
ГЛАВА X.
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ.
§ 93. Задача приближенного интегрирования. Если невоз-ь
можно вычислить точное значение интеграла j f(x)dx, то приме-а
нчются методы приближенного интегрирования. Так как всякий опре-
деленный. интеграл можно геометрически представить в виде площади плоской кривой, то тем самым задача приближенного вычисления
интеграла сводится к приближенному измерению площади.
§ 94. Правило трапеций. Площадь, ограниченную к р и во й у =/(х), можно с достаточной точностью заменить суммой площадей вписанных трапеций. Разобьем для этого отрезок оси ОХ от х = а до х — Ь на п равных частей и обозначим длину такой части через Дх (черт. ПО). Так как площадь тра-
пеции равна произведению полусуммы длин параллельных оснований на высоту, то будем иметь:
площадь первой трапеции = (j/0 + У)) Ьх,
А»
площадь второй тоапеции = -i- (у, -|- j'.,) Ах, А
площадь л-ой трапеции = - -()• х +уп) Ах.
Складывая площади этих трапеций, получим:
сумма площадей трапеции = %- (у0 -|- 2yl-[- 2_y3-J-.. •+2уп_1-ИУв) ^х’
Правило трапеций состоит в том, что искомую площадь S мы полагаем приближенно равной сумме площадей трапеции’.
s= • «Ч-Л-х+уЛ)Дх- 0)
Очевидно, что чем на большее число делений мы разобьем интервал (а, Ь) оси абсцисс, тем с большей точностью сумма площадей трапеции будет представлять величину искомой площади, ограниченной кривой.
12
Пример. Вычислить x*dx правилом трапеции.
1
Решение. Разобьем интервал оси ОА'отх=1 дох =12 на одиннадцать равных частей. Будем иметь:
Искомая площадь ограничена нрявой у = х*. Подставляя в это уравнение значения абсцисс х = 1, 2, 3.12, найдем значения соответствующих ординат;
у = 1, 4, 9,..., 144. Следовательно, по формуле (1) получаем:
$=(4-Н4-94 16+25+36-Н9+64-1-Ы+100+121 + -1.144 } - 1 = 577-^.
Эта же площадь, вычисленная при помощи интегрирования, выражается числом:
Г Гх3!12 2
/""Ы, -575з-
Следовательно, в данном случае правило трапеций даст ошибку, меньшую трети процента.
§ 95. Правило Симпсона (параболическая формула). Вместо того чтобы точки деления кривой соединять хордами и заменять иско-
мую площадь суммой площадей трапеций, можно получить лучшее приближение к искомой площади, проводя через точки делений, лежащие на кривой, дуги парабол и заменяя искомую площадь суммой площадей, ограниченных этими дугами и ординатами, соответствующими точкам делений. Через какие - нибудь три точки, взятые
на кривой, можно провести параболу с вертикальной осью; ряд дуг таких парабол
теснее прилегает к кривой, чем ломаная линия, состоя-
щая из хорд, соединяющих последовательно точки, лежащие на кривой.
Разобьем теперь интервал на оси ОХ от х = а = ОМ0 до х»Ь— = ОМ„ на четное число частей п длиною Дх. Через каждые три последовательные точки Ро, Pit Ра; Р2, Ра, Р4;... проведем дуги парабол с вертикальными осями (черт. 111). Тогда получим:
площ. криволин. параболич. трапеции 2И0 Ро Р9/Иа = площ. трапеции 2И0Р0РаЛ1а-]-площ. сегмента параболы Ро
площ. трапеции iM0P0P,Afa = y (Уо+Ув) ’ 2Д* = (Ув + Л) д*,
площ. параболич. сегм. PqP, Рй=двум третям описанного параллелогр.
Следовательно:
площ. первой параболической трапеции A70 Ро Р2 /Иа =
2 Дх
= (Уо +Л)+ у (2Л —Уо—У2Дх) = у O0-F4у, 4-уа),
Таким же образом: Дх площ. второй параболич. трапеции = (уа4~ 4у3 4~А)>
площ. третьей параболич. трапеции = —(у4 4" 4УБ~ЬУв) О
площ., последней параболич. трапеции = (у „4- 4у _ t 4_У,).
Складывая площади всех параболических трапеций, получаем:
Дх
“У (Уо + 4У1 + 2уэ 4- 4у3 2у< Н- ... 4- 2у„ _, 4--4у„_х +уп).
Следовательно, по формуле Симпсона (п — четное число) получаем: иском, площ. = S =~ (у0 + 4yt 4- 2уа + 4_у8 2у4 4-... 4-у„). (II)
Как и в случае правила трапеций, чем большее число делений п мы возьмем, тем получим более точные приближения к искомой площади.
1°
Пример. Вычислить по правилу Симпсона интеграл j х* dx. о
Решение. Разобьем интервал от х = 0 до х = 10 на 10 частей. Будем иметь:
Ь-а 10—0 , .
-------- —гр— = 1 = Ах. п 10
Искомая площадь ограничена кривой у«=х8. Подставляя в это уравнение абсциссы х-=0, 1. 2,..., 10, найдем соответствующие ординаты _у = 0, 1,8, 27.. 1 000. Следовательно, по формуле (II) получаем:
S L(0 + 44-16+1084-1284-5004-432+1 3724-1 024 + 2 916+1000)-2500
Ннтегрнрованмем находим:
ю
/Г П ю x«dx = Hr =2500. L« J.
Таким обрааом в данном примере формула Симпсона дала результат, совпадающий с точным значением искомой площади.
УПРАЖНЕНИЯ.
1. Вычислять интеграл последнего примера по правилу трапеций, разбивая интервал интегрирования на 10 частей.
Отв. 2525.
5
2. Вычислить у*при помощи обоих правил, разбивая интервал интегрн-i
рования на 12 частей.
Отв. По правилу тралений 1,6182; по прагчлу Симпсона 1,6098.
it
3. Вычислить у x8 9dx при помощи обоих правил, полагая 10. 1 Oms. Трапеции 3 690; Симпсон 3660. 10
4. Вычислить У Igm-vtA' при помощи обоих правил, полагая п = 10. 1 Отв. Трапеции 6,0656; Симпсон 6,0896.
5. Вычислить /' dx / -j при помощи обоих правил, полагая п = 6. и 1 0ms. Трапеции 1,0885; Симпсон l,090G. 60*
6. Вычислить J slnxdx при помощи обоих правил, полагая п = 10. 0
Т. Вычислить а J* jfldx при помощи каждого из правил, полагая п — 12. 2 10
8. Найти ошибку, получавшуюся при вычислении J л * dx по правилу Симп-0
сона при л =• 10.
1
9. Вычислить по правилу Симпсона f ^*dx, полагая п = 10.
и
ДОКАЗАТЕЛЬСТВО ОСНОВНОЙ ТЕОРЕМЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
(Для преподавателей)
§ 1. Формулировка теоремы. Основная теорема интегрального исчисления формулируется так:
всякая непрерывная функция f(x) имеет первообразную, т. е. служит производной некоторой функции F(x)
F'(x)=f(x).
Речь теперь идет о том, каким образом дать этой важнейшей теореме интепзального исчисления совершенно точное доказательство. Тонным же доказательством называется такое, которое не делает никаких пропусков в рассуждениях, не прибегает к наглядности и не ссылается на очевидность там, где ее, может быть, совсем и не имеется.
§ 2. Обычные приемы доказательства основной теоремы. Их недостатки. Этих приемов два: геометрический и аналитический.
Первый прием, собственно, не заслуживает названия „доказательства**, так как это не есть точное доказательство, но лишь некое рассуждение, посредством которого стремятся оправдать основную теорему. Сущность этого прие- у м/
ма состоит в том, что на плоскости XOY /
чертят непрерывную линию, имеющую ' /
своим уравнением у (х) и обозначают через F(x) площадь АахМ. Как только ' ,:х'
это сделают, тогда все дальнейшее уже Г(х)
хорошо выходит, так как в действитель-______________________
пости, из чертежа 1 немедленно следует, 0 а г х
что производная функция F (х) в точно- qepT j
сти равна данной f(x). Но доказательство основано на наглядности и, собственно, с этой кажущеюся очевидностью здесь, просто, предлагают помириться: ведь нисколько не очевидно, что между кривой y=f(x), осью абсцисс ОХ и двумя ординатами: неподвижной аА и подвижной хМ имеется, вообще, „площадь*, вдобавок выражаемая числом. Что фигура АахМ есть кусок (т. е. часть) плоскости, это, в самом деле, очевидно. Но что этот кусок измеряется определенной „площадью* — это нисколько не очевидно, особенно когда непрерывная линия y=f (х) делает бесконечное множество извивов, вроде тех, что^показаны на чертеже 2.
Если бы данная линия была многоугольником (см. черт. 3) тогда самый факт наличия площади был бы, действительно, очевидным. Но когда этого нет, тогда доказать существование площади у данной фигуры АахМ столь же трудно, как и существование первообразной F(x) у данной непрерывной функции / (х). Здесь наглядность совершенно обманчива и, собственно, единственный путь доказать существование площади у фигуры АахМ — это прибегнуть к двойным интегралам.
Второй прием, весьма совершенный с точки зрения точности, вместе с тем очень труден и, надо сознаться, не только непригоден для начинающих, но и исторически как раз обратен тому пути, который первоначально был проделан наукой. Сущность этого приема состоит
Черт. 2.
в том, что сначала доказывают существование определенного анте-ь
грала / f(x)dx, т. е. существование предела интегральной суммы 3
S =/ (%0) Дхо +/ (-S) Дх14 • • • 4-7 Дхп_р
предполагая данный отрезок [а, Ь\ разбитым на малые отрезочки Дхр...» Дхп_х и предполагая, что длина наибольшего на них с течением времени стремится к нулю.
Что в этих условиях интегральная сумма S стремится к совершенно определенному пределу, отнюдь независящему от способа разбивать основной отрезок [а, Ь\ на отрезочки bxv Дхр.. .,йхп_г лишь бы все они (и средн них самый крупный) бесконечно умалялись, —г это обстоя» тельство должно быть точно установлено, и современная наука полагает, что она его устанавливает со всею строгостью. Но, во всяком случае, это доказательство — длинное, трудное и недоступное для начинающих.
Затем, когда доказательство существования предела интегральной суммы S проделано и, значит, существование определенного инте-
i>
грала у*f(x)dx установлено, тогда делают верхний его пределb пере»
менныи, обозначают его просто буквой х, а переменное интегриро* ванне обозначают какою-нибудь другою буквою, напр. а, т. е. рассматривают выражение
X ff№ а
уже как функцию его верхнего предела х. Обозначив эгу функцию чрез F(x), т. е. написав равенство
X
F(x} = J‘f(*)<h,
U
затем уже без труда устанавливают, что F(x) и есть первообразная функция для данной f (х), т. е. имеет ее своею производной
F' (x) = f(x).
Таким образом, существование первообразной для всякой непрерывной функции f (х) является установленным.
Но здесь и заключается главный недостаток этого приема доказательства основной теоремы интегрального исчисления: и исторически, и фактически вычисление определенного интеграла всегда происходит при помощи первообразной, и никогда не наоборот. В указанном же приеме первообразная получается при помощи определенного интеграла.
Ввиду этого Лебег и предложил свой знаменитый прием доказывать основную теорему интегрального исчисления без интегрального исчисления.
Метод Лебега
§ 3. Правильная сходимость. Сначала Лебегом вводится такое важное определение:
бесконечный ряд ut (х) «9 (х) + ... u, (х) -j- ... ,с о с т а в-ленный из каких-нибудь функций, называется правильно-сходящимся, если имеется такой сходящийся знакоположительный ря-д что
|а1(х)|<Д1, |и3(х)| < Av.... |iz„ (х)| <
Из этого определения сразу следует, что всякий правильно-схо-дящийся ряд и, (х) -{- ця (х) + и. (х) + ... есть ряд абсолютно-
сходящийся, потому что ряд абсолютных величин его членов | ut (X) 14~ +1 «а (л) I + • • • +1 (х) I + • • • обязательно сходится, имея свои члены соответственно меньшими членов сходящегося знакоположительного ряда At -|-Лг+ ... -|-Дп... Р
§ 4. Лемма Лебега. Важная лемма вта формулируется так:
Лемма Лебега. Правимно-сходящийся ряд «1 (х) + (х) +... производных дает в сумме опять производную.
Доказательство. Дадим себе, прежде всего, отчет в том, что именно нам дано и что от нас требуется установить.
Прежде всего, нам дан некоторый правильно-сходящийся ряд
в(х) = ц1(х)4-«,(х)-|-... 4-и. (х)4-..., (1)
т. е. такой ряд, для которого заранее имеется сходящийся знакоположительный ряд
, Л,+ • • •• (2)
члены которого превышают соответсттенно абсолютные величины данного ряда (1):
(«Д^КЛр |и2(х)| < Л2,..., к„(х)|< Лп>...
Но самое главное это то, что при этом прибавлено, что данный ряд(1) есть ряд производных. Это значит, что функции их (х), и, (х).ип (х),...
суть соответственнЬ производные от некоторых непрерывных функций U1 (х), £/2(х).(Jn(x),... на отрезке [а, 0, т. е. что мы имеем-
{/, (х) = ut (х), U'a (х) = иг (х),..., £/'(х) = ип (х),...
В этих условиях от нас лемма Лебега требует доказать, что сумма и (х) ряда (1) есть тоже производная от некоторой непрерывной функции U(х). '
Переходим к доказательству леммы Лебега.
Первый шаг. Прежде всего установим, что ряд первообразных
[Ь\ (х)- и, (01 Н- [(/, (х) - иг (0] -|- ... -I- (X) - ия (01 + ... (3)
есть ряд правильносходящийся; здесь буква с обозначает какое-нибудь заранее выбранное постоянное число, взятое на отрезке (a ^xsgd]
Для этого достаточно только применить теорему Лагранжа о конечном приращении. Действительно, она нам дает равенство
W„(x)-lZ,(r) = (x-c)t/n (U = (x-^)«,(!n),
где L есть число, промежуточное между с и х, т. е. лежащее на отрезке [с, X] и, значит, принадлежащее основному отрезку [a, Z»]; поэтому имеем | ип (Е„) | < Ля. И так как |х — с | < | Ь — а|, то заключаем, что
|С7.(ж) —4A.(<r)| < |fr—«1 -
и, следовательно, ряд (3) имеет абсолютные величины своих членов соответственно меньшими, чем знакоположительный сходящийся ряд
— а| • Ai -j- | b — а | • A3 -f- ... -f- lb— a| • A„~~ ...
А это и доказывает, что ряд (3) есть правильчо-сходящийся.
Второй шаг. — Установим наконец, что сумма U(x) пра-вильно-схолящегося ряда(З) есть первообразная для суммы и(х) данного ряда (1).
Действительно, написав, что
и (4 = [Ui (X) - и, (01 + [U, (х) - иг (с)] +.... -I-
+ (£/в(х)- ЦД0)+ ... (3*)
вы постараемся доказать, что
Для этого же достаточно доказать, что будем иметь
<t Дх '
лишь только | Дх | сделается достаточно малым; здесь е обозначает заранее заданное положительное число, малое сколь угодно.
Так как знакоположительный ряд (2) есть сходящийся, то егочможно
остановить на таком члене Ат, чтрбы остаток был меньше чем —, т. е.
О
Ат -|-1 -J- Ат 4 2 -|- ... < . О
«)
Остановим на этом же самом месте оба ряда (1) и (3*).
Введя обозначения
а (х) = ut (X) + иг (X) 4- ... 4- ип (х); р (X) = (х) + иа+3 (X) 4- . ..
S(x)=[C/1 (х) - Ц (с)] 4-... 4- [СТ, (х) - U. (с)];
мы понятно имеем
и(х) = о(х)4-р(х) и t/(x) = S(x)4-/?(x) и, следовательно, можем написать
Шх + Дх)-Шх)_ Г5(х + ^)-5(х)_ 1
дх L ьх ' 'J
4- [ /?(Х+Ад2~/?(Х)~] +1 -р (х)]=7« +4+4
(5)
где JpJgH J3 обозначают первую, вторую и третью квадратную скобку предыдущего равенства.
Так как для всякого целого п, имеем Un (х) = ип (х), то, имея И виду, что т есть число постоянное и раз навсегда выбранное для данного е, мы получаем
S'(x) = o(x).
Поэтому, для Дх достаточно малого, мы должны иметь
5(х4-Дх) — S(x) «
------о(х) <у.
(61
С другой стороны, мы имеем
₽(х4-Дх)-^(х) = 6/^.1(х4Дх)-£/и+1(х) Дх Дх
, ^ж+г^ + Ах)-^2(х) ,
‘ Дх “Г • • •
“ “-Н4 + ft.+iДх) + вм+а (* + в«н^Дх) + • • ••
где, по теореме Лагранжа, количества 0„l+2,... обозначают числа, содержащиеся между 0 и 1. Из этого равенства мы сразу заключаем, что
141= <А +А т
Наконец, мы сразу находим, что
IЛ I = Ip (X) I = I Им+1 (X) 4- “т+3 (Х) + • • • I <4п+1 +
+ Л.»+з + •••< у * . (.8)
Сопоставляя равенство (5) с неравенствами (6), (7) и (8), мы полу-' чаем
£/(х + Ах) U(x) и(х> <|711 + 1Л| + |7з|< ‘ ^е.
и О и
А это и обнаруживает, что и(х) есть производная, так как £Г(х)аи(х).
§ 5. Полигональные функции. Непрерывная функция Р(х) называется полигональной, если кривая у = Р (х) изображается геометрически в виде многоугольника с конечным числом прямолинейных сторон (черт. 4). Указанное определение имеет
чисто-геометрический характер. Аналитически это определение будет выражаться так: непрерывная функция Р(х) есть полигональная, когда отрезок [л, б] можно разделить точками cv c,,...cm на такие части [а„ с,], [CpCj,..[ст, А], в каждой из которых функция Р(х) есть линейная.
Из этого определения сразу следует, что р а э н о с т ь Pt (х) — Ра (х) двух полигональных ф у н к ц и й Pt (х) и Ра (х) есть опять полигональная функция. Действительно, мы можем разделить отрезок [а, А] на части, в каждой из которых Pt (х) есть линейная; деля каждую из них на части, во всякой из которых Р2 (х) есть линейная, мы этим самым весь отрезок [а, 6] разделили на части, в каждой из которых обе функции Р,(х) и Ра(х) одновременно суть линейные. А так как раз-
ность двух линейных функций есть опять линейная функция, то отсюда и следует, что Р, (х) — Р2 (х) есть полигональная функция.
Точки полигональной линии у=*Р(х), в которых соединены две
различные прямые, называются вершинами полигональной линии.
Полигональная линия у=р (х) называется элементарной, если она состоит лишь из двух прямых, из которых первая (т. е. левая) лежит на оси абсцисс (черт. 5). Непрерывная функция р (х) соответствующая
элементарной полигональной кривой, называется элементарной поли-
гональной функцией.
Теорема 1. Всякая полигональная функция Р(х) есть сумма постоянного числа К и ограниченного числа т элементарных полигональных функций р, (х),
р.(х),...,от(х), т. е. Р(х) = К+ +A (*)+Р-2 (*)+•••+/>„ (х).
Доказательство. Пусть рассматриваемая полигональная линия у=Р (х) изображена на чертеже в. Если мы начальную ординату аА кривой обозначим чрез К и вычтем из Р(х), то полученная разность Р (х)—К изобразится геометрически в виде полигональной линии _у = Р(х) — К с начальной ординатой равной
нулю (см. черт. 7). Отсюда следует, что, продолжив первую сторону аЕ, мы получим элементарную полигональную линию ОаЕ; пусть р{ (х) есть соответствующая
ей элементарная полигональная функция. Ясно, что, если мы вычтем из Р(х) — К функцию/>1 (х), то полученная разность Р(х) — — /С—рх (х) изобразится в виде полигональной линии у = Р (х)—
— К—А(х), У которой ордината у(х) будет равна нулю нс только в точ ке х = а, но и дальше, вплоть до точки ct (см. черт. 8). Поступим точно так же и дальше, продолжив первую сторону q G. Мы таким образом получим элементарную полигональную линию. Пустьpt(x) есть соответствующая ей элементарная полигональная функция. Ясно, что, если мы вычтем нз Р(х) — К—Р\(х) функцию р2(х), то полученная разность Р(х) — К—Рх(х)—Р^х) изобразится в виде полигональной линии j = P(x) — л—РЛХ) — Pi(x)i У которой ордината у(х) будет равна нулю уже вплоть до точки са (см. черт. 9). Ясно, что про-
цесс можно продолжать сколько угодно дальше, пока мы не получим, наконец, такую полигональную кривую у = Р (х) — К—рх(х) — ... —рт (х), у которой ордината у(х) равна нулю на всем отрезке [а, 6]. Ясно, что тогда мы и будем иметь желаемое разложение произвольно данной полигональной функции Р (х) на постоянное К и на сумму элементарных полигональных функций рх (х), р2(х).....Рт(х) так как
будем иметь тождество:
Р(х) = К-\-рх (х) +А(х) + ... +/>т (х)
на всем отрезке [а, Ь\.
Теорема 1L Всякая полигональная функция есть производная.
Доказательство. Доказательство разбивается на следующие шаги: Первый шаг. — Всякое по-
стоянное К есть производная. Чтобы видеть это, достаточно взять функцию Кх, производная которой равна К.
Второй шаг. — Элементарная полигональная функция р(х), имеющая вершину в начале координат, есть производная.
Чтобы видеть это, достаточно рассмотреть чертежи 10 и 11. На чертеже 10 изображена элементарная по-
лигональная функция р (х), равная нулю для х отрицательных и равная линейной функции /(х)длях положительных. На чертеже И изображена первообразная F(x),
U равная нулю для х отрицательных и равная ха для х положи-
касающейся в начале координат к осн абсцисса ОХ.
Ясно, в самом деле, что F (х) = 0, если х отрицательно или равно нулю, и что F'(x) = |tx для х положительного, потому что ==|1Х.
Третий шаг. — Всякая элементарная полигональная функция/>(х) есть производная.
Действительно, если р(х) имеет вершину в точке с, то р(х— с) есть элементарная полигональная функция с вершиной в начале координат. Поэтому, р(х — с) есть производная от некоторой непрерывной функции F(x), т. е.
р(х — c) = F'(x).
Меняя в этом равенстве х на x-j-c, мы получим
р (х) = F' (х 4- с) = [F (х -f- г)]'
и, значит, р (х) есть производная.
Четвертый шаг. — Всякая полигональная функция Р(х)есть производная.
Действительно, в силу теоремы I, мы можем разложить Р(х) на постоянное К и на элементарные полигональные функции Pt(x), рл(х),.. .,рт(х), т. е. можем написать
Р(х) = К(х) 4-?9(х)4-... -F/’Jx).
Так как pt (х) есть производная от некоторой непрерывной функции ГДх), т. е. pt (х) = Ft' (х), то ясно, что
ЛГх4-Г1(х) + Га(х)Н-...4-Гт(х)
есть первообразная для Р(х) и поэтому Р(х) есть производная.
§ 6. Доказательство основной теоремы интегрального исчисления. Пусть /(х) есть какая-нибудь функция, непрерывная на отрезке [а, £]. Это значит, что для всякого наперед заданного положительного числа е мы будем иметь неравенство
|Р(х')-Р(х")|<.
всякий раз, как величины х* и х" аргумента будут сближены между собою меньше чем на некоторое положительное число ц, т. е. всякий раз, как будет удовлетворено неравенство
|х' — Х"|<7).
Вспомнив это свойство непрерывности функции на отрезке, разделим весь отрезок [а, />] на части меньшие чем т], при помощи точек деления xI,x.J,...,x<1x<H,... х,^, и восстании в этих точках деления перпендикуляры к оси ОХ (черт. 12). Построенные перпендикуляры пересекут рассматриваемую непрерывную кривую j =/(х) соответственно в точках Afp Afa,..., Af Р лежащих на дуге
АВ кривой близко друг к другу и к конечным точкам А и В. Соединяя всякие две соседние из этих точек прямолинейными хордами, мы получим некоторую полигональную линию у = Р (х), вписанную в нашу кривую дугу АВ.
Ясно, что вершины этой полигональной Линии лежат все на нулевой дуге АВ.
19 Ввв. 1858. — Гр а ал иль Луаип, ч. II, Иагегрлльжов жечжяекжа
Докажем, что полигональная функция Р(х) такова, что мы всюду на отрезке [а, Z>] имеем неравенство
|/(х) —Р(х)| < 2«.
Для доказательства возьмем какое-нибудь число X, а^х^Ь. Рассматриваемая точка х попадет на некоторый отрезок [хр xf+J, так что мы имеем неравенство а;<х<х(+1. Вследствие того, что точки х( и х<+1 с®лижены между собою меньше чем на т„ а точка х находится между ними, то
I*—*(|< л-
Поэтому, мы имеем |/(х)-/(х,)|<«. (9)
Рассмотрим, с другой стороны, разность Р(х)—/(х,). Это есть линейная функция на отрезке [л.,х(+1], уничтожаюицяся при х = хр потому что полигональная линия у = Р(х) имеет все свои вершины лежащими на кривой y = f(x) и, значит: Р(х^ —/(х,1. Если мы теперь положим х = Л'<4_1, то будем иметь в силу равенства /5(xi_|_1) =/(xi_f_1) следующее неравенство:
|Р(х,.+1)-/(х.)| = |/(хж)-/(хр| < г,
потому что |х>+1 — х(| < т). Таким образом, линейная функция Р(х) — —fkxi) уничтожается на одном конце отрезка [х,, Х| (1 ], а на другом конце по абсолютной величине меньше, чем «. Отсюда следует, что рассматриваемая линейная функция Р(х)—/(х() имеет все свои абсолютные величины на отрезке [x^x.^J мен ь-шими числа г. В частности, поэтому, мы должны иметь:
\Р(х)—/(*.)! <•• do,
Сопоставляя неравенства (9) и (10), мы находим
!/(х) — Р(х)|<2г. (Ц>
Полученный результат следует формулировать так:
каково бы ни было положительное число е, всегда можно найти такую полигональную функцию Р (х), которая отличается от данной непрерывной функции /(х) меньше чем на 2е, т. е. |/(х,— Р(х)|<2е.
Перейдем теперь к заключительному предложению.
Теорема 111. Всякая непрерывная функция f(x) есть сумма праеильно-сходящегося ряда полигональных функций.
Доказательство. Возьмем8 — • Согласно предыдущему, имеется
такая полигональная функция Р„(х), что
2
l/(*) — (12>
Заставляя целое п безгранично увеличиваться, мы на основании этого неравенства заключаем, что *
lim^» (х)=/(х). (13)
Заметив это, построим теперь бесконечный ряд
P1(jC)+lP9(x)-Pk(x)]-J . . . -L [Р„ (х) - Р^ (х)] 4- ... (14) Этот ряд есть сходящийся и имеет своею суммою данную функцию /(х), потому что сумма п членов этого ряда в точности равна Рп (х) и так как мы имеем равенство (13).
Следовательно, мы можем написать:
/(х) = Р, (х) [Р2 (х) - Р, (XI] -J- ... + [Р„ (X) - Р^ (X,) 4- ... (15)
С другой стороны, обозначим общий член этого ряда просто чрез Р„(х), полагая
Pj(*) = £i(*) и
Ясно, что Р„(х) есть полигональная функция. Кроме того мы имеем
le.wi - Л w - р^,(х; ।=। VW ~ - ,/(х) - ₽„ (хм ।
- |/(Х) - (X) I + |/(Х)- Р„ (X) | < А + 2 6
Таким образом, ряд (15) можно переписать в виде
/(X) = Л (X) + Р2 (X) . . + р„ (х) + . . . . (16)
g
где Р„ (х) есть полигональная функция и где | Р„ (х) | < —г,. Так как л»
-1
есть сходящаяся геометрическая прогрессия, то формула (16)
представляет правильно-схолящийся ряд полигональных функций, имеющий своею суммою данную непрерывную функцию /(х).
Основная теорема интегрального исчисления
„всякая непрерывная функция f(x) есть производная*
вытекает теперь как прямое следствие леммы Лебега (§ 4), теоремы II (§ 5) и равенства (16).
Действительно, в силу теоремы И всякий член ряда (16) есть производная, и ряд (16) есть правильно-сходящийся. Поэтому, по лемме Лебега,/(х) есть производная.
ТАБЛИЦА ИНТЕГРАЛОВ ДЛЯ СПРАВОК.
Помещаем таблицу интегралов для справок. На первых порах следует обращаться к этой таблице возможно реже, а то и совсем не пользоваться ею. Но когда вывод этих интегралов будет усвоен и понят хорошо, то можно пользоваться этой таблицей, собственно говоря, только для сбережения времени и труда при решении практических задач.
Некоторые элементарные формы'
3. у* rf/(x) = J f'[x) dx=f(x)+С.
' /'”" = •^рг+с'"+-1-
5. J-^- = 1пх+С.
* Формы, содержащие целые степени от я 4- Ьи
7. Д + + С. п + - 1.
8. у* F(x, а + bx)dx.
Попробовать одну из подстановок
z = a -f- bx, xz = a -J- Ьх.
0. ^-~^ = ^[а + Ьх-а\п(а + Ьх)] + С.
ю. f^^=i[i{a+bx}2~2a(a+bx}+,t'м* + м]+с.
11 /^гИ|,1,+1'1+^Ы+с'
14. /• dx 1 Г at 3 / -TTTS =-£T e+«x-2a ln(* + M a— 4-£ J (a 4- bx)2 IP L я 4- bx J
15. f dx = 1 1_. Д4-6-Г . r J x (a 4- bx)2 о (я 4“ bx) a3 x '
16. /* xdx 1Г 1 . fl ~| _ J (a+bx)» a±bx 1 2(fl4- bx? J + Формы, содержащие at 4-x1, e’ — x2, fl 4- bxn, a 4- bx2-.
H. Г dx 1 . x , г. Г dx , . _ J d2+x2 a***a+C’ J T+^ = arCtgX + C
18. Г dx _ 1 a + x Г dx 1 x — a J a2—x2 2flln a — x 1 C' J a2-x2 2fl‘‘" x + a + C
19. f dx 1 Г~ъ J a + bx* _/^arctgxK — 4-Спря fl>0 и 4>0-
20. Г dx 1 . a + bx J — 2ab a-bx 1
21. Jxm (a 4- bxn)pdx = m-n + l( a_|_ftx")p+‘ fl (m —«4-1) /•«„ b(np + m + l) b(np + m + l)J x «
22. /ж’(« + »х")’^= x „4‘+£’ +
xm(a-4-Z>xV
___________1__________b(m-n-[-np—V)b /"_dx_____ ~ (m-Y)axm~l(a + bxn)t>-i (m-l)a J хт~п{а^-Ьхп)р '
/dx
x™(a + &rV =
___________1__________. m — я 4- пр — 1 Г dx___ ~ an(p—\)xm-*(a + bxn)p~i an(p-l) J x" (a 4-&rV“1 ’
25. J* (a 4- fex”)p rfx = (д 4- frx”)p~*~1 _ b(m — n — np — \) /* (a 4- bx”)pdx ~ в(т-1)хя-1 e(m-l) J x’»-»
26. Г (а 4- bx”)1* dx {a-}-bxn)p . anp Г (g-Ь ftx")p~1dr J xm ~ (np—m+l)xm~l np—m+lj
27. C (a-Y bxn)pdx _ J X™ = хта~те+1 fl (я —«4-1) Г x,a~*dr b(m—np 4- 1)(fl4- bx")*-1 b(m - np 4-1) J (e _|_ bx?)p '
28. f x™ dx _
(<i -j- bxn)p
Х"> + ‘
m J- n — np14-1 Г x~ dx
an(fT- )) J (y.|_7x")P-r
29.
1
30.
31.
32.
34.
(a» 4- x-')n ~ 2 (n—I) a? [ (as _|_ X2)n“l
’ dx _ 1 Г x______________
(аЧ-5х»)п-2(л— l)a |_(a 4-5X»)"-1
x dx 1 Г dz
--------«=-o /-----------r*c z
(a 4- 5x»)n 2 J (a + bz)n
' x?rix
(a 4- 5x»)“ dx x(a-4- 5x"j
1 dx
(a» + x2)’ dx
(a 4- 5X3)1
________— x 1 Г _______________dx 26(n—l)(a :-5x2)n_| ~2b\.n 1) J (a-|-5x2)'
1 . АЛ
s — in —- ——H ЛЛ a ф h rn
1
36.
37.
38.
39.
dx x- (a + 5X2)'* a J x-' (a bx*)' T+~bx^ ~ 2b " (?' ' ~b j ' C’ x-dx _ x_____________а Г_____dx______
a -j- bx? b b J a ••[ • bx- ' • dx _______________1 jn _
x (a 4- 5x2) — 2a П dx ___________________1
x* (a 4- 5X2) ax
dx x
dx (a
к Г a J a |-5x2‘
(аЦ-5х3)2 2a (a 4-5X2) 2a J a 4- bx?
Формы, содержащие yra -j- 6x:
2 (2a — 36x) ^(а +~bxj»' 155» т
2 (8a2 —12a 5x4- 155=x«) V(a + bx)*
40.
41.
1055»
42.
43.
15ft3
а
41.
45.
46.
-LlnX^
2 (2a - bx) .____
— 35*-----Уа + 1
2(8g»-4a5x4- 35»х»)
4- С, для a < 0. — a
Формы, содержащие х'1 а2:
48. [ (х2 + dx = ^ /х2"+ a2 J- -у- In (x + yG^T?-’) + C.
49. J’ (x2 + a2)« dx = -*(2x2 + 5o-->) /is 'j. & + -?-* In (x+/лТТ^)-| C. n
50. f (x2 + a2)2' dx = _|_ -JjL Г (x2 + ~lax.
J Л -f* I n “h 1 J
n -J-2
r M J- дй *
51. J х(хЧ-а*)г dx = ~— +9------+ C.
52. /'x2 (x2 + а2)1 Л = v (2-^ + «2) У*2 + ? ’n (x+/^+^) + С.
1 о о
.53. Г------- In (X + с.
j (х» + а2)7
Xs (хя + а3)
61. Г.^.Л-^dx = / , д|п£±Га2 + .у2
J х х
1
.-•> Г (х3 + а1) * dx Yа2 + х2 , . , . , г-^—.—_ , _
Ъ?. j ------------=---г-— -----F- In (х + V а2 -|- х2) 4 С.
Формы, содержащие Ух2 — а2:
€3. [ (л2 — a1)* dx = /л2 -G-’ — I" (х /.г2'-4 -) ' С.
64. [(х2- о5)2 dx = 4 (2x2— 5а2)/хз-а2 + 1а (х + /л2 - а2) 4 с. J о о
»>4э
66. Гх (xt-a2)2 dx = fj. * -ь С. J П -f- х
у. 1 „ _____ -4 _____
67. / хЦх»— a2)2 dx = 4-(2ха—в2)/х2—а2—!□ (х4- У‘х2-а-') + С. J о о
68. У*---dx , - = In (х 4- /х2 - а2) 4- С.
(х2 — а2)2
69. f-----J- =------. -4 С.
J -L а2/х«-а2
(х2—а2)2
7°. У----XdX - = Vх2-д24- С.
(jfi — d2)*
71. f----4. С.
(х2—а2)2
72. У----—=~у==4-Щх4-/72^ё) + С.
(х^-Л2-
73. /*---——— = — arcsec 4 + С f-----r^L=- = arcsec х 4- С.
J J_a 2 J х/х2-1
х (х2 — а2)2
74 Г_____dx. . с
' J _L а2х +С'
х2(х2-а2)2
_» Г dx У х2 — а2 .1 х . „
73, J _L = 2о2х2 + 2а2 1ГС,€С а + С‘
х^х2— а2)2 '
1
/(х2 — а2)2 dx _;------ а . „
:--—<-------— Ух2 — а2 — arccos — 4- С.
г
77. у.С^-ар2^ =_liz_g._|.ln(x+Tr^rr^) + c. Формы, содержащие V& — х2: 1
78. Ла2 - x^’dx = 4/^Г=Г^+-?-“ГС81в 4-+с-э
79. /*(«2 - х2)2 dx = -4 (5а2 - 2x2) /.р - х2 4- - arcsin — J- С. J в о а
80.
81.
82.
83.
84.
85.
86.
87.
«8.
89.
90.
9!.
92.
93.
” т — -1
/, . _ а , х (а3 — х2) * . flSn Г, _ , z ,
(«• - жч л_ _L—2_ + _ту -,=) л.
я ***
• t f х2 (а2 - х2) 3 dx = -£- (2*3 - в3) У^-х3 + 4- arcsin — -г С. J о о л
dx
= arcsin
= arcsin х -|- С.
(в3 — х2) dx
(в2-*3)
(а3 — х3) x*dx
(а3 —х2)
x*dx s (я2-х2)3
4- С.
— arcsin — 4- С. а
J 1 т 'mJ
(в2 —х2)3 (а3-х3/
х2 (а2 - х»)3
dx
1 хЧа2— х3)3
Х*=^_л__1_1п_______*____
2а3х2 1 2a3
Гdx . _ а 1п JL+Y*-** _ь с.
J X X
1 /• (Я* - х2)2 . . х . _
/ —----;---dx =------------ — arcsin-к С.
J х2 х а
Формы, содержащие У Чах — х3, - г лJ:
з
94. Гх" /2дх—x«rfx = - -iLJj2'’1-|-
•/ т -у 2
Л. ~г~ })д ‘ т к
95.
96.
97.
S3.
99.
100.
101.
101
103.
104.
/dx _ У2ах — .r’ _j_ ">—i _ f__dx____
xm y'2ax - x* “ (2m-l)oxM (2m-l)u’J x“ “ */2лг - x*
Г xndx _ x"~1/2ax-x* (2м — Пд Г xn ldx
J V2ax — x* m + « J У2ах — x* *
dx x/2ax-xa
dx з (2ax — x2)'-
»
<2rx —x2): j _m — 3 ’/*У2дх —x3
(2гл —3)ax"‘ '(2m-3)eJ x" i
ax
ax=- + C.
Зах» ---+ a2 Yr^ax — x1
----------, - + C.
-- а У2лх — x* (2ax--x®)!
F(x. V?ax - x’) dx — fFiz + a,
dx
F (x, /2ex 4- xs) dx =
Формы, содержащие a-ybx^cX2;
F dx 2 . 2'x + b _ ,, - .
Юэ. / —-- - = -------- arctg —— —-4- С, где £-<4at
J a 4- bx -r ex’ Y^ac — b2 У 4ac — b3
lftR Г dx 1 . Чсх + Ь-У*^ 4ac „
J a 4- bx 4 - ex2 yb2 — 4ас Чех 4^4- V — 4cc
когда •.
10T. / л . — J„. |л +c
d . bx — ex у у;. j_ цвс -yCp 4^. — 2cx -1- b
108. /’- In <2cx 4- b 4- 2 /7/74-6x4-ex*) + C
У a 4- bx 4- ex'- у c
109. У* /a-|-6x4-cx«rfx =
“ ~C + bx + сх3 ~ У' s’- In (2ex4- 64- 2 /ё /л 4- 6x4-cx^4-C 8eT
,,л Г dx 1 2cx—b . _
t' Г d4-6x — ex2 /с /ft*4-4ec f
111. f Va-^bx^cx2 dx =
2ex — b -r——г-; J bs-l-iac , iex—b , -
---—6 + ‘<-«-+—+ c
In (2ел-{ b 4- 2 yrc/a4-ftx4-cx2)4-C. 2сТ
ИЗ.
х dx
Ve + ftx -^сх*
сх- . b 2сх — 6
---------arcsin ____________
— V Ь*+4ас
2с-
Другие алгебраические формы.
114. У tfx = F(e+x)(6+.?j + (а - b)In ( /^+7+У6+7) + С.
115. У ^х = У(о- х) (Ь + ~х) ? (а 4 I» arcsin |А±| + С.
116. у |/ Лг = • - У(а 4- х) (ft — х) — (л 4- 6) arcsin 4- С.
117. У " ' * dx = — К1 — х2 + arcsln х 4- С.
118. Г —--------dx - = 2arcsin 1/ ——* + С.
J /(X —а)(3 —х) г р—а
Показательные и тригонометрические формы.
119. Г r° dx = #- + С.
J 1па
120. УехЛг = «14-С.
121. Г enxdx= — +C.
122. у* slnxrfx = — cosx 4- С.
113. У cosxrfx = sin.r -|-С.
121. уtgxtfx = Insecx = — lncosx-1-С.
125. у ctg х dx = Ih sin x 4- C.
126. f sec x dx = ( -**- = In (sec x 4- tg x) + In tg + C.
127. cosec xdx= J’ —= In (cosec x — ctgx) = In tg 4 C.
128. у sec3x dx = tgx 4* C.
129. у cosec2 x dx = — ctg x 4- C.
130. / sec x tg x dx = sec x 4- C.
131. j cosecxctgxdr = — cosec x -|- C.
132. / sln’xdr=4- — -j-sln2x4C-/ J 4
133. J cosaxdx = 4^sl" 2x4 C.
134. Г . n j sin"-1 x cos x . я —1 /• , / sin xdr= 1 / sin” xdx. J n n J
135. Г n J cos"-1 x sin x . л —1 /* __a J / cos" x dx= -j / cos" J X dx. / Л n J
136. Г dx 1 cosx n — 2 /* dx J sln"x л —1 sin"-1 x л —1 J sln"-2x ’
137. Г dx _ 1 . sin x . л — 2 Г dx J cos”x л —1 cos’*-*x л—1 J cos"-2 x "
138. /* m . n j cos’"-*x sin"+ 1 x , m— 1 f _ / cos’"xsin”xdx= — — / cos" •xslnnxdx. / m -j- n m n J
139. Aos’” X sin" Xdx= x 4- "ll f cos1" x sin”-2x dx / т + л /n-f-л./
140. Г dx = 1 . 1 / sin”xcos"X л—1 sin”-*xcos"-1 X | л» +л —2 /* dx л—1 J sin*" x cos"-2 x
141. Г dx 1 1 p f sln"1 xco*"x m—1 sin’"-1 xcos"-1 x rn 4 л — 2 /* dr от —1 J slnm-2xcos"x ’
142. Г cos”x dx cosm+1x m~ д + 2 Г cos” x dx ! sin"x (d— l)sin"-1 x л —1 J sin”-2x
143. f coswxdx cosm-1x । от — 1 Г cos*"-axdx * sin"x (от — л)з1п”-1х ' m — nj sln"x
144. C . n . cos”+,x i p / sin cos"xdx= т 6. > «4-1
145. /*sin” x cos x dr= >,П X Ц- G ' Л -f* 1
146. f tg”xdx=.^_-1x — у tg”-axdx4C
147. f ctg”xdr= — _ j* ctg"-’xdx4C.
148. . /* . , . sin (от 4 я) x . sin (от —л) X . _ / sin mx sin Л-V dx= T ' + — 4- C. ' 2 (m + n) 1 2 (от — л) '
149. Г , . sin (от 4 л)X . sin (от — л)х . / cosотхcosnxdxg=—Т-.-Ц— т-4-£ ' 2 (от 4 л) 1 2 (от — л) *
/, . соз(т-(-л)х cos (гл — л)х . _
sinтхcos пхdx=------'-----------------+ С.
2(/л + я) 2(т — л)
/dx 2 . (. / а — Ь. х \ .
—гч--------= - arctg 1/ ——; tg ) + С, если а> J.
a-f-ftcosx у (Р—& ь \ Г a-{-b ь 2 /
«/г 1 / * -«• tg 4-+ /м7®
152. / --------= —^г= In--------------------------[- С, если a <&
J o + *cosx V&-d*
Г dx 2 fltg'2* + &
153. / ---:------- r arctg — r______—|- С, если a > b.
J e+isinx Vcfi—Ь» Yai — P
154. - Лг , «tg -тг+Ъ— — а* / — = — !п + С, если а < Ь. J а + bsinх УЬ2 — о2 atgy4-44-У6«—й«
155. J в2 cos2 х5* slnE х ab arclg ( а ) + С Г ах , . е“® (a sin лх — л cos лх) . „ / sin лх dx= s , 4- С.
156. J аъ+гР 1 /* - , . е3 (sin х — cos х) . „ j г sinxdx= i 4- C.
f e” cos nxdx= e<a (я sin 7 + g C°S ПХ~ + C.
157.1 * flJ + w3
/- . e® (sin x + cos x) . ~
tr cos xdx=---i-----------— + C.
хеая dx = (ox - 1) + C.
159. f Xя e^dx = —— - — /* x”-1 e“tfx.
J ' a a J
160. [ a”axndx = хП^хП----------- C dHa,xn~idx.
J m In a mU\a J
/a*dx____________a®_____. In а Г <^dx
x" - (m — IJx”-1 и — 1 J xT'‘“* "
162. У* e°®cos"xrfx =
e°®cos”—1 (acosx + nsinx) n(n—1) Cja^n-s
-----------------------------C°S XttX’
163. f x**cos ax dx=^-^-(ax sin ax-{-m cos ax)— ”* fJ^~*cosaxdx.
J и* J
Логарифмическая формы.:
164. /* 1пдгЛг=х1пх — х + С.
= In (In х) + In ж +in* х + С.
166-
167.
№8.
e“* In xdx =
169. f x"ln’*x</x . Ji2tlln’,x---------/* x™ In"-1 xdx.
J m -f-1 m +1J
x” + 1 ,n+1 C xndx
(л-l)lnn-‘x + л - 1 J lnn-‘x’
ОлетстветыЯ редактор. И. Я. Акуиикай. Технический редактор В. Д. Фишки.
Саане в набор 3/V1 1934 г. Подписана к печати 21/VIII 1934 г.
Формат 62ХМ *1,» ГХТИ № 96. Бум. листов 9'|, Тип. эн. в 1 бум. л. 110976. Уамв. Гаавлтв М В-94+36. Тираж 35 009-авт. л. 26*;. Заказ М №>4.