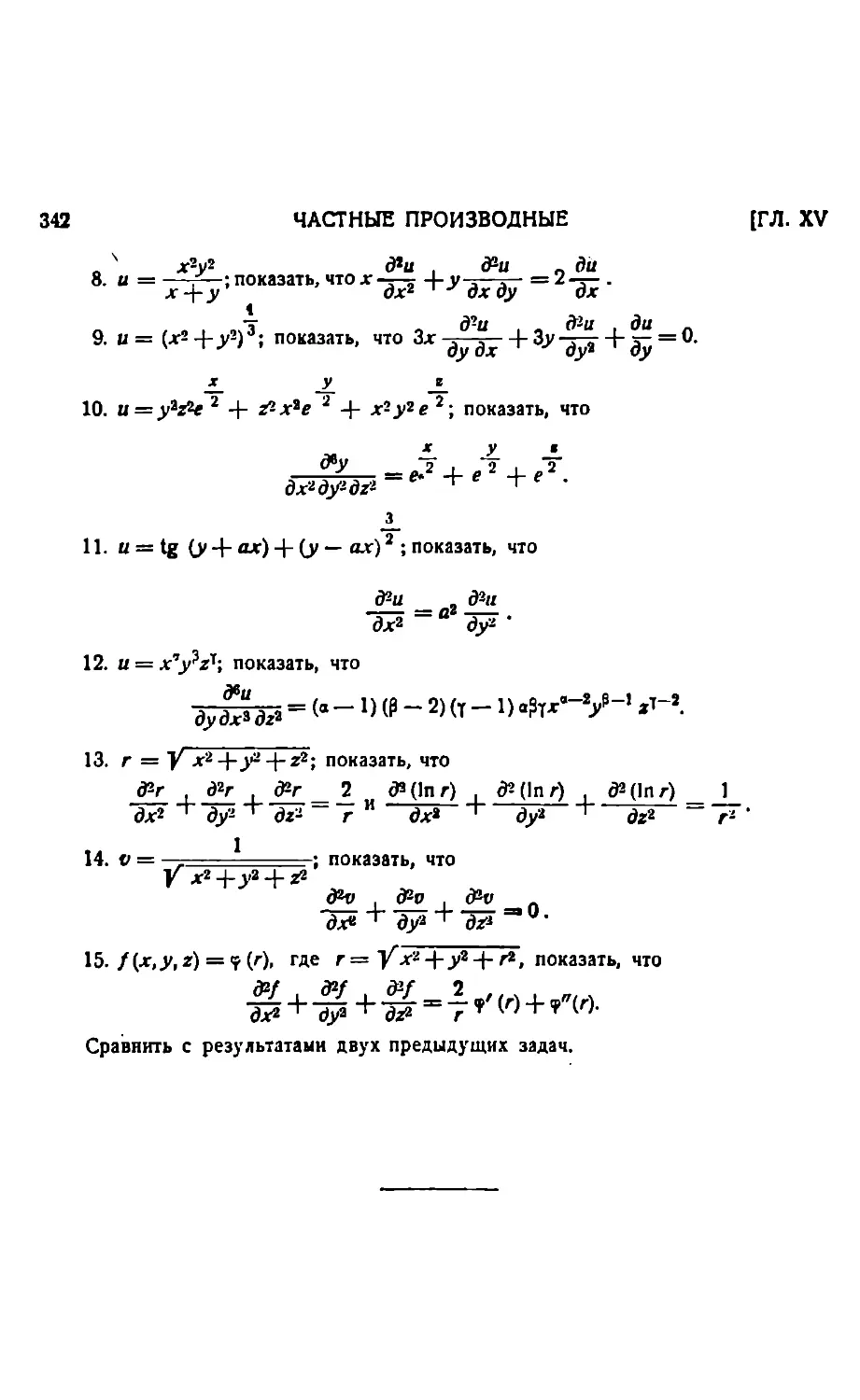Текст
КУРС ДИФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
ЧАСТЬ ПЕРВАЯ
ДИФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ОНТИ-ГТТИ—1834
КУРС
ДИФЕРЕНЦИАЛЬНОГО
И ИНТЕГРАЛЬНОГО
ИСЧИСЛЕНИЯ
ЧАСТЬ I
ДИФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Лопущен в качестве учебника в 1J34 г. Всесоюзный комитетом по высшему техническому образованию при ЦИК СССР
, онти
ГОСУДАРСТВЕННОЕ ТЕХНИКО-ТЕОРЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО МОСКВА 1934 ЛЕНИНГРАД
Выпускаемый в свет стандартным изданием Грэнвиль-Лузин, часть I—„Дифгренцнальное исчисление* и часть II — .Интегральное исчисление “ представляет собою, переработку для втузов печатавшегося раньше учебника под тем же самым заглавием.
Благоприятное отношение учащихся нашей страны к этому учебнику — о чем свидетельствует самое число (четырнадцать) его изданий— побуждает нас сохранить основную его установку, ориентирующуюся целиком на понимание учащимся и читателем излагаемого материала.
Из двух основных моментов действия всякого вообще учебника на учащегося: путем усвоения, т. е. вбиранием памятью материала, и путем понимания, мы совершенно сознательно остановились на втором: понимании.
К этому нас побуждало вовсе не то указание, которое обычно делают в защиту этой точки зрения, что выпадение какой-нибудь важной части материала из памяти приводит в расстройство и весь вообще казавшийся хорошо*усвоенным материал. Это, конечно, верно, но мы имели в виду неизмеримо более важное соображение: инициативу учащихся. Эта инициатива может притти и всегда приходит лишь от совершенного понимания материала, и вовсе не от легкости его усвоения.
Инициатива, смелое и вместе с тем точное обращение с материалом, является самой большой драгоценностью, и практика западной инженерии очень тонко понимает это. Для иллюстрации достаточно указать, что Запад выработал два типа инженера. Первый тир получает во втузе математики — и вообще теории — ровно столько, сколько ему практически понадобится в его непосредственной деятельности; обучение этого рода инженеров ориентируется на легкость усвоения предлагаемого ему материала. Второй же тип получает во втузах математику, вообще говЬря, почти в том же самом объеме, но излагаемую совершенно иначе; обучение этого рода инженеров ориентируется уже на совершенное понимание, для чего отводится'' на теорию несколько больше времени. Инженеры первого рода хорошо справляются со стандартизированным производством: там, где нужны лишь шаблон и точность его выполнения, эти инженеры вполне на своем месте, но достаточно заказчику лишь немного изменить деталь требуемого им устройства, отступив от выработанного фабрикой шаблона, и инженеры первого рода внезапно становятся совершенно беспомощными. В таких случаях заказчика обычно отсылают к инженерам второго рода. Эти последние, вообще говоря, имеют не больше чисто технических сведений по требуемому
предмету, но в их руках драгоценная инициатива, т. е. умение ориентироваться в новой обстановке, выходящей из шаблона, и они с наилучшим успехом доводят порученное им дело до конца, на основе превосходно заложенного в них понимания принципов, по дороге пополняя самостоятельно недостающие йм сведения.
Едва ли нужно указывать на то, что эта способность к инициативе, получающаяся лишь на основе совершенного понимания принципов, исключительно драгоценна для нашей страны, в которой при ведущемся строительстве мы имеем дело с все время изменяющимися условиями.
В условиях ориентировки на понимание нисколько не страшны дефекты памяти, так как самый ход однажды понятого материала не позволяет утратиться существенному, деталь же легко восстановить по справочнику. Ориентировка на понимание кажется громоздкой лишь вначале; но на деле затраченное на понимание время с лихвой окупается в дальнейшем, так как при правильно понятых основаниях дисциплины дальнейший материал часто принимает характер лишь упражнений в давно известном, чем создается уже экономия и времени.
Таким образом мы отказались от сколь-нибудь значительного сокращения в принципах математического анализа. В частности, в части I мы сократили лишь вдвое против прежних изданий „Введение в анализ", не рискуя делать дальнейшего его сокращения, потому что это угрожало бы уже ясности понимания для учащихся ').
Такова принципиальная сторона той платформы, на которой построен предлагаемый учебник. Относительно тех или иных деталей изложения мы не отстаиваем нашей позиции, ч^отому что предлагаемый учебник в дальнейшем будет, конечно, подлежать ряду изменений.
Теперь придется более подробно остановиться на части II учебника, впервые выходящей в сильно переработанном виде сравнительно с еще довоенным переводом английского подлинника Грэнвиля.
Часть II посвящена интегральному исчислению, и первый вопрос, который встал перед нами, — как он встает и перед всяким, кто приступает к изложению интегрального исчисления, — это । был вопрос: с чего здесь начинать?
В этом вопросе нет'полного единодушия среди авторов: одни начинают с неопределенных интегралов, другие предпочитают начать с определенных интегралов. Взгляды тех и других аргументируются достаточно искусно; те и другие имеют стойких сторонников и пламенных защитников. ч
Если мы теперь обратимся к большинству курсов и трактатов математического анализа как наших, так и заграничных, не пренебрегая и простыми учебниками, то наблюдаем вот какую картину: большинство курсов анализа бесконечно малых, написанных в конце XIX в., предпочитает начать с неопределенных интегралов, и, напротив, большинство курсов начала XX в. начинает с определенных интегралов.
Спрашивается, какая причина побудила многих авторов отказаться от выработанного путем долгого научного и педагогического "опыта изложения, начинающегося с неопределенных интегралов и принявшего вид
*) При первом чтении могут быть опущены §§ 29 и 34 и доказательства теорем §§ 37, 38 и 47.
стройной и строгой системы, и перейти к обратному порядку изложения. Без сомнения, причины этому были не педагоги еского характера (так как система изложения вполне сформировалась и устоялась), а уже научного калибра. Повышенная строгость к принципам математики, компрометирующее анализ открытие Вейерштрассом недиференцируемых непрерывных функций, его стремление арифметизировать весь анализ, как и всю математику, зарождающаяся теория функций с ее открытием все более и более широких определений определенного интеграла — вот истинная причина тому, что изложение интегрального исчисления получило „обратный ход**. К этому присоединились еще указания исторического характера, так как, в самом деле, задача суммирования бесконечно малых исторически возникла почти одновременно с задачей о проведении касательных и вначале никак не была с нею связанней. И практика начала XX в. стала вырабатывать педагоигческие пути изложения интегрального исчисления определенных интегралов.
Спрашивается, в настоящий момент: каково положение вопроса с точки зрения строгой науки? Отвечая на этот вопрос, мы должны признать, что при современном состоянии науки вопрос не имеет никакой остроты, и не потому, что он уже решился в определенную сторону, но потому, что его решение совершенно безразлично: обе точки зрения могут быть сделаны одинаково научно строгими. Таким образом, при научной равноценности обоих способов изложения, вопрос должен быть перенесен совсем на другую почву: на почву чисто педагогического искусства, умения ярко выразить идеи того или другого способа изложения, личных склонностей или привычки преподавателя. Для учащегося обе системы одинаково хороши или одинаково дурны, смотря по тому, в руках какого преподавателя они находятся: обе могут принести одинаковый плод. Но для преподавателя вопрос вовсе не безразличен, так как в его руках должна иметься книга для учащихся, такая, согласно которой он мог бы преподавать, следуя своему способу изложения.
Это важное обстоятельство побудило нас дать в части II сразу оба способа изложения, скомбинировав материал таким образом, чтобы его без всяких изменений можно было начать излагать по желанию: либо с определенных, либо с неопределенных интегралов.
Преподаватели и учащиеся, которые желают начать изложение и изучение с определенных интегралов, должны начать читать^ с главы I, где даются: понятие о суммировании бесконечно малых, научные вопросы, выдвинувшие задачу суммирования бесконечно малых, понятие определенного интеграла, прием решения задачи суммирования бесконечно малых, и, наконец, глава заканчивается понятием неопределенного интеграла. Далее, преподаватель и читатель должны переходить к чтению остальных глав по порядку так, как они следуют в учебнике.
Преподаватель н учащиеся, которые желают начать изложение и изучение с неопределенных интегралов, должны, опустив совсем главу I, начать читать прямо с главы II, где излагаются основные понятия из теории неопределенных интегралов, и перейти затем к чтению дальнейших глав, в которых сначала заканчивается теория неопределенных интегралов, а потом дается изложение определенных интегралов для тех, кто здесь прошел полностью неопределенные интегралы.
В научном отношении такая свобода маневрирования достигается отказом определять неопределенный интеграл через определенный интеграл. Основная теорема интегрального исчисления: «всякая непрерывная функция имеет первообразную" может быть доказана прямо без всякого интегрального исчисления. Справедливость этого, кажущегося парадоксальным, утверждения была показана еще Лебегом.
Этот важнейший факт вполне соответствует историческому ходу вещей. Интегральное исчисление, в современном изложении, состоит из двух частей: определенных и неопределенных интегралов, исторически назвавшихся: „квадратуры" и «обращение касательной". То, что задача о „квадратуре" решается во всех случах, в которых решается задача об «обращении касательной", — это обстоятельство стало известным лишь Лейбницу и Ньютону, и в установлении связи этих двух великих задач заключается открытие анализа бесконечно малых этими двумя великими мыслителями. До них бесконечно малые и их суммирование в различных частных случаях прекрасно было известно. Но лишь они двое дали систематический прием отыскания квадратур помощью „обращения касательной". Короче говоря, в руках создателей анализа бесконечно малых неопределенные интегралы были лишь инструментом фактического суммирования бесконечно малых. Роль неопределенных интегралов несколько напоминала роль современных методов суммирования расходящихся рядов.
Таким образом вначале развития анализа бесконечно малых не могло быть и речи о том, чтобы определять неопределенный интеграл при помощи суммирования бесконечно малых, так как суммирование бесконечно малых (вообще, в конечном виде нам недоступное, потому что процесс этот бесконечен) как раз и совершалось помощью неопределенных интегралов, отыскиваемых сторонним, но совершенно конечным, путем.
И лишь впоследствии порядок этот был извращен, и начали определять неопределенный интеграл помощью суммирования бесконечно малых.
Эти идеи и положены в основу изложения нашей части И. Ради педагогических соображений, для учащихся втузов существование первообразной просто постулируется. Психологически это для учащегося не представляется изумительным и неприятным, так как, отыскивая фактически неопределенные интегралы, он приобретает если не уверенность, то склонность рассматривать всякую данную ему непрерывную функцию f (х) как производную от ее первообразной, которую ему в „большинстве случаев" удается найти.
По просьбе профессоров и преподавателей я, однако, прилагаю в виде добавления развитое указание Лебега.
Недостаток времени не позволил мне лично изложить теорию дифе-ренциальных уравнений; это изложение было сделано проф. Н. П. Тарасовым, которому принадлежит превосходный набор задач на все отделы обеих частей.
Москва 3 июня 1934 г.
Акад. Николай Лузин.
ОГЛАВЛЕНИЕ.
Стр.
Предисловие................................................. 3
Глава I.
ЧИСЛА.
Рациональные числа 11. — Практическое значение рациональных чисел 12. — Сопоставление рациональных чисел с точками прямой линии 12.— Несоизмеримые отрезки 12. — Иррациональные числа 13. — Представление рациональных чисел в виде десятичных дробей 15. — Действительные числа 16. — Абсолютная величина 17.—Деление на нуль невозможно 17.
Глава П.
ПЕРЕМЕННОЕ ФУНКЦИЯ.
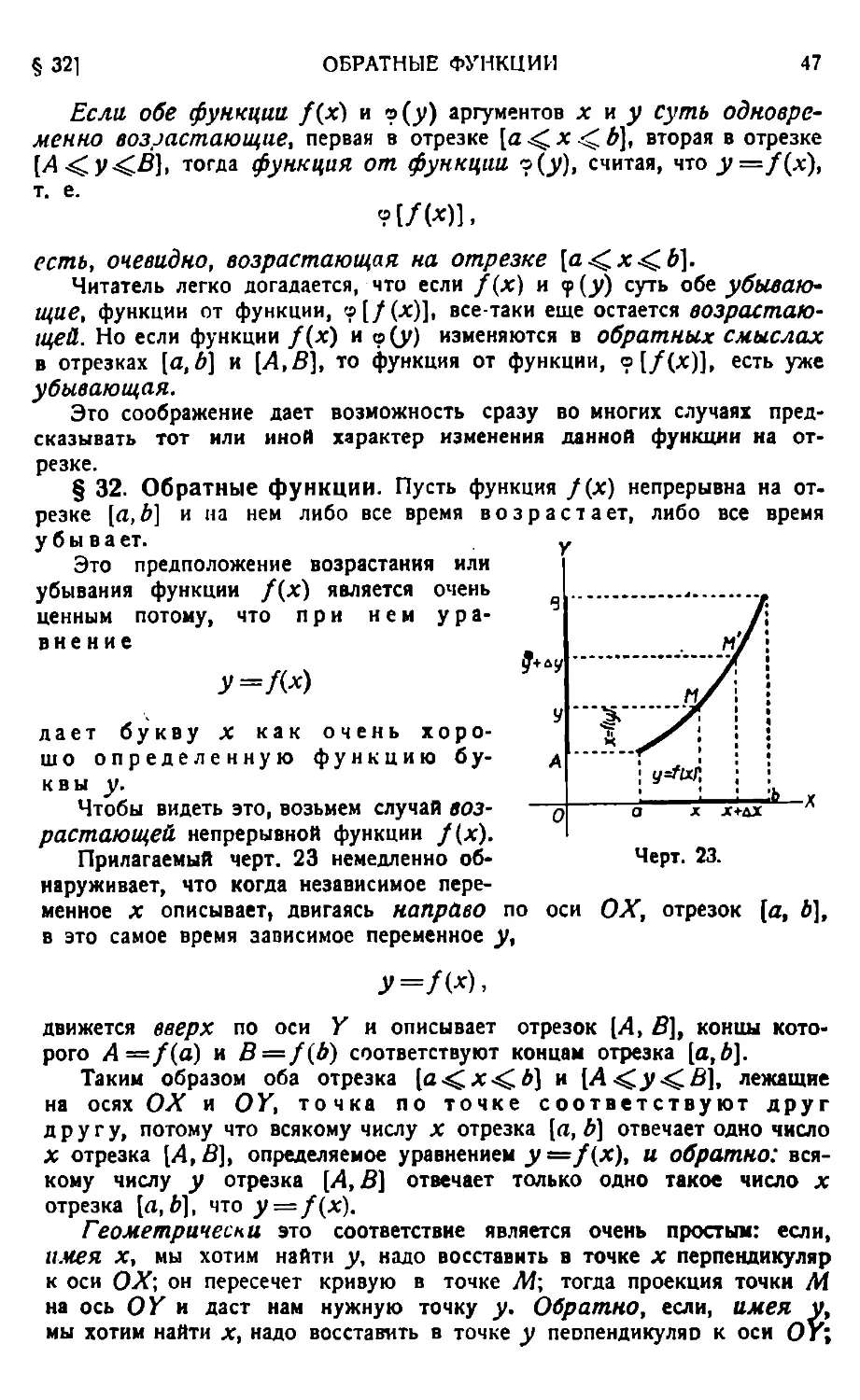
О величинах вообще 19. — Переменная величина 20. — Постоянная величина 20. — Геометрическое изображение величин 21. —Область значений переменного 22. — Отрезок и промежуток 22. — Монотонное и колеблющееся изменения величины 24. — Ограниченная величина 25. — Приращение переменной величины 27. — Постоянная величина как переменная 28. — Функция 29. — Зависимое и независимое переменные 29. — Характеристика функции 29. — Вычисление функций 32.— Область изменения аргумента 33. — Приращение функции 34. — Геометрическое изображение функций 35. — Геометрическое изображение приращения функции 36. — Классификация функций 37. — О различном происхождении функций 42. — Функция от функции 44. — Возрастающие и убывающие функции 45. — Обратные функции 47.
Глава Ш.
ТЕОРИЯ ПРЕДЕЛОВ.
Предел переменного 53. — О способах переменной величины приближаться к своему пределу 55. — Бесконечно малые 57. — Связь понятия предела и бесконечно малого 59. — Основные свойства бесконечно малых 59. — Основные теоремы о пределах 63. — Понятие о бесконечно большом 66. — Связь бесконечно большого и бесконечно малого 68. — Непрерывность функций 70. — Свойства непрерывных функций 75. — Основная теорегма о непрерывных функциях 78.— Типы разрывов функций — 79. Устранимый и неустранимый разрывы 81. — Кажущийся разрыв и так называемая .истинная величина* функции. Раскрытие неопределенностей — 82. Два замечательных предела: отношение синуса к дуге — 86; число е 88. — Сравнение бесконечно малых друг с другом 97. — Порядки бесконечно малых 100. — Равносильные бесконечно малые 101. —Первый принцип анализа бесконечно малых 106.- Приложение первого принципа 108.
Глава IV.
ДИФЕРЕНЦИРОВАНИЕ.
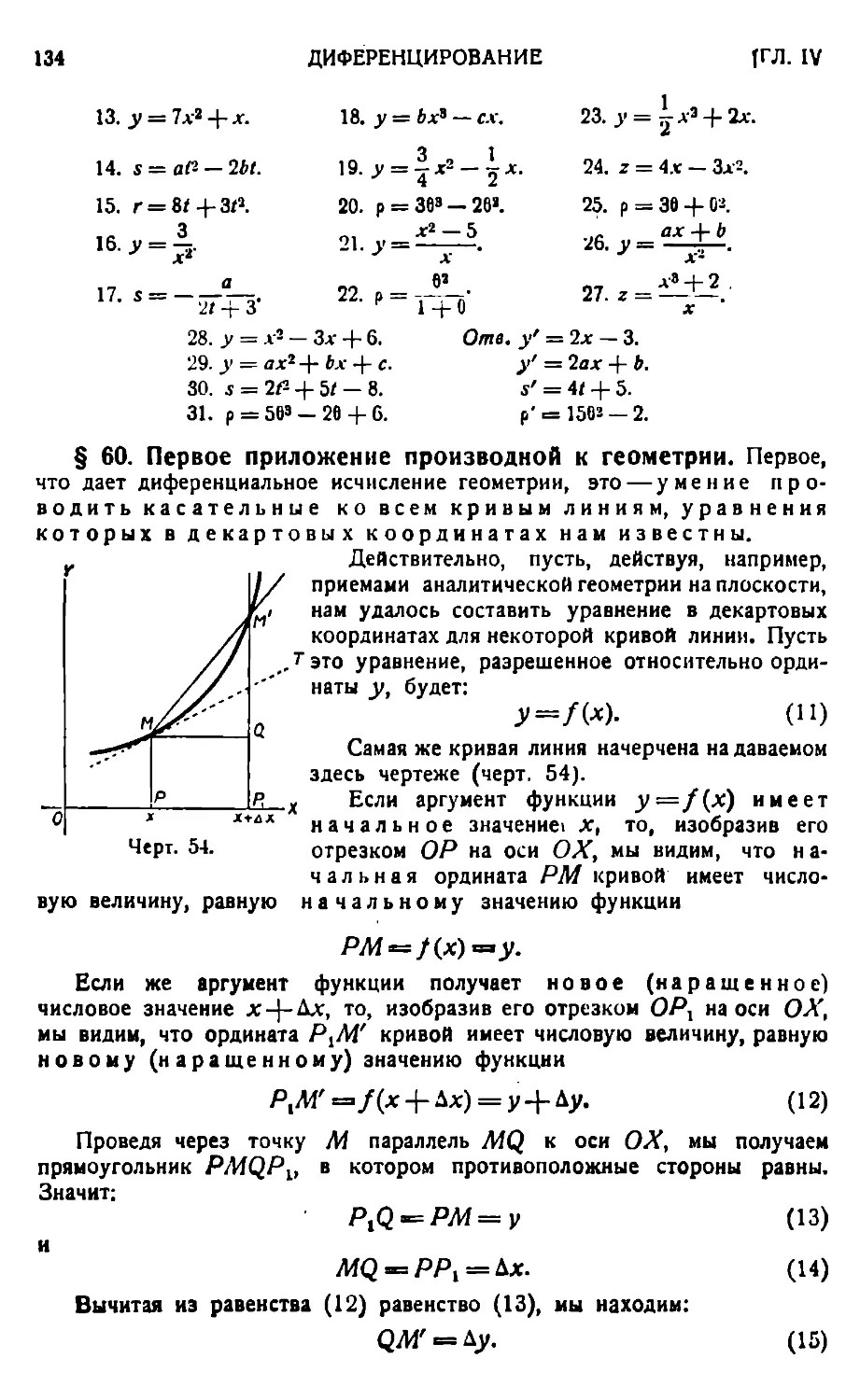
Введение 123. — Сравнение приращений 125.— Производная функции одного переменного — 126. Различные обозначения производной 128. — Диференци-руемые функции 131. — Общее правило днференцирования 132. — Первое приложение производной к геометрии 134.
. Гл ABA V.
ПРАВИЛА ДИФЕРЕНЦИРОВАНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.
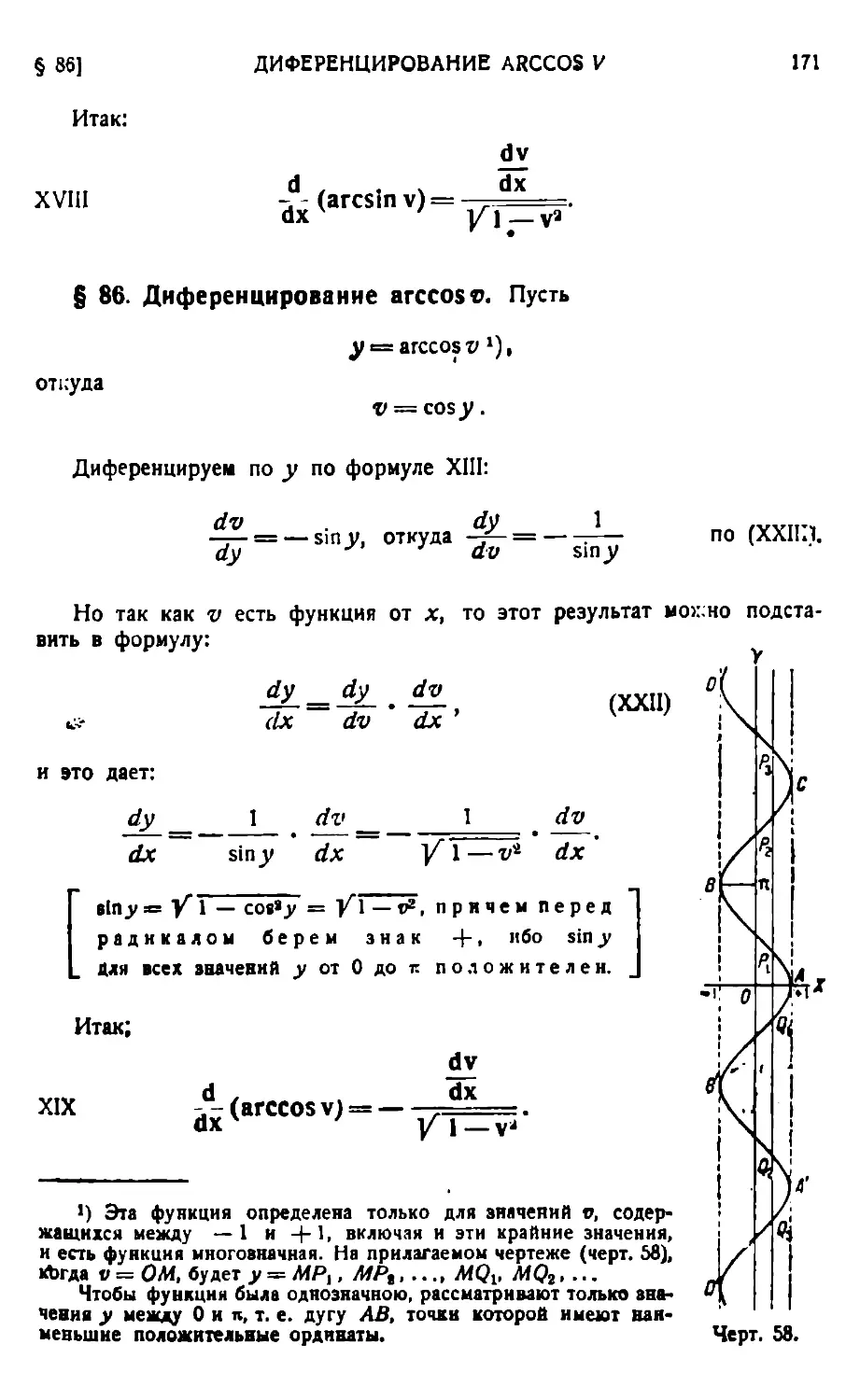
Важность общего правила 138. — Диферепцирование постоянного 140. — Ди-ференцирование переменного по самому переменному. 140. — Диференцнрование суммы (алгебраической) 141. — Диференцнрование произведения постоянного на переменное 141. — Диференцнрование произведения двух переменных 142. — Диференцнрование произведений любого конечного числа переменных 142. — Дн-ференцирование степенной функции с постоянным показателем 143. — Диферен-цирование частного 1-13. — Диференцнрование функции от функции 149 — Практика правила диференцирования функций от функции 153. — Диференциро-ванне обратной функции 155. — Диференцнрование логарифма 156. — Диференци-рование простой показательной функции 157. — Диференцнрование общей показательной функции 158. — Практика диференцирования логарифмических функций 159. — Диференцнрование sin о 164. — Диференцнрование cos V 165. — Дифе-ренцирование tg v 165. — Диференцнрование etg v 166. Диференцнрование sec <о 166.—Диференцнрование cosec v 166.—Диференцнрование arcsin о 170.—Ди-ференцирование arccos v 171.—Диференцнрование arctg v 172.—Диференцнрование arcctg v 172. — Неявные функции — 175. Диференцироьание неявных функций 177.
Глава VI.
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ.
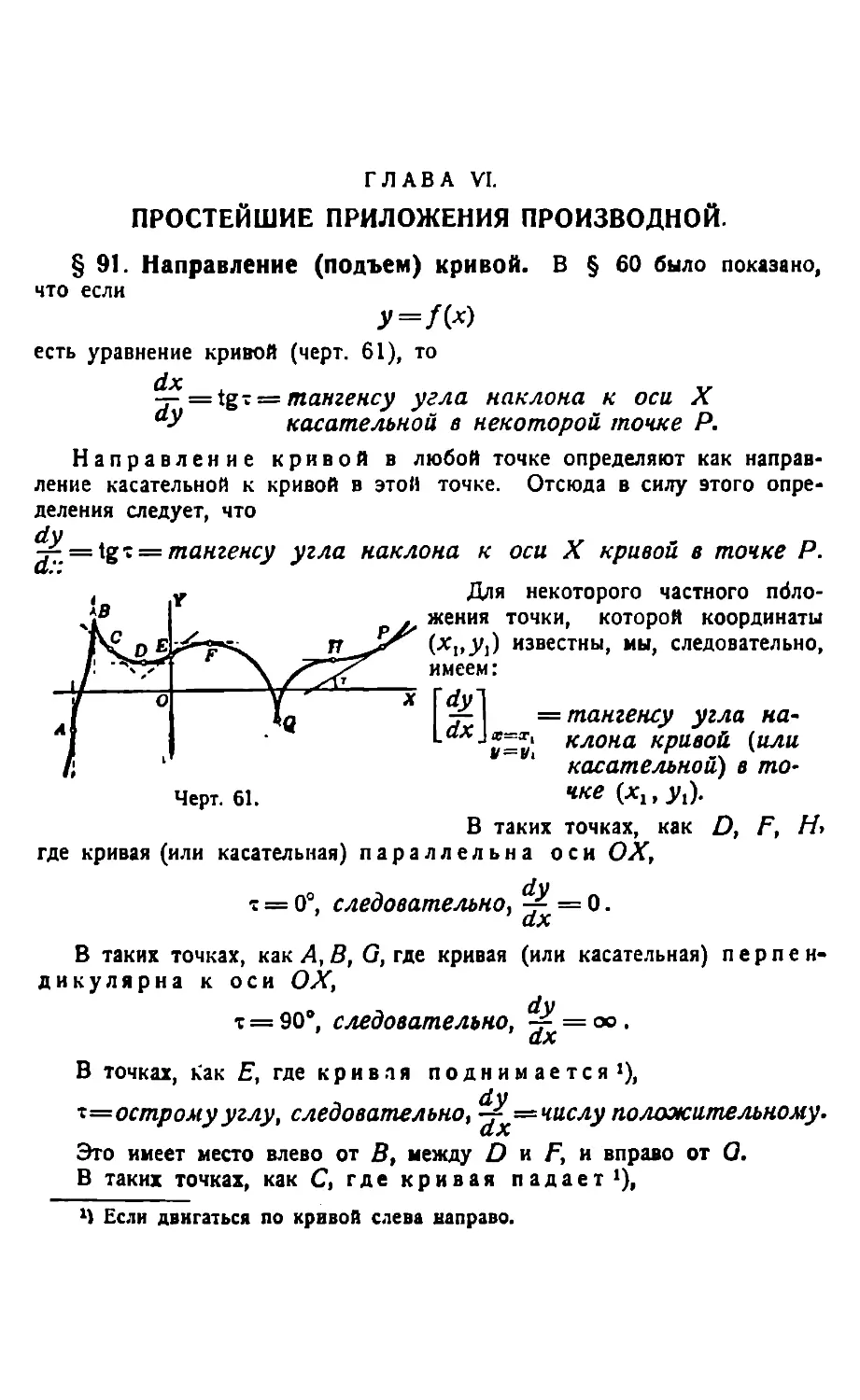
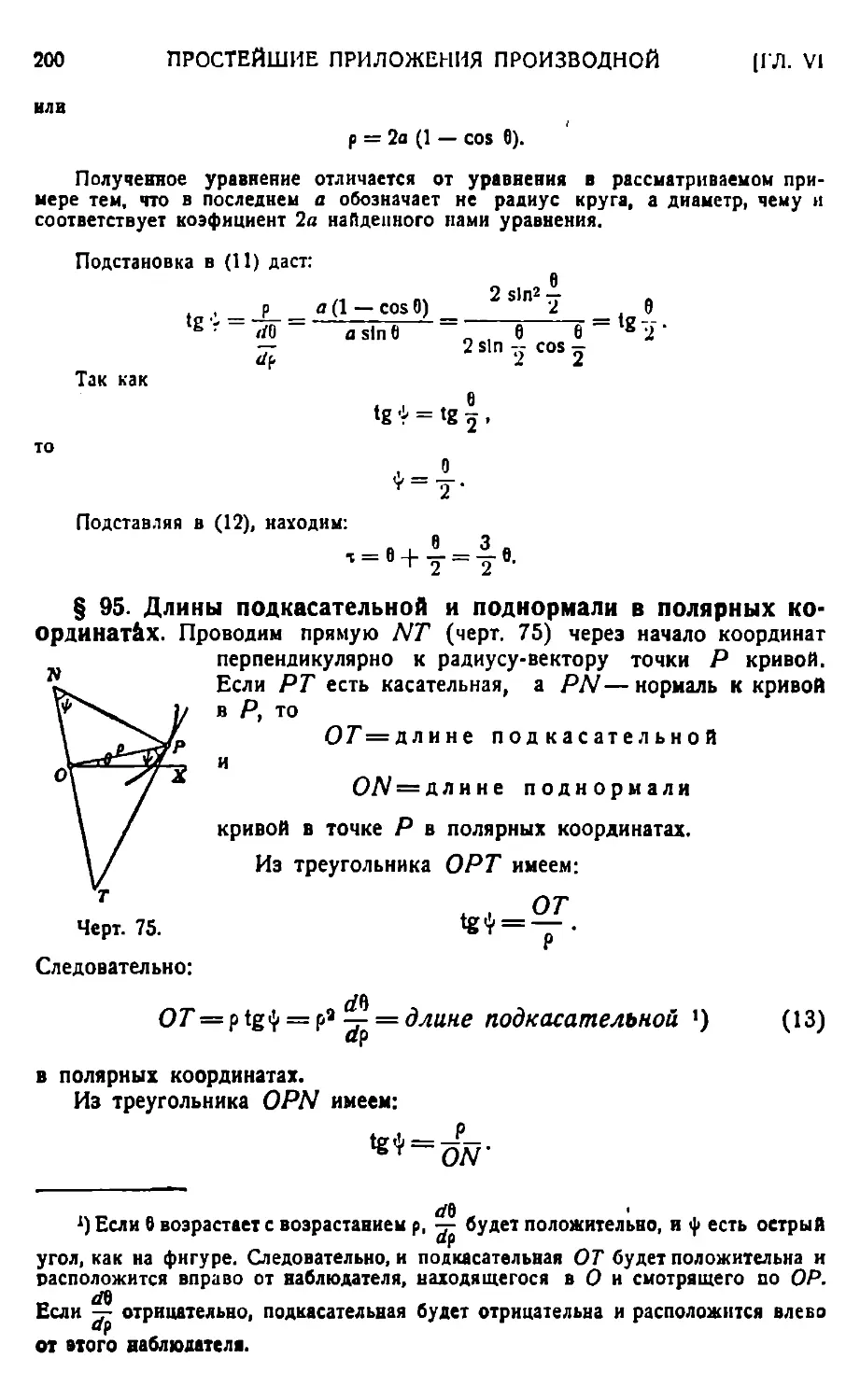
Направление кривой 182. — Касательная и нормаль, подкасательная и поднормаль (в прямоугольных координатах)— 187. Параметрические уравнения кривой 191.— Угол между радиусом-вектором и касательной 198. — Подкасательная и поднормаль в полярных координатах 200. — Отделение кратных корней у многочленов 203. — Приложение производных в механике: скорость 208. — Компоненты скорости 209. — Производная как отношение скоростей 210. — Тангенциальное ускорение 211. — Компоненты тангенциального ускорения 211.
Глава VII.
ПОСЛЕДОВАТЕЛЬНОЕ ДИФЕРЕНЦНРОВАНИЕ.
Определение последовательных производных 217. — Обозначения 217.— л-я производная 218. — Формула Лейбница 219. — Последовательное диференци-рование неявных функций — 220.
Глава VIII.
МАКСИМУМЫ И МИНИМУМЫ. ТОЧКИ ПЕРЕГИБА. ВЫЧЕРЧИВАНИЕ КРИВЫХ.
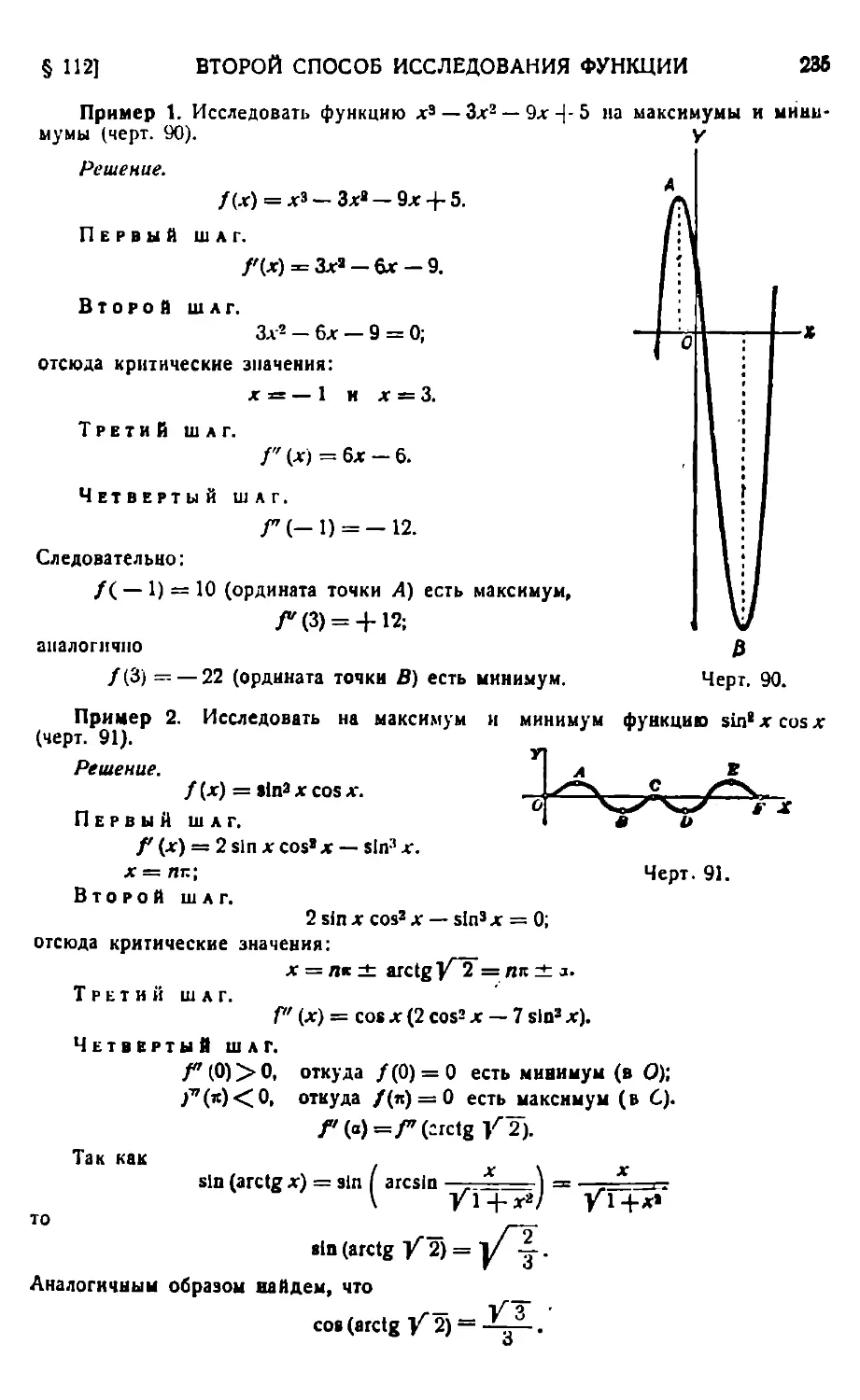
Введение 223.— Функции возрастающие и убывающие 226. — Признаки возрастания и убывания функций 227. — Максимальное и минимальное значения функции 229. — Першай способ исследования функции па максимумы и минимумы 231. — Второй способ исследования функции на максимумы и минимумы 233. — Общие указания для решения задач на максимумы п минимумы 240. — Точки перегиба 248. — Вычерчивание кривых 251.
Г л а в а IX.
ДИФЕРЕНЦИАЛЫ.
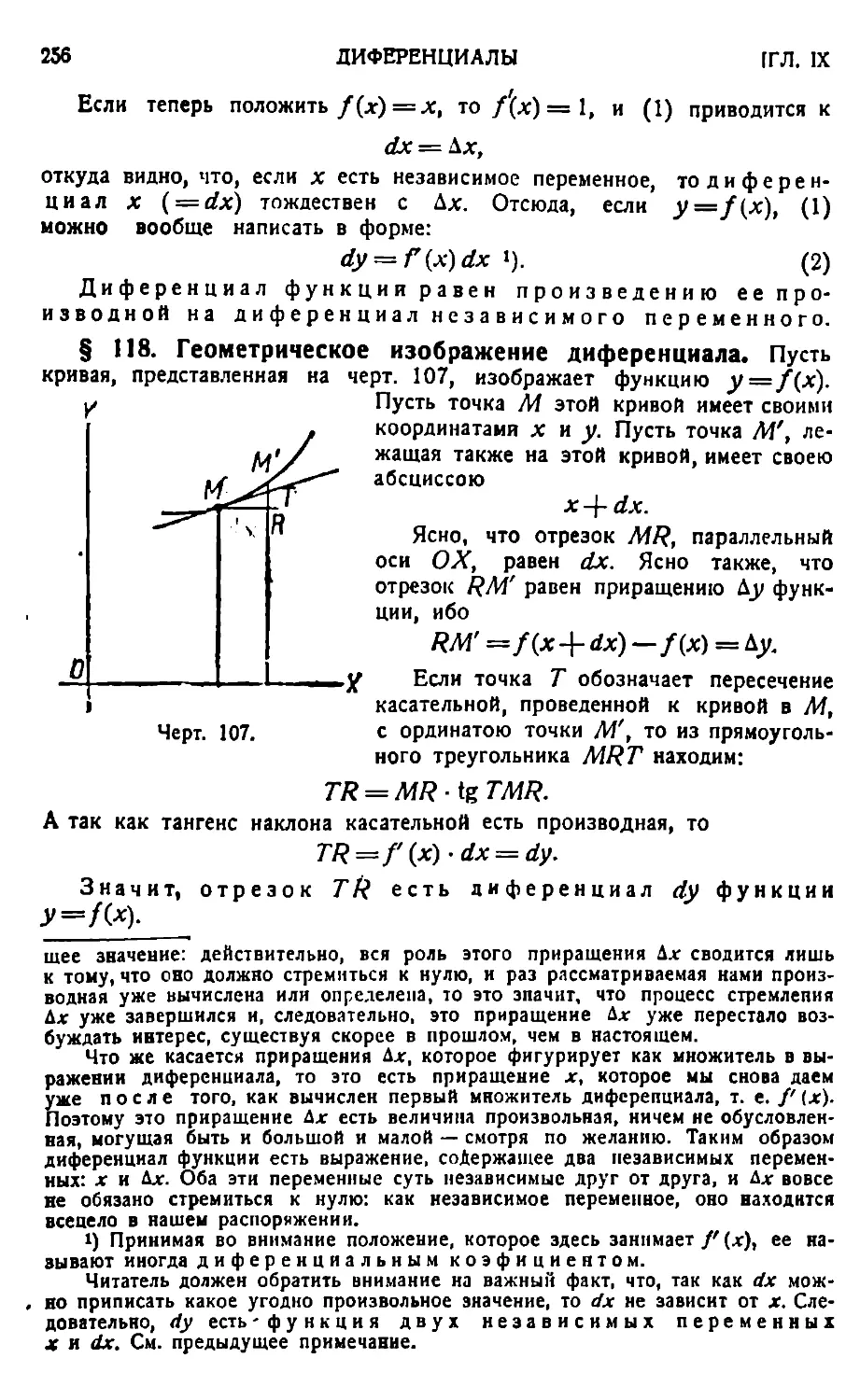
Введение 255. — Определения 255. — Диференциал функции и приращение функции 257. — Геометрическое изображение диференциала 256. — Важность диференциала функции 258. — Производная дуги в прямоугольных координатах 260. — Производная дуги в полярных координатах 261. — Формулы для нахождения диференциалов функций 262. — Диференциалы высших порядков 264.
ГлаваХ.
СКОРОСТЬ ИЗМЕНЕНИЯ.
Производная, рассматриваемая как отношение двух скоростей — 268. Упражнения 270.
Глава XI.
ЗАМЕНА ОДНИХ ПЕРЕМЕННЫХ ДРУГИМИ.
Замена зависимого и независимого переменных одного другим 275. — Замена зависимого переменного 276. — Замена независимого переменного 277. — Одновременная замена зависимого и независимого переменных 279.
Глава ХИ.
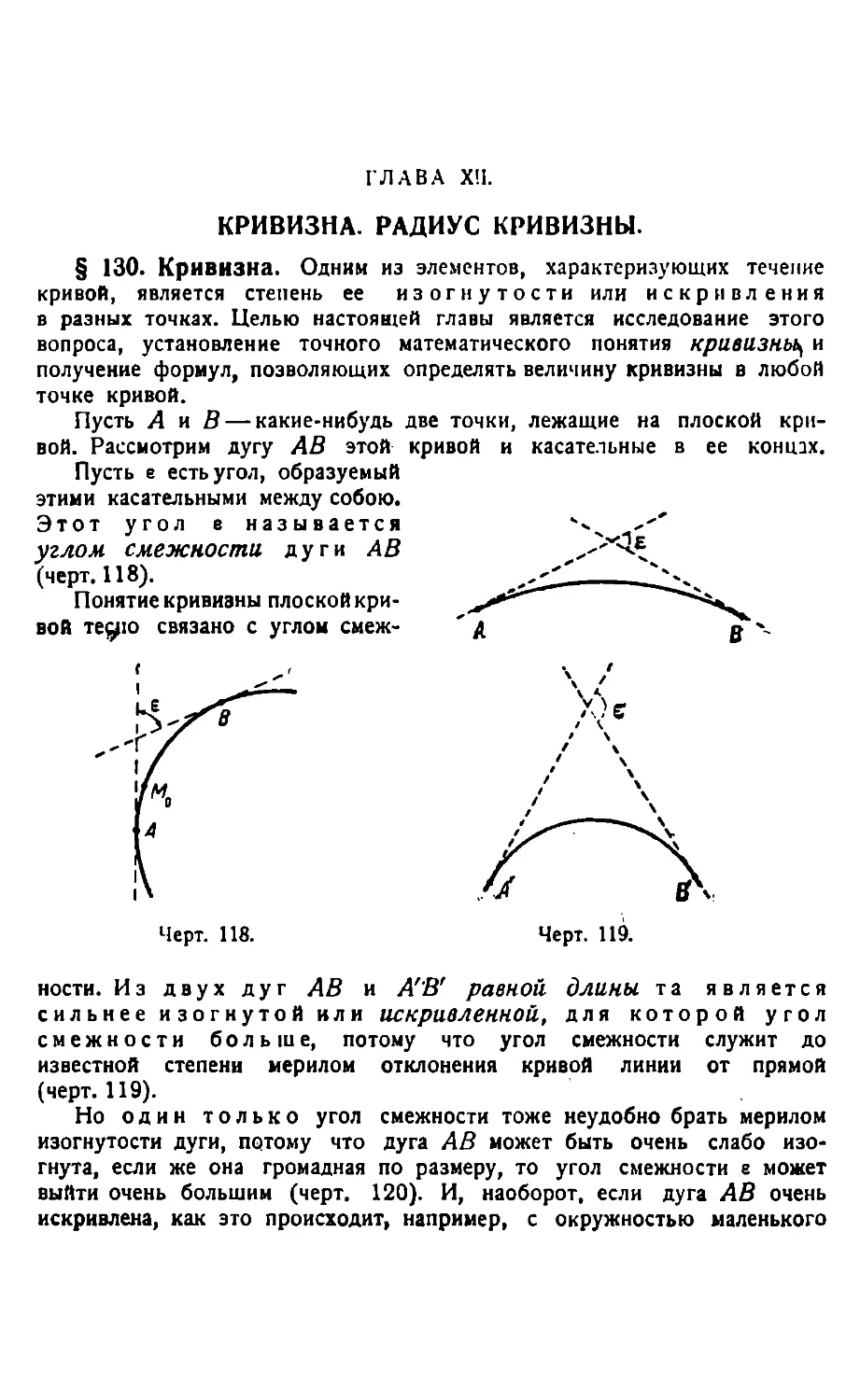
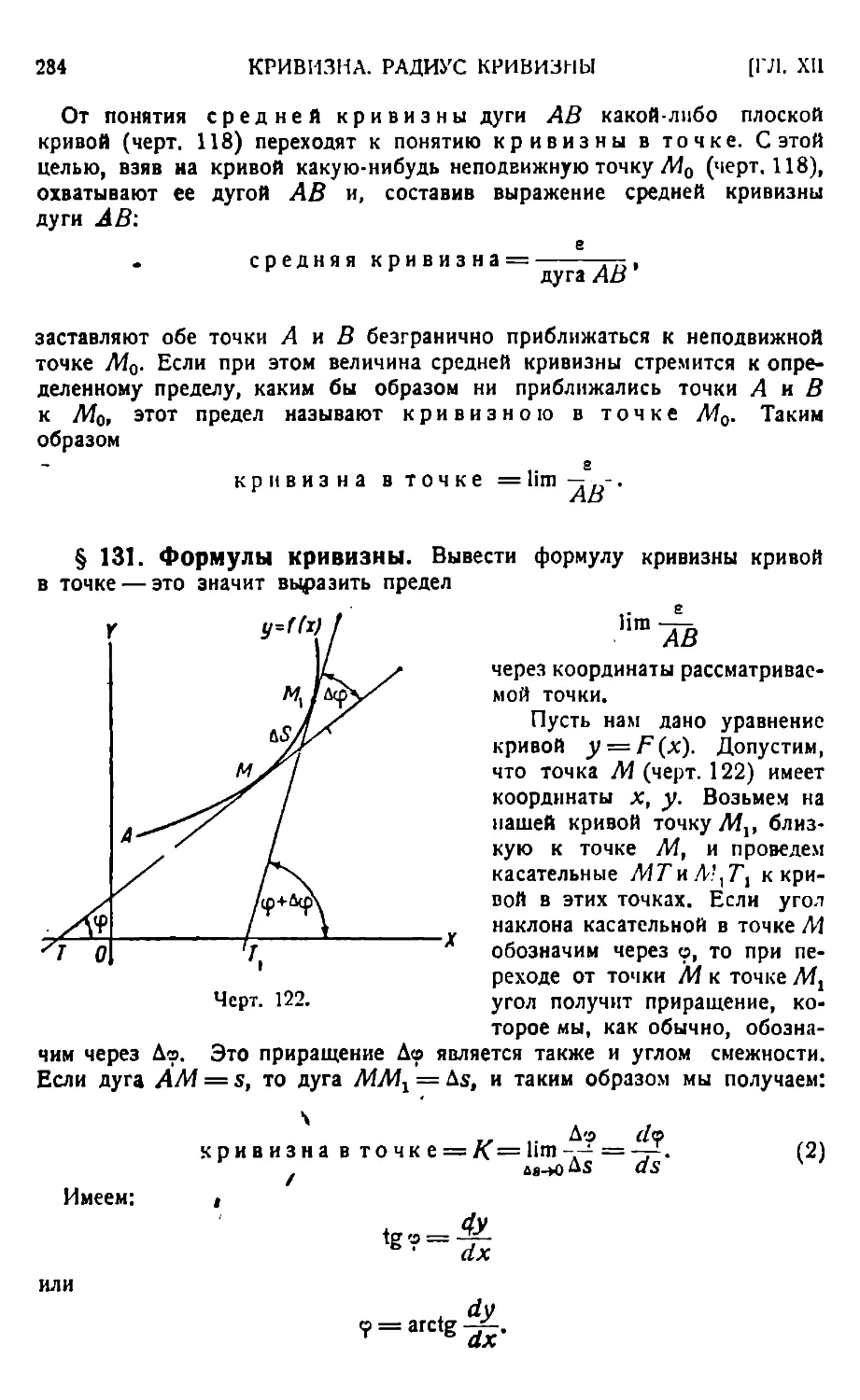
КРИВИЗНА. РАДИУС КРИВИЗНЫ.
Кривизна 282. — Формулы кривизны 284. — Формула кривизны для случая, когда кривая задана уравнениями в параметрической форме 286.—Формула кривизны в полярных координатах 287.—Радиус кривизны 288. —Кург кривизны 289.
Глава XIII.
ТЕОРЕМА О КОНЕЧНОМ ПРИРАЩЕНИИ. НЕОПРЕДЕЛЕННЫЕ ФОРМЫ.
Теорема Ролля 293. — Теорема Лагранжа о конечном приращении — 294. Формула Тейлора 296. — Максимумы и минимумы, рассматриваемые аналитически 297. — Теорема Коши 299. — Неопределенные формы 300. — Вычисление начения функции, принимающей неопределенную форму 300. — Раскрытие неопределенной формы £ 302. — Раскрытие неопределенной формы 304. — Раскрытие неопределенности вида 0 • со 306. — Раскрытие неопределенности сс-оо 307. — Раскрытие неопределенных форм 0°, l", оо° 308.
Глава XIV.
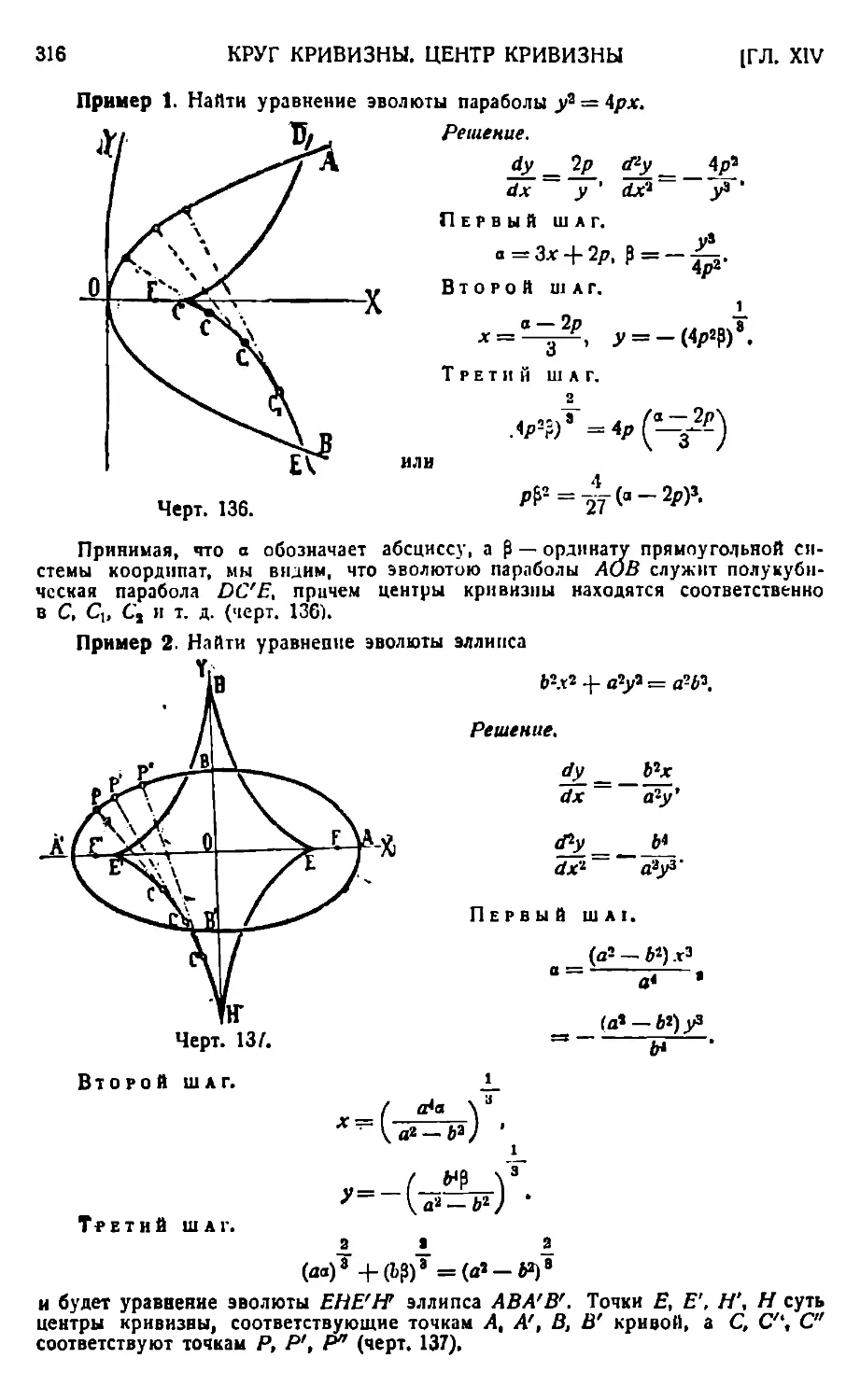
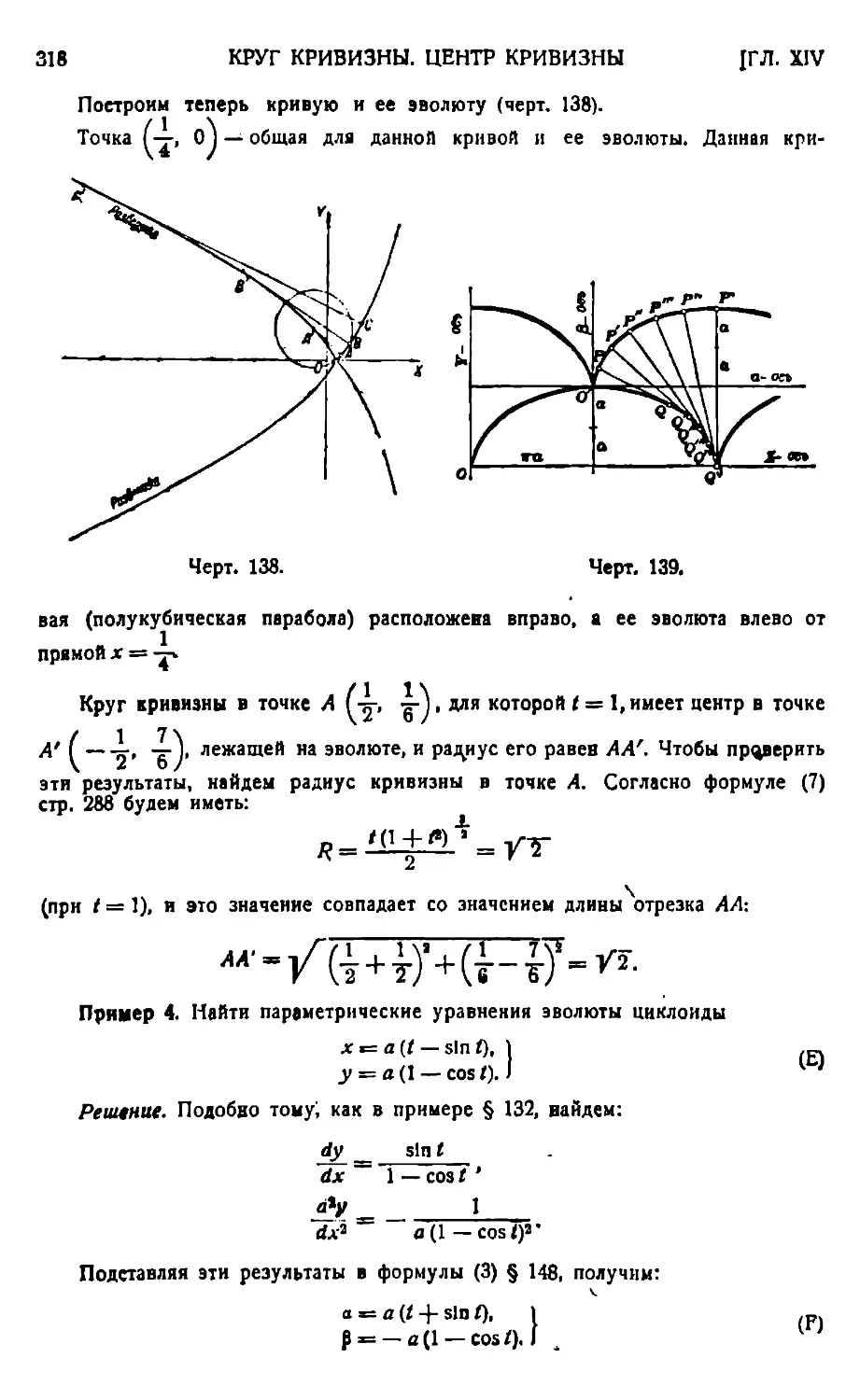
КРУГ КРИВИЗНЫ. ЦЕНТР КРИВИЗНЫ.
Круг кривизны. Центр кривизны 311,—Центр кривизны как предельное положение пересечения нормалей в смежных точках 314. — Эзолюты 315. — Свойства эволюты 319. — Инволюты и их .механическое построение 320.
Глава XV.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ, ЧАСТНЫЕ И ПОЛНЫЕ ДИФЕРЕНЦИАЛЫ.
Непрерывные функции двух и более независимых переменных 323. — Частные производные 324. — Геометрическая интерпретация частных производных 325.— Полное приращение 328. — Полный диференциал 330.—Производные и диферен-циалы сложной функции одного независимого переменного 331. — Диференци-рование неявной функции 335. — Последовательные частные производные 340.— Теорема о порядке днференцирования 340.
Глава XVI.
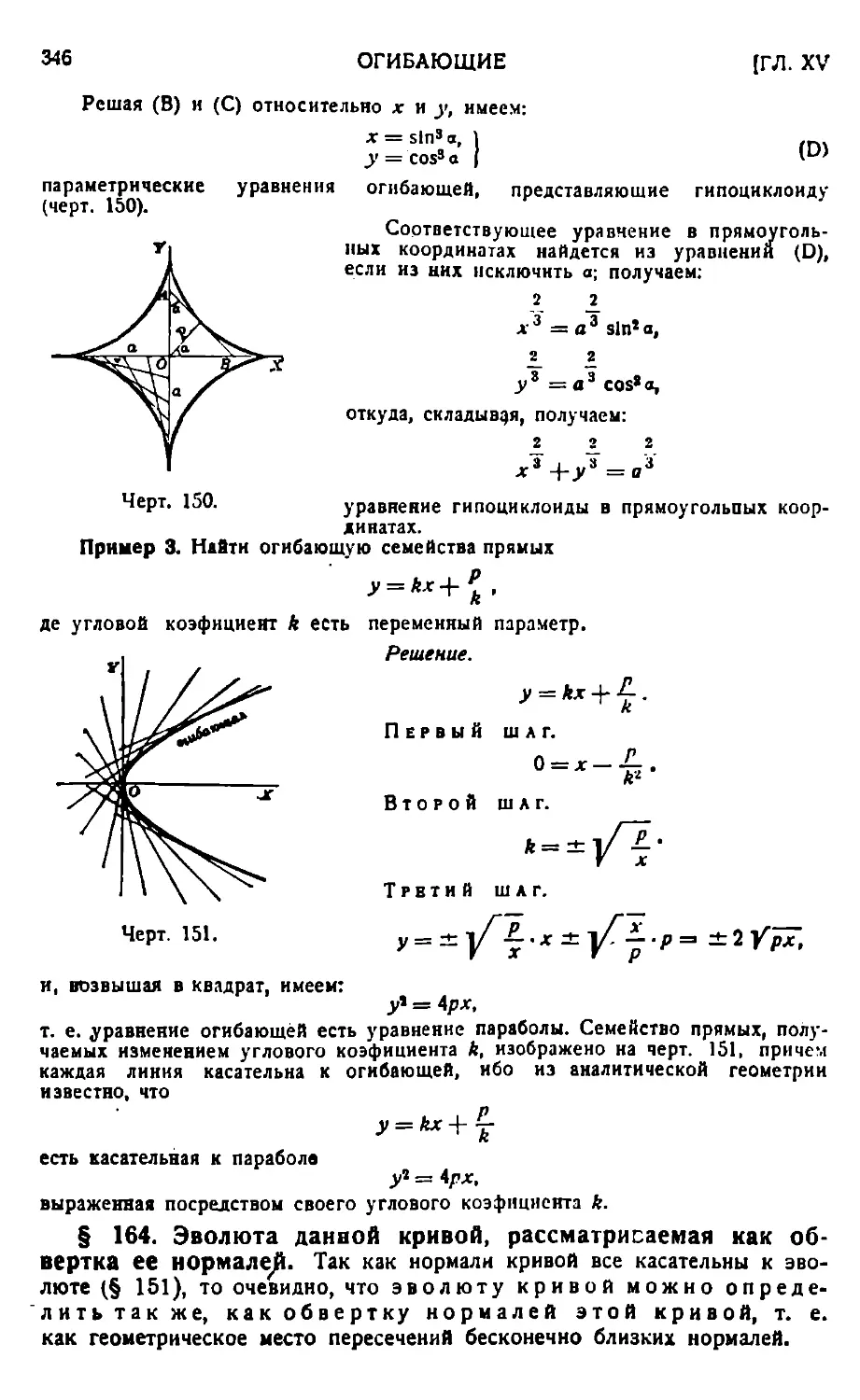
ОГИБАЮЩИЕ.’
Семейство кривых. Переменный параметр 343. — Огибающая семейства кривых, зависящих от одного параметра 343. — Эволюта данной кривой, рассматриваемая как обвертка ее нормалей 346. — Два параметра, связанные одним условным уравнением 347.
Глава XVII.
РЯДЫ.
Бесконечные последовательности 351. — Ряды 353. — Необходимый признак сходимости 354. — Достаточные признаки сходимости. Сравнение рядов 356. — Признак сходимости Даламбера 356. — Ряды с чередующимися знаками 35$.—у Абсолютная сходимость 360.
Глава XVIII.
РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯДЫ.
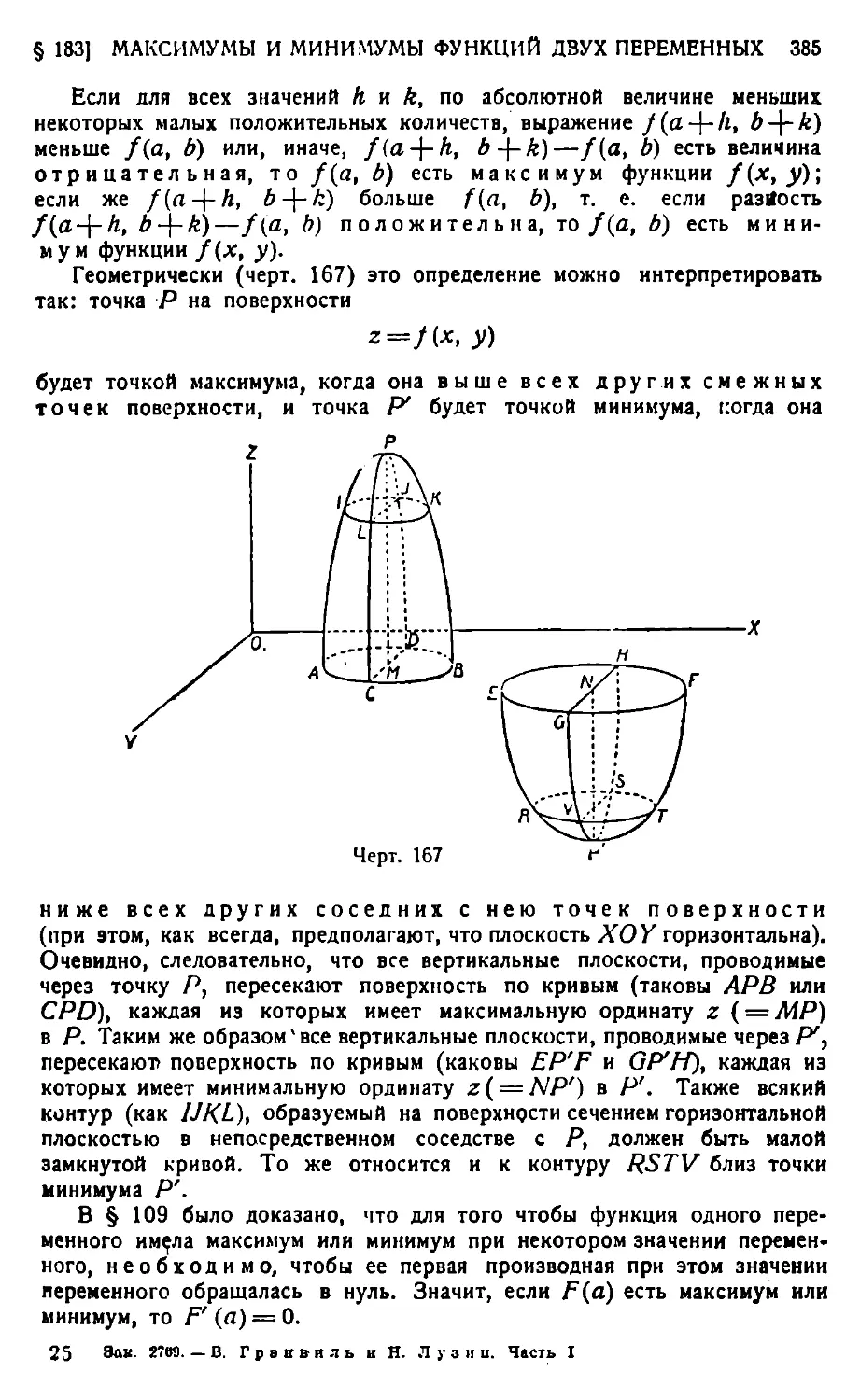
Ряды функций 363. — Степенные ряды 364. — Разложение функций в ряды 367.— Ряд Тейлора 368. — Формула Маклорена и ряд Маклорена 371. — Вычисления посредством рядов 378. — Приближенные формулы, выводимые из рядов 379.— Ряд Тейлора для двух и большего числа переменных 381. — Максимумы и минимумы функций двух независимых переменных 384.
Глава XIX.
АСИМПТОТЫ. ОСОБЫЕ ТОЧКИ.
Прямолинейные асимптоты 391. — Нахождение асимптот по способу стремления к пределу отрезков на осях координат 391. — Способ определения асимптот для алгебраических кривых 392. — Асимптоты в полярных координатах 396. — Особые точки 397. — Определение касательной к алгебраической кривой и данной на ней особой точке 398. — Узлы 400. — Точка возврата 401. — Уединенные или изолированные точки 402. — Особые точки трансцендентных кривых 403.
Глава XX.
ПРИЛОЖЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ.
Касательная линия и нормальная плоскость к кривой двоякой кривизны 405. — Касательная плоскость к поверхности 407. — Нормаль к поверхности 409. — Другая форма уравнений касательной прямой к кривой двоякой кривизны 411.— Другая форма уравнения нормальной плоскости к кривой двоякой кривизны 412.
Глава XXI.
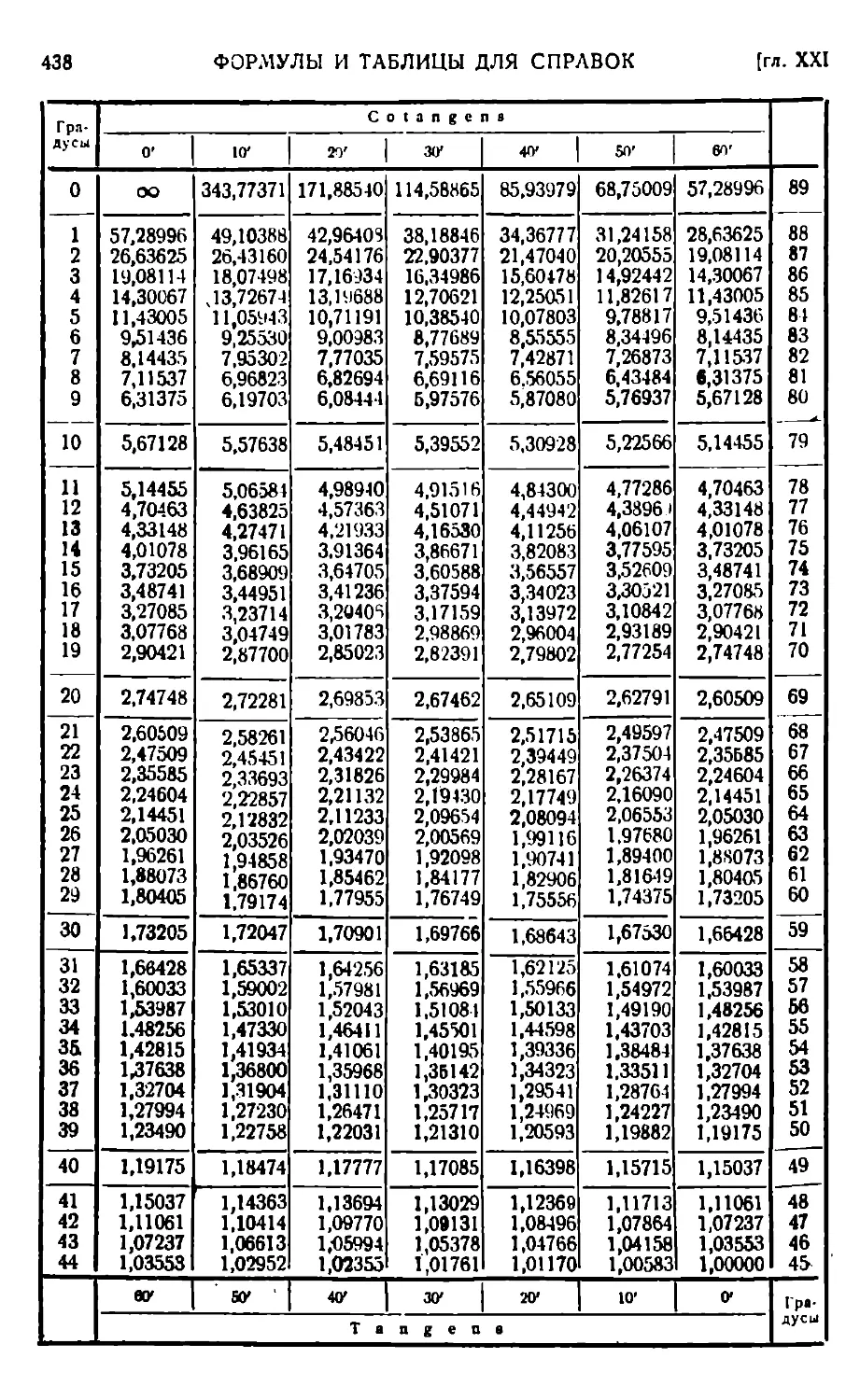
ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ СПРАВОК.
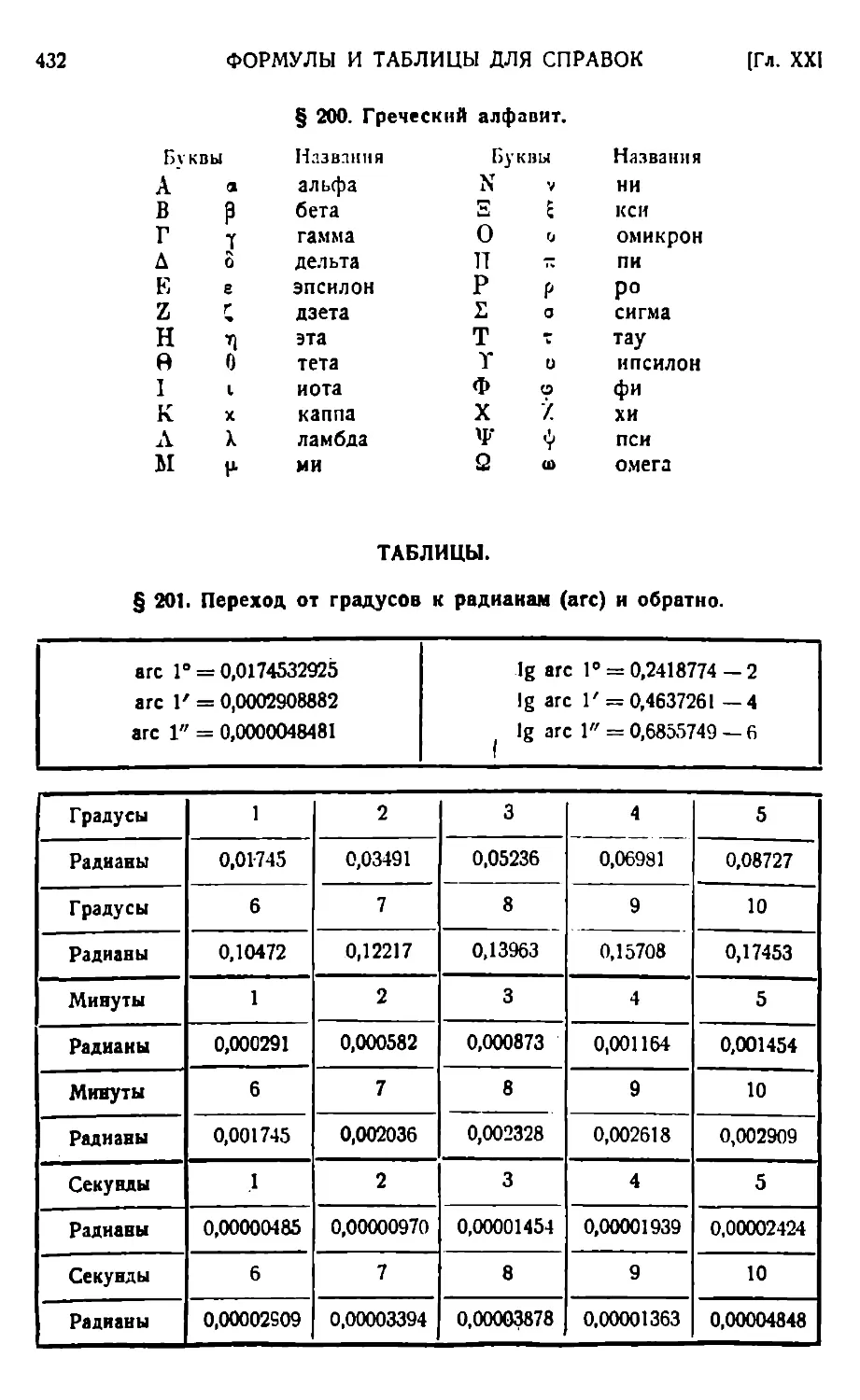
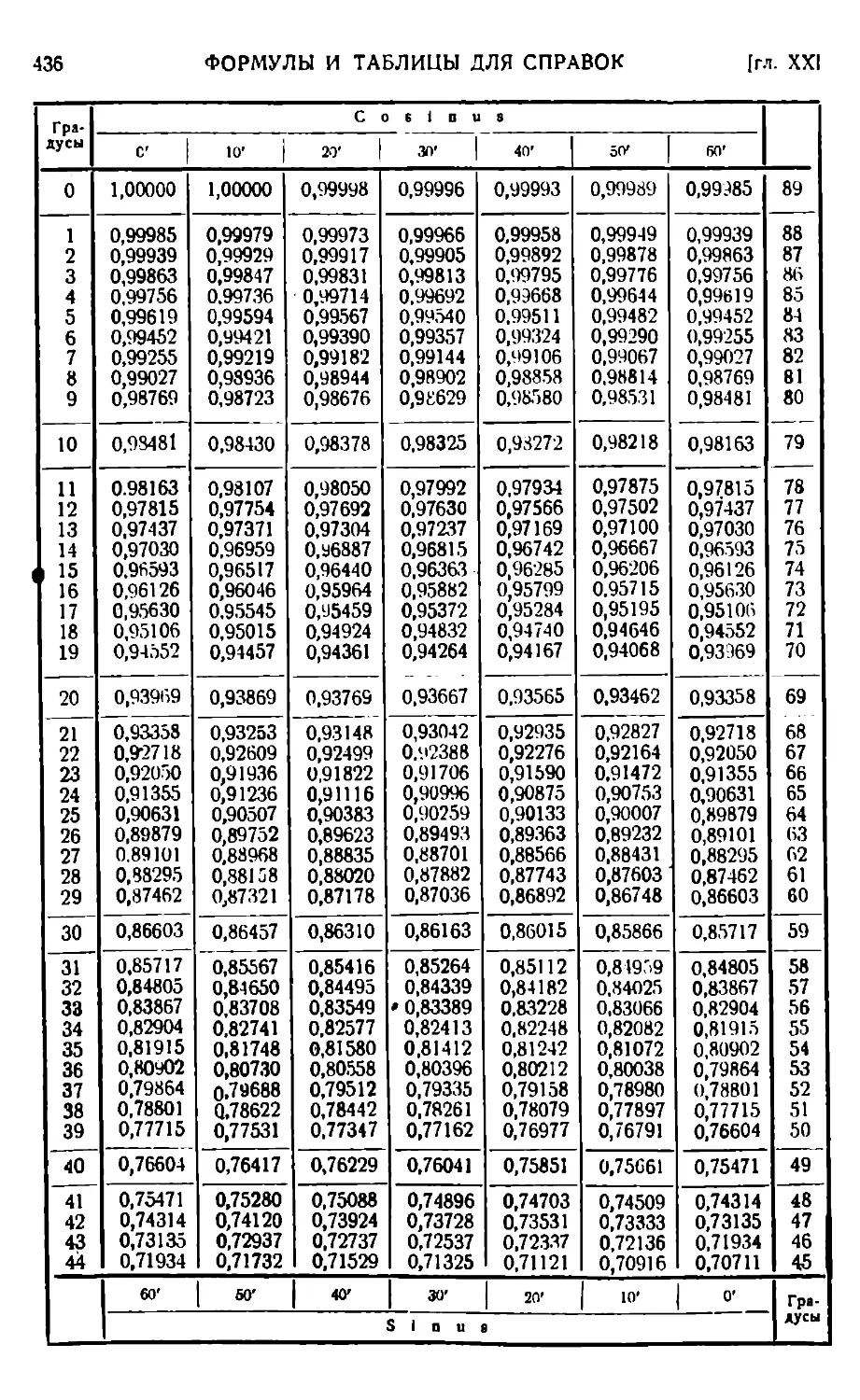
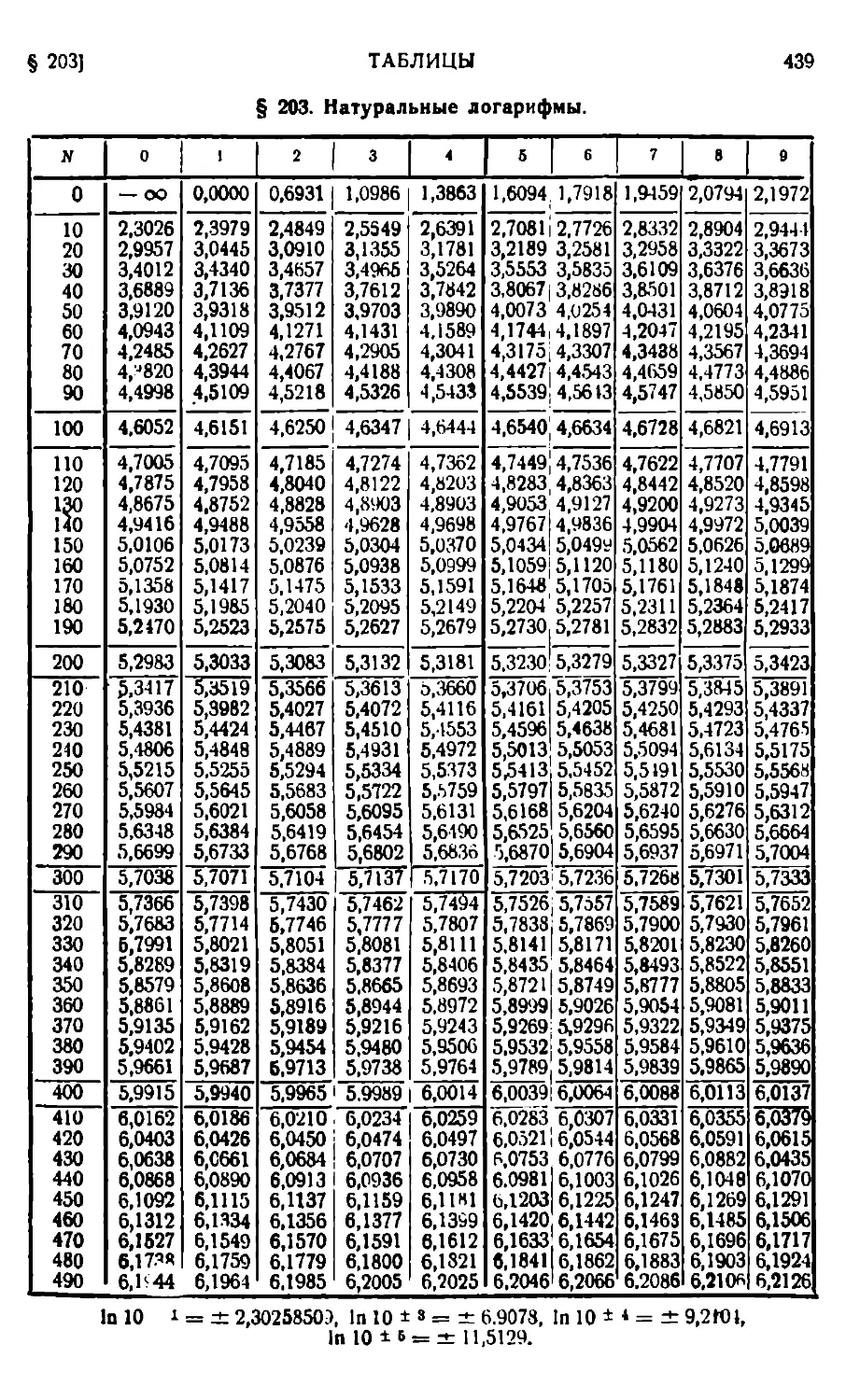
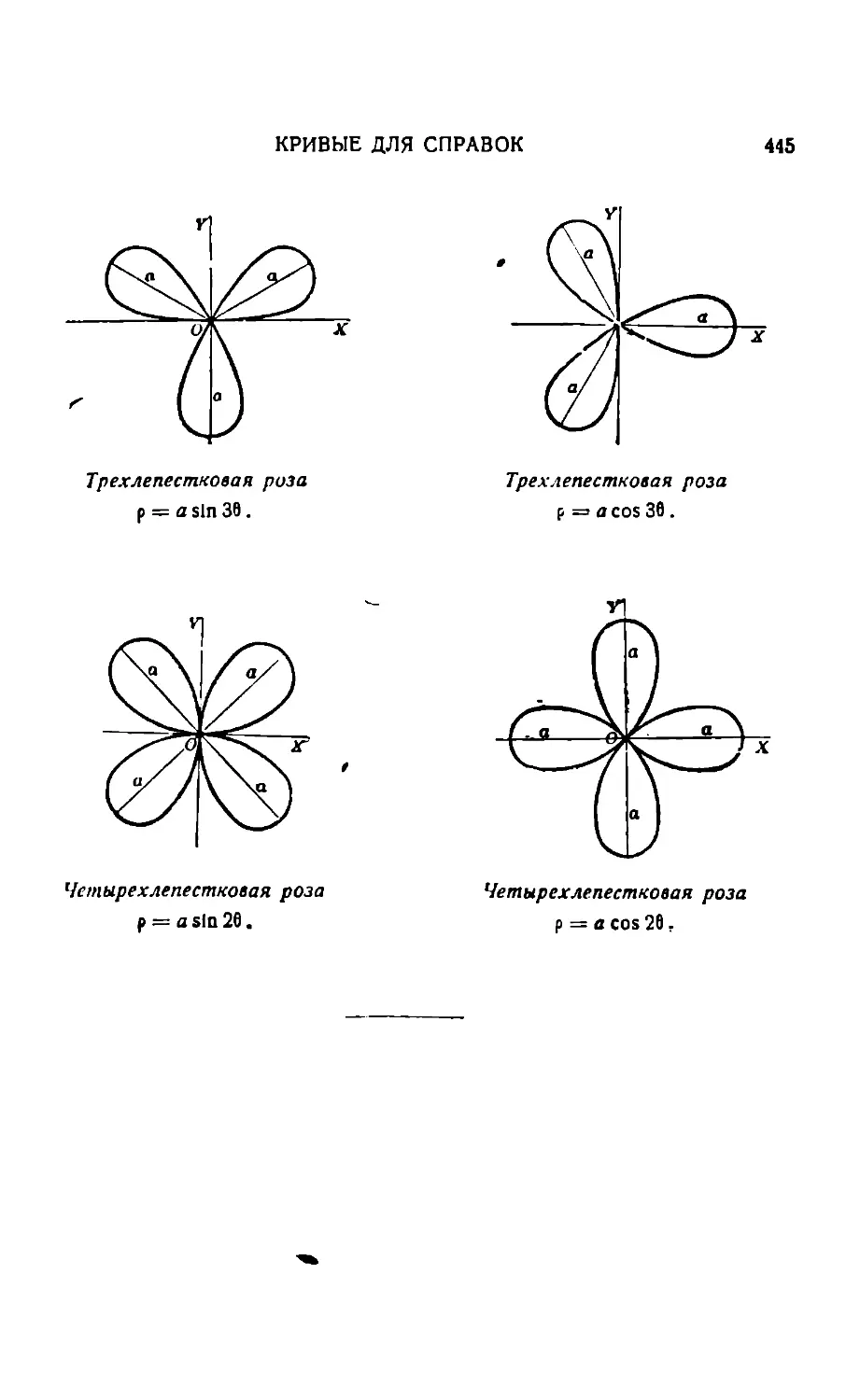
Алгебра 414. — Геометрия 415. — Тригонометрия 416. — Аналитическая геометрия 417. — Детерминанты 423. — Диференциальное исчисление 424. — Геометрия в пространстве 431. — Греческий алфавит 432. — Переход от градусов к радианам (аге), и обратно — 432. Некоторые значения тригонометрических функций 434. — Правило знаков 434. — Таблицы значений тригонометрических функций 435. — Натуральные логарифмы чисел 439. — Кривые для справок 441.
ГЛАВА I.
ЧИСЛА.
§ I. Рациональные числа. Все целые и дробные числа, как положительные, так и отрицательные, — включая сюда число нуль — называются рациональными числами. Читатель еще в арифметике ознакомился с начальными свойствами этих чисел и с их употреблением.
Проделывая над этими числами четыре действия арифметики: сложение, вычитание, умножение и деление, мы получаем опять рациональные числа. Значит, этим путем мы не получим никаких новых чисел.
§ 2. Практическое значение рациональных чисел. С точки зрения практики, рациональных чисел совершенно достаточно для производства всевозможных измерений.
Собственно говоря, задача фактического измерения заданной величины есть неопределенная задача. Пусть, например, надо измерить длину некоторого прямолинейного отрезка, который нам дан физически. Самые концы его всегда ведь несколько неопределенны, потому что всегда можно заменить данный отрезок другим, столь нечувствительно от него отличающимся, что мы не обнаружим этой подмены: для этого достаточно, чтобы разница длин обоих этих отрезков лежала за порогом чувствительности наших инструментов.
Таким-то образом и имеется бесчисленное множество рациональных чисел, чрезвычайно близких друг к другу, каждое из которых вполне можно принять за „истинную* длину нашего физического отрезка. Свободой такого выбора на практике очень часто и пользуются. Так как результат какой-нибудь арифметической выкладки изменится весьма мало, если мы слегка изменим те числа, над которыми производится самая выкладка, то для удобства вычислений обычно сохраняют очень небольшое количество десятичных знаков измеряемой величины. Так, например, часто просто принимают — = 3,14, отбрасывая все остальные десятичные знаки у более точного значения к = 3,141592653...
Значит, рациональных чисел вполне достаточно для нужд измерительной практики, потому что они позволяют выполнять измерения с какой угодно степенью пгочности. Но одних только рациональных чисел уже становится недостаточно, когда мы хотим решать вопросы геометрии, механики и теоретической физики с абсолютной точностью', здесь необходимо уже знание так называемых иррациональных чисел.
§ 3. Сопоставление рациональных чисел с точками прямой линии. Ряд рациональных чисел всюду плотен, так как между любыми двумя такими числами мы всегда можем найти сколько угодно промежуточных рациональных чисел. Поэтому на первый взгляд кажется, что для новых чисел в ряде рациональных чисел как будто уже не остается никакого промежутка.
Тем не менее в таком ряду всюду имеются просветы, как это становится ясным, если рассмотреть соответствие между рядом рациональных чисел и точками прямой линии.
Возьмем прямую линию Х'Х (черт. 1), бесконечную в обе стороны, и на ней положительное направление: слева направо. На этой прямой мы выберем неподвижную точку О, которую будем называть началом координат, и примем определенную единицу длины е для измерения отрезков. Очевидно, можно построить отрезок, длина которого равна заранее заданному рациональному числу а, и отложить его от начала О вправо, либо влево, смотря по тому, будет ли а положите ----1—- 17-------------х тельно или отрицательно. Этим путем
е мы получаем совершенно определенную
1 1 концевую точку М, которую можно
Черт. 1. рассматривать как точку, соответствую-
щую рациональному числу а '); это число а называется абсциссою точки М. Следовательно, можно ска-
зать, что всякому рациональному числу соответствует одна — и только одна — точка на прямой. Ясно, что абсциссы таких точек М суть рациональные числа.
§ 4. Несоизмеримые отрезки. Но имеются и такие длины, которые
несоизмеримы с
данною единицею дл и н ы. Так? из геометрии известен пример диагонали квадрата, сторона которого есть единица длины а). Отложив подобную длину от начала О, — что проще всего можно сделать, заставив диагональ квадрата ОС, вращающуюся около О как твердый стержень, упасть на нашу прямую,— мы получим точку N (черт. 2), которая не соответствует никакому рациональному числу и у которой, строго говоря, нет никакой абсциссы. А так как
существует бесчисленное множество длин, несоизмеримых с единицею масштаба, то прямая линия в бесконечное число раз богаче индиви-
]) На чертеже а взято положительным.
2) Предание приписывает это открытие греческому философу Пифагору, т. е. относит ко времени около 2500 лет тому назад. Геометрическое рассуждение Пифагора о взаимной несоизмеримости стороны и диагонали квадрата встречается почти во всяком учебнике элементарной геометрии.
Вот аналитическое рассуждение.
Если диагональ соизмерима со стороной, длина диагонали ОС выразится некоторым рациональным числом, которое всегда можно написать в виде несократимой дроби — .А так как квадрат гипотенузы ОС равен сумме
дуальными точками, нежели ряд рациональных чисел индивидуальными числами. Это сравнение ведет, следовательно, к признанию некоторой неполноты в системе рациональных чисел, тогда как прямой линии мы приписываем всю полноту и совершенное отсутствие просветов, т. е. непрерывность.
Если представить себе рациональные точки черными и непрозрачными, а все другие точки — прозрачными, то мы, став против света и держа нашу прямую перед глазами, увидали бы пробивающиеся всюду бесконечно тонкие лучи света, прошедшие через точки, соответствующие концам несоизмеримых с выбранною единицей длины отрезков.
§ 5. Иррациональные числа. Если мы желаем изучать прямую линию арифметически, то, так как система рациональных чисел оказывается недостаточной, является необходимость в расширении нашей системы чисел таким образом, чтобы она обладала такою же полнотою или непрерывностью, как и прямая линия. Это достигается введением иррациональных чисел, определяемых только при посредстве рациональных чисел. Рамки этой книги не дозволяют нам развить обычную арифметическую теорию иррациональных чисел; вследствие этого мы только останавливаем внимание читателя
па существовании иррациональных X-—I-1111 ii!iiiiliiiJ»hliiiili^liiiiliniLuiLiiJiiiiiuiJiuJui % чисел и на следующем положении: О М
иррациональные числа совершенно заполняют все Черт. 3.
просветы, существующие
в системе рациональных чисел, т. е. мы принимаем, что всякой точке прямой соответствует число, рациональное или иррациональное, называемое абсциссою этой точки, и обратно.
Арифметически же иррациональные числа представляются в виде бесконечных десятичных дробей.
Чтобы видеть, как это выходит, представим себе, что нам нужно измерить с абсолютною точностью длину несоизмеримого отрезка ОМ, лежащего на прямой X' X (черт. 3). С этою целью мы прикладываем к прямой X'X идеальную измерительную линейку, разделенную на метры, дециметры, сантиметры, миллиметры и так
квадратов д^у.\ катетов, то = I2 + 1:- Отсюда = 2 и, значит, Р2 = 2q-. 7
Правая часть этого равенства есть число четное. Значит, число р обязательно должно быть тоже четным, т. е. р = 2р'. Подставив это значение числа р в предыдущее равенство, мы получаем 4р'2 = 2да, отсюда 2р'2 = д2.
Левая часть этого равенства есть число четное. Значит, число q обязательно должно быть тоже четным, т. е. q = 2g'.
Таким образом дробь — на самом деле пишется в виде ^,т. е. является Я 2q
сократимой дробью на 2. А так как была взята несократимой, то полученное прдтиворечие и обнаруживает невозможность соизмеримости диагонали со стороной.
далее до бесконечности. Слово .метр" здесь взято только в смысле единицы длины: существенно лишь то, что каждое деление нашей линейки разделено на десять следующих, более мелких делений, так что дециметр обозначает просто * */10 единицы длины, сантиметр */ioo» миллиметр ‘/1000 и т- д-
Для измерения длины отрезка ОМ мы заставляем начало отсчета линейки совпасть с началом координат О и затем прочитываем на линейке, сколько всего целых единиц („метров") укладывается в ОМ, начиная от точки О; пусть это будет а0 метров *). Затем мы последовательно прочитываем на нашей линейке, сколько всего к найденной целой части можно добавить десятых долей („дециметров"), потом сотых долей („сантиметров"), потом тысячных долей („миллиметров") и так далее до бесконечности, никогда не переступая при этом конца М измеряемого отрезка. Пусть мы прочли на нашей линейке добавочных аг дециметров 2), сантиметров, Од миллиметров и т. д.; каждая из этих цифр ап не больше 9, потому что каждый раз к получаемой длине нами всегда добавляется полное количество десятичных долей рассматриваемого рода, так что остаток от отрезка ОМ оказывается постоянно уже меньше такой доли, и, следовательно, десятичных долей следующего рода уложится не более девяти. Ясно поэтому, что усиление какой-нибудь цифры ап хотя бы одной единицею заставит нас переступить вправо через конец Af, т. е. мы получим уже больший отрезок, чем ОМ. Значит, последовательно получаемые нами длины
t ^1 I ^1 I ^9 I ^1 f I «я
°о» аоЧ-7о» ао । То^Тоо’ 00 То Too юоо и т‘ л' являются десятичными приближениями по недостатку измеряемой несоизмеримой длины ОМ с точностью до метра, дециметра, сантиметра, миллиметра и т. д.
Так как отрезок ОМ по предположению несоизмеримый, наш измерительный процесс не может закончиться на конечном шаге, потому что конец М никогда не попадет ни на одну из делящих точек линейки. Итак, если мы для памяти выпишем подряд одну за другой прочитанные на линейке цифры, отделив самую первую от остальных запятой, то н a Li нескончаемый процесс измерения развернет перед нами единый цельный бесконечный символ
По> Л|rt2a3 • • •
состоящий из бесконечного множества цифр, поставленных рядом друг с другом, и навиваемый бесконечною десятичною дробью.
Для цели точного измерения этот бесконечный символ, разумеется, служить не может, потому что нельзя же на самом деле сложить, в буквальном смысле этого слова, бесконечно много слагаемых
*) На чертеже л0 взято равным нулю.
*1 На чертеже а, взято равным 6.
Оо _|_ £1- -J. i). Однако указанный бесконечный сим-
вол Oq, a^ag... ап ... очень удобен для приближенного измерения С любою степенью точности. Действительно, мы уже знаем, что, обрывая этот бесконечный символ остановкой на Л-м месте нашего процесса, мы получаем конечную десятичную дробь^j^a1a2a3 ... ап, являющуюся приближением по недостат юДЬ змепяемой длины ОМ с точностью до y-jyr единицы; усилив же последнюю цифру ап на одну единицу, т. е. взяв вместо ап цифру а„4-1, мы получаем приближение по избытку с той же самой точ-
ностью ДО jgH- .
§ 6. Представление рациональных чисел в виде десятичных дробей. До сих пор мы предполагали, что измеряемый отрезок ОМ несоизмерим. Однако ясно, что указанный процесс измерения годится и для того случая, когда ОМ соизмерим с единицею, т. е. когда точка М. имеет абсциссою некоторое рациональное числ0 в этом случае наш бесконечный символ о0, а1а^ай ... ап ...
Я
также послужит к получению десятичных приближений рационального
числа —. Только в этом случае, как нас учит элементарная арифме-Я
тика, бесконечная десятичная дробь а0, аха^а3 ... ап... становится периодической (простой или смешанной), и в арифметике в этом случае пишут условное равенство *):
р
—— а0, a^gOg... ап... ,
р
выражающее только ту мысль, что рациональное число постоянно
*) Никто никогда не мог и не может сложить в буквальном смысле этого слова бесконечно много слагаемых. И если говорят о .сумме* членов бесконечно убывающей геометрической прогрессии вроде -j + -у + ... + + • • • .
то читатель должен все время иметь в виду, что сумма эта не настоящая, а есть лишь предел суммы $,,, составленной из первых п членов, к которому она стремится при беспредельном возрастании числа п взятых членов.
-) Читатель не преминет отметить здесь всю условность этого равенства: настоящее равенство ,«" должно писаться собственно лишь тогда, когда обе его части, левая и правая, суть истинные числа. Здесь же налево стоит истинное число — , а направо лишь бесконечный символ, позволяющий получать для этого числа его десятичные приближения. Истинным это условное равенство становится только тогда, когда цифры ап, начиная с некоторого номера т, сплошь равны нулю:от+1 = от_|_а = ат+3 = ... = 0.‘ В этом случае мы имеем
Р . fli । а3 , ат
уже истинное равенство = а0 + +100 4“ • • • + . в котором сумма,
стоящая направо, составлена из конечного числа слагаемых, которые все можно фактически сложить.
содержится между двумя конечными десятичными дробями, одну из которых получают, останавливая бесконечную дробь на какой-нибудь л-й ступени процесса, а другую получают, увеличивая на единицу последнюю цифру остановленной дроби, причем обе эти дроби сближены * 1 между собой •
Этим обозрением арифметики и пользуется математический анализ, называя иррациональным числом просто всякую непериодическую бесконечную десятичную дробь а0, aia3a3... а . и считая это иррациональное число большим всякого приближения по недостатку и меньшим всякого приближения по избытку.
Таким образом, например, пишут:
1^51,4142136... ,
т: = 3,1415926... , £ = 2,7182818...
Читатель должен понимать, что никакого таинственного смысла в этих равенствах нет, потому'что бесконечный символ, стоящий направо, есть просто инструмент, при п о м о щ и к ото р о г о у к а з ы-вают точку jia прямой или — что то же самое — при помощи которого указывают то отверстие (просвет) в ряде рациональных чисел, которое называется „числом ]/2“ и которое лежит между д е с ятичными приближениями 1,414213 и 1,414214, разность которых равна одной миллионной.
§ 7. Действительные числа. Все рациональные и иррациональные числа называются действительными или вещественными числами. Ясно, что действительные числа располагаются в порядке их возрастания; из двух неравных действительных чисел а и Ь одно всегда больше другого. Всякое положительное число больше нуля; всякое отрицательное число меньше нуля. Сам же нуль нейтрален и является границей положительных и отрицательных чисел.
Символ > читается: больше чем; символ<читается: меньше чем.
Поэтому, чтобы показать, что число а больше числа Ь, пишут: а>Ь. Формула а>0 указывает, что число а положительно. Точно так же формула Ь < 0 указывает, что Ь отрицательно.
Все такие формулы называются неравенствами. Неравенства можно умножать на положительные числа. Так, если а < Ь, то справедливо неравенство ас < Ьс, если с — положительное число. Наоборот, умножая какое-нибудь неравенство на отрицательное число, необходимо переменить самое направление неравенства на обратное. Так, если а < Ь и d отрицательно, то ady> bd.
Символ ^читается: больше или равно, а символ ^читается: меньше или равно. Поэтому, если а не превосходит числа Ь, пишут: а^Ь.
В этой книге, если не сделано оговорки, рассматриваются только действительные числа.
§ 8. Абсолютная величина. Под абсолютной величиной действительного числа а понимают его величину, взятую положительно. Абсолютная величина числа а обозначается символом | а |. Так:
|5|= +5 и |-7|= +7; )01 = 0.
ИЗ этого определения прямо следует, что
абсолютная величина алгебраической суммы не больше суммы абсолютных величин слагаемых, т. е.:
Например:
|7 — 3 + 8 — 131< 74-3 4- 8 -1-13.
Абсолютная величина разности бсчьшеили равна разности абсолютных величин, т. е.;
\a — b\^\a\ — \b\.
Чтобы убедиться в справедливости этого предложения, возьмем тождество — b) = a. В силу предыдущего предложения об абсолютной величине суммы мы имеем | д | -| 4 л — £ | ^>| а |. Отсюда, перенося |А| в другую часть со знаком минус, мы получаем окончательно |а — d | 1 а | — |А|, что и надо было обнаружить.
Упомянем еще о следующем предложении, также вытекающем из самого определения абсолютной величины:
Абсолютная величина произведения и частного в точности равна произведению и частному абсолютных величин, т. е.
|а-b • с • d| = |a| |&| • |с| • |d| и = КГ -
§ 9. Деление на нуль невозможно. При всех* математических расчетах, теоретических или практических выкладках читатель неизменно должен руководиться одним из самых важных правил математического анализа:
Деление на нуль безусловно недопустимо ни в одном случае.
Это можно обнаружить самым отчетливым образом.
есть неопределенность. В самом деле, частное двух чисел есть
такое третье число, что если мы помножим на него делитель, то получим делимое. Но всякое число при умножении на нуль дает нуль.
Значит, выражает собою
любое число и поэтому есть полная не
определенность.
а
- не имеет никакого смысла, если а отлично от нуля. В самом
деле, так как произведение всякого числа на нуль есть нуль, то нет н и-какого числа, которое, будучи помноженным на нуль, дало бы число а, отличное от нуля.
бак. 2760. — П. Гранвиль и Н. Л узив. Часть 1
2
Итак, деление на нуль есть действие и «допустимое.
Кажущийся парадокс. Дли того чтобы научить читателя осторожности в обращении с нулем, мы сейчас докажем равенство 1 = 2 и попросим читателя самого отыскать то место, где рассуждение грешит против вышеуказанного правила.
Возьмем число а, отличное от нуля, и число Ь, равное а. Очевидно, имеем равенство ab = а2. Вычитая из обеих частей этого равенства Ь2, получаем:
ab — Ь2 — а2 — Ь2.
Разлагая на множителей левую и правую части, имеем:
Ь(а — b) = (a-\-b) {а — Ь).
Опуская общий множитель у левой и правой частей, находим: b = a-\-b,
и так как по сделанному предположению число b равно числу а, то из последнего равенства следует, что
а = 2а.
Деля обе части этого равенства на число а (что вполне законно, ибо число а отлично от нуля), мы находим окончательно:
1=2.
ГЛАВА II.
ПЕРЕМЕННОЕ И ФУНКЦИЯ.
§ 10. О величинах вообще. Не следует смешивать число и величину. Число всегда отвлеченно, так как получается в результате измерения. Напротив, величина всегда конкретна, потому что является качеством предмета.
Величины бывают самых разнообразных родов. Всякая наука, изучающая природу, имеет дело со своими собственными величинами, характерными для нее. В физике, например, температура, теплоемкость, удельный вес, сила электрического тока суть величины. В механике величинами являются скорость, масса, тяжесть. Даже в геометрии имеются величины: длина линий, углы, площади, объемы и т. д.
Несмотря на чрезвычайное разнообразие величин, у всех у них имеется одно общее свойство: каждая величина может быть измерена единицею величины этого же самого рода. Так, длина измеряется единицею длины—метром', температура измеряется единицею температуры— градусом-, сила электрического тока измеряется ее единицею — ампером и т. д. Как было уже указано, результатом такого измерения является всегда отвлеченное число, выражающее собою меру рассматриваемой величины в принятой для нее единице масштаба.
Отвлеченное число, получающееся как результат измерения данной конкретной величины единицею масштаба этого же рода,' называется значением рассматриваемой величины.
Таким образом значение величины есть всегда отвлеченное число.
Подобно всем другим наукам, математический анализ также имеет свою собственную величину: „математическую величину*, и притом столь гибкую, что она оказывается способной воплотиться в любую конкретную величину наблюдаемой действительности.
Математическая величина есть просто буква, например х или а, которая может становиться тем или иным отвлеченным числом. Это отвлеченное число называется „значением* математической величины х или а. Про это отвлеченное число, приписываемое букве х или а, говорят, что оно .принимается* математической величиной, т. е. буквой х или а.
Ясно, что благодаря такой точке зрения на величину вообще математический анализ достиг чрезвычайной гибкости, так как любую конкретную величину, наблюдаемую в жизни, всегда можно обозначить буквой х или а, а про числовое значение этой конкретной величины, полученное лутем ее измерения, всегда можно выразиться, что „оно принимается буквою*, т. е. приписать это отвлеченное число нашей букве, как ее „значение**.
§ II. Переменная величина. В текущей жизни почти все конкретные наблюдаемые величины являются переменными, т. е. изменяющимися с течением времени, хотя бы и немного. Если я бросаю вверх камень, его расстояние х до поверхности земли есть, разумеется, величина переменная, потому что это расстояние св чала увеличивается, пока камень уносится вверх, а затем начинает уменьшаться, когда камень, достигнув высшей точки, начнет падать, и под конец станет равным нулю, когда камень, упав, будет покоиться. Значит, в этом случае расстояние х есть величина переменная, т. е. имеющая в различные моменты времени различные значения.
Мы сказали, что в жизни почти все величины, являются переменными. Даже там, где внимательное наблюдение как будто дает величину постоянную, более тонкое измерение точным и чувствительным прибором обнаруживает, что наблюдаемая величина все-таки есть переменная, например рост читателя в течение одних только суток. Привычка заставляет нас считать этот рост в продолжение одного дня одним и тем же. На самом же деле измерение точным прибором обнаруживает, что утром рост всегда немного выше, чем вечером, когда накопившаяся за день усталость, какой бы незначительной она ни казалась, заставляет неизбежно мускулы ослабевать и делает организм ниже.
Как общее правило, всякая величина наблюдаемой действительности есть переменная. Лишь научное мышление видит в текущей жизни постоянные величины, например, когда речь идет о законах сохранения энергии или количества материи. Мы уже видели, что математический анализ всякую конкретную величину обозначает буквою. И так как конкретная величина все время меняется, то математический анализ должен сообразно этому предполагать, что эта буква все время меняет свои численные значения.
Например, если в случае брошенного камня буква х обозначает расстояние его до земли, то числовое значение буквы х зависит от времени и меняется непрерывно, сначала увеличиваясь, а потом убывая до нуля и оставаясь, далее, нулем, если мы не трогаем камня и пренебрегаем мелкими сотрясениями почвы, которые всегда имеются. Таким образом:
Переменной величиной математический анализ называет букву, например х, которая с течением времени изменяет свое числовое значение.
Следовательно, если х есть переменная величина, то буква х обозначает в разные моменты времени различные числа. То число, которое обозначает буква х в данный момент, называется значением переменной величины х в данный момент. Это значение вообще изменяется от момента к моменту. Это обстоятельство часто выражают словами, говоря, что „переменное х последовательно проходит через ряд значений** или что „буква х пробегает ряд значений**.
Переменные величины обозначаются последними буквами латинского алфавита: х, у, z, а также и, v, t, w.
§ 12. Постоянная величина. Величина, которая совсем не изменяется, носит название постоянной величины. В силу непрестанной изменчивости жизненных процессов было бы затруднительно привести пример постоянной величины, наблюдаемой прямо из жизни. Зато
наука дает большое число примеров постоянных величин. Так, в геометрии сумма углов в треугольнике есть величина постоянная, каким бы образом ни менялся треугольник, как бы ни вытягивались или укорачивались его стороны и как бы ни изменялись его углы. Другой пример из геометрии же — это отношение длины окружности к ее диаметру, остающееся всегда тем же самым (равным ~, где ~ = 3,141592653.. какие бы окружности, большие или маленькие, мы ни брали.
Постоянные величины принято обозначать первыми буквами латинского алфавита: а, Ь, с,...
Среди постоянных величин полезно различать абеолютные постоянные и параметры. Первые сохраняют в любых условиях и при всяких заданиях одно и то же определенное числовое значение, например 2, 5, V7, я и т. д. Параметры же суть лишь произзольные постоянные, т. е. относительно них условно соглашаются рассматривать их в пределах одного вопроса как величины не меняющиеся, но которые в пределах другого вопроса могут иметь совсем другие значения, хотя точно так же не меняющиеся.
Например, рассматривая какую-нибудь одну прямую линию в аналитической геометрии, мы пишем:
а b где х, у суть «текущие координаты* движущейся точки, описывающей своим движением нашу прямую, следовательно, истинные переменные величины; коэфициенты же а, b суть параметры, потому что остаются постоянными, коль скоро мы выбрали определенную прямую; во они изменятся и будут другими, если мы перейдем от данной прямой к какой-нибудь другой прямой, также данной.
§ 13. Геометрическое изображение величин. Оно тоже самое, какое употребляется и для изображения отвлеченных чисел. Для этого прежде всего берут прямую линию
Х'Х, снабженную выбранной едини- г,___________д_______м
ней масштаба е и положительным д " * *
направлением (слева направо). ’ •
Если хотят геометрически изобра- Черт. 4.
зить постоянную величину а, то
для этого ищут на прямой Х'Х ту точку А, абсцисса которой (т. е. длина отрезка ОА, измеренная единицею масштаба е) как раз равна значению постоянной величины а. Так как а есть постоянная величина, то ее значение сохраняется все время нейзменным и, значит, точка А будет неподвижной. Таким образом:
Постоянная величина геометрически изображается неподвижною точкою прямой линии (черт. 4).
Если хотят геометрически изобразить переменную величину х, то прежде всего вспоминают, что ведь она меняется с течением времени, проходя различные числовые значения. Поэтому сначала рассматривают переменную величину х, захватывая ее в какой-нибудь определенный, хотя и произвольный, момент времени. В этот самый момент х принимает некоторое совершенно определенное числовое значение; и в этот же самый момент мы поступаем с х точно так же, как поступали раньше при геометрическом изображении постоянного числа а, именно находим на прямой Х'Х ту точку Л4, абсцисса которой как раз равна числовому
значению переменной величины х в этот момент. Такая точка М отыскивается легко и будет единственной (черт. 4).
Но с течением времени х изменяет числовое значение. Следовательно, в другие моменты времени точка М будет находиться в других местах на нашей прямой Х'Х, т. е. будет двигаться. Таким образом:
Переменная величина геометрически изображается движущейся точкой прямой линии.
§ 14. Область значений переменного. Мы знаем, что всякая переменная величина х с течением времени проходит через ряд различных числовых значений, принимая их одно за другим. Часто очень полезно обратить внимание на эти принимаемые переменной величиной х числовые значения и выделить их совокупность отдельно от прочих чисел. Эта совокупность числовых значений, принимаемых переменной величиной х, и называется областью ее значений.
Не следует думать, что раз х есть величина переменная, то уже тем самым она способна принимать всякие значения. Например, если х есть число шахматных партий, выигрываемых каким-нибудь опытным шахматным игроком со дня его рождения, то х увеличивается (изменяется) стечением времени, значит, есть переменная величина. Но х может принимать только целые положительные значения, ибо нельзя, например, выиграть Y2 партий. Значит, областью значений переменной величины х в этом случае явится некоторая сравнительно небольшая группа целых чисел.
После того, что мы говорили о геометрическом изображении переменной величины, ясно, что область значений переменной величины х геометрически изобразится просто в виде некоторого собрания точек прямой Х'Х: это будет совокупность тех самых точек, на которых побывает движущаяся точка .44, потому что абсцисса всякой такой точки и является тем значением, которое примет х в некоторый соответствующий момент времени.
На приведенном примере шахматного игрока область значений переменного х изобразится просто в виде некоторого собрания точек с целыми абсциссами.
§ 15. Отрезок и промежуток. При изучении переменной величины, наблюдаемой в п р и р о д е, ,приходится прежде всего следить за ее изменением, т. е. за движением по прямой линии Х'Х точки Л4, изображающей изучаемую переменную величину х. При этом часто оказывается, что область изменения такой (т. е. взятой из природы} переменной величины имеет только два типа.
Первый тип: отрезок. Переменное х в этом случае принимает только такие значения, которые заключены между числами а и Ь в широком смысле этого слова, т. е. обязательно включая сюда и самые пограничные числа а и Ь, которые также принимаются переменным х (черт. 5). Это обстоятельство, связывающее изменение переменного х, записывают в виде двойного неравенства-равенства:
а < х < Ь.
С геометрической точки зрения область изменения переменного х состоит в этом случае из совокупности точек, лежащих между точками
а и Ь, с непременным присоединением к ним и самих точек а и Ь. Такая область изменения называется отрезком и сокращенно обозначается через [а^х^Ь] или просто [а, Ь].
Граничные точки а и b включены в область и называются концами отрезка. Ясно, что точка а есть самая левая точка отрезка, а точка b — самая правая точка отрезка. Таким образом всякий отрезок [а, 6] всегда замкнут своими концами а и Ь. Отрезок можно изобразить схематически в виде черт. 6.
Второй тип', промежуток. Переменное х в этом случае принимает только те значения, которые заключены между числами а и b в узком смысле этого слова, т. е. отнюдь не принимая зна-
Чсрт. 5. Черт. 6.
чений самих граничных чисел а и Ь. Это обстоятельство, связывающее изменение переменного х, записывают в виде двойного строгого неравенства:
а < х < Ь.
С геометрической точки зрения область изменения переменного х состоит в этом случае из совокупности точек, лежащих строго между точками а и Ь, самые же точки а и Ь теперь уже выключаются из области. Такая область изменения называется промежутком и сокращенно обозначается через (а<х <. Ь) или просто через (а, Ь).
Черт. 7. Черт. 8.
Граничные точки а и Ь уже не входят в область и называются границами для промежутка. Из сказанного ясно, что всякая неподвижная точка М промежутка (а, Ь) всегда отлична от обеих границ а и Ь и, значит, отстоит от них на некоторое конечное (существенно положительное и не нулевое) расстояние. Поэтому точка N промежутка является окруженной с обеих сторон только точками этого же промежутка (чер^ 7). Здесь мы имеем дело с чрезвычайно важным свойством всех промежутков, которое обычно выражают словами:
Всякая точка промежутка есть его внутренняя точка.
Отсюда следует, что, какую бы мы ни взяли точку промежутка, по обе стороны от нее окажутся опять точки этого же промежутка. Поэтому в отличие от отрезка промежуток не может иметь ни самой левой, ни самой правой точки. По этой причине в отличие от отрезка промежуток не имеет концов: -точки а и Ь являются границами для промежутка, но в него не входят.
Итак, промежуток открыт с обеих сторон, будучи без концов, и схематически его можно изобразить в виде черт. 8.
Не следует путать отрезок с промежутком. Хотя отрезок богаче промежутка лишь на две точки, однако разница между ними крайне важна для математического анализа
Читатель, прочитавший только что изложенное, без всякого сомнения, почувствует живейшее недоумение и крайнее неудобство мыслить промежуток как не имеющий концов и постарается самостоятельно каким-нибудь образом устранить кажущуюся .нелепость". Однако пусть читатель знает, что здесь нет никакой нелепости и что все дело только в привычке к такого рода фактам. Для того чтобы облегчить действительно нелегкое дело приспособления, мы советуем читателю проделать следующий .умственный опыт": пусть читатель попробует представить себе, что он разламывает прямую линию X' X в какой-нибудь точке Р и отделяет друг от друга получившиеся две части. Ясно, что самая точка перелома Р войдет лишь в одну часть (черт. 9), будучи ее истинным концом, а другая часть уже
X___________ 7 станет открытой, потому что точка
перелома Р не может появиться в двух
Черт. 9. экземплярах и быть сразу и в одной
и в другой части прямой.
К тому же самому выводу читатель придет, если попробует окрасить в какую-нибудь краску все точки прямой Х'Х, имеющие существенно положительную абсциссу: тогда самой левой окрашенной точки у читателя не будет, потому что всякую положительную абсциссу можно разделить пополам, и, значит, влево от каждой окрашенной точки будет иметься опять окрашенная точка.
§ 16. Монотонное и колеблющееся изменения величины. Всякая переменная величина х меняется с течением времени. Те значения, которые х принимает раньше других, называются предшествующими, а те, которые принимаются ею позже, называются последующими.
Если переменное х изменяется та-ким образом, что всякое последующее у* Q______________“ . —X
его значение больше, чем предшеству- *
ющее, тогда переменная величина х Черт. 10. называется возрастающей.
Геометрически возрастающая переменная величина х изобразится точкою 7И, перемещающеюся постоянно вправо (черт. 10).
Аналогично, если переменное х изменяется так, что всякое последующее его значение будет меньше, чем предшествующее, тогда х называется убывающей переменной величиной.
Геометрически убысающая величина изобразится точкою М, двигающейся все время влево.
Переменные величины возрастающие и переменные величины убывающие называются все вместе монотонными величинами. Переменная величина, изменение которой немонотонно, называется колеблющейся.
Хороший пример немонотонной величины представляет маятник. Если
’) Терминоли! ию мы устанавливаем русскую, переводя иностранные .сегмент*— отрезком, а .интервал*—промежутком.
мы обозначим через х расстояние центра тяжести тяжелого свинцового шарика, подвешенного на нитке, до точки его равновесия, тогда при качании маятника х попеременно то возрастает, то убывает. Следовательно, х уже не будет все время монотонной величиной.
Примером реальной возрастающей величины является прежде всего само время, отсчитываемое от определенной даты. Время обычно обозначают буквой t (первая буква латинскаго слова tempus — время). По самой своей природе время t является возрастающей величиной. Переменные величины Р, t3 и т. д. также являются возрастающими, потому что, когда время t растет, увеличивается и его квадрат /а, и его куб t3, и т. д.
,, 1 1 1
Наоборот, —, —, -=• и т. д. суть каждая в отдельности убываю-t
щие величины, потому что, когда время растет, растут и знаменатели указанных дробей. А известно, что дробь, у которой знаменатель растет, а числитель остается неизменным, убывает по своей абсолютной величине.
Наконец, величина x = sin t есть колеблющаяся. Чтобы усмотреть это, возьмем окружность, радиус которой равен единице и у которой диаметр А В неподвижен, а радиус ОМ подвижный (черт. И). Пусть угол, образуемый этим подвижным радиусом ОМ ____
с горизонтальным неподвижным радиусом ОА, у"< равен времени t, т. е. /АРМ = t. В этих [ Л \\\
условиях наша окружность становится в некотором {___/с\\ ]1 1
роде идеальными математическими часами, fit D P /4 " в которых единственная подвижная стрелка ОМ \ г
равномерно движется по циферблату, вечно обхоДя окружность и указывая время углом АОМ. В начале времени, когда £ = 0, стрелка ОМ проходит Черт. 11. через неподвижный радиус ОА и раз за разом обходит всю окружность в эпохи 2-, 4~, 6-, 8к,... секунд. При этих условиях ясно, что перпендикуляр МР, равный sin t, т. е. равный х, то возрастает до-]-1. то убывает до—1; значит, х есть колеблющаяся переменная величина, неустанно совершающая размахи между -|-1 и — 1.
§ 17. Ограниченная величина. Переменная величина х называется ограниченной, если, начиная с некоторого момента времени, ее абсолютная величина |х| сделается и будет впредь постоянно оставаться меньше некоторого одного и того же положительного числа А.
Иначе говоря, переменная величина х есть ограниченная, если, начиная с некоторого момента времени, сделается верным и будет оставаться таковым неравенство:
И<А
где А есть неизменное положительное число.
Наоборот, если нельзя найти такое положительное число А, чтобы абсолютная величина | х| оказывалась постоянно меньше его, начиная с некоторого момента времени, тогда такая переменная величина х называется неограниченной.
Например, если t есть время, переменная величина х, определенная равенством;
х = sin t.
есть ограниченная величина, потому что синус не может превосходить по абсолютной величине единицу.
Кстати заметим, что эта переменная величина все время остается по абсолютной величине меньше или равной единице.
Но отнюдь нет надобности удовлетворять неравенству | х | < А все время, чтобы быть ограниченной величиной; достаточно, если оно будет верным, лишь начиная с некоторого момента.
Так, например, переменная величина х, определенная равенством:
1
х ~ t ’
где t есть время, отсчитываемое от начального момента 1 = 0, есть опять-таки ограниченная величина, потому что, начиная хотя бы с Г>2, мы имеем | х | < -i-, несмотря на то, что она очень велика, когда t еще мало.
Но само время t, его квадрат, Л, его куб, Г8, н т. д. суть, очевидно, величины уже неограниченные, потому что они с течением времени превзойдут любое постоянное число А. Неограниченной величиной окажется также и t sin t, ибо хотя она и равна нулю при I кратных двум прямым, т. е. когда /=10°, 2-18СР, 3-1а0°, 4-180°,. . но зато, когда t = 90-, 5-90-1, 9-90°,. . ., вообще (4л +1)-90°, где л —целое, то синус равен единице, и, следовательно, вся величина ZsinZ сделается равной просто времени t, а оно безгранично возрастает*
Очень важно узнать, каким геометрическим свойством обладает ограниченная величина х. С этой целью отложим от начала координат О вправо и влево постоянную длину А. Мы получим тогда на нашей прямой Х'Х неподвижный отрезок CD. Ясно,
что все точки внутри этого отрезка CD имеют абсциссу, по абсолютной величине меньшую А, потому что их расстояние до начала О
г, С 0 0
л.—_1
М
Черт. 12. меньше, чем А. Наоборот, все точки, лежа-
щие вне этого отрезка CD, имеют абсциссу, по абсолютной величине большую, чем А, потому что расстояния таких
точек до начала координат О, очевидно, превышают А (черт. 12).
Построив указанный неподвижный отрезок CD, возьмем нашу пере-
менную ограниченную величину х и нанесем изображающую ее подвижную точку Л1, у которой абсциссою служит х. Так как, начиная с некоторого определенного момента времени и дальше в любой момент, мы должны иметь неравенство |х| < А, то из сказанного ясно, что движущаяся Мочка М, начиная с некоторого момента времени, должна попасть внутрь неподвижного отрезка CD и впредь там
и оставаться.
Ясно также и обратное: если некоторая движущаяся точка М, у которой абсцисса обозначена через х, попадает, начиная с некоторого момента времени, на неподвижный отрезок CD и впредь внутри него остается, то абсцисса х такой точки М есть ограниченная величина. Действительно, начиная с этого момента и при всем дальнейшем изменении х мы будем иметь неравенство |х[ < А, что и обозначает, что х есть ограниченная величина.
Итак, всякая ограниченная величина х геометрически изображается движущейся точкой М, которая, начиная с некоторого момента, остается на конечном неподвижном отрезке.
Ясно, что только ограниченные величины изображаются таким движением точки. *
Точка, изображающая неограниченную переменную величину, будет выходить из всякого отрезка, как бы велик он ни был.
§ 18. Приращение переменной величины. Изучение какой-либо переменной величины начинается обычно с того, что наблюдают то приращение, которое она получает, когда переходит от прежнего (т. е. раннего) числового значения к новому (т. е. более позднему).
Если переменная величина х, имея некоторое числовое значение х', примет некоторое другое числовое значение х", то разность
между новым и прежним значениями называется приращением переменного, потому что эту разность как раз и нужно прибавить к прежнему значению х', чтобы получить новое значение х!'.
Действительно, если эту разность обозначим через h, т. е. если напишем: ,. , ,
х — х =h, то отсюда получим:
т. е. новое значение равно прежнему плюс приращение.
Приращение h обозначается еще и другим способом, и должно сказать, что этот другой способ предпочтительнее первого. Именно, по-латыни разность называется differentia', так как буквой d в диферен-циальном исчислении обозначается важное понятие „диференциала*, то для обозначения приращения берется буква А — .дельта“ греческого алфавита, соответствующая латинскому d. *) Сообразно этому принято писать приращение х" — х' в виде значка
Ах', который читается так: ^дельта икс прим*. Этот значок есть единое целое, и нельзя отделить А или рассматривать его как множитель, стоящий при х!. Значит, новое значение х" теперь напишется в виде: х'-|-Ах'.
Подобным же образом, если переменное у перейдет от у к новому значению, получив приращение Ду', то новое значение напишется
Точно так же новое значение для переменного z пишется: z'-j-Az' и т. д. Значки Дх', Ду', Az7 и т. д. очень удобны, потому что сразу видно, для какого переменного берется приращение.
х) См. греческий алфавит в последней главе.
Сделаем оцно важное примечание: число х7, которое мы назвали .старым значением1*, .прежним значением**, называется обычно просто первоначальным значением, и его чаще всего обозначают той же буквой х, что и самую переменную величину х, т. е. без значка „прим" вверху.
Сообразно этому первоначальное значение переменной величины х будет х, а новое значение будет х-|-Дх.
Чтобы геометрически изобразить приращение Дх переменной величины х, изобразим точкой М первоначальное значение х, а новое ее значение х-|-Лх изобразим точкою N (черт. 13). Значит, отрезок C-J
$авен х-|--Дх. Отсюда следует, что от-X* f И N у резок MN, направленный от старой точ-
Черт. 13. ки М к новой точке N, и есть гео-
метрический образ приращения Дх.
Если бы новое положение N было левее старого М, то отрезок AhV был бы направлен влево, и приращение Дх было бы отрицательным, потому чго новое значение х-|-Дх оказалось бы меньше старого х.
§ 19. Постоянная величина как переменная. На первый взгляд понятия переменной величины и постоянной величины столь противоположны, что их нельзя и сравнивать. На самом деле очень часто бывает полезно рассматривать постоянную величину как частный случай переменной величины.
Делается это вот зачем: нередко, изучая какую-нибудь формулу, можно на первый взгляд подумать, что имеют дело с истинной переменной величиной, и только внимательное изучение ее обнаруживает, что это не переменная, а постоянная величина.
Например, лицо, не знающее тригонометрии или забывшее ее, легко может счесть сумму
sin21 -|- cos2 t за переменную величину, так как, когда меняется время », изменяются и оба слагаемых суммы. Но известно, что эта сумма всегда равна единице.
Аналогично, можно думать, что дробь
1-<2 (1-0(1+/ + «2) есть переменная величина, потому что числитель имеет другой вид, чем знаменатель. На самом же деле числитель равен знаменателю, и дробь есть просто 1.
И геометрически также может случиться, что постоянная величина явится частным случаем переменной. Например, если точка М движется как-нибудь на плоскости, ее расстояние х от наблюдателя вообще меняется, т. е. является переменной величиной. Но если точка М бежвт по кругу, в центре которого стоит наблюдатель, то х будет постоянной величиной, равной радиусу этого круга.
Включить постоянную величину в разряд переменных можно вот каким образом: переменной величиной х мы выше назвали букву, проходящую последовательно через ряд значений. Но в частном случае эти значения могут оказаться все равными друг другу. В этом случае переменное х является на самом деле постоянной величиной С.
Приращение йС постоянной величины С равно нулю, потому что всякое новое значение всегда равно старому значению (раз все значения равны между собой), и поэтому их разность есть нуль:
ДС=0.
Обратное предложение, очевидно, верно: величина, у которой приращение всегда равно нулю, есть величина постоянная.
Ясно также, что всякая постоянная величина С есть величина ограниченная, ибо ее абсолютная величина остается неизменной и, следовательно, меньше некоторого постоянного числа.
§ 20. Функция. Наблюдение текущей жизни с очевидностью убеждает нас в том, что одни переменные величины, зависят от других. Наиболее общим образом ту переде тую величину, которая зависит от другой, называют функцией этой д угой.
Почти все величины, наблюдаемые в действительности, зависят одни от других, будучи связаны между собою. Почти все научные проблемы имеют дело с соотношениями величин, а в опытах повседневной жизни мы постоянно сталкиваемся с обстоятельствами, подтверждающими эту зависимость одной величины от другой. Так, тяжесть, которую может поднять человек, зависит от его силы, считая другие обстоятельства одинаковыми. Равным образом расстояние, которое пробегает мальчик, зависит от времени, т. е. есть функция времени. Площадь квадрата есть функция его стороны, объем шара есть функция его радиуса и т. д.
Математический анализ выделяет отдельно понятие функции и изучает свойства функций независимо от того, есть эти функции в природе или же пока их еще там не найдено.
§ 21. Зависимое и независимое переменные. Второе переменное, значения которого находятся всецело в нашем распоряжении, т. е. то, которому можно приписать какие угодно значения в пределах, зависящих от частной задачи, называется независимым переменным, или, еще иначе, аргументом. Первое же переменное, значение которого вполне определится, коль скоро дается значение независимого переменного, называется переменным зависимым, или функцией.
Часто, когда мы рассматриваем два такие связанные одно с другим переменные, от нас самих зависит, какое из них принять за независимое переменное. Но всякий раз, как такой выбор уже сделан и нами после такого выбора написаны некоторые формулы, менять дальше роли независимого и зависимого переменных уже нельзя, по крайней мере без больших предосторожностей и без введения надлежащих дополнительных формул.
Одна какая-нибудь переменная величина (зависимое переменное) может оказаться в действительности функцией одновременно двух или даже большего числа других переменных величин (независимых переменных, или аргументов). Например-, цена предлагаемой материи есть функция ее качества и ее количества-, площадь треугольника есть функция основания и высоты-, объем прямоугольного параллелепипеда есть функция трех его ребер и т. д.
§ 22. Характеристика функции. Мы уже указали на то обстоятельство, что современное естествознание изучает зависимости в природе одних переменных величин от других, т. е. занимается изучением функций. Делается это вот зачем: когда зависимость „изучена*, иначе говоря, когда открыт тот закон, по которому одни переменные величины зависят от других, то этот закон, раз он нам стал известен, позволяет впредь предсказывать наступление явлений. Какое это имеет практическое
значение, — достаточно вспомнить предсказание приливов и отливов с указанием их высоты.
Открытие закона, по которому одна переменная величина зависит от другой, — это одна из целей, которые ставит себе всякая ветвь естествознания. Она считается осуществленной, когда удается выразить зависимость наблюдаемой переменной величины у от другой наблюдаемой переменной величины х помощью математических знаков, т. е. помощью формулы.
Например, механика ищет зависимость длины пути S, пройденного падающим в пустоте телом, от времени t, в течение которого падало это тело. И когда механика пишет эту зависимость в виде формулы:
где ^=981, то вопрос решен до конца, так как закон открыт.
Всякая формула есть не что иное, как указание тех математических действий, которые надо произвести над величинами, входящими в форму у. Таким образом:
Всякая формула, дающая зависимое переменное у, есть не что иное, как совокупность тех действий, которые надо произвести над независимым переменным и над коэфициентами, чтобы получить у.
Так, например, уравнение
v = 3x2 + <g * ~ sin*
УЯ= 2®-|-/^6
ясно указывает, чтд именно нужно проделать ели некотсрыми постоянными числами, чтобы получить у.
Часто случается, что одна и та же функция у от независимого переменного X много раз встречается в каком-либо исследовании. Чтобы не выписывать каждый раз полностью формулу, выражающую зависимость у от л, что явилось бы крайне затруднительным, когда выражение у через л очень громоздко В, согласились обозначать эту формулу сокращенно, одною буквою. Именно, согласились писать:
У =/(*), обозначая значком /(л) рассматриваемую формулу, содержащую независимое переменное л. Это равенство читают так: „игрек есть функция от икса* или еще короче: „игрек есть эф от икси.
В этом обозначении букву f называют характеристикой функции, причем она обозначает просто совокупность тех действий, которые надо проделать над величиной х, чтобы получить величину у.
Если в одном и том же исследовании встречается несколько различных функций аг одного и того же переменного л, будет неудобно и вызовет крайнюю путаницу употребление одной и той же буквы для
В Например, формула движения луны занимает более восьмидесяти страниц.
обозначения различных характеристик этих функций. Так, если встреча-
ются функции:
у - Зх2 4- 1, z = 1g х, 1 = Ух, и — sin
то лучше писан, сокращенно:
1
л28
и т. д.,
у=/(х), z = F(x), / = Ф(х), « = ?(х), v = ty(x), io = a>(x) и т. д.
Но если одна и та же зависимость связывает разные пары букв, можно и должно употребить ту же самую букву для характеристики, потому что вид зависимости остается один и тот же. Так, например,
если
Зхз4-1 ~lgA-4-8
зц2-[-1
— 1g «4-8 ’
У
и V
то следует писать сокращенно:
j=/(x) и v=f(u),
потому что совокупность действий та же самая. Таким образом всякая характеристика в течение одного рассуждения необходимо должна обозначать одну и ту же совокупность действий; для обозначения различных совокупностей действий должны употребляться различные характеристики.
По поводу сокращенного способа письма
У = Дх)
следует заметить, что он удобен и не ради устранения одной только громоздкости: часто бывает так, что, наблюдая в природе изменение переменной величины у, зависящей от х, мы еще не успели открыть математическую структуру этой зависимости, т. е. еще не умеем изобразить у в виде математической формулы, содержащей х, потому что от нас еще скрыта совокупность математических действий, дающих у. В этом случае самая зависимость у от х сказывается только в том, что изменение величины х вызывает изменение величины у, и постоянство х сопровождается постоянством у.
Здесь именно особенно удобен сокращенный способ письма:
y=f(x),
потому что характеристика f как раз обозначает эту еще нам не известную совокупность действий. В этом же случае зависимость величины у от х облекается в форму соответствия: мы говорим, что у есть функция от х, если всякому рассматриваемому значению х соответствует определенное значение у.
Следует сказать, что читатель уже, собственно, знаком с такого рода символическим обозначением. Так, когда он в тригонометрии встречает у = sin х, у = cos х, у = tgx, у = ctg х, у = arcsin х и т. д.
или даже в алгебре
то буквы sin, cos, tg, ctg, arcsin, 1g как раз и обозначают характеристику функций, прямое выражение которых через х не может быть дано элементарной математикой.
Наконец, когда переменное z является функцией многих, например двух, независимых переменных х и у, то пишут:
*=/(*, у),
где/ (х у) обозначает формулу, известную или еще не известную, содержащую, кроме коэфициентов, переменные х и у.
§ 23. Вычисление функций. Если w есть функция от независимых переменных х, у, ..., z и если '/ есть ее характеристика:
w = f(x, у, ..., г),
то самое значение, принимаемое зависимым переменным w, когда независимые переменные х, у, ..., z сделаны соответственно равными а, Ь, ..., с:
х = а, y = b,..., z = c, обозначается так:
/(а, Ь, ..., с).
Так, например, если
. . \ х — y + z
* (х, у, z) = —,
Ф (1, 2, 3) = 2 3 = —,
11 ’ • P-|-2J д’
ф (2 1 3) = 2 ~ = —
’ °' 23 + 1« 5’
♦ (Я, 1)=’=’+1-2.
Если
/(х) = л’-9х-|- 14, то
f(y) =yi— 9у + 14, /(в) = а2 — 9д-|-14, /(*+1) = (д+1)2-9(6+ 1)4-14 = а’-7д+6, /(0) = 0-9-0 4-14 = 14, Z( — 1) = ( — 1)2 — 9-(— 1)4-14 = 2?, /(3) = 32-9-34-14= -4, /(7) = 72 —9-74-14=0.
Пусть
<f(x, у) = sin (х 4-у);
тогда (в, b) = sin (а 4- ь),
^-,°J = sm^2- 4- 0) = slny = l, ?(7’-т) = 51п(т-т) = 51п0 = 0’ ф(т5’’ —'5’) = Sln(fo—5‘) = S,n16= 4" ’ й • °)=sin ё + °)=s,n П=012588
(с точностью до половины четвертого десятичного знака); значение sin взято из таблицы.
§ 24. Область изменения аргумента. По определению функции y=f(x) зависимое переменное у получает вполне определенное числовое значение всякий раз, как аргументу х нами дано определенное числовое значение. Но отсюда отнюдь еще не следует, что мы можем давать аргументу х решительно всякие числовые значения. Как общее правило, из которого почти нет исключения, у каждой формулы f{x) имеются такие исключительные значения аргумента X, при которых формула разрушается, утрачивая всякий математический смысл. Эти исключительные значения аргумента х называются особыми для оассматриваемой формулы.
Так, например, функция
особой величиной аргумента имеет х = 5, потому что при х = 5 делитель делается нулем, и величину у уже вычислять невозможно, ибо делить на нуль нельзя.
При особых величинах аргумента функцию прямо по формуле нельзя вычислять, потому что формула утрачивает при этих значениях аргумента всякий числовой смысл. Но кроме особых значений х приходится часто избегать давать х такие величины, при которых формула дает Мнимые значения для у, хотя и вполне определенные. В задачах практики нередко приходится избегать давать х такие значения, при которых у мнимое, потому что практике часто с мнимыми числами нечего делать.
Например, функция y = Vx
мнима, когда х отрицателен. Приходится, следовательно, ограничиваться положительными значениями х.
Функция
У =logax
при основании а положительном становится мнимой, если х отрицателен: ведь отрицательные числа не имеют действительных логарифмов.
Аналогично, функции:
у = arcsinx,
у = arccosx
бессмысленны для х вне отрезка [—1 х < 1 ], потому что синус и косинус не могут быть больше 1 и меньше—1.
Напротив, функции:
А'2 — 2х 4- 5, sin х, arctg х
можно вычислять при всяких конечных действительных х.
Всякая функция y—f(x) имеет свою собственную совокупность всех допустимых для нее значений аргумента х. Эта совокупность допустимых значений аргумента называется областью существования функции.
Зак. 27G9. — В. Гранвиль н Н. Л у з и н. Часть I 3
Пример. Найти совокупность допустимых значений аргу. мента функции 1 + х + У41 — х, приняв во внимание одни только действительные значения.
Решение. Чтобы первое слагаемое было действительным, надо, чтобы подкоренное выражение 1 -^х было положительным или нулем. Поэтому х> — 1. С другой стороны, чтобы второе слагаемое не дало мнимого числа, надо, чтобы х<Ц. Значит, область существования есть отрезок [— 1].
§ 25. Приращение функции. Мы увидим дальше1), что для дифе-ренциального исчисления в высшей степени важно уметь находить приращения функций, потому что полное знание функции дается нам лишь тогда, когда мы знаем ее изменение, т. е. приращения, приобретаемые ею, когда начинает изменяться аргумент.
Итак, пусть у = /(х) есть изучаемая функция.
Предположим, что аргумент сначала имеет некоторое значение х, а затем получает приращение Дх. Тогда новое значение а) аргумента будет х-|~Дх.
Но раз аргумент изменился и перешел от старого значения х к новому значению x-j-Дх, то изменится и зависимое переменное, перейдя от старого значения у к некоторому новому значению у4-Ду» где ty есть приращение функции, вызванное приращением Дх аргумента.
Но если аргумент имел старое значение, то и значение функции тоже было старым. Значит:
у=/(*).
А если аргумент получил новое значение, то и значение функции тоже сделалось новым. Следовательно,
У + =/(* + МУ
Вычтя из этого равенства предыдущее, мы находим основное, важнейшее по следствиям и по приложениям равенство:
Ду=/(х4-Дх)—/(х).
Таким образом:
Чтобы вычислить приращение Ду функции у =/(х), надо сделать следующие шаги:
Первый шаг. Заменить в формуле /(х), дающей функцию, старый аргумент х на новый, наращенный аргумент х-}-А-К« Получим новое значение /(х-[-Дх) нашей функции.
Второй шаг. Взять старое значение /(х) функции.
Третий шаг. Вычестьиз н о в о го з и а ч е н и я /(х-|- Дх) ее старое значение /(х). Разность /(х-[-Дх)—/(х) и есть искомое приращение Ду функции.
ПРИМЕРЫ.
1. Найти приращение функции у = х1.
Решение. Первый шаг (замена первоначальной величины х на наращенную величину аргумента х-|-Дх) дает:
(х4-Дх)а.
Второй шаг (взятие функции при старом аргументе) даст х-.
*) См., например, вею гл. IV.
-) См. о приращении переменного вообще в этой главе, § 18.
Третий ш а г (составление разности новой и старой величин функции) даст формулу приращения:
Ду = (х + Дх)’--хз которая после вычисления и упрощения принимает вид: Ду = 2х Дх -I- (Дх)’.
2. Найти приращение функции у = У~х.
Решение. Согласно общему правилу имеем:
Это приращение после преобразований представится в виде:
Дх
*у =
3. Найти приращение функции у = 5 — З.г-|-4х3.
Отв. Ду = ( - 3 4- 12jc2) Дх + 12х (Дх)’ + 4 (Дх)’.
§ 26. Геометрическое изображение функций. Мы уже видели, что всякая величина изображается точкою. Легко также геометрически изобразить всякую функцию.
Пусть нам дана некоторая
функция у аргумента х:
У=/(х). значению переменного х отвечает одна
Это значит, что всякому совершенно определенная величина переменного у.
Заметив это, возьмем прямоугольную систему координатных осей XOY на плоскости. Пусть Р есть такая точка, у которой абсцисса равна х. Если мы восставим к оси абсцисс перпендикуляр в этой точке Р, то на этом перпендикуляре всегда можем отыскать такую единственную точку М, ордината которой РМ в точности равна величине/(х) нашей функции (черт. 14). Значит, мы имеем:
ОР = Х, PM = y=f(x).
Вообразим, что наше построение мы проделали для всех значений, которые можно дать переменному х. Тогда во всех точках Р оси абсцисс будет восставлено по перпендикуляру, и на всяком перпендикуляре будет отложено по отрезку РМ, данной функции у, когда аргумент имеет значение абсциссы точки Р.
В результате концы М восставленных перпендикуляров будут образовывать геометрическое место точек, простирающееся таким же точно безграничным образом, как простирается сама ось абсцисс ОХ, потому что всякой точке Р оси абсцисс отвечает своя собственная точка М этого геометрического места. Мы можем поэтому назвать это геометрическое место точек М кривою (черт. 15).
Таким образом:
Всякая функция f(x) может быть изображена геометрически такою кривою, ордината которой у в любой точке х оси абсцисс в точности равна значению J(x) функции, когда ее аргумент равен абсциссе х.
М
</
01
х Р
Черт. 14.
X
равному значению
Обратно, если мы имеем кривую, пересекаемую всякой прямой, перпендикулярной к оси абсцисс, в одной только течке, то такая кривая изображает вполне определенную функцию, именно ту, значения которой равны ординатам кривой при значениях аргумента, равных абсциссам.
Это обстоятельство можно выразить весьма кратко, сказав: у всякой кривой ордината есть функция абсциссы.
В результате функция и кривая оказываются так тесно связанными друг с другом, что не приходится удивляться тому, что математик, естественник и статистик отождествляют в уме эти два понятия и, говоря о функциональной зависимости, своим воображением еидят соответствующую кривую.
§ 27. Геометрическое изображение приращения функции. Раз всякая функция y=f(x) изобразима геометрически в виде кривой, то весьма важно получить геометрическое изображение ее приращения Ду.
Пусть данная функция
У =f(x)
изображена геометрически в виде кривой (черт. 16).
Пусть точка Р на оси X изображает первоначальное значение аргумента, т. е. пусть отрезок ОР равен х.
Тогда ордината РМ кривой в этой точке равна значению рассматриваемой функции при этом значении аргумента. Следовательно, имеем равенства:
х = ОР, у = f(x) = РМ.
Дадим х приращение Дх; тогда новым значением аргумента будет х &х- Если точка Р' изображает геометрически это новое значение аргумента, то направленный отрезок РР' (от точки Р к точке Р') изобразит приращение Дх. Ордината же Р'М' кривой в точке Р', очевидно, равна величине рассматриваемой функции для нового значения аргумента. Следовательно, мы имеем равенства:
Дх =« РР', f(x 4- Дх) = Р'М'.
Но величина функции при новом значении аргумента есть, очевидно, новое значение функции, которое равно старому значению у плюс приращение Ду. Следовательно:
у -(- Ду = Р'М'.
Теперь достаточно провести через точку М параллель к оси X, чтобы иметь прямоугольник РМ(±Р', в котором сторона P'Q равна у.
Следовательно:
геометрически приращение Ьу функции изображается отрезком QA4'.
§ 28. Классификация функций. Предварительное замечание. Здесь рассматриваются функции у только от одного независимого переменного х. Всякая такая функция у пишется в виде:
У =/(*).
где f(x) есть формула, содержащая х и дающая величину рассматриваемой функции у. Эта формула является совокупностью математических действий, проделываемых над аргументом х, и ясно, что, чем больше этих действий и чем они труднее выполняемы, тем более сложной является сама функция j=/(x) и тем ее труднее изучить.
Поэтому, прежде чем приступить к изучению всяких функций f(x), естественно постараться сначала их расклассифицировать по признаку простоты указанных в формуле f(x.) действий.
Однозначные и многозначные функции.
Переменное у называется однозначною функцией другого переменного х, если каждому значению х соответствует одно и только одно значение у. Так, в уравнении
у есть однозначная функция от х.
Если каждому значению второго переменного соответствует не одно, а несколько значений переменного у, то оно называется многозначною функцией от х. Например, уравнение
_у2-= 5х
определяет у как двузначную функцию от х, потому что
у = ±У5х.
Аналогично равенство
у = arctg х
определяет у как многозначную функцию от а>, потому что числу ее значений нет конца при всяком данном значении переменного х. Например, если х = 0, то, очевидно, у = пп, где число п обозначает нуль или любое целое число.
Многочлены.
Так называются такие функции f(x), которые получаются из х только тремя первыми действиями арифметики: сложением, вычитанием и умножением. Эти действия должны Сыть притом проделаны конечное число раз.
Из элементов алгебры известно, что когда все эти указанные действия выполнены, когда все скобки раскрыты и все подобные члены соеди-
пены в один, то многочлен можно написать по убывающим степеням аргумента х, например:
у — 2х3 — 5х2 -|- 2х — 3,
у = ах2 Ьх 4- с
и т. д. Самый старший член пишется первым. Его степень называется степенью всего многочлена. Так, первый многочлен есть кубический, второй — квадратный.
Рациональные функции.
Если к сложению, вычитанию и умножению мы прибавим еще действие деления, то получающиеся при помощи этих четырех действий (проделанных конечное число раз) функции называются рациональными. Эти функции, разумеется, не содержат радикалов, относящихся к аргументу, и если мы выполним все указанные действия, то эти функции пишутся довольно просто: в виде отношения двух многочленов.
Например, если
2х— 3 Зх —2
х—1 ' х-Н . „
У------------—
X — 2
то эта же самая функция у после выполнения указанных действий напишется гораздо проще:
_ 7х*4-5х8 — 23х2 4-11x4-2
У х8 — х
Явные алгебраические функции.
Если к четырем предыдущим действиям — сложению, вычитанию, умножению и делению — мы присоединяем еще одно действие — извлечение радикалов любых степеней: квадратных, кубичных и т. д., то получаемые от выполнения этих пяти действий1) (в конечном, разумеется, числе) функции называются явными алгебраическими.
Так:
^4x4-1 —/л + 7 у х1—6
есть явная алгебраическая функция.
Явные алгебраические функции вообще очень сложны и редко могут быть упрощены.
х) Читатель должен помнить, что в расчет берутся лишь действия, проделываемые над теми частями формулы, куда аргумент х входит на самом деле, но отнюдь не принимаются во внимание действия, проделываемые над козфи-цаентами, ибо последние дают опять только коэфициенты же. Например, функция У 2№ — 6х-|-8 есть просто многочлен третьей степени, так как радикал У2 считается просто за один из коэфициентов, притом этот радикал можно обозначить одною буквою и написать весь многочлен в виде ах3— 6х-|-8. Здесь радикала уже нет, и а есть постоянное число, ве содержащее буквы х.
Важно, однако, заметить, что, проделывая надлежащие преобразования, все радикалы можно устранить. Но это достигается ценою того, что мы получаем такое равенство, где буква у встречается уже в квадрате, кубе и в еще более высоких степенях. Например, явная алгебраическая функция
допускает вот какие преобразования:
у — У1-|-х = У1 —х,
(у— V* 4-х)а= 1 —х,
— 2у /1+х + (1 4- х) = 1 — х,
>24-2х = 2у/Г+х, (>2 + 2х)2 = 4у2(1+х), и окончательно:
у1 — 4у® 4ха = 0, где уже нет радикалов, но где у входит в высоких степенях.
Как общее правило, следует отметить, что
всякая явная алгебраическая функция у=f(x) после надлежащих преобразований, предпринятых для удаления радикалов, приводит к уравнению вида:
Р(х,у) = 0.
где F есть многочлен от двух букв х и у, т. е. к уравнению вида:
А (х)уп 4- B(x)yn-i 4- С (х)уп~2 + ... + G(x)>+H(x) — О, где А (х), В (х), С (х) ,...,Н (х) суть многочлены от одной только буквы х.
Неявные алгебраические функции.
Предыдущий результат наводит вот на какие размышления. Выше мы назвали функцией всякое зависимое переменное j/, зависящее от аргумента х, и обозначили у через /(х):
y=fW, где f (х) есть формула, выражающая у через х, т. е. указывающая совокупность математических действий, которые нужно проделать над х, чтобы иметь у. Если эта совокупность действий еще пока нам неизвестна, то мы все-таки удерживаем прежнее обозначение
>=/(*),
где /(х) обозначает как раз эту самую не известную нам пока совокупность математических действий.
Функция у называется явной, если известны все те действия, которые должны быть проделаны над аргументом х, чтобы получить у.
Если же для определения функции у аргумента х нам дано лишь уравнение, содержащее обе буквы, у и х.
F(x,y) = 0,
решение которого и определяет функцию у, и если мы не умеем решить это уравнение относительно буквы у или если мы не хотим его решать, то тогда у называется неявною функцией аргумента х.
Неявная функция у становится тотчас же явною, если мы решим уравнение F(x,y) = 0 относительно буквы у; в этом случае y=j(x) обозначает найденную при решении совокупность действий над х. Если же мы не умеем решить уравнение F(x,y)~0 относительно буквы у или забыли его решение, тогда в способе писать y=f(x) значок fix) обозначает эту неизвестную нам или забытую нами совокупность действий над х.
Если F(x,y) обозначает многочлен от двух букв хи у, то неявная функция у, удовлетворяющая уравнению f(x,y) = 0, называется алгебраической, неявной функцией от буквы Д'.
Сперва можно подумать, что всякая неявная алгебраическая функция у обращается в явную алгебраическую функцию, стоит только решить уравнение F (х,у) = Ъ помощью радикалов. На самом деле не всякое алгебраическое уравнение разрешимо при помощи радикалов, и, значит, класс алгебраических неявных функций более широк, чем класс явных алгебраических функций, т. е. написанных при помощи радикалов.
Так, например, уравнение
>6 + j' + x = 0
уже неразрешимо относительно буквы у помощью радикалов любых степеней и в любом количестве, если бы даже мы их выписывали миллионы. Значит, это уравнение определяет букву у как существенно неявную алгебраическую функцию от х, которая никогда не сделается явной, пока мы ограничиваемся рассмотрением первых пяти действий: сложения, вычитания, умножения, деления и извлечения радикалов.
Читатель не преминет отметить, что каждый из рассмотренных четырех классов функций — многочлены, рациональные функции, явные алгебраические, неявные алгебраические — объемлет все предыдущие. Так, многочлен есть частный случай рациональной функции (когда ее знаменатель есть единица), рациональная функция есть частный случай явной алгебраической (когда все радикалы извлекаются), и, наконец, явная алгебраическая функция есть частный случай неявной алгебраической (когда уравнение разрешимо в радикалах).
Трансцендентные функции.
/Понятие трансцендентной функции является одним из наиболее слабых и уязвимых мест современного математического анализа, потому что до сих пор еще не имеется прямого и положительного определения трансцендентной функции, с перечислением и классификацией всех трансцендентных действий. Такой каталог трансцендентностей пока невозможен.
Поэтому в настоящее время ограничиваются совершенно отрицательным определением трансцендентной функции, а именно: трансцендентной функцией называется всякая неалгебраическая функция (ни явная, ни неявная).
Вначале математический анализ имеет дело лишь со следующими простейшими трансцендентными функциями (так называемыми элементарными трансцендентностями)'.
1. Степенная трансцендентность: это есть функция вида: х“,
где а есть иррациональное число *) например ху'г.
2. Показательные функции, где аргумент находится в показателе:
3. Тригонометрические функции* 2), т. е. | |
sin х, cos х, tgx, ctgxr sec x, cosec x. \ J
4. Круговые (обратные тригонометри-чески e) функции3): ,,
1 ' Черт. 17.
arcsinx, arccosx, arctgx, arcctgx.
В высших же ветвях математического анализа изучаются еще и другие трансцендентные функции (например ценные для механики эллиптические функции и др.).
р
л / ft
’) Дробная степень не дает ничего нового, так как х обозначает у хр , следовательно, есть явная алгебраическая функция. Иное дело — и р рациона л ь н а я степень.
2) Во всем дальнейшем изложении мы станет задавать углы не в градусах, минутах и секундах, но отвлеченным образом, считая за единицу угла не 1/мо Долю окружности, но так называемый .радиан*: это есть тот самый угол, который стягивает дугу, выпрямленная длина которой в точности равна радиусу. Если принять за единицу меры углов радиан, то величина любого угла АОВ выразится в высшей степени просто и естественно: это есть отношение длины выпрямленной дуги АВ к радиусу /?.
Так, на черт. 17 угол АОВ будет измерен по формуле:
Например, если бы дуга АВ оказалась вдвое длиннее радиуса ОА, то угол ЛОВ был бы просто равен 2:
Z АОВ = Ч.
Легко сообразить, какова мера радиана в градусах: угол в 90° стягивает дугу, длина которой равна . Значит, на единицу выпрямленной дуги придется дробь 90° : -у = 57° 17'44,8". Таким образом радиан в старой мере равен при-1 ближенно 57°17'44,8".
а) Равенство у = arcsln х читается так: игрек равен углу, синус которого! есть х (по-латыни угол или дуга называется агсрв^ГВааЧэц, написанное соотно-j
§ 29. О различном происхождении функций. С формальной точки зрения переменная величина у есть функция переменной величины х:
У =/(*), когда всякой числовой величине х отвечает совершенно опре елейная числовая величина у. под этим следует понимать только то обстоятельство, что когда дается числовая величина для х, то мы умеем вычислить или вообще каким-то образом определить соответствующую числовую величину у.
Эта формальная точка зрения является, собственно говоря, лишь логической схемой, в которую мы укладываем самые разнообразные по своей природе функциональные зависимости, почти не сводимые друг на друга.
I. Наше уменье вычислять у, зная X, может проистекать из знания тех аналитических операций, которые следует произвести над х, чтобы получить у.
Таков, например, случай, когда у есть многочлен от х или рациональная функция.
II. Полная определенность у при знании х может проистечь из фактов геометрической природы.
Например, мы можем вообразить идеальную окружность радиуса 1, на которой измеряются дуги (углы) х. Координаты точки М суть, очевидно, cosx и slnx, если дуга QM обозначена через х (черт. 18). Эти координаты, cosx Hsinx, мы можем определять с безграничной точностью, но сущность аналитических действий, которые надо проделать над х, чтобы иметь cosx и sinx, нам остается неизвестной. Поэтому здесь значки cos х и sin х не стоят большего, чем самый общий функциональный значок /(х).
III. Наконец, зависимость у от х может проистекать из фактов механического (кинематического) характера.
Чтобы видеть это, заметим сначала, что очень удобно представлять себе букву х как время и, значит, рассматривать ось Х'Х как род прямолинейного часового циферблата, где время будет отмечаться точкою, равномерно движущеюся вправо, пробегающею единицу длины в единицу времени и проходящею через начало координат О в момент начала отсчета времени. Тогда всякий промежуток длины (а, а') можно рассматривать как промежуток времени, и, следовательно, можно рассматривать точку с абсциссой х как движущуюся от точки а к точке а' по оси ОХ.
Пусть теперь y—f(x)— какая-нибудь функция, определенная на отрезке [а, а']. Всякой точке х этого отрезка отвечает определенная
шение между буквами у и х есть не что иное, как перефразировка первоначального уравнения х = sin у.
Например, равенство (первоначальное) tg = 1 можно написать в виде:
= arctg 1.
величина у и, значит, отвечает определенная точка у на оси OY, ордината которой есть у. По мере того как течет время х, изменяется и величина у. Это значит, что точка у движется вдоль оси OY. Теперь важно знать, каким образом она движется.
С этой целью заметим, что данная нам функция y=f(x) заставляет отвечать всякой точке х отрезка [а, а'] определенную точку М, лежащую на плоскости с абсциссою х и ординатою у = f(x).
Когда точка х движется от точки а к точке а', точка М вычерчивает на плоскости дугу некоторой кривой, идя от точки А (с координатами а, Ь) к точке А' (с координатами а', Ь'). Эта дуга (черт. 19), являющаяся следом (траекторией) движущейся по плоскости точки М, и позволит нам легко проследить за движением по оси OY точки у соответственно движению точки X. Точка у в момент времени а (т. е. х = а) находится в точке Ь, в момент времени а’ (х = o') она нахо
Черт. 19.
дится в точке Ь'- поэтому в промежуток времени (а, а') она движется по оси OY, начав с положения b и придя под конец в положение Ь'. Второй чертеж ясно показывает, что точка у во время своего движения может выйти из отрезка [Ь, У].
Сказать, что мы знаем движение точки у по оси Y и промежуток времени (а, а'), это значит сказать, что мы знаем во всякий момент времени х (между а и а'), показанный нашими прямолинейными часами ОХ, положение движущейся точки у.
Значит, ордината у движущейся тонки есть функция времени х.
Однако эти функции, как бы даваемые самою природою, т. е. вытекающие из движения и описывания идеальных графиков, обладают одним особенным свойством, присущим далеко не каждой функции: нет графики, нет движения без непрерывности, и читатель, без сомнения, пожелает глубже войти в смысл этого слова. С другой стороны, нельзя представить себе кривую, у которой ордината у при возрастании х также 1 е возрастала бы или не убывала бы или не оставалась постоянной, или г.о крайней мере мы не в состоянии представить себе кривую, которая не могла бы быть рассеченной на такие части; мы не можем вообразить себе: ни движения, которое не совершалось бы в определенном направлении, ни движущейся по оси Y точки, которая не поднималась бы или
не спускалась бы и которая, идя от одного положения к другому, не прошла бы всех промежуточных положений, и т. д.
Все эти свойства движения и графика связаны с непрерывностью.
§ 30. Функция от функции. Среди разнообразных приемов получения функций все более и более сложных одним из самых важных является образование так называемых „функций от функций*.
Вот сущность этого приема.
Предположим, что /(х) есть какая-нибудь данная нам функция, определенная на отрезке [а х Ь\. Пусть ее величина при изменении аргумента х от а ло b остается всегда заключенной между двумя числами А и В.
Пусть теперь «(.у) есть некоторая функция аргумента у, также нам данная, определенная как раз на отрезке или на отрезке
еще более широком, т. е. содержащем отрезок [А В].
Если теперь мы будем рассматривать букву у как во всякий момент равную по величине первой функции /(х), то тогда <?(_у) или <? [/(х)] окажется просто обыкновенной функцией аргумента х. В знак ее происхождения она называется „функцией от функции*1, причем первая функция аргумента х, т. е. /(х), называется внутренней, а вторая функция с аргументом у, т. е. ®(_у), называется внешней.
Ясно, что полученная таким образом новая функция F(x) аргумента х, написанная явно:
/?(х) = ?[/(х)] или неявно:
f /г(х) = ®Су),
(читая, что
J =/(•*)»
определена везде на отрезке [а х Ь], ибо всякой величине х этого отрезка отвечает вполне определенная величина у и, значит, вполне определенное число ®(у).
Разумеется, мы можем продолжать и дальше: если величина функции ® (у) все вр^мя содержится в том отрезке, где определена некоторая третья функция аргумента Z, например o(z), то можно рассматривать 4>(z) опять как функцию первоначального аргумента х, написав ее или явно в виде:
*{?[/(*)]) или неявно в виде:
считая, что
где полагаем, что
м т. д.
Здесь кроется некоторое общее понятие, которым читатель уже пользовался много и много раз. Так, функция sin2x есть не что иное, как функция у\ где у замещено через sin х; функция У1 -|- sin2 х есть просто Уz, где z замещено через 1 -f-_y2, а буква у, в свою очередь, за
мешена через sin х. Функция л1ое°г может быть рассматриваема как av, где у замещен через logn х; притом д1ог°® есть просто х (если х > 0), как это следует из теории логарифмов (см. дальше § 63).
Более того: можно утверждать, что всякая написанная в конечном виде функции аргумента х (т. е. выраженная через конечное число элементарных знаков, вроде у, 1g. sin и т. д) составляется повторным применением „функции от функции'. Читатель скоро убедится в этом, если станет разбивать любые сложно написанные функции аргумента х на повторные применения принципа „функции от функции".
Пример. Разбить функцию
у = V 1 -Ь 1g (3 + cos а 1 ® ) на повторные процессы функции от функции.
Решение. Ясно, что написанная функция составлена так:
у = Уz , z - 1 + 1g «. и = 3 + cos v, v = af, t = Ух.
§ 31. Возрастающие и убывающие функции. Одна из важнейших задач математического анализа состоит в изучении изменения функций. Самым простым изменением функции является такое, при котором функция возрастает или убывает. Дадим точное определение, что нужно понимать под этим.
Непрерывная функция у =f(x), заданная на отрезке [а, £], называется возрастающей на этом отрезке, если чем больше будет взятая величина аргумента х, тем бдльшим станет соответствующее значение функции. И аналогично, /(х) называется убывающей на отрезке [а, А], когда увеличение величины аргумента х влечет за собою, наоборот, уменьшение значения функции.
С аналитической точки зрения это значит, что из неравенства
Xj <х2 следует неравенство:
/(х1)</(х2), если функция возрастает, и неравенство:
/(хх) > /(х2), если функция убывает.
С геометрической точки зрения возрастающая функция изображается кривой, поднимающейся направо вверх, а убывающая функция изображается кривой, наоборот, опускающейся направо вниз (черт. 20 и 21).
У возрастающей функции самая малая величина (минимум) на отрезке [а, достигается* в левом конце, х = а, а самая большая величина (максимум) достигается в правом конце, х = Ь. У убывающей, наоборот, максимум имеется в левом конце, х = а, а минимум — в правом конце, х = Ь.
Если аргумент х растет от а до Ь, соответствующая точка М движется по кривой, а ее проекция т на ось Y движется по этой оси, проходя все промежуточные точки от /(л) до f(b), причем каждая промежуточная точка будет пройдена по одному только разу. Поэтому
в случае возрастающей функции y=f(x) движение тонки т будет постоянно вверх, а в случае убывающей функции у =f(x) движение точки т совершается постоянно вниз (черт. 20, 21).
Было бы весьма естественным предположить, что всякая непрерывная функция на отрезке [a, й], не являющаяся на нем все время возрастающей или убывающей, позволяет разрезать этот отрезок [а, й] на конечное число таких более мелких отрезков [a, o'], [с', с"], [с",с'"].[с(р\й], на каждом из которых рассма-
триваемая функция возрастает или убывает. К этому как будто склоняет и черт. 22, указывающий ясно, как надо сделать разрезы.
Но на самом деле это не так: возможность такого разрезания отрезка [а, й] вовсе не следует логическим образом из определения непрерывности. Читатель должен быть предупрежден заранее, что имеются такие функции y=f(x), которые удовлетворяют определению непрерывности и которые тем не менее не возрастают и не убывают (и не постоянны) ни на каком мелком отрезке, являющемся частью отрезка [л,й].
Такие функции не имеют, конечно, геометрического и механического характера. Нельзя себе представить ни кривой, которая бы нс шла вверх или вниз, ни такого прямолиней--* кого движения точки т по оси Y, при котором ни в какой момент времени нельзя было бы сказать, что точка т поднимается или опускается. Но такие функции не войдут в нашу книгу.
Полезно сделать следующие простые указания.
Если А есть положительное число, то обе функции /(л) и Af(x) изменяются в одном и том же самом смысле: если одна возрастает, то и другая тоже; если первая убывает, вторая — тоже.
Напротив, если А есть отрицательное число, функции /(л) и Af(x) изменяются в противоположных смыслах: если одна из них возрастает, другая убывает. Если функции /(х) и g(x) обе вместе сразу либо возрастают, либо убывают, то то же самое делается с их суммою /(x)-|-g(x). Если к тому же эти функции еще и положительны, то то же самое можно сказать еще и об изменении их произведения
/(х) • g(x), которое возрастает или убывает вместе с функциями/(л) и g(x). Наконец, если функция /(х) положительна и возрастает, функция
убывает; если /(х) положительна и убывает, возрастает.
Если обе функции /(х) и э(^) аргументов х и у суть одновременно возрастающие, первая в отрезке \а.^х^Ь\, вторая в отрезке [ДСу^В], тогда функция от функции считая, что j=/(x), т. е.
?[/(*)].
есть, очевидно, возрастающая на отрезке [д<<х<;б].
Читатель легко догадается, что если /(х) и <р(_у) суть обе убывающие, функции от функции, ®[/(х)], все-таки еще остается возрастающей. Но если функции /(х) и © (у) изменяются в обратных смыслах в отрезках [а, Ь\ и [Д,В], то функция от функции, © [/(х)], есть уже убывающая.
Эго соображение дает возможность сразу во многих случаях предсказывать тот или иной характер изменения данной функции на от-
резке.
§ 32. Обратные функции. Пусть функция /(х) непрерывна на отрезке [д,Ь] и на нем либо все время возрастает, либо все время
у б ы в а ет.
Это предположение возрастания или убывания функции /(х) является очень ценным потому, что при нем уравнение
>=/(*)
дает букву х как очень хорошо определенную функцию буквы у.
Чтобы видеть это, возьмем случай возрастающей непрерывной функции /(х).
Прилагаемый черт. 23 немедленно об
наруживает, что когда независимое пере-
менное х описывает, двигаясь направо по оси ОХ, отрезок [а, й],
в это самое время зависимое переменное у,
У=№,
движется вверх по оси Y и описывает отрезок [Д, 5], концы которого Д =/(д) и B=f(b) соответствуют концам отрезка [д,д].
Таким образом оба отрезка [д<;х-С^] и [Д-Cj-C^l. лежащие на осях ОХ и OY, точка по точке соответствуют друг другу, потому что всякому числу х отрезка [я, Z>] отвечает одно число х отрезка [Д, В], определяемое уравнением y=f(x), и обратно: всякому числу у отрезка [Д, В] отвечает только одно такое число х отрезка [д, fr], что у = /(х).
Геометрически это соответствие является очень простым: если, имея х, мы хотим найти у, надо восставить в точке х перпендикуляр к оси ОХ\ он пересечет кривую в точке М; тогда проекция точки /Й на ось OY и даст нам нужную точку у. Обратно, если, имея у, мы хотим найти х, надо восставить в точке у пеопендикуляо к оси Or;
он пересечет кривую в точке М; тогда проекция точки М на ось ОХ и даст нам нужную точку х.
Так как геометрически обе оси координат, ОХ и OY, играют симметричную роль в наших рассуждениях, то мы можем рассматривать у тоже как независимое переменное, т. е. как аргумент, а букву х— как функцию этого аргумента, т. е. мы имеем новую функцию:
x = F(y). (2)
Ясно, что числа х, у, удовлетворяющие этому уравнению, суть те же самые, которые удовлетворяли и прежнему уравнению (1):
У=Нх\
потому что они — координаты той же самой точки М. Поэтому уравнение (2):
x = F(y)
надо рассматривать просто как прежнее уравнение (1), у=/(х), только разрешенное относительно буквы у.
Ясно, что с геометрической точки зрения и прежнему уравнению (1), y = f(x), и новому уравнению (2), x = F(y), соответствует та же самая кривая линия, телько для уравнения (1), у = /(х), осью независимого переменного является ось ОХ, а для уравнения (2) осью незави-мого переменного является ось OY.
Говоря образно, для наблюдателя, идущего по оси ОХ и имеющего голову направленной вверх в положительном направлении оси OY, уравнением кривой линии будет прежнее уравнение (1):
У=/(х),
а для другого наблюдателя, идущего по оси OY (служащей теперь для него осью его „абсцисс') и имеющего голову в положительном направлении оси ОХ (оси, играющей теперь для него роль его .ординат"), уравнением той же самой кривой станет новое уравнение (2):
x = F(>).
Обе функции, /(х) и F(y), называются взаимно обратными друг по отношению к другу.
Ясно, что новая функция F(y\ как и старая функция /(х), есть также возрастающая на всем отрезке [Д< Z?]. Рассматр; вая же чертеж, читатель уверится в том, что функция F(y) непрерывна на этом отрезке’).
Если бы данная функция /(х) была убывающей на отрезке [а^х<: £], тогда уравнение (1), y=f(x), определило бы букву х как обратную функцию x = F(y) аргумента у.
Черт. 24 показывает, что теперь обратная функция F(y) есть уже убывающая непрерывная функция.
Ч Читатель не преминет отметить, что мы обращаемся просто к наглядности чертежа.
Если же данная функция f(x) не будет возрастающей или убывающей на отрезке [а тогда уравнение (1):
y=f(x), будучи разрешено относительно буквы х, даст обратную функцию:
x = F(y),
непременно многозначную и, чаще всего, притом разрывную.
Чтобы понять причину этого, достаточно взглянуть на прилагаемый черт. 25, где изображена геометрически непрерывная функция f(x),
которая до точки с возрастает, потом до точки d убывает, потом снова начинает возрастать.
Читатель ясно видит, что если мы разрешим уравнение y=f(x) относительно буквы х, то обратная функция
x = F(y)
ведет себя следующим образом: на отрезке [Л, а] она однозначная и возрастающая; на отрезке [a, р] она трехзначная, потому что всякая параллель оси ОХ, проведенная через точку у этого отрезка, пересечет кривую в трех точках; наконец, в точке у = р обратная функция F (у) скачком переходит от значения к значению, много большему, рА (так как для наблюдателя, движущегося по оси OY, ее .ордината", упиравшаяся в точку К, соскальзывает с этой точки при прохождении наблюдателя через точку р и начинает упираться уже в точки, соседние с L) и далее течет уже непрерывно и возрастая.
В частности, именно по этой причине обратная функция для у = х1, т. е.
есть функция многозначная, так как х2 есть убывающая на промежутке (— оо< х < 0), а на промежутке (0<х<-|-оо) она, наоборот, возрастает.
вак. 2769. — В. Гранвиль и Н. Лузин. Часть I 4
УПРАЖНЕНИЯ.
1. Дано /(х) = х3 — 10х24-31х — 30; показать, что
/(0)= -30,
/(2) = 0, /(3)=/(5), /(1)>/(-3), /(-!) = -6-/(6),
2. Дано
/(>) =У3-Ю3'2 + 31>-30, f(a) = as — 10х2 + 31а - 30, f(az) = — 10a2z3 4- 31 az - 30,
f(x - 2) = x» - 16x2 4- 83x - 140, /(x 4- h) = x3 + (ЗЛ - Ц» x”-
4-(3ft2-20ft 4-31 )x 4-4' Л8 - 10ft2 4- 31ft - 30.
9
3x4-v
найти
F (3, 1J; F(2, 0); F(0, 2); F (1, - -1) .
Отв. 1-1; 1-1; -1; 1-1.
3. Дано F (x) = 2®; найти
F(0), F(3), r(l),
Л(_1), F(-3), F(-l).
4. Если
/(x) = x3 - 10x2 4- 31x - 30,
<p (x) = x* — 55x2 - 210x - 216,
показать, что
/(2) = т(-2),
/(3) = <?(-3),
/(5) = <?(-4), /(0) 4- ? (0) + 246 = 0.
5. Если
?(x) = x(x-l)(x4-6)^x-l) (x4-|), показать, что
<р(0) = <?(1) =<₽(-6) = ? (-1) = q> A)-=0.
6. Полагая
/(x) = 2x«-x‘4-7x2 —3,
показать, что /(3) = /(— 3) и вообще /(zn) =/( — m).
7. /(x) = x24-3. Найти
f(x+l); /W4-1; /(x2); [/(X)]2; f(2Jt); 2f(x).
Отв. x24-2x 4-4; x24-4; x‘4-3; x14-6x24-9; 4x24-3; 2x24-6.
8. Уравнение с одним неизвестным изображено в виде /(х) = 0. Как записать, что числа 3 и — 1 являются корнями этого уравнения?
Оотв./(3)=/(-1)=0.
9.
показать, что
1 ч
Ч- (х) = л3 + -L - Зх - -; ' ' xJ х
10. Если /(х) = а1, показать, что
/О)-/«=/Су + 2).
V __ 1
И. Ф(у) = ; показать, что
Ф(Я)~фСя) _ я—Я 1 + Ф(я)ф(я) i+яя’
12- /(?) = cos ?; показать, что
13. Дано
показать, что
ч
14. Дано
показать, что
/(?)=/( — '?) =—/(" — ?) = —/0'4 '?)•
F(0) = tgO;
F(20)
_ 2F(8)
“ 1-[^(6,Р ‘
?w = 'gf+J;
15. /(x) = x!; найти , ] (2)s /(b); /(6).
Отв. 2; 120; 720.
Примечание. Согласно смыслу символа х! = 1 2• 3-4.. .х, аргумент х может принимать только целые значения.
16. Определить область существования функций:
а) |/24-х4-j/5-х, i/r+Zz 1Л£2 /1 + х + |/х-2‘
с) р/m —х + у'х — л.
d) arcslnx-e_x
е)
а — х
Отв. -L- 2 < х 5.
Отв. Функция имеет смысл для любого конечного значения х, не меньшего 2: 2 < х < 4* оо.
Отв. Функция имеет смысл для любого конечного значения х: — оо <х <, 4- оо.
Отв. — 1 < х < +1.
Отв. Функция имеет смысл при всех значениях х, отличных от а.
17. Найти приращение функции
Ч> (х) = х2 + 2.v — 4, соответствующее переходу аргумента от значения х = 2к значению х = 4.
Отв. Д? (х) = 16.
' 4*
18. Дана функция у = х-. Заполнить пустые места в нижеследующей таблице:
19 Найти обратные функции для каждой из следующих функций:
1. 4х — 8. Отв. Х ~j~-8 .
4
а + Ьх сх — а
с * Ь •
3. cos2 х. arccos Ух.
4. Показать, что если /(х) = [/ а — хп > то
/[/(х)) = х.
Найти для этой функции обратную ей функцию.
ГЛАВА 111.
ТЕОРИЯ ПРЕДЕЛОВ *).
§ 33. Предел переменного1 2). Мы рассматриваем переменную величину х, которая изменяется все время. Изменяясь стечением времени, переменное х принимает последовательно бесконечное множество числовых значений, через которые оно .проходит".
Для нас особенно существенным будет то обстоятельство, что переменное х изменяется все время. Это значит, что переменное х никогда не перестает меняться. Поэтому никакое из значений, принятых переменным х, не будет самым последним, так как за каждым значением, принятым переменным х, имеются еще дальнейшие значения, через которые наше переменное х пройдет несколько позже 3 * * * * В).
Читатель должен с самого же начала чрезвычайно внимательно отнестись к этому в высшей степени важному факту. Ведь нельзя представить себе, что имеется какой-то самый последний момент времени, за которым уже совсем пет никакого времени; аналогично, нельзя представить себе на прямой линии какую-то самую последнюю точку, за которой дальше наша прямая уже перестает простираться; нельзя, наконец, вообразить себе какое-то самое большое натуральное число, к которому уже нельзя было бы прибавить одну единицу и тем самым еще более увеличить его.
1) Упражнения к этой главе, соответствующие отдельным параграфам, приложения в конце главы.
’) Теория пределов возникла лишь полтора века спустя после открытия диференциального и интегрального исчислений и обязана своим созданием
французскому ученому Коши (Cauchy, 1789—1857). Теория пределов не является
самостоятельной дисциплиной, но имеет лишь служебное и вспомогательное значение, будучи предназначена к 'Строгому обоснованию диференциального
и интегрального исчислений. Появление теории пределов было в свое время
продиктовано прямой необходимостью, так как накопившиеся недоразумения
и противоречия (кажущиеся или действительные) при дальнейшем развитии диференциального и интегрального исчислений сделали почти невозможным ни ясное понимание сущности этих исчислений, ни просто хорошее их изложение.
В истории математического анализа насчитываются три эпохи (включая современность), когда накопившиеся недоразумения принуждали к пересмотру его основ. Создание теории пределов было делом первой из этих эпох.
в) Выше, в § 19, мы согласились рассматривать постоянную величину как переменную (такую, которая последовательно проходит через ряд значений,равных друг другу). Читатель не должен при рассмотрении предела переменной величины изгонять постоянные величины только на том основании, что .они совсем не изменяются*. Для нас важно, собственно, не то, что переменная величина х изменяется все время, а важно то, что она нами рассматривается все время независимо от того, проходит ли она через ряд существенно различных или между собою равных значений.
Изменение переменного х может протекать весьма разнообразно. Но среди всех возможных изменений переменного х заслуживает особенного внимания такое изменение переменной величины 1", про которое обычная речь выражается такими словами: „переменное х стремится к постоянной величине аи, „переменное х безгранично приближается к а“, „х становится соседним с а", „х с течением времени нечувствительно мало отличается от а“ и т. д.
Все эти фразы достаточно ярко указывают, в чем дело: характер изменения переменного х должен быть таким, что отличие х от а все более и более сглаживается с течением времени. Но фразы эти опасны в том отношении, что всякая из них имеет свой собственный оттенок, что может легко отразиться на самом понимании основного явления. Поэтому все они должны быть заменены математическим описанием, т. е. математическим определением-.
мы говорим, что переменное х стремится к пределу а, если абсолютная величина разности х — а со временем сделается и будет потом все время оставаться меньше любого малого положительного числа в, т. е. если, начиная с некоторого момента, будет все время справедливым неравенство:
]х —а|<е,
Черт. 26. каково бы ни было по своей малости по-
ложительное число е.
Геометрически наличие предела у переменной величины истолковывается очень просто. В самом деле, изобразим в виде точки М переменную величину х, а-в виде точки Л — постоянную величину а. Так как х есть переменное, и а постоянное, то точка М есть движущаяся, а точка А неподвижна.
Выберем теперь произвольно какое-нибудь положительное число е; выбор его произволен, но раз мы его сделали, то в дальнейшем следует рассматривать е уже как совершенно определенное число, не подлежащее никакому дальнейшему изменению. Взяв е, мы откладываем вправо и влево от неподвижной точки А отрезок длины е. Мы получим на прямой Х'Х небольшой неподвижный отрезок длины 2г с центром в неподвижной точке А (черт. 26k
Теперь, по мере того как будет протекать время, точка будет как-нибудь двигаться по прямой Х'Х. Но раз число а есть предел переменной величины х, точка М кончит тем, что непременно попадет на этот неподвижный отрезочек и будет там с этих пор оставаться все время, потому что разность х — а по абсолютной величине сделается и останется меньше е, по определению предела. А эта разность и есть расстояние подвижной точки М до неподвижной точки А, ее предела.
Таким образом: сказать, что движущаяся точка М стремится к неподвижной точке А как к своему пределу, это значит просто сказать, что точка М движется так, что попадет со временем на любой заранее выбранный нами маленький отрезочек, охватывающий А, и будет впредь там оставаться.
Но то, каким именно образом будет двигаться в дальнейшем точка М внутри вышеупомянутого отрезочка, попав на него, это отнюдь не указывается и не предрешается: это движение может быть весьма разнообразным; мы увидим сейчас, что точка М может итти к А или справа, или слева, или даже попеременно то с той, то с другой стороны.
Из указанного геометрического истолкования предела переменной величины следует, что
одна и та же самая переменная величина х может иметь не более одного предела а.
В самом деле, если бы пределов было два разных, то одна и та же движущаяся точка М при дальнейшем своем движении оказалась бы одновременно вблизи двух совершенно разных точек, что невозможно.
Но переменная величина может иногда совсем не иметь никакого предела.
Например, переменная величина х, определенная равенством:
х = sin t,
где буква t обозначает время, совсем не имеет никакого предела, потому что мы знаем (см. стр. 25), что синус будет колебаться все время между 1 и — 1 и, значит, не может приближаться ни к какой постоянной величине1).
Когда переменное х стремится к пределу а, это записывают символически в виде:
limx = a или в виде х-*а.
Выше мы сказали, что всякую постоянную величину а можно рассматривать как переменную (такую, которая проходит через ряд значений, равных а). Из самого определения предела переменной величины следует, что рассматриваемая величина а имеет своим пределом а. Это можно выразить, сказав:
предел постоянной величины есть она сама:
11m а = а.
§ 34. О способах переменной величины приближаться к своему пределу. Для ясного понимания идеи предела переменной величины надо иметь в виду, что переменная величина может стремиться к своему пределу различными способами: переменная величина может или все время быть меньше своего предела, или быть все время больше своего предела, или как бы колебаться около своего предела, т. е. проходить через бесчисленное множество значений, попеременно то бдльших, то меньших этого предела; наконец, переменная величина может во время процесса своего изменения и стремления к пределу неограниченно большое число раз проходить через значение, в точности равное самому пределу. Иллюстрируем все эти обстоятельства на примерах, частью уже хорошо известных.
х) Так как буква t ооозначает время (в физическом смысле), то t непрерывно и безгранично увеличивается, ч потому sin / никогда не перестает колебаться между +1 и - 1.
I. Переменное меньше своего предела.
Если число сторон правильного вписанного в окружность многоугольника неограниченно увеличивается, то пределом площади этого многоугольника служит площадь круга. В этом случае переменное всегда меньше своего предела.
II. Переменное больше своего пределл.
Подобно этому, если рассмотреть описанный около окружности правильный многоугольник, то при безграничном увеличении числа его сторон площадь круга явится попрежнему пределом площади этого многоугольника. Но теперь уже переменное всегда больше своего предела.
III. Переменное, приближаясь к
КОЛЕБЛЕТСЯ ОКОЛО
Бесконечная геометрическая прогрессия
СВОЕМУ ПРЕДЕЛУ, НЕГО.
2'4 8 “
имеет первый член at = 1 и знаменатель прогрессии q = —. л» Отсюда сумма sn ее первых а членов найдется по формуле:
2
1-1
, =!=£=_ " •—ч .
2. _1
3 ’ 2rt'
2 2
3 3
Если число взятых членов, т. е. п, неограниченно увеличивается, то сумма sn становится переменной величиной, пределом которой, очевидно, 2 „ служит —. Итак: О
2_ 3 ’
lim $, п -> со
где нижний символ п -> оо просто только указывает, что число членов п неограниченно возрастает. Вместе с тем, очевидно, что имеем:
2 2
sn<-— для п четного и s„> — для п нечетного, и О
1
-7, а во втором случае оно прибавляется.
2 потому что в первом случае при вычислении sn из — вычитается сущест-
2 венно положительное число — О
Поэтому, суммируя два, три, четыре и т. д. первых членов прогрессии, мы находим, что рассматриваемые суммы попеременно то меньше, „ 2
то больше —.
О
Итак, в этом случае переменное безгранично долго колеблется около своего предела, будучи то меньше, то больше его.
V. Переменное, стремясь к своему пределу, бесконечно МНОГО РАЗ ДЕЛАЕТСЯ ЕМУ РАВНЫМ ВО ВРЕМЯ СВОЕГО ИЗМЕНЕНИЯ.
В указанных выше примерах переменное никогда не достигало своего предела. Но это есть лишь просто случайное обстоятельство, которое отнюдь нельзя возводить в общее правило. В самом деле, из самого определения предела переменного ясно, что самая сущность этого определения состоит просто только в том, что абсолютная величина разности между переменным и его пределом, т. е. |х — а|, должна в некоторый момент сделаться и в дальнейшем остаться меньше любого данного положительного числа в, как бы мало оно ни было. И ни о чем другом здесь больше не говорится.
Рассмотрим пример. Переменная величина х, определенная равенством:
sin t
Х~Г'
где буква t обозначает время, имеет, очевидно, своим пределом нуль, когда время t безгранично возрастает. Действительно, числитель, будучи синусом, никогда не больше единицы; значит, при любом t имеем:
откуда виу им, что х стремится к нулю, когда t безгранично растет, т. е. limx = 0.
Ясно, с другой стороны, что эта переменная величина х во время своего изменения бесконечно много раз принимает в точности значение 0: это происходит всякий раз, когда время t (= угол t) делается равным т., 2т., Зт, 4к, 5it,... ит. д. ( = целому числу полуокружностей).
Итак, в этом случае переменное, стремясь к своему пределу, бесконечно много раз в точности принимает его величину во время своего изменения.
§ 35. Бесконечно малые. Мы теперь вводим самое основное понятие, на котором строится весь математический анализ.
Определение. Переменная величина называется бесконечно малой, если она имеет своим пределом нуль. Следовательно, если х есть бесконечно малое, то мы должны писать:
limx = 0 или х->0.
Чтобы понять самую сущность бесконечно малого, необходимо разумеется, вернуться к определению предела, которое мы дали несколькими страницами выше (см. стр. 54). Там мы установили, что когда какая-либо переменная величина х стремится к пределу а, то разность х — а по абсолютной величине сделается и останется меньше е, т. е. |х — а| < е. Теперь в нашем случае, когда х есть бесконечно малое, его предел а есть нуль: а = 0. Поэтому разность х — а есть просто х, и абсолютная величина |х — а| есть просто | х |>
Из сказанного ясно, что переменная величина х называется бесконечно малой, если она себя ведет так, что ее абсолютная величина | х |, начиная с некоторого момента, сделается и будет все время в дальнейшем оставаться меньше любого положительного числа е, как бы мало оно ни было, т. е. если мы с известного момента постоянно будем иметь удовлетворенным неравенство:
|х| <8.
Для правильного понимания самой сути дела учащийся должен себе хорошо отметить, что бесконечно малое по самому своему определению есть всегда переменная величина и что поэтому никакое постоянное число, как бы мало оно ни было, никогда не есть бесконечно малое. Читатель должен остерегаться пользоваться сравнениями или уподоблениями вроде, например, следующего: „один сантиметр есть величина бесконечно малая по сравнению с диаметром солнца1*.
Эта фраза') совершенно неправильна.
, Эбе величины: и сантиметр и диаметр
X' у солнца суть величины постоянные и, зна-
" чит,| к о н е ч и ы е, только, разумеется,
Черт. 27. одна значительно меньше другой. При-
том и сантиметр вовсе не представится маленькой величиной, если мы, например, сравним его с „толщиной волоса**; а для движущегося микроба сантиметр явится пространством колоссальной величины. Чтобы избавиться впредь от всяких рискованных сравнений и субъективных, случайных уподоблений, читатель твердо должен помнить, что никакая постоянная величина не является бесконечно малой, так же как никакое число, как бы мало оно ни было.
Поэтому, в сущности говоря, было бы гораздо правильнее употреблять не термин „бесконечно малое", но термин „бесконечно умаляющееся**, как более ярко выражающий идею переменности. Согласно традиции мы, однако, сохраним прежний термин 2).
Исключением из всех чисел является нуль, который мы будем считать величиной бесконечно малой, несмотря на то, что нуль есть число постоянное. Вспомнив о том, что было сказано о величине постоянной, рассматриваемой как переменная, условимся и в данном случае считать нуль за величину переменную, принимающую в течение процесса изменения все время одно и то же значение. Так как предел величины, принимающей значения, только равные нулю, есть нуль, то, следовательно, нуль можно считать величиной бесконечно малой. Такого рода точка зрения позволит нам в дальнейшем сокращать формулировку большого числа определений и теорем.
1) Еще сравнительно недавно (в самом конце прошлого века) это сравнение делалось в университетских лекциях по математическому анализу.
2) Термин .бесконечно умаляютe"etя* вполне согласуется с построением русской речи. Он предложен И. И. Жегалкиным.
Геометрически, если мы изобразим бесконечно малую величину в виде точки М на прямой Х'Х, то получим движущуюся точку перемещающуюся по этой прямой таким образом, что, каким бы малым отрезочком длины 2е мы ни охватили начало координат О, точка М в некоторый момент времени попадет на этот отрезочек и в дальнейшем будет двигаться только внутри его (черт, 27).
§ 36. Связь понятия предела и бесконечно малого. Легко усмотреть зависимость, которая имеется между переменной величиной, стремящейся к пределу, и бесконечно малым. В самом деле, если какая-либо переменная величина х стремится к пределу а, то разность х— а будет, очевидно, бесконечно малой величиной, потому что согласно определению предела мы должны иметь, начиная с некоторого момента, неравенство |х — а|<е, каково бы ни было заданное положительное число г. А это неравенство именно и характерно для бесконечно малого.
Отсюда, обозначая разность х — а через а, т. е. написав х — — а = а, мы получим:
х = а о, из чего и выводим, что
всякая переменная величина, стремящаяся к пределу, разбивается на сумму двух с п аг з ем ых: первое слагаемое есть постоянное число, являющееся пределом рассматриваемой переменной в е л и ч и н ы, второе же слагаемое есть бесконечно малое.
Обратное также очевидно: если какая-либо переменная величина х написана в виде суммы двух слагаемых:
х = а -а,
из которых первое, а, есть постоянное число, второе же, а, есть бесконечно малое, то такая переменная величина х стремится к постоянному а как к своему пределу:
Пт х = а или х -> а.
Эта зависимость и устанавливает связь теории пределов и теории бесконечно малых.
§ 37. Основные свойства бесконечно малых. Свойства эти следующие.
Свойство /. Алгебраическая сумма а — Р-р*(+••• 5х ограниченного числа бесконечно малых есть опять бесконечно малое.
Действительно, пусть число бесконечно малых а, р, 7,..., у. не превышает целого постоянного т. Зададимся каким-нибудь положительным
е _ .
числом в и возьмем его т-ю часть: —. Так как а есть бесконечно т
малое, то наступит такой момент времени 7\, начиная с которого мы уже будем иметь |а|<-^. Точно так же, раз р бесконечно мало, наступит такой момент времени Т2, начиная с которого справедливо
неравенство |р[< — • Аналогично, для 7 имеем неравенство: 171 < — • tn т
начиная с эпохи Т3. И так далее. Наконец, для последнего слагав/
мого <а имеем неравенство | «• | < ~ • начиная с эпохи Тт.
Пусть Тк есть наибольшая из всех величин Г,, Тъ..., Ть..., Тп.
Тогда ясно, что за эпохой 7\ мы уже одновременно будем иметь )довлетворенными все неравенства:
Но так как всегда
Iе -Р + тН- • • -гр1 <1«|-г 1РИ-1П+ • • • + 1:4, то, значит, за упомянутой эпохой мы будем иметь:
или окончательно:
l«— P + l+• • •+р1 < е.
что и обнаруживает бесконечную малость алгебраической суммы а — 0-|“ 7 . + |а, что и требовалось доказать.
Читатель должен обратить внимание на то, что свойство I говорит не только об арифметической сумме бесконечно малых, но и о более общей алгебраической сумме, т. е. о такой, члены которой присоединяются друг к другу не только при помощи знака -|-, но еще и при помощи знака—. Значит, как частный случай мы получаем предложение: разность а—£ двух бесконечно малых аир есть опять бесконечно малое.
Примечание. Доказанное свойство I бесконечно малых существенно предполагает, что общее число т складываемых бесконечно малых все время остается ограниченным.
Эта оговорка крайне необходима, потому что свойство I может оказаться прямо ложным, когда общее число складываемых бесконечно малых не остается ограниченным, но, например, безгранично растет по мере того, как каждое слагаемое стремится к нулю. В этом случае сумма e + ₽ + 7j- ... + р- этих бесконечно малых может оказаться уже не бесконечно малой. Этим обстоятельством все время и пользуется интегралоное исчисление.
Например, пусть имеем л переменных величин а, fl, 7,каждая из которых равна —, т. е.
Когда общее число их л неограниченно увеличивается, каждая из этих величин, очевидно, стремится к нулю; следовательно, это будут бесконечно малые величины. И, однако, их сумма
остается все время равной единице.
Свойство II. Произведение х-а ограниченной переменной величины х на бесконечно ма л ое а есть опять бесконечно малое.
Действительно, раз х есть величина ограниченная, имеется такое неизменное положительное число А, что,начиная с некоторой эпохи 7\, мы постоянно будем иметь неравенство |х| < А.
Зададимся теперь положительным числом е. Так как а есть бесконечно малое, то, начиная с некоторой эпохи Т2, мы будем иметь соблю-8
<Т'
Но так как всегда
|х • а| = |х| • |а|, то, значит, за эпохами Тх и Т2 мы будем иметь:
| JC • <х | < А • — = г
или окончательно:
|х а | < е , что и доказывает бесконечную малость произведения х • а.
Читатель уже знает, что всякая постоянная величина есть величина ограниченная (стр. 29). С другой стороны, он легко усмотрит, что всякая переменная величина х, имеющая предел, есть величина ограниченная. Действительно, раз х имеет предел, XL_£_______М—» 4 х
то X можно написа.ь (стр. 59) в виде х а
х = а-\-а, где а есть предел перемен- Черт. 28.
ноги х и а есть бесконечно малое.
Но тогда, начиная с некоторой эпохи Т, мы должны иметь неравенство | х | < | а |-|-1, потому что для бесконечно малого а мы, начиная с некоторого момента, должны иметь |а|< 1. А это и обнаруживает ограниченность величины х.
Таким образом как частный случай мы получаем предложение:
Произведение С • а постоянной величины С на бесконечно малое а и произведение х-а переменной величины х, стремящейся к пределу, на бесконечно малое а суть опять бесконечно малые.
Прежде чем перейти к последнему основному свойству бесконечно малых, мы нуждаемся во вспомогательном предложении:
Лемма. Если переменная величина х имеет предел а, отличный от нуля (т. е. если а ф 0), тогда -!• есть ограниченная величина.
Действительно, отметим на прямой Х'Х неподвижную точку А с абсциссою а и подвижную точку М с абсциссою х (черт. 28). Так как переменная величина х имеет а своим пределом, то подвижная точка М должна безгранично приближаться к неподвижной точке А. Существенно важно, что число а отлична от нуля (т. е. а^=0) и, следовательно, неподвижная точка А отстоит от начала координат О на
расстояние | а |. А так как точка М должна безгранично приближаться к точке А, то отсюда вытекает, что с течением времени точка М отойдет от начала координат О и будет, начиная с некоторого момента вре-
мени, отстоять от него на расстояние большее, чем . Значит, начи-Л
2 X
ная с некоторого момента времени, мы будем
i i Iа I 1Л
ство I х I > Нг • и так как
1
И’
постоянно иметь неравен-
то, начиная с некоторого момента времени, мы будем иметь сохраняю
щимся неравенство:
что и доказывает ограниченность переменной величины —.
Теперь последнее основное свойство бесконечно малых величин таково:
Свойство III. Частное — от деления бесконечно ма
лого а на переменную величину х, стремящуюся к пределу а, отличному от нуля, есть опять бесконечно малое.
а
Действительно, частное — можно написать в виде произведения:
/ 1 \
I — I • ’ > \х / 1 и так как в силу предыдущей леммы — есть ограниченная величина, а а бесконечно мало, то, прилагая свойство II бесконечно малых, мы имеем свойство III доказанным.
Примечание. Оговорка, делаемая свойством III о том, что предел а знаменателя х отличен от нуля, в высшей степени важна по двум причинам:
Во-первых, если бы предел а был равен Нулю, то само доказательство леммы, на которую опирается вывод свойства 1П, становится никуда не годным, потому что в доказательстве этой леммы всюду стоит в знаменателе число |а|, т. с. куль; а по условию на нуль делить нельзя. Таким образом доказательство леммы становится бессмысленным.
Во-вторых, если знаменатель х частного — имеет пределом нуль (т. е. если а = 0) и, значит, если этот знаменатель сам есть тоже бесконечно малое, то тогда свойство 111 может стать ложным. Дело в том, что тогда частное вообще уже не есть бесконечно малое; этим обстоятельством все время и пользуется диференциальное исчисление. _ а
Пусть, например, имеем частное —, в котором числитель и знаменатель суть а д
равные бесконечно малые. Это частное все время равно единице, ибо — = 1 и, значит, уже не есть бесконечно малое.
Свойство 1И здесь перестает иметь силу именно вследствие того, что предел знаменателя а есть число, равное нулю.
§ 38. Основные теоремы о пределах. Доказанные свойства бесконечно малых без труда позволяют установить следующие три основных теоремы из теории пределов.
Теорема /. Предел алгебраической суммы ограниченного числа переменных равен такой же алгебраической сумме пределов отдельных складываемых переменных. В символах:
lim (х—У~~г 4- • • -р/) = limx — lim у 4*lim
Теорема II. Предел произведения ограниченного числа переменных равен произведению пределов отдельных перемножаемых переменных. В символах:
lim (х -у z.. .O = (linix) (limj) • (limz)... (lim i).
Теорема III. Предел частного двух переменных равен частному пределов отдельных переменных, если только предел знаменателя не равен нулю. В символах:
[ х\ lim х lim — ] = ---, если hmу zt 0.
\У ] limj/
Эти все три теоремы постоянно употребляются в каждой задаче, содержащей отыскание предела той или другой переменной величины. Поэтому эти теоремы имеют самое важное значение.
Формулируя их, мы, понятно, предполагаем, что предел каждого переменного существует.
Доказательство теоремы 1.
Докажем ее, например, для случая алгебраической суммы трех слагаемых х—y~\~z- Пусть пределы переменных х, у и z соответственно равны числам а, b и с. Значит (см. стр. 59), мы можем написать равенства:
* = л4®> ^ = *4-?. 2 = с4'Т>
где а, р и 7 — бесконечно малые. Беря теперь алгебраическую сумму этих равенств, мы получаем:
х—J>4- z = (а — Ь 4- с) 4-(а — ₽ 4- 7).
В силу свойства I скобка (а — 04“l) есть бесконечно малое. Поэтому (см. стр. 54) первая скобка (а — b4-с), будучи постоянным числом, является пределом переменной величины х—y-f-z, т. е.
lim (х —у 4~ 2) = а. — b 4~ с — Нт х — limj lim z, что и требовалось доказать.
Доказательство теоремы П.
Докажем ее сначала для случая только двух множителей х-у.
Пусть пределы х и у суть соответственно а и Ь\ следовательно, имеем:
х = а4"а-
>=*4-₽’-
Отсюда, перемножая, находим: = + = + + +
Легко видеть, что выражение, стоящее в скобке, есть бесконечно малое. Действительно, каждое слагаемое, стоящее в скобках, ар, аР» бесконечно мало в силу свойства II бесконечно малых. Но раз скобка бесконечно мала, то число ab есть предел переменной величины х -у, т. е.
1 im (х у) = ab = (lim х) • (lim у).
А теперь легко уже без всяких вычислений доказать нашу теорему для трех, четырех и вообще любого ограниченного числа множителей.
Например, имеем для трех множителей х, у и z следующие равенства:
lim (х у z) = lim ([х у] • z) = lim [х • у] • lim z = lim x • limу • lim z.
Доказательство теоремы III.
Пусть пределы x и у суть соответственно а и Ь, причем мы предполагаем, Зто ЬфО. Можем писать:
х==а-|-я, у = ь+ь
где аир суть бесконечно малые.
х
Сделаем вот какую выкладку: напишем — и вычтем из этого пере-
„ а
менного его предполагаемый предел ; если после этого вычитания у
нас окажется в результате бесконечно малое, то постоянное число
b
« х явится тогда на самом деле пределом переменной величины — :
х а___а а а___аЬ-\-зЬ — ab — а$ — яр
У Ъ ь-Ф ₽ ь ^+р) ь*+ь?
В числителе находится бесконечно малое, потому что уменьшаемое Ьл и вычитаемое ар — бесконечно малые как произведения постоянного на бесконечно малое (свойство II). А знаменатель есть' переменная величина, стремящаяся к пределу Ь2, отличному от нуля, ибо Z>p есть бесконечно малое.
Значит, в силу свойства III вся полученная нами дробь есть бесконечно малое. Поэтому
/ х \ a lim х
lim — == — = ----------
\ у ) о limy
причем lim у ф 0, что и требовалось доказать.
Очевидно, что если одно или несколько из переменных в этих теоремах будут заменены постоянными, то наши рассуждения не теряют силы и вышеприведенные теоремы останутся верными. Действительно, любую постоянную величину законно рассматривать как переменную величину, у которой все ее значения оказываются (случайно) равными между собою. Очевидно, что такая „переменная* величина имеет предел (согласно определению понятия предела), который равен, понятно, этой же самой постоянной величине. Это замечание и делает предыдущие теоремы применимыми и к постоянным величинам.
К доказанным основным теоремам I, II и III теории пределов можно присоединить еще две следующие теоремы: IV и V, почти очевидные, употребление которых весьма частое.
Теорема IV. Если две переменные величины остаются всегда равными между собою и если одна из них стремится к пределу, тогда и другая будет стремиться к тому же самому пределу.
Действительно, если две переменные величины остаются всегда равными между собою, то это значит, что мы имеем дело, собственно, только с одной переменной величиной, лишь по-разному обозначенной. А так как величина предела не зависит от обозначения переменной величины, то теорема IV доказана.
Теорема V. Если переменная величина остается заключенной все время между двумя переменными величинами, стремящимися к одному и тому же пределу, она необходимо стремится к тому же самому пределу.
Действительно, пусть согласно условию lim х = с и lim у = с, и пусть переменное z все время содержится между х и у, т. е. х < z<y. Возьмем прямую линию Х'Х и изобразим на ней в виде точек пере- О___________,„£„я М ? г
менные величины х, у и постоянную 1 с j j у
величину с. Пусть точка /И имеет абсциссу х, точка М имеет абсциссу у, Черт. 2J.
и точка С имеет абсциссу с (черт. 29).
Так как переменные величины х и у имеют своим пределом с, то обе подвижных точки Л1 и W должны безгранично приближаться к неподвижной точке С. Зададимся теперь произвольным положительным числом е и заключим неподвижную точку С в середину отрезочка длины е. Ясно, что обе подвижных точки М и безгранично приближаясь к неподвижной точке С, должны, начиная с некоторого момента времени, обе попасть внутрь этого отрезочка и впредь в нем и оставаться все время. Теперь изобразим в виде точки Р переменную величину z. Так как величина z заключена между величинами х и у, точка Р обязана быть промежуточной между точками М и N. Но если обе эти точки, начиная с некоторого момента, будут находиться на построенном отрезочке, охватывающем неподвижную точку С, то на этом же отрезочке должна будет находиться и наша точка Р, начиная с этого момента времени. А это и обнаруживает (см. стр. 54), что переменная величина z имеет своим пределом с, lim z = c.
Зак. 2760. — В. Гранвиль п Н. Прайн. Часть I 5
§ 39. Понятие о бесконечно большом (бесконечности: -д- оз, — оо и оо). В математическом анализе встречаются три символа:
-J- оо, — оо и просто оо, называемые .положительной бесконечностью", „отрицательной бесконечностью" и просто „бесконечностью";
Эти символы в анализе играют весьма заметную роль, но, к сожалению, само появление их представляется делом весьма деликатным и нередко сопровождается огромною опасностью, потому что влечет за собою у лиц, не приобревших опыта в математических рассуждениях, нескончаемые неясности, иллюзии, недоразумения, парадоксы и очень часто приводят к грубейшим ошибкам при числовых выкладках.
Первоосновой всех этих недоразумений является то бессознательно вкрадывающееся в еще неопытный ум искушение, которое приглашает нас считать эти символы числами. Это искушение, повидимсму, столь сильно, что часто приходится слышать вырывающиеся невольно фразы: „возьмем конечное число", „пусть а есть какое-нибудь конечное число" и т. д. А между тем такая квалификация рационального или иррационального числа прилагательным конечное является, собственно, бессмысленной и излишней: по самой природе своей всякое без исключения число всегда „конечно", потому что всякое без исключения число а, рациональное или иррациональное, всегда содержится между такими двумя целыми числами т и п, из которых одно меньше его, а другое его превосходит:
т < а < л;
всякое же целое число как собрание ограниченного количества единиц— положительных или отрицательных — всегда, понятно, является „конечным* числом.
Всякое число, рациональное или иррациональное, по самой своей природе всегда „конечно", и это обстоятельство должно настолько вытекать из его природы, что, собственно, не должно подниматься и речи о прозваний их „конечными": обычно в жизни никогда не поднимают разговора о вещах, и без того ясных всякому.
Аналогично, всякая постоянная величина есть необходимо „конечная", потому что измеряется рациональным или иррациональным числом.
Бесконечных чисел нет, бесконечных постоянных величин а также нет. И если математический анализ вводит свои символы -|-оо, —оо и оо, то вовсе не как некоторые таинственные числа, предназначенные для выражения таких идей, как: „безграничность в пространстве", „вечность во времени* и т. п. Назначение символов -|- оо, — оо и оо в математическом анализе, так сказать, более, прозаическое.
Роль с и м вол о в —|—оо,—оо и оо состоит только в ука-вании на то или иное поведение переменных величин, „конечных" во всякий момент времени.
Определение Л Переменная величина х называется положительной бесконечно большой, или, короче, положитель
ною бесконечностью., если ее изменение будет иметь следующий характер: х со временем сделается и впредь будет всегда оставаться больше любого, выбранного по произволу положительного числа N (/V > О), каким бы большим N ни было, т. е. если осуществится и останется в силе неравенство:
х > /V.
В этом случае мы иногда станем говорить, что х „неограниченно увеличивается'', и будем это символически обозначать в виде условного равенства: „ ,
Um х= -{-оо.
Это условное равенство, ради участия в нем знака предела 11m, а также еще ради однообразия в произношении с предыдущими обозначениями (когда предел у переменного х действительно имелся), иногда произносят так: „х приближается к пределу, равному плюс бесконечность**.
Хотя это символическое равенство, lim х= -г00» и устное вышеприведенное его прочтение и представляют практические удобства, однако чересчур сильная привычка к нему может создать теоретическую опасность: может X' 0___________У , У
бессознательно усвоиться та мысль, что бесконечность есть какое-то число вроде Черт. 30.
обычных конечных чисел и что оно, стало быть, подчинено действиям арифметики. А этот взгляд на бесконечность как на постоянное число легко может вызвать у учащегося неправильные представления и повлечь впоследствии даже к ошибкам в вычислениях (особенно при обращении с интегралами между бесконечными пределами) 1).
Учащийся должен хорошо помнить, что бесконечность не есть предел в настоящем смысле (как мы выше его определили), ибо бесконечность не есть число: и бесконечно большое, и бесконечно малое суть прежде всего величины переменные, в каждый момент времени имеющие определенное числовое (конечное) значение.
Геометрически бесконечно большая положительная величина х изображается весьма просто: это есть попросту движущаяся точка М, перемещающаяся по прямой Х'Х Таким образом, что со временем уйдет вправо за всякую грань N, какую только мы ни выберем, и будет впредь двигаться лишь аа этой гранью (черт. 30).
Определение //. Переменная величина х называется отрицательной бесконечно большой, или, короче, отрицательною бесконечностью, если ее изменение будет иметь
*) Математическому анализу стоило много времени и труда освободиться от взгляда на бесконечность как на постоянное число. Это очищение анализа вызывается существеннейшими теоретическими соображениями и в настоящий момент может считаться почти законченным. К сожалению, старый взгляд на бесконечность как на постоянное число еще до сих пор имеет следы в уцелевшей прежней терминологии и символизации (вроде цитированного выше), что нередко влечет аа собой недоразумения н всегда создает большие педагогические трудности.
следующий характер: х со временем сделается я будет впредь оставаться менее произвольно выбранного отрицательного числа —N (N > 0), каким бы большим по своей абсолютной величине N оно ни было нами выбрано, т. е. если осуществится и сохранится неравенство:
х< — N.
В этом случае мы иногда станем говорить, что х „неограниченно убывает.* *)> и будем записывать это символически в виде условного равенства:
lim х = — оо.
Это равенство иногда читают так: „х приближается к пределу, равному минус бесконечность*.
Геометрически бесконечно большая отрицательная величина х изобразится в виде движущейся точки М, в некоторый момент уходящей влево за всякую грань —N и впредь XL-h____Ц____________X там остающейся (черт. 31).
-N" Наконец, если переменное х ме-
Черт. 31. няет свой знак от времени до
времени, но его абсолютная величина |х| неограниченно увеличивается, тогда мы просто называем переменную величину х бесконечно большой или скажем, что „х стремится к бесконечности*, и напишем;
lim х = со.
Геометрически бесконечно большая величина х изображается просто в виде точки М, безгранично удаляющейся от начала координат О, но могущей двигаться прыжками так, что точка М оказывается попеременно то по одну сторону от начала координат О, то по другую его сторону.
Все оговорки, сделанные выше, сохраняются и здесь: бесконечностьоо не есть число, а есть ничто иное, как способ называть такое изменение переменной величины х, в силу которого она неограниченно увеличивается по абсолютной величине.
§ 40. Связь бесконечно большого и бесконечно малого.
Связь эта самая тесная.
Пусть х есть бесконечно большое, т. е. lim х = оо. Разделим единицу на х и полученную таким образом дробь обозначим через а:
Легко видеть, что а есть бесконечно малая величина.
!) Читатель не должен здесь быть введен в заблуждение некоторым недостатком русского языка. Мы здесь говорим, что х .неограниченно убывает", но это вовсе не значит, что х „мало* по абсолютной величине, т. е. мало в арифметическом смысле. По абсолютной величине х здесь громадно,, превышая миллионы и миллионы единиц, но оно .мало* в алгебраическом смуСле, потому что является коллоссальным отрицательным числом. Поэтому слово .убывает* надо здесь понимать в алгебраическом смысле.
Действительно, зададимся каким-нибуд произвольным положительным числом в. Так как х есть бесконечно большая переменная величина, то наступит такой момент времени, начиная с которого мы все время будем иметь неравенство |х|> —. Отсюда мы заключаем на основании ра
венства
3| =
1
И ’
что
|а| < 1 :
т. е. ] а | < в. А это неравенство и характеризует бесконечно малую величину, что и требовалось доказать.
Обратно, если а есть какая-нибудь бесконечно малая величина, никогда не обращающаяся в нуль, то величина х, определенная равенством
1
х = —, а
есть бесконечно большая.
Действительно, пусть М есть произвольно взятое большое положи-1 тельное число. Обозначим через е положительное количество тт, т. е.
N
1 положим е = —. Так как а есть бесконечно малое, то, начиная N
с некоторого момента, мы будем все время иметь неравенство |а | < е. Значит, в силу
равенства
1
мы, начиная с этого момента времени, будем постоянно иметь неравенство :
|X|>± = /V,
т. е. | х | > АЛ А это неравенство как раз характеризует бесконечно большую величину, что и требовалось доказать.
Итак, единица, деленная на бесконечно большое, есть бесконечно малое; единица, деленная на бесконечно малое, не обращающееся никогда в нуль, есть бесконечно большое.
Это обычно символически записывают в виде условных равенств:
!- = 0;
1
— = оо О ’
относительно которых читатель должен помнить, что эти равенства не настоящие, так как бесконечность не есть число, а также по
тому, что на нуль делить нельзя. Только так и надо понимать эти „равенства1*, которые некоторые авторы записывают даже в виде:
оо-1 = ( и О-1 = оо,
пользуясь просто тем соглашением, делаемым в элементах алгебры, < 1 -1
в силу которого всякую дробь — можно написать в виде а
ОС
„ X 1
Если а есть положительное бесконечно малое, тогда — есть по-а
ложительная бесконечно большая величина; если а есть отрица-тельное бесконечно малое, тогда - есть отрицательная бесконечно 1 1
большая величина; если а меняет свой знак, — тоже изменяет знак, а
Читатель очень легко освоится с
этим, когда изобразит функцию
в виде кривой (черт. 32).
Когда х весьма мало по абсолютной величине, у весьма велико по абсолютной величине; в этом случае точка М с координатами х, у находится чрезвычайно близко к оси Y и очень далеко от оси Л. Вся кривая состоит из двух бесконечных ветвей, из которых левая ветвь асимптотически приближается к осн Y внизу слева и к оси X снизу, а правая ветвь асимп-
тотически приближается к оси Y вверху справа и к оси X сверху:
говоря, что кривая асимптотически приближается к прямой, мы просто хотим указать на то, что точки этой кривой приближаются сколь угодно близко к этой прямой, лишь бы их координаты,
та или другая, были достаточно велики по абсолютной величине.
Начерченная кривая называется равносторонней (равнобокой) гиперболой.
§ 41. Непрерывность функций. Пусть нам дана некоторая функция y=zf(x) на отрезке (а, />]. Для того чтобы подойти к понятию о
ее непрерывности на этом отрезке, мы сначала просто отметим, что непрерывность функций у = /(х) на отрезке [а, Ь] вызывает в нас представление о том, что численная величина у изменяется „очень слабо** при „очень малом* изменении величины аргумента х. Это выражают еще иначе, сказав, что величины f(x') и /(х") функции „очень близки* друг к другу, когда величина х" и х" аргумента суть „соседние* друг другу, т. е. „мало** отличаются один от другого.
Все эти фразы, смысл которых один и тот же, наводят на мысль сказать: если функция j (х) непрерывна на отрезке [а, 6], то разность
/(х")—fW) должна быть „очень мала" по абсолютной величине всякий раз, как разность х" — х' очень мала по абсолютной величине.
Однако такая формулировка непрерывности функции f (х) на отрезке [а, 6] еще очень далека от ясности и точности. Если мы вдумаемся в это обстоятельство, то увидим, что оно происходит от двух причин:
Во-первых, совершенно неизвестно, какое количество следует считать „очень малым" и Какое „не очень малым", потому что понятие „очень малого* расплывчато и неясно; надо иметь в виду, что одно и то же количество может являться и „очень малым" и „очень большим", если оно рассматривается в различных обстановках ’)•
Во-вторых же, прекрасно может случиться, что хотя разность /(х")—f (х') в самом деле „очень мала", когда разность х"— х' „очень мала", однако первая разность /(х")—f (х7) может вырасти в весьма внушительную величину, если мы сблизим несколько сильнее величины х' и х" аргумента; но такое предположение плохо вязалось бы с нашим представлением непрерывности.
Все эти затруднения сразу пропадут, если мы скажем, что непрерывность функции у = f (х) на отрезке [д, />] состоит в том, что разность f (х")—/(х7) должна бесконечно умаляться всякий раз, когда разность х" — х! бесконечно умаляется.
Эго определение есть уже совершенно точное, но в таком виде оно еще не очень удобно для вычислений, когда требуется проверять непрерывность какой-либо заданной функции.
Чтобы притти к уже совсем удобному определению непрерывности функции f (х), мы сначала отмечаем, что разность х"— х' есть не что иное, как приращение аргумента (см. § 18), и можно поэтому ее обозначить в виде Дх', так как х" — х7 = Ах7; что же касается разности /(хд)—/(х7), то это есть, очевидно, приращение функции (см. § 25, 27), потому что мы имеем х" = х'4_Лх', и, значит, рассматриваемая разность есть просто /(х7~)-Дх7)—/ (х7).
Вот теперь точное математическое определение непрерывности функции на отрезке:
Функция у — f(х), определенная только на отрезке [а, д], включая его концы, называется непрерывной на этом отрезке, если ее приращение Aj/=/(x4-Ax)—f (х) бесконечно умаляется независимо от х, когда Дх беско-нечно умаляется, т. е. (см. черт. 33) мы должны иметь:
lim Ау = 0, когда lim Дх = 0.
Функция f (х), которая не является непрерывной на отрезке (а, Ь}, называется разрывной на этом отрезке. В этом случае доказывается а),
’) Так, например, длина в один сантиметр „очень мала* для движущегося на полном ходу поезда, который пробежит эту длину в долю секунды, и .очень велика* для движущегося микроба, которому нужно несколько лет, чтобы пройти это расстонние.
Доказательство этой глубокой и тонкой теоремы следует искать в более обширном трактате математического анализа. Рамки настоящей книжки не позволяют нам входить в дальнейшее рассмотрение, и мы здесь ограничиваемся тем, что просто предупреждаем читателя об истинности этой теоремы. /
что такая функция /(л) непременно отрезке [а, А] хотя бы одну точку точку х0, что приращение функции
7(*o + *) — f W
уже не стремится к нулю, когда приращение умаляется (см. черт. 34).
должна иметь на разрыва, т. е. такую
ti, аргумента бесконечно
О а ’ г.&г
Черт. 33.
Черт. 34.
Из определения непрерывности и точек разрыва вытекает, что испытание непрерывности всякой заданной функции f (х) на каком-либо отрезке [а, Ь] должно происходить по следующему правилу.
Черт. 35.
Правило испытания на непрерывность
Первый шаг. В функцию / (х) вместо х подставляем х Дх, что дает нам новое значение / (х -|- Дх) функции.
Второй шаг. Вычитаем старое значение f(х) функции из ее нового значения / (х -[- ^х) и таким образом находим приращение функции Ду=/(х-(-Дх)—f(х).
Третий шаг. Ищем предел найденного выражения /(х-|-Дх)—/(х), рассматривая букву х как постоянное и делая Дх бесконечно умаляющимся. Если получим lim Ду = О для всякой точки х отрезка [л, Ь], то функция /(х) непрерывна на этом отрезке.
Учащийся должен вполне освоиться с этим правилом, прилагая его к большому числу примеров.
Три подобных примера приводим со всеми деталями вычислений.
Пример 1. Испытать непрерывность функции х!.
Решение. Положив у = л2, проделываем последовательно шаги, указанные в общем правиле.
Первый шаг.
у -|- Ду = (х + Дх)2 = х2 4- 2л • Дл + (Дх)3.
Второй шаг.
у + Ду = х2 -|- 2л • Дл -|- (Дл)2
Ду = 2л • Дх + (Дл)2
Третий шаг. Рассматриваем букву х как постоянное; ясно, что тогда оба слагаемые бесконечно умаляются, когда Дх бесконечно умаляется. Значит, lim Ду = О для всякого конечного х. Поэтому функция ха непрерывна на всяком отрезке [а, Д], как это можно видеть прямо из черт. 35.
Пример 2. Испытать непрерывность функции sinx.
Решение. Полагаем у = sin х.
Первый шаг;
у -|- Ду = sin (х -|- Дх).
Второй шаг:
у -|- Ду = sin (х + Дх)
у = sin X
Ду = sin (х + Дх)—sin X
Вспомнив из тригонометрии, что •«. „ , я — b a-j-b
sina — sino = 2sin- -- • cos—
мы (полагая a = x Дх и b = x) имеем:
Ду = 2-sin— • cos ^x + -2- J.
Третий шаг. Делаем Дх бесконечно умаляющимся. Тогда, очевидно, и Дх
sin -у будет также бесконечно умаляющимся. Так как оба других множителя:
_ ( , Дх\
2 и cosix-]-—) суть величины ограниченные, а .произведение ограниченной величины на бесконечно малое есть опять бесконечно малое* (§ 37),
то видим, что limДу = 0. Поэтому функцая sinx непрерывна на всяком отрезке [л, £>], как это можно видеть из черт. 36.
Пример 3. Испытать непрерывность функции i-.
Решение. Полагаем у = —. х
Первый шаг.
y + Ay=_J_
Второй шаг. Делаем вычитание:
> + ^=^7
1
__________________>, = 7______________
Ду = 1 _ 1 = х ~ ) = _ Д*
у х-±&х х (х + Дх) х ха -f- х Дх
Третий шаг. Рассматриваем букву х как постоянное. Ясно, что когда мы делаем Дх бесконечно умаляющимся, то знаменатель ха-|-х-Дх есть переменная величина, имеющая х® своим пределом. А мы знаем, что .частное от деления бесконечно малого на переменную величину, стремящуюся к пределу, отличному от нуля, есть опять бесконечно малое* (§37). Поэтому мы
имеем lim Ду = 0 для всякого х, отличного от нуля. Поэтому функция — непрерывна на всяком отрезке [а, а'], не содержащем начала 0. Черт. 37 показывает, что начало 0 есть точка разрыва функции —, так как по мере приближения к нему величины функции уходит либо в — оо (если двигаться к началу 0 слева), либо в = оо (если двигаться к нему справа).
Примечание. Очень важно заметить следующее: выражение Ду — f(x -f- Дх) — — fix) после того, как оно вычислено, оказывается содержащим и букву х, и количество Дх. Поэтому выражение Ду есть, собственно, функция двух независимых переменных: хиДх. Значит, если мы на какой-нибудь плоскости возьмем прямоугольные оси координат и по горизонтальной оси будем откладывать величины х, а по вертикальной — количества Дх, то всякой точке М (х, Дх), имеющей абсциссою ОР = х и ординатою МР = Дх, будет отвечать определенная численная величина выражения Ду. Отсюда сле-
дует, что доказывать, что выражение Ду бесконечно умаляется независимо отх, — это значит доказывать, что выражение стремится к нулю всякий раз, как точка Af(x, Дх) приближается к отрезку [л, б|. лежащему на оси абсцисс, следуя любой дорожке. Поэтому-то доказывать это всегда чрезвычайно трудно: пусть, например, читатель попробует доказать, что Ду первого примера, Ду = 2х • Дх + (Дх/2 бесконечно умаляется независимо от х или, что еще труднее, что Ду третьего примера, Ду = — ~• ^х бесконечно умаляется тоже незави-
симо от х.
' В первом примере это возможно сделать, лишь предполагая, что само хне возрастает бесконечно, а в третьем примере это возможно сделать лишь предполагая, что х не стремится к нулю, и притом нужные для этого рассуждения очень трудны. Лишь во вто-. п , Ах ( . Дх\ ром примере, где Ду = = 2 sin -?- • cos ( х 1, бесконечное умаление выражения Ду независимо от х, достигается нами сравнительно легко, так как здесь 2 и cos ( х-|- — \ суть величины, ограниченные независимо отх.
Это показывает, насколько трудно доказывать бесконечное умаление выражения Ду независимо отх. Напротив, доказывать бесконечное умаление того же самого выражения Ду, рассматривая букву х как постоянное, очень легко, как показывают нам те же самые примеры. При этом перед нами сразу же обнажаются и точки разрыва рассматриваемой функции /<х)у
Ведь действительно, раз мы доказали, при всяком постоянном х, принадлежащем отрезку [а. б], выражение Ду бесконечно умаляется, то отсюда сразу становится ясным, что функция f(x) непрерывна на отрезке [о, о]. В самом деле, если /(х) не есть непрерывная на этом отрезке, то, как замечено выше, на нем непременно должна лежать хотя бы одна точка разрыва ха. А тогда мы и не
Дх
I
Черт. 38.
имели бы нашего равенства 11m Ьу^О уже для постоянного х, равного х0, т. е. х = х0, чего .третий шаг* не допускает.
Поэтому-то для обнаружения непрерывности какой-либо функции /(х) на отрезке [а, 6] совершенно достаточно доказывать равенство lim Ду = 0 при постоянном х. Геометрически это значит, что мы заставляем точку М (х, Дх) (черт. 38) приближаться к оси абсцисс, следуя лишь по прямым линиям, перпендикулярным к этой оси (так как * постоянно), а не по любым дорожкам. Последнее всегда трудно и не выгодно.
§ 42. Свойства непрерывных функций. Мы ограничимся здесь простым описанием важнейших свойств, которыми обладают непрерывные функции. Свойства эти выводятся логически из самого определении непрерывности функции. Однако мы, оставаясь в рамках этой книги, откажемся »т этого выгода и просто будем рассматривать эти свойства как очевидные, по крайней мере для таких непрерывных функций, которые
. имеют геометрическое или механическое (кинематическое) происхождение.
Свойство I. Среди численных значений, принимаемых на отрезке непрерывной на нем функцией, всегда имеется как самое большое (максимум), так и самое малое (минимум) значение.
Геометрически (черт. 39) это
означает, что непрерывная кривая
y=f(x) на отрезке [а, а'] всегда имеет и самую большую ординату У(х') и самую маленькую ординату /(х"), так что все течение функции /(х) на отрезке [а, Ь} остается ограниченным этими двумя числами fix') и f(x").
Отсюда следует, что непрерывная функция на отрезке не может стремиться к бесконечности (ни к-|-оо, ни к — оо), потому что все ее течение на целом отрезке должно быть ограниченным.
Примечание. Для разрывных функций свойство I может быть ложным. Например, функция /(х), определенная следующим правилом:
,, . „ ,1 , (\\ 1
/(х)=х —х- для, х±2 и f ( %) ~ в
получается удалением из целой параболы у = х — х- ее самой высокой точки (вершины) (черт. 40), имеющей абсциссой 1 и ординатой i, и опусканием ее вдвое ниже. Ясно, что полученная функция /(х) есть разрывная и что она уже не имеет максимума, потому что f ( ) = g, 8 не 4*
Свойство II. Непрерывная функция, изменяющая свой знак, проходит через нуль.
Геометрически это означает, что непрерывная кривая у =/(х), соединяющая две точки А и В, расположенные по разные стороны оси абсцисс, должна непременно пересечь эту ось в некоторой промежуточной точке с (черт. 41).
Более общим является то предложение, что непрерывная функция f (х\ достигающая на отрезке [a, максимума М и минимума т, должна на отрезке [а, д] принять любое промежуточное значение L, где т < L < М.
Это предложение сводится, впрочем, к предыдущему, так как функция <р(х)=/(х)— L есть, очевидно, тоже непрерывная и изменяет на
Черт. 41.
отрезке [а, А] свой знак. Действительно, в силу свойства I имеется такое х', что f(x?) = m, и такое х", что f (х"]=- М, и поэтому:
? (х') — т — КО и «(х") = М — L > 0.
Следовательно, з (х) проходит на отрезке [а, Ь\ через нуль, т. е. имеется на этом отрезке такое с, что с(с) = 0, откуда f(c) = L.
Примечание. Для разрывных функций свойство II может быть ложным. Например, функция f(x), отрицательная влево от с, положительная вправо от с и положительная для самого с, f(c)>0, меняет свой знак на [о, 6], ио не проходит через нуль (черт. 42).
Черт. 43.
Свойство III. Непрерывная функция стремится к совершенно определенному пределу, когда ее аргумент сам стремится к пределу. К тому же этот предел lim/(х) нашей функции в точности равен ее значению /(limx), вычисленному для предела аргумента, т. е.
limy (х) =/(lim х).
Доказательство. Пусть аргумент х (черт. 43) стремится к пределу х0, т. е. пусть
11m х = х0.
Это означает, что разность х— х0 есть бесконечно умаляющаяся величина; поэтому, обозначив ее через Дх0, т. е. написав:
х — х0 = Ах0, мы имеем:
х = х0 -|- Дх0 и
lim Дх0 = 0.
Возьмем теперь соответствующее приращение функции
/(Хо + ДХе)— /(*)•
Так как функция /(х) непрерывна на отрезке [а, Ь], где лежат обе величины х0 и х0-|-Дх0 аргумента, то это приращение бесконечно умаляется, когда Дх0 бесконечно умаляется.
Но здесь /(х0) есть постоянное, потому что х0 постоянно. Уменьшаемое же /(х0-)-Дх0) есть переменная величина, потому что х0 -|- Дх0 = х, и, зйачит, это уменьшаемое просто можно написать как/(х), где х переменно. И так как разность переменной величины и постоянного только тогда бесконечно умаляется, когда это постоянное есть предел рассматриваемой переменной величины, то отсюда следует, что /(х0) есть предел переменной величииы /(х0-|- Дх0); значит:
Пт/(х04-Дх0)=/(х0).
Но так как х3-}-Дх0 = х и х0 = 11шх, то, делая эту замену, мы находим:
Hm /(х) = /(limx).
Свойство III часто выражают следующим алгебраическим образом. Чтобы понять его, читателю следует обратиться к той первой теореме теории пределов, которая в словесной формулировке гласит: «предел суммы равен сумме пределов" (см. § 38) и которая математически записывается в виде равенства:
lim(x — y-j-z-j- • • • + Л = (limx — limy-}- lim Z-j-... -}- lim/}.
Вот это последнее равенство нередко читают так, сообщая этому прочитыванию алгебраический характер: „если надо найти предел скобки, можно переходить к пределу под знаком скобки" !)•
Теперь аналогичным образом читают математическую запись свойства III непрерывных функций
lim/(x) = /(limx), выражая это в виде следующего общего правила:
') Сумму х — у + z + ... +<,о которой идет речь, часто выписать всю трудно, если она очень длинна; тогда ее пишут короче в виде Ех, где Е есть знак суммы, за которым выписывается либо первый, либо так называемый .общий* член рассматриваемой суммы.
Пользуясь этим Обозначением, указанная первая теорема теории пределов выписывается следующим образом:
lim Ex = 2 limx и прочитывается так: „Если надонайти предел суммы, можно перейти к пределу под знаком суммы*.
Общее правило. Если надо найти предел непрерывной функции, можно переходить к пределу под знаком функции.
Из всего сказанного выше читатель видит, что эта возможность перехода к пределу под знаком функции, /(limx), имеется лишь у непрерывных функций: разрывные функции не допускают такой возможности, потому что равенство lim/(jc) = /(lim х) вполне характеризует непрерывные функции.
§ 43. Основная теорема о непрерывных функциях. Выражение свойства Ш непрерывных функций р форме только что указанного общего правила позволяет нам очень легко притти к одной из важнейших теорем анализа.
Основная теорема. Сумма, разность, произведение и частное двух непрерывных функций есть опять непрерывная функция, если только знаменатель частного не обращается в нуль; в этом последнем случае, вообще говоря, имеем разрыв.
Доказывать эту теорему нет никакой необходимости, потому что она является только новой формулировкой уже известных читателю теорем о пределах (см. § 38), лишь выраженных на языке непрерывных функций.
Примечание 1. Ясно, что не только сумма двух и произведение двух непрерывных функций суть непрерывные функции, но точно так же алгебраическая сумма и, соответственным образом, произведение ограниченного числа непрерывных функций:
T(x)-4(Jf)4-...+»W И т (х) • ф(х) . .. ш (х) суть непрерывные функции. Ибо помощью скобок всегда возможно, например, представить сумму и произведение трех функций как сумму и произведение двух функций:
ф (х) — -!> (х) + ш (х) = [? (х) - ф (X)] + ш (ж)
И
ф (х) • 6 (х) • ш (х) = (V (х) • О (х)1 • W (х).
Но теорема может стать и ложной, если число слагаемых или множи
телей не остается ограниченным, но, напримёр, безгранично возрастает, т. е. когда речь идет о бесконечных рядах, члены которых суть непрерывные
функции: сумма такого ряда может оказаться уже разрывной функцией. ф (л*) Примечание 2. Если в отношении двух непрерывных функций
знаменатель ф (х) уничтожается в какой-либо точке х0, ф (х0) = О, много ос и ований ждать разрывности функции /(х) =
то есть
ф (х) .
Г7-: 8 ЭТОЙ
Ф(х)
точке Хо. Например, функция — разрывна в начале координат О (см. § 42), хотя
знаменатель х везде непрерывен; разрыв этой функции обусловлен уничтожением знаменателя в точке х = 0.
' Только что доказанное предложение немедленно влечет два важных следствия.
Следствие 7. Всякий многочлен \
ахп + Ьх"-14- схп 2 ... 4-gx 4- h,
где коэфициенты a, b, с,..., g и h — постоянные числа, есть функция, везде непрерывная, ибо всякий многочлен образован
из аргумента х при помощи действий сложения, вычитания и умножения, которые не приводят к разрывным функциям.
Следствие 2. Всякая рациональная функция
ахп 4- Ьхп~1 gxh
Ахт 4- Вхт 1 + ..•+ Кх + L есть функция, непрерывная всюду, кроме, быть может, таких точек х0, в которых знаменатель уничтожается, т. е. к^оме, быть может, корней уравнения
А хт 4- Вхт~14- ... + Кх 4- L = о,
иб» числитель и знаменатель непрерывны всюду как многочлены; значит, разрывы хЛ могут притти лишь с уничтожением знаменателя.
§ 44. Типы разрывов функций. Свойство III непрерывных функций легко можно представить себе и геометрически.
В самом деле, изобразим данную нам функцию
У = /(х),
непрерывную на отрезке [а, Ь], в виде геометрической кривой (черт. 44).
Ясно, что свойство III теперь обозначает, что длина подвижной ординаты хМ безгранично приближается к длине неподвижной ординаты х0Л'0, когда переменная абсцисса х безгранично приближается к постоянной абсциссе х0, потому что длина подвижной ординаты равна /(х), а длина неподвижной ординаты равна /(х0), и потому что в силу свойства III мы имеем:
iim/(x) =/(xu),
когда limx = x0.
Здесь х0 есть, разумеется, какая-нибудь (и притом безразлично, какая именно) точка отрезка [а, А], на котором рассматриваемая функция/(х> непрерывна.
К сказанному прибавим, что совершенно неважно, каким именно способом осуществляется приближение переменной абсциссы х к постоянной абсциссе х0: абсцисса х может безгранично приближаться к ха как справа, так и слева. Единственное исключение предста-, вляется лишь тогда, когда неподвижная точка х0 служит концом отрезка [а, £]. Ясно, что если х0 = п, то точка х может приближаться лишь справа к точке х0; если же х0 = Ь, то х должна приближаться только слева к х0. Во всех же других случаях подвижная точка х может приближаться и слева и справа к неподвижной точке х0, и в обоих случаях мы должны иметь;
lim/(x)=/(x0).
Если же функция /(х) не является непрерывной на отрезке [а, £], то мы знаем (см. § 42), что тогда у функции /(х) непременно имеется точка разрыва (хотя бы одна), т. е. такая точка х0, что мьп уже не имеем равенства
lim/(x) = /(x0),
когда х безгранично приближается к х0.
Читатель должен заметить, что это может произойти только по одной
из следующих двух причин:
I. Или /(х) совсем не имеет никакого предела, когда точка х приближается к х0 с какой-нибудь стороны (справа или слева).
Геометрически это обстоятельство может быть изображено так,
Черт. 45.
Черт. 44.
как показано на черт. 44 и 45.
Это есть изображение разрыва справа в точке х0. В первом случае кривая колеблется справа от х0 бесчисленной множество раз, причем ее г размах не убывает до нуля;
во втором случае кривая уходит в бесконечность. Ясно, что аналогичные случаи могут оказаться и по левую сторону абсциссы х0 (что тогда даст разрыв сле-/ ва в точке х0).
II. Или хотя f(x) и имеет пределы справа и слева в точ-
ке х0, но по крайней мере один из этих двух пределов заведомо не равен f(x0).
Геометрически это обстоятельство может быть изображено так, как показано на черт. 46 и 47.
Из чертежей видно, что /(х) имеет оба предела в точке х0: и справа и слева. Но в первом случае эти пределы и, значит, по крайней мере
один из них отличен от значения /(х0)рассматриваемой функции /(х) в самой точке х0; во втором случае, хотя оба эти предела и равны между собой, но зато отличны от /(х0).
Часто для обозначения
Черт. 46. Черт. 47. • этих обоих пределов — пре-
дела функции справа от точки х0 и предела функции слева от точки х0 — употребляют некоторые особенные обозначения, которые читатель должен знать и самый смысл которых он должен ясно понимать, чтобы не быть введенным в заблуждения и ошибки. Эти обозначения таковы:
предел/(х) справа от точки х0 обозначается:
/(Хо + О)»
предел /(х) слева от точки х0 обозначается:
/(хо-О).
Вот каким образом приходят к этим обозначениям: возьмем положительное число г, г > 0, и рассмотрим два значения функции:
/(х0Н-е) и /(Хо — е).
Ясно, что первое из них является значением функции справа от точки разрыва х0, а второе — слева от нее. Если мы теперь заставим наше
положительное число е безгранично убывать до нуля, lim s = О, то /(х.,--е) будет переменной величиной, стремящейся к вполне определенному пределу (так как предполагается, что справа от точки х имеется предел); вот этот самый предел и обозначается символическ и(условно) через / (х0 -Ь 0). Аналогично, предел переменной величины / (х0— е) обозначают через /(х0— 0). Итак, согласно этому условию мы имеем:
f(x0 -Г 0) = НтД*о + е)
и
f(xo — °) = lim f(x0 — в)-• ->0
Но читатель должен быть предупрежден, что эти обозначения
/(лГо + О) и /(х0—0)
являются условными, так сказать стилизованными, т. е. выбранными таким образом, чтобы эти обозначения несли на се б е от п е ч а т о к самого происхождения тех количеств, которые они выражают *)•
§ 45. Устранимый и неустранимый разрывы. Черт. 44, 45, 46 изображают случай неустранимого разрыва функции: изучая эти чертежи, мы сразу убеждаемся в том, что никаким изменением численного значения функции /(х) в самой точке х0 никогда нельзя добиться того, чтобы в рассматриваемой точке х0 пропал разрыв и была восстановлена непрерывность. Действительно, какое бы численное значение мы ни давали нашей функции /(х) в точке х0, на черт. 44 никогда не исчезнет бесчисленное множество колебаний, на черт. 45 не исчезнет уход функции /(х) в бесконечность, и на черт. 46 — резкая разорванность течения кривой.
Наоборот, черт. 47 дает ясное понятие о так называемом устранимом разрыве функции. Это есть тот случай, когда оба предела функции /(х) в точке х0 равны друг другу, но неравны величине /(х) функции в самой точке разрыва х0, т. е. когда (символически):
/(*о + °) =/(*о — 0) ^/(х0).
Если в случае черт. 45 график являет нам картину ветки кривой, разорванной на две части, причем одна из них поднята (или опущена) выше другой, то черт. 47 просто изображает одну ветку кривой, целость которой нарушена только тем обстоятельством, что из нее вынута одна точка (абсциссы х0) и помещена вне кривой.
*) Буквально же (т. е. стационарно, не символически) их понимать, разумеется, невозможно, так как прибавление или отнятие нуля от х0 нисколько не изменит хп, потому чтох0 + 0 = х0 и х0 — 0 = х0, и, значит, обозначения /(х0-|-0)и f(x0 — 0) тогда не могут дать ничего ценного или интересного, выражая при грубом не символическом понимании их просто величину функции /(х) в самой точке х0, которую и без того .можно было бы прекрасно написать в виде /(х0).
Зак. 2769. — В. Гранвиль u Н. Лузин. Часть I 6
Простейшим примером такого разрыва является функция, равная всюду нулю, кроме начала координат, где она имеет величину, равную -j- 1, т. е.
f(x) = 0, если хфО и У(0) = —j-1.
Ясно, что, возвращая вынутую точку обратно „на ее место", т. е. полагая
/(х0)=/(ло + 0)=/(х0-0),
мы восстанавливаем нарушенную непрерывность функции. Поэтому такой разрыв называется устранимым разрывом.
Читатель отнюдь ис должен думать, что все описываемые случаи разрывов функции .слишком отвлеченны-, имеют лишь .теоретический” интерес и «никогда* не встречаются на практике. Напротив, современная техника как раз имеет дето с описываемым поведением функций. Например, при возведении строения сплошь и рядом балка рассчитывается нагруженной неравномерно: в одной ее части нагрузка одна, а в непосредственно прилегающей к ней части нагрузка уж? совершенно другая. Это соответствует как раз неустранимому разрыву (левый график) для функции, задающей нагрузку. Резкая (сосредоточенная) нагрузка балки в одной точке соответствует устранимому разрыву функции, задающей нагрузку.
§ 46. Кажущийся разрыв и так называемая «истинная величина” функции. Раскрытие неопределенностей. Случается, что функция выражается формулой/которая утрачивает числовой смысл при каком-нибудь значении аргумента.
Например, функция
_______ (х—JCo)®_________ х:' — Зх2 • х-0 ф- Зх • х2 — хя0
при х = х0 не равна ничему, потому что числитель и знаменатель дроби оба обращаются при значении аргумента х — х0 в нуль. В этих условиях формула, разумеется, невычислима.
Однако такое повреждение при X = х0 формулы /(х), дающей функцию у = f (х), отнюдь не означает, что повреждена в этой точке и самая функция у =f (х). Часто бывает, что формула /(х) повреждается при х = х0, переставая служить для вычисления величины/(х), потому что утрачивает всякий смысл в точке хл, в то время как сама функция y=^f(x) не представляет ничего особенного в этой точке, имея в ней столь же гладко: течение, как и в соседних точках.
Говоря самым общим образом, когда какая-нибудь формула /(х), содержащая букву х, утрачивает численный смысл при каком-нибудь исключительном значении х0 аргумента х, тогда естественно ожидать в этой точке х0 какой-нибудь неприятности для течения функции, например неустранимого разрыва. Но часто случается, что можно дать такую численную величину функции у в точке х0, что эта функция станет уже на отрезке [я, А] непрерывной.
Ясно, что для этого функция у должна стремиться к определенному пределу, когда аргумент х стремится к точке х0, причем этот предел должен быть одинаковым независимо от того, стремится ли аргумент х к точке х0 возрастая или убывая (т. е. слева или справа от точки х0).
Ясно, наконец, что, давая функции у эту предельную величину как ее значение в самой точке х0, мы делаем функцию у непрерывной в точке х0. Такой устранимый разрыв называется кажущимся разрывом, и предельное значение функции у в точке х0 называется ее „истинной, величиной'1 в этой точке.
Геометрически истинная величина функции у изобразится точкой, вставляемой между правой и левой ветвями функции, стремящимися к этой точке (черт. 48).
Таким образом, когда это обстоятельство случается, тогда находят искомую величину функции y=f(x) в такой точке х0, просто вычисляя /(хо-|-О)и /(х0— 0). Если оказывается, что эти количества равны друг другу, то считают, что в точке х0 повреждена не сама функция,
а лишь дающая ее формула, и просто часто принимают за f (х0) общую величину
Ж 4-0)=/ (х0-о), называя ее в этом случае истинной величиной функции в точке х0. Мы знаем, что этим восстанавливается непрерывность функции J (х) в точке х0.
Иногда это восстанавливание величины функции у = /(х) делается чисто алгебраически, именно так, что надлежащими элементарными алгебраическими переделками в данной формуле: сокращениями, приве
дением подобных членов и т. д. устраняется повреждение формулы
для х = х0, без изменения численных величин функции в других точках.
Из сказанного явствует, что естественно рассматривать этот случай как случай кажущегося разрыва, обязанного не недостатками самой функции (в геометрическом смысле), а лишь некоторому недостатку дающей эту функцию формулы, утрачивающей случайным образом свой
численный смысл при х = х0.
Например, формула
Г(х) = (зх« 4- —Ц)---Ц-
* \ 1 X— 1 / X— 1
перестает служить для вычисления величины функции при х=1, потому что тогда два знаменателя обращаются в нуль.
Если мы раскроем скобки и „сократим** члены
то этим самым мы нисколько не изменяем величины функции для значений аргумента х, отличных от нуля, но тогда рассматриваемая формула переходит в другую формулу:
Ф (х) = 3x2.
которая дает уже непрерывную функцию и величина которой для х = 1 равна 3.
Так как имеем равенство:
/(х) = Ф(х)
для всех х, отличных от единицы, то отсюда заключаем, что
/(1-Ь0) = 3 и /(1 —0) = 3.
Поэтому, полагая просто /(1) = 3, мы восстанавливаем непрерывность функции и устраняем кажущийся разрыв, происшедший от разрушения формулы /(л) при х = 1.
Другим примером того, что подобная утрата численного смысла той или иной формулой может произойти чисто случайно, читатель заметит из того обстоятельства, что достаточно написать любую непрерывную функцию /(х) в виде:
х/(х)
X
или в виде:
[4+/w -4’
как новая формула уже утрачивает численный смысл при х = 0.
Но далеко не всегда столь простым чисто алгебраическим сп о с о б о м удается восстановить непрерывность 'функции и открыть ее истинное значение в точке х0, в которой разрушается формула. Так, например, формула
sin х х ’
очевидно, разрушается при х = 0, потому что мы получаем нуль в знаменателе. И устранить этот нуль никаким чисто алгебраическим способом нельзя. Однако функция у = /(х), даваемая этой формулой, непрерывна при х = 0, как мы докажем немного дальше (см. § 48), и мы найдем, что /(04-0)= 1 и /(0 — 0) = 1, так что „истинной величиной" функции /(х) в точке х = 0 будет единица *).
Находить .истинную величину" функции /(х) вообще дело очень трудное, потому что в самой точке х0 формула утрачивает смысл, и для нахождения предела lim /(х), когда х стремится к х0, прибегают обычно к пиференциальному исчислению, даю'щему могучее средство к определению истинных величин функций, называемое иногда „раскрытием неопределенности1*, так как функция /(х) неопределенна в точке х = х0.
Неопределенность функции /(х) в точке Х = ХО происходит оттого, что форыула /(х) утрачивает смысл, когда йолагают в ней х = х0. Эта утрата смысла чаще всего происходит от того, что функция
Читатель не должен думать, что всякий устранимый разрыв надо непременно устранять. Следует устранять лишь кажущиеся разрывы, проистекающие от формул, становящихся невычислпмыми при каких-нибудь частных значениях х0 аргумента, потому что они происходят от несовершенства формул.
Но если самая функция (т. е. график) имеет разрыв, хотя бы и устранимый, то тут уже ничего поделать нельзя, так как такой разрыв здесь выражает дей-'ствительность (например нагрузку балки в одной точке).
в точке х = х0 принимает вид -. Но неопределенность может проистечь еще и потому, что функция f(x) в точке х — х0 примет один из следующих семи видов неопределенности:
/
О, —, 0 • оо, оо — оо, 0°, ос0, О"*0.
0 ос
Правила раскрытия этих неопределенностей изложены в главе XIII.
Упомянем, наконец, что часто говорят про „истинную величину" функции при х= 4“00 или при X = —оо и при этом пишут символы /(-1~ оо) и /(— оо). Эти слова и символы употребляются в чисто переносном слысле, и под этим надо разуметь лишь предел функции f(x), когда аргумент х безгранично возрастает или безгранично убывает, так что
/(-}-оо) обозначает просто lim /(х), когда х->4*°°> и
/(— оо) обозначает просто lim /(х), когда х->—оо.
В заключение мы приведем таблицу простейших пределов, играющих особенно важную роль при изучении математического анализа. В этой табличке буква с всюду обозначает число, существенно не равное нулю.
В форме пределов В сокращенной, часто употребляемой форме
1. lim — = оо; х > 0 X 2. lim сх = ос; х -> оо 3. lim — = оо; х -+а> С 4. lim — = 0; . х->оо х \ 5. lim ах = -|- оо, если fl < 1; С — = оо. 0 С • оо = оо. оо — = оо. с — = 0. оо а-°°= 4-ос.
ДГ-> — ОО 6. lim ах = 0, если а <1; о+°° = 0.
х-> + оо 7. lim ах =0, если а >1; ^° = 0.
— GO 8. lim ах = 4-ос, если а > Г, а+“ = -J-оо.
X > 4- оо 9.1imlogex = — оо для а > 1; 10ge 0 = — ОО.
Х->0 10.1imlogex = -4-ос для а> 1; loge(4-oo)=4-oo.
Выражения, написанные во втором столбце, не следует рассматривать как выражения численных равенств (оо не есть число); это просто — символические равенства, под которыми надо разуметь соотношения, указанные в первом столбце) и только так их и нужно понимать.
§ 47. Два замечательных предела. Для изучения диференциаль-ного исчисления существенно необходимо познакомиться с нижеследующими двумя замечательными пределами, без знания которых невозможно обойтись.
1. Предел отношения синуса к дуге. sinx
Речь идет об отыскании предела отношения ———, когда аргумент х
стремится к нулю, т. е. надо, вычислить
ного пути А МВ,
Возьмем окружность радиуса 1 и в ней угол АОВ, равный 2х. Так как мы измеряем углы не в градусах, а отвлеченным образом (см. § 28), то 2х есть просто выпрямленная дуга ЛМВ окружности.
Но из элементарной геометрии известно, что прямолинейный путь АСВ короче криволиней-1й, в свою очередь, короче обходного ломаного
пути ADB, состоящего из отрезков двух касательных. Поэтому мы имеем неравенства:
ACB<AMB<ADB.
Но АСВ = 2sinx, АМВ = 2х и HD5 = 2tgx. Значит, 2 sin х < 2х < 2 tg х,
откуда, деля все на 2sinx, находим х в первой четверти;
1 < <——• sin х cos х
Ясно, что если х безгранично умаляется, cos х имеет пределом 1, следовательно:
lim —-— = 1. х-> О cosx
х
И так как дробь * оказывается в силу предыдущих неравенств заключенной между переменной величиной —-— и еепре-3 COS X
целом 1, то (теорема V, § 38) предел этой дроби тоже равен единице.
Значит: lim = х.->о Sin X
и, следовательно:
sin х .
lim--------= 1.
Здесь мы предполагали, что аргумент х приближается к нулю, будучи положительным.
Но если положительный аргумент х переменит свой знак на обрат-„ sin (— х)
ный и станет —х, то отношение-----.— не изменит своей величины,
( —х)
ибо числитель и знаменатель одновременно переменят свои знаки, и, значит, отношение их останется прежним:
sin ( — х) s’n х ( — х) ~ х „ » sin х
Отсюда мы заключаем, что отношение --- имеет во всех случаях
своим пределом 1, через какие бы числа ни стремясь к нулю *), т. е.:
• sinx
всегда имеем lim— - = 1. когда lim х — О х
Если мы рассмотрим функции' sin х
проходило переменное х,
в начале координат, то
то читатель видит, что она имеет кажущийся разрыв в начале координат х = 0, где ее „истинная величина** (т. е. предел для х, стремящегося к нулю) равна единице.
И так как знаменатель уничтожается лишь рассматриваемая функция нигде не имеет никаких разрывов. Так кац . - sin х
перемена знака аргументов х функцию не изменяет, то кривая у = —-— симметрична относительно оси У. Знак функции зависит от знака sin х, когда х возрастает от 0 до -j- оо- Притом функция стремится к нулю, когда х стремится к ибо числитель по абсолютной величине не
превышает 1, а знаменатель возрастает до -|-оо.
Сказанного достаточно, чтобы видеть, что график функции
sin х 1
будет таким, как это изображено на черт. 50.
Можно сказать, что хотя кривая и колеблется около оси абсцисс Х'Х, то возвышаясь над нею, то уходя под нее, однако колебания эти затухают, так как ордината у кривой стремится к нулю, когда х возрастает до оо.
*) Однако, разумеется, х не делается никогда в точности равным нулю во „ sin X
время процесса своего изменения, ибо, иначе, отношение - временами переставало бы иметь смысл.
88
П. Число е Непера.
Различные системы логарифмов. Вспомним сначала самое определение логарифма^даваемое элементарною алгеброю.
Логарифмом числа N при основании а, а> 1, называется тот показатель степени т, в которую нужно возвысить основание а, чтобы получить число N. Это определение записывается математической формулой в виде равенства:
am = N.
Чтобы помнить, что вании а, обычно пишут
показатель т есть логарифм числа А/ при осно-напоминающее об этом обстоятельстве равен-
ство:
/п = I oge /V.
Значш, имеют всегда такое тождество'. a"^N =
справедливое для всякого числа N.
Так как нам надо изучить функцию loga х, то естественно в этом тождестве заменить число N через х, что даст опять тождественное соотношение:
а,оеаХ =х.
Обозначая величину функции loga х через у:
y = \oga х,
мы видим, что предыдущее тождественное соотношение напишется в виде: t
av = х.
Это важное уравнение показывает, что логарифмическая функция есть функция, обратная показательной.
Чтобы иметь график логарифмической функции _y = logax, напишем это уравнение в виде х = av и будем рассматривать букву у как аргумент, а букву х как функцию аргумента у. Здесь ясно следующее:
1. Если у = О, то х = 1 при любом а.
2. Если у возрастает до оо, тогда и х возрастает до оо.
3. Если у убывает до —оо, тогда х, оставаясь положительным, стремится к нулю.
Поэтому, если мы начертим кривую х = av, рассматривая сначала ось OY как ось независимого переменного и затем переходя к обычному рассмотрению оси ОХ как оеи независимого переменно/о, мы немедленно усматриваем из черт. 51, что:
1. Логарифмическая функция logax есть непрерывная возрастающая функция в промежутке (а не в отрезке) (0 < х < оо).
2. Для отрицательных значений аргумента х функция logax не существует: отрицательные числа не имеют логаоифмов (эти логарифмы мнимы).
3. log'll =0 при любом основании а.
До этой точки логарифмическая кривая течет под осью ОХ: логарифмы, чисел, меньших единицы, отрицательны-, после этой точки кривая возвышается над осью ОХ: логарифмы чисел, больших единицы, положительны. Прих, безгранично возрастающем, logax также безгранично возрастает, что условно ’) записывают в виде символи-(еского равенства:
10g (4-оо)= -j- оо.
Натуральные логарифмы, переход от них к обыкновенным логарифмам, и обратно. Мы видим, что пенкой базе а > 1 соответствует своя собственная логарифмическая кривая у =logax и, значит,своя собственная система логарифмов. Таким образом систем логарифмов имеется бесчисленное множество.
Но на самом деле употребительны только две системы логарифмов:
I. Система логарифмов Бригга, называемых иногда обыкновенными или десятичными логарифмами. В этой системе за базу а взято число 10, а = 10.
II. Система логарифмов Непера, называемых часто натуральными или гиперболическими логарифмами. В этой системе за базу а взято одно особенное иррациональное число, обозначаемое буквою €, приближенную величину которого нетрудно запомнить:
е = 2,7 1828 1828 459045 ...
Таким образом, если у есть десятичный логарифм числа х, то имеем 10v = x, и если у есть натуральный логарифм числах, то имеем ei'=x.
При первом знакомстве с теорией логарифмов кажется вполне естественным взять за основание (базу) системы логарифмов число 10, т. е. употреблять всегда бригговы логарифмы. Эта естественность обусловливается прежде всего нашей привычкой выражать целые числа в десятичной системе счисления и пользоваться десятичными дробями в наших выкладках: таким образом взять число 10 за базу логарифмов побуждают, собственно, соображения практического порядка.
Однако более глубокое знакомство с логарифмами и логарифмическими функциями обнаруживает, что принятие числа 10 за базу является случайным обстоятельством и влечет за собою в дальнейшем такое усложнение формул, которое не может быть оправдано ни теоретическими, ни даже практическими соображениями.
Напротив, уже в элементах диференциального исчисления представляется наиболее* целесообразным принять за базу системы логарифмов не число 10, а вышеуказанное иррациональное число
е = 2,7 1828 1828 459045...
Только при употреблении этого иррационального числа е как базы логарифмов формулы получают наиболее простой вид. Два иррациональных числа: е и ~ = 3,141592653... играют исключительно важную роль в математике: первое, е, в анализе, второе, - — в геометрии.
!) Читатель не должен забывать, что бесконечность не есть число и поэтому на самом деле не имеет никакого логарифма. Приводимое равенство есть лишь условная запись для памяти.
Логарифмы с базою е называются натуральными, логарифмами (или логарифмами Непера) и обозначаются просто
InV
без указания базы. Обозначение же lg N удерживается для десятичных логарифмов (логарифмов Бригга).
Мы предполагаем, что читатель из элементарной алгебры знаком с употреблением логарифмов Бригга lg N и умеет обращаться с таблицами этих логарифмов.
На первый взгляд может показаться, что одновременно с таблицами бригговых (десятичных) логарифмов, lg N, необходимо иметь еще и таблицы натуральных логарифмов, In N.\ На самом деле это не так, потому что имеется очень простой способ перехода от одной системы логарифмов к другой, так что никакой новой таблицы уже не требуется.
В самом деле, пусть у есть логарифм числа х при базе а, т. е. av = х.
Логарифмируя обе части этого равенства натуральными логарифмами, мы получаем:
jlna = lnx. (1)
Следовательно, если известен натуральный логарифм In х числа х, мы будем иметь логарифм этого числа х при любой базе а простым умно- •
жением натурального логарифма на множитель М = . Этот множи-
тель называется иногда модулем базы а. Значит, помножая всю таблицу натуральных логарифмов на модуль М базы а, мы немедленно получим таблицу логарифмов с базою а.
Этот модуль М можно вычислить 'еще иначе: положим в предыдущем равенстве (1) х = е. Тогда 1пе=1 (потому что всегда имеем
loge а = 1 при любой базе а), и, значит, у = ——. Но, с другой стороны, у = log„ х = log„ е. Значит:
|ог-е=1Л=м
И обратно: если известен логарифм числа х при базе а, мы немед-лено получим натуральный логарифм этого числа простым умноже-
1 /п
нием на число -тт, как показывает равенство (1).
М
В частности для десятичных (бригговых) логарифмов
а =10 и М = 0,434294481903. ..,47 = 2,302585092994...,
М
ln = ~lg, 1g =/И-In.
Чтобы переходить от одних логарифмов к другим, надо пользоваться .. 1
умножением на М и
Число е. Мы уже знаем, что наиболее целесообразной в теоретическом отношении является такая система логарифмов, в основание которых принято не число 10, а особенное иррациональное число е, называемое числом Непера или просто числом е, приближенная величина которого легко запоминаема:
б? = 2,7 1828 1828 459045...
Такая система логарифмов называется системой натуральных (или неперовых, или гиперболических) логарифмов. Натуральный лога рифм какого-нибудь числа А обозначается просто
In А.
Самое введение в математический анализ числа е совершается при помощи следующей важной леммы:
, / , 1 \«
Лемма. Выражение!14— , г д е п есть целое поло-\ п)
жительное число, стремится к вполне определенному пределу, когда число п безгранично возрастает. Этот предел больше 2 и меньше 3.
Действительно, вспомним бином Ньютона:
(а 4-Ь)п = ап4-у.ап~'Ь + ап~‘^ + ...
1 1 • £•
п(п — 1) (п—2)...(п— L2-3...A
„я— k i,k I ,п
а о -f- • •
и положим в нем
а = 1 и о — п
Тогда получим:
1 . п(л — 1) 1
п 1 • 2 *
л(п —1).. ,(л —&4-1) 1^ , 1
' ‘~г" 1 ,2.3... k ' пк ' ““г пп ‘
Полученную формулу крайне выгодно написать несколько иначе, так, чтобы выступили наружу* ее основные свойства:
(1 \п 1/ 1\ 1/ 1 \ / 21
!4-,7 =Ж+-А- 1 - i + г4-з 1 - +•••
И ] 1 • Z \ II) 1 • X • О \ ПI \ п /
Для того чтобы понять, как это делается, читатель должен просто обратить свое внимание на общий (А-й) член предыдущей формулы и
заметить, что в его числителе всех скобок имеется k— 1 и что по сокращении первого множителя л со знаменателем пк у нас в знаменателе к—1
останется л , значит, столько же множителей л, сколько в числителе скобок. А тогда, деля каждую скобку на одно л, мы и получаем выведенную последнюю формулу.
Свойства же последней формулы следующие:
С одной стороны, каждая из скобок есть число положительное, отсюда, заменяя всякую из этих скобок через нуль, мы получим в правой части нашего последнего равенства меньше того, что там ранее имелось: значит, всегда
(1+-Г>2-
\ п !
С другой стороны, каждая из этих скобок меньше единицы отсюда, заменяя всякую из них единицею, а каждое из чисел 2, 3, 4....находящихся в знаменателях перед скобками, просто двойками,
мы получим в правой части нашего последнего равенства больше того, что там ранее имелось, значит:
(1 \п 111 1
1 + 2)<1 + 1 + 1 + ^ + - + ...+_.
Но правая часть этого неравенства всегда меньше 3, как читатель легко убедится, вспомнив убывающую бесконечную геометрическую прогрессию:
2=‘ + т + т+-5- + Гб+г2-Ь-
Итак, для любого целого положительного числа п мы имеем всегда:
/ 1 \п
2< I-}-— <3. \ л /
Пусть теперь целое положительное число л начинает безгранично возрастать. Посмотрим, что происходит тогда с написанным выше разложением
('+41'
Прежде всего надо отметить, что возрастает число слагаемых в этом разложении и что, кроме того, все слагаемые этого разложения положительны. Затем следует заметить, что каждое слагаемое, рассматриваемое в отдельности, также возрастает по своей величине, ибо всякая скобка
с увеличением числа л начинает возрастать, неограниченно приближаясь к своему пределу 1>
Так как сумма всех этих слагаемых и дает величину выражения
/ 1 \п
1+-) ,
\ п]
то отсюда необходимо заключить, что с увеличением целого положительного числа п выражение
возрастает по своей величине.
Итак, когда п безгранично возрастает, выражение
ест^ положительная переменная величина, все время возрастающая, но остающаяся все время меньше 3. Поэтому эта переменная величина необходимо стремится к пределу *), когда п безгранично возрастает, причем этот предел, очевидно, не меньше 2 и не больше 3, раз сама переменная величина
6+-Г \ п /
всегда находится между этими границами.
Доказанная лемма позволяет дать следующее определение
Определение. Предел выражения
(i+-y\ \ п /
когда натуральное число п возрастает безгранично, называется неперовым числом и обозначается буквою е:
/ 1 \п
Пт 1-I-— =е, п-юо\ п /
Мы выше видели, что число е заключено между 2 и 3. Приближенная а) величина е следующая:
£ = 2,718281828459045.
!) Отметим, что далеко не всякая переменная величина имеет предел. Так например, sin п не стремится ни к какому пределу, когда п безгранично возрастает, потому что эта переменная величина все время колеблется между —1 и +1, подходя по временам как угодно близко к любому заданному заранее числу в, лежащему в границах [—1, -|-1].
Но, опираясь на теорию иррациональных чисел, нетрудно доказать, что всякая возрастающая переменная величина, остающаяся притом всегда меньше некоторого числа, необходимо стремится к пределу. Не имея возможности расширить рамки нашей книги, мы примем этот факт просто как принцип, не входя в его обоснование Геометрически этот принцип эквивалентен утверждению, что точка, движущаяся в одном, всегда в том-же самом направлении и не уходящая бесконечно далеко, необходимо приближается к некоторому определенному предельному положению.
2) Число е как иррациональное может быть изображено лишь приближенно конечной десятичной дробью. i
П р и м е н а н и е. На примере числа е читатель ясно видит, как нельзя быть легкомысленным h неосторожным в обращении с пределами и с бесконечностью. Ведь читатель прекрасно мог „рассуждать* и так: „Мне надо найти предел
к. гда л безгранично увеличивается; очень хорошо: я и сделаю п = оо. Тогда
И, значит: 1+—= 1+0= 1. оо
Значит, мне надо 1 возвысить в бесконечную степень. Но так как
12=1, р= 1........1«= 1,
то и в пределе я получу 1°° = 1. Значит:
Заключение, как мы видим, совершенно ложное и происходящее от того, что читатель в выражении / 1 X»
(1+л)
сначала в скобке сделал п = оо, положив
11m — = 0, л
и уже потом в показателе скобки ( )п сделал п = оо. На самом же деле бесконечность оо не есть число, и сначала вычислять
1 + — при л-»- + оо и уже после этого вычислять ( )” при л-> + оо недопустимо. п
В действительности нужно л безгранично увеличивать одновременно и в скобке, и в показателе скобки. И когда мы это будем делать, то мы и увидим, что f 1 + —Y* = 2,7,..., а не 1.
Л-Н“сс\, л / |
Читатель безусловно прав, когда в отдельности заключал, что lim fl 4--1Л = 1
/ П->4-со\ л J и что '
Um 1П=1. П->4-ОО
Порознь так рассуждать можно. Когда л еще пока обозначает число (целое, положительное и, значит, конечное), читатель, вычисляя выражение
имеет право сначала вычислить внутри скобки сумму 1 -|----и уже потом
вычислить степень скобки ( )п. Но с бесконечностью этого нельзя делать, потому что она не есть число, и тут уже надо одновременно увеличивать л: и В скобке, и в показателе. В
Мы только что доказали, что выражение
где п означает натуральное число (т. е. целое положительное), имеет своим пределом число Непера е, когда п безгранично увеличивается: '
Простые выкладки ') обнаруживают, что рассматриваемое выражение продолжает иметь своим пределом число Непера е не только тогда, когда п, будучи натуральным числом, безгранично увеличивается, но и тогда, когда п стремится к оо, пробегая все положительные числа, как целыеД так и дробные и даже иррациональные. Более того, оказывается, что предел будет тот же самый, если п даже стремится к — со, пробегая все отрицательные (соизмеримые или несоизмеримые) числа.
Таким образом имеется предложение:
(1 \п ' 1 + 7г) = е-
когда переменное п неограниченно увеличивается по абсолютной величине, пробегая какие угодно значения: |п|->-|-оо.
Из этого предложения вытекает следующая важная теорема, ради которой, собственно, в математический анализ введено чйсло Непера е.
j_
Теорема. Функция аргумента х непрерывна
в точке х = О, стремясь к числу Непера е как к пределу, когда аргумент х стремится к нулю.
Доказательство. Аргумент X в выражении функции
1 1
у = (1-|-х)« (
может быть каким угодно: как положительным, так и отрицательным, за одним лишь исключением: он не может быть равным нулю, потому что при х = 0 формула
дающая функцию у, разрушается, переставая иметь какой-либо смысл.
г) Читатель может найти эти выкладки в более обширном курсе по математическому анализу. Мы не приводим их, потому что они длинны, не интересны и не могут дать читателю никакой новой мысли. Простая же проверка указываемого ниже факта еще не может служить оправданием помещения ее в кратком учебнике анализа.
Таким образом мы как будто бы сначала в праве ожидать при х = О разрыва рассматриваемой функции
£ j> = (i4-x)-.
Однако это лишь кажущийся разрыв, и .истинная величина" функции
в точке х = 0 равна числу Непера е.
Для того чтобы убедиться в этом, положим:
1 х = —. п Тогда выражение
(14-*? перепишется в виде:
(1 \п 14--) • п /
Если х безгранично приближается к нулю безразлично каким способом, т. е. пробегая по положительным или отрицательным числам, абсолютная величина переменного п безгранично возрастает, так что:
Inl-^-Uoo.
А мы видели, что в этих условиях
/ 1 \»
lim I 1 -!-I — е.
\ л /
Следовательно, численная величина функции
У = (1 4-х)1
безгранично приближается к числу Непера е, когда абсолютная величина |х| аргумента х безгранично умаляется.
Полное построение графика рассматриваемой функции не может быть произведено без диференциального исчисления, т. е. помощью одних только элементарных методов. Забегая вперед, мы укажем читателю, что график функции
у ='(1 4-х)*
имеет вид, изображенный на черт. 61.
Таким образом это есть непрерывная кривая, аналогичная одной ветви гиперболы. Она спускается из 4~00 ПРИ значении х = — 1 и идет, все время ниспадая, но, однако, оставаясь все время выше прямой J=l. К этой последней кривая безгранично приближается, когда аргумент х стремится к 4- оо. Итак, кривая имеет две асимптоты: прямую х = — 1 и прямую _у=1, к которым она безгранично приближается.
Ось Y пересекается нашей кривой в точке у = е, как мы это и обнаружили. Таким образом разрыв кривой
у= (1 +%)*
при х = 0 был лишь кажущимся, обязанным не недостаткам самой кривой, а лишь недостатку выражающей ее формулы
(1 4- ху,
случайно утрачивающей свой числовой смысл при х = 0.
Тот факт, чта функция >
убывает на всем промежутке
(—1<х< 4-оо),
можно обнаружить, лишь употребляя могущественные методы диференциального исчисления.
Натуральные логарифмы обладают следующим характерным свойством: по мере приближения величины а к нулю как своему пределу — бевразлично каким способом — мы всегда будем иметь равенство:
lim —— = lim In | (1 -|- <*)
а->0 Ч а-Ц) [_
In lim (1 -[-а)" =1пе=1,
ибо логарифм есть непрерывная функция, и, значит, можно переходить к пределу под его знаком (см. § 42).
§ 48. Сравнение бесконечно малых друг с другом. Когда опыт или наблюдение дают нам несколько величин
а, Ь, с, d /
одной и той же природы (объемы, веса, теплоемкости и т. д.), то первое, что мы стараемся сделать, — это узнать, во сколько раз одна из этих величин больше или меньше другой. Обычный путь для этого такой: одну какую-нибудь из этих величин берут за единицу масштаба (например величину а) и при помощи ее измеряют все остальные величины b, с, d, т. е. составляют отношения
bed
”“ • ' * ' * • • • ж
> а а а
показывающие, во сколько раз эти величины превосходят (или меньше) величину а. При помощи этого приема в дальнейшем делается излишним рассмотрение самих величин, так как все вопросы сводятся к выкладкам над числами.
Аналогичным образом поступают и тогда, когда теоретические рассмотрения приводят нас к нескольким бесконечно малым
«, 3>• • •
7 Залг. 278В. — В. Гренвпль и Н. Лузин. Чисть I
И в этом случае в целях сравнения этих бесконечно малых между собою избирают одно из этих бесконечно малых как основное бесконечно малое (как бы единицу масштаба), например бесконечно малое а, и с ним сравнивают остальные бесконечно малые
?> 1, З.---, составляя отношения:
JL т Л
а * а ’ а '
Только теперь эти отношения уже не являются числами, а лишь переменными величинами, и вполне понятно, что в целях сравнения бесконечно малых интересуются пределами, этих переменных величин.
Вот важнейшие относящиеся сюда понятия.
бесконечно малое [3 называется бесконечно малым высшего порядка (высшей малости), чем а, если отношение р
— стремится к нулю, т. е. если а
lim — = 0. а
Таким образом, например, если *
Р = За2 — а3,
то р есть бесконечно малое высшего порядка, чем а, ибо
В / За2 — а® \
lim — = lim I------) = lim (За — а2) = 0.
а \ а J
Наоборот:
бесконечно малое р называется бесконечно малым низшего порядка (низшей малости), чем а, если отноше-? к
ние — стремится к бесконечности, т. е. если а 3
Нт — — оо. а
Например, если
р = 5/а + а2, то р есть бесконечно малое низшего порядка, чем а, ибо
потому что а есть бесконечно малое, стоящее в знаменателе дроби, числитель которой есть конечное число, не равное нулю; значит:
5
§ 48] СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ДРУГ С ДРУГОМ 99 есть бесконечно большая величина. Са,мо же а есть бесконечно малое, и, следовательно:
lim i = 0.
Читатель не должен обмануться терминологией: сказать, что есть бесконечно малое высшего порядка, чем а, это значит сказать, что оно „гораздо быстрее" стремится к нулю, чем а. Значит, оно является бесконечно малым не только в сравнении с конечными количествами, но
к ' к Р
даже по отношению к самому бесконечно малому а, ибо стремится
к нулю. Таким образом, будучи исчезающе м^лым по отношению к а, бесконечно малое 3 высшего порядка является более мелким по своей величине, чем а.
Наоборот, если р есть бесконечно малое низшего порядка, чем а, то это значит, что оно „гораздо медленнее" стремится к нулю» чем а, т. е. что оно крупнее по своей величине, чем а.
Теперь естественно ввести определение бесконечно малых одинакового порядка:
бесконечно малые а и 3 называются бесконечно малыми одинакового порядка (одинаковой малости), если з
их отношение -^-стремится к пределу, отличному и от нуля и от бесконечности.
ч При этом нет необходимости пробовать оба отношения:
так как если
lim — = С, а
где постоянное С не есть ни нуль, ни бесконечность, то и .. а 1 1,т7=с’
1 где число тоже не есть ни нуль, ни бесконечность.
Таким образом, например, если
P=7a-j-3a2,
то 3 есть бесконечно малое одинакового порядка с а, ибф
11m — = lim ( — — — \ — цт за) — 7. « 01 у a J
Ясно, что одинаковость порядка есть свойство взаимное, ибо если 3 одинакового порядка с а, то и а одинакового порядка с 3-
Одинаковость порядка указывает на „сравнительно одинаковые размеры или величины" рассматриваемых бесконечно малых, т. е. на одинаковую „быстроту" их стремления к нулю.
К этому нужно добавить еще одно определение, собственно, отрицательного характера:
бесконечно малые а и (3 называются несравнимыми между собою, если их отношен не-* не стремится ни к какому пределу, ни к конечному, ни к бесконечности.
Так, например, если
то хотя р и есть бесконечно малое (ибо величина синуса не превосходит по абсолютной величине единицу, и значит |р |а |, откуда и следует бесконечная малость величины р), однако отношение
1 и 0, потому что вследствие чего никакого предела
не стремится ни к какому пределу, когда а, убывая, пробегает все числа между тогда увеличиваясь, пробегает все числа между 1 н + оо,
sin — все время колеблется между—1 и -|-1. Поэтому здесь нет lim — .
а
Существование несравнимых между собою бесконечно малых есть, по существу, новое явление, которому нет примера у постоянных количеств, так как всякие две постоянные величины всегда имеют отношение и, значит, всегда сравнимы между собою.
Прибавим, наконец, что свойства „быть высшего порядка* и „быть низшего порядка" также взаимны между собою, потому что если бесконечно малое р есть высшего порядка, чем а, то а есть, наоборот, бесконечно малое низшего порядка, чем р, ибо если
lim — =0, а
то отсюда следует, что
I- а lim-- = ос.
Р
§ 49. Порядки бесконечно малых. В предыдущем параграфе говорилось о порядке бесконечно малых лишь с качественной точки зрения, без количественной оценки этого порядка: мы просто говорили о том, что р высшего порядка, чем а, и не говорили, насколько высок этот порядок и каким образом его измерить или оцеьить.
Чтобы притти к этой оценке, рассмотрим безграничный ряд таких бесконечно малых:
а, а2, а3, а1, ..., а”, ...
ж
Легко видеть, что всякое следующее бесконечно малое есть более высокого порядка, чем все предыдущие, так как если
т < п, то
lim = lim а”-’" = 0, а
ибо разность п—т есть целое положительное число.
Раз так, тб явилось естественным рассматривать безграничный ряд бесконечно малых
_ «3 -И
а, а*, а , . .., i > • • •
как своего рода шкалу бесконечно малых, по которой можно мерить порядки бесконечно малых.
В связи с этим стало принятым называть а9 бесконечно малым второго порядка, а3 — называть бесконечно малым третьего порядка и вообще а” называть бесконечно малым n-го порядка. Само а называется бесконечно малым первого порядка, если, оно принимается за основное бесконечно малое. Далее, понятие порядка бесконечно малого расширилось и на дробные и даже на иррациональные показатели:
бесконечно малое ап называется бесконечно малым rt-го порядка, каков бы ни был положительный показатель п.
Отсюда следует:
Общее правило. Если мы принимаем за основное бесконечно малое а и если мы хотим найти порядок бесконечно малого р, мы должны постараться найти Этакое положительное число л, чтобы [3 оказалось такого же порядка, как и бесконечно малое а", т. е. чтобы предел lim -Д- = С а
оказался конечным числом, отличным от нуля (т. е. чтобы С ф 0 и С ф °°)- В этих же условиях мы скажем, что бесконечно малое р есть п-го порядка.
Пример. Найти порядок бесконечно малого
, ₽ = 4а3 + 7а2 — 5зв.
Решение. Так как чем выше порядок бесконечно малого, тем оно мельче, то среди членов, составляющих .3, естественно остановить внимание на самом крупном бесконечно малом, т. е. па члене 7аг. Поэтому естественно попробовать, не будет ли р второго порядка.
Делаем вычисление:
Иш = lim ( 4°3 + 7*~ ~ 5з8 ) = lim (4а + 7 - 5а6) =
= lim 4а + 7 + Ит (— 5а6) = 0 + 7 4- 0 = 7.
Значит, р в самом деле — бесконечно малое второго порядка.
§ 50. Равносильные бесконечно малые. Для планомерной и быстрой оценки порядков бесконечно малых, не зависящей от случайных угадываний и попыток, весьма важно ввести следующее определение:
Определение. Два бесконечно малых а и р называются ₽ оавносильными друг другу, если их отношение имеет а пределом единицу, т. е. если
lim —= 1.
а v
Равносильность бесконечно малых а и р обозначается символом а~Р-
Из этого определения следует, что понятие равносильности есть понятие взаимное, т. е. если р равносильно а, то и а равносильно р, ибо если
3 а
- Пт—=1, то и lim —— 1.
а р
Далее ясно, что всякое бесконечно малое а равносильно самому себе, т, е. а — а, ибо
lim — = 1, а
и что равносильные бесконечно малые суть бесконечно р малые одного и того же порядка, так как их отношение
• а
стремится к пределу 1, отличному от нуля (и от бесконечности).
Как пример равносильных бесконечно малых укажем на равносильность бесконечно малых а и sin а, ибо из § 77 мы знаем, что
Значит, а — sin а.
Затем так же ясно, что два бесконечно малых, а и р, равносильные третьему бесконечно малому 7, будут равносильны друг другу, т. е. если а — 7 и р~7, то и а~р.
Действительно, раз мы имеем равенства: •
lim—=1 и lim—=1, то отсюда находим:
а I a f \
Пт т = lira — • v =
Р \ 7 Р /
= lim — • lira X =1 • 1 = 1.
7 Р
Заметим, наконец, что бесконечно малое 7, содержащееся между двумя равносильными бесконечно малыми аир, а~Р, само равносильно им. Действительно, раз бесконечно малые аир равносильны друг другу, то
а р
lira-7-=1 и lim — = 1.
р а
И так как бесконечно малое у во всякий момент находится всегда заключенным между ними, то имеем во всякий момент:
или а < 7 < р или а > т > р, откуда, деля каждое из этих неравенств на а (причем совершенно безразлично, какой знак имеет бесконечно малое а), мы получим всегда одно из неравенств:
1<±<2 „ли l>i>_, а а а а
₽ а так как отношение — имеет пределом единицу, то, следовательно, и
а
У lim — = 1, т. е. т— а. а
§ 51. Относительно равносильных бесконечно малых весьма важным является следующее предложение, обнаруживающее их сущность:
Теорема. Бесконечно малые а и р тогда и только тогда равносильны одно другому, когда их разность р^-а есть бесконечно малое более высокого порядка, чем они сами.
Действительно, если разность р — а двух бесконечно малых аир имеет более высокий порядок, чем а, то это значит, что
lim ------ = 0.
а
Отсюда же следует, что
lim f —--1 ) = 0,
\ а /
или, наконец,
lim — = 1, а
что и показывает равносильность -бесконечно малых аир.
Обратно, если бесконечно малые аир равносильны друг другу, то
lim —= 1; а
8 отсюда следует, что переменная* величина --1 имеет своим пределом
а
нуль, т. е.
lira ( —-1^ = 0.
\ а / ,
Это же равенство можно написать в виде:
8 — а lim1-----= 0,
а
откуда и следует, что разность р — а имеет более высокий порядок, чем а, что и требовалось доказать.
Доказанная теорема очень важна, потому что обнаруживает, каким именно процессом можно получать равносильные бесконечно малые.
Рассмотрим, в самом деле, два равносильных друг другу бесконечно малых а и р. Обозначим через о их разность.:
8 = р — а.
Мы знаем, что аир одного и того же порядка и что 8 есть бесконечно малое уже высшего порядка. Из предыдущего равенства следует:
р = а4-а.
Значит, бесконечно малое а, равносильное бесконечно малому р, получается из р отбрасыванием (зачеркиванием или опусканием) у него части высшего порядка.
Это замечание важно, так как имеет уже практический интерес: имея сумму двух бесконечно малых а-]-8 разных порядков, мы просто зачеркиваем бесконечно малое высшего порядка; полученное новое бесконечно малое а равносильно всей сумме а-{-8.
Пример. Из сложного бесконечно Малого
3 sin а — 5аа
получить более простое, равносильное ему. 1
Решение. Так как sin а есть бесконечно малое первого порядка, а член 5а3 третьего порядка, то мы просто зачеркиваем его и таким образом получаем более простое бесконечно малое 3sina, равносильное данному первоначально
3 sin я — 5а3, т. е.
3 sin а — 5з3 ~ 3 Sin а.
Чтобы сделать совсем практическим это правило, докажем сначала следующее предложение:
Лемма. Сумма р -|- f 8 -]-Хограниче иного числа бесконечно малых р, 7, 8, ..., К высшего порядка, чем а, есть бесконечно малое опять более высокого порядка, чем а.
В самом деле, обозначим эту сумму через а:
° = P-H+S+. • 4- х.
Так как каждое из бесконечно мальЫ р,„Т, 8, ..., X есть более высокого порядка, чем бесконечно малое а, то имеем:
В t 8 X
lim —= 0, lim—= 0, lim — = 0, ...,lim— = 0, а а , а а
откуда и следует, что отношения
JL JL ± ... 1 а ’ а ’ а ’ ‘а суть величины бесконечно малые. Так как эти отношения имеются согласно предположению в ограниченном числе, то по первоначальному
свойству I бесконечно малых (см. § 38) сумма этих отношений есть величина бесконечно малая. Значит:
llm (1+1+А + ...+2А=о, \ а а а а /
откуда
в _1_ -г _j_ г _л_.. । х lim OU-—' •••Т = о.
а
Значит, рассматриваемая сумма
есть опять бесконечно малое более высокого порядка, чем а, так как а lim — = 0, а
что и требовалось доказать.
Доказанная лемма сразу приводит к следующему практическому правилу для отыскания равносильных бесконечно малых:
Практическое правило (упрощения бесконечно малых): если имеется сумма a-f-p-f-7ограниченного числа бесконечно малых и если среди членов этой суммы имеется лишь один член наиболее низкого порядка, то можно зачеркнуть все остальные члены, так как вся сумма равносильна этому одному члену.
Чтобы оправдать это правило, возьмем сумму
0 = а + ?+‘г+5+--- -Н ограниченного числа каких-нибудь бесконечно малых
а, Р, 7, 3, ..., X
и допустим, что среди них только одно имеет самый низкий порядок; пусть это бесконечно малое наинизшего порядка будет а. Тогда бесконечно малые р, у, о,..., X будут более высокого порядка, чем а. Зна-<ит, по предыдущей лемме, их сумма
(Р + -Г + 8Н----+Х)
будет также бесконечно малое более высокого порядка, чем а.
Написав теперь всю данную нам сумму о бесконечно малых в виде о = «+(? + т + 8-Н.• + >•), мы видим, что скобка представляет собою бесконечно малое высшего порядка, чем первое слагаемое а. Значит, согласно изложенному выше, вся сумма о равносильна а:
а~а, что и требовалось доказать.
Правило это формулируют иногда не совсем верно, говоря, что при отыскании равносильных бесконечно малых можно пренебречь бесконечно малыми высших порядков. Дело
в следующем: фраза ьта совершенно верна, если член на и низшего порядка имеется в сумме только один; мы доказали выше законность именно такого пренебрежения. Но если членов наинизшего порядка будет несколько, то они могут взаимно уничтожиться, и тогда правило пренебрежения свелось бы к тому, что и вообще все члены можно вычеркнуть.
Пример!. Упростить бесконечно малое
£ = (1 — cos а) -|- 16а3 — 6а5 + За — 42а4.
Решение. Так как
1 — cos а = 2 sin2 у, то скобка (1 — cos а) есть величина бесконечно малая и притом второго порядка, так как '
. ° °
sn2 2’
. а
и, значит, sin у есть бесконечно малое первого порядка, а его квадрат.
sin2 имеет второй порядок. Так как среди всех членов, образующих бесконечно малое р, член За наинизшего порядка, и притом только один, то, зачеркивая все остальные члены, мы получаем р—За.
Пример 2. Упростить бесконечно малое
Р = (1 — cosa)2 + 3a-j-16а3 + 5а‘ — За + ба3.
Решение. Член (1 — cosa)2 четвертого порядка, ибо (1 — cosa) второго порядка. Так как наннизшнх членов За и —За два и они взаимно уничтожаются, то после приведения получим:
Р = (1 - COS a)2 + 16a3 + 5a4 -f- 6a\
Теперь наинизший член 16a3 только один. Отсюда
Р~ 16a3.
Отметим, наконец, что если при отыскании порядка бесконечно малого р мы нашли, что этот порядок равен п, п>0, потому что
lim-4 = С, Л
где С есть число, отличное от нуля и от бесконечности, то беско
нечно малое р равносильно бесконечно малому Са*.
Р ставляя отношение видим, что оно имеет своим Са
Р 1 . 3 с
11т с1,т?“сL
Действительно, со-
пределом единицу:
§ 52. Первый Принцип Анализа бесконечно малых. Математический анализ пользуется бесконечно малыми как в высшей степени ценным инструментом для отыскания глубоко скрытых соотношений между конечными количествами соотношений, которые" ускользают от нашего ума, когда мы пользуемся другими методами, и которые вскрываются, когда мы прибегаем к бесконечно малым.
Анализ бесконечно малых состоит из двух ветвей: диференциального исчисления и интегрального исчисления. Оба эти исчисления широко пользуются рассмотрением бесконечно малых, но употребляют их по-разному.
Диференцнальное исчисление рассматривает конечные количества, между которыми надо открыть соотношения, как пределы отношений бесконечно малых.
Интегральное исчисление рассматривает конечные количества, между которыми надо открыть соотношения, как пределы сумм безгранично возрастающего числа бесконечно малых.
В связи с э'тим оба указанных исчисления сильно заинтересованы в упрощении бесконечно малых и притом в таком их упрощении, которое не изменяет ни в какой степени и ни в каком отношении окончательных результатов.
Мы формулируем теперь так называемый первый принцип анализа бесконечно малых, называемый еще иначе принципом диференциального исчисления. '
Первый принцип бесконечно малых (принцип диференциального исчисления). При отыскании предела отношения двух бесконечно малых каждое из них можно заменить равносильным бесконечно малым, не изменив нисколько этого предела.
а
В самом деле, пусть надо отыскать lim —, где а и 3 — какие-нибудь Р
сложные бесконечно малые. Пусть а равносильно а' и р равносильно 3', так что а ~ а' и 3 — ?' Допустим, что бесконечно, малые а' и £' гораздо проще данных первоначально бесконечно малых аир.
Из тождества a' af а 3 ° ’ 3 * ?' заключаем, что а' а' ,. а 3
lim .-J- = lim — • lim -j- • lim ? а 3 ?
А так как а и а' равносильны, так же как и р и р', то
а и '
lim-lr = 1,
3
тку да а' а
lim-7-7- = lim —, 3 3
что и доказывает первый принцип бесконечно малых.
Читатель отметит всю силу и все значение этого принципа, рассмотрев хотя бы такой пример. *
Пример. Найти предел от ношен и я двух бесконечно малых 8а3 — 4аг + 3 sin а — 6а7 4* 18 (I — COS я) 1Ш 4а7 + (1 - COS а)3 4- 2а - 17 а6 4- ба3 “
Решение. Заменим числитель и знаменатель этого отношения равносильными бесконечно чалыми, для чего, как мы знаем, надо просто зачеркнуть члены высших порядков (если член низшего порядка один в числителе и соответственно один в знаменателе).
Так как (1—cos а) есть бесконечно малое второго порядка, то наиннзший член в числителе только один: 3sina, и наиннзший член в знаменателе тоже только один: 2a.
Значит, в силу принципа искомый предел равен просто
§ 53. Приложение первого принципа. Мы уже знаем (§ 41), что если какая-нибудь функция
непрерывна на отрезке [а х Ь], то приращение Ьу этой функции д.У = /(*+д*)—/(*)>
возникающее от получения аргументом х приращения Дх, есть величина бесконечно малая, когда приращение Дх аргумента бесконечно мало.
Значит, наличие заданной непрерывной функции
У =/(*)
влечет за собою обладание двумя бесконечно малыми величинами Дх и Ду. из которых первое, Дх, находится всецело в нашем распоряжении, завися только от нашего желания; второе же, Ду, есть уже несвободное бесконечно малое, ибо его величина обусловливается величиной бесконечно малого Дх.
Таким образом у нас имеются две одновременно бесконечно малые величины Дх и Ду.
Основною задачею диференциально го исчисления является сравнение этих двух бесконечно малых путем рассмотрения их отношения
Ау
Дх
и вычисления предела этого отношения.
Итак, основною задачею диференциального исчисления является определение предела отношения некоторых двух специальных бесконечно малых. И читатель легко теперь оценит значение и помощь, оказываемую первым принципом анализа бесконечно малых при отыскании предела этого отношения.
Этот предел, постоянно рассматриваемый диференциальным исчислением, получил особое имя и называется производной отданной непрерывной функции y = f(x). Это название оправдывается тем обстоятельством, что рассматриваемый предел, разумеется, зависит от
_ Ду
буквы х, ибо для различных значений аргумента х отношение будет различным и различным же будет и предел этого отношения, т. е. он будет зависеть от аргумента х. Поэтому это будет некоторая новая функция аргумента х, выведенная (произведенная) отданной функции у=/(х). Она-то и называется производной и обозначается иногда просто f(x) или у'.
Пример 1. Найти производную функции у = х2.
Решение. Вычисляем сначала приращение этой функции:
Ду = (х + Дх)2 - х2 = х2 + 2хДх + (Дх)2 — х2, значит:
Ду = 2хДх (Дл)2.
Составляем отношение:
Ду 2хДх + (Дх)2 Дх “ Дх
Если приращение Дх стремится к нулю, то приращение функции Ду есть бесконечно малое, являющееся суммою двух бесконечно малых различных порядков (бесконечно малое Дх, как находящееся в нашем распоряжении, считается за основное): первого 2хДх и второго (Дх)2. Отсюда, вычеркивая бесконечно малое высшего порядка, на основании первого принципа имеем:
„ Ду „ 2хДх „ Нт = Нт —г— = 2х. Дх Дх
Значит, производная от х- есть 2л, что мы напишем в виде:
(х2)' = 2х.
Пример 2. Найти производную функции у = х2.
Решение. Вычисляем приращение Ду этой функции:
Ду = (х -|- Дх)2 — х2 = х8 + Зх2Дх + Зх (Дх)2 4- (Дх)2 — х2, Ду = Зх2Дх + Зх (Ах)2 + (Дх)2.
_ Ду ,
Составляя отношение и вычеркивая бесконечно малые высших поряд-
ков, имеем: д 3хаДх
lim = Urn —т— = Зх2.
Дх Дх
Значит, производная от х3 равна Зх2, т. е. (х3)' = Зх2'.
УПРАЖНЕНИЯ.
К §33.
1. Показать, что lim cos х = 1. Х->0
Решение. Нам надо показать, что, начиная с некоторого значения х и при всем дальнейшем изменении х, будет оставаться справедливым неравенство:
| cos х — 11 < в ял я всякого произвольного, положительного, сколь угодно малого числа е. Согласно известным формулам имеем:
I cos х — 11 = 11 — cos х | = 2 sin2 )*-.
Из тригонометрии известно, что '
| sin а | < о I.
Полагая ° = получаем:
2sin’ Т<2(т)2 = 4<хг
Таким образом можем написать:
I cos х — 11 < л 2-
Следовательно, если мы покажем, что х2<е, то тем самым установим справедливость и нашего неравенства:
| cos х — 11 < е.
Так как х неограниченно приближается к нулю, то наступит такой момент, когда |х| станет меньше с и при всем последующем изменении будет оставаться меньше е, как бы мало е ни было. Так как по существу вопроса мы можем считать х величиною, меньшею единицы, то подавно будем иметь:
|х|2 = Х2<«, • что и доказывает справедливость требующегося неравенства.
2. Показать, что lim = у ш-их> х
Решение^Составляем основное неравенство: У
|^-’|<- *
и производим следующие преобразования:
l*L±3_2l |2.< + з_ I |2 + 2_2[ = |3| 3 .
I х I I х х I I х- I I X I |х|
Следовательно, нам нужно показать, что, начиная с некоторого значения х и при всем дальнейшем изменении х, дробь станет и будет оставаться меньше любого наперед заданного положительного числа е, как бы мало е ни было:
3 „
1—; <Е-
И
Но, очевидно, для этого нужно, чтобы было справедливым неравенство:
Так как х неограниченно возрастает, то среди значений х требующееся значение необходимо найдется. Очевидно также, что и при дальнейшем возрастании х последнее неравенство будет оставаться справедливым. А тогда будем иметь:
3
I* I< Е’
3. Показать, что
lim fl +— 1.
х-ко к х /
4. Показать, что
„ Зх - 5 3
Нт-^-
5. Показать, что
11m
4.
6. Показать, что
.. 7-/2х V 2 2х - 2 •
вправо от отрезка АВ = а. Будем
7. Точка С лежит ограниченно вправо. Показать, что
11т ~ВС ~
точку
С удалять ве-
2
Решение. Обозначим длину отрезка ВС через х. Тогда АС = а х.
Составляем неравенство:
/
(если
Так как в данном случае все величины положительны вление движения вправо положительным и предполагать, что точки располагаются слева направо в порядке букв алфавита, которыми они обозначены), го
считать напра-
а
а
Так как длина х неограниченно возрастает, то, начиная t некоторого значе-(I J
ния х>~ и ПРИ всем дальнейшем движении точки С, будем иметь:
* в
8. Точка С к левому концу
лежит внутри отрезка АВ — а и неограниченно приближается отрезка. Показать, что
Нт 4^ = 0.
оС.
лежит внутри отрезка АВ = а и неограниченно приближается
9. Точка С
к правому концу отрезка. Показать, что
и АВ 1
Пга АС ~ Е
34.
ри х, стремящемся к нулю, предел переменной величины ' slnx
У = -7-
есть единица. Исследовать, каким способом эта переменная величина приближается к своему пределу.
Решение. Пусть х приближается к нулю каким угодно способом. Так как
sin (— а) = — sin а, , sin X
то дробь —— для х, близкого к нулю, будет положительна как для положительных, так н для отрицательных значений х. Принимая во внимание неравен-
ство | sin х | < | х [, заключаем, что при любом значении х (близком к нулю) есть правильная положительная дробь. Следовательно, разность 1-------будет оставаться всегда положительной. А это означает, что пере-
менная у приближается к своему пределу, оставаясь меньше его.
2. При х, стремящемся к а, предел переменной величины
у = х — а
есть нуль. Выяснить способ приближения у к своему пределу.
3. При х, стремящемся к нулю, переменная величина у = e*slnx
имеет своим пределом нуль. Выяснить способы приближения этой переменной к своему пределу: 1) если х принимает только положительные значения; 2) если х изменяется, принимая только отрицательные значения; 3) если на изменение х не накладывается никаких условий.
4. Предел y = -^-Vx при х, стремящемся к а-, есть а. Выяснить способ приближения у к своему пределу.
К § 35, 36, 37.
1. Показать, что sinx при х-> О есть величина бесконечно малая.
Решение. Нам надо показать, чю, начиная с некоторого значения х и при всем дальнейшем изменении х, для всякого положительного сколь угодно малого числа е будет соблюдаться неравенство:
I sin2 х | < е.
Так как х стремится к нулю, то, начиная с некоторого значения х, абсолютная величина | х | будет только убывать при изменении х. Поэтому какое бы постоянное положительное малое число е мы ни задали, обязательно найдется значение х, удовлетворяющее неравенству | х |< е и условию, что это неравенство будет оставлться справедливым и для всех последующих значений х. Атак как | sin х | < I х |, то тем самым будет осуществляться и неравенство:
I sin х | < е.
2. Показать, что
lim cosx = 0. к
® * а’
Решение. Так как нам надо показать справедливость неравенства:
| cos х | < с,
относящегося к абсолютной величине cosx, то, будет ли х приближаться к изменяясь в первой четверти или во второй или принимая значения, соответствующие то дугам,
лежащим в первой четверти, то во второй, — на справедливость написанного неравенства это обстоятельство не будет оказывать никакого влияния. Поэтому
какое бы постоянное, как угодно малое, положительное число е мы ни за-
дали (например ОР) (черт. 52), в силу того, что х->-у, всегда наступит такой момент, когда х примет значение, при котором | cos х | станет меньше е (на нашем чертеже, например, при х = AR их — APR' и при последующем изме-
нении х будет оставаться меньше е. А это и значит, что cos х при х есть величина бесконечно малая.
К § 38.
1. Показать, что
lim sin х = 1.
2
Решение.
sin ж = cos
На основании теоремы IV можем написать:
lim slox = lim cos
Положим
Тогда, при х -> ,
Следовательно (задача 1 к § 33):
разность у — х -► 0, т. е. у -* 0.
lim sinx = lim cos
X
у — xj = lim cos у = 1.
2. Показать, что
lim tg x = 0. x-M>
2
Указание. Применить теорему III.
3. Показать что,
4. Показать, что
lim ctgx = 0.
2
lim
1
- 2‘
lim
= 5.
lim [3 (sin a + 2 COS a) — ctg a] = 3.
lim
2 cos x — 3 tg x _ .. ? ’ .a
з
5.
6.
7.
9/ — Р
8. lim ~~=0.
г->з /14- 1
9. На отрезке длиною а, как на гипотенузе, построен равнобедренны# треугольник. Катет этого треугольника служит гипотенузой нового равнобедренного треугольника, и т. д. Найти предел суммы площадей треугольников.
' Отв.
К § 39 и 40.
1. Показать, что secx при х -> у есть величина бесконечно большая.
2. Показать, что
lim cosec х = оо.
♦ х-И)
8 Зак. 2168. — В. Г р а к о и л ь и П. Луаны. Часть I
lim tgx = со.
3. Показать, что
4. Показать, что
К § 46.
Во всех нижеследующих примерах требуется найти истинное значение
Hm ctgx = оо.' х-М>
функции при указанном в каждом отдельном случае значении аргумента.
1. х® — 1 _ 1 Отв. 3.
1 при X = 1.
Решение. Так как
л3~1 _ (х-1) (х2 + а-+1) _ . х— 1 х- 1 Г-*-Г
при всех значениях х, за исключением х=1, то
Нт = 11т (х2 + х + 1) = 3.
Ж->1 Х — 1 х->1
2. — - при х = 1. Отв. 0. х (х — 1)
4xs + Зх2 — 5х _ _ 5
3. l-5 при х = 0. Отв. ——, 6ж Ь
Указание. Сократить дробь на х.
4. хЗ(х-З) (2х+1) п_и„_3 (х - 3) (X - 2) Р 3‘ Отв. 189.
5. х2 + Зх-Ю 3x2 --5х -2 "Р"* = 2- Отв. 1.
6. £±W±iy_ приз, = _2. п 2 Отв. — — О
7 — Г1 + 2/2—5Т + 3 , , /2 + 4Г2-7< + 2 "РИ ' ‘ Отв. 0.
(хЦ-й)"-. Л хп (л — целое положительное число) при h = 0,
Отв. лх’*-1.
Решение. Разлагая (x + h)n по формуле бинома Ньютона, получаем:
„П | — 1». I П(П— 1) ^я~-2 «Л I I ьП „»»
(х + Л)"-х"_Х + "* А + —2--------Л»+...+Л -х
h ~ h ч “
= лх""1 + xn~3h + я(я ~ \(я л”’ 8Л« + ... + Л’*”1,
z о!
откуда следует, что при Л -> 0 выражение
h
п /Г+х-1 Л _ 1
9. ---------- при х = 0. Отв.
Решение.
откуда
X — 1 = X =___________1
X х(/1+х+1)~ /Г+1-ri ’
/Г+^-1 1 1
lim---------= Jim г ----= —,
х-нэ х х-н> у 1 + х + 1 2
Замечание. При определении предела иррациональной дроби прием переноса иррациональности из числи|елч в знаменатель (или наоборот) весьма часто быстро приводит к цели.
/х + й - / х h
10.
11.
12.
Решением
___1______1
/х + Л V х
Л
V у-^-<Р—а
/ У+Л’ - ь
при Л = 0.
при Л = 0.
при у = 0.
Отв. ---— .
2 V х
1
2х/х‘
£ а
// + Ц2-Д = ( /У +д2-«'> {VУ"' Ч-дНв) (1<У24-й2-|-й) = '+ ^-|-й
'/?+р - ь “ (уу-»+Т2 _ Ь) (к ?Т^+*) (// + “Ч-д) /?’+^+в ’
»-х> Vу2 + д’ + а а
— yf х
13. —------ прих = 1. Отв. 3.
/ х - 1
Решение.
х2- /7 = / х (/Г3 - 1) = /х (/х- 1) (х+ /х+1)
/х-1 /х-1 /х-1
(разность /х3 — 1 есть .разность кубов*);
lim х (х + /х + 1) = 3.
.Г-Н
14. 1 при t = 1. Отв. — •
V t-\ 3
Решение.
= (1/7-1) (р + 1) (^ + ^~/ +1) =
]//-i (/7-1) (/7 + 0 (у77+ /7 +1)
= (/1 + D (/-1)____= /~/ +1
О -1) (к 7-+к' 7 +1) у 7+^7 +1
2 Следовательно, предел данного выражения при t -> 1 равен *у. о
х
15. -т---- прих = 0. Отв. 1.
sin х г
16. при <р = 0. Отв. 1.
Решение.
lim *** Ф-я> Ф
sin ? 1
f cos ?
= 1.
17.
при х = 0.
Отв. 2.
Решение,
sin 2х 2 sin 2х
Обозначим
2х=у. При х = 0, = 0. Следовательно, будем иметь:
„ sin2x ..
11m ------= lim
= 2.
18.
sin2 х _
—5— при х = 0.
Отв. 1.
19.
при х = 0.
Отв. 0.
20.
1 — sin t
Решение.
2 '
при / = -J
Отв. 0.
, . , sin —— sin t
1 — Sin t 2
7"'
7 +
2 cos---
s,n——
2 *
cos
-J + Z sln—2—
2 t 2
Предел первого сомножителя при t -> равен нулю. Для нахождения предела второго сомножителя положим
2 ~ *
2
При t = -у переменная х = 0. Следовательно, будем иметь:
2 *
sln-^— lim ---—
sin x , = 11m--------= 1,
откуда окончательно:
21
- T — * 2 2
2
1 — sin t . n . n lim ----= 0-1=0.
sin2 v—sin’ й
- - "РИ у = a-
n sin 2a
Отв. —д— 2a
Решение.
sin-y —sin2 л _ (sin_у 4- sin a) (sin у — sin а) _
>'2 „2 ~ (у (у _ д)
п. У~Ьа у— а у-}-а . у — а
2 sin < cos — • cos sin —
- у+а ‘ у-а ’
2
откуда видно, что при у -> а предел первой дроби равен:
2 sin д cos « _ sin 2л 2л — 2л ’
а предел второй — единице. Следовательно, искомый предел равен sin 2л ~2а~'
22.
Отв. |.
Решение.
Разделим числитель и знаменатель на 15х; тогда
будем иметь:
sin 5х sln3x _ 1
15х 15х — 3
sin 5х . 1 sin Зх Зх
5х
1 _ 5
5 3 *
откуда видно,
что при х -> О отношение
sin 5х
——стремится к 4-sin Зх 3
23-
Решение.
(" - г) tg у Положим
Отв. 2.
при г = п.
Тогда
Пт (п — е) tg -у= Нт * S-H)
= Нт
2 cos у
cos
sin
24.
при х = О
У 1 — cos х
2
= 2
Решение.
2
lim — - --= lim
»-м> у 1 —cosx t-»o
1 — cos х
2
= Нт
Sin —
25.
Xs sin х Л
—----------при х = 0
4(1 — cosx)s
Отв. 1.
26.
— sin-j----------- при Л = 0.
27.
Ърих=-
От. % „ 1 Отв. .
2
h
Решение. Положим х = ^-4-у. Тогда будем иметь:
lira tg Чх ctg (х + = lim ctg 2у • tg у = lim (1 ~ = 1.
К \ 4 / v-M) * 1g у 1
^4
28; arcslin х ПрИ х = 0. Отв. 1.
Решение. Положим тогда
Следовательно.-
29.
arcsin х=у,
X = sin у.
arcsin х у ,
Jim--------------= lira —f— = 1.
.г-x; x j»-m> s'n .У
arctg a (arctg a + 2) a (arctg a — 3)
при a = 0.
Отв. — . о
It
•y —у — arccos^
30.----------------------------------при у = 0. Отв. 0.
у + у —arccosy
Решение s arccos у = t, у = cos t. % я
—у — arccosy у — cos t — t
lim ---------------= lim ---------------
y*° -£-+y — arccosy + cos < — t
Положим
Тогда будем иметь:
u
~ — cos t - t lira -------------------
у + cos t - t
,, и — sin и lim —--u_>o u + sin u
1 sin lim -------= 0.
«-m> 1 4.
~ u
31. Определить значения /( — 0) и /(4-0) функции
Ome./<-0)^ -1: /( + 0)= 4.1.
Решение. Как известно, абсолютная величина функции
стремится к единице при х, стремящемся к нулю. Но когда х пробегает по отрицательным значениям, функция /(х) остается всегда отрицательной.
Поэтому
/(-0)=-1.
Очевидно:
/(4-0)= -И-
Следовательно, в точке, где х = 0, функция имеет разрыв.
32. Определить значения /( — 0) и /(4*0) функции
/ (х) = arcctg .
Отв. f ( - 0) = f (4- 0) = 0.
К § 48-52.
1. Показать, что при х -* у cos х есть величина того же порядка малости, что и ctg х.
2. Если порядок величины a (lim а — 0) принять за единицу, то какими числами выразятся порядки бесконечно малых
-° ~ -, i/ sin а, 1 — cos а 7 Отв. 1; -4 ; 2.
а “ и
Решение. 1
а ... (Sin а)3 ,
lim -----= — 1; lim -J——— = 1;
<i->o в__ «-ю о э
а — 1
1 2 51П’ O’ 1
Пт’-^Л^Нп,-----------' =i-
а-ю а2 а-м) °* *
3. Бесконечно малые р и у имеют относительно бесконечно малой а соответственно порядки 2 н 4. Определить порядки бесконечно малых
₽±Т, ₽Т, Отв. 2; 6; 2.
Решение. Из условий задачи имеем:
lim = a; lim ~ = Ь, а* а4
или
4=я+’; -^г=ь+'{'-
где и суть бесконечно малые (см. § 36); отсюда
х
= да14- фа2; у = Ьа* 4" 'j'»4. следовательно:
Р ± у = да2 4- 9а2 ± 6а4 iz
откуда видно, что р±у — величина второго порядка малости относительно а;
lim --у-Т- = а.
а2
Аналогичным образом определяются порядки малости и остальных величин.
4. Показать, что если дуга окружности данного радиуса R стремится к нулю, то хорда, стягивающая г ту дугу, есть бесконечно малая того же порядка, что и рассматриваемая дуга, а стрела (отрезок между хордой и дугой радиуса, перпендикулярного к хорде) — высшего порядка. Определить порядок малости стрелы относительно хорды.
0
Черт. 53.
Решение. Обозначим радиальную меру угла АОВ через а (черт. 53). Тогда дуга
АВ = Ra, а хорда АВ = 2R sin у; откуда
АВ Ctfsin-^-1, когда а-> 0;
В АВ Ra
CD = R -— OD = R — R cos -y =1R sin2 .
Следовательно:
CD 27?sin2-^-AB~ *e ’
откуда видно, что стрела CD — бесконечно малая второго порядка малости относительно дуги АВ, а следовательно, и относительно хорды АВ.
5. Показать, что при х-у 0 бесконечно малые величины 2 (tg х — sin х) и
х3 равносильны. __________
6. Показать, что при х->0 бесконечно малые величины |/х’4-Ух3и tg х У~х равносильны.
Решение.
tg Ух Ух ~ i/х Ух (см. пример 16, стр. 115):
/л3 + Ух3' = ’ х3 + хУх Ух Ух Г х УУ
|’ х У х + 1 —► 1 при х—► 0.
А так как две бесконечно малые, равносильные порознь третьей, равно сильны между собой (см. § 50), то
Ух3 + Ух3 ~tg f/x Ух.
7. Пользуясь теоремами § 51 и 52, найти пределы следующих выражений:
sin Зх S,n 2 arcslnx arctg Зх
sin 2х* tg 2х ’ sin 4х ' arc sin 2x _ 3 11.3
Ome. -2 , 4 , 4 , 2 •
Решение. Так как
' sin x ~ x; tg x~x; arcslnx ~x; arctg x ~ x,
то вопрос сводится к нахождению пределов выражений (х->0):
Зх У_. Зх 2х’ 2х ’ 4х 2х
8. Решить, применяя теоремы о равносильных бесконечно малых, примеры 15, 16, 17 и 20 данные на стр. 115—116.
9. Доказать, что если а — а' и то ар~а'рл.
Решение. Из условия задачи следует:
lim -Л- = 1, llm-L=l.
ай а В
Следовательно: lira —= 11m —? • lim-£7-= 1-1.
а'р а р
arctg — «arcsin — • arctg
,0. ------------*---------
S|n 1 . tg * . Sin -!= « arctg ~
x x V x V x Y x
11 lim ln 0 + + 4x2)
,r^oo In (1 -x + 2x2-7.v2) '
Оте. 2.
Отв. — 2.
Решение. Покажем прежде всего, что
1п(1-]-а)~а при я->0:
1’
„ In (1 + а)
lim -----!—- = lim In (1 + а)
а->0 ® а*>0
= In е = 1
(с.1, стр. 97). Поэтому
1Ч'”,(’1пА2-',етг)-
7 Отв.------.
п
Решение. Положим
Тогда будем иметь:
и I < -V — 7 Um sin —=—
х->? \ 2
lim
У>0
+
ДОПОЛНИТЕЛЬНЫЕ ПРИМЕРЫ И ЗАДАЧИ НА НАХОЖДЕНИЕ ПРЕДЕЛОВ.
Показать, что
1. lim х->оо
0.
3. lim 1 = — oo, ei x — a ели х, приближаясь к значению а, возрастает.
4. lim ДГ-HJ ——- = + оо, если x, приближаясь к значению а, убывает.
5. lim Х-ъоо Зх2—1 2х °°‘ 6. lim ул-оо 4>2 + 1у - 1 2уг = 2.
7. lim x-*oo 2х24-5х —3__2 Зх2 — 7х — 1 3 JB. lim 4 —z _ 8z -|- 3 £ " 8 '
9. lim x->oo 2х2 + Зх - 2 _ 2х* + 5 10. lim Х->ОО х» — 4х - 7 х2 + 2 = 1.
И. lim X->0 3x3+ бх2 2л4 15х2 “ »• 11 11ш 2<з+ ЗР _ Р оо.
13.
lim X-XJO
5х2 —2х
= оо.
14. lim (Ухф 1 - Ух) = 0. Х-КЗО
15. Нт (Ух»ф1-х) = 0. Х->СО
16. Пт (Ух3 + ах + Ь-Х-Кзо
- + *) = *--'.
18. lim = оо.
Л. /(1 - »1п х)2
1.24-2- 3+...+Л(л-1-1)_1
2э. нтп-----------q-----------= .
Л-XJD П «
/ 1 \л+3
28. lim (1 + — ) =е.
п-ю \ nJ
29. Нт [л {In (л4* 1) — In л}] = 1. П->СО
30. Нт (1 + cot х)6,е'х = е5.
31. Как изменяются корни квадратного уравнения дх!+6х + се=0, если коэфициевты Ь и с остаются постоянными (Ь ф 0), а коэфициент а стремится к нулю? __
32. В прямоугольном треугольнике один из катетов равен х, а другой 2 Ух. Найти предел разности между гнппотенузой и катетом х и предел отношепия гипотенузы к тому же катету при х —> оо.
Отв. 2; 1.
33. Отрезок длины а прямой разделен на л частей, и на каждой части по одну и ту же сторону прямой построен правильный треугольник. При неограниченном возрастании п получающаяся при этом построении ломаная линия приближается к отрезку. Стремится ли и длина ломаной к длине а отрезка?
ГЛ ABA IV
ДИФЕРЕНЦНРОВАНИЕ.
§ 54. Введение. Теперь мы должны перейти уже к систематическому исследованию того, каким именно образом изменяете» величина у рассматриваемой функции /(х) при изменении аргумента х.
Основная задача диференциального исчисления и состоит в планомерной оценке этого изменения функции.
Исследуя задачи этого именно рода, Ньютон ') и пришел к открытию основных начал диференциального исчисления — этого могущественного научного орудия в руках современного естествоиспытателя.
Приращение. Указанная планомерная оценка изменения величины функции, происходящего по причине изменения величины аргумента, достигается сравнительной оценкой приращений функции и аргумента.
Вообще приращением какой-либо переменной величины, переходящей от прежнего числового значения к новому, называется тот прибавок, который надо придать к ее прежнему значению для того, чтобы получить ее новое значение. Значит, приращение переменной величины есть просто разность между новым значением и прежним, получаемая вычитанием прежнего значения из нового9).
Приращение переменной величины х обозначается символом Дх, так что если прежнее значение этой переменной величины обозначено буквою х, то новое (приращенное) ее значение будет:
х-{-Дх.
Символ Дх произносится „дельта х“. Предупреждаем, что символ этот никоим образом нельзя читать „дельта, умноженное на х* или „дельта раз х“, потому что буква Д неотделима от буквы х, без которой она не имеет никакого смысла; читатель уже знаком с аналогичным явлением в элементарной алгебре, где 1g А имеет определенный числовой смысл, обозначая логарифм числа А, тогда как буквы 1g, отделенные от буквы А, не имеют никакого смысла (числового).
’) Исаак Ньютон (1642—1727) был человек выдающейся гениальности. Он развил учение о днференциальном исчислевии под именем флюксий. Хотя Ньютон уже пользовался им в своих исследованиях еще в 1670 г., но впервые обнародовал его лишь в 1687 г. в своем сочинении „Phllosophiae Natural!» Principia Mathertiatlca'. Это было главным произведением Ньютона. По словам Лапласа, .оно навсегда останется самым превосходным из всех творений человеческого ума1*.
'-) Для более подробного знткомства с понятием приращение читатель должен обратиться к § 25 и '.7.
Очевидно, что приращение переменной величины вовсе необязательно положительно: оно будет отрицательным, когда новое значение меньше прежнего, что будет, например, тогда, когда переменная величина убывает. Аналогичным образом
Ду означает приращение у,
Дг означает приращение z,
До означает приращение переменного о,
Д/(х) означает приращение функции f (х) и т. д.
Если в равенстве y=f(x) независимое переменное х получит приращение Дх, то под \у всегда разумеют соответствующее приращение функции / (х), т. е. приращение зависимого переменного у.
Мы уже сказали, что приращение Ау функции у есть тот прибавок, который надо придать прежнему значению функции, чтобы иметь новое ее значение. Сообразно этому, вычисляя это приращение Ду, всегда надо помнить, к какому именно начальному (прежнему) значению у оно придается; надо помнить также и о начальном (прежнем) значении аргумента х, которому соответствует начальное (прежнее) значение функции, равно как и о том приращении к нему Дх аргумента х, которое вызвало приращение Ду функции.
В качестве примера рассмотрим функцию
у = х2.
Если начальное значите аргумента есть х = 10, то начальным значением функции будет у =100. Если новое значение аргумента 12, то это значит, что приращение аргумента Дх = 2. Новым значением функции будет 144, и, значит, приращение функции Ду = 44. Если же новое значение аргумента равно 9, то это значит, что приращение аргумента Дх=—1. Но тогда новое значение функции есть 81, и, следовательно, ее приращение Ду= —19.
Вообще, если функция у = f (х) — возрастающая (как, например, х2 в промежутке 0 < х < оо), то ясно, что если Дх положительно, то и Ду будет положительным, и если Дх отрицательно, то и Ду тоже будет отрицательным. Значит, оба приращения, Дх и Ду, в этом случае имеют всегда одинаковые знаки.
Если же функция у=f (х) — убывающая, то положительному Дх отвечает, очевидно, отрицательное Ду, потому что новое значение у меньше прежнего, а отрицательному Дх сувечает уже положительное Ду, ибо теперь новое значение функции больше прежнего. Значит, Дх и Ду в этом случае всегда будут противоположных знаков.
Наконец, мы знаем (см. § 41), что если функция
непрерывна и если приращение Дх аргумента стремится к нулю:
_ lim Дх = 0,
то и приращение Ду функции также будет стремиться к нулюг
lim Ду = 0,
т. е. оба приращения, Дх и Ду, суть одновременно бесконечно малые.
§ 55. Сравнение приращений. Возьмем функцию
У = х\ (1)
Пусть начальное значение аргумента есть х, и пусть это начальное значение X получает приращение Дх.
Значит,
X есть начальное (прежнее) значение аргумента и
х-|-Лх есть новое (наращенное) значение аргумента.
Так как, когда аргумент имеет прежнее значение, то и вся функция имеет тоже прежнее значение, то обе части равенства
У = х9 (1)
являются начальным (прежним) значением функции.
Когда же аргумент делается новым (наращенным), то и соответственное значение функции становится точно так же новым (наращенным); поэтому обе части равенства
у-|-Ду = (х4-Дх)2 (2)
являются новым (наращенным) значением функции.
Чтобы найти приращение Ду функции, нам теперь достаточно просто вычесть из нового равенства (2) прежнее равенство (1). Это вычитание нам даст:
Ду = (х 4~ Дх)2 — х2,
или, раскрыв скобку и сделав приведение подобных членов:
Ду = 2х • Дх (Дх)2. (3)
Мы теперь получили приращение Ду функции, выразив его через начальное зньчгние х аргумента и через приращение Дх аргумента.
Если это приращение Дх аргумента начинает стремиться, к нулю, т. е. делается бесконечно малым, lim Дх = О, то и соответственно приращение Ду функции также будет стремиться к нулю, lim Ду = 0, т. е. также будет бесконечно малым, как это обнаруживает найденная величина (3) приращения Ду функции.
Таким образом мы рмеем два бесконечно малых:
Дх и Ду.
Чтобы сравнить между собою эти два бесконечно малых, разделим второе, Ду, на первое, Дх, т. е. составим отношение:
*У Ьх
Для вычисления величины этого отношения достаточно просто разделить обе части равенства (3) на Дх, что дает нам:
4х=2х+Дх '4)
Чтобы видеть, каким образом одновременно изменяются приращения Ах и Ау, возьмем определенное числовое начальное значение аргумента, например возьмем х = 4.
В этом случае предшествующая формула (4) нам даст:
lim iX-kO
ау_
Ах
= 8.
Если мы хотим проследить тщательнее, каким образом изменяется отношение приращений Ду и Ах, когда приращение Дх начинает делаться все меньше и меньше, обратимся к табличке:
1 [анальное значение X аргумента Новое значение аргумента Приращение Дх аргумента Начальное значение у функции Новое значение функции Приращение Ау функции Ду Дх
4 5,0 1.0 16 25 9 9
4 4,8 0,8 16 23.04 7,04 8,8
4 4,6 0,6 16 21,16 5,16 8,6
4 4,4 0,4 16 19,36 3,36 8,4
4 4.2 0,2 16 17,64 1,64 8,2
4 4,1 0,1 16 16,81 0,81 8,1
4 4,01 0,01 16 16.0801 0,0801 8,01
Мы видим, что по мере уменьшения приращения Дх аргумента уменьшается и приращение Ау функции, но их отношение равно последовательно числам:
9; 8,8; 8,6; 8,4; 8,2; 8,1; 8,01;
Ду к
мы видим здесь на деле, что отношение — — постепенно приближается
к числу 8. И мы, в самом деле, теоретически уже знаем, что это отношение можно как угодно близко подвести к 8, сделав надлежаще малым приращение Дх аргумента, ибо
lim ^ = 3
Дх-н) Дх
при начальном значении х = 4 аргумента.
§ 56. Производная функции одного переменного. Основное определение диференциального исчисления таково:
Производная данной функции есть предел отношения приращения этой функции к приращению независимого переменного, когда это последнее приращение приближается к нулю как своему пределу.
Когда предел этого отношения существует и есть конечное число, тогда говорят, что данная функция д и ф е р е н ц и ру е м а, или что она имеет производную (обладает производной).
Вышеприведенное словесное определение можно дать в более сжатой символической (математической) форме следующим образом.
Дана непрерывная функция y=fW. (5)
Пусть аргумент х получает приращение Дх. Тогда величина у функции получит приращение Ьу, и новым значением функции будет
_у + Ду=/(х-|-Дх). (6)
Чтобы' получить приращение &у функции, достаточно вычесть из равенства (6) равенство (5); находим:
Ду=/(*4-М—/(*)• (7)
Разделив обе части этого равенства на приращение Дх аргумента, имеем :
Ьу_ _ /(х4-Дх) —/(х)
Дх Дх
Так вот, предел этого отношения, когда приращение Дх аргумента приближается к пределу, равному нулю, по только что данному словесному определению, и есть производная.
Оказалось по мере развития естествознания, что разрешение весьма многочисленных и крайне разнообразных задач сводится к вычислению пределов отношений вида (8). Поэтому предел отношения (8) получил особое имя „производная", и ему дано особенное стилизованное обозначение, такое, в котором как бы уцелели для нашей памяти следы самого происхождения этого предела. Именно производная обозначается символом
dy dx ’
так что мы имеем:
аУ _ lim ДУ
dx д^-^оДх или, &олее подробно:
dy /(х + Дх)—/(х)
dx 4х_>о Дх
(9)
(Ю)
Это равенство и определяет производную от функции^ [или от /(х)] по переменному х.
Процесс отыскания производной от функции называется диферен-
ц и р о в а н и е м ее.
Следует хорошо заметить себе, что производная есть предел отношения, но отнюдь не отношение пределов, ибо последнее
отношение ввиду того, что Дх и Ду суть бесконечно малые, т. е. О
имеющие своим пределом нуль, должно написаться в виде —, а это прямая
бессмыслица и полная неопределенность,
§ 57. Различные обозначения производной. До перехода к своему пределу, значит, во всякий момент времени, приращения Дх и Ду всегда конечны и имеют определенные числовые значения. При этом первое приращение, Дх, т. е. приращение аргумента, как всецело находящееся в нашем распоряжении, всегда может быть взято отличным от нуля. Поэтому отношение
Ду Дх до своего перехода к пределу есть в действительности дробь, ибо до перехода к пределу тут есть и числитель и знаменатель, причем этот последний отличен от нуля.
Когда же мы отыщем предел этого отношения, т. е. когда мы вычислим производную
dx ’
то эта производная есть просто только отвлеченное число (как вся-кий*вообще предел) и уже не дробь, ибо в этом отвлеченном конечном числе, вычисленном как предел, мы не в состоянии более различать ни числителя, ни знаменателя, Поэтому на символ
dx
нельзя смотреть как на постоянную дробь, но его следует рассматривать лишь как предел некоторой переменной истинной дроби. Тот факт, что эта переменная истинная дробь ранее писалась нами Ду в виде отпечатлелся в
Дх
дела этой истинной дроби в что символ производной
несколько стилизованном ооозначении пре-
<У „ виде . по читатель должен помнить
dx t
dy dx
отнюдь не есть истинная дробь и что поэтому отдельные частицы этого символа
dy и dx
суть лишь символические (условные) числитель и знаменатель, не имеющие в отдельности пока ни малейшего числового смысла, если их брать порознь 9- Значит, все части символа являются крепко связанными "Г 1) В дальнейшем, именно в главе X(в учении о диференциале), читатель по-знакомится с возможностью рассматривать символ производной как истинную дробь, с конечными числителем и знаменателем, но эта возможность достигается там ценой введения нового независимого переменного, другого, чем х. Пока же читатель должен отказаться от толкования символа как дроби и должен рассматривать его как нечто цельное, без числителя и без знаменателя.
между собою одним общим смыслом и неотъделимы друг от друга (вроде того, как неотделимы буквы 1 и g друг от друга в символе лога-
рифма 1g/V). Поэтому мы должны рассматривать символ ~~ как нечто
цельное.
rfv
То обстоятельство, что символ производной не есть настоящая
дробь, и позволяет так свободно обращаться с этим символом, как ни-dy
когда не рискнули бы, если бы символ был истинной дробью, с на-
стоящим числителем и знаменателем. Так, производная функции
не только обозначается в виде
dx
или
но даже так:
df(x) dx ’
сильно опуская вниз значок функции f (х). Зд :ь на символ
dx ’
очевидно, надо смотреть лишь как на слозо производная, которое он и заменяет. '
Так, например, производная от функции у = х2 может бить написана в виде rf(x2) d .
—или — Аналогично производная от функции
у = 3xJ — 6х + Vx
может быть обозначена через
^(Зх*-6х+ГГ).
Читатель отметит, что отношение приращений
Ьх
до своего перехода к пределу зависит от двух переменных величин: а) от начального значения х аргумента и Ь) от величины приращения Дх аргумента.
Так, например, когда рассматривают функцию у = ха, то согласно Д_у сделанным выше вычислениям имеют для отношения выражение:
= 2х Дх. Дх
9 Зак. ЭТОТ_В. Г р в ив и ль в Н. Лузин. Часть I
и &У
по когда ищут предел этого отношения приращений, заставив приращение Дх аргумента стремиться к нулю, т. е. делая 11m Дх = О, тогда, разумеется, этот предел
Um ¥
перестает уже зависеть от исчезающего Дх, потому что во время отыскания указанного предела
Um £
Дф->0 начальное значение х аргумента предполагается постоянной величиной, а всякий вообще предел переменной величины есть величина Ду
постоянная. Поэтому предел lim - будучи величиной постоянной, мо-жет оказаться зависящим только от начального значения аргумента, т. е. только от буквы х. Значит, этот предел
г &у lim ——, ix -> о ^Х
т. е. сама производная
rfy
dx'
окажется выражением, содержащим только букву х, т. е, это будет некоторая новая функция буквы х (аргумента х).
Эта новая функция аргумента х, будучи выведена из данной функции y=f(x) аргумента х или, иначе говоря, будучи произведенной данной функцией y^=f(x), и получила по этой причине имя производной функции от данной функции y=f(x).
То обстоятельство, что эта новая функция выведена из данной функции jz=/(x) помощью некоторого процесса, или, еще иначе, что она произведена данной функцией у=/(х) помощью некоторого процесса, часто ставят на вид, обозначая производную просто такими символами:
У или /' (х),
т. е. постановкой вверху функции ударения, или штриха (').
Таким образом, если данная функция есть
У=Дх'),
то ее производная пишется шестью способами:
dv
unu
dx dx ’
d d r.
~dx?
У или f'(x).
Наиболее часто для производной от данной функции у = /(х) пишут равенство:
читая его вслух следующим образом: производная от у по х равна вф прим (штрих) икс.
Символ же d dx' рассматриваемый сам по себе, называется знаком диференциро-в а н и я и просто показывает, что функцию, за ним написанную, нужно продиференцировать по букве х.
Пример. Вычислить и изобразить производную от ф у и к-ции у = ла.
Решение. Согласно сделанным выше для этой функции вычислениям Ду Ду
имеем для отношений приращений ~ выражение = 2х + Дх. Заставляя в этом равенстве приращение аргумента Дх стремиться к нулю, т. е. делая Л W
Пт Дх = 0, мы находим Пт = 2х, ибо Дх есть бесконечно малое; значит, 4*->оДх
производная от функции у = ха равна в точности 2х. Найденный результат записывают, наконец, в виде одного из шести равенств:
^ = 2х; ^-у = 2х; у' = 2х; ^^ = 2х; (х*) = 2х; (х!)'=2х.
dx dxJ J dx dx' ' ' '
§ 58. Диференцируемые функции. Легко видеть, что только непрерывные функции у =f(x) могут обладать производными.
Действительно, раз производная от функции y=f(x) существует
Ду при начальном аначении х аргумента, то это значит, что отношение есть переменная величина, стремящаяся к совершенно определенному конечному числовому пределу (к . производной), когда приращение Дх стремится к нулю. Следовательно, тем самым это отношение есть ограниченная переменная величина (§17). С другой стороны, величина Дх есть бесконечно малая, ибо по условию КтЛх = 0. А так как произведение ограниченной переменной величины на величину бесконечно малую есть опять величина бесконечно малая (§ 37), то отсюда следует, что произведение
есть величина бесконечно малая. Значит, имеем:
Нт Ду = 0.
А это и есть определение непрерывности функции у =/(х) в точке х (§ 41).
Таким образом разрывные функции заведомо не имеют никакой производной в точках разрывов.
Однако обратное заключение не всегда верно; в самом деле в настоящее время найдены функции, которые, будучи непрерывными, тем не менее не имеют производной. Но такие функции не часто встречаются в прикладной математике, а в этой книге будут рассматриваться только диференцируемые функции, т. е. функции, имеющие производную для всех значений независимого переменного, ва исключением разве некоторых отдельных его значений.
§ 59. Общее правило диференцирования. Из определения производной следует, что процесс диференцирования функции у=/(х) распадается на следующие отдельные ступени.
Первый шаг. В фу н к ци lore место х подставляем что дает новое значение функции, т. е. .у-|-Ду.
Второй шаг. Вычитаем данное значение функции из ее нового значения и таким образом находим приращение Ду функции.
Третий шаг. Делим остаток Ду (т. е. приращение функции) на Дх (т. е. на приращение независимого переменного).
Четвертый шаг. Находим предел этого частного, когда Дх (приращение независимого переменного) приближается к пределу, равному нулю. Это и будет искомая производная.
Учащийся должен вполне освоиться с этим правилом, прилагая его к возможно большему числу примеров.
Три подобных примера приводим со всеми деталями вычислений.
Пример 1. Диференцировать Зх2-|-5.
Решение. Положив у = Зх2 + 5, прилагаем последовательные шаги, указанные в общем правиле.
Первый шаг.
у Ду = 3 (х + Дх^2 + 5 = Зх2 + 6х • Дх + 3 (Дх)2 + 5. Второй шаг.
у + Ду = Зх2 + 6х • Дх + 3 (Дх)2 + 5
у_____= Зх2______________4-5
Ду = 6х • Дх + 3 (Дх)2 Третий шаг.
= бх + 3 • Дх.
Дх 1 Четвертый шаг.
Можно написать ответ еще так:
(Зх2 + 5) = 6х.
Пример 2. Диференцировать х3 — 2х + 7.
Решение. Полагаем
у = х3 - 2х + 7.
Первый шаг.
у + Ду = (х + Дх)3 — 2 (х + Дх) + 7 =
= х3 + Зх2 • Дх + Зх • (Дх)2 + (Дх)3 - 2х — 2 Дх + 7.
Второй шаг.
_у 4- Ду = х3 4- 3x2. Дх 4-Зх • (Дх)3 + (Дх)3 —2х—2 • Дх + 7
у = х3 — 2х +7
Ду = Зх2 • Дх + Зх • (Дх)3 4- (Дх)3 - 2 • Дх
Третий шаг.
£ = Зл-2 + Зх . Дх + (Дх)3 - 2.
Четвертый шаг.
£ = Зх2 - 2.
Или: dx
4- (х3 — 2х 4- 7) = Зх2 ~2. dx '
Пример 3. Дифференцировать Л.
Решение. Полагаем с У ~~ х-Первый шаг.
v+A-y = (х4-Дх)2' Второйшаг. !
_ с с _ — с-Дх(2х 4- Дх)‘
•У — (х 4-д*) 2 х3 ~ х2 (х 4-Дх)2 Третий шаг.
Ду _ 2х 4- Аг Дх “ С ‘ х2(х4-Дх;2
Четвертый шаг. dy 2х ’ 2с
dx х- • х- х3 Или: d / с \______________________________2с
dx \х3) ~ х3 ’
УПРАЖНЕНИЯ.
Применяя общее правило диференцирования (стр. 132), найти производные
следующих функций:
1. > = 3x2. owe. £ = бх. dx
2. у = х2+2. - £ = 2х.
3. _у = 5 —4х. £= — 4. dx
da
4. s = 2/2—4. 5т = 4Л at
5. v = l. '/ ^=_± У jc z dx x3
fi *+2 rfv 2
x dx л-
7. _y = x3. Отв. ^=3х». dx
8. у = 2л-2 - 3. - $l = 4x. ut
9. у = 1 - 2x3. ^ = -6X2. ax
10. p = flO2. ^ = 2“0.
11. dy 4 dx ~ Xs'
12. 3 dy _ 6»
У x- — 1 dx (x3 — I )*
13. у = 7х* 2 * ч * * * + х.
14. s—aV- — 4bt.
15. г = 8/-|-3/2.
18. у = Ьх2 — сх.
19. J =
20. р = 3в8 —26*.
21., = ^.
J х
22- ₽ = -Лп-
23. у = ^-ла + 2х.
24. z = 4x — Зх2.
25. p = 30 + 02. _ ax + b
26. v ------J—.
X
28. у = x2 — Зх + 6.
29. у = ax2 + bx + c.
30. 5 = 2/24-5/ — 8.
31. p = 503-20 4- 6.
Отв. у' = 2x — 3. у' = 2ях 4- b. s' = 414- 5. p' = 1502 — 2.
§ 60. Первое приложение производной к геометрии. Первое, что дает диференциальное исчисление геометрии, это — умение проводить касательные ко всем кривым линиям, уравнения которых в декартовых координатах нам известны.
Действительно, пусть, действуя, например, приемами аналитической геометрии на плоскости, нам удалось составить уравнение в декартовых координатах для некоторой кривой линии. Пусть .гэто уравнение, разрешенное относительно ординаты у, будет:
j=/(x). (11)
Самая же кривая линия начерчена на даваемом здесь чертеже (черт. 54).
х Если аргумент функции y=f(x) имеет
начальное значение! х, то, изобразив его
отрезком ОР на оси ОХ, мы видим, что н а-
ч а л ь н а я ордината РМ кривой имеет число-начальному значению функции
0
Черт. 54.
вую величину, равную
РМ = /(х) *=ау.
Если же аргумент функции получает новое (наращенное) числовое значение х-|-Дх, то, изобразив его отрезком ОРХ на оси ОХ, мы видим, что ордината PiM' кривой имеет числовую величину, равную новому (наращенному) значению функции
Р1УИ'=/(х-|-Лх) = у4-Ду. (12)
Проведя через точку М параллель AfQ к оси ОХ, мы получаем прямоугольник PMQPV в котором противоположные стороны равны. Значит: Р^^РМ=у (13)
и AfQ^PP^Ax. (14)
Вычитая из равенства (12) равенство (13), мы находим: QM' = ty. (15)
Равенства (14) и (15) показывают, что горизонтальный катет 7WQ прямоугольного треугольника AfQAf' равен приращению Дх независимого переменного, а вертикальный его катет QM' равен приращению Ьу функции.
По этой причине прямоугольный треугольник AfQAf' называется треугольником приращений. Он играет важную роль в многочисленных геометрических исследованиях.
Из тригонометрии известно, что один катет равен другому катету, умноженному на тангенс противолежащего угла. Отсюда
Ду = Ал • tg QMM', т. е.
~^ — tgQMM',
Ду что словесно выражается так: отношение приращений
с геометрической точки зрения является тангенсом наклона секущей (хорды) ММ' к горизонту (оси О Л).
Если теперь мы станем приближать приращение Дх аргумента к нулю как к пределу, весь чертеж приходит в движение. Точка Рх начинает двигаться, безгранично приближаясь к неподвижной точке Р, соответствующей начальному значению х аргумента. Движение точки Рх увлекает подвижную ординату Р^М',' которая начинает безгранично приближаться к неподвижной начальной ординате РМ. Вследствие этого движения подвижной ординаты РХМ' ее конец, т. е. точка М', начинает скользить по кривой, безгранично приближаясь к начальной неподвижной точке М этой кривой. Вследствие же всех этих движений секущая (хорда) ММ' также приходит в движение, начиная поворачиваться около неподвижной начальной точки М.
Это, конечно, предполагает рассматриваемую кривую у=/(х) непрерывной при начальном значении х аргумента.
Если рассматриваемая функция у^=/(х) диференцируема при начальном значении х аргумента, тогДа отношение приращений
ьу Ьх
стремится к определенному числу как к пределу, когда приращение Дх стремится к нулю. Геометрически это означает, что вращающаяся секущая (хорда) ММ' безгранично приближается к некоторому предельному положению Л/Г, ибо раз тангенс наклона секущей безгранично приближается к некоторому числу как к пределу, то и сам наклон (т. е. угол с горизонтом) этой секущей тоже стремится к пределу, откуда и следует, что сама секущая ММ' приближается к некоторой предельной прямой МТ.
Эта предельная прямая МТ, к которой безгранично приближается поворачивающаяся секущая (хорда) ММ', когда точка М' безгранично приближается к точке М, называется касательной, проведенной к кривой в точке М.
Так как тангенс наклона касательной, tg QMT, есть предел тангенса наклона секущей, tg QAf/W', и так как этот последний тангенс есть Ду отношение приращений, tg Q/ИЛт = то отсюда следует, что п р о-
dv Ду
изводная будучи пределом отношения приращений и яв-
ляется не чем иным с геометрической точки зрения, как тангенсом наклона касательной к горизонту. Таким образом производная функции y=f (х):
dy .. А> dx _>о Ах
^^/(х+М-Лх), дх->0 Ах
есть тангенс наклона касательной, к оси ОХ:
Эта-то именно задача о проведении касательной и привела Лейбница ’), со своей стороны, к открытию диференциального исчисления.
Пример 1. Провести касательную к обыкновенной параболе у = х2 (черт. 55).
7 Решение. Днференцируя по общему правилу
\ / (§ 59), имеем:
\ / g=2x = tgPrM.
\ я где прямая МТ изображает искомую касательную
\ /] к параболе. С другой стороны, ордината РМ = ха
У! и абсцисса ОР = х. Из прямоугольного треугольника
------/__________I—* РТМ находим: О Т Р
тп пч * птч х" х ОР
TP-PM>zigPTM - i ртм~ 2х~ 2“ 2 '
Черт. 55. 5
Значит, если хотят иметь касательную в точке М к обыкновенной параболе, надо отыскать середину Т отрезка ОР и соединить прямой точки Т и М: полученная прямая и будет касательной.
Пример 2. Вычислить наклон касательной к обыкновенной . 1. параболе в вершине, а также в точке х =
Решение. Для отыскания наклона касательной в вершине полагаем в формуле tg РТМ = гх предыдущего примера х = 0. Тогда tg РТМ = 0, что показы-
*) Готфрид-Вильгельм Лейбниц (1646—1716) был уроженцем Лейпцига. Его выдающаяся гениальность сказалась оригинальными исследованиями в различных областях знания. Свое открытие диференциального исчисления впервые он обнародовал в форме краткой записки, появившейся на страницах ученого журнала .Acta Eruditorum' в Лейпциге, в 1664 г. Известно, однако, что уже существовала рукопись Ньютона о флюксиях и что слухи о ней дошли в то время и до Лейбница. В настоящее время, повидимому, твердо установилось убеждение, что и Ньютон и Лейбниц пришли к открытию диференциального исчисления друг от друга независимо. Принятая ныне система обозначений была введена Лейбницем. Эта система обозначений более удобна, чем система обозначений, употреблявшаяся Ньютоном.
г зет. что и самый угол РТМ равен нулю. Значит, касательная параллельна горизонту ^оси ОХ).
Для отыскания наклона касательной в точке х = нашей параболы полагаем х= J в формуле tg РТМ = 2х; это дает tg РТМ = 1, что означает, что угол РТМ = 45°.
Пример 3. Провести касательную к кубической парабол е у = х3 (черт. 56).
Решение. Днференцирз'я по общему правилу (§ 59) функцию у = х3, мы находим:
у Ду = (х + Дх)2 = х3 + Зх2 • Дх + + Зх (Дх)2 + (Дх)3,
Ду = Зх2 • Дх -I- Зх • (Дх)2 + (Дх)3,
^ = Зх2 + Зх.Дх + (ДхА
(t V’
Переходя к пределу, имеем ^ = 3х2. Итак, считая, что касательная есть прямая ТМ, имеем tg РТМ = Зх2. С другой сторокы, катет РМ = х3, ибо это есть ордината у. Значит, другой катет РМ х
ТР-РМ^Р™ = ^РТМ=^Ъ- Отсюда ТГ1 х ОР -
отрезок /Р = -5’ = —-. Поэтому, если хотят о о
иметь касательную к кубической параболе, надо
разделить отрезок ОР на три равные части и взять правую точку деления Прямая ТМ, проведенная через точки Т и М, и есть искомая касательная.
УПРАЖНЕНИЯ.
Найти наклоны касательных к нижеперечисленным кривым в указанных точках и сделать соответствующие геометрические построения.
1. у = х2 — 4 в точке, где х = 2. Отв. 4.
2. у = 6 — Зх2 х= 1. — 6.
3. у = х3 X = — 1. 3.
, 2 1
4. у = — J X х — — 2. 2'
5. у = х —х3 х = 0. • 1.
6. у = —Ц J X — 1 х = 3. _ 2 4'
7-У = |х2 х = 4. 4.
8. у = X3 — 2х + 3 х = 1. 0.
9. у = 9 — х3 х = — S. 6.
10. Найти наклоны касательной к кривой у = 2х3—6х-|-5: а) в точке, для которой х = 1, Ь) в точке, где х = 0.
Отв. а) 0; Ь) — 6.
И. а) Найти наклоны касательных к двум кривым: у = 3х2 — 1 и у = 2х24~3 в точке их пересечения; Ь) под каким углом они пересекаются?
Отв. а) ±: 12, ±8; b) arctg ~.
ГЛАВА V.
ПРАВИЛА ДИФЕРЕНЦИРОВАНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ.
§ 61. Важность общего правила. Общее правило дифе-ренцирования, данное в предыдущей главе, § 59, есть правило основное, которое найдено прямо из определения производной, и крайне важно, чтобы учащийся тщательно освоился с ним. Однако процесс приложения этого правила к примерам вообще есть вещь утомительная или даже трудная; вследствие этого, для облегчения труда по диференцированию некоторых часто встречающихся употребительных функций, из общего правила были выведены особые специальные правила.
Найдено было полезным выразить эти правила посредством формул, список которых следует за сим. Учащийся должен не только каждую формулу удержать в памяти, но и уметь соответствующее правило выразить словами. В этих формулах и, 1) и w означают переменные количества — именно функции от х; все эти переменные предполагаются диференцируемыми.
Формулы днференцирования.
I. de п . . — = 0 (с есть постоянное).
п. £-1. dx
ш. d , . , du , dv dw dx dx 1 dx dx
IV. d . . dv . . _— (cv) = c-^- (С есть постоянное).
V. d . . dv . du dx dx 1 dx
VL d , . , . dVt . . . dv9 . dx (V^e-.V.) = (V8VB...Vj-^i+ (VJV....V.) dxa 4- ... 1 I ч dV ••• + (vlv9...v„_1)-d7.
vn. (v") = (n есть постоянное).
Vila. (xn) = nx" 1 (п есть постоянное). du dv , . v u —
VIII. d /u\ _ dx dx ' dx \v / — v2 du
Villa. d /u\ dx . . (с есть постоянное). dv c —
Vlllb. d /с\ dx , . — 1 - 1 = —— (с есть постоянное). dv
IX. d „ . , dx (iogav) = loe«e • v • dv
IXa. d dx — (In v) = — . dx4 ' v
X. d , dv — (a*) = a In a • 3-. dx v ' dx
Ха. d . r. , dv 'dx e ) — e dx ‘
XI. 4-(u’) = vu'-1 • д—In u • . dx 7 dx ‘ dx
XII. d . . . dv dxv ’ dx
XIII. d . . . dv dx k ' dx
XIV. d .. . 1 dv dx b V cos2v dx ‘
XV. d . . . 1 dv dx 6 ' sin*v dx
XVI. d , . sin v dv •3—(sec v) = —5- • 3— . dxv cosJv dx
XVII. d , . cos v dv dx ' sin2v dx dy
XVIII. d / . . dx — (arcsin v) = r . dx v ' у 1 — v2 dy
XIX. d . dx x 3— (arccos v = . dx Y1 —v2
dy
XX, -Д- (arctg v) - —dX— . dx 4 в /1 + v> dy
XXI. -^-(arcctg v) = — dX .
dx s/ 1;- v2
VVII dy dy du
XXII. -^ = -i. . — где у есть функция и.
dx du dx J
Xftll. Д, где у есть функция х.
dx dx ’ J
dy
§ 62. Диференцнрование постоянного. Функция, о которой известно, что она сохраняет одно и то же значение (см. § 19) для всякого значения независимого переменного, есть постоянное количество, и можно ее обозначить буквою с:
у = с.
Когда х получает приращение Дх, функция не изменяет своей величины, т. е. Ду = 0, и
£ = О.
Дх
Поэтому мы имеем и
Но
Следовательно:
I
Ит^-0.
Дх—> О
de dx
= 0.
Итак, производная постоянного есть нуль.
§ 63. Диференцнрование переменного по этому же самому переменному. Пусть
Следуя общему правилу, § 59, имеем:
Первый шаг. у -|- Ду == х Дх.
Второй шаг. Ду = Дх.
Третий шаг. ^=1. Дх
§ 65] ДИФЕРЕНЦИРОВАНИЕ СУММЫ (АЛГЕБРАИЧЕСКОЙ) 141
Четвертый шаг.
dx
Следовательно:
Итак, производная переменного по этому самому переменному равна единице.
§ 64. Диференцирование суммы (алгебраической). Пусть
у = и 4- v — w.
Следуя общему правилу, имеем:
Первый шаг.
у -f- Ду = и Ди + V Д'» — W — A^-
Второй Третий шаг. ШАГ. Ду = Ди 4~ А^ — Sw. Sw Дх ’
Ду Дх Ди ~ Дх 1 Дх
Четвертый шаг. dy du j dv dw
dx dx । dx dx'
[Применяя теорему I § 38.]
Следовательно:
... d . . . du . dv dw
111 j-(u4-v —w) = -j-4-j------j •
dx ' ’ dx 1 dx dx
Подобным же образом доказывается теорема и для алгебраической суммы любого конечного числа функций.
Итак, производная алгебраической суммы конечного числа функций равна той же алгебраической сумме их производных.
§ 65. Диференцирование произведения постоянного на переменное. Пусть
у = CV.
По общему правилу:
Первый шаг.
у4-Ду = с(® 4_Дг') = cv-{-c • йу.
Второйшаг.
Ду — с • Дт*.
Третий шаг.
Ду__ b.v
йх~С &х'
Четвертый шаг.
dy________________________ dv
dx~ ’ dx'
[Прилагая теорему II § 38].
Отсюда
d . . dv
IV. (cv) = с — •
dx dx
Итак, производная от произведения постоянного на переменное равна произведению постоянного на производную от пере-пенного.
§ 66. Диференцнрование произведения двух переменных.
Пусть
_у = иъ.
По общему правилу:
Первый шаг. /
у-]-Ду = (и 4- Ди) (v + Дт») = uv 4- и • Ди -f- v • Ди 4* Ди • Д'».
Второй шаг.
Д^ = и . Дт/ 4- v . д« 4~ Ди . д^.
Третий шаг.
Ду Дг1 , Ди , . Др
* =И ’ л---Г® • а-ЬДы ‘ •
Дх Дх 1 Дх Дх
Четвертый шаг.
"Прилагаем теорему II § 38. Когда Дх приближается к пре-" делу 0, Ди приближается также к пределу 0, так что Нт(д«.^)=0.
Отсюда
,, d , . dv । du
V. -r- (uv) = u —Fv — •
dx v ' dx 1 dx
Итак, производная произведения двух переменных равнг. первому переменному, помноженному на производную второго, плюс второе переменное, помноженное на производную первого.
§ 67. Диференцнрование произведения любого конечного числа переменных. Разделив обе части V на uv, даем ему вид:
d , . du dv dx _dx .tix uv ~ и ' v '
Следовательно, взяв произведение п переменных: y = ^v2...v(1, можем написать:
d . . dvx d . . Ж 37 , К dvx dx , dv2 dx , d , ,
dvx dv2 dva dx . dx . dx у - V, ‘v2 ! T-3^- ...4- 1 dx vn
/множив обе части на v^v^.. .Уп, найдем:
VL (v1v2...vn) = (vav8...vn)^4-(v1v9...v(,)^24- -
dv
... 4-(V1Va...Vn-l)^? •
Итак, производная произведения конечного числа переменных равна сумме всех произведений, составленных умножением производной от каждого переменного на произведение всех остальных переменных.
§ 68. Диференцирование степенной функции с постоянным показателем. Если каждый из п множителей в VI будет равен у, то VII A (v»)+nv"-1 • •
dx v ’ 1 dx
Если v = x, уравнение дает:
VII
А (X") = ПХЯ 1 dx4 '
Правило VII доказано только для случая п целого положительного. Но в § 76 будет показано, что эта формула остается верною для какого угодно значения п, так что имеем следующий общий результат:
Производная степени переменного с постоянным показателем равна произведению показателя на степень переменного с показателем, единицею меньшим, и на производную этого переменного.
§ 69. Диференцирование частного. Пусть
U I Л
V=—, ффо.
z v Т
По общему правилу:
Первый
ШАГ.
иЦ-Ли
Второй
ш л г.
Ду
и -р Ди и____v • Дн — и.Ьу
у {у 4- Дф)
а-]-v
Третий
шаг.
Дц v‘ Дх
&у
Ду Дх____________Дх
Дх у (у -|- Д у)
Четвертый шаг.
du dv
dy dx dx
dx~ t»a
[Прилагая теоремы II и Hi, § 3S.]
Следовательно: du dv
v______u---
VIII. ____J>.
dx \ v / vi
Итак, производная дроби равна произведению знаменателя на производную числителя минус произведение числителя на производную знаменателя,—все разделенное на квадрат знаменателя.
Если знаменатель есть количество постоянное, то. положив v—c в VIII, имеем:
du
V111. .
dx \ с / с
Гив»^=^.=о.1 |_ dx dx J
Можно еще вывести Villa из IV так:
du
d / и\ _ 1 du _ dx dx\ с / с dx~ с
Итак, производная частного от разделения переменного на постоянное равна производной переменного, разделенной на это постоянное.
Если числитель будет постоянной величиной, то, положив и=с в VIII, найдем:
dv
vnib А. =__________dx.
dx \ v / v-
ГИб0^ = 4£=о.]’
L dx dx J
Итак, производная частного от разделения постоянного на переменное равна минус произведению постоянного на производную переменного, разделенному на квадрат переменного.
Следуя выведенным до сих nojr правилам, мы теперь уже в состоянии диференцировать всякую явную алгебраическую функцию одного независимого переменного.
ПРИМЕРЫ.
Диференцировать следующие функции:
1. у = х8.
Решение.
4^ = -£-(л3) = Зл« по Vila.
dx dx '
[Я = 3]
2. у = ах* — Ьх-.
Решение.
Q = -!L(ax*- Ьх1) = -4- (ах*) - 4~ (^2) = п0 111
dx dx ' dx ' dx '
. = a-4- (*«) - b ±(x») = по IV
dx dx
**$ax? — 2bx no Vila
3. > = х8+5. Решение.
Решение.
5. у = (х2 - 3)6. »
Решение.
^- = 5(х2-3)«-£-(х2-3) = dx ' 'dx
[р = ж* —3 и л=5)
= 5 (х3 - 3)< • 2х = 10х (х3 - 3)<
по 111 по Vila и I.
по Ill по IV и Vila.
по VH
Можно бы было разложить эту функцию посредством бинома Ньютона, затем приложить III и т. д., но указанный ход короче.
6. у = У в3 — х2.
Решение.
= -4—(а3 — д -)2 = — (а2 — х3) * -j- (а- —х2) = по УП
dx dx' ' 2 ' 'dx
Jp = a> — .v’ и n = -- 1
7. у = (Зх2 + 2) У1 + 5x2.
Решение.
% = (Зх2 + 2)-^ (I + 5л2)2 + (1 + 5х=У (Зх2 + 2) = по V
[и = Зх» + 2 и v = (1 + Зх’)'1]
= (Зх24-2)-А(1+5х2Г2 .-^(1+5х2) + (1+5х2)2-6х= по VII
_L 2 " Т> Д‘
= (Зх24-2)(1 +5х2) 2 • 5х + 6х • (1 + 5x2ja =
8- У
5х(Зх2 + 2) УТ+5х2
6х У 1 4-5x2 =
45г8 4- 16х У Г4-5хГ-
д» + х2
У а2 —х2’
Ю Зак. 2769. — В. Гранвиль и Н. Лузин. Часть I
Решение.
_ <«= _ +х, _ (а,+л («, _ х,-:
dx а1 — х2
по VIII
2х (а- — х2) 4- х (л2 + х2) _ = £ — (а5 —х2)2
умножая числитель и знаменатель на (а> — х’)'1’
За2х — х3 а” ’
(л2-*2)-
9. >, = 5х< 4-Зх2 — &
10. у = Зсх2 — 8dx 4- 5г.
И. у = ха + ь.
12. у = х» 4- пх 4* л.
13. /(Х) = ух3 - ±х2 + 5.
14. /(x) = (a4-*)x24-cx4-d.
15. (а 4- Ьх 4- сх2) = 6 4" 2сх.
16. — Зу 4- 6) = Smjr’”-1
17. (2х“2 4- Зх~8) = - 4х~8 -
18. — (Зд-« - $) = - 12д-б - I. аз
19. А( 4х’24-х2)=2х~'24-2 dx \ /
20. — 4> 2)=-2у~34-2>
2!. ^(2х3 + 5) = бх2.
22. ^-(3/3-2/2) = 15/'-4/.
23. 4г (аб14- 66) = 4а63 4 Ь. OU
27. r= ct34-rf624-ee. 7 £ 2
28. > = 6х’2 4-4х3 4-2х2. 29
29. у= y& + -j/x+ 1.
Эх’4.
g= 20x3 4-6*.
= бсх — 8rf. dx
^- = (a + b)xa+b-1
= лх”-14- л.
dx
/'( v) = 2x2- Зх.
/'(х) = 2(а4-*)х4-с.
d I 1 i
24. 4- 5-2а 2 = - За 2. da \ /
d I - -
25. 4г $/34-< 1=15/3-/ a t \ /
26. 4- (2х12 - х») = 24х“ - 9х». ах
^^3e^ + 2dt) + e.
5 3 £
^-=21х8 4-Юх 2 4-Зх3. «х
dy _ 3 ,_1___1
^“г/зх^зр/х2 •«’*
30. v = l+*x±^. X dy а dx'~C~xi' ч
X® - 1 х® — х — хя -4- а 32. у = ~ з - -• ха ^ = -?х3 — 5х3+2х ’+4* 3’ ОХ 0 0 А 1 dy _ 2хд +х+2х2 — За dx 2. 2х2
33. у = (2х« + X» - 5;’. 34. /(х) = (а + Ьс)т. 35. /(х) = (1+4x3) (1+2x3). 36. / (х) = (д + х) V а-х. = 6х (Зх + 1) (2x3 _]_ хз _ 5)2. К h |f —- f'(x) = ~(a+bx^*. f (x) = 4x (1 - Зх + Юл-3). . . a — 3x f(x) = — ,. 2 V a — x
37./(х) = (д + х)т (4 + х)п. +(x) = (д + x)m(b + x)4A + ."--I. |_а-гх b —xj
38.> = ±. X dy _ n dx x*^1
39. у = х (д2 + X9) < д2 - х2. dy _ a4 + д2х2 — 4x* tfx-
40. Вычислить нижеследующие производные:
a)^(2x3-4x + 6). е)^(6+а/2)2. и^хЗ-дЗ^.
Ь)^-(д<’ + ^-9). с)*5в( зез-гез'+бв). d)^(2x3 + x)3. .. 2х* 4L У - _ х» ‘ 42. у = * д + х 43‘ 5 (1 + о® ‘ 44./(*) = ^±^. о “р* О 45. /(#>--=1— у а — Ь\>- 3 8 ^^(хЗ-азЛ П^(5 + 2/)3. K)^(4-’’5J‘ Ю^/д + ьГ7. 1°л1<1+9'2- +2х J' rfy 8ft3xs — 4x3 dx {Ifl — x2)2 rfy _ 2д dx ~ (д + x)* ’ ds _ 3P +13 л (i + t)»-P(s\- (s + 2)^+_41 /(S)“ (s + 3)« • /40) (д -8вЯ)э
4в. F(f)=y/~ 47. ФСУ)-(Г^)”. F(r) = -. d-r)Vl-r2 У(у)=.-тУт~1 .
2х’— 1 48.<?(х)=-^^=. х у 1 + ха . ^)=_1±±4-. Х’(14-Х2)3
49. ( 'j = - dX \(в + х)т (6+Х)"/ m(ft + x) +л(в-Ьх) (а+ X)m+1(Z> + .v)n4’1"
50. А /±1^=^ dx Ya + х — У а — х/ ая + a Ya1 — х2 Х2 Y — х*
Указание. Сначала привести к рациональному виду знаменатель.
51. у= Vlpx.
52. у = А/д» —х2.
54. r= Va^ + cV<?з.
= Р. dx у ' dy __ blx /
dx ~ а2у' dv_ = _ лГ!-dx V х '
dr _ V а + Зе?
“ 2/?
du ve~* . пл~1 dv ~ d ‘ с~
Х.р = <!±£.
Vq-l
dp (q — 2)Yq + 1 dq
(9-1?
57. J =
dy _ пу
dx ~ х /1 - х2'
58. Дано
(д + х)в = а» + 5а‘х + Юа’х1 + 10а2хЗ 5ах* + х6;
найти диферендированием (а-}-*)'-
59. Зная, что
1 __ .-ч+1
, • =1 + х4-х2+... +хп,
вывести днференцированием сумму ряда:
1 4-2х + Зх»+ ... + лх"“,> где л — любое целое положительное число.
Отв. их"+х-(л + 1)х"+1
(Х-1Г-
60. Вычислить нижеследующие производные:
§ 70. Диференцнрование функции от функции. Отсылая учащегося, желающего получить ясное представление о том, что такое есть .функция от функции1, к § 30, в котором понятие .функции от функции** всесторонне выяснено, переходим к дифе-ренцированию функции от функции.
Мы видим чрезвычайную практическую важность этого вопроса, потому что большинство явлений действительности выражается формулами функции от функции у =/ [? (х)], где функции /и в свою очередь не очень просты, а сами часто являются опять функциями от функций.
Пусть же имеем функцию от функции
=/(?(*)]• (О
Вводя промежуточный аргумент и, мы эту сложную зависимость (1) разбиваем на цепочку двух более простых зависимостей:
(2)
j =/(«); и = ф(х).
Чтобы отыскать желаемую производную функции от функции у=/[?(х)], будем поступать согласно общему правилу (§ 59 предыдущей главы): дадим последнему (истинному) аргументу х приращение Дх; тогда функция от функции у, будучи функцией аргумента х,
Ду
получит приращение Ду. Пишем отношение и, заставив приращение
Ах стремиться к нулю, ищем предел этого частного, который и будет z/y искомой производной :
«» ах дх-ьпАх
С другой стороны, обратим внимание на цепочку зависимостей (2). Из нее мы видим, что когда аргумент х получит приращение Дх, то величина и, будучи функцией аргумента х, и = о (х), получит в свою очередь некоторое приращение Ди. Но так как величина у зависит от величины и, то по причине получения промежуточным аргументом и приращения Ла эта величина у получит приращение Ду.
Это окончательное приращение Ду мы по произволу можем рассматривать либо как вызванное одним только приращением .Дх благодаря прямой зависимости (1), у=/[?(х)], буквы у от буквы х, либо как вызванное приращением Да промежуточного аргумента и благодаря косвенной зависимости, y—f(u), буквы у от буквы и.
Итак, имеем три приращения:
Дх, Ли и Ду.
Если приращение Дх стремится к нулю, то приращение Ди тоже стремится к нулю, потому что функция и = »(х) предполагается непрерывной; наконец, приращение Ду также будет стремиться к нулю, ибо и функция у также предполагается непрерывной.
Написав тождество
Дх Ди Ад' ’
видим 9, что предел левей части есть произведение пределов правой:
Av Ду .. Ди
lim — ~ lim • lim -—. Дх Ди Дх
dv
Первый предел, lim есть искомая производная функции ог
Ди
функции у =/['? (д')1 по аргументу х;третий предел, lim —, есть про-
Дх du ,, . . ,,
— = л (х) функции и по аргументу х. Что касается второго
Ду .
lim то это есть производная функции у по аргументу и:
• Ди du 1 4 '
промежуточному аргументу, который мы ввели, заменив
им функцию <р(х).
Поэтому окончательный результат выразится следующим образом: d<£ dy du dx ~ du
Таким образом, если y=f(u), где и = ф(х), то производная функции у по аргументу х равна производной у по аргументу и, умноженной на производную и по аргументу х.
Пример 1.
изводная
предела,
т. е. по
dx’
(ХХП
= 2и2 —4, и = Зх2-|-1.
Найти dx
Решение.
dy . du с
du dx
подставляя найденные производные в формулу (ХХП), получим:
= 4и • 6х = 24х (Зх2 4- 1;.
Пример 2.
Решение. Положим
тогда
^- = 2х. dx
у = (х» + 3)«».
х» + 3 = и;
= uw = i00u« du
Следовательно:
& = lOOu08 2х = 100 (х» + 3)» • 2х = 200х (х2 + З;»
!) Мы здесь предполагаем, что приращение Ди ве равно нулю, ибо иначе мы просто не могли бы написать отношения раз у него в знаменателе стоит нуль. Однако все окончательные выводы остаются верными и в этом случае.
Если бы мы имели дело с более длинной цепочкой зависимостей, например с цепочкой из четырех зависимостей:
y=f(uy, и = »(:); -y = 6(w); ад = Ф(х),
то на основании тождества
Ду Au Av Aw Ах Au Av Aw Ax
мы, рассуждая, как раньше, и переходя. к пределу, получили бы формулу диференцирования функции от функции для случая цепочки из четырех зависимостей:
dy dy du dv dw dx du dv dw dx
Формулу эту словесно можно прочесть так: производная функции от функции равна произведению всех проме* жуточных производных на последнюю производную.
§ 71. Возвращаясь к формуле (XXII), выведенной для случая самой короткой цепочки (2) из двух только зависимостей у =f(u)‘, и = <р(х), мы можем воспользоваться этими зависимостями и можем переписать формулу (XXII) в следующем виде:
(XXII*)
Эта формула словесно читается так: производная функции от какого угодно аргумента и по какому угодно неза-висимому переменному х равна производной данной функции, помноженной на производную аргумента.
Можно еще переписать основную формулу (XXII), пользуясь цепочкой у = /(и); и = <? (х), в виде:
= f{u) <(х), (XXII**)
ал
или, наконец, вспомнив, что у есть функция от функции:
У =/[?(*)].
мы можем написать ее более распространенным образом в виде:
^/[?(*)]=/'[?(*)] •'/00-
Самой надежной для практического пользования все-таки является основная формула (XXII), потому что при ее употреблении не может возникнуть никаких недоразумений.
Формула (XXII**) является для начинающего обычно более привлекательной, .потому что тут нет никаких вспомогательных, а на деле мне мешающих букв и, а есть только функции настоящего переменного х‘. Но читатель должен быть предупрежден относительно того, что формула (XXII**) может повлечь недоразумения: наиболее опасным является множитель /'[®(х)]. Опасность его состоит в том, что этот множитель
говорит нам сразу о двух действиях: а) действии диференцирования, символизируемом значком штриха, и Ь) алгебраическом действии подстановки, символизируемом квадратными скобками [ ], в которые и вставляется функция v(x). Надо в высшей степени твердо помнить, какое из этих действий делается сперва и какое потом: первым производится действие диференцирования ('), причем оно ведется, собственно, по ненаписанному аргументу [ ], и уже вторым, когда диференцирование выполнено и закончено, производится алгебраическая подстановка в окончательном результате в ненаписанный аргумент [ ] функции <з (х); значит, во всех местах у функции / делается вставка
Если же спервр вставить функцию <р(х) в ненаписанный аргумент, а потом продиференцировать, то читатель, наверное, получит ошибку, ибо тогда он получит просто
{/[?(*)])'.
т. е. самую производную функции от функции, а не промежуточную производную f [<р (х)].
Иными словами, читатель твердо должен помнить, что хотя символ Л*)
и обозначает производную от функции /(х), так что мы имеем:
однако, например, символ
f (2х) /
отнюдь не обозначает производной от функции /(2х), ибо таковая вдвое больше, чем /'(2х). Действительно, обозначив через у функцию /(2х),
у=/(2х),
мы видим, что имеем дело с функцией от функции, ибо это уравнение разбивается на цепочку двух уравнений помошью введения промежуточного аргумента и:
4 _у=/(а); ц = 2х.
Но тогда формула (XXII) диференцирования функции от функции нам даст: , , ,
= = -2 = 2 ./'(2х).
dx du dx J v J '
> Значит, производная функции /(2x) вдвое больше числа /'(2х).
d d d d
Обозначение производных через —, -г- , — , -т— , ... более на-r е dx du dv dw
дежное, потому что, употребляя его, учащийся не сделает ошибки. Если же не пользоваться этим обозначением, то производную от функции / (2х) надо обозначить через
[/(2х)Г, а отнюдь не через
/(2х).
Числовая разница между ними та, что [/(2х)]' вдвое больше, чем f'(2x). Теоретическая же разница между ними та, что в [/(2х)]' сначала вставляют в /( ) аргумент !?х и уже потом диференцируют (по х), а в f (2х), наоборот, сначала диференцируют функцию /( ) по пустому аргументу ( ) и уже потом вставляют вместо ( ) количество 2х.
Таким образом далеко не безразлично, сначала ли вставить в функцию /( ) количество а(х) и уже потом диференцировать, или, наоборот, сначала получить диференцированием/'( ) и уже потом вставить 'р(х). Результат вычислений зависит от порядка этих двух действий, и формула (XXII**) говорит нам о том, что
{/[?(*)])' =7 [?(*)] • ?'(х).
Если же не обращать внимания на порядок этих двух действий, то ошибка будет состоять в забвении множителя ?'(х).
§ 72. Практика правила диференцирования функций от
функций. Читатель не преминет заметить, что формула VI,
#-(*") =
dx
= nv
п—1
dv
dx
представляет
собою
применение выведенной формулы
производной функции от функции и что большинство примеров, данных на стр. 145, можно было бы решить, пользуясь этой формулой. Равным образом и в дальнейшем вместо того, чтобы пользоваться уже готовыми формулами таблицы производных (стр. 138—140), можно во всех случаях применять формулу производной функции от функции. Поэтому остановимся более подробно на практике применения этой формулы.
Ради наибольшей теоретической ясности мы были «вынуждены в тексте нашего изложения изображать различными буквами и, v, w,... те функции, которые вложены одна в другую в цепочках зависимостей.
Учащийся в самом начале своего обучения диференцированию м о-жет сначала подражать этому, чтобы выучиться хорошо распознавать функции от функций.
Пример диференцирования при отсутствии навыка.
Найти производную функции у = (!-]-х )".
Чтобы распознать здесь функцию от функции, читатель может обозначить внутреннюю функцию буквой и, как мы это делали выше; тогда он получит цепочку зависимостей:
у — ип\ и = 1 4- У~х,
откуда, применяя татель напишет:
dy dy
dx du
правило диференцирования функции от функции, чи-
du _ dua d(l-\-Vх) n-i 1
dx du dx nu 2]/x
= n (1 + Г7)”-1
ибо согласно формуле (VII) мы имеем:
dVх _ 1 ~dx~ 2/х ‘
Но читатель должен пользоваться лишь короткое время своим правом вводить буквы u, v, W,... и должен в дальнейшем поскорее освободиться от этой ненужной привычки, пока еще она не слишком сильно в него вкоренилась. Привычка вводить буквы и, V, W,... чрезвычайно затягивает выкладки и заставляет терять из виду самый ход вычислений; но, самое главное, она вредна для ума, ослабляя воображение.
Повторим предыдущий пример, не вводя никаких букв, т. с. так, как надо всегда делать.
Пример диференцирования при навыке.
Найти производную от(1-|-/х)п.
Надо говорить себе так: производная от (1 -1- х)п равна производной от (1 /х)п по 1 ]/х, т. е.
п (14-/Х)"-1,
умноженной на производную 1-]-Ух по х, т. с.
1
2]/х
Значит, искомая производная равна:
В соответствии с изложенным рассмотрим на примере формы записей, которых следует придерживаться читателю.
/ ___ 2 \8»
Найти производную функции у — I ух* -|-----j-l .
3-й способ записи, к которому читатель должен в конце концов перейти:
УПРАЖНЕНИЯ.
Пользуясь правилом диференцирования функции от функции, найти производные следующих функций:
§ 73. Диференцнрование обратной функции. Пусть х = ?(>).
Если обратная функция существует, обозначим ее
>=/(х). (3)
Днференцируя (3) по у, найдем:
1 * ~dy п0 (ххп)
[предполагая, что и /(х) днференцируемы] или
! _ &У (1х dx ау ' Следовательно, если (У) отлично от нуля, то получим:
dy _ 1
dx — dx (ХХШ)
dy
или
,(x>=F7w' <ххш’)
Итак, производная от обратной функции равна обратному значению производной от прямой функции.
§ 74. Диференцирование логарифма. Пусть
У = loge« ')•
Диференцируя по общему правилу § 59 и рассматривая v как пере-
менное независимое, имеем:
Первый шаг.
у Ад'= ,og. (v "Ь Av).
Второй шаг.
Ад = loga (v Н- Av) — logav = logo
Третий шаг.
v -4- Av v
, ( i । Av \
=!°g h
[Разделяя логарифм на v и в то же самое время умножая показатель! скобок на v, мы изменяем форму выражения, но не его величину.]
Четвертый шаг. . log е 2). dv v °
~ Дю ~
По мере приближения Дю к пределу, равному нулю, — также
приближается к пределу, равному нулю 3j. Следовательно: (Др \ До Др
1 4----) = е, по теореме § 47, полагая а = —/
v / v
Итак: dy d . 1
-j— = -г- (!°g«v) = log„e • — dv dv v 6 ' b v '
।
Так как v есть функция от х и требуется диференцировать log„v по х, то нужно обратиться к формуле (XXII) диференцирования функции от функции, именно:
dy dy dv , dx d v dx '
Подставив
значение ~~, dv
находим:
dy , \ dv
-- = log.e • — • -г-.
dx Б a v dx
i) Учащийся пе должен забывать, что эта функция определена только для положительных значений основания а и переменного с.
2) Если мы проделаем третий и четвертый шаг общего правила без преобразования правой части равенства, то получим: Третий шаг.
Ду _ Ioga (Ю + д») — 10ga V
Дю ~ Дю
Четвертый шаг.
tfy О = -у- — неопределенность
Следовательно, предел правой части не может быть найден непосредственно после трепего шага, и проделываемые ниже преобразования необходимы.
Так как log ю есть функция непрерывная.
Итак,
dv
1Х Д (logev) = lcgae -^-.
Если а = е, то формула примет вид: dv d .. ч dx
IXa з— (In v) =----.
dx4 ' v
Итак, производная от логарифма переменного равна произведению модуля *) системы логарифмов на производную переменного, деленному на это переменное.
§ 75. Диференцирование простой показательной функции.
Пусть
у = а\ при условии а > 0.
Берем от обеих частей логарифм по основанию е:
Iny = vlna, или 1пу 1 v = ---- • 1пу.
In a In а
Диференцируя по у, по формуле IXa, имеем: dv 1 1
dy In а у и по формуле (XXIII), относящейся к обратным функциям, находим:
-/- = 1па • у,
* dv
или
.
-±- = Inn • а . dv
Так как v есть функция х и требуется диференцировать а* относительно х, мы должны обратиться к формуле (XXII) для диференцирования функции от функции, именно:
dy __ dy dv dx~ dv * dx'
i) Логарифм числа e при каком-нибудь основании а (т. е. log^e) называется модулем системы, которой основание есть а. В алгебре доказывается, что логарифм числа N при основании а можно найти по формуле:
log N In N log N = log e • log N = -—-— ==-.
° ° ' Ina
Модуль обыкновенных,'или бригговых, логарифмов (основание 10) есть lg е = lgI0 е = 0,434294 ...
Подставляя значение -г—, найдем: dv
dy . „ dv
= In a • a • ——. dx dx
Итак:
X
d . , г dv
—(а ) = 1п а • а • dx 7 dx
, dv
Ха
Если а = е, формула примет вид:
^(e’)^eV-dx dx
Итак, производная от постоянного с переменным показателем равна произведению натурального логарифма постоянного на постоянное с переменным показателем и на производную показателя.
§ 76. Диференцнрование общей показательной функции.
Пусть
у = ’)•
Взяв логарифмы обеих частей по основанию е, получаем 1п_у = t/lnu, или v In U
у = е .
Диференцируя по формуле Ха, имеем:
dx dx' ’ \
du dx . , dv
-----kin и • —— и 1 dx
по V
= tiv
v •
du \
dx . , dv I -----pin и- —I.
и 1 dx
XI
Следовательно:
A(tt«) = vu”-1 dx 7
du . , 4dv
-г-4-In u • if —. dx 1 dx
Итак, производная от показателем равна сумме мых сперва д и ф е р е н ц и р о в а н и е и по VII, показатель как количество принимая постоянным основание.
Пусть v = постоянному п\ в таком случае XI приводится к z..n\____________________„,.я—1 du,
di^ т -di-
переменного с переменным двух результатов, получае-рассматривая постоянное, а затем поХ,
Но это есть формула, найденная в § 68; следовательно, VII остается верною для всякого значения п.
i) u может принимать здесь только положительные значения.
Пример 1. Диференцировать у = In (х2 + а).
Решение.
dy __ dx^x + а _ no IXa
dx x- 4- a
|v = x»+a|
_ 2x - x5 + a ‘
Пример 2. Диференцировать y = — x-.
Решение.
dV
—' - =---------= по IXa
ax J_
(1-хз)1
__ 1
’ (1 _ X2) - ( _ 2x)
_ 1 * по VII
“ » ’ Д2 - I
(I-X’)3
Пример 3. Диференцировать у = ая v’.
Решение.
g -lna.aa^(3x=)= поХ
= 6x In a • аЯл .
Пример 4. Диференцировать y = Ьее'+зс\ Решение.
= ^c'+x’-^(c= + x=)= no Ха
= гЛхе^+Л
Примерб. Диференцировать у = х‘*.
Решение.
dx = W 1п V ~di = по XI
= Zx**-» + x**lnx.Z =
= еххеХ н- In х) .
§77. Практика диференцирования логарифмических функций. При диференцировании логарифмических функций, вместо применения сразу формул IX и 1Ха, мы можем иногда ради упрошения сперва воспользоваться одним из преобразований элементарной алгебры. Так, пример 2 предыдущего параграфа можно было бы решить следующим образом.
Пример 1. Диференцировать у = 1пУ1 — х2.
Решение. Можно сначала написать у в форме, свободной от радикала:
у = у 1п (1 — Xs).
Отсюда
dy 1 dx u _ 1 - 2х _ х
dx = 2 1 — xs “ 2 ‘ 1 - vs “ г2 - Г "° '
Пример 2. Диференцировать у = In
,/ l + xs V 1 - х-‘
Решение. Упрощая имеем:
> = у[1п(14-х’)-1п (1 - xs)J.
. ,[#(» +х’) dy 1 dx 4 ' dx '
~di~l. L Г+х» 4 -xs
no IXa
x , x _ 2x
1 + xs + 1 — xs = 1 — x*'
Когда приходится диференцировать показательную функцию, и именно переменное с переменным показателем, то лучше всего сначала взять логарифм функции, а затем диференцировать. Так, пример 5 § 76 изящнее решается следующим образом.
Пример 3. Диференцировать у = х .
Решение. Взяв от обеих частей логарифм:
In _у = е* • In х, диференцируем обе части по х:
или
1 dv е* d „ . . , d , r
----г- — — (In x) + In х • — (cr) = у dx dx 1 dx
X 1 , . X = e---k In x • e ,
x 1
£х=еМт+1пх)=
no IXa и V
= /x^ (y + lnx).
Пример 4. Диференцировать у = (4x2 —7)г+Уж’~5 •
Решение. Берем логарифм:
In у = (2 4- У х2 — 5) In (4х2 — 7).
Диференцируем обе части по х;
J. .^ = (2 + /л2-5) . - + In (4х2 - 7) • ,
у dx 4х- — 7 ' у хг — 5
^=х(4х2-7г+^ Г8(2+/^5) Ш (4х» — 7) 1 Лс 4л2-7 Ух2-5
Г(х- 1) (х-2)
V (х —3)(х —4) \
В случае, когда функция состоит из нескольких множителей, иногда выгоднее, прежде чем диференцировать ее, взять логарифм. Так:
Пример 5. Диференцировать у =
Решение. Взяв логарифм, имеем:
In у = у [In (х — 1) + In (х — 2) — In (х — 3) — In (х — 4)]. Диференцируем обе части по х:
1 1 Г 1 . t___________1________1_1 =
у dx 2 [ х — 1 ' х — 2 х — 3 х — 4 I
= 2х’-10х + 11
(х — 1) (х—2) (х —3) (х —4) ’ или dy 2.v2 — 10x4-11 •
dx ~ £ £ £ £ *
(х-1)а (х-2)3 (х-3)2 (г— 4)3
УПРАЖНЕНИЯ.
Диференцировать функции: 1. ^ = 1п (х + а). Отв. = dx 1 *4- a‘
2. у = In (ох + 6). dy __ dx a ax-±b ’
q 1 1 4- X 3. у = In . J 1 — X dy = dx 2 1 — X2'
1 4-х3 4. у = In . Л 1 —Xs dy _ dx 4x 1 —X»’
е ОХ аУ _ ax
5. у = е . dx ae •
6. у ~ е^\ dy__ dx 4ete+6.
1.у = \и (х34-х). dy _ dx 2x4-1 X a 4- x ’
8. у = ln (Xs-2x4-5). dy _ 3xa — 2
dx Xs—2x4-5 ’
9. у = log^x-hx3). dy _ dx , 2-|-3x2 10g</- 27+7»
10. у = х In х. dy _ dx In X 4* 1 .
ll./(x) = ln(x’). /'(x) = £
12./(x) = lnsx. / f (X) = 31n2x
13. /(x)=ln^if. Г(Х) 2a
a3 —x3’ 1
14./(х) = 1п (х-Ь VI 4-х3). /'(X)
Vi-l-x3 ’
15. у = а**. dy _ dx . e® x = in a-a • e t
11 Вак. 27вв. — В. Грвквиль и Н. Луин. Часть 1
16. у=. Ьх*. = 2х • In Ь • 6®*. dx
17. у = 7®’+1т . -^- = 2 In 7 .(х+1)7х’+ dx 1
18.> = СО’-Х*. ~~ = — 2х In с • с“’~‘г’. dx
19. г »» а . dr е . — = а -Ina.
2О.г = а™. dr a1”' In a db 0
21. s = ?*+t’ . ^- = 2teb'+t\ dt
22. и = ае^ ° . da _ ae^"* dv ~ 2/V "
23. р = е«1п’. ^ = ^1B’(i + m9).
24. [е®(1 - х2)] = ех (1 - 2х - ха).
25 -?£1_
25 (еЧ-1Я
26. ~ (x« «“) = x™ (ax + 2). 27. у = In • dy dx i _|_ •
28.y=^^-e~Tj. <L = lf fi +c"^ dx 2 V +c ;•
„ г® — e~x 29. у = —- — . e“ + e~x 30. у = xnax. dy 4 dx ( 6х + e~x * ‘ = л® x’*-1 (л + x In a).
31. y= Xх. Xх (Inx 4-1).
2 32. у = x* . dy _ x®(l — Inx) dx x2
33. у = x1" *. $!= Inx2 • xlnF-i. dx
34. / (_y) = In у • ev. Г (У) = ev (in.у -I-
35./(s) = -!^-. . 1 — s In s ™
36. /(x) = In (In x).
37. F (x) = In4 (In x). F'(x) « X In X
38. (x) = In (In* x). ’/(Х) = Tin x •
Л 1 V 39. <?(у) = 1п|/ 40. /(х) = In /х34-1Ч-х f{x}~ /i-м3’
41. у=х*“*. g-°-
42. > = е®Е. ^• = e®a’(l + lnx)x®. aX
43.,. «• 45. w = о® °. Л? „е" dv \ V J
й = (тУ(1пв-1п/-1)-
47. у = х®”. = ха’”+"-1 (л 1пх+ 1). аХ
48. у =хяХ. ^=хХХ ГХ1П Х + 1П’Х + X ) •
1 49. у = aVa’-^ , dy ху In а dx (а3-х®) 2
50. у = ех[хп-пхп~1 4-л(л-1)хп~2 -• • • ]. “£ = егхп.
51. Вычислить следующие производные:
а) з- Х21пХ. dx 0 d ». e* In x. dx k) ^Щ(а® + И.
Ь) Тх^~^ g) dx 1) 1g (x3 4- 5x).
d , 3x4-1 d 1 d 2 4-х»
с) ZF 1п ГТ • dx х 4- 3 h) dx xlnx m) dx e3^
d) d , 1 - ха -г- In • /14-х D £ In x» /1 4- x3. ax n) ^(x3 + <J2)e
d Ух d ( I d . rt , . о
е) dx j) h(I) • o) d^(xa+4x>
. _ (*+ I)3 ____<* + П (5ха+14х + 5)
7 (x+'2js(x+'3>- dx (х + 2)«(х + 3р
Указание. В этом и в следующих номерах, прежде чем диференцировать, взять от обеих частей логарифмы.
53. у =
(х-1)* £ 7 (х—2)* (х-4)®
54. у = хY 1 — х (1 -f- х).
dy = (х- 1)2Jx» + 30x-97)
dx 1 io
12(х — 2)4 (х—31®
dy 2 4-х — 5х*
dx 2 / 1 —х ‘
(1
’•-v = 7T^
56. у = л* (а + Зд- )3 (а — 2л)2.
57. , _ Й4±^. У х — а
dy _ 1 + Зх» — Чх*
dx~ 2.
(1-х2) ®
= 5х‘ (в-|-Зх)2(а—2х)(аг-|-2ох—12x2).
dy _ (х - 2д) /х то
dx ~ 3
(х-а)а
§ 78. Диференцирование sin v. Пусть y = sin v.
Рассматривая v как независимое переменное, по общему правилу § 59 имеем:
Первый шаг. #
у Ду = sin (v -J- Av).
Второй шаг.
Ду = sin (v -|- Ди) — sin v
Д-у sin— i). £
Третий шаг.
Ау
-- = cos Дг>
, Дг/ sin-7-
Д-v
Четвертый чи а г.
dy
= cos v, av
/ > А«\ / sin — \
так как Um I —5— 1 = 1 § 47, Av = o\ /
\ 2 /
и
/ До \
lim cos о4--7 = coso.
До = 0 \ 2 /
*) Пусть
Складывая
откуда
А = v + Ди
В = у
А + В = Чу + До, , 1 До
у (А + В) = у + -у.
А = и + До В= и вычитая ,
1 До
у(А — В)= 2 •
Подставляя эти значения А, Я у И + В), -у (А — В), выраженные через о и До, в известную тригонометрическую формулу:
sin А — sin В = 2 cos у (А + В) sin у (А — В),
_ / , До\ До •
мы найдем sin (о + До) — sin о = 2 cos I о Ц- — ) sin —.
Так как v есть функция от х и требуется диференцировать sin v по х, мы должны обратиться к формуле (XXII) диференцирования функции от функции, именно:
dy dy dv dx d v dx '
r, dy
Подставляя значение ~ из четвертого шага, имеем: dv
dy dv
-f- = cos v — . dx dx 4
Итак, d /• \ dv
XII (sin v) = COS V — .
Правило легко формулировать.
§ 79. Диференцирование cos V. Пусть
у = cos V. 1 la основании известной формулы нз тригонометрии можно написать: j'=sin (2_
Диференцируя по формуле XII, имеем:
dy /it \ d 1 it \ / — \h dv\ . dv
_z_ = cos-----------------y=cos—----------1/ —— = — sinx/—.
dx \ 2 ) dx\2 ) \ 2 / \ dx] dx
[Так как cos — v ) = sin t>.]
Итак:
d / x j dv
XIII ^(cosv)= — sin V — .
§ 80. Диференцирование tg v. Пусть
y = tgv.
На основании определения тангенса можно написать:
__sin v cos v '
Диференцируем по формуле VIII:
d . , . . d , . . dv ... dv dv
, cos г/— (sin p)—sinir—7- (cos V) COS2T>----HSin2^— -3—
dy_ dxK '_______________dx4 _____________dx 1_____dx _ dx
dx co&v cos2x* cos-v‘
Итак:
d x 1 dv dx cos2v * dx’
§ 81. Диференцнрование ctg v. Пусть у = ctg V .
На основании определения котангенса можно написать:
У ~ tg v *
Диференцируем по формуле Vlllb: . — * dy __________ dx ______________dx __________1 dv
dx tg2» cos2» • tg2?/ sin2г/ dx '
Итак: d , . ч 1 dv
CT S<cl<!v>=—Stas ik?
§ 82. Диференцнрование seco. Пусть
у = sec v.
По определению секанса можно написать:
1 V =------.
J cost/
Диференцируем по формуле Vlllb:
Итак:
XVI
d ( . dv
. —г~ (cos v) Sinv-J—
dy_____dx_________________
dx cos2,» cos9»
d . . slnv
j-(sec v) =----—
dx' 7 cos2 v
dv dx’
§ 83. Диференцнрование cosec v. Пусть у =» cosec V.
По определению косеканса можно написать: 1 sin® '
Диференцируем по формуле "Vlllb: d . , . dv
dy-57 co,t,-5T dx sin2'» sin9'»
Итак:
СТП — (cosec v) = -“
dx' ' sin9v dx
§ 84] ПРИМЕРЫ 167
§ 84. При выводе наших формул применение общего правила § 59 (т. е. четырех шагов) было необходимо только в следующих случаях: d . , . du , dv dv) (Алгебраическая Ш ах(и+^ dx -dx.
V d . . dv . du — (uv) = U — k- V -Г-dx ' dx 1 dx (Произведение)
du du
VIII d / и \ dx dx (Частное)
dx\v / v3
dv
IX d .. ч . dx л(1ог.®) = 1о6,е. v . (Логарифм)
XII d , . . dv (Синус)
XXII dy d\> dv dx dv dx ' (Функция от функции)
От этих формул зависят и все формулы, которые будут выведены далее. А отсюда следует, что вывод фундаментальных формул диференцирования включает вычисление только двух пределов, представляющих некоторые затруднения, а именно:
= l Нш (1 -4- v)v =е § 47-
•=о\ v / в=о 1
ПРИМЕРЫ.
Диференцировать функции:
1. у = sin ах2.
= cos аХ* (ах2) = по XII
dx dx '
If = ax’] = 2ax cos ax2.
2. у = tg V1 - x. t
= sec2 /Г^х - (1 - x)2 = по XIV
dx dx'
(r = Vi“)
1
= sec2 Vr^.y(l-x) 2(-l) =
____sec2 /T~~v 1
2 — x . cos2 Vе! — x-2• Yl — x
3. y = cos3x, что можно записать так: у = (cosx)2.
~ со 3 (cosx)2 -^-(cosx) = по VII
[notoi X л = 3]
=c3cos2x( — sinx)= по ХШ
e — 3 sinx COS1 X.
4. у = sir их sin” х.
~ = sin их (sin х)п sin” х (sin пх) = по VII
[n = sln л.г и о- в1пл X]
= sin пх-п (sinx/‘-1 (sin х) sin’*xcos пх — (их) = по XII
= п sin их sin”—1 х cos х + л sin” х cos пх =
= л sin” ~1 х (sin их cos х + cos лх sin х) =
= л sin”-1 х sin (л -|- 1) х.
УПРАЖНЕНИЯ.
Диференцировать функции: 1 «. соллс Отв. dy a sin ax
2. 3. 4. 5. 6. 7. 8. 9. 0. 11. 12. 13. 14. 15. 16. 17. y = tg(ax + i). у = sin2 X. у = cos4 X2 . Ду) = sin 1у cos v. F(x) = ctg2 5х. ' F(0) = tg е — е. /(?) = <? Sin ? н- cos т. f(f) = sin9/cos t. r=a cos 28. r = a У cos 20 . r = a(l — cos 0). r = a sin9 -5-. V (in cos x) = — tg X. d 2 — (In tgx) = dx ' 67 sin 2x ~ (In sin1 x) = 2 ctgx. tgx-J sec x dx — cos'- ax p a . dx cos2 (ax + b) = sin 2x. dx -j - = — 6 x cos2 x2 sin x2. dx f(y) == 2 cos 2y - cosy — sin 2y • sin у. F'(x) = — 10 ctg 5x • cosec2 5x. 5'(0) = tg20. /'(•?) = ? COS ? . Д11) = sin21 (3 cos21 - sin2 0. ~ = —2fl sin 28. dlt dr _ a sin 26 <10 У cos 20 dr . n ^=«510 6. dr 8 6 -^ = fl sin- j cos7. dy , . -J- = sinx 4- cosx. dx
18. 19. 1 , / 1 +sln X V = in 1/ -J—! j ' r 1 — sin X у = 1п ш(7+т)‘ • dy 1 dx cosx * dy _ 1 dx cosx
20. 21. Дх) = sin (x + e) COS (x Дх) = sin(lnx). -fl). /'(x) = cos 2x.
22.
23.
24.
25.
26.
27.
23.
29.
30.
/(*) = tg (Inx). /'W = sec2 (In x) X
a ds a a sinT
s = cos — . dt * • »
, 1 dr 2cos^
r = sin -Г7 . ~dl> ~ 63 '
p = sin (cos q). dp__ dq — sin q cos (cos q).
у = еЛлх. dy__ dx eeln x. cos x.
y = a*tnx. dy _ dx naif • sec2 nx • In a
у = ecoe т sin х. = e'os х (cos х — sin2 х).
>’ = ea!lnsinx. = e®(ctgx-|-lnslnx).
(xn e,ln x) = xn-1 eBla x (n + x cos x).
31. Вычислить следующие Производные:
a) sin 5x2. dx f) -г- coscc in x. dx d a—o coe t K) ~dte
b) cos (a — bx). g) ~ sin3 2x. Б dx ,4 d ( . t 2f\ *) 7^7 slnVC0S~4_ • dt \ 3 3 /
. d L ax С)Л d r h) -r- cos2Inx. dx d . d , b т)-^С,8в-2-d
d) ctgVax. d d n) -7- V 1 +cos2?. d
e) — sec e10. dx I) dx ln (sin' o) -7- In Y 1 — 2 sin2 s. ds
32. (e°® cos mx) = enx (a cos mx — m sin mx).
oo z/ax 1+cosO n 2 sinO
31 = ~Т~1~7>ч«'й • Omt- f (°) = — П---ТТТйЗ•
1 — cos 0 (1 — cos OJ2
34. . ea,>(flsine — cos ф) /(») /'(f) = eaTsinf. c
35. /(s) = (sctgs)2. f (s) = 2s ctg s (ctg s — s cosec2 s).
36. *• = 4- tg3 e — tg e + e. 0 ^ = ‘8‘в-
37. y = x81n®.
38. у = (sinx)*. = (sinx)“()nslnx-|-xctgx).
39. у = (sin X)* ® = (sin x)‘l ®(1 + sec2x In sin x).
40. у = X -f- In COS (x — y) • dy 2 dx "1+tgx-
41. Из sio 2х = 2 sin к cos х диференцированием вывести cos 2х = cos2 х — sin2 х. 42. Из ..
. 71 -р I 77А
sin —х • sin
sln я + sin 2х 4- ... -f- sin nx =---------
s,nT
диференцированием вывести л , x . 2л + 1 1 f , л \г
-у sin sin-у— X — -у I sin - X )
cos х + 2 cos 2х + ... + л cos nx --------------------------
sin’у
(л = целому положительному числу).
§ 85. Диференцирование arcsin v. Пусть
следовательно:
у = arcsin V1)-,
p = siny.
Диференцируя по у по формуле XII, получим;
dv dy 1
—г— = cos v, откуда —- =--------
dy dv cosy
по (XXIII).
Но так как v есть функция от х, то этот результат можно подста-
dy dy dv dx dv dx*
(XXII)
вследствие чего найдем:
вить в
Черт 57.
dy _ 1 dv____1 dv
dx cosy dx У1—v2 dx
cosy = У1 — sin’y = У 1 — v2; перед радикалом берем знак-f-, нбо cosy для всех значений у от —- до положителен.
1 ' 2 2 _____ »
х) Необходимо напомнить, что эта функция определена только для значений v, содержащихся между—1 и +1, включая и эти крайние значения, и что у есть функция многозначная, так как существует бесконечное множество дуг, которых синусы все равны V. Так, на прилагаемой фигуре (черт. 57, который представляет функцию v = arcsin v) для v = ОМ будет у = MPV МР,, МРа,.... MQi, AiQg, ... Чтобы иметь дело с функциею однозначною, рассматриваются только значения у, лежащие между — у и +у (включая последние), т. е. точки дуги АОВ; таким образом из всех дуг, которых синус равен v, рассматривается дуга, точки которой имеют наименьшие по абсолютной величине ординаты.
Итак: dv
XVIII -f- (arcsin v) = r dx
dx ' ' у i _ va
§ 86. Диференцирование arccos г. Пусть
откуда
= arccos г* *), v — cos .у.
Диференцируем по у по формуле XIII:
dv . dy \
dy J dv siny
Но так как v есть функция от х, то этот результат мох вить в формулу:
(ххп) dx dv dx
и это дает:
dy __ 1 dv_____ 1 dv
dx sin j dx Y1—v* dx
ein> = V1 — сое» у = —v2, прячем перед
радикалом берем знак -|-, ”6° sin У для всех значений у от 0 до к положителен.
Итак;
dv
XIX ,d (arccos v) ---,-dX- —.
dx' 1 /1—va
>) Эта функция определена только для значений v, содержащихся между —1 и —|- 1, включая и эти крайние значения, и есть функция многозначная. На прилагаемом чертеже (черт. 58), КЪгда v = ОМ, будет у = AfPj, MPt, ..., AfQp MQ2,
Чтобы функция была однозначною, рассматривают только значения у между 0 и п, т. е. дугу АВ, точки которой имеют наименьшие положительные ординаты.
по (XXIII].
но подста-
У
Черт. 58.
§ 87. Диференцнрование arctg о. Пусть j/ = arctg-y>);
следовательно:
Диференцируя по у по формуле XIV, находим: dv „ dy I
—— = sec2y, откуда —— =—т— по (XXIII).
dy dv 5ес2у v '
Но так как v есть функция от х, то результат можно подставить в формулу: dy dy dv
dx dv dx ’
и это дает: dy _ 1 dv _ 1 dv
dx у dx I-]- 'У2 dx
[sec2у = 1 + tg2y = 1 + v2]. Итак:
dv
§ 38. Диференцнрование arcctg©2). Следуя методу предыдущего dv
XXI ^-(arcctgvj^—j-^.
параграфа, найдем:
Черт. 60.
>) Эта функция определена для всех значений v и есть функция многозначная, как ато ясно видно из ее графика (черт. 59). Чтобы сделать ее однозначною, рассматриваем только те значения у, которые лежат между — у и + у, т. е. /дугу, ординаты точек которой имеют наименьшие по абсолютной величине значения.
2) Это — функция, определяемая для всех значений V, притом многозначная, как видно из черт. 60. Чтобы сделать ее однозначною, рассматриваем только те значения у, которые лежат между О и я.
§ 88] ПРИМЕРЫ.
Диференцировать:
1. у = arctg ох’.
Решение.
dy _ dx lax
dx ~ 1 + (ax2)2 “ 1 + d‘x*
|u = ax’).
2. у = arcsin (3x — 4x3).
Решение.
-£-(3x—4x3) dy _ dx _
tfx ~ /1 - (3X - 4x3)2 ”
(a = 3x - <r«]
3— 12x2
/ 1 — 9x3+24^— 16x«
___3 _
/1 -x»‘
по (XX).
по (XVIII)
УПРАЖНЕНИЯ.
1. y= arcsin — . z a
2. у = arcctg (x1 — 5).
•’x
3. у = arctg—-
4. у = arctg "Kl — x.
5. у = arctg .
6. у = arcsin —. /2
7. /(x) = x Vai _ л-2 a’ агс$|п .
8. f (x) ™ V a* —x* + a arcsin —. CL
9. в = arcsin (3r—1).
10. f = arctg r~^~ a . 6 1 — ar
dv Отв. —-— 1
dx V tP—Xi
dy — lx
dx l + (x’^5?-
dy 2
dx 1 4-x2’
1
dx 2(2 —x)
dy _ a
dx aa-|-x2 ’
dy ___________1_______
tfx “ /i _ 2x - x« ’
/'(-r)=-’/e3-x2.
/'И-(М)’-
db _ 3
dr ~ V 6r-9r’‘
d<f _ 1
ar ~ 1 4- r*‘
х
11. -т- (х arcsln х) = arcsin х dx '
12. -^-(tg 6 arctg 6) = sec2 в arctg в
13. — [In (arccos 0] =------------
dt arccos t *
14. f(y) = arccos(iny).
15. /(в) = arcsln Vsin fi.
it t, •. z ,/”1 — COS?
16. f (?) = arctg 1/ —:------.
r 1 + cos ?
17. p = etI'**. ev — e~v 18. u = arctg-----------.
e«_ e~t 19. s = arccos—---------
e‘ + e~‘
20. y = x“ceiI11.
21. у = exx arctg x.
22. у = arcsin (sin x).
__ . 4slnx 23. у = arctg 5-^-------—.
J • 3-f-о cos x в x — a
24. у = arcctg----1- In 1/ —:—.
J 6 x 1 r x 4- a i z] _|_x\ * 1
25. > = ln (r^x) “ 2*arctg x'
26. у = У”1 — x2 arcsin x — x.
x** — 1
27. у = arccos —=-----.
x2n 4- 1
28. Найти следующие производные: a) ~ arcsin 2x2. f) X-t3 ’ dx dt
tgQ
1 4- 62’
1 — fl'
P ( y) —---------1------.
У V1 — (Iny?
/' (0) = у V1 4- cosec в.
/'(?) = 4-
dp _ e‘rct« ч ~dq ~ '1 4-<7s ‘ du _ 2
dv ev-\-e~v ds __ 2
dt e* 4- *
dy _ -ЛГСВ1Пx f arcsln x Inx \ dx \ x •
lx агс ‘C-v C1 +ln *)] •
^ = 1. dx dy _ 4
dx “54-3 cos x ‘ dy______2ax3
dx ~ x* — a* ‘
dy _ x3 dx ~ 1 — x*‘ dy x arcsln x dx ’
dy _ 2nxn~l dx x2’* 4- 1 ‘
4-
b) 4x B) ~3t *w°'e at k> ^7 arcsln^ 1 ~J/2 ’
- d . 2x c) arcctg T. d) (x arccos x). h) tg arctg ?2. 1) arclg (In 3 az). i) arcsln a'. m) У1—t2 arcsin t.
e) ^-x2 arcctg ax.
В нижеследующих примерах читатель должен научиться диферениированию обратных функций.
Читатель должен отнестись к формуле (XXIII) диференцирования обратных функций:
Он
dx должен отыскать ,
29.
30.
31.
32.
1 + in у' aln^+J
33.
V .«o<a v
dy 1 dx ~ dx * ~dy
и найденное подставить в формулу (XXIII).
dy _ 2 УТ+у _ 2х
dx 2 +Зу 2у4-3у» ‘
dy _ 2 /1 4- cosy _ 2
dx sin у У*2^
dy = (1 4- InyP _ ya dx iny xy — x2’
'-V0=p. %.---------y=.
dx gi
dy _ 14-y* dx x '
~ — cosec.c. dx
$L = V\_4e-4 • dx
34.
35.
36.
х = 2arctg (ev).
ev -f- Уе~у — 4 Х = 1П--------------
Показать, что геометрический смысл формулы (ХХП1) состоит в том, что
касательная к кривой образует с осями координат дополнительные углы.
§ 89. Неявные функции. Читатель уже познакомился выше с обратными функциями и их диференцированием.
Он уже знает, что если /(х) есть какая-нибудь данная и хорошо известная нам функция, то буква у называется обратной функцией поотношениюк' ношением:
/(х), если эта буква у связана с буквою х соот-
•*=/(>)•
решить это уравнение относительно буквы у, т. е.
от этой связи, то мы получаем тогда обратную
Если нам удается освободить букву у написанную явным образом через букву х. например, случай обратной функции:
Х = 2 + ЗУ
У — 5 ' это уравнение относительно буквы у, мы получаем обратную
функцию, Таков,
Решая функцию у, написанную уже явным образом:
X — 3 ’
Но не всегда и не во всех случаях возможно разрешение уравнения
относительно буквы у, т. е. освобождение ее из этого уравнения. И следует сказать, что на практике, к сожалению, большею частью именно
и представляется тот случай, когда мы не умеем или не можем освободить из этого уравнения букву у, выразив ее в известных знаках действий над х. И тогда нам ничего иного не остается, как просто ввести совершенно новый значок, обозначающий зависимость буквы у от буквы х.
Таков был у нас случай*, когда мы имели функцию, обратную тригонометрической, и когда, имея зависимость
х — siny
п не умея решить это уравнение относительно буквы у просто писали:
у = arcsin х,
введя новый значок „arcsin*. Введение этого значка мы сделали по необходимости, ибо иначе никак нельзя выразить букву у через букву х помощью других известных нам значков.
Таков был, в сущности говоря, даже случай обыкновенного логарифма, когда мы, имея зависимость
Х=Ю»
и не умея освободить из нее букву у, просто согласились писать:
y = Lgx,
введя новый значок „'Lg*, называя его „логарифмом* и изучая его как новую функцию, хотя взятый сам по себе, без породившего его первоначального прямого уравнения х=10*, он ничего не означает, — подчеркивая этим всю меру нашего незнания.
Но случай этот исключительный, и, как общее правило, невозможно выразить явным образом обратную функцию у через букву х, т. е. невозможно в подавляющем большинстве случаев решить уравнение:
x=f(y)
относительно буквы у, освободив ее из него.
Тем меньше у нас шансов ожидать разрешимости относительно буквы у, если вместо уравнения:
х— /(J) = O,
имеющего все-таки специальный вид, ибо буква х входит только один раз и притом только в первой степени, у нас имеется любое уравнение, связывающее друг с другом вместе буквы х и у:
/(х,у) = 0.
Здесь знак /(X, у) обозначает любое выражение содержащее буквы х и у.
Если уравнение
f(x,y) = o,
связывающее две буквы, хну, разрешается относительно буквы у, тогда это значит, что буква у является явною функцией буквы х. Если же мы не умеем решить уравнение
f(x,y) = О
относительно буквы у или если не хотим это сделать, видя, что получится слишком громоздкое выражение для у, то тогда количество у рассматривается как неявная функция независимого переменного х *)•
Например, уравнение
ха — 4у 4- 7 = О, пока оно не разрешено относительно буквы у, определяет у как неявную функцию буквы х. Решение же этого уравнения относительно буквы у — здесь очень легкое — дает у как явную функцию буквы х: х84-7
У = -Т~'
Равным образом уравнение
ха-|-у2 — а = 0, пока оно не решено относительно буквы у, определяет у как неявную функцию х. Но явное выражение у через х и здесь возможно, ибо
у = V а — ха.
Напротив, уже уравнение
не может быть разрешено явным образом относительно буквы у и, значит, определяет у как неявную функцию буквы х.
§ 90. Диференцирование неявных функций. Когда у определяется как неявная функция от х при помощи уравнения:
/(*.>) = °.
то в случае неразрешимости этого уравнения относительно буквы у мы на первый взгляд находимся в безвыходном положении, если нам нужно иметь производную
dx'
Действительно, на первый взгляд кажется, что, прежде чем отыскать
dy dx ’
производную
надо сначала найти выражение у черех х, т. е.
*) При этом, понятно, мы должны твердо быть уверенными в том, что уравнение /(х,у) = 0 для всякого числа х известной области имеет хотя бы один корень yr, даже если мы его не умеем вычислить. Если же такого корня нет, тогда не может быть и разговора ни о какой функции у, явной или неявной.
12 Зак. 2769. - В. Гранвиль и Н. Лу.’иа Часть I
превратить неявную функцию в явную. А так как это последнее не всегда возможно, как, например, в случае уравнения
ах6 2х’у—у7х — 10 = 0,
то кажется, что в этом случае надо отказаться от определения производ-dy
НОЙ dx
Выход нз этого положения дает следующее правило1).
Правило. Имея уравнение /(х,у) = 0, надо продифе-рен пировать все его члены, рассматривая укакфунк-циюх по правилу функции от функции, и результат приравнять нулю, т. е. надо вычислить
df(x,y) dx
Тогда
получим уравнение относительно и с к о< rfy •
мой производной , которую оттуда и освобождаем,
решая его.
Приложим это
правило к отысканию -f- из уравнения;
ахв-[-2х8у—j7x— 10 = 0
часть при неявной функции всегда будет нуль, а
Так как левая производная постоянного есть нуль, то имеем:
d(ax*-\-2x*y—У’х—10) dx
Или иначе:
dax* . d2x*y dylx d 10
dx dx dx dx
по теореме диференцирования суммы [формула (III)].
Вынося постоянные за знак диференцирования и применяя правило о производной произведения, мы находим:
6охв + 2 • Зх«у + 2х8-^ — 7у« & х—у' = 0. ил
~ , dy
Собирая члены, в которые входит искомая , вместе, а все другие перенося вправо, имеем:
(2х8 — 7ув) = у7 — бах6 — 6x’j,
*) Правило это будет оправдано в главе XV. В производную можно подставлять только соответственные значения х и у, удовлетворяющие данному уравнению /(ж,у) -0,
откуда, решая относительно искомой производной, имеем, наконец:
dy _ у1 — бах1 — 6х*у
dx~~ 2x3 —7у°
Читатель замечает, что результат содержит сразу обе переменные величины х и у, причем они должны, понятно, удовлетворять первоначальному уразнению:
axs -J- 2х3у —yix — 10 = 0.
УПРАЖНЕНИЯ.
Диференцировать, применяя 1. yi = 4px. вышеуказанное правило, следующие функции: „ dy 1р dx у
2. 3. 4. 5. 6. х3+у2 = И!. Ьях- + а-уЗ = аЧ». у3 — Зу -|- 2ах = 0. 1 1 1 х2 +уа = а2 . з. L з. Xs +ys = а2 . dy _ х dx у " dy b-x dx ~ a2y' dy 2a
dx 3(1—y2)' dy — лГ~У dx V x " dx r x
7. 4-S II dy b2x dx~ a'y‘
8. 9. 10. 11. 12. 13. 14. у2—2ху4-02 = О. х9+у3— Заху = 0 гУ — Vх dy у dx y — x’ dy аУ — x3 dx ~ y2 — ax’ dy jp — xy Iny
р3 = a2 sec 20. р3 cos 0 = а2 sin 30. cos (uo) = cv. 6 = cos (0 + *?) • dx x2 — xy in x ’ dp _ a2 sin 20 db~ p dp 3a2 cos 30 + P2 sin 6 db — 2pcos0 du _ c 4- и sin (uv) dv —v sin (uv) ’ db sin (0 4- <p)
d? 14- sin (0 4" f)
15. ЛУ Найти из следующих уравнений:
а) х* = ау. Ь) х24-4у3= 16. с) 03х3 — аяуЗ = а2^3. d) у2 = х34-в. е) х2 —у2 = 16. f) xy 4~y2 4~ 4x = 0. k) tg X-f- y3 = 0. g) yx2 — y3 = 5. 1) cosy 4* 3-С3 = 0. h) x3—2xe=y3. m) xctgy4"У = 0. 1) x3y® 4- 4y = 0. n) y3 = In x. j) y2 - sin 2x. o) e®’ 4- 2y® - 0.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ.
Проднференцировать слсдуюШйе функции:
1. arcsin У1 — 4х-.
2. лехг .
3. In (sln£j
4. arccos —.
У
б’ 1 4- Inx'
7. In sec (1 — 2x).
8.
9. г 1 cos t
10. arcsin (1 — cos x) .
,, L 2s
11. arctg --------.
У s2 - 1 s/ 2
12. (2x—1)1/ r 1 -j- *
x3 arcsin x . (x3+ 2) VI — x-
13- 1 + 9
14. tg24-4-In sec2 4-. О о
15. arctgyCe2® |-е_аг).
17. x*”.
Отв. — 2
eI’(2x24-1).
1 * ° 2-ctgy.
a
у УУ — я-я2 «
(e2 - л2?
In X
(1 4-In X)2
— 2tg(l—2x).
xe2-Sx(2 — 3x).
coscc t.
_1_ 2 '
________2
(1 —5s2) / S’ — 1 ‘
7 4-4x V~~2~~ 3(l+x)K 14- x-
л2 arcsin x.
23. In sin2 у.
24. eax In sin ax.
25. sin3 f cos 7.
1 2
1Я (Ж)’(х’-1)4'
IB.
хг
19.
20. arctg У1 — x2.
z2
21.
cos z
22. e‘«r2-
27 m + x <?W ‘rCtg X 14-m2 ’ VT+x2’
28. tg2 x — In sec2 x.
on 3 In (2 cos x 4* 3 sin x) 4- 2x 13
30. arcctg — 4- In 1/ X । Д • 6 x r x + a
31. (In tg3x-x3)3.
£ £
32. 2-3/2 + 4fa +<2
(1-|-х)(1-2х)(2 + х) (34-х)(2-Зх)
34. arctg (In Зх).
35. y\a-bxn),,‘.
36. in/^-ex-)"*.
/ \й 4-1
37. my
38. 1/ (2~3x>3.
V l -£4x '
39. COS X *
40. e*lnsinx.
41. . X arcsin —— V1 + X'
42. arctg ax.
43. a'in’"“
44. ctg3 In (ax).
45.
46.
i
(1 — 3x2)ex .
In
)/l — x?
ГЛАВА VI.
ПРОСТЕЙШИЕ ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ.
§ 91. Направление (подъем) кривой. В § 60 было показано, что если
У = /(х)
есть уравнение кривой (черт. 61), то dx х v
— =tgr = тангенсу угла наклона к оси X касательной в некоторой точке Р.
Направление кривой в любой точке определяют как направление касательной к кривой в этой точке. Отсюда в силу этого определения следует, что dy v - г.
= = тангенсу угла наклона к оси X кривой в точке Р.
Для некоторого частного пбло-жения точки, которой координаты (XpyJ известны, мы, следовательно, имеем:
dyl
-f- = тангенсу угла на-
клона кривой {или касательной) в точке {хх, у,).
В таких точках, как D, F, где кривая (или касательная) параллельна оси ОХ,
„о , dy
т = о, следовательно, = О. dx
В таких точках, как Л,В, G, где кривая (или касательная) перпендикулярна к оси ОХ, » , dv
т = 90°, следовательно, -f = оо. dx
В точках, как Е, где кривая поднимается ’), 1 dv
~=острому углу, следовательно, числу положительному.
Это имеет место влево от В, между D и F, и вправо от Q.
В таких точках, как С, где кривая падает1),
Ц Если двигаться по кривой слева направо.
t = тупому углу, а потому = отрицательному числу.
Эго имеет место между В и D и между F и G.
1.
а)
Ь)
d) е)
ПРИМЕРЫ. №
Дана кривая у = — х- 4- 2 (см. черт. 62).
Найти Найти Найти Найти Найти
. - g л т-и*- “‘у
т, если х = 1.
т, если х = 3.
точки, где кривая параллельна оси ОХ.
точки, где т = 45°.
точки, где кривая параллельна прямой (линия АГ) 2х — Зу = 6.
= х2 — 2х = тангенсу угла наклона dx
Диференцируя, имеем
следовательно,
следовательно,
Решение.
кривой к оси ОХ в любой точке, а>«’=[;Ц«=1-2=-';
135° = 90° +45°.
b)*4aL-9-c-3i 1 = arctg 3.
с) т = 0°, tg т = ~ = 0; следовательно, х2 — 2х =
— 0. Решая это уравнение, находим, что х = 0 или 2, что дает точки С и D, где кривая (или касательная)
d) % = 45°, tg т = =1; следовательно, х2 — 2х = 1. Решая, имеем:
параллельна оси ОХ.
что дает две точки, для которых тангенс угла наклона кривой (или касательной) есть 1.
2
е) Тангенс угла наклона прямой равен у; следовательно:
2
х» - 2х = 4.
«5
Решив относительно х, находим:
х-1 _у 3 , вто дает точки Е и F, где кривая (или касательная) параллельна прямой АВ.
Так как кривая в любой точке имеет то же самое направление, как и касательная к ней в этой точке, то угол между двумя общей точке равен углу, образуемому их касательными в
2. Под каким углом пересекаются окружности х*4-у3 * * * * * — 4х = 1, (А)
Xя+У— 2у = 9? (В)
Решение. Решая совместно эти уравнения, находим точки пересечения (3, 2) и (1,-2) (черт. 63): dy 2 — х ,.. _ „
- -у из (А) по § 90. dy х dx~ 1 — у
кривыми в их этой точке.
из (В) по § 80.
~ = тангенсу угла наклона к оси X касательной к кривой (А)
в точке (3, 2'
—— j 3= —3 = тангенсу угла наклона к оси X касательной к кривой В' в точке (3, 2).
Формула для нахождения угла между двумя прямыми, угловые коэфнциенты которых суть и ij, такова:
* 1+V*/
Подстановка дает:
-4+3 tg«=—Ц- = 1.
откуда
6 45°.
Таков же и угол пересечения в точке (I, — 2).
УПРАЖНЕНИЯ.
1 Найти тангенс угла наклона к осн ОХ кривой
У l-j-x* в начале координат. Отв. tg т = 1.
2. Какой угол с осью ОХ образует касательная к кривой
X2j2 = fl3(x+>) в начале координат? Отв. -t = 135°.
3. В каком направлении точка, описывающая кривую
у = Зха — х, стремится двигаться в момент, когда х= 1? Отв. Параллельно прямой, угловой коэфицнент которой есть 5. 4. Показать, что для прямой линии есть величина постоянная.
5. НайтиНаклон к оси ОХ кривой
у = 2 sin х + 3 cos х
в точке, гдех = -^-. Отв. УЗ —
6. Найти абсциссы точек, в которых кривая
у = х3 - 3jfi - 9х + 5 параллельна оси, ОХ. 7. Найти абсциссы точек, в которых кривая Отв. х = 3; х = — 1.
у (х — 1) (х — 2) = х — 3 параллельна осн ОХ. 8. В какой точке кривой = 2л° Отв. х = 3 * V2.
тангенс угла ее наклона к оси ОХ равен 3? Отв. (2, 4).
9. В каких точках окружности v2+>2 = r£
О
тангенс угла наклона касательной к оси ОХ равен — —? •
~ f ,3г 4г' ( Зг 4г\
Отв. (+5.4-5; ‘*(--5-.-5>
10. Где касательная к параболе
у = х2 - 7х + 3 параллельна прямой у = 5x4-2?
Отв. (6, — 3).
11. Найти абсциссы точек кривой
у = х + sin 2х, в которых касательные параллельны прямой _у = 2x4-3.
Отв. х = -£ + ля.
О
12. Показать, что синусоида у = sin х пересекает ось ОХ каждый раз под углом в 45° или в 135°.
13. Найти точки, в которых касательная к окружности
перпендикулярна к прямой
х’4-у«= 169
Ьх 4- 12> = 60.
Отв. ( + 12, 4-5) и ( — 12, — 5).
14. Найти точку, в которой касательная к параболе у2 — 4ах параллельна линии х 4-> = 2.
Отв. (а, — 2а).
15. Под какими углами прямая
Зу- - 2х - 8 = 0 пересекает параболу
У- = 8^? ! ! ,
Отв. arctg -т- и arctg — .1 О о
16. Найти угол пересечения параболы _у2 = 6х с окружностью
Л-5 4-_у2=16.
Отв. arctg °-Уз. «3
17. Показать, что ветви гиперболы х;—_у2=5 пересекаются с эллипсом
под прямыми углами.
18. Показать, что
и циссоида1)
окружность х2 +_у2 = 8ах
а) перпендикулярны вначале;
Ъ) пересекаются под углом в 45° в двух остальных точках.
‘) Пусть ODA (черт. 64) —круг диаметра ОА и АТС—касательная к кругу в точке А. Проведем через точку О какую-нибудь прямую, которая пересечет окружность в точке D и прямую LK в точке Е. Отложим на отрезке ОЕ отрезок OD, равный DE. Геометрическое место точек Р образует кривую, называемую циссоидой.
Черт. 64.
19. Найти угол пересечения параболы
х2 = 4ау
с локоном *)
_ 8а3
х* 1 + 4а2"
20. В скольких точках кривая
у = х3 — 2№ + х — 4
Отв. arctg 3.
параллельна оси ОХ? Каковы эти точки? / 1 101 \
Отв. В двух: (1,-4) и
21. Найти углы пересечения парабол у = 3х3 — 1 и _у = 2х23.
Отв. arctg
22. При каком соотношении между коэфицнентами конических сечений
ajx2 + b.y1 = 1 и а**? + — 1
они пересекаются под прямыми углами?
vj Og ?3 за начало координат, 2а. Соединим точки угол МОР через 0.
Чтобы найти уравнение циссоиды, примем точку О прямую ОА за ось ОХ и положим диаметр круга равным А и D и опустим перпендикуляр МР на ОА. Обозначим Будем иметь:
ОЕ = 2а sec О, OD = 2а сов в, откуда
DE = ОЕ — OD = 2а (sec 9 — cos 6). Следовательно:
OP = 2а (sec в — cos 0). Итак:
х = ОМ = OP cos в = 2а (1 — cos 3 в) = 2а sin2 в, но так как
. я МР у sin в = = г________,
ОР / х2 +
то получаем:
*) Пусть ОБА (черт. 65) — круг, ОА — диаметр круга и LK — касательная к окружности в точке А. Проведем из точки О какую-нибудь прямую, которая у пересечет окружность в точке В и каса-
тельную LK в точке С. Через точку В
I - проведем прямую, параллельную пря-
мой ЬК"; пусть Р — точка пересечения ( Т/вГ***^ этих ПРЯМЫХ- Геометрическое место то-
-—I чек Р дает кривую, называемую локо-
1 -1 • 0"w' ном Аньези.
Чтобы получить уравнение этой кри-Черт, 65. вой, примем точку О аа начало коор-
динат и ОА за ось ОУ. Диаметр круга положим равным 2а. Продолжим отрезок СР до пересечения с осью ОХ в точке М. Будем иметь:
0М = х, МР-у, ОА = МС<=2а.
§ 92. Уравнения касательной и нормали; длины подкасательной и поднормали в прямоугольных координатах. Уравнение прямой линии, проходящей через точку (хр у,) и имеющей угловой коэфициент k, есть
У— У1 = к(х — X,).
Если эта прямая касательна к кривой АВ (черт. 66) в точке Р^ (хп у,),
то по § 60
k = tg т =
' dy ' dx
dxY
Следовательно, уравнение касательной TPY в точке (xi> У1) бУдет:
у— = (*-*:)•
(1) Черт. 66.
Так как нормаль по самому своему определению есть прямая, перпендикулярная к касательной, то ее угловой коэфициент будет:
1 dx.
~k dyY
А так как ола также проходит через точку касания Px(xlt yj, то уравнение нормали P^N (черт. 66) будет:
«л (2)
Из треугольника ОМС получаем:
МР ОВ_ОВ-ОС МС^ОС ОС» "
Соединим точки Я и В. Угол ОВА прямой и поэтому
ОВОС=ОА».
Далее
ОС® = ОМ» + м&.
Следовательно:
МР= ОА»
МС ом» + мс»' т. е. у _ 4о» 2а ~ х» ^-4а* или
8а»
<fy
*) Под этим символом подразумевается, что сперва нужно найти , затем в результат подставить xt вместо х и yt вместо у. Учащийся должен остере-
Отрезок касательной между точкою касания и осью ОХ называется длиною касательной (ГР|), а проекция этого отрезка на ось ОХ называется длиною подкасательной (ТМ). Подобно этому имеем длину нормали (P,N) и длину поднормали (MN).
Из треугольника ТР,М имеем:
tg-
Л.'Р, dv-i
ТМ ~ dx;
отсюда
(
ТМ = = у, = длине подкасательной ’).
tg- J dy,
(3)
Из треугольника MP,N имеем:
tg-
мр;
откуда
MN = MP, tg т —у, ~ = длине поднормали (субнормаль) 2). (4)
Длину касательной (ТРЛ и длину нормали {P,N) можно найти прямо из чертежа, ибо каждый и'этих отрезков есть гипотенуза прямоугольного треугольника, катеты которого известны. Таким образом
7-р, = / =
=У1
= длине касательной.
P,N =
(5)
(6)
Впрочем, советуем учащимся, вместо того чтобы пользоваться формулами (5) и (6) для нахождения длин касательной и нормали, вычислять эти отрезки прямо из чертежа.
гаться понимать символ так, будто он обозначает производную от yj по Л], ибо это не имело бы смысла, так как х, и yt суть величины постоянные, а не переменные; между тем всякое диференцирование необходимо предполагает непрерывное изменение величины той буквы, по которой диференцируют.
]) Если подкасательная простирается вправо от Г, ее считают положительной; если влево — отрицательной.
2) Если поднормаль простирается вправо от М, ее считают положительной; если влево — отрицательной.
УПРАЖНЕНИЯ-
!. Найти уравнения касательной и нормали, длины подкасательной, поднормали, касательной и нормали в точяе (а, а) циссоиды (черт. 67).
Решение.
dy____ Зах- — Xs
dx ~ у(2а — xp' Отсюда
//v 1 За® — д®
-i = —---------------- = 2 = угловому коэфициенту,
dx Jx^i а (2а — ау
у--а
Подстановка в (1) дает:
у = 2х — а.
Подстановка в (2) дает:
2у + х = За.
Подстановка в (3) дает:
ТМ = у = длине подкасательной.
Подстановка в (4) дает:
MN = 2а = длине поднормали.
Затем
PT = V ТМ2 -|- Л4Г- = — + о2 = 5 = длине касательной,
Черт. 67.
PN = ]/”М№ + МР2 = 4а® 4- а® = а5 = длине нормали.
2. Найти уравнения касательной и нормали к эллипсу
х2 — 2ху — х = О
в точке, для которой х = 1.
Отв. В точке (1, 0).. ,2у = х — 1; у 4- 2х = 2.
. » (1. 1).. 2у = х4-1; j4-2x = 3.
3. Найти уравнения касательной и нормали, длины подкасательной и под нормали к окружности
х®4-у = г»
в точке (xj, ух).
4. Показать, что подкасательная параболы у- = $рх делится вершиною пополам и что поднормаль постоянна и равна 2р.
л. Найти уравнение касательной в точке (х^уО:
а) к эллипсу ^4-^ = 11 Ь) к гиперболе — = 1.
Ome.a)^4-Vf=i;b)^_^ = i.
6. Найти уравнение касательной и нормали к локону:
_ 8а3
У ~ 4а2 4- -V2
в точке, где х = 2а. Отв. х 4- 2,у = 4а; у = 2х — За.
7. Доказать, что в любой точке цепной линии !)
« Л ( а . а \
>=т\е +е /
длины поднормали и нормали равны соответственно: / 2х 2х \
8. Найти уравнения касательной и нормали, длины подкасательной н поднормали для каждой из нижеследующих кривых, в указанных точках: а) у = .г3 в точке (-Ь, . е) у = 9 — ха в точке ( — 3, 0).
Ь)_у* 2 = 4х в точке (9, — 6). f) х2 = бу в точке, в которой х = — 6.
с) х2 + 5у2 = 14 в точке, в которой J = 1 g) х2 — ху-$-2х — 9 = 0 в точке (3, 2). d) ха-|-.у2=25 в точке (— 3,-4). h) 2ха — уа = 14 в точке (3,-2).
9. Найти уравнение касательной к коническому сечению:
дх2 + Uxy + суа + Idx + 2еу +f= 0
в точке (xlt
Отв. ax,x + b (ytx + Xj_y) + cyy + d(x! + x) + e + _y) +/= 02).
10. Показать, что уравнение касательной кривой
Н)’+(Я-г
в точке (а, Ь) есть
£ + ^=2 а 1 Ь для всех значений п.
11. Доказать, что длина подкасательной к кривой у = а? постоянна и равнапк-
12. Найти уравнение касательной к параболе уг = 20х, образующей угол в 45° с осью ОХ. Отв. у = х -|- 5.
13. Найти уравнения касательных к окружности
х2+>2 = 52, параллельных прямой 2х4-3> = 6.
Отв. 2х-|-3_у zt 26 = 0.
14. Найти уравнения касательных к гиперболе
4х2 — 9_уа-|-36 = 0, перпендикулярных к прямой 2_у-|-5х=10.
Отв. 2х — 5у±8 = 0.
15. Показать, что для равносторонней гиперболы
2ху = а2 площадь треугольника, образуемого касательною и координатными осями, постоянна и равна а2.
2) Цепной линией называется кривая, по которой располагается однородная гибкая нить, подвешенная за два конца.
2) Относительно примеров 3, 5 и 9 учащийся должен заметить, что если в уравнениях касательной стереть указатели, то эти уравнения обратятся в уравнения самих кривых.
16. Найти уравнения касательных и нормалей к кривой у4 = 2ха — х®
в точках, для которых х = 1.
Отв. В точке (1, 1) . ,.2у = х-|-1; у-|-2х = 3.
, » (1,— 1)... 2у= — х — 1; у — 2х = — 3.
17. Показать, что сумма отрезков, образуемых касательной к параболе
1 1 1
2 2 3
X + у =а
на осях координат, постоянна и равна а.
18. Найти уравнение касательной к кривой
хЗ(х+» = а5(х-у) вначале. Отв. у = х.
19. Показать, что для гипоциклоиды *)
2. 2 2.
3,3 3
х +у = а
отрезок касательной, содержащийся между осями координат, имеет постоянную величину, равную а1.
20. Показать, что у кривой я
у = ал® подкасательная имеет постоянную величину.
21. Показать, что у кривой
Ж» +
2 с+/с8-У> касательная имеет постоянную длину1).
§ 93. Параметрические уравнения кривой. Пусть уравнение кривой будет:
F(x,y) = 0. (7)
Если х дается как функция третьего переменного, например а, называемого параметром, то, подставляя в уравнение (7) вместо буквы
х ее выражение через параметр а, мы тотчас же замечаем, что у также будет функцией от а и, следовательно, функциональное соотношение (7) между хну может быть вообще заменено системой двух уравнений:
X =/ (а), 1 у = ? («); J
(8)
каждое значение переменного а дает значение для х и значение для у. Уравнения (8) называются параметрическими уравнениями кривой.
(8) исключить а, то, очевидно, в результате должно
Если из уравнений получиться соотно-
шение (7). Для примера возьмем уравнение окружности (черт. 68):
х9+у2 = га, или у = г2 — Xя.
*) Вывод уравнения гипоциклоиды см. в сноске на стр. 196.
а) Вследствие этого сама эта кривая называется кривою равных к аса* тельных (tractrix).
Пусть
х = г • cos а; тогда
у — г • sin а, и получите^ система:
x = r-cosa, I ,g
у = г • sin a. J
Это — параметрические уравнения круга, представленного на прилагаемом чертеже, причем а есть параметр.
Исключая а из уравнений (9), для чего нужно их возвысить в квадрат и сложить, найдем попрежнему:
х® -f- J® = г® (cos2 a -j- sin® a) = r®, уравнение круга в прямоугольных координатах. Очевидно, что если а изменять от 0 до 2~, то точка Р(Х, у) опишет полную окружность.
В § 98 мы займемся исследованием движения точки Р, определяемого уравнениями вида:
у = ?(0-
Эти уравнения называются параметрическими уравнениями траектории, причем время t есть параметр. Так, в примере 2, стр. 212, уравнения
X = vx cos о • t,
Sin ? -t
в действительности суть параметрические уравнения траектории брошенного тела, причем время t есть параметр. Исключение t даст уравнение траектории в прямоугольных координатах:
, ёх~
У = х tg о-------f------.
2г*! cos® <р
Так как в системе (8) у дается как функция а, а a — как функция х, то по (XXII)
dy____dy da_____dy 1 da
dx da dx da dx dx
da da
Таким образом, если даны параметрические уравнения кривой, то можно найти уравнения касательной и нормали, длины подкасательной и поднормали в данной точке кривой, если сначала найти из (XXIV) значение
в этой точке, а потом подставить в формулы (I), (2), (3) и (4) Последнего параграфа.
ПРИМЕРЫ.
L Найти уравнения касательной и нормали, длины подкасательной и поднормали для эллипса
х = a cos <р, j' = isln<y
(Ю)
в точке, для которой у = — . Решение. Так как параметром служит ?, то
— = — a sin v, d? dy . -J- = b cos ф.
Подстановка в (XXIV) даст: dy b cos <p , . M
jjj e----a sin у = УГЛ0В0МУ коэфициенту в любой точке.
Подставляя <р = в данные уравнения (10), находим точку касания:
Следовательно:
Подстановка в (1) §
или
4У1 = _ь_'
dxt а
92 дает уравнение касательной: b Ь ( а \ У-77^------------7 И-ZT^ •
bx + ay = abY 2.
х) Как указывает прилагаемый черт. 69, проведем большой гательные круги эллипса. Через точки о и С, взятые на одном и том же лели к кутся в
радиусе, проведем парал-осям координат. Эти две линии пересе-точке Р (х, .у) на эллирсе, ибо
х = ОА = OB cos <f = acos у = АР = OD = ОС s(n ? = b sin?
или
— = cos
Т = аМ-
Возвышая в квадрат и складывая, находим: 1*3 v2
+ $3 = cos* 9 + sin* ф = 1,
н малый вспомо-
Черт. 69.
т. е. уравнение эллипса в прямоугольных координатах. Иногда <р называют эксцентрическим углом эллипса (на черт. 69 обозначен буквой Ф).
Подстановка в (2) § 92 дает уравнение нормали: b а / а v >-77тг = Т|х-^)>
13 Ви. ЭТв. — В. Гранвиль и Н. Л у з в и. Часть I
или _
(ax-by)V 2 =
Подстановка в (4) и (3) § 92 дает:
Ъ / b \ &
длина поднормали = - [---=---------,
aj ау 2
длина подкасательной =
АН)
а
У 2
2. Даны уравнения циклоиды *) в параметрической форме: х = а (8 — sin 8), у = а (1 — cos 6),
где 6 — переменный параметр. Найти длины подкасательной, поднормали, касательной и нормали в точке, для которой 8 = -^.
Решение.
= а (1 — cos 6); = a sin 8.
flo ао
Подставляя в (XXIV), имеем: dy sin 8 . , „
-г- = ---------f- = угловому коэфициенту в любой точке.
dx 1 — cos О _ п , Ina \ dy.
Так как 6 = —, точка касания будет -----------а, а и
2 \ 2 / (iXt
Подставляя в (3), (4), (5) и (6) § 92, имеем:
длина подкасательной = а, длина поднормали = а, Примечание. Проводим (черт, метр МВ и соединяем Р с В:
длина касательной = аУ'Л длина нормали = aVT.
70) касательную РТ, вертикальный диа-
dy
ЪМТР = £
sin 8
1 — cos 6
„ ,6 9
2sin-y • cos-y
2 sin» А
2
“‘т-
>) Кривая, которую описывает точка окружности круга, катящегося без скольжения по неподвижной прямой, называется циклоидою (черт. 70). Пусть радиус катящегося круга равен а. Р — производящая кривую точка, а М — точка его касания с неподвижною прямою ОХ, называемою базою. Если длина дуги МР равна ОМ, то точка Р коснется базы в О, полагая, что круг катится влево. Называя угол
Черт. 70. PGM буквою 6, имеем:
х — ОМ — NM = аО — a sin 8 — а (8 — sin 6), У = PN = МС— АС = а — a cos 8 = а (1 — cos 8);
таковы параметрические уравнения циклоиды, причем угол 8, на который катящийся круг поворачивается, будет параметром. OD = 2па называется базою одной арки циклоиды, а точка V называется ее вершиною. Исключив 6, найдём уравнение циклоиды в прямоугольных координатах:
х а • arccos ) — V 2ау — у» .
Отсюда
Также
/_РВМ= Л,
так как измеряется половиною дуги МР, измеряющей центральный угол 6, к
ZAPB--L-4-.
Сравнивая, находим:
£МТР= £АРВ.
Следовательно: касательная к циклоиде всегда проходит через высшую точку производящего круга.
УПРАЖНЕНИЯ.
Найти уравнения касательной и нормали, длины подкасательной и поднормали к каждой из следующих кривых в указанных точках:
Под- Под-
коса- нор-
Касательная Нормаль тель- маль пая
1. х = fl, Чу = /; /=1. х-4у + 1 =0, 8х + 2у- 9 = 0, 2, 1.
2
2. Х = Л > = /3; / = 2. 12х —j — 16 = 0, х + 12> —98 = 0, —, 96.
о
’ 9 а
3. x = fl, у = Р; t=\. Зх-Чу-\=0, Чх + Зу- 5 = 0, 4, 4.
4. х = Че*,у = е~‘; t = 0. х + Чу — 4 = 0, Чх — у — 3 = 0, — 2, —
5. x=sin Z,y/=cos2/;/=4 4-4х — 3 = 0, 4у — Чх — 1=0, — — I.
6. х = 1 — /, у = fl; t = 3. 11. х = cos,/ _y. = sin 2/; -T
7. х = 3/, у = 6/ -/=;/ = 0. 12. x = Зе~*, У = 2ee; / = 0-
8. х = fl, у = t; t = 2. 13. x = sin /, у = 2 cos /; II *1”
9. Ю. х = fl, у = fl; t = — 1. х = 2 — t, у = 3&; t = 1. 14. x = 4 cos /, у = 3 sin t; 15. x = ln(/4-2), y = t, / = 2.
Для нижеследующих кривых найти длины: а) подкасательной, Ь) поднормали, с) касательной, а) нормали в любой точке.
1. Кардиоида ')
х = а (2 cos t — cos 4t),
у = о (2 sin / — sin 2t .
От». a) у ctg j t\ b) _ytg-|-t; c)—=^-; d) — sin cos у t
l) Кардиоида представляет собой частный вид кривой, называемой эпициклоидой.
Эпициклоидой называется кривая, которую описывает точка окружности, катящейся извне по другой окружности.
2. Гипоциклоида (астроида) *)
х = 4а соьв t.
у = 4а sin3t.
От». a)-^ctg/; b)-ytgr; с) ; d)
Пусть О — центр неподвижной окружности, С — центр катящегося круга, N — точка соприкосновения обеих окружностей и Р (х, у) — точка, описывающая эпициклоиду (черт. 71). Предположим, что точка k представляет собою положение точки Р, при котором Последняя находилась на неподвижной окружности.
Следовательно, KN = NP.
Примем О за начало координат и ОК за ось ОХ. Опустим на ось ОХ перпендикуляры CL и РМ, проведем прямую PS параллельно ОХ и пусть R — точка пересечения этой прямой с перпендикуляром CL. Пусть а —радиус катящейся окружности и Ь — радиус неподвижного круга, 6 —угол ОСР и / — угол КОС. Будем иметь:
KN = bt, NP = ab.
Таким образом
bt = аО.
Далее, имеем:
х = ОМ = OL 4- LM = ОС cos КОС - СР cos SPC =
= (д + &) cos t — a cos (t 4- 0) = (а -|- b) cost — a cos а-~- • t-
y = MP = LC—RC = ОС sin КОС - СР sin SPC = = (я -J- b) sin t — a sin (/ 4- 8) =
= (я 4" b) sin t — a sin —t.
В частном случае, когда а = Ь, кривая носит наименование .кардиода". Как легко видеть, уравнения кардиоды имеют вид, данный в примере.
г
1) Гипоциклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по другой окружности, соприкасаясь с ней внутренним образом (черт. 72). Следуя методу, данному при выводе уравнения эпициклоиды (стр. 195, сноска 1), легко получим уравнения этой кривой:
, . . b — а,
х = (b — a) cos 14- a cos —— t, у = (b — a) sin / — a sin а t.
3. Эвольвента круга *) х = a (eos 14* t sin t), у = a (sin! — I cos /).
Отв. a) у ctg t; b) у tg t; c) ; d) .
4. Параметрические уравнения трактрисы (см. задачу 21 на стр. 191) имеют вид;
х = а ( In tg у + cos и ) , у — a sin и.
Показать, что касательная к трактрисе в любой точке имеет постоянную длину.
В частном случае при b = 4а после элементарных преобразований получим уравнения:
х = а (3 cos t + cos 3/) = 4а cos31,
у = a (3 sin t — sin 3/) = 4а sin3t.
В этом частном случае гипоциклоиду называют астроидой.
') Предположим, что на окружность круга навернута нить. Если возьмем конец этой нити и будем ее развертывать, сохраняя ее все время в натянутом положении, то конец нити опишет при этом кривую, называемую эвольвентой круга (черт. 73). Пусть О — центр круга, а—радиус и А — конец нити в навернутом на окружность положении. Примем О за начало координат и ОА за ось ОХ. Пусть Р(х, у) — произвольная точка эвольвенты, РК — касательная к кругу и t — угол ХОК. Таким образом дуга представляет собой часть развернутой нити н поэтому
KP = AK=at
Радиус ОК образует угол t — с осью OY. Следовательно, проекция этого радиуса на ось ОХ будет равна:
OK cost = a cos t
и на ось OY:
OK cos j = a sin Д
Касательная КР образует с осью ОХ угод 1-у и с
Поэтому проекции КР на оси координат соответственно будут равны:
КР cos ( /j — = a t sin t,
КР cos (к — t) = — at cos t
Координаты точки P являются проекциями отрезка ОР на осн координат. ОР является замыкающей ломаной ОКР. Поэтому будем иметь:
х = a cos t -|- at sin t = a (cos t +t sin /), y-a sin t—at coa e (sin t — at cos I).
§ 94. Угол между радиусом-вектором, проведенным в точку на кривой, и касательною к кривой в этой точке. Пусть уравнение кривой в полярных координатах будет:
Р=/(0).
Пусть на кривой (черт. 74) дана точка Р(р, 6). Если 6, которое принимаем за переменное независимое, примет некоторое приращение ДО, то соответствующее приращение р пусть будет Др. Обозначим буквою Q точку
________(р-4-Ар. «H-AG)
—-%7'р Проведем к OQ перпендикуляр РР. Тогда т 4г OQ = р Др, РР = р sin ДО
и
Черт. 74. OP = р cos Дй.
Таким образом:
tg PQP = — =--------—------=-------Р~1П .
g RQ OQ — OR р-)-Др — р cos ДО*
Угол между радиусом-вектором ОР и касательной РТ обозначим буквою Если теперь приближать ДО к нулю, то: а) точка Q будет неограниченно к точке Р;
Ь) секущая QP будет приближаться к как к своему предельному положению
с) угол PQR будет приближаться к пределу.
Следовательно:
приближаться
касательной РТ и
как к своему
, . р sin ДО р sin ДО
tg6= lim ——---------------— = lira -------—--------
д1_0р4-Др —рсовДО AS->02рsln3 ДО _|_Др 2
Г ДО^
I ибо р — р cos ДО = р (1 — сов ДО) = 2р Bin2 -у I
р sin ДО
*= Ьш---------—-------=
"-’,02psin«^ .
_______2 Др ДО 1 до
[разделив числитель и знаменатель на ДО] sin ДО Р-
а
= Нш --------ТЕ----•
М’>в sin — . ДО 8,п 2 , Др ₽sl"T-Tr+iii
Так как
/Др\ dp / . Д6\
11Ш -т-т = —, Игл sin — I = О, дв->о\Д’/ «ч дб+оХ 2 /
также по § 47
L 2 J то
***-£• (И)
de
Из треугольника ОРТ имеем:
т = 6-Н- 02)
Пример. Найти фит для кардиоиды *).
р = a (cos 0). Решение.
= a sin в.
Разделив теперь второе уррвневие на первое, будем иметь:
р = tg t, откуда найдем:
cos/ = /д-'s + У» ’ Поставив найденное вна.еиие для cos/ в уравнение, определяющее хг, получим
или
х'» -|- уз = Ча У х/2 =Уа—2ах7 Воспользовавшись теперь формулами перехода от прямоугольных координат к полярным, будем иметь:
р« » Чар — 2ар cos в,
х) Уравнение кардиоиды в полярных координатах может быть получено из уравнений ее в параметрическом виде:
х = а (2 cos t — cos 2/), у — а (2 sin t — aln 2/)-(см. пример 1, стр. 195) следующим образом.
Воспользуемся черт. 71. Перенесем начало координат в точку К. Формулы преобразования будут.
х = х' + а, у = у'.
Параметрические уравнения примут тогда вид:
х' = а (2 cos t — cos 2/ — 1) = а (2 cos t — cos* t + sin* t — sin* t — cos’ t) =
= 2a cos/ (1 — cos/), y‘ = a (2 sin / — sin 2/)» a (2 sin / — 2 sin / cos /) = 2 sin / (1 — cos /).
или
р = 2а (1 — cos 6).
Полученное уравнение отличается от уравнения в рассматриваемом примере тем, что в последнем а обозначает не радиус круга, а диаметр, чему и соответствует коэфициент 2а найденного нами уравнения.
Подстановка в (11) даст:
Так как
_ p _ a (1 — cos 0) _
B ' //0 ~
<Zp
a sin в
2 sln2 -5-
в в 2 sin — cos
= tg®.
tg 'J' = tg 2 •
то
£ 2 '
Подставляя в (12), находим:
8 _ 3
2 2
§ 95. Длины подкасательной и поднормали в полярных ко*
Ординатах. Проводим прямую NT (черт. 75) через начало координат перпендикулярно к радиусу-вектору точки Р кривой. Если РТ есть касательная, a PN — нормаль к кривой 1/ в Р, то
\ Л'хА ОГ=длине подкасательной
\ '/ ON = длине поднормали
\ / кривой в точке Р в полярных координатах.
\ / Из треугольника ОРТ имеем:
т ♦ , от
Черт. 75. tg^ = —.
Следовательно:
ОТ = р = р9 — = длине подкасательной ’) (13)
в полярных координатах.
Из треугольника OPN имеем:
*) Если 6 возрастает с возрастанием р, будет положительно, и | есть острый угол, как на фигуре. Следовательно, и подкасательная ОТ будет положительна и расположится вправо от наблюдателя, находящегося в О и смотрящего по ОР. Если отрицательно, подкасательная будет отрицательна и расположится влево от втого наблюдателя.
Поэтому
ON=
~т = = длине поднормали
tg ф ab г
(14)
в полярных координатах.
Длину касательной РТ и длину нормали PN в полярных координатах можно найти из чертежа: каждая есть гипотенуза соответствующего прямоугольного треугольника.
Пример. Найти длину подкасательной и поднормали в полярных координатах для лемнискаты г):
р2 = a1 cos 20.
Решение, Диференцируя по 0 как функцию неявную, находим:
2р =-2а2 sin26, ао
ИЛИ dp _ a- sin 20 rffl- р
Подставляя в (13) и (14), имеем:
„ р3 a2 sin 20
длина подкасательной =-----„ , , длина поднормали =--------------.
в2 sin 20 р
Если желательно выразить результаты в функции 0, находим из данного уравнения р в функции 0 и подставляем. Таким образом в данном примере найдем:
р = ± а У cos 20, и, следовательно: ____
длина подкасательной = i a ctg 20 У cos 20'.
УПРАЖНЕНИЯ.
1. В круге p = 2rsln0 выразить фит через 0.
Отв. ф = 0, т = 20.
0
2. Для параболы р = a sec3 -у показать, что т -|- ф = к.
3. Показал^ что для лемнискаты р2 = a2 cos 20
2ф = к + 40.
*) Лемнискатой называется геометрическое место точек, произведение расстояния которых до двух данных точек Р и Q (PQ = 2т) есть величина постоянная, равная т2.
Для вывода уравнения лемнискаты расположим полюс О посредине расстояния между точками Р и Q (черт. 76). Тогда будем иметь:
РМ • QM = т\ _____*
Выражая Р и Q по известной формуле три- [ \
гонометрии, приходим к уравнению: т------------------------Г4
Кр2 + т2 -f- 2/ир cos 0 • Ур2 -f- т2 — 2/лр cos в = т2, х У
ткцхв получаем: Черт. 76.
(р2 m2)2 — 4m2p2 cos2 в = m1, p4 = 4m2p2 cos2 6 — 2m2p2, p2 = 2/n2 (2 cos2 в — 1), P2 = 2m2 cos 20.
Полагая 2m2 = а2, окончательно находим: в2 к a2 cos 26,
4. Показать, что для логарифмической спирали р = е°’ угол имеет постоянную величину. Так как касательная образует с радиусом-вектором постоянный угол, эта кривая называется также равноугольною спиралью.
5. Дана конхоида
р = a sin» —;
О показать, что л = 4ф.
6. Показать, что для архимедовой спирали
р = аб имеем:
tg | = в.
Вычислить для
9 = 2я и для
9 = 4л.
От», ф = 80°57' и 85’27'.
7. Показать, что прямая р соа в 2а пересекается с окружностью р = 5а sin 9 , 3 под углом arctg —.
О 6
8. Показать, что параболы р = a sec2 =- и р = b cosec2 — пересекаются под пря* мыми углами.
9. Найти углы пересечения линий
р — a sin в, р = а sin 29.
Отв. Вначале 0°; в двух других точках arctg 3
10 Найти наклоны нижеперечисленных кривых в указанных точках:
а) Р = a (1 — cos 9), 0 II to| а Отв. —1.
Ъ) Р = a sec2 9, p = 2a. 3.
с) Р = a sin 49, в начале. 0, 1, оо, — 1.
d) ₽г = a2 sin 49, в начале. 0, 1, оо, — 1.
е) Р = a sin 39, в начале. о. /з,- /з.
f) Р = a cos 39, в начале.
К) Р = a coe 29, в начале.
Ь) Р = a sin 26, 0 II ►Iя
ж «
t) Р = a sin 39, ’“6-
ж Я
!) Р = <70, 6в 2’
к) р9 = a.
1) Р = A 0 = 0.
11. Показать, что спираль Архимеда ₽ = аО и гиперболическая спираль Р = -д пересекаются под прямыми углами.
12. Найти угол, обравуемый пересечением параболы р = авес2у и прямой р <1п 9 = 2a. Отв. 45*.
13. Показать, что две кардиоиды р = а (1 -|- cos в) и р = а(1—cost) пересекаются под прямыми углами.
14. Найти длины подкасательной, поднормали, касательной и нормали в произвольной точке спирали Архимеда р = «и.
От». Подкасательная равна у;
поднормаль о;
касательная У а1 + р2 J
нормаль У аг -|- р2.
(Читателю следует отметить, что длина поднормали постоянна.)
15. Найти длины подкасательной, поднормали, касательной и нормали логарифмической спирали р = а‘.
От». Подкасательная равна ;
1П Л
поднормаль pin а;
1 + !—>-;
1 In га
нормаль р У1 -|- In2 а.
Заметим, что при а = е подкасательная равна поднормали и касательная равна нормали.
16. Найти углы, образуемые пересечением кривых:
р = а (1 + cos 6), р = b (1 — cos в).
От». 0, у.
17. Показать, что длина подкасательной гиперболической спирали р = ® постоянна.
18. Показать, что равносторонние гиперболы р2 sin 28 = в2, р2 cos 28 = И1 пересекаются под прямыми углами.
§ 86. Отделение кратных корней у многочленов. Рассмотрим многочлен л-й степени:
ахп-\-Ьхп^л ф-сх"-гф- ... -\-px-\-q,
расположенный по нисходящим степеням буквы х. Эту букву х мы будем считать независимым переменным, а коэфициенты его, т. е. буквы а, Ь, с,...,р н q, будем считать данными постоянными числами, причем первое из них, число а, будем считать отличным от нуля а ф0, потому что иначе данный многочлен был бы не степени л, а ниже.
Известно уже из элементов алгебры, что число а называется корнем данного многочлена, если этот многочлен делается равным нулю, когда подставляют в него вместо буквы х рассматриваемое число а, т. е. когда справедливо равенство:
аз” + “1-ф са" ~ *-I- ... ф-ра-Н = 0.
Относительно корней, их существования и их свойств в высшей алгебре доказываются следующие два основных предложения, на справедливости которых мы не будем останавливаться и которые мы просто примем беа доказательства:
Теорема!. Всякий многочлен л-fl степени* axn-j-bxn~i-[-cxn~2-j- ... q
якеет в точности л корней, а, р, f, v, не более и не менее. Эти корни могут быть какими угодно, т. е. различными друг от друга или совпадающими друг с д,ру-гом, действительными или мнимыми, положительными или отрицательными, соизмеримыми или несоизмеримыми, дробными или целыми.
Теорема П. Если a, р, (,..., у. и v сутьвсе лкорней данного многочлена л-й степени
ox" -J- 6х" 1 СХ рх q,
то данный многочлен может быть представлен как произведение л разностей:
а(х — а) (х —р) (х —у).. .(х—и.) (х — v) буквы х последовательно со всеми корнями, т. е. имеем тождество:
axn-}-bxn~1Jr ... -\-px-\-q = а(х — а) (х—?).. .(х —(х —v), справедливое для всякого значения буквы х.
Если среди всех л корней
а, р, 7,. .., [л, '> данного уравнения л-й степени
ox" -f- bx —ex -J- ... рх -J- q = 0 (15)
имеются корни, равные между собою, то тогда мы говорим, что данное уравнение (15) имеет кратные корни. Смотря по тому, сколько именно раз встречается рассматриваемый корень среди всех корней а, р, 7> ..., н> v> мы говорим, что рассматриваемый корень обладает такою-то кратностью: так, если рассматриваемый корень встречается среди а, р, у, ..., ц, v лишь два раза, мы называем его в этом случае двукратным; если он встречается три раза, мы называем его трехкратным и т. д.
Корни, встречающиеся среди а, р, у, ..., u, v лишь по одному разу, мы называем, п р о с т ы м и или однократными корнями.
Например, уравнение
х* — 7х» 4- 9х2 -Н 27х — 64 = О имеет корни:
3, 3, 3, —2.
Следовательно, 3 есть трехкратный корень, а —2 простой. В силу теоремы II это уравнение может быть написано в виде:
(X —3)» (х4-2) = 0.
На первый взгляд кажется, что для того, чтобы узнать, имеет ли данное уравнение кратные корни, единственное средство — это решить уравнение и затем посмотреть, имеются ли среди его корней равные
§ 96] ОТДЕЛЕНИЕ КРАТНЫХ КОРНЕЙ У МНОГОЧЛЕНОВ 205 или же таковых совсем нет. Но решение алгебраического уравнения есть вообще операция крайне тягостная, причем трудности этой операции быстро возрастают с повышением степени уравнения. Поэтому являемся вполне целесообразным изобретение такого приема, который еще до решения данного уравнения обнаружил бы существование или несуществование у предложенного уравнения кратных корней. Мы сейчас увидим, что диференциальное исчисление дает такой прием, причем можно, не решая уравнения, не только убедиться в существовании кратных корней (когда они есть), но еще, кроме того, можно и отобрать все кратные корни, отделив их от простых корней, притом все это можно сделать, не решая данного уравнения.
В самом деле, пусть f(x) есть многочлен, имеющий члсло а своим кратным корнем, и притом именно кратности т. Ясно, что в силу теоремы II многочлен f(x) напишется в виде произведения, в котором будет содержаться в точности т множителей, равных разности х — а, остальные же множители будут существенно отличны от х — а, т. е.
/(к) = (х —а)т-©(х), П6)
где через ©(х) мы обозначаем произведение всех остальных множителей, существенно отличных от разности х — а.
Ясно, что <р (х) есть многочлен, уже не имеющий числа а- своим корнем, так как в противном случае многочлен ©(х) содержал бы в своем составе (в виде множителя наряду с другими множителями) хотя бы один множитель, равный (х — а); но тогда это значило бы, что число а есть не /n-кратный корень многочлена /(х), а кратности более высокой. Итак:
© (а) ф 0.
Диференцируя (16), находим:
/' (х) = (X — а)”1 ф (х) ф- т (X — а)’" -1? (х) или
/'(х) = (х-а)"‘-1 [//гз (Х)4- (X-а)©'(х)]. (17)
Выражение в квадратных скобках в правой части равенства (17) есть многочлен. Легко видеть, что число а не будет корнем этого многочлена. Действительно, заменяя в этом многочлене переменное х на а, мы । его обращаем в
/п? (а)4- (а — а) <?'(а) = m<f (а) ф 0
— число, отличное от нуля, ибо
т ф 0 и ф (а) ф 0.
Равенство (17) поэтому нас учит тому, что число а есть в точности (т — 1)-к ратный корень производной f'(x). В частности, когда /п=1, мы видим, что простой корень данного уравнения /(х) = 0 ни в каком случае не может оказаться корнем производного уравнения /' (х) = 0, потому что для последнего необходимо, чтобы /п> 1.
- Итак, если в /(х) множитель (х — а) содержится в точности т раз, то в /’(л) этот самый множитель встречается в точности т — 1 раз.
Составим теперь общий наибольший делитель многочленов
/(X) И /(X).
Иа элементов алгебры мы знаем, что составление общего нанболь* шего делителя двух данных многочленов есть действие, совершенно аналогичное отысканию общего наибольшего делителя двух данных натуральных чисел: и в том и в другом случае он отыскивается путем последовательного деления одного многочлена на другой, затем делителя на первый остаток, первого остатка на второй остаток и т. д. до тех пор, пока не получим остатка, равного нулю, т. е. до тех пор, пока деление не завершится нацело. Тогда последний остаток, не равный нулю, и будет общим наибольшим делителем.
Из сказанного ясно, что общий наибольший делитель многочленов /(х) и /'(х) будет содержать множитель (х — а) в точности т — 1 раз, т. е. а есть его (т.— 1)-кратный корень.
Если /(х) имеет еще некоторый другой кратный корень р кратности г, то в силу предшествовавшего это число р есть (г—1)-кратный корень общего наибольшего делителя.
Итак, общий наибольший делитель м н ого ч л ен о в /(х) и/'(х) имеет своими корнями лишь кратные корни данного многочлена/(х), причем каждый из этих кратных корней данного многочлена /(х) является корнем общего наибольшего делителя кратности на единицу ниже; простые корни данного м но го ч л е н а/(х) совсем не являются корнями общего наибольшего делителя.
Можно, таким образом, высказать следующее правило для нахождения кратных корней уравнения /(х) = 0.
Первый шаг. Находим/(х).
Второй шаг. Находим общий наибольший делитель для /(х) и /'(х).
Третий шаг. Находим корни общего наибольшего делителя. Всякий из различных корней общего наибольшего делителя встречается в /(х) одним разом больше, чем в общем наибольшем делителе.
Если случится так, что общий наибольший делитель совсем не содержит х, то /(х) не имеет кратных корней, и описанный выше процесс отделения кратных корней делу решения уравнения ничем не поможет, а только обнаружит, что данное уравнение/(х) = 0 лишено кратных корней.
Пример. Решить уравнение
х3 — 8х2 + 13х — 6 = 0.
Решение. Пусть
/(х) = х3 — 8х3-|-13х — 6.
Первый шаг.
Г (х) = Зл’ - 16х 4-13.
Второй шаг. Заметим, что при нахождении общего наибольшего делителя для удобства вычислений мы можем делимое, делителя и промежуточные остатки при последовательном делении умножать на постоянного множителя: то обстоятельство, что общий наибольший делитель (О. Н. Д.) функции / (х)
и ее производной /'(х) будет отличаться от О- Н. Д., который находятся обычным образом, т. е. без указанных упрощений, на постоянного множителя, не окажет влияния на разыскание корней, так как уравнения, получавшееся путем приравнивания нулю О. Н. Д., все равно можно сокращать или умножать на постоянного множителя. Поэтому при делении /(х) на /'(х), чтобы не иметь первый член дробным, умножим предварительно /(х) на 3:
ч ч ч -гю об ся — 1 1 1 1 н 39х-- 13х - 26х- - 18| Зх» - 16х + 13 х «4- 8 - 18 * 1
^умножим оста- 94 2 _ ток на — 3) — 24х« - Зх»- - 78х+ 54 - 128х + 104 50х— 50 - 16х + 13 |х - 1 1 8
’ о л
Зх»- - Зх Зх — 13 (остаток умно- \ /
О. Н. Д. = х —1. _ - - 13x4 - 13х- - 13 жили на >/»)• - 13
0
Третий шаг.
Черт. 77.
х — 1 = 0, откуда х = 1.
Так как 1 является простым корнем уравнения х— 1 = 0, то он будет двукратным корнем данного первоначально уравнения, т. е. левая его часть содержит множителем (х—I)2. Разделив х8 — 8х2 4-13х — 6 на (х—1)*, находим второй множитель (х—6), который дает корень 6. Следовательно, корни нашего уравнения суть 1, 1, 6. Начертив график функции (черт. 77), мы видим, что при х = 1, т. е. при х, равном двукратному корню, кривая касается оси ОХ, но не пересекает ее J).
УПРАЖНЕНИЯ.
По способу § 96 решить следующие 10 уравнений.
1. х® — 7х»4-16х- 12 = 0. Отв. 2, 2, 3.
2. х4 _ бх» — 8х — 3 = 0. -1, -1, -1,3.
3. х8 - 7х3 + 9х2 + 27х — 54 = 0. 3, 3, 3, - 2.
4. х* - 5х® -,9х» + 81х — 108 = 0. 3, 3, 3, - 4.
5. х» + бх3 + х» — 24х + 16 = 0. 1, 1, -4, -4;
6. Х4 _ 9x3 _|_ 23х» - Зх - 36 = 0. 3, 3, -1, 4.
7. х* — бх3 + 10х» - 8 = 0. 2, 2, 1 zt У3.
8. х6 — х4 — 5х3+ха+8х + 4 = 0, - 1, - 1, - 1, 2, 2.
9. х» — 15Х3 + 10х» + 60х — 72 = 6. 2, 2, 2, - 3, - 3.
10. х» — Зх4 - 5х3 + 13х» + 24х + 10 = 0. - 1, -1, -1, з± у^т
Показать, что следующие четыре уравнения не имеют кратных (равных) корней.
11. х® + 9л2 4- 2х - 48 = 0.
12. х4—15х»-10х + 24 = 0.
13. х4-Зх3-6х»+ 14х + 12 = 0.
14. хп- ап = 0.
<) Так как первая производная для каждого кратного корня обращается в нуль, то ось X касательна к кривой во всех точках, соответствующих кратным корням. Если кратный корень встречается четное число раз, то в такой точке кривая функции не пересекает оси X (черт. 77); если же он встречается нечетное число раз, то кривая пересекает ось ОХ, в то же самое время касаясь ее.
15. Показать, что условие, чтобы уравнение
имело двукратный корень, есть 4<73 + г2 = 0.
16. Показать, что условие, чтобы уравнение х« 4- Зрх2 4- г = 0 имело двукратный корень, есть г (4р3 4-г) = 0.
§ 97. Приложения производной в механике. Скорость. Рассмотрим движение некоторой точки, описывающей кривую АВ (черт. 78). змеряемое по траектории от некоторой постоянной точки, например А, до некоторого положения точки Р будет s, а соответствующее протекшее время пусть будет t. Каждому значению времени. / соответствует некоторое положение точки Р на траектории, а следовательно, и некоторое расстояние (или пройденный путь) s. Таким образом 5 есть некоторая функция от /, и можно написать:
s =/(/).
Пусть теперь t принимает приращение Л/; соответственно этому s примет приращение As, и
As
-г-. = в е л и ч и н е средней скорости ')
усть расстояние, и
Черт. 78.
точки Р в течение промежутка времени Л/. Если Р двигается равномерным движением, то вышеуказанное отношение будет иметь одну и ту же величину для всякого промежутка времени и будет представлять
величину скорости в любой момент.
В общем случае какого угодно движения, равномерного или нет, мы определяем величину скорости® в любой момент как предел As ., -
отношения -т-т, когда А/ приближается к пределу нуль; т. е. зг
V — Нт
As A?
или
ds dt
(18)
Итак, скорость в любом движении, по величине, есть производная расстояния (пройденного пространства) по времени.
Чтобы показать, что это вполне согласуется с нашим представлением о скорости, которое мы уже имеем, найдем скорость падающего тела в конце двух секунд.
2) Скорость определяется как быстрота, изменения места со временем и есть количество векторвое, т. е. имеющее, кроме величины, еще и определенное направление. Следует поэтому отличать величину скорости (что есть просто число) от самой скорости (каковая имеет, кроме числовой величины^ вше д определенное направление).
Опыт показал, что тело, падающее свободно из состояния покоя, в пустоте, вблизи поверхности земли, приблизительно следует закону:
S = 4,9/2, где s равно пройденному телом пространству в метрах, t равно времени в секундах. Прилагаем общее правило § 59.
Первый шаг.
S 4- Д$ = 4,9 (t + Д/)2 = 4,9Р 4- 9,8/ • Д/ 4- 4,9 (Д/)2.
Второй шаг.
Д$ = 9,8/ • Д/ 4- 4,9 (Д/)«.
Третий шаг.
— = 9,8/ 4- 4,9Д / = величине средней скорости в продолжение М промежутка времени М, считая его от не-
которого определенного момента времени ’).
Полагаем / = 2.
= 19,6 4~ 4,9Д/ = средней скорости в течение проме-М жутка времени Ы по прошествии
двух секунд падения.
(19)
Наше представление о скорости тотчас подсказывает нам, что (19) вовсе не представляет действительной скорости в конце двух секунд: в самом деле, если Д/ взять даже весьма малым, положим Д/ равным какой-нибудь 1/1Оо или 7юоо секунды, все равно (19) даст только среднюю скорость в течение соответствующего малого промежутка времени. Но то, что мы разумеем под скоростью в конце двух секунд, есть предел средней скорости, когда Д/ уменьшается до нуля; т. е. скорость в конце двух секунд по (19) есть 19,6 М’сек. Таким образом даже обычное представление о скорости, получаемое из опыта, включает идею о пределе, или согласно нашему обозначению
х* = lim ( — I = 19,6 м!сек.
Приведенный пример хорошо иллюстрирует понятие о предельном значении. Учащийся должен освоиться с представлением, что предельное значение есть вполне определенная величина, но не есть нечто лишь приблизительное. Это не есть значение, при котором 4,9Д/ означало бы как угодно малую величину; это есть предельное значение переменной величины 19,6 4~ 4,9Д/, когда Д/уменьшается до нуля, и это значение в точности равно 19,6.
§ 98. Компоненты скорости. Координаты х и у точки Р, движущейся в плоскости XOY, суть также функции времени, и их движение можно определить посредством двух уравнений:
^ = ?(09).
Это — параметрические уравнения траектории.
*) &з есть пространство или расстояние, пройденное в течение времени Д/.
а) Уравнение самой траектории в прямоугольных координатах найдем, исключив t из этих уравнений.
14 Зак. 2760. — В. Грэпвпль и Н. Лузин. Часть I
Горизонтальная слагающая vx скоростиv есть, как известно из механики, скорость по оси ОХ проекции М точки Р; следовательно, это есть скорость изменения х со временем. Итак, по (18), заменяя $
через х, имеем:
dx
V = —
х dt
(20)
Подобным же образом находим, что вертикальная слагающая, или скорость изменения
у со временем, есть
v
__dy v~at'
(21)
Изображая скорость и ее компоненты векторами, на черт. 79 тотчас находим:
или
ds /"ldx\2 j (dyX*
v=di=V (•*) +(з/
(22)
формулу, дающую скорость по величине для любого момента.
Если угол, образуемый направлением скорости с осью ОХ, назовем т, то из чертежа, принимая во внимание (18), (20) и (21), имеем:
v. Sin T = -i = V dy dx dy dt dt . vu dt = —; cost = —=-^-; tgi- = -« = —. (23) ds v ds vx dx 4 dt dt ~cti
§ 99. Производная как отношение скоростей. Можно получить механическое истолкование производной и в том случае, когда уравнение траектории задано не в параметрическом виде, а в обычной форме:
где х ну изменяются со временем, т. е. являются некоторыми функциями от t. Продиференцируем обе части равенства по t, помня, что направо стоит сложная функция от I. Применяя формулу функции от функции, имеем:
dt r w dt
Перепишем это соотношение в следующем виде:
dy dt . dy
dt
(24)
*) Скорость v всегда направлена по касательной к траектории.
_ , dy
Таким образом производная измеряет отношение скорости изменения со временем^ к скорости изменения со временем х.
Пример. Точка движется по параболе бу = хг таким образом, что когда х = 6, абсцисса возрастает со скоростью 2 м)сеК. С какой скоростью возрастает ордината?
Решение. Диферепцируя по t, находим:
.dy . dx dv 1 dx
dt dt dt 3 dt
Итак, в любой точке параболы (скорость изменения у) = х X (скорость из-О
dx
менения .с); по условию задачи, при х = 6, =2 м/сек. Подставляя в (А), на-
ходим:
(А)
= 4- • 6 • 2 м/сек — 4 м!се к. al 3
Таким образом в заданной точке ордината изменяется по величине вдвое быстрее абсциссы.
§ 100. Тангенциальное ускорение. Ускорение (полное) есть один из важнейших векторов, характеризующих движение. При криволинейном движении ускорение его выражается весьма сложным образом.
Оставляя в стороне полное исследование этого вопроса, мы рассмотрим здесь только так называемое тангенциальное ускорение.
Это есть вектор, направленный по касательной к траектории движущейся точки. Его величина j равна:
или
(25)
Иначе говоря, величина j тангенциального ускорения является мерою изменения скорости в данный момент времени по направлению касательной к траектории.
В частном случае, когда рассматриваемое движение прямолинейно, тангенциальное ускорение является в то же время и полным ускорением.
§ 101. Компоненты тангенциального ускорения. Следуя тому же плану, как и при нахождении компонентов скорости, получаем компоненты тангенциального ускорения, параллельные осям ОХ и OY-. Ж
dvx. . _dvy
~dt '' Jy—~dt
(26)
Так же _______
/=£=/(t)
Эта формула дает величину тангенциального ускорения.
ПРИМЕРЫ.
1. Опыты показали, что тело, свободно падающее в пустоте у поверхности земли, приблизительно следует закону:
s = 4.9Р, где s равно пространству (высоте) в метрах, t равно времени в секундах. Найти величины скорости и ускорения:
а) в любой момент;
Ь) в конце первой секунды;
с) . ,, пятой ,
Решение.
s= 4,9 Г. (А)
а) Диференцируя, имеем:
Й = 9-8z-ul
или по (18):
v = 9,81 м/сек. (В)
Диференцируя еще раз, имеем:
^ = 9,8, или по (25):
j = g = 9,8 м/сек-, (С)
откуда видно, что ускорение падающего тела есть величина постоянная; другими словами, что скорость возрастает на 9,8 м в каждую секунду падения.
Ь) Для нахождения v и j в конце первой секунды подставляем в (В) и в (С) t=l;
v = 9,8 м/сек, j = g = 9,8 м/сек1.
с) Для нахождения v и j в конце пятой секунды подставляем в (В) и в (С) 1 = 5;
v = 49 mJ сек, j = g = 9,8 м/сек-.
2. Если пренебречь сопротивлением воздуха, то уравнения движения брошенного тела будут:
х = о, cos <р • t, у = pj sin • t — 4,9P,
где Vj — начальная скорость, ? — угол метания с горизонтом, t — время полета в секундах, причем хну выражаются в метрах.
Найти величины скорости, тангенциального ускорения, компонентов скорости, компонентов тангенциального ускорения:
а) в любой момент;
Ь) в конце первой секунды, если даны vx = 30 м/сек, <р = 30°;
с) найти направление движения в конце первой секунды.
Решение. Из (20) Я (21)
a) vx = Vi cos tp; vy = sin <p 9,8Z.
Из (22)______________________________________________
v = — 19,6 Vit sin ф + 96Z2.
Из (25) и (26)
^ = ^ = 0; jy = - gy = — 9,8; j = —g=-9,8.
Ъ) Подставляя в результаты t = 1, Wj = 30, у = 30°, находим:
vx = 26 м/сек, jx = gx = 0.
Vj, = 5,2 м/сек, jv= —gy= — 9,8 м/cetfl.
v = 26,4 м/сек, j = — g = — 9,8 м/сек*.
v 5.2
c) tg,= ^- = -2g-, т — 11°19' = углу направления движения с горизонтом.
УПРАЖНЕНИЯ.
1. Законы прямолинейных движений заданы нижеследующими уравнениями; найти в указанные моменты времени длину пути, скорость и ускорение.
a) s = f> + 2fi; / = 2 Ь)л = Р + 2Г, / = 3. с) 5 = 3 — 4/; 1 = 4. d)x = 2t — l3; /=1. е)у = 2< — I3; 1 = 0. f) Л = 20/+ 16/2; t= ю. g) s = 2 sin t; t = ^r .
4
h) у = a cos t = 1-
i) s = 2est; t = 0.
)) s = 2/a — 3/; / = 2.
k) s = 4 +t3; t = 3.
1) _y = 5 cos2/; / = -£.
Q
m) s = b sin ; I = 2.
4
Отв. s=16, v = 20, j = 16.
s = 15, v = 8, j = 2.
s = — 13, v = — 4, j = — 0.
x = 1, v = 0, j = — 2.
у = 0, v = 2, j = 0.
h = 1 800, v = 340, j = 32
s = /2 v = /2 j = - /2
s = 2, v = 6, j = 18. n) x = ae~2i; 1=1. o)-s = y + W2; t = t0.
4 р),= 101Пт-р; / = 1.
2. Снаряд обладает начальной скоростью 200 м/сек и имеет направление, образующее угол в 45° с горизонтом. Найти:
а) скорость и направление в конце третьей и шестой секунды;
Ь) составляющие скорости в те же моменты времени. Закон движения тот же, что в примере 2, стр. 212.
111 94
Отв. а) При / = 3, v = 180,3 м/сек, -t = arctg,
82 48 при t = 6, v = 163,6 м/сек, т = arctg
Ь) при t = 3, vx = 141,4 м/сек, vy = 111,94 м/сек
при t = 6, Vx = 141,4 м/сек, vv = 82,48 м/сек.
3. Высота (5) в метрах, кально вверх со скоростью
какой достигает в t секунд тело, брошенное верти-vt метров в секунду, дается формулой:
J = vtl - 4,9/2.
Найти: а) величины скорости и ускорения в любой момент и, если Pj = 100 м/сек, найти величины скорости п ускорения:
Ь) в конце второй секунды, с) , „ пятнадцатой секунды.
Сопротивлением воздуха пренебрегаем.
Отв. a) v = Vj — 9,8/, j = — g= — 9,8;
b) v = 80,4 м/сек, j = — g— — 9,8 м/сек3-, c) v= —47 м/сек, J= — g = —9,8 м/сек3.
4. Пушечное ядро, выпушенное вертикально вверх, вылетает со скоростью 196 м/сек. Найти: а) величину его скорости в конце десятой секунды; Ь) сколько времени оно поднимается до наибольшей высоты. Условия те же, что в упражнении 2.
Отв. а) 98 м/сек-, Ь) 20 секунд.
5. Поезд выходит со станцил и через t часов находится на расстоянии s = Z9 + 2/3 + 3/ километров от станции отправления. Найти величину его ускорения: а) в конце t часов и Ь) в конце 2 часов.
Отв. a) j = 6/ + 4; b) j = 16.
6. В момент t часов поезд находится на расстоянии у t* — 4/3 -f-16/8 километров от точки отправления. Найти: а) скорость и ускорение поезда; Ь) в какой момент поезд остановится и изменит направление; с) описать характер движения поезда за первые десять часов.
2t
Отв. a) v = Z3 — 12Р 4-32/, j = 3/2-у+32;
Ь) в конце четвертого и восьмого часа;
с) поезд будет двигаться вперед в течение первых четырех часов; обратно — в течение вторых четырех часов; снова вперед по истечении первых восьми часов.
7. Найти ускорение, если a) v = P-f-2/; / = 3. b)v = 3/ — I3; 1 = 2.
с) o = 4siny; t = у,
d) v — a cos 3/; t = у. е)о = 5е2', /=1.
дано:
Отв. J = 8. у =-9. j=V3.
J = — За. j = 10е2.
8. Расстояние (в метрах), проходимое точкою в / секунд, выражается формулою:
а = 30/-6Р.
Найти величины скорости и ускорения в конце 23/t секунд.
Отв. о = 0, j = — 12.
6. Дано « = 2/-|-З/2 + 4/3 метров; найти величины скорости и ускорения: а) в начале; Ь) в конце 5 секунд.
Отв. а) о = 2 м/сек, J = 6 м/сек-;
b) v = 332 м/сек, j = 126 м/сек-.
9. Дано
*= у+М«, где а и б— постоянные; найти величины скорости и ускорения в любой момент.
Ome.v = -± + Ы, j = ^ + 2b.
10. В конце I секунд тело обладает скоростью 3/2-|-2/ метров в секунду; найти величину его ускорения: а) в любой момент; Ь) в конце 4 секунд.
Отв. a) j = 6/ -|- 2 м/сек3-, b) j = 26 м/сек3.
И. Вертикальный компонент скорости точки в конце / секунд есть
vy = ЗР — 21 + 6 м/сек.
Найти вертикальный компонент ускорения: а) в любой момент; Ь) в конце 2 секунд.
Отв. а) 7„ = 6/ — 2; Ь) 10 м/сек2.
12. Если точка движется по прямолинейной траектории так, что 5= /7 то показать, что величина ускорения отрицательна и пропорциональна кубу скорости.
13. Если расстояние в метрах, проходимое точкою в t секунд, дается формулою:
5=101п^-4-< 4 + то найти величины скорости и ускорения: а) в конце 1 секунды; Ь) в конце 16 секунд.
2 Ота. a) v = — 2 м/сек, j = -= м/сек-;
О
b) v = — -у м/сек,} = ± м/сек"-.
14. Если пройденный путь дается формулою: $ = ae* -f- Ье~*, то показать, что величина ускорения всегда равна пройденному расстоянию.
15. Дано гЛ s = a cos ;
найти величину ускорения.
Отв. j =---— .
4
16. Если точка, отнесенная к прямоугольным осям координат, движется так, что
х = a cos t + Ь, у = a sin t -f- c, то показать, что се скорость постоянна по величине.
17. Если путь движущейся точки есть синусоида х = at, у = b sin at, то показать:
а) что слагающая скорости по оси ОХ имеет постоянную величину;
Ь) что величина тангенциального ускорения точки в любой момент пропорциональна ее расстоянию от осн ОА’.
18. Если точка движется так, что х = ^, y=t\ то:
а) показать, что ее траектория есть полукубическая парабола у"- = •**;
Ь) найти v_, vv, v,
с) . Д. jy, Г,
d) если 1 = 2 секундам, то найти v, j, положение точки (т. е. ее координаты) и направление движения. х _______
Отв. b) vx = 27; vy = 3P; v = t/4 -f-97»;
c) yx = 2; jy = f>t; y=2/T+9P; d)v = 8/I6; / = 2/37; x = 4;
у = 8. Направление определяется , углом наклона касательной к траек-
тории в данный момент времени.
-3.
19. Даны нижеследующие законы движения. Найти в указанные моменты времени vx, vy, v, jx, jy, j положение точки (ее координаты) и направление
движения.
а) x = t\ y = t-> 1 = 2.
Ъ) x=t, t =1.
с) x = 2i. У = Г- + 3; 1 = 0.
d) X = 1 - /=, y = 2f. t = 2. n_
е) x = a sin t. у = acos t; t=4-
0 x = 2 sin I, j> = 3coet; t = n.
я) x = sin/, у = cos 2t; '=7-
h) x = 2Z, у = Зе*; t = 0.
i) x = 3t, у = In I; t = 1.
j) x = Z, y = 12/-1; 1 = 3.
ГЛАВА vn.
ПОСЛЕДОВАТЕЛЬНОЕ ДИФЕРЕНЦИРОВАНИЕ.
§ 102. Определение последовательных производных. Мы видели, что производная функции от х вообще также есть функциях. Эта новая функция также может быть диференцируемл, и в этом случае производная этой первой производной называется второю производною первоначальной функции. Подобно этому производная второй производной называется третьею производною и т. д. до п-й производной. Так, если
= 12х3,
dx
= 72x,
d Г d ( dy\ dx [dx \dx]
и T. Д.
§ 103. Обозначения. Символы для последовательных производных обыкновенно пишутся сокращенно следующим образом:
d / dy\__d?y
dx \dx) dx2’
d ’ d I dy\' d /<Py\ (fly dx dx \ dx) dx \dx9/ dx3’
d / d"~'y \ dny
dx \ dx"-1 / “ dx" ’
Если y=f(x), то последовательные производные обозначают еще так:
или
'lv.
d , d9 (fl d4 d”
..........
218 ПОС ЛЕДОВ AT ЕЛЬНОЕ ДИФЕРЕНЦИРОВАНИЕ [ГЛ. V1J
§ 104. /z-я производи для n-Й производной Обычный прием состоит первых производных, столь кона их образования; затеь 1ЯЯ. Для некоторых функций можно фактически найти общее выражение в функции буквы п. в нахождении нескольких последовательных ких, сколько будет нужно для раскрытия за-t, по индукции, пишут л-ю производную.
Пример 1. Дано у = еах\ найти dxn
Решение. ахУ ’
Отсюда -^ = апе“, dxn
Пример 2. Дано у = In х; „ d”v наити — dxn
Решение. dy 1 dx ~ ~х' d*y _ _1_ dx1 х*' <fiy 1 -2 dx* = X3 ’ d*y 1-2.3 dx* x* ’
Отсюда *
dx” ' x”
(f'v
Припер 3. Дано у = sin х; найти dx
Решение.
dy dx
. ( . к
cosx = sin ( х +
S=isin(x+ ) = C0S(x+T)=sln(x+2- -5)’
g=Asln(x + 2^) = cos(x + 2.j) = sin(x + 3^). Отсюда
§ 105. Формула Лейбница для я-й производной произведения. Эта формула выражает п-ю производную произведения двух переменных в функции этих переменных и их последовательных производных.
Если и и v суть функции х, то в силу (IV) имеем:
d , . du , dv
— {uv) = -г- v 4- и . dx dx dx
Диференцируем снова по x:
d* . . (Pu . du dv . du dv . d*v W = dx? + dx ~di + di Tx+" d* =
d*u , ndu dv , d2v
= -5-:,^-t-H-U-t-t:.
dx1 1 dx dx ' dx1
Подобно этому
d* . . cPu , d*udv , d*u dv . 9 du cPv , du <Pv . d*v_
dx* dx*0 1 dx*dx dx* dx ‘ dx dx* ' dx dx* И dx*
d*u . _ d2u dv , _ du cPv . d*v
dx* dx* dx 1 dx dx* 1 dx*
Продолжая дальше, убедимся, что численные коэфициенты следуют тому же закону, как коэфициенты биномиальной теоремы, и что указатели производных соответствуют показателям биномиальной теоремы ’)• Заключая затем по способу математической индукции от /п-й производной произведения к (/п4~1)-й> мы легко докажем формулу Лейбница:
4“ (Г и . d” rudv . я(я—l)d” 2u <Pv
-
dudn 'v , d'lv --------r U---. dxdxn~l 1 dxn
(1)
Пример 1. Даиоу — exInx; найти по формуле Лейбница
Решение. Пусть
и = ех, v = In х, имеем:
du х dv 1
dx dx х
d*u _ х <flv 1 dx*~e ' dx*= ~~x*
d*u _ у cPv____2_
rfx3- e ' dj^~ л®'
Подставляя в (1), находим:
d*y dx®
= e* In x
Зех Зе* . Чех ,1 . .3 3 . 2 \
Т'“^ + ^’ = г( + X~P + ?)-
(flu d9v
Ч Для пополнения этого соответствия рассматриваем и и v как и
Пример 2. Дано у = найти по формуле Лейбница —, dx ‘
Решение. Пусть
и = х-, v = е01;
^- = 2х,
dx dx ’
£“ = 2, —,= а2е^,
dx2 dx2 '
d*u л dx3~0. Q ДД* й? “ в е 1
— = апеах
ахп
имеем:
Подстановка в (1) дает:
Q =xbneax-i-2an-1nxeax-t-n(n-i)an-2eax=an-2eaxl^2 + 2axn+n (л—1)]-dxn
§ 106. Последовательное диференцирование неявных функ* </ау
ций. Чтобы иллюстрировать процесс, найдем ; из уравнения гиперболы
Ь2х3 — <Ру2 = а2Ь2.
Диференцируя по х, как в § 90, находим:
2dax —2aav^ = 0 •'dx
или
dy = b*x
dx (Ру (А)
Диференцируя еще раз и замечая, что у есть функция от х, получаем;
aWy—а2Ь2х~ d*y_______________dx
dx2 а*у2
dy
Подставляем вместо -f- ее значение из (А): dx '
/ b2x\ a2b2v—a2b2x [ — I
= у \а2у) = __ ^а(^>аха —аау») dx2 а*у2 а*у3
Но в силу данного уравнения
Ь2х2 — а-у2 = а2Ь2. Следовательно: (Ру _ Ь* dx2~ а2у*‘
УПРАЖНЕНИЯ.
Для каждой функции найти производную, порядок которой указан справа.
1. у = 4х® — бх- 4- 4х + 7.
2. /(х)=-147.
3. /Су)=У.
4. у = Xs !п х.
g = 12(2x-l).
,iv(х)в ьа-з^-ч
J W (1 _ x)5
/VI (jf) = 1.2 • 3 • 4 • 5-6.
diy _ A rfr*- x'
6. у = (x — 3) ё** + 4xex + x.
7. J = -fG“ +₽"“)•
8. /(x) = ax’ 4-6x4- c.
9. /(x) = In (x 4-1).
10. f (x) = In (erT 4- e-JC).
11. r=sinaO.
12. r=tgi».
13. r — In sin 7.
14. /(0 = e~1 cos t.
15. /(0) = У вес 20;.
16. p = 4- a’) arctg A
17. y = ax.
<Ру _ n(n -|- l)c
t/x’ xn-^2
§ = 4^[(х-2)г4-х + 2].
£y = _L(J dx2 2a \
Г" (x)=0. flvx = -______-__
J (x-f-l)1
f”' (x) =
a-
8 (eT - e~x) (е«4-е-х)з
—sj = a* sin aO = a*r. au*
18. _y = ln(l-|-x).
19. у = cos ax.
20. _y = xn—1lnx.
^=6sec*?-4sec»?.
(Pf
= 2 ctg у cosec3
/Iv (0 = - 4e_/ cos t = — 4/(0.
/"(9) = 3[/(6)]’-/(6).
<Pp _ 4as
dq3 ~ (aJ 4- q2)r
^ = (lna)"a».
dx
^У = (- и»-11-2- -<я-1)
rfx” (14~x)n •
d”v n ( - it \
—= a”cos| ax 4- b
rfx” V T 2 J
_ 1 ‘2 ••»(« — 1) p целое положи*
fjxn x L тельное число..
21.
22. Если у = a® sin x, то доказать,
^У — 2( 1 )п 1*2*3 ... п
dxn (14-х)"+1‘
что
<г-у dx3
2^ 4-2j = 0, dx J
23. Если y = a cos(lnx)4-6sln(lnx), то доказать, что
<^У । dy dx*^ x dx
24. у = х2ахх. = д*( In а)” 2 [(х In а + л)2 — л]. dx
25. у = ех ж. dnv v — = . (* + »)
26. f еХ sin х- /<”> <*>-(/ 2) Vslnfx +1").
27. Показтть, что формулы величины ускорения (25) и (26) § 100 и 101 можно написать в виде: _
. _ (fls _ Лг . (fly
J ~ dt2’ Jx~ dt2’ dfl'
28. _у2 = 4ах. fly 4«2 dx2 ~~ y3 ’
29. b2x2 + a2y2 = a2b2. d2y _ b* _ (fly 3Aex dx2 a’-y3’ dx3 a^y3'
30. x*+y' = fl. (fly r2 dx2 y3’
31. yt+y = x^ d3y 24x dx3 (1 4_2y)“’
32. ax2-f-2Axy — by2 = 1. (fly _ h2 — ab dx2 (hx+byp ’
33. у2 — 2ху = а2. (fly a2 (fly _ 3a*x dx2 (y — x)» ’ dx3 (y — x)y
34. sec ? cos 6 = c. ^0 _ tg26 — tg2? df2 tg3 в
35. e = tg(? + B). rf3Q 2 (5 4- 8fi2 4- 30 ‘) rf?3 0s
36. In (u 4- v) = и — V. (flv _ 4(u4"v) . du2 («4-v 4-1)5’ '
37. eu-f-и = ev -j-v. -£“+”) (eu-ev) du2 (ev 4- l)a
38. s = 1 + te*. (f~S 3 — S dt2 (2 — j/ *
39. e’ + st — e = 0. = s (2 —s)e*4-2^ dt (e* 4- 0*
40. _y8 -|- Xs — 3axy = 0. (fly _ 2a3xj dx2 (y2 — nx)3 ‘
41. y1 — Imxy + xa — a = 0. d2y _ a (m2 — 1) djfl ~ (y — mx)3'
42. у = sin (x 4- >). d*y = —У dx2 [1 — cos(x4-.y)ls
43. e®+w = xy. 44. ax2 4- 2Лху 4- by2 4- , 4- Igx 4- If у 4- e = 0. d*y._ y[(x-l)2 + (y-l)2] dx2 x2(y-l) , d2y _ abe -|- fgh. — af2 — h^1 — eh2 dx2 ~ (hx + by 4-y )8
45. Найти вторые производные от следующих функций:
a) In (a 4- v) == и — v. b) е“4-“ = ^®4-°-c) j = 1 4- te3. d) e? 4" st — c = 0. e) y3 4- x* — 3axy = 0. f) y2 — Imxy 4- x2 — a = 0. " g) J = sin(x4-j). h) ex+« = xy.
ГЛАВА VIII.
МАКСИМУМЫ И МИНИМУМЫ *). ТОЧКИ ПЕРЕГИБА. ВЫЧЕРЧИВАНИЕ КРИВЫХ.
§ 107. Введение. Многие вопросы прикладного характера приводят к необходимости исследовать функцию, имеющую наибольшее (максимум) или наименьшее (минимум) * 2) значение сравнительно со всеми другими близкими значениями, и весьма важно знать, при каких значениях независимого переменного функция принимает указанное наибольшее или наименьшее значение. Пусть, например, требуется определить измерения прямоугольника, имеющего наибольшую площадь из всех прямоугольников, какие могут быть вписаны в круг радиуса 5 см. Рассмотрим данный круг и впишем в него какой-нибудь прямоугольник. Положим основание = х; тогда высота = ]/100 — х2, и площадь S прямоугольника выразится, очевидно, следующим образом:
S = x У 100 —х’. (1)
То, что существует прямоугольник с наибольшей площадью, можно установить путем таких рассуждений.
Заставим возрастать основание (= х) до тех пор, пока оно не станет равным 10 см (диаметр круга); при этом высота = У 100 — ха будет уменьшаться до нуля, и площадь S обратится также в нуль. Пусть теперь уменьшается до нуля основание; тогда высота будет возрастать до 10 CMt и площадь S снова обратится в нуль. Следовательно, интуитивно очевидно, что существует такой вписанный прямоугольник, площадь которого больше площадей всех других вписанных прямоугольников. Нетрудно догадаться, что когда прямоугольник обратится в квадрат, то площадь его станет наибольшей из всех возможных; но эта догадка остается пока простым предположением.
Более надежный метод решения вопроса состоит, очевидно, в построении и исследовании графика функции (1). Для облегчения вычерчивания графика заметим, что
а) согласно смыслу задачи величины X и S положительны;
Ь) значения х содержатся между 0 и 10 включительно.
]) Доказательства, данные в этой главе, опираются главным образом на геометрическую интуицию. Аналитическое рассмотрение вопроса о максимумах и минимумах будет дано в § 139.
2) Функция может иметь несколько максимумов и несколько минимумов, как это показывает черт. 85 на стр. 228.
Составим теперь таблицу значений (черт. 80).
х и S и вычертим график
X S
0 1 2 3 4 5 6 8 9 10 0,0 9,9 19,6 28,6 36,6 43,0 48,0 49,7 48,0 39,6 0,0
Что НАМ ДАЕТ ИССЛЕДОВАНИЕ ГРАФИКА?
а) Если он аккуратно выполнен, мы можем весьма точно определять значение площади прямоугольника для любого значения х, измеряя длину соответствующей ординаты. Так, например, когда х = ОМ = 3 см, S = МР = 28,6 см* и когда х = ON = 4,5 см:
S = NQ^ 39,8 см*.
Ь) Кривая имеет единственную горизонтальную касательную RS. Ордината TH точки Т касания больше всех других ординат. Отсюда заключаем: один из вписанных прямоугольников имеет, очевидно, наибольшую площадь сравнительно с площадью любого другого из прямоугольников. Другими словами, мы можем отсюда заключить, что функция (1) имеет одно наибольшее значение (максимум). Мы не можем найти точно это значение (= НТ), измеряя соответствующую ординату, но мы его легко найдем, воспользовавшись методами анализа. Нами замечено, что в точке Т касательная горизонтальна; следовательно, наклон кривой в этой точке равен нулю (пример 1, стр. 183). Поэтому, чтобы определить абсциссу точки Т, найдем первую производную функции (1), приравняем ее нулю, и решим получающееся таким образом уравнение относительно х. Будем иметь:
S = x /100 — х*, ds 100 —2х2
dx ~ /ТоО —л2’ 100 —2ха _р /100 —х2~ ’ х = 5 /2.
Подставляя это значение х в выражение, определяющее высоту, получим: ________
высота = /100 — х* = 5 У~2.
Итак, прямоугольник наибольшей площади, вписанный в данный круг, является квадратом и площадь его
5 = 51/2-51/2 = 50 см2.
Следовательно, длина ординаты НТ равна 50.
Возьмем другой пример. Требуется сделать деревянную коробку, объем которой должен содержать 108 см3. Коробка открыта сверху и имеет квадратное дно. Каковы должны быть ее размеры, чтобы на нее пошло наименьшее количество материала?
Обозначим через х длину стороны основания коробки и через у ее высоту. Так как объем коробки известен, то у можно выразить функцией от х. В самом деле:
объем = х2у = 108, откуда
108
Х2 •
Теперь мы можем выразить через х число М квадратных сантиметров дерева, потребное для того, чтоб^и сделать коробку: площадь основания = х2 см2. *
И * 432
площадь четырех боковых сторон = 4ху =----см2.
* X
Следовательно:
Ж = х» + ^-. (2)
Построим график функции (2) (черт. 81).
X М
1 433
2 220
3 153
4 124
5 111
б 108
7 111
8 118
9 129
10 143
Что'ДАЕТ НАМ ИССЛЕДОВАНИЕ ЭТОГО ГРАФИКА?
а) Если он тщательно выполнен, мы можем измерить ординату, соответствующую какому-нибудь значению х длины основания коробки, и определить таким образом число квадратных сантиметров дерева, требующегося для построения коробки.
15 Зак. 2769. — В. Г р е и в п л ь и Н. Лузин. Часть I
Ь) Кривая имеет единственную горизонтальную касательную /?5. Ордината точки касания имеет наименьшую длину сравнительно со всеми другими ординатами. Отсюда мы заключаем: очевидно, существует коробка, на которую пойдет наименьшее количество дерева, чем. на всякую другую. Другими словами, мы заключаем, что функция (2) имеет одно наименьшее значение (минимум). Найдем интересующую нас точку графика, пользуясь методами анализа. Диференцируя функцию (2) для нахождения наклона кривой в любой точке, получим:
dM п 432
= 2-х------
dx х2
В наиболее низкой точке графика наклон равен нулю. Поэтому
2х
432 х2
= 0;
отсюда следует, что когда х = 6, необходимое количество материала для коробки будет наименьшим.
Подставляя найденное значение х в формулу (2), найдем, что
М = 108 см2.
Существование наименьшего значения функции М можно показать также путем следующего рассуждения. Предположим, что дно коробки изменяется, увеличиваясь от очень маленького квадрата до очень большого. В первом случае высота коробки очень велика, и поэтому количество необходимого материала тоже очень большое. Во втором случае высота становится очень малой, и поэтому для основания коробки при том же объеме коробки, потребуется большое количество дерева. Следовательно, функция М, отправляясь от очень большого значения, убывает, затем возрастает до другого тоже большого значения. Отсюда следует, что ее график должен иметь наиболее низкую точку, соответствующую размерам, при которых построение коробки будет наиболее экономичным.
Перейдем к подробному исследованию вопроса о максимумах и
минимумах.
§ 108. Функции возрастающие и убывающие. Функция назы-
вается возрастающею,
Черт. 82.
когда она возрастает при возрастании переменного и, значит, убывает при убывании переменного. Функция называется убывающею, когда она убывает при возрастании переменного и, значит, возрастает при его убывании.
Геометрическое изображение функции ясно показывает, возрастающая ли она или убывающая. Для примера рассмотрим функцию
<jx, график которой (черт. 82) есть геометрическое место уравнения:
у = ах (а > 1).
Если двигаться по кривой слева направо, то кривая поднимается, т. е. по мере возрастания х функция у все время возрастает. Следовательно, а* есть функция, возрастающая для всех значений х.
С другой стороны, рассмотрим функцию (а — х)8, геометрическое изображение которой (черт. 83) есть геометрическое место уравнения:
у = {а — х)8.
В этом случае, по мере того как мы двигаемся вдоль кривой слева направо, кривая падает, т. е. по мере возрастания х функция постоянно убывает. Следовательно, (а — х)8 есть функция, убывающая для всех значений х.
Что функция может то возрастать, то убывать, показывает геометрическое изображение (черт. 84) уравнения:
_у = 2х« —9х9-|-12х —3.
По мере того как мы передвигаемся по кривой слева направо, кривая поднимается, пока мы не достигнем точки А, затем — от А до В — она падает, а вправо от В идет все время поднимаясь.
Следовательно:
а) от х = — оо до х = 1 функция возрастает;
Ь) от х = 1 до х = 2 она убывает;
с) от х = 2 до х = -}- оо функция возрастает.
Учащийся должен тщательно изучить кривую, чтобы заметить, что делается с функцией при х = 1 и при х = 2. Очевидно, А к В суть точки поворота. В А функция от возрастания переходит к убыванию; в В имеет место обратное. В А и в В касательная (или кривая), очевидно ’)» параллельна оси ОХ (черт. 84), и, следовательно, угловой коэфициент касательной равен нулю.
§ 109. Признаки, определяющие, возрастает ли функция или убывает. Из черт. 84 видно, что в такой точке, как С, где функция
У=/(Х) возрастает, касательная образует острый угол с осью ОХ; следовательно, угловой коэфициент
tg"
dy dx
=/'(*)
есть положительное число.
х) Слово «очевидно* в этом месте употреблено лишь в геометрическом смысле, т. е. очевидность, о которой здесь идет речь, есть геометрического (но не логического) порядка.
Подобно этому в такой точке, как D где функция убывает, касательная составляет с осью X тупой угол; следовательно, угловой коэфи цие нт'
есть отрицательное число ').
Итак, следовательно, чтобы функция могла перейти от возрастания к убыванию, или, наоборот, необходимо и достаточно, чтобы первая производная ее меняла знак. Но для непрерывной производной это может случиться только при переходе ее через нулевое значение. Так на черт. 85, следя за ходом кривой, усматриваем, что производная (т. е. угловой коэфициент касательной) изменяет знак в точках А и В, где ее значения равны нулю. Итак, вообще в точке поворота будет:
й(О
Почти во всех приложениях, имеющих важное значение, производная является непрерывной, но интересно отметить случай, когда производная
(равная угловому коэфициенту касательной) меняет знак при переходе через бесконечность 2). Очевидно, это имеет место в точках В, Е, G на черт. 85, где касательные (и, значит, кривая) перпендикулярны к оси X. В таких особенных точках поворота имеем:
^=/W = oo,
или, что то же самое:
') Обратно, для данного значения х,
если /’ (х) > 0, то / (х) в о з р а с т а е т в этой точке;
если f (х)<0, то /(х) убывает в этой точке.
Если f (х) = 0, то без дальнейшего исследования нельзя решить, возрастает ли / (х) или убывает в точке х.
-) Под этим нужно разуметь, что ее обратная величина проходит через значение нуль.
§ ПО. Максимальное и минимальное значения функции »). Максимум функции есть такое ее значение, которое больше любых значений, в непосредственной близи ему предшествующих и за ним следующих.
Минимум функции есть такое ее значение, которое меньше любых ее значений, в непосредственной близи ему предшествующих и за ним следующих.
Так на черт. 84 видно, что функция имеет максимальное значение МА (=у = 2) при х=1 и минимальное значение NB (=jf=l) при х — 2.
Учащийся должен заметить себе, что максимум не есть необходимо наибольшее из всех возможных значений функции, а также, что минимум не есть необходимо такое значение, которое меньше всех других значений функции. В самом деле, на том же чертеже видим, что функция (у), имеет вправо от В значения, большие максимума УЙД, а влево от А — значения, меньшие минимума NB.
Функция может иметь несколько максимумов и несколько минимумов. Пусть черт. 85 представляет график функции f(x).
В точках В, D, G, /, К функция имеет максимум, в точках С, Е, Н, J—минимум. Чертеж показывает, что некоторые минимумы функции могут быть больше максимумов; так, минимальные значения в С и Н больше максимального значения в К-
В обыкновенных поворотных точках С, D, Н, I, J, К касательная (или кривая) параллельна ОХ\ следовательно, угловой коэфициент
В особенных точках поворота В, Е, G касательная (или кривая) перпендикулярна к ОХ, так как здесь угловой коэфициент
^7 =/'(*) = 00 •
Итак, чтобы функция имела максимальное или минимальное значение, необходимо одно из этих условий. Но этого условия недостаточно; в самом деле, в точке F, например, угловой коэфициент есть нуль, а в точке А он равен бесконечности, и, однако, ни в той, ни в другой из этих точек функция не имеет ни максимума, ни минимума. Нам еще нужно знать, каков будет ход изменения функции в соседстве с каждою такою точкою. Таким образом в точках максимального значения В, D, G, I, К функция переходит от возрастания к убыванию, а в точках минимального значения С, Е, Н, /совершается переход функции от убывания к возрастанию. Итак, из § 109 следует, что в точках максимума угловой коэфициент
]) Читатель должен помнить, что вообще определения и доказательства, данные в этой книге, приложимы только для точек, где функция непрерывна.
(3)
(4)
230 МАКСИМУМЫ И МИНИМУМЫ. ТОЧКИ ПЕРЕГИБА [ГЛ. VIII должен изменяться с плюса на минус, а в точках минимума угловой коэфициент
должен изменяться с минуса на плюс, если двигаться по кривой слева вправо.
В таких точках, как Ли/7, где угловой коэфициент также есть нуль или бесконечность, но при этом таких, что они не являются ни точками максимума, ни точками минимума, угловой коэфициент .
%—гм dx J '
не меняет знака.
Итак, можно высказать следующие общие условия для максимума и минимума функции при некоторых значениях переменного:
/(х) имеет максимум, если /'(х) = 0; И « , ч
j (х) меняет знак с плюса на минус; /(х) имеет минимум, если f'(x) = 0; И хг , ч
/ (х) меняет знак с минуса на плюс;
Значения независимого переменного для поворотных точек функции называются критическими значениями; так, х = 1 и х = 2 суть критические значения переменного для функции, графическое представление которой дает черт. 84. Критические значения для точек поворота, где касательная параллельна оси ОХ, очевидно, мы найдем, приравняв первую производную нулю и найдя из полученного уравнения действительные значения х, как в § 91 *).
Для определения знака первой производной в точках, близких к изучаемой точке поворота, подставляем в нее сперва значение переменного немного меньшее соответствующего критического значения, а потом немного большее * 2) его. Если в первом случае получаем плюс (как в L, см. черт. 85), а во втором получаем минус (как в М), то функция (=_у) имеет в этом промежутке максимальное значение (ка:: в I).
Если первая подстановка дает минус (как в Р), а вторая плюс (как в 7V), то функция (у) имеет в этом интервале минимальное значение (как в С).
Если в обоих случаях знак будет тот же (как в Q и в R), то функция (у) не имеет в этом интервале ни минимума, ни максимума (как в F)8).
Резюмируем теперь наши результаты в форме сжатого практического правила.
*) Подобно этому, если желаем исследовать, имеет ли функция особенные точки поворота, где касательная перпендикулярна оси ОХ, приравниваем нулю обратную величину первой производной и решаем это уравнение.
2) Под термином .немного меньше* следует понимать значение аргумент-, между ближайшим меньшим корнем (критическим значением) и рассматриваемым; под выражением .немного больше/ разумеют любое значение между рассматриваемым корнем и ближайшим большим.
•) Подобная же дискуссия, очевидно, имеет силу и для особенных новостных точек В, Е и G.
§ 111. Первый способ исследования функции на максимум и минимум. Практическое правило.
Первый шаг. Ищем первую производную функции.
Второй шаг. Приравниваем первую производную нулю *) и ищем действительные корни полученного
уравнения, которые и дадут критические значения переменного. -
Третий шаг. Разлагаем производную на множители; если это — функция алгебраическая, то разлагаем ее на линейные множители.
Четвертый шаг. Взяв в рассмотрение одно из этих критических значений, испытываем первую производную сначала для значения немного меньшего, а затем для значения немного большего этого критического значения. Если знак производной будет снач ала пл юс,
потом минус, то для рассматриваемого критического значения переменного функция имеет максимум; но если производная переходит с минуса на плюс, то функция имеет минимум. Если же знак не изменяется,
то нет ни максимума, ни минимума.
Пример 1. Исследовать на максимум и минимум функцию (х — I)1 2 * * (х1)^ Решение.
/(х)=(х-1)2(х-|-1)3.
Первый шаг.
Г (х) = 2 (х - 1) (х + -j- 3 (х - 1)3 (х + I? = (х - 1) (х + 1)3 (эх - 1).
Второй шаг.
(х - 1) (х + 1Н5х - 1) = 0, откуда критические значения х = 1, — 1, -у . Третий шаг.
Г (х) = 5 (х - 1) (х + 1)’ (х-1) .
Четвертый шаг. Исследуем сначала для критического значения х=1 (С па черт. 86).
Если х 1, то /'(х) = 5 (— ) (+ )s ( +) = —, . х>1, тоГ(х) = 5( + )(+)2( + ) = +, Заключаем, что при х=1 фунция имеет минимум f(l) = 0, равную ординате точки С.
Исследуем теперь для критического значения
х = 4- (В на черт. 86). Черт. Е5.
О
При x<il, /'(х) = 5(-)( + )а(-)=+. и
. х>1 у/(х) = 5(-)( + Р( + ) = -. □
Следовательно, при х = -у функция имеет максимум, равный / ^-yj = + 1,10эУ2 (равную ординате точки В).
1) Если первая производная при некотором значении независимого пере-
менного обращается в бесконечность, то исследуем функцию для такого крити-
ческого значения переменного, ибо и в этом случае она может иметь максимум
или минимум, как в В, Е или G (черт. 85). См. предыдущую выноску.
Рассмотрим, наконец, функцию для критического значения х = — 1 (точка Л на черт. 86).
Прих<—1, /'(х) = 5( —)(-)2( —) =+,
. х>—1, /' (х) = 5(-)( + )а(-) = +.
Следовательно, когда х = —1, функция не имеет ни максимума, ни минимума.
Пример 2. Исследуем функцию:
sin х (1 + cos х) на максимум и минимум.
Решение.
f(x) = sin х (1 cos х).
Первый шаг.
/' (х) = — sin2x -j- (1 cos х) cos х = 2 cos2 х + cos х — 1. Второй шаг.
2 cos2 х + cos х — 1 =0.
Решал это квадратное уравнение, находим корни:
1
COSX = y или —1, откуда критические значения:
x = zty или п.
Третий шаг.
/'(х) = 2 (cos х - (cos х + 1).
Четвертый шаг. Исследуем функцию сначала для критического значения:
х“‘з •
При х < у, /' (х) = 2 ( + )( + ) = +,
. х>|, /(х) = 2(-)( + ) = - •
Итак, при я
Х“з функций имеет максимум
Исследуем для критического значения х = —
Прих<-у, /(х) = 2(-)( + ) = -.
• х>~%' Лх) = 2( + )( + ) = +. Следовательно, при
•я
х~~ ~3
функция имеет минимум
Исследуем функцию для критического значения х = л.
При х<«, /'(х) = 2(-)( + ) = -
. Х>к, /'(х) = 2 ( — )( + ) = —.
Следовательно, когда х = л, функция не имеет ни максимума ни минимума
Так как косинус есть функция периодическая, то критические значения вообще суть
х = 2ил + -у и Лл, О
где п — какое угодно целое число. Следовательно, функция имеет бесчисленное множество максимальных значений, равных каждое
и бесчисленное множество минимальных значений, равных каждое
-4 о.
Пример 3. Исследовать на максимум и минимум функцию: о а—Ь(х — с)3.
Решение.
2^ /(х) = а-4(х-с)3,
З(х-с)3
Так как х = с есть критическое значение, для которого /' (х) =оо, но f (х) не обращается в бесконечность, то исследуем максимальное и минимальное значения функции для х = с.
При х < с, f (х) = п Х>с, /'(Х) = —.
Следовательно, при х = с = ОМ функция имеет максимум (черт. 87):
/(с)«= а = МР.
§ 112. Второй способ исследования функции на максимум И минимум. Из условия (3) § 110 ясно, что в соседстве с максимальным значением /(х) при переходе по кривой слева вправо
/' (х) изменяется с плюса на минус1).
Следовательно, f'(x) есть функция убывающая, а из § 109 нам известно, что ее производная, т. е. вторая производная самой функции [=/"(х)], отрицательна или нуль.
Подобно этому из условия (4) § ПО нам известно, что в соседстве с минимальным значением /(х)
/'(х) изменяется с минуса на плюс.
Следовательно, /'(х) есть функция возрастающая, а по § 109 из этого следует, что f" (х) положительна или нульг'
Учащийся должен заметить, что если /"(х) непрерывна, то она положительна не только в точках минимума (какова А на черт. 88), но и в таких точках, как Р.
1) Предполагается, что f (х) непрерывна и что /"(х) существует.
В самом деле, когда точка проходит через Р, двигаясь слева направо угловой коэфициент
tg т = =f (х)
Б dx J '
есть функция возрастающая.
Говорят, что в такой точке кривая вогнута вверх.
Подобно этому, если fu(x) непрерывна, то она отрицательна не только в точках максимума (какова, например, В на черт. 89), но и в таких точках, как Q. В самом деле, когда точка проходит через Q,
двигаясь слева направо, угловой коэфициент
,CT=^=/'W
есть функция убывающая.
Черт- 89. Говоря г, что в такой точке
Черт. 88.
кривая
Итак, мы имеем следующие достаточные минимума функции / (х) для некоторых значений
вогнута вниз, условия максимума и переменного:
/(х) имеет максимальное значение, если /'(х) = 0, а Г(х) отрицательна.
f(x) имеет минимальное значение, если /'(%) = О, а/”(х) положительна.
(6)
Соответствующее практическое правило будет таково.
Первый шаг. Ищем первую производную функции.
Второй шаг. Приравниваем первую производную нулю и из полученного уравнения находим действительные корни, которые и дадут критические значении переменного.
Третий шаг. Ищем вторую производную.
Четвертый шаг. Подставляем во вторую производную вместо переменного каждое критическое значение. Если получится результат отрицательный, то для йены-туемого критического значения функция имеет максимум; если же результат подстановки будет положителен, то функция имеет минимум1).
1) Если f (х) = 0 или не существует, приведенное правило является недостаточным, хотя и в атом случае также может быть максимум или минимум; в таких случаях обращаемся к первому основному методу. Обыкновенно пользуются вторым методом, и если процедура нахождения второй производной не слишком утомительна или продолжительна, то вообще метод этот кратчайший
Пример 1. Исследовать функцию х3 — Зх2 — 9х5 на максимумы и мини-
мумы (черт. 90).
Решение.
/(х) = х3 — Зх» — 9х-|-5.
Первый шаг.
/'(х) = Зх» - 6х - 9.
Второй шаг.
Зх2 - бх — 9 = 0;
отсюда критические значения:
х=—1 и х = 3.
Третий шаг.
/" (х) = 6х - б.
Четвертый шаг.
1) = - 12. Следовательно;
/( — 1) = 10 (ордината точки А) есть Л(3) = +12;
аналогично
/(3) = — 22 (ордината точки В) есть
Пример 2. Исследовать на максимум (черт. 91).
Решение.
/ (х) = sin2 х cos х.
Первый шаг.
Черт. 91.
f (х) = 2 sin х cos» х — sin3 х.
х= nr.;
Второй шаг.
2 sin х cos» х — sin» x = 0;
отсюда критические значения:
х = пк ± arctg Y 2 = nit ztz а.
Т РЕТ И Й Ш АГ.
f" (х) = cos х (2 cos2 х — 7 sin3 х).
Четвертый шаг.
У (0)>0, откуда /(0) = 0 есть минимум (в О);
Г(*)<0| откуда /(я) = 0 есть максимум (в С).
Г (.)=/*(«ctg/2).
Так как / х \ х
sin (arctg х) = sin I arcsin „_= ,_____гт
\ У1+х»У /14-х» ТО
sin (arctg / 2) = 1/ .
F О
Аналогичным образом найдем, что г- УТ • cos (arctg У 2) = .
Следовательно:
т. е. f"(а) < 0. Такны образом /(а) есть максимум (в А), /" (п — а) > 0, т. е. /(тс —а), есть минимум (в В) и т. д.
Замечание. Нахождение максимума н минимума часто можно упрощать, пользуясь следующими началами, непосредственно вытекающими из нашего исследования предмета:
1) Максимальное и минимальное значения непрерывно и функции должны чередоваться.
2) Если с есть некоторое положительное постоянное, то cf(x) будет максимум или минимум для таких, и только для таких, значений х, при которых f(x) получает максимальное или минимальное значение.
Если с отрицательно, то cf (х) будет макси м ум, когда / (х) есть минимум, и наоборот.
Отсюда при определении критических значений переменного х и испытании их на максимум и минимум можно опускать любой постоянный множитель.
3) Е с л и с есть количество постоянное, то
Г (л) и с-(-/(х)
принимают максимальное и минимальное значения для тех же самых значений х.
Итак, при нахождении критических значений х и при испытании их постоянный член может быть опущен.
УПРАЖНЕНИЯ.
Найти максимумы и минимумы следующих функций:
1. 3x3-9Х2 _ 27х-(-30. Отв. х = — 1 дает шах = 45; х = 3 дает min = — 51.
2. 2x3 _ 21x2 + 36х - 20. х = 1 „ шах = — 3; х = 6 „ mln =—128.
3. ~~2x24-3x4-1. О , 7 х = 1 „ max = у; х = 3 „ min = 1.
4. 2х’ _ 15Х2 4- 36х 4- 10. х = 2 » max = 38; х = 3 „ min = 37.
5. х3 — 9ха-(-15х — 3. x = 1 , max = 4; x = 5 , mln =—28.
6. хз-Зх3 4-6x4-10. Ни max ни mln.
7. х®~5х«4-5хз4-1. x = 1 дает max <= 2; x = 3 , min = — 26; x = 0 ни шах ни mln.
8. Зх5- 125хЗ-|-2 160х. x = — 4 и 3 дают max; х = —3 ц4 , min.
9. (х —3)*(х —2). 7 4 x = у дает max = ; x = 3 „ mln = 0.
10. (х — 1)з (х - 2)2. 8 x = — дает max; x = 2 . mln; x = 1 нет ни max ни mln.
11. (х- 4)» (х 4-2)*. x = — 2 дает max; 2 x = у дает mln; x = 4 нет ни max ни mln.
12. (х-2)-’(2х4-1)‘.
Отв. х = — у дает max;
11 х = дает mln;
16
х = 2 нет ни max
ни mln.
13. (x-J-l)3 (х-5)3.
_L 2
14. (2x —a)3 (x-a)3, (a >0).
1
х = у дает max;
х = — 1 и 5 дают mln.
15. x(x — l)»(x+l)s.
16. x (a + x)2 (a - x)», (a > 9)
2а
х = -у- дает max;
х = а дает min;
а
х = у нет ни max ни mln.
1
х = ~2 дает шат!
х = 1 и — у дают mln;
х = — 1 нет пи max ни min.
а
х = — а и -х- дают mln;
о
а
х = — у дает max;
х = а нет ни max ни min.
17. b + c(x-a)3', (a>0, c<0).
1
18. a — b(x — c)3.
19. - ~ .
x — 10
20. (a>0).
a — 2x
х = а дает max = Ь.
1 ~ X + X2
1 +x —X2 ’
Ни max ни mln.
х= 4 дает шах;
х = 16 „ min;
х = 10 нет ни max ни min.
а
х— — дает mln;
4
а
х = а и х = у нет ни max ни min.
21.
22.
xi - 3x + 2 x3 + 3x + 2 •
(x —a) (b-x)
(a>0, t>0).
24 _____“_______
4x» - 9x2 + 6x
ни mln;
х = У~2 дает min;
х = — YTдает max.
lab
х = —p-r дает max;
<2 -f- О
x = 0 дает mln.
х = 1 дает max = 10;
х = у , min = 8.
94
°’ Зл*-1-20x3 +60л+1 •
26. 2х»-j-Зх»— 36x4-17.
Нет ни max ни mln.
х = 2 дает mln = — 3;
х = — 3 дает max У 98.
28. а^ + Ъв-^, (в>0, 4>0, А>0).
29. Xе, (1<х<-[-ос).
£
30. Xх, (1<х< + оо).
31. cosx-j-sinx, (0<х<2те).
32. sln2x—х,
33. х + tg х.
34. sin x + cos 2x, ^0<*<yV
35. 2tgx —tgax, (o<x<y).
36. Амплитуда бросания OA (черт. 92)
Отв. x = e дает min.
In b — In a x -------ТГГ--- дает min =
2k
= 2/дГ x = — дает mln. x = e дает max. x — дает max = V~T; 4
5те , ,/--sr
x = —г- дает min = - V 2.
4 те x = -= дает mu; О
я x = — -г- дает min. о
Ни max, ни mln.
, 1 х = arcsin -г дает max;
4 те
х = у дает mln.
X х = у дает шах.
ядра в пустоте дается формулою:
R р? sin 2? g
где Oj — начальная скорость, g—ускорение тяжести, Ф —угол бросания с го-прн данной начальной скорости, д давал бы наибольшую ампли-туду- Отв. Ф=45°.
37. Полное время полета брошенного тела в последней задаче дается формулою:
2р, sin ф g
Под каким углом оно должно быть брошено, чтобы время полета было наибольшее?
Отв. ф = 90°.
38. Время, нужное шару, чтобы скатиться вниз по наклонной плоскости (черт. 93) АВ, дается формулою: ______
Г = 2 1/~—-— .
Г £51п2ф
Если пренебречь трением и т. п., каково должно быть значение ф, чтобы тело скатилось в кратчайшее время? Отв. ф™45°.
39. Если принять в расчет сопротивление воздуха, то отклонение маятника от вертикали можно представить формулою:
О = ае~ke cos (nt +е).
Показать, что наибольшие Элонгации происходят через равные промежутки времени.
40. Требуется измерить возможно точным образом некоторую неизвестную величину х. Положим, что для этого сделано было п одинаково тщательных наблюдений этой величины, давших результаты:
я1» °1> °3..ап-
Погрешности этих наблюдений, очевидно, суть
X - аи х — аъ X - о3....X - ап,
из которых некоторые положительны, другие отрицательны.
Известно, что наиболее вероятное значение х есть то, которое сумме квадратов погрешностей, т. е. сумме
(х - + (х — а+ (х - оа)« +... + — ля)*,
дает наименьшее значение. Показать, что наиболее вероятным значением будет среднее арифметическое наблюдений. в
41. Момент изгиба в точке В бруска длины I, равно-
мерно нагруженного, дается формулою: f
1 1 '------------------------------------1----
Л, = _ю/х__юЛ церт м
где w — нагрузка на единицу длины. Показать, что максимум момента изгиба приходится в центре бруска.
42. Если полный расход на каждую милю (1,596 км) для электрического проводника есть
W=Pr+^ + b,
где Z — сила тока в амперах, г—сопротивление в омах на каждую милю н t и b — величины, не зависящие от i и г, то какого сопротивления проводник является наиболее экономным при данных /, t и ft?
Оте. г = —.
i
43. Подводный телеграфный кабель состоит из сердцевины, сделанной из медной проволоки, и из оболочки, состоящей из непроводящего материала. Если х означает отношение радиуса сердцевины к толщине оболочки, то известно, что скорость сигнализации пропорциональна
Показать, что наибольшая скорость достигается, если
1
X = —.
V е
44. Принимая, что энергия, отдаваемая электрическим элементом, дается формулою:
Р= (.r + Rf
где Е — постоянная электровозбудительная сила, г—постоянное внутреннее сопротивление, R — внешнее сопротивление, доказать, что Р имеет максимум, когда
/? = г.
45. Если батарея из тп элементов сгруппирована в т рядов по л элементов, соединенных последовательно, причем т рядов соединены параллельно, то ток дается формулою: тп^
С— mR-\-nr ’
где Е — электровозбудительная сила каждого элемента, г — внутреннее, a R — внешнее сопротивления каждого элемента. Показать, что ток достигает максимума, когда Rm^rn, т. е. когда полное внутреннее сопротивление равно полному внешнему сопротивлению.
240 МАКСИМУМЫ И МИНИМУМЫ. ТОЧКИ ПЕРЕГИБА [ГЛ. VIII 46. Сила, с которою круговой электрический ток радиуса а действует да небольшой магнит, ось которого совпадает с осью круга, пропорциональна X
(в2 + х*)2 где х—расстояние магнита от плоскости круга. Доказать, что сила достигает максимума при
Х = у .
47. В А и В имеем два источника теплоты, напряжения которых соответственно равны а и Ь. Полное напряжение теплоты в расстоянии х от А дается формулою: а ь
л Р a / = +
Sr; Л .-.4. Показать, что температура в Рбудет наименьшая, если
Черт. 95. = j/*
х \/ а т. е. если расстояния ВР и АР относятся, как кубичные корни из соответствующих напряжений теплоты. Расстояние Р от А будет:
л х= —i------г-
а3 4- 63
48. Доказать, что при любом значении х
§ 113. Общие указания для решения задач на максимум и минимум. До сих пор давалась функция и требовалось найти ее максимум или минимум. Но не всегда так бывает: обыкновенно мы сами должны бываем составить функцию по данным условиям задачи, а затем уже исследовать эту функцию в отношении максимума и минимума.
Для составления функции нельзя дать правила, которое прилагалось бы во всех случаях, но для обширного круга задач могут служить руководством следующие общие указания:
а) Написать функцию, определение максимума или минимума которой решает задачу.
Ь) Если полученное выражение для функции содержит больше одного переменного, то условия задачи дадут достаточно соотношений между переменными, чтобы все их можно было выразить в функции одного переменного.
с) К полученной функции одного переменного прилагаем одно из наших двух правил нахождения максимальных и минимальных значений.
d)B задачах, какие дает практика, обыкновенно легко сказать, какое критическое значение даст максимум и какое минимум, так что в приложении четвертого шага наших правил не всегда встречается надобность.
ЗАДАЧИ.
1. Из квадратного жестяного листа (черт. 96), сторона которого а, желают сделать открытый сверху ящик возможно большего объема, вырезая равные квадраты по углам, удаляя их и затем загибая жесть, чтобы образовать бока ящика. Какова должна быть длина стороны у вырезаемых квадратов?
Решение. Пусть сторона малого квадрата равна х-, следовательно, сторона квадрата, образующего дно ящика, равна а — 2х, а объем его
V = (а — 2х)’х;
такова функция, максимум которой нужно найти, выбирая надлежащим образом х. Прилагаем правило.
Первый шаг. *----- ° “
dV
уу =4 (а ~ 2х)3 - 4х (д - 2х) = а3 - 8ах + 12х3.
Второй шаг. Решая уравнение
* я3 — 8ах12х3 = О,
находим критические значения:
1 1 '". 1
а
Черт. 96.
и
6'
а х = у дает минимум, и материала для ящика не а
-g дает максимальный
Из чертежа 96 видно, что жесть будет вынута вырезкою, Обычным испытанием найдем, что х = 2а3 объем, равный Итак, сторона у вырезаемых квадратов составляет шестую долю стороны данного квадрата.
2. Известно, что прочность балки с прямоугольным поперечным сечепием (черт. 97) изменяется прямо пропорционально ширине и квадрату вышины. Каковы будут размеры балки наибольшей прочности, какую только можно выпилить из крумого бревна, диаметр которого равен
Решение. Пусть х будет ширина, у — вышина балки; по условию балка будет иметь наибольшую прочность, когда функция х>3 достигает максимума.
Из чертежа имеем:
в этом случае вся останется никакого.
Черт. 97.
<П
уг = (Р _ х-; следовательно, нужно исследовать функцию: /(x) = x(d3-X3).
Первый шаг.
f(x) = —2х3 + — х3 = <Р — Зх».
Второй шаг.
— Зх3 = О, d х =
/3 есть критическое значение, при котором функция чаем, что если балка выпилена так, что
вышина = 1/ •= диаметра г О
ширина = V диаметра Г «1 то балка будет иметь наибольшую прочность.
16 Зак. 2798. — В. Гранвиль в Н. Лузин. Часть I
откуда
получает максимум. Заклю-
бревна;
бревна,
; ибо
3. Какова ширина прямоугольника максимальной площади, который можно вписать в данный сегмент ОАА' параболы (черт. 98)?
Указание. Если
ОС = Л, ВС=/г — х и РР' = 2у,
то площадь прямоугольника PDD'P' будет;
2(Л-х)>.
Но так как точка Р лежит на параболе
Черт. 98.
У = 2рх,
то исследуемая функция будет:
2 (Л — x)V 2рх.
2 Отв. Ширина равна -у Л. j
4. Найти высоту копуса максимального объема, который можно вписать в шар данного радиуса г (черт. 99).
Указание. Объем конуса равен
Черт. 100.
7
но
X* = ВС • CD = у (2г — у)-, поэтому исследуемая функция будет:
/O) = y>,(2r-j).
Отв. Высота конуса равна V
5. Найти высоту цилиндра максимального объема, который можно вписать в данный прямой конус 1черт. 100).
Указание. Пусть АС = г и ВС = А. Объем ци-
линдра равен пх*_у- Но из прямоугольных треугольников АВС и DBG имеем:
г : х = Л : (А—_у), откуда
г(А—_у)
А ’
Таким образом исследованию подлежит функция:
Отв. Высота равна -д- А.
О
6. Разделить а на такие две части, чтобы их произведение было максимум.
Отв. Каждая часть равна у.
7. Разделить 10 на такие две части, чтобы сумма их квадратов была наименьшей.
Отв. Каждая часть равна 5.
8. Разделить 10 на такие две части, чтобы сумма удвоенной одной и квадрата другой была наименьшей.
Отв. 9 и 1.
9. Найти число, которое превышало бы свой квадрат возможно большим
числом.
Отв. 1.
10. Какое число, сложенное с ему обратным, дает возможно меньшую сумму?
Отв. 1.
11. Показать, что из всех прямоугольников, имеющих данный периметр, наибольшую площадь имеет квадрат.
12. Требуется выделить прямоугольную площадку земли в 216 ж2, огородить ее забором и разделить загородкой, параллельной одной из сторон площадки, на две равные части. Каковы следует выбрать размеры сторон площадки, чтобы на постройку заборов пошло наименьшее количество материала?
Отв. 12 м и 18 м.
13. Проволокой 20 м длины требуется огородить клумбу, которая должка иметь форму кругового сектора. Какой следует взять радиус круга, чтобы площадь клумбы была наибольшей?
Отв. 5 м.
14. Требуется огородить забором прямоугольный участок, который имел бы данную площадь. Если часть уже выстроенной каменной стены принять за одну из сторон забора, то каковы должны быть размеры площадки, чтобы постройка обошлась возможно дешевле?
Отв. Сторона, параллельная стене, должна быть вдвое длиннее каждой из двух остальных сторон.
15. Показать, что из всех прямоугольников, которые могут быть вписаны в данный круг, наибольший периметр имеет квадрат.
16. Показать, что из всех равнобедренных треугольников, вписапных в данный круг, наибольший периметр имеет равносторонний треугольник.
17. Найти прямоугольный треугольник наибольшей площади, имеющий гипотенузою отрезок, длина которого равна h.
Отв. Длина каждого катета равна /Т
18. Резервуар, который должен иметь квадратное дно и быть открытым сверху, нужно выложить внутри свинцом. Каковы должны быть его измерения, чтобы выкладка требовала наименьшего количества свинца, если он должен вмещать 32 л воды?
Отв. Вышина 2 м, сторона основания 4 м, т. е. вдвое больше вышины.
19. Если внутренняя поверхность такого же бака равна 48 какова наибольшая возможная емкость бака?
Отв. 32 ма.
20. Каковы наиболее экономичные размеры цилиндрического парового котла данной емкости?
Отв. Диаметр равен длине котла.
21. Найти размеры цилиндрической коробки заданной вместимости v, которую нужно изготовить из картона с наименьшей затратой материала (коробку нужно сделать без крышки).
з/" о
Отв. Радиус основания равен высоте, равен 1/ —. Г Л
22. Изготовить из куска картона 30X14 сж3 коробку (без крышки) наибольшей вместимости, вырезая равные квадраты по углам и затем загибая картон для образования боков коробки.
Отв. Вырезаемые квадраты должны быть размером 3X3 см.
23. Кровельщик желает сделать открытый желоб наибольшей вместимости, у которого дно и бока были бы шириною в 10 см и бока были бы одинаково наклонены ко дву. Какова должна быть ширина желоба наверху?.
Отв. 120 см.
24. Нормандское окно имеет форму прямоугольника, завершенного полукругом. Дан периметр фигуры. Каковы должны быть ее размеры, чтобы окно пропускало наибольшее количество света?
Отв. Радиус круга равен высоте прямоугольника.
25. Принимая, что прочность бруска с прямоугольным поперечным сечением прямо пропорциональна ширине и кубу вышины, найти ширину бруска наибольшей прочности, который можно вырезать из бревна в 16 см диаметром. _
Отв. Ширина равна 8 см.
26. Найти высоту прямоугольника, имеющего наибольшую площадь, вписанного в прямоугольный треугольник, основание которого равно Ь, а высота равна h.
Отв. Высота прямоугольника равна —.
27. Найти высоту прямого цилиндра с наибольшим объемом, который может быть вписан в шар радиуса г.
2г
Отв. Высота равна TTv-• г d
58. Найти высоту прямого цилиндра с наибольшей боковой поверхностью, который может быть вписан в данный шар.
Отв. Высота равна г/2 .
29. Показать, что из всех прямых цилиндров данного объема наибольшую поверхность имеет тот, у которого осевое сечение — квадрат.
30. Найти высоту прямого конуса с наименьшим объемом, описанного около данного шара.
Отв. Высота равна 4г, а объем — двум объемам шара.
31. Прямой конус с наибольшим объемом вписан в данный прямой конус, причем вершина внутреннего конуса находится в центре основания данного конуса. Показать, что высота внутреннего конуса составляет треть высоты данного конуса.
32. Из круглого железного диска радиуса г требуется сделать конус наибольшего объема. Каков должен быть радиус основания этого конуса?
/ 2~ Отв. г 1/ F О
33. Требуется построить палатку в форме правильной четырехугольной пирамиды. Найти отношение высоты палатки к стороне основания при условии, чтобы при данной площади боковой поверхности объем палатки был наибольшим.
Отв. —Д^-. /2
34. Равнобедренный треугольник данного периметра р вращается около основания. Какими следует выбрать основание и высоту треугольника, чтобы объем тела вращения был наибольшим?
Отв. Основание высота -4-2. 4 4
35. Дока3ать, что конический шатер данной вместимости требует наименьшего количества материи, когда его высота в /2 раз больше радиуса основания.
36. Найти наибольшую емкость конической палатки, которую можно сделать из материи размера $ квадратных единиц.
п 41 Г~$
Отв. - в 1 / —.
/27 у г-
37. Проволока 12 м длиной разрезана на шесть частей, из которых две части одного размера и четыре части другого. Первые два куска согнуты в виде квадратов н вершины этих квадратов соединены оставшимися четырьмя кусками так, что вся фигура представляет собой прямоугольный параллелепипед. Как надо разрезать проволоку, чтобы объем этого параллелепипеда был наибольший?
Отв. Четыре ч сти по 1 м, две части по 4 м.
38. Длина и периметр поперечного сечения почтовой посылки в сумме должны составлять 60 см. Найти наибольший объем посылок: 1) если посылка имеет форму прямоугольного параллелепипеда с квадратным поперечным сечением; 2} посылка имеет форму цилиндра. я ООО
Отв. 1) 2 000 см*; 2) см\
39. Чтобы по возможности уменьшить трение жидкости о стенки канала, площадь, орошаемая водой, должна быть возможно меньшей. Показать, что лучшей формой открытого прямоугольного канала с заданным периметром поперечного сечения является такая, при которой ширина канала превышает
вдвое его высоту.
40. Степа, имеющая 27 м высоты, отстоит на 8 ж от дома, превышающего вышину стены. Найти какова должна быть наименьшая длина лестницы, которая опиралась бы одним концом о землю с внешней стороны стены по отношению к дому, касалась бы в промежуточной точке стены и другим концом достигала бы дома. „ ,— 4
Отв. 13 УТЗ. ,
41. Бревно длиной 20 м имеет форму усеченного конуса, диаметры оснований которого соответственно 2 м и 1 ж. Требуется вырубить из бревна балку с квадратным поперечным сечением, ось которой совпадала бы с осью бревна и объем которой был бы наибольшим. Каковы должны быть размеры балки?
Отв. Длина балки 13*/, м; сторона основания поперечного сечения U/з м.
42. Против пункта А берега, на расстоянии 3 км от него, на якоре стоит корабль. На расстоянии 9 км от берега, против пункта В, стоит другой корабль. Расстояние от Л до 8 составляет 5 км. Шлюпка с первого корабля должна доставить пассажира на берег и затем проследовать ко второму кораблю. Каков наикратчайший путь шлюпки? q
43. Миноносец стоит на якоре в 9 км от ближайшей точки берега; с миноносца надо послать гонца в военный лагерь, расположенный в 15 км, считая по берегу от ближайшей к миноносцу точки берега. Если гонец может делать пешком по 5 км в час, а на веслах по 4 км в час, то в каком пункте берега он должен пристать, чтобы поспеть в лагерь в кратчайшее время?
Отв. В 3 км от лагеря.
44. Электрическая станция расположена на одном берегу реки, имеющей в ширину b километров, и фабрика на противоположном на расстоянии а километров, считая от проекции на другой берег пункта, где находится станция. Найти наиболее экономичный способ для подводки тока к фабрике, если стоимость подвески проводов над землей составляет т рублей, а прокладка кабеля под водой л рублей за километр.
_ 6m 6л
Отв. а----_______- км по земле; , — км под водой.
Ул2 - т» /л« - т2
45. В данный момент времени лодка находится в пункте А и движется в направлении АВ со скоростью 10 км/час; другая лодка находится в пункте С и движется по направлению АС со скоростью 20 км/час. Угол между направлениями АВ и АС составляет 60°. Через сколько времени лодки будут находиться на наиболее близком расстоянии друг от друга?
Отв. Через 1п/14 часа.
46. Корабль движется на север со скоростью 10 км/час. Другой корабль находится на 190 км дальше на север от первого и имеет курс Ю. 60°. В., двигаясь со скоростью 15 км/час. Через сколько времени расстояние между кораблями будет наименьшее?
Отв. Через 7 часов.
47. Картина 1,4 м вышиной повешена на стену так, что ее нижний край на 1,8 м выше гЛЗЗа наблюдателя. На каком расстоянии от стены должен стать наблюдатель, чтобы его положение было наиболее благоприятным для созерцания картины?
Отв. 2,4 ж.
У Казание. Положение наблюдателя будет наиболее благоприятно, когда угол зрения (угол в вертикальной плоскости, образуемый лучами зрения, проведенными к верхнему и нижнему краям картины) будет наибольшим.
48. Полоса жести шириною а должна быть согнута в виде открытого цилиндрического желоба (профиль желоба имеет форму кругового сегмента). Найти значение центрального угла ?, опирающегося на дугу этого сегмента, при котором вместимость желоба будет наибольшей.
Отв. ? = г., т. е. профиль желоба имеет форму полукруга.
49. Груз IF поднимают рычагом, причем сила F приложена к одному концу, а точка опоры находится недругом конце рычага (черт. 101). Если груз привешен в точке, находящейся на расстоянии а сантиметров от F точки опоры, а стержень рычага весит w граммов на каж-Г — '_____j дый сантиметр длины, то какова должна быть длина рычага,
Jmnjinrmiteiawl чтобы сила, потребная для поднятия груза, была наименьшей?
* ~
1 , л, Отв. х = 1/ -------.
Черт. 101. г w
50. Электрическую дуговую лампу требуется повесить прямо над центром круглой площадки в 30 м в диаметре. Принимая, что сила освещения прямо пропорциональна косинусу угла, под которым свет падает на освещаемую площадку, и обратно пропорциональна квадрату расстояния от источника света; спрашивается: на какой высоте надо повесить лампу, чтобы она всего лучше освещала дорожку, которою обведена площадка? 15
Отв. На высоте - __ м.
УТ
51. Какие пропорции надо придать жестяной цилиндрической кружке данной емкости в целях наибольшей экономии, если все ее части (крышку, дно и боковую поверхность) нужно вырезать из прямоугольных кусков жести любого размера, так что обрезки составят прямой убыток?
Отв. Если х — радиус основания, а у — высота кружки, то х: у = к: 8.
Указание. При вырезывании боковой поверхности кружки никакой потери материала не будет. Для решения задачи следует составить выражения для объема v кружки и площади s двух квадратных кусков жести, из которых вырезываются дно и крышка кружки. Так как — = 0 (о — постоянная ds величина) и — = 0 (условие, при котором потеря материала будет наименьшая), то, лродиференцнровав s и v по х, мы получим два уравнения, dy содержащие (у есть функция от х). Исключение из этих урав-
нений дает соотношение между х и у.
52. На отрезке длиною /, соединяющем два источника света —силы и силы Z2, найти наименее освещенную точку. (Яркость освещения обратно пропорциональна квадрату расстояния предмета от источника света.)
ЛЯГ
Отв. Расстояние от источника силы /. равно / п -._J—гт=. pi + р.
53. Найти длину кратчайшего отрезка, который делит равносторонний треугольник на две равновеликие части.
Отв. d = ——
54. На странице книги печатный текст должен занимать S квадратных сантиметров. Верхнее и нижнее поля должны быть по а сантиметров, правое и левое — по о сантиметров. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
Отв. Длина страницы по нижнему краю равна 26 4- -~
» , , боковому , , +1/
55. Гирю весом Р килограммов тянут за веревку, составляющую с горизонтом угол а. Коэфициент трения гири о пол равен /. Каков должен быть угол а, чтобы усилие, необходимое для того, чтобы сдвинутьгирю с места, было наименьшим? п L .
Отв. а = arctg /.
Указание. Сила трения равна произведению f на горизонтальную составляющую равнодействующей сил, действующих на гирю. С другой стороны, эта сила равна горизонтальной составляющей натяжения веревки.
56. Стальная балка длиною 25 м перемещается вдоль дороги, имеющей 12,8 м в ширину, и затем направляется в узкий проход, расположенный перпендикулярно к дороге. Пренебрегая шириной балки, определить, какова должна быть наименьшая ширина прохода. 5 4 дс
57. Пароход потребляет в час 0,3 + 0,001 о8 тонны угля (у — скорость парохода в час, выраженная в километрах). Найти скорость парохода, дающую наибольшую экономию расхода топлива. ,.. „
Отв. у/ 150 км!час.
58. Принимая, что энергия, затрачиваемая на перемещение парохода, пропорциональна кубу его скорости, найти, какова будет наиболее вкономнчная скорость, если пароход идет против течения, а скорость течения составляет с километров в час. 3
Отв. Скорость равна-у с.
У казание. Расстояние, проходимое пароходом в 1 час, равно v — с, где v — скорость парохода, развиваемая пароходом в стоячей воде.
59. Найти на прямой у = х точку, сумма квадратов расстояний которой от точек (— а, 0), (а, 0) и (0, Ь) была бы наименьшей. . b ь .
Отв- (-6"’ "б-}
60. На окружности у2-|-х2 = а2 найти точку, сумма квадратов расстояний которой от точек (2а, 0); (0, 2а) была бы наименьшей.
Отв. (у/г “/г).
61. На оси параболы у- = 1рх дана точка на расстоянии а от вершины; найти абсциссу ближайшей к ней точки кривой. Qma х = а_р
62. В прямоугольной системе координат дана точка (Хд, ул), лежащая в первом квадранте. Провести через эту точку прямую так, чтобы она образовала с положительными направлениями осей координат треугольник наименьшей площади. Отв. Прямая отсекает на осях отрезки 2х0 и 2jg.
63. В прямоугольной системе координат через точку (хд, у») проведена прямая, отрезок которой между осями имеет наименьшую длину. Показать, что эта длина равняется
/ 2 —\_1
I 8 • j а.
64. Найти наименьшую длину отрезка касательной к эллипсу 68х8 + а8у8 = — аЧй, заключенного между осями координат. дтв в_|_$
65. Найти измерения прямоугольника наибольшей площади, вписанного в эллипс
Ь2х8 + а2у2 = а2*8
Отв. Стороны прямоугольника: н ЬУ~2.
66. Найти эллипс, площадь которого будет наименьшей нз площадей всех эллипсов, которые можно описать около данного прямоугольника. (Площадь эллипса с полуосями а, b равна nab.)
Отв. Площадь эллипса равна у площади прямоугольника.
67. Найти на данной прямой точку, сумма квадратов расстояний которой от двух данных точек была бы наименьшей.
Отв. Точка лежит посредине расстояния между основаниями перпендикуляров, опущенных из данных точек на данную прямую.
68. Найти на данной прямой точку, сумма расстояний которой от двух данных точек была бы наименьшей.
Отв. Прямые, соединяющие искомую точку с данными, наклонены к данной прямой под равными углами.
69. В прямоугольной системе координат (XYZ) дана прямая
у = тх -\-b, г = nx-f-c.
Найти расстояние прямой от начала координат.
Отв. а= + +
Г 1Н-т1 2 + л2
Указание. Расстояние d точки (х, у, z), взятой на прямей, от начала координат, определяется формулой:
<Р = х» +у2 4- х2 = х2 + (тх + Ь)г + (mx + cf =
= х2 (1 + m2 + л2) -J- 2х (mb + лс) + *2 + с2.
70. Дан ряд чисел:
1- /т, 1/Т, f/T, р'Т,...,
доказать, что наибольшее число в этом ряде есть Y 3.
Указание. Исследовать на максимум функцию^ = у х непрерывно изменяющегося переменного х. Результат этого исследования покажет, какое целое значение следует выбрать для х для ответа на поставленный вопрос.
§ 114. Точки перегиба. Определение. Точки перегиба отделяют дуги, вогнутые вверх, от дуг, вогнутых вниз. Так, если кривая
, j=/(x) (черт. 102) изменяет (как в В) вогнутость
z о вверх (как в Л) на вогнутость вниз (как в С), или наоборот, то такая точка В называется точкою пере-' гиба.
д-------------j- Исследование § 112 сразу показывает, что в точке
А будет/* (х) > 0, а в точке С будет J"(x) < 0. Но Черт. 102. при перемене знака функция должна пройти через значение, равное нулю *): следовательно, в точке перегиба f(x) = 0.
Решая это уравнение, мы ндйдем абсциссы точки перегиба. Чтобы определить направление закривления в смежности с точкою перегиба, исследуют f (х) для значений х, сперва „немного меньших*, потом „немного больших* абсциссы этой точки.
Если f (л) меняет знак, мы имеем точку перегиба, а полученные знаки укажут направление изгиба в соседстве с точкой перегиба *)•
1) Предполагается, что/Чх) и f(x) непрерывны. Решение примера 2, стр. 250
показывает, как исследуют случай, когда и /' (х) и J" (х) обе бесконечны.
Читатель должен заметить, что поблизости с точкою, где кривая вогнута вверх (как в А), она лежит выше касательной, а в точке, где кривая вогнута вниз (как в С), она лежит ниже касательной. В точке перегиба (как в В) касательная, очевидно, пересекает кривую (прикасаясь в то же самое время к ней).
Итак, имеем следующее правило для нах9ждения точек перегиба кривой, уравнение которой естьз>=/(х), правило, содержащее также указания для исследования кривой в смежности с такою точкой.
Первый шаг. Ищем f (х).
Второй шаг. Полагаем //,(х) = 0 и на- ""Х.
ходим действительные корни уравнения. Черт. 103 * 2)
Третий шаг. Разлагаем /" (х) на множители.
Четвертый шаг. Исследуем f" (х) для значений х, сперва „немного меньших*, потом „немного больших* каждого корня уравнения //,(х) = 0. Если при этом /"(х) меняет знак, мы имеем точку перегиба.
Если /"(х)>0, кривая вогнута вверх (-|-).
Если (х) < О, кривая вогнута вниз (—) (черт. 103).
ПРИМЕРЫ.
Исследовать следующие кривые на точки перегиба и на направление изгиба.
1. у = Зх4 — 4л3 -|- 1 (черт. 104). Решение.
/ (х) = Зх4 — 4х3-|-1.
Первый шаг.
/"(х) = 36x2-21с.
Второй шаг.
36x2 _ 24х = 0, 2
откуда x = -q-H х = 0 — критические значения. О
Третий шаг.
Г(х) = 36х (х-у).
Черт. 104.
Четвертый шаг. Если х < 0, f (х) > 0, а если х > 0, /" (х) < 0.
Отсюда: кривая вогнута вверх — влево, и вогнута вниз — вправо от х =
на черт. 104). Если
2
х<4, Л(х)<0;
О
(-4
о
Ч Точки перегиба Можно также определить как такие точки, гдо
, d-y п d*y
а) -/г- = 0 и —меняет знак,
' dx2 dx*
или
.. rf*x п (Рх
Ь) -гт- =0 и -з-т- меняет знак.
' dy1 dy*
2) Это правило легко запомнить, сказав: сосуд, имеющий форму кривой, там, где она вогнута вверх, содержит (-|-) воду, а там, где она погнута вниз, не содержит (— ) воды.
Иногда это правило называется также правилом дождя: падающий на кривую сверху дождь собирается (-(-) там, где кривая вогнута вверх, и скаты-
вается (—) с нее там, где она вогнута вниз.
а если 2 х>4. /"(х)>0.
О
Следовательно, кривая вогнута вниз—влево, и вогнута вверх — вправо от 2
х = -х- (В на чертеже).
3 Очевидно, кривая вогнута вверх Л (0,1) и В (у, и вогнута вверх
2. (_у — 2)3 = (х — 4) (черт. 105).
Решение.
всюду влево от А, вогнута вниз между всюду вправо от В.
у = 2 + (х-4)8.
Ш А Г.
dx
(Ру dx*
2
1 , .ч а
3-(х-4) ,
Второй шаг. При х = 4 в первая и вторая производные бесконечны.
Четвертый шаг. При х < 4,
?<>».
dx*
& при х>4,
Заключаем, что касательная в точке (4, 2) перпендикулярна к оси X и что влево от (4, 2) кривая вогнута вверх, а вправо от (4, 2) она вогнута вниз. Значит точка (4, 2) является точкой перегиба.
УПРАЖНЕНИЯ.
1. у = х*.
2. у = 5 — 2х — х2.
3. y = xs.
4. > = х8— Зх2 — 9x-f-9.
5. у = а + (х — 6)3; (Ь > 0).
6. = -ах« + 2а»; (а>0).
7. х8 — 36х2 + а'-у = 0.
8. у-=*х*.
9. у — х* — 12х3 + 48х2 — 50.
Отв. Всюду вогнута вверх.
Всюду вогнута вниз.
Вогнута вниз влево и вогнута вверх вправо от точки (0, 0).
Вогнута вниз влево и вогнута вверх вправо от (1, —2).
Вогнута вниз влево н вогнута вверх вправо от (Ь, а).
Вогнута вниз влево н вогнута вверх вправо от
(’ I •)
Точка перегиба
Всюду вогнута вверх.
Вогнута вверх влево от х = 2; вогнута вниз между х = 2 и х = 4; вогнута вверх вправо от х » 4.
“ эти* '“>»> Отв. Вогнута вниз между 2а 3 \ ( УТ* 2 е)’ вогнута вверх вне этих точек.
11. у = х + 36х2 — 2х3 —х* Точки перегиба при х = 2 и х = —3.
12- Вогнута вверх влево от точки (-М-1.), вогнута вниз между точками / а \ (—За, 4 а ) и (0> ОН вогнута вверх между точками (0, 0) и (за,-|-а вогнута вниз вправо от точки / 9 \
2 ф’+фт-= (а>(У, 6>0). Точки перегиба при . а х = :£ - У 2
9 14. у = а—Ух— Ь. 15. у = 8ШХ. Точка перегиба при х = Ъ. Точки перегиба при х = п-, где п — любое целое число и нуль.
16. > = tgx. Точки перегиба при х = лк, где л — какое угодно целое число и нуль.
17. у«=хе~®. х = 2 дает точку перегиба.
18. Показать, что функции ех и In х не имеют точек перегиба.
19. Показать, что кривая
j(xe+a2) = x имеет три точки перегиба, лежащие на прямой линии
х — 4а3у = 0.
20. Показать, что абсциссы точек перегиба кривой у* = /(х) удовлетворяют уравнению:
l/'(x)F = 2/(x)-/"W.
§ 115. Вычерчивание кривых. Элементарный способ вычерчивания (построения) кривой по заданному уравнению в прямоугольных координатах, способ, с которым читатель уже хорошо знаком, состоит в решении данного уравнения относительно у (или х), в вычислении у (или х) по произвольным значениям, задаваемым х (или у), в построении определяемых таким образом точек и в нанесении кривой, проходящей через эти точки, руководствуясь при этом соображением о непрерывности кривой; вычерченная таким образом кривая является приблизительным образом искомой кривой. Этот способ исключительно кропотливый, и когда уравнение кривой выше второй степени, формула
252 МАКСИМУМЫ И МИНИМУМЫ. ТОЧКИ ПЕРЕГИБА (ГЛ. VIII решения такого уравнения может оказаться весьма неудобной для вычисления значений зависимого переменного; этот способ может оказаться и совершенно непригодным, потому что не всякое уравнение разрешимо относительно у (или х).
Обычно требуется установить только вид кривой, и сведения, которые нам предоставляет анализ, дают возможность определить форму кривой путем небольшого числа выкладок.
Первая производная дает наклон кривой (касательной к кривой) в точке; вторая производная дает возможность определить интервалы, в которых кривая выпукла или вогнута книзу, и точки перегиба, разделяющие эти интервалы; точки максимума и минимума дают представление о том, где кривая достигает наибольшего подъема и наибольшего спуска, т. е. характеризуют гребни и впадины кривой.
Нижеследующее правило дает читателю руководство для работы по вычерчиванию кривых.
Правило для вычерчивания кривых.
(Прямоугольные координаты.)
Первый шаг. Найти первую и вторую производные и по правилам, изложенным в § 111, 112, определить абсциссы точек максимума и минимума и точек перегиба.
Второй шаг. Вычислить ординаты, соответ-Ч I ствующие абсциссам, найденным при первом шаге. Й/ Вычислить, кроме того, координаты нескольких -/• дополнительных точек, которые необходимы для ' ; более точного представления вида кривой. Соста-| вить таблицу, подобную приводимой в нижесле-i : дующем примере.
Третий шаг. Построить найденные точки и начертить кривую, соответствующую результатам, представленным в таблице.
j Если значения ординат окажутся очень большими, то _ .—по реи ординат следует выбрать меньший масштаб с таким расчетом, чтобы кривая могла уместиться на предназначенном для вычерчивания листе бумаги. Удобно пользоваться для вычерчивания кривой миллиметровой Черт. 106. бумагой.
ПРИМЕРЫ.
Вычертить кривые по нижеследующим уравнениям. Найти также уравнения касательных и нормалей к этим кривым в точках перегиба.
1. у=х2—9ха + 24х—7.
Решение. Воспользуемся данным выше правилом.
Первый шаг.
у' = 3x2 18г + 24; f = бх - 18
Зх2 - 18х + 24 = 0; х = 2 и 4.
6-2 - 18 = - 6 < 0;
6 • 4 —-18 = + 6> 0;
6х- 18 = 0;
х = 2
х = 4
х = 3
лает max. дает mln.
6 .'.v — 3)< 0 при х <
3 и 6 (х — 3) > 0 при х > 3.
Второй шлг.
X У У' У" Выпуклость и вогнутость
0 2 — 7 13 + 0 max | вогнута книзу
3 4 11 9 0 0 4- точка перегиба min выпукла книзу
6 29 4- +
Третий шаг. Построив точки, приведенные в таблице, и вычертив кривую, получим черт. 106.
Чтобы найти уравнения касательной и нормали в точке перегиба Pi (3, 11), воспользуемся формулами (1) и (2), стр. 187. Получим: Зх+_у = 20— уравнение касательной и Зу—х = 30 — уравнение нормали.
2. у = х® — 6х2 — 36х + 5. Отв. max ( — 2, 45); mln (6, — 211);
точка перегиба (2, — 83); урав-нениекасательной:_у + 4х — 13= = 0; уравнение нормали: 48_у — — х + 3 986 = 0.
3. у = х* — 2х2+ 10. max (0, 10); min 1, 9); точки
, 1 85\
перегиба ( cfc —п- .
\ У /
4. у = i х4 — Зх2 + 2. max (0, 2); mln (zt
точки перегиба (±1, —
5 , _ б* max (1» 3); min ( — 1, — 3); точ-
14-х» ки перегиба (0, 0); 3;
6. у = 12х — х3. max (2,16); min (— 2, — 16); точка
перегиба (0, 0).
7. 4> + х® - Зх2 + 4 = 0. max (2, 0); mln (0, - 1).
8. у = х® — Зх2 — 9х + 9.
9. 2у + Xs—9х + 6 = 0.
15. j = (х+1) 6 7 8 9 (х —5)а.
16. у =
х + 2 х® ’
10. у = х® - 6x2 _ 15х + 2.
11. У (1 + х») = х. 8а®
12. у = , , .
J х3+4а-
13. у = е~х’.
14->= Ча-
17. j = x»-3x2- 24х.
18. у = 18 + Збх - Зх2 - 2х®.
19. у = х — 2cosx.
20. у = Зх — х3.
21. j = х® — 9х2 + 15х — 3.
254 МАКСИМУМЫ И МИНИМУМЫ. ТОЧКИ ПЕРЕГИБА
ГЛАВА IX.
ДИФЕРЕНЦИАЛЫ.
§ 116. Введение. До сих пор мы рассматривали производные, употребляя для обозначения производной от у = f(x) символ
g-=rw. (1)
Особенно же мы всюду старались дать понять читателю, что выражение
dx
рассматривалось не как дробь, в обыкновенном смысле слова, с чистителем dy и с знаменателем dx, а как особый символ для обозначения предела частного .
к Ьу
Ьх
по мере приближения Дх к пределу, равному нулю.
Однако же встречаются задачи, в которых весьма выгодно рассматривать dx и dy как количества отдельные, и особенно это полезно в приложениях интегрального исчисления. Объясним, каким образом это достижимо.
§ 117. Определения. Если f(x) есть производная от /(х) для некоторого частного значения х, а Дх —произвольно выбранное приращение х, то д и ф е р е н ц и а л' от /(х), обозначаемый символом df(X), определяется равенством:
<№)=/'(*)•**• (А)
Итак, диференциал функции, в силу самого его определения, есть не что иное, как произведение /'(х)Дх производной /' (х) от этой функции на произвольное число Дх, которое рассматривается как приращение независимого переменного х1)-
*) Читатель должен отдать себе ясный отчет в том, что это приращение Дх независимого переменного х, входящее как множитель в диференциал, не имеет ничего общего с тем приращением Дх независимого переменного, которое употребляется при вычислении производной f (х).
В самом деле, хотя при вычислении производной Г(х) как предела отно-
шений
_ цт /(х + Дх) —/(х) нт -7— = нт-------г------
и приходится говорить о приращении Дх независимого переменного, тем нс менее совершенно ясно, что вто приращение Дх употребляется лишь как средство определить или вычислить производную, т. е. имеет лишь преходя-
Если теперь положить f(x) = x, то /(х) = 1, и (1) приводится к
dx = tax,
откуда видно, что, если х есть независимое переменное, то диферен-циал х ( = dx) тождествен с Дх. Отсюда, если y=f(x), (1) можно вообще написать в форме:
dy = f(x)dx ’). (2)
Диференциал функции равен произведению ее производной на диференциал независимого переменного.
§ 118. Геометрическое изображение диференциала. Пусть кривая, представленная на черт. 107, изображает функцию y=f(x).
у Пусть точка М этой кривой имеет своими
, координатами х и у. Пусть точка М', ле-
'/ жащая также на этой кривой, имеет своею
д/ абсциссою
x + dx.
v п Ясно, что отрезок MR, параллельный
оси ОХ, равен dx. Ясно также, что отрезок RM' равен приращению Д_у функции, ибо
RM' =f(x -j- dx) — /(х) = Ду.
J2 , — . I------- у Если точка Т обозначает пересечение
I касательной, проведенной к кривой в М,
Черт. 107. с ординатою точки М', то из прямоуголь-
ного треугольника MRT находим:
TR = MR- tg TMR.
А так как тангенс наклона касательной есть производная, то
TR = f (х) • dx = dy.
Значит, отрезок ТR есть диференциал dy функции У=/(х).
шее значение: действительно, вся роль этого приращения Дх сводится лишь к тому, что оно должно стремиться к нулю, и раз рассматриваемая нами производная уже вычислена или определена, то это значит, что процесс стремления Дх уже завершился и, следовательно, это приращение Дх уже перестало возбуждать интерес, существуя скорее в прошлом, чем в настоящем.
Что же касается приращения Дх, которое фигурирует как множитель в выражении диференциала, то это есть приращение х, которое мы снова даем уже после того, как вычислен первый множитель диференциала, т. е. /'(х). Поэтому это приращение Дх есть величина произвольная, ничем не обусловленная, могущая быть и большой и малой — смотря по желанию. Таким образом диференциал функции есть выражение, содержащее два независимых переменных: х и Дх. Оба эти переменные суть независимые друг от друга, и Дх вовсе не обязано стремиться к нулю; как независимое переменное, оно находится всецело в нашем распоряжении.
1) Принимая во внимание положение, которое здесь занимает/'(х), ее называют иногда диференциальным коэфициентом.
Читатель должен обратить внимание на важный факт, что, так как dx мож-, но приписать какое угодно произвольное значение, то dx не зависит от х. Следовательно, dy есть - функция двух независимых переменных х и dx. См. предыдущее примечание.
§ 119. Приращение функции и днференциал функции. Непосредственно из чертежа читатель видит, что приращение функции by = RM' и днференциал функции dy = RT отнюдь не равны друг другу. Их разность ТМ' есть отрезок между касательной и самой кривой.
Рассмотрим этот вопрос с аналитической точки зрения.
Пусть независимое переменное х получает приращение Ах. Вычислим соответствующее приращение функции, а также ее днференциал.
Для приращения Ду мы находим равенство:
д.У=/(х + дх) -/(*)•
Если теперь мы станем приращение Дх независимого переменного приближать к нулю, то, как известно,
и, значит, разность
/(х + дх)-/(х) игл-------------
Г(х),
f(x -1- Дх) — / (х)
Дх
/(х)
есть величина бесконечно малая; обозначим ее через е:
/(х + дх)-/(х) Дх
Г (х) = «.
Из этого равенства мы заключаем, что
/(х + Дх) — /(х) = f (х) Дх -|- е Дх, или, приняв во внимание, что левая часть этого равенства есть приращение функции Ду, а первое слагаемое правой части есть дифе-ренциал dy этой функции, мы заключаем, что г.
±y = dy г8 • дх. (3)
Это основное равенство (3) говорит нам, что приращение Ду функции и днференциал dy функции отличаются друг от друга на бесконечно малое высшего порядка, чем Дх = dx.
В общем случае производная /'(х) не равна нулю, и, значит, дифе-ренциал функции dy=f'(yc)±x есть бесконечно малое первого порядка относительно приращения независимого переменного Дх. Но тогда в • Дх есть бесконечно малое порядка выше первого, и, значит, бесконечно малое приращение Ду функции и диференциал dy этой функции суть равносильный друг другу бесконечно малые (см. § 50 гл. Ill), т. е. Ду«</у, и, следовательно:
По этой причине на практике часто вместо сложного по своей природе приращения Ду функции берут более простой ее диференциал dy.
17 Зак. 27вв_В. Гравии ль в Ы. Луции. Часть I
Пример 1. Возьмем функцию у = Xs 4- 5х2 — 4х 4- 6.
Если независимое переменное х получит приращение Дх, то приращение Уу функции будет: •
Ду = (х + Дх)8 + 5 (х Дх)2 — 4 (х + Дх) + 6 — Xs — 5х2 4* 4х — б.
Приведение подобных членов дает:
Ду = (3x2 4- Юх _ 4) • Дх 4- (Зх 4- 5) • (Дх)8 4- (Дх)8.
Но, пренебрегая членами высших порядков, мы получим: (Зх8 4- 10х — 4) • Дх, а это и есть диференциал rfy нашей функции, как легко убедиться, вычислив у' = Зх® 4- 10х — 4.
Диференциал функции есть главная часть приращения функции, получающаяся зачеркиванием членов высшей малости.
Пример 2. В технике весьма часто применяется приближенная формула: V^+T =а+^.
где b есть число малое сравнительно с а. Пояснить происхождение этой формулы.
Решение. Положим /(х) = Г14-х , Д/ (х) = f (х 4- Дх) - f (х) да dF (х) = f (х) Дх, откуда
f (х + Дх) да/ (х) + /' (х) Дх.
При х = 0 получаем:
/(Дх) ^/(0) 4-Г (0) Дх = /Г 4- —~ Дх = 1 4- - Дх. 2/1 2
Преобразовав к виду a J/1 4- ~ и положив ~ = Дх, найдем:
а/(Дх) = п-j/l + А « а (1 + ± - А) = о 4-А.
§ 120. Важность диференциала функции. Важность диферен-циала функции состоит в том, что его вид остается неизменным даже в том случае, когда берут другое независимое переменное.
Действительно, пусть J . ч
есть функция независимого переменного и. Тогда, по только что сказанному, диференциал dy этой функции напишется в виде:
dy = f (и) • du. (2*)
Пусть теперь мы взяли за независимое переменное другое переменное, например х, таким образом, что прежнее независимое переменное и стало теперь, в свою очередь, некоторой функцией буквы х, например:
« = ? (X).
Тогда буква у стала зависящей уже от независимого переменного х, ибо теперь
>»=/[?(•*)]•
Если мы хотим вычислить диференциал dy функции у в этом новом предположении, то должны написать;
dy={f№)]Y -dx. (4)
Можно подумать, что мы получили совсем другое выражение для диференциала dy. Но на самом деле на основании теоремы о производной функции >от функции мы имеем:
(/['? (*)])' =/' [?(*)] • <?' (х) =/'(«) • /(х).
Значит, равенство (4) перепишется в виде:
dy =f («) • ?' (х) • dx. (4*)
Но так как выражение </ (х) • dx есть, очевидно, диференциал функции и, ибо du = <?' (х) dx, то равенство (4*) перепишется, в свою очередь, в виде: dy=f'(u)du, (4**)
и, значит, мы снова возвратились к тому виду (2*) диференциала, который был нами написан в предположении, что буква и есть независимое переменное. Таким образом мы приходим к чрезвычайно важному свойству диференциала,выражающемуся словесно следующим образом:
Формула диференциала
dy = /' («) • du справедлива во всех случаях: как в том случае, когда и есть независимое переменное, так и в три случае, когда и есть функция другого независимого переменного; в этом последнем случае под множителем du надо понимать диференциал функции и.
Как применение этого важного для анализа свойства диференциалов допустим, что у есть функция независимого переменного х, например у — /(х). Тогда производная функции у по х, т. е. /' (х), напишется в виде: dy
dx '
Пусть в некоторый момент рассуждения мы увидели, что и буква у, и буква х зависят обе от некоторого переменного t, так что, например;
= 'НО и X = (/), по что при этом зависимость между у и к остается» старой, т. е.
Н0=/['М0]-
Тогда отношение (5) будет равно
«Г (0 • dt ?' (f) • dt или, сокращая на dt (что имеем право сделать, ибо dt, будучи дифе-ренциалом независимого переменного t, есть любая величина), это отношение становится равным
У (0
770 ’
(5)
(6)
Но, с другой стороны, применяя правило диференцирования функций от функций к равенству (5), мы получим:
О)=/'[? (01 •?'('),
и, значит,
О)
Мы видим, что даже при взятии другого независимого переменного t вместо прежнего х формула (5) по прежнему обозначает производную у по х.
dx
В частности, — обозначает производную обратной функции для/(х), т. е. производную относительно у функции х = F(y), которую мы получим, решив относительно буквы х уравнение:
_У=/(Х).
§ 121. Производная дуги в прямоугольных координатах. Пусть 5 будет длина *) дуги АР (черт. 108), измеряемая от постоянной точки А кривой. Обозначая соответственные приращения знаками Дх, Ду, As, из прилагаемого чертежа имеем:
(хорда PQ)2 = (Дх)2 -|- (Ду)2.
Умножая и деля первую часть на (дугу PQ)2 [ = (Д$)2], получим:
хорда PQ \2
дуга PQ 5)
(Дх)2 + (Ду)2.
Черт. 108.
Разделив обе части на (Дх)2, находим:
/ хорда PQ \а / Д$ \2___ . /Ду \а
\ дуга PQ / \Дх/ \Дх/ ’
Отсюда, приближая Дх к пределу нуль, получаем:
Zrfs \а__. . (dy \а
\с/х/ ~ ' \dx) '
вследствие того, что lim (—= 1 ’)• Следовательно:
• pq-о\ луга PQ /
ds dx
(7)
1) Относительно определения понятия „длины дуги* кривой см. часть вторую этой книги.
-) Эго равенство вытекает из понятия длины дуги: отношение хорды к дуге, ею стягиваемой, стремится к единице, когда хорда стремится к нулю. Для случая круга это было установлено точно, а именно, в § 47 было доказано равенство:
lim slnx = 1
•0-0 х
Подобно этому, разделив (А) на (Ду)9 и переходя к пределу, имеем:
Из того же чертежа имеем: п Дх Дх C0S — хорда PQ As
хорда PQ As
[умножая числитель и знаменатель в обоих случаях на дугу PQ = As].
По мере приближения делу т, а отношение дуги Следовательно: dx C0S7 = ~di'
дуга PQ хорда PQ ’
хорда PQ
(7*)
Дх к пределу нуль, 6 приближается к пре-PQ к хорде PQ приближается к единице.
sinT = -^. (8)
ds
Употребляя символы диференциалов, можем (7) и (7*) написать так:
ds =
(9)
ds =
(Ю)
Чтобы легче запомнить соотношения от циалами dx, dy, ds, заметим, что они в фиктивным 9 прямоугольным треугольником торого есть ds, катеты dx и dy, а угол при основании т. Таким образом ds = У (dx)--[- (Jy)2,
а разделив на dx или dy, найдем (7) или (7*) соответственно.
Так же из чертежа имеем: dx dy
cos т = , , sin т = -г- , ds ds
а это — соотношения (8).
§ 122. Производная дуги в полярных координатах. В нижеследующем обращаемся к чертежу, символам и сокращениям § 94.
Из прямоугольного треугольника PRQ (черт. ПО) имеем:
(хорда PQ)9 = (Р/?)9 (/?Q)a = (р sin ДО)9-}-(р Др — р cos ДО)9 = = p9sin2 ДО—I— ( 2р sin9 4- Др I .
(6) до (10) между диферен-точности даются некоторым (черт. 109), гипотенуза ко-
') Мы называем этот треугольник .фиктивным* потому, что то, что дано на черт. 109, в сущности, не является этим прямоугольным треугольником: вертикальный катет, собственно, равен Ду, а не dy, а гипотенуза криволинейна. Однако, пренебрегая бесконечно малыми высших порядков, мы можем криволинейный прямоугольный треугольник, изображенный на чертеже, считать за прямоугольный. А тогда его элементы, стороны и углы, тождественны с элементами фиктивного треугольника.
Умножая и деля первую часть на (дуга PQ)9 [ = (As)2], а затем деля па (ДО)2, находим:
/ хорда PQ V
\ дуга PQ /
Переходя к пределу с приближением Д6 к нулю, имеем:
откуда
dh V р 1 \d6j
В диференциалЯх получим следующее выражение: 1
Г /J. \o-12
•</в.
ds =
(И)
(12)
dt
с
том-
Эти соотношения между р й диференциалами ds, dp и ностью изображаются фиктивным прямоугольным треугольником (черт. 111), гипотенуза которого есть ds, а катеты суть dp и pdO. Имеем:
ds = /(pdO)2 4- (dp)2,
a ho разделении на dO находим (11).
Обозначая угол между dp и ds буквою (черт. Ill), тотчас имеем:
1^ = РЗ-.
а это есть формула (И) § 94.
§ 123. Формулы для нахождения диференциалов функций. Так как диференциал функции равен произведению ее производной на диференциал независимого переменного, то отсюда прямо следует, что формулы для нахождения диференциалов будут те же, что и формулы, служащие для нахождения производных, данные в § 61, если каждую из них умножить на dx. Таким образом имеем:
1. d(c) = O. 4. d(cv) = Qdv.
• 2. d(x) = dx. 5. d (uv) = и dv 4~ v du.
3. d(u-j-v — w) = dv-j-dv—dw.
6. d= (v9va...vn)dvl 4-(v^g... v,) dv94-...
...-|-(wiva.‘-vn-t)
7. d(vn) = livn~'dv.
7а. d(xn) = пхп~'dx.
_ . / и \ v du — и dv
8. a I — I — ——--------•
\ v J
„ . / и \ dii
8a. d — = —
\ c / c
/ с \ c dv
8b. d — =----------
\ v] v*
9. d(logei>) = loga e-
10. d(a”) = av In a dv.
10a. d (<?”) — c’dv.
11. d(uv)=vii',~ldu -j-In и • uvdv.
12. d (sin v) = cos v dv.
13. d(cosz>) = — sinz/rft/.
14. d (tg v) = sec2 v dv.
15. rf(ctgt>) = — cosec2 vdv.
. sinw .
16. a (sect/) = —^—dv.
4 cos2 v
. cos г» ,
17. d (cosec v) =------„ - dv.
sin2 v
18. d (arcsin v) = . .
V \—v*
dv
19. d (arccos v) =------------.
/1—
20. d (arctg v) = -^~
1 -j-VJ
21. d (arcctg v) = — ;.
1 -4- V’-
22. d^ = ~-dv, где v dv
есть функция v.
Чтобы найти диференциал, проще всего обыкновенный способом найти производную и результат умножить на dx. Поэтому действие на хождения диференциала обычно называется днференцированием, хотя .«о сих пор под этим мы понимали операцию взятия производной.
Пример 1. Найти диференциал от —-
х + 3
У ~~ л _с з •
Решение.
. н М + 3 \ _ (х2 + 3) d(x + 3) - (х+3) d (х2 + 3)
* - ' 1^+3?----------------<!“+3?-----------------
(X2 + 3) dx — (х + 3) • 2х dx (3 — 6х - х») dx
~ (х2+’3)2 •
(^ + 3)a
Пример 2. Найти dy из ^х2 - а V = в»62.
Решение. ‘ 2b2x dx — 2а2у dy = 0,
откуда . Ь-х . dy— л-dx. J <Ру
Пример 3. Найти tfp из р2 = a2 cos 20.
Peiuetfu. 2р dp = — аг sin 20 • 2rf0, откуда . a2 sin 20 dp =---------------------------------------аа.
Р
Пример 4. Найти d(arcsln (34 — 4/®)].
Решение.
d [arcsln (ЗГ — 4/3)]
d(31-4fl)________3 (1 - 4P) dt
У1 — (3t-4t»)»_ У1 -t*(3 —4«4»’
§ 124. Диференциалы высших порядков. Так как диференциал функции вообще есть также функция независимого переменного, мы можем диференцировать ее диференциал. Рассмотрим функцию:
y=f(x).
d (dy) называется вторым диференциалом от jr (или от функции) и обозначается символом
d*y.
Подобным же образом, третий диференциал от yt d(d(rfy)l пишется так:
(/«у и т. д. до n-го диференциала от у.
dny.
Так как dx, т. е. диференциал независимого переменного, не зависит от х, то, диференцируя dx по х, нужно рассматривать dx как количество постоянное *). Зная . это, мы придем к весьма простым соотношениям между последовательными диференциалами и последовательными производными. Таким образом
dy =f(x) dx, и
ибо dx рассматривается как постоянное.
Так же
d*y=f”<x)(dx)* и вообще
<у=/";(х) (dx)n.
Разделяя обе части каждого выражения на степень ах, стоящую во второй части, находим обыкновенное обозначение производных:
^Х=/"(х), (х),...,
dx* , dt ' ' dxn
Пример 1. Найти третий диференциал от
у = jfl — 2х3 + Зх — 5.
Решение.
dy = (5г* — 6х3 + 3) dx, <Ру = (20x3 _ 12х) (dx)2, (Ру = (60x3 _ 12) (dx?.
Примечание. Очевидно, это — третья производная функцип, умноженная на куб диференциала независимого переменного. Разделяя на (dx)1, получаем третью производную:
-^- = 60х3 — 12.
]) Ибо, как было сказано выше, dx не зависит от х, и, значит, относи тельно х это есть величина постоянная.
УПРАЖНЕНИЯ.
Найти диференциалы следующих функций:
1. у = ах3 — Ьх2-[- ex 4- d.
Отв. dy = (Зал2 — 1Ьх 4- с) dx.
Б_ А
2. у = 2х 2 — Зх3 4* 6х“ 1 + 5.
3. _у = (а2-х2)&.
3
4. у = /14-х2.
, х2"
5. у =----------.
(14-х2)"
6. у = In V 1 — X2.
7. У =(еа’4-е_х)3.
8. у = In х.
10. р = tg ? 4- sec ?•
П- ' = 4-tg36 4-tg0. □
12. /(х) = (1пх)>.
13. ?«-------^-г-
(1-*)»
,, .Fxlnx . . J Inxdx 14Л^ + 1П(1-Х)1=(Г^Г
15. rf[arctgln>]=yTn^r].
. Г cos ? 1 i . ?! dy
16‘1.2Sin2<y 2 ntg2]= sin3?
dy = — lOx (a2 — x2)'<fx. dy — X dx.
J 2/w2”-1 . аУ=.. .
dy x2 — Г dy = 2 (e2® - a-8®) dx. dy = ex (in x 4- y) dx.
\ «*+<-• i
. 1 4-sin? .
7p =--- d?.
r COS2 ?
dr = sec* 6 dfl.
. 3(lnx)2dx f (x)dx = -±-^-------.
...... 3fldt t'(f)dt =------j-.
(1 -f2)2
Для каждой из нижеследующих кривых найти диференциал дуги, а также косинус и синус угла касательной с осью ОХ.
17. у3 = 1рх (парабола).
Отв. ds = у V p^+y^dx-, у cost = _ ;
V Р2 4-У2
18. х24->2 = 25 (окружность).
у COS т - ;
д
А £ i
19. х» 4"у2 = •
_ . 5dx
Отв. ds =---
У
sin т = — —. О
Отв. ds =
20.
62х2 fl2j'2 = а2Ь- (эллипс). ________________
_ j 1 , /~ а* — т2хг Отв. ds— — у —г-----------j-
а V в2 — л2
cos ~
sin
bx
21.
№ уЗ
tfT ~ fr = 1 (гипербола).
m2x2 — г
—5----=- dx, где т — } а- - Ь*
х1 — а2 '
cos т = —; sin т —
У mW — а»
22. у = ах3 (кубическая парабола).
bx
Отв. ds = У1 -|- 9а2х* dx; 1 , Зал2
-------; sin т = — -—. -4- Эа-х1 V1 + 9а2х‘
COST =
23. у2 = ах2 (полукубическая парабола). _____
_ J У 4х3 4- г . Отв. ds = -—~------cfx;
2х
2х . Зу
cos т = — -------; sin т = ——--------.
У 4 л2-|-9 У 4x2-f-9
24. х = a (t — sin /); у = а (1 — cos t} (циклоида).
Отв. ds = 2a sin dt; cos - = sin у; sin т = cos —.
25. x = a cos3 6; у = a sin3 8 (гипоциклоида).
Отв. ds = За sin 0 cos 6 rfO; cos т = — cos 0; sin т = sin 0.
26. x = fl (A cos t — cos kf); у = a(k sin t -Отв. ds = 2 ka sin dt; cos т =
Для каждой из нижеследующих кривых, и ?, найти диференциал дуги.
27. р = а? (архимедова спираль).
28. р = — (гиперболическая спираль).
29. р = fl<? (логарифмическая спираль).
30. р = п sin ф (окружность).
31. р = в (1 — cos ?) (кардиоида).
32. р = a sec2 4- (парабола).
Найти <Ру для следукЛиих функций:
33. a) x*-y2 = a"-. b) x2 = 4fly. g) p = esec3
с) у + e~x. 1 1
d) xy = fl. h) X« 4-y« :
e) у = In sec x. 1) y2 = ax3.
f) p = 2a tg 8 sin 6. ji _y = lnx.
•sin АО (эпициклоида).
А -|- I . . . А -|- I
- COS —4— t; sin Т =: sin —t.
заданных в полярных координыах р
Отв. ds = а У 1 -|- ф3^.
= 1
ds = р У1 -р (In я)2 df.
ds = a df.
ds = 2a sin у d<f.
ds = -^-.
cos3|-
2 k) 4A=y3.
3 • .0
1) p = a sec2 у.
~a* ’ m) p = 1 + sin6.
n) p6 «= a.
34. Вычислить приближенно приращения функции у = х3 — 5х -|- 80
при переходе переменного х от значения х = 4 к значению х = 4,001. Сравнить приближенный результат с точным.
Отв. Лу «0,003. Точное значение отличается от приближенного в шестом десятичном знаке.
35. Зпая, что lg10200 = 2,30103, найти lglo200,4. Сравнить полученный результат с данными таблицы.
36. Объяснить происхождение приближенной формулы, весьма часто применяющейся в технике:
где |6| есть число малое сравнительно с [д|.
ГЛАВА X.
СКОРОСТЬ ИЗМЕНЕНИЯ.
§ 125. Производная, рассматриваемая как отношение двух скоростей. Пусть
>=/(*)
будет уравнение кривой, производимой движением точки Р (черт. 112). Ее координаты хну можно, следовательно, рассматривать как функции времени, как указано в § 98. Диференцируя по /, имеем:
dt J W dt
(О
Во всякий момент скорость изменения с течением времени у (или функции) равна произведению ее производной на скорость изменения с течением времени независимого переменного.
Или, переписав (31) в форме:
dy
dt \ dv
dt
(2)
Производная измеряет отношение скорости изменения с течением времениу к скорости изменения х.
„ ds
Так как есть скорость изменения с течением времени длины дуги то из (22) § 98 имеем:
WWW соотношение, указываемое вышеприведенным чертежом.
В качестве руководства при решении задач, аналогичных приводимым далее, можно пользоваться нижеследующим правилом:
Первый шаг. Сделать чертеж, иллюстрирующий задачу. Обозначить через х, у, z и т. п. величины, изменяющиеся с течением времени.
Второй шаг. Установить соотношение между рассматриваемыми переменными, соответствующее произвольному моменту времени.
Третий шаг. Продиференцировать соотношение по времени.
Четвертый шаг. Составить перечень известных и искомых величин.
Пятый ш а г. Подставить значения известных величин в результат, полученный путем диференцирования (третий шаг) и решить относительно неизвестных.
Пример 1. Человек приближается со скоростью 8 км/час к подножью башни, вышиною в 60 м. Какова скорость его приближения к вершине башни в момент, когда он находится на расстоянии 80 м от ее основания?
Решение. Применим вышеприведенное правило.
Первый шаг. Сделаем чертеж (черт. 113). Пусть х —расстояние человека от подножья башни и у — расстояние от вершины в произвольный момент времени.
Второй шаг. Из прямоугольного треугольника имеем:
>2 = х« + 3 600.
Третий шаг. Диференцируя, получаем: _ rfy „ dx ^-dt=2x^t
или
dy _ х dt ~ у
Четвертый шаг.
x = 80,
dt '
(А)
dx i „ = 8 км/час,
у = /Р +Уб70 = 100, -^ = ?
Пятый шаг. Подставляя в (А), находим: dv 80 0 _ .
-dt = 100-8 = 614 КМ/ЧаС-
Пример 2. Точка движется по параболе бу — х1 таким образом, что когда .V = 6, абсцисса возрастает со скоростью 2 м/сек. С какою скоростью возрастают в тот же самый момент ордината и длина дуги?
Решение.
Первый шаг. Строим параболу (черт. 114).
Второй шаг.
Третий шаг.
бу = х2.
к dy dx &-dt~2x-dt
или
Четвертый шаг.
dy x dx dt ~ 3’~dt‘
(В)
х = 6,
•«* * 6=6,
dx „ ,
—— = 2 мсек, dt
dt
-^ = ?
dt
Пятый шлг. Подставляя в (В), находим: ^=|-.2 = 4ж/с^.
Подставляя в (3), стр. 268, получаем:
/ 2»+'4» = 2 / 5" м/сек.
Из первого результата мы видели, что в точке Р (6,6) ордината, изменяется по величине вдвое быстрее абсциссы.
Если рассматривать точку Р (—6,6), то будет — - 4 м/сек.
Знак минус означает, что при возрастании абсциссы ортииата убывает.
Пример 3. Круглый металлический диск расширяется от теплоты так, что его диаметр равномерно увеличивается на 0,01 мм/мин. С какою скоростью увеличивается его площадь, если радиус равен 2 см?
Решение. Пусть ренцируя по времени
радиус х, и площадь кружка у. Имеем у = тех5; и дифе-t
n dx Tt=2nx-—f
(С)
Итак, в каждый момент, площадь диска возрастает в квадратных сантиметрах в 2шг раз быстрее, чем возрастает радиус в линейных сантиметрах:
х =2, ~ = 0,0^ & = ? dt t't
Подставляя в (С), получаем:
—У? = 2л • 2 • 0,01 = 0,04л см/сен. dt '
лампа повешена на высоте 12 м над прямою горизон-
Пример 4. Дуговая .
тальною дорожкою, по которой идет человек, рост которого равен *1,5 м. Насколько удлиняется его тень, если он удаляется от лампы со скоростью 49 м/мин?
Решение. Пусть расстояние человека от точки, лежащей непосредственно под лампою L, будет х, а длина его тени у. Из черт. 116 имеем:
откуда
у: (у + х)= 1,5:12,
2 7
т. е. удлинение тени или 7 м/мин.
Диференцируем:
dy _ 1 dx _ dt ~ 7 * ~dt ’
составляет 1/7 пути, пройденного человеком в то же время.
УПРАЖНЕНИЯ.
1. В параболе j2 = 12х, если х возрастает равномерно со скоростью 2 см/сек, то с какою скоростью возрастает у, когда х = 3 с.к?
Отв. 2 см/сек.
2. В какой точке параболы предыдущего примера абсцисса и ордината возрастают с одинаковою скоростью?
Отв. (3,6).
3. В функции _у = 2х*-|-6 каково значение х в точке, в которой у возрастает в 24 раза быстрее х?
Отв. х = ± 2.
4. Ордината точки, описывающей кривую хг -(-У = 25, убывает со скоростью 1,5 см/сех. С какой скоростью изменяется абсцисса точки, когда ордината становится равной 4 см)
Отв. = 2 см/сек.
at
5. При каком значении х функция 2х2 —4 убывает в 5 раз быстрее, чем х возрастает?
Отв. х = — 4-.
4
6. Найти значения х в точках, где скорость изменения функции хз _ 12x2 + 45х _ 13
равна нулю. отв. х — л и о.
7. Какому значению х отвечают точки, где х1 —5х*-{-17х и х8 —Зх изменяются с одинаковою скоростью?
Отв. х = 2.
8. В какой точке эллипса 16х; 9у-’ = 400 ордината у убывает с такою же скоростью, как х возрастает? , jg.
\ 8)
9. Дапо у = х3 — 6х2Зх-|-5; найти точки, в которых скорость изменения ординаты равна скорости изменения тангенса угла касательной к кривой с осью ОХ. Отв. х = 1 и 5.
10. Где в первом квадранте дуга увеличивается вдвое против синуса?
Отв. При 60°.
Точка движется по кривым, уравнения которых даны ниже. Как изменяется
дуга в каждом случае?
11. у = х* = 1; х = 4. Отв. = 3. at at
dx - ~ ds
12. у = 2х; ~ = 2; х = 2. -Л = / 5. dt dt
п. г,-». 4W’'13-
dx . ds
14. x2 + 4j* = 20; 1, J-=1. ^ = /2.
„ dx
15. v = .v3; —yr = 3, x = —3. at
16. у = x3; & = 4, у = 8.
17. Сторона равностороннего треугольника имеет 24 см длины и увеличивается со скоростью 3 см!час\ как велико приращение площади?
Отв. 36 смЧчас.
18. Найти скорость изменения площади квадрата, если сторона Ь увеличивается со скоростью а единиц в секунду? „ „ ,
Отв. 2аЬ кв. ед. в сек.
19. а) Объем сферического мыльного пузыря увеличивается во сколько раз быстрее радиуса? Ь) Если радиус его равен 10 см и увеличивается со скоростью 1,25 см/сек, то каково приращение объема?
Отв. а) в 4пг® раз быстрее;
Ь) 500л смъ!сек.
20. Лестница длиною в 10 м одним концом прислонена к вертикальной стене, а другим опирается о горизонтальный пол. Нижний конец отодвигают от стены со скоростью 2 м/мин. а) С какою скоростью опускается верхний конец лестницы, если основание ее находится в 6 м от стены? Ь) Когда оба конца лестницы двигаются с одинаковою скоростью? с) Когда верхний конец лестницы опускается со скоростью 1 м/мин(
Отв. а) l’/а м/мин',
Ь) когда отстоит от стены на м;
с) когда отстоит от стены на 2 Y 5 м.
21. Баржу, палуба которой на 3 м ниже уровня дока, тянут к нему по* средством каната, привязанного к кольцу в полу дока, причем канат тянут воротом, находящимся на палубе, со скоростью 2 м/мин. С какою скоростью баржа движется к доку, если удалена от него на 4 ж?
' Отв. 2.5 м/мин.
22. Вагон, стоящий на верхнем пути, находится на высоте 10 м прямо над нижним вагоном, причем их пути пересекаются под прямым углом. Если скорость верхнего вагона равна 30 км/час, а нижнего 18 км/час, то с какою скоростью они удаляются друг от друга 4 минуты спустя после встречи?
Отв. 34,9 км/час.
23. Один корабль плывет к югу со скоростью 6 км/час, другой к востоку со скоростью 8 км/час. В 4 часа пополудни второй пересекает путь первого в точке, где первый проходил 2 часа тому назад, а) Как изменялось расстояние между кораблями в 3 часа пополудни? Ь) Как в 5 часов пополудни? с) Когда расстояние между ними не изменялось?
Отв. а) Уменьшалось на 2,8 км/час,
Ь) увеличивалось на 8,73 км/час, с) в 3,28 пополудни.
24. Предполагая, что объем ствола дерева пропорционален кубу его диаметра и что последний равномерно увеличивается из года в год с ростом дерева, показать, что скорость роста, когда диаметр равен 0,9 ж, в 25 раз больше, чем когда диаметр равен 18 см.
25. Железнодорожный поезд, проходя мимо леса длиною 800 м, движется со скоростью 79,2 км/час. Путь имеет форму параболы _у3 = 600 х, и поезд
движется по направлению, обозначенному на чертеже стрелкой. Солнце всходит в тот момент, когда поезд проходит мимо леса. С какой скоростью тень S локомотива 4 движется вдоль леса в момент, когда локомотив находится против края леса?
Решение.
Л = 600Х,
или
т/х _ у dy dt ~ 3QQ‘~dt
Черт. 117. dx . Подставляя это выражение для в формулу:
ds 1/(dx\2 1
~dt~ V \ dt J + U J ’
получаем: fds\^_(y_ *У\г,(*У\'
\~dtj “ k300 ‘ dt J '\dt J •
= 79,2 км/час = 22 м/сек, у = 400 и = ?
Подставляя в (D), находим:
откуда
= 13,2 м/сек.
26. Поезд и воздушный шар отправляются в один и тот же момент из одного пункта. Поезд движется со скоростью 50 км/час, а воздушный шар поднимается со скоростью 10 км/час. С какой скоростью они удаляются друг от друга?
Отв. 51 км/час.
27. Человек, рост которого равен 1,8 м, удаляется от истаиника света, находящегося на высоте 3 м, со скоростью 6,34' км/час. С какой скоростью перемещается тень от его головы?
Отв. 15,85 км/час.
23. Солнечные лучи образуют угол в 30° с горизонтом. С высоты 19,2 м брошен камень. С какой скоростью перемещается по земле тень от камня в момент прикосновения камня к земле?
Отв. 33,6 м/сек.
29. Якорь моторной лодки лежит на дне реки, на глубине 5,4 м. Цепь от якоря проходит через шкив блока, находящегося на носу лодки на высоте 1,8 м над водой. Если цепь накручивается со скоростью 30 см/сек, то с жакой скоростью движется лодка в момент, когда оставшаяся часть цепи составляет 9 м?
Отв. 0,5 м/сек.
30. Человек поднимает груз при помощи блока, укрепленного на стене на высоте 15 м от земли. Человек тянет веревку со скоростью 3 м/мин и в то же время удаляется от стены со скоростью 1,5 м/мин. С какой скоростью будет подниматься груз в конце второй минуты? Л
Отв. 3,29 м/мин.
31. Вода течет по трубке в резервуар, имеющий форму полушара, со скоростью 5 см3/сек. Диаметр резервуара составляет 35 см. С какой скоростью моднимается вода в резервуаре:
а) когда уровень ее достигает половины Ц£1соты резервуара,
Ь) в момент, когда вода наполнит резервуар (объем шарового сегмента равен i г. г- Л + т-лЛ3, где h — высота сегмента).
2 о
32. Песок, сыплющийся на землю из трубы, образует кучу, имеющую форму конуса, высота которого все время остается равной радиусу основания. Если песок падает со скоростью 2 м'чсек, то с какой скоростью возрастает высота кучи в момент, когда она становится равной 1,5 ж?
33. Бумажный змей находится па высоте 50 м, имея при этом яеревку распущенной на 67 м. Предполагая, что змей перемещается горизонтально со скоростью 4 км/час, найти с какой скоростью раскручивалась веревка во время подъема змея?
34. Раствор наливается в фильтр конической формы, радиус основания которого равен 6 см, а высота 24 см, со скоростью 2 см3/сек и фильтруется со скоростью 1 см3/сек. С какой скоростью поднимается уровень раствора, когда: а) раствор наполняет фильтр на !/3 высоты, Ь) раствор наполняет весь фильтр. Л
' * г Отв. а) 0,079 см3/сек.}
Ь) 0,009 см*/сек.
35. Лошадь бежит по кругу со скоростью 20 км/час. В середине круга находится электрическая лампа. С какой скоростью перемещается тень лошади вдоль забора, расположенного по прямой линии, являющейся касательной к кругу в точке, откуда лошадь начинает бежать, в момент когда лошадь пробегает */а часть окружности?
Отв. 40 км/час.
18 Зак. 2769. — В. Гранвиль и П. Лузин. Часть I
36. Ребро куба ранпо 24 см. С какой скоростью изменяются объем и поверхность куба, если каждое ребро его возрастает со скоростью 0,02 см j мин?
37. Коническая воронка радиусом 8 см и такой же высоты наполнена раствором, который фильтруется со скоростью 2 см*]мин. С какой скоростью опускается уровень жидкости в момент, когда он находится на расстоянии 2 см от вершины?
35. Угол увеличивается с постоянной скоростью. Показать, что тангенс и синус увеличиваются с одинаковой скоростью, когда угол равен 0°, и что тангенс возрастает в 8 раз скорее при угле в 60°.
36. Камень, привязанный на веревке длиной 1,5 м, вращают со скоростью 20 об/мин. В момент разрыва веревки камень продолжает лететь по касательной к кругу. С какой скоростью он удаляется от центра круга по истечении 0,01 сек. после момента разрыва веревки (предполагая, что на него не действуют никакие другие силы).
Отв. 6,6 м!сек.
ГЛАВА X’.
ЗАМЕНА ОДНИХ ПЕРЕМЕННЫХ ДРУГИМИ.
§ 126. Замена зависимого и независимого переменных одного другим. Иногда бывает желательно преобразовать выражение, содержащее производные от у по х, в эквивалентное выражение, содержащее производные от х по у, считая, следовательно, у независимым переменным. Примеры покажут нам, что в некоторых случаях такая замена приводит к более простым выражениям. Например, иногда х дается в задаче как явная функция от у; тогда бывает выгоднее иметь дело
. dx сРх
с формулами, содержащими и т. д., нежели с формулами, за-
dy day о ,
ключающими и т. п. Займемся изысканием формул, необхо-
dx dx- т г j >
димых для выполнения таких преобразований.
Пусть будет у =/(х); по формуле (XXIII) § 61 имеем:
= (dx ±0\ dx dx * \ dy '
dy
dy , dx
Эта формула и дает в функции от ~г-dy
Формула (XXII) показывает, что
(1)
или
Но
и по (1):
(Ру d / dy \ d / dy \ dy dx* dx \ dx ) dy \ dx / dx ’
(Py df 1 \ dy dx* dyt dx | dx ’
\ "У /
(Px
d / 1 \ dy -ay I dx j / dx \a
\dy J \ dy )
dy 1 dx dx'
dy
Подстановка в (А) дает: d3x d3y_______________________ dy7
dx? I dx \3' \ dy )
и этой формулой d?y dx?
выражается в функции dx d3x dy И dy*'
Подобно этому d3x dx_______________________________d?x \2
d3y___ dy3 dy \ dy3)
dx3 I dx\b
\~dy)
(2)
и т. д. Такое преобразование называется заменою независимого переменного х на у.
Пример. Заменить независимое переменное х на у в уравнении:
\dx2} dx dx3 dx- \dx) ' '
Решение. Подставляем из (1), (2) и (3):
уравнение более простое.
§ 127. Замена зависимого переменного. Пусть
У = /(*),
(А)
и пусть в то же время у будет функцией от z, например:
j = ?(z). (В)
„ dy d?y dz d2z
Производные -^и т. д. нужно выразить через -т-, -т— и т. д.
U X ил Ил UX
Вообще, Z по (В), есть функция от у, а так как у в силу (А) есть функция от х, то очевидно, что z есть функция от х. Отсюда, по (ХХП)
§61, имеем:
dy___dy dz_____ , .dz
dx dz dx ? ^Z' dx'
(4)
Так же
<?У dx3
dz d ,. . . . d?z
зг-гг(*)+тюл.-
Но
tz \ 11 \ dz hi \ dz
J-'? (z) = ~r ? (z) -j- = <? (z) -J— dx ' dz ' dx T dx
Отсюда
dx3 '
(5)
Подобным же образом найдем и высшие производные. Это преобразование называется заменою зависимого переменного_уна z, причем независимым переменным всюду остается х.
Поясним этот процесс примером.
Пример. Дано уравнение
<Ру _ , 2(1 + у) / dy \3 dx* 1 \dx )'
заменить зависимое переменное у на z посредством соотношений:
Решение. Из (D) имеем:
У = tg z-
(D)
dy dx
sec2z ~ dx
Подставляя в (С), находим:
sec2*-^7 +2sec2ztgz(-g)'=I +
2 0+tgz) l-|-tg2z
sec2z
dz у dx) '
а по упрощении:
§ 128. Замена независимого переменного. Пусть у будет некоторая функция от х, и вместе с тем пусть х (а следовательно, и у) будет функцией нового независимого переменного t. Требуется
rfy (Ру dx ’ dx*
и т.
д.
выразить в функции новых менным t. По (XXII) § 61
производных, имеющих независимым пере-
d\> _ dy dx dt ~ dx dt
или
dy
dy — d£ dx dx’
dt
Так же
( ^У\ d*y d / dy\ d I dy\dt dt \ dx / dx* —~dx \ dx) ~ dt \ dx I dx~ dx_
dt
(6)
Но, диференцируя (6) по t, имеем:
(dy\ dx d*y dy d-x
dt | dt dt* di dt2
dx I / dx \8
~dt ] \ dt )
Следовательно:
dx d2y dy (Px
d*y dt dt* dt dt* ,_v
~dx*~ (dx у (}
\ dt )
и т. д. для высших производных. Такое преобразование называется заменою независимого переменного х на t. Обыкновенно лучше решать примеры вышеуказанным способом, чем пользоваться готовыми формулами.
Пример. Заменить независимое переменное х на t в уравнении: х,ё+'ж+>’=0 <Е)
посредством соотношения: л=е'. (F)
Решение dx = Л л следовательно;
£ = (О)
Так же dy _ dy dt dx ~ dt dx’ следовательно:
<»> Затем
£y_ = e-t .-t( dy}JL _dy tdt_
dx- dx\dt) dt dx dt \ dt J dx dt dx’
Подстановка сюда из (G) дает: = ,-tt ffiy_ e-*t dx* dt2 dt
Подстановка (F), (H), (G) и (E) дает: по упрощении, находим:
Хотя формулы, выведенные в диференциальном исчислении, вообще содержат производные от у по х, но такие формулы, как (6) и (7), употребляются в особых случаях, когда уравнения кривых даются в параметрической форме. Подобные примеры встречались в § 93 и встретятся и впоследствии.
§ 129. Одновременная замена независимого и зависимого переменных. Нередко желательно бывает заменить одновременно оба переменные. Важный случай этого рода представляет преобразование прямоугольных координат в полярные. Так как
X = р cos 0
и ' £
у = р sin б, то уравнение
/(х, _у) = 0
после подстановки превращается в уравнение с переменными р и О, определяющее, следовательно, р как функцию 0. Таким образом р, х и у суть все функции от 0.
Пример. Преобразовать формулу радиуса кривизны (6) § 134.
L (А)
d-v dx-
в полярные координаты.
Решение. Так как в формулах (б) и (7) § 128 t есть независимое переменное, от которого зависят х и у, можно в этом случае положить Г=0, что дает:
dy ___ dd
dx ~ dx
dO
dx <Py______ dy (Px
(Py d0‘ dfP d6 d& dx'- ~ ( dx у
(B)
(С)
Подставляя (В) и (С) в (А), находим: з
ГГ-^Уд-МНП2
„ dO ) + dO /
или
dx (Py dy (Px ~do do» de’ “Ж
7 dry \ dO )
£
\ .L. (J!? V] 2
dO J ~ГД d6 J J
dx (Py dy (Px
16 d6» dO d6*
Но так как
x = p соя e 11
у = p sin 6,
то будем иметь: dx , „ . о ^Р. -d(j=-psin6 + c°s6-,^
-& = p cose + sine
-g- = -pcos0-2sln0 4j +cose-^;
S ~p S,n ® + 2COS°^ + sln 0 -Si-
Подставляя в (D) и упрощая, имеефокончательно:
в
. 2
R
d2?
р tfO2
УПРАЖНЕНИЯ.
В следующих четырех уравнениях заменить независимое переменное х на у. £ 2
£ 2
1. R
Отв. R =
dx*
9 —У-dx*
= 0.
3. х
&=0. dx
dy*
^_23,Л_О. dy- dy
d?x ( dx'?
= 0.
4.
dx* ’ Отв.
Заменить зависимое переменное у на z в уравнении:
=2<1+>’>гй' /-’+*•
„ , , .. rf*z dz d*z , , ,
Отв. (z + 1) -j-,. = — -j-z + z2 4-' dx* dx dx* 1 1
В следующих восьми уравнениях заменить независимое переменное.
6. — т-~—5 ;г- + т-^—а = °« x = cost dx2 1 — х- dx 1 — х2 Ome- ~dt* +-v = °-
7. (1 — Х2)^ — X ~~ = 0х = cos z. 4 dxJ dx ’ ^ = 0. dz*
8. d-^—^-^ + a’a^O, у = sinx. g+^“=o-
9. x = l. dx2 1 dx ‘ x2 z g+^-o.
10. .rfSp rf2® dv' n t Xs -7~5 + Зх2—. 4- X — + V = 0, X = e. djfl * dx2 1 dx 1 ' Лз + ^=°-
11. d*y . 2x dy , v „ , „ dx* * 1 + x» dx । (1 + x2)2 °’ X tg 0 </2y , „ d62+-y_0-
12. d*u . du —rz -г- sh -—sec2 s = 0, x = arctg t. ds* 'ds 6
Отв. (1-H2)^ 4- (2f4-HarctgO^4-J = O.
13. х^^+а2у = 0, х= -. Отв. ^ + -^ + а2у = 0.
dx2 J z dz2 1 z dz J
В следующих четырех примерах уравнения даны в параметрической форме.
„ _ dy d"-y
Найти —и в каждом случае dx dx2 J
x = 7 + f-, y = 3 + t2-3t*.
14.
15.
16.
17.
x = ctgi, _y = sin3f.
Отв. -j- = — 3 sin41 cos t; dx
x = a (cos 14-1 sin /), у = a (sin t — t cos t).
Отв. =
dx
2t
18.
1У.
1-t x = l+7- * x = 2t, у = 2 x = a cos t, y=b sin t. x = 1 - t2, у = t\ Преобразовать
iL dx
принимая х = р cos 8, у = р sin 8.
Отв. ^- = 1-6/’, ^=-6. dx dx2
= 3 sin51 (4 — 5 sin21). dx2 '
<Py 1
dx2 at cos3 t ‘
^=0.
dx2
Отв.
22-Пусть f(x, _y) = 0 будет уравнение кривой. Найти выражейе для тангедса угла наклона кривой к оси ОХ, в полярных координатах.
pcose + sine %
Отв. ------------------------з- •
х — р sin 8 -J- cos 6
ГЛАВА XII.
КРИВИЗНА. РАДИУС КРИВИЗНЫ.
§ 130. Кривизна. Одним из элементов, характеризующих течение кривой, является степень ее изогнутости или искривления в разных точках. Целью настоящей главы является исследование этого вопроса, установление точного математического понятия кривизны^ и получение формул, позволяющих определять величину кривизны в любой точке кривой.
Пусть А и В — какие-нибудь две точки, лежащие на плоской кривой. Рассмотрим дугу АВ этой кривой и касательные в ее концах.
Пусть е есть угол, образуемый этими касательными между собою. Этот угол е называется углом смежности, дуги АВ (черт. 118).
Понятие кривизны плоской кривой те^ю связано с углом смеж
ности. Из двух дуг АВ и А'В' равной длины, та является сильнее изогнутой или искривленной, для которой угол смежности больше, потому что угол смежности служит до известной степени мерилом отклонения кривой линии от прямой (черт. 119).
Но один только угол смежности тоже неудобно брать мерилом изогнутости дуги, потому что дуга АВ может быть очень слабо изогнута, если же она громадная по размеру, то угол смежности е может выйти очень большим (черт. 120). И, наоборот, если дуга АВ очень искривлена, как это происходит, например, с окружностью маленького
радиуса, но очень мала по длине, то угол смежности е может выйти очен малым и, значит, не обнаружить искривленности дуги должным образом.
Поэтому берут мерилом, искривленности какой-нибудь дуги АВ кривой (черт. 118) отношение
е ~АВ
угла смежности в к длине дуги АВ и называют это отношение средней кривизной дуги АВ.
Из всех кривых окружность является единственной кривой, одинаково искривленной во всех ее частях, потому что она может, вращаясь около центра О, двигаться сама по себе, всюду сама С собой совпадая. Никакая другая плоская кривая этим свойством уже не обладает. Поэтому естественно ожидать, что средняя кривизна любых дуг у одной и той же окружности, будет
одна и та же. Это значит, что средняя кривизна дуги АВ окружности не зависит от размера (т. е. длины) этой дуги и, следовательно, есть величина постоянная для данной окружности, зависящая только от ее радиуса. Легко проверить это ожидание. Известно, что угол смежности в дуги окружности равен углу между радиусами, проведенными в концы этой дуги. Поэтому (черт. 121), обозначая через е угол смежности, мы видим, что угол АОВ равен в. Но с другой стороны, мера угла е есть отношение длины дуги АВ к радиусу г. Значит, имеем:
АВ • =-----.
г
Отсюда, деля обе части этого равенства на дугу АВ, видим, что
Таким образом средняя кривизна всякой дуги окруж-1 ноет и радиуса г есть величина постоянная, равная —.
Эту величину у называют просто кривизною окружности.
От понятия средней кривизны дуги АВ какой-либо плоской кривой (черт. 118) переходят к понятию кривизны в точке. С этой целью, взяв на кривой какую-нибудь неподвижную точку /Ио (черт. 118), охватывают ее дугой АВ и, составив выражение средней кривизны дуги АВ:
е . средняя кривизна =--------,
дуга АВ
заставляют обе точки А и В безгранично приближаться к неподвижной точке 7И0. Если при этом величина средней кривизны стремится к определенному пределу, каким бы образом ни приближались точки А и В к 7И0, этот предел называют кривизною в точке MQ. Таким образом
.. а кривизна в точке = lim —
§ 131. Формулы кривизны. Вывести формулу кривизны кривой
в точке — это значит выразить предел
,im7s через координаты рассматриваемой точки.
Пусть нам дано уравнение кривой у = /?(х). Допустим, что точка М (черт. 122) имеет координаты х, у. Возьмем на нашей кривой точку Afp близкую к точке М, и проведем касательные Л47'иЛ'17'1 к кривой в этих точках. Если угол наклона касательной в точке М обозначим через <р, то при переходе от точки М к точке угол получит приращение, которое мы, как обычно, обозна-
чим через До. Это приращение Дер является также и углом смежности. Если дуга AM = s, то дуга ММ}=№, и таким образом мы получаем:
„ До г/<?
кривизна в точке = л = 11т. дв-юДз as
(2)
Имеем;
tgo =
4у
dx
или . dy <? = arctg^
Диференцируем по s:
(Ру dx dx2 ds
ds
(А)
Ho
Подставляем в
а так как
ТО
ds
(3)
Так как нам задано уравнение кривой y = F(x), то при данном зна* чении х мы можем вычислить значения первой н второй производных; а так как кривизну мы выразили через , этм производные, то, следовательно, полученная формула даст нам теперь возможность определять величину кривизны через координаты рассматриваемой точки. Таким образом наша цель достигнута.
Пример. Найти кривизну параболы
у2 = 4рх
в точке (р, Чр).
Решение.
dy _ Чр <Ру _ Чр dy _ 4р2 dx ~ у ’ dx2 ~ у2 dx ~ У
Подставив в (3), имеем: * =---------------------------—
(У! + 4рi) 2 * * * * *)2 это дает кривизну в любой точке. В точке (р. 2р) » к 4pt = - 4р' = - L 4 16/2 4/2 -р'
(4р’ + 4р5)2
§ 132. Формула кривизны для случая, когда кривая уравнениями в параметрической форме. Если кривая уравнениями:
задана
задана
то имеем:
db dy_dt _ >/(£) dx d?~ <f' (t) ‘ dt
_ <&У -L. - J -
Для нахождения диференцируем по аргументу t обе части написанного равенства:
d ( dy\__ di dy\ dx (Py dx_______d*y ,
~di\dx]~dx\dx)' dt~ dx2 ’ dt dxa' 9 ’
d Гj/(0 = '/Wffl —y'WW dt[<?'(t).
Следовательно:
<Ру_ -?"(*)/(0
rfx» &' (OJ*
Подставляя полученные выражения в формулу кривизны (3) и производя элементарные преобразования, найдем:
2
{[?w+И'(0]’|2
(Ру dy (Рх dy dx* ' dx dP’ dt
аГ •
И)
( dx^\^ , t dy 2
1 dt ) + \ dt / J
Пример. Найти кривизну циклоиды
х = a (t — sin t), у — a (1 — cos /).
i) Хотя в нашей книге важно знать только абсолютную величину кривизны
К, но можно объяснить геометрический смысл и знака. Всюду в нашей книге
берется при радикале j/~ 1 + положительный знак. Следовательно, К
будет либо положительной либо отрицательной соответственно тому, будет ли
4^ положительна или отрицательна, т. е., в силу § 114 будет ли кривая вогнута
ах-
вверх, или она будет вогнута вниз.
Решение, dx ,, _ dy
— = а (1 — cos f), a sin f,
tPx <Py
| ^>=asln'’ ^ = ecos'-
Подставляя в формулу (4), найдем:
a cos t -а(1 — cos/) — aslnt-asint К= -j =
[вз (1 _ cos /)Э + a2 sin2 Г] 2
cos t — 1 1
= —T'
2 2 a • (1 — cos /) 4a sin 2
§ 133. Формула кривизны в полярных координатах. Пусть кривая задана уравнением в полярных координатах
Р=/(9).
Тогда длина S дуги кривой и угол 7 наклона касательной к кривой в рассматриваемой точке будут также зависеть от 9, т. е. могут быть рассматриваемы как функции параметра 0. Поэтому по формуле (3), можем написать:
do
А ds ds
d0
Согласно формулам (12) и (11) § 94, имеем:
? = ’i' + °. = arctg
de
где — угол между касательной к кривой и радиусом-вектором. Поэтому
/ dp \ 2 d*p
dv d n. & . p । . \ d6 / P d62 .
^=_w+8)=-„Ilg^+1= ! +<• de p г de)
Из § 122, формулы (11) мы знаем, что
*=1/P> + №V de у v ~ ^de }
r, - ds ...
Подставляя найденные выражения зтг и в (А) и производя эле-ментарные преобразования) получим:
3 з
Пример. Найти кривизну логарифмической спирали р = es1 в любой точке.
Решение.
rfp 4i)
= =а?;
= а?>
Подставив в (5), найдем:
р/1+»а -
§ 134. Радиус кривизны. По аналогии с окружностью [см. (1) § 130] радиус кривизны кривой в некоторой точке определяется как обратная величина кривизны кривой в этой точке. Обозначая радиус кривизны буквою R, имеем:
К
или, подставляя значения К из уравнений (3), (4) и (5):
3
dx2
(6)
I Z^yV]2 \dt) + nd d2y dx rf2x dy dF Tt~~d^ ~dt
(7)
(8)
Пример 1. Найти радиус кривизны в?любой точке цепной линии f ж _ Д \ v = а).
Решение.
= Де ° - е а)- = -L U °’ + е а).
dx 2 ’ dx* 2а
Подставляя в (6), имеем:
еа +е а еа+е °
2а 2а
>) Знак радиуса кривизны одинаков со знаком кривизны, т. е. плюс или минус, смотря по тому, будет ли кривая обращена вогнутостью вверх или вниз.
§ 135. KpyF кривизны. Рассмотрим на кривой какую-нибудь точку Р (черт. 123). Мы можем построить в каждой точке кривой круг, имеющий ту же кривизну, что и кривая в этой точке.
Этот круг строится следующим образом: проводим нормаль к кривой в точке Р в направлении вогнутости кривой. Берем на нормали расстояние Рс, равное радиусу кривизны Р кривой в точке Р. Из точки с как из центра описываем круг радиусом Р. Следовательно, кривизна круга равна
123.
т. е. совпадает с кривизной кривой в точке Р. Круг, построенный таким образом, называется кругом кривизны кривой в точке Р.
В общем случае круг кривизны кривой в точке пересекает кривую в этой точке, как это наглядно показывает черт. 123.
Подобно тому как касательная к кривой, характеризуя направление кривой в точке, помогает лучше представлять себе течение кривой в точке, круг кривизны способствует лучшему представлению о кривизне кривой в точке.
В § 148 круг кривизны будет определен как пре-% Черт,
дельное положение круга, пересекающего кривую в трех точках, т. е. методом, аналогичным методу определения ной (см. § 60).
Пример. Найти радиус кривизны равносторонней гиперболы ху = 12 в точке (3, 4) и построить круг кривизны в этой точке (черт. 124).
касатель-
1. Найти радиус кривизны нижеследующих кривых в указанных точках; вычертить каждую кривую и построить соответствующий круг кривизны.
а) &х2 -|- а2_у3 = а2/»5, (а, 0). Отв. R =
’si дЗ
Ь) 6-'х2 4- а2_у3 = в3б3, (0, б). R = 6-.
*) Во всех случаях вычисляется абсолютная величина кривизны и радиус кривизны. Постоянные величины всюду предполагаются положительными.
19 Зак. 278». — В. Гранвиль и Н. Лузин. Часть I
R 36'
R = 2.
4 2 d+9x^
Л\ —“
бХ! В 1 2
/? = у(40) . R ~ 116’
R = -£ К ЗЬ'
R = 2a.
«=±-
_ (^Хд+Д^;)2 К ~ а*Ь*
с) у = х* — 4х» - 18х», (0, 0).
d) 16У = 4х« - х«, (2, 0).
е)_у = х3, (Xvj-j).
f) у = х’, (4. 8).
Е)У = 8х, (|,з).
2
"> И’+Ш’’1' <*»>.
i) х- = 4ау, (0, 0).
j)(y-x)2 = x\ (0,0).
к) 62хг — а-у2 = а’б2, (хр у^.
1) ex = sinj, (х^). jn)j = sinx, (у, 1).
п) у = cos х, /Т,.
о) у = In х, х = е.
р) 9 v = Xs, х = 3.
q) 4у2 = Xs, х = 4.
г) х4-у- = а2, у = 0. в)х2 + 2у2 = 9, (1.-2).
2. Найти радиус кривизны кривой а2у = Ьх2 + сх2у вначале.
Отв. R = ~. ID
on «о а2(а— х)
3. Показать, что радиус кривизны кривой у2 =-——- в вершине pa-
fl
вен Г
4. Найти радиус кривизны кривой у = In sec х в точке (xb jit).
Отв. R = sec xv
11 1
5. Найти К в любой точке параболы х2 + у2 = в2. 1
Отв. К ----------—.
2(x-|-j)2
6. Найти R в произвольней точке гипоциклоиды
1 2 1 1
х*+у3=в3. Отв. 3 (аху)2.
7. В какой точке кривая у = ея имеет наименьший радиус кривизны.
о™. (-±1„2,к?.).
8. Показать, что в точке перегиба любой кривой радиус кривизны принимает бесконечно большое значение.
Найти радиус кривизны нижеследующих кривых в любой или в указание?! точке:
|х = ЗР
9. Кривая { _ ...
н | > = 3t — t»,t = 1.
{х = a cos31, у = а sin81, t = fj.
{x = a (cos t -|- / sin t),
у = a (sin t — t cos 0. t = у.
{x = a (m cos 14- cos mf), у — a (m sin t — sin mt), t = tl
Ота, R = 6.
10.
11.
12.
13.
Окружность p = a sin 6.
14.
Спираль Архимеда p = лв.
15.
Кардиоида p = a (1 — сов 6).
Лемниската р8 = a8 cos 26.
6 Парабола р = a sec8
Л 0
18. Кривая р = a sin8 -у.
16.
17.
19. Трисектриса p = 2a cos fl — a. Равносторонняя гипербола p8cos2fl = a3.
20.
21.
v а (1 — е8)
Коническое сечение р = -------г-
1 cos о
Отв. R = 3a sin cos tt.
Отв. R = ~. Л
г, 4та Отв.---;
т— 1
Отв. R
Ome.R = ±
£
(рг4д-)а ' p2 + 2a2 ’
R = ^V2TP.
О
P fl
R = 2a sec3
R = ^-a sin8 ~ 4 о
3
a(5 — 4cosfl)3 " 9 — 6 cos fl
ps Отв. R = ~. a‘
а
a(l — е®)(1 — 2e cos 0 4-е’)2 С//лв.-----------------------------
(1 — е cos О)3
Найти радиусы кривизны нижеследующих кривых в указанных точках; вычертить каждую кривую
а) -с = Z8, x = t\ х = sin t, d) x = 1 -1,
22.
b) c)
и
2y = t;
у = fi;
у --- cos 2t;
у = Г3;
построить / = 1.
e = i.
6 t = 3.
соответствующий круг кривизны: e)x = Z, y=6/-1;
f) x = 2ef. у = e~f;
g) x = sin t, у = 2 cos t;
h) x = P, y=fl+2t; t
t = 2.
t = 0.
4 1.
Кривизна К кривой в точке, являясь пределом отношения д—:
К = lim
Аз > О
As ~ Из*
представляет собою скорость изменения направления касательной относительно дуги кривой (или, как говорят, просто направления кривой) в данной точке (см. § 91).
23. Путь, по которому идет автомобиль, представляет собою эллипс х2+16у2 = 16. С какой скоростью автомобиль меняет направление:
а) когда он проходит через конец большой оси,
Ъ) когда он проходит через конец малой оси,
с) когда он находится на расстоянии двух километров от малой оси,
d) когда он находится на одинаковых расстояниях от оси? (За единицу длины принят километр.)
Отв. а) 4 радиана на километр.
b) Vie радиана на километр.
24. Пароход движется по дуге полукубической параболы 4_у2 = х3. Если предположим, что линия берега совпадает с осью ОУ и что за единицу длины принят километр, то с какою скоростью изменяет пароход свое направление, когда он находится на расстоянии одного километра от берега?
Отв. 2,/ia радиана на километр.
25. Военное судно 120 м длины изменяет свое направление на 30°, переместившись при этом на расстояние, равное длине судна. Чему равен радиус круга, по которому движется судно?
Отв. 229,29 м.
26. С какой скоростью меняет свое направление мотоциклетка, перемещаясь по кругу, имеющему 1[гкм в диаметре?
Отв. 4 радиана на километр.
29. Железнодорожное полотно имеет форму кривых, приближающихся к виду дуг нижеперечисленных кривых. С какой скоростью меняет направление движения паровоз в указанных точках? (Единица длины — километр.)
а) у = х3, (2, 8). d) у = < х = 0.
Ь) у = х2, (3, 9). е) у = cos х, х = у.
с) х2—у2 = 8, (3, 1). f) р8 = 4, 9 = 1.
При укладке железнодорожных рельсов, вследствие большой скорости движения поездов, нельзя резко переходить от прямолинейного участка к кривой части пути. Для постепенного изменения направления при соединении прямолинейных участков с кривыми вводятся поэтому переходные кривые. В качестве переходных кривых употребляются обыкновенно дуги кубической параболы.
28. Переходная кривая железнодорожного полотна имеет форму дуги кубической параболы у = -|-х3. С какой скоростью локотомив меняет направление, еле-О
дуя по этой дуге (единица длины — километр), когда он проходит:
а) через точку (3, 9); Ь) через точку (2, 8/3); с) через точку (1, Vs)-
Отв. а) ——j- радиана на километр;
(82р
Ь) ----у- радиана на километр;
. (17f
с) ----j— радиана на километр.
(2)Т
ГЛАВА XIII.
ТЕОРЕМА О КОНЕЧНОМ ПРИРАЩЕНИИ. НЕОПРЕДЕЛЕННЫЕ ФОРМЫ.
§ 136. Теорема Ролля. Пусть у =f(x) будет непрерывная однозначная функция от х, обращающаяся в нуль при х = а и х = Ь, и допустим, что f (х) изменяется непрерывно при изменении х от а до Ь. Такая функция графически может быть представлена непрерывною кривою, касательная которой непрерывно поворачивается, как показывает черт. 125. Геометрическая интуиция тотчас покажет нам, что, по крайней мере, при одном значении х, лежащем между а и Ь, касательная будет параллельна оси ОХ (как, например, в точке Р), т. е. что тангенс угла наклона кривой к оси ОХ [равный/' (х)] будет нулем. Это и есть геометрическое пояснение теоремы Ролля'.
Если /(х) пр и х = а и х = b обращается в нуль и если /(х) и /'(х) непрерывны для всех значений х от х = а до х = Ь, то /'(х) обращается в нуль, по крайней мере, при одном значении х между а и b ').
. 125.
Черт. 126.
Теорема эта, очевидно, верна; в самом деле, по мере того как х возрастает от а до b, f(x) не может постоянно возрастать или постоянно убывать, в то время как х возрастает, потому что /(а) = 0
') Черт. 126 представляет график функции, которая претерпевает разрыв непрерывности между а и Ъ. Черт. 127 дает график непрерывной функции, которая не имеет первой производной для подобного же промежуточного значения х = с. В том и другом случае, как видно, между х = а и х = Ь не существует такой точки на кривой, где касательная (или кривая) была бы параллельна QX.
и f(b) = 0. Следовательно, по крайней мере, при одном значении х между а и b функция /(х) должна перестать возрастать и начать убывать, или же перестать убывать и начать возрастать; а для такого частного значения х первая производная должна быть нулем (§ 112).
§ 137. Теорема Лагранжа о конечном приращении. Рассмотрим постоянное число Q, определяемое равенством:
./(*)-/«).-Q (А)
Ь — а
j tf) -/(а) - (* - а) Q = 0. (В)
Пусть F(x) будет функция, образуемая заменою постоянного b на переменное х в левой части (В), т. е.
F(x) =/(х) —/(а) - (х - о) Q. (С)
Из (В):
F(*) = 0,
а из (С):
следовательно, по теореме Ролля (§ 136), F (х) *) должна быть нулем, по крайней мере, для одного значения х между а и Ь, например, для хР Но, диференцируя (С), имеем:
F'(x)=/(x)-Q.
Следовательно, так как
/?,(х1) = 0, то и r(*i)-Q = o,
Q
Подставляя это значение Q в (А), мы и получаем теорему о конечном приращении'.
(1)
где о значении хг известно только то, что оно лежит между а и А9).
!) Если F (х) н F'(x) непрерывны, что в силу (С), очевидно, будет осуществлено, если f (х) есть непрерывная функция между а и Ь.
2) Теорема о .конечном приращении*, выражаемая равенством (I), получила свое имя потому, что ее можно написать в виде равенства:
f(b)-f(a)=f'
которое обнаруживает, что конечное приращение f(b) — f(a) функции /(х) равно соответственному конечному приращению b — а независимого переменного х, помноженному на величину производной f (х), взятой в некоторой промежуточной точке х,, заключенной между а и Ь,
Теорему о конечном приращении легко интерпретировать геометрически. Пусть кривая, данная на прилагаемом чертеже (черт. 128), будет геометрическим местом функции:
. J=/W-
Возьмем
ОС = а и OD = b\ /(а) = СА и f(b) = DB, что дает:
АЕ = Ь — а и ЕВ =f(b) — / (а).
Отсюда угловой коэфициент хорды АВ будет:
ЕВ_ f(b)—f{a) АЕ b — а ’
и теорема о конечном приращении просто утверждает, что на кривой существует, по крайней мере, одна точка между А и В (например Р),
для которой касательная (или кривая) параллельна хорде АВ. Если абсцисса точки Р будет х„ то угловой коэфициент касательной а Р будет /' (х,), и мы имеем:
Читатель должен начертить кривые, которые показывали бы, что в рассматриваемом интервале может быть и более одной такой точки, а с другой стороны,
должен начертить и такие кривые, которые
пояснили бы, что теорема может быть и неверна, если для некоторого значения х между а и Ъ функция /(х) претерпевает разрыв или если /' (х) не существует.
Освобождая (1) от дробей, формулу можно представить еще в виде:
f{b)=f(a)-\-(b — a)f'(xJ. (2)
Пусть b = а Да, следовательно:
Ъ — а = Да,
и, так как xL есть число, лежащее между а и Ь, то можно написать: Xj = a-|-6 • Да,
где 0 — положительная правильная дробь 1). Подставляя в (5), получим теорему о конечном приращении в другой форме:
/(a-t-Да)—/(а) = Да-/'(а + °-дя) 0 < 6 < 1. (3)
*) Точнее: в есть число, заключенное между нулем и единицею: О<0<1, •
могущее, в частном случае, оказаться и иррациональностью.
§ 138. Дальнейшее развитие теоремы о конечном приращении; формула Тейлора. Следуя методу последнего параграфа, положим, что постоянное число R определяется равенством:
f(b)-f(a)-(b-a)f(d)- 1 (b - а)= R = 0. (А)
Пусть F (х) будет функция, образуемая заменою b на х в левой части уравнения (А), т. е. пусть
F(x) =/(х) —/(а) — (х — а)/ (а) — ~ ц (В)
Из (А) имеем F(£) = 0; а из (В) будет F(a) = 0, следовательно, по теореме Ролля, по крайней мере, одно значение х, лежащее между а и Ь, например хп обратит F' (х) в нуль. Отсюда, так как
F' (х) =f'(x) —f (а) — (х — a) R, то
F' (хх) =f (xj — f (а) — (Xj — a)R = 0.
Так как
F(x1) = 0 и
F'(a) = 0,
то очевидно, что F' (х) также удовлетворяет условиям теоремы Ролля, так что ее производная, т. е. F"(x), должна, по крайней мере, при одном значении х, лежащем между а и хр например при х = ха, обращаться в нуль, а следовательно, х2 также лежит между а и Ь. Но
F(x)=f (*)-#, следовательно:
/?’(х2)=Г(х2)-/? = 0, н R=f{x^.
Подставляя этот результат в (А), находим:
(а<х2<Ь). (С)
Таким же образом, определяя постоянное число 5 посредством равенства :
f(b)-f(a)-{b-d)f (а)- -Ц (b-af /' (а)- —(Ь-а)» 5=0, 1 ’ а 1 • Z * и
можем вывести равенство:
/(А)=/(а)+(6-а)/(а)4^(^_а)2Ла)+—2ф-(6-а)Г^8) (а < х8 < Ь), где х8 находится между а и Ь.
(D)
Продолжая тот же процесс, придем к общему результату !):
(6 (b-tf (п) (Е)
1-2...(и — 1)' (}+1.2...л/ 1 J
(а < Xj < b\
где Xj лежит между а и Ь. Формула (Е) называется формулой Тейлора.
§ 139. Максимумы и минимумы, рассматриваемые аналитически. Пользуясь результатами последних двух параграфов, можем теперь дать общее исследование максимальных и минимальных значений функций о д н о г о и е з а в и с и м о г о п е р ем е н и о г о.
Дана функция /(х). Пусть h будет как угодно малое положительное число; в таком случае определения, данные в § 109, можно выразить следующим образом:
если для всех значений х, отличных от а, в интервале [а — A, a-\-ti\, разность -
/(х)-/(а) (А)
есть число отрицательное, то говорят, что f(x) имеет максимум при х = а\
если, с другой стороны, разность
/(х)-/(а) (В)
есть число положительное, то говорят, что /(х) имеет минимум при х = а.
Рассмотрим следующие случаи.
I. Пусть /' (а) ф 0.
Из (2) § 137, заменяя b на х и перенося /(а) в левую часть, имеем:
f(x) —f{a) = (х — a) f' (xj) (а < х, <х). (С)
Так как f (а) ф 0, а функция f (х) по предположению непрерывна, то h можно выбрать настолько малым, чтобы f' (х) нигде не обращалась в нуль и имела тот же знак, как и f (а) для всех значений х в интервале [а — Л, a-f-Л]. Следовательно, /' (xj имеет тот же знак, как и Но х — а изменяет знак сообразно тому, будет ли х меньше или больше, чем а. Следовательно, согласно (С), разность
/ W — f (а)
будет также менять знак, и в силу (А) и (В) /(а) не будет ни максимум, ни минимум. Этот результат согласуется с исследованием, данным в § 109, где было показано, что для всех значений х, для которых /(х) имеет максимум или минимум, первая производная f'(x) должна обращаться в нуль.
х) Предполагается, что /(х), f (х).........../"> (х) существуют во всем
промежутке [а, 6].
(Е)
(F)
И. Пусть /' (а) = 0, а /" (а) ф 0.
Из (С) § 138, заменяя Ь на х и перенося /(а) в левую часть, имеем;
/(х) -/ (я) = Г (ха) (а < х2 < л). (D)
Так как /'’(а)фО, а /"(х) по предположению непрерывна, то наш интервал [а — h, а Л] можно выбрать настолько малым, чтобы знак /я(х2) был одинаков со знаком /"(а). Знак же (х — а)3 меняться не может. Следовательно, вторая часть (D) не будет менять знака, и разность
будет иметь один и тот же знак для всех значений х в промежутке [а — h, и, сверх того, знак этот будет одинаков
со знаком f (а). Итак, из наших определений (А) и (В) следует, что
/(а) есть максимум, если а /"(а) отрицательна-,
f (а) есть минимум, если f (а) = О, а /"(а) положительна.
Это — те же условия, что и (4) и (5) § 112. III. Пусть /'(а) =/"(а) = 0, а /'"(а)фО.
Из (D) § 138, заменяя b на х и перенося в левую сторону /(а), имеем:
/ (х) -/(а) = -r-J-T - а>3/"' <*з) (а < х3 <х). (G)
Как и прежде, /"'(х8) будет иметь знак величины f'"(a}. Но, когда х, увеличиваясь, проходит через а, количество (х — а)8 меняет знак с минуса на плюс. Следовательно, разность
/(*)—/(«)
должна менять знак, и /(а) не есть ни максимум, ни минимум. IV. Пусть / (а) = /' (а) = ... =/п-1) (а) = 0, а /п)(а) ф 0. Продолжая исследование, как указано в I, II и III, найдем, что если первая производная от /(х), не обращающаяся в нуль при х = а, будет четного порядка ( = «), то
/(а) есть максимум, если /(п)(а) отрицательна’, (4) /(а) есть минимум, если fln\a) положительна ’). (5)
Если первая производная функции /(х), не обращающаяся в нуль при х = а, будет нечетного порядка, то f{a) не будет ни максимум, ни минимум.
Пример 1. Исследовать функцию х’ —9х*-|-24х— 7 ва максимальные и минимальные значения.
Решение.
f(x) = х»—9x2 4- 24х - 7.
f'(x) =3х»— 18x4-24.
1) Как и в § 109, критическое значение х = а найдем, приравняв нулю первую производную и определяя действительные корни полученного уравнения.
Решая
Зх»-18x4-24 = 0, ’
паходим критические значения х = 2 и х = 4. Таким образом /'(2)«=0 и /'(4) = О.
Диференцируем вторично: f (х) = 6х — 18.
Так как /" (2) = — 6, из (4) заключаем, что /(2) = 13 есть максимум-Так как f" (4) = 4- 6, из (5) заключаем, что /(4) = 9 есть минимум.
Пример 2. Исследовать на максимум и минимум функцию ех + 2cosx -f-Решение.
f(x) = ех 4- 2 cos х 4* е~х, f' (х) = е® — 2 sin х — е~х = 0 при х = 0 f" (х) = е® — 2 cos х 4~ ® = 0 при х = О, /"(x) = ex4-2sinx — е~х =0 прих = 0, /,v(x) = ех 4- 2 cos х е~® = 4 при s = 0.
Следовательно, в силу (5) /(0) = 4 есть минимум.
УПРАЖНЕНИЯ.
Исследовать на максимумы и методом последнего параграфа.
1. Зх* —4х»-|-1.
2. х» - бх» + 12х 4- 48.
3. (х-1)« (х + 1)з.
4. Исследовать х* — 5х* -J- 5х3
5. Исследовать Xs — 3х34-3х-
минимумы следующие функции, пользуясь
Отв. х = 1 дает mln = 0;
х = 0 не дает ни max, ни mln.
Отв. х = 2 не дает ни max, ни min.
Отв. х = 1 дает min = О, 1
х = у дает max;
х = — 1 не дает ни того, ни другого. 1 при х = 1 и х = 3.
Отв. х = 1 дает шах; х = 3 дает mln.
7 при х = 1.
Отв. х = 1 не дает ни max, ни mln.
6. П оказать, что, если первая производная, не обращающаяся в нуль при х = а будет нечетного ( = л) порядка, то /(х) при х = а будет возрастающей либо убывающей функцией, смотря по тому, будет ли /^(а)>0 или<0.
(6)
§ 140. Теорема Коши. Относительно двух функций /(х) и F(x) эта теорема утверждает, что
F(d)-F(a) “ Г(х0
где л, лежит в интервале [а, 6], a F'(x) не должна в этом интервале -обращаться в нуль.
Доказательство. Умножая обе части (6) на Р (хг) и перенося (xj влево, находим, что наша теорема требует, чтобы уравнение
р (Х) — f' = о F(A) — F(a) r 1 * 1 J w
лежащий между а и b. Чтобы можно было применить 136), попытаемся построить такую функцию, произ*
имело корень хи теорему Ролля (§
1) х = 0 есть единственный корень уравнения:
— 2 Bin к — в~* = 0.
водною которой была бы левая часть уравнения, притом, чтобы эта функция обращалась в нуль при х = а и х = Ь. Такой функцией будет:
W~F(<I)1 “ —/<«>].
потому что при x = а и x = b она обращается в нуль, и следовательно, по теореме Ролля, ее производная должна обращаться в нуль при некотором значении х, лежащем между а и Ь, например при
Х = хи т. е.
F(b) — F(a)
F'(.xi)—j'(xi) = 0,
а это и есть формула (6).
§ 141. Неопределенные формы. Когда при некотором частном значении независимого переменного формула, дающая функцию, принимает одну из форм:
0 оо , оо
—, —, 0 • оо, оо — оо, 0°, оо°, 1 ,
0 оо
то говорят, что функция неопределенна, и для этого значения независимого переменного функция данным аналитическим выражением (формулой) не определяется (см. гл. IV, § 46). Пусть, например, имеем:
f(x)
F(xy
и пусть для некоторого значения
будет:
/(О) = 0,
переменного, например для х = а, F(a) = 0.
Для этого значения переменного х наша функция не определена, потому что деление на нуль невозможно, и потому мы можем приписать ей какое угодно значение.
Из сказанного выше (§ 46) очевидно, что желательно приписать функции такое значение, которое делало бы ее непрерывною при х = а, если это только возможно.
§ 142. Вычисление значения функции, принимающей неопределенную форму. Если формула, дающая функцию /(х), при х = а принимает неопределенный вид, то
lim/(x) >) se->a
принимается за значение этой функции при х = а.
Допущение этого предельного значения делает /(х) непрерывною при х = а. Это согласуется с изложенным в § 46, а также и с практическими примерами гл. IV, где вычислено несколько функций, прини-_ 0
мающих неопределенную форму -у.
:) Вычисление этого предельного значения называется раскрытием неопределенности.
Так, при х = 2 функция, данная формулой:
х9— 4 х — 2 '
£
0 ’
принимает вид
но
lim ЯГ-MJ
х2 —4 х — 2
4.
Следовательно, 4 следует взять за значение функции при х = 2. Поясним графически тот факт, что, если принять 4 за значение функции для х = 2, то при х = 2 функция становится непрерывной.
Пусть
х2 — 4
х — 2 ’
У =
Это уравнение можно написать в виде: _у(х —2) = (х —2) (х4-2) или
(х —2)(j—х —2) = 0.
Приравнивая нулю каждый множитель в отдельности, имеем:
х = 2 и у^х-^2.
Геометрическими местами этих уравнений служат две прямые, А В и CD (черт. 129). Так как на прямой АВ существует бесчисленное множество точек, у которых абсцисса будет 2, то очевидно, что при х = 2 (= ОМ) значением у (или функции) может быть какое угодно число, но, когда х отлично от 2, то из черт. 129 видно, что соответственное значение у (или функции) всегда может быть найдено из
_У = х-|-2,
уравнения прямой CD. Также, когда х = 2, мы находим на CD
у = МР = 4, что, как мы знаем, было также предельным значением у (или функции) при х = 2; и из геометрических соображений очевидно, что если за значение функции при х = 2 принять 4, то функция при х = 2 становится непрерывной.
Подобно этому многие примеры гл. IV поясняют, каким образом можно находить предельные значения некоторых функций, принимающих неопределенные формы, употребляя соответствующие алгебраические или тригонометрические преобразования, и каким образом вообще эти предельные значения делают соответствующие функции непрерывными в рассматриваемых точках. Но более общие способы раскрытия неопределенностей основаны на методах диференциального исчисления.
ПРАВИЛО ЛОПИТАЛЯ.
§ 143. Раскрытие неопределенной формы ~. Дается функция f(x) °
вида - такая, что /(а) = О и F(a) = 0, т. е. что при под-
О становие а вместо х формула принимает неопределенную форму —. Требуется, следовательно, найти °
lim я»а F (X)
Принимая f(x) и F(x) за те самые функции, которые рассматривались в § 140, и заменяя в (6) § 140 букву Ь на х, имеем:
/(х) _ /' (х,) ^(х) F (XJ [ибо/(д) = 0 и F(e) = 0].
Так как Хх лежит между х и а, то, когда х приближается к а, хх гоже приближается к а как к своему пределу, и мы имеем:
Iim /w _1im f'M ’)
22f(x) f'uo !Lr(x) •
Следовательно, если частное от деления /'(х) на F'(x) не принимает при х = а неопределенной фзрмы, можем напирать:
Нт
iZ F(x) F1 (а) ’ где
/(а) = 0, F(a) = 0, Г'(а)ф0. Отсюда
правило раскрытия неопределенности вида
диференцируем в отдельности числитель и знаменатель функции и находим новые числитель и знаменатель 2). Значение этой новой дроби для данного значения 3) переменного будет предельным значением первоначальной
i) Полагая, что, по к некоторому пределу.
2) Предостерегаем
обычной ошибки, диференцирования всего выражения по правилу дифференцирования дроби.
з) Если а = оо, подстановка х = j приводит задачу к вычислению предела для 2 = 0; таким образом
дроби.
мере приближения х к а, дробь -^г/ приближается
учащегося от весьма неосмотрительной, но довольно
Следовательно, правило имеет силу и в этом случае.
Если же случится, что
т. е. что первые производные также при х = а обращаются в нули, , 0
то мы опять имеем дело с неопределенною формою —, и правило сно-
ва можно приложить уже к отношению:
/=*(*)’
что дает:
/(X) _ Г(д) X™ F(x) F” (а)
Если будет также
(а) = 0,
мы таким же образом найдем: f(x) Г (д)
F(x) F'" (а)
и т. д.
Может встретиться необходимость повторить этот процесс большое число раз.
Пример 1. Вычислить Дх) х’ - Зх + 2 ,
Е(х) “хз-хз-х + l при X-L
Решение. ) Г х-з — Зх 1) “ 1x3 —х» —
1-3 + 2
1 — 1 — 1 +
0
•q-: неопределенность.
3x2 _ з 3x2 _ 2х - 1
3-3 0
-я—й—г- = -j;-: неопределенность. О ““ л ~“ х и
6х 6х —2
6_____3
6 — 2 2 *
Пример 2. Вычислить
„ ех — е~х — 2х иш--------------
Решение.
/(0) _рх
f (0) “ L
1-1-0 0
у-: неопределенность.
0-0
л aniA Ja = o
+ е~х —2 1 _ 1+1-2
1 —cosx Ja, = 0“
О
-у: неопределенность.
1 - 1
/ (0) Г
F"(0) ~ L
1 — 1 О
о *
у-: неопределенность.
F" (0) |_ cos х
1
УПРАЖНЕНИЯ.
Вычислить црн помощи правила Лопиталя нижеследующие выражения 1).
1. lim X2—16 —я-; stt- Oms x2 + x — 20 ~ 8_ 9 12. lim tg 6 4- sec В — 1 tg 6 — sec b + 1 ‘ Отв. 1.
2. lim о. lim d л->1 X —1 xn — 1* In X x — Г £ n 1. 13. lim 14. lim z-ta sec2? — 2 tg ? . 1 -|- cos 4? Г az — z® a4—2a3z-|-2az3—z* 1 2 • — oo.
4. lim х-И) ex-e~ x sin X 2. 15. lim (ex — e~>3 (x — 4) e* — e2x Ge*.
5. lim ХЧЮ tgx —X 2. 16-,lm X->1 xa + x~2
X — slnx ‘ x3 —1 •
6. lim 'Ч In sin X (K-2X)2- ___1_ 8 ’ 17. lim x3-|-8 .2 x® + 32’
7. Um х->0 8. lim 9. lim 4^-0 10. lim 11. lim v+o a*-b* r3—ar2 Г3 — В — arcsln 6 sin3 0 slnx —sin <p x —<? ev + siny — 1 ln(l+y) a ln b- 0. _1. 6‘ cos <?. 2. 18. lim X->0 19. lim X-»( 20. lim 21. lim x-H> sln2x x — sin X ) *3 In cos(x — 1) Il . nx 1-sln — tgx — slnx sln3x
найти
§ 144. Раскрытие неопределенной формы—. Чтобы
Л*)
lim с. . , х->а F (х)
когда
и
lim/(х) = оо
lim F(x) = оо, а?->а
т. е. когда при х = а функция
/(х)
F(x)
принимает неопределенный вид—, мы следуем правилу, данному в § 143
О для раскрытия неопределенности вида —.
Ч Продиференцировав, учащийся должен в каждом случае сперва привести результат к простейшему виду и только после этого подставлять значение неизвестного.
144] РАСКРЫТИЕ НЕОПРЕДЕЛЕННОЙ ФОРМЫ 5 305
ОО
Итак, правило раскрытия неопределенности вида—:
диференцируем отдельно числитель и отдельно знаменатель. Значение этой новой дроби для данного значения переменного и будет предельным значением первоначальной дроби1)*
В случае, если новая дробь окажется неопределенною для данного значения переменного, повторяем тот же процесс.
Для доказательства правила должно показать, что
если
/(х) f'(a)
™'F(xj-F(ay
lim/(x) = oo, lim F(x) = оо.
x>a x->a
(А)
Во-первых, допускаем, что
х+а F(X) где I есть определенное число.
Из теоремы Коши, § 140, видим, что равенство /(х)— f(b) F(x) — F(b) F'(Xl) (заменяя b и а соответственно через х и Ь) справедливо при заданных х и b и при некотором частном значении хг удовлетворяющих неравенствам: a<x<x1<£< a-\-h, где b— число произвольное, а F' (х) не должна обращаться в нуль в промежутке [я, а-|-^]* Из (Л) имеем:
/ (x)-f (b) = [F (x) - F (*)],
или
Разделим
Пусть в иметь:
F(x) равенстве
/'(*,) Г. F(b)'
L F(x)'
(В)
так как
=f(b) + [F(x)-F(*)].
на F (x): f(x) _ f(b) F{x)
(B) x приближается к а как к пределу. Будем
Л(Х) x-ta
4.^=0, x-ta F (X)
F' (X0
lim lim _. .
F(x)
о .
i) F (*) и Fr (х) по предположению — функции непрерывные.
20 Зак. 2700. — В. Грека и ль и И. Лузин. Часть I
Пусть теперь h приближается к пределу, равному нулю; тогда х1 будет приближаться к пределу а, и получится:
fix) f'(a}
l?eF(x) F'(a)'
Можно показать, что правило остается верным если
Пример. Вычислить
Решение.
/(0) Г Inx
F(0) [cosecx
-------- при x = 0, cosec x
— оо
——: неопределенность.
sln2x
F'(0)
_— cosec х • ctgx_
x=0
0
—: неопределенность.
1
2'slnxcosx
T=«-
§ 145. Раскрытие неопределенности вида 0 со. Если функция /(х) •» (х) принимает неопределенную форму 0 • оо при х = а, мы переписываем данную функцию в виде:
. fix') / о(х)\
/(х) • ? (х) = J-y- I или
I ? (Х) \ /( х) J
0 оо
так, чтобы она могла принять или вид — или приводя таким образом вопрос к § 143 или к § 144.
Пример. Раскрыть неопределенность sec Зх • cos 5х при х = у. Решение.
[sec Зх • cos 5х]__^_ «я оо • 0: неопределенность, 2
Подставляем вместо зесЗх, что дает функции вид: со» 5х _ / (х) cos Зх F (х) '
\ 2 J Гео» 5х 1 0
-7Тх = L^-J,₽ix= неоп₽меленность-/А27 •
Лт; Г—slnSx-5 1
( я \ I — sin Зх • 3 Л
з
§ 146. Раскрытие неопределенности оо — оо. Вообще возможно преобразовать такое выражение в дробь, которая примет один из видов: О оо
— или ---.
О оо
Пример. Раскрыть неопределенность sec х — tg х при х = у.
Решение. ,
[sec х — tg xk^-JL = оо — оо : неопределенность. 2
По правилам тригонометрии . 1 sin х 1 — sin х /(х)
sec х — tg х =--------=---------= -=7—7.
> ь cosx cosx cosx F(x)
•Цу) ri-slnxl 1-1 0
----°----o’1 иеопРеделишость-
/Z(t) = Г —cosx~l 0 0
L-s*nxJx=£ -1
УПРАЖНЕНИЯ.
1. Um X->ao fX* 4- d Отв. c 13. 11m (it — 2r) tg x. к Omi. 2.
2. 1. ctgx lim -г-5—• ф-м> Inx — 00. 14. 1. . fl lim ж sin—. ажо < a
3. <> In x 11m . аько xn 0. 15. Um xnlnx(n>0). o»O 0.
4. lim —. ®-и» e® 0. 16. Um (1 — tg 6) sec 26. a К "7 1.
5. e® 11m —• as-и» Inx 00. 17. Hm (a* - tg 4a,J к
6. Hm lnsln2x. a>-»0 InSlnx lim *830 1. 18. 19. нт Г 2 1 1 1
7. 3. S-hIx»— 1 X— If lim Г 1 x 1 “ 2 • -1.
*-»i [In x In xj'
8. ln (’“t) Um 1 — < tg? 1 0. 20. Um (seed —tg6). a 0.
9. , Inx Um —r—. ®-x> ctgx 0. 21. Um Г 2 1 1 1
[sin» If 1 — cos ?J "5 ‘
10. lim xInslnx. ®-M) Hm xctgих. 0. 22. 23. 1
11. s' 0. [у — 1 fn>J* h Г ’ к 1 2 ' к»
12. lim -x—. v-^00 eay JS [4z 2z(e« + l)J 8 •
24. Показать, что
lim х-ко
X + sin X X — sin X
существует, но не может быть вычислен по правилу диференцирования числи теля и знаменателя.
Решение.
lim
11m
Х-КО
14
1-
sln X
X sin X
= 1,
х -|- sin х _ х —sinx —
так как
lim — =0(| sinx [< 1). X-KO x
Однако отношение производных числителя и знаменателя, равное:
♦
1 + COS X _
1 — COS X ~~
2 cos2 у
2 sin2 у
= ctS2f .
не стремится ни к какому пределу при х-> оо, откуда и следует, что правило диференцирования числителя и знаменателя неприменимо.
§ 147. Раскрытие неопределенных форм 0°, ос°. Дана функция вида:
' /(х)9(г).
Чтобы функция могла принять одну из трех вышеуказанные форм, для известного значения х должно быть
/(х) = 0, ср (х) = 0, что дает 0°; или
/(х)=1, <?(х) = оо, что дает 1"6;
или
/(х) = оо, ?(х) = 0, что дает оо°.
Пусть
взяв от обеих частей логарифм, имеем:
1п_у = <р(х)1п/(х).
В каждом из вышеприведенных случаев логарифм от у (функции) принимает неопределенный вид:
О • оо.
Раскрытие этой неопределенности способом, указанным в § 145, лает предел логарифма функции. Но последний равен логарифму предела функции; таким образом предел функции известен *)•
1) Так, если 11л1п<у = а, то 11m у^еа.
Пример 1. Вычислить хх, если х = 0.
Решение. Функция при х = 0 принимает неопределенный вид 0°. Пусть
отсюда 1пу = х In х = 0 • (— оо), если х = 0.
Ио § 143 . 1пх — ОО 1пу = —= , если х = 0. 1 оо
По § 146 1пу = —- — = — х = 0 при х = С-
Так как у = Xх, и In Xе = 0, то [^ = 0 = ’• 1
Пример 2. Вычислить (1 4- х)х, если х = 0.
Решение. При х = 0 эта функция принимает неопределенный вид I'1'.
Пусть 1
v = (l 4-х)7; следовательно:
]пу = In (1 + х) = оо • 0, если х = 0.
По § 145 , 1п(1+х) 0 л Jnj, = J = — при х = 0.
По § 144 1
Так как 1пу = —- = —4— = 1, если х = 0. 1 Ц-х у = (1+х)“
и £ ln(l+x)x =1.
то [(1+х)г1в = о = г-
Пример 3. Вычислить (ctg х)’*“ * при х = 0.
Решение. Пусть При х = 0 эта функция принимает неопределенный вид оо®. у = (ctg x),in «;
тогда in> = sin х • In ctg х = 0 • oo, если x =
По § 145 , In ctg x oo rt lay = — = —, если x = 0. ' cosec x oo
По § 146 — cosec* x . etgx sinx л л fn у = — = —5— = 0, если x = 0. — cosec x • ctg x cos’ x
Так как и то
у = (ctgx)eln®, In (ctg x)Bin ® = 0; [(ctgx)Bta*]x=0 = l.
УПРАЖНЕНИЯ.
Вычислить при помощи правила Лопиталя следующие выражения:
1. 2. limx1-<г. 1. ( 1 \‘К!Г 11m ( — ) ®-»о \ х ) Отл.—. е * &
3. Hm(slnO)tg’. ч 1.
4. Нт (1+ — Y V-ио \ У / 1 е“.
5. lim (е^ + х)®. ®-М) 1 1
6. Нт (ctgx)lnx. ®-м> 1 1 е ’
7. Нт (1 +пг)е. «-М> еп.
8. , г Нт (tg-^-) . Отв.—. ?->1 \ в 4 У е
9. п 1 . — _ -т’п Нт (cos тб)8 е 2 6-М)
10. Нт (1 + sin х)0* ®. е.
11. 11m (-l-i-iY; е\ \ X /
12, llmtctgx)®. 1.
г-*О
. пх / х 20 2
13. Пт (2 ®-м> \ в / е".
ГЛАВА XIV.
КРУГ КРИВИЗНЫ. ЦЕНТР КРИВИЗНЫ.
§ 148. Круг кривизны *) Центр кривизны. Если через три точки Ро, Ри Ръ плоской кривой провести круг, и если точки и Р2 приближать к Ро, двигая их по кривой к Ро жению, то круг, вообще говоря, и по величине и по положению будет приближаться к некоторому предельному кругу, называемому кругом кривизны кривой в точке Ро. Центр этого круга называется центром кривизны.
Пусть уравнение кривой (черт. 130) будет:
как к их предельному поло*
I? — радиус
а
.у =/(*).
(1)
и пусть х0, xlt х2 будут абсциссы, а Уо> Ур Уч ординаты точек Ро, Ри Pt соответственно; (а', {/) — координаты центра, проходящего через эти три точки. Уравнение этого круга будет:
круга,
(х - в')2+(у—?')а=Я'2;
так как координаты точек Ро, Plt Р.2 должны удовлетворять этому уравнению, то мы имеем:
(Хо - а')’ + (Уо - Р'Р-Р'2 = 0, (х1-а')2 + (^-Ю2-^а = °. (2)
(л-2-а')а-Ш-Ю’-Я'а = 0. J
Рассмотрим теперь функцию х, определяемую уравнением:
F (х) = (х — а')а 4- (у — р')2 — Р'2, где у заранее нужно заменить функцией /(х) из (1). Из уравнений (2) находим:
F(xo) = O, F(Xj) = 0, F(x2) = 0.
!) Иногда называется также соприкасающимся кругом. Следует делать различие между соприкосновением и простым касанием:£о-прикосновение есть частный случай касания, именно это есть касание веЖ<а сильное, тесное, т. е. касание высшего порядка.
По теореме Ролля (§ 136) F'(x) должна обращаться, в нуль, по крайней мере, при двух значениях X: одном, лежащем между х0 и *!> например х', и другом, лежащем между хг и х2, например х"\ т. с.
F'(x,) = 0, F'(x") = Q.
По той же самой причине F"(x) должна обращаться в нуль при некотором значении х, лежащем между х' и х", например при х9; т. е.
F"(x9) = 0.
Следовательно, элементы *) а', р' и R' круга, проходящего через Ро> и Рг> Должны удовлетворять трем уравнениям:
F(xq) = 0, F'(x') = 0, F"(xa) = 0.
Пусть теперь точки Рх и приближаются к Ро как к предельному положению; тогда х„ ха, х', хг и х3 все будут приближаться к х0 как к пределу, и, следовательно, элементы а, р, Р соприкасающегося круга
определятся из трех уравнений:
Р(Хо) = 0, F'(x0) = Q, Р"(Хо) = О, или, опуская значки:
(х-а)а + (у-р)’ = /?>,
(х — а) + О — Р)^ = 0, продиференцировав (А); и
(А)
(В)
(С)
продиференцировав (В).
Решая (В) и (С) относительно
X — а и у — р,
находим
предполагая, что
(D)
Т. е. координаты центра круга (а’, р') и величина его радиуса R'.
отсюда координаты центра кривизны суть:
dx2
dx*
Подставляя значения х— а ну— риз (D) в (А) и решая относительно R, находим:
3
dx*
отодвигается, и радиус кривизны обращается
что тождественно с (6) § 134. Отсюда предложение:
Теорема. Радиус круга кривизны равен радиусу кривизны.
Из § 114 мы знаем, что в точке перегиба (какова точка Q на черт. 132).
^ = 0.
dx*
Следовательно, по (3) § 133 кривизна ^=0; а из (6) § 134 и из (3) этого параграфа усматриваем, что по мере приближения второй производной к нулю а, Р и вообще беспредельно возрастают. Это значит, что если предположить, что Р вместе со своею касательною двигается по кривой к Р', то в точке перегиба Q кривизна обращается в нуль, вращение касательной на мгновение останавливается, и, по мере того как направление вращения изменяется, центр кривизны неограниченно в бесконечность.
Пример. Найти координаты центра кривизны параболы у* = 4рх, соответствующие: а) любой точке кривой; Ь) ее вершине (черт. 133).
Решение.
dy 1р. (Ру ______4р2
Лсв у ’ Л*а= ’
л) Подставляя в (3), имеем:
„ _ „ । У’ + 4Р2 2Р У3 о„|9п “-* +—7—•= 3х + 2а
й _ . У' + 4ра у3 _ у3
Р У У- *4/- 4р-‘
Следовательно, центр кривизны, соответствующий любой точке кривой, есть
(3*+г* -$)•
Ь) Центр кривизны, соответствующий вершине (0, 0), есть (2р, 0).
§ 149. Центр кривизны как предельное положение пересечения нормалей В смежных точках. Пусть уравнение кривой будет:
С/а.й^ У=/(Х). (А)
Уравнения нормалей к кривой в двух смежных точках Ро и Р, будут!):
(Хо-Л)4-с/о-П^- = о,
С(аУе) \
PtUa.yt>
Черт. 134.
Если нормали пересекаются в С' (a', р') (черт. 134), то координаты этой точки (а', р') должны удовлетворять обоим уравнениям, что дает:
(*о — аЭ + (Уо — ₽Э = о>
(^-«') + СУ1-Р')-^- = о.
Рассмотрим теперь функцию от х, определяемую уравнением: с (х) = (х — a') -j- (у — р') где у заранее нужно заменить через /(х) из (А).
Уравнения (В) показывают, что
<Р(хо) = О, ?(х1) = 0.
Но по теореме Ролля, § 136, <р'(х) при некотором значении х, ле* жащем между Хо и х,, например при х = х/, должна обращаться в нуль. Следрвательно, <? и Р' определяются уравнениями:
<?(*о) = О, ?'(хЭ = 0.
Если теперь Pt будет приближаться к Ро как к предельному поло* жению, то Х' будет приближаться к х0, давая
<?(Xq) = 0, Ч>'(*о) = О,
и, значит, С' (а', р') будет приближаться к некоторому предельному положению, а именно к центру кривизны С (а, р), соответствующему
*) На основании (2) § 92, причем X и Y суть текущие координаты.
точке Ро на кривой. Для доказательства, опустив указатели и написав
два последних уравнения в виде:
/
усматриваем, что, решая их относительно а' и 0', получим те же результаты, что и решая (В) и (С) § 148 относительно а и {5. Отсюда: Теорема. Центр кривизны С, соответствующий точке Ркривой, есть предельное поло
жение точки пересечения нормали к кривой вРс соседней нормалью.
§ 150. Эволюты. Геометрическое
место центров кривизны данной кривой называется эволютой этой кривой. Рассмотрим круг кривизны, соответствующий точкеРкривой. Если точкаР будет двигаться по данной кривой (черт. 135), то можно предположить, что вместе с нею катится по кривой и соответствующий круг кривизны, причем его радиус изменяется, будучи всегда равен радиусу кривизны кривой в точке Р. Кривая, описанная центром круга,
и будет эволютою кривой РР7.
Формула (3) § 148 дает координаты (а, 0) любой точки эволютц, выраженные в функции координат соответствующей точки (х, у) данной кривой. Но у есть функция х, следовательно:
dx*
(Ру djp
тотчас дают нам параметрические уравнения эволюты в функции параметра х.
Чтобы найти обыкновенное уравнение эволюты в прямоугольных координатах, исключим из этих двух выражений х. Нельзя дать общего способа исключения, который был бы приложим во всех случаях, ибо удобоприменимый метод зависит от формы данного уравнения. Тем не менее, в большинстве случаев можно находить уравнения эволюты в прямоугольных координатах, поступая следующим образом.
Общие указания для нахождения эволюты,’.
Первый шаг. Ищем а и 0 на (3) § 148.
Второй шаг. Решаем два полученные уравнения относительно х и у, выражая их в функции а и 0.
Третий шаг. Эти значения х и у подставляем в данное уравнение. Это и дает нам соотношение между переменными а и 0, представляющее уравнение эволюты.
Пример 1. Найти уравнение эволюты параболы у2 = 4рх.
Черт. 136.
Решение.
dy__ 2р (Ру__ 4р9
dx~~'
Первый шаг.
“ = 3х + 2р.₽ = -^.
Второй шаг.
>' = -0/’2₽)7-
Третий шаг. 2 . ои.Т . /а — 2р\ .^Р-?) = 4Р\~з)
4
pp=_t.(a_2p)J
Принимая, что а обозначает абсциссу, а ₽ — ординату прямоугольной системы координат, мы видим, что эволютою параболы АОВ служит полукубн-чсская парабола DC'E, причем центры кривизны находятся соответственно в С, Си С, и т. д. (черт. 136).
Третий шаг.
(aa)® +(Ьр)Т = (а’-6»)‘5
и будет уравнение эволюты EHE'If эллипса АВА'В'. Точки Е, Е’, Н\ Н суть центры кривизны, соответствующие точкам А, А', В, В' кривой, а С, С'1, С" соответствуют точкам Р, Р', Р" (черт. 137).
Если уравнения кривой даны в параметрической форме, то начинаем с отыскания
dx dx*’ как в § 131, из
АУ. dy dt -te=-d*J (А)
dt dx d*y dy d*x d*y _~dy ~dt* — ~dF dt2 dx* ~ V ’ (B)
\ dt)
а затем подставляем результаты в формулы (3) § 148. Это и даст параметрические уравнения эволюты в функции того самого параметра, который фигурирует в данных уравнениях.
Пример 3. Параметрические уравнения кривой суть:
Найти уравнения эволюты этой кривой в параметрической форме, построить кривую и эволюту, найти радиус кривизны в точке t = 1 и построить в этой точке круг кривизны.
Решение, dx t (Рх _ 1 dy __ t'2 (Ру _ 1
~dt ~ ~2 ' ~di*~ 2' ~dt~ 2 ' ~dt2~~2'
Подстановка в формулу (А) и (В) и затем в (3), § 148 дает:
Эти соотношения и являются уравнениями эволюты в параметрической форме. Давая различные числовые значения параметру t, вычислим соответствующие значения х, у, а, 0 из формул (С) и (D) и представим результат вычислений в виде прилагаемой таблицы.
t X У а ₽ t X У а ₽
3 2 3 2 1 0 2 5_ 4 13 16 1 2 2 4 9 2 4 3 9 16 1 6 0 85 2 _ 35 4 91 32 1 2 2 4 15 2 19 3 3 2 6 0 -1 3 2 о -3 2 2 13 16 5 4 2 2 _ 1 6 9 16 _ 4 3 9 2 1 2 _ 91 32 _ 35 4 _1_ 6 — 3 _ 19 3
Построим теперь кривую и ее эволюту (черт. 138).
вая (полукубическая парабола) расположена вправо, а ее эволюта влево от прямой х =
Круг кривизны в точке А (у, , для которой t = 1, имеет центр в точке
/ 1 7\
А' ( —j, -g-J, лежащей на эволюте, и радиус его равен АА. Чтобы проверить эти результаты, найдем радиус кривизны в точке А. Согласно формуле (7) стр. 288 будем иметь:
= VT
(при t = 1), и это значение совпадает со значением длиньЛотрезка АА:
АЛ "V(4+т) +(т_г) =
Пример 4. Найти параметрические уравнения эволюты циклоиды
x = e(( —slnf), 1
у = а (1 — cos t) J 1 1
Решение. Подобно тому; как в примере § 132, найдем:
dy _ sin £ dx 1 — cos t * d*y__________1
dxi~ fl(l—cos/)2'
Подставляя эти результаты в формулы (3) § 148, получим:
а = a (t + sin Z). I rF)
₽ = —а(1 — cos/). I . 4 '
Примечание. Если исключить t из уравнения (F), то получится уравнение эволюты OO'Q'' черт. 139), отнесенное к осям О'а и СУр. Координаты точки О относительно этих осей суть ( — т.а, — 2а). Преобразуем уравнения (F), отнеся их к новым осям ОХ и OY; получим:
а о= х — яа, ₽=.у-2а, t = V — я.
По подстановке в (F) и по упрощении уравнения эволюты будут: х = а{1' — sin/'), 1 у = а(1 — cos/'). I
(G)
Так как (О) и (Е) тождественны по форме, то заключаем, что эволюта циклоиды сама есть циклоида, производящий круг которой равен производящему кругу данной циклоиды.
§ 151. Свойства вволюты. Диференцируя а и £ уравнений (3) § 148 по х, имеем:
dy / <fly\3 day / dy у d3y di dy dx\dxa/ dx3 \ dx / dx* dx= dx / d?y V )
\dx»/
dy / (Ру у_d*_y___/ dy у d*_y
dp dx \ dx9 / dJc® \dx/ ~dx3 dx ~ / (fly у *
\ dx2 )
Разделяя затем (В) на (А), получаем:
d£_ = 1_ da dy ’
dx
(С)
Ио наклона касательной к в соответственной точке Р (черт. 140).
Подставляя два последних результата в (С), находим:
равно
равно
тангенсу угла наклона касательной
тангенсу угла данной кривой
Так как тангенс угла наклона одной касательной равен отрицательному обрат-
к «волюте
ному значению тангенса другой, то касательные взаимно перпендикулярны. Но прямая, перпендикулярная к касательной в Р, есть нормаль к кривой. Итак, нормаль к данной кривой есть касательная к ее эволюте.
Из (А) и (В) для дуги $ эволюты находим:
/ d£|2__/ da \8 / V______
\ dx] \dxj ' \ dx /
3 dy/ (Ру V dx \ dx9 /
diy dx9
I dy^\2 (Py j2 \ dx/ dx9
Но это тождественно результату, получаемому ди^еренцированием R [формула (6) § 134] по х и затем возвышением в квадрат. Следовательно:
Черт. 141.
\ dx/ \ dx /
или
ds= ±dR,
т. e. радиус кривиз.ны данной кривой возрастает или убывает ровно настолько, насколько возрастает дугаэво-люты1). В приложении к нашей фигуре (черт. 140) это значит, что
РхСх — РС = лк ССХ 2).
Длина дуги эволюты равна разности между радиусами кривизны данной кривой, касательными к этой дуге в ее концевых точках8).
Так, в примере 3 предыдущего параграфа замечаем, что если QVPV( = 4а) навернуть влево на эволюту, то упадет в О', откуда заключение:
Длина дуги циклоиды (например OO'QV) равна восьми
радиусам производящего круга.
§ 152. Инволюты и их механическое построение. Представим себе, что некоторая гибкая линейка согнута в форме кривой СХСО (черт. 141), т. е. в форме эволюты кривой РХРО, и предположим, что нить длины Рв, одним концом укрепленная в Со, огибает эту линейку (или кривую). Из результатов последнего параграфа ясно, что если эту нить развернуть и натянуть, то свободный конец ее опишет кривую РХРО Отсюда и название эволюта (т. е. развертка) кривой СХСО.
1) Мы не делаем в этом месте различия между приращением функции и се диференциалом, законность чего здесь будет далее ясна из интегрального исчисления.
s) Вывод лишь приблизителен: только интегральное исчисление строго выводит это равенство.
„ dR
•) Принимается, что не изменяет знака.
Кривая Р,Р9 называется инволютой кривой CiC6. Очевидно, любая точка нити опишет инволюту, так что данная кривая имеет бесчисленное множество инволют, но только одну эволюту.
Инволюты PtP9, Pt, Pj Р, называются параллельнымикри-в ы м и, ибо расстояние между любыми двумя из них, измеряемое по их общим нормалям, постоянно.
Читатель ради упражнения должен построить параболу и эллипс (§ 150) по их эволютам.
УПРАЖНЕНИЯ.
Найти координаты центра кривизны и уравнение эволюты для каждой из нижеследующих кривых:
. _ , х2 v2 , п (а2 + Ь9) х3 0 (а2 + 62)У
1. Гиперболы —л- — ~ — 1. Отв. а =-1—Н— ; 9 = — --' ;
г а- Ь1 а4 5 г Ь*
-1.1 2
эволюта (аа) * — (ftp) 3 = (а2 -|- б2) 8 .
2 2 2 1 a 2 1.
2. Гипоциклоиды х J +у 3 = а 3. Отв. а = х + Зх3 у 3; 9 =у + 3^ 3 у ’’
_2 2 2
эволюта (а 4- р)3 (а — Р)8 = 2d 3 .
3. Найти координаты центра кривизны кубической параболы у3 = аРх. Отл а-в4+15-у4 — 9/
Отва~--6а2у 2а* '
4. Показать, что для параболы х 2 -]-у 2 = а 3 имеет место соотношение а+р = 3(х+у).
5. Дано уравнение равнобочной гиперболы 2ху = аг; показать, что
,+ р =
(у + х)3 а2
, 9.z(y~x)!>
Р а2
_ _ 2
Отсюда уравнение эволюты (а р)8 — (а — Р) 3 = 2а 3 . Найти параметрические уравнения эволют следующих кривых в функции
параметра t:
6. Гипоциклоиды^
7. Кривой ,{^ГзГ—А
8 Клиной |x = a(cosZ + «slnO, в. кривой [y = a(Sin/_rcoSq.
9. Кривой (JZ?L6.
10. Кривой (
I а = a cos31 -|- За cos t • sin2 t, • | p = asln3Z-|-3acos,<'Sin3X.
j а = 4(1+2П-<<),
| p= -4Я
J a = a cos t,
| P = a sin I.
. —
p = 3P-1.
I а = 4-ЗЛ,
I p= -2A
21 Зак. 27Э9. — В. Гранвиль и II. Лузин. Часть I
11. Кривой сч . 1 Яй II II Н => Отв. J a= -2P, I P = 3/2.
12. Кривой х = 4t, a= — P, [ P=ll +3/2.
13. Кривой Ч h 111 to <£> ^l a = 7 — 3P, p= -2/».
х = 2t, At — fl ° = —4— ’
14. Кривой y = — f? {y з1' .12 + 5P " 6/ '
15. Кривой h . II I co|t-* JSi 4Р+12/ “ 3 ’ 2P+P . P“ 2 *
l У = P.
x = 2t, 12P + 9
16. Кривой 3 J = T. 4/3 O..27 + 4P P “ 6/ ’
17. х = 4 — P, у = 2/. 22. x = t, у = fl.
18. х — 21, у = 16 — P. 23. x = sin t, у = 3 cos t.
19. x = t. у = tin /. 24. x = I — cos t, у = / — sin /.
20. 4 х=у, у = 3/. 25. x = cos4 /, у = sin4 /.
21. Х=Р, 26. x = a sec /, у = b tg /.
27. Полукубической параболы х3 = ay3.
Отв. a = Эх3 X 2a : ’“* (*+?)/?!
эволюта 729а02 «= 16 [2а + V а? — 18аа]2 [ /а» - 18аа - а].
28. Трактрисы х «д а In д —• Т^а3—у3 .
- а + Va3-j2 а3
Отв. а = a In —‘— -----— ; 0 = —:
У У
эволюта р = ° + в “ ).
ГЛАВА XV.
ЧАСТНЫЕ ПРОИЗВОДНЫЕ. ЧАСТНЫЕ И ПОЛНЫЕ ДИФЕРЕНЦИАЛЫ.
§ 153. Непрерывные функции двух и более независимых переменных. Функция f(x, у) двух независимых переменных х и у по определению непрерывна для значения (а, Ь) переменных (х, у), если lim/(x, у) =f(a, b), х-*а У+Ь
все равно, каким бы способом х и у ни приближались к своим пределам а и Ь. Иногда это определение кратко выражают, говоря, что весьма малое изменение одного или обоих независимых переменных одновременно производит весьма малое изменение значения функции *).
Поясним это геометрически и л представляемую уравнением:
Рассмотрим на поверхности постоянную точку Р, мп которой х = а и у = Ь.
Приращения независимых переменных х и у назовем Дх и Ду, а соответствующее приращение зависимого переменного z назовем Дг, и пусть
X-}-Ax, .У + Д.У» z-j-Дх
будут ординаты точки Р' (черт. 142).
Значение функции будет:
z=f(a, Ь)~МР.
Если в точке Р функция непрерывна, то, каким бы образом Дх и Ду ни приближались к пределу, равному нулю, Дх будет также приближаться
I
П
Черт. 142. я этого рассмотрим поверхность, , У)-
:) Это будет понятнее, если читатель просмотрит § 41—43 о непрерывных функциях одного переменного.
к пределу • нуль, т. е. откуда бы точка Р7 ни приближалась по поверхности к точке Р, М'Р' будет всегда приближаться к совпадению с МР.
Подобное же определение удерживается и для непрерывной функции более чем двух независимых переменных.
Во всем нижеследующем рассматриваются только такие значения независимых переменных, для которых функция непрерывна.
§ 154. Частные производные. Так как в функции z — f(x> у)
х и у независимы, то можно предположить, что х изменяется, в то время как у остается постоянным, или наоборот.
Производная от z по х, когда изменяется х, а у остается постоянным *), называется частною производною от z по хи обозна-dz ..
чается символом . Можно, следовательно, написать: дх
dz _ /(х4-Дх, y)—f{x, у)‘
дх Ах
(А)
Подобно этому, когда х остается постоянным1), а у изменяется, частная производная от z по у будет:
^ = 11_ ГЛ*’ уЧ-aj)—7(х, j)'
ду ду-м) [ Ду J *
dz d,. df
Вместо -v пишут также-— т(х, у) или подобным же
дх } дх' дх
(В)
образом
dz д .. . df
вместо пишут ^/(х, у) или
Во избежание всяких недоразумений для обозначения частного диференцирования всюду принято д круглое 2). Впрочем, употребительны и другие обозначения, каковы
Л У), fy(x, у); Dxf, Dvf.
Наше обозначение можно распространить и на функцию какого угодно числа независимых переменных. Так для функции
u = F(x, у, z)
имеем три частные производные: ди ди ди дх’ ду’ дг’
или др др др дх ’ ду ' dz'
Пример 1. Найти частные производные от Z = ДА'5 + 26ху 4 су-.
*) Постоянные значения надо подставлять в функцию до диференцирования. ’) Введенное Якоби (1804—1851).
Решение.
~ = 2ах + 2Ьу, дх J
рассматривая у как постоянное;
^ = 2Ьх+2су, рассматривая х как постоянное.
Пример 2. Найти частные производные от и = sin (ах + by + cz).
Решение.
= a cos (ах + by 4-«), рассматризая у и z как постоявные;
= b cos (ах by + cz) рассматривая х и z как постоянные;
— = с cos (ах + by + cz), oz
рассматривая у и х как постоянные.
В
Черт. 143.
Обращаемся снова к функции
*=/(*. у);
... dz
посредством (А) мы определили как предел отношения приращения функции (считая у постоянным) к приращению переменного х, когда это приращение х приближается к пределу нуль. Подобным же образом (В) dz определяет .
§ 155. Геометрическая интерпретация частных производных. Пусть уравнение поверхности, представленной на прилагаемом чертеже (черт. 143), будет:
z=f(x, у).
Проведем плоскость EFGH через точку Р (где х = а, у = Ь) поверхности параллельно плоскости XOZ. Так как уравнение этой плоскости есть
то уравнение сечения JPK, отмечаемого ею на z=f{x, Ь),
если EF рассматривать как ось OZ, а ЕН—как ось ОХ. В этой плос-dz dz dz , ..~.п
кости -х— означает то же самое, что -7— , и, следовательно*-^ — (еМТР дх dx 'дх
равно тангенсу угла наклона к оси ОХ касательной к сечению JK в точке Р.
поверхности, будет:
Подобным же образом, если провести плоскость BCD через Р параллельно плоскости YOZ, ее уравнение будет;
х = а, ппт dz dz
и в плоскости сечения DPI производная означает то же, что .
Отсюда =tgAf7'P равно тангенсу угла наклона коси OY касательной к сечению DI в точке Р.
Пример. Дан эллипсоид 24^12^6 ’
найти тангенс угла наклона к осям ОХ и ОУ сечений эллипсоида, образуемых: а) плоскостью у = 1 в точке, где х = 4 и г положительно; Ь) плоскостью х = 2 в точке, где у = 3 и z положительно.
, Решение. Рассматривая у как постоянное, имеем: 2х , 2г dz _ 14 + У дх -0,
откуда
Если же х постоянно,
dz _ х дх~ 4г ’
то
откуда
а) Для у = 1 и х = 4
12 ф 6 ду и’
________У_ ду Чх'
следовательно:
Ь) Для х = 2 и у •= 3
следовательно:
dz___
ду~ 2
УПРАЖНЕНИЯ.
Найти частные производные функций:
1. u = xe-f-3x,y — >8.
О/пв
2. и = Ах1 -г Вху + Су* 4- Dx + Еу -|- F.
= 3x2 + бху, дх 1 J
g»2Ax4-By + D;
^Вх + 2Су4-£.
3. и = (ах2+ бу2 + «2)п.
4. u= arcsln —. V
п ди 2апхи
итв- дх~ ах-by2cz- '
ди_____2Ьпуи
ду ~ ах- + + с г- ’
ди _ 2cnzu
dz ах2 + by2 -|- cz2 ’
ди _ 1
дх У у2 — х2 *
ди________х
ду У Ууг — хз *
6. и = a&y2z + бху3** 4" О'® 4~ dxz3.
Отв. — 3ax2y2z -|- Ьу3г* -|- dz3;
ди
= 2ах3уз + 3f>x>2z* + бсу5;
gj = ахву2 4- 4bxy2z2 + 3dxz2.
7.
8.
и = х3у2 — 2ху* 4- Зх!_у3; показать, что ди , ди , х з- 4- У з~ = 5а.
дх 1 ' ду ху
и = —г—; показать, что х4- у ’
ди , ди
9. и = (у — х) (z — х) (х — >); показать, что
За , ди . ди дх'.ду'дг
10. ueln(eJf4*e>'); показать, что
ди .ди
еху
11. и = —-----; показать, что
вх + еУ
^4.^ = (x+j,-l)tt
дх 1 ду 1 ’
12. и=хууТ; показать, что ди , ди , . ...
х Л Ту “(ж + у + ° и) “•
13. и = In (х® 4-У8 4- ~~ 3xyz); показать, что ди . ди . ди _ 3
дх ду "Г dz ~ x-j-y + z'
14. и = exslny + е* sin х; показать, что
15. и = In (tgx-|- tgy + tg 2); показать, что
sin 2х ~ + sin 2у + sln 2* "г = 2. дх 1 ду dz
16. Пусть высота прямого круглого конуса будет у, а радиус его основания х. Показать: а) что если основание остается без изменения, то объем изменяется в пх2 раз быстрее высоты; Ь) что если высота остается без изменения,
2 го объем изменяется в -x-пху раз быстрее радиуса основания.
J
л» у’
17. Точка движется по эллиптическому параболоиду z = — + в плоскости, параллельной плоскости XOZ. Если х = 3 м и возрастает со скоростью 9 м!сек, то найти: а) скорость изменения г со временем; Ь) величину скорости точки; с) направление ее движения.
Отв. a) vt = 6 м/сек-, b) v = ЗУТз Mjcetc,
2
с) т = arctgу — угол, составляемый с плоскостью XOY.
18. Если на поверхности предыдущей задачи точка движется в плоскости, параллельной плоскости YOZ, то, полагая, что у = 2 и возрастает со скоростью 5 MfceK, найти: а) скорость изменения z со временем; Ь) величину скорости точки; с) направление ее движения.
Отв. а) 5 м/сек; Ь) 5 У~2м1сек; с) = у- — угол с плоскостью XOY
§ 156. Полное приращение. Пусть дана непрерывная функция двух переменных z=f(x, у). Если х и у получают одновременно приращения Дх и Ьу, то функция z получает приращение, называемое полным приращением в отличие от приращения функции, образующегося от изменения только одного переменного, с чем мы встретились при рассмотрении понятия частной производной. Обозначая полное приращение функции через Дг, можем написать:
Дг=/(х4-Дх, y-f- &у)— f (х, у). (А)
Когда Дх и Ду одновременно стремятся к нулю, точка (х-j- Дх, у -}-Ду) на плоскости XOY движется каким-нибудь образом к точке (X, у), а значение функции f(x уДх, у-]-Ду) стремится к значению /(х, у). Заставим точку (x-f-Дх, у-|-Ду) приближаться к точке (х, у), следуя по определенному пути, именно сперва по прямой, параллельной оси ОХ, а затем по прямой, параллельной оси OY. Очевидно, при этом точка (х-|-Дх, .у + Ду) переместится сперва в точку (х, y-f-Ду), а затем из этой точки — в точку (х, у) (см. черт. 144; на чертеже приращение Ду взято отрицательным).
Соответственно этому способу перемещения точки значения функции z=f(x, у) будут тоже изменяться определенным образом: от значения /(х-(-Дх, у-[-Ду) мы перейдем сперва к значению /(х, у-|-Ду), а затем от этого значения к значению /(х, у). Таким образом полное приращение функции мы можем представить следующим образом:
Дх = [/(х4-Дх, у + Ду)— Дх, у4-Ду)]4-1/(X, уЧ-Ду)— Дх, у)].
Рассматривая первую квадратную скобку, мы видим, что переход от значения /(х4-Дх, У4"4У) к значению f(x, у4~Ду) происходит при постоянном значении переменного у, именно при значении у -f-Ду. Следовательно, приращение /(х4~Дх, у 4~ Ду)—/(х, у4“Ду) является результатом изменения только одного х, а потому к этой разности можно применить формулы, относящиеся к функции одного переменного; применим в частности формулу Лагранжа (§ 137). При этом заметим, что теперь в формуле Лагранжа нужно поставить не просто производную, а частную производную, по аргументу х, соответственно тому, что написанное приращение соответствует изменению х при постоянном у4~Ду (§ 155). Итак, можем написать:
f(x + Дх, у + Ду) —/ (х, у Ду) =/' (х 4- б.Дх, у 4- Ду) Дх,
где — правильная положительная дробь.
Этот результат очевиден и с геометрической точки зрения: при переходе от значения /(х4~Дх, у 4-Ду) к значению /(х^у-^АУ) точка Р' перейдет в точку Р", следуя поповерхности z =^f (х, .у) вдоль плоской
кривой, лежащей в плоскости, параллельной плоскости XOZ, на расстоянии у 4- Ду от нее (черт. 145). И чертеж показывает, что в некоторой точке между точками Р' и Р" касательная будет параллельна секущей. А это свойство
Y
Лсу, j- j
и.ч'Ш
О
Черт. 144. Черт. 145.
плоской кривой как раз и составляет геометрический смысл формулы Лагранжа (§ 137).
Рассуждая совершенно аналогичным образом, мы применим формулу Лагранжа для разности, стоящей во второй квадратной скобке, и таким образом будем иметь:
/ (X, У+Ду) —f (X, у) (х, у 4- 02Ду) Ду.
Итак, полное приращение можно представить в следующем виде:
Дг = f’x (х 4- Дх, у+Ду) дх 4- f'y (х, у 4- еаДу) Ду. <в)
Допустим теперь, что частные производные нашей функции также непрерывны.
Это означает, что разности
Л (* + 6A*. .У+ Ау) —Л (х> У) == ei >
/у(х’ -у + 6Ау)—Л (х> У) = %
при Дх->0 и Ду-+О будут стремиться к нулю, т. е. величины ех и ва будут бесконечно малыми.
Из последних равенств будем иметь:
Л + °1Дх» У + ДУ) =Л (х> У)+а1 > f'y (х, У + =fy (X, У) + «,, и равенство (В) может -быть представлено в следующем виде:
д^ =Л (х> У> Lx +Л У) ^У + е1Дх + аг^У • (с)
§ 157. ПОЛНЫЙ диференциал. Напомним сперва, что приращение одного переменного y = f(x) выражается соотношением:
Ду = f (х) Дх 4- еДх,
где е -> О, когда Дх -> 0. Первое слагаемое /' (х) Дх было названо диференциалом функции:
dy = f (х) Дх.
Следовательно, приращение функции отличается от диференциала на бесконечно малое высшего порядка сравнительно с Дх или диференциал есть главная часть приращения функции, получающаяся зачеркиванием членов высшей малости. ч
В формуле (С) предыдущего параграфа слагаемые etAx и еаДу также являются членами высшего порядка малости. И по аналогии с понятием диференциала функции одного переменного, полным диференциалом функции Z =/ (х, у} мы назовем главную часть полного приращения, т. е. сумму
Л о, .у)д*+4'(*, зОАу-
Обозначая полный диференциал функции символом dz, таким образом получим:
=fx (х, Дх 4-^ (х, у) Ьу.
Для случая, когда х и у являются независимыми переменными Дх = dx, Ly = dy, а потому
dz =fx (х, у) dx 4-/у' (х, у) dy или
<•)
Аналогично, полным диференциалом функции трех независимых переменных и (х, у, z) называется выражение: . ди , . ди . . ди .
du = , dx4- -т— dy4- -3— dz. (Г)
дх 1 ду J dz ' 7
В дальнейшем мы увидим, что формулы (1) и (1') сохраняют свой вил в том случае, когда переменные х, у, Z не являются независимыми.
В главе, излагающей учение о диференциале функции одного переменного, было показано, что на практике часто вместо сложного по своей природе приращения функции берут более простой ее диференциал. Получающаяся при этом ошибка не имеет существенного значения вследствие того, что приращение отличается от диференциала на член высшей малости.
Совершенно аналогичную роль для практики играет и полный диференциал функции многих переменных.
Рассмотрим применение полного диференциала для вычисления погрешностей ад таком примере.
Пример. Период качания простого маятника выражается формулой:
Г = 1/ — ,
г g где Z—длина маятника и g — ускорение силы тяжести. Найти погрешность в определении Т, обусловливаемую небольшими погрешностями при измерении Z и g.
Решение. Обозначим погрешности, имеющиеся при измерении I и g, соответственно через dl и dg. Получающаяся благодаря этому погрешность при вычислении периода Т является приращением АГ. Заменяя АГ через dT, получаем:
Относительная погрешность:
dT_^(dl_dg\
r~2U g)'
Отсюда заключаем:
|-М(1тН>
т. е. абсолютная величина относительной погрешности, получающейся при вычислении Т, не превышает полусуммы абсолютных величин относительных погрешностей, имеющих место при измерении / и g.
§ 158. Производные и диференциалы сложной функции, одного независимого переменного. Мы уже рассмотрели диферен-цирование сложной функции (или функции от функции) одного переменного. Если, например:
У =/(«),
TO
rfy__ dy du
~dx~ du ' dx’
Рассмотрим теперь функцию двух переменных, зависящих от одного и того же независимого переменного. Пусть
z=f(x, у), где х и у суть функции третьего переменного t. Наша задача состоит „ dz в нахождении производной dz kz Как известно, -г- = lim . Если дадим аргументу t приращение at м-ьв &t
Д/, то х и у получат приращения Дх и Ду, а функция z — полное приращение Дг. Взяв формулу (С) и разделив обе части эт<уо равенства на Д/, получим: >
Ьг . Дх . . Ду . Дх , Ду
S=1, (х, Л +4 (х. У) -£+=, .
Переходя теперь к пределу при Д/->0, будем иметь: dz j . . dx . .г , . dy
потому что пределы последних двух слагаемых равны нулю, так как limet = 0 и Нгае2 = 0.
Итак: dz dz dx , dz dy
di dx dt ' dy ' dt '
Подобно этому, если
«=/(*, у, z), причем х, у, 2 суть все функции от t, имеем: du_ _ du_ dx , ди_ dy da rf? dt dx dt ' dy dt ' dz dt ' '
и t. д. для любого числа переменных J).
Если у будет функцией х, и и будет в действительности функцией одного только переменного х, то формула (1) примет вид:
du_ _ da . da_ dy_ . .
dx dx ' dy dx ’ ' '
i) В действительности это лишь частный случай общей теоремы, которую можно формулировать так:
Если и есть функциа независимых переменных х, у, г,..., из которых каждое, в свою очередь, есть функция независимых переменных г, $, то (при известных условиях относительно непрерывности)
ди _ ди дх ди ду ди дх . дг~ дх дг' ду dr ‘ dz Or'"’’
, ди ди
и подобные же выражения для и т. д.
(4)
Подобным же образом (2) даст: du ди . ди dy , ди dz dx дх' ду dx' dz dx'
_ ди du
Читатель не должен забывать, что и имеют совершенно
ди различный смысл. Частная производная составляется в предположении, что изменяется только одно частное переменное х, тогда как
du.
-4—= llm
dX Дх>0
где Да есть полное приращение переменного и, производимое изменениями всех переменных — изменениями, зависящими от изменения Дх независимого переменного 1). В отличие от частных произ-du du
водных-т;- и -т— называются полными производными относи-dt dx
тельно t и х соответственно а).
Пример 1. Дано и = sin у , х = е‘, у — t2; найти ™.
Решение.
ди 1 х ди х х dx t dy
— = — COS— , -ч- —-5 COS — , -7T = e , -~=2/.
дх у у ду у- У dt dt
Подставляя
Пример 2.
Решение.
в (1), найдем: du .. е‘ е Л=('-2)Тз‘0*7
Дано и = е" (у — г), у = a sin х, z = cos х; найти 4^. ах
du nr . . du qt du я,.
= ae (y — z), 4- — e , - == — eax;
dx dy dz
dy dz
-- = a cos x, — = — sin x.
dx dx
ди .
что есть производная функция и по букве х, той
*) Можно сказать, самой, которая лишь явным образом фигурирует в формуле, изображающей эту функцию u=f{x, y,z), тогда как — есть производная функции и по букве х, содержащейся в и= f (х, у, z) не только явно, но еще и неявно, так как предполагается, что буквы у и z тоже некоторые функции буквы х.
~ ,, ди
«) Нужно заметить, что имеет совершенно определенное значение для лю-. ди . .
бой точки (х, _у). между тем как зависит не только от точки (х, >), но и от
того частного направления, т. е. от , которое будет избрано, чтобы достичь этой точки.
Подставляя в (4), имеем:
= ее" (у — д) +ае“ сов х 4- е0* sin х = е** (а2 +1)sln *•
Примечание. В примерах, подобных вышеприведенному, можно было бы посредством подстановки выразить и явно в функции независимого переменного и затем прямо диференцировать, но вообще этот процесс был бы длиннее, а в некоторых случаях и вовсе был бы неприменим.
Формулы (3) и (4) весьма полезны во всех приложениях, относящихся к вопросу изменения функций многих переменных относительно времени. Правило решения задач при этом остается то же, какое изложено на стр. 269 за исключением того, что вместо диференцирования повременив (третий шаг) мы находим частные производные и подставляем их в формулу (1) или (2). Разъясним сказанное на примере.
Пример 3. Высота кругового конуса, равная 100 м, уменьшается со скоростью 10 м!сек\ радиус основания равен 50 м и возрастает со скоростью 5 м]сек. Как изменяется объем конуса?
Решение. Пусть х — радиус основания и у- высота ковуса. Тогда объем
dV 2 17 = 3^’
Подставляем в формулу (2). dV 2
О
ду ~~ 3
dx , 1 . dy
•зг+т’-'л
Так как х = 50, у = 100, = 5, = — 10,
dt „dt
то
4^=4-’' -6000 . 5 — 4’'2 500-10 = 2 5004-л3/сек. at о о о
* Умножая равенства (1) и (2) на dt, получаем выражения для полных диференциалов функций z = j(x,y) и u=f(x,y,z):
, dz , , dz ,
dz=^dx+^dy, (6)
. du , . du . . du .
dx-^dx + ^dy + ^dz. (6)
Полученные формулы показывают, что полный диференциал функции нескольких переменных х, у,... выражается через эти переменные и их duфepeнцuaлы совершенно так же, как и полный диференциал функции, когда х, у,... считаются независимыми переменными.
у
Пример 4. Даво и = arctg найти du.
Решение, ди _ у ди _ х
дх ~ хР—у3’
Подставив в (5), имеем:
du = ^-y~^dx. х?+у* '
Пример 5. Основание и высота прямоугольника содержат соответственно 5 и 4 см. В некоторый момент они начинают непрерывно возрастать со скоростями 2 см/сек и 1 см[сек соответственно. С какою скоростью в этот момент возрастает площадь прямоугольника?
Решение. Пусть основание будет х, высота у, следовательно, площадь будет:
Отсюда
и = ху.
да да
Их ду = х'
Подставляя в (1), имеем:
du dx . dy dt У dt dt'
(A)
Ho x = 5 см, у = 4 см, = 2 cMjceK, = 1 см]свк.
Отсюда:
= (8 5) см^сек = 13 c.rfjceK.
Примечание. Если рассматривать du как бесконечно малое приращение площади, производимое бесконечно малыми приращениями dx и dy, то очевидно, что du есть сумма двух тонких полосок, прибавленнных к обеим сторонам (черт. 146). В самом деле, по умножении (А) на
dt имеем:
du = у rfx 4- х dy, где у dx — площадь вертикальной полоски, xdy— площадь горизонтальной полоски.
Но полное приращение Ди, производимое приращениями dx и dy, очевидно, есть Ди =у dx-}- xd^-}-dxdy.
Отсюда очевидно, что малый прямоугольник (черт. 146) в правой вершине сверху ( = dxdy) есть разность между Ди и du. Эта фигура иллюстрирует тот факт, что полное приращение и полный диференциал функции нескольких переменных, вообще говоря, не равны между
Черт. 146.
собою (см. § 156 и 157).
§ 159. Диференцирование неявной функции. Уравнение
/1х,у) = 0
(А)
определяет либо х, либо у как неявную функцию другого переменного1). Оно представляет любое уравнение, содержащее х и у, в котором все члены перенесены в левую часть. Пусть
«=/(*. j);
следовательно:
du _ df_ . д/ dy dx~ дх' ду dx' Но в силу (А)
/(х,у) = 0, т. е.
!) Предполагается, что малое изменение величины Же изменение величины у.
х производит лишь мало
так что
дх ду dx '
dv \
Решая относительно *), найдем: dx
dx df \dy* )’ (7)
формулу диференцирования неявной функции.
Эта формула в форме (В) эквивалентна процессу, указанному в § 90 для диференцирования неявных функций, и все примеры § 90 можно решить, пользуясь формулой (7). Так как
Лх,у) = 0 (А)
для всех допустимых значений х и у, то можно сказать, что (7) дает относительные скорости изменения с течением времени х к у, удерживающие f(x, у) от всяких изменений. Геометрически это значит, что точка (х, у) должна двигаться по кривой, уравнение которой есть (А), а (7) определяет для любого момента направления ее движения.
Пример 1. Дано x«y1 + s!ny = 0; найти
Решение. Пусть
/(x..>) = ^y*-|-slny,
Тх = = 4х!>у3 + cosy ‘
Из (7) находим:
dy_ = _ 2ху«
dx 4х2у34-cosy ’
Пример 2. Если х, когда оно проходит через значение х == 3 дм, возрастает со скоростью 2 дм/сек, то с какой скоростью должно изменяться у, когда у=1 дм, для того чтобы функция 2хуг — Зхгу сохраняла постоянную величину?
Решение. Пусть
/(х, у) = 2ху2 — Зх2у;
находим частные производные этой функции по х и по у:
^-=2у’-6ху, -g=4xy-3r2.
Подставляя в (7), имеем:
</у 2у» — бху dx ~~ 4ху — Зх2
или
аУ
dt_____2уз — бху
dx ~ 4ху — Зх2'
dt
_ ди ди
1) Предполагается, что и существуют.
но х = 3, у = 1, ~ = 2; отсюда dy п 2 . , "Л = — 2Тб дм1сеК'
Пусть Р будет точка (х, у, z) на поверхности да ной уравнением:
u = F (х, у, z) = О, (С)
и пусть PC и АР будут сечения, производимые плоскостями, проведенными через точку Р параллельно плоскостям YOZ и XOZ соответственно. Для точек кривой АР переменное у остается постоянным, следовательно, в силу (С) z есть неявная функ1 ия одного х, и в силу (7) имеем;
dF dz___ . дх
дх ~dF' dz
чем определяется наклон кривой АР в точке Р (§ 155).
„ dz dz
В левой части вместо -т- написано , ибо dx дх
чально было неявной функцией х и у, но (8) выведено нии, что у остается постоянным.
Подобно этому наклон кривой PC в точке Р дается dF , dz __ ду
ду ~ dF' dz
(8)
в силу
(С) Z первой:-в предположе-
равенством:
(9)
УПРАЖНЕНИЯ.
В следующих шести примерах найти полные производные, употребляя формулы (2), (3) или (4).
1. и = г3 + у3 + zy, z = sin х, у = ех.
Отв. — Зе3х + ех (sin х + cos х) -f- sin 2х.
„ . , . х „ du ех(1-4-х).
2. и = arctg (ху), у = ех. Отв. — = ~ .
• dx 1 + хгезх
3. и = In (а2 — р2), р = a sin 0. du dU = -2tg0.
4. и = о2 + vy} v = In s, у — es. du ds j 1
5. и = arcsin (г — s), г = 3/, s = 4Р. du 3
dt у 1 —r2
6. 22 (у — z) tt — - u — /7 «1п г г —X СПС г du = e0Jfslnx.
а* +1 Вак. £769. — В. Грапвпль л Н. Л у в и к. Часть I dx
В следующих восьми примерах найти полные диференциалы, пользуясь формулами (5) и (6).
7. и = Ьуах4* сх- + gv3 + ex. Отв. du = (by1 -|- lex -j-e)dx-j-
+ (2by* + 3gy-)dy.
8. и = 1пх>|. Отв. du = у dx -|- In х dy.
9. и=/1п'. du = veln x In у cos x dx -1 ^4— dy. J J 1 yl — Bin* J
10. ц = х1п< . (Iny . Inx . \ du = u\ x х+—аУ)'
11. 5 Z и = —- 5 — t 2(sdt — tds) (s-tr •
12. и = sin (pq). du = cos (pq) \qdp -j-p dq].
13. и = xyc. du = x'-*’-1 (_уд dx-)-zx In xdy-}-xy In x dz),
14. » = tg41i><itg4. + +
lS.,_|+Z+£. л_(1_.£)л+(1_'),,+
+ (W>
16. и = arctg + arctg . У •*
. _ x
17. и = arcsin — .
У
du = 0.
у dx — xdy yV y1 — x2
18. Принимая, что уравнение, характеризующее совершенный газ, есть
vp = RT,
где v — объем, р — давление, 7"—абсолютная температура, а 7? — постоянное, каково будет соотношение между диференциаламн dv, dp, dTt
Отв. vdp-\- pdv = R dT.
19. Воспользовавшись результатом задачи 18, найти, как изменяется р при следующих данных:
Г = 300° С, р = 1 000 kz]m\ о =14,4 л3.
и при условии, что при изменении t до 301° и v до 14,5 м- изменение р протекает равномерно.
Отв. — 3,26 кг/лА.
20. Сторона треугольника имеет длину 2,4 м и возрастает со скоростью 10 см/сек вторая сторона длиною 1,5 м уменьшается со скоростью 5 см!сек. Угол, заклю ценный между этими сторонами, составляет 60° и возрастает со скоростью 2° в секунду. Как изменяется площадь треугольника?
Отв. Возрастает со скоростью 413 см^сек.
21. Как изменяется третья сторона треугольника предыдущей задачи?
р. Отв. 12,32 см]сек.
22. Сторона прямоугольника имеет 2$ см длины и увеличивается со скоростью 5 см1сеп. Другая сторона длиною 37,5 см уменьшается со скоростью 2.5 cm/cck. Как изменяется площадь прямоугольника в конце второй секунды?
Отв. Возрастает со скоростью 74,82 смг1сек.
23. Ребра прямоугольного параллелепипеда имеют длины 7,5 см, 10 см и 12,5 см, и каждое из них возрастает со скоростью 0,5 см/свк. Как изменяется объем параллелепипеда?
24. Змей перемещается горизонтально со скоростью 0,6 м/сек и подни^ мается вертикально вверх со скоростью 1,5 м/сек. С какой скоростью раскручивается веревка?
? Оте. 1,61 м/сек.
25. Человек, стоя на пристани, притягивает лодку за веревку, которую он тянет со скоростью 0,6 м/сек. Руки его находятся на высоте 1,8 м над носом лодки. С какой скоростью движется лодка в момент, когда она находится на расстоянии 2,4 м от пристани?
Отв. 0,75 м/сек.
26. Объем и радиус цилиндрического котла возрастают соответственно со скоростью 27 дм3/мин и О.иОЗ дм/мин. Как изменяется длина котла в момент, когда объем его становится равным 1,18 м3 и радиус 0,6 ж? t
Отв. 0,234 дм/мин.
27. Вода вытекает из конического фильтра высотою 20 см и имеющего диаметр основания длиною 15 см со скоростью 0,0125 см3/час. С какой скоростью уменьшается площадь поверхности воды, когда уровень воды опустится на 10 с.и?
28. Пусть хну — координаты некоторой точки относительно прямоугольной системы координат, а г и 6 — полярные координаты той же точки. Показать, что
х dy — у dx = г2 dO2, dx2 -f- dy2 = dr2 -|- r2 d№.
29. Закрытый ящик, имеющий в длину 10 см, в ширину 8 см и в вышину
7 см, сделан из дощечек, имеющих -у см в толщину. Определить приближенно объем затраченного на ящик материала.
Отв. 206 см3.
30. Ускорение g вычислено из формулы:
Найти допущенную при этом погрешность в зависимости от небольших погрешностей, допущенных при измерении ли/.
w Zds—lgtdt
Отв. Абсолютная погрешность dg =-------— .
Относительная В остальных примерах найти —, пользуясь 31. (ха + У2)1 — а2 (х2 - у2) = 0. Отв. . dg ds 2dt формулой (7).
dy dx = _ £ . 2(x24-y2) —Д2 > 2(x24-y2)4-a2 '
32. Р1 —е*4-ху = 0. dy dx = ex-y еУ + х'
33. sin (ху) — еху — х2у =• 0. dy dx _ у [cos (xy) — е*У — 2x] x [x е^У — cos (xy) ]
34. sin х siny 4- cos х cos у — у = 0. dy sin (x — y)
dx sin (x — y) — 1 ’
35. ух =ху. dy yxy~* — y* in у
dx xy*-1 — xy in X
36- f(x, у) — f(y, х) = 0. Показать, что производная может быть выражена при помощи дроби, числитель которой получается из знаменателя перестановкой букв х и у (ср. задачу 35).
§ 160. Последовательные частные производные. Рассматривая функции многих независимых переменных, возьмем какую-нибудь функцию / (х, у, z) трех аргументов х, у, Z. Рассмотрим частные производные ее
соответственно по этим аргументам н назовем их первыми производными (или частными производными первого порядка).
Предположим, что каждая из них, в свою очередь, имеет первые производные по аргументам х, у и г; для данной функции f (х, у, z) они будут называться вторыми производными (или частными производными второго порядка). Так, например, первые производные для f или df
-j- относительно х, у и z напишутся в виде: f" f " f" J хх> J xy ’ 1 xz ’
ИЛИ d*f d2f dxdx’ dxdy' dxdz' t df
Точно так же первые производные f у или — относительно х, у и z напишутся в виде:
/у* > fyy ’ fyz или
д-f d*f Jff дудх' дуду' dyuz и т. д.
§ 161. Порядок диференцирования безразличен. Эти обозначения упрощаются, когда возможно изменять порядок диференцирования.
Читатель легко убедится на многочленах в том, что порядок диференцирования для них, в самом деле, безразличен.
Пример. Возьмем f(x, у, z) = Зл^у3 — 7xy2z + 2xz3.
Имеем:
fx — 12л3/3 — 7y2z-}- 2zs, /у = 9л*_у2 — 14xyz.
Следовательно:
/ту = З6х3_у2 — 14yz и
fyx = 36x3ja — 14yz.
Итак, окончательно:
xy fyx"
Это правило о безразличии для результата того порядка, в котором производится диференцнрование, имеет силу не для одних только многочленов. Оно сохраняет полную силу для всякой частной производной, какого бы она порядка ни была, лишь бы она была непрерывной, и может утратить свою силу лишь тогда, когда рассматриваемая частная производная становится разрывной.
Мы обращаем внимание читателя на всю важность возможности изменять порядок диференцирования для самого обозначения частных производных. В силу этого безразличия порядка диференцирования та частная производная функции f(x, у, г), которая получается в результате р-кратного диференцирования по х, кратного диференцирования по .у и r-кратного диференцирования по г, напишется просто в виде:
dxfdy^dz' ’
где п обозначает сумму всех порядков диференцирования, п =р-\-Я Г-
Мы повторяем, что этот способ изображать частные производные законен лишь тогда, когда безразличен порядок диференцирования (на-
пример тогда, когда q^-r есть непрерывная функция от всех
бы
ве-
по-
трех аргументов).
Часто бывает нужно написать такой символ, который изобразил величину частной производной для йекоторой избранной системы личин аргументов. В этом случае пишут:
/г2 У О’ го)’ хРуЧг'" (Хо'Уо’
для того чтобы обозначить тот численный результат, который лучается, когда аргументы х, у, Z заменяются соответственно числами д‘о, yQ и z0 в рассматриваемых частных производных.
Пример. Дано и = х3у — Зх2_у3; проверить, что .
Решение. = Зх2у — бху3; = Зх2—18-гу3; = х3 — 9х2у2,
дх ду дх ду
— Зх® — 18ху3; требуемое проверено.
д-и
УПРАЖНЕНИЯ.
1. « = cos (х -f-у); проверить, что .
«в -4- х2 (Ри \сРи
2. и = '—г; проверить, что -д . • • = -ч1 . .
у» — х2 дудх дх ду
д'и дР-и
3. и =у In (1 + проверить, что .
. г д3и даи
4. и = arctg - ; проверить, что .
5. и = sin (О2?); проверить, что .
6. и = 6e*y2z + 3^ x2z2 -|- 2егх3у — xyz; воказать, что
7. и = ехуг; помазать, что = U + ^хУг + и-
QX Оу О»
„ х2у2 д*и . &и „ ди
8. и = —г—; показать, что х-5-5 4-у = 2-3- .
х-\-у дх2 1 J дхду дх
9. и = (х2 + V2)3; показать, что Зх + 3> -4-^- + = 0. ' ‘ х » • дудх ду2 ду
X у Z
10. и=у2#е 2 4- &х2е 2 + х2у2е2; показать, что
3
11. и = tg (у + ах) + (у — ах)2 ; показать, что
д2и . д2и — = п2________ .
дх2 ду2
12. и = х’_у3хт; показать, что
_ (. - I) W - 2) (, -1>
13. г = У х2+_>'24-г2; показать, что
X — J- — - 2 <ln ') । ^(|пг) । & (In г) _ J дх2 ”1 ду2 ' дг2 г И дх2 ду2 dz2 ~ г
1
14. v = ; показать, что
V х2-\-у2-\-^ i^v d2v , <^0
dx® ду2 ' дх2 =
15. / (х, у, z) = <? (г), где г — Yх2 + у2 + г2, показать, что
2 ,(г) + 1Аг) dx2 + ду2 + dz2 г Т { } + т (
Сравнить с результатами двух предыдущих задач.
ГЛАВА XVI.
ОГИБАЮЩИЕ.
§ 162. Семейство кривых. Переменный параметр. Уравнение кривой, кроме переменных х и у, вообще говоря, содержит некоторые постоянные, от которых зависят размеры, вид и положение этой кривой. Так, например, геометрическое место уравнения
(А)
есть окружность, центр которой лежит на оси X на расстоянии а от
начала, а размеры зависят от радиуса г.
Если предположить, что а принимает ряд значений, то получится соответствующий ряд окружностей, отличающихся своими расстояниями от начала, как показывает черт. 148.
Всякая система кривых, получаемых таким образом, называется семейством кривых, а количество а, постоянное для одной какой-
либо из этих кривых, но изменяющееся при переходе от одной Кривой к другой, называется переменным параметром.
Как видно будет далее, встречаются и такие задачи, где число таких параметров два или больше. Вышеприведенный ряд кругов называется семейством, зависящим от одного параметра. Чтобы показать, что а входит в качестве
переменного параметра, условились вносить вол; таким образом пишут:
/(х, у, а) = 0.
Черт. 148.
его в функциональный сим-
§ 163; Огибающая семейства кривых, зависящих от одного параметра. Все кривые семейства могут касаться одной или нескольких линий, как это показано на черт. 148. В таком случае эту кривую (или эти несколько кривых) называют огибающей данного семейства. Дадим способ нахождения уравнения огибающей семейства кривых.
Предположим, что кривая, заданная уравнениями в параметрической форме:
X = <? (а), У = ф (а), (А)
касается каждой из кривых семейства:
f{x,y, а) —О, (В)
причем параметр а один и тот же как в уравнениях (А), так и в уравнении (В).
Тангенс угла наклона касательной к кривой (А) в любой точке есть dy _ (а) dx у' (а) ’ ' '
и тангенс угла наклона к (В) определяется соотношением:
(D) dx fy (x, у, a)
Поэтому, если кривые (А) и (В) касаются друг друга, то подъемы их в точках касания (для одного и того же значения а) должны быть равны, что дает;
У (а) /Лх< У> а)
<?'(“) /у(х, У, а)
или
Z (х> у>а) ?' (а)+4 (х> У’а) (а)=°- (Е)
По предположению, при всяком значении а кривая (А) касается соответствующей этому значению а кривой семейства (В); поэтому для всякого значения а координаты (х, у), определяющиеся уравнениями (А), будут удовлетворять уравнению соответствующей кривой (В). Следовательно, для всякого значения а справедливо равенство:
/[?(а)> •>(«), «] = 0, (F)
получаемое подстановкой х и у из уравнений (А), в уравнение (В).
Поэтому полная производная левой части (F) по а должна быть равна нулю для всякого значения а, т. е.
Z(x> У> У, «О’/(«)+/(*» У. а) = °-
где
* = ?(*), _у = ^(а).
Принимая во внимание соотношение (Е), получаем:
Z (*, У, “) = 0. (Н)
Отсюда заключаем, что координаты точек огибающей удовлетворяют уравнениям (В) и (Н):
f(x, у, а) = 0 и / (х, у, а) = 0, (I)
т. е. что параметрические уравнения огибающей могут быть найдены решением уравнений (I) относительно х и у, откуда х и у определяются как функции параметра а.
Общие указания для нахождения уравнений огибающей в параметрическом виде.
Первый шаг. Диференцируем уравнение семейства кривых по п е рем е н н о м у п а р а м е т ру, рассматривая все другие величины, входящие в уравнение, как постоянные.
Второй шаг. Решаем получаемое таким образом уравнение и данное уравнение семейства кривых относительно х и у. Получаемый результат и будет представлять собой параметрические уравнения огибающей.
Замечание. Если желательно получить уравнение огибающей в прямоугольных координатах, то следует исключить параметр а из параметрических уравнений огибающей или из уравнения семейства (В), и уравнения (Н).
Пример 1. Найти огибающую семейства прямых
X COS а + у Sin а = р, (Л)
где а —переменный параметр.
Решение.
х cos a -f-y sin а = р. (А)
Диференцируя (А) по а, имеем:
— х sin я+у cos а = 0. (В)
Умножая (А) на cos я и (В) на sin а и вычитая (В) из (А), находим:
х = р cos я.
Подобным же образом, исключая х из (А) и (В), имеем: у = р sin я.
Параметрические уравнения обвертки (огибающей) будут, следовательно:
х = р cos я, 1
у = р Sin Я, J
где я — параметр. Возвышая уравнения (С) в квадрат и складывая, найдем:
Х2+у2 = />2 уравнение обвертки в прямоугольных координатах, представляющее окружность (черт. 149).
Пример 2. Найти огибающую семейства прямых, образуемого прямой линией, имеющей постоянную длину а и движущейся так, что ее концы всегда находятся на двух постоянных прямоугольных осях.
Решение. Пусть АВ = а (данная длина) н пусть
xcosa+ysin«-p = 0 (А) Черт. 149.
будет уравнение прямой АВ. Так как АВ движется, I
постоянно скользя концами по осям, то я и р буду; изменяться. Но р можно выразить в функции я
В самом деле:
АО = АВ cos я = a cos я, и р = АО sin я = a sin я cos a.
Подстановка в (А) дает: х cos я-|-у sin я — д sin я cos я = 0, (В)
где я есть переменный параметр. Диференцируя (В) по я, находим:
— х sin я -|- у cos я 4* a sin2 a — a cos2 я = 0. (С)
Решая (В) и (С) относительно х и у, имеем: х = sin8 а, | у = cos8 а J
(D)
параметрические уравнения (черт. 150).
огибающей, представляющие гипоциклоиду
Соответствующее уравнение в прямоугольных координатах найдется из уравнении (D), если из них исключить а; получаем:
2 2
х 3 = а 3 sin8 а,
2 2
у 3 = а3 COS8 а,
откуда, складывая, получаем:
2 2 2
х3+>3 = а3
уравнение гипоциклоиды в прямоугольпых координатах.
Пример 3. Найти огибающую семейства прямых
де угловой коэфициеят k есть
У = кх+Р, переменный параметр.
Решение.
у=кх+£ •
Первый шаг.
0 = х — —
А2
Второй шаг.
Третий шаг.
и, возвышая в квадрат, имеем:
у» = Арх, т. е. уравнение огибающей есть уравнение параболы. Семейство прямых, получаемых изменением углового коэфициента А, изображено на черт. 151, причем каждая линия касательна к огибающей, ибо из аналитической геометрии известно, что
У = кх+Т
есть касательная к параболе
у» = 4рх, выраженная посредством своего углового коэфициента А.
§ 164. Эволюта данной кривой, рассматриваемая как обвертка ее нормале^Й. Так как нормали кривой все касательны к эволюте (§ 151), то очевидно, что эволюту кривой можно определить так же, как обвертку нормалей этой кривой, т. е. как геометрическое место пересечений бесконечно близких нормалей.
Интересно также заметить, что, найдя параметрические уравнения обвертки по способу предыдущего параграфа, мы будем иметь координаты х и у центра кривизны; так что здесь мы имеем другой способ нахождения координат центра кривизны. А если затем исключить переменный параметр, то будем иметь соотношение между х и у,' которое является уравнением эволюты (обвертки нормалей) в декартовых координатах.
Пример. Найти эволюту параболы уг = 4/>х, рассматривая ее как обвертку пормалей параболы.
Решение. Уравнение нормали в точке (х', у') есть
у-у'=-Тр(х-х'}‘
по (2), § 92. Так как рассматриваются нормали для всех точек кривой, то х' и у' будут изменяться. Исключая х' посредством уравнения у'- = 4рх', предста-
вим уравнение нормали в виде:
у У Яр- 2р
Рассматривая у как переменный параметр, мы ищем огибающую этого семейства нормалей. Диференцируя (А) по у', имеем:
- 3/ 2_ *
“ 8р2 2р ’
а решая относительно х, находим:
3/» + 8р"-
Х~ 4Р
(А)
(S)
Подставляя это значение х в (А) и решая относительно у, имеем:
У= -
(С)
Следовательно, (В) и (С) представляют координаты центра кривизны параболы. Рассматриваемые совместно уравнения (В) и (С) суть параметрические уравнения эволюты в функции параметра у. Исключение у' из (В) и (С) дает:
21ру^ = 4 (х — 2/>)3
уравнение эволюты параболы в прямоугольных координатах. Тот же результат найден был выше в примере 1 § 150 иным способом.
§ 165. Два параметра, связанные одним условным уравнением. Встречаются задачи, где выгоднее употреблять два параметра, связанные одним уравнением, выражающим некоторое геометрическое свойство, чем пользоваться одним только параметром, выражая другой через него. Так, пример последнего параграфа содержит два параметра х' и у’, связанные уравнением кривой. В этом случае х! мы исключили, оставив только один параметр уУ
Но когда исключение выполнить трудно, то как данное уравнение, так и вспомогательное уравнение, связывающее оба параметра, можно диференцировать по одному из параметров, рассматривая каждый из параметров как функцию другого. Для уяснения себе этого процесса рассмотрим следующую задачу.
Пример. Найти огибающую семейства эллипсов, оси которых совпадают с осями координат, а площадь имеет постоянную величину.
Решенче.
х- у .
= 1 * (А)
есть уравнение эллипса, в котором а и b — переменные параметры, связанные уравнением:
ita* = к, (В)
где tzab есть площадь эллипса, полуоси которого равны а и Ь. Диференцируя (А) и (В\ рассматривая а и b как переменные, а х ну как постоянные, получим, употребляя диференциалы: из (А)
и нз (В)
xzda yzdb _ яз +' Ьз - °
b da -|- a db = 0.
Перенося в каждом соотношении один из членов во вторую часть и деля почленно получающиеся уравнени>]. находим:
ь
Черт. 153 ху = ±х~.
Огибающая представляет собою пару сопряженных равносторонних гипербол (см. черт. 153).
УПРАЖНЕНИЯ.
1. Найти огибающую семейства прямых
у = 2тдг + т*, где т — переменный параметр.
Отв. х = — 2тэ, у = — 3m4; или 16у3 + 27х4 = 0').
2. Найти огибающую семейства парабол у* = а (х — а), где а — переменный параметр.
Отв. х = 2а, у = ± а; или у = ±-у х.
3. Найти огибающую семейства окружностей
*+(у-₽)« = /•, где ₽ — переменный параметр.
Отв. х=±г.
1) Когда ответ дается в двух видах, то первый представляет решение
в параметрической форме, второй — в форме одного уравнения.
4. Найти уравнение кривой, касательными к которой служит семейство прямых _________
у = тх Yа2т- -|- ft2, где угловой коэфициент т есть переменный параметр.
Отв. Эллипс ft2x2 + a2>* = аЧ2.
5. Найти огибающую семейства окружностей, диаметрами которых служат двойные ординаты параболы
у2 = 4рх.
Отв. Парабола у2 = 4р(р-}- х).
6. Найти огибающую семейства окружностей, диаметрами которых служат двойные ординаты эллипса
ft’x3 4- а2/- = аЧ2.
Отв. Эллипс +
7. Круг движется так, что его центр постоянно находится на параболе
у2 — 4ах,
а окружность его проходит через вершину параболы. Найти уравнение огибающей окружностей.
Отв. Циссоида у2 (х + 2а) -|- х3 = 0.
8. Найти огибающую семейства, состоящего из всех окружностей, центры которых лежат на осн ОХ, а радиусы имеют одинаковое для всех окружностей значение R.
Отв. Две параллельные прямые у = ztz R.
9. Найти эволюту эллипса
Ь2х2 + а2у2 = аЧ2,
если уравнение нормали дано в форме
by = ах tg ? — (а2 — b2) sin ?, где эксцентрический угол есть параметр.
_ a2-ft2 , ft2-! а2 ,
Отв. х =--------cos2 <?, у =-г---sin3 э;
а ft т’
, 2 JL 1
или (ах)3 +(ау)3 = (а2—ft2)3.
10. Найти эволюту гипоциклоиды
2 2 2.
х3 +>3 =а3,
нормаль которой дается уравнением:
у cos х — х sin х = a cos 2х, 4
где х — параметр.
2 г 2
Отв. (х+>)3 +(х— = 2а3.
11. Найти огибающую кругов, проходящих через начало и имеющих центры на гиперболе
х2-у2 = (*.
Отв. Лемниската (х2 -|-у2)2 = 4с2 (х2 — _у2).
12. Найти огибающую прямой, образующей на осях отрезки, сумма которых равна с.
1 £ 1 Отв. Парабола х3+у2=с*.
13. Найти огибающую семейства эллипсов Ьгх3 + а3у* = л263, если с^тма ил полуосей равна с.
Черт. 154.
_2 £ 2.
Отв. Гипоциклоида xs + ys =с3.
т4. Найти огибающую эллипсов, оси которых совпадают, причем расстояние между концами большой и малой осей сохраняет постоянную величину, равную /.
Отв. Квадрат, стороны которого выражаются уравнениями (х с!:у)3 = Р.
15. Ядра выбрасываются пушкою с начальной скоростью о0. Предполагая, что пушке может быть дано любое наклонзние и что опа находится всегда в одной и той же вертикальной плоскости, найти огибающую всевозможных траекторий, пренебрегая сопротивлением воздуха.
Указание. Уравнение любой траектории есть
. 1 FX3
> = xtga-—, 2t>0 cos3 a
где a — переменный параметр.
Отв. Парабола у = ~(черт. 154). 2g 2о0
16. Найти уравнение огибающей каждого из семейств кривых, заданных нижеследующими уравнениями, где t — переменный параметр:
а) (х-0»+у»=1-Л
Ь) х« + (у-Л2 = 2Г.
с) (х-Па+>3= -2-<2-1-d)x3 + b'-02 = |f.
е) у = tx + Р.
f; х = 2ty + Р.
Е) У = tx + у-
h) y3 = t(x + 2t).
1) (х— 0s + J2 = 41.
j) x2+ty-i)2 = 4-/2.
к) (х-П2 + (у-02 = А
1) (X-/)2 + (y + 02=^
n) y = t(x- 21).
о) х = -^ + /.
Р) (x-/)2 + 4j2 = f.
ГЛАВА XVII.
РЯДЫ.
§ 166. Бесконечные последовательности. Последовательность чисел ип «2 ,.. .. называют бесконечной, если за каждым членом
этой последовательности имеется еще один. Такова, например, последовательность целых чисел 1, 2,..., л,...
Сказать, что последовательность задана, эт0 значит сказать, что дан способ вычислить каждый член, когда известно его место, вычислить ип, когда дано л; таковы, например, последовательности:
I2, 22, З2,..., л2,...,
2, 4, 8, .... 2я,...,
12 3 л
2’3’4 л+1’"”
УПРАЖНЕНИЯ.
Написать n-й член нижеследующих последовательностей:
1. 1,3,9,27,... 2. — а, + а2, — а2, + а4,... - X2 Xя .г4 3' х,~2‘ 3 ’ 4 • •• 4. 4,-2,-f-1,-1,... Зу 5v3 7v3 2 ’ 5 ’ 10 Отв. 3я 1 (-а)п. _1" л 2л + 1 л л2+1 У '
Выписать четыре первых члена каждой из последовательностей, л-й член которых дан ниже:
1. пгх£ Отв. х, 4№, 9хя, 1бх*.
2. —Отв. *, 1+/л 2 1 + V 2 1 + /3 1 + V4
-,3 4 5 6
Ота. 2 ’ э > 28 ’ 65 •
12 11 2 ’ 4 ’ 6 ’ 16
С изменением п меняется и ип\ можно сказать, что ип есть функция от п. Может случиться, что при неограниченном возрастании п величина иа будет иметь своим пределом некоторое число А:
lim и=А.
П+.-О Я
Мы скажем тогда, что последовательность и.2,..., ип,.. . имеет число А своим пределом. Так, например, из написанных выше после довательностей третья имеет своим пределом нуль, а четвертая единицу.
Если на прямой линии мы расположим точки с абсциссами и,, и2,..., ып,...,то эти точки в конце концов все окажутся заключенными в отрезке с центром в точке А и как угодно малом. Вне такого отрезка будет находиться лишь конечное число точек последовательности (ср. § 33, черт. 26).
§ 167. Для заданной последовательности и,, и2....... ип,. . . чрез-
вычайно важно уметь установить, имеет ли она предел, даже если бы мы не могли точно вычислить величину этого предела.
Укажем ряд случаев, когда существование этого предела легко установить.
Допустим, что члены последовательности идут, все время возрастая или, вернее, не убывая, когда п неограниченно возрастает; другими словами, допустим, что для всякого п имеем:
“л+1 > "»•
Могут представиться два случая:
или и„ неограниченно возрастает вместе с л, т. е., как бы велико ни было число Р, члены последовательности, начиная с некоторого, сказываются все больше Р\ это именно имеет место в последовательности целых чисел 1, 2,...,л,...;
или же все числа , и2,..., гг„ ,... меньше некоторого фиксированного числа Q, и тогда ил при неограниченном возрастании п стремится к пределу А, меньшему или равному Q.
Читатель легко этому поверит; предложение это покажется ему достаточно правдоподобным, если он рассмотрит на прямой точки , и2,..., и„,..., абсциссы которых равны числам и,, иа,.... и„ .
Каждая точка по предположению правее предыдущей или совпадает с ней; значит, либо точки неограниченно удаляются, либо, если они должны все оставаться левее некоторой фиксированной точки Q, им приходится скопляться впереди некоторой точки А, к которой они неограниченно приближаются, или с ней совпадают; точка А находится левее Q или совпадает с Q.
Строгое доказательство изложенных фактов выходит из рамок этого курса.
Вот предложение, которое в силу его чрезвычайной важности мы здесь приводим, хотя и без доказательства.
Для того чтобы последовательность и1( и,,..., и,,,... имела предел, не-
обходимо и достаточно, чтобы каждому числу « соответствовало такое целое число р, что | ип — ит | < а для всех целых чисел п и т, превосходящих р.
Что это условие необходимо, вполне очевидно: если Um ип = А, то все члены п -> оо последовательности, начиная с некоторого, содержатся в интервале (Л — а, А + »); их взаимная разность меньше чем 2а, и, значит, достаточно тогда принять а<-^-. Что условие достаточно, это менее очевидно: ясно, однако, что если оно выполнено, то все члены последовательности, начиная с р-го, принадлежат интервалу (ир — е, Up-|-e), который так мал, как угодно; заменяя точками ип числа ип, мы предчувствуем, что точки и,, u2, ... , un, ... кончат тем, что сгруппируются около некоторой точки Л. Это можно доказать и строго.
§ 168. Вот примеры последовательностей, не имеющих пределов:
1, 2, 3,..., п,...,
—1, 2, — 3,1)"л,...,
О, 1, 0, 1,...,
'• I- 1+т>-- ,+&’ 2ГМ--
В третьей последовательности члены попеременно равны нулю и единице; они не могут неограниченно приближаться ни к какому числу.
В последней л-й член, если п четно, имеет вид 1 + , он очень бли-
эок к единице, если п. (или р) очень велико; если п нечетно, то л-й
1 „ Z
член имеет вид ; он очень близок к нулю, если л (или р) очень велико. Члены попеременно близки к единице и к нулю; нет постоянного числа, к которому ип неограниченно приближается, когда л неогра
ниченно возрастает.
Среди последовательностей, не имеющих предела, заслуживают внимания те, в которых ип неограниченно возрастает при неограниченном возрастании л; такова, например, первая из написанных выше последовательностей ; в этих случаях удобно говорить, что ия стремится к -|- оо, и писать lim и„ = оо; но надо твердо помнить, что это только обоз-п-юо
начение и что ия не имеет предела (см. § 39).
§ 169. Ряды. Когда бесконечная последовательность ult u2,..., и„,... задана, называют рядом символ
ы1 + ыа4" •••
е котором члены последовательности написаны с сохранением их порядка так, как если бы их прибавляли друг к другу; назы-
ваются членами ряда.
Обозначим через сумму л первых членов ряда;
5ж = «1 + «а+•••+«••
Если Sn стремится к определенному пределу 5, когда л неограниченно возрастает, то ряд называют сходящимся, и число S его суммой. Если же Sn не имеет предела, то ряд называют расходящимся', в этом случае он не имеет суммы.
Зак. 2709_В. Гранвиль и Н. Лузин. Часть t
23
Рассмотрим, например, ряд
а4-яг + а/'а+ • • • + лг’ + • • • »
члены которого образуют геометрическую прогрессию со знаменате* лем г; сумма п первых членов его
Предположим, что |r|< 1. Тогда
Значит, когда ]/'[<!, геометрическая прогрессия есть ряд сходя-fl щийся, и его сумма равна -j----
Напротив, ряд
1 4-1 4-1 + • • • 4-1 4- • • •
расходится, так как сумма его п первых членов равна п, т. е. неограниченно возрастает.
Но ряд .может расходиться и без того, чтобы Sn безгранично возрастало вместе с п. Таков, например, ряд
Здесь Sn либо единица, либо нуль, смотря по тому, будет ли п нечетное или четное; S„ при неограниченном возрастании п не стремится ни к какому пределу.
Так как сумма сходящегося ряда есть число совершенно определенное, тогда как суммы расходящегося ряда вообще не существует, то в любой задаче, где встречается бесконечный ряд, необходимо определить, сходится он или расходится. Это та же проблема, как и существование предела некоторой последовательности; вопрос сводится к тому, чтобы установить, стремится ли к какому-нибудь пределу, когда п неограниченно возрастает.
§ 170. Необходимый признак сходимости. Для всякого ряда «1 + «2+ •••+“»+•••
имеем:
= “14- • • • 4- «„-14-> sn- 1 «14- • • • 4- «н—1 >
а потому
Если ряд сходится, то S„ стремится к определенному пределу S; Snl стремится к тому же самому пределу, а потому их разность и„, т. е. П-й член ряда, стремится к нулю при неограниченном возрастании п.
Поэтому необходимое условие для сходимости ряда таково:
lim ип = 0.
П->оо
Другими словами, если n-й член ряда не стремится к нулю, когда ц. неограниченно возрастает, то ряд расходится. Таков, например, ряд у 1 -pi 4-1 -1-1 -j-...
Но это условие не является достаточным, т. е. если п-Л член ряда стремится к нулю, .мы еще не можем утверждать, что ряд сходится. В самом деле, так называемый гармонический ряд 1+12+4+---+4+---
расходится, хотя . .
Hm un = lira I — 1=0. n-х» n-юо \ tl /
Чтобы доказать расходимость этого ряда, напишем его в виде:
и для сравнения подпишем под ним ряд
Каждый член верхней строки больше или равен соответствующему члену нижней строки; но сумма членов, сгруппированных в каждой скобке нижней строки, равна */2; Поэтому сумму первых членов в нижней строке можно сделать как угодно большой, если только взять достаточное число членов; следовательно, и сумма п первых членов верхнего ряда неограниченно возрастает при неограниченном возрастании п, т. е. ряд расходится.
Необходимо упомянуть следующее предложение, вполне аналогичное теореме, которую мы привели без доказательства, когда говорили о пределах: для того чтобы ряд сходился, необходимо и достаточно, чтобы каждому числу t соответствовало такое целое число /и, что | Sn+p — Sn |< * для всех целых чисел л, превосходящих т, и для всех целых чисел р. Мы не будем опираться на это предложение и приводим его лишь ввиду его важности.
§ 171. Достаточные признаки сходимости. Сравнение рядов.
До сих пор мы рассматривали самые общие ряды. Остановим теперь наше
внимание на одном частном случае, а именно на рядах с положительными членами. Этот частный случай тем более важен, что, как мы увидим
в дальнейшем, к нему приводится огромное большинство других случаев.
Итак, пусть
«1 + ца4- • • • + “» + • • •
ряд с положительными членами; ясно, что при всяком п имеем:
•^n+i >\>
поэтому возможны Два случая: либо S„ неограниченно возрастает при неограниченном возрастании п, и тогда ряд расходится; либо су^ма п первых членов остается при всяком п меньше некоторого постоянного числа А; в этом случае ряд сходится, и его сумма меньше или равна А (см. § 169).
Это замечание приводит нас немедленно к следующему способу узнать, сходится или расходится ряд с положительными членами.
Пусть
+ ••• (V)
ряд с положительными членами, относительно которого мы знаем, сходится он или расходится; сравним с ним данный ряд:
И1 ~\~и2 + • • • Ч" Un Ч- • • • (и)
Допустим, что ряд (v) сходится, и пусть для всех значений п имеем un^,vn'i тогда ряд (и) тоже сходится, потому что сумма его первых п членов не больше суммы п первых членов ряда (v) и, следовательно, его суммы v, значит, сумма ряда (и) не превосходит V.
Допустим, что ряд (v) расходится и что для всех значений п имеем сумма п первых членов ряда (v) может превзойти любое положительное число; и подавно это будет иметь место для ряда (и), значит, он расходится.
Пример 1. Исследовать ряд
Решение. Каждый член данного ряда, кроме первого, меньше соответствующего члена геометрической прогрессии:
2 ' 22 23 21 2а 2'*
а этот ряд сходится (§ 169), следовательно, и данный ряд сходится.
Пример 2. Исследовать ряд
Решение. Этот ряд расходится, так как его члены больше соответствующих членов гармонического ряда, который, как мы видели в § 170, есть ряд расходящийся.
§ 172. Признак сходимости Даламбера. Принимая за ряд (v) геометрическую прогрессию с положительным знаменателем, мы приходим к одному чрезвычайно удобному для практики признаку сходимости, открытому Даламбером.
Рассмотрим отношение п 1-го члена ряда к n-му, т. е. отношение
Допустим, что
U ,. lim —= р. »4->ОО ип *
Нам придется различать три случая:
1. Если р < 1, то ряд сходится. В самом деле, как только п ста-“n+t
нет достаточно большим, отношение —— будет заключено в интервале «я
(р — е, р-f-е), где е — очень малое число. Поэтому, полагая г = р-|-е, имеем для всех п, начиная с некоторого т, неравенство:
поэтому
“m+l < rUm I «т+2 < Г“т^ i “m+3 < 'Ч. I • • •
Следовательно, каждый член нашего ряда, начиная с /71-[-1-го, меньше соответствующего члена геометрической прогрессии
которая сходится, так как г<1 (г как угодно мало отличается от р, а р< 1, значит, и r< 1). Поэтому и данный ряд тоже сходится1).
2. Если р> 1, ряд расходится. В самом деле, как только п станет достаточно большим:
как бы мало ни было е, значит, -Д^> 1, т. е. и ,, > следова-’ Цп нт*
тельно, члены ряда идут возрастая, т. е. не могут стремиться к нулю при неограниченном возрастании п, значит, ряд расходится.
]) При исследовании вопроса о сходимости ряда мы имеем право не обращать внимания на любое конечное число первых членов. В самом деле, сравним между собою два ряда
И1 + и2+ ... +om + «w+i + «„l+a+ ... и
Ит+1 + “я»+2 + •1 •
Докажем, что эти ряды или одновременно сходятся, или одновременно расходятся. Действительно, если есть сумма п первых членов первого ряда, a — сумма л первых членов второго ряда, то
Так как при неограниченном возрастании п величина т не меняется, то либо lira 5П существует, тогда существует и Um sn (и обратно), либо оба эти предела одновременно не существуют.
3. Если р=1, ряд может и сходиться и расходиться. Это легко видеть на следующих примерах.
Рассмотрим для различных значений р ряд:
! + 2?+ 3P+4P-F + (л_|_ !)₽+•’•
Отношение “„+1 1
\ "Г" п ) поэтому . . .
/«„.Д 1 1
lim = lim7--------------П₽=р=1( = р)-
П->оо \ и>п / 11-Ко / | I * j А
Следовательно, при всяком р, будет р = 1. Но мы сейчас увидим, что при р 1 ряд расходится, а при р > 1 он сходится. В самом деле, если р=1, данный ряд обращается в гармонический, расходимость которого уже была доказана. Если р<С,1, то члены данного ряда больше соответствующих членов гармонического ряда, значит, он расходится.
Наконец, если р > 1, имеем:
при р > 1 представляет геометрическую прогрессию со знаменателем, меньшим единицы, и, следовательно, сходится. Но сумма первых членов данного ряда меньше соответствующей суммы для этой прогрессии, как показывают предыдущие неравенства, поэтому данный ряд сходится.
Мы убедились, что в случае, когда р= 1, признак Даламбера не решает вопроса о сходимости ряда; здесь нужны более тонкие исследования, выходящие из рамок этого курса.
Пример 1. Исследовать вопрос о сходимости ряда
1 + Т + Ь2 + 1-2-3 + 1 -2-3-4 + • • • + 1-2...(л—Л) + 1 -2...Л + ’' *
Решение, л-й член есть
следовательно:
/"п+1\ { 1
11m _Д±1 = пт —— --------
n-юо \ / n-ко \ I • 2 • 3... п
1
~2...(л — 1)
_v ( 1-2-3...(л-1)
=Л« ( 1-2-3...(Л-1), л
,im =0 ( = ₽)’ п->оо у п /
поэтому, в силу случая 1, ряд сходится. Сумма его равна неперову числу е. Пример 2. Исследовать ряд
1 I 1 '2д. 1 -2'3 ! '
10 + 10^ + 103 + ••• Решение.
поэтому
(ип+Д .. /1 • 2.. .л (л +1) 1-2-3...л
hm I —— I = lim I-----------—------:----------
»>со\ и ] „-юо у юп+1 ю"
1-2-3.. .л (л + 1) • 10”\ --------------1 = hm
1-2-З...Л-10’,+1 / tw-oo
и в силу случая 2 ряд расходится х).
Пример 3. Исследовать ряд
1 -2^3-4^5-6^ Решение.
_ 1
11,1 — (2л — 1) 2д ’ поэтому
. .. /мп+1\_ .. Г (2л-1)2л 1
п-^ \ «„ ) ,£> (2л + 1) (2л + 2)]
Признак Даламбера ничего не дает. Но сходимость ряда можно доказать, заметив, что его члены меньше соответствующих членов ряда:
1 + 22 + 32 + 43 + >
в этот ряд сходится (ср. пример в случае 3, полагая р = 2).
§ 173. Ряды с чередующимися знаками. Так называют ряды, в которых члены попеременно положительны и отрицательны; таков будет ряд:
Ki — иа~}~ив— яа+---+(— Ч»+• • (“)
если предполагать, что все числа к,, щ,..., ия,... положительны.
Если
и .
lim ил = 0, п>ос
то ряд (ц) сходится, и его сумма 5
1) Можно было бы убедиться в расходимости этого ряда, доказав, что ип
не стремится к нулю с возрастанием л. Это имеет место и во всех случаях,
когда признак Даламбера указывает па расходимость.
Доказательство. Рассмотрим сумму S2n первых 2п членов ряда; ее можно написать в двух видах:
52П = («I — «2) + (“з — — «<;)+•••+ («2п-1 — И2,.)
И
S2n =U!- (U2 - «.)-(U^Ub)~ (U2n_2 - U^) - U*
Каждая разность в скобках положительна (или равна нулю).
Поэтому из первой строки мы видим, что 52я есть величина поло- ' жительная (или равная нулю) и возрастает вместе с л; из второй строки видно, что S2|| Up Положительные величины S2n возрастают с л, оставаясь все время меньше числа и^, значит (§ 167), они стремятся к определенному пределу S, меньшему или равному uv Равенство
"*2n-f-l = ^2П 4“ И2»>4-1»
в котором и2„+1 стремится к нулю при неограниченном возрастании п, показывает, что и S2n+1 стремится к тому же пределу S; значит, данный ряд сходится и имеет S своей суммой.
Замечание. Если мы примем сумму S равной сумме л первых членов ряда и, — в,-}- ... -|-(— l)”-1un, то мы сделаем ошибку, абсолютная величина которой будет меньше ип^, так как отброшенный нами ряд есть тоже знакочередующийся, и его первый член есть (—l)"un+1, а потому его сумма по абсолютной величине меньше или равна Un+1.
Пример. Исследовать ряд с чередующимися знаками
1 — — 4--— — + ..
2 г 3 4
Решение. Так как
lim ип = lim — = 0, п->со П->СО Л
то ряд сходится. Если принять его сумму равной
Z о п
мы сделаем ошибку меньше, чем
1
п + 1’
§ 174. Абсолютная Сходимость. Ряд называется абсолютно или безусловно сходящимся, если сходится ряд, полученный из данного заменой всех членов их абсолютными величинами (иначе говоря, заменой всех минусов на плюсы).
Таков, например, ряд:
i_2._l.1_2
2а “ о® 44 ~
Этот ряд сходится абсолютно, потому что ряд
1-!_1 -lIj-1 X
1 2а ~ З2 ‘ 4а '
сходится (§ 172).
Чрезвычайно важным является следующее предложение, которое мы приводим без доказательства.
Всякий абсолютно сходящийся ряд есть ряд сходящийся.
Эта теорема позволяет для широкого класса рядов свести вопрос об их сходимости к вопросу о сходимости ряда с положительными членами. В самом деле, заменив все члены ряда их абсолютными величинами, мы получим ряд с положительными членами; допустим, что, применив к нему один из признаков сходимости для рядов с положительными членами, мы доказали его сходимость; тогда и данный ряд сходится.
Не следует, однако, думать, что сходимость всякого ряда, члены юторого и положительны и отрицательны, может быть исследована та-Мш способом; в самом деле, существуют ряды, которые сходятся без того, чтобы сходиться абсолютно. Такие ряды называют условно или не абсолютно сходящимися.
Например, ряд
сходится (§ 173), но не абсолютно, потому что ряд
1J- —+ —+ —+ ••• ' 2 3 4
расходится.
УПРАЖНЕНИЯ.
Применив признак Даламбера, показать, что нижеследующие ряды сходятся:
, 1,2,3,4 Д1.1.1д_
!• 2 "Ь 2» "Ь 23 + 24 ‘ 4. 1 , 2! + 3! + ' ’
о 1 1-3 1-3-5 , ,.2,2-5, 2-5-8 . 2-5-8-11 ,
3 *’3-6 + 3-6-9+1 +1-5+1-5-9 + 1.5-9.13+”*
3‘ 1-2-3 + 1-2-3-4-5 6' "з + 9+27“*"'•*
+ 1 -2...7 + ‘
Путем сравнения рядов показать сходимость нижеследующих рядов. Показать также, что признак Даламбера для этих рядов неприменим.
7. 1+—1— +_L= + —1—+...
Указание. Сравнить с рядом
1 +— + -1-т 2Р ЗР
Указание. _ 1 _ 1 1
"п ~ л (л 4- 1) ~ л2 4- п< п‘1'
Показать, что нижеследующие ряды расходятся.
У к а з а и в е.
у+т+у+--- =4(1 + т+у+---)-
П L2 + L±JJ +
10 ' 10» ' 10s Г"'
Указание. Применить признак Даламбера.
У Казани е.
_ 1 + л 1 4- л _ 1
“п ~ 1 + л’-^ 1 + 2л 4- л» “ 1 + л •
13.2+4+4+---н-г+4+4+А+-
Указание.
±+±>1. л л2 ^л
Выяснить, какие из нижеследующих рядов сходятся абсолютно и какие не абсолютно:
15 i-l+l_±+l_ З2 ' 5» 9»
„ * . 1 1 1
Сходится абсолютно, так как | | = ija <
16 ±-1 1+1 1-1.1 +
2 2 2»"*'3 2s 4 2*"Г’”
17 _!__L 4-—__,
1п2 In Зт In 4
, । 1 1 , 1
+ Г2 /3+ /4
,n sin а , Sin 2а , sin За , 1У* 1 + 4 + 9 +••• л , [sin ла| . 1
Сходится абсолютно, так как и_ | =-5— < —г.
" п* п*
'-т+|-т+т-•••
»• Н4У
Указание. См. задачу 9.
ГЛАВА XVIII.
РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯДЫ.
§ 175. Ряды функций. В предыдущей главе мы рассматривали ряды, членами которых были постоянные числа. Мы переходим теперь к более общему случаю, а именно, будем предполагать, что члены ряда являются функциями переменного х.
Пусть
/а(х),..., Д(х),...
бесконечная последовательность функций, определенных на отрезке [а, д]; составим ряд
А (х) +Л W +/. (X) 4-... 4-А (х) +... (t)
Когда х принимает определенное значение, например х = х0, каждая функция /,(х), /2(х),..., /о(х),... принимает тоже определенное значение Д (х0), /2(х0),..., /п(х0),..., так что ряд (f) превращается в уже знакомый нам числовой ряд. Для различных значений х мы имеем, вообще, различные числовые ряды. Эти ряды при некоторых значениях х могут сходиться, при других расходиться. Если ряд (f) сходится при всех значениях х отрезка [а, 6], говорят, что ряд сходится на отрезке [а, 6]; тогда его сумма будет функцией х, которую можно вычислить с наперед заданной точностью для всех х на отрезке [а, Ь\.
Если F(x) есть эта функция, то можно писать:
F W =л (X) 4-Л (х) +... +Л (X) + ...
Обратно, если дана функция F(x) и если мы умеем найти ряд (I), который сходится для всех значений х на отрезке [а, Ь] и его сумма для каждого значения х равна F(x), то говорят, что г(х) разложена
Так, например, в § 169 главы XVII мы видели, что геометрическая прогрессия с первым членом а и знаменателем г, где
|Г| < 1, а _ сходится и имеет сумму • _Поэтому для всех значений х отрезка
[—a, 4“a]i гАе с — положительное число, меньшее единицы, ряд
14-л+х»4-...4-х"-|-...
сходится, н его сумма равна .
Мы можем написать:
г±_=1+х + л2+...4_х«+...
и сказать, что правая часть равенства есть разложение левой части в ряд по целым положительным степеням х.
§ 176. Степенные ряды. Среди рядов, членами которых являются функции переменного х, важнейшую для анализа роль играют ряды вида: + + ••• (а)
Здесь а0, ап,... — постоянные числа, которые называют
коэфициентами ряда-, ряд называется степенным, так как члены идут по возрастающим степеням х; он вполне определен, когда дана последовательность его коэфициентов.
Рассмотрим ряд с положительными членами, составленный из абсолютных величин коэфициентов данного степенного ряда, т. е. ряд
I aol + 1 I + | <4.1 + • • • + I ап 1+ • • •
Предположим, что существует вполне определенный предел отно-
шения
а ,.
п+1
а„
; пусть, следовательно:
где L — вполне определенное конечное число. Тогда
lim 1а"+1Л + I Ifln+1 I |х|_/ I у| lim —; й-— = Пт — — л = L х , п-хо | апХ | n-х» | аП |
при ВСЯКОМ X.
Поэтому в силу признака Даламбера ряд с положительными членами
l*ol + l*i*l + ... Н-|пХ1 + ••• • (а*)
сходится, если только
L И < 1,
а, значит, данный степенной ряд сходится абсолютно, если L |х| < 1-Отсюда следует, что при £ = 0 степенной ряд сходится абсолютно при всех конечных значениях х; если же L ф 0, то он сходится абсолютно для всех тех х, для которых
1
т. е. для значений х, заключенных в отрезке
2_' L
. Этот отре-
L’
зок называют интервалом, сходимости. Покажем, что вне этого интер-
вала, т. е. когда
1*1
1
L •
ряд расходится.
В самом деле, тогда члены ряда (а*), начиная с некоторого, идут возрастая, ибо
г это выражение при достаточно большом п близко к А|х|>1.
Поэтому п-й член ряда (а*), а следовательно, и ряда (а), не стремится к нулю, значит, ряд (а) расходится.
Наконец, если
1
£’
то о сходимости или расходимости ряда ничего нельзя сказать. Другими словами, в концевых точках интервала сходимости ряд может и сходиться и расходиться. Например, ряд
л2 . № х* .
х~2- + — Т+-
имеет интервалом сходимости отрезок [—1, 1]. Действительно, ряд
абсолютных величин его коэфициентов есть гармонический ряд
1 + ~2 + У + ••+у+ •••
Поэтому
Iа I /1 1 \
lim — + ,- = lim I —г—г : — 1 = 1 (= L).
П>оо | I п->оо \Л “р 1 П )
Значит, данный ряд сходится абсолютно, если — 1 < х < 1; он
расходится, если х < — 1 или х > -|- 1.
Если х = — 1 или же х = 4~ 1» сразу ничего сказать нельзя. Но при х = — 1 наш ряд обращается в
_ J__J_____________L_
2 3 4 ” п
т. е. в ряд, получаемый из гармонического заменой всех плюсов на ' минусы; ясно, что он расходится. Напротив, при х = -|-1 получается
ряд с чередующимися знаками
1-L+-1— 1
2^3 4
° ♦»
а этот ряд сходится (см. § 173 предыдущей Черт’ 155,
главы). Графически мы представим интервал сходимости этого ряда, как это сделано на черт. 155.
Концевые точки интервала отмечены кружками, если в них ряд сходится: в данном случае кружком отмечена точка -|- 1» так как ПРИ X = 4" 1 ряд сходится.
Замечание. Мы сделали предположение, что 11m ’,есть конеч-|вл|
ное число L. Если предположить, что при неограниченном возрастании п отпо-I Ял4-1 I
шение — , тоже неограниченно возрастает ’). то ряд расходится при всех
I ап I
значениях х кроме х = 0, потому что его п-й член при всяком х кроме х = 0 неограниченно возрастает по абсолютной величине.
Случай, когда отношение не стремится ни к какому пре-
делу, мы здесь не рассматриваем.
УПРАЖНЕНИЯ.
При каких значениях переменного сходятся следующие ряды:
Графическое представление интервала сходимости.
1. 1+х + х’ + х’+...
Отв. — 1<х<4-1. х2 х3 х* - х — 2а + 4» + • • •
Отв. — I < х < 1.
Отв. — 1<х<1.
4. 1 + х -j- j—j + утугз + • • • Отв. Все значения х.
5 1 92 | _____——4
°’ 1-2^ 1-2-3-4 1-2-3...6 '
Отв. Все значения в.
5 ф____У3- - I ______________?1__
т 1-2-3 ' 1-2-3-4-5 1-2...7
Отв. Все значения <?.
, sin a sln3a , Sin5a
7- “1- 3~ + ~5, — ~ • • •
Отв. Все значения a cosx . cos2x cos3x .
«• -77- + -^--+^—+•••
С me х>0. л i j । 1 *г1п2а . х31п3я ,
” | + '|"«+-ПТ + П2Тз+-
Отв. Все значения х.
Черт. 166-164.
!) Можно считать, что тогда lim - , । = 4- оо.
п->оо |в„|
10.
1 х2 1 -За5 1.3-5 .г’ , 2 3 + 2 • 4 5 + 2 • 4 • 6' 7
Отв. -1<х<1 1).
1к 1+х + 1 + хг+1+л-з+---
Отв. х > 1.
12. 14-х + 2л-2 + Зх’+...
,, X3 . хб х’
13’ х 3 + 5 7 + •••
14. 10х + 100x2 + 1 ОООх’Н- ...
Графическое представление интервала сходимости.
0 *1
Черт. 165 и 166.
15. 1 + х + 2! х2 + 3! Xs + ...
16. х + х^ + х® + х1® + ...
§ 177. Разложение Функций в ряды. Часто случается, что заданная функция /(х) выражается через аргумент х при помощи такого действия, которое мы не умеем произвести непосредственно над числовой величиной независимого переменного х; таковы даже элементарные трансцендентные функции, например:
sinx, cosx, Inx, еТ и т. д.
Для того чтобы иметь возможность вычислять величины таких функций при заданном значении переменного, мы постараемся найти для них разложения в степенные ряды и заменить, таким образом, недоступное нам прямо трансцендентное действие некоторым конечным (хотя иногда и большим) числом элементарных действий (сложений и умножений).
Задача, следовательно, ставится так: дана функция /(х); требуется найти такой степенной ряд, который сходится (хотя бы в некотором отрезке) и имеет суммой функцию /(х). Если такой ряд найден, мы пишем:
/(х) = а0 + ахх + а,х9 + • • • + + • • •
То, что ряд сходится в данной точке х0 и имеет суммой /(х0), это по самому определению сходимости ряда значит, что
lim [a0-f- ахх0+ ... 4-апх"1 =/(*<»); п->со
другими словами, взяв достаточно большое п и вычислив величину а0-|-а1х0+ ... +апХо, мы будем иметь приближенно величину /(xj, причем можно получить приближение с любой наперед заданной степенью точности.
Ближайшей нашей целью явится указание способа, который позволит разлагать в степенные ряды целый обширный класс функций. Этого мы достигнем с помощью рядов Тейлора и Маклорена.
*) Сходимость этого ряда при х = zt 1 мы оставляем недоказанной.
§ 178. Ряд Тейлора. В § 138 главы ХШ мы познакомились с формулой Тейлора. Если в этой формуле заменить букву b буквой х, то она примет вид:
/ W =/(«)+(а) + (“)+(«)+•••
J___а\________ /-(’«-I) (д) I_(Х Д>_ f(n) ( к
1 1 -2-3...(л— I)7 1 1 -2.3... п/ 1 Ш
где хх лежит между а и х.
Эта формула дает изображение /(х) в виде суммы некоторого многочлена, расположенного по степеням (х— а), и добавочного члена, называемого остаточным членом,
(Х а) f(n)( х
1-2-З...Л7
Этот член существенно отличается от остальных, потому что число х, зависит от х, тогда как в остальных членах степени разности (х — а) помножены на постоянные коэфициенты.
Сделаем теперь предположение, что этот остаточный член стремится к нулю при неограниченном возрастании числа п, т. е.
Ita
П->оо А Д
В таком случае из формулы Тейлора получаем равенство: /
/(x) = lim /(а)
П->00
х а (х — д)2
(х —Д)п1
1 -2... (л — 1)
I т
(п-1,(а)
Поэтому, если мы рассмотрим степенной ряд, расположенный по
степеням х—а:
то предыдущая формула покажет, что он сходится и имеет суммой /(х), так как /(х) есть как раз тот предел, к которому стремится сумма п первых членов ряда при неограниченном возрастании л.
Мы имеем тогда право писать:
/W -/(«)+X~rf "(«)+••• + .“’"/"(а)... (И)
Степенной ряд, стоящий в правой части равенства (II), называется рядом Тейлора1) для функции/(х). Говорят, что данная функция/(х) разложена в ряд Тейлора.
!) Обнародован доктором Брук Тейлором (1685- 1731) в его „Methodus Incrementorum**, London 1715.
Очень важно обратить внимание на следующее обстоятельство: если только данная функция /(х) имеет в точке а производные всех порядков, то ее ряд Тейлора формально всегда может быть написан, так как известны тогда все его коэфициенты /(а), /'(а),/" (а),...,/<п) (а),... Но не следует думать, что этот ряд обязательно должен сходиться к функции /(х). Прежде всего он может оказаться расходящимся для некоторых значений х (или даже для всех значений х, кроме х = а); далее, может оказаться, что он сходится, но его сумма не равна данной функции /(х). Из равенства
следует, что если остаточный член стремится к нулю, ряд Тейлора сходится к функции /(х); если остаточный член стремится к определенному пределу, отличному от нуля, то ряд сходится, но не к функции /(х), и, наконец, если остаточный член не стремится ни к какому пределу или если он неограниченно возрастает, то ряд расходится. Следовательно:
ряд Тейлора изображает функцию / (х) для тех и только для тех значений х, для которых остаточный член формулы Тейлора стремится к нулю при неограниченном возрастании числа п.
Из сказанного следует, что, для того чтобы пользоваться рядом Тейлора для вычисления величины функции /(х), недостаточно еще уметь написать его, т. е. вычислить или просто знать все его коэфициенты. Необходимо исследовать остаточный член и пользоваться рядом Тейлора для вычисления /(х) лишь для тех значений х, при которых этот остаточный член стремится к нулю.
Напомним еще раз, что остаточный член формулы Тейлора
1-2...П7
где X} лежит между а и х, не следует смешивать с общим членом ряда Тейлора
<х—°) у<»)(а),
1 • Z. . .71
Если остаточный член стремится к нулю, то ряд Тейлора сходится и сумма его равна /(х), тогда как, если общий член стремится к нулю, ряд может даже и расходиться.
К сожалению, исследование остаточного члена формулы Тейлора нередко представляет существенные трудности. Поэтому обычно стараются тем или иным способом обойтись без этого исследования, пытаются косвенным путем доказать, что ряд Тейлора сходится именно к функции /(х). Мы не имеем возможности указывать здесь те способы, которыми этого достигают.
24 Зак. 2709. — В. Гранвиль н Н. Л уз ив. Часть I
Пример 1. Разложить inx по степеням х — 1. Решение.
/(х) = 1пх, /(1) = 0.
У’(х) = -^, Г(1) = -1.
2
' Г'(х) = р. /"'(!) = 2.
/<"’ (х) = --1)Т1 /(л) (1) - (-1)”“* 1 • 2 • 3.. .(л - 1).
Подставляя в (II), находим:
!пх= (х—1) —— (х—1)г-[--i-(x —I)8—... л О
Остаточный член имеет вид:
(х-1)" ,_ пп-1 Ь2-3...(л-1)в ( - I)""1 / х-1 1-2*3... л . х” л \ хх
где xt заключено между 1 и х.
Отрицательные значения х мы не будем рассматривать, так как для них 1п х не имеет смысла. Если 1<х<2, то х—1<1, а так как 1<х,<х, х j 1
то------< 1, и остаточный член по абсолютной величине меньше, чем—,
хг л
т. е. стремится к нулю, когда л неограниченно возрастает. Поэтому ряд Тейлора сходится к Inx при 1<х<2. Аналогичное можно было бы доказать и для 0<х<1, но для этого пришлось бы брать остаточный член в несколько иной форме. Если же х>2, то можно легко доказать расходимость ряда, потому что его члены уже не будут стремиться к нулю. Для х = 2 ряд обращается в уже знакомый нам сходящийся ряд:
Мы видим теперь, что его сумма равна In 2.
Когда дается функция суммы двух чисел а и х, т. е. /(а-]-х), то часто желательно иметь разложение функции по степеням одного из этих чисел, например х. Для этой цели употребляют ряд Тейлора в другой форме, получаемой из (И) заменою х на а-|-х, а именно:
/(а + х) =/(а) +(а) + ^У' (а) + (а) + * * - (И!)
Пример 2. Разложить sin (а х) по степеням х.
Решение. Имеем:
л /(a + x)«=Bin(fl + x).
Отсюда, полагая х «= 0:
/(л) = line, /'(в) = соав, f (в) я» — sin a, /w(a)«t —созя,...
Подставляя в (III), получаем: X х^
sin (д -|- х) = sin а -|- у cos а — j—sin а
П273 С£”а+-'
§ 179. Формула Маклорена и ряд Маклорена. Если в формуле Тейлора (I) положить а = 0, мы получим так называемую формулу Макл орена:
X х^ х$
f (X) =f (0) 4- у f (0) + ^/" (0) + (0)4-...
1 1 • X 1 ' Z ' О
где х, лежит между 0 и х. Это — частный случай формулы Тейлора. Правая часть есть сумма некоторого многочлена, расположенного по возрастающим степеням х, и остаточного члена.
Положив а = 0 в формуле (П), получим ряд Маклорена1)*'
/(х) =/(0) -4 (0) 4- ^/"(О)+т^тз/w (°) + • • • м
Эр— весьма употребительный частный случай ряда Тейлора, и потому все, что сказано было об остаточном члене и о сходимости ряда Тейлора, сохраняет силу и для ряда Маклорена.
Хотя ряд Маклорена имеет более простой вид, чем ряд Тейлора, и потому пользоваться им для вычислений легче, но это не всегда возможно. Так, например, In х может быть разложен в ряд Тейлора по степеням (х—1) (см. пример 1 предыдущего параграфа), но его нельзя разложить в ряд Маклорена, так как и сам 1пх, и все его производные обращаются либо в —оо, либо в -|-оо при х = 0, а потому не могут быть подставлены в качестве коэфициентов ряда.
Прежде чем переходить к примерам разложения в ряд Маклорена, укажем, каким образом для широкого класса функций может быть доказано стремление к нулю остаточного члена формулы Маклорена и, следовательно, сходимость ряда Маклорена к функции /(х), разложенной в этот ряд.
Допустим, что все производные /(я)(х) п0 абсолютной величине меньше некоторого постоянного положительного числа Р, каково бы ни было х и каково бы ни было целое число п. Тогда остаточный член по абсолютной величине меньше, чем
1 • 2...1Г
Iх поэтом* 172^3
Но ряд
1 - Ь — 4- - J-----—------1- .. . -!------------L...
' 1 ^1 *2^ 1 *2*3 ‘ ' 1 -2-З...Л
сходится, как показывает признак Даламбера, для всех значений х.
стремится к нулю при всяком х; Р — число
постоянное, поэтому остаточный член стремится к нулю np:i всех значениях х, т. е. ряд Маклорена сходится к /(х) при всех значениях х.
’) Назван по имени Колина Маклорена (1698—1746) п впервые опубликован в его .Treatise of Fluxions*, Edinburgh 1742. В действительности этот ряд дан Стирлингом (1692—1770).
24* t
Пример. Разложить cosx в ряд Маклорена и доказать, что этот ряд сходится при всех значениях х именно к cosx.
Решение. Сначала последовательно диференцируя, а потом полагая х = О,
найдем: /(х) = созх, /(0)=1. /'(х) = —sinx, /,(0) = 0. f" (х) = — cos х, f" (0) = — 1. (х) =г sin х, f" (0) = 0. /Iv(x) = cosx, /IV(0) = l. /v (x) = - sin x, /v (0) = 0. /VI(x) = - cos x, fNl (0) = - 1. И T. д. и T. Д.
Подставляя б (VS имеем:
, X2 . X1 X* . 1-2’1.2-3-4 1-2 -3-4-5-6 1
Остаточный член стремится к нулю при всех значениях х, так как (х) = = zt cos х или zt sin х (смотря по тому, чему равно л), и, следовательно, для всех л и для всех х, |/<п) (х)|С1. Поэтому в силу только что сделанного замечания ряд сходится именно к cos х для всех значений х.
Подобным же образом найдем разложение для sin х:
sin г-х-Г^з+-Г2.^4 75-- 1.9^..7 + • • •
Доказательство того, что этот ряд сходится именно к sin х для всех значений х, было бы полным позтореиием того, Что сказано относительно ряда для cos х.
УПРАЖНЕНИЯ *).
1. Разложить е® по степеням х —2.
Отв. е® = еэ + ез (Х_ 2) + (х- 2)= + • • •
2. Разложить х3 — 2х2 -|- 5х — 7 по степеням (х — 1).
Отв. - 3 + 4 (х - 1) + (х - I)3 + (х - I)3.
3. Разложить 3_у3 — 14_у-|-7 по степеням разности .у —3.
Отв. - 8 + 4(> - 3) 4- 3 СУ — ЗА
4. Разложить 5г2 + 7z + 3 по степеням разности г — 2.
Отв. 37 + 27 (г - 2) + 5 (л - 2)3.
5. Разложить 4х3—17х3 4-11x4-2 по степеням разности х — 4.
6. Разложить бу1-}-бу3 — 17_у2-|-18у — 20 по степеням j'4'4.
7. Разложить е® по степеням х4~ 1.
8. Разложить sin х по степеням х — а.
9. Разложить cos х по степеням х — а.
!) Исследование остаточного члена ввиду представляющихся при этом исследовании трудностей обязательным при решении нижеследующих задач не предполагается.
10. Разложить cos (а + х) по степеням х.
Отв. cos (а -|- х) = cos а — х sin а —z—= cos а + — —= sin а 4-1*2 1 • л • «5
11. Разложить In (х + й) по степеням х.
Отв. In (х + й) = 1пй + -£ .
12. Разложить по степеням й функцию
1+Л + £ + £+£+
13. Разложить по степеням й функцию (х 4* й)”
Отв. (Л + л)’* = Л" + лЛп-1х + —"~1\"~8лг +
+ ^n-l>ln-2)w-1J +
1 • Z • О • • •
Сходится при I X I < I й |.
Замечание. Это разложение верно, каково бы ни было л: целое, дробное или иррациональное, положительное или отрицательное. Когда п — целое положительное число, ряд обращается в конечную сумму, и мы получаем известную из алгебры формулу бинома Ньютона.
14. Разложить cos х по степеням разности х — у.
1 1 ( ъ\ 1 / я\2 , 1 / п\з ,
Отв. COSX = —т=----7=(Х — _------7= х---7 4----— X------ 4" • • •
/2 /2\ 4/ 2/2\ 4/ 6/ 2 \ 4/
15. Разложить V х по степеням разности х —4.
Отл 2 1х-4 (-г-4)1 . (х-4)8
Ome.Vx- 2 4- -j---------64^+“512-----------
16. у = /(х);. полагая by=f(x + dx)-f (х), показать, что
а w . <^У f <&У । । <**у ।
Aj = rfy + ^f4--3f + ••• +-#+•••
Решение.
, , , . х (х) dx* , f"' (х) ЛгЗ ,
/ (х 4- dx) =f (х) 4-Г (х) dx 4- —^21-г—-------1---
Замечая, что f (х) dx = dy, f" (x) dx- = d*y и т. д. н перенося] f (х) из правой части в левую, получаем требуемое разложение.
Проверить нижеследующие разложения функций в ряд Маклорена и доказать их сходимость к данной функции для всех значений х:
_ г X® X® х^
17л е® = 1 4- у 4-уту 4-ртутд4*
Решение. Остаточный член формулы Маклорена будет иметь вид:
хп ~,eXl л!
где X] лежит между 0 и х. Так как е® меньше некоторого постоянного положительного числа Р, каково бы ни было х, то
М2 ^<Р М2 л!. л!
11о ряд 1 + у + ±1 + • •
сходится для всех значений х, так как
, .. п«4-1
L = lim ——
И->оо ап
ши :—;—гтг = 11,11 —;—г п->оо (Л + 1)1 »-»соЛ-[-1
|х|”
Следовательно, стремится к нулю при п -> оо при всяком х, Р — число постоянное, поэтому остаточный член стремится к нулю при всех значениях х, а это и значит, что ряд Маклорена сходится при всех значениях к функции е*.
,о .х , , х1пя , л-In2 л , х3In3а ,
18. а = 1 Н-----1- —j,— Н------а*---h • • •
Решение. Разложение функции а® следует непосредственно из разложения функции в®: так как ах = е* — ст|пл, то из разложения с1 (см. предыдущую задачу) немедленно получаем разложение, данное в ответе. Можно было бы получить тот же результат, вычисляя коэфициенты ряда Маклорена и непосредственно последовательным диференцированнем функции о®.
Исследование вопроса о стремлении к нулю остаточного члена разложения ведется совершенно аналогично тому, как это сделано в задаче 17.
„ t t Л’х» . *5x5 *’х’ .
19. sin kx — kx---si—' ~5]-------7J—г • • •, где * постоянно.
Решение.
,_ t J , Р , Р L_. *3Х® , ^Х®
sin kx — sin t — t 3! -Ь 5! • • • — *x 31 + 51 ‘ •
Остаточный член имеет вид: (*i)» где (xi) = — kn cos kxt или
ct*nsin*Xj. Так как Л —постоянное число, a |cos*x|, или | sin kx [ не превосходят единицу, то
1/(п) (Жа) I
ЛЛх”
Ряд с общим членом —сходится абсолютно при всех значениях х, так как Л!
Следовательно, остаточный член разложения стремится к нулю, т. е. полученный ряд сходится к функции sin kx при всех значениях х.
20 в-*® = 1 — Lx + fe2x2- — 4- .
м. е * ft* т 21 31 + 41
Проверить разложения в ряд Маклорена и указать, пользуясь признаком сходимости рядов (§ 176), при каких значениях ряды сходятся.
21. 1п(1+х) = х- + + у--------
Отв. Сходится, если — 1 <х<-f 1.
. х3 х3 х4
22. In (1 — х) — х 2 3 4 — ' • •
Отв. Сходится, если — 1 <х< 1.
Отв. Сходится при всех значениях х
Решение.
f (х) = sin2 х;
f (х) = 2 sin х cos х = = sin 2x;
f" (x) = 2 cos 2x;
f" (x) = — 23 sin lie, /Iv (x) = — 23 cos 2x;
/v (x) = 2< sin 2x, Z71 (x) = 2B cos 2x;
f (0) = 0.
/"(0) = 2.
(0) = 0.
/Iv (0) = - 2s.
/V (0) = 0.
/VI (0) = 25
2x2 23X* r5,B Vi A
SInaj;=-2r-^r+ir-?8r+ •••+(-63 4C5 86*
24. e6.sln0 = 0 + 62 + v- 5~Г~2—fi
О 1 • Z .. . и 1 * 2 ... О
22n—i^2tt (2л)!
Отв. Сходится для всех значений 0. х3 х5 X7
25. arctg х = х—у + у—уН--------------
Отв. Сходится, если — 1 < х< 1.
Решение, f (х) = & или (1 4-х2)/'(х) = 1.
Вычисляя л-ю производную от левой части по формуле Лейбница (см. гл. Vlil, § 105), получаем:
1+х2; f'(x).
!Ш£гЭ-2« '/w-rw
-<* 7VГ И = /1"+1)№
dxn dxn
Следовательно, л-я производная левой части имеет вид:
(1 + х2)/(,‘+1) (х) 4- л • 2х/п) (х) + л(" ~ 1} • 2/”-1) (х) = 0
(все производные правой части равны нулю). Подставляя сюда х = 0, найдем формулу:
/("+у (0) 4- п (л -1) /<”—г> (0) = 0, которая позволяет по известному значению какой-нибудь производной при х«=0 вычислять при этом значении х производную порядка выше на 2. Таким образом, зная, что f (0) = 1, последовательно получаем:
f" (0) = — 1 • 2 = - 2!; fy (0) = 4; ..., /2*+1) (0) = (- l)k (2Jfe) I
Для определения значений при х = 0 производных четного порядка находим сперва непосредственным диференцированием:
f (х) =_______—----
7 1 (1 4- хзр ’
откуда f° (0) а 0. Из выведенного общего соотношения видим, что при х = 0 все производные четных порядков обращаются в нули.
Следовательно: X® X® — 1 Х2” 2
arctgx = x-----+ у----------(-I)”’1 ^+...
Легко убедиться, что ряд сходится при — 1 < х < 1.
, 1 х» 1 • 3 х® , 1 • 3 • 5 х’ .
26. arcsinx — х + 2’3+2 - 4' 5 ^2-4-б’ 7 *" ”
Отв. Сходится, если — 1 < х < 1.
Решение.
f'(x) = -7=L=- или V 1 - xV' (х) = I-
У 1 —хя
Диференцируя обе части, находим:
Г (х) - -7--*= Р (*) = О у 1 — х2
или
(]_х®)Г(х)-х/'(х) = 0.
Применяя к каждому члену левой части формулу Лейбница, находим л-ю производную от полученного выражения:
1— х* f" (х) - 2х; f" (х) - 2; /IV(x)
0; /v(x)
х; Р (х) 1; Г (х)
0; Р" (х)
0; /Iv(x)
0; /*+2) (х)
0; /п+1) (х)
(1 - х2)/п+2)(х) — л • 2х/’^(х) - П (Л2, • 2/п)(х) ~ х/(п+1) (х)—n/n)x = 0.
Полагая х = 0, получаем формулу:
/(»+!) (0) _ Л2 у(л) (0) = 0>
позволяющую при х = 0 по данному значению какой-нибудь производной вычислить значение производной порядка высшего на 2. Так как Р (0) = 1, то последовательно находим: '
7"(0) = 1;
/v (0) = 3 3;
/га(0) = 5-5-3.3;
/“ (0) =7.7-5-5.3.3
и т. д. Из соотношения
(1-х2)Г(х)-х/' (х) = 0
видим, что Р’ (0) = 0, откуда из найденной выше общей формулы замечаем, что все производные четного порядка при х = 0 обращаются в нули. Следовательно :
. . Ьх» , ЬЗ х». 1 -3-5 х’ .
arc sin х = х Ч—s—4- я— • -г, + „ - 4-
2-3 '2-4 5 '2-4-6 7 ' ...
1.3... (2л - 1) Х2М-1
‘ * ' + 2-4- • -2л 'Зл-|- 1 + • • •
Обычным способом легко найдем, что полученный ряд сходится для значений— 1<х<-{-1. Можно было бы показать, что ряд сходится также при х = ± 1, но вследствие весьма трудного исследования этого вопроса мы доказательства сходимости ряда для х = 3:1 здесь не приводим.
27. Найти три члена разложения каждой из следующих функций:
a) tg х, b) sec х, с) е00в *, d) cos lx, е) arc cos x, f) .
Вычислить значения нижеследующих функций, используя разложение в ряд каждой функции и беря достаточное число членов ряда, чтобы результаты удовлетворяли указанной точности.
28. е = 2,7182.
Решение. Воспользовавшись разложением в ряд функции е1 (пример 17) и положив в нем х = 1, получим:
е = 1 + 1 + -pyj + m1-2-3-4 + 1-2-3-45 + " ' '
Первый Второй Третий Четвертый Пятый Шестой Седьмой Восьмой член == 1,00000 . = 1,00000 . = 0,50000 . = 0,16667 (деля третий член на 3) „ = 0,04167 (деля четвертый член на 4) . = 0,00833 (деля пятый на 5) „ = 0,00139 (деля шестой на 6) „ =0,00019 (деля седьмой на 7)
Складываем: е = 2,71825. Здесь верны первые четыре знака.
29. йп 1 = 0,8415.
Решение. Полагая х = 1 в ряде для sin х, находим: . , - 1 1 ’ 1 5П1-1 1-2-з+ 1-2-3-4-5 1-2...7 1 ”•
Суммируя отдельно положительные и отдельно отрицательные члены, мы паходим следующие приближенные равенства:
1 = 1,00000
1.2.3-4.5 = 0,<|1М33
i~T^ = °.16667 1 / • и
1 2-3-4-5-6-7
= 0,00019
1,00833
0,16686
Отсюда:
- sin 1 = 1,00833 - 0,16686 = 0,84147,
где верны 4 десятичных знака, так как сделанная погрешность меньше Jт. е. меньше 0,900003. В самом деле, мы производили вычнсле-
ние с знакочередующимся рядом, в котором погрешность при замене его суммы первыми л членами меньше (л-{-1)-го члена (см. § 173).
Очевидно, величина sin 1 может быть вычислена с любой желаемой степенью точности, если только взять достаточное число членов ряда.
30. arctg (1) = 0,1973 ...
31. cos 1 = 0,5403 ...
32. cos 10° = 0,9848 . . .
33. arcsln 1 = 1,5708 . ..
34. sin 4 = 0,7071 ...
4
35. sin 0,5 = 0,4794 . . . 2» 23
36. е’ = 1+2+£ + зГ +
37. /7= 1,6487...
= 7,3891 ...
§ 180. Вычисления посредством рядов.
I. Вычисление числа ж посредством рядов.
Е примере 25 предыдущего параграфа мы видели, что . . Xs . хь х7 .
arctg х = х-у +т--+ ...
Полагая х = 1, получим формулу Лейбница:
«=1„1+1_Л+ 4 3^5 7 -
которая позволяет вычислить число Можно было бы также воспользоваться рядом примера 26, дающим разложение арксинуса, полагая в нем х = у , и получить таким образом величину . Но оба эти ряда сходятся чрезвычайно медленно (т. е. надо взять очень большое число членов, чтобы вычислить п с большим числом верных десятичных знаков). Поэтому на практике обычно пользуются другими рядами, я-
п. Вычисление логарифмов посредством рядов.
Ряды играют важную роль в составлении таблиц логарифмов.
Формула 2 s
1п(1+х) = ^-~ + ~ . ..
1X0
(см. пример 21 предыдущего параграфа) верна только для значений х, заключенных. между — 1 и + 1; однако она могла бы служить для вычисления логарифмов всех целых чисел, если ее применять последовательно к каждому из них.
В самом деле, пусть р — целое число; полагая в предыдущей формуле х = ,
получим:
если бы 1л 2 был известен, эта формула позволила бы найти 1п 3, In 4, ...; вычисления, довольно длинные для маленьких значений р, стали бы легки для больших значений р; однако более скоро можно притти к результату, пользуясь другой формулой, которую мы сейчас выведем.
Из формулы , ।
1п^=1п (1 + х)-1п (1-х),
подставляя вместо In (1 + х) и In (1 — х) соответствующие ряды (примеры 21 и 22 § 179, найдем >):
. 1 -f-х „Г х3 . Xs . х7 1
ln = 2 [х + т+5 + 7 + • •• J '
лот ряд сходится, если — 1 <х< 1.
Пу"Ь 1+_х _М
1-х N'
ОТКУМ M-N .
Х M-\-N ’
тогда для всех положительных значений М и N всегда будем иметь |х | < 1.
1) Мы воспользовались здесь предложением, которое оставляем без доказательства: если два ряда сходятся, то сходится и ряд, полученный путем почленного сложения (или вычитания) данных рядов, причем его сумма равна сумме (или разности) сумм этих рядов.
Подставляя в написанный выше ряд, имеем:
In N- In M In N - 2 M + N + з _|_ N j + j + N J + • • J •
Этот ряд сходится для всех положительных чисел М и N, причем мы будем их выбирать так, чтобы ряд сходился быстро.
Положив М = 2 и N=l, получим:
1"2-2 [тЧ-?+г1+г4+"]-ми14’“
( л , п M—N 1 \
ибо In N = In 1 — 0, а -г.-.—г; = -л- .
\ М + N о)
Полагая М = 3 и N = 2, найдем:
1« 3-10 2 + 2 [1-1 . ] = 1,02361229 ...
Этим способом надо вычислить только логарифмы простых чисел, а лога* рифмы составных чисел найдутся при помощи теорем 9, 10, 11 главы XXI. Так 1п 8 = 1п (23) = 3 in 2 = 2,07944154 ....
In 6 = In 3 In 2 = 1,79175947 . . .
Все это — не перовы, или натуральные, логарифмы, т. е. логарифмы, взятые при основании е = 2,71828 . . . Если желают найти бригговы или обыкновенные, логарифмы, основание которых равно 10, то стоит только изменить основание посредством формулы (см. § 47):
)g10 х = lg10 е In х — 0,434294481903 ... In х.
Таким образом
lg10 2 = 0,434 In 2 = 0,434 • 0,693 = 0,301 • -
Когда действительно составляют таблицы логарифмов, то лишь немногие табличные значения вычисляют посредством рядов, остальное же находят при помощи теорем теории логарифмов и различных остроумных уловок в видах экономии труда.
УПРАЖНЕНИЯ.
Вычислить по способам настоящего параграфа следующие логарифмы: ! log, 5 = 1,6094 ... 3. loge 24 = 3,1781 . . .
2. Ioge10 = 2,3025 ... 4. log,10 5 = 0,6990 ...
§ 181. Приближенные формулы, выводимые из рядов. Интерполяция. В двух предыдущих параграфах мы вычисляли функцию при помощи соответствующего степенного ряда, подставляя данное значение х в известное число членов этого ряда, причем число членов зависело от степени точности, которой мы желали достигнуть. Практически это значит, что мы считаем функцию приближенно равной обыкновенному многочлену с постоянными коэфициентами. Для примера рассмотрим ряд
sin х = х -+ 1,2.з.4.5 — 1.2-3-4-5-6-7
Это — ряд с чередующимися знаками как для положительных, так и для отрицательных значений х. Следовательно, принимая sin х приближенно равным сумме первых п членов, мы делаем ошибку, численно меньшую (п -f- 1)-го члена (см. замечание § 173). Примем, например, sin х = х и найдем, при каких значениях х это допущение даст три верных десятичных знака. Для этого положим
Ьтсюда | х | < р/0,006 ( = 0,1817), т. е. замена sin х черев х даст результат, верный до трех десятичных знаков, когда х лежит между +10°,4 и — 10°,4.
Если пренебречь всеми членами ряда, следующими за членом, содержащим хп-1, то мы делаем ошибку, выражаемую остаточным членом:
Отсюда можно найти, при каких значениях х многочлен представляет функцию с желаемой степенью точности: для этого^надо написать неравенство:
|/?1<предела погрешности
н решить его относительно х; при этом предполагается, что максимальная величина (xj известна.
Так, например, если хотят найти; при каких значениях х формула
X3 ein х = х — -г-о
имеет два верных десятичных знака (т. е. ошибка меньше 0,01), то знля, что |Z<’»> (xt)|<l, мы получаем:
|..2.t4.5|<№
т. е.
|i?o|<M’
или
5 _ |х|<^/1,2;
у 1,2 немного больше единицы.
Поэтому, если х<1, то формула х—дает для sinx значение, верное о
до двух десятичных знаков; значит, вычисление sin х по этой формуле верно до двух десятичных знаков для всех углов, лежащих между — 57° и -j- 57°.
Так как для огромного большинства практических задач требуется точность только до двух или трех десятичных знаков, то выгода приближенных формул, выводимых из рядов, становится очевидной.
Разлагая sin х в ряд Тейлора по степеням разности х — а, получим:
sin х = sin а + (х — a) cos а — (х — а)2 ——h • • •
Отсюда получаем приближенную формулу для всех значений х, близких к определенному значению а:
sin х = sin х + (х — a) cos а.
Перенеся sin а в любую часть равенства и разделив все равенство на х — а, будем иметь:
sin х — sin а -------------- cos а. х — а
Так как cos а есть величина постоянная, то найденное соотношение показывает, что при значениях, близких к значению а, синус получает приращение, пропорциональное приращению аргумента.
Например, пусть а = ЗСР = 0,5236 радиана, и предположим, что требуется по вышеприведенной формуле вычислить sin 31° и sin 32°. Будем иметь:
sin 31° = sin 30° 4- 0,01745 cos 30° >) = 0,5000 4- 0,8660 • 0,01745 = = 0,5000 + 0,0151 = 0,515’.
*) х — а = 1° = 0,01745 радиана.
' sin 32° = sin 30° + 0,03490 cos 30е = 0,5302.
Это исследование иллюстрирует принцип, именуемый интерполяцией при помощи первых разностей.
В общем случае ряд Тейлора дает наем следующую приближенную формулу: / (х) = f (а) + (х — а) /' (а). (1 j
Если постоянная величина Д (в)ф0, эта формула показывает, что отношение приращения функции к приращению независимого переменного для всех значении х, незначительно отличающихся от а, есть величина постоянная.
Очевидно, однако, что эта формула может применяться только с предосторожностью, так как если абсолютная ошибка при применении этой формулы будет незначительной, относительная ошибка может оказаться столь большой, что результат вычисления будет непригоден для применения.
В таком случае необходимо применить интерполяцию при помощи вторых разностей. Для этого мы возьмем в ряде Тейлора одним членом больше, что даст следующую приближенную формулу:
/ (х) = / (а) + (х - a) f (а) + у {а) (2)
Значения sin 31° и sin 32°, вычисленные выше, имеют только три верных десятичных знака. Если желательно получить большую точность, можно воспользоваться формулой (2), которая для / (х) = sin х дает:
I । z \ (х — д'я ,
sin х = sin а + (х — a) cos а — 5— sln л
Пусть а = 30° = 0,5236 радиана. Тогда
sin 31° = sin 30°+ 0,01745 cos 30° - (°-01^45)3 sln gQe =
= 0,50000 + 0,01511 — 0,00008 =
= 0,51503.
sin 32° = sin 30° + 0,03490 cos 30° - <2-°3490)3 sjn зо« =
= 0,50000 + 0,03022 - 0,00030 =
= 0,52992.
Эти результаты дают четыре верных десятичных знака.
УПРАЖНЕНИЯ.
. Применяя формулу (1), вычислить значения следующих функций:
a) cos 61°, положив а = 60°. с) sin 85°,1, положив а = 85°.
b) tg 46°, положив а = 45°. d) ctg 70°,3, положив а = 70°.
2. Применяя формулу (2), вычислить значения следующих функций:
/а) sin 11°, положив а =10°. с) ctg 15°,2, положив а =15°.
b) cos 86°, положив а = 85°. d) tg 69°, положив а = 70°.
д-3 Х3 д-5
3. Вычертив графики функций х, х — —, х — — + ^ сравнить их с гра-<j! о! 01 Г
фиком функции sin X.
§ 182. Ряд Тейлора для двух и большего числа переменных. Для функция двух или большего числа переменных можно найти разложение в ряд Тейлора путем введения некоторого вспомогательного переменного, сводя тем самым эту новую задачу к уже изученной задаче для функции одного переменного.
Пусть дана функция двух переменных
/(х, у).
Дадим х приращение h, у— приращение k\ наша задача — разложить функцию
/(x + A,j4-A)
по степеням h и k.
Введем вспомогательное переменное t и составим выражение:
f(x + ht, y-\-kt).
Если будем считать х, у, h и k параметрами и рассматривать это выражение как функцию t, то можем написать:
F(t)=f(x + ht, y + kt}.
При i=l мы будем иметь y-j-A).
Разложим функцию F (t) в ряд Маклорена по степеням t\ будем иметь:
F(t)(0) 4- J- F’(0)4- ... + 7-2--FW(0) 4- . ..
Найдем теперь выражения для последовательных производных функции F(t) через х, у, h и k. Полагая
х-|- ht = a,
у+м=?,
будем иметь:
F(0=/(«, р),
причем а и 3 суть функции t\ поэтому для нахождения F' (0 надо диференцировать по формуле для сложной функции (§ 71); получим:
Г ( да dt^~ dfidt'
Но по самому определению а и 3 имеем:
Далее: dF_dFdx dF_ др ду да дх да и д$ ду 00 ’
но так как по определению а и 0 имеем:
то
dF^dF да в дх 00 = ду’
Поэтому окончательно находим:
„<?F, . dF .
FI‘>=Txh+^k-
3S3
Если в этой формуле заменить F(t) через F' (t), то получим: . dF , .[.^F., d’Fl . . Г, d2F . .d’Fl
F" (t) = --— h -4—3— k = h h-s—„ k t—-7- -4- k h-\—3—I- k -5—7.
4 7 dx 1 dy dx2 dxdy] 1 [ dxdy 1 dy2
или d’F d’F d’F
F° (Л = A’ + 2hk 4- A’VJ. k ’ dx2 * dx dy 1 dy2
Таким же образом находим третью производную: d’F d’F d’F d’F
F" ОТ - + 3W +
и т. д. для производных высших порядков.
Так как, при £=0, F (t) заменяется функцией f(x, у), то мы имеем: F(0)=/(x, _у).
F'" (0) = Л’ ?(+ЗЛ’А 7ГЯГ + 3+ k*и т- л-4 7 dx8 1 dx2dy 1 dxdy2 1 dy8
Подставляя эти результаты в ряд Маклорена для F(t), получим: (x-\-ht, y-\-kl) =
у \ dx 1 dy) 1 1.2\ dxdy 1 dy2] 1
Чтобы перейти от f(x-\-ht, y-\-kt) к f{x-}-h, заменяем t единицей и тогда находим окончательное разложение в ряд Тейлора для функции двух независимых переменных:
+Л(*,^+2**Д+*,^)+- от
Подобно этому для трех переменных:
/(жЧ-Л, + zH-/)=/(x, JF, 2) + л^+а^+/^4-
+1 • 2\h dx2+k d>’+Z dz2^2hkdx dy^2kldydz^2lhdzd^ J +'"( V) и т. д. для скольких угодно переменных.
ПРИМЕРЫ.
1. Дано
f(x,y) = Ax2 + Bxy + Cy2 разложить
/(•* + /'. у + л)
по степеням h и А.
Решение.
^ = 2/х + Ву, ^ = Вх + '2Су, ^ = 2А; Й = 2С- лЧг = в-дх 1 л ду дх2 ду2 дхду
Производные третьего и всех высших порядков равны нулю.
Подставляя в ряд Тейлора (111), найдем:
f(x + h, y + k} =
= Ах2 + Вху + Су2 + (2Ах + By) h + (Вх + 2Су) k + Ah2 + Bhk + Ck2.
2. Дано
f(x, у, z) = Ax2 4- By2 + Cz2-, разложить
/(* + *. У+ *. z + Л по степеням h, k и I.
Решение.
д/=2Ах; *2Ву, d/ = 2Cz; g = 2A; ^=2В; ^=2С;
дх оу dz дл2 ду2 dz2
_ &f &f _ 0 дх ду ду dz dz дх
Производные третьего и высших порядков все равны нулю.
Получаем, подставив в ряд Тейлора для трех переменных (VI):
f (х 4" й> у + k, z 4- I) =
-Ах2 + By2 + Cz2 + 2Axh + 2Byk + 2Czl + Ah2 + Bk2 + Cl2.
УПРАЖНЕНИЯ.
1. Дано
/(x, у, z) = Ax2 + By2 + Cz2 + Dxy Eyz + Fzx-, разложить
f(x-\-h, y + k, z + 0 по степеням h, k, I.
Ome. f(x + h. у 4- ft, z 4- /) = (Ax2 4* By2 4-. Cz2 4* Dxy 4 - Eyz 4- Fzx) 4-4- [(2Ax 4- Dy 4- Fz) h 4- (2By + Dx + Ez)k +
4- (2Cz 4- Ey 4- Fx) /] 4- (Aft2 4- BA2 4- C/2 4- Dhk 4- Ekl 4- Flh).
2. f(x, y) = ?®slny; разложить f(x+h, у 4-А) п° степеням ft н ft, ограничиваясь членами третьего измерения относительно Л и А.
Оте. h sin (у 4* А) = е® siny 4" 0х (Л sin у 4- ft cosy) 4-'
в® е®
+ jj- [(Л2 — A2) siny 4- 2ftft cosyl 4- gj- [(Л — ЗЛА2) sin у 4- (ЗЛ2А — ft8) cosy] 4- ...
§ 183. Максимумы и минимумы функций двух независимых переменных. Мы говорим, что функция /(л, у) имеет максимум при х = а, у = Ь, если, каковы бы ни были смежные сайд значения х и у, величина /(а, Ь) всегда больше /(х, у). Подобно этому говорят, что функция /(х, у) имеет минимум при х = а, у = Ь, если величина f{a, b) всегда меньше /(х, у), каковы бы ни были хну, смежные сайд.
Эти определения в аналитической форме можно выразить следующим образом.
Если для всех значений h н k, по абсолютной величине меньших некоторых малых положительных количеств, выражение f(a-{-II, b-{-k) меньше /(а, Ь) или, иначе, f(a-{-h, b-{-k)—f(a, b) есть величина отрицательная, то /(л, Ь) есть максимум функции f(x,y)‘, если же b-\-h) больше f(a, b), т. е. если разйость
/(а-|-А, b —/(а, Ь) п о л о ж и те л ь н а, то /(а, Ь) есть мини-
мум функции f(x, у).
Геометрически (черт. 167) это определение можно интерпретировать так: точка Р на поверхности
Z =J (X, у)
будет точкой максимума, когда она выше всех других смежных точек поверхности, и точка Р' будет точкой минимума, когда она
ниже всех других соседних с нею точек поверхности (при этом, как всегда, предполагают, что плоскость ХО Y горизонтальна). Очевидно, следовательно, что все вертикальные плоскости, проводимые через точку Р, пересекают поверхность по кривым (таковы АРВ или CPD), каждая из которых имеет максимальную ординату z ( = МР) в Р. Таким же образом * все вертикальные плоскости, проводимые через Р', пересекают) поверхность по кривым (каковы EP'F и GP'ET), каждая из которых имеет минимальную ординату z( = NP') в Р'. Также всякий контур (как UKL), образуемый на поверхности сечением горизонтальной плоскостью в непосредственном соседстве с Р, должен быть малой замкнутой кривой. То же относится и к контуру RSTV близ точки минимума Р'.
В § 109 было доказано, что для того чтобы функция одного переменного им^ла максимум или минимум при некотором значении переменного, необходимо, чтобы ее первая производная при этом значении переменного обращалась в нуль. Значит, если Р(а) есть максимум или минимум, то F' (а) = 0.
25 Зак- — В. Гранвиль и Н. Л у з и в. Часть I
Подобно этому для функции двух переменных докажем предложение: для того чтобы f(x, у) имела максимум или минимум при х = а, у = Ь, необходимо, чтобы
-^= 0; 0 при х = а, у = Ь.
дх ду J
Доказательство. Если придать переменному у значение Ь и менять только переменное х, то функция /(х, у) примет вид f(x, b), т. е. станет функцией только одного переменного х. Раз /(а, Ь) есть максимум (или минимум), то /(а, Ь) больше (или меньше), чем /(х, Ь), каково бы ни было х, близкое к а. Это значит, что функция /(х, Ь) одного переменного имеет максимум (минимум) в точке а. А для этого
необходимо, чтобы ее производная ^/(х, обратилась в нуль при
х = а. Но производная /(х, Ь) есть не что иное, как частная производная функции /(х, у) по переменному х; поэтому ^должно обра-
титься в нуль при х = а, у = Ь. Заставляя теперь х принять значение а х df
и меняя только у, докажем таким же образом, что должно обращаться в нуль при х = а, у = Ь. Теорема доказана.
При изучении функций одного переменного мы видели, что когда первая производная обращается в нуль в некоторой точке, то в этой точке может оказаться максимум или минимум, или"ни то ни другое. В § 139, изучая формулу Тейлора, мы довели до конца исследование вопроса о максимумах и минимумах функций одного переменного. Для функций двух переменных исследование значительно более сложно; поэтому мы ограничимся указанием достаточных условий, которые позволят нам решать приводимые ниже задачи.
Разложим f(a-\-h, b-[-k) в ряд-Тейлора [(III), § 182], заменив х буквою а, а у—буквою Ь\ найдем:
/(а+Л, *+*>=/(«, д)+Л A^-f-
+ гЦ (А’ 2АА тТ + ) +*’
1 1-2\ дх1 1 дхду 1 ду*] 1
(III*)
где частные производные нужно вычислить для х = а ny=b,tR означает сумму всех невыписанных членов. Все эти члены содержат h и k в степенях выше второй.
Так как в точке максимума или минимума = О и ^~ = 0, то по перенесении /(а, Ь) в левую часть равенства (I) получим:
Если левая часть равенства (III**) сохраняет вполне определенный знак, то мы имеем либо максимум, либо минимум, причем максимум, если
знак отрицательный, минимум, если знак положительный; если же знак меняется, мы не имеем ни максимума, ни минимума.
Такиу образом все сводится к решению вопроса о знаке левей, а следовательно, и правой части равенства (III**).
Но правая часть равенства (Ш**)_есть сумма двух выражений, из которых мы сначала изучим первое.
Обозначая кратко значения частных производных второго порядка при х = а, у = Ь через
g-A; »L = B; ^С.
дх2 дх ду ду2 исследуем квадратный трехчлен
Возможны три случая: 1) его корни мнимы, 2) корни действительны и различны, 3) корни действительны и равны.
Первый случай произойдет, когда В2— АС < 0, второй — когда В2 — ДС>0 и третий при В2— АС = 0.
Если корни мнимы, то трехчлен сохраняет свой знак (не обращаясь в нуль ни при каких действительных значениях h. и k}\ этот знак совпадает со знаком А (или С, потому что знаки А и С в этом случае одинаковы).
Если корни действительны и различны, трехчлен обязательно меняет свой знак.
Наконец, если корни равны, то знак сохраняется, но трехчлен может обратиться в нуль.
Отсюда мы выводим такое следствие: пусть
А <32/6»/ / д2/ у.
1л — дх2 ду2 \dxdy/ ’
тогда
дх2 -1- 2hk dx dy Vk2^-1 R dy2 < 0, если Д;
h2^-п дх2 2hk d2/ dx dy 1 dy2 > 0, если Л \ > 0 и > 0 ; dx2
h^. " dx2 -I- 2hk dx dy 1 Л dy2 меняет знак, если Д <0;
-|- 2hk W dx dy 1 dy2 не меняет знака, но может обращаться в нуль, если Д = 0.
Детальное исследование, выходящее из рамок этой книги, показывает, что величина R, входящая в правую часть равенства (III**), может оказать влияние на знак этой правой части лишь в последнем из четырех вышеупомянутых случаев, т. е. при Д = 0; во всех остальных случаях знак правой, а следовательно, и левой части этого равенства совпа-
дает со знаком
дх2 1
J!L+k,^L. дх ду ' ду2
Исследование знака величины 7? чрезвычайно сложно, поэтому мы ограничимся замечанием, что случай Д = 0 следует считать сомнительным. Окончательно полученные результаты можно резюмировать в виде следующего правила нахождения максимумов и минимумов функции /(х, у) двух Переменных.
Первый шаг. Решаем совместно уравнения:
Второй шаг. Вычисляем для полученных значений х ну выражение:
ду / ду V дх* ду*
Третий шаг. Функция будет иметь:
d*f I дУ \
максимум, если А>0 и < 0 ^или < 0 j,
, d*f ( d*f \ минимум, если Д > 0 и > 0 ^или > 0 |,
ни максимум ни минимум, если Д < 0.
Вопрос остается нерешенным, если Д = 0.
Следует заметить, что, пользуясь этим правилом, мы можем не найти некоторых максимальных и минимальных значений. В самом деле, если пара значений х и у, определяемая первым шагом, обратит Д в нуль, то найденная точка может быть и точкой максимума, и точкой минимума, и ни тем ни другим. Для таких значений необходимо более детальное исследование. Тем не менее формулированного правила достаточно для решения многих важных задач.
Вопроса о максимумах и минимумах функций трех и большего числа независимых переменных мы разбирать не будем.
ПРИМЕРЫ.
Пример 1. Исследовать функцию
Заху — х3 — у3 на максимумы и минимумы.
Решение.
f (х, v) = Заху — х* — Vs.
Первый шаг. *
= 3x2 = 0;
=Зах-Зу3 = 0. ду '
Решая вти уравнения совместно, находим: х = 0, у = 0; х = а, у = а.
Второй
шаг.
д2/ с W „ д2/
д-з = — 6х; = 3а; х-л = — бу;
дх- дх ду о*2 л
= 3Sx> -9а2.
Третий вательно, при
При х = а, у = а имеем Д — 21аъ, Д
*{=-6а,
ах2
ШАГ.
(0. 0)
При х = 0, у = 0 имеем Д = — 9а2, т. е. Д < 0, и, следо-нет ни максимума ни минимума.
0, а так как
то при
имеем максимум.
Подставляя в данную
функцию
в точке максимума равна а?.
а на такие три части, чтобы их произведение было
находим, что ее величина
Пример 2. Разделить максимумом.
Решение. Пусть первая часть будет xt вторая у; тогда третья часть будет: а — (*+>) = а — х — у, и исследуемая функция будет
/(*. у} — (а — х — у) ху.
Перцый шаг.
££ = ау-2ху—у^ = 0; = ах - 2ху - х’- = 0.
Решая эти уравнения совместно, находим, что одна пара решений !) есть: а а
х ~ "3 ’ У ~ 3 производится на три равные части).
ШАГ,
«=-2,; „_2х_2,: ^--2,;
дх* дх ду ду-
Д = 4ху — (а — 2х — 2у)2. ш а г. Ес.'и
(т. е. деление
Второй
Третий
а а
3’ У~ 3 ’
то
а так как
д'-f 2
дхг~ За>
то, очевидно,
при
д =
> = а
а а
3 ’ у ~ 3
а3 наше произведение имеет максимум; величина его равна
*) Мы не исследуем случая, когда x=j = 0, или х = 0, у —а, или х = в, у = 0, так как во всех этих трех случаях произведение ху = 0, и поэтому ясно, что получается минимум.
УПРАЖНЕНИЯ.
1. Найти минимум функции х2 4- ху + у2 — ах — by.
Отв. 4- (ab — с. - - Ъ2). □
2. Исследовать на максимум и минимум функцию sin х + sin у + cos (х + у)
Отв. При х=у = -^- имеем max = 1,5.
Зл при х=у— у имеем пип.
3. Показать, что функция хеУ + х sin у пе имеет ни шах, ни min.
4. Исследовать на максимум и минимум функцию х* у* — х2 + ху-у-.
Отв. При х = 0, у = 0 имеем max, при х=у = +—и при
, х = — у=±- у 3 имеем mln.
5. Показать, что значение, при котором функция (ох 4- fry 4- с)2
X2 4-У2 4-1 достигает максимума, равно а2 4* Ь- 4* с2.
6. Исследовать на максимум и минимум функцию и = ху(х4-у-1).
Отвл При х=у=—- имеем mln = — ^=. ' d 27
7. Показать, что поверхность прямоугольного параллелепипеда данного объема имеет минимум, когда тело есть куб.
8. Показать, что наиболее экономичные размеры для прямоугольного бассейна данного объема суть: квадратное основание и глубина, равная половин: стороны основания.
9. Палатка имеет форму цилиндра с насаженной на него конической верхушкой. При каких размерах на изготовление такой палатки заданного объема v потребуется наименьшее количество материи?
Отв. Если х — радиус основания палатки,у — высота цилиндрической части, z— высота конической верхушки, то пропорции размеров определяются соотношениями:.
z о г______
/х^+^ = '3 ; 2j= ^x2 + z<
10. Показать, что из всех треугольников, имеющих данный периметр, наибольшую площадь имеет равносторонний треугольник.
11. Найти наибольший прямоугольный параллелепипед, какой можно вписать в эллипсоид.
Отв. Размеры параллелепипеда: 2-^=, 2-^^, 2^^. Объем:
УказаниЕ. Положить v = xyz и подставить значение г, определенное из уравнения вллипсонда. Получим функцию
’’“-М'-э-’Э,
только двух переменных.
ГЛАВА XIX.
АСИМПТОТЫ. ОСОБЫЕ ТОЧКИ.
§ 184. Прямолинейные асимптоты. Асимптотой к кривой
называют предельное положение ’) касательной, точкй касания которой
удаляется на бесконечное расстояние от начала * 2).
Так, в гиперболе асимптота Доесть предельное положение касательной РТ, по мере того как точка касания Р удаляется вправо в бесконечность (черт. 168). В случае алгебраических кривых употребительно следующее определение: асимптота есть предельное положение секущей, к которому она приближается, по мере того как обе точки пересечения секущей с ветвью кривой удаляются в бесконечность, двигаясь
Черт. 163.
Q движутся вверх, уда-
вдоль этой ветви в одном и том же направлении. Например, асимптота АВ есть предельное положение секущей PQ, по мере того как Р и ляясь в бесконечность.
§ 185. Нахождение асимптот по способу стремления к пределу отрезков на ОСЯХ координат. Уравнение касательной к кривой в точке (Xj.yJ, в силу (1) § 92, есть:
Полагая сначала у = 0 и решая относительно х, затем полагая х = О и решая относительно у и обозначая отрезки на осях координат буквами х и у., соответственно имеем:
dx, xt — xL —у - j—= отрезку на оси
ОХ,
yt=yl — х^- = отрезку на оси OY.
Так как асимптота должна проходить в конечном расстоянии от начала, то один или оба эти отрезка по мере удаления точки касания
1) Мы предполагаем, что асимптота, согласно самому ее определению, должна проходить в конечном расстоянии от начала. Очевидно, что кривая, у которой нет бесконечных ветвей, не может иметь действительной асимптоты.
2) Иногда, но не так точно, определяют асимптоту к кривой как касательную, точка касания которой находится в бесконечности.
(х„ в бесконечность должны приближаться к некоторым конечным предельным значениям. Если
lim (х() = а и lim (j/,) = b, то уравнение асимптоты найдем, подставив эти предельные значения а и Ь в уравнение:
Если известен только один из этих пределов и если известно, что
,. I dy\ \ lim -г-1- = т, \dxx )
то будут даны один из отрезков и угловой коэфициент, так что уравнение асимптоты будет:
у =* тх 4- b или х = — 4- а. ' т
Пример 1. Найти асимптоты к гиперболе
_ сГу Ь2.т . Ь 1 . / dy\ Ь
Решение. - = и т = - -.
V
„ а2 &
Также х, = — и у< — — отсюда при х = у = оо эти отрезки обращаются в нули. Следовательно, асимптоты проходят через начало ("м. черт. 168), и уравнения их суть:
ь
у — 0 = rt —(х— 0), или ау = ±Ьх.
Этот способ часто сопровождается осложнениями, а потому на практике не употребителен. Более удобный способ определения асимптот для алгебраических кривых дается в следующем параграфе.
§ 186. Способ определения асимптот для алгебраических кривых. Дано алгебраическое уравнение с двумя переменными:
/(х, у) = 0. (А)
Если по освобождении от дробей и от радикалов это уравнение будет л-й степени, то его можно будет расположить по нисходящим степеням одного из переменных, например у, в виде:
ауп + (ь и + с)У’-1 + (dx= -’г ех+/)У*-2 +... = 0 »). (В)
Для данного значения х это уравне! ие определяет вообще п значений у.
Предполагается, что а и Ь одновременно оба не равны нулю, так как при этом асимптота не была бы вполне определена.
В нижеследующем читателю придется припомнить следующую теорему алгебры: дано уравнение л-й степени:
Ауп + Byn-1 + Суп~2 4 Dyn~2 -j-... = 0.
Если А приближается к пулю, то один из корней (значение у) приближается кбесконечн )сти.
Случай I. Определить асимптоты кривой {В), параллельные осям координат. Исследуем сначала асимптоты, параллельные оси OY. Уравнение любой такой асимптоты будет вида:
х = /г, (С)
и она должна иметь по крайней мере две точки пересечения с (В), имеющие бесконечные ординаты.
Во-первых. Пусть в (В) а не равно нулю, т. е. член, содержащий уп, существует. В этом случае для всякого конечного значения х уравнение (В) даст п значений у, которые будут все конечны. Следовательно, все прямые (С) будут пересекать кривую (В) в точках, имеющих конечные ординаты, и потому асимптот, параллельных оси ОУ, не имеется.
Во-вторых. Положим теперь, что а = 0, но b и с — не нули. Из алгебры известно, что один из корней ( = у) уравнения (В) будете этом случае бесконечен для всякого конечного значения х, т. е. всякая произвольная прямая (С) пересекает кривую (В) только в одной точке, имеющей бесконечную ординату. Если теперь будем иметь к тому же, что
Ьх с = О, или
то исчезнут два первых члена в уравнении (В), и, следовательно, два его корня будут бесконечны. Это значит, что (В) пересекается с (D) в двух точках, имеющих бесконечные ординаты, и, следовательно, (D) е с ть уравнение асимптоты к (В), параллельно й о с и OY.
В-третьих. Если в уравнении (В)
a — b = c = Q,
то имеются два значения х, делающие у в уравнении (В) бесконечным, именно — значения, удовлетворяющие уравнению:
dx^ex-f-^0- (Е)
Решая (Е) относительно х, найдем дв>е асимптоты, параллельные оси ОY.
Подобным же образом, располагая/(х, у) по нисходящим степеням х, можем найти асимптоты, параллельные оси ОХ. Отсюда следующее правило для нахождения асимптот, параллельных осям координат:
Первый шаг. Приравниваем нулю коэфициент при высшей степени х в уравнении. Это даст все асимптоты, параллельные оси ОХ.
Если А и В приближаются к нулю, то два корня приближаются к бесконечности.
Если А, В и С приближаются к нулю, то три корня приближаются я бесконечности и т. д.
Второй шаг. Приравниваем нулю коэфициент при высшей степени у в уравнении. Это даст все асимптоты, параллельные оси OY.
Примечание. Естественно, что, если одни или оба эти коэфициента не содержат х (или у), то они не могут равняться нулю, и соответственных асимптот не имеется.,
Пример 1. Найти асимптоты кривой а2х = у (х — а';2.
Решение. Располагая члены по степеням х, имеем:
ух2 — (2ау в2) х + д2у = 0.
Приравнивая нулю коэфициент при высшей степени х, находим у = 0: это и есть асимптота, параллельная оси ОХ. Она совпадает с осью ОХ.
Расположив члены по степеням у, имеем:
(х — а>-у — а2х = 0.
Приравнивая нулю коэфициент при у, имеем дважды х = а, что указывает, что АВ есть двойная асимптота, параллельная оси OY. Если эту кривую исследовать по нижеуказанному методу для асимптот, наклонных к осям, то нашли бы, что таких асимптот нет. Следовательно, единственные асимптоты у данной кривой суть к
у = 0 и х = а (черт. 169).
Черт. 169 Черт. 170
Случаи \\.'Определить асимптоты, наклонные к координатным осям. Дано алгебраическое уравнение:
/(X,J) = O. (F)
Рассмотрим прямую
y = mx-{-k. (G)
Требуется т и k определить так, чтобы прямая (G) была асимптотою к кривой (F).
Так как асимптота (черт. 170) есть предельное положение секущей по мере удаления двух точек пересечения ее с одною и тою же ветвью кривой в бесконечность, то полученное в результате исключения у из (F) и (G) уравнение относительно х, именно:
f(Xi mx-y-k) = Q (Н)
должно имет два бесконечных корня. Но это требует, чтобы исчезали коэфициенты при двух высших степенях х. Приравнивая эти коэфициенты, получим два уравнения, из которых и можно определить требуемые значения т и k. Подстановка этих значений в (G) даст уравнение асимптоты. Отсюда—следующее правило для нахождения асимптот, наклонных к осям координат:
Первый шаг. Заменяем в данном уравнении у количеством mx-\~k и развертываем.
Второй шаг. Располагаем члены по нисходящим степеням буквы х.
Третий шаг. Приравниваем нулю коэфиииенты двух высших степеней *) х и решаем полученные уравнения относительно т и k.
Четвертый шаг. Подставляем найденные д л я т и k значениявформулу:
у = тх -j- k.
Это идаст искомые асимптоты.
Пример 2. Исследовать на асимптоты кривую у3 = 2ах! — х®.
Решение. Так как ни один член не содержит х иу одновременно, то очевидно, что асимптот, параллельных осям координат, нет. Для нахождения наклонных асимптот исключим у из данного уравнения при помощи соотношения у = тх к. Это даст:
(тх + А)3 = Чах"- - х3, а расположив члены по степеням х, получим: (1 + т3) х3 + (Зш-А — 2а) х3 + 3A1 2mx -f- А3 = 0. Приравниваем нулю два первых коэфициента 1 -|- т3 = 0 и Зт2А — 2а = 0.
2 Решая, находим т = — 1, к = — а. Подставляя в у = тх + к, имеем: , 2 > = _х + _а;
это есть уравнение асимптоты АВ (черт. 171).
ПРИМЕРЫ.
Первые восемь кривых исследовать на асимптоты по способу §185, а остальные — по способу § 186.
1. у = ес. Отв. у = 0.
2. у = «“**• у = 0.
3. у = 1п х. х = 0.
= + > = е'
5. У = tg х. Отв. х = тде п — любое нечетное число.
1
6. у = ех — 1. Отв. х = 0, у = 0.
1) Если слуужтся, что чл.'на, содержащего хп—\ нет или значение т, полученное приравниванием пулю первого коэфициента, обращает второй коэфн-циент в нуль, то, приравняв нулю коэфиииенты при х” и хп—а, получим два уравнения, из которых можно найти значение т и к. В этом случае, вообще
говоря, найдем для каждого т два значения k, т. е. по паре параллельных наклонных асимптот. Подобно этому, если обратится в нуль коэфициент при хп~2, каждое значение т даст по три параллельных наклонных асимптоты, и т. д.
7. у3 = 6х2 -{- л3. Отв. у = х + 2.
8. Показать, что парабола ве имеет асимптот.
9. у3 = а3 — л3. хЗ
10. Циссоида _у2 = г-----.
J 2г — х
11. у2а = у2х + л3.
12. >2(л2+ 1) = л3(л2- 1).
13. у2 (л — 2а) = л3 — а3.
14. х2у2 = д2(л=-|-У).
15. у (л- - ЗЬх + 2b2) = л3 - Зал2 +
Отв. у -f- х = 0.
л = 2г.
л - а.
у = ±х.
х = 2а, у = zt: (л + в).
л - - а, у = zt а.
Отв. х — Ь, х = 2Ь, у -f- За = л + ЗЬ.
дЗ
16. у = с + • Отс- У = с, х = Ь.
17. Лист л®-[-.у3 — Заху = 0. у -|- л -|- а = 0.
18. Локон Аньези х2у = 4а2(2а —у). у = 0.
19. ху2 + Х'У — °3- Отв. л = 0, у = 0, л + у = 0.
20. л3 + 2х2у — ху2 - 2у3 + 4_у2 -\-2ху+у = \.
Отв. х 2у = 0, л4~.У = 1» х—_у= — 1.
§ 187. Асимптоты в полярных координатах. Пусть /(р, 6) = 0 будет уравнение кривой PQ, имеющей асимптотою прямую CD (черт. 172).
Так как асимптота должна проходить в конечном расстоянии (= ОЕ) от начала, а точка касания удалена в бесконечность, то очевидно, что радиус-вектор OF, проведенный в точку касания, параллелен асимптоте, а подкасательная ОЕ к нему перпендикулярна. Или, говоря точнее, расстояние асимптоты от полюса есть предельное значение полярной подкасательной, по мере
того как точка касания отодвигается в бесконечность.
Для определения асимптоты к полярной кривой поступаем следующим образом:
Первый шаг. Находим из уравнения кривой значения 6, делающие р = оо1). Эти значения 6 дают направления асимптот.
Второй шаг. Найти предел полярной подкасательной.
по мере того как 0 приближается к каждому из таких значений, помня, что в то же самое время р приближается к бесконечности.
1) Если уравнение можно написать в виде полинома относительно р, то эти значения 6 можно найти, приравняв нулю коэфициент высшей степени р (см. выноску на стр. 392).
Третий шаг. Если предельное значение полярной подкасательной конечно, то соответственная асимптота в этом расстоянии от начала существует и параллельна радиусу-вектору, проведенному в точку касания. Если этот предел положителен, то асимптота расположена вправо; если отрицателен, то она находится влево от начала, если смотреть в направлении бесконечного радиуса-вектора.
ПРИМЕРЫ.
1. Исследовать на асимптоты гиперболическую спираль р = у .
Решение. Когда 0 = 0, р = оо. Затем
£*_ _____2- ---------------
откуда подкасательная равна /о
М о» ( tP\_ (
= -------------Г
следовательно.
11ml р2 -г- = — а,
e-M)L J Черт. 173.
количеству конечному. Таким образом в этом случае подкасательная для всех значений 0 имеет одну и ту же величину. Следовательно, асимптота ВС кривой параллельна полярной оси ОА и проходит над нею в расстоянии а (черт. 173).
Исследовать на асимптоты следующие кривые.
2. р cos 0 = a cos 20.
Отв. Асимптота кривой перпендикулярна к полярной оси и лежит в расстоянии а влево от начала.
3. р = a tg 0.
Отв. Кривая имеет дсе асимптоты, перпендикулярные к полярной оси и в расстоянии а от начала, по обе стороны от него.
1
4. Lttuus (жезл) рв2 — т. Отв. Полярная ось.
5. р = a sec 20.
Отв. Четыре асимптоты, лежащие на одинаковом расстоянии у от полюса и наклоненные под углом 45° к полярной оси.
6. (р — a) sin 0 = Ь.
Отв. Одна асимптота, параллельная полярной оси и лежащая над нею в расстоянии Ь.
7. р = a (sec 20 + tg 20). тс
Отв. Две асимптоты, параллельные ’’ = 41 по обе стороны от полюса, в расстоянии а от него.
8. Показать, что полярная ось служит асимптотою к обеим ветвям крнвой еа sin 0 = a3 cos 20.
9. Парабола р = । _ cos д- • Отв. Не имеет асимптот.
§ 188. Особые точки. Дана кривая уравнением: /(х, >) = 0.
Всякая точка кривой, для которой
называется особою точкою кривой. Все другие точки называются обыкновенными точками кривой.
Так как
dy __ дх
dx ~ df’ ду то очевидно, что в особой точке направление кривой (или ее касательной) неопределенно, ибо угловой коэфициент принимает вид —. В следующем параграфе будет показано, каким образом можно находить касательные в такого рода точках.
§ 189. Определение касательной к алгебраической кривой в данной на ней особой точке. Если данное уравнение преобразовать к новым осям координат, параллельным прежним, но с началом в рассматриваемой точке на кривой, то известно, что новое уравнение не будет иметь постоянного члена. Таким образом уравнение можно написать в виде:
/ (х, у) = ах + by + (ex’ 4- dxy + еу^ 4-
+ (A*8+^2J' + Axy94-I>8) + --- = 0- (А)
Уравнение касательной к кривой в данной точке (служащей теперь началом) будет:
У
• X. х=0 V-0
(В)
Пусть у = тх будет уравнение прямой, проходящей через начало О и другую точку Р, взятую на кривой (А). Значит, если Р приближается к О, двигаясь по кривой, то из (В) имеем:
= (С)
dx ' '
Пусть О будет обыкновенная точка. Тогда, очевидно, а и b не исчезают одновременно, ибо для точки (0,0) из (А) имеем:
df_h
. — Д, -j — о* дх ду
Заменив в (А) у через тх, разделим на множитель хи будем приближать х к нулю как к пределу. Очевидно, (А) обратится в *)
а 4- Ьт = 0.
Отсюда из (В) и (С) имеем:
ах 4~ by = 0,
х) По разделении на х останется алгебраическое уравнение относительно т, коэфиииенты которого будут функциями х. По мере приближения х к пределу нуль имеет силу теорема, что один из корней этого уравнения относительно т будет приближаться к пределу, равному — .
§ 189J ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ В ОСОБОЙ ТОЧКЕ 399 уравнение касательной. Левая часть, как видно, состоит из членов первой степени уравнения (А).
Если О не есть обыкновенная точка, то будет а = Ь = 0. Допустим, что с, d, е не обращаются одновременно в нуль. Поступая по предыдущему (но разделяя уже на ха) и приближая х к пределу нуль, найдем, что будет
c-\-dm-\- ет2 = 0, или из (С):
По подстановке из (В) имеем:
ex2 dxy + СУ2 = °. (Е)
уравнение пары касательных в начале. Мы видим, что левая часть состоит из членов второй степени уравнения (А). Такая особая точка кривой называется двойной точкою, на том основании, что в этой точке кривая имеет две касательные.
Так как в точке (0, 0) из (А) имеем:
о <*7 w о
чЦ: = 2с, j—j- = d, хЛ = 2е,
дх2 дхду ду2
очевидно, что (D) можно написать в форме:
=0
дх2 ' дх dy\dx) х=й' dy2\dx] '
=• У=о
Подобным же образом, если
a = b = c = d=e = 0,
то в начале будет тройная точка, а уравнение трех касательных будет;
/х8 4~ gx2y hxy2 -f- iy2 = 0.
И т. д.
Желая исследовать вид кривой в данной точке, необходимо решить задачу о касательной в этой точке. Вышеприведенные результаты показывают, что эту задачу можно решить простым исследованием, перенеся начало в эту точку.
Отсюда имеем следующее правило для нахождения касательной в данной точке.
Первый шаг. Переносим начало в рассматриваемую точку.
Второй шаг. Располагаем члены полученного уравнения по восходящим степеням х ну.
Третий шаг. Приравниваем нулю группу членов низшей степени. Это и даст уравнение касательной в этой точке (начале).
Пример 1. Найти уравнение касательной к эллипсу:
5ха + 5у2 2ху — 12х — 12у = 0
в начале координат.
Решение. Приравнивая
нулю члены низшей (первой) степени, имеем:
- 12х - 12> = 0,
или
X + J = о, это,следовательно, и есть уравнение касательной РТ в начале (черт. 174).
Пример 2. Исследовать кривую
Зл-2 - ху -2у* + 4- X3 - 8у® = 0 на касательные в начале.
Решение. Приравнивая нулю члены низшей (второй) степени, имеем:
или
Зх3 — ху — 2уа = 0,
(х — >) (Зх + 2у) = 0,
причем х —у = 0 есть уравнение касательной АВ, а Зх -{- 2у = 0 — уравнение касательной CD. Следовательно, начало есть двойная точка кривой (черт. 175).
Так как корни квадратного уравнения (F)
2--/- 4- = О
ду2 \dx) ' dx dy\dx) ' дх2
могут быть действительные неравные, действительные равные, либо мнимые, нужно рассмотреть три случая двойных точек, соответственно тому, будет ли разность
(гл
\ дх ду / дх2 дх2 ' '
положительна, нуль или отрицательна
/ d2f V § 190. Узлы ЬгЧг э \дхду/
ОУ
дх2 ду2
0. В этом случае (F) дает для
углового коэфициента два действительных неравных значения,
так что в рассматриваемой особой точке мы имеем две различные действительные касательные к кривой. Это значит, что через точку кривая проходит в двух различных направлениях, или, другими словами, в этой точке пересекаются две ветви кривой. Такую особую точку называют действительною двойною точкою кривой, или узлом. Следовательно, в узле должны быть удовлетворены условия:
/(х, У) = °, = 0, ^=0,
1 v ’ дх ду
дх ду / дх2 ду2
Пример 1. Исследовать на особые точки лемнискату у2 = х2 — х*
Решение. Здесь
/(х, j)=jS-x2 + x< = 0.
Затем
4^ = + 4х> = 0, 4^- = 2у = 0.
дх ду
Точка (0, 0) есть особая точка, так как трем уравнениям. В точке (0,0) имеем:
-0, ^ = 2.
ду2
^=-2
дх2 ’ Ъхду
Отсюда
( дЧ \« _ \dx dy) dx2 и начало есть двойная точка проходят в различных направлениях две члены низшей (второй) степени, находим:
у2 — х2 = 0, или у = х н у = — х, f уравнения двух касательных АВ и CD в этой особой точке или в узле (0,0) (черт. 176).
ее координаты удовлетворяют этим
которую ветви кривой. Приравнивая нулю
^=4, ду2
(узел), через
/ d2f \* d2f дЧ
§ 191. Точка возврата —зА • хЛ=0. В этом слу-
э г\дхду) дх* ду2 J
чае уравнение (F) дает для углового коэфициента два действительных и равных значения, следовательно, имеем две совпадающие касательные. Это значит, что обе веиви кривой, проходящие через эту точку, каса-тельны друг к другу. Когда кривая удаляется от касательной в разные стороны от точки касания, то особая точка называется точкою соприкосновения; если она удаляется от точки касания в одну сторону, она называется Точкою возврата. Есть два рода точек возврата.
Точка возврата первого рода. Когда обе ветви кривой лежат по разные стороны от общей касательной. '
Точка возврата второго рода. Когда обе ветви лежат по одну сторону от общей касательной ').
Следующие примеры поясняют, как определяется род особых точек, о которых идет речь.
Пример 1. Исследовать на особые точки кривую а*у2 = а2х*— xfi.
Решение. Здесь f(x, у) = а*у2 — в2.г* х6 = 0,
= - 4в2х» + 6x5 = о, = 2гНу = 0, дх ду J
и (0,0) есть особая точка, так как удовлетворяет всем трем уравнениям. Затем, для точки (0,0) имеем:
^-0 -П ^-9^4
дх2 ’ дхду ’ ду2 '
&f А
Y
Черт. 177.
откуда
х) Подразумевается, в соседстве с особой точкой.
26 Зак. 2789. — В. Гранвиль я Н. Л у а и и. Часть I
а так как кривая симметрична относительно ОУ, то начало есть точка соприкос новения. Приравнивая нулю члены низшей (второй) степени, получаем у- = О, уравнение, показывающее, что обе касательные совпадают с ОХ (черт. 177).
Пример 2. Исследовать на особые точки кривую у'- = х3.
Решение. Имеем:
f(x, У) = у3-х3 = 0.
9f__ дх
df
откуда видно, что точки (0,0) имеем:
откуда
Однако это не относительно у, иуеем:
есть точка
особая точка есть (0,0). Затем для
^=0, дх-
_*/_0 — — 2 дхду ' ду3~£>
соприкосновения, ибо, решая данное уравнение
расположена только вправо от ОУ, ибо для отрн-
а это показывает, что кривая расположена только вправо от ОУ, ибо для отрицательных значений х ордината у мнима. Следовательно, начало есть точка возврата, и так как обе ветви лежат по обе стороны от общей касательной, то это есть точка возврата первого рода. Приравнивая .нулю члены низшей (второй) степени, получаем уравнение у3 = 0, показывающее, что обе общие касательные совпадают с осью ОХ (черт. 178).
Пример 3. Исследовать на особые точки кривую (_у — х2)2 = х6.
Решение.' Поступая, как в предыдущем примере, находим точку возврата (0,0), причем общая касательная к обеим ветвям совпадает с осью Решая относительно у, имеем:
к
ь
Г-2
ОХ
Для всех у принимает чення, а это чалом обе ветви лежат над общей касательною. Следовательно особая точка (0,0) есть Ьлчка возврата второго рода (черт. 179).
значений х, лежаших между 0 два различных положительных показывает, что в соседстве с
и 1, зна-на-
§ 192. Уединенные или изолированные точки
дх* денные тельных сечения тельной кривой,
точкою.
• -^£<0. В этом случае значения углового коэфициента, най-из уравнения (В), мнимы. Следовательно, действительных каса-в этом случав нет; особая точка есть действительная точка пере-мнимых ветвей кривой, и координаты ни одной иной действи-точки в непосредственном соседстве не удовлетворяют уравнению Такая уединенная точка называется изолированною
Пример 4. Исследовать кривую уг = х* — х* на особые точки.
Решение. В этом случае особою точкою кривой служит точка (0,0), и для нее
<У
dx
zt / — 1-
Следовательно, начало есть изолированная точка. Решая уравнение относительно у, находим:
у = ± X Ух — 1.
Это ясно показывает, что начало есть изолированная точка кривой, ибо нет значений х, лежащих между 0 и 1, которые давали бы действительные значения для у (черт. 180).
Черт. 180.
§ 193. Особые ТОЧКИ трансцендентных кривых. Кривая, уравнение которой содержит трансцендентные функции и не может быть приведено к одним только алгебраическим функциям, называется трансцендентною кривою. Такая кривая может иметь концевую точку, в которой внезапно обрывается, вследствие разрыва непрерывности функции; либо угловую, в которой оканчиваются две ветви кривой, не имея общей касательной, вследствие разрыва непрерывности производной.
Пример 1. Показать, что кривая у = х1пх имеет концевую точку в начале координат.
Решение. Абсцисса х не может быть отрицательным числом, ибо числа отрицательные не имеют логарифмов; поэтому кривая простирается только вправо от OY. При х — 0 и у = 0. Для всякого положительного значения х имеется только одно значение у, так что кривая состоит только из одной ветви, оканчивающейся в начале, которое, следовательно, и служит концевою точкою
Пример 2. Показать, что кривая у = ——у- (черт. 182) имеет угловую точку 1 +е7 в начале координат.
Решение' Имеем: t
_ 1 , ех
dx - ( -У 1-|-еж \х (1-|-в*./
Когда х положительно и стремится к пределу нуль, в конце концов будет:
и
^=0. dx
Когда х отрицательно и стремится к пределу нуль, в конце концов будет:
у = 0 и = 1. J dx
Следовательно, обе ветви встречаются в начале координат, причем одна имев1? касательной ось ОХ, а другая — прямую АВ, составляющую с осью ОХ угол в 45° (черт. 182).
ПРИМЕРЫ.
1. Показать, что кривая _у2 = 2х2 + х3 обладает узлом в начале координат, причем угловые коэфиииенты касательных суть zt V 2.
2. Показать, что начало служит узлом кривой _у2 (в2-|-х2) = х2 (а2 —х2) и что касательные служат биссектрисами углов между осями.
3. Доказать, что точка (д, 0) есть узел кривой у2 = х (х — в)2 и что угловые коэфицие*ты касательных суть zt Y а.
4. Доказать, что точка соприкосновения кривой а3у2 — 2аЬх2у — х® = 0 находится в начале координат.
5. Показать, что точка соприкосновения кривой _у2 = х®-|--г4 лежит в начале координат.
6. Показать, что циссоида у2 = ?а_х имеет точку возврата первого рода
в начале координат.
7. Показать, что у кривой у3 = 2ах2 — х3 имеется точка возврата первого
рода в начале координат.
8. Показать, что для кривой (_у — х2)2 = х“ начало служит точкою возврата первого рода, если п<4, и точкою возврата второго рода, если п >4.
9. Показать, что кривая х* — 2ах2у — аху2 + а2у2 = 0 обладает точкою
возврата второго рода в начале координат.
10. Показать, что начало есть изолированная точка кривой у2 (х2 — а2) = .г*.
11. Показать, что у кривой у2 = х (а -|- х)2 имеется изолированная точка (-д, °).
12. Показать, что начало координат будет изолированною точкою кривой ау2 — х3 + Ьх2 = 0, когда а и Ь имеют одинаковый знак, и будет ее узловою точкою, когда знаки а и Ь противоположны.
13. Показать, что начало координат будет тройною точкою кривой х4 4--|- 2ах?у — ау3 = 0 и что угловые коэфиииенты касательных суть 0, + 1^2
14. Показать, что
точки пересечения кри
“«(т)’+ (*)’
с осями
суть точки возврата первого рода.
15. Показать, что ни одна кривая второго или третьего порядка относительно переменных х и у не может иметь точки возврата второго рода.
16. Показать, что кривая у = — имеет концевую точку в начале коор-
= 1
динат.
17. Показать, что кривая.у = х arctg — имеет угловую точку в начале и что . я
угловые коэфиииенты касательных суть ± .
ГЛАВА XX.
ПРИЛОЖЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ.
§ 194. Касательная линия и нормальная плоскость к кривой двоякой кривизны, уравнения которой даны в параметрической форме. Читатель уже знаком с параметрическим представлением
плоской кривой. Распространим это понятие пусть координаты какой-либо точки (х, у, z) кривой двоякой кривизны даны как функции некоторого независимого переменного t, например:
х ='? (О, У = (0, 2 = у (О- (А)
Исключение параметра t из этих уравнений, взятых попарно, дает проектирующие цилиндры кривой на координатные плоскости.
Пусть точка Р (х, у, z) (черт. 183) соответствует значению параметра t, а точка Р' (х Дх, у 4- Ду, z-j-Дх) соответствует значению £-{-Д/, причем Дх, Ду, Дх суть
на кривые в пространстве:
Черт. 183.
приращения х, у, z, соответствующие при-
ращению Д^ и находимые из уравнений (А). Из аналитической геометрии известно, что косинусы углов секущей (диагонали) РР' пропор-
циональны количествам
Дх, Ду, Дх;
или, разделив на Д/ и обозначая углы секущей с осями координат буквами а', р',
cos а' : cos р' : cos 7' =
Дх , Ду Дх дГ • “Д£ ‘ "дГ
Пусть теперь Р', двигаясь по кривой, приближается к Р.
Очевидно, Д0 а следовательно, и Дх, Ду, Дх будут приближаться к пределу, равному нулю, секущая РР' будет приближаться к касательной к кривой в точке Р как к своему предельному пЪложению, и
получится:
_ dx dy "dz
где a, p, у суть углы с осями координат касательной (или кривой) в точке Р. Таким образом уравнения касательной к кривой
X = ? (0, У = (0, z = X (0
в точке (х, у, z) будут:
Х-х Y-y Z—z
dx dy_ dz ’ k '
dt 'dt dt
а уравнение нормальной плоскости, т. е. плоскости, проходящей через точку (х, у, z) перпендикулярно к а-сательной, будет:
4-+4- 4-°-
> С»*'
где Д', У, Z текущие координаты. Ujrnwp. Найти уравнения касательной линии и нормальной плоскости к винтовой линии (где 6—параметр):
х = a cos О, 9 у = a sin О,
z = 60,
а) в любой точке; Ь) когда 6 = 1-1).
Решение.
dv d*
--в- = вСО5в = Х, ~^ = Ь.
Подстановка в (1) и (2) дает для точки (х, у, *): Х-х Y-y Z-z ..
——— = —= —&--------------уравнения касательной,
и
—у(Х — х)Ц-х (Y — (Z— г) = 0 — уравнение нормальной плоскости.
Когда 6 = 2к, точка касания будет (а, 0, 2Ьп); это даст:
X- а = Y-Ъ _Z-2br. О а Ь или
X = a, bY = aZ— ЧаЬк — уравнения касательной, и 2б2к = 0 — уравнение нормальной плоскости.
*) Винтовую линию можно определить как такую кривую, начерченную на
прямом круглом цилиндре, которая пересекает все его образующие под одним и тем же углом.
Дозьмем 02 по оси цилиндра (черт. 164), а точку выхода на ОХ в Р& Пусть а равно радиусу основания цилиндра и 0 равно углу вращения. По определению
PN PN г . , .
•сП =-------— —г = к (пост.)
SN дуга РйЫ ав
ИЛИ г = сАО.
Пусть ak = bi тогда z будет равно М. Затем у = MN •= a sin 6; х = ОМ = a cos 6.
УПРАЖНЕНИЯ.
Найти уравнения касательной липни и нормальной плоскости к каждой из нижеследующих кривых в указанных точках:
1. х = 2/, у = Р, z = 4Р; t = 1. Отв. —;
2 2 10
. х +У + 8z — 35 = 0.
2. х = Р - 1, у = t + 1, z = Р; t = 2. Отв. = ^-=-5- = ;
4x-j-y+ 2z — 111 =0.
3. x = ,3-i,j, = < + /2( 0 * _у-2 _ *~2 .
z = 4P-3t + l;/= 1. 3 3 ~ 9 ’
x+y + 3z-8 = 0.
4. x — t, у = sin t, z = cos t\ t = .
От,.
4 1 — 1
16x + v~2y - /Tz - 4- = 0.
5. x = at, у = bp, z = ct\ / = 1. 7. x = t y = J t _ 3-t. z _ 0
6. x = t, у = 1 - P, y „
г — зр । 4/. t _ _ 2. 8. x = a sin t, у = b cos t, z = t\ t = .
9. Найти направляющие косинусы касательной линии к кривой х = Р, у = Р, z — I* в точке, где х = 1.
§ 195. Касательная плоскость к поверхности. Прямая линия называется касательной к поверхности в точке Р, если она служит предельным положением секущей, проходящей через Р и через близкую точку Р' на поверхности, когда Р', двигаясь по поверхности, приближается к Р. Докажем следующую весьма важную теорему.
Теорема. Все касательные линии к поверхности в данной точке1) лежат вообще в одной и той же плоскости, называемой касательной плоскостью в этой точке.
Доказательство. Пусть уравнение данной поверхности будет:
F (х, у, z} = 0,
(А)
а данная на поверхности точка пусть будет Р (x^y^z). При приближении точки Р' к Р по кривой С, лежащей на поверхности и проходящей через точки Р и Р', секущая РР' будет приближаться к положению касательной к кривой С в точке Р. Пусть уравнения кривой С будут:
х = с?(/),^ = <>(0, z = z(0. (В)
Уравнение (А) должно тождественно удовлетворяться этими значениями, и так как полный диференциал от (А), если х, у, z определяются уравнениями (В), должен равняться нулю, то
dx . dF dy . dF dz dx dt * ~3y dt dz di
J) Предполагается, что рассматриваемая точка есть dF др бая) точка поверхности, т. е. что в этой точке
в (C)
обыкновенная (не осо-dF
не все равны нулю.
Это уравнение показывает, что касательная к С, косинусы углов которой с осями пропорциональны dx dy dz ~dt ’ ~dt ' ~dt ’
перпендикулярна ’) к прямой, которой косинусы углов с осями определяются отношениями:
dF . df\ № дх ’ ду ’ dz ’ и так как С есть какая угодно кривая на поверхности, проходящая через точку Р, то тотчас заключаем, что если заменить точку Р (х, у, z) точкою Рх (х„ у,, z,), то все касательные к поверхности в точке Р1 лежат в плоскости * 2)
^(*-^)+^-л)+^(г-г-)=03,> (3)
это, следовательно, и есть уравнение плоскости, касательной в точке (хх, ур z,) к поверхности, данной уравнением:
F (х, У, z) = 0.
В случае, когда уравнение поверхности дано в форме z=f(x, у), полагаем
F{x,y, z)=f(x,y)-z = 0. (D)
Имеем:
ЭР = о/ <?z = =
дх дх дх ' ду ду ду ' dz
Вычисляя эти количества для точки (xv yv zt) и подставляя в (69), получим:
= (4)
это, следовательно, есть касательная плоскость в точке (х,,у,. z,) к поверхности, уравнение которой дановформе *=/(*> >)•
') Из аналитической геометрии в пространстве известно, что если две прямые, которых косинусы углов С ОСЯМИ суть COS a,, COS Р,, COS Т, и COS Ogi cos cos Ta взаимно перпендикулярны, то
cos a, COS ft + COS'P, cos p, -|- COS ft COS ft = 0.
2) Косинусы углов нормали с осями к плоскости (3) пропорциональны dFi dFt dFt dx, ’ dy,' dz,'
Следовательно, как известно из аналитической геометрии, (С) есть условие, что касательные, которых косинусы углов с осями суть cos a, cos р, cos т, перпендикулярны к этой нормали, т. е. что касательные лежат в этой плоскости.
а) Сопасно нашим обозначениям dF\ dF} dFt dzx dz^ dx, ’ dy, ’ dz, ’ Sjq ’ dy, суть значения частных производных для точки (х„ у,, z,).
В § 157, формула (1), мы нашли полный диференциал функции и (или z) от х и у, именно:
, dz . /С.
Теперь мы можем дать геометрическую интерпретацию этого результата. Касательная плоскость к поверхности z =f (х, у) в точке (х, у, z), по формуле (4) есть
(F>
где X, Y, Z суть переменные координаты любой точки плоскости. Подставив в (F)
X = x-\-dx и y=j/-|-rfy, найдем:
/у dz . । dz . . —,
Z — z— rfx4--4— dy. (G) dx 'dy-'
Сравнивая (E) и (G), имеем: dz = Z — z. (H)
Отсюда: Теорема. Полный диференциал функции f (х, _у), соответствующий прира-
щениям dxn dy, равен со- церт
ответствующему приращению координаты z касательной плоскости к поверхности z = f(x, у).
Так, на прилагаемом чертеже (черт. 185) РР' есть касательная плоскость к поверхности PQ в точке Р (х, у, г).
Пусть АВ = dx и CD = dy.
Тогда dz = Z — z = DP’ — DE = EP'.
§ 196. Нормаль к поверхности. Нормалью к поверхности в дайной точке называется прямая, проходящая через эту точку перпендикулярно касательной плоскости к поверхности в этой точке.
Косинусы углов с осями всякой прямой, перпендикулярной к касательной плоскости (3), пропорциональны dFx dFx dF, dxx ’ dyx ’ dzx
Следовательно, уравнения нормали ]) к поверхности F (х, у, z) = 0 в точке (xn ух, zx) с у т ь;
х — _ у—ух _ z — zx
дЛ, dF± dFx • w
dxx dyx
*) См. выноску 2 стр. 408.
Подобным же образом из (4) имеем следующие уравнения нормали к поверхности z=f(x, у) в точке (хр г,):
х — х^У—У1 z — z;
0zx — 1 ' '
Пример. Найти уравнение касательной плоскости и уравнение нормали к шару х2+у24-а2 = 14 в точке (1, 2, 3).
Решение. Пусть
F(x, у, а) = х2-[-_у2а2 — 14, откуда
^-= 2х — = 2v ^ = 2z-дх iX' ду у' dz '
х, — 3'1 = 2> *1 3 3,
е потому
s.t Р=6.
vX| дуд dzj
Подстановка в (3) дает уравнение касательной плоскости:
2(х-1)-НСу-2) + 6(а-3) = 0 или
х + 2у + За = 14.
Подстановка в (5) дает уравнения нормали:
х—1 у — 2 а — 3
2 - 4 “ Т" или
а = Зх и 2а = Зу.
УПРАЖНЕНИЯ.
1. Найти уравнение касательной плоскости и уравнения нормали к эллипсоиду 4х* + 9у* + 36а2 = 36 в точке, где х = 2, у= 1, а а положительно.
Отв. Касательная плоскость есть
- 8(х-2) + 9Су-1) + в/Й^а--|- /й)=0;
* ,-2 ,-1 ’-I’"11
"Г"’" , еуп •
2. Найти уравнение касательной плоскости к’ эллиптическому параболоиду с = 2ха4-4у^ в точке (2, 1, 12).
Отв. 8х Ц- 8у — я = 12.
3. Найти уравнения нормали к однополостному гиперболоиду х2— 4у2 + 2а» = в
в точке (2, 2, 3).
Отв. у + 4х = 10, Зх — а = 3.
4. Найти уравнение касательной плоскости к двуполостному гиперболоиду ^_У?_^. = 1 а* 1>* с*
в точке (хр _ур ах).
пт. У>У _ *1* _ I
От1, а» b‘i «з 1"
§ 197] ДРУГАЯ ФОРМА УРАВНЕНИЙ КАСАТЕЛЬНОЙ 411
•
5. Найти уравнение касательной плоскости в точке (xt, yt, zx,) к поверхности ax2 + ^2+cz2_]_rf = o.
Отв. axjx 4- byty + cz{z + d = 0.
6. Показать, что уравнение касательной плоскости к шару
х* + У + + 2 Lx 4- 2Му + INz + D = 0 в точке (хх, уи Zi) есть
xix 4- У\У 4" г1г + L (х 4- X]) 4- М (у 4-.У1) 4- А/ (л 4- *i) 4- = о.
7. Найтя уравнение касательной плоскости в любой точке поверхности
2 2_ 2 2
х* +ув +** = «’
и показать, что сумма квадратов отрезков на осях, образуемых касательной плоскостью, есть величина постоянная.
8. Показать, что тетраедр, образуемый координатными плоскостями с любой касательной плоскостью к поверхности хуг = а3, имеет постоянный объем.
9. Найти уравнение касательной плоскости и уравнения нормали к следующим поверхностям в указанных то
а) 2x2 4-4у2 _ 2 = 0; (2, 1, 12) Ь) х3 4- 4у« — л3 = 0; (1, 2, — 1 С) х2 4-У4-гг=П: О, 1, 1).
§ 197. Другая форма уравнений касательной прямой к кривой двоякой кривизны. Если рассматриваемая кривая будет кривая АВ пересечения двух поверхностей Fix,у, z) = 0viG (х,у, z) = 0, то касательная линия РГвточ-ке Р (xp yv zj будет пересечением касательных плоскостей CD и СЕ в этой точке, ибо она будет касательна к обеим
лежать в обеих касательных плоскостях (черт. 186). В силу (3) уравнения двух касательных плоскостей в Р суть:
d) 3x2 _|__у2 _ 2z = 0; X = 1, у = 1.
е) х2у* + 2х z3 = 16; х = 2, у = 1.
f) X3 4- Зу 4- 2z2 = 9; у = 1, z = 1.
Черт. 186. поверхностям и. следовательно? должна
д<7<, . । <?Oi , . , <?О., . _
эг;(г_£1)=0-
(7)
Взятые совместно, уравнения (7) суть уравнения касательной линии РТ к кривой двоякой кривизны АВ. Уравнения (7) можно написать в более сжатой форме:
Х—Хх = у—У! = Z — Z, .
dFt дС, dFidGl дР\д£. dG, dFx dG, dF, dGx v J
t dyY dzx dzx dyt dzi дхг dxt dz{ ~dxx dyx dyt dxt
или, употребляя детерминаты:
X — X, У—Ji z—z. (9)
dF, dF, dy, dz, dG, dG, dF, dF, dz, dx, dG, dG, dF, dF, dx, dy, dG, dG,
dy, dz, dz, dx, dx, dy.
§ 198. Другая форма уравнения нормальной плоскости к кривой двоякой кривизны. Нормальную плоскость к кривой двоякой кривизны в данной точке мы уже определили как плоскость, проходящую через эту точку перпендикулярно к касательной линии к кривой к этой точке. Так, на предыдущем чертеже, PHI есть нормальная плоскость к кривой АВ в точке Р. Так как эта плоскость перпендикулярна к касательной, выражаемой уравнением (9), то тотчас же имеем:
dFx dFt dy, dz, dG, dG, dy, dz.
(x—x,) +
dl\df\ dzt dxx dG, dG, dz, dx.
(У~Ji) +
dF, dF, 3x7 dy, dG, dG, dx, dy,
(z — z,) = 0(10)
уравнение нормальной плоскости к кривой двоякой кривизны.
Пример. Найти уравнения касательной линии и уравнение нормальной плсскости
в точке lr. г, г |^2) к кривой пересечения шара с цилиндром, уравнения которых суть х2 -f- у2 + z2 = 4г2 и x2-j-y2 = 2rx (черт. 187).
Решение. Пусть
o,
или
Черт. 187.
=2г/2, dz,
^1 = 0. dz,
= "*- = •
d.r, ’ dyi
dG, =0 dx, ’ dy,
Подставим в (9):
уравнения касательной РТ в точке Р к кривой пересечения.
Подстановка в (10) дает уравнение нормальной плоскости:
или
/2x-z = 0.
УПРАЖНЕНИЯ.
1. Найти уравнения касательной ливни к окружности х2 _|__уз 4. гг = 25,
________________ х 4~ z = 5 в точке (2, 2]/^ 3, 3). _
Отв. 2х + 2 УЗу + 3z = 25, х + z = 5.
2. Найти уравнение нормальной плоскости к кривой х2 4-J2 4- z2 = г2, х2 — гх + >2 = О
в точке (Xj, jp zj.
Отв. 2_yjZiX — (2xj — г) z^y — rytz = 0.
3. Найти уравнения касательной прямой и нормальной плоскости к кривой 2х2 -|- ЗУ + z2 = 9, z2 = 3x24-_y2 в точке (1, — 1, 2).
4. Найти направляющие косинусы касательной к кривой xyz = 1, _у2 = х в точке (1, 1, 1).
5. Найти направляющие косинусы касательной к кривой у = х2, z2 = 1 — у в точке (0, 0, 1).
6. Уравнения винтовой линии (спирали) суть х2 + уъ = г2
Показать, что в точке (хр ух, zx) уравнения касательной линии суть: c(x-xi) +у, (z - z,) = 0. с (у - л) - -vi (* — о, а уравнение нормальной плоскости есть
yix-xiy-c(z-zl) = 0.
7. Кривая двоякой кривизны произведена пересечением конуса, уравнение которого —^„- = 0 с шаР0М x2+_y2-|-z2 = г2. Показать, что
в точке (;q, ух, zt) уравнения касательной прямой к кривой суть:
с2 (я2 — ft2) Xi (х — xj = — a2 (ft2 + с2) zx (z - zj, с2 (а2 — ft2) у! (у — ух) = 4- 62 (с2 4- а2) Zj (z — zL), а уравнение нормальной плоскости
а2 (б2 4- с2) j’jZjX — ft2 (с2 4- а2) ZjXjу — с2 (а2 - 6») x^z = 0.
ГЛАВА XXL
ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ СПРАВОК.
ФОРМУЛЫ ДЛЯ СПРАВОК.
§ 199. Для удобства читателя даем следующий список элементарных формул.
Алгебра.
1. Бином Ньютона (л— целое положительное):
(а + Ь)п =ап + -?-ап~1 Ь + П ап—2 + -(-Л ~ }а""3 6» + ...
1 1 • Z 1 • £ • О
... + M"-i)(»-2lu^-* + d e„_kьк + _ + ь,
Пишут также:
(а + Ь)п = ап + С1п а”-1 Ь + С® а^Ь* + ... + Г* ап~к Ьк ь
где Сп есть число сочетаний из л предметов по й, т. е. ' it _ л (л — 1) (л — 2)...(л — й + 1) _ л!
l-2-З...й ~(n — k)'.k'.'
2. л! = 1-2-3-4... (л — 1) • л.
3. В полном квадратном уравнении ах* -f- Ьх + с = 0 имеем:
— Ь + У йа — 4ас х1.2 “ 2а ’
если Ь* — 4ас>0, корни действительны и различны,
„ Ь* — 4ас = 0 . и . равны;
в Ьг — 4ас <0 а мнимые.
4. В приведенном квадратном уравнении
< х* -I- рх + q = 0 имеем:
р = сумме корней с обратным ( —) знаком:
q = произведению корней с прямым ( 4*) знаком;
Р 2
5. В арифметической прогрессии
e + ((7 + rf) + (a + 2rf) + (a + 3rf)+... +/
имеем:
. л -f-1 2а -j- (п — 1) d
/ = a+ (л - l)d; s= -y- -п =------------------^-2------
• л.
6. В геометрической прогрессии
а + ар 4- аф + aq* + ... 4- I имеем:
7. Сумма членов бесконечной геометрической прогрессии а 4- ад 4* aqt + ... 4- aqn 4- ...
при — 1 < q < 4-1 равна:
. ат — ” г
8. ат • ап = am+n: —- = am-n; а п = V ат, а0 = 1. ап
9. ]gab = Iga4-lg6; lg-y- = lga — Igft.
10. lga” = nlge;
11. Igl «=0; 1g i = — 1g a.
Примечание. В формулах 9, 10 и 11 символ 1g обозначает логарифм при любом основании. Логарифм при основании а пишется: log ,
12. elog.a.V = дг. 10gfte=i.
13. In обозначает натуральный логарифм, т. е. lge
1g . десятичный » т. е. lglc
1g У = (In W)-0,4342945.
Основание натуральных логарифмов е = 2,7 1828 1828 459045...
Геометрия.
14. Сторона правильного вписанного треугольника равна г-У 3.
. я я квадрата . г • УЪ.
. „ . шестиугольника , г.
' /т-1
, „ , десятиугольника , г -—------.
15. Площадь треугольника с периметром 2р и сторонами а, Ь и с равна: Д = / р(р — а)(р—Ь)(р — с).
16. Площади подобных многоугольников относятся, как квадраты сходственных сторон.
17. Окружность круга равна 2яг = nd. d*
18. Площадь , , пг* = к——. \
4 г d
19. . сектора , а-у = а—, где s есть длина дуги сектора.
20. Боковая поверхность правильной усеченной пирамиды равняется полусумме периметров ее оснований, умноженной на апофему.
21. Объем призмы равен S’h.
22. Объем пирамиды равен - 5 • h. о
23. Объем прямого кругового цилиндра равен .
4. Боковая поверхность прямого кругового цилиндра равна Inrh = ndh.
25. Полная поверхность прямого кругового цилиндра равна
2пг(г + Л) = га/ (у+л).
26. Объем прямого кругового конуса равен = -ру-. О 1Z
__ г- , T-dl
27. Боковая его поверхность равна иг/ = ——.
28. Полная его поверхность равна itr (г-]-/) = -^ (у -Н ) •
29. Объем усеченного кругового конуса равен кЛ (/?’ 4- Rr + г4).
и
30. Боковая его поверхность равна
i»(A? + r) V Л2 + (/?-г)2.
4 , r-tfl
31. Объем шара равен у zr«= -у- .
32. Поверхность шара равна 4кг2 =
33. Поверхность шарового пояса равна произведению его высоты на окружность большого круга, т. е. 2кгЛ = rdft.
Примечание. В формулах 14 — 33 г означает радиус, d — диаметр, Л — высоту, S — площадь основания, / — образующую.
Тригонометрия.
34. tgx
sinx .
cosx ’
35. secx
1 cosx ’
. cosx . 1
6 sinx 6 tgx 1 cosec X = —;----.
sinx
36. sln2x-|- cos2x = 1; 1 + tg2x = scc2x; 1-|-ctg2 x = cosec2 x.
37. sinx = 4^1— cos2x; cosx = ct У1 — sin’ x.
„„ tgx 1
38. sin x = :------ ; cos x = _.
~V l+tg2x t+tg-.v
39. sinx = cos (y — x); cosx = sln(y — x); tgx = ctg(y — x ,40. sin (n — x) = sin x, cos (n — x) = — cos x, tg (n — x) = —tgx.
41. Sin(x + y) = Sin x cosy + cos xslny,
sin (x — y) = sin x cos у — cos x sin y,
cos(x +y)= cosx cosy — sinx sin y, cos(x —y)= cosxcosy + sinxslny.
42 tg(x4-v) = +!«>-; tg (x-y) = ^-У-
42. Ig 1.x-j-y; l-tgx-tgy’ igH У) l-|-tgx.tgy
43. sin2x = 2sinxcosx, cos2x = cos2x — sin2x, tg 2x =
44. sin 3x = 3 sin x — 4 sin3 x, cos 3x = 4 cos8 x — 3 cos x.
- x , , / 1 — cos x x _ /”1 + cos x
45. slny = *J/ ------j---, cosy = =t|/ -------:
2tg x
1 — tg3A ‘
X 1 — COS X tg T----------sm7"
sinx
1 + cosx’
4b 1 — cos x = 2 sin2 у ;
1 + cos x — 2 cos!
7 ’
47. sin х 4- sin у = 2 sin —у- cos х 2 , х — у! х Ч-у
sin X — sin у = 2 sin —2^- cos —, х -|- у х — у
cos х + созцу = 2 cos —2^ cos —2~' х -|~ у х —у cosx —cosy =— 2 sin—sin — а b с „ _
48. —;—т- = —;—~ = D — закон синусов; здесь и есть диа-sln A sin В sin С
метр круга, описанного около треугольника.
49. аа = 6а + с3 — 26с cos А — закон косинуса.
* А tgT =
т . А
50. sln-j-
— b)(p — c) _
Ьс
, А psln
(Р —6)(Р —с) . р (р — а) ’
а~ В С cos-^-.cos-y
2g • sin Я sin A - sin С ’
здесь периметр треугольника есть 2р, его площадь есть g.
51. sin х = у,
cos х = у; tg *=У', ctg х=у;
х = arcsin у х = arccosy х = arctg у х = arcctg у
обратные круговые функции.
Аналитическая геометрия.
1. На плоскости.
52. Расстояние d между точками (х^ у,) и (ха, fy:
d = /(*1 — ХгР + (Л ~У>)2-
53. х лх^-|-тхг, _ координаты Точки, делящей отрезок
с концами (х1г у,) и (ха, у2) в отношении т :п;
х, + х2 у. + У1 х=—------------------------координаты средины отрезка с концами
(Xi, yt) и (х2, уа).
54. х = х04-х', у =у0 — преобразование к новому началу (х0, у0).
55. Преобразование к новым осям, образующим угол а со старыми: x = x'cosa— у' sins, у = хУ sin а +у cos а.
| выражение прямоугольных координат через полярные.
57. р= V х3 + у3,
<р = arctg выражение полярпых координат через прямоугольные.
58. Различные формы уравнения прямой:
общее уравнение прямой: Ах4-Ву+С=0; (а)
нормирующий множитель:
1 л М =------г - - ; его знак противоположен знаку О.
zt/Aa4-fl3
Зак. 2709. —|в. Гранвиль и Н. Луз и и. Часть I 27
нормальное уравнение прямой:
xcosa +> sin а — р = 0; (Ь)
уравнение с угловым коэфициентом:
У = kx 4- Ь; (с)
уравнение в отрезках:
' («
уравнение пучка прямых с центром в точке (х', у')’, у — у' — k(x — х'); (е)
уравнение прямой, проходящей через две данные точки (хр yt) и (х^ у2):
Х-Х^ = Л—У1_. , (f)
*»-*! Уа~У1
Это же самое уравнение можно написать еще иначе, именно в виде детер-
минанта третьего порядка:
который при раскрытии дает:
X у 1
ЧЛ 1
х2Уа 1
= 0,
х (У1 —уг} + У (х2 - Xj) + (Xjyj - хгуд) = 0.
59. Угол 0 между двумя прямыми с угловыми коэфициентами и
tg8 =
А=А_. 1 + *Л ’
условие параллельности этих прямых:
л1 = *а;
условие перпендикулярности втих прямых:
' >= 4-
60. Расстояние точки (хг .у 4 до прямой Ах 4- By 4- С — 0:
•ЧУ)1 х2 у21 ЧУэ1
61. 4 = 4=4
, _ Лсд + Byt 4- С zt V + *
•—площадь треугольника с вершинами в точках (Хд.Уд), (х^У2) и (хВ1 у3);
то же самое в раскрытом виде:
д = — у К*зЛ ~ — <хзУ1 “ Х1У^ + (ЧУг ~ х2У1)г
62. Уравнение окружности с центром в точке (я, ₽) и радиусом г: (хга)»4-(У-?)г = А
63. Общее уравнение окружности:
х2 4-У2 4- 2ах 4- 2by 4- с = 0.
64. Уравнение эллипса с полуосями а и Ъ:
65. Уравнение гиперболы с полуосями а и Ь:
66. Касательная к эллипсу в точке {х', >'):
• хх' уу' _
а2 -Г - *’
касательная к гиперболе в точке (х', у'): в
•УХ' уу'_ _ ,
а2 й2 “
67. Уравнение гиперболы, отнесенной к асимптотам:
ху = т, где т = (а2 4- Ь-).
68. Фокусы эллипЖ^я^ Ь',:
0) и (—У?--й2,0);
эксцентриситет эллипсе:
/ а2 — 62 е = —--------,
а
0<е<1;
директрисы эллипса:
I
длина фокального радиуса-вектора, исходящего из правого фокуса до точки
(х, у) эллипса: г = а — ех;
свойство фокальных радиусов-векторов эллипса: г-}- г' = 2а.
69. Фокусы гиперболы:
(4- /в2-]-*2, 0) и (—УаЧ^.О);
эксцентриситет гиперболы: ______
директрисы гиперболы: У а2 4- й2 е = !, а 1 <е< + оо; , а а х = Н , х = ; е е
длина фокального радиуса-вектора, исходящего из правого фокуса до точки (х, у) правой ветви гиперболы: \
It г=ех — а\
свойство фокальных радиусов-векторов гиперболы:
г' — г = 2 а.
70. Уравнение параболы: -
у2 = 2рх\
уравнение касательной к ней в точке (х', уУ.
фокус параболы: >/=р(х4-х'); & »)••
директриса параболы:
длина фокального радиуса-вектора параболы:
r=x+ Р--
2 ’
эксцентриситет параболы:
е = 1.
71. Общее уравнение кривой второго порядка, отнесенное к центру:
Ах"- + Вху + Су"- + D = 0.
Если
Если
Вг — 4АС<0, имеем эллипс.
Если
Вг — 4ЛС>0, имеем гиперболу.
В1 — 4АС=0, имеем параболу.
72. Уравнение для угловых коэфициентов асимптотических направлений: СЛ! 4-ВЛ + А = 0 ,
(Л — угловой коэфициент),
‘s2?=/пВв-;
7 есть угол, образуемый осью кривой с осью абсцисс.
2. В пространстве.
73. Расстояние между двумя данными точками (xI( ylt zt) и (Xj, у^ Zj):
/ = V(Х1 - Х2)« + (Л -yrf + U, - Ztf.
74. Координаты середины отрезка с концами (хр yt, zj и (хг, уъ z3):
г — Х* + Х- • v__ ~|-J'z . _ _ zt Ч~ га
2 ’ у~ 2 * 2
75. Соотношение между углами я, р и 7, образуемыми прямой с осями координат:
cos2 я + cos2 р 4- cosaT = 1.
COS ? = COS Я COS я' 4- COS Р cos Р' 4- cos 7 cos f', . , _ 1‘cos a cosp I2 . I cosp cosy I2 I cosy COS Я |2 1 ~ I COS a' CCS P' I I COS P' COS f' I "• I COS 7' COS a' I 1
76.
или
sin2 v=(cos я cosP'—cos a'cos p)24-(cos p cos 7'—cos P'cos t)24-(cos f cos я'—cos т'созя)2; есть угол между направлениями (я, р, 7) и (я', Р', 7').
77. Преобразование к новому началу (х0, у0, г0):
х = х'4-хо, у=у'4-Уо. 2 = z'4-z0-
78. Преобразование направлений осей:
х = х' cos я 4- у cos р 4- z' cos 7 ~х
у = х' cos У 4- У1 cos р' 4- г' cos 7' —
z = х7 cos я" )-у' cos Р" 4-cos 7"
Z
79. Преобразование координат через эйлеровы углы:
х = д/ (cos <р cos ip — sin 7 sin 6 cos 0) — у* (cos 9 sin <p 4- sin cos ip cos 6) 4-4- z? sin ysin 0),
у = X' (sin 9 COS Ip 4- cos <P Sin Ip COS 0) — y> (sin If Sin Ip — cos <? COS <p cos 6) — — Zr COS f sin 0,
Z = X1 sin Ip sin 6 4- j/ COS tp sin 6 4- z! cos 6.
X' Y> Z'
T д' P' t' a" p"
80. х = р cos cos 0 |
у = р cos <р sin 6 | выражение прямоугольных координат через полярные; z = р sin <р j
<р — широта, в — долгота, р — радиус-вектор.
81. р = /ж«+‘>’ + Г-z
<f = arctg - . __ выражение полярных координат через прямо-
¥Х‘~ЬУ2 угольные.
6 = arctg
82. Различные формы уравнения плоскости: общее уравнение:
Ах 4~ By 4" Cz -|- Z) = 0; (а)
нормирующий множитель:
М =----_______________; его знак противоположен знаку D.
^)Га- + з>+с*
COS а = М • А cos ,3 = М • В cos f = Л1 • С
направление нормали к плоскости;
нормальное уравнение:
х cos з 4* .у cos 3 + 2 cos t — р = 0; уравнение в отрезках:
(Ь)
(с)
ЛД' + ВВ' 4- СС'
83. cos? = r______—т-----------r-r ... —угол между двумя плоско-
/А- + В» + С2 • V А'- + В'2 + С'2
стями, данными уравнениями: Ах 4- By 4- Cz 4- D = 0 и А'х 4- В'у 4- C'z-\-D' = 0; условие параллельности плоскостей:
_А__ А' ” В' С ’
условие перпендикулярности плоскостей:
АА' + ВВ' 4- СС' = 0.
84. Расстояние точки (хь yt, г,) до плоскости Ах 4- By 4- Cz 4- D = 0:
_ Axt 4- АУ: 4~ Czt 4- D dt V A^ + B^ + C1'
85. Уравнение плоскости, проходящей через точки (xlt zj, (xj, y^ z2) и (хь Уъ z3):
X у z 1
хьУ12^ x2ytz21 хзу3га1
= 0.
86. Объем тетраэдра с вершинами в точках (xb ylt zj, . . . , (-ч* 2t>.
2 б
х1У121^ X^y^Z-jl XjyjZgl х1У^
87. Различные формы уравнений прямой: симметрические уравнения прямой:
х — а у—b г —с . .
тпр
т cos а = —. - --- ,
Vrrfi + n^+p-
cos о ______5_____ углы", образуемые прямой с осями
р /m2 4-„2_|_p2 координат;
р cos т = —у -
/m2 + лз + р2
несимметрические уравнения прямой: \
х = тг а; у.— nz Ь; (Ь)
уравнения прямой, проходящей через две данные точки (xlt yt, zj и (хг,у2,г2):
x-xt _ y-yi = z-zx
X2- - Xi У2—У1 *2—*1
„„ ,, m n p
88. Условие параллельности двух прямых:— = —=
условие перпендикулярности двух прямых: тт' + пп' -\-рр' = 0.
8д‘т-\п"р" = л'р" — л’р'
\р' п=\р^" = р'т” — р”т' угловые коэфициенты (т, л, р)
|т' л '=|т"л" = т’п"'— т”п'
прямой, перпендикулярной к двум прямым с угловыми коэфициентами
(и', л', р') и (т", п", р"}.
90. Угол между прямой и плоскостью:
sin ? = ------тА + пВ + рС _ , .
/m2 4- л2 + рз • / Аа + Bi + С*
условие параллельности прямой и плоскости: mA-j-пВ-j-рС = 0;
I „ т л р
условие перпендикулярности прямой и плоскости: .
91. Уравнение сферы с центром в точке (а, 0, у) и радиусом R: (X-a)2 4.(>_₽)2+(2_T)2 = /?2.
92. Уравнение эллипсоида с полуосями а, Ь, с:
д2 * b2 Т с» — и
93. Уравнение однополостного гиперболоида:
Т J, 94. Уравнение двуполостного гиперболоида:
дЗ /,2 Т С2
95. Касательная плоскость к эллипсоиду:
> ^+^+4-=1;
а2 62 с2
касательная плоскость к однополостному гиперболоиду: хх' jj/ лг' _
а2 б 2 с2
касательная плоскость к двуполостному гиперболоиду:
I гг' cP bi т с-
96. Уравнение конуса: ,
” 4г+-£г--?=о.
в2 Ь2 с2
97. Эллиптический параболоид:
х3. . уг-
2р 2Ч
гиперболический параболоид: о
Z ~ 2р 2а ‘ 63. Касательная плоскость к эллиптическому параболоиду:
—+ ^- = г + г';
Р Ч касательная плоскость к гиперболическому параболоиду: хх' уу' , ,
-----^—=-z-\-z'.
Р Ч
Детерминанты.
89. Детерминант второго порядка:
правило диагоналей:
100. Детерминант третьего порядка:
а Ь с а'Ь'с' а"Ь"с"
а
= с" + a'b"c + а"6<У — a”b'c — cb"c' — e'ftc*»
правило диагоналей:
101. Детерминант четвертого порядка:
abed a' b' е d' а" Ь" с" d" a'"b'"d"d’"
bed V d d' b"'e''d"'
-a"’
bed b'c'd' b"c"dn
дравило миноров (приведение к детерминантам третьего порядка).
102.
Диференциыьное исчисление.
Неравенства для абсолютной величины:
103.
|a —6|>|«| —|Z»|.
Формулы теории пределов:
lim(x — y-j- г) = limx — lim_y -|- 11m z;
lim(x-_y • z) = limx • limj • lim z;
lim
если
11m у '
104.
11ш у ф 0.
Замечательные пределы: Hm = 1;
11m
1
-) = е = 2,7 1828 1828 459045 ...
п 1 9 ’
или еще иначе:
lim (1 + а)’ = е.
105. Производная:
_ n_ 4.V /(* + Дх)— f(x)
—= нт —— = Hm ------------т--------•
Ал->0 Дг-»0
Производная есть тангенс угла наклона касательной к оси ОХ.
106. Формулы диференцирования:
постоянное:
4^ = 0;
аргумент:
^=1; dx
сумма — разность:
d (и у — w) _ du . dv dw t dx ~ dx' dx dx *
произведение:
d (uv) du . dv
dx dx 1 dx
частное;
d
функция от функции:
dx
du dv
---- V — и • -- dx-dx
V»
__dy du
обратная функция:
dx du dx
показательные функции:
dy _ 1 ~dx~ ~dx*
dy
df dx
dAa ., , .
—— = Ах • 1п А; dx
§ 199] логарифмы:
dlnx 1 dlogax_ logae dx ~ x ’ dx ~ x ’
степень:
=„rn-l.
квадратный корень:
d У~х _ 1
dx ~ 2 /7 ’ тригонометрические функции:
d sin x dx
= cos x;
d cos x dx
sin x;
!!££ = _l_ = 1 + tg2X- =______1- =
dx cos8x । ь • sin2x
круговые функции: d arcsin x _ 1 . rf arccos x _ ____1
dx у 1 — x~ dx V1 -
(1 4-ctg2x);
x2 ’
darctg x _ 1 rfarcctgx _ 1
dx ~ 1 + x2 ’ dx ~ 1 -j-x2
107. Уравнение касательной:
параметрический вид:
f yt Y-y = ^r(X-x).
Уравнение нормали:
параметрический вид:
Длина касательной:
параметрический вид:
Длина нормали: параметрический вид:
dx
Длина подкасательной:
У' dy'
параметрический вид: x't
У
yt
Длина поднормали: dv
параметрический вид:
108. Угол радиуса-вектора и касательной:
dti
Длина подкасательной:
Рг~. Р ^Р Длина поднормали:
d0’
109. Скорость движения s=f(t) есть: « = =/'(/)• Тангояциальное ускорение движения $ = /(/) есть:
( 1 dt dt'i J ( ’
Компоненты скорости v движения x =/(<)> J' = '}'(0 суть: dx dy
V = — I г = —•
® dt ’ У dt 9
Компоненты тангенциального ускорения j движения х = f(t), у = <f(t) суть: 1 f _ ^tx. • _ &У
JU~~dp'
ПО. Производные высших порядков
/'(X), /'(х), /"’(X), ...; /п’(х) или
dy <Ру _ <Ру tf^y
dx’ dx1’ dx° ' ’ dxn"
Формула Лейбница:
о + u^v'+ (% u(n~ V+.. •+ су*- V + ... +™(Я).
где С* = (биномиальный коэфмциент),
111. Максимум и минимум: если
/'(х) = 0 или не существует и /"(х)> 0—минимум; если
/'(х) = 0 или не существует и /"(х)<0— максимум.
112. Точка перегиба:
f" (х) = О или не существует и f" (х) меняет анак при переходе значений аргумента х от значении меньших х к значениям большим х; f" (х) 4= О-
ИЗ. Диференциал:
dy = /'(x)rfx.
Формулы диференциалов:
</С=0;
d (х) = dx;
d (i: -j- v — w) = du -j- dv — dw;
d
d (ut>) = du v + и • dv; и \ du-v — и-dv
02
dxa = ax'
dx
Л4® = Xя InXrfx; d log .x = ^.X . ; xlnX dx
dex = eTdx;
ds’ix = cosxdx;
. , dx
d arcsln x = —
. dx
d tg x =---—;
6 cos2x
d cos x = — sin xdx; dx sln2x ’
etgx
rfsecx = tgxsecxrfx;
. i dx
d arctg x= z-j—
d arccos x = — d arcsln x;
d arcctg x = — rf arctg x;
, rdx
d arcsec x = —7
114. Неизменность вида диференциала:
dy=f (и) du
независимо от того, является ли буква и в соотношении y=f{u) аргументом или в свою очередь функцией.
115. Диференциал дуги:
ds = /(<fx)24-(d>)2.
Производная дуги:
dx Г \dx)
Полярные.координаты:
диференциал дуги:
ds= У(р<Л)»+(</рр,
производная дуги:
116. Переход от одного независимого переменного к другому
dy dx dx ’ ~dt~
(Ру dx dy d-x
<Ру df1 dt dx dt-
\ dt I
117. Кривизна К: декартовы координаты:
«----------—-------77;
полярные координаты:
р ₽ d№ du ) К------------------
Радиус кривизны:
R = ~K'
Координаты а, р центра кривизны:
Нормаль к данной кривой есть касательная к ее эволюте. Радиус кривизны данной кривой возрастает или убывает ровно на столько, на сколько возрастает дуга эволюты.
118. Теорема о конечном приращении:
где а<с<6.
Конечная формула Тейлора:
/(*) =/(«) + (» - «)Л (а) + (в) + ...
• • +(в)+ где а<с<6.
Теорема Коши:
/(»)-/(*) Г (с)
<н&) —<»(а) »'(*)’
119. Неопределенные формы: О О раскрываются посредством*
х->а ?(х) ' <?'(Х)
120. Частные производные функции z=f(x,y):
dz dz
•j- и j—* dx dy
или
Полный диференциал:
. dz . . dz .
Их^Лх + ^Чу, или'
Производная неявной функции /(x,y) = 0! df
dy __ dx
dx~"~ df '
dy
121. Огибающая семейства f(x, у, a) = 0
получается исключением а из уравнений
fix, у, а) = 0 и
у, а) = 0.
122. Ряд
“1 + “2 + “в + • • • + И« + • • •
Необходимый признак сходимости:
11m и_ = 0.
П-Н-оо
Признак Даламбера: если
ия । j
Нт —— < 1 — сходимость; п++» ип
если
11m п+ >1 — расходимости n->fOO ио
Знакопеременный ряд (убывающий)
“1 —Иа+«з-“4 + --« сходится, если
11m u_ = 0.
n->4-oo
123. Разложение функции в ряд Тейлора:
/(х) = /(а) + / (а) + (^^-2 /" («) 4- ... + /») (а) + ...
Разложение функции в ряд Маклорена:
f W=/(0)+х/ (0) + Г (°) + • • • + т.-2-.з" д /(п) (0)+...
X X® X® хп
^=1+^+-2Г+з!- + --- + ^Г + -’
X Xs Xs X7
slnx- 31 + 51 71 +••• •
хЗ . х4 Xе .
cosx — 1 2| + 4! g] + • •• 1
х х2 х^ х&
1п(1+х) = -- 2 + — - + ;
1п’±^==2(х+4+4+4+...): ln(a+'x) = lna + 2|^i + -l(55^) |
, хЗ , X5 X7 ,
arctg х = х J" + -5-7- + • • •
124. Ряд Тейлора для функции /(х, .у): у + ^)=/(х, У) + [л +л;|£] +
+_1_ГЛ,^- + 2ЛА;Д_ + Л2^1 н„-1 1 -2 L йх- 1 дхду dy2J г
125. Максимум и минимум функции /(х, >): необходимые условия:
и достаточные условия: д= ? дхз <J2/ ХЗ
максимум, если и минимум, если к Д>0 #4<о; дх- Д > 0 дх ду J
и
126. Особые точки кривой /(х, _у) = 0:
эу у дх ду )
___d'f дх2 ду-
>0 — узлы,
= 0 — точка возврата, < 0 — уединенная точка.
Геометрия в пространстве.
127. Уравнение касательной к кривой
х = <р (0, у = 'г' (0, = z W
имеет вид:
Х-х _ Y-y Z—z
dx dy dz
~dt ~dt ~dt
Уравнение нормальной плоскости
=) 4г - °-
128. Касательная плоскость к поверхности
F (х, у, z) = 0 имеет вид;
+ +(2-^=0.
Касательная плоскость к поверхности
*=f(x, у) г-’--тУх-^ + %<у-л-
Нормаль к поверхности F (х, у, z) = 0
имеет вид:
X- -х У —у Z — z
dF dF dF •
дх ду ~Sz
129. Если кривая дана уравнениями:
f(x,y, z) = 0
и
* ? (x, y, z) = 0,
то уравнения касательной прямой:
Х-х _ Y~y _ Z—z
df df df df df df ’
ду dz dz dx dx dy
df д-f df d? df df
ду dz dz dx dx dy
уравнения нормальной плоскости:
df df df df df df
ду dz dz dx , dx dy
(Х-х) / + (У -J) . a +(Z-z) a У =0.
df df df df df df
~ду ~3z dz dx dx dy
§ 200. Греческий алфавит.
Буквы Названия Бу киы Названия
А а альфа N V ни
В ₽ бета е КСИ
Г т гамма 0 омикрон
д 0 дельта 11 — пи
Е е эпсилон Р р ро
Z г дзета Е а сигма
н •п эта Т ь тау
R 0 тета Y и ипсилон
I йота Ф о фи
к X каппа X Z хи
А к ламбда 'F пси
М ми 2 (О омега
ТАБЛИЦЫ.
§ 201. Переход от градусов к радианам (аге) и обратно.
аге Iе = 0,0174532925 1g arc 1° = 0,2418774 —2
аге Г = 0,0002908882 1g arc 1' = 0,4637261 —4
arc 1" = 0,0000048481 1g arc 1" = 0,6855749 — 6
Градусы 1 2 3 4 5
Радианы 0,01745 0,03491 0,05236 0,06981 0,08727
Градусы 6 7 8 9 10
Радианы 0,10472 0,12217 0,13963 0,15708 0,17453
Минуты 1 2 3 4 5
Радианы 0,000291 0,000582 0,000873 0,001164 0,001454
Минуты 6 7 8 9 10
Радианы 0,001745 0,002036 0,002328 0,002618 0,002909
Секунды 1 2 3 4 5
Радианы 0,00000485 0,00000970 0,00001454 0,00001939 0,00002424
Секунды 6 7 8 9 10
Радианы 0,00002909 0,00003394 0,00003878 0,00001363 0,00004848
аге а 0 а / // аге в а
0 (Г
1,0 57 17 44,806 0,005 0,004 0 0 17 12 11,32 45,06
0,003 0 10 18,79
0,9 51 33 58,33 0,002 0 6 52,53
0,8 45 50 - 11,84
0,7 0.6 40 в 25,36 38,88
34 22 0,001
0,5 28 52,40 0 3 26,26
38 55
0,1 22 5,92
0,3 17 11 19,14
0,2 11 27 32,96 0,0009 • 0 3 5,64
0,0008 0 2 45,01
0,0007 0,0006 о 2 24,39 3,76
0 2
0,1 5 43 46,48 0,0005 0 0 I 1
43,13 22,51
0,0004
0,0003 0 1 1,88
0,09 5 9 23,83 0,0002 0 0 41,25
0,08 4 35 1.18
0,07 0,06 4 0 38,54 15,89
3 2 2 1 26 51 17 43 0,0001 0 6 20,63
53,24
0,05 0,04 0,03
30,59 7,94
0,02 1 8 45,30 0,00009 0 0 18,56
0,00008 0 0 16,50
0,00007 о о 14,44
34 22,65 0.0С006 0 0 12,38
0,01 0 0 0 0 0
0,00005 0,00004 10,31 8,251
• 0,00003 0 0 6,188
0,009 0 30 56,38 0,00002 0 0 4,135
0,008 0 27 30,12
0,007 0,006 о 24 20 3,85 37,59
0 0,00001 0 0 2,063
Зак. 2709. — В. Гранвиль u Н. Лузин. Часть I
28
Угол в радианах Угол в градусах sin cos tg ctg sec cosec
0 0 0 1 0 ОО 1 оо
К т 90 1 0 оо 0 оо 1
л 180 0 —1 0 оо -1 оо
Зп ~Т 270 —1 0 ОО 0 оо —1
2z 360 0 1 0 оо 1 оо
Угол в радианах Угол в градусах sin COS ‘g ctg sec cosec
0 0 0 1 0 оо 1 оо
я т 30 1 2 Уз~ 2 Уз 3 Уз 2/~3 3 2
к т 45 /2~ 2 У"2 2 1 1 /Т /т
я 7 60 Уз~ 2 1 2 Уз /~з 3 2 2Уз 3
к т 90 1 0 ОО 0 оо 1
Правило знаков.
Квадрант sin cos tg ctg sec coscc
I + + -г + + +
II + — — — • — +
III — + -i- — —
IV — + — — + —
§ 202. Таблицы тригонометрических функций.
Градусы Sinus
0- ю- 20' 30' 40' | 50- 6tf
0 0,00000 0,00291 0,00582 0,00873 0,01164 0,01454 0,01745 89
1 0,01745 0,02036 0,02327 0,02618 0,02908 0,03199 0,03490 88
2 0,03490 0,03781 0,04071 0,04362 0,04653 0,04943 0,05234 87
3 0,05234 0,05524 0,05814 0,06105 0,06395 0,06685 0,06976 86
4 0,06976 0,07266 0,07556 0,07846 0,08136 0,08426 0,08716 85
5 0,08716 0,09005 0,09295 0,09585 0,09874 0,10164 0,10453 84
6 0,10453 0,10742 0,11031 0,11820 0,11609 0,11898 0,12187 83
7 0,12187 0,12476 0,12764 0,13053 0,13341 0,13629 0,13917 82
8 0.13917 0,14205 0,14493 0,14781 0,15069 0,15356 0,15643 81
9 0,15643 0,15931 0,16218 0,16505 0,16792 0,17078 0,17365 80
10 0,17365 0,17651 0,17937 0,18224 0,18509 0,18795 0,19081 79
11 0,19081 0,19366 0,19652 0,19937 0,20222 0,20507 0,20791 78
12 0,20791 0,21076 0,21360 0,21644 0,21928 0,22212 0,22495 77
13 0,22495 0,22778 0,23062 0,23345 0,23627 0,23910 0,24992 76
14 0,24192 0,24474 0,24756 0,25038 0,25320 0.25601 0,25882 75
15 0,25882 0,26163 0,26443 0,26724 0,27004 0,27284 0,27564 74
16 0,27564 0,27843 0,28123 0,28402 0,28680 0,28959 0,29237 73
17 0,29237 0,29515 0,20793 0,30071 0,30348 0,30625 0,30902 72
18 0,30902 0,31178 0,31454 0,31730 0,32006 0,32282 0,32557 71
19 0,32557 0,32832 0,33106 0,33381 0,33655 0,33929 0,34202 70
20 0,34202 0,34475 0,34748 0,35021 0,35293 0,35565 0,35837 69
21 0,35837 0,36108 0,36379 0,36650 0,36921 0,37191 0,37461 68
22 0,37461 0,37730 0,37999 0,38268 0,38537 0,38805 0,39073 67
23 0,39073 0,39341 0,39608 0,39875 0,40141 0,40408 0,40674 66
24 0,40674 0,40939 0,41204 0,41469 0,41734 0,41998 0,42262 65
25 0,42262 0,42525 0,42788 0,43051 0,43313 0,43575 0,43837 64
26 0,43837 0,44098 0,44359 0,44620 0,44880 0,45040 0,45399 63
27 0,45399 0,45658 0,45917 0,46175 0,46433 0,46690 0,46947 62
28 0,46947 0,47204 0,47460 0,47716 0,47971 0,48226 0,48481 61
29 0,48481 0,48735 0,48989 0,49242 0,49495 0,49748 0,50000 60
30 0,50000 0,50252 0,50503 0,50754 0,51004 0,51254 0,51504 59
31 0,51504 0,51753 0,52992 0,52250 0,52498 0,52745 0,52992 58
32 0,52992 0,53238 0,53484 0,53730 0,53975 0,54220 0,54464 57
33 0,54464 0,54708 0,54951 0,55194- 0,55436 0,55678 0,55919 56
34 0,55919 0,56160 0,56401 0,56641 0,56880 0,57119 0,57358 55
35 0,57358 0,57596 0,57833 0,58070 0,58307 0,58543 0,58779 54
36 0,58779 0,59014 0,59248 0,59482 0,59716 0,59949 0,60182 53
37 0,60182 0,60414 0,60645 0,60876 0,61107 0,61337 0,61566 52
38 0,61566 0,61795 0,62024 0,62251 0,62479 0.627Q6 0,63932 51
39 0,62932 0,63158 0,63383 0,63608 0,63832 0,64056 0,64279 50
~40 0,64279 0,64501 0,64723 0,64945 0,65166 0,65386 0,65606 49
41 0,65606 0,65825 0,66044 0,66262 0,66480 0,66697 0,66913 48
42 0,66913 0,67129 0,67344 0,67559 0,67773 0,67987 0,68200 47
43 0,68200 0,68412 0,68624 0,68835 0,69046 0,69256 0,69466 46
44 0,69466 0.69675 0,69883 0,70091 0,70298 0,70505 0,70711 45
60' | 50’ | 40" 30' 20- 10' О' Гра-
с о в 1 п И 9 дусы
Гра- с 0 6 i П U 8
дусы С’ 10' 20' зо' 40’ 50- 60’
0 1,00000 1,00000 0,99998 0,99996 0,99993 0,99989 0,99985 89
1 0,99985 0,99979 0,99973 0,99966 0,99958 0,99949 0,99939 88
2 0,99939 0,99929 0,99917 0,99905 0,99892 0,99878 0,99863 87
3 0,99863 0,99847 0,99831 0,99813 0,99795 0,99776 0,99756 86
4 0,99756 0.99736 0,99714 0.99692 0,99668 0,99644 0,99619 85
5 0,99619 0,99594 0,99567 0,99540 0,99511 0,99482 0,99452 84
6 0,99452 0,99421 0,99390 0,99357 0,99324 0,99290 0,99255 83
7 0,99255 0,99219 0,99182 0,99144 0,99106 0,99067 0,99027 82
8 0,99027 0,98936 0,98944 0,98902 0,98858 0,98814 0,98769 81
9 0,98769 0,98723 0,98676 0,98629 0,98580 0,98531 0,98481 80
10 0,98481 0,98430 0,98378 0,98325 0,98272 0,98218 0,98163 79
11 0.98163 0,98107 0,98050 0,97992 0,97934 0,97875 0,97815 78
12 0,97815 0,97754 0,97692 0,97630 0,97566 0,97502 О’,97437 77
13 0,97437 0,97371 0,97304 0,97237 0,97169 0,97100 0,97030 76
14 0,97030 0,96959 0,96887 0,96815 0,96742 0,96667 0,96593 75
। 15 0.96593 0,96517 0,96440 0,96363 0,96285 0,96206 0,96126 74
16 0,96126 0,96046 0,95964 0,95882 0,95799 0.95715 0,95630 73
17 0,95630 0.95545 0,95459 0,95372 0,95284 0,95195 0,95106 72
18 0,95106 0,95015 0,94924 0,94832 0,94740 0,94646 0,94552 71
19 0,94552 0,94457 0,94361 0,94264 0,94167 0,94068 0,93969 70
20 0,93969 0,93869 0,93769 0,93667 0,93565 0,93462 0,93358 69
21 0,93358 0,93253 0,93148 0,93042 0,92935 0,92827 0,92718 68
22 0,9-2718 0,92609 0,92499 0.92388 0,92276 0,92164 0,92050 67
23 0,92050 0,91936 0,91822 0,91706 0,91590 0,91472 0,91355 66
24 0,91355 0,91236 0,91116 0,90996 0,90875 0,90753 0,90631 65
25 0,90631 0,90507 0,90383 0,90259 0,90133 0,90007 0,89879 64
26 0,89879 0,89752 0,89623 0,89493 0,89363 0,89232 0,89101 63
27 0.89101 0,88968 0,88835 0,88701 0,88566 0,88431 0,88295 62
28 0,88295 0,88158 0,88020 0,87882 0,87743 0,87603 0,87462 61
29 0,87462 0,87321 0,87178 0,87036 0,86892 0,86748 0,86603 60
30 0,86603 0,86457 0,86310 0,86163 0,86015 0,85866 0,85717 59
31 0,85717 0,85567 0,85416 0,85264 0,85112 0,84939 0,84805 58
32 0,84805 0,84650 0,84495 0,84339 0,84182 0,84025 0,83867 57
33 0,83867 0,83708 0,83549 • 0,83389 0,83228 0,83066 0,82904 56
34 0,82904 0,82741 0.82577 0,82413 0,82248 0,82082 0,81915 55
35 0,81915 0,81748 0,81580 0,81412 0,81242 0,81072 0,80902 54
36 0,80902 0,80730 0,80558 0,80396 0,80212 0,80038 0,79864 53
37 0,79864 0.79688 0,79512 0,79335 0,79158 0,78980 0,78801 52
38 0,78801 0,78622 0,78442 0,78261 0,78079 0Д7897 0,77715 51
39 0,77715 0,77531 0,77347 0,77162 0,76977 0,76791 OJ6604 50
40 0,76604 0,76417 0,76229 0,76041 0,75851 0,75661 0,75471 49
41 0,75471 0,75280 0,75088 0,74896 0,74703 0,74509 0,74314 48
42 0,74314 0,74120 0,73924 0,73728 0,73531 0,73333 0,73135 47
43 0,73135 0,72937 0,72737 0,72537 0,72337 0,72136 0,71934 46
44 0,71934 0,71732 0,71529 0,71325 0,71121 0,70916 0,70711 45
60' 60' «У 30' 20' 10' о- Гра-
Sinus дусы
Гра- Т a n g е □ S
дусы о- 10' | 20' ЗУ 40' W | 60'
0 0,00000 0,00291 0,00582 0,00873 0,01164 0,01455 0,01746 89
1 0,01746 0,02036 0,02328 0,02619 0,02910 0,03201 0,03492 88
2 0,03492 0,03783 0,04075 0,04366 0,04658 0,04949 0,05241 87
3 0,05241 0,05533 0,05824 0,06116 0.06408 0,06700 0,06993 86
4 0,06993 0,07285 0,07578 0,07870 0,08163 0,08456 0,03749 85
5 0,08749 0,09042 0,09335 0,09629 0,09923 0,10216 0,10510 84
6 0,10510 0,10805 0,11099 0,11394 0,11688 0,11983 0,12278 83
7 0,12278 0,12574 0,12869 0,13165 0,13461 0,13758 0,14054 82
8 0,14054 0,14351 0,14648 0,14945 0,15243 0,15540 0,15838 81
9 V - 0,15838 0,16137 0,16435 0,16734 0,17033 0,17333 0,17633 80
10 0,17633 0,17933 0,18233 0,18534 0,18835 0,19136 0,19438 79
11 0,19438 0,19740 0,20042 0,20345 0,20648 0,20952 0,21256 78
12 0,21256 0,21560 0,21864 0,22169 0,22475 0,22781 0,23087 77
13 0,23087 0,23393 0,23700 0,24008 0,24316 0,24624 0,24933 76
14 0,24933 0,25242 0,25552 0,25862 0,26172 0,26483 0,26795 75
15 0,26795 0,27107 0,27419 0,27732 0,28046 0,28360 0,28675 74
16 0,28675 0,28990 0,29305 0,29621 0,29938 0,30255 0.30573 73
17 0,30573 0,30891 0,31210 0,31.530 0,31850 0,32171 0,32492 72
18 0,32492 0,32814 0,33136 0,33460 0,33783 0,34108 0,34433 71
19 0,34433 0,34758 0,35085 0,35412 0,35740 0,36068 0,36397 70
20 0,36397 0,36727 0,37057 0,37388 0,33720 0,38053 0,38386 69
21 0,38386 0,38721 0,39055 0,39391 0,39727 0,40065 0,40403 68
22 0,40403 0,40741 0,41081 0,41421 0,41763 0,42105 0,42447 67
23 0,42447 0,12791 0,43136 0,43481 0,43828 0,44175 0,44523 66
24 0,44523 0,44872 0,45222 0,45573 0,45924 0,46277 0,46631 65
25 0,46631, 0,46985 0,47341 0,47698 0,48055 0,48414 0,48773 64
26 0,48773 0,49134 0,49495 0,49858 0,50222 0,50587 0,50953 63
27 0,50953 0,51319 0,51688 0.52057 0,52427 0,52798 0,53171 62
28 0,53171 0,53545 0,53920 0,54296 0,51637 0,55051 0,55431 61
29 0,55431 0,55812 0,56194 0,56577 0,56962 0,57348 0,57735 60
30 0,57735 0,58124 0,58513 0,58905 0,59297 0,59691 0,60086 59
31 0,60086 0,60483 0,60881 0,61280 0,61681 0,62083 0,62487 58
32 0.62487 0,62892 0,63299 0,63707 0.64117 0,64528 0,64941 57
33 0,64941 0,65355 0,65771 0,66189 0,66608 0,67028 0,67451 56
34 0,67451 0,67875 0,68301 0,68728 0,69157 0,69588 0,70021 55
35 0,70021 0,70455 0,70891 0,71329 0,71769 0,72211 0,72654 54
36 0,72654 0,73100 0,73547 0,73994 0,74447 0,74900 0,75355 53
37 0,75355 0,75812 0,76272 0,76733 0,77196 0,77661 0,78129 52
38 0,78129 0,78598 0,79070 0,79544 0,80020 0,80498 0,80978 51
39 0,80978 0,81461 0,81946 0,82434 0,82923 0,83415 0,83910 50
40 0,83910 0,84407 0,84906 0,85408 0,85912 0,86419 0,86929 49
41 0,86929 0,87441 0,87955 0,88473 0,88992 0,89515 ’ 0.90040 48
42 0,90040 0,90569 0,91099 0,91633 0,92170 0,92709 0,93252 47
43 0,93252 0,93797 0,94345 0,94896 0,95451 0,96008 0,96569 46
44 0,96569 0,97133 0,97700 0,98270 0,98843 0,99420 0,00000 45
60’ 5J’ 40' 30' 20' 10’ О’ Гра-
С
о t а п g е 4 S
Градусы Cotangens
о- 10* 20' 30* 40' 50' 60'
0 оо 343,77371 171,88540 114,58865 85,93979 68,75009 57,28996 89
1 57,28996 49,10388 42,96408 38,18846 34,36777 31,24158 28,63625 88
2 26,63625 26,43160 24,54176 22,90377 21,47040 20,20555 19,08114 87
3 19,08114 18,07498 17,16934 16,34986 15,60478 14,92442 14,30067 86
4 14,30067 ,13,72674 13,19688 12,70621 12,25051 11,82617 11,43005 85
5 11,43005 11,05943 10,71191 10,38540 10,07803 9,78817 9,51436 84
6 9,51436 9,25530 9,00983 8,77689 8,55555 8,34496 8,14435 83
7 8,14435 7,95302 7,77035 7,59575 7,42871 7,26873 7,11537 82
8 7,11537 6,96823 6,82694 6,69116 6..56055 6,43484 6,31375 81
9 6,31375 6,19703 6,08444 6,97576 5,87080 5,76937 5,67128 80
10 5,67128 5,57638 5,48451 5,39552 5,30928 5,22566 5,14455 79
11 5,14455 5,06584 4,98940 4,91516 4,84300 4,77286 4,70463 78
12 4,70463 4,63825 4,57363 4,51071 4,44942 4,3896 । 4,33148 77
13 4,33148 4,27471 4,21933 4,16530 4,11256 4,06107 4,01078 76
14 4,01078 3,96165 3.91364 3,86671 3,82083 3,77595 3,73205 75
15 3,73205 3,68909 3,64705 3,60588 3,56557 3,52609 3,48741 74
16 3,48741 3,44951 3,41236 3,37594 3,34023 3,30521 3,27085 73
17 3,27085 3,23714 3,20405 3,17159 3,13972 3,10842 3,07768 72
18 3,07768 3,04749 3,01783 2,98869 2,96004 2,93189 2,90421 71
19 2,90421 2,87700 2,85023 2,82391 2,79802 2,77254 2,74748 70
20 2,74748 2,72281 2,69853 2,67462 2,65109 2,62791 2,60509 69
21 2,60509 2,58261 2,56046 2,53865 2,51715 2,49597 2,47509 68
22 2,47509 2,45451 2,43422 2,41421 2,39449 2,37504 2,35685 67
23 2,35585 2,33693 2,31826 2,29984 2,28167 2,26374 2,24604 66
24 2,24604 2,22857 2,21132 2,19430 2,17749 2,16090 2,14451 65
25 2,14451 2,12832 2,11233 2,09654 2,08094 2,06553 2,05030 64
26 2,05030 2,03526 2,02039 2,00569 1,99116 1,97680 1,96261 63
27 1,96261 1',94858 1,93470 1,92098 1,90741 1,89400 1,88073 62
28 1,88073 1,86760 1,85462 1,84177 1,82906 1,81619 1,80405 61
29 1,80405 1/79174 1,77955 1,76749 1,75556 1,74375 1,73205 60
30 1,73205 1,72047 1,70901 1,69766 1,68643 1,67530 1,66428 59
31 1,66428 1,65337 1,64256 1,63185 1,62125 1,61074 1,60033 58
32 1,60033 1,59002 1,57981 1,56969 1,55966 1,54972 1,53987 57
33 1,53987 1,53010 1,52043 1,51084 1,50133 1,49190 1,48256 56
34 1.48256 1,47330 1,46411 1,45501 1,44598 1,43703 1,42815 55
за 1,42815 1,41934 1,41061 1,40195 1,39336 1,38484 1,37638 54
36 1,37638 1,36800 1,35968 1,35142 1,34323 1,33511 1,32704 53
37 1,32704 1,31904 1,31110 1,30323 1,29541 1,28764 1,27994 52
38 1,27994 1,27230 1,26471 1,25717 1,24969 1,24227 1,23490 51
39 1,23490 1,22758 1,22031 1,21310 1,20593 1,19882 1,19175 50
40 1,19175 1,18474 1,17777 1,17085 1,16398 1,15715 1,15037 49
41 1,15037 1,14363 1,13694 1,13029 1,12369 1,11713 1,11061 48
42 1,11061 1,10414 1,09770 1,09131 1,08496 1,07864 1,07237 47
43 1,07237 1,06613 1,05994 1,05378 1,04766 1,04158 1,03553 46
44 1,03553 1,02952 1,02355 1,01761 1,01170 1,00583 1,00000 45
еси SV ‘ 40» 30' 20* 10’ О' Гр«-
дусы
Т а П g е п 8
§ 203. Натуральные логарифмы.
N 0 1 2 3 4 б 6 7 8 9
0 — оо 0,0000 0,6931 1,0986 1,3863 1,6094.1,7918 1,9459 2,0794 2,1972
10 2,3026 2,3979 2,4849 2,5549 2,6391 2,70811 2,7726 2,8332 2,8904 2,9444
20 2,9957 3,0445 3,0910 3,1355 3,1781 3,2189 3,2581 3,2958 3,3322 3,3673
30 3,4012 3,4340 3,4657 3,4965 3,5264 3,5553 3,5835 3,6109 3,6376 3,6636
40 3,6889 3,7136 3,7377 3,7612 3,7842 3,80671 3,8286 3,8501 3,8712 3,8918
50 3,9120 3,9318 3,9512 3,9703 3,9890 4,0073 4,0254 4,0431 4,0604 4,0775
60 4,0943 4,1109 4,1271 4,1431 4,1589 4,1744,4,1897 4,2047 4,2195 4,2341
70 4,2485 4,2627 4,2767 4,2905 4,3041 4,3175.4,3307 4,3438 4,3567 4,3694
80 4,J820 4,3944 4,4067 4,4188 4,4308 4,4427,4,4543 4,4659 4,4773 4,4886
90 4,4998 4,5109 4,5218 4,5326 4,5433 4,5539 4,5613 4,5747 4,5850 4,5951
100 4,6052 4,6151 4,6250 | 4,6347 4,6444 4,6540 4,6634 4,6728 4,6821 4,6913
110 4,7005 4,7095 4,7185 4,7274 4,7362 4,7449 4,7536 4,7622 4,7707 4,7791
120 4,7875 4,7958 4,8040 4,8122 4,8203 4,8283 4,8363 4,8442 4,8520 4,8598
130 140 4,8675 4,8752 4,8828 4,8903 4,8903 4,9053 4,9127 4,9200 4,9273 4,9345
4,9416 4,9488 4,9558 4,9628 4,9698 4,9767 4,9836 4,9904 4,9972 5,0039
150 5,0106 5,0173 5,0239 5,0304 5,0370 5,0434 5,0499 5,0562 5,0626 5,0689
160 5,0752 5,0814 5,0876 5,0938 5,0999 5,1059 5,1120 5,1180 5,1240 5,1299
170 5,1358 5,1417 5,1475 5,1533 5,1591 5,1648 5,1705 5,1761 5,1848 5,1874
180 5,1930 5,1985 5,2040 5,2095 5,2149 5,2204 5,2257 5,2311 5,2364 5,2417
190 5,2470 5,2523 5,2575 5,2627 5,2679 5,2730, 5,2781 5,2832 5,2883 5,2933
200 5,2983 5,3033 5,3083 5,3132 5,3181 5.3230! 5,3279 5,3327 5,3375 5,3423
210 5,3417 5,3519 5,3566 5,3613 5,3660 5,3706 5,3753 5,3799 5,3845 5,3891
220 5,3936 5,3982 5,4027 5,4072 5,4116 5,4161 5,4205 5,4250 5,4293 5,4337
230 5,4381 5,4424 5,4467 5,4510 5,4553 5,4596 5,4638 5,4681 5,4723 5,4765
240 5,4806 5,4848 5,4889 5,4931 5,4972 5,5013 5,5053 5,5094 5,6134 5,5175
250 5,5215 5,5255 5,5294 5,5334 5,5373 5,5413 5,5452 5,5491 5,5530 5,5568
260 5,5607 5,5645 5,5683 5,5722 5,5759 5,5797 5,5835 5,5872 5,5910 5,5947
270 5,5984 5,6021 5,6058 5,6095 5,6131 5,6168 5,6204 5,6240 5,6276 5,6312
280 5,6348 5,6384 5,6419 5,6454 5,6490 5,6525 5,6560 5,6595 5,6630 5,6664
290 5,6699 5,6733 5,6768 5,6802 5,6836 5,6870 5,6904 5,6937 5,6971 5,7004
300 5,7038 5,7071 5,7104 5,7137 5,7170 5,7203 j 5,7236 5,7268 5,7301 5,7333
310 5,7366 5,7398 5,7430 5,7462 5,7494 5,75261 5,7557 5,7589 5,7621 5,7652
320 5,7683 5,7714 5,7746 5,7777 5,7807 5,7838 5,7869 5,7900 5,7930 5,7961
330 5,7991 5,8021 5,8051 5,8081 5,8111 5,8141 5,8171 5,8201 5,8230 5,8260
340 5,8289 5,8319 5,8384 5,8377 5,8406 5,8435 5,8464 5,8493 5,8522 5,8551
350 5,8579 5,8608 5,8636 5,8665 5,8693 5,8721 5,8749 5,8777 5,8805 5,8833
360 5,8861 5,8889 5,8916 5,8944 5,8972 5,8999 5,9026 5,9054 5,9081 5,9011
370 5,9135 5,9162 5,9189 5,9216 5,9243 5,9269 5,9296 5,9322 5,9349 5,9375
380 5,9402 5,9428 5,9454 5,9480 5,9506 5,9532 5,9558 5,9584 5,9610 5,9636
390 5,9661 5,9687 6,9713 5,9738 5,9764 5,9789 5,9814 5,9839 5,9865 5,9890
400 5,9915 5,9940 5,9965 । 5.9989 I 6,0014 6,0039 6,0064 6,0088 6,0113 6,0137
410 6,0162 6,0186 6,0210 6,0234 6,0259 6,0283 6.0307 6,0331 6,0355 6/5375
420 6,0403 6,0426 6,0450 6,0474 6,0497 6,0521 6,0544 6,0568 6,0591 6,0615
430 6,0638 6,0661 6,0684 6,0707 6,0730 6,0753.6,0776 6,0799 6,0882 6,0435
440 6,0868 6,0890 6,0913 6,0936 6,0958 6.0981 6,1003 6,1026 6,1048 6,1070
450 6,1092 6,1115 6,1137 6,1159 6,1181 6,1203 6,1225 6,1247 6,1269 6,1291
460 6,1312 6,1334 6,1356 6,1377 6,1399 6,1420 6,1442 6,1463 6,1485 6,1506
470 6,1527 6,1549 6,1570 6,1591 6,1612 6,1633 6,1654 6,1675 6,1696 6,1717
480 6,17’« 6,1759 6,1779 6,1800 6,1821 6,1841 6,1862 6,1883 6,1903 6,1924
490 6,ls44 6,1964 6,1985 6,2005 6,2025 6,2046' 6,2066 6.2086 6,2106 6,2126
In 10 1 = i 2,30258503, In 10 ± з = * 6.9078, In 10 ± 1 = ± 9.2ГО4, In 10 ± з = з: 11,5129.
N 0 1 2 3 4 6 6 7 8 9
500 6,2126 6,2165 6,2186 6,2206 6,2226 6,2246 6,2265 6,2285 6,2305 6,2324
510 6,23*44 6,2364 6,2383 6.2403 6,2422 6,2442 6,2461 6,2480 6,2500 6,2519
520 6,2538 6,2558 6,2 77 6,2596 6,2615 6,2644 6.2653 6,2672 6,2691 6,2710
530 6,2729 6,2748 6,2766 6,2785 6,2804 6,2823 6,2841 6.2860 6,2879 6.2897
540 6.2916 6,2934 6,2953 6,2971 <1,2989 6,3008 6,3026 6,3044 6,3063 6,3081
550 6,3099 6.3117 6,3135 6,3154 6,3172 6,3190 6,3208 6,3226 6,3244 6,3261
560 6.3279 6,3297 6,3315 6,3333 6,3351 6,3368 6,3386 6,3404 6,3421 6,3439
570 6 3456 6,3474 6,3491 6,3509 6,3526 6,3544 6.3561 6,3578 6,3596 6,3613
580 6,3630 6,3648 6,3665 6,3682 6,3699 6,3716 6,3733 6,3750 6,3767 6,3784
590 6,3801 6,3818 6,3835 6,3852 6,3869 6,3886 6,3902 6,3919 6,3936 6,3953
600 6,3969 6,3986 6,4003 6,4019 6,4036 6,4052 6,4069 6,4085 6,4102 6,4118
610 6,4135 6,4151 6,4167 6,4184 6.4200 6,4216 6,4232 6,4249 6,4265 6,4281
620 6,4297 6,4313 6,4329 6,4345 6,4362 6,4378 6,4394 6,4409 6,4425 6,4441
630 6,4457 6,4473 6,4189 6,4505 6,4520 6,4536 6,4552 6,4568 6,4583 6,4599
640 6,4615 6,4630 6,4646 6,4661 6,4677 6,4693 6.4708 6,4723 6,4739 6,4754
>650 6,4770 6,4785 6,4800 6,4816 6,4831 6,4846 6,4862 6,4877 6,4892 6,4907
660 6,4922 6,4938 6,4953 6,4968 6,4983 6,4998 6,5013 6,5028 6,5043 6,5058
670 6,5073 6,5088 6,5103 6,5117 5,5132 6,5147 6,5162 6,5177 6,5191 6,5206
680 6,5221 6,5236 6,5250 6,5265 6,5280 6,5294 6,5309 6,5323 6,5338 6,5352
690 6,5367 6,5381 6,5396 6,5410 6,5425 6,5439 6,5453 6,5468 6.5182 6,5497
ТОО 6,5511 6,5525 6,5539 6,5554 6,5568 6,5582 6,5596 6,5610 6,5624 6,5639
710 6,5653 6,5667 6,5681 6,5695 6.5709 6,5723 6,5737 6,5751 6,5765 6,5779
720 6,5793 6,5806 6,5820 6,5834 6,5848 6,5862 6,5876 6,5889 6,5903 6,5917
730 6,5930 6,5944 6,5958 6,5971 6,5985 6,5999 6,6012 6,6026 6,6039 6,6053
740 6,6067 6,6080 6,6093 6,6107 6,6120 6,6134 6,6147 6,6161 6,6174 6,6187
750 6,6201 6.6214 6,6227 6,6241 6,6254 6,6267 6,6280 6,6294 6,6307 6,6320
760 6,6333 6,6346 6,6359 6,6373 6,6386 6,6399 6,6412 6,6425 6,6438 6,6451
770 6,6464 6,6477 6,6490 6,6503 6,6516 6,6529 6,6542 6,6554 6,6567 6,6580
780 6,6593 6,6006 6,6619 6,6631 6,6644 6,6657 6,6670 6,6682 6,6695 6,6708
790 6,6720 6,6733 6,6746 6,6758 6,6771 6,6783 6,6796 6,6809 6,6821 6,6834
800 6,6846 6,6859 6,6871 6,6884 6,6896 6,6908 6,6921 6,6933 6,6916 6,6958
810 6,6970 6,6983 6,6995 6,7007 6,7020 6,7032 6,7044 6,7056 6,7069 6,7081
820 6,7093 6,7105 6,7117 6,7130 6,7142 6,7154 6,7166 6,7178 6,7190 6,7202
830 6,7214 6,7226 6,7238 6,7250 6,7262 6,7274 6,7286 6,7298 6,7310 6,7322
840 6,7334 6,7346 6,7358 6,7370 6,7382, 6,7393 6,7405 6,7417 6,7429 6,7441
850 6,7452 6,7464 6,7476 6,7488 6,7499 6,7511 6,7523 6,7534 6,7546 6,7558
860 6,7569 6,7581 6,7593 6,7604 6,7616 6,7627 6,7639 6,7650 6,7662 6,7673
870 6,7685 6,7696 6,7708 6,7719 6,7731 6,7742 6,7754 6,7765 6,7776 6,7788
880 6,7799 6,7811 6,7822 6,7833 6,7845 6,7856 6,7867 6,7878 6,7890 6,7901
890 6,7912 6,7923 6,7935 6,7946 6,7957 6,7968 6,7979 6,7991 6,8002 6,8013
900 6,8024 6,8035 6,8046 6,8057 6,8068 6,8079 6,8090 6,8101 6,8112 6,8123
910 6,8134 6,8145 6,8156 6,8167 6,8178 6,8189 6,8200 6,8211 6,8222 6,8233
920 6,8244 6,8255 6,8265 6,8276 6,8287 6,8298 6,8309 6,8320 6,8330 6,8341
930 6,8352 6,8363 6,8373 6,8384 6,8395 6,8405 6,8416 6,8427 6,8437 6,8448
940 6,8459 6,8469 6,8480 6,8491 6,8501 6,8512 6,8522 6,8533 6,8544 6,8554
950 6,8565 6,8575 6,8586 6,8596 6,8607 6,8617 6,8628 6,8638 6.8648 6,8659
960 6,8669 6,8680 6,8690 6,8701 6,8711 6,8721 6,8732 6,8742 6,8752 6,8763
970 6,8773 6,8783 6,8794 6,8804 6,8814 6,8824 6,8835 6,8845 6,8855 6,8865
980 6,8876 6,8886 6,8896 6,8906 6,8916 6,8926 6,8937 6,8947 6,8957 6,8967
990 6.8977 6,8987 6,8997 6,9007 6,9017 6,9027 6,9037 6.9047 6,9057 6,9068
hi'lO * • = X 13,8155, In 10 ± 7 = 16,) 181, In 10 ± з = 18,4207.
КРИВЫЕ ДЛЯ СПРАВОК.
Для удобства читателя здесь помещены некоторые из наиболее известных кривых, встречающихся ч тексте.
Кубическая парабола
Полукубическая парабола
у = ах3.
у-= ах3.
Циссоида Диоклеса у- (2а — х) = Xs. р = 2а sin 6 tg 0 .
Локон Аньези х2у = 4а2 (2а —у).
Лемниската Бернулли (.Г2 4-^)2 =fl2(x2_>2). р2 = а2 cos 20 .
Конхоида Никомеда х2у2 = (у + а) (б2-/-), р -= a sec 0 i b.
х = a arccos
х = a arccos I 1 —— ) — \ а )
— '/Зоу—у-’.
i х = а (6 — sin в),
I у = а (1 — cos 0).
+ / Чау - у* .
i х = а (0 sin 8), ( у = а (1 — cos 6).
Цепная линия
Парабола
Гипоциклоида с 4 заострениями
2 2?
з.з "з
’ + У = а .
( х = a cos8 8, \ v = a «in9 в .
2 £ 3
(ax)a + (by)3 = (а9-*9)".
Кардиоида л-2 +>,2 + аХ = а р = а (1 — cos 0).
Декартов лист л3 -J-j3 — Зл.гу = 0.
Улитка р = а — b cos 0.
Спираль Архимеда р = аб.
Логарифмическая или равноугольная спираль р = ео8 или In р = а0 .
/Кезл (Lituus) р'-в = а-.
Гиперболическая или обратная спираль
Р<1 = а.
Параболическая спираль (р — а)2 = 4ас0.
Логарифмическая кривая у = In х.
Показательная кривая у = е*.
Кривая вероятностей х = е~х3.
Трехлепестковая роза
р = a sin 30.
Чстырехлепестковая роза
р = a sin 20.
Четырехлепестковая роза р = a cos 20 г
ОтветствеввыА редактор Я. Ахушский. Слака вабор 10/V 1934 г. Формат 03 X *4'/м- Упоив. Главлита М В—88831. ТехввческиА редактор 0. В. Персиянинова. Бум. листов 14. Подписала к печати 10/VII 1934 г. ГТГИ М 77. Тип. эв. в 1 бум. л. 110.979. Тираж 35.000—авт. л. 38*/,. Задав N 3709-
УЧЕБНИКИ И УЧЕБНЫЕ ПОСОБИЯ, УТВЕРЖДЕННЫЕ ВСЕСОЮЗНЫМ КОМИТЕТОМ ПО ВЫСШЕМУ ТЕХНИЧЕСКОМУ ОБРАЗОВАНИЮ ПРИ ЦИК СССР
ВЫХОДЯТ В СВЕТ
ПОССЕ, К. А.
КУРС ДИФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Допущен в качестве учебника в 1934 г. Всесоюзным комитетом по высшему техническому образованию ври ЦИК СССР.
ПОССЕ, К. А.
КУРС ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Допущен в качестве учебника в 1934 г. Всесоюзным комитетом по высшему техническому образованию при ЦИК СССР.
ГРЕНВИЛЬ В. и ЛУЗИН, Н. Н.
КУРС ДИФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
Часть II. Интегральное исчисление.
Допущен в качестве учебника в 1934 г. Всесоюзным комитетом по высшему техническому образованию.
УЧЕБНИКИ И УЧЕБНЫЕ ПОСОБИЯ, УТВЕРЖДЕННЫЕ ВСЕСОЮЗНЫМ КОМИТЕТОМ ПО ВЫСШЕМУ ТЕХНИЧЕСКОМУ ОБРАЗОВАНИЮ ПРИ ЦИК СССР
ВЫШЛИ ИЗ ПЕЧАТИ
ПРИВАЛОВ, И. И.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Допущен в качестве учебника в 1934 г. Всесоюзным комитетом по высшему техническому образованию.
Цена 3 р., пер. 60 к.
.ЦУБЕРБИЛЛЕР, О. Н.
ЗАДАЧИ И УПРАЖНЕНИЯ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Допущено в качестве учебного пособия в 1934 г. Всесоюзным комитетом по высшему техническому образованию при ЦИК СССР.
Цена 3 Рч.90 к.,,'пер. 60 к.
9 ДУБНОВ, Я. С.
ЗАДАЧИ И УПРАЖНЕНИЯ ПО ДИФЕРЕНЦИАЛЬНОМУ ИСЧИСЛЕНИЮ Допущено в качестве учебного пособия в 1934 г. Всесоюзным комитетом по высшему техническому образованию при ЦИК СССР.
Цена 3 р., пер. 1 р.