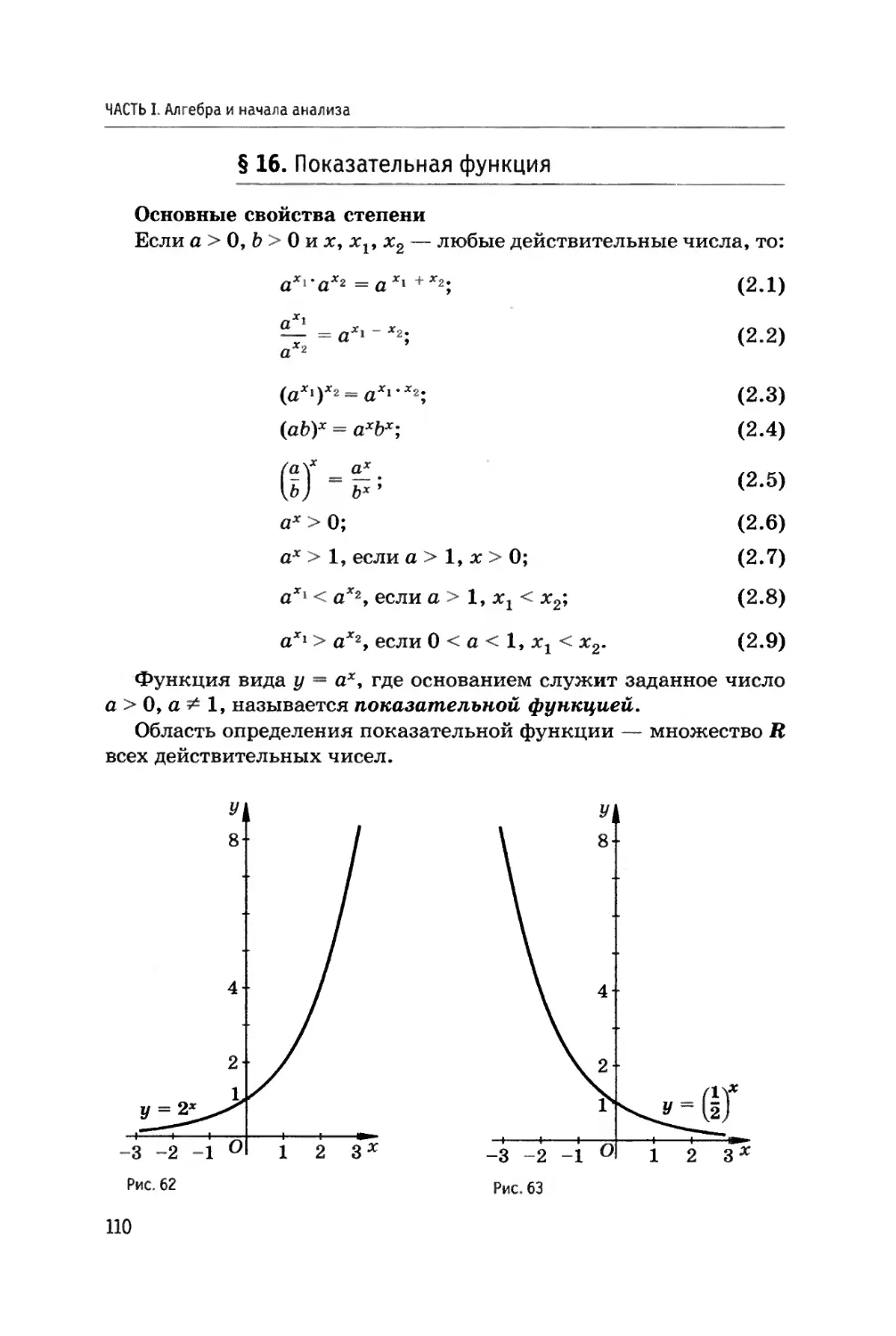
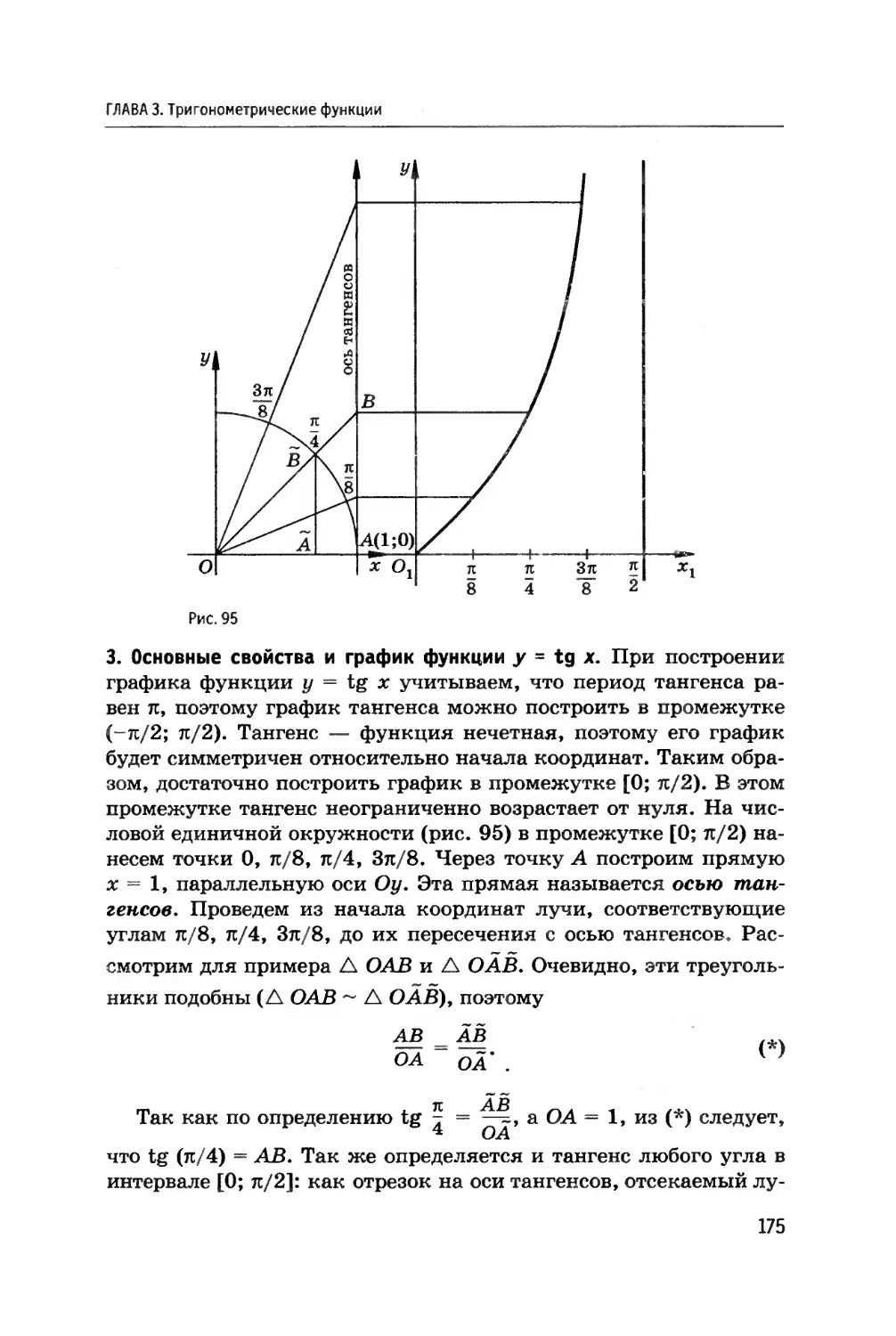
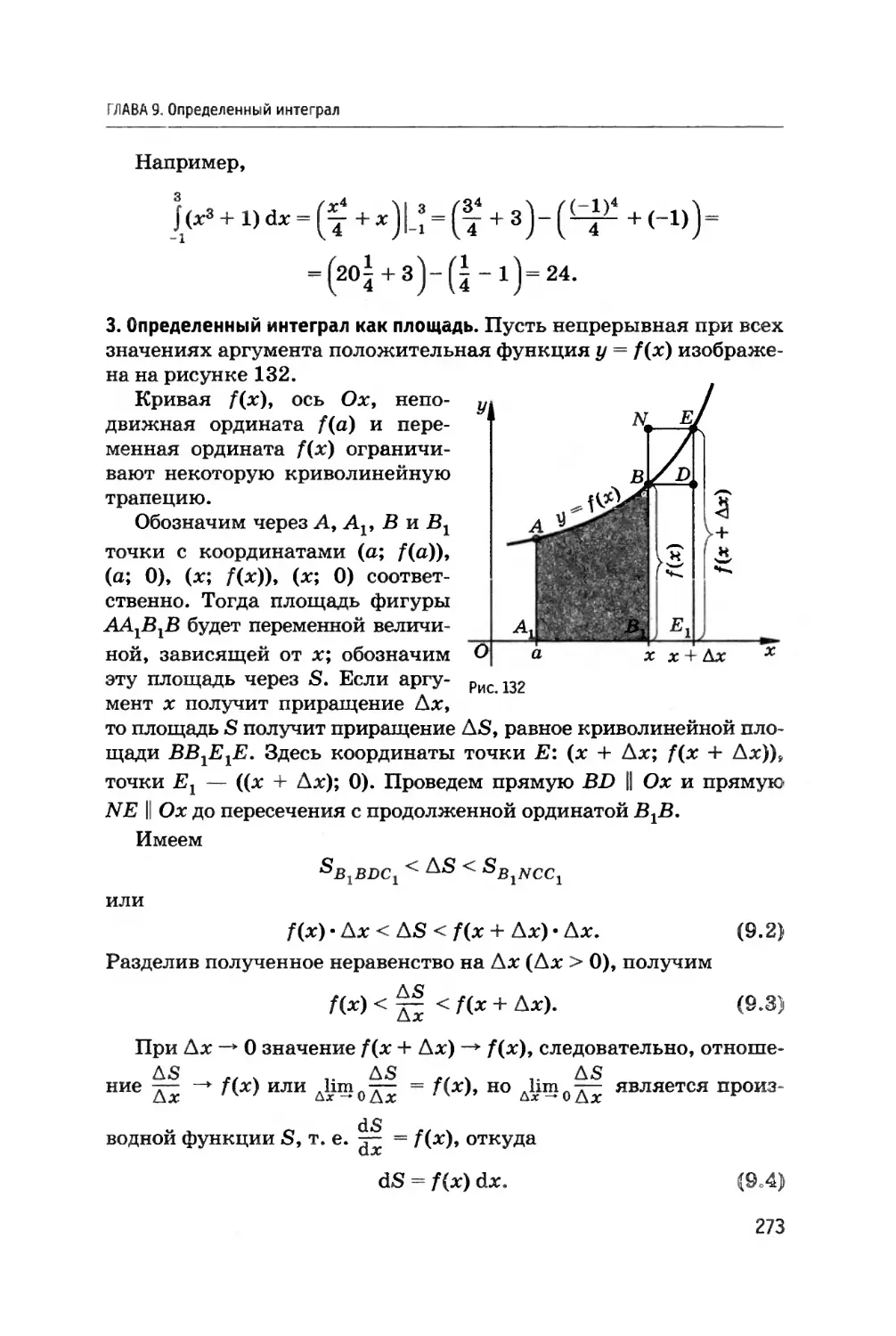
Автор: Богомолов Н.В. П.И. Самойленко.
Теги: математика учебные пособия и учебники по математике учебник
ISBN: 978-5-358-08334-9
Год: 2010
Текст
Н. В. Богомолов, П. И. Самойленко
МАТЕМАТИКА
Рекомендовано
Федеральным государственным учреждением
«Федеральный институт развития образования»
в качестве учебника для использования
в учебном процессе образовательных учреждений,
реализующих программы
среднего профессионального образования
7-е издание, стереотипное
СРЕДНЕЕ
ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАНИЕ
Москва
р роф а
2010
УДК 51(075.32)
ББК 22.1я723
Б74
Рецензенты:
доктор физ.-мат. наук, проф.
И. И. Баврин
(Московский государственный педагогический университет);
А. Н. Рубцова
(Санкт-Петербургский технический колледж управления
и коммерции)
Богомолов, Н. В.
Б74 Математика : учеб, для ссузов / Н. В. Богомолов,
П. И. Самойленко. — 7-е изд., стереотип. — М. : Дрофа,
2010. — 395, [5] с. : ил.
ISBN 978-5-358-08334-9
В учебнике рассмотрены основные разделы математики, охватываемые
действующими программами для техникумов: алгебра, начала анализа,
дифференциальное и интегральное исчисления, дифференциальные урав-
нения, аналитическая геометрия на плоскости, стереометрия, элементы
теории вероятностей и математической статистики. Приведено большое ко-
личество примеров с решениями. Издание является одной из книг учебно-
го комплекта, в который также входят «Сборник задач по математике»
Н. В. Богомолова и «Сборник дидактических заданий по математике»
Н. В. Богомолова и Л. Ю. Сергиенко.
Для студентов техникумов гуманитарного направления, финансо-
во-экономических, технических, строительных, сельскохозяйственных.
Может быть использован школьниками старших классов общеобразо-
вательных школ, слушателями курсов по подготовке в вузы и учителями
школ.
УДК 51(075.32)
ББК 22.1я723
ISBN 978-5-358-08334-9
© ООО «Дрофа», 2002
Предисловие к первому изданию
Настоящее издание представляет собой учебник
по математике для учащихся техникумов и являет-
ся одной из книг учебного комплекта, в который
также входят «Сборник задач по математике»
Н. В. Богомолова и «Сборник дидактических зада-
ний по математике» Н. В» Богомолова и Л. Ю. Сер-
гиенко. Материал, изложенный в книге, соответст-
вует действующим программам для техникумов как
гуманитарного направления, так и финансово-эко-
номических, технических и строительных.
Учебник охватывает материал, относящийся к
алгебре, началам анализа,
дифференциальному и
интегральному исчислениям,
дифференциальным
уравнениям, аналитической геометрии на плоскос-
ти, стереометрии, а также элементам теории вероят-
ностей и математической статистики.
В книге приведено большое количество тщатель-
но подобранных примеров, снабженных решения-
ми. К каждой теме прилагается блок вопросов, по-
зволяющих проконтролировать понимание теорети-
ческих положений, определений и доказательств.
Учебник с успехом можно использовать как при
занятиях под руководством преподавателя, так и
для самостоятельной работы. Он также полезен
школьникам старших классов общеобразователь-
ных школ, слушателям курсов по подготовке в вузы
и учителям школ.
Математические обозначения
= равно
* не равно
~ приближенно равно
< меньше
> больше
< меньше или равно
> больше или равно
а абсолютная величина числа а
+ (плюс) сложение
- (минус) вычитание
• умножение, например, а • Ъ или ab (знак умножения часто опуска-
ется)
, , а
: или -, или / —деление, например, а : о, или - , или а/Ь
ат а в степени т
квадратный корень
i квадратный корень из -1; i — J-i
корень степени т при 2
logfc логарифм при основании Ь. Если нет необходимости указывать ос-
нование, то пишут log
1g логарифм при основании 10 (обыкновенный или десятичный лога-
рифм)
In логарифм при основании е = 2,71828... (натуральный логарифм)
(),[],{} скобки
п! факториал; и! = 1 • 2 • 3 •... • п
± перпендикулярно
II параллельно
w подобно
АВ отрезок прямой между точками АиВ
Д треугольник: ДАВС
А плоский угол
и дуга: иАВ
° градус
' минута > при обозначении величины плоского угла или дуги
" секунда
4
Если обозначение ° (градус),' (минута) или " (секунда) относится
к числу, содержащему десятичную дробь, то оно ставится над запя-
той, например, 6°5', 27; 8°4'2",9.
При обозначении угла отвлеченным числом подразумевается, что
это число есть отношение данного угла к радиану; радиан есть цент-
ральный угол, длина дуги которого равна радиусу; радиан =
= 57°,29578...
п отношение длины окружности к диаметру
sin синус
cos косинус
tg тангенс
ctg котангенс
sec секанс
cosec косеканс
arcsin арксинус (у = arcsin х; у есть дуга, синус которой равен х)
arccos арккосинус
arctg арктангенс
arcctg арккотангенс
Для обозначения степени функции показатель степени ставится
при знаке функции; например, sin2 х (синус квадрат икс) есть (sin х)2.
а, Ь, с, ... постоянные величины (применяются преимущественно пер-
вые буквы латинского алфавита)
х, у, z, и, ... переменные величины (применяются преимущественно
последние буквы латинского алфавита)
/()» ф()» ), Ф( )> ••• функции одного аргумента; например, /(х)
ОО бесконечность
lim предел
—* стремится, например, х —* a, lim (1 + х)1/х = е
А приращение (греческая прописная буква дельта)
d дифференциал
'" обозначения первой и второй производных, например, f\x), f"(x)
d dy
— первая производная одного переменного; например,
п
L сумма, например, У uk = их + и2 + ... + ип
k = 1
J интеграл
ь
J определенный интеграл с нижним пределом а и верхним пределом b
а
2 комплексное число, сопряженное с 2, например, z = х + iy, z = х - iy
гт п(п - 1) ... (п - т + 1)
С ' = ------------;-------- число сочетании из п элементов по т
п т\
Tt!
А™ = п(п - 1)(п - 2)...[п - (т — 1)] = - число размещений из п
(и — т)1
элементов по т
5
Рп = п! число перестановок из п элементов
.г» .ь
1а знак двойной подстановки; например, F(x) 1а = F(b) - F(a)
е принадлежит; например, а е А — элемент а принадлежит множест-
ву Л
с содержится; например, NcZ, множество N содержится в множестве Z
а вектор
АВ вектор, начало которого в точке А, конец в точке В
i, j единичные векторы осей прямоугольной системы координат
—> —> равенство, сложение (сумма), вычитание (разность) векторов
AB+CDI
а • Ь скалярное произведение векторов а и b
N множество натуральных чисел
Z множество целых чисел
Q множество рациональных чисел
I множество иррациональных чисел
R множество действительных (вещественных) чисел
С множество комплексных чисел
[а; Ь] замкнутый промежуток (отрезок) с началом а и концом b
(а; Ь) открытый промежуток (интервал) с началом а и концом Ь
(а; Ь], [а; Ь) полуоткрытые промежутки с началом а и концом b
<=> если А «В, то из А следует В и наоборот
=> если А => В, то из А следует В
Латинский алфавит
Греческий алфавит
Аа — а
ВЬ — бэ
Сс — цэ
Dd — дэ
Ее — е
Ff —
Gg -
Hh —
li —
Jj -
Kk —
LI —
Mm —
Nn —
Oo —
Pp -
Qq —
Rr —
Ss —
Tt —
Uu —
Vv —
Ww—
Xx —
Yy —
Zz —
эф
re (же)
xa (ani)
и
йот (жи)
ка
эль
эм
эн
о
пэ
ку
эр
эс
тэ
У
вэ
дубль-вэ
икс
игрек
зэт
Аа —
вр -
Гу -
Дб —
К ~
Нт] —
000 —
h —
Кк —
КК —
Мц —
Nv —
—
Оо —
Пл —
Рр -
Ха —
Тт —
Фер —
Хх -
Yu —
—
£2со —
альфа
бэта
гамма
дельта
эпсилон
дзэта
эта
тэта
йота
каппа
лямбда
мю
ню
кси
омикрон
пи
ро
сигма
тау
фи
хи
ипсилон
пси
омега
7
ЧАСТЬ I. АЛГЕБРА
И НАЧАЛА АНАЛИЗА
ГЛАВА I. Линейные и квадратные
уравнения и неравенства. Элементы
вычислительной математики
§ 1. Рациональные числа. Иррациональные числа.
Понятие о мнимых и комплексных числах
1. Натуральные числа. Одним из основных понятий математики яв-
ляется понятие числа. Исторически первыми возникли в практи-
ке и были введены в науку натуральные числа.
Натуральные числа используют в связи со счетом количества
отдельных предметов, например при подсчете количества книг
на полке, количества деталей, изготовленных за смену, и т. д.
Натуральные числа образуют бесконечное множество, которое
принято обозначать через N:
# = {1,2, 3, 4,...}.
2. Дробные числа. Для практических целей натуральных чисел
оказалось недостаточно, в частности при делении чисел, при из-
мерении длин отрезков и различных физических величин воз-
никла необходимость расширения множества целых чисел введе-
нием долей единицы и количества этих долей.
Например, если некоторая величина разделена на п частей и
взято т таких частей, то вводится новое так называемое дробное
т
число — , где тип — натуральные числа.
3. Отрицательные числа. Практическая потребность привела к вве-
дению отрицательных чисел, чтобы иметь возможность измерять
величины, способные изменяться в двух противоположных на-
правлениях от выбранной точки отсчета. Например, при измере-
нии сил, действующих на пружину, растягивающие пружину си-
лы можно считать положительными, а сжимающие пружину —
отрицательными.
8
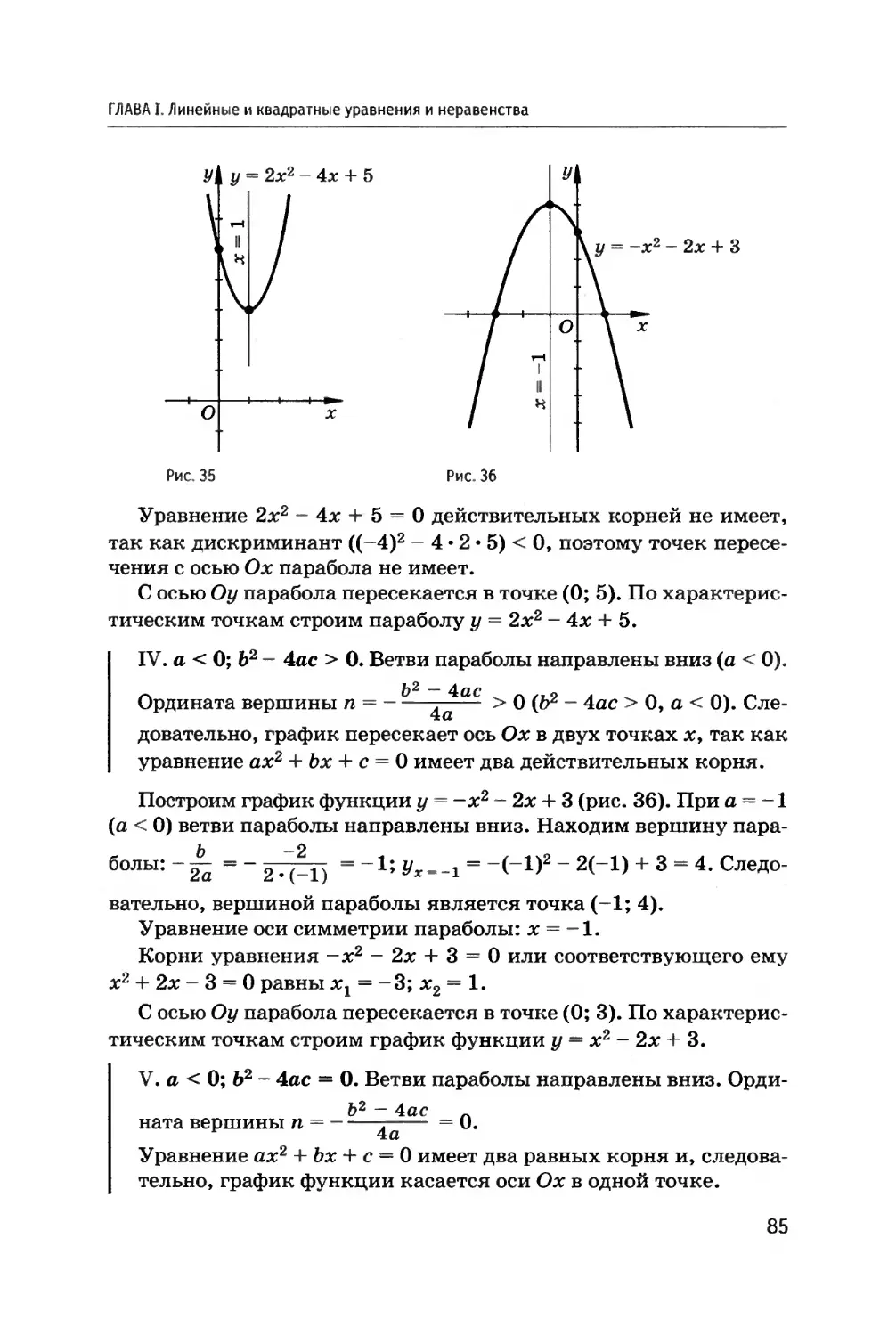
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Таким образом, каждому числу, натуральному или дробному,
сопоставляется отрицательное число. Если число (положитель-
ное) обозначать буквой а (или +а), то соответствующее ему про-
тивоположное (отрицательное) число записывается как -а.
К этим числам присоединяется число 0, соответствующее на-
чалу отсчета как положительных, так и отрицательных чисел.
4. Множество целых чисел. Натуральные числа, им противополож-
ные (отрицательные) и число 0 составляют множество Z целых
чисел.
Целые числа могут быть записаны в виде дробей, например
5. Множество рациональных чисел. Множество, состоящее из поло-
жительных и отрицательных целых и дробных чисел и числа О,
называется множеством рациональных чисел. Обозначим его че-
рез Q. Таким образом, всякое рациональное число может быть
натуральное число.
Следовательно, N содержится в И, a Z в Q. Символически это
записывается следующим образом: N cz Z cz Q. Знак с обозначает
включение или принадлежность одного множества другому.
Другими словами, Z есть расширенное множество N, Q — рас-
ширенное множество Z, и, таким образом, Q является расширен-
ным множеством N.
6. Основные законы действий над рациональными числами. Укажем
основные законы действий над рациональными числами и неко-
торые отношения между ними. Основными действиями над чис-
лами являются сложение и умножение, а основным отношением
между ними является сравнение чисел, т. е. установление того,
какое из двух чисел больше (меньше), если такое сравнение воз-
можно.
I. Переместительный или коммутативный закон сложения:
а + b = b + а.
II. Сочетательный или ассоциативный закон сложения:
(а + Ь) + с = а + (Ь + с).
III. Сложение рационального числа с нулем:
а + 0 = а.
9
ЧАСТЬ I. Алгебра и начала анализа
IV. Сложение рационального числа с соответствующим ему
числом противоположного знака:
а + (-а) = О.
V. Переместительный или коммутативный закон умножения:
a*b = b • а.
VI. Сочетательный или ассоциативный закон умножения:
(а • Ь) • с = а (Ъ • с).
VII. Умножение рационального числа на единицу:
а • 1 = а.
VIII. Умножение не равного нулю рационального числа на
число, равное отношению единицы к этому числу (такие числа
а и - называются взаимно обратными):
= 1 для а О.
IX. Распределительный, или дистрибутивный, закон умно-
жения относительно сложения:
а(Ь + с) = а* b + а* с.
Введем знак =>. Запись А => В обозначает, что из А следует В.
X. Свойство транзитивности:
a<b, b < с а < с.
XI. Правило сложения неравенств: для любого числа с
a<b=>a + c<b +с.
XII. Правило умножения неравенств на число, отличное от
нуля:
а <Ъ => а* с <Ь* с при с > О,
а <Ь => а*с > Ь*с при с < О.
7. Представление рациональных чисел десятичными дробями. Любое
положительное и отрицательное целое число можно представить
в виде обыкновенной дроби со знаменателем, равным единице,
3 5
например, 3 = у , -5 = - j .
Число 0 можно представить в виде обыкновенной дроби с чис-
„ О О
лителем, равным нулю: 0=7 = х ....
10
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Величина дроби не изменится, если числитель и знаменатель
дроби умножить или разделить на одно и то же число, не равное
нулю, например, z
D
1 = 1 • 3 = 3 . 18 = 3 • 6 = 3
2 2*3 6’24 4 • 6 4 ’
Если знаменатель обыкновенной дроби есть степень числа 10,
то эту дробь можно представить в виде конечной десятичной
дроби.
Например, =0,7;
19Z = i 97.
100 ’ ’ 1000
= 0,187; = -0,3;
13
10
Если знаменатель обыкновенной дроби содержит в себе ка-
кие-либо простые множители, отличающиеся от 2 и 5, и эти
множители не сокращаются с числителем, то такая дробь не
обращается в десятичную.
Подобные дроби можно обращать лишь в приближенные деся-
тачные: || = -Ц- = 0,52389...; = 0,2648... .
21 3 • 7 ос З2 • 7
8. Периодические дроби. Существуют рациональные числа, кото-
рые нельзя записать в виде конечной десятичной дроби, напри-
1 4
мер, з , ~ у •
Бесконечная десятичная дробь, у которой одна или несколько
цифр неизменно повторяются в одной и той же последователь-
ности, называется периодической десятичной дробью, а сово-
купность повторяющихся цифр называется периодом этой
дроби.
Периодические дроби бывают чистыми и смешанными. Чис-
той периодической дробью называется дробь, у которой период
начинается сразу же после запятой, например, 3,171717... . Сме-
шанной называется дробь, у которой между запятой и первым
периодом есть одна или несколько неповторяющихся цифр, на-
пример, 0,231919... .
Периодические дроби сокращенно записывают следующим об-
разом: 3,171717... — 3(17); 0,231919... — 0,23(19), т. е. период
дроби заключают в скобки. Например, число 3,(17) читается: три
целых и 17 в периоде.
11
ЧАСТЬ I. Алгебра и начала анализа
Бесконечная десятичная дробь, получающаяся при обраще-
нии обыкновенной дроби, должна быть периодической.
Каждое рациональное число можно представить в виде конеч-
ной периодической десятичной дроби.
Например, рациональное число уу делением 7 на 11 можно
представить периодической десятичной дробью 0,(63).
Конечные десятичные дроби можно записывать в виде беско-
нечных десятичных дробей:
0,27 = 0,27000... = 0,27(0); -4,73 = -4,73000... = -4,73(0).
Целые числа также можно записывать в виде бесконечных де-
сятичных дробей:
17 = 17,000... = 17(0); - 8 = -8,000... = -8(0).
Можно утверждать, что каждое рациональное число предста-
вимо в виде бесконечной периодической десятичной дроби.
Верно и обратное утверждение.
Любая бесконечная периодическая дробь является рациональ-
ным числом.
9. Обращение чистой периодической десятичной дроби в обыкновен-
ную. Обыкновенная дробь, знаменатель которой после сокраще-
ния не содержит множителей 2 и 5, обращается в чистую пери-
одическую десятичную дробь.
Чтобы обратить чистую периодическую десятичную дробь в
обыкновенную, нужно ее период сделать числителем, а в знаме-
нателе записать цифру 9 столько раз, сколько цифр в периоде.
Например,
П ГАЧ - § - 2 .
0,(6) 3,
3,05 = 3^; 0,(057)-^
19
333 ’
10. Обращение смешанной периодической десятичной дроби в обыкно-
венную. Обыкновенная дробь, знаменатель которой после сокра-
щения вместе с другими множителями содержит множители 2
или 5 или оба множителя, обращается в смешанную периодиче-
скую дробь. Например,
|| = =0,5(3); | =0,8(3); ± =0,0(142857); || =0,9(4).
12
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Чтобы обратить смешанную периодическую дробь в обыкно-
венную, достаточно из числа, стоящего до второго периода,
вычесть число, стоящее до первого периода, и полученную
разность взять числителем, а знаменателем написать цифру 9
столько раз, сколько цифр в периоде, со столькими нулями,
сколько цифр между запятой и периодом.
Например,
0,5(3)=
48 = 8 .
90 15’
0,0(142857) =
142857 - 0
9999990
142857
9999990
94—9
0,9(4) =
85 17
90 18’
п _______ 345 3
0,3(45) - 990
342 = 19
990 55 ’
Исключение составляют бесконечные периодические десятич-
ные дроби с периодом 9. Например:
0,6(9)
63
90
0,76(9) =
769 - 76
900
693 = 77
900 100
= 0,77.
Любая бесконечная периодическая десятичная дробь с пери-
одом 9 равна некоторой конечной десятичной дроби, поэтому при
представлении рациональных чисел десятичными дробями необ-
ходимо исключить из рассмотрения бесконечные периодические
десятичные дроби с периодом 9.
11. Иррациональные числа. Потребности логического развития ма-
тематики и ее практических приложений показали недостаточ-
ность множества рациональных чисел для решения многих за-
дач.
Покажем, что не существует рационального числа, квадрат
которого равен 2. Задача сводится к решению уравнения х2 = 2.
Очевидно, что не существует такого целого числа, квадрат кото-
рого равен 2, ибо I2 < 2, а 22 > 2.
13
ЧАСТЬ I. Алгебра и начала анализа
Допустим, что такое число найдется среди дробных чисел, по-
этому будем считать, что дробь х = — несократима, т. е. числа тип
взаимно простые. Предположим, что имеет место равенство
= 2, тогда т2 = 2п2. Отсюда следует, что натуральное число
т2 — четное, так как 2п2 — число четное. Если т2 — четное, то
и т — четное, т. е. т = 2р, где р — натуральное число. Имеем:
(2р)2 = 2п2 или 4р2 = 2п2, 2р2 = п2, т. е. число п2 также четное, от-
сюда следует, что и п — четное.
Приходим к выводу, что числа тип четные, т. е. не явля-
ются взаимно простыми. Это противоречит первоначальному
предположению, что тип — взаимно простые. Следователь-
но, не существует такого дробного числа, квадрат которого ра-
вен 2.
Из доказанного вытекает, что диаго-
наль квадрата несоизмерима с его сторо-
ной, т. е. не имеет общей меры со сторо-
ной квадрата, равной 1 (рис. 1). Такой вы-
вод противоречит нашему интуитивному
представлению о том, что любой отрезок
имеет длину. Длина диагонали квадрата
со стороной, равной единице, не может
быть выражена рациональным числом*.
На числовой оси при принятой единице
Рис j измерения всякому рациональному числу
соответствует одна и только одна точка.
Если каждую из этих рациональных точек представить не-
прозрачными (черными), а все другие точки прозрачными, то на
числовой оси образуется множество просветов, которые будут со-
ответствовать числам V 2 , л/3 , л и множеству других чисел, не
являющихся рациональными. В отличие от рациональных чисел
эти числа называются иррациональными. Таким образом, чис-
ловая ось полностью заполняется точками, соответствующими
рациональным и иррациональным числам, и просветов на число-
вой оси не будет.
Данное открытие приписывают греческому философу Пифагору
[ПиОосуорад], жившему около 2500 лет тому назад. Не исключено, что
сведения о существовании несоизмеримых отрезков восходят к глуби-
нам ассиро-вавилонской культуры.
14
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Иррациональные числа представляют собой множество I всех
бесконечных непериодических десятичных дробей.
Иррациональное число больше всякого приближения по не-
достатку и меньше всякого приближения по избытку. Приведем
примеры иррациональных чисел:
J2 = 1,4142136... (1,414213 < J~2 < 1,414214),
л = 3,141592653589...,
е = 2,718281828459045... (е — основание натуральных лога-
рифмов),
1g 5 = 0,6989700... .
12. Действительные числа. Множество Q всех рациональных чисел
и множество I всех иррациональных чисел называется множест-
вом R действительных или вещественных чисел, т. е. Q <= R,
I a R. Другими словами, действительным числом называется ко-
нечная или бесконечная десятичная дробь.
Множество действительных чисел обладает всеми свойствами
I—XII множества рациональных чисел Q (см. п. 6). Множество
неотрицательных действительных чисел обозначают jR+, а мно-
жество отрицательных действительных чисел обозначается R_.
Множество называется конечным, если оно состоит из конеч-
ного числа элементов, в противном случае оно называется беско-
нечным.
Множество R всех действительных чисел называют числовой
прямой, а сами действительные числа — точками числовой
прямой.
Наиболее часто встречаются следующие числовые множества:
замкнутый промежуток (или отрезок) с началом а и концом Ъ
[а; Ь] или а < х < Ь;
открытый промежуток (или интервал) с началом а и концом
Ъ (точки а и b не включаются):
(а, Ь) или а < х < Ь;
полуоткрытые промежутки с началом а и концом Ъ:
(а, д] или а < х < Ъ и
[а, Ь) или а < х < Ь,
число Ъ - а называется длиной промежутка с концами а и Ъ;
15
ЧАСТЬ I. Алгебра и начала анализа
бесконечные промежутки (лучи, полупрямые)
(а, +оо) или а < х < +оо,
(-оо, а) или -оо < х < а,
[а, +оо) или а < х < +оо,
(-оо, а] или -оо < х < а;
числовая прямая
(-ОО, +оо) = R ИЛИ -ОО < X < +оо.
13. Абсолютная величина (модуль) действительного числа. Под абсо-
лютной величиной (модулем) действительного числа а понима-
ют его величину, взятую без знака. Поэтому следует отличать аб-
солютную величину действительного числа от его алгебраиче-
ской величины, которая всегда записывается или представляется
мысленно со знаком. Абсолютная величина числа а обозначается
символом |а|. Например, |+5| = 5, |-31 = 3, | ±01 = 0.
Каждому положительному действительному числу а соответ-
ствует отрицательное действительное число -а.
По определению абсолютная величина (модуль) числа | а | рав-
на самому числу а, если а — положительное число, или числу
- а, если а — отрицательное число:
(
j а, если
-а, если
а > 0,
а < 0.
Абсолютная величина нуля равна нулю.
Например,
|4| = 4;|-4| = -(-4) = 4.
Из определения абсолютной величины следует:
|а | > 0; |-а| = |а|; а < |а|.
Например, если | а | > 10, то а > 10 или а < -10.
14. Деление на нуль. Деление на нуль всегда является недопусти-
мым действием.
4x^0 0
1) Выражение — неопределенность, так как выражает со-
бой любое число т = т; 0 = 0 • m = о\
2) Выражение не имеет смысла. Пусть = ?п, а = 0 • ?п = 0,
но а * 0. Нет такого числа ?п, которое, будучи помноженным на
нуль, дало бы число, отличное от нуля.
16
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Следовательно, обе формы q и q являются только кажущи-
мися математическими формулами: первая бесполезна, вто-
рая бессмысленна.
Нуль есть число нейтральное, оно не является ни положитель-
ным, ни отрицательным, а является лишь границей положитель-
ных и отрицательных чисел.
15. Понятие о мнимых и комплексных числах. Для решения многих
задач физики, электротехники и других наук оказалось недоста-
точно множества действительных чисел.
Приведем следующий пример. Для уравнения х2 + 1 = 0 фор-
мально х = ± J-1, т. е. это уравнение в множестве действитель-
ных чисел решения не имеет, так как не существует действитель-
ного числа, квадрат которого равен — 1.
В связи с этим возникла потребность нового расширения по-
нятия числа. Комплексными числами называются числа вида
z = а + bi, где а и Ь — действительные числа, а число i, определяе-
мое равенством i2 = -1, называется мнимой единицей*.
Два комплексных числа 2г = аг + Ь^ и z2 = а2 + b2i называются
равными, если аг = а2 и Ьх = Ь2.
Запись комплексного числа в виде z = а + bi называется алгеб-
раической формой записи комплексного числа. Действительное
число а называется действительной частью комплексного числа
z = а + Ы, а Ы — его мнимой частью.
Любое действительное число а содержится в множестве комп-
лексных чисел, его можно представить в виде а — а + 0 • i. Числа
0, 1 и i записываются соответственно в виде 0 = 0 + 0*i, в этом
случае комплексное число 0 совпадает с числом 0 множества дей-
ствительных чисел, 1 = 1 + 0*гиг = 0 + 1*г. При а = 0 комплекс-
ное число а + bi обращается в чисто мнимое число Ы.
Два комплексных числа называются взаимно сопряженными
(обозначаются z и z), если их действительные части равны, а мни-
* Еще в XVI в. итальянские математики Джероламо Кардано [Car-
dano] (1501—1576) и Раффаэле Бомбёлли [Bombelli] (ок. 1526—1572) до-
пускали существование квадратных корней из отрицательных чисел и
ввели символ J-1. Символ i был введен академиком Петербургской ака-
демии наук Леонардом Эйлером [Euler] (1707—1783). Термин же «комп-
лексное число» был предложен немецким математиком Карлом Гауссом
[Gau/J] (1777—1855).
17
ЧАСТЬ I. Алгебра и начала анализа
мне отличаются знаками. Например, числу z — — 3 4- 5/ сопря-
женным будет число z = -3 - 5/, числу 2 = 5-7/ сопряженным
будет число 2 = 5+7/. При решении квадратного уравнения
х2 - 2х + 2 = 0 получаем два взаимно сопряженных корня хг —
= 1 - / д/2 и х2 = 1 + /»/2 .
Комплексные числа вида а + bi и — а — bi называются противо-
положными.
Множество комплексных чисел обозначается буквой С. Мно-
жество действительных чисел R содержится в множестве С комп-
лексных чисел: R <z С, следовательно, NcZcQcftcC.
16. Геометрическая интерпретация комплексных чисел. Комплексное
число 2 — а + bi можно изобразить точкой плоскости с координа-
тами (а; Ь). Плоскость хОу, на которой изображаются комплекс-
ные числа, называется комплексной плос-
М <а\Ъ)
Рис. 2
костью (рис. 2). При этом действительные
числа изображаются точками оси абсцисс,
которую называют действительной осью,
а чисто мнимые числа — точками оси ор-
динат, которую называют мнимой осью.
Любое комплексное число 2 = а + bi
единственным способом определяется его
действительной и мнимой частями. Каж-
дому комплексному числу z = а + bi в
комплексной плоскости соответствует единственная точка
М(а; &), и, обратно, каждой точке (а; Ь) плоскости хОу соответст-
вует единственное комплексное число. Например, число 2 = 3 + 2/
изображается точкой с абсциссой 3 и ординатой 2 (рис. 3). Число
2 = 0 + 3/ изобразится с точкой (0; 3) на оси ординат, которую мы
условились называть мнимой осью (рис. 4). Сопряженные числа
2 = 2 + /и2 = 2- / расположены симметрично относительно дей-
ствительной оси (рис. 5).
Рис. 5
18
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Таким образом, между множеством комплексных чисел и мно-
жеством точек плоскости хоу существует взаимно-однозначное
соответствие. Каждому действительному числу z — а + 0 • I соот-
ветствует точка (а; 0) на оси абсцисс, и всякому мнимому числу
z = 0 + bi соответствует точка (0; Ь) на оси ординат. Числу z = i со-
ответствует точка (0; 1).
Комплексное число z — а 4- b • i можно геометрически изобра-
зить в виде вектора ОМ — z с началом в точке О (0; 0) и концом в
точке М(а; Ь). Следовательно, каждой точке М(сг, Ь) будет соот-
ветствовать один и только один вектор ОМ (рис. 2).
Модулем комплексного числа z = а + Ы называется действи-
тельное число г = Jo? л^Ъ2. В геометрической интерпретации мо-
дуль — это длина радиуса-вектора ОМ: | ОМ | = г = Ja2 + Ь2. Чис-
ло г может быть либо положительным, либо равным нулю при
а = 0 и Ъ = 0.
Модуль комплексного числа называется также абсолютной ве-
личиной этого числа. При b = 0 имеем |а + 0• i| = Ja2 + О2 = |а|,
т. е. модуль действительного числа есть абсолютная величина
этого числа.
♦ ПРИМЕР
Найти модули комплексных чисел z1 = 4 + Зг; г2 = -1 - 2i.
РЕШЕНИЕ.
Угол (р между действительной осью Ох и вектором ОМ
(см. рис. 2), отсчитываемый от положительного направления
действительной оси, называется аргументом комплексного числа
z = а + Ы. Если отсчет ведется против движения числовой стрел-
ки, то величина угла считается положительной, а если по движе-
нию часовой стрелки — отрицательной. Для числа z = 0 аргумент
не определен.
Из геометрической интерпретации комплексных чисел выте-
кают следующие свойства:
19
ЧАСТЬ I. Алгебра и начала анализа
I. Длина вектора z равна |z|.
II. Точки z — а + Ыи2 = а-Ы симметричны относительно дей-
ствительной оси.
III. Точки 2 и -г симметричны относительно точки О.
IV. Число zt 4- z2 геометрически изображается вектором, по-
строенным по правилу сложения векторов (правилу парал-
лелограмма), соответствующих точкам и г2 (рис. 6).
V. Расстояние между точками 2г и г2 равно Izj - z21.
17. Сложение и вычитание комплексных чисел, заданных в алгебраиче-
ской форме. Действия над комплексными числами удовлетворяют
основным законам действий над рациональными числами I—IX
(см. п. 6). Законы действий X—XII к комплексным числам не
применимы. Между комплексными числами не существует поня-
тий «больше» или «меньше».
Сложение двух комплексных чисел выполняется по формуле
(at + bYi) 4- (а2 + b2i) = (а1 + а2) + (Ьг 4- b2)i.
Например, суммой двух комплексных чисел zx = 3 4- 4i и z2 =
= -5 4-3/ является z = zA 4- z2 = (3 - 5) 4- (4 4- 3)i = —2 + 7i.
Сумма двух сопряженных комплексных чисел z = a +bi nz =
= a - bi равна z + z = 2a.
Представим геометрически сумму двух комплексных чисел
—>
zx = 1 + 2i и г2 = 4 4- i. Числу zx = 1 4- 2i соответствует вектор ОМр
-------------------------->
а числу z2 = 4 4- I — вектор ОМ2 (рис. 7). Суммой этих векторов
—>
является вектор ОМ, представляющий собой диагональ паралле-
—> —»
лограмма, построенного на векторах ОМХ и ОМ2.
Рис. 6
М (г = 5 + 30
О
Рис. 7
20
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Вычитание двух комплексных чисел определяется как дейст-
вие, обратное сложению. Разность двух комплексных чисел на-
ходится по формуле
(а1 4- bti) - (а2 + b2i) = (аг - а2) 4- (Ьг - b2)i.
Например, разность двух комплексных чисел zx = 4 - 3/ и z2 =
= - 3 4- 5i равна
z = 2Х - z2 = (4 - 30 - (-3 4- 50 = (4 4- 3) + (-3 - 5)i = 7 - 8i.
Разность двух сопряженных комплексных чисел z = а 4- bi и
z = а - Ы равна а 4- bi - а 4- bi = 2Ы.
18. Умножение комплексных чисел, заданных в алгебраической форме.
Умножение двух комплексных чисел выполняется по формуле:
(аг + &!0(а2 + Ь20 = (aia2- &1&2) + (ai^2 + а2^1^-
Правило умножения распространяется и на большее число
сомножителей.
♦ ПРИМЕР
Найти произведение комплексных чисел: 1) = 2 4- 3i и z2 =
-- -1 - i; 2) 2г - 3 - 2i, z2 = 1 + 4i и z2 = 2 - i.
РЕШЕНИЕ. 1) • z2 = (2(—1) - 3(—1)) 4- (2(-1) 4- (-l)3)i = (-2 4- 3) 4-
4- (-2 - 3)i = 1 - 5i;
2) zx • z2 = (3 - 20(1 4- 40 = 3 + 12i - 2i - 8i2 = 3 4- lOi 4- 8 =
= 114- 100
• 22 • 23 = (H 4-100(2 - 0 = 22 - Hi 4- 20i - 10i2 = 22 4- 9i - 10 =
= 32 4- 9i.
Приведем соотношение, представляющее собой интересную зависи-
мость в области действительных чисел. Пусть даны два произведения с
комплексными числами:
(Gj 4- Ь^)(а2 4- b2i) = (ага2 - btb2) 4- (а^ 4- c^bji, (а)
(ai - Ь^)(а2 - b2i) = (ага2 - ЬгЬ2) - (а1Ь2 4- a2br)i. (р)
Перемножив левые и правые части равенств ((X) и (р), получим:
(п24- &2)(п24- fc2) = (аАа2 - Ь,Ь2)2 4- (а.Ь2 4- а2&.)2.
JL JL Л. JL X
21
ЧАСТЬ I. Алгебра и начала анализа
Последнее равенство содержит только действительные числа, из чего
следует, что при умножении двух чисел, каждое из которых есть сумма
двух квадратов, получается произведение, представляющее собой также
сумму двух квадратов.
Рассмотрим примеры:
(1 + 9)(4 + 25) = 10•29 = 290 = I2 + 172,
(1 + 4)(9 + 25) = 5 • 34 = 170 = I2 + 132,
(1 + 25)(9 + 16) = 26 • 25 = 650 = 52 + 252.
При перемножении сопряженных чисел z = a + binz = a — bi
получим z • z = (а + bi)(a — bi) = а2 - b2i2 = а2 + Ъ2 = г2, где г — мо-
дуль каждого из сомножителей. Итак, произведение двух сопря-
женных комплексных чисел является действительным числом,
равным г2, т. е. квадрату их общего модуля.
Равенство
а2 + b2 = (а + bi)(a - bi)
(1.1)
показывает, что сумму квадратов двух действительных чисел
можно разложить на комплексные множители. Это разложение
на множители невыполнимо в множестве действительных чисел.
♦ ПРИМЕР
Используя формулу (1.1), разложить на комплексные множи-
тели: 1) 4т2 4- 9п2; 2) а + Ь; 3) 2 + J 5 ; 4) 5.
РЕШЕНИЕ.
1) 4т2 + 9п2 = (2т)2 + (Зи)2 = (2т + 3ni)(2m - 3ni);
2)a + b= (J~a)2 + (Jb)2 = (Ja + ijb)(j~a -ijb)\
3)2+ = (a/2)2 + (4j5)2 =(J2 +i475)(j2 -il/5);
4) 5 = 1 + 4 - I2 + 22 - (1 + 2i)(l - 2i).
19. Деление комплексных чисел, заданных в алгебраической
рорме
.п
Деление комплексных чисел рассматривается как действие, об-
ратное умножению, и производится по формуле
Поясним предыдущую формулу. Умножим делимое и делитель
на число, сопряженное делителю:
22
ГЛАВА I. Линейные и квадратные уравнения и неравенства
а2 ^2* (а2 ^2*)
aj ~ b%i2
^1^2^ ' Л ; 11 + ^1^2 ®1^2 ^1^2 4” (^2^1 Oj^2)Z
«2 + Ь2
«2 + Ь2
♦ ПРИМЕР
Найти частное от деления числа zr = 3 + 41 на число z2 = 2 - 3i.
РЕШЕНИЕ.
3 + 41
г2 2 - 3i
(3 + 4t)(2 + 3i) = 6 + 9i + 8z + 12t2
(2 - 3i)(2 + 3i) 4 - 9i2
= -6 17 . = _ 6 17 .
13 + 13 1 13 + 13 1‘
6 + 17i - 12
4 + 9
20. Возведение комплексных чисел в степень. Возведение комплекс-
ного числа 2 = а + Ы в степень п (п е N) будем рассматривать как
частный случай умножения комплексных чисел:
2п — 2 • 2 • ... *2.
Найдем натуральные степени мнимой единицы i:
i2 = -1, i3 = i2 • i = -i, i4 = i2 • i2 = (-1)(-1) = 1, i5 = i4 • i = i, i6 =
= i4 • i2 = 1 • (-1) = -1, i7 - i4 • i3 = 1 • (-1) = -i, i8 = i4 • i4 = 1.
Учитывая, что i4 = 1, имеем i4n +1 = i • i4n + 2 = -1, i4n + 3 = —i, где
пе N.
♦ ПРИМЕР 1
Вычислить i55.
РЕШЕНИЕ. При делении числа 55 на 4 имеем: 55 = 52 + 3 = 13*4 + 3,
ПОЭТОМУ i55 = jl3*4 + 3 = J . j3 _ _ j.
♦ ПРИМЕР 2
Вычислить: 1) гг = (1 + i)2, 2) г2 = (1 + i)3, 3) г3 = (1 + г)4, 4) z4 =
= (3 - 2i)2, 5) 25 = (1 + i)17, 6) 26 = (1 - L)-3.
РЕШЕНИЕ.
1) 2j = 1 + 2i + i2 = 1 + 2i - 1 = 2i;
2) z2 = (1 + 02(l + 0 = 2i(l + 0 = -2 + 2i;
23
ЧАСТЬ I. Алгебра и начала анализа
3) 23 = (1 4- 02(1 + О2 = 2i • 2i = 4i2 = -4;
4) z4 = 9 - 12i + 4i2 = 9 — 12i — 4 = 5 - 12i;
5) z5 = (1 + i)16(l + i) = ((1 + О4)4 (1 + О = (-4)4 (1 + i) = 256(1 + 0;
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие числа называются натуральными? Какое обозначение введено
для множества натуральных чисел?
2. Какие числа входят в множество целых чисел? Какое обозначение при-
нято для этого множества?
3. Какое множество называется множеством рациональных чисел и как
это множество обозначается?
4. Перечислите основные законы действий над рациональными числами.
5. Какие обыкновенные дроби обращаются в конечные десятичные?
6. Какие обыкновенные дроби выражаются только приближенными деся-
тичными?
7. Какие десятичные дроби называются бесконечными периодическими?
8. Что называется периодом бесконечной периодической десятичной дроби?
9. Какие периодические дроби называются чистыми и смешанными и как
сокращенно они записываются?
10. Как записываются целые числа и конечные десятичные дроби в виде
бесконечных периодических дробей?
11. Любая ли бесконечная периодическая десятичная дробь является рацио-
нальным числом?
12. Как обратить чистую периодическую десятичную дробь в обыкновенную?
13. Как обратить смешанную периодическую десятичную дробь в обыкно-
венную?
14. Какое исключение представляет собой бесконечная периодическая де-
сятичная дробь с периодом 9?
15. Какие числа называются иррациональными и как обозначается множе-
ство иррациональных чисел?
16. Докажите, что не существует числа, квадрат которого равен 2.
17. Какие числа называются действительными и какое для них введено
обозначение?
18. Какими свойствами обладает множество действительных чисел?
19. Что называется числовой прямой?
24
ГЛАВА I. Линейные и квадратные уравнения и неравенства
20. Что называется числовым отрезком?
21. Что называется числовым интервалом?
22. Какие промежутки называются полуоткрытыми?
23. Какие промежутки называются бесконечными?
24. Что понимается под абсолютной величиной действительного числа?
25. Почему нельзя делить на нуль?
26. Какие числа называются комплексными и мнимыми?
27. Как геометрически представляется комплексное число?
28. Что называется модулем комплексного числа?
29. Как выполняется сложение и вычитание комплексных чисел?
30. Как геометрически представляется сумма двух комплексных чисел?
31. Как выполняется умножение комплексных чисел?
32. Как выполняется деление комплексных чисел?
33. Как выполняется возведение в степень мнимых и комплексных чисел?
§ 2. Метод координат
Прямоугольная система координат на плоскости позволяет в
наглядной форме (в виде графиков) представлять различные
функциональные зависимости и решать уравнения и системы
уравнений графическим способом.
Две взаимно перпендикулярные оси (ось абсцисс Ох и ось ор-
динат Оу) и точка пересечения — начало координат образуют
при выбранной единице масштаба декартову систему коорди-
нат*.
Из школьного курса математики известны правила постро-
ения точек и линий по их координатам, поэтому кратко укажем
только основные положения метода координат.
Плоскость, на которой расположены координатные оси, назы-
вается координатной плоскостью. Абсциссой х любой точки
плоскости называется число, выражающее в принятом масштабе
расстояние от этой точки до оси Оу, взятое со знаком плюс, если
точка лежит справа от оси Оу, и со знаком минус, если слева. Ор-
динатой у любой точки называется число, выражающее расстоя-
* Система координат называется декартовой по имени французского
философа, математика и физика Рене Декарта [Descartes; латинизиро-
ванное имя Cartesius — Картезий] (1596—1650), разработавшего метод
координат; Декарт одним из первых ввел понятия переменной величины
и функции.
25
ЧАСТЬ I. Алгебра и начала анализа
II х<0
у>о
о
III х < О
У <0
Рис. 9
х
IV х>0
У<0
ние от этой точки до оси Ох, взятое со знаком плюс, если точка
лежит выше оси Ох, и со знаком минус, если ниже.
Числа х и у, определяющие положение точки на плоскости, на-
зываются прямоугольными координатами точки. На рисунке 8
изображены точки К, М, N, соответствующие своим координатам.
Каждой паре (х; у) действительных чисел соответствует одна и
только одна точка М(х; у) на координатной плоскости, для кото-
рой абсцисса равна х, а ордината равна у; каждой точке на коор-
динатной плоскости соответствует одна и только одна пара чисел —
координат этой точки.
Множество точек х = 0 образует ось Оу, поэтому графиком
уравнения х == 0 является ось Оу.
Множество точек у = 0 образует ось Ох, поэтому графиком
уравнения у = 0 является ось Ох.
Множество точек у = х образует прямую, проходящую через
начало координат и делящую I и III квадранты пополам.
Знаки координат по четвертям (квадрантам) показаны на ри-
сунке 9. На рисунке 10 изображены графики уравнений х == 1 и
у = -1.
§ 3. Погрешности приближенных значений чисел
1. Абсолютная погрешность и граница абсолютной погрешности прибли-
женных значений чисел. Модуль (абсолютная величина) разности
между точным числом х и его приближенным значением а назы-
вается абсолютной погрешностью приближенного значения чис-
ла х и обозначается через а, т. е. |х - а| = а.
Число а называется приближенным значением точного числа
х с точностью до Да, если абсолютная погрешность приближен-
ного значения а не превышает Да, т. е. |х - а| < Да.
26
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Число Да называется границей абсолютной погрешности
приближенного числа а. Существует бесконечное множество чи-
сел Да, удовлетворяющих приведенному определению, поэтому
на практике стараются подобрать возможно меньшее и простое
по записи число Да.
По известной границе абсолютной погрешности Да находятся
границы, в которых заключено точное значение числа х*:
(х = а ± Да) <=> (а - Да < х < а + Да).
♦ ПРИМЕР 1
Даны приближенные значения числа х = : а1 = 0,6; а2 = 0,66;
а3 = 0,67. Какое из этих приближений является лучшим?
РЕШЕНИЕ.
3
-0,6 =
2
3
15
аз
-0,66 =
-0,67 =
33
50
100
150’
300
300’
а
3
2
3
3
2
Лучшим приближением числа х является а3 = 0,67.
♦ ПРИМЕР 2
Длина детали х (см) заключена в границах 33 < х < 34. Найти
границу абсолютной погрешности измерения детали.
РЕШЕНИЕ. Примем за приближенное значение длины детали сред-
нее арифметическое границ: а = (33 + 34)/2 = 33,5 (см). Тогда
граница абсолютной погрешности Да приближенного значения
длины детали а не превзойдет 0,5 см.
Величину Да можно найти и как полуразность верхней и нижней
границ, т. е. Да = (34 - 33)/2 = 0,5 см.
Длина детали х, найденная с точностью до Да = 0,5 см, заключе-
на между приближенными значениями числа х (1.2):
33,5 - 0,5 < х < 33,5 + 0,5; х = 33,5 ± 0,5 (см).
♦ ПРИМЕРЗ
Площадь квадрата равна 24,5 ± 0,4 (см2). Найти границы из-
мерения площади квадрата.
* Символ <=> означает, что если А <=> В, то из А следует В и наоборот.
27
ЧАСТЬ I. Алгебра и начала анализа
РЕШЕНИЕ. По формуле (1.2) находим:
24,5 - 0,4 < х < 24,5 + 0,4; 24,1 < х < 24,9 (см2).
2. Верные и значащие цифры числа. Цифра иг приближенного числа
а называется верной в широком смысле, если граница абсолют-
ной погрешности числа а не превосходит единицы того разряда, в
котором записывается цифра т.
Цифра т приближенного числа а называется верной в стро-
гом смысле, если граница абсолютной погрешности числа а не
превосходит половины единицы того разряда, в котором записа-
на цифра т.
В числах, полученных в результате измерений или вычисле-
ний и используемых при расчетах в качестве исходных данных,
а также в десятичной записи приближенного значения числа все
цифры должны быть верными.
Наиболее употребительна такая запись приближенного числа
(например, в математических таблицах), при которой цифры вер-
ны в строгом смысле.
Граница абсолютной погрешности Да находится непосредст-
венно по записи приближенного значения а числа х. Например,
если в приближенном числе а = 1976 цифры верны в строгом
смысле, то граница абсолютной погрешности Да = 0,5, т. е. равна
половине последнего разряда числа 1976.
Цифры в записи приближенного числа, о которых неизвестно,
являются ли они верными, называются сомнительными.
Значащими цифрами приближенного числа называются все
его верные цифры, кроме нулей, стоящих перед первой цифрой
(слева направо), отличной от нуля.
♦ ПРИМЕР 1
Найти границу абсолютной погрешности приближенного зна-
чения 0,1978 числа х, все цифры которого верны в строгом
смысле.
РЕШЕНИЕ. Граница абсолютной погрешности этого числа равна
0,00005, т. е. половине единицы последнего разряда, сохраняе-
мого в записи.
♦ ПРИМЕР 2
Указать верные цифры (в широком смысле) следующих чисел:
1) 2,73 ± 0,056; 2) 4,627 ± 0,0008; 3) 3,732 ± 0,06; 4) 562 274 ±
± 500.
28
ГЛАВА I. Линейные и квадратные уравнения и неравенства
РЕШЕНИЕ. 1) Граница погрешности Да = 0,056 не превосходит еди-
ницы разряда десятых (неравенство 0,056 <0,1 верное). Следова-
тельно, верными являются цифры 2 и 7.
2) Так как Да = 0,0008 < 0,001, то все цифры приближенного
числа 4,627 верные.
3) Так как Да = 0,06 <0,1, верными являются цифры 3 и 7.
4) Так как Да — 500 < 1000, то верны цифры 5, 6 и 2.
♦ ПРИМЕРЗ
За приближенное значение числа 26,7 взято число 27. Явля-
ются ли цифры числа 27 верными?
РЕШЕНИЕ. Так как |26,7 - 27| = 0,3 < 1, то цифры 2 и 7 — верные
в строгом смысле.
3. Относительная погрешность приближенного значения числа. Отно-
сительной погрешностью 8 приближенного значения а числа х
называется отношение абсолютной погрешности а этого прибли-
жения к числу а:
(1.3)
Так как абсолютная погрешность а обычно бывает неизвестна,
то на практике оценивают модуль относительной погрешности
некоторым числом е, которое заведомо не меньше этого модуля:
|8| < £.
Число £ называется границей относительной погрешности.
Границей относительной погрешности а приближенного зна-
чения а называется отношение границы абсолютной погрешнос-
ти Да к модулю числа а:
(1.4)
Чем меньше относительная погрешность, тем выше качество
измерений или вычислений. Относительная погрешность — ве-
личина безразмерная, что позволяет сравнивать качество измере-
ний величин разной размерности.
Зависимость относительной погрешности от числа значащих
цифр иллюстрируется данными, приведенными в таблице 1.
29
ЧАСТЬ I. Алгебра и начала анализа
Таблица 1
Число Наименьшее число Наибольшее число Граница абсолютной погрешности Относительная погрешность наибольшего числа Относительная погрешность наименьшего числа
Однозначное 1 0 0.5 0,56 = 5,6% 0.5 = 50%
Двузначное 10 99 0,5 0,005 = 0,5% 0,05 = 5%
Трехзначное 100 999 0,5 0,0005 = 0,05% 0,005 = 0,5%
Четырех- значное 1000 9999 0,5 0,00005 = 0,005% 0,005 = 0,05%
Из таблицы видно, что три верные значащие цифры обеспечи-
вают точность результата (относительную погрешность) от 0,05%
до 0,5%. В технических расчетах, не требующих высокой точнос-
ти, достаточно бывает обеспечить точность результата порядка
десятых долей процента. Поэтому в таких расчетах принято вы-
полнять вычисления с тремя значащими цифрами.
В ряде задач границу абсолютной погрешности находят по
данной относительной погрешности и модулю приближенного
значения величины:
(1.5)
♦ ПРИМЕР 1
В результате измерений получили, что длина карандаша рав-
на 16 см, а длина комнаты равна 730 см. Что можно сказать
о качестве этих двух измерений?
РЕШЕНИЕ. Будем считать границу абсолютной погрешности изме-
рений равной ±0,5 см. Найдем относительные погрешности этих
измерений (1.3):
0 5
“ = 0,0312 ~ 3,1% (при измерении длины карандаша);
0,5
730
= 0,000685 ~ 0,07% (при измерении длины комнаты).
Следовательно, качество измерения длины комнаты значительно
выше, чем качество измерения длины карандаша.
♦ ПРИМЕР 2
Найти относительную погрешность числа 6,8, если обе цифры
его верны в строгом смысле.
30
ГЛАВА I. Линейные и квадратные уравнения и неравенства
РЕШЕНИЕ. По условию Да = 0,05; поэтому согласно (1.4)
еа = = 0,00735 = 0,7%.
♦ ПРИМЕРЗ
Какие цифры числа 4,86 при относительной погрешности,
равной 0,03%, являются верными?
РЕШЕНИЕ. В соответствии с формулой (1.5) находим
Да = 4,86 • 0,003 = 0,0146 < 0,2;
а — 4,86 ± 0,02.
Верными являются первые две цифры 4 и 8.
4. Округление и погрешность округления. Округление десятичной
дроби состоит в отбрасывании единиц младших разрядов начи-
ная с некоторого. Полученное число принимается в качестве при-
ближенного значения дроби. Абсолютная погрешность, допус-
каемая при округлении, называется погрешностью округления.
Рассмотрим три способа округления положительных десятич-
ных дробей: округление с недостатком, округление с избытком и
округление с наименьшей погрешностью.
* Округление с недостатком до единиц некоторого разряда со-
стоит в отбрасывании единиц всех младших разрядов.
♦ ПРИМЕР
Округлить с недостатком до сотых, десятых и единиц число
54,376.
РЕШЕНИЕ: Имеем 54,37; 54,3; 54. Погрешности округления соот-
ветственно равны 0,006; 0,076; 0,376.
При округлении с избытком до единиц некоторого разряда
число единиц данного разряда увеличивают на единицу.
♦ ПРИМЕР
Округлить с избытком до сотых, десятых и единиц число 24,368.
РЕШЕНИЕ. Имеем 24,37; 24,4; 25. Погрешности округления соот-
ветственно равны 0,002; 0,032; 0,632.
Наиболее часто применяемым является правило округления
с наименьшей погрешностью (правило округления десятичных
дробей). Это округление производится по следующим правилам:
1) единицы младших разрядов отбрасываются;
2) число единиц данного разряда не изменяется, если следую-
щая цифра дроби меньше 5, и увеличивается на единицу, если
следующая цифра больше или равна 5.
31
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕР
Округлить с наименьшей погрешностью до сотых, десятых и
единиц число 32,467.
РЕШЕНИЕ. Имеем 32,47; 32,5; 32. Погрешности округления соот-
ветственно равны 0,003; 0,033; 0,467.
Из правил округления можно сделать вывод, что при округле-
нии с недостатком и с избытком погрешность может быть больше
половины единицы последнего сохраняемого разряда, но не пре-
вышает единицы этого разряда.
При округлении с наименьшей погрешностью она не превы-
шает половины единицы последнего сохраняемого разряда.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется абсолютной погрешностью приближенного числа?
2. Что называется границей абсолютной погрешности?
3. Какие цифры приближенного числа называются верными в широком
смысле и в строгом смысле?
4. Какие цифры приближенного числа называются значащими?
5. Что называется относительной погрешностью приближенного числа?
6. Что называется границей относительной погрешности приближенного
числа?
7. Как зависит относительная погрешность от числа значащих цифр?
8. Как связаны границы абсолютной и относительной погрешностей?
9. Что называется округлением десятичной дроби?
10. Что называется погрешностью округления?
11. Как производится округление с недостатком?
12. Как производится округление с избытком?
13. Как производится округление с наименьшей погрешностью? Перечис-
лите правила этого округления.
§ 4. Действия над приближенными
значениями чисел
1. Сложение приближенных значений чисел. Граница абсолютной по-
грешности суммы приближенных значений чисел равна сумме
границ абсолютных погрешностей этих чисел:
Д (а + Ъ) = Да + Д&
(1.6)
32
ГЛАВА I. Линейные и квадратные уравнения и неравенства
где а и Ъ — приближенные значения чисел; Да и ДЬ — границы
абсолютных погрешностей соответствующих приближений.
Граница относительной погрешности суммы вычисляется по
формуле:
(1.7)
♦ ПРИМЕР 1
Найти сумму S приближенных значений следующих чисел:
6,8 ± 0,05; 4,3 ± 0,05 и 3,575 ± 0,0005.
РЕШЕНИЕ. Имеем:
S = 6,8 + 4,3 4- 3,575 = 14,675,
Д8 = 0,05 4- 0,05 4- 0,0005 = 0,1005.
Граница абсолютной погрешности 0,1005 заключена в пределах
0,05 < 0,1005 < 0,5. В приближенном значении суммы верными
являются лишь две цифры (в разрядах десятков и единиц). Полу-
ченный результат округлим до единиц: S = 14,675 = 15.
♦ ПРИМЕР 2
Найти сумму 8 = 75 + УН , взяв приближенные значения
корней с точностью до 0,001. Определить границу абсолютной
погрешности Д8 и границу относительной погрешности es.
РЕШЕНИЕ. Имеем
8 = + 7 П = 2,236 4- 3,317 = 5,553 « 5,55.
По формуле (1.6)
Д8 = 0,0005 + 0,0005 = 0,001.
Согласно формуле (1.7)
AS 0,001
s 5,55
= 0,00018.
2. Вычитание приближенных значений чисел. Граница абсолютной
погрешности разности двух приближенных значений чисел рав-
на сумме границ их абсолютных погрешностей:
Д (а — Ь) = Да 4- Д&.
(1.8)
2-9664
33
ЧАСТЬ I. Алгебра и начала анализа
Граница относительной погрешности разности вычисляется
по формуле
Да + ДЬ
(1.9)
♦ ПРИМЕР
Вычислить разность двух приближенных значений чисел
а = 5,863 ± 0,0005 и Ь = 2,746 ± 0,0005. Определить Д (а - Ь) и
РЕШЕНИЕ. По формуле (1.8) находим границу абсолютной погреш-
ности разности (а - Ь):
А(а-Ь) = 0,0005 + 0,0005 = 0,001.
В приближенном значении разности цифра в разряде тысячных
не может быть верной, так как Д (а — Ь) > 0,005. Поэтому
а - b = 5,863 - 2,746 = 3,117 ~ 3,12.
В приближенном числе 3,12 все цифры верные.
По формуле (1.9) находим относительную погрешность раз-
ности:
ео , = = 0,00032 к 0,03%.
О у X iu
3. Умножение приближенных значений чисел. Формулы для оценки
границ абсолютной погрешности произведения (частного) слож-
ны, поэтому на практике сначала находят относительную по-
грешность произведения (частного), а затем границу абсолютной
погрешности произведения (частного).
Формулы для границ абсолютной погрешности Ду
и относительной погрешности е некоторых функций
У
Для у = ад: Ду = д • Да + а АЬ, е = — + ; (1-Ю)
У Cl и
для у = abc: Ау = |Ьс\ • Да + |ас| • Дд + |ад| • Де,
Да Дд
Де
(1.11)
для у = ал:
для у = а2:
Ду = пап —
v у а
А А * лДа
Ду = 2а • Да, е = 2— ;
(1.12)
(1.13)
34
ГЛАВА {.Линейные и квадратные уравнения и неравенства
для у = а3:
&.у = За2 • Да, е = 3 — ;
у а
дляу =
для у = 3Ja:
для у =
а .
ь:
&У =
(1Л4)
(1.15)
(1.16)
(1.17)
♦ ПРИМЕР
Найти верные цифры произведения двух приближенных зна-
чений чисел а = 0,3862 и b = 0,8.
РЕШЕНИЕ. Имеем а*Ъ = 0,3862*0,8 = 0,30896. Границы абсолют-
ной погрешности сомножителей равны 0,00005 и 0,05. По форму-
ле (1.10) находим относительную погрешность произведения
= 0,00005 0,05 = n n q
«ь 0,3862 0,8 и»ио°-
По формуле (1.5) находим границу абсолютной погрешности про-
изведения
A (ab) = (аЬ)гаЬ = 0,30896 • 0,063 = 0,0195;
0,005 < 0,0195 < 0,05.
Полученный результат означает, что в произведении одна верная
цифра (в разряде десятых): 0,30896 ~ 0,3.
4. Деление приближенных значений чисел. Определение границ абсо-
лютной и относительной погрешностей при делении осуществля-
ется с помощью выражений (1.17).
♦ ПРИМЕР
Найти границу абсолютной погрешности частного двух при-
ближенных значений чисел а — 8,36 ± 0,005 и b = 3,72 ± 0,004.
РЕШЕНИЕ. Имеем: £ == =2,25.
Ь 3,72
По формуле (1.17) находим границу относительной погрешности
частного:
= 0,005 0,004
е°/б 8,36 + 3,72
= 0,002 = 0,2%
35
ЧАСТЬ I. Алгебра и начала анализа
По формуле (1.5) находим границу абсолютной погрешности ча-
стного:
= ?£„,.,= 2,25-0,002-0,0045.
Ъ и
Полученный результат означает, что в частном все три цифры
верные.
5. Возведение в степень приближенных значений чисел и извлечение из
них корня. Для определения абсолютной и относительной погреш-
ностей при возведении в степень и извлечении корня используют
формулу (1.12) и выражения для ее частных случаев (1.13—
1.16).
♦ ПРИМЕР 1
Вычислить относительную погрешность, допущенную при вы-
числении площади квадрата, если приближенное значение
стороны квадрата равно I = 68 ± 0,5.
РЕШЕНИЕ. По формуле (1.13) получим
г682= 2^ =0,015= 1,5%.
♦ ПРИМЕР?
Вычислить относительную погрешность, допущенную при из-
влечении квадратного корня из числа 76,8 ± 0,05.
РЕШЕНИЕ. По формуле (1.15) получим
Елг. = = °’0003 = °’03% •
6. Вычисление с наперед заданной точностью. В предыдущих задачах
по известным границам погрешностей данных определялись гра-
ницы погрешностей результата. Теперь рассмотрим обратную за-
дачу, в которой нужно установить, с какой точностью необходи-
мо знать данные, чтобы обеспечить некоторую наперед заданную
точность результата.
♦ ПРИМЕР 1
С какой точностью надо измерить длину стороны квадрата,
чтобы при вычислении его площади граница абсолютной по-
грешности площади не превышала 1 см2? Грубое (приближен-
ное) значение стороны квадрата равно 9 см.
36
ГЛАВА I. Линейные и квадратные уравнения и неравенства
РЕШЕНИЕ. Так как площадь S = а2, то по формуле (1.13) AS =
= 2а • Аа, откуда
= 0,0556-0,1 (см).
Итак, если измерить величину а с погрешностью, не превышаю-
щей 0,1 см, то погрешность площади не превысит 1 см2.
♦ ПРИМЕР?
С какой точностью надо измерить длину ребра куба а, чтобы
при вычислении его объема граница абсолютной погрешности
не превышала 100 см3? Грубое (приближенное) значение ребра
куба равно 80 см.
РЕШЕНИЕ. Так как объем V = а3, то по формуле (1.14) АГ = За2 • Аа,
из чего следует, что
100
= 0,005 (см).
Таким образом, если измерить величину а с погрешностью, не
превышающей 0,005 см, то погрешность значения объема не пре-
высит 100 см2.
7. Вычисления с приближенными числами без подсчета погрешностей.
Во многих случаях вычислительной практики возможно упрос-
тить вычисления с приближенными числами без подсчета по-
грешностей, применяя правила подсчета цифр*.
Правила подсчета цифр
I. При сложении и вычитании приближенных чисел в резуль-
тате следует сохранять столько десятичных знаков, сколько
их в том из приближенных чисел, у которого наименьшее чис-
ло десятичных знаков.
II. При умножении и делении в результате следует сохранять
столько значащих цифр, сколько их имеет то из приближен-
ных данных, у которого число значащих цифр наименьшее.
III. При возведении в квадрат и куб в результате следует со-
хранять столько значащих цифр, сколько их имеет возводи-
мое в степень приближенное число. Последняя цифра квадра-
та и тем более куба при этом менее надежна, чем последняя
цифра основания.
* Эти правила были разработаны профессором В. М. Брадисом
(1890—1975).
37
ЧАСТЬ I. Алгебра и начала анализа
IV. При извлечении квадратного и кубического корней в ре-
зультате следует брать столько значащих цифр, сколько их
имеет подкоренное (приближенное) число. Последняя цифра
квадратного и тем более кубического корня при этом более на-
дежна, чем последняя подкоренного числа.
V. При вычислении промежуточных результатов следует
брать на одну цифру больше, чем рекомендуют предыдущие
правила.
VI. Числа, которые имеют больше десятичных знаков, чем
другие (при действиях первой ступени), или больше значащих
цифр (при действиях второй и третьей ступени), следует пред-
варительно округлять, сохраняя одну лишнюю цифру.
При применении всех правил подсчета цифр следует избегать
нулей, помещенных в конце приближенных чисел вместо неиз-
вестных цифр.
Применяя правила подсчета цифр, следует помнить, что они
не дают гарантии точности последней цифры результата. Эта по-
следняя цифра может иметь погрешность, достигающую в от-
дельных случаях нескольких единиц, но малые значения этой
погрешности более вероятны, чем большие.
При вычислениях с приближенными числами на микрокаль-
куляторе необходимо руководствоваться «Правилами подсчета
цифр»*.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Как вычисляется граница абсолютной погрешности суммы приближен-
ных значений чисел?
2. Как вычисляется граница относительной погрешности суммы прибли-
женных значений чисел?
3. Как вычисляется граница абсолютной погрешности разности двух при-
ближенных значений чисел?
4. Как вычисляется граница относительной погрешности разности при-
ближенных значений чисел?
5. Как вычисляется граница относительной погрешности произведения и
частного приближенных значений чисел?
* Брадис ВуМ. Четырехзначные математические таблицы: для обще-
образовательных учебных заведений. — М.: Дрофа, 2008.
38
ГЛАВА I. Линейные и квадратные уравнения и неравенства
6. Как вычисляется граница относительной погрешности степени прибли-
женного значения числа?
7. Как вычисляется граница относительной погрешности квадратного и
кубического корней из приближенных значений чисел?
8. Как применяются «Правила подсчета цифр» при сложении и вычитании
приближенных значений чисел?
9. Как применяются «Правила подсчета цифр» при умножении и делении
приближенных значений чисел?
10. Как применяются «Правила подсчета цифр» при извлечении квадратно-
го корня и при возведении в квадрат приближенных значений чисел?
§ 5. Линейные уравнения с одной переменной
1. Основные определения. В математике любое предложение, отно-
сительно которого можно сказать, является оно истинным либо
ложным, называется высказыванием.
Если из высказывания А следует высказывание В, то это запи-
сывается следующим образом:
А => В (из А следует В).
Если из высказывания А следует высказывание В, а из выска-
зывания В следует высказывание А, то они называются равно-
сильными и обозначаются: А <=> В.
Равенство с одной переменной называется уравнением с од-
ной переменной, если нужно найти те значения переменной, при
которых получается верное числовое равенство.
Корнем или решением уравнения называется значение пере-
менной, при подстановке которого в уравнение получается вер-
ное числовое равенство.
Уравнения называются равносильными, если множества их
решений равны.
Линейным уравнением с одной переменной х называется
уравнение вида
ах + b = О,
где аиЬ — действительные числа.
Решение линейных уравнений и уравнений, сводящихся к ли-
нейным, основано на следующих теоремах:
I. Если к обеим частям уравнения прибавить одно и то же чис-
ло, то получится уравнение, равносильное данному.
39
ЧАСТЬ I. Алгебра и начала анализа
II. Если обе части уравнения умножить или разделить на одно
и то же число, не равное нулю, то получится уравнение, равно-
сильное данному.
♦ ПРИМЕР 1
Решить уравнение j х 4- g = 0.
РЕШЕНИЕ. Имеем:
1 3 ( 3\ 3
4 8 V 8) * U) Л 2 ’
♦ ПРИМЕР 2
Решить уравнение 6 - 2х -
6х — 4
5
РЕШЕНИЕ. Умножив обе части уравнения на 15, получим:
О — V* fi V ““ Л
6 - 2х - о = к « 90 - ЗОх - 10 + 25х = 18х - 12 «
3 5
—Q2
-ЗОх + 25х-18х = -12-90+ 10 <=> -23х = -92 « х = -Ц = 4.
Ио
Линейное уравнение ах + Ъ = 0 может иметь только одно реше-
ние, или совсем не иметь решения, или иметь бесконечное мно-
жество решений. Поясним это с помощью примеров:
1) уравнение 5х + 4 = 0 имеет единственное решение х = -5/4;
2) уравнение Зх = 0 имеет единственное решение х = 0;
3) уравнение 0 • х + 2 = 0 не имеет решения, так как при любом
значении х произведение 0*х = 0и0 + 2#0;
4) уравнение 0*х = 0 имеет бесконечное множество решений,
любое число является решением этого уравнения.
2. Дробно-рациональные уравнения. К линейным уравнениям при-
водятся и некоторые уравнения, содержащие переменную в зна-
менателе дроби.
Рассмотрим приемы решения таких уравнений.
, 2х — 9 Зх
Приведем уравнение к целому виду, умножив все члены урав-
нения на произведение (2х - 5) • (2 - Зх). Учитывая, что на нуль
делить нельзя, каждый из знаменателей 2х — 5 и 2 — Зх не может
быть равен нулю. Если бы значение х оказалось равным 5/2 или
2/3, то уравнение не имело бы решения.
40
ГЛАВА I. Линейные и квадратные уравнения и неравенства
2х - 9 _ Зх
< 2х — 5 2 — Зх
2х - 5 * О
2 - Зх ** О
(2х - 9)(2 - Зх) - Зх(2х - 5) - 2(2х - 5)(2 - Зх) = О,
8х + 2 = О,
Выполнив преобразования, как и в предыдущем примере, по-
лучим:
х 2
+ 3 = 0,
х-3 + х + Зх-6 = 0,
х 2
4х - 8 = О,
х * 2
Корень х = 2 оказался посторонним. Уравнение не имеет реше-
ния.
III.
3(3х - 1)
(х - 3)(х + 3) ’
Имеем:
х + 3
х + 1
3(3х - 1)
(х - 3)(х + 3) *
(х + 1)(х + 3) - (х - 2)(х - 3) - 3(3х - 1) = О,
х # -3,
х 3
О • х = О,
Уравнение имеет бесконечное множество решений. Корнем
является любое действительное число, кроме х = - 3 и х = 3.
41
ЧАСТЬ I. Алгебра и начала анализа
2х + 1 - 5 + 4х - 6х 4-18 = О,
х * 3
О*х 4- 14 = О,
х 3.
Ни при одном значении переменной х сумма 0 • х 4- 14 не мо-
жет быть равной нулю. Уравнение корней не имеет.
♦ ПРИМЕР
Разделить 850 на две части так, чтобы 8% первой части в сум-
ме с 24% второй части составили 12% всего числа.
РЕШЕНИЕ. Пусть часть I равна х, тогда часть II будет равна 850 - х,
при этом 8% от части I равны 0,08х, 24% от части II равны
0,24(850 - х) и 12% от 850 равны 0,12 • 850.
Составим уравнение
0,08х 4- 0,24(850 - х) = 0,12 • 850.
Упростив его, получим:
-0,16х = -102 => х = 637,5.
Следовательно, часть I равна 637,5; часть II равна 850 - 637,5 =
= 212,5.
3. Графический способ решения линейных уравнений. Уравнение вида
ах = Ь, к которому может быть сведено любое линейное уравне-
ние, можно решить графическим способом.
На одном и том же чертеже построим графики двух функций:
у = ах и у = Ъ. Если эти графики пересекутся, то абсцисса их точ-
ки пересечения и будет корнем уравнения ах = Ъ.
Если графики не будут иметь точки пересечения, то уравнение
не будет иметь корней.
Рассмотрим три случая.
I. а # 0. Графиком функции у = ах будет прямая, проходящая
через начало координат, наклоненная к оси Ох под некоторым
углом а (рис. 11). Графиком функции у = b является прямая, па-
раллельная оси Ох. Эти две прямые пересекаются в единственной
точке М. Абсцисса точки пересечения - и есть корень уравнения
ах = Ъ.
42
ГЛАБАI. Линейные и квадратные уравнения и неравенства
Рис. И
II. а = О, Ъ О. В этом случае прямая у = ах совпадает с осью
Ох, а прямая у = Ъ параллельна оси Ох (рис. 12). Прямые у = ах и
у = b оказались параллельными. Эти прямые не имеют точки пе-
ресечения, поэтому уравнение ах — Ъ не имеет корней.
III. а — b = 0. В этом случае прямые у = ах и у — Ъ совпадают,
сливаясь с осью Ох (рис. 13). Можно утверждать, что эти прямые
пересекаются в каждой точке оси Ох, поэтому любое число явля-
ется корнем уравнения ах = Ь.
♦ ПРИМЕР
Графически решить уравнение 2х = 5.
РЕШЕНИЕ. Строим прямые у = 2х и у = 5 (рис. 14). Эти прямые пе-
ресекаются в точке (5/2; 5). Абсцисса 5/2 является корнем урав-
нения 2х = 5.
4. Основные свойства модуля (абсолютной величины). Модуль дейст-
вительного числа |х| равен самому числу х, если х положительное
число, или равен числу -х, если х отрицательное число. Модуль
нуля равен нулю.
Например, если |х| = 5, то по определению модуля х = 5 или
х = - 5.
Vi
у-Ь(Ь = О)
у = ах (а — 0)
Рис.13
Рис. 14
43
ЧАСТЬ I. Алгебра и начала анализа
Свойства модуля
I. Два противоположных числа имеют один и тот же модуль:
|а| = |-а|, модуль числа не изменится, если число умножить на
(-1).
II. Модуль не может быть отрицательным числом: |а| > 0.
III. Число не может быть больше своего модуля: а < а
IV. Модуль суммы действительных чисел не больше суммы их
модулей:
|а + b\ < |а| + |6|.
V. Модуль разности двух чисел не меньше разности модулей
этих чисел:
VI. Модуль произведения нескольких чисел равен произведе-
нию их модулей:
|а • &| = |а| • |Ь
VII. Модуль целой степени какого-либо числа равен степени
его модуля:
|ал| = |я |п.
VIII. Модуль частного двух чисел равен частному их модулей:
Ь * 0.
5. Системы и совокупности двух предложений. Системой двух пред-
ложений А(х) и В(х) называется предложение, которое записы-
вается с помощью фигурной скобки (здесь А(х), В(х) — уравне-
ния или неравенства с одной переменной):
А(х),
В(х).
Число х0 называют решением системы, если оно является ре-
шением каждого из предложений А(х) и В(х).
Совокупностью (объединением) двух предложений А(х) и
В(х) называется предложение «А(х) или В(х)», которое записы-
вается с помощью квадратной скобки:
[ А(х),
LB(x).
44
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Число х0 называется решением совокупности, если х0 явля-
ется решением хотя бы одного из предложений А(х) или В(х).
Например, переход от уравнения (ах + b)(cx + d) = 0 к сово-
купности уравнений выражается соотношением:
((ах + &)(сх + d) — 0)
ах + b = 0,
Lex + d = 0,
т. е. ах + Ъ = 0 или сх + d = 0.
6. Уравнения, содержащие переменную под знаком модуля. При реше-
нии уравнений, содержащих переменную под знаком модуля, бу-
дем руководствоваться определением модуля:
если х > 0,
если х = 0,
если х < 0.
♦ ПРИМЕР 1
Решить уравнение |х| = 3.
РЕШЕНИЕ. По определению модуля:
Решим это уравнение графическим способом. Построим гра-
фики функций у = |х| и у = 3 (рис. 15). Для построения графика
функции у = |х| строим прямые у = хиу = -х. График функции
у = |х| есть сплошная линия, симметричная относительно оси ор-
динат и расположенная выше оси абсцисс (|х| — число положи-
тельное, следовательно, график расположен выше оси абсцисс).
При х > 0 график совпадает с прямой у — х, а при х < 0 — с пря-
мой у = -х. Далее строим прямую у ~ 3. График функции у = х
пересекается с прямой у = 3 в двух точках и М2 с абсциссами
х = Зи х = - 3, которые являются корнями уравнения |х| = 3.
Ук
Рис. 15
Рис. 16
45
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕР 2
Решить уравнение |х - 2| = 4.
РЕШЕНИЕ. По определению модуля:
Графическое решение этого уравнения дано на рисунке 16.
♦ ПРИМЕРЗ
Решить уравнение |6 - 2х| = Зх + 1.
РЕШЕНИЕ. Правая часть уравнения положительна или равна нулю:
Зх + 1 > 0. Данное уравнение представляет собой совокупность
двух смешанных систем:
(|6-2х| = 3х + 1)
6 — 2х = Зх + 1,
Зх + 1 > 0;
6 - 2х = -(Зх + 1),
Зх + 1 > 0
Г х = 1,
[решения нет.
Число х = - 7 не является корнем уравнения, так как - 7 < -1/3.
Следовательно, уравнение имеет решение х = 1.
При графическом решении этого уравнения (рис. 17) графики
у — |6 - 2х| и у = Зх + 1 пересекаются в единственной точке с абс-
циссой х = 1, которая и является корнем данного уравнения.
♦ ПРИМЕР4
Решить уравнение |4 - 2х| = х — 5.
РЕШЕНИЕ. Имеем:
(|4- 2х| = х- 5)
4 - 2х = х - 5,
х - 5 > 0;
4 - 2х = —(х - 5),
х - 5 > 0
решения нет
решения нет.
46
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Рис. 17
Рис. 18
Графическое представление решения этого уравнения (рис. 18)
показывает, что график уравнения у = |4 - 2х| не имеет точек пе-
ресечения с графиком у — х - 5, следовательно, уравнение не име-
ет решений.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение уравнения с одной переменной.
2. Как записывается в общем виде линейное уравнение?
3. Какие уравнения называются равносильными?
4. Что называется корнем уравнения?
5. Сформулируйте теоремы, на основании которых решаются линейные
уравнения.
6. Какой вид имеют линейные уравнения, имеющие одно решение, не
имеющие решения и имеющие бесконечное множество решений?
7. Какие уравнения называются дробно-рациональными?
8. Как выполняется графическое решение линейных уравнений?
9. Как графически изображается линейное уравнение, имеющее одно реше-
ние, не имеющее решения и имеющее бесконечное множество решений?
10. Дайте определение модуля действительного числа.
11. Перечислите основные свойства модуля действительного числа.
12. Что называется системой двух уравнений с одной переменной?
13. Что называется совокупностью двух уравнений с одной переменной?
14. В чем состоит различие между системой и совокупностью двух уравне-
ний с одной переменной?
15. Как выполняется решение линейных уравнений, содержащих перемен-
ную под знаком модуля?
16. Как графически выполняется решение линейных уравнений, содержа-
щих переменную под знаком модуля?
47
ЧАСТЬ I. Алгебра и начала анализа
§ 6. Линейные неравенства
1. Неравенства и их основные свойства. Два алгебраических выраже-
ния или два числа, соединенные знаком больше или меньше, на-
зываются неравенствами.
Неравенства могут быть как числовыми: 5 > 3; -8 < — 3;
-7 < 5, так и алгебраическими: а > Ь; а2 > 0; а + Ъ < с + d.
Любое положительное число больше нуля: 7 > 0; 3/4 > 0.
Любое отрицательное число меньше нуля: -6 < 0; -5/7 < 0.
Любое положительное число больше любого отрицательного
числа: 8 > -3; - 7 < 2; 3 > - 3.
Из двух положительных чисел большим считается то, абсо-
лютная величина которого больше: 13 > 7; 4 < 8.
Из двух отрицательных чисел большим считается то, абсо-
лютная величина которого меньше: -5 > -9, так как |-5| < |— 9|;
-6 < -1, так как |-6| > |—1|.
Решением неравенства называется значение переменной,
при котором неравенство истинно (обращается в верное числовое
неравенство). Решить неравенство — значит найти множество его
решений.
Неравенства называются равносильными, если множества их
решений равны.
Основные свойства неравенств
I. Если к обеим частям неравенства прибавить (или отнять) од-
но и то же число, то получится неравенство, равносильное дан-
ному:
если а > Ъ и т — любое число, то а + т > b + т.
II. Если обе части неравенства умножить или разделить на од-
но и то же положительное число, то получится неравенство,
равносильное данному:
если а > b и т > 0, то ат > Ът.
III. Если обе части неравенства умножить или разделить на од-
но и то же отрицательное число, то знак неравенства изменит-
ся на противоположный:
если а > Ъ и т < 0, то ат < Ът.
IV. Если а < b и Ъ < с, то а < с.
48
ГЛАВА I. Линейные и квадратные уравнения и неравенства
V. Правило сложения неравенств:
>Ъ
>d
а + с > b + d,
т. е. неравенства одного смысла можно почленно складывать*.
Например:
1) -8 <-4
+ 2> 1
-6 <-3;
-4
-2
VI. Два неравенства противоположного смысла можно почлен-
но вычитать, в результате получится неравенство одного
смысла с уменьшаемым:
а - с > b - d.
VII. Правило умножения неравенств:
О < а < Ъ
О < с < d
ас < bd.
В частности, если 0 < а < Ъ, то ап < Ьп для любого натурального
числа п > 0.
2. Линейные неравенства. Линейным неравенством называется
неравенство вида ах + Ъ > 0 (или ах + Ъ < 0), где анЬ — действи-
тельные числа.
♦ ПРИМЕРЫ 1—4
Решить неравенство.
1. х + 4 > 2 - Зх.
РЕШЕНИЕ. Имеем:
(х + 4 > 2 - Зх) <=> (4х > -2) (х > —0,5), —0,5 < х < +оо.
При сложении двух неравенств противоположного смысла в ре-
зультате может получиться неравенство любого смысла и даже равенст-
во, поэтому для такого сложения нельзя дать общего правила.
49
ЧАСТЬ I. Алгебра и начала анализа
5х - 2
6
РЕШЕНИЕ. Умножив обе части неравенства почленно на 12, полу-
чим
(4(4 - Зх) < 3(2х - 1) - 2(5х - 2)) (-8х < -15)
15
8
X < +оо.
3. (2х - I)2 - 8х < (3 - 2х)2.
РЕШЕНИЕ. Получаем
((2х - I)2 - 8х < (3 - 2х)2) <=>
<=> (4х2 - 4х + 1-8х<9 - 12х + 4х2) <=> (0 < О • х < 8).
Данному неравенству удовлетворяет любое значение х,
— оо < х < +оо.
4. (х - 2)2 - 2х + 10 < (3 - х)2.
РЕШЕНИЕ. Имеем
((х - 2)2 - 2х + 10) < (3 - х)2)
4 - 2х + 10 < 9 - 6х + х2) <=> (О < 0 • х < -5).
Данное неравенство решений не имеет.
3. Системы и совокупности линейных неравенств с одной переменной.
Неравенства (х) < 0, f2 (х) < 0, записанные в виде
fj(x) < О, (а)
/2(х) < О, (р)
образуют систему двух неравенств с одним неизвестным х.
Неравенства (а) и (р) могут содержать различные знаки неравен-
ств >, <, <, >. Система может содержать большее количество не-
равенств: три, четыре, ....
Число х является решением системы (а) — (р), если х удов-
летворяет каждому неравенству системы.
Чтобы найти решение системы неравенств, чаще всего посту-
пают следующим образом.
| I. Находят решение каждого неравенства системы.
| II. Изображают найденные решения на числовой прямой.
III. Используя построенное изображение и определение поня-
тия решения системы, находят множество ее решений.
50
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Множество решений системы может иметь различную струк-
туру : содержать одну или несколько изолированных точек; яв-
ляться промежутком числовой прямой; быть объединением изо-
лированных точек и промежутков. Решение системы может не
содержать ни одной точки; в этом случае говорят, что система ре-
шений не имеет. Система неравенств не имеет решений, если хо-
тя бы одно из неравенств системы не имеет решений.
Для решения системы линейных неравенств рекомендуется
привести ее к стандартному виду, т. е. записать одним из сле-
дующих трех способов:
Знаки неравенств в системах могут быть различными.
♦ ПРИМЕРЫ
Решить систему неравенств [1—4].
1. !бх + 2 > Зх - 4,
2х + 1 >4х - 7.
РЕШЕНИЕ. -
6х + 2 > Зх — 4,
2х + 1 > 4х - 7
О,
<=> —2 < х < 4.
РЕШЕНИЕ.
51
ЧАСТЬ I. Алгебра и начала анализа
3. 2(2х - 1) > 3(1 4- х),
РЕШЕНИЕ.
(2(2х - 1) > 3(1 4-х),
14х - 2 > 3 + Зх,
14 - 2х < Зх - 16
<=> х > 5, 5 < х < 4-00.
РЕШЕНИЕ.
Зх - 8 < 2х - 10,
2 - 5х > 6 - 6х
система не имеет решения.
Неравенства /\(х) < О, f2(x) < О, записанные в виде
Л(х)< О,
/2(х) < О,
(а)
(?)
образуют совокупность двух неравенств с одним неизвест-
ным х. Так же как и система неравенств, совокупность нера-
венств (а) и (р) может содержать различные знаки неравенств >,
<, >, <. Совокупность может содержать большее количество не-
равенств: три, четыре, ....
Число х является решением совокупности неравенств (а) и
(р), если х удовлетворяет хотя бы одному неравенству сово-
купности.
Чтобы найти решение совокупности неравенств, чаще всего
поступают следующим образом.
| I. Находят решение каждого неравенства совокупности.
| II. Изображают найденные решения на числовой прямой.
III. Используя построенное изображение и определение поня-
тия решения совокупности, находят множество решений сово-
купности.
Множество решений совокупности может содержать одну или
несколько изолированных точек; являться промежутком число-
вой прямой; быть объединением изолированных точек и проме-
52
ГЛАВА I. Линейные и квадратные уравнения и неравенства
жутков. Решение совокупности может не содержать ни одной
точки; в этом случае говорят, что совокупность не имеет реше-
ний. Совокупность неравенств не имеет решений, если каждое
неравенство совокупности не имеет решений.
♦ ПРИМЕР 1
Решить неравенство
(2х + 1)(3х - 6) > 0.
РЕШЕНИЕ. Решение сводится к решению совокупности систем ли-
нейных неравенств:
(2х + 1)(3х - 6) > 0
0
о
о
о
I
— « или 2
♦ ПРИМЕРЫ
Решить совокупность неравенств [1, 2].
1.
РЕШЕНИЕ.
2. Г4 - Зх < 5(2 - х),
1.2 - Зх > х - 18.
РЕШЕНИЕ.
Г4 - Зх < 5(2 - х),
|_2 - Зх > х - 18
-4х >16,
4х > 4
-ОО < X < -4 ИЛИ 1 < X < 4-00.
4 - Зх < 10 - 5х,
_2 — Зх > х - 18
3,
-оо < х < 3.
Замечание. Неравенство х < 5 является решением второго не-
равенства совокупности.
53
ЧАСТЬ I. Алгебра и начала анализа
4. Дробно-рациональные неравенства. Дробно-рациональным нера-
венством с одной переменной х называется неравенство, которое
с помощью равносильных преобразований можно привести к виду*
где av а0, bv b0 и х — действительные числа (знак неравенства
может быть любым другим: <, <, >).
♦ ПРИМЕРЫ
Решить неравенство [1 — 3].
0.
РЕШЕНИЕ. Решение этого нелинейного неравенства с одной пере-
менной сводится к решению совокупности двух систем линейных
неравенств с одной переменной, так как дробь положительна в
том случае, если ее числитель и знаменатель имеют значения од-
ного знака. Поэтому
’ 2х - 3 > 0,
11 Зх - 6 > 0;
I 2х - 3 < 0,
! Зх - 6 < 0
-оо < х < - или 2 < X < +ОО.
2. ——- < 0.
2х - 3
РЕШЕНИЕ. Дробь отрицательна в том случае, если ее числитель и
знаменатель имеют значения разных знаков. Поэтому:
х - 4 >0,
2х - 3 < 0;
I х - 4 < 0,
I 2х - 3 > 0
решения нет,
* Рассматривающиеся в данном разделе неравенства являются част-
ным случаем дробно-рациональных неравенств, числители и знаменате-
ли которых представляют собой многочлены более высоких степеней от-
носительно переменной х.
54
ГЛАВА I. Линейные и квадратные уравнения и неравенства
РЕШЕНИЕ.
3 — 6х
2х + 1
3 — 6х . е- гЛ _ /3 — 6х + 10х + 5
---------F 5 > 0 <=> ------------------
2х + 1 / \ 2х + 1
5. Простейшие неравенства, содержащие переменную под знаком моду-
ля. При решении неравенств, содержащих переменную под зна-
ком модуля, необходимо использовать определение модуля
х > О,
х < О
при
при
(1-18)
и равносильные преобразования
(1.19)
Неравенства (1.19) графически представлены на рисунке 19.
На рисунке 20 графически представлены равносильные преобра-
зования
(|х| > а)
(х < -а или х > а).
(1.20)
♦ ПРИМЕР 1
Решить неравенство 1) |х - &| < а; 2) |х - > а.
Рис. 19
Рис. 20
55
ЧАСТЬ I. Алгебра и начала анализа
Рис. 21
Рис. 22
РЕШЕНИЕ. 1) По формуле (1.19) имеем
|х - д| < а
Ъ - а < х <Ъ + а.
Графически это решение представлено на рисунке 21.
2) По формуле (1.20) получаем:
(|х - д| > а)
(х <Ь — а или х > Ь + а).
Данное решение графически представлено на рисунке 22.
♦ ПРИМЕР 2
Решить неравенство: 1) |х| < 3; 2) |х — 3| > 2; 3) |3х + 8| < 4.
РЕШЕНИЕ. 1) По формуле (1.19) имеем
2) По формуле (1.20)
х < 1 или х > 5.
3) По формуле (1.19) имеем
Зх>-12,
Зх <-4
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется неравенством?
2. Какие выражения называются алгебраическими и какие числовыми не-
равенствами?
3. Что называется решением неравенства?
4. Какие неравенства называются равносильными?
5. Перечислите основные свойства неравенств.
56
ГЛАВА I. Линейные и квадратные уравнения и неравенства
6. Какие неравенства называются линейными?
7. Какие неравенства не имеют решения?
8. Какому неравенству удовлетворяет любое число?
9. В каких случаях решение неравенства сводится к решению совокупнос-
ти неравенств?
10. Как записываются решения неравенств вида |х| < а и |х| > о?
§ 7. Системы линейных уравнений
1. Решение системы двух линейных уравнений с двумя переменными.
Решением системы двух линейных уравнений с двумя перемен-
ными
+ Ь1У = ср
будем называть пару чисел (х0; у0), которая каждое уравнение
этой системы обращает в верное числовое равенство.
Приведем различные способы решения подобных систем на
примере следующей системы:
I 4х - 3z/ = -1,
I Зх + 4г/ = 18.
I. Способ подстановки. Этот способ заключается в том, что
из одного уравнения данной системы выражают какую-либо
из переменных через другую переменную и найденное для этой
переменной выражение подставляют в другое уравнение сис-
темы, в результате чего получают уравнение с одной перемен-
ной.
+4у-18
3-(3 - 1)
4
II. Способ алгебраического сложения. Этот способ состоит в
том, что все члены каждого из уравнений умножают на соответ-
57
ЧАСТЬ I. Алгебра и начала анализа
ственно подобранные множители так, чтобы коэффициенты при
одной и той же переменной в обоих уравнениях оказались проти-
воположными числами, а затем уравнения почленно складыва-
ют, в результате чего получают уравнение, содержащее только
одну переменную.
12х - 9у = -3,
— 12х- 16у = -72
-75
Ш. Грас]эический способ. Каждое из уравнений системы пред-
ставляет собой линейную функцию, график которой прямая ли-
ния. Если эти прямые имеют общую точку пересечения, то коор-
динаты этой точки и будут корнями решения системы.
18 - Зх
3
Рис. 23
Прямая определяется двумя точками. Для построения первой
прямой (рис. 23) возьмем точки (-1; -1) и (5; 7), для построения
второй — точки (-2; 6) и (6; 0). Чтобы упростить построение гра-
фиков, следует подбирать такие точки, в которых обеим перемен-
ным соответствуют целые числа. Построенные прямые пересе-
каются в точке с координатами (2; 3) — эти координаты являют-
ся корнями данной системы х = 2, у = 3.
Графический способ решения
системы по сравнению с первыми
двумя способами требует значи-
тельно большего времени, поэтому
для решения систем уравнений он
применяется редко. Преимущест-
вом графического способа реше-
ния системы является его нагляд-
ность. Необходимо отметить, что
некоторые уравнения можно ре-
шить только графическим спосо-
бом.
58
ГЛАВА I. Линейные и квадратные уравнения и неравенства
2. Однородные и неоднородные, совместные и несовместные системы
двух линейных уравнений с двумя переменными. Если в системе двух
линейных уравнений
оба свободных члена сг и с2 равны нулю, то система называется
однородной. Например, система
Зх - 2у = О,
17х + 5у = О
однородная, ее решение (0; 0).
Графический способ решения этой системы (рис. 24) также по-
казывает, что прямые Зх-2# = 0и7х + 51/ = 0 пересекаются в на-
чале координат, т. е. х = 0, у = 0.
Если хотя бы один из свободных членов сх или с2 не равен ну-
лю, то система называется неоднородной. Например, система
| х + 2у = 10,
Зх - 4у = 0
неоднородная, ее решение (4; 3). Рисунок 25 иллюстрирует гра-
фический способ решения этой системы.
Система линейных уравнений, имеющая одно решение, назы-
вается совместной. Любая однородная система совместна.
Система линейных уравнений, не имеющая ни одного реше-
ния, называется несовместной. Система
не имеет решения, так как
рисунке 26 прямые х + у =
3 * 0, т. е. система несовместна. На
3 и х 4- у = 0 параллельны, следова-
Рис. 24
Рис. 25
59
ЧАСТЬ I. Алгебра и начала анализа
Рис. 26
Рис. 27
тельно, не имеют общих точек, и данная система уравнений не
имеет решения.
Система двух линейных уравнений с двумя переменными мо-
жет иметь бесконечное множество решений. Например, система
Зх - у = 5,
6х - 2у = 10
имеет бесконечное множество решений, так как любое решение
уравнения Зх - у = 5 будет и решением уравнения 6х - 2у = 10.
На рисунке 27 прямые Зх - у = 5 и 6х - 2у = 10 совпадают, т. е.
каждая точка первой прямой одновременно является и точкой
второй прямой, следовательно, система имеет бесконечное мно-
жество решений.
Таким образом, при решении системы линейных уравнений
необходимо выяснить, является ли она совместной, и если она
совместна, найти ее решение.
3. Решение системы двух линейных уравнений с двумя переменными в
общем виде. Решим систему двух линейных уравнений
(1.21)
в общем виде.
Исключим переменную у. Для этого умножим обе части перво-
го уравнения системы на д2, а второго — на (-fex) и, сложив соот-
ветствующие уравнения почленно, получим:
60
ГЛАВА I. Линейные и квадратные уравнения и неравенства
В результате пришли к уравнению с одной переменной х:
(а1^2 ~ а2^1)Х ~ ^2с1 ~ ^1С2
(1.22)
Чтобы исключить переменную х, умножим обе части первого
уравнения (1.21) на (~а2), а второго — на av Сложив их, полу-
чим:
ц^о2х а2Ь^у a2с j
6Z^6ZgX “Г” а^Ь2у
^1^2^ — ^2^1У = ^1С2 — а2^1*
Таким образом приходим к уравнению с одной переменной у:
(^1^2 — ^2^1^У ^1^2 ~~ ^2^1* (1.23)
Из уравнений (1.22) и (1.23) образуем систему
(^1^2 _ й2&1)х = ^2С1 “ &1С2»
(aYb2 - a2bjy = агс2 - а2сг (1.24)
Если arb2 - а2Ьг 0, то система (1.24) имеет единственное ре-
шение:
^2С1 ^1^2 а1С2 а2С1
х =------------, у =------------
arb2 - a2br ахЬ2 - а2Ьг
(1.25)
Решение системы (1.24) является также и решением системы
(1.21), что легко проверить подстановкой найденных значений
(1.25) для х и у в систему (1.21).
Выражение aYb2 - а2Ьх называется определителем второго
порядка и обозначается символом
b
(1.26)
Определитель (1.26), составленный из коэффициентов при пе-
ременных данной системы, называется определителем систе-
мы и обозначается знаком Д:
(1.27)
Числа av bv а2, Ъ2 называются элементами определителя,
причем элементы at и Ь2 образуют главную диагональ, а элемен-
ты а2 и t»i — побочную диагональ. Таким образом, определитель
второго порядка равен произведению элементов главной диагона-
61
ЧАСТЬ I. Алгебра и начала анализа
ли минус произведение элементов побочной диагонали, как это
показано стрелками:
Аналогично составляются определители Дг и Д„, которые со-
ставляются из определителя Д заменой столбца коэффициентов
при соответствующей переменной столбцом свободных членов:
Система двух линейных уравнений с двумя переменными
(1.21) совместна при условии, что определитель системы (1.27)
имеет единственное решение, которое находится по формулам
ci
с2 ^2
а\ bi
а2 Ь2
а1 Ь1
а2 Ь2
(1.28)
Формулы (1.28) называются формулами Крамера*.
Если определитель системы Д = 0, то система является либо
несовместной (когда Д„ # О, Д„ 0), либо неопределенной (когда
А = Д„ = 0). В последнем случае система сводится к одному урав-
л у
нению, а другое является следствием этого уравнения.
Условие несовместности можно записать в виде
gi _ £i
а2 Ь2 с2 *
а условие неопределенности — в виде
Ь2
* Габриэль Крамер [Cramer] (1704—1752) — швейцарский матема-
тик. Крамер установил правила решения системы п линейных уравне-
ний с п переменными (правило Крамера) и заложил основы теории опре-
делителей.
62
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Приведем примеры решения системы двух линейных уравне-
ний с помощью определителей.
♦ ПРИМЕРЫ
Решить систему уравнений [1—3].
lJ4x- 3j/ = -l,
I Зх + 4у = 18.
РЕШЕНИЕ. Так как Д =
= 4*4- 3 • (-3) = 25, система сов-
местна и имеет единственное решение, которое находится по фор-
мулам (1.28):
18
3 18
25
= 3
2.
Зх - 2у = 1,
6х - 4у = 2.
РЕШЕНИЕ. Находим
= 3(-4) - 6(-2) = О.
Свободные члены пропорциональны коэффициентам при пере-
3 -2
менных: х = —т
6 -4
Поэтому данная система равносильна одно-
му из уравнений, например первому, и следовательно, имеет бес-
конечное множество решений.
РЕШЕНИЕ. Определим Д =
4 _6 “х
Здесь свободные члены не пропорциональны коэффициентам
2 —3 2
при переменных -
~ ; поэтому данная система несовмест-
О
на, т. е. не имеет решения.
63
ЧАСТЬ I. Алгебра и начала анализа
4. Решение систем трех линейных уравнений с тремя переменными.
Рассмотрим систему трех линейных уравнений с тремя перемен-
ными
(1.29)
Определителем третьего порядка, составленным из чисел
а1» ^1» с1» а2» ^2» с2» аз» ^з» сз» называется число, определяемое ра-
венством
ai
а2 ^2
а3 &3
(1.30)
Формула (1.30) представляет собой разложение определителя
третьего порядка по элементам первой строки.
Система (1.29) имеет единственное решение при условии, что
определитель системы Д # 0. Это решение находится по форму-
лам Крамера
(1.31)
где
Если же Д = 0, то система является либо неопределенной, либо
несовместной. В том случае, если система однородная, т. е. имеет
вид
' агх + Ъ2у + срг = 0,
а2х + b2y + с2г = 0,
а3х + b3y + c3z = 0,
и Д 0, то она имеет единственное решение: х = 0, у = 0,
2 = 0.
Если определитель однородной системы Д = 0, то система сво-
дится либо к двум независимым уравнениям (третье является их
следствием), либо к одному (следствиями которого являются ос-
64
ГЛАВА I. Линейные и квадратные уравнения и неравенства
тальные два). В обоих случаях однородная система имеет беско-
нечное множество решений.
♦ ПРИМЕР
Решить систему уравнений
7х — Зу + 5г = 32,
5х + 2у + z = 11,
2х - у + 3z = 14.
РЕШЕНИЕ. Имеем:
= 7(6 + 1) + 3(15 - 2) + 5(-5 - 4) = 49 + 39 -45 = 43;
32
11
14
14
5
9
11
14
= 129.
По формулам (1.28) получаем:
= 129 =
43
5. Решение систем трех линейных уравнений с тремя переменными ме-
тодом Гаусса. Методом Гаусса является способ решения системы
линейных уравнений путем последовательного исключения пере-
менных и сведения ее к треугольной системе уравнений.
Подробно и последовательно изложим решение системы трех
уравнений с тремя переменными методом Гаусса на примере сис-
темы уравнений (а — у):
2х - 4у + 3z == 1,
< Зх - у + 5г = 2,
х - 2у + 4г = 3.
(а)
(₽)
(у)
3 - 9664
65
ЧАСТЬ I. Алгебра и начала анализа
1) Из данной системы получим уравнение, не содержащее х.
Умножив уравнение (а) на 3 и (р) на (-2), получим:
2х - 4 г/ + 3z = 1 |«3
6х - 12г/ + 9г = 3; (6)
Зх- у + 5г = 2 |-(-2)
-6х + 2у — 10а = -4. (е)
2) Сложим полученные уравнения (5) и (е):
+ 6х — 12г/ + 9z = 3
-6х + 2у - Юг = -4
-Юг/ - z = ~l.
3) Из исходной системы получим уравнение, не содержащее х
и у. Уравнение (у) умножим на (-2):
х - 2у + 4г = 3 | • (-2)
-2х + 4г/ - 8z = -6 (О
4) Сложим уравнения (а) и (£):
5) Получена треугольная система
2х - 4г/ + Зг = 1,
-Юг/- г = -1,
01)
(А)
(к)
6) Из (к) находим 2*. 2—1.
7) Из (О) находим г/: - Юг/ - 1 = -1; у = 0.
8) Из (т|) находим х: 2х - 0 + 3 = 1; х = — 1.
Ответ: х = -1, у = 0, г = 1.
♦ ПРИМЕР
Решить систему уравнений
-2х + 5г/ - 6г = -8,
' х + 7г/ - 5г = -9,
4х + 2г/ - г = -12.
66
ГЛАВА I. Линейные и квадратные уравнения и неравенства
РЕШЕНИЕ. Имеем:
1) х + 7у- 5г = - 9 | -2
2х 4- 14г/ - Юг = -18;
2) -2х + 5г/ - 6г = - 8
+ 2х + 14у- 10z = -18
19у - 16г = -26.
3) х+ Чу- 5г = -9 |*(-4)
—4х - 28г/ + 20г = 36.
4) -4х - 28г/ + 20г = 36
+ 4х + 2у - г = -12
-26у + 19г = 24.
(X)
(Ю
Таким образом, получили два уравнения (X) и (ц), содержащие
у и г. Умножим (X) на 26:
19у - 16г = - 26 -26
494г/ - 416г = -676, (v)
а (ц) на 19:
-26у + 19г = 24 |-19
-494j/ + 361г = 456.
Сложив (v) И (5)» получим
494г/ - 416г = -676
+ -494{/ + 361г = 456
-55г = -220.
5)
лл 220 л
6) г = -гг- = 4.
эЬ
-2х + 5г/ - 6г = - 8,
Юг/ - 16г = - 26,
-55г = -220.
7) 19г/ - 16 • 4 = -26 => у = 2.
8) -2х + 5 • 2 - 6 • 4 = -8 => х = -3.
Ответ: х = -3, у = 2, г = 4.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие уравнения с двумя переменными называются линейными?
2. Как решаются системы двух линейных уравнений с двумя переменными
способами подстановки, алгебраического сложения и графическим?
67
ЧАСТЬ I. Алгебра и начала анализа
3. Какие системы двух линейных уравнений с двумя переменными назы-
ваются однородными и неоднородными?
4. Какие системы двух линейных уравнений с двумя переменными назы-
ваются совместными и несовместными? Приведите примеры.
5. Как графически изображаются решения совместной и несовместной
систем двух линейных уравнений с двумя переменными?
6. Как графически изображается решение системы однородных линейных
уравнений с двумя переменными?
7. Как графически изображается решение системы двух линейных урав-
нений с двумя переменными, имеющей бесконечное множество реше-
ний?
8. Как решается в общем виде система двух линейных уравнений с двумя
переменными?
9. Как составляется определитель второго порядка и каким знаком он обо-
значается?
10. Как составляются определители Ду и Л?
—*
11. Как записываются формулы Крамера для решения системы двух линей-
ных уравнений с помощью определителей?
12. При каком значении определителя Д система двух линейных уравнений
с двумя переменными имеет одно решение?
13. Как записываются условия несовместности и неопределенности реше-
ния системы двух линейных уравнений с двумя переменными?
14. Как записываются формулы Крамера для решения системы трех линей-
ных уравнений стремя переменными?
15. При каком значении определителя Д система трех линейных уравнений
стремя переменными имеет бесконечное множество решений?
16. Как решается система трех линейных уравнений с тремя переменными
методом Гаусса?
§ 8. Квадратные уравнения
1. Квадратное уравнение общего вида ах2 + Ьх + с = 0. Уравнение, в ко-
тором левая часть является многочленом второй степени относи-
тельно переменного х, а правая часть равна нулю, называется
квадратным уравнением.
Уравнение
ах2 + Ьх + с = 0, а^О
называется уравнением общего вида.
(1.32)
68
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Напомним вывод формулы корней квадратного уравнения об-
щего вида:
Ь Ь2 _ Ь2 с \ // b \2 _ Ь2 — 4ас \
2аХ + W ” W “ а ) + 2а ) ~ 4а2 )
Jb2 — 4ас
Jb2 — 4ас
2а
(1.33)
По формуле (1.33) легко вычисляются корни квадратного
уравнения (1.32).
♦ ПРИМЕРЫ
Решить уравнение [1—2].
1. Зх2 - 8х + 4 = О.
РЕШЕНИЕ. По формуле (1.33) имеем
= 8 ± 7в2 - 4 • 3 • 4 = 8 ± J16 = 8 ± 4 .
х1.2 2’3 6 6 *
2. х2 - 5х + 6 = О.
РЕШЕНИЕ. По формуле (1.32) находим
_ 5 ± 725-4-6 = 5 ± 1 .
х1,2 2 2 ;
2. Исследование корней по дискриминанту. Дискриминантом квад-
ратного уравнения называется подкоренное выражение в фор-
муле (1.33):
D = Ь2 - 4 ас.
В зависимости от величины дискриминанта D рассмотрим три
случая.
69
ЧАСТЬ I. Алгебра и начала анализа
I. D > О. В этом случае оба корня — числа действительные и
разные.
♦ ПРИМЕР
Решить уравнение 5х2 + 7х + 2 = 0.
РЕШЕНИЕ. Имеем:
Р = 7х2 - 4 • 5 • 2 = 9 0;
= -7 ± Л2- 4 • 5 • 2 = -7 ± 3
Х1.2 2-5 10 ’
-7-3 . -7 + 3 _ 2
Х1 ю 1,х2 ю 5’
Корни Xj и х2 действительные и разные.
II. D = О. В этом случае х, 2 = —b(2.a. Оба корня действитель-
ные и равные.
♦ ПРИМЕР
Решить уравнение 9х2 + 24х + 16 = 0.
РЕШЕНИЕ. Находим:
О = 242 - 4 • 9 • 16 = 576 - 576 = О; х, , = =-1.
2 • У
Уравнение имеет два равных корня.
III. D < О. В этом случае подкоренное выражение отрицатель-
но и уравнение действительных корней не имеет. Оба корня —
сопряженные комплексные числа.
♦ ПРИМЕР
Решить уравнение х2 - 4х + 13 = 0.
РЕШЕНИЕ. Получаем:
D = 42 - 4 • 13 = 16 - 52 = -36 < 0;
_ 4 ± 7^6 _ 4 ±6/ _
Х1 2 2 2 Z “Л1'
Корни — сопряженные комплексные.
3. Приведенное квадратное уравнение. Если все члены уравнения
(1.32) разделить на а (а * 0), получим
70
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Положив - = р и - = д, придем к уравнению
х2 + рх + q = О.
(1,34)
Уравнение (1.34) называется приведенным в отличие от урав-
нения общего вида (1.32), которое называется неприведенным.
Решим уравнение (1.34) по формуле (1.33):
Таким образом, получена формула для решения приведенного
квадратного уравнения:
(1.35)
♦ ПРИМЕР
Решить уравнение: 1) х2 - 5х + 6 = О, 2) х2 + 6х + 8 = О.
РЕШЕНИЕ. По формуле (1.35)
2) Хъ 2 = -3 ± 79-8 = — 3 ± 1;
х1 - -3 - 1 = -4, х9 = -3 + 1 = -2.
А £л
4. Решение квадратного уравнения (1.32) для случая, когда коэффици-
ент b четное число (Ь - 2к). Уравнение (1.32) в этом случае принима-
ет вид
ах2 + 2kx + с = 0.
Тогда по формуле (1.33)
J4fe2 — 4ас _ -2fe ± 74(fe2 — ас)
2а 2а
(1.36)
-2fe + 2лД2 — ас
2а
71
ЧАСТЬ I. Алгебра и начала анализа
Получили формулу для случая четного b = 2k:
(1.37)
использование формулы (1.37) упрощает вычисления.
♦ ПРИМЕР
Решить уравнение
1) Зх2 - 8х + 4 = 0; 2) 5х2 - 26х - 24 = 0.
РЕШЕНИЕ. По формуле (1.37)
= 13 ± 7169 + 5-24 = 13 ± 7289 = 13 ± 17 .
XL 2 5 5 5 ’
13 - 17 = 4 = 13 + 17
5 5 * Х2 5
5. Неполные квадратные уравнения. Квадратное уравнение (1.32) на-
зывается неполным, если один из коэффициентов b или с или оба
одновременно равны нулю. Если М 0 и с 0, уравнение (1.32)
называется полным.
Неполные квадратные уравнения могут быть трех видов:
ах2 = 0, ах2 + с = 0, ах2 + Ъх = 0.
I. Уравнение ах2 = 0 удовлетворяется только при х = 0. Таким
образом, хх = х2 = 0.
II. Уравнение ах2 + с = 0 равносильно уравнению х2 = -сfa
(а 0). Если одновременно а > 0, с > 0 или а < 0, с < 0, уравне-
ние действительных корней не имеет, так как х2 не может быть
отрицательным числом. В этом случае уравнение ах2 + с = 0
имеет два мнимых корня:
Если а и с имеют разные знаки, то -с/а будет положительным
числом, и в этом случае уравнение имеет два действительных
корня.
72
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Например, уравнение 2х2 + 8 = 0 имеет два мнимых корня:
Xj = -2i, х2 = уравнение х2 = 49 имеет два действительных
корня: Xj = -7, х2 = 7.
Ш.Уравнение вида ах2 + Ъх = 0 равносильно уравнению х(ах +
+ Ь) = 0. Корни этого уравнения: х2 = 0, х2 = - - (а 5й О). В этом
CL
случае один из корней всегда равен нулю.
Например, уравнение Зх2 - 5х = О имеет два корня: хт = О,
х2 = 5/3; уравнение х2 + 4х = О имеет два корня: хх = 0, х2 = —4.
6. Свойства корней квадратного уравнения (теорема Виета)*.
нтн
Теорема Виета устанавливает связь между корнями и коэффи-
циентами приведенного квадратного уравнения.
ТЕОРЕМА ВИЕТА (ПРЯМАЯ)
Сумма корней приведенного квадратного уравнения равна ко-
эффициенту при неизвестном в первой степени, взятому с об-
ратным знаком, а их произведение равно свободному члену.
Иначе говоря, если хх и х2 — корни уравнения х2 + рх + q = 0, то
Xi + х2 р,
Х1 • Х2 = q.
(1.38)
ДОКАЗАТЕЛЬСТВО
что и требовалось доказать* **.
Франсуа Виет, Вьет [Viete] (1540—1603) — французский матема-
тик. Виет первым ввел в уравнениях обозначения неизвестных и коэф-
фициентов при неизвестных буквами.
** Для полного квадратного уравнения ах2 + Ьх + с = 0 соответствующая
_ . b с
зависимость выражается следующим образом: хг + х2 = — , хг • х = - .
73
ЧАСТЬ I. Алгебра и начала анализа
ОБРАТНАЯ ТЕОРЕМА ВИЕТА
Если сумма каких-либо чисел хг и х2 равна (—р), а их произве-
дение равно д, то эти числа являются корнями квадратного
уравнения х2 + рх + q = О.
♦ ПРИМЕР 1
Найти корни квадратного уравнения х2 - 9х + 20 = 0.
РЕШЕНИЕ. Применяя выражения (1.38) к данному уравнению, по-
лучаем:
Легко установить, что этой системе удовлетворяют только числа
4 и 5, т. е. хх = 4, х2 = 5.
♦ ПРИМЕР 2
Составить квадратное уравнение, корни которого равны:
РЕШЕНИЕ. По обратной теореме Виета имеем:
1) J хх + х2 = -2 + 4 = 2,
j хх • х2 = (-2) • 4 =-8.
Следовательно, заданным корням соответствует квадратное урав-
нение х2 — 2х - 8 = 0;
19 5
Таким образом, х2 + х + s — 0 <=* 24х2 + 38х + 15 = 0.
J.Z о
♦ ПРИМЕРЗ
Найти знаки корней уравнения 15х2 + х - 10 = 0, не решая
его.
РЕШЕНИЕ. Здесь а > 0, Ъ > 0, с < 0, D = Ъ2 - 4ас > 0, так как с < 0.
Следовательно, уравнение имеет два различных корня. По теоре-
те . Ь 1
ме Виета имеем х. +х9 = — = ~ т?»
1 2 а 15
Ю тт
15. Произведе-
ние корней — отрицательное число, следовательно, корни имеют
74
ГЛАВА I. Линейные и квадратные уравнения и неравенства
различные знаки. Сумма корней — отрицательное число, следо-
вательно, больший по модулю корень отрицателен.
♦ ПРИМЕР 4
Найти знаки корней уравнения 5х2 - х - 10 = 0, не решая его.
РЕШЕНИЕ. Здесь с < 0, поэтому D = Ъ2 - 4ас > 0, и уравнение имеет
„ ,1 10
два корня. По теореме Виета получим: х, + х9 = -=, х. • х9 = - .
Произведение корней — величина отрицательная, следовательно,
корни имеют разные знаки. Сумма корней — положительное чис-
ло, поэтому положительным является больший по модулю корень.
7. Разложение квадратного трехчлена на линейные множители. Квад-
ратным трехчленом называется многочлен вида ах2 + Ьх + с
или х2 + рх + q при а 0.
Корнями квадратного трехчлена называются те значения
переменной х, при которых трехчлен обращается в нуль.
Пусть хр х2 — корни квадратного трехчлена ах2 + Ьх + с. В си-
лу теоремы Виета имеем
b
а
следовательно,
ххх2) = а(х(х - Xj) - х2(х - Xj)) =
= а(х - Xj)(x - х2).
Получили формулу разложения квадратного трехчлена на ли-
нейные множители
ах2 + Ьх + с = а(х - хг)(х - х2).
(1.39)
♦ ПРИМЕР 1
Разложить на линейные множители квадратные трехчлены:
1) 9х2 + 6х - 8; 2) -20х2 + 7х + 6.
РЕШЕНИЕ. Имеем:
1) Корнями трехчлена 9х2 + 6х - 8 являются хх = — х » х2 = х,
следовательно, по (1.39)
9х2 + 6х- 8 = 9(х+ |Yx- |)= (Зх + 4)(3х - 2).
75
ЧАСТЬ I. Алгебра и начала анализа
2) Корни трехчлена -20х2 + 7х + 6 равны Xj = -
этому
-20х2 + 7х + 6 = -20 (х + |)(х - =
= (5х + 2)(3 - 4х).
-(5х + 2)(4х - 3) =
♦ ПРИМЕР 2
Сократить дробь: 1)
2х2 - 9х + 10
2х2 + х — 15
4 — За — а2
За2 + 4а + 1
РЕШЕНИЕ. 1) Чтобы сократить дробь, ее числитель и знаменатель не-
обходимо разложить на линейные множители по формуле (1.39):
2х2 — 9х + 10 _ 2(х — 2)(х — 5/2) _ х — 2
2х2 + х — 15 2(х + 3)(х — 5/2) х + 3 ’
2) Аналогично
а2 + За — 4
За2 + 4а + 1
(а + 1)(а - 4)
3(а + 1)(а + 1/3)
4 — а
8. Биквадратные уравнения. Уравнение четвертой степени, содер-
жащее только четные степени переменной, называется биквад-
ратным:
ах4 4- Ьх2 + с = 0.
(1.40)
Для решения биквадратного уравнения применим подстанов-
ку х2 = 2.
♦ ПРИМЕР
Решить уравнение х4 - 13х + 36 = 0.
РЕШЕНИЕ. С помощью соответствующей подстановки получим
уравнение z2 - 13г + 36 = О, корни которого равны гг = 4, г2 = 9.
Таким образом,
9. Уравнения, левая часть которых разлагается на множители. Одним
из основных методов решения алгебраических уравнений являет-
ся метод разложения на множители. Его суть состоит в том, что
в уравнении F(x) = 0 левую часть раскладывают на множители,
76
ГЛАВА I. Линейные и квадратные уравнения и неравенства
т. е. представляют в виде /\(х) • /2(х) = и> следовательно,
заменяют данное уравнение равносильной ему совокупностью.
fi (х) = О,
L/2(x) = 0.
♦ ПРИМЕР
Решить уравнение:
1) х3 - 2х2 - 8х = 0; 2) х3 - 5х2 - х 4- 5 = О.
РЕШЕНИЕ. 1) Левая часть уравнения раскладывается на множите-
ли. Для нахождения корней исходного уравнения приравниваем
каждый сомножитель нулю и решаем совокупность уравнений:
(х3 - 2х2 - 8х = О) <==> (х(х2 - 2х - 8) = 0)
[х = 0,
[ х2 - 2х - 8 = 0
хг = —2, х2 = 0, х3 = 4.
2) Разложим на множители левую часть уравнения и прирав-
няем каждый сомножитель нулю. Решив совокупность уравне-
ний, получим корни исходного уравнения:
(х3 - 5х2 - х + 5 = О) *=> (х2(х — 5) - (х — 5) = 0)
« ((х - 5)(х + 1)(х - 1) = О) <=>
• х-5 = 0,
х + 1 = О,
х - 1 = О
Xj = — 1, х2 = 1, х3 = 5.
10. Двучленные уравнения. Уравнения вида
ах" 4- Ь = 0,
где а, Ь — действительные числа, причем а # 0, называются дву-
членными. В общем случае они имеют п комплексных корней.
В некоторых частных случаях такие уравнения могут быть
решены методом разложения на множители.
♦ ПРИМЕР
Решить уравнение:
1) х4 - 16 = 0; 2) х3 - 8 = 0.
РЕШЕНИЕ.
1) (х4 - 16 = 0)« ((х2 - 4)(х2 + 4) = 0) ~ ((х + 2)(х - 2)(х2 + 4) = О)
х 4- 2 = О,
х - 2 = О,
х2 4- 4 = О
х = -2,
х = 2,
нет решения;
77
ЧАСТЬ I. Алгебра и начала анализа
(х3 - 8 = О) <=> ((х - 2)(х2 + 2х + 4) = О)
рх - 2 = О,
х2 + 2х + 4 = О
А
г х = 2,
I нет решения;
11. Дробно-рациональные уравнения с одной переменной. Канониче-
ским видом дробно-рационального уравнения называется пред-
ставление этого уравнения в виде
п - 1
- =0
’о
(а)
т т-1 1
где коэффициенты ап и Ьт отличны от нуля.
Обычно при решении уравнения (а) его заменяют равносиль-
ной системой
о
п
[ т т-1 1 О
Затем корни первого уравнения подставляют в неравенство и от-
брасывают те из них, которые этому неравенству не удовлетворяют.
♦ ПРИМЕРЫ.
Решить уравнение [1, 2].
1. --------------i------- = 0.
3(3х - 7)
РЕШЕНИЕ.
!) 3(3х - 7) х )
2х(х — 2) — 6(х — 2)(3х — 7) _ q
/3х(3х - 7)
\ 6х(х — 2)(3х — 7)
6х(х - 2)(3х - 7) 5* 0
(Их2 - 61х + 84 = 0)
6х(х - 2)(3х - 7) * 0
11’
6х(х - 2)(3х - 7) * 0
I
11
I
11’
11 » 2
9
3
78
ГЛАВА I. Линейные и квадратные уравнения и неравенства
о х + 4 , х — 4 _ 64
• • I •
х — 4 х + 4 х2 — 16
РЕШЕНИЕ.
(х - 4)(х + 4) О
|х2- 16 = 0,
] (х - 4)(х + 4) О
(х - 4)(х + 4) О.
При х = ±4 обе части исходного уравнения не имеют смысла.
Поэтому корни квадратного уравнения х2 - 16 = О не являются
корнями данного уравнения. Уравнение не имеет решений.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какое уравнение называется квадратным уравнением общего вида и
какое приведенным квадратным уравнением?
2. Выведите формулу корней квадратного уравнения общего вида.
3. Какое выражение называется дискриминантом квадратного уравнения
общего вида?
4. Как по дискриминанту определяется характер уравнения?
5. Какие уравнения называются неполными квадратными?
6. Приведите примеры неполных квадратных уравнений и укажите спосо-
бы их решения.
7. Докажите теорему Виета о свойстве корней квадратного уравнения.
8. Приведите примеры решения квадратного уравнения с использованием
теоремы Виета.
9. Как составляется квадратное уравнение по его корням?
10. Как можно найти знаки корней квадратного уравнения, не решая урав-
нения?
11. Какое выражение называется квадратным трехчленом и как находятся
его корни?
12. По какой формуле квадратный трехчлен раскладывается на линейные
множители?
13. Какое уравнение называется биквадратным и как находятся его корни?
14. Какое уравнение называется двучленным и как находятся его корни?
79
ЧАСТЬ I. Алгебра и начала анализа
§ 9. График квадратной функции.
Графическое решение квадратного уравнения
1. Квадратная функция у = ах2 + Ьх + с и ее частные случаи. Квадратной
функцией (квадратным трехчленом) называется функция вида
у — ах2 4- Ьх 4- с, (1-41)
где а,Ьис действительные числа, а # 0. При Ь = 0 и с = 0 квад-
ратная функция имеет вид
у = ах2. (1-42)
При а = 1 имеем квадратную функцию простейшего вида
у = х2. Построим по точкам график функции у = х2 (рис. 28):
X со 1 -2 -1 0 1 2 СО
9 4 1 0 1 4 9
График функции у = ах2 4- Ьх 4- с (и ее частных случаев) назы-
вается параболой. На рисунке 28 в точке (0; 0) парабола касается
оси Ох. Эта точка называется вершиной параболы, а ось Оу —
осью симметрии параболы.
Функция у = х2 не изменяет своих значений при изменении
знака аргумента: (-х)2 = х2. Такие функции называются четны-
ми. Наименьшее значение функция имеет в точке (0; 0).
Далее построим на одном чертеже (рис. 29) графики функций
у = ах2 при а = 1/2; а = 1; а = 2; а — -1/2.
Рис. 28
Рис. 29
80
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Из построенных графиков видно, что при а > 0 ветви параболы
направлены вверх, а при а < О вниз, при а, большем по абсолют-
ной величине, ветви парабол располагаются ближе к оси симмет-
рии Оу.
Рассмотрим график функции вида у — а(х - т)2, например,
график функции у = 2(х - З)2, и сравним его с графиком функции
у = 2х2 (рис. 30). Вершиной параболы у = 2х2 служит точка (0; 0),
а осью симметрии — прямая х = 0. При смещении графика впра-
во по направлению оси Ох на 3 единицы точка с координатами
(0; 0) переходит в точку с координатами (3; 0), а прямая х = 0 —
в прямую х — 3. Поэтому вершиной параболы у = 2(х - З)2 являет-
ся точка (3; 0), а осью симметрии — прямая х = 3. Так как а = 2 > 0,
ветви параболы направлены вверх.
Из построения графика у = 2(х - З)2 следует, что он получен
переносом графика у = 2х2 по оси Ох вправо на 3 единицы.
График функции у == а(х + т)2 при т > 0 можно получить смеще-
нием графика ах2 влево на расстояние т. Ветви параболы направле-
ны вверх, если а > 0, и вниз, если а < 0. Вершина параболы находит-
ся в точке (-лг; 0), а осью симметрии служит прямая х = -т. На ри-
сунке 31 представлен график функции у = 2(х + 4)2. Построение
здесь выполнено параллельным переносом графика у — 2х2 влево
на 4 единицы.
2. График функции/ = а(х - т)2 + л. График функции у = а(х - т)2 + п
можно получить смещением параболы у = а(х- т)2 по направле-
Рис.30
Рис. 31
81
ЧАСТЬ I. Алгебра и начала анализа
Рис. 32
нию оси симметрии вверх на
расстояние п, если п > 0, и вниз на
расстояние -п, если п < О. Верши-
на этой параболы находится в точке
(т; и), а осью симметрии является
прямая х = т. При а > 0 ветви па-
раболы направлены вверх, а при
а < 0 — вниз.
На рисунке 32 изображен гра-
фик функции у = 2(х - З)2 - 2. Он
получен из графика функции у =
= 2(х - З)2 смещением его вниз на
2 единицы по оси симметрии.
3. График функции у = ах2 + Ьх + с. Выделяя полный квадрат в квад-
ратном трехчлене
у = ах2 + Ьх + с,
получаем
= ах2 + Ьх + с — а(х2 + - х + -
\ а а
Ь2
4а2
Ь2 — 4ас
4а2
( , Ъ \2 Ъ2 — 4ас
= а х + ---------.
V 2а ) 4а
Это выражение имеет вид
у = а(х - т)2 + и,
где т = -Ь/2а, п = ~(b2 — 4ас)/4а.
Отсюда следует, что графиком функции у = ах2 + Ьх + с явля-
ется парабола с вершиной в точке
№ — 4ас
4а
и с осью сим-
метрии х = -
Ъ
2а '
При построении графика параболы у — ах2 + Ьх + с необходи-
мо знать ее характеристические точки: координаты вершины
и точки пересечения параболы с осями координат.
4. Исследование и построение графика квадратной функции (квадратно-
го трехчлена) у = ах2 + Ьх + с. При построении графика квадратной
функции у = ах2 + Ьх + с могут представиться следующие случаи.
82
ГЛАВА I. Линейные и квадратные уравнения и неравенства
I. а > О, Ь2 - 4ас > О. В этом случае (а > 0) ветви параболы на-
правлены вверх. Ордината вершины п = -
fr2 — 4а<?
4а
< 0 (Ь2 -
- 4ас > 0, а > 0), следовательно, вершины параболы располо-
жены ниже оси Ох. Так как ордината любой точки оси Ох рав-
на 0, при у = 0 имеем квадратное уравнение ах2 + Ьх + с = 0.
По условию дискриминант Ь2 — 4ас > 0, поэтому уравнение
имеет два действительных различных корня — абсциссы то-
чек пересечения параболы с осью Ох.
Функция у = ах2 + Ьх + с принимает наименьшее значение в
вершине параболы
Ь2 — 4ас
4а
. Уравнение оси симмет-
рии параболы имеет вид х = -
Ъ
2а *
Построим график функции у — х2 - 6х + 8 (рис. 33). При а = 1
(а > 0) ветви параболы направлены вверх. Находим координаты
вершины параболы:
-6 Ь2 - 4ас (-6)2 -4-8
2-1 д; 4а 4-1
Следовательно, вершина параболы (наименьшее значение функ-
ции у = х2 - 6х + 8) находится в точке (3; — 1).
Ординату вершины можно вычислить и другим способом, для
этого в функцию нужно подставить значение найденной абсцис-
сы:
г/г _ ч = З2 - 6 • 3 + 8 =-1.
w Л и
Ось симметрии параболы проходит через вершину параболы,
следовательно, уравнение оси: х = 3.
Для нахождения точек пересечения параболы с осью Ох ре-
шим уравнение х2 — 6х + 8 = 0: его корни хг = 2, х2 = 4.
Находим точку пересечения параболы с осью Оу: при х = 0 по-
лучим у = 8.
Получили характеристические точки, по которым легко по-
строить график функции.
II. а > 0; Ь2 - 4ас = 0. Ветви параболы направлены вверх. Ор-
дината вершины равна нулю (Ъ2 — 4ас = 0), поэтому вершина
параболы лежит на оси Ох.
Уравнение ах2 + Ьх + с = 0 в этом случае имеет два равных
корня.
83
ЧАСТЬ I. Алгебра и начала анализа
Рис. 33
Построим график функции у = х2 4- 2х 4- 1 (рис. 34). При а = 1
(а > 0) ветви параболы направлены вверх. Находим вершину па-
раболы:
J/x-i=(-D2 + 2(-l) + l = 0.
Следовательно, вершина параболы находится в точке (-1; 0).
Уравнение оси симметрии параболы: х = -1.
Корни уравнения х2 4- 2х 4-1 = О равны: х, 2 ~ ~1> т. е« график
функции касается оси Ох в точке (—1; О). С осью Оу парабола пе-
ресекается в точке (О; 1). По найденным характеристическим
точкам строим график функции у = х2 4- 2х 4- 1.
III. а > 0; Ь2 — 4ас < О. Ветви параболы направлены вверх. Ор-
дината вершины п = -
Ь2 — 4ас
4а
О (Ь2 - 4ас < 0, а > О), следо-
вательно, вершина расположена выше оси Ох и парабола с
осью Ох не пересекается. Уравнение ах2 4- Ьх 4- с = 0 действи-
тельных корней не имеет.
Построим график функции у = 2х2 - 4х 4- 5 (рис. 35). При а = 2
(а > 0) ветви параболы направлены вверх. Находим вершину па-
- b -4
раболы: - = - -—-
г 2а 2 • 2
= 2*124-5 = 3. Следовательно,
вершина параболы находится в точке (1; 3).
Уравнение оси симметрии параболы: х = 1.
84
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Рис. 36
Уравнение 2х2 — 4х + 5 = О действительных корней не имеет,
так как дискриминант ((—4)2 — 4 • 2 • 5) < 0, поэтому точек пересе-
чения с осью Ох парабола не имеет.
С осью Оу парабола пересекается в точке (0; 5). По характерис-
тическим точкам строим параболу у = 2х2 - 4х + 5.
IV. а < 0; Ъ2 — 4ас > О. Ветви параболы направлены вниз (а < 0).
— 4ас о
Ордината вершины п = -г-— > 0 (д2 - 4пс > 0, а < 0). Сле-
довательно, график пересекает ось Ох в двух точках х, так как
уравнение ах2 + Ьх + с = 0 имеет два действительных корня.
Построим график функции у = —х2 - 2х + 3 (рис. 36). При а = — 1
(а < 0) ветви параболы направлены вниз. Находим вершину пара-
- ь
болы: - тг-
2а
= Ух—1 = -(-I)2 - 2(-1) + 3 = 4. Следо-
вательно, вершиной параболы является точка (-1; 4).
Уравнение оси симметрии параболы: х = -1.
Корни уравнения -х2 - 2х + 3 = 0 или соответствующего ему
х2 + 2х - 3 = 0 равны хг = -3; х2 = 1.
С осью Оу парабола пересекается в точке (0; 3). По характерис-
тическим точкам строим график функции у = х2 - 2х + 3.
V. а < 0; Ь2 - 4ас = 0. Ветви параболы направлены вниз. Орди-
ната вершины п = —
Ь2 — 4ас
= 0.
Уравнение ах2 + Ьх + с = 0 имеет два равных корня и, следова-
тельно, график функции касается оси Ох в одной точке.
85
ЧАСТЬ I. Алгебра и начала анализа
Рис.37
Построим график функции у = -х2 +
+ 2х - 1 (рис. 37). При а = -1 ветви па-
раболы направлены вниз. Находим вер-
шину параболы: -
2а
ух = 1 = ~ I2 + 2 • 1 — 1 = 0, следовательно,
вершина параболы находится в точке
(1; 0).
Уравнение оси симметрии параболы
х = 1.
Корни уравнения -х2 + 2х — 1 = О
равны хх 2 = 1, т. е. график функции
касается оси Ох в точке х = 1.
Парабола пересекается с осью Оу в точке (О; —1). По характе-
ристическим точкам строим график функции у = -х2 + 2х - 1.
VI. а < О; Ъ2 - 4ас < О. Ветви параболы направлены вниз. Ор-
Ь2 — 4ас
дината вершины п =---г-—
О (Ъ2 — 4ас < 0, а < 0). Следо-
вательно, вершина параболы лежит ниже оси Ох. Уравнение
ах2 + Ьх + с = 0 действительных корней не имеет. Поэтому па-
рабола расположена ниже оси Ох и с ней не пересекается.
Построим график функции у = —х2 — 2х - 3 (рис. 38).
При а — -1 (а < 0) ветви параболы направлены вниз. Находим
координаты вершины: -
-2
-3 = -2.
Вершина параболы находится в точке (-1; -2).
Уравнение оси симметрии параболы х = -1.
Уравнение —х2 - 2х - 3 = 0 действительных корней не имеет, и
парабола с осью Ох не пересекается.
Парабола пересекается с осью Оу в точке (0; -3). По характе-
ристическим точкам строим график функции у = -х2 — 2х — 3
(рис. 38).
Установлено шесть возможных случаев исследования и по-
строения графика функции у = ах2 + Ьх + с.
5. Графический способ решения квадратного уравнения. Квадратное
уравнение графически можно решать двумя способами. Первый
способ заключается в построении параболы у = ах2 + Ьх + с и на-
86
ГЛАВА I. Линейные и квадратные уравнения и неравенства
хождении корней уравнения ах2 + Ьх + с = 0 как абсцисс точек
пересечения параболы с осью Ох. Как было установлено в п. 4
при исследовании графика квадратной функции, если парабола
пересекает ось Ох в двух точках, соответствующее уравнение
имеет два действительных корня, если касается оси Ох, то урав-
нение имеет два равных действительных корня, и если не пересе-
кает оси Ох, то уравнение действительных корней не имеет.
Иначе можно уравнение ах2 + Ьх + с = 0 представить в виде
ах2 = —Ьх — с. Обозначив левую и правую части этого уравнения
через у, получим две функции: квадратную и линейную: у = ах2 и
у = -Ьх + с. Корни этих функций должны быть одними и теми
же. Следовательно, координаты точек пересечения этих графи-
ков и будут корнями исходного уравнения. Построив на одном
чертеже графики функций у = ах2 и у — -Ьх - с, найдем коорди-
наты точек их пересечения. Если парабола у — ах2 имеет две об-
щие точки с прямой у = — Ьх - с, то уравнение имеет два действи-
тельных различных корня. Если эти графики имеют одну общую
точку, то уравнение имеет два равных действительных корня, ес-
ли общих точек они не имеют, то уравнение действительных кор-
ней не имеет.
Представим графическое решение квадратного уравнения
х2 - х - 6 = 0 (рис. 39). Приведем уравнение к виду х2 = х + 6. По-
строим графики функций у = х2иу = х + 6. Парабола у = х2 и
прямая у — х + 6 пересекаются в двух точках: (-2; 4) и (3; 9). Сле-
довательно, корни уравнения х2 - х — 6 = О равны x1 — -2tx2 = 3.
Рис. 39
87
ЧАСТЬ I. Алгебра и начала анализа
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Приведите примеры частных случаев квадратной функции / = ах1 2 + Ьх + с.
Как называется график квадратной функции?
2. При каких значениях коэффициента а ветви графика функции / = ах2 +
+ bx + с направлены вверх (вниз)?
3. Как расположены ветви параболы по отношению к ее оси симметрии
при различных значениях коэффициента а (о > 1,0 < а < 1)?
4. Как строится график функции / = а(х - т)2 + п?
5. Как найти абсциссу вершины параболы, если она пересекается с осью
0x2
6. По каким формулам вычисляются координаты вершины любой парабо-
лы?
7. Какие точки графика функции у = ах2 + Ьх + с называются характеристи-
ческими?
8. Приведите шесть вариантов построения графика функции / = ах2 + Ьх + с.
9. Укажите способы графического решения квадратного уравнения.
§ 10. Квадратные неравенства.
Решение неравенств методом промежутков
1. Графическое решение квадратного неравенства. Квадратным на-
зывается неравенство
ах2 + Ьх + с > О
или
ах2 + Ьх + с < 0.
(1.43)
(1.44)
Умножив обе части неравенства (1.44) на (-1), получим нера-
венство (1.43), поэтому достаточно изучить приемы решения не-
равенства (1.43). При решении квадратного неравенства будем
исходить из построения графика квадратного трехчлена, т. е. па-
раболы у = ах2 + Ьх + с.
Для решения неравенства (1.43) достаточно знать, при каких
значениях аргумента х график трехчлена ах2 + Ьх + с находится
в верхней полуплоскости. Результаты исследований квадратного
трехчлена (§ 9) отвечают на этот вопрос.
Рассмотрим основные случаи решения квадратного неравен-
ства.
ГЛАВА I. Линейные и квадратные уравнения и неравенства
I. Если а> 0 nD = Ь2 — 4ас > О, то график квадратного трехчле-
на ах2 + Ьх + с находится в верхней полуплоскости, кроме ду-
ги, отсекаемой осью абсцисс.
Неравенство (1.43) справедливо при х < хг и при х > х2, где хА
и х2 — корни квадратного трехчлена и хг < х2.
Рассмотрим более подробно подобное решение на примере не-
равенства х2 + 2х - 3 > О (рис. 40).
Так как а = 1 (а > 0), ветви параболы у = х2 + 2х - 3 направле-
ны вверх. Дискриминант D = 22 — 4 • 1 • (-3); D > 0, поэтому трех-
член х2 + 2х - 3 имеет два действительных корня: хх = — 3, х2 = 1
(в этих точках парабола пересекает ось Ох). Для построения пара-
болы находим ее вершину:
b
2а
-2
2 •(-1)
+ 2*(-1) — 3 = —4, т. е. координаты вершины равны (-1; -4).
Уравнение оси симметрии параболы: х = -1. Точка пересечения
параболы с осью Оу имеет координаты (0; -3).
Таким образом, трехчлен х2 + 2х - 3 имеет положительные
значения в точках, лежащих выше оси Ох, т. е. исходное нера-
венство справедливо при
П. Если а > 0 и D = 0, то график трехчлена находится в верх-
ней полуплоскости за исключением точки касания с осью Ох.
Неравенство (1.43) справедливо при всех значениях х, кроме
х = -Ь/2а.
Подобный вариант рассмотрим на примере неравенства х2 +
+ 2х 4-1 > 0 (рис. 41).
Рис. 40 Рис. 41
89
ЧАСТЬ I. Алгебра и начала анализа
При а = 1 (а > 0) ветви параболы направлены вверх. Дискри-
минант D = 22- 4*1*1 = 0, следовательно, трехчлен имеет два
равных корня: xr = -1, х2 = -1. Таким образом, вершина парабо-
лы — точка ее касания с осью Ох (-1; 0). Уравнение оси симмет-
рии параболы: х = -1. С осью Оу парабола пересекается в точке
(0; 1).
Значение трехчлена х2 + 2х + 1 положительно во всех точках,
лежащих выше оси Ох, за исключением точки (-1; 0). Поэтому
III. Если а > 0 и D < 0, то график трехчлена расположен в
верхней полуплоскости и неравенство (1.43) справедливо при
всех значениях х.
Рис. 42
Подобный случай рассмотрим на приме-
ре неравенства 2х2 - 4х + 5 > 0 (рис. 42).
При а = 2 (а > 0) ветви параболы на-
правлены вверх. Дискриминант D — (-4)2 -
-4’2*5; D < 0; следовательно, трехчлен
2х2 — 4х + 5 действительных корней не
имеет и парабола с осью Ох не пересекает-
= 2* I2 - 4* 1 + 5 = 3; ко-
ординаты вершины составляют (1; 3).
Уравнение оси симметрии: х = 1. Точка пересечения с осью Оу
имеет координату (0; 5).
Трехчлен является положительной величиной при всех значе-
ниях х, поэтому
IV. Если а < 0 и Р > 0, то в верхней полуплоскости содержится
часть графика, ограниченная дугой параболы и осью Ох.
Неравенство (1.43) справедливо при хг< х < х2, где хх и х2 —
корни трехчлена и х2 < х2.
Подобный случай отразим с помощью неравенства — х2 + 6х -
- 5 > 0 (рис. 43).
При а = -1 (а < 0) ветви параболы направлены вниз. Дискрими-
нант D = 62 - 4 • (-1)(-5); D > 0. Корни уравнения х2 - 6х + 5 = 0
90
ГЛАВА I. Линейные и квадратные уравнения и неравенства
равны Xj = 1, х2 = 5. Координаты вершины параболы определя-
ются как -
b
2а
= 3, ух_ 3 = -З2 + 6 • 3 - 5 = 4, т. е. рав-
ны (3; 4). Уравнение оси симметрии: х = 3. Точка пересечения па-
раболы с осью Оу имеет координаты (0; -5).
Значение трехчлена —х2 4- 6х - 5 является положительным во
всех точках промежутка 1 < х < 5.
V. Если а < 0 и D = 0, то график трехчлена расположен в ниж-
ней полуплоскости, кроме точки касания с осью Ох, поэтому
неравенство (1.43) решения не имеет.
Подобный вариант представлен с помощью неравенства —х2 +
+ 4х - 4 > 0 (рис. 44).
При а = -1 (а < 0) ветви параболы направлены вниз. Дискри-
минант D = 42 - 4(-1)(-4) = 0, следовательно, парабола касается
оси Ох в точке - №
2а
= 2, т. е. координаты вершины па-
раболы равны (2; 0). Уравнение оси симметрии параболы — х = 2.
Точка пересечения с осью Оу имеет координаты (0; -4).
Неравенство -х2 + 4х - 4 > 0 выполняется при тех значениях
х, при которых точки параболы лежат выше оси Ох, но таких то-
чек нет, следовательно, данное неравенство не имеет решения.
VI. Если а < 0 и D < 0, то график трехчлена лежит в нижней
полуплоскости и неравенство (1.43) решений не имеет.
Соответствующий случай рассмотрим на примере неравенства
-2х2 + 4х - 3 > 0 (рис. 45).
При а = -2 {а < 0) ветви параболы направлены вниз. Дискрими-
нант D = 42 - 4(-2)(-3); D < 0, следовательно, парабола не пересе-
Рис. 43
Рис. 44
Рис. 45
91
ЧАСТЬ I. Алгебра и начала анализа
кает ось Ох, Определяем вершину параболы: -
4
2•(-2)
ух = j = -2 • I2 + 4*1 - 3 = -1, т. е. координаты вершины равны
(1; -1). Уравнение оси симметрии параболы: х = 1. Точка пересе-
чения параболы с осью Оу имеет координаты (0; -3).
Неравенство -2х2 + 4х - 3 > 0 выполняется только при тех
значениях х, при которых точки параболы лежат выше оси Ох,
но таких точек нет. Данное неравенство решения не имеет.
2. Решение неравенств методом промежутков (интервалов). Если ле-
вую часть неравенства можно разложить на линейные множите-
ли, то его можно решить методом промежутков.
Для нахождения промежутков знакопостоянства на числовой
прямой отмечают все точки, в которых функция Р(х) обращается
в нуль или претерпевает разрыв. Эти точки разбивают числовую
прямую на несколько промежутков, внутри каждого из которых
функция Р(х) сохраняет свой знак. Знак может измениться толь-
ко при переходе через корни сомножителей.
На примере неравенства (х + 3)(х — 2)(х - 5) > 0 рассмотрим
этот метод.
Многочлен Р(х) = (х + 3)(х - 2)(х - 5) обращается в нуль в точ-
ках xt = -3, х2 = 2 и х3 == 5. Эти точки разбивают всю число-
вую прямую (рис. 46) на следующие промежутки: -оо < х < -3,
-3<х<2, 2<х<5, 5<х< +оо.
Рассматривая промежутки справа налево, находим знак функ-
ции по знаку каждого из промежутков.
В промежутке 5 < х < 4-оо выберем любое число, входящее в
него, например х = 6, которое подставим в каждый из сомножи-
телей многочлена Р(х), чтобы найти знак Р(х)*.
При х = 6 имеем sgn Р(х) = (+)(+)(+) = (+)• Таким образом, при
любом значении числа х, взятом из промежутка 5 < х < +оо, не-
равенство соблюдается, следовательно, любое число из этого про-
межутка является решением данного неравенства.
Далее рассмотрим промежуток 2 < х < 5. Приняв, например,
х = 4, получим sgn Р(х) = (+)(+)(“) = (“)• Следовательно, лю-
бое число из промежутка 2 < х < 5 не является решением нера-
венства.
* Для обозначения знака некоторого выражения принято использо-
вать термин sgn (от лат. signum — знак).
92
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Рис. 46
Рис. 47
Для промежутка -3 < х < 2 положим, например, х = О, тогда
sgn Р(х) = (+)(-)(-) = (+). Следовательно, этот промежуток слу-
жит решением неравенства.
Для промежутка -оо < х < -3 примем х = -10, тогда sgn Р(х) =
= (-)(-)(-) = (-). Числа из этого промежутка не являются реше-
ниями неравенства. Таким образом, решением неравенства явля-
ются промежутки
Из решения видно, что знаки на числовой прямой чередуются,
причем для всех значений х, расположенных правее самого боль-
шого корня, многочлен Р(х) будет положительным, и все сомно-
жители будут также положительными. Поэтому при решении не-
равенств методом промежутков достаточно правый промежуток
взять со знаком «+», остальные промежутки (справа налево) бу-
дут иметь чередующиеся знаки.
График на рисунке 47 иллюстрирует решение неравенства
х2 - 7х + 10 > 0. Данный трехчлен имеет корни хг — 2, х2 = 5. Эти
корни отмечаем на числовой оси и строим кривую знаков. Так
как Р(х) > 0, решением неравенства являются промежутки
-оо <х<2, 5<Х< 4-00.
♦ ПРИМЕР
Решить неравенство:
1)
3; 2)
х + 3
х — 1
РЕШЕНИЕ. 1) Путем преобразований получим
2(х - 7/2) <()
х — 2
V « (х - 2) о
Умножив обе части последнего неравенства на i—5— , х 5* 2,
придем к (х - 2)(х - 7/2) < 0. Точки х = 2 и х = 7/2 называют-
ся «выколотыми точками» и обозначаются обычно на графике
(рис. 48) кружочком. Решением неравенства является промежу-
ток 2 < х < 7/2.
93
ЧАСТЬ I. Алгебра и начала анализа
Рис. 48
Рис. 49
2) Получаем
О
(х + 3)(х - 1)
О .
2
2
Умножив обе части последнего неравенства на —
(х^ -3, х 1), получим (х + 3)(х + 1)(х — 1) > 0. На графике,
представленном на рисунке 49, отмечены промежутки решения:
-3 < X < -1, 1 < X < +00.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие неравенства называются квадратными неравенствами?
2. Как решаются квадратные неравенства графическим способом?
3. Перечислите возможные варианты решения квадратных неравенств гра-
фическим способом.
4. При каком расположении графика квадратного трехчлена решением не-
равенства служит множество всех действительных чисел?
5. В каких случаях квадратное неравенство не имеет решения?
6. Какие неравенства можно решать методом промежутков?
7. Объясните с помощью примеров применение метода промежутков при
решении неравенств.
§ 11. Иррациональные уравнения
и иррациональные неравенства
1. Иррациональные уравнения. Уравнение, содержащее переменную
под знаком корня, называется иррациональным.
Решение иррационального уравнения основано на преобразова-
нии его к рациональному уравнению. Это достигается возведением
обеих его частей в одну и ту же степень (иногда несколько раз).
При возведении обеих частей иррационального уравнения в чет-
ную степень получается уравнение, являющееся следствием исход-
ного. Уравнению-следствию удовлетворяют все корни исходного
уравнения, но могут появиться и корни, которые не являются кор-
нями исходного уравнения, так называемые посторонние корни.
94
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Поэтому все найденные корни уравнения-следствия проверяют под-
становкой в исходное уравнение и посторонние корни отбрасывают.
Исходное иррациональное уравнение равносильно смешанной
системе, состоящей из уравнения-следствия и ограничений, опре-
деляемых областью допустимых значений переменных. В этом слу-
чае посторонние корни не будут входить в область допустимых
значений переменной, и проверять их подстановкой в исходное
уравнение не требуется. При возведении обеих частей ирраци-
онального уравнения в нечетную степень получается уравнение,
равносильное данному.
♦ ПРИМЕР
Решить иррациональное уравнение: 1) *Jx2 — 7 = 3; 2) — 5 =
РЕШЕНИЕ. 1) Возводим в квадрат: (х2 — 7 = 9) (х2 = 16) <=> х12 = + 4.
Подставив полученные корни в исходное уравнение, видим, что
они удовлетворяют ему.
2) Подкоренные выражения не должны быть отрицательными:
х- 5 >0, f х > 5,
3 - х > О 1х < 3.
Полученная система неравенств решения не имеет, не имеет
их, таким образом, и исходное уравнение.
(27(х - 1)(2х - I))2 = (27 - Зх)2,
х > 1,
х < 9
х2 - 150х + 725 = О,
1 < х < 9
Г* = 5,
Lx = 145,
1 < х < 9.
Последней системе отвечает единственное решение х — 5.
+ х 4- 2 = 4,
х2 + 2х = 4 - 4х
О < х < 2
6х = 4,
О < х <
Решение х = 2/3 удовлетворяет исходному уравнению.
95
ЧАСТЬ I. Алгебра и начала анализа
2. Иррациональные неравенства с одной переменной. Решение ирра-
ционального неравенства с одной переменной сводится к реше-
нию равносильной ему системы рациональных неравенств или
совокупности систем иррациональных неравенств.
Простейшие иррациональные неравенства имеют вид:
'Vftx) > a, nJf(x) < a, nJf(x) < ф(х), nJf(x) > ф(х),
nJf(x) < лл/<р(х), 'Vf(x) > п7<р(х).
Решение неравенства вида 2kJf(x) > а сводится к двум случаям:
1) если а > 0, то исходное неравенство равносильно неравенст-
ву f(x) > a2k;
2) если а < 0, то решением исходного неравенства является
пустое множество.
❖ ПРИМЕР
Решить неравенство: 1) ^2х - 5 > 7; 2) -х < -3.
РЕШЕНИЕ. 1) 2х — 5 > 49. Следовательно, 27 < х < +оо.
2) Решением неравенства Jb - х < -3 является пустое множе-
ство, так как ни при каком значении х корень четной степени не
может быть отрицательным числом.
Неравенство 2V/(x) > ф(х) равносильно совокупности двух
систем неравенств:
| ф(х) > О,
f (х) > О,
. /(х) > ф2*(х)
I Ф(х) < О,
I f(x) > 0.
Например,
х + 1 > 0,
< х + 3 > 0,
х + 3 > х2 +
f X + 1 < 0,
1х+3>0
2х + 1,
(7х + 3 > х + 1)
х2 + х - 2 < 0,
Данной совокупности удовлетворяет х е [-3; 1).
96
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Неравенство 2kJf(x] < ф(х) равносильно системе трех нера-
венств
ф(х) > О
/ (х) < ф2(х).
Например
>0,
13 > О
13 <х
13
3 *
О
I
I
нет решения,
4
Таким образом, решением системы является х е (4; +оо).
Решение неравенства 2k*Jf(x) > 2^Ф(х) сводится к решению
равносильной системы неравенств
/(х) > 0,
< ф(х) > 0,
/(х) > ф(х).
Например,
Полученной системе удовлетворяет х g (2/3; 3].
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие уравнения называются иррациональными?
2. В каких случаях появляются посторонние корни иррационального урав-
нения?
3. Каким способом может быть устранено появление посторонних корней
иррационального уравнения?
4. Приведите примеры различных способов решения иррациональных не-
равенств.
4 - 9664
97
ЧАСТЬ I. Алгебра и начала анализа
§ 12. Нелинейные системы уравнений
с двумя переменными
При решении систем уравнений используют правила, позво-
ляющие преобразовать данную систему в равносильную ей.
I. Одно из уравнений системы можно заменить на равносиль-
ное.
II. Если одно из уравнений системы имеет вид х = А (А — вы-
ражение, не содержащее х), то в остальных уравнениях систе-
мы можно заменить переменную х на ее выражение А.
III. Любое уравнение системы можно заменить на уравнение,
получающееся при его сложении с любым другим уравнением
системы.
IV. Любое уравнение системы можно умножить на выраже-
ние, не обращающееся в нуль.
♦ ПРИМЕР
Решить систему уравнений:
РЕШЕНИЕ. 1) Складывая первое уравнение системы с удвоенным
вторым, получаем:
Следовательно,
2) Положим z = - (х 0, у * 0). Тогда z + - = —, откуда г. = 5,
У 2 О
г2 = |. Таким образом, исходная система распадается на совокуп-
ность двух систем, каждая из которых решается способом подста-
новки:
98
ГЛАВА I. Линейные и квадратные уравнения и неравенства
J X = 5у,
124г/2 = 24
х2 — у2 = 24
5’
- = - < о нет решения.
Ь 5’ -2^=24
х2 — у2 = 24 L 25
Таким образом, получаем два решения: (хг = -5, уг = -1) и
(х2 = 5, у2 = 1).
§ 13. Простейшие задачи линейного
программирования с двумя переменными
1. Общие понятия. Задачи, в которых отыскивается максимум или
минимум некоторой функции при наличии ограничений на пере-
менные, называются задачами математического программи-
рования.
Линейное программирование — это наука о методах исследо-
вания и отыскания наибольших и наименьших значений линей-
ной функции*, на неизвестные которой наложены линейные ог-
раничения. Соответствующая функция называется функцией це-
ли или линейной формой F.
Функция цели совместно с системой ограничений образует ма-
тематическую модель рассматриваемой задачи.
Решение задачи линейного программирования состоит из трех
этапов: 1) постановки задачи и составления ее математической
модели; 2) выбора соответствующих методик (алгоритмов) для
решения задачи и проведения вычислений по этим методикам;
3) интерпретации модели в исходных условиях.
Система ограничений сводится к т линейных уравнений или
неравенств с п переменными, где т < п. Системы, в которых пе-
ременных больше, чем уравнений, называются неопределенны-
ми. Неопределенные системы приводятся к определенным (т. е.
системам, содержащим столько уравнений, сколько имеется пе-
ременных) путем последовательного приравнивания к нулю соот-
ветствующего числа переменных.
* Линейной называется функция вида у = ах + Ь. Графиком линей-
ной функции является прямая линия.
99
ЧАСТЬ I. Алгебра и начала анализа
В системе из двух уравнений с тремя переменными можно по-
лучить три решения, приравнивая поочередно нулю хр х2 и х3.
Например, система
имеет три решения:
Математическое линейное программирование требует ото-
брать неотрицательные решения неопределенных систем линей-
ных уравнений, при которых линейная форма принимает макси-
мальное или минимальное значение.
♦ ПРИМЕР
Найти наибольшее значение линейной формы Z = 2х± + х2 при
следующих условиях:
РЕШЕНИЕ. Учитывая, что хг > 0 и х2 > О, строим прямые 3xt + х2 = 9
Рис. 50
и 2xj 4- 4х2 = 16 только в I четверти
(рис. 50). Множеством точек, коор-
динаты которых удовлетворяют
системе неравенств (а), является
выпуклый многоугольник OAED
(многоугольник решений). Верши-
ны А, Е и D многоугольника нахо-
дим, решая системы уравнений:
100
ГЛАВА I. Линейные и квадратные уравнения и неравенства
Среди множества этих точек надо найти такие, в которых
функция Z = 2хг + х2 принимает наибольшее значение. Построим
прямую 2хг + х2 = О, т. е. х2 — -2хг При увеличении Z эта пря-
мая перемещается параллельно самой себе. Наибольшего зна-
чения Z достигает в одной из вершин многоугольника. Нахо-
дим значения функции Z — 2хг + х2 в вершинах многоугольни-
ка: Zo = О, ZA = 2*3 + 1-0 = 6, ZE = 2-2 + 1-3 = 7, = 2-0 +
+ 1-4 = 4.
Таким образом, при хг = 2, х2 = 3 функция Z — 2xt + х2 дости-
гает наибольшего значения Zmnv — 7.
1 HUA
2. Задача составления оптимального плана. Требуется составить план
выпуска двух видов изделий на четырех участках цеха, чтобы по-
лучить максимальную прибыль от сдачи этих изделий. При этом
накладываются следующие ограничения: время работы на участке
I не превышает 16 ч, на участке II — 30 ч, на участке III — 16 ч
и на участке IV — 12 ч.
Цеху начисляется прибыль: 3 тыс. р. при реализации одно-
го изделия вида М и 4 тыс. р. при реализации одного изделия
вида N.
В таблице указано время, необходимое для изготовления каж-
дого из этих двух видов изделий на каждом из участков. Нуль оз-
начает, что изделие на данном участке не изготовляется:
Изделие Участки
J II III 1 IV
М 4 3 0 2
N 2 6 4 0
Возможное время работы участка, ч 16 30 16 12
Обозначим через ху число изделий вида М, а через х2 число из-
делий вида N.
На участке I затрачивается 4х1 часов на изготовление изделий
вида М и 2х2 часов на изготовление изделий вида N, т. е. всего
4хг + 2х2 ч. Так как время работы на участке I не превышает
16 ч, то 4Xj + 2х2 < 16.
101
ЧАСТЬ I. Алгебра и начала анализа
На участке II затрачивается 3xt часов на изделия вида М и
6х2 часов на изделия вида N, всего не более 30 ч, т. е. Зхг + 6х2 < 30.
На участке III затрачивается 0 часов на изделия вида М и
4х2 часов на изделия вида N, т. е. 4х2 <16.
На участке IV затрачивается 2хг часов на изделия вида М и
0 часов на изделия вида N, т. е. 2хг <12.
Общая прибыль цеха составляет Зхг + 4х2 тыс. р., где Xj > 0
и х2 > 0.
Таким образом, ограничения сводятся к системе линейных не-
равенств
{4хл + 2х9 < 16, Зх. + 6х9 < 30, 4х9 < 16,
2х* 12, хг > 0, х2 > 0}.
На множестве решений этой системы неравенств требуется
найти наибольшее значение линейной формы Z = 3xj + 4х2.
Построив прямые 4xt + 2х2 = 16, Зхг + 6х2 = 30, 4х2 = 16 и
2хг = 12, получим замкнутый многоугольник OABCD (рис. 51).
Вычислим координаты его вершин:
2х, = 12,
[ Х2 = 0
; 2xj = 12,
3Xj + 6х2 = 30
А(6; 0);
В(6; 2);
С(2; 4);
=> Р(0; 4).
Рис. 51
Подставив координаты вершин
в выражение линейной формы,
получим: ZA = 3*6 + 4*0 = 18;
= 3 • 6 + 4 • 2 = 26; Zc = 3-2 +
+ 4*4 = 22; = 3*0 + 4*4 = 16.
В точке В(6; 2) линейная форма
достигает максимума: Zm&x — 26.
Таким образом, наибольшая
прибыль от сдачи двух видов из-
делий составляет 26 тыс. р. Она
будет получена, если цех изгото-
вит 6 изделий вида М и 2 изделия
вида N.
102
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
ГЛАВА 2. Функции.
Степенная, показательная
и логарифмическая функции
§ 14. Функции и их основные свойства
1. Функции. Переменная у называется функцией переменной х, ес-
ли каждому допустимому значению х соответствует определен-
ное значение у.
Символически функциональная зависимость между перемен-
ной у (функцией) и переменной х (аргументом) записывается с
помощью равенства у = f(x), где f означает совокупность дейст-
вий, которые надо произвести над х, чтобы получить у.
Числовое значение функции, соответствующее данному чис-
ловому значению аргумента, называется частным значением
этой функции. Например, функция у = /(х) при х = а принимает
значение у = f(a).
Областью определения (существования) функции называет-
ся множество всех действительных значений аргумента, при ко-
торых она может иметь действительное значение.
Например, для функции у — х областью определения является
множество всех действительных чисел R; для функции У = ~ об-
ластью определения является множество R кроме х = 0.
Множеством значений функции называется множество всех
действительных значений функции у, которые она может прини-
мать.
Например, множеством значений функции у = х + 1 является
множество R, множеством значений функции у = х2 + 1 является
множество действительных чисел, больших или равных 1.
Для задания функции необходимо и достаточно задать закон со-
ответствия, по которому для каждого значения аргумента можно
указать единственное значение функции и ее область определения.
Функция может быть задана аналитически (формулой), табли-
цей, графиком или каким-либо другим способом.
♦ ПРИМЕР
Найти область определения функции: 1) у = Jx + х — 1;
2)у =
Зх - 2
2х 4- 6
103
ЧАСТЬ I. Алгебра и начала анализа
Рис.52
РЕШЕНИЕ. 1) Областью определения данной
функции является общая часть областей
определения каждого из слагаемых. Для
первого слагаемого х > 0, для второго
х > 1. Областью определения функции
служит промежуток х > 1.
2) Функция определена для всех значений х, удовлетворяю-
щих неравенству
> 0. Таким образом,
На рисунке 52 показаны области определения данной функции.
2. Четные и нечетные функции. Функция у — f(x) называется чет-
ной, если при всех значениях х в области определения этой функ-
ции при изменении знака аргумента на противоположный значе-
ние функции не изменяется, т. е. /(-х) = /(х). Например, парабо-
ла у = х2 является четной функцией, так как (-х)2 = х2. График
четной функции симметричен относительно оси Оу.
Функция у = f(x) называется нечетной, если при всех значе-
ниях х в области определения этой функции при изменении зна-
ка аргумента на противоположный функция изменяется только
по знаку, т. е. /(-х) = -f(x). Например, функция у — х3 — нечет-
ная, так как (-х)3 = -х3. График нечетной функции симметри-
чен относительно начала координат.
Свойством четности или нечетности обладает не всякая функ-
ция. Например, функция /(х) = х2 + х3 не является ни четной, ни
нечетной: /(-х) = (—х)2 4- (~х)3 = х2 - х3; х2 + х3 х2 — х3.
♦ ПРИМЕР
Исследовать на четность и нечетность функцию: 1) у =
2)*/ =
определенную на всей числовой оси.
РЕШЕНИЕ. Подставляем на место аргумента (-х).
1)
3(-х)4 - 2(-х)2
— функция четная;
104
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
3(-х)2 + 4 Зх2 + 4 Зх2 + 4
— функция нечетная;
2)
ни нечетной.
— функция не является ни четной,
3. Возрастающие и убывающие функции. Среди множества функций
есть функции, значения которых с увеличением аргумента толь-
ко возрастают или только убывают. Такие функции называются
возрастающими или убывающими.
Функция у = f(x) называется возрастающей в промежутке
а < х < 6, если для любых хг и х2, принадлежащих этому проме-
жутку, при хг < х2 имеет место неравенство /(Xj) < /(х2).
Функция у = /(х) называется убывающей в промежутке а < х < Ь,
если для любых хг и х2, принадлежащих этому промежутку, при
хх < х2 имеет место неравенство /(х1) > jf(x2).
Как возрастающие, так и убывающие функции называются
монотонными, а промежутки, в которых функция возрастает
или убывает, — промежутками монотонности.
Например, функция у = х2 при х < 0 монотонно убывает, а при
х > 0 монотонно возрастает. Функция у = х3 на всей числовой оси
монотонно возрастает, а функция у — -х3 на всей числовой оси
монотонно убывает.
4. Обратная функция. Если функция у = /(х) принимает каждое
свое значение только при единственном значении х, то такую
функцию называют обрати мой.
Например, функция у — Зх + 5 является обратимой, так как каж-
дое значение у принимается при единственном значении аргумента
х. Напротив, функция у = Зх2 не является обратимой, поскольку,
например, значение у = 3 она принимает и при х = 1, и при х = -1.
Пусть у = f(x) — обратимая функция. Это означает, что каж-
дому у из множества значений функции соответствует одно опре-
деленное число х из области ее определения такое, что /(х) — у.
Решив это уравнение относительно х, получим уравнение х =
= ф(^), в котором у является аргументом, ах — функцией этого
аргумента. Поменяв местами в соответствии с принятыми обозна-
чениями х и у, получим у = ф(х).
Функция у = (р(х) называется обратной к функции у = f (х).
Областью определения обратной функции является множество
значений исходной функции, а множеством значений обратной
функции является область определения исходной функции.
105
ЧАСТЬ I. Алгебра и начала анализа
Рис. 53
График обратной функции у = (р(х)
симметричен графику функции у — f(x)
относительно биссектрисы I и III коорди-
натных углов. Проиллюстрируем это на
примере линейной функции у = Зх + 4
(рис. 53). Из исходной функции следует
уравнение х = (у - 4)/3. Поменяв местами
х и у, получим обратную функцию у = (х -
- 4)/3. Построив соответствующие графи-
ки, убеждаемся в их симметрии относи-
тельно прямой у = х.
Для всякой непрерывной функции (такой, которая не имеет
точек разрыва) существует монотонная однозначная и непре-
рывная обратная функция.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Сформулируйте определение функции.
2. Что называется областью определения функции?
3. Что называется областью изменения функции?
4. Какими способами может быть задана функция?
5. Как находится область определения функции?
6. Какие функции называются четными и как они исследуются на четность?
7. Какие функции называются нечетными и как они исследуются на нечет-
ность?
8. Приведите примеры функций, которые не являются ни четными, ни не-
четными;
9. Какие функции называются возрастающими? Приведите примеры.
10. Какие функции называются убывающими? Приведите примеры.
11. Какие функции называются обратными?
12. Как расположены графики прямой и обратной функций?
§ 15. Степенная функция
Функция вида у = х\ где k — действительное число, называет-
ся степенной функцией с показателем k.
Свойства и график степенной функции существенным образом
зависят от показателя степени k. Рассмотрим различные возмож-
ные варианты.
I. Показатель степени k = 2п — четное натуральное число.
В этом случае областью определения функции у — х2п является
множество R всех действительных чисел; множеством значе-
106
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
ний — неотрицательные числа (у > 0); функция является чет-
ной ((-х)2п = х2п); функция — убывающая на промежутке
х < 0 и возрастающая на промежутке х > 0.
На рисунке 54 приведены графики функций у = х2 и у — х4.
II. Показатель степени k = 2п - 1 — нечетное натуральное
число.
Такая степенная функция у = х2п ~ 1, где п — натуральное чис-
ло, обладает следующими свойствами: ее область определения —
множество В, множество значений — множество JR, функция
является нечетной, так как (-х)2п " 1 = -х2л “ функция —
возрастающая на всей действительной оси.
Графики, изображенные на рисунке 55, соответствуют функ-
циям у = х3 и у = х5. (Отметим, что в частном случае при п = 1 по-
лучаем функцию у = х с графиком биссектрисы первого и третье-
го квадрантов.)
III. Показатель степени k = -2п, где п — натуральное число.
В этом случае областью определения функции у = х 2п =
является множество R, кроме х = 0; множеством значений —
положительные числа у > 0; функция является четной, так
как
2п = —; функция — возрастающая на
Y ОС) ОС
0 и убывающая на промежутке х > 0.
промежутке
Рис. 54
Рис. 55
107
ЧАСТЬ I. Алгебра и начала анализа
Рис. 56
Рис. 57
На рисунке 56 представлены графики функций у = —% и у = —.
ОС х
IV. Показатель степени k = ~(2п — 1), где п — натуральное
число.
Областью определения такой функции у — х <2п — 2п_ г яв-
ОС
ляется множество R, кроме х — 0; множеством ее значений —
множество R, кроме у = 0; функция — нечетная, так как
-х)
2п - 1
; функция является убывающей на проме-
жутках х < 0, х > 0.
На рисунке 57 приведены графики функций у = ЯУ=~5
ОС ОС
Рис. 58
Рис.59
108
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
у = хк; k > О
10 3 2 3
Рис. 60
Рис. 61
V. Показатель степени k —
положительное действительное
нецелое число.
Областью определения такой функции являются неотрица-
тельные числа х > 0, множеством значений — неотрицатель-
ные числа у > 0; функция — возрастающая на промежутке
х > 0.
На рисунке 58, а представлены графики функций у = х1/2 и
у = х1/3 (показатель k < 1), на рисунке 58, б — графики функций
z/ = х2/3 и у = х^3 (показатель k > 1).
VI. Показатель степени k — отрицательное действительное
нецелое число.
Такая функция обладает следующими свойствами: область оп-
ределения — положительные числа х > 0; множество значе-
ний — положительные числа у > 0; функция — убывающая на
промежутке х > 0.
Этот случай проиллюстрирован графиками на рисунке 59:
На графиках рисунка 60 в I квадранте представлены кривые,
соответствующие функциям у = xk при k > 0, на графиках рисун-
ка 61 — при k < 0.
109
ЧАСТЬ I. Алгебра и начала анализа
§ 16. Показательная функция
Основные свойства степени
Если а > О, b > 0 и х, хр х2 — любые действительные числа, то:
ах1-ах2 = а Х1 + х2;
(2.1)
(2.2)
(а*1)*2 = а*1 * х2;
(ab)x = ахЬх;
fa'f _ ах .
UJ ~ Ъх ;
ах > 0;
ах > 1, если а > 1, х > 0;
ах* < а*2, если а> 1, х. < х?;
Л м
аХ1 > аХ2, если 0 < а < 1, хг < х2.
(2.3)
(2.4)
(2.5)
(2.6)
(2.7)
(2.8)
(2.9)
Функция вида у = ах, где основанием служит заданное число
а > 0, а 1, называется показательной функцией.
Область определения показательной функции — множество R
всех действительных чисел.
рис. 62 Рис. бз
ПО
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
Рис. 64
Рис. 65
Множество значений показательной функции — множество
всех положительных чисел у > 0.
Показательная функция у = ах является возрастающей при
а > 1 на множестве всех действительных чисел и убывающей при
0 < а < 1. Это следует из свойств (2.8—2.9).
Построим графики показательных функций у = 2х (рис. 62) и
Г1\х
у = Н (рис. 63) и перечислим их основные свойства.
✓
График функции у — 2х проходит через точку (0; 1) и располо-
жен выше оси Ох. Если х > 0 и возрастает, график быстро подни-
мается вверх; если х < 0 и убывает, график быстро приближается
к оси абсцисс, никогда не достигая нуля.
Г1\х
График функции у = I I также проходит через точку (0; 1).
Если х > 0 и возрастает, то график быстро приближается к оси
абсцисс, никогда не достигая нуля; если х < 0 и убывает, то гра-
фик быстро поднимается вверх.
Так же выглядят графики любых функций у = ах при а > 1
(рис. 64) и при 0 < а < 1 (рис. 65).
§ 17. Логарифмическая функция
1. Понятие о логарифме числа. Задача определения показателя сте-
пени х в простом соотношении 2х — 8 оказывается неразрешимой
с применением известных шести математических действий. Опре-
111
ЧАСТЬ I. Алгебра и начала анализа
Рис. 66
делив тем не менее, что х = 3, записать ре-
шение этой задачи с помощью известных
математических знаков невозможно.
Правда, эту задачу легко решить графи-
ческим способом нахождением точки пере-
сечения графиков у = 2х и у — 8 (рис. 66);
это точка (3; 8). Графический способ иног-
да позволяет решить задачу, неразреши-
мую с применением обычных математиче-
ских приемов.
В общем виде задача ах = N разрешима
только с введением нового математическо-
го действия. Это действие называется на-
хождением логарифма числа N по осно-
ванию а, что записывается таким образом:
loga N = х.
(2.10)
Логарифмом положительного числа N по основанию а (а > 0,
а * 1) называется показатель степени, в которую нужно воз-
вести число а, чтобы получить число N.
Например, 25 = 32, поэтому log? 32 = 5; 2 3 = 3, поэтому
log2 (1/8) = -3; 5° = 1, поэтому log5 1=0; 102 = 100, поэтому
log10 100 = 2; а1 = а (а > 0, а 1), поэтому loga а = 1.
Подставим в выражение ах = N в качестве х его представление
по (2.10). Тогда получим
(2.11)
Это равенство называется основным логарифмическим тож-
деством. Оно справедливо при N > 0, а > 0, 1. Например,
2log28 = 8; i/3logi/s7 = 7; a 31og«x = (alogflX )“3 = x~s.
2. Свойства логарифмов. Рассмотрим некоторые свойства логариф-
мов, используемые при выполнении различных преобразований
и решении уравнении.
Пусть а > 0, М > 0, N
любое действительное число,
тогда
log (MN) = log М + log АГ;
м
loga -ft = loga M - loga N;
(2.12)
(2.13)
112
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
loge Мп = п loga М; (2.14)
loga = 1 Iog0 М. (2.15)
По основному логарифмическому тождеству (2.11) имеем
а'°г“М = М, (2.16)
а1оеЛ=Лг. (2.17)
Перемножив равенства (2.16) и (2.17), получим
log „Л/ + logjv ЛЖ-АГ
а 6а ®а =MN,
из чего по определению логарифма находим loga (MN) = loga М +
+ loga N, т. e. выражение (2.12) доказано.
Разделив равенство (2.16) на (2.17), получим
logaM - k>gaN = М
а N 1
откуда по определению логарифма получим выражение (2.13).
Возведем основное логарифмическое тождество (2.11) в сте-
пень с показателем п, получим
ап1ое<^ = м",
из чего по определению логарифма получим выражение (2.14).
Наконец, (2.15) является частным случаем (2.14).
Отметим, что из условия log„ х — logrt у (а > 0, а # 1) следует,
что х = I/, т. е. если логарифмы двух чисел по одному и тому же
основанию равны, то равны и сами числа.
3. Логарифмирование. Действие нахождения логарифма числа на-
зывают логарифмированием. Если одночленное выражение со-
ставлено из положительных чисел с применением действий ум-
ножения, деления, возведения в степень и извлечения корня, то
логарифм такого выражения вычисляется с использованием фор-
мул (2.12—2.15).
Например, прологарифмируем по основанию 2 выражения
х. - 144 • 3 40 и х9 = а5(Ь2 4- 1)/(Ь3 + 4) при а > 0, b > 0.
1_
Имеем
log2 Xj = 4 log2 14 + | log2 40,
log2 x2 = 5 log2 a + Iog2 (b2 + 1) - log2 (b3 + 4).
113
ЧАСТЬ I. Алгебра и начала анализа
4. Потенцирование. Действие, обратное логарифмированию, назы-
вается потенцированием. Этим действием с использованием
формул (2.12—2.15) по логарифму выражения восстанавливает-
ся само выражение.
♦ ПРИМЕР
Определить хр х2 их3, если:
log3 xt = 3 log3 12 + 4 log3 26 - log3 19,
2 1
log2 X2 = 3 log2 12+2 log2 14,
log3 x3 — log3 a + 2 log3 (a + b) - log3 (a - b) (a > 0, b > 0, a > b).
РЕШЕНИЕ. Имеем:
log3 = log3
123 • 264
19
следовательно, хг =
123 • 264
19 ’
log9 x9 = logJ 122/3 • 141/2 L следовательно, x9 = 122/3 • 141/2;
. . a(a + b)2
log3 x3 = log3———
a — о
следовательно, x3 =
a(a + b)2
a — b
5. Десятичные и натуральные логарифмы. Десятичным логариф-
мом числа называется логарифм этого числа по основанию 10.
Такой логарифм записывается следующим образом:
lg а = log10 а.
Десятичные логарифмы чисел, составляющих некоторую сте-
пень числа 10, легко вычисляются, например,
10° = 1,
101= 10,
102 = 100,
10-1 = 0,1
1g 1 = о,
1g 10 = 1,
1g 100 = 2,
lg 0,1 = -1.
Логарифмы остальных чисел определяются либо с помощью
таблиц, имеющихся в различных справочниках, в частности, в
четырехзначных таблицах В. Брадиса (см. с. 38), либо с примене-
нием микрокалькуляторов. Например, по таблице находим, что
1g 124 = 2,093 — это означает, что 1О2,093 ~ 124.
Целая часть логарифма, в нашем примере число 2, называется
характеристикой, а дробная часть — мантиссой.
Натуральным логарифмом числа называется логарифм это-
го числа по основанию е, где е — иррациональное число, прибли-
114
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
женно равное 2,718. Логарифм числа по основанию е записывает-
ся следующим образом: In b = log. Ъ. Число е представляет собой
Ci--
сумму*:
Выведем соотношения, с помощью которых можно связать на-
туральные и десятичные логарифмы.
Пусть N = 10х, N = тогда х = 1g Nt у = In N. Очевидно, что
тогда 10х = еу. Прологарифмировав обе части этого равенства по
основанию 10, получим
х 1g 10 = у 1g е или х = у 1g е,
следовательно,
_ х
У ~ Ige ’
поэтому
lnN =
IgN
Ige *
По таблице логарифмов можно определить 1g е = 0,4343;
1
0,4343
= 2,303, следовательно,
In N = 2,303 1g N,
lg N = 0,4343 In N.
6. Логарифмические тождества. Выведем формулу перехода от лога-
рифма по одному основанию к логарифму по другому основанию
log. N = —Ц- log. N.
ьь logab &а
(2.18)
Запишем основное логарифмическое тождество N = bloSbN
Прологарифмируем это тождество по основанию а:
Используя свойства логарифма степени (2.14), получаем
из чего и следует (2.18).
* Более подробно о числе е будет сказано в § 43 п. 2.
115
ЧАСТЬ I. Алгебра и начала анализа
Формула (2.18) при а = 10 и а = е дает формулы перехода к де-
сятичным и натуральным логарифмам:
Множитель
logab
logd N =
log& N =
IgN.
Igb ’
InW
lnb *
(2.19)
(2.20)
в (2.18) называется модулем перевода от
системы логарифмов с основанием а к системе с основанием Ь.
В частном случае при N = а
. 1
log. а = 7-г ,
так как loga a = 1.
♦ ПРИМЕР
Вычислить: 1) Xj = log125 5; 2) х2 = log1/16(l/2).
РЕШЕНИЕ. По формуле (2.21) находим
- _ 1 _ - 1 = _L__ = л
1 log5125 3 ’Ж2 log1/2(l/16)
Докажем тождество
logftN=|log N (a>0, a;* l,fc^0, N>0).
и гС
Из основного логарифмического тождества (2.11)
, log bN
N = (ak) *k ,
(2.21)
(2.22)
иначе
fclog kN
aK
Прологарифмировав это равенство по основанию а, получим:
loga N = k loga* N loga a = k loga* N,
из чего и следует тождество (2.22).
Например, приведем log х к основанию 2. По (2.22):
10g х = log 1/2 X = 2 log2 х.
Любой логарифм можно представить в виде отношения двух
логарифмов, взятых по одному и тому же основанию, т. е.
116
ГЛАВА 2. Функции. Стеленная, показательная и логарифмическая функции
logoW = logfrN
logaM logbM
(a > 0, a * 1, b > 0, b * 1, N > 0, M > 0).
(2.23)
Из (2.18) следует, что
1 v = log«N =
logaM log^Af
что и требовалось доказать.
Докажем тождество
log, N = log mNm (a > 0, a * 1, N > 0).
(2.24)
Пусть log, N = n, тогда an = N; возведем это равенство в сте-
пень т:
(ап)т = Nm или (ат)п = Nm
откуда п = log mNm, из чего и следует (2.24).
cl
Например, log4 25 == log22 52 = log2 5.
7. Логарифмическая функция, ее график и основные свойства. Лога-
рифмической называется функция вида
у = log, X,
(2.25)
где а < 0, а # 1.
Логарифмическая функция у — log, х и показательная функ-
ция у = ах, где а > 0, а # 1, взаимно обратны. Решив уравнение
у = log, х относительно х, получим х = ау; поменяв местами х и у,
придем к показательной функции у = ах. Графики этих функций
при а = 2иа = 1/2 приведены на рисунках 67 и 68.
Рис. 67
Рис. 68
117
ЧАСТЬ I. Алгебра и начала анализа
А
у = loge х
а > 1
У = loga Х
0<а< 1
аг > а2
Рис. 69
Рис. 70
Область определения логарифмической функции — множест-
во всех положительных чисел.
Множество значений логарифмической функции — множест-
во R всех действительных чисел.
Логарифмическая функция у = loga х на промежутке х > 0 при
а > 1 монотонно возрастает и при 0 < а < 1 монотонно убывает.
Если а > 1, логарифмическая функция на промежутке 0 < х < 1
принимает отрицательные значения, а на промежутке х > 1 —
положительные значения.
Если О < а < 1, логарифмическая функция на промежутке
О < х < 1 принимает положительные значения, а на промежутке
х > 1 — отрицательные значения.
График любой логарифмической функции расположен правее
оси ординат и проходит через точку (1; 0).
На рисунке 69 приведены графики логарифмических функ-
ций с различными основаниями при основаниях а > 1, на рисун-
ке 70 — при основаниях а, лежащих в пределах 0 < а < 1.
♦ ПРИМЕР
Найти области определения функции: 1) у = log7 |х|; 2) у —
= log4 (х2 + х 4- 1); 3) у = log3 (х 4- 6) + log1/2(6 - х).
РЕШЕНИЕ. 1)х*0;
2) х2 4- х 4- 1 > 0, квадратное уравнение х2 4- х -г 1 = 0 действи-
тельных корней не имеет (см. § 10 п. 1), следовательно, х е R;
3) необходимо одновременное выполнение неравенств (х 4- 6) > 0
и (6 — х) > 0, следовательно, -6 < х < 6.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Приведите определения степенной, показательной и логарифмической
функций.
118
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
2. Приведите определение логарифма числа по данному основанию.
3. Как связаны между собой графики показательной и логарифмической
функций?
4. Укажите области определения и области изменения показательной и
логарифмической функций.
5. Перечислите основные свойства показательной функции при о > 1 и при
0<а<1.
6. Перечислите основные свойства логарифмической функции при а > 1 и
при 0< а< 1.
7. Сформулируйте основное логарифмическое тождество.
8. Перечислите основные свойства логарифмов.
9. Приведите доказательства логарифмических тождеств.
§ 18. Показательные уравнения.
Системы показательных уравнений
1. Показательные уравнения. Уравнение, содержащее переменную в
показателе степени, называется показательным.
При решении показательных уравнений вида
а/(«) = а<р(*) (д > о, а * 1)
используется следующее свойство:
= а<₽(*)) <=> (/(х) = ф(х)).
Преобразование показательного уравнения к виду af^ = аФ<х)
выполняется многими способами. Рассмотрим некоторые из них.
I. Способ уравнивания оснований. Проиллюстрируем его на
- 1 ч f * 1 2 А
примере следующих уравнении: 1) П-1ОК
1) Левую часть уравнения представим в виде
= 128; 2)2
, « .2х 2х 2х
(о,12б) =8 =(23 * * *) ,
правую — в виде 128 = 27. Тогда 3 • 2х = 7, х = 7/6;
пч 1
2) правую часть уравнения можно представить в виде (х_2);
й с(х-2) _ о(х-2) к(х-2)
умножая обе части уравнения на 5 , приходим к 2 *5 —
= 1, иначе, 10(х " 2) = 1, в то же время правую часть этого уравне-
ния можно представить в виде 1 = 10°, отсюда х - 2 = 0, х = 2.
119
ЧАСТЬ I. Алгебра и начала анализа
II. Логарифмирование обеих частей уравнения. Применение
основного логарифмического тождества. Решим следующие
уравнения: 1) 32х “3 = II1 -х; 2) 3х = 8.
1) Прологарифмировав обе части уравнения по основанию 10,
получим (32х "3 = II1 ’*) ((2х - 3) 1g 3 = (1 - х) 1g 11) ~ (2х 1g 3 -
- 3 1g 3 = lg 11 - х lg 11) ** (2x lg 3 + x lg 11 = lg 11 + 3 lg 3) «
[x(2 lg 3 + lg 11) = lg 11 + 3 lg 3 )<=> (x =
Igll + 31g3 \
21g3 + Igll /
2) Согласно основному логарифмическому тождеству (2.11)
имеем 8 = 310638, тогда (3х = 8) (3х = 310638 ) <=> х = log3 8.
К этому результату можно прийти, логарифмируя обе части
уравнения по основанию 3: (3х = 8) <=> (х log3 3 = log3 8) <=>
<=> х = (log38)/(log33). Из последнего выражения согласно тожде-
ству (2.23) следует х = (Ig8)/(lg3).
п а 0,903 ~ 1 on
С использованием таблиц получим х = х -т== ; х ~ 1,89.
III. Преобразование к квадратному уравнению. Решим урав-
1 95
нения: 1)5*+^ = 30; 2) 6 • 22* - 13 • 6* + 6 • З2* = 0.
1) Умножим все члены уравнения на 5х:
52х - 30 • 5х + 125 = 0.
Решив это уравнение относительно 5х, получим два корня:
Х1 х2
5 = 5, 5 = 25. Следовательно, хх = 1, х2 = 2;
2) преобразовав второй член уравнения, получим 6 • 22х —
- 13 *2Х* 3х 4- 6*32х = 0. Разделив все члены уравнения на 32х
(при этом 32х # 0), получим относительно переменной (2/3)х квад-
ратное уравнение 6 • (2/3)2х - 13 • (2/3)х + 6 = 0.
Решив это уравнение, получим
(2/3)х* = 2/3, (2/3)*2 = 3/2,
следовательно, хх = 1, х2 = — 1.
IV. Способ группировки. Проиллюстрируем этот способ на
примере решения уравнения
52х+1 + 7х + 1-175х-35 = 0.
Преобразуем это уравнение:
120
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
(5 • 25х 4- 7 • Iх - 25х • 7х - 35 = 0) ~ (25х(5 - 7х) - 7(5 - 7х) = О)
« ((5 - 7Х)(25Х - 7) = 0) (5 - 7*1 = О, 25*2 -7 = 0).
Следовательно, хг = log7 5, х2 = log25
2. Системы показательных уравнений. Решение систем показатель-
ных уравнений основано на свойствах показательной и логариф-
мической функций. При этом часто используются метод подста-
новки и алгебраическое сложение. Рассмотрим несколько приме-
ров решения систем показательных уравнений:
1) J 3х-5^ = 75,
1з*'-5х = 45;
2) J 4х* 5*, = 16,
1 2 • 3х = 18;
3) J 3х-3^ = 27,
I 3х + Зу = 12.
1) Перепишем данную систему в виде
Перемножив уравнения системы, получим
(3х + у • 5х + у = З3 • 53) <=> (15х + у = 153) « (х 4- у = 3).
Разделив первое уравнение на второе, получим:
(3* - «• 5" = З1 • 5) ® Г(3/5>*-к = З"1 • 5)=>
« ((3/5)* ’ » = (3/5)“1) « (х - у = -1).
Решение данной системы сводится к решению равносильной
ей системы
(х = 1, у~ 2).
2) Прологарифмировав каждое из уравнений, получим:
Из второго уравнения имеем: х 1g 3 = 2 1g 3, т. е. х = 2. Подставив
это значение х в первое уравнение, получим: 4 1g 2 4- у 1g 5 = 4 1g 2,
следовательно, у 1g 5 = 0, т. е. у = 0.
Таким образом, решением системы является (х = 2, у = 0).
Этим же способом можно было решить и предыдущую систему.
121
ЧАСТЬ I. Алгебра и начала анализа
3) Согласно свойствам корней квадратного уравнения (1.35),
3х и Зу служат корнями уравнения z2 - 12г + 27 — 0. Решив по-
следнее, находим Zj = 3; z2 = 9. Следовательно, 3х = 3, х = 1 и Зу = 9,
у = 2 и, наоборот, 3х = 9, х = 2 и Зу = 3, у = 1. Итак, получаем два
решения: (х} = 1, уг — 2), (х2 = 2, у2 = 1).
§ 19. Показательные неравенства
ГТ Г Г Чф1(х) Чф2<*) Л
Неравенства вида ах > с, ах < с, f(x) > f(x) , где а > О,
а 1, с > 0, называются простейшими показательными нера-
венствами.
Имеют место следующие равносильные преобразования, выте-
кающие из свойств возрастания или убывания показательной
функции:
: а > 1,
1 '
х > loga с;
| 0 < а < 1,
! 1 х < log с;
а > 1,
х < logo с;
0 < а < 1,
х > loga с;
(2.26)
(2.27)
-z <М*) ,,
f(x) > f(x)
> 1,
(рх(х) > Ф2(х),
0<ftx)<l,
<рг(х) < ф2(х).
(2.28)
♦ ПРИМЕР
Решить неравенство:
1) 3х > 4;
2) 6х2-7*+12> 1;
3)(х + 3)<х2-51 + 6>> 1.
РЕШЕНИЕ. 1) Применив преобразование (2.26), получим х > log3 4.
2) Представив правую часть неравенства в виде 1 = 6°, полу-
чим 6х2 - 7х +12 > go, 0ТСЮда х2 — 7х + 12 > 0. Следовательно, х < 3
или х > 4.
122
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
3) Представим правую часть нера-
венства в виде 1 = (х + 3)°. Тогда, со-
гласно (2.28), получим совокупность
двух систем:
Рис. 71
[х + 3> 1,
1 х2 - 5х + 6 > 0;
|0<х + 3< 1,
I х2 - 5х + 6 < О
Вторая из этих систем решения не имеет, а из первой следует
Решение (-2 < х < 2 или х > 3) проиллюстрировано схемой,
приведенной на рисунке 71.
§ 20. Логарифмические уравнения.
Системы логарифмических уравнений
1. Логарифмические уравнения. Уравнение, содержащее перемен-
ную под знаком логарифма или в основании логарифма, называ-
ется логарифмическим. Проиллюстрируем различные способы
решения таких уравнений с помощью следующих примеров:
1) log 16 - log 2 = 1/2.
logx(16/2) = 1/2,
< x > 0,
X 5е 1
[xV2 = 8,
Решением является x = 64.
2) lg (x - 3) + lg(x - 2) = 1 - lg 5.
Учитывая, что 1 = lg 10, потенцируем:
lg(x - 3) • (x - 2) = lg(10/5),
x > 3
+ 4 = 0,
Данной системе удовлетворяет единственное решение х = 4.
123
ЧАСТЬ I. Алгебра и начала анализа
3) 1g2 х + 1g х2 = 1g2 2 — 1.
Данное уравнение преобразуем к квадратному, решив которое
относительно переменной 1g х (по 1.32), получим:
1g2 х 4- 21g х + (1 - 1g2 2) = О,
х > О
Hg (2х) = -1,
|_lg (x/2) = —1,
x > 0
2x = IO1,
x/2 = 10-1.
Корнями исходного уравнения являются хг = 0,05 и х2 = 0,2.
4)xlgx= 100х.
Логарифмируя обе части уравнения по основанию 10 и решая
затем полученное квадратное уравнение, находим
1g х 1g х = 1g 100 + 1g x,
x > 0,
lg2 x - 1g x - 2 — 0,
0
~lgx = —1,
_lg x = 2,
x > 0,
x 1.
Исходному уравнению удовлетворяют корни хг == 0,1 и х2 = 100.
2. Системы логарифмических уравнений. Решение систем логариф-
мических уравнений основано на свойствах логарифмических
функций.
Решим для примера систему уравнений
log х - 31ogj/ = 2,
log2 х = 4 - log2y.
РЕШЕНИЕ. Здесь х > 0, у > 0. Имеем
log х - З/log х = 2,
У
log2 х = log2 16 - log2 у
[[log x = -l
^Llogyx = 3,
x = 16/y
J logjx - 2 log x - 3 = 0,
”1x=l6/{/
r _; I У
К ’ \x-16/y,
I* 16/г/ Дх =16/г/
нет решения,
f x = 8,
Решением исходного уравнения является (8; 2).
124
ГЛАВА 2. Функции. Степенная, показательная и логарифмическая функции
§ 21. Логарифмические неравенства
Неравенства вида loga х > с, loga х < с (а > 0, а # 1) называются
простейшими логарифмическими неравенствами.
При решении таких неравенств используют следующие преоб-
разования:
loga х > с
loga х < с
(2.29)
(2.30)
10g/(x) ф^Х) > log/(x) ф2(х)
Ф1(х) > О,
Ф2(х) > О,
/(X) > 1,
Ф1(х) > ф2(х),
0</(х)<1,
Ф1(х) < ф2(х).
(2.31)
Решим следующие неравенства: 1) log2 х > 36; 2) 2 +
+ log2 (х + 1) > 1 - log1/2 (4 - х2).
РЕШЕНИЕ. 1) Очевидно, что
(|log1/2x| > 6)
log1/2 х > 6,
log1/2x<-6.
Используя равносильные преобразования (2.29) и (2.30), полу-
чаем
log1/2x>6,
log1/2x<—6
0 < х < (1/2)6
х > (1/2)-6
0<х<(1/64),
х > 64.
Решение неравенства представлено схемой (рис. 72).
2) Имеем
log1/2 (4 - х2) =
log2(4 — X2) _ log2(4 — X2)
log 2( 1/2) “ -log22
-log2 (4 - x2).
125
ЧАСТЬ I. Алгебра и начала анализа
Рис. 72
Тогда, перенеся единицу в левую
часть неравенства, получим
1 4- log2 (х + 1) > log2 (4 — х2
(log
2 2(х 4-1) > log2 (4-х
2
Используя далее равносильные преобразования (2.31), придем
к системе
х 4-1 > О,
4 - х2 > О,
2(х4-1)>4-х2
х > -1,
х2 — 4 < О,
х2 4- 2х - 2 > О
>
нет решения,
ГЛАВА 3. Тригонометрические функции
§ 22. Радианное измерение дуг и углов
1. Радианная мера дуги и угла. Известна градусная мера измерения
ю 1
углов и дуг: 1° =
части длины окружности, 1° = 60', 1' = 60".
В дальнейшем будем применять еще одну единицу измерения
дуг и углов — радиан.
Длины дуг /х и 12 двух концентрических окружностей, соответ-
ствующих одному и тому же центральному углу, пропорциональ-
ны их радиусам Rx и R2 (рис. 73):
т. е. при одном и том же центральном угле отношение длины ду-
ги окружности к ее радиусу не зависит от длины радиуса. При из-
менении центрального угла величина этого отношения изменяет-
ся. Поэтому отношение 1/R может служить мерой дуги и соответ-
ствующего ей центрального угла.
126
ГЛАВА 3. Тригонометрические функции
Рис. 73
Рис. 74
Отношение длины дуги окружности I к длине ее радиуса R на-
зывается радианной мерой а этой дуги:
(3.1)
При радианном измерении дуг за единицу измерения прини-
мается дуга, длина которой равна радиусу этой дуги. Эта дуга на-
зывается радианом (рис. 74).
При радианном измерении углов за единицу принимается
центральный угол, опирающийся на дугу в один радиан. Такой
угол также называется радианом.
Число радиан в данной дуге (и в соответствующем ей цент-
ральном угле) является радианной мерой этой дуги (и соответст-
вующего ей центрального угла).
Из формулы (3.1) следует, что окружность имеет радианную
меру, равную 2п радиан
—= 2л.
Полуокружности соответствует п рад.
2. Формула перехода от градусного измерения к радианному. Пусть ду-
ге в а градусов соответствует дуга, равная а радиан, тогда из про-
порции
180°
получим формулу перехода от градусного измерения к радианному:
л
180 ’а’
(3.2)
127
ЧАСТЬ I. Алгебра и начала анализа
При а = 1° по формуле (3.2) получим радианную меру дуги
а = ds •г ~ °>0175
loU
Приведем таблицу зависимости между градусной и радианной
мерами для некоторых часто встречающихся дуг (углов):
Г радусы 30° 45° 60° 90° 180° 270° 360°
Радианы я/6 тс/4 тс/З тс/2 тс Зтс/2 2я
♦ ПРИМЕР
Найти радианную меру дуги, равной 210°.
РЕШЕНИЕ. По формуле (3.2) получаем а —
тс
180
• 210° =
3. Формула перехода от радианного измерения к градусному. Из форму-
лы (3.2), выражая дугу или угол а через а, получаем формулу пе-
рехода от радианного измерения к градусному:
180°
а = ----- *а.
тс
При а = 1 рад получим градусную меру одного радиана:
180°
• 1 = 57°17'44,"8 ~ 57,°3.
♦ ПРИМЕР
Найти градусную меру угла, равного 7я/4.
1 ЯЛ°
РЕШЕНИЕ. По формуле (3.3) получим а =------
7тс
= 315°.
4
4. Длина дуги окружности. По формуле (3.1) находим
l = a-R. (3.4)
I Длина дуги окружности равна радианной мере дуги, умножен-
| ной на радиус этой дуги.
При R = 1 длина дуги равна ее радианной мере. Это обсто-
ятельство делает радианную меру весьма удобной для вычисле-
ния длин дуг.
Ф ПРИМЕР
Колесо радиуса R — 0,35 м повернулось на угол а = 72°36'.
Найти длину пути, пройденного точкой на ободе колеса.
128
ГЛАВА 3. Тригонометрические функции
РЕШЕНИЕ. Так как значение радиуса колеса дано с двумя значащи-
ми цифрами, по таблице Брадиса (см. с. 38) находим радианную
меру 72°36', равную 1,27, с тремя значащими цифрами (одна
цифра запасная). По формуле (3.1) находим
I = 0,35 • 1,27 « 0,443 « 0,44 (м).
Формула для длины дуги, измеренной градусной мерой, имеет
более громоздкую форму
2nR _ nRa
360° *а- 180°
(3.5)
5. Площадь кругового сектора. Если центральный угол измеряется
градусной мерой, то площадь сектора определяется выражением:
_ 7TjR2(X
сект 360 •
(3.6)
Если центральный угол измеряется в радианах, то, подставив
в формулу (3.6) значение а из формулы (3.3), получим более
простую формулу для вычисления площади сектора:
q — . 160 п = — /q 71
5сект 360 П а 2aR *
♦ ПРИМЕР
Вычислить площадь сектора круга радиуса 0,76 м, если ради-
альная мера дуги сектора равна 1,12 рад.
РЕШЕНИЕ. По формуле (3.7) находим
1 19
^сект = ’ °»762 °»56 ‘ °’578 ~ °’324 °’32 (м2)‘
6. Линейная скорость при вращательном движении. Скорость любой
точки твердого тела во вращательном движении называется ли-
нейной скоростью.
Линейная скорость v при равномерном движении точки по ок-
ружности радиуса R выражается формулой
2nR
(3.8)
где Т — период вращения, т. е. время (в с), за которое совершает-
ся один полный оборот точки.
Зависимость линейной скорости v от радиуса R и числа оборо-
тов п, совершаемых точкой в 1 с, выражается формулой
v = 2nRn.
(3.9)
5 - 9664
129
ЧАСТЬ I. Алгебра и начала анализа
Число оборотов п и период вращения Т связаны соотношением
(ЗЛО)
♦ ПРИМЕР 1
Колесо, радиус которого равен 0,45 м, в минуту совершает при
равномерном вращении 120 оборотов. Найти линейную ско-
рость точки, находящейся на ободе колеса.
РЕШЕНИЕ. Число оборотов колеса в секунду равно п — 120/60 = 2.
По формуле (3.9) определяем линейную скорость точки на ободе
колеса: v = 2п • 0,45 • 2 = 1,8л (м/с).
♦ ПРИМЕР 2
Найти период вращения точки колеса, находящейся на рас-
стоянии 0,61 м от его центра и вращающейся равномерно с ли-
нейной скоростью v = 5,8 м/с.
РЕШЕНИЕ. Из (3.8) находим период вращения Т:
2nR _ 2л • 0,61
v ~ 5,8
= 0,65 (с).
7. Угловая скорость при вращательном движении. Угол, на который
поворачивается радиус любой точки равномерно вращающегося
твердого тела за 1 с, называется угловой скоростью. Угловая
скорость выражается в рад/с.
Угловая скорость со и период вращения Т связаны формулой
2л
<о= у
рад/с.
(3.11)
Через число оборотов в секунду п угловая скорость со выража-
ется как
со = 2пп.
(3.12)
Линейная скорость v точки, находящейся на расстоянии R от
оси вращения, и ее угловая скорость со связаны соотношением
v = соВ.
(3.13)
♦ ПРИМЕР 1
Найти угловую скорость и период вращения равномерно вра-
щающегося вала, делающего 540 оборотов в минуту.
130
ГЛАВА 3. Тригонометрические функции
РЕШЕНИЕ. Число оборотов в секунду составляет п = 540/60 = 9.
Подставляем это значение в (3.12):
со = 2пп - 2я • 9 = 18я рад/с.
По (3.10) получаем Т = 1/9 (с).
♦ ПРИМЕР 2
Найти угловую скорость равномерно вращающегося колеса с
радиусом 0,81 м, если линейная скорость точки на его окруж-
ности равна 324 м/с.
РЕШЕНИЕ. По формуле (3.13)
со = б = (ГБ7 = 400 (рад/с).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие величины принимаются за единицу при градусном и радианном
измерении дуг (углов)?
2. При решении каких задач удобнее применять радианное измерение дуг
(углов) по сравнению с градусным?
3. Выведите формулы перехода от градусного изменения к радианному и
от радианного к градусному.
4. Чему равна градусная мера дуги в 1 рад?
5. Чему равна радианная мера дуги в 1°?
6. По какой формуле вычисляется длина дуги, измеренная в радианах?
7. По какой формуле вычисляется площадь сектора, центральный угол ко-
торого измерен в радианах?
§ 23. Обобщение понятия дуги (угла)
1. Единичный круг и единичная окружность. В прямоугольной систе-
ме координат хОу построим круг с центром в начале координат и
с радиусом, равным 1. Будем называть этот круг единичным
кругом., а его окружность — единичной окружностью.
Точку пересечения А(1; О) единичной окружности с осью Ох
примем за начало отсчета дуг, а положительную полуось Ох — за
начальную сторону центрального угла, образуемого подвижным
—»
радиусом-вектором ОМ* с осью Ох (рис. 75).
* Радиусом-вектором называется вектор, направленный из начала
координат в произвольную точку плоскости.
131
ЧАСТЬ I. Алгебра и начала анализа
Рис.75
ук
Рис. 76
2. Положительные и отрицательные дуги и углы. Вращение ради-
—>
уса-вектора ОМ от положительной полуоси Ох против движения
часовой стрелки назовем положительным, а дугу \jAM = а, обра-
зуемую концом радиуса-вектора ОМ, и соответствующий этой
дуге центральный угол ААОМ — также положительными. Вра-
щение радиуса-вектора ОМ от положительной полуоси Ох по ча-
совой стрелке назовем отрицательным, а дугу \jAOMx, образуе-
мую концом радиуса-вектора ОМ, и соответствующий централь-
ный угол Z. АОМХ — отрицательными.
Если отсчет дуг вести против движения часовой стрелки, то
дуги равны иАВ = тс/2, \jABC = тс, kjABD = Зл/2 и иАВА = 2л. Ес-
ли отсчет дуг вести по часовой стрелке, то дуги <jAD = — тс/2,
uADC = -тс, <jADB — -Зтс/2 и uADA = -2тс.
Дуга, равная нулю (нулевая дуга), имеет совпадающие точки
А и М. Центральный угол равен нулю, если радиусы-векторы ОА
и ОМ совпадают.
3. Дуги и углы, ббльшие 2л (360°). Во многих задачах приходится
рассматривать вращения, большие полного оборота (например,
вращение колеса). Поэтому понятие дуги (угла) необходимо обоб-
щить: ввести дуги (углы), большие полного оборота (большие 2я).
—»
Пусть точка М (конец радиуса-вектора ОМ), вращаясь в положи-
тельном направлении от начала отсчета дуг — точки А, соверши-
ла один полный оборот, а затем описала дугу иАМ = о^ (рис. 76).
Тогда общая дуга а, которую описала точка М (угол, на который
132
ГЛАВА 3. Тригонометрические функции
Рис. 77
Рис. 78
—>
повернулся радиус-вектор ОМ), составляет а = 2л + ар где
О < eq < 2л (в градусной мере a = 360° + cQ.
Существует бесконечное множество дуг (углов), имеющих дан-
ное начало А и данный конец М (данные начальную и конечную
сторону угла).
Множество этих дуг (углов) как положительных, так и отри-
цательных можно выразить общей формулой
a = 0Cj + 2лА
(0 < 04 < 2л),
где k е Z (множеству целых чисел).
В градусном выражении (3.14) модифицируется в
a = 04 + 360° • k (0 < 04 < 360°).
(3.14)
(3.15)
♦ ПРИМЕР 1
Указать на единичной окружности точку М дуги \jAM = 5л.
РЕШЕНИЕ. По формуле (3.14) получим 5л = 2л *2 4- л. Конец дуги
и AM отмечен на рисунке 77.
♦ ПРИМЕР 2
Указать на единичной окружности точку, соответствующую
углу a == -770°.
РЕШЕНИЕ. По формуле (3.15) a = -(360° *2 + 50°). Соответствую-
щий угол изображен на рисунке 78.
♦ ПРИМЕРЗ
Выразить в общем виде дуги единичной окружности: 1) абс-
циссы концов которых равны нулю; 2) ординаты концов кото-
рых равны нулю.
133
ЧАСТЬ I. Алгебра и начала анализа
РЕШЕНИЕ. Концы дуг л/2 и Зл/2 имеют абсциссы, равные нулю,
следовательно, множество концов дуг с абсциссой, равной нулю,
выразится формулой л/2 + nk, keZ. Концы дуг Ойл имеют орди-
наты, равные нулю, следовательно, множество концов дуг с орди-
натой, равной нулю, соответствует itk, k е Z.
4. Единичная числовая окружность. Пусть каждому действительному
числу а на единичной окружности соответствует точка М(а) —
конец дуги \jAM, для которой kjAM имеет величину а.
Такую единичную окружность будем называть числовой еди-
ничной окружностью. Для числовой единичной окружности
должны быть заданы: начало отсчета А, положительное направ-
ление движения и единица измерения дуг — радиус этой окруж-
ности, равный единице.
Длина всей числовой единичной окружности равна 2л. Поэто-
му, если два числа отличаются друг от друга на целое, кратное
2л, то им на числовой единичной окружности будет соответство-
вать одна и та же точка. Если два числа соответствуют одной и
той же точке числовой единичной окружности, то их разность бу-
дет кратной 2л.
Установим соответствие между точками числовой оси и точка-
ми числовой единичной окружности. Каждому действительному
числу на числовой оси соответствует точка Р(а) (рис. 79), причем
каждой точке числовой оси соответствует одна и только одна точ-
ка числовой окружности. Это соответствие можно представить
«наматыванием» в положительном или отрицательном направле-
ниях числовой оси на числовую единичную окружность, причем
наматывание начинается от их общих нулевых точек (нуля на
числовой оси и точки А на числовой единичной окружности).
В то же время каждой точке числовой окружности на числовой
оси соответствует не одна, а бесконечное множество точек число-
вой оси, что можно установить качением числовой единичной ок-
Рис. 79
134
ГЛАВА 3. Тригонометрические функции
ружности (вправо или влево) по числовой оси, начав качение от
их совмещенных нулевых точек.
На рисунке 79 точки Мх и соответствуют углу, равному 1 рад.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение единичной окружности. Как записывается уравне-
ние единичной окружности?
2. Какие дуги в единичной окружности называются положительными (от-
рицательными)?
3. Как в общем виде обозначить множество положительных (отрицатель-
ных) дуг и углов?
4. Каким условиям должна удовлетворять единичная числовая окруж-
ность?
5. В чем заключается соответствие между точками числовой оси и точками
числовой единичной окружности, имеющими общие нулевые точки?
§ 24. Тригонометрические функции
числового аргумента
1. Определение тригонометрических функций числового аргумента. Об-
ласти их определения и значений. Каждому действительному числу
соответствует единственная точка М(а) на числовой единичной
окружности, и каждая точка М(а) этой окружности однозначно
определена ее абсциссой и орди-
натой, т. е. абсцисса и ордината
являются функциями числа а:
х = /(а) и у = ср (а), причем абсцис-
са и ордината по абсолютной ве-
личине не превышают единицы
(М < 1, |у| < 1)-
Абсцисса х точки М(а) число-
вой единичной окружности на-
зывается косинусом числа а
(рис. 80)*:
cos а = х. (3.16)
Рис. 80
* Начала тригонометрии с использованием единичного круга были
впервые изложены Леонардом Эйлером в 1747 г.
135
ЧАСТЬ I. Алгебра и начала анализа
Ордината у точки М(сс) числовой единичной окружности на-
зывается синусом числа а:
sin а = у.
(3.17)
Функции cos а и sin а определены для любого действительного
числа а, следовательно, область их определения: a е R.
Функции cos а и sin а ограничены, так как каждая из них мо-
жет принимать любое числовое значение, не превосходящее по
абсолютной величине единицы: |cos а| < 1 и |sin а| < 1, т. е. мно-
жеством значений функций sin а и cos а является промежуток
[-1; 1].
Отношение синуса числа а к его косинусу называется танген-
сом числа а:
. Sind /О ю\
tg а = ----. (3.18)
& cosa ' '
Следовательно, tg а есть отношение ординаты точки М(а) чис-
ловой единичной окружности к ее абсциссе.
Функция tg а не определена для тех значений аргумента а,
при которых cos а = 0 (абсцисса х равна нулю), т. е. тангенс не
определен для значений аргумента ±л/2, ±Зл/2, .... Множество
значений аргумента а, для которых cos а = О, выражается форму-
лой a = л/2 4- я/?, k е Z. Следовательно, область определения тан-
генса — все действительные числа, кроме чисел вида я/2 + я/г,
keZ.
Область изменения функции tg a — множество всех действи-
тельных чисел.
Рис. 81
В точке А(1; 0) числовой единич-
ной окружности (рис. 81) проведем
касательную, выбрав на ней поло-
жительное направление, одинако-
вое с положительным направлени-
ем оси Оу. За начало отсчета на этой
оси, которую назовем осью танген-
сов, примем точку А(1; 0).
Пусть точка М(а) — любая точка
числовой единичной окружности,
кроме точек (0; 1) и (0; —1), т. е. то-
чек, лежащих на оси Оу. Продол-
—>
жив радиус-вектор ОМ до пересече-
ния с осью тангенсов, получим на
136
ГЛАВА 3. Тригонометрические функции
ней точку N (если бы точка М(ос) лежала на оси ординат, это по-
строение нельзя было бы выполнить). Точка N лежит на оси тан-
генсов выше точки А, если точка М(а) лежит в первой или треть-
ей четвертях, и ниже А, если М(а) лежит во второй или четвертой
четвертях.
Из подобия треугольников ОММг и ONA следует взаимная
пропорциональность сторон:
Тангенс числа а равен ординате точки N (ординате точки пере-
сечения продолженного радиуса-вектора ОМ с осью тангенсов).
Таким образом, каждой точке М(а) числовой единичной окруж-
ности (за исключением точек (О; 1) и (О; -1)) соответствует точка
на оси тангенсов. Установленная зависимость наглядно показы-
вает, как при изменении числа М(а) изменяется ордината точки
N, т. е. изменяется величина тангенса.
Отношение косинуса числа а к его синусу называется котан-
генсом числа а:
ctg а =
cos а
sin а *
(3.19)
Следовательно, ctg а есть отношение абсциссы точки М(а)
числовой единичной окружности к ее ординате.
Функция ctg а не определена для тех значений аргумента, для
которых sin а = 0 (ордината у равна нулю), т. е. котангенс не оп-
ределен для значений аргумента 0, тс, 2тс, ... . Множество значе-
ний аргумента а, для которых sin а = 0, выражается формулой
а = тс/г, k е Z. Следовательно, об-
ласть определения котангенса —
все действительные числа, кроме
чисел вида тс/г, k е Z.
Область изменения функции
ctg а — множество всех действи-
тельных чисел.
В точке В(0; 1) числовой еди-
ничной окружности (рис. 82) про-
ведем касательную, выбрав на ней
положительное направление, оди-
наковое с положительным направ-
лением оси Ох. За начало отсчета
Рис. 82
137
ЧАСТЬ I. Алгебра и начала анализа
на этой оси, которую назовем осью котангенсов, примем точку
В. Пусть точка М(а) — любая точка числовой единичной окруж-
ности, кроме точек (1; 0) и (-1; 0), т. е. точек, лежащих на оси
—>
Ох. Продолжив радиус-вектор ОМ до пересечения с осью котан-
генсов, получим на этой оси точку Р (если точка М(а) лежит на
оси абсцисс, это построение выполнить нельзя). Точка Р лежит
на оси котангенсов правее точки В, если точка М(а) лежит в пер-
вой или третьей четвертях, и левее В, если М(а) лежит во второй
или четвертой четвертях.
Из подобия треугольников ОММг и ОВР следует:
Следовательно, каждой точке М(а) числовой единичной ок-
ружности за исключением точек (1; 0) и (-1; 0) соответствует точ-
ка на оси котангенсов. Эта зависимость наглядно показывает из-
менение величины котангенса с изменением М(а).
Определим еще две тригонометрических функции, использую-
щиеся значительно реже первых четырех.
Величина, обратная косинусу числа а, называется секансом
числа а:
sec а = ——. (3.20)
cosa v '
Функция sec а не определена, как и tg а, для значений аргу-
мента я/2 + nk, k е Z. Следовательно, область определения секан-
са — все действительные числа, кроме чисел вида л/2 + nk, k е Z.
Область изменения функции sec a — множество всех действи-
тельных чисел.
Величина, обратная синусу числа а, называется косекансом
числа а:
cosec а =
1
sina *
(3.21)
Функция cosec а не определена, как и ctg а, для значений ар-
гумента nk, ke Z. Следовательно, область определения косеканса —
все действительные числа, кроме чисел вида nk, kE Z.
Область изменения функции cosec a — множество всех дейст-
вительных чисел.
138
ГЛАВА 3. Тригонометрические функции
§ 25. Знаки, числовые значения и свойства
четности и нечетности
тригонометрических функций
1. Знаки тригонометрических функций. Из определений тригономет-
рических функций следует, что знаки косинуса и секанса совпа-
дают со знаком абсциссы точки М(а) числовой единичной окруж-
ности (рис. 83, а), а знаки синуса и косеканса — со знаком орди-
наты точки М(а) (рис. 83, б). Знаки тангенса и котангенса
находим по знакам синуса и косинуса одного и того же аргумента
(рис. 83, в).
2. Вычисление числовых значений тригонометрических функций для
значений аргументов: 0, л/2, я, Зл/2,2л. Из определения тригономет-
рических функций следует:
1) cos О = 1, sin О = О, tg О = - О,
cosO 1
ctgO =
cos О
sin О
не определен;
О
к л • к 1 х 71 соз(л/2) _ О _ л
2) cos 0, sm 2 1, ctg 2 sin(7l/2) 1 °»
sin(x/2)
cos(x/2)
не определен;
О
- л . sinit О
cos л = -1, sm я = О, tg л =--------- = —т
” cos л -1
cos л -1
sinx = ~0 не опРеДелен
Рис. 83
139
ЧАСТЬ I. Алгебра и начала анализа
.ч Зп „ . Зл 1 х го /оч cos (3 л/2) О Л
4) cos 2 0, sin 2 l,ctg(3n/2) sin(3K/2) -1
tg (Зл/2) =
sin(3Tt/2)
cos(3ft/2)
не определен;
О
5) cos 2л = 1, sin 2л = 0, tg 2л =
sin 2 л
cos 2 л
О
1
cos 2 л 1
= б не определен.
3. Вычисление числовых значений тригонометрических функций для
аргументов л/6, л/4 и л/3. На числовой единичной окружности по-
строим дугу иАМ = л/6 (рис. 84, а). Проекцию точки М на ось
Ох обозначим через Мх. В треугольнике МХОМ угол /- МХОМ =
= л/6, гипотенуза ОМ — 1, катет МХМ = 1/2 (свойство катета, ле-
жащего против угла, равного л/6).
По теореме Пифагора катет ОМХ —
71 - (1/2)2 = ТЗ/2. Из
определения тригонометрических функций получим
cos (л/6) = а/З /2, sin (л/6) — 1/2,
tg (л/6) = 1/7з = 73 /3, ctg (л/6) = Уз.
На числовой единичной окружности построим дугу иАМ = к/4
(рис. 84, б). Проекцию точки М на ось Ох обозначим через Мх.
В треугольнике МХОМ угол Z. МХОМ = л/4, гипотенуза ОМ = 1,
катет ОМХ = МХМ.
По теореме Пифагора 2(ОМХ)2 = 1, следовательно, ОМХ = ММХ =
= л/2 /2. Из определения тригонометрических функций получим
Рис. 84
140
ГЛАВА 3. Тригонометрические функции
cos (л/4) = л/2 /2, sin (л/4) = J2 /2,
tg (я/4) = 1, ctg (л/4) = 1.
На числовой единичной окружности построим дугу иАМ = л/3
(рис. 84, в). Проекцию точки М на ось Ох обозначим через Мг
В треугольнике М^ОМ угол Z. МХОМ = л/3, гипотенуза ОМ = 1,
катет ОМХ — 1/2 (свойство катета, лежащего против угла, равно-
го л/6). По теореме Пифагора катет М.М = J1 - (1/2)2 = J3 /2.
По определению тригонометрических функций получим
cos (л/3) = 1/2, sin (л/3) = а/З /2,
tg (л/3) = ,/3, ctg (л/3) = 7з /3.
В таблице 2 приведены значения основных тригонометрических
функций для наиболее часто встречающихся значений аргумента.
Таблица 2
а° 0° 30° 1 45° 60° 90° 180° > 1 270° 360°
а, рад 0 я 6 0,5236 п 4 0,7854 л 3 1,0472 л 2 я Зл 2 2л
sin а 0 1 2 0,5000 J2 2 0,7071 Л 2 0,8660 1 0 -1 0
cos а 1 Л 2 0,8660 72 2 0,7071 1 2 0,5000 0 -1 0 1
tga 0 а/3 3 0,5773 1 1,0000 а/3 1,7320 не су- щест- вует 0 не су- щест- вует 0
ctg а не су- щест- вует 7з _- 1,7320 1 1 1,0000 1 а/3 3 0,5773 0 не су- щест- вует 0 не су- щест- вует
4. Свойства четности и нечетности тригонометрических функций. Свой-
ства четности и нечетности функций были рассмотрены в § 14,
п. 2. Исследуем на четность тригонометрические функции.
На числовой единичной окружности построим точки Мг и М2
(рис. 85), полученные поворотом точки А(1; 0) на углы а и -а со-
ответственно. Эти точки симметричны относительно оси Ох. Точ-
141
ЧАСТЬ I. Алгебра и начала анализа
Рис. 85
ки М j и М2 имеют одну и ту же абс-
циссу и равные по абсолютной вели-
чине, но противоположные по знаку
ординаты. По определению тригоно-
метрических функций эта абсцисса
является косинусом, а ординаты —
синусами соответствующих углов.
Следовательно,
cos (-а) — cos а,
sin (-а) = -sin а,
(3.22)
(3.23)
т. е. косинус является четной функ-
цией, а синус — нечетной.
Легко показать, что тангенс и котангенс представляют собой
нечетные функции:
tg (-а) =
sin (-а)
cos (-а)
-sina
cos а
-tga,
таким образом,
tg (—а) = -tg а, а # л/2 + life, k е Z.
Аналогично
ctg (-а) =
cos (-а) _ cos а
sin(-a) -sina
-ctg а,
и соответственно
ctg (—а) = -ctg а, а # nkt keZ.
(3.24)
(3.25)
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определения тригонометрических функций числового аргумента
и укажите области их определения.
2. Какие тригонометрические функции являются ограниченными и какие —
неограниченными?
3. Как определяются знаки тригонометрических функций по четвертям?
4. Как найти числовые значения тригонометрических функций для значе-
ний аргумента 0, л/2, л, Зл/2,2л?
5. Вычислите числовые значения тригонометрических функций для значе-
ний аргумента л/6, л/4 и л/3.
6. Какие тригонометрические функции являются четными и какие — не-
четными? Почему?
142
ГЛАВА 3. Тригонометрические функции
§ 26. Изменение тригонометрических функций
при возрастании аргумента от 0 до 2л
1. Изменение косинуса и синуса. Изменение функций cos а и sin а
при возрастании аргумента а от 0 до 2л легко проследить по изме-
нению абсциссы и ординаты движущейся точки М(а) по единич-
ной числовой окружности в положительном направлении от точ-
ки А(1; 0) (рис. 80).
2. Изменение тангенса. Для значений аргумента а < л/2, близких к
л/2, значения функции tg а положительны и неограниченно воз-
растают.
Неограниченность возрастания tg а при а —> л/2 (а < л/2) мож-
но проследить по изменению ординаты точки N (рис. 81). При
а л/2 ордината точки N может превзойти по величине любое
сколь угодно большое наперед заданное положительное число,
следовательно, tg а —* +оо при а —* л/2 (а < л/2).
Во второй четверти функция tg а принимает отрицательные
значения, и при возрастании аргумента а в промежутке (л/2; л]
ее значения возрастают от — оо до 0.
При изменении аргумента а в III и IV четвертях функция tg а
изменяется так же, как в I и II четвертях соответственно.
3. Изменение котангенса. Для значений аргумента а > 0, близких
к нулю, значения функции ctg а неограниченно возрастают и по-
ложительны. Следовательно, в промежутке 0 < а < л/2 функция
ctg а убывает от +оо до 0.
Убывание котангенса можно проследить по изменению абс-
циссы точки Р (рис. 82) при а —► 0 в промежутке (0; л/2]. Для зна-
чений а, близких к нулю, абсцисса точки Р может превзойти по
величине любое сколь угодно большое наперед заданное положи-
тельное число, следовательно, при а —► 0 в промежутке (0; л/2]
значение ctg а —► +оо.
Во II четверти функция ctg а принимает отрицательные значе-
ния и при возрастании аргумента а в промежутке [л/2; л) функ-
ция ctg а убывает от 0 до - оо.
При изменении аргумента а в III и IV четвертях функция ctg а
изменяется так же, как в I и II четвертях соответственно.
4. Изменение секанса и косеканса. Из определения функций sec а
(3.20) и cosec а (3.21) следует, что знаки их совпадают со знаками
функций cos а и sin а соответственно, а также, что одновременно
с убыванием и возрастанием функций cos а соответственно воз-
143
ЧАСТЬ I. Алгебра и начала анализа
растает и убывает функция sec а, и одновременно с возрастанием
и убыванием функции sin а соответственно убывает и возрастает
функция cosec а.
Изменение тригонометрических функций по знаку и величи-
не по четвертям тригонометрического круга представлено в таб-
лице 3.
Таблица 3
Функция 0 I четверть 90° 1 II четверть 180° III четверть 270° IV четверть 360° 1
sin а 0 возрастает +1 убывает 0 убывает ' -1 возрастает 0
cos а +1 убывает 0 убывает ___ возрастает 0 возрастает +1
tga 0 возрастает ”^”00 возрастает 0 возрастает возрастает 0
ctg а Too убывает 0 убывает 4.00 убывает 0 убывает Too
sec а +1 возрастает ^Ноо возрастает -1 убывает 4^00 убывает +1
cosec а Too убывает возрастает Too > возрастает -1 убывает q=oo
§ 27. Основные тригонометрические тождества
Если две тригонометрические функции от одних и тех же ар-
гументов имеют одну и ту же область определения и принимают
равные значения при всех допустимых значениях аргументов, то
они называются тождественно равными. Равенство, справед-
ливое при всех допустимых значениях аргументов, называются
тождеством.
1. Основное тригонометрические тождество. Сумма квадратов синуса
и косинуса одного и того же аргумента равна единице:
sin2 а + cos2 а « 1. I (3.22)
144
ГЛАВА 3. Тригонометрические функции
Пусть точка 7И(х; у) единич-
ной окружности (рис. 86) полу-
чена поворотом точки А на про-
извольный угол а. Тогда по оп-
ределению функций sin а и cos а
ее (точки М) координаты: х =
= cos а и у = sin а. Поскольку
точка М принадлежит единич-
ной окружности, ее координаты
удовлетворяют уравнению х2 +
4- у2 = 1, из чего и следует тож-
дество (3.22).
Рис. 86
2. Зависимость между тангенсом и котангенсом. По определению tg а =
sina
cos а
и ctg а =
cos а
sina
. Перемножив эти выражения, получим
tg а • ctg а = 1, а * itk/2, ke Z.
(3.23)
Из (3.23) следует:
ctga
а rcfe/2, ke Z,
1
ctg a = г—
6 tga
а Ф rcfe/2, k e Z,
(3.24)
(3.25)
3. Зависимость между тангенсом и косинусом. Разделив обе части ра-
венства (3.22) на cos2 а, получим
1 4- tg2 a =
—5“, a * s + я&, k g Z.
cosza
(3.26)
4. Зависимость между котангенсом и синусом. Разделив обе части ра-
венства (3.22) на sin2 а, получим
1 4- ctg2 a =
sin2 a
(3.27)
5. Доказательство тригонометрических тождеств. При доказательстве
тригонометрических тождеств возможно использование следую-
щих приемов: преобразование обеих частей тождества к одному и
тому же выражению, преобразование левой части к правой и пра-
вой к левой, доказательство того обстоятельства, что разность
между правой и левой частями равна нулю.
Докажем тождество
1 — cosa
sina
sina
1 + cosa ’
(3.28)
a rc.fe, k e Z.
145
ЧАСТЬ I. Алгебра и начала анализа
Умножим числитель и знаменатель левой части тождества на
(1 + cos а):
(1 — cosa)(l + cosa)
sina(l + cosa)
1 — cos2a
sina(l + cosa)
sin2 a
sin(l + cosa)
sing
1 + cosa
Тождество доказано. При преобразованиях использовано ос-
новное тригонометрическое тождество (3.22).
Для доказательства тождества (3.28) можно также использо-
вать свойство пропорции: (1 — cos a)(l 4- cos a) = sin2 a <=> 1 - cos2 a =
= sin2 a <=> sin2 a = sin2 a.
Тождество доказано.
§ 28. Выражение тригонометрических функций
через другие тригонометрические функции
С использованием основных тригонометрических тождеств и
следствий из них можно одну тригонометрическую функцию вы-
разить через любую другую тригонометрическую функцию от то-
го же аргумента.
1. Выражение тригонометрических функций через синус. Из тождества
(3.22) имеем: cos a = ±71 ~ sin2a. В формулах, содержащих ра-
дикалы, знак «+» или «-» ставится в зависимости от того, какой
четверти принадлежит аргумент а.
Подставив это выражение cos а в выражения (3.18) и (3.19),
определяющие функции tg а и ctg а, получим:
tga =
sin a
±71 — sin2a
7C
a # x + л/г, k e Z;
ctg a =
±л/1 — sin2a
sin a
a * л/г, k e Z.
♦ ПРИМЕР
Вычислить значения cos a, tg a и ctg a, если sin a = -4/5,
л < a < Зл/2.
РЕШЕНИЕ, cos a = - 71 - (~4/5)2 = - | ; tg a = -4~
Э <5/ D
1 3
tga 4 ’
146
ГЛАВА 3. Тригонометрические функции
2. Выражение тригонометрических функций через косинус. Из тожде-
ства (3.22) имеем sin а = ±71 ~ cos2a. Подставив это выражение
для sin а в (3.18) и (3.19), получим:
. ±71 — cos2a , п , , , „
tg a =-------------, а и + к/г, k е Z;
ь cosa 2
ctga =
±71 ~ sin2a
sin а
а * л/г, ke Z.
♦ ПРИМЕР
Вычислить значения sin а,
л < а < Зл/2.
tg а и ctg а, если cos а = -4/5,
РЕШЕНИЕ, sin а =
1 4
ctga = -— = 3.
& tga 3
3. Выражение тригонометрических функций через тангенс. Из тожде-
ства (3.26) получим cos2 a =
+ nk, ke Z. Отсюда
cos a = —------------ , a л/2 + л/г, ke Z.
±71 + tg2a
По определению функции tg a имеем sin a = tg a • cos a, a
* л/2 + л/г, k e Z. Подставив сюда найденное выражение для
cos а, получим
sin a = -г === -, aл + nk, ke Z.
71 +tg2a
По формуле (3.25) имеем
ctga=t^
a $ /г, k e Z.
♦ ПРИМЕР
Вычислить значения sin a, cos a и ctg a, если tg a = — 73,
л/2 < a < л.
РЕШЕНИЕ. Имеем: ctg a = -
7з
sin a
cos a =
147
ЧАСТЬ I. Алгебра и начала анализа
4. Выражение тригонометрических функций через котангенс. Из тож-
дества (3.27) получим sin2 а =---—-, а nk, k е Z, поэтому
1 + ctg2a
sin а =
По определению функции ctg а имеем cos а = ctg a*sin а,
а # nk, keZ.
Подставив сюда найденное выражение для sin а, получим
cos a =
ctga
a & nk, keZ.
По формуле (3.24)
1
tg a = -г—
ctga
♦ ПРИМЕР
Вычислить значения sin a, cos a и tg a, если ctg a = 73 /3,
л < a < Зл/2.
РЕШЕНИЕ, tg a = 3/7з = J3 ; sin a = . Л;/.- = - 73 /2; cos a =
-71 + 1/3
=: . 1 = _ 1
3 -7i +1/3 2
В таблице 4 приведены выражения основных тригонометриче-
ских функций через другие тригонометрические функции.
Таблица 4
sin a cos a tga ctg a
sin a sin a ±71 _ sin2a sing ±71 “ sin2 a ±71 - sin2a sina
cosa ±71 — cos2a cos a ±71 ~ cos2 a cosa cosa ±71 _ cos2a
tga tga 1 tga _1_ tga
±71 + tg2a ±71 + tg2a
ctg a 1 ctga ctga ctg a
±71 + ctg2a ±71 + ctg2a
148
ГЛАВА 3. Тригонометрические функции
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Как изменяются основные тригонометрические функции с возрастани-
ем аргумента от 0 до 2л (по четвертям)?
2. Какие тригонометрические выражения называются тождественно рав-
ными?
3. Докажите основные тригонометрические тождества. При каких допус-
тимых значениях аргумента тождества справедливы?
4. Выразите тригонометрические функции через синус, косинус, тангенс и
котангенс соответственно.
§ 29. Периодичность тригонометрических функций
Функция /(а) называется периодической, если существует по-
ложительное число X О, называемое периодом, такое, что ра-
венство /(а ± X) = /(а) удовлетворяется при любом допустимом
значении аргумента а.
Периодами являются также числа вида па, п е Z, п 0. На-
именьший положительный период для функций sin а и cos а ра-
вен 2л, а для функций tg а и ctg а равен л.
Свойство периодичности тригонометрических функций при
k е Z выражается тождествами:
cos а = cos (а + 2nk);
sin а = sin (а + 2nk);
tg а = tg (а + nk);
ctg а = ctg (а + itk).
(3.29)
(3.30)
(3.31)
(3.32)
Докажем справедливость формулы (3.29) методом от против-
ного. Для этого докажем, что 2л — основной (наименьший поло-
жительный) период для функции cos а. Покажем, что не сущест-
вует такого положительного числа X (0 < X < 2л), для которого ра-
венство (3.29) было бы верным для всех допустимых значений а.
Допустим, что периодом функции cos а является число X
(0 < X < 2л), т. е. cos (а + X) = cos а. Положим а = О, тогда
cos (0 + X) = cos 0 = 1, но cos X = 1 только в точке А(1; 0) числовой
единичной окружности (рис. 85), для которой X = 2л/г. Но дуга,
измеряющаяся числом 0 < X < 2л, не оканчивается в точке
А(1; 0), а потому косинус соответствующего угла не равен 1. По-
лученное противоречие показывает, что не существует положи-
тельного числа 0 < X < 2л, для которого было бы справедливо ра-
венство cos (а + X) = cos а.
149
ЧАСТЬ I. Алгебра и начала анализа
Наименьшим положительным значением X является число 2л,
так как X = О, ±2л, ±4л,... для cos X = 1, из чего следует, что cos а —
периодическая функция с периодом, равным 2л.
Таким же образом доказывается справедливость равенств
(3.30—3.32).
♦ ПРИМЕР 1
Вычислить: 1) 2 cos (4,5л) + sin (19л/3); 2) sin (-300°) -
-tg (-150°).
РЕШЕНИЕ. 1) На основании свойств периодичности тригонометри-
ческих функций:
2 cos (2л • 2 4- 0,5л) 4- sin (2л • 3 + л/3) = 2 cos 0,5л 4- sin (л/3) =
= 0 + Тз/2 = Тз/2.
2) Прибавив по одному периоду к каждому из аргументов, по-
лучим:
sin (-300° 4- 360°) - tg (-150° + 180°) = sin 60° - tg 30° =
= Тз/2- 7з/з = 7з/б.
♦ ПРИМЕР 2
Найти период функции: 1) ух = cos х/2; 2) у2 = sin 2х 4- cos Зх;
3) у3 = sin (Зх/2) 4- sin (2х/3).
РЕШЕНИЕ. 1) Обозначим искомый период через X, тогда получим:
cos (х 4- 4- Х)/2 = cos х/2, или cos (х/2 4- X/2) = cos (х/2), следова-
тельно, Х/2 — 2л, т. е. X = 4л.
2) Найдем период каждого из слагаемых:
sin 2(х 4- Xj) = sin 2х, 2Xj = 2л, Xj = л;
cos 3(х 4- Х2) = cos Зх, ЗХ2 = 2л, Х2 = 2л/3.
Каждое число, кратное периоду, само является периодом, по-
этому общее кратное чисел Xj и Х2 является периодом функции у2.
Наименьшее общее кратное чисел л и 2л/3, равное наименьшему
общему кратному числителей периодов Xj и Х2, составляет 2л.
3)
Имеем sin
ЗХ!
~2~
sin
. 2х
sm -Х-; sm
О
3
2Х2
= sin
2х 2Х2
Т,-з”
= 2л, Х2 = Зл.
150
ГЛАВА 3. Тригонометрические функции
Наименьшее общее кратное числителей периодов Хх и Х2 равно
12л, следовательно, период функции у3 равен 12л.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение периодической функции.
2. Являются ли числа, кратные наименьшему периоду, периодами функ-
ции?
3. Какие числа являются периодами функций синуса и косинуса?
4. Какие числа являются периодами функций тангенса и котангенса?
5. Приведите примеры вычисления периодов тригонометрических функ-
ций.
§ 30. Формулы приведения
Формулы приведения позволяют привести тригонометриче-
ские функции углов (л/2)/г ± a, k с Z к тригонометрическим
функциям угла а.
1. Свойство полупериода косинуса и синуса. На числовой единичной
окружности отметим произвольную точку М и точку N такую,
что <jMN = л (рис. 87). Точки М nN симметричны относительно
начала координат. Поэтому соответствующие координаты этих
точек равны по абсолютной величине и противоположны по зна-
ку. Точке М соответствуют координаты (—х; у), точке N — коор-
динаты (х; -у). Следовательно,
cos а = —cos (а ± л);
sin а = —sin (а ± л).
(3.33)
(3.34)
Функции косинуса и синуса при
увеличении или уменьшении аргу-
мента на л изменяются только по зна-
ку.
♦ ПРИМЕР
Вычислить: 1) /х = sin (5л/6);
2) f2 = cos (5л/4); 3) f3 = cos (-210°).
РЕШЕНИЕ. Используя формулы (3.33—
3.34), получим:
1) = -sin (5л/6 - л) = -sin (-л/6) =
Рис. 87
= sin (1/2)= 1/2;
151
ЧАСТЬ I. Алгебра и начала анализа
2) f2 — —cos (5л/4 — л) = —cos (л/4) = - 7з /2;
3) f3 = -cos (-210° + 180°) = -cos (-30°) - -cos 30° = - 7з /2.
2. Тригонометрические функции взаимно дополнительных аргументов.
Два аргумента, в сумме составляющие л/2, называются взаимно
дополнительными. Такими являются, например, л/6 и л/3 или
2л/3 и -л/6.
Рис. 88
Числовая единичная окруж-
ность симметрична относитель-
но прямой у = х (биссектри-
сы I и III координатных уг-
лов). Пусть дуги иАМ = ос и
(jBN = -а (рис. 88), тогда точ-
ки М и N симметричны отно-
сительно прямой у = х. При
отражении в прямой у = х оси
меняются местами: ось абсцисс
переходит в ось ординат и наобо-
рот.
Сравнивая координаты точек
M(cos a; sin а) и 2V(cos (л/2 - а); sin (л/2 - а)), замечаем, что абс-
цисса точки N равна ординате точки М и, наоборот, ордината
точки N равна абсциссе точки М, из чего следует:
sin (л/2 - а) = cos а;
cos (л/2 - а) = sin а.
(3.35)
(3.36)
Таким образом, выявлена зависимость между синусом и коси-
нусом взаимно дополнительных аргументов. Применив формулы
(3.35—3.36), установим зависимости между тангенсом и котан-
генсом взаимно дополнительных аргументов:
, , ,л . sin(n/2 - а)
tg (л/2 - а) = ——---------*
сов(л/2 — а)
cosa
sin а
= ctg а,
tg (л/2 - а) = ctg а, а * лй, k е Z. (3.37)
Аналогично
ctg (л/2 - а) - cos(,I/2 ~ а)
sin(K/2 — а)
sin а
cosa
= tga
ctg (я/2 — а) = tg а, а * л/2 + л/г, k € Z. (3.38)
152
ГЛАВА 3. Тригонометрические функции
Формулы тригонометрических функций взаимно дополни-
тельных аргументов обычно применяются для приведения триго-
нометрических функций к положительному аргументу, меньше-
му л/4 (45°).
♦ ПРИМЕР
Вычислить: 1) f1 = sin (2л/3); 2) f2 = cos (5л/6).
РЕШЕНИЕ. 1) = sin (л/2 - (-л/6)) = cos (-л/6) = cos (л/6) = J3 /2;
2) f2 = cos (л/2 - (-л/3)) = sin (-л/3) = -sin (л/3) = - л/3 /2.
3. Тригонометрические функции аргумента (л/2 +а). Докажем тождества:
sin (л/2 + а) = cos а;
cos (л/2 + а) = —sin а;
tg (я/2 + а) = —ctg а;
ctg (л/2 а) = —tg а.
(3.39)
(3.40)
(3.41)
(3.42)
Для доказательства тождеств (3.39—3.42) в тождествах
(3.35—3.38) заменим аргумент (а) на аргумент (-а) и, применяя
свойства четности и нечетности, получим, например,
sin (л/2 - (-а)) = cos (-а) = cos а,
т. е. (3.39). Так же доказываются тождества (3.40—3.42).
♦ ПРИМЕР
Вычислить: 1) /х = sin 150°; 2) f2 = ctg (2л/3).
РЕШЕНИЕ. 1) fx = sin (90° + 60°) = cos 60° = 1/2;
2) f2 = ctg (л/2 + л/6) = -tg (л/6) = - 73 /3.
4. Тригонометрические функции аргумента (л - а). Докажем тождества:
sin (л — а) = sin а;
cos (л — а) = —cos а;
tg (л - а) = -tg а;
ctg (л — а) = —ctg а.
(3.43)
(3.44)
(3.45)
(3.46)
Для доказательства тождеств (3.43—3.44) в тождествах
(3.33—3.34) заменим аргумент (а) на аргумент (-а) и, применив
свойства четности и нечетности, получим, в частности,
sin (л + (-а)) = -sin (-а) = sin а,
т. е. тождество (3.43).
Аналогично доказывается тождество (3.44).
153
ЧАСТЬ I. Алгебра и начала анализа
Свойства (3.45—3.46) можно доказать, применив свойство пе-
риодичности тангенса и котангенса и свойства их нечетности.
♦ ПРИМЕР
Вычислить: 1) Д = cos 150°; 2) f9 = tg 120°.
* х
РЕШЕНИЕ. 1) /, - cos (180° - 30°) = -cos 30° = - 73 /2;
2) f2 = tg (180° - 60°) = -tg 60° - - J3 .
5. Тригонометрические функции аргумента (те + а). Докажем тождества:
sin (те + а) = —sin а;
cos (те + а) = —cos а;
tg (те + а) - tg а;
ctg (те + а) = ctg а.
(3.47)
(3.48)
(3.49)
(3.50)
Тождества (3.47—3.48) являются видоизмененными тождест-
вами (3.33—3.34), а тождества (3.49—3.50) являются формулами
периодичности тангенса и котангенса.
♦ ПРИМЕРЫ
Вычислить: 1) Д = sin 225°; 2) f2 = ctg 240°.
РЕШЕНИЕ. 1) Д = sin (180° + 45°) = -sin 45° = - J2 /2;
2) Д = ctg 60° = Уз /3.
6. Тригонометрические функции аргумента (Зте/2 - а). Докажем тож-
дества:
sin (Зте/2 — а) = —cos а;
cos (Зте/2 — а) — —sin а;
tg (Зте/2 — а) = ctg а;
ctg (Зте/2 — а) = tg а.
(3.51)
(3.52)
(3.53)
(3.54)
Тождества (3.51) и (3.53) можно доказать следующим образом:
sin (Зте/2 - а) = sin (те + (те/2 - а)) = -sin (те/2 - а) = -cos а,
tg (Зте/2 - а) = tg (те/2 - а) = ctg а.
Тождества (3.52) и (3.54) доказываются аналогично.
♦ ПРИМЕР
Вычислить: 1) Д = sin 600°; 2) f2 = cos 225°.
РЕШЕНИЕ. 1) Д = sin 240° = sin (270° - 30°) = -cos 30° = - J3 /2;
2) Д - cos (270° - 45°) = -sin 45° = - J2 /2.
154
ГЛАВА 3. Тригонометрические функции
7. Тригонометрические функции аргумента (Зл/2 + а). Докажем тож-
дества:
sin (Зл/2 + а) — —cos а;
cos (Зл/2 + а) = sin а;
tg (Зл/2 + а) = —ctg а;
ctg (Зл/2 + а) = —tg а.
(3.55)
(3.56)
(3.57)
(3.58)
Заменив в тождествах (3.51—3.54) аргумент (а) на аргумент
(-а) и применив свойства четности и нечетности, получим тожде-
ства (3.55—3.58).
♦ ПРИМЕР
Вычислить: 1) fx = sin 330°; 2) f2 = cos 315°.
РЕШЕНИЕ. l)ft = sin (270° + 60°) = -cos 60° = -1/2;
2) f2 = cos (270° + 45°) - sin 45° = 72 /2.
8. Тригонометрические функции аргумента (2л - а). Докажем тожде-
ства:
sin (2л — а) = —sin а; (3.59)
cos (2л — а) = cos а; (3.60)
tg (2л — а) = —tg а; (3.61)
ctg (2л — а) = —ctg а. (3.62)
Согласно свойству периодичности и нечетности, имеем
sin (2л - а) = sin (-а) = -sin а.
Тождества (3.60—3.62) доказываются аналогично.
♦ ПРИМЕР
Вычислить: 1) == sin 300°; 2) f2 = cos 330°.
РЕШЕНИЕ. 1) = sin (360° - 60°) = -sin 60° = - J3 /2;
2) f2 = cos (360° - 30°) = cos 30° = Тз /2.
Рассмотренные формулы приведения представлены в таблице 5.
Применяя формулы приведения, рекомендуется пользоваться
следующими правилами:
I. Если угол а откладывается от оси Ох, то наименование приво-
димой функции, т. е. функции аргумента (-а), (л ± а), (2л - а),
не изменяется. Если угол а откладывается от оси Оу, то на-
именование приводимой функции, т. е. функции аргумента
(л/2 ± а), (Зл/2 ± а), заменяется на сходное (синус на косинус,
тангенс на котангенс и наоборот).
155
ЧАСТЬ I. Алгебра и начала анализа
И. Знак, с которым нужно брать тригонометрическую функ-
цию в правой части, находится по знаку левой части в предпо-
ложении, что 0 < а < л/2.
Таблица 5
Функция аргумент sin (р COS ф tgф йдф
<р = -а -sin а cos а -tga -ctg a
Ф - л/2 - а cos а sin а ctg а tga
Ф = л/2 + а cos а -sin а -ctg а -tga
<р = я-а sin а -cos а -tga -ctg a
<р = л + а -sin а -cos а tga ctg a
Ф = Зл/2 - а -cos а -sin а ctg a tg a
Ф = Зл/2 + а -cos а । sin а -ctg a -tga
Ф = 2я-а -sin а cos а -tga -ctg a
♦ ПРИМЕР
Составить формулу приведения для tg (Зл/2 + а).
РЕШЕНИЕ. Так как угол а откладывается от оси Оу, то в правой час-
ти формулы оказывается функция «котангенс». Формула верна
при всех допустимых значениях аргумента а, следовательно, она
верна и для О < а < л/2, но в этом случае дуга (Зл/2 4- а) оканчи-
вается в четвертой четверти, в которой функция тангенса являет-
ся отрицательной. Тогда tg (Зл/2 + а) = -ctg а.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие формулы называются формулами приведения?
2. При каких вычислениях необходимо знание формул приведения?
3. В чем заключается свойство полупериода синуса и косинуса?
4. Сформулируйте правила названий тригонометрических функций при
составлении формул приведения.
5. Сформулируйте правила знаков при составлении формул приведения.
156
ГЛАВА 3. Тригонометрические функции
§ 31. Тригонометрические функции
алгебраической суммы двух аргументов
(формулы сложения)
Формулами сложения называются формулы, выражающие
тригонометрические функции углов (а ± р) через одноименные
функции углов аир. Приведем эти формулы:
sin (а + р) = sin а
sin (а — р) = sin а
cos (а + р) = cos а
cos (а — р) = cos а
cos р + cos а sin р;
cos р — cos а sin р;
cos р — sin а sin р;
cos р + sin а sin р;
(3.63)
(3.64)
(3.65)
(3.66)
tg (а + Р) =
tga + tgp
1 - tgatgp ’
а * +!),₽# f^(2fe +
1), tg a tg p * 1;
(3.67)
tg (a - p) =
tga - tgp
1 + tgatgp ’
a * [|)(2fe + !),₽# (|)(2fe +
а nk, p Ф
1), tg a tg p * 1;
(3.68)
(3.69)
rcfe, а Ф —p + rcfe;
ctg (a - p) — LI,
ctgp — ctga
а Ф nk, p Ф itk, а Ф p + nk.
(3.70)
В выражениях (3.67—3.70) k g Z.
1. Косинус разности двух аргументов. Косинус разности двух аргу-
ментов равен сумме произведения косинусов и произведения си-
нусов этих аргументов (3.66).
Отложим на единичной окружности (рис. 89) дуги, соответст-
вующие углам аир; пусть М nN — точки, в которых оканчива-
ются эти дуги: Z. АОМ = a, Z AON — р.
Координаты точек М и N в системе координат хОу:
хг = cos а, у г = sin a; х2 = cos р, у2 = sin р;
тогда квадрат расстояния между точками М и N выражается со-
отношением:
157
ЧАСТЬ I. Алгебра и начала анализа
Рис. 89
(MN)2 — (х2 - xt)2 4- (у2 ~ уг)2 — (cos р - cos а)2 4- (sin р - sin а)2 =
= (cos2 р 4- cos2 а - 2 cos р cos а) + (sin2 р + sin2 а - 2 sin р sin а) =
= (cos2 р + sin2 р) 4- (cos2 а 4- sin2 а) - 2 (cos а cos р + sin а sin р) =
= 2 - 2 (cos а cos р 4- sin а sin р). (*)
Повернем оси координат на угол р. Тогда направление оси абс-
цисс Ох' совпадет с направлением луча ON. Радиус ОМ составит с
осью Ох' угол, равный (а - р).
Координаты точек М и N в системе координат х'Оу':
х[ = cos (а - р), у{ = sin (а - р); х2 =1, у2 — 0;
тогда квадрат расстояния между точками М и выражается со-
отношением*:
(MN)2 = (х2 - х{)2 4- (у'2 - у{)2 = [1 - cos (а - р)]2 4- sin2 (а - р) =
= [cos2 (а - р) 4- sin2 (а - р)] 4-1 - 2 cos (а - р) =
= 2 - 2 cos (а - р). (**)
Приравняем выражения (*) и (**):
2-2 cos (а - р) = 2 - 2(cos а cos р 4- sin а sin р),
отсюда получаем выражение (3.66).
* Это соотношение основано на формуле (10.18) гл. 10, § 70, п. 1.
158
ГЛАВА 3. Тригонометрические функции
2. Косинус суммы двух аргументов. Заменив в формуле (3.66) аргу-
мент р на аргумент (-р), получим: cos (<х + Р) = cos a cos (-Р) +
+ sin а sin (- р). Воспользовавшись свойствами четности косинуса
и нечетности синуса, получим (3.65).
3. Синус суммы двух аргументов. По формуле приведения (3.36) име-
ем sin (а + р) = cos (л/2 - (а + Р)) = cos ((л/2 - а) - р). Далее по
(3.66) получим формулу (3.63).
4. Синус разности двух аргументов. Заменив в формуле (3.63) аргу-
мент р на аргумент (-р), получим sin (а - р) = sin а cos (~р) +
+ cos а sin (-р). Используя свойства четности косинуса и нечет-
ности синуса, приходим к (3.64).
5. Тангенс суммы двух аргументов. Имеем
, , . Q4 sin(a + р)
tg (« + ₽)------
cos (a + Р)
sinacosP + cosasinp
cos a cos Р — sin a sin Р
Разделив почленно числитель и знаменатель на cos a cos р О,
получим:
tg (a + р) =
sinacosP cosasinP
cos acos P cos acos P
cosacosP _ sinasinP *
cos acos p cosacosP
т. e. формулу (3.67). Формула (3.67) имеет место при всех допусти-
мых значениях аргумента, т. е. таких, при которых тангенсы углов
а, р и (а + р) имеют смысл. Следовательно, для каждого из рассмат-
риваемых углов значение косинуса не должно быть равным нулю.
6. Тангенс разности двух аргументов. Заменив в (3.67) р на (~р) и вос-
пользовавшись свойством нечетности тангенса, получим выраже-
ние (3.68):
tg (a - р) = tg (a + (-Р)) =
tga + tg(-p)
1 - tgatg(-p)
tga - tgP
1 + tgatgp ’
7. Котангенсы суммы и разности двух аргументов. Формулы (3.69) и
(3.70) выводятся аналогично тому, как это было сделано для фор-
мул сложения и разности тангенсов.
♦ ПРИМЕР 1
Вычислить: 1) sin 15°; 2) cos 15°; 3) f1 = sin 70° cos 40° -
- cos 70° sin 40°; 4) f2 = cos (a + p), если cos a = 3/5, cos p = 4/5,
a e (л/2; л), p e (л; Зл/2).
159
ЧАСТЬ I. Алгебра и начала анализа
РЕШЕНИЕ. 1) sin 15° = sin (45° - 30°) = sin 45° cos 30° - cos 45° sin 30° =
2) cos 15° = cos (45° - 30°) = cos 45° cos 30° + sin 45° sin 30° =
= ^(л/з +1);
3) /, = sin (70° - 40°) = sin 30° = 1/2;
4) вычислим sin а и sin p с учетом четверти, которой принадле-
жат углы аир:
sin а = 71 - (3/5)2 = 4/5, sin р = -71 - (4/5)2 = -3/5.
Подставив исходные данные и найденные значения в формулу
(3.65), получим:
cos
♦ ПРИМЕР 2
Решить уравнение: sin 2х cos х = cos 2х sin х.
РЕШЕНИЕ, sin 2х cos х - cos 2х sin х = 0, т. е. sin (2х - х) = 0
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выведите формулы сложения для основных тригонометрических функций.
2. При каких значениях аргумента формулы tg(a ± р) и ctg (а ± р) не
имеют смысла?
3. Выведите формулу сложения для косинуса разности двух углов. Как из
нее получить остальные формулы сложения?
4. Приведите простейшие примеры применения формул сложения.
§ 32. Тригонометрические функции
удвоенного аргумента
Рассмотрим формулы сложения для такого частного случая,
когда слагаемые аргумента равны. При этом получим формулы,
выражающие тригонометрические функции двойного угла 2a че-
рез тригонометрические функции одинарного угла а:
sin 2а = sin (а + а) = sin a cos а + sin a cos а — 2 sin a cos а;
cos 2а = cos (а + а) = cos a cos а - sin a sin а = cos2 а - sin2 а;
tg 2а = tg (а + а) =
tga + tga
1 - tgatga
2tga
160
ГЛАВА 3. Тригонометрические функции
Таким образом, формулы для тригонометрических функций
удвоенного аргумента при а * л/2 + л&, а * л/4 + л/2й, k е Z име-
ют следующий вид:
sin 2а = 2 sin а cos а;
cos 2а — cos2 а — sin2 а;
(3.71)
(3.72)
(3.73)
tg 2а =
2tgq
1 — tg2a
Формула для косинуса удвоенного аргумента может выгля-
деть иначе:
cos 2а = cos2 а - sin2 а = cos2 а - (1 - cos2 а) = 2 cos2 а - 1.
cos 2а = cos2 а - sin2 а = (1 — sin2 а) - sin2 а = 1 - 2 sin2 а.
Итак, получены формулы, позволяющие косинус удвоенного
аргумента выражать только через косинус или только через си-
нус этого аргумента:
cos 2а = 2 cos2 а - 1;
cos 2а = 1 — 2 sin2 а.
(3.74)
(3.75)
Ф ПРИМЕР 1
Выразить: 1) tg За через tg а; 2) sin За через sin а.
РЕШЕНИЕ. 1) tg За = tg (2а + а) = tg2a + tga
1 — tg2atga
2tga
1 — tg2a
+ tga
2tga
• tga
3tga - tg3a.
1 - 3tg2a *
2) sin 3a = sin (2a + a) = sin 2a cos a + cos 2a sin a =
= 2 sin a cos a cos a + (cos2 a - sin2 a) sin a = 2 sin a cos2 a +
+ sin a cos2 a - sin3 a — 3 sin a cos2 a - sin3 a — 3 sin a (1 - sin2 a) -
- sin3 a = 3 sin a - 4 sin3 a = sin a (3 - 4 sin2 a).
♦ ПРИМЕР 2
Вычислить cos 2a, если sin a = -0,3.
РЕШЕНИЕ. Применив формулу (3.72), получим: cos 2а = 1 - 2(~0,3)2 =
= 0,82.
6 - 9664
161
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕРЗ
Решить уравнение: sin х • cos х = 1/2.
РЕШЕНИЕ. Умножив левую и правую части на 2, получим
2 sin х cos х = 1, sin 2х = 1 => 2х = л/2 + 2nk,
х — п/4 + nk, keZ.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выведите формулы тригонометрических функций удвоенного аргу-
мента.
2. При каких значениях аргумента функция tg 2а не имеет смысла?
3. Приведите примеры вычислений с использованием формул удвоения.
§ 33. Тригонометрические функции
половинного аргумента
Выразим тригонометрические функции аргумента а через
тригонометрические функции аргумента а/2.
Заменив в формулах (3.74—3.75) аргумент а на аргумент а/2,
получим
cos а = 2 cos2 ? ~ 1 или
cos а = 1 - 2 sin2 или
1 + cosa
2
1 — cosa
2
— cos2
= sin2
a
поэтому
a , /1 + cosa
C0S 2 =±V------2----;
. a , /1 — cosa
Sln 2 = 1J-----2----
(3.76)
(3.77)
причем знак перед корнем
определяется по
четверти,
которой
принадлежит аргумент а.
Разделив почленно равенство (3.77) на равенство (3.76), полу-
чим
‘е i = ± J
1 — cosa
1 + cosa
a # я + 2ick, k е Z.
(3.78)
162
ГЛАВА 3. Тригонометрические функции
Знак перед радикалом надо выбирать так, чтобы он совпадал
со знаком tg (а/2), иначе говоря, знак (+), если а/2 принадлежит
I или III четвертям, и знак (-), если а/2 принадлежит II и IV чет-
вертям.
Соответственно
1 4- cosa
1 — cosa
a * 2nk, ke Z.
(3.79)
Вместо формул (3.78—3.79) можно получить формулы, даю-
щие рациональное выражение а/2 через тригонометрические
функции аргумента а. Имеем равенство
tg (a/2) =
sin(a/2)
cos(a/2)
cos (a/2) # 0.
Умножив числитель и знаменатель правой части на 2 cos (a/2),
получим
a _ 2sin(a/2)cos(a/2)
2 ” 2cos2(a/2)
при этом числитель 2 sin (a/2) cos (a/2) = sin a, а знаменатель
2 cos2 (a/2) =14- cos a, поэтому
tg (a/2) = 1 , a # n + 2nfe, k e Z. (3.80)
Аналогично можно доказать следующие равенства:
tg (a/2) =
1 — cosa
sina *
(3.81)
ctg (a/2) =
1 4- cosa
sina
(3.82)
ctg (a/2) =
sina
1 — cosa
(3.83)
В равенствах (3.81), (3.82) левая и правая части имеют различ-
ные области определения. В равенстве (3.81) левая часть имеет
областью определения а п 4- 2 л/г, а правая часть имеет областью
определения a л/г, k е Z. В равенстве (3.82) области определе-
ния левой и правой частей: a # 2л/г VLCL^nk соответственно, k g Z.
В равенстве (3.83) области определения совпадают: a # 2nk, ke Z.
Используя соотношения (3.81, 3.82) при решении тригонометри-
ческих уравнений, необходимо учитывать несовпадение их об-
ластей определения.
163
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕР
Найти sin (а/2), cos (а/2), tg (а/2), если sin а = 0,6, а е (0; л/2).
РЕШЕНИЕ. По основному тригонометрическому тождеству cos а ==
= J1 -^0,36 = 0,8. По формулам (3.76), (3.77) находим:
sin (а/2) =
- 0,8 = __ J10
2 л/и*1 10 ’
COS
0,8 ЗЛО
2 ^U,y 10
tc (а/2) = 8*п(а/2) _ 1
tg(a/Z) cos(a/2) 3-
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выведите формулы тригонометрических функций половинного аргу-
мента.
2. При каких значениях аргумента формулы tg (а/2) и ctg (а/2) не имеют
смысла?
3. Покажите, что в формулах (3.81) и (3.82) имеет место несовпадение об-
ластей определения левой и правой частей формул.
4. Приведите простейшие примеры применения формул для тригономет-
рических функций половинного угла.
§ 34. Выражение тригонометрических функций
через тангенс половинного аргумента
Все тригонометрические функции любого аргумента выража-
ются рационально через тангенс половины этого аргумента. Вы-
разим sin а и cos а через tg а/2. По формулам (3.71), (3.72) имеем
sin а = 2 sin (а/2) cos (а/2),
cos а = cos2 (а/2) - sin2 (а/2).
Разделив правые части этих равенств на 1 — sin2 (а/2) 4- cos2 (а/2),
получим
sin а — 2sin(a/2)cos(a/2)
sin2(a/2) + cos2(a/2)
cos a =
cos2(a/2) — sin2(a/2)
sin2(a/2) + cos2(a/2)
Разделим правые части этих двух равенств на cos2 (a/2):
164
ГЛАВА 3. Тригонометрические функции
sin а =
2tg(a/2) .
1 + tg2(a/2) ’
cos а =
1 - tg2(a/2)
1 + tg2(a/2) *
Из формул (3.84), (3.85) следует:
tg а =
2tg(a/2) ,
1 - tg2(a/2) ’
ctg а =
1 - tg2(a/2)
2tg(a/2) ’
(3.84)
(3.85)
(3.86)
(3.87)
Полученные формулы теряют смысл при всех а = n(2k 4- 1),
ke Z.
♦ ПРИМЕР
Вычислить выражение
5cosa - 3
lOsina + 1
если tg (а/2) = 3.
РЕШЕНИЕ. По формулам (3.84), (3.85) получаем: sin a =
3
1-9
cos a =--
1+9
4
ё, следовательно,
5 cos a — 3 _ -4 — 3
lOsina + 1 6 + 1
§ 35. Преобразование произведения
тригонометрических функций в сумму
В вычислениях, относящихся к тригонометрическим функци-
ям, часто встречаются случаи, когда необходимо преобразовать
произведение тригонометрических функций (sin a cos Р, cos a cos p,
sin a sin p) в алгебраическую сумму.
Сложив почленно равенства (3.63), (3.64), получим:
sin (a + р) + sin (а - р) = 2 sin a cos р,
откуда
sin a cos р = з [sin (а + Р) + sin (а - Р)].
(3.88)
Складывая почленно равенства (3.65), (3.66), получим
cos (a + р) + cos (a - р) = 2 cos a cos p,
165
ЧАСТЬ I. Алгебра и начала анализа
откуда
cos a cos р = 1 [cos (а + р) + cos (а — Р)]. (3.89)
Л
Вычитая из равенства (3.89) равенство (3.88), получим
cos (а - р) - cos (а + р) = 2 sin а sin р,
откуда
sin а sin Р = | [cos (а — Р) — cos (а + р)]. (3.90)
♦ ПРИМЕР
Представить в виде суммы произведение: 1) /* = sin 25° sin 5°;
2) f2 = cos (x/2) cos (x/3) cos (x/4).
РЕШЕНИЕ. 1) По формуле (3.90) f
— (cos 20° - cos 30°
cos
COS x COS 7
2 4
cos
x x
COS “Г COS о + COS 7 cos
4 3 4
( 3x
: COS -T-
! V 4
13x
cos 12
4
5x
12
cos
7x
12
2
cos12
Формулы (3.88), (3.90) можно использовать для понижения
степени функций вида sin2 х, cos2 х, sin3 х. В частности,
sin2 х = sin х sin х = - (cos 0 - cos 2х) = 5 (1 — cos 2x);
cos2 x = cos x cos x = 5 (cos 0 + cos 2x) = з (1 4- cos 2x);
sin3 x = sin2 x sin x =
- s cos 2x sin x = « (sin x - sin x cos 2x) =
Сл J и
2
= x sin x - - (sin 3x - sin x) = 5 sin x - j sin 3x
iu 4 JU 4
1 .
7 sm x =
4
= j (3 sin x — sin 3x).
Таким образом, получена формула для синуса утроенного ар-
гумента:
sin Зх = 3 sin х - 4 sin3 х.
(3.91)
166
ГЛАВА 3. Тригонометрические функции
Аналогично
е$§3 х — cos2 х cos х = I g 4- gCos 2x jcos x = cos x + % cos 2x cos x =
4
4
= (3 cos x 4- cos 3x).
Получена также формула для косинуса утроенного аргумента:
cos Зх = 4 cos3 х — 3 cos х, (3.92)
Таким же образом можно привести к алгебраической сумме:
cos5 х = cos3 х cos2 х = I -z cos x 4- 7 cos 3x
2
3
8
8
o.3 o.l
cos 3x + - cos x cos 2x+ q
О о
, 3
x+8
5
g cos
cos 3x cos 2x =
5
16
16
8 2
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выведите формулы преобразования произведения тригонометрических
функций в сумму.
2. Как выполняется понижение степени тригонометрических функций?
§ 36. Преобразование алгебраической суммы
тригонометрических функций в произведение
Представим суммы и разности тригонометрических функций
в виде произведения тригонометрических функций от других ар-
гументов.
1. Сумма синусов. По формуле (3.88) имеем
sin (А 4- В) 4- sin (А — В) = 2 sin A cos В.
Пусть А 4- В = а, А - В = р. Решив систему
167
ЧАСТЬ I. Алгебра и начала анализа
относительно аргументов А и В, получим
Тогда
sin а + sin 0 — 2 sin
(3.93)
2. Разность синусов. Заменим в (3.93) аргумент р на аргумент (-р):
sin а
sin (- р) = 2 sin ——- cos —5
или
(3.94)
sin a — sin 0 = 2 sin —cos —5
3. Сумма косинусов. Заменим в выражении cos a + cos p косинус
каждого аргумента синусом дополнительного аргумента и вос-
пользуемся соотношением (3.93). Тогда
cos а + cos р = sin
o . (Tt/2 - a) + (тс/2 - 0)
= 2 sm
cos (я/2 - a) - (Tt/2 - p) _
2
2
= 2 sin
2 2
Таким образом,
cos
= 2 cos —cos
2
(3.95)
cos —2
cos a + cos 0 = 2 cos
4. Разность косинусов. Аналогично с помощью формулы (3.94) вы-
водится выражение для разности косинусов:
cos а - cos P = sin I 5 - a
= 2 sin ” a) “ (7l/2 “ P)
cqs (л/2 - a) + (тс/2 - P) _
2
2
~— sin
= 2 sin
cos
= 2 sin
= 2 sin
2 sin 2
cos a — cos 0=2 sin —
sm
(3.96)
2 2
2
168
ГЛАВА 3. Тригонометрические функции
5. Сумма тангенсов. По определению функции тангенса:
tg а + tg р =
sina
cosa
sinP _ sinacosp + cosasinp _ sin (a + p)
cosP cosacosp cosacosP ’
или
tg a + tg p =
sin (a + P)
cosacosp *
a # 5 + nfe, p * 5 + nk, k e Z. (3.97)
6. Разность тангенсов. Заменив в (3.97) аргумент р на аргумент
(~Р), получим
tg a + tg (-р) =
sin(a — Р)
cosacos(-P) *
т. е.
tg a - tg p =
sin (a — P)
cosacosp *
+ icfe, P * 5 + rcfe, k e Z. (3.98)
7. Преобразование выражений (1 + cos a). (1 - cos a), (1 + sin a) и (1 - sin a)
в произведение. Заменив в формулах для косинуса удвоенного ар-
гумента (3.74—3.75) аргумент а на аргумент а/2, получим
cos а = 2 cos2 (а/2) - 1, cos а = 1 - 2 sin2 (а/2),
тогда
1 + cos а = 2 cos2 (а/2),
1 — cos а = 2 sin2 (а/2).
(3.99)
(3.100)
Заменив синус аргумента а на косинус дополнительного аргу-
мента и воспользовавшись (3.99), получим:
1 + sin a = 1 + cos
\ _ 2 п/2 - a - о 2 (п
a 1= 2 cos2---5— = 2 cos2 7 ~ х ь
т. е.
1 4- sin a — 2 cos2
(3.101)
Аналогично
1 - sin a = 1 - cos
A o . 2 я/2 “ a о • 2 (n « A
- a = 2 sin2 -L—x— = 2 sm2 7-75 ,
) A \4 2 J
или
1 — sin a = 2 sin2
(3.102)
169
ЧАСТЬ I. Алгебра и начала анализа
8. Условия равенства одночленных тригонометрических функций. Если
синусы двух аргументов равны (sin х = sin у), то sin х - sin у = 0.
Тогда по (3.94)
9 Х ~ У * + У _Г, «
& sm q vos q О
sin^=0,
cos —= 0 | = л + Ttk, ke Z.
Следовательно, условием равенства sin х = sin у является сово-
купность
х - у = 2л&,
! х 4- у = (2fe 4- 1)л, k g Z. (3.103)
Аналогично с использованием (3.96) можно показать, что для
равенства cos х = cos у необходимо и достаточно выполнение од-
ного из следующих условий:
(3.104)
Для того чтобы тангенсы двух аргументов были равны (tg х =
= tg у), необходимо, чтобы тангенс каждого из двух аргументов
существовал и чтобы sin (х - у) = 0 (из (3.98)); следовательно,
х- у — л&, k g Z.
(3.105)
♦ ПРИМЕР 1
Преобразовать в произведение:
1) jfj = cos (л/5) - cos (7л/10); 2) f2 = ctg (2л/7) - ctg (л/7);
3) f3 = cos2 a - sin2 p.
РЕШЕНИЕ. 1) По формуле (3.96) = 2 sin (9л/20) sin (л/4) =
= л/2 sin (9л/20);
2)___выразив котангенсы через тангенсы, используем формулу
(3.98): f2 = tg (л/2 - 2л/7) - tg (л/2 - л/7) = tg (Зл/14) - tg (5л/14) =
______ sin (л/7)_________
cos(3k/14) • cos(5k/14) ’
3) используя формулы (3.99—3.100) и (3.95), получаем:
= 5 Г2 cos 2(a jt„.P)
2L 2
1 - cos2В 1 . о
-------z—- = х (cos 2a 4- cos 2р) =
Li Li
cos P) = cos (a + p) cos (a - p).
2 -
170
ГЛАВА 3. Тригонометрические функции
t ПРИМЕР 2
Преобразовать в произведение выражение: 1) = 1 + sin а +
+ cos а; 2) f2 == sin х + sin 2х + sin Зх.
РЕШЕНИЕ. 1) Преобразуя выражение (1 + cos а) по формуле (3.99) и
используя формулу удвоенного аргумента (3.71), получаем:
2) преобразуем в произведение сумму двух первых слагаемых
по (3.93), а третье слагаемое преобразуем по формуле удвоенного
аргумента (3.71):
о . Зх х
2 sm -5- cos х
zS
о . Зх „ х . . Зх х
= 2 sm 2 cos х cos « = 4 sm -5- cos x cos x
Z Z Z Z
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выведите формулы для преобразования алгебраической суммы триго-
нометрических функций в произведение.
2. При каких значениях аргумента формулы для суммы tg а ± tg р не име-
ют смысла?
3. Выведите формулы для преобразования выражений (1 ± cos а) и
(1 ± sin а) в произведение.
4. Запишите условия равенства одноименных тригонометрических функций.
§ 37. Свойства тригонометрических функций
и их графики
1. Свойства функции у - sin х и ее график. Используя рассмотренные
свойства тригонометрических функций и формулы приведения,
построим график функции у = sin х. В силу периодичности функ-
ции синуса достаточно построить график в промежутке [-л; л],
так как в промежутках таких, как [-Зл; -л], [л; Зл], [Зл; 5л],
график синуса будет иметь тот же вид, что и в промежутке [-л; л].
В указанных промежутках график получается путем сдвига гра-
171
ЧАСТЬ I. Алгебра и начала анализа
Рис. 90
фика синуса в промежутке [—я; я] влево или вправо. Учитывая
свойство нечетности синуса, достаточно построить график в про-
межутке [0; я], так как в промежутке [-я; О] график будет сим-
метричен графику на отрезке [0; я] относительно начала коорди-
нат. По свойству дополнительного аргумента (3.43) заключаем,
что точки х и (я - х) симметричны относительно точки я/2,
поскольку, когда аргумент х пробегает промежуток [0; я/2], ар-
гумент (я - х) пробегает в обратном направлении промежуток
[я/2; я]. Поэтому (так как график функции у = sin х симметричен
относительно прямой х = я/2) можно ограничиться построением
графика в промежутке [0; я/2].
В промежутке [0; я/2] функция у = sin х монотонно возраста-
ет от 0 до 1. Для приближенного построения графика функции
у = sin х на числовой единичной окружности в промежутке [0; я/2]
отметим точки, соответствующие дугам 0, я/8, я/4, Зя/8, я/2
(рис. 90). Затем нанесем эти значения аргумента на ось Охг (здесь
Рис. 91
172
ГЛАВА 3. Тригонометрические функции
л/2 составляет ~ 1,57 длины радиуса
единичной окружности). Построив ор-
динаты, соответствующие значениям
синусов этих аргументов, и соединив
их плавной линией, получим кривую,
приближенно представляющую собой Рис-92
график синуса. Построение графика будет тем точнее, чем боль-
ше точек будет нанесено.
На рисунке 91 изображен график функции синуса в проме-
жутке [0; л], полученный отражением графика рисунка 90 отно-
сительно прямой х = л/2. На рисунке 92 показан график функ-
ции синуса в промежутке [-л; л], полученный из графика
рисунка 91 отражением его относительно начала координат. Гра-
фик синуса называется синусоидой. На рисунке 93 изображена
синусоида на интервале (-2л; 2л).
Основные свойства функции у = sin х
I. Область определения функции — множество R всех действи-
тельных чисел.
II. Множество значений — отрезок [-1; 1].
III. Функция является периодической с периодом Т = 2л.
IV. Функция у = sin х нечетная.
V. Функция у = sin х принимает значения, равные нулю, в
точках х — nkt ke Z;
— наименьшие значения, равные -1, при х = -л/2 + 2л&, k е Z\
— наибольшие значения, равные 1, при х = л/2 + 2л&, k е Z.
VI. Функция принимает положительные значения на интерва-
лах (2лЛ; л + 2л&), k е Z;
— отрицательные значения — на интервалах (л + 2л/г; 2л + 2л&),
keZ.
Рис. 93
173
ЧАСТЬ I. Алгебра и начала анализа
VII. На отрезках [-л/2 + 2л/г; л/2 + 2л/г], k е Z функция явля
ется возрастающей, на отрезках [л/2 4- 2nk; Зл/2 + 2л/г], k g Z
функция является убывающей.
2. Основные свойства и график функции у •- cos х. График функ-
ции у = cos х можно построить исходя из соотношения COS X =
= sin (х + л/2). Из этого выражения следует, что график функции
у — cos х получается из графика функции у = sin х путем сдвига
графика функции синуса влево на л/2 (рис. 94). График косинуса
называется косинусоидой.
Основные свойства функции cos х
I. Область определения функции — множество R всех действи-
тельных чисел.
II. Множество значений — отрезок [-1; Л-
III. Функция является периодической с периодом Т = 2л.
IV. Функция у = cos х четная. График функции симметричен
относительно оси Оу.
V. Функция у — cos х принимает значения, равные нулю, в
точках х = л/2 + л/г, к g Z;
— наименьшие значения, равные -1, при х == (-л + 2л/г), к е Z
— наибольшие значения, равные 1, при х = 2л/г, /г е Z.
а л
VI. Функция принимает положительные значения на интерва -
лах (-л/2 + 2 л/г; л/2 + 2л/г), k е Z.
Функция принимает отрицательные значения на интервалах
(л/2 + 2л/г; Зл/2 + 2л/г), k е Z.
VII. На отрезках [-л + 2л&; 2л/г], /г е Z функция является воз-
растающей, на отрезках [2л/г; л + 2л/г], /г е Z функция являет-
ся убывающей.
174
ГЛАВА 3. Тригонометрические функции
Рис. 95
3. Основные свойства и график
функции у - tg х. При построении
II
графика функции у = tg х учитываем, что период тангенса ра-
вен тс, поэтому график тангенса можно построить в промежутке
(-я/2; я/2). Тангенс — функция нечетная, поэтому его график
будет симметричен относительно начала координат. Таким обра-
зом, достаточно построить график в промежутке [0; я/2). В этом
промежутке тангенс неограниченно возрастает от нуля. На чис-
ловой единичной окружности (рис. 95) в промежутке [0; я/2) на-
несем точки 0, я/8, я/4, Зя/8. Через точку А построим прямую
х == 1, параллельную оси Оу, Эта прямая называется осью тан-
генсов. Проведем из начала координат лучи, соответствующие
углам я/8, я/4, Зя/8, до их пересечения с осью тангенсов. Рас-
смотрим для примера Д ОАВ и А ОАВ. Очевидно, эти треуголь-
Л/
ники подобны (Д ОАВ ~ Д ОАВ), поэтому
АВ = АВ
ОА ОА .
(*)
к АВ
Так как по определению tg = —=, а ОА = 1, из (*) следует,
4 ОА
что tg (я/4) = АВ. Так же определяется и тангенс любого угла в
интервале [0; я/2]: как отрезок на оси тангенсов, отсекаемый лу-
175
ЧАСТЬ I. Алгебра и начала анализа
ЬЭ1Й
Рис. 96
чом, ограничивающим соответст-
вующий угол. Учитывая это, строим
график функции tg х.
На рисунке 96 изображен график
тангенса в промежутке (-л/2; л/2),
полученный отражением графика в
промежутке [О; л/2) относительно
начала координат. График тангенса
называется тангенсоидой. На ри-
сунке 97 представлена тангенсоида,
полученная последовательным пере-
носом графика рисунка 96 вправо и
влево на отрезки, кратные л.
Основные свойства функции у = tg х
I. Область определения — множество всех действительных чи-
сел х * л/2 + л/г, ke Z.
II. Множество значений — множество R всех действительных
чисел.
III. Функция у = tg х периодическая с периодом Т = л.
IV. Функция у = tg х нечетная. График функции симметричен
относительно начала координат.
V. Функция у = tg х принимает значения, равные нулю, при
х = л/г, k е Z;
— положительные значения на интервалах (л/г; л/2 + л/г), ke Z,
— отрицательные значения на интервалах (-л/2 Чл/г; к/?), k е Z.
VI. Функция у = tg х возрастает на следующих интервалах:
(-л/2 + nk; л/2 + л&), ke Z.
Рис. 97
176
ГЛАВА 3. Тригонометрические функции
Рис. 98
4. Основные свойства и график функции у - ctg х. Для построения
графика функции у = ctg х воспользуемся тождеством ctg х = - tg
(х + л/2). Из этого тождества следует, что для построения графи-
ка котангенса необходимо сдвинуть график тангенса на л/2 влево
вдоль оси Ох и отразить полученную кривую относительно оси
Ох, График котангенса (рис. 98) называется котангенсоидой.
Графики тангенса и котангенса состоят из бесконечного мно-
жества одинаковых периодически повторяющихся ветвей.
Основные свойства функции у — ctg х
I. Область определения — множество всех действительных чи-
сел х * Ttk, keZ.
II. Множество значений — множество R всех действительных
чисел.
III. Функция у = ctg х периодическая с периодом Т = л.
IV. Функция у = ctg х нечетная.
V. Функция у — ctg х принимает значения, равные нулю при
х = л/2 4- л/г, k е Z;
— положительные значения на интервалах (nk; л/2 + л/г), /г g Z°
— отрицательные значения на интервалах (—л/2 + л/г; л/г), /г g Z,
VI. Функция у = ctg х является убывающей на каждом интер-
вале (л/г; л + л/г), /г g Z,
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Постройте график синуса. С помощью графика опишите поведение
функции синуса при изменении аргумента.
2. Таким же образом опишите поведение функций/ = cosх,у = tg х,у = ctgx.
177
ЧАСТЬ I. Алгебра и начала анализа
§ 38. Обратные тригонометрические функции
1. Функция, обратная синусу. Известно, что областью определения
функции у — sin х служит вся числовая ось: х g R и каждому зна-
чению аргумента соответствует только одно значение функции из
промежутка [-1; 1], а каждому значению функции соответствует
множество значений аргумента.
Для функции, обратной синусу, необходимо установить вза-
имно-однозначное соответствие между значениями аргумента и
соответствующими значениями функции, чтобы избежать много-
значного соответствия.
Для этого из множества значений аргумента рассматривают
промежуток значений х е [-л/2; п/2]. Каждому значению аргумен-
та из этого промежутка будет соответствовать только одно значение
функции у е [-1; 1]. Таким образом, множества значений аргумен-
та и функции взаимно-однозначно отображаются друг на друга.
Следовательно, функция синуса в промежутке -п/2 < х < п/2 имеет
монотонно возрастающую обратную функцию. Эта функция назы-
вается арксинусом и обозначается у = arcsin х*.
Функция у = arcsin х, заданная на промежутке [-1; 1], моно-
тонно возрастает от -п/2 до п/2 (рис. 99). График функции
у = arcsin х симметричен графику функции у = sin х (—п/2 < х < п/2)
относительно прямой у — х.
Из определения функции у — arcsin х следует, что sin у = х,
у 6 [-я/2; п/2].
Областью определения функции у = arcsin х является отрезок
[-1; 1], множеством значений — отрезок [-п/2; п/2].
Из определения функциц у = arcsin х следует, что
arcsin (-х) = -arcsin х.
Главный угол (дуга), arcsin х, есть угол (дуга), содержащийся
в промежутке от -п/2 до я/2 (-п/2 < arcsin х < п/2), синус ко-
торого равен х:
sin (arcsin х) = х.
♦ ПРИМЕР
Вычислить значение arcsin х при: 1) хг =
7з/2; 2) х2 = -1/2;
3) х3 = 3.
* Arcus — дуга (лат.).
178
ГЛАВА 3. Тригонометрические функции
РЕШЕНИЕ. 1) arcsin хх = л/3, так как sin (л/3) = «/3 /2;
2) arcsin х2 = -л/6, так как sin (-л/6) = -1/2;
3) arcsin х3 не имеет смысла, так как число 3 не входит в об-
ласть определения функции arcsin х.
2. Функция, обратная косинусу. Рассмотрим функцию у = cos х на
промежутке 0 < х < л. В этом промежутке функция монотонно
убывает от 1 до -1. Следовательно, множество значений аргумен-
та 0 < х < л и множество значений функции -1 < х < 1 взаимно
отображаются друг на друга. Поэтому функция у = cos х в проме-
жутке 0 < х < л имеет монотонную убывающую обратную функ-
цию. Эту функцию называют арккосинусом (рис. 100) и обозна-
чают у = arccos х. Функция у = arccos х, заданная на промежутке
X G [-1; Л, монотонно убывает от л до 0.
Из определения следует, что равенство у = arccos х равносиль-
но утверждениям: cos у = х, у g [0; л].
Областью определения функции у = arccos х является отрезок
[-1; 1], множеством значений — отрезок [0; л].
Из определения функции у — arccos х следует, что
arccos (—х) = л - arccos х.
Главный угол (дуга), arccos х, есть угол (дуга), содержащийся
в промежутке от 0 до л (0 < arccos х < л), косинус которого ра-
вен х:
cos (arccos х) = х.
Рис. 99 Рис. 100
179
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕР
Вычислить значение arccos х яля* 1) хг = 1/2; 2) х2 = - J2 /2;
3) х3 = /2.
РЕШЕНИЕ. 1) arccos хг = п/3; 2) arccos х2 = Зл/4; 3) arccos х3 = п/6.
3. Функция, обратная тангенсу. Функция у = tg х в промежутке
— тс/2 < х < л/2 монотонно возрастает от - оо до 4-оо. Поэтому мно-
жество значений аргумента х g (-л/2; л/2) и множество значе-
ний функции у g R взаимно-однозначно отображаются друг
на друга. Таким образом, для функции у = tg х на промежутке
(-л/2; л/2) существует монотонно возрастающая обратная функ-
ция (рис. 101). Эта функция называется арктангенсом и обозна-
чается: у = arctg х.
Функция у = arctg х, заданная на промежутке (-оо; +оо), мо-
нотонно возрастает от - л/2 до л/2.
Из определения следует, что равенство у = arctg х равносильно
следующим утверждениям: tg у — х, у е (-л/2; л/2). Также по
определению arctg (-х) = -arctg х.
Приведем значения функции arctg х для некоторых значений
аргумента: arctg Js /3 = л/6, arctg 1 = л/4, arctg 7з = л/3.
Главный угол (дуга), arctg х, есть угол (дуга), содержащаяся
между -л/2 и л/2 (—л/2 < arctg х < л/2), тангенс которого ра-
вен х:
tg (arctg х) = х.
4. Функция, обратная котангенсу. Функция у = ctg х в промежутке
0 < х < л монотонно убывает от - оо до +оо. Таким образом, мно-
жество значений аргумента х е (0; л) и множество значений
функции у е R взаимно-однозначно отображаются друг на друга.
Поэтому функция у = ctg х на промежутке (0; Зл) имеет монотон-
но убывающую обратную функцию. Такую функцию называют
арккотангенсом и обозначают у = arcctg х.
Из этого следует, что равенство у = arcctg х равносильно сле-
дующим утверждениям: ctg у — х, у е (0; л).
Областью определения функции у = arcctg х является проме-
жуток (-оо; -гоо), т. е. множество R всех действительных чисел, а
множеством значений — интервал (0; л).
Из определения функции у = arcctg х следует, что
arcctg (—х) = л - arcctg х.
180
ГЛАВА 3. Тригонометрические функции
УЬ
Рис. 101
Рис.102
График функции у — arcctg х изображен на рисунке 102.
Приведем значения функции у = arcctg х для некоторых аргу-
ментов: arcctg /3 = л/6; arcctg 1 = л/4; arcctg О = п/2.
Главный угол (дуга), arcctg х, есть угол (дуга), содержащийся
между О и л (О < arcctg х < л), котангенс которого равен х:
ctg (arcctg х) = х.
Функции у = arcsin х, у = arccos х, у = arctg х, у = arcctg х на-
зываются обратными тригонометрическими функциями.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. На каком промежутке изменений аргумента задается функция/ = arcsin х?
2. Дайте определение функции / = arcsin х.
3. Укажите область значений функции / = arcsin х.
4. Постройте график функции/ = arcsin х.
5. Охарактеризуйте таким же образом функции / = arccos х, у = arctg х,
/ = arcctg х.
§39. Построение дуги (угла) по данному значению
тригонометрической функции. Простейшие
тригонометрические уравнения
1. Решение уравнения sin а = а. Построим единичную окружность
(рис. 103), а также график функции у = а.
Рассмотрим случай |а| < 1; тогда прямая у = а пересечет еди-
ничную окружность в точках и М2, симметричных относи-
тельно Оу. Так как а — sin а, то точка Мг получается из точки
181
ЧАСТЬ I. Алгебра и начала анализа
Рис.103
.4(1; 0) поворотом на угол, равный arcsin а, а точка М2 — пово-
ротом на угол, равный (тс - arcsin а). Множество углов, дуги ко-
торых оканчиваются в точке Mv определяется выражением
а = arcsin а + 2 л/г, k ±1, ±2,...» а множество углов, дуги которых
оканчиваются в точке М2, определяется выражением а = п -
- arcsin а + 2л/?, k = ±1, ±2,... или а = -arcsinа + л(1 + 2k), fee Z.
Так как (-1)" = 1 при п = 2fe (т. е. при четном п) и (-1)" = -1
при п = 2k + 1 (т. е. при нечетном п), то можно объединить выра-
жения для а в одну формулу:
а = (-)1л arcsin а + лп, п е Z.
(3.106)
Рассмотрим теперь случай, когда а = +1. Точка В(0; 1) отвеча-
ет случаю а = 1, а точка С(0; -1) — случаю а = -1. Множество уг-
лов, дуги которых оканчиваются в точке В, выражается форму-
лой а “ л/2 + 2?cfe (fe е Z), а множество углов, дуги которых окан-
чиваются в точке С, — формулой а = - л/2 + 2nk (k е Z).
Отметим, что если |а| > 1, то уравнение sin а = а не имеет кор-
ней.
Уравнение sin а = а для а е [-1; 1] на отрезке а е [-л/2; л/2]
имеет только один корень. Этот корень лежит в промежутке
[0; л/2], если а > 0, и в промежутке [-л/2; 0), если а < 0.
♦ ПРИМЕР 1
Построить дугу, соответствующую arcsin (4/5) и arcsin (—4/5),
лежащую в пределах [-л/2; л/2].
РЕШЕНИЕ. Решение выполним графическим способом (рис. 104),
uAMj соответствует arcsin (4/5), u4M2 соответствует arcsin (-4/5).
182
ГЛАВА 3. Тригонометрические функции
♦ ПРИМЕР 2
Решить уравнение sin а = 1/2.
РЕШЕНИЕ. На единичной окружности имеются две точки, для кото-
рых sin а = (1/2) : ах = arcsin (1/2) = л/6, а2 = я - arcsin (1/2) =
= я - л/6. Таким образом, решение определяется выражениями
а = л/6 + 2л/г и а = -л/6 + л(2& + 1), где k = ±1, ±2,... или общим
выражением
а = (-1)п л/6 + лп, п е Z.
2. Решение уравнения cos а - а. Построим единичную окружность и
проведем прямую х = а, параллельную оси Оу (рис. 105)
Если |а| < 1, то прямая х = а
пересекает единичную окруж-
ность в точках М2, симмет-
ричных относительно оси Ох.
Так как а = cos а, точка Мх по-
лучается из точки А(1; 0) пово-
ротом на угол, равный arccos а,
а точка М2 — поворотом на угол,
равный (-arccos а). Множество
углов, дуги которых оканчива-
ются в точке М19 определяется
выражением а = arccos а + 2л&,
r = XI, XZ, ...» а множество уг- Рис 105
лов, дуги которых оканчивают-
ся в точке М2, определяется выражением а = —arccos а + 2л&,
k = ±1, ±2, ... . Эти две формулы можно объединить в одну:
а = ±arccos а + 2л&, k е Z.
(3.107)
Если а = ±1, тогда точка А(1; 0) отвечает случаю а — 1, а точка
В(-1; 0) отвечает случаю а = -1. Множество углов, дуги которых
оканчиваются в точке А, выражается формулой а — 2лfe, k е Z9
а множество углов, дуги которых оканчиваются в точке В, —
формулой а = я + 2л& = л(2& + 1), k g Z.
Отметим, что если а > 1, то уравнение cos а = а не имеет корней.
Уравнение cos а = а для а е [-1; 1] на отрезке а е [0; л] имеет
только один корень. Этот корень лежит в промежутке [0; л/2], ес-
ли а > 0, и в промежутке (л/2; л], если а < 0.
Приведем примеры решения некоторых уравнений типа
cos а = a: cos а = 0 => а = arccos 0 = л/2; cos а = - л/2 /2 => а =
183
ЧАСТЬ I. Алгебра и начала анализа
= arccos (~л/2 /2) = л - arccos (72/2) = тс - л/4 = Зл/4; cos а =
= -3/4 а = тс - arccos (3/4).
♦ ПРИМЕР 1
Построить дуги, соответствующие arccos (4/5) и arccos (-4/5),
лежащие в пределах [0; л].
РЕШЕНИЕ. Решение выполним графическим способом (рис. 106):
uAMj соответствует arccos (4/5), \jAM2 соответствует arccos (-4/5).
♦ ПРИМЕР 2
Решить уравнение cos а = 1/2.
РЕШЕНИЕ. На единичной окружности имеются две точки, для кото-
рых cos а = 1/2: 04 = arccos (1/2) = л/3, а2 = arccos (1/2) = -л/3.
Таким образом, решение определяется общим выражением
а = ±л/3 + 2л/г, k е Z.
3. Решение уравнения tg а = а. Известно, что функция tg а может
принимать любые действительные значения. Поэтому уравнение
tg а = а имеет корни при любом значении а.
Построим единичную окружность и ось тангенсов (рис. 107).
На оси тангенсов отметим точку N, ордината которой равна а. Че-
рез эту точку и начало координат проведем прямую, которая пе-
ресекает единичную окружность в точках и М2. Из выводов
§ 37 п. 3 следует, что ордината а на оси тангенсов равна тангенсу
угла Z. OAMV Поскольку tg а == а, точке Мх соответствует угол,
равный arctg а, а точке М2 — угол, равный arctg а + л. Множест-
Рис. 106
Рис.107
184
ГЛАВА 3. Тригонометрические функции
во всех решений уравнения tg а = а записывается следующим об-
разом:
а = arctg а + л/г, k е Z. (3.108)
Уравнение tg а = а имеет на интервале а е (-л/2; л/2) для лю-
бого a е R только один корень. Этот корень заключен в проме-
жутке [0; л/2], если а >0, и в промежутке (-л/2; 0), если а < 0.
Приведем примеры решения некоторых уравнений типа tg а = а:
tg а = 7з => а = arctg л/3 = л/3; tg а = -1 => а = arctg (-1) =
= -arctg 1 = -л/4.
♦ ПРИМЕР
Построить дуги, соответствующие arctg (6/5) и arctg (—4/5),
лежащие в пределах (-л/2; л/2).
РЕШЕНИЕ. Решение проиллюстрировано рисунком 108: иАМ1 соот-
ветствует arctg (6/5), uAM2 соответствует arctg (—4/5).
4. Решение уравнения ctg а - а. Уравнение ctg а “ а имеет корни
при любом значении а, так как функция ctg а может принимать
любые действительные значения.
Построим единичную окружность и ось котангенсов (рис. 109),
которая имеет уравнение у = 1. На этой оси отметим точку N? абс-
цисса которой равна а. Через эту точку и начало координат про-
ведем прямую, которая пересекает единичную окружность в точ-
ках Мг и М2. Аналогично рассуждениям, приведенным в § 37
п. 3 для функции tg а, можно показать, что абсцисса точки а соот-
Рис. 108
Рис. 109
185
ЧАСТЬ I. Алгебра и начала анализа
ветствует котангенсу угла
Z. AOMV Так как а — ctg а, точ-
ке Мх соответствует угол, рав-
ный arcctg а, а точке М2 — угол,
равный arcctg а + л. Множество
всех решений уравнения ctg а = а
записывается общей формулой
Рис. ИО
жутке (0; л/2], если а
а = arcctg а + л/г, k е Z. (3.109)
Уравнение ctg а = а имеет для
любого а е R на интервале
а е (0; л) только один корень,
Этот корень заключен в проме-
> 0, и в промежутке (л/2; л), если а < 0.
Приведем примеры решения некоторых уравнений типа
ctg а = a: ctg а = л/З /3 => а = arcctg (J3 /3) = л/3; ctg а = -1 => а =
= л + arcctg (-1) = л - arcctg 1 = л - л/4 = Зл/4.
♦ ПРИМЕР
Построить дуги, соответствующие arcctg (3/5) и arcctg (-6/5),
лежащие в пределах (0; л).
РЕШЕНИЕ. Решение проиллюстрировано рисунком 110: оА/И соот-
ветствует arcctg (3/5), uAM2 соответствует arcctg (-6/5).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Запишите в общем виде решение уравнения sin а = а. Приведите приме-
ры решения таких уравнений.
2. Проведите такой же анализ решения уравнений cos а = a, tg а = о, ctg а = а.
§ 40. Тригонометрические уравнения
1. Простейшие тригонометрические уравнения. Простейшими назы-
ваются тригонометрические уравнения, рассмотренные в § 39.
Они имеют вид sin х = /и, cos х = m, tg х = т, ctg х = тп, где т —
данное число. Приведем примеры более сложных уравнений та-
кого типа.
❖ ПРИМЕР 1
Решить уравнение:
3) cos (cos х) = 1/2.
1) sin 2х = 1/2; 2) tg (Зх + 2) = -1;
186
ГЛАВА 3. Тригонометрические функции
РЕШЕНИЕ. 1) По формуле (3.106) 2х — (—1)" л/6 4- лп, следователь-
но, множество корней уравнения имеет вид х = (-1)" л/12 4- лп/2,
п g Z;
2) из формулы (3.108) следует, что Зх 4- 2 = -л/4 4- л/?; следова-
тельно, множество корней уравнения имеет вид х = - 2/3 — л/12 4-
+ лЛ/3, k е Z;
3) из формулы (3.107) следует, что cos х = ±л/3 + 2nk, ke Z,
последнее уравнение не имеет корней, так как при любом k е Z
модуль его правой части |±л/3 4- 2л/г| > 1.
♦ ПРИМЕР 2
Решить уравнение: 1) sin2 х = иг, т е [0; 1]; 2) tg2 х = т, т > 0.
РЕШЕНИЕ. 1) Уравнение распадается на два:
sin х — Jm , х — nk 4- (-1)* arcsin Jm,
sin x = - Jm x = nk- (-l)ft arcsin Jm ,keZ.
В этой записи множители (— l)ft, регулирующие знаки вторых
членов, являются лишними, так как в зависимости от четности
или нечетности k знаку «+» в первом решении соответствует знак
«-» во втором и наоборот. Поэтому оба решения можно объеди-
нить в одно:
х = nk ± arcsin Jm .
2) Уравнение распадается на два:
х = л/г 4- arctg Jm
х = nk - arctg Jm
tg x = Jm, x = л« 4- arctf
tg x = - Jm x — nk- arcfy
<=> x = nk ± arctg Jm , k e Z.
2. Уравнения, сводящиеся к квадратным. Уравнение, являющееся
или сводящееся к квадратному относительной одной тригономет-
рической функции, решается вначале как квадратное, а затем
сводится к решению простейшего тригонометрического уравне-
ния.
♦ ПРИМЕР 1
Решить уравнение 2 sin2 х - 7 sin х 4- 3 = 0.
РЕШЕНИЕ. Обозначим sin х = у, получим уравнение 2у2 - 7у 4- 3 = 0.
Его корни ух = 1/2, у2 = 3. Таким образом, исходное уравнение
свелось к решению простейших уравнений sin х = 1/2 и sin х = 3.
187
ЧАСТЬ I. Алгебра и начала анализа
Решением первого уравнения является х = (-1)* л/6 4- л/г, ke Z,
второе уравнение не имеет решения.
Ф ПРИМЕР 2
Решить уравнение 4 cos2 х + sin х - 1 = 0.
РЕШЕНИЕ. Заменой cos2 х на (1 - sin2 х) сводим исходное уравнение
к квадратному: 4 sin2 х - sin х - 3 = 0. Обозначив sin х = у, полу-
чим уравнение 4у2 - у - 3 = 0. Его корни yt = 1, у2 = -3/4. Итак,
исходное уравнение свелось к решению двух простейших уравне-
ний: sin х = 1, sin х = -3/4. Их корнями являются хг — л/2 4- 2л&,
х2 = (- l)ft arcsin 7 4- nk, ke Z.
X Уравнения, решаемые разложением левой части на множители. Мно-
гие тригонометрические уравнения, правая часть которых равна
кулю, решаются разложением левой части на множители.
Ф ПРИМЕР 1
Решить уравнение tg х cos х + tg х - cos х - 1 = 0.
РЕШЕНИЕ. Уравнение можно привести к виду (cos х 4- l)(tg х - 1) = О,
при этом необходимо исключить возможные корни х л/2 + л/г.
cos х = -1,
tgx= 1,
х * л/2 4- nk
~х = л(2/г 4- 1),
х = л/4 + л/г,
х л/2 + nk
' х = л(2& + 1),
х = л/4 4- л/г,keZ.
Ф ПРИМЕР 2
Решить уравнение tg3 х - tg х = 0.
РЕШЕНИЕ. Уравнение приводится к виду tg x(tg2 х - 1) = 0, х л/2 4-
+ nk.
"х = л&,
X = ±л/4 4- л/?,
х л/2 4- itk
Xj = Ttk,
х2 = ±л/4 4- л/г, k е Z.
4. Уравнение a sin х + b cos х = с. Частным случаем уравнения подоб-
ного вида является уравнение со свободным членом, равным ну-
лю, например sin х - cos х = 0. Поделим уравнение на cos х, полу-
чим tg х — 1 = О. Решением этого уравнения является х = л/4 4-
4- л/г, k е Z. Так как при делении на выражение, содержащее не-
известное, могли быть потеряны корни, необходимо проверить,
188
ГЛАВА 3. Тригонометрические функции
не являются ли корни уравнения cos х = 0 корнями данного урав-
нения. Если cos х — 0, то из исходного уравнения следовало бы,
что sin х = 0. Однако sin х и cos х не могут быть одновременно
равны нулю, так как они связаны соотношением sin2 х + cos2 х = 1.
Следовательно, при делении уравнения a sin х + b cos х ~ 0, где
а * 0, Ъ * 0, на sin х или cos х получаем уравнение, равносильное
данному.
Если уравнение имеет вид
a sin х + b cos х = с,
а * 0, b * 0, с 0, то его можно решить следующим образом. Раз-
делим обе части уравнения (*) на </а2 + Ъ2 , получим
sin х
cos х =
Введем вспомогательный аргумент \|/ такой, что
а
cos у = .
Ja2 + b2
sin у =
Такое число существует, так как
Поэтому уравнение (**) можно записать в виде
с
sin х cos y + cos x sin v = ~--------
J a2 + b2
По (3.63) последнее уравнение сводится к уравнению
sin (х + у) =
которое является простейшим тригонометрическим уравнением.
♦ ПРИМЕР
Решить уравнение 3 sin х + 4 cos х = 5.
РЕШЕНИЕ. По отношению к уравнению (*) здесь а = 3, b — 4t с — 5
Ja2 + b2 = 5. Разделив обе части на 5, придем к уравнению
3 . , 4
ё Sin X + ё COS X = 1.
5 5
189
ЧАСТЬ I. Алгебра и начала анализа
Введем вспомогательный аргумент у такой, что sin у = 4/5,
cos v = 3/5. Исходное уравнение запишется в виде sin х cos у +
+ cos х sin у = 1, sin (х + у) = 1, откуда
х + у = л/2 + 2л/?, где у = arccos (3/5),
х = л/2 — arccos (3/5) + 2л/?, k е Z.
5. Однородные уравнения*. Однородными называют тригономет-
рические уравнения, у которых левая часть является одно-
родным многочленом относительно sin х и cos х, а правая часть
равна нулю. Такие уравнения сводят к уравнениям относительно
tgx.
♦ ПРИМЕР 1
sin2 х - 4 sin х cos х + 3 cos2 х = 0.
РЕШЕНИЕ. Уравнение приводим к виду
tg2 x-4tgx + 3 = 0,
cos х 0
tgx = 1,
। tg х = 3,
х л/2 + л/?
~х = л/4 + л/?,
< х = arctg 3 +
л/?,
х * л/2 + л/?
х = л/4 + л/?,
I
| х = arctg 3 + л/?, k е Z.
♦ ПРИМЕР 2
Решить уравнение
2 sin2 х + 5 sin х cos х + cos2 х - 4 = 0.
РЕШЕНИЕ. Умножив свободный член на 1 = sin2 х + cos2 х, получим
однородное уравнение
2 sin2 х + 5 sin х cos х + cos2 х — 4 sin2 х - 4 cos2 х = 0
или
2 sin2 х - 5 sin х cos х + 3 cos2 х = 0.
Далее поступаем так же, как и в предыдущем случае:
2 tg2 x-5tgx + 3 = 0
tgx= 1,
tg х = 3/2
Гх = л/4 + л/?,
1 х = arctg (3/2) + л/?, k g Z.
Однородными называются уравнения, в которых каждое слагае-
мое имеет одну и ту же степень.
190
ГЛАВА 3. Тригонометрические функции
6. Уравнения, решаемые с помощью введения вспомогательного аргу-
мента. Некоторое число а можно рассматривать как значение
тригонометрической функции от аргумента, называемого вспо-
могательным, так как при любом значении а имеют место ра-
венства tg (arctg а) = a, ctg (arcctg а) ~ а и при a < 1 равенства
sin (arcsin а) = а и cos (arccos а) = а. Таким образом, алгебраиче-
скую сумму любых двух чисел можно представить в качестве ал-
гебраической суммы тригонометрических функций и, следова-
тельно, применять формулы преобразования алгебраической
суммы тригонометрических функций в произведение.
♦ ПРИМЕР 1
Преобразовать в произведение с помощью введения вспомога-
тельного уравнения выражение: 1) = а/2 sin а + 1; 2) f2 =
= 4 cos2 а - 1; 3) а + Ъ.
РЕШЕНИЕ. 1) = J2 (sin а + 1/2) = J2 (sin а + sin (л/4)). По фор-
муле (3.93) последнее выражение приводится к
2 J2 sin (л/8 + а/2) cos (а/2 - л/8);
2) f2 = 4(cos2 а - 1/4) = 4(cos а - l/2)(cos а + 1/2) = 4(cos а +
+ cos (jc/3))(cos а - cos (л/3)).
По формулам (3.95) и (3.96) последнее выражение можно при-
вести к виду 4 • 2 cos (а/2 + л/6) cos (а/2 - л/6) • 2 sin (а/2 + л/6) х
х sin (л/6 - а/2).
Согласно формуле (3.71) имеем
4 sin (а + л/3) sin (л/3 - а);
3) /3 = а(1 + b/а) == а(1 + tg <р) = a(tg (л/4) + tg ф).
Используя формулу (3.97) и обозначение ф = arctg (&/а), при-
ходим к уравнению
sin(rc/4 + ф) _ aA/2sin(ft/4 + ф)
соз(л/4)со8ф совф
♦ ПРИМЕР 2
Решить уравнение sin х + J3 cos х — 2.
РЕШЕНИЕ. Используем метод вспомогательного аргумента:
sin х + -$- cos х ]= 2 cos (л/3) sin х +
J X
+ sin (л/3) cos х 1= 2 sin (х + л/3).
191
ЧАСТЬ I. Алгебра и начала анализа
Таким образом, исходное уравнение преобразуется к виду
2 sin (х + л/3) = 2 <=> (х + л/3 = л/2 + 2т№) <=> х = л/6 + 2л&, k е Z.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие тригонометрические уравнения называются простейшими?
2. Что понимается под решением тригонометрического уравнения?
3. Перечислите основные способы решения тригонометрических уравне-
ний.
4. Выведите формулы преобразования выражений (1 ± cos а) и (1 ± sin а)
в произведение.
5. Как выполняются преобразования с помощью вспомогательного аргу-
мента?
§ 41. Тригонометрические неравенства
Простейшими тригонометрическими неравенствами называ-
ются неравенства
sin х < m, sin х > m, cos x < m, cos x > m, tg x < m, tg x > m,
ctg x <m, ctg x > тп, где m — данное число.
Решить простейшее тригонометрическое неравенство — зна-
чит найти множество всех значений аргумента, которые обраща-
ют данное неравенство в верное числовое неравенство.
Ф ПРИМЕР 1
Решить неравенство: 1) |sin х| > 1/2; 2) cos х > -1/2.
РЕШЕНИЕ. 1) Решение иллюстрируется рисунком 111: здесь точке
Mj соответствует угол л/6, М2 — угол 5л/6, М3 — угол л/6 + л,
М4 — угол 5л/6 + л. Неравенство выполняется для л/6 < х < 5л/6
ил/6 + л<х< 5 л/6 + л. Общим решением служит неравенство
л/6 + nk < х < 5л/6 + nk, keZ.
2) Данное неравенство иллюстрируется рисунком 112: здесь
точке Мг отвечает угол 2л/3, а точке М2 — угол -2л/3. Общим
решением неравенства является
-2л/3 + 2л/г < х < 2л/3 + 2лА, k g Z.
$ ПРИМЕР 2
Решить неравенство: 1) tg х > л/3; 2) sin (х/2) > 1/2.
192
ГЛАВА 4. Пределы
Рис. 111
Рис. 112
РЕШЕНИЕ. 1) Учитывая свойство неограниченности функции tg х,
имеем tg х е (7з; +оо). Исходному неравенству удовлетворяют
дуги из промежутка х е (л/3; л/2). Так как периодом для функ-
ции tg х является число л, общим решением является неравенство
л/3 + л/г < х < л/2 + л/г, /г е Z.
2) Поскольку л/6 + 2л/г < х/2 < 5л/6 + 2л/г, решение имеет вид:
л/3 + 4л/г < х < 5л/3 + 4л/г, /г е Z.
ГЛАВА 4. Пределы
§ 42. Предел переменной величины
1. Понятие о числовой последовательности. Рассмотрим функцио-
нальную зависимость у = х2:
Здесь значениями аргумента х являются натуральные числа,
а функцией является числовая последовательность у.
Числовой последовательностью называется нумерованное
множество чисел, расположенных в порядке возрастания но-
меров, т. е. являющееся функцией от натурального аргумента.
7 - 9664
193
ЧАСТЬ I. Алгебра и начала анализа
В общем виде числовая последовательность записывается сле-
дующим образом:
Число ип называется общим числом последовательности.
Зная формулу общего члена последовательности, можно най-
ти любой ее член (например, в арифметической и геометрической
прогрессиях).
2. Характер изменения переменной величины. В математике и ее при-
ложениях постоянно используются переменные величины.
Переменная величина может быть возрастающей, убывающей
или переходить от возрастания к убыванию или наоборот.
Переменные, которые в процессе изменения или только воз-
растают, или только убывают, называются монотонными.
По характеру изменения переменные величины подразделя-
ются на ограниченные и неограниченные.
Переменная величина у называется ограниченной, если начи-
ная с некоторого ее значения выполняется неравенство
где М — постоянное положительное число.
Например, значения функции sin х являются ограниченными
величинами, так как |sin х|
функции tg х являются ограниченными величинами.
Некоторые переменные являются неограниченными величи-
нами, например, значения функции тангенса при изменении ар-
гумента от 0 до л/2 неограниченно возрастают. Каким бы боль-
шим ни было положительное число N, значение tg х при х —* л/2
превзойдет по своей величине это число N.
3. Бесконечно малая величина. Среди различных переменных ве-
личин особое место занимают бесконечно малые величины.
1. На отрезке [-л/4; л/4] значения
Переменная величина а называется бесконечно малой, если
она при своем изменении становится и затем остается по абсо-
лютной величине меньше любого наперед заданного сколь
угодно малого положительного числа е:
Например, дробь 1/х при неограниченном возрастании абсо-
лютной величины х является бесконечно малой величиной. Как
бы мало ни было данное положительное число е при неограничен-
194
ГЛАВА 4. Пределы
ном возрастании г, величина 1/х станет и останется меньше е,
т. е. 11 /х| < е.
Легко показать, что функция у = sin х при х —* 0 есть величи-
на бесконечно малая, т. е. sin х —* 0.
Не следует смешивать бесконечно малую величину с ничтож-
но малой, так как бесконечно малая является величиной пере-
менной, а ничтожно малая остается постоянной.
Иначе говоря, никакая постоянная величина не может быть
бесконечно малой, так как она по абсолютной величине не может
стать меньше любого, сколь угодно малого наперед заданного по-
ложительного числа. Исключение из всех постоянных величин
составляет нуль, ибо нуль всегда меньше любого, сколько угодно
малого, положительного числа. Поэтому нуль считается беско-
нечно малой величиной.
Примерами бесконечно малых величин могут служить зна-
чения функций: у = х2 при х —> 0; у = х - 1 при х —* 1, у = 2х при
X -ОО.
4. Бесконечно большая величина.
Переменная величина у называется бесконечно большой, ес-
ли, каким бы большим ни было наперед заданное положитель-
ное число N, абсолютная величина у становится и при даль-
нейшем изменении остается больше этого числа N:
Ы > N.
Термин бесконечно большая величина определяет характер
изменения переменной величины, поэтому бесконечность не яв-
ляется числом. Каким бы большим ни было постоянное число,
оно является конечным.
Например, функция у = ctg х при х —* 0 неограниченно возрас-
тает, т. е. ctg х +оо. Как бы велико ни было наперед заданное
положительное число N, найдется такое значение аргумента х,
близкое к нулю, для которого ctg х станет и в дальнейшем будет
оставаться больше этого числа. Следовательно, ctg х является ве-
личиной бесконечно большой при х —* 0.
5. Связь бесконечно малой величины с бесконечно большой. Между
бесконечно малой и бесконечно большой величинами существует
связь, а именно:
I. Если х — величина бесконечно большая, то обратная ей ве-
личина -
является бесконечно малой.
195
ЧАСТЬ I. Алгебра и начала анализа
II. Если х — величина бесконечно малая, то обратная ей вели-
чина ~ является величиной бесконечно большой.
Например, если у — бесконечно большая величина, прини-
мающая значения 1, 10, 100, 1000, ...» у + оо, то 1/х получает
соответственно значения 1, (0,1), (0,01), (0,001), ... (1/х) -*• 0,
т. е. оказывается бесконечно малой величиной.
Наоборот, если а — бесконечно малая величина, принимаю-
щая значения 1, (0,1), (0,001), (0,0001), ...» а -* 0, то 1 /а получа-
ет соответственно значения 1, 10, 100, 1000, ... (1/а) —* +оо, т. е.
оказывается бесконечно большой величиной.
6. Понятие о пределе переменной. Рассмотрим разность между
площадью круга и площадью вписанного в этот круг правильного
многоугольника: при неограниченном удвоении числа его сторон
эта разность становится сколь угодно малой.
Пусть переменная х в процессе изменения неограниченно при-
ближается к числу 2 и при этом принимает значения: х = 2,1;
2,01; 2,001; 2,0001 ... или х = 1,9; 1,99; 1,999; 1,9999 ... .
В каждом из этих случаев абсолютная величина разности
|х - 2| -* 0, причем в первом случае значения переменных в про-
цессе изменения остаются большими 2, а во втором случае —
меньшими 2.
Для приведенных значений переменной х абсолютная величи-
на разности |х - 2| принимает значения: 0,1; 0,01; 0,001; ..., т. е.
модуль |х - 2| есть величина бесконечно малая. В этом случае
число 2 называется пределом переменной.
Постоянная а называется пределом переменной х, если раз-
ность х - а = а есть величина бесконечно малая.
Для обозначения предела используется символ lim*.
В частности, для предыдущего примера можно использовать
запись lim х = 2.
Говорят также, что переменная х стремится к пределу а, если
разность х - а = а есть величина бесконечно малая.
Из равенства х - а = а следует, что х = а + а. Таким образом,
можно сформулировать утверждение.
Переменная величина х, имеющая своим пределом число а,
может быть представлена в виде суммы двух слагаемых: по-
стоянной а (предела а) и бесконечно малой а.
* limes — предел (лат.), limite (фр.).
196
ГЛАВА 4. Пределы
Справедливо и обратное утверждение.
Если переменная величина х является суммой числа а и беско-
нечно малой а, то а есть предел переменной х.
Из определения предела следует, что:
I. Предел бесконечно малой равен нулю.
Если lim а = 0, то разность а — 0 = а есть величина бесконечно
малая.
II. Если lim а = 0, то а есть величина бесконечно малая.
Из равенства lim а = 0 следует, что разность а - 0 есть величи-
на бесконечно малая, но а — 0 = а; значит, а есть величина беско-
нечно малая. Другими словами, переменная, имеющая своим
пределом нуль, является величиной бесконечно малой.
III. Постоянную можно рассматривать как переменную, принимающую
одно и то же числовое значение, а постоянную, равную нулю, как беско-
нечно малую.
Покажем, что предел постоянной с равен самой постоянной с,
т. е. lim с = с. Пусть переменная х принимает одно и то же посто-
янное значение с, тогда х - с = с — х = 0, т. е. разность х — с = О
есть величина бесконечно малая. Отсюда следует, что lim х = с,
т. е. lim с = с.
Исходя из определения бесконечно малой величины, понятие
предела можно сформулировать в следующей форме:
Число а называется пределом переменной величины х, если
разность |х - п| в процессе изменения х становится и при даль-
нейшем изменении х остается по абсолютной величине мень-
ше любого наперед заданного положительного числа е, как бы
мало это число ни было:
♦ ПРИМЕР
Пусть переменная у =
в процессе изменения аргу-
мента х принимает соответствующие числовые значения. Оп-
ределить lim у при х —* 1.
РЕШЕНИЕ. Составим таблицу значений аргумента х и функции у:
X 1.1 1.01 1.001 1,0001 * в в
5,1 5.01 5,001 5,0001 в в в
197
ЧАСТЬ I. Алгебра и начала анализа
Можно заметить, что у —► 5 при х —*• 1, но для того, чтобы дока-
зать, что lim у = 5, необходимо показать, что (у — 5) 0, т. е. что
разность (у — 5) является бесконечно малой величиной.
Выполним преобразования:
х2 + Зх - 4
х2 — 2х + 1
х — 1
(х — 1)
X — 1
Сокращение на (х - 1) корректно, так как при х —* 1 величина
х не может принимать значения х = 1 и, таким образом,
знаменатель не может оказаться равным нулю.
Разность (х - 1) -* 0 при х —* 1, т. е. является величиной беско-
нечно малой. Поэтому по определению число 5 является преде-
лом переменной у:
х2 + Зх - 4
lim---------
х—1 X — 1
В дальнейшем будут рассмотрены более рациональные прие-
мы вычисления предела функции.
7. Основные свойства бесконечно малых.
I. Бесконечно малая величина при перемене ее знака на проти-
воположный остается бесконечно малой.
В определении бесконечно малой величины (4.1) фигурирует
абсолютная величина переменной, поэтому равенство (4.1) спра-
ведливо при изменении ее знака.
II. Если а и Р — бесконечно малые, то их сумма и разность то-
же величины бесконечно малые.
Процесс изменения аир при их приближении к нулю может
быть различным, но по определению для сколь угодно малого по-
ложительного числа е величины аир станут и будут оставаться
меньше е/2, т. е. |а| < е/2, |р| < е/2, следовательно,
|а| + |р|<е.
(4.2)
Известно, что абсолютная величина суммы меньше или равна
сумме абсолютных величин слагаемых, т. е. |а + р| < |а| + |р|, по-
этому из формулы (4.2) следует, что |а + р| < £. Таким образом,
сумма а + р есть величина бесконечно малая.
198
ГЛАВА 4. Пределы
Бесконечно малая Р при перемене ее знака остается бесконеч-
но малой; из предыдущего заключения следует, что разность
а - р есть тоже бесконечно малая величина.
III. Алгебраическая сумма конечного числа бесконечно малых
слагаемых есть величина бесконечно малая.
Это утверждение может быть доказано методом математиче-
ской индукции с использованием предыдущего свойства.
IV. Произведение ограниченной величины х и бесконечно ма-
лой а есть бесконечно малая величина.
В процессе изменения величин х и а, начиная с некоторого мо-
мента будут сохраняться неравенства:
где т — положительное число, ас — некоторое наперед заданное
сколь угодно малое положительное число. Перемножив левые и
правые части неравенств получим
|х||а
Известно, что абсолютная величина произведения равна про-
изведению абсолютных величин: |х||а| = |х • а|, поэтому |х • а| < £,
т. е. произведение х • а является бесконечно малой величиной.
V. Произведение постоянной на бесконечно малую есть вели-
чина бесконечно малая. Произведение нескольких бесконечно
малых есть величина бесконечно малая. Целая положительная
степень бесконечно малой есть величина бесконечно малая.
Эти утверждения справедливы, так как любое число и любая
бесконечно малая величина являются ограниченными.
VI. Частное от деления двух бесконечно малых может быть ве-
личиной постоянной, или бесконечно малой, или бесконечно
большой.
8. Теоремы о пределах.
ТЕОРЕМА I
Переменная величина не может иметь двух различных пределов.
ДОКАЗАТЕЛЬСТВО. Допустим, что переменная х имеет два различ-
ных предела А и В, тогда по определению предела получим
х - А = а, х - В = р,
где аир — бесконечно малые.
199
ЧАСТЬ I. Алгебра и начала анализа
Вычитая из первого равенства второе, получаем
х-А-х4-В = а- р или а - р = В - А.
Левая часть этого равенства содержит разность двух бесконечно
малых, т. е. величину бесконечно малую; правая часть является ве-
личиной постоянной. Бесконечно малая может равняться постоян-
ной только в том случае, если постоянная равна нулю, следователь-
но, В - А = О, А = В, т. е. переменная имеет только один предел.
СЛЕДСТВИЕ. Если две переменные величины, имеющие пределы,
при всех своих изменениях равны между собой, то равны и их
пределы.
ТЕОРЕМА II
Предел суммы конечного числа переменных, имеющих преде-
лы, равен сумме пределов этих переменных.
ДОКАЗАТЕЛЬСТВО. Пусть переменные х и у имеют пределами числа
А и В, т. е.
lim х = A, lim у = В.
По определению предела имеем:
х - А = а, #-В = р,
где аир — бесконечно малые. Сложив эти равенства, приходим
к соотношению (х 4- у) — (А 4- В) = а 4- р.
По определению предела имеем lim (х + у) = А 4- В. Учитывая
формулу (4.3), получаем
lim (х 4- у) = lim х 4- lim у.
ТЕОРЕМА III
Предел разности переменных, имеющих пределы, равен раз-
ности пределов этих переменных.
ДОКАЗАТЕЛЬСТВО. Принимая во внимание, что разность можно рас-
сматривать как алгебраическую сумму, теорема II может быть
распространена на разность переменных.
ТЕОРЕМА IV
Предел произведения конечного числа переменных, имеющих
пределы, равен произведению пределов.
ДОКАЗАТЕЛЬСТВО. Пусть переменные х и у имеют своими пределами
величины А и В, тогда по определению предела имеем
х = А 4- a, f/ = B + p,
где аир бесконечно малые. Перемножив эти равенства, получим
ху = АВ 4- Ар 4- Ва 4- ар или ху - АВ = Ар 4- Ва 4- ар.
200
ГЛАВА 4. Пределы
Левая часть представляет собой разность между произведени-
ем переменных ху и постоянной АВ, а правая часть — сумму бес-
конечно малых, которая с учетом свойства III является также бес-
конечно малой величиной. Поэтому разность (ху - АВ) — величи-
на бесконечно малая, следовательно, по определению предела
lim (ху) = АВ
или
lim (ху) = lim х • lim у.
Эта теорема может быть доказана для любого конечного числа
переменных сомножителей.
СЛЕДСТВИЕ 1. Предел произведения постоянной величины на пере-
менную, имеющую предел, равен произведению постоянной на пре-
дел переменной, т. е. если а — постоянная, ах — переменная, то
lim (ах) = a lim х. (4.4)
По теореме IV
lim (ах) = lim а • lim х,
но lim а = а, из чего и следует формула (4.4).
СЛЕДСТВИЕ 2. Предел степени переменной, имеющей предел, равен
той же степени предела переменной, т. е.
lim хт = (lim х)т. (4.5)
Число хт является произведением т одинаковых сомножите-
ли
лей х, хт = х • х • ... • х , тогда
lim хт = lim (х • х •... • х) = lim х • lim х •... • lim х — (lim х)т.
СЛЕДСТВИЕ 3. Предел корня из переменной, имеющей предел, равен
корню той же степени из предела переменной, т. е.
lim mJx =
"i/limx.
(4.6)
Представив mJx в виде степени х1/т,
получим:
lim mJx = lim x1/m = (lim x)1/m = "1/limx .
ТЕОРЕМА V
Предел частного от деления двух переменных, имеющих пре-
делы, равен частному от деления пределов делимого и делите-
ля при условии, что предел делителя не равен нулю, т. е.
lim - = , lim у * 0. (4.7)
у limy р 7
ДОКАЗАТЕЛЬСТВО. Пусть lim х = A, lim у = В, В # 0.
201
ЧАСТЬ I. Алгебра и начала анализа
Опустим доказательство существования предела - ввиду
сложности изложения, поэтому докажем только, что этот предел
равен частному от деления lim х на lim у.
X
Положим - = z, тогда х = yz. Полагая, что х, у и г имеют пре-
У
делы, применим теорему IV о пределе произведения:
lim х = lim у • lim z или А = В lim z,
из чего следует, что
1- А
lim 2 = — .
а
С учетом введенных обозначений получим формулу (4.7).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какая последовательность называется числовой последовательностью?
2. Каким может быть характер изменения переменной величины?
3. Какому условию должна удовлетворять ограниченная переменная вели-
чина? Приведите примеры ограниченных переменных величин.
4. Дайте определение бесконечно малой переменной. Приведите примеры
бесконечно малых величин.
5. Какую переменную называют бесконечно большой?
6. Какая связь существует между бесконечно малой и бесконечно большой
величинами?
7. Сформулируйте определение предела переменной величины.
8. Перечислите основные свойства бесконечно малых.
9. Перечислите теоремы о пределах переменных и следствия из них.
§ 43. Предел функции
1. Вычисление предела функции. Пусть функция у = f(x) имеет сво-
им пределом число A: lim f(x) = А, причем f(x) изменяется в за-
х — *о
висимости от изменения переменной х. Необходимо учитывать,
что при неограниченном стремлении переменной х к числу а
(х а) само число а исключается из значений, принимаемых пе-
ременной х. Дадим определение предела функции в точке.
Число А называется пределом функции f(x) в точке х0 и обо-
значается lim /(х) = А, если для любого числа е > 0 существу-
X Хо
ет число 5 > 0 такое, что для всех х, удовлетворяющих условию
|х - х0| < 5, где х х0, выполняется неравенство |/(х) — А| < е.
202
ГЛАВА 4. Пределы
При вычислении пределов функции используются теоремы,
которые формулируются без доказательств.
ТЕОРЕМА I
Если существуют пределы функций f(x) и ф(х) при х —* а, то
существует также и предел их суммы, равный сумме пределов
функций f(x) и ф(х):
Jim (f(x) 4- ф(х)) = lim f(x) + lim ф(х).
ТЕОРЕМА II
Если существуют пределы функций f(x) и ф(х) при х —► а, то
существует также и предел их произведения, равный произве-
дению пределов функций f(x) и ф(х):
lim (/(х) • ф(х)) = lim /(х) • lim ф(х).
Л U Л U A U
ТЕОРЕМА III
Если существуют пределы функций f(x) и ф(х) при х —► а, пре-
дел функции ф(х) отличен от нуля, то существует также пре-
дел отношения
f(x}
Ф(х)
равный отношению пределов функций
/(х) и ф(х):
СЛЕДСТВИЕ 1. Постоянный множитель можно вынести за знак пре-
дела:
Jim, (kf(x)) = k Jim, f(x).
СЛЕДСТВИЕ 2. Если n — натуральное число, то справедливы соотноше-
ния: lim хп = ап. lim nJx = nJa .
х а х —• а
СЛЕДСТВИЕ 3. Предел многочлена (целой рациональной функции)
F(x) = atxn “ 1 + а2хп ~2 + ... + ап_ jXn " 1 + ап
при х -* а равен значению этого многочлена при х = а, т. е.
lim F(x) = F(a).
СЛЕДСТВИЕ 4. Предел дробно-рациональной функции
апхл + алхп ~ 1 + ... + а .х + а„
Г(х) = —------------------—--------
boxm + biXm ‘ 1 + ... + bm _ гх + Ът
203
ЧАСТЬ I. Алгебра и начала анализа
при х —> с равен значению этой функции при х = с, если с прина-
длежит области определения этой функции, т. е.
Нтс Г(х) = Г(с).
Рассмотрим некоторые нестандартные ситуации, возникаю-
щие при вычислении пределов функций.
1. Функция представляет собой дробь, предел знаменателя
5
которой равен нулю. Например, для Д = -------- определим
4х — 8
lim fv Теорему III о пределе частного применять нельзя, так как
lim (4х — 8) = 0. Таким образом, знаменатель Д есть величина
X '-'Г £
бесконечно малая, а обратная ей величина
таким обра-
зом, есть величина бесконечно большая, поэтому lim Д = со.
Л * £
2. Функция представляет собой дробь, пределы числителя и
знаменателя которой равны нулю. Например, для /2 =
Зх2 — 2х
2х2 — 5х
определим lim Д. Непосредственной подстановкой вместо аргу-
X * V **
мента его предельного значения вычислить lim Д нельзя, так
как при х —> 0 это вычисление сведется к определению отноше-
ния двух бесконечно малых величин.
Разложим числитель и знаменатель на множители, чтобы со-
кратить дробь на общий множитель, значение которого стремит-
ся к нулю при х —* 0, и таким образом сделать возможным приме-
нение теоремы III. При этом не производится сокращения на
нуль: по определению предела функции аргумент х стремится к
своему предельному значению, никогда не достигая этого значе-
ния. Имеем
lini Д = lirn
х • о * 2 х — о
(Зх - 2)
Inn------------
X 0 / Л _ ЕГ \
3-0-2
2-0-5
2
5‘
Подобный случай будет иметь место и при определении Jimo Д
Здесь необходимо умножить числитель
и знаменатель на сопряженный знаменателю множитель
и затем, сократив дробь на х, вычислить
204
ГЛАВА 4. Пределы
lim f.
с - о ' •
lim
♦ ПРИМЕР
- sina
Определить lim-----
а —> о a
РЕШЕНИЕ. При вычислении такого предела нельзя применить те-
орему III о пределе частного, так как при a —> 0 и числитель, и
знаменатель дроби стремятся к нулю.
Обратимся к рисунку 81, на котором изображен единичный
тригонометрический круг с дугой u AM = a (0 < a < л/2). Очевид-
но, что МгМ < u AM < AN или sin a < a < tg а. Последнее нера-
венство можно записать в виде
sin a
sina
a <-----.
cosa
Так как sin a > 0, то, разделив это неравенство на sin а, получим
1 < - < 1
sina cosa
или
1 > > _1_ (*
a cosa ’ v
При a —> О функция cos a -* 1 и неравенство (*) принимает вид
- > sina 1
a
Следовательно, lim
sina
a
Эквивалентными называются бесконечно малые, предел от-
ношения которых равен единице.
В последнем примере sin а и a — эквивалентные бесконечно
малые при a —> 0. Величины tg а и а при ос —> 0 также оказывают-
ся эквивалентными бесконечно малыми:
.. tga ,. sina/cosa sina
hm -s— = hm----------- = lim------ =
a->o a a-»o a a-»oacosa
.. /sina 1 > sina .. 1 ,
= lim -----•---- = hm-------• hm------ = 1 • 1 = 1.
a->o\ a cosa J a->o a a-> о cosa
205
ЧАСТЬ I. Алгебра и начала анализа
Отметим без доказательства, что отношение двух бесконечно
малых величин можно заменить отношением эквивалентных ве-
личин, например,
,. sinax .. ах .. а а
lim = lim т— = lim -г = г .
х->о sinox х-^obx b о
3. Функция представляет собой разность двух бесконечно
больших величин при стремлении аргумента к некоторому зна-
чению. Например, для функции f4
12
определим
lim^. Здесь, выполнив действие вычитания, получим дробь,
числитель и знаменатель которой стремятся к нулю при х —* — 2.
Далее поступаем, как и в случае с функцией f2; сократив дробь на
(х + 2), находим
х2 — 2х — 8
1 ----------------
оо I О
_(Х+.2И* - 41....
°°(х + 2)(х2 — 2х + 4)
.. (х — 4)
hm —----------------------
4. Некоторые слагаемые функции пределов не имеют. На-
пример, определим f5 для функции /5 = х3 - 6х2 + 5х — 1.
Первые три слагаемых при х —> °° пределов не имеют, поэтому
нет возможности непосредственно воспользоваться следствием 3.
Вынося х3 за скобки, получаем:
X — оо
и —з — бесконечно малые и их пре-
_ 6 5
при х —* 00 величины - , —
делы равны нулю
5. Знаменатель функции является величиной бесконечно
5
большой. Например, определим lim^ /6 для f6 = ----. Так как
^1 эс I 1
знаменатель при х —* сю становится величиной бесконечно боль-
шой, то обратная ему функция
становится при х —► бес-
конечно малой. Произведение бесконечно малой на ограничен-
206
ГЛАВА 4. Пределы
ную величину
есть величина бесконечно малая, сле-
довательно, lim^ /6 = 0.
6. Функция представляет собой дробь, числитель и знамена-
тель которой — величины бесконечно большие. Например, опреде-
2х + 3
лим limm f7 для функции /7 =------. При непосредственном приме-
х "00 5х + 1
нении теоремы III приходим к выражению —. Поэтому для вычис-
ления lim^ f7 необходимо числитель и знаменатель разделить на х:
2х + 3
5х + 1
lim = lim
х * 00 ' ( X —> СО
2+0 _ 2
5 + 0 5 ‘
7. Функция представляет собой разность бесконечно боль-
ших величин. Например, определим lirn fs для функции f8 =
= х - л/х2 — 4. Умножив и разделив функцию на выражение
х + 7х2 “ 4х , получим
2. Число е. Натуральные логарифмы. Функция z =
при п
имеет предел, выражающийся иррациональным числом; это чис-
ло принято обозначать через е:
Приведем значения функции 1 + - при увеличивающихся
значениях аргумента п.
Л 5 10 100 1000 10 000 100 000
1 Н- 2.4883 2.5937 2,7048 2.7169 2,7181 2,7182
207
ЧАСТЬ I. Алгебра и начала анализа
Можно заметить, что при п > 10 000 четыре первые знака зна-
чения функции остаются неизменными. Число 2,718 является
приближенным значением числа е. Более точное его значение:
6 = 2,7182818285.
Если обозначить а = - , то можно записать:
п
е = lim (1 + а)1/Га.
Q —* ОО х Л
Число е принято за основание логарифмов, называемых нату-
ральными. Натуральный логарифм числа N, как уже было отме-
чено в § 17, п. 5, принято обозначать In N — log,, N'.
С
♦ ПРИМЕР
Вычислить: 1) L. = lim 1 + - ; 2) L9 =
' 1 х “* со I ОС I 7
РЕШЕНИЕ. 1) Имеем: L. = lim
7 1 X С
х/3)•3
= lim
х/3
= 1/е.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Перечислите теоремы и следствия из них, на которых основано вычис-
ление предела функции.
2. Что представляет собой число е?
§ 44. Непрерывность функции
1. Приращение аргумента и функции. Для функции у = f(x) разность
двух значений аргумента хх и х2, лежащих в области определе-
ния функции, называется приращением аргумента и обознача-
ется символом Дх, т. е. х2~ хг = Ах.
Разность двух значений функции у± — ffx^) иу2 = f(x2) (из мно-
жества значений функции, которые она может принимать), соот-
ветствующих значениям аргумента х^ и х2, называется прираще-
нием функции и обозначается символом Ау, т. е. Ay = f(x2) -
~ f(x1) = y2-y1.
208
ГЛАВА 4. Пределы
Если х2 > хр то Дх > 0; если же х2 < хр то Дх < 0. Соответ-
ственно и приращение функции Дг/ > 0, если у2 > уг и Дг/ < 0, ес-
ли y2<yv
Пусть аргумент х получил приращение Дх, тогда новое значе-
ние аргумента есть х 4- Дх, а соответствующее ему значение
функции есть у + Дг/ = /(х 4- Дх). Чтобы найти приращение функ-
ции, нужно из нового значения функции вычесть первоначаль-
ное:
у 4- Д г/ = f (х 4- Дх)
= /(*)
ку = f(x 4- Дх) - /(х)
♦ ПРИМЕР
Найти приращение функции у = х2 4- х 4- 1, если аргумент х
изменил свое значение от хт = 2 до х2 = 2,5.
РЕШЕНИЕ. Приращение аргумента Дх = х2 - хх = 0,5. Вычислим
значения функции у^х^) и */2(х2):
Ух = Лхт) = f(2) = 22 4- 2 4- 1 = 7,
у2 = f(x2) = /(2,5) = (2,5)2 4- 2,5 4- 1 = 9,75.
Тогда
^У = У2~Ух = 9,75-7 = 2,75.
2. Непрерывность функции. Функция f(x) называется непрерывной
в точке х = а, если
Иша /(х) = f(a).
Можно дать другое определение непрерывности функции.
Функция у = /(х) называется непрерывной в точке х = а, ес-
ли она в этой точке определена и бесконечно малому прираще-
нию аргумента соответствует бесконечно малое приращение
функции, т. е. lim Дг/ = 0.
Если условие непрерывности функции в некоторой точке на-
рушено, то такую точку называют точкой разрыва функции.
Степенную, показательную, логарифмическую и тригономет-
рические функции, а также их различные комбинации называют
элементарными функциями. Для элементарных функций спра-
ведливы следующие утверждения:
209
ЧАСТЬ I. Алгебра и начала анализа
I. Область непрерывности элементарной функции совпадает
с ее областью определения, т. е. элементарная функция непре-
рывна во всей области определения.
II. Элементарная функция может иметь разрыв только в от-
дельных точках какого-либо промежутка, но не во всех его
точках.
III. Элементарная функция может иметь разрыв только в той
точке, в которой она не определена.
Функция называется непрерывной в промежутке (замкну-
том или открытом), если она непрерывна во всех точках этого
промежутка.
♦ ПРИМЕР 1
Исследовать на непрерывность функцию у = Зх.
РЕШЕНИЕ. Функция у = Зх определена для всех действительных
значений аргумента х, т. е. х е R. Область непрерывности функ-
ции совпадает с ее областью определения.
Найдем приращение функции Az/, если аргумент х получает
приращение Ах.
у 4- Az/ = 3(х + Ах)
У = Зх
Az/ = 3 Ах
Тогда
.lim Az/ = .lim (3 Ах) = 3 .lim Ax = 0.
Лх -* а Лх — a v z Лх -* а
Равенство дИт а Ау — 0 справедливо при любом конечном зна-
чении х, поэтому функция у = Зх непрерывна при любом значе-
нии х.
♦ ПРИМЕР 2
Исследовать на непрерывность функцию у = х2 — 2 при х = 3.
РЕШЕНИЕ. Предел функции: lim (х2 - 2) = ( lim х)2 - 2 = З2 - 2 =
X ~* о X * о
= 7; значение функции /(3) = З2 - 2 = 7, т. е. предел функции при
х -* 3 равен значению функции при х = 3. Следовательно, функ-
ция у = х2 - 2 в точке х = 3 непрерывна.
Однако не все функции и не при любых значениях аргумента
непрерывны. Например, функция у = - при х = 0 имеет разрыв.
210
ГЛАВА 5. Производная
Функция у = --- имеет разрыв при х = 5; функция у = —-
х — 5 х2 — 4
имеет разрывы при х = -2 и х — 2; функция у = tg х имеет разры-
вы при х = л/2 + л&, k g Z.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется приращением аргумента и приращением функции?
2. Сформулируйте определения непрерывности функции.
3. Приведите примеры функций, имеющих разрывы.
ГЛАВА 5. Производная
§ 45. Скорость изменения функции
Если для некоторой функции у = f(x) при изменении аргумен-
та х на некоторую величину Ах функция у изменяется на Ду, т. е.
у + Ду = f(x + Дх), то приращение Ду функции, соответствующее
приращению Дх аргумента,
Ду = f (х + Дх) - f(x).
Средней скоростью изменения функции у для промежутка
значений аргумента от х до х + Дх называется отношение
Ду = fix + Дх) - /(х)
Дх Дх
_ Ду
Отношение -г2 показывает, сколько единиц приращения
функции приходится на единицу приращения аргумента.
Мгновенной (истинной) скоростью изменения функции при
данном значении аргумента х называется
.. Ду .. fix + Дх) - fix)
hrn -г— = Alimn----т------
х-OAr Дг — 0 /\х
Для линейной функции у = kx + b средняя скорость —'
истинная скорость изменения функции .lim
= k совпадают;
числовое значение истинной скорости равно коэффициенту k.
211
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕР 1
Найти среднюю скорость изменения функции у = Зх2 - 6 при
изменении х от хА = 3 до х2 = 3,5.
РЕШЕНИЕ. 1-й способ. Приращение Дх = 3,5 - 3 = 0,5. Значения
функции уг (Xj) = 3 • З2 — 6 = 21, у2(х2) = 3 • 3,52 — 6 = 30,75. При-
ращение функции Ду = 30,75 - 21 = 9,75. Средняя скорость изме-
нения функции:
Ду = 9,75
Дх 0,5
= 19,5.
2-й способ. Значение функции при х = х2:
у + Ду = 3(х + Дх)2 - 6 = Зх2 + 6х Дх + 3(Дх)2 — 6.
Поэтому Ду = 6х* Дх + 3(Дх)2; приращение аргумента Дх = 0,5.
Тогда
Ау _ 6 • 3 • 0,5 + 3 • (0,5)2
Дх 0,5
= 19,5.
♦ ПРИМЕР 2
Прямолинейное движение точки задано уравнением S = 3t2 -
- 2t + 5, здесь пройденный путь S выражен в м, время t — вс.
Найти скорость движения точки в момент tQ = 5.
РЕШЕНИЕ. Значение <8 + Д8 составляет
S + Д8 = 3(t + ДО2 - 2(t + ДО + 5,
поэтому
Таким образом,
Д8 = 6t Д* + 3(Д02 - 2 At.
AS = GtAt + 3(At)2 - 2At
At At
= 6t + 3 Д* - 2.
Истинная скорость v движения точки в момент t:
Л s
v А11П?О -(6f + 3 At - 2) = 6t - 2.
Тогда истинная скорость движения точки в момент t0:
р(5) = 6 • 5 - 2 = 28 (м/с).
♦ ПРИМЕРЗ
Закон падения материальной точки в пустоте выражается фор-
мулой S = i gt2, где g — ускорение силы тяжести (g = 9,8 м/с),
212
ГЛАВА 5. Производная
t — время, S — путь, пройденный точкой за время t. Опреде-
лить скорость движения точки в момент времени I.
РЕШЕНИЕ. Подобное движение является неравномерным, так как
его закон выражается квадратной функцией. Значение S 4- AS со-
ставляет
S + AS = 5 g(t2 + 2t At + (At)2),
Li
поэтому
AS = l^(2t At + (At)2),
следовательно,
Ag^lg2tAt + (At)2=lg(2t + At).
\ It Li Z—Ж Ir Ы
Поскольку отношение -г- зависит и от t, и от A t, понятие ско-
рости неравномерного движения может быть отнесено только к
определенному моменту времени t. Так как средняя скорость за-
висит от At, она тем точнее характеризует состояние падающей
точки в момент t, чем меньшим выбирается отрезок At.
Мгновенная скорость v падения точки в момент времени t оп-
ределяется как
и. здесь — средняя скорость. Поэтому
lim
Af а
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Как вычисляется скорость изменения функции?
2. Что называется мгновенной скоростью изменения функции?
3. Чему равны средняя и истинная скорость линейной функции?
4. Как вычисляется мгновенная скорость при неравномерном движении?
§ 46. Производная функции
1. Определение производной функции. Пусть функция у = f(x) опре-
делена на некотором промежутке, х — точка этого промежутка и
число Ах таково, что х + Ах тоже принадлежит этому промежут-
ку. Тогда производной функции у = /(х) называется предел отно-
213
ЧАСТЬ I. Алгебра и начала анализа
шения приращения функции &у к приращению аргумента Дх
при Дх -* 0:
АНтЛ -т-2, = . lim_
Дх —* О Дх Дх * о
f(x + Дх) - f(x)
(5.1)
если этот предел существует.
Если производная существует для каждого значения х в облас-
ти определения функции f(x), то она представляет собой новую
функцию от аргумента х.
Процесс вычисления производной называется дифференциро-
ванием.
С физической точки зрения производная от /(х) в точке х
представляет собой скорость изменения функции /(х) относи-
тельно ее аргумента при данном значении х.
Производная функции имеет следующие обозначения: у', /'(х),
dy ..г
Алгоритм определения производной функции
вычисляют приращение
Ду = ftx + Дх) - f (х);
находят среднюю скорость изменения функции
Ду =
Дх
вычисляют истинную
стремлении Дх -» 0
/~(х + Дх) - /(х).
Дх
скорость изменения функции при
lim
Нт + Л*) ~ Л*)
ДХ
или
lim;— =/'(х).
Дх — оДх ' v f
(5.2)
♦ ПРИМЕР
Определить производную функции у = х2 при х = 2.
РЕШЕНИЕ. Вычисляем:
у + Ду = (х + Дх)2 = х2 +
2х Дх + (Дх)2,
214
ГЛАВА 5. Производная
следовательно,
Ду = 2х Лх + (Дх)2.
Средняя скорость изменения функции
Ду _ 2хДх + (Дх)2
Дх Дх
= 2х + Лх.
Тогда истинная скорость изменения функции
Jim_^r^ = Jini (2х + Дх) = 2х.
Дх—ОДх Дх — о ' '
Находим значение производной при х = 2:
у' = 2-2 = 4.
их = 2
2. Связь производной функции с непрерывностью. Сформулируем за-
висимость между непрерывностью и наличием производной
функции.
Если функция /(х) имеет производную при некотором значе-
нии аргумента х, то при этом значении х данная функция не-
прерывна.
Допустим, что при некотором значении х функция f (х) имеет
производную, т. е.
у = Jim .-г— .
* Дх-ОДх
По определению предела
где а — 0 при Дх -* 0, отсюда Лу = у' Лх + а Дх. Находим предел
этого выражения при Дх -* 0:
.limп Лу = .lim _ {у' Дх) + Нт . (а Дх) = 0.
Дх — О v Дх — 0 ' Дх —• 0 ' '
Так как
Jim_ (у' Дх) = 0, Jim _ (а Дх) = 0,
Ах -» 0 ’ Дх - 0 v '
то АПтл Лу = 0.
Дх * 0 и
Функцию у = f(x) при данном значении х называют непрерыв-
ной, если бесконечно малому приращению аргумента х соот-
ветствует бесконечно малое приращение функции у, т. е. если
Jirn Дг/ = 0.
Дх — 0 &
215
ЧАСТЬ I. Алгебра и начала анализа
Рис. 113
3. Геометрический смысл производной. Касательной к данной кри-
вой в данной ее точке А называется предельное положение секу-
щей АВ, когда точка В, перемещаясь по кривой, неограниченно
приближается к точке А.
Прямая, проходящая через точку А перпендикулярно каса-
тельной, называется нормалью к кривой в точке А.
Рассмотрим непрерывную кри-
вую у = f(x) (рис. 113).
Отметим на этой кривой фикси-
рованную точку А(х; z/), а также
перемещающуюся по кривой точ-
ку В(х + Дх; у + Ду). Тогда рас-
стояние от точки В до оси абсцисс
BBj = у + Ay = f(x 4- Дх).
Проведем прямую АВ, пересе-
кающую кривую /(х) в точках А и
В, и прямую АВ2, параллельную
оси Ох.
Обозначим в прямоугольном треугольнике Д АВВ2 угол
А ВАВ2 = р, тогда tg р =
Ду
Дх
т. е. с геометрической точки зрения
tg р равен тангенсу угла наклона секущей АВ к оси Ох.
При Дх -* О точка В, перемещаясь по кривой /(х), неограни-
ченно приближается к точке А, секущая АВ, поворачиваясь около
точки А, стремится занять предельное положение касательной в
точке А к кривой /(х). При этом р —> а, где а — угол, образуемый
касательной AM с положительным направлением оси Ох, т. е.
lim В = a, lim tg р = tg а.
Дх — О г ’ Дх — О ° “
Из равенства tg р =
следует, что
.lim _ tg р = .lim
Дх — О Дх —
о Дх
или
AltaotgP = &I,
но lim tg р = tg а, поэтому у'х = tg а или у 'х = /г, где k — угловой
ил V
коэффициент касательной AM к графику функции у = /(х) в точ-
ке А, равный тангенсу угла наклона касательной к оси Ох, т. е.
f'(x) = tg а= k.
(5.3)
216
ГЛАВА 5. Производная
Итак, производная функции у = f(x) в точке А равна угловому
коэффициенту касательной, проведенной к графику функции
у = f(x) в этой точке А.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется средней скоростью изменения функции?
2. Дайте определение производной функции.
3. Сформулируйте общее правило нахождения производной функции.
4. Какая связь существует между непрерывностью функции и ее произ-
водной?
5. Объясните геометрический смысл производной.
§ 47. Формулы дифференцирования
1. Производная постоянной. Пусть у = С, где С — постоянное число.
Тогда
у + Ду = С;Ду = у4-Ду-у = С- С = 0;
Ay 0 л / 1. Ау л
т— = -т— = 0; у — А1нпл-т— = 0.
Дх Дх v лх — оДх
Производная постоянной равна 0:
С' = 0.
(5.4)
2. Производная функции у = х. В этом случае
у 4- Ду = х 4- Дх; Ду = х 4- Дх - х = Дх;
Ду _ Дх
Дх Дх
= 1; у' = lirn = lim 1 = 1.
* v Lx — о Дх
Производная функции у = х равна 1:
(5.5)
3. Производная алгебраической суммы функций. Для вывода ограни-
чимся суммой двух слагаемых у = и 4- v, где ини — функции от
аргумента х, имеющие производные по х:
у + Ду = и + Ди 4- v 4- Ди;
Ду = и 4- Ди 4- v 4- Ди - и - и = Ди 4- Ди;
, .. Ду ,. /Ди , Ди
У = ЛптЛ-т— = ,hni -т— 4- -т—
У Аг —ОДх Ах —О^Дх Дх
А ,. Ди , Ди
= Jini 7— 4- Alim_-r—.
J Лх-»0Дх Ах —‘ ОДх
217
ЧАСТЬ I. Алгебра и начала анализа
Слагаемые правой части являются производными функций и
и v, поэтому у' = и' 4- v' или
(u 4- v)' = и' + и'. (5.6)
Вывод можно распространить на алгебраическую сумму ко-
нечного числа слагаемых.
Производная алгебраической суммы конечного числа функ-
ций равна сумме производных слагаемых.
Например, у = 1 + х, тогда у' = 1.
4. Производная произведения двух функций. Пусть у — uv, где ии и —
функции от аргумента х, имеющие производные по х.
Находим:
у + Ai/ = (и 4- Дп)(у 4- Ли) = uv + и Av + v Au 4- Au Av;
Ay = uv + и Av 4- v Au 4- Au Av — uv = и Av 4- v Au 4- Au Av;
, Ay Av
у = .lim .-г— = Jimn и .hmnT-
Ar-ОДх Дх — О Лх-ОДх
Au
+ ЛИтп v lirn -г—
Дх — О Дх — 0 Дх
. .. л 1- Av
4- Jim„ £хи Ашпл-т— .
Лх — 0 Дх — О Дх
(а)
Функции и и v не зависят от Ах, поэтому будем считать их по-
стоянными; по определению
Jim
Дх —’
оДх
Функция и дифф
еренцируема, следовательно, она непрерыв-
на, поэтому lim Аи = 0, и последний член в (а) равен нулю.
Тогда имеем:
(uv)' = uv' + vu'.
(5.7)
Производная произведения двух функций равна сумме произ-
ведений первой функции на производную второй и второй на
производную первой.
5. Производная произведения постоянной на функцию. Пусть у = Си
где С — постоянная, а и = /(х), имеющая производную по х:
у' = (Си')' = Си' 4- иС' = Си' 4- и- О,
(Си)' = Си'.
(5.8)
218
ГЛАВА 5. Производная
Производная произведения постоянной на функцию равна
произведению постоянной на производную функции (постоян-
ную можно выносить за знак производной).
6. Производная частного. Дана функция у = , где и и и — функции
аргумента х, имеющие производные по г (о * 0). Тогда
У + &у =
и + Ди
. •
v + Др
vu' — uv'
Здесь, как и при выводе формулы (5.8), принято, что и и v не
зависят от Дх и lim „Ду = 0.
Ах • 0
Итак,
vu/ — uvz
V2
(5.9)
Производная частного равна дроби, числитель которой есть
разность между произведением делителя на производную де-
лимого и произведением делимого на производную делителя,
а знаменатель есть квадрат делителя.
7. Следствия. Из (5.9) следует:
I. Если знаменатель дроби есть постоянная С, у = я , то
е.
(5.10)
219
ЧАСТЬ I. Алгебра и начала анализа
Если знаменатель дроби — постоянная величина, то производ-
ная дроби равна производной от числителя, деленной на зна-
менатель.
(j
II. Если числитель дроби есть постоянное число С, у = - , то
2
у - Су _ Си'
V2 у2
v
СгУ
V2
Если числитель дроби — постоянная величина С, то производ-
ная равна числителю С, умноженному на производную знаме-
нателя и деленному на квадрат знаменателя, взятому с проти-
воположным знаком.
8. Понятие о сложной функции. Пусть дана функция у = Jx2 + 1.
Обозначим х2 + 1 через и. Тогда у = Ju зависит от х через вспомо-
гательную переменную и, а переменная и является функцией ар-
гумента х.
Если для функции у = 1g sin х функцию sin х обозначить через
и, то получим у = 1g и. В этом случае у также зависит от х через
вспомогательную переменную и, которая является функцией ар-
гумента х.
Такого рода функции называются сложными функциями или
функциями от функции.
В общем виде такие функции могут быть представлены сле-
дующим образом:
у = f(u), и = ф(х).
(5.12)
9. Производная сложной функции. Для нахождения производной от
сложной функции рассмотрим равенства (5.12).
Если х получит приращение Дх, то и получит приращение Ди,
а у получит приращение &у (Аи * 0, Дх 0).
Функции f(u) и ф(х) непрерывны, поэтому из Дх —* 0 следует,
что Ди —* 0, Дг/ —* 0.
Отношения
Ду
Ди
имеют пределы
Ди ,,, ч Ди ,, ч
.limп -г— = f (и), .lim,, -г— = ф(х).
Ди — 0 Ли ' Дх — О Дх v '
220
ГЛАВА 5. Производная
Имеем очевидное равенство
Ду _ Ду в Ди
Дх Ди Дх ’
из которого следует
&У г &У
А11тл-т— = А11тлт—
Дх — 0 Дх Ди—ОДх
ИЛИ
= Г(и)<р'(х).
Иначе, если сложная функция у(х) = /!(<р(х)), то
= f'(№ (*))<₽ '(х).
(5.13)
(5.14)
Если у является дифференцируемой функцией от u, а и явля-
ется дифференцируемой функцией от х, то производная у по х
равна произведению производной функции у по и на производ-
ную функции и по х.
10. Производная степени с целым положительным показателем. Пусть
функция у = ип, где и = /(х), п — целое положительное число,
т. е. у является сложной функцией.
Допустим, что функция и имеет производную по х. Рассмот-
рим, в частности, функцию у = и2. Найдем производную этой
функции по формуле (5.7):
(и2У = (и*и)' = и' • и + и* и' = 2и* и'.
Докажем методом математической индукции, что равенство,
справедливое для (ипУ = пип ~ ги'9 будет справедливо и для (izrt+1)' =
= (п + 1)ипи',
Представим ип + 1 в виде ип* и и по (5.7) найдем производную
произведения:
(ип + х)' = (ип • и)' = {ип)'и + и'ип = пип Чс'и + и'ип —
— пипи' + и'ип — ип • и'(п + 1) = (и + 1)ипи'.
Следовательно, если (ип)'= пип ~ *и'9 то и (urt+ *)' = (п + 1)ипи'.
Указанный закон верен для (ипУ и для (ип + 1)', т. е. он верен
для любого целого положительного числа п.
Итак, для любого целого положительного показателя п
(ипУ = пип ~ 1и'. (5.15)
Если и = х, то
(х«у = пхп 1.
(5.16)
221
ЧАСТЬ I. Алгебра и начала анализа
Приведем доказательство того обстоятельства, что формула
(5.15) справедлива для любого значения п 0.
Прологарифмируем равенство у = ип по основанию е, тогда
in у = п In и;
здесь In у — сложная функция. Продифференцируем это соотно-
шение по правилу дифференцирования сложной функции:
отсюда
, 1 ,
У =пУ~
поэтому
у' = пип • - • и' = п • ип ~ 1 • и'
v и
где п — любое число, п 0.
Например, у = Зх4, z = 5х“2/5. Тогда
11. Производная
I»
у' = 3 • 4х3, Z = 5
-2х“7/5.
ункции у =
При вычислении производной
функции у = Ju , где и = f(x), заменим корень дробным показате-
лем и применим формулу (5.15)
(Л )' - (u1/2)' = 1 и1/2 - !«' = 5 =
Хи Z-
(5.17)
При и = х имеем
(5.18)
Например, у — Jsx2 — 1, тогда у' = —. .
222
ГЛАВА 5. Производная
12. Производная функции у = -. При выводе формулы производной
функции -, где и = f(x), заменим
на
тогда
(5.19)
При и = х имеем
(5.20)
Например, у = , тогда у' = -
13. Применение формул дифференцирования. Определим производ-
ные некоторых функций:
1) у = 4х3 + 2х2 4- х - 5; 2) г = -—-; 3) и = 37(х3 + I)2 ;
х + а
4) v = x2*Jx2 — 1.
Используя формулы (5.4)—(5.6), (5.8), (5.16), получаем:
1) у' = (4х3)' 4- (2х2)' + х'~ (5)' = 12х2 4- 4х 4- 1;
2) учитывая формулы (5.4) и (5.9), получаем:
, _ (х — а)(х + а) — (х + а) (х — а) _ х + а — х + а
(х 4- а)2 (х 4- а)2
2а ф
(х 4- а)2 ’
3) по формуле (5.14) находим
и' = ((х3 4- I)2/3)' = | (х3 4- 1)-V3(X3 + | (Хз + 1)-1/з. Зх2 =
4) используя формулу (5.14), получаем:
223
ЧАСТЬ I. Алгебра и начала анализа
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Чему равна производная постоянной? Приведите доказательство.
2. Чему равна производная аргумента? Приведите доказательство.
3. Как вычисляется производная алгебраической суммы функции, произ-
ведения и частного функций?
4. Какую функцию называют сложной? Приведите примеры сложных
функций.
5. Как вычисляется производная сложной функции?
6. Выведите формулу производной степени для целого положительного
показателя.
§ 48. Геометрические приложения производной
Геометрический смысл производной обсуждался в § 47, п. 3.
Изобразим кривую, являющуюся графиком функции, и отме-
тим на ней точку А(хг; уг) (рис. 114).
Производная функции у = f(x) при х = xY равна угловому ко-
эффициенту касательной МА, проведенной к кривой в точке с
абсциссой х = хг:
ki = A*i) = te ct,
X = X.
где а — угол между касательной к данной кривой, проведенной
через точку А, и положительным направлением оси Ох.
Уравнение касательной MN к кривой у = /(х), проходящей че-
рез точку А(Хр уг), имеет вид
У “ У! = - Xj).
(5.21)
Так как по определению нормаль к кривой в точке перпенди-
кулярна касательной, проведенной в этой точке, а условием пер-
Рис. 114
пендикулярности прямых является
соотношение kl9k2 = -1 между их уг-
ловыми коэффициентами, то уравне-
ние нормали NA имеет вид
У - = ~г&)(ж Х1)-
(5.22)
Направление кривой в каждой ее точке
определяется направлением касатель-
ной к ней в этой точке, поэтому для на-
224
ГЛАВА 5. Производная
хождения угла наклона кривой в данной ее точке надо вычислить
угол между касательной, проведенной в этой точке, и осью Ох.
♦ ПРИМЕР 1
Найти угол наклона параболы у — х2 — х + 1 к оси Ох в точке
Xj = -1.
РЕШЕНИЕ. Для вычисления угла наклона кривой найдем у'(х^у.
у' = 2х - 1; y'OcJ = -3; k = tg а = —3. По таблице определяем
а = 108°26'.
♦ ПРИМЕР 2
К параболе у — Зх2 - х в точке хг = -1 проведены касательная
и нормаль. Составить их уравнения.
РЕШЕНИЕ. Ордината точки касания у(— 1) составляет 3(-1)2 - (—1) =
= 4, т. е. координаты точки касания: (—1; 4). Угловой коэффици-
ент /?х= равен у'(-1) = (Зх2 - х)* = = (6х - 1)х= = -7.
Составим уравнение касательной, подставив в (5.21) коорди-
наты (-1; 4) и значение k = -7:
у - 4 = -7(х + 1) => 7х + у + 3 = 0.
Составим уравнение нормали, воспользовавшись (5.22):
1
-7
у - 4 = - —= (х + 1) => х - 7у + 29 = 0.
♦ ПРИМЕРЗ
Найти координаты точки А, в которой касательная к параболе
у — х2 - х - 12 образует угол в 45° с осью Ох.
РЕШЕНИЕ. Находим тангенс угла наклона касательной, проведен-
ной в искомой точке к оси Ох:
tg а = у' = (х2 - х - 12)' = 2х - 1.
По условию угол а равен 45°, следовательно, tg 45° = 1 = 2х — 1,
поэтому х = 1. Находим ординату искомой точки: у(1) — I2 — 1 -
-12 — -12. Таким образом, координаты точки А: (1; —12).
♦ ПРИМЕР 4
Найти, под каким углом ось Ох пересекает параболу у = х2 + х.
РЕШЕНИЕ. Уравнение оси Ох: у = 0. Поэтому решим систему
8 - 9664
225
ЧАСТЬ I. Алгебра и начала анализа
Корни этой системы хг = -1; х2 — 0. Парабола пересекает ось Ох
в точках А(-1; 0); В(0; 0;).
Находим угловые коэффициенты касательных к параболе в
точках А и В:
у' = (х2 + х)' = 2х + 1; Аг = 2(—1) + 1 = -1; /г _0 = 2 • 0 + 1 = 1.
Вычислим углы dj и а2, образуемые касательными к параболе
с осью Ох в точках А и В:
= _i = tg ai = -1 => at = 135°;
kx „ о = tg а2 = 1 а2 = 4^°.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Чему равна производная при данном значении аргумента с геометриче-
ской точки зрения?
2. Запишите уравнения касательной и нормали, проведенных через дан-
ную точку на кривой.
3. Как находится направление кривой в каждой ее точке?
4. Как вычисляется угловой коэффициент касательной в данной точке
кривой?
§ 49. Физические приложения производной
При прямолинейном движении точки скорость v в данный мо-
х . dS
мент t = tQ есть производная от пути В по времени вычислен-
ная для момента t
Ускорение а в данный момент t = t0 есть производная от ско-
рости v по времени вычисленная для момента tQ.
о-
♦ ПРИМЕР 1
Точка движется прямолинейно по закону S = 2t3 + t2 - 4. Най-
ти величину скорости и ускорения в момент времени t0 — 4 с.
РЕШЕНИЕ. Скорость движения точки в любой момент времени t:
dS
dt
Тогда скорость движения точки в момент t0:
v(t0) = 6 • 42 + 4 • 2 = 104 (м/с).
226
ГЛАВА 5. Производная
Ускорение движения точки в любой момент времени t:
а=^ =12/+ 2.
at
Тогда ускорение движения точки в момент времени г0:
а(г0) = 12 • 4 + 2 = 50 (м/с2).
При вращательном движении угловой скоростью называется
скорость со изменения угла поворота <р за время t. Угловая ско-
рость равна производной угла поворота ср по времени t:
dip
“=d7-
Угловое ускорение Е равно производной от угловой скорости со
по времени t:
dco
е” df *
♦ ПРИМЕР 2
При торможении маховик за t (с) поворачивается на угол ср =
= 3 + 8г - г2. Найти: 1) угловую скорость со в момент времени
tQ = 3 с; 2) угловое ускорение е в момент 3) момент времени
г*, когда вращение прекратится.
РЕШЕНИЕ. 1) Угловая скорость со равна 8 — 2г. Тогда в момент вре-
мени t0 угловая скорость составляет 8 — 2 • 3 = 2 (рад/с); 2) угло-
вое ускорение е равно —2; таким образом, в любой момент време-
ни оно составляет е = — 2; положив со = 0, найдем
8 - 2г* = 0; t* = 4 (с).
Движение прекратится в момент г*, так как в этот момент угло-
вая скорость со(г*> = 0.
Пусть при нагревании тела его температура Т изменяется в за-
висимости от времени по закону Т = f(t). Тогда скорость нагрева-
dT
ния тела — это производная температуры тела по времени — .
♦ ПРИМЕРЗ
Закон изменения температуры тела Т задан соотношением Т =
= 0,2г2, где t — время. С какой скоростью нагревается тело в
момент времени t0 = 10 с?
РЕШЕНИЕ. Скорость нагревания тела составляет 0,4г. Тогда в мо-
мент времени г0 эта скорость равна 0,4 • 10 = 4.
227
ЧАСТЬ I. Алгебра и начала анализа
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Как определяется скорость изменения функции при данном значении
аргумента?
2. Как определяется ускорение прямолинейного движения точки при дан-
ном значении аргумента?
3. Какие физические задачи решаются с применением производной?
§ 50. Производные тригонометрических функций
1. Производная синуса. Пусть функция у = sin и, где и = f(x). Нахо-
дим производную синуса по общему правилу:
у + Ay = sin (и + Ди);
Ди = sin (и + Ди) - sin и.
Выполним преобразования по формуле разности синусов (3.94):
Ди — 2 cos
Ди
sin
Тогда
Ду
Дх
( , Ди \ . Ди
COS и + -7^ Sin -7Г
У множим числитель и знаменатель полученной дроби на
Ду _ 2cos(u + Ди/2) • sin(Au/2) * Ди/2
Дх Дх . Ди/2
— cos
и +
Ди \ sin(Au/2) . Ди
~2 J (Ди)/2 ’ Дх ’
Так как функция дифференцируема по х, Ди —* О при Дх —► 0:
, Ди \ 8ш(Ди/2)
Jim л и Ч—х- Jim л -т-т—. .
Ди~о^ 2 уДи —о (Ди)/2
lim
п опк 1- sma
С учетом примера на с. 205, в котором вычисляется Ahm0 — ,
имеем
.. ( . Ди J .. sin(Au/2) - Ди ,
Jimл cos и + -77- = cos и, Jimл —77—. ,о = 1, Jim л-т— = и .
Ли -» 0 2 ) * Ли — о (Ди)/2 ’ Дх — ОДх
Поэтому
(sin и)' = cos и*и'. (5.23)
228
ГЛАВА 5. Производная
При и = х имеем
(sin х)' = cos х.
(5.24)
2. Производная косинуса. Пусть у = cos и, где и = f(x). Поскольку с
учетом формулы для функции дополнительного аргумента (3.35)
sin (л/2 — и) = cos и, определение производной косинуса сводится
к (5.23):
(cos и)' — sin (л/2 - и)' = [cos (л/2 - и)]( л/2 - и)' =
= sin и (—и)' = - sin и • и'.
Следовательно,
При и = х
(cos иУ — — sin и • и1.
cos х = —sin х.
(5.25)
(5.26)
3. Производная тангенса. Пусть у = tg и, где и = f(x). С учетом опре-
деления тангенса и правила дифференцирования сложной функ-
ции (5.14) получаем
(sinu) cos u — (cosu) sinu
cos2u
С учетом соотношений (5.23) и (5.25) получим
(tg и)' =
(cosu • cosu + sinu • sinu)u
cos2u
(cos2u + sin2u)u'
cos2 и
1
COS2U
Итак,
(tg uy
COS2U
(5.27)
Если и = x, то
(tg хУ
1
COS2X
= 1 + tg2 X.
(5.28)
4. Производная котангенса. Пусть у = ctg и, где и = f(x). С учетом
того, что ctg и = г— , воспользуемся соотношением (5.19):
WO И
1 1,1,
• 2 / 2 * 9 * • 2 *
sirru/cos^u COSzlZ sinzu
229
ЧАСТЬ I. Алгебра и начала анализа
Таким образом,
(ctg и)' = - -т4- • (5-29)
sinzu
При и = х
(ctg х)' = - = -(1 + ctg1 2 * * х). (5.30)
♦ ПРИМЕР
Определить производные функции 1) f(x) =——s*nx; 2) <р(х) =
1 + sinx
= ctg х - tg X.
РЕШЕНИЕ. 1) Учитывая формулы (5.14) и (5.24), находим
ГМ =
(1 — sinx) (1 4- sinx) — (14- sinx/(l — sinx)
(14- sinx)2
-cosx(l 4- sinx) — cosx(l — sinx) _ _ 2cosx .
(1 4- sinx)2 (1 4- sinx)2 *
2) по формулам (5.28) и (5.30) получаем
1 (^0 • 2 2
sinzx COSZX
cos2x 4- sin2x
sin2 x cos2 x
4
(2sinxcosx)2 sin22x ’
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Приведите формулы для нахождения производных синуса и косинуса.
2. Выведите формулу производной тангенса. При каких значениях аргу-
мента производная тангенса не имеет смысла?
3. Выведите формулу производной котангенса. При каких значениях аргу-
мента производная котангенса не имеет смысла?
§ 51. Производные обратных
тригонометрических функций
1. Производная арксинуса. Пусть у = arcsin и, где и — f(x). По опре-
делению арксинуса
sin у = и. (*)
Функция sin у — сложная, так как у = у(и), а и = и(х), следова-
тельно, у = у(х).
230
ГЛАВА 5. Производная
Дифференцируем обе части (*) по х:
(sin у)' = и' => cos у • у' = и\
следовательно, у =
cosy
Воспользуемся соотношением cos Д — sin2 у (здесь квадрат-
ный корень берется со знаком (+), так как arcsin и с [—л/2; л/2],
а на этом отрезке cos у 0), тогда
(arcsin и)' —
(5.31)
При и — х
(arcsin х)' =
(5.32)
2. Производная арккосинуса. Пусть у = arccos и, где у = f(x). Так как
arccos и = л/2 - arcsin и, то
(arccos и)' =
- arcsin и = (0 - arcsin и)' —
л/1 ~ W2
Таким образом,
При и — х
(arccos иУ = —
(5.33)
ц/
л/1 ~ U2
(arccos хУ = —
(5.34)
3. Производная арктангенса. Пусть у = arctg п, где и — /(х). Из опре-
деления арктангенса следует: tg у = и. Дифференцируя по х, по-
лучим
(tg уУ = и
cos2
откуда
у' = cos2 у • и'.
231
ЧАСТЬ I. Алгебра и начала анализа
Так как
cos2 у —
1
1 + tg2!/ ’
то
Следовательно,
При и = х
(arctg и)' =
(arctg х)' =
(5.35)
(5.36)
4. Производная арккотангенса. Пусть у = arcctg и, где и = /(х). Так
как arcctg и = л/2 - arctg и, то
(arcctg и)' = (л/2 - arctg и)' = О - (arctg и)' = -
Итак,
При и = х
(arcctg и)' = —
(arcctg х)' = —
(5.37)
(5.38)
♦ ПРИМЕР
Найти производную функции: 1) f(x) = 2 arcsin х + arccos х;
2) ф(х) = arcctg 7х ; 3) ф(х) = (arccos Зх)2.
РЕШЕНИЕ. 1) Имеем Л(х) = — - -г------ = г ’
71 — х2 л/1 — X2 л/1 — X2
2)<р'(х) = -1 = ^ = _2(1 +х)75:
3) \/(х) = 2 arccos Зх • —-------- .
v 71 - (Зх)2
=- 2 arccos Зх
6arccos3x
71 - 9х2
71 - 9х2
3
232
ГЛАВА 5. Производная
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выведите формулы производных арксинуса и арккосинуса.
2. При каких значениях аргумента существуют арксинус, арккосинус и их
производные?
3. Выведите формулы производных арктангенса и арккотангенса.
4. При каких значениях аргумента существуют арктангенс, арккотангенс и
их производные?
§ 52. Производная логарифмической функции
Производная функции у = In и, где и = f(x), вычисляется по
формуле:
(1П и)’ = U~.
(5.39)
Доказательство, ввиду его сложности, не приводится. Если
In X = -
(5.40)
Производная десятичного логарифма у = 1g и вычисляется по
формуле
(lg и)' = 0,4343 • £.
(5.41)
При и — х
(lg х)' = 0,4343 • i .
Л-
(5.42)
Здесь 0,4348 = 1g е — модуль перехода от натуральных лога-
рифмов к десятичным (см. § 17, п. 5), lg N = 0,4343 In N.
Также без доказательства приведем выражение для определе-
ния производной от логарифма по любому основанию:
• <5-43)
Значения производных
функций:
от логарифмов тригонометрических
м ч, 1 / ч, sinx .
(In cos х) =----- (cos x) =---------- — tg x;
cosx v cosx
(5.44)
(In sin x\ =
1
sinx
(sin x)' =
cosx
sinx
= ctg x;
(5.45)
233
ЧАСТЬ I. Алгебра и начала анализа
(In tg X)' = (tg х)' =
1 = 1 = 2
cos2x sin х cos х sin2x
(5.46)
<ln ctg X)' = (ctg XY = -
1 = _ 2
sin x cos x sin2x *
/ 1
\sin2x
(5.47)
♦ ПРИМЕР
Найти производную функции: 1) f(x) = In (ax2 + 6); 2) <p(x) =
= In J2x; 3) \|/(x) = lg (2x + 1).
РЕШЕНИЕ. 1) По формуле (5.39) находим:
Г(х) =
2ах
______ •
ах2 + b ’
2) учитывая формулы (2.12) и (2.15), получаем
ф'(х) =
(In 2 + In х)Т = 0 + Л ;
3) по формуле (5.41) находим
// \ 0,4343 . 1 кf
V (*) = (2х + 1) =
X > X
0,8686
2х + 1 ‘
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выпишите формулы для вычисления производных функций у = In и,
У = 1д и-
2. Приведите примеры вычисления производных сложных функций, вклю-
чающих функции натуральных и десятичных логарифмов.
§ 53. Производные показательных функций
Пусть у = аи — показательная функция, причем и = п(х), а а —
постоянное число. Прологарифмируем выражение для у по осно-
ванию е:
In у = и In а;
(*)
здесь у — сложная функция аргумента х.
Продифференцируем равенство (*):
— = и' In а
У
234
ГЛАВА 5. Производная
тогда
у' = уи' In а = аии' In а,
т. е.
(а“У = аи In а* и’. (5.48)
При и = х
(ахУ — ах In а. (5.49)
Если а = е, то
(еиУ = еи In е и = еи • и',
таким образом,
еи = еи-и\ (5.50)
при и = X
(ехУ = ех, (5.51)
т. е. производная от функции ех совпадает со значением самой
функции.
♦ ПРИМЕР
Определить производную функции: 1) f(x) = З2*2; 2) F(x) =
= In х • ех; 3) ф(х) = х2ех; 4) \/(х) = 5 In х + ех.
РЕШЕНИЕ. 1) По формуле (5.48) имеем
f (х) = З2*2 In 3 (2х2)' = З2*2 In 3 • 4х;
2) F\x) = (In х)'ех + (ех)' In х = - ех + ех In х = ех(- + In х\
ЭС V X j
3) ф'(х) = (х2)'ех + (ех)'х2 — 2хех + ехх2 ~ хех(2 + х);
4) \/(х) = 5 + ех.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выведите формулу для производной от функции у = аи.
2. Выведите формулу для производной от функции у = еи.
3. Приведите примеры вычисления производных сложных функций, вклю-
чающих в себя показательные функции.
235
ЧАСТЬ I. Алгебра и начала анализа
ОСНОВНЫЕ ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
С' = О (С — постоянная)
х' = 1
(и + V - w)' = и' + v' - w' {и, v, iv — функции от х)
(Си)' = Си'
(uv)' = u'v + uv'
(и'х vu’ — uv’
(jjj——
(sin x)' = cos x
(cos x)' = -sin x
(tg x)' = —= 1 + tg1 2 x
coszx
(ctg xY = - = -(1 + Ctg2 X)
bill л>
(In sin x)' = ctg x
(xn)' = nxn 1
(In cos x)' = - tg x
(ex)' = e
(In tg x)' = . 29;
sin 2.1
(In ctg x)' = -
2
sin2x
(ax)' — ax In a
(In x)' = i
(arcsin x)' = .
7i -x2
z XZ 1
(arccos x) = —.
7i — x2
(arctg x)'= —
(arcctg x)' = - ~~9
§ 54. Производная второго порядка.
Физический смысл производной второго порядка
1. Производная второго порядка. Если существует производная от
производной у' функции у = /(х), то она называется второй произ-
водной или производной второго порядка, т. е.
у" = (Г(х)Г = г\х).
236
ГЛАВА 5. Производная
♦ ПРИМЕР
Найти вторую производную функции у = х3.
РЕШЕНИЕ. Находим первую производную: у' = (х3)' = Зх2. Полагая
первую производную функцией, вычисляем вторую производ-
ную: (у')' — (Зх2)' = 6х, у" = 6х.
2. Физический смысл второй производной. Пусть точка движется
прямолинейно по закону S = /(<); здесь S — путь, пройденный
точкой за время t. Скорость движения точки, как было установ-
лено в § 49, есть производная пути по времени v = S' = f\t).
Если точка движется неравномерно, то скорость за промежу-
ток времени Д£ получит приращение Ду. Отношение 77 показы-
вает изменение скорости в единицу времени; оно называется
средним ускорением за промежуток времени от t до t + At.
Если приращение At -*• 0, то t 4- Д£ t, а среднее ускоре-
ние
At
будет стремиться к ускорению а в данный момент време-
ни t, т. е.
а = lim = v' = S”.
At — О
Следовательно, ускорение а прямолинейного движения точки
в данный момент времени равно второй производной пути по вре-
мени.
♦ ПРИМЕР
Точка движется прямолинейно по закону S « 3t2 - 2t + 4. Вы-
числить скорость и ускорение точки в момент времени t0 = 6 с.
РЕШЕНИЕ. Имеем:
v = S' = (Ы2 -2t + 4)' = 6t - 2.
При t = t0
уо = 6 • 6 - 2 = 34 (с).
Ускорение а равно
а = S" = (6t - 2)' = 6.
Ускорение является постоянной величиной при любом значе-
нии времени t, т. е. движение точки происходит с постоянным ус-
корением.
237
ЧАСТЬ I. Алгебра и начала анализа
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется производной второго порядка?
2. Что называется средним ускорением?
3. Что называется ускорением прямолинейного движения точки?
4. Как по закону движения точки S = f(t) находится ускорение точки?
ГЛАВА 6. Исследование функций
с помощью производных
§ 55. Возрастание и убывание функций
Рис. 115
Основные понятия о возрастающих и убывающих функциях
даны в § 14, п. 3.
Возрастание и убывание функции у = f(x) характеризуется
знаком ее производной: если на некотором промежутке f'(x) > О,
то функция на этом промежутке возрастает; если же f'(x) < 0, то
функция на этом промежутке убывает.
На промежутке возрастания функции
у — f(x) касательная к графику функ-
ции образует с осью абсцисс острый угол,
и график функции направлен вверх,
т. е. f'(x2) = k2 = tg а > 0, 0 < а < л/2
(рис. 115), а в промежутке убывания
функции касательная к графику образует
тупой угол, и график функции направлен
вниз, т. е. f\xY) = &! = tg 0 < О, л/2 < 0 < л.
♦ ПРИМЕР
Найти промежутки возрастания и убывания функции: 1) f(x) —
= х2 - Зх + 13; 2) F(x) = х3 - 6х2 + 4; 3) <р(х) = ^ ; 4) V(x) = In х.
РЕШЕНИЕ. 1) Производная f'(x) — 2х — 8; она принимает значение,
равное нулю (f'(x) = 0) при х = 4. Вычислив значения f\x) для
любого значения х > 4 (например, f'(5) = 2), заключаем, что на
этом интервале производная f'(x) > 0, следовательно, функция
f(x) на этом интервале возрастает, и наоборот, Л(1) = ~6, при
х < 4 производная f'(x) < 0, следовательно, на этом интервале
функция f(x) убывает (рис. 116);
238
ГЛАВА 6. Исследование функций с помощью производных
2) F'(x) = Зх1 2 - 12х; корни произ-
водной xt = 0, х2 = 4. Вычислив зна-
чения производной на отдельных
интервалах, делаем относительно по-
ведения функции заключение, про-
иллюстрированное рисунком 117;
3) областью определения функции
Ф(х) является вся числовая прямая,
кроме точки х = 0. Производная ф'(х) =
= - ~2. Производная ф'(х) < 0 при
всех значениях х из области определения функции, следователь-
но, функция убывает на интервалах хе (-со; 0), х е (0; 4-оо);
4) область определения функции ф(х) — интервал х е (0; оо).
Производная \|/(х) = - на этом интервале всегда положительна.
Следовательно, функция ф(х) является возрастающей на всей об-
Рис. 116
Рис. 117
ласти определения.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие функции называются возрастающими и убывающими?
2. Объясните, как применяется производная для нахождения промежутков
возрастания и убывания функции.
3. Сформулируйте практическое правило исследования функции на воз-
растание и убывание.
§ 56. Исследование функций
на максимум и минимум
1. Понятие о максимуме и минимуме функции. Сформулируем прави-
ло определения тех значений аргумента, которые отделяют уча-
стки возрастания функции от участков убывания и наоборот.
Рассмотрим графики функций /(х) (рис. 118) и ф(х) (рис. 119).
Если слева от некоторого допустимого значения х = х0 функция
У ~ f(%) возрастает, а справа убывает, то значение х = х0 называ-
ется точкой максимума данной функции, т. е. функция у = /(х)
при х = х0 имеет максимум. Если слева от точки х = х0 функция
у = (р(х) убывает, а справа — возрастает, то значение х = х0 назы-
вается точкой минимума данной функции, т. е. функция у =
= ф(х) при х = х0 имеет минимум.
239
ЧАСТЬ I. Алгебра и начала анализа
Рис. 118
Рис. 119
Точка максимума служит границей перехода функции от воз-
растания к убыванию, а точка минимума — границей перехода
функции от убывания к возрастанию.
Необходимо отметить, что функция может иметь либо только
один максимум (например, функция у = -х2) или только один
минимум (например, функция у = х2), либо множество максиму-
мов и минимумов (например, у = sin х), либо не иметь ни макси-
мума, ни минимума (например, у = tg х).
Точка х0 называется точкой максимума функции f(x), если су-
ществует такая окрестность точки х0, что для всех х х0 из
этой окрестности выполняется неравенство /(х) < /(х0).
Точка х0 называется точкой минимума функции f(x), если су-
ществует такая окрестность точки х0, что для всех х х0 из
этой окрестности выполняется неравенство /(х) > /(х0).
Точки минимума и точки максимума называются точками
экстремума.
2. ПРИЗНАКИ МАКСИМУМА И МИНИМУМА ФУНКЦИИ. Пусть на графике
рисунка 118 точка А соответствует максимуму функции у = /(х)
при х = х0. В точках, расположенных левее точки А, касатель-
ные образуют острые углы с положительным направлением оси
Ох. Тангенсы этих углов положительны; следовательно, и произ-
водные в этих точках положительны, т. е. /'(х) — tg a; f\x) > О
при х < х0.
В точках, лежащих правее точки А, касательные образуют ту-
пые углы с положительным направлением оси Ох, следователь-
240
ГЛАВА 6. Исследование функций с помощью производных
но, и производные в этих точках отрицательны, т. е. f\x) — tg а2;
f\x) < 0 при х > х0.
Так как производная функции непрерывна, то при переходе
производной от положительных значений к отрицательным она
пройдет через нуль при х = х0, т. е. f'(x0) = 0.
Точки, в которых производная функции равна нулю, называ-
ются стационарными.
Если при переходе через стационарную точку (такую, в кото-
рой производная функции равна нулю) х0 функции /(х) ее про-
изводная меняет знак с положительного на отрицательный,
т. е. слева от точки х0 значение f'(x) > 0, а справа от точки х0
значение /(х) < 0, то точка х0 является точкой максимума
функции /(х).
Если f'(x) = 0 в некоторой точке, то это значит, что угловой ко-
эффициент касательной к графику функции в соответствующей
точке также равен нулю, т. е. касательная в этой точке парал-
лельна оси абсцисс.
Исследуем таким же образом график, изображенный на ри-
сунке 119. Здесь точка х0 соответствует минимуму функции (р(х)
при х = х0. Производные в точках, лежащих правее точки В, яв-
ляются положительными (углы р2 острые, тангенсы этих углов
положительны), и наоборот, производные в точках, лежащих ле-
вее точки В, являются отрицательными (углы — тупые, соот-
ветствующие тангенсы меньше нуля). Так как производная функ-
ции непрерывна, то при переходе производной от отрицательных
значений к положительным она обратится в нуль при х = х0.
Если при переходе через стационарную точку х0 функции /(х)
ее производная меняет знак с отрицательного на положитель-
ный, то точка х0 является точкой минимума функции /(х).
Признаки экстремума функции являются необходимыми и до-
статочными.
Отметим, что функция может иметь экстремум в точке, в ко-
торой эта функция не имеет производной (в качестве примера
можно указать функцию у(х) — |х|; f'(0) не существует; х = 0 —
точка минимума функции). Стационарные точки, а также такие,
в которых функция не имеет производной, в совокупности назы-
ваются критическими точками этой функции-
241
ЧАСТЬ I. Алгебра и начала анализа
Рис. 120
Существуют функции, в которых первая
производная, обращаясь в нуль при х =
— х0, не меняет знака при переходе аргу-
мента через Хц. В таком случае функция в
этой точке не имеет экстремума. Пример
подобной функции у = \|/(х) приведен на
графике рисунка 120. Таким образом, об-
ращение первой производной в нуль явля-
ется необходимым, но не достаточным ус-
ловием существования экстремума.
3. Практические правила исследования функции на максимум и мини-
мум с помощью первой производной. Необходимо придерживаться
следующего алгоритма:
I. Найти производную f\x) функции /(х).
II. Найти критические точки функции у = f(x), т. е. точки, в
которых /'(х) обращается в нуль или терпит разрыв.
III. Исследовать знак производной f\x) в промежутках, на ко-
торые найденные критические точки делят область определе-
ния функции f(x). При этом критическая точка х = х0 есть
точка минимума, если производная меняет знак при переходе
через х = х0. Если же в соседних промежутках, разделенных
критической точкой х = х0, знак производной не меняется, то
в точке х = х0 функция не имеет ни максимума, ни минимума.
IV. Вычислить значения функции в точках максимума и ми-
нимума.
♦ ПРИМЕР
Исследовать на экстремум функцию: 1) /(х) = х2 — 4х; 2) <р(х) =
= -х2 + 5х - 6; 3) \|/(х) = х3 - Зх2.
РЕШЕНИЕ. 1) Находим f'(x) = 2х - 4. Полагая f\x) - 0, получим
единственную критическую точку х = 2. В этой точке /(2) = -4.
Слева от точки х = 2 производная f'(x) имеет отрицательные зна-
чения, справа — положительные. Характер графика /(х) пред-
ставлен на рисунке 121;
2) находим <р'(х) — -2х + 5. Приравнивая производную к нулю,
получаем критическую точку х = 2,5. В этой точке ср(2,5) = 0,25.
Слева от критической точки х = 2,5 производная функции <р(х)
имеет положительные значения, справа — отрицательные. Гра-
фик соответствующей функции представлен на рисунке 122;
242
ГЛАВА 6. Исследование функций с помощью производных
Рис. 121 Рис. 122 Рис. 123
3) находим \|/(х) = Зх2 - 6х. Уравнение производной имеет два
корня: Xj = 0, х2 = 2. В этих точках \|/(0) = О, а \|/(2) = —4. Произ-
водная имеет положительные значения слева от точки х = О и
справа от точки х = 2 и отрицательные значения между этими
точками. График, приведенный на рисунке 123, характеризует
функцию у(х).
4. Исследование функции на максимум и минимум с помощью второй
производной. Если f'(x) — производная от функции у — /(х), то
производная от f' (если она существует) называется второй про-
изводной (или производной второго порядка). Для второй про-
изводной употребляются следующие обозначения: у", у",
d2y
dx2
или
d2f(x)
dx2
Алгоритм исследования функции у = f(х)
на экстремум с помощью второй производной
I. Найти производную f\x).
II. Найти критические точки данной функции, в которых
Г(х) = 0.
III. Найти вторую производную f"(x).
IV. Исследовать знак второй производной в каждой из крити-
ческих точек. Если при этом вторая производная окажется от-
рицательной, то функция в такой точке имеет максимум, а ес-
ли положительной, то — минимум. Если же вторая производ-
ная равна нулю, то исследование функции нужно произвести
с помощью первой производной.
V. Вычислить значения функции в точках максимума и мини-
мума.
243
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕР
Исследовать на экстремум с помощью второй производной
функцию: 1) f(x) = х2 - 2х — 3; 2) ф(х) = х3 - 9х2 + 24х - 12.
РЕШЕНИЕ. 1) Находим производную f\x) = 2х — 2. Из уравнения
/'(х) = 0 получаем критическую точку х = 1. Находим вторую
производную f”(x) = 2. Так как вторая производная в критиче-
ской точке положительна, то при х = 1 функция имеет минимум:
Л™ = Л1) = -4;
2) находим производную ф'(х) = Зх2 - 18х + 24 и корни произ-
водной: Xj = 2, х2 = 4. Определим вторую производную ф"(х) = 6х —
- 18. Знаки второй производной в критических точках: <р"(2) =
= 6*2- 18; ф"(2) < 0, т. е. при х = 2 функция имеет максимум;
ф"(4) = 6*4- 18; ф"(4) > 0, т. е. при х = 4 функция имеет мини-
мум. Вычислим значения функции в точках хг и х2:
«Ртах = Ф(2> = 23 - 9* 22 + 24 - 2 - 12 = 8,
Фтт = Ф<4) = 43 - 9 • 42 + 24 • 4 - 12 = 4.
Итак, функция имеет максимум в точке (2; 8) и минимум в
точке (4; 4).
5. Наименьшее и наибольшее значения функции. Сформулируем алго-
ритм определения наибольшего и наименьшего значения функ-
ции, непрерывной в некотором промежутке.
I. Найти критические точки, принадлежащие заданному про-
межутку, и вычислить значения функции в этих точках.
II. Найти значения функции на концах промежутка.
III. Сравнить полученные значения: минимальное и макси-
мальное из них являются соответственно минимумом и макси-
мумом функции в рассматриваемом промежутке.
♦ ПРИМЕР 1
Найти наименьшее и наибольшее значения функции /(х) =
= х2 - 4х + 3 на отрезке х е [0; 3].
РЕШЕНИЕ. Имеем: f'(x) = 2х - 4; х = 2 — критическая точка. Нахо-
дим /(2) = -1. Вычисляем значения функции на концах проме-
жутка: /(0) = 3, /(3) = 0. Наименьшее значение функции /(2) =
= -1 и достигается ею во внутренней точке промежутка, а наиболь-
244
ГЛАВА 6. Исследование функций с помощью производных
шее значение /(0) = 3 и достигается на
левом конце промежутка (рис. 124).
♦ ПРИМЕР 2
Из всех прямоугольников с одинако-
вым периметром найти тот, у кото-
рого площадь наибольшая.
РЕШЕНИЕ. Обозначим периметр прямо-
угольника через р, длину одной из сто-
рон прямоугольника через х, тогда
длина другой стороны равна (р - 2х)/2 =
= р/2 - х. Обозначив площадь прямо-
угольника через р, получим
Рис. 124
Исследуем функцию на максимум и минимум с помощью вто-
рой производной: у' = р/2 — 2х; критическая точка х — р/£. Вто-
рая производная у" = -2. Вторая производная отрицательна, сле-
довательно, функция имеет максимум при х — р/4, Таким обра-
зом, из всех прямоугольников с одинаковым периметром
наибольшую площадь имеет квадрат.
♦ ПРИМЕРЗ
Закон прямолинейного движения тела задан уравнением
8 = -*3 + 9t2 - 24* - 8.
Найти максимальную скорость движения тела (S (м), t (с)).
РЕШЕНИЕ. Скорость движения тела — первая производная от пути
по времени:
v = S' = -З*2 + 18* - 24.
Исследуем функцию u(t) на максимум и минимум с помощью
второй производной: v' = —6* + 18; критическая точка t = 3; v" = -6.
Вторая производная отрицательна, следовательно, скорость яв-
ляется наибольшей при t = 3. Найдем величину скорости в мо-
мент t = 3:
г(3) = 3 • З2 + 18 • 3 - 24 = 3 (м/с).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение максимума и минимума функции.
2. Приведите примеры функций, имеющих один максимум или минимум,
множество максимумов и минимумов.
245
ЧАСТЬ I. Алгебра и начала анализа
3. Приведите примеры функций, не имеющих ни максимума, ни минимума.
4. Укажите необходимые и достаточные признаки максимума и минимума
функции.
5. Укажите признаки существования максимума и минимума функции.
6. В каких случаях функция не имеет ни максимума, ни минимума?
7. Изложите практические правила исследования функции на максимум и
минимум с помощью первой производной.
8. Как исследуется функция на максимум и минимум с помощью второй
производной?
9. Как находится наименьшее и наибольшее значения функции?
§ 57. Направление выпуклости графика
Кривая у = /(х) называется выпуклой вниз в промежутке
а < х < Ь, если она лежит выше касательной к кривой, проведен-
ной в любой точке этого промежутка (рис. 125).
Кривая у = f(x) называется выпуклой вверх в промежутке
а < х < Ь, если она лежит ниже касательной к кривой, проведен-
ной в любой точке этого промежутка (рис. 126).
Промежутки, в которых график функции обращен выпукло-
стью вверх или вниз, называются промежутками выпуклости
графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком
функции у = /(х), характеризуется знаком ее второй производ-
ной.
Рис. 125
Рис. 126
246
ГЛАВА 6. Исследование функций с помощью производных
Если в некотором промежутке f"(x) > О, то кривая выпукла
вниз в этом промежутке; если же f"(x) < 0, то кривая выпукла
вверх в этом промежутке.
♦ ПРИМЕР 1
Исследовать на выпуклость кривую f(x) — - в точках хг = -2
X
и х2 — 1.
РЕШЕНИЕ. Находим первую и вторую производные /(х): f'(x) =
1 2
= —2 ♦ — -3 . Подставляя значения хх = - 2 и х2 = 1, получим
Г(-2) = 2 • , /"(2) < 0; Г'(1) = I > /"(1) > 0. Следовательно, в
\ J
точке х = -2 кривая выпукла вверх, а в точке х — 1 — выпукла
вниз.
♦ ПРИМЕР 2
Найти промежутки выпуклости кривой: 1) <р(х) = х3; 2) /(х) =
= х4 - 2х3 + 6х - 4.
РЕШЕНИЕ. 1) Находим <р'(х) = Зх2, ф"(х) = 6х.
В промежутке хе (-оо; 0) имеем (р"(х) < 0,
т. е. в этом промежутке кривая выпук-
ла вверх; в промежутке х е (0; +оо)
вторая производная <р"(х) > 0, т. е. в этом
промежутке кривая выпукла вниз
(рис. 127);
2) находим f\x) = 4х3 - 6х2 4- 6, f"(x) =
= 12х2 - 12х. Вычисляем корни второй
производной: xi = 0; х2 = 1. В промежут-
ках х е (-©о; 0) и х е (1; +оо) выполняется
Рис. 127
неравенство /"(х) > 0, т. е. в этих промежутках кривая выпукла
вниз, а в промежутке хе (0; 1) имеет место неравенство f"{x) < 0,
т. е. в этом промежутке кривая выпукла вверх. Более подробно
эта зависимость f(x) будет исследована в § 58, примере 2.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Как определяется выпуклость кривой вверх и вниз?
2. Что понимается под промежутком выпуклости графика функции?
3. Как исследуется функция на направление выпуклости с помощью вто-
рой производной?
ЧАСТЬ I. Алгебра и начала анализа
§ 58. Точки перегиба
Точка графика функции у = f(x), разделяющая промежутки
выпуклости противоположных направлений этого графика, на-
зывается точкой перегиба.
Точками перегиба могут служить только критические точки,
принадлежащие области определения функции у = /(х), в которых
вторая производная f"{x) обращается в нуль или терпит разрыв.
Если при переходе через критическую точку х = х0 вторая про-
изводная f"(x) меняет знак, то график функции имеет точку пе-
региба (х0; /(х0)).
Правило нахождения точек перегиба графика
функции у = f(x)
I. Найти вторую производную f"(x).
II. Найти критические точки функции у = /(х), в которых
f"(x) обращается в нуль или терпит разрыв.
III. Исследовать знак второй производной f"(x) в промежут-
ках, на которые найденные критические точки делят область
определения функции у = /(х). Если при этом критическая
точка х = х0 разделяет промежутки выпуклости противопо-
ложных направлений, то х = х0 является абсциссой точки пе-
региба функции.
IV. Вычислить значения функции в точках перегиба.
♦ ПРИМЕР 1
Найти точку перегиба кривой: 1) f(x) = 6х2 - х3; 2) (р(х) = х +
РЕШЕНИЕ. 1) Находим f\x) = 12х — Зх2, f"(x) = 12 - 6х. Полагая
f"(x) — 0, получим единственную критическую точку х = 2. Так
как в промежутке -оо < х < 2 имеем f"(x) > О, а в промежутке
2 < х < +оо имеем f"(x) < 0, то при х = 2 кривая имеет точку пере-
гиба. Находим ординату этой точки: f'(2) = 16. Итак, точка пере-
гиба имеет координаты (2; 16);
2) находим (р'(х) = (х+ ” 21 = 1 + | х2/3; (р"(х) = | • | х-1/3 =
= —— . Здесь критической является точка х — О, в которой вторая
производная терпит разрыв.
248
ГЛАВА 6. Исследование функций с помощью производных
Вторая производная <$"(х) < О в промежутке -оо < х < О и
<р"(х) > 0 в промежутке 0 < х < +оо, т. е. кривая (р(х) имеет точку
перегиба при х = 0; координаты этой точки (0; -2).
♦ ПРИМЕР 2
Построить график функции /(х) = х3 - 6х2 4- 9х - 3, используя
предыдущие исследования.
РЕШЕНИЕ. 1. Функция определена на всей числовой прямой, т. е.
х е R.
2. Данная функция не является ни четной, ни нечетной и не
является периодической.
3. Находим точку пересечения графика с осью Оу: при х = 0
значение функции /(0) = — 3. Точки пересечения графика функ-
ции с осью Ох найти затруднительно, так как для этого необходи-
мо решить кубическое уравнение f(x) = 0.
4. Находим производную f'(x) = Зх2 - 12х + 9. Критиче-
ские точки функции /(х): xt = 1, х2 = 3. Эти точки делят область
определения функции на три промежутка: (-оо; 1), (1; 3),
(3; +оо).
В первом и последнем из них f\x) > 0, в промежутке хе (1; 3)
производная f'(x) < 0. Следовательно, в промежутках х е (-<х>; 1),
х е (3; +оо) функция возрастает, а в промежутке хе (1; 3) —
убывает. При переходе через точку Xj производная меняет знак
с плюса на минус* а при переходе через точку х2 — с минуса
на плюс. Таким образом, (1; 1) — точ-
ка максимума, а (3; —3) — точка ми-
нимума.
Находим вторую производную
f"(x) = 6х - 12; из решения урав-
нения f”(x) — 0 получаем х = 2. Точ-
ка х = 2 делит область определе-
ния функции на два промежутка
х е (-оо; 2) и х е (2; +оо). В первом из
них f" < 0, т. е. кривая выпукла
вверх, а во втором f" > 0, т. е. кривая
выпукла вниз. Получили точку пере-
гиба (2; -1).
По полученным точкам построим
приближенный график данной функ-
ции (рис. 128).
И
Рис.128
249
ЧАСТЬ I. Алгебра и начала анализа
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие точки графика называются точками перегиба?
2. Как исследуется функция на точки перегиба с помощью второй произ-
водной?
3. Сформулируйте правила исследования функции на точки перегиба.
4. Что необходимо знать для построения графика функции?
Глава 7. Дифференциал функции.
Приложение дифференциала
к приближенным вычислениям
§ 59. Сравнение бесконечно малых величин
Приведем примеры сравнения бесконечно малых величин при
делении их друг на друга; в этих ситуациях могут представиться
различные варианты. Пусть а, а* 1 2 3 4 и 2а — бесконечно малые. Тог-
да возможно:
1) отношение а2/а = а — бесконечно малая величина;
2) отношение а/а2 = 1/а — бесконечно большая величина;
3) отношение 2а/а = 2 — конечная величина;
4) отношение а/а = 1.
Первое отношение показывает, что а2 составляет малую часть
от а, следовательно, стремится к нулю быстрее, чем а. Из второго
отношения видно, что делитель а2 стремится к нулю быстрее, чем
делимое а, т. е. при а —*• О величина 1/а —*• следовательно, яв-
ляется величиной бесконечно большой. Из третьего отношения
следует, что бесконечно малые а и 2а стремятся к нулю с одина-
ковой скоростью, поэтому при их изменении отношение 2а/а ос-
тается постоянным. Такие бесконечно малые называются беско-
нечно малыми одного порядка малости, а если их отношение
равно единице, то они называются эквивалентными.
Введем следующие определения:
I. Если аир — бесконечно малые величины и lim (а/Р) = О, то
а называется бесконечно малой высшего порядка малости по
сравнению с р.
II. Если lim (а/Р) = а (а * 0), то бесконечно малые аир одного
порядка малости.
III. Если lim (а/р) = со, то а называется бесконечно малой низ-
шего порядка малости по сравнению с р.
250
ГЛАВА 7. Дифференциал функции. Приложение дифференциала к приближенным вычислениям
IV. Если lim (а/р) = 1, то бесконечно малые а и Р называются
эквивалентными.
♦ ПРИМЕР
Сравнить порядки малости следующих величин: 1) х2 + х3 и х,
если х —* 0; 2) 5х + Зх2 и х, если х 0; 3) sin х и tg х при х —* О;
4) Jx и х при х ~* 0.
РЕШЕНИЕ. Имеем:
1) lim
== lim (х + х2) = О, бесконечно малая (х2
имеет высшии порядок малости по сравнению с х;
2) lim
lim (5 + Зх) = 5, бесконечно малые (5х +
+ Зх2) и х одного порядка малости;
.. sinx sinx
d) hm -— — hm -----------
x —otgx x — osmx/cosx
tg x одного порядка малости;
lim cos х = 1, величины sin х и
4) lim
lim
бесконечно малая Jx имеет низ-
ший порядок малости по сравнению с х.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Перечислите различные варианты сравнения бесконечно малых величин.
2. Приведите примеры бесконечно малых высшего порядка малости.
3. Приведите примеры бесконечно малых одного порядка малости.
4. Какие бесконечно малые называются эквивалентными?
5. Когда отношение бесконечно малых стремится к бесконечности?
§ 60. Дифференциал функции
1. Понятие о дифференциале функции. Пусть дана функция у = /(х),
, Ду „
ее производная у = д11т 0 . По определению предела перемен-
~ Ду
нои имеем: -г2-
= у' 4- а, где а — бесконечно малая при Дх
0
с ледовател ьно,
Ду = у' Дх + а • Дх.
(7.1)
251
ЧАСТЬ I. Алгебра и начала анализа
При уменьшении Дх первое слагаемое у'Lx уменьшается про-
порционально Дх, второе слагаемое а • Дх уменьшается быстрее,
чем у' Lx. Сравним их:
аДх _ а
у'Lx ~ у' ’
т. е. отношение —, — бесконечно малая при у' * О. Отсюда следу-
ет, что а Дх бесконечно малая высшего порядка малости по срав-
нению с у'Lx.
В формуле (7.1) первое слагаемое у'Lx называется главной
частью приращения функции у = f(x).
Главная часть у'Lx приращения функции у = f (х) называется
дифференциалом функции. Дифференциал функции У = f(x)
обозначается символом dy, т. е.
dy = у' Lx.
(7.2)
Дифференциал аргумента у = х найдем по (7.2): dy = х' Дх =
= Дх или
dx = Дх, (7.3)
т. е. дифференциал аргумента равен приращению аргумента, по-
этому равенство (7.2) запишем в виде
Из формулы (7.4) следует
производной:
= у' dx. (7.4)
возможность нового обозначения
т. е. производная функции у = /(х) есть отношение дифференци-
ала функции к дифференциалу аргумента.
Заменив в выражении (7.1) слагаемое у'Lx дифференциалом
функции dy, получим
Ly = dy + a* Lx.
(7.6)
В выражении (7.6) слагаемое а • Дх есть величина бесконечно
малая высшего порядка малости по отношению к dy, поэтому
слагаемое а • Дх можно отбросить, допустив незначительную
ошибку, и тем меньшую, чем меньше Дх.
Получили важное для приближенных вычислений равенство
Ly ~ dy.
(7.7)
Для линейной функции у — kx + Ъ значение Ly = dy.
252
ГЛАВА 7. Дифференциал функции. Приложение дифференциала к приближенным вычислениям
Дифференциалом второго порядка называется дифференциал
от дифференциала первого порядка
d2y = f"(x) dr2.
(7.8)
♦ ПРИМЕР 1
Найти дифференциал первого порядка функции: 1) у = (х3 -
- 2)“; 2) z = л/х2 - 1.
РЕШЕНИЕ. По формуле (7.4) имеем:
1) &У = ((*3 “ 2)4)' dx = 4(х3 - 2)3(х3 - 2)' dx = 4(х3 - 2)3 * Зх2 dx =
= 12х2(х3 - 2)3 dx;
2) dz = (Jx2 — 1 У dx =
(х2 - 1)' dx =
2xdx
♦ ПРИМЕР2
Найти дифференциалы второго порядка функции у = е х.
РЕШЕНИЕ. По формуле (7.8)
у' = (е~х)' = е~х(-х)' = - е~х;
у" = (~е~х)" = - е~х{-х)' = е~х;
d2y = у" dx2 = е~х dx2.
2. Геометрический смысл дифференциала функции. На рисунке 129
изображен график функции у = /(х), направленный выпуклостью
вниз. На кривой отмечены точки М и N с координатами (х; у) и
(х 4- Дх; у + Ду) соответственно. В точке М к кривой проведена
касательная, которая пересека-
ет ось абсцисс под углом а. Обо-
значим через Рг проекцию точ-
ки N на ось Ох, через Р — про-
екцию точки М на вертикаль,
опущенную из точки N на ось
Ох, и через Т — точку пересече-
ния касательной с этой верти-
калью. Тогда
PtN = у + ку = f(x + Дх),
Рис. 129
PN = Ду.
253
ЧАСТЬ I. Алгебра и начала анализа
Угловой коэффициент k касательной равен производной функ-
ции f(x), т. е. k = tg а = у' = f\x).
Из А МРТ имеем: PT = tg а*МР; по формуле (7.3) Ах = dx,
т. е. MP = dx, следовательно, учитывая формулу (7.4), получаем
РТ = у' dx = dy.
Дифференциал dy функции у = /(х) представляет собой прира-
щение ординаты касательной, проведенной в данной точке
кривой.
Поскольку PN = PT + TN, приращение функции Аг/ = dy + TN,
тогда, согласно формуле (7.6), TN = а Ах, т. е. TN представляет со-
бой часть приращения функции, которая при Ах —► О является
бесконечно малой высшего порядка малости по сравнению с Ах.
В рассматриваемом случае приращение Аг/ превышает диффе-
ренциал dy на. величину а • Ах:
Аг/ — dy = а • Ах.
Приращение Аг/ может оказаться и меньше dy, например, ког-
да кривая у = /(х) будет направлена выпуклостью вверх.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение дифференциала функции.
2. Как обозначается дифференциал функции?
3. Чему равен дифференциал аргумента?
4. Что называется дифференциалом второго порядка?
5. Объясните геометрический смысл дифференциала функции.
§ 61. Приложение дифференциала
к приближенным вычислениям
1. Абсолютная и относительная погрешности. Рассмотрим функцию
у = f(x). Предположим, что величина х получена непосредствен-
ным измерением или в результате приближенного вычисления.
Тогда при нахождении величины х допускается некоторая по-
грешность Ах.
Пусть х — приближенное значение аргумента (измеряемой ве-
личины), Ах — абсолютная погрешность величины х, Ах/х —
относительная погрешность величины х, а (х + Ах) — истинное
значение измеряемой величины (Ах может быть как положи-
тельным, так и отрицательным числом).
254
ГЛАВА 7. Дифференциал функции. Приложение дифференциала к приближенным вычислениям
Тогда х определяет приближенное значение функции /(х),
а (х + Дх) — ее истинное значение f{x + Дх), из чего следует, что
абсолютная погрешность функции
Ду| = |(х + Дх)-/(х)|.
При близких к нулю значениях Дх величину Ду можно при-
ближенно заменить дифференциалом dy:
Ду = /(х + Дх) - /(х) — f{x) dx = dy.
Выгода замены приращения функции Ду ее дифференциалом
dy состоит в том, что dy зависит от Дх линейно, а Ду представля-
ет собой обычно более сложную зависимость от Дх.
Полагая Ду ~ dy, получим выражение для относительной по-
грешности е величины у:
♦ ПРИМЕР
Сравнить относительные погрешности при вычислении пло-
щади круга радиуса г = 125 см, считая, что абсолютная по-
грешность равна: 1) приращению площади круга; 2) диф
ренциалу площади круга.
РЕШЕНИЕ. 1) Находим приращение Д£ площади круга и относи-
тельную погрешность Д8/8 при вычислении площади круга
S = яг2. Будем считать, что погрешность при измерении радиуса
не превышает ±0,5 см. Имеем Д8 = л(г + Дг)2 - лг2 = л(2г Дг +
+ (Дг)2) = л(2 • 125 • 0,5 + 0,25) = 125,25л;
AS = 125,25k
S к • 1252
= 0,008016 -0,8%;
2) найдем дифференциал dS и относительную погрешность
dS/S при вычислении площади круга:
dS = 2лг dr = 2л-125-0,5 = 125л;
О KTZ
dr
Таким образом, относительная погрешность при вычислении
площади круга равна удвоенной относительной погрешности, по-
лученной при измерении радиуса:
dS
S
= 2- — = 2-^| =0,8%.
г 125
255
ЧАСТЬ I. Алгебра и начала анализа
Итак, во втором случае вычисления значительно проще и вы-
полнены без ущерба для точности вычисления.
Определим относительную погрешность приближения при за-
мене приращения AS дифференциалом dS:
AS - dS = 125,25л - 125л = 0,25л;
AS - dS = 0,25л
dS 125л
= 0,002 = 0,2%.
2. Вычисление приближенного числового значения функции. Пусть да-
на функция у = f(x); приращение этой функции Аг/ = f(x + Ах) -
- /(х), ее дифференциал dz/ = f'(x) dx. При достаточно малых
(близких к нулю) приращениях аргумента Ах будем считать, что
Аг/ ~ di/, т. е. что приращение функции приближенно равно ее
дифференциалу.
Заменив приращение функции ее дифференциалом, получим
f'(x) dx = f(x + Ах) - /(х),
из чего следует
/(х + Ах) ~ Дх) + f'(x) dx. (7.9)
Применение этой формулы дает значительное упрощение вы-
числения числового значения функции; геометрически это соот-
ветствует замене участка кривой отрезком касательной.
Ф ПРИМЕР 1
Найти приближенное значение приращения функции у = 2х3 +
+ 5 при х = 2 и Ах = 0,001.
РЕШЕНИЕ. Имеем:
Аг/ ~ dz/ = 6х2 dx = 6 • 22 • 0,001 = 0,024.
Точное значение приращения
Аг/ = 2(х 4- Ах)3 + 5 - 2х3 — 5 = 6х2 Ах + 6х(Дх)2 + 2(Ах)3 =
= 6 • 4 • 0,001 + 6 • 2 • 0,000001 + 2 • 0,000000001 = 0,024012002.
♦ ПРИМЕР 2
На сколько увеличится при нагревании объем шара радиуса
В, если его радиус удлинился на величину АВ?
РЕШЕНИЕ. Объем шара вычисляется по формуле V = (4/3)nR3. Счи-
тая приращение АВ аргумента R малым, заменим приращение
объема шара его дифференциалом: AV = dV. Следовательно, для
вычисления приращения объема шара достаточно найти диф
ренциал функции V = | тсВ3, т. е. dV = 4лВ2 dB.
256
ГЛАВА 7. Дифференциал функции. Приложение дифференциала к приближенным вычислениям
♦ ПРИМЕРЗ
Найти приближенное значение функции /(х) = 5х3 - 2х + 3
при х = 2,01.
РЕШЕНИЕ. Полагая х = 2 и Дх = 0,001, получаем
f(2) = 5 • 23 - 2 • 2 + 3 = 39;
f(x) = 15х2 - 2; f (2) = (15 • 22 - 2) = 58; /'(2) Дх = 0,58.
По (7.9) /(2,01) = 39 + 0,58 = 39,58.
Сравним с точным значением функции: /(2,01) = 5-(2,01)3 -
- 2 • 2,01 + 3 = 39,583005.
3. Формулы для приближенных вычислений. Применяя соотношение
(7.9), легко получить различные формулы для нахождения при-
ближенных числовых значений. Рассмотрим формулы, имеющие
практическое значение в приближенных вычислениях.
Выражение для приближенного вычисления степеней:
(х + Дх)л ~
(7.10)
Приведем частные случаи формулы (7.10):
1) и = 2: (х + Дх)2 ~ х2 + 2хДх;
2) п — 3; (х + Дх)3 « (х3 + Зх2)Дх;
3) х = 1, (1 + Дх)л ~ 1 + пДх.
Выражение для приближенного вычисления корней:
(7.11)
Рассмотрим частные случаи формулы (7.11):
Дх .
2jx ’
Выражение для приближенного вычисления обратных вели-
чин:
(7.12)
Приведем частные случаи формулы (7.12):
9 - 9664
257
ЧАСТЬ I. Алгебра и начала анализа
2)х= 1:
~ 1 - Дх;
3) х = 1, Дх < 0: -т— ~ 1 4- Дх.
' х - &х
Выражения для приближенного вычисления синусов и тан-
генсов малых углов: sin х ~ х; tg х ~ х.
♦ ПРИМЕР
Найти приближенное значение: 1) (4,012)2; 2) л/1,006;
1,004 ’
РЕШЕНИЕ. 1) Полагая в соотношении (7.10) х = 4, Дх = 0,012, полу-
чим (4 + 0,012)2 ~ 42 4- 2 • 4 • 0,012 = 16,096 ~ 16,1; точное значе-
ние составляет 16,096144;
2) полагая в формуле (7.11) х = 1, Дх = 0,006, получаем
71 + 0,006 « 1 + 0,006/2 = 1,003;
3) полагая в (7.12) х = 1, Дх = 0,004, получаем 1/(1 4- 0,004) ~
~ 1 - 0,004 = 0,996.
4. Вычисления по способу строгого учета погрешностей. При вычисле-
ниях нередко возникает необходимость знать границы допущен-
ной погрешности промежуточных вычислений и окончательного
результата. Такой способ ведения приближенных вычислений
называется способом строгого учета погрешностей. Для этого не-
обходимо знать, как вычисляются границы относительных по-
грешностей алгебраической суммы, произведения, степени, кор-
ня и частного.
Покажем, что относительная погрешность е произведения не
превышает суммы относительных погрешностей ее сомножите-
лей. Пусть дана функция у = uv, где и = f(x) и v = <р(х). Пролога-
рифмируем ее и найдем дифференциал:
1 1 .1 du du , dy
In у = In и 4- In v; — =-----1- — .
* у и v
Так как абсолютная величина суммы не превышает суммы аб-
солютных величин слагаемых, то
du । dv
и v
du
v
du
и
258
ГЛАВА 7. Дифференциал функции. Приложение дифференциала к приближенным вычислениям
или
е(ир) =
du । du
и v
(7.13)
Покажем, что относительная погрешность е частного не пре-
вышает суммы относительных погрешностей делимого и делите-
ля. Пусть дана функция у = u/v, где и = f(x) ни = <р(х). Пролога-
рифмировав и взяв дифференциал от функции у = и!и, получим
, , , du du du
in u = In и - In v; — ----------------.
27 у и v
Так как абсолютная величина разности не превышает суммы аб-
солютных величин уменьшаемого и вычитаемого, то
dt/ _ du
У и
du
или
du
(7.14)
Покажем, что относительная погрешность степени е равна от-
носительной погрешности основания, умноженной на показатель
степени. Пусть дана функция у = хп. Прологарифмируем ее и
найдем дифференциал:
In у — п In х
Относительная погрешность равна
(7.15)
Отметим частные случаи:
«X « Z Ox ZxdX
2) п = 3: е(х3) = 3—.
Покажем, что относительная погрешность корня равна отно-
сительной погрешности подкоренного числа, деленной на показа-
тель степени корня. Пусть дана функция у = nJx. Прологарифми-
руем ее и найдем дифференциал:
, 1 1 du 1 dx
In у = - In х; — = - • — .
259
ЧАСТЬ I. Алгебра и начала анализа
Относительная погрешность
(7.16)
Отметим частные случаи:
l)n = 2:e(TS)= | v!
di JC
2)n = 3:e(?£) = |y.
♦ ПРИМЕР 1
Длина прямоугольника составляет и — 60 м, ширина составля-
ет v = 23 м. Погрешность при измерении длины не превышает
0,3 м, а при измерении ширины — соответственно 0,2 м. Опре-
делить границы погрешности, которая допускается, если пло-
щадь прямоугольника принимается равной 60*23 = 1380 м2, и
относительную погрешность.
РЕШЕНИЕ. Имеем: |diz| < 0,3, |dt>| < 0,2. При наихудших условиях
du| = 0,3, |du| = 0,2. Найдем абсолютную погрешность произведе-
ния:
d(uu) = v du + и dt> = 23 • 0,3 + 60 • 0,2 = 18,9 — 19 (м2).
Это наибольшая величина абсолютной погрешности, которую
можно допустить, принимая площадь равной 1380 м2. Округляя
погрешность в сторону увеличения и принимая ее равной 20 м2,
найдем границы погрешности при вычислении площади. Таким
образом, площадь не превосходит 1380 + 20 = 1400 (м2) и не мо-
жет быть менее 1380 - 20 = 1360 (м2).
Относительную погрешность вычислим по формуле (7.13):
, . 0,3
е<“р> = go
1 2
200 + 230
-0,014 = 1,4%.
♦ ПРИМЕР 2
Для нахождения плотности тела определены его масса тг =
= 484 г и масса вытесненной им воды т2 = 62 г. Абсолютные
погрешности Д/П] = 0,5 г и Лт2 = 0,4 г. Найти относительную
погрешность при вычислении плотности тела р.
РЕШЕНИЕ. Так как р = uij/m2, то по (7.14)
do dm, dm? 0 5 0 4
= —! + —? = тб7 + = 0,00103 + 0,00645 = 0,00748 ® 0,7%.
о Шл тч 484 62
260
ГЛАВА 8. Неопределенный интеграл
♦ ПРИМЕРЗ
Найти относительную погрешность, допущенную при измере-
нии объема куба, если ребро равно 12,5 см. Абсолютная по-
грешность Дх = 0,05 см.
РЕШЕНИЕ. Полагая dx = 0,05 см, по формуле (7.15) имеем
рГх31 = 3 — = 3 • 0’05 = 15 ~ л 012 = 1 2°/
Е(х ) d х d 12 5 1250 1,2/
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение абсолютной и относительной погрешностей.
2. Выпишите формулу для вычисления приближенного числового значе-
ния функции.
3. Выпишите формулы для приближенных вычислений степени, корня, об-
ратной величины.
4. Выпишите формулы для вычисления границ относительной погрешнос-
ти алгебраической суммы, произведения, частного, степени и корня.
ГЛАВА 8. Неопределенный интеграл
§ 62. Неопределенный интеграл
и его простейшие свойства
•L
кых задач дифференциального исчисления является задача на-
хождения скорости изменения какой-либо функции, т. е. задача
нахождения производной (или дифференциала). На практике
часто приходится решать обратную задачу: зная скорость измене-
ния функции, найти эту функцию; эта операция называется ин-
тегрированием. Это означает, что необходимо найти функцию
F(x) по одному из выражений dF(x) = f(x) dx или F\x) — f(x), где
f(x) — известная функция.
Искомая функция F(x) называется первообразной функцией
по отношению к функции /(х).
Первообразной функцией для данной функции /(х) называет-
ся такая функция F(x), производная которой равна jf(x) (или,
что то же самое, дифференциал которой равен f(x) dx).
Например, первообразной функцией для функции Зх2 явля-
ется х3, ибо (х3)' = Зх2. Но эта первообразная не единственная,
261
ЧАСТЬ I. Алгебра и начала анализа
а только одна из многих, так как функции х3 - 3, х3 + 2 и вообще
х3 + С, где С — произвольная постоянная, тоже являются перво-
образными для f(x) = Зх2, ибо (х3 + С)' = Зх2.
Действительно, если на некотором промежутке функция F(x)
является первообразной для функции /(х), то для этой последней
будет первообразной и любая функция вида
Ф(х) = Е(х) + С, (8.1)
где С — постоянная.
Покажем, что этим выражением исчерпывается все множест-
во первообразных, т. е. что любую первообразную для /(х) можно
получить из равенства (8.1) при некотором значении С.
Пусть F(x) и Ф(х) — две функции, являющиеся первообразны-
ми для функции /(х) на некотором промежутке. Тогда на этом
промежутке
(Ф(х) - Е(х))' = Ф'(х) - Г(х) = /(х) - f (х) = О,
из чего следует, что Ф(х) - F(x) = С и поэтому Ф(х) = F(x) + С.
Обращаясь к геометрической интерпретации только что дока-
занного утверждения, можно сказать, что графики всех первооб-
разных для данной функции f(x) представляют собой семейство
таких кривых, которые могут быть получены из любой из них
путем ее сдвига вдоль оси ординат (рис. 130).
Если F(x) — какая-либо первообразная функция для /(х), то
выражение F(x) 4- С, где С — произвольная постоянная, назы-
вается неопределенным интегралом от функции /(х) и обозна-
чается символом J f (х) dx.
Рис. 130
При этом функция /(х) называется
подынтегральной функцией, а выра-
жение /(х) dx называется подынте-
гральным выражением, знак J называ-
ется знаком интеграла.
Согласно определению неопределен-
ного интеграла, можно записать
if (х) dx = F(x) + С. (8.2)
Операция нахождения первообраз-
ной по данной функции называется ин-
тегрированием*.
* От integratio — восстановление (лат.).
262
ГЛАВА 8. Неопределенный интеграл
♦ ПРИМЕР
Найти: 1) [ ; 2) [ — .
J cos2x J х
РЕШЕНИЕ. 1) Находим функцию, производная которой равна-----:
COS
cosx2 *
Следовательно,
f dx , . ~
---2~ = tg X + С.
J COS2X
2) Находим функцию, производная которой равна - : (In х)' =
= i , где х е (0; +оо). Следовательно, J
(In |х|)' = , следовательно, J = In
О < X < +оо.
dx
— = In х + С. Заметим, что
х
х| 4- С, где —оо < х < 0 или
2. Основные свойства неопределенного интеграла.
I. Производная неопределенного интеграла равна подынтег-
ральной функции, а дифференциал неопределенного интегра-
ла равен подынтегральному выражению:
(f /(х) dx)' = f(x), (8.3)
d I f(x) dx = f(x) dx. (8.4)
Эти свойства непосредственно вытекают из определения неоп-
ределенного интеграла.
II. Неопределенный интеграл от дифференциала функции ра-
вен сумме этой функции и произвольной постоянной:
f dF(x) = F(x) + С. (8.5)
Для доказательства воспользуемся определением неопреде-
ленного интеграла:
I f (х) dx = F(x) + С,
но
dF(x) = /(х) dx, f(x) = F'(x),
следовательно,
j dF(x) = F(x) + C.
263
ЧАСТЬ I. Алгебра и начала анализа
III. Постоянный множитель можно выносить за знак неопре-
деленного интеграла:
f af(x) dx = a J f{x) dx, a * 0. (8.6)
Докажем формулу (8.6):
(af(x) dx)' = a(f(x) dx)' = ajf(x),
из чего следует формула (8.6).
IV. Интеграл от алгебраической суммы функций равен алгеб-
раической сумме интегралов от этих функций, т. е.
f (fi(x) “ f2(x> + М*» dx = f Мх) dx “ I 4(x) dx + f dx- (8.7)
По формуле (8.3) имеем (J(/j(x) - /2(х) + /з(х)) dxX = Л(х) ~
- f2(x) + 4<х>» из чего и следует (8.7).
ЙЮ.Й
3. Табличные неопределенные интегралы. Принимая во внимание,
что интегрирование есть действие, обратное дифференцированию,
получим табличные интегралы с помощью таблицы производных.
Приведем таблицу первообразных (постоянная С везде опуще-
на и подразумевается).
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
III. J х" dx = » (д * “!)•
IV. f | In \а + 6х|.
J а + bx b
V. [— =1п|х|.
J X
VI. f d* = arctg х.
J 1 + x2
VIII. [ . = = arcsin x.
J 1 - x2
IX. j ex dx = ex.
X. J In x dx = x In x - x.
Г ax
XI. ax dx = 7— .
J Ina
XII. J cos x dx = sin x.
XIII. J sin x dx — -cos x.
XIV. f = tg x.
J COS2X
dx
sin2x
264
ГЛАВА 8. Неопределенный интеграл
§ 63. Непосредственное интегрирование
Непосредственным интегрированием принято называть вы-
числение неопределенных интегралов путем приведения их к
табличным с применением основных свойств.
Отметим, что если операция дифференцирования совершается
формально, то далеко не так обстоит дело с интегрированием —
например, нет формул для интегрирования произведения или ча-
стного функций. Поэтому существуют обширные таблицы интег-
ралов (приведенная выше является весьма неполной) и возникает
задача — так преобразовывать вычисляемые интегралы, чтобы
их можно было свести к табличным.
Один из приемов, используемых при вычислении интегралов,
называется методом замены переменных. Он заключается в
преобразовании интеграла J f(x) dx в интеграл J F(u)du, который
легко вычисляется по какой-либо из табличных формул интегри-
рования.
♦ ПРИМЕР 1
Вычислить методом замены переменных интеграл: 1) J tg х dx;
2) J sin (ах 4- b) dx; 3)
xdx
sin2(x2 + 1)
РЕШЕНИЕ. 1) Так как sin х dx = —d(cos х), то
J tg х dx = f = -In |cos x| 4- C;
J cosx 1 1
2) так как d(ax 4- ft) = a dx, to dx = - d(ax 4- b). Следовательно,
J sin (ax 4- b) dx = J sin (ax 4- b) • - d(ax 4- b) =
= ~ ! sin (ax 4- b) d(ax + b) = cos (ax 4- b) + C;
3) так как xdx= x d(x2 4- 1), to
d(x2 4- 1)
sin2(x2 4- 1)
x dx
sin2(x2 + 1)
Ctg (x2 4- 1) 4- C.
265
ЧАСТЬ I. Алгебра и начала анализа
♦ ПРИМЕР 2
Найти интеграл методом замены переменной:
1) Ц = f (2х3 + 1)4х2 dx; 2) L> = J
xdx
(x2 + I)3 ’
РЕШЕНИЕ. 1) Положим 2x3 + 1 = и => 6x2 dx = du => x2 dx = (1/6) du.
Таким образом,
6 Ju4du 6 * 5 +C 30u5 + C 30(2x3 + I)5 + C;
2) положим x2 4- 1 = и => 2x dx = du => x dx = (1/2) du. Нахо-
дим
1
4(x2 + I)2
♦ ПРИМЕРЗ
Методом замены переменной найти интеграл:
= Г tg kx dx; 2) I2 = [4^;3)Z3 = f —.
' 1 J ' 2 J smu z 3 J cosu
РЕШЕНИЕ. 1) Имеем =
sinfex
cosfcx
dx. Положим cos kx
- k sin kx dx = du => sin kx dx = -(1/A) du. Следовательно,
f — = — |ln |u| + C = — |In |cos kx\ 4- C;
ft J U R R
2) так как sin u = 2 sin(u/2) cos(u/2), to I2 =
_______du________
2sin(u/2)cos(u/2)
Разделив и умножив знаменатель на cos (u/2), получим
du
tg(u/2)cos2(u/2)
Положим tg (u/2) = z
1
cos2(u/2)
9 du = dz
du
cos2(u/2)
= 2 dz.
Таким образом,
266
ГЛАВА 8. Неопределенный интеграл
3) имеем 13 =
du
sin(n/2 + и)
Положим л/2 + и = z => du = dz.
Поэтому
+ C = ln
♦ ПРИМЕР 4
, л/2 + и
tg г-
+ C = ln
Найти интеграл методом замены переменных:
1)/1 = р5*I. 2х
dx; 2) 12 =
3x2 + rxdx; 3) 13 =
(а > 0).
РЕШЕНИЕ. 1) Положим 5х2 = и => 10х dx = du => х dx = (1/10) du.
Таким образом,
10 P“du ю 10 In 3
g5x2
101n3
+ C;
+ C =
2) положим -Зх2
Таким образом,
- 6х dx = du => х dx = -(1/6) du.
3) имеем I3 =
. Положим x/a = и => dx = a du.
Таким образом,
______dx_______
л/о2(1 — (x/a)2)
= arcsin и + С = arcsin—I- C.
При помощи подстановок ах + Ь = иитх = и нетрудно вычис-
лить следующие интегралы (постоянная С везде опущена и под-
разумевается) :
I. fe(ax + b>dx=-e(ax + fe).
а
п. \g^Ax=^.
III. J sin (ax + b) dx = - i cos (ax + &), a 0.
IV. J cos (ax + b) dx = sin (ax 4- b), a 0.
,r f dX 1 x / . LA
V. —Й------ = ~ tg (ax + b).
cos2(ax + b) a
267
ЧАСТЬ I. Алгебра и начала анализа
VI. [ —--------- = - i ctg (ах + Ъ).
* sin2(ax + b) а
VII. Г , dx = - arcsin ~ х, т > 0.
J Л2 - т2х т k
Отыскание функции по заданной производной или по диффе-
ренциалу — задача неопределенная, так как jf(x)dx означает мно-
жество первообразных функций вида у = F(x) + С, отличающихся
друг от друга постоянным слагаемым С; величина С может прини-
мать любые числовые значения, если на первообразную функцию
не наложено никаких начальных условий. Чтобы из множества
первообразных функций выделить одну определенную функцию,
должны быть заданы начальные условия. Под начальными усло-
виями понимается задание частных значений х и у для первооб-
разной функции у = F(x) + С, по которым находится определен-
ное значение С, удовлетворяющее этим начальным условиям.
♦ ПРИМЕР
Найти функцию, производная которой у' = 2х - 3, если при
х = 2 эта функция принимает значение, равное 6.
РЕШЕНИЕ. Имеем у' = 2х -
3, или = 2х - 3, т. е. dy = (2х - 3) dx.
Интегрируя обе части последнего равенства, находим значение
J dy = f (2х - 3) dx; С* + у = х2 - Зх 4- С2. Полагая С2 - Cj = С, полу-
чим у = х2 - Зх + С. Нашли общее выражение функций, имею-
щих своей производной у' = 2х - 3.
Вычислим С при заданных значениях х = 2 и у = 6. Подставив
в выражение для функции эти значения, получим 6 = 22 — 3*2 +С,
откуда С = 8. Таким образом, функция, удовлетворяющая задан-
ным начальным условиям, имеет вид у = х2 — Зх + 8.
§ 64. Геометрические приложения
неопределенного интеграла
Рассмотрим случаи использования неопределенного интегра-
ла при построении графика функции.
♦ ПРИМЕР 1
Найти уравнение кривой, если угловой коэффициент каса-
тельной в каждой ее точке равен 2х.
268
ГЛАВА 8. Неопределенный интеграл
РЕШЕНИЕ. Согласно условию, угловой ко-
эффициент k = 2х. Известно, что k =
= tg а =
следовательно,
dp
dx
т. e. dp = 2x dx. Интегрируя, получим
J dp = J 2x dx; p = x2 + C.
Найдено семейство кривых, для ко-
торых угловой коэффициент касатель-
ной в любой точке равен 2х. Эти кривые
отличаются друг от друга на посто-
янную С. При С = 0 получим параболу
р = х2 с вершиной в начале координат
Рис. 131
(рис. 131), при С = 1 — параболу у = х2 + 1 с вершиной в точке
(0; 1), при С = - 2 — параболу у = х2 - 2 с вершиной в точке (0; -2)
ИТ. д.
♦ ПРИМЕР 2
Составить уравнение линии, если угловой коэффициент каса-
тельной в любой точке касания равен р/х.
РЕШЕНИЕ. Согласно условию, угловой коэффициент k = р/х; так
как k =
dp
dx
из чего, разделив переменные, получим
dp .
dx ’
dw dx __
— = — . Интегрируя, находим
= 1т:1п^ = 1пх+с-
Произвольную постоянную полагаем для удобства равной
In С.
Потенцируя, получим у = Сх — уравнение семейств прямых,
проходящих через начало координат.
♦ ПРИМЕРЗ
Найти уравнение кривой, проходящей через точку (0; 1), у ко-
торой касательная в любой точке кривой имеет угловой коэф-
фициент, равный ординате точки касания.
dp
dx
РЕШЕНИЕ. Согласно условию, имеем угловой коэффициент k =
Из начальных условий находим In 1 = 0 + С, т. е. С = 0; следова-
тельно, у = ех.
269
ЧАСТЬ I. Алгебра и начала анализа
§ 65. Физические приложения
неопределенного интеграла
Рассмотрим несколько ситуаций» когда при решении задач
кинематики используются неопределенные интегралы.
♦ ПРИМЕР 1
Скорость прямолинейного движения точки изменяется по за-
кону v — St2 + 4. Найти закон ее движения, если за время t — 2 с
точка прошла 20 м.
РЕШЕНИЕ. Обозначим путь, пройденный точкой за время i, через S.
Так как v = = 3t2 4- 4, то dS = (3f2 4- 4) dt. Интегрируя, полу-
чим J dS = J (3£2 + 4) dt; S = t3 + 4t + C.
Используя начальные условия, найдем 20 = 23 4- 4 • 2 4- С, т. е.
С = 4. Итак, закон движения точки имеет вид S = t3 4- 4£ 4- 4.
♦ ПРИМЕР 2
Найти закон движения свободно падающего тела при постоян-
ном ускорении g, если в начальный момент движения тело на-
ходилось в покое.
РЕШЕНИЕ. Известно, что ускорение а прямолинейно движущегося
тела есть вторая производная пути S по времени t или производ-
ная от скорости v по времени t, т. е. а =
d2S _ dv
dt2 df
. Так как а = g,
то т- = g => dt? = g dt. Интегрируя, получим
f dt> = J g dt; v * gt 4- Cr
Используя начальные условия (у = 0 при t = 0), имеем 0 = g • 0 4-
4- Ср т. е. Сх = 0. Таким образом, скорость движения тела изменя-
ется по закону v = gt,
„ ~ _ dS dS
Найдем теперь закон движения тела. Так как v = , то =
= gt, или dS = gt dt. Интегрируя, получим
J dS = J gt dt; S =
4- C2«
Используя начальные условия (S — 0 при t = 0), имеем 0 =
= g*02/2 4- C2, C2 = 0. Итак, закон движения падающего тела
имеет вид S = gt2/2.
270
ГЛАВА 9. Определенный интеграл
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какое действие называется интегрированием?
2. Какая функция называется первообразной для данной функции/(х)?
3. Чем отличаются друг от друга различные первообразные функции для
данной функции/(х)?
4. Дайте определение неопределенного интеграла.
5. Дайте определение подынтегральной функции и подынтегрального вы-
ражения.
6. Какой геометрический образ соответствует неопределенному интегра-
лу If (х) dx?
7. Как проверяется результат интегрирования?
8. При каком условии справедливо равенство J/(x) dx = F(x) + С?
9. Чему равны производная и дифференциал неопределенного интеграла?
10. Чему равен неопределенный интеграл от дифференциала функции Г(х)?
11. Сформулируйте основные свойства неопределенного интеграла.
12. Укажите ограничения на параметр п для табличного интеграла
J xn dx =
— + С(х>0).
п + 1
13. Выпишите формулу для интеграла jxndx при л = -1.
14. В чем заключается метод замены переменных при отыскании неопреде-
ленного интеграла?
ГЛАВА 9. Определенный интеграл
§ 66. Основные свойства и вычисление
определенного интеграла
1. Понятие об определенном интеграле. Сформулируем без доказа-
тельства теорему Ньютона—Лейбница*.
ТЕОРЕМА НЬЮТОНА—ЛЕЙБНИЦА
Пусть f — данная функция, F — ее произвольная первообраз-
ная. Тогда
J f(x) dx = f(b) - F(a).
(9.1)
* Английский физик и математик Исаак Ньютон [Newton] (1643—
1727) и немецкий математик и физик Готфрид Лейбниц [Leibniz, Leib-
nitz] (1646—1716) являются основоположниками дифференциального и
интегрального исчисления.
271
ЧАСТЬ I. Алгебра и начала анализа
Приращение F(b) - F(a) любой из первообразных функций
F(x) + С при изменении аргумента от х = а до х — b называется опре-
деленным интегралом.
Формула (9.1) носит название формулы Ньютона—Лейбница.
Разность F(b) — F(a) записывают в виде F(x)|^ .
ъ
Алгоритм нахождения определенного интеграла J f(x) dx
а
I. Найти первообразную функцию F(x) для функции f(x).
II. Вычислить значение F(x) при х = b (6 называется верхним
пределом).
III. Вычислить значение F(х) при х = а (а называется нижним
пределом).
IV. Вычислить разность F(b) - F(a).
Приведем примеры:
Л/6
J cos х dx = sin х [J76 = sin - sin 0 = %
2. Основные свойства определенного интеграла. Перечислим основ-
ные свойства определенного интеграла:
I. При перестановке пределов интегрирования знак опреде-
ленного интеграла изменяется на противоположный:
Ь а
J /(х) dx = - j /(х) dx.
в ь
II. Постоянный множитель подынтегрального выражения
можно выносить за знак определенного интеграла:
ъ ь
J kf(x) dx = k J jf(x) dx.
a a
III. Определенный интеграл суммы функций равен сумме опре-
деленных интегралов этих функций:
ь ь ь
J (f(x) + Ф (х)) dx = J f (х) dx + f ф(х) dx.
а а а
272
ГЛАВА 9. Определенный интеграл
Например,
3. Определенный интеграл как площадь. Пусть непрерывная при всех
значениях аргумента положительная функция у = /(х) изображе-
на на рисунке 132.
Кривая f(x), ось Ох, непо-
движная ордината f(a) и пере-
менная ордината /(х) ограничи-
вают некоторую криволинейную
трапецию.
Обозначим через А, Ар В иВ1
точки с координатами (a; f(a)),
(а; 0), (х; /(х)), (х; 0) соответ-
ственно. Тогда площадь фигуры
AAjBjB будет переменной величи-
ной, зависящей от х; обозначим
эту площадь через S. Если аргу-
мент х получит приращение Дх,
Рис. 132
то площадь S получит приращение ДВ, равное криволинейной пло-
щади ВВ Е Е. Здесь координаты точки Е: (х + Дх; /(х + Дх)),
точки Ех — ((х + Дх); 0). Проведем прямую BD || Ох и прямую
NE || Ох до пересечения с продолженной ординатой ВгВ.
Имеем
^B1BDC1 < < SB^NCCi
или
f (х) • Дх < AS < f(x + Дх) • Дх.
Разделив полученное неравенство на Дх (Дх > 0), получим
/(х) <
ДВ
Дх
/(х + Дх).
(9.3)
При Дх -* 0 значение f(x + Дх) -* /(х), следовательно, отноше-
AS .. ДВ . .. AS
ние Дх или Дх™0Дх = но д^ШоДх является произ-
водной функции S, т. е
= f(x), откуда
dS = /(х) dx.
(9.4)
273
ЧАСТЬ I. Алгебра и начала анализа
Проинтегрировав обе части предыдущего равенства, получим
J d8 = J f(x) dx или
8 + Cj = J f(x) dx. (9.5)
Пусть F(x) — первообразная функция для /(x), тогда
f /(x) dx = F(x) + C2. (9.6)
Из сравнения равенств (9.5) и (9.6) получим:
S + Cj = F(x) + С2
или
8 = F(x) + С, С2 - Ci = С.
(9.7)
Для вычисления С в равенстве (9.7) положим х = а, тогда пло-
щадь AAiBjB = 8 = 0. Следовательно, 0 = F(a) + С, откуда С =
= ~F(a),
Равенство (9.7) примет вид 8 = F(x) - F(a), что можно запи-
ь
сать в виде определенного интеграла F(x) - F(a) = J f(x) dx.
а
Итак, переменная площадь 8 примет вид
X
S = J f(x) dx = F(x) - F(a).
a
(9.8)
Для вычисления постоянной площади, ограниченной пло-
щадью криволинейной трапеции АА^ВуВ, положим в формуле
(9.8) х = Ь, тогда
ь
8 = J f(x) dx = F(b) - Ffa).
a
(9.9)
Следовательно, площадь фигуры 8, ограниченной кривой
у = /(х) (/(х) > 0), осью Ох и прямыми х = а и х = Ь, выражается
определенным интегралом
ь
S = J f (х) dx.
а
(9.10)
В этом выражении заключается геометрический смысл опре-
деленного интеграла.
♦ ПРИМЕР
Вычислить площадь фигуры, ограниченной данными линиями:
1) у = х2, у = 0, х = 2, х = 3; 2) у2 = х, у = 0, х = 1, х = 4;
3) у = sin х, у = 0, х = 0, х = л; 4) у = х2, у = 2х.
274
ГЛАВА 9. Определенный интеграл
РЕШЕНИЕ. 1) Данная фигура изображена
на рисунке 133. По (9.10)
= 6,5 (кв. ед.);
2) данная фигура изображена на ри-
сунке 134. По (9.10), где f(x) = Jx,
= |(8-1) =
Рис. 133
3) искомая площадь ограничена по-
луволной синусоиды и осью Ох:
л
S = J sin х dx = -cos х |*= -cos л + cos 0 = 1 + 1 = 2 (кв. ед.);
о
4) данная фигура представлена на рисунке 135. Для вычисле-
ния точек пересечения заданных линий необходимо решить сис-
тему уравнений
Искомая площадь равна разности площадей:
(кв. ед.).
Рис. 134
Рис. 135
275
ЧАСТЬ I. Алгебра и начала анализа
Рис. 136
4. Определенный интеграл как предел суммы. Рассмотрим функцию
у = /(х), непрерывную в промежутке а < х < Ъ. Пусть функция
в этом промежутке является положительной и возрастающей.
Выделим площадь фигуры
АА^В^В (обозначим ее через В),
ограниченную кривой у = f(x),
прямыми х = а, х = b и осью Ох
(рис. 136). Здесь точки А, В,
Вг имеют координаты (а; /(а)),
(а; 0), (b; /(b)), (Ь; 0) соответ-
ственно. Эта площадь равна
ь
S=jf(x)dx. (9.11)
Разделим отрезок АГВ} на п равных частей, каждую из кото-
рых обозначим через Дх. Площадь фигуры состоит из суммы
площадей прямоугольников (Вр) и суммы площадей криволиней-
ных треугольников (Вд); S = Bg + S^:
s-sQ = s^.
(9.12)
Абсциссы точек деления обозначим через xv х2, ...» хп _ р а со-
ответствующие им ординаты через /(хх), /(х2), ..., f(xn _ t).
Сумма площадей всех прямоугольников
S = f(a) Дх + /(Xj) Дх + ... + f(xn _ х) Дх
или
В»£/(х)Дх. (9.13)
а
Если число делений п отрезка AjBj неограниченно увеличивать,
то Дх —* 0, и величины Вд и Вд станут переменными. При этом ус-
ловии Вд будет величиной бесконечно малой. Расположим криво-
линейные треугольники в прямоугольнике ABCD: основанием это-
го прямоугольника является отрезок Дх, высотой — отрезок (/(b) —
- /(а)), а площадью — произведение |/(Ь) - /(а)| Дх. При этом
Вд<|/(Ь)-/(а)|Дх. (9.14)
При Дх —* 0 произведение постоянной |/(b) - /(а)| на бесконеч-
но малую Дх есть величина бесконечно малая, тогда и Вд — бес-
конечно малая.
276
ГЛАВА 9. Определенный интеграл
Таким образом, левая часть формулы (9.12) — величина бес-
конечно малая, тогда по определению предела равенство (9.13)
принимает вид
S = lim So = £ /(х) Дх. (9.15)
Л v
а
Сравнивая формулы (9.11) и (9.15), получаем
г Ь
J /(х) dx = Jim X /(х) Дх- (9.16)
а а
Правая часть равенства (9.16) называется пределом интег-
ральной суммы.
| Определенный интеграл с конечными пределами равен преде-
лу интегральной суммы, число слагаемых которой неограни-
I ченно растет, и каждое слагаемое стремится к нулю.
Отметим, что вывод не зависит от вида функции (она может
быть убывающей, возрастающей, возрастающей на одних участ-
ках и убывающей на других).
Итак, интегрирование есть процесс суммирования, т. е. на-
хождение целого путем суммирования его частей. Отметим, что
символ J есть удлиненная буква S.
5. Вычисление определенного интеграла методом замены переменной.
При вычислении определенного интеграла методом замены пере-
ъ
менной (способом подстановки) определенный интеграл J /(х) dx
а
преобразуется с помощью подстановки и = <р(х) или х = у(и)
в определенный интеграл относительно новой переменной и. При
этом старые пределы интегрирования а и Ъ заменяются соответ-
ственно новыми пределами интегрирования аир, которые нахо-
дятся из исходной подстановки.
♦ ПРИМЕР
з
Вычислить определенный интеграл: 1) = j (2х — I)3 dx; 2) 12 =
2
1 л/З/З
= f (2х3 + 1)4х2 dx; 3) 13 - J -т=== •
О Тг/з V4 - 9х2
РЕШЕНИЕ. 1) Введем новую переменную интегрирования с по-
мощью подстановки 2х - 1 — и. Дифференцируя, получаем 2 dx —
= du, откуда dx = (1/2) du. Находим новые пределы интегрирова-
277
ЧАСТЬ I. Алгебра и начала анализа
ния. Подставляя в соотношение 2х - 1 = и значения х = 2 и х = 3,
соответственно получим их^2 — 2* *2 — 1=3, их = 3 = 2*3 — 1 = 5.
п т 1 f 3 Л 1
Следовательно, 1г = 5 J иа аи — %
о
= |(54 - З4) = 68;
О
3
2) положим 2х3 + 1 = и; тогда 6х2 dx = du, х2 dx = du/6. Вычис-
ляем новые пределы интегрирования: их „ 0 = 2u О3 + 1 = 1, ux = 1 =
= 2 • I3 + 1 — 3. Таким образом,
б J “4 dlZ 6 * 5 30 (З5 815 *
3) преобразуем подкоренное выражение: 4 - 9х2 = 4(1 - (Зх/2)2).
Положим Зх/2 = и, откуда dx =
2du/3. Найдем новые пределы
интегрирования: = 2 * ~3
2 ’ и/з/з 2 * 3
/3 „
. Следо-
вательно,
3
_ 2 1
з 3*2
J2/2
73/2
г du
2
= х arcsin и
О
73/2
72/2
arcsin
- arcsin
2
§ 67. Физические приложения
определенного интеграла
1. Вычисление пути, пройденного точкой. Путь S, пройденный точкой
при неравномерном движении по прямой с переменной скоро-
стью v = f(t), v > 0 за промежуток времени от tx до t2, вычисляет-
ся по формуле
*2
S = J f(t) di.
(9.17)
♦ ПРИМЕР 1
Скорость движения точки изменяется по закону v = (3i2 + 2t +
+ 1) (м/с). Найти путь S, пройденный точкой за 10 с от начала
движения.
278
ГЛАВА 9. Определенный интеграл
РЕШЕНИЕ. По формуле (9.17) имеем
10 ю
S = J (3t2 + 2t + 1) dt = (t3 + tz + t)|0 = IO3 + 102 + 10 = 1110 (m).
0
♦ ПРИМЕР 2
Скорость движения точки v = (9i2 - 8t) (м/с). Найти путь S,
пройденный точкой за четвертую секунду.
РЕШЕНИЕ. Здесь пределами интегрирования являются tx = 3, t2 = 4.
Следовательно,
4 4
S = J (9*2 - St) dt = (3t2 - 4t2) |3 = 83 (м).
з
♦ ПРИМЕРЗ
Два тела начали двигаться одновременно из одной точки в одном
направлении по прямой. Первое тело движется со скоростью
I?! = (dt2 4- 2t) (м/с), второе — со скоростью v2 = (4t + 5) (м/с).
На каком расстоянии S друг от друга они окажутся через 5 с?
РЕШЕНИЕ. Очевидно, что искомая величина есть разность расстоя-
ний, пройденных первым и вторым телом за 5 с:
Sj = J (6t2 + 2t) dt = (2t3 + t2) Io = 275 (м);
О
S2 - J (4t + 5) dt = (2t2 + 5t) Io
0
= 75 (m).
Таким образом, S = Sx - S2 = 200 (m).
♦ ПРИМЕР 4
Тело брошено с поверхности земли вертикально вверх со ско-
ростью v = (39,2 - 9,8t) (м/с). Найти наибольшую высоту Нтах
подъема тела.
РЕШЕНИЕ. Тело достигнет наибольшей высоты подъема в такой мо-
мент времени tQt когда v = 0, т. е. 39,2 - 9,8£0 = 0, следовательно,
i0 = 4 (с). Находим:
Hm8x = 1 (39,2 - 9,8t) dt = (39,2t - 4,9t2) |‘ = 78,4 (м).
О
279
ЧАСТЬ L Алгебра и начала анализа
2. Вычисление работы. Работу А, произведенную переменной силой
f(x) при перемещении по оси Ох материальной точки от х — а до
х = Ь, находим по формуле
А = J f(x) dx. (9.18)
При решении задач на вычисление работы силы, связанных
с растяжением—сжатием пружин, основываются на соотноше-
нии
F = kx, (9.19)
где F — сила; х — абсолютное удлинение пружины, вызванное
силой F, k — коэффициент пропорциональности.
♦ ПРИМЕР 1
Укорочение х винтовой пружины при сжатии пропорциональ-
но приложенной силе F. Вычислить работу А силы F при сжа-
тии пружины на 0,04 м, если для сжатия ее на 0,01 м нужна
сила 10 Н.
РЕШЕНИЕ. По формуле (9.19) F = /?«0,01, следовательно, k =
= 1000 (Н/м), поэтому в данной задаче F = ЮООх, т. е. f(x) =
= ЮООх. Работу найдем по (9.18), полагая а = 0, b = 0,04:
0.04
A- J
о
„ .0.04
ЮООх dx = 500х2 |
= 0,8 (Дж).
♦ ПРИМЕР 2
Для растяжения пружины на = 0,04 м необходимо совер-
шить работу Aj = 20 Дж. На какую длину 12 можно растянуть
пружину, совершив работу, равную 80 Дж?
РЕШЕНИЕ. По формуле (9.18) работа Ах = J kl dZ, т. е.
о
0,04 » 0,04
20= J kldl = k^ = 0,0008/?,
о Z о
откуда k — 20/0,0008 = 25 000 (Н/м). Тогда
^2 12 ^2
80 — f 25 000 Z dZ = 25 000 = 12 500Z^,
0 0
откуда Z| =80/12 500; 12 = 0,08 (м).
280
ГЛАВА 9. Определенный интеграл
♦ ПРИМЕРЗ
Цилиндрическая цистерна с радиусом
основания г = 0,5 м и высотой Н — 2 м
заполнена водой. Плотность воды р =
= 1000 кг/м3. Определить работу А, ко-
торую необходимо произвести, чтобы
выкачать воду из цистерны.
РЕШЕНИЕ. Вес воды, заполняющей цис-
терну, равен
Р = mg,
где т = pV — масса воды,
цистерны, g — ускорение
Таким образом,
Рис. 137
V — объем
свободного падения (g = 9,8 м/с2).
Р = pVg.
Чтобы поднять слой воды dx на высоту х, необходимо совершить
работу
dA = dPx,
где dP = pg dV — вес выделенного слоя, dV — его объем. Так как
dV — л г2 dx, получим
dA = pgnr2x dx.
Для того чтобы получить выражение для работы А, следует
взять определенный интеграл в пределах от 0 до Н:
А = j pgjcr2x dx — pgnr2 J x dx = pgitr2 ==
0 о
= 1000 • 9,8 • 3,14 • 0,25 • f - 15 400 (Дж).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выпишите формулу Ньютона — Лейбница и объясните ее смысл.
2. Приведите основные свойства определенного интеграла.
3. Объясните, в чем заключается геометрический смысл определенного
интеграла.
4. В чем заключается соответствие между пределом интегральной суммы и
определенным интегралом?
281
ЧАСТЬ I. Алгебра и начала анализа
§ 68. Понятие о дифференциальном уравнении
1. Общие понятия о дифференциальных уравнениях. Дифференциаль-
ным уравнением называется уравнение, связывающее между со-
бой независимую переменную х, искомую функцию у и ее произ-
водные или дифференциалы.
Символически дифференциальное уравнение записывается
следующим образом:
F(x, р, у') = 0, F(x, у', у") = 0, F(x, у, у\ у", ..., у™) = 0.
Дифференциальное уравнение называется обыкновенным, ес-
ли искомая функция зависит от одного независимого переменно-
го.
Порядком дифференциального уравнения называется поря-
док старшей производной (или дифференциала), входящей в дан-
ное уравнение.
Решением (или интегралом) дифференциального уравнения
называется такая функция, которая обращает это уравнение в
тождество.
Общим решением (или общим интегралом) дифференциаль-
ного уравнения называется такое решение, в которое входит
столько независимых произвольных постоянных, каков порядок
уравнения. Так, общее решение дифференциального уравнения
первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называ-
ется решение, полученное из общего при различных числовых
значениях произвольных постоянных. Значения произвольных
постоянных находятся при определенных начальных значениях
аргумента и функции.
График частного решения дифференциального уравнения на-
зывается интегральной кривой.
Общему решению дифференциального уравнения соответству-
ет совокупность (семейство) всех интегральных кривых.
Дифференциальным уравнением первого порядка называет-
ся уравнение, в которое входят производные (или дифференци-
алы) не выше первого порядка.
2. Дифференциальные уравнения с разделяющимися переменными.
Дифференциальным уравнением с разделяющимися переменны-
ми называется уравнение вида
du /•/ ч z х
g = f(x) (p(z/).
282
ГЛАВА 9. Определенный интеграл
Для решения этого уравнения нужно сначала разделить пере-
менные:
й)= f{x} dx’
а затем проинтегрировать обе части полученного равенства:
IЙ) -J dx-
♦ ПРИМЕР 1
Найти общее решение уравнения х(1 4- у2) dx = у dy,
РЕШЕНИЕ. Разделив переменные, получим
х dx = -.
1 + у2
Проинтегрируем обе части полученного уравнения:
J х dx = J iydy2 ; | In (1 + у2) + | In С,
У
Так как произвольная постоянная может принимать любые
числовые значения, то для удобства дальнейших преобразований
в качестве такой постоянной приняли In С. Потенцируя по-
следнее равенство, получим
х2 = In С(1 4- у2).
Это и есть общее решение данного уравнения.
♦ ПРИМЕР 2
Найти частное решение уравнения 8 tg t dt 4- d8 = 0, удовлет-
воряющее начальным условиям 8 = 4 при t = л/3.
РЕШЕНИЕ. Разделив переменные, получим
tg t dt 4- =0.
О
Проинтегрируем обе части полученного уравнения:
J tg t dt 4- f — = In C; -In cos 14- In 8 = In C
J о
или In S = In С 4- In cos t;
8 = C cos t.
283
ЧАСТЬ I. Алгебра и начала анализа
Это общее решение данного уравнения. Для нахождения значе-
ния произвольной постоянной С подставим значения t — л/3 и
S = 4 в выражение для общего решения: 4 = С cos (л/3), или
4 = С/2, откуда С = 8.
Следовательно, искомое частное решение, удовлетворяющее
указанным начальным условиям, имеет вид S = 8 cos t.
♦ ПРИМЕРЗ
Найти закон движения тела по оси Ох, если оно начало дви-
гаться из точки М(4; 0) со скоростью v = 2t 4- 3Z2.
РЕШЕНИЕ. При прямолинейном движении скорость есть производ-
ная от пути по времени. Обозначив путь через х, имеем v = ;
тогда
~ = 2t 4- 3t2 => dx » (2t + 3£2) dt.
Проинтегрировав, получим x — t2 + t3 4- С. Используя начальные
условия, найдем С. Так как х = 4 при t = 0, то, подставив эти зна-
чения в общее решение, находим С = 4. Итак, закон движения те-
ла имеет вид х = t3 4- t2 4- 4.
$ ПРИМЕР 4
Составить уравнение кривой, проходящей через точку М(2; -3)
и имеющей касательную с угловым коэффициентом k = 4х - 3
РЕШЕНИЕ. Согласно условию, имеем
dy
dx
= 4х - 3 => dz/ = (4х - 3) dx.
Проинтегрировав, получим у = 2х2 - Зх 4- С. Используя на-
чальные условия (х = 2, у = -3), находим С = — 5. Следовательно,
искомое уравнение имеет вид у = 2х2 — Зх - 5.
3. Линейные дифференциальные уравнения первого порядка. Уравне-
ние вида
dy
dx
+ • у = ф(х) = 0,
где /(х) и ф(х) — функции переменной х, называется линейным
дифференциальным уравнением первого порядка. В частном
случае /(х) и ф(х) могут быть постоянными величинами.
284
ГЛАВА 9. Определенный интеграл
Это уравнение приводится к уравнению с разделяющимися пе-
ременными с помощью подстановки у = иг, где и и z — новые
функции аргумента х.
♦ ПРИМЕР 1
Найти общее решение уравнения -------------= (х + I)3.
ах X "1" х
РЕШЕНИЕ. Данное уравнение является линейным: здесь f(x) =
ф(х) = —(х - I)3. Положим у = иг и продифференцируем
это равенство по х:
Подставив теперь выражения для у и з^ в исходное уравнение,
получим
2uz
X + 1
= (х + I)3
или
2и
х + 1
Так как одну из вспомогательных функций и или z можно вы-
брать произвольно, то в качестве и возьмем одно из частных ре-
„ du
шении уравнения з-------
чД Л'
= 0. Разделив в этом уравнении пе-
ременные и интегрируя, получим
du _ 2dx _q Г du _ g Г dx .
и х + 1 ~ ’J « ~ J х + 1 ’
In и = 2 In (х + 1) => и = (х + I)2,
произвольную постоянную принимаем равной нулю, так как на-
ходим одно из частных решений.
Подставим теперь выражение для и в уравнение (*), тогда по-
лучим
ИЛИ
(х + 1)
= (X 4- I)3
dz
dx
285
ЧАСТЬ I. Алгебра и начала анализа
Отсюда находим
2
,1 dz = J (х + 1) dx; z = х * + С.
Зная и и z, получаем общее решение данного уравнения:
у = иг = (х +
I)2
(х + I)2
2
(Xt1)4 + С(х + I)2.
♦ ПРИМЕР 2
Найти частное решение уравнения cos xdy + у sin х dx = dx,
если у = 1 при х = 0.
РЕШЕНИЕ. Разделив все члены данного уравнения на cos х, придем
к уравнению
dy . , 1
л + У tg х =-----,
dx v cosx
которое является линейным. Положим у
dy dz
= иг; тогда = и-т-
dx dx
Подставив выражения для у и
в (**), получим:
1
COSX ’
или
dz , (du , . \ 1
+4di +utgxr^-
Для отыскания и получаем уравнение
+ tg х dx = 0,
из которого следует
J = -/ tg х dx; In и = In cos x => и = cos x.
Подставляя выражение для и в уравнение (**), приходим к
dz 1 dz 1
COS X . 1 л ,
dx cosx dx cos2x
z = tg X + С.
286
ГЛАВА 9. Определенный интеграл
Следовательно, общее решение исходного уравнения:
у = uz = cos х (tg х + С) = sin х 4- С cos х.
Используя начальные условия, получаем 1 = sin 0 4- С cos О,
откуда С = 1. Таким образом, искомое частное решение имеет вид
у = sin х 4- cos х.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какое уравнение называется дифференциальным?
2. Что называется решением дифференциального уравнения?
3. Какие решения дифференциального уравнения называются общим и
частным?
4. Как решаются дифференциальные уравнения с разделяющимися пере-
менными?
5. Какое уравнение называется линейным дифференциальным уравне-
нием первого порядка?
ЧАСТЬ 2. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОМ
ГЕОМЕТРИИ НА ПЛОСКОСТИ
ГЛАВА 10. Прямая на плоскости
и ее уравнения
§ 69. Векторы на плоскости.
Основные понятия и определения
1. Понятие вектора. Преобразование фигуры F на плоскости, при
котором ее произвольная точка с координатами (х; у) переходит в
точку с координатами (х + а; у + Ь), где а и b — постоянные, на-
зывается параллельным переносом. Параллельный перенос за-
дается формулами
Xj = х + а, ух = у + Ь,
(Ю.1)
где (Xjj уг) — координаты точки, в которую переходит точка (х; у)
при параллельном переносе.
Отрезок называется направленным, если один из его концов
считается началом отрезка, а другой — его концом. Вектором
называется направленный отрезок. Вектор обозначается симво-
—> -> - -> ->*
лом АВ либо а, Ъ, ...» х, у . Точка А называется началом, а точка
—>
В — концом вектора АВ.
—>i —>
Расстояние АВ называется длиной (модулем) вектора АВ.
—»
Вектор АА, концы которого совпадают, называется нулевым
вектором. Длина нулевого вектора равна нулю. Понятие направ-
ления для нулевого вектора не вводится.
Каждый вектор, отличный от нулевого, вполне характеризу-
ется своим направлением, длиной и точкой приложения.
* Существует также практика обозначения векторов путем набора
их наименования жирным шрифтом, например АВ либо а, Ъ, а также с
черточкой вместо стрелки наверху: АВ, а, Ъ.
288
ГЛАВА 10. Прямая на плоскости и ее уравнения
Два вектора называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых. Нулевой вектор
считается коллинеарным любому вектору.
Если два ненулевых вектора а и Ъ коллинеарны, то они могут
быть направлены либо одинаково^ либо в противоположные сторо-
ны. В первом случае векторы а и b называются сонаправленными
(a 11 Ь), во втором — противоположно направленными (a U д).
Два вектора называются равными, если они совмещаются па-
раллельным переносом, т. е. если существует параллельный пе-
ренос, который переводит начало и конец одного вектора соответ-
ственно в начало и конец другого вектора. Другими словами, рав-
ные векторы сонаправлены и равны по модулю, т. е. если а = Ь, то
a tt Ъ и |ct| = |д|, и, наоборот, если векторы сонаправлены и равны
по модулю, то они равны, т. е. если a ft Ъ и |а| = р|, то а = Ъ.
Любой вектор равен самому себе: а = а. Если а = b и b = с, то а = с.
Из любой точки плоскости можно
отложить единственный вектор, рав- /N
ный данному вектору. Построение /
вектора MN, равного вектору а, на- /
зывается откладыванием вектора /
а от точки М (рис. 138). f /
Чтобы построить вектор MN = а, / •
проведем из точки М луч, сонаправ- а ™
ленный с вектором а, и отложим на /
нем отрезок MN такой, что MN = |а|. /
---> '
Тогда MN = а. Рис. 138
♦ ПРИМЕР
Параллельный перенос перево-
дит точку А(2; 3) в точку А(-3; 2).
В какую точку В(хх; У1) он переве-
дет точку В(3; -1)?
РЕШЕНИЕ. Используя формулу (10.1),
находим значения а и Ь, соответст-
вующие параллельному переносу точ-
ки А в точку А: -3 = 2 + а, 2 = 3 + Ь,
т.е. а — -5, b — -1. Далее, х± = 3 — 5 =
= -2, У1 = -1 - 1 = -2, т. е. (-2; -2) —
координаты точки В (рис. 139).
Рис.139
10 - 9664
289
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
2. Сложение и вычитание векторов. Умножение вектора на число. Сло-
жение векторов. Для того чтобы построить сумму векторов а и Ъ,
нужно выбрать произвольную точку и отложить от нее вектор
—_> —> -*
АВ = а и затем от точки В отложить вектор ВС = Ь. Тогда вектор
—> _» —» —> —>
АС является искомой суммой а + b = АВ + ВС = АС (рис. 140).
Вектор с называют замыкающим вектором, а векторы а и b — со-
ставляющими векторами. Этот способ построения называется
правилом треугольника. Правило треугольника можно сформу-
лировать и так: если А, В и С — произвольные точки плоскости,
Сумму двух данных векторов а и b можно построить и иначе.
Откладывая от произвольной точки О (рис. 141) векторы О А = а
—> -> —>
и ОВ = Ь, построим параллелограмм ОАСВ. Тогда вектор ОС (где
|ОС| — диагональ параллелограмма) является искомой суммой:
а + b = ОА + OB = ОА +
—> —> -
АС = ОС = с. Этот способ построения на-
зывается правилом параллелограмма.
Чтобы построить сумму п данных векторов а19 а2, ..., ап, нуж-
но от произвольной точки О отложить вектор av затем от конца
вектора аг отложить вектор а2 и т. д. (рис. 142). В заключение
от конца вектора dn . j необходимо отложить вектор ап. Тог-
да вектор, начало которого совпадает с началом вектора а19 а ко-
нец — с концом вектора ап, является искомой суммой с = d1 + а2 +
Два вектора называются противоположными, если их сумма
равна нулевому вектору. Вектор, противоположный вектору а,
Рис. 140
Рис.141
290
ГЛАВА 10. Прямая на плоскости и ее уравнения
Рис. 142
Рис. 143
обозначают со знаком минус', —а. Таким образом, а + (~а) » 0. Не-
нулевые противоположные векторы имеют равные длины и про-
тивоположные направления (рис. 143).
Вектор с называется разностью векторов а и Б, если с + Ь = а.
Чтобы вычесть из вектора а вектор Ь, достаточно прибавить
к вектору а вектор, противоположный вектору Ь, т. е. а — b = а +
+ (-&) (рис. 144).
Другой способ построения разности векторов а и Ъ состоит
в следующем. Откладывая от произвольной точки О векторы
—» > —>
ОА = аи ОС — Ъ, получим ОВ = а — Ь (рис. 145).
Произведением ненулевого вектора а на число т называет-
ся вектор, имеющий направление вектора а, если т > 0, и проти-
воположное направление, если т < 0. Длина этого вектора равна
произведению длины вектора а на модуль числа т. Произведение
вектора а на число т обозначается та. При любых т и а векторы
та и а коллинеарны и
\та\ = | т | • |d |.
Рис. 144
Рис. 145
291
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
3. Угол между двумя векторами и между вектором и осью. Углом меж-
ду двумя ненулевыми векторами а и Ъ называется угол между на-
правлениями этих векторов ср, где 0 < <р < 180°. Угол <р = 0, если
a ft fl, и <р = 180°, если a П Ь.
Прямая, на которой выбрано положительное направление и
задана единица измерения длины, называется осью.
Вектор е, имеющий длину |е| = 1 и направление, совпадающее
с направлением оси, называется единичным вектором (ортом)
этой оси.
Если а 0 и ё — вектор единичной длины, направление кото-
рого совпадает с направлением вектора а, то а = а • ё.
Углом между ненулевым вектором а 0 и осью I называется
угол между направлениями оси и вектора; 0 < < 180°.
Проекцией вектора на ось называется отрезок на оси, начало и
конец которого являются проекциями начала и конца вектора.
Длина этого отрезка считается положительной, если направле-
ния вектора и оси совпадают, и отрицательной, если их направ-
ления противоположны (рис. 146). Иначе говоря, если угол а
между положительным направлением оси и направлением векто-
ра составляет меньше 90°, то проекция является положитель-
ным числом, и отрицательным, если этот угол является тупым
(90° < р < 180°).
Отметим, что если угол между осью и вектором равен 90° (век-
тор перпендикулярен оси), проекция вектора равна нулю.
Проекция вектора а 0 на ось I равна длине этого вектора, ум-
ноженной на косинус угла <р между осью и вектором (рис. 147):
at — |d| cos (р. (10.2)
Проекция суммы векторов равна сумме его проекций.
4. Прямоугольная система координат. Пусть на плоскости задана па-
ра единичных взаимно перпендикулярных векторов i и /, отло-
женных от некоторого начала — точки О (рис. 148). Такую пару
Рис. 146
Рис.147
292
ГЛАВА 10. Прямая на плоскости и ее уравнения
*4
М
Рис. 148
Рис. 149
векторов называют прямоугольным базисом на плоскости. Со-
вокупность начала О и прямоугольного базиса (i, /) называют
прямоугольной или декартовой* системой координат на плос-
кости. Точку О называют началом координат, а векторы i и j —
координатными векторами.
Вектор, направленный из начала координат в произвольную
точку М плоскости хОу, называется радиусом-вектором точки М
t —>
и обозначается г = ОМ.
Проекции вектора г на координатные оси называются коорди-
натами вектора. Координаты вектора г = ОМ кратко обозначают-
ся следующим образом: г — (х0; у0).
Координаты радиуса-вектора г = ОМ являются одновременно
координатами точки М, т. е. конца радиуса-вектора г.
—>
Если начало вектора АВ не совпадает с началом координат, то
координаты вектора АВ и координаты его конца различны, это
показано на рисунке 149. В таком случае проекции вектора АВ
на оси координат соответственно равны:
х х& ~ х^, у ув ~ уЛ. (10.3)
Разложение вектора а в базисе (i, j) имеет вид
а = xoi + yoj, (10.4)
где i — единичный вектор на оси Ох, / — единичный вектор на
оси Оу (рис. 148).
О Декарте см. § 2.
293
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
Числа и у0 называются координатами вектора а в базисе
G. У)-
Векторы xQi и yoj называются составляющими (или компо-
нентами) вектора а.
Если начало вектора а находится в точке А(ха; уА), а конец —
в точке В(хв; ув), то разложение вектора а записывается в виде
> “* ->
а = АВ = (хв - xA)i + (ув - yA)j. (10.5)
Если в базисе (i, 7) заданы векторы а = (хг; уг) иЬ = (х2; z/2), то:
I. Координаты суммы двух (или более) векторов равны суммам
соответствующих координат слагаемых, т. е.
а + b = (Xj + х2; уг + у2).
II. Координаты разности двух векторов равны разностям соот-
ветствующих координат этих векторов, т. е.
а - b = (хх - х2; уг - у2).
III. Координаты произведения вектора на число равны произ-
ведениям соответствующих координат данного вектора на это
число, т. е.
та = (тх}; тух).
Условие коллинеарности двух векторов а = (Хр уг) и b = (х2; у2)
имеет вид
хх = тх2; ух — ту2, (10.6)
т. е. если соответствующие координаты двух векторов пропорцио-
нальны, то векторы коллинеарны.
Если т > 0, то векторы а и b имеют одинаковое направление,
если т < 0, то направление векторов противоположно.
♦ ПРИМЕР 1
Найти проекцию ах вектора а на ось х, образующую с векто-
ром угол а = 60°, если |а| — 6.
РЕШЕНИЕ. По формуле (10.2)
аг = |а| • cos а = 6 • cos 60° = 6 • (1/2) = 3.
•Аг
♦ ПРИМЕР 2
-> -> —>
Выразить через единичные векторы i, 7 вектор АВ, если коор-
динаты начала и конца вектора составляют соответственно
(-2;-1), (4;-3).
294
ГЛАВА 10. Прямая на плоскости и ее уравнения
РЕШЕНИЕ. По формуле (10.5)
АВ = (4 - (-2))/ + (-3 - (-!))/ = 6/ - 2/.
5. Длина вектора. Углы, образуемые вектором с осями координат. Дли-
на вектора а = (х; у) определяется следующим образом:
(Ю.7)
Длина вектора АВ = (хв - хА; ув — уА) находится по формуле
|АВ| = J(xB - хА)2 + (ув - уА)2 . (10.8)
С помощью формулы (10.8) вычисляется также расстояние
между двумя точками на плоскости (соответствующее доказа-
тельство будет дано в § 70, п. 1).
—>
Углы, образуемые вектором АВ с осями координат Ох и Оу,
определяются соотношениями:
cos а =
7(хв - хА)2 + (ув~уА)2
COS Р =
J(*в - хд)2 + (Ув - Уа?
(10.9)
У в - У А
♦ ПРИМЕР 1
Определить длину вектора |АВ|, если А(1; 1), В(4; —3).
РЕШЕНИЕ. По формуле (10.8)
|АВ| = 7(4 - 1 )2 + (—3 - I)2 = 5.
♦ ПРИМЕР 2
Найти единичный вектор того же направления, что и вектор
а = (3; 4).
РЕШЕНИЕ. Длина вектора а составляет |а| = л/32 + 4 2 = 5. Единич-
ный вектор ё того же направления, что и вектор а:
Каждая проекция вектора е в пять раз меньше соответствую-
щей проекции вектора а, поэтому е _i; z j ]•
295
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
♦ ПРИМЕРЗ
Найти косинусы углов, образуемых заданным вектором АВ
с осями координат, начало и конец вектора: А(2; —3), В(1; 4).
РЕШЕНИЕ. По формуле (10.9) имеем:
1-2 -* п 1 К
cos а = . .......— = -== — -0,1J2 ;
7(1 - 2)2 + (4 + З)2 ТбО
cos В = =4= = 0,772 .
7(1 “ 2)2 + (4 + З)2 750
6. Скалярное произведение двух векторов. Скалярным произведени-
ем двух ненулевых векторов называется число, равное произве-
дению длин этих векторов на косинус угла между ними.
Скалярное произведение векторов а и Ь обозначается симво-
лом а • Ъ. Таким образом, если обозначить через <р угол между век-
торами а и Ь, то
d'b = |a|*|b| coscp. (10.10)
Скалярное произведение двух векторов равно модулю одного
из них, умноженному на проекцию другого вектора на направле-
ние первого:
а-Ь = |а|-6 =|&|-аЛ. (10.11)
Скалярным квадратом вектора а называется скалярное произ-
ведение а • а. Скалярный квадрат вектора равен квадрату его длины:
а-а = а2. (10.12)
Необходимым и достаточным условием перпендикулярности
двух ненулевых векторов а и b является равенство нулю их ска-
лярного произведения:
(а * 0, b * 0, d'b = 0) « а ± Ь), (10.13)
Необходимое и достаточное условие коллинеарности двух век-
торов а и b заключается в соотношении:
а-£ = ±|а||Ь|, (10.14)
при этом знак плюс соответствует случаю d И Ь, а знак минус —
случаю а П Ь.
Скалярное произведение векторов а(хх; уг) и Ь(х2; у2) выража-
ется через их координаты по формуле
d'b = хгх2 +ууу2. (10.15)
296
ГЛАВА 10. Прямая на плоскости и ее уравнения
Угол (р между двумя векторами уг) и 6(х2; у2) определяет-
ся формулой
cos (р =
*1*2 + У1У2
(10.16)
Из формулы (10.16) следует, что если векторы аиЬ перпенди-
кулярны, то
*1*2 + У1У2 = °-
(10.17)
♦ ПРИМЕР 1
—>
Найти скалярное произведение векторов а(-3; 2) и 6(4; 3).
РЕШЕНИЕ. По формуле (10.15)
d*6 = (-3)*4 + 2* 3 =-6.
♦ ПРИМЕР 2
Вычислить угол у между векторами а(— 4; 3) и 6(3; —4).
РЕШЕНИЕ. По формуле (10.16) находим:
cos у =
-4•3 + 3 • (-4)
л/(-4)2 + З2 • 7з2 + (—4)2
= -0,96,
из таблиц находим, что у= 163°,7.
♦ ПРИМЕРЗ
____ >
Проверить, перпендикулярны ли векторы а(— 3; 2) и 6(4; 6).
РЕШЕНИЕ. По формуле (10.17) находим
(-3) • 4 + 2 • 6 = 0,
->
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение вектора.
2. Какие векторы называются коллинеарными?
3. Какие векторы называются равными?
4. Как производится сложение и вычитание векторов?
5. Дайте определение угла между векторами.
6. Дайте определение угла между вектором и осью.
7. Какой вектор называется единичным?
8. Как находится проекция вектора на ось?
9. Как записываются координаты радиуса-вектора?
10. Как записывается формула разложения радиуса-вектора по координат-
ным осям?
297
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
11. Перечислите правила действий над векторами, заданными своими ко-
ординатами.
12. Сформулируйте условие коллинеарности двух векторов.
13. Как вычисляется длина вектора?
14. Как вычисляются углы, образуемые вектором с осями координат?
15. Дайте определение скалярного произведения двух векторов.
16. Сформулируйте условие перпендикулярности двух векторов.
17. Как выражается скалярное произведение двух векторов через их коор-
динаты?
18. По какой формуле вычисляется угол между двумя векторами?
§ 70. Метод координат
Как было уже установлено, в декартовой системе координат
на плоскости каждой точке плоскости соответствует пара дейст-
вительных чисел х и у (ее координат), которые определяют поло-
жение точки на плоскости. Наоборот, каждой паре действитель-
ных чисел хну соответствует одна точка плоскости.
Метод координат широко применяется в различных областях
математики. Рассмотрим две задачи, имеющие приложения во
многих разделах аналитической геометрии.
1. Расстояние между двумя точками. Пусть даны две точки А(хг; у}) и
В(х2; у2) (рис. 150). Требуется найти расстояние между ними.
Построим прямоугольный треугольник, гипотенузой которого
является отрезок АВ, а катетами — отрезки АС и ВС, параллель-
ные осям Ох и Оу и равные соответствующим проекциям отрезка
АВ на эти оси. В Д АВС катет АС = х2 — хр а катет ВС = у2- уv
Обозначим отрезок АВ через d. Тогда по теореме Пифагора
d= J(x2 - хх)* 1 2 + (у2 - уг)2 .
(10.18)
2. Деление отрезка в данном отношении. Пусть даны две точки А(х}; уг)
и В(х2; у2) (рис. 151). Найдем точку С(хс; z/c), делящую отрезок
в отношении
АС _ т
Проведем через точки А, В и С прямые, параллельные осям
координат, получим при этом следующие подобные треугольни-
ки: Д ACD ~ Д СВЕ.
298
ГЛАВА 10. Прямая на плоскости и ее уравнения
Vk
Рис. 150
Рис. 151
Поэтому
AD = CD _ АС .
СЕ BE СВ ’
согласно условию,
АС _ т
СВ п
Отсюда
X — Ху
х2 — х
У^У1
У2 - У
Решив эти уравнения относительно х и г/, получим
У =
У1 + ^У2
1 + X
(10.19)
Формулы (10.19) справедливы для любых двух точек А и В
плоскости.
При делении отрезка пополам, т. е. в отношении X = 1, форму-
лы (10.19) принимают вид:
(10.20)
♦ ПРИМЕР
Точка С делит отрезок АВ в отношении (3 : 5). Концами отрез-
ка служат точки А(2; 3) и В(10; 11). Найти точку С.
РЕШЕНИЕ. По формулам (10.19), находим
2 + 3/5*10
1 + 3/5
3 + 3/5*11
1 + 3/5
299
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Как определяется положение точки на плоскости?
2. Как вычисляется расстояние между двумя точками?
3. Как определяется середина отрезка между двумя данными точками?
4. Как находится точка, делящая отрезок в данном отношении?
§ 71. Уравнения прямых
1. Уравнения прямых, параллельных осям координат. Уравнение осей
координат. Выберем точку (а; 0) и проведем через эту точку пря-
мую, параллельную оси Оу (рис. 152). Уравнением этой прямой
является х = а. При а — 0 прямая сольется с осью Оу. Таким обра-
зом получим уравнение оси Оу: х = О.
Если через точку (0; Ь) проведем прямую, параллельную оси
Ох, то уравнением этой прямой является у = Ь. При b = 0 прямая
сольется с осью Ох; таким образом, уравнение оси Ох: у = О.
Итак,
х = а — уравнение прямой, параллельной оси Оу;
х = 0 — уравнение оси Оу;
у = Ь — уравнение прямой, параллельной оси Ох;
у — 0 — уравнение оси Ох.
(10.21)
2. Уравнение прямой, проходящей через начало координат. Через про-
извольную точку М(х; у), х О, у 0 и начало координат прове-
дем прямую, которая образует с осью Ох угол а (рис. 153).
Опустив из точки М на ось Ох перпендикуляр получим
треугольник ОММХ, из которого следует, что у = x*tg а; поло-
жив tg а = /г, получим уравнение
у - kx
Рис.152
300
(10.22)
Рис.153
ГЛАВА 10. Прямая на плоскости и ее уравнения
Координаты любой точки прямой ОМ удовлетворяют получен-
ному уравнению, формула (10.22) является уравнением прямой,
проходящей через начало координат; здесь k — угловой коэ
it и
и-
циент, равный тангенсу угла наклона прямой к положительному
направлению оси Ох. Если а — острый угол, то k > 0, если а —
тупой угол, то k < 0. При а = 90° функция тангенса не имеет чис-
лового значения, т. е. отсутствует возможность записи уравнения
прямой с помощью углового коэффициента.
♦ ПРИМЕР
Составить уравнение прямой, проходящей через начало коор-
динат под углом 135°.
РЕШЕНИЕ. Угловой коэффициент k = tg 135° = -1. Уравнение пря-
мой: у — — х.
3. Уравнение прямой с угловым коэффициентом и начальной ординатой.
Пусть прямая, не параллельная
оси Оу, пересекает ось Оу в точке
А(0; а), а ось Ох пересекает под
углом а (рис. 154). Выберем на
прямой произвольную точку
В(х; у). Построим прямоуголь-
ный треугольник Д АВС такой,
что катеты АС и ВС параллельны
осям Ох и Оу соответственно.
В этом треугольнике катет ВС =
— у - а, А ВАС — а. Имеем tg а ==
Рис. 154
У ~ а
или у = tg а • х + а.
Обозначив tg а = k, получим уравнение прямой с угловым ко-
эффициентом k и начальной ординатой а:
у = kx + а.
(10.23)
При а = 0 получаем уравнение прямой, проходящей через на-
чало координат: у = kx; при k = 0 — уравнение прямой, парал-
лельной оси Ох: у — а; при /г = 0 и а = 0 — уравнение оси Ох: у = 0.
♦ ПРИМЕР 1
Прямая наклонена к оси Ох под углом 60° и имеет начальную
ординату а = — 2. Составить уравнение прямой.
РЕШЕНИЕ. Угловой коэффициент прямой k = tg 60° =
л/3. По фор-
муле (10.23) уравнение прямой: у = л/3 х - 2.
301
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
♦ ПРИМЕР 2
Найти уравнение прямой, проходящей через точку А(2; -4) и
наклоненной к оси Ох под углом 45°.
РЕШЕНИЕ. Угловой коэффициент прямой k = tg 45° = 1. Координа-
ты точки А должны удовлетворять уравнению прямой, поэтому
-4 = 1 • 2 4- а, где а — ордината точки пересечения прямой с осью
Ох, откуда а = -4 — 2 = -6. Получим уравнение прямой: у = х - 6.
4. Общее уравнение прямой. Всякая прямая линия определяется
уравнением первой степени. В этом можно убедиться, рассматри-
вая уравнения (10.21—10.23).
Эти уравнения легко получить из уравнения
Ах + By 4- С = О
(10.24)
при различных значениях коэффициентов А, В и С.
С
I. В = 0, А & О, С * 0 => Ах 4- С — О. Положив — а, получим
х = а, следовательно, уравнение Ах + С = О является уравнением
прямой, параллельной оси Оу.
П.А = 0, В*0, С*0
By 4-С = 0. Положив — -г = &, получим
у = Ь. Следовательно, уравнение By 4-0 = 0 определяет прямую,
параллельную оси Ох.
III. В = 0, С = 0, А^О => Ах = 0. Уравнение Ах = 0 является
уравнением оси ординат х = 0.
IV. А = 0, 0 = 0, В^О => By = О. Уравнение By = 0 является
уравнением оси абсцисс у = 0.
V. С = О, А О, В & 0 => Ах 4- By = 0. Положив - = = k, получим
уравнение у = /гх, определяющее прямую, проходящую через на-
чало координат.
VI. А # О, В О, С # О. Уравнение (10.24) можно преобразовать
к виду у = - о х - -=. Положив - -=
= а, получим уравне-
ние прямой с угловым коэффициентом и начальной ординатой
(10.23).
Следовательно, уравнение (10.24) включает в себя все рассмот-
ренные уравнения прямых, поэтому его и называют общим урав-
нением прямой.
Уравнение первой степени (10.24) при любых значениях А, В
и С (исключая А = В = 0) определяет прямую линию.
302
ГЛАВА 10. Прямая на плоскости и ее уравнения
♦ ПРИМЕР 1
Построить прямую 2х - Зу + 6 = 0.
РЕШЕНИЕ. Построим эту прямую по двум точкам ее пересечения с
осями координат. Положив в исходном уравнении последова-
тельно х = 0, у = 0, получим точки (0; 2) и (—3; О). Соединив эти
точки (рис. 155), получим прямую 2х - Зу + 6 = 0.
♦ ПРИМЕР 2
Найти угловой коэффициент k и начальную ординату а пря-
мой Зх + 2у — 6 = 0.
РЕШЕНИЕ. Преобразуем это уравнение к виду y = kx + a:y = — ~х + 3.
з
Поэтому k = - о , а = 3.
5. Уравнение прямой в отрезках на осях. В примере, проиллюстриро-
ванном рисунком 155, показано, как построить прямую по точ-
кам на осях координат, т. е. по отрезкам, которые она отсекает на
координатных осях.
Прямая Ах + By + С = 0 отсекает на осях Ох и Оу отрезки в том
случае, если все ее коэффициенты не равны нулю. Преобразуем
уравнение Ах + By 4- С = 0 в уравнение прямой в отрезках на осях:
Ах + By = -С
-С/В
Положив ^ = -п,Ь = -т;, получим уравнение в отрезках на осях
^+1=1, (10.25)
здесь а и Ь — отрезки, отсекаемые прямой на осях Ох и Оу
(рис. 156).
Рис. 155
303
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
Прямая (10.25) пересекает ось Ох в точке а и ось Оу — в точке
Ь; в этом легко убедиться, подставив в (10.25) последовательно
значения у = 0 и х = 0.
♦ ПРИМЕР
Найти отрезки, отсекаемые прямой Зх - 2у - 12 = 0 на осях
координат.
РЕШЕНИЕ. Следуя предшествующему ходу рассуждений, получим:
На оси Ох прямая отсекает отрезок, равный 4, на оси Оу — рав-
ный -6 (т. е. ниже оси абсцисс).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Запишите уравнения прямых, параллельных осям координат, а также
осей координат.
2. Запишите уравнение прямой, проходящей через начало координат.
3. В каких случаях угловой коэффициент является величиной положитель-
ной и в каких — отрицательной?
4. Запишите уравнение прямой с угловым коэффициентом и начальной
ординатой.
5. Проведите исследование общего уравнения прямой, перечислите част-
ные случаи.
6. Какими способами можно построить прямую Ах + By + С = О?
7. Выведите уравнение прямой в отрезках на осях.
8. Как построить прямую, используя уравнение прямой в отрезках на
осях?
§ 72. Системы прямых
1. Уравнение пучка прямых. Составим уравнение прямой, проходя-
щей через точку М(хг; у^. Пусть прямая
у = kx + b
проходит через эту точку, тогда
уг = kxx + b.
(10.26)
(10.27)
В уравнении (10.27) два неизвестных параметра: k и Ъ. Исключим
параметр b: b = ух - kxv Подставив это значение Ъ в формулу
304
ГЛАВА 10. Прямая на плоскости и ее уравнения
(10.26), получим уравнение, содержащее только один неизвест-
ный параметр k:
у = kx + уг~ kxx
или
у - ух = k(x-xx),
(10.28)
здесь k может принимать любые числовые значения, поэтому че-
рез точку М(х^ у^) может проходить не одна прямая, а множест-
во прямых (за исключением прямой, перпендикулярной оси Ох,
так как в этом случае k = tg 90°).
Уравнение (10.28) называется уравнением пучка прямых.
♦ ПРИМЕР
Записать уравнение пучка прямых, проходящих через точку
М(2; -3).
РЕШЕНИЕ. Координаты точки М подставим в формулу (10.28); по-
лучим у + 3 = k(x - 2).
2. Уравнение прямой, проходящей через две данные точки. Составим
уравнение прямой, проходящей через две произвольные точки
М1(х1; у J и М2(х2; у2). Пусть точка Мх является центром пучка
прямых и искомая прямая, таким образом, окажется одной из
прямых пучка, проходящей через точку М2.
Подставим в формулу (10.28) вместо текущих координат коор-
динаты точки М2: У2~ Уг = k(x2 - хх), отсюда
У2 -Уг
х2 — Хх
(10.29)
Таким образом, получена формула для вычисления углового
коэффициента прямой, проходящей через две заданные точки.
Подставив выражение (10.29) в формулу (10.28), получим урав-
нение прямой, проходящей через две данные точки:
У~У1 =
У2 ~У\
х2 — хг
(10.30)
или
У - У1
Уг ~ У1 х2 ~ xi
305
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
♦ ПРИМЕР
Записать уравнение прямой, проходящей через точки Mj(2; 3)
иМ2 (-3; 4).
РЕШЕНИЕ. Угловой коэффициент k = (4 - 3)/(-3 - 2) = —1/5 по фор-
муле (10.29). Подставим значение k и координаты Му в уравне-
ние (10.30):
у — 2 = — | (х - 2) => х + 5у — 12 = 0.
3. Угол между двумя прямыми. Определим угол между двумя непа-
раллельными прямыми по их уравнениям. Пусть даны две пря-
мые: у = kyX + by и у = k2x + b2, Оп-
Рис. 157
ределим угол между этими прямы-
ми (рис. 157).
Обозначим углы, образуемые
данными прямыми с положитель-
ным направлением оси Ох, через
04 и а2, а угол между прямыми —
через (р. Для Л АВС угол ос2 явля-
ется внешним, поэтому он равен
сумме внутренних, с ним не смеж-
ных, т. е. а2 = 04 + (р, следователь-
но, (р = а2 - 04.
Если углы равны, то равны и тангенсы этих углов, поэтому
tg (р = tg (а2 — 04). По формуле для тангенса разности двух углов
(3.68)
tga2 - tgotj
1 + tga2tg04 ’
но tg 04 = ky, tg a2 = k2y поэтому
(10.31)
По формуле (10.31) можно вычислить угол между двумя пря-
мыми по их угловым коэц
••Til
ициентам.
♦ ПРИМЕР
Найти острый угол между прямыми Q: Зх + — 12 = 0 и R:
5х - 12г/ - 16 = 0.
306
ГЛАВА 10. Прямая на плоскости и ее уравнения
РЕШЕНИЕ. Уравнение Q преобразуем к виду у = - х + 3, уравнение
тх
5 4
к виду у = 75 х - 5, следовательно, угловые коэффициенты
1Z о
3
прямых Q и R соответственно = - 7
kR — tg • По формуле (10.31)
tg<p =
5/12 - (-3/4)
1 + (5/12)(-3/4)
56
33
1,697.
Значению tg ф 1,697 соответствует угол (р « 59°,5.
4. Условие параллельности двух прямых. Если прямые параллельны,
то их углы с осью Ох равны, поэтому и их угловые коэффициен-
ты равны, т. е. условием параллельности двух прямых является
равенство их угловых коэффициентов: = k2.
Справедливо и обратное утверждение. Если — /?2, то в выра-
жении (10.31) числитель равен нулю, в этом случае тангенс угла
между прямыми tg ф = О, т. е. ф = 0 или ф = 180°.
♦ ПРИМЕР
Составить уравнение прямой Llt проходящей через точку
(-2; 4) параллельно прямой L: 2х - Зу + 6 = 0 (рис. 158).
РЕШЕНИЕ. Для прямой L угловой коэффициент kL = 2/3, тогда и
для прямой угловой коэффициент kL = 2/3. Следовательно,
уравнение прямой у - 4 = 5 (х + 2) или 2х - Зу 4-16 = 0.
А о
5. Условие перпендикулярности двух прямых. Если прямые перпенди-
кулярны, то углы ф! и ф2, под которыми они пересекают ось Ох,
различаются на 90е, ф2 = ф] + 90° (рис. 159), поскольку внешний
Рис. 158
Рис. 159
307
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
угол треугольника равен сумме двух внутренних, с ним не смеж-
ных. Соответственно равны друг другу и тангенсы углов: tg ф2 =
= tg (<р! 4- 90°), но по формуле (3.41) tg (cpj 4- 90°) = —ctg фр следо-
вательно, tg (р2 = _ctg Ф1 или tg ф2 = -
1
4&Ф1
. Заменив tg ф1 и tg ф2
на k2 и kx, получим k2 = - -
или
1 4- krk2 = 0.
Справедливо и обратное утверждение. Пусть k2 = - т-. Тогда
«1
tg ф2 = = -ctg ф. = tg (ф. + 90°). Следовательно, ф2 = ф, 4- 90°,
т. е. угол между данными прямыми равен 90°, а это и значит, что
они перпендикулярны.
6. Пересечение прямых. Чтобы найти точку пересечения прямых
Ах + By 4- С = 0 и Ах 4- By 4- С = 0, необходимо решить систему
этих уравнений, так как точка пересечения двух прямых являет-
ся их общей точкой, и, следовательно, координаты точки пересе-
чения должны удовлетворять каждому из уравнений прямых.
♦ ПРИМЕР
Найти расстояние от точки М(6; 8) до прямой L: 4х 4- Зу 4- 2 = 0
(рис. 160).
РЕШЕНИЕ. На прямой L необходимо найти точку А, которая бы-
ла бы основанием перпендикуляра, опущенного из точки М на
L : 4х 4- Зу 4- 2 = 0
прямую L,
Угловой коэффициент прямой L:
4
kL = - 5 . Угловой коэффициент пер-
пендикуляра k± будет обратным по
величине и противоположным по
, 3 ~
знаку, т. е. k t = j . Составим уравне-
ние прямой, проходящей через точ-
ку М, с угловым коэффициентом k L:
у - 8 = j (х - 6) => Зх - 4у 4-14 = 0.
Рис. 160
308
ГЛАВА 11. Кривые второго порядка
Решим систему уравнений прямой L и перпендикуляра:
4х 4- Зу + 2 = О,
Зх - 4у + 14 = О
(х = -2, у = 2).
Таким образом, точка А имеет координаты (-2; 2). По (10.18) рас-
стояние между точками А и М:
AM = 7(6 + 2)
(8 - 2)2 = J64 '+ 36 = 10.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выпишите уравнение пучка прямых.
2. Выпишите уравнение прямой, проходящей через две данные точки.
3. Как можно вычислить угловой коэффициент прямой, проходящей через
две данные точки?
4. Как вычисляется угол между двумя прямыми через их угловые коэффи-
циенты?
5. Сформулируйте условие параллельности двух прямых.
6. Сформулируйте условие перпендикулярности двух прямых.
7. Как находится точка пересечения двух прямых?
8. Как найти расстояние от данной точки до прямой?
ГЛАВА 11. Кривые второго порядка
§ 73. Окружность
1. Уравнение окружности с центром в начале координат.
Окружностью называется геометрическое место точек, одина-
ково удаленных от точки, называемой центром.
Пусть центр окружности с радиусом R находится в начале ко-
ординат О. Выберем на окружности произвольную точку М(х; у).
По (10.18) расстояние между двумя точками ОМ = R= Jx2 + у2
или
(11.1)
Координаты любой точки окружности удовлетворяют (11.1).
2. Уравнение окружности с центром в произвольной точке. Пусть ок-
ружность радиуса R имеет центр в точке С (а; Ь). Выберем на ок-
309
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
ружности произвольную точку М(х; у). Также по (10.18) полу-
чим СМ = R— *!{х — а)2 + {у — Ъ)2 или
(х — а)2 + (у- b)2 = R2.
(11.2)
♦ ПРИМЕР
Составить уравнение окружности с центром С(-3; 4) и ра-
диусом R = 5.
РЕШЕНИЕ. По формуле (11.2) получаем
(х + З)2 4- {у - 4)2 - 25.
3. Уравнение окружности как частный случай общего уравнения второй
степени. Раскроем скобки в (11.2) и перегруппируем члены:
х2 4- у2 - 2ах - 2Ьу 4- а2
+ b2 - R2 = 0.
(И.З)
Умножив все члены уравнения (11.3) на А * 0, получим
Ах2 +Ау2 - 2Аах - 2АЪу 4- Аа2 + Ab2 -AR2 = 0. (11.4)
Положим -2Аа = В, — 2АЬ = С, Аа2 4- Ab2 — AR2 = D, тогда выраже-
ние (11.4) принимает вид
Ах2 4- Ау2 + Вх 4- Су 4- D = 0.
(И.5)
Уравнение (11.5) является частным случаем общего уравне-
ния второй степени, имеющего вид
Ах2 4- Вху 4- Су2 4- Dx 4- Ёу 4- F = 0.
(11.6)
Уравнение окружности (11.5) отличается от (11.6) тем, что в нем
коэффициенты при однородных членах х2 и у2 равны, а член, со-
держащий ху, отсутствует.
♦ ПРИМЕР
Найти координаты центра С и радиус R окружности х2 4- у2 -
- 8х - 10 у -8 = 0.
РЕШЕНИЕ. Дополним двучлены (х2 — 8х) и (у2 - 10t/) до полных
квадратЪв:
х2 - 8х 4- 16 4- у2 - 10у 4- 25 = 16 4- 25 4- 8
или (х - 4)2 + (у — 5)2 = 49. Таким образом, центр С имеет коорди-
наты (4; 5), R = 7.
310
ГЛАВА 11. Кривые второго порядка
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Выпишите уравнение окружности с центром в начале координат и с ра-
диусом, равным /?.
2. Выпишите уравнение окружности с радиусом R и с центром в произ-
вольной точке.
3. Как получить уравнение окружности в общем виде и чем оно отличается
от общего уравнения второй степени?
4. Где расположены центры окружностей, заданных уравнениями х2 + (у -
- Ь)2 = R2 и (х - а)2 +у2 - R2?
§ 74. Эллипс
Рассмотрим кривую второго порядка
(П-7)
здесь а > О, Ъ > 0, а > Ь. Кривая, заданная уравнением (11.7), на-
зывается эллипсом.
Из уравнения (11.7) следует, что
< 1 или |х| < a, 11/| < Ъ.
Из последних двух неравенств следует, что эллипс есть кри-
вая, ограниченная прямоугольником со сторонами 2а и 26 и с
центром в начале координат (рис. 161).
Из уравнения (11.7) следует также, что если М(х; у) принадле-
жит эллипсу, то точки с координатами (х; -у) (—х; у), (—х;—у) то-
же принадлежат эллипсу. Из этого следует, что эллипс симмет-
ричен относительно осей координат и начала координат. Начало
координат — центр симметрии называется центром эллипса.
Точки пересечения осей коорди-
нат — осей симметрии с эллип-
сом Аг(а; 0), В^О; 6), А2(-а; 0),
В2(0; -Ь) — называются верши-
нами эллипса. Отрезок оси Ох
длиной 2а между вершинами Аг
и А2 называется большой осью,
а отрезок оси Оу длиной 26 меж-
ду вершинами Вг и В2 называет-
Рис. 161
ся малой осью эллипса.
311
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
Благодаря симметрии эллипса относительно осей координат
для анализа его формы достаточно изучить его часть, содержа-
щуюся в одной из координатных четвертей, например х > 0, у > 0.
Из уравнения (11.7) получим
- л/а2 — х2 ,
а
отсюда следует, что графиком эллипса в I четверти является не-
прерывная кривая, ординаты которой убывают от & до 0 при дви-
жении от точки Вх до точки Аг
Введем некоторое число с > 0 такое, что
с2 = а2 - &2, с < а. (11.8)
На оси абсцисс отметим точки Fj(-c; 0), Р2(с; 0). Эти точки на-
зываются фокусами эллипса. Так как с < а, фокусы и F2 ле-
жат между вершинами Ах и А2.
Расстояния и г2 от любой точки М на кривой эллипса до фо-
кусов Fx и F2 назовем радиусами точки М. Длину гх находим как
расстояние между точками М и Fv По (10.18)
г. = 7(х + с)2 + i/2 = /(х + с)2 + Ь2 - Мр .
Аналогично
После преобразований получим гх =
г. + г2 = 2а. (11-9)
Равенство (11.9) дает возможность сформулировать определе-
ние эллипса.
Эллипсом называется геометрическое место точек М, для каж-
дой из которых сумма расстояний гг и г2 до двух данных точек
Fr и F2 (фокусов) есть величина постоянная.
Число
е = --, 0 < е < 1
а
(11.10)
называется эксцентриситетом эллипса. Эксцентриситет харак-
теризует степень вытянутости эллипса.
Если в уравнении (11.7) положить b = а, то оно превратится
в уравнение окружности с радиусом а (это видно из сравнения
312
ГЛАВА 11. Кривые второго порядка
с выражением (11.1)). При этом с = 0, т. е. координаты фокусов
совпадают с координатами центра эллипса — окружности.
Таким образом, окружность можно рассматривать как част-
ный случай эллипса.
♦ ПРИМЕР 1
Составить уравнение эллипса, если расстояние между фокуса-
ми равно 6, а большая ось равна 10.
РЕШЕНИЕ. Из условия следует, что а = 5, с = 3. По формуле (11.8)
находим квадрат малой оси: b2 = 52 — З2 =16. Согласно формуле
(11.7) уравнение эллипса
25
♦ ПРИМЕР 2
Составить уравнение эллипса, фокусы которого находятся в
точках (—4; 0), (4; 0), а эксцентриситет е — 0,8.
РЕШЕНИЕ. По условию с = 4, е = - = 0,8. Получаем значение боль-
а
шой оси а = 5. По формуле (11.8) Ъ2 = 52 - 42 = 9. Следовательно,
уравнение имеет вид
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Объясните геометрический смысл параметров, входящих в уравнение
эллипса.
2. Дайте определение центра симметрии и осей симметрии эллипса.
3. Какие точки называются фокусами эллипса?
4. Дайте определение эллипса.
5. Что называется эксцентриситетом эллипса?
6. Какая существует связь между уравнениями эллипса и окружности?
§ 75. Гипербола
Рассмотрим уравнение
^2 ~ ^2 = (11.11)
Кривая, отвечающая этому уравнению, называется гипербо-
лой (рис. 162).
313
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
Рис. 162
Из формулы (11.1) следует,
что 1 или |х| > а. так что все
аг 1
точки гиперболы лежат вне по-
лосы |х| < а, кроме точек Aj(-a; 0)
и А2(а; 0), лежащих на границе
полосы и называемых вершина-
ми гиперболы. Отрезок длиной
2а между ними называется дей-
ствительной осью гиперболы.
При этом в отличие от эллипса
гипербола является неограни-
ченной кривой, что следует из
модификации уравнения гипер-
болы у2 = ~2 (х2 ~ а2) или
7х2 - а2 . (11.12)
В самом деле, |z/| —► оо при х —► ±оо.
Если точка М(х; у) принадлежит кривой гиперболы, то, оче-
видно, и точки (-х; у), (х; -у), (-х; -у) тоже принадлежат этой
кривой. Таким образом, гипербола симметрична относительно
осей координат и относительно начала координат, являющегося
центром гиперболы.
Из формулы (11.11) следует, что гипербола не пересекает оси
Оу, так как если положить х = 0, то (11.11) преобразуется в
J/2
уравнение — ^2 = 1, не имеющее действительных корней. Отрезок
длиной 2Ь от точки (0; -Ъ) до точки (0; Ь) на оси Оу называется
мнимой осью гиперболы.
Благодаря симметрии гиперболы относительно осей коорди-
нат для ее построения и анализа достаточно изучить поведение
кривой в одной из координатных четвертей, например в I четвер-
ти, т. е. в области х е [а, 4-оо), у 0. Из выражения (11.12) следу-
ет, что при изменении х от а до 4-оо ордината у возрастает от 0
до 4-ОО. При этом у < ~х; это означает, что гипербола в I четверти
лежит под прямой
; У=Ьах’
проходящей через начало координат. Прямая, определяемая
уравнением (11.13), называется асимптотой гиперболы.
314
ГЛАВА 11. Кривые второго порядка
При х -* +оо разность ординат асимптоты и гиперболы 8 -* О.
В самом деле, 8 =
8 -* 0 при х —► 4-оо. Таким
образом, асимптота и график гиперболы неограниченно сближа-
ются при неограниченном возрастании абсциссы х.
Учитывая симметрию гиперболы относительно координат-
ных осей, можно построить график этой функции на всем ко-
ординатном поле: график имеет две ветви, пересекающие ось
Ох в точках (-а; 0) и (а; 0), абсолютные значения ординат неогра-
ниченно увеличиваются с ростом абсолютного значения абсцисс,
будучи ограниченными значениями ординат асимптот, имеющих
Ь
уравнения: у = ±- х.
Положим
с2 = а2 + Ь2, (11.14)
очевидно, с > а. Точки F1(-c; 0), Р2(с; 0) называются фокусами
гиперболы. Из равенства (11.14) следует, что фокусы Р* и F2 ле-
жат за вершинами гиперболы и, следовательно, вне полосы
|х| < а. Расстояния т\ и г2 от любой точки М(х; у) гиперболы до
фокусов называются радиусами точки М.
Длину радиуса = MFX определим по формуле (10.18):
+ У2 =
Аналогично
7(х - с)2 4- у2 =
(11.16)
Вычтя (11.15) из (11.16) и наоборот, получим соотношение
1^-^!= 2а, (11.17)
благодаря которому можно сформулировать определение гипер-
болы .
Гиперболой называется геометрическое место точек М, для
каждой из которых разность расстояний гх, г2 до двух данных
точек (фокусов) есть величина постоянная: — г2 = 2а (правая
ветвь); г2 - г* = 2а (левая ветвь).
315
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
Величина
(11.18)
называется эксцентриситетом гиперболы; поскольку с > а, ве-
личина е > 1.
Если в уравнении гиперболы (11.11) b = а, то это уравнение
сводится к х2 - у2 = а2. Такая гипербола называется равнобоч-
ной. Асимптоты такой гиперболы имеют уравнения у = ±х.
♦ ПРИМЕР 1
2
= 1. Найти координаты
Дано уравнение гиперболы:
ее вершин и фокусов, определить ее эксцентриситет и соста-
вить уравнения асимптот.
РЕШЕНИЕ. Если пользоваться предшествующими обозначениями,
то а = 9, Ъ = 12. По формуле (11.17) с = ±л/81 + 144 = ±15. Следо-
вательно, вершины гиперболы имеют координаты (-9; 0) и (9; 0),
с 15 5
а фокусы — (-15; 0) и (15; 0). По формуле (11.18) е = - = 77 = к .
Подставив значения а и b в выражение (11.13), получим уравне-
ния асимптот: у = ±х х.
v 3
♦ ПРИМЕР 2
Составить уравнение гиперболы, если ее асимптоты заданы
уравнениями у = ± -=•
О
х и она проходит через точку М(6; —4).
Подставим в выражение
РЕШЕНИЕ. По формуле (11.13) - = .
О о
(11.11) координаты точки М и решим систему уравнений
2
д =
а ~ 3
Получаем уравнение гиперболы: - %- = 1.
1Z о
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Объясните геометрический смысл параметров, входящих в уравнение
гиперболы.
316
ГЛАВА 11. Кривые второго порядка
2. Дайте определение центра симметрии и осей симметрии гиперболы.
3. Какие точки называются фокусами гиперболы?
4. Дайте определение гиперболы.
5. Что называется эксцентриситетом гиперболы?
6. Какая гипербола называется равносторонней?
§ 76. Парабола
1. Парабола с вершиной в начале координат. Рассмотрим уравнение
кривой второго порядка
(11.19)
Уравнение (11.19) называется уравнением параболы, число р
является параметром параболы.
Парабола является неограниченной
кривой, так как у = +J2px -* оо при
х —* оо. Парабола имеет только одну
ось симметрии — ось Ох, называемую
осью параболы, и не имеет центра
симметрии. Точка пересечения оси па-
раболы с кривой называется вершиной
(Р2 А
параболы. Точка F ; 0 (рис. 163) на-
зывается фокусом параболы.
Проведем прямую
(11.20)
называемую директрисой парабо-
лы. Расстояние d от любой точки
М(х; у) параболы до директрисы со- Рис. 163
ставляет d = | МК\ = х + 5 .
Вычислим расстояние г от точки М до фокуса параболы F:
317
ЧАСТЬ 2. Элементы аналитической геометрии на плоскости
Сопоставляя г и d, можно сделать вывод, что г = d, и сформу-
лировать определение параболы.
Параболой называется геометрическое место точек М, для
каждой из которых расстояние г до данной точки F (фокуса)
равно расстоянию d до данной прямой (директрисы).
Если в уравнении (11.19) поменять местами переменные х и у,
то получим уравнение
х2 = 2ру
(11.21)
параболы, для которой осью симметрии служит ось Оу. Решив
уравнение (11.21) относительно у, получим у =
х , а положив
5- = а, придем к уже известному из курса алгебры виду уравне-
ния параболы у = ах2.
Если для параболы осью симметрии служит ось Ох, то при
р > 0 ее ветви направлены вправо, при р < 0 — влево. Когда же
осью параболы является ось Ор, то если в уравнении (11.21) р > О,
то ветви параболы направлены вверх, если р < 0, то ветви парабо-
лы направлены вниз.
♦ ПРИМЕР 1
Составить уравнение параболы с вершиной в начале коорди-
нат, если ее фокус F находится в точке (3; 0).
РЕШЕНИЕ. Используем предшествующие обозначения: фокус F
имеет координаты f ; oj, отсюда р/2 = 3, р = 6. По формуле
(11.19) уравнение параболы имеет вид у2 = 12х.
♦ ПРИМЕР 2
Составить уравнение параболы с вершиной в начале коорди-
нат, если ее директрисой служит прямая х — — 4.
РЕШЕНИЕ. Расстояние от директрисы до начала координат состав-
ляет р/2, следовательно, р = 8. Уравнение параболы имеет вид
у2= 16х.
♦ ПРИМЕРЗ
Составить уравнение параболы с вершиной в начале коорди-
нат, симметричной относительно оси Оу и проходящей через
точку 7И(4; 2).
318
ГЛАВА 11. Кривые второго порядка
РЕШЕНИЕ. Уравнение такой параболы имеет вид (11.21). Подставив
в него координаты точки М, найдем, что р = 4. Уравнение парабо-
лы имеет вид х2 = 8у.
2. Параболы со смещенной вершиной. Пусть парабола имеет верши-
ну с координатами (а; 6). Если ось симметрии такой параболы па-
раллельна оси Ох, то ее уравнение имеет вид
{у - Ь)2 = 2р(х - а) (11.22)
(при р > 0 ветви направлены вправо, при р < 0 ветви направлены
влево); если же ось параболы параллельна оси Оу, то уравнение
такой параболы имеет вид
(х - а)2 = 2р(у - Ъ) (11.23)
(при р > 0 ветви направлены вверх, при р < 0 — вниз). В каждом
из этих уравнений расстояния от фокуса параболы до ее вершины
и от вершины до директрисы равны и составляют р/2.
♦ ПРИМЕР
Составить уравнение параболы, имеющей вершину А с коор-
динатами (1; 2) и проходящей через точку М(4; 8), если ось
симметрии параболы параллельна оси Ох.
РЕШЕНИЕ. Подставим в уравнение (11.22) координаты вершины А
и точки М: (8 - 2)2 = 2р(4 — 1), откуда р = 6. Подставив теперь в
уравнение (11.22) найденное значение р и координаты вершины
А, получим {у - 2)2 = 12(х - 1).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какой смысл имеет параметр, входящий в уравнение параболы с верши-
ной в начале координат?
2. Что называется осью симметрии параболы?
3. Что называется вершиной, фокусом и директрисой параболы?
4. Каким свойством обладает директриса параболы?
5. Дайте определение параболы.
6. Как записывается уравнение параболы, если ее ось совпадает с осью
Оу7.
7. Что определяет направление ветвей параболы?
8. Запишите уравнения параболы с вершиной в точке (о; Ь) и осями, па-
раллельными осям Ох и Оу. о
319
ЧАСТЬ 3. ЭЛЕМЕНТЫ СТЕРЕОМЕТРИИ
ГЛАВА 12. Прямые и плоскости
в пространстве
§ 77. Основные понятия стереометрии
1. Определения и обозначения. Стереометрией* называется раздел гео-
метрии, в котором изучаются фигуры в пространстве. В стереомет-
рии свойства геометрических фигур устанавливаются с помощью
доказательства теорем**, которые основываются на аксиомах*** —
математических предложениях, принимаемых без доказательства.
Основными фигурами в пространстве являются точка, прямая и
плоскость. Длй обозначения точек будем использовать прописные
буквы латинского алфавита — А, В, С, ..., прямые будем обозна-
чать строчными буквами латинского алфавита — а, д, с, ... и плос-
кости — строчными буквами греческого алфавита — а, р, у,... .
2. Основные свойства плоскости. Введем группу аксиом, выражаю-
щих основные свойства плоскостей в пространстве.
Т.Через любые три точки, не лежащие на одной прямой, мож-
но провести плоскость, и притом только одну.
II. Если две различные плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту точку.
III. Если две точки прямой принадлежат плоскости, то вся
прямая принадлежит этой плоскости.
Следствием этих аксиом являются следующие теоремы.
ТЕОРЕМА I
Через прямую и точку вне ее можно провести плоскость, и
притом только одну.
* От греч. GTEped^ — объемный, пространственный и ЦЕТрОЕСО — мера.
** От греч. ОЕСОрЕСО — рассматриваю.
*** От греч. a^LOCO — считаю достойным, настаиваю, требую.
320
ГЛАВА 12. Прямые и плоскости в пространстве
ДОКАЗАТЕЛЬСТВО. Данная точка и две точки прямой составляют три
точки, не лежащие на одной прямой. По аксиоме I через них про-
ходит единственная плоскость. По аксиоме III данная прямая ле-
жит в этой плоскости.
ТЕОРЕМА II
Через две пересекающиеся прямые можно провести плос-
кость, и притом только одну.
ДОКАЗАТЕЛЬСТВО. На каждой из прямых можно взять по одной не-
общей точке. Вместе с точкой пересечения прямых они образуют
три точки, не лежащие на одной прямой. По аксиоме I через них
проходит единственная плоскость. По аксиоме III обе прямые ле-
жат в ней.
ТЕОРЕМА III
Через две параллельные прямые можно провести единствен-
ную плоскость.
ДОКАЗАТЕЛЬСТВО. По теореме I через одну из параллельных прямых
и произвольную точку другой прямой можно провести плоскость,
и притом только одну.
3. Взаимное положение прямых и плоскостей в пространстве. Взаим-
ное расположение прямых в пространстве можно свести к сле-
дующим случаям.
I. Прямые пересекаются, тогда они лежат в одной плоскости
(рис. 164, а).
II. Прямые параллельны — тогда они тоже лежат в одной
плоскости (в частном случае совпадают) — рисунок 164, б.
III. Прямые не пересекаются и не параллельны — такие пря-
мые называются скрещивающимися (примером такого рода пря-
мых могут служить ребра куба — рис. 164, в).
Возможны следующие варианты взаиморасположения прямой
и плоскости в пространстве:
а) б) в)
Рис. 164
321
ЧАСТЬ 3. Элементы стереометрии
Рис. 165
I. Прямая лежит в плоскости (рис. 165, а).
II. Прямая и плоскость имеют одну общую точку, в которой
они пересекаются (рис. 165, б).
III. Прямая и плоскость не имеют ни одной общей точки — в
этом случае они называются параллельными (рис. 165, в).
Плоскости в пространстве могут принимать следующие поло-
жения относительно друг друга:
I. Плоскости совпадают.
II. Две плоскости не имеют общих точек — в этом случае
они называются параллельными.
III. Две плоскости могут пересекаться по прямой — в этом
случае они не имеют других общих точек вне этой прямой.
Рис. 166
♦ПРИМЕР
Построить точку пере-
сечения данной прямой
а с данной плоскостью а
(рис. 166).
РЕШЕНИЕ. Выберем на плос-
кости а произвольную точ-
ку A, A g а. Через точку А
и прямую а проведем плос-
кость р. Она пересечет плос-
кость а по некоторой пря-
мой Ь. В плоскости Р нахо-
дим точку С пересечения
прямых а и b — эта точка и
является искомой.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какой раздел геометрии называется стереометрией?
2. Какие предложения называются аксиомами?
3. Какие предложения называются теоремами?
4. Сформулируйте аксиомы плоскости и следствия из них.
322
ГЛАВА 12. Прямые и плоскости в пространстве
5. Назовите возможные варианты взаимного положения прямых в про-
странстве.
6. Перечислите возможные варианты взаимного положения прямой и
плоскости в пространстве.
7. Приведите возможные варианты взаимного положения двух плоскостей
в пространстве.
§ 78. Параллельность прямой и плоскости.
Параллельные плоскости
1. Параллельные прямая и плоскость. Определение параллельности пря-
мой и плоскости было сформулировано в предыдущем параграфе.
Прямая и плоскость называются параллельными, если они не
пересекаются.
ТЕОРЕМА
Если прямая, не принадлежащая плоскости, параллельна ка-
кой-нибудь прямой в этой плоскости, то она параллельна и са-
мой плоскости.
ДОКАЗАТЕЛЬСТВО. Пусть а — плоскость, Ъ — не лежащая в ней пря-
мая и а — прямая в плоскости а, параллельная прямой b
(рис. 167, а). Проведем через прямые а и Ь плоскость р. Она от-
лична от а, так как прямая Ъ не лежит в плоскости а. Плоскости
аир пересекаются по прямой а. Если бы прямая b пересекала
плоскость а, то точка пересечения принадлежала бы прямой а.
Это невозможно, так как а II Ь. Следовательно, прямая b не пере-
секает плоскость а, значит, а || а, что и требовалось доказать.
6)
а)
Рис. 167
323
ЧАСТЬ 3. Элементы стереометрии
ТЕОРЕМА
Если плоскость проходит через прямую, параллельную другой
плоскости, и пересекает эту плоскость, то линия пересечения
плоскостей параллельна первой прямой.
ДОКАЗАТЕЛЬСТВО. Пусть прямая b лежит в плоскости р, b II а, а плос-
кости аир пересекаются по прямой а (рис. 167, а). По условию
be р, а е р. Допустим, что прямые b и а пересекаются. Тогда пря-
мая b и плоскость а тоже пересекаются, что противоречит усло-
вию b II а. Следовательно, допущение, что прямые а и b пересе-
кутся, неверно и b II а, что и требовалось доказать.
Следствием последней теоремы является следующее утверж-
дение.
Если две прямые параллельны и через каждую из них прохо-
дит плоскость и эти плоскости пересекаются, то линия пересе-
чения параллельна каждой из двух прямых.
Это утверждение можно пояснить с помощью рисунка 167, б:
если be р; с е а; b || а, то линия пересечения плоскостей а парал-
лельна прямым b и с.
2, Угол между скрещивающимися прямыми. Углы с соответственно
параллельными и одинаково направленными сторонами равны.
О скрещивающихся прямых (см. § 77, п. 3) можно сказать, что
это прямые, не лежащие в одной плоскости.
Углом между двумя скрещивающимися прямыми называется
угол между их параллельными и одинаково
направленными сторонами, проходящими
через произвольную точку.
Для построения такого угла у между
двумя скрещивающимися прямыми а и b
(рис. 168) выберем произвольную точку М
и проведем через нее прямую а, а II а. Че-
рез эту точку проведем прямую b9 b II Ъ.
Один из полученных четырех попарно рав-
ных углов (обычно острый) у принимает-
ся за угол между скрещивающимися пря-
мыми.
Если угол между скрещивающимися
прямыми а и b прямой, то такие прямые на-
зываются взаимно перпендикулярными.
324
ГЛАВА 12. Прямые и плоскости в пространстве
3. Параллельные плоскости. В § 77, п. 3 было отмечено, что две
плоскости называются параллельными, если они не пересека-
ются.
ТЕОРЕМА (признак параллельности двух плоскостей)
Если две пересекающиеся прямые одной плоскости соответ-
ственно параллельны двум прямым другой плоскости, то эти
плоскости параллельны.
ДОКАЗАТЕЛЬСТВО. Пусть прямые а и Ъ плоскости а пересекаются в
точке А (рис. 169). Прямые а и b лежат в
плоскости Р: а II а, b II Ъ. Допустим, что
плоскости аир пересекаются по прямой I.
По условию плоскости а и Р проходят через
параллельные прямые а и о, следователь-
но, их линия пересечения I II а, такого же
рода рассуждения можно провести относи-
тельно прямых Ь и £>, т. е. III Ь. Получилось,
что через точку А проходят две прямые а и
Ь, параллельные прямой Z, что невозможно,
поэтому а || р.
Сформулируем без доказательств свой-
ства параллельных плоскостей.
Рис. 169
I. Если две параллельные плоскости пересечены третьей плос-
костью, то линии пересечения параллельны.
II. Через точку, не лежащую в данной плоскости, можно про-
вести единственную плоскость, параллельную данной.
III. Если две плоскости параллельны третьей, то они парал-
лельны.
IV. Отрезки параллельных прямых, заключенные между па-
раллельными плоскостями, равны.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Назовите признак параллельности прямой и плоскости.
2. Как найти угол между скрещивающимися прямыми?
3. Какие плоскости называются параллельными?
4. Сформулируйте признак параллельности плоскостей.
325
ЧАСТЬ 3. Элементы стереометрии
§ 79. Перпендикулярные прямые и плоскости
1. Прямая, перпендикулярная к плоскости. Прямая, пересекающая
плоскость, называется перпендикулярной этой плоскости, если
она перпендикулярна любой прямой в плоскости.
ТЕОРЕМА О ДВУХ ПЕРПЕНДИКУЛЯРАХ
Прямая, перпендикулярная двум пересекающимся прямым
на плоскости, перпендикулярна этой плоскости.
ДОКАЗАТЕЛЬСТВО. Пусть a t b, а е а, Ь е. а, k ± а, k ± & (рис. 170).
Случай 1. Прямые а, b проходят через точку О пересечения
прямой k с плоскостью а. Проведем на плоскости а через точку О
некоторую прямую с, не совпадающую с прямыми а и Ь. Отметим
на прямой k некоторый вектор ОК, на прямой с — некоторый
—> —> —»
вектор ОС. Докажем, что ОК • ОС = 0.
Разложим ОС на векторы, лежащие на прямых а и Ь: векторы
ОА и ОВ. Тогда ОС = ОА + ОВ и
ОК-ОС = ОК-ОА + ОК-ОВ.
(12.1)
—> —> —> —> —> —>
Но OK ± ОА, OK J_ ОВ, тогда скалярные произведения ОК • О А ~
= |ОК||ОА| cos 90° = О, ОК- ОВ = |(Ж||ОВ| cos 90° = О, следова-
—> —> —> —>
тельно, по формуле (12.1) ОК • ОС = О. Это значит, что ОК ± ОС,
т. е. k ± с.
В качестве прямой с была выбрана любая прямая, проходя-
щая через точку О. Но любая прямая на плоскости а параллельна
какой-либо из прямых, проходящих через точку О, поэтому мож-
k
К
но сказать, что из перпендику-
лярности прямых k и с следует,
что k ± а.
Случай 2. Прямые а, b и с
не проходят через точку О. Про-
ведем через точку О прямые
а || а, Ъ || &, с || с. По условию k ± а,
k ± 6, поэтому k ± а, k ± Ь. Та-
ким образом, доказательство сво-
дится к предыдущему случаю.
Рис. 170
326
ГЛАВА 12. Прямые и плоскости в пространстве
2. Зависимость между параллельностью и перпендикулярностью пря-
мых и плоскостей. Приведем без доказательств теоремы о парал-
лельности прямых и плоскостей в связи с их перпендикулярно-
стью.
ТЕОРЕМА I
Если плоскость перпендикулярна к одной из параллельных пря-
мых, то она перпендикулярна и к другой, и наоборот, если две
прямые перпендикулярны к плоскости, то они параллельны.
ТЕОРЕМА II
Если прямая перпендикулярна к одной из параллельных
плоскостей, то она перпендикулярна и к другой, и наоборот,
если две плоскости перпендикулярны к одной прямой, то они
параллельны.
3. Перпендикуляр и наклонная. Если через
точку Айа провести прямую АВ ± а, то 4
основание перпендикуляра — точка В — \
называется проекцией точки А на плос- \
кость а, а длина отрезка АВ — длиной ____________X-------
перпендикуляра (рис. 171). Прямая АС, у \ /
не параллельная и не перпендикулярная / • j
к плоскости а, называется наклонной, (/
а точка С — основанием наклонной. От- рис 17i
резок ВС, соединяющий основания пер-
пендикуляра и наклонной, называется проекцией наклонной.
ТЕОРЕМА
Если из точки, лежащей вне плоскости, провести к ней пер-
пендикуляр и наклонные, то:
1) перпендикуляр короче всякой наклонной;
2) те из наклонных равны, которые
имеют равные проекции; А
3) из двух неравных наклонных / к
больше та, которая имеет большую / V
проекцию. / у.
ДОКАЗАТЕЛЬСТВО. 1) Пусть точка А ё a, -----------
АВ ± а, АС — наклонная, ВС — про-
екция наклонной (рис. 172). Так как (в \
АВ _L а, то Д АВС — прямоугольный, в ____ а__________)
нем АС — гипотенуза, АВ — катет, по-
этому АС > АВ. Рис. 172
327
ЧАСТЬ 3. Элементы стереометрии
2) Отложим от точки В в разных направлениях два равных от-
резка BD и BE и из точек D и Е проведем наклонные в точку А.
Тогда Д ABD = Д АВЕ (по двум катетам), следовательно, AD — АЕ.
3) Отложим от точки В в разных направлениях два неравных от-
резка BD < ВС и из точек В и С проведем наклонные в точку А. От-
ложим на прямой ВС отрезок BE = BD, В треугольнике АЕС угол
А АЕС — тупой, поэтому АС > АЕ, следовательно, АС > AD.
ТЕОРЕМА (обратная)
Если из точки вне плоскости провести к ней перпендикуляр и
наклонные, то равные наклонные имеют равные проекции, а
большая наклонная имеет большую проекцию.
Доказательство легко провести методом от противного.
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
Прямая, проведенная на плоскости через основание наклон-
ной перпендикулярно к ее проекции, перпендикулярна к са-
мой наклонной.
ДОКАЗАТЕЛЬСТВО. Пусть АВ — перпендикуляр к плоскости а, АС —
наклонная и, таким образом, отрезок ВС является проекцией АС
на плоскость а (рис. 173). Проведем через
К точку С прямую a g а такую, что
\ а ± СВ.
\ —» —»
Скалярное произведение СВ*СА =
j = CD*СВ + CD*BA. По условию CD х
J х СВ = 0. Так как ВА ± a, CD ± ВА, по-
ct D
------——этому и CD • ВА = 0. Следовательно,
Рис. 173 CD • С А = 0, т. е. CD ± СА, поэтому а ± СА.
ТЕОРЕМА (обратная)
Прямая, проведенная на плоскости через основание наклон-
ной перпендикулярно к ней, перпендикулярна к ее проекции.
4. Угол между прямой и плоскостью. Углом между прямой и плоско-
стью называется острый угол между прямой и ее проекцией на
эту плоскость.
ТЕОРЕМА
Острый угол между прямой и ее проекцией на плоскость мень-
ше угла между этой прямой и любой другой прямой, лежащей
на этой плоскости.
328
ГЛАВА 12. Прямые и плоскости в пространстве
ДОКАЗАТЕЛЬСТВО. Пусть прямая АВ
является наклонной по отношению
к плоскости а, прямая СВ — ее про-
екция на плоскость а, прямая BD —
произвольная прямая на плоскости
а, не совпадающая с ВС (рис. 174).
Из произвольной точки Е е ВА опус-
тим на плоскость а перпендикуляр
EF. Так как ВС является проекцией
прямой ВА, то точка F е ВС. Отло-
жим на прямой BD отрезок ВК = BF
и соединим точки К и Е. Тогда, по-
Рис. 174
скольку EF ± a, EK > EF. В треугольниках ВЕК и BEF сто-
рона BE является общей, BF = ВК и EK > EF. Следовательно,
А КВЕ > А РВЕ.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определение прямой, перпендикулярной к плоскости.
2. Как формулируется теорема о двух перпендикулярах?
3. Какая прямая называется наклонной к плоскости?
4. Что называется проекцией наклонной на плоскость?
5. Как формулируется теорема о трех перпендикулярах?
6. Как определяется угол между прямой и плоскостью?
§ 80. Двугранные и многогранные углы
1. Двугранные и линейные углы. Прямая, лежащая в плоскости, де-
лит плоскость на две части, каждая из которых называется полу-
плоскостью. Полуплоскость ограничена с одной стороны пря-
мой.
Часть пространства, ограниченная двумя полуплоскостями,
общей ограничивающей их прямой, называется двугранным уг-
лом. Полуплоскости двугранного угла называются гранями, об-
щая прямая — ребром.
Двугранный угол принято обозначать следующим образом:
аАВр; здесь аир — грани, АВ — ребро двугранного угла.
Два двугранных угла считают равными, если их можно сов-
местить.
329
ЧАСТЬ 3. Элементы стереометрии
Плоскость, перпендикулярная ребру
двугранного угла, пересекает его грани по
двум полупрямым. Угол, образованный
этими полупрямыми, называется линей-
ным углом двугранного угла (рис. 175).
Все линейные углы двугранного угла
равны между собой.
Двугранный угол называется острым,
прямым, тупым или развернутым в зави-
симости от их линейного угла.
ТЕОРЕМА
Если двугранные углы равны, то равны их линейные углы.
ДОКАЗАТЕЛЬСТВО. Пусть двугранные углы аАВр и аАВр равны меж-
Рис. 176
ду собой; Z. MKN — линейный угол
двугранного угла аАВр, a Z. MKN —
линейный угол двугранного угла
аАВр (рис. 176). Совместим равные
двугранные углы аАВр и аАВр: тог-
да совместятся их ребра АВ и АВ,
грани а и а, а также р и р. Они со-
ставят один двугранный угол, в ко-
тором проведено два линейных угла:
Z. MKN и Z. MKN, следовательно,
Z. MKN = Z. MKN.
ТЕОРЕМА (обратная)
Если линейные углы двугранных углов равны, то равны и са-
ми двугранные углы.
Теорема доказывается от противного.
2. Площадь проекции плоской фигуры. Проекцией фигуры на плос-
кость является фигура, ограниченная линиями — проекциями
линий, ограничивающих исходную фигуру.
ТЕОРЕМА
Площадь проекции многоугольника на плоскость равна про-
изведению площади этого многоугольника на косинус угла
между плоскостью многоугольника и плоскостью проекции.
330
ГЛАВА 12. Прямые и плоскости в пространстве
ДОКАЗАТЕЛЬСТВО. Докажем теоре-
му для треугольника, так как
площадь любого многоугольни-
ка может быть представлена как
сумма площадей треугольников.
Пусть Д АВС е р, Д АВгС яв-
ляется проекцией треугольника
АВС на плоскость а, угол между
плоскостями аир составляет ф
(рис. 177). В треугольнике АВС ₽ис177
из вершины В опустим высоту BD. По теореме о трех перпенди-
кулярах ее проекция ВХВ является высотой треугольника АВХС,
а угол (р = Z. BDBX — линейный угол двугранного угла аАСр. Сле-
довательно, площадь АВ с = ^АС • DB19 но DBX = DB cos ф, тог-
да sa АВхс = \aC*DBcqs<$ = 8лАВС COS ф.
3. Перпендикулярные плоскости. Если две плоскости, пересекаясь,
образуют прямые двугранные углы, то они называются взаимно
перпендикулярными.
ТЕОРЕМА
Если плоскость проходит через перпендикуляр к другой плос-
кости, то она перпендикулярна к этой плоскости.
ДОКАЗАТЕЛЬСТВО. Пусть а — плоскость,
Ь — перпендикулярная ей прямая, р —
плоскость, проходящая через прямую Ь,
MN — прямая, по которой пересекаются
плоскости аир (рис. 178). Докажем, что
а _!_ р. Проведем в плоскости а через точ-
ку пересечения прямой b с плоскостью а
прямую а, а ± MN. Проведем через пря-
мые а и Ъ плоскость у. Она перпендику- рис
лярна прямой MN, поскольку MN ± а,
MN ± Ь. Так как прямые а ± &, то плоскости a -L р.
ТЕОРЕМА (обратная)
Если две плоскости взаимно перпендикулярны и к одной из
них проведен перпендикуляр, имеющий общую точку с другой
плоскостью, то он лежит в этой плоскости.
Доказательство можно провести методом от противного. Исхо-
дя из этой теоремы можно сформулировать следствие.
331
ЧАСТЬ 3. Элементы стереометрии
СЛЕДСТВИЕ. Если две пересекающиеся плоскости перпендикуляр-
ны третьей плоскости, то их линия пересечения перпендикуляр-
на этой плоскости.
4. Многогранный угол. Многогранным углом называется часть
пространства, ограниченная несколькими плоскими углами, у
которых вершина общая, а стороны попарно общие. Каждые три
следующие друг за другом общие стороны не лежат в одной плос-
кости.
Общая вершина плоских углов, образующих многогранный
угол, называется вершиной многогранного угла, плоские углы —
гранями, общие стороны плоских углов — ребрами. В зависи-
мости от числа граней многогранные углы могут быть трехгран-
ными, четырехгранными и т. д.
Многогранный угол называется выпуклым, если сечение его
любой плоскостью, пересекающей все грани, является выпуклым
многоугольником (рис. 179, а). В противном случае многогран-
ный угол называется невыпуклым (рис. 179, б).
ТЕОРЕМА
В трехгранном угле каждый плоский угол меньше суммы двух
других плоских углов.
ДОКАЗАТЕЛЬСТВО. Пусть угол Д SKMN — трехгранный угол и
KSN > Д KSM, Д KSN > A MSN (рис. 180). В грани KSN про-
ведем прямую SP, образующую с SN угол Д PSN = Д MSN, и от-
ложим на прямых SP и SM равные отрезки SD — SB. Через точки
В и D проведем плоскость, пересекающую ребра SK и SN в точ-
ках А и С. Рассмотрим образовавшиеся треугольники: Д CSD =
= Д CSB по двум сторонам и углу между ними (Д BSC = Д DSC
по построению, SD = SB по построению, сторона SC — общая).
Следовательно, ВС = DC.
Рис. 179
Рис. 180
332
ГЛАВА 12. Прямые и плоскости в пространстве
В треугольнике АВС имеем АС < АВ + ВС или AD 4- DC < АВ 4-
+ ВС, но так как DC — ВС, то AD < АВ,
В треугольниках ASD и ASB сторона AS — общая, SD =
= SB и AD <АВ, из чего следует, что
Z-ASD<Z.ASB.
Прибавив к левой части последнего равенства угол Z_DSC, а к
правой — равный ему угол A BSC, получим:
A ASD 4- A DSC < A ASB 4- A BSC
или
A ASC < A ASB 4- А ВВС,
что и требовалось доказать.
Следствием этой теоремы является следующее утверждение.
Всякий плоский угол трехгранного угла больше разности двух
других его плоских углов.
♦ ПРИМЕР
Доказать, что если два плоских угла трехгранного угла острые
и равны между собой, то проекция их общего ребр^на плос-
кость третьего угла есть его биссектриса.
РЕШЕНИЕ. Пусть А АВВ = А АВС —
SA на плоскость СВВ (рис. 181).
Проведем АХК ± SB, АгМ ± SC.
По теореме о трех перпендику-
лярах АК ± SB, AM ± ВС. Тре-
угольники ASK и ASM равны
(A AS В — A ASC, гипотенуза АВ —
общая), следовательно, SK — SM,
АК = AM, но АгК и АгМ —
проекции равных наклонных, по-
этому АгК = АгМ. Таким образом,
Д ArSK = Д AtSM, т. е. ВА — бис-
сектриса угла А ВВС.
острые; ВА* — проекция ребра
Рис. 181
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется двугранным углом? Его ребром? Гранями?
2. Что называется линейным углом двугранного угла?
3. Какая существует зависимость между двугранными углами и их линей-
ными углами?
333
ЧАСТЬ 3. Элементы стереометрии
4. Какие плоскости называются взаимно перпендикулярными?
5. Сформулируйте признак перпендикулярности плоскостей.
6. Что называется многогранным углом? Его вершиной? Ребрами? Гра-
нями?
ГЛАВА 13. Многогранники и площади
их поверхностей
§ 81. Многогранники и их основные свойства
1. Понятие о многогранниках. Тело, ограниченное плоскими много-
угольниками, называется многогранником (рис. 182). Много-
угольники, ограничивающие многогранник, называются граня-
ми, их стороны — ребрами, а вершины — вершинами много-
гранника.
Грани, имеющие общее ребро, называются смежными. Отре-
зок, соединяющий две вершины многогранника, не принадлежа-
щие одной грани, называется диагональю многогранника.
Многогранники различают по форме и по числу граней.
Многогранник называется выпуклым, если отрезок, соеди-
няющий любые две внутренние точки многогранника, не пересе-
кает его поверхности; в противном случае многогранник называ-
ется невыпуклым, например, на рисунке 182 изображен невы-
пуклый многогранник.
2. Призма. Призмой называется многогранник, у которого две
грани — равные многоугольники с соответственно параллельны-
ми сторонами {основаниями призмы), а все остальные грани (бо-
ковые) пересекаются по параллельным прямым (рис. 183). Ребра
Рис.182
Рис. 183
334
ГЛАВА 13. Многогранники и площади их поверхностей
оснований называются сторонами оснований, общие ребра бо-
ковых граней — боковыми ребрами.
Призму называют прямой, если плоскости боковых граней
перпендикулярны к плоскостям оснований. Непрямая призма
называется наклонной. Прямую призму называют правильной,
если основанием ее служит правильный многоугольник. Призмы
могут быть треугольными, четырехугольными и т. д. На рисунке
183 изображены шестиугольные призмы (слева прямая, справа
наклонная).
Боковые ребра призмы равны между собой, боковые грани яв-
ляются параллелограммами. Боковые грани прямой призмы —
прямоугольники.
Отрезок, соединяющий две вершины призмы, не лежащие в
одной грани, называется диагональю призмы (на рис. 184 изо-
бражена одна из диагоналей А. С).
Перпендикуляр, опущенный из точки
плоскость другого основания, называется
рис. 185 — высота призмы й).
Плоскость, проходящая через два бо-
ковых ребра призмы, не лежащих в одной
грани, называется диагональной плоско-
стью. Сечения, образующиеся от пересе-
чения диагональной плоскости с гранями
призмы, называются диагональными се-
чениями. На рисунке 184 изображено ди-
агональное сечение АА^С^С.
Если плоскость сечения перпендику-
лярна боковым ребрам призмы или их
продолжениям, то она называется пер-
пендикулярным сечением.
Свойства правильной призмы
I. Боковые грани равны между собой.
II. Двугранные углы при них равны
между собой.
III. Любая точка оси призмы равно-
удалена от всех вершин любого из ос-
нований призмы.
IV. Любая точка оси равноудалена от
всех граней призмы.
одного основания на
высотой призмы (на
Рис. 184
Рис. 185
335
ЧАСТЬ 3. Элементы стереометрии
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется многогранником?
2. Что называется гранями, ребрами и вершинами многогранника?
3. Какой многогранник называется призмой?
4. Что называется диагональю, высотой и диагональным сечением призмы?
5. Какая призма называется прямой?
6. Какая призма называется правильной?
§ 82. Параллелепипед
Призма, основаниями которой являются параллелограммы,
называется параллелепипедом. Грани параллелепипеда, не
имеющие общих вершин, называются противолежащими.
ТЕОРЕМА
Противолежащие грани параллелепипеда параллельны и равны.
Доказательства теоремы приводить не будем. Из теоремы сле-
дует, что любая грань параллелепипеда может быть принята за
его основание.
ТЕОРЕМА
В параллелепипеде диагонали пересекаются в одной точке и
делятся в ней пополам.
Рис. 186
ДОКАЗАТЕЛЬСТВО. Пусть ACU BDlt CAV DBr — диагонали паралле-
лограмма Р (рис. 186). Через параллельные ребра АгВг и DC про-
ведем сечение A^B^CD, в котором стороны А1В1 = DC, AXBX II DC,
так как AjBj = АВ и DC = АВ. Следовательно,
сечение A^jCD является параллелограммом.
Диагонали параллелепипеда АгС и B±D явля-
ются диагоналями параллелограмма, поэто-
му эти диагонали пересекаются и в точке пе-
ресечения делятся пополам. Диагональ А^С
пересекает диагональ АСГ в точке О и делится
в ней пополам.
Следовательно, все четыре диагонали про-
ходят через одну точку и делятся в ней попо-
лам, что и требовалось доказать.
Параллелепипед, боковые ребра которого
перпендикулярны его основанию, называется
336
ГЛАВА 13. Многогранники и площади их поверхностей
прямым. Непрямой параллелепипед на-
зывается наклонным, все его грани явля-
ются параллелограммами.
Прямой параллелепипед, основанием
которого является прямоугольник, назы-
вается прямоугольным, Вее грани прямо-
угольного параллелепипеда являются
прямоугольниками.
Прямоугольный параллелепипед, все
ребра которого равны, называется кубом.
Все грани куба являются квадратами.
ТЕОРЕМА Рис-187
Квадрат диагонали прямоугольного параллелепипеда равен
сумме квадратов трех его измерений.
ДОКАЗАТЕЛЬСТВО. Пусть в прямоугольном параллелепипеде Р
имеем а, Ъ, с — непараллельные ребра, d — диагональ (рис. 187).
Сторона с перпендикулярна основанию ABCD, следовательно,
она перпендикулярна диагонали основания АС, Из треугольника
АА^С следует, что d2 = АС2 + с2. Из треугольника АВС следует,
что АС2 = а2 + ВС2, но ВС2 — Ъ2, поэтому
d2 = а2 + Ъ2 + с2.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какая фигура называется параллелепипедом?
2. Какая фигура называется кубом?
3. Какие свойства параллелепипеда следуют из того, что эта фигура явля-
ется частным случаем призмы?
4. Сформулируйте свойства противолежащих граней параллелепипеда.
5. Сформулируйте свойства диагонали параллелепипеда.
f 83. Пирамида
1. Основные понятия. Пирамидой называется многогранник, од-
ной из граней которого служит многоугольник (основание пира-
миды), а остальные грани (боковые) суть треугольники с общей
вершиной (вершина пирамиды) (рис. 188). Общие стороны боко-
вых граней называются боковыми ребрами пирамиды. По осно-
ванию лежащего в основании многоугольника пирамиды делятся
на треугольные (тетраэдр), четырехугольные и т. д.
12-9664
337
ЧАСТЬ 3. Элементы стереометрии
Рис.189
Перпендикуляр, опущенный из вершины пирамиды на плос-
кость ее основания, называется высотой пирамиды (h на
рис. 189).
Сечение пирамиды плоскостью, проходящей через два боко-
вых ребра, не лежащих на одной грани, называется диагональ-
ным сечением пирамиды.
Пирамида, основанием которой является правильный много-
угольник и вершина проектируется в центр основания, называет-
ся правильной.
Высота боковой грани правильной пирамиды, опущенная из
вершины пирамиды, называется апофемой (а на рис. 189).
Основные свойства правильной пирамиды
I. Боковые ребра, боковые грани и апофемы соответственно
равны.
II. Двугранные углы при основании равны.
III. Двугранные углы при боковых ребрах равны.
IV. Каждая точка высоты равноудалена от всех вершин осно-
вания.
V. Каждая точка высоты равноудалена от всех боковых граней.
2. Параллельные сечения. Опишем свойства сечений пирамиды, па-
раллельных плоскости основания.
ТЕОРЕМА
Если пирамида пересечена плоскостью, параллельной основа-
нию, то
1) боковые ребра и высота пирамиды делятся этой плоскостью
на пропорциональные части;
2) сечением этой плоскости является многоугольник, подоб-
ный основанию;
338
ГЛАВА 13. Многогранники и площади их поверхностей
3) площади сечения и основания от-
носятся друг к другу как квадраты их
расстояний от вершины.
ДОКАЗАТЕЛЬСТВО. Пусть в пирамиде Р вы-
сота OS делится сечением AjBjCp парал-
лельным основанию АВС, на отрезки
ООг и OjS (рис. 190).
1)Так как А1В1 || АВ, BlC1 II ВС, ... ,
AjOj || АО, то
ААг _ ВВг ВВг _ CCj AAj _ ООг
A.S = B^S * BjS = C[S ’ — ’ A^S ~ OfS ‘
В каждой из этих пропорций содержатся
Рис. 190
попарно равные отно-
шения, поэтому
АЛ1=ВВ1= =ОО1
AXS BjS •” OtS'
2) Треугольники: A AjSBj A ASB, A BiSCl ™ A BSC, тогда
из чего следует
т. е. стороны сечения пропорциональны сторонам основания
АВ ВС
А1С1
АС ‘
Стороны одноименных углов в основании и сечении взаимно
параллельны, поэтому соответственные углы равны и по опреде-
лению подобных треугольников
A AlB1C1 ~ А АВС.
(*)
3) Из (*) следует, что площадь сечения S„OTI и площадь основа-
ния Восн подчиняются соотношению
«се.
339
ЧАСТЬ 3. Элементы стереометрии
Треугольники AjSO и ASO подобны, Д AjSBj ™ Д AS В, поэтому
_ AXS AlBl _ ArS
OS ~ AS’ ~AB ~ ~AS ’
следовательно,
Из (**) и (***) следует, что
«сеч OiS2
«осн OS2 *
Доказательство легко распространяется на случай пирамиды с
любым числом граней.
3. Усеченная пирамида. Часть пирамиды, заключенная между ее ос-
нованием и секущей плоскостью, параллельной основанию, на-
зывается усеченной пирамидой (рис. 191).
Основание и соответствующее сечение усеченной пирамиды
называются основаниями усеченной пирамиды. Основания усе-
ченной пирамиды являются подобными многоугольниками, их
стороны попарно параллельны, поэтому боковые грани усечен-
ной пирамиды являются трапециями.
Перпендикуляр, проведенный из какой-либо точки одного ос-
нования на плоскость другого, называется высотой усеченной
пирамиды (h на рис. 191).
Сечение усеченной пирамиды плоскостью, проходящей через
два боковых ребра, не лежащих в одной грани, называется диа-
Рис. 191
гональным сечением (затемнено на
рис. 191).
Усеченная пирамида называется пра-
вильной , если она составляет часть пра-
вильной пирамиды.
Высота боковой грани правильной
усеченной пирамиды называется ее апо-
фемой (а на рис. 191).
Основные свойства правильной усеченной пирамиды
I. Боковые ребра, боковые грани и апофемы соответственно
равны.
II. Двугранные углы при основании равны.
III. Двугранные углы при боковых ребрах равны.
340
ГЛАВА 13. Многогранники и площади их поверхностей
IV. Каждая точка оси равноудалена от всех вершин основания.
V, Каждая точка оси равноудалена от плоскостей боковых гра-
ней.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется пирамидой? Ее вершиной? Основанием? Высотой?
2. Что называется диагональным сечением пирамиды?
3. Какая пирамида называется правильной?
4. Сформулируйте теорему о свойстве параллельных сечений пирамиды.
5. Что называется усеченной пирамидой?
6. Что называется правильной усеченной пирамидой?
§ 84. Площади поверхностей многогранников
1. Площади боковой и полной поверхностей призмы. Площадью боко-
вой поверхности призмы называется сумма площадей ее боковых
граней; площадью полной поверхности — сумма площадей всех
ее граней.
@ ТЕОРЕМА
Площадь боковой поверхности призмы равна произведению
периметра сечения, перпендикулярного боковым ребрам приз-
мы, на длину бокового ребра.
ДОКАЗАТЕЛЬСТВО. Проведем доказательство на примере треуголь-
ной призмы, которое легко распространить на случай призмы с
любым, числом граней. Пусть в призме
П плоскость а перпендикулярна реб-
рам, АА1 = BBj = CCj = Z, Р — периметр
сечения А^2С2 (Рис* 192). Боковая
площадь В5ох = <8АЛ1В1В + SBBiC1c +
+ Scc л А . По построению А2В? являет-
ся высотой параллелограмма ААгВВ^
площадь которого, таким образом, рав-
на ^АА,В.В = ^'^2^2* аналогии пло-
щади других граней равны соответствен-
но I• В2С2 и I ’ С?А2. Таким образом,
Рис. 192
^бок + ^2^2 ^2^2^
что и требовалось доказать
341
ЧАСТЬ 3. Элементы стереометрии
В прямой призме периметр перпендикулярного сечения равен
периметру основания, поэтому S6oK = 1РОСК.
2. Площадь боковой поверхности параллелепипеда. Прямой паралле-
лепипед является частным случаем прямой призмы, поэтому
площадь его боковой поверхности равна S6oK = IP^.
3. Площадь боковой и полной поверхности пирамиды. Площадью боко-
вой поверхности пирамиды (полной и усеченной) называется сум-
ма площадей всех ее боковых граней, площадью полной поверх-
ности — сумма площадей всех ее граней.
ТЕОРЕМА
Площадь боковой поверхности правильной пирамиды равна
половине произведения периметра основания на апофему пи-
рамиды.
ДОКАЗАТЕЛЬСТВО. Пусть в n-угольной пирамиде Р — периметр осно-
вания, а — апофема. В правильной пирамиде все п боковых гра-
ней являются равными между собой треугольниками. Пусть ос-
нование любого из этих треугольников равно д, тогда = Ьа/2У
следовательно, площадь боковой поверхности равна
1 1
S6OK = nSA = 2 nba = 2 Ра-
Очевидно,
ПОЛИ
^бок + ^осн*
4. Площадь боковой и полной поверхностей усеченной пирамиды.
В правильной n-угольной усеченной пирамиде все боковые грани
являются равными между собой трапециями. Обозначим длины
их оснований через Ь и Ь1У высотой в них служит апофема а. Тог-
да площадь трапеции равна S ™ (Я- Ьг)а/2У тогда
S6OK = nS^n = nl(b + bja = 2 (Р + Л)а,
где Р и Р1 — периметры оснований усеченной пирамиды. Таким
образом, площадь боковой поверхности усеченной пирамиды рав-
на произведению полусуммы периметров ее оснований на апо-
фему.
342
ГЛАВА 13. Многогранники и площади их поверхностей
§ 8b. Правильные многогранники
Выпуклый многогранник называется правильным, если все
его грани являются правильными многоугольниками с одним и
тем же числом сторон и в каждой вершине многогранника схо-
дится одно и то же число ребер.
В правильном многограннике все многогранные углы равны
между собой, все двугранные углы равны между собой.
Существует всего пять видов правильных многогранников
(рис. 193): правильный тетраэдр, гексаэдр (куб), октаэдр, додека-
эдр, икосаэдр*.
Правильный тетраэдр имеет 4 грани, являющиеся правиль-
ными треугольниками, в каждой вершине сходится 3 ребра. Пра-
вильный тетраэдр является треугольной пирамидой, у которой
все ребра равны.
Тетраэдр
Додекаэдр
Рис. 193
Икосаэдр
* Названия правильных многогранников имеют греческое происхож-
дение; буквально они означают: четырех-, шести-, восьми-, двенадцати-,
двадцатигранник.
343
ЧАСТЬ 3. Элементы стереометрии
Гексаэдр (куб) имеет 6 граней, являющихся квадратами, в
каждой вершине сходится по 3 ребра. Гексаэдр является прямо-
угольным параллелепипедом с равными ребрами.
Октаэдр имеет 8 граней, являющихся равносторонними тре-
угольниками, в каждой его вершине сходится по 4 ребра.
Додекаэдр имеет 12 граней, являющихся правильными пяти-
угольниками. В каждой вершине додекаэдра сходится по 3 ребра.
Икосаэдр имеет 20 граней, являющихся равносторонними
треугольниками, в каждой его вершине сходится по 5 ребер.
Теоремой Эйлера установлена зависимость между числом вер-
шин любого выпуклого многоугольника В, числом его граней Г и
числом его ребер Р: В - Р + Г = 2.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие многогранники называются правильными?
2. Сколько существует видов правильных многогранников? Охарактери-
зуйте их.
ГЛАВА 14. Фигуры вращения
и площади их поверхностей
§ 86. Цилиндр
1. Основные понятия. Круговым цилиндром называется фигура,
образованная вращением прямоугольника вокруг одной из его
сторон (рис. 194, а).
Пусть прямоугольник ОАВС вращается вокруг стороны ОА,
тогда ОА — ось вращения — является осью цилиндра, ОС — R —
радиус цилиндра, СВ — образующая цилиндра.
Стороны прямоугольника ОС и АВ, перпендикулярные оси
вращения, при вращении образуют основания цилиндра — круги
с центрами в точках О и А и с радиусами R. Образующая цилинд-
ра СВ и ось ОА являются высотой цилиндра h.
Образующая цилиндра при вращении образует его боковую
поверхность. Вся поверхность цилиндра состоит из боковой по-
верхности и суммы двух оснований.
Плоскость, проходящая через ось цилиндра, называется осе-
вым сечением и представляет собой прямоугольник, две стороны
которого являются образующими цилиндра, а две другие — диа-
344
ГЛАВА 14. Фигуры вращения и площади их поверхностей
метрами оснований цилиндра (се-
чение а на рис. 194, б). Цилиндр,
осевое сечение которого является
квадратом, называется равно-
сторонним цилиндром.
Сечение стороны плоскостью,
параллельной его оси, дает пря-
моугольник, две стороны кото-
рого служат образующими ци-
линдра, а две другие являются
равными между собой хордами
окружностей оснований (сечение
Р на рис. 194, б).
Плоскость, параллельная оси
цилиндра и отстоящая от нее на
а)
Рис. 194
расстояние, равное радиусу окружности основания и содержа-
щая в себе одну образующую цилиндра и не имеющая с поверхно-
стью цилиндра других общих точек, называется касательной
плоскостью.
Плоскость, проходящая через ось цилиндра и образующую, по
которой касательная плоскость касается цилиндра, перпендику-
лярна к касательной плоскости.
2. Площадь поверхности цилиндра. Если мысленно разрезать боко-
вую поверхность цилиндра по образующей СВ и развернуть ее на
плоскость, то получится прямоугольник, длина основания кото-
рого равна длине окружности основания цилиндра 2л7?, а высо-
та — высоте цилиндра h; этот прямоугольник является разверт-
кой цилиндра.
В качестве площади боковой поверхности цилиндра принима-
ется площадь развертки, равная 2т: Rh.
Площадь полной поверхности цилиндра S состоит из суммы
площадей двух оснований — кругов — и площади боковой по-
верхности цилиндра, т. е. S = 2nR2 + 2nRh или
S = 2nR(R + h).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какое тело называется цилиндром?
2. Дайте определения основания, высоты, образующей и боковой поверх-
ности цилиндра.
3. Какое сечение называется осевым сечением цилиндра?
345
ЧАСТЬ 3. Элементы стереометрии
4. Какая плоскость называется касательной плоскостью к цилиндру?
5. Что принимают в качестве площади боковой поверхности цилиндра?
6. Выпишите формулы для вычисления площадей боковой и полной по-
верхностей цилиндра.
§ 87. Конус
1. Основные понятия. Круговым конусом называется фигура, об-
разованная при вращении прямоугольного треугольника вокруг
одного из его катетов (рис. 195).
Пусть прямоугольный треугольник АВО
вращается вокруг катета ОВ, тогда О В —
ось вращения — является осью конуса;
В — вершина конуса; ОА = R — радиус ос-
нования конуса; О — центр круга, лежаще-
го в основании конуса; АВ = L — образую-
щая конической поверхности; OB — h —
высота конуса.
Сечение конуса плоскостью, проходя-
щей через его ось, называется осевым сече-
нием конуса.
Осевым сечением конуса является рав-
нобедренный треугольник, у которого боко-
вые стороны — образующие конуса, а основание — диаметр осно-
вания конуса.
В сечении конуса плоскостью, перпендикулярной к его оси,
образуется окружность.
В сечении конуса плоскостью, проходящей через его вершину
и пересекающей его поверхность, получается равнобедренный
треугольник, боковыми сторонами которого служат образующие
конуса, а основанием — хорда окружности основания.
Плоскость, проходящая через образующую конуса и перпен-
дикулярная к плоскости осевого сечения, проходящей через ту
же образующую, не имеет с поверхностью конуса других общих
точек, кроме точек этой образующей; она называется касатель-
ной плоскостью.
2. Площадь поверхности конуса. Если мысленно разрезать боковую
поверхность конуса по образующей АВ (рис. 196) и развернуть ее
на плоскость, то получим круговой сектор, радиус г которого ра-
вен образующей конуса АВ = L , а длина дуги сектора равна длине
346
ГЛАВА 14. Фигуры вращения и площади их поверхностей
окружности основания конуса 2nR.
Следовательно, площадь боковой по-
верхности конуса S равна площади
развертки боковой поверхности кону-
са, т. е. площади сектора АВА:
_ л:г2а _ тега . г
^сект ’ 360 180 • 2 ’
Здесь а — угол при вершине разверт-
г яга ,
ки, г — радиус сектора, г = £, = I —
длина дуги сектора.
Тогда SceKT = I • . Заменив в этом выражении I на 2лЯ и г на L,
получим
S = S = itRL,
сект
(14.1)
где R — радиус основания конуса, L — его образующая.
Площадь полной поверхности конуса 5ПОЛН = + SOCH, где
= kR2> тогда
^полв = + L).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какое тело называется конусом?
2. Дайте определения основания, вершины, оси, высоты и образующей
конуса.
3. Какое сечение конуса называется осевым?
4. Какая плоскость называется касательной плоскостью к конусу?
5. Что принимается в качестве площади боковой поверхности конуса?
6. Какая фигура лежит в сечении конуса плоскостью, перпендикулярной к
его оси?
7. Выпишите формулы для вычисления площадей боковой и полной по-
верхностей конуса.
§ 88. Усеченный конус
1. Основные понятия. Часть конуса, заключенная между его осно-
ванием и секущей плоскостью, параллельной основанию, назы-
вается усеченным конусом.
347
ЧАСТЬ 3. Элементы стереометрии
Пусть прямоугольная трапеция АОО^В (рис. 197) вращается
вокруг ее боковой стороны ОО,, перпендикулярной к основанию
трапеции АО. Вторая боковая сторона трапеции АВ служит обра-
зующей усеченного конуса. Две параллельные стороны являются
радиусами R и г трапеции. Описываемые ими круги служат сето-
ваниями усеченного конуса.
Ось усеченного конуса GOY является его высотой h.
Часть конической поверхности, ограничивающая усеченный
конус, называется его боковой поверхностью.
2. Площадь поверхности усеченного конуса. Пусть L — образующая
усеченного конуса, х — образующая дополненной части конуса,
R — радиус нижнего основания, г — радиус верхнего основания
(рис. 198).
По формуле (14.1)
8бок = 71(L + х) - лгх = TtRL + n(R- r)x.
Из подобия треугольников АОР и ВО,Р следует:
А.
X
После преобразований получим
R — г
Lr
Подставим значение х в (*):
= tiRL + TtrL = n(R + r)L
Вбок = + n(R-r)*
Рис. 197
P
Рис. 198
348
ГЛАВА 14. Фигуры вращения и площади их поверхностей
или
— + 2тгг
бок 2
(14.2)
Площадь боковой поверхности усеченного конуса равна произве-
дению полусуммы длин окружностей основания на образующую.
Полная площадь поверхности усеченного конуса равна
^полн = + r)L + nR2 + ПГ
ИЛИ
ПОЛИ
= it(LR + Lr + R2 + r2).
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какое тело называется усеченным конусом?
2. Дайте определение высоты усеченного конуса.
3. Как вычисляется площадь боковой поверхности усеченного конуса?
§ 89. Сфера и шар
1. Основные понятия. Поверхность, образованная вращением полу-
окружности вокруг ее диаметра, называется сферой (рис. 199).
Сфера — это геометрическое место точек пространства, равно-
удаленных от одной точки (центра) и образующих поверх-
ность, называемую сферой или шаровой поверхностью.
Тело, ограниченное шаровой поверхностью, называется шаром.
Отрезки прямых, соединяющих центр с точками сферы, назы-
ваются радиусами. Отрезок прямой, соединяющей две точки
сферы, называется хордой сферы. Хорда, проходящая через
центр, называется диаметром сферы.
следствия из нее.
ТЕОРЕМА
Сечение сферы плоскостью есть окруж-
ность.
СЛЕДСТВИЯ
I. Если секущая плоскость не проходит че-
рез центр сферы, то радиус окружности се-
чения меньше радиуса сферы.
Рис. 199
349
ЧАСТЬ 3. Элементы стереометрии
II. Сечение имеет наибольший радиус, если плоскость сечения
проходит через центр сферы. Это сечение называется боль-
шим кругом сферы.
III. Плоскость большого круга есть плоскость симметрии сферы.
IV. Радиусы сечений, плоскости которых равноудалены от
центра сферы, равны.
2. Касательная плоскость к сфере. Плоскость, имеющая с поверхно-
стью сферы одну общую точку, называется касательной плоско-
стью к сфере.
ТЕОРЕМА
Плоскость, проходящая через конец радиуса сферы и перпен-
дикулярная к нему, является касательной плоскостью.
ДОКАЗАТЕЛЬСТВО. Пусть ОА — радиус сферы (рис. 200), А е а, плос-
кость а ± ОА. Пусть произвольная точка В е а. Соединим точку
В с центром сферы О. Тогда ОА < ОВ (перпендикуляр короче на-
клонной), следовательно, точка В лежит вне сферы, таким обра-
зом, плоскость а содержит единственную точку А сферы, т. е. яв-
ляется касательной плоскостью.
Прямая, лежащая в касательной плоскости к сфере и проходя-
щая через точки касания, называется касательной прямой к
сфере. Все касательные к сфере, проведенные из данной внешней
точки, равны между собой.
Две пересекающиеся сферы по линии их пересечения образу-
ют окружность. Эта окружность лежит в плоскости, перпендику-
лярной к прямой, соединяющей центры пересекающихся сфер.
3. Части шара и сферы. Часть шара, отсекаемая плоскостью, назы-
вается шаровым сегментом (рис. 201). Часть сферы, отсекаемая
плоскостью, называется сферическим сегментом. Площадь сфе-
Рис. 200
рического сегмента, иначе называемого
шаровым сводом, определяется как
S = 2nRh, где R — радиус шара, h — вы-
сота шарового сектора.
Часть шара, заключенная между дву-
мя параллельными секущими плоскос-
тями, называется шаровым слоем
(рис. 202), Сферическая поверхность ша-
рового слоя называется шаровым по-
ясом. Расстояние между параллельны-
350
ГЛАВА 14. Фигуры вращения и площади их поверхностей
ми секущими плоскостями h называется высотой шарового слоя.
Площадь шарового пояса определяется как S ~ 2nRh, где R — ра-
диус шара.
Часть шара, образованная вращением кругового сектора во-
круг оси, проходящей через его центр, называется шаровым сек-
тором (рис. 203). Шаровой сектор можно рассматривать как
сплошную или полую фигуру, в зависимости от этого он называ-
ется сплошным или полым. В качестве высоты шарового сектора
h принимают высоту его сферической поверхности (проекцию
хорды, стягивающей дугу сектора, на ось вращения). Площадь
поверхности шарового сектора определяется как S = тсЯ(2Д + г),
где R — радиус шара, г — радиус основания шарового сегмента,
охватывающего шаровой сектор.
Вывод соотношений, определяющих площади сферического
сегмента и шарового пояса, будет дан в § 90, п. 4, 5.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Дайте определения сферы и шара.
2. Какое сечение называется большим кругом сферы?
3. Какая плоскость называется касательной плоскостью к сфере?
4. Дайте определения шарового сегмента и сферического сегмента.
5. Дайте определения шарового слоя и шарового пояса.
6. Что называется высотой шарового слоя?
7. Дайте определение шарового сектора.
8. Что принимают в качестве высоты шарового сектора?
§ 90. Площадь поверхности сферы и ее частей
1. Дифференциал дуги. Длина дуги. Рассмотрим кривую у — f(x).
Найдем длину кривой между двумя ее точками А и В (рис. 204).
Пусть I — переменная длина дуги иАМ, измеряемая от фикси-
рованной точки А кривой до перемещающейся по кривой точки
М. Каждому значению абсциссы х соответствует определенное
351
ЧАСТЬ 3. Элементы стереометрии
Рис. 204
положение точки М на кривой
и, следовательно, определен-
ное значение длины I дуги
\jAM9 т. е. 1 = I (х). Пусть дуга
kjMN — это приращение AZ ду-
ги от точки М(х; у) до точки
Nix + Дх; у + Д^}; здесь Дх и
Др- — приращения переменных
х и у соответственно.
Из прямоугольного треугольника MNP следует, что
(MN)2 = Дх2 + Др2,
откуда
(M^)2
Длина Д/ дуги uMN эквивалентна длине хорды MN, так как
при замене длины дуги <jMN длиной хорды MN погрешность
5 —► 0 (5 = Д/ - MN) при MN -* 0, поэтому
2 Д/ L ,
ИЛИ — = 1 + т2 I .
М\2
Следовательно,
д/
hrn —
х -оДх
л lim л
Дх — о
Отсюда
dZ =
•dx
(14.3)
dZ называется дифференциалом дуги.
Проинтегрируем выражение (14.3) и получим длину дуги
между точками А и В с абсциссами а и Ь соответственно:
а
dx.
♦ ПРИМЕР
Найти длину L окружности х2 + у2 — R2.
РЕШЕНИЕ. Проди
ни»;
еренцировав уравнение окружности, получим
2х + 2р^р = 0, т. е.
«Аг
352
ГЛАВА 14. Фигуры вращения и площади их поверхностей
По формуле (14.4) вычислим длину дуги четверти окружности,
выбрав в качестве пределов интегрирования значения О и В:
R
= R arcsin = jR(arcsin 1 - arcsin 0) = R(n/2).
R о
Следовательно, длина L окружности
L = 4Z = 4В(л/2) = 2лВ.
2. Площадь поверхности вращения. Предел, к которому стремится
площадь поверхности, образованной вращением ломаной
М^Мг..Мп_ уМп, вписанной в дугу МОМЛ, при неограниченном
Рис. 205
увеличении числа ее звеньев, называется площадью поверхно-
сти, образованной вращением дуги МОМЛ.
Вычислим площадь поверхности, образованной вращением
элемента иАВ дуги, заданной уравнением у ~ /(х), вокруг оси Озе
(рис. 205). Будем считать функ-
ции f (х) и f (х) непрерывными в
промежутке [а; &], где а и Ь —
абсциссы точек А и В соответ-
ственно. Разделим дугу АВ на п
частей и соединим точки де-
ления хордами, т. е. впишем в
дугу ломаную линию. Рассмот-
рим одну из хорд, ограниченную
точками, которые обозначим че-
рез М(х; у) и N(x + Дх; у + Д(/).
Найдем приближенные выражения для площади поверх-
ности, образованной участком <jMN кривой, заменив кривую
У = Ах) хордой MN. Площадь поверхности, образованную хордой
MN, можно приближенно принять равной площади боковой по-
верхности усеченного конуса к, описанного вращением хор-
ды MN. Радиусами основания этого конуса являются ординаты
у и у + Ду, высотой — отрезок Дх и образующей — хорда MN =
То е. по (14.2)
^бок. К = 4 2 + *1д*2 + Лу2 = п(2у + Ay) JДх2 + Ау2
353
ЧАСТЬ 3. Элементы стереометрии
Вся площадь поверхности, описанной ломаной АВ, равна
£ п(2у + Ду) 7Дх2 + Az/2 = £ л(2у + Дг/) /1 + (^1 Дх =
х - а х - a N /
j у di. (14.5)
= % п(2у + Ду) • Д/.
х = а
Таким образом, площадь S поверхности, образуемой враще-
нием дуги иАВ, является пределом, к которому стремится эта
интегральная сумма при Дх —* О, Ду —*• 0, поэтому
S = Jim 0 % п(2у + Ду) Ы = 2л
х — и
Выражение (14.5) является формулой для вычисления площа-
ди поверхности тела вращения; здесь дифференциал дуги dZ опре-
деляется по формуле (14.3). Функция у = /(х) и дифференциал
дуги dZ должны быть выражены через одну и ту же переменную.
Площадь, образованная вращением дуги АВ вокруг оси Оу,
определяется уравнением
S = 2тс f х dZ, (14.6)
р
где pv.q — ординаты точек А и В соответственно.
3. Площадь поверхности сферы. Пусть поверхность сферы образова-
на вращением полуокружности х2 + у2, — R2 вокруг оси Ох. Про-
дифференцируем уравнение окружности у = Jr2 — х2:
dx _ -2х _х _ _ х
dy 2 Jr2 - х2 Jr2 - х2 у
Найдем дифференциал дуги
г» пн
dZ =
dx
Подставив найденное значение в выражение (14.5), получим
R
= 2тсй J dx = 2itRx
-R
R
= 2tiR(R + R) = 4/itR2.
-R
Площадь поверхности сферы равна учетверенной площади
большого круга этой сферы:
S == 4лК2.
354
ГЛАВА 14. Фигуры вращения и площади их поверхностей
Рис. 206
Рис. 207
4. Площадь поверхности сферического сегмента. Пусть сегмент, обра-
зованный из сферы радиуса R, имеет высоту h (рис. 206). Как и в
предыдущем случае,
у — Jr2 - х2, dZ =
Rdx
Jr2 - x2 ’
тогда площадь поверхности сферического сегмента S составляет
R
S = 2n [ 7й2 - х2
R- h
Rdx
л
= 2nR I dx = 2nRx
= 2nR(R — R + h) = 2nRh,
t. e. площадь поверхности сферического сегмента равна произве-
дению длины окружности большого круга этого сегмента на его
высоту.
5. Площадь поверхности сферического пояса. Пусть сферический по-
яс образован из сферы радиуса Л, имеет высоту h и пусть то осно-
вание сферического пояса, которое расположено ближе к диамет-
ральному сечению, отстоит от него на отрезок а (рис. 207). Как и
в предыдущем случае,
Bdx
s = 2n j Jr
а
J dx = 2nRx
Тогда площадь поверхности сферического пояса S составляет
а + h а
2 - х2 = 2лЯ
л/в2 “ х2
— 2nR(a 4- h - а) =
т. е. площадь поверхности сферического пояса равна произведе-
нию длины окружности большого круга на высоту пояса.
355
ЧАСТЬ 3. Элементы стереометрии
Рис. 208
♦ ПРИМЕР
Вычислить площадь поверхности, образо-
ванной вращением дуги параболы у1 2 = 4х во-
круг оси Ох, ограниченной точками 0(0; 0)
и А(3; 2л/3 ) (рис. 208).
РЕШЕНИЕ. Преобразуем уравнение параболы: у =
= 2х1/2. Продифференцировав, получим
dy
dx
= х 1/2. По формуле (14.5)
j 2xV2 71
о
S = 2тс
. z -1/2.2 ,
+ (х ) dx,
подведем х1/2 под знак корня: S = 4л J Jx + ldx. Положим х + 1 =
о
= г, тогда dx = dz, с учетом изменения пределов интегрирования
получим
4 4
S = 4л J z1/2dz = 4я • | z3/2 = (8 - 1) = (кв. ед.).
1 1
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется дифференциалом дуги?
2. По какой формуле вычисляется длина дуги?
3. Как вычислить длину окружности по формуле длины дуги?
4. Как определяется площадь поверхности вращения?
5. Выпишите формулу для вычисления площади поверхности вращения.
6. Вычислите площади поверхности сферы, сферического пояса и сфери-
ческого сегмента.
ГЛАВА 15. Объемы многогранников
и тел вращения
§ 91. Объемы прямых параллелепипедов,
призмы и цилиндра
1. Основные понятия. Величина части пространства, занимаемого
геометрическим телом, называется объемом этого тела. Вычис-
лить объем тела или измерить объем — означает вычислить отно-
356
ГЛАВА 15. Объемы многогранников и тел вращения
шение его к объему, принятому за единицу измерения; за едини-
цу измерения объема принимают объем куба, ребро которого рав-
но единице измерения длины. Такая единица называется
кубический единицей»
Основные свойства объемов
• I. Объемы равных многогранников равны.
Г
1
t II. Объем многогранника, состоящего из суммы нескольких
I многогранников, равен сумме их объемов.
Два многогранника, имеющие равные объемы, называются
равновеликими. Всякие два равносоставленных многогранника
являются равновеликими.
Если один многогранник составляет часть другого, то его
объем меньше объема другого многогранника.
2. Объем прямоугольного параллелепипеда. Рассмотрим ситуацию,
когда все три измерения а, Ь, с прямоугольного параллелепипеда
выражаются целыми числами а = т, b = р, с = q. Тогда плоскос-
тями, параллельными граням, параллелепипед разбивается на
mpq единичных кубов, а потому его объем V равен произведению
abc:
V = abc.
(15.1)
Пусть все три измерения прямоугольного параллелепипеда
выражаются дробными числами:
где т,р^п — натуральные числа. В этом случае единичный куб
разделен на п3 равновеликих кубов. Объем такого малого куба ра-
1
вен —з, а прямоугольный параллелепипед содержит mpq таких
малых кубов. Тогда объем параллелепипеда равен сумме объемов
этих малых кубов:
тл 1 mpq .
V = —5 mpq = — • - •21 = abc.
п3 п п п
Наконец, рассмотрим общий случай, когда измерения а9 Ъ и с
выражены любыми действительными числами. Пусть их прибли-
жения с недостатком выражаются числами ар Ьр с19 а прибли-
жения с избытком — числами а2, Ь2, с2; объемы параллелепипе-
357
ЧАСТЬ 3. Элементы стереометрии
дов с этими измерениями выражены через V\ и V2 соответствен-
но. Это значит, что
или
V<
аг • &1 • сг
где
_ . 1 ь 4- 1 1
а2 а} + *()л » ° 2 °1 + Юл » С2 С1 *" Юп ’
При п —*• оо число -* О, поэтому разность 8 = а2*Ь2*с2 -
- ах • Ьг • cv 8 —* 0, т. е. число V сколь угодно мало отличается от
abc или
V = abc.
Таким образом, какими бы ни были измерения a g Р, b е R,
с € R, объем прямоугольного параллелепипеда выражается соот-
ношением (15.1).
Следовательно, справедливо и другое соотношение для опреде-
ления объема прямоугольного параллелепипеда
V = S*h, (15.2)
где S — площадь основания (S = db), h — его высота (h = с).
3. Объем прямой треугольной призмы. Рассмотрим треугольную
призму Р (рис. 209). Дополним ее до параллелепипеда, проведя
через ребра ВВ1 и PDj плоскости, па-
Рис. 209
раллельные граням AA^D^D и АА^В^В.
Обозначим ребро, по которому они пе-
ресекутся, через CCj, ССг || ВВГ Приз-
ма Р равна призме Р, так как если сов-
местить их равные основания Д ABD к
Д BCD, то совместятся и их боковые
ребра, равные между собой и перпенди-
кулярные к плоскости основания. Сле-
довательно, объем треугольной призмы
Р равен половине объема параллелепи-
педа, т. е.
Р 2 ^ABCD ’ &ABD *•
358
ГЛАВА 15. Объемы многогранников и тел вращения
Таким образом, объем прямой треугольной призмы равен про-
изведению площади ее основания на высоту:
V = S*h.
(15.3)
4. Объем многоугольной прямой призмы. Пусть Р — п-угольная пря-
мая призма с высотой h (рис. 210). Через одно из боковых ребер
призмы проведем диагональные плоскос-
ти, тогда призма Р окажется составлен-
ной из (п - 2) треугольных призм с той же
высотой Л; площади их оснований обозна-
чим через Sx, S2, ...» Sn _ 2.
Объем V прямой призмы Р равен сумме
объемов всех прямых треугольных
призм, т. е.
здесь S = + S2 + ... + Sn_2 — площадь
Рис.210
(15.4)
основания призмы Р, следовательно,
т. е. объем любой прямоугольной призмы равен произведению
площади основания на высоту.
5. Объем прямого кругового цилиндра. В качестве объема цилиндра
принимают предел объема правильной вписанной в него или опи-
санной вокруг него призмы при неограниченном увеличении чис-
ла ее сторон.
Представим себе цилиндр с радиусом основания R и высотой
h. Впишем в цилиндр и опишем вокруг него правильные призмы
с п гранями, объемы которых равны и V2 соответственно. Оче-
видно, Vt<V< У2, где V — объем цилиндра, но V\ — V2 = S2h,
где Sj и S2 — площади оснований вписанной и описанной призм
соответственно, тогда
Slh<V<S2h, (15.5)
Известно, что
= л7?2, = nR2.
Следовательно, обе части двойного неравенства (15.5) имеют
один и тот же предел nR2k, тогда объем цилиндра
V (15.6)
359
ЧАСТЬ 3. Элементы стереометрии
Объем прямого кругового цилиндра равен произведению пло-
щади его основания на высоту.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Что называется объемом тела?
2. Как определяется действие вычисления объема тела?
3. Перечислите основные свойства объема тела.
4. Выпишите формулы для определения объема прямоугольного паралле-
лепипеда и прямой призмы и поясните смысл входящих в них парамет-
ров.
5. Можно ли применить формулу объема прямой призмы для вычисления
объема прямого параллелепипеда?
§ 92. Объем геометрической фигуры с заданными
площадями поперечных сечений
1. Применение интегральной суммы к вычислению объема тела. Объ-
емы фигур с заданными площадями поперечных сечений можно
вычислять с применением определенного интеграла.
Пусть геометрическая фигура F заключена между параллель-
ными плоскостями а и Р (рис. 211), перпендикулярными оси Ох.
Обозначим через а и Ъ (а < Ь) абсциссы пересечения плоскостей а
и Р с осью Ох. Пусть плоскость у также перпендикулярна к оси
Ох и пересекает ее в точке с абсциссой х, х е [а; &].
В сечении фигуры F плоскостью у получаем некоторую фигу-
ру, которую назовем поперечным сечением и обозначим его пло-
щадь через 8(х). Площадь S(x) задана. Это значит, что любому
значению х е [а; Ь] соответствует определенная площадь попереч-
ного сечения S(x), иначе говоря, S является функцией перемен-
ной х. Предположим, что S(x) непрерывна на [а; &].
Для вычисления объема V
фигуры F разделим промежу-
ток [а; Ь] на п частей. Пусть
абсциссы точек деления удов-
летворяют неравенствам:
Рис. 211
Рассмотрим объем пояса
между сечениями с абсциссами
360
ГЛАВА 15. Объемы многогранников и тел вращения
xk и xk + ДхА. Заменим этот объем объемом прямого цилиндра
(призмы), высота которого равна ДхА, а основание равно S(xft),
тогда этот объем ДVk = S(xk) • Дхй. Объем тела, составленного из п
таких цилиндров (призм), выражается интегральной суммой
X S(xk) • Дхk.
k = i
Объем фигуры из п цилиндров (призм) отличается от объема
фигуры F тем меньше, чем меньше промежутки ДхА. Назовем
объемом V фигуры F предел интегральной суммы
V= lim
Лхк - О
ZS(xfe) Дхй.
Поскольку
lim
Дх* - О
ь
X S(xft ) ДхА = J S(x) dxft,
а
объем фигуры с заданными площадями поперечных сечений
ь
V = j S(x) dxfe. (15.7)
а
Для призматических или цилиндрических тел функция <S(x)
является величиной постоянной (если в качестве оси Ох принять
прямую, перпендикулярную к основанию), равной площади ос-
нования; для других тел, например конических, площадь £(х)
изменяется в зависимости от расстояния между сечением и осно-
ванием. В этом случае для вычисления объема тела по формуле
(15.7) нужно найти зависимость площади сечения 8(х) от рас-
стояния между этим сечением и одним из оснований тела. Это ос-
нование может быть как плоскостью, так и линией или точкой
(например, вершиной конуса или основанием шара).
2. Объем наклонной призмы (наклонного цилиндра). В наклонной
призме (цилиндре) с площадью основания S и высотой h площадь
сечения S(x) = S. Тогда по (15.7) объем V этого тела
о
т. е. объем наклонной призмы (цилиндра) равен произведению
площади его основания на высоту.
Сформулируем другое соотношение для определения объема
наклонной призмы (цилиндра).
361
ЧАСТЬ 3. Элементы стереометрии
Рис. 212
М ТЕОРЕМА
Объем наклонной призмы равен
произведению площади перпен-
дикулярного сечения на боковое
ребро.
ДОКАЗАТЕЛЬСТВО. Пусть Р — наклонная
призма, боковое ребро АА1 = Z, q —
плещадь сечения у, перпендикуляр-
ного ребрам призмы, h — ее высота и
S — площадь основания призмы
(рис. 212). Пусть высота призмы h об-
разует с боковым ребром ААг угол а,
тогда угол между плоскостью основа-
ния и плоскостью у также равен а.
Из треугольника ААгО находим высоту h = l cos а. Поскольку
q — это проекция треугольника основания АВС на плоскость у,
площадь q = S cos а, из чего следует: S = g/cos а. Подставим в
(15.8) значения h и S, получим V — (g/cos a) I cos а, т. е.
(15.9)
что и требовалось доказать.
3. Объем пирамиды. В пирамиде площади основания 3 и параллель-
ных ему сечений S(x) относятся как квадраты их расстояний от
вершины (§ 83, п. 2). Примем в качеств® оси Ох в пирамиде пря-
мую, перпендикулярную к основанию, с началом в вершине пи-
рамиды, таким образом, пределы интегрирования в (15.7) равны
а = 0, b = h. Таким образом,
&(х) _ х2
~S Ь2
или
S(x) = х2.
Тогда объем пирамиды V равен
h
V- Js(x)dx=^2
О
Таким образом, объем пирамиды равен одной трети произведе-
ния площади ее основания на высоту:
(15.10)
362
ГЛАВА 15. Объемы многогранников и тел вращения
4. Объем усеченной пирамиды. Представим себе усеченную пирами-
ду с площадями нижнего и верхнего основания, равными SH и SE
соответственно и высотой h. Пусть высота полной пирамиды, об-
разованной продолжением ребер усеченной до их пересечения в
одной точке, равна h + Н.
Объем усеченной пирамиды V равен разности между объемом
полной пирамиды и объемом пирамиды, дополняющей усечен-
ную до полной:
(*)
По свойству параллельных сечений в пирамиде
S„ = (h + Я)2 Js~„ _ h + Н
Sb Нг JSB н '
Преобразуя пропорцию, получим
Отсюда
Подставив (**) в (*) и упростив, приходим к формуле
(15.11)
5. Объем тела вращения. Пусть фигура, ограниченная линиями
у = f(x), х = а, х = д, у = О, вращается вокруг оси Ох (рис. 213).
Найдем объем V полученного тела вращения F.
Сечение тела F плоскостью, перпендикулярной к оси Ох в точ-
ке х, является кругом с радиусом
У ~ т. е. площадь этого сече-
ния S(x) = пу2, тогда по (15.7)
ь
V = п J у2 dx. (15.12)
а
Если же фигура, ограничен-
ная линиями х = f(y), у = р, у = q
и х = 0, вращается вокруг оси Оу,
Рис. 213
363
ЧАСТЬ 3. Элементы стереометрии
то объем V полученного тела вращения определяется выраже-
нием
q
V = л J х2 dy.
р
(15.13)
6. Объем конуса. Пусть конус, полученный в результате вращения
прямоугольного треугольника ОБА вокруг оси Ох (рис. 214), име-
ет радиус основания R и высоту Л. Составим уравнение образую-
щей ОА:
y = xtga=~x,
где а — угол между осью конуса и его образующей.
По (15.12) объем V конуса составляет
То э. объем конуса вычисляется по формуле
V = I nR2h.
О
(15.14)
7. Объем усеченного конуса. Пусть усеченный конус, образованный
вращением прямоугольной трапеции ОАВС вокруг оси Ох, имеет
радиусы большего и меньшего оснований R и г соответственно и
высоту h (рис. 215). Уравнение образующей АВ этого конуса имеет
вид у = kx + Ь9 здесь угловой коэффициент k = tg cl (R — r}/h9 a —
угол между осью конуса и его образующей, Ъ — ордината образую-
щей в точке х = О, Ь = г. Тогда уравнение образующей имеет вид
Рис.214 Рис.215
364
ГЛАВА 15. Объемы многогранников и тел вращения
По (15.12) объем V усеченного конуса
h
При интегрировании применим подстановку
h ~ ' h —
Находим новые пределы интегрирования:
о
du.
Таким образом
R
,, Г h
, nh
du =----
яЛ
——— (Я3 - гЗ)
3(1? - г)
или
V = -^(R2 + г2 + Яг),
о
(15.15)
8. Объем шара. Пусть образующей шара является полуокружность
с центром в начале координат х2 + у2 = R2, у 2s О, тогда у2 = R2 — х2.
Объем v половины шара составляет
тогда объем V шара
(15.16)
О
Можно также выразить объем шара через диаметр D = 2R\
V=|nD3. (15.17)
9. Объем шарового сегмента. Пусть шаровой сегмент, образованный
вращением половины кругового сегмента АВС шара с радиусом R
вокруг оси Ох, имеет высоту h (рис. 216). Тогда по (15.12) его
объем V равен
365
ЧАСТЬ 3. Элементы стереометрии
ИЛИ
(15.18)
10. Объем шарового слоя. Рассмотрим шаровой слой, образованный
вращением вокруг оси Ох криволинейной трапеции, ограничен-
ной дугой окружности у = *]R2 — х2, прямыми х = аи х = Ьи осью
Ох (рис. 217). Таким образом, а и b — расстояния от центра шара
до секущих плоскостей, R — радиус шара; высоту шарового слоя
обозначим через h = Ь - а. По (15.12) объем V шарового слоя равен
V=K J (Я2 - х2) dx - я (н2х - j V = л(я2&- j -Лга+ j )=
a J а '
= я (й2(& - а) - Ь-^- )= я (в2(& - а) - (Ь ~ а>(Ь^ аЬ + )=
я (tfh - —
ИЛИ
V = nR2h — 5 nh(a2 + ab + Ь2).
О
(15.19)
Если шаровой слой задан радиусами оснований шарового слоя
гг и г2 (Fj > г2) и высотой слоя Л, то его объем может быть вычис-
лен по формуле
V = |«fe(3r2 + 2г| + Л2) (15.20)
Рис. 216 Рис. 217
366
ГЛАВА 15. Объемы многогранников и тел вращения
или
V = |(лг| + nr%)h + |лй3.
(15.21)
11. Объем шарового сектора. Пусть шаровой сектор образован вра-
щением кругового сектора ОАВ вокруг оси Ох (рис. 218). Его
объем можно представить себе как сумму объемов конуса ОВС и
шарового сегмента СВА. Обозначим радиус шара через R и высо-
ту шарового сегмента через h.
Обозначим точку проекции точек В и С на ось Ох через D. Тог-
да (из треугольника ODB) квадрат радиуса основания конуса R
составляет
R2 = R2 - (В - h)2 = 2Rh - h2.
По формулам (15.14) и (15.18) объем V шарового сектора равен
V= = n(2Rh - й2)(Л - Л) + тгЛ2(й - 5 |=
о \ О J
= 5 (2В2/? - 2Rh2 - Rh2 + h3 + 3Rh2 -h3)=^ nR2h
о о
или, если отбросить знак тильды, объем шарового сектора с ради-
усом R и высотой h равен
V= lnR2h.
О
(15.22)
12. Объемы других тел вращения. Приведем примеры вычисления
объемов тел, образованных вращением различных кривых.
Рис. 218
Рис. 219
367
ЧАСТЬ 3. Элементы стереометрии
Рис. 220
Рис. 221
I. Объем тела, образованного вращением вокруг оси Ох фигу-
ры, ограниченной полуволной синусоиды у = sin х на промежут-
ке х е [ 0; л] и осью Ох (рис. 219).
По формуле (15.12)
Я л
vr Г . о j f 1 ~ cosx , л/ sin2x Y л2 z - .
/ = л I sin2 x ax = л I -x--dx = x x---x— I = -x- (куб. ед.).
J J Z Z k Z Л z
о 0 /f0
И. Объем тела, образованного вращением вокруг оси Ох фигу-
ры, ограниченной линиями у2 = 2х, х = 0, х = 2и1/ = 0 (рис. 220).
Такая фигура называется параболоидом вращения.
По формуле (15.12)
е 2
V = п J 2х dx = лх2 о = 4л (куб. ед.).
о
III. Объем тела, образованного вращением вокруг оси Оу фигу-
ры, ограниченной линиями у = х х2, у = 2,I/ = 4 и х = 0 (рис. 221).
По формуле (15.13)
f I4
V = л | 2у dy = пу2 к = 12л (куб. ед.).
2
IV. Объем тела, образованного вращением вокруг оси Ох пло-
щадки, ограниченной полуэллипсом
и осью Ох (рис. 222). Такое тело вращения называется эллипсо-
идом.
368
ГЛАВА 15. Объемы многогранников и тел вращения
Рис. 222
Рис. 223
Из уравнения эллипса следует, что
У2 = “5 О*2 ~ *2)-
Фигура симметрична относительно оси Оу, поэтому вычислим
объем половины фигуры и:
Объем всего эллипсоида составляет
V = 2v = х nab2 (куб. ед.).
V. Объем тела, образованного вращением вокруг оси Ох пло-
щадки, ограниченной гиперболой
и прямыми у = 0, х = 2а (рис. 223). Такое тело вращения называ-
ется гиперболоидом.
Из уравнения гиперболы следует, что
У2 = (*2 “ &2)-
Тогда по формуле (15.12)
13-9664
369
ЧАСТЬ 3. Элементы стереометрии
Рис. 224
VI. Объем тела, образованного вращени-
ем вокруг оси Ох площадки, ограниченной
линиями у2 = 4х и у — х (рис. 224).
Решив систему
I У2 = 4х,
\у = х,
находим точки пересечения параболы и пря-
мой: 0(0; 0) и А(4; 4). Таким образом опреде-
ляем пределы интегрирования: х = 0 и х = 4.
Объем тела вращения представляет собой
разность объемов параболоида, образованно-
го вращением кривой у2 = 4х и конуса, обра-
зованного вращением прямой у = х. Тогда
4 4
V = л J 4х dx - л j
о о
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Объясните, как используется формула для вычисления объема тела по
площади его поперечного сечения.
2. Как вычисляется объем наклонной призмы?
3. Выведите формулу объема пирамиды.
4. Выведите формулу объема усеченной пирамиды.
5. Как вычисляется объем тела вращения?
6. Выведите формулу объема полного и усеченного конусов.
7. Выведите формулу объема шара.
8. Выведите формулы объема шарового сегмента и шарового слоя.
ЧАСТЬ 4. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
ГЛАВА 16. Элементы комбинаторики
и теории вероятностей
§ 93. Элементы комбинаторики
Группы, составленные из каких-либо элементов, называются
соединениями.
Различают три основных вида соединений: размещения, пере-
становки и сочетания.
Задачи, в которых производится подсчет возможных различ-
ных соединений, составленных из конечного числа элементов по
некоторому правилу, называются комбинаторными. Раздел мате-
матики, занимающийся их решением, называется комбинатори-
кой.
1. Размещения. Размещениями из п элементов по т называются
такие соединения, которые отличаются друг от друга либо сами-
ми элементами (хотя бы одним), либо порядком их следования.
Число размещений из п элементов по т обозначается симво-
лом А™ и вычисляется по формуле
А™ = п х (п — 1) х (п — 2)х ... х (п — (т — 1)). (16.1)
2. Перестановки. Перестановками из п элементов называются та-
кие соединения из п элементов, которые отличаются друг от дру-
га лишь порядком следования элементов.
Число перестановок из п элементов обозначается символом Рп.
Перестановки представляют собой частный случай размещения
из п элементов по п в каждом, т. е.
Рп = А* = п х (п - 1) х (п - 2)х ... х 1. (16.2)
Таким образом, число всех перестановок из п элементов равно
произведению последовательных чисел от 1 до п включительно.
Произведение 1 • 2 • ... • п первых натуральных чисел обозначает-
371
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
ся знаком п\ (читается «n-факториал»), причем формально полага-
ют 0! = 1,1!= 1. Поэтому равенство (16.2) можно записать в виде
Рп = и! (16.3)
С использованием формулы (16.3) выражению (16.1) можно
придать вид
Рп = п\
п-т (П ~ 7П)! ’
(16.4)
При решении задач удобно использовать очевидное равенство
А™ + 1 = (л ~ тп) А™.
И ft
(16.5)
3. Сочетания. Сочетаниями из п элементов по т называются такие
соединения, которые отличаются друг от друга хотя бы одним
элементом.
Число сочетаний из п элементов по т обозначается символом
С™ и вычисляется по формуле
С - ТГ • (16.6)
‘ т
которую можно записать также в виде
п!
т\(п — т)!
(16.7)
или
ПХ(п + 1) X ... х (п — (т — 1))
т\
(16.8)
По определению полагают С„ = 1 и С„ = 1. Кроме того, при ре-
шении задач используются формулы, выражающие основные
свойства сочетаний:
С™ = сп-т
(16.9)
(16.10)
♦ ПРИМЕР 1
Найти число размещений: 1) из 10 элементов по 4; 2) из п 4- 4
элементов по п - 2.
РЕШЕНИЕ. Согласно формуле (16.1) получим
1) А*о =10 х 9 х 8 х 7 = 5040;
2) А"= (и 4- 4) х (п + 3) X ... х(п + 4 - (п - 2 - 1)) = (п 4- 4) X
X (п 4-3) X ... х 8 X 7.
372
ГЛАВА 16. Элементы комбинаторики и теории вероятностей
♦ ПРИМЕР?
Решить уравнение А ® = 30 А (4„ _ 2).
РЕШЕНИЕ. Используя формулу (16.1), перепишем уравнение в виде
п (п - 1) ... (и - 4) = 30 (п - 2)(п - 3)(п - 4)(п - 5).
Учитывая, что и > 6, разделим обе части на (п - 2)(и - 3)(п - 4);
имеем п(п - 1) = 30(п - 5), отсюда пг = 6, п2 = 25.
♦ ПРИМЕРЗ
Составить все возможные перестановки из элементов: 1) 1;
2) 5, 6; 3) а, Ъ, с.
РЕШЕНИЕ. 1) (1> : = 1;
2)(5, 6), (6, 5) :Рг = 1-2 = 2;
3) (а, Ь, с), (а, с, д), (д, а, с), (д, с, а), (с, а, d), (с, Ь, а);
=1-2-3 = 6.
О
♦ ПРИМЕР 4
Вычислить значения выражений: 1) 5! + 6!; 2)
4) С4 +С».
РЕШЕНИЕ. 1) 5! + 6! = 5 • 4 • 3 • 2 • 1 + 6 • 5 • 4 • 3 • 2 • 1 = 120 + 720 =
= 840;
Ц; “ 52'50!~ 5°! “ 52 ’ 51 = 2652
3) пс формуле (16.7) получим
£13 =
15 13!(15 - 13)
15- 14-13!
13!-2 - 1
15 • 7 = 105;
4!(6 - 4)!
6-5-4!
4!-2 -1
+ 1 = 15 + 1 = 16.
+ С? =
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие соединения называются размещениями?
2. Выпишите формулу для числа размещений из п элементов по т.
3. Какие соединения называются перестановками?
4. Выпишите формулу для числа перестановок из п элементов.
5. Какие соединения называются сочетаниями?
6. Выпишите формулу для числа сочетаний из п элементов по т.
373
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
§ 94. Элементы теории вероятностей
1. Случайные события, вероятность события. Изучение каждого явле-
ния в порядке наблюдения или производства опыта связано с осу-
ществлением некоторого комплекса условий (испытаний). Вся-
кий результат или исход испытания называется событием.
Если событие при заданных условиях может произойти или не
произойти, то оно называется случайным. В том случае, когда
событие должно непременно произойти, его называют достовер-
ным, а в том случае, когда оно заведомо не может произойти, —
невозможным.
События называются несовместными, если каждый раз воз-
можно появление только одного из них. События называются сов-
местными, если в данных условиях появление одного из этих со-
бытий не исключает появления другого при том же испытании.
События называются противоположными, если в условиях
испытания они, являясь единственными его исходами, несов-
местны.
Вероятность события рассматривается как мера объективной
возможности появления случайного события.
Классическое определение вероятности
Вероятностью события А называется отношение числа исходов
т, благоприятствующих наступлению данного события А, к
числу п всех исходов (несовместных, единственно возможных
и равновозможных), т. е.
Р(А)=^
(16.11)
Вероятность любого события не может быть меньше нуля и
больше единицы, т. е. О < Р (А) < 1. Невозможному событию соот-
ветствует вероятность Р (А) = 0, а достоверному — вероятность
Р(А)=1.
♦ ПРИМЕР 1
В лотерее из 1000 билетов имеются 200 выигрышных. Выни-
мают наугад один билет. Чему равна вероятность того, что
этот билет выигрышный?
РЕШЕНИЕ. Общее число различных исходов есть п = 1000. Число
исходов, благоприятствующих получению выигрыша, составляет
т = 200. Согласно формуле (16.11), получим Р (А) — 200/1000 =
= 1/5 = 0,2.
374
ГЛАВА 16. Элементы комбинаторики и теории вероятностей
♦ ПРИМЕР 2
Из урны, в которой находятся 5 белых и 3 черных шара, выни-
мают один шар. Найти вероятность того, что шар окажется
черным.
РЕШЕНИЕ. Обозначим событие, состоящее в появлении черного ша-
ра, через А. Общее число случаев п = 5 4- 3 = 8. Число случаев тп,
благоприятствующих появлению события А, равно 3. По форму-
ле (16.11) получим Р (А) = т/п = 3/8 — 0,375.
♦ ПРИМЕРЗ
Из урны, в которой находятся 12 белых и 8 черных шаров, вы-
нимают наудачу два шара. Какова вероятность того, что оба
шара окажутся черными?
РЕШЕНИЕ. Обозначим событие, состоящее в появлении двух чер-
ных шаров, через А. Общее число возможных случаев п равно
числу сочетаний из(12 + 8) элементов по два. Тогда
- «ь - «н? - '»»
Число случаев т, благоприятствующих событию А, составляет
По формуле (16.11) находим вероятность появления двух черных
шаров Р (А) = т/п = 28/190 = 14/95 = 0,147.
♦ ПРИМЕР 4
В партии из 18 деталей находятся 4 бракованных. Наугад вы-
бирают 5 деталей. Найти вероятность того, что из этих 5 дета-
лей две окажутся бракованными.
РЕШЕНИЕ. Число всех равновозможных независимых исходов п
равно числу сочетаний из 18 по 5, т. е.
5
18
18 • 17 • 16 • 15 * 14
1-2-3-4-5
= 8568.
Подсчитаем число исходов иг, благоприятствующих событию А.
Среди 5 взятых наугад деталей должно быть 3 качественных и
2 бракованных. Число способов выборки двух бракованных дета-
лей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:
375
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
Число способов выборки трех качественных деталей из 14 имею-
щихся качественных равно
С3 = 14*13* 12 з«л
1*2*3
Любая группа качественных деталей может комбинироваться с
любой группой бракованных деталей, поэтому общее число т
комбинаций составляет
т - С% • С?4 =6*364 = 2184.
Искомая вероятность события А равна отношению числа исхо-
дов т, благоприятствующих этому событию, к числу п всех рав-
новозможных независимых исходов:
Р(А) = 2184/8568 = 0,255.
2. Теоремы сложения вероятностей. Приведем из без доказательств.
ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ НЕСОВМЕСТНЫХ СОБЫТИЙ
Вероятность одного из нескольких попарно несовместных со-
бытий, безразлично какого, равна сумме вероятностей этих со-
бытий:
Р(А 4- В) = Р(А) 4- Р(В); (16.12)
Р(АХ + А2 + ... 4- Ak) = P(AJ 4- Р(А2) + ... + P(Aft). (16.13)
ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ СОВМЕСТНЫХ СОБЫТИЙ
Вероятность появлениях хотя бы одного из двух совместных
событий равна сумме вероятностей этих событий без вероят-
ности их совместного появления:
Р(А 4- В) = Р(А) 4- Р(В) - Р(АВ). (16.14)
Для трех совместных событий имеет место формула
Р(А + В + С) = Р(А) 4- Р(В) 4- Р(С) - Р(АВ) -
- Р(АС) - Р(ВС) 4- Р(АВС). (16.15)
Событие, противоположное событию А (т. е. ненаступление со-
бытия А), обозначают через А. Сумма вероятностей двух противо-
положных событий равна единице
Р(А)4-Р(А)= 1. (16.16)
Вероятность наступления события А, вычисленная в предпо-
ложении, что событие В уже произошло, называется условной
376
ГЛАВА 16. Элементы комбинаторики и теории вероятностей
вероятностью события А при условии В и обозначается через
РВ(А) или Р(А/В)*. Если А и В — независимые события, то
Р(В) - Р(В/А) = Р(В/А). (16.17)
События A, Bt С, ... называются независимыми в совокупнос-
ти, если вероятность каждого из них не меняется в связи с на-
ступлением или ненаступлением других событий по отдельности
или в любой их комбинации.
♦ ПРИМЕР 1
В ящике в случайном порядке разложены 20 деталей, причем
пять из них стандартные. Рабочий берет наудачу три детали.
Найти вероятность того, что по крайней мере одна из взятых
деталей окажется стандартной (событие А).
РЕШЕНИЕ. I СПОСОБ. Очевидно, что по крайней мере одна из взятых
деталей окажется стандартной, если произойдет любое из трех
несовместных событий: В — одна деталь стандартная, две не-
стандартные; С — две детали стандартные, одна нестандартная и
D — три детали стандартные.
Таким образом, событие А можно представить в виде суммы
этих трех событий: А = В + С + D. По теореме сложения имеем
Р(А) — Р(В) 4- Р(С) + P(D). Находим вероятность каждого из этих
событий (см. задачу 4, п. 1):
Р(А) =
15
15-14
20
1-2-3 35.
20 • 19 • 18 76 *
Р(С) =
15
5-4
15
20
20 • 19 • 18 38 ’
Р(Л) =
5-4-3
20 • 19 • 18
20
Сложив найденные величины, получим
114 ’
7б + 38
1 _ 137 - П ЙО1
114 228 °»601*
II СПОСОБ. События А (хотя бы одна из трех взятых деталей оказа-
лась стандартной) и А (ни одна из взятых деталей не оказалась
стандартной) являются противоположными; поэтому Р(А) + Р(А) =
= 1 или Р(А) = 1 - Р(А).
* Читается Р от А при условии В.
377
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
Вероятность появления события А составляет
= 15 °14*13 1-2-3 91
C2Q 1-2-3 ’ 20-19-18 228*
Следовательно, искомая вероятность есть Р(А) = 1 - Р(А) = 1 -
- 91/228 = 137/228 = 0,601.
♦ ПРИМЕР 2
Найти вероятность того, что наудачу взятое двузначное число
окажется кратным либо 3, либо 5, либо тому и другому одно-
временно.
РЕШЕНИЕ. Пусть А — событие, состоящее в том, что наудачу взятое
число кратно 3, а В — в том, что оно кратно 5. Найдем Р(А + В).
Так как А и В — совместные события, то воспользуемся форму-
лой (16.14):
Р(А + В) = Р(А) + Р(В) - Р(АВ).
Всего имеется 90 двузначных чисел: 10, 11,..., 98, 99. Из них
30 являются кратными 3 (благоприятствуют наступлению собы-
тия А); 18 кратными 5 (благоприятствуют наступлению события
В) и 6 — кратными одновременно 3 и 5 (благоприятствуют
наступлению события АВ). Таким образом, Р(А) = 30/90 = 1/3,
Р(В) = 18/90 = 1/5, Р(АВ) = 6/90 = 1/15, т. е. Р(А + В) = 1/3 +
+ 1/5 - 1/15 = 7/15 = 0,467.
3. Теоремы умножения вероятностей. Приведем их также без доказа-
тельств.
ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ НЕЗАВИСИМЫХ СОБЫТИЙ
Вероятность совместного появления (или произведения) двух
независимых событий равна произведению вероятностей этих
событий
Р(АВ) = Р(А) • Р(В). (16.18)
Вероятность появления нескольких событий, независимых в
совокупности, вычисляется по формуле
Р(А1А2 ... Ап) = Р(А,) • Р(А2) •... • Р(АП). (16.19)
ТЕОРЕМА УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ ЗАВИСИМЫХ СОБЫТИЙ
Вероятность совместного появления (или произведения) двух
зависимых событий равна произведению одного из них на ус-
ловную вероятность второго при условии первого:
Р(АВ) = Р(А) • Р(В/А) = Р(В) • Р(А/В). (16.20)
378
ГЛАВА 16. Элементы комбинатооики и теории вероятностей
♦ ПРИМЕР 1
В одной урне находятся 4 белых и 8 черных шаров, в другой —
3 белых и 9 черных. Из каждой урны вынули по шару. Найти
вероятность того, что оба шара окажутся белыми.
РЕШЕНИЕ. Пусть А — появление белого шара из первой урны, а В —
появление белого шара из второй урны. Очевидно, что события
А и В независимы. Найдем Р(А) = 4/12 = 1/3, Р(В) = 3/12 = 1/4.
По формуле (16 20) получим Р(АВ) = Р(А)-Р(В) = (1/3)-(1/4) =
= 1/12 = 0,083.
♦ ПРИМЕР 2
В ящике находится 12 деталей, из которых 8 стандартных. Ра-
бочий берет наудачу одну за другой две детали. Найти вероят-
ность того, что обе детали окажутся стандартными.
РЕШЕНИЕ. Введем следующие обозначения: А — первая взятая де-
таль стандартная; В — вторая взятая деталь стандартная. Веро-
ятность того, что первая деталь стандартная, составляет Р(А) =
= 8/12 = 2/3. Вероятность того, что вторая взятая деталь окажет-
ся стандартной при условии, что была стандартной первая деталь,
т. е. вероятность события В при условии А равна Р(В/А) = 7/11.
Вероятность того, что обе детали окажутся стандартными, на-
ходим по теореме умножения вероятностей зависимых событий:
Р(АВ) = Р(А) • (В/А) == (2/3) • (7/11) = 14/33 = 0,424.
4. Формула полной вероятности. Формула Байеса*. Пусть события (ги-
потезы) Вр В2, ..., Вп образуют полную группу событий и при на-
ступлении каждого из них, например В., событие А может насту-
пить с некоторой условной вероятностью Р(А/В£). Тогда вероят-
ность наступления события А равна сумме произведений
вероятностей каждой из гипотез на соответствующую условную
вероятность события А:
Р(А) = Р(ВХ) • Р(А/В;) + Р(В2) • Р(А/В2) + ... +
+ Р(В„) • Р(А/ВП). (16.21)
Здесь Р(ВГ) + Р(В2) + ... + P(Bn) = 1. Формула (16.21) называется
формулой полной вероятности.
* Байес Томас {Bayes Thomas, 1702—1761) — английский матема-
тик и философ.
379
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
Пусть событие А может наступить лишь при условии появле-
ния одного из несовместных событий (гипотез) Bv В2, ...» Вп9 ко-
торые образуют полную группу событий. Если событие А уже
произошло, то вероятности гипотез могут быть переоценены до
формуле вероятности гипотез
Р(В£) • P(A/BJ
Р(В‘/4) “ ' Р(Л) ’ (1б‘22)
которая носит также название формулы Байеса. Здесь Р(В./А) —
вероятность каждой из гипотез после испытания, в результате
которого наступило событие A; P(A/Bi) — условная вероятность
события А после наступления события В,, а Р(А) находится по
♦*
формуле полной вероятности (16.21).
♦ ПРИМЕР 1
На склад поступили детали с трех станков. На первом станке
изготовлено 40% деталей от их общего количества, на втором —
35% и на третьем 25%, причем на первом станке было изго-
товлено 90% деталей первого сорта, на втором — 80% и на
третьем — 70%. Какова вероятность того, что взятая наугад
деталь окажется первого сорта?
РЕШЕНИЕ. Введем следующие обозначения: Вх — деталь изготовле-
на на первом станке, В2 — на втором станке и В3 — на третьем стан-
ке; событие А — деталь оказалась первого сорта. Из условия сле-
дует, что Р(ВХ) = 0,4, Р(В2) = 0,35, Р(В3) = 0,25, Р(А/ВХ) = 0,9,
Р(А/В2) = 0,8 и Р(А/В3) = 0,7 Следовательно,
Р(А) = Р(ВХ) • Р(А/ВХ) + Р(В2) • Р(А/В2) + Р(В3) • Р(А/В3) =
= 0,4 • 0,9 + 0,35 • 0,8 + 0,25 • 0,7 = 0,815.
♦ ПРИМЕР 2
В первом ящике имеются 8 белых и 6 черных шаров, а во вто-
ром — 10 белых и 4 черных. Наугад выбирают ящик и шар.
Известно, что вынутый шар — черный. Найти вероятность то-
го, что был выбран первый ящик.
РЕШЕНИЕ. Введем обозначения: Вх — был выбран первый ящик; В2 —
был выбран второй ящик; А — при проведении двух последователь-
ных испытаний выбора ящика и выбора шара был вынут черный
шар. Тогда Р(ВХ) = 1/2, Р(В2) = 1/2. Вероятность извлечения черно-
го шара после того, как выбран первый ящик, составляет Р(А/ВХ) =
380
ГЛАВА 16. Элементы комбинаторики и теории вероятностей
= 6/14 = 3/7. Вероятность извлечения черного шара после того, как
выбран второй ящик, равна Р(А/В2) = 4/14 = 2/7.
По формуле полной вероятности находим вероятность того,
что вынутый шар оказался черным:
Р(А) = P(BJ • Р(А/ВХ) + Р(В2) • Р(А/В2) =
= (1/2) • (3/7) + (1/2) • (2/7) = 5/14.
Искомая вероятность того, что черный шар был вынут из пер-
вого ящика, вычисляется по формуле Байеса:
Р(ВТ/А) =
PCBJ-PCA/Bj) _ (1/2)-(3/7) _3
Р(А) 5/14 5
= 0,6.
5. Повторение испытаний. Формула Бернулли. Если производятся ис-
пытания, при которых вероятность появления события А в каж-
дом испытании не зависит от исходов других испытаний, то та-
кие испытания называются независимыми относительно со-
бытия А.
Вероятность того, что в п независимых испытаниях, в каждом
из которых вероятность появления события А равна р (где 0 <р < 1),
событие А наступит ровно k раз (безразлично, в какой последова-
тельности), находится по формуле Бернулли:
?„(*) = "! ьч, • Рк^к = СпРКЧп ' (16.22)
к!(71 ~ к)!
гдед = 1 -р.
♦ ПРИМЕР
Вероятность попадания в цель при одном выстреле составляет
р = 0,8. Найти вероятность четырех попаданий при шести вы-
стрелах.
РЕШЕНИЕ. Здесь п = 6, k = 4, р = 0,8, q = 0,2. По формуле Бернулли
находим
Рб(4) =
6!
4!(6 - 4)!
• (0,8)4 • (0,2)4 • (0,2)6-4 =
= • (0,8)4 • (0,2)2 = 0,246.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. Какие случайные события называются достоверными и какие невоз-
можными?
2. Какие события называются несовместными?
381
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
3. Какие события называются совместными?
4. Какие события называются противоположными?
5. Дайте классическое определение вероятности.
6. Сформулируйте теорему сложения вероятностей несовместных собы-
тий.
7. Сформулируйте теорему сложения вероятностей совместных событий.
8. Чему равна сумма вероятностей двух противоположных событий?
9. Что называется условной вероятностью события?
10. Какие события в совокупности называются независимыми?
11. Сформулируйте теорему умножения вероятностей независимых событий.
12. Сформулируйте теорему умножения вероятностей зависимых событий.
ГЛАВА 17. Элементы математической
статистики
§ 95. Основные задачи и понятия
1. Задачи математической статистики*. Установление закономернос-
тей, которым подчинены массовые случайные явления, основано
на изучении статистических данных — результатах наблюдений.
Первая задача математической статистики — указать способы
сбора и группировки (если данных очень много) статистических
сведений.
Вторая задача математической статистики — разработать ме-
тоды анализа статистических данных в зависимости от целей ис-
следования.
Изучение тех или иных явлений методами математической
статистики служит средством решения многих вопросов, выдви-
гаемых наукой и практикой (правильная организация технологи-
ческого процесса, наиболее целесообразное планирование и др.).
Итак, основная задача математической статистики состоит в
создании методов сбора и обработки статистических данных для
получения научных и практических выводов.
2. Генеральная и выборочная совокупности. Пусть требуется изучить
совокупность однородных объектов относительно некоторого ка-
* Термин «статистика» происходит от латинского слова status — со-
стояние.
382
ГЛАВА 17. Элементы математической статистики
чественного или количественного признака, характеризующе-
го эти объекты. Например, если имеется партия деталей, то каче-
ственным признаком может служить стандартность детали, а ко-
личественным — контролируемый размер детали.
Иногда проводят сплошное обследование, т. е. обследуют каж-
дый из объектов совокупности относительно признака, которым
интересуются. На практике, однако, сплошное обследование при-
меняется сравнительно редко. Например, если совокупность со-
держит очень большое число объектов, то провести сплошное об-
следование физически невозможно. Если обследование объекта
связано с его уничтожением или требует больших материальных
затрат, то проводить сплошное обследование практически не име-
ет смысла. В таких случаях случайно отбирают из всей совокуп-
ности ограниченное число объектов и подвергают их изучению.
Выборочной совокупностью или просто выборкой называют
совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объек-
тов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) назы-
вают число объектов этой совокупности. Например, если из 1000
деталей отобрано для обследования 100 деталей, то объем гене-
ральной совокупности N — 1000, а объем выборки п = 100.
Замечание. Часто генеральная совокупность содержит конечное чис-
ло объектов. Однако если это число достаточно велико, то иногда в целях
упрощения вычислений или для облегчения теоретических выводов до-
пускают, что генеральная совокупность состоит из бесчисленного мно-
жества объектов. Такое допущение оправдывается тем, что увеличение
объема генеральной совокупности (достаточно большого объема) практи-
чески не сказывается на результатах обработки данных выборки.
3. Выборка с возвращением и без возвращения. Репрезентативная вы-
борка. При составлении выборки можно поступать двояко: после
того как объект отобран и над ним произведено наблюдение, он
может быть либо возвращен, либо не возвращен в генеральную
совокупность. В соответствии со сказанным выборки подразделя-
ют на выборки с возвращением и без возвращения.
Выборкой с возвращением называют выборку, при которой
отобранный объект (перед отбором следующего) возвращается в
генеральную совокупность.
Выборкой без возвращения называют выборку, при которой
отобранный объект в генеральную совокупность не возвраща-
ется.
383
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
На практике обычно пользуются выборкой без возвращения.
Для того, чтобы по данным выборки можно было достаточно
уверенно судить об интересующем нас признаке генеральной со-
вокупности, необходимо, чтобы объекты выборки правильно его
представляли. Это требование коротко формулируют так: выбор-
ка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка
будет репрезентативной, если ее осуществить случайно: каждый
объект выборки отобран случайно из генеральной совокупности,
если все объекты имеют одинаковую вероятность попасть в вы-
борку.
Если объем генеральной совокупности достаточно велик, а вы-
борка составляет лишь незначительную часть этой совокупности,
то различие между выборкой с возвращением и без возвращения
стирается; в предельном случае, когда рассматривается бесконеч-
ная генеральная совокупность, а выборка имеет конечный объем,
это различие исчезает.
4. Способы отбора. На практике применяются различные способы
отбора. Принципиально эти способы можно подразделить на два
вида.
1. Отбор, не требующий расчленения генеральной совокупнос-
ти на части, к нему относятся:
а) простой случайный бесповторный отбор;
б) простой случайный повторный отбор.
2. Отбор, при котором генеральная совокупность разбивается
на части, к нему относятся:
а) типический отбор;
б) механический отбор;
в) серийный отбор.
Простым случайным называют такой отбор, при котором
объекты извлекают по одному из всей генеральной совокупности.
Осуществить простой отбор можно различными способами. На-
пример, для извлечения п объектов из генеральной совокупности
объема N поступают так: выписывают номера от 1 до N на кар-
точках, которые тщательно перемешивают и наугад вынимают
одну карточку; объект, имеющий одинаковый номер с извлечен
ной карточкой, подвергают обследованию; затем карточка воз-
вращается в пачку и процесс повторяется, т. е. карточки переме-
шиваются, наугад вынимают одну из них и т. д. Так поступают п
раз; в итоге получают простую случайную выборку с возвращени-
ем объема и.
384
ГЛАВА 17. Элементы математической статистики
Если извлеченные карточки не возвращать в пачку, то выбор-
ка будет простой случайной без возвращения.
При большом объеме генеральной совокупности описанный
процесс оказывается очень трудоемким. В этом случае пользуют-
ся готовыми таблицами «случайных чисел», в которых числа
расположены в случайном порядке. Для того чтобы отобрать, на-
пример, 50 объектов из пронумерованной генеральной совокуп-
ности, открывают любую страницу таблицы случайных чисел и
выписывают подряд 50 чисел; в выборку попадают те объекты,
номера которых совпадают с выписанными случайными числа-
ми. Если окажется, что случайное число таблицы превышает
число N, то такое случайное число пропускают. При осуществле-
нии выборки без возвращения случайные числа таблицы, уже
встречавшиеся ранее, следует также пропустить.
Типическим называют отбор, при котором объекты отбирают-
ся не из всей генеральной совокупности, а из каждой ее «типиче-
ской» части. Например, если детали изготовляют на нескольких
станках, то отбор производят не из всей совокупности деталей,
произведенных всеми станками, а из продукции каждого станка
в отдельности. Типическим отбором пользуются тогда, когда об-
следуемый признак заметно колеблется в различных типических
частях генеральной совокупности. Например, если продукция
изготовляется на нескольких машинах, среди которых есть более
и менее изношенные, то здесь типический отбор целесообразен.
Механическим называют отбор, при котором генеральная со-
вокупность «механически» делится на столько групп, сколько
объектов должно войти в выборку, и из каждой группы отбирает-
ся один объект.
Например, если нужно отобрать 20% изготовленных станком
деталей, то отбирают каждую пятую деталь; если требуется ото-
брать 5% деталей, то отбирают каждую двадцатую деталь и т. д.
Следует указать, что иногда механический отбор может не
обеспечить репрезентативности выборки. Например, если отби-
рается каждый двадцатый обтачиваемый валик, причем сразу же
после отбора производят замену резца, то отобранными окажутся
все валики, обточенные затупленными резцами. В таком случае
надо устранить совпадение ритма отбора с ритмом замены резца,
для чего надо отбирать, скажем, каждый десятый валик из двад-
цати обточенных.
Серийным называют отбор, при котором объекты отбирают из
генеральной совокупности не по одному, а «сериями», подверга-
385
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
ющимися сплошному обследованию. Например, если изделия из-
готовляются большой группой станков-автоматов, то подвергают
сплошному обследованию продукцию только нескольких стан-
ков. Серийным отбором пользуются тогда, когда обследуемый
признак колеблется в различных сериях незначительно.
Подчеркнем, что на практике часто применяется комбиниро-
ванный отбор, при котором сочетаются указанные выше способы.
Например, иногда разбивают генеральную совокупность на се-
рии одинакового объема, затем простым случайным отбором вы-
бирают несколько серий и, наконец, из каждой серии простым
случайным отбором извлекают отдельные объекты.
§ 96. Статистическое распределение выборки
1. Основные понятия. Пусть из генеральной совокупности извлече-
на выборка, причем х1 наблюдалось п1 раз, х2 наблюдалось п2 раз,
xk наблюдалось nk раз и — п — объем выборки. Наблюдаемые
значения х. называют вариантами, а последовательность вари-
ант, записанных в возрастающем порядке, — вариационным ря-
дом. Числа наблюдений называют частотами, а их отношения к
объему выборки nx/n = Wi — относительными частотами.
Статистическим распределением выборки называют пере-
чень вариант и соответствующих им частот или относительных
частот. Статистическое распределение можно задать также в ви-
де последовательности интервалов и соответствующих им частот
(в качестве частоты, соответствующей интервалу, принимают
сумму частот, попавших в этот интервал).
Заметим, что в теории вероятностей под распределением по-
нимают соответствие между возможными значениями случайной
величины и их вероятностями, а в математической статистике —
соответствие между наблюдаемыми вариантами и их частотами,
или относительными частотами.
♦ ПРИМЕР
Составить распределение относительных частот, если задано
распределение частот выборки объема п = 20:
xt 2 6 12
"i 3 10 7
386
ГЛАВА 17. Элементы математической статистики
РЕШЕНИЕ. Найдем относительные частоты, для чего разделим час-
тоты на объем выборки:
~ - 0,15; W2 - = 0,50; W3 = - 0,35.
Составим распределение относительных частот:
*1 2 6 12
0.15 0.5 0,35
Сумма относительных частот составляет 0,15 4- 0,5 4- 0,35 = 1.
2. Эмпирическая функция распределения. Пусть известно статисти-
ческое распределение частот количественного признака X. Вве-
дем обозначения: пх — число наблюдений, при которых наблюда-
лось значение признака меньше х, п — общее число наблюдений
(объем выборки).
Относительная частота события X < х равна пх/п. Если х будет
изменяться, то, вообще говоря, будет изменяться и относитель-
ная частота, т. е. относительная частота пх/п есть функция от х.
Так как эта функция находится эмпирическим (опытным) путем,
то ее называют эмпирической.
Эмпирической функцией распределения (функцией распре-
деления выборки) называют функцию F*(x), определяющую для
каждого значения х относительную частоту события X < х.
Итак, по определению
f *(Х) = ,
где пх — число вариант, меньших х, п — объем выборки.
Таким образом, для того чтобы найти, например, F*(x2), надо
число вариант, меньших х2, разделить на объем выборки:
FW = V '
В отличие от эмпирической функции распределения выборки
интегральную функцию F(x) распределения генеральной сово-
купности называют теоретической функцией распределения.
Различие между эмпирической и теоретической функциями со-
стоит в том, что теоретическая функция F(x) определяет вероят-
ность события X < х, а эмпирическая функция F*(x) определяет
387
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
относительную частоту этого же события. Из теоремы Бернулли
следует, что относительная частота события X < х, т. е. F*(x)
стремится по вероятности к вероятности F(x) этого события. Дру-
гими словами, числа F*(x) и F(x) мало отличаются одно от друго-
го. Уже отсюда следует целесообразность использования эмпири-
ческой функции распределения выборки для приближенного
представления теоретической (интегральной) функции распреде-
ления генеральной совокупности.
Такое заключение подтверждается и тем, что F*(x) обладает
всеми свойствами F(x). Действительно, из определения функции
F*(x) вытекают следующие ее свойства:
1) значения эмпирической функции принадлежат отрезку [0,1];
2) F*(x) — неубывающая функция;
3) если хх — наименьшая варианта, то F*(x) = 0 при х < хх;
если xk — наибольшая варианта, то F*(x) = 1 при х > xk.
Итак, эмпирическая функция распределения выборки служит
для оценки теоретической функции распределения генеральной
совокупности.
♦ ПРИМЕР
Построить эмпирическую функцию по данному распределе-
нию выборки:
варианты х
частоты п.
РЕШЕНИЕ. Найдем объем выборки: 12 + 18 + 30 = 60. Наименьшая
варианта равна 2, следовательно, при х < 2
^*(х) = 0.
Значение X < 6, а именно хх = 2 наблюдалось 12 раз; следова-
тельно, при 2 < х < 6
Значения X < 10, а именно х1 = 2 и х2 = 6 наблюдались 12 + 18 =
= 30 раз; следовательно, при 6 < х < 10
F *(х) = = 0,5.
Так как х = 10 — наибольшая варианта, то при х > 10
F*(x) = 1.
388
ГЛАВА 17. Элементы математической статистики
1,2-
6,8 -
0,4
2 4
6 8 10 12 14
Рис. 225
Искомая эмпирическая функция
Г*(х) = <
О при х < 2,
0,2 при 2 <х < 6,
0,5 при 6 < х < 10
1 при х > 10.
График этой функции изображен на рисунке 225.
3. Полигон и гистограмма. В целях наглядности строят различные
графики статистического распределения и, в частности, полигон
и гистограмму.
Полигоном частот называют ломаную, отрезки которой со-
единяют точки (хр Hj), (х2, и2),..., (xk, nk). Для построения поли-
гона частот на оси абсцисс откладывают варианты хр а на оси ор-
динат — соответствующие им частоты nf. Точки (хр щ) соединя-
ют отрезками прямых и получают полигон частот.
Полигоном относительных частот называют ломаную, от-
резки которой соединяют точки (хр W’1), (х2, W2), ..., (xft, VTfc).
Для построения полигона относительных частот на оси абсцисс
откладывают варианты х;, а на оси ординат соответствующие им
относительные частоты ИЛ. Точки (хр W.) соединяют отрезками
прямых и получают полигон относительных частот.
На рисунке 226 изображен полигон относительных частот сле-
дующего распределения:
389
ЧАСТЬ 4. Элементы теории вероятностей и математической статистики
В случае непрерывного признака целесообразно строить гис-
тограмму, для чего интервал, в котором заключены все наблю-
даемые значения признака, разбивают на несколько частичных
интервалов длиной h и находят для каждого частичного интерва-
ла nt — сумму частот вариант, попавших в i-й интервал.
Гистограммой частот называют ступенчатую фигуру, со-
стоящую из прямоугольников, основаниями которых служат час-
тичные интервалы длиной h, а высоты равны отношению п2/Л
(плотность частоты).
Для построения гистограммы частот на оси абсцисс отклады-
вают частичные интервалы, а над ними проводят отрезки, парал-
лельные оси абсцисс на расстоянии njh.
390
ГЛАВА 17. Элементы математической статистики
ni
Площадь i-ro прямоугольника равна h ° ~г = п> — сумме частот
it
вариант i-ro интервала; следовательно, площадь гистограммы
частот равна сумме всех частот, т. е. объему выборки.
На рисунке 227 изображена гистограмма частот распределе-
ния объема п = 100, приведенного в таблице 6.
Таблица 6
Частичный интервал длиной h = 5 Сумма частот вариант частичного интервала nt ni Плотность частоты — П
5-10 4 0,8
10-15 6 1,2
15-20 16 3,2
20-25 36 7,2
25-30 24 4,8
30-35 10 2,0
35-40 4 0,8
Гистограммой относительных частот называют ступен-
чатую фигуру, состоящую из прямоугольников, основаниями ко-
торых служат интервалы длиною Л, а высоты равны отношению
WJh (плотность относительной частоты).
Для построения гистограммы относительных частот на оси
абсцисс откладывают интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии WJh. Площадь i-ro пря-
wi
моугольника равна h • = Wt — относительной частоте вариант,
попавших в i-й интервал. Следовательно, площадь гистограм-
мы относительных частот равна сумме всех относительных
частот, т. е. единице.
ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ
1. В чем заключается задача математической статистики?
2. Что называется выборкой?
3. Дайте определения генеральной созокупности и объема совокупности.
4. Как различаются выборка с возвращением и выборка без возвращения?
5. Охарактеризуйте возможные способы выбора.
6. Дайте определение эмпирической функции распределения.
7. Что называется полигоном частот и гистограммой частот?
391
Оглавление
Предисловие ..................................... 3
Математические обозначения....................... 4
Латинский алфавит................................ 7
Греческий алфавит................................ 7
ЧАСТЬ 1. АЛГЕБРА И НАЧАЛА АНАЛИЗА
ГЛАВА 1. ЛИНЕЙНЫЕ И КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА.
ЭЛЕМЕНТЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
§ 1. Рациональные числа. Иррациональные числа.
Понятие о мнимых и комплексных числах........................................... 8
§ 2. Метод координат. 25
§ 3. Погрешности приближенных значений чисел....... 26
§ 4. Действия над приближенными значениями чисел. 32
§ 5. Линейные уравнения с одной переменной. 39
§ 6. Линейные неравенства. 48
§ 7. Системы линейных уравнений........................... 57
§ 8. Квадратные уравнения........................... 68
§ 9. График квадратной функции. Графическое решение
квадратного уравнения.......................... 80
§ 10. Квадратные неравенства. Решение неравенств
методом промежутков................................. 88
§ 11. Иррациональные уравнения и иррациональные
неравенства......................................... 94
§ 12. Нелинейные системы уравнений
с двумя переменными................................. 98
§ 13. Простейшие задачи линейного программирования
с двумя переменными................................. 99
ГЛАВА 2. ФУНКЦИИ. СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ
И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
§ 14. Функции и их основные свойства............. 103
§ 15. Степенная функция.......................... 106
392
§ 16. Показательная функция......................... ПО
§ 17. Логарифмическая функция...................... 111
§ 18. Показательные уравнения.
Системы показательных уравнений............... 119
§ 19. Показательные неравенства.................... 122
§ 20. Логарифмические уравнения. Системы
логарифмических уравнений..................... 123
§ 21. Логарифмические неравенства.................. 125
ГЛАВА 3. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
§ 22. Радианное измерение дуг и углов.............. 126
§ 23. Обобщение понятия дуги (угла)................ 131
§ 24. Тригонометрические функции числового
аргумента..................................... 135
§ 25. Знаки, числовые значения и свойства четности
и нечетности тригонометрических функций............ 139
§ 26. Изменение тригонометрических функций
при возрастании аргумента от 0 до 2я............... 143
§ 27. Основные тригонометрические тождества........ 144
§ 28. Выражение тригонометрических функций
через другие тригонометрические функции............ 146
§29. Периодичность тригонометрических функций...... 149
§ 30. Формулы приведения........................... 151
§ 31. Тригонометрические функции алгебраической
суммы двух аргументов (формулы сложения)............ 157
§ 32. Тригонометрические функции удвоенного
аргумента.......................................... 160
§ 33. Тригонометрические функции половинного
аргумента.......................................... 162
§ 34. Выражение тригонометрических функций через
тангенс половинного аргумента...................... 164
§ 35. Преобразование произведения тригонометрических
функций в сумму.................................... 165
§ 36. Преобразование алгебраической суммы
тригонометрических функций в произведение........... 167
§ 37. Свойства тригонометрических функций
и их графики....................................... 171
§38. Обратные тригонометрические функции.......... 178
§ 39. Построение дуги (угла) по данному значению
тригонометрической функции. Простейшие
тригонометрические уравнения....................... 181
393
§ 40. Тригонометрическиеуравнения .................186
§ 41. Тригонометрические неравенства............. 192
ГЛАВА 4. ПРЕДЕЛЫ
§ 42. Предел переменной величины.................. 193
§ 43. Предел функции...............................202
§ 44. Непрерывность функции........................208
ГЛАВА 5. ПРОИЗВОДНАЯ
§ 45. Скорость изменения функции.................. 211
§ 46. Производная функции......................... 213
§ 47. Формулы дифференцирования................... 217
§ 48. Геометрические приложения производной........224
§ 49. Физические приложения производной............226
§ 50. Производные тригонометрических функций.......228
§ 51. Производные обратных тригонометрических
функций.......................................230
§ 52. Производная логарифмической функции..........233
§ 53. Производные показательных функций............234
§ 54. Производная второго порядка. Физический
смысл производной второго порядка.............236
ГЛАВА 6. ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
§ 55. Возрастание и убывание функций...............238
§ 56. Исследование функций на максимум и минимум...239
§ 57. Направление выпуклости графика...............246
§ 58. Точки перегиба...............................248
ГЛАВА 7. ДИФФЕРЕНЦИАЛ ФУНКЦИИ. ПРИЛОЖЕНИЕ
ДИФФЕРЕНЦИАЛА К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
§ 59. Сравнение бесконечно малых величин...........250
§ 60. Дифференциал функции........................ 251
§ 61. Приложение дифференциала к приближенным
вычислениям ..................................254
ГЛАВА 8. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 62. Неопределенный интегоал и его
простейшие свойства................................ 261
§ 63. Непосредственное интегрирование..............265
394
§ 64. Геометрические приложения
неопределенного интеграла...........................268
§ 65. Физические приложения неопределенного
интеграла...........................................270
ГЛАВА 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 66. Основные свойства и вычисление
определенного интеграла............................ 271
§ 67. Физические приложения определенного интеграла ... 278
§68. Понятие о дифференциальном уравнении..........282
ЧАСТЬ 2. ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
ГЛАВА 10. ПРЯМАЯ НА ПЛОСКОСТИ И ЕЕ УРАВНЕНИЯ
§ 69. Векторы на плоскости. Основные понятия
и определения..................................288
§ 70. Метод координат...............................298
§ 71. Уравнения прямых..............................300
§ 72. Системы прямых................................304
ГЛАВА 11. КРИВЫЕ ВТОРОГО ПОРЯДКА
§ 73. Окружность....................................309
§ 74. Эллипс....................................... 311
§ 75. Гипербола.................................... 313
§ 76. Парабола..................................... 317
ЧАСТЬ 3. ЭЛЕМЕНТЫ СТЕРЕОМЕТРИИ
ГЛАВА 12. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
§ 77. Основные понятия стереометрии.................320
§ 78. Параллельность прямой и плоскости.
Параллельные плоскости.............................323
§ 79. Перпендикулярные прямые и плоскости...........326
§80. Двугранные и многогранные углы................329
ГЛАВА 13. МНОГОГРАННИКИ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
§ 81. Многогранники и их основные свойства..........334
§ 82. Параллелепипед................................336
§ 83. Пирамида..................................... 337
395
§84. Площади поверхностей многогранников.......... 341
§ 85. Правильные многогранники......................343
ГЛАВА 14. ФИГУРЫ ВРАЩЕНИЯ И ПЛОЩАДИ ИХ ПОВЕРХНОСТЕЙ
§ 86. Цилиндр.......................................344
§ 87. Конус.........................................346
§ 88. Усеченный конус.............................. 347
§ 89. Сфера и шар...................................349
§ 90. Площадь поверхности сферы и ее частей........ 351
ГЛАВА 15. ОБЪЕМЫ МНОГОГРАННИКОВ И ТЕЛ ВРАЩЕНИЯ
§ 91. Объемы прямых параллелепипедов,
призмы и цилиндра...................................356
§ 92. Объем геометрической фигуры с заданными
площадями поперечных сечений........................360
ЧАСТЬ 4. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ
СТАТИСТИКИ
ГЛАВА 16. ЭЛЕМЕНТЫ КОМБИНАТОРИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
§ 93. Элементы комбинаторики ...................... 371
§ 94. Элементы теории вероятностей................. 374
ГЛАВА 17. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
§ 95. Основные задачи и понятия ....................382
§ 96. Статистическое распределение выборки..........386
Учебное издание
Богомолов Николай Васильевич
Самойленко Петр Иванович
МАТЕМАТИКА
Зав. редакцией Т. Д. Гамбурцева
Редактор Е. А. Вольмир
Художественное оформление А. А. Абрамова
Технический редактор Н. И. Герасимова
Компьютерная верстка Т. В. Рыбина
Корректор Н. С. Соболева
Санитарно-эпидемиологическое заключение
№ 77.99.60.953.Д.010105.09.08 от 22.09.2008.
Подписано к печати 12.02.10. Формат 60 х 90 */16-
Бумага типографская. Гарнитура «Школьная». Печать офсетная.
Усл. печ. л. 25,0. Тираж 6000 экз. Заказ № 9664.
(ХЮ «Дрофа».
127018, Москва, Сущевский вал, 49.
По вопросам приобретения продукции
издательства «Дрофа» обращаться по адресу:
127018, Москва, Сущевский вал, 49.
Тел.: (495) 795-05-50, 795-05-51. Факс: (495) 795-05-52.
Торговый дом «Школьник».
109172, Москва, ул. Малые Каменщики, д. 6, стр. 1А.
Тел.: (495) 911-70-24, 912-15-16, 912-45-76.
Сеть магазинов «Переплетные птицы».
Тел.: (495) 912-45-76.
Интернет-магазин: http://www.drofa.ru
Отпечатано с предоставленных диапозитивов
в ОАО «Тульская типография». 300600, г. Тула, пр. Ленина, 109.