Текст
Сборник задач по сопротивлению материалов
f
ПОД РЕДАКЦИЕЙ В. К.КАЧУРИНА
СБОРНИК ЗАДАЧ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
Под редакцией
В. к. КАЧУРИНА
Допущено Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
физико-математической литературы
МОСКВА 1970
С95
С 23
УДК 620.10
КОЛЛЕКТИВ АВТОРОВ?
Н. М. БЕЛЯЕВ, Л. А. БЕЛЯВСКИЙ, Я. И. КИПНИС, Н. Ю. КУШЕЛЕВ и А. К. СИНИЦКИЙ
Сборник задач по сопротивлению материалов под редакцией В. К- Кач урина. Главная редакция физико-математической литературы изд-ва «Наука», М., 1970, 432 стр.
В сборнике представлены задачи иа все основные разделы курса сопротивления материалов: растяжение — сжатие, сложное напряженное состояние и теории прочности, сдвиг и смятие, кручение, изгиб, сложное сопротивление, кривые стержни, устойчивость элементов конструкций, методы расчета по допускаемым нагрузкам и по предельным состояниям, динамическое и длительное действие нагрузок.
Всего в сборнике 888 задач, часть из которых со многими вариантами. Все задачи даны с ответами. Некоторые задачи снабжены решениями или указаниями.
Рисунков 612, таблиц 9.
Николай Михайлович Беляев, Лев Александрович Белявский. Яков Исаевич Кипнис. Никита Юрьевич Кушелее и Анатолий Константинович Синицкий СБОРНИК ЗАДАЧ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
М., 1970 г., 432 стр. с илл.
Редактор И. К. Снитко
Техн, редактор С. Я- Шкляр Корректор И. Б. Мамулова
> - — — Сдано и набор 26/V1 1970 г. Подписано к печати 13/Х1 1970 г. Бумага 60x90*/,.. Физ. печ. л. 27. Услоан. печ. л. 27. Уч.-нзд. л. 27.01. Тираж 250 000 экз. Т-15496.
Цена книги 86 коп. Заказ А» 1268.
Издательство «Наука» Главная редакция физико-математической литературы. Москва. В-71. Ленинский проспект, 15.
Ордена Трудового Красного Знамени Первая Образцовая типография имени А. А. Ждаксв.-, Главио.тнграфирома Комитета по печати при Совете Министров СССР Москва, М-54, Валовая, 28
15-70
ОГЛАВЛЕНИЕ
Предисловие......................................................... 5
Таблица перевода единиц силы и напряжения системы СГС в систему СИ 6
Общие для всех задач данные......................................... 6
Глава 1. Осевое растяжение и сжатие................................. 7
§ 1. Статически определимые системы.......................... 7
§ 2. Статически неопределимые системы.........................25
§ 3. Учет собственного весв...................................46
§ 4. Гибкие нити..............................................50
Глава 2. Сложное напряженное состояние. Теории прочности..........55
§ 5. Аналитические и графические методы определения напряжений 5Q.
§ 6. Деформации. Потенциальная энергия......................61
| 7. Тонкостенные сосуды.....................................65
§ 8. Контактные напряжения..................................72
Г л в в а 3. Сдвиг и смятие..........................................74
§ 9. Болтовые и заклепочные соединения........................74
§ 10. Сварные соединении..................................... 80
§11. Врубки, шпонки, другие элементы конструкций..............83
Г л в в а 4. Кручение...............................................88
§ 12. Кручение стержней круглого сечения......................88
§ 13. Кручение стержней прямоугольного сечения................96
§ 14. Винтовые пружины с малым шагом ........................98
§ 15. Конструкции, работающие на сдвиг и на кручение.........102
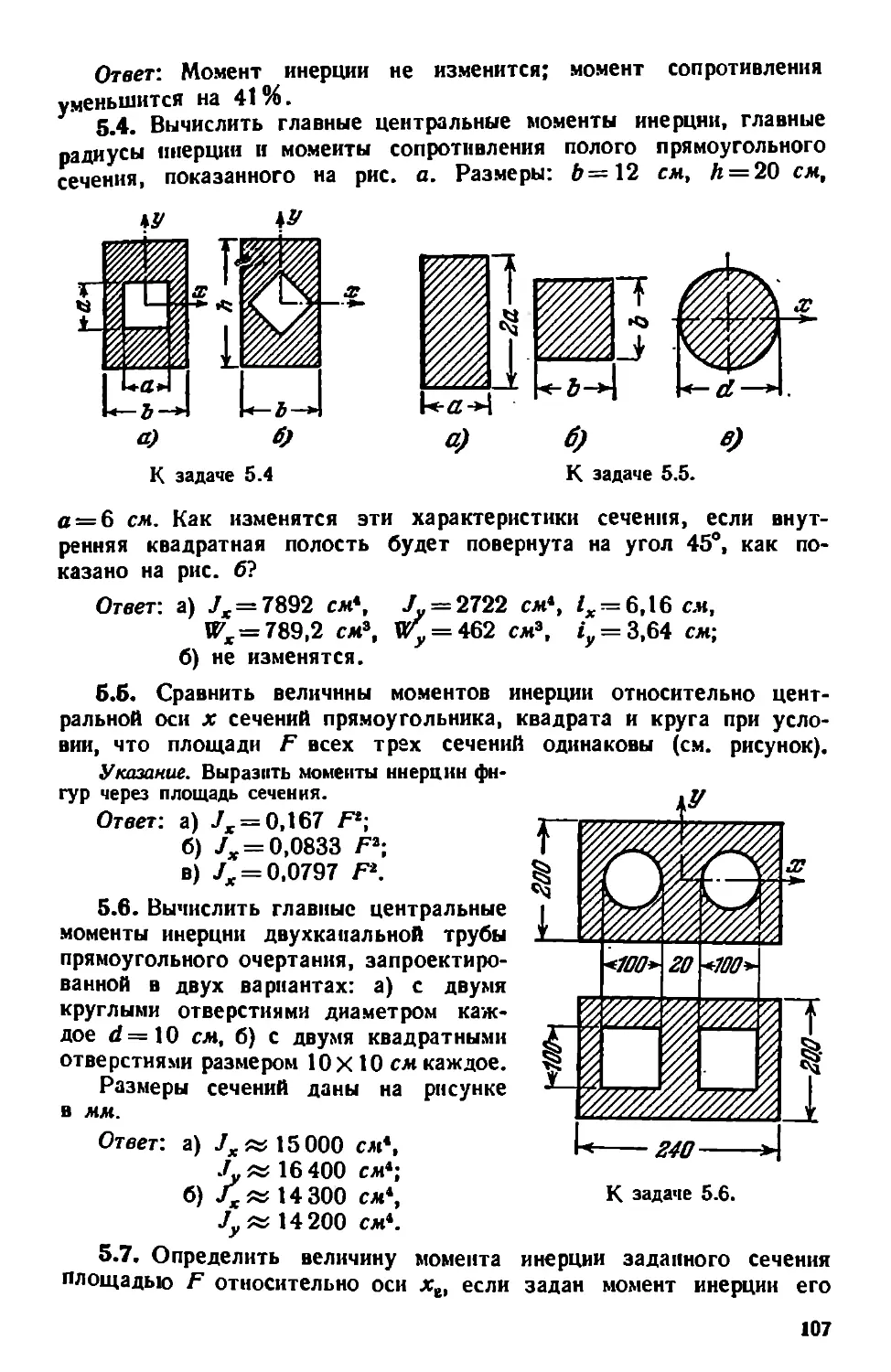
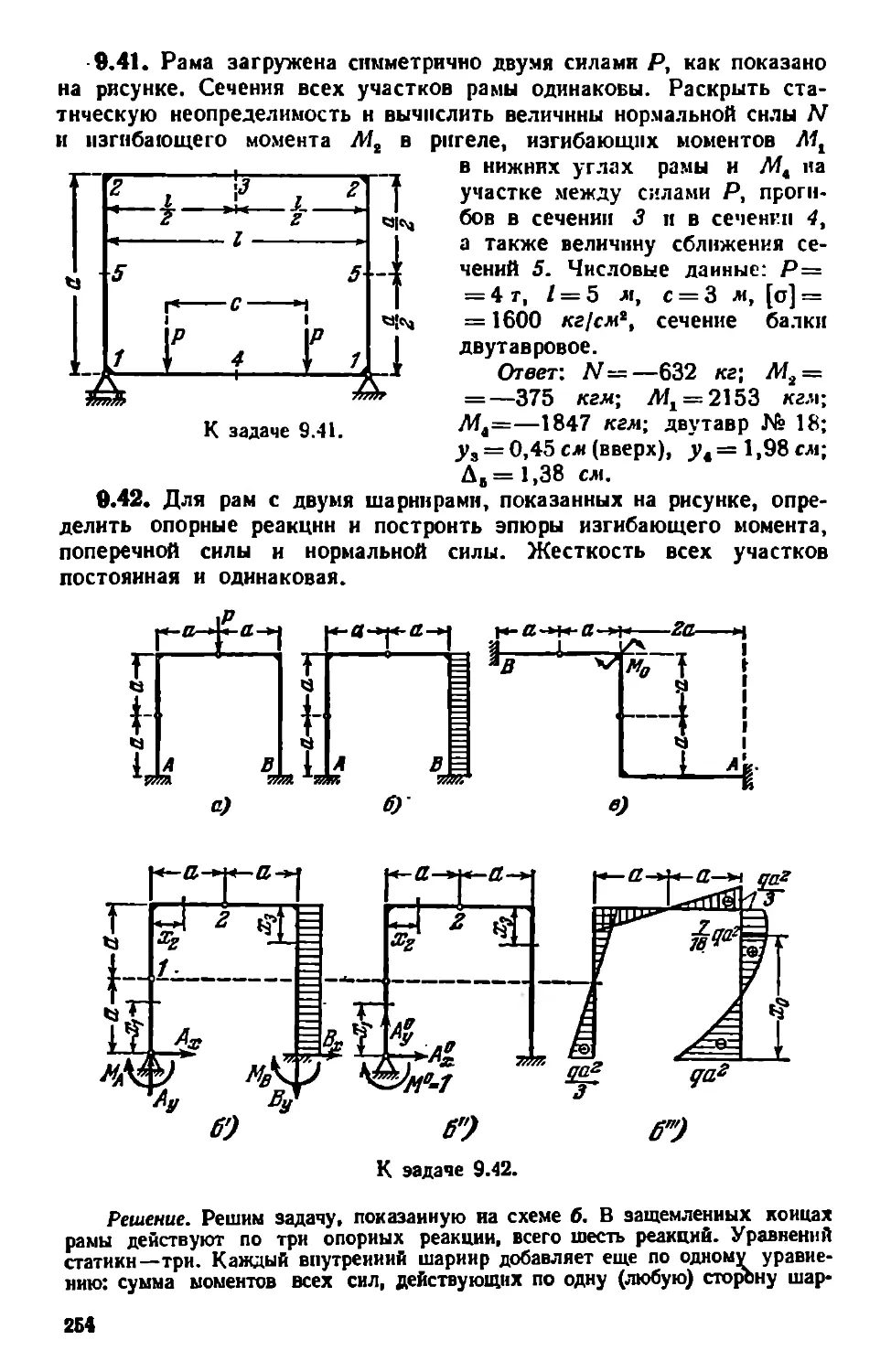
Глава 5. Геометрические характеристики плоских фигур.................106
§ 16. Геометрические характеристики сечений, имеющих оси симметрии .........................................................106
§ 17. Геометрические характеристики несимметричных сечений . . 116
Глава 6. Плоский изгиб. Внутренние усилия и напряжения ...... 125
§ 18. Эпюры поперечных сил и изгибающих моментов............125
§ 19. Нормальные напряжения при изгибе......................142
§ 20. Касательные напряжения при изгибе. Центр изгиба .... 154
§ 21. Главные напряжения при изгибе. Полная проверка прочности балок................................................. 165
Глава 7. Деформация н перемещения при изгибе......................173
§ 22. Аналитические методы определения перемещений..........173
§ 23. Графоаналитический и графический способы определения перемещений при изгибе . .......................................185
3
§ 2- 1. Энергетические методы определении перемещений.......195
§ 25. Определение перемещений в балках любым способом .... 204
Глава 8. Составные балки. Балки псремеииого сечения...............212
§ 26. Составные балки.......................................212
§ 27. Балки переменного сечения.............................220
Глава 9. Статически неопределимые системы.........................228
§ 28. Балки ................................................228
§ 29. Рамы..................................................246
Глава 10. Сложное сопротивление...................................258
§ 30. Косой и пространственный изгиб........................258
§ 31. Виецеитрешюе растяжение или сжатие....................271
§ 32. Одновременное действие продольных и поперечных сил . . . 282
§ 33. Изгиб и кручение......................;...............289
§ 34. Общий случай сложного сопротивления...................298
§ 35. Тонкостенные стержни..................................306
Глава 11. Кривые стержни..........................................320
§ 36. Напряжении в кривых стержнях..........................320
§ 37. Определение перемещений...............................326
§ 38. Статически неопределимые кривые стержни...............331
§ 39. Толстостенные трубы и составные цилиндры..............334
Глава 12. Устойчивость элементов конструкций......................338
§ 40. Устойчивость сжатых стержней..........................338
§ 41. Расчеты па устойчивость в сложных случаях.............347
§ 42. Продольно-поперечный изгиб............................352
Глава 13. Расчеты по допускаемым нагрузкам и по предельным состояниям .............................................................356
§ 43. Расчеты по допускаемым нагрузкам при растяжении пли сжатии н при кручении...........................................356
§ 44. Расчеты по допускаемым нагрузкам при изгибе...........363
§ 45. Метод «расчетных предельных состояний*................369
Глава 14. Динамическое и длительное действие нагрузок.............374
§ 46. Влияние сил инерции...................................374
§ 47. Напряжения и деформации при колебаниях................382
§ 48. Напряжения и деформации при ударе.....................389
§ 49. Переменные напряжении.................................399
§ 50. Ползучесть и релаксация напряжений....................408
Приложения .......................................................418
ПРЕДИСЛОВИЕ
Предлагаемый «Сборник задач» составлен тем же коллективом авторов, который неоднократно перерабатывал и дополнял «Сборник задач по сопротивлению материалов» покойного члена-корреспондента АН СССР Н. М. Беляева (издания II—XI). В настоящем «Сборнике» сохранено некоторое количество задач, принадлежащих Н. М. Беляеву, сохранена в основном структура и общая направленность его «Сборника». Поэтому авторы, являющиеся бывшими учениками и сотрудниками Н. М. Беляева, сочли своим долгом возглавить авторский коллектив именем своего учителя.
«Сборник» в основном предназначен для решения задач студентами, а потому особо сложные задачи, интересные дли лиц, более глубоко изучающих сопротивление материалов, в нем не приведены. Наиболее типичные задачи даны с решениями. Наряду с задачами, имеющими разнообразные условия, почти в каждом разделе помещены комплексные задачи с общим условием и большим количеством вариантов схем или цифровых данных. Эти задачи могут быть использованы для контрольных работ или для индивидуальных домашних заданий.
Так как изучение курса сопротивления материалов в высших учебных заведениях и расчетная работа в проектных и конструкторских организациях пока еще ведутся в системе единиц СГС и так как все ТУ и нормы пока составлены в той же системе, то и в настоящем «Сборнике» применена система СГС. Однако несколько примеров и задач по каждому разделу приведены в системе СИ для приобщения учащихся к этой последней.
Между авторами материал «Сборника» распределен следующим образом: Н. М. Беляеву принадлежат отдельные задачи в риде разделов; Л. А. Белявским составлены §§ 12—15, 24, 25, 27—29, 36—39; Я. И. Кипнисом—§§ 9—11, 16—23, 26; Н. Ю. Кушелевым — §§ 1—8, 43—45 и Приложения; А. К. Синицким —§§ 30—35, 40—42, 46—50; В. К. Качурин дал темы отдельных задач в риде разделов, им же осуществлено редактирование «Сборника».
В. К. Качурин
ТАБЛИЦА ПЕРЕВОДА ЕДИНИЦ СИЛЫ И НАПРЯЖЕНИЯ СИСТЕМЫ СГС В СИСТЕМУ СИ
1 кг=9,81 н,
1 т =9810 н,
1 хг/сж®=0,981 • 10ь я/ж®,
1 кг/ммг=0,981 • 10® «/ж*.
ОБЩИЕ ДЛЯ ВСЕХ ЗАДАЧ ДАННЫЕ
Если нет специальных указаний в условии задачи, то при ее решении необходимо принимать следующие средине значении указанных величин:
В системе СГС I В системе СИ (кг смг) ; (н л*)
Модуль упругости стали при растяжении или сжатии.......................................£ = 2-10®
Модуль упругости алюминия и дуралюмипа . .£ = 0,7-10е
Модуль упругости чугуна....................£=1,2-10®
Модуль упругости меди......................£=1-10®
Модуль упругости дерева вдоль волокон . . . . £ = 1 • 10®
Модуль упругости стали при сдвиге..........0 = 8-10®
Объемный вес стали...........................у = 7,8-10~®
кг/см*
Температурный коэффициент линейного расширения стали ...................................... а=125-10-7
£ = 2-10» £ = 0,7-10» £=1,2-10» £=1-10» £=1-10*° 0 = 7-1010 у = 8,8-10-« (я/ж»)
Температурный коэффициент линейного расширения меди..................................
Коэффициент поперечной деформации стали . >
а= 165-10-1 р=0,30
Г Л Л В A- 1
ОСЕВОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
§ 1. Статически определимые системы
1.1. Поршень цилиндра паровой машины (см. рисунок) имеет диаметр 40 ем, а шток поршня—диаметр 5,6 см. Давление пара равно
К задаче 1.1.
10 ат (1 ат = 1 кг/смг = 9,81 • 10» н/м*). Найти наибольшее напряжение в штоке и соответствующее изменение его длины во время одного хода машины. Длина штока равна 75 см, материал штока — сталь.
Решение. Обозначим: диаметр цилиндра D = 40 см, диаметр штока d = 5,6 см, длину штока 1 = 7Бсм, давление пара q = 10от=10кг/смг=9,81-10»л/ма, модуль упругости £ = 2-10е кг/сма= 19,62-1010 я/л«а. Площадь поршня равна nDs
Fj==0,785 • 40s = 1256 см* = 0,1256 ма
Усилие в штоке (пар слева) составит
Р = F,q = 1256 • 10 = 12 560 кг=0,1256 • 9,81 • 10» = 1,23 • 10» н (сжатие).
Площадь сечения штока равна
Д/Р
F, = =0,785 • 5,6s = 24,65 см2 = 2,465• 10"» м».
4
Напряжение в штоке получится следующим:
„ Р 12560 „ 1,23-10» с 1Л,. , ,
£, 24,65 5 Окг^с-*’ —2,465-ю-’-5'10
7
а укорочение штока будет равно
.. Р1 12560 75 ПЛ1О1 1,23-10»-75-10-*
Д/-££г-210’!-24,б5 0,0,91 си 19.6210W-2.465 10-»-19 ’ ° М'
1.2. Каково должно быть допускаемое напряжение при расчете на статическую нагрузку для материала винта стяжки железнодорожных вагонов, если напряжение при трогании поезда с места не должно превосходить предела текучести стали? Принимаем предел текучести от = 0,6о„, а предел прочности ов = 50 кг]мм-. Учесть, что напряжении при внезапном трогании поезда с места вдвое больше, чем при постепенном.
Ответ: \500кг/смг.
1.3. Чугунная колонна высотой 3л1 имеет кольцевое поперечное сечение с наружным диаметром 25 см и внутренним диаметром 20 см. Она нагружена сжимающим усилием 50 т. Найти напряжение в поперечном сечении, абсолютное и относительное укорочения колонны.
Ответ: о = — 283кг,'см3; Д/ = 0,71 лом; е = 2,36-10-4.
1.4. Определить допустимую нагрузку на деревянную стойку круглого поперечного сечения диаметром 20 см, если сжимающее напряжение в ней не должно превышать 40 кг/см3.
Ответ: 12,57 т.
1.5. Стальной стержень круглого сечения растягивается усилием
10 т. Относительное удлинение не должно превышать а иа" пряжение не должно быль больше 1200кг;см3. Найти наименьший диаметр стержня, удовлетворяющий этим условиям.
Ответ: 3,57 сл1.
1.6. Определить диаметр каждого из двух болтов, соединяющих обе части разъемной головки шатуна (см. рисунок); усилие в
К задаче 1.6.
шатуне Р= 12 800 кг; допускаемое напряжение дли материала болтов равно [о] = 600 к г/сл!2.
Ответ: 37 мм.
1.7. Рабочее давление (превышение над наружным) в цилиндре двигателя д=10 ат; внутренний диаметр цилиндра 350л<л1 (см. рисунок). Какое количество болтов диаметром 18л<.и- необходимо, дли
в
того, чтобы прикрепить крышку к стенке цилиндра, если допускаемое напряжение дли материала болтов равно 400 кг/см2?
Ответ: 10 болтов.
К задаче 1.7.
2m
2М
\2
К задаче 1.8.
1.8. Определить напряжения в сечениих 1—1 и 2—2 и полное удлинение стального стержни, нагруженного, как показано на рисунке, если площадь его поперечного сечения равна 4 см-.
Решение. Мысленно рассекаем стержень сечением 1—/ н отбрасываем хотя бы правую часть. Можно было бы отбросить и левую часть, но обычно для упрощения решения отбрасывается та часть стержня, к которой приложено большее число сил. Для того чтобы уравновесить силу 2 т, приложенную к оставшейся левой части, равнодействующая внутренних сил в сечении I—/ должна равняться тоже 2 т и быть направленной вправо, в наружную сторону от оставшейся части. Таким образом, в сечении /—/ усилие растягивающее н равно Nt = 2T. Путем подобных рассуждений устанавливаем, что в сечении 2—2 усилие тоже растягивающее и равно /Уг=1 т. Теперь мы можем определить напряжения. В сечении /—/ напряжение равно
G1_1=^ = 2^=500^.
а в сечении 2—2
Ns 1000 ,
а2 _ в—-j? = =2э0 кг/см*.
Так как усилие в левом участке (длиной 1 л) не равно усилию в правом участке (длиной 2 л<), то деформации каждого участка надо определять отдельно. Полная деформация стержня получится путем суммирования деформаций (алгебраического, если они разных знаков) отдельных участков. В нашем случае
.... . л» .МЛ _200°. 100 , 1000-200 п с
А ДМ-Д^в EF + EF 2-10в-4 + 2-10»-4 —0,05СЛ—0,5 *Ж'
1.9. Найти напряжения во всех участках представленного на рисунке стального стержни и полную его деформацию. Поперечное сечение стержня равно 5cai2.
К задаче 1.9.
Ответ: В левом участке о = 800 кг!смг, в среднем участке <т =: О, в правом участке О =— 400 кг/см-; Д1 = 0.
9
1.10. Изображенный на рисунке стальной стержень имеет в правой части сплошное круглое, а в левой части кольцевое сечение.
Определить напряжения в обеих частях стержня и полное его удлинение.
Ответ. В левом участке а=531 кг/см2, в правом участке 0=397 кг,смг\ Д/=0,132жж.
1.11. Полиэтиленовая трубка кольцевого поперечного се-
К задаче 1.10.
чения имеет наружный диаметр 5сж. Опа растянута силой 240 кг. Определить необходимую толщину стенки при допускаемом напряжении 34кг/сжа.
Ответ-. 5 жж.
1.12. Стяжка диаметром с( = 30жж растянута усилием Р (см. рисунок), вызывающим в ней напряжение 800 кг!см2. Чему должна
Кирпич
К задаче 1.12.
равняться сторона а квадратной шайбы, если допускаемое напряжение на смятие (местное сжатие) кирпичной кладки равно 10 кг/см2? Ответ: 24 см.
1.13. Деревянный брус шириной р=15сж опирается на кирпич
иую кладку^ (см. рисунок). Через дается давление 3 т. На какую кладку, если допускаемое напряжение на смятие древесины бруса поперек волокон 12 кг/см2, а допускаемое напряжение смятия кладки Юкг/сж2? Давление полагать равномерно распределенным по поверхности соприкасания.
Ответ: 20 см.
этот конец бруса на кладку пере-длнну а нужно завести брус на
К задаче 1.13.
1.14. Трос растянут усилием 7,5т. Он состоит из проволок диаметром 2 жж. Допускаемое напряжение для троса, учитывая наклон проволок в нем, равно [а] = 3000 кг 1см2. Определить число проволок в тросе.
Ответ: 80 проволок.
10
1.15. Под воздействием приложенной нагрузки представленный на рисунке стержень удлиняется на 0,2 мм. Модуль упругости алюминия принят равным 0,75- 10е кг/см?, а бронзы 1,Ы0* кг[см2. Определить величину нагрузки Р.
Ответ: 3670 кг.
SUM
U Алюминий
10сч-А^-10см-Л^-10см-^
БрМЗЛ
К задаче 1.15.
1.16. При испытании пробным загружением стальной фермы моста разность показаний тензометра, поставленного на одном из элементов фермы, оказалась равной 12 мм. База тензометра (длина, на которой производится измерение деформации) равна 20мм, его коэффициент увеличения 1000. Определить напряжения в исследуемом элементе.
Решение. Определяем напряжения по закону Гука. Абсолютная деформация равна разности показаний тензометра, деленной па его увеличение:
Л'“Т-ТИо=°-0|2“'
Относительная деформация равна отношению абсолютной деформации к базе прибора:
Напряжения равны
<т= Ее = 2-10’ 0,0006= 1200 кг/см»
1.17. Какая необходима минимальная база у тензометра, предна-виаиенного для испытания стальной детали, если его увеличение равно 1000, точность отсчета равна 0,1 мм, а напряжение должно быть измерено с точностью не менее 10 кг/см2?
Ответ: 20 мм.
1.18. Во время испытания проволоки диаметром 1,2 мм при помощи тензометра с базой 10 см под нагрузкой 10 кг было измерено удлинение 0,08 мм. Чему равен модуль нормальной упругости материала проволоки?
Ответ: 1,1-10е кг-см2.
1.19. При изменении нагрузки на 10 т разность отсчетов тензометра, поставленною на деталь с поперечным сечением 10 см2, оказалась равной 25 мм. База тензометра 100 мм, его увеличение — 500. Чему равен модуль упругости материала этой детали?
Ответ: 2-10е кг/см2.
11
1.20. При подвешивании некоторого груза к стальной проволоке длиной 3 я и диаметром 1,6 ям ее удлинение оказалось равным 1,5 мм. Затем тот же груз был подвешен к медной проволоке длиной 1,8 я с диаметром 3,2 яя, и в этом случае удлинение получилось равным 0,39 мм. Зная модуль упругости стальной проволоки, определить модуль упругости медной.
Ответ: 1,15-10’ кг)см2.
1.21. Клеть шахтного подъемника подвешена к тросу с площадью поперечного сечения 100 мм2, длина которого при нагружении его только весом клети равна 100 я. При загрузке клети рудой весом 350 кг удлинение троса оказалось равным 3 см. Определить модуль упругости троса.
Ответ: 1,75 • 10’ кг!см2.
1.22. Во время испытания образца на растяжение при некоторой нагрузке разность отсчетов тензометра № 1, измерявшего продольные деформации, оказалась равной 10,4 яя, а тензометра № 2, измерявшего поперечные деформации,—равной 7,8 мм. Тензометр № 1 имел базу 20 яя, а тензометр № 2—60 яя. Увеличения обоих тензометров были одинаковы. Найти коэффициент Пуассона.
Ответ: 0,25.
1.23. Стальной стержень круглого поперечного сечения диаметром 30 яя растянут на испытательной машине усилием 12,5 т. С помощью тензометров на длине 50 мм измерено его удлинение, оказавшееся равным 0,43 яя, и изменение его диаметра, равное 0,007 яя. Определить модуль упругости и коэффициент Пуассона материала стержня.
Ответ: Е — 2,06-10’ кг/см2; р, = 0,271.
1.24. Определить величину изменения диаметра D тонкого кольца с поперечным сечением F, выполненного из материала с модулем Е,
К задаче 1.25.
под влиянием равномерно распределенного внутреннего давления интенсивности q.
Ответ: AD = -^=.
1.2Б. В бетонную стену заделан стальной стержень (рис. а). Для его выдергивания необходима силаР=2т. Этому препятствуют силы сцеплення, равномерно распределенные по его длине. Площадь поперечного сечеиия стержня 2 см2, длина I = 40 ся, изменения напряжения в сече-
fl— 15 ся. Построить эпюру (график)
ниях по длине стержня и найти его удлинение.
Решение. В любом сечении коны и раины
на части стержня длиной а напряжения однна-
2000
2
= 1000 кг/с.и2.
12
На части стержня длиной Z равнодействующая сил сцепления из условия равновесия должна равняться силе Р. По условиям задачи эта сила распределена равномерно по длине I, следовательно, на единицу этой длины придется снла р = Р//.
Возьмем сечение на расстоянии х от правого конца стержня. Тогда правее сечения равнодействующая сил сцепления будет равна
„ Р
N = рх = — х.
Отбросив левую часть стержня, нз условия равновесия правой, оставшейся части получаем, что усилие в сеченни равно N. Тогда напряжения в сечении на расстоянии к от правого конца стержня будут равны
, % N Рх F -lF .
На правом конце стержня прн х=0 они рав1(ь? нулю, на расстоянии / от правого конца напряжения
Pl Р at=jp- = ^-=lOOO кг/см*.
Эпюра напряжений по длине стержня представлена на рис. б. Удлинение части стержня длиной а будет равно
.. Ра 2000-15 _с .... Д,° —££ = 2-10"-2~7’5'10 СМ'
Для определения удлинения части стержня длиной Z выделим на расстояниях от правого его конца бесконечно малую часть стержня длиной dx. Усилие в этом сеченин было определено ранее. Тогда удлинение этой бесконечно малой части длины стержня будет равно
. , N dx Pxdx
&dx = -EF~TET-
Удлинение части длины стержня Z получим путем интегрирования:
,, С. л CPxdx_ Pl 2'00-40 . 10-м
A'l-jAdx-j [EF 2£f~2-2-10e-2~
о о
Полное удлинение AZ всего стержня будет равно
AZ = AZz+AZ„ = 1 • 10-*4-7,5-10"»= 17,5-10"» сж=0,175 мм.
1.26. Стержень квадратного поперечного сечения растягивается силами Р=150 кг (см. рисунок). Он ослаблен сквозным отверстием
К задаче 1.26.
диаметром 2 мм. Чему должна равняться сторона сечения а при допускаемом напряжении для материала стержня, равном 1000 кг/сжа?*) Ответ: 5 мм.
*) В задачах 1.26—1.28 распределение напряжений как в ослабленных, так и в неослабленных поперечных сечениях предполагается равномерным.
13
1.27. Стальная полоса шириной 20 см и толщиной 20 мм ослаб-
лена болтовым отверстием диаметром 25 мм, расположенным на оси полосы. Определить допустимое растягивающее полосу усилие, если известно, что предел прочности материала полосы равен 48 кг/мм2,
кс, представляют собой квадраты.
а коэффициент запаса принят равным трем.
Ответ: 56 т.
1.28. Стальная полоса (см. рисунок) растянута продольными силами. Она ослаблена заклепочными отверстиями диаметром 20 мм. Каким наибольшим усилием может быть растянута полоса, если допускаемое напряжение равно 1600 кг/снП
Ответ. 28,8 т.
1.29. Поперечные сечения отдельных частей конструкции, изображенной на рисун-Определить размеры сечений
при следующих допускаемых напряжениях на местное сжатие (смятие): для стали [ос]=1400 кг[см2, для чугуна [оч]=1000 кг/см2,
Стальная
★Бутовая клаВка
д г
Грунт
1
''ШмашггЖ
К задаче 1.29.
К задаче 1.30.
для тесаного камня [ок] = 40 кг/см2, для бутовой кладки [о6] = = 15 кг/см2, для грунта (песок) [ог] = 5 кг/см2. Нагрузка Р= 100 т, собственным весом частей конструкции пренебречь.
Ответ: Сечение стальной колонны 10x10 см, сечение чугунного башмака 50x50 см, сечение тесаного каменного цоколя 82x82 см, сечение бутового фундамента 142x142 см.
1.30. Две стойки круглого поперечного сечения диаметром 10 см нагружены, как указано на рисунке. Соединение горизонтальных
элементов со стойками полагать шарнирным. Определить напряжения в сечениях верхней, средней и ннжней частей обеих стоек.
Ответ: Все напряжения сжимающие (в кг/см2).
В левой стойке: В правой стойке!
в верхней части 8,3 в верхней части 5,7
в средней части 21,6 в средней части 1,3
в нижней части 15,3 в ннжней части 20,4
1.31. Определить напряжения в опасном сечении подвески АВ,
ослабленной заклепочными отверстиями (см. рисунок). В точках С, D, Е, F передаются иа конструкцию давления по 20 т.
Ответ: 659 кг/см2.
Сечение т-п
К задаче 1.31.
1.32. Сила Р=10т нагружает конструкцию, как указано на рисун-
ке. Все стержни одинакового поперечного сечения, состоящего из двух равнобоких уголков 80x80x8. Определить напряжения в стержнях.
Ответ: аАВ = 305 кг/см2-, аАС = 406 кг/см2-,
авс= — 509 кг! см:1-, aCD = — 305 кг /см1.
1.33. Бревно А при помощи двух канатов ВАС, расположенных по концам бревна, поднимается по наклонной плоскости BD (см, ри
сунок). Концы нижних ветвей канатов закреплены, как показано на рисунке. К концам верхних ветвей канатов приложены силы Р. Проверить прочность канатов, если вес бревна 300 кг, рабочая площадь поперечного сечения каната 1,17 см2 и допускаемое напряжение для него [а] = = 55 кг/см2. Силы трения не учитываются. Ответ: о = 41,5 кг/см2 < 55 кг/см1.
1.34. Проволока диаметром 5 мм и длиной 600 мм, приводящая в движение
железнодорожный сигнал, расположена на роликах, как указано на рисунке. Определить, какое перемещение А при усилии 200 кг
15
надо дать концу проволоки в сигнальной будке, если перемещение другого ее конца у сигнала должно быть равно а = 17,5 см.
К сигналу
К задаче 1.34.
Провесом проволоки между роликами и силой трения между проволокой и роликами пренебречь.
Ответ: 48 см.
1.36. Две проволоки, одна стальная, другая медная, имеют одинаковую длину и нагружены одинаковыми осевыми растягивающими усилиями. Медная проволока имеет диаметр 1 мм. Чему равен диаметр стальной проволоки, если обе проволоки удлиняются иа одинаковую величину?
Ответ: 0,71 мм.
1.36. Жесткая балка АВ, деформацией которой пренебрегаем, закреплена и нагружена, как указано на рисунке. Стержень 1 — стальной, сечением 10 см2, стойка 2—деревянная, сечением 10x10 см, стержень 3 — медный, сечением 30 см2. Определить опускание тонки С.
Ответ: 0,5 лсм.
1.37. Определить увеличение объема стального стержня длиной 5 м, растянутого силой 25 т. Явление протекает в упругих пределах.
Ответ: 2,5 с л Iя.
1.38. На тягах 1 и 2 горизонтально подвешен жесткий брус (см. рисунок), деформацией которого пренебрегаем. На каком расстоянии а от тяги 1 должен быть помещен груз Р, чтобы и после
16
деформации брус остался горизонтальным? Какие в этом случае будут напряжения в тягах, если Р = 3 т?
Ответ: с = 1,08 м; а, = 330 кг/см2; а, = 440 кг /см2.
1.39. Жесткий брус АВ нагружен н закреплен, как указано иа рисунке. Тяга 1 стальная, круглого сечения диаметром 25 лы1, стойка 2
К задаче 1.38. К задаче 1.39.
деревянная, квадратного сечения 20x20 см. На каком расстоянии х от опоры нужно поместить силу Р, чтобы опускание конца бруса А было в два раза меньше опускания конца В? Какое значение должна иметь сила Р, чтобы в этом случае опускание точки С равнялось I ля? Чему тогда будут равны напряжения в тяге /ив стойке 2? Деформацией горизонтального стержня 3 пренебречь.
Ответ: х = 8,1 см; Р= 41,4 т; at = 234 кг/см2; а2 = —101 кг/см2.
1.40. Брус АВ подвешен на трех стержнях одинакового поперечного сечения площадью 10 см2 (см. рисунок). Определить напряжения в стержнях, а также величину и направление перемещения
К задаче 1.41.
точки А, если стержни стальные. Сила 6 т направлена вдоль стержня 2, как то показано на рисунке.
Ответ: с1 = аэ = 0; аг = 600 кг/см2, перемещение горизонтально и равно 1,95 лы1.
1.41. Водонепроницаемый щит удерживается деревянными распорками АВ (см. рисунок) от опрокидывания давлением воды. Распорки
!7
поставлены через каждые три метра. Подобрать круглое сечение распорки, если для дерева допускаемое напряжение на сжатие в нашем случае равно [ст] = 30 кг!смг.
Решение. Выделим часть щита длиной (перпендикулярно к плоскости чертеж»), равной 3 м. На эту длину приходится одна распорка. Гидростатическое 2-2 давление воды, действующее на выделенную часть щита, равно Э--^- = 6 т. Оно направлено горизонтально и приложено на высоте, равной 1/3 глубины воды, т. е. на 2/3 м от дна. Давление щита на распорку в точке В, равное сжимающему усилию в распорке, находим по правилу рычага:
Рз=6-Д=4-т.
О* «5 о
Необходимая площадь поперечного сечения распорки равна _ Р 4000 ... .
F=й=з^б=44-5 см'
Диаметр распорки равен
45,2 ]/Z=2 7.5 см.
г я Г 3,14
1.42. Определить наибольшее допустимое расстояние между подкосами, удерживающими от опрокидывания водонепроницаемый щит
К задаче 1.42.
К задаче 1.43.
(см. рисунок). Подкосы деревянные, круглого поперечного сечения диаметром 15 см. Допускаемое напряжение для материала подкосов принять равным 20 кг/см*.
Ответ. 1,88 м.
1.43. Определить диаметр круглого поперечного сечения тяг 1 и 2 (см. рисунок). Допускаемое напряжение для материала тяг равно 1000 кг!см2.
Ответ. dt ^25,2 мм; de = 42,4 мм.
1.44. Конструкция ABCD, деформацией которой пренебрегаем, прикреплена к фундаменту при помощи стержней 1, 2 и 3. Вес конструкции и боковое давление на нее указаны на рисунке. Подо
18
брать сечение стоек 1 и 3 и раскоса 2 из четырех равнобоких уголков каждое, если [а] =1000 кг!см*.
Ответ. Сечение стойки 1 — из уголков 80x80x8, раскоса 2—из уголков 63x63x6 и стойки 3—из уголков 32x32x4.
1.45. Мостовая балка опирается на «подфермениые камни» А и
В, как указано на рисунке. По балке перемещаются два связанных между
К задаче 1.44.
собой груза по 15 т каждый. Определить размеры подферменников в плане при самом невыгодном положении нагрузки, если допускаемое напряжение для кладки под под-ферменниками равно 9 кг!см*, а сами под-ферменники в плане представляют собой квадраты. Собственным весом балки и под-ферменных камней пренебречь.
Ответ. 55x55 см.
К задаче 1.45
1.46. Жесткий стержень (см. рисунок) нагружен силой Р и удерживается от опрокидывания наклонной стальной тягой АВ круглого
поперечного сечения диаметром 20 мм. Определить наибольшую до-
К задаче 1.46.
пустимую нагрузку Р и горизонтальное перемещение точки приложения силы. Допускаемое напряжение для материала тяги равно 1600кг/сма.
Ответ; Р -- 2,01 т; 6 = 5 мм.
К задаче 1.47.
1.47. На рисунке представлен подъемный кран. Его оттяжка АД является тросом с поперечным сечением 500 мм*, Допускаемое напряжение для троса равно 800 кг[см*. Какова грузоподъемность
19
крана (величина максимального груза Р) из условия прочности оттяжки?
Ответ: 6,67 т.
1.48. К двум стержням подвешен груз Р, как изображено на рисунке. Стержень I круглого поперечного сечения диаметром 30 мм
с допускаемым напряжением материала 1600 кг/см?, а стержень 2 тоже круглого поперечного сечения, но диаметром 40 мм и с допускаемым напряжением материала 600 кг/см11. Какой наибольший груз Р может выдержать эта конструкция?
Ответ: 13 т.
1.49. Жесткий брус АВ весом Р подвешен при помощи системы пеньковых канатов АСЕ, BDF, CD (см. рисунок). Все канаты одина-
кового сечения диаметром 25 мм, причем полезная площадь сечения составляет лишь 75°/0 от площади, заключенной в периметре каната. Определить наибольший вес бруса Р, если для канатов [о] = 100 кг/см*.
Ответ: 695 кг.
1.50. Стальные стержни, прикрепляющие жесткую конструкцию к фундаменту (см. рис. а), выполнены следующим образом: стержень 1 — из четырех уголков 50x50x5, стержень 2 — из двух швеллеров №12, стержень 3—из одного двутавра № 20. Определить напряжения в стержнях и полное перемещение шарнира К.
а)
К задаче 1.50.
Решение. Для определения усилий в стержнях мысленно разрежем стержни и в местах разрезов приложим неизвестные пока усилия, предполагая их все растягивающими (см. рис. б). Равнодействующая горизонтальной нагрузки бу
20
дет равна Р=2,5-4 = 10 т и приложена на высоте 2 м от шарнира К. После этого составляем уравнения равновесия для усилий в стержнях и равнодействующей нагрузки:
2х=Р-Д\ = 0, ^тк=— Р-2-Л'3-1=0, £т£=-Р-2+Л'г1=0,
откуда Л\ = Р;
откуда N3= — 2Р;
откуда Л'2 = 2Р.
Таким образом, наше предположение о знаке усилий для стержней 1 и 2 оказалось правильным, а для стержня 3—неправильным.
Из сортамента определяем площади поперечных сечений стержней:
стержня/ Р> = 4x4,80= 19,2 сл2; стержня 2 Р2=2х 13,3 =26,6.сл2; стержня 3 Р3 = 26,8 смг.
Имея значения усилий и площади поперечных сечений, можно подсчитать напряжения в стержнях:
ог=
ULl
Fi
Р _10000
Pi “ 19,2
522 кг/см2;
N2 2Р 2-10000 ,
о2- —F* =- 26>6 -752 кг/см ;
N3_ 2Р 2-10 000 _
F3~ F3~ 26,8 -
747 KZlctfi.
Для того чтобы найти полное перемещение шарнира К, определим сначала его горизонтальное и вертикальное перемещения. В нашем случае горизонтальное перемещение равно удлинению стержня /:
Д/гор = Д/1 = ^1=^1=фт^°=0,0261 сл = 0,261 мм; Г j С 1и
вертикальное перемещение равно удлинению стержня 2:
. .. Л^2/2 о2/2 752-100 Л с п о-тс
Л'всрт = Д 1г = -Л- = -р = о ini, = 0.0376 см=0,376 мм.
Lil 2 С Z-1U”
Полное перемещение шарнира К получится геометрическим суммированием горизонтального и вертикального перемещений:
Д = /дг2ор + Л2ерт = V0,261*+0,376* = 0,45 мм.
1.Б1. Груз Q подвешен к шарнирно-стержневой системе АСВ (см. рис. а). Стержень АВ дуралюминовый, стержень ВС стальной. Допускаемое напряжение для стали и дуралюмина принято одинаковым и равным [о] = 1500 кг/см*. Подобрать площади поперечных сечений стержней и найти горизонтальное и вертикальное перемещения точки С.
Указание. Для определения перемещения точки С разъединим в ней стержни и изобразим их новые длины ДС] и ВС2, увеличив старые иа Д/1=СС1 и Д/2=ССа (см. рис. б). Для того чтобы найти новое положение точки С, сведем вместе удлиненные стержни, вращая их вокруг точек А н В. Точки Cj и С2 будут перемещаться по дугам CjC3 и С2С3, которые по их малости могут быть приняты за прямые, перпендикулярные к АСХ и ВС2. Тогда отрезок СС3 п будет искомым перемещением Д. Обозначая угол, составленный этим отрезком с вертикалью, через р, получаем систему уравнений
а —
cos (а2 — р) ’ cos (а2— Р) •
21
№ этих уравнений определяем Р, а затем Д и его вертикальную и горизои* тальную проекции.
Ответ. Рис = 3,46 с-**2; Ряс = 4,88 см3;
Дгор = 2,6 мм; Дторт = 5 Л1л».
К задаче 1.51.
1.52. Жесткий брус CD, деформацией которого можно пренебречь, нагружен, как указано на рисунке, и подкреплен деревянным подкосом АВ. Было измерено опускание точки D; оно оказалось равным 3 лл1. Чему равны напряжения в подкосе? Если поперечное сечение подкоса квадратное с размерами 20 X 20 сл1, то какова нагрузка Р?
Ответ: а = — 43,3 кг/с;.':1; Р=5,78 т.
К задаче 1.53.
К задаче 1.52.
1.53. В изображенном на рисунке кронштейне стержень АС стальной» а стержень ВС деревянный. Допускаемое напряжение для стали KJ= 1600 кг/см*, для дерева [од] = 40 кг/см3. Подобрать диаметр d круглого сечения стального стержня и сторону а квадратного сече-нкя деревянного н определить горизонтальное, вертикальное и полное смещение узла С.
Ответ: d=*27 мм; а =16,4 см; Дгор = 2,4 мм;
Двсрт = 6,2 мм; Д = 6,64 лги.
1.54. Силой Р нагружен представленный на рисунке кронштейн. Оба стержня сильные. Верхний состоит нз двух швеллеров № 12(
22
нижний—из двутавра № 24. Допускаемое напряжение на растяжение принято равным 1600 кг/см2, а на сжатие—1000 кг/сж®. Определить наибольшую допустимую нагрузку Р и вертикальное перемещение узла приложения нагрузки.
Ответ! Р = 34,8 т; Д --- 2,70 мм.
К задаче 1.54.
К задаче 1.55.
1.55. К двум тягам одинакового поперечного сечения F= 1 см2, выполненным из одинакового материала с модулем Е= 1 • 10е кг/см2, подвешен груз Р=1т (см. рисунок). Определить перемещение точки подвеса груза. Как изменится это перемещение, если угол а=52°?
Ответ. 0,2 см. Увеличится в два раза.
1.56. При испытании на растяжение стального стержня диаметром 6 мле и длиной между головками 30 лмг была получена представленная на рис. а диаграмма. Диаметр шейки в месте разрыва оказался равным 3,1 л.и. Определить условные и истинные характеристики материала и построить диаграмму истинных напряжений.
Решение. Рассматривал диаграмму (на рис. а), мы видим, что пределу пропорциональности соответствует нагрузка Р„ —650 ка=6380 н, пределу
23
текучести — нагрузка Рт = 710 кг=6970 н, пределу прочности — нагрузка Ря = = 1150 кг= II 280 н н моменту разрыва—нагрузка Рразр=610 кг = 5990 н. Так как площадь первоначального поперечного сечения образца равна
£=^=^=28,3 жл2=2,83-10_# м\ 4 4
то соответствующие условные (отнесенные к первоначальной площади поперечного сечения) механические характеристики будут равны:
предел пропорциональности
Р АЗЯП
a" = /=2^I^=2-25-10e^2-
предел текучести
°г = у=2,83-10_& = 2,48' Ю8
предел прочности
о«=т=да^=3-98-10вн/л2-
На той же диаграмме замечаем, что полное остаточное удлинение разорванного образца составляет Д/разр=5,8+3,3 = 9,1 мм. Тогда относительное остаточное удлинение после разрыва будет равно
6 = А^эп 100 = -Ц.. 100=30,3%. • л)
Площадь поперечного сечения шейки в месте разрыва равна
£ш = =?-= 7>55 жж2=7,55.ю-е м*.
Тогда относительное остаточное уменьшение площади поперечного сечения после разрыва будет равно
Ф==28,32^37’55 = 0.731 = 73,1 %.
Переходим к определению истинных характеристик. Для этого предварительно необходимо найтн предельное равномерное остаточное удлинение Д/раВ1|. Из диаграммы видно, что оно равно Д/равн = 5,8 лгм; тогда относительное предельное равномерное остаточное удлинение составит
_А/равн _5,8_ еРавн— i — 30 — и,1аЛ‘
Истинное напряжение, соответствующее пределу прочности, определяем по формуле
5В= ов (1 +еравн)=3,98-10« (1 +0,193) = 4,76-10« н/ж*.
а истинное напряжение в момент разрыва
5разр=^=7^-в = 7.92.10ан/Л*.
Истинное относительное предельное равномерное остаточное удлинение находим по формуле
г₽авИ = 1п (1+еравн)==1п (1 +0,193) = 0,1765,
24
а истинное относительное остаточное удлинение при разрыве—по формуле eH3? = ,nTZ7^ = ln 1—0.731 =1,ЗН-
По данным истинным характеристикам строим диаграмму истинных напряжения, представленную на рнс. б.
§ 2. Статически неопределимые системы
1.57. Размеры поперечного сечения короткой железобетонной колонны 25x25 см. Она снабжена арматурой в виде четырех продоль
ных, симметрично расположенных стальных стержней, каждый диаметром 20 лы<. Колонна нагружена продольной сжимающей силой 60 т. Модуль упругости бетона принять в десять раз меныним модуля упругости стали. Определить напряжения в бетоне и в арматуре*).
Ответ: св = — 81 кг/см*; ас = — 813 кг/см*.
1.58. Короткая стойка из двутавра № 36 усилена двумя бетонными стержнями сечением 20 X 20 см каждый. Определить напряжения, возникающие в двутавре до усиления и в двутавре и бетонных стержнях после усиления, если Р=100т. Передача дав-
Г
лении осуществляется, как указано иа рисунке, через абсолютно жесткую подушку А. Отношение модулей упругости стали и бетона принять равным 10.
Ответ: До усиления ос = —1615 кг/см*; после к задаче 1.58. усиления <JC = —705 кг/см*, а6 = — 70,5 кг/см*.
1.59. Определить усилия в сечениях стержней, показанных на
рисунке (стр. 26) на участках /, // и ///. Закрепление концов всех
стержней абсолютно жесткое. Ответ:
материала.
1.60. Найти напряжение в тросе, состоящем из. центральной стальной проволоки диаметром 5 мм и девяти медных проволок
’р
е)
ж)
и
ш
у
К задаче 1.59.
диаметром 2,5 лги, окружающих первую, считая проволоки параллельными. Растягивающее усилие в тросе равно 500 кг.
Ответ: ом = 6,0 кг/им*; <тс = 12,0 кг/мм*.
1.61. Между неподвижными точками А и В (см. рисунок) до приложения нагрузки горизонтально протянута стальная проволока диаметром 1 лея, находящаяся в ненапряженном состоянии (ее собственным весом пренебречь). Какую gT С* необходимо приложить нагрузку Р
А т~ **~[^ в точке С посредине длины прово-
Г’ л локи и какое в этом случае воз-
никает напряжение в ней, если вер-К задаче 1.61. тнкальное перемещение точки С до-
стигнет СС' = 4,5сл1?
Решение. Абсолютное удлинение одной половины проволоки после приложения силы Р будет равно разности длин СВ н С’В:
Д/ = /100а-Н.52 - ЮО=0,1 см.
26
.-^=0.001.
Тогда напряжение п проволоке мы можем получить, используя закон Гука
о = £е=210° 0.001 = 2000 кг/см2.
Зная напряжение, определяем усилие в проволоке:
4 14-0 1®
fl = PF = 200 - ’ , =15,7 кг.
4
Точка С' будет находиться в равновесии под действием силы Р и двух усилий N.
Р/2 N
Из подобия треугольника сил и треугольника ССВ находим, что -r-g- = inn . .
1W» 1 откуда
P~2 4>5 ioo,l ~ 100,1 - ’4 кг'
1.62. Между неподвижными точками А и В (см. рисунок к задаче 1.61) без натяжения горизонтально протянута стальная проволока диаметром 1 л«л1, собственным весом которой мы пренебрегаем. К точке С посредине длины проволоки прикладывается нагрузка Р. Когда удлинение проволоки достигло 0,5%, опа порвалась. Чему в этот момент равен груз Р, какова величина опускания точки С и каково значение предела прочности проволоки? Считать, что проволока наклепана и до момента разрыва она имеет лишь упругие деформации.
Ответ; Р= 15,7 кг; СС = 10 см; а„= 100 кг/мм2.
К задаче 1.63.
f.63. Стальной болт пропущен сквозь медную трубку, как показано на рисунке. Шаг нарезки болта равен 3 л«лс. Какие напряжения возникают в болте и трубке прн завинчивании гайки на 1/4 оборота?
Ответ; ос= 1274 кг 1см-; ои = — 364 кг/сл1®.
1.64. Чугунный цилиндр длиной 1,50 Л1 имеет внутренний диаметр 25 см и толщину стенок 25 леи. Торцы цилиндра закрыты жесткими крышками, через центры которых пропущен стальной болт, стянутый гайками. Гайки подвернуты настолько, что растягивающее усилие в болте равно 20 т. Затем к каждой крышке прикладываются растягивающие усилия 20 т. Определить напряжение в болте, если его рабочая длина равна 150 елц а поперечное сечение 35 смг.
Ответ; 692 кг[см2.
27
1.65. Лопнувший во время работы чугунный диск предположено исправить, стянув бандажом из мягкой стали. Наружный диаметр диска равен 80 см. Для возможности насадки бандаж будет предварительно нагрет. Каков должен быть внутренний диаметр бандажа до нагрева, если напряжения в нем после насадки должны равняться ЮООкг/сл:2? Ввиду массивности диска по сравнению с бандажом диск считать недеформируемым.
Ответ: 79,96 см.
1.66. Жесткий брус, деформациями которого пренебрегаем, подвешен па трех стержнях и нагружен, как указано на рис. а. Стержень 1 медный, сечением 1 сл»2; стержень 2 стальной, сечением
К задаче 1.66.
1,5 ел:2; стержень 3 алюминиевый, сечением 2 сл:2. Определить напряжения в стержнях.
Решение. Предполагаем, что все усилия растягивающие и что брус ваймет после деформации стержней новое положение, изображенное на рис. 0. Кам известно, для плоской системы параллельных сил статика дает лишь два уравнения равновесия. Составим эти два уравнения:
1) Ns-bOO—Ws-2,25 + P-1,50=0,
2) 2"'e = Ni-2,25+Na-l,25—Р-0,75=0.
Для составления третьего необходимого уравнения рассмотрим деформации (рис. б). Из трапеции, изображенной на рисунке, можно составить следующее соотношение:
Д/э—А/, Л/г — А/,
2,25 ~ 1,00 ’
которое преобразуем к виду
1.25А/,—2,25А/2+А/э = 0.
Выразим в этом уравнении деформации через усилит
, к ^ 200 оу JVg*150 'V3'200 П
1,2 100-1 • 2 100-1,5 0,7-100-2 ‘
После Сокращения имеем
3) 2,5^-1,125^+ 1,437Уэ=0.
28
Совместно решая уравнения I), 2) н 3), получаем
17( =0,018Р = 0,018-3000 = 55 кг.
Ni = 0,568P=0,568-3000= 1705 кг.
Л/3 = 0,414Р = 0,414-3000= 1240 кг.
Проверим полученные значения:
2 W = 55+1705+1240 = 3000 кг = Р.
Напряжения в стержнях соответственно равны
Ni 55 „ , , N2 1705 _
а. = =т = 55 кг/см2, с2 = ~ =1135 кг/см2,
Г*1 1 Г 2
и3 = =620 кг! см2.
*"э х
1.67. Определить усилия в стержнях 1, 2 и 3. Заштрихованные элементы считать абсолютно жесткими. Площади поперечного сечения
стержней указаны на рисунках. Модули упругости материалов всех стержней одинаковы.
29
Ответ к задаче 1.67.
1.68. Железобетонная колонна квадратного поперечного сечения армирована четырьмя стальными стержнями, площадь поперечного сечения которых составляет 1 % от площади поперечного сечения колонны. Допускаемое напряжение для бетона равно 60 кг!см*, для арматуры 1200 кг/см*. Отношение модулей упругости стали и бетона равно 10. Колонна несет нагрузку 100 т. Каковы должны быть стороны сечення колонны и диаметр стержней? Состояние материала считать упругим.
Ответ: с = 39 см; d = 22 лш.
1.69. Жесткий брус закреплен одинакового поперечного сечения и
с помощью системы стержней одного материала (см. рисунок).
30
Значения размера х:
Вариант Схема а 6 в г е 3
1 0 0 0 0 0 0
а а а а а
2 2 ~2 "2 ~2 2
3 а а а а а
3 3 3
4 ~2а ~2а 2U
5 2а
Принимая Р=18т и [ст] = 1600 кг/см*, определить площадь поперечного сечения стержней.
Ответ.
1.70. Жесткий брус АВ подвешен на трех тягах и нагружен, как указано на рис. а, силой Р. Подобрать площадь поперечного сечения
К задаче 1.70.
тяг, если тяга / стальная, тяга 2 медная, с площадью поперечного сечения в три раза большей, чем площадь тяги /, а тяга 3
91
дуралючшшвая, с площадью сечения в дг.а раза большей тяги 1. Допускаемые напряжения принять следующими: для стали [ос]= 1600 кг/см2, для меди [ан] = 600 кг/см2, для дуралюмина [а ] = 1200 кг/сж2.
Решение: Предположим, что все три тяги будут растянуты. Брус АВ после нагружения займет новое положение А'В', изображенное па рис. б. Направление соответствующих реакции точек подвеса тяг также изображено па этом рисунке. Составим уравнение равновесия—суммы моментов относительно точек С и D:
'^1тс=Л'г- 1,5« + Л'8-2,5а—Р-п = 0, (1)
2mD=/V1-2,5o4-A'i!-o—Р-1,5а = 0. (2)
Удлинения всех тнг можно связать следующей зависимостью:
Д/о Д^З Д^1 Д^2 ПСЛ1 Л I 1 С Л I Л
—=----2=—\-=—-, откуда 2.5Д/,— Д/, —1,5Д/.=0.
а 1,5а 1
Заменим в этом уравнении значения удлинений нх выражениями: NJi .. Л’..-0.6Л .. - N3-0,7h , Д/2- - и Д/э- ’ . /-сП 1-ыГг *д^а
Тогда Л\-0,6Л Nih tt.Na0,7h . 2’5 £MF, EcFi *’5 £,F3 "°-
Учтем, что F2 = 3F, и F3=2Fi и подставим модулей упругости:
/У20,6'1 Л'?.
’ 110» 3F, 210»-F, ’
в последнее уравнение значения
А'з-0,7Л
0,7-1C»-2Fj —°’ (3)
После выполнения сокращений и упрощений уравнения (1), (2) и (3) приводятся к следующей системе:
1.5Л'2+2,5М,уР. 2,5Л'14-2У2=1,5Р. Л'2 — — 1.5/V,=0.
Решив эту систему, получаем
Л\=0,39Р = 0,39-30000= 11 700 кг, Nt = 0.52Р=0,52 •30 000 = 15 600 кг, Л'3=0,09Р=0,09-30 000 = 2700 кг.
Исходя из условий прочности, достаточны были бы следующие площади поперечных сечений:
_И700 f,3s[oc]- 1600 -7,32СЛ’
Nt 15 600 .
[oj 600
F>=-i£f-15Sr2'26"A Но необходимо выполнить заданные в условии соотношения площадей. Так как f 26 F
•=^ = =-535 > 3, а р? < 2, то за исходную возьмем площадь F2 = 26 см2. Тогда • I 7,32 г ।
F1 = ^=^=8,67 см- и Fa=%-F3 = %- -26= 17,33 см2. О о о о
Обе эти площади больше необходимых по условиям прочности, что допустимо. Если бы в качестве исходных мы взяли полученные из условий прочности площади Fi или F3, то, соблюдая заданные соотношения, площади сечений остальных тяг оказались бы меньше допустимых по условиям прочности. Итак, окончательно принимаем: F,=8,67 см2, Ft=26 смг, F3= 17,33 см2.
Я2
Недогрузка стержней 2 п 3 является характерной особенностью статически неопределимых систем, у которых иа предельном напряжении, как правило, работают лишь самые слабые звенья, в данной конструкции тяга 2.
1.71. Три стержня, шарнирно скрепленные в одной точке (см. рисунок), имеют одинаковое поперечное сечение. Определить площадь поперечного сечения, принимая [о] = 1600 кг/сж2.
Ответ: 3 см2.
К задаче 1.71.
К задаче 1.72.
1.72. Жесткая балка поддерживается подвесками, как показано на рисунке. Первая подвеска должна иметь площадь сечения в два раза большую, чем вторая; для материала подвесок принять допускаемое напряжение [а] = 1600 кг/см2. Определить площадь сечения подвесок.
Ответ: f\ = 7,5 см2; Рг = 3,75 см2.
1.73. Три стержня кронштейна (см. рисунок) выполнены из одного материала. Сечение первого 2 см2, второго 3 см2 и третьего 4 см*. Определить напряжения в стержнях.
Ответ: O!=1268 KzjcM2; о, = 268 кг/см2; о8 = — 864 кг/см2.
К задаче 1.74.
1.74. Определить опускание точки С системы из пяти стальных стержней одинакового поперечного сечения площадью 5 см2 (см. рисунок).
Ответ: 0,895 мм.
1.75. Четыре стержня, поддерживающие жесткую конструкцию (см. рисунок), выполнены из одного материала и имеют одинаковые
33
поперечные сечения площадью жения.
Ответ: Oj = 1330 кг/см2;
о3 = — 525 кг/см1-,
F=25 см2. Определить в них напря-
аа = 525 кг/см2-, о4 = — 1330 кг/см*.
К задаче 1.76.
1.76. Жесткий стержень прикреплен к стене при помощи шарнира (см. рисунок), стальной тяги и деревянного подкоса. Подобрать сечение тяги и подкоса, если площадь сечения подкоса должна быть в десять раз больше площади сечения тяги, а допускаемые напряжения равны: для стали [ос] = 1600 кг/см*, для дерева [од] = 60 кг/см*.
Ответ Fc = 50 см2; Fn = 500 см2.
1.77. В изображенной па рисунке конструкции стержень 1 чугунный с [о,] = 800 кг/см2, стержень 2 медный с [ом] = 600 кг/см* и
стержень 3 стальной с [ос] = 1200 кг/см2. Площади поперечных сечений стержней 1 и 2 одинаковы, сечение же стержня 3 вдвое меньше. Подобрать сечения стержней.
Ответ: Ft = Fz = 24,6 cm2; Fs=12,3 cm2.
1.78. В изображенной на рисунке конструкции стержни 1 стальные с площадями сечений Fc=10cjh2, а стержни 2 медные с площадями сечений FM = 20 см2. Допускаемые напряжения равны: для
34
стали [ос] = 1600 кг/сма, для меди наибольшую возможную нагрузку Р. Ответ: 32,8 т.
[о J = 600 кг! см2. Определить
К задаче 1.79.
К задаче 1.80.
1.79. Жесткая конструкция прикреплена к фундаменту при помощи шарнира и двух стержней (см. рисунок). Стержень 1 стальной ([ос] = 1600 кг/сж2), стержень 2 чугунный ([о,] = 1000 кг/см2). Их площади сечений соответственно равны: /\. = 30 см2, F4 = 50 см2.
Определить максимальную допустимую нагрузку Р.
Ответ: 112,5 т.
К задаче 1.81.
1.80. Абсолютно жесткая балка АВ, нагруженная посередине своей-длины силой Р=162 т, опирается на три симметрично поставленные короткие стойки. Крайние стойки бетонные, с размерами квадратного поперечного сечения 30x30 см, средняя стойка деревянная, с размерами прямоугольного поперечного сечения 15x30 см. Определить напряжения в стойках.
Модуль упругости бетона принять равным удвоенному модулю упругости дерева.
Ответ: об = — 80 кг/см2', ой=—40 кг)'см2.
ЗБ
1.81. Квадратная плита опирается иа четыре симметрично расположенные стойки одинакового поперечного сечения, одинаковой длины и из одинакового материала (см. рисунок стр. 35). Определить величину усилия в каждой стойке, пренебрегая деформацией плиты.
Ответ: Л\ = —ОДР; Мг = — 0.25Р; W8 = — О,IP.
1.82. Жесткая прямоугольная плита опирается на четыре одинакового с 1ения, длины и материала стойки, расположенные в ее углах, как указано на рисунке (стр. 35). Определить величину усилия в каждой стойке от нагрузки Р.
Ответ: Nt = —1,5 т; Nt = — 4,5 т; Na = — 8,5 т; Nt = — 5,5 т.
1.83. Определить напряжения в сечениях стержней, показанных на рисунке, на участках /, II, III. Плоскости А и В абсолютно
О) б) в) г) д)
К задаче 1.83.
неподатливы. Принять а = 0,5 л, F= 100 см*, Р= 150 т, 6 = 0,1 мм.
Зазоры 6 имеют указанный размер до приложения нагрузки Р.
После ее приложения они закрываются.
Ответ:
^^^^Схемы НнпряТ''^^-жен п я а 6 в е д
°! °1И 1133 —367 1633 133 —1367 1160 —340 —170 980 —520 -520 238 475 —1025
Напряжения в кг/см*
36
1.84. Жесткий брус (см. рис. а) прикреплен к фундаменту при помощи шарнира С и двух стальных тяг одинакового поперечного сечения. Левая тяга выполнена короче проектного размера на величину А = 5 мм. Определить напряжения в тягах после сборки конструкции.
Решение. После сборки конструкции жесткий брус займет наклонное положение, изображенное на рис. б. При этом левая тяга удлинится на величину Д/л, а правая удлинится на величину Д/п. В точках прикрепления появятся реакции Na и N„, в шарнире С—реакции Л и Я.
Составим уравнения равновесия—сумму моментов всех сил относительно шарнира С:
a sin 30°—Яд-dsin 60°=0, откуда
,, с sin 30° 3 0,5 ,, , „„„
N" ~ b sin 60° Wj,-1 -0,866 (а)
В остальные два уравнения равновесия войдут не интересующие иас реакции Л и Н, поэтому мы их и ие пишем. Для составления дополнительного уравнения обратимся к рассмотрению деформаций.
Из рис. б видно, что
Но
Такнм образом.
Лл а га-т~
Д—Д/
Л —ц ц‘л м л sin 30° sin 60°
(Д-Д<д) sin 60° , sin30°-A/n
87
или
Д—Д/д sin 30° 0,5
Д/п sin 60° 0,866 ’ ’
откуда 1,73Д/П+Д/л = Д. (б)
Выразим Д/л и Д/п через усилия Na и N„:
л/ EF “EFsin 30°
л/ N„t
п~ EF ~EF sin 60° *
Подставим в уравнение (б) найденные значения Д/д п Д/п:
уз NtJ . ЛЦ _ д ’ EF sin 60° TEF sin 30° ’
или
Na+Na=^f. (в)
Разделим обе части уравнений (а) и (в) на F и учтем, чти
тогда
ап=1,73ол, оп + од = -^-.
Решая совместно эти уравнения, получаем, что
_ ДЕ 0,184-0,5-2-10® ООЛ , .
Од = 0,184 —=-------2^---------=920 кг/см*.
nw^E 0.317-0.5-2-10® ,
ап = 0,317 — =-------птгт:----=1585 кг/см*.
1.85. В изображенной на рисунке конструкции стальные стержни 1 выполнены длиннее проектного размера па 1 мм каждый. Их сечение /71 = 25см®, а сечение чугунных стержней 2 равно Л, = 40 см3. Определить напряжения в стержнях после сборки конструкции.
Ответ: о1= — 321 кг/см2-, ов = — 284 кг/см2.
К задаче 1.85.
1.86. Стальной стержень АВ, имеющий длину / = 4л, нижним концом опирается на жесткий фундамент, а верхним прикреплен к
38
балке потолочного перекрытия (см. рисунок). Податливость балки CD в точке А определяется коэффициентом а = 0,03 мм/т, т. е. под действием силы 1 т, приложенной в точке А, балка прогибается на 0 03 мм. Если сила Р = 50 т, а площадь поперечного сечения стержня /=30 сж2, то чему равны напряжения в стержне на участках АК и КВ?
Ответ: аАК=767 кг/см2; окв = — 900 кг/см2.
1.87. Два жестких бруса соединены, как показано иа рисунке, тремя стержнями. Крайние стержни стальные, с площадью сечения верхней части, равной 16 см2, и нижней части 10 см*; средний стержень медный, с площадью сечения, равной 20 см2. Между верхним
К задаче 1.87.
К задаче 1.88.
концом среднего стержня и верхним брусом поставлена без натяга пружина с коэффициентом податливости а = 1,25-10”* см/кг (осадка пружины на 1 кг нагрузки). При заданной нагрузке определить напряжения в соединительных стержнях.
Ответ: В верхней части стального стержня а = —90 кг (см*, в его нижней части а= 1026 кг/см2, в медном стержне о= 144 кг/см*.
1.88. Жесткий брус покоится на трех стойках (см. рисунок). Крайние стойки стальные, одинакового поперечного сечения, площадью 20 см2, средняя стойка чугунная, площадью сечения 50 см2. Между крайними стойками и брусом помещены без натяга одинаковые пружины с коэффициентом податливости, равным а= 5-10“® см/кг. Между средней стойкой и брусом до приложения нагрузки был зазор Д = 0,5 мм.
Определить напряжения в стойках.
Ответ: ос = — 500 кг/см2; о, = — 300 кг!см*.
1.89. Изображенные на рисунке стержни подвергаются нагреванию на t°. Определить наибольшее по абсолютной величине напряжение, если стенки, между которыми расположены стержни, абсолютно неподатливы.
39
Принять Еч = 1 • 10* кг] см*, Еы = 0,8-10* кг/см1, ач = ас, /°=40, / = 0,5ж, 6 = 0,1 Л1Ж.
К задаче 1.89.
Ответ:
Схема а б в г д
Абсолютная величина напряжения, кг/см* 667 1333 1020 600 396
1.90. Стальные рельсы, длина которых составляет 12,5 я, укладываются при температуре 4-10°. Между рельсами оставляется зазор а = 4мм. При какой температуре зазор исчезает? Каков будет зазор зимой при температуре —40°? Какие напряжения будут летом при температуре 4-50°?
Ответ: 4*35,6°; 11,8 «ж; —360 кг/см*.
К задаче 1.91.
1.91. Температура стержней 1 и 2, поддерживающих жесткий брус АВ (см. рисунок), после сборки конструкции может повыситься 40
на 60°. Стержень 1 стальной, площадью сечения 20 см’, стержень 2 медный, площадью сечения 80 см*. Пренебрегая собственным весом бруса, определить возникающие в этом случае в стержнях 1 и 2 напряжения.
Решение. Предположим, что после повышения температуры брус АВ займет положение А'В. изображенное на рнс. 6. Предположим, далее, что стержень / растянут усилием Л/р а стержень 2 сжат усилием Nt. Чтобы исключить реакции Rb » Н. в качестве уравнения равновесия возьмем сумму моментов относительно шарнира В:
'£mB = Nl-2a— N2-a=0,
откуда
/Vt = 2/V|. (I)
Из рис. б видно, что удлинения стержней / и 2 связаны отношением
= (2)
Деформации AZi и Д/, будут вызваны усилиями Nx и Nt и повышением температуры:
AZi = -g^+aJ
Л/ /
Д/2=-0-+аи/ДЛ
Эти значения деформаций подставим в уравнение (2):
AZ =2 £-^-+ам/ Az) .
После подстановки условия (1), произведя сокращения н преобразования, получаем
., 2FcF1(all — ac) At 2 2-10»-20 (165-10-’—125-10-’) 60
"' = 1+<Ы' =-----------’ 2-Ю--20------------
+ £mF2 1 + 4 l-10«-80
II из условия (1)
= 2Д\ =2-6400 = 12 800 кг.
Положительные знаки у Nx и Nt указывают на то, что направление усилий было выбрано правильно и стержень / действительно растянут, а стержень 2 сжат. Следовательно, напряжения равны:
О1 = ^=512° = 320 кг/см*.
, ".1_1^=_16ою/сЛ
1 я oU
1.92. Жесткий брус (см. рисунок), кроме шарнирной опоры, поддерживается еще двумя стальными тягами одинакового поперечного сечения площадью 40 см*. После установки тяг температура повысилась пряжения в тягах.
К задаче 1.92.
на А/ = 4- 20°. Определить на-
Ответ: ох =—470 кг[см*-, а,= —542 кг[см*.
41
1.93. Стальные стержни 1 с поперечным сечением площадью 20 см1 и медные стержни 2 с поперечным сечением площадью 30 см* шарнирно соединены в точке С (см. рисунок) при температуре tt = 15°. Определить напряжения в стержнях при понижении температуры конструкции до tt=—45°.
Ответ: ас=104 кг [см*; а„ =—57 кг/см*.
К задаче 1.93.
к другу при температуре 4-45,5’ и сжаты силами,
К задаче 1.97.
1.94. Определить напряжения в стержне АВ задачи 1.86, если сила Р отсутствует, но температура стержня понизилась на 40°.
Ответ: о = 690 кг!см*.
1.9Б. Инварная трубка с поперечным сечением 30 см* и длиной 40 см и медная трубка тех же размеров поставлены впритык друг 0°. Затем они нагреты до температуры не позволяющими измениться их общей длине. Какова величина этих сил и чему равна длина каждой из трубок при повышенной температуре? Для инвара ая = 0 и £„ = 2-10e кг/см*.
Ответ: Р = 15,0 т; /м = 40,01 см; /„ = 39,99 см.
1.96. Между неподвижными точками Л и В при температуре /0 — 0° горизонтально подвешена без натяжения стальная проволока диаметром 1 мм (см. рисунок к задаче 1.61), весом которой пренебрегаем. Температура проволоки может повыситься до /, = 4- 50° и понизиться до /2= —50°. Допускаемое напряжение для материала проволоки равно [а] =
= 2000 кг/см*. Определить, какую нагрузку Р можно подвесить к проволоке в точке С посредине ее пролета при трех указанных температурах.
Ответ: При 0° нагрузка Р=1,4 кг; при —50° нагрузка Р = 0,32 кг; при +50о нагрузка Р=1,79 кг.
1.97. Груз Р=4,5т передается через жесткую плиту на сплошной стальной цилиндр площадью 15 см* и полый медный цилиндр площадью 20 см*. Сила действует по оси обоих цилиндров (см. ри
43
сунок). После приложения нагрузки температура может повыситься на 30°. Найти распределение нагрузки до и после изменении темпе-
ратуры.
Ответ: До изменения температуры Рс = 2,7 т, Р„ = 1,8 т, после изменения температуры РС=1,26 т, Рм = 3,24 т.
1.98. Стальное ленточное кольцо толщиной 6 xixi необходимо натянуть на стальной же цилиндр диаметром 30 см; внутренний диаметр ленточного кольца равен 29,98 см. Насколько необходимо повысить температуру кольца, чтобы оно стало скользить по поверхности цилиндра? Какое растягивающее напряжение возникает в кольце,
когда оно примет ту же температуру, что и цилиндр, если деформацией последнего можно пренебречь?
Решение. Средний диаметр ленточного кольца до его нагрева равен
<1 = 29,98 + 0.6 = 30,58 см.
Чтобы кольцо могло скользить по цилиндру, необходимо, чтобы внутренний его диаметр стал по крайней мере равен диаметру цилиндра, т. е. чтобы он увеличился на
Ad = 30 — 29,98 = 0.02 см.
На эту величину Ad увеличится и средний диаметр кольца. Тогда относительно увеличение диаметра составит
Ad 0,02 е d 30,58 6,54 ’ 0 '
Приравняем это значение в относительному увеличению диаметра, вызванному повышением температуры:
в=а-А1, откуда
в_6,54-10-«
ДГ-а“ 125-Ю-7
К задаче 1.99.
После того как кольцо в горячем состоянии будет надето, оно постепенно остынет до первоначальной температуры, т. е. по сравнению с нагретым состоянием его температура уменьшится на Д<=52,2°. Так как деформацией цилиндра мы пренебрегаем, то кольцо не имеет возможности уменьшить свой диаметр; следовательно, для определения в нем напряжений можем воспользоваться формулой а = ЕаД< = 210«-125-10-’-52.2= 1308 кг/см*
или
а=£е = 210«-6,5410-«=1308 кг/см1.
1.99. Короткий чугунный стержень свободно вставлен в стальную трубку, которая в свою очередь свободно вставлена в алюминиевую трубку (см. рисунок). Определить напряжения в стержне и трубках (поперечными деформациями пренебречь) при действии силы Р, сжимающей систему через посредство жесткой плиты.
Решение. Нагрузка Р распределится между чугунным стержнем, стальной н алюминиевыми трубками. Равенство нулю суммы проекций всех сил на
43
вертикаль лает
Рч+*>с+'>. = *>-
Это единственное уравнение статики, которое мы можем составить.. Обратимся к рассмотрению деформаций. Деформации (укорочение) всех трех стержней равны между собой, следовательно,
Д/„ = Д/с=Д/а.
Отсюда можно составить два уравнения деформации:
Д/„ = Д/С и Д/ч = Д/а.
Выразим деформации через нагрузки:
=_Р£ „ р-‘ Р*1
ЁЧГЧ ECFC E4F4 EaFa'
Выразим в уравнении равновесия и в уравнениях деформации силы через на-Рч ?с Р,
пряжения, имея в виду, что ^L=o4, и г± = аа> и сократим в урав-
•ч *‘с 'а
нениях деформации длину Z. Тогда уравнение равновесия и уравнения деформации примут следующий внд:
o4F4+acFc+aaFa = P;
Совместное решение этих трех уравнений дает Значения напряжений. Онн равны
Р
ч.л 9 «Л. 2 5,5»—2,5* 0,7 8.5»-5,5»\-1е0'сг/"‘’ 3,!4 2,5» 1 + -J-2-+ L2 ’ 2,5» )
F 9.10®
<Т£=Й:<Тч=Г2ТТо'’ •160 = 300 KZ‘CMi‘
Е 0 7-10»
в-=Е!с’=ТЗЛ5» ’,80= 105 кг/сл1’
Все напряжения сжимающие.
1.100. Жесткий брус подвешен на трех стальных стержнях одинакового поперечного сечения площадью 20 см-. Средний стержень
К задаче 1.100.
выполнен короче проектного размера на 6 — 0,5 мм (см. рисунок). Определить напряжения в стержнях после сборки конструкции.
Ответ: at=—143 кг (см2-, ot = 715 кг (см2', о8=—429 кг [см2.
44
1.101. Жесткий брус подвешен на трех стержнях одинакового поперечного сечения площадью 10 см1, ио выполненных из разных материалов (см. рисунок). Определить напряжения в стержнях после
К задаче 1.101. К задаче 1.102.
повышения их температуры на А/=4-30°. Для инвара а„ = 0 и
£м = 2-10’ кг!см\
Ответ: ос =—142 кг)смг’, ом=—166 кг/см1; о, = 527 кг/см*.
1.102. Жесткая конструкция (см. рисунок) прикреплена к фунда-
менту при помощи шарнира и трех тяг с одинаковой площадью попе-
речного сечения и одинаковой длиной. При допускаемом напряжении (о] = 1600 кг[сн? подобрать площадь сечения тяг.
Ответ: 7,65 см1.
1.103. Бетонная стойка АВ с обоими защемленными концами (см. рисунок) в среднем своем сечении должна быть нагружена вдоль оси силой
К задаче 1.103.
Р=32 т. Какой площади сечения нужно поставить две стальные тяги /, чтобы растягивающие напряжения в верхней части бетонной стойки после нагружения не превосходили 5 кг[смП Чему
45
в этом случае будут равны напряжения в тягах и в нижней части стойки? Модуль упругости для бетона при растяжении и при сжатии принять одинаковым и равным Еб= 1,5-10* кг/см*.
Ответ: F = 2X120 смг; ат=66,7 кг/см*-, аб=—5 кг/см*.
1.104. Жесткая балка первоначально опиралась правым концом на чугунную стойку площадью сечения 100 см2 и не имела промежуточных опор. Затем были поставлены две промежуточные деревянные стойки круглого сечення диаметром 25 см (см. рисунок). На сколько процентов можно увеличить нагрузку после установки промежуточных стоек при условии, что напряжения в чугунной стойке останутся первоначальными?
Ответ: На 41%.
§ 3. Учет собственного веса
1.105. Определить наибольшие сжимающие напряжения и полное укорочение бетонной колонны постоянного сечения высотой 10 м, если один кубический метр бетона весит 2400 кг, а его модуль упругости равен 2-10* кг/смг.
Ответ: 2,4 кг/см2-, 0,06 лиг.
1.106. Клеть подъемника, весящая 1,6 т, подвешена на двух
тросах на глубине Л =140 л». Площадь, поперечного сечения каждого
К задаче 1.107.
троса равна 1,25 смг, погонный метр его весит 1,5 кг. При предварительном испытании троса было установлено, что при нагрузке 1000 кг отрезок троса длиной в 1 м удлиняется на 0,5 мм. Чему равны напряжения у верхнего и нижнего концов троса и какое он будет иметь полное удлинение?
Ответ: ов = 808 кг/см*', ан = б40 кг)смг\ Ы = 6,35 см.
1.107. Площадь поперечного сечения столба, изображенного на рисунке, изме-няется в соответствии с формулой Fx = Fo .
Определить полное укорочение столба от собственного его веса при известных у и Е.
Решение. Выделим на расстоянии х от вершины бесконечно малую часть столба высотой dx. Ее объем dV=Fxdx=F0-^ dx. Объем верхней части столба Л
высотой х будет равен о о
а вес этой части
40
Укорочение бесконечно малого объема столба высотой dx под воздействием веса вышележащей части столба высотой х будет равно
Л yFpX2h dx __ ух dx
EFX 2hEFox 2E ’
а укорочение всего столба
h h
о 0
1.108. Определить полное укорочение от собственного веса конуса высотой h с радиусом основания риала у и
Ответ:
модуле упругости Е.
уЛ2 6£ • Определить полное укорочение представленного на рисунке стержня с веса, если материала
Ответ:
1.109.
учетом его собственного известны объемный вес у и модуль упругости Е. 3 Ра । Зуд* Т £F"* "2£~‘
1.110. Определить с учетом собственного веса перемещение сечения m—п приведенного на рисунке стержня с поперечным сечением F, модулем упругости Е и объемным весом материала у.
Ответ,- ^+v£+£)£+g.
R при объемном весе мате-
К задаче 1.109.
К задаче 1.110.
2F
Р
ч
1.111. При какой длине разорвется только от собственного веса стальной стержень, вертикально подвешенный за верхний конец? Предел прочности стали принять равным 50 кг/мм*.
Ответ: 6,41 км.
1.112. Определить размеры квадратного поперечного сечения каменного столба высотой 10 лс, нагруженного силой 65 т. Удельный вес кладки равен 2, допускаемое напряжение на сжатие равно 10 кг/см2. Определить напряжения в верхнем и среднем сечениях столба. Какими получились бы по расчету размеры поперечного сечения, если нс учитывать собственный вес столба?
Ответ: 90x90 см; ов= —8 кг)см2, оср = —9 кг/ся2; 81 Х81 см.
1.113. Определить площади поперечных сечений ступенчатой стойки высотой 40 м, сжатой силой 100 т, имеющей четыре участка одинаковой длины. Удельный вес материала стойки равен 2, допускаемое напряжение равно 8 кг)см2. Построить эпюру распределении напряжений по длине стойки.
Ответ: 1,67 я2; 2,23 я2; 2,97 м2; 3,95 я2.
47
иого веса оудут п
К задаче 1.116.
1.114. Штанга бурильного агрегата длиной 120 ж представляет собой стальную трубку с внутренним диаметром 25 мм, закрепленную верхним концом и нагруженную на нижнем конце продольной растягивающей силой 2 т. Определить толщину стенки штанги в двух предположениях: с учетом и без учета собственного ее веса. На сколько процентов действительные напряжения с учетом собствен-:вышать величину допускаемых, если штангу спроектировать без учета ее собственного веса? Допускаемое напряжение [о] = 1000 кг/см?.
Ответ: 2,5 мм; 2,3 жж; 9%.
1.115. Определить объем кладки мостовой опоры высотой 42 м, нагруженной сжимающей силой Р = 400 т, в трех случаях: 1) опора постоянного сечения, 2) ступенчатая из трех частей одинаковой длины и 3) в виде бруса равного сопротивления. Материал кладки имеет объемный вес 2,2 т/м3, а допускаемое напряжение равно 12 кг 1см?.
Ответ: V, = 610 ж3; V2 = 261 ж3; V3 = 209 ж3.
1.116. На рисунке представлен поперечный разрез кирпичной стены шестиэтажного здания. От чердачного перекрытия и кровли на погонный метр стены действует нагрузка = 6 т/м, от междуэтажных перекрытий <72 = 4 т/м и от пола нижнего этажа 03 = Зт/ж. Эти нагрузки приложены вдоль оси стены. Объемный вес материала стены и фундамента равен 2 т/м3. Определить наименьшие толщины стен в каждом
этаже при допускаемом напряжении [о] = 6 кг/см? и ширину фундамента при допускаемом давлении на грунт, равном 5 кг/см3.
Ответ: ^=11,5 см; Ьг = 2\ см; Ь3 = 32 см;
bt = 44,5 сж; bt = 59 см; bt = 76 см;
&ф= 125 сж.
На основании теплотехнических расчетов полученные минимальные размеры толщин стен верхних этажей увеличиваются. Кроме того, все размеры должны быть приведены в соответствие со стандартными размерами кирпичей.
1.117. Вертикальный стальной стержень с площадью поперечного сечения F и длиной / = 300 ж работал с продольной нагрузкой Р при напряжении 6 кг/мм3. Не меняй ни размеров сечения стержня, ин нагрузки на него, требуется нарастить стержень в длину, считая возможным повышение допускаемого напряжения до 6,5 кг/мм3. Насколько длиннее можно сделать стержень?
Ответ: На 64,1 ж.
1.118. Определить наибольшие растягивающие и сжимающие напряжения в поперечных сечениях стержня, изображенного на рис. а. Объемный вес материала стержня у, а модуль упругости Е. Площадь поперечного сечения верхней части F1( иижией Fv
48
Решение. Обозначим верхнюю реакцию А и нижнюю В. Предположим, что обе онн направлены вверх. Тогда единственное уравнение равновесия — сумма проекций на вертикальную ось—дает, что вес стержня равен сумме реакций:
yFja+yFJb = A-\-B. (1)
Таким образом, система оказывается статически неопределимой. Обратимся к рассмотрению деформаций. Для перехода к основной системе отбросим нижнюю опору. Нагрузим основную систему реакций В (см. рис. 6). Так как полная деформация равна нулю, то укорочение стержня, вызванное реакцией В, должно равняться его удлинению, вызванному собственным его весом. Это условие и будет дополнительным уравнением деформации. Укорочение стержня от реакции В равно
К задаче 1.118.
Удлинение стержня, вызванное его собственным л/ vF2ba_ybt Г, , / а
Л'С~2Е +2Е+ EF2 ~2Е + J
Приравняем выражения (2) и (3):
£(1+|£) <[i+^y+ \ о г 2 С. L \ О }
весом, равно
+ 2У?1-
(3)
откуда
В-—-
’+2ТГ’
Р Fl
b F.
а из уравнения (1)
Л=yFifl + yFjb— В=yFiO+yFtb—
после несложных преобразований получаем
о Ft a F2 Ь F.
+ 2-^ a Fz Ь_Г\ a F2 Наибольшее растягивающее напряжение будет равно
л _VaFi
А—Г
” F* 2‘ i-i-ALi
« Ft а наибольшее сжимающее
В _ yb
F2 2
4»
1.119. Железобетонная колонна указанных на рисунке размеров нагружена только собственным весом. При объемном весе железо-
бетона, равном
2,5 т/м3, определить напряжение в бетоне и в арматуре колонны. Отношение модулей упругости стальной арматуры и бетона принять равным 15, диаметр арматуры 25 лен.
Ответ: о6 = —1,7 кг/см2: ос = — 25,5 кг/см2.
1.120. Бетонная колонна постоянного сечения жестко защемлена своим верхним и нижним концами. Какую предельную длину может иметь колонна, если растягивающие напряжения в бетоне не должны превышать 5 кг/см2? Объемный вес бетона принять равным 2,5 т/л13.
Ответ: 40 м.
§ 4. Гибкие нити
-*\25см м-
К задаче 1.119.
1.122. Трос положенным на
1.121. Гибкая нить с точками подвеса на одном уровне изготовлена из материала, имеющего вес единицы объема 8 г/см3 и допускаемое напряжение 3000 кг/см2. Определить предельные значения проле-f 1 1
тов при -у-=род и -pj. Увеличением напряжения у опор пренебречь.
Ответ: 300 м и 3000 м.
весом 1 кг/м подвешен с провесом 1 м к двум рае-одном уровне опорам, находящимся на взаимном
расстоянии 40 м. Определить величину натяжения троса.
Ответ: 200 кг.
1.123. Висячий мост поддерживается двумя стальными цепями. Пролет цепей равен 120 лс, а их стрела провисания 10м. Собственный вес конструкции моста вместе с временной (полезной) нагрузкой составляет 6 т/м. Определить необходимую площадь поперечного сечения каждой цепи при [о] = 4000 кг/см2.
Ответ: 142,5 см®.
К задаче 1.124.
1.124. Полная нагрузка на цепь изображенного на рисунке висячего моста равномерно распределена по пролету и равна 5т/лс. Определить необходимое сеченне оттяжек АВ и CD при допускаемом напряжении для них, равном 3000 кг/см2.
Ответ: 295 см2.
60
1.12Б . Стальная проволока круглого сечения площадью 0,5 см\ пролетом 1=80 м перекинута через блок В и натянута грузом 0=350 кг, как изображено на рисунке. Определить стрелу провисания f в двух случаях: 1) проволока нагружена только собствен-
ным своим весом и 2) на проволоке между точками А и В намерз слой льда толщиной 1 см. Удельный вес льда 0,9. Трением в блоке пренебречь.
Ответ: = 0,90 м; /2 = 2,07 м.
1.126. Определить натяжения в стальной и алюминиевой частях проволочного сталеалюмннневого
К задаче 1.125.
кабеля, подвешенного к двум опо-
рам, расположенным на одинаковом уровне, с пролетом I и при стреле провисания кабеля /. Площадь стальной части кабеля Fc, алюминиевой Fa, объемные веса и модули упругости равны соответственно ус, уа, Fc и Fa.
Ответ:
Н (ТЛ + Т^аИ2 . Н (Ycfc + Yafa)/2
1.127. Якорная цепь, удерживающая баржу,—стальная, сечением 5 см2. В точке установки якоря она горизонтально касается дна (см. рисунок). Определить расстояние I от баржи до якоря, если величина горизонтального усилия, вырывающего якорь, равна 100 кг.
Ответ: 18,8м
К задаче 1.127.
1.128. Горизонтальное расстояние между опорами провода сечением 1 см2 равно 37 м. Одна опора ниже другой на 30 см, и наиннз-шая точка провода расположена на 90 см ниже нижней опоры. Определить горизонтальное расстояние от нижней опоры до наиннз-шей точки провода и натяжение в этой точке, если удельный вес провода равен 8 г/см3.
Ответ: 17,1м; Н= 131 кг.
1.129. Определить натяжение в нижнем сечении несущего троса, поддерживающего провод электрической железной дороги (см. рисунок), при уклоне Z = 30°/оо, пролете / = 75 м и нагрузке q = 1,6 кг/м
51
троса. Расстояние по вертикали наиболее пониженной точки троса от вершины более высоко расположенной опоры равно f = 3 ж.
Ответ: Н = 667 кг.
К задаче 1.129.
U--------I --------н
К задаче 1.130.
1.130. Плавающая в воде баржа (см. рисунок) передает на якорную цепь горизонтальное усилие /7= 36 т. Полная длина цепи 45 ж, а вертикальное расстояние от точки прикрепления цепи к барже до дна равно 9 ж. Погонный вес цепи в воде равен 50 кг/м. Определить горизонтальное расстояние между якорем и точкой подвеса цепи к барже.
Ответ: 43,8 ж.
1.131. При помощи стального троса, погонный вес которого 3 кг/м., а площадь сечения 4 см2, корабль пришвартован к берегу (см. рисунок). Какими уснлнямн корабль относит от берега, когда трос
провисает по кривым 1, 2 и 5? Нижняя точка кривой 2—у ее левого закрепления, нижняя точка кривой 1—левее левого закрепления, а кривой 3— правее и на одном уровне с нижней точкой кривой 1.
Ответ: fit = 143 кг; На = 60 кг; Нв = 25 кг.
1.132. Стальной провод должен быть подвешен к двум точкам, находящимся на одном уровне и отстоящим на 30ж друг от друга.
62
Провод подвешивается при температуре 4-35°. Чему должна равняться первоначальная стрела провисания, чтобы при температуре—25° напряжения не превышали 3000 кг/см*? Провод нагружен только своим собственным весом.
Решение. Условие прочности для провода имеет вид
Н 1
°- F
Так как нагрузкой на провод является только собственный его вес. то q= yF-1 и условием прочности будет 2^- < [о].
После сокращения на площадь сечения провода находим необходимую
стрелу провисания:
уР 7,8-10-8-30а-104 ' 8[с]~ 8-3000
=2,92 см.
Эту стрелу провисания должен иметь провод в опасном состоянии, т. е. при температуре —25°. Чтобы найти стрелу провисания при подвеске провода, необходимо перейти от его состояния при Zj = —25е к его состоянию при /а= +35°. Как известно, два состояния провода связаны между собой следующим кубическим уравнением:
L 24П1 J
EFqjP 24
Произведем в этом уравнении следующие замены:
На=|£. Н, = Н = |оИ и <7i = <72=? = ?F.
Of 2
Тогда уравнение запишется так:
.2 3 12 Г Угр It 3^-п
,2 8 1 [24[с]2 + (<а Z,) Е_Ра 64 £“°’
После подстановки числовых данных оно принимает вид
+1й.ю-^+Я)-ЭД _
3-7,8 10-»-3000«
64-2-10» “°’
а после сокращения
/| + 2Б15/2—14 860= 0,
откуда /2 = 5,82 см. Это и будет необходимая первоначальная стрела провисания.
1.133. Многожильный алюминиевый провод сечением 95млса подвешен к опорам, ресположенным на одном уровне и находящимся на взаимном расстоянии 100 л:. Стрела провисания провода равна 4 м. Найти увеличение напряжений при понижении температуры на 50°, если вес погонного метра провода равен 0,257 кг, коэффициент линейного расширения а = 23 • 10“*, модуль упругости Е *= 0,63 X10* кг)см2.
Ответ: Напряжения увеличатся на \\ кг/см2.
1.134. Между двумя опорами, расположенными на одинаковом уровне н отстоящими одна от другой на расстоянии /= 100 м, летом
63
подвешивается многожильный сталеалюминневый провод при температуре t2 = 4-25°. Площадь сечения провода Р=120жж*. В дальнейшем температура понижается до t2 = —53 и происходит обледенение провода, при этом слой льда достигает толщины Юля. Одновременно провод подвергается горизонтальному давлению ветра интенсивностью 24 кг на 1 мг вертикальной проекции провода, покрытого слоем льда. Кроме того, предусматривается, что зимой температура может понизиться до ta = — 40°, но без одновременного обледенения и ветра.
Какова должна быть первоначальная стрела провисания провода, чтобы при наихудших условиях напряжения в нем не превышали 1000 кг/см1, если вес 1 пог.м провода равен 0,491кг, его наружный диаметр 15,2 мм, a=19-10-e, Е— 0,82-10® кг!см1, удельный вес льда равен 0,9?
Ответ: 1,42 ж.
ГЛАВА 2
СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ. ТЕОРИИ ПРОЧНОСТИ
§ Б. Аналитические и графические методы определения напряжений
2.1. Стержень диаметром бел» растянут вдоль своей оси усилием 245-103 н (25 т). Определить величину нормального н касательного напряжений по сечению, нормаль к которому составляет угол 30° с осью стержня. Определить, по какому сечению касательные напряжения достигают максимума, и вычислить их величину.
Решение. Найдем напряжение по сечению,перпендикулярному к осн стержня: Р Р 4-245-1№ ,
ao~F~ mP/4 “ 3.14-0.062 - 867 10 Н,М ‘
Нормальное и касательное напряжения по наклонному сечению определяются по формулам
оа= о0 cos2a=867-10*-0,8662 = 650- 10е н[м?.
та =^ sin 2а=86721°6 0,866=375-10» h/jh2.
Касательные напряжения достигают максимума по сечениям, наклоненным к осн стержня под углом 45°. Их значение равно
_о0_ 867-Ю»
Тщах— 2 — 2
433-10» н/лР.
2.2. Стержень с квадратным поперечным сечением размером 10х10сл1 сжат вдоль осн силой 50т. Определить полные напряжения в поперечном сечении и в сечении, образующем угол 30° с поперечным.
Ответ: р0 = о0 = 500 кг/см2; р, = 433 кг/см2.
2.3. Стержень прямоугольного поперечного сечения с отношением сторон 5:1 растянут вдоль оси силой 32т. Допускаемое касательное напряжение принято равным 800 кг/см1. Определить размеры сечения.
Ответ: 2 X Юсм.
2.4. В растянутом вдоль осн стержне нормальные напряжения по одному из наклонных сечений равны 750 кг/см2, а касательные 433 ке!смг. Определить наибольшие нормальные напряжения и угол между заданным наклонным и поперечным сечениями.
Ответ; 1000кг/см2; 30°.
Ы
2.5. Наибольшее нормальное напряжение в растянутом вдоль оси стержне равно 400 кг/см-, а по одному из наклонных сечений касательное напряжение равно 173 кг/см2. Определить угол наклонного сечения ио отношению к поперечному и значение действующего по нему нормального напряжения.
Ответ: а, = 30э, аЯ1 = 300 кг/см?-, а* = 60°, аа' = 100 кг/см?.
2.6. При испытании на сжатие бетонного кубика размером 20x20x20 см перед его разрушением нормальное напряжение по сечению, наклоненному под углом 45° к направлению усилия, оказалось равным —45 кг/см2. При какой нагрузке разрушился кубик?
Ответ: 36 т.
2.7. Полное напряжение по одному из сечений, проведенных через выбранную точку элемента конструкции, равно 600 кг/см?, н оно наклонено к этому сечению под углом 60°. По второму сечению, перпендикулярному к первому, нормальное напряжение равно нулю. Определить наибольшее нормальное напряжение по опасному сечению, проведенному через эту точку.
Ответ: 654 кг/см?.
2.8. По заданным ot и а2 (рис. а), или а, и ая (рис. б), или а2 и а, (рнс. в) определить аналитически или графически оа и та в
К задаче 2.8.
сечении под углом а. Определить наибольшие касательные напряжения в элементе.
Заданные величины Ответ
Вариант 01. кг’см* Оа. кг'см* оя. кг'см * <х° кг 1см*
1 1000 500 0 30 875
2 1000 500 0 -60 625
3 300 300 0 л тобой 300
4 800 0 —200 60 50
5 800 0 —200 -30 550
6 300 0 —300 45 0
7 300 0 -300 30 150
8 300 0 —300 —60 —150
. 9 0 —200 -600 60 -500
10 0 —200 —600 —30 —300
50
2.9. В стенке резервуара главные напряжения равны бООкг/см* и 1200 кг/см2. Определить нормальные и касательные напряженки для сечения, нормаль к которому составляет угол 30° к направлению наибольшего главного напряжения. Найти положение сечения, нормального к стенке, с наибольшим касательным напряжением и вычислить обе составляющие напряжения по этой площадке.
Ответ: <уа = 1050 кг/см*-, та = 260 кг/см1-, тгаах — 300 кг/см--, атах- = 900 кг/см2.
2.10. Главные напряжения в точке элемента, находящегося в плоском напряженном состоянии, равны 1200 кг/см2 и 450кг/сма. Определить положение сечения, в котором полное напряжение наклонено под наименьшим углом к сечению.
Ответ: Под углом 58°30' к сечению с наибольшим главным напряжением.
2.11. По заданным оа, и та(т₽ =—та) (см. рисунок) определить аналитически или графически величину и направление главных напряжений и изобразить элемент, находящийся под воздействием только одних главных напряжений.
К задаче 2.11.
Вариант Заданные величины, кг/см2 Ответ
ач °0 т а шах а. кг [см*
1 400 200 100 441
2 Б00 300 —200 623
3 —200 300 200 370
4 —400 200 -300 324
5 —100 —200 100 —38
6 —200 —400 —400 —112
7 500 0 200 570
8 0 600 300 724
9 —400 0 200 83
10 0 —800 250 72
11 500 500 100 600
12 —400 -400 —200 —200
13 0 0 250 250
14 —600 400 0 400
' 67
2.12. Определить аналитически или графически нормальное от и касательное тт напряжения по указанному (см. рисунок) наклонному сечению в элементе, по граням которого известны нормальные и касательные напряжения.
К задаче 2.12.
Вариант Заданные пеличпны Ответ, кг!смг
С . а хе см3 кЦсн* та ’ кг/см3 Vе с У т г
1 800 0 400 30 254 546
2 600 0 200 —60 323 —360
3 400 0 —200 —30 127 —273
4 200 0 —400 60 396 273
5 —1000 0 400 —30 —404 633
6 —800 0 300 60 —460 -496
7 —600 0 —200 30 —377 —360
8 —400 0 —400 -60 —446 373
9 700 200 —300 —30 315 —366
10 600 400 —200 60 623 187
11 500 300 100 30 363 137
12 400 200 400 -60 596 -287
13 400 -600 200 30 —23 533
14 500 -300 200 -60 323 —446
15 300 -500 —200 -30 —73 —446
16 200 —400 —200 60 —77 146
17 —100 —400 200 —30 -2 -30
18 —200 —500 200 60 —598 30
19 —300 -500 —300 30 —90 —63
20 —400 -600 —300 -60 -810 63
2.13. По граням АС и СВ треугольного элемента, изображенного на рисунке, действуют одинаковые сжимающие нормальные напряжения — 500 кг/см* и касательные напряжения, а грань АВ не нагружена. Определить значение касательных напряжений по граням АС и СВ и величину и направление главных напряжений.
Ответ: т = 500 кг!см?\ ot = 0; оэ = — 1000 кг/см2.
2.14. Кубик с ребром 10 мм был испытан на сжатие. При нагрузке 6300 кг он разрушился по октаэдрической плоскости, т. е.
68
по плоскости, равнонаклоненной ко всем трем его граням (см. рисунок). Определить нормальное, касательное и полное напряжения в этом сечении в момент разрушения.
К задаче 2.14.
Решение. Главные напряжения в рассматриваемом кубике равны а(=о2=0, о8=—6300 кг/см1.
Октаэдрическое нормальное напряжение определяется по формуле Рокт = °| + ? + °3 = -^=-2100 кг/сж>.
а октаэдрическое касательное напряжение—по формуле
»<жт=уК (П|—а»)*-!- (а2—о8)а+(о8—о,)а = ^- |о3|= ^6300 = 2970 кг/см2.
Полное напряжение равно
Рокт = V о’кт+^кт= /(-2100)^ + 2970^ = 3630 кг/см2.
2.1Б . Определить октаэдрические нормальное и касательное напряжения для элемента, находящегося в указанном в таблице напряженном состоянии.
Вариант
Заданные главные пппряжения. кг/км*
а1 I о. I о,
1
2 3
4
5 6
7
8
12 12
12
12
10
10
8
—8
10
10
8
—8
8
—10
—10
8
—10
—10
—12
—12
—12
—12
10 4,67 3,33 —2
2 —3,33 —4,67 —10
3,77 9 9,5 9,93 9,93
9.5 9
3,77
2.16. На грани элементарного кубика, вырезанного нз стального ствола орудия, действуют напряжения: 55 кг/мм2, 42 кг/мм2 и —35 кг/мм2. Определить наибольшее касательное напряжение и подсчитать расчетные напряжения по 111 и IV теориям прочности.
89
Решемие. Главные напряжения соответственно равны
О! = 55 кг/мм2, о2=42 кг/мм2 н о3= — 35 кг!млР.
Наибольшие касательные напряжения определяются по формуле о3 554-35 _
^тах— 2 2 кг/лл .
Расчетное напряжение по III теории прочности равно °1П=01—о3=554-35 = 90 кг/мм*.
Расчетное напряжение по IV теории прочности равно у "о. г_______________________________
O|V= —2~ —°г)а+(°1—°s)2 + (°2—°з)2 =
= 0,707 / (55 — 42)2 4- (55 + 35)2 4- (42 4- 35)2 = 84 кг/мм2.
2.17. Вычислить расчетные напряжения по I и II теориям прочности при указанных главных напряжениях (р. = 0,3).
Вариант Заданные главные напряжения. кг/см3 Ответ, ке/см*
О, о. С, °! °И
1 1200 1000 800 1200 1660
2 1200 1000 —800 1200 1460
3 1200 —1000 800 1200 1600
4 1200 —1000 —800 1200 1740
5 800 1000 —1200 4-1000 или —1200 1740
6 1000 —800 —1200 4-1000 или —1200 1600
7 800 —1000 —1200 4-800 или —1200 1460
8 —800 —1000 —1200 —1200 660
2.18. Вычислить расчетные напряжения по Ш и IV теориям прочности при указанных главных напряжениях.
Вариант Заданные главные напряжения, жг/ом1 Ответ, кг/см*
о. * С. ’ill °iv
1 1200 1000 800 400 346
2 1200 1000 -800 2000 1910
3 1200 —1000 800 2200 2030
4 1200 —1000 -800 2200 2110
5 800 1000 —1200 2200 2110
6 1000 -800 —1200 2200 2030
7 800 —1000 —1200 200 1910
8 —800 —1000 —1200 400 346
60
2 19 Проверить прочность чугунной детали при величине главных напряжений 150 кг/см2, —400 кг/см2, —600 кг/см2. Допускаемые напряжения для данной марки чугуна: на растяжение [а+] = =300 кг/см2, на сжатие [а_] = Ю00 кг/см2. Руководствоваться теорией прочности Мора.
Решение. Обозначим: Oj = 150 кг/см2, о2 = — 400 кг/сж2 и о3 = — 600 кг/рР.
Условие прочности на растяжение по Мору имеет вид
В нашем случае
ЧОО
150 + 600^=330 кг/см2 > 300 кг/см2.
Оно не удовлетворено. Расчетное напряжение превышает допускаемое на 10»/о. что недопустимо.
Мы получили бы такой же результат, если бы вычислили расчетное сжимающее напряжение и сравнили его с допускаемым напряжением на сжатие в соответствии с преобразованным условием
2.20. Вычислить расчетное сжимающее напряжение по теории прочности Мора для случаев:
Вариант Заданные величины Ответ
Ot, кг/см* (Тз. кг/см*
1 100 —600 4 1000
2 —100 —700 5 1300
3 350 —250 3 1300
4 300 100 4 1100
5 300 0 4 1200
6 0 —700 5 700
§ 6. Деформации. Потенциальная энергия
2.21. Главные напряжения в стальной стенке котла равны 3-10’ н/м2 и 6-10’ н/м2. Определить главные относительные деформации. Какое напряжение в направлении ot вызовет в этом направлении такую же относительную деформацию при линейном напряженном состоянии? Определить запас полной потенциальной энергии, накопленной в 1 см3 материала стенки котла. Принять Е = 2-10“ н/м2 и Ц = 0,3.
Ответ: е, = 2,55-10-*; е2 = 0,6.10-*;
а = 5,1 • 10’«/л»2; и = 8,55-10“3 нм/см2.
2.22. Во время испытания стального листа на простое растяжение при напряжении 1500 кг/см2 на длине 250 мм было измерено Удлинение, равное 0,2 лея. Чему будут равны главные деформации,
61
если этот лист добавочно нагрузить таким же напряжением в поперечном направлении? Чему будут равны эти деформации, если добавочные напряжения в поперечном направлении будут сжимающими?
Ответ: При добавочном растягивающем напряжении = Д/2= =0,14 мм; при добавочном сжимающем напряжении Д/, = 0,26 мм Ыг = — 0,26 мм.
2.23. Элемент, вырезанный нз стальной детали, находится в плоском напряженном состоянии (см. рисунок). Определить изменение длины диагонали.
Ответ: 37-1О-3 мм.
2.24. При прохождении поезда через мост в одной из точек стальной балки при помощи тензометров были измерены удлинения в горизонтальном и вертикальном направлениях. В горизонтальном направлении разность отсчетов тензо-600кг/см* метра оказалась равной +8 мм при
его базе 20 мм и увеличении 1000; в вертикальном направлении разность отсчетов тензометра оказалась равной —12 мм при его базе 100 мм и том же увеличении.
Определить нормальные напряжения в горизонтальном и вертикальном направлениях.
Ответ: В горизонтальном направлении а = 800 кг/см1, в вертикальном направлении а = 0.
2.25. . Напряженное состояние элемента, выделенного из стальной детали, находящейся в плоском напряженном состоянии, представлено на рис. а. Его относительные деформации (см. рис. б)
150ке/смг
К задаче 2.23.
Г— 1—И
а) 6)
К задаче 2.25.
равны: ех = 5,32-10-4, еу = —1,82-10‘4, у = 1,19-10-3. Определить величину и направление главных напряжений.
Ответ: а, = 1600 кг/см*; а3 =— 600 кг/см2; ах повернуто относительно горизонтали на 30° по часовой стрелке.
2.26. Определить модуль объемной деформации и наибольшие по абсолютной величине относительные деформации для стального
02
элемента, находящегося в объемном напряженном состоянии, при указанной величине главных напряжений.
Вариант Заданные значения главных напряжений, кг/см*. Ответ
1 + 150, + 300, + 450 С1 = 157-10-’
2 + 150, +300, —450 е3 = —293-10-’
3 + 150, —300, —450 «3 = —202-10-’
4 + 150, —300, + 450 е3= —240-10-"
5 —150, —300, —450 е3= —157-10“’
6 —150, +300, —450 et = 240-10’
7 —150, —300, + 450 ei = 293-Ю-’
8 —150, + 300, + 450 et = 202-10-’
К= 1,667-10’ кг/ся».
2.27. Определить раздельно энергию изменения объема и энергию изменения формы для элементарного кубика, выделенного из стальной детали, находящегося в объемном напряженном состоянии, при указанных значениях главных напряжений.
Вариант Заданные значения главных напряжений, кг/см1 Ответ, кг/см*
<*| (7, 03 ИФ
1 1000 700 400 0,147 0,585-10-1
2 1000 700 —400 0,558-Ю-1 0,353
3 1000 —400 —700 0,333-10-» 0,535
4 —400 —700 —1000 0,147 0,585-10-1
2.28. Толстая плита имеет квадратное в плане гнездо глубиной 10 мм н с поперечными размерами 10,001 X 10,001 мм. В это гнездо
вставлен медный кубик размерами 10 X ХЮхЮлш, который затем нагружается сверху силой 1000 кг, как то указано на рисунке. Полагая плиту недеформи-руемой, определить все три главных напряжения в кубике. Коэффициент поперечной деформации для меди принять равным 0,32.
Решение. Сжимающие напряжения по верхней н нижней граням кубика будут наибольшими, поэтому обозначим их а3. Они равны
К задаче 2.28.
оэ=——qp=—1000 кг/см*.
Ввиду симметрии гнезда и кубика в плане два остальных главных напряжения одинаковы:
а1=о2.
63
Одинаковы и соответствующие относительные деформации е, н е2. Они равны
ei — ег —
10,001 — 10 10
ю-«.
1
Значение относительной деформации С| при объемном напряженном состоянии определяется формулой
ei=-g-|<Ji—p«J»+o3)J.
Положив а2=о,. решаем это равенство относительно ох:
О1=Ол = Д1±1!£з * - 1-ц
Подставив значения е, н о3, получаем
2.29. В толстой плите, деформацией которой пренебрегаем, высверлено на некоторую глубину цилиндрическое гнездо диаметром 2 см, в которое плотно, без зазоров, вставлен стальной цилиндрический стержень. Затем этот стержень нагружается сжимающей силой 2 т. Определить все три главных напряжения в стержне.
Ответ. <з1 = <зг = —273 кг 1см2, о3 =—638 кг/см2.
2.30. В толстой недеформируемой плите пропилен сквозной паз шириной и глубиной по 1 см. В этот паз плотно, без зазора, вставлен дуралюминовый параллелепипед размером в плане 1X1 см, который затем нагружается так, как указано на рисунке. Определить
главные напряжения в параллелепипеде. Какая должна быть его высота h до нагружения, чтобы после деформирования его верхняя грань была заподлицо с верхней поверхностью плиты? Для дуралю-мина |1 = 0,33.
Ответ. а, = 0, а2 =—264 кг/см2, а3 = — 800 кг/см2’ h= 10,01 мм.
2.31. В толстой абсолютно жесткой плите высверлено цилиндрическое гнездо. В него плотно, без зазора, вставлен медный патрон в виде полого тонкостенного цилиндра (см. рисунок). Затем внутрь патрона наливается жидкость, которая сжимается с помощью поршня до давления ^=100 ат. Определить главные напряжения в материале патрона. Трением между патроном и плитой пренебречь. Увеличением среднего диаметра патрона в связи с малой толщиной его
С4
стенок также пренебречь. Коэффициент поперечной деформации дли меди принять равным 0,32.
Ответ. ох = 0, аа = —32 кг/см*, о8 =—100 кг]сма.
2.32. В толстой абсолютно жесткой плите просверлено сквозное круглое отверстие, через которое пропущена, как то изображено на рисунке, тонкостенная латунная трубка. Трубка вставлена в отверстие настолько плотно, что в пределах толщины плиты из-за
трения продольные деформации трубки отсутствуют. Чему равны главные напряжения в отрезке трубки, проходящем через плиту, если трубка подвергается внутреннему давлению 9 = 200 ат? Коэффициент поперечной деформации для латуни ц = 0,32.
Ответ. = = —94 кг!смг, а3 = —200 кг!см-.
§ 7. Тонкостенные сосуды
R-75m
К задаче 2.35.
2.33. Определить толщину стенки чугунной водопроводной трубы диаметром 120 см при высоте напора 100 м. Допускаемое напряжение на растяжение чугуна принять равным 200 кг!см*.
Ответ. 30 м.и.
2.34. Какую максимальную высоту напора можно допустить в випипласто-вой водопроводной трубе с наружным диаметром 54 мм и внутренним диаметром 50 мм? Допускаемое напряжение на длительное растяжение винипласта можно принять равным 80 кг/сма.
Ответ: 61,5 .и.
2.35. Вертикально стоящий цилиндрический сосуд диаметром 50 см испы
тывает внутреннее рабочее давление 20 ат и, кроме того, нагружен через днище вертикальными силами, равномерно расиредблеи-
С5
ними по его торцу, равнодействующая которых R = 75 т. Устойчивость конструкции обеспечивается жесткими ребрами и диафрагмами, не показанными на рисунке. Определить толщину t стенки сосуда, если допускаемое напряжение [а] = 800 кг{см2 и принята IV теория прочности. Какая необходима толщина t, если бы была принята Ill теория прочности?
Решение. Наибольшее растягивающее напряжение, направленное перпендикулярно к образующей, равно
qD 20-50 500 , , о, = ^ = —= — кг/см2.
Напряженке вдоль образующей получится как алгебраическая сумма напряжений, вызванных внутренним давлением и сжимающей силой:
qD R 20-50 75 000 228 , .
°3 4/ nDt 41 3,14-50/ “ / Кг,СМ '
Промежуточное главное напряжение, направленное перпендикулярно к цилиндрической поверхности, можно полагать о2 = 0- Таким образом, мы имеем плоское напряженное состояние. Условие прочности по IV теории в этом случае имеет вид
V О1Т Оз—ОЛ<М-
Подставим в него полученные ранее выражения для ot и о3 и значение [о]:
Из этого неравенства имеем /Ss 0,805 см. Принимаем /=8 мм.
Если бы применялась 111 теория прочности, то условие прочности имело бы вид
ох—оэ<[о].
В нашем случае
откуда /^0,973 см ~ 10 мм.
Применение IV теории прочности уменьшает вес конструкции.
2.36. Проверить прочность стенки цилиндрического котла диаметром 250 см, находящегося под рабочим давлением 10 ат. Толщина стенки 12 мм, допускаемое напряжение для нее равно 900 кг/см2. Применить IV теорию прочности.
Ответ-. aIV = 900 кг/см2 = [а].
2.37. Котел имеет диаметр цилиндрической части 200 см. Он находится под рабочим давлением 16 ат. Подобрать толщину стенки котла / при допускаемом напряжении 1000 кг/см2, основываясь на III теории прочности. Какая была бы необходима толщина при использовании IV теории прочности?
Ответ: По III теории прочности /= 16 льи; по IV теории / = 14 мм.
2.38. Кислородные баллоны представляют собой стальные цилиндрические сосуды с наружным диаметром 25 см и толщиной стенки 10 мм. Каков будет запас прочности стенки баллона, если рабочее
и
давление в нем достигнет 30 ат? Предел прочности принять равным 51 кг) мм*. Применить IV теорию прочности.
Ответ'. 15.
2.39. Стальной стержень круглого поперечного сечения диаметром d = 50 лои заключен в трубчатую рубашку из титанового сплава с толщиной стенки /=1 мм (см. рисунок). Стержень сжат силами р=24 т. Определить главные напря-
жения в стержне и трубке. Трением _______________
между стержнем и трубкой пренебречь. /Цл У Г я »
Модуль упругости титана принять рав-
ным Ет=1,2-10’ кг/см*. Ш____J1_ 3
Решение. Мысленно вырежем из тела
стержня у его цилиндрической поверхности К задаче 2.39.
элементарный кубнк с ребрами, равными
единице, ориентированный так, что две грани параллельны поперечному сечению стержня, а две другие—его цилиндрической поверхности. По граням, параллельным поперечному сечению, напряжения будут сжимающими н наибольшими по абсолютной величине. Обозначим их оэ. Они равны
Р о3=-г
4Р _ 4-20000
nd2'- 3.14-53
1218 кг/елр.
При сжатии в продольном направлении стержень в поперечном направлении будет расширяться, тем самым растягивая трубчатую рубашку, создавая в ней внутреннее давление с интенсивностью q. В свою очередь трубка будет передавать на стержень сжимающее боковое .давление той же интенсивности q. Таким образом, второе главное напряжение в пашем элементарном кубике будет
о2 = — q.
Наконец, благодаря тому, что относительные деформации в тангенциальном и радиальном направлениях одинаковы (периметр круга всегда имеет ту же относительную деформацию, что н его диаметр), последнее главное напряжение в кубике будет тоже равно —<?:
Oi = a2 = — q.
Трубчатая рубашка представляет собой тонкостенный цилиндр. Напряжения, растягивающие его перпендикулярно к образующей, при наличии внутреннего давления q равны
°~2t ' откуда
Напряжений, параллельных образующей, в трубке не будет, так как в этом направлении отсутствует нагрузка (силы трепня между стержнем и трубкой приняты равными нулю).
Как известно, в тонкостенных стержнях напряжения в третьем направлении (перпендикулярно к поверхности трубки) принимаются равными нулю. соето* °бРаэом’ ТРУБКУ можно считать находящейся в линейном напряженном
Для определения величины напряжений о0 обратимся к рассмотрению Деформаций. Относительная деформация диаметра стального стержня при однородной деформации одинакова с относительной деформацией в том же
направлении вырезанного из стержня кубика:
ес = е2[о2—рс (О! + as)l = 1 — q — цс (—7 -|- п3)].
В свою очередь относительная деформация диаметра титапоиой трубки, одинаковая с относительной деформацией ее периметра, равна ег — . Изменение
диаметра стержня равно изменению диаметра трубки, т. е. рс = ег. Подставим к это равенство значения деформаций:
-^-1—9—цс (—?+о3)]=
п заменим q его выражением через ол:
Решив это уравнение относительно о0 и подставив численные значения всех величии, найдем напряжение о0:
а0 =
0,3-1218 _1С . . .
I Е ~~ 0 1 2-10° — 5 кг!см~-
2 4-(1-к) + ^ 2-^(1-0,3)+-^
—РсОз
Первое н второе главные напряжения в стальном стержне будут равны
Oj = о2
2-0,1-215
8.6 кг!см1.
2.40. Стальная трубка диаметром 30 см с толщиной стенки 1 мм заполнена бетоном (так называемый «бетон в обойме»). Бетон в трубке в направлении ее оси сжат силой 60 т. Найти главные напряжения в бетоне и растягивающее напряжение в стейке трубки. Модуль упругости бетона принять равным 0,14-10" кг/см-, его коэффициент поперечной деформации равным 0,18. Решить эту задачу также в предположении, что толщина стенок трубки велика и ее деформацией можно пренебречь.
Ответ. 1) = о2 = —1,35 кг/см1, аэ = —85 кг) см-, агр =
= 202 кг/смг;
2) ст, = аг = —18,6 кг/см*, а3 = —85 кг/емг.
2.41. В стальную трубку длиной 50 ли1 с внутренним диаметром 50 леи п внешним 56 мм вставлен алюминиевый цилиндр той же длины с диаметром 50 лиг. Цилиндр вдоль своей оси сжат силой 20 т. Определить укорочение алюминиевого цилиндра. Найти эту же величину в предположении, что внутренний диаметр стальной трубки на 0,1°/0 больше диаметра алюминиевого цилиндра. Коэффициент поперечной деформации алюминия принять равным 0,35.
Ответ: 1) Д/ =—0,066 мм; 2) Д/ =—0,071 лм1.
2.42. На полый медный цилиндр с внешним диаметром d — 50 см и толщиной стенок = 4 мм плотно насажен полый стальной цилиндр с толщиной стенок tc = 2 лиг. Определить наибольшее допустимое внутреннее давление в этом сосуде, если для меди [ом] = 400 кг/см-, а для стали [ас] = 1600 кг/см*. Напряжениями, параллельными осп цилиндров, пренебречь.
68
Решение. Относительные деформации диаметров и периметров обоих цилиндров одинаковы:
ес = ем»
тогда
<тс <тн
откуда
сс Ес 2-10" ом-£м Ы0«
Разрежем сосуд диаметральным продольным сечением (см. рисунок) на две части и составим условие равновесия одной части в виде суммы проекций
всех сил иа ось у, перпендикулярную к плоскости разреза:
2oM/HZ + 2ас1с1 —q ld = 0
(разницей между внешним и внутренним диаметрами медного цилиндра пренебрегаем). Учтем, что ос = 2ом:
2o„tHl+4oMZcZ—q Id=О, откуда
_2ом (Гм +2/с)
d
При определении допускаемого давления необ- К задаче 2.42.
ходимо ориентироваться иа медный цилиндр, так как при давлении, вызывающем в стальном цилиндре напряжение o'z, равное допускаемому [ос]= 1600 кг/см2, в медном цилиндре напряжение ом будет равно f^i=800 кг/см-, что больше допускаемого для меди ом = 400 кг/см1.
Положим ом = [ом]; тогда
2 [<»«](<«+ 2/с) 2-400 (0,4 + 2 0,2) „
q= 1 . ——=---------- '--------*=12,8 кг/см- х 13 ат.
и OU
2.43. Цилиндр из алюминиевого сплава с внутренним диаметром 100 мм и толщиной стенки 2 льи заключен в чугунную рубашку с толщиной стенки 5 мм. Давление газов в цилиндре равно 30 ат. Определить напряжения, растягивающие стенки цилиндра и рубашки. Продольными напряжениями пренебречь.
Ответ: оа = 145 кг/см2; ач = 248 нг/см*.
2.44. Сферический газгольдер диаметром 5 м имеет толщину стенки 30 мл. Он наполнен газом, находящимся иод рабочим давлением 6-10ь н/мг. Определить растягивающее напряжение в стенке газгольдера.
Ответ: 25-10е н)м-.
2.45. Какое максимальное рабочее (избыточное над наружным) давление газа может выдержать тонкая сферическая оболочка воздушного шара-зонда диаметром 1 ж, выполненная из полиэтиленовой пленки толщиной 1 мм? Для полиэтилена высокого давления принять [о] = 50 кг/см*.
Ответ: 0,2 ат.
.69
2.46. Определить главные напряжения в опасном сечении конического резервуара с толщиной стенки t = 4 мм, представленного на рисунке. Резервуар подвешен за верхний край и полностью заполнен водой.
Решение. Как известно, для определения нормальных напряжений в меридиональном направлении ат и в тангенциальном направлении at имеются формулы
_ Y»g« m 2t cos а
h~Ty)y и °l =
Y tg « t cos а
(Л—У} У.
где у—объемный вес жидкости, а у— расстояние от вершины конуса до сечения. где определяются напряжения. Найдем максимум этих напряжений в зависимости от растояния у. Для этого t приравняем нулю производные от выраже-
.._________ ний для а- и по у:
К задаче 2.46.
В сечеиин АВ
^2.= М=0,
dy 2t cos a V 3 yJ ’
3
откуда yt=—h (в сечении AB) и
^.=^_(Л_2у)=0. dy t cos a'
h
откуда Уг=-£ (в сечении CD). Таким образом, мы имеем два опасных сечения.
тахоя =
Ytga 2t cos a
/»=
3yft2tga
16/ cos a
3 0,001-5002-0,364
16 0,4-0,940
45,4 кг/см*
я
Y tg a [, 3 Л 3 . Зу/P tg a t .
at = /----I ft—— ft ) — ft=-X—-— = ma x am=45,4 кг/см3.
* t cos a \. 4 J 4 16/ cos a "
В сечении CD
_ у tg a / 2 ft Y ft _y/.Mg a 0,001-500»-0,364
m 2t cos a \ 3 2)2 6/cos a- 6-0,4-0,940 ’ '
я
ytga/. h\ h yft»tga 0,001-500*-0,364 .
maxof=; - I h—— ) —= * —=—. h .- —=60,5 кгсм3.
t cos a \ 2)2 41 cos a 4-0,4-0,940
2.47. Для хранения нефти применен резервуар в виде усеченного -конуса с толщиной стенки 10 мм, опирающегося на меньшее основание (см. рисунок). Определить наибольшие напряжения в меридиональном и тангенциальном направлениях. Удельный вес нефти принять равным 0,95.
Ответ: от — —59 кг/см'-, о, = 203 кг!см'.
70
2.48. Проверить по III теории прочность сосуда с толщиной стенки 2 jwjw, имеющего форму параболоида, подвешенного за верхний край (см. рисунок). Сосуд заполнен жидкостью до уровня h.
К задаче 2.47.
Удельный вес жидкости 1,1. Допускаемое напряжение для материала стенки равно 200 кг/см2. Прочность проверить на высоте верхнего
уровня жидкости.
Ответ-. о|и = 158 кг/см2 < [ст] = 200 кг/см2.
2.49. Резервуар для бензина имеет форму тела вращения и размеры, представленные на рисунке. Он подвешен за верхний край и полностью заполнен бензином с удельным весом 0,7. Толщина стенки резервуара равна 5 мм. Прочность стенки в месте сопряжения цилиндрической и конической частей резервуара обеспечена специальным кольцевым поясом. Определить в стенке резервуара наибольшие нор
мальные напряжения в меридиональном и тангенциальном направлениях.
Ответ: max а„ = 39,5 кг/см1-,
max ut = 52,5 кг/см*.
К задаче 2.50.
2.50. Вертикально стоящий цилиндрический резервуар с полусферическим днищем доверху заполнен водой (см. рисунок). Толщина боковых стенок и днища равна 2 jhjh. Определить наибольшие нормальные напряжения в цилиндрической и сферической частях конструкции.
Ответ: max o,,u, = 200 кг/см2-, тахоСфер= 125 кг/см2.
7ft
§ 8. Контактные напряжения
2.51. Определить расчетные напряжения по IV теории прочности в стальном шариковом подшипнике, схема которого представлена на рисунке. Радиус шарика /?, = 2,5 Л1Л, радиус желоба /?2 = 3 мм, радиус кольца R3 = 30 мм. Давление на наиболее нагруженный шарик подшипника равно Р = 40 кг.
Решение. Необходимые расчетные формулы, графики и таблицы приведены в гл. IX курса проф- Н. М. Беляева «Сопротивление материалов». На них в дальнейшем и будут даны ссылки.
Найдем коэффициенты уравнения эллипса касания:
2R,
2RZ
К задаче 2.51.
--J -и,ООО. +я) -°-2,в5'
Тогда отношение А к В равно А
0,035
В 0,2165 °’1615-
По этому отношению из таблицы 10 курса находим а: а=0,772.
Подсчитаем наибольшее нормальное напряжение:
°ш»х = «
|/Р£а (Я2-/?!)2 И (RtR&
= 0,772
3/40(2-10«)*-(3—2,5)* , 2
У (2,5-3)*-----------L = 32' Кг/ММ -
Расчетное напряжение в опасной точке внутри материала равно O|V = 0,6-отах = = 0,6-321 —193 кг/мм1. Из графика на рис. 92 курса по значению отноше-д
пия -j- = 0.1615 находим коэффициенты п:
Л] =0,23 и л2 = 0,24.
Тогда расчетное напряжение в центре эллипса касания составит o’|V= л, отах =0,23-321 =74 кг/м»?.
а расчетное напряжение иа конце большой полуоси того же эллипса равно °iv =n2°max=0-24'321=77 кг/мм*.
2.52. При вдавливании на прессе Брпнеля закаленного стального шарика диаметром 10 мм в испытуемую плоскую стальную деталь пластические деформации в детали (появления отпечатка) начинают образовываться при значении наибольшего контактного напряжения отах=100 кг/мм*. Определить величину нагрузки на шарик в этот момент.
Ответ: 1 кг.
72
2.53. Через два одинаковых стальных цилиндра указанной па рисунке длины передается равномерно распределенная нагрузка интенсивностью 500 кг/см. Определить необходимый диаметр цилиндров d, если наибольшее напряжение по поверхности соприкасания не должно превосходить 100 кг/мм-.
Ответ'. 70 леи.
2.54. Определить наибольшее допустимое давление Р на шарнирно-подвижную опору мостовой фермы с двумя стальными цилиндрическими катками диаметром d = 100 жл1 и длиной / = 900 мм, лежащими на стальной же плите (см. рисунок). Наибольшее допустимое напряжение у поверхности опирания катков равно 110 кг] мм1.
Ответ: 311 т.
2.55. Определить минимально необходимый диаметр соприкасающихся под прямым углом стальных цилиндров одинакового диаметра, нагруженных, как указано на рисунке, силами Р= 1 т. Допускаемая величина наибольшего напряжения па поверхности соприкасания равна 120 кг/мм*.
Ответ: 116 мм.
ГЛАВА 3
СДВИГ И СМЯТИЕ
§ 9. Болтовые и заклепочные соединения
3.1. Из условий прочности стали на срез и смятие определить величину допускаемой нагрузки Р, которую можно приложить к тяге болтового соединения, изображенного на рисунке, при допускаемых
К задаче 3.1. К задаче 3.2.
напряжениях: на срез [т] = 800 кг/см2 и па смятие [ос]=2400 кг/см*. Размеры элементов соединения: <1 = 50 мм; / = 20 мм; /{^12мм.
Ответ: Р = 24 т.
3.2. Для испытания круглых стержней на срез применяется при* способление, размещаемое между подвижной и неподвижной травер* сами одного из прессов (см. рисунок). Определить наибольший диаметр стального стержня, который может быть подвергнут срезу на прессе силою 60 т, если временное сопротивление испытуемой стали при срезе тв = 300 Мн/м2. Выяснить, какие напряжения смятия возникнут во вкладных втулках проушин при испытании такого стержня, если толщины проушин / = 0,03 м, /, = 0,02 ли
Решение. Стержень подвергается срезу по двум сечениям. Усилие, необходимое для перерезывания стержня диаметром d, Р=2^-т1и откуда диаметр
74
Так как сила пресса задана в тоннах, то, переходи к системе единиц СИ, имеем
Р=60 т к 60-9807 н ж 0,59 Мн.
Следовательно,
d=
2-0,59
3,14-300
х 0,036 м.
Напряжения смятия, возникающие в высокопрочных вкладных втулках проушин, будут
ос
—__0159_____Q Мн/м2
id ~0,03-0,036 ’ ' '
Разумеется, такие же напряжения смятия возникнут н в материале болта. В системе единиц СГС ответом будет
d as 3,6 см; ос as 5560 кг/см2.
3.3. Коленчатый рычаг,'нагруженный силою P—V2, т, поддерживается стальным шарнирным болтом в точке А и роликовой опорой
в точке В (см. рисунок). При допускаемых напряжениях на срез и смятие стали [т] = 1200 кг/см* и [<тс] = 2500 кг/см2 определить
необходимый диаметр болта.
К задаче 3.3.
если расстояние между опорами рычага I = 75 см, размер а = 50 см, а толщина t = 3 см.
Указание. Давление, передающееся на болт, определить как полную реакцию в точке А из условия равновесия рычага.
Ответ; d = 2,8 см.
К задаче 3.4.
3.4. Болт диаметром d = 100 -мм, работающий на растяжение, опирается головкой на лист (см. рисунок). Определить диаметр головки D и высоту ее t, если растягивающие напряжения в сечении болта и =1000 кг/см2, напряжения смятия по площади опирания головки ос = 400 кг/с.ч2 и напряжения среза головки т = 500 кг/см*.
Ответ; 0=187 лыс; Г = 50 мм.
3.5. Через стальной валик болтового соединения передается усилие Р = 48 т (см. рисунок). Из условий прочности валика на срез и смятие, а также листов — на растяжение определить необходимый диаметр валика и размеры сечения листов (b, и /2) при
75
допускаемых напряжениях для стали: на растяжение [<т] = 1600 кг/см2, на срез [т] = 950 кг/см* и на смятие [<тс] = 2500 кг/см1.
Ответ: d=40 леи; 6 = 102,5 лис; /, = 24 ле.м; /2=16 леи.
К задаче 3.5.
К задаче 3.6.
3.6. Кронштейн из листов толщиною /=16 леи прикреплен к стене четырьмя анкерными болтами (см. рисунок). Определить необходимый диаметр болтов (без учета продольных усилий) из усло-
вия прочности их на срез и смятие [т] = 800 кг/см.1, [ас] = 2400 кг/см?,
при допускаемых напряжениях если кронштейн поддерживает подкрановую балку, передающую на него давление Р = 23 т.
Ответ: d — 30 лыс.
3.7. Стык двух листов толщиною /=10 леи, перекрытый двумя накладками толщиною /, = 6 Л1.и каждая, растягивается силами Р=24 т (см. рисунок). Определить необходимое
количество заклепок диамет-
К задаче 3.7. ром d = 20 мм и разместить
их в плане, если допускаемые напряжения приняты: для заклепок — на срез [т] = 1000 кг/см2, на смятие [стс] = 2400 кг/см* и на растяжение листов [ст] = 1600 кг/см*.
Решение. Заклепки двухсрезиые. Необходимое количество их из условия прочности на срез должно быть
л
Р
Л/р
2 —М
2-24 000 3,14-22-1000
ж 4.
По условию прочности на смятие требуется
Р _ 24 000 nSiM[oc] —1-2-2400 - 3, Следует расставить с каждой стороны стыка по Б заклепок.
7G
Для размещения их в плане надо определить необходимую ширину листов. Из условия прочности на. растяжение рабочая площадь сечей ня листа должна быть
_ Р 2400 .,
“1600 10 с"'-
Рабочая ширина листа (за вычетом ослабления заклепочными отверстиями) должна быть
. F„ 15
Ь„ = -^-=у = 15 см.
Полная ширина b = b,,-]-md, где т — число заклепок в поперечном сече-пнн. Прн ширине Ь^15 см число заклепок в поперечном ряду должно быть не менее т = 2; тогда сечение будет ослаблено двумя отверстиями и полную ширину листов следует принять Ь= 154-2-2= 19 см. Пять заклепок целесообразно разместить в шахматном порядке. Приняв шаг и --3d и расстояния от осей заклепочных отверстий до краев листов и накладок но c = 2d, размещаем заклепки, как показано па рисунке.
3.8. Какое количество заклепок диаметром d-- 20 льи необходимо будет поставить в стыке двух листов, рассмотренном в задаче 3.7, если при тех же данных стык будет перекрыт не двумя, а одной накладкой толщиною / = 12 Л1.н? Разместить заклепки в плане.
Ответ: 8 заклепок с каждой стороны стыка.
3.9. Два листа толщиною t— 10 мм соединены внахлестку шестью заклепками диаметром d — 20 л.н (см. рисунок). Определить величину допускаемых растягивающих усилий Р и необходимую ширину листов b при допускаемых напряженных: па растяжение [о] = 1600 кг/см*, на срез [т] = 1200 кг/см1 и па смятие [стс]=-3200 кг!см-.
Ответ: Р — 22 т; b -=180 льн.
К задаче 3.9. К задаче 3.10.
3.10. Стык двух листов сечением 10x150 лл, перекрытый двумя накладками толщиною /, = 6 мл каждая, растягивается силами 7’=12,5 т. Проверить прочность заклепочного соединения, если с каждой стороны стыка поставлено по две заклепки диаметром rf = 20 мм, при допускаемых напряжениях: [о] = 1600 кг)см-, [tJ = == 1000 кг/см2, [ос] =3200 кг!см-.
Ответ: Для листа: omdX = 1140 кг!см- < 1600 кг/сл1;
для заклепок: г = 996 кг) см'1 < 1000 кг'см-;
ос = 3120 кг)см1 < 3200 кг/см-.
3.11. Цилиндрический стальной котел диаметром 0=1,5 лл, с толщиной стенок / = 10лм1 имеет продольный шов, перекрытый
77
К задаче 3.11.
двумя накладками толщиною = 6,0 мм каждая, присоединенными к стенке котла двумя рядами заклепок (с каждой стороны стыка) диаметром d = 20 мм. Заклепки размещены в шахматном порядке с расстоянием между рядами е = 45 мм и с шагом в каждом ряду а= 100 мм (см. рисунок). Проверить прочность стыкового соединения при допускаемых напряжениях: на растяжение стали [о] = 1200 кг/см*, на срез [т] = 800 кг/см*, на смятие [ос] = =2400 кг/см*. Рабочее давление пара внутри котла q = 12 ат.
Решение. Нормальные напряжения в стенке котла, направленные перпепдп-_ , qD
кулярно к образующей = складываются в усилия, растягивающие стык. Вырезав полоску шириною а= 10 см так, что па ней размещаются две заклепки,
найдем величину усилий, растягивающих эту полоску и воспринимаемых двумя двухсрезиыми заклепками:
P = ctF = ^-al = l-^~ . 10 = 9000 кг.
Проверка прочности заклепок на срез и смятие дает
2Р 2 9000
T=^=3J4^2 =715 кг,сма < 800 кг'с^
°с=т£=Т^’=2250 кг,см* < 2400 Ke/CMi-
Произведем также проверку прочности стенки котла на растяжение по сечению ш—л, ослабленному одним заклепочным отверстием, и условно ио зигзагообразному сечению mt—л,, ослабленному двумя отверстиями.
Сечение m—л. Площадь сечения нетто
F„ = (fl-d)/ = (I0—2)1=8с.и».
Р 9000
Напряжение <?=•=—=—5—= 1125 кг/см2 < 1200 кг/см*. гн О
Сечение тх—nt. Площадь сечения брутто и нетто
F«p=(f + (тУ+ег) « = (у+К^+Т52)-1= П.725 см*.
FK=F6f—2td= 11,725 - 2-1 -2 = 7,725 сж2.
Напряжение о=тг-=-=т=5= = 1165 кг/см2 < 1200 кг/см*. л хО
Таким образом, все условия прочности соблюдены.
3.12. Цилиндрический стальной котел диаметром D= 1,0 -и, изготовленный из листов толщиною < = 10мм, соединенных продольным швом, подвергается внутреннему рабочему давлению д — 12 ат. Шов перекрыт накладкой, прикрепленной к стенке котла заклепками диа
78
метром d = 23 лис, размещенными с каждой стороны стыка в два ряда (см. рисунок к задаче 3.11).
Проверить прочность стыкового соединения, если шаг заклепок каждого ряда а = 100 мм, расстояние между рядами с = 50 мм. Допускаемые напряжения принять по данным задачи 3.11.
Ответ: о = 780 кг/см* < 1200 кг! см1-, т = 720 кг/см2 < 800 кг/см*-ос = 1300 кг/см1 < 2400 кг/смг.
3.13. Раскосы стальной стропильной фермы, состоящие каждый из двух равнобоких уголков 80x80x8 льи, присоединяются к ниж-
нему поису с помощью косынки толщиной / = 8 Л1Л1 (см. рисунок). Усилия в раскосах равны Nt = —Мг — = 14 т.
1) Определить необходимое количество заклепок диаметром d — = 17 лсл1 для присоединения каждого из раскосов к косынке при допускаемых напряжениях на срез [т] = = 1000 кг! см'1 и па смятие [ос] =
=2600 кг) см1. 2) Найти также число заклепок, необходимое для прикрепления косынки к нижнему поясу фермы, если угол наклона раскосов к поясу равен 45°, а сечение пояса состоит из двух уголков 75x75x6 лит.
Ответ: пг = 4; пг = 6.
К задаче 3.14.
3.14. Стык нижнего пояса стропильной фермы, состоящего из двух уголков 80x80x8 мм, перекрыт двумя накладками из таких же уголков и косынкой толщиной 8 мм, присоединенными с помощью заклепок диаметром d = 20 мм (см. рисунок). Пояс растягивается усилиями, вызывающими в ослабленном сечении нормальные напряжения amax = 1400 кг!см-. Определить необходимое количество заклепок из условий прочности на срез и смятие при допускаемых напряжениях [т] = 1000 кг/см1, [ос] = 2400 кг/см1 н разместить их в стыке.
Указание. Заклепки горизонтальных полок одиосрезные, а вертикальных—четырехсрезиые.
Ответ: N = 30 т; с каждой стороны стыка требуется приблизительно 10 площадей среза и 8 площадей смятия, что обеспечивается 5 заклепками. В горизонтальных полках л, = 2 (2 площади смятия), в вертикальных ле = 3 (2x3 = 6 площадей смятия).
7»
§ 10. Сварные соединения
3.15. Определить необходимую длину фланговых швов для соединения внахлестку двух полос сечением 10x80 мм и 10x100 мм (см. рисунок), растягиваемых продольными силами Р. Допускаемые напряжения принять: на растяжение полос [о] = 1600 кг)см1, на срез швов [та] = 900 кг/см1. Учесть возможный непровар в начале и в конце каждого шва по 5 мл (/=/расч + 2 X 5 мм).
Ответ: lp = 10,2 см; I = 11,2 см.
3.16. Стальная полоса с размерами сечения b = 0,1 м и / = 0,01 м, растягиваемая усилием Р=15-10*н, приваривается к фасонному
листу внахлестку одним лобовым и двумя фланговыми швами (см. рисунок). Определить наименьшую длину фланговых швов, необходимую для прикрепления полосы к фасонке, при допускаемых напряжениях на срез швов [тэ]=910т h[m\
Решение. Проверка прочности лобовых швов условно производится па срез. Принято считать, что усилие, воспринимаемое всеми швами, равномерно распределяется по рабочему нч сечению. Следовательно,
Р
Т’ 0,7/ (Ь + 21р)
Отсюда расчетная длина флангового шва
'-=4 (етга -‘) =4 UhV» -•
Проектную длину шва (при учете ослабления непроваром только на одном конце) следует принять /=0,069-(-0,005 = 0,074 м.
3.17. Стальная полоса сечением 0,01x0,24 м приваривается внахлестку к фасонному листу с помощью двух фланговых и одного прорезного шва размером />, = 0,02 м н /, = 0,1 м (см. рисунок). Определить необходимую длину фланговых швов, если полоса растя-тиваетсн усилием Р=360 кя, а допускаемое напряжение на срез швов принято [тэ] = 8104 кя/.и2. Ослабления швов вследствие непровара не учитывать.
Ответ: I х 0,2 .и.
ЕЭ
3.18. Стойка фермы, состоящая из двух швеллеров № 12, прикрепляется к фасонке с помощью фланговых швов (см. рисунок), а) Определить необходимую рабочую и проектную длину швов, если катет шва принят t = 10 лш, допускаемое напряжение па срез шва
К задаче 3.18.
[та] = 1000 кг! см?, а нормальные напряжения в сечении стойки а=1530 кг/см?, б) Выяснить, какая потребуется рабочая длина фланговых швов, если стенка каждого швеллера будет дополнительно приварена прорезным швом длиною 85 н шириной 10 мм (см. рисунок к задаче 3.17).
Ответ: а) /р=150 мм, /=160 мм; б) /р=8,9 см.
3.19. Стык двух листов, перекрытый двумя накладками, растягивается силами Р = 24 т (см. рисунок), а) Определить длину фланговых швов, необходимую для прикрепления накладок, если толщина листов t = 10 лыс, толщина накладок /, = 8 мм, а допускаемое напряжение на срез швов [тэ] = 1000 кг/см?. Непровар длиною 5 мм
учесть только па одном конце каждого шва. б) Сравнить размеры сварного стыка (ширина и
К задаче 3.20.
длина накладки) е размерами клепаного соединения, полученного при тех же данных в задаче 3.7. Оценить экономию металла листов, получаемую при замене клепаного соединения сварным.
Ответ: а) /=112 мм; б) для сварного стыка />=150 .нл1, />, = = 130льи, /. = 225 мм; для клепаного Ь= 190 лгм, />, = 190 мм н L = 400 Л1Л1. Экономия только основного металла листов составляет 21%.
3.20. Сварной стык стальной полосы сечением 80x8 лои* осуществлен крестообразным соединением с помощью прокладки,
81
приваренной к полосе четырьмя торцевыми швами, как показано па рисунке. Определить величину напряжений в сечении швов, если катет шва / = 10лии, а растягивающие напряжения в сечении полосы
К задаче 3.21.
о= 1500 кг/см2. Учесть ослабление шва вследствие непровара на концах.
Ответ: тэ = 905 кг/см*.
3.21. Определить длину фланговых швов, необходимую для приварки равнобокого уголка размерами 110x110x8 лги к фасонному листу при допускаемом напряжении па срез швов [тэ] = 1000 кг/см2. Уголок растягивается усилием Р=20 т, катеты швов приняты равными t = 8 мле (см. рисунок).
Решение. Общая длина обоих боковых швов может быть определена из условия прочности их на срез:
Z = /1 + /г0 7/ =о 7.о>8. looo = 35,8 см' (а)
Растягивающее усилие Р приложено в центре тяжести уголка, отстоящем от обушка на расстоянии z0 = 3cjh. Так как линия действия усилия Р проходит на разных расстояниях от левого и правого швов, то доли этого усилия, приходящиеся на каждый из них, обратно пропорциональны расстояниям до швов z0 и Ь—г0, т. е. Р1:Рг = (Ь—г0):г0. В таком же от-
ношении следует распределить и длины швов:
Zl:/2 = (6-z0):z0=^^=2,67,
или ll = 2,67ls... (б)
Решая совместно с (а), найдем /х=26,05 см и /г = =9,75 см.
Проектную длину при учете непровара примем /,=27 см и = 11 см.
3.22. По данным предыдущей задачи определить необходимую расчетную длину фланговых швов при условии, что полка уголка будет приварена с торца дополнительным лобовым швом. Принято условно считать, что лобовой шов работает на сдвиг равномерно по длине Ь.
Ответ: /х = 18,05 см; /2 = 6,75 см.
3.23. Стержень сварной фермы, состоящий из двух исравнобоких уголков размерами 125х X 80x12, прикреплен к фасонке с помощью
К задаче 3.23.
фланговых швов толщиной ?=12 мм (см. рисунок). Растягивающие
напряжения в сечении стержня о= 1500 кг) см1. При допускаемых напряжениях на срез швов [тэ] = 1100 кг[смг а) определить необходимую рабочую длину швов /х и 1г; б) как следует изменить толщину катетов швов 1, прикрепляющих обушки уголков, чтобы длины
всех фланговых швов были одинаковыми? Ответ: а) /х = 25,2 см, /2 = 12,8 см;
б) ? = 2,36 см.
82
§11. Врубки, шпонки, другие элементы конструкций
3.24. Для испытания древесины на сдвиг применяется приспо* собление, устанавливаемое па одном из прессов (см. рисунок). Выяснить, какое усилие должно создаваться прессом, если временное сопротивление образцов на скалывание вдоль волокон может достичь
К задаче 3.24.
120 кг) см2. Найти также величину наибольших напряжений смятия при испытании. Размеры образца на рисунке даны в мм.
Ответ: Р = 720 кг; ас = 360 кг/см2.
3.25. Два бруса прямоугольного сечения размерами b = 0,12 м и Л = 0,18 м, работающие на растяжение, соединены прямым зубом
глубиною с = (см. рисунок). Определить величину допускаемого растягивающего усилия Р (в ньютонах) и размеры врубки в метрах при допускаемых напряжениях: на растяжение [а] = 10’ н/м2; на скалывание вдоль волокон
К задаче 3.25.
[т] = 1 • 10е н/м2 и смятие вдоль
волокон [<тс] = 8-10в н/м2. Стягивающие врубку болты в расчет
не принимаются.
Ответ: Р = 4,32 • 10* н; а « 0,36 м.
3.26. Стык пояса фермы, состоящего из брусьев сечением 20x22 см2, перекрыт стальными накладками с отогнутыми полками,
К задаче 3.26.
врезанными в брусья (см. рисунок). Определить необходимый размер а и глубину врезки с при допускаемых напряжениях на скалывание
83
К задаче 3.27.
вдоль волокон [т] = 10 кг/см2 и иа смятие [oj = 50 кг!смг, если растягивающее усилие в поясе N = 5 т. Стягивающие болты в расчет не принимаются.
Ответ, а = 25 см; с = 5 см.
3.27. Соединение стропильной ноги с затяжкой выполнено с помощью лобовой врубки (см. рисунок). Определить необходимые размеры соединения (a, d, е, с), если сжимающее усилие в подкосе равно Р= 7 т, угол наклона крыши а = 30°, размеры сечения брусьев: Ь= 15 см и Л = 20 см. Допускаемые напряжения приняты: на растяжение и сжатие вдоль волокон [а] = 100 кг/см-, на смятие вдоль волокон [aj = 80 кг/смг, на смятие поперек волокон [аво] = = 25 кг/см2, па смятие под уг
лом 30° к волокнам [аэп] = 50 кг/см? п иа скалывание вдоль волокон [т]=10 кг/см*. Соединительный болт и силы трения в расчет не принимаются.
Решение. Разложив силу Р на две составляющие, вертикальную и горизонтальную, получим
Р,= Р sin а = 7000-0,5 = 3500 кг, Р2=Р cos а = 7000-0,865 = 6055 кг.
Эти силы уравновешиваются реакцией опоры R = P2 и растягивающим усилием в затяжке N = Рг. Сила Р2 вызывает смятие затяжки по площади опирания па опорную подушку (перпендикулярно к волокнам). Напряжения смятия
Р Р 3500
*с=^«1<Чо1. откуда «^-^=— = 9,33^.
Такую же длину с должна иметь площадь опирания подкоса на затяжку; конструктивно она принимается значительно больше.
Усилие Рг вызывает смятие вертикальной площадки в месте контакта торца стропильной ноги с затяжкой (Fc = bd); при этом смятие подкоса происходит под углом к волокнам, затяжки — вдоль волокон. Из условия прочности на смятие подкоса имеем
Рг , , Рг 6055 „„
^<10301. откуда 5=8.07 0».
Это же усилие вызывает появление скалывающих напряжений в выступающем конце затяжки (на длине е). Из условия прочности па скалывание вдоль воло-р
коп получим Следовательно,
3.28. Опорный узел стропильной фермы выполнен из брусьев сечением Л = 20 см, 6=18 см, соединенных при помощи врубки с шипом шириною */36. Стропильная нога наклонена к затяжке иа угол а = 40° и сжата усилием Р = 3 т (см. рисунок). Определить наименьшие необходимые размеры соединения (л, с, d, I) при допус-84'
на
1г, на смятие под углом 40° на скалывание вдоль волокон [т] =
каемых напряжениях: на смятие вдоль волокон [ас] = 85 кг/см2, смятие поперек волокон [afl0] = 25 кг/см-к волокнам [а40| = 45 кг/см2 и = 8 кг/слС1. Трения по липни т—п не учитывать.
Ответ: а = 4,3 см; с — = 6,4 см; d ~ 8,5 см; 1= 17 см. Конструктивно размеры а и с обычно принимаются больше расчетных.
3.29. Стык двух сосновых брусьев размерами 6=16 см и А = 20 см осуществлен с помощью шести дубовых шпонок и сосновых накладок (см. рисунок). Определить необходимые размеры шпонок cud, а также расстояние между ними а, если брусья растягиваются усилием Р=12т. Проверить также прочность брусьев на растяжение. Допускаемые напряжения принять: а) для сосны: на растяжение [а] = 100 кг/см1, на смятие в торен [стс] = 100 кг/см2, на скалывание вдоль волокон [т] = 10 кг/см1;
К задаче 3.29.
б) для дуба: на смятие поперек волокон [а„п] = 25 кг/см2 и па срез поперек волокон [тео] = 12 кг/см2. Работа стягивающих болтов не учитывается.
Указание. Размеры дубовых шпонок cud определяются из условия прочности на срез н смятие в предположении, что усилие Р распределяется между шпонками поровну. Расстояние а между шпонками определяется из условпя р прочности сосны на скалывание вдоль волокон под действием усилия Ро =— , Л передающегося одной шпонкой.
Ответ: = 10,4 см; d = 5,0 см; а — 12,5 см; а = 94 кг/см2.
3.30. Стык двух брусьев квадратного ссчеппя 20x20 см перекрыт двумя стальными накладками с приклепанными к ним призматическими шпонками (по 6 шпонок в каждой накладке), врезанными в брусья на глубину d = 2 см (см. рисунок).
«5
Из условий прочности на растяжение и смятие дерева определить величину допускаемого растягивающего усилия Р, которое может быть передано через стык, если допускаемые напряжения при-
К задаче 3.30.
ияты: на растяжение [а] = 120 кг/см1, на скалывание вдоль волокон [т] = 12 кг/см- и на смятие [стс] = 100 кг/см2. Найти также расстояние а между шпонками, считая, что усилие распределяется между ними поровну. Стягивающие болты в расчет не принимаются.
Ответ: Р = 24 ООО кг; а = 16,7 см.
3.31. Подкосы деревянного моста опираются на стойку, составленную из двух брусьев, при помощи дубовых подушек («коротышей»), врубленных в стойку на глубину с, и сг (см. рисунок). Разная глубина врубок с, и сг(е = с1 — ct = 1 см) предохраняет зуб ВАС от скалывания (след площади скалывания смещается па линию ВО, показанную пунктиром).
Определить необходимую длину подушки а и глубину врубок с, и с2, если сжимающее усилие в подкосе Р=18,4 т, угол наклона а = 45°, размеры сечения брусьев стойки: b = 15 см, Л = 24 см, а допускаемые напряжения приняты: на смятие вдоль волокон [ас] =110 кг/см2, на смятие поперек волокон [ав0] = 25 кг/см2, на смятие дуба под углом 45° к волокнам [ом] = 70 кг/см2 и на [т] = 12 кг/см2. Определить также наи
меньший диаметр подкоса, требующийся по условию прочности подушки на смятие.
Указание. Длина подушки а определяется нз условия прочности на скалывание вдоль волокон, а суммарная площадь, через которую передается продольное усилие на стойку, £ = (с1-|-с2)Л—нз условия прочности на смятие.
Ответ: а = 45 см; с,л;3 см; с2х2 см; d=18,3 см.
3.32. Круглый стальной стержень, растягиваемый силой Р= 18 т, укреплен на детали с помощью чеки прямоугольного сечения (см. рисунок). Из условий прочности на растяжение, срез и смятие стали определить диаметр стержня d, необходимую длину а хвостовой его
N
К задаче 3.31. скалывание вдоль волокон
8в
части, а также размеры поперечного сечення чеки t и h (без учета ее работы на изгиб). Допускаемые напряжения принять: [а] = ж 1600 кг!см\ [т] = 1000 кг/см2 и [<тс] = 3200 кг/см*.
Ответ'. d = 4,62 см; /=1,22 см; h = 7,4 см; а = 9,33 см.
К задаче 3.32.
К задаче 3.33.
3.33. В листе толщиною t продавливается круглое отверстие. Определить наименьший диаметр пуансона из условия, что напряжения смятия на его торце в четыре раза выше временного сопротивления срезу вырубаемого металла. Схема вырубного штампа показана на рисунке.
Ответ, d — t.
3.34. Проверить прочность зубьев храпового колеса па срез и смятие, если нормальное давление на зуб в момент торможении Р=3200 кг. Размеры зуба (см. рисунок): ширина основания а = 24 мм, толщина / = 20 лм«, высота зуба h =16 мм.
Определить также необходимый диаметр болта, на который опирается собачка, нз условия прочности на срез и смятие. Допускаемые напряжения принять: на срез [т] = 700 кг/смг, на смятие [а] = ®= 1200 кг)смг.
Ответ: т = 667 кг/см? < 700 кг)смг;
ас = 1000 кг!смг <1200 кг/смг;
d = 1,33 см.
ГЛАВА 4
КРУЧЕНИЕ
§12. Кручение стержней круглого сечения
4.1. Определить диаметр сплошного стального вала круглого сечения, передающего крутящий момент Л1К=1,6 тм, если допускаемое напряжение на сдвиг [т] = 800 кг/см2, а допустимый угол закручивания [<р] = 0,6° на один метр длины вала.
_ . Л1„ , . лг’
Решение. Из условия прочности вала ттах = ^ <|т|, где и^-у, на-tr р Z
3 ЛТлГ- 3 ‘ ----------
ходим г =
2Л1К з <2.160000
= V “jTeoo" =5'° сл’
Из условия жесткости вала Ф = 1ф|. где
t-i J р
^/"2Л1кГ300 ‘
а [ф] = ~ • вычисляем г =
= 5,9 см.
^,С = Я№кг1смг, 2-160000-100-300
800 000-9.86 “
Ответ: d 11,8 см.
4.2. Напряжения у поверхности вала ттах = 800 кг/см2. Чему равны касательные напряжения в том же поперечном сечении на расстоянии четверти радиуса от поверхности вала?
Ответ: 600 кг!см2.
4.3. Сплошной стальной вал диаметром 10 см и длиной 6 м закручен на угол 4е. Чему равно наибольшее касательное напряжение?
Ответ: 465 кг/емт.
4.4. Определить грузоподъемность [Л1к] стального стержня круглого сечения диаметром 20 мм при допускаемом напряжении [т] —-= 1000 кг!см-. Чему равна величина угла закручивания участка стержня длиной 100 см?
Ответ: 1570 кгем; 0,125 рад.
4.5. Стальной образец круглого сечения диаметром 20 мм испытывается на кручение на машине, стальной вал которой имеет диаметр 40 мм. Образец и вал имеют общую геометрическую ось. Предел пропорциональности материала образца при растяжении равен 3200 кг/см2. Какова наибольшая величина касательных напряжений
83
в вале машины в тот момент, когда наибольшие касательные напряжения в образце достигнут предела пропорциональности при сдвиге, который следует определить, пользуясь третьей теорией прочности?
Ответ. 200 кг'см1.
4.6. Стержень из мягкой стали диаметром 25 мм удлиняется на 0,122 мм на длине 20 см при растяжении силой 6 т. Этот же стержень закручивается на угол 0,75° на длине 20 см при нагружении крутящим моментом 2 тем. Определить величину Е, G и р..
Ответ: 2- 10е кг /см-; 8-10® кг!см*; 0,25.
4.7. При испытании на кручение стального образца длиной 20 см и диаметром 20 мм установлено, что при крутящем моменте 1632 кгем угол закручивания равен 0,026 рад. Предел упругости достигнут при крутящем моменте 2700 кгем. Определить величины модуля упругости при сдвиге и предела упругости при кручении.
Ответ: 8-10* кг/см-; 1720 кг/см2.
4.8. Стальной стержень диаметром 10 мм закручивается на испытательной установке. Крутящий момент увеличивается ступенями по 15 кгем. Среднее значение разности приращения показаний приборов, измеряющих углы поворота двух сечений, равно 3,8 мм. Расстояние между сечениями 100 мм. 1 мм шкалы прибора обозначает 1/2000 рад. Чему равен модуль упругости при сдвиге?
Ответ: 8,05-10® кг/см*.
4.9. На стальной вал через 5 шкивов действуют пары сил, показанные на рисунке. Построить эпюру крутящего момента, подобрать диаметр вала при [т] = 900 кг!см1 и определить величину угла
М^ЮОкгм Мг=200кгм Мз=300кгм Н4=300кгм Мв=200шм
поворота правого концевого сечения вала по отношению к левому. Затем первую и четвертую пары сил поменять местами и решить задачу при этом измененном условии.
Ответ: 7 см; 0,000365 рад; 7,7 см; 0,000728 рад.
4.10. Сравнить веса сплошных валов одинаковой длины, стального и из алюминиевого сплава, спроектированных с одинаковым углом закручиванияпрн одинаковых крутящих моментах. Модуль упругости при сдвиге, алюминиевого сплава равен 2,7-10® кг/см-, а его объемный вес равен 2,6.
Ответ: Стальной вал на 750/0 тяжелее алюминиевого.
4.11. К стержню круглого поперечного сечения, защемленному правым концом, приложены две одинаковые крутящие пары сил М
69
(см. рисунок). Диаметр левого участка стержня 40 мм, диаметр правого участка 60 мм. Наибольшее касательное напряжение в стержне на
правом участке 800 кг/см2. Чему равно наибольшее касательное напряжение на левом участке стержня?
Ответ: 1350 кг/см*.
4.12. К стальному валу приложены крутящие пары сил: Л11 = = 11 420 кгсм, Af, = 27 160 кгсм, /И3 = 50 000 кгсм. Длины участков вала (см) показаны на рисунке. Диаметр крайних участков вала 40 мм;
к——>w 150 ----—120—
К задаче 4.I2.
диаметр вала на среднем участке 60 мм. Построить эпюру крутящего момента и график нарастания угла закручивания, отсчитываемого от левого торцевого сечения I вала. Подсчитать, чему равны касательные напряжения у поверхности вала на каждом его участке и угол закручивания вала между сечениями 2 и 4?
Ответ: 910 кг/см* на всех участках; 0,0113 рад.
4.13. Сплошной вал радиусом г усилен надетой на него трубой внутренним радиусом г и наружным R. Вал и труба изготовлены из одного материала н работают как одно целое. Чему должно равняться отношение R:r, чтобы описанное усиление вала увеличило его грузоподъемность вдвое?
Ответ: 1,26.
4.14. Полый стальной вал с наружным диаметром </, = 75 мм и внутренним da = 50 мм имеет длину 1 я. Он закручивается на 1° парой сил с моментом 350 кгм. Чему равны наибольшие касательные напряжения в вале? Определить величину модуля упругости при сдвиге.
во
Решение. Наибольшее касательное напряжение
»ni«x=^7^. где J/> = ^(di—<Ф=249 сж«;
_35 000-3,75
Тп>а» ~ 249
527 кг/см2.
Модуль упругости при сдвиге иаходнм из формулы для угла закручивания
G
Л1и-<_35000-100-180 л-249
8,05-10» кг!См2.
4.15. Полый стальной вал длиной 1,8 jh нагружен по концам двумя парами сил с моментами Л1 = 0,6 гм. Определить наружный п внутренний диаметры вала, если угол закручивания не должен превосходить 2°, а касательные напряжения 700 кг/см2.
Ответ: 90,4 мм; 72,4 мм.
4.16. Наружный диаметр полого вала в два раза больше внутреннего. Этот вал па 20% легче сплошного вала, запроектированного при допускаемом напряжении на сдвнг 600 кг/см1. Чему равны наибольшие касательные напряжения в полом вале при одинаковых крутящих моментах?
Ответ: 581 кг/см1.
4.17. Сравнить веса двух валов, размеры которых подобраны для одного и того же крутящего момента при одинаковых допускаемых напряжениях. Первый вал сплошной, второй—трубчатый с отношением внутреннего диаметра к наружному, равным 0,6.
Ответ: Рт:Рс = 0,702.
4.18. Определить диаметр сплошного стального вала, передающего мощность 80 л. с. при 180 об/мин, при допускаемом напряжении 480 кг/см2 и допускаемом угле закручивания 1° на метр длины вала.
Указание. Сначала вычислим величину крутящего момента:
.. 225 000-/V 225000-80 о, „„
М“= - ~ = 3,14-180 =31 850 КХМ'
л-л
Затем из условия прочности и из условия жесткости находим необходимый диаметр вала.
Ответ: 7 см.
4.19. Вал диаметром 90 мм передает 90 л. с. Определить предельное число оборотов вала, если допускаемое касательное напряжение равно 600 кг/см2.
Ответ: Не менее 75 об/мин.
4.20. Сплошной стальной вал диаметром 90 мм при скорости вращения 150 об/мин передает 50 л. с. Длина вала между шкпвамн 4 м. Определить наибольшее касательное напряжение в вале н угол, на который один шкив повернется относительно другого.
Ответ: 167 кг/см2; 1°4'.
4.21. Сплошной вал круглого сечения был запроектирован в предположении определенной скорости его вращения. Затем было решено
01
повысить скорость в 20 раз. Как изменился диаметр вала после пересчета его при неизменных остальных данных?
Ответ: Уменьшился в 2,71 раза.
4.22. Для определения диаметра вала сплошного сечения можно пользоваться формулой d = k f/'N:n. Какое значение имеет величина k при допускаемых напряжениях [т] = 600, 800 и 1000 кг/см2?
Ответ: 8,5; 7,7; 7,1.
4.23. Лебедка поднимает груз Р= 1,6 т со скоростью v = 0,6 м/сек. Считая, что вал лебедки работает только на кручение, и пренебрегая вредными сопротивлениями, подобрать диаметр сплошного вала лебедки, вращаемого со скоростью 200 об/мин, при допускаемом напряжении |т] = 450 кг/см2.
Указание. Мощность, передаваемая валом; A = P-v= 1,6-0,6 = 0,96 тм/сек. Скорость вращения вала со = 2О,9 рад/сек. Крутящий момент Л1к = Л:со = 46лгм. Определение диаметра производится из условия прочности вала.
Ответ: 37 мм.
4.24. Полый стальной вал с наружным диаметром dt = 100 мм н внутренним d2 = 50 мм при вращении со скоростью 80 об/мин закручивается на угол 1,8° на длине 2,7 м. Какую он передает мощность? Чему равно наибольшее касательное напряжение в вале?
Л1„-п-л w-Jd-G л 15
жем написать следующее:
я-15-я-<6-я-п п’-15-5*8-10»-80 _
“ 100-32/-225 000 — 100-32-270-225000
Величина ттаж определится по формуле
4.25. Определить диаметры полого стального вала, передающего мощность 7000 кет при 100 об/мин, если наибольшее касательное напряжение в вале 600 кг/см2, а внутренний диаметр составляет 0,6 от наружного.
Ответ: 40,5 см и 24,3 см.
4.26. При определении мощности турбины был измерен угол закручивания вращаемого ею стального вала, который на длине 6 м оказался равным 1,2°. Наружный и внутренний диаметры вала равны 25 см и 17 см. Скорость вращения вала 250 об/мин. Вал выполнен из стали. Определить мощность, передаваемую валом, и возникающие в нем наибольшие касательные напряжения.
Ответ: 2160 кет; 349 кг/см2.
4.27. Карданный вал автомобиля при двух режимах работы передает одну и ту же мощность—23 л. с. Скорость вращения вала в одном случае 108 об/мин, а в другом—60 об/мин. Каков должен быть наружный диаметр вала, если отношение внутреннего диаметра к наружному равно 0,9, а допускаемое касательное напряжение
[т] = 4Q0 кг/см1? Как изменятся наибольшие касательные напряжения в вале при переходе от большой скорости к малой?
Ответ; d=10,0 см. Увеличатся в 1,8 раза н достигнут допускаемого значения.
4.28. Средний диаметр трубы 30 см, а толщина стенок / = 8 лл. Определить величину касательных напряжений, возникающих в материале трубы при действии на нее крутящего момента Л1к=1,15 тм.
Указание. При кручении тонкостенных труб касательные напряжения возле внутренней и наружной поверхностен трубы очень мало отличаются друг от друга, а потому расчет следует вести иа среднее значение напряжений, которое можно определить по формуле
Мц ’ ^Ср
где гср—средний радиус кольцевого сечения.
Полярный момент инерции кольцевого сечения можно подсчитать такхсе по приближенной формуле
Jp = 5р2^ = гс2р.2л.гср./= 2лгс3р/.
М Формула для среднего значения напряжений в трубе примет вид т =--7—.
?лгсре
Ответ: т= 101,5 кг/см3. При точном вычислении полярного момента инерции наибольшее напряжение ттах =104,5 кг/см3.
4.29. К тонкостенной стальной трубе со средним диаметром 12,5 см приложены но концам нары сил, скручивающие трубу моментом 62,5 тем. Какова должна быть толщина стенок трубы, чтобы касательные напряжения не превосходили 800 кг/см2? Чему равен угол закручивания трубы иа длине 1 м?
Ответ: 0,32 см; 0, 016 рад.
4.30. Стальной трубчатый вал передает мощность 75 кет при вращении со скоростью 100 об/мин. Толщина стенок составляет 1/50 среднего диаметра сечения. Определить величину этого диаметра из условия, чтобы угол закручивания не превышал 1° на 3 м длины. Чему при этом равны касательные напряжении?
Ответ: 17,8 см; 413 кг/см2.
4.31. Стальной вал трубчатого сечения длиной 1,8 -н, средним диаметром 30 см. при толщине стенок 3 мм вращается со скоростью 100 об/мин. Какую мощность он передает, если среднее касательное напряжение в стенке вала равно 630 кг/см3? Чему равен угол закручивания вала?
Ответ: 275 кет; 0,542°.
4.32. Концы стержня круглого сечения защемлены; в промежуточном сечении приложена пара сил с моментом Л1=1200 кгм (см. рисунок, схема а). Расстояние Ь = 2а. Чему равны наибольшие касательные напряжения в стержне, если его диаметр 8 см?
Указание. Уравнение статики: Мд+ Мя = М. Система однажды статически неопределима. Выберем за основную (статически определимую) систему стержня
93
Фв— Но так
м„=
схему б. При загружеиин этой схемы ларами М и Мв (схема в) и при условии, что <ря=0, схема в станет эквивалентной схеме л. Рассмотрим теперь раздельно действие иа стержень пары М (схема г) и пары Мя (схема д). Сечение В , Маг,
в схеме г повернется иа угол Vb~gj~ в схе" ме д поворот того же сечения Мв(а+Ь) , =------------— (в другую сторону).
как фя=Фв+ *Рв=0, находим
= • М, а Л4д = —-М. Строим эпюру
крутящего момента (е). Из эпюры видно, что иа левом участке касательные напряжения больше, чем на правом.
Ответ: 795 кг!см\
4.33. Стержень круглого сечения с защемленными концами подвергается действию двух равных и одинаково направленных пар сил с моментами по 800 кгм (см. рисунок). Раскрыть статическую неопределимость и определить угол поворота среднего сечения 7—1 стержня. Диаметр стержня равен 10 см, длина каждого из крайних участков а = 60 см, а длина среднего участка (> = 80 см.
Ответ: Мд = М в =800 кгм; 21'.
4.34. К стержню круглого сечения, защемленному концами, приложены две равные и противоположно направленные пары сил с моментами по 1000 кгм диаметр стержня при допускаемом напря
жении иа сдвиг 600 кг/см2. Чему, равен угол поворота среднего сечения стержня?
Ответ: 8,27 елц 0.
К задаче 4.33.
К задаче 4.34.
4.35. Диаметр левой части стержня, защемленного иа концах равен 6 см, а правой—5 см. Общая длина стержня а-|-&=3,3 м (см. рисунок). Определить размеры а и b из условия, чтобы крутящий момент, приложенный в месте изменения диаметра стержня,
В4
вызывал в каждой части стержня одинаковые наибольшие касательные напряжения.
Ответ: а = 1,8 я; b = 1,5 м.
4.36. Медная трубка наружного диаметра 7,5 см помещена внутри стальной трубки такого же внутреннего диаметра. Толщина стенок обеих трубок одинакова и равна 3 лыс
Концы трубок жестко скреплены между .__________ г\
собой, и в месте скрепления приложены ;
пары сил с крутящими моментами по . р г > I j
100 кгм. Длина трубок 3 м. Модуль упру- । । i'
гости меди при сдвиге равен 4-10' кг/см2. Как распределяется крутящий момент
между трубками? На какой угол закрутятся трубки? Чему равны наибольшие касательные напряжения в стенках трубок?
Указание. Назовем Ми крутящий момент, приходящийся на медную трубку, и Мс—на стальную. Уравнение статики свяжет эти два момента с моментом приложенной пары. Так как трубки жестко соединены по концам между собой, углы закручивания их должны быть одинаковыми.
Ответ: 28,2 кгм и 71,8 кам; 1,38°; 120 кгм/см2 и 260 кг!см2.
4.37. Стальной стержень круглого сечения диаметром 25 мм имеет цилиндрические выступы А и В. К боковым поверхностям выступов
Л Ь
К задаче 4.37.
плотно прилегает стальная трубка наружного диаметра 75 мм и толщиной стенки 1,25 мм (см. рисунок). Перед надеванием трубки стержень был закручен парами сил с моментами Мо = 7,5 кгм. После того как трубка была приварена к обоим выступам, крутящие моменты с концов стержня были сняты. Какой величины моменты будут взаимодействовать между стержнем и трубкой? Чему равны наибольшие касательные напряжения в стержне п в трубке?
Указание. Считаем, что выступы А и В не деформируются. Угол <р0, па который был закручен стержень парами сил Мо, после удаления этих пар уменьшится на ту величину, на которую закрутится трубка (<рт). Следовательно, стержень останется закрученным на угол <рс = «р0—<рт (1). Равенство же моментов взаимодействия между стержнем и трубкой (Мс и AfT) представляет второе уравнение (2). Из совместного решения этих уравнений находится величина взаимодействующих моментов, а затем и касательные напряжения.
Ответ: /Мт = Л1С = 6,85 кгм; JC:JT = 0,0975. Напряжения: 223 кг)см2 в стержне и 65 кг/см2 в трубке.
§ 13. Кручение стержней прямоугольного сечения
4.38. Стальной стержень прямоугольного сечения с размерами сторон 2 см на 3 см (см. рисунок) загружен двумя крутящими парами с моментами по 2 тем каждая. Вычислить величину касательных напряжений, возникающих в поперечном сечении у поверхности стержня по линиям АВ и CD. Определить величину угла закручивания стержня при его длине 1 м.
К задаче 4.38.
Указание. При расчетах па кручение стержней прямоугольного сечения пользуются следующими данными:
Момент инерции прямоугольника при кручении Ju=a-b*, где b—меньший из двух размеров сторон прямоугольника.
Момент сопротивления прямоугольника при кручении 07н= P-f.
Наибольшее касательное напряжение, возникающее в сечении посредине длинной стороны.
Мк
max де'*
Наибольшее касательное напряжение посредине короткой стороны сече*
Коэффициенты а, Р и у зависят от величины отношения h/b.
Значения этих коэффициентов приведены в следующей таблице:
ft b ! 1.5 1,75 2.0 2 5 3.0 4.0 0.0 в,0 10.0
а 0,140 0,294 0,375 0,457 0,622 0,790 1,123 1,789 2,456 3,123
р 0,208 0,346 0,418 0.493 0,645 0,801 1,128 1,789 2,456 3,123
У 1.0 0,859 0,820 0,795 0,766 0,753 0,745 0,743 0,742 0,742
Решение. Для данной задачи й:Ь=1.5. Находим по таблице значения коэффициентов: а=0,294, Р = 0,346 и у=0,859.
. 2000
Наибольшее напряжение TmaX = Q-34g g =772 кг/см*.
Напряжение посредине короткой стороны ттах = 0,859-722 = 620 кг/см1.
МЛ1 2000-100 „„„„ ,
Угол закручивания <₽ = — = = 0.0532 рад.
£6
4.39. Стержень имеет круглое сечение па среднем участке и квадратное, вписанное в круг, на крайних участках. На стержень действуют крутящие пары сил = 11 тем и (см. рисунок). Какую величину должна иметь крутящая пара сил Ма, чтобы наибольшие касательные напряжения на среднем и на крайних участках были одинаковы? Концентрацию напряже-
ний в местах резкого изменения сечения не учитывать.
Ответ: 3 тем.
4.40. Дверная пружина (см. рисунок) выполнена из стального прута АВ квадратного сечения 6 x6 мм2. Прут прикреплен верхним концом А к двери, а нижним
В—к притолоке. Найти величину силы Р, с которой нужно тянуть за ручку дверь, повернув ее на 90°, и угол, на который нужно предварительно закрутить прут, чтобы при открытой двери наибольшие напряжения в материале прута не превышали 5000 KefCM2. Длина прута 2 м. Ширина двери 1 м.
Ответ: 2,25 кг; 87°.
4.41. Определить размер стороны квадрата поперечного сечения вала, передающего 100 л. с. при 120 об/мин. Касательные напряжения нс должны превышать 450 кг/см*.
Ответ: 86 мм.
4.42. Сплошной вал круглого сечения обжат на части длины так, что ссченне приобрело форму квадрата, равновеликого с кругом. Во сколько раз наибольшие напряжения в квадратной части вала больше, чем в круглой, если крутящий момент по всей длине вала одинаков? Концентрацию напряжений в месте изменения формы сечения не учитывать.
Ответ: В 1,35 раза.
4.43. Определить отношение весов двух равнопрочных валов круглого и квадратного поперечных сечений.
Ответ: 0,81.
4.44. Прямоугольное цриеречное сечение стержня имеет ширину 4 см. Какова должна быть высота сечения, чтобы наибольшие касательные напряжения в нем были такими же, как в стержне круглого поперечного сечения диаметром 5 см? Оба стержня загружены парами сил с одинаковыми крутящими моментами.
Ответ: 6,5. см.
S7
4.45. Стержень прямоугольного поперечного сечении нагружен двумя парами сил с крутящими моментами по 60 кгм. Допускаемое напряжение иа сдвиг [т] = 1400 кг/см*. Какова должна быть высота поперечного сечения, если ширина его 20 мм?
Ответ: 4,28 см.
4.46. Определить из условия прочности по касательным напряжениям при [т] = 1000 кг/см- величину допустимого крутящего момента
К задаче 4.47.
для пустотелого стержня прямоугольного поперечного сечения с размерами, показанными на рисунке (в мм).
Указание. При решении задачи воспользоваться данными учебника Н. М. Беляева «Сопротивление материалов», табл. 17 иа стр. 216.
Ответ: 90 тем.
4.47. Стальной стержень двутаврового сечения с размерами, показанными на рисунке (в мм), испытывает действие двух скручивающих пар, приложенных по концам стержня и равных 100 кгм каждая. Чему равны наибольшие касательные напряжения? Где они возникают? Чему равен угол закручивания стержня на длине 100 см.
Указание. Воспользоваться данными учебника Н. М. Беляева «Сопротивление материалов», стр. 218—219.
Ответ: 500 кг/см1: посредине полок, вблизи наружной поверхности их; 0,032 рад.
§ 14. Винтовые пружины с малым шагом
4.48. Стальная цилиндрическая винтовая пружина круглого сечения диаметром 20 мм сжата осевой силой в 100 кг. Средний диаметр витков пружнны 160 мм. Число витков 8. Определить наибольшее касательное напряжение в стержне пружины, величину осадки и полную потенциальную энергию деформации пружины.
Решение. Наибольшее касательное напряжение в стержне
Р , Мк Р , 2PR 100 „ , .
ттах р + № л 6 кг/СМ.
98
, 4PR*n 4-100-8-3 _ft.o
Осадка пружины *=-^г~ = 8-10»-1* = 2,048 Слс Р-Х
Полная потенциальная энергия деформации пружины U =—= 1 02,4 кгсм.
4.49. Цилиндрическая винтовая пружина, изготовленная из б-мм стальной проволоки, имеет 10 витков. Наружный диаметр витка пружины 66 мм. Определить осевую растягивающую силу, при которой наибольшее касательное напряжение в стержне не превосходит 2400 кг!см*. Чему равны при этой силе удлинение пружины, полная работа упругой деформации и жесткость пружины (т. е. сила, необходимая для растяжения пружины на 1 см)?
Ответ; 32,3 кг; 5,38 сж; 86,9 кгсм; 6 кг/см.
4.50. Для образования винтовой* пружины на барабан диаметром 5 см должно быть навито столько стальной проволоки диаметром 6 мм, чтобы пружина под нагрузкой в 9 кг давала осадку в 2,5 см. Определить необходимую для этого длину проволоки (без учета длины концов пружины и наклона витков). Чему равен угол закручивания проволоки между концами пружины?
Ответ: 361 см; 51°15'.
4.51. При испытании для установки зеркальных измерительных приборов иа образце пластинки прибора 1—1 и 2—2 (см. рисунок) прижимаются к образцу струбцинами с двумя одинаковыми стальными цилиндрическими пружинами 3—3 и 4—4. Сколько витков должна иметь каждая из пружин, если при деформации их на 10 мм нажатие упорного винта иа пластинку должно равняться 400 г? Какие возникнут при этом максимальные касательные напряжения в пружинах? Диаметр проволоки пружин 0,5 мм, диаметр витка 4 мм.
Ответ: 49 витков; 1730 кг! см2.
4.52. Витки буферной винтовой стальной пружины имеют средний
диаметр 20 см. При осадке пружины иа 5 см она должна поглощать 50 кгм энергии, причем наибольшие касательные напряжения в стержне пружины не должны превышать 1750 кг)смг. Определить диаметр стержня пружины и число витков.
К задаче 4.51.
Р - X
Решение. Потенциальная энергия пружины (7 = —^—= 5000 кгсм. Отсюда Р=2000 кг.
Наибольшее напряжение в материале стержня пружины
Р 2PR ттвх=й75-+-^=1750 кг/см2.
99
Подставив в эту формулу числовое значение Р, получим
г 4 2/?= 2,75г’.
Методом постепенного подбора найдем, что г = 2 см.
.. XGr4 5-810»2« „
Число витков п = = 4-___ = 8.
4.53. Во сколько раз изменится диаметр стержня пружины и число витков, если в условие предыдущей задачи внести изменение: пружина должна поглощать 100 кгм энергии?
Ответ: Диаметр увеличится в 1,27 раза, а число витков увеличится до 11.
4.54. Винтовая цилиндрическая пружина под нагрузкой в 200 кг должна давать полную осадку (до соприкасания витков) в 8 см. Допускаемое напряжение на сдвиг 1800 кг!смл. Стальная проволока при изготовлении пружины навивается на барабан диаметром 16 см. Определить диаметр проволоки, число витков пружины н ее полную высоту. Чему равен теоретический вес такой пружины?
Указание. Радиус витка пружины выразить через Ро+Г- где Рв—радиус барабана. Из условия прочности получится уравнение Рв +1,5г = 14,13га.
Ответ: 17,4 мм; ~7 витков; ~20 см; ~ 7,2 кг.
4.55. Предохранительный клапан диаметром 7,5 см, прижатый пружиной под некоторым начальным усилием Ро, должен открываться при давлении на клапан в 8 ат, после того как пружина сожмется на 2 см. У полностью разгруженной пружины расстояние между витками в свету равно 5 мм, а при открытом клапане пружина сохраняет запас деформации в 16 мм. Средний диаметр витков пружины 6 см, а диаметр стального стержня пружины 12 мм. Определить необходимое число витков, величину начального усилия и наибольшее касательное напряжение в стержне пружины.
Решение. Усилие, передаваемое клапаном на пружину при достижении давления в клапане в 8 ат, равно Р = 353,2 кг. Под начальным усилием Рв пружина должна дать осадку
Ао = 0,5л—1.6—2 = 0,5л—3,6 (см).
При увеличении усилия от Ра до предельного значения Р осадка пружины возрастет, на 2 см. Напишем дважды формулу для осадки пружины
4(Р-Р0)/?’л
Gr*
0.5п-3,6 = -4-Г?Р— иг*
(1)
(2)
Из совместного решения этих двух уравнений получаем л = 12,1 я 12 витков. 3X0=2,45 см. Затем из пропорции (Р—Рв):Р0 = 2:2,45 находим величину Ро.
Ответ: 12 витков; 194 кг; 3430 кг/см2.
4.56. Стержнем винтовой цилиндрической пружины служит тонкостенная стальная трубка. Пружина нагружена осевым усилием такой
106
величины, что среднее значение касательного напряжения в стержне пружины равно 3000 кг/см2. Определить потенциальную* энергию, приходящуюся на 1 кг металла. Воспользоваться указанием к задаче 4.28.
х%
Ответ: -2GC^~ = 7’22
4.57. Винтовая цилиндрическая пружина квадратнфго сечения 10X10 выполненная из стали, имеет 12 витков ,со средним радиусом 5 см. Определить наибольшую силу, которой можно. нагрузить- пружину при допускаемом напряжении . на скалывание 2800 кг/см-. Чему будет равна осадка пружины при действии этой силы?
Ответ: 112 кг; 9,42 см.
4.58. Стальная труба с наружным диаметром 20 см и толщиной стенки 2 см разрезана винтовым цилиндрическим ходом с шагом 3 см (плюс толщина реза) так, что образовалась пружина в 10 витков. Эта пружина была затем нагружена осевым усилием 900 кг, растягивающим пружину. Чему равно удлинение пружины, наибольшие касательные напряжения в ней и полная потенциальная энергия пружины?
Ответ: 10,9 см; 3076 кг/см2; 4905 кгем.
4.59. Внутри стальной цилиндрической винтовой пружины круглого сечения диаметром 3 см помещена вторая пружина, с сечением диаметром 2 см. Средний диаметр наружной пружины 16 см, а внутренней —10 см. Обе пружины одинаковой высоты и имеют по 10 витков каждая. На пружины действует нагрузка 2000 кг. вызывающая одинаковую осадку обеих пружин. Чему равна нагрузка на каждую из кружим, их осадка п наибольшие касательные напряжения в каждой из них?
Ответ: 1104 и 896 кг; 5,6 см; 1822 и 3139 кг 1см2.
.4.60. Две пружины с одинаковым средним радиусом витков R= 10 см изготовлены из стальной проволоки круглого сечения диаметром d = 2 см. Пружины вставлены между двумя неподвижными плоскостями. Между пружинами помещается нагрузочная плита, как это показано на рисунке, жестко скрепленная с концами пружин. Через плиту на пружины передается осевая нагрузка Р = 450 кг,
вниз. Не учитывая веса плиты, определить, как распределяется нагрузка между пружинами, если верхняя пружина имеет 4 витка, а нижняя — 5 витков. Чему равно вертикальное перемещение плиты? Какой величины достигают касательные напряжения в стержнях каждой пружины?
Ответ: 250 и 200 кг; 5 см; 1672 и 1338 кг/см2.
4.61. Коническая стальная рессора круглого сечения диаметром 2 см сжимается силой 400 кг. Радиус оси верхнего витка пружины
К задаче 4.60.
направленная
101
равен 4 см, а нижнего—10 см. Определить величину наибольших касательных напряжений в стержне пружины и число витков, если осадка пружины равна 6,5 см.
Указание. Расчет конических пружин дан в учебнике Н. М. Беляева, стр. 210.
Ответ: 2675 кг!смг\ 8 витков.
4.62. Кузов пассажирского вагона весит со всем оборудованием 18 т и покоится на 32 стальных конических пружинах квадратного •сечения 3x3 см. Число витков в каждой пружине 6. Допускаемое напряжение на скалывание при статическом загруженни 2000 кг [см2. .Наибольший радиус витка 12 см, а наименьший—6 см. Какое количество пассажиров можно поместить в вагоне, считая, что пассажир и его багаж весят в среднем 100 кг? Какова будет средняя осадка пружин при порожнем вагоне и в присутствии всех пассажиров?
Ответ: 104 чел.; 1,9 см и 3 см.
§15. Конструкции, работающие на сдвиг и на кручение
4.63. Кронштейн, прикрепленный к колонне при помощи шести заклепок (см. рисунок), нагружен силой Р = 2400 кг. Определить полное усилие, приходящееся на наиболее загруженную заклепку.
Решение. Приведем силу Р к центру заклепочного соединения А. Сила Р, перечеркнутая одни раз, распределяется равномерно между шестью заклепками. На каждую из них придется усилие Ро = 400 кг, направленное вертикально вниз. Силы же Р, перечеркнутые два раза, создают пару Ре, которая скручивает заклепочное соединение. Предполагаем по аналогии с кручением стержней, что усилие Рв в каждой заклепке, вызываемое парой сил Р-е, пропорционально расстоянию рк заклепки от центра А и направлено каждое перпендикулярно своему радиусу ри. Из рисунка видно, что pt= 12,5 см, ра=7,5сж.
102
е=250 лл = 25 см. Из сказанного следует, что Р1:Р2 = 12,5:7,5; Р1=-уР1 (см. рис. 6). Очевидно также, что P, = P3=P4 = Pt и P2 = Pt. Момент, скручивающий соединение, Ми=Ре=2РцРк-
Подставив числовые значения, получим урввненне
к
2400-25 = 4” • Pt.12,54-2Pt-7A
О
Из уравнения находим Р4=610 кг, а Р1=1017 кг.
Из двух средних заклепок 2 н 5 более загруженной является заклепка 5, воспринимающая полное усилие S5 = P5-|-Po=610-|-400 = 1010 кг. Из четырех крайних заклепок наиболее нагруженными являются заклепки 4 и 6 (см. рнс. б и в). Полные усилия в этих заклепках прн cos а=0,6 равны:
S4=Se = У10172+4002+2-1017-400-0,6 = 1300 кг.
Следовательно, наиболее загруженными являются заклепки 4 и 6, принимающие на себя полное усилие 5=1300 кг каждая.
4.64. Заклепочное соединение, изображенное на рисунке, прини-
мает нагрузку от силы Р = 3,5 т. Диаметр заклепок 20 мм. Заклепки работают на одиночное перерезывание. Определить величину
касательных напряжений в наиболее загруженной заклепке.
Ответ: 704 кг!см*.
4.65. Кронштейн из толстого стального листа передает на стальную колонну вертикальное усилие Р=3000 кг посредством болтового соединения, показанного на рисунке. Болты работают на одиночное перерезывание. Их диаметр 23 мм. Допускаемое напряжение «а срез 1000 кг/см2. Каков допустимый разрез выноса консоли е?
Ответ: Не более 87 см.
4.66. Сплошной вал диаметром 10 см, работающий на кручение, имеет стык, перекрытый трубчатой муфтой, приваренной по торцам к стыкуемому валу (см. рисунок на стр. 104). Материал муфты и вала одинаковый, с допускаемым напряжением на сдвиг 600 кг/смл. Внутренний диаметр муфты 10 см, наружный—12 см. Определить
103
допустимый крутящий момент. Какие будут при этом напряжения в материале сварного шва?
Ответ: 1053 кгм; 792 кг/см-.
К задаче 4.66.
4.67. Вал диаметром d„=10 см работает при наибольших касательных напряжениях ттах = 700 кг/см2. Две его части соединены при помощи фланцевого соединения на болтах, расположенных на равных расстояниях один от другого по окружности радиусом R =10 см. Напряжения на срез в болтах диаметром 20 мм не должны превышать 600 кг!см2. Сколько болтов должно иметь фланцевое соединение?
Указание. Крутящий момент, воспринимаемый валом, Мк = 0,5лгат1Пах передается па фланцевое соединение на п болтах; MK=P-R-n, где Р—усилие, приходящееся па один болт: Р=лг|(т].
Ответ: 8 болтов.
4.68. Две трубы соединены при помощи фланцев шестью болтами диаметром 40 мм. Болты расположены на окружности на расстоянии по хорде 20 см один от другого. Допускаемое напряжение на одиночное перерезывание в болтах равно 600 кг/см2. Какой крутящий момент может быть передан этим соединением? Чему равны напряжения смятия болтов о стенку фланца, если толщина стенки 16 мм?
. Ответ: 9,04 тм; 1177 кг[см2.
. 4.69. Два сплошных вала диаметром 80 мм и 100 мм соединены при помощи фланцев четырьмя болтами. Болты диаметром 20 мм расположены на двух взаимно перпендикулярных диаметрах па расстоянии 10 см от оси валов. Соединение передает крутящий момент 800 кгм. Вычислить наибольшие касательные напряжения в каждом нз валов и касательные напряжения в болтах.
Ответ: В кг [см.2: 795, 408 и 636.
4.70. Во фланцевом соединении, передающем крутящий момент 25 тем, на окружности радиусом 7,5 см поставлено симметрично 4 болта диаметром 25 мм. Один из болтов вышел из строя. Определить, какая нагрузка придется на каждый из трех оставшихся болтов и чему будут равны касательные напряжения в ннх.
Указание. Нужно найти центр тяжести трех оставшихся болтов и усилия, в них возникающие, как это было объяснено в решении задачи 4.63. Момент
IM
усилий н трех болтах относительно их центра тяжести равен' крутящему моменту, а равнодействующая равна нулю.
Ответ: Два болта, расположенные на концах одного диаметра, будут нагружены больше, чем третий болт: Р' = Р"=1317 кг: р"' = 833 кг. Напряжения в болтах соответственно ;равны 269 п 170 кг!смг.
4.71. Шкив, вращающий вал со скоростью 200 об^шн, передает 125 л. с. сплошному валу диаметром 75 мм. Шкив соединен с валом при помощи шпонки сечением 10X10 ммг и длиной 100 мм. Определить касательные напряжения в шпонке и напряжения смятия шпонки о стенку канавки.
Ответ: 1194 кг!см-\ 2388 kzIcm1.
4.72. Две части полого вала (наружный диаметр 60 мм, а внутренний—30 м.и) соединены кулачковой муфтой (наружный диаметр
К задаче 4.72.
100 мм, а внутренний—60 мм), как это показано на рисунке. Наибольшие касательные напряжения в материале вала равны [tj. Какую часть этих напряжений составляют скалывающие напряжения т в основании зубцов муфты, еслп считать напряжения равномерно распределенными по сечению основании каждого зубца?
Ответ: т = 0,396 [т].
ГЛАВА 5
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ ФИГУР
§ 16. Геометрические характеристики сечений, имеющих оси симметрии
5.1. Вычислить осевые и центробежный момент инерции площади прямоугольника относительно осей х и у, совпадающих с двумя его сторонами, имеющими размеры: 6 = 24 см, 6 = 30 см.
bh3
Ответ: 7=^-=216 000 см1;
о мл Jv=-^ =138 200 см1;
У J
W/.2
J, = -^-=129 600 см*.
5.2. Определить величину главных центральных моментов инерции и моментов сопротивления сечения прямоугольного бруса, ослабленного круглым отверстием (см. рисунок), при заданных размерах:
К задаче 5.2. К задаче 5.3.
Ответ: Jx = 7375 см1; J =2160 см1;
Wx = 737,5 см3; w£=360 см3.
5.3. Выяснить, как изменятся момент инерции и момент сопротивления квадрата со стороной а относительно осн х, если сечение повернуть на угол 45°, оставив ось х горизонтальной (см. рисунок).
100
Ответ: Момент инерции не изменится; момент сопротивления уменьшится на 41%.
J 5.4. Вычислить главные центральные моменты инерции, главные радиусы инерции и моменты сопротивления полого прямоугольного сечения, показанного на рис. а. Размеры: &=12 см, Л = 20 см.
К задаче 5.4
К задаче 5.5.
а = 6 см. Как изменятся эти характеристики сечения, если внутренняя квадратная полость будет повернута на угол 45°, как показано на рис. б?
Ответ: a) 4 = 7892 см*, /„ = 2722 см*, /х = 6,16 см, Wx= 789,2 см3, = 462 см3, iy = 3,64 см;
б) не изменятся.
5.5. Сравнить величины моментов инерции относительно центральной оси х сечений прямоугольника, квадрата и круга при условии, что площади F всех трех сечений одинаковы (см. рисунок).
Указание. Выразить моменты ннерцин фигур через площадь сечения.
Ответ: a) Jx = 0,167 F3;
б) Jx = 0,0833 F3;
в) 4 = 0,0797 F3.
5.6. Вычислить главные центральные моменты инерции двухканальной трубы прямоугольного очертания, запроектированной в двух вариантах: а) с двумя круглыми отверстиями диаметром каждое d = 10 см, б) с двумя квадратными отверстиями размером 10 X 10 см каждое.
Размеры сечений даны на рисунке в мм.
Ответ; а) 4 « 15000 см*, Jy& 16 400 см*;
б) 4» 14 300 см*, 4 « 14 200 см*.
5.7. Определить величину момента площадью F относительно оси хЕ1 если
К задаче 5.6.
инерции заданного сечения задан момент инерции его
107
относительно осн хг (см. рисунок). Расстояния от центра тяжести сечения до осей и xt соответственно равны а1 и аг.
Ответ: JXi = JXi + F(al — aj).
518. Сравнить величины главных центральных моментов инерции и гл'авных радиусов инерции трубчатого прямоугольного сечения,
К задаче 5.7.
К задаче 5.8.
запроектированного в двух вариантах (см. рисунок): а) с круглым отверстием и б) с квадратным отверстием трубы (одинаково рас* положенными по высоте сечения). Вычислить также наименьшие моменты сопротивления сечений относительно центральной осп х.
Решение. Для варианта а): площадь сечения F = 8o2 = L^ = 7,215a2; расстояние от центральной осн прямоугольника хо до центра тяжести трубчатого Sxo _ ла2 а па3 па3 п „сс
сечения j/c= у*, где Sxo = f у и Ус= - -0,0550.
Момент инерцнн сечения относительно центральной оси ж вычисляем по формулам перехода к параллельным осям [jx =£(-'хо+^2)]:
Jx= рПУГ" +8а2 (0-055о>2] ~ + V (у+°.°55о)2] « 10,33а*.
Относительно вертикальной оси у момент инерцнн будет
. 4а (2а)3 12“
~=2,62а«. С4
Главные радиусы инерции:
»л =
10,33
7,215
а2 = 1,2а;
Для варианта б), выполнив аналогичный расчет, найдем:
Г = 7о2; ус = 0,07о; Jx= 10,3a*; /,,=2,59а*; ix= 1,22a; 1^=0,610.
Моменты сопротивления сечений относительно главной осн х будут:
а) Wx=±_№. !/imx 2,055a
UZ -A-IW. ’ * Wmax 2,07a
=5,027o3;
4,976a3.
108
6.9. Деревянная балка составлена из трех одинаковых досок, склеенных между собой в виде двутавра (см. рисунок). Определить величину главных центральных моментов инерции и моментов сопротивления площади двутавра, если размеры сечения каждой доски равны 5x24 см.
Ответ: Jx = 56660 см*; Jy = \\ 770 см4;
IFX = 333O см3; Wy — 980 см3.
5.10. Составная балка из двух швеллеров № 33, перекрытых листами 300X14 мм (см. рисунок), проектируется в двух вариантах:
К задаче 5.9.
К задаче 5.10.
а) сварной—с прикреплением листов к полкам швеллеров фланговыми швами; б) клепаный—с присоединением листов к полкам швеллеров при помощи заклепок диаметром d = 23 мм. Вычислить момент инерции и момент сопротивления сечения относительно осн х для обоих вариантов и сравнить полученные результаты.
Указание. Для учета ослабления сечения заклепочными отверстиями следует подсчитать момент инерции четырех отверстий, не заштрихованных па (<ца \
-|g-4-d/c* 1, причем соб-
( dt* \ ственным моментом инерции заклепочного отверстия можно пренеб-
речь. Момент инерции всего сечения J1( = 4p—
Ответ: a) Jx=40 800 см*; 1Рх = 2280 см3;
б) Jx = 34 300 см*; Wx = l920 см\
5.11. Определить величину главных центральных моментов инерции, моментов сопротивления и радиусов инерции симметричных сварных сечений, составленных из прокатных профилей (см. таблицу). Совместили работа элементов составного сечения обеспечивается соединительными элементами, показанными пунктиром. *
Ответ: См. таблицу.
109
К задаче 5.1!
№ схемы Схема сечения Состав сечения (размеры в лсм) Ответ в см*
Вариант а) Вариант б) а) б)
I II 2 уголка 100x100x10 6=10 2 уголка 80x 80x8 6=8 ч"’ х” II II 00 сл ** 00 ь- со *т сч —' со II II
11 Л 2 уголка 80x80x8 6 = 8 2 уголка 100x100x10 6=10 ч"’ х” II II -Ъ. ко — со — N0 ч*4 х"” II II О СЛ СО 0) 00 00
111 пг UL? ни 4 уголка 125x125x10 6=10 Л=400 4 уголка 100x100x10 6=8 Л=300 II II s 8 о § 8 сч о II II
IV . а 4 уголка 140 x90x10 лист 12x240 4 уголка 110x70x8 лист 200х Ю х^ II h о о ° 8 ч*4 х” II II — сл S о о
V ШЯ Г" 2 швеллера № 36 Двутавр№14 2 швеллера № 30 Двутавр №14 7Д.=21 680 7^=11600 /Л.= 11 6G0 7^ = 8566
VI - tx 1 х 2 швеллера № 22 с=100 2 листа 280x10 2 швеллера № 16 с =100 2 листа 250x8 7х=П630 7^ = 6740 Jx=4320 7^ = 3880
110
К задаче 5.11 (продолжение)
№ схемы Схема сечения Состав сечения (размеры в лсм) Ответ в см*
Вариант а> Вариант б) в) 6)
VII 5 2 швеллера № 36 2 листа 240x12 2 швеллера Ns 22 2 листа 280x10 7х = 41570 Jy= 13070 7x=11630 7^=11 380
VII! cS в> а зь 2 двутавра № 14 2 листа 240 x8 с=!20 2 двутавра № 30 2 листа 300x12 с = 150 7х=3250 7^=3180 7X=31 700 7^=11300
IX 03 н Т*—^->1 Д’ 4 уголка 50x50 x5 2 листа 200x6 с =130 4 уголка 90x90x8 2 листа 220x8 с=160 7х=2260 Jy=2!70 7x=5850 7^=8600
X &Зв£И 1 4 уголка 70x70x7 4 листа 200x6 4 уголка 100x100x10 4 листа ЗООхЮ Jv=5940 Jy = 5940 7x = 31190 7^=31 190
XI а 4 уголка 140x90x10 лист 240х 10 4 уголка 160x100x12 лист 300x12 7x=4060 7^=4070 7x=8880 7y=6110
XII ) х *4 уголка 80x 80x8 2 полки 180x10 стенка 600x10 4 уголка 100X100X10 2 полки 240Х10 стейка 900x10 7X = 89615 7^=1595 Jx=297 380 7^=3880
111
6.12. Установить, как изменятся главные центральные моменты инерции и моменты сопротивления круглого сечения, если абсциссы всех точек окружности увеличить в п раз, как показано на рисунке пунктиром.
Ответ:
Jx увеличитси в п раз; Jy— в п3 раз;
1ГЛ. увеличится в п раз; Wy— в л2 раз.
К задаче 5.12.
К задаче 5.13.
Б.13. Определить положение центра тяжести и вычислить моменты инерции площади полукруга относительно главных центральных осей инерции фигуры (см. рисунок).
Решение. Расстояние от вспомогательной осп до центра тяжести сечения определяется по формуле
где
S*,= J VidF, а Г = 0,5лг2. F
Для вычисления статического момента площади $Х1 выделим элементарную Г
полоску dF = b (у) dy. Тогда SX1 = J b (у) yt dyt. i. о
Переходя к полярным -координатам, найдем
Ь (у) = 2r sin <р, р1 = гсозф, dpi=—гзтфЛр.
Подставляя под знак интеграла и имея в виду, что при изменении ух от нуля до г угол ф изменяется от л/2 до нуля, получим
о
Р Q|l)3 (Г) 9
SXl=—2г* \ Б1п'гф созф4ф=2гэ;—у-£ = -д-г3.
л/2 •
2г? 4г Следовательно, Ус=—^=-. Для определения момента инерцнн полукруга относительно центральной оси х воспользуемся формулой перехода к параллельным осям. Зная, что момент инерции площади полукруга относительно вспомогательной осн Хц совпа-
112
лающей с диаметром, равен половине момента инерции круга относительно , 1 пг* пг*
той же оси, т. е. что JX|=y , найдем
Jx
, _ , ЯГ*
Jx, РУс~ g
пг2 16г2_лг4Л 64 \
2 ’ 9л2 “ 8 V 9л2/
«0.1! г*.
Момент инерции сечения относительно другой главной осп
Jy = 0,5^ = ^« 0,39г4.
6.14. Вычислить моменты инерции площади кругового сегмента, опирающегося на центральный угол 2<р0—120°, относительно осей х и у, проходищих через центр окружности (см. рисунок).
К задаче 5.14.
Указание. Выделив па произвольном расстоянии у от оси х элементарную полоску шириной Ь(у) и высотой dy, где b (у) = 2r sin <р, y = r cos<p и dy=—г sin <рdtp (см. задачу 5.13), найдем
y2dF=—2г4^5Щ2ф cos2 ф Лр= зт22ф</ф=^-Фо <•
Момент инерции рассматриваемой площади сегмента относительно другой осн у можно подсчитать как сумму моментов инерции элементарных. полосок (прямоугольников) с основанием ау и высотой b (у):
го Фо
, C&(y)dy 8г3 f . , . .. 2г*С . ; .
Jy= J jg =-j2 J 51П3ф( —Г31Пф)<!ф = —j 81Л4.фЛр =
V1 Фо О
2г4 /3 sin фу sin 4ф0\ ='3'^‘8Ч>О—Г~+~зГ~Г
Ответ: Jx = (4<р0—sin 4<р0)« 0,315г4;
= (,2(Ро—8 sin 2<j, + sin4<p0) » 0,1 lr4. r
113
Б.1Б. Найти величину главных центральных моментов инерции и моментов сопротивления сечения мостового быка, показанного на рисунке. Воспользоваться результатами решения задачи 5.13.
Ответ: Jx 4,785а1; Jy = 73а*;
Wx » 4,785а3; Wy = 18,3а3.
6.16. Пользуясь результатами решения задачи 5.13, определить значения главных центральных моментов инерции и главных радиусов инерции площади сечения, имеющего форму
К задаче 5.15.
К задаче 5.16.
диуса а (см. рисунок). Как изменятся эти характеристики сечения при повороте осей хну на 45°?
Ответ: 1) Jx = Jy « 86,2а1, lx = iy as 1,7а;
2) не изменятся.
Б.17. Мостовой брус выпилен из бревна диаметром d — 2r = 24 см, обтесанного с двух сторон на глубину а = 3,5 см (см. рисунок).
------d------
К задаче 5.17.
К задаче 5.18.
Пользуясь результатами решения задачи 5.14, определить момент инерции и момент сопротивления сечения бруса относительно центральной оси х.
Указание. Выразить момент инерции каждого из срезанных сегментов через радиус и центральный угол 2<р.
Ответ: J, = ^-(4а—sin 4а) = 8140 см1; ИТ, « 0,56г3 = 958 см3. * о л
114
Б.18. Из круглого бревна диаметром d необходимо выпилить брус прямоугольного сечения, момент сопротивления которого относительно центральной оси х имел бы наибольшее возможное значение. Определить из этого условия размеры сечения b и Л (см. рисунок).
Ответ: 6 = 4/3”; А = 4/б”; 4 = /2. О О и
6.19. Определить величину главных центральных моментов инерции сечения: а) тонкостенного кругового цилиндра, б) тонкостенного полуцилиндра (см. рисунок), считая толщину стенок t пренебрежимо малой по сравнению с радиусом г.
КУ
а)
К задаче 5.19.
Указание. Рекомендуется предварительно подсчитать полярный момент инерции кольца Jj,= ^ (FdF, выразив dF=trd<p.
Ответ: a) Jx = Jy = nrst:
2г
б) ус = — « 0,638г, J, к, 0,3r3t, Jv « l,57r3t
Б.20. Вычислить главные центральные моменты инерции и главные радиусы инерции площадей: а) равностороннего треугольника,
б) равнобокой трапеции и в) правильного шестиугольника, вписанного в круг радиуса г (см. рисунок).
115
Ответ: a) JA. = J =^-^«0,018а‘, /_=<„ =—4=-« 0,204а; у 96 ‘ 2Кб
б) Jx = ~ bh3 « 0,12bh3, Jv = b3h к 0,312b3h, 1UO л It)
К задаче 5.21.
iy = 0,4566;
в) Л = ^ = Цр-«0,54/-‘,
. . г у 30 л . -z<
/* = I>’ = —12“ ~ 0,4o6r-
5.21. Для двутавра с полками различной ширины, изображенного па рисунке (размеры даны в мл<), определить положение центра
тяжести сечения и вычислить момент инерции и наименьший момент сопротивления
площади фигуры относительно центральной оси х.
Ответ: ус= 10,8 см; Jx =25470 см*; Wx = 1330 см3.
§17. Геометрические характеристики несимметричных сечеинй
Б.22. Найти значения осевых и центробежного моментов инерции площади треугольника относительно осей х и у, совпадающих с его катетами. Воспользовавшись полученными результатами, определить также осевые и центробежный моменты инерции треугольника относительно центральных осей х0 и уп и найти положение главных осей инерции фигуры (см. рисунок).
Указание. Выделив элементарную полоску площадью dF = b(y)dy, подсчитать моменты инерции как интегралы:
Б.23. Найти величину центробежного момента инерции площади сечения равнобокого прокатного уголка 125x125x10 (см. Приложения, табл. 1) относительно центральных осей х и у, параллельных
116
полкам (см. рисунок). Как изменится значение центробежного момента инерции Jxy, если повернуть сечение вокруг вертикали на 180° (горизонтальной полкой влево)?
Установить, какова будет погрешность определения величины Jxy, если подсчет выполнить, разбив уголок на два прямоугольника, пренебрегая закруглениями.
К задаче 5.23. К задаче 5.24.
Ответ: 1) •/*>, = ^2^-” sin 2а = — 211 см* (а < 0);
2) Jx>1 = 211 см* (изменится знак угла а);
3) Jxy=—215 сл‘; погрешность 1,9%.
Б.24. Определить координаты центра тяжести сечения иер'авНо-бокого уголка, показанного па рисунке, найти положение главных центральных осей инерции площади фигуры и вычислить моменты инерции относительно этих осей. Сечение, размеры которого показаны на рисунке в мм, рассматривать как состоящее из двух прямоугольников (без учета закруглений).
Ответ: хг=1,2 см; ус = 3,7 см; а= 14с23'; Jx = = 150 cjh4;
J, = 15,7 слг*.
Б.25. Определить координаты центра тяжести сечения, составленного из листа 200x10 лип и равнобокого прокатного уголка 90 х 90 х 9 (см. рисунок); найти положение главных центральных осей инерции, вычислить значения главных моментов инерции и построить эллипс инерции фигуры. Размеры на рисунке даны в см.
Решение. Выпишем и подсчитаем геометрические характеристики отдельных элементов сечении.
- 1)Лпст: площадь сечения F, = 20 см3. Собственные моменты инерции: ,о 1-203 0 20-1» „ .
Jx=—р— =667 сл|*. Jy== д; 2 с.ч4.
2) Уголок (см. Приложения, табл. 1):
Г2=!5,Ссл<3, j5=J® = 118 cm*. Jmax= 186 см*. Jm|n=48,6 СМ*, J% = An»"/.™,. si)1 2а = _ ’86-48д6= _w 2,55
2
117
1. Определение координат центра тяжести сечения.
Выбрав вспомогательные осн xt и ylt подсчитаем статические моменты сечеиня. S^F^i+Faiд=20-10+15,6-2,55=239,7 см3,
Syi=+FtXi t=20 • 0,5 +15,6 • 3,55=65,2 он».
Расстояние от осей х± и j/j до центра тяжести сечения:
sy, XC~F1+F1
65,2
35,6
= 1,83 см.
239,7
35 6 -6.72 см.
2. Определение положения главных центральных осей инерции.
Через найденный центр тяжести сечеиня проведем новые вспомогательные оси хс и Ус> параллельные полкам уголка, и вычислим осевые и центробежный
К задаче 5.25.
моменты инерции сечеиня относительно этих осей, пользуясь формулами перехода к параллельным осям. Вычисления удобно свести в таблицу.
К задаче 5.25
Таблица моментов инерции сечения
Л? элементов сече* пня Их площади F. СМ* Координаты ц.т. площадей, см Моменты инерции площадей, см*
J —/0 + + Fxc!/c
хс “с 4 J*c У с •'«'С J° Fxc^c Jxcrc
1 2 20 15,6 -1,33 1.72 Л тог 3,28 —4,17 о: 667 118 215 272 882 380 2 118 35 46 37 164 0,00 —68,7 —87 —112 —87 —181
785 487 1272 120 81 201 —69 —199 —268
118
Таким образом, 7Х(?=1272 см4, 7>с=201 см* и 7ХсУс= —«268 см*.
Угол наклона главных осей к осям хс и Ус определяется из условия
9а,- 2Jxcyc -2-268
tg 2а0 - 20 J _ 127$ 0,501.
Отсюда
2ao=26°36', a0=13°I8', 511100=0,23, cosa0 = 0,973, bin 2a4 = 0,443.
3. Вычисление главных центральных моментов инерции.
Пользуясь формулами перехода к повернутым осям, получим
Jx=Jxc cos2 «о + Jyc sin2 a# — JXcyc sin 2ao = = 1272-0,973* 4-201 -0,2324-268 0,443= 1336 c.u‘, Jy = JXc sin2 a0 + Jyc cos2 a0 + JXcyc sin 2a0 = = 1272-0,23*4-201 -0.9732— 268-0,443 = 137 cm*.
Можно также воспользоваться формулами, не содержащими тригонометрических функций, получив те же значения Jx и Jy:
Jmax — 0,5 mln
[(^с+^с) ± У<4-V :-4J'C J •
Проверка арифметических выкладок (7х4--1у = -1*с4--1ус=const): Jx+Jy = = 1336 4-137 = 1473 см*, 7^4-7^=1272 4-201 = 1473 см*.
Положение главных осей инерции показано на рисунке. Так как угол а0 > 0, то откладываем его от оси хс против хода часовой стрелки до главной оси х. Заметим, что если Jxcyc < то главиая ось, относительно которой момент инерции имеет наибольшее значение, проходит через 1-й квадрант. Из сопоставления найденных величии видно, что Jx = 7|Лах= Jlt aJy = = J2.
Главные моменты инерции сечения можно определить также графически, пользуясь кругом Мора (рис. б). Отложив в выбранном масштабе координаты точек Da(0E = JXc, EDa = JX(.yc) и D? (0El = Jyc, ElD9=JycX(;), строим круг Мора так же, как при графическом определении главных напряжений по заданным ах, хху и ау, хух.
4. Построение эллипса инерции сечения.
Уравнение эллипса инерции имеет вид ——4--Ет-=1. Здесь ix и iv—глав-‘у й
иые радиусы инерции сечения—являются полуосями эллипса:
137
35,7 — "96 см-
Отложив радиусы инерции перпендикулярно к соответствующим осям в том же масштабе, в каком вычерчена фигура, строим на них как на полуосях эллипс инерции (см. рисунок).
Б.26. Для сечения, рассмотренного в задаче 5.25, аналитически (по формулам перехода к повернутым осям) и графически (с помощью круга Мора и по эллипсу) определить величину моментов инерции относительно осей и и v, наклоненных иа угод а = 30° (см. рис. а) к главным осям.
Указание. Круг Мора строится на разности главных центральных моментов инерции как иа диаметре (см. задачу 5.25). На эллипсе инерции радиус
119
инерции /„ измеряется как расстояние от оси и до касательной 'к эллипсу, параллельной этой осн: Ja = ilF.
К задаче 5.26.
Ответ: /„=1035 см*; /г = 438 см4; /иг = 518 см*. Графическое решение показано на рисунке.
5.27. Для зетовых сечений, изображенных на рисунке—толстостенного (а) и тонкостенного с отбортованными полками (б), найти положение главных центральных осей инерции, определить величины
а) б)
К задаче 5.27.
К задаче 5.28.
главных моментов инерции п главных радиусов инерции сечений. Размеры на рисунке даны в льи.
Ответ: а) а0 =—26°25', J* = 70 400 см*, Jy = 5400 см*, ix=\7,7 см, i =4,9 см;
б) а0=— 31°15', /Л. = 78100 см*, Jy = 6000 см*, /„ = 25,5 см, 1у = 7,\ см.
5.28. Определить координаты центра тяжести составного сечения из двух швеллеров № 12, вычислить моменты инерции фигуры относительно центральных осей, параллельных сторонам сечении (/„ , Jy , Jx у ), и затем аналитически и графически определить
120
угол наклона а, главных осей к осям хсОус, величину главных моментов инерции фигуры Лмх и Jmin и главных радиусов инерции.
Ответ: хг = 8,23 см, yr — 9,77 см; J, =7\3cm*,Ju -465 см1; с •'*- *с у с
J, у =—223 сл1«; ао = ЗО°15'; JmaK = 845 см\ / .=332 см\ Л с “ С u шеи •
*тах=~5-63 СМ’ Zmin=3-54 СМ-
5.29. Для составных несимметричных сечений из прокатных профилей: 1) найти координаты центра тяжести фигуры; 2) определить положение главных центральных осей инерции; 3) аналитически и графически (построением круга Мора) определить величину главных моментов инерции, главных радиусов инерции и построить эллипс инерции сечения. Форма и размеры сечений в мм даны на рисунках в таблице.
Ответ: См. таблицу (цифры округлены).
К задаче 5.29
схемы Схема сечения Вариант Состав сечения (размеры в мм}. Ответ
Координаты центра тяжести в см Угол с осью *с Главные моменты инерции В CJH*
хс "с а ^тах J . •min
1 а) Швеллер № 18 L 80 X 80 X 8 —0,37 11,51 —П°40' 1565 245
б) Швеллер № 24 L 125X125X12 — 1,95 16,10 —15°50' 4390 1155
2 Ed —> а "с а) Швеллер № 18а L 90x 90 x8 0,33 6,50 —13°30' 1730 320
б) Швеллер № 24 L ЮОхЮОхЮ 0,40 8,45 —11“ 4200 580
3 а с I, *1 м- 1 1 а) Швеллер № 20; л. 200X10 L 100x100x10; с=|2 0,48 5,45 17-10' 2885 1065
б) Швеллер № 30; л. 260x12 L 140x140x12; с = 10 0,84 8,0 11-55' 11700 3000
121
К задаче 5.29 (продолжение)
1 № схемы Схема сечения Вариант Состав сечения (размеры в jmjw) Ответ
Координаты центра тяжести в с.« Угол с осью *с. Главные моменты инерции в см*
Лс »с а Алах ^rnin
4 а) Швеллер Хе 14; л. 240x10 L 125 х 80 х Ю 0,93 11,35 —28с50' 6175 855
Г~|
б) Швеллер Хе 16; л. 240x10 L 160 X 100x12 0,21 10,5 —34°05' 7070 2060
5 а) Швеллер Xs 20; л. 180x10 L 80 X 80 х 8 16,55 7,5 35°05' 4500 1080
л б) Швеллер Xs 14; л. 180x10 L НО х ПО х 8 13,4 8,8 —40° 3300 600
6 чщ а) Швеллер Xs 30; л. 200x10 L 100X100X10 12,05 9,15 —21’25' 10980 3020
~г 4? J* б) Швеллер Xs 24; л. 240X10 L 110x110x8 13,9 6,67 44° 7500 3300
7 t а) Швеллер Xs 16; л. 240x10 L 125X80X10 1,30 14,0 —17’15' 4370 520
б) Швеллер Xs 20; л. 300x12 L 125X80X12 1,21 17,3 —13’10' 8870 790
-> л <- 'С
8 а) Швеллер Xs 16; л. 240X10 L 140x140x10 16,0 10,7 37° 15' 6310 1180
1 ♦ 1
б) Швеллер Xs 14; л. 240X10 L 125x125x10 14,2 10,7 31°10' 5380 910
122
К задаче 5.29 (продолжение)
3 3 к о Схема сечения Вариант Состав сечения (размеры в мм) Ответ
Координаты центра тяжести н см Угол с осью хс Главные моменты инерции а сии*
хс "с а, J так ^mln
9 а) л. 240x10; L 100X100X10 L 160x100x10 3,55 п.о 9°30* 5580 1140
А i feLrr» «У*- «) л. 240x10; L 90x 90x8 L 180X110X10 3,85 9,9 16°05' 5420 1280
10 I а) л. 300 х 12 2 L 140x140x12 14,6 15,0 20°05' 13350 1080
б) л. 400 х 12 2 L 160x160x12 16,6 20,0 16°25' 28500 1680
11 —у I йша,! а) л. 300 X 12; L 140x140x12 2 L 90x 90x9 7,6 14,7 10°15' 12700 1300
б) л. 300 X 12; L 160x160x12 2 L 110x110x8 9,87 14,85 12°50' 13770 1330
12 X а) 2 швеллера №12; л. 240x10 L 160X100X10 1,91 13,1 —18°40' 5720 900
б) 2 швеллера № 16; л. 360X10 L 160x100x12 1.71 19,0 —6°55' 17000 1300
Обозначения: L—уголок, л.—лист.
123
Б.ЗО. Для параллелограмма, имеющего основание й = 30 см, высоту Л = 40 см и угол наклона боковой стороны к вертикали <р = 45°, определить осевые и центробежный моменты инерции площади относительно центральных осей хс и ус, из которых ось хс параллельна основанию; найти направления главных осей инерции и подсчитать величины главных моментов инерции. Решение провести в буквенном виде с последующим подсчетом числовых значений.
Ответ: Jx =^-= 160000 см*,
С 12
J = §(Л' tg* ф + W Г 250 ООО
Лс>с = ^4еф= 1600(Ю
tg2а = ----1 = 3,555 и а == 38°8',
Jmax = 371 000 с-и4 и Jmin = 39 000 см*.
К задаче 5.31.
5.31. Показать примерное расположение главных центральных осей инерции и эллипсов инерции для каждой из фигур, изображенных на рисунке.
ГЛАВА 6
ПЛОСКИЙ ИЗГИБ. ВНУТРЕННИЕ УСИЛИЯ И НАПРЯЖЕНИЯ
§ 18. Эпюры поперечных сил и нагибающих моментов
6.1. Построить эпюры поперечных сил и изгибающих моментов для балок, схемы загружения которых показаны иа рисунке*).
(р*2т/м
4“3т/м
К задаче 6.1.
!!!Н11»Н»Н!НН|
равномерно распределенной нагрузкой интенсивностью q, парой сил с моментом Ma = qa- и сосредоточенной силой P=qa (см. рисунок), составить в буквенном виде выражения Q(x) и М (х), построить эпюры Q и Af и вычислить наибольшие по абсолютному значению величины изгибающего момента и поперечной силы, если д = 2т/м и а = 2м.
1=2м---->Г
*) Здесь и далее в ответах даны наибольшие дю абсолютным значениям ординаты эпюр Q н М. Знаки показывают их направление.
125
\Мп 1 гг О 1
отарам
Решение. 1) Определение опорных реакций
Направив реакции опор в точках А н В вверх (горизонтальная реакция На заведомо равна пулю), составим уравнения моментов относительно опор А и В:
2>в=0,
— А-За—Мв—P-2a + 3qa- 1,5а = 0.
Отсюда
Л= (—qa2—2qa2-}- l,5qa2) = 0,5qa.
o Q
^мА=о,
В-За + Р-а—3qa- 1,5а—Л1о = 0, откуда B=l,5qa.
Проверка: У У=0. Л4-В+
+ Р—3qa=0.
2) Составление аналитических выражений Q (х) и М (х).
участка, в пределах которых выраже
ния Q и М будут различны. Для составления этих выражений необходимо рассмотреть два сечения между силами: сечение 1—1 левее силы Р иа первом участке н сечение 2—2 справа от иее. При этом целесообразно рассматривать ту часть балки, к которой приложено меньше сил, н выбирать начало координат так, чтобы уравнения были возможно проще; хг отсчитываем от опоры А, а х2—от опоры В. Уравнения Q (х) и М (х) примут вид:
К задаче 6.2.
Сила Р разделяет балку па два
для 1-го участка (0<xt<a):
<2 (х1) = Л — qxl=0,5qa—qxlt М (xl) = Axi + Mo-^-=0,5qax1+qa2—^-i для 2-го участка (0<хг<2а):
Q (*s) = — B+qxt=— l,5qa+qxt. М (Xt)=Bxs—^=l,5qaxa—^.
Уравнения Q (х) и М (х) показывают, что поперечная сила изменяется иа каждом участке балки по закону прямой, а изгибающий момент—по квадратной параболе.
3) Построение эпюр Q и М
Построение графиков функции Q (х) и М (х) производим, придавая переменным Xi и х2 определенные значения [для Q(x) не менее двух на каждом участке, а для М (х) не менее трех]. Подсчеты выполнены в табличной форме.
По приведенным в таблице значениям построены эпюры Q и М. Положительные значения поперечных сил н изгибающих моментов откладываем вверх (в некоторых курсах принято строить эпюры М на растянутых волокнах балки, т. е. откладывать положительные значения моментов вниз).
Эпюра Q изображается двумя параллельными наклонными прямыми; эпюра М ограничена параболическими кривыми, причем наибольшие значения изгибающий момент имеет в сечениях, где Q=0. На первом участке Мтая = 9
— ~^qa2 (при Xi = 0,5a). Для отыскания наибольшего момента иа втором
128
Абсциссы сечения Поперечная силе <2(х) Изгибающий момепт M (x)
*1 = 0 Qi = Л = 0,5да Мг = Mo — qa2
*i = 0,5a Mi = qa2+0,5qa - 0,5aqa2 О о
*1 = а Q1 = 0,5^a—qa=— 0,5qa M i = qa2+0,5qa2—=?a®
*2=0 Qs=—l,5?a M2=0
*2=а — M2=l,5qa2-^-=qc?
*2 = 2а Qt=—1,5qa+2qa=Ooqa Mt= l,5qa-2a—^^=qa2
участке исследуем уравнение М (xj) иа максимум:
dM (*2) . Л .
—" =0=—Q2 (знак минус, так как ось *2 направлена влево);
dM (*») , _ п . _
— —- *' = 1,5qa—qx^=0, откуда xt = 1,5 а. аХ%
Подставляя это значение в уравнение М (х£, получим „ , , , с ?(1,5а)« 9 .
Afmax= 1.5?а- 1,5а—---g--—=-&- ?а«.
К задаче 6.3.
т. е. такое же значение, как и иа первом участке. Вид полученных эпюр показан иа рисунке. Обратим внимание на то, что в эпюре Q имеется скачок на величину силы P = qa в сечении под силой, а в эпюре М получен скачок иа величину Мо в опорном сечении, где приложена пара сил. Характер кривых, ограничивающих эпюру М, находится в соответствии с дифференциальной зави-d2M
симостью ц^Г = <7- Так как q<0 diM
(направлено вниз), то < 0, т. е. кривизна эпюры отрицательна, и, значит, выпуклость кривой должна быть направлена в сторону положительных ординат М, что н получено.
Расчетные значения Q и М, как это видно из эпюры, соответственно равны: QmBx = |1.5?a| = l,5-2.2=6r, Мтак = 9 9
= д- qa-= 2-2«=9 тм. о о
6.3. Построить эпюры Q и М для балки длиною I = За = 6 м, защемленной одним концом и нагруженной сплошной равномерно рас
пределенной нагрузкой q = 1 т/м, сосредоточенной силой P = qa = 2 т и парой сил с моментом Мй — да2 = 4тм, как показано на рисунке.
127
Ответ: QmaM = 2qa = 2 • 1 • 2 = 4 т; Мтак = qa2 = 1 22 —• 4 тм (см. рисунок).
Примечание. Вид эпюры М позволяет судить о характере изогнутой оси балки. Если М > 0, то кривизна кривой изгиба также положительна ( —= -^4>(Й \ Р Е* ) и балка изгибается выпуклостью вниз; при М < 0—выпуклостью вверх. Точка, где Л1 = 0, соответствует точке перегиба изогнутей оси. Примерный вид изогнутой осн показан иа рисунке пунктиром (направление перемещения свободного конца—вверх или вниз—выясняется расчетом).
6.4. Консоль ной нагрузкой и
длиною / = 3а нагружена равномерно раенределен-сосредоточенпымн силами (см. рисунок). Установить,
задаче 6.4.
К
при. каких значениях сил Р момент в заделке обратится в нуль. Построить эпюры Q и М при найденных значениях сил и убедиться в том, что площадь эпюры Q равна нулю.
Указание. Учесть, что М= J Qdx+Al0, где ^Qdx равен площади эпю-О II
ры Q на длине х до рассматриваемого сечения, а Мв = Л4Х=О = 0.
Ответ:
Схема • 6 6 а а е
Сила Р 2 кэ| со «о 0,3ql сч
Л1тах •Г 8 18 0,08ql2 81 ’ &
6.5. Для балок, защемленных одним концом (схемы 1—6) и для шарнирно опертых по концам простых балок (схемы 7—12), нагруженных, как показано на рисунке, построить эпюры поперечных сил
128
И изгибающих моментов. При заданных иа схемах цифровых величи-нак нагрузок и размеров вычислить наибольшие по абсолютным значениям величины Q и Л4.
„ , М0-8тм д-2т/м ° ♦,
Р=2т М‘>2ЛШ
2тм
д=2т/м
ШШШ1
g=2mfi^8mM
3)
1=2м
В).
Р=2т
Ht=4mM ,--2т/м
1=4м
!!!!!!!!!!!!!!!!!!!!{
2т/м
Ма^1тм q=2m/H
Р=4т
К задаче 6.5.
2гпм 1т/м
Ответ:
Для консолей (схема Xs) 1 2 3 4 5 6
Q, т 4 —2 —4 6 2 —2
М, тм 8 4 4 — 12 3 2
Для двухопориых балок (схема Ns) 7 8 9 10 11 12
<?. т —3 -5 —3 2 2,33 —2,25
М, тм —8 6,25 8 5 3,33 1,74
6.6. Построить эпюры Q и М для балки иа двух опорах пролетом I = За, несущей нагрузку, распределенную на длине 2а по закону треугольника (см. рисунок).
Решение. Опорные реакции определяем из уравнении равновесия, заменив распределенную нагрузку ее равнодействующей, равной площади треугольника
129
o = ^-q-2a = qa и приложенной в центре тяжести треугольника; получаем 5 4
л = у9°- B=-$qa.
Составим выражения Q (х) и М (х) для каждого из участков балки. В сече-
К задаче 6.6.
тельно, п 5 Qi =§?«
нии 1—1 (рассматриваем левую часть, для которой х( меняется от нуля до х( = 2а)
0.1 = А—<о(х),
/И1 = ЛХ1—<о(х) v-
Здесь со (х)— грузовая площадь, расположенная слева от сечения и равная площади треугольника с основанием и высотой q(xl) = = ? ^ • т- е- “ М • Следова"
id 4a *
Mi = -^qaxi- w
Для сечеиня 2—2, рассматривая правую часть (0^хв^а), получим 4 4
Qi = — у qa. = у qaxt.
На первом участке поперечная сила изменяется по квадратной параболе, а изгибающий момент—по кубической параболе. На втором участке эпюры Q и/И ограничены прямыми линиями. Значения ординат Q и М в пределах каждого участка приведены в таблице.
X QW м w
х1 = 0 О м II <о| сл 8 M1 = 0
xt = a Л 11 Ql=36?e .л 17 2
Xj = 2a Qi = -4?a
*2 = 0 О W II 1 <о| s м,=о
хг=а о II 1 <О| 8 Л12=у9а2
130
По данным таблицы построены графики—эпюры Q и М.
Наибольшее значение изгибающего момента найдем, исследуя уравнение Mi на максимум:
^!1=q 5 „в_£1=0.
dxi 1 9 ’ 4а
Отсюда абсцисса опасного сечения (х,=х0)
х0=| /20=^ Г5. О о
Подставляя в уравнение Mv получим
Мтах у Г5 —(Г5 )8 « | qa>.
Наибольшее значение поперечной силы равно (см. эпюру Q)
Л 5
Qmax— g
6.7. Балка, защемленная одним концом, несет сплошную нагрузку,
распределенную по всей длине балки / по закону трапеции (см.
рисунок). Построить эпюры Q и абсолютному значению величины поперечной силы и изгибающего момента.
Указание. Для составления уравнений Q (х) и М (х) рекомендуется разделить нагрузку иа равномерно распределенную интенсивностью и треугольную с наибольшей ординатой 9о=?я—?!•
Ответ:
М и вычислить наибольшие по
к 0=2(7,/; M = -f<7,/*.
К задаче 6.7.
К задаче 6.8.
6.8. Построить эпюры Q и М для балки иа двух опорах с консолями, загруженной по схеме, показанной на рис. а, при следующих данных: а = 1,5 м, д, = 1т/м, <7, = 3</, = 3 т/м, Р = 2^,а = 3т, Af0=y9,aa = 3 т/м. Изобразить также примерный вид изогнутой оси балки, руководствуясь характером эпюры М.
Ответ: Эпюры Q(t) и М(тм) изображены на рис. бив.
Примерный вид изогнутой оси показан иа рис. г. На участках ЕС и DF, где М < 0, выпуклость изогнутой оси направлена вверх; на участке CD—вниз, так как М > 0; точки С и D, где /И=0, являются точками перегиба.
131
6.9. Построить эпюры Q и Л4 дли балок, несущих нагрузку, распределенную по треугольнику, и вычислить наибольшие по абсолютному значению величины Q и Л/. Доказать, что в схемах 1—3 площадь эпюры Q равна опорному моменту, а в схемах 4—6 равна нулю.
К задаче 6.9.
Ответ: 1) Q=^, 2) Q=qa, M=—qa\ 3) Q=^ , ;
4) <?—f. 7И = ^; 5)0=f,
6.10. Балка пролетом I, шарнирно опертая по концам, несет сплошную нагрузку, распределенную по параболическому зако-
Q .,.,w
К задаче 6.10.
Поперечная сила и изгибающий выражениями (см. рисунок)
Q(x) = 4 — (о (х) =
ну, выражающемуси уравнением q(x) = lf(/x—Xя). Построить эпюры Q и М.
Решение. Элементарная нагрузка, приходящаяся иа отрезок балки длиною dx, равна da>=q(x)dx. Опорные реакции вследствие симметрии равны А = В = <л/2, где со—грузовая площадь, ограниченная параболой и равная со =
I I
= J q (*) Лх=Ц § (lx—x-) dx=^ ql. о о
Следовательно, А = В = ^-. момент в сечении с абсциссой х даются
М (х) = Ах—§ du (х—Xj) = у х
х
J 9 (xj dxt (л —Xj).
132
Однако проще, не составляя выражений для Q (х) и М (х), получить их из • и &М . . ,
дифференциальных зависимостей. Из равенства =~ЧМ (знак минус
взят, так как q < 0—направлена вниз), интегрируя дважды, получим:
1) ^=QW=—y?W<br+Q0; О
2) М (х) = — У dx У g (x)dx+Qox + Af0. о о
Произвольные постоянные интегрирования Qo и Мо определяются из граничных условий при х = 0. Так, иа левой опоре Q0=A=^-, а Мо = О. Ин-О
теграл
y?(x)dx=^y (Zx-x2)dx=^-(^-£). о о
Значит,
О 1Л_____(. _6х» 4хЗ\
ч W р 2 з J f з - з р । р J .
. 4<7 С /х2/ х®\ о/ ql ( 2хэ х*\
А4 (х) — /г J 2 3 / dx^' 3 Х~ 3 V Z* *" I*) ’
о
Для построения эпюр Q (х) и М (х) по точкам подсчитаем ординаты этих уравнений (см. рисунок):
при х=0 Q = Q0=^-, М = М„=0;
при х = у Q=0, M=^qP = MmaKi
при х=/ Q = QZ= —At = Afz=O.
О
6.11. Для балок, несущих сплошную нагрузку, распределенную по криволинейному закону, построить эпюры Q и М и вычислить
К задаче 6.11.
наибольшие значения поперечной силы и изгибающего момента, если: а) ?(х) = ?5(2/_х); б) <7(х) = ^-; в) g(x) = gsin^ (см. рисунок).
* 4
133
Ответ: a) Q = ~^ql, б) Q = —в) <?=^, О О JV
ял № ял ял ql*
^=~T; л1=-12-;
6.12. Как изменятся расчетные значения Q н М для балок а) и б), рассмотренных в задаче 6.11, если нагрузку развернуть на 180°, расположив «тяжелую» ее часть у свободного конца консоли?
Ответ: a) Q =— ^ql, М=—6) Q =— М = —
6.13. Построить эпюры Q и М для балки пролетом I, нагруженной по всей длине равномерно распределенной моментной нагрузкой интенсивностью m (см. рисунок).
m m
«ЯГЯЯ№
...д8М11| ,,ЖЙИ£Я Эпюрам ---га—-X-д—►
К задаче 6.13. К задаче 6.14.
Решение. Направим реакцию А левой опоры вниз, а реакцию В правой опоры вверх. Величина опорных реакций определяется из уравнений равновесия:
2мд = 0, Al—ml = 0, A=m-2МЛ = О, Bl—ml=0, B = m.
Следовательно, опорные реакции численно равны m н направлены в противоположные стороны: левая А—вниз и правая В—вверх (если m выражается в кгм/м, то суммарный момент M=ml имеет размерность кем, а реакция
М \
А= — В= у выражается в кг j . Поперечная сила в произвольном сечении с абсциссой х равна
Q (х) = — А = — т.
Изгибающий момент
М (х) =— Ах+тх=0.
Таким образом, равномерно распределенная моментная нагрузка уравновешивается моментом, создаваемым опорными реакциями, причем балка не изгибается.
Ответ: См. рисунок.
6.14. Построить эпюры Q и М дли балок, нагруженных равномерно распределенной моментной нагрузкой (см. рисунок), если а = 2 м, т = “2 тм(м.
134
з
Ответ: a) Q = 0; /И =— ma=—4 тм; 6) Q=—m=3 т, М = — ma = — 4 тм.
6.15. По заданным эпюрам поперечных сил и изгибающих моментов изобразить схемы закрепления и нагружения балок и определить величины приложенных к ним сил. Ординаты эпюр Q даны в тоннах,
К задаче 6.15.
эпюр М—в тм, а длины—в метрах (см. рисунок). Криволинейные участки эпюр очерчены по квадратной параболе.
Ответ: a) q = ± 1. т/м; б) q = 0,5 т/м, М = 2 тм;
в) q = ± 3 т/м.
6.16. -Построить эпюры поперечных сил и изгибающих моментов для четырехопорной балки с двумя промежуточными шарнирами, изображенной на схеме. Вычислить наибольшие ординаты эпюр Q и М, если а = 2 м, b = 1 м, с = 3 м, /, = 4 м, 12 = 3 м и /э = 4 м.
а) £ Р=2т А в д=2т/м —,М0=2тм V в
Ш1Ш1Ш!!!
А ^3 7 к г- и fa
ч J 1г д *!’ 1з 1
IIIIIIIIIIIIII 1 1
£| г А Я/ Ъ\ 1 .1 Lo
щт
К задаче 6.16.
Указание. Проще всего расчленить балку на подвесную (/ — //) и двеосиов-иые (£—/ и //—D), как показано иа схеме б. Заменив давления, передающиеся от подвесной балки через шарниры, реакциями R2 и R2, вычисленными для двухопориой балки I—II, построить эпюры Q и М для каждой из балок в отдельности.
Можно поступить и иначе. Так как изгибающий момент в шарнире равен нулю (шарнир момента передать не может), то в дополнение к уравнениям статики для всей системы можно составить уравнения моментов относительно шарниров I и II (рассматривая силы, расположенные слева или справа от них) и приравнять их нулю. Это позволит определить все опорные реакции и строить эпюры Q и М обычным путем, как для бесшарнириой балки.
Ответ: Q = 3 т; М = —11 тм.
133
6.17. Построить эпюры Q и М для балок с шарнирами, схемы которых приведены на рисунке, и вычислить наибольшие по абсолютному значению величины поперечной силы и изгибающего момента.
Ответ: a) Q = 10 т, Л1 = — 8 тм; б) Q = — 12 т, /И = — 15,2 тм; в) Q= — 3 т, М = — 4 тм; г) Q = 4 т, Л! = 8 тм.
М0=8тм~
д=2тп/м
н1нн»1н»ин».шн»»1!
д-=2^т^-3т \р=3т
!ННМН»ВН»НН»1»»И
1т/м \p~3lT!
д=2тп/м
а) 9
К задаче 6.17.
6.18. При проектировании консольных мостов с подвесными пролетами приходится решать задачу о иаивыгоднейшей их разбивке. Для балки, изображенной на чертеже, установить, при каком соотношении размеров а:/:/, значения изгибающих моментов в опасных
(Г
!!!»ННННН»!!НМНН!НН»НН!И»Н»НН|
•A. I sS
I— Ua
\П
I
К задаче 6.18.
сечениях подвесных и основной балки (посредине пролетов и над опорами В и С) будут по абсолютной величине одинаковы. Определить также величину наибольшего изгибающего момента.
Ответ: a = 0,146/; /.=0,853/; д шах
6.19. Пользуясь принципом независимости и сложения действия сил, построить эпюры Q и М для балки, изображенной иа рис. а.
Решение. Рассматриваем балку отдельно под действием равномерно распределенной нагрузки 9=1 т/м (рис. б) и отдельно под действием сосредоточенной силы (рис. в). Для получения суммарной эпюры Q или М в случае, если графики имеют одинаковые знаки, достаточно приложить их одни к другому. Если графики имеют разные знаки, их следует наложить одни иа другой (см. задачу 6.20).
136
Результаты сложения эпюр показаны иа рис. гид. Для придания эпюрам обычного вида можно привести их к горизонтальной нулевой оси, для чего суммарные ординаты откладываются от горизонтальной оси вверх или вниз в зависимости от знака.
К задаче 6.19.
в.20. Пользуясь методом сложения действия сил, построить эпюры Q и М для балки, изображенной иа рисунке.
Р=3т ___________д=4и1/м
I!!!!!!!!!!!'!!!!!!!}}!!!1
К задаче 6.20.
Ответ: См. рисунок на стр. 138.
6.21. Применяя метод сложения действия сил, построить эпюры изгибающих моментов и поперечных сил для балок, изображенных на рисунке.
Ответ: a) Q = —1 т, Л1 =— 2 тм; б) Q = 6 т, М = — 5 тм;
в) Q = — 7 т, М = — 10 тм; г) Q = — 5,5 г, М =— 6 тм;
д) Q = — 3,5 т, Л1 = 6тм; е) Q = 8,6r, М = — 8 тм.
137
6.22. Балка пролетом I, несущая равномерно распределенную нагрузку интенсивностью д, имеет две консоли длиною а каждая.
ф=2т/м ^M0=2mM
»НН»НН1»1»»Т
VW],
Ь--4м—
Pt=4m №3т
tT=4m/M
А----S--
I!I!!f11!H1Ш?!t!I!
3m—J
!!!»!»й!!П1111!
К задаче 6.21.
а) Найти длину консоли а (в долях пролета /), при которой изгибающий момент посредине пролета будет равен нулю, б) Установить, ,ри какой длине консолей а величина наибольшего изгибающего момента в опасных сечениях балки будет наименьшей.
Указание. Воспользоваться методом сложения действия сил, построив эпюры М отдельно от нагрузки, лежащей иа консолях, и отдельно отзагружеиия среднего пролета.
Ответ: а) а = 0,5/; б) а = -^- У~2.
6,23. Двухосная тележка подъемного крана перемещается по двум подкрановым балкам пролетом /=10л1. Расстояние между осями те-
К задаче . 6.23.
лежки с — 1,2 Л1 (см. рисунок). Найти опасное положение тележки, при котором изгибающий момент будет иметь наибольшее значение, в двух случаях: а) при отсутствии груза на крюке, когда давления от колес крана, передающиеся на каждую балку, одинако-
вы и равны = Рг = 2 т, и б) при наличии груза на крюке, когда Pt = 5 т и Рг = 1 т. Подсчитать величины Afmax.
Указание. Обозначив расстояние от левой опоры А до первого груза Рг через х, выразить величину опорных реакций в виде функций от х, составить затем выражение для изгибающего момента в сечении под силой и исследовать его иа максимум.
I с
Ответ: а) х = -^---^- = 4,7 л», Л!тах=8,84 тм;
б) х = у—^=4,9 л«, Afmax=14,'4 тм.
6.24. Пользуясь графическим методом, построить эпюры Q и М дли балки пролетом 1 = 5 м, загруженной равномерно распределенной нагрузкой д = 4 т/м и парой сил с моментом Л10 = 10 тм (см. рисунок).
138
Решение. Изгибающий момент в любом сечении балки может быть выражен произведением М (х) = Нт\, где Н—полюсное расстояние в силовом многоугольнике, отложенное в масштабе сил, а т]—ордината веревочного многоугольника, измеренная в масштабе длин.
Выбрав масштаб длин, вычерчиваем схему балки и нагрузки. Для построения силового многоугольника заменяем распределенную нагрузку несколькими сосредоточенными силами, например Р1 = Р2=Рэ = Рв = Р, = 4 г, а пару сил Мо—двумя противоположно направленными силами Р4 н Рл бесконечно большой величины, образующими пару с моментом /Ио= 10 тм.
Масштаб длин
|ИЧ| I -----I---1
О 1 2 Зм
Масштаб сил । । । । । । О 4 8 12 10 20 24
К задаче 6.24.
В принятом масштабе сил при произвольном положении полюса строим силовой, а затем и веревочный многоугольники. При проведении стороны веревочного многоугольника, параллельной лучу 3—4, в сечении, где приложена пара Мо, получаем разрыв иа величину момента внешней пары (луч 4—5 параллелен силам Р4 и РЛ, так как линия, соединяющая полюс О с концом силы Р4. пересекается с ней в бесконечности). Поскольку отрезок 4—5 по величине пропорционален моменту Af0=Wifo- то т]0 = . В рассматриваемом примере Мо=
=10 тж, а полюсное расстояние принято Я = 18 т. Следовательно, т)0 = |~ = 1с =0,555 м. Это расстояние и отложено в масштабе длин в сторону положительных ординат эпюры М (Мо > 0), что позволяет достроить веревочный многоугольник с замыкающей А— В. Проведя в силовом многоугольнике от полюса луч А—В, параллельный замыкающей, находим опорные реакции ас = А и Ьс=В.
Построение эпюры Q для системы приложенных к балке сосредоточенных сил сводится к последовательному откладыванию сил, начиная с опорной реакции А, в выбранном масштабе. При увеличении числа сосредоточенных сил ступенчатая эпюра Q в пределе обратится в наклонную прямую, а веревочный многоугольник—в веревочную кривую, представляющую собой эпюру М.
Как видно из построенных графиков, Л =8 т, В =12 т, а наибольший изгибающий момент А4тах=Ят;1Пах, где измеренная в масштабе длин наибольшая ордината i)max=0.89 м.
Ответ: Q ——12 т; Л4=16тм.
139
6.2Б . Для балки, рассмотренной в задаче 6.2, построить эпюры поперечных сил и изгибающих моментов графическим способом, приняв а = 2 м и д = 4 т/м.
Ответ: Q « 12 т; М « 18 тм.
6.26. Графическим способом построить эпюры Q и 7И для главной балки моста, загруженной системой из 9 сосредоточенных сил, заменяющих давление колес локомотива и тендера (см. рисунок). Нагрузка дана в килоньютонах, размеры—в метрах.
Ответ: Qmax=805 кн; Л1П1ах=4403 кн-м.
6.27. Построить эпюры продольных сил, поперечных сил и изгибающих моментов для стержней рамы, изображенной на рисунке. Найти наибольшие по абсолютному значению величины N, Q и М при 1 = 4 м и д=2 т/м.
К задаче 6.27.
Решение. Опорные реакции определяются нз уравнений статики:
2> = 0, ql—HB = Q,
£у=о, -Яд + Яя = 0, 2>д = 0, Ял/-^=0,
откуда или
откуда
/Уд = 9/ = 8 Т;
т.
а) Продольная сила в сечении равна сумме проекций на ось стержня всех внешних сил, приложенных к отсеченной части рамы. В сечении 1—I, рассматривая нижнюю часть стойки АС, получим Л\= Яд = 4 т (растяжение). Эго усилие остается постоянным по длине стойки.
В сечении 2—2 (рассматривая левую отсеченную часть рамы АС—2) имеем продольную силу Nt = —ql=— 8 т (сжатие).
В сечении 3—3 стойки BD нз рассмотрения ннжней ее части найдем N#= = — Рц —— 4 т (сжатие). Эпюра сил N показана на рис. б.
б) Поперечная сила равна сумме проекций на плоскость сечения внешних сил, приложенных к отсеченной части рамы. Считают ее положительной, если
140
внешние силы поворачивают отсеченную часть относительно центра сечения по ходу часовой стрелки.
В сечении 1—/: Qi =—qyi, приyt = 0 Q=0;npn yt = l Qt = — ql = — 8 г.
В сечении 2—2: Q2 = — Ra =— 4 г.
В сечеиин 3—3: Q3 = Hb = 8 т.
Эпюра сил Q показана на рнс. в.
в) Изгибающие моменты вычисляем, как и для балок, считая их положительными, если момент растягивает внутренние волокна, показанные на рис. а пунктиром *).
Эпюры М строим на сжатых волокнах, как и для балок.
Выражения для изгибающих моментов будут:
В сечении /—/: М1=> — ; при j/i = 0 /И1=.= 0; при yl==l =
ар пр
В сечении 2—2: Л12 = — Яд-х —V : при х = 0 М2= — при х = /
M3 = -qP.
В сеченнн 3—3: М3 = — Нц-у2; при у = 0 М3 = 0; при у = 1 М3 = — qt*.
Эпюра М изображена на рис. г. Наибольшую по абсолютному значению величину имеет момент в узле D; здесь MD= — ql* = — 2-42 = — 32 тм.
Ответ: — 8 т; Q=St; М =— 32 тм.
6.28. Как изменятся эпюры N, Q и М, если горизонтальная нагрузка q будет приложена к правой стойке BD рамы, рассмотренной в задаче 6-27, и направлена справа налево?
Ответ: Изменятся вид и знаки эпюр: Л/ = 4 т; Q = 8 т; Л1= 16 тм.
К задаче 6.29.
6.29. Построить эпюры продольных, поперечных сил и изгибающих моментов для рам, схемы которых приведены на рисунке. Вычислить наибольшие по абсолютному значению величины N, Q и М.
) Иначе говоря, каждый стержень рамы можно рассматривать как балку, пунк1ЯЯ часть К0Т0Р°й расположена по внутреннему обводу рамы, показанному
141
Ответ-.
Внутрен. усилия Размер* ность Наибольшие значения внутренних усилий
° й 4 4 д е ж
N 7 —4 —2 4 —8 —4 —6 4,5 -2,8
М ТМ 8 10 12 —9 —4 12 2,4 16
Q т —4 2 6 6 4 6 4,5 4
§ 19. Нормальные напряжения при изгибе
6.30. Для балок, сечения которых показаны на рисунке, изобразить эпюры распределения нормальных напряжений по высоте, считая изгибающий момент в сечении положительным.
К задаче 6.30.
шарнирно опертая но концам, несет
-> Ъ~-
Установить, как выгоднее расположить сечения, имеющие только одну ось симметрии, в плоскости которой действует изгибающий момент, если материал балки чугун, лучше работающий на сжатие, чем на растяжение.
Ответ: Повернуть сечение так, чтобы наиболее удаленные от нейтральной оси точки оказались в сжатой зоне.
6.31. Балка трубчатого прямоугольного сечеиня пролетом / = 4 м, равномерно распределенную нагрузку д = 3 т/м (см. рисунок). Определить величину наибольших нормальных напряжений в опасном сечении балки, а также величину напряжений в точке С того же сечения, если размеры его равны: В=12сж, Н =20 см, Ь = = 6 см и h= 10 см.
К задаче 6.31.
Решение. Наибольшие напряжения в опасном сечении:
О — ^тах vmax---пу >
у
где Мтал—изгибающий момент в опасном сечении (посредине пролета), равный ^max=_g"= “g- = 6 тм: Wy—момент сопротивления сечения относительно
142
Jy
нейтральной оси у, определяемый по формуле Wy =—— . Момент инерции се-гшах
чения относительно нейтральной оси равен
^ = ВН»^=12.2Оз 6.1О>=75оосж<
Расстояние от той же оси до наиболее удаленной от нее точки zmax= Н 7500
= Д-=10сл<. Следовательно, №^ = -^-=750 смэ, а наибольшие напряжения
в опасном сечении балки
М 6-10*
«п,ах=800 кг/см».
Для вычисления нормальных напряжений в точке С воспользуемся формулой
°с = %^ = ~ . 5 = - 400 кг/см*.
Jy iuw
Знак «минус» взят потому, что точка С расположена в сжатой эона (М > 0, гс < 0).
6.32. Деревянная балка прямоугольного поперечного сечения пролетом /=6л, свободно опертая по концам, нагружена равномерно распределенной нагрузкой q = 4 кн/м и сосредоточенной силой Р=20 кн, приложенной посредине пролета (см. рисунок). Размеры сечения балки: 0,12x0,20 м.
я_______У
К задаче 6.32.
ншннннш
it —г—-Д»-
К задаче 6.33.
Определить величину наибольших нормальных напряжений в опасном сечении балки.
Ответ: атах=15-10в н/лс2.
в.ЗЗ. Для балки, изображенной на рисунке, построить эпюры Q и М и определить величину наибольших нормальных напряжений в опасном сечении. Вычислить также напряжения в точке С того же сечения, расположенной на расстоянии а = 4 см от нижней кромки. Пролет балки 1 = 2 м, размеры сечения: ft = 20 еле, Л = 30 см. Нагрузки: q = 2 т/м, Мо = 1,2 тм.
Ответ-. сттах « 93 кг/см--, ас = — 68 кг/см2.
6.34. Балка прямоугольного сечения пролетом 1 = 5а = 5 м нагружена, как показано на рисунке (см. стр. 144). Определить интенсивность нагрузки q, если наибольшие нормальные напряжения, возникающие в опасном сечении балки, атах=121 кг/см2, а размеры сечения ft =12 см и Л = 20 см.
Ответ: Mm!a = 2,42qa2; q = 400 кг/м.
143
6.3Б . Деревянная балка круглого сечения диаметром d = 27 см шарнирно оперта по концам и нагружена двумя сосредоточенными силами Р=2 т каждая, приложенными на равных расстояниях а = 1 м от опор. Определить величину наибольших нормальных напряжений в опасном сечении балки, если пролет ее 1 = 3 м.
Ответ: атах = 104 кг/сж2.
К задаче 6.34.
К задаче 6.36.
6.36. Нормальные напряжения, возникающие пол действием силы Р в точке С балки треугольного сечения, изображенной на рисунке, равны ас = 300 кг/см2. Определить величину наибольших по абсолютному значению нормальных напряжений в опасном сечении балки, где М = Мтм.
Ответ: <ттах=1200 кг/см2 (сжатие).
6.37. Пустотелая балка прямоугольного поперечного сечеиия пролетом 1 = 4 м свободно оперта по концам. Какую сосредоточен-
Ь----Z?
6.37.
К задаче
напряжение
принять
ную силу Р можно безопасно приложить посредине пролета в вертикальной плоскости при допускаемом напряжении [о] = 500 кг/см*"} Размеры сечеиня показаны на рисунке в сантиметрах.
Ответ: Р = 5400 кг.
6.38. Дверной проем перекрывается двумя рядом расположенными балками, воспринимающими давление от веса лежащей над проемом стены Qo = 4,8 т. Считая балки свободно опертыми по концам и принимая давление кладки равномерно распределенными по длине пролета I = 3,0 м, подобрать необходимое сечение балок в двух вариантах: а) из двух двутавров; б) из двух швеллеров. Допускаемое [о] = 1600 кг/см2.
Решение. Наибольшая величина изгибающего момента
М
-Qi!
max— g
4,8-3 8
= 1.8
тм.
Из условия прочности на изгиб определяем необходимый момент сопротивления сечения двух балок:
W =
180000
1600
= 112,5 см2.
144
По таблицам нормального сортамента (см. Приложения) ищем сечение с подходящим моментом сопротивления (каждая балка должна иметь сечение с моментом сопротивления не менее ГГ = О,5-112,5 » 56 ел3). Для варцанта а) подходит двутавр № 12 (№ = 58,4 см3); для варианта б)—швеллер № 14 (1Р = 70,2 см8).
6.39. Подобрать двутавровое сечение консольной балкн, несущей равномерно распределенную нагрузку q = 2 т/м (см. рисунок), если
Lzz-U— I =2а-%&-а^
К задаче 6.39.
длина консолей а = 2 м, пролет I = 2а = 4 м, а допускаемое напряжение [а] = 1600 кг/см1.
Ответ. Двутавр № 22а.
6.40. По проекту проем в стене предположено перекрыть двумя балками двутаврового профиля № 12. Затем было решено заменить их одной балкой большего профиля. Определить необходимый номер двутавра и выяснить, какое из решений экономичнее.
Ответ. Двутавр №18. Это решение дает около 30% экономии
мсталла.
6.41. Балки пролетом 1 = 6 м спроектированы из брусьев квадратного сечения со стороною Ь = 20 см. На стройке нх заменили круглыми бревнами с такой же площадью сечения, а) Как изменится величина наибольших нормальных напряжений в опасном сечении в результате замены? б) Какой следует выбрать диаметр бровей, чтобы обеспечить проектную прочность?
Ответ: а) Увеличится на 18%;
б) d = 23,3 см.
6.42. Балка квадратного сечения, защемленная одним концом, нагружена сосредоточенной силой Р, приложенной на другом конце параллельно Как изменится величина повернуть вокруг оси вместив линию действия квадрата, при условии, больших напряжений в
стороне квадрата, силы Р, если балку на угол 45°, со-енл с диагональю что величина наи-. опасном сечении в
обоих случаях одинакова?
Ответ: Уменьшится на 29,3%.
6.43. Тормозное устройство состоит из тяги и ломаного рычага АВС, свободно поворачивающегося вокруг шарнирного болта в точке В (см. рисунок). При торможеннии в тяге развивается усилие Р=150 кг, вследствие ..с
лодка прижимается к колесу в точке С. Определить величину напряжений, возникающих в опасном сечении рычага, ослабленном
К задаче 6.43.
чего тормозная ко-
145
болтовым отверстием, если короткое плечо рычага а = 0,25 м, сечение его—прямоугольник с размерами Ь = 2 см, Л = 6 см, а диаметр болтового отверстия d = 30 мм.
Ответ: отах=1430 кг!смг.
6.44. Для балки, схема загружения п размеры которой показаны на рисунке, по наибольшему изгибающему моменту подобрать сечение в двух вариантах: а) двутавровое (сталь прокатная) п б) прямоугольное (сосна)—при отношении высоты сечения к ширине hlb = 3l2. Допускаемые напряжения принять для стали [о] = 1600 кг{см3, для дерева [а] = = 120 кг/см3.
Решение. Эпюры Q и М изображены на рисунке. Л41пах = 2тж = 2- 10е кгем. Из условия прочности на изгиб имеем:
М 2-10» Вариант
= 125 сж*. По сортаменту (Приложения) находим двутавр № 18, момент сопротивления которого IF =143 cjh3 (с запасом 14%), либо двутавр № 16 (IF = 109 см3—перенапряжение около 13%). Принимаем двутавр № 18.
(?=2т/м
Мо=2тм
Р=2т^
1=3м
К задаче 6.44.
I
Вариант б): IF^-y^-= 1668 сж*. Так как для прямоугольника
__ ЬЛ» Ь /З.у 3,, . 3/8J668 ,с . 3 u
IF=-?-=-7-« I-д-b ) =-о’Ь3, TOb^s 1/ —=—= 16,45 см, h=-7-b = 24,7 см.
О О \ £. / О г о 2
Примем брус 17x25 сл2.
6.4Б. Для балок, схематически изображенных на рисунке (в таблице), при заданных продольных размерах и нагрузках построить эпюры поперечных сил и изгибающих моментов и подобрать сечение по наибольшему изгибающему моменту в одном из двух вариантов: а) прокатный профиль (сталь) и б) круглое или прямоугольное сечение (сосна)—при заданном отношении hfb. Допускаемые напряжения принять для стали [о] = 1600 кг/сж8, для дерева [а] = 120 кг/сж’.
Ответ: См. таблицу (схемы 1—10 для консолей, схемы 11—20 для двухопорных балок).
6.46. Чугунная труба, наполненная водой, перекрывает пролет /=12 ж (см. рисунок). Рассматривая трубу как балку, шарнирно опертую по концам, определить величину наибольших
опасном сечении, если наружный диаметр трубы £> = 25 см, внутренний d = 23 см, а удельный вес чугуна у = 7,8.
Ответ: <тП1ах = 412 кг {см3.
К задаче 6.46. нормальных напряжений в
146
К задаче 6.45
№ схемы и варианта Схема балки н нагрузки Размеры и нагрузки Ответ
Вид сечения или отношение Л/ft а р а м. Q м W № профиля или размеры сечения, ем
и т т/ч тм т тм сма
1 а) 1 б) в—j •*^0 7 двутавр h/b =1,5 2 1 1 1 1 2 2 1 1,0 1 —4 -2 250 1670 двутавр № 22 6=16,45
см * яи I!!III1!I!1 двутавр Л/д = 3/2 1 2 4 4 4 2 1 2 4 4 1 2 62,5 1670 двутавр Xs 12 6=16,45
3 а) 3 б) й г*-^ д k- g - -« > двутавр круг 2 1 2 2 2 4 2 1 6 6 =3 375 2500 двутавр Хе 27 d = 29,4
4 а) 4 б) Iff r*ffi у 1 2 швеллера h/b=-2 2 1 0,5 0,25 1 1 2 0.5 -4,5 -2,25 —2 500 1670 швеллер Хе 24 t = 13,6
СП 1 2 двутавра Л/6 = 5/2 2 0,5 2 1 4 2 2 0,125 14 3,5 —26 —1,68 1625 1355 двутавр Х« 40 6= 10,9
К задаче 6.45 (продолжение)
№ схемы и варианта Схема балки и нагрузки Размеры и нагрузки Ответ
Вид сечеиня или отношение h/b а р Q Л1в Q м UZ № профиля или размеры сечении, СМ
м т т/м тм т тм СМЛ
6 а) 6 б) , л&г* q двутавр круг 2 1 8 2 4 2 16 2 =2 8 1 500 833 двутавр № 30а d = 20,4
7 а) 7 б) <7 Г*-Мя 2 двутавра 6/6 = 2 2 1 6 2 3 2 6 1 -6 _о 12 2 750 1670 двутавр Хз 27 6=13,6
п rL „ Л р
а -J а 4
8 а) б) q Г~М0 _ двутавр Л/Л = 4/3 2 2 3 2 3 2 3 2 3 2 3 2 177 1670 двутавр № 20 6=17,8
ппипи У К
1ПШИ1Ш
<-/7 *4
4” — Mof двутавр А/6 = 5/3 2 1 2 0,5 2 1 4 0,5 —6 -1,5 8 1 500 833 двутавр № 30а 6=12,2
9 а) 9 б)
IIIIIIIIII1I
h д -3
10 а) lU б) q 2 швеллера круг 2 1 4 1 2 1 8 1 8 2 24 3 1500 2500 швеллер № 40 d=29,4
iRSHHH! 1
1НШЧНЧ/7 а п*—cl^—* 1 н
К задаче 6.45 (продолжение)
№ схемы и варианта Схема балки и нагрузки Размеры нагрузки Ответ
Вид сечения или отношение Л/д а Р Q м„ <5 м UZ .V? профиля или размеры сече-иия. см
.и т т/м тм т тм С .4’
11 а) 11 б) «1^7 у тжшншиа t г- а? двутавр hlb = 3l2 2 2 4 2 2 1 4 2 3 1.5 4 2 250 1670 двутавр № 22а 6=16,45
12 а) 12 б) «г 2 двутавра круг 3 2 6 4 2 2 1 1 3,37 2,25 2,61 1,74 163 1450 двутавр № 14 d = 24,5
Г Is 1
И а) U б) •*Т^7 Я двутавр А/6 -=4/3 2 1 — 2 1 16 2 8 2 12 1.5 750 1250 двутавр № 36 6=16,2
14 а) И б) ,д. "" г*^7 Я 2 двутавра Л = 26 2 i — 1 2 2 0,25 — 11 -2,75 15,1 1.9 916 1580 двутавр № 30 6=13,3
|!Н1!111!1!И
,—га.—-
СЛ Ок ш -пЛ'г Я \Р двутавр Л/6 = 4/3 2 1 6 3 I 1 оо См 6,25 3,12 11,52 2,88 722 2400 двутавр № 36 6 = 20,1
штшптшвн
^гг-За
К задаче 6.45 (продолжение)
№ схемы и варианта Схема балки и нагрузки Размеры нагрузки Ответ
Вид сечения или отношение h/b а Р Q м. Q М № профиля или размеры сечения, см
м т т/м тм т тм СМ*
16 а) 10 б) *-M0 двутавр круг 1 0,5 2 1 2 2 2 0,5 4,0 2,0 6,0 1,5 375 1250 двутавр № 27 d = 23,3
17 а) ' б) *1 2 швеллера h/b = 3/3 2 1 4 2 2 2 4 1 4,67 2,34 4,0 1,0 250 833 швеллер Xs 18а 5=12,2
Ж R> i & k
io а) 18 б) 1Л& 2 швеллера h/b = 4/3 2 1 5 5 2 2 4 2 4,6 4,6 5,78 2,89 330 2405 швеллер >5 20а 5 = 20,1
ferX—4a «
19 а) 1а б) Г Mo двутавр круг 2 2 3 2 3 2 3 2 3,75 2,5 -3,09 —2,06 -193 1718 двутавр № 20а d = 25,8
1 ihiiiiiz ifi
20 а) м б) "о- f V двутавр h!b=3/2 4 2 1 0,75 2 3 4 1,5 5,0 3,75 —4 -1,5 250 1250 двутавр Xs 22а 5=14,9
Для прямоугольных сечений дано отношение h/b.
9.47. Определить величину допускаемой силы Р, которую можно безопасно приложить к балке из ковкого чугуна пролетом 1 = 4 м (см. рисунок), при допускаемых напряжениях: на растяжение чугуна [о] = 300 кг/см3, на сжатие [ос] = 1000 кг/см2. Размеры сечения показаны на рисунке в лш.
К задаче 6.47.
Решение. Построив эпюру изгибающих моментов, найдем величину Р1
Л1шах=-^-. Для составления условия прочности необходимо вычислить момент инерции сечения относительно главной центральной оси у. Рассматривая сечение как состоящее из трех прямоугольников, найдем:
1) Площадь сечения F=2-2-20 + 4-30 = 200 см3.
2) Статический момент площади относительно осн уг, проходящей через основание фигуры, 5^=2-20-2 (10+4)4-4-30-2= 1360 см3.
3) Расстояние до центра тяжести сечения гс=-2дд- = 6,8 см.
4) Момент инерции сечения относительно оси у по формулам перехода к параллельным осям:
Jy=2 [^+2-20(10+4—6.8)3] 4
М
Условие прочности имеет вид: отах = —р25 г, 2< [<т|, где г1>2—расстояние , Jy ' '
от осн у до наиболее напряженных точек сечения.
а) В растянутой (нижней) зоне сечения Zj = 6,8cjh.
б) Для сжатой (верхней) зоны сечения г3=24—6,8= 17,2 см.
Условия прочности:
а) иа растяжение прн изгибе:
Р/ , , „ 4(<*Ну 4-300-9740 ,Qnn
4j^^<[o], откуда Р = -^-]— =----6,8• 400 = 4300 Кг'
б) на сжатие прн изгибе:
4[oc]Jv 4-1000-9740 /’<-^=-17Ж-=5650 KZ-
Скевндио, что допускаемая нагрузка не должна превышать Р = 4300 кг, что определяется условием прочности чугуна на растяжение.
ЧО .43
^-+30-4 (6,8—2)2 =9740 см*.
в.48. Балка таврового профиля длиною 1 = 1,4 м, защемленная одним концом, нагружена в вертикальной плоскости сосредоточенной силой Р, приложенной на другом свободном конце коисоли. Размеры
151
сечения даны на рисунке в мм. Определить величину силы Р и значение наибольших сжимающих напряжений, если растягивающие напряжения в опасном сечении отах = 424 кг/см2.
Ответ: Р = 825 кг; атах =—932 кг 1см3.
6.49. Определить величину наибольших растягивающих и сжимающих напряжений в опасном сечении балки пролетом I = 2 м, защемленной одним концом и загруженной в вертикальной плоскости но
20
К задаче 6.48.
К задаче 6.49.
всей длине равномерно распределенной нагрузкой ^=3 т/м. Сечение балки — неравнополочный двутавр; размеры сечения даны на рисунке в мм.
Ответ: отах=254 кг/см3; omin =—452 кг[см3.
6.50. Балка корытного профиля, изображенного на рисунке (размеры даны в Л1м), свободно лежит на двух шарнирных опорах и загружена двумя равными силами Р—2 т каждая, отстоящими на
К задаче 6.50.
К задаче 6.51.
одинаковых расстояниях от опор а —2,2 ж. Материал балки—сплав с пределом прочности па растяжение ов=18 кг{мм3 и на сжатие овж = 40 кг/мм3. Определить коэффициенты запаса прочности на растяжение и сжатие при изгибе для точек опасного сечения балки.
Ответ: На растяжение А, = 1,8; на сжатие Аа = 2,96.
6.51. Колонка станка, ослабленная несимметрично расположенным круглым отверстием для направляющей стойки, подвергается чистому изгибу в плоскости хОг моментом М = 6 тм.
152
Определить величину наибольших нормальных напряжений в сечении колонки, показанном на рисунке, если г =15 см. Расстояние между центрами внешней и внутренней окружностей равно с = 0,25 г.
Ответ: огпах = 287 кг/см2.
6.52. Балка, защемленная одним концом, длиною I = 1,5 м, несет сплошную нагрузку Qo, распределенную по закону треугольника.
К задаче 6.52.
Сечение балки, прямоугольное, пустотелое, с несимметрично расположенной полостью, показано на рисунке (размеры в мм), а) Определить величину нагрузки Qo при допускаемом напряжении [о] = = 1000 кг/см2, б) Установить, как изменится величина нагрузки Qo, если она будет распределена равномерно по длине балки.
Ответ: a) Qo = 750O кг. б) Уменьшится в 1,5 раза.
6.53. При испытании чугунной балки (Е= 1,2- 10е кг/см2) по схеме, изображенной на рисунке, снимались показания тензометров 1 и 2.
К задаче 6.53.
Средние приращения показаний от ступени нагружения Р=5 т оказались равными Дл, =—15 мм, &п3 = 5 мм. Определить величину момента инерции сечения относительно главной центральной оси у, если высота сечения ft = 24 см, а = 0,6 м, база тензометров I = 20 мм, коэффициент увеличения А =1000.
Ответ: 7^ = 6000 см*.
6.54. Подпорная стенка, поддерживающая насыпь, состоит из круглых свай, обшнтых досками—каждая шириною А = 0,2 м (см. Рисунок). Расстояние между сваями I = 1,2 м, высота стенкн ft = 1,5 м.
153
Давление на подпорную стенку возрастает по линейному закону от pt = 5 кн/м3 (от действия нагрузки, возвышающейся над стенкой) до р4=1,8 кн/м3. Вследствие податливости грунта место защемления сван принимается ниже уровня грунта на величину а (рис. б).
Рассматривая доски обшивки как балки, шарнирно опирающиеся на сван, и принимая размер а = 0,25 м, подобрать диаметр сваи d и толщину досок t при допускаемых напряжениях иа растяжение и сжатие дерева при изгибе [о] = 10 мн/м3.
Указание. Каждая промежуточная свая воспринимает давление от части обшивки площадью ш=Ы. Следовательно, интенсивность давления изменяется по высоте сваи от <у1 = р1/ до q^=p±l- Подсчитав Л4тах> подбирают сечение сван. Что касается обшивки, то в невыгоднейших условиях находится нижняя доска, работающая как балка на двух опорах пролетом /, нагруженная равномерно распределенной нагрузкой Чь=рф (давление на кв. м внизу равно рг, а на пог. м при ширине доски b м в b раз больше).
Ответ: d = 0,26 м; t = 0,044 м.
6.55. Боковая обшивка рамы, изображенной на рисунке, передает на стойку равномерно распределенное давление от ветровой нагрузки 9 = 500 кг]м. Стойки и ригель рамы проектируются из двух одинаковых швеллеров. Из условия прочности на изгиб определить необходимый номер швеллера, если а = 2 м, а допускаемое напряжение [о] =1400 кг 1см3.
Ответ: Два швеллера № 36.
§ 20. Касательные напряжения при изгибе. Центр изгиба
6.56. Показать направление касательных напряжений, передающихся через ступенчатый разрез abed от правой части балки на левую и обратно, при положительном и отрицательном значении поперечной силы Q в сечении (см. рисунок). Определить также ве
164
личину касательных напряжений по горизонтальной площадке Ьс, если Q = 3200 кг, b = 12 см и h = 20 см.
Ответ: т = 15 kzJcm*.
6.57. Прн допускаемых напряжениях на растяжение и сжатие при изгибе [о] = 1600 кг/см* и на срез [т] = 1000 кг/см2 подобрать
К задаче 6.56.
К задаче 6.57.
по сортаменту двутавровое сеченне балки пролетом / = 3 я, нагруженной двумя равными силами Р=18 т, приложенными на одинаковых расстояниях от опор а = 0,35 м (см. рисунок).
Решение.
Отах = >8 Т, Мтп = Ра= 18-0,35 = 6,3 тм.
Из условия прочности прн изгибе находим
^тах_8.3-106 ддд , [о] ~ 1600 -J92c*-
По сортаменту (см. Приложения) находим подходящий профиль—двутавр № 27а с моментом сопротивления IF = 407 см*. Наибольшие нормальные напряжения будут
®max = ^22 = 6 407°6 = 1550 Кг1СМ* < 1600 кг!см*-
Произведем проверку прочности по касательным напряжениям. По таблице для двутавра № 27а имеем:
момент инерцнн сечения относительно нейтральной оси у 7^ = 5500 см4; статический момент полусечення относительно осн у =229 см*-, ширина сечения на уровне нейтрального слоя b (?)=6=0,6 см.
По формуле Журавского найдем
т .Qmax^ maK Jyb (z)
18000-229 5500 0,6
1250 кг/см* > 1000 кг/см*.
Для обеспечения прочности сечения на сдвиг следует увеличить номер профиля. Попробуем двутавр № 30:
Jy = 7080 см*. SJ = 268 см*, 6 = 0.65 см, = =»050 кг/см* > 1000 кг/см*.
Перенапряжение составляет 5%, что допустимо. Сечение пришлось выбрать нз условия прочности на срез.
Ответ: Двутавр № 30.
155
6.58. Подобрать прямоугольное сечение деревянной балки, защемленной одним концом и загруженной, как показано на схеме, при от. ношении сторон прямоугольника Л:/> = 3:.2, если а = 0,25 м, q= 1 т/м P=\0qa, [о] = 100 кг/сл12 и [т] = 12 кг/см2. *
Ответ: b=\7 см: Л = 25,5 см.
6.59. Определить величину нормальных н касательных напряжений, возникающих в опасном сечении мостового бруса под давлением колес локомотива—Р=96кн от каждого рельса (см. рисунок). Размеры
7 Р\ у
L За,-
К задаче 6.58.
поперечного сечения бруса: b = 21
см, Л = 28 см. Считать, что брус
опирается на продольные балки моста шарнирно н имеет пролет, равный расстоянию между осями их /=2м.
Ответ: отах « 7000 кн/м*: ттах = 2450 кн/м*.
6.60. Подобрать сечение консольной балки двутаврового профиля,
нагруженной, как показано на
,Р=12т P=12m.
4000-
К задаче 6.60.
рисунке. Допускаемые напряжения принять [о] =1600 кг/см2, [т] = = 1000 кг!см*.
Ответ: Двутавр № 27.
6.61. Балка двутаврового профиля проектируется на действие изгибающего момента УИ0 при поперечной силе Qo. Для испытания конструкции изготовлена модель
балки, геометрически подобная проектируемой, со всеми размерами, уменьшенными в л раз. Испытание модели производится уменьшенными нагрузками, причем изгибающий
момент н поперечная сила Qt в модели в одинаковое число раз меньше, чем Мо и Qo. Установить, как отличается величина наибольших касательных напряжений (шахт,) в модели от max т0 в оригинале, если наибольшие нормальные напряжения в обеих балках одинаковы.
Ответ: В модели max т, в л раз меньше, чем в проектируемой балке.
6.62. Сравнить два варианта а) и б) трубчатого прямоугольного сечения балки, работающего на изгиб в вертикальной плоскости,
исходя из условий прочности по нормальным и по касательным напряжениям. Размеры сечеиня: b=\2 см, Л = 20 см, а = 8 см (см. рисунок).
Ответ: По нормальным напряжениям оба варианта равнопрочны; по касательным—более выгоден вариант а) (тб = 5,73та).
156
6.63. Балка пролетом 1=3 м, свободно опертая по концам, нагружена двумя равными сосредоточенными силами Р=\2т каждая, приложенными на одинаковых расстояниях а = 0,7 ж, от опор. Проверить прочность сечения при допускаемых напряжениях на изгиб = 600 кг [см2 и на срез [т] = 200 кг/см2. Размеры сечения (см. рисунок): Ь = 24 см, d = 20 см.
К задаче 6.62.
К задаче 6.63.
Указание. Статический момент полукруга относительно основания равен
Sy =|2<р-
Ответ: отак = 508 кг/см*
тт.х=160 кг/см*
< 600 kzIcm1-, < 200 кг/см*.
6.64. Балка пролетом / = 4 м с двумя равными консолями по а = 0,5 м загружена, как показано на рис. а. Определить величину наибольших нормальных и касательных напряжений в опасном сечении
К задаче 6.64.
балки, если в точках С касательные напряжения равны тс=100 кг/см*. Размеры сечения и расстояния до точек С показаны на рис. б в мм.
Ответ: отах = 700 кг/см*-, ттак=112 кг/см2 (z0=7 см, Jy = 337Q см*}.
6.65. Построить эпюру распределения вертикальных составляющих касательных напряжений по высоте сечения балки, имеющего форму равнобедренного треугольника. Поперечная сила Q направлена “Доль осн г.
137
Решение. Из закона парности касательных напряжений следует, что полное
касательное напряжение в точках контура совпадает по направлению с гранями АС и ВС; в любой же точке сечения оно может быть принято направленным к вершине треугольника. По формуле Журавского, выведенной в пред
положении равномерного распределения т по ширине сечения, определяются
К задаче 6.65.
только составляющие т, параллельные оси г и равные
т_ 0^ Jyb (г) ‘
(а)
Для произвольной точки, лежащей на линии Ь(г), статический момент сдвигающейся относительно нейтральной осн у площади S® — Вого; площадь заштрихованного треугольника
г®=г + у(4Л-г)=4(Л+г)-
Следовательно,
Sj=yb(2) (I Л-г) (| + г)=^(2Л8+ЗЛг-9г’), а
Касательные напряжения изменяются по параболическому закону. Подставляя , Wt8
момент инерции треугольника Jv=-=?-. получим
т=^(2Л1+ЗАг-9г2)- (б)
Исследуя уравнение для т на максимум, найдем
^=ЗЛ—18г=0, откуда г = -^-;
Следовательно, т=ттах при z=h/(>, т. е. на средней линии треугольника.
30 3 Q
Подставляя это значение г в (б), получим ттах=^=-^- . Для построе-
ния эпюры т по высоте сечения дадим переменной г еще три значения: 1) при г=0 т=4--§; 2) при г=-|-Л т=0 н 3) прн г=— ^-т=0.
О Г о о
Ответ: См. рисунок.
6.66. Балочка уголкового профиля 50x50x5 мм подвергается изгибу в вертикальной плоскости. Построить эпюру распределения касательных напряжений по сечению и найти их величину в точке К (при 2^=20 жж) и т1Пак(2 = 0), если поперечная сила в сечении, параллельная оси г, равна Q = 2r.
Указание. Для вырезанного элемента по методу Д. И. Журавского найти значение т по площадке, параллельной осн х (рис. а). По закону парности
1Б8
такие же напряжения действуют вдоль полок:
6СО145*
T=V’ где52=Уг<,г=-ЭТ= j zdz-F. г
Q№
Ттак ~ 2Jy /2
1000 кг!см\
Ответ: См. рис. б). тк = 695 кг/см2:
К задаче 6.66.
6.67. Построить эпюры .распределения касательных напряжений, возникающих в стенке и в полках двутаврового профиля, изображен-
ного на чертеже, если по-
перечная сила в сечении Q = 16 т и направлена вдоль оси z. Размеры сечения: 6 = 36 сж, Л ==40 сж, /=2 сж, 6=1,2сж.
Решение. По формуле Журавского величина касательных нал ряжений равна:
действующих вдоль стенки т =_^_
действующих вдоль полок
Здесь §2 н Sy —статические моменты сдвигающейся части сече-
ния относительно нейтральной
оси У\ b(z) = 6—толщина стенки; t—-толщина полки и Jv—момент ралыюн осн у, равный
К задаче 6.67. инерции сечения относительно цент-
, _6(Л-2ГРГЫэ /Л_/ут 1,2-36» /36-2» , „ „ 1(МЛ
---12—+2[-i2+W(k“2_J J=~i2- + 2k_i2-+36-219l)«
к 56 700 сж*.
159
При постоянных ширине сечения Ь (г) = в н толщине полки t изменение вел» чины касательных напряжений зависит только от изменения величины статического момента. Для точек 1 и 3, принадлежащих стейке в месте сопряжения ее с полками,
$i,s = bt = 36,2-19 = 1368 см3.
Для точки 2, лежащей на нейтральной оси,
s» = $max = $1 + ^5^ • (Л~2<)6= 1368+18-9-1,2= 1560 см3.
Для произвольной точки с абсциссой у, принадлежащей полке,
При у = 0 $£=684 см3; при У = -^- ${, = 0.
В стейке статический момент изменяется по параболе, а в полке—по прямой. Величины касательных напряжений в стенке двутавра (рис. б):
, „ QS, 16 000-1368 ооо , .
в точках 1 и 5Т1>8=7-Л=-5ТОТ5.=322 кг/сл<»;
„ QSj 16 000-1560 .
в точке 2 56 700+2- =367 KS/CM '
Касательные напряжения, действующие вдоль полок, изменяются по закону прямой линии; наибольшие значения близ точек 1 и 3 равны:
Q$l 16 000-684 ос , .
таХТ>= 56760-2 а 96 Кг/СМ -
Поток касательных напряжений, действующих вдоль стенки параллельно Q, растекается по полкам в противоположные стороны (рис. а). В точках перехода от стенки к полкам т2 и ту имеют характер местных напряжений и методами сопротивления материалов не могут быть определены.
6.68. Сечение балки имеет форму неравнополочного двутавра (на рисунке размеры в см). Найти значения касательных напряжений
К задаче 6.68.
в точках /, // и /// стенки двутавра и наибольшую величину касательных напряжений ту в полках (параллельных осн у), если поперечная сила в сечении Q= 18 т и направлена вверх. Построить эпюры
160
точках и по каким площадкам
К задаче 6.70.
распределения касательных напряжений хг по высоте стенки и ту по ширине полок.
Ответ. zc = 12 см; тх> j = 102 кг!смг; т,. „ = 212 кг!см';
хг, in = 191 кг)см*; xyi, = 51 кг!смг; ху, HI = 95 кг/см*.
6.69. Балка П-образного профиля (размеры даны в мл<) подвергается изгибу в вертикальной плоскости xz. В опасном сечении q х==12т, Л11Пах = 5 гм. Определить величину наибольших нормальных и касательных напряжений, построить эпюры распределения касательных напряжений хг по высоте стенок и ху по ширине горизонтальной полки. Выяснить, в каких касательные напряжения будут наибольшими.
Ответ. zc = 11,5 см; J ш & 3750 см'; оп)ах=1530 кг(смг; тахту = 96 кг)смг (в точке /); тахт, = 212 кг/см* (в точке 5); т, = 144 кг)смг (в точке 2);тах та = = 765 кг/см2 (в точке 4 по площадке, наклоненной на угол а = 45° к оси балки).
6.70. Швеллер № 30 подвергается изгибу в плоскости наименьшей жесткости xz. Построить эпюры распределения касательных
напряжений ху и т,, действующих вдоль стенки н вдоль полок, если поперечная сила в сечении Q = 6,54 т и направлена вдоль оси z. Уклона полок не учитывать, считая толщину их постоянной.
Ответ: тахту = 613 кг]смг; тахт, = 280 кг [см* (см. рисунок).
6.71. а) Определить величину наибольших нормальных и касательных напряжений в опасном сечении прямоугольной трубчатой
К задаче 6.71.
балки, загруженной, как показано иа схеме, если Р = 24т, /=4л и ° = 0,6 ж. Размеры сечения: b = 24 см, /г —20 см и 1 = 2 см. б) Построить эпюры распределения касательных напряжений вдоль
Ml
вертикальных н горизонтальных стенок сечения, в) Установить, как изменятся эпюры ту и т2, если в нижней горизонтальной стенке трубы сделать продольный разрез, как показано на рис. в.
Ответ', а) оП)ах= 1565 кг/сл(а, ттак = 365 кг/см*;
б) эпюры т показаны на рис. б в кг!см°\ в) не изменятся.
6.72. Построить эпюру распределения касательных напряжений для тонкостенной балки*), работающей па изгиб в вертикальной
а) 6) в) г)
К задаче 6.72.
плоскости, если поперечная сила в сечении Q=16 т. Сечение балки имеет вид швеллера с загнутыми полками (рис. а); толщина стенок профиля t = 4 мм, размер а = 20 см.
Выяснить также, как изменится величина и вид эпюр т, если полки швеллера будут отогнуты наружу, как показано на рис. в.
Ответ: 1) тП)ак = 763 кг/см*; эпюра т показана на рис. б;
2) ттах = 630кг/сж»; эпюру т см. иа рис. г.
6.73. а) Для несимметричного тонкостенного двутавра, подвергающегося изгибу в плоскости, параллельной полкам, определить
положение центра изгиба сечения**) и построить эпюры распределения касательных напряжений, если Q = 35 т. Размеры сечении: Л = 36 см, bt = 45 см, 62 = 30 см, — 2 см, 6=1 см. б) Пользуясь результатами решения, найти положение центра изгиба симметричного двутавра и тавра.
*) Для тонкостенных профилей полные размеры считают совпадающими с осевыми, рассматривая толщину малой по сравнению с прочими размерами сечения.
** ) Общее решение задачи об определении коордннвт центра изгиба дается в главе 10. Здесь рассматриваются простейшие задачи для сечений, имеющих одну ось симметрии, на которой и располагается центр изгиба сечеиня.
162
Указание. Из условия равенства нулю момента всех касательных усилий относительно центра изгиба А (см. рисунок) следует, что Qiei = Qaez> где qi = С ndF и $ rtdF. Так как касательные напряжения в полках, опре-F, F.
п ы w Qs<" Qs'*‘
являемые по методу Д. И. Журавского, равны т. = -, , и т2 = , -
J yt J J у12
[здесь S"’=y (у—z2), a Z®J], то- выразив т„ т2 и dF
через г, находим Q, и Q2, а затем и е, и ег, имея в виду, что Qi+Qa = Q, а е,-|-еа=Ло-
Ответ: a) е, =—= 8,7 см; = 672 кг/см2. !+<£•
б) Для симметричного двутавра (ft, = ft2) е, = О,5йо; для тавра (при ft2 = 0) е, = 0.
6.74. Найти положение центра изгиба равнобокого уголка, рассмотренного в задаче 6.66. Закруглений в полках не учитывать.
Ответ: Центр изгиба лежит в точке пересечения касательных усилий, т. е. осей полок.
6.75. Определить положение центра изгиба сечения тонкостенной балочки, подвергающейся изгибу в вертикальной плоскости. Построить
К задаче 6.75.
также эпюру распределения касательных напряжений по профилю, если Q = 7 т, а сечение представляет собой круговое полукольцо радиусом г = 25 см и толщиной 6 = 0,25 см (см. рисунок). Установить, как изменятся е и ттзх, если сечение будет иметь вид разрезного кольца (рис. б).
Решение. Центр изгиба лежит на оси у, например, в точке А *). Если поперечная сила Q проходит через центр изгиба, то сечение не скручивается. Так как Q — равнодействующая касательных усилий в сечении, то сумма моментов этих усилий dT (dT = т dF=r6ds) относительно любой точки плоскости
*) Для открытых профилей центр изгиба всегда расположен со стороны, противоположной раскрытой части профиля, что освобождает от необходимости Учитывать знаки Sy, р и е.
163
равна моменту поперечной силы относительно той же точки. Выбрав в качестве полюса точку О, имеем
(а)
Для полукольца (рис. о) р = г, a ds = rd<p. Статический момент сдвигающейся (заштрихованной) части сечения относительно осп у равен
я/2
Sj = J г dF = J (г sin <р) бг d<p = г2б cos ф. Fe ф
Момент инерции сечения относительно той же оси
я/2 (* (‘ лг®6
Jy=\ z2dF = 2 \ (г51Пф)2бг«/ф=—2— > о
Расстояние до центра изгиба от точки О будет
я/2
1 С -о J 2 .. . 2г*б 4г 4-25 о
e = -j— \ Stf>as = -j— \ r-о созф-г-г//ф=-у—=— =—— = 31,8 см.
J у " у J Jу Л о, 14
Касательные напряжения в любой точке равны
QSg_ <?г2 cos ф _2Q cos ф . 2Q 2-7000
J/ Jy ллб ’ Т,пах~лг6~ 3.14-25-0.25 '
Для разрезного кольца (рис. 6) получим
Sg = r26(l — cosqp); /^ = лг36; е = 2г=50 см.
тш» не изменится.
6.76. Пользуясь результатами решения задачи 6.75 (формула (а)),
определить положение центра изгиба тонкостенного швеллера, по-
К задаче 6.76.
казанного иа рисунке. Размеры сечения: й = 200 лии, b =* 80 мм, 6 = 5 мм. Определить также величину наибольших касательных напряжений, если поперечная сила в сечении Q = 6 т и направлена параллельно оси z.
Указание. Выбрав полюс на оси стенки в h h
точке О, получим р=-^- н $° = (Ь—Прн вычислении момента инерцнн сечения собственными моментами инерции площадей полок пренебречь.
01,1
Ответ: е = =2,82 см\ ттм=274 кг/см2.
6.77. Построить эпюру распределения касательных напряжений по контуру профиля и найти положение центра изгиба сечения тонкостенной балочки, подвергающейся изгибу в вертикальной плоскости,
164
если поперечная сила в сечении Q= 1000 кг. Размеры профиля: а = 30 мм, 6 = 2 мм и а = 45°. Момент инерции сечения относительно оси у 23,7 см*.
Указание. Выбрав полюс в точке О пересечения полок, воспользоваться формулой (а) из задачи 6.75.
К задаче 6.77.
Ответ: Эпюра т показана ттак = 702 кг/см3-, е т 2,3 см.
на
рис. б; т, = 512 кг/см*-.
§21. Главные напряжения при изгибе. Полная проверка прочности балок
6.78. Определить величину и направление главных напряжений
о, и оэ в точке С балки прямоугольного сечения, работающей на
изгиб в вертикальной плоскости. Размеры сечения: 6 = 5 см, Л = 12 см (см. рисунок). Изгибающий момент в сечении 7И = 1,2 тм; поперечная сила Q = 4 г.
К задаче 6.78.
iz
К задаче 6.79.
Ответ: ох = 512 кг 1см3', о3 = — 12 кг/см3; а = — 8°20'.
6.79 Балка двутаврового профиля Л& 27 подвергается изгибу в плоскости xOz. Изгибающий момент в опасном сечении М=—4,85 тм, поперечная сила Q = —13,7 т. Определить величину
165
и направление главных напряжений в точках С, и Сг опасного сечения аналитически и графически (с помощью кругов Мора). Точки Cj И Сг лежат на оси стенки (см. рисунок).
Ответ: В точке С, ot = 1565 кг/см2, аа = — 355 кг 1см*, а = 25°30'; в Точке Сг Oj = 355 кг/см2, а8 = —• 1565 кг/см2, а = 65°30'.
6.80. Балка прямоугольного трубчатого сечения (см. рисунок) работает на изгиб
вертикальной плоскости. Изгибающий момент в сечении М = 7,6 тм, поперечная сила Q = 36 т.
Размеры сечения: В = 12 см, 77 = 20 см, t = 2 см, 6 = 1,5 см. Выяснить, в какой из точек сопряжения горизонтальной и вертикальной стенок, С или D, величины главных растягивающих напряжений имеют ббльшую величину.
Ответ: В точке D (max ос==1427 кг/см2, max aD = 1592 кг/см2).
6.81. Балка двутаврового профиля № 27 свободно оперта по концам и нагружена в плоскости стенки сосредоточенной силой Р, приложенной посредине пролета 7. Определить величину пролета балки из условия, что в опасном сечении наибольшие нормальные напряжения атах и растягивающие главные напряжения а, (в точке С стенки двутавра у сопряжения ее с полкой) равны между собой. Найти также = 1560 кг/см2.
Ответ: I « 150 см; Рта 15,5 т.
6.82. Балка, свободно опертая кальной плоскости двумя сосредоточенными силами Р=7 т каждая (см. рисунок), а) Подобрать двутавровое сечение балки (по сортаменту) при допускаемых напряжениях [а] = 1600 кг/см2 и [т] = = 1000 кг/см2, б) Найти величину нормальных и касательных напряжений по площадке, наклоненной на в
К задаче 6.80.
в
величину силы Р, если аП)ах =
по концам, нагружена в вертн-
правее сечения под силой
угол <р=30° к оси балки, «очке С, взятой непосредственно в четверти высоты балки.
Указание. Определение напряжений может быть произведено по формулам
по
наклонной площадке в точке С
оа=ая cos2a+oy sln2a—тх sin 2a,
тв = —g—- sin 2a+rx cos 2a,
где a*=oc, 0^=0, tx = re и a—угол между направлением ax и нормалью к площадке.
Ответ: а) Двутавр № 24; б) a„ = 673 кг[см\ тв = 616 кг/см2.
160
К задаче 6.83.
6.83. Определить величину нормальных, касательных и главных напряжений в точке С двутавровой балки № 40, пролетом 1 = 4 м, свободно лежащей иа двух опорах и нагруженной посредине силой р= 15 т. Точка С расположена под силой Р непосредственно левее ее и выше нейтрального слоя на 10 см. Найти также величину нормальных н касательных напряжений в той же точке С по площадке, наклоненной к оси балки на угол 30°.
Указание. См. задачу 6.82. Прн известных значениях и о3 легко вычислить оа н та по формулам: оа=о1 cos2 а,-|-+ о3 sin3 а1( т„=01 2°3- sin 2а„ где а,—угол между направлением и нормалью к площадке.
Ответ: ас = — 792 кг/смг; тс = 248 кг/см2-, at = 71 кг!см2\ os = — 863 кг/см2; a, = — 46°; ae = — 412 кг/см2; тв = — 467 кг/смг.
6.84. Балка пролетом I = 6 л», свободно опертая по концам, несет сплошную равномерно распределенную нагрузку интенсивностью
К задаче 6.84.
<7 = 5 т/м. Сечение балки—прямоугольник со сторонами b =15 см и А = 40 см. Построить траектории главных напряжений а, и а3*), проходящие через точку nlt лежащую на пересечении нейтрального слоя с сечением 1—1, взятым на расстоянии о = 0,1 м от левой опоры А (см. рисунок).
Решение. Для построения траекторий ох и о3 следует провести ряд сечений через 10—20 см н определить величины изгибающего момента и поперечной силы в каждом из них.
Вследствие симметрии нагрузки достаточно рассмотреть половину балки (например, левую). Построение траекторий главных напряжений начинаем
*) Траекториями главных напряжений называются линии, направления которых в каждой точке совпадают с направлениями ох или о3.
187
с заданной точки nt. Так как на нейтральной оси балкн о=0 (чистый сдвиг), то О( н О^ направлены под углами а= £ 45° к оси балки. Учитывая, что tg 2а = —•у, найдем (прно=0 нт > 0) 2а = —90° п а = — 45° (от осях до00.
Продолжив найденные в точке /ц направления ot и о3 до встречи со смежными сечениями А—0 и 2—2 (точки л0 и л2), надо найти направления главных напряжений в этих точках. Например, для точки пг имеем
Aft = ^.2f-^=¥.0.2-54?: = 2,9 тм.
Qs=^—9-2a = ^-5-0,2= 14 т. bha 15-403
Момент инерции сечения относительно нейтральной осн у Jy=-^-=—— = = 80000 см*; расстояние от осн у до точки л. z2=10 см; статический момент л с(л.) Ъ (К- 15 /402
нижележащей части сечения 5;, == 1 —г 1=-гг* —
» 2 \ 4 у 2 \ 4
Нормальные и касательные напряжения в точке Hj будут
Мггг 2,9-10» 1Л „ 17=-8Лог- 10=36 'сг/сл -QS<2) 14 000-2250 п„ _,__л
’ Jb 8-10»-15 -2Ькг!см-
2250 см1.
°(2)
(2)
Направление ох в точке л2 определится углом а2:
2т 2-26
tg2a2 = — —=— 1.44, 2а2=—55°10' н а2 = — 27э35'.
О оо
Под этим углом продолжаем линию ot до сечения 3—3 и т. д. Что касается точки л0, то Мо = 0 и направление сг составляет угол —45°. Непосредственно правее сечения А—0 в верхней точке Ко о> вертикально. Вписывая в полученные ломаные линии плавную кривую, найдем траекторию главного напряжения ot> проходящую через заданную точку л2. Подобным же образом строится и траектория оа, что рекомендуется выполнить самостоятельно.
Ответ: См. рисунок.
6.85. По данным задачи 6.84 построить траекторию главного растягивающего напряжения alt проходящую через точку л'2, лежащую в сечении 2—2 выше нейтрального слоя на 10 см (см. рисунок к задаче 6.84).
Ответ: В точке л2 угол наклона траектории а, составляет с горизонталью 117°35' (против хода часовой стрелки).
6.86. Двутавровая балка № 20, свободно лежащая на двух опорах пресса, подвергается испытанию на изгиб сосредоточенной силой, прикладываемой посредине пролета равными ступенями АР=Зг. Измерение упругих деформаций производится с помощью электро-тензометров (датчиков сопротивления), наклеенных в четвертях пролета в точках нейтрального слоя под углами 45° к оси балки.
Определить величину коэффициента Пуассона материала балки, если отсчитываемое по шкале измерительного прибора приращение показаний тензометров от каждой ступени нагружения составляет в среднем Ал =10,6 деления, а цена деления прибора с = 1-10~* (в единицах относительного удлинения).
168
Указание. Измеренное по показаниям датчиков относительное удлинение материала е4&=с-Дл. Имея в виду, что в точках нейтрального слоя изгибаемой балки материал находится в условиях чистого сдвига, и выразив е45 через главные напряжения ot и о3, легко составить уравнение, из которого определяется коэффициент Пуассона р.
Ответ: р = 0,3.
6.87. Балка пролетом / = 3 л«, свободно опертая по концам, нагружена сплошной равномерно распределенной нагрузкой q= 1 т/л« и двумя равными силами Р= 16 т, приложенными на одинаковых расстояниях от опор а = 0,3 л« (см. рисунок).
К задаче 6.87.
При допускаемых напряжениях на растяжение и сжатие при изгибе [о] = 1600 кг/см2 н на сдвиг [т] = 1000 KejcM3 подобрать двутавровое сечение балки и, пользуясь энергетической теорией, произвести полную проверку прочности принятого сечения. Уклона полок двутавра и закруглений в местах сопряжений со стенкой не учитывать.
Решение. Эпюры Q н М построены на рис. а. (2шак = 17,5 m (в сечениях над опорами), а Мтая=5,95 тм (посредине пролета). Из условия прочности на изгиб находим
W ^П1ах = 5'95'10- = 372 см3 |о| 1600
По сортаменту подходит двутавр № 27 =371 см3), если сечение удов-
летворит всем условиям прочности.
О S
Проверка прочности на сдвиг. Тщ,,™ ту та» ДдЯ двутавра № 27 7^ = 5010 см*. Sroax = 210 см3, 6 = 0,6 см. Следовательно,
тш„ = 1^^>.оё° =1220 кг/с“* > 1000
Условие прочности иа сдвиг пе соблюдено, номер профиля необходимо увеличить. Попробуем двутавр № 30, геометрические характеристики которого
169
JУ = 7080 см*, Smax = 268 см3, 6 = 0,65 см, t = 1,02 см:
“VI 1018 » 1000
(перенапряжение составляет менее 2%, что вполне допустимо).
Проверка прочности по главным напряжениям. В опасных сечениях, где М = Л4тах и Q = Qmax, прочность материала балки обеспечена. Заметим, что в сечении, где М = Мтт, Q = 0, а там, где Q = Qmax, Л< = 0. Для этих сечений проверка прочности по главным напряжениям сведется к проверкам но наибольшим нормальным и по наибольшим касательным напряжениям. Более опасным может оказаться сечение под силой, где хотя М < Л4тах н Q < Qmax, но эффект нх совместного действия может вызвать высокие напряжения в точках, где о н т достаточно велики. Такими точками являются точки Cj и Сг стенки двутавра у мест сопряжения ее с полкой. Эпюры ант, иллюстрирующие сказанное, приведены на рис. б. Для точек С\ и С2 произведем проверку прочности по главным напряжениям в соответствии с IV (энергетической) теорией прочности.
В сечениях под силой Af = 5,21 тм, Q = 17,2 m (см. эпюры). Напряжения в точках С
(гс = А_/=^_1>02= 13,98 см; S^ = Snm- ® (Jt-1 V =
= 268_2Ц8г.0.65 = 204 сл.з):
Ос = ^=5^™8 =1030 ^, Qtf, 17 200-204 .
Т<? “ JyS 7080-0,65 - 763 ,СМ ’
Расчетные напряжения по IV теории прочности:
o'V = j/ Ос+3тС= /10302+3-7633= 1680 кг/см3 > 1600 кг/см3.
Наиболее опасными оказались точки Cj и С2, где Орасч = 1680 кг/см*. Перенапряжение 5% допустимо.
К задаче 6.88.
6.88. По данным задачи 6.87 построить эпюру распределения наибольших главных напряжений по высоте двутаврового профиля №30 (вдоль оси г) в сечении под силой (где Q > 0).
170
Указание. Эпюру о, можно построить путем подсчета значений о, т н с, = о/2 + У(о/2)2 +т2 Для нескольких точек по высоте сечения. Проще, однако, решить задачу графически, используя построенные на рис. а эпюры о и т. _________
Так как при графическом построении выражение У(о/2)2 -г т2 можно рассматривать как гипотенузу прямоугольного треугольника с катетами, равными о/2 и т, то, взяв из графиков о н т, построенных в одном масштабе, отрезок, равный о/2, добавляем к нему отрезок, равный гипотенузе bd=bc треугольника abc (рис. в), для чего достаточно развернуть этот отрезок Ьс до горизонтали, как показано на рис. б. В местах сопряжения полок со стенкой построенный график показан условно.
Интересно отметить, что если т1Пах > отах, то график имеет максимум вблизи точки D.
Ответ: См. рис. б.
6.89. При допускаемых напряжениях на растяжение и сжатие при изгибе [а] = 1600 кг!смг и на срез [т] = 1000 кг]см2 подобрать сечение консольной балки двутаврового сечения, загруженной, как показано на рисунке, и произвести полную проверку прочности по IV (энергетической) теории прочности.
а)
К задаче 6.89.
Путем построения кругов Мора или аналитически определить также величину и направление главных напряжений в каждой из пяти точек, указанных на рис. б, и построить эпюру ot для сечеиня балки над левой опорой, если Р=14 т, а = 0,5 м и / = 2,5 м. Сравнить также вид эпюр Oj, полученных в задачах 6.Е8 и 6.89, и объяснить причину различия в направлениях выпуклости кривых, ограничивающих эпюры ах.
Ответ: Сечение—двутавр № 30а; Орасч = 1660 кг/см2.
Эпюра ах показана на рис. 6.
6.90. Балка прямоугольного трубчатого сечения пролетом 1 = 3 м шарнирно оперта по концам и нагружена двумя равными силами Р=23т каждая, приложенными на одинаковых расстояниях а = 0,5 м от опор. Размеры сечения даны на рисунке в см.
Пользуясь IV (энергетической) теорией прочности, произвести полную проверку прочности сечення при допускаемых напряжениях
171
[a] = 1600 кг/см? и [т] = 1000 кг/см2. Построить также эпюры распределения главных напряжений at и о3 по контуру сечения.
Ответ: отах=1530 кг/см2-, ттах = 687 кг/см2; oj,v = 1598 кг/см2.
Эпюра Oj — см. рис. б.
К задаче 6.90.
6.91. Проверить прочность балки из легкого сплава, подвергающейся изгибу в вертикальной плоскости, при допускаемых напряжениях
[о] = 1000 кг/см2 и [т] = 700кг/см2, если изгибающий момент в опасном сечеиии Л4 = 60 т.н, а поперечная сила Q = 30 т. Воспользоваться теорией наибольших относительных деформаций (II теория прочности), приняв величину коэффициента Пуассона = 0,3. Построить также эпюры распределения главных напряжений по контуру сечения, показанному на рисунке (размеры в мм).
Ответ: отах = 721 кг/см2-, ттах =
= 411 кг/см2; a{>v = 692 кг/см2 (в горизонтальных полках у точек сопряжения с вертикальными стенками).
ГЛАВА 7
ДЕФОРМАЦИЯ И ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ*)
§ 22. Аналитические методы определения перемещений
7.1. Стальная балка прямоугольного поперечного сечения, защемленная одним концом, изгибается парой сил с моментом А40 = 1 кгм, приложенным на другом свободном конце (см. рисунок). Длина балки 1=1 м, размеры сечения: Ь = 6 см, Л = 0,5 см. Путем интегрирования приближенного дифференциального уравнения изогнутой оси балки определить величины наибольшего прогиба и угла поворота концевого
сечения и сравнить их с результатами точного решения.
Решение. Балка подвергается чистому изгибу: Q=0, Мд = М0 и М(х) — М0. Приближенное дифференциальное уравнение изогнутой осн имеет вид EJy"=Mtt, где
, Ml» 6-0.5’ .
J=-\2=~i2~=0.062а см*.
Проинтегрировав его дважды, получим
EJy' = Mox+C (1),
EJy = ^-+Cx+D. (II)
К задаче 7.1.
Произвольные постоянные интегрирования С н D найдем из условий закрепления балки в сечении А:
1) В точке А при х = 0 0л~У(Х=О)=0; подставляя в (I), найдем С=0.
2) Также прн х=0 /л=У<х=о> = 0; подставляя в (II), получим D=0.
Таким образом, уравнения (I) и (11/ примут вид
EJy' = Mex. EJy = -^.
•) Во всех задачах этой главы положительное направление прогибов принято вверх—в сторону положительной осн ординат у. Положительное направление углов поворота сечення—против хода часовой стрелки, если ось абсцисс х направлена слева направо.
173
Наибольшие значения перемещений получим прн (в точке В): ~ в уравнения (1) н (11),
100-100* лл = 4,0 см.
®тах—®В— У[х—1) н /шах — Подставляя
найдем
fi 100 100 ____________
в EJ 2-10’ 0,0625 ’ ’ lB~ 2EJ “2-2-10’ 0,0625
Знаки Он/ показывают, что сечепне В поворачивается против хода часовой стрелки, а прогиб /я направлен вверх.
Более точные результаты можно получить нз уравнения для кривизны: — = . Так как при чистом изгибе М (х) = Л10=const, тон p = const, т. е.
ось балки изгибается не по параболе, как это следует нз уравнения (II), а но дуге окружности, описанной радиусом
EJ 2-10’ 0,0625 ₽= мг---------100—=1250 см-
Теперь перемещения легко найтн из геометрических соображений (см. рисунок). Угол Од определяется как отношение дуги длиною I к радиусу р, а прогиб—как отрезок AD = AC—CD. Следовательно, вв=7=1^=0,08, ИЛИ вв = 4°34'-
/в = р—р cosO = p(l — cos 4®34') = 1250(1—0,99684)=3,95 см.
Расхождение между точным н приближенным решениями для ' прогиба составляет около одного процента; для угла поворота результаты совпадают с точностью до третьего знака. Заметим, что для обычно применяемых в конструкциях балок большой жесткости, например двутавровых, погрешность приближенного решения с помощью дифференциального уравнения еще меньше (порядка 0,05—0,1%) в сторону некоторого преувеличения перемещений.
7.2. Балка пролетом 1=\ м, свободно лежащая на двух шарнирных опорах, изогнута по дуге окружности. Сечение балки прямоугольное со сторонами Ь = 6 см и й = 4 см.
Прогиб, измеренный посредине пролета, оказался равным /=6,25 мм. Определить величину модуля упругости материала и радиус кривизны оси балки при условии, что наибольшее нормальное напряжение атах = [о] = 100 кг/см2.
Ответ: Е=1-10‘ кг/см2; р = 20 м.
7.3. Балка круглого сечения диаметром d и длиною /, защемленная одним концом, подвергается изгибу под действием равномерно распределенной нагрузки интенсивностью q кг/м. Определить кривизну оси балки в сечении, где 0тах = [о].
Указание. Выразить кривизну и напряжения через изгибающий момент в опасном сечении.
~ I 2 [о]
Ответ: — = -£/.
р Ed
7.4. Балка симметричного сечения высотою h и длиною I защемлена одним концом и нагружена силой Р на другом конце, вызывающей в опасном сечении наибольшие напряжения о1Пах = [о]. Найти величину прогиба в сечении под силой, выразив его через размеры балки и допускаемые напряжения.
9/2
Ответ;
174
7.5. Для балок, защемленных одним концом (см. рисунок), путем интегрирования дифференциального уравнения изогнутой осн определить значения углов поворота и прогибов па свободном конце при следующих данных: а) 1 = 2 м, q = 3 т/м, 7ИО = 3 тм, сечение — двутавр № 20; б) I = 2 м, Р = 2 т, Л10 = 2 тм, сечение —двутавр № 18.
Ответ, а) 0 = = -0,0054, /=^-^- = 0;
n Mol PP _ f_M0P PP
6) Q—EJ 2EJ —°. f 2EJ 3EJ ~~ °,516 CM.
7.6. Определить углы поворота опорных сечений 0Л и 0Я и прогибы / посредине пролета для шарнирно опертых балок двутавро-показанных на ри-
при следующих данных: м, q = 3 т/м, сечение — № 27j б) I = 6 м, q = 2 т/м,
вого сечения, сунке, а) / = 2 двутавр
Cf
a)
A
в
i
^-Мр д
q
Л рШПШЛШ в г—-х.
&
a)
ИППИШИЦП
К задаче 7.5.
ИП»„1ПГГ„1
в
I
К задаче 7.6.
Мо = 8 тм, сечение —двутавр № 36; в) I = 4 м, q = 2 т/лс, Л10 = 4 тм, сечение—двутавр № 30.
Ответ: а) 0Л =—0в =—0,001, /=—0,062 см;
б) 0Л=—0,0097, 0В = О,О127, /= — 1,94 см;
в) 8А = —0Я = —0,0094, /=—1,04 см.
7.7. Подобрать во сортаменту двутавровое сечение балки пролетом / = 8 ль шарнирно опертой по концам и нагруженной равномерно распределенной нагрузкой q = 4 т/м, из условия, чтобы наибольший прогиб не превосходил допускаемого [/]=^q/; проверить также прочность принятого сечения, приняв [о] = 1600 кг!смг.
Ответ: Двутавр № 55; отах=1608 кг/см*« [о].
7.8. Путем интегрирования дифференциальных уравнений изогнутой оси с применением метода уравнивания произвольных постоянных определить величину наибольшего прогиба в пролете и опускание точки приложения силы для балки, изображенной на рисунке. Найти также углы поворота опорных сечений Л и В.
Решение. Опорные реакции равны:
А =---i—"(вниз), В= 1 1 —- (вверх).
175
Так как в балке выделяются два участка для М (х), необходимо составить t . .. .. 1 каждого участка. Решение упрощается, если
выражения моментов па каждом участке составлять, отсчитывая абсциссы сечений 1—1 и 2—2 от одного начала координат (например, от точки Л) и рассматривая каждый раз одну нту же отсеченную часть балки (у нас—левую). Тогда
дифференциальные уравнения для
Г I Я
i-ZZ->
'7
Mt = — Ах,
Л12 =— Лх-|-В (х— Интегрирование будем вести без раскрытия скобок, для второго участка— по переменной (х—Z), обращающейся в нуль при х=1. Это скажется
К задаче 7.8.
лишь на величине произвольных постоянных, приводя к уравниванию соответствующих постоянных для обоих участков. Получим:
Первый участок Второй участок
EJyi =— Ах EJy"2 =— Ах+В (х—Z) + Л10 (х—1)°
EJy; = -~ + C1 (1) EJy2 =---У + В(Х~<)2 + -Ч(х—Z) + C, (III)
УЕ
Р
-1~3а-
Лх3 Ах® В(х—Z)8 Л40(х—Z)2
fVj,! =-—+Схх+Dt (II) EJy2 ---g—|--6 - + —£-g—- 4-
+ С2х-Юа (IV)
Из уравнений (11) и (IV) видно, что изогнутая ось балки состоит из двух кривых. Так как прн упругой деформации ось балки представляет собой неразрывную плавную линию, то в точке сопряжения кривых (точка В) онн должны иметь общую касательную и общин прогиб:
1) при x=Z У1 = уг, н 2) прн x=Z ;/i = {/2.
По первому условию из (!) н (III) получим С1 = С2 = С. Из второго условия по (II) н (IV) найдем D1=D2 — D. Значения произвольных постоянных С и D определяются из условий закрепления балки на опорах А и В, где прогибы равны нулю:
3) прн х=0 £/1=0 и, следовательно, D=0; АР
4) прн x=l yt=y2=0, откуда С=— (из (II) или нз (IV)).
Величина наибольшего прогиба в пролете найдется из уравнения (II). Если £/i = «/max, то / =0. Приравняв (!) нулю, найдем необходимое значение х, соответствующее утях:
Ах* , АР I
°=—r+v X=W
Подставляя это значение х в (II) и заменяя А и С их значениями, получим Утп = Ь
Ра+Мв Р , Ра+М0 Р Ра+М„ (Ра + М2)Р ' 6Z " 3 /3 + 6Z / 3 9 / 3 ’ 9£ J V 3
Величину прогиба в сеченнн под силой найдем нз уравнения (IV) прн х = 1+а н y = fD:
EJfD=-Pa+M°(l +а)» + Р(а+^ + М° «»+—°- + Pag.-M,>Z8(1-|-а)1
. _ Pa2(Z+a)+M0oZ
Ггз 3EJ
176
Наконец, углы поворота опорных сечений можем определить из уравнения (I) прн х=0 н при х = 1:
Л ' era п (Ра+М0)Р а (Ра + МЛ1
Од=У1<х-о». или EJ6a = C=------'6f °' , откуда 0л=!—$EJ •
Л „ ст _ (Ра + Мв}Р , (Ра + М0)Р (Ра+Мв)1
0В-У1«-1>. т. е. £J0B =----------+-----6/------------3~^’
0д
(Ра + М0)1
~ 3EJ
Полученные результаты отвечают принципу позволяя разделить перемещения, вызванные по отдельности сосредоточенной силой Р и парой Л10.
Обращаем также внимание на то, что из-за равенства произвольных постоянных на смежных участках (Ct = C2 и D1 = Da) уравнение (IV) для второго участка можно переписать в виде EJy =
= D+Cx-^| +*(^ + ^F'Z.
О |1 О Z
(IVa) Слева от вертикальной черты расположены члены, входящие в уравнение кривой первого участка, справа—дополнительные члены, входящие в уравнение второго участка (т. е. уг = !/, + Уаоп}-
Примерный вид изогнутой оси показан па рисунке пунктиром.
7.6. Используя метод уравни-
незавнснмости действия сил.
К задаче 7.9.
вання произвольных постоянных интегрирования дифференциального уравнения изогнутой оси, опре-
делить: для балок, защемленных одним концом, прогиб и угол пово-
рота сечения на свободном конце; для шарнирно опертых балок — углы поворота опорных сечений (0л и 0В), прогибы посредине пролета (/с) и на свободном конце (/д).
Л , Ра2 (31 — a) Q Ра2
Ответ, а) /— 6£у ,0— 2£j ;
Л qcfl(3a-(-4b) п_ qa2 .
v> J — 24EJ ’ 6EJ ’
n _ Pal _ Pal . _ Pal2
Va—ьёТ' Vf>-~3ET’ 'с-ТьЁТ'
. _ Pa2(l + a) .
/d~ 3EJ
_4 p . qa2l p __ qa2l
Г) f2£7
f _ qa*(4l + 3a)
Jo— 24EJ
qa2l2
32EJ'
m
7.10. Выяснить смысл и размерность произвольных постоянных интегрирования дифференциального уравнения изогнутой оси балки,
т. е. начальных параметров, входящих в уравнение упругой линии. Найти также по методу начальных параметров прогиб и угол поворота концевого сечения балки, пзображен-
№ I__V
ипшншпшш
К задаче 7.10.
ной на рисунке.
Решение. Представив приближенное дифференциальное уравнение изогнутой оси в виде, не требующем составления выражения для М (х), имеем:
£7/ = Л4(х), (1)
W" = Q(x) (2) и EJy™ = q(x). (3)
Интегрируя уравнение (3) четыре раза, получим:
х
1) EJy,'’~\q(x)dx+Cl, о
2)
3)
4)
EJy'= J dx J q (x) dx+Cix+C,, о о
EJy'= j dx J dx J q (x) dr+£^+C8x+C3. 0 0 0
EJy = JdxJdxJdxJ9(x) dx+^+^+Csx + Ct. 0 0 0 0
Значения входящих в эти уравнения произвольных постоянных определяются из условий в начале координат при х=0. Используя равенства (1) и (2), получим: C1 = £Jya_o> = Q(x=O)=Po, Ca = EJy'x-.<n = Me. Кроме того, при х=0 Cs = £Jj,(x—o) = £J0o н С4 = EJy(X=m = EJf0.
Таким образом, произвольные постоянные интегрирования являются начальными параметрами, т. е. геометрическими и силовыми факторами прн х=0, чем определяется и нх размерность: fe и в0—прогиб и угол поворота начального сечения, а Рв и Л40—сосредоточенная сила и момент в начале координат.
Уравнение изогнутой оси через начальные параметры напишется так:
. Л , 1 Af0x2 ^ = fo+6ox4-£j ~2~
(а)
В случае равномерно распределенной нагрузки q (x) = g0=const и послед-
ний член уравнения после четырехкратного интегрирования получит значение
<7<Л4 24
, а уравнение (а) примет вид
„ f -Lfi г J- ’ rM°Xa РоХЭ I ?»**]
У Ао+вох+^j [ 2 6 24 J '
Воспользуемся нм для определения перемещений в заданной балке. Так как в начале координат (точка Д) нет нн силы, ни момента, т. е. Рв=0 и Л4в=0, а нагрузка qB=—q (направлена в сторону отрицательной осн у), то
17В
уравнения Прогибов и углов поворота примут вид
0=А>+ео*~^?р £,’*=0°_‘йГг
Начальные параметры /0 и 0О определим из условия закрепления балки
аР
в сечении В: прн х=1 у=0 и при х = / у' = 0, откуда н
, -
Io~~8EJ~'a-
Прн рациональном выборе начала координат решение может быть упрощено. Рекомендуется решить эту же задачу, приняв начало координат в точке В и направив ось х влево. Как изменятся при этом начальные параметры?
Ответ: /о = О; 0„ = 0; Мо-----Pe = ql; bA~-gj;
8EJ'
7.11. Пользуясь методом начальных параметров, определить линейные и угловые перемещения в балках, схемы которых приведены в задачах 7.5 и 7.6.
7.12. Методом начальных параметров определить величину наибольшего прогиба (/тах), а также прогиб посредине пролета (/с) в балке пролетом /, несущей сплошную нагрузку, распределенную
по треугольнику (см. рисунок).
Указание. Интенсивность нагрузки
q(x)=—q у. Четыре раза интегрируя эту функцию, получим последний член уравнения (а) (см. задачу 7.10):
f-ir- К задаче 7.12. 0 0 0 0
Ответ-. /тах = — 0,00652 (при х = 0,52/); /с --0.00651 £7 •
7.13. Для балок, несущих сплошную нагрузку, изменяющуюся по трапеции, определить: а) для консоли (рис. а)—угол поворота
б)
К задаче 7.13.
и прогиб концевого сечения; б) для шарнирно опертой балки (рис. б) — углы поворота на опорах и прогиб посредине пролета.
179
Указание. Удобно разделить нагрузку на равномерно распределенную qt=— qt и изменяющуюся по закону треугольника (рнс. a) q \x) = q -j-, где 7 = —(qt—qt). Уравнение изогнутой осн примет вид
Ответ: а)
u-f +0х + — 1
У — + [ 2! ' 3! 41 5! ]’
n _ (3<7i+qj Р (Ug. + ^ge)** .
24Ё7 ’ J “ I20EJ-
б) Од
(6qx+lqt)P о _(7ql + 6ql}P t___________5(gl+?2)/*
~ 360Ё7 ’°я- 360/77 ' 7 768EJ
7.14. При расчете балок, перекрывающих проемы в кирпичных стенах зданий, нагрузка на балку принимается от веса части расположенной над ней кладки, распределенной по параболе (рнс. а).
К задаче 7.14.
К задаче 7.15.
Считая балку шарнирно опертой по концам (рис. б), определить величину наибольшего прогиба, если закон изменения нагрузки описывается уравнением д(х)=^(/—л).
«-0,0106-^-.
Ответ: f=
5760EJ
7.1 Б. Определить углы поворота опорных сечений п прогиб посредине пролета для шарнирно опертой по концам балки, несущей нагрузку, изменяющуюся по параболическому закону. Рассмот-реть два варианта загружения балкн (см. рисунок): а) ч(х) = ^- и
Ог.ет:а)0л-----gggj, 0,-^ , /---------0.00306-g-;
6'е' = -Й7' в->=»7' f-----------«.««'б-g-.
7.16. Стальная балка двутаврового профиля № 40 длиною Z = 12 и поднимается краном с помощью троса, укрепленного посредине балки. Определить величину наибольших нормальных напряжений и
1Ю
наибольших прогибов от действия собственного веса в двух вариантах: а) при изгибе балки в плоскости наибольшей жесткости; б) то же в плоскости наименьшей жесткости.
Ответ: а) отах=107 кг/см2, /тах = 0,24 см;
б) Отах =1180 кг/см*, /тах = 6,82 см.
7.17. Пользуясь методом начальных параметров, определить величину наибольшего прогиба и углы поворота опорных сечений
К задаче 7.17.
деревянной балки, изображенной на рисунке. Сечение балки—прямоугольник со сторонами Ь= 15 см и h = 20 см, пролет 1 = 3а = 6м. Интенсивность нагрузки, приложенной на длине 2а, q=X),3 т/м.
4 2
Решение. Опорные реакции: A=-^-qa, B=-^qa. Начало координат при-О о
мем в точке А.
Для балки, разделенной на два или более участков, при нагружении ее силами, парами и равномерно распределенной нагрузкой общее уравнение изогнутой осн может быть написано в виде
y-f,+ »ох+-ёД-гГ + -31-+-4Г- Л +
1 ГМ, (х-Ол,)» , Р. (х-ау)3 । g, (x-y-| ' EJ [21 3! 41 J'
Здесь /0, 0О, Мо и Ро—начальные параметры (см. задачу 7.10); q0—интенсивность равномерно распределенной нагрузки на первом (от начала координат) участке; Л1,, Pt-, qi—силовые факторы, появляющиеся в начале второго (и каждого последующего) участка при х=О{. Девая часть равенства, отделенная вертикальной чертой, представляет собой уравнение изогнутой оси в пределах только первого участка; все уравнение в целом описывает кривую только последнего участка балки (а нашем случае—второго). Следовательно, как ив задаче 7.8, !/2=У1+Удоп- Из этих соображений нагрузку qt первого участка следует продолжить до конца балки, восстановив нарушенную схему нагружения добавочной нагрузкой на втором участке <?, = — q0, направленной вверх (см. рисунок).
В рассматриваемой балке начальные параметры (точка Д): /о=О, Afo=O, Pa = A = -^qa;
нагрузки: q0= — q, М,=0, Р,=0, qi=q (af = 2a).
Уравнение упругой линии примет вид
п „ , 1 ( 4 дах» д(х—2а)*
g-VoX-t-Ej 6 24 Д'1- 24EJ '
. Значение начального параметра 0о найдем из условия равенства нулю прогиба на опоре В (у = 0 при х=3а). Подставляя х = 3о, получим
О=е,-Зо+^Г| fffl(3fl)?-^(3o)«+^l, откуда 0о=—•
1S1
Окончательный вид уравнений прогибов и углов поворота:
1 y~EJ , 1 У ~ЁТ
[ — ga3x +-|-дох3 ( — ®.90э+А?0Х2_
I । g (х—2а)* 24,/24EJ
। Ч (*~ 2а)3 6 Л1 6EJ •
(а)
(б)
Для отыскания наибольшего прогиба надо найти абсциссу х, при которой У=Ушах, т. е. / —0. В балках рассматриваемого типа наибольший прогиб располагается около середины пролета, поэтому рассматриваем только часть уравнения (б), относящуюся к первому участку:
qx3 2 . , 8 , п
V—з^24-9^’=0-
ftnax —
0,8да* EJ ’
Решая уравнение методом последовательного подбора, найдем х = 1.445а. Подставляя х в уравнение (а), для первого участка получим
• Г 8 . , ... , 2 1Я (1,445а)*1
-g-^-g-fla3- 1.445а+у да (1,445а)3-g1 24 j =
Для получения числового ответа подсчитаем жесткость балки:
/=^=^^.= 10000 сл*, £7 = Ы0*-10< = 10» кгем3.
Следовательно,
_ 0,8да* _ 0.8-0.3-2*-10* _
/шах Ej — j-Ю» Л,О1СМ.
Углы поворота опорных сечений: 0л=!/<х—з». 0я=£/<х-зо>- Из (6) имеем
Sqa3 8,0-3-23-107 д . О.З-23.1О7
°л= “9Ё7=—9-10» = -°'0213- ®в-§Ё7—9-----------10»---= 0-0187-
7.18. Для балок, рассмотренных в задаче 7.9, определить прогибы и углы поворота указанных на схемах сечений, пользуясь методом начальных параметров.
Ответ: См. задачу 7.9.
7.19. Определить величину прогибов посредине пролета и на свободном конце балки, изображенной на рисунке, если P = qa. Каковы будут эти прогибы, если равномерно распределенную нагрузку q распространить на всю длнну балки?
10»
Ответ:
7.20.
оси, либо
с
ШНННШНМН!
а
'Ц
К задаче 7.19.
qw
да* f qtfi
4EJ' 'О
П /с— £/ • ю— 48EJ’ JC~ lEJ'JD~bEJ'
Интегрированием дифференциальных уравнений изогнутой пользуясь универсальными уравнениями метода начальных
181
параметров, найти значения прогибов посредине пролета (/с) и на свободном конце (fD) для балок, изображенных на рисунке.
Ответ: a) fc =
Ра (3Z2 —4а=) 24EJ
г _Pab(l—о);
2EJ ’
. _ ql (8/з - 4 b21 + b3) _qbc(3l-—b2)
°* Jc ~ ЗЫЕ J ' 'D ~ 43EJ
7.21. Определить величину прогиба посредине пролета двух-опорной балки, несущей нагрузку, распределенную на половине пролета по закону треугольника, в двух вариантах: а) левая половина балки не загружена; 6) правая половина загружена равномерно распределенной нагрузкой (см. рисунок).
К задаче 7.22.
Указание. В схеме б следует догрузить правую половину балки треугольной нагрузкой вверх н вниз.
Ответ: а) /=—0,0375 gj
б) /=-0,171g.
7.22. Определить значения прогибов в сечениях под силой (/D) и в шарнирах (/с) для балок с шарнирами в пролете (см. рисунок). Сечение считать по всей длине постоянным.
Указание. Расчленить балку на основную н подвесную, заменив отброшенную связь силами, передающимися через шарнир. При составлении уравнения изогнутой оси для подвесной балки учесть, что начальный прогиб для нее /0=fc, где fc—прогиб в точке С основной балки.
Ответ: а) /с =
64<7О4 , __29qa*
~3EJ~' ^d~~3ET'’
128ф1« . _ 62qa* ,
ЗЕ J ’ •'О - ЗЕ J ’
64<?а4 , __94qa*
~~EJ~ * Jd-HeT'
Д83
7.23. Балка пролетом I нагружена силой Р, приложенной посредине пролета. Определить величину перемещения А подвижной опоры при расположении опорных точек Л и В на оси балки, выразив его через прогиб / под силой.
Решение. Перемещение Д может быть определено как разность между длиной изогнутой осн и проекцией ее на горизонталь (см. рисунок):
A=l(ds—dx). Имея в виду, что 4s =
К задаче 7.23.
dx3-|-dp2, или ds=dx 1 -f
и раскладывая бином по формуле Ньютона, найдем приближенно ds« я dx р -f-у (y')2j • Отсюда для Д получим
A=Udx [14-1 (у')21 -dx
или Д = у J (у')2 dx. (а)
/
Остается выразить у'. Для заданной балки уравнения прогибов и углов поворота имеют вид (вследствие симметрии достаточно рассмотреть половину пролета):
_ Ах3_____ РР , Рх* , _ Ах2 РР Рх2
у-°<>х+бЁТ~~16Ё7 Х~гТ2Ё7' У ~°о + 2Ё7~~'16Ё7+4Е/ '
„ . -с .fl
Выразив производную у через прогиб f под сплои при
, РР \
'=-48Ё7)’ П0ЛуЧНМ
, РР (3 12х2\ f („ 12х2\
У ~ 48EJ \l Р )~ I \ Р )’
Подставляя в (а), найдем искомое перемещение:
'р /2 /, 12х2\.
д = 2 j 2/2 \ Р ) dx' о
и
Ответ: А = 2,4 у.
7.24. Используя решение задачи 7.23, найти сближение концов оси балки пролетом /, шарнирно опертой по концам и нагруженной сплошной равномерно распределенной нагрузкой q.
Ответ: А = 2,49 у, где /=—•
7.26. Балка двутаврового профиля № 55 пролетом 1=8 м опирается нижними полками по концам на шарнирные опоры и несет равномерно распределенную нагрузку q = 4 т/м.
а) Определить перемещение подвижной опоры (по величине и направлению), считая, что оно совпадает с удлинением нижних волокон балки, б) Уточнить, как повлияет иа величину этого перемещения искривление оси балки (см. задачу 7.23).
1Ь4
ol3
Ответ: a) A = — 0,428 см (в сторону увеличения пролета);
б) на 1,3% в сторону уменьшения.
7.26. Для экспериментального определения величин и направлений главных напряжений применяют метод лаковых покрытий. При нагружении в тех точках поверхности исследуемой детали, где удлинения достигают определенной
величины, в лаковом покрытии возникают трещины, перпендикулярные к направлениям главных растягивающих напряжений. Для оценки чувствительности лака, т. е. величины относительного удлинения е, прн котором появляются трещины, применяется тарировочиое устройство.
К задаче 7.26.
схематически показанное на рисун-
ке. Стальная балочка, защемленная одним концом, покрывается лаком и подвергается изгибу с помощью винта, передающего давле
ние на свободный конец балки (точка В). Прогиб в точке В изме-
ряется индикатором.
Определить чувствительность лака и величину напряжений в стали, вызывающих появление трещин в лаковом покрытии, если при прогибе f=l,4, мм трещины распространились на расстояние а = 20 см от заделки. Пролет балочкп Z = 60 см, размеры сечения: 6 = 30 мм, Л = 10 мм.
Ответ: е = = 2 • 10 о = £е = 400 кг/см3.
§ 23. Графоаналитический и графический способы определения перемещений при изгибе
7.27. Графоаналитическим способом определить величину прогиба и угла поворота концевого сечения для балок, изображенных на рисунке.
°””- ,) ч /-----9 =
, ЬРа3 2М0п2 2М0а Ра3
7 ' 6EJ EJ ’ °— EJ 2EJ *
18S
7.28. Графоаналитическим и аналитическим способами определить углы поворота опорных сечений и прогибы посредине пролета в двух вариантах загружения шарнирно опертой по концам балки равными опорными моментами (см. рисунок).
Ответ: а) 0Л=-0В=-^, /с=-^; б) 0Л = 0В =
7.29. Графоаналитически определить величину прогиба и угла поворота сечения на свободном конце балки, защемленной одним
концом и нагруженной, как показано на рис. а. Результаты проверить аналитически.
Решение. Построив эпюру изгибающих моментов для заданной балки (рнс. б), рассматриваем ее как сплошную фиктивную нагрузку, направленную вниз (М < 0). Опорные закрепления фиктивной балки (нулевая ось
К задаче 7.29.
К задаче 7.28.
Л*—В* эпюры М) выбираем в соответствии с условиями закрепления заданной Л1* Q*
балки. В сечении Д нет ин прогиба, ни поворота, т. е./д =-=-=-=0 и 0д=-=-?=О; CJ Си
поэтому оставляем конец Д* свободным (Л4^=0, Q*=0). Сечению В, где fB jc 0 и 0В # 0, соответствует защемление фиктивной балки в точке В4* (Л4^ Ф 0 и ?£ 0). Именно эти величины М J и нас и интересуют.
Для их определения заменим сплошную фиктивную нагрузку грузовыми площадями <ot, <о2 и а>3, т. е. сосредоточенными фиктивными силами, приложенными в центрах тяжести каждой нз площадей. Напомним, что площадь, ограниченная параболой n-й степени (заштрихованной па рнс. в), равна п , (л -f-1) а
<о=-----ah, а расстояние до центра тяжести хс= , о>; Для «дополни-
п -J-1 & \п "г *)
телыюй» (пезаштрпхованной) параболы n-ой степени ah и хс= а.
Так как эпюра изгибающих моментов очерчена двумя квадратными параболами (л = 2), то грузовые площади будут
2 да3 да3 да3 ga3 1 да* да3
ttx=3-Vfl=3 ; Шз = -3 '-Ta = ~6-
180
Плечи этих сил относительно заделки (сечение В*): „ 3 13 а , 3 3
Ci = 2a—у п= g-п] сх = -^-+а = -^-а; с3 = —а.
Изгибающий момент и поперечная сила от фиктивной нагрузки в се* чеинн fl* будут равны:
Л /на* 13 . qa3 За qa3 3 \ 17 .
= <о2с2 —(оэсэ= — • у й + -у * y + lT ' ~ia) = _Т2? ’
Искомые перемещения соответственно будут f 17gn4 „ _Q*_ 9°*
'B~EJ=Z 12EJ ’ B~EJ~ EJ '
Для аналитической проверки полученных результатов рекомендуется выбрать качало координат в точке А, догрузив правую половину балки нагрузкой q вверх и вниз.
7.30. Используя принцип независимости действия сил, графоаналитически определить величину прогиба и угла поворота сечения на свободном конце консоли, нагруженной, как показано на рисунке.
Указание. Построить две фиктивные балки, т. е. две эпюры изгибающих моментов: от распределенной нагрузки q и от сосредоточенной силы Р (см. рис. б), определить перемещения от каждой нз нагрузок в отдельности и сложить их алгебраически.
Ответ- е=з&-
7.31. Графоаналитическим способом определить величину прогиба посредине пролета и углы поворота опорных сечений для балки, изображенной на рисунке.
Указание. Эпюру изгибающих моментов (рис. б) удобно разбить на два равных треугольника и параболический сегмент. Площадь сегмента квадратной
187
2 параболы, ограниченного произвольной хордой а-b (рис. в), равна <о = -^- he.
о
Если балка загружена равномерно распределенной нагрузкой q, то высота . 9е®
сегмента п = —, а расстояние от концов сегмента до центра тяжести его О
хс = с/2.
Отегт. fc = 0.
9go* . _ 7<7«з
48EJ ‘ В~48ЕГ
7.32. Для балки, изображенной на рис. а, графоаналитически
определить прогиб посредине пролета (/с) и углы поворота опорных
сечений (0Д н 0Я.) Проверить результаты аналитически.
Указание. См. задачу 7.31 (рис. б). Можно также воспользоваться приемом расчленения эпюры М, как это показано на рис. в—д. Уравнения изгибающих моментов (при отсчете абсцисс от одного начала координат):
Mt=Ax; Ms = Ax—P(x—а)—• _ <?(х—п)2
2
Строим соответствующие эпюры от А, от Р и от q:
Мд = Ах (рис. в); Мр = —Р (х—а) (рис. г); Мд= —Ч(Х2 Ф- (рне.д).
К задаче 7.33.
К задаче 7.32.
Эпюра М расчленяется на составляющие, которые строятся от каждой силы в отдельности, как для консоли, защемленной на правом конце (М = МА-\-Мр ); суммарный момент на опоре В равен нулю. От каждой нз эпюр графоаналитически определяются перемещения, которые затем
суммируются.
„ . , I3qa* . _ 19?о» . 7да*
Ответ. fc— 48EJ , Од — 48fJ , 16EJ’
7.33. Графоаналитически и аналитически определить угловые перемещения опорных сечений и прогиб посредине пролета для балки при следующих данных (см. рис.): а = 2 м, q = 2 т)м, Мо = qa* = 8 тм и £7=12 10» кгем*.
Отвез: 0Л = — да = — 0,00108; 0в = да = 0,00069;
^ = 0,95 см, ЧОС v
188
7.34. Для балки с консолью графоаналитически определить величину прогибов посредине пролета (/г) и на свободном конце (fD), а также углы поворота опорных сечений (0zl и 0Л) и концевого сечения (6D), если принять М0 = Ра.
Указание. Для определения Q* п М* удобно разделить фиктивную балку (рис. б) ка подвесную длиною I и основную (консоль длиною а), как показано па рис. в. Можно воспользоваться также методом расчленения эпюры (см. задачу 7.32).
_ , РаР .
Ответ: fc = jEJ- f D=
=_™(3/+2Й):ОД=-0Я=™:
»о-
7.36. Прогиб на свободном конце балки измеряется с помощью индикатора при различных положениях груза в пролете. На каком расстоянии х от левой опоры А следует поместить груз показание индикатора?
К задаче 7.34.
Р, чтобы получить наибольшее
Указание. Выразить фиктивную реакцию в точке В в виде функции от расстояния х и исследовать ее на максимум (см. рис. б).
Ответ: х=-±=я> 0,5771.
ишшнннн!
я) А р
L—a——а—»4<—а.—*
К задаче 7.35.
К задаче 7.36.
7.36. Для балок, изображенных на рисунке, графоаналитическим методом определить величину прогибов посредине пролета (/с) и иа свободном конце консоли (/D). Найти также углы поворота левого опорного и правого концевого сечений (0Д и 0D), если а = 2 м, a EJ —10- 10е кгем2. Воспользоваться указаниями к задачам 7.31, 7.32 и 7.34.
139
Ответ:
Схема Прогибы, см Углы поворота
1с hi % «О
а —1.2 1.87 —0,00934 0,00934
б —0,667 1,33 —0,0040 0,00667
в — 0,33 0,73 —0,00167 0,00367
7.37. Элемент машины представляет собой балку пролетом /,
опирающуюся одним концом на шарнирно подвижную опору, а
К задаче 7.37.
другим—на вертикальные направляющие, вдоль которых свободно (без трения) скользит ползун, жестко связанный с балкой (см. рисунок). Графоаналитическим методом определить величину прогибов в точках А и С и угол поворота на опоре в двух случаях: а) если к балке будет приложена сосредоточенная сила Р в
середине пролета; б) если та
„ i f п₽р
Ответ: a) fA------
рр
же сила будет приложена к ползуну.
РР
6EJ' РР
16EJ’
А _3₽р. 8EJ*
А _ РР vb--^F-
7.38. Двутавровую балку № 24 предположено испытать сосредоточенной силой Р, приложенной посредине пролета. Считая балку
шарнирно опертой по концам, выбрать пролет балки I и необходимую величину нагрузки Р из условия, чтобы наибольшие нормальные напряжения и наибольший прогиб достигли допускаемых значений. Принять [о] = 1600 кг!см‘, [/] = 0,5 см.
Ответ: I = 300 см; Р= 6150 кг.
7.39. Пользуясь принципом независимости действия сил, графоаналитически определить величину прогибов посредине пролета
балки, изображенной на рисунке.
К задаче 7.39.
(/с) и на свободном конце (/о) для
190
Указание. Определить прогибы от каждой из нагрузок в отдельности (см. рно. б и в) и сложить их с учетом знаков.
„ - 7^о*
Ответ-. fc------з^-j
13<?а«
JD~ \2EJ ’
7.40. Зная, что для консоли, загруженной по всей длине равномерно распределенной нагрузкой q, прогиб на свободном конце по
абсолютному значению равен
/=
а угол поворота
0 =
из геометрических соображений
qi*
8EJ’
qla
&EJ '
определить: а) величину прогиба
В G
К задаче 7.40.
К задаче 7.41.
и угла поворота концевого сечения консоли, загруженной на половине длины; б) значения прогиба и угла поворота того же сечения, если нагрузку, распределенную по длине АВ = а, переместить на участок ВС такой же длины.
Ответ-, а) /с=-^
ес=
qa3 6Ё7’
41ga* Л 7qa3
= 24 Е/’ °с— 6EJ "
7.41. Установить, как изменится величина прогиба посредине подвеской балки, если нагрузку, равномерно распределенную на Длине 2а (рис. а), заменить сосредоточенной силой P*=2qa, приложенной посредине пролета (рис. б).
Отвеп а) /= —1
6) /=
7.42. Балка пролетом I, шарнирно опертая по концам, несет нагрузку только от собственного веса. Установить, как изменятся наибольшие нормальные и касательные напряжения, углы поворота опорных сечений и прогиб посредине пролета, если все
191
размеры балки увеличить в л раз. Каково булет изменение наибольших напряжений и перемещений, если изменить условии опирания балки?
Ответ: 1) Прогиб увеличится в ла раз; все прочие величины — в л раз.
2) При действии только собственного веса эти соотношения не зависят от схемы опирания балки.
7.43. Для балки, изображенной на рисунке, графически определить величину и направление прогибов посредине пролета (/с) и на свободном конце (/о), если пролет / = 6 м, длина консоли а = 2 м, Л10 — 2тм, Е — 2-10* кг/см2, J = 3500 см*. Проверить полученные результаты графоаналитически.
Решение. Определение прогибов сводится к построению эпюры изгибающих моментов от фиктивной нагрузки. Вычерчиваем схему балки а выбранном масштабе длин и строим для нее эпюру изгибающих моментов. Принимая
I.I Illi -I---1
1 0 1 2 3 4 5 6 м
Масштаб фиктивных сил
|пн|1 1-^ н-1 н-^.1—
10 2 4 В В 10 12тмб
К задаче 7.43.
площадь эпюры М за сплошную фиктивную нагрузку, разбиваем ее на ряд грузовых площадей ы2 11 т- Д-. т- е- заменяем сплошную нагрузку сосредоточенными фиктивными силами, приложенными в центрах тяжести грузовых площадей и равными
ci)I=(0j = 2 тм2, со3=а>4 = 4 тм2, со6 = соб = 2 тм2.
Выбрав масштаб фиктивных сил, строим силовой многоугольник при произвольно взятом в том же масштабе полюсном расстоянии Н. Положение полюса О по высоте также произвольно. Точка О размещается слева от линии
192
сил, если они откладываются по обходу слева направо; направление фиктивных сил выбирается в зависимости от знака эпюры М-. если М > 0, то <о > 0, т. е. откладывается вверх.
Учитывая симметрию фиктивной нагрузки, размещаем полюс па середине высоты суммы сил, проводим лучи А— I, 1 — 2 и т. д. и строим веревочный многоугольник, начиная от точки А. Чем больше число грузовых площадей <о, тем ближе веревочный многоугольник к кривой, изображающей изогнутую ось балки с увеличением в
ЕJ . (. М* , Hi] т] \
—раз ( М9 = Нц; так как f = -=rr, то f=-=rf=-l-\.
П \ EiJ I2JRJ
Замыкающая веревочного многоугольника АВ проводится так, чтобы удовлетворить условиям закрепления заданной балки (так как /д = 0 и /в=0, то т]д=0 и т]я=0). Остается измерить в масштабе длин ординаты т]с » Лд от замыкающей АВ до соответствующих сторон веревочного многоугольника 3—4 и 6—В (продолженной до вертикали D'D). Они оказались равными
т]С=175сл1, t]D=200 см.
Так как полюсное расстояние принято нами И=8 гм2, а жесткость
EJ = 7 -10е кгем2 = 700 тм2, то соответствующие прогибы будут . Н 8175 _ ^с-Е/Лс- 700 -2с“’ , 8-200 __
^D~ 700 ~2,3 СМ~
Графоаналитическое решение дает 7М<р2
fD=^f-=2,2ScM.
1с- 4EJ - 2 см.
7.44. Пользуясь графическим методом, построить изогнутую ось и определить величину прогибов посредине пролета (/с) и на свободном конце консоли (fD) для двух балок, показанных на рисунке, если
Р=4 т, / = 4а = 4 ж
и а)
EJ = 400 тм2.
Проверить результаты построения графоаналитически.
Ответ, а) /с = 2 см, fy „
fD = —2,33 см; ------1------
б) /г =—1,83 см, v
f= 1,5 слс.
7.46. Построить изогнутую ось балки с шарниром и определить величину прогибов в шарнире (/с) и в сечении под силой P(fn\. если жесткость балки EJ = 2400 тм2 (см. рисунок на стр. 194). Проверить результаты графического решения аналитически.
193
Указание. Так как заданная балка расчленяется на основную и подвесную балки, следует провести две замыкающие: одну HjCj для основной балки, направленную вдоль первой стороны веревочного многоугольника (так как 0л=О и /л = 0). и другую С]/?! для подвесной балки, проходящую через
шарнир Ct и опору (рис. б). Веревочную кривую можно привести к горизонтальной нулевой осн (см. рис. в).
Ответ: fc =—1,77 см; /о = 0,8 см.
7.46. Графоаналитически и графически определить вертикальное перемещение шарнира С для балок, изображенных на рисунке, если
К задаче 7.46.
Л4О = 6 тм. Двутавровое сечеиие балки подобрать по наибольшему изгибающему моменту при допускаемом напряжении [а] = 1600 кг/см1, 1 = 3 м.
Ответ: a) fc =— -^т =— 1,8 см (двутавр № 27); OL J
б) /с = ^Т=1.8сл1.
7.47. Для балок с шарнирами, рассмотренных в задаче 7.22, при заданных размерах и нагрузках графическим способом определить величину прогибов в шарнире (/с) к на свободном конце (/с). Построить изогнутую ось балки, приведенную к горизонтальной нулевой линии.
Ответ: См. задачу 7.22.
194
§ 24. Энергетические методы определения перемещений
7.48. Пользуясь зависимостью между потенциальной энергией деформации, накопленной в элементах кронштейна, показанного на рисунке, и работой внешних сил, определить величину вертикального перемещения узла, в котором приложена сила Р, равная 12 т. Стальная оттяжка имеет сечение 10 см2, а подкос из сосны —250 см2.
Ответ: 0,273 см.
7.49. На балку пролетом Z, шарнирно опертую по концам, в середине пролета действуют сосредоточенная вертикальная сила Р и сосредоточенный момент М. Жесткость балки EJ постоянна. Чему равна потенциальная энергия деформации балки?
/и/a мН
Ответ‘ 96£7+24Ё7‘
7.60. Балка пролетом I постоянного сечеиня с жесткостью EJ и высотой h испытывает чистый изгиб. Подсчитать количество потенциальной энергии, накопленной балкой, предполагая, что наибольшие нормальные напряжения в балке равны допускаемым [о].
„ 2 [а]2 Л
Greer..
7.61. Рама, показанная на рисунке, имеет одинаковых размеров ригель и стойки, жестко соединенные между
собою и изготовленные
К задаче 7.51.
К задаче 7.52.
этих элементов рамы а = 100 см. Велн-Р, стремящейся переместить подвижную 600
Длина силы равна
из двутавров № 10. чина горизонтальной опору рамы влево, потенциальной энергией изгиба чину перемещений левой опоры
Ответ: 4- = 2,525 см.
О tZJ
7.62. К балке на двух опорах, пролетом 2а = 4 м, прикреплена жестко на правом конце стойка высотой а = 2 м Дем. рисунок).
кг. Пользуясь зависимостью между и работой силы Р, определить вели-рамы.
195
К верхнему концу стойки приложена горизонтально сила Р = 900 кг. Как балка, так и стойка выполнены из двутавров № 16. Пользуясь тем, что работа внешних сил равна потенциальной энергии изгиба, вычислить величину горизонтального перемещения точки приложения силы Р. Значительно ли изменится величина перемещения, если при вычислении учесть также и потенциальную энергию сжатия балки?
Ответ-. 4,12 см; увеличится лишь на 0,009 см.
7.53. Двутавровая стальная балка № 22 пролетом 6 м оперта одним концом па шарнирно неподвижную опору, а другим — на винтовую цилиндрическую пружину. Диаметр оси пружины 10 см, диаметр стержня пружины 2 см, число витков 6. Подсчитать количество потенциальной энергии, накопленной этой системой под действием силы Р—2 т, приложенной посредине пролета балкн. Пользуясь зависимостью между потенциальной энергией и работой внешних сил, найти затем величину вертикального перемещения среднего сечения балки.
Ответ. 3640 кгсм; 3,64 см.
7.64. Определить при помощи теоремы Кастильяио прогиб балки в сечении С (см. рисунок, схема а), а также углы поворота концевых сечений балки.
К задаче 7.54.
Решение. В точке С нужно приложить дополнительную силу Рд> чтобы затем вычислить прогиб, как сумму интегралов:
1 С м dMi^ . 1 С «
Ус~ EJ J М1 дРл dx+ EJ J Мг дРа dx-(о) (Ь)
' Покажем балку с заданной нагрузкой и силой Рл, отметив абсциссы текущих сечений jq и х2 (схема б). Вычислим опорные реакции:
А = ~^ + Ря^. В=^+Рл±,
затем вычислим все подынтегральные величины:
М1=Мо-Мо^ + Ря±Х1,
190 '
После вычисления частных производных нужно принять Рл равным нулю. . Искомый прогиб
Р ° 6Е/(а + 6)*
Для определения угла поворота левого конца балки А нужно подсчитать опорные реакции для заданной схемы а загружения балки, составить выражения М (х), взять производную по заданному моменту Л1о и вычислить следующий интеграл:
о 1 С « , . ЯМ (х) . 1 С ал Л х\л а М»1
°А~ EJJ М W дМ0 dx~ EjyM°\X I ) dx~3EJ ' о о
Для определения угла поворота правого конца балки В надо рассмотреть новую схему в загружения балки, где, кроме заданного момента Мо на левом конце балки, приложен еще Л1Я иа правом конце В. Вычислив опорные реакции, изгибающий момент М (х), частную производную М (х) по Мя для этой схемы в, составляем интеграл, определяющий величину искомого угла поворота:
i i
а 1 (м Z Ч (X) 1 С , X \ X М01
°в~ EJJMM dM*dx~ EJj M°V I J I dx 6EJ • о 0
Все три ответа имеют положительный знак. Это означает, что прогиб Ус направлен вниз (как и сила Рд), угол поворота на левой опоре—по часовой стрелке (как и Л10, по которому брали частную производную) и угол поворота на правой опоре—против часовой стрелки (как направлен Мя).
7.ББ. Определить при помощи теоремы Кастильяно прогиб сечения С и угол поворота сечения D для балок, показанных на
а) ’
К задаче 7.55.
рисунке. Р=2,1т, М = 2,1 тм, д=1,2т/м, а=1м, сечение балок — двутавр №12.
S Ро& Pcfi
Ответ: а) —=—2,5 см, ==гт- = 0,015 рад; О С J J
7 Ма2 „ г. Ма л ,
б) —г--Б7-=—3,5 см, -7^=7=0,0025 рад; О C.J IZCJ
в) -§1ё = -0’916 см> -^=-0,0093 род.
7.66. Определить способом Максвелла—Мора прогиб и угол поворота конца консоли стальной балки, загруженной, как показано на рисунке. Р=2 т, q=3 т/м, 1 = 4 м, а=1 м, 7=3500 см*.
197
Решение. Перемещение сечеиня балки (прогиб или угол поворота) по Максвеллу—Мору выражается следующей суммой:
Х'' С М • М° dx
д = 2- J —Ё1 •
(/)
Здесь Л1(х) или М—изгибающий момент в текущем сечении балки прн заданной схеме загруження (см. схему о), а М°—изгибающий момент в том
К задаче 7.56.
же сечении от загружения единичной нагрузкой. При отыскании прогиба за единичную нагрузку принимается груз Р°=1, приложенный в том сечении, где отыскивается прогиб (см. схему б).
Проведем параллельно следующие вычисления:
Загружеиие по схеме а
хг
2 ’
Загружеиие по схеме б '
Bo = poJL=2.t
М°=—1 -Xi=—*1.
Л1°2 = -уХ2.
Теперь вычисляем прогиб у как сумму двух интегралов:
•0,667 см.
Раг(а+0 даР * 3EJ 24EJ
Знак <мпиус» показывает, что прогиб направлен в сторону, противоположную направлению силы Р°.
Для определения угла поворота конца консоли рассмотрим еще одно * состояние загружения (схема в), когда иа конце консоли приложен момент Л4°=1. Опорная реакция правой опоры прн этом состоянии загружения и единичные изгибающие моменты выразятся так:
Л^ = 1, Л1? = у-.
IBS
Значения же Mj и М2 от заданной нагрузки (схема а) вычислены ранее. Искомый угол поворота определится из следующей суммы интегралов:
EJ&= f jM2-M$dx = §-Px-l-dx + § (Sg-Q-S*} ±-dx.
о о о 0 4
e= Г— P -l(3a+2/)+^-l :EJ =0,0062 pad.
7.67. Определить способом Максвелла—Мора величину прогиба сечения С и угла поворота сечения D для баЪок, показанных на
К задаче 7.57.
рисунке. Р=1,8т, TH = 1 тм, ^=1,2 т/м, а=1 м, сечение балок — двутавр № 10.
Ответ: а) —~—0>884 сл», —=—0,00505 рад;
б) ^=0,632 см, — = —0,00842 рад; в) —^f = —0,2525 см,
*lc,J ОС J 1OZSJ
--^ = —0,002525 рад.
7.68. Определить способом Верещагина угол поворота конца левой консоли стальной балки АВ, нагруженной, как показано на рисунке. Жесткость балки равна EJ = 4 • •10е кгсм2.
Решение. Любое перемещение Л при нескольких участках за-гружеиия балки вычисляется в следующей форме:
,,о
д = 'У'®Л4с
EJ ’
где со—площадь эпюры изгибающего момента от заданной нагрузки, а Л1° —ордината эпюры изгибающего момента от единичной нагрузки Р» = 1 или М° = 1, приложенной в том сечении, где отыскивается
К задаче 7.58.
перемещение. Ордината М ° берется
в том сечении участка балки, против которого приходится центр тяжести эпюры изгибающего момента от заданной нагрузки на этом участке.
199
Применим принцип сложения действия сил и построим отдельно эпюры изгибающего момента: от силы Р (эпюра б), от нагрузки q в пределах пролета (эпюра в), от нагрузки q на консоли (эпюра г). Подсчитаем площади этих эпюр (грузовые площади);
«в, = • 1 1 = 0,5 тм, <i)2 = -^-1-4 = 2 тм2,
<оа = -^--1-4 = -|-т.н2, w4 = -~1-4 = 2 т.н2, О О
1 1 о 2 1
<о5 = _.1.2=у тм2.
Приложим к балке момент М° = 1 иа конце левой консоли (схема д) и построим эпюру изгибающего момента от этой единичной нагрузки (схема е). Вычислим значения ординат Л4°, приходящихся против центров тяжести грузовых площадей, показанных иа схемах б, в и а. Эти ординаты отмечены на схеме е. Затем вычислим величину искомого угла поворота сечения Л:
£Л0л = -О,5-1-2| + у-4-24“4'О = _Б’™2-
7-Ю7
°^=—Г4Лб5Г=-°-0029 род-
D балок, показанных па
7.59. Пользуясь методом Верещагина, определить величину прогиба сечеиня С и угла поворота сечеиня
К задаче 7.59.
рисунке. Жесткость каждой балки EJ=8-108 кгсм2, Р=1,2 т, М = 0,8 тм, = 1,6 т/м, а = 1 м.
Ра3 9РдЗ
Ответ: а) ==у = 0,50 см, —=—0,01 рад;
б) -^ = 0,25 см, —^ = —0,0067 рад; OtJ &E.J
в) ^£ = 0,625 см, — 2g = —0,005 рад.
7.60. Определить горизонтальное перемещение опоры В рамы, показанной на рисунке, под действием равномерно распределенной нагрузки. Найти также вертикальное перемещение сечения С и угол поворота сечения D. Жесткость всех трех участков рамы одинаковая и постоянная.
Решение. Задача может быть решена при помощи теоремы Кастильяно, прн помощи интегралов Максвелла—Мора или методом Верещагина. Применим метод Верещагина. От заданной нагрузки (схема а) построим эпюры изгибающего момента (схема б). Покажем положения центров тяжести площадей
200
и подсчитаем величину площади каждого участка эпюр:
2 <?Л2 , qh3 “‘ = -3-2-Л=-3-
1 qh- qh2a “2- 2 ~2~а~~
Приложим к раме силу Р°=1 в месте искомого перемещения по его направлению (схема в). Построим от этой единичной нагрузки эпюру изгибающего момента (схема г) и отметим иа каждом участке этой эпюры ординату.
Ю ff) в) г)
К задаче 7.60.
соответствующую положению центра тяжести площади каждого участка эпюры от заданной нагрузки:
= M°=h.
О
Горизонтальное перемещение опоры В рамы определится суммированием следующих произведений:
• I (qh* 5 qh2a \_
Ав = ёД-3--8Л + — h) =
Для определения вертикального перемещения сечения С нужно приложить в этом сечении рамы силу Р°=1, действующую вертикально, и для этого состояния загружения построить эпюру изгибающего момента, а затем вычислить ординаты этой эпюры, соответствующие положениям центров тяжести площадей эпюр от заданной нагрузки (схема б). Далее следует снова выполнить операции по перемножению площадей эпюр от заданной нагрузки на вычисленные, как указано выше, ординаты эпюр от единичной нагрузки. Просуммировав эти произведения и разделив иа жесткость, получим величину вертикального перёмещеиия сечеиия С.
Дли определения угла поворота сечения D нужно рассмотреть состояние эагружеиня рамы моментом М°=1, приложенным в сечеиии, где требуется определить угол поворота. Затем вновь выполнить операции, аналогичные перечисленным выше.
Л оЛ2о2 _ qh2a
Ответ'Ус- — -з2ЁЗ> 0О-Т2Ё7-
7.61— 7.63. Определить любым энергетическим методом величину вертикального перемещения сечения А(уА), величину горизонтального перемещения сечения В(Дв) и величину угла поворота сечения С(0с) показанных на рисунках статически определимых рам постоянной н одинаковой иа всех участках жесткости EJ.
С отрицательным знаком указаны в ответах перемещения, направленные вниз п влево. Отрицательный угол поворота—по часовой Стрелке.
201
Ответ к задаче 7.61:
Схема EJyA EJ*B Ej.ec
а 384 & 1 „ 12 А
б Тб^ -ГбРсЭ
0 -Те*"' у Мак 4- Ма 6
г ±PV(a + h) О -4-р/ш 0
202
Ответ к задаче 7.62:
Продолжение ответа к зад. 7.63.
Схема EJyA EJ.bg EJOC Схема EJ-Va EJ-bg EJ-ec
и — Ма-и -^Ма- О —| Ма н ~iqa*
к T2qal 7 . 1 , Vfl3 0 iqa* ~rqa3
л о| сл *0 о ы о п 4- Ра3 6 . w| КЗ "О a и 4- Pa3 D
м 1 — 13!’°3 р 1 . -6qa 1 . 12 qa
§ 25. Определение перемещений в балках любым способом
7.64. Путем вычисления перемещений в балках проверить на двух частных примерах, показанных на рисунке, справедливость теоремы о взаимности перемещений.
К задаче 7.64.
Л РГ-а о о Ml
Ответ: y1—yi — ; 6t — 02 — 24£j •
7.65. Балка иа двух опорах с консолью загружена, как показано на рисунке. Какой величины должны быть сила Р, чтобы прогиб конца консоли равнялся нулю?
Ответ: 10 г.
д=3т/м
m А I
р,-----зм------
К задаче 7.66.
К задаче 7.65.
7.66. Балка на двух опорах загружена сосредоточенным моментом, как показано на рисунке. Определить величину прогиба в сечении, где приложен момент, и угол поворота на каждой из опор.
204
л Mab(a—b) o M(a2+2ab—2b?)
Ответ: у — 3EJ (a + b) • ^A~ GEJ (a + b) ’
M(b2 + 2ab—2a2)
6EJ (a+b) •
7.67. Для балок, защемленных одним концом п загруженных, как показано на рисунке, определить величину прогиба свободного конца
К задаче 7.67.
ук и величину угла поворота сечения посредине пролета балки О-Для упрощения подсчетов принять P = qa и M = Pa = qa*.
Ответ: yK = k 0 = Л' • ; значение числовых коэффициен-
тов k и k' приводятся ниже в таблице.
1 Схема k к' Схема ь Схема it Л' Схема и к’
а д и 1 1 1 ьэ| — !g| сл оо| м 1 2 0 6 б е К 23 24 7 24 0 _ 1 2 0 1 6 в ж л 19 8 41 24 7 6 тг |c«J U5 |<о сч |л 1 1 1 г в м 13 24 29 24 _2_ 3 1 3 5 6 1 3
7.68. Симметричные двухконсольные балки загружены симметричной нагрузкой, как показано на рисунках в таблице на стр. 206. Определить в буквенном виде величину прогиба конца консоли ук, величину прогиба посредине пролета ус и величину угла поворота сечения на левой опоре.
205
К задаче 7.68 (см. стр. 205).
7.69. Стальная двутавровая балка № 24, защемленная одним концом, пролетом 2 м загружена равномерно распределенной нагрузкой интенсивностью 600 кг/м. Какой величины сосредоточенную силу Р можно приложить дополнительно на свободном конце балки, чтобы наибольшие нормальные напряжения не превышали 1600 кг/см-, а наибольший прогиб не превосходил 1/300 пролета балки?
Ответ: Р=1280 кг (из условия жесткости).
7.70. Приняв прогиб балки в среднем сечении (см. рисунок) при загрузке по схеме а за единицу и сравнивая между собой нагрузки балок на остальных трех схемах рисунка, установить, чему будут равны прогибы среднего сечения этих трех балок. Путем сравнительных подсчетов определить, во сколько раз наибольший прогиб балки по схеме в меньше прогиба посредине пролета балки а.
Ответ. 1) 0,5; 0; 0,5; 2) в 16 раз.
20в
7.71. Определить величины прогибов и углов поворота в сечениях А и В двух балок, показанных на рисунке, различных по
К задаче 7.70.
условиям закрепления, а затем изобразить примерный вид изогнутой оси этих балок.
К задаче 7.71.
Ответ: а) уА = — , Ув = 0, 0л = ~, 0в = 0;
2Р«3 Л о ЬРа- о Ра1
б) Уа-~ 2ЁТ' Ув — 0’ е-4-6ЁТ' ев-—6Ё7
(слева от шарнира) и 0В = О (справа от шарнира).
К задаче 7.72 (см. стр. 203).
Схема UopuuiiT Номер двутавра Ответ
Ус. СМ »к- см Вл рад
9 «J я А ° i о 4 а -М q PI ппннпГннггл^ ] 1 2 27 27 —0,866 —0,931 0,266 0,196 —0,01067 —0,00931
q N 1111111111111 ГГТП1 1 2 33 30а 0,169 —0,343 —0,474 —0,129 0,00068 —0,00343
н * — у -► 1 1 2 27 30 —0,067 —0,799 —0,566 0,494 —0,00133 —0,00659
*7/ 1 2 27 18 —0,498 0 2,413 —0,711 —0,00732 —0,00518
ь Л _
- V ТТЛ! 1 2 24а 18 —0,658 0 0,844 —0,194 —0,00438 0
1 2 24а 33 —1,272 —0,881 1,37 0,89 —0,00965 —0,00678
207
7.72. Определить величины прогибов одноконсольных балок (показанных на рисунках в таблице на стр. 207) посредине пролета и на конце консоли, а также величину угла поворота сечений иа левой опоре. Пролет балок / = 4а = 4 м, длина консоли а = 1 л. Предварительно подобрать номер двутавра сечения балки при допускаемом напряжении 1600 кг/см1. Нагрузка для каждой схемы балки задается в двух вариантах: 1) q=2 т/м, Р>=4 т, Л4 = 6 тм; 2) q=4 т/м, Р=6 т, М = 2 тм.
7.73. Для указанных на рисунке балок на двух опорах определить величину прогиба в сечении С и угла поворота на правой опоре В. Предварительно подобрать сечение каждой двутавровой балки из условия прочности при допускаемом напряжении 1600 кг/см1 или воспользоваться данными о номерах двутавров, указанных в таблице с ответами. Предлагается два варианта загружения балки: 1) q = 2 т/м, Р=4 т, Л/=6 тм и 2) q=4 т/м, Р=6 т, Л1 = 3гл. Пролет балок I = За = 6 м. На какую величину Дус изменится прогиб каждой балки, если учесть ее собственный вес?
К задаче 7.73.
Схема Вариант Номер двутавра Ответ
ус. СМ Од. рад ЛУ(.. см
м с 1 1 2 33 40 —1,355 — 1,197 0,00926 0,00806 —0,031 —0,022
IIIIIIIHIII]
£ ... е> i (Г 1 1
-►/7 । 1 2 27а 30 —1,212 —1,319 0,00707 0,00675 —0,045 —0,038
.111111 1 .8
с ж IT
1 2 36 45 — 1,295 —1,117 0,00822 0,00692 -0,027 —0,017
НИИ IIIIIIIHIII
!к С С £ q м 8
IIIIIIIHIII 1 2 27 30 0,355 —1,130 —0,00488 0,00832 —0,046 —0,038 X.
k р * Л* с
,111111 1 2 27 20 —0,444 0 0,00866 0,00785 —0,046 —0,084
с р я а
IIIIIIIHIII 'i 1 2 27а 36 —1,858 — 1,046 0,01192 0,00775 -0,045 —0,027
ZZ—* р й?
208
7.74. Определить в буквенном выражении величину прогибов балок, показанных на рисунках. Прогибы определить в середине пролета CVC) и на конце консоли (jK).
7.75. Балки двутаврового сечения загружены, как показано на рисунках на стр. 210. Определить величины прогибов посредине пролета (_ус) и на конце консоли (ук), а также величину угла поворота на правой опоре. Длина участка а = 2 м. Нагрузка для каждой схемы балки задается в двух вариантах: 1) Л1 = 2 тм, Р=3 т, д=1 т/м; 2) М = 3 тм, Р—2 т, д — 2 т/м.
Номер двутавра следует определить из условия прочности при допускаемом нормальном напряжении 1600 кг/см-. Можно также взять иомер двутавра нз таблицы (графа 3).
После определения числовых значений величин перемещений подсчитать, какие следует назначить номера двутавров, чтобы наибольший прогиб в середине пролета балки не превышал 1,6 см, а на конце консоли 1 см.
7.76. Для двутавровых балок с шарнирами, показанных иа рисунках иа стр. 210, при размерах и нагрузках, указанных в таблице иа стр. 211, построить эпюры изгибающего момента, подобрать помер двутавра при допускаемом нормальном напряжении 1600 кг/см*, а затем определить величину прогиба в шарнире yz и на свободном конце консоли ук.
209
К задаче 7.75 (см. стр. 203).
J ж Ответ
Схема iptt а пт дпуташ услови очностп Зг ЗЕ е дпу-вра из ловпя ‘СТКО- и
о
а) р и 1 24а -3,16 1,23 0,00878 30а
А i & - 2 20 —2,54 —1,63 0 24
б) | м 1 ! Р 1 1 1 27 2,4 —3,87 —0,01533 40
А । J р ; я 2 22а 2,87 —4,42 —0,01732 36
в) 1 ; 1 24а —3,16 1,49 0,00878 30а
i - 1 2 22а —0,96 —1,67 —0,00478 27
1 Я !р —2,13
—0,27 —0,00667
г) маании 1 27 36
А । । Аг 1 ГТ 2 30 —2,64 0,75 0,008 36
д) ! М । я 1 18 3,10 —4,40 —0,01805 27а
А 1 2 22а 2,87 —4,18 —0,01735 36
1 1 гпт тт Г 1 20а -4,61 2,30 0,01642 30
е) А. 1 2 30 —2,92 1,84 ' 0,01120 36
к —2d >><
К задаче 7.76. (См. стр. 209).
210
К задаче 7.76. (См. стр. 209 и 210),
Схема Вариант '1 Размеры, jm Нагрузка Ответ
/. 1, а, а, р Q м„ "max № профиля Прогибы, см
т т/м тм ' тм Ус «к
1 а б в 3 4 3 5 4 5 1 3 1 1 1 1 10 8 5 4 2 2 16 10 8 27,2 11,0 13,6 55 36 40 —0,77 0,65 —1.12 -0,01 —0,71 —0,01
2 а б в 4 3 4 4 4 4 2 1 2 2 1 2 2 3 1 4 2 2 8 10 4 44,0 19,0 22,0 65 45 50 —1,07 — 1,44 —1,38 0,56 0,45 0,72
3 а б в 4 3 5 2 5 6 1 3 1 1 2 2 10 10 6 1 2 2 8 12 4 14,0 8,4 4,3 40 30а 24 2,25 1,13 2,51 —0,99 1,80 —1,18
4 а б в 4 4 4 5 3 4 1 1 1 3 1 1 4 3 4 2 2 2 14 10 10 12,5 8,0 5,3 36 30а 24а 1,60 0,88 —0,31 —0,71 —0,64 —1,01
5 а б в 4 4 5 3 5 4 1 1 2 2 2 2 1 2 3 2 1 2 6 10 12 6,0 6,0 13,0 27 27 40 —0,12 —0,36 —1,02 —0,13 1,78 0,61
6 а б в 5 6 4 3 3 3 1 1 1 2 1 1 1 4 2 4 2 4 8 6 8 17,4 12,5 12,3 45 36 36 0,55 0,96 0,56 —0,93 —0,57 - 0,38
’7 а б в 6 5 4 3 4 3 1 1 1 1 1 2 2 4 4 4 1 2 10 8 8 19,4 5,9 5,7 45 27 27 0,71 0,68 0,65 —0,20 +0,02 — 1,18
8 а б в 4 4 4 3 5 3 1 2 1 1 1 1 8 ' 2 2 4 1 4 9 , 8 2 9,0 8,0 7,3 33 30а 30 —0,21 —1,89 —0,19 —0,24 0,46 0,20
9 а б в 2 3 2 3 4 4 1 1 1 2 2 2 2 5 12 1 2 2 6 10 24 7,0 14,0 30,0 30 40 55 0,73 0,54 0,40 —1,69 —1,43 —1,11
10 а б в 6 4 3 4 3 2 2 2 1 2 1 1 1 2 4 2 4 2 6 8 4 6.3 12,0 4.0 27а 36 22а 0,48 —0,90 0,18 0,48 0,50 —0,33
ГЛАВА 8
СОСТАВНЫЕ БАЛКИ. БАЛКИ ПЕРЕМЕННОГО СЕЧЕНИЯ
§ 26. Составные балки
8.1. Подобрать двутавровое сечение сварной подкрановой балкн при допускаемых напряжениях: на растяжение и сжатие при изгибе [а] = 1600 кг!см-, на срез основного металла [т]=1000 кг/см* и на срез швов [тэ] = 800 кг/см-. Балка нагружена четырьмя равными силами по Р=40 т каждая (рис. а). Произвести полную проверку прочности принятого сечения по IV теории прочности и проверить жесткость балки при [/] = ggg I = 1,6 см. Собственный вес балки не учитывать.
а) в) г}
К задаче 8.1.
Решение. Эпюры поперечных сил и изгибающих моментов показаны на рис. a. Qraax=80 т> Л1тах=120 тм. Необходимый момент сопротивления сечения
М 120-10»
W > J l'nax lzu 7500 э (о| 1600 см •
Так как в таблице нормального сортамента нет двутавра с нужным моментом сопротивления, необходимо спроектировать составное сечение из листового металла—стенки и двух полок, соединенных сварными швами.
212
а) Предварительное назначение размеров сечения производится путем при-кидочных расчетов из конструктивных соображений, с последующей корректи* ровкой размеров по результатам поверочного расчета.
Высота стенки может быть взята по эмпирической формуле:
1,2 /^=1,2 V7500= 104 см
(IF —в сл3). Толщина стенки 6 выбирается из условия прочности на сдвиг, но не менее 0,6 см во избежание выпучивания ее. Так как поперечная сила Q почти полностью воспринимается стенкой, то, рассматривая ее как прямоугольник высотою h и толщиной 6, можно условно считать
_ 3Qmax гТ| 0ТКуДа $> 3<?шах _ 3 80 000 | 2
*тах- 2Л6 «т. откуда 02 (т] Л “ 2 1000-100 ’
Примем ft = 100 см и 6=1,2 см.
Для предварительного назначения размеров сечения полки допускают, что изгибающий момент в основном (на 80—85%) воспринимается полками в виде
пары сил N с плечом, примерно равным Л (рис. о). Следовательно, N = —.
Усилия N вызывают растяжение и сжатие полок. Поэтому площадь сечения полки
N _0,8М 0,8120-10® ,
nSS:[o]~ л [о] г- 100-1600
Ширину полок по конструктивным соображениям обычно принимают F 60
Ь к (0,3 -j- 0,4) Л. Приняв 6 = 30 см, найдем толщину полки: 1=—=^ = 2см.
Для уточнения намеченных размеров надо подсчитать момент инерции и момент сопротивления сечения относительно центральной оси:
J>=^+2^+w^y]=l^+2(^+2.30.5p)=412(X)0cj.., 1F„= -^-=-?5ЮО=79ОО сл3 > 7500 сл’.
zmax W
Сечение можно несколько уменьшить, например, изменив размеры полок. При-кидочиыми подсчетами найдены наиболее подходящие размеры сечения каждой полки: 6=31 см и t= 1,8 см. Тогда моменты инерции и сопротивления будут
ооо АЛЛ
Jv=389000 см*. TFV = ^; „ =7500 см\
что и требуется.
Статический момент полусечеиия относительно нейтральной осн
Sy=bt + . А=31.1,8• 50,9 +1 ’2 B100i = 2840 +1500 = 4340 сл®.
Z Z 4 о
б) Поверочный расчет принятого сечения. Наибольшие нормальные и наибольшие касательные напряжения соответственно равны
°тах= = 1600 кг/см*. т„,ах= =740 кг/см2 < [т].
Проверка по главным напряжениям в соответствии с энергетической теорией прочности должна быть произведена для наиболее напряженных точек в двух сечениях под силами: а) где Q = Qmax и б) где Л4 = Л4тах.
213
Наиболее напряженными оказались точки и К у мест сопряжения
-стенки с полками в сечении, где Af = Afmax (рис. в). Расчетные напряжения:
о’с = у/~ Oq + Зт® = 1598 кг/см1.
с™ = у/~оД4-Зт^ = 1670 кг/см-.
Переиапряжение (в точке К полки) составляет 4,3%, что допустимо.
в) Проверка прочности сварных швов. Продольная сдвигающая сила, воспринимаемая двумя фланговыми швами, препятствующими сдвигу полки ртно-
QSn
сительио стенки, на участке длины е равна Т = —=-^е. Площадь сечения двух
Jy
швов иа той же длине е (рис. г) равна F3=2-0,7 <эе= 1,4/8е, где t3— толщина шва.
от-
Т Qs"
Из условия прочности швов на срез -?-<[т8] найдемt3^ . у— ,
Г в 1>4 Jy [Тэ]
куда /8 = 0,52 см. Примем /8=6 мм.
г) Проверка жесткости сечения. Для оценки жесткости балки необходимо сравнить величину наибольшего прогиба- с допускаемым. Пользуясь одним нз способов определения перемещений при изгибе, находим величину прогиба оси балки посредине пролета. Наибольший прогиб равен
t 45Ра8 45-40 000 100s ,
f~ 2EJ “2-210«-389 000 ’ 6 см <
Заметим, что можно подобрать и другие вполне удовлетворительные варианты сечения.
8.2. Для перемещения тяжелых грузов сооружены временные подмости из имевшихся на строительстве прокатных швеллеров № 24. Каждая балка, перекрывающая пролет I = 6 ж, составлена из четырех швеллеров, склепанных полками
и стенками при помощи заклепок диаметром d = 17 мм, поставленных с шагом е=120 жж (см. рисунок). Поперечная сила в опасном сечении Q= 12 т, изгибающий момент М = 18 тм. Учитывая ослабление сечения заклепочными отверстиями, проверить прочность балки, а также прочность наиболее напряженных вер-
тикальных заклепок при до-К задаче 8.2. пускаемых напряжениях [ст] =
= 1600 кг/см? и [т] = 1000 кг/сж2.
Ответ: J6f = 29 200 сж4; ./„=26 000 сж4; «${[= 735 сж3; отах= = 1670 кг/сж-, ттак = 267 кг/см2-, т3 = 795 кг/см*.
8.3. Балка, свободно лежащая на двух опорах, составлена из двух рельсов типа 1-а, склепанных полками (см. рисунок). Площадь сечения каждого рельса F0 = 55,6cm2, момент инерции его площади относительно собственной центральной оси JPo=1476 сж4, расстояние от подошвы рельса до его центра тяжести Zc = 6,96 сж, диаметр заклепок d = 20 жж. Определить необходимый шаг заклепок е при
214
допускаемых напряжениях на срез [т] = 1000 кг/см*, если наибольшая величина поперечной силы в сечении балки Q= 12,25 т.
Ответ: е = 110 мм.
8.4. Пролетное строение временного моста проектируется из двух продольных сварных балок, расположенных параллельно, как показано на рисунке. Сечение каждой балки составлено из листа 10 X
К задаче 8.4.
Х800 мм (стенка) и двух полос (полки) 20x255 .мм, приваренных к стенке фланговыми швами с катетами t3 = 5 -им. Проверить прочность сечения, если изгибающий момент в опасном сечении моста Л4 = 140 тм, поперечная сила в том же сечении Q=120t, а допускаемые напряжения: [а] = 1600 кг/см2, [т] = 1000 кг/см? и [тэ] =
= 850 кг/см?. Воспользоваться энергетической теорией прочности.
Ответ: ог1Пах= 1370 кг/см*-, ттах = 810 кг/см2; а'р = = 1688 кг!см2 > [о]; т8 = = 835 кг/см2.
8.5. Рассмотреть два варианта усиления подкрановой балки двутаврового профиля № 65, осуществляемого путем прикрепления к полкам двутавра продольных полос сечением 20x240 мм:
К задаче 8.5.
а) с помощью сварки сплошными фланговыми швами и б) при помощи заклепок диаметром d = 30 мм (см. рисунок). Сравнить величины наибольших нормальных и касательных напряжений, вычисленных после усиления балки в каждом из вариантов, с теми, какие были до усиления. Определить также необходимую высоту катета швов fa в сварном варианте и наибольший допустимый шаг заклепок е в клепаном, если поперечная сила в опасном сечении Q= 100 т, а допускаемые напряжения на срез швов и заклепок [т] = 1000 кг/сма. При вычислении касательных напряжений момент инерции и статический момент сечения принимать брутто.
219
Ответ: а) сварной вариант: — = 0,515, — = 0,92, /„ = 5,5 мм; °о то
б) клепаный: -^- = 0,68; — = 0,92; е = 18,3 см.
Оо т0
8.6. Составная клепаная балка коробчатого поперечного сечения работает на изгиб в вертикальной плоскости. Изгибающий момент в опасном сечении Л1 = 800 кнм, поперечная сила Q = 480 кн. Сечение составлено из двух вертикальных и двух горизонтальных листов с одинаковыми поперечными размерами й = Л = 60 см, / = 1 см п четырех равнобоких уголков 75x75x8 мм, соединенных при помощи заклепок диаметром d = 23 мм (см. рисунок). Принимая ослабление сечения
К задаче 8.7.
заклепочными отверстиями 15% (от J6p), произвести проверку прочности балки и определить наибольший допускаемый шаг е горизонтальных поясных заклепок, если допускаемые напряжения приняты: иа растяжение и сжатие при изгибе [о] = 16 кн/см2; па срез основного металла и заклепок [т] = 10 кн/см2 и на смятие [стс] — 25 кн/см2.
Ответ: отах=15,9 кн/см2 < 16 кн/см2; ттах = 4,4 кн/см2 < < 10 кн/см2; е = 0,129 ж.
8.7. Проверить прочность клепаной подкрановой балки двутаврового сечения, составленной из стенки сечением 1350x12 лш2, четырех равнобоких уголков 140x140x12 Л1Л1 и поясных листов 350x10 мм2 (по два листа в каждой полке), соединенных при помощи заклепок диаметром d = 23 мм (см. рисунок), если изгибающий момент в опасном сечении М = 240 тм, поперечная сила Q=80 т, а допускаемые напряжения приняты: на растяжение и сжатие при изгибе [о] =1300 kzIcm2, иа срез основного металла и заклепок [т] = 800 кг/см2 и иа смятие заклепок [ос] = 2500 кг/см2. Шаг двухрядных поясных заклепок, размещенных в шахматном порядке, а = 130 мл1.
Указание. Ослабление горизонтальных листов считать двумя заклепками в каждой полке, вертикального листа—в соответствии с фактическим их размещением (см. рисунок) и каждого уголка—двумя заклепками — вертикальной и горизонтальной.
216
Ответ: сттах=1235 кг/см3 < [ст]; ттах = 540 кг/см3 < [т]; т3= =780 кг/см3 < [т]; стс = 2360 кг/см3 < [стс].
8.8. Два двутавра № 30а укладываются один поверх другого и изгибаются силой Р=10т, прикладываемой посредине пролета 1 = 6 м (см. рисунок). В этом положении полки двутавров свариваются, после чего нагрузка снимается. Определить величину нормальных напряжений в крайних волокнах сечения балки посредине пролета: а) при нагружении силой Р, б) после снятия нагрузки.
К задаче 8.8.
К задаче 8.9.
Сварочных (усадочных) напряжений не учитывать.
Ответ: а) ст = 1450 кг/см2-, стост--±270 кг/см1.
8.9. При допускаемых напряжениях [ст] = 1400 кг/см3 определить: а) величину допускаемой нагрузки Р, которую можно приложить посредине составной, балки, рассмотренной в задаче 8.8, если уло
жить ее на опоры, как показано на рисунке (при I — 6 м); б) какую силу Р, можно было бы приложить к составной балке из тех же двутавров, сваренных полками, но без предварительного изгиба? Сравнить величины допускаемых нагрузок.
Ответ: а) Р = 14,1 т; б) Pt = = 11,8 т, Р:Р, « 1,2.
8.10. С целью увеличения грузоподъемности имеющихся иа строительстве двутавровых балок № 60 (Л = 60 см) предложено разрезать каждую бал-
К задаче 8.10.
ку, как показано иа рис. а, а затем сварить обе половины по рис. б. Выяснить, как можно будет изменить величину допускаемой нагрузки на балку (в %) после осуществления проекта (учесть ослабление балки вырезами), если о = -у = 15см, с = 50 см.
Проверить также прочность сварных швов при допускаемом напряжении на срез [тэ] = 920 кг!см1, если Qmax = 20 т.
Ответ: В варианте б) грузоподъемность балки может быть повышена на 53%; тэ = 800 кг/см2 <920 кг/см3.
217
8.11. Деревянная составная балка пролетом 1 = 6 м, свободно опертая по концам, нагружена двумя равными силами Р=4,5ткаж-дая, приложенными на одинаковых расстояниях а = 2 м от опор. Балка составлена из двух сосновых брусьев сечением каждый 20 X 28 см,
соединенных при помощи сосновых же колодок и связанных болтами (см. рисунок)*). Размер каждой колодки с = = 40 см, h = 41 = 8 см. Проверить прочность балки и соединительных элементов при
допускаемых напряжениях: на
К задаче 8.11. растяжение и сжатие при из-
гибе [о] = 120 кг!см-, на смятие вдоль волокон [стс] = 125 кг/см2 и на скалывание вдоль волокон [т] = 12 кг) см2. Диаметр болтовых отверстий d — 2 см. Некоторая
податливость соединения учитывается снижением момента сопротивления сечения на 15%.
Указание. Момент инерции сечения при учете ослабления равен J„ = Jgp — — ДУ, где ДУ—момент инерции ослабления болтовым отверстием и вырезом под колодку. Момент сопротивления при учете податливости соединения принимается равным И7ц=0,85-----— .
zmax
Прочность соединения проверяется иа действие продольной сдвигающей _ Ощах^м , „п _ ,
силы Т =----у—-—е, где Jy и SJJ берутся брутто (расстояние между осями ко-
лодок е=2 с).
Ответ: а) Для балки: J6p = 293 000 с.и4; Jn = 263 000 cm*i №„=8000 см3; сттах=113 кг!см2.
б) Для колодок: Т = 9630 кг; стс = 120 кг/см2; т = 12 кг/см2.
8.12. Деревянный брус сечением 20x20 см2 усилен стальной полосой толщиною t = 20 мм, прочно склеенной с деревом и совместно с ним работающей на изгиб (см. рисунок). Определить величину нормальных напряжений в дереве н в стали, если изгибающий момент в опасном сечении балки М = 2,9 тм, а отношение модулей упругости материалов FCT: Дд = 20.
Решение. Балку, составленную из разных материалов, условно рассчитывают, заменяя ее сечение «приведенным! сечением из одного материала, эквивалентным заданному. Из условия эквивалентности и иа основании гипотезы плоских сечений следует, что е = е0 (черточка над буквой показывает, что соответствующее относительное удлинение относится к «приведенному» элементу сечения, а е0—к основному).
*) Колодками называются соединительные элементы, воспринимающие давления со стороны соединяемых брусьев торцами—вдоль волокон. Элементы, на которые давления передаются поперек волокон, называются шпонками. Стягивающие болты при расчете соединения не учитываются.
218
Так как е=~, то ±^-=Д^-. Так, если сталь заменяется деревом, то £ ° £
= 20, т.е. величина напряжений в деревянной полосе, заменяющей
Од *-Д
стальную, должна быть в 20 раз меньше, чем в стальной; поэтому ширину
— Е
полосы Ьо следует заменить шириной b = b0 -^ = 2ОЬо = 400 см (рис. 6). На-to
оборот, если дерево заменять сталью, то в приведенном сечении ширина
_ £
Ь=Ь0 -~ = \ см (рис. в). В обоих случаях приведенное сечение имеет вид £ст _
, , — Мг у
тавра, расчет которого на изгиб производится по формуле о = „ - , где Jy— J у
момент инерции приведенного сечения относительно оси у, проходящей через его центр тяжести.
Для сечения, замененного деревянным по рис. б, имеем:
Расстояние от оси бруса до центра тяжести сечения
- 2-400(10+1) см
с f 400 + 800
Момент инерции приведенного сечения
__ 9П опэ 400-93
/у=£!12±Г- + 400.7,332+-^^- + 800(11—7,33)2=45 700 сж*.
Расстояния до крайних волокон тавра от центральной оси:
~гл = Ю-l-7,33 =17,33 см, ^=10+2—7,33=4,67 см.
Нормальные напряжения в крайних фнбрах приведенного сечения: М1А 2,9-10»-17,33 11Л , „
°» = -T2L=---------«ТОО-------= П0 Кг/СМ"‘
Jy 2,9-10*-4,67 .
оВ = —=------------45 700-----= 30 кг/см'-
Действительные напряжения в крайних точках А и В будут: в дереве Од= ПО кг/см2-, в стали Од = ав =30-20 = 600 кг/сж2.
219
Рекомендуется проверить полученные результаты для сечения, «приведенного! к стали по рис. в.
К задаче 8.13. = 1600 кг/см2,
, 8.13. Защемленный одним концом деревянный брусок длиною I = 50 см и размерами сечения 6 = 2 см и 6 = 5 см, усиленный двумя стальными полосами толщиною каждая t = 2,5 мм и шириною 6 = 20 мм (см. рисунок), нагружен на свободном конце силою Р в плоскости xz. Считая совместную работу элементов сечения полностью обеспеченной, найти величину допускаемой нагрузки Р при допускаемых напряжениях для дерева [ад] = 100 кг/см2 и для стали [ост] = если отношение модулей упругости ЕЛ:ЕВТ = 1:20.
Ответ: Р = 93 кг.
§ 27. Балки переменного сечения
8.14. Балка, показанная на рисунке, имеет сеченне постоянной ширины b и переменной высоты h(x). Найти наибольший прогиб балки /11)ах м сравнить его с наибольшим -прогибом /0 балки такого же пролета и с той же нагрузкой, ио постоянного сечения.
К задаче 8.14.
Решение. Обозначим Мв изгибающий момент, а И70 момент сопротивления сечения в защемлении балки. Условие равного сопротивления изгибу выразится так:
М(х) _М0 г-т1 max-W' (х) “ W'0-,aj-
Подставив буквенные значения М (х), Af0, W (х) и 1Г0, получим qx2 6 _ ql2 6
откуда находим законы изменения высоты и момента инерции сечения: h(x) = hB±, J(x) = JB~.
Напишем уравнение изогнутой оси балки:
£J^dx2~ 2 * EJ° P'dx2 2 ’ EJty 2 ' x*
Интегрируем это уравнение:
EJBy’=— — lnx-f-С
220
и определим величину С из условия, что при х=1 у’ =0:
С = ^1п/, £Jo!/'=-^lnx + ^lnZ.
Интегрируем вторично:
EJBy = -4’х1п x + ^x+^+xhiZ + D.
При х=1 у=0; поэтому D=—
Окончательное уравнение прогибов:
EJBy = — (хInх—х—xln 74-/).
Приняв х=0 и так какх1пх—х1п/ = —xln-^- ПР11 этом тоже Рав,,° нулю, находим величину наибольшего прогиба балки:
f - ql* -if
/max 2EJB lo'
П римечание. При решении этой задачи, а также некоторых других задач параграфа 27 считаем, что в поперечных сечениях балки нормальные напряжения направлены горизонтально, хотя в действительности в верхних и нижних волокнах направление напряжений параллельно поверхности балки.
8.15. Две балки равного сопротивления имеют одинаковое квадратное сечение в защемлении и загружены одинаковыми силами на свободном конце. У первой балки меняется ширина, у второй — высота. Какая будет легче? У какой из них наибольший прогиб будет больше?
Ответ: : ф2 =Д :f2 = 3:4.
8.16. Из соснового бревна изготовлен брус переменной ширины с постоянной высотой Л = 10 см. Один конец бруса защемлен, а на другом, свободном конце приложен груз Р= 300кг. Пролет бруса 1 = 1,2м. Какой должна быть ширина бруса в защемлении Ьв и наименьшая ширина b на свободном конце при допускаемых напряжениях [о] = 100 кг!смг и [т] = 12 кг/см2? На какой длине а от свободного конца должна быть выдержана наименьшая ширина бруса? Определить прогиб Д свободного конца бруса. Чему будет равен прогиб конца бруса, если считать, что ширина сечения меняется по линейному закону от Ьв в защемлении до 0 иа свободном конце?
Ответ: t0 = 21,6 яа 22 см; Ь = 3,75 «4 см; а = 22,2 « 22 см;
Pl Pl3
л ----/•—ST.’-1’41 СЛ
8.17. Балка равного сопротивления изгибу, защемленная одним концом, имеет квадратное поперечное сечение и несет равномерно распределенную но всей длине нагрузку интенсивностью q. По какому закону должна изменяться сторона квадрата, если задана
221
величина допускаемого нормального напряжения [а]? Чему равен прогиб свободного конца балки?
_ , 3<?хг , 3ql*
Ответ-. =
8.18. Балка на двух опорах имеет форму равного сопротивления изгибу при прямоугольном поперечном сечении постоянной высоты h. Балка загружена равномерно распределенной нагрузкой интенсивностью q. Зная высоту балки, величину пролета, допускаемые напряжения и модуль нормальной упругости, вычислить величину наибольшего прогиба, предполагая, что на опорах ширина балки сходит на нет.
Ответ-
8.19. Стальная балка круглого поперечного сечения диаметром 12 см оперта по концам и загружена посредине пролета, равного2,4м, грузом Р= 1800 кг. Определить величину наибольшего прогиба балки. Чему станет равен прогиб, если балке придать форму равного сопротивления изгибу?
ЗР/з
Ответ’. —0,255 см; . опс., =—0,458 см.
oUt J Q
8.20. Стальная полоса длиной 126 см и шириной 5 см опирается по концам на шарнирные опоры. Толщина полосы в середине про-(2х\1/
у I /з. Под действием силы Р, приложенной посредине пролета, прогиб под силой равен 2,4 см. Чему равна сила Р?
Ответ: 32 кг.
К задаче 8.21.
8.21. Балка из соснового бруса переменной ширины имеет форму и размеры, показанные на рисунке (схема а), причем Ьо = 3&1. Силы Р=200кг каждая. Найти наибольший прогиб.
222
Решение. Применим графоаналитический способ. Построим эпюру М (схема б). Моменты инерции сечений балки иа трех ее участках соответственно равны:
Приведем эпюру М (х) к эпюре балки одинаковой жесткости EJB па всех участках. Для этого ординаты эпюры М (х) на участках I увеличим в 3 раза, на участках II— в отношении а:х, а иа участке 111 оставим без изменения (схема в). Вычислим площади фиктивной нагрузки coj и <о2, а затем фиктивную опорную реакцию R$:
“>>=¥• «2=i-pa-. R*='-ip<t-ио о
Фиктивный изгибающий момент в середине пролета
Л,*= “V Р^+^Ра2 Gh+W +4 Ра‘ * 1п=---------------Ра9'
w О о \ о У / 3 о 54
107Рс3
Величина наибольшего прогиба /=—= —1,41 см.
Если предположить, что на участках / ширина балки меняется так же, как и на участках II, то наибольший прогиб
8.22. Балка равного сопротивления изгибу, показанная на рисунке, меняет ширину прямоугольного сечения Ь(х) от нуля на опоре А до Ьо на опоре В по линейному закону. Значение Ьо затем сохраняется на всем участке ВС. Определить величину прогиба сечения С графоаналитическим способом.
Ответ: +
К задаче 8.22.
К задаче 8.23.
8.23. Деревянная балка пролетом 2Z = 80 см защемлена левым концом. На правом, свободном конце балки приложена сила Р = 200кг. Диаметр одной части балки!3 см, другой—10 ext (см.рисунок). Чему равны наибольшие нормальные напряжения в сечениях I—7 и II—//? Найти величину прогиба свободного конца балки. Влиянием концентрации напряжений пренебречь.
Указание. Для определения величины прогиба удобно применить теорему Дастильяно. Отношение J4:Ji = 2,86. Выражение для величины искомого
223
прогиба имеет следующий вид:
I 21
1=^г f Рх* dx + ir f Pxi dx=Sr (1 +21б) •
cJj J J 3cJj \ 2,00 /
0 /
Положительный знак в ответе для прогиба означает, что направление
прогиба совпадает с направлением силы Р, по которой вычислялись частные производные.
Ответ: 011 = 0,910!; о, = 81 кг/см4; 0,3 см.
8.24. Из сосновой доски изготовлена балка со ступенчатым изменением сечения, показанная на рисунке. Пренебрегая влиянием концентрации напряжений, вычислить наибольшие нормальные напряжения, наибольшие касательные напряжения и наибольший прогиб
балки от действия силы Р = 400кг.
Ответ: 94 кг/см2: 12,5 кг/см2: —0,054 см.
К задаче 8.25.
К задаче 8.24.
нормальное напряжение в любом
8.25. Чему равно наибольшее
сечении балки переменного сечения, показанной па рисунке?
Ответ: атах
8.26. Стальная полоса переменной ширины имеет размеры, пока» занные на рисунке. Р=10кг. Вычислить наибольшие нормальные напряжения и наибольший прогиб полосы.
• ПР/3
Ответ: ami = 273 кг/см2: f = — = 1,25 см.
J q
224
8.27. Определить необходимую ширину Ьп стальной полосы, показанной на рисунке, при допускаемом напряжении [сг] = 1500 кг/см* от действия силы Р = 40кг, а также наибольший прогиб балки.
17Р/3
Ответ-. b0 = 4 см; f= —тёгг — ~2’66 см-J q
8.28. Стальная рессора (см. рисунок) составлена из девяти листов, образующих брус равного сопротивления изгибу постоянной
высоты, и десятого листа таких же размеров, как самый длинный из девяти. Ширина каждого листа Ь = = 6см, толщина t = 1 см. Пролет
К задаче 8.28.
К задаче 8.27.
рессоры £=108 см. Найти прогиб рессоры посредине ее пролета при значении Р= 1200 кг.
Решение. Изобразим рессору как брус переменной ширины с размерами, показанными в нижней части рисунка, в плане. Начало координат примем в точке пересечения проекций боковых граней бруса. Для определения прогиба применим теорему Кастильяпо с учетом переменного значения момента инерции сечения балки:
«Цх) =
60
С М (х) дМ (х) J £J(x) * дР 6
Ь»ТГ6=6О-Й=Х’ JW = J»TT6’
Д1(х) = Р(х-6), ™Щ=х-б,
—
Для рессоры из девяти листов (без верхнего) прогиб при тех же остальных условиях оказался бы равным
р/з /=^=10,5 см.
225
8.29. Стальная рессора (см. рисунок) состоит из десяти листов
шириной 7,5 см и толщиной 10 мм. Пролет рессоры 1 м. Допускаемое напряжение [а] = 4000 кг]см-. Определить грузоподъемность рессоры
К задаче 8.29.
и величину прогиба посредине пролета.
Ответ: [Р] = 2000кг; /=
[«И Р с = _—=-бсм.
8.30. Стальная рессора равного сопротивления изготовлена из полос шириной 8 см и толщиной 8 мм. Сколько нужно полос, если рессора в середине пролета несет груз Р=1280 кг при допускаемом
напряжении [о] = 3000 кг/см-, а величина пролета рессоры I = 80 см?
Вычислить величину осадки рессоры под указанным грузом.
Ответ: 10 полос; 3 см.
8.31. Балка переменного сечения (см. рисунок) пролетом I = 5,4 м
лежит на двух опорах и несет равномерно распределенную нагрузку интенсивностью q. Балка составлена из двутавра № 30 и двух нар
К задаче 8.31.
листов; первая пара листов размерами 115 X 10 мм приварена к полкам двутавра; листы второй пары размерами 95X10 мм приварены к листам первой пары. Допускаемое напряжение [а] = 1400 кг/см2. Определить величину допустимой нагрузки [^], теоретические длины и листов первой и второй пары и величину прогиба балки посредине пролета. Сравнить с прогибом балки постоянного сечения, несущей нагрузку той же интенсивности.
Указание. Сначала следует вычислить грузоподъемность двутавровой балки (с профилем № 30): [Мо]=6608 кгм. Затем, подсчитав J и W сечения с двумя горизонтальными листами и с четырьмя листами, определить грузоподъемность, соответствующую этим профилям: (714,] = 11 040 кгм и [Л42] = = 14 620 к&м. Далее по величине [Л4.2] находится допустимая интенсивность равномерно распределенной нагрузки. Для определения теоретического места начала и обрыва горизонтальных листов выражение М (х) приравнивается
226
с [Afo] и [Л411- Величину прогиба удобно вычислить при помощи теоремы Кастильяио, суммируя три интеграла, по числу участков балки разной жесткости.
Ответ'. 4т/м', 4,00 м; 2,66 м; —1,37 см; —1,24 см.
8.32. Балка переменного сечения, имеющая, в целом постоянную высоту, составлена из двух сосновых брусьев переменной высоты, соединенных по боковым граням листами из толстой фанеры. Размеры
Р
К задаче 8.32.
балки показаны на рисунке. Найти наибольшее нормальное напряжение в балке и величину прогиба свободного конца ее под действием силы Р = 500 кг.
Ответ: 121,5 кг/см8; -^2,5 см.
8.33. Балка переменной высоты образована из двух швеллеров, скрепленных с двумя стальными листами. На рисунке указаны все
К задаче 8.33.
размеры балки. Определить величины наибольших нормальных напряжений в балке и величину прогиба ее свободного конца под действием силы Р=9т.
Ответ: 1500 кг/см*', ~\,7 см.
Указание. Задачи 8.32 и 8.33 проще всего решить графическим способом.
ГЛАВА 9
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
§ 28. Балки
9.1. Раскрыть статическую неопределимость стальной балки, показанной на рисунке, определить опорные реакции, построить эпюры изгибающего момента и поперечной силы, подобрать двутав-4 нормальном напряжении 1600 кг/см1, определить величину наибольшего прогиба балкн, сравнив с наибольшим допускаемым прогибом, равным 0,002 пролета балки.
Решение. Из уравнений статики устанавливаем следующие зависимости:
Нв = 0, A + B = qa, (1) 3Ba-MB = M0+Q~. (2)
При двух уравнениях—три неизвестных. Применим при раскрытии статической неопределимости метод интегрирования дифференциального урав-
нения изогнутой оси балки с использованием приема уравнивания произвольных постоянных интегрирования (см. решения задач в § 22). Начало координат примем в точке В, в защемлении балки, чтобы произвольные постоянные С и D оказались равными нулю. Составляем дифференциальное уравнение упругой липни и _ интегрируем его дважды:
ровое сечение
q=2m/M n)\ кптпппн
б)
6).
при
М0=2тм У
У
, В
। „ । н—а=2м-^-
ЬгггпттМШть, . I
2а=4м-
'В
К задаче 9.1.
EV = flx-AfB-Af0(x-2a)»-g (X 22o)3 .
EJy’ = B~-MBx-M0 (x-2a)-q (*~~2fl)3+C, Z D
rr n*3 .x .. (x—2a)2 (x—2a)* _ _
EJy^=B-^—MB-^~M0K-2 g' 24 ' 4-Cx-l-D.
22B
Записываем следующие три *1=0, *1=0. х4=3а, подставив это значение х2 в симость:
условия для определения неизвестных величин: отсюда 0=0;
> С=0.
!/; = 0;
Ух = 0;
Уг=°;
уравнение
(3)
—3
прогибов, получим следующую зави-9Ва—9Мв = М0 + ^~.
Для определения величины Мв решаем совместно уравнения (2) и (3):
(2) ЗВа-Мв=М0+-^-(3) 9Ва-9Мв = М9+^-
Мв=^ Мо+Ц <7а2=-|+-^ = 2.56 тм.
Далее из уравнений (2) и. (1) находим В=1,43 т н Л = 2,57 т.
Обычными приемами строим эпюры поперечной силы и изгибающего момента (схемы б и в). Наибольший изгибающий момент Л1тах=3,14 тм. Подбираем размеры балки: №г=-^-= = 196 см3. Нужен двутавр № 20а:
W = 203 сл3, J = 2030 сл4, EJ = 4,06 10е кгсм-.
Прежде чем вычислять перемещения, рекомендуется переписать уравнения углов поворота и прогибов, подставив в них все известные числовые величины: £7у' = 0,715х3—2,56х—2 (х—4)—-Ь (х-4)3, О EJy=0,238х3— 1,28х2— (х—4)2 —1 (х-4)«.
Приемами, объясненными в § 22, определяем, что сечение с наибольшим прогибом находится иа правом участке балки и имеет абсциссу х0 = 3,58 л.
У .
. А
а) ТППIIII11111111
(1)
(И)
Это значение подставляем в уравнение (11) и устанавливаем, что наибольшая величина прогиба /=1,35 см, т. е. на 12% больше допустимой: [,']= 1,2см. Приняв вместо двутавра № 20а следующий по порядку двутавр № 22 (7=2550 см*, 117 = 232 сл3), снизим величину наибольшего прогиба до 1,18 см. Наибольшие нормальные напряжения в опасном сечении уменьшатся при новом профиле до 1355кг/сл2.
9.2. Раскрыть статическую неопределимость стальной двутавровой балки, показанной на рисунке, определить опорные реакции, построить эпюры поперечной силы и изгибающего момента, подобрать сечение балки при допускаемом нормальном напряжении, вычислить величину прогиба в сечении, отстоящем на 2 м от опоры А.
г*--а=5м
К задаче 9.2.
равном 1600 кг/см*, н
I
229
Решение. Составляем уравнения статики:
Л + В + С=9(а+6), (1)
Д(с + Ь) + ВЬ-1-(^+Ь); —0. (2)
Для раскрытия статической неопределимости применим дважды общее уравнение прогибов:
EJy=Ejy0+Eje0-^r+Yi M(*-/o)S +Х--Х^,оР+^<?(Х41/о)* : в сечении В
ЕМАа + А-£—^- = 0; (3)
в сечении С
£/еЛ(а+6)+Л^±^+В-^—glc+b)* =0. (4)
Решив все четыре уравнения, получим Л=4,05 т, В =10,53 т и С =1,42 т.
Эпюры поперечной силы и изгибающего момента построим обычными приемами (схемы б и в).
Необходимый момент сопротивления сечения
Подходит двутавр Ns 24: W =289 см3. 7 = 3800 см*, £7 = 3800-2-10* = = 7,6- 10е кгсм3.
Для вычисления любого перемещения нужно определить сначала из уравнения (3) величину £70л (учтя, что Л =4,05 т):
£7ел=_^+_^=40Л25
л 6 т 24 6
. 2-125 155 ,
+Т=~24: ™ -
Для определения искомого прогиба подставляем в общее уравнение прогибов значение * = 2 м:
Е1«—^•2+4’05-т-2-2* ------^-=8,85 тм3.
24
Отсюда у = 8,85:7,6= 1,16 см.
9.3. Раскрыть статическую неопределимость стальной двутавровой рисунке.
27
а) А
6)
Ре
К задаче 9.3.
балки, показанной иа Построить эпюры по-
перечной силы и изгибающего момента. Подобрать сечение при
допускаемом нормальном напряжении 1600 кг/см3. Определить величину прогиба в сечении С. Р1=8т, Р,= 16т, о=60 см, Ь=2а= 120 см, с=За=180 см.
1111
230
Решение. Обозначим иа рисунке (схема а) опорные реакции Н, В, D н М& Составим уравнения статнкн:
W=0, (1) P1-f-Pi = B-f-D, (2)
-P1(a+6+c) + B(6+c)-Pic + A1D=0 (3')
или
—6Р1в+5Ва—3P2a + MD=0. (3*)
За лишнюю неизвестную примем опорную реакцию В. Основная расчетная система показана на рисунке (схема б). Загрузим балку заданной нагрузкой (силами Р) и лишней неизвестной В (схема в). Для того чтобы балка схемы в была эквивалентна балке схемы а, к схеме а следует добавить условие совместности деформаций fa—®- Применим теорему Кастильяио:
а b Ь+с \
j " > Л+ j м>тяг •j *)-а о о Ь '
М3, М2 н М3— изгибающие моменты в текущих сечениях каждого из трех участков балки. Жесткость EJ примем постоянной. Вычислим подынтегральные величины:
^-=0;
дМ2
М3=—Р1(х3+а’) + Вх3—Р2(хЙ—Ьу, ^г-=х8.
Подставим эти величины под интегралы уравнения fa—®-
Ь+с Ь+с
J (-Р1хг-Р1ах+Вх^)<1х+ J (—Pax2+P2bx)dx=0.
о ь
f ‘в дВ
Л12= — Pi (ха + а) + Вх2,
После интегрирования заменим, по условию задачи, бис через а, а Р3 через Pi и после вычислений получим B=2,164Pi = 17,31 т, а затем нз уравнений статнкн найдем D = 6,69 т и Мо=5,67 тм.
Далее обычными приемами строим эпюры Q и М, используя при этом составленные ранее выражения для Л4,, М3 и М3 (см. схему а). Необходимый
m Mmrn 637 ООО _ п
момент сопротивления сечен ни W = - — 1600 сл^‘ Подход,,т ДВУ"
тавр № 27а: IF = 407 сж3, 7 = 5500 сж*.
Для определения прогиба сечения С нужно вычислить производную потенциальной энергии по силе Р2, приложенной в сечении С. Сила В рассматривается теперь как известная сила. В выражения Mi и М2 сила Р2 не входит. Для упрощения вычислений выгодно положение текущего сечения на третьем участке отсчитывать от силы Р2 (см. схему д):
М3=----^(За+^ + В^+д^-Рл, -^- = -х„
За
fc=-gj-^ (3P1ax + PIx2—2Bax—Bxi+P2x-)dx. а
Выполнив интегрирование и подставив все числовые значения, получим fc=+0,24 сж. Положительное значение прогиба обозначает, что направление прогиба совпадает с направлением силы Р2.
231
9.4. Раскрыть статическую неопределимость п определить опорные реакции стальной балки, показанной на рисунке, построить эпюры Q и М.
Решение. Балка один раз статически неопределима. Для раскрытия неопределимости применим способ сравнения перемещении. За лишнее закрепление принимаем опору С. Основная система показана на рис. б. Загрузим
К задаче 9.4.
Необходимый момент сопротивления тавр № 16: 1Г=109 см3, 7 = 873 см*.
балку заданной нагрузкой (схема в) и лишней неизвестной силой С (схема г). Прогиб балки в сечении С под действием заданной нагрузки обозначим через fcq, а под действием силы С—через В заданной балке в сечении С имеется опора, следовательно, fc = 0 пли
fcg + f" = O- (П
Величину прогибов feq и [ес удобней всего брать в готовом виде из таблиц наиболее распространенных прогибов. Эти таблицы приводятся в справочниках и и некоторых учебниках.
£^=-ф-. (2)
cP
EJfee=~^T П1 + /я)- (3)
О
На схемах дне приведены данные для вычисления тех же прогибов графоаналитическим способом.
Подставив выражения (2) и (3) в (1), найдем величину опор-Г Qli _ пои реакции С=_ -
g
= 2[ =0,381 г. Затем из уравнений статики вычислим Л =1,714 ти В = 2,667 т.
Далее обычными приемами строим эпюры Q и М (схемы ж и э).
Ц7 Мщах 147 000 g слз Дву-
Io] 1600 Д У
9.5. Раскрыть статическую неопределимость стальной двутавровой балки, показанной на рисунке, построить эпюры Q и М, подобрать сечение при [о] = 1600 кг!смг и определить величину прогиба конца консоли.
Решение. Применим способ Максвелла—Мора. За лишнюю неизвестную примем реакцию А. Основная статически определимая балка показана па схеме б. Эту балку загружаем дважды: заданной нагрузкой и силой А (схема в) и единичной силон Р°=1 (схема г). Интеграл Мора, выражающий прогиб
232
в сечении А, должен быть ранен нулю:
J M(x)-M°dx=0. (О
Левый участок балки не рассматриваем, так как на этом участке изги-
бающий момент от единичной нагрузки равен нулю.
На втором участке
М(х) = Ах--^Х^—", М° = Р°х=х,
о о
Отсюда А = 17 т. Эпюры Q и М построены иа схемах д и е. | Мшах | = = 8 тм. Нужен момент сопротивления 117=500 ел®. Подойдет двутавр № 30а.
Для определения прогиба при составлении интеграла Мора прикладываем в конце консоли силу Р° =1 и от этого же места ведем отсчет абсцисс текущих сечений, как это показано па схеме ж).
EJy = 1+а 1+а
= С —xdx-j- С А(х—a)xdx.
Взяв интеграл, после подстановок получим EJy — —13,33 гл3, у ж—0,86см, т. е. перемещение направлено вверх,
К задаче 9.5.
против направления силы Р°.
9.6. Раскрыть статическую неопределимость стальной двутавровой балки, показанной на рисунке (стр. 234), построить эпюры Q и М, подобрать сечение при [а] = 1600 кг/см*, а также определить величину угла поворота сечения на левой опоре.
Решение. За лишнее закрепление примем левую опору; основная система балки показана на схеме б. Эта балка загружается заданной нагрузкой и лишней неизвестной А (схема в). Применим далее способ Верещагина. Условие равенства пулю прогиба на опоре А при пользовании этим способом для балки постоянной жесткости записывается так:
»И0=0.
Для составления этой суммы строим эпюры изгибающего момента: от распределенной нагрузки (схема г), от Мо (схема д), от лишней неизвестной А (схема е). На каждой эпюре указываем характерные ординаты, а в центре тяжести каждого участка эпюры—стрелку и рядом с ней величину каждой грузовой площади в тмг. Затем нагружаем основную систему балки единичной нагрузкой Р°=1, приложенной в том сечении балки, где действует лишняя неизвестная А, по ее направлению (схема ж). Строим эпюру единичного изгибающего момента М° (схема а); па этой эпюре выделяем ординаты, прнходя-
233
щиеся против центров тяжести фиктивных нагрузок, отмеченных нами на схемах г, д, е. Затем вычисляем сумму произведений каждой площади ш нз схем г, д, е на соответствующую
К задаче 9.6.
ординату нз схемы в, а именно:
9
— 18-4—27-2 —12-1 +
4
+ 4,5Л-2 + 4,5Л-2 = 0.
Отсюда Л=5,92 г, а нз уравнений статики В = 3,49 т и С=2,59 7. Эпюры поперечной силы н изгибающего момента для всей балки в целом строятся обычными приемами (схемы и, к). При Afmax = 8 тм нужен двутавр № 30а.
Для определения угла поворота на левой опоре расчетную схему балки следует загрузить в сечении А единичным моментом Л1°=1 (схема л); эпюра изгибающего момента от М0 = 1 показана на схеме м. Производим вычисления, аналогичные показанным выше:
2
EJQA= — 18-1—27 - 12 X
О
1 2
Ху +4,5-5,92 + 4,5-5,92-у , EJGa = 4,4tm2, 6л =0,0028 рад.
9.7. Двухпролетная деревянная балка загружена, как показано на рисунке. Раскрыть статическую не-
определимость, вычислить опорные реакции, построить эпюры М и Q и подобрать прямоугольное сечение балки при отношении Л:& = 2 и при допускаемом напряжении [ст] = 100 кг!см2.
Решение. Балка одни раз статически неопределима. Для раскрытия неопределимости применим теорему о трех моментах. За лишнее неизвестное примем изгибающий момент на средней опоре. Построим для обоих пролетов, как для двух отдельных балок, эпюры изгибающего момента от нагрузки, расположенной иа каждом пролете. Обозначим стрелками равнодействующие грузовых площадей со с указанием расстояний а и Ь этих со от крайних опор (схема б). Затем составим формулу трех моментов:
Значения величии, входящих в формулу: 32
Л1л = Мс=0, ©!=— 2 тм2, соа=8 гл8, <1)3=—— гл8,
4 10 „ .
О1 = уЛ, Оа = уЛ, 63=2 м.
234
После подстановки в формулу этих данных получаем 2Мв-10=-6- (-2-^+8— + ^) = -56, Мд=—2,8 тж.
На схеме в показана эпюра М (х) от Мд для обоих пролетов.
К задаче 9.7.
Из уравнений статики находим величину опорных реакций: А = 1,47 г, В = 6,17 т, С=3,3 т. Затем строим эпюры Q н М (схемы г и д). Подбираем сечение: необходимый момент сопротивления TF = ^lnax = ' =3070 сж3;
[OJ
так как IF=^-=^5, то h= J/36 840 = 33,3 сж=34 см, b=0,5h= 17см. о 12 v
9.8. Для каждой из девяти балок, показанных на рисунке (стр. 236), раскрыть статическую неопределимость любым способом, определить опорные реакции и вычислить величину наибольших изгибающих моментов. Для схем ж, з, и полагать, что Ах = Вх = 0.
Ответ:
•) л=Ар, я=Нр, мв=^Р1, мв-^Р1-, Q Г, 1 Q
б) Л = |9/, в = у9/, MB= — ±ql\ =
. . 97ИО „ 9Л10 .. 1 .. м 9 ..
в) Л— 81 * &— 41 * — 8^°’ —16^°’
235
Г) Л = р(ц-|?), B = -3Pf-, Мв=^Ра, МА = -Ра-д) Л = ?о (1+ |у), В = — MB = ±qa2, MA = — ±qa3i
$ j| 111111 п । rm 11111111111 iti i in rm i~m~|/? H----------------------------1--------------------h‘
К задаче 9.8.
ец=-|Л B:—мд=|Л1о, MA = -M0;
ж) Л = Р, МА = МВ= — Ра^-Ь, мР = Ра^ъ>
з) А=^, MA = MB= — ^qP, M = ^qP (в середине
пролета);
н)Л = 0, МА = МВ---Л40 М = МО^-Ь (в середине
пролета).
23в
9.9. На рисунке показаны однажды статически неопределимые балки с различными схемами их загружения. Расстояния на схемах указаны в метрах. Раскрыть статическую неопределимость любым способом, определить опорные реакции, построить эпюры поперечной силы н изгибающего момента.
К задаче 9.9.
Ответ: Указаны опорные реакции и экстремальные значения изгибающего момента. Перечисление ведется слева направо.
а) —1,64 7, —1,64 тм, 1,08 тм, 1,64 т, —0,56 тм;
б) —3,36 ТМ, 3,84 т, 0,48 тм, 2,16 тм, 2,16 т;
в) —1,125 Т, —2,25 тм, 1,75 тм, 1,125т, —0,125 тм;
г) —2,25 тм. 3,56 т, 0,92 тм, 0,44 т;
д) 1,31 Т, 1,74 тм, 2,69 т, —2,75 тм;
е) —1,75 ТМ, 1,44 т, 1,64 тм, 2,56 т;
ж) 2 Т, —4 тм, —2 т, 2 тм;
з) 0,5 тм, —0,5 т, —1 тм, 2,5 т;
») 4,5 т, —3,0 тм, — 1,5 т, 1,5 тм;
к) —0,25 т, —0,5 тм, 2,5 т, 0,77 тм, 1,75 т;
л) —0,28 т, —0,56 тм, 2,06 т, 1,22 тм, 1,22 т;
м) 0,125т, 0,25 тм, —2,25 т, —1,9/4-2,1 тм, 2,125 т.
9.10. На рисунке (стр. 238) приведены схемы загружения статически неопределимых балок, образованные наложением некоторых схем задачи 9.9. Построить эпюры поперечной силы и изгибающего момента (можно воспользоваться решениями задачи 9.9).
237
Ответ (см. пояснение к ответу задачи 9.9):
а) —1.5 т, —1,5 тм, 0, 1,5 тм, 1,5 т;
б) 3,69 т, 3,4 тм, —1,24 тм, 0,31 т;
а) 0,5 тм, —2,125т, —0,625 тм, 1,13 тм, 2,122 т;
г) —2 т, —2/+2тм, 0, —2/4-2 тм,' 2 т;
д) 2,03 т, 1,03 тм, 0,06 тм, 0,44 т, — 1,47 тм;
е) 2 т, 1 тм, 0, — 1 тм, —2 т.
К задаче 9.10.
9.11. Двутавровая стальная балка № 40 длиной £ = 8м оперта по концам на шарнирные жесткие опоры, а посредине пролета поддерживается чугунной трубчатой колонной высотой Н=^м (см. ри
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
К задаче 9.11.
сунок). Наружный диаметр колонны 16 см, внутренний—12 см. Балка несет равномерно распределенную нагрузку интенсивностью 2 т/м. Определить усилие в чугунной колонне и наибольшие нормальные напряжения в балке и напряжения в колонне. Чему будет равна реакция средней опоры, если эта опора будет жесткой?
Указание. Уравнение совместности перемещений в точке В:
5 qL* BL3 _ВН 384 ‘ ECJ 4&E,.J~E4F'
отсюда вычисляется величина усилия в колонне В:
_ Ь qL . . Ес 48HJ . П1ое В~8Р где k-1 + — .-^-1,0135.
Ответ' В = 9870 кг; напряжения в балке 395кг/сл1г, в колонне 112 кг/см2. При жесткой опоре В = 10000 кг.
233
9.12. Стальная двутавровая балка № 22 длиной 4 ле опирается
по концам на шарнирные жесткие опоры, а посредине длины—на деревянную стойку высотой 8 м с площадью поперечного сечения 400 смг. В одном метре от опор приложены две силы Р = 3т каждая. Найти наибольшие нормальные напряжения в балке и на
пряжения в стойке.
Ответ: 469 кг!см*; ~10 кг)см?.
9.13. Двутавровая стальная балка № 22 защемлена одним кон-
цом в стене, а второй конец балки поддерживается вертикальным стальным тяжем диаметром 25 жм (см. рисунок). Балка загружена
равномерно распределенной нагрузкой интенсивностью Зт/м. Определить величину усилия и напряжений в тяже и наибольших нормальных напряжений в балке. Как изменятся усилие и напряжения, если тяж, установленный до загружения балки, оказался на 2,5 мм длиннее восьми метров?
Ответ: 3230 кг; 656 кг/см*; 1640 кг/см?;
3090 кг; 627 кг[см-; 1830 кг [см?. К задаче 9.13.
9.14. В месте соединения двух ба-
лок АВ и CD (см. рисунок) приложена сила Р. Как распределится эта сила между балками, если известны отношения нх пролетов и жесткостей: = 3:2 и EJt:ЕJ2 = 4:5?
Ответ: Pj « 0,19Р; Pt « 0,81 Р.
К задаче 9.14.
К задаче 9.15.
9.1Б. Две балки прямоугольного сечения одинаковой длины и ширины, из одного материала, положены одна на другую, как показано на рисунке. Высота верхней балки в два раза меньше, чем нижней. Как распределится нагрузка между балками?
Ответ: Pi = */eP; Рл = а19Р.
9.16. Балка, показанная на рисунке,
К задаче 9.16. загружена равномерно распределенной
нагрузкой по всей длине. Какое предельное значение может иметь сила Р, приложенная посредине левого пролета, чтобы конец балки иа правой опоре не поднимался?
Ответ: P=4ql.
239
9.17. Двухпролетная неразрезная балка загружена по всей длине равномерно распределенной нагрузкой. Как должны относиться нрэ-леты балкн I и а (см. рисунок), чтобы
реакция правой опоры оказалась равной нулю?
Ответ: а = 0,433/.
9.18. Балка, защемленная одним
К задаче 9.17. концом и поддерживаемая на другом
конце шарнирно подвижной опорой, нагружена равномерно распределенной нагрузкой q по всему пролету /. Насколько нужно приподнять или опустить опору, чтобы сделать величину наибольшего положительного изгибающего момента в пролете равной величине отрицательного момента в защемлении?
л/4
Ответ; Приподнять на 0,013 gj.
9.19. Деревянная балка квадратного сечения 30x30 см длиной 3 м подвешена на трех стальных тягах длиной по 2 я и площадью поперечного сечения по 8 см2 каждая. Две тяги поддерживают балку по концам, третья — посредине. На балку действует посредине ее длины сила Р=13т. Определить величину напряжений в тягах и наибольших нормальных напряжений в балке.
Ответ: В средней тяге 1425 кг/см2, в крайних —100 кг/см2, в балке 27 кг/см2.
9.20. Двутавровая балка № 55 установлена на трех двутавровых стойках Кг 20. Стойки делят длину балки на два пролета по 1,5 м. Высота стоек 3 м. После установки балкн средняя стойка нагрета на 40°. Определить величину усилия в средней стойке, напряжений в стойках и наибольшего нормального напряжения в балке от нагревания стойки.
Ответ: 11 100 кг; 414 кг/см2; 207 кг/см2; 417 кг /см2.
9.21. Балки расположены перекрестно, как показано на рисунках. В местах пересечения балок при отсутствии нагрузки низ верхних балок касается верха нижних балок без нажима. Размеры балок обозначены на рисунке, причем
а= 100 см, ft =12 см, h = 20 см.
Определить, чему равны опорные реакции и наибольшие нормальные напряжения в каждой из верхних и нижннх балок под действием силы Р= 1200 кг.
Ответ: я) В = 200 кг, А = 400 кг, 25 кг/см2, б) В = 658 кг, А = 271 кг, 420 кг/см2, в) В = 474 кг, А= 63 кг, 103 кг/с м®,
12,5 кг/см2;
295 кг/см2;
257 кг/см2
и 51 кг/см2 в крайних балках.
9.22. Раскрыть статическую неопределимость двухпролетных балок, показанных на рисунке, определить опорные реакции, построить эпюры поперечной силы и изгибающего момента.
240
К задаче 9.21.
|7w. ....1пш
Ц4-______________^nilllllllllllinr
Зм-S*------4м—
Л*-2м-<\
г)
1т/м
liiiiiiiiiiiiiimnii
fab
е)
К задаче 9.22.
241
Ответ к задаче 9.22 (см. стр. 240 и 241):
Схема Реакции опор. Т Поперечная сила Изгибающий момент
А в С макс. МИН. макс. мнн.
а —1.27 4,79 2,48 3,52 —2,48 1,54 —1,55
б 3,21 6,63 1,16 3,21 —4,79 2,57 —3,18
в 2,06 6,89 4,05 2,95 —3,94 3,10 —2,82
г 2,14 2,94 1,92 2,08 —1,92 1.27 —1,32
д 3,76 1,90 1.34 1,76 —2 0,90 —2
е 3,99 4,27 —1,26 2,99 —3,01 1.48 —2,52
9.23. Балки, показанные на рисунке, поддерживаются в точке В упругой опорой с коэффициентом податливости а, который выражает в см величину осадки от 1 т нагрузки на упругую опору.
В___g
1.1iiiiiiiiiiiiiiiHiiiiiiiiiiiiiiil
liiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
fl)
I
Л
К задаче 9.23.
Полная нагрузка на каждую балку равна Q и распределена равномерно по длине балки. Чему равно давление на опору В?
Ответ: а) В = • -у, где k = 1 + ;
х. „ 3 Q . . . 3EJa
б) Wft=14—р~-
9.24. Балка длиной Z, весом Q, с моментом инерции J лежит иа трех одинаковых упругих стойках (по концам и посредине длины балкн). Для укорочения стойки на 1 см требуется осевое усилие 5. Чему равна нагрузка В, приходящаяся на среднюю стойку?
_ „ Q 192£J + 5/»s
Ответ. В— 8 • 72EJ + i3S •
9.25. Двутавровая балка № 18 длиной 6 л лежит на трех деревянных стойках круглого поперечного сечения диаметром 25 см и высотой 4 jh. Две стойки поддерживают балку по концам, третья — в середине пролета. Балка нагружена по всей длине равномерно распределенной нагрузкой интенсивностью q = 2 т/м. Определить усилия и напряжения в стойках и наибольшие нормальные напряжения в балке.
Ответ: 7480 кг; 2260 кг; 15,3 кг[см*; 4,6 кг[смг; 1545 кг[смг.
242
9.26. Определить грузоподъемность балок, защемленных обоими концами н нагруженных симметрично, как показано на рисунке. Горизонтальные реакции в защемлении считать равными нулю. Вычислить величину наибольшего прогиба.
В схеме а сечение прямоугольное, 12x30 см2, пролет 1 = 6м, [о] = 100 кг (см-, материал балки — сосна. В схеме б сечение —
К задаче 9.26.
двутавр № 10, пролет 1 = 4 м. В схеме в сечение—двутавр № 20, пролет / = 6л1. Для двутавровых балок [о] = 1600 кг/см2.
Ответ: а) 2400 кг, —1,0 см; б) q = 700 кг(м, —0,96 см;
о) 400кг/м, —1,1см.
\2Р ЗР
F-------1—М
Ц—Д51— а)
у_______ПТТТ1-П11ТПТТТ1Д
--0,61— в)
I)
К задаче 9.27.
9.27. Балки, защемленные обоими концами, загружены несимметрично, как показано на рисунке. Раскрыть статическую неопределимость, найти опорные реакции и построить эпюры Q и М.
Ответ:
Схема А МА Характерные ординаты изгибающего момента в пролете мв в
а б в г 1.312Р -4 0,1512g/ 0,15gZ —0.346PZ 0.4М —0,0396g/2 —0,033g/2 0.310PZ, —0.104PZ —0,56М —0.52М 0.44М ' 0.48Л1 0,0209g/2, 0,0323g/2 Mm„=0,0215g/2 —0.634PZ 0 —0,0684g/2 —0,05g/2 3.688P 0,4488g/ 0,35gZ
9.28. Нераэреэная балка имеет два пролета одинаковой длины /. Левый конец балки защемлен, остальные две опоры шарнирные.
243
ПосрЪдине левого пролета приложена сила Р. Чему равны опорные реакции?
„ 9 т 17 п 25 „ 3 п
Ответ. &Р1; ^Р; ^Р; 56 Р.
9.29. Неразрезная балка с пролетами и lt защемлена левым концом и свободно оперта правым. На расстоянии а от свободно опертого конца приложен груз Р. Чему равен момент в защемлении и на средней опоре (а < /2)?
Ра(Ц — о2)
Ответ: Л13 = 1 ^ср = —2М>-
9.30. Двутавровые неразреэные балки загружены симметричной нагрузкой, как показано на рисунке. Р = 6т, д-Ьт/м. Раскрыть любым способом статическую неопределимость, вычислить опорные
К задаче 9.30.
реакции, построить эпюры Q и М, подобрать помер двутавра при [о] = 1600 кг/см2 и вычислить величину прогиба в среднем сечении балки.
Ответ:
Схема A, гп В. m Mmin- mM •''max' mM Двутавр !/. CAI
а —0,62 3,62 —2,85 5,85 № 27 —1,23
б 2,58 3,42 —2,01 6,19 № 27 0,72
в 8,31 —2,31 —6,00 0,92 № 27 —0,23
г —1,60 13,20 —7,34 9,48 № 33 —1,4
д 8,71 10,49 —4,29 9,49 № 33 0,79
е 4,77 —0,77 —2,00 0,31 № 18 —0,30
244
9.31. Стальная балка с моментом инерции сечения J и длиной / оперта по концам на жесткие шарнирные опоры, а в двух промежуточных сечениях — на стальные колонны высотой h. Все три пролета балки равны между собой. При отсутствии нагрузки все четыре опоры находятся на одном уровне. Балка загружена нагрузкой, равномерно распределенной по всей длине. Найти необходимую площадь поперечного сечения опор F из условия, чтобы усилия в стойках и реакции крайних опор были одинаковы.
л - 486JA
Ответ: F=-^~.
9.32. Раскрыть любым способом статическую неопределимость и построить эпюры' поперечной силы и изгибающего момента для неразреэных балок, показанных на рисунке.
1т/м
а) ъ
I1IIIIIIIIIIIIIIIIIIII
к--4 —
12т/м б)
lllflllllllllllllllllllllll
2т
4
К задаче 9.32.
Ответ (указаны наибольшие значения Q а) 2,46 т; —2,20 т; 1,54 тм; —1,86 тм. б) 3,95 т; —4,05 т; 1,91 тм; —2,18 тм.
1m
А
2,20 т; 1,54 тм;
4,05 т; 1,91 тм; 2m 2m 1т/м I | a)
Z1 обоих знаков):
liiiiiiiiiiHiiiiiiiii
б)
Зт
I 2т/м
t—4
г)
4m < А В
2—^---4
6т
Вт
-*Ы-3-4т
2
4-
2т/м___
е) П~Г 111111 I t 111IJJll НI
*В 4
- ----6-----
4т
1_____В
**—3----
12m 2т/м
д|111111ПП|||||||||||||1ПТПП77 ---------------8--------- 4т/м
в-----
К задаче 9.33.
9.33. На рисунках показаны трехпролстные неразрезные балки с различными схемами загружения. Раскрыть любым способом стати-
A ^b‘ ‘
4m/м
liiiiiiiiiiiil
С
и
В
liiKiiiiiiiil
Л
Л
С
6
245
ческую неопределимость, найти опорные реакции и построить эпюры Q и М. Длина участков балок указана на рисунке в метрах. Ответ:
Схема A. m В. m С, m D, m "max- mM "min- mM
а о.п 5,67 3,46 —0,24 1,78 — 1,79
б 0,60 5,62 4,07 —0,29 2,42 — 1,80
в 5,20 7,80 —1,20 0,20 3,36 — 2,40
г 7,05 —5,18 9,20 4,93 4,93 — 4,30
д 3,14 9,46 16,97 6,43 10,34 —12,51
е 6,59 18,47 27,13 13,81 10,15 15,13
9.34. Четырехпролетная неразрезная балка с равными пролетами выполнена из деревянного бруса. Длина балки 8 м. Отношение высоты поперечного сечения к ширине равно 1,5. Балка загружена по всей длине равномерно распределенной нагрузкой интенсивностью q = 700 кг/м. Определить размеры бруса при [о] = 80 kzJcm2.
Ответ: 10x15 см.
9.35. Четырехпролетная нераэрезная балка двутаврового сечения № 22 имеет крайние пролеты по 3 м, а средние по 4 м. Балка загружена по всей длине равномерно распределенной нагрузкой, интенсивность которой на крайних пролетах ql = 2 т/л», а на средних пролетах ?а = 3 т/м. Определить наибольшие нормальные напряжения в балке и указать, в каком сечении они действуют.
Ответ: 1912 кг/см* в сечении на средней опоре.
§ 29. Рамы
9.36. Раскрыть статическую неопределимость стальной рамы двутаврового сечения, одинакового на всех участках рамы, построить эпюры поперечной силы, изгибающего момента и нормальной силы, подобрать номер двутавра и определить величину угла поворота сечения С. Рама имеет шарнир в сечении D, способы закрепления опор рамы, нагрузка и размеры показаны на рисунке. Числовые данные: 9 = 4 т/ж, 1 = 5 м, а = 4 м, с = 3 м, [о] = 1600 кг/см2.
Решение. Покажем на схеме а опорные реакции и напишем уравнения статики:
Нд = Нв. (I)
A + B = qa, (2)
Ла+Яд(/-С) + Л1л=0. (3)
Наличие шарнира позволяет написать еще два уравнения: сумма моментов относительно шарнира всех сил, взятых по одну сторону шарнира, равна нулю:
Ва—^--Нвс=0, (4')
НА1+МА=0. (4’)
249
Любое из уравнений (4) является дополнением к первым трем уравнениям статики. Так как неизвестных пять, то задача является однажды статически неопределимой.
К задаче 9.36.
За <лишнее» неизвестное примем Нв (схема б). Для того чтобы рама по схеме б была эквивалентна заданной раме (схема о), к схеме б нужно добавить условие:
двго₽=о.
Применим теорему Кастильяио. Так как ДВГо₽=^г> то
(5)
7И (x)^^-dx—0.
Oil в
(5')
Вычисляем сумму интегралов уравнения (5') по участкам:
л гг дМг
он в
$(-ffBx)(-x)dx=^. о
На втором участке в выражение изгибающего момента войдет момент от реакции В, которую предварительно нужно выразить в зависимости от Яд,
247
пользуясь уравнением (4'):
д-« с д.ча
В = Нв- + -^, 0<х4<а. Ms=-HBc+HB^x+^-^.. ^=-^х-с
На третьем участке 0<x3<Z, Mt = —Мд — Ндх; учитывая (!) н (4*), пишем Ma=HB(l—х),
I дМ; С I9
^=1-1. \нв(1-ху*х=нв±.
о
Сумму вычисленных интегралов приравниваем на основании уравнения (5') пулю:
Нв<? Нвс9а qcn9 Яя!а н _24 г
—+-3----------24------~=°’ "в = 27«°.51 т.
Из уравнений статики находим остальные опорные реакции: Нд = Нв = -= 0,51 т, МА = —2,55 тм, В = 8,38 т, Л = 7,62 т.
Далее обычными приемами строим эпюры поперечной силы (схема в), изгибающего момента (схема а) и нормальной силы (схема д). Находим положение сечения с наибольшим изгибающим моментом (х0 = 2,095 м) и величину Afmax = 7,26 тм. Необходимый момент сопротивления 117 = 454 см9. Берем двутавр № 30: 117 = 472 cjhs, J = 7080 cjh4, F=46,5 см-.
Наибольшие нормальные напряжения от изгибающего момента а = = 726 000:472= 1538 кг/смг\ сжимающие напряжения от нормальной силы в любом сечении второго участка а = 510:46,5= II кг/см--, суммарные наибольшие сжимающие напряжения в верхних волокнах рамы (в сечении при хг = = 2.095 л)атах= 1538-|-11 = 1549 кг/см- < 1600 кг,'см-.
Для определения угла поворота сечения С приложим в этом сечении основной системы рамы (схема б) дополнительный момент Мс (схема е). Угол поворота сечения С
а 1 V Г и / > ЭМ (х) .
0С“ EJ J М W dMc dx’
(О
Значения изгибающего момента М (х) па трех участках рамы у нас уже „ сШ (х)
вычислены. Значения же вычислим для схемы е\ опорные реакции, от с
вызываемые моментом Мс, показаны иа этой схеме. Запишем значения изгн-х
бающих моментов от действия Мс’. Л41=0, Л13=Л1С—Alf —, Л43=0.
Производная отлична от нуля только иа втором участке, где она равняется = 1 ——; следовательно, для определения угла поворота сече-оМс о
ini я С нужно вычислить лишь один интеграл на втором участке рамы:
248 '
9.37. Раскрыть статическую неопределимость рам, показанных на рисунке, н построить эпюры нормальной силы, поперечной силы и изгибающего момента при следующих данных: Р — 4 т, М9 = 4тм,
К задаче 9.37.
д — 2 т/м, а —2 м, с = 3 м. Жесткость рамы постолппаи и одинаковая на обоих участках.
Ответ:
Схема A. m Л11. тм 1 Схема Л. m М,. тм
3M0(a-i-2c) о (0о 0,364 ЪРс- —7,1
2а(а-|-Зс) 2н(а + 3с)
б ЗЛ1°С -1 636 0 728 ЗРа* 0 89 —5,33
u(o+3c) 1,bJ° с 2с(3о-|с)
в Зда(а-|-4С) -0,182 'НС Р(24а-;-5с)_ 1б(3а + с) ’ —0,75
8(а-|-Зс) ’
<?с3 — I 227 —6,546 3 9Р —0,72
г 2а(а + 3с) ’
249
9.38. Раскрыть статическую неопределимость рам, загруженных, как показано на рисунке, построить эпюры нормальной силы, поперечной силы и изгибающего момента прн следующих данных: Р=4 т, с = 3 м, а = 4 м, q = 2 т/м, Af0 = 6 тм. Жесткость рам постоянна и одинакова на всех участках.
К задаче 9.38.
Ответ (Н—горизонтальная составляющая опорной реакции):
Схема Н, m М,. тм Мл, тм
а б в г 8д(2д + 3с) ’ -02 3^_=-0 8 8(2д + 3с) ** - 0 8 Рс(4д + 3с) „ 8(2д+3с) ' ?с*(2д + с) 8(2д-|-Зс) ’ ££!_=_! ,88 4(2д+3с) ’ ?Моа _ (2Д+ЗС) ’2>82
4д(2д-|-Зс) ’ Зуд(д+2с) „ 4(2д + 3с) ’ . =0 79 д (2д + Зс) 4(2д+3с) 9?да(д+2с)а 32(2д + 3с)« (2д + 3с) 3118
9.39. Рама замкнутого контура загружена по длине ригеля равномерно распределенной нагрузкой интенсивностью q = 2 т/м. Размеры рамы: а = 5м, 2с = 6 м (см. рисунок, схема а). Раскрыть статическую неопределимость рамы, считая жесткость всех участков одинаковой и постоянной, построить эпюры нормальной силы, поперечной силы и изгибающего момента, подобрать двутавровое сечение рамы при [о] = 1600 кг/см2 н определить величину прогиба сечения посредине ригеля.
Решение. Опорные реакции находятся нз уравнений статики: А = В = = qc=6 т, Нд=0. Для определения внутренних усилий разрезаем раму сечением так, чтобы не нарушить симметрии рамы и симметрии загружеиня; таким
250
разрезом может быть разрез посредине ригеля, по сечению С. Для сохранения прежних условий работы рамы прикладываем в проведенном сечении усилия Мс> N& Qc (схема б). Вертикальное перемещение сечения С возможно; горизонтальное же перемещение и угол поворота сечення С равны нулю; в силу симметричности равна нулю поперечная сила Qc. Покажем теперь одну половину рамы, слева от сечення “ ...
усилия со стороны другой части рамы, обозначив их для краткости М и N. Это основная система в. Усилия, передающиеся от правой части рамы иа левую в сечении Н, не показываем. так как эти усилия в выражения изгибающих моментов не войдут. Запишем условия: А™р = ® и 6с=0, при соблюдении которых схема в станет эквивалентной заданной схеме.
Далее решение можно вести любым способом. Применим канонические уравнения метода снл:
&Nq + N + М вдг м = О,
М 6ММ=0; индексы обозначают: первый—место перемещения, второй—причину перемещения.
Для вычисления перемещений, перечисленных в канонических уравнениях, применим метод Верещагина. На расчетной схеме половины рамы в
С, и передающиеся в этом сечении
,4
(1)
(2)
i
О)
iiiiiiiiiiiiiiimiiiiiiiiiiiiimil
К задаче 9.39.
iiiiiiiiimiii
покажем все действующие на раму
нагрузки: д, М и N, затем построим отдельно эпюры изгибающего
момента
К задаче 9.39.
от нагрузки д (схема г), от нормальной силы № = i (схема д) и от изгибающего момента Л1°=1 (схема е). Формула Верещагина: А = У тЛС (см. задачу 9.6).
251
Пользуясь построенными эпюрами, вычислим произведения <оЛ4“: А»,— •«— & С +2«>.
•«—g<3,+ «). W=sMl = y' 14-ас-1=-|-(а4-2с), hw=~2 -yа+oc-a = -g-(a+3c), вд1Л1= lcl + lal + lcl=a4-2c.
О) зс) з) и)
К задаче 9.39.
Подставим вычисленные значения суммы произведений а>-Л1 ° в канонические
К задаче 9.39.
уравнения:
Л/ -g-(a-|-3c) + М (а-|-2с)=
= ф(а+2с), (1)
N у (а+2с) + М (а + 2с)=
= ^(3п+4с). (2)
Решив эти уравнения, получим
N= ; =0,939 т я 0,94 т, в (а 4-6с)
м qcl За2+16са+12с®
М ~ “6 аг + 8са+12с»
Величина изгибающего момента в левом верхнем углу рамы
MD= М— у-=5,016— 9 = —3,984 г.и.
5,016 ™.
Изгибающий момент в нижнем углу рамы
MA = MD+N-a = — 3,9844-0,939-5 = 0,711 тм.
Эпюры М, N и Q построены на схемах ж, з, и. Подбираем сечение: лужей двутавр № 24а: W =317 сж3, J =3800 сж*.
Решение получается более простым, если величины перемещений выражать не в буквенной форме, как приведено в настоящем решении, а в числовой. Однако в этом случае труднее заметить допущенные ошибки.
252
Для определения прогиба сечения С рассмотрим .ригель как простую балку с равномерно распределенной нагрузкой и моментами Л1д = —3,984 тм на опорах. От этих нагрузок строим эпюры изгибающего момента и следом за ними эпюру единичного изгибающего момента от силы Р° = 1, приложенной в сечении С. Все эти эпюры показаны иа схеме к.
Подсчитаем половины площадей первых двух эпюр:
(й1=18 тм2 и о)2=11,952 тм2.
Ординаты эпюры единичного момента, соответствующие положениям центров тяжести первых двух эпюр:
. ,о .,0 3
Л11=77ж и Л12=— м.
10 4
Сумма произведений й) Л1° составит
2 (13-Ц- 11,952 • А) =2 (16,876—8,964) = 15,82 тм».
„ Г * 15,82-10® _по
Искомый прогиб Ус = 2.10а.зе0()=2,08 см.
9.40. Рамы постоянной жесткости загружены симметрично, как показано на рисунке. Раскрыть статическую неопределимость, построить эпюры нормальной силы, поперечной силы и изгибающего
момента. Вычислить величину изменения расстояний между сечениями 1—1 и 2—2 вследствие деформации рамы.
Ответ-.
Схема Л', Al, M, Ди Asa
/у 0,5Р PZ (Z + 2a) PP PP (Z + 4a) PPa2
8(Z + a) 8(l + a) 96(Z-|-a) 32 (Z-f-a)
б 0,5$Z Ч (I + За) qP Qi* (Z + 5a) qPa2
24(Z + a) 12 (Z 4-a) 192 (l + a) 48 (Z 4-a)
в 2Л40('+«) ± 0,5 Mo , Mol 2(Z + 2a) 0 0
Z(Z + 2<z)
253
9.41. Рама загружена симметрично двумя силами Р, как показано на рисунке. Сечения всех участков рамы одинаковы. Раскрыть статическую неопределимость н вычислить величины нормальной силы М
ригеле, изгибающих моментов Л72
и изгибающего момента ТИ2 в
в нижних углах рамы и иа участке между силами Р, прогибов в сечении див сечении 4, а также величину сближения сечений 5. Числовые данные: Р = = 4 г, I = 5 л, с = 3 л, [о] = = 1600 кг/смг, сечение балки двутавровое.
Ответ: N——632 кг; Л12 = = —375 кгм; ^ = 2153 кгм; Mt=—1847 кгм; двутавр № 18;
= 0,45 см (вверх), j>4=1,98cm;
Д,= 1,38 см.
9.42. Для рам с двумя шарнирами, показанных на рисунке, опре-
делить опорные реакции н построить эпюры изгибающего момента, поперечной силы н нормальной силы. Жесткость всех участков
постоянная и одинаковая.
К задаче 9.42.
Решение. Решим задачу, показанную иа схеме б. В защемленных концах рамы действуют по три опорных реакции, всего шесть реакций. Уравнений статики—три. Каждый внутренний шарнир добавляет еще по одном/ уравнению: сумма моментов всех сил, действующих по одну (любую) сторону шар-
254
нира, относительно шарнира равна нулю. В раме два шарнира. Следовательно, всего имеем пять уравнений статики. Таким образом, рама один раз статически неопределима. Выберем за лишнюю неизвестную опорный момент Мд, тогда основной системой будет рама, показанная иа рис. б'. Основную систему загрузим заданными силами и лишней неизвестной Мд. Обозначим иа рис. б' все опорные реакции и составим пять уравнений статики:
Дх + Вх = 2q а, (1)
Ау = Ву, (2)
2?а«—Ву-2а—Мд— Мв=0, (3)
Сумма моментов сил относительно точки Г. Аха—Мд=0. (4)
То же относительно точки 2: Ах-2а—МА—Ауа=0. (5)
Мл Мл Из уравнений (4) и (5) находим следующие зависимости: Ах=—-, Ау = -^-.
Основная система станет эквивалентной заданной, если будет выдержано условие 0Л=О. (6)
Для раскрытия условия (6) применим способ Максвелла—Мора:
M(x).M«dx=0.
(ft
Покажем на рис. .6* основную систему, загруженную единичной силой М° = 1. Обозначим далее иа схемах б' и б* положение текущих сечений абсциссами х(, х2, х3, а затем вычислим все подынтегральные величины для каждого из трех участков рамы:
0«£x1(s2a, М = Ма-— -xt = MA (1--V а \ a J а
0<х2<2а,
М = Мд — ^~’ 2а + ^ 2а-х2 = -Мд (1-^). =
0<х3<2а, Мэ = Л4л-^(2а-х8) + ^А.2а-^ = а а 2
^Ma + Ma.^-S^. = Ma MS = (1+^).
Подставляем вычисленные величины в интеграл Максвелла—Мора: 2а 2а 2а
| (-£)*—+£('-гр-Ч м> (1+1)‘л-2а
4 ? о+-?)*-»
Мл (v+f »+“•)—г «“Ч-2**-
Отсюда Мд=^-, а далее из уравнений статики находим все остальные реакции, величины которых указаны ниже в ответе.
Эпюра изгибающего момента построена на рис. б'".
255
Ответ к задаче 9.42 (см. стр. 254):
Схеме Ая Дд) МА Л<в Мщах Место Л<тах
а *р 30 Ир 30 В правом верхнем углу рамы
6 Ча 3 Яа 3 3 qa2 1 . 18 ?в х0=-|-а от В
в м„ За мв За м0 3 w| ю е В сечении, где приложен Мо
К задаче 9.43.
260 ,
9.43. Раскрыть статическую неопределимость рам, показанных на рисунке (стр. 256), имеющих постоянную, одинаковую на всех участках жесткость, при действии равномерно распределенной нагрузки q = 2 т/м. Размеры элементов рам: I -- 5 .и, а = 4 м, с = 3 м.
Ответ (Нв—горизонтальная составляющая реакции опоры B)i
Схема Ив. m В. m Мщах» тм Afmin» тм
а —0,368 3,816 2,536 — 1,84
б 5,03 —1,515 6,33 — 5,91
в 2,68 0,86 6,6 — 4,3
г —2,65 5,25 8,25 — 6,89
д 0,983 4,615 7,7 — 2,46
е —1,33 3,17 3,32 — 11,16
ж —0,805 5,006 2,24 — 8,98
3 —4,915 —0,106 0,425 —15,25
и —3,729 0,979 3,86 — 1,08
к -0,0896 4,123 3,97 — 0,27
л 0,14 3,72 3,88 — 0,70
9.44. Двухпролетная рама загружена, как показано на рисунке. Материал балок АВ и ВС и стойки BD одинаковый. Моменты инерции! балок J6 и стойки Jc. Размеры частей рамы показаны на
Г
С.
iiiiiiiiiiiiiiiii
К задаче 9.44.
рисунке. Составить выражения для сжимающей силы в стойке, изгибающего момента в балке слева от узла В и изгибающего момента в стойке снизу от того же узла.
Ответ: M—q2 [1 +4(2^_а)] ; М6 s^+a)
Л4е = /Иб.а; а = й
ГЛАВА 10
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
f 30. Косой и пространственный изгиб
10.1. Деревянная балка прямоугольного поперечного сечения, шарнирно опертая по концам (шаровые шарниры), нагружена посредине пролета сосредоточенной силой Р. Плоскость действия нагруз-
К задаче 10.1.
кн составляет угол <р с вертикальной плоскостью, проходящей через ось балки (см. рисунок). Определить нормальные напряжения в точках Л, В, Си О, построить эпюры изменения этих напряжений по сторонам сечения АВ, ВС, CD и ОЛ; проверить прочность балки при [о] = 100 кг/см*. Определить также полный прогиб балки посредине пролета по величине и по направлению.
Решение. При косом изгибе нормальные напряжения в любой точке опасного сечения с координатами у и г вычисляются по формуле
pt 300
Так как Мтах=у =800 •
= 60 000 кгем, cos <р = cos 12° = =0,978, sin <p = sin 12°=0,208,
. feh® 12-20® вплп . _ hb3 20-12®
Jy =-jg-= 12 =8000 см* и Jz =- = —^-=2880 сл‘, то
Г-60000 Сет' +S") =7-3"+'л-
268
В точке Л с координатами рд=+в см и г^ =—10 см Ол =—7,34-10 + + 4,33-6=—47,4 кг]смг-, подобно этому находим Од=—7,34-10—4,33-6 = -с__99,3 кг/слР, сс— +47,4 кг/см2 и Од=99,3 кг/см*. Наибольшие напряже-
нии возникают в точках В и D сечения; здесь omax=oD= —од=99,3 кг/см1 < < [о] = 100- кг/см*. Эпюры изменения нормальных напряжений вдоль сторон сечении даны на рисунке.
Наибольший прогиб балки будет в сечении посредине пролета. Составляющие этого прогиба в направлении осей у и г могут быть вычислены по формулам
Pyla РР sin <р . РгР Pl3 cos <р '•У-48£TZ— 48ЕЛ Н ^~48Ё77_ 48EJv *
Полный прогиб будет равен
« V PZP /~sin2<P , cos2(P _ Pl*
+ J2 “ 48EJnp„’
W
1 /"sin2<p , cos2<p „ Г /0,208V . /0,978V nnnn..„ ,, . 1^-y -тг^-ц-у bw) +(mw) ="™li2 ** Таким образом,
Приравнивая нулю выражение для нормальных напряжений!
o=7,34z+4,33y=0, находим таигеис угла наклона нейтральной линии к осн yi tgH7l=Hb0-59=tg30033'-Направление прогиба будет перпендикулярно к нейтральной линии сечения П будет составлять с направлением оси г угол а=30°33'.
10.2. Какое положение займет нейтральный слой в балке прямоугольного поперечного сечения, если плоскость действия нагрузки будет совпадать с одной из диагональных плоскостей (см. рисунок)?
Ответ: Совпадет с другой диагональной плоскостью.
10.3. Дощатые обрешетины кровли, шарнирно опертые на стропила, подвергаются действию вертикально направленной равномерно распределенной нагрузки q (см. рисунок). Определять наибольшую
2В0
допускаемую величину этой нагрузки при [о] = 100 кг)см* и вычислить полный прогиб обрешетины посредине ее пролета.
Ответ: 146 кг/м; 1,47 см.
10.4. При установке на опоры двутавра № 70, предназначенного для работы на изгиб в вертикальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка, и стенка двутавра отклонилась от вертикали на угол <р = 2°. Определить связанное с этим увеличение наибольших нормальных напряжений и полного прогиба двутавра.
Ответ: Напряжения увеличились на 51,5%, полный прогиб—на 99%.
10.5. Шарнирно опертая по концам балка длиной 4 ж несет равномерно распределенную нагрузку интенсивностью q = 500 кг)м. Поперечное сечение балки — швеллер № 18. Стенка швеллера наклонена к плоскости действия нагрузки под углом <р = 5° (см. рисунок). Определить нормальные напряжения в точках А, В, С и D опасного сечення балки
К задаче 10.6.
и построить эпюры этих напряжений по линиям АВ, ВС и CD. Определить также величину и направление наибольшего прогиба балки. Кручение швеллера во внимание не принимать.
Ответ: оА = —309 KejcM*; ов= —1019 кг/смг; ос= + 626 кг/см*-, oD = 4-1336 кг!см*; /=1,14 см; а = 47°57' (к плоскости стенки).
10.6. Двутавровая балка, шарнирно опертая по концам, посредине пролета 1 = 5 м нагружена сосредоточенной силой Р = 800 кг. Плоскость стенки двутавра составляет угол <р = 20° с плоскостью действия нагрузки (см. рисунок). Подобрать сечение балки при допускаемом напряжении [о] = 1600 кг!смг.
Решение. Условие прочности в данном случае имеет такой вид: .. /cos® sin<p\ 800-500 /0,94 0,342\ ,
Wy + Wz )~ 4 t Wy + Wz J l°] — 1600кг/сл| нли
800-500 /0,94 0,342\_58,75 21,38
4-1600 Wy + Wz J ~ Wy + Wz *
2С0
Сечение подбираем путем последовательных проб. Возьмем, например, двутавр № 20. Подставляя в условие прочности значения = 184 см2 н №г = 23,1 сл3, имеем
Л5Г+^Т=0,319 + 0,925= 1,244 > L 104 ZO,1
Условие прочности не удовлетворяется, максимальное напряжение будет иа 24,4% больше допускаемого. Необходимо увеличить номер двутавра. Испробуем № 22, имеющий ^ = 232 сл? и 11^ = 28,6 сл3. Теперь
%Г+ЭТ=0,253 + 0,748=’’001~1-
Перенапряжение в 0,1 % допустимо. Останавливаем свой выбор на двутавре №22
10.7. Деревянный брус прямоугольного поперечного сечении, защемленный одним концом, нагружен на другом конце сосредоточенной силой Р (см. рисунок). Полагая, что Л:й=1,5, подобрать размеры сечения бруса при допускаемом напряжении [о] = 100 кг/см*. Определить величину и направление наибольшего прогиба.
Ответ: Л =19,9 сж«20 см; /=0,93 см; а = 52°25' с осью г.
К задаче 10.8.
10.8. Стропильные ноги крыши отстоят друг от друга на 3 м и наклонены к горизонту под углом 30°. К ним прикреплены обрешетины нз швеллеров № 20 на расстоянии 2 м друг от друга. Ветровая нагрузка, направленная перпендикулярно к плоскости крыши, имеет интенсивность = 75 кг/м2, а собственный вес кровли, действующий вертикально, имеет интенсивность д3 = 50 кг/м2 (см. рисунок). Определить в опасном сечении нормальные напряжения в точках А, В, С н D и построить эпюры этих напряжений по линиям АВ, AD и DC. Скручивание швеллера во внимание не принимать.
Ответ: оА = —273 кг/см2; ов = + 105 кг/см2; ос= + 446 кг/см2; cD = +67 кг/см2.
10.9. Деревянная балка прямоугольного поперечного сечения длиной 2,4 м, шарнирно опертая по концам, нагружена посредине
261
пролета сосредоточенной силой Р. На установленных в опасном сечении балки тензометрах А и В (см. рисунок), с базой 20 мм и
К задаче 10.9.
увеличением в 1000 раз, при этом отмечены такие изменения отсчетов: А—уменьшение на 9 мм, В — увеличение на 6 мм. Определить величину и направление нагрузки Р, а также величину наибольшего нормального напряжения в балке.
Ответ: Р=839 кг; <р=26°34' к вертикали; огоах = 75 кг/см2.
10.10. Защемленная одним концом двутавровая балка № 24а длиной 1,4 м, нагруженная на свободном конце сосредоточенной силой Р, прогнулась под силой на 3 мм. Направление прогиба совпало с биссектрисой угла между главны-
ми осями инерции поперечного сечения балки. Определить величину и направление силы Р, а также наибольшее растягивающее напряжение в балке.
Ответ: Р=1765 кг; <р = 3°55' к вертикали; о1Пвх=1184 кг/см2.
К задаче 10.11.
10.11. Балка прямоугольного поперечного сечення изгибается в плоскости, наклоненной к плоскости хг под углом <р (см. рисунок). Построить графики, иллюстрирующие зависимость наибольшего нормального напряжения и полного прогиба балки от величи-
на
иы угла <р. Величину нагрузки при любом значении ф считать одной и той же. При каком угле ф нормальное напряжение будет самым большим? Рассмотреть случай, когда h:b = 2. Выполнить такие же построения для двутавра №18.
Ответ: Эпюры о1ПаХ = Ф1(ф) и /==Фа(ф) для прямоугольного сечения приведены на рисунке.
Для краткости обозначено:
max о при <р О тахо при <р = 0
1F совф + ^г sin ф,
/ при ф О
/ при ф = 0
Наибольшее нормальное напряжение имеет место прн условии, что 1g ф= WJWZ. Для прямоугольного сечения с отношением Л:Ь = 2 лтах = 2,236 при ф = 6з°26'; для двутавра № 18 лл)ах = 7,83 при ф=82°40'. Таким образом, плоскость наименьшей грузоподъемности не совпадает с плоскостью наименьшей жесткости.
б) в)
К задаче 10.12.
г)
10.12. В результате изгиба балок, поперечные сечения которых изображены на рисунке, центры тяжести сечений переместились в указанных направлениях.Опреде
лить для каждой из балок положение плоскости действия внешних сил (угол ф с осью z).
Ответ: а) ф = 20°; б) ф = 35°; в) ф = 8°; г) ф = 60°.
10.13. Уголок 80x80x7 мм длиной 1,6 м работает как балка с одним защемленным концом; на свободном конце он нагружен сосредоточенной силой Р=100 кг, направление которой проходит через центр изгиба сечения (см. рисунок). Определить в опасном сечении положение нейтральной линии и нормальные напряжения в тс
К задаче 10.13.
А, В и С. Найти также
величину и направление наибольшего прогиба уголка.
283
Решение. Нормальные напряжения в любой точке опасного сечения уголка равны
/sin <р созф \ /sin 45° , cos 45° \
о=Л4-х 1"7гг/+т772;=₽ч^гг/+^г2)=
= 100.160-0,707 + 2L) =419у + 108,8г.
Приравнивая последнее выражение нулю, находим тангенс угла наклона нейтральной линии к осн г:
tga =-у-= дг—0,26 = tg(—14°33')-
Координаты точек А, В и С имеют такие значения (см. рисунок):
гл=— гс= у=-=-^=5,66 см. ув=—г0У2 =
= —2,23 }/’ 2 = —3,15 см, г„=0.
Подставляя эти координаты в формулу для вычисления о, имеем О/ = 419х Х2.5+108,8-5,66= 1664 кг/см2, Ос=419-2,5—108,8-5,66 = 433 кг] см* и Од = = -419-3,15= —1322 кг/см*.
Наибольший прогиб уголка равен
Pl3 cos ф 3EJy
Jy sin ф
Jz СС5ф
101-0,707 у 27-0,707 )
,85 см.
2
Направление прогиба перпендикулярно к нейтральной линии сечения.
10.14. Обрешетина кровли зетового сечения № 14 (ОСТ 29) работает как шарнирно опертая по концам балка пролетом 2,5 м, нагруженная равномерно распределенной нагрузкой интенсивностью q, плоскость действии которой проходит через центр изгиба сечении (см. рисунок). Положение главных центральных осей сечения указано на рисунке: Р = 21°48', Ууо = 847 см*, Уг=61,4 см*, 0 = 65 лгм, Л = 140 мм.
Определить наибольшую допускаемую величину нагрузки при допускаемом напряжении [о] = 1600 кг]см*, а также величину и направление полного прогиба обрешетины от этой нагрузки посредине пролета.
Ответ: 1,5 т/м; 0,57 см; 34°26' к вертикали.
10.15. Шарнирно опертая по концам балка несет посредине пролета длиной 3,2 м сосредоточенную нагрузку Р. Поперечное сечение балкн — швеллер № 24 (см. рис. а). К стенке швеллера на протяжении всей длины балки предположено приварить уголок 125 X 125 X X 12 мм (см. рис. б). Положение главных центральных осей предполагаемого сечения балкн показано на рис. б; моменты инерции относительно этих осей равны: Jy = 4671 см* и Уг = 873 см*.
При допускаемом напряжении [сг] = 1600 кг/см2 определить наибольшую допускаемую величину нагрузки Р; а) для одного швеллера
264
и б) для швеллера с приваренным к нему уголком, полагая, что плоскость действия нагрузки в обоих случаях параллельна плоскости стенки швеллера и проходит через центр изгиба сечения. Опре-
К задаче 10.14.
делить также наибольший прогиб балки в первом и во втором случае, считая, что Р=4 г.
К задаче-10.15.
Ответ: а) Р=4840 кг, /=0,47 см; б) Р=4396 кг, / = 0,51 см; добавление уголка снижает допускаемую величину нагрузки на 9,2% и увеличивает прогиб балки на 8,5%.
Схемы закрепления и нагружения балок
Схемы поперечных сечений балок
К задаче 10.16.
10.16. Для изображенных на рисунке балок найти положение нейтральной линии (угол а с осью .у), определить в опасном сече-
265
яии наибольшие нормальные напряжения, построить эпюры этих напряжений по сторонам сечения и найти величину наибольшего прогиба балки. Плоскость действия нагрузки во всех случаях совпадает
К задаче 10.16.
Л» 11/п Схема балки и сечения Пролет 1 Нагрузка Размеры сечення Угол Ф Ответ
Угол а /max Ощах
м СМ кг/см*
1 1—А 1.5 Л4о = О,4 тм 12x20 см 60е 78°16' 1,38 97,2
2 1—Б 1.4 Л4о=О,2 тм двутавр № 12 30° 82°8' 1,77 1443
1 3 1— В 2,0 Л4о = О,6 тм швеллер №27 60° 87°55' 1,98 1492
4 2—А 2,0 Р =80 кг 10x15 см 45° 66°2' 1,32 75,4
5 2—Б 1.5 Р =200 кг двутавр № 16 30° 83°22' 0,97 1273
6 2--В 1.4 Р =300 кг швеллер № 22 60° 87°38' 0,79 1552
7 3—А 2.0 q =2 кг/см 10x25 см 45° 80»55' 1,37 95,0
8 3—Б 1.2 д =3 кг/ см двутавр № 14 30° 82°46' 0,47 1168
9 3—В 2.4 q =2 кг/ см швеллер № 24 45° 85°54' 1.41 1481
10 4—А 2.5 Мо=О,6 тм 12x30 см 60° 84°43' 0,94 88,8
11 4—Б 3,0 М» = 0,8 тм двутавр № 27 45° 87°2' 1,23 1516
12 4—В 2.2 Л4о = О,3 тм швеллер № 14а 30° 79°39' 0,80 1463
13 5—А 2,5 Р =250 кг 9х 15 см 45° 70°12' 0,67 87,3
14 5—Б 4.0 Р =1200 кг двутавр № 36 60° 88°44' 1.34 1542
15 5—В 2.4 Р =400 кг швеллер № 14 30° 80°54' 0,64 1388
16 6—А 3.2 д =6 кг/см 16x24 см 60° 75°37' 0,89 90,0
17 6—Б 5.0 д =4 кг/ см двутавр № 40 60° 88°50' 2,12 1326
18 5—В 4,0 д = 1,2 кг/см швеллер № 16 45° 85“9' 2,24 1415
с вертикальной плоскостью v, проходящей через центр изгиба сече-
ния—точку О. Балки
К задаче 10.17.
прямоугольного сечения—деревянные, остальные балки — стальные. Данные о размерах балок и величине нагрузки приведены в таблице; там же помещены и ответы.
10.17. Чугунный брус треугольного поперечного сечения (см. рисунок), шарнирно опертый по концам, в плоскости, параллельной стороне АВ, изгибается сосредоточенной силой Р, приложенной посредине пролета 7=1,8 м. Определить необходимые размеры поперечного сечения бруса, если допускаемое напряжение для чугуна на растяжение равно 400 кг {см?, а на сжатие — 1200 кг[см\
Ответ: h~ 18 см.
10.18. Чугунный брус с поперечным сечением в виде трапеции (см. рисунок) имеет длину 1,2 м, защемлен одним концом и нагружен на другом конце сосредоточенной силой Р, направление которой проходит через центр тяжести поперечного сечения О и точку С. Определить нормальные напряжения в вершинах углов трапеции и
266
наибольший прогиб бруса. Е = 1,2-10е кг/см*, J =4455 сж4, /г = = 1875 сж4.
Ответ: ол = 391 кг}см*-, ов = 109 ке1смг\ ас=—603 кг/см1-. Од = 246 кг/см?-, /=0,58 см.
10.19. Балка с поперечным сечением в виде полукруга, имеющая длину 2 ж и шарнирно опертая по концам, нагружена равно
К задаче 10.19.
мерно распределенной нагрузкой интенсивности q (см. рисунок). Определить наибольшие растягивающие н сжимающие напряжения в опасном сечении балки, а также наибольший прогиб ее.
Решение. Центр тяжести сечення балки находится в точке О на расстоя-4г 4-10 . . ,,
пии г0 = =-==-=-, =4,24 см от диаметральной оси yt. Моменты инерции о Л О О| 14
_ _ ЛГ«
сечения относительно главных центральных осей у и г равны Jz=—— = о
Ej’H8L°?. = 3927 см* н Jy = Jy-zlF=^--4,24*X х?л^=1098 сл.
Угол наклона нейтральной линии к осн у определяем по формуле
Jv logs tga=-2-tg<p=^-0,364 = 0,1018=tg 5°48,6'.
J g
Наибольшие нормальные напряжения возникнут в точках, наиболее удаленных от нейтральной линии; это будут точки В и А (точка, в которой линия НК, параллельная нейтральной оси, касается контура сечення). Опасное сечение балки будет посредине пролета; в этом сечении
/sin<p , cos ср \ 4-2002 ( 0,3420 0,9397 \
= 1,74 у— 17,12 г.
Нормальное напряжение в точке В с координатами уя = г=Ю см и гл = •=—г0=—4,24 см будет растягивающим; оно равно ов= 1,74-10-|-17,12 X X 4,24 и 90 кг/см*.
267
Координаты точки A: za — OD = CD—OC=r cosa—z0= 10-0,9949—4,24 = = 5,71 ел! и уд=—AD=—ZCsina=—rsina= — 10-0,1012= —1,01 см. Напряжение в точке А будет сжимающим; оно равно
од= —1,74-1,01 — 17.12-5,71 = —99,5 кг/см*.
Наибольший прогиб балки находим по формуле
5<?/’ f cos2 tp sin2q> 4 -200’ _ f /0,9397 V2 / 0,3420 V n 79
, = 184£ V _^-+_7Г = 384Л05 F ПОЭТ,) + V 3927-,) '
10.20. Деревянный брус с поперечным сечением, изображенным на рисунке, шарнирно оперт по концам. Посредине пролета 1 = 3 м
на брус действует сосредоточенная сила Р, направленная под углом 60® к оси симметрии сечения. При допускаемом напряжении [о] = = 110 кг 1см* определить наибольшую допускаемую величину силы Р. Jy = 333\ см*, ./г=1949 см*.
Ответ: 388 кг.
10.21. Деревянная балка, защемленная одним концом, изгибается силами Рг и Рг (см. рисунок). Подобрать прямоугольное сечение балкн с отношением высоты h к ширине Ь, равным 2, н определить полный прогиб ее в сечении
А по величине и направлению,* [о] = 100 кг!см*.
О>вет: 9X18 см; /д = 1,98 см (под углом 80°52' к вертикали).
10.22. Двутавровая балка № 40, шарнирно опертая по концам
пролета 5 м при горизонтальном положении стенки, временно использована в качестве опоры для горизонтально расположенного домкрата, установленного на расстоянии 2 м от одной нз опор (см. рисунок). Учитывая собст-
К задаче 10.21.
К задаче 10.22.
венный вес балки, определить наибольшую допускаемую нагрузку на домкрат. Для материала балки [о] = 1600 кг/см*.
Ответ: 11 т.
268
10.23. Двутавровая балка № 36 защемлена одним концом и нагружена в плоскости наибольшей жесткости равномерно распределенной нагрузкой интенсивности q, а в плоскости наименьшей жесткости— сосредоточенными силами Pt н Р. (см. рисунок). Определить в опасном сечении балки наибольшее нормальное напряжение, а также величину и направление полного прогиба в сечениях В, С, D и Н.
Решение. Для двутавра № 36 по сортаменту /г = 516 см*. Jy= 13380 см*. ^7=743 см3 и W'z = 71,l см3. Эпюры изгибающих моментов в вертикальной (Му) и горизонтальной (Мг) плоскостях представлены на рнс. б. Опасным будет сечение С или сечение А.
В сечении С, где МуС=0,72 тм, а МгС=0,96 тм, наибольшее растягивающее напряжение будет в точке ft; оно равно
max а (С) = ск== 97 +1350 = 1447 кг/си<’-. у W* / 40 /1*1
В сечении А, где Л4уд = 2,88 тм, а Л4гд = 0,72 тм, наибольшее растягивающее напряжение возникает в точке N:
тахО(Л)=Ол, = ^ + ^=^^+?|^ = 388+1012=1400 кг/см3.
*Т у *Т j / «0 /1)1
Более опасным оказывается сечение С.
Интегрирование дифференциальных уравнений изогнутой осн балки в вертикальной и горизонтальной плоскостях приводит к таким выражениям для прогибов:
fz=— Ф1 (6m2—4m3-|-m*)
и
fy = Фа { 8 (р-1) т3-12 (р-2) тг | Ас-Р (2m -1)31 сн ) =
= Фг Г 14m3—9m2 | дС- Н (2m-1)31 сн I ,
х Р, 2200 п,е Л ql* 10-2404
т~ I • р^р1 ~ 800 - 2,75, Ф1~ 24£/у_24-2 10*.13380 - 0’0517 СМ
269
А Pxl3 800-2403 „оло
Фг- 48£J “ 48-2-10«-516 “°1223 СМ'
Подставляя в формулы для вычисления fyH f2 значения т: т=1/4, т = = 1/2, т=3/4 и т=1, находим составляющие полного прогиба в направлении той и другой главной оси инерции в сечениях В, С, D и Н, Величину полного прогиба определяем по формуле
а угол а между направлением полного прогиба и осью z находим из выражения tga.= fylfz. Результаты соответствующих вычислений приведены в таблице. Изогнутая ось балки представляет пространственную иривую.
Селение fv. СМ h. см t. СМ tga a Примечание
в с D Н —0,0767 —0,1116 4-0,1116 4-0,8093 —0,0163 —0,0549 —0,1035 —0,1550 0,0785 0,1244 0,1522 0,8240 +4,695 4-2,034 —1,078 —5,222 +77’59' +63’49' —47’10' —79’10' Положительные значения угла a откладываются от оси z по направлению движения часовой стрелки
10.24. Для балок, схемы которых изображены на рисунке, определить величину наибольших нормальных напряжений в опасном сечении, а также величину и направление (угол с вертикальной осью
К задаче 10.24.
сечения) полного прогиба в сечении А. Варианты балок: а) деревянная, круглого сечения диаметром d; б) деревянная, прямоугольного сечения с отношением Л:£ = 2; в) стальная, двутаврового сечения;
270
г) стальная, корытного сечення (считать, что в этом случае плоскость действия внешних снл проходит через центр изгиба сечения). Концы балок на схемах 1 и 2 защемлены, а на схемах 3 и 4 закреплены шарнирно как в вертикальной, так и в горизонтальной плоскости; одна из двух опор неподвижная. Во всех случаях высота сечения балкн параллельна вертикальной оси z. Данные о размерах балок н величине нагрузки приведены в таблице; там же помещены п ответы.
К задаче 10.24
№ п/п Схема балкн н вид сече* ння Размеры сечення Длина, .« Нагрузки Ответ
1 а Р, т ч. кг/см м. кгм а max. кг/см1 1 А' СМ а
1 1—а d= 16 см 1.5 1,0 0,2 104,4 0,73 17’17'
2 1—5 ft = 20 см 1.8 1.0 0,3 135,0 1,18 42°9'
3 1—в № 12 1.2 0,8 0,2 — 1512 0,66 75’38'
4 1—г № 14 1.4 0,9 0,2 1381 0,62 72®26'
5 2—а d= 12 см 1.0 0,4 0,2 — 150 100,2 0,80 79031’
6 2—5 Л= 18 см 1.2 0,5 0,4 — 120 90,5 0,80 81’30'
7 2—в № 18 1.6 0,6 1.0 200 1507 1,55 86’24'
8 2—г № 20 2.0 0,8 2,0 100 1540 0,96 67’35'
9 3—а d= 18 см 3,0 — 0,4 4 —— 94,5 0,93 28’4'
10 3—б ft = 24 см 2,4 — 0,6 6 —— 100,0 0,52 69’27'
11 3—в № 20 2,8 — 0,4 7 — 1585 0,82 79’10'
12 3—г № 24 3,6 0,3 10 1524 0,80 61’43'
13 4—а d= 14 см 2,4 — —— 3 140 95,5 0,87 37’52'
14 4—6 ft=20 см 3,0 4 100 97,5 0,93 46’51'
15 4—в № 16 2,2 10 150 1589 0,79 77017'
16 4—г № 18 2,8 — — 8 160 1589 0,96 72°9'
§ 31. Внецентренное растяжение или сжатие
10.26. Деревянная стойка прямоугольного поперечного сечения нагружена продольной сжимающей силой Р = 90кн, приложенной в точке N (см. рисунок). Определить положение нейтральной оси сечення и построить эпюры нормальных напряжений по сторонам прямоугольника.
Решение. Для нахождения напряжений в поперечном сечении стойки воспользуемся формулой
’-я,+^+¥)-
В данном случае Р = — 90 000 н (сила сжимает стойку), F = bh= 15 -20 = =300 см* = 0,03 мг, ур=гр=3 см, а квадраты радиусов инерции поперечного
сечения равны л ftft» ft^ 20* 100 . г 15* 75 ,
у F~ 12Wi~ 12 ~ 12 ~ 3 СМ'' ‘г~ F~ \2bh~ 12 ~ 12 ~ 4 СМ
271
Подставляя значения Р, F, уР, гр, i* и i® в формулу для вычисления напряжений, имеем (у и z в ел)
° = -ЛГбг( 1+У^+^г)=-3.10«(1-|-0.16{,4-0,09г)н/л<’. v,uo \ /и 1W /
Положение нейтральной осп найдем, полагая, что о = 0; получаем уравнение
14-0,16(/4-0,09z=0, откуда при z=0
ау = — g-Jjg = — 6,25 см (точка К), а при 0=0
вг=—р-^ = —11,1 см (точка М).
Нейтральная ось сечения проходит через точки К и М.
Так как нормальные напряжения линейно зависят от координат у н z, то для построения эпюр нх изменения вдоль сторон сечения достаточно вычислить величину напряжений в вершинах углов прямоугольника. В точке А с координатами Уд =—7,5 см н зд = —10 см.
Oj = -3-10« (1—0,16-7.5—0,09-10) = 3,3-10е н/л2 = 3.3 Мн/м1 (растяжение).
Аналогично вычисляются напряжения и в остальных угловых точках: ср= = —2,1 Мн/м2, ос=—9,3 Мн/м2 п aD= — 3,9 Мн/м2; в этих точках имеет место катке. Эпюры напряжений показаны иа рисунке.
10.26. Определить необходимую толщину стальной полосы шириной 18 ел, растягиваемой двумя параллельными ее оси силами 9 т, приложенными посредине толщины на расстоянии 5 см от края полосы; [о] = 1600 кг/см2.
Ответ: 7,3 мм.
272
10.27. Нормальное напряжение в точке А сжатого бруса (см.
рисунок) равно 12 кг/см2 Чему равно напряжение в точке С?
Ответ: 48 кг/см1 (сжатие).
(растяжение), в точке В
оно равно нулю.
К задаче 10.27.
К задаче 10.29.
10.28. В точках А двух колонн приложены сжимающие силы (см. рисунок). При этом в точках С обеих колонн сжимающие напряжения оказались одинаковыми. Сравнить напряжения в точках В колонн.
Ответ: В колонне круглого сечения напряжение будет больше на 20%.
10.29. В точках А и В колонны прямоугольного сечения (см. рисунок) приложены одинаковые силы. Как изменится наибольшее сжимающее напряжение в колонне, если одну из сил удалить?
Ответ: Не изменится.
Ю.ЗО.Провернть прочность нижней части бетонного столба прямоугольного поперечного сечения (см. рисунок). Допускае-
{Р=600ка
л
-40ОН*
К задаче 10.30.
а)
0 К задаче 10.31.
мое напряжение па растяжение равно 7 кг] см1, на сжатие — 70 кг/ся?. Ответ: max <тр = 6,3 кг/см1 < 7 кг/см2-, max осж = 9,7 кг!см2 < 70 кг/см2.
10.31. Основание для стойки сделано из бруса с поперечным сечением 20x30 см (см. рнс. а). Определить наибольшее нормальное напряжение в основании стойки, если сжимающая ее сила Р = 36т.
>73
Чему будет равно это напряжение, если основание стойки сделать из бруса с поперечным сечением 20x20 см (см. рис. б)?
Ответ: а) 120 кг!см'1-, б) 90 кг/см*.
10.32. От какого вида напряжений (растяжение или сжатие) произойдет разрушение бетонной колонны прямоугольного поперечного сечення (см. рисунок), если сжимающая ее сила будет приложена: а) в точке Л? б) в точке В? Предел прочности бетона при
сжатии в шесть раз больше предела Зависимость между о и в считать линейной вплоть до разрушения.
Ответ: а) сжатие; б) растяжение.
прочности при растяжении.
К задаче 10.33.
К задаче 10.32.
10.33. При сверлении детали на шпиндель А сверлильного станка (см. рисунок) передается осевое давление 1,6 т. Определить диаметр d круглой чугунной колонны В, если допускаемое напряжение на растяжение равно 350 кг/смг.
Ответ: 125 мм.
10.34. Короткая деревянная стойка с поперечным сечением в виде полукруга диаметром d = 20 см нагружена продольной сжимающей силой Р, приложенной в точке Л— посредине ширины и толщины стойки (см. рисунок). Определить наибольшую допускаемую величину
К задаче 10.35.
К задаче 10.34.
силы Р, если допускаемое напряжение [о] = 100 кг!см*. Какую силу Р можно было бы приложить к стойке, если бы она работала на простое сжатие?
Ответ: 9,68 т; 15,7 т.
10.35. К крестовине CDEF, жестко скрепленной со стальной трубой АВ (см. рисунок), симметрично подвешены четыре одинаковых
274
груза Р=100кг. Труба АВ имеет наружный диаметр 60 мм при толщине стенки 2 мм. Определить наибольшее растягивающее напряжение в трубе при четырех грузах, а также в том случае, если один из грузов будет снят.
Ответ: ПО кг/смг; 1256 кг/сж2.
10.36. Колонна с поперечным сечением, изображенным па рисунке, сжата продольной силой, приложенной в точке А. Определить, во
К задаче 10.36.
К задаче 10.37.
сколько раз максимальное нормальное напряжение в данном случае меньше того, которое возникло бы в колонне, если бы толщина ее стенок везде была одинаковой и равной 6 см.
Ответ: В 1,15 раза.
10.37. Столб, служащий для подвески одиночного трамвайного провода, состоит из двух швеллеров № 16 (см. рисунок). Учитывая вес провода, вес консоли, к которой подвешен провод, и собственный вес столба, определить наибольшие растягивающие и сжимающие напряжения в сечении у основания столба.
Ответ: -j-Пб кг/см*', —130 кг 1см1.
10.38. Короткая двутавровая стойка №55, нагруженная центрально приложенной сжимающей силой Р=180т (см. рис. а), «усилена» швеллером № 18, приваренным к стойке по всей ее длине (см. рис. б). Чему было равно наибольшее сжимающее напряжение в двутавровой стойке и чему оно равно в стойке, «усиленной» швеллером?
Ответ; а) 1579кг/сжа; б) 1707 /сг/сж2.
10.39. На короткую стойку двутаврового сечения, шарнирно закрепленную по концам, через кронштейн передается нагрузка Р = 6,5т (см. рисунок). Определить необходимый номер двутавра при допускаемом напряжении 1600 кг)смг.
Ответ; № 22.
10.40. Двутавровые стойки CD поддерживают балкн АВ, по которым уложены пути узкоколейной железной дороги (см. рисунок). Определить необходимый номер двутавра при загружении вагонами обоих путей или одного из них^ если собственный вес конструкции,
275
передающийся на одну [а] = 1400 кг!смг.
Ответ: № 36.
стойку, равен Q=12t, Р = 8т, а=\м и
P=180m Р*180тп
VmWzW/SZVP.
’*\Z75\Z75\*~
NB55
а)
К задаче 10.38.
10.41. Кран для подъема и перемещения грузов до 8 т (см. рису
нок) опирается на бетонный фундамент, причем ось АВ крана про-
ходит через центр фундамента. Считая, что вес крана, равный 18 т
К задаче 10.41.
(без веса груза Р и веса противовеса Q), приложен к фундаменту в точке С па расстоянии 0,6 м от оси АВ, определить размер стороны а фундамента так, чтобы в основании фундамента не было растягивающих напряжений. Определить, чему
К задаче 10.42.
при выбранном значении а будет равно наибольшее давление на грунт. Объемный вес бетона равен 2,2 т/м3.
Ответ: 3,68 м «3,7 м; 16,1 т/м®.
10.42. Стальная полоса растягивается центрально приложенными силами Р (см. рисунок). Какой глубины а может быть сделана в по-
276
лосе односторонняя выточка при условии, что наибольшие нормальные напряжения в ней не превысят 1500 кг/см2? Концентрацию напряжений в выточке во внимание не принимать.
Ответ: 20,7 мм.
10.43. При отливке полой стальной колонны прямоугольного сечения толщина двух параллельных стенок ошибочно была сделана
неодинаковой (см. рисунок). Полагая, что сжимающая колонну продольная нагрузка приложена в точке А, определить наибольшую допускаемую величину этой нагрузки, если [о] = 1600 кг! см2. Для сравнения
-60^-90-^-110-^\40 к—150—^^—150—
Размеры в мм
К задаче 10.43.
К задаче 10.44.
определить наибольшую величину нагрузки в предположении, что толщина стенок колонны везде одинакова (50 jhjh).
Ответ: 594,7 т; 640 т, т. е. па 7,6% больше.
10.44. Насколько (в процентах) увеличится наибольшее сжимающее напряжение в короткой стойке квадратного поперечного сечения со стороной а, сжатой центрально приложенной силой Р, если в ней сделать: а) одну врубку, как указано на рисунке? б) две такие одинаковые врубки с противоположных сторон стойки?
Ответ: На 70,2%; на 33,3%.
10.4Б. Стойки, поперечные сечения которых изображены па рисунке (стр. 278) подвергаются действию продольной сжимающей нагрузки Р, приложенной внецентренно. Для некоторых точек напряжения, найденные экспериментальным путем, известны; на рисунке величина напряжений в этих точках указана в кг'см2.
Определить для каждой нз стоек величину нагрузки Р и координаты точки ее приложения, а также величину наибольшего сжимающего напряжения.
Ответ: а) Р=6т, ур= -|- 2 см, zp =— 4с.«, тахо = 80 кг/см2;
б) Р= 15 т, УР = + 0,22 см, zp = 9,5 см, тахо = = 1584 кг/см2.
10.46. Уголок 140x140x12 мм растягивается двумя силами Р— 15 т, приложенными в концевых сечениях в точках К. (см. рису-
277
иок). Определить положение нейтральной оси и напряжения в точ-
ках А, В к С сечения уголка. Найти наибольшего прогиба уголка, если его длина равна 2 м. Кручение уголка во внимание не принимать.
также величину и направление
Размеры а мм
К задаче 10.45.
К задаче 10.45.
Указание. Наибольший прогиб уголка определяется по формуле
Направление прогиба перпендикулярно к нейтральной оси сечения.
Размеры в метрах
К задаче 10.47.
изображены на рисунке
Ответ: ау =— 12,25 см, az= 4-3,37 см, о^ = — 512 кг/см1, ов=+1216 кг/сл2,
Ос= + 234 кг/см*, f=0,355 см.
10.47. На рисунке изображены горизонтальные сечения быка двухпутного железнодорожного моста. Вес быка 3200 т. В точках /, 2, 3, 4, 5, 6, 7 и 8 на бык передаются одинаковые силы веса пролетных строений моста, каждая из которых равна 120 т. Кроме того, в точках 1 н 2 на бык передаются одинаковые силы веса поезда, проходящего по одному нз пролетных строений; каждая из них равна 210 т. Определить положение нейтральной оси, а также наибольшие и наименьшие сжимающие напряжения в горизонтальном сечении быка у основания.
Ответ: ау = — 26,6 м; аг = — 86,6 м; Фтах = 49,2 Т/м*; Oniin= 33 т/м*.
10.48. Стальные стержни длиной / = = 1,5 л<, поперечные сечения которых (размеры указаны в см), растягиваются
продольными силами Р, приложенными в концевых сечениях в точ-
ках, отмеченных звездочками. Найти отрезки, отсекаемые ней-
тральной линией вд осях координат, вычислить нормальные напряжения
278
К задаче 10.48.
К задаче 10.48
№ схемы Координаты точек нейтральной оси Напряжения в точках сечення. кс/см* Прогиб f. CM
о„, см а2, см °А ав ас °D 0 max
1 4-0,75 4-2,67 +375 -625 + 125 + 1125 1125 0,49
2 4-0,96 —1,56 + 1672 +281 —1005 +386 1672 0,57
3 —1,15 4-1,48 —919 +331 + 1493 +243 1493 0,45
4 —1,25 —1,25 + 1273 —764 —764 +1273 1695 0,41
5 4-6,04 —2,27 + 1342 —443 +784 +115 1403 0,30
6 —0,54 —3,30 —532 + 1580 4-949 —1164 1580 0,55
7 —0,53 —2,49 +23 + 1283 +747 —514 1283 0,45
8 4-0,77 +2,17 —280 +412 —70С + 1524 1524 0,41
9 —0,63 +1.05 + 1415 —454 +ю — 1415 0,54
270
в точках А, В, С и D, построить эпюры изменения этих напряжений вдоль сторон сечения и определить стрелу прогиба / стержня посредине его длины. Для стержней, сечения которых изображены иа схемах 4 и 5, определить также величину наибольших нормальных напряжений. Напряжения, возникающие в результате изгибно-крутильной деформации тонкостенных стержней, не учитывать. Ответы помещены в таблице.
10.49. На рисунке изображены поперечные сечения: прямоугольные, корытное и шестиугольное, а также их ядра сечений. Как будет
К задаче 10.49.
проходить в каждом из этих сечений нейтральная ось, если перпендикулярная к плоскости сечения сила будет приложена в точке Л?
Ответ: Пройдет через точки В и С.
10.60. На рисунке изображено квадратное поперечное сечение каменного столба. Продольная сжимающая столб сила Р приложена
на границе ядра сечения в точке К, лежащей на диагонали ОС. Чему равны напряжения в точках А, В, С и D?
К задаче 10.50.
К задаче 10.51.
Ответ: ол = 0; од=оо = —стс = —2-^.
10.51. Как будет менять свои размеры ядро сечения двутавра (см. рисунок), если толщина стенки d последнего будет уменьшаться? Какие предельные размеры оно будет иметь при уменьшении d до нуля?
Ответ: Ья = ~
10.52. На рисунке изображены поперечные сечения трех полых колони. Определить размеры ядра сечения для каждой из колонн: а) при наличии и б) при отсутствии в них внутренней полости.
280
Ответ: 1) в полых колоннах: а) Л„ = 2г„ = 42,9 см, Ья*=2уя— == 68 см; 2) Ля = b„ = 112,4 см; 3) ft„ = Ья = de = 72,0 см; б) в сплошных колоннах: 1) йя = 26,7 см, />я = 50 см; 2) ЛЯ = ЬЯ = 66,7
К задаче 10.52.
3) Ля = Ья — (1Я — 50 см. Во всех случаях в полых сечениях размеры ядра сечения больше, чем в сплошных сечениях.
10.53. Построить ядро сечення для каждого из поперечных сечений, изображенных на рисунке.
Ответ:
Сече-лис Координаты ядра Сече-ппе Координаты ядра
Ул г» Ул
1 0 -|-1,4 4 м -1,18 +2,36 м 0 0
2 0 +0.181Л
0 —0,144/t
±0,268& -0.052Л
3 0 +0,242 л +0,478 м —0,676 м ±0,467 м ±0,461 м 0 0
4 —0,118а ±0,253а
—0,206а 0
+0.165а ±0,354а
281
§ 32. Одновременное действие продольных н поперечных сил
10.Б4. Кирпичный столб квадратного поперечного сечения 1 х 1 л, высотой 5 я нагружен своим собственным весом н поперечным равномерно распределенным давлением ветра, равным 80 кг/м.2 (см. ри-кладкп равен 1,6. Определить
сунок). Удельный вес столба
величину наибольшего и наименьшего сжимающих напряжений в основании столба.
Ответ: ол =—2 т/м2; оя = = —14 т/я2.
10.55. Деревянный столб АВ круглого поперечного сечения диаметром 15 см (см. рисунок) удерживает канат, который натянут силой Р. Считая столб в сечении В защемленным, определить наибольшее возможное натя-
К задаче 10.54.
Л
d
К задаче 10.55.
жение каната, если допускаемое напряжение для дерева равно [о] = 100 кг/см*.
Ответ: 787 кг.
10.56. Столб диаметром 20 см несет на высоте 5 я над землей две группы горизонтальных проводов: А и В (см. рисунок). Воспринимаемое столбом горизонтальное усилие от группы проводов А равно 100 кг, от группы проводов В—150 кг. Передающийся иа столб
1^=150ке Р
К задаче 10.57.
К задаче 10.56.
вес проводов обеих групп равен 280 кг; вес столба 90 кг. Определить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении столба у земли.
Ответ: max араст = 83 кг/см2-, max 0^= 85,4 кг 1см1.
10.57. Определить нормальное напряжение в трубке, на которой укреплено седло велосипеда (см. рисунок), если нагрузка Р = 800 к.
282-
К задаче 10.59.
^Наружный диаметр трубки равен 24 мм, внутренний—21 мм. Конец В трубки считать защемленным.
Ответ: 113,9 Мн!м2.
10.68. Заводская труба в виде полого усеченного конуса имеет высоту 32 л<; наружный диаметр верхнего сечения трубы равен 2 м, наружный диаметр основания — 3,5 м; толщина стенки соответственно равна 25 см и 1 Л1. Вес 1 л? кладки трубы равен 1,6 т.
Определить наибольшую величину ветровой нагрузки на 1 м2 вертикальной проекции трубы, при действии которой в основании трубы не будет растягивающих напряжений. Давление ветра по диаметральному сечению трубы считать распределенным равномерно.
Ответ: 89,5 кг/м2.
10.59. Двутавровая балка ВС настенного крана шарнирно соединена со стойкой DE и тягой АС (см. рисунок). Определить наибольшее нормальное напряжение в поперечном сечении балки при грузе Р=4 г.
Ответ: 976 KijcM2.
10.60. Стойка DE настенного крана
(см. рисунок к предыдущей задаче) составлена из двух швеллеров №16, сваренных стенками; плоскость стенок параллельна плоскости чертежа. Определить наибольшее сжимающее напряжение в поперечном сечении стойки, расположенном непосредственно под точкой А. Считать, что груз Р = 4 т находится в точке С.
Ответ: 557 кг/см2.
10.61. Деревянная шпренгельиая балка прямоугольного поперечного сечения с отношением Л:ft = 1,5, шарнирно опертая по концам,
^•=Б00кг/м
К задаче 10.61.
К задаче 10.62.
нагружена равномерно распределенной нагрузкой (см. рисунок). Определить размеры поперечного сечения балки при допускаемом напряжении 100 кг/см2 и диаметр стальных тяг AD и DB при [о] = = 1200 кг/см2. Считать, что балка АВ в сечении С имеет шарнир.
Ответ: ft =17,6 см; ft=ll,7 см; </=12,6 мм.
10.62. По деревянной балке АВ с помощью лебедки волоком перемещается груз Q=1 т (см. рисунок). Сечение балки прямоугольное (высота ft = 30 см, ширина ft = 10 см, пролет / = 6 м).
£83
Коэффициент трения между грузом и балкой считать равным /= 0,4. Определить положение груза, при котором в балке возникает наибольшее сжимающее напряжение, и величину этого напряжения. Груз Q считать сосредоточенным, усилие троса лебедки — приложенным на уровне низа груза.
Ответ: х = 2,97 л«; <?„,„ = 99,3 кг/смг.
10.63. Трубка нз тонкой прорезиненной ткани диаметром 6 см заклеена по концам. В трубку накачан воздух под давлением (добавочным к атмосферному) 1,2 ат. Трубка положена концами на две опоры, расстояние между которыми равно 30 см, и нагружена сосредоточенной силой Р посредине пролета.
Полагая, что трубка способна работать на изгиб только до того момента, когда в какой-либо точке ее сечения возникнут сжимаю-
К задаче 10.64.
щие напряжения, определить наибольшую допускаемую величину силы Р. Местные давления силы и опорных реакций не учитывать.
Ответ: 3,39 кг.
10.64. Защемленный в стену коленчатый стержень прямоугольного поперечного сечения нагружен двумя сосредоточенными силами Р2 и Р2 (см. рисунок). Для каждого
из участков стержня построить эпюры изгибающего момента и продольной силы, а также определить наибольшие нормальные напряжения; Р2 = 360 кг, Р2 = 7200 кг, 1 = 50 см, а = 30 см, h = 6 см, Ь = 4 см, а = 60°.
Ответ: о, = 358 кг/см2; ои = 1078 кг!смг.
10.65. Наклонно установленная балка АВ длиной I в сечении С нагружена вертикально направленной сосредоточенной силой Р (см. рисунок). Построить эпюры изменения по длине балки изгибающего
момента и продольной силы. Определить величины наибольших растягивающих и сжимающих напряжений для различных вариантов расположения верхней шарнирной опоры. Вид поперечного сечения и его
284
размеры, длина балки, положение и величина нагрузки указаны в таблице; там же помещены ответы. Во всех случаях высота балки параллельна направлению действия силы.
К задаче 10.65
10.66. Консольная балка составлена из двух скрепленных между собой неравнобоких уголков (см. рисунок); на нее действуют две силы: Pt = 20 т, параллельная оси х и приложенная посредине высоты сечения на свободном конце балки (в точке К), и Рг = 750 кг.
К задаче 10.66.
направление которой, перпендикулярное к оси х, проходит через центр изгиба среднего сечения балки. Определить положение нейтральной линии и величину нормальных напряжений в точках А, В и С защемленного сечения, а также полное перемещение центра тяжести О свободного конца балки.
285
Данные для контроля решения. Силовые факторы в защемленном сечении равны: W=20000 кг, Afy=48400 кгсм и Л4, = 75000 кгсм. Нормальные напряжения в любой точке защемленного сечения определяются по формуле 0 = 450,5 —54,5г—153р. Составляющие полного перемещения точки О находим
К задаче 10.67.
по формулам
f f H f _P^L lx EF> iy~4SEJ2 'г~ 8EJy '
Ответ: ay = 2,94 cm; az = 8,26 cm;
СТд=1578 кг!смг; ав=—1177 кг/см2;
<jc=964 кг/см* и
= /0,045» 4- 0,064» + 0,136’ = 0,157 cm.
10.67. Изображенная на рисунке стойка сжимается силой Р3, приложенной в точке С поперечного сечения, и изгибается силами Р3 и Ря. Считая допустимым применение принципа независимости действия сил, построить эпюру
изменения изгибающего момента по высоте стой-
ки и в опасном сечении последней определить наибольшие растягивающие и сжимающие напряжения. Вид попереч-
ного сечения и его размеры, положение и величина нагрузок указаны в таблице; там же даиы ответы.
10.68. На рисунке схематически изображены короткие стойки и различные варианты их поперечных сечений. Верхний конец каждой стойки нагружен продольной сжимающей силой Plt приложенной
286
в точке К, и поперечной силой Pt, направление действия которой проходит через центр изгиба сечеиия.
Определить наибольшее нормальное напряжение в стойке; найти
в сечении у ее основания положение
К задаче 10.68.
нейтральной оси и нормальные напряжения в точках А, В, С и D; указать координаты точки Н, через которую нейтральная ось проходит в любом поперечном сечении. Из-гибно-крутильные деформации тонкостенных стоек не учитывать.
а=Ц8м
К задаче 10.69.
Данные о величинах нагрузок и Р2 приведены в таблице; там же помещены и ответы.
К задаче 10.68
№ сечения Pl. т р.. т Ответ
Qyt СМ аг, см ад. кг/см9 °В-кг/см9 ос. кг/см9 ал. кг/см9 °max-кг/см9
1 2 3 4 1.8 2,5 12 6 0.16 0,30 2 1 + 1.81 + 1.13 —14,9 —13,7 -1,78 -Н.05 -1,66 + 1.47 —102,6 -88,4 —1045 +268 +21.4 +68,8 —1532 —57 г77,Ъ + 12.0 +565 -1063 —46,4 —31,7 + 1051 —738 102.6 91.4 1625 1125
Координаты точки В во всех случаях равны Ун—^ 11 iH=az.
19.69. Каменная подпорная стенка, поперечный разрез которой изображен на рисунке, поддерживает земляную насыпь. Удельный вес кладки равен 1,8. Давление земли направлено горизонтально и
t8T
распределено по высоте стенки по закону треугольника; наибольшее давление у основания ^max = 1,5 т/м1. Определить величину наибольшего и наименьшего сжимающего напряжения в основании стенки.
Решение. Выделим из стенки по ее длине участок в 1 м; этот участок стенки можно рассматривать как брус, защемленный ннжнпм концом, изгибаемый давлением земли и сжимаемый собственным весом. Сечение бруса в основании стенки будет наиболее напряженным. Наибольшее н наименьшее сжимающие напряжения в этом сечении могут быть вычислены по формуле o*n«x п: 2?
umln F т W' ’
Сила N равна собственному весу выделенного участка стенки: W^Qi+Qo, где Qi—вес треугольной, a Qz—прямоугольной призмы. Так как
Q, =2-Л (Ь—а) 1у =2 4.5 (2—0,8) -1 • 1.8= 4,86 г, а (?2 = Шу=4,5 0,8-1 • 1,8 =
= 6,48 т, то jV = 4,86 + 6,48= 11,34 г.
Изгибающий момент М равен сумме моментов сил веса Q, и Qa и равнодействующей давления земли Н вокруг центральной оси основания стенки zi
M=Qi (а+Ц^-2Л-(?2 Ь^ + ’па^ . 2. = 4,86-0,2- 6,48 0,6+
Так как
F = b/ = 2-l=2 я2 и
/ы 1-г2
W'= W'2 = -^-=—^- = 0,67 л»,
то
max 11.34_г2,15_
°mln 2 0,67
5,67 Т 3,22 т/я2.
Таким образом,
Отах = ОД =—8.89 т/я3 И Omin = Од =— 2,45 т/м3.
10.70. На рисунке схематически изображены два варианте поперечного разреза бетонной плотины высотой 7 м. Принимая удельный вес бетона равным 2, определить необходимую ширину
плотины (а, и а2) так, чтобы в ее основании не возникало растя» гивающих напряжений.
Ответ: а, = 3,93 м; о2 = 3,52 м.
288
10.71. Каменный бык косого в плане моста (см. рисунок) в верхнем сечении нагружен вертикальной силой Р1 = 100 т (вес пролетного строения моста и проходящего по мосту в точке О, и горизонтальной силой Р2 = 20 т (сила торможения поезда), параллельной сторонам АВ и CD сечения быка. Объемный вес кладки последнего равен 2 т/м3. Положение главных осей инерции поперечного сечения быка и и v указано на рисунке, Ju= 8,94 ж4 и /,, = 33,4 .п4. Определить наибольшее и наименьшее сжимающие напряжения в горизонтальном сечении быка у его основания.
Ответ: огоах = од= — 59,5 т/жг; oniin = =сс =—2,4 т/м*.
поезда), приложенной
§ 33. Изгиб и кручение
10.72. На вал (см. рнс. а) насажены два шкива, через шкивы перекинуты ремни, ветви которых параллельны друг другу и наклонены к горизонту на первом шкиве под углом 30°, иа втором — под углом 45°. От первого шкива ремень идет к
электромотору; в этом ремне усилие в сбегающей ветви вдвое больше, чем в набегающей. От второго шкива ремень идет к станку; в этом ремне усилие в набегающей ветви вдвое больше, чем в сбегающей. Станок имеет мощность 100 л. с.\ вал делает 200 об/мин. Используя четвертую теорию прочности, определить необходимый диаметр вала при допускаемом напряжении 800 кг/см*.
Решение. Вал подвергается изгибу, а часть его, расположенная между шкивами, и скручиванию. Крутящий момент определяется по формуле
.. 2250 „ 2250-100
М“~ лп Л'_3,14-200 - 3''8 КгМ'
Обозначим натяжение набегающей ветви ремия, надетого иа первый шкив, через tx, тогда натяжение сбегающей ветви по условию равно 21Для вращающего шкив момента, равного крутящему моменту Л4К, имеем
М1 = Л1И=-^- D/i,
где D,—диаметр первого шкива; отсюда
. 2МК 2-35800 оп_
'*= ОГ=“80“=895 *г:
для второго шкива аналогично
, 2М„ 2-35 800 ,1Й
1*= оГ=~1бо-=716 кг'
289
Таким образом, в сечениях, где посажены шкнвы, вал нагружен наклон-иши силами
К,=3/,=3-895 = 2685 кг и Я, = 3/, = 3-716 = 2148 кг.
Кроме того, в тех же сечениях действуют вертикальные силы, равные весу шкивов: Qi =80 кг и Qa = 120 кг.
К задаче 10.72.
Для вычисления наибольшего изгибающего момента определим сначала изгибающие моменты в вертикальной и горизонтальной плоскостях. Для этого разложим силы ₽а и R. на вертикальную и горизонтальную составляющие; вертикальные составляющие сложим с весами шкивов. Тогда вертикальная иагрузка от первого шкнва будет равна
Р\ = Qj.-Ь Rt sin 30°=804-2685-0,5= 1422 кг,
290
а от второго шкива
р'а = Q2+R2sin 45°= 1204-2148-0,707= 1639 кг.
Горизонтальная нагрузка от первого шкива равна
Р\ = Ri cos 30°=2685-0,866 = 2325 кг, а от второго шкива
Pa = Racos45°=2148-0,707=1519 кг.
При этом нагрузки Р\ и Ра направлены в противоположные стороны (см. рис. в).
Для нагрузок Р\ и Ра, действующих в вертикальной плоскости, определяем обычным путем реакции: Л'=2716 кг и В'=345 кг, и строим эпюру изгибающих моментов Л1и = Л1у(см. рис. б). Аналогично этому от нагрузок Pj и Ра, действующих в горизонтальной плоскости,, определяем опорные реакции: А* = 2341 кг н В'=1535 кг, и строим эпюру изгибающих моментов Л1’ = Л12(см. рис. в).
Результирующий изгибающий момент может достигнуть наибольшего значения либо на опоре А, либо в сечении С, так как обе эторы моментов представляют собой ломаные линии с вершинами в этих сечениях. Величина результирующего момента в этих сечениях равна
МА = (мл)2 + (М’л)а = /711*4-1163» = 1363 кгм
И
Мс = (м'с)2 4- (Мд)8 = /259» 4-П51» =1181 кгм.
Таким образом, опасным сечением является сечение А. Эпюра результирующего изгибающего момента представлена иа рис. г.
Расчетный момеит по четвертой теории прочности равен
Л4р1СЧ=}/ГA15j4-0.75A1»= /1363»4-0,75-358»= 1398 кгм.
Необходимый диаметр вала находим по формуле
. 5/32-139800
V л [о] ~ г 3,14-800 -12,1 СЛ‘
10.73. Сплошной стальной вал круглого поперечного сечения в опасном сечении подвергается действию крутящего момента AfK = 1 кнм и изгибающего момента AfH =1,2 кнм. Из условия прочности по третьей теории прочности определить необходимый диаметр вала, если допускаемое напряжение [а] = 80 MhJm^. Какой диаметр должен был бы иметь вал, если расчет произвести, пользуясь четвертой теорией прочности?
Ответ. 126 мм; 124 мм.
291
10.74. Полый стальной вал, внутренний диаметр которого должен составлять 0,6 наружного, в опасном сечении подвергается действию изгибающего момента Л1и == 9 тм и крутящего момента /Ик =- = 12 тм. Определить наружный и внутренний диаметры вала при допускаемом напряжении [о] = 1200 кг]смг, использовать теорию наибольших касательных напряжений.
Ответ: 245 мм; 147 мм.
10.75. Полый чугунный вал с наружным и внутренним диаметрами, соответственно равными 160 мм н 100 мм, передает мощность 200 л. с. при 100 об/мин. Расстояние между опорными подшипниками равно 1,2 м; посредине этого расстояния к валу приложена поперечная сосредоточенная сила 3 т. Определить величину наибольшего расчетного напряжения в опасном сечении вала, пользуясь второй теорией прочности; у, = 0,25.
Ответ: 409 кг/см-.
10.76. Определить наибольшее расчетное напряжение в стальном стержне АВ круглого поперечного сечения, нагруженном двумя одинаковыми грузами Р=100ка, приложенными, как указано на рисунке. Чему будет равно наибольшее расчетное напряжение и стержне,
если один из грузов будет снят? Использовать четвертую теорию прочности.
Ответ: 1273 кг!смг; 1518 кг!смг.
10.77. Стальной коленчатый стержень ABCD закреплен, как указано на рисунке. Участок АВ имеет круглое поперечное сечение диаметром 125 мм. Сила 2 т приложена в точке М перпендикулярно к плоскости чертежа. Пренебрегая касательными напряжениями от поперечной силы, определить в наиболее опасной точке сечения тп главные напряжения и расчетные напряжения по третьей и четвертой теориям прочности.
Ответ: Uj = 451 кг/см-; о3 =—54 кг/смг; <гр[[| = 505 кг]см-; <т„ =480 кг!смг.
₽iv '
10.78. Дорожный знак укреплен на полой круглой стойке с наружным диаметром 80 мм (см. рисунок). Используя третью теорию
прочности, определить толщину стенки стойки при допускаемом напряжении [о] = 800 кг]смг, если наибольшая ветровая нагрузка на знак равна 150 кг]»?.
Ответ: 2,36 мм « 2,4 мм.
10.79. Из условии прочности по теории наибольших касательных напряжений определить наибольшую допускаемую величину груза Р,
которую можно поднять при помощи ворота (см. рисунок). Вал ворота круглого поперечного сечения диаметром 30 мм. Допускаемое напряжение для материала вала [о] = 800 кг/см1.
Ответ: 79 кг.
К задаче 10.78.
К задаче 10.79.
10.80. Два одинаковых шкива А и В насажены на вал (см. рисунок). Ведущий шкив А передает 10 л. с. при 100 об]мин. Обе ветви ремня на шкиве А горизонтальны, на шкиве В вертикальны. Натяжение ремней: Т2=150ка, 7\ > Та. Диаметры шкивов равны
К задаче 10.80.
К задаче 10.81.
60 см. Из условия прочности по третьей теории , прочности определить необходимый диаметр вала при допускаемом напряжении [о] = 800 кг]смг.
Ответ: 60 мм.
10.81. Оба конца стального бруска АВ квадратного сечення 20x20 мм защемлены. Посредине пролета /=160 см к бруску жестко прикреплена стальная поперечина CD такого же сечения, длиной а = 30 см; на свободном конце ее приложена сила Р — 30 кг (см. рисунок). Определить расчетные напряжения в бруске АВ и
293
поперечине CD по теории наибольших касательных напряжений и па*ги перемещение точки D в направлении действия силы Р.
Ответ: о^д = 704 кг] см*; oCD = 675 кг/см*', /=9,4 леи.
10.82. Определить диаметр вала АВ цилиндрической зубчатой передачи (см. рисунок). Крутящий момент на зубчатом колесе /
К задаче 10.82. К задаче 10.83.
равен 30 кгм. Использовать четвертую теорию прочности. Собственными весами зубчатых колес пренебречь. Допускаемое напряжение [а] = 800 кг]см*. Какой диаметр вала следовало бы взять на основе третьей теории прочности?
Ответ: 56,2 ми; 57,8 мм.
10.83. Дуралюминовая труба с наружным диаметром 80 мм и толщиной стенки 5 мм скручивается равномерно распределенными по ее длине моментами интенсивностью m = 30 кгм/м и изгибается равномерно распределенной, поперечной нагрузкой интенсивностью 9 = 20 кг]м (см. рисунок). Определить в опасном сечении трубы расчетное напряжение по третьей теории прочности, а также найти наибольшие прогиб и угол закручивания трубы. £ = 7>10* кг/см*, G = 2,7 • 10s кг/см*.
Ответ: <гр1СЧ = 612 кг]см*; /=3,48 см; <р = 0,03 рад = 1°43,3'.
10.84. Используя теорию наибольших касательных напряжений, определить необходимые размеры шейки вала, щеки и мотылевой шейки кривошипного механизма, схематически изображенного на рисунке. Направление действия силы Р и реакций в подшипниках перпендикулярно к плоскости кривошипа. Передаваемая от двигателя мощность N=50 л. с. при л = 200 об/мин. Допускаемое напряжение [о] = 800 кг/см", R = 56cm, at = 18 см, a, = 15 см.
Решение. Значения момента МЛ н силы Р находим по формулам А10 = 71 620 —=71 620— я 17 900 кгем и Р=^=Ц^*=597 кг. Опорная П zUv К «5U
„ р реакция в сечении и равна .
Шейка вала на участке CD подвергается кручению и изгибу. Крутящий момент на этом участке постоянен и равен AfK = Alo=17900 кгем, а изгибающий момент меняется по линейному закону, достигая наибольшего значения
294
В сечении С, где Мн = М”'ах=-^- a^-g—18 = 5370 кгсм (см. эпюры М иа рисунке). Таким образом, опасным оказывается сечение С. Из условия прочности по третьей теории прочности
0расч=1^/л1* + Л1^<[о] следует, что
Перенося реакцию D и пару сил Мо в сечение С, убеждаемся, что щека кривошипа также подвергается кручению и изгибу. Крутящий момент по
Щеки кривошипа. (ВС)
„ 8950кгсм
Эпюрам*
______ 1*7/3!
ч ! ! т
Эпюра Ми Мотыпевая шейка (АВ)
Эпюра Мх
I
: Эпюра Ми Шейна вала (СН) | Эпюрам*
К задаче 10.84.
длине щекн не меняется и равен Л1к=-^-а1=5370 кгсм, а изгибающий момент меняется по линейному закону, уменьшаясь от сечения С к сечению В.
р
В сечении С МЯ = МО= 17900 кгсм, а в сечении В Ма = М0—^-/?=17900— 597
—30 =8950 кгсм (см. эпюры М иа рисунке). Таким образом, опасным
оказывается сечение С. Так как изгибающий момент действует в плоскости наибольшей жесткости щекн кривошипа, то наибольшее расчетное напряжение в сечении С будет в точке К на осн г; здесь
М„ 6Л10 6 • 17 900 _ 17 190
°K~WV~ bh* ~b(2,5b)a ’
а
Мк а ™ 5370 -6380
T*-Y W'n-Y ₽63—0,7660,6456» ЬЛ •
295
Прн -у =2,5 р = 0,645 и у=0,766 (см. таблицу значений а, Р и у к задаче 4.38 в § 13). Из условия прочности
Орасч = V °х + 4тЛ- = К 17 190*+ 4-6380* < [о]
находим
. з/17 190*+4-6380* „„
1/ -----отт;----= 2,79 см » 2,8 см
Г OVV
и ft=2,5b = 2,5-2,8 = 7 см.
Перенося реакцию D и пару сил Мо в сечение В, замечаем, что мотыле-вая шейка также подвергается изгибу и кручению; крутящий момент на р
участке АВ постоянен и равен МК=МО—^-7? = 8950 кгсм, а изгибающий момент растет от сечения В к сечению А. В сечении В Л1И = -^- Pat = 5370 кгсм. Р 597
а в сечении Л Л1н=-^-(а14-а2)=-^-(184-15)=9850 кгсл (см. эпюры М на рисунке). Поэтому опасным будет сечение А. Из условия прочности находим
К32*/” *»
Участки кривошипного механизма слева от сечения А находятся в более благоприятных условиях, чем рассмотренные участки АВ, ВС и CD.
10.85. Стальной стержень АВС квадратного поперечного сече-
ния 3x3 см, изогнутый в виде полукруга, защемлен концом С
н стену и нагружен ма
К задаче 10.85.
свободном конце силой Р=100 кг (см. рисунок). Определить наибольшие расчетные напряжения в сечениях В и С стержни, используя четвертую теорию прочности. Найти вертикальное перемещение точки А.
Решение. Сила Р вызывает изгиб и скручивание стержня АВС. В произвольном сечении тп, наклоненном к сечению А под углом ф (см. рисунок), изгибающий момент
MH = P-HA — PRsin <р, а крутящий момент
Мн = Р НК = PR (1 - cos ф).
В сечении В прн ф= у М„ = Мк= PR. Наибольшее нормальное напряжение от изгиба в этом сечении равно
Л1Н_6РЯ omax-ttZH— fl3
6-100-20
З3
444 кг/см-'.
наибольшее касательное напряжение
от кручения в том же сечении
ттах
Л4К PR 100 20 1|7и-₽а3- 0,208-3®
356 кг/см1
296
(для квадратного сечения коэффициент Р = 0,208 —см. таблицу к задаче 4.38 в § 13). Дополнительными нормальными напряжениями, возникающими' в результате скручивания криволинейного стержня, по нх малости в данном- случае пренебрегаем.
Наибольшее расчетное напряжение по четвертой теории прочности в сечении В равно
max ора£Ч = j/" о„1ах 4-Зт® ах = К4442 + 3-3562 я 760кг/см*.
В сечении С при <р = л Л1и=0 и Л1И=2Р7?; поэтому о = 0, а ттах => = 2-356 = 712 кг/см*. Расчетное напряжение в этом сечении равно
max орасч = |/"Зт^ах= К Зттах = 1,732-712= 1233 кг/см*.
Сечение С находится в худших условиях, чем сечение В.
Перемещение конца А стержня АВС в направлении действия силы Р определим с помощью теоремы Кастильяно; прн этом учтем потенциальную энергию изгиба и скручивания стержня. В элементе стержня длиной ds = Rdtp потенциальная энергия изгиба и кручения равна
dUu + dUK
M*Rd<f M%Rd<p 2EJ„ 4 2GJT ’
Потенциальная энергия в объеме всего стержня
л
КМ* Мк 2ET„+2Gj-J^-
о
По теореме Кастильяно
{л~дР
Rd<p.
Так как ^ = flsinq>, (1—costp), G = 8-10» кг/см*=0АЕ.
Jg=— и 7к=сха* = 0,14а* (см. вышеупомянутую таблицу значений a, Р н у), то о
3-3,14-100-203 /о I \ ПС1
— 34-2-10« 0,8-0,14/ 0,5 См'
10.86. Стальная прямоугольная скоба круглого поперечного сечения диаметром 25 мм защемлена двумя концами в стену и нагружена силой Р (см. рисунок). Из условия прочности по теории наибольших касательных напряжений определить наибольшую допускаемую величину силы Р, если допускаемое напряжение [а] = 800 кг/см*. Найти также вертикальное перемещение точки А.
Указание. В каждом из защемленных сечений возникает вертикальная реакция, равная Р, опорный момент Мо = у Ра в вертикальной плоскости
297
и опорный момент 7И0 вокруг оси ВС или DH; последний определяется нз dU Л „
условия ---: = 0. Вследствие симметрии потенциальную энергию изгиба и
дМ0
скручивания достаточно вычислить лишь на участках АВ н ВС.
Ответ: 120 кг; 0,07 лип.
10.87. Кулачковый вал диаметром 28 ми, укрепленный в подшипниках А, В и С, нагружен, как схематически указано на ри-
К задаче 10.86.
сунке; Р = 80 кг, 1 = 32 см, а — = 4 см и е — 5 см. Раскрыть статическую неопределимость, построить эпюры крутящего и
К задаче 10.87.
изгибающих моментов и вычислить в опасном сечении вала расчетное напряжение по теории наибольших касательных напряжений.
Ответ: 560 кг/см*.
§ 34. Общий случай сложного сопротивления
10.88. Какие углы а с плоскостью поперечного сечения стержня составят площадки, по которым произойдет разрушение материала: а) при простом растяжении, б) при кручении и в) при одновременном кручении и растяжении, если по плоскости поперечного сечения к моменту разрушения о = 0,8ттах? Рассмотреть случаи, когда материал находится в хрупком и в пластическом состоянии. Использовать первую и третью теории прочности.
Ответ: Материал в хрупком состоянии: а) а = 0°, б) а = 45°, в) а = 34°6'; материал в пластическом состоянии: а) а = 45°, б) а = 0°, в) а=10°54'.
10.89. Трубчатый стержень с наружным и внутренним диаметрами, соответственно равными 80 мм и 60 мм, скручивается парой сил с моментом 400 кгм. Какое наибольшее растягивающее усилие, может быть дополнительно приложено к стержню, если допускаемое напряжение [а] =1600 кг)смг? Использовать четвертую теорию прочности.
Ответ: 27,3 т.
10.90. Из условия прочности по третьей теории прочности определить наружный и внутренний диаметры полого вала, подвергающегося одновременному кручению парой сил с моментом 4 тм и растяжению осевой силой 30 т. Допускаемое напряжение [а] =1200 кг/см2; отношение rfBBm>:<4aP:= 0,6.
Ответ; аиар=159 мм; rfBByTp = 95 мм.
288
10.91. Вал диаметром 22 см, имеющий на конце консоли длиной 45 гребной винт, передает мощность 4000 л. с. при 300 об/мин. Тяговое усилие на винте 17 т, вес винта 2 т. Определить величину главных напряжений в наиболее опасной точке иа поверхности вала и построить диаграмму, показывающую изменение главных напряжений в этой точке за время одного оборота вала. Определить величину расчетного напряжения в той же точке по энергетической теории.
Ответ, max at = + 527 кг/см\ шах о3 = — 396 кг/см1-, = = 802 кг/см*.
10.92. Стальная труба, имеющая внутренний диаметр 80 мм и толщину стенки 5 мм, подвергается действию сжимающего осевого усилия 4000 кг п крутящего момента 300 кгм. Пользуясь третьей теорией прочности, определить наибольшую допускаемую величину внутреннего (избыточного над атмосферным) давления, которому могла бы быть дополнительно подвергнута труба, если [о] = = 1200 кг/см*. Считать, что внутреннее давление не вызывает в трубе продольных напряжений. Определить угол наклона к оси трубы площадок, по которым будут действовать наибольшие касательные напряжения.
Ответ. 17,8 ат, 10°48'.
10.93. Определить размеры прямоугольного поперечного сечения
щекн коленчатого вала, нагруженной, как указано на рисунке. Отно-
шение сторон Л:6 = 2. Применить теорию наибольших касательных напряжений; [о] = = 800 кг/см*.
Решение. Наиболее опасной точкой в сечении является одна из следующих:
1) точка А, в которой нормальные напряжения от силы N и моментов Му и Мг будут одного зивка (сжатие); в этой точке не будет касательных напряжений;
2) точка В, в которой касательные напряжения от кручения будут наибольшими, а сжимающие нормальные напряжения возникнут только от силы N н момента Mz;
3) точка С, в которой касательные напряжения от кручеиня будут несколько меньше, чем в точке В, зато сжимающие нормальные
напряжения возникнут от силы N и момента Му, большего, чем момент Мг.
Составим условия прочности материала для каждой из этих точек по третьей теории прочности.
Геометрические характеристики сечеиия, выраженные через размер Ь
щекн:
&
и П7и=₽Ь3 = 0,49363 (при h:b = 2 коэффициент Р = 0,493—см. таблицу к задаче 4.38 в § 13).
299
Условие прочности материала в точке А, наиболее удаленной от осей у и z. имеет вид
. . INI , |Mvl , 2000 , 30000 , 10000
расч <^ = 1^1=1^ + — + — = _+—_ + — =
=-^-4—й—<|с]=800 кг/см2.
О о°
Считая, что | вд | = [о], получим такое уравнение для определения Ь:
8006s—10006 — 75 000 =0 или 6*—1,256—93,75 = 0;
путем подбора находим 6 = 4,6 см.
Нормальное напряжение в точке В равно , , |W| , \М,] 1000 , 30000
|ай l=-rL+-L^1 = -Tr- + —.
а касательное напряжение
|МК| _ 20 000 -40 570 ,тя|_ “ 0,4936s - 6s ’
Условие прочности:
Считая, что расч ов = [о], получим уравнение
6’ — 1,563 6s + 93,756 — 1Г 690=0;
путем подбора находим 6 = 4,8 см.
Нормальное напряжение в точке С равно
. . | N | , I му I 1000 , 45 000
1°с1=—+-1У7 = _6^+_б5-’ а касательное напряжение
прн h:b = 2 у=0,795.
Условие прочности получает такой вид:
Г г . aJF , / / 1000 , 45 000/32 250\2 , , опп , , расчос = |/ Ос + 4тс =у —ьз-) +4 ("Й") l0^ 800**/"»2.
Полагая, что расчос=|о], имеем уравнение
6« — 1,563 6* — 140,63 6 — 9665 = 0;
путем подбора находим 6 = 4,7 си.
Наиболее опасной оказывается точка В. Размеры щекн вала необходимо принять равными 6 = 4,8 см н /i=2-4,8 = 9,6 см.
10.94. Стержень прямоугольного поперечного сечення 10x4 см скручивается парой сил с моментом 100 кгм и растягивается центрально приложенной силой 6 т. Определить величину наибольшего расчетного напряжения по третьей теории прочности.
Ответ: 506 кг/см2.
10.95. Мотылевая шейка коленчатого вала нагружена, как показано на рисунке. Из условия прочности по четвертой теории проч
300
ности определить необходимый диаметр шейки при [о] = 1200 кг)см2. Указать координаты опасной точки.
Ответ: 68 лии; у0 — — 2,72 см; 20 =— 2,04 слг.
10.96. Щека коленчатого вала прямоугольного поперечного сечения 3x8 см нагружена, как показано на рисунке. Определить
взаимно перпендикулярных уси-
К задаче 10.97.
положение нейтральной оси и, используя третью теорию прочности, найти расчетные напряжения в трех наиболее опасных точкак поперечного сечення щекц (в вершине угла прямоугольника и в серединах его сторон).
Ответ: Оу = — 0,375 см; аг = 4-1,33 см; о_=100 Мн/м2; oPj = 105,4 Мн/м2; оР1 = 82,1 Мн/м2.
10.97. Острие резца токарного станка (см. рисунок) при обточке детали подвергается действию трех лий: Ра—сопротивление резанию в узком смысле слова, Ра — радиальное усилие, стремящееся отжать резец назад, и Р3—осевое усилие, параллельное оси детали, или усилие подачи.
Определить расчетные напряжения по энергетической теории прочности в трех наиболее опасных точках и в центре сечении АВ резца (считая последний в этом сечении защемленным) прн условии, что Pt = 60 кг, Ра = = 0,15Р1 и Ps = 0,35Pl. Расчет произвести с учетом и без учета
касательных напряжений от поперечных сил. Показать, какие напряжения действуют по граням элементов, выделенных в упомянутых точках.
Ответ: С учетом поперечных сил: 1692 кг/см2, 1305 кг/сл!2, 604 кг/см2, 212 кг/см2; без учета поперечных сил: 1692 кг/см2, 1286 кг[см2, 472 кг/см2, 10 кг[см2.
301
10.98. Для изображенных на рисунке стержней круглого и прямоугольного поперечных сечений определить наибольшие расчетные напряжения по третьей теории прочности.
Ответ. 1) 850 кг/см2-, 2) 100,4 кг[см2; 3) 95 кг/см2; 4) 88,3 кг [см2.
10.99. Определить величину трех составляющих перемещения, а также величину полного перемещения конца А стального коленчатого стержня ABCD круглого поперечного сечения (см. рисунок). Нагрузка Р= 100 кг.
Решение. Перемещение точки А в направлении силы Q=l. равно
7 С ~ 2£JB
100-20 30» 2-2-10е-12,57
= —0,0358 см;
точка А по вертикали перемещается в направлении, противоположном направлению силы Q=l, т. е. вверх.
Перемещение в направлении силы Н= 1 будет
{н = ”2И= 100-25-30а =0,0148 см.
,н 2EJ* 2-2-10е-12,57
Перемещение в направлении силы 2=1 равно
ь=т [т+-wr+i(й +в+э'!',+3,'м J"
_ 100 Г 30 20»-25-2-10е 1
~2-10» [12,57 ‘8-106-2-12,57 ‘3-12,57 Х
X(20e+25s+3-20»-30+ 3- 25»-30)J =0,2035 см.
Полное перемещение точки А в пространстве
/= т/ +f*H +/*= j/"0,03582-|-0,0448»+0,2035»=0,212 см.
302
10.100. Определить величину вертикальных смещений точек А :-ц В стального коленчатого стержня прямоугольного поперечного сечения (см. рисунок); Р=1000 кг, Л1в=1 тм, 1Х=1 м, /,=0,8k, ^.= 1 м, Ь = 8 см и Л = 12 см.
Ответ. /л = 0,71 см; /в=1,54 см.
К задаче 10.99.
10.101. Для изображенных на рисунке стальных коленчатых стержней построить эпюры продольной силы, крутящего и изгибающих
К задаче 10.101.
моментов на каждом из участков стержня, определить по тре-тьей теории прочности наибольшие расчетные напряжения и найти
303
перемещение центра тяжести сечения А в направлении, указанном стрелкой К. Размеры стержней и величины нагрузок указаны в таблице; там же помещены и ответы.
К задаче 10.101
№ схемы н вари-анта Размеры, см Нагрузки, кг Ответ
d А ь 1, 1, Р, ря р, арвСЧ’ кг {см* /> см
1а 6 __ . 60 80 80 120 9000 894 0,57
16 5 — — 90 60 — 100 60 4000 1091 0,90
2а 4 — — 30 40 60 50 30 2000 878 0,45
26 7 — — 50 80 40 120 100 8000 644 0,23
За 5 3 60 30 20 75 45 2500 997 0,85
36 — '9 5 70 40 60 250 400 6000 1330 0,87
4а 6 — — 60 80 60 90 200 3000 1161 1,49
46 8 — — 80 90 60 160 300 9000 962 1,31
5а 9 — — 80 60 90 600 900 750 1227 0,75
56 7 — —. 70 50 80 600 400 200 1612 1,90
6а 10 6 40 60 50 500 600 9000 1500 0,45
66 8: 4 40 30 40 360 200 4000 1550 0,37
7а 5 — 40 50 40 100 80 4000 1021 0,57
76 4 — • — 30 20 40 60 80 3000 979 0,25
8а — 6 4 30 50 — 180 160 3800 840 0,19
86 — 8 3 60 40 — 200 150 6000 1623 0,73
9а 5 6 6 50 30 50 120 100 5000 1547 0,69
96 8 9 6 60 50 40 400 500 8000 1517 0,55
10.102. Для каждого из участков коленчатого стержня АВСН (см. рисунок) построить эпюры продольной силы, крутящего и изгибающих моментов и, используя теорию наибольших касательных
К задаче 10.102
Е Е № схемы н варианта Размеры стержня см Размеры сечений, мм Углы N. л.с. л. об/мин Q, кг Ответ
а< а» 1 К О d b h h b а 6 V
1 2 3 4 5 6 7 8 9 1—а 1—С 1—в 11—а 11-6 П-в 111—а 111—6 111—в 8 10 12 И 15 15 24 20 15 8 15 10 18 10 12 16 10 10 20 18 16 25 24 20 80 90 80 40 28 25 30 40 50 40 30 32 60 36 40 60 40 50 30 27 28 100 68 40 90 30 32 65 32 20 60 14 12 но 80 50 96 35 45 3 1.8 2.5 45° 60° 90° 20° 18° 24° 30° 0° 90° 0° 30° 30° 45° 45° 90° 30° 0° 0° 30° 0° 0° 45° 0° 90° 150 100 9 145 250 500 300 300 600 500 70 0 60 90 0 60 120 80 Q Q Q »а.£2 з-а.32 в-а.32 II II II II II II || II II II II II Ю N5 — рОсЛОО — до<л°^)—00 * * * £ 3 Л * £ * s Ы 36 П £ р 1? IO И Ю
304
К задаче 10.102.
напряжений, рассмотреть один из следующих вариантов решения задачи:
а) найти наибольшее расчетное напряжение;
б) установить наибольшую допускаемую величину веса груза Q или мощности N;
в) определить размеры круглого и прямоугольного сеченнй стержня.
Касательные напряжения от поперечных сил во внимание не при* ннмать. Основное допускаемое напряжение [о] = 800 кг/см*.
Необходимые для расчета данные приведены в таблице; там же помещены и ответы.
§ ЗБ. Тонкостенные стержни
10.103. Для профиля, изображенного на рис. а, определить положение центра изгиба, построить эпюру главных секториальных координат и вычислить величину секториальиого момента инерции.
Решение. Так как сечение симметрично относительно осн г, то центр тяжести С н центр изгиба А будут лежать на этой оси. Расстояние гс центра тяжести сечеиия от средней линии нижией полкн равно
_Syo_ —4.0,5-8—8 0,4-4 28,8 _
*с~ F ~4-0,5 + 8-0,4+6-0,5 = 8,2“ ’ СМ'
Для нахождения расстояния гд от центра тяжести сечения С до центра изгиба А воспользуемся формулой
где Se>B—сектормально-линейный статический момент сечеиия относительно полюса С и главной центральной оси инерции у, a —момент инерции
К задаче 10.103.
сечення относительно главной центральной оси инерции г. Принимая за начало отсчетов точку О1( строим вспомогательную эпюру секториальных площадей со, (см. рис. б).
Секторнально-линейный статический момент определяется из выражения
F
308
интеграл может быть вычислен по способу Верещагина путем* умножения площадей эпюры <оо на ординаты эпюры расстояний у (см. рис. в), лежащие под центрами тяжести площадей. Для правой половины, верхней полки.пло-_ 1 ,, '. a a h—гс
щадь эпюры <i)0 положительна и равна F1 = -^-(h—zc) • — 2 2 2 о
а ордината эпюры у под центром тяжести площади Fx положительна и равна 2 а а , о< а3 ,, . _
У1 = у • таким образом 5(1)^=-^-(й—Zc)6n- Для левой половины
верхней полки F2 ——з* (h—Zc)a-, а ордината у2 = —так что S” = О о ШО1/
а3
=-^ (Л—£с) 6ц. Аналогично этому для правой и левой половин нижней полки находим
с'" _ civ _Л “ 24 Zc°n’
Полная величина секторнально-лннейпого статического момента равна S^ = 2 (S^„+ O=4le3("-Zc)-b3Zc,=
[4® • (8 - 3,51) - 63 - 3,51] = -19,62 мА
Момент инерции сечення относительно оси г равен /«6® + (а3 + Ь®) 6П 80,4® + (4®+6®)0,5 _
J,=-------12------------т——=в.п
и координата центра изгиба ^<i)ow 19,62 гл==~~77=П7тТ=1,68 см'
Принимая теперь точку А за главный секторнальный полюс, а точки Ot и О2 за главные нулевые секториальные точки, строим эпюру главных секте-о 4
риальных координат (см. рис. г). При этом <о/>=—ci>b=-=-|zO1| = 6,17-^- = " 2
= 12,34 сл® и а>н——шО=4‘|го31= 1,83~=5,49 см2. 2 2
Для вычисления секториального момента инерции Jlo=^<£^dF снова вос-F
пользуемся способом Верещагина. Для правой половины верхней полки имеем / 1 а 2 - 1 - 2
2 2 " 3 б
для левой половины верхней полки
J’u> =4’ =Т а6п“о;
для левой и правой половин нижней полки
поэтому
j»= 2 (<o+-Q=y 6" («®d + b“o)=¥ (<• 12,34®+6 6,49®)= 131,7 см2.
307
10.104. Для профилей, изображенных на рисунке, определить положение центра изгиба (точки Д), построить эпюру главных секториальных площадей, определить наибольшую ординату этой эпюры
iz
60*3
< * 40-**
100*3
,60*5
40*5-
160*5
7)
40*3
80*2
9)
У
И
К задаче Ю.Ю4.
^nui и вычислить велнчнпу секториального момента инерции. Размеры на рисунке даны в мм.
Ответ:
1)3'д=2л=0; | озгт1вх | = 18 см*-, Зш= 518,5 смв;
2) уА ——1,85 см, дл=0; | Сйтах | = 22,05 см2; Уш=726 см°;
= |сот1Х| = 45 смг; Ju,= 10220 смв;
4)Ул = гА = 0; |<огаах| = 27 смг; Jw = 3995 смв;
80S
5) _ул = 0, zA ——1,41 см; ||(omix| = 12,95 см2; 7Ш= 150,5 см*; 6)>д = 0, 4-1,41 см; |(отах| = 12,95 см2; /ш=150,5 сл’;
7) уА =— 0,78 см, гл = 0; | (отах | = 16,1 см2; J(o = 289,5 сл’;
8) уА = — 1,33 см, zA = 0; | (0тзх | = 16 см2; J„, = 319,5 см’;
9) уА -- — 3,64 см, zA = 0; | (omax | = 57,45 см2; /,„ = 9890 сл’;
10) УА — — 2,31 см, za = G; |(omax | = 12,15 см2; /ш= 189 см’;
И)>л-^ = 0; |=И,2 см2; /ш = 112,5 см’;
12) yA = zA = Q; | (omax | = 33,35 см2; /ш = 2500 см’.
10.105. Стержень с поперечным сечением, изображенным на рис. а, растягивается двумя силами Р=1200 кг, приложенными в точках К (см, рис. а и б). Определить величину нормальных напряжений в точках В, G, Н, L, Q и R и построить эпюру распределения этих напряжений по поперечному сечению стержня.
Решение. Геометрические характеристики поперечного сечения стержня:
Площадь поперечного сечения F=0,25 (6-|-2-4 + 2-2) = 4,5 см2.
Расстояние между центром тяжести сечения С и точкой О (рис. в), расположенной посредине высоты н толщины стенкн профиля,
^о_0,25(2-4.2 + 2.2-4)_| Ус — р — 5 1, / о см.
Момент инерции сечения относительно главной центральной оси инерции у
Jy = 0,25 ^(62 + 2-2’4-2-4 0t252) + 2.4-32 + 2.2.42J = 38,85 см*.
Момент инерции сечения относительно главной центральной оси инерции г
/г=0,25 (6 0,25г4-2-2-0,2524-2-4’) + 6-1,78»+
4-2-4 0,222 + 2-2-2,222] = 12,45 см*.
Эксцентриситеты точки К приложения силы Р по отношению к главным осям инерции равны гР=-^=3 см и ур—-^- — Ус=-^г—1,78 =0,22 см.
Для нахождения положения центра изгиба построена вспомогательная эпюра секторнальных координат <оо прн полюсе и начале отсчетов в точке О (рнс. в) и эпюра расстояний точек профиля от осн у (рис. г).
Расстояние уА центра изгиба от средней линии стенки профиля вычислено по формуле
УА Jy 38,85
51,35
38,85
1,32 см.
При построении эпюры главных секторнальных координат со точка А принята за главный секториальный полюс, а точка О—за главную нулевую секторнальнуюточку. Эпюра со изображена на рис. д. Значения секторнальных
Зв»
20*2,
J| ч
60*2,5 -i и JnM
ДЧ*1Ъ
Н :
а)
К задаче 10.105.
координат в точках В, G, Н, L, Q н R равны:
о>л = — g)£ = i/zi~ = 1,32-—=3,96 см2; и>а — —^q = ^b—^=3,96—
=— 3,04 см2; <i>H= — v>R=<>>0+a(b+yA) = — 8,04 + 2(44-1,32) = 2,6 см2.
Секториальный момент инерции вычисляем по способу Верещагина:
+4.8,042 . J-rbg+l • 2,62 /2—| ^61,95 см2.
Для определения нормальных напряжений имеем формулу
1 ,УрУ , zp2\ , Да F + Jz + Jy)+ *
а=Р
Величина бимомеита в сечениях, где приложены силы Р, равна
В=Втт = Р<^=Р (<ов-^) = 1200 (з,96—• у) =
= —1200-2,04=—2448 кгсм2.
Таким образом.
ff=^+iaT^^+^z-S“=266i7+21'l9!,+92'68z-39’fi2<,><
Значения координат точек и величины нормальных напряжений,; вычисленных по последней формуле, приведены в таблице и иа эпюре распределения напряжений по. поперечному сечению стержня (рис. е). Наибольшее нормальное напряжение возникает в точке G:ao=910 кг/см2.
Точки Величи и в D G н О L N <? я
У. см Z, см <0, см2 а, кг/см2 —1,78 +3 +3,96 +351 +0,46 +3 0 +554 +2,22 +3 —8,04 +910 +2,22 +5 +2.6 +674 —1,78 0 0 +229 —1,78 —3,96 +107 +0,46 0 —2 +2,22 -3 +8.04 -282 +2,22 —5 —2,6
00*4
120*4' О
tfcJLk*
К задаче 10.106.
Ц4
Размеры в нм
10.106. Стержень с поперечным сечением, изображенным на рисунке, растянут двумя силами Р=6 т, приложенными в концевых сечениях. Определить величину наибольшего растягивающего и сжимающего напряжений в поперечном сечении стержня в предположении, что: а) силыР приложены в центрах тяжести О концевых сечений и б) в концевых сечениях приложены по две силы Р/2 в точках К, посредине толщины стенок (см. рисунок).
Ответ: а) о=375 кг/см2 (растяжение); б) а= 1530 кг/см2 (растяжение) и 0 = 781 кг/см2 (сжатие).
10.107. Изображенный на рисунке стержень
Р=1,5 т, приложенными в точках и Kt концевых сечений. Опреде
нагружен силами
811
лить величину нормальных напряжений в точках В, D, G, Н, LhN промежуточного сечения и построить эпюру распределения этих напряжений по поперечному сеченню стержня.
Ответ: aD = — ав = 210 кг!см*-, он — — ос=1450 кг/см9-, оЛ= = — oL = 1050 KzjcM*.
К задаче 10.107.
40*2
'20*2
Е
Размеры в мм
В0*2-
\го*2>
40*2
К задаче 10.108.
10.108. Стержень, поперечное сечение которого изображено на ртсунке, растягивается центрально приложенными силами Р= 1600 кг. Определить наибольшие растягивающие и сжимающие напряжения в стержне.
Ответ: 0=1164 кг/см1 (растяжение), 0 = 364 кг!см* (сжатие).
10.109. Стальной стержень корытного профиля (см. рис. а) длиной 1 = 2 м, защемленный одним концом, нагружен на другом конце сосредоточенной силой Р = 200 кг, приложенной посредине ширины полки (см. рнс. б). Определить величины наибольших нормальных н касательных наприжеиий.
Решение. А. Геометрические характеристики поперечного сечения стержня.
Площадь поперечного сечения: Г =15,6 см*.
Момент инерции относительно главной центральной оси у: Jy = 652,8 см*. Момент инерции сечеиия при чистом кручении: /к= 1,649 сл*. ,
Секториальио-лииейный статический момент сечеиия относительно полюса О и главной осн инерции z (см. рис. а и д), вычисленный по способу Верещагина (см. решение задачи 10.103):
5^ = —2160 сл».
Координата центра изгиба
S
УА = -у* = ~ 3.31 см.
Jy
Эпюра главных секторнальных координат со для главного секторнальиого полюса А и главной нулевой секториальиой точки О изображена иа рис. е. Секториальный момент инерции, вычисленный по способу Верещагина, равен /ш=4370 см*.
Эпюра секторнальных статических моментов S^, приведена на рис. ж. Для точки 0 5^=49,5 см*. для точки В 5шв = 24,85 см* и для точки О 5шО= = —12,45 см*.
Обычные статические моменты относительно оси у части поперечного сечеиия, расположенной по одну сторону от точки, в которой определяются касательные напряжения, равны: для точки D S„D=21,1 сл», для точки В SyB=36 см* и для точки О Sy0 = Sy miK = 47,25 сл».
312
7722
у
______________t
7722.
&
н
Эпюра б(кг/смг)
К задаче 10.109.
313
Изгибпо-крутильная характеристика стержня:
8 10» 1,649
2-10°-4370
=0,0123 — : см
aZ=0,0123-200 = 2,46; shaZ=5,79 и chaZ = 5,88.
Эксцентриситет приложения нагрузки по отношению к центру изгиба 8
сечения равен е=-^-4-|:/д | = у}-3,31 = 7,31 см.
Б. Силовые факторы в любом сечении стержня
Решение дифференциального уравнения бимоментов в рассматриваемом случае имеет такой вид (см. Н. М. Беляев, Сопротивление материалов, изд. 1954 г. и более поздние, стр. 552):
Р с Ре
В =-----г—;sha(Z—х), Л4ш=-г—;cha(Z—х) н
a ch al ' ' ш ch al ' '
Ре
^K=EhaZIch aZ—Cha(Z—*)]•
Изгибающий момент и поперечная сила при плоском изгибе вокруг оси у равны: Му = —Р (I—х) и Q = -|-P. Эпюры изменения силовых факторов по длине стержня представлены иа рис. е. Наибольшего значения В, Мш и Му достигают в защемленном сечении, где при х=0:
„ _ Ре sh al
«т.х---acha/
200-7,31-5,79 0,0123-5,88
= 117 300 кгем2,
Л4шт1Ж = Ре=200-7,31 = 1462 кгем, Му тах =—Р1=—200-200=—40000 кгем.
Момент чистого кручения наибольшего значения достигает на свободном конце стержня, т. е. прн x=Z:
max
^chai =^^(5.в8-1) = 1213 кгем.
в этом же сеченни
.. Ре 200-7,31 оло
Мш ~ ch al 5,88 —249 “а*’
Поперечная сила по длине стержня не меняется: Q=P = 200 кг.
В. Нормальные и касательные напряжения
Нормальные напряжения в защемленном сечении вычисляются по формуле
z—
мутахг В ы 40000 117300 „
а=——+-Т-==—652T8Z- «70-<o=-61,3z-26,8<o.
Значения координат гнои нормальных напряжений в точках В, D, Н, К, L и N сечения приведены в таблице. По данным таблицы построена эпюра а (см. рис. о).
Точки Величины'''-'-^ н О в к L N
г, см <0, см2 а, кг/см* —7,5 4-35,2 —484 —7,5 0 4-460 —7,5 —24,8 4-1126 4-7,5 4-24,8 —1126 4-7,5 0 —460 4-7,5 —35,2 4-484
314
Касатешше напряжения в защемленном сечении складываются из напряжений от поперечной силы Q н от изгибно-крутящего момента Мю:
. г . — У i шах 5Ш Т-Т<? + Т“- + /шб •
Наибольшего значения касательные напряжения достигают в точке О, где направления Тр и тш совпадают:
200-47,25 1462-12,45 „ „ . 1П . .
ттах — То — 652,8-0,4 + 4370-0,4 — 36,24-10,4 46,6 кг/см .
В точках D и L, где направления Тр и тш ие совпадают, 1462-49,5 200-21,1 о_ с ... 1С о , ,
XC.L~ 4370-0,6 652,8-0,6 27,6 10,8 16,8 •
в точках В н К (направления Тр и тш тоже не совпадают) 200-36 1462-24.8 „ _о ., ,
’*•'"652,8-0,4“ 4370-0.4 - 27,6 20,8-6,8 ^см •
На свободном конце стержня касательные напряжения складываются из напряжений чистого кручения и напряжений от поперечной силы;
Л4кв t = Tk+Tq=_^ + —.
Наибольшего значения касательные напряжения в этом сечении достигают о точках В и К у наружной поверхности стержня, где
1213-0,6 200-36 лсп , ,
Tmix — хв.к— 1 649 +б52.8-0.6~441>4 + 18-4 « 460 «*/«* •
10.110. Дуралюминовый стержень длиной 1= 1 м, концы которого закреплены от поворота вокруг продольной оси, но могут свободно депланировать, нагружен парой сил с моментом Л40=10 кглц приложенной посредине пролета в плоскости, перпендикулярной к осп стержня (см. рис. а). Поперечное сечение стержня изображено на рис. в.
Определить величины наибольших секторнальных нормальных и касательных напряжений, наибольших напряжений чистого кручения и угла закручивания сечения стержня посредине пролета. Е=7-105 кг/см*, G = 2,7-106 кг/см\
Данные для контроля решения. Секториальиый момент инерции сечеиия /ш=289,6 см*. Иэгибно-крутильиая характеристика стержня а=0,0178 см-1. Решение дифференциального уравнения бнмоментов для данного случая см.: Н. М. Беляев, Сопротивление материалов, изд. 1954 г. н более поздние, стр. 552. Эпюры изменения В, Мш и М* по длине стержня даны иа рис. б.
Ответ: Наибольшие секториальные нормальные напряжения будут в точках Н и N среднего сечения стержня: оШ1Пах=1110 кг/см*. Наибольшие секториальные касательные напряжения возникают в точках G и М того же сечения: тштах = 44,7/сг/слг2. Касательные напри-жения в опорном сечении стержня, складывающиеся из напряжений
315
чистого кручения и напряжений от изгибно-крутящего момента Л1Ш, наибольшего значения достигают в точках G и М\
т1Пах тн + тш = 187,5 -|- 31,4 а; 219 кг!с.чг.
Угол закручивания среднего сечения стержня по отношению к
Б(кгсмг)
К задаче 10.110.
опорным сечениям определяется из выражения
//2
ив.
“о 4GJKchy4 '
10.111. Стальной стержень длиной 1 = 2 м, оба конца которого защемлены, посредине пролета нагружен парой сил с моментом Л10, действующей в плоскости, перпендикулярной к оси стержня (см. рис. а). Поперечное сечение стержня изображено на рис. б.
316
Построить эпюры изменения силовых факторов по длине стержня, определить величину момента Л1в так, чтобы наибольшие секто-риальные нормальные напряжения не превышали 1500 кг!см\ найти наибольшие секториальные касательные напряжения и напряжения чистого кручения, а также угол закручивания среднего сечення стержня.
60*4-
'ЮО*4
Размеры в мм,
30*4-
К задаче 10.111.
Ответ. 2И0 тах = 5020 кгсм «50 кгм; тш max = хп = 156 кг!смг (в защемлении); тктах = 369 кг!см* (при х = 50 см); xltтак = 471 кг!смг (при х = 50 см); ф = 0,078 рад.
X, см Силооые X. факторы \ 0 25 50 75 100
В, кг/смг —95640 —42510 0 +42510 +95640
Мш, кгсм 2500 1837 1633 1837 2500
М*. кгсм 0 663 867 663 0
10.112. Защемленный одним концом стальной стержень трубчатого сечении с продольным разрезом (см. рисунок) скручивается парой сил с моментом Л10 = 20 кгм, приложенной на свободном конце стержня. Определить наибольшие секториальные нормальные к касательные наприження, наибольшие касательные напряжении чистого кручения и угол поворота свободного конца стержня.
Для сравнения определить касательные наприження н угол закручивания в стержне такого же трубчатого сечения без продольного разреза.
Ответ: оштах = 161 кг/см? (в защемлении); тштах=12,8 кг) см* (в защемлении); тк тах = 622 кг)смъ (на свободном конце); ф = 0,124 рад. В стержне без разреза татах=17,7 кг[смг и ф = 0,00037 рад.
317
10.113. Защемленный одним концом стальной7 стержень двутаврового сечения на свободном конце нагружен силой Р= 60 кг, дей-
ствующей вдоль средней наибольшие нормальные и
К задаче 10.112.
линии полки (см. рисунок). Определить касательные напряжения, наибольший угол закручивания н перемещение центра тяжести свободного конца стержня в направлении действия силы Р.
К задаче 10.113.
Ответ. ошах=1251 кг) см2; ттах=154 кг!см2; ф = 0,0444 рад', f— 1,56 см.
10.114. Алюминиевый стержень двутаврового поперечного сече-
ння, концы которого закреплены от поворота вокруг продольной
оси, но могут свободно депланировать, нагружен парами сил с моментом 2И0, действующим в плоскости одной из полок (см. рисунок).
Определить наибольшую величину момента 2И0, при которой наибольшие нормальные напряжения в стержне не превысят [о] = 800 кг!см\ Найти величину наибольших секториальных касательных напряжений и напряжений чистого кручения. £ = 7-10* кг) см3.
О=2,7-Ю6 кг/см2.
Ответ: Af0 max = 1440 кгем; тш max = 11,3 кг[см2; тк шах = 95,8 кг/см2.
К задаче 10.115.
К задаче 10.116.
10.115. Стальной стержень корытного профиля, концы которого вакреплены от поворота вокруг продольной оси, но могут свободно
318
декламировать, нагружен посредине пролета I=1,6 м силой />=250 кг, приложенной, как указано на рисунке; а =10 см.
Определить величину наибольших нормальных и касательных напряжений в поперечном сечении стержня.
Ответ: omiK=1629 кг[см*' тт1Х = 466 кг! см2.
10.116. Стальной стержень длиной / = 90 см, концы которого закреплены от поворота вокруг продольной оси, но могут свободно деплаиировать, нагружен равномерно распределенной нагрузкой интенсивности q. Поперечное сечение стержня—неравнополочный двутавр (см. рисунок). Нагрузка q приложена посредине высоты стенки.
Определить наибольшую величину нагрузки q, при которой нормальные напряжения в стержне не превысят 1600 кг[см2. При нагрузке g = 5 кг1см определить наибольшие нормальные и касательные напряжения и угол поворота среднего сечения стержня вокруг продольной осн.
Ответ. ?т„ = 6,59 кг)см‘, omax = 1214 KzfcM*-, ттах = 258 кг/см*; ф = 0,0324 рад.
ГЛАВА 11
КРИВЫЕ СТЕРЖНИ
§ 36. Напряжения в кривых стержнях
11.1. Построить эпюры изгибающего момента, поперечной силы и нормальной силы для кривых стержней, показанных на рисунке. Ось стержней — круговая кривая.
К задаче 11.1.
Ответ:
Схема AI (ф) Q «Г) N (<p)
а Рг (1 — coscp) P sin <p P cos <p
б —Рг sin <р — P cos <p P sin <p
е Рг ^sin<p—sin y) P cosq> —P sinep
г О.б^г2 sin2 ф sin 2<p —9rsin2<p
11.2. Кольцо с разрезом по горизонтальному диаметру, показанное на рисунке, имеет высоту сечения к=10см и ширину b = 5 см; радиус кривизны внутренних волокон кольца /?а = 6 см. Кольцо сжато силами Р=4 т, как показано иа рисунке. Определить напряжения в сечении АВ по линиям 1—1, 2—2, 3—3, 4—4, 5—5 и
320
(>'—0, после, чего построить эпюру распределения напряжений но высоте сечения АВ.
Решение. Площадь поперечного сечеиия F=50 см2. Радиус кривизны оси стержня ₽0=11 см. Радиус кривизны нейтрального слоя вычисляем по формуле Л Ю 10
r~ Rt~ 8 “0,9798^10,2 См’ ХпЪ ,пз
Расстояние от главной оси у0 до нейтральной оси CD z0=R0—г=11,0—10,2 = 0,8см.
Статический момент сечеиия относительно нейтральной осн CD 3 = 50-0,8 = 40 см3.
Напряжения от нормальной сжимающей силы
, N —4000 __ , „ „
ст——=—=;—= — 80 кг/см2. Напряжения от Г OU
М М = где
S pi S
Zi—координаты точек, отсчитываемые от иейтраль-же точек, Изгибающий
изгибающего момента
К задаче 11.2.
ной оси CD, р;—координаты тех отсчитываемые от центра кривизны.
момент в сечении
АВ
7И 44 000
равен М =4000-11=44000 кгсм. Отношение у= =1100 кг[см2.
Вы*
11 Сб. еадач
321
числяем коэффициенты а/ для шести zj = z1=5,8 см, z2=3,8 см, г3= 1,8 см, г} = —0,2 см, г6=—2,2 см,
Zb = z0= —4,2 см,
линий сечения АВ: р1= 16 см, рг=14 см, р3= 12 см, р4 = 10 см, рь=8 см, рв = 6 см.
<4=0,363,
<4=0,272,
<4=0,150,
<4 =—0.020.
<4 =—0,275, <4 =—0,700.
Полные нормальные напряжения по тем же шести линиям сечения АВ: ол=о1 = —80 + 1100 0,363=—80+399=319 кг/см*, о2 = — 80 +1100 •0,272 = — 80 +298 = 218 кг/сж», с3=— 80 + 1100 0,150=— 80 + 165 = 85 кг/см2, о4=—80+1100-—0,020=—80— 22= —102 кг/см*, оь = -80+1100- —0,275= —80 —305= —385 кг/см-, ал = с0= — 80+1100- —0,700= —80— 770= —850 кг/см*.
По этим числам построена эпюра распределения нормальных напряжений по сечению АВ, показанная на рисунке (стр. 321). CD—нейтральная ось прн изгибе моментом М\ ML—нейтральная ось при совместном действии М и N.
11.3. Стержень прямоугольного сечення шириной 4 см и толщиной 6 см имеет форму, показанную на рисунке. Радиус Ro оси стержня 7 см. На расстоянии 12 см от центра среднего сечения приложены две равные силы по 1 т каждая, направленные так, что стремятся разогнуть стержень. Найти наибольшие нор
мальные напряжения и построить эпюру распределения напряжений по высоте среднего сечения стержня.
Ответ: 750 кг!смг-, —341 кг!смъ (г = 6,55 сж*)).
11.4. Найти грузоподъемность крюка прямоугольного поперечного сечения. Радиус внутренней поверхности крюка 15 см, наружной—25 см, ширина сечения 7,5 см. Линия действия вертикальной силы проходит через центр кривизны крюка. Допускаемые нормальные напряжения равны 700 кг!см-.
Ответ: 3380 кг (г =19,58 см).
*) В ответах к задачам 11.3—11.13 указаны в скобках величины радиусов кривизны нейтрального слоя г, вычисленные с округлением для дальнейших подсчетов при решении каждой задачи.
322
11.5. Кольцо, изображенное иа рисунке, выполнено из стержня круглого сечения диаметром 8 см. Внутренний диаметр кольца 12 см. Кольцо сжато силой 20000 н. Найти напряжении в точках А и В.
Решение. Определим величину радиуса кривизны нейтрального слои кольца и выпишем остальные расчетные данные:
d3 64
г =------у____ =---------г =9,58 см
4(K0_j/4fl*_<₽) 4(100— К400—64)
(см. Н. М. Беляев, Сопротивление материалов, стр. 252, формула (21.26));
nd2
z„=R0—r= 10—9,58 =0,42 см; 77=^-=50,25 см*;
радиусы кривизны крайних волокон: 7?^ =14 см, Rj) = 6 см; координаты их: г.д = 4 4-0,42=4,42 см, гд=4—0,42 = 3,58 см.'
Напряжения в крайних волокнах определятся по формулам
А~ F ' Fz0 Ra F\ ' z0RaJ
т(,+^)—8Ю-,О,(,+Йт)-
= — 398-10* (1 -f-14,2) = -605-10» н/м*.
11.6. Кривой стержень круглого сечения диаметром 10 см имеет радиус кривизны внутренних волокон 5 см. Изгибающий момент вызывает во внутренних волокнах стержня растягивающие напряжения, равные 200 кг/см*. Чему равны напряжения в наружных волокнах стержня?
Ответ; 89,5 кг!см* (г = 9,27 см).
11.7. Определить наибольшие растягивающие и сжимающие напряжения в опасном сечении крюка, поднимающего груз Р= 10 т.
Размеры крюка даны на рисунке. За кругл е-кР ния углов в поперечном сечении не пока-
JLLrL заны и при расчетах не учитываются.
К задаче 11.7.
Решение. Опасным является сечение АВ. Положение центра тяжести сечения определится расстоянием с ат внутренней грани:
Л (27,,+^) 1214 _пп с= ----=5.09 см.
З^+Ьа) 311 ’
11
823
Радиус кривизны нейтрального слоя находится по формуле
Л^г+Л ___________я 2____________ 125,5 lng-л-м ~ (3+20.А) lnf-S
Остальные данные, необходимые для вычисления напряжений: Я0=Я2+с= 8+5,09= 13,09 см, г0=/?0—л = 13,09—12,22 = 0,87 см, S = FzB= 5,5-12-0,87=57,4 сл*3, г! = Л—с+г0= 12—5,09 + 0,87 = 7,78 см, г«=с—zo=5,09—0,87 = 4,22 см.
Определяем напряжения:
+ +'0^13.09 .<р_|5г+,.mo.iss, „1С*.
+ WgO 13.09 .^.^-ио.-тзз
11.8. Крюк имеет трапецеидальное сечение с основанием 5 см на внутренней стороне и 2,5 см на внешней. Высота опасного сечения 10 см; радиус кривизны внутренних волокон 10 см. Линия действия силы проходит через центр кривизны крюка. Какой груз может поднять крюк при допускаемом напряжении, равном 1000кг/сж2?
Ответ: 3281 кг (г = 13,9 см).
11.9. Поперечные сечения кривого стержни имеют формы и размеры, показанные на рисунке. Там же показаны н величины радиуса кривизны внутренних волокон стержня. Найти отношение напряжений в крайних волокнах кривого стержня к напряжениям в тех же волокнах прямого бруса такого же сечения от действия одинаковых изгибающих моментов.
Ответ: а) 1,285; 0,795 (г=1,35й, с = 0,4Л);
б) 1,44; 0,78 (г = 0,88Л).
324
11.10. Определить наибольшие и наименьшие нормальные напряжения в стержне, показанном на рисунке, от нагрузки Р=5 т.
Ответ: 1178 кг/сма и—1088 кг/см2 (г= 18,52 см, с = 4,07 сж).
11.11. Кривой стержень имеет поперечное сечение в форме кольца. Размеры обозначены на рисунке. Определить величину допустимого момента [7И], если d = 2 см, а допускаемые напряжения [о] = 850 кг/сж2.
К задаче 11.11.
Указание. При вычислении J — исходить из формулы (31.25), прпведен-F
ной па стр. 592 «Сопротивления материалов* Н. М. Беляева, изд. 1951—1965 гг. В условиях данной задачи этот интеграл оказывается равным 0,26га!, а радиус кривизны нейтрального слоя г=2,8854.
Ответ: [7И] = 80 кгм.
11.12. Поперечное сечение кривого стержня — равнобедренный треугольник высотой h, равной ширине основания. Радиус кривизны внутренних волокон (основания треугольника) равен 2h. Стержень изгибается положительным моментом величиной 2000 кгем. Определить напряжения у внутренней поверхности стержня и в вершине угла, если Л = 3 см.
Ответ: —1000 кг)см2-, 1482 кг/сж2 (г = 2,31Л).
11.13. Вычислить радиус кривизны нейтрального слоя при изгибе кривого стержня парой сил. Поперечное сечение стержня — двутавр с разными полками. Размеры указаны на рисунке (стр. 326). Числовые значения этих размеров следующие: Ь3 = 3 см, Ь3 = 1 см, Ь1 = 2 см, 7?в = 3 см, Лх = 1 см, Л2 = 2 см, h3 = 1 см.
Решение. Точное решение дает следующий результат:
Р Ь]/?, + + ^3^3
Г С dF . . ₽! . - Rt R3
JT bllnVMnF3+M,4
____2 + 2 + 3_ _ 7 о. 7 . . 3 , Q, 4 “1,577
21п -+1H у + 31п у
4,44 см.
325
При сложном поперечном сечении интегрирование становится трудным и его заменяют суммированием -~* разбивая сечение иа полоски малых размеров. Для приближенного решения рассматриваемой задачи разделим сечение иа 8 полосок высотой по 5 мм каждая. Границы полосок указаны на рисунке пунктиром. Вычисление знаменателя формулы, приведенной в начале решения, дано в таблице.
№ полоски ДГ, смг р. см AF:p, см
1-. 1.0 6,75 0,1481
2 1.0 6,25 0,1600
3 0.5 5,75 0,0870
4 0,5 5,25 0,0952
5 0,5 4,75 0,1053
6 0,5 4,25 0,1177
7 1.5 3,75 0,4000
8 1.5 3,25 0,4617
Сумма 1,5750
Результаты приближенного вычисления знаменателя формулы для нахождения величины радиуса кривизны нейтрального слоя кривого стержня оказались очень близкими к точному.
§ 37. Определение перемещений
11.1 . Найти вертикальное и горизонтальное перемещения и угол поворота сечеиия А кривого стержня, загруженного моментом Мл. Ось стержня—круговая кривая ра-
диуса а (см. рисунок).
Решение. Воспользуемся теоремой Кастильяио. В Точке А прикладываем дополнительные силы Ру, Рц, Мд. Рассматриваем только второй участок кривого стержня от сечеиия, где приложен Л10, до заделки, так как иа первом участке кривого стержня Л4(ф)=0.
Вертикальное перемещение точки п/4
1 С лл , х дМ (ф) л
= М^-5р^аЛр.
о
М (<p) = A1(1+PVzasln ( j+ф
= а sin
ЭМ (ф) dPv
п/4
Va=Jj У Л*©*1 sln (у+ ф) а<*ф = 0,707 О
320
Горизонтальное перемещение точки А:
n/i
1 Г >4 I \ дМф ^=ЁТ] M^d^adlP.
о
Угол поворота сечеиия А: п/4
QA=il J ^(<p) = A4o + ^,
о Я/4
®Л=^Г j Мо.1.айф=0,785-^. о
дМ (ф)
Положительные знаки ответов означают, что направление каждого перемещения соответствует направлению дополнительной силы.
11.15. Для каждой схемы кривого стержня, показанного на рисунке, определить угол поворота, вертикальное и горизонтальное
перемещения свободного конца с учетом влияния нормальной силы на величину перемещения.
827
Ответ к задаче 11.15 (см. стр. 327):
Схема °А «А ХА
а 2EJ М&2 EJ 0,571
6 Ра2 EJ пРс? nPa 4EJ + 4EF Ра3 Ра 2EJ 2EF
в Ра2 0,571 ТУ РсР Ра 2EJ 2EF 0 ^6 Ра3 F пРа 0,356 EJ + 4EF
г ЗлМда 2EJ Mffl2 EJ 5.71^
д Ра2 EJ ЗпРсР ЗпРа 4EJ + 4EF Ра2 Ра 2EJ 2EF
е 571^ 5,71 EJ Ра3 Ра 2EJ 2EF о 065 Рд3 4-3пРа 9,065 EJ 1 4EF
11.16. Определить величину вертикального перемещения свободного конца кривого стержня постоянного сечения, показанного па рисунке. Ось стержня — четверть окружности радиуса а. Рассмотреть
К задаче 11.16.
три схемы загружения стержня: а) вертикальная нагрузка интенсивностью q распределена равномерно по горизонтальной проекции стержня, б) нагрузка интенсивностью q радиального направления распределена равномерно по оси стержня, и в) равномерно распределенная нагрузка интенсивностью q направлена в любой точке осн стержня по касательной к его осп.
328
Указание. Применим теорему Кастнльяно, учтя влияние иа перемещение также и нормальной силы:
п/2 Я/2
1 С ..<>М * С
'J~EJ J М дР ad,p + EF J 'V dP ad<₽-о о
Здесь Р—дополнительная сила, приложенная вертикально к свободному концу кривого стержня (см. рисунок).
Сначала вычислим отдельно зависящие от Р и одинаковые для всех трех схем величины изгибающего момента и нормальной силы:
М = Р a sin ф и N = —РвШф;
частные производные их по 0 соответственно равны азтф и—51Пф.
Затем вычисляются изгибающий момент и нормальная сила, зависящие от равномерно распределенной нагрузки интенсивностью q. Их значения;
. ?a2sin29 а) N = — qa sin2 ф;
6) M=2qa2s\n2 у, N = — 2<?asin2
в) M = qa2 (ф—sin ф). ^ = 0aзinф.
Эти данные подставляются в указанные выше два интеграла.
, оа* . 2оа2 ?а‘ . qa2
Ответ: a) + ; б) 2EJ ^~2EF ’
4 E J V 4 ) EF 4 •
11.17. Кривой стержень имеет форму камертона с размерами, показанными на рисунке. Вычислить величину абсолютного сближения
К задаче 11.17.
концов стержня под действием двух сил Р, сжимающих камертон.
Ответ: ~ [2a2 (2a + 3b) + 6nRa (a + b) + 12R* (2a + b) + ЗлЯ3]. DC J у
329
Интегралы, встречающиеси при вычислении перемещений и кривых стержнях с круговой осью (Пономарев С. Д. н др.. Расчеты-на прочность в машиностроении, 1956, том 1, стр. 589)
Подынтегральное выражение Значение определенного интеграла в пределах:
от 0 до а от Одоя/2
sin tp dtp cos tp dtp sin*tpdtp cos2tp dtp sin^ dtp cos*tp dtp tp sin tp dtp tp cos tp dtp tp2 sin tp dtp tp2 cos tp dtp tp sin2 tp dtp tp cos2tp dtp sin tp cos tp dtp sin tp cos2tpdtp sin2tp cos tp dtp sin2tp cos2tp dtp sin 2<p dtp cos 2tp dtp tpsin2tpdtp tp cos 2tp dtp 1 — cos а sin а —|-sin2a+y а jsin2a+-l-a i cos3a-|cosa + | j^sin 3a-|- — sin a sin a—a cos a cosa-|-asina—1 2a sin —(a2—2) cos a—2 2a cos a-|-(a2—2) sin a 1 , 1 . „ 1 „ , 1 -r-a-—T-a sin 2a—g- cos2a-|--g-4 о о 1'1 1 1 — a2+—asin2a— cos 2a—— у sin 2a 4-(l — cos3 a) 0 4- sin3 a 1 1 • „ ya-gsmta 1 1 о у-у cos 2a 1 - A sin 2a 1 • n 1 —- sin 2a——a cos 2a 4 2 1 a 1 • a 1 — cos 2a+ -% a sin 2a—— 1 1 Л т л т 3 2 2 3 1 ?- 1 л 2 т-2 16 4 л2 1 16 4 1 2 1 3 1 3 л Тб 1 0 л т 1 2
830
§ 36. Статически неоиределимые кривые стержни
' 11.18. Для двухшарнирной арки, ось которой очерчена по полуокружности (см. рисунок), построить эпюры изгибающего момента, нормальной силы и поперечной силы от действия вертикальной силы Р, приложенной в вершине арки.
К задаче 11.18.
Решение. Эта система однажды статически неопределима. За лишнюю неизвестную принимаем горизонтальную составляющую реакции опоры В. Из уравнений статики находим А = В=0,5Р и Нд=Нд = Н. Для определения величины И воспользуемся условием, что горизонтальное перемещение опоры В
равно нулю:
Дд=0 или
(S)
331
- ' В' силу симметрии арки и нагрузки иа нее можно рассматривать при интегрировании только половину арки. Тогда
л/2
§ £— (1 — совф) + sin <pj a sin <р-а d<p=O.
о
р
Вычислив интеграл, получим Я = —.
Ординаты эпюр М (<р), N (<р) и Q (<р) вычисляем по уравнениям:
, Ра , , Ра . „ /cosq> 1 , sirup\
М (<р) = — -у (1 — cos«p)+— sinrp=Pa(—2"l—„ J’
,,, , Р Р . _ (cos <р , sin <р\
N (ф) = _ — СОЗф — — 81Пф = — Р ( ———- ), X Л \ X JV у
Р Р . _ Z cos <р sin ф\
Q (ф) =— cos ф—2 sin ф= Р ( —7^-----2х 1-
Максимального значения М (ф) достигает при Q (ф) = 0; таким образом, cos ф 5|п ф__^ 15ф=-^-=0,637, ф = 32°30'. При этом же значении ф достигает максимума и N (ф). Ординаты эпюр через каждые 15° показаны иа рисунке (схемы б, в н г).
11.19. Для двух шарнирной арки, загруженной, как показано па рисунке, построить эпюры изгибающего момента, нормальной силы и поперечной силы.
Ответ: А — В = На~Нв = 0,5Р. Для правой половины арки:
Л1 (ф) = 0,5Ра (sin ф + cos ф— 1), N (ф) = — 0,5P(cos ф -f- sin ф), С(ф) = 0,5Р(со8ф—зшф). Mmm = 0,207Pa п
л
ALax = 0,707Р
при ф = 45е.
К задаче 11.20.
. 11.20. Ось кривого стержня очерчена по четверти окружности радиуса а. Способы закрепления концов стержня и варианты его загружения показаны на рисунке. Определить опорные реакции,
332
построить эпюры изгибающего момента, нормальной силы и поперечной силы и вычислить величину перемещения Д опоры В.
Ответ: а) В =0,9 — , ’ а ’ Д =0,042^; tt J
б) В=0,637Р, Д = 0,036
в) В=1,408Р, рп3 Д =0,081
Ординаты усилий (для построения эпюр) показаны в таблице.
Схема ф Усилия 0‘ 30° 45° СО’ 90°
а М:М0 Na:M0 Qa:M0 0 0 —0,900 —0,450 0,450 —0,779 —0,636 0,364 0,636 —0,636 0,221 0,779 —0,450 0,100 0,900 0
б М-.Ра N:P Q-.P 0 1 —0,637 —0,183 1,183 —0,051 —0,157 1,157 0,257 —0,051 1,051 0,548 0,363 0,637 1
в М-.Ра N:P Q-.P 0 — 1,408 . 1 0,311 —1,720 0,161 0,294 —1,703 —0,273 0,164 — 1,570 —0,720 —0,408 — 1 —1,408
б при <p = 32°30' <? = о. М = - -0.185Ра, А’=1 I85P
в при <р = 35°22' <2=0, м = 0,318Ра, А’ = - 1.727Р
11.21. Звено цепи в форме двух круговых полуколец радиусом а и двух прямолинейных участков длиной 21 растягивается силами Р,
как показано на рисунке. Определить изгибающие моменты в сечениях А и В. Приняв / = а, найти Ма и At в при этом упрощении, а также определить, на какую величину Д увеличится расстояние между точками В.
„ .. Ра л—2
Ответ-. Л1А =-s- •----j-;
л+2 —
+—
Мв = Ра----МА = — 0,111Ра;
л+2— а
К задаче 11.21.
РлЗ
2Ив = 0,389Рв; Д =0,229 .
333
11.22. Насколько увеличится диаметр стального кругового кольца, растягиваемого силами Р = 2т, действующими вдоль диаметра? Радиус кольца а =10 см, сечение прямоугольное с высотой (в плоскости изгиба) 2 см и шириной 3 см. Чему равны наибольший и наименьший изгибающие моменты в кольце?
Ра9
Ответ: 0,15-gj =0,075 см; 0.3185Р (в сечении, где приложена сила) = 6370 кгсм; —0,1815Р =—3630 кгсм.
Мв = — 0,403Рс;
11.23. Вычислить изгибающие моменты в сечениях Ап В звена, показанного иа рисунке, от действия сжимающих изменение А расстояния А—Л?
Ответу МА = 0,597Ра;
Л = 1,023~.
С J
сил Р. Чему равно
11.24. Для кривого стержня, показанного на рисунке, вычислить величину вертикальной и горизонтальной составляющих реакции опоры В.
м м
Ответ: В„ = 0,188-^; Д,= 1,117—.
У ’ а х а
11.25. Определить, как распределится нагрузка Р между кривыми брусьями 1 и 2, показанными на рисунке. Влиянием нормальной силы пренебречь. Какое горизонтальное усилие X передается от одного бруса к другому в шарнирном узле А7 Чему равны вертикальное и горизонтальное перемещения узла Д?
рл3
Ответ. Р^О.бввР; Ра=0,312Р; Х=0,438Р;.ул = 0,02б^; хА=0.
§ 39. Толстостенные трубы и составные цилиндры
11.26. Длинная бетонная труба, имеющая внутренний диаметр 1 л>, заложена на глубине 35 м от поверхности воды. Считая давление воды равномерно распределенным по поверхности трубы, определить необходимую толщину ее стенок, исходя из условий прочности по теории наибольших напряжений, а затем найти, чему равны расчетные растягивающие напряжения у внутренней поверхности трубы по теории
334
наибольших деформаций. Допускаемые напряжения для бетона на сжатие 15 кг/см*-, коэффициент поперечной деформации р. = 0,16.
Решение. Наружное давление, равномерно распределенное по поверхности трубы, р1 = у-Ц= I -35 = 35 тл/л2 = 3,5 кг/см1. Нормальные напряжения в радиальном и в тангенциальном направлениях
аг
11 О£ =
где г\—радиус наружной, a гг—радиус внутренней цилиндрической поверхности трубы; г—расстояние любой площадки в поперечном сечении трубы от ее оси.
Так как труба длинная, то для сечений, удаленных от ее концов, деформацию в направлении оси трубы (ег) следует считать равной нулю, т. е.
откуда
ez=y К—Ц (Ог+ <М1 = °.
= р (ог + О() = — 2gPi —= const.
Напряжения аг, о( н о2 по всей толщине трубы сжимающие. Наибольшее нз них по абсолютной величине—тангенциальное у внутренней поверхности трубы. Здесь при г = гг =50 см
при этом ог=0.
Условие прочности по теории наибольших нормальных напряжений имеет вид
2р
| оэ I = I шах а( | = 1 < [осж],
П—г2
откуда
Следовательно, стенки трубы должны иметь толщину t = rj—га=68,5 —50 = = 18,5 см.
Расчетные растягивающие напряжения у внутренней поверхности трубы по теории наибольших деформаций
ог, = О1—И (Р»+аэ)=аг—р (of + Oz)=0+p(-^ir+2p—= \ Г! — Г2 Г1 — Г 2 /
=2рГ1 •-^Н->(1+р) = 2-0,16-3,568^502 . 1,16 = 2,77^2,8 кг/см*.
Г । Г 2 ’
11.27. Длинная стальная труба, имеющая внутренний диаметр 4 см и толщину стенок 5 мм, подвергается внутреннему равномерно распределенному давлению 270 к.г]см- и наружному равномерно распределенному давлению 90 кг/см*. Считая деформацию в направлении оси трубы равной нулю, определить главные напряжения и
335
наибольшее расчетное напряжение в материале трубы иа основе энергетической теории прочности.
Ответ: Главные напряжения: 410, 96 и —90 кг/см2; расчетное напряжение 438 кг!см2.
11.28. Стальной цилиндр имеет диаметры: наружный—200 мм и внутренний —150 мм. По торцам цилиндра имеются днища. Цилиндр подвергнут внутреннему давлению в 400 ат. Считая нормальные напряжения, параллельные оси цилиндра, равномерно распределенными по поперечному сечению, определить величину расчетного напряжения в стенке цилиндра по третьей и четвертой теориям прочности.
Ответ: 1828 кг/см2; 1582 кг/см2.
11.29. Длинный полый стальной цилиндр, имеющий наружный диаметр 200 мм, подвергается действию внутреннего давления 350 ат. Определить необходимую толщину стенки цилиндра при допускаемом напряжении 2000 кг/см2 по третьей и четвертой теориям прочности.
Ответ: 19,4 мм; 16,7 мм.
11.30. На длинный сплошной стальной вал диаметром 160 мм надета в горячем состоянии стальная же муфта одинаковой с валом длины, имевшая до нагревания наружный диаметр 240 мм и внутренний—159,8 мм. Определить: а) давление, которое возникает по поверхности соприкасания вала и муфты после остывания, б) растягивающие напряжения у наружной н внутренней поверхностей муфты и в) наибольшие сжимающие напряжения в вале.
Ответ: а) 695 кг/см2: б) 1122 кг/см2 п 1806 кг/см:1: в) 695 кг/см2 по всей толщине).
К задаче 11.31.
11.31. Два длинных стальных цилиндра показаны в разрезе на рисунке. Цилиндр а) имеет наружный диаметр 240 мм и внутренний диаметр 120 мм. Цилиндр б) образован из двух труб: первая имеет наружный диаметр 180 мм и внутренний—120 мм; вторая труба
336
имела до нагрева наружный диаметр 240 лгм, а внутренний — 179,865 мм. Вторая труба была нагрета и надета на первую.
Пользуясь третьей теорией прочности, определить величину допустимого внутреннего давления [р] для каждого из цилиндров при допускаемом напряжении 3000 кг/см2. Вычислить величину тангенциальных, радиальных и продольных нормальных напряжений в обоих цилиндрах в точках, взятых на расстоянии 60, 90 и 120 млг от осн цилиндров.
Ответ- Прн остывании между трубами цилиндра 6) возникнет давление 243 кг/см1. Допустимые внутренние давления: [р]о = 1125 кг/см2 н [р]б = 1453 кг/см2. Напряжения, возникающие при действии этих давлений, показаны в виде графиков иа рисунке.
11.32. Полый стальной сферический сосуд с внутренним диаметром 50 см предназначен для хранения газа, сжатого под давлением 800 ат. Исходя нз условия прочности по третьей теории прочности, определить необходимую толщину стенок сосуда при[о] = 2500кг/сл!8. Какую толщину должны иметь стенки закрытого цилиндрического сосуда из той же стали и с тем же внутренним диаметром?
Ответ: 61 мм; 125 лм(.
ГЛАВА 12
УСТОЙЧИВОСТЬ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
§ 40. Устойчивость сжатых стержней
12.1. Определить наименьшую гибкость стержня, при которой для вычисления критического усилия еще применима формула Эйлера, если стержень выполнен:
а) из стали с пределом пропорциональности ап = 2200 кг)смг и модулем нормальной упругости Е = 1,9 • 10® кг!смг:
б) из 3,5% никелевой стали сап = 4900 «г/см2 и £= 2,15-10® «г/см2;
в) из дуралюмина с on = 1770 «г/см2 и Е = 7 • 10® «г/см2;
г) из сосны с оп = 160 кг!см- и £=10® кг/смл.
Ответ: а) 92,3; б) 65,8; в) 62,5; г) 78,5.
12.2. Какой из двух стержней одинаковой длины, условия закрепления и нагружения которых также одинаковы, является более гибким—стержень квадратного или круглого сечения с равной площадью?
Ответ: Гибкость второго иа 2,3% больше.
12.3. Пользуясь формулой Эйлера, найти отношение величин критических усилий для работающих в одинаковых условиях стоек,
К задаче 12.3.
поперечные сечения которых, изображенные на рисунке, имеют одинаковые площади.
Ответ: Рм:Рм:РмгРм'.РмгРм= 1 -.0,955:0,333:4,56:4,35:2,38.
338
12.4. Определить величины критической силы и критического напряжения для сжатой стойки двутаврового поперечного сечения № 27. Оба конца стойки шарнирно оперты (шаровой шарнир). Длина стойки 4 м. Материал — сталь с пределом пропорциональности оп = 2000 кг/см1 и модулем упругости £ = 2-10° кг!см3.
Решение. Двутавр № 27 имеет F=40,2 см3, Jmia= Jy=200 см* и «min = = 1у = 2,54см. Гибкость стержня . ц1 1-400 1С_С .
—7~. о сл — 157,5 > Х0(№Д—я 1/
•min '
таким образом, применима формула Эйлера. Критическое усилие равно
EJ ге|пл2 2-10е-260-9,87
W (1-400)2-------------- 32 0оикг,
критическое напряжение
—=3,14 °п
2-108-9S,d'
м, шириной 25 мм и
Рк 32080 , -
ак=-^-=^оу-=798 кг/см3.
12.Б. Используя формулу Эйлера, подобрать по сортаменту па продольную сжимающую нагрузку Р— 12,5 т двутавровое поперечное сечение стойки длиной 2,6 м. Один конец стойки защемлен, второй оперт шарнирно. Материал—ст. 3. Коэффициент запаса устойчивости Лу = 2.
Указание. Из формулы Эйлера определяется необходимое значение J затем по сортаменту устанавливается номер профиля, для которого Jmin = jy имеет такую же или несколько большую величину.
При этом
т. е. формула Эйлера применима.
12.6. Определить величину допускаемого сжимающего усилия и допускаемого напряжения для стойки прямоугольного поперечного сечения 12x20 см, длиной 6 м, из дерева с модулем упругости Е=0,9 X Х10‘ кг/см2 и пределом пропорциональности <тп=150 кг/см- (см. рисунок, на котором показаны две проекции стойки). Коэффициент запаса устойчивости ky = 3.
Ответ: 6580 кг; 27,4 кг/см?.
12.7. Прямой стальной стержень длиной толщиной 2,5 мм изогнут в виде лука с упругим прогибом посредине, равным 5 см. Его концы связаны тетивой. Определить усилие в тетиве и наибольшее напряжение в стержне.
Ответ: Р = РИ « 6,45 кг; агоах« 1250 кг/слР (сжатие при прогибе 5 см).
12.8. Двутавр № 24 длиной 5 м защемлен обоими концам» в стены при температуре 15°. При какой температуре двутавр начнет
1
339
терять устойчивость, если стены считать: а) абсолютно жесткими, б) податливыми с коэффициентом податливости каждой стены k = = 2-10-в см/кг и в) абсолютно жесткими при шарнирном закреплении концов двутавра?
Ответ, а) 87°; б) 127°; в) 33°.
12.9. Трубчатая дуралюминовая стойка, имеющая длину 1,8 ж и наружный диаметр 60 мм, нагружена продольной сжимающей силой Р=10т. Оба конца стойки защемлены. Определить необходимую толщину стенки трубы, если для принятой марки дуралюмииа при 0 X 80 критическое напряжение по опытным данным равно сгк = 3360—28Х (кг/см2); коэффициент запаса устойчивости Ау = 2.
Ответ: /«б мм.
12.10. Определить допускаемую величину нагрузки на стойку с поперечным сечением, изображенным на рисунке (швеллеры состав-
лены стенками вплотную и сварены). Длина стойки 1,5 м, концы ее защемлены. При вычислениях исполь-
V ,320*10
№22
К задаче 12.10.
22J
~___О_
Уо .хе
X
\С
d=20
----------320-
Размеры в мм
К задаче 12.11.
_зовать формулу Ясинского: <тк = 3100—11,4Х (кг/сж2). Коэффициент запаса устойчивости Ау= 1,8.
Ответ: 64 300 кг.
12.11. Пользуясь таблицей значений коэффициента снижения допускаемого напряжения, определить наибольшую допускаемую величину нагрузки на шарнирно опертую по концам стойку длиной 6 ж, составленную из двух швеллеров № 22 и двух листов 320 X 10 жж из ст. 3 (см. рисунок). Листы и швеллеры скреплены заклепками диаметром d = 20 мм. Основное допускаемое напряжение [о] = = 1600 кг/см".
Решение. Так как по сортаменту для одного швеллера № 22 F=26,7 см2, Jx = 2110 см* н Jy= 151 см*, то для всего сечення F = 2(26,7 + 32-1) = = 117,4 см*, /у = 2|^51 + 26,7(16-8,2 + 2,21)г+1^] = 11 110«сж« н 1Х = = 2 ^2110+Ц^-+32-1-11.52) = 12 690 см* > 1у.
Наименьший радиус инерции сечення стойки
,/77 ,/~П~По
imin iy у у 117,4 —9,73 см.
340
Гибкость стержня
•rain
Значении коэффициента ф
Г ибкость X=-HL-min Значения <р для 1'ибкость А=-г-min Значения <р для
стали марок 3 и 4 сталп марки 5 чугуна дерева стали марок 3 и 4 стали марки 5 чугуна дерева
0 1,0 1.0 1.0 1.0 по 0,52 0,43 0,25
10 0,99 0,98 0,97 0,99 120 0,45 0,37 — 0,22
20 0,97 0,96 0,91 0,97 130 0,40 0,32 — 0,18
30 0,95 0,93 0,81 0,93 140 0,36 0,28 0,16
40 0,92 0,89 0,69 0,87 150 0,32 0,25 — 0,14
50 0,89 0,85 0,57 0,80 160 0,29 0,23 — 0,12
60 0,86 0,80 0,44 0,71 170 0,26 0,21 0,11
70 0,81 0,74 0,34 0,60 180 0,23 0,19 — 0,10
80 0,75 0,67 0,26 0,48 190 0,21 0,17 — 0,09
90 100 0,69 0,60 0,59 0,50 0,20 0,16 0,38 0,31 200 0,19 0,16 0,08
Из таблицы значений <р—коэффициента снижения допускаемого напряжения прн продольном нзгнбе—путем линейной интерполяции находнм для ст. 3 «р=0,852. Допускаемое сжимающее уснлне равно
[P)=<p[o]F = 0,852-1600-117,4 м 160000 кг.
Поперечное сеченне стойки ослаблено четырьмя отверстиями под заклепки, прнчем
F„ = F6p-4d(tn 4-<шв)= 117,4 - 4 2(1+0,95)= 101,8 см*.
Из условия прочности
р °max=p" 1°] г н
следует, что
[о] £„=1600-101,8= 162 900 кг.
Таким образом, допускаемое сжимающее уснлне на стойку должно быть назначено по условию устойчивости: [Р]=160 т.
12.12. Стойка состоит из четырех уголков 100 X 100 X10, скрепленных планками (см. рисунок). Оба конца стойки шарнирно оперты,
ее длина 6 ж, она сжата силой 1 Мн. Определить размер стороны а поперечного сечения стойки. Материал—ст. 3; [сг] = 160 Л1н/лс2.
При вычислении момента инерции поперечного сечения стойки считать уголки жестко соединенными между собой. Увеличение гибкости стойки за счет соединения уголков не вполне жесткой решеткой во внимание не принимать.
Ответ: 21,9 см.
К задаче 12.12.
12.13. Из условий устойчивости и прочности определить наибольшую допускаемую величину сжимающей нагрузки на колонны, попе-
341
К задаче 12.13
№ п/п Схема поперечного сечения Состав сечения Диаметр заклепок. мм Вид закрепления Длина КОЛОППЫ. м Ответ: допускаемая нагрузка. т
1 Оси заклепок Два швеллера № 16 Два листа 250 x 8 мм 5,5 6.6 7 3.5 96.6 104,0 104,1 80,8
Е =К №16 У -да 17 а б в
^-200-^
лп Четыре уголка 70 х х70х7 мм Два листа 200x 6 леи Два листа 290x6 мм 14 а б в г 6 8 10 2 125,0 128.6 133.5 138,9
2 +200- ’1
рЬ—«4 31L1
[L №36 Два швеллера № 36 Два швеллера К: 22 20 9 205,0 211,5 234,6 192,7
3 \ю22 3 140 . В *- б в г 12 6 5
1Г ^-350- 1
4 1 -240- №14 Два двутавра К: 14 Два листа 240X8 jmjm 17 а б в г 3 7 1Г 3 100,3 91,8 85,4 79,7
Четыре уголка 100х X 100x10 мм Два листа 300х X10 мм' Одни лист 240 X
5 ПТ t 20 а б в г 7 5 10 4 126,8 212,5 190,9 102,7
1 — 300 *-4 X10 мд
6 i~i rj-: -U> Четыре уголка 140х Х9ОХ1О мм Один лист 200 X 10 мм 20 а б 6 6 107,4 142.2
[ -200+ Г _1 в г 10 3.5 128,8 85,1
342
речные сечения которых схематически изображены ниже. Использовать таблицу значений коэффициента снижения допускаемого напряжения <р. При проверке прочности совмещенными в одном сечении считать не более четырех заклепок. Материал—ст. 3; основное допускаемое напряжение [ст] =1600 кг/см2.
Способы закрепления концевых сечений колонн: а) оба конца шарнирно оперты; б) один конец оперт шарнирно, второй защемлен; в) оба конца защемлены; г) один конец защемлен, второй свободен от закрепления. Данные о составе сечения и длине колонн приведены в таблице; ответы помещены там же.
12.14. Из условия устойчивости с помощью таблицы значений коэффициента снижения допускаемого напряжения ф определить размеры поперечного сечения деревянной стойки, нагруженной продольной сжимающей силой Р = 20 т. Один конец стойки оперт шарнирно, второй защемлен, длина ее I = 3 м; сечение стойки прямоугольное с отношением сторон А:д = 2:1. Основное допускаемое напряжение [о] = 100 кг/см2.
Решение. Выразим основные геометрические характеристики поперечного сечения н гибкость стойки через размер Ь. Имеем
F — bh — 2b, Jraill — 12 — 6»
’min —
Jmln _ у/ _ Ь
F г 6-2Ь- 2 Уз ц1 _0,7-300-2 Уз 728 ‘min ~ Ь “ Ь •
Необходимую величину b найдем путем проб. Вначале ориентировочно принимаем, что q>=0,5; тогда
_ Р 20000 . _/У ,/400
F =^==бУТОб = 400 сЛ н b=V ~2 = У
При этом А. = ^р = 52, ф = 0,782 и
[оу1 = ф1а] = 0,782 100 = 78,2кг/С.^ >одсГ1„=-^=^^=51 кг/см2.
728
Сечение сильно недонапряжеио. Испробуем b = 12 см; теперь Х=-^- = 60,7,
ф = 0,702, F=2-12* = 288 см2 и [oj = 0,702-100 = 70,2 кг/см2 » anpflrT =
20000 , У
= -оой- = 69'° кг/с*-
Принимаем Ь=12сл< и h = 24 см.
12.15. Из условия устойчивости с помощью таблиц значений коэффициента снижения допускаемого напряжения ф определить размеры поперечных сечений сжатых стержней, схематически изображенных в таблице. Материал стержней: 1) дерево с основным допускаемым напряжением [о] = 100 кг/см2, 2) чугун с [о] = 1200 кг/см2, 3) ст. 3 с [о] = 1600 кг/см2 и 4) ст. 5 с [о] = 1800 кг[см2.
343
К задаче 12.15
№ п/п Схема поперечного сечення Матерная Способ закрепления Длина стержня. м Сжимаю-* щая нагрузка, т Ответ: размер сечення, см
1 “Т о 4 Дерево а б 3 4 9 12 12,0 12,5 11,8 Н.2
1 1 в г 4 1.6 15 6
2 — 1 «а Дерево а б в г 3.6 5 5 2 14 25 40 18 18,6 21,9 24,3 20,9
3 Чугун а б 5.2 4.8 4.5 2,8 120 80 90 22,5 16.6 15,0 22,9
pv>YS^Y i-д-» I 1 г ПО
4 — "Т гз 1 Чугун а б в 4.8 3,8 4,2 85 60 70 21,8 15,1 14,3
г 3.2 90 25,7
=|т S'?
5 Сталь 5 а б 3,2 3,6 38 70 10,0 12,0
8 2.4 80 100 13,9 15,8
^-^Zd—^- I г
Сталь 3 а б 3,6 4,5 5,0 2,2 28 65 120 25 27—а 40
6 в г 50 30—а
Способы закрепления концевых сечений стержней: а) оба конца шарнирно оперты; б) один конец оперт шарнирно, второй защемлен; в) оба конца защемлены; г) один конец защемлен, второй свободен от закрепления.. Данные о длине стержней и величине сжимающей нагрузки приведены в таблице.
Указание. Руководствоваться решением задачи 12.14.
344
12.16. Подобрать сечение колонны из четырех равнобоких угол* ков (см. рисунок) иод сжимающую нагрузку 60 т. Длина колонны 3,75 м; концы ее шарнирно оперты. Материал — ст. 3; основное допускаемое напряжение [о] =1600 кг/см2.
Решение. Подбор сечеиня производим путем проб. Вначале принимаем Ф=0,5. Необходимая площадь сечения колонны
г Р 60000 ,
Гб₽_ф|а] 0,5-1600 75
Из сортамента вндно, что эту площадь можно получить, беря четыре уголка 100x100x10 мм с Ft =19,2 смг, Jx=179 см* и г0 = 2,83 см. При этом для всего поперечного сечення колонны
F6p = 4Fi = 4 • 19.2 = 76,8 см2 и
JXt=4 [179 + 19,2 ^2,83-h^yj = 1568 см*.
Радиус инерции поперечного сечеиия
, - 1/2^- 1/15Й_.152сл<
V р - V 76,8“1,52
Гибкость колонны
ц1 _1-375 Г“Т52 - 83-
К задаче 12.16.
frlDwu
По таблице значений ф для ст. 3 находим ф=0,732. Допускаемое напряжение равно [Оу]=ф[а] = 0,732-1600= 1171 кг/см*. Действительное напряжение
Р 60000 „О1 , , °ДСЙСТВ—р& --- 76 8 -7^ кг1см
значительно меньше допускаемого, поэтому выбранное сеченне будет сильно педонапряжено.
Возьмем уголки 90x90x8 мм с площадью Г1=13,9сл2, 7х=106сл« и zt = 2,51 см. Для всего поперечного сечення колонны теперь имеем
Гбр = 4-13,9 = 55,6 см* и
7^=4 [106+13,9 (г,51 +^У] =928 см*. .
Радиус ннерцнн поперечного сечення
= l/rS = 4109 см-
х<> Г 55,6
Гибкость колонны
Z-k3Z2-917
4,09
По таблице значений ф находим ф = 0,675. Допускаемое напряжение равно [оу] = 0,675-1600 ~ 1080 кг/см*. Действительное напряжение
°действ = т=гтг= Ю79 кг/см1 я |ov]= 1080 кг/см*, ии ,0 "
Остановимся иа уголках 90x90x8 мм.
345
Проверим прочность колонны. Ослабленная отверстиями под заклепки площадь поперечного сечения равна
Fн = Fвр—2d • 2/ = 55,6 — 2 • 2 2 0.8 = 49.2 см-.
Сжимающее напряжение в ослабленном сеченни
°=1220 кг/см* < [о] = 1600 кг/см*.
Прочность материала запроектированной колонны вполне обеспечена.
12.17. Определить диаметр подкоса АВ кронштейна (см. рисунок) из дерева с основным допускаемым напряжением [ст] = 11 Мн/м*.
Оба конца подкоса считать шарнирно опертыми. Равномерно распределенная по балке CD нагрузка q = § Мн/м.
Т Ответ: 20,95 см х 21 см.
12.18. Жесткая конструкция ABCD поддерживается стержнями DH, СН 1 и CG (см. рисунок); в узлах D, С, G и Н крепления стержней шарнирные. Вес конструкции Q=100t, боковое давление Р=20т. Подобрать одинаковые поперечные сечения стержней из парных равнобоких уголков при
основном допускаемом напряжении [о] = 1600 кг!см*-, материал — ст. 3.
Ответ: У голки 125 X 125 х 9 мм.
12.19. Подобрать под сжимающую нагрузку 20 т поперечное сечение раскоса стропильной фермы из двух равнобоких уголков (см. рисунок); длина раскоса 2 м; концы его шарнирно оперты. Материал— ст. 3; основное допускаемое напряжение [ст] = 1600 кг/см2.
К задаче 12.19.
Указание. При вычислении момента инерции поперечного сечення считать уголки жестко соединенными между собой. Увеличение гибкости раскоса за счет соединения уголков ие вполне жесткой решеткой во внимание не принимать.
Ответ: Уголкн 70x70x 6 мм.
346
§ 41. Расчеты на устойчивость в сложных случаях
12.20. Определить наименьшую длину стержня квадратного поперечного сечения 10x10 см, защемленного одним концом и свободного от закрепления на другом конце, при которой он потеряет устойчивость под действием собственного веса, если стержень изготовлен: а) из стали с объемным весом у = 7,8 г/см3 и модулем упругости £=2-10® кг!см3, б) нз дуралюмииа с у = = 2,6 г/см3 и £=7-10® кг/см3 и в) из дерева с у = 0,6 г/см3 и £=10® кг/см1.
14
EJ я3
Указание. Воспользоваться формулой (gl)Kf=—, где |.i=i.i2.
Ответ: а) 25,6 м; б) 26,0 л«; в) 22,2 м.
12.21. Шарнирно- опертая по концам деревянная стойка диаметром 20 см н длиной 7 м нагружена двумя Р
Pi=-~-, приложенной в верхнем концевом •Э
2
и Р2 = -=- Р, приложенной в сечении на рас-•Э
а = 0,5/ от конца стойки (см. рисунок).
силами:
К задаче 12.21.
сечении, стоянии
Определить наибольшую допускаемую величину сжимающей нагрузки P = Pl+Pi.
Указание. Применить формулу Эйлера
для вычисления коэффициента длины ц, зависящего от условий нагружения стойки, воспользоваться прн а = Z/2 таблицей *)
Pl+Pt т- л 1.0 1,25 1.5 1,75 2,0 3,0
р 1.0 0,95 0,91 0,89 0,87 0,82
или приближенной формулой **)
р=-7?= 1/ ! + (">—1)(®~Д: sin 2ал V где а=-%- и т = —1^Р* . у т г \ / » “i
Коэффициент запаса устойчивости /гу = 3; £ = 10® кг/см3.
Ответ: [PJ = 2620 кг; [Р2] = 5240 кг; [Р] = 7860 кг.
12.22. Шарнирно опертая по концам деревянная стойка прямоугольного поперечного сечения 12x20 см, длиной 3,5 ж сжата
•) См. Н. М. Беляев, Сопротивление материалов, Гостехнздат, изд. 1954 г. н более поздние, стр. 629, таблица 30.
** ) См. А. Н. Митинский, А. К. Синнцкнй, Сборник примеров и задач по прикладной теории упругости, ЛИИГВФ, 1936.
347
продольной силой Р = 10 т. В нижией половине стойка усилена двумя досками сечением 3 X 20 см каждая (см. рисунок). Проверить устой-
К задаче 12.22.
чивость стойки, полагая, что коэффициент запаса устойчивости Ау = 3, а Е= 0,9-10® кг)смг. Использовать формулу Эйлера
р ___£Jtminn2
к~ (Ц/)2 '
Указание. Для вычисления коэффициента длины р, зависящего от соотношения моментов инерции Jt и Jt, воспользоваться таблицей
Jx п=т 1.0 0,8 0,6 0,5 0,4 0.3 0,2
и 1,00 1,06 1,16 1.24 1,35 1,51 1,82
нлн приближенной формулой
, /0,822п+0,589 (1 +«г) Jt
V —-------------------• п=тг
(см. сноски на стр. 347).
Ответ: Р = 10 т < [Ру] = 10,2 т.
12.23. Защемленная в нижнем сечении стальная колонна высо
той 6 м изготовлена из четырех равнобоких уголков 100 X100 х 12 лы<,
скрепленных решеткой из распорок и диагоналей (см. рисунок). Размер стороны колонны в верхнем сечении равен ал = 30 см, в нижнем — а2 = 60 см.
Определить наибольшую допускаемую величину сжимающей колонну нагрузки Р, если основное допускаемое напряжение [сг] = 1600 кг/см*.
Указание. Коэффициент длины за счет соединения уголков решеткой нз распорок н диагоналей принять равным р-1 = 1.1. а коэффициент длины р2 за счет переменности момента инерции сечення колонны взять нз таблицы ниже, где n = J1/Ji; за расчетное принять сечение в защемлении (см. сноски к задаче 12.21).
К задаче 12.23.
Л 0 0.1 0.2 0,3 0.4 0,5 0,6 0.8 1
»1 6.25 2.71 2,47 2,35 2,28 2,21 2,16 2,07 2
Ответ: 125,6 т.
12.24. Определить величину критической силы для стального стержня с поперечным сечением, изображенным на рис. а. Длина стержня 2 м, концы
его шарнирно оперты. Сжимающая нагрузка приложена в центре тяжести сечения. Предел упругости материала сгу = 32 кг] мм*.
348
Решение. Геометрические характеристики сечения:
Площадь сечения Р=12сж2; расстояние от средней линии стенки до центра тяжести сечення С ус=2,4 см.
Моменты инерции сечення относительно главных центральных осей инерции Jy=280,9 см* и Jz ~ 75 сж1. Момент инерцин сечення при чистом кручеинн JK=0,717 сж1.
Расстояние от точкн О до центра нзгнба сечеиия А равно Уа =—3,54 см. Эпюра главных секторнальных координат ш приведена на рнс. б. Главный секторнальный момент инерцни 7Ш=3485 см*.
Расстоянне от главной осн ннерцни г до центра нзгнба сечення = j/c + | </д | = 2,4 + 4-3,54 = 5,94 см. Особая характеристика сечен ня
г^у+^= ^Ц±^+5.942 « 65 см*.
Эйлерова крнтнческая снла в плоскости наибольшей жесткости
£Ag=210«-2M,9-9.87 * 138 500 кг.
У /2 2002
крнтнческая сила в плоскости наименьшей жесткости
Рг=^=2_^^«37 000кг.
200г
Снла, соответствующая крутильному эффекту.
К задаче 12.24.
(2l0*t!?'9’87+8-io6°-717)=з5 25°кг-
Величина критической снлы но Власову
_ (Py+P.u) К(РУ+ Pj2r4-4PyP.,/2 (r--og)~
В“ 2(r2—о^)
(138500+35250) 65— К (138500+35250)2 • 652—4 -138500 •35250 • 65 • (65—5,942) “ 2 (65 — 5,94-) “
= 30 550 кг.
Потеря устойчивости стержня происходит в нзгнбио-крутнльной форме; величина критической снлы по Власову в
37 000 ,
30 550 1
раза меньше эйлеровой.
12.25. Определить наибольшую допускаемую величину сжимающей нагрузки на стальной стержень длиной 1,8 м, поперечное сечение которого изображено на рисунке. Концы стержня шарнирно оперты, сжимающая нагрузка приложена в центре тяжести сечения. Коэффи-
349
циент.запаса устойчивости йу = 2,5. Предел упругости материала оу = 32 кг!мм*.
Ответ: 24,4 т (потеря устойчивости происходит в изгибной форме).
12.26. Стальной стержень с поперечным сечением, изображенным на рисунке, сжимается центрально приложенной продольной силой. Концы стержня шарнирно оперты. Определить величину критической
50*3
50*3
С
100*3
I-
50*3-
50*3
К задаче 12.26.
К задаче 12.25.
3=3
оо*г
К задаче 12.27.
силы в предположении, что стержень имеет длину: а) 2,4 м и б) 2,6 м. Найти наибольшую длину стержня 1так, при которой он еще теряет устойчивость в чисто крутильной форме.
-Ответ: а) РК = РВ = Рш = 5120 кг < 5710 кг = Рэ—стержень теряет устойчивость в чисто крутильной форме; б) Рк = Р3 =4870 кг < <Рш = 5120кг—стержень теряет устойчивость в чисто изгибной форме; при / = /тах = 2,54 ж Рк = Рэ = Рв = Рш = 5120 кг.
12.27. Дуралюминиевый стержень корытного профиля (см. рисунок) сжимается продольной силой, приложенной в центре тяжести поперечного сечения. Концы стержня шарнирно оперты; длина его равна 80 см. Определить величину критической силы в предположении, что полка швеллера имеет длину: а) b = 24 мм и б) b = 26 мм. Найти наибольшую величину Ь, при которой стержень теряет устойчивость еще в чисто изгибной форме. Е = 7 • 106 кг/см2- 0=2,7-106 кг/см*-, предел упругости оу = 2000 кг!смг.
Ответ: а) Рк = Рэ=4145 кг — стержень теряет устойчивость Рк = Рв = 4885 кг—стержень теряет устойчивость в изгибно-крутильной форме; &тах = 2,52 см; РК = РЭ = =РВ =4750 кг.
12.28. Проверить прочность и устойчивость плоской формы изгиба балки двутаврового сечения № 60, лежащей на двух шарнирных опорах и нагруженной равномерно распределенной
нагрузкой (см. рисунок). Допускаемое напряжение [о] =1600 кг/см*, коэффициент запаса устойчивости Ау=1,7.
в чисто изгибной форме; б)
?=18т/м
--------------- Т
4 ""Ал»
L-----i=bm-----J
К задаче 12.28.
350
Решение. В плоскости наибольшей жесткости, в которой действует поперечная нагрузка, проверяем прочность балки. Момент сопротивления сечения балки относительно осн х по сортаменту равен Ч7х=2510 си2. Наибольшее нормальное напряжение в сечении посредине пролета будет
Л4тах <7/2 18-8002 .
amax=-^=^;=T25io-=574 кг/см* < [а] =1600 ка/сж2.
При проверке устойчивости плоской формы изгиба используем условие устойчивости
‘/действ ^ [?] — ~k~P
где С] и С2—соответственно жесткости балкн прн изгибе и при кручении, а 0—коэффициент, зависящий от типа нагрузки, условий закрепления концов балкн н величины отношения
а
B~Ci \h) ’
где в свою очередь Л—высота поперечного сечення балки.
В данном случае
Ci = EJ„щ = EJy = 2-10» 1720 = 344• 107 кгем* и
C3 = GJK = G^ l(h—2t)<P+2bt*]-,
О
здесь b н t—ширина и толщина полки, h н d—высота и толщина стенкн двутавра, а т]—коэффициент, зависящий от формы сечения; для двутаврового сечения т)= 1,2. Таким образом.
1 2
С2 = 8-10» • —1(60— 2-1,78)-1,112+19-2- 1,78SJ=9,33-107 кгем*. О
Отношение
9.33-107 / 800 \2 л _ а»=-344ЛбГ 1-60-) =4*’2-
По найденному значению Од в таблице 33 курса «Сопротивление материалов» Н. М. Беляева (иэд. 1954 г. и более поздние, стр. 649) в случае распределенной нагрузки, лежащей на балке, шарнирно опертой по концам, путем интерполяции находим 0 = 02 = 29,04. Теперь
[ <7 J К344-107• 9,33 107 = Гв.9 кг/см > <7действ=18 кг/см.
Таким образом, в данном случае при назначении величины нагрузки приходится исходить нз проверки на устойчивость.
12.29. Шарнирно опертая по концам стальная балка прямоугольного поперечного сечения 50x6 мм (высота 50 мм параллельна плоскости действия нагрузки) нагружена сосредоточенной силой Р, приложенной посредине пролета. Определить длину балки и величину силы Р из условия равной прочности н устойчивости плоской формы изгиба, если [о] = 1600 кг/см* и fty=l,7.
Ответ: /=136 см; Р= 118 кг.
351
12.30. Защемленная одним концом в стену стальная балка прямоугольного поперечного сечения шириной 2 см, высотой 12 см и длиной 3 м нагружена равномерно распределенной нагрузкой интенсивности q. Из условий прочности и устойчивости плоской формы изгиба балки определить наибольшую допускаемую величину нагрузки q. Коэффициент запаса Ау=1,8; [а] =1600 кг] см2.
Ответ: 1,71 кг/см.
12.31. Сварная балка двутаврового сечения, составленнаи из стальных листов 150x16 мм (полки) и 500x12 мм (стенка), шарнирно оперта по концам и нагружена сосредоточенной силой Р= 10 т посредине пролета 1=6 м. Определить величину коэффициента запаса устойчивости ky и величину наибольшего нормального напряжения в балке при изгибе.
Ответ: fty = 2,06; <ттах=897 кг/см2.
§ 42. Продольно-поперечный изгиб
12.32. Двутавр № 36 длиной 1 = 5 м, концы которого в плоскости наибольшей жесткости закреплены шарнирно, а в плоскости наименьшей жесткости защемлены, нагружен продольными сжимающими силами N=70 т и поперечной силой Р=2,5 т, приложенной посредине пролета (см. рисунок). Проверить прочность и устойчивость двутавра, если [а] = 1600 кг/см2 и коэффициент запаса прочности k = 1,7. Использовать точное и приближенное решения задачи. Определить наибольший прогиб двутавра.
Решение. Проверка устойчивости в плоскости наименьшей жесткости. По сортаменту двутавр № 36 имеет Г = 61,9 см2.
двутавра в этой плоскости защемлены, то гибкость его равна
imin = »y = 2,89 см- Так как концы
К задаче 12.32.
±L
•tnin
0,5-500 2,89
= 86,5.
Коэффициент снижения допускаемого напряжения ф=0,711; допускаемое усилие
(Л') = ф (о) £ = 0,711-61,9-1600 =
= 70 400 кг х W = 70 000 кг.
Проверка прочности в плоскости на иболь ш е й ж ест к ост и
А. Точное решение. Проверку прочности производим по формуле
ст₽асч—f+4В7* • у,
/ Г Nk
где у ЁТ~' —коэффициент запаса прочности.
Так как Jx= 13^380 см* и Й7К=743 см3, то
500 _/70 000- b?_L_Q 5272-^, 30°12,4', и 2 V 2-10* 13380 ’
352
0, 5822 н наибольшее расчетное сжимающее напряжение
70 000 , 2500-500 0,5822 11О1 , ... , ... , ,
Opaci = -ёу-д- + 4.743— ‘ сГ5272 =1 >31 + 464 = 1595 кг/см*<[о] = 1600 кг/см3.
Наибольший прогиб балки определяем по формуле
/max — Q/o jyg
f PP 2500-5003 W '® — 48£уж—48-2.10® • 13380 речной нагрузки. Так как
=0,243 см—прогиб от одной только попе-
U=-L |/-"-=50° 1/ 70 000 =0,4043-23404 2 V EJX 2 V 2-10®-13 380 ’
tg 17=0,4279 и U3=0,4043s=0,06611, то /тах = 3-0,243 • °’427?-^МЗ=0,243-1,07«0,26 см.
Б. П риближенное решение. Для проверки прочности используем формулу N Afmax f. , mkn \ - .
"раем == Г + ’ +
W ,, EJxii2
где п=^-, /VK=/V,=—/Т~• k~коэффициент запаса прочности, а т—коэффициент, зависящий от типа поперечной нагрузки; при наличии равномерно распределенной нагрузки т= 1,029; прн сосредоточенной силе посредине пролета т = 0,823; прн действии сосредоточенных пар сил в концевых сечениях балки т= 1,234. В данном случае т = 0,823, Afmax=-|-P/ = -|-. 2500-500 =
= 312500 кгсм и N NP 70000-500?-
П~ NK~EJxJtl~ 2-10»-13 380-9,87 ’
Поэтому
70000 , 312500/, , 0,823-1,7-0,0663\ 11О,
«Грасч — -61 9 + 743 1 — 1,7.0,0663 ) 1131 +420.6-1,10о —
= 1595 кг/см2 < |а|= 1600 :а/слР.
Наибольший прогиб балки равен
/max = у—д=0,243 - 7-±^=0,243 -1.07 = 0,26 см.
Результаты точного и приближенного решений задачи практически совпадают.
12.33. Шарнирно опертая по концам балка двутаврового сечения длиной 1 = 5 м сжата центрально приложенными продольными силами
N=30 т и в плоскости наибольшей жесткости песет равномерно распределенную нагрузку интенсивности д=550 кг/м (см. рисунок). В направлении, перпендикулярном к плоскости стоики двутавра, пролет балки разделен связями пополам. При допускаемом напряжении [о] = 1600 кг/см* подобрать поперечное сечение балки. Использовать
лптшшш
К задаче 12.33.
приближенное решение задачи. Коэффициент запаса прочности k-= Ответ: Двутавр № 24.
12 GC. задач
353
12.34. Стальной стержень диаметром 30 лж и длиной 2 м, шарнирно опертый по концам, нагружен осевыми сжимающими силами 800 кг и поперечной силой 5 кг, приложенной посредине его длины. Ось стержня расположена горизонтально. Используя приближенное решение задачи, определить величину наибольшего прогиба и величину наибольшего сжимающего напряжения в стержне: а) пренебрегая собственным весом стержня и б) учитывая вес стержня.
Ответ: а) 1,8 мм, 261 кг 1см2; б) 4,2 лл, 439 кг 1см2.
12.ЗБ. Балка АВ кронштейна длиной / = 2 лц шарнирно закрепленная в сечениях А и В, несет сосредоточенную поперечную нагрузку Р=600 кг, приложенную посредине пролета. Поперечное се-чеине балки составлено из двух неравнобоких уголков 80x50x6 мм;
К задаче 12.35.
уголки составлены большими полками вплотную и сварены (см. рисунок). Проверить прочность и устойчивость балкн в предположении, что узел А не может перемещаться в направлении, перпендикулярном к плоскости чертежа. Использовать точное решение задачи, [о] =1600 кг/см2; А =1,6.
Ответ: Усилие в стержне АВ, равное AT,B=1120 кг, меньше [Ру] = 12,65 т; арасч=1615 кг/сл|‘а«[о] (растяжение).
12.36. Деревянная стойка прямоугольного поперечного сечения (см. рисунок) длиной 2 м шарнирно оперта по концам, причем шар
ниры помещены иа оси стойки, и сжата продольными силами N, приложенными в точках А концевых сечений. Из условий прочности
п устойчивости определить наибольшую допускаемую величину силы N. Использовать приближенное решение задачи. Основное допускаемое напряжение [о] = 100 кг/см2; ft = 2,5.
Ответ: 7,95 т«8 т.
12.37. Швеллер № 16 растянут силами N, приложен-
К задаче 12.37.
ными в концевых сечениях посредине высоты и толщины стенкн (см. рисунок). Определить напряжения в точках А и В, а также наибольший прогиб швеллера: а) не учитывая влияния продольных сил на деформацию, т. е. применяя принцип независимости действия сил, и б)
учитывая это влияние.
354
Указание. Используя приближенное решение задачи, для вычисления °тах в случае б) применить формулу
N _ Ne 7. тп \
a™*'~F +j^xAB (J 1+np
e—эксцентриситет силы N; n и m—см. задачу 12.32.
Ответ: а) од =—344 кг!см2, ав = +596 кг]см2, A,ax=L47 см; б) 04 = 18 kzJcm2, ав = +454 кг)см2, /тах = 0,83 см.
12.38. Алюминиевая трубка растянута силами М=70 кн, приложенными в концевых сечениях посредине толщины стенки (см. рисунок). Учитывая влияние продольных сил на изгнбную деформацию
К задаче 12.38.
трубки, определить наибольшие растягивающие и сжимающие напряжения и наибольший прогиб трубки. Использовать точное решение задачи. Е=7-10* Мн/м2.
Данные для контроля решения. Основные формулы:
2(сьа-1) /шах-/о w2chL/
_N/., eF \ ®max F ^‘yZchl//*
где
f NeP 8EJ
и e—эксцентриситет приложения силы
N.
Ответ: +88,1 Мн/м2; —22,9 Мн/м2; 1,07 см.
12.39. Уголок 90x90x9 мм длиной 2 м сжат силой 10 т. Стержень первоначально прямой, концы его шарнирно оперты; эксцентриситет сжимающей силы в плоскости наименьшей жесткости, в направлении к вершине уголка, равен 7 мм. Определить величину наибольшего прогиба уголка, а также величины наибольших сжимающих и растягивающих напряжений в нем. Использовать точное решение задачи.
Ответ: 6,25 мм; —1624 кг/см2; +111 кг!см2.
12.40. Если ось уголка, рассмотренного в задаче 12.39, будет иметь первоначальную кривизну в плоскости наименьшей жесткости со стрелкой 2 мм, tq каковы будут стрела прогиба и величина наибольших сжимающих и растягивающих напряжений в уголке? Предполагается, что влияния эксцентриситета и первоначальной кривизны складываются.
Ответ: 9,7 мм; —1882 кг[см2; +308 кг/см2.
12’
ГЛАВА 13
РАСЧЕТЫ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ И ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
§ 43. Расчеты по допускаемым нагрузкам при растяжении или сжатии н при кручении
13.1. Определить допускаемую нагрузку Ртак для стержня, изображенного на рисунке. Площадь поперечного сечения стержни F= 100 см2, допускаемое напряжение для материала [о] = 1800 кг1см2.
Решение. Задача статически неопределима. Решив ее обычным методом, получаем следующие выражения для опорных реакций:
А = Р-4т н В = р-Гь-a+b a+b
> b, то В > А. Эти значения опорных реакций соответствуют упругой стадии работы стержня.
Прн увеличении нагрузки Р первыми до предела текучести дойдут напряжения в поперечных сечениях нижней части стержня (так как В > А). После достижения предела текучести дальнейший рост напряжений в нижней части стержня невозможен. Таким образом, Вшах = Гат. Дальнейшее увеличение нагрузки приведет к увеличению напряжений в верхней части стержня до предела текучести. Тогда
Атах = f стт-
Дальнейший рост нагрузки невозможен, так как весь материал стержня течет.
Из условия равновесия найдем соответствующее значение нагрузки:
Ртах = Л max + Bmax = for+ = 2^т-
Введем коэффициент запаса k. Тогда допускаемая нагрузка будет равна
Р _Рн1ах_2Гот_9р |о|
max k ~ k 11
так как допускаемое напряжение (о] = ^-. В пашем случае Pniax=2-100-1800 = 360000 кг=360 т.
356
13.2. Определить допускаемую нагрузку для стержней, изображенных на рис. а, б и в. Поперечное сечение верхней части каждою из стержней равно 100 см2, нижней части—200 см2. Допускаемое напряжение для материала 1200 кг/см2.
Ответ: а) 360 т; б) 360 т; в)
240 т.
//fzzzzzzz
К задаче 13.3.
13.3. В конструкции, изображенном па
рисунке, зазор Д такой величины, что он исчезает еще до достижения нагрузкой Р значения 100 т. Поперечное сечение стержня 50 см2, допускаемое напряжение для материала 2000 кг/см2. Найти допускаемую нагрузку Ртах. Ответ: 200 т.
13.4. Сплошной стальной цилиндр вставлен в полый латунный цилиндр так, что их оси совпадают. Оба цилиндра через абсолютно жесткую плиту сжаты центральной нагрузкой Р, как указано на рисунке. Определить величину нагрузки в
цилиндров потечет. Предел текучести
момент, когда материал обоих
стали от. с = 25-107н/Л12 латуни от. я= 15-10* н/м3.
Ответ. 643 • 10s н.
13.Б. Определить величину безопасной нагрузки Р для конструкции, изображенной на рисунке. Деформацией балки пренебречь. Площадь поперечного сечения стержня 1 равна 10 елг2, предел текучести
357
его материала 2600 кг/см2; площадь поперечного сечения стержня 2 равна 15 см2, предел текучести материала этого стержня 1200 кг! см2. Коэффициент запаса равен 2.
Ответ. 21,2 т.
13.6. Короткая железобетонная колонна имеет квадратное поперечное сечение размером 25 X 25 см. Ее арматура состоит из четырех стальных стержней диаметром 20 мм. Определить величину безопасной нагрузки при значении допускаемого напряжения для бетона [а6] = 80 кг/сла, а для арматуры [ос] = 1800 кг/см2. При определении площади сечения бетона полагать ее равной полной площади поперечного сечения колонны *).
Ответ: 72,6 т.
13.7. Четыре стержня, с одинаковым поперечным сечением площадью 4 см2, одинаковой длины и выполненные из одного материала, удерживают жесткую плиту, нагруженную силой Р, как показано на рисунке. Определить безопасную величину этой силы, если [о] = 1600 кг /см2.
Ответ: 18,3 т.
К задаче 13.7.
3
г t
2
Р=30тп,°‘3м
К задаче 13.8.
13.8. К трем стальным стержням с одинаковым поперечным сечением площадью F подвешена абсолютно жесткая балка, нагруженная, как указано на рисунке. Определить площадь поперечного сечения F при [о] = 1600 кг!см2.
Решение. Пользуясь обычными приемами, находим усилие в стержнях в упругой стадии нх работы. Они будут равны:
в первом стержне /У1 = 0,403Р,
во втором стержне /Уг = 0,345Р,
в третьем стержне W3 = 0,252P.
Отсюда видно, что в упругой стадии наиболее нагружен стержень /. При возрастании нагрузки Р в нем раньше, чем в других стержнях, напряжения достигнут предела текучести <тт. Усилие в этом стержне тогда будет равно
ЛГ[=атР.
*) В задачах 13.6, 13.10—13.12 коэффициенты запаса прочности принимаются одинаковыми для разных материалов.
358
В этот момент напряжения в стержнях 2 и 3 еще не равны пределу текучести. Прн дальнейшем росте нагрузки напряжения и, следовательно, усилие в стержне / будут оставаться неизменными, усилия же н напряжения в стержнях 2 и 3 будут увеличиваться до тех пор, пока напряження в стержне 2 (наиболее нагруженном из оставшихся) в свою очередь не дойдут до предела текучести и усилие в нем не станет равно
= =<jTF.
Это состояние конструкции является предельным, так как дальнейшее увеличение нагрузки Р невозможно. Действительно, стержни I н 2 будут деформироваться без увеличения усилий, а жесткая балка начнет вращаться вокруг шарнира ее прикрепления к стержню 3.
Рассмотрим условия равновесия прн достижении конструкцией предельного состояния. Для этого составим сумму моментов усилий в стержнях и предельной нагрузки Рпред относительно шарнира прикрепления балки к стержню 3:
aTF-2,7+aIF.l,2-Pnpcfl-l,5=0.
Разделим это уравнение иа коэффициент запаса k и учтем, что
£и£2 = Р н £ = к к
[о] F- 1,2+[о] F-2,7—Р-1,5 =0,
откуда
1,5Р 101(1,2+2,7)
1,5-30000
1600-3,9
= 7,22с.на.
13.9. Подобрать поперечные сечення на рисунке. Допускаемое напряжение для материала стержней равно 1600 кг/см2.
Ответ: а) 25 см2; б) F„ = 33,3 см2, FB=16,7 см2.
13.10. Железобетонная колонна квадратного поперечного сечения нагружена силой 100 г. Колонна армирована четырьмя стальными стержнями, площадь поперечного сечения которых составляет 1 °/0 от площади поперечного сечения кото-лонны. Допускаемое напряжение для бетона равно 60 кг/см2, для стали 1200 кг/см2. Чему равна сторона а сечення колонны туры d?
Ответ; а = 37 см; d = 21 мм.
стержней, представленных
К задаче 13.9.
н диаметр стержней арма-
13.11. Определить площади поперечных сечений стержней, к которым подвешена абсолютножесткая балка (см. рисунок на стр. 360), нагруженная силой Р= 10 т. Крайние стержни стальные, средний—дур-алюмнновый, площадь поперечного сечения среднего стержня в полтора раза больше площади поперечного сечення каждого из крайних. Допускаемые напряжения для стали равны 1600 кг/см2, для дуралюмнна 1200 кг!см2; коэффициенты запаса одинаковы.
Ответ: Fc = 2 см2; Гл = 3 см2.
359
Примечание. В этой и последующих задачах принимается, что дуралюмип и некоторые другие материалы обладают пределом текучести, определяемым по нормированному удлинению.
13.12. Определить площади поперечного сечения стержней конструкции, изображенной иа рисунке. Стержень 1 стальной, [стс] =
К задаче 13.11.
= 1200 кг/см1-, стержень 2 дуралюмнновый, [стд] = 800 кг/см2; стержень 3 латунный, [стл] = 600 кг1см2. Площади поперечного сечении стержней /г1 = /гэ = 2/:'1.
Ответ: f\ = 8,33 см’; F2 = F3 = 16,66 см2.
13.13. Жесткая конструкция А, нагруженная силой Р=2-10* н, удерживается в равновесии тремя стержнями одинакового сечения,
К задаче 13.13.
К задаче 13.14.
как изображено на рисунке. При допускаемом напряжении для материала стержней [ст] = 16 • 107 н/м2 определить площадь поперечного сечення стержней.
Ответ: 10 см2.
13.14. Определить наружный диаметр трубчатого стержня с толщиной стенки, составляющей 0,1 этого диаметра. Стержень подвергается скручиванию. Величина крутящего момента Л4к = 0,9 тм. Материал стержня имеет предел текучести tT = 1400 кг/см2, коэффициент запаса й = 2.
Решение. Выделим в пределах сечения (см. рисунок) бесконечно тонкое кольцо с радиусом р н толщиной dp. Его площадь равна
dF=2rtpdp.
360
Предельным будет значение крутящего момента, когда по всему поперечному сечению стержня касательные напряжения достигнут предела текучести тг. Момент усилия, созданного этими напряжениями по площади бесконечно тонкого кольца, взятый относительно центра тяжести сечеиия, раней
dAlT = 2лр dp ттр.
Определим теперь суммарный момент внутренних сил. Он будет равен
'н 9 г з
Mr= jdA1T = j 2лр2 dprT=-y лтт (г® —г®) =-у лг®тт [*~(“) ]• F
__ R
Введем обозначение а = -“== — и учтем, что допу скаемое значение крутящего «и Gi
... . Л1Т —
момента [Ми] = -~. Тогда
М 9 т
lA1Kl = Y = y^f
Условие прочности МК<(Л4К], принимает вид
О к откуда
3 Г зЩ;
'l,Si V 2лтт(1 — а3)"
В пашем случае г„=тн—0,ldH = rH—0,2гн=0,8гн, откуда а= —=0,8 гн и
“ Г 3-2-1),9-10»
V 2-3,14-1400(1 — 0.83)-5 СМ’’
таким образом, dH=2r11 = 2-5 = 10 см.
13.16. Стержень круглого поперечного сечении скручивается парой сил с моментом Мк = 3600 кгм. Определить диаметр сечення стержня при [т] = 800 кг/см*.
Ответ: 12 см.
13.16. Определить величину коэффициента запаса прочности стержня кольцевого поперечного сечении с наружным диаметром 12 см п с внутренним диаметром 10 см при его скручивании. Величина крутящего момента равна 1 • 104 нм, предел текучести материала стержня tT= 1 • 10е н/м*.
Ответ: 1,9.
13.17. Стержень круглого поперечного сечеиия имеет два участка с диаметрами сечений 10 см и 12,5 см. По концам стержня приложены скручивающие его две пары сил. Определить наибольшую величину момента этих пар сил, если допускаемое касательное напряжение равно 1000 кг/см*.
Ответ: 2,61 тм.
13.18. Определить наибольшие значения моментов пар сил, скручивающих стержень, имеющий два участка с круглыми поперечными
361
сечениями разного диаметра (см. рисунок). Допускаемое касательное напряжение равно 900 кг1см3.
Ответ: = 1,21 тж; Mt = 1,15 тм; М3 = 2,36 тм.
13.19. Определить при допускаемом напряжении [о] = 1200 кг/см3 диаметр стержня круглого поперечного сечения, защемленного обоими
К задаче 13.18.
К задаче 13.19.
концами и нагруженного, как указано на рисунке, парой сил с моментом Мо = 3 тж. Материал пластичный, применить третью теорию прочности. Насколько стержень стал бы тяжелее, если бы был рассчитан по способу допускаемых напряжений?
Решение. Из решения этой задачи в упругой стадии известно, что по мере возрастания нагрузки, пока наибольшие касательные напряжения не достигнут предела текучести, левый реактивный момент будет больше правого. Когда все сечение левого участка будет охвачено текучестью, левый реактивный .момент перестанет возрастать. Правый реактивный момент будет продолжать увеличиваться до тех пор, пока все сечение и правого участка также не будет вовлечено в пластическую деформацию. Дальнейшее увеличение нагрузки невозможно, состояние конструкции является предельным. В этом случае, так как сечение стержня постоянно, оба реактивных момента равны между собой.
Из условия равновесия очевидно, что каждый из реактивных моментов равен
МА = МВ = ^, откуда крутящий момент
Мм=~=^-= 1,5 тм = 1,5-10* кгсм.
На основании третьей теории прочности допускаемое касательное напряжение [т] = 0,5[о]. В нашем случае
[т J=0,5 [о] = 0,5-1200 = 600 кг/см3.
Диаметр сечения будет равен з d^2 I
3 Л1К о з Г 3-1,5-10* __________2 1/ ______-_______ 9 9 см
2 л [т) У 2-3,14-600 см’
Определим диаметр стержня прн расчете по способу допускаемых напряжении. Наибольший крутящий момент в упругой стадии работы стержня будет равен
о 9
Л4Л=-г- Л40,=-=- • 3=2 тм=2-10® кгсм,
н 3 3
3G2
а диаметр стержня
“ / 2^К а^2У м^Г2
2-2-10*
3,14-600
12 см.
Таким образом, этот стержень, рассчитанный по способу допускаемых напряжений, получился бы тяжелее рассчитанного по способу допускаемых нагрузок на
12=—9,92
9,93
100 = 47%.
13.20. Стержень круглого поперечного сечения с двумя участками разного диаметра жестко защемлен обоими концами и нагружен, как указано на рисунке. Определить диаметры его поперечных сечений, если [т] = 300 кг!см2.
Ответ: d = 8,6 см.
К задаче 13.21.
13.21. Определить безопасное значение Л40 для стержня, представленного на рисунке. Диаметр стержня 7 см, допускаемое напряжение для материала [тт] = 1500 кг/см2.
Ответ: 0,54 тм.
§ 44. Расчеты по допускаемым нагрузкам при изгибе
13.22. Определить коэффициент повышения расчетной грузоподъемности двутавровой балки № 30, нагруженной в плоскости ее стенки, и найти для этой балки безопасную величину изгибающего момента при [сг] = 1600 кг/см2.
Указание. Коэффициентом повышения расчетной грузоподъемности называется отношение
2S
n~W ’
показывающее, во сколько раз грузоподъемность, рассчитанная по способу допускаемых нагрузок, больше таковой, определенной по способу допускаемых напряжений. В этой формуле S—статический момент полусечеиия балки относительно нейтральной оси, a W —момент сопротивления всего сечения относительно этой же оси.
Ответ: л = 1,13; [УИ] = 8,57 тм.
S63
К задаче 13.24.
13.23. Определить допускаемую интенсивность равномерно распределенной по пролету нагрузки для двутавровой балкн № 24, нагруженной в плоскости наибольшей жесткости. Балка имеет пролет 6 ж с шарнирными опорами по концам. Допускаемое напряжение равно 1600 кг/см2.
Ответ. 1,16 т/м.
13.24. Стальная балка пролетом 1 = 4 м с шарнирными опорами по концам нагружена посередине пролета силой Р. Поперечное сечение балки представлено на рисунке. Определить допускаемую величину силы Р, если предел текучести материала ат= = 2400 кг/см2, а коэффициент запаса равен k = 1,6. Как изменится величина допускаемой нагрузки прн расчете по допускаемым напряжениям?
Решение. Известно, что прн пластическом изгибе нейтральная ось делит площадь поперечного сечеиия пополам. При этом условии в нашем случае нейтральная ось должна проходить в пределах нижней полк», так как площадь последней больше площади остальной части сечения.
Найдем расстояние г0 до нейтральной оси ул иэ условия равенства площадей: 25z0 = 5 • 10 + 2,5 • 20+(5—г0) • 25,
откуда г0 = 4,5 см. Статический момент площади верхней части сечення относительно нейтральной оси равен
S,= 10-5-23-|-20-2,5-10,5 + 25-0,5-0,25= 1678 сж3,
а статический момент площади нижней части равен
S2 = 25-4,5-2,25 = 253 см3.
Допускаемый нагибающий момент будет равен
IMl=(S1+S2)^ = (1678+253)^ = 2900000 кгсж = 29 тм.
К 1.0
К задаче 13.25.
41Л41 4-29
Допускаемая нагрузка равна [Р] = —!у!- = —= 29 т. При расчете по допускаемым напряжениям Р оказывается равным 20 т. Снижение расчетной 29—20 грузоподъемности составит ——-100 = 31%.
13.25. Определить предельно допустимый пролет I для шарнирно опертой по концам балки таврового сечення (см. рисунок), нагруженной посередине пролета сосредоточенной силой Р= 12 г. Допускаемое напряжение для материала балки равно 1600 кг/см3.
Ответ: 4 ж.
13.26. Подобрать сечение прокатной двутавровой балки пролетом 6 м, с шарнирными опорами по кон
цам, нагруженной в третях пролета двумя сосредоточенными силами ио 2 т каждая. Какой будет необходим номер балки, если
364
вести расчет по способу допускаемых напряжений? Принять [<т] = 1600 кг! см2.
Ответ. № 22; № 22а.
13.27. Определить размеры прямоугольного поперечного сечення балки, защемленной одним концом и нагруженной на свободном конце сосредоточенной силой 540 кг. Высота сечения равна удвоенной его ширине, длина балки 1 jh, допускаемое напряжение равно 2000 кг/с.н2. Насколько потребуется больше материала, если рассчитать эту балку по способу допускаемых напряжений?
Ответ: 3x6 см; на 37%.
13.28. Определить диаметр балки круглого поперечного сечения, свободно лежащей па двух шарнирных опорах и нагруженной посередине пролета сосредоточенным моментом 4 тм. Допускаемое напряжение материала балки равно 1000 кг/см1. На сколько процентов увеличится диаметр, если рассчитать его по способу допускаемых напряжений?
Ответ: 10,6 с.н; на 22%.
13.29. Балка круглого трубчатого сечения с двумя шарнирными опорами но концам нагружена равномерно распределенной нагрузкой.
Пролет балки 6 м, наружный диаметр ее сечения 25 см, внутренний—20 см, допускаемое напряжение равно 1600 кг/см2. Определить допу-
стимую интенсивность нагрузки.
Ответ: 4,48 т/м.
13.30. Балка длиной 2 м защемлена одним концом п нагружена равномерно распределенной нагрузкой интенсивностью 104 н/м. Ес поперечное сечение представлено на рисунке. Определить размер а при допускаемом напряжении 108 н1м-.
Ответ: а = 6,13 см.
13.31. Сварная балка длиной 6 jh, сечение которой изображено па рисунке, имеет по концам шарнирные
К задаче 13.30.
К задаче 13.31.
опоры и нагружена двумя силами Р, приложенными на расстоянии 2 м от каждой опоры. Прн допускаемом напряжении для материала 1600 кг/см2 определить наибольшее значение сил Р. Устойчивость
балки считается обеспеченной.
Ответ: 39 т.
13.32. Для определения изгибающего момента при пластической деформации во время гнутья арматуры (стальных стержней круглого поперечного сечения) практически используется формула М = 250 d3, где d—диаметр стержня в см, М—момент в кгсм. Какой предел текучести материала предусматривается этой формулой?
Ответ: 1500 кг/см2.
13.33. Определить величину допускаемой нагрузки Р для изображенной иа рис. а балки. Ее сечение—двутавр № 24, допускаемое
365
напряжение [<j] = 1600 кг/см9. Сравнить с грузоподъемностью балки> рассчитанной по способу допускаемых напряжений.
К задаче 13.33.
Решение. Пока наибольшие напряжения в поперечном сечении балки не превысят предела упругости, эпюра изгибающего момента имеет вид, представленный на рис. б. Следовательно, при дальнейшем увеличении нагрузки пластический шарнир сначала образуется в сечении под силой 2Р, а затем в защемлении. При этом эпюра моментов будет иметь вид, представленный на рис. в. Соответствующее значение силы обозначим Рт. Нвпишем выражение для изгибающего момента в сечении, где приложена сила 2РТ:
мт=ас-ав=.
Из этого уравнения находим Рт:
_ MT(/-J-b) т (26—а) с ’
Учтем, что Л1т=25от. Тогда
_2SoT(/+b)
1 (26—в) с ’
Для получения допускаемой нагрузки введем коэффициент запаса k и примем во внимание, что
и £= [oj:
2S[o](t+b)
1 J~ (26—а)с *
Из таблиц сортамента для двутавра № 24 находим статический момент полу-сечения S= 163 см9. Тогда
2-163-1600-(330+130) (2-130-^60)200 — *
366
При расчете по допускаемым напряжениям (рис. 6) Л4тах = 0,898 Р как=89,8 Р кгем.
Из условия прочности -= [о] имеем
89,8P=W'[o], откуда
»_У-Н 89,8 •
Из сортамента находим W = 289 смг; следовательно, _ 289-1600 р=-щ-=5,5°кг-
Уменьшение расчетной грузоподъемности равно 6000—5150, пп - —.-100=14.2%.
13.34. Определить допускаемую нагрузку Р для балки, изображенной на рисунке. Балка выполнена из двутавра № 20, допускаемое напряжение равно 1600 кг/см3.
Ответ: 6660 кг.
а и tpZm/M
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIHI
15м—1,5м—** I*-- 1=4и---»|
К задаче 13.34. К задаче 13.35.
13.35. Подобрать двутавровое сечение балки, изображенной на рисунке, при [<j] = 1600 кг/см3. Устройство опор таково, что горизонтальные опорные реакции отсутствуют.
Ответ: № 16.
13.36. Подобрать прямоугольное поперечное сечение для балки, представленной на рисунке. Отношение высоты поперечного сечения
500кг/м \500кг
IIIIIHHIIIHIIIIiniltllll
|---------1jS В ;
--70см—**30s*? U---1м---Л^Ц5м^Ц5м^
К задаче 13.36. К задаче 13.37.
к его ширине-£-= 1,6, допускаемое напряжение [о] = 1000 кг/см*.
Ответ: 3,71x5,94 см.
13.37. Определить диаметр круглого поперечного сечения балкн, изображенной на рисунке, если допускаемое напряжение равно 1400 кг 1см*
Ответ: 31 мм.
387
13.38. Подобрать ссченис балки, представленной па рис. а. Опоры устроены так, что горизонтальные реакции равны нулю. Поперечное сечение балки составлено из двух сваренных прокатных швеллеров. Оно показано па рис. б. Допускаемое напряжение равно 1600 кг/см*.
Ответ: Два швеллера № 14а.
К задаче 13.38.
13.39. Найти коэффициент запаса прочности для балки, представленной на рисунке. Сечение балки—двутавр № 22, предел текучести ее материала равен 2600 кг/см3.
Ответ: 2,27.
3m
К задаче 13.39.
2,5т/м
....IIUIIIIIHIIIIIIIIIIIIIIUIHIHII
О tn
«—2м—2м—ч
К задаче 13.40.
13.40. Определить коэффициент запаса прочности для балки, изображенной на рисунке. Ее сечение—прямоугольник шириной 4 см и высотой 10 см, предел текучести материала 2000 кг/см3.
Ответ: 2,32.
13.41. Балка, выполненная из двутавра № 30, защемлена левым концом С, правый же ее конец А шарнирно соединен с вертикальной тягой АВ, в свою очередь шарнирно скрепленной в точке В с опорой (см. рисунок). В сечении D балка нагружена сосредоточенной силой Р. Определить величину предельной нагрузки, если площадь поперечного сечения тяги АВ равна F— 4 см2, а предел текучести материала балки и тяги одинаков и равен сгт = 2400 кг/см2.
Решение. Выход конструкции из строя может произойти по одной из двух схем, в зависимости от соотношения размеров балки и тяги. При одной схеме потечет материал тяги и образуется пластический шарнир в сечении С защемления балки, соответствующая эпюра изгибающих моментов изображена иа рис. б. При большем сечении тяги выход из строя конструкции может произойти по другой схеме: раньше, чем потечет материал тяги, образуются пластические шарниры в сечениях С и D балки; соответствующая эпюра изображена на рнс. в. Необходимо рассмотреть оба варианта выхода конструкции из строя.
Рассмотрим первый вариант (эпюра б). Усилие в тяге при наступлении в ней текучести обозначим Nt. Тогда
M^=Pja-Nr(a+b).
Положив A4I=2SoI н Nr=FoT, получаем
2SoT= Pta— Fcj (о-(-Ь),
363
откуда
PT=^I2S4-F(fl + b)L
Для двутавра № 30 из сортамента имеем S=268 см3. Следовательно, = [2-268 + 4 (800+100))= 12 400 кг.
Рассмотрим второй вариант выхода конструкции из строя (эпюра в). В этом случае
.. Р-^ь ь
Мг = ——Г — М а+Ь
а-\-Ь '
откуда
Рт = ^(0 + 2Ь) = ^(а + 2й).
Следовательно,
Р-
^-foo0(800 + 2’|00)= 16080 кг'
Предельной нагрузкой будет меньшая из двух полученных, т. е. 12 400 кг = 12,4 т.
К задаче 13.41.
4м—
К задаче 13.42.
13.42. Схема конструкции представлена на рисунке. Балка выполнена из двутавра № 20, площадь поперечного сечения вертикального стержня равна 3 с.н2. Предел текучести материала балки равен 2800 кг/см3, предел текучести материала стержня 2400 кг)см3. Определить предельное значение силы Р.
Ответ: 5810 кг.
§ 45. Метод «расчетных предельных состояний»*)
13.43. Проверить прочность центрально растянутого элемента конструкции, выполненного из двух швеллеров № 20. Ослабление сечения заклепочными отверстиями диаметром 20 мм показано на
*) В этом параграфе терминология н методы расчета даются в соответствии со «Строительными Нормами н Правилами» («СН и П»), Стройиздат, Москва, 1962-1965.
369
рисунке. Материал швеллеров—ст. 3. Элемент растянут усилием от постоянной нагрузки 18 т и от временной нагрузки 28 т.
Решение. В соответствии с методом РПС (расчетных предельных состояний) проверка прочности центрально растянутых стальных элементов производится только по первому предельному состоянию—по несущей способности. При этом условие прочности имеет вид
N”ni + N”nt
К задаче 13.43.
н
где N” — нормативное усилие от постоянной нагрузки, Л/"— нормативное усилие от временной нагрузки, nt—коэффициент перегрузки для постоянной нагрузки, пг—коэффициент перегрузки для временной нагрузки, Fn — поперечное сечение нетто, 7? — расчетное сопротивление, m — коэффициент условий
работы.
В нашем случае Л’® = 18 000 кг, Л/" = 28 000 кг. Согласно <СН и П», значения коэффициентов перегрузки могут быть приняты следующими: пх= 1,1 и пг=1,4. Из сортамента имеем для швеллера №20: площадь сечення Г ='23,4 см2, толщина полки 7=9 мм и толщина стенки 4 = 5,2 мм. Тогда FH =2-23,4 — 4-2-0,9 — 4-2-0,52 = 35,4 см2. Расчетное сопротивление R есть произведение нормативного сопротивления 7?н на коэффициент однородности, для стальных элементов на коэффициент перехода и в некоторых случаях на коэффициент условий работы. В нашем случае коэффициент условий работы учтен отдельно. Для ст. 3 значение R = 2100 кг/см2. Коэффициент условий работы принят /п=0,8. Тогда
^Л1+^"иг 18 000-1,1+28 000-1,4 ,
------------=----------35Л---------=1665
и /?./п = 2100-0,8= 1680 кг/см2.
Так как 1665 < 1680, то условие прочности удовлетворено.
35,4
13.44. Проверить прочность центрально растянутого элемента деревянной конструкции, выполненного из двух сосновых досок, каждая сечением 5x20 см. Конструкция защищена от увлажнения. Усилие от постоянной нагрузки равно 2 т, от временной нагрузки 8 т. Ослабление сечения составляет 20% от его площади. Коэффициенты перегрузки равны: от постоянной нагрузки 1,1 от временной нагрузки 1,3. Расчетное сопротивление (с учетом коэффициента условий работы) равно 80 кг/см2.
Ответ. 78,8 кг!см2 < 80 кг/см*.
13.45. Определить по первому предельному состоянию допустимую величину временной нагрузки на короткий бетонный столб квадратного сечения размером 50x50 см. Постоянная нагрузка на столб (включая его собственный вес) составляет 70 т. Коэффициент перегрузки от постоянной нагрузки 1,1, от временной—1,3. Бетон марки 100 с расчетным сопротивлением 40 кг!см*. Коэффициент условий работы равен 1.
Ответ: 17,7 т.
13.46. Определить диаметр короткой деревянной стойки круглого поперечного сечения, не имеющей ослаблений, нагруженной постоян
370
ной нагрузкой 20 т и временной нагрузкой 30 т. Коэффициенты перегрузки равны: для постоянной нагрузки 1,1, для временной нагрузки 1,4. Расчетное сопротивление (включая коэффициент условий работы) принять равным 130 кг/см2.
Ответ: 25 см.
13.47. Подобрать двутавровое сечение элемента, растянутого постоянным усилием 17 7 и временным усилием 30 7. Коэффициент перегрузки для постоянной нагрузки равен 1,1, для временной нагрузки 1,3. Сечение ослаблено в полках четырьмя заклепочными отверстиями диаметром 23 мм. Материал—ст. 5 с расчетным сопротивлением 2300 кг]смг. Коэффициент условий работы включен в значение расчетного сопротивления.
Ответ: № 24.
13.48. Проверить по первому предельному состоянию прочность короткой железобетонной стойки квадратного поперечного сечения размером 30x30 см, армированной восемью гладкимм стержнями диаметром 20 мм. Стойка центрально сжата постоянной нагрузкой 60 т с коэффициентом перегрузки 1,1 и временной нагрузкой 30 т с коэффициентом перегрузки 1,3. Применен бетон марки 150, стальная арматура класса A-I.
Решение. Проверка на прочность центрально сжатого железобетонного элемента в соответствии с <СН и П» при отсутствии продольного изгиба производится ио формуле
^"^1 + + Fа^а-
В нашем случае, так как площадь сечення арматуры меньше 3% площади бетона, последняя определяется без вычета площади арматуры:
F6 = 30-30 = 900 см*.
Площадь сечення арматуры
Расчетное сопротивление бетона марки 150 на сжатие в железобетонных элементах равно
₽б=65 кг]см'-.
Расчетное сопротивление круглой арматуры класса А-1 равно Ra = 2100 кг]см1. Тогда
N+ N”n2 = 60000-1,1+30000-1.3 =105000 ла
И F6₽6+fa₽a = 900-65 + 25,2-2I00=IH 400 кг.
Так как 105 m < 111,4 m, то прочность стойки обеспечена.
13.49. Короткая железобетонная стойка имеет квадратное поперечное сечение и армирована четырьмя стальными стержнями периодического профиля (снабженных винтовой нарезкой) класса А-П. Стойка сжата постоянной нагрузкой 50 т с коэффициентом перегрузки 1,1 и временной нагрузкой 20 т с коэффициентом перегрузки 1,4. Процент армирования принять равным 2, бетой марки 200 с R6 = = 80 кг[смг. Для принятой арматуры /?а = 2700 кг[см\ Коэффициент
371
условий работы равен 1. Определить сторону сечения стойки и диаметр стержня арматуры.
Ответ: 25x25 см; 20 ля.
13.50. Проверить ио первому (на прочность) и по второму (па жесткость) предельным состояниям балку двутаврового профиля № 30 пролетом 1 = 4 м. Балка нагружена постоянной равномерно распределенной нагрузкой (включая ее собственный вес) интенсивностью ^, = 1 т/м с коэффициентом перегрузки л, = 1,1 и временной сосредоточенной нагрузкой Р2 = 5 т с коэффициентом перегрузки 1,4, приложенной посередине пролета. Опоры балки шарнирные, расположены но ее концам, материал балки—ст. 4. Ослабление в расчетном сечении отсутствует. Предельный прогиб не должен превышать 1/400 пролета. Коэффициент условий работы принять равным /и = 0,9.
Решение. Условие прочности по первому предельному состоянию имеет вид
</!m.
В рассматриваемом случае
Л4" =
М'^ + Л^'л.
М% =
_ 10-400®
8 8
5000-400
4 4
= 2-10* кгсм.
= 5-106 кгсм.
момент сопротивления №'„ = 1ГбР=472 см3 (так как в опасном сечешш отсутствует ослабление), Л1=1,1 и л2=1,4. Определим левую часть условия прочности:
Лфц+Лфч 2 10»-1,1 +5-10»-1,4 .
W„ ~ 472 ”1735 кг/'м •
Расчетное сопротивление для ст. 4 равно ₽ = 2100 кг/см2. Теперь определим правую часть условия прочности:
₽-m = 2I00-0,9 = 1890 кг/см2.
Так как 1735 < 1890, то условие прочности (первое предельное состояние) удовлетворено.
В соответствии со вторым предельным состоянием на основании требований <СН и П» наибольший прогиб (только от временной нагрузки и без коэффициента перегрузки) не должен превышать нормированной величины. Для стали модуль упругости принимается равным £ = 2,1-10е кг/см2. Из сортамента для двутавра № 30 имеем 7 = 7080 ел*.
В рассматриваемом случае
/max р2г- 5000-400® I I
I 48£7Ср ~ 48-2,1 - 10е-7080 “466 < 400’
Таким образом, условие жесткости (второе предельное состояние) также удовлетворено.
13.51. Определить предельную временную нагрузку Р для деревянной балки круглого поперечного сечения диаметром 24 см, пролетом 6 я, с шарнирными опорами по концам. Постоянная нагрузка, включая собственный вес балки, равномерно распределенная с иитен-
372
сивностью 100 кг/м; коэффициент перегрузки для нее равен 1,1. Коэффициент перегрузки для временной нагрузки принят равным 1,3, расчетное сопротивление, с включенным коэффициентом условий работы, равно 160 кг/см3. Ослабление момента сопротивления в расчетном сечении равно 10%. Модуль упругости древесины равен 1-10ь кг/см3, предельный прогиб не должен превышать 1/250 пролета. Схема временной нагрузки представлена на рисунке. Расчет произвести
Р Р Р Р Р
К задаче 13.51.
по первому и второму предельным состояниям. Прн определении прогиба ослабление сечения во внимание не принимать.
Ответ: Р = 257 кг.
13.52. Двутавровая балка длиной 4 м защемлена одним концом и на свободном конце нагружена
сосредоточенной силой 2 т. Постоянная нагрузка, включая собственный вес балки, равномерно распределена по ее длине. Интенсивность этой нагрузки 0,3 т/м. Для сосредоточенной силы коэффициент перегрузки взят равным 1,4, для распределенной нагрузки —1,1. Материал балки—ст. 5, с расчетным сопротивлением 2300 кг)см3 и модулем упругости 2,1-10е кг1см~. Коэффициент условий работы принят равным 1, предельный прогиб от временной нагрузки не должен превышать 1/200 пролета. В защемлении сечение полок ослаблено
800кг 800кг
1 1200кг/м
HiiiiiiiiiiiiiiiiiiiiiiiiiiiiHiiiiiiiil
'Т ! - : ¥
к— Хи—1м 1м —х
четырьмя заклепочными отверстиями диаметром 26 мм. Подобрать номер двутавра. Расчет произвести по первому и второму предельным состояниям.
Ответ: № 40.
13.53. Подобрать ио первому и второму
К задаче 13.53. предельным состояниям прямоугольное сечение деревянной балки с отношением высоты к ширине сечення, равным 1,5. Балка нагружена, как указано на рисунке. Коэффициент перегрузки для равномерно распределенной постоянной нагрузки равен 1,1, коэффициент перегрузки для сосредоточенной временной нагрузки равен 1,3. Расчетное сопротивление равно 150 кг/см3, предельный прогиб—1/250 пролета, модуль упругости материала балки 1-10ь кг/см3. В опасном месте сечение ослаблено сквозным вертикальным отверстием для болта диаметром 25 мм. Ответ: 14x21 см.
ГЛАВА 14
ДИНАМИЧЕСКОЕ И ДЛИТЕЛЬНОЕ ДЕЙСТВИЕ НАГРУЗОК
§ 46. Влияние сил инерции
пня стержня
14.1. Груз весом 3 т поднимается равноускоренно с помощью стального троса, причем за первые две секунды он поднимается на высоту 4 jh. Площадь поперечного сечення троса 5 см2, .длина его 90 jh, объемный вес материала 7,2 г/см3. Определить наибольшее нормальное напряжение в тросе без учета и с учетом его собственного веса.
Ответ: 722 кг]см*; 800 кг/см2.
14.2. Стальной стержень круглого поперечного сечения, длиной /= 1,6 jh, несущий на обоих концах грузы Р = 3 кг, равномерно вращается вокруг горизонтальной оси О—О, делая 600 об/мин (см. рисунок). Определить необходимый диаметр поперечного сече-при допускаемом напряжении [о] = 1200 кг/см2. Найти удлинение стержня.
Решение. Сила инерции Рд, возникающая вследствие вращения груза Р, может быть вычислена по формуле
р .
Д g 2 1800g
Здесь ш—угловая скорость вращения груза, п—соответствующее число оборотов в минуту, g—ускорение силы тяжести.
Для нахождения силы инерции Рд, возникающей вследствие вращения самого стержня, выделим на расстоянии х от осн вращения элемент стержня длиной dx. Сила инерции ЛРД , действующая на выделенный элемент, равна
Fy . , Fyn2n2 .
dP„ = — dxafix=— x dx;
Д g 900g
здесь F—площадь поперечного сечення стержня.
силы инерции Рд в сечении тп стержня найдется путем сумми-
рования элементарных снл инерции надлине стержня отсечения тп до груза Р:
К задаче 14.2.
Величина
374 ’
Нормальное напряжение в сечен нн тп представляет сумму динамических напряжений от сил инерции Рд и Рд (статическими напряжениями от веса груза и самого стержня по малости их пренебрегаем):
Наибольшее растягивающее напряжение в стержне, очевидно, будет у осн вращения, т. е. при х=0; поэтому условие прочности запишется так:
л?п21 ( Р . I \ -
1800g F +v 4
откуда
nd3 4Рл2п~1
~ 4 7200g [ oj—л2п2Ру
Подставляя числовые данные в выражение для F, находим
- 4-3-9,87-6003-160
7200-1200-981—9,87-6003-0,0078-1603
= 1,06 см
мм.
И
Удлинение элемента стержня длиной dx, выделенного возле сечення тп, равно
.А1 dx nW- [Pl , fP .
dAZ_a“£~I800£g |_f+ 1Д4 J J
а удлинение всего стержня
1/2 1/2
о о
/Р у/\ 9,87-600.160® / 3-4 ,0,0078.160 \
~1800g£\F + 61800-981-2-10« \ 3,14-1,Г3 * 6 ) СМ’
14.3. Чугунный стержень круглого поперечного сечения, несущий па свободном конце груз Р (см. рисунок), вращается вокруг гори-
зонтальной оси О—О с постоянной угловой, скоростью 120 сек-1. Определить величину груза Р, при которой произойдет разрушение стержня, если предел прочности чугуна при растяжении равен 1600 кг/см2, а объемный вес его 7,2 г/см3.
Ответ: 5 кг.
14.4. Двигатель весом 600 кг установлен на бетонном фундаменте высотой 40 см, шириной 60 см и длиной 80 см. Объемный вес бетона равен 2 г/м3. Неуравновешенная часть вращающегося якоря весит 2 кг и находится на расстоянии 15 см от оси вращения.
Определить наибольшее сжимающее напряжение у подошвы фундамента от его собственного веса, веса
гомм.
двигателя и вертикальной составляющей силы инер-
К задаче 14.3.
ции, считая, что направление последней совпадает с вертикальной осью симметрии фундамента. Рассмотреть два случая: а) двигатель не работает, б) двигатель делает 2000 об[мин.
375
напряжения, возникающие в результате колебаний фундамента и от горизонтальной составляющей силы инерции, не учитывать.
Ответ: а) 2,05 т/м2; б) 4,85 т/м2.
14.5. Противовес подъемника (см. рисунок) весит 4,2 т. При торможении поднимающегося подъемника опускающийся противовес
испытывает ускорение, равное 1,
К задаче 14.5.
м/сек2. Определить диаметры болтов А и В противовеса, если для материала болтов [о] = 320 кг/см2 и [т] = 200 кг/см2. Число болтов: А—два, В—один.
Ответ: dA=3\ мм; dB = = 39,3 леи.
К задаче 14.6.
14.6. Длинный стальной тонкостенный барабан (см. рисунок) вращается вокруг оси О—О, делая 600 об/мин; он укреплен на осн вращения только по торцам. Определить нормальные напряжения в выделенном из стенки барабана кольце АВ, пренебрегая влиянием закреплений барабана в торцевых сечениях, если средний диаметр последнего равен 2 ж.
Ответ: 314 кг/см2.
14.7. Наибольшая безопасная окружная скорость для чугунных маховиков принимается равной 25 м/сек. Пренебрегая влиянием спиц и считая удельный вес чугуна равным 7,4, определить наибольшее растягивающее напряжение в ободе маховика при указанной окружной скорости.
Ответ: 4,71 Мн/м2.
14.8. Скорость вращения чугунного маховика за 0,5 сек равномерно изменяется с 300 до 200 об/мин. Обод маховика веент 800 кг, радиус инерции его равен 40 см. Определить величину крутящего момента н наибольшего касательного напряжения, возникшего вследствие этого изменения скорости в вале, на который насажен маховик, если диаметр вала равен 80 мм.
Ответ: 27 330 кгсм; 272 кг/см2.
14.9. На вал диаметром 60 мм насажен маховик с моментом инерции 6000 кгсмсек2; скорость вращения вала равна 400 об/мин. Внезапно начинает действовать тормоз, останавливающий маховик через 20 оборотов; вал с маховиком отключаются от двигателя до пуска в ход тормоза. Определить величину наибольшего касательного напряжения в вале. Треннем в подшипниках пренебречь.
Ответ; 988 кг/см2.
376
14.10. Кожаный ремень шириной 15 см и толщиной 6 мм перекинут через шкив диаметром 1 м и передает 28 л. с. Шкив вращается с постоянной скоростью н делает 450 об/мин. Вес 1 см3 ремня равен 1 г. Определить напряжения в ремне без учета и с учетом возникающих в нем сил инерции, если отношение усилий в набегающей и сбегающей ветвях ремня равно 2,5.
Ответ: 16,5 кг/см2; 22,2 кг/см2.
14.11. Сплошной стальной диск насажен па вал. В диске сделано круглое отверстие (см. рисунок). Определить наибольшее нормальное
К задаче 14.12.
напряжение в опасном сеченнн вала, вызванное наличием этого отверстия, если вал вращается с постоянной угловой скоростью w=40 сек-1. Напряжения в результате колебаний вала не учитывать.
Ответ: ТА кг/см2.
14.12. Рамка ABCD (см. рисунок) вращается вокруг вертикальной осн О—О со скоростью 240 об/мин. Все стержни рамки стальные, круглого поперечного сечення; в узлах А, В, С и D они шарнирно скреплены между собою. Определить диаметр стержней AD и ВС при допускаемом напряжении 1000 кг/см2.
Ответ: 25,1 мм.
14.13. На двух балках корытного профиля № 20 установлена лебедка весом 800 кг, поднимающая груз Р = 3 т с помощью
Лебедка.
Ж
У Р=Б00кг
К задаче 14.14.
стального троса (см. рисунок). Площадь поперечного сечения троса F=5cm2. Подъем груза происходит с постоянным ускорением Ь м/сек2.
377
Учитывая вес груза, лебедки и собственный вес балок, определить величину наибольшего нормального напряжения в балках и в тросе.
Ответ: max <тб= 1253 кг/см2: 0^ = 845 кг/см?.
14.14. Груз Р равноускоренно поднимается на тросе, навернутом на шкнв (см. рисунок). Площадь поперечного сечения троса F= 1 см2. Определить наибольшее расчетное напряжение в тросе и в опасном сечении вала по третьей теории прочности, если ускорение движения равно 0,8 м/сек2. Массу троса, вала и шкива при расчете не учитывать.
^ии Ответ: отр = 649 кг/см2: расч оиау„ = 892 кг/см2.
' I 14.15. Стальной стержень АВ квадратного по-
г перечного сечення 1 X 1 см2, несущий на концах А
А _____S. и В грузы, опускается на стальной проволоке с по-
стоянной скоростью 2,4 м/сек (см. рисунок). Опреде-'Мкг 'Р лить прогибы концов стержня, наибольшее нормаль» К задаче 14 15 ное напРпжение в нем1 а также напряжение в проволоке, если скорость опускания в течение 0,5 сек равномерно уменьшится в трн раза. Массой стержня АВ пренебречь. Ответ: /=0,249 см; шах аАВ= 1194 кг/см2; Опрое1 = 507 кг/см*. 14.16. Определить наибольшее нормальное напряжение в спарнике локомотива, движущегося с постоянной скоростью v= 120 км/час (см. рис. а). Продольное сжимающее спарник усилие равно 18 г. Рассмотреть два варианта поперечного сечения (см. рнс. б).
К задаче 14.16.
Ответ: 1) 1474 кг/см*; 2) 1254 кг/см2. Во втором варианте, несмотря на уменьшение сечеиия, напряжения примерно на 15% меньше.
14.17. Определить наибольшее нормальное напряжение в стальном шатуне АВ для четырех вариантов поперечного сечення: круглого, квадратного, прямоугольного и двутаврового, имеющих одинаковую площадь поперечного сечения F=9 см2 (см. рисунок). Кривошип ОВ делает 600 об/мин.
Считать, что центробежные силы инерции направлены перпендикулярно к оси шатуна и по длине его меняются по линейному закону. Продольное сжимающее усилие в шатуне равно 2,5 т.
Ответ: 1) 1627 кг/см2\ 2) 1419 кг [см2; 3) 1134 кг/см? и 4) 963 кг/см2.
378
14.18. Люлька качелей, весящая вместе с людьми 300 кг, прн помощи стержней А подвешена к стальному валу О—О (см. рисунок). Определить необходимый диаметр вала при допускаемом напряжении
К задаче 14.17.
К задаче 14.18.
800 кг!смг. Считать, что масса люльки сосредоточена в точке В на расстоянии 4 я от оси вращения. Наибольший угол подъема люльки над горизонтом равен 45°.
Ответ: 6,96 см « 7 см.
14.19. Стальной стержень АВ, жестко скрепленный со стержнями
KL и MN, несущими на концах шипннкахАиВ вокруг оси О—О, делая 200 об!мин (см. рисунок). Определить наибольшие нормальные напряжения в стержнях, пренебрегая нх собственным весом.
К и М грузы Р, вращается в под-
К задаче 14.20.
К задаче 14.19.
Ответ: = =27 кг!см--, аАВ = 1281 кг/см2.
14.20. Стержень АВС прямоугольного поперечного сечения 2x6 ям, изогнутый по дуге окружности радиуса /?= 10 см, вращается вокруг вертикальной осн О—О с постоянной угловой скоростью о> = 20сек~1. В точках А и С к стержню прикреплены грузы Р=180 г (рнс. а).
379
Определить наибольшее нормальное напряжение в стержне и горизонтальное смещение точки А или С. Массой стержня пренебречь.
Решение. Сила инерции Ря в данном случае (очень гибкий стержень) должна быть вычислена по формуле
₽д = у“2(Л + /д).
где /д—горизонтальное смещение точки С (нли Л) кривого стержня под действием сил Р и Рд (рис. б).
Применяя для определения {я теорему Кастнльяно и пренебрегая влиянием поперечной н продольной снл, последовательно находим
дЛ1д
Ma=PR(\ — cos a)—PflPsina, Vp— =— Л sin а
^д и
Я/2 / = -^=Л /д дРя J
О
EJ Ма дРя dx~
Я/2
=|j У (Рд sin2a—Psin а(1 —cos а)]4а =-^^(лРд—2Р).
О
Подставляя полученный результат в выражение для Рл, имеем Рд=-^о>’-[я+^(лРд-2Р)]. откуда
27(1—РЯФ)
Нд— 2—пЯФ7 ’
где
для краткости обозначено Ф = н
7 = —/?ы2. g
Так как
0,60,2®
ЫР
12 - 12
10
0,0004 сл4,
Ф 2-2-10е-0,0004 0,00625 кгсМ
>
то
_ 0,18-10-20* .о
7=------—------= 0,734 кг.
„ 2-0,734(1— 0,18-10 0,00625) п_оо
Рд= 2-3,14.10-0.00625-0,734 = 0782 кг'
Горизонтальное перемещение точки С равно ^-ет^-^’-ТгпДоом'3-14-0-782- 2-0’18’-0-655 ".
По малости кривизны стержня нормальное напряжение в нем вычисляем по формуле для прямого бруса. Максимальное нормальное напряжение в любом сечении стержня равно
Ад Мд [ 1 fl
шах Од =—+—= (Pflsin a-f-P cos а) Нг+^г
PR
V
380
Приравнивая нулю производную этого выражения по а, находим значение угла Од, определяющего положение сечення, в котором величина шах <тд будет
0 782
наибольшей; имеем tga0 = -g- = -7^-f^-= 4,344, a0 = 77°2', sinao=0,9745 и Г v, 1О
cos a0 = 0,2243.
Таким образом,
шахОд = (0,782 0,9745-1-0,18 0,2243) + -9^1?= 1563 кг/сл’-.
В сечении В, для которого a = 90°, max <тл= 1511 кг/см1 * * 4, что меньше найденного выше значения на 3,3%.
Нетрудно заметить, что при определенных значениях Р, R и со знаменатель формулы для Рл может стать равным нулю, т. е. сила инерции, напряжения в стержне и смещение точки С получат бесконечно большие значения. В данном случае это будет иметь место, например, при Р х 2,5 кг или при «критическом! значении скорости <о = <окр = 74,5 сек-1. Очевидно, однако, что рост напряжений приведет к разрушению стержня при скорости, несколько меньшей, чем критическая. Вместе с тем следует отметить, что при больших деформациях вышеприведенные формулы становятся неточными, а основанные на ннх расчеты ненадежными.
Числитель формулы для Рп также может оказаться равным нулю, но это случится лишь при значениях Р, сильно превышающих те, при которых разрушение стержня произойдет даже при статической нагрузке.
14.21. Регулятор вращается вокруг оси О—О с постоянной скоростью 120 об/мин (см. рисунок). Считая стержень ВС абсолютно жестким, определить наибольшее нормальное напряжение в стальном стержне АВ регулятора, а также горизонтальное смещение груза Р. Стержень АВ считать невесомым.
Указание. Руководствоваться решением предыдущей задачи.
Ответ: 1910 кг/см-\ 1,91 см.
К задаче 14.21.
14.22. Груз весом Р
К задаче 14.22.
1 кг вращается с постоянной угловой скоростью си = 18 сек-1 в горизонтальной плоскости, удерживаемый
стальной пружиной, имеющей до деформации длину / = 20 см ^см.
рисунок). Найти удлинение пружины и наибольшее касательное напряжение в ней, если она имеет 30 витков при среднем радиусе витка
4 см и радиусе проволоки 3 мм. Трением груза о горизонтальную
381
плоскость пренебречь. Определить критическую скорость вращения груза, при которой деформация пружины неограниченно возрастает.
Ответ. 12,9 см; 1062 кг/см2; 28,8 сек-1.
14.23. Сплошной стальной диск одинаковой толщины вращается с постоянной угловой скоростью 200 сек-1 вокруг центральной оси, перпендикулярной к его срединной плоскости. Определить наибольшее нормальное напряжение в диске, если его диаметр равен 90 см.
Ответ: 266 кг/см2.
14.24. Равномерно вращающийся вокруг центральной осн, перпендикулярной к его срединной плоскости, стальной диск постоянной толщины, диаметром 80 см имеет центральное отверстие диаметром 10 см. Определить наибольшее допускаемое число оборотов диска, при котором максимальное нормальное напряжение в нем не превысит 1200 кг/см2.
Ответ: 3410 об/мин.
§ 47. Напряжения и деформации при колебаниях
70*70*7мм
14.2Б. Определить частоту собственных продольных колебаний: 1) деревянной стойки круглого поперечного сечення диаметром 15 см и длиной 120 см, нагруженной продольной сжимающей силой 10 т; 2) стальной стойки двутаврового сечения № 20, длиной 1,5 лц сжатой силой 15 т; 3) кирпичного столба квадратного поперечного сечения 80x80 см, высотой 1,8 я, сжатого силой
1 Л 30 т. Задачу решить без учета массы стоек * 3 *
' и столба, нижнне концы их считать защем-г ленными. Для кирпичной кладки принять Е = 3.1 о4 кг/см2.
Ответ: 1) 120,2 сек-1; 2) 152,9 сек-1;
3) 186,8 сек-1.
14.26. Электродвигатель весом 1,3 т
К задаче 14.26. укреплен в узлах А двух кронштейнов ВАС, каждый из которых выполнен из стержней АВ и АС, представляющих парные равнобокие уголки. Стержни кронштейна шарнирно соединены между собой и со стеной (см. рисунок). Определить период и частоту собственных колебаний двигателя на кронштейнах.
Ответ: t0 = 0,025 сек; соо = 249,4 сек-1.
14.27. Электродвигатель весом Р= 1300 кг, укрепленный на кронштейнах (см. предыдущую задачу), делает 2400 об/мин. Неуравновешенные массы двигателя сводятся к грузу 1,5 кг, вращающемуся на расстоянии 3 см от оси двигателя в плоскости симметрии конструкции.
Пренебрегая силами сопротивления и рассматривая лишь вертикальные вынужденные колебания системы, вычислить коэффициент нарастания колебаний и динамический коэффициент, а также определить величину наибольшего нормального напряжения в стержнях кронштейна.
382
Решение. Из решения задачи 14.26 известна частота собственных колебаний системы: О)о=249,4 сек-1. Частота изменения возмущающей силы равна
яп 3,14-2400
“=зо =—зб—=251>3 ’
Коэффициент нарастания колебаний равняется я 249,42
Р-ш2_ш2-251,32-249,42 66Л
Центробежная сила инерции за счет неполной уравновешенности частей двигателя может быть вычислена по формуле
Н=т<^г=^251,32-3я 290 кг.
Уо1
Динамический коэффициент равен
где Ь//—статическая деформация кронштейна от половины наибольшей величины возмущающей силы, а бр—статическая деформация кронштейна от половины веса электродвигателя. Очевидно, что
бр Р 1300
поэтому
ka= 14-0,223-66,4= 15,8.
Наибольшее нормальное напряжение возникает в стержне АС; оно будет равно
Nac^ Р . 1300-15,8 1ПОЛ , .
*^тах— р — р ^д— ;д 55 —1090 кг/см .
14.28. Стальная цилиндрическая винтовая пружина, имеющая 12 витков при среднем диаметре витка 8 см и диаметре проволоки 6 мм, растянута грузом 12 кг. Определить частоту собственных продольных колебаний груза.
Ответ; 13,1 сек-1.
14.29. К цилиндрической винтовой пружине подвешены два одинаковых груза; оба груза вместе растягивают пружину на 3 см. Один из грузов внезапно снят. Определить период возникающих вследствие этого продольных колебаний, а также наибольшее значение скорости и ускорения колеблющегося груза.
Ответ; tt = 0,246 сек; v= = 38,4 см!сек; £=981 см.)сек1.
14.30. Для записи колебаний конструкций применяется виброграф (см. рисунок), в котором ча<
подвешенного на пружине, весьма мала (в сущности, груз должен оставаться неподвижным относительно земли). Определить вес груза Р, при котором частота собственных колебаний его на пружине.
К задаче 14.30. собственных колебаний
383
имеющей 20 витков при среднем диаметре витка 28лш и диаметре проволоки 2 лиц будет равна 10 сек-1.
Ответ: 3,58 кг.
14.31. Наружный диаметр полого стального вала равен 150льи, внутренний—100 лиц длина его 2 л1, один конец защемлен, а второй снабжен шкивом, имеющим момент инерции Jo = 10 000 кгсмсек3. Определить наибольшее касательное напряжение в сечении вала и наибольший угол закручивания его, если к шкиву в плоскости, перпендикулярной к оси вала, будет приложен момент М, изменяющийся по закону М = Моsinсо/, где Л4о = 800кгл(, а со = 36сек-1. Силами сопротивления при расчете пренебречь.
Решение. Так как полярный момент инерции сечення вала равен
•'л=т('нар-'вИут) (7>5*—5«) = 3988сл«*.
то жесткость его при кручении будет
„ GJP 8-10»-3988 1СО_
С = -г-=—==---------= 1595-10* кгсм.
I ZUU
Частота собственных крутильных колебаний вала со шкивом равна
<оо =
=39,94 сек-1.
силы задана (со = 36 сек-1), то
5,33.
1595-10* 10*
Поскольку частота колебаний вынуждающей i
коэффициент нарастания колебаний будет
_ cog 39.942
Р~ cog- со’- 39.942—362
Угол закручивания вала под действием момента Л10 найдется по формуле М01 80 000-200
<Fo=GJ;= 8.10-.3988 = 0-00502-
Амплитуда вынужденных колебаний и, следовательно, наибольший угол закручивания вала при действии момента М = Мо sin со/ будут равны
А = <ртах = фор = 0,00502-5,33 = 0,0267.
Соответствующее углу закручивания (pmax наибольшее касательное напряжение в вале можно определить из пропорции
*Чтах тшзх _<pmax _
То Л1о Фо откуда
Тп,ах=^ р=^^Рр=80^87’5 5,33 = 802 кг[см3.
14.32. Определить частоту и период собственных колебаний груза на балке (см. рисунок), пренебрегая массой балки.
Ответ: а) 36,6 сек~1 и 0,172 сек; б) 157,2 сек-1 и 0,04 сек; в) 15,9 сек-1 и 0,394 сек; г) 118,8 сек-1 и 0,0529 сек; д) 39,6 сек-1 и 0,159сек; е) 27,4 сек-1 и 0,229сек.
384
14.33. Для демонстрации явления резонанса электромотор весом Р— 9 кг установлен на шарнирно опертой по концам стальной балке
1ВООкг\ \4т
о) I- j ]C г) |z" I l IW27.
S’ швел- я
L----1iBm----*лераМ16
К задаче 14.32.
прямоугольного поперечного сечення 6x100 мм. Пролет балки I— 1,2м. На оси электромотора укреплен стержень АВ, несущий на конце В
груз весом Q, = 300e, расположенный на расстоянии 10 см от осн электромотора (см. рисунок).
Установить число оборотов электромотора, при котором наступит явление резонанса. Определить амплитуду колебаний и наибольший прогиб балки, а также максимальное нормальное напряжение в балке при резонансе. Силы сопротивления считать пропорциональными скорости колебательного движения; коэффициент затухания колебаний л принять равным 3 сек~1. При расчетах учесть собственный вес балки.
К задаче 14.33.
Решение. Момент инерции н момент сопротивления поперечного сечения балкн равны
, bh? 10-0.6® Л1О а т b№ 10-0.6®
?=— = ———=0,18 см4 и №==-=—-— = 0,6с.н3. 12 12 О О
13 Сб. задач
883
Действительный статический прогиб балки в сечении, где установлен электромотор, находим по формуле
_ рр_ _5QP___P_/ 5 х
,£д 48£J ^384 EJ ~ 48 EJ \ 8 4 ) ’
где
Q = f/T= 10-0,6-120-0,0078 = 5,62 кг
—собственный вес балкн. Подстанляя числовые значения, находим
Г _ 1203
'£д—48-2-10°-0,18
(9+4-5.62)-
1,25 см.
Приведенный статический прогиб балки в том же сечении равен
fcn 48EJ V +35Q)~48-2-10»-0.18
(9+gs.62)
= 1,175 см.
Частота собственных колебаний электромотора иа балке
С0о =
е_ = fcn
Вследствие вращения груза Qo = 300 г возникает центробежная сила инерции. Когда частота изменений возмущающей силы <о=^ будет равна частоте собственных колебаний электромотора на балке <о0, наступит явление резонанса. Поэтому критическое число оборотов электромотора равно
ЗОшо 30-28,9
пир =-^=—зд4-=276 об/мин.
Наибольшая величина возмущающей силы Н равна центробежной силе инерции от груза Qo:
И = — &г = г=• 28,92 • 10=2,56 кг.
g g 981
Коэффициент нарастания колебаний, имея в виду, что <>>=<оо, вычисляем по формуле
₽ =
=^=^5=4,82.
2 2л 2-3
Динамический коэффициент равен
йд = 1 + ^ ₽ = 1 +----₽ = 1 +-----------------4,82 = 1,99.
Гса 9 + 4.5,62
о О
Здесь t HP 'н —48£J ’
386
Амплитуда вынужденных колебаний
А = /„₽ =---------Р/сд = (*д- Шел = 0.99-1.25= 1,24 ель
О
Наибольший прогиб балки равен
7д=/сл+А = fcakn= 1,25-1,99 = 2,49 см, а наибольшее нормальное напряжение
/ pi Qi \ / Q \ 1кд
max <тд = тах <т£*д= j *д = (Р+у) 4^ =
= (9+^)-Л 1.99 = 590-1,99= 1173 кг/см*.
\ Z / 4*U,O
14.34. Решить предыдущую задачу в предположении, что электродвигатель установлен не па балке, а на четырех симметрично расположенных цилиндрических винтовых пружинах, каждая из которых имеет десять витков при среднем диаметре витка 6см и диаметре проволоки 5мм. Определить критическое число оборотов электромотора, наибольшую деформацию и наибольшее касательное напряжение в пружинах. Весом пружин пренебречь. Коэффициент затухания колебаний принять равным 4 сек-1.
Ответ: 339 об/мин', 2,26 см; 832 кг/см1.
14.35. Электромотор укреплен посредине пролета двух шарнирно опертых по концам стальных балок корытного профиля № 18 (см. рисунок). Двигатель делает 1500 об/мин. Центробежная сила инерции.
возникающая вследствие неполной уравновешенности вращающихся частей двигателя, равна 150 кг. Учитывая собственный вес балок и пренебрегая силами сопротивления, найти динамический коэффициент и наибольшее нормальное напряжение в балках.
‘ Ответ: 2,38; 393 кг/см*.
14.36. На двух одинаковых деревянных балках укреплен двигатель, делающий 1400 об/мин (см. рисунок). Подобрать прямоугольное поперечное сечение балок при отношении Л: 6 =1,5 так, чтобы частота собственных колебаний двигателя на балках была приблизительно на 30% больше частоты возмущающей силы. Считая, что наибольшая величина возмущающей силы равна 40 кг, определить наибольшее нормальное напряжение в балках. Массой балок и силами сопротивления пренебречь.
Ответ: h= 15 см; таход= 13,8 кг/см*.
13*
387
14.37. Двигатель, укрепленный на конце консольной балки нз двух уголков, делает л = 800 об/мин (см. рисунок). При работе двигателя возникает центробежная сила инерции, равная 5 (кг) = 10-4 л2. Определить наибольшее нормальное напряжение в балке. Найти число оборотов двигателя, при котором возникает явление резонанса, и определить соответствующее наибольшее нормальное напряжение. При расчетах учесть силы сопротивления, пропорциональные скорости колебательного движения. Коэффициент затухания колебаний принять равным 5 сек-1. Массой балки пренебречь.
Ответ. 1108 кг/см2; лкр = 847 об/мин; 1289 кг/cat2.
14.38. Двойная рессора легкого экипажа имеет шесть листов шириной 40 мм и толщиной Змм (см. рисунок). Статическая нагрузка на рессору равна 80 кг. На одном участке дорога имеет ряд небольших ухабов, расположенных волнами длиной 0,5 at, так называемую
К задаче 14.37.
I I
К задаче 14.38.
«гребенку». При какой скорости движения будет наблюдаться явление резонанса?
Ответ. 11,6 км/час.
14.39. Опытным путем было установлено, что период собственных колебаний груза весом 200 кг, расположенного посредине пролета I = 6 м двутавровой балки № 24, равен 0,35 сек. Стенка балки расположена горизонтально. Определить величину модуля Г'1 нормальной упругости материала, учитывая при расчете I собственный вес балки.
Ответ. 2,09-10° кг/см2.
14.40. Каменный столб квадратного поперечного сечения 1,8 X 1,8 лг опирается на скалу, залегающую на ъыУ/мЬ-Жл. неизвестной глубине от поверхности земли (см. рисунок). । Объемный вес кладки столба предположительно равен | | 2 т/м3. Опытным путем были определены: а) прогиб
хЪяЖг. верхнего конца столба при действии горизонтальной СКОПИ силы Р=6т, оказавшийся равным 4,5мм, и б) период собственных поперечных колебаний столба при отсут-14И4О1е ствин силы Р, равный 0,32 сек.
Считая столб заделанным в скалу и полагая, что насыпной грунт никакого влияния на работу столба не оказывает, определить глубину залегания скалы и модуль упругости кладки.
Ответ. 4,47 м; 58 400 кг/см2.
388
§48. Напряжения и деформации при ударе*)
14.41. Сила Р=2,7т мгновенно, но без удара приложена в узле А кронштейна ВАС (см. рисунок). Чему равен коэффициент запаса прочности конструкции, если Fr = 4 см2, F2 = 100 см2, ав1 = 4000 кг 1см2 и ав2 = 300 кг/см1.
Ответ: 2,49.
14.42. Вертикальный стержень, статически растянутый силой Р, удлиняется на 1,5 лиг. Определить удлинение стержня, если тот же груз растянет его, падая с высоты бльм.
Ответ: бльи.
14.43. Определить величину наибольшего нормального напряжения в стальном ступен-
К задаче 14.43.
чатом стержне (см. рисунок), подвергающемся действию улара при падении груза Р=400кг с высоты /7=6льи; F=2cm2, 1 = 5м.
Какое наибольшее напряжение возникнет в стержне, если на кольцевой выступ А для смягчения удара поместить цилиндрическую винтовую пружину, которая при действии статической нагрузки, равной 1 кг, сжимается на 4-10-3ж.и?
Ответ: 1349 кг/см2-,
732 кг/см2.
14.44. Сравнить величину наибольшего растягивающего напряжения в каждом
Размеры в. vm
К задаче 14.44.
из трех стальных стержней (см. рисунок),
подвергающихся продольному удару грузом 250 кг, обладающим в
момент удара кинетической энергией 20 кгем. Ответ: иа = 881 кг/см2-, иа:об: о» = 1:2,43:2,08.
14.46. Стержень, имеющий длину 80 см и площадь поперечного
сечения 5 см2, подвергается продольному растягивающему удару прн
*) При отсутствии специальных указаний в условиях задач этого параграфа последние решаются без учета массы рассчитываемых элементов конструкций; прн этом в случае удара, вызванного падением груза, вычисление динамического коэффициента производится по точным формулам (см. курс «[Сопротивление материалов» Н. М. Беляева, изд. 13-е, 1962, формулы (36.10), (36.11) и (36.12)).
389
падении груза 200 кг. Кинетическая энергия груза к моменту соударения равна 15 кгсм. Найти напряжение в стержне при ударе в предположении, что он изготовлен: а) из стали; б) из дерева; в) из резины (£=100 кг/см2).
Ответ, а) 429 кг/см2; б) 135 кг/см2; в) 80 кг/см2.
14.46. Крышки цилиндра крепятся к фланцам с помощью стальных болтов. Вследствие резкого повышения давления внутри цилиндра
К задаче 14.46.
болты воспринимают кинетическую энергию удара 60 кгсм. Определить необходимое количество болтов для каждого из двух вариантов крепления, изображенных на рисунке. Допускаемое напряжение равно 500 кг/см2.
Ответ. На одну крышку: а) 120шт.; б) 12шт.
14.47. Груз Р=1,5т с постоянной скоростью г» = 2,4м/сек опускается па сматывающемся с барабана лебедки проволочном тросе. Когда длина троса между грузом и лебедкой оказывается равной / = 180 м, происходит резкое торможение барабана, и груз останавливается. Площадь поперечного сечення троса £=5сма, вес погонного метра 9 = 2,1 кг/м, модуль упругости Е= 1,6-10* кг/см2.
Определить наибольшее нормальное напряжение в тросе и его удлинение без учета и с учетом его веса.
Решение. Пренебрегая весом троса, для вычисления наибольшего напряжения в нем прн внезапном торможении лебедки воспользуемся формулой Р 1500
оя=асйд, где ос =—=—=—=300кг/см2, а динамический коэффициент Г о
_ Г&EF Г 2402-1,6- 10е-5
V gPl~l+V 981-1500-18000_&,1Л
Здесь единицей перед радикалом учитывается статическое действие нагрузки (прн о=0).
Таким образом, динамическое напряжение равно
од = 300-5,17= 1551 кг/см2, а удлинение троса
Д,я = Д,с.Лд = !^_^. 5,17 = 3,375-5,17= 17,45 см.
l,D-lUu-5
390
При решении задачи с учетом собственного веса троса динамический коэффициент должен быть вычислен по формуле
где р—отношение
Лд1 = 1 +
SEF гРИУ+ЪГ
приведенной массы троса
3g
Ql 3g
к массе ударяюще-
го груза —, т. е.
В=—------g-=-gL= 2,1-180 = 0,084.
р 3g Р ЗР 3-1500 ’
Таким образом, динамический коэффициент равен
*41 = 1 +
2402-1,6-10®-5
981-1500-18000(1+0,084)
Наибольшее нормальное напряжение в тросе будет
. P + ql . 1500 + 2,1-180 ... 100„ , „
max б„=----=-£— Лд1 =------=-------5,01= 1882 кг см2,
“ F “ 5
а полное удлинение его
л/ ь P+Wql _ 1500 +0,5-2,1-180
Д/д — Д/сКд1— /Лд| । 6-10®-5 -18000 5,01 ~ 19,05см»
Пренебрегая собственным весом троса, мы в данном случае существенно снижаем в нем расчетные значения напряжений н деформаций.
14.48. Определить наибольшее напряжение в тросе и его удлинение (см. предыдущую задачу), если между тросом и грузом будет помещена цилиндрическая винтовая пружина, имеющая 30 витков при среднем диаметре витка 15 см и диаметре стержня пружины 3 см. Найти также наибольшее касательное напряжение в пружине, если О = 8-10® кг/см2.
Задачу решить: а) без учета н б) с учетом веса троса.
Ответ: а) 789 кг!см2, 8,87 см, 6136 кг/см2;
б) 1046 кг)см2, 10,59 см, 6503 кг!см2.
14.49. Груз Р = 40 кг подвешен на стержне; качаясь, он ударяется о груз Q = 60 кг, лежащий на гладкой горизонтальной плоскости и связанный со стеной стальной пружиной (см. рисунок). Пружина имеет 20 витков при среднем радиусе витка 8 см и радиусе
К задаче 14.49.
К задаче 14.50.
стержня 7,5 мм. К моменту соударения груз Р обладает кинетической энергией Т = 800 кгсм.
891
Определить наибольшее касательное напряжение в пружине и се осадку: а) при наличии груза Q и б) прн отсутствии его; трением последнего о горизонтальную плоскость пренебречь.
Ответ: а) 503 кг/см1 и 6,44 см; б) 1257 кг/см? и 16,1 см.
14.50. Вагонетка А катится по рельсам тупикового пути и останавливается двумя симметрично расположенными по отношению к осн пути упорами В (см. рисунок). Вагонетка имеет два буфера, снабженные стальными цилиндрическими винтовыми пружинами, такие же буфера поставлены и на упорах В. Каждая пружина имеет 12 витков прн среднем диаметре витка 16 см и диаметре стержня пружины 2,5 см.
Учитывая только деформацию пружин, определить максимальную допустимую скорость движения вагонетки к моменту удара, прн которой наибольшие касательные напряжения в пружинах не превысят [т] = 3000 кг/см2. Чему будет равна осадка каждой пружины прн ударе?
н наибольшее касательное напряжение в
Указание. Осадку пружины
ней max тд следует выразить через максимальную силу инерции при ударе Ра. Величина Рд определится из условия прочности: тахтд<[т], а предельная р
скорость о1Пак — из условия, что кинетическая энергия вагонетки Т = -^ f’max РДХД равна потенциальной энергии динамической деформации пружин: ид=4 — %—
Ответ: 3,75 м/сек; 13,4 см.
14.51. Определить наибольшее допустимое число оборотов вращающегося сплошного стального диска диаметром 0 = 80 см и толщиной t = 8 жлс, насаженного на стальной вал диаметром 60 мм, так, чтобы при внезапном торможении вала в сечении, расположенном на расстоянии 1,6 ж от диска, наибольшее касательное напряжение в вале не превышало 1000 кг/см2.
Указание. Момент инерции массы диска определить по формуле
32g
а кинетическую энергию удара прн торможении—по формуле 7’ = —Jmo>2.
Ответ: 100 об/мин.
14.52. На стальной вал диаметром 100 мм насажены два маховика с одинаковыми моментами инерции Jm = 8000 кгсмсек2. Расстояние между маховиками 3 м. Один маховик постоянно заклинен па вале, а другой, свободно вращающийся со скоростью 30 об/мин, посредством особого приспособления можно мгновенно сцепить с валом и таким образом привести в движение всю систему.
Определить наибольшее касательное напряжение в поперечном сечении вала в момент сцепления с ним второго маховика.
Ответ: 1003 кг/см2.
14.53. Груз Р со скоростью 2 м/сек опускается с помощью стального троса, намотанного па шкив А; последний насажен па вал ВС. Когда длина троса оказывается равной 30 м, происходит остановка вра-
392
щения вала в сечении В (см. рисунок). Момент инерции шкива 100 кгсмсек2, модуль упругости троса Е= 1,7-10® кг/см*. Пренебрегая массой шкива, троса и вала, определить растягивающее напряжение в тросе и наибольшее касательное напряжение в сечении вала.
Ответ: 1822 кг) см?-, 425 кг! см2.
14.54. Двутавровая балка № 60, шарнирно опертая по концам, посредине пролета 1 = 4 м подвергается удару грузом Р=800 кг, падающим с высоты /7=5 см. Стенка двутавра расположена вертикально.
Определить наибольшее нормальное напряжение н наибольший прогиб балкн без учета и с учетом ее массы.
Решение. Для балки № 60 по сортаменту
а вес единицы длины 9=104 кг/м. Наибольшее нормальное напряжение при статическом нагружении силой Р = 800 кг равно
. Р1 800-400 о , тах бс = 4^-= 4.251о = 31 ’9 кг/см ‘
120СМ-
Тормоз
□27
\Л,^Вмм
\Р=50кз
К задаче 14.53.
J,=75 450 см* н «7_ = 2510 с.ч’.
а статический прогиб в месте приложения силы
РР 800-400»
fc~ 48EJX~ 48-2-10«-75 450
= 0,00707 см.
Пренебрегая массой балки, динамический коэффициент вычисляем по формуле
/nej Г о е _______
1 + Т-=1+У 1+0Дб7б7=1 + ^,414,4-6л38-6-
Следует иметь в виду, что эта формула становится весьма неточной при эиа-2// ченнях -т— >100, как в данном случае; при учете массы балки ее допустимо ' w inn
использовать и при значениях -j— > 100.
Наибольшее нормальное напряжение в балке при ударе равно max Од=max ос-йд = 31,9-38,6= 1231 кг/см\ а наибольший прогиб ее
/д=/с-йд=0,00707-38,6 = 0,273 см.
Статические составляющие напряжения и деформации от собственного веса балкн здесь не учтены.
Прн учете массы балки динамический коэффициент должен быть вычислен по формуле _________
/2Н
1+ (1 + ₽)/с ’
„О 17
где 1 -|- р = 1 -|-а , причем для балкн па двух шарнирных опорах а=-5=- ;
Г оо
393
Q=ql= 104-4 = 416 кг—вес балки. Таким образом,
Лд - 1 +
2-5
1+-!?-.<* т 35 еоо
, , И 14.6
+ 1,2526 - 34-6-
Теперь наибольшее нормальное напряжение в балке равно
max °я= 8W7+W7 *д= 8®7(<г+2РЛд)= 8-2510 (416 + 2-800-34.6) =
= 1112 кг/см2, а наибольший прогиб ее
f 5Q/s _ Р/’ЛЛ _ (5 , пь Р
'л ~ 3MEJX + 48EJX ~ \8 Q + PkaJ 4HEJX~
- (4 416+•»-*•) 4В 2.Х.^Т - 0-2«
Первые члены последних выражений представляют статическое напряжение и статический прогиб балки под действием ее собственного веса, не учтенные в предыдущем расчете.
Учет массы балки приводит в данном случае к снижению вычисленного напряжения н прогиба примерно в 1,1 раза.
14.55. Шарнирно опертая по концам балка подвергается посредине пролета 1 = 2 м удару при падении груза 200 кг, обладающего к моменту соударения с балкой кинетической энергией 120 кгсм. Сеченне балки—швеллер № 30, стенка швеллера расположена горизонтально. Определить наибольшее нормальное напряжение и наибольший прогиб балки. Чему будут равны наибольшие напряжения и наибольший прогиб, если концы балки будут защемлены?
Ответ: В шарнирно опертой балке шах од= 1366 кг/см1 и fa = = 0,304 см; в балке, защемленной по концам, шах од= 1234 кг/смг и Д = 0,137 см. При статическом нагружении за счет защемлении концов балки наибольшие напряжения уменьшаются в 2 раза, а наибольший прогиб—в 4 раза; при ударе в данном случае напряжения снижаются лишь на 9,7%, а прогиб—в 2,2 раза.
14.56. На шарнирно опертый по концам деревянный брус прямоугольного поперечного сечения 12 X 24 см посредине пролета I = 4 м с высоты 5 см падает груз 100 кг. Определить наибольшее нормальное напряжение и наибольший прогиб бруса при изгибающем ударе в плоскости: а) наибольшей жесткости и б) наименьшей жесткости.
Ответ: а) 97,5 кг/смг и 1,08 см; б) 107,4 кг/см? и 2,39 см.
14.57. Каковы будут наибольшее нормальное напряжение и наибольший прогиб бруса (см. предыдущую задачу), если при изгибающем ударе в плоскости наибольшей жесткости величина падающего груза будет в 5 раз больше?
Ответ: 246 кг/см* и 2,73 см; напряжение и деформация увеличились не в 5 раз, а лишь в 2,5 раза.
14.58. Льдина, плывущая со скоростью 1 м/сек, ударяется о деревянную сваю круглого поперечного сечения (см. рисунок). Опреде
394
лить наибольшее нормальное напряжение и наибольший прогиб сваи при ударе, если модуль упругости дерева Д = 8-10‘ кг/см2. Сваю в нижнем сечении считать защемленной.
Ответ: ~100 кг/см2; 3 см.
^d‘Z5cM
15икг
К задаче 14.58.
14.59. Определить высоту падения груза Р, при которой свободный конец консольной двутавровой балки в результате удара коснется неподвижной плоскости (см. рисунок).
Ответ: 5,73 см.
14.60. Груз 200 кг движется горизонтально и ударяется о балку, которая при этом прогибается на 5 см. К моменту соударения груз имеет скорость 2 м!сек. Какая стати
ческая нагрузка, приложенная в том же сечении балки, вызовет тот же прогиб?
Ответ: 1631 кг.
14.61. Консольная балка АВ из двух швеллеров № 22 подверглась удару при падении груза Р в сечении С (см. рисунок). Наибольший прогиб на конце консоли оказался равным 8 мм. Определить высоту падения груза и наибольшее нормальное напряжение в балке. Д=2-10ь Мн/н.2.
Ответ: 6,06 мм; 163,7 Мн/м*.
К задаче 14.62.
14.62. Двутавровая балка № 24 опирается на шарнирные опоры. Груз падает на балку посредине пролета со скоростью 50 см/сек к моменту удара (см. рисунок). Определить наибольшее нормальное
395
напряжение и наибольший прогиб балки в результате удара, предполагая, что: а) опоры балки абсолютно жесткие; б) опоры балки представляют упругие конструкции; смещение каждой из них на единицу приложенной к ней нагрузки равно 4-10-4 см/кг', в) опоры балкн абсолютно жесткие, но посредине пролета на балке лежит груз того же веса, что и ударяющий груз. Массой балки во всех случаях пренебречь.
Ответ, а) 1736 кг/ми2, 0,544 см; б) 1083 кг/см2, 0,339 см; в) 1319 кг/см2, 0,413 см.
14.63. Модель стальной балки иа двух шарнирных опорах, изготовленная из той же стали в -4- натуральной величины, была ис-О
пытана на удар сосредоточенной нагрузкой, приложенной посредине пролета. Нагрузка и высота ее падения также были взяты в три раза меньшими, чем в действительной балке. Динамический коэффициент, определенный опытным путем (из сравнения статической и динамической деформации модели балки), оказался равным четырем.
Определить величину динамического коэффициента в действительной балке в двух вариантах: а) пренебрегая при расчете собственным весом балки, составляющим 70% веса падающего груза, и б) учитывая этот вес.
Ответ: а) 6; б) 5,43.
14.64. Швеллер № 24 длиной 8 м с помощью крана опускается
на две опоры со скоростью 0,8
.Лптпишш*,
К задаче 14.64. длине швеллера, потенциальная может быть вычислена по формуле
1 1 1
Г Mndx _ 1 С / Qalx
J 2EJV ~ 2EJV J 4“^"
0 z z 0
м/сек (см. рисунок). Определить наибольшее нормальное напряжение и наибольший прогиб швеллера при ударе его об опоры.
Решение. Для швеллера Ns 24 Jy = = 208 сл1; №^ = 31,6 см3 и вес единицы длины q = 24 кг/м. Кинетическая энергия швеллера при ударе равна
_ Qc»2 24-8-802
Т—2>g81- --626,3 кгем.
В предположении, что силы инерции 9д будут равномерно распределены по энергия его динамической деформации
' 0
q2„la ^-800*
_ 4A _____ 4 A________r?
2WEJy 240 • 2 • 10® • 208 '
Из равенства T = Ua находим величину силы инерции:
/626,3 . ,
3282‘=0,437 кг/СЛ’
306
Наибольшее нормальное напряжение в швеллере от собственного веса и сил инерции будет равно
(?с + ?,) V (0.24 +0,437)-8002
тахоя=—~— =-------------^зу-g-----=1714 ю/ой»,
а наибольший прогиб
5(<?с + ?дН4 5 (0,24 + 0,437)-800»
fa = 3MEJy “ 384-2-10»-208 = 8,68 см'
14.65. Стальная листовая рессора, шарнирно опертая по концам, имеет 9 листов сечением 50x8 льм2. Груз 50 кг падает на рессору посредине ее пролета 1=1 м с высоты 3 сл. Сравнить наибольшие нормальные напряжения и наибольшие прогибы в рессоре и в балке постоянного сечения, имеющей момент инерции и момент сопротивления такие же, как рессора посредине пролета.
Ответ: В рессоре /д=1,62 см и max од= 1033 кг/см2; в балке постоянного сечения /д=1,58 см и max од= 1513 кг/см2.
14.66. Деревянная балка круглого поперечного сечения, шарнирно опертая по концам и имеющая длину 4 м, посредине пролета подвергается удару горизонтально движущимся телом, обладающим в начальный момент удара кинетической энергией 800 кгсм. Определить диаметр поперечного сечення балки так, чтобы наибольшее нормальное напряжение в ней не превышало 100 кг;см2, а максимальный прогиб был не более 1 см.
Ответ: 25,7 см та 26 см.
14.67. В рамах, изображенных на рисунке, определить наибольшее нормальное напряжение и прогиб в месте удара. Сечение
К задаче 14.67.
стержней каждой рамы—парные равнобокие уголки, составленные полками вплотную.
Ответ: а) 595 кг/см2, 1,87 см; б) 2022 кг/см2, 1,057 с.ч;
в) 1862 кг/см2, 0,93 см.
337
14.68. На балку АВ, защемленную в сечении А и шарнирно опертую в сечении В (см. рисунок), посредине пролета падает груз Р, скорость движения которого к моменту соударения с балкой равна 60 см/сек. Определить наибольшее нормальное напряжение в балке и прогиб ее в месте удара.
Ответ: 1724 кг/см*', 0,375 см.
14.69. Балка АВ, одни конец которой защемлен, а второй лежит на шарнирно опертой балке CD, подвергается удару падающим грузом в сечении В (см. рисунок). Обе балки деревянные, одинакового
К задаче 14.68.
ст)Вэ
К задаче 14.69.
прямоугольного сечения; Л = 24 см, ft =12 см. Определить величину коэффициента запаса прочности конструкции, если временное сопротивление дерева при изгибе ств = 500 кг/см2.
Указание. Условие совместности динамической деформации балок имеет такой вид:
, _(Рд-«Я)^я _*&>
Гл - Гав - Гео- ^rj - i8EJ .
между балками в сечении В. Условие равенства кинетической энергии удара и потенциальной энергии деформации балок:
T = P(H + fa) = Ua =
*д 1СД ,(Pn-R^AB
96EJ 6EJ
Совместное решение этих уравнений приводит к определению Ra и Ра.
Ответ: 4,08.
14.70. Стальной коленчатый стержень ABCD, несущий на концах А и D грузы, вращается с постоянной »уг вертикальной оси О—О (см. рисунок).
Определить наибольшее расчетное напряжение в стержне при внезапной остановке вращения. Использовать третью теорию прочности. Собственным весом стержней пренебречь.
Решение. Кинетическая энергия грузов в момент остановки вращения равна р„а prfriW 3-3.14S-30M52
7=2 2i’=“i-= Т30^=-----------98Ь 30*--= 6’79 КгСМ-
где кд—сила
'\ГН J
«— д —й*- а-15см-*
- О Л=20мм
14.70.
К задаче
30 об/мин
0
В
С
А
898
Потенциальная энергия деформации стержней АВ, ВН, НС и CD при изгибе и кручении равна
и--2 (4 +4р-^+4 =зтг+^+^=
* / OZLJy OL J ц UJp
Рд ( FJ \
=3£ГЛ'3 + ОЗ+ОР =
64Рд ( 2- 10е 1 \
=1ГГТО*.ЗЛ4.2« 153+15 202 • W 4? =
= 0.004005Р’
д
Из равенства T=Ua следует, что сила инерции прн ударе
Рл V 0,004005 ~41,2 кг'
Наибольшие нормальные и касательные напряжения возникают в сечении И стержня ВС:
М 32Р„а 32-41.2-15
шаход-^— - 314 23
=786 кг/см1, Мк \6P.l max тд = -™Л-=----г-
“ wp ла’ 16-41,2-20
----3,14-2’----524 кг,См3'
Расчетное напряжение по третьей теории прочности равно
арН1 = 1/ max Од+4-тах Тд =
л, й=32шк, С ---------
ь*-25см
Квадрат 30*30мм\ §
25см—м Л
I
Р=1,5кз
К задаче 14.71.
14.71. Стержень АВ круглого поперечного сечеиия вращается в подшипниках Л и В вокруг оси О—О, делая 100 обрит. Со стержнем АВ жестко связан стержень CD квадратного сечення, несущий на конце груз Р (см. рисунок).
Пренебрегая весом стержней АВ и CD, определить наибольшее нормальное напряжение в стержне CD и расчетное напряжение по четвертой теории прочности в стержне АВ при внезапном торможении системы в сечении В.
Ответ: max oCD = 893 кг/см2; расч Оав= 1334 кг/см2.
§ 49. Переменные напряжения*)
14.72. Определить величину предела выносливости при симметричном цикле изменения напряжений для подвергающегося изгибу ступенчатого стержня круглого поперечного сечения с галтелью в месте перехода от одного диаметра к другому (см. рисунок). Стержень изготовлен из углеродистой стали (ст. 30) с временным
*) В этом параграфе для определения масштабных коэффициентов н коэффициентов концентрации напряжений при расчетах на переменные нагрузки используется таблица 37 и кривые иа рис. 626—629 курса «Сопротивление материалов» Н. М. Беляева, изд. 1954 г. и более поздние.
399
сопротивлением ов = 55 кг!ммл и пределом выносливости в случае симметричного цикла при изгибе сг^1=25 кг/ммл, определенным лабораторным путем на образцах диаметром 7—10 мм.
Решение. Величина предела выносливости детали (в данном случае ступенчатого стержня) может быть определена по формуле
«кл«м ’
где о" ।—предел выносливости для образца малого размера, с^д—действитель-
ный (эффективный) коэффициент концентрации напряжений, а ам— масштабный
Г=5мм
К задаче 14.72.
В данном случае при
коэффициент. При этом значение акл можно найти, используя зависимость
«кд=1-г<?(«кт-1)-
Здесь акт—теоретический коэффициент концентрации напряжений, a q—коэффициент чувствительности материала к местным напряжениям. Значения сскт н q можно найти в курсе «Сопротивление материалов» Н. М. Беляева.
5
=——0,0625 из таблицы 37 упомянутого курса
следует, что акт=1,75. При этом значении с^т для стали с оп —55 кг/мм2 по графику на рис. 626 путем линейной интерполяции находим величину коэффициента q — 0,53. Теперь
акл= 1-}-0,53х(1,75—1)= 1,4.
Значение масштабного коэффициента устанавливаем по кривой 2 рнс. 629; для стержня диаметром 80 мм имеем ан=1,57. Таким образом, искомая величина предела выносливости будет
25
о“д. = i а 1 = 11,4 кФ**1-
14.73. Решить предыдущую задачу в предположении, что стержень изготовлен из легированной стали: а) 20Х с характеристиками ов = 80 кг!ммг и о" , = 38 кг/лл2; б) 25ХНВА с характеристиками ов = 110 кг) мм* и сг“ j = 50 кг! мм*.
Ответ, а) = 12,6 кг/лл2;
б) о™ =15,1 кг/лл2.
14.74. Определить величину предела выносливости при симметричном цикле изменения напряжений для деталей, схемы н размеры которых помещены в таблице (см. рисунок). Стержни изготовлены: а) из углеродистой стали (ст. 20) с характеристиками: <тв = 50 кг/лл2, o*i = 16 кг!ммл, o“j=22 кг/лл2 и т^( = 13 кг/лл2; б) из легированной стали 40ХН с характеристиками: ов = 90 кг/мм*, olj = 29кг/лл2, о" 1 = 40 кг [мм* и т* f = 24 кг/лл2.
Ответы приведены в таблице.
400
К задаче 14.75
Линии оливных напряжений: а) опытная \ 0 условно
V спрямленная
№
и \
14.75. Определить величину предела выносливости при переменном изгибе: а) для полированного образца малого размера из углеродистой стали (ст. 20), имеющей о” = 30 кг/лгл!1 н о1^, = 20 кг/.нл<2; коэффициент асимметрии цикла, или характеристика цикла, г=—0,2;
б) для детали круглого поперечного сечения диаметром 60 лии из стали 12ХНЗА, имеющей сгв = = 95 кг!мм.*, сг^* = 72 кг!ммг п сг’Д , = =45кг/л(л12; характеристика цикла г =4-0,4. Использовать спрямленную диаграмму предельных (опасных) напряжений в координатах оя—оа (см. рисунок).
Решение. Выведем общую формулу
для определения <зг—предела выносливости прн цикле с характеристикой г —по заданным значениям о_х и о+1=ов. Из подобия треугольников АОС и BDC (см. рисунок) следует, что
BD__D£ АО~ОС ’
или
401
Подставляя в последние равенства значения стг = ——сг и аог = —%—ог, находим
=_________2Р+1О-1______
r (I— л)о+1^-(1гл)а_,
Для образца из ст. 20 имеем
9-40-90
<'=<0.2=30(,+о2)<20(,--02)=23,1 кг/ММ2.
Тангенс угла наклона луча ОВ к осп <зт равен
_ Одг _1-Г__1+0.2__, г-
— о;лг ~1-j-г — 1—0.2—
Если диаграмму <зт—<за построить в масштабе напряжений, то величину ог можно найтн прямо по графику, проведя луч О В под углом в; ог = от+ол = =OD+DB.
Аналогично для детали из стали 12ХНЗА найдем o“a = o“«4 = = 18,1 кг/мм1.
14.76. Пользуясь спрямленной диаграммой предельных (опасных) напряжений в координатах от—атах (см. рисунок), показать, что
Линии
К задаче 14.76.
для нахождения величины ог по заданным значениям ио+1 = ов можно применять формулу, выведенную при решении предыдущей задачи. Показать также, что тангенс угла наклона прямой OF 2
коси ст равен tg£ = утру.Определить для полированных образцов малого размера из углеродистой стали с характеристиками ов = 120 кг!мм1 и о®, = 45 кг/мм2 значения пределов выносливости, соответствующих на диаграмме °т—Gn,ax отрезкам: a)DE;6)FG, если tgP = l,5; в) KL, если сг^п = OZ. = 20,9 кг!мм2.
Указание. Прн выводе формулы для ог использовать подобие треугольников AFH н АВО.
Ответ: а) 65,5 кг/мм2; б) 77,1 кг/мм2; в) 58,1 кг/мм2.
14.77. Определить величину предела выносливости при переменном кручении валика диаметром 45 лглс, изготовленного из стали 20ХНВА, для которой = 60 кг/мм2 и т* t = 28 кг/мм2. Напряжения меняются от -J-0,3Tmax до + ттах. Валик снабжен шпоночной канавкой; коэффициент ант считать равным 1,6. Использовать диаграмму предельных напряжений в координатах от—отах.
Ответ: 24,1 кг/мм2.
402
14.78. Определить величину допускаемого напряжения для балки, изготовленной из углеродистой стали (ст. 35) с характеристиками а" = 370 Мн!м* и о” ( = 280 Мн/м2 и подвергающейся переменному изгибу при цикле с коэффициентом асимметрии г =—0,6. Основной коэффициент запаса прочности считать равным k0 = 1,7, действительный коэффициент концентрации напряжений акд=1,56, масштаб-
ный коэффициент ам = 1,72, динамический коэффициент Ад = 2.
Решение. Допускаемое напряженке прн постоянной нагрузке равно
[°""]=-ir=T77=218 Мн,м^ допускаемое напряжение прн симметричном цикле находим по формуле
К задаче 14.78.
^О^д^кД^м
1.7.2.Т56.1,72 ЧТ2=30-7
Для нахождения допускаемого напряжения при цикле с характеристикой г воспользуемся спрямленной диаграммой допускаемых напряжений (см. рисунок). Из подобия треугольников MNC it АОС следует (см. аналогичный вывод в задаче 14.75), что
[0,1 =_____.
1,1 (l+Olo.J + Cl-г)[о+1|
Подставляя в эту формулу числовые данные, получаем
Го,,д1 = |о"д 1 =_________2 30,7-218________—27 1 Мн!*Р
I r I I -O.eJ (|—0,6)-30,7+(14-0,6)-218 27J Мн'м ’
14.79. Пользуясь спрямленной диаграммой допускаемых напряжений (см. рисунок к предыдущей задаче), определить величину допускаемого напряжения для вала, изготовленного из стали 25ХНВА с характеристиками т* = 60 кг1мм* и т^(=30 кг 1мм2 и испытывающего переменное кручение. Крутящий момент меняется от 0,6Л4тах до Afmax. При вычислениях принять Ао = 1,6, анд=1,85 и ам = 1,46.
Ответ. 19,9 кг/мм*.
14.80. Допускаемые напряжения для детали из стали 40ХН равны: при симметричном цикле 12 кг/лии2, при постоянной нагрузке 50 кг!мм2. Определить величину допускаемого напряжения в следующих случаях:
1) для цикла с характеристикой г=—0,5;
2) для цикла со средним напряжением сгт=10 кг!мм2:
3) для цикла с наименьшим напряжением omln =—8 кг/мл12;
4) для цикла, при котором аа= 1,4 ат;
5) для циклов, определяемых на диаграмме рнс. к задаче 14.78 у глами: а) 0 = 30° и б) 0 = 60°.
Ответ: 1) 14,8 кг/мм2; 2) 19,6 кг/мм2; 3) 14,5 кг/мм2; 4) 23,2 кг/мм2; 5а) 16,6 кг /мм2 и 56) 17,6 кг/мм2.
403
14.81. Балка прямоугольного поперечного сечения, ослабленная ниточками (см. рисунок), в плоскости наибольшей жесткости подвергается действию изгибающего момента, меняющегося от —0,5Afmax до 4-Л4тах. Балка изготовлена из стали 12ХНЗА с характеристиками ств = 95 кг/мм2, а" = 72 кг/мм2 и <т“1=40 кг/мм2. Принимая основной коэффициент запаса прочности равным Ао = 1,8, определить допускаемую величину изменится значение радиус выточки будет 6 мм при глубине 6 лш?
Допускаемое напряжение
наибольшую Л4п,ах. Как ^Чпах. если увеличен до
Решение.
прн постоянной нагрузке равно °'т 72
^=14=40 кг/мм2. «О 1 »о
Величину допускаемого напряжения для балки при симметричном цикле изменения напряжений определим по формуле
1 ,J *0«кд«и
,нд
Теоретический коэффициент концентрации напряжений, определенный для от-г 3
ношения —=—=0,05 но кривой / рис. 628 (см. курс «Сопротивление мате-п oU
риалов» Н. М. Беляева), равен avT=2,25. При этом значении акт коэффициент чувствительности для стали с ов=95 кг/см2 будет q = 0,785 (рис. 626). Поэтому действительный коэффициент концентрации напряжений
анд= 14-0,785 (2,25 — 1) = 1,98.
Масштабный коэффициент по кривой 3 рис. 629 для d(H) =72 мм равен двум. Таким образом,
10-»]- = 1,8.?°9Г2=5’61 'И/ЛЛ2-
Характеристика цикла нзмеиення напряжений г=—^^*п,|с = — 0,5. До-
Л1тах
пускаемое напряженке для этого цикла находим по формуле
, х г , 2 ГаЗМГоВД11 2-5,61-40
[ оид1_Г 0"Д 1=________1 +4L -1J______________________;________________
L < J I -0.6J (1— г)[о^,]4-(14-/-)[ о"я1] (14-0,5)40-Ь(1—0,5)5,61
=7,15 кг/мм2.
Так как момент сопротивления ослабленного сечения балки равен Wi« 2,5-6* ,с . , ж
W = -т—=——7—=15 см2, то наибольшее допускаемое значение изгибающего 6 6
момента будет равно
Мтак = 1Г[о^д0 sJ = 15-715=10 730 кгсм st 107 кгм.
Повторяя приведенные выше выкладки для того случая, когда радиус выточки равен 6 мм, последовательно находим: акТ=1,8; q = 0,785; акд=1,63; аи=2; [ а^^б.вг кг/мм2\ [о"д0 5] = 8,60 кг/мм2 и Мщах =129 кгм (увеличение больше чем на 20%).
404
14.82. Стержень круглого поперечного сечения, ослабленный круглым поперечным отверстием, подвергается изгибу в плоскости наименьшей жесткости (см. рисунок). Изгибающий момент меняется от М = 200 кгм до М — Мтах = 700 кгм. Стержень изготовлен из углеродистой стали (ст. 15), для которой ств = 45 кг/мм2, о" = 26 кг/мм* и ] = 22 кг)ммг. Проверить прочность стержня, если основной коэффициент запаса прочности равен 1,7.
Ответ: одс'1"в-=^^- = 9,02 кг! мм* < Го'!д| = 9,08 кг/мм2.
,пах 7/ ,о L r J
К задаче 14.82.
К задаче 14.83.
14.83. Стержень прямоугольного поперечного сечення с галтелью (см. рисунок), изготовленный из углеродистой стали (ст. 35) с характеристиками ав = 55 кг/мл14, <т° = 28 кг! мм2 и сг^( = 18 кг/мм2, подвергается действию сжимающей нагрузки, величина которой меняется от 0,15Ртах до Ртах. Определить наибольшую допускаемую величину Ртах, если коэффициент запаса прочности k0 — 1,8, а динамический коэффициент /гя = 2.
Ответ: 3,4 т.
14.84. Цилиндрическая винтовая пружина имеет 10 витков прн среднем диаметре витка D=18 ям и диаметре проволоки d = 4 мм. Пружина изготовлена нз хромованадневой стали с характеристиками тт=100 кг/мм2 и 1^ = 35 кг1мм*. Пружина предварительно сжата на 4 мм; наибольшая амплитуда деформации пружины во время работы равна ± 3 мм. Проверить прочность пружины при коэффициенте запаса прочности k0 = 1,8. Коэффициент концентрации напряжений считать равным единице.
Решение. Наибольшая деформация пружины Лтах = 44-3 = 7 мм, наименьшая Хпйп = 4—3=1 м.ч. Соответствующие значения сжимающей пружину силы находим нз выражения для осадки пружины
Р-™-Ь
F 8nD»А
8-10»-0,4* 8-1,8s-10
Х=43,9Х.
Прн k=Xniin = 0,l см />П,-|П = 43,9-0,1 =4,39 кг; при ^=Х1т1ах=0,7 см Рп,ах = 43,9-0,7=30,7 кг. Наибольшее касательное напряжение в пружине равно
8PD ( , d \ maXT = ^-(l1 + 2DJ) =
8-1.8Р 3,15-0,4»
1
403
Наименьшее и наибольшее напряжения цикла будут т|П-|П = 79,6-4,39 = 349 кг/см1 349
и тт„= 79,6-30,7 = 2445 кг/см2, а характеристика цикла Л = 2445 = 0,1
Допускаемые напряжения [т+1| и [t_J при коэффициенте запаса прочности k0= 1,8 будут равны
[т+11=р=7-Б=55.5 кг/ммг и [т_1] = ^=^ = 19,4 кг/мл?.
Допускаемое напряжение для цикла с характеристикой г=0,143
Zfr+dlT-J
1т0»«4з] —
2-55.6-19.4
(1+0,143) 19,4+ (1—0.143) 55.6 30,9 кг1мм*-
Наибольшее действительное напряжение ттах=2445 кг/см- значительно меньше допускаемого напряжения |т0143] = 3090 кг/см-.
14.85. Вал круглого поперечного сечения диаметром d = 90 мм, имеющий в месте перехода к диаметру 0=110 мм галтель радиусом 6 лиц изготовлен из углеродистой стали (ст. 45) с характеристиками ов = 75 кг/ммг, = 45 кг/ммг, ( = 35 кг)ммг, т* = 22 кг/лии1 и т* j = 20 кг/леи2. Вал при вращении изгибается парой сил с моментом Л1И и скручивается парой сил с моментом Л4К, меняющимся от 0,5Л4™ах до Л4™ах = 1,5 Л1К. Принимая основной коэффициент запаса прочности k0= 1,8, а динамический коэффициент для переменных составляющих
Лд = 2, определить наибольшую допустимую величину /Ин и Мя.
циклов нормальных и касательных напряжений
прочности вала, подвергающегося одновременному из-
Решение. Условие гибу и кручению, может быть записано так:
о™
.max к
В этом выражении о™ах и т™а* мальиых н касательных напряжений в опасном сечении вала, а [ —допускаемые напряжения для вала при изгибе и при кручении, опре-
деляемые в зависимости от характеристик гя и гя циклов нормальных и касательных напряжений.
Наибольшие действительные значения напряжений равны
—наибольшие действительные значения нор-[о«] н
атах =
М™* 32Л4„ 32 М„ _ .. 11 =-----5=-------=0,01397 М„
И7и л<Р 3,14-Э3 "
п
.max к
Установим теперь пых напряжений при
М™к 16Л4"’ах 16-1,5Ма
. “ . =----5—=-------------5=0,01048 Л+.
Wp жР 3,14-Э3 к
величину допускаемых напряжений. Цикл нормаль-иэгибе будет симметричным; величину допускаемого
4V8
напряжения определим по формуле
^<ЛдвЕЛ®М
Значения коэффициентов, входящих в знаменатель этой формулы, найдем по соответствующим таблицам и графикам (см. задачи 14.72 н 14.81): ант=1,73, д = 0,65, авд=1,48 и ам=1,62. Так как й0=1,8 и Лд=2, то
[ °-Л11= 1,8-2-1,48-1,62 = 405 кг1см*-
Характеристика цикла касательных напряжений при кручении равна ги = 0,5. Величину допускаемого напряжения в случае симметричного цикла при кручении определяем по формуле
тк
[т“д |-
1 11 k^a^a.*
Здесь (ант=1,45, д = 0,57) акд=1,26, ам=1,62, й0=1,8 и Ад=2. Поэтому
I т-"1 =1,8-2-1,26-1,62=272 кг/см2’
Допускаемое напряжение при кручении в случае постоянной нагрузки равно
2200 ЦТ
= 1222 кг/см2.
а для цикла с характеристикой гк=0,5
[<!=№]=
2-1222-272
(1+0,5) 272+(1 — 0,5) 1222
=653 кг/смг.
и | тгк]- а также нан-
Подставляя в условие прочности значения деппые ранее значения <s™a* и т™ах, получаем уравнение
К0,01397\1 /0,01048\21
405 ) + V 653 J J
М2„ = 14,478-10-io М* < 1,
откуда
/Юхо 10® max
7078=3^565 ~ 26 300 кгсм я М* =1.5-26 300 « 39500 кгсм.
14.86. Ступенчатый вал с диаметрами d = 50 лии и 0 = 60 мм имеет в месте перехода галтель радиусом 4 льи. Вал подвергается переменному изгибу с кручением. Нормальные напряжения при изгибе меняются от omin =—6 кг! мм1 до отяж = + 6 кг)ммг, касательные напряжения при кручении изменяются от tmin = 0 до тшах = 5 кг!мм*. Материал вала—углеродистая сталь (ст. 45), для которой ов = 60 кг!мм2, о” = 42 кг!ммг, о" 1 = 25 кг/лси2, = 22 кг/мм* и т“1 = 16 кг) мм2. Определить величину коэффициента запаса прочности.
Ответ: 1,73.
407
14.-87 . Вал круглого поперечного сечения диаметром 100 мм, снабженный кольцевой полукруглой выточкой радиусом 8 мм и глубиной 10 мм, изготовлен из стали 12ХНЗА с характеристиками сгв = 95 кг/мм?, о” = 70 кг/мм?, о“1 = 45 кг!мм?, т* = 40 кг!мм? и тх1 = 24 кг!мм?. При вращении вал изгибается парой снл с моментом 7Ии = 300 кгм и скручивается парой снл с моментом, меняющимся от 0,7 АТках до Af™ах.
Определить наибольшую допускаемую величину крутящего момента. Коэффициенты концентрации напряжений принять равными: при изгибе анд=1,8, а при кручении ака = 1,56; масштабный коэффициент считать равным двум, а основной коэффициент запаса прочности Ло = 1,7.
Ответ: /Ик = 1079 кгм.
§ 50. Ползучесть и релаксация напряжений
Стержни прямоугольного поперечного сечення 20x30 мм, растянутые силой 3 т тырех разных сталей: а) углеродистой
\ кг J час
б) углеродистой
ХЮ’|а
в) хромомолибденовой стали (2,08% Сг, 0,5°/0Мо);
Л = 0,14-10-1®
\ кг i г) молибденовой \п 1 кг} час Определить относительное удлинение каждого нз стержней на стадии равномерной (установившейся) ползучести через 10000 часов.
14.88.
при температуре 540°С, изготовлены из че-
стали (ст. 45); л = 3,9;
стали (ст. 15); л = 3,05;
1 .
час ’
стали (0,52% Мо); л = 4,6;
А = 0,14х
Л = 0,12х
п = 3,55;
А = 0,6х
час ’
Указание. Использовать формулу еп=ерп/ = Ло"/.
Ответ: а) 4,70%; б) 2,05%; в) 0,321«/о; г) 0,156%.
14.89. Стальной стержень длиной 20 см, с площадью поперечного сечения 0,5 см2 растянут силой 200 кг прн температуре 540° С. Определить наибольший срок службы стержня, при котором удлинение его не превышало бы 2,5 мм, а действительное напряжение было бы вдвое меньше предела длительной прочности.
Стержень изготовлен из углеродистой стали (ст. 45), для которой при указанной температуре модуль нормальной упругости £т= 1,75-10® кг/см2; скорость равномерной ползучести прн /^1000 часов можно определить по формуле v n = kcn, где л = 3,9
(СМ^ \п 1
— J ' — > а предел длительной прочности—по формуле ов( = j , причем сго = 45ОО кг[см?, Р = 0,8^ hv = 0,2.
40S
Деформацию при неравномерной ползучести считать вдвое большей деформации при нагружении.
Ответ-. Из расчета па предельную величину деформации ползучести /тах = 7000 часов, из расчета па длительную прочность ^шах = 6460 часов.
14.90. Кронштейн из двух трубок АВ и АС (см. рисунок), на-
ружный и внутренний диаметры которых 40 мм и 34 мм, поддерживает груз весом Р при температуре 425° С. Определить наибольшую допускаемую величину этого груза так, чтобы скорость вертикального смещения узла А при равномерной ползучести не превышала 10~* см)час. Найти величину вертикального смещения узла А до начала ползучести и через 6 месяцев после нагружения, пренебрегая деформацией неустановившейся ползучести. Материал трубок— углеродистая сталь; £т=1,75- 10е >
соответственно равны
К задаче 14.90.
fCMz\n 1 л = 5,4 и А = 0,18-10-21 ( — ) • — . ' ’ \ кг ) час
Ответ: Ртах = 1280 кг; /вЛ = 0,096 см (/ = 0) и /П/1 = 0,535 см (I = 6 мес.).
14.91. Колонна прямоугольного поперечного сечення 80x80 см из бетона состава 1:3:6 с водоцементным отношением 0,55, арми-
Время, сутки
К задаче 14.91.
рованная шестнадцатью симметрично расположенными стальными стержнями диаметром 25 лив, сжимается силой Р-=300 т при температуре 20°С. Построить график изменения с течением времени напряжений в бетоне к арматуре, если модуль упругости арматуры Еа = 2 • 10° кг)см\ среднее значение модуля упругости бетона 2,8-10® кг/см1, а деформация ползучести бетона может быть определена . at
по формуле en = ^-j-^ , где а = 10е —хсут, ft = 3,5x см*
X10* кг]смг (t измеряется в сутках).
Решение. Из условия равновесия следует, что P=o^F^ + aaFa, где оа и Об—нормальные напряжения в арматуре и в бетоне, а £а= 16-^-=16 • — X
X 3.14-2,6* = 78,5 см* и £б = 80-80—£а = 6400— 78,5 = 6321,5 см- — площади сечений арматуры и бетона.
409
Полагая, что поперечные сечения колонны остаются плоскими, т. е. относительные деформации бетона eg и арматуры еа равны, и имея в виду, что при указанной температуре явление ползучести имеет место только в бетоне, можно составить следующее условие совместности деформаций:
а, °б . 1
ea~Ea~e6~E6 + °6a+bt ‘
откуда
’-<’6(Й+г+й)”°“л+в,)-где
Л_*а—Eat 2-1W 2f
Е6 2,810® ’ ‘ а+bt 10»+3,5-10*/ —1+0,035/‘
Из условия равновесия и формулы (1) следует, что
Р = о6 (Fg+Fa (Л + £t)] = об ^прнв
И ___________________Р Р
6 ^б + ^а И + В») F пряв
Результаты вычисления по формулам (1) и (2) напряжений оа н <jg для разных значений времени t, прошедшего после нагружения колонны, приведены в таблице. По данным таблицы построены графики изменения напряжений в бетоне и арматуре (см. рисунок).
t, сутки 0 10 30 (месяц) 100 365 (год) 1100 (3 года) 1830 (5 лет) 3650 (10 лет)
og, кг/см2 43,6 37,3 32,7 28,9 27,2 26,7 26,6 26,5
оа, кг/см2 311 819 1190 1492 1634 1675 1684 1690
Данные таблицы и графики показывают, что с течением времени происходит перераспределение нагрузки между бетоном и арматурой; напряжения в бетоне вначале быстро, а затем все медленнее понижаются, а в арматуре увеличиваются. Если в начале ползучести нагрузка на бетон была равна р6 =ogFg = 43,6-6322 = 275 600 кг, а на арматуру Pa = oaFa = 311-78,5= 24,4
= 24 400 кг, т. е. отношение ₽ = Pa:Pg = gyg-g=0,09, то через год после нагружения Pg=27,2x 6322= 171 700 кг, Ра= 1634-78,5= 128300 кг и р =
14.92. По данным опытов лаборатории сопротивления материалов Ленинградского политехнического института им. М. И. Калинина, при растяжении труб из полиэтилена низкого давления, изготовляемого Охтинским химическим комбинатом, зависимость между напряжением и> относительной деформацией как при кратковременном, так и при длительном действии нагрузки может быть выражена формулой е = j» проверенной в диапазоне температур от +10° до
410
+ 65° при значениях е от 0 до 0,12. Коэффициенты а и b зависят
от продолжительности действия нагрузки (/):
_ °i+^
-1 + М
н
o2+62Z
1 + c2z ’
в свою очередь коэффициенты о„ о2, blt b2, с, и с2 зависят от температуры; их значения приведены в таблице.
Пелн-ЦННЫ X. 7. °C Раз-мерность 10° 20° 30° 40° 50" 60’
а1 кг/см2 18100 12200 7800 4S50 3100 2850
Ь1 кг /час -см2 63,2 73,8 76,2 70,9 59,0 38,5
с! \/час 0.015 0,0345 0,0494 0,0548 0,0533 0,0420
а2 безразм. 75.7 53,8 37,3 26,5 22,9 22,0
1/час 0,039 0,196 0,345 0,485 0,613 0,732
Сг 1/час 0,0023 0,0140 0,0266 0,0400 0,0541 0,0688
Пользуясь вышеприведенными формулами и таблицей, для трубы из полиэтилена низкого давления, имеющей площадь поперечного сечения 2 см2 и растянутой силой: 1) 240 кг при температуре + 10°С, 2) 140 кг при температуре -|-30оС и 3) 110 кг при температуре 4-50° С, определить величину относительного удлинения сразу после нагружения и через 3000 часов после этого.
Решение. При температуре + 10°С сразу после нагружения, т. е. прн 1=0, Р 240 коэффициент a = aj= 18 100 кг/см2 и Ь=а2=75,7; напряжение о = —= -^-=
=120 кг/см2', поэтому относительное удлинение равно Е=~—Ъо =
120
= 18 100—75,7 -120=°-0131~1 *31 % -
Через 3000 часов после нагружения коэффициенты а и Ь принимают такие значения:
а
1+CiZ
18 100+ 63,2-3000
1+0,015-3000
4515 кг/см2
и
а2+Ь2Г_75.7 + 0,039-3000 Ь~ 1+с2/ — 1+0,0023-3000 —
Таким образом,
120
е=4515—24.4-i20=0,0756~7'56%-
Ответ: При 7’ = 30°С и / = 0 е = 0,0135;/ = 3000 час., е = 0,107. При Т=50°С и/ = 0 е = 0,0299;/ = 3000 час., е = 0,112. У
14.93. Бесконечно длинная тонкостенная полиэтиленовая труба, имеющая наружный диаметр 70 мм при толщине стенки 3 лл.
411
подвергается действию внутреннего равномерно распределенного давления 2 кг/см2 прн температуре 4-50° С. Определить через год после нагружения величину коэффициента запаса прочности.
а) А, — по отношению к пределу длительной прочности о/дп — напряжению, прн котором разрушение материала происходит в конце заданного промежутка времени (здесь о,-—интенсивность напряжений, вычисляемая по формуле
о,- = у= /(а> — о,)' + (о2—о3)2 -г (о3—о, )2,
где о,, о2 и о3—главные нормальные напряжения); значения о/дп могут быть определены по эмпирической формуле
п ____ао ~Ь Ь01
1-|-Со* ’
где’ для полиэтилена низкого давления (при Т — 50°С) ай = 110 кг/см2, Ь.. = 0,365 кг/см2 час и с0 — 0,0097 —!—;
° 01 час
б) Л2— по отношению к предельному статическому сопротивлению о1псс, отвечающему увеличению диаметра трубы на 3°/0 (предельным статическим сопротивлением называется то наибольшее напряжение, при котором начавшаяся ползучесть еще может через некоторое время прекратиться, вызвав деформацию определенной величины); дли нахождения о,-псс можно использовать формулу
_ те,-а'"сс — 14-пе,- ’
где ef = ^V(e,—е2)2 + (е2—е3)а + 1ез—ei)s — интенсивность деформаций; при заданной температуре т = 2770 кг/см2 и л = 52.
Указание. Деформацию в направлении осн трубы считать равной нулю, величиной нормального напряжения радиального направления пренебречь, коэффициент поперечной деформации считать равным половине.
Ответ: Л, = 2,08; Л2=1,85.
14.94. Бесконечно длинная стальная труба, наружный диаметр которой равен 0 = 60 мм, а толщина стенки 2,5 мм, подвергается действию внутреннего равномерно распределенного давления 50 ат при температуре 420°С. Найти изменение диаметра трубы в процессе равномерной ползучести в течение 3000 часов. Материал трубы — углеродистая сталь; скорость равномерной ползучести может быть определена по формуле и>п = -^г=Асуп, где л =5,9 и А = 0,65-10-20f^-Y* • — .
т г j рп dt \кг J час
Ответ: ДО = 5,85 ми; Онов = 65,85 мм.
14.95. Полый стальной стержень круглого поперечного сечения с наружным и внутренним диаметрами, соответственно равными 40 мн и 20 мм, скручивается парами сил с моментом ЛГК при температуре 540° С. Определить наибольшую допускаемую величину крутящего
412
момента так, чтобы через 6 месяцев после нагружения угол закручивания на единицу длины стержня 0 не превышал 0,005 рад/см, а наибольшее касательное напряжение в стержне было бы не более половины предела длительной прочности материала. Построить эпюры распределения касательных напряжений по сечению стержня сразу после нагружения и через 6 месяцев.
Стержень изготовлен из углеродистой стали, для которой при заданной температуре модуль сдвига GT = 6-10‘ кг!см*, стадия неравномерной ползучести продолжается /о = 500 час., причем соответствующая деформация ползучести в три раза больше, чем деформация при нагружении; скорость равномерной ползучести ®рп = йт'‘, где л = 3,9, a k = = 1,3- 1O-1S = пРедсл длительной прочности может быть
определен по формуле тяп = • причем т0 = 2000 кг/см*, р =
= 1,17-!— и v = 0,12. час’
Указания и данные для контроля решения. Момент инерции сечення полого стержня при ползучести вычисляется по формуле
л = 3,9,
(^тах ^о)
Условие жесткости имеет такой вид:
®тах = ®н + ®и/>п = +
или, после подстановки численных значений,
Мв+3.18-10-“М®-’< 17 700 (мел).
Путем последовательных проб находим Л4к=3180 кгсм.
Так как тдп = —=475 кг/см*, а р^"х. то нз условия
Ч-Р'тах
длительной прочности
кгсм
Ртах ^Ртах
Таким образом, наибольшая допускаемая величина крутящего момента: Мк = 3180 кгсм. Эпюры т приведены на рисунке.
14.96. Цилиндрическая винтовая пружина предохранительного клапана, работающая при температуре около 450° С, имеет 8 витков при среднем диаметре витка D = 28 мм п диаметре стержня пружины d = 4 мм; диаметр тарелки клапана равен О0 = 32 жя. Перед
413
постановкой в гнездо клапана пружина была сжата на Хо = 16 мм. Определить, при каком давлении внутри цилиндра будет открываться клапан в начале работы установки и через /, =720 час. Через сколько часов работы (Q давление при открытии клапана снизится вдвое против начального?
Материал пружины—хромомолибденовая сталь; GT=6,75-10® кг/см*, скорость равномерной ползучести v= йт", причем л = 8,5 и
1 V
— ] деформацией неравномерной ползучести можно пренебречь.
Указание. Осадка пружины должна определяться по формуле
. ktCxJpDn~l где А =---------- н
2n-ljn рп
с°- Cjd*
—жесткость
пружины прн
/=0.
Суммарное давление на тарелку клапана Р прн t=0 равно Р0 = уЛ.
1-0
Ро 4Р0 , , 4Р D
поэтому q0=-£-=—при t = l, ?i =----------, а Р определяется нз уравне-
F nD* nD2
ння Р+АРП = РО.
Ответ: При t = 0 ^О = 2,45 ат; при t = /, = 720 час. 1,37 ат; /2 = 2200 час.
14.97. Балка двутаврового сечения № 12 длиной 0,8 м, защем
на свободном конце сосредоточенной силой Р при температуре около 500° С. Определить наибольшую допускаемую величину силы Р так, чтобы через 9000 часов после нагружения наибольшее нормальное напряжение в балке не превышало половины предела длительной прочности материала одп, величину которого можно вычислить по формуле адп = t ; для заданной температуры <т0 = =3080 кг/сж2, В = 0,4—!— н v = =0,15. При решении задачи ста-
ленная одним концом, нагружена
К задаче 14.97.
дией неравномерной ползучести пренебречь, скорость равномерной ползучести определять по формуле т/рп = Аоп, где л = 4 и k —
(CJ^ \ п 1
— ) • —. Построить эпюры распределения нормаль-
К2 у час
ных напряжений по высоте сечения балки сразу после погружения и
через 9000 часов.
414
Указание. Прн ползучести нормальное напряжение в любой точке сечення па расстоянии г от нейтральной осн у определяется по формуле
о=-^~ гЧп
С —
в момент инерции сечення—по формуле Jyn= \ г п dF. При вычислении Jya F
уклоном полок и закруглениями в углах двутавра допустимо пренебречь.
Данные для контроля решения. J^,„ = 99,1 сч3.-6, одпаЛ200 кг/см-.
Ответ: Р=475 кг; эпюры а приведены на рисунке.
14.98. Для балок, схемы которых изображены на рисунках, вывести формулы для определения наибольшего прогиба /тах при изгибе в условиях равномерной ползучести материала, если скорость равномерной ползучести т/рп = йа".
Решение. Рассмотрим, например, схему 5). Дифференциальное уравнение изогнутой оси балки в условиях равномерной ползучести при ие изменяющемся во времени изгибающем моменте М имеет такой внд:
Выбирая начало координат на свободном конце балки, можем написать; х л2 qax2
Qx — Qo-r н Л4 = . Поэтому дифференциальное уравнение для /
I О Си
имеет вид
dx2 jn &Ча ln '
уч
где
Интегрируя это уравнение, последовательно находим
dx (Зл+1)ln+C Н f (3n+l)(3n+2)Z"+Cx+D’
Так как прн х=1 ^=0 и /=0, то постоянные интегрирования равны
Apn+i APin+»
С~ Зл+1 И U~ Зл + 2 *
Таким образом, в любом сеченин балкн
АР (п+1> (Зл+1) (Зп 4-2)
[3n +1-(Зл + 2) у + (у)3"”] •
Прн х=0
Х,2<п + 1> kl / — /max — 3л + 2 — „ уч где в данном случае
л"/2<П+1» ф = —----------.
(Зл + 2)-6п
415
Схемы балок
Формулы для ф
Схемы балок
I-
К задаче 14.98
Формулы для Ф
мпг
2
«1
,Т—~
(Зп 4-2) 6»
з) <
ff
шшшшППшг
I-
рЩп + 2 п 2
; 1/
2
Р
.1 2
рцп+з
(Т+2)2«<«+М
дЩМЛ+М
(п+1)2»+*
q'^a^a + , ®K 21+1
qn^ 2л + 3
Мп м.
7?fz—b
Va^-1-Za-^a.
Л4"
-jT(/’-4fl’)
О
N
р
\к
рпяп + 1
Фк=——
ж РпапР ®Л=----—
„ . . W qnl* . , a-/1
Если n = 1, to /max=— • . что отвечает формуле fnaK=^j- при
отсутствии ползучести.
Ответ: Общая формула /тах = -^-Ф; значения Ф (по абсолют-
'vn ной величине) даны в таблице.
14.99. Стержни прямоугольного поперечного сечения высотой Зсм, шириной 2 см н длиной 60 см изготовлены из четырех разных сталей (см. задачу 14.88). Каждый из стержней работает как шарнирно опертая по концам балка, нагруженная посредине пролета сосредоточенной силой Р= 100 кг. Определить в стержнях наибольшее нормальное напряжение и наибольший прогиб на стадии равномерной ползучести через 10 000 часов.
Ответ: а) Ст. 45: 0-,..,. = 449 кг/см*, / = 1,57 см;
б) ст. 15: оп„ = 437 кг/см', /„„=1,12 см;
в) хромомолибденовая сталь: отах = 422 кг/см*, /тах = = 0,06 см;
г) молибденован сталь: отах = 430 кг/см?, /так = 0,035 см.
14 св. задач
У
ПРИЛОЖЕНИЯ
СОРТАМЕНТ ПРОКАТНОЙ СТАЛИ В СООТВЕТСТВИИ С ГОСТ 8239—56*, 8240—56*, 8509—57, 8510—57, ДЕЙСТВУЮЩИМ НА 1 ИЮЛЯ 1963 г.
Таблица 1. Двутавры
№ профилей Вес 1 пае. м, кг Размеры, мм Площадь сечеиия, см* Справочные величины для осей
h ь d t X — X V — У
Jk IV. ‘х J У ‘у
см* см3 см см1 см* СМ* СМ
10 9,46 100 55 4,5 7,2 12,0 198 39,7 4,06 23,0 17,9 6,49 1,22
12 11.5 120 64 4,8 7,3 14,7 350 58,4 4,88 33,7 27,9 8,72 1,38
14 13,7 140 73 4,9 7,5 17,4 572 81,7 5,73 46,8 41,9 11,5 1,55
16 15,9 160 81 5,0 7.8 20,2 873 109 6,57 62,3 58,6 14,5 1,70
18 18,4 180 90 5,1 8,1 23,4 1290 143 7,42 81,4 82,6 18,4 1,88
18а 19,9 180 100 5,1 8,3 25,4 1430 159 7,51 89,8 114 22,8 2,12
20 21,0 200 100 5,2 8,4 26,8 1840 184 8,28 104 115 23,1 2,07
20а 22,7 200 ПО 5,2 8,6 28,9 2030 203 8,37 114 155 28,2 2,32
22 24,0 220 ПО 5,4 8,7 30,6 2550 232 9,13 131 157 28,6 2,27
Таблица 1 (продолжение)
Ki профилей Вес 1 пог. м, кг Размеры, мм Площадь сечения, см* Справочные величины для осей
Л ь а t X — X У—и
S* J,
см* СМ см* см* СМ* см
22а 25,8 220 120 5,4 8.9 32,8 2790 254 9,22 143 206 34,3 2,50
24 27,3 240 115 5,6 9,5 34,8 3460 289 9,97 163 198 34,5 2,37
24а 29,4 240 125 5,6 9,8 37,5 3800 317 10,1 178 260 41,6 2,63
27 31,5 270 125 6,0 9,8 40,2 5010 371 11,2 210 260 41,5 2,54
27а 33,9 270 135 6,0 10,2 43,2 5500 407 11,3 229 337 50,0 2,80
30 36,5 300 135 6,5 10,2 46,5 7080 472 12,3 268 337 49,9 2,69
30а 39,2 300 145 6,5 10,7 49,9 7780 518 12,5 292 436 60,1 2,95
33 42,2 330 140 7,0 11,2 53,8 9840 597 13,5 339 419 59,9 2,79
36 48,6 360 145 7,5 12,3 61,9 13 380 743 14,7 423 516 71,1 2,89
40 56,1 400 155 8,0 13,0 71,4 18 930 947 16,3 540 666 85,9 3,05
45 65,2 450 160 8,6 14,2 83,0 27 450 1220 18,2 699 807 101 3,12
50 76,8 500 170 9,5 15,2 97,8 39290 1570 20,0 905 1040 122 3,26
55 89,8 550 180 10,3 16,5 1'4 55 150 2000 22,0 1150 1350 150 3,44
60 104 600 190 11.1 17,8 132 75 450 2510 23,9 1450 1720 181 3,60
65 120 650 200 12,0 19,2 153 101 400 3120 25,8 1800 2170 217 3,77
70 138 700 210 13,0 20,8 176 134 600 3840 27,7 2230 2730 260 3,94
70а 158 700 210 15,0 24,0 202 152 700 4360 27,5 2550 3240 309 4,01
706 184 700 210 17,5 28,2 234 175 370 5010 27,4 2940 3910 373 4,09
Таблица 2. Швеллеры
№ профилен Вес 1 пае. м, IU Ризиеры, Ji.il Площадь сечения Справочные величины для осой г»
h ь а t JC — X у — У
Jx J Ч Wu
см' ем* ем* см ем* ем* см* СМ СМ
5 4,84 50 32 4,4 7,0 6,16 22,8 9,10 1,92 5,59 5,61 2,75 0,954 1,16
6,5 5^90 65 36 4,4 7.2 7,51 48,6 15,0 2,54 9,00 8,70 3,68 1,08 1,24
8 7,05 80 40 4,5 7,4 8,98 89,4 22,4 3,16 13,3 12,8 4,75 1,19 1,31
10 8'59 100 46 4,5 7,6 10,9 174 34,8 3,99 20,4 20,4 6,46 1,37 1,44
12 10,4 120 52 4,8 7,8 13,3 304 50,6 4,78 29,6 31,2 8,52 1,53 1,54
14 12,3 140 58 4,9 8,1 15,6 491 70,2 5,60 40,8 45,4 11,0 1,70 1,67
14а 13^3 140 62 4,9 8,7 17,0 545 77,8 5,66 45,1 57,5 13,3 1,84 1,87
16 14,2 160 64 5,0 8,4 18,1 747 93,4 6,42 54,1 63,3 13,8 1,87 1,80
16а 15,3 160 68 5,0 9,0 19,5 823 103 6,49 59,4 78,8 16,4 2,01 2,00
18 16,3 180 70 5,1 8,7 20,7 1090 121 7,24 69,8 86,0 17,0 2,04 1,94
18а 17,4 180 74 5,1 9,3 22,2 1190 132 7,32 76,1 105 20,0 2,18 2,13
20 18,4 200 76 5,2 9,0 23,4 1520 152 8,07 87,8 113 20,5 2,20 2,07
20а 19,8 200 80 5,2 9,7 25,2 1670 167 8,15 95,9 139 24,2 2,35 2,28
22 21,0 220 82 5,4 9,5 26,7 2110 192 8,89 НО 151 25,1 2,37 2,21
22а 22,6 220 87 5,4 10,2 28,8 2330 212 8,99 121 187 30,0 2,55 2,46
24 24 ;о 240 90 5,6 10,0 30,6 2900 242 9,73 139 208 31,6 2,60 2,42
24а 25,8 240 95 5,6 10,7 32,9 3180 265 9,84 151 254 37,2 2,78 2,67
27 27'7 270 95 6,0 10,5 35,2 4160 308 10,9 178 262 37,3 2,73 2,47
30 3U8 300 100 6,5 11,0 40,5 5810 387 12,0 224 327 43,6 2,84 2,52
33 36^5 330 105 7,0 11,7 46,5 7980 484 13,1 281 410 51,8 2,97 2,59
36 41,9 360 110 7,5 12,6 53,4 10 820 601 14,2 350 513 61,7 3,10 2,68
40 48,3 400 115 8,0 13,5 61,5 15 220 761 15,7 444 642 73,4 3,23 2,75
Таблица 3. Уголки равнобокие
№ профилей Размеры, мм Площадь профиля Вео. 1 пае. м Справочные величины для осей
Ь <1 « — д — »« — <» <1 “х» г.
J л макс '*0 макс 7ю МИН '»'о мин
СМ* кг см* СМ см* см см1 см см* см
2 20 3 4 1,13 1,46 0,89 1,15 0,40 0,50 0,59 0,58 0,63 0,78 0,75 0,73 0,17 0,22 0,39 0,38 0,81 1,09 0,60 0,64
2,5 25 3 4 1,43 1,86 1,12 1,46 0,81 1,03 0,75 0,74 1,29 1,62 0,95 0,93 0,34 0,44 0,49 0,48 1,57 2,11 0,73 0,76
2,8 26 3 1,62 1,27 1,16 0,85 1,84 1,07 0,48 0,55 2,20 0,80
3,2 32 3 4 1,86 2,43 1,46 1.91 1,77 2,26 0,97 0,96 2,80 3,58 1,23 1,21 0,74 0,94 0,63 0,62 3,26 4,39 0,89 0,94
3,6 36 3 4 2,10 2,75 1,65 2,16 2,56 3,29 1,10 1.09 4,06 5,21 1,39 1,38 1,06 1,36 0,71 0,70 4,64 6,24 0,99 1,04
Таблице 3 (продолжение)
422
№ профилей Размеры, мм Площадь профиля Вес 1 пог. м Справочные величины для осей
Ь d X—X х,-з, St-У» X,-*! г.
J ® •/®а макс '*0 макс Jvo МИН МИН J4
СМ1 кг см» СМ см* см см* см см* ем
3 2,35 1,85 3,55 1,23 5,63 1,55 1,47 0,79 6,35 1.09
4 3,08 2,42 4,58 1,22 7,26 1,53 1,90 0,78 8,53 1,13
3 2,65 2,08 5,13 1,39 8,13 1,75 2,12 0,89 9,04 1.21
4,5 45 4 3,48 2,73 6,63 1,38 10,5 1.74 2,74 0,89 12,1 1,26
5 4,29 3,37 8,03 1,37 12,7 1,72 3,33 0,88 15,3 1,30
3 2,96 2,32 7,11 1,55 11,3 1,95 2,95 1,00 12,4 1,33
5 50 4 3,89 3,05 9,21 1,54 14,6 1,94 3,80 0,99 16,6 1,38
5 4,80 3,77 11.2 1,53 17,8 1,92 4,63 0,98 20,9 1,42
3,5 3,86 3,03 11,6 1,73 18,4 2,18 4,80 1.12 20,3 1,50
5,6 56 4 4,38 3,44 13,1 1.73 20,8 2,18 5,41 1.U 23,3 1,52
5 5,41 4,25 16,0 1,72 25,4 2,16 6,59 1,10 29,2 1,57
4 4,96 3,90 18,9 1,95 29,9 2,45 7,81 1,25 33,1 1,69
6,3 63 5 6,13 4,81 23,1 1,94 36,6 2,44 9,52 1,25 41,5 1.74
6 7,28 5,72 27,1 1,93 42,9 2,43 11.2 1.24 50,0 1,78
4,5 6,20 4,87 29,0 2,16 46,0 2,72 12,0 1,39 51,0 1,88
5 6,86 5,38 31,9 2,16 50,7 2,72 13,2 1,39 56,7 1,90
7 70 6 8,15 6,39 37,6 2,15 59,6 2,71 15,5 1,38 68,4 1,94
7 9,42 7,39 43,0 2,14 68,2 2,69 17,8 1,37 80,1 1,99
8 10,7 8,37 48,2 2,13 76,4 2,68 20,0 1,37 91,9 2,02
Таблица 3 (продолжение)
423
№ профилей Размеры, мм Площадь профиля Вес 1 пае. м Справочные величины для осей
b а х-х г.
Jx <> J*o макс % макс J!'O МИН МИИ J*i
СМ: К. ем* СМ см* см ем* см СМ* СМ
5 7,39 5,80 39,5 2,31 62,6 2,91 16,4 1,49 69,6 2,02
6 8,78 6,89 46,6 2,30 73,9 2,90 19,3 1,48 83,9 2,06
7,5 75 7 Ю,1 7,96 53,3 2,29 84,6 2,89 22,1 1,48 98,3 2,10
8 11,5 9,02 59,8 2,28 94,9 2,87 24,8 1,47 113 2,15
9 12,8 Ю,1 66,1 2,27 105 2,86 27,5 1,46 127 2,18
5,5 8,63 6,78 52,7 2,47 83,6 3,11 21,8 1,59 ’ 93,2 2,17
6 9,38 7,36 57,0 2,47 90,4 3,11 23,5 1,58 102 2,19
8 80 7 10,8 8,51 65,3 2,45 104 3,09 27,0 1,58 119 2,23
8 12,3 9,65 73,4 2,44 116 3,08 30,3 1,57 137 2,27
(5 10,6 8,33 82,1 2,78 130 3,50 34,0 1,79 145 2,43
7 12,3 9,64 94,3 2,77 150 3,49 38,9 1,78 169 2,47
У уи 8 13,9 10,9 106 2,76 168 3,48 43,8 1,77 194 2,51
9 15,6 12,2 118 2,75 186 3,46 48,6 1,77 219 2,55
6,5 12,8 10,1 122 3,09 193 3,88 50,7 1,99 214 2,68
7 13,8 10,8 131 3,08 207 3,88 54,2 1,98 231 2,71
8 15,6 12,2 147 3,07 233 3,87 60,9 1,98 265 2,75
10 100 10 19,2 15,1 179 3,05 284 3,84 74,1 1,96 333 2,83
12 22,8 17,9 209 3,03 331 3,81 86,9 1,95 402 2,91
14 26,3 20,6 237 3,00 375 3,78 99,3 1,94 472 2,99
16 29,7 23,3 264 2,98 416 3,74 112 1,94 542 3,06
424-
Таблица 3 (продолжение)
№ профилей Размеры, мм Площадь профиля Вес 1 пол. м Справочные величины для осей
Ь d JC-Л я,-хв Pt- и» z.
•/ ® макс макс мни МИИ
ем' кг см* см ЛК4 см см* ем CM* CM
НО 7 15,2 11,9 176 3,40 279 4,29 72,7 2,19 308 2,96
11 8 17,2 13,5 198 3,39 315 4,28 81,8 2,18 353 3,00
8 19,7 15,5 294 3,87 467 4,87 122 2,49 516 3,36
9 22,0 17,3 327 3,86 520 4,86 135 2,48 582 3,40
12,5 125 10 24,3 19,1 360 3,85 571 4,84 149 2,47 649 3,45
12 28,9 22,7 422 3,82 670 4,82 174 2,46 782 3,53
14 33,4 26,2 482 3,80 764 4,78 200 2,45 916 3,61
16 37,8 29,6 539 3,78 853 4,75 224 2,44 1051 3,68
9 24,7 19,4 466 4,34 739 5,47 192 2,79 818 3,78
14 140 10 27,3 21,5 512 4,33 814 5,46 211 2,78 911 3,82
12 32,5 25,5 602 4,31 957 5,43 248 2,76 1097 3,90
10 31,4 24,7 774 4,96 1229 6,25 319 3,19 1356 4,30
11 34,4 27,0 844 4,95 1341 6,24 348 3,18 1494 4,35
12 37,4 29,4 913 4,94 1450 6,23 376 3,17 1633 4,39
16 160 14 43,3 34,0 1046 4,92 1662 6,20 431 3,16 1911 4,47
16 49,1 38,5 1175 4,89 1866 6,17 485 3,14 2191 4,55
18 54,8 43,0 1299 4,87 2061 6,13 537 3,13 2472 4,63
20 60,4 47,4 1419 4,85 2248 6,10 589 3,12 2756 4,70
Табляца 3 (продолжение)
№ про-филей Размеры, мм Площадь профиля Вес 1 пог, м Справочные величины для осей
b d X — X *0—«0 !Л>-(С Х,-Х, Z,
МАКС макс Jvo мин '»о МЛН ,/®i
СМ9 кг см* см ел* ем см* см см* ем
11 38,8 30,5 1216 5,60 1933 7,06 500 3,59 2128 4,85
18 1OU 12 42,2 33,1 1317 5,59 2093 7,04 540 3,58 2324 4,89
12 47,1 37,0 1823 6,22 2896 7,84 749 3,99 3182 5,37
13 50,9 39,9 1961 6,21 3116 7,83 805 3,98 3452 5,42
14 54,6 42,8 2097 6,20 3333 7,81 861*- 3,97 3722 5,46
20 200 16 62,0 48,7 2363 6,17 3755 7,78 970 3,96 4264 5,54
20 76,5 60,1 2871 6,12 4560 7,72 1182 3,93 5355 5,70
25 94,3 74,0 3466 6,06 5494 7,63 1438 3,91 6733 5,89
30 111,5 87,6 4020 6,00 6351 7,55 1688 3,89 8130 6,07
ООП 14 60,4 47,4 2814 6,83 4470 8,60 1159 4,38 4941 5,93
16 68,6 53,8 3175 6,81 5045 8,58 1306 4,36 5661 6,02
16 78,4 61,5 4717 7,76 7492 9,78 1942 4,98 8286 6,75
18 87,7 68,9 5247 7,73 8337 9,75 2158 4,96 9342 6,83
20 97,0 76,1 5765 7,71 9160 9,72 2370 4,94 10 401 6,91
25 250 22 106,1 83,3 6270 7,69 9961 9,69 2579 4,93 11 464 7,00
25 119,7 94,0 7006 7,65 11 125 9,64 2887 4,91 13 064 7,11
28 133,1 104,5 7717 7,61 12 244 9,59 3190 4,89 14 674 7,23
30 142,0 111,4 8177 7,59 12 965 9.56 3389 4,89 15 753 7,31
Таблица 4. Уголки неравнобокне
№ про-филеВ Размеры, мм Площадь профиля Вес 1 пог.м Справочные величины дЛя осей
В ь d х—х у—и X1-JT1 У1-»1 и — и
J* Jv <у Расстояние от центра тяжести 4/в МИИ Расстояние от центра тяжести х® JII мни МИИ Угол наклона оси tg а
см1 кг ем* СМ СМ* СМ CM* см см* см ем* см
2,5/1,6 25 16 3 1,16 0,91 0,70 0,78 0,22 0,44 1,56 0,86 0,43 0,42 0,13 0,34 0,392
3,2/2 32 20 3 1,49 1,17 1,52 1.01 0,46 0,55 3,26 1,08 0,82 0,49 0,28 0,43 0,382
4 1,94 1,52 1,93 1,00 0,57 0,54 4,38 1,12 1.12 0,53 0,35 0,43 0,374
4/2,5 40 25 3 4 1,89 2,47 1,48 1,94 3,06 3,93 1,27 1,26 0,93 1,18 0,70 0,69 6,37 8,53 1,32 1,37 1,58 2,15 0,59 0,63 0,56 0,71 0,54 0,54 0,385 0,381
4,5/2,8 45 28 3 4 2,14 2,80 1,68 2,20 4,41 5,68 1,43 1,42 1,32 1.69 0,79 0,78 9,02 12,1 1,47 1,51 2,20 2,98 0,64 0,68 0,79 1,02 0,61 0,60 0,382 0,379
Таблица 4 (продолжение)
Размеры. ИЛ( Справочные величины для осей
Пло- X- - X У- ~У - х. У -Vi и — и
№ профилей в ь d щадь профиля Вес 1 пог. м Jx ix Jv '.V J*i Расстояние от центра тяжести Уь Jv\ МИН Расстояние от центра тяжести •^в мин гв мин Угол наклона осн tg а
см* кг ем* см см* ем СМ* см см* ем см* см
5/3,2 50 32 3 4 2.42 3,17 1,90 2,49 6,17 7,98 1,60 1,59 1,99 2,56 0,91 0,90 12,4 16,6 1,60 1,65 3,26 4,42 0,72 0,76 1,18 1,52 0,70 0,69 0,403 0,401
5,6/3,6 56 36 3,5 4 5 3,16 3,58 4,41 2,48 2,81 3,46 10,1 Н.4 13,8 1,79 1,78 1.77 3,30 3,70 4,48 1,02 1,02 1,01 20,3 23,2 29,2 1,80 1,82 1,86 5,43 6,25 7,91 0,82 0,84 0,88 1,95 2,19 2,66 0,79 0,78 0,78 0,407 0,406 0,404
6,3/4,0 63 40 4 5 6 8 4,04 4,98 5,90 7,68 3,17 3,91 4,63 6,03 16,3 19,9 23,3 29,6 2,01 2,00 1,99 1,96 5,16 6,26 7,28 9,15 1,13 1,12 1.11 1,09 33,0 41,4 49,9 66,9 2,03 2,08 2,12 2,20 8,51 10,8 13,1 17,9 0,91 0,95 0,99 1,07 3,07 3,73 4,36 5,58 0,87 0,86 0,86 0,85 0,397 0,396 0,393 0,386
7/4,5 70 45 4,5 5 5,07 5,59 3,98 4,39 25,3 27,8 2,23 2,23 8,25 9,05 1,28 1,27 51 56,7 2,25 2,28 13,6 15,2 1,03 1,05 4,88 5,34 0,98 0,98 0,407 0,406
7,5/5 75 50 5 6 8 6,11 7,25 9.47 4,79 5,69 7,43 34,8 40,9 52,4 2,39 2,38 2,35 12,5 14,6 18,5 1,43 1.42 1,40 69,7 83,9 112 2,39 2,44 2,52 20,8 25,2 34,2 1.17 1.21 1,29 7,24 8,48 10,9 1,09 1,08 1,07 0,436 0,435 0,430
8/5 80 50 5 6 6,36 7,55 4,99 5,92 41\6 49,0 2,56 2,55 12,7 14,8 1.41 1,40 84,6 102 2,6 2,65 20,8 25,2 1,13 1.17 7,58 8,88 1,09 1,08 0,387 0,386
Продолжение табл. 4
№ профилей Размеры, мм Площадь профиля Вес 1 пог.м * Справочные величины для осеЛ
В » d X — X У— у Х1 — X, V1 — V1 и — и
J-t <« Jn '.V Расстояние от центра тяжести у9 JV1 МНН Расстояние от центра тяжести г0 X эх > 5 X Угол наклона ОСЯ tg а
см1 W CM* см ем* с,и вм* см ем4 ем см> см
5,5 7,86 6,17 65,3 2,88 19,7 1,58 132 2,92 32,2 1,26 11,8 1,22 0,384
9/5,6 90 56 6 8,54 о,70 70,6 2,88 21,2 1,58 145 2,95 35,2 1,28 12,7 1,22 0,384
8 11,18 8,77 90,9 2,85 27.1 1,56 194 3,04 47,8 1,36 16,3 1.21 0,380
6 9,59 1,53 98,3 3,2 30,6 1,79 198 3,23 49,9 1,42 18,2 1,38 0,393
10/6,3 7 11.1 8,70 113 3,19 35,0 1,78 232 3,28 58,7 1,46 20,8 1,37 0,392
1UU 8 12,6 9,87 127 3,18 39,2 1,77 266 3,32 67,6 1,50 23,4 1,36 0,391
10 15,5 12,1 154 3,15 47.1 1,75 333 3,40 85,8 1,58 28,3 1,35 0,387
6,5 Н.4 8,98 142 3,53 45,6 2 286 3,55 74,3 1,58 26,9 1,53 0,402
11/7 но 70 7 12,3 9,64 152 3,52 48,7 1,99 309 3,57 80,3 1,6 28,8 1,53 0,402
8 13,9 10,9 172 3,51 54,6 1,98 353 3,61 92,3 1,64 32,3 1,52 0,400
7 14,1 11 227 4,01 73,7 2,29 452 4,01 119 1,8 43,4 1,76 0,407
12,5/8 8 16 12,5 256 4 83,0 2,28 518 4,05 137 1,84 48,8 1,75 0,406
]2о во 10 19,7 15,5 312 3,98 100 2,26 649 4,14 173 1,92 59,3 1.74 0,404
12 23,4 18,3 365 3,95 117 2,24 781 4,22 210 2 69,5 1.72 0,400
14/9 8 18 14,1 364 4,49 120 2,58 727 4,49 194 2,03 70,3 1,98 0,411
14и ъи 10 22,2 17,5 444 4,47 146 2,56 911 4,58 245 2.12 85,5 1,96 0,409
Продолжение табл. 4
№ профилей Размеры, мм Площадь профиля Вес 1 пог.м Справочные величины для осей
В ь d Х — Х У- У Xi — У1 -у, и — и
J у Расстояние от центра тяжести j/0 Расстояние от центра тяжести Jt0 Z 35 > Я Угол наклона осп tg а
ел’ кг см* ем см* СМ см* ем СМ* ем СМ* ем
9 22,9 18 606 5,15 186 2,85 1221 5,19 300 2,23 по 2,2 0,391
16/10 160 100 10 25,3 19,8 667 5,13 204 2,84 1359 5,23 335 2,28 121 2,19 0,390
12 30 23,6 784 5,П 239 2,82 1634 5,32 405 2,36 142 2,18 0,388
14 34,7 27,3 897 5,08 272 2,8 1910 5,40 477 2,43 162 2,16 0,385
18/11 180 ПО 10 28,3 22,2 952 5,8 276 3,12 1933 5,88 444 2,44 165 2,42 0,375
12 33,7 26,4 1123 5,77 324 3,1 2324 5,97 537 2,52 194 2,40 0,374
11 34,9 27,4 1449 6.45 448 3,58 2920 6,5 718 2,79 254 2,75 0,392
20/12,5 200 125 12 37,9 29,7 1568 6,43 482 3,57 3189 6,54 786 2,83 285 2,74 0,392
14 43,9 34,4 1801 6,41 551 3,54 3726 6,62 922 2,91 327 2,73 0,390
16 49,8 39,1 2026 6,38 617 3,52 4264 6,71 1061 2,99 367 2,72 0,388
12 48,3 37,9 3147 8,07 1032 4,62 С212 7,97 1634 3,53 604 3,54 0,410
25/16 250 160 16 63.6 49,9 4091 8,02 1333 4,58 8308 8,14 2200 3,69 781 3,50 0,408
18 71,1 55,8 4545 7,99 1475 4,56 4358 8,23 2487 3,77 866 3,49 0,407
20 78,5 61,7 4987 7,97 1613 4,53 10410 8,31 2776 3,85 949 3,48. 0,405
4УУВ1₽'|*явв®^
Таблица 5. Секториальные геометрические характеристики прокатных двутавров (ОСТ 10016—39)
№ профиля Се кто риал ь-иыП момент инерции /<0. Секторналь-ная площадь для крайней точки профиля е'тах, см* Секторналь-и ый момент сопротивлении UZf0, см* Момент инерции прн чистом кручении 7н’ см* Упругая изгиб-но-крутнльная характеристниа Q=l/
10 644,3 15,25 42,26 2,873 0,04122
12 1 353 20,10 67.33 4,243 0,03457
14 2 560 25.54 100,23 5,911 0,02966
16 4 879 32,25 161.30 8,406 0,02562
18 8 219 38,90 211,28 11,37 0.02295
20" 13 121 46,15 284,31 14,81 0.02074
13 857 47,05 294.50 17,85 0,02215
22" 22 773 55,91 407,33 20,32 0.01844
23 930 56,90 420,55 24,08 0.01958
24° 33 799 64,48 524,15 25,57 0,01698
с 35 426 65,57 540.25 30.12 0,01800
27° 52 987 76,68 690,99 31 ,93 0,01515
г76 55 414 77.92 711,21 37,60 0,01608
а 76 704 88,38 867,93 38,83 0.01389
306 80 114 89,75 892.60 45,78 0,01475
с 83 612 91.13 917,50 55,23 0,01587
о 107 160 100.69 1064,3 46, 19 0,01281
ззь 111 780 102,21 1093.6 54,49 0,01363
с 116 520 103.73 1123.3 65.74 0.01466
а 154 820 115, 19 1344,0 56.85 0,01183
366 161 210 116.85 1379,6 66,72 0,01256
с 167 760 118.51 1415.6 79,99 0.01348
а 228 900 134,13 1706.6 68,75 0.01070
406 237 950 136 00 1749.6 80,68 0,01137
С 247 210 137.85 1793.3 96.55 0,01220
а 376 630 159.75 2357.6 95,31 0.009819
456 390 770 161,86 2414,4 HI ,3 0,01041
С 405 220 163.96 2471.5 131.8 0,01113
а 61 1 990 187.10 3270,9 131,2 0,009038
506 633 900 189,44 3346.2 150,3 0,009504
С 656 270 191.79 3421.8 174,9 0.01007
о 906 350 216,79 4180.8 159,9 0,008198
556 937 220 219,36 4272.5 182,7 0,008617
С 968 720 221,94 4364.8 211,5 0,009119
а 1 349 900 251,22 6373,4 195,6 0.007427
606 1 393 200 254,04 5484.2 221,9 0,007790
с 1 437 300 256.86 5595.7 255,3 0,008226
| Е=2 К П р и ы е ч а )0 000 кг/см*. н и е. При вычислении z принято: С = 800 000 ке/см*;
430
Таблица 6. Секториальиые геометрические характеристики прокатных швеллеров (ОСТ 10017—30)
№ профиля Координата центра изгиба ха. см Секторн-альныП момент инерции J .см* U) Секториальиые площади Секториальиые моменты сопротивления Момент инерции при чистом кручении J*. см* Упругая на-гнбно-кру-тнльпая характеристика 1/CJH а= V ЯГ-он-’
см* С1)я. см* «Ч-см* см*
5 1,08 24.91 2.70 4.26 9.22 5,85 1.350 0,1437
в.5 1,15 64.88 3.86 6.36 16.80 10.21 1.497 0.09375
8 1.22 141.8 5.15 8.75 27.57 16.20 1.940 0,07219
10 1.34 354.8 7.19 12.71 49.35 27.92 2,727 0.05411
12 1 .48 768.3 9.54 17.31 80.51 44.39 3.634 0.04245
14° 1 .58 1 512 12.03 22.63 125.74 66.85 4.815 0.03483
1.39 I 711 11,46 23.85 149,32 71.75 6,248 0.03730
16? 1.68 2 760 14.74 28.63 187,23 96,40 6.306 0,02950
1.48 3 099 14.03 30.09 220.87 103.00 8.227 0 03180
ISfc 1.83 4 745 17.68 35.32 268.41 134.34 8,128 0,02555
1.57 б 292 16.83 37,02 314,50 142.95 10.50 0.02749
20? 1 .94 7 698 21.27 42.46 361,95 181,28 9.84 0.02207
1.73 8 560 20.24 44.45 422.87 192,57 12.50 0.02359
2.07 11 593 24.84 23,63 49.60 466.69 233.73 11.66 0.01958
1 ,86 12 863 51.88 544.42 247.15 14.60 0.02079
а 2.10 15 326 27.48 55.21 557.74 277.59 13,21 0,01812
246 1.88 17 007 26.10 57,75 651,56 294,50 16,47 0,01921
С 1.67 18 640 24.91 60.09 748.35 310,21 21.31 0.02087
а 2.14 24 337 31 85 66.46 764,11 366,19 16.25 0.01595
276 1.91 26 883 30,23 69.39 889,34 387,42 20,34 0.01698
С 1.70 29 355 28.82 72.10 1018.6 407,14 26.34 0.01848
а 2.26 36 645 37.21 76.54 984.87 478,78 20.39 0,01456
306 2.03 40 436 35.23 79.98 1147,8 505.61 25.01 0,01535
с 1.80 44 104 33.59 83,06 1313.0 530.97 31.75 0.01656
а 2.25 52 630 41.39 88,54 1271,7 594,43 24.29 0,01326
336 2.02 57 844 39,27 92,27 1473.2 626,93 29.92 0,01404
с 1.80 62 890 37,44 95,69 1679,8 657,23 38.04 0,01518
а 2.47 92 189 49.50 104,55 1862.2 881.77 38.91 0.01268
366 2.24 100 430 47,30 108,51 2123,4 925,54 46.56 0.01329
с 2.02 108 420 45,36 112.18 2390.2 966,48 57,18 0.01417
а 2.43 148 100 55,78 121.67 2655,1 1217.2 59.74 0.01240
406 2.21 160 100 53.51 125.86 2991,7 1272.1 70,78 0.01298
С 2.00 171 870 51.51 129,80 3336.4 1324.0 85.72 0.01378
Е = 2 При ыечанн 100 000 кг/см*. е При вычислении а принято : 6=800 000 т/см*;
431
Таблица 7. Коэффициенты ф
Г нбкость Значения ф для
стали марок 4 3. 2, ОС стали (MapKH стали СПК 1угуиа дерева
0 1,00 1,00 1,00 1,00 1,00
10 0,99 0,98 0,97 0,97 0,99
20 0,96 0,95 0,95 0,91 0,97
30 0,94 0,92 0,91 0,81 0,93
40 0,92 0,89 0,87 0,69 0,87
50 0,89 0,86 0,83 0,57 0,80
60 0,86 0,82 0,79 0,44 0,71
70 0,81 0,76 0,72 0,34 0,60
80 0,75 0,70 0,65 0,26 0,48
90 0,69 0,62 0,55 0,20 0,38
100 0,60 0,51 0.43 0,16 0,31
ПО 0,52 0,43 0,35 — 0,25
120 0,45 0,36 0,30 — 0,22
130 0,40 0,33 0,26 — 0,18
140 0,36 0,29 0,23 — 0,16
150 0,32 0,26 0,21 0,14
160 0,29 0,24 0,19 — 0,12
170 0,26 0,21 0,17 — 0,11
180 0,23 0,19 0,15 —- 0,10
190 0,21 0,17 0,14 — 0,09
200 0,19 0,16 0,13 — 0,08
432