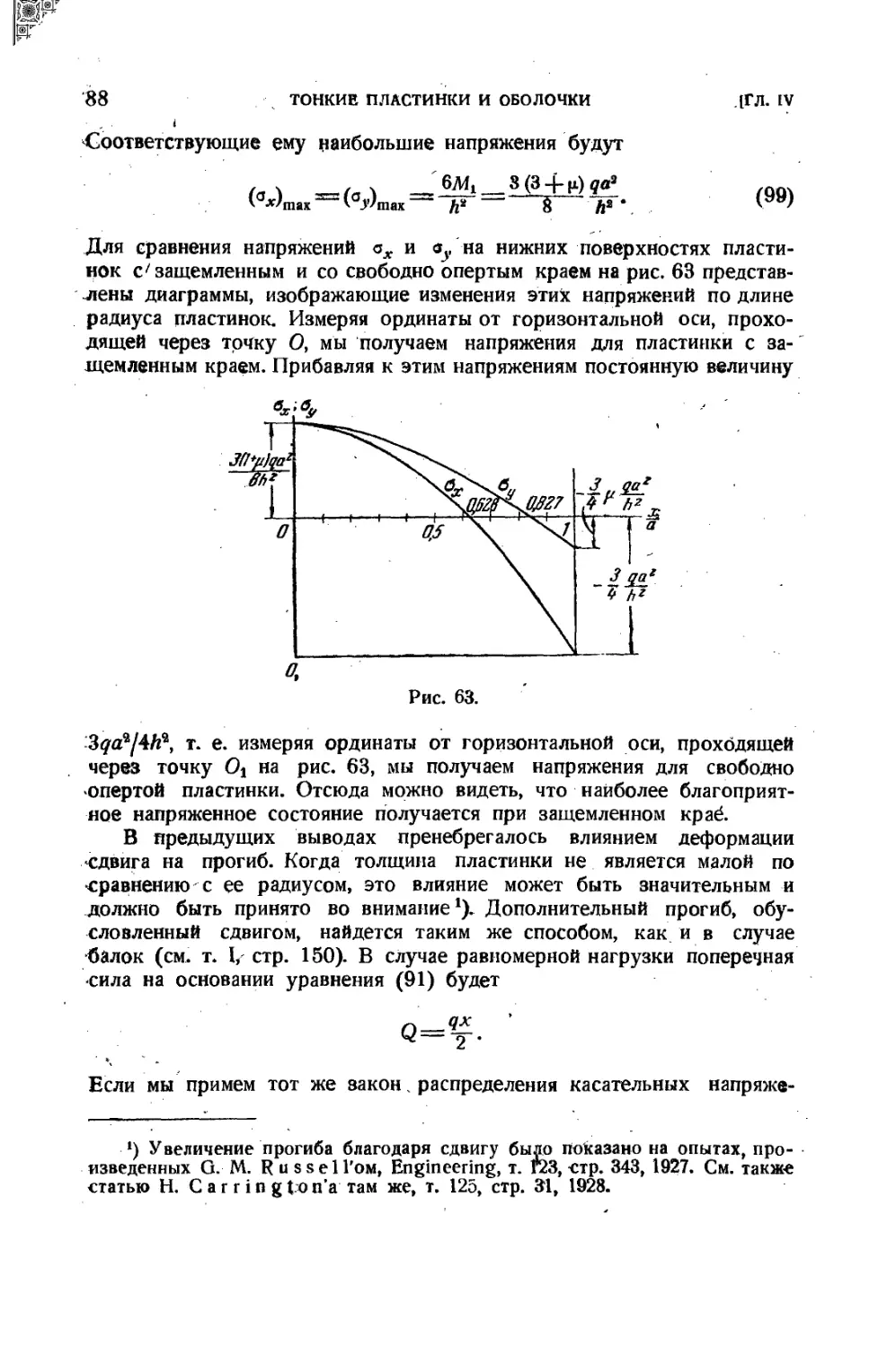
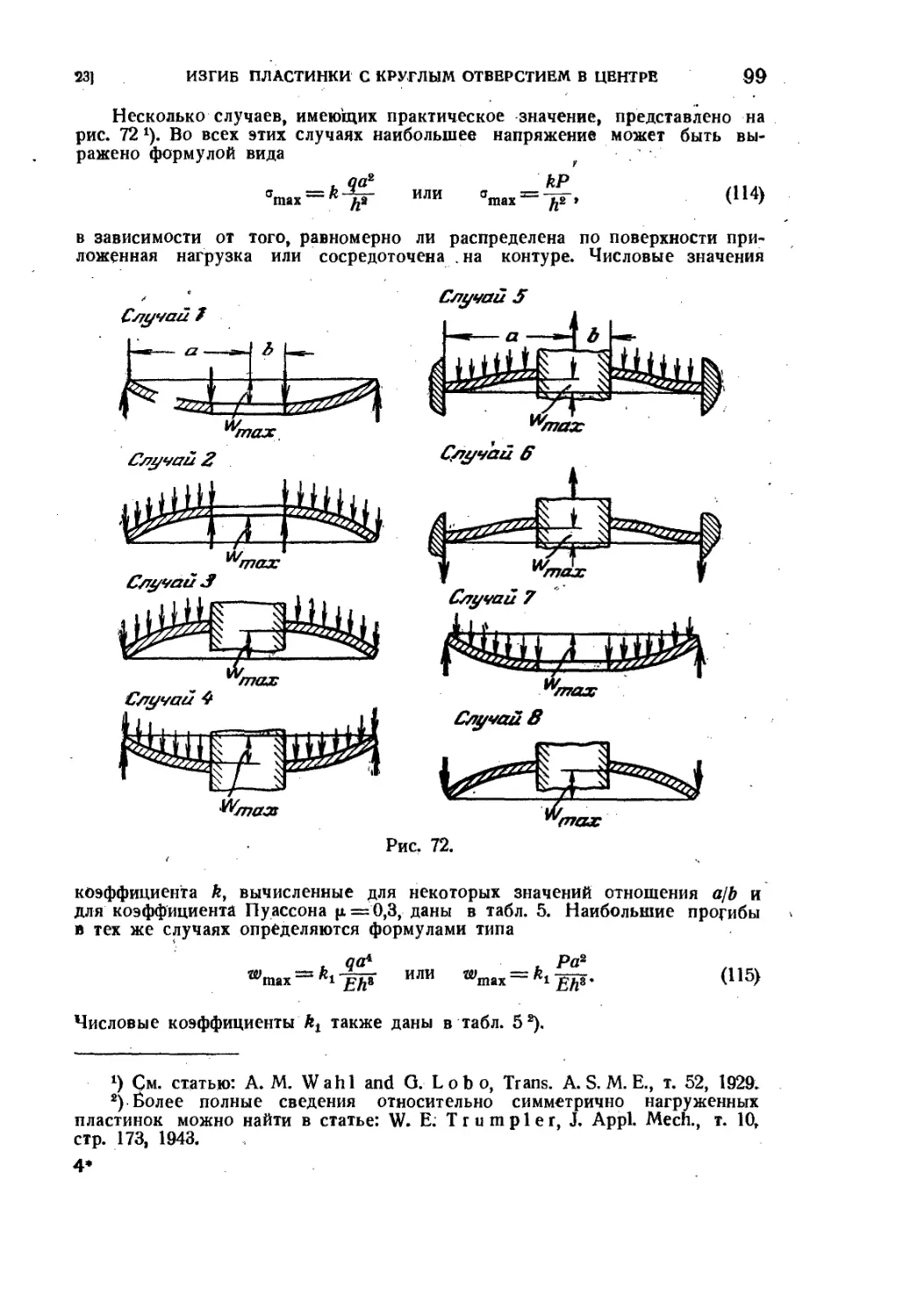
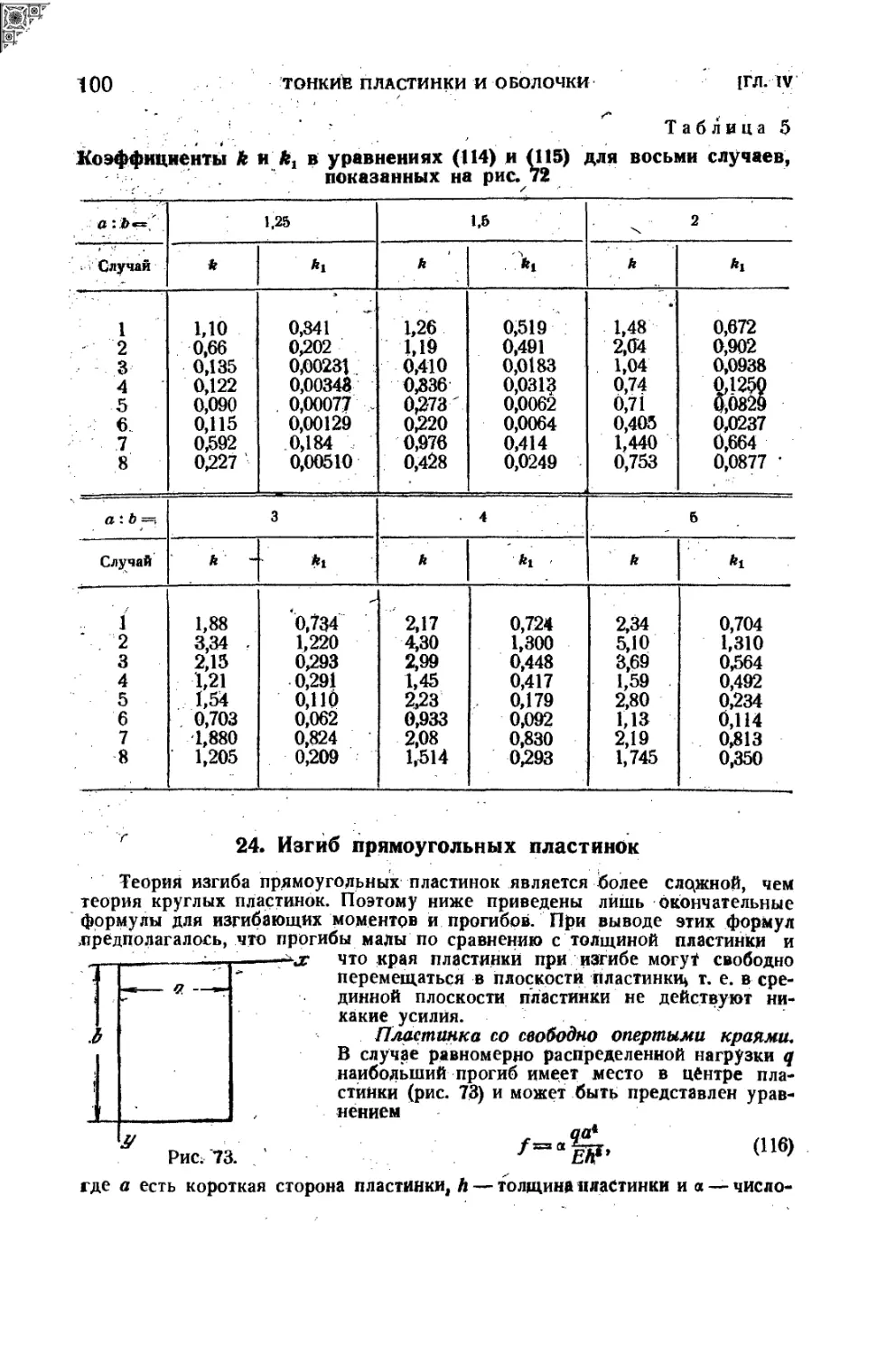
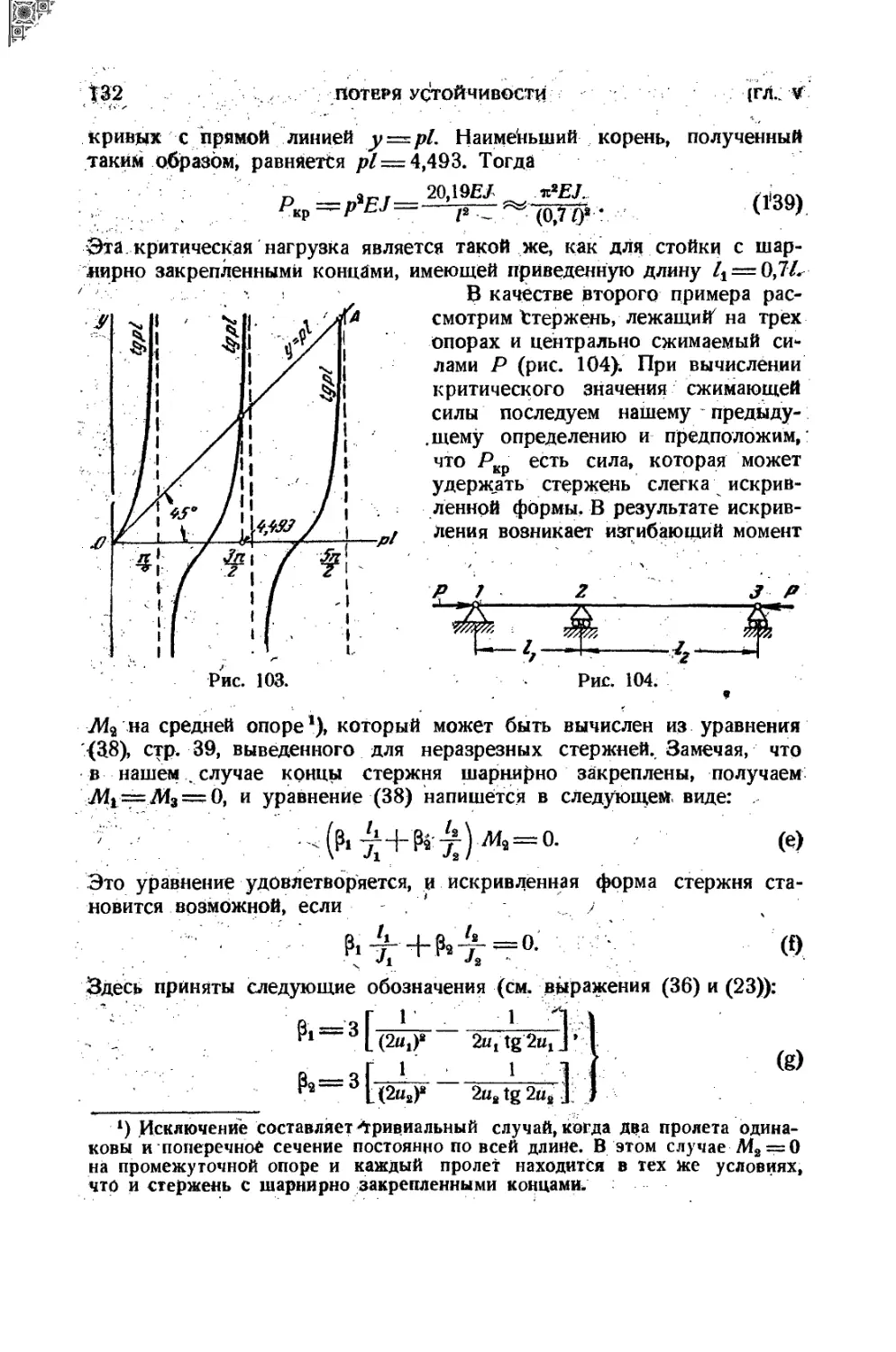
Текст
с. п. ТИМОШЕНКО
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
ТОМ ВТОРОЙ
БОЛЕЕ СЛОЖНЫЕ ВОПРОСЫ
ТЕОРИИ И ЗАДАЧИ
. ПЕРЕВОД В. Н. ФЕДОРОВА
С ТРЕТЬЕГО АМЕРИКАНСКОГО ИЗДАНИЯ
ПОД РЕДАКЦИЕЙ И. К. С Н И Т К О
ИЗДАТЕЛЬСТВО <НАУКА>
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1965
II f^^^Tgl'
6.05
Т 39
УДК 620.10
STRENGTH OF MATERIALS
PART ir
ADVANCED THEORY
AND PROBLEMS
by
S. TIMOSHENKO
Professor Emeritus of Engineering Mechanics
Stanford University
THIRD EDITION
D. VAN NOSTRAND COMPANY, INC. '
PRINCETON, NEW JERSEY
TORONTO LONDON
NEW YORK
Техн. редактор И.
Степан Прокофьевич Тимошенко
Сопротивление материалов, т. И
М., 1965 г., 480 стр. с илл.
Редактор Я. К Снитко
Ш. Аксеаьрод
Корректор О. А. Сигал
Сдано в набор 12А' 1965 г. Подписано к печати 8/IX 1965 г. Бумага 60X90Vie Физ печ
л. 30. Условн. печ. л. 30. Уч.-изд. л. 29,73. Тираж 37 500 экз. Цена книги 99 коп
Заказ № 1721
Издательство «Наука»
Главная редакция физико-математической литературы
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография № i «Печатный Двор» имеий А. М. Горького «ГлавполигоаЛ-
прома» Государственного комитета Совета Министров СССР по печати, ГатчинскаяГ 26,
ОГЛАВЛЕНИЕ
Из предисловия к первому американскому изданию 6
Предисловие ко второму американскому изданию 8
Предисловие к третьему американскому изданию 9
Глава I. Балки на упругом основании 11
\. Балки неограниченной длины И
2. Полубесконечные балки 20
3. Балки конечной длины на упругом основании 23
Глава II. Балки, подверженные одновременному действию
осевых^ и поперечных нагрузок , 30
4. Одновременное действие осевых сжимающих и поперечных
нагрузок 30
5. Неразрезные сжатые стержни 38
^. Растянутый стержень с поперечной нагрузкой 41
7. Представление кривой изгиба тригонометрическим рядом 45
8. Прогиб б()усьев с малой начальной кривизной 51
Глава III. Особые задачи при изгибе балок.... ^... 54.
9. Местные напряжения при изгибе балок 54
10. Касательные напряжения в балках переменного поперечного
сечения 58
И. Полезная ширина тонких полок 60
12. Ограничения метода наложения 64
Глава IV. Тонкие пластинки и оболочки , . . 69
13. Изгиб пластинки по цилиндрической поверхности 6Э
14. Изгиб длинной, равномерно нагруженной прямоугольной
пластинки 71
15. Изгиб длиннь|х прямоугольных пя;астин©к, имеющих
первоначальную малую цилиндрическую кривизну 76
16. Чистый изгиб в двух перпендикулярных направлениях 77
17. Температурные напряжения в пластинках 81
18. Изгиб круглых пластинок, нагруженных симметрично
относительно центра 82
19. Изгиб равномерно нагруженной круглой пластинки ......... 85
20. Изгиб круглых пластинок переменной толщины .. J ....... . 90
21. Изгиб круглой пластинки, нагруженной в центре , , . „ ^ » . . . . 92
22. Изгиб круглой пластинки, нагруженной концентрически...... 94
28. Изгиб симметрично нагруженной круглой пластинки с круглым
отверстием в центре 96
1*
^^^'^^Лш^
4 ОГЛАВДЕНИЕ
24. Изгиб прямоугольных пластинок . 100
25. Тонкостенные сосуды, подверЛкенные внутреннему давлению . . ЮЗ
26. Местные напряжения изгиба в тонкостенных сосудах 108
27. Температурные напряжения в цилиндрических оболочках 115
28. Кручение круглого Кольца под действием моментов, равномерно
распределенных по его оси . 117
Глава V. Потеря устойчивости стержней, пластинок и оболочек 124
29. Продольный изгиб призматических стержней (простые случаи). , 124
30. Продольный изгиб призматических стержней (более сложные
случаи) ..... ^ ............ 131
31. Энергетический метод определения критических сжимающих
нагрузок • 137
32. Продольный изгиб призматических стержней под действием
равномерно распределенных осевых сил . . . 141
83. Продольный изгиб стержней переменного поперечного сечения 143
34. Влияние поперечной силы на величину критической нагрузки. . 145
35. Продольный иэгиб составных стержней . , 146
36. Неупругий продольный изгиб прямолинейных колонн 150
31. Устойчивость круглых колец и труб под действием внешнего
давления ................... . 156
38. Устойчивость прямоугольных пластинок ■ 162
39. Выпучивание балок, не имеющих боковых опор 167
if л аГв а VI. Деформации, симметричные относительно оси 173
40. Толстостенный цилиндр 173
41. Напряжения, вызываемые горячей посадкой 177
4^. Вращающийся диск йостояиной толщины 180
43., Вращающийся диск переменной толщины 187
44. Температурные напряжения в длинном полом цилиндре...... 191
fr-пЖА а VII. Кручение . 196
4ё. Валы некругового поперечного сечения 196
46. Мембранная аналогия 198
47. Кручение прокатных профилей 204
48. Кручение тонкостенных трубчатых стержней . . 206
49. Кру^чение тонкостенных стержней открытого профиля, в
которых предотвращено искажение некоторых поперечных сечений 212
50. Совместный изгиб и кручение тонкостенных стержней открытого
профиля . .... 222
51. Крутильная форма потери устойчивости тонкостенных стержней
открытого профиля 227
52. Потеря устойчивости тонкостенных стержней открытого профиля
от одновременного действия изгиба и кручения \ 231
53. Продольные нормальные напряжения в скручиваемых стержнях 237
54. Цилиндрическая пружина с большим шагом витка 241
Глава VIII. Концентрация напряжений . . ..... 248
55. Концентрация напряжений в растянутых или сжатых элементах 248
56. Напряжения в пластинке с круглым отверстием 249
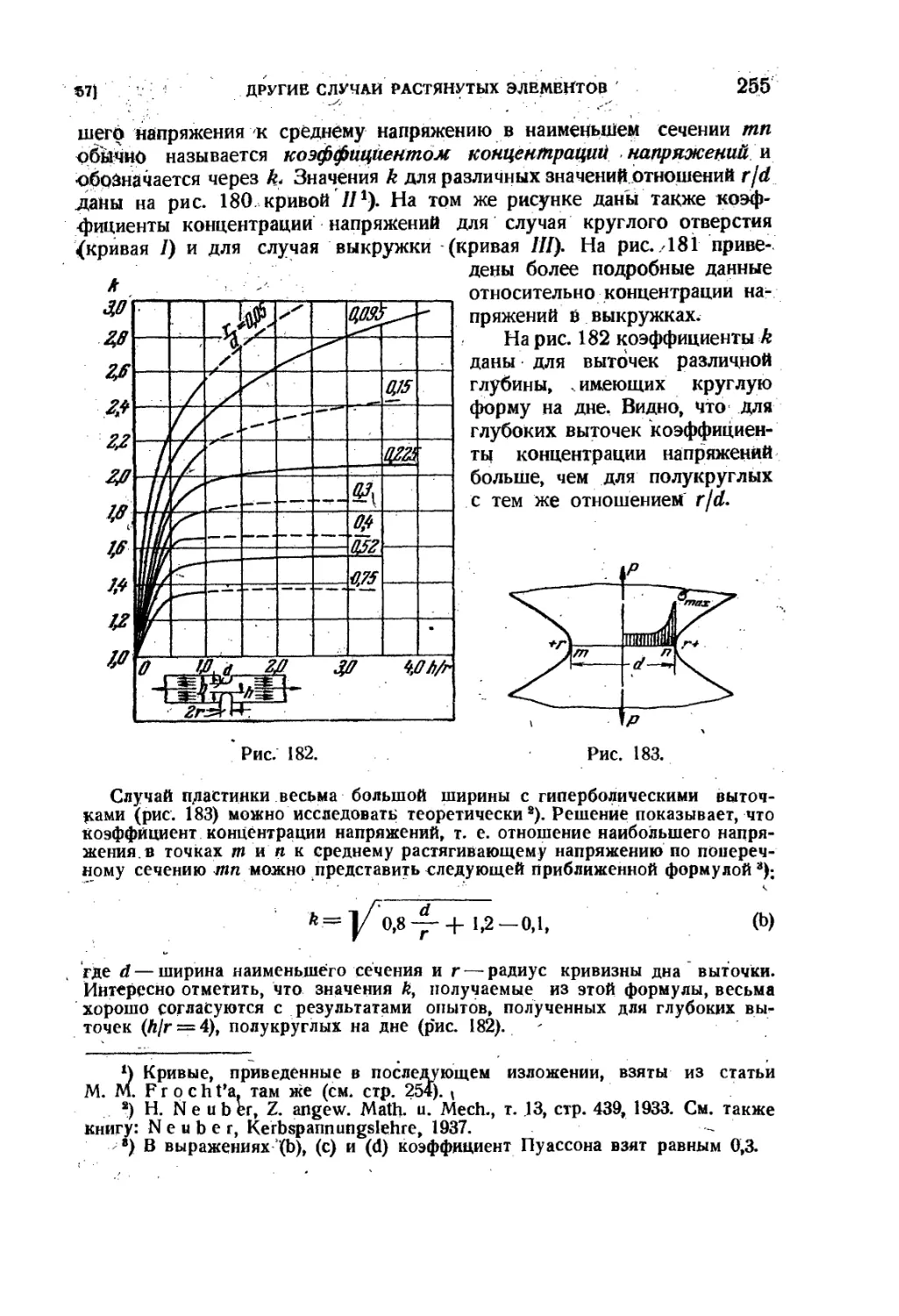
57. Другие случаи концентрации напряжений в'растявутых элементах 253
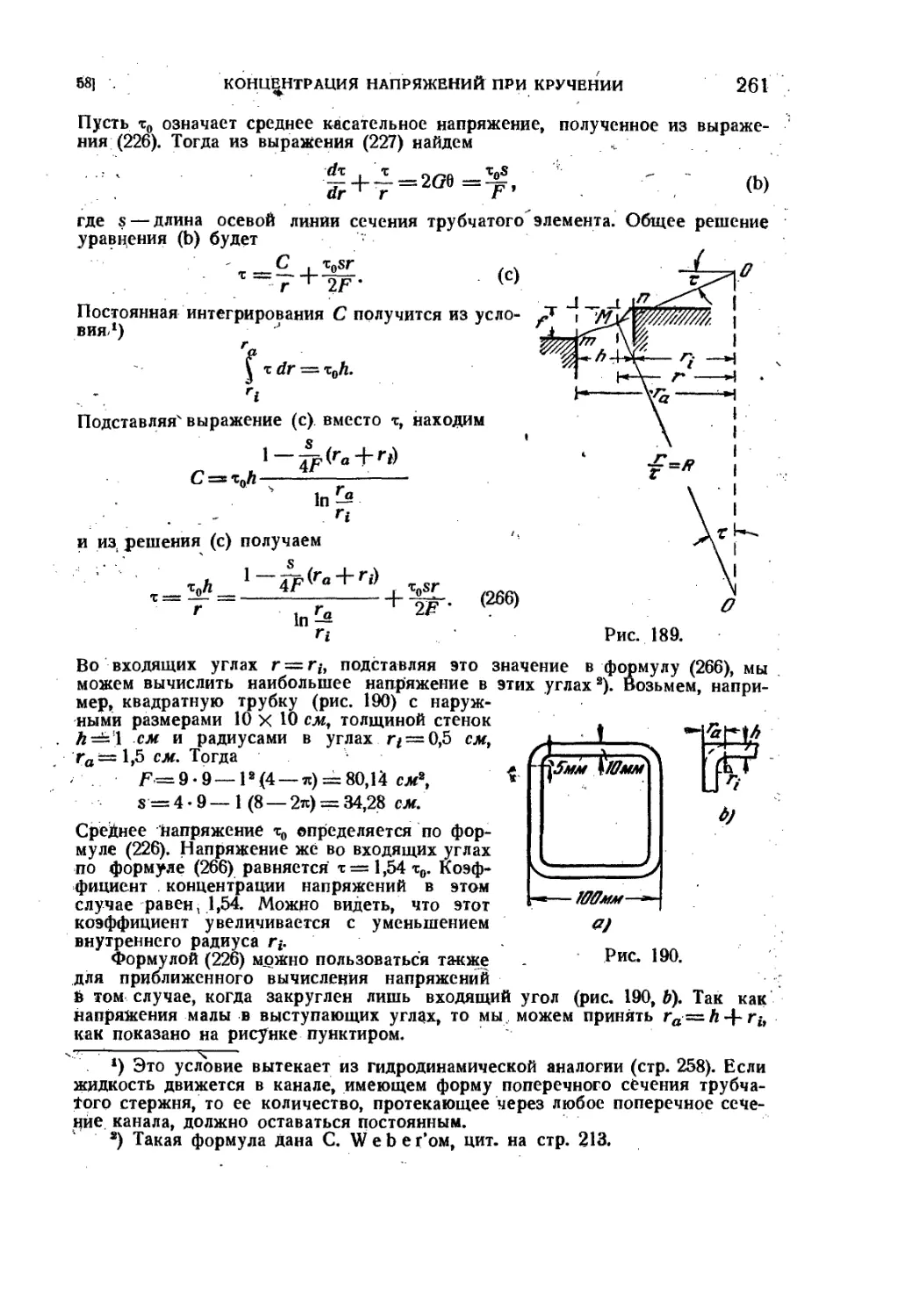
58. Концентрация напряжений при кручении . 258
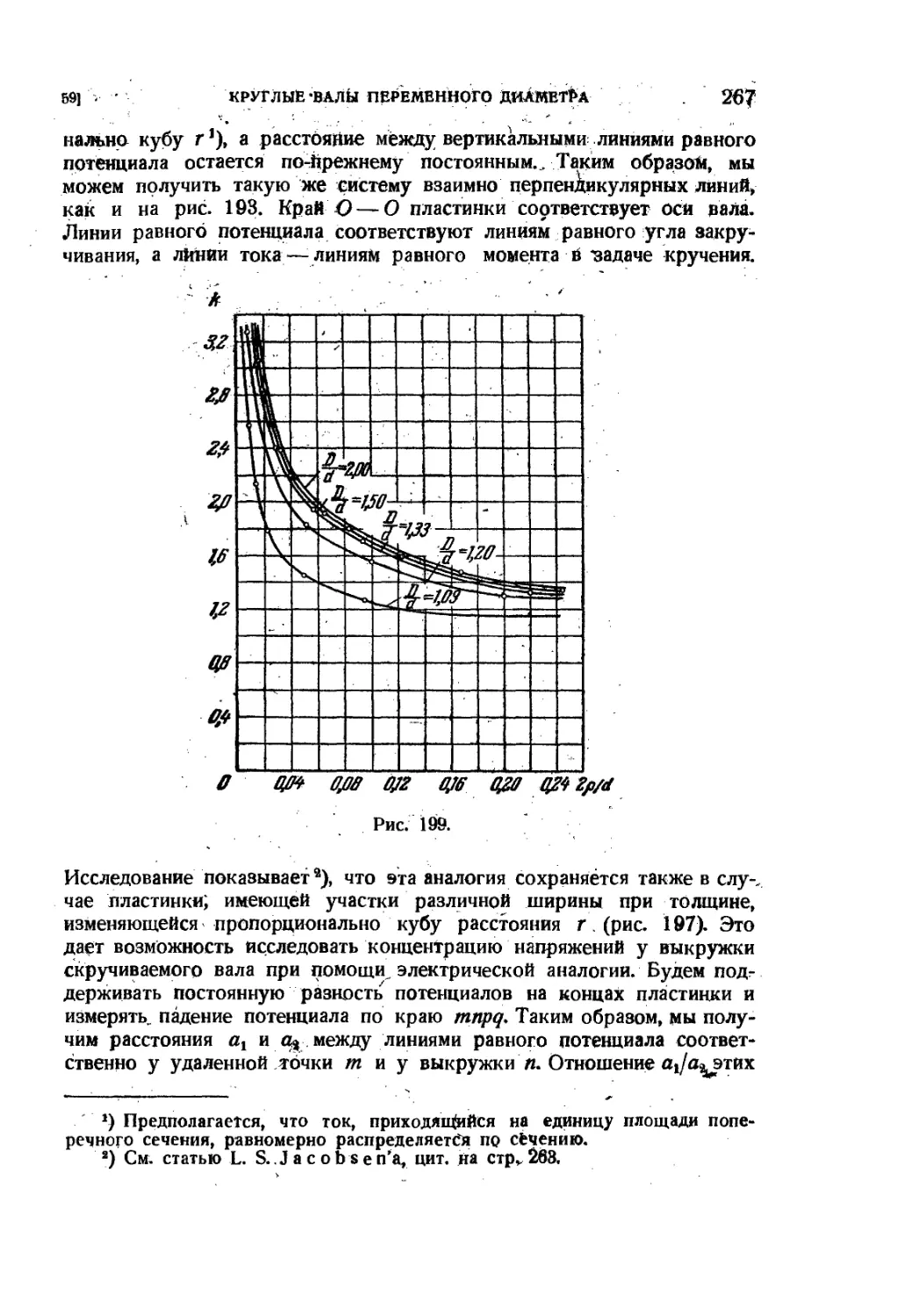
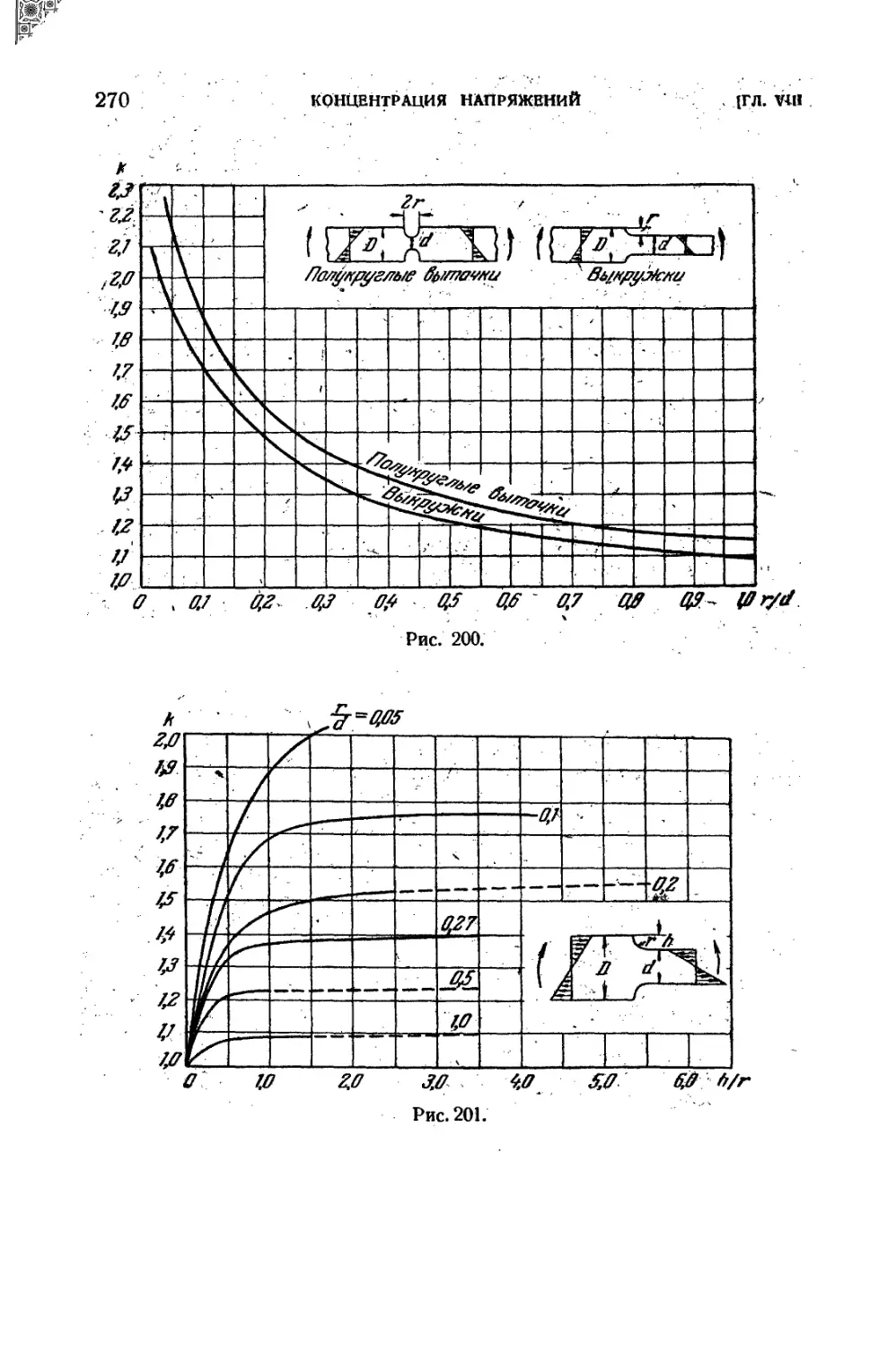
59. Круглые валы переменного диаметра . 262
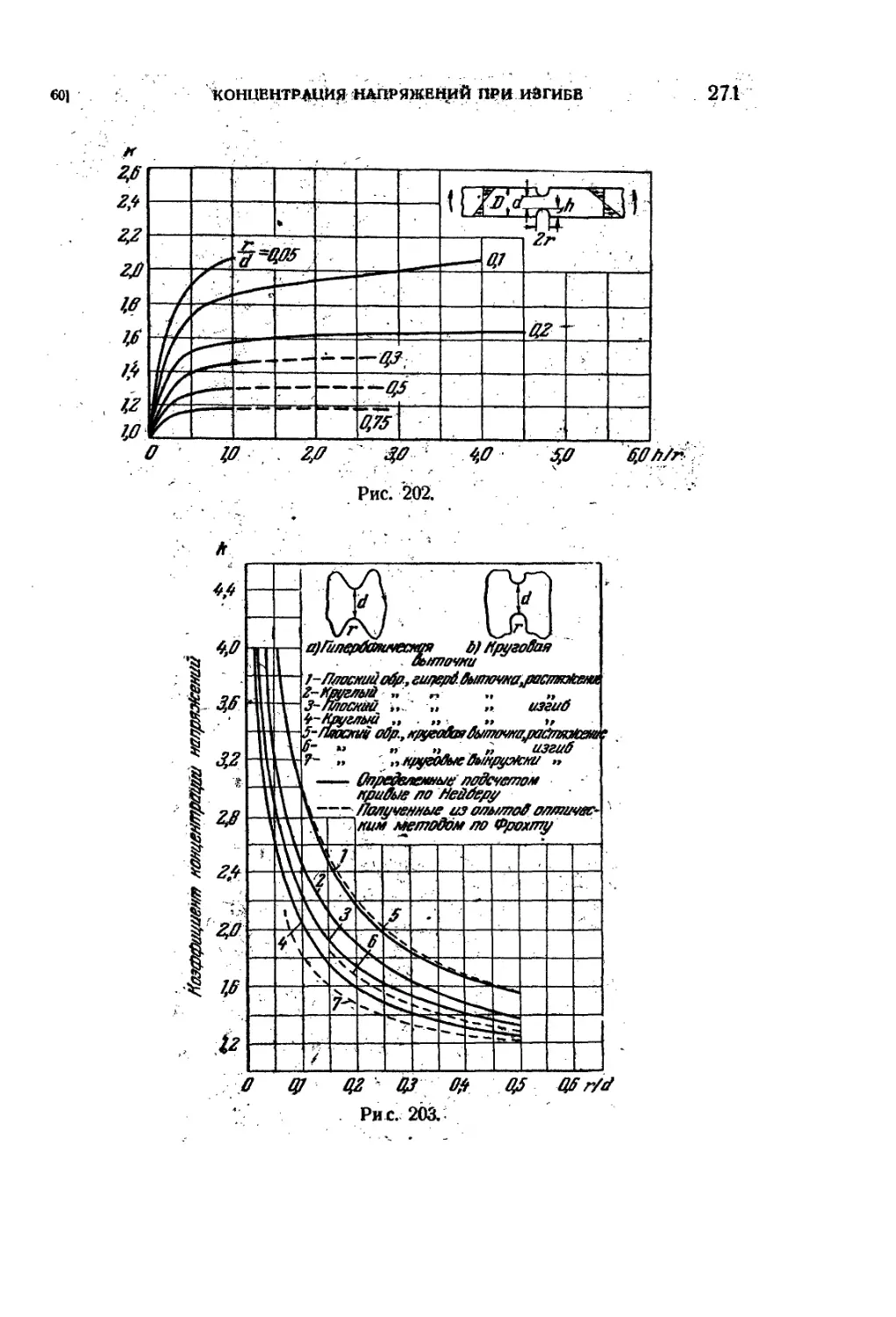
60. Концентрация напряжейий при изгибе. - 268
61. Исследования концентрации напряжений с помощью моделей. . 273
62. Оптический метод измерения напряжений. . 276
63. Напряжения при касании шаров и лщяйндров 281
ОГЛАВЛЕНИЕ б
Глава IX. Деформации за пределом упругости • ,• • 287
64. Системы из идеально пластических материалов . - : 287
65. Предельное сопротивление систем 294
66. Чистый изг^ балок, материал которых не следует закону Гука 304
67. Изгиб балок поперечной наУрузкой за пределом упругости ... 310
68. Остаточные напряжения, вызываемые неупругим изгибом .... 312
69. Кручение за пределом упругости 816
70. Пластические деформации толстостенных цилиндров под
действием внутреннего давления 320
Глава X. Механические свойства материалов . ...; 326
71. Общие соображения 326
72. Испытания на растяжение хрупких материалов 328
73. Испытания на растяжение пластических материалов . 332
74. Испытания образцов из монокристалла в упругой области .... 335
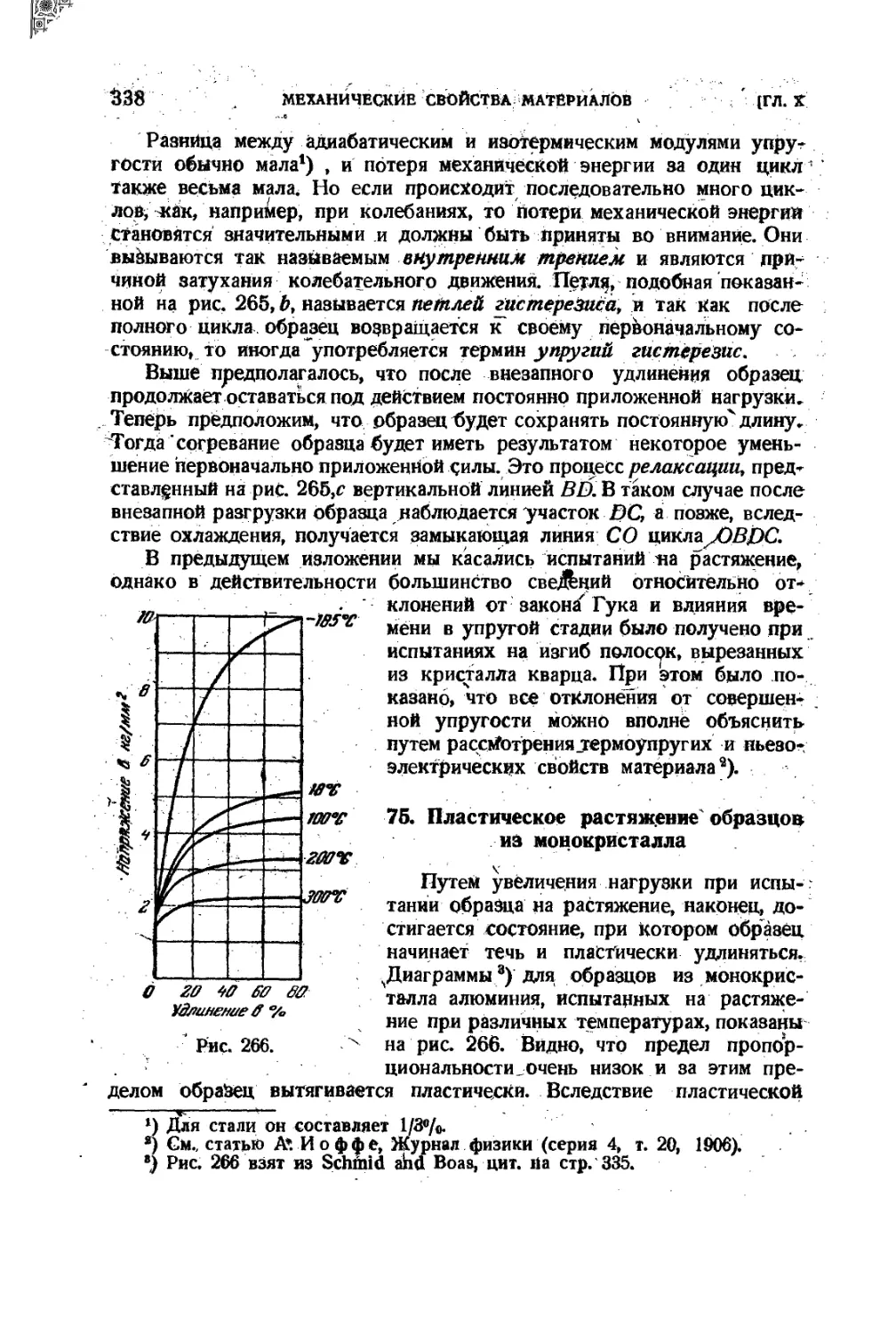
75. Пластическое растяжение образцов из монокристалла ....... 338
76. Испытания на растяжение мягкой стали в упругой области . . . 341
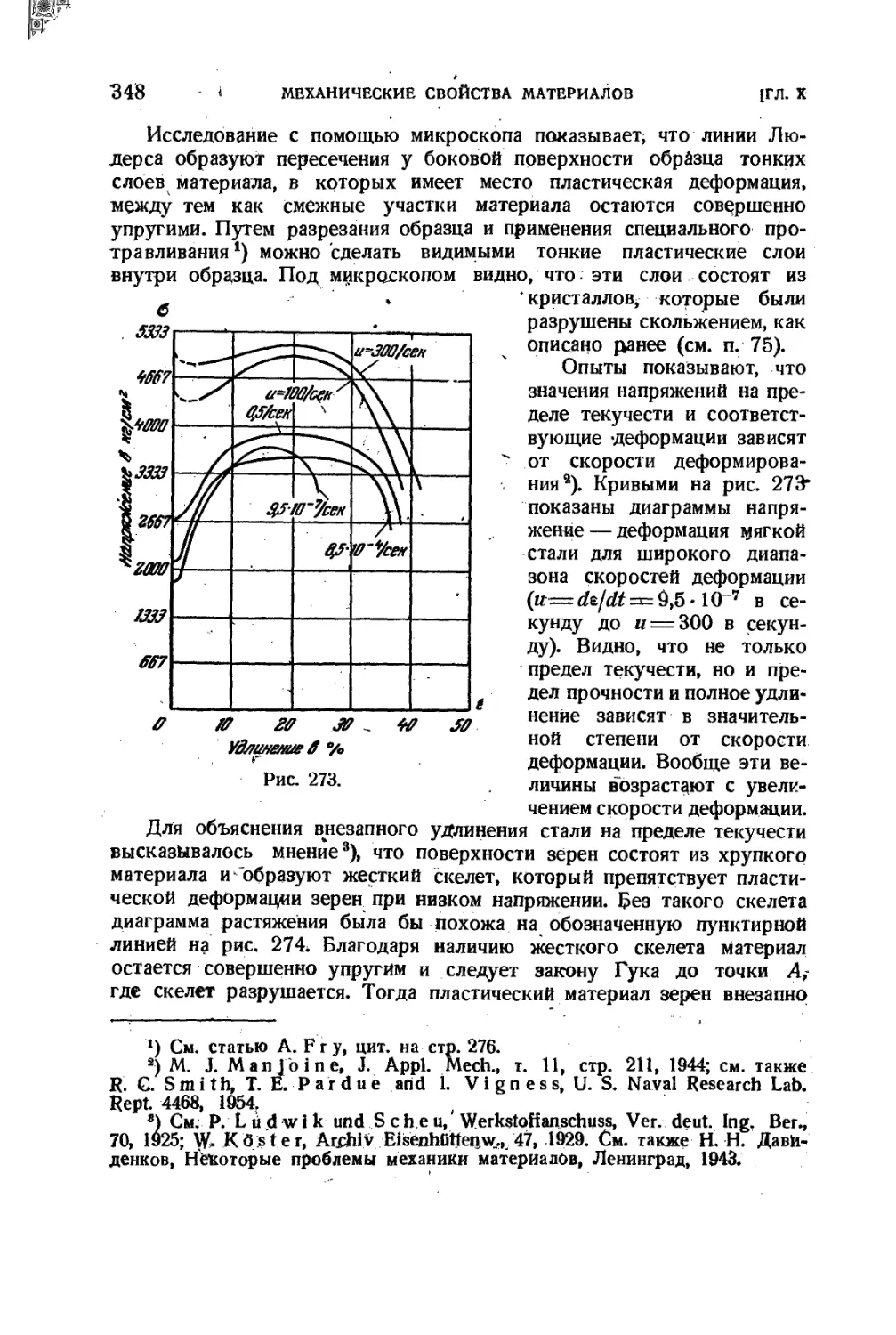
77. Предел текучести .> 346
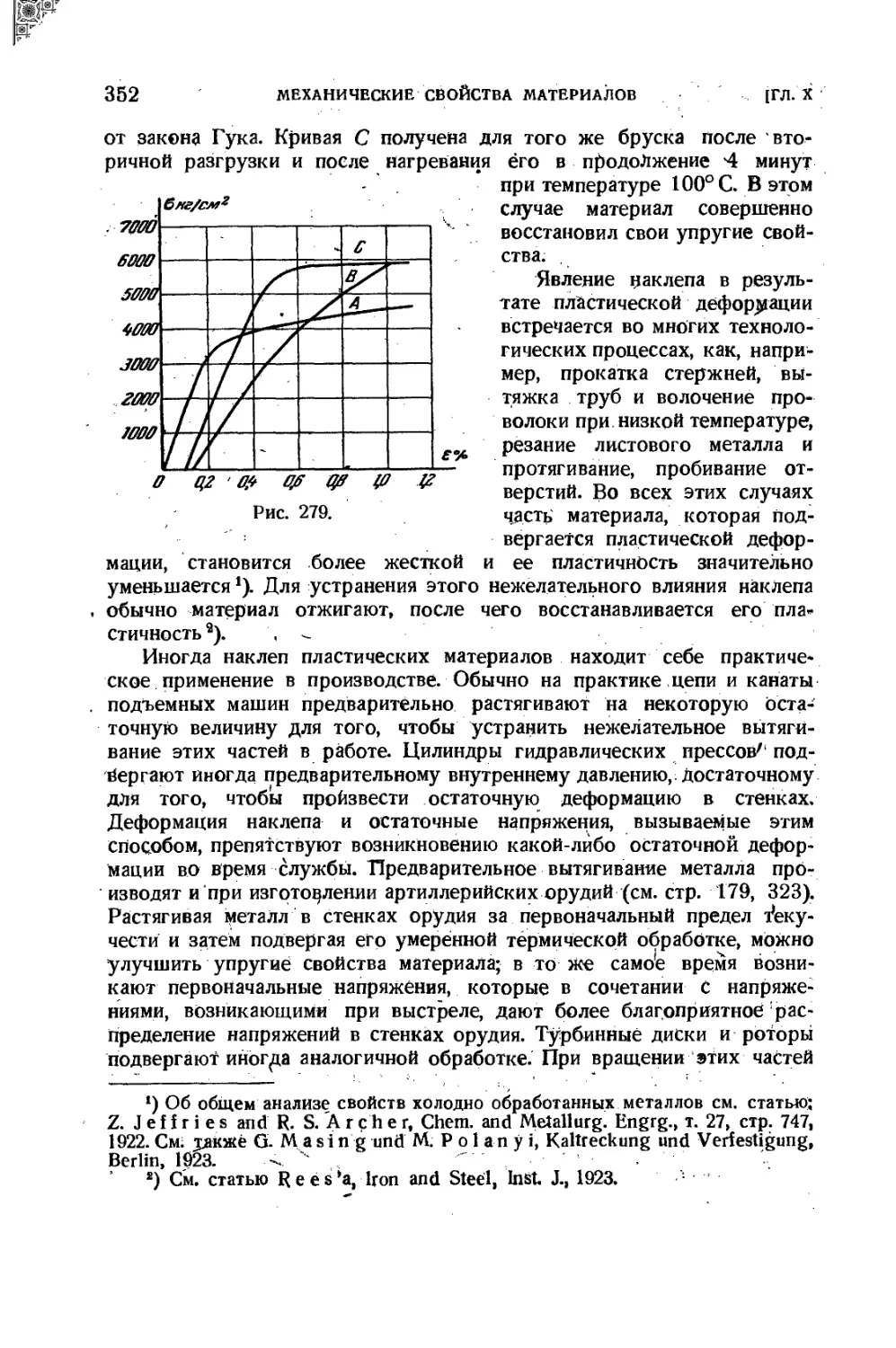
78. Растяжение стали за пределом текучести 349
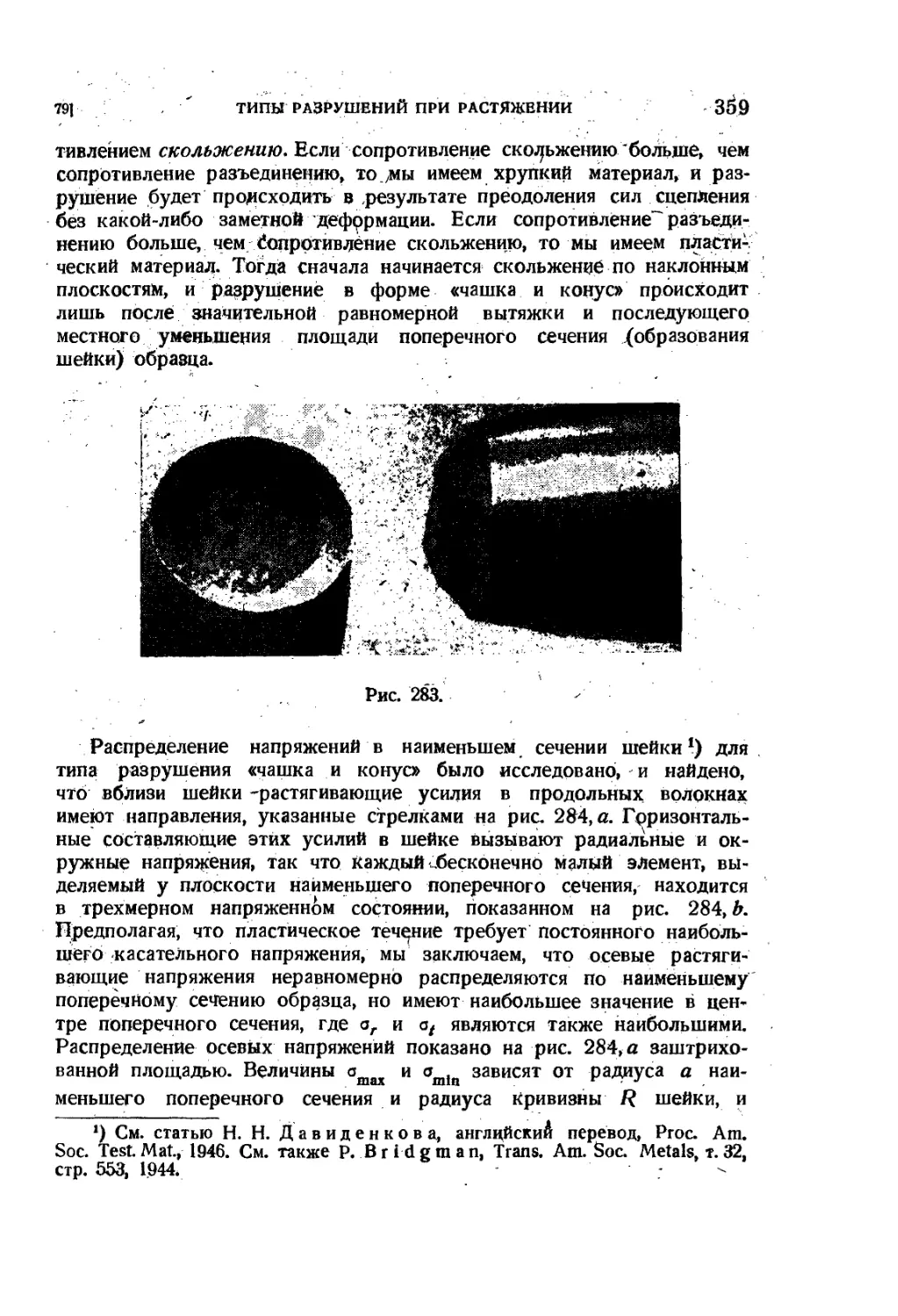
79. Типы разрушений при растяжении 358
80. Испытания на сжатие , 362
81. Испытания материалов при сложном напряженном состоянии , . 365
82. Теории прочности 370
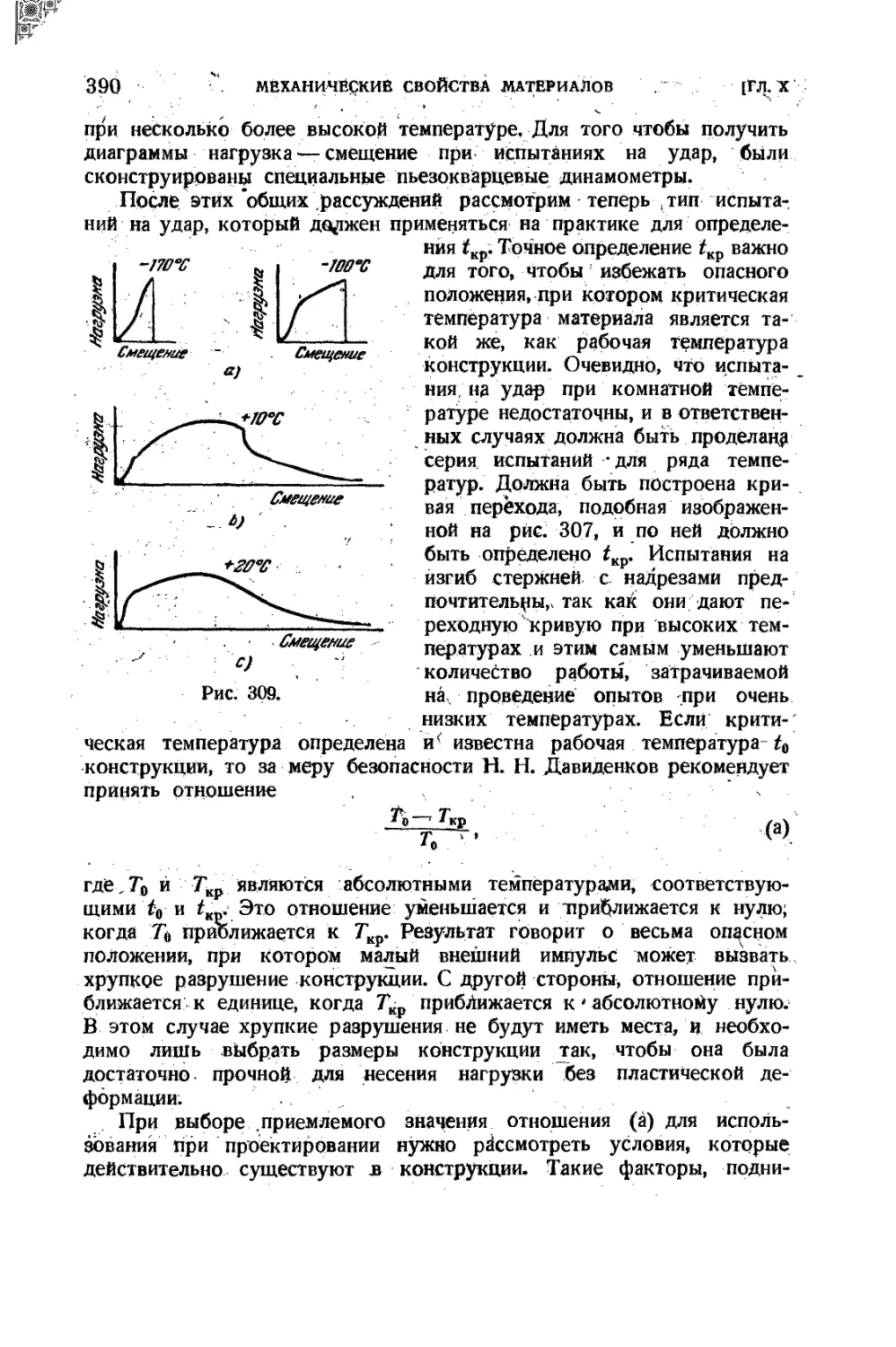
83. Испытания на удар. . 384
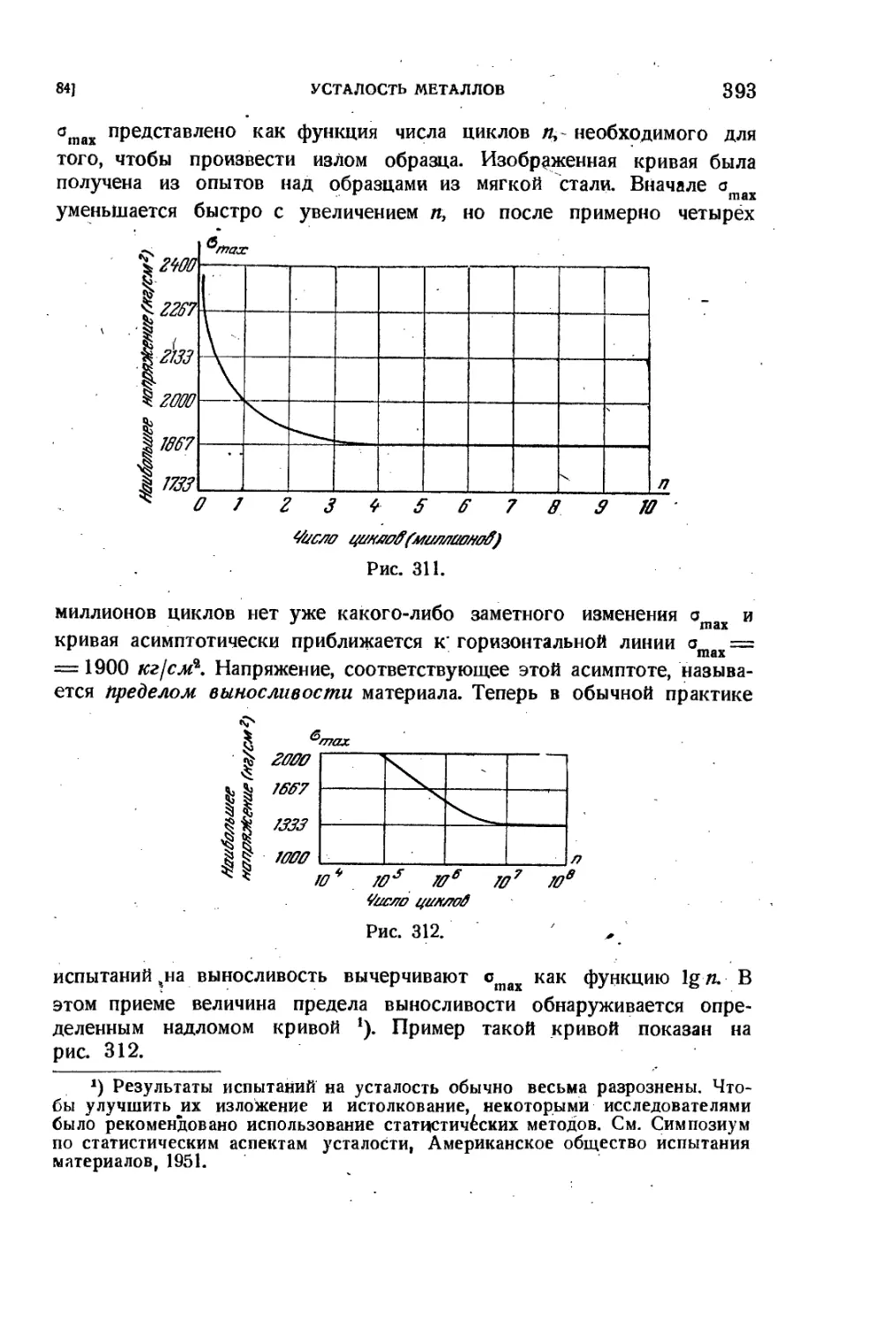
84. Усталость металлов 391
' 85. Усталость металлов при сложном напряженном состояний .... 399
86. Факторы, влияющие на предел выносливости 403
87. Усталость и концентрация напряжений 408
88. Уменьшение влияния концентрации напряжений на усталость . . 415
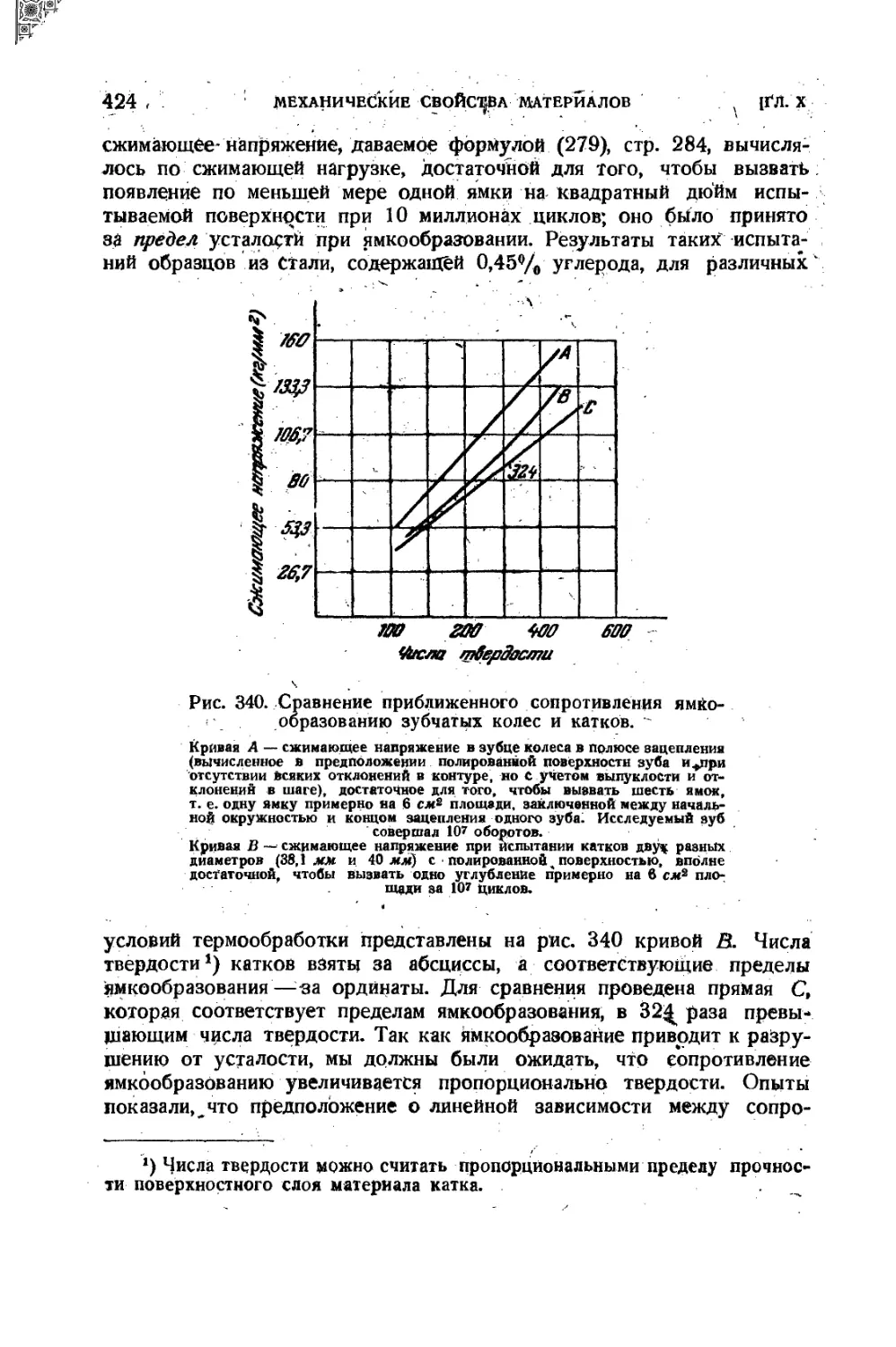
89. Разрушение поверхности при усталости 422
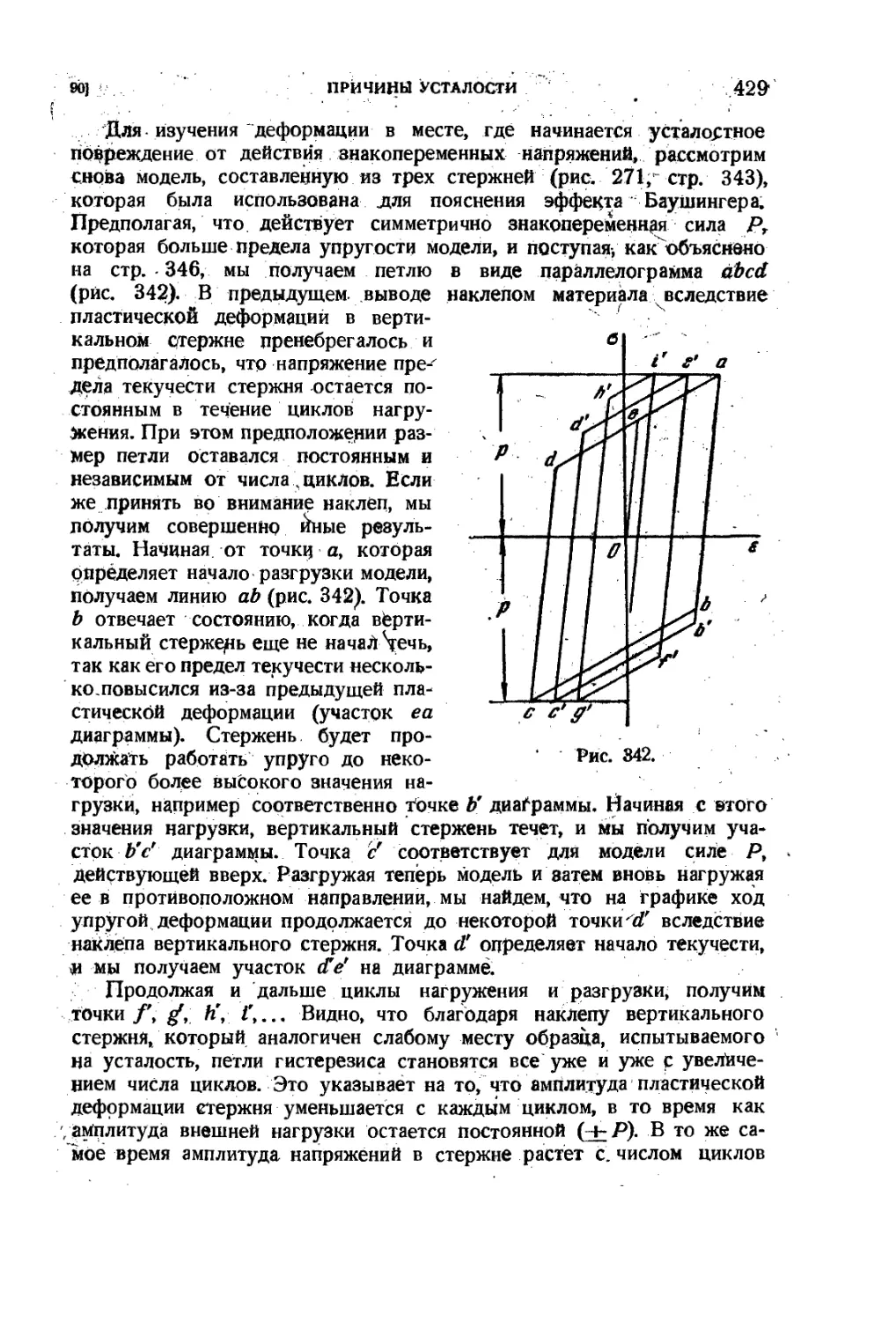
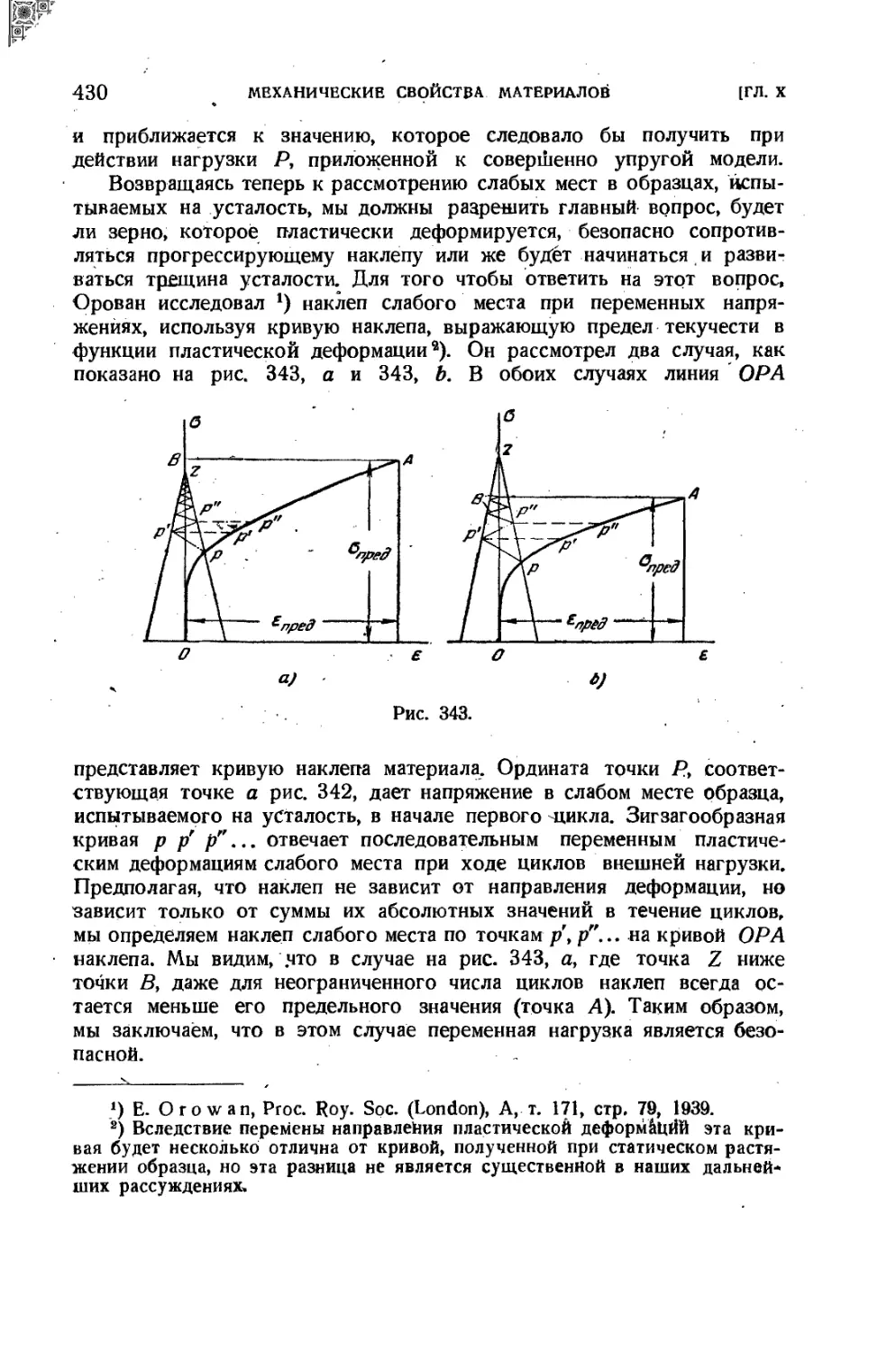
90. Причины усталости 425
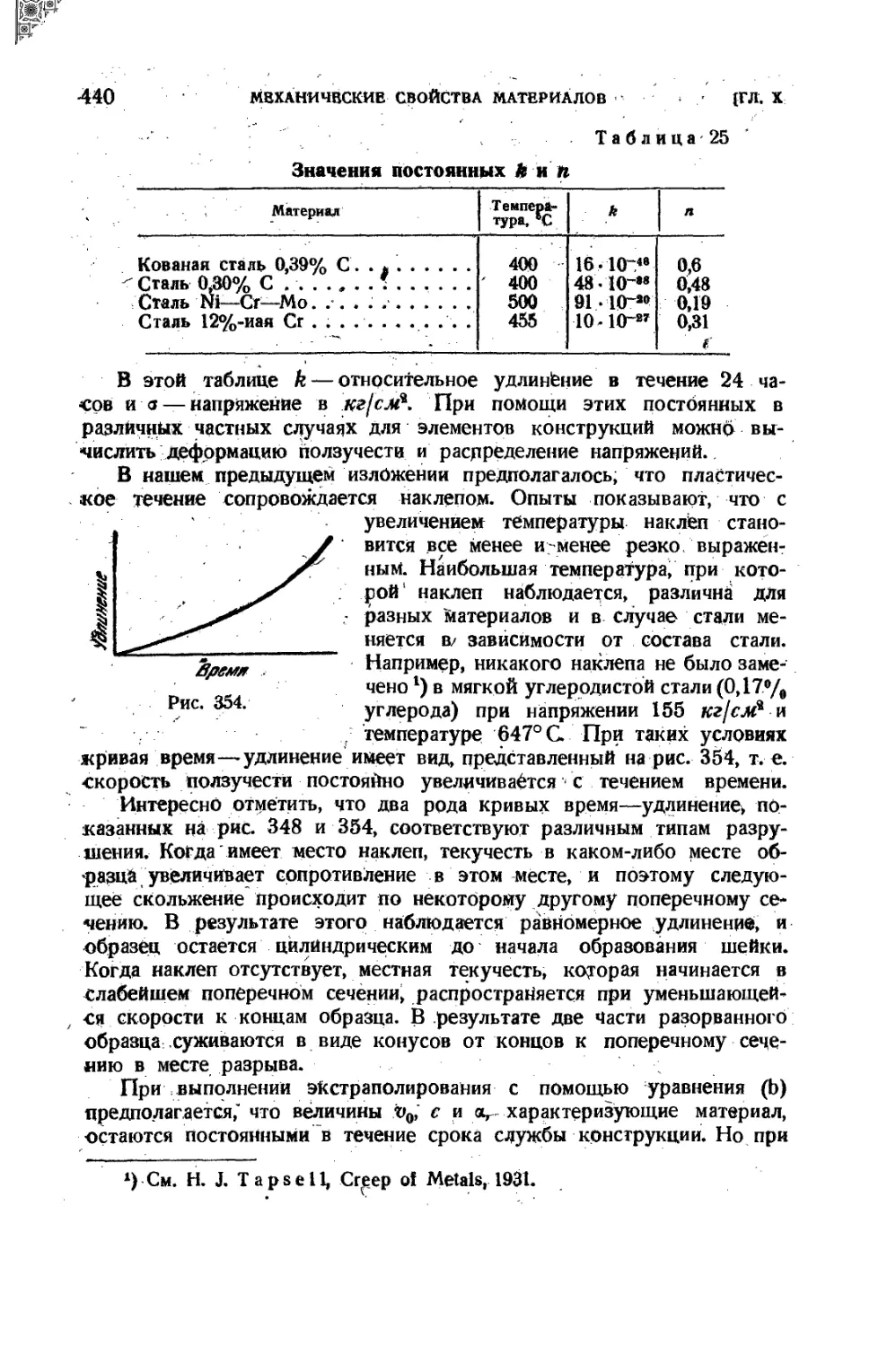
91. Механические свойства металлов при высоких температурах , . 431
92. Изгиб балок при высоких температурах 441
93. Релаксация напряжений ^ 444
94. Ползучесть при сложном напряженном состоянии 447
95. Частные случаи двумерной ползучести . 450
96. Рабочие напряжения ! . . . 456
Обозначения 470
Именной указатель .^-. 472
Предметный указатель , 476
к^^ЖТЯ"'
из ПРЕДИСЛОВИЯ к ПЕРВОМУ АМЕРИКАНСКОМУ ИЗДАНИЮ
Второй том сопротивления материалов написан главным образом
для аспирантов, инженеров-исследователей и проектировщиков. Автор
стремился написать книгу, которая содержала бы новейшие
достижения драктической важности в области сопротивления материалов и
теории упругости. В большинстве случаев дан полный разбор задач,
представляющих практический интерес. Только в сравнительно
немногих случаях даны лишь окончательные результаты более сложных
задач, решения которых нельзя получить, не выходя за пределы
обычного для инженеров объема знаний по математике. При этом разобраны
практические приложения результатов и в то же время даны ссылки
на литературу, в которой можно найти полный вывод решения.
В первой главе рассмотрены , более сложные задачи изгиба
призматических стержней. Подробно разобраны важные задачи изгиба
стержней, лежащих на упругом основании, и даны приложения теории
по исследованию напряжений в рельсах и трубах. Также разобрано
приложение тригонометрических рядов к исследованию задач изгиба
и выведены важные приближенные формулы для случаев
одновременного действия продольных и поперечных нагрузок.
Во второй главе подробно развита теория кривых брусьев.
Приложение этой теории к проектированию машин иллюстрировано
анализом напряжений в крюках, маховых колесах, звеньях цепей,
поршневых колесах и кривых трубах.
Третья глава содержит теорию изгиба пластинок. В ней подробно
рассмотрены случаи изгиба пластинок по цилиндрической поверхности
и симметричный изгиб круглых пластинок; даны практические
приложения. Приведены также некоторые данные относительно изгиба
прямоугольных пластинок под действием равномерной нагрузки.
из ПРЕДИСЛОВИЯ К ПЕРВОМУ АМЕРИКАНСКОМУ ИЗДАНИЮ 7
В четвертой главе разобраны задачи о распределении напряжений
в элементах, имеющих форму тела вращения и нагруженных
симметрично. Эти задачи особенно важны при проектировании сосудов,
подверженных внутреннему давлению, и вращающихся машинных частей.
Уделено внимание напряжениям растяжения и изгиба в тонкостенных
сосудах, напряжениям в толстостенных цилиндрах, напряжениям
насаживания элементов, а также динамическим напряжениям, возникающим
Б роторах и во вращающихся дисках под действием сил инерции,
и напряжениям от неравномерного нагревания.
Пятая глава содержит теорию потери устойчивости сжатых
стержней и тонких пластинок вследствие упругой неустойчивости. Эти
задачи являются чрезвычайно важными во многих новейших
сооружениях, где размеры поперечных сечений сведены к минимуму, благодаря
применению более прочных материалов и желанию уменьшить вес.
Во многих случаях разрушение инженерных сооружений объясняется
упругой неустойчивостью, а не недостаточной прочностью самого
мате]риала,
В шестой главе рассмотрена неправильность в распределении
напряжений, вызываемая резкими изменениями поперечных сечений
вследствие наличия отверстий и вырезов, и рассмотрено практическое
значение концентрации напряжений. - Описан также оптический метод,
который оказался весьма полезным при исследовании концентрации
напряжений. Объяснена мембранная аналогия в задачах кручения нее
приложение к исследованию концентрации напряжений во входящих
углах, а также в прокатных и трубчатых сечениях. Рассмотрены также
валы переменного диаметра, и при объяснении местных напряжений
у выкр5гжек таких валов использована электрическая аналогия.
В последней главе рассмотрены механические свойства материалов.
Здесь внимание направлено скорее на общие принципы, чем на
описание стандартных методов испытаний материалов. Изложены результаты
новейших исследований механических свойств монокристаллов и
указано их практическое значение. Такие вопросы, как усталость
металлов и их прочность при высокой температуре, представляют
значительный практический интерес при проектировании современных машин.
Эти вопросы трактуются главным образом со ссылками на новейшие
достижения в этих областях.
В заключение рассмотрены различные теории прочности.
Разработан важный вопрос о связи между этими теориями и методом
MiW
8 ПРЕДИСловив ко ВТОРОМУ АМЕРИКАНСКОМУ ИЗДАНИ1р
установления допускаемых напряжений цри различных напряженных
СОСТОЯНИЯХ.
Уже было упомянуто, что книга написана отчасти для учебных
целей, но она также может.быть использована для более
углубленного изучения. Автор, на основании своего опыта, разделил книгу на
три таких курса: 1) курс^ заключающий в себе главы I, III и V,
предназначен главным образом для аспирантов, интересующихся инженернб-,
строительным делом; 2) курс, содержащий главы Hi III, IV и VI, —
для аспирантов, главный интерес которых представляет
машиностроение; 3) курс, использующий главу VII как основу и сопровождаемый
демонстрированием опытов в лаборатории по испытанию материалов.
Автор полагает, что такой курс, в котором рассматриваются
основные механические свойства материалов и устанавливается зависимость
между этими свойствами и допускаемыми напряжениями,
применяемыми при различных условиях проектирования, имеет первостепенное
практическое значение, и изучению такого курса должно быть
уделено большое внимание в нашем инженерном образовании.
ПРЕДИСЛОВИЕ КО ВТОРОМУ АМЕРИКАНСКОМУ ИЗДАНИЮ
При подготовке к новому изданию этого тома общий характер
книги оставлен неизменным, были лишь приложены усилия к тому,
чтобы сделать ее более полной и современной путем включения
нового теоретического и экспериментального материала, отражающего
новейшие достижения в области анализа напряжений, и
экспериментального исследования механических свойств строительных материалов.
Нрболее важные изменения, внесенные во второе издание,
сводятся к следующему: ,
1. Более полно рассмотрены задачи, относящиеся к изгибу,
сжатию и кручению гибких и тонкостенных конструкций. Такого рода
конструкции находят в настоящее время широкое применение в
аэропланах, и было сочтено нужным включить в новое издание больше
задач из этой области. '
2. Добавлена глава о пластических деформациях, трактующая изгиб
и кручение балок и валов за пределом упругости, а также
пластическое течение материала в толстостенных цилиндрах, подверженных
действию высоких внутренних давлений.
ПРЕДИСЛОВИЕ к ТРЕТЬЕМУ АМЕРИКАНСКОМУ ИЗДАНИЮ 9
/ ■ . ' • ■ '■
■ ">.■■■.
3. Внесено значительное количество нового материала
экспериментального характера, относящегося к поведению строительных
материалов при высоких температурах^ и к усталости металлов под
действием знакопеременных напряжений, особенно в тех случаях,
где усталость металлов сочетается с высокой концентрацией напря*
жения.
4. Сделаны важные дополнения в части книги, посвященной
балкам на упругом основании; к главам по теории кривых брусьев и
теории пластинок и оболочек; и к главе о концентрации напряжений,
в которую были включены некоторые позднейшие результаты
оптических испытаний.
Со времени появления первого издания этой книги были
опубликованы три книги более углубленного характера: «Теория упругости»,
«Теория устойчивости систем» и «Теория пластинок и оболочек».
Ссылки на эти книги сделаны в различных местах этого тома,
особенно в тех случаях, когда даются лишь конечные результаты без
полного математического вывода.
Можно надеяться, что, е упомянутыми выше добавлениями книга
будет давать представление о современном состоянии учения о
сопротивлении материалов и может быть полезна как для аспирантов,
интересующихся строительной механикой, так и для
практиков-инженеров, имеюиХих дело со сложными задачами исследования напряжений.
С- П. Тимошенко
Пало Альто, Калифорния
12 июня 1941 г.
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ АМЕРИКАНСКОМУ ИЗДАНИЮ
При подготовке нового издания этой книги было добавлено
значительное количество материала. Включены ссылки на новейшую
литературу, внесены новые задачи для самостоятельного решения и
дополнительные иллюстрации. Большинство изменений внесено в главы
о кручении, пластических деформациях и механических, свойствах
материалов.
Что касается кручения, то была рассмотрена задача о скручивании
трубчатых стержней с несколькими контурами, а также продольный
изгиб при кручении тонкостенных стержней открытого профиля. Каждый
testTH"
10 ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ АМЕРИКАНСКОМУ ИЗДАНИЮ
ИЗ этих вопросов является важным при проектировании тонкостенных
конструкций, которые являются составляющими частями самолетов.
В главе о пластических деформациях рассмотрены основные принципы
проектирования по предельному состоянию. Представлено несколько
примеров применения метода к проектированию стро1^тельных конструкций.
Много дополнений было сделано в главе о механических
свойствах материалов, и одна эта глава теперь содержит свыше 160
страниц. Цель такого расширения главы заключается в сосредоточении
внимания на новейших достижениях в области экспериментального
изучения свойств строительных материалов. Рассмотрены следзтощие
вопросы: 1) влияние несовершенств на предел прочности хрупких
материалов и «масштабный эффект»; 2) сравнение результатов
испытаний образцов' из монокристаллов и поликристаллов; 3) испытание
материалов в условиях плоской и пространственной задачи и
различные теории прочности; 4) сопротивление удару; 5) усталость металлов
при различных напряженных состояниях и методы повышения
сопротивления усталости частей машин; 6) сопротивление материалов при
высоких температурах, явление ползучести и использование данных
испытаний ползучести при проектировании. Для читателя, который
желает расширить в дальнейшем свои познания в этих вопросах,
будут полезны многочисленные ссылки на новейшую литературу.
Наконец, в заключительном параграфе книги приводятся достаточно
подробные сведения для надлежащего выбора рабочих напряжений.
Автор надеется, что с этими добавлениями книга будет более
полной для изучения расширенных курсов по механике материалов,
а также более полезной для инженеров-исследователей и
конструкторов при проектировании машин и сооружений.
В заключение автор выражает благодарность профессору Стан-
фордского университета Джемсу М. Гиру за его помощь и
многочисленные советы при просмотре книги и при чтении корректур.
С Тимошенко
Станфордский университет
10 февраля 1956 г.
ГЛАВА1
БАЛКИ НА УПРУГОМ ОСНОВАНИИ
1. Балки неограниченной длины
Рассмотрим призматическую балку, опирающуюся по всей своей длине
на сплошное упругое основание таким образом, что, когда балка
изгибается, интенсивность равномерно распределенной реакции в
каждой точке пропорциональна прогибу в этой точке *). При таких
условиях реакция, приходящаяся на единицу длины балки, может быть
представлена выражением ky, в котором у есть прогиб, а УЬ —
постоянное число, обычно называемое коэффициентом основания ^). Этот
коэффициент представляет собой реакцию на единицу длины балки при
ее прогибе, равном единице. Простое предположение, что
непрерывная реакция основания пропорциональна прогибу, дает
удовлетворительные результаты во многих случаях практики. Например, в случае
железнодорожного пути полученные при этом предположении
решения хорошо согласуются с действительностью^). При исследовании
*) Балка уложена на постель из материала, способного сопротивляться
как силам, действующим вниз, так и силам, действующим вверх.
^) По предложению Н. И. Фусса, k называется коэффициентом тгостели
(прим. перев.).
8) См. S. Timoshenko и В. F. Langer, Trans. А. S. М. Е., т. 54,
стр. 277, 1932. Теория изгиба балок на упругом основании разработана
Е. Winkleг'ом. Die Lehre von der Elastizitat und Festigkeit,Prague, стр. 182,
1867. См. также Н. Zimmermanп. Die Berechnung des Eisenbahn — Ober-
baues, Berlin, 1888. Дальнейшее развитие теории можно найти в следующих
источниках: Н а у а s h i, Theorie des Tregers auf elastischer Unterlage, Berlin,
1921 (русский перевод: Теория расчета балок на упругом основании,
ГНТИ, 1930. Прим. ред.); W i е gh аг d t, Z. angew. Math. u. Mech., т. 2, 1922;
К. V. S a n d e n and Schleicher, Beton u. Eisen, тетрадь 5, 1926;
Pasternak, Beton u. Eisen, тетради 9 и 10, 1926; W. P r a g e r, Z. angew. Math. u.
Mech., T. 7, стр. 354, 1927; M. A. Biot, J. Appl. Mech., т. 4, стр. A-1, 1937;
M. H e t e'n у i, Beamson Elastic Foundation, Ann. Arbor, 1946. (Ha русск.
яз. в 1930 г. вышла книга: А. Н. Крйлов, О расчете балок на упругом
основании. — Прим. ред.)
l^rXr^TS''
12 БАЛКИ НА УПРУГОМ ОСНОВАНИИ {ГЛ. I
изогнутой ОСИ балки мы пользуемся дифференциальным уравнением *)
£'Л^===9. / (а)
где q означает интенсивность нагрузки, действующей на балку. Для
ненагруженной части балки нагрузкой является лишь непрерывно
распределенная реакция со' стороны основания интенсивностью ky.
Следовательно, ^= — ky, и уравнение (а) получается в таком виде:
>Л0=-*> О)
Используя обозначение .
V 4EJ,
общее решение уравнения A). можно представить в следующем виде:
J = е^^ (Л cos рдг 4- В Sin ^х) 4- ^е-^ (Ccos^x-\-D sin ^х). (b)
Это можно легко проверить подстановкой уравнения (Ь) в
уравнение A). В частных случаях постоянные интегрирования А, В, С и D
должны быть определены из известных
условий для некоторых точек.
В качестве примера рассмотрим слу- ^
чай одного сосредоточенного груза,
^-^ действующего на бесконечно длинную
^("^ балку (рис. 1,д), взяв начало координат
\ ^fff(ffffiii'i^^i^ff0fff^. g точке приложения силы. Вследствие
-w симметрии достаточно рассмотреть лишь
^j часть балки справа от груза (рис. 1,^).
Для применения к этому случаю общего
Р"^- ^- - решения уравнения (Ь) необходимо
сначала найти произвольные постоянные.
Логично предположить, что в точках, бесконечно удаленных от силы
Р, прогиб и кривизна оси балки обращаются в нуль. Это условие
может быть выполнено лишь в том случае, ^сли постоянные А и В^
в уравнении (Ь) принять равными нулю. Следовательно, уравнение'"
изогнутой оси для правой части балки получается в таком виде:
y^e-^iCcos^x-j-Dsin^x). (с)
Остальные две постоянные интегрирования Си D найдутся из
условий в начале координат при д:=0. В этой точке изогнутая ось балки
*) См. С. Тимошенко, Сопротивление материалов, т. I, уравнение (80),
стр. 125.
1] БАЛКИ НЕОГРАНИЧЕННЬЙ длины jS
должна иметь горизонтальную касательную, поэтому
или, подставляя значение у из уравнения (с), получаем
e"P*(Ccos Рдг4-^5шрдг4- Csin pAT — Dcos pA;)j(^o==0,
откуда C=D.
Поэтому ура$нениё (с) получается в таком виде:
jj/==C<?-P^(cos.pAr4-sinpAr). (d)
Последовательные производные этого уравнения будуг.
g = -2pC«?-P*8inpAr.
|^=2р*Са-^(81прлг-со8рд;), (е)
^з = 4р«Са"^со8рдг. (О
Постоянная С теперь может быть определена из условия, что при
л:=0 поперечная сила для правой части балки (рис. 1,^) равна — Р/2.
Знак минус вытекает из принятого нами условия относительно знаков
для поперечных Ьил (см. т. I, стр. 71). Тогда
, (оь=о=(а=о=-^м.^г=о=-4.
или, пользуясь уравнением (f), получаем
£Л4Р«С=^,
откуда
^ Р
^fEJg-
Подставляя это значение С в уравнения (d) и (е), получаем
следующие уравнения для прогиба и изгибающего момента:
V=;
Ж = — £Л ^ = - ^ е-Р^ (sin рдг - cos рлг). D)
График каждого из выражений C) и D) представляет собой
волнообразную кривую с постепенно уменьшающейся амплитудой. Длина а
этих волн определяется периодом функций cos рдг и siri рлг, т. е.
а = -р- = 2,г|/-у. E)
14
БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. I
Чтобы упростить вычисление прогибов, изгибающих моментов и по
перечных сил, приведена таблица (табл. 1), в которой приняты еле
дующие обозначения:
<f == е~^ (cos рлг -}- sin ^х),
^ = — e~P-*'(sin ^х — cos ^х)у
6 = е-Р-^ cos Pat, с = е-Р' sin рх
F)
На рис. 2 показаны графики функций ^ и t}).
Пользуясь обозначениями F) и уравнениями (d)—-(f), получим:
M=~Ej.^^.=^Hm
Q:
^■'^0=-f »№■*>■
G)
По этим уравнениям и табл. 1 можно вычислить прогиб, угол наклона
касательной, изгибающий момент и поперечную силу для любого
-02
О
A2
о,е
0.8
<№|||
/
9>
^
г ,
3
4
3
о
г 3
Рис. %.
•^
j3j:
поперечного сечения балки. Наибольший прогиб и наибольший
изгибающий момент имеют место в начале координат и соответственно
равняются
S = (^)j.=o
Жо = (Ж)^,=о = 4р-
(8)
(9)
Пользуясь решением C) для одиночного груза и принципом
сложения действи^т сил, можно легко получить прогиб, вызываемый
в бесконечно длинной балке на упругом основании любым другим
видом нагрузки.
БАЛКИ НЕОГРАНИЧЕННОЙ ДЛИНЫ
15
а
1=;
а
CD
SB
»
>>
•8-
В
К
ф
ВР
се
s
со
00.
S-
&
СМ
v>—4
О
05
■*—4
О
г-
05
г—^
Q
О
■^
у—^
о
ел
со
Y—1
о
й
^—4
о
? 11111
ю
■ч<
С<1
о
О
(N
О
г~-
г~
о
с^^^
-*
(N
О
О
1
«о
«о
05
О
ел
г~-
о
о
I
г—t
S
о
о
•4f
г
г-
■^
о
о
1
00
о
о
о
о
о^
о
ю
05
О
О
со
^—4
о
о
1
■^
г~-
о
о
ю
см
уттЩ
о
1
■^
ю
о
о
г-
*—(
»—ч
о
о
1
00
со
о
о
00
о
г—t
о
8
^—4
о
9?
Q
ь
111
со
см
8
ч—1
о
о
^-^^^-^^.^
а>
ч—«
о
о
111
■^
05
О
1 1 1
CD
СО
О
о
8
о
г—*
г-
со
со
о
ел
о
о
со
о
о
о>
о
оо
со
г~-
гч
CD
г^
о
^
(N
О
00
О
«о
00
CJ
о
о
1
ел
со
о>
00
»—ч
(N
О
г~-
г~-
о
г~-
о
00
ю
CJ
о
о
•4f
о
о
о
со
гм
о
г~-
VQ
S
о
■^
о
<м
о
о
г~-
о
о
ел
г~-
*—(
о
ел
г~-
S
о
ю
m
*—(
о
m
00
о
о
о
й
*—ч
о
ел
00
8
о
V—4
»—*
О
8
о
о
о
а>
о
о
о
CJ
§
о
см
00
8
о
1
г-
*«*
о
о
ел
00
о
о
о
ю
г-
о
о
со
г-
S
1
"*
8
о
г^
00
о
о
о
о>
ю
о
о
.о
Cjp
<''*>
о
о
1
ел
■W—Щ
о
о
о
■^
00
о
о
о
«D
4rt*
^ь
о
^^^^^^^^^^^
о
Tf
о
«—<
CD
(N
О
■*
г~-
V—1
CD
О
^
■^
00
о
ел
(N
о
со
(N
со
^.
о
3
■^
оз
§
со
о
о
со
lii
■^
о
со
■^
оз
а>
»—ч
со
о
00
ел
г~-
со
о
Tf
■^
со
гч
Ci
со
о
со
V—1
со
О
S
•*
S
¥—4
со
о
г-
сч
т
сч
о
«о
Tf
CD
о>
О
00
о
00
00
о
1—'
о
г~-
Tf
г~-
CD
С5
см
о
о
»—*
vO
*—ч
о
00
■^
г~-
о
00
сч
о
о>
о
*—'
о
ел
■^
CD
см
CD
см
о
о
сч
г~-
о
о
о
ю
ы
^
см
о
ел
*—ч
S
о
1—
1Q
^*J
о
а>
у
8
11
со
см
«о
см
8 S.
о
о
00
8
о
??
о
о
о
1
*—ч
ю
«о
гм
CJ
С^)
о
S?
о
о
о
m
г~-
о
о
о
со
сч
о
о
см
^
^^J
о
о
1,
00
CJ
о
о
о
оз
ел
8
о
-*
*—^
8
п
(»
ю
00
V—t
о
см
о
о>
ю
8
«?
со
ю
см
«—<
00
*—'
о
\о
со
С^)
о
9
о о 00
8 о ел
-н со
<Р 00 «D
^ <э сэ"
00 Tf ю •—1 ел
об «D —I со ел
00 IQ -*
■^ со с^
сГ сэ с? <э сэ"
2: g
со
ел
о
о
г~- оо
g S
CD
00
>-ч 00 Г~ Г~-
—1 «о Г~- >*<
о о о о
с^ с^ с^ см
111111111
§r~. .—1. r^Tf.-ioOr^'^C^COCDQS
OincD00C0CMO)vr5'-400r~O>
O>CDC^r~-C^«DO3C0r~-Q'*00
О <?i o>^o>^oq_oo^r~- Ф,<1С2,'Л_1П^'Ч^со^со^с^
_Гоо~о'о'о"о"<э'сГос5'оо~ооо~сз' <э
lO ел
С5 CD
«л tn
о о о о о о о о о г-Г i—T 1—г г—» г-н* »^ г-ц" т-ч*
la
ВАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ.1
ЕВ
I
С
юотсооо'^оч^'З'с^'г!
м С<| cS5 *-■-- Tir S S Ж S
^ 8„ S S 8^ t S I S. t
III I 111 I T +
}Q
s
^ ^ -. - =^ о ^
o, cj, c^ о © СЭ, Ф,
о © о o^ c> с? с?
ОТ ^ ОТ Op r~ Ю ■Tf
Сч ^ Cn '•^ '•"** '■^ '•■^ ^*< ч"** ^D ©
<^^^^GJ,©_©.©©0_C9_©_ ©_ ©^ Q^ Q_ ©^
Ф © © ■ ^^ CD © g5^ вр CSS © © © © © © ^^ ©
Tj<OOCJ, СО—«СО—<COCJ00in(NOT
s
c^ ©^ ©^ © ©
■* (N --I
So ©
© О
Qj^C5_CJ_0©©_00©0
^©'сГ©©©©сГ. ©"©"c?
^©1П©МЮГ~ОООТв>ООООГ~СОЮ>*<СО
illi S is § i s s i i1зД i
сГ©'©'сГсГсГ<5"© о<зГ©'о©'о ©■© ©
•*1П_СОГ^вООТ©л— (N«rt<inC0r~00OTO
1п'ю'1огГю 1о'«£Г«сГ«£ГсгГс£Г«сГс£Г«о'со~со~г^
©ЮФг^юооеосу
f«M *-| со Ю
от
г^ 3 CJ
00 о ifo
© от -^ оо ю со
т»ч ^-™ ь'J U J ^и^ ~^г ^"^ *'-'•' vy W ч,^ ъ ■ t> г** «"^ C*J fcO 00 CD
22:£i2Sg^8S§ggoS8888S
«- о- о- о- о- о о- о- »- о- о- о- о- о- о- Y f f
«о ■«*< со 00 (N
t-- 00 со '—' Ю
2 S i 8 "^
от
со 00 со
с^ © г~-
8 8 g с5
со © г~-
от ю ©
«о со
см 00
X ж X ^ ?s. я^
CD С5 о CD \^ CS^
t f t f f T11 f 111 f t f f ?■
g g S S « 2 ffl :? 2 8 t: S S ffl S? "° "^ "^
fb^ T-M »—1 ,»ц^'4—I v-rt Ti^ ^*4 •**( О Ф
?T?TttTTTt:7T1t1
CO CD 00 CS CO r~-
»?5 •* CO © c<i —',
*-J. ©^ o_ © © ©_
о © ©
•4f(Nr~.OTi*'©©©rl<©OTC0C0 ri —• (N 00 от
rtiS3COTO^S?5c5iQK«b©(N<»?co(N©oo
(NOTc5Tfi^ScpSc4e»3«5^2:2;3£:2::S:2S
.—. о © © © © © ©■ © © <si_ ^ o_ ©^ e^ ©_ ©^ o_
(sTcTo'©©"©'®'"© ©■©©© ©■©■©сэ'сь'сГ
. ox
OOOT©—<CMCO'*lOCOr--00OT©—l<NCO_Tt<in
ц
БАЛКИ НЕОГРАНИЧЕННОЙ ДЛИНЫ
17
Для примера рассмотрим случай равномерной нагрузки, определенной
по длине / бесконечно длинной балки (рис. 3). Возьмем какую-либо точку А,
и пусть с п Ь представляют расстояния
от этой точки до конца -нагруженного
участка балки. Прогиб в точке А,
вызываемый элементарной нагрузкой q dx,
получится из уравнения C) путем
подстановки в него q dx вместо Р, что дает
?'^-*^.^-р(со8рл: + 81прл:).
Щт1г
Рис. 3.
Следовательно, прогиб в точке А, вызываемый нагрузкой, распределенной
по всей длине /, будет
b с
У-=^ \ J^e-P'(cospA;4-sinp^:L-| |^ е^Р* (cos рх + sin И =
= ^B —г-р* COSP& —г-р'^созрс). (g)
Бели с и 6 велики^ то значения е~Р* и е~Р'= будут малыми, и прогиб
(уравнение g) будет приблизительно раве^ qik, т. е. в точках, удаленных от конца
нагруженного участка балки, изгибом балки можно пренебречь и можно
предположить, что равномерная нагрузка q непосредственно передается
упругому основанию. Взяв точку А в конце нагруженного участка балки,
мы будем иметь с = 0, ^==/, *-p'=cospc = 1. Предполагая, что I велико, мы
имеем также г~Р^ cos р & esw 0. Тогда y=qi2k, т. е. в этом случае прогиб
составляет лишь половину полученного выше значения.
Подобным же образом при помощи уравнения D) можно вывести
выражение для изгибающего момента в точке А.
Если точка А взята вне нагруженного участка балки и если величины b
-и с представляют соответственно большее и меньшее расстояние от этой
точки до концов нагруженного участка балки, то прогиб в точке А будет
равняться -
ь
с
^ ^^ ■ е-И (cos рл: -f sin рлг)
WEJ,
2k
(е-р*^ cos рс — г-р" cos Щ.
(h)
величиной, мы получаем для про-
а;
Когда с = 0, а Ь = 1 является большой
гиба значение q/2k, что совпадает с
нашим предыдущим заключением. Когда
расстояния b и с увеличиваются, то
прогиб, согласно уравнению (К),
уменьшается, приближаясь к нулю, если b п с
весьма велики.
Случай пары сил, действующей на
бесконечно длинную балку (рис. 4, а)
может быть также разобран при помощи
решения C) для одиночного груза.
Действие момента пары эквивалентно действию
двух рил Р, показанных на рис. 4, &7
если Ре приближается к Mq, в то время как е стремится к нулю. Пользуясь
6J
3^
18 БАЛКИ НА УПРУГОМ ОСНОВАНИИ |ГЛ. I
первым из уравнений G), находим прогиб в расстоянии лг от начала
координат:
Из уравнений G) имеем
^ = -2рСфх).
и уравнение кривой прогибов от действия пары Мо получается в виде
у^М^ц^х). A0)
Дифференцируя это уравнение, получаем
M = ~-EJ,^=.^H^x), A0')
О- FJ ^'^ - ^«РшЖИ
Q — EJ,-^- 5-«р(Р^).
Пользуясь этими уравнениями и таблицей 1, мы можем легко вычислить
прогиб, угол наклона касательной, изгибающий моменг и поперечную силу
для любого поперечного сечения балки.
Рассмотрим теперь случай нескольких грузов, действующих на беско-,
нечно длинную балку. В качестве примера разберем изгиб рельса,
вызываемый давлением колес паровоза. Излагаемый здесь метод определения
напряжений в рельсах основан на допущении, что под рельсом имеется
сплошное упругое основание. Это допущение дает довольно хорошее
приближение *), так как расстояние между шпалами мало по сравнению с длиной
волны а изогнутой оси, определяемой по уравнению; E). Чтобы получить
значение k коэффициента основания, нужно нагрузку, необходимую для того,
чтобы вызвать осадку шпалы, равную единице, разделить на расстояние
между шпалами. Предполагается, что шпала симметрично нагружена двумя
грузами, соответствующими давлениям рельсов. Допустим, например, что
шпала получила осадку в 0,75 см под каждым из двух грузов по 4000 кг и
что расстояние между шпалами равно 55 см; тогда
4000 л, , о
*^6J53^ = ^''^^/^-^-
В случае расположения на рельсе одного колеса, вызывающего давление Р,
для определения наибольшего прогиба и наибольшего изгибающего момента
пользуемся уравнениями (8) и (9). Наибольшее напряжение в рельсе от
изгиба будет . г—;=г7-
_^W__P Р ^/4£Л ,..
°тах— ^^ ~~ A^W" AW V к ' ^^
где W— момент сопротивления рельса *).
*) См. статью автора «Прочность рельсов». Вестник Института инженеров
путей сообщения (Петербург), 1915 г. и статью автора в Ргос. 2-d Internat
Congr. Appl. Mech., Zurich, 1926. См. также сноску на стр. 11.
2) При написании выражения (i) предполагалось, что элементарная
формула при изгибе балки может быть применена к поперечному сеиению, где
приложен груз Р. Более детальные исследования показывают, что вследствие
местных напряжений следует ожидать значительного отклонения от
элементарной формулы (i).
11
БАЛКИ НЕОГРАНИЧЕННОЙ ДЛИНЫ
19
Для возможности сравнивать напряжения в рельсах, поперечные
сечения котор>1Х геометрически подобны, уравнение (i) представим в
следующем виде:
_ Р гУТг *
F
max
AW
Vf-
(j)
где F—площадь поперечного сечения рельса. Так как второй множитель
правой части уравнения (j) остается достоянным для геометрически подобных
поперечных сечений и так как третий множитель не зависит от размере!*
рельса, то наибольшее напряжение обратно пропорционально площади
поперечного сечения, т. е. обратно пропорционально весу рельса,
приходящемуся на единицу его длины.
Приближенное значение наибольшего давления ^„j^x на шпалу получится
путем умножения наибольшей осадки на расстояние между шпалами и на
коэффициент основания. Таким образом, пользуясь уравнением (8), получаем
4
Я
max
РР
2k
Ik
Щ
-W
kl*
4ЕЛ
(к)
•Отсюда видно, что давление на шпалу зависит главным образом от
расстояния / между шпалами. Надо также заметить, что величина k в обоих
выражениях (j) и (к) находится под корнем четвертой степени. , Поэтому ошибка
в определении величины k повлечет за собой значительно меньшую ошибку
В величинах а^^^х и R^^^.
Когда на рельс действует несколько грузов, следует пользоваться
принципом сложения действия сил. Для иллюстрации метода расчета разберем
численный пример. Возьмем рельс, момент инерции сечения которого /j, =
= 1830 см^, а расстояние между шпалами такое, что k = 100 кг/см^', тогда
по формуле B) находим
3 по формуле E)
■Vir=V
100
4 • 2 . 10« • 1830
НО:
а =
2тс
690 см.
Возьмем для примера систему четырех колес равных давлений, находящихся
на расстоянии 165 см одно от другого. Если мы примем начало координат
в точке контакта первого колеса, то значения ^х для других колес будут, те,
которые даны в табл. 2. Там же приведены соответствующие значения
функций «риф, взятые из табл. 1.
Таблица 2
Грузы
рл:
Ф
9 • •
12 3
0
1
1
1,5
—0,207
0,238
3,0
—0,056
—0,042
4
45
0!008
—0,013
Складывая влияние всех четырех грузов, находящихся на рельсе,
бающий момент под первым колесом определяем по уравнению D):
изги-
л*.=^<'
•0,207 — 0,056 4-0,008):
: 0,745 |,
20
БАЛКИ НА УПРУГОМ ОСНОВАНИИ
1ГЛ. Г
т. е. изгибающий момент в этом случае иа 25,5о/0 меньше, чем в случае
одного груза. Поступая таким же образом, для точки контакта второго колеса
получаем
Ж» = ^ (I — 2.0,207 — 0,056) = 0,530 —..
Видно, что благодаря действию смежных колес изгибающий момент под
вторым колесом гораздо меньше, чем поД первым. Это обстоятельство
подтверждается мйогочисленными опытными данными, полученными при измерении
напряжений в железнодорожных рельсах.
Пользуясь уравнением C) и значениями, приведенными в последней
строчке таблицы 2, находим следующий прогиб под первым колесом:
Л = ^A+0,238-0,042-0,013)=1,183^.
Подобным образом определяются прогибы и в других точках. Отсюда
следует, что метод наложения может быть-легко применен, к исследованию изгиба
рельса, вызываемого любой системой грузов, как угодно расположенных.
Выполненный расчет основан на предположении, что опоры рельса могут
развивать отрицательные реакции. Так как обычно между рельсом и
костылями имеется зазор, то при перемещении рельса вверх возникает небольшое
сопротивление, что приводит к увеличению изгибающего момента в рельсе
под первым и последним колесами. Тем не менее,-в общем, изложенная
теория изгиба рельса, вызываемого статической нагрузкой, вполне
удовлетворительно согласуется с результатами проделанных опытов.
ЗАДАЧИ
1. Пользуясь данными таблицы 2, построить эпюру изгибающих
моментов для рельса, полагая, что давления колес равны 16 т. Такая эпюра должна'
показать, что в сечениях посередине между
колесами моменты отрицательны; это указывает ^&
то, что при движении паровоза рельс подвергается
действию Знакопеременных напряжений от
изгиба, которое в конечном результате может
вызвать трещины усталости.
2. Найти изгибающий момент посередине
нагруженного участка балки, показанной на рис. 3,
и угол наклона изогнутой оси на левом конце
этого участка.
3; Найти прогиб в произвольной точке А на
участке треугольной нагрузки, приложенной к
бесконечно длинной балке на упруголг основании (рис. 5),
Ответ, Поступая так же, как при выводе уравнения (g), стр^ 17, мы
Рис. 5,
получаем
1
[^ фс) - ф фЬ) - 2р/е фЬ) + щ.
2. Подубесконечные балки
Если длинная балка на упругом основании изгибается силой Р и
моментом Мо, приложенными на конце балки, как показано на рис. 6, мы опять
можем использовать общее решение (Ь) предыдущего параграфа. Так как
прогиб и изгибающий момент приближаются к нулю, если расстояние
X от нагруженного конца увеличивается, мы должны в решении положить
21
ПОЛУБЕС14оНЕЧИЫБ БАЛКИ
21
Л = В = 0; получим
у = е-И (С cos рлг + £> sin ^х).
(а>
Для определения постоянных интегрирования С » D имеем условия в на*-
чале коорЗаинат, т. е. под грузом Я:
^*^-(^L=o='
М
01
EJ,
%
(Ашшшшш'
Подставляя в эти уравнения значение у из
уравнения (а), получаем два линейных уравнения
относительно С и Д из которых находим
Р
Подставляя эти
значения в
уравнение
Рис. е.
(а), получаем
У = 2Б8£7-1^* cos ^х — Що (cos рдг — sin рл:)]
или, пользуясь обозначениями F),
2р
(И>
З; = ^ {Рв (рд:) - рЖо [в (рд:) - С (рх)}}.
Чтобы найти прогиб под грузом, мы должны в уравнение (И) подставить
jc = 0. Тогда
/=(y)j(-o =
1
(Я-рМД
A1'>
2р8£^4
Выражение для угла наклона касательной получится путем
дифференцирования уравнения A1). Для конца, т. е. при д:!=0, это будет
\йх)х==<з'
WEJz
При помощи уравнений A1') и A2) на основе принципа наложения можно^
решать и более сложные задачи. Возьмем, например, равномерно
нагруженную бесконечно длинную балку на
упругом основании, имеющую
свободно опертый конец (рис. 7, а).
Реакция R на конце найдется из того
условия, что прогиб на опоре равен
нулю. Замечая, что на большом
расстоянии от опоры изгиб балки
является незначительным и что ее
осадка может -быть принята равной
qjk, мы можем вычислить значение /?
путем подстановки в уравнение AГ)
Жо = 0 и f=q]k. В результате
найдем
R = 2^^EJ.
^ * ~р*
A3)
Рис. 7,
Уравнение изогнутой оси в этом
случае получается путем вычитания
прогибов, определяемых из уравнения A1) для Р=/?, Л!о = 0, из равномерной
осадки qjk балки, что дает
y=-^-^^^Rco&^x =.^{\—1Г^^а>&Щ. A4)
3^
22
БАЛКИ НА УПРУГОМ ОСНОВАНИИ
1ГЛ.1
В случае балки с заделанным концом (рис. 7,6) величины реакции JR и
момента Mq получаются из условий, что на опоре прогиб и угол наклона
касательной равны нулю. Замечая, что на большом расстоянии от опоры
прогиб равен q/k и пользуясь уравнениями AГ) и A2), мы получаем
следующие уравнения ') для вычисления J^ и Мо.
1
|- = -^^,<^ + Р^«)
'И
откуда
^ = 2р4г/^ + 2Р^«)'
Л1о = -2р«£/^-|-, ;? = 4Р=
EJ,
Я Я
-±— —г- _±,
A5)
Минус в выражении для М^ указывает на то, что момент имеет направле-
;ние, обратное показанному стрелкой слева на рис. 7, 6.
ЗАДАЧИ
1. Получить уравнение изогнутой оси полубесконечной балки на упругом
основании, шарнирно закрепленной на конце, при действии момента М^ (рис. 8).
Решение. Реакция в шарнире получается из
уравнения AГ) путем подстановки /=0, что
; дает Р=^^М(^. Подставляя это значение Р в
уравнение A1), получаем
%
Mfl
Рис. 8.
2р*£/,
е~^^ sin ^х =
Жо
2р«Е/,
С (И- A6)
Последовательным дифференцированием находим:
dy 2рзл1о
dx
чм,
М = —£/;
d^y
"^ dx''
d^y _
dx"
М,Ьфх),
(b)
2. Найти изгибающий момент Мо и силу Р, действующие на конец полу-
^есконечной балки на упругом основании (рис. 9), если прогиб / и угол
а наклона касательной на этом конце
jr даны.
Решение. Значение М^ и Р
получаются из уравнений A1') и A2) путем
подстановки заданных величин / и
{dyldx)x.^ — a.
j 3. Вывести уравнение изогнутой
^^ оси полубесконечной балки на
упругом основании, е(;ли на балку
действует груз Р, приложенный на рассто-
А (рис. 10).
Рис. 9.
янии с от ее свободного конца
*) В уравнениях AГ) и A2) подставлено Р = —/?, так как
положительное направление для реакции принято вверх.
3]
БАЛКИ КОНЕЧНОЙ ДЛИНЫ НА УПРУГОМ ОСНОВАНИИ
2а
Решение. Предположим, что балка продолжена влево от конца А, как
показано штрихами. В таком случае уравнение C) дает изогнутую ось длж
л->0, и в поперечном сечении А фиктивной
бесконечной балки мы имеем из уравнений G)
и используя условия симметрии:
(с)
Чтобы получить требуемое уравнение
изогнутой оси полубесконечной балки, свободной
на конце А, мы, очевидно, должны наложить
прогиб полубесконечной балки, вызываемый
силами, показанными на рис. 10,6, на
прогиб фиктивной бесконечной балки. При
помощи уравнений (8), (И) и (с) таким путем получаем для л:>0'
д, = g .р М+^ {06 IP(^ + с)]-f рже [р (лг + сI-РМ № (а:+с)]} = ^ у (Рл:)-{-
+ ^{в(Рс)е[Р(д: + с)]+14^(Рс)е[Р(л:4-с)]-1ф(Рс)С1Р(А: + с)]}. (d)-
Это выражение может быть также использовано при —с <: л: < 0; в этом,
случае мы должны х подставлять в «рфл:) в ее абсолютном значении.
3. Балки конечной длины на упругом основании
Изгиб балки конечной длины на упругом основании может быть также.
исследован при помощи решения C) для бесконечно длинной балки с
использованием и принципа наложения *).
Чтобы иллюстрировать метод решения,
рассмотрим случай балки конечной длины
со свободными концами, которая
нагружена двумя симметрично приложенными
силами Р (рис. 11, а). В подобных
условиях находится шпала под действием
давлений от рельсов. К каждому из трех
участков балки может быть приложено
общее решение (Ь) п. 1, а постоянные
интегрирования могут быть найдены из
условия на концах и в точках
приложения грузов. Однако требуемое решение
может быть получено значительно легче
путем наложения решений для двух
родов нагружения бесконечно длинной
балки, показанных на рис. 11,6 и И, с.
На рис. 11,6 две силы Р действуют на
бесконечно длинную балку. На рис. II, с
бесконечно длинная балка нагружена
внешними силами Оо и моментами Мо
непосредственно в точках Л и В, которые-соответствуют свободным концам
*) Этот метод расчета был разработан М. Hetenyi, Final Report 2.
Congr. Internat. Assoc. Bridge and 'Struct. Eng. Berlin, 1938. Смотри также
его «Beams on Elastic Founa>, стр. 38.
Рис. 11.
ш
•24
БАЛКИ НА УПРУГОМ ОСНОВАНИИ
{ГЛ.!
.дачной балки (рис. 11, а). Легко видеть, что при надлежащем выборе сил Оо
« моментов Жо изгибающий момент и поперечная сила, вызываемые силами Р
в поперечных сечениях А к В бесконечной балки, показанной на рис. 11, &,
могут стать равными нулю. Тогда средний участок бесконечной балки будет
■находиться в тех же условиях, что и конечная балка, представленная на
рис. 11, а, и все необходимые величины, относящиеся к изгибу последней
^алки, будут получены путем наложения решений, найденных по рис.
11,* и И, с.
Чтобы вывести уравнения для определения надлежащих значений Мр и
Ч?о. рассмотрим сечение А бесконечно длинной балки. Принимая начало
координат в этой точке и пользуясь уравнением G), найдем, что изгибающий
момент М' и поперечная сила Q', вызываемые в этой точке двумя силами Р
<рис. 11, Ь), будут
М
4р
{ф[Р(/-с)] + ф(^)},
С?'==-1-{е[р(/-с)] + е(рс)}. (а)
-Момент М" и поперечная силд Q", вызванные р той же точке силами,
показанными на рис. 11, с, получаются при помощи уравнений G) совместно
•<: уравнениями A0'), что дает
Q
МоР,
(Ь)
0"=-^[1-в(р/)]-^[1-<Р(р/I.
11адлежащие значения М^ и Qo теперь получатся из уравнений
М'4-М" = 0, С?'4-0" = 0,
■которые могут быть решены в каждом частном случае при помощи
таблицы 1. После того как Мо и Qo будут найдены, прогиб и изгибающий
момент в любом поперечном сечении действительной балки (рис. И, а) могут
^ыть получены при помощи уравнений G), A0) -и A0') методом наложения.
(с)
Р
А
ie
^ш
р
В
А
Щ
^ X. ^ I
2 ЛС 2 '\ff
Рис. 12.
Рис. 13.
Частный случай, показанный на рис. 12, решается на основе этих же
соображений,' если принять с = 0. Поступая, как объяснено выше, получаем
для прогибов на концах и посередине следующие выражения:
2Рр ch|/4-cos|/^
к sh р/ + sin Р' '
:^а=Уь
(d)
Уе —
и Р^ Р'
k shp/4-sinp/
Изгибающий момент посередине равен
М^=-
2Р
Р shpz-f stop/*
(е)
(t)
3]
ВАЛКИ КОНЕЧНОЙ ДЛИНЫ НА УПРУГОМ;, ОСНОВАНИИ
2Ь^
Случай одного груза посредине (рис. 13) может быть гакйсе получен из.
предыдущего, показанного на рис. 11, о. Необходимо лишь принять с = 1!2№
подставить Р вместо 2Р. Таким путем мы получим для прогибов посередине
и на концах следующие выражения: /'
. р/ р/
Уа—Ур — -J- shp/+ stop/
PPchp/-f cosp/4-2
2* shpz+sinpz •
Ус
Для изгибающего момента под грузом находим
Р chp/—cosp/
Мс^
# shp/ + sinp/'
(i>
Метод, примененный для симметричной задачи, приведенной на рис. 11, в,,
может быть также использован в антисимметричной, показанной на рис. 14, а.
В этом случае Q^ik М^^булут представлять также антисимметричную систему,
как показано на рис.-14, с. Для определения надлежащих значений Оо и М^
можно написать систему уравнений, подобных уравнениям (а), (Ь) и (с). Как
только С?о и ^0 будут вычислены, все необходимые параметры, касающиеся
изгиба балки, показанной на рис. 14, а, могут быть легко получены
наложением случаев, 'представленных на рис. 14, ft и 14, с.
Рис. 14.
Рис. 15.
Имея решение для симметричного и антисимметричного нагружений
балки, мы можем легко получить решение для любого рода нагружения,
используя принцип наложения. Например, решение для несимметричнога
случая, показанного на рис. 15, а, получается наложением решений
симметричного и антисимметричного случаев, показанных на рис. 15, ^ и 15, с.
Задача, показанная на рис. 16, может быть решена таким же способом. В
каждом случае задача сводится к определению надлежащих значений сИл Ов »
моментов Мд из двух уравнений (с).
При исследовании изгиба балок конечной длины мы замечаем, что
действие сил, приложенных к одному концу балки, на прогиб другого конца
-26
БАЛКИ НА УПРУГОМ ОСНОВАНИИ
[ГЛ. Г
зависит от значения величины р/. Эта величина возрастает с увеличением
длины балки. В то же время, как можно видеть из таблицы 1, функции ^, ф
и 6 быстро убывают, и при р/, превышающем некоторое значение, мы можем
предположить, что сила, действующая на одном конце балки, имеет лишь
незначительное влияние на другом конце. Это дает нам право, рассматри-
гвать балку как бесконечно длинную. В таком случае в уравнениях (Ь) можно
^пренебречь величинами ср (р/), ф (р/) и 6 (р/) по сравнению с единицей; тогда
уравнения (с) значительно упрощаются.
Вообще рассмотрение изгиба балок конечной длины приводит нас,
естественно, к разделению их йа три группы:
I. Короткие балки, р/<0,60.
II. Балки средней длины, 0,60<р/<5.
III. Длинные балки, р/>5.
При рассмотрении балок группы I мы можем совершенно пренебречь
1Изгибом и принимать эти балки абсолютно жесткими, так как прогиб от
изгиба обычно ничтожно мал по сравнению с осадкой основания. Взяв, напри-
Aiep, случай груза посредине (рис. 13) и положив р/ = 0,60, мы найдем по
i
А
I
Г71
'
\у
R
а}Ъ
А
Ьм,Ш
Рис. 16.
Рис. 17.
Ь)
3
•приведенным ранее формулам для у а и ус, что разница между прогибом
посредине и прогибом на конце составляет лишь около половины процента
от полной осадки. Это указывает на то, что осадка основания получается
с очень хорошей точностью, если рассматривать балку бесконечно жесткой
(И пользоваться для определения осадки формулой
_у =
kV
Характеристикой балок группы II является то обстоятельство, что сила,
действующая на одном конце балки, оказывает значительное влияние на
другом конце. Следовательно, такие балки нужно рассматривать как балки
конечной длины.
В балках группы III мы можем допустить при исследовании одного конца
балки, что другой ее конец бесконечно удален. Поэтому балку можно
принимать за бесконечно длинную.
В предыдущих рассуждениях предполагалось, что балка опирается на
-сплошное упругое основание, но полученные результаты можно также при-
31 БАЛКИ КОНЕЧНОЙ ДЛИНЫ НА УПРУГОМ ОСНОВАНИИ 27
менить и в том случае, когда балка опирается на большое число
равноотстоящих упругих опор. В качестве п|римера такого рода рассмотрим
горизонтальную балку А^ (рис. 17), поддерживающую систему равноотстоящих,
вертикальных балок, которые несут равномерно распределенную нагрузку q ^).
Все балки являются свободно опертыми на концах. Обозначая через Е/, и Zj,
соответственно жесткость при изгибе и длину вертикальных балок, мы
находим, что прогиб их посредине
у 384 £Л 48£Л' ^*'
где /^ есть давление произвольной вертикальной балки на горизонтальную
балку. Решая уравнение (j) относительно /?, мы находим, что горизонтальная,
балка АВ находится под действием сосредоточенной силы (рис. 17, с),
величина которой равняется
_, 5 , 48ЯЛ ...
/? = y9'i ^У- (к>
Полагая, что расстояние а между вертикальными балками мало по
сравнению с.длиной / горизонтальной балки и заменяя сосредоточенные силы
равноценной равномерной нагрузкой, как показано на рис. 17, с, заменяем также
ступенчатое распределение нагрузки (указанное на рисунке прерывистой;
линией) непрерывно распределенной нагрузкой интенсивностью
где
Тогда дифференциальное уравнение изогнутой оси для балки АВ будет
EJ-~i = gi—ky. (m)
Отсюда видно, что горизонтальная балка находится в условиях равномерно
нагруженной балки на упругом основании. Интенсивность нагрузки и
коэффициент основания даны выражениями A).
Для определения прогиба балки мы можем применить фанее поясненный
метод наложения или непосредственно проинтегрировать уравнение (ш).
Пользуясь последним способом, мы можем написать общий интеграл
уравнения (т) в следующем виде:
3» = ^ + Ci sin рл: sh ^х -j- Cg sin рлг ch рд: -}- Cj cos ^x sh ^x + Q cos ^x ch ^x. (n>
Взяв начало координат посредине (рис. 17, с), мы заключаем по условию
симметрии, что
Cg = Сз = ^J•
Подставляя это в уравнение (п) и пользуясь условиями для свободно
опертых концов
Ч.4=''' @).-4='''
') Различные задачи такого рода встречаются в корабельных
конструкциях. Довольно полное изложение таких задач дано И. Г. Бубновым в его
книге «Строительная механика корабля», Петербург, т. 2, 1914. См. также
П. Ф. Попкович, Строительная механика корабля, Москва, т. 2, ч. 1,
стр. 318—814, 1946.
■28
БАЛКИ НА УПРУГОМ ОСНОВАНИИ
1ГЛ.1
«юлучаем
Oj — —■=i-
k co8p/ + chp/ '
С,=:-%
2cds^ch|.
k cosp/4-chp/
Тогда уравнение изогнутой"оси будет
_5i
у =
2 sin Y sh Y
cospZ + chpf
sin pje sh рл: —
2co8^ch^
cosp/ + chp/
ЗПрогиб посередине получим, положив л: = 0, что дает
о Р' »,Р'
2coe!jch^
созрл: сЬрлг].
^.=0=1'
1
(о)
(р)
cospf + chp/
Подставляя это значение в уравнение (к), находим реакцию средней опоры
вертикальной балки, которая пересекает балку АВ в ее середине. Интересно
■отметить, что эта реакция может получиться отрицательной; это, указывает
на то, что горизонтальная балка действительно поддерживает вертикальные
"балки, если она достаточна жестка. В противном случае прогиб некоторых
вертикальных балок может увеличиться.
ЗАДАЧИ
1. Найти общее выражение для изогнутой оси балки, представленной на
рнс, 12.
Ответ.
2Рр chрд:coe^(l — x) + ch^(t — х)cos^х
shp/4-sinp/
2. Найти прогибы на концах и изгибающий момент посредине балки, из-
4гибаемой двумя равными и противоположными парами сил М,^ (рис. 18).
Ответ.
v,P' Р' , иР' • Р'
sh!--COS ~-+ ch i^ an !j
y^T
— = _ 2MoP' shpf —staff
Уа = Уь
k shp/ + sinp/ '
Mc = 2M„
sh p/ 4- sin p/
P
Рис. 18.
Рис. 19.
3. Найти прогиб и изгибающий момент посредине балки с шарнирными
асонцами (рис. 19). Harpj^sKa приложена посредине балки.
51 БАЛКИ КОНЕЧНОЙ ДЛИНЫ НА УПРУГОМ ОСНОВАНИИ 29
Ответ. ' . — -
4. Найти прогиб и изгибающий момент посередине равномерно нагружен-
балки
Omeek
яой балки с шарнирными концами (рис. 20).
1Ш.
Ус
1 —
о U Р' Р'
2ch^cos5^
chpz + cosp/
Мс'
ifl
1
\
тг"т 1 ■ 1 :.в t
^^ 1 —_^
^\
Л1 . Ы
Р« chpZ + cospr
Рис. 20.
Рис. 2i.
5. Найти изгибающие моменты на концах балки с защемленными
концами; балка несет равномерно распределенную нагрузку и груз посредине
<рис. 21).
Ответ.
М,:
д shpZ —sinp/
р shpz-fsinp/ 2^8 shpZ + sinpZ *,
6. Найти уравнение изогнутой оси балки на упругом основании с грузом
на одном конце (рис. 22).
Ответ. i
У =
2РР
Р
[sh р/ cos ^х ch р (/ — л:) — sin pZ ch рл: cos р (l -- л:)].
Рис. 22.
Рис. 23.
7. Балка на упругом основании с шарнирными концами изгибается парой
сил Же, приложенной на конце (рис. 23). Найти уравнение изогнутой оси
балки.
Ответ.
2М S*
'^""fe(ch^Pf-co8^PO^''^^^ smPA:shp(/ —д:)-со8р/ shрд:sinр(/-jr)|.
ГЛАВА П
БАЛКИ, ПОДВЕРЖЕННЫЕ ОДНОВРЕМЕННОМУ ДЕЙСТВИЮ
ОСЕВЫХ И ПОПЕРЕЧНЫХ НАГРУЗОК
4. Одновременное действие осевых сжимающих
и поперечных нагрузок
Начнем с простой задачи о стержне с шарнирными концами,
нагруженном одной поперечной силой и центрально сжатом двумя
равными и противоположными силами б' (рис. 24). Предполагая, что
стержень имеет плоскость симметрии, в которой действует сила Р, мы
принимаем, что изгиб происходит в этой же плоскости.
Дифференциальные уравнения изогнутой оси для двух участков стержня будут
X, (а)
I
dx^'
I
A-^х).
A7)
Пользуясь обозначением
о о
представим решения уравнений (а) и (Ь) в следующем виде:
V = d cos рх -)- Са sin рх — -^х, (с)
у = Сз cos рх ~\- Ci sin рх —
Рс
Рис. 24.
РA — с)
SI
{1-Х), (d)
Так как прогибы на концах стержня обращаются, в нуль, заключаем,
что Ci = 0, Сз = —Citg/?/.
Остальные две постоянные интегрирования найдутся из условий
неразрывности деформаций в точке приложения груза Р, которые
требуют, чтобы уравнения (с) и (d) давали один и тот же прогиб и
один и тот же угол наклона касательной при х=/—с. Таким путем
4] ОСЕВЫЕ СЖИМАЮЩИЕ И ПОПЕРЕЧНЫЕ НАГРУЗКИ 31
получаем *
d sinр(I--с) == Ci[sinр(I~~ с) ~tgр1 cosрA~ с)], • ^
Р
Qp cos (I — с) = Cip [cos рA— c)-\-tg р1 sin р (I — с)]-{- -^,
откуда
„ Psinpc „ Psrnp(l — с)
Sp sin рГ ^* Sptg/;/ •
Подставляя Ca в уравнение (с), получаем для левого участка стержня
Psinpc Рс ^-.Qv
и дифференцированием находим
^ dy Psinpc Рс
dx Ssinp/ ^ Si'
d^y Pp sin рс .
-j^ = ^ . \ sm px.
dx^ Ssinpl '^
A9)
Соответствующие выражения для правого участка стержня получатся
подстановкой (/ — х) вместо х и (I — с) вместо с и изменением
.знака dyjdx в уравнениях A8) и A9). Эти подстановки дают
^ = ^Ш^^'»''('—)-^V-*('--X B0)
В частном случае, когда груз Р приложен посредине, имеем с = 1[2,
и вводя обозначение
AEJ— 4 — "• ^^"^^
получаем из уравнения A8)
Первый множитель в уравнении B4) представляет прогиб, вызванный
действием одной лишь поперечной нагрузки. Второй множитель
указывает, в какой пропорции прогиб, вызванный силой Р, увеличивается
от действия осевых сжимающих сил б'. Когда 5 мало по сравнению
с эйлеровой нагрузкой (S^ = EJiz^jP), величина и мала и второй
множитель в уравнении B4) приближается к единице; это указывает на
то, что при этом условии влияние на прогиб осевых сжимающих сил
незначительно. Когда 5 приближается к эйлерову значению, величина и
mm
32 БАЛКИ под ДЕЙСТВИЕМ ОСЕВЫХ и ПОПЕРВЧ)Н[ЫХ НАГРУЗОК 1ГЛ. 11
приближается к значению «/2 (см. формулу B3)) и второй множитель
в уравнении B4) неограниченно увелиливается, как и нужно было
ожидать 'из нашего прежнего изучения вопроса о критической силе
(см. J. I, стр. 223).
Наибольшее значение изгибаюш.его момента имеет место под си-
лей jP, это значение получается из второго уравнения A9), которое
Опять видим, что первый множитель в уравнении B6) представляет
изгибающий момент, вызываемый действием только лишь силы Р,
в то время как второй множитель является коэффициентом
увеличения, оценивающим влияние осевой
силы ^ на наибольший изгибающий
-X момент. .
Имея решение задачи для одной
поперечной силы Р (рис. 24), можем
легко получить решение для случая
^^^- ^^- сжатого стержня, изгибаемого царой
сил, приложенной на конце (рис. 25).
Необходимо только предположить, что в нашем предыдущем
изложении расстояние с бесконечно уменьшается и приближается к нулю,
в то время как Рс остается постоянным и равным М^. Подставляя
Pc=Mff и slnpcs=pc в уравнение A8), мы получаем уравнение изо-
откуда
гнутой оси .4 / •
. ^—T\wi;r'~Tj' ^^^^
dy ___ 7Ив tpco&px \\
их 5 \ sinpZ / ;•
Углы наклона касательных к оси балки на концах будут
/^^ —^о/_£ IWA^oZfif 1 \_\ f07\
\<?л:]дг=о ~" S \sinJ0/ / j"~ 6EJ " \2« sin 2а Bи)*/' ^"^'^
1^\ \-LMb(_£ ^\ — Wo( 1 1 \ (оо^
\dxlx==i~~ S \tgpl 1 }~SEj''\2utg2u Bа)* j* ^''''^
Снова первые множители в уравнениях B7) и B8), взятые с
надлежащими знаками, представляют углы наклона касательных,
вызываемые действием только однбй пары сил Mq (см. т. I, стр. 141), а
вторые множители представляют влияние осевой силы .S.
Рассматривая уравнения A8) и B6), видим, что поперечная сила Р
и пара сил Ж© входят в эти выражения линейно, в то время как
осевая сила входит в те же выражения в более сложном виде, так
как р также содержит .S (см. уравнение A7)). Из этого заключаем,
что если в точке С (рис. 24) приложены две силы Р и Q, прогиб
4] ОЙЕВЫЁ СЖИМАЮЩИЕ И ПрПЕРЕЧННЙЕ НАГ^»УЗКИ ' 33
В какой-либо точке можно полз^ить налож€ни(^м ^прогибов,
вызываемых грузом Q и осевыми силами ^, на прогиб, вызываемый грузом Р
и теми же осевыми силами. Подобное з^клюдение можно применить
и в случае пар сил, приложенных на одном конце б^лки.
Это заключение относительно применения принцйда наложени»
можно легко обобщить й распространить на случай нескольких гру--
зов (рис. 26). Для/ кажщбго
участка сжатого, стержня
можно написать уравнение,
подобное уравнениям (а) и
(Ь), и можно получить
решение, подобное решениям (с)
и (d). Постоянные интегри- Рис 26.
рования можно найти из _^
условий непрерывности в точках приложения грузов и из условий
на концах сжатого стержня. Таким путем можно показать, что
"прогиб в какой-либо точке сжатого стержня является линейной функцией
грузов Pj, Pg, ... и что прогиб в какой-либо точке можно получить
наложением прогибов, вызываемых в этой точке каждым из
поперечных грузов, действующим совместно с осевой силой «S.
Рассмотрим общий случай, когда действуют л сил и т из этих
сил приложены справа от поперечного сечения, для которого
вычисляется прогиб. Выражение для этого прогиба получается при по^
мощи уравнения A8) для сил Pj, Р^, ..., Р^ и уравнения B0) для
сил Рт+1> Рщ+Ч' ••'* Рп- Таким путем находим требуемый прогиб:.
Если вместо сосредоточенных сил имеется" равномерно распрёде-'
ленная нагрузка интенсивностью q^ действующая на сжатый стержень^
то каждый элемент q dc этой нагрузки, взятый на расстоянии с от
правого конца, можно рассматривать как сосредоточенную силу.
Подставляя его вместо Р,- в уравнение B9,) и заменяя суммирование
интегрированием, получаем следующее уравнение для изогнутой оси:
1 — х 1 — х
l — x l—x
2 С П^ Тимошенко, т. 11
34
БАЛКИ ПОД ДЕЙСТВИЕМ ОСЕВЫХ И ПОПЕРЕЧНЫХ НАГРУЗОК
[ГЛ. П
Выполняя интегрирование, находим
y=w
cos
COS
pi
Jq JC {^l JCf,
2S
, . g
-'^raax W £ Sp2\cOSM
2
1
. M*\ ^0^ COSM,
1 ——
2
C0)
C1)
24
u*
Дифференцированием уравнения C0) легко получаем вйражения для
угла наклона касательной и для изгибающего момента. Угол наклона
касательной на левом конце стержня равен ,;
fdy\ ql^
{dx}x=^o~'2S
/«4
\ Pi
\ 2
'"4ё7 1
C2)
«"
Наибольший изгибающий момент будет нбсредине и равен
^(l-cosf) ^;.2(l-cosa)
Ж
max
= -^Л^^'.-''-
^—2
Scos
pi
8
M^COSM
C3)
Пользуясь решением для случая пары сил совместно с решениями
для поперечных нагрузок и применяя метод наложения, мы можем
легко решить, различные статически
неопределимые случаи изгиба сжатых
стержней. Взяв в качестве примера
случай равномерно нагруженного сжа-
трго.хтержня с одним заделанным
концом (рис. 27), найдем изгибающий
момент Же в заделанном конце из того
условия, что этот конец не
поворачивается при изгибе. Пользуясь уравнениями B8) и C2), это условие
представляем в следующем виде:
ql« tgu—u,Mol( 3 3
Рис. 27.
24Е/ I
— и"
3
3£/\2atg2a Bм)
-7^ =0.
откуда
Ж„
C4)
ql^ 4tg2uiigu—u)
8 a(tg2M —2м) •
В случае равномерно нагруженного сжатого стержня с обоими
заделанными концами моменты Жо на концах получатся из уравнения
д[ь tgH—м , Mp/f 3 3 •] MqI ( 6 6
.2м sin 2м
24EJ 1
м»
'[:
3EJl2utg2u B
3 1 МрП
uyj 6EJ [1
B
О,
4)
ОСЕВЫЕ СЖИМАЮЩИЕ И ПОПЕРЕЧНЫЕ НАГРУЗКИ
35
откуда
ql^ tg и—и
Ма= —
12 1
«*tg«
C5)
Из уравнений C4) и C5) видно, что значения статически
неопределимых моментов получаются умножением соответствующих моментов,
возникающих от действия только одной поперечной нагрузки, на
некоторые коэффициенты увеличения.
Необходимые вычисления можно значительно упростить при
помощи готовых численных таблиц, содержащих коэффициенты
увеличения *). В табл. 3 даны коэффициенты увеличения для равномерно
нагруженного сжатого стержня при следующих обозначениях:
_!__._ и*
cos и 2 . , ч 2 A — cos и)
сро(м) =
^f,{u).
24
и*
«""cosu
Когда наибольший изгибающий момент для сжатого стержня
найден, численно наибольшее напряжение получится сложением сжи-
Таблица 3
Коэффициенты увеличения моментов для равномерно нагруженных
сжатых стержней
и =
Ч'о(«)= '
to(«) =
.« =
fo («) =
Фо(«) =
0
1,000
1,000
0,90
1,494
1,504
0.10
1,004
1,004
1,00
1,690
1,704
0,20
1,016
1,016
1,10
1,962
1,989
0.30
1,037
1,038
1.20
2,400
2,441
0,40
1,070
1,073
1.30
3,181
3,240
0,50
1,114
1,И7
1,40
4,822
4,938
0,60
1,173
1,176
1.45
6,790
6,940
0.70
1,250
1,255
ч
1.50
11,490
11,670
0.80
1,354
1,361
It
~2~
С»
СО
мающего напряжения от силы б' с наибольшим напряжением от изгиба,
что дает .
М
max
■max
w
(е)
где F vi W — соответственно площадь поперечного сечения стержня и
момент сопротивления площади. Взяв в качестве примера равномерно
^) Различные частные случаи поперечно нагруженных сжатых стержней
были рассмотрены А. П. Ван-дер-Флитом, Известия Собрания инженеров
путей сообщения, С.-Петербург, 1900—1903 гг. Численные таблицы
коэффициентов увеличения даны в этой работе.
36 ; БАЛКИ |10Д ДЕЙСТВИЕ]У10СЁВЫХ и ПрГШРБЧИЫХ HAfPitaOK 1ГЛ. tl
нагруженный стержень с шарнирными койцами, лолучим из фор-
ЗИуЛЫ C3) -:
■max
ql^ 2A—cos й)
8Vr а^сози
(f)
При подборе надлежащих размеров поперечного сечения сжатого
стержня необходимо сначала установить зависимост!^ между
продольной; и поперечной нагрузками. Если условия тйкбвыу что осевая сила 5
остается постоянной, а может изменяться только поперечная
нагрузка q, то наибольшее напряжение по уравнению (f)
пропорционально, нагрузке q. Тогда требуемые размеры поперечного сечения
прочатся подстановкой в это уравнение о^/А вместо о^ах» где k —
коэффициент безопасности по отношению
к пределу текучести материала *).
Если условия такие, какие
показаны для, стержня Ав на рис. 28,
т. е. осевая сила iS изменяется'в том
же отношении, что и поперечная
нагрузка 9, .вопрос о выборе
безопасных размеров становится более
сложным. Правая часть уравнения (f) уже
не является линейной относительно q^
так как величина и, определяемая по
уравнению B3), такжЪ зависит от
величины q. Благодаря этому об-
стбятельству наибольшее напряже-
• ниё по уравнению (f) увеличивается
Б большей степени, чем нагрузка q, и если .мы поступим, как в
предыдущем случае, и подставим в это уравнение a^fk вместо Ощах.
то действительный коэффициент безрпасности конструкции будет
м^ньш^ чем k и нагрузка, при которой начнется текучесть, будет
меньше чем kq. Чтобы удовлетворить условиям безопасности,
воспользуемся уравнением (f) дли определения условий начала текучести и
Рис. 28.
запишем
^т- р "Т"
'^рЗЙт)
8 IF и|ссв«.
(g)
Так как S^ в каждом частном случае (например,, как на 'рис. 28)
является некоторой функцией q^., а «определяется по уравнению B3),
то правая часть уравнения (g) для любых принятых значений 7= и W
является функцией предельного значения нагруаКи q^^ а это значение
можно найти из уравнения путевй последовательных попыток. Зная q^^
мы определим безопасную нагрузку q-^jk для принятых размеров
*) Предполагается, что" материал стержня имеет ясно выраженный
предел TteKy^ecTH а^
41
ОСЕВЫВ СЖИМАЮЩИЕ Й П0ПВР]ЕЧН1|1е НАГРУЗКИ
.Шу
поперечного сечения сжатого стержня. "Повторягя эти вычйСлейия
несколько раз, мы тйожем окончательно найти размеры, поперечного
сечения*), которые будут соответствовать требуемому коэффициенту
безопасности k. Подобный метод был применен ранее в п. 59 т, 1.
(Расчет колонн на основании предполагаемых неточностей, стр. 232.)
■■':••"> 'ЗАДАЧИ ■■ ^ " ■ ,
1. Размеры сжатого стержня АВ на рис 28 таковы, что его эйлерова
нагрузка равнё lOipO кг. Пользуясь таблицей 3, найти коэффициенты увелиг
чения <fo(«) и ^(j(«), если а=45° и flf=1000 *сг.
Ответ, (ро (и) ==2,01; фо («)?= 2,03.
2. Найти угол наклона касательной на левом конце cikaToro стержня
с шарнирными концами, который нагружен в середине грузом Р и осевыми
силами S. ■■' '
_ (dy\ Р\—costt Р/^ I—costt
^'"«^'^- feUo=2S'-^5rir==,16£/ I. . ^ •
■ ■ ■ , . ' ■ ■ 4. ' - '
3. Найти углы наклона касательных на концах Сжатого стержня,
несущего треугольную нагрузку (рис. .29).
S "
г
V
-./г*
¥
\
<'
- {*А 1 ^
^^ ^ ■ S
г
Рис. 2§.
Рис. 30.
Решение. Подставляя в уравнение B9) щс dc/l вместо Pi и заменяя
суммирование интегрированием, находим
1~^х 1—х
sin рх
"~ 5/> sin
N о
О
I I
smp\
с)йа.
l—x
l—x
Дифференцируя это по Jf, яаходим, что
\dx}x=^o бр^ЕГ^ ''' [dxJx^i ^^EJ^ *''
где а и р являются функциями, определяемыми по уравнениям C6) (см.
ниже п. 5).
*) Этот метод расчета сжатых стержней был разработан К. С. Заврие-
вым; см. Известия Института инженеров путей сообщения (С.-Петербург),
1913 г.
38 БАЛКИ под ДЕЙСТВИЕМ ОСЕВЫХ И ПОПЕРЕЧНЫХ НАГРУЗОК (ГЛ. II
'4. Найти углы наклона касательных на концах сжатого стержня,
симметрично нагруженного двумя грузами Р, как показано на рис. 30.
\cos^ /
5. Сжатый стержень с заделанными концами нагружен, как показано
на рис. 30. Найти изгибающие моменты Мд на концах. ^
Решение. Моменты Мо найдутся из услойий, что концы стержня не
поворачиваются. Пользуясь ответом предыдущей задачи, а также уравнениями
B7) и B8), получаем для вычисления Мд следующее уравнение:
MqI MqI Р /сов pb Л__п
6ЕГ" + 3£7+'^'—^-М-0.
; откуда
.. 2PEJ и cospb Л
" SI tgtt\cosu Г
Если Ь = 0, получим случай стержня, нагруженного грузом 2Р,
сосредоточенным посредине.
б. Неразрезные сжатые стержни
В случае неразрезного сжатого, стержня мы поступим так же, как и
в случае неразрезных балок (см. т. I, стр. 175), и рассмотрим два смежных
, пролета (рис. 31) ^). Пользуясь уравнениями B3), B7) и B8) и вводя следую-
щие обозначения для п-го пролета при u^=jpj-:
^r 1
P« ^|Btt„)« 2a„tg
2u„sin2a„ ,_..„, ^ ,
(db)
If, ' ' ...
b = *-^^f^. C7)
мы заключаем, что угол наклона касательной на правом конце п-го пролета
(рис. 31, а), вызываемый концевыми моментами Mnli и Л1„, равняется
~Р"ЗЕ/„~""~61ЛГ' ^^
Угол наклона касательной, 'Вызываемый на левом конце (п + 1)-го пролета
м<;^ментами Л1„ и Л1„+„ равняется
*) Теория принадлежит Н, Zimmermanп'у, Sitzungsber. Akad. Wis-
sensch., Berlin, 1907 и 1909.
51
НЕРАЗРЕЗНЫЕ СЖАТИЕ СТЕРЖНИ
39
Если нет поперечной нагрузки, действующей на двух рассматриваемых
пролетах, то выражения (а) и (Ь) должны быть равны ме^ду собой, поэтому
получаем ' .
П^Л1„_, + 2(р„-^ + Р„^4^]л1„+а„^.,^Л1„+,=0. C8)
•'П ^ •'П •'n+l/ •'П+1
Таково уравнение трех моментов для неразрезного сжатого стержня, если
не имеется поперечной нагрузки на двух рассматриваемых пролетах.
'М.
'гт-1
п~1
^^л-.
Ч,
/т*/
Рис. 31.
Если же действует поперечная нагрузка, то соответствующие углы
наклона касательных, вызываемые этой нагрузкой, должны быть добавлены
к выражениям (а) и (Ь). Взяв, например, случай равномерной нагрузки дп и
Чп+и действующей на пролетах п и п -f-1 в направлении сверху вниз, мы
найдем соответствующие углы наклона касагельных из уравнения C2) и
вместо выражений (а) и (Ь) получим
Р«
SEJn
MnLyU
М
*Л+1'
П+1*Л+1
+р,
6£/„
Mnln+i.
— Тп
Чп11
приравнивая эти два выражения, мы находим
24EJn '
"+^ 24EJ„
+ Т
'n+i
(с)
(d)
Jn
\ •'n •'n+l/ •'П+1
— In
Яп1%
AJn
"in+i.
gn+i^n + 1
4/.
n+l
C9)
Это уравнение трех моментов для сжатого стержня с равномерной
нагрузкой в каждом пролете. Оно подобно уравнению трех моментов для нераз-
резной балки и совпадает с ним,
когда S = 0 и функции о, р, -у
становятся равными единице.
Для любого иного вида
поперечной нагрузки мы должны изменить
только правую часть уравнения C9),
которая зависит от поворота
смежных концов двух пролетов,
вызываемого поперечной нагрузкой. Взяв,
например, , случай трапецеидальной
нагрузки, показанной на рис. 32, и
разделив нагрузку на две части:
равномерно распределенную нагрузку и нагрузку по треугольнику, мы
воспользуемся для равномерных нагрузок членами, уже написанными в правой
Рис. 32.
ifF
40 БАЛКИ йод ДЕЙСТВИЕМ ОСЕВЫХ и ПОПЕРЕЧНЫХ НАГРУЗОК [ГЛ. И
части уравнения^39), К этим членам мы должны добавить члены,
соответствующие треугольным нагрузкам. Пользуясь выражениями для углов
наклона касательных в задаче 3 предыдущего параграфа, мы находим, что два
члена, которые мы должны добавить к правой части уравнения C9) в
случае нагрузки, показанной на рис. 32, будут
Р Jn • Р -fn+i. ■ *
где Од и Рп+1 .определяются выражениями (Щ. 'Если на рассматриваемых
пролетах действуют сосредоточенные силы, то требуемые ' выражения для
яоворотов легко получаются из общего уравнения изогнутой оси B9).
Вычисление моментов из уравнения трех моментов C9) можно
значительно упростить при помощи числовых таблиц функций о, р и 7 ^).
При выводе уравнения C9) предполагалось, что момент М^ на п-й опоре
имеет одно и то же значение для обоих смежных пролето*. Однако
встречаются чглучаи, когда на опоре приложен внешкий момент М^, как показано
на рис. 31, с; тогда следует иметь в виду различие между значениями
изгибающих моментов слева и справа от опоры. Соотношение между этими
двумя {Моментами дается уравнением статики 2): Мп—М^ — Л1^ = 0, откуда
К = М„-Л1«. ' (f)
Уравнение C9) в таком случае заменяется следующим уравнением:
^ Л1я.1+ 2р„ ^ м„+2р„^., ^ м; + ««+17^' Мп^, =
Если опоры неразрезного сжатого прямого стержня не находятся на
одной прямой, то в правую часть уравнения C9) или D0) должны быть вне^
сены дополнительные члены, зависящие от разностей в уровнях трех
последовательных опор. Наличие осевых сил не влияет на эти члены, и они будут
такими же, как и в с;лучае балки без рсевой нагрузки (см. т. 1, стр. 177).
ЗАДАЧИ
1. Написать правую часть уравнения трех моментов, если имеется
сосредоточенная сила Р в ;(и4'1)-м пролете на расстоянии й„+1 от опоры п + Ь
Ответ.-:^S—{^£!B:^^M^
2. Написать правую часть уравнения трех моментов, если п-й пролет
нагружен так, как показано на рис. 30, стр. 37, и если на п + Ьм пролете
не имеется нагрузки.
^) Такие таблицы можно найти в книге А. S, N i 1 е s and J. S. Newell,
Airplane Structures^ New York, т. 2, 1943; см.- также книгу автора «Theory of
Elastic Stability», New York, 19*5; русский перевод: Устойчивость упругих
систем, 1955, Гостехиздат, Москва, i
2) Направление Mf^, указанное на рис' 31, с, принято за положительное
направление внешнего момента.
6]
РАСТЯНУТЫЙ СТЕРЖЕНЬ С ПОПЕРЕЧНОЙ НАГРУЗИЛИ
41
Ответ. Пользуясь рещением задачи 4 стр. 38, мы получим следующее
выражение:
■)•
л*/
Рис. 33.
3; Нййтй правую часть уравнения трех моментов, если нагрузка такая,
как показано на рис. 33.
Ответ.-^^1-^^^^^-Ьп
/'«cos^
■)■
6. Растянутый стержень с поперечной нагрузкой
Если растянутый стержень подвергается действию растягивающих
сил 5 и поперечной нагрузки Р (рис. 34), то мы можем написать Диф^
ференциальное уравнение изогнутой оси дли каждого участка стержня
точно таким же образом, как это
сделано для сжатого стержня в п. f.
Необходимо лишь изменить знак при 6".
В таком случае вместо величин р* й и\
определяемых соответственно
уравнениями A7) и B3), мы будем иметь
—jD^ и —и^^ а вместо р и^м мы будем
иметь р |/— 1р=:р/ и и i/— 1 =н£. Подставляя -г- 6", р1 й id вместо
S, р и и в формулы, полученные для сжатого стержня (рис. 24),
мы получим необходимые формулы для растянутого стержня,
показанного на рис 34. При выполнении этой подстановки мы
воспользуемся известными зависимостями:
sin «/=^ishа, cosH/ = chH, tgui = itb.u.
Таким .путем мы получим для левого участка растянутого стержня
(рис. 34) из уравнений A8) и A9):
Рис. 34.
Pshpc . , Рс
dx Sshp/"'^-^^ Sr dx*
Ppshpc
Sshpl
shpx.
D1)
D2)
Подобные формулы можно .также поЛучить для правого -участка
при помощи уравнений B0) — B2). .Имея уравнение изогн)гтой оси
mm
42 БАЛКИ под ДЕЙСТВИЕМ ОСЕВЫХ И ПОПЕРЕЧНЫ?; НАГРУЗОК [ГЛ. II
для случай одного груза Р, действующего на растянутый стержень»
мы можем легко получить уравнение изогнутой оси для любого рода
нагрузки, используя метод наложения. " '
Рассматривая, например, равномерно нагруженный растянутый
стержень и пользуясь уравнениями C0) и C1), мы получаем
у=^
ch
(^--)
наибольший же прогиб будет
chf-
Н-^-^(^ —лг);
' 1 + "^
J/шах = (y\_i = mTj 5~ = 384 Ш ^1 <">' <^^>
где
... 1 , цз
, . сЬи ^ 2
<Pi(«) = 5 ♦
24
Угол наклона касательной к изогнутой оси на левом конце по
уравнению C2) станет ^
{ЁУ\ — Я^' Ц—th» ,44^
\dx)x=^o'~'24EJ _l^„, • ^^^^
3
^и»
Наибольший изгибающий момент, который в этом случае будет
посредине пролета, получится из уравнения C3):
где
2(chK—1)
1'1(и)
tt*chtt
Отсюда видно, что наибольший прогиб и наибольший изгибающий
момент получаются умножением соответствующих выражений для
свободно опертой балки без осевой нагрузки на множители «р^ (и) и
^i(m), которые зависят от величины осевой растягивающей силы 6".
Числовые значения этих множителей даны в табл. 4*).
В случае изгиба растянутого стержня парой сил, приложенной на
правом конце, уравнение изогнутой оси получается из уравнения B6),
*) Различные случаи изгиба растянутых стержней исследованы в статьях
А. П. Ван-дер-Флита, цит. на стр. 35, а также И. Г. Бубнова, цит. на стр. 27.
Табл. 4 взята из последней книги.
6}
РАСТЯНУТЫЙ СТЕРЖЕНЬ С ПОПЕРЕЧНОЙ НАГРУЗКОЙ
43
Таблица 4
Множители для определения прогибов и наибольших изгибающих
моментов поперечно нагруженных растянутых стержней
и
0
0,5
1,0
1,5
2.0
2,5
3,0
3,5
4,0
4,5
5,0
5,5
6,0
Vl
1.000
0,908
0,711
0,523
0,380
0,281
0,213
0,166
0,132
0,107
0,088
0,074
0,063
<Рз
1,000
0,976
0,909
0,817
0,715
0,617
0,529
0,453
0,388
0,335
0,291
0,254
0,223
Ф1
1,000
0,905
0,704
0,511
0,367
0,268
0,200
0,153
0,120
0,097
0,079
0,066
0,055
Фз
1,000
0,984
0,939
0,876
0,806
0,736
0,672
0,614
0,563
0,519
0,480
0,446
0,417
Фв
1,000
0,972
0,894
0,788
0,673
0,563
0,467
0,386
0,320
0,267
0,224
0,189
0,162
и
6,5
7,0
7,5
8,0
8,5
9,0
9,5
10,0
10,5
11,0
11,5
12,0
VI
0,054
0,047
0,041
0,036
0,032
0,029
0,026
0,024
0,021
0,020
0,018
0,016
<Рз
0,197
0,175
0,156
0,141
, 0,127
0,115
-t),105
0,096
0,088
0,081
0,075
0,069
4-1
0,047
0,041
0,036
0,031
0,028
0,025
0,022
0,020
0,018
0,017
0,015
0,014
—1
Фз
0,391
0,367
0,347
0,328
0,311
0,296
0,283
0,270
0,259
0,248
0,238
0,229
Фв
0,139
0,121
0,106
0,093
0,083
0^074
0,0615
0,060
0,054
0,050
0,045
0,042
которое напишется так:
MqIx sbpx\
^~ S \l shpl j
D6)
Если имеются две равные и противоположные пары сил,
приложенные к концам растянутого стержня, уравнение изогнутой оси
получится с помощью метода наложения:
Мо(х_ sh рх\ ■ МрП — X $ЪрA — л:)"|
Mo
S
^ chp(i—x)
2
D7)
Из этого уравнения мы находим прогиб посредине и угол наклона
касательной на левом конце растянутого стержня:
Mpchu—1 MqI^ chu — 1
Су),
{dxJx=o
chu
8£J 1 , . '
-K- и ch и
M
D8)
-^pthu
MJtha
2EJ u'
Изгибающий момент посредине равен
w.=4=-^-'(SL
м,
1
• ch ц"
D9)
imw
44 БАЛКИ ПОД'ДЕЙ€Т61{11Е»1 ОСЕВЫХ И ПОПЕРЕЧНЫХ НАГРМЗОК {ГЛ, П
^ . \. '■ - ■
Имея уравнение изогнутой оси для растянутого стержня с
шарнирными кощамй, изгибаемого Поперечной нагрузкой и парами сил на
концах, мы можем легко получить различные статически
неопределимые случай изгиба растянутых стержней rio методу наложения.
Взяв, "например, случай равномерно нагруженного растянутого стержня
с заделанными концами и воспользовавшись уравнениями D4) и D8),
мы .получим изгибающ.ие моменты Ж^ на концёх из уравнения
ql^ It—Щц , M^l th» __^
otKyfla
где
24£У 1 , r2EJ и
3
^о = —121 -— — ybitO' E0)
, , ч и —thu
-^u^thu
■ i :0
■ . '' ' ' ■■. ^
Числовые значения функций фз (н) даны в таблице 4. При помощи
уравнений D6) и D9) изгибающий момент посредине получится равным
л. _ge2(<^h»-l) дПи~ти _q^6(shu--u)__ql\ ,.
^1~1Г u^chu ~I2 ,^ —24 u«sh« —M'^^W- E1)
о
Прогиб посредине определяется уравнениями D3) и D8), которые
дают >..
1 и*
_/V _^ 5 д1*аГи~^^^Т ql* (u^thц)(chц — 1)_
Ушах—ЛУ)^_|--384 £/ 5^^, 16EJ и* Shu ~"
24
-=ШЕТ^^<^г E2)
где.
.V 24/и» ttCh tt — tt\
Функции ^1, ..., ^ раэны единице при w == О, т. е. когда
действует только поперечная нагрузка. Когда продольная растягивающая
сила yвeличивaeтcЯj каждая из этих функций уменьшается, т. е.
продольные растягивающие силы уменьШак)Т прогибы и изгибающие
моменты в поперечно нагруженные растянутых стержнях. Применения
вышеприведенной таблицы будут даны ниже при рассмотрении изгиба
тонких пластинок (см. стр. 72).
7J
ПРЕДСТАВЛЕНИЕ КРИВОЙ ИЗГИБА "ТРИГОНОМЕТРИЧЕСКИМ РЯДОМ
..ЗАДАЧИ,-.■ ■ .. . .
Ь Найти наибольший п]рогиб и наибольший изгибающий момент дяяг
растянутого ^тержня, нагруженного посредине. ^
Р/» и'—ЛЬи ., Pnbt^ .
Ответ.
(У)
max
4НЩ 1
м
и«
max
и
2. HafttH изгибающие моменты ТИо «а концах растянутого стержня, с
заделанными концами, симметрично нагруженного двумя Силами Р,, как рока*,
зано на рис. 30.
Решение. Изгибающие моменты г н& концах
получатся из уравнения
Р
S
I М^1 thи _^
3, Найти изгибающие моменты. Ц» концах
растянутого стержня с заделанными концами, нагруженного
треугольной нагрузкой, показанной на рис. 29.
y^aaaMUif. Воспользоваться решением задачи 3 на
стр. 37, а также уравнением D6).
4. Найти наибольший прогиб ц наибол^шц^ - из-
^Ш
Рис. 35.
гибающий момент для стержня, показанного, на
рис. 35. ~» '
Указание. Считать стержень, как половину растянутого стержня,
нагруженного посредине.
7* Представление.кривой изгиба тригонометрическим рядом
При рассмотрении изгиба балок иногда очень удобно представить
кривую изгиба в виде тригонометрического ряда*). Это имеет то преимущество,
что по всей длине пролета ^справедливо
единое математическое выражение
изогнутой оси. Взяв случай балки с
опертыми концаь^и *), показанного на рис. 36,
можно охарактеризовать прогиб в любой
ее точке следующим рядом:
. -пх , . 2ялг ,
y = ai sm -j^ -f- «2 sin ^-7—r
-f- e, sm -y- -f- -..
iv
Геометрически это означает, что ' ^ рдс. зб.
изогнутая ось может быть поЛучена
наложением простых синусоид; таких, какие показаны на рис. 36, ft, с ц d
^) См. статью аатсфа «Применение нормальных координат к
исследованию изгиба стержней и пластинок», Известия Киевского политехнического
института, 1909; cw. также И. М. Westergaard, Proc. Am^ Зое. Civ. Engrs.,
т. 47, стр. 455 — 533.
. ^) В других случаях расчет становится слишком сложным для
большинства практических целей. ^
mm
46 БАЛКИ под ДЕЙСТВИЕМ ОСЕВЫХ И ПОПЕРЕЧНЫХ НАГРУЗОК [ГЛ. Н
И т. д. Первый ,член ряда (а) представляет первую кривую, второй член
представляет вторую кривую и т. д. Коэффициенты Oj, «g, а^ ряда дают
наибольшие ординаты этих синусоид, а числа 1, 2, 3,;.. дают число полуволн.
Надлежащим выбором коэффициентов а^, а^, ... ряда (уравнением (а)) можно
представить любую изогнутую ось ^) со степенью точности, которая зависит
от числа взятых членов. Эти коэффициенты можно вычислить путем раст
смотрения потенциальной энергии деформации балки (т. I, уравнение A91),
стр. 268), которая определяется выражением
^^=¥5©)'- . <ь>
Вторая производная от у на основании уравнения (а) будет
S
d4 т.^ . 7ZX 2М , 2ял: 3%* . Зпх
^^3=—а, — ЯП—— flB-TTsin-^ ««-^sm-y-...
В уравнение (Ь) входит квадрат этой производной, который содержит члены
двух родов: .
" «л*"* - <> ппх „ ' п^т^-к* , тх , тих
a%-^sm^-j- и 2апат—-p^^n^sin—^.
Непосредственным интегрированием можно показать, что
]
. „ П-пХ . I
sm^——dxz=-^
и
. ппх , т-пх . -
sm—р- sin —J— dx = 0 при пфт.
Следовательно, в интеграле уравнения (Ь) все члены, содержащие
произведения коэффициентов такие, как Од, а^ обращаются в нуль и остаются
только члены с квадратами этих коэффициентов. Тогда
п=со
^=^A*-«Ц-2М + 3*.о| + ...) = :|^ ^пЧ%. E3)
в предыдущем Изложении (см. т. I, уравнение (а), стр. 303")) было
показано, что если упругая система претерпевает малое перемещение из своего
положения равновесия, то" соответствующее увеличение потенциальной
энергии деформации системы равно работе, совершенной внешними силами на
таком перемещении. Когда упругая кривая представлена рядом (а), беск9-
нечно малые перемещения можно получить бесконечно малыми вариациями
коэффициентов а„ а^, «з» ••• Если любому коэффициенту а„ дать
приращение dan, то вместо члена Оп sin (nnx/l) мы будем иметь в ряде (а) член
*) См. Byerly, Fourier Series and Spherical Harmonics, §§ 19 — 24. См.
также Osgood, Advanced Calculus, стр. 391, 1928. ,
2) См. также S. Timoshenko and D. H. J о u n g, Theory of Structures.
New York, стр. 229, 1945.
-f] ПРЕДСТАВЛЕНИЕ КРИВОЙ ИЗГИБА ТРИГОНОМЕТРИЧЕСКИМ РЯДОМ 47
(вп -\- dan) sin (nnx/l), другие же члены останутся без изменения. Это прирэт
щение dOn коэффициента о„ представляет дополнительный бесконечно малыйг
прогиб, изображаемый синусоидой «?«„ sin (ияд://), наложенной на
первоначальную кривую. На этом дополнительном прогибе внешние силы совершают
работу. В случае только одного груза Р, придоженного на расстоянии с от
левой опоры, точка приложения груза претерпевает вертикальное
перемещение dan sin (nizx/l) и груз совершает работу, равную
dan (s»n^) Р- (с)
Приращение потенциальной энергии деформации, определяемой по
уравнению E3), вследствие приращения dOn коэффициента а„ равняется
dU = -^dan = -~-n*andan. (d)
Приравнивая это работе, определяемой уравнением (с), получаем
-2j^^'^an = P sin-J-,
откуда
2Р/3 1 . тс
Из этого уравнения мы можем определить каждый из коэффициентов ряда (а),
и уравнение кривой изгиба получится в таком виде:
2Р/3 / . -ПС . 1ZX , 1 . 2яс . 2-кх , \
00
2Р/» \1 1 , nizc , ппх ,-„
При помощи этого уравнения можно вычислить прогиб для любого значе-^
ния X. Например, прогиб, посередине, когда груз находится посредине
(с = л: = //2) будет
2
Взяв только один первый член этого ряда, получим ч,
2Р/3 р/з
/=
EJtz* 48,7ЕГ
Сравнение с ур;авнением (90) т. I (стр. 130) показывает, что мы получили 48,7,
в то время как точное значение было 48, так что ошибка, сделанная при
использовании только одного первого члена вместо всего ряда, составляет
около 1,5в/о. Такая точность достаточна во многих.практических случаях; мы
будем Иметь другие примеры, где достаточная точность получится при
использовании только одного члена ряда (а).
На основании решения, полученного для одного груза, можно
исследовать с помощью метода наложения более сложные задачи. Например,
рассмотрим балку, несущую равномерно распределенную нагрузку
интенсивностью д. Каждый элементарный груз д dc, находящийся на расстоянии
с от левой* опоры, вызывает прогиб, получаемый по уравнению E4) при
к^^жТИ"'
48 БАЛКИ ШД ДЕЙСТВИЕМ ОСЕВЫХ И ПОПЕРЕЧНЫХ НДГРУВОК (ГЛ. П
подстановке S него Р«Si?4<;, равный
00
S
. п%с . mix
sm —г- sin ■
^y^2qdcl> > •" / - /
EJn* Amd in?'
n=« 1
И|1тегрируя это по с в пределах от с = О до с = /, получаем прогиб,
вызываемый всей нагрузкой:
п = 1, 3, Ъ, • • •
Если мы воспользуемся только ойним первым членом, прогиб посредине
равномерно нагруженной балки будет
. 4?/* ql^
гы 7e,5EJ'
сравнивая это решение с t04Hbi?ii решением
находим, что ошибка при использовании только первого члена в этом случае
составляет меньше 1/2*/о.
Тригонометрический ряд (а) особенно удобен в том случае, когда в
дополнение к поперечной нагрузке балка подвергается действию продольной
сжимающей или растягивающей силы. В случае балки, показанной на рис. 37,
шарнир В приближается к неподвижному шарниру А при изгибе балки на
величину, равную разности между длиной изогнуто^ оси и длиной хорды AB^).
Для пологой кривой эта разность равняется (см. т, I, <:тр. 157)
I
=т1Ш'- ■ '^)
X
б
Если реличина у эааана уравнением (а), то квадрат ее производной
содержит члены двух виаов:
„п*я* аПпх ^ _ - nmii^ mix mux
^^-jr^^ I ^ 2a„fl^-^^-cos-pCos—p.
Интегрированием можно показать, что
-'■ г ''■... ■ I
J, ппх . I с ппх тпх .л у
cos'-у-"л: = -2"; I cos-y-cos—^йл: = 0 пряпфт.
..,, .,■.." о - ' ) ■ '
Тогда уравнение для определения Х получится в таком виде:
оо
^=^2 «X. E7)
;^*) При малых Прогибах продольное относительное укорочение балки под
действие:м осев(^ силы можно считать постоянным. :
^]
ПРЕДСТАВЛЕНИВ КРИВОЙ ИЗЩБЛ ТРЙГОИОАШТРИЧЕСКИМ РИДОМ
т
Для вычисления коэффидиентор «ь «а, «j, ... в ряду (а) мы опять
рассмотрим работу, со9ерщснную"*внещними силами на бесйойечно малом nef)e-
мещении <fа« sin (я«;с//) из положения равновесия. В. случае, представленном
на рис. 37, при таком деремещенйи и груз Р и продольная сила 5
совершают работу. Перемеш^ение X вследствие прира[1цевия dd^ коэффициента а^
увеличивается на величину > ^ ' .
Тогда работа, совершенная силой S,
будет равна
■ я*'
Рис. 37.
Эта работа прибавляется к работе (выражение (с)), совершенной поперечной
силой, и сумма этих работ приравнивается приращению потенциальной эне]р-
гии (уравнение (d)). Это дает нам следующее уравнение для определения
любого коэффициента а„ в уравнении (а):
Psin
«тсс
d(^n + S ^ п*«п'^вй == -5«г «*«п <?«я.
2/
откуда
2Р/»
^'^'^EJn
2/«
sin
«яс
у
Обозначив отношение продольной силы к критическому значению осевой
нагрузки (см. стр. 31) через a = S/V£/«', получаем
2Р/«
1
^"~^Ё/7с«иЧи'-
в)
sin
«тес
Подставляя ЭТО значение в уравнение (а), придаем уравнение кривой изгиба
следующий вид:
2Р/* /1 . тес . «лг ,
1 , 2яс . 2тед:
^nr^sin-^-sin
г+-)=
EJ;
00
^ V 1
^' tmc . ппх
sm -ч—sm—7-.
E8)
п ■■
сравнивая это с уравнением E^, выведенным для случая только
поперечной нагрузки, видим, что прогиб бруса увеличивается благодаря дейетвию
продольной сжимающей силы S. Мы уже знаем, что первый'член ряда (а)
представляет хорошее приближенное значение для прогиба бруса;
следовательно, увеличение прогар, вызываемое продольной силой, может быть
приближенно представлено отношением I: A— в).
Это заключение также справедливо в том случае, когда действует
несколько поперечных грузов в одном и том же направлении или когда на
балку действует непрерывная нагрузка. Обозначая через/о наибольший
прогиб, вызываемый действием только одной поперечной нагрузкой, мы можем
с достаточной точностью предположить, что при одновременном действии
ш
50 БАЛКИ под ДЕЙСТВИЕМ ОСЕВЫХ Й ПОПЕРЕ»^НЫХ НАГРУЗОК [ГЛ. 1Г
сжимающих сил S и поперечной нагрузки наибольший прогиб будет равен
/=1^. E9)
Зто выражение для наибольшего прогиба можно* применить также и для
вычисления изгибающих моментов в сжатом стержне. Например, в случае
равномерно нагруженного сжатого стержня с шарнирными концами
наибольший изгибающий можно вычислить по следующей приближенной формуле:
Л4тах = ^' + Г^. F0)
Если продольная сила является растягивающей, а не сжимающей, то
разобранный выше ме1;од сохраняет силу, необходимо лишь в выражение
для изогнутой оси E8) подставить — а вместо а. Если мы воспользуемся
только первым членом в этом выражении, то для прогиба посередине
полечим следующую приближенную формулу:
где /о означает прогиб, вызываемый только поперечными грузами.
Необходимо заметить, что в случае продольных растягивающих сил а может быть
больше единицы и что точность приближенного выражения F1) уменьшается
с увеличением а. Например, в случае равнрмерно распределенной нагрузки
ошибка в уравнении F1) при о = 1 составляет приблизительно 0,3"/в. При
о = 2 ошибка равна 0,7о/о и при о =10 она равна 1,7«>/о.
В случае бруса с заделанными концами для вычисления прогиба
посередине пролета можно вывести следующее приближенное выражение,
аналогичное выражению F1):
4
1 +
f=-^^, F2)
где /о есть прогиб посередине, вызываемый действием только одних
поперечных нагрузок, а а, имеет то же значение, что и ранее. ,
Применение этих приближенных формул будет показано ниже 'при рас-
рмотрении, прогибов тонких прямоугольных пластинок. Метод
тригонометрического ряда также может быть распространен на расчет балбк переменного
поперечного сечения ^).
ЗАДАЧИ
1. Пользуясь бесконечным рядом, вывести уравнение кривой изгиба
балки, показанной на рис. 36, а, если на нее действует пара сил, приложен-
•»ная на левом конце.
Решение. Принимая с за весьма малую величину и подставляя Рс = М,
sin (nnc/l) S5S5 (rrnc/l) в ряд E4), мы полу-
-^ ' чаем _
J'
'i
пт
6
гу-
1
J '
S
.
ппх
2М1'' \1 1 . ил,
п==1
2. Составить уравнение изогнутой
оси свободно опертого сжатого стержня.
Рис. 38. нагруженного, как показано на рис. 38.
^) См. статью М. Hetenyi, J. Appl. Mech., т. 4, стр. А-49, 1937.
S]
ПРОТИВ БРУСЬЕВ С МАЛОЙ НАЧАЛЬНОЙ КРИВИЗНОЙ
61
00
Ответ, у^^ ^ WW=^['^
ппа
cos—j-j sm
nnx
3. Найти прогиб / конца В вертикальной колонны АВ. Колонна заделана
в Л и нагружена в В, как показано на рис. 3&.
Ответ.
/=
где
3£71—о'
_PBlf
Рис. 39.
8. Прогиб брусьев с малой начальной кривизной
Если брус с малой начальной кривизной изгибается
только одними поперечными силами, то прогибы можно
вычислять по методу, применяемому для Прямого бруса.
Однако условия будут совершенно иными, если имеются
кроме поперечных сил еще и продольные силы. Малая лачальная кривизна
вносит значительное изменение в действие этих продольных сил на прогиб.
Решение этой сложной задачи можно значительно упростить, используя
тригонометрический ряд для представления как начальной формы кривой,
так и прогибов, вызываемых изгибом *). Предполагаем, как и ранее, что
кривой брус имеет плоскость симметрии, в которой действуют внешние
силы, и считаем, что этот брус свободно опирается на концах. Пусть з'о
означает начальные ординаты осевой линии бруса, измеряемые от хорды,
соединяющей центры тяжести концов, и 3*1—прогибы, вызываемые внешними
силами, так что полные ординаты после изгиба будут равны
У=Уй-\гУу
Пусть для начальной изогнутой оси мы имеем ряд
yfi = biSm-j--\-bssm—j--\-..
и пусть прогиб, вызываемый грузом, будет
У1
. их , . 2пх
«1 san -у- 4- '^а s»n -J-
(а)
(b)
(с)
В этом случае можно -воспользоваться тем же 1самым выражением
(уравнение E3)) для потенциальной энергии деформации, что и для прямых брусьев.
Для нагрузки, показанной на рис. 37, необходимо при вычис;?ении работал,
совершенной продольными .силами S, заменить величину X (см.
выражение E6)) величиной
о о
,00 00 ,
F3)
*) См. статью автора, «Festschrift zum 70 Geburtstage August РбррЬ,
Berlin, стр. 74, 1924.
imw
Ш БАЛКИ под ДЕЙСТВИЕМ ОСЕВЫ?; и ПОПЕРЕЧНЫХ НАГРУЗОК {ГЛ. Й
Это явл111ется продольным перемещением одного конца изогнутого стержня
относительно другого конда при изгибе.
Поступим т;ак же, как и в сагучае прямых брусьев (стр. 49) и дадим
стержню бесконечно малый дополнительный прогиб «?«„ sin (ятсдг//). Работа,
произвед1енная продольными силами S при этом прогибе, равна
Работа же, совершенная грузом Р, равна
& приращение потенциальной энергии деформации по уравненик! E3У будет
'■;'■' . ■ ' ■; ЕМ ■ ^
Уравнением для вычисления я;, является ,,
■ ( ■
-gj-n*Me« — Я sm ~^-rffl^ 4-S-^ (e„ + fc„) rfe„,
откуда
' '^"'^' EJn*n* — Sn'n*P • ,
Подставляя уравнение (с) и пользуясь, обозначением о = ^гг-г, получаем
'•■'.■; JbJ'n
(. тсс . тслг . 2яс . 2кх \ /, ■ их . . 2ил: \
F4)
■ " ■ \ ■
Первый член правой части уравнения F4) представляет прогиб прямого
бруса (см: уравнение E8)), в то время как второй дает дополнительный
прогиб благодаря начальной кривизне. ч
Возьмем, например, брус, который имеет начальный прогиб Уо^=Ь sin (тел://).
Наибольший прогиб будет посредине пролета и равняется Ь. Если на брус
действуют только одни продольные силы 5 (Р = 0), хо прогиб посередине,
вызываемый этим CHJia^Hf получается из уравнения F4) путем подстановки
Р=:0, *1==Д (&д =s=>^sir,..i==:0. Тогда
absm—z-
Полные ординаты осевой линии после изгиба будут равны
«д «in -г .
I * * ... тех • х> . -пх ,->_»
( ■•■■■,■ .- ' ^^
Благодаря продольным сжимающим силам S ординаты осевой линии
увеличиваются в отношении 1;A-^о), т. е. увеличение opAHHat зависит от вели-
8)
ПРОГИБ БРУСЬЕВ С МАЛОЙ НАЧАЛЬНОЙ КРИВИЗНОЙ ' 53^
ЧИНЫ а, которая представляет собой отношение продольной силы' к
критической силе.
Если вместо сжимающих сил на брус действуют продольные
растягивающие силы, то в предыдущие урярнения вместо а необходимо подставить —о.
В частном случае, в котором у^ =ж Ь sin(iix/l), ординаты осевой линии яЬслё
деформадии получатся рйвйыми
>'-rpsm-y. ^ F6).
Отсюда видно, что продольвая растягивающая сила уменьшает начальные
ординаты. Взяв^ например, продо^яькую силу, равную ее критическому зна-
1 TtX ■ '
чснию (а = 1), мы иайдем:-^у = rir * sin-у^, т. ё. эта продольнйл сила
уменьшает начальные ординаты изогнутой оси бруса наполовину.
ГЛАВАШ
ОСОБЫЕ ЗАДАЧИ ПРИ ИЗГИБЕ БАЛОК
9. Местные напряжения при изгибе балок
Элементарная формула для напряжения при изгибе в
призматических стержнях дает удовлетворительные результаты только на
некотором расстоянии от точки приложения груза. Вблизи этой точки будут
•неправильности в распределении напряжений. В случае узкого
прямоугольного поперечного сечения эти
неправильности можно изучить при
помощи строгого решения для
распределения напряжений в бесконечно
большой пластинке, подверженной
действию сосредоточенной силы Р
(рис. 40). Сила Р действует в
срединной плоскости пластинки и
перпендикулярно ребру пластинки. В
этом случае распределение
напряжений является простым
радиальным распределением напряжений *).
Такой элемент, как показанный у
точки А, подвергается простом)'
сжатию в радиальном направлении,
и напряжение будет
0^ = k
Pcos6
br
(а)
где г есть радиальное расстояние от точки приложения груза ш Ь —
толщина пластинки. Коэффициент k определяется из того
обстоятельства, что напряжения а^ распределенные по длине полуокружности.
^) См. S. Timoshenko and J. N. G о о d i е г. Theory of Elasticity,
New York, стр. 85, 1951. Местные напряжения в заделанных балках,
подверженных действию сосредоточенной нагрузки, были изучены Е. W. Р а г к е s,
Proc. Roy. See, Д., т. 231, № 186, стр. 37W—387, 1955.
9] МЕСТНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ БАЛОК .55^^
показанной на рисунке пунктиром, находятся в равновесии с силой Р^
Следовательно,
я/2
— 2Ь \ a^cosBrdb=:P.
о
2
Подставляя вместо о^ его выражение (а), мы получаем Л=—, иурав-
нение (а) становится
— 2Рсо8в ,„_.
Если мы рассмотрим горизонтальную плоскость тп в расстоянии h
от ребра пластинки (рис. 4D), то нормальное напряжение, действующее
по этой плоскости, будет .
о„ = О- cos* е = J—- = —j-r-. F8>
Отсюда видно, что давление быстро уменьшается -с увеличением угла б.
Также видно, что напряжения увеличиваются с уменьшением
расстояния А. Зная напряжения, вызываемые действием одного
сосредоточенного груза и пользуясь методом наложения, мы можем легко разобрать
случаи, в которых действует несколько грузов.
Если сосредоточенная сила действует в средине прямоугольной
балки узкого поперечного сечения высотой h, то большие напряжения-
кследствие концентрации, определяемые по формуле F7), накладываются
иа напряжения от изгиба балки, и. в результате получается сложное
распределение напряжений вблизи точки приложения груза. Эти
неправильности в распределении напряжений, вызываемые сосредоточенным
грузом, косят местный характер и имеют важное значение лиш^
в области, непосредственно примыкающей к точке приложения груза.
Если мы рассмотрим поперечное сечение балки на расстоянии от
груза большем, скажем, чем половина высоты балки, то
распределение напряжений в этом поперечном сечении достаточно точно будет
определяться по простой формуле для балок.
Определяя равнодействующую горизонтальных составляющих рг-^
диальных давлений ba^dB для каждой половины очерченного
пунктиром полукруга на рис 40, а, можно показать, что сосредоточенная
сила Р вызывает расклинивающее действие, представленное на рис. 40, Ь
двумя равными и противоположными силами величиной PJtz. В случае
балки высотой Л и толщиной b эти силы, действующие на
расстоянии Ш2 от оси балки, вызывают в срединном поперечном сечении не
только растягивающие напряжения, определяемые формулой
^в
ОСОБЫЕ ЗАДАЧИ ПРИ ИЗГИБЕ ВАЛОК
1ГЛ. Ш
ло также й напряжения от изгиба, даваемые выражением
ч(с)
-ft котором PA/2tc есть изгибающий момент, вызываемый
горизонтальными силами Р/тс, у — расстояние от оси балки, принятое
положительным вниз; и /j == ph^ll2 — момент инерции поперечного сечения.
Накладывая напряжения уравнений (Ь) и (с) на'напряжения от изгиба,
•определяемые по обычной форму^1е для балок, находим, что растяги-
•вающеё напряжение в наиболее удаленном волокне балки
нагруженного поперечного сечения равня(ется
К)
у=-
4 Ш1"
■abh
ЗР
vbh
~Т4 M*V Зя /]•
(d)
Второй член в скобках представляет собой нап|}яжение, вызываемое
расклинивающим действием груза Р. Видно, что в случае коротких
лбалок это напряжение достигает значительной величины.^
а)
Ь)
Рис. 41.
""Уравнение(|а) было выведено для балки узкого прямоугольного
поперечного сучения, йо оно может быть использовано для двутавро-,
вых балок. Дреддолагая^что местное действие груза Р будет восйрй-
ниматься полностью стенкой балки, опять получим расклинивающие
силы Р/тс, и соответствующие напряжения будут
Р
■jtF'
2л J~
где F vi Jg будут соот|йб1Тственно представлять площада и момент
инерции поперечного сечейия балки. Накладывая эти напряжения на
9)
МЕСТНЫЕ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ БАЛОК
бГ
напряжения, Ьпределяейые по простой формуле Хдя балок, мы
получаем формулу для определения наибольшего растягивающего
напряжения ,
, \ iPl РН\ h , Р .^
■■•■■..' '2 . ...■._■■..■ .■■-:■■■
Напряжение, вычисленное по этой формуле, удовлетворительно сод-яа*-:
суется с результатами опы^ой*), —
Чтобы исследовать местные напряжения на рпорах балки узкого
прямоугольного поперечного сечения, мы можем использовать
известные рещения*) для двух случаев клина, нагруженнЬго, как показано
на рис/41. В этих случаях опять имеем простое радиальное
распределение напряжений и можем воспользоваться формулой (а) для
радиального сжимающего напряжения. Постоянная k для случая сжатия
клина (рис. 41, а) находится из уравнения
Р,
откуда
А==
/ , 8т2а\
(« + -2Т)
Тогда из уравнения (а) получаем напряжение
Pcose
. / , sin2a\
^'■(" + -2-)
F9)
В случае изгиба клина (рис. 41, Ь) угол 6 опять измеряется ог
направления силы Р, и уравнение статики
становится /
Ъ \ о^ COS QrdBz=:-— р,
, (п/2)-^а -
откуда
k=
I
siri2a*
,2 Рис. 42.
Тогда мы получаем для радиального сжимающего напряжения
^) См. статью Arnold W. Hendry, Ргос. Soc. Exp. Stress. Annal.,
T. 7, стр. 91, 1949.
*) См. Timoshenko and Goodier, Theory of Elasticity, стр.96-
1951. .{
h^^'t^^iSf^
8 ОСОБЫЕ ЗАДАЧИ ПРЛ ИЗГИБЕ ВАЛОК [ГЛ. 1П
формулу
Pcos6
"г^ -7 ШЩ'^ G0)
br{a 2-)
Отсюда видно, что если- 6 больше ?г/2, радиальное напряжение
получается положительным, т. е. растягивающим.
Объединяя два решений, по уравнениям F9), и G0) можем
получить распределение радиальных напряжений у опоры прямоугольной
€алки (рис. 42).
10. Касательные напряжения в. балках переменного
поперечного сечения
Пользуясь уравнением G0) предыдущего параграфа, рассмотрим
теперь напряжения от изгиба в консоли, имеющей форму клина
{рис. 41, Ь). Взяв поперечное сечение тп, перпендикулярное оси х,
лолучим (см. т. I, уравнения A7) и A8), стр. 41)
My 4 tg^ g sin^ 6
(a)
, __«r „i„ oB—f. ley tg^asin^e
еде
/j = 2jctga, J^==-Y2-, M = — Px.
По нейтральной плоскости клина 6 = тс/2 и нормальные и
касательные напряжения становятся равными нулю. Наибольшие нормальные
и касательные напряжения имеют место при 6 = (ic/2) -\- а. Они могут
быть вычислены из уравнений (а), что дает
(Ь)
/ \ о Mh
(°^)так = —Р24'
Р
('^Ху)гаах=^Рбй'
где
л 4 tg^ а COS* а
Р Т 2а —sin 2а'
При а =5°, 10°, 15° и 20° коэффициент р имеет соответственно
значения 1,00, 0,970, 0,947 и 0,906.
Из первой формулы (Ь) видно, что наибольшее нормальное
напряжение а^ приблизительно такое же, какое получается на основании
обычной формулы для балок, при условии, что угол а достаточно
мал. При а = 20° ошибка, получающаяся при использовании простой
10)
КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ В БАЛКАХ ПЕРЕМЕННОГО СЕЧЕНИЯ
69»
формулы для балок, как это видно из значения коэффициента р,
составляет приблизительно Юу^. Наибольшее касательное .напряжение^,
определяемое по второй формуле (Ь), приблизительно в три раза
больше среднего касательного напряжения Pjbh и имеет место в
точках, наиболее удаленных от нейтральной оси. Этот результат прямо-
противоположен полученным для призматических стержней (т. ^1,
стр. 106). Во многих случаях практики касательные напряжения не
имеют большого значения и рассматриваются лишь нормальные
напряжения при изгибе. Тогда формула для определения наибольшего
напряжения от изгиба, выведенная для призматических балок, может быть
также использована с достаточной точностью для стержней
переменного поперечного сечения при условии, что изменение поперечного'
сечения не является слйшкрм резким.
/%, ^
В предположении, что простая формула для балок ' может быть
использована с достаточной точностью при вычислении нормальных
напряжений от изгиба в балках переменного поперечного сечения, ве-;^
личина касательных напряжений в этих балках может быть вычислена^
при помощи метода, уже примененного для призматических- балок
(см. т. I, стр. 105). Предположим, что прямоугольная балка
переменной высоты h и постоянной ширины b изгибается грузом Р„
приложенным на конце (рис. 43). Взяв два смежных поперечных сечения тп
и ШхЩ и вырезав элемент тт-фа горизонтальной плоскостью аЪ,
найдем величину касательных напряжений Ху^ из уравнения равновесия,
этого элемента
(fi + dh)/2 . ft/2
b J (a^-^dajdy — b laj,dy = bxy^dx.
(c>
где
\2Pxy
bh
8 » "Jf
+Ш'^=Щ^+ШУЛ
imtW
ЩО ОСОБЫЕ ЗАДАЧИ ПРИ ИЗШБЕ БАЛОК 1ГЛ. IU
'■■<•''■■' ' . ., ■ "
Лодстабляя'В уравнение (с), получаем
юткуда
^■- ■ V
Если ft дано как некоторая .функция jv, то из этого уравнения
можно легко вычислить г^^^.. Предположим, напримф, что Л является
'мЩй^йной функцией х и что hy~=:2h^ (рис. 43). Тогда имеем Л=1ЙоA -i-x/i)
и получаем из уравнения (d) '^j'jc^^^ ■а^г тЧ~(^) ( ^Y )г ^''^^^^^
1ВИДН0, что распределение касательных напряжений зависит т только
«от j/i, но также и от расстояния л; от нагруженного конца. При x=Q
мы получаем распределение напряжений по параболе, как для
призматической прямоугольной балки. Для заделанного конца при jc===/
Д1олу«1аем ,
Это распределение напряжений показано на рис. 43 заштрихованной
т1лощадью.
формула (d) была выведена в предположении частного случая на-
грузке1<ия, показанного на рис. 43. Замечая, »Гто изгибающий момент
« этом случае равен Рх, и подставляя М в (d) вместо Рх, получаем
dMdh
X
, 6 /Л» Л d {М\ ' .
У" bh*dx
которое можно применить для любого нагружения балки;
11. Полезная ширина тонких полок
Формула для простого изгиба (см. т. I, уравнение E5), стр. 87)
показываем, что нормальные напряжения в балке пропорциональны
расстЪяййю 6т нейтральной оси. Это заключение справедливо до тех
пор, пока мы имеем дело с балками, для которых размеры
поперечного сечёнйЯ; малы по сравнению с их длиной, и до тех пор, пока
мы рассмз^грйваем точки, находяш1иеся на значительнрм расстоянии от
концов 6aj^KHi В практических приложениях мы иногда применяем
■балки с широкими полками,.для которых элеменйрная формула балки
не может быть применена с достаточной точностью. Возьмем в
качестве примера^-случай балки, состояш,ей из р^ра и широкой полки,
как показано *йа рис» 44v Предполагая, что балка свободно оперта на
концах и нагружена в срединной плоскости д:у» мы замечаем, что
имеются касательные напряжения, действующие между полками и реб-
tl]
ПОЛ)^НАЯ ШИРИНА ТОНКИХ ПОЛОК
611
ром по поверхностям WW фис. 44, а) и направленйые, как показано
на рис. 44, Д Видно, что 9tH напряжений стремятся уменьи1ить про^
гиб ребра, т.е. сделать его более жестким. В то же самое время
они вызывают сжатие полок. Рассматривая полку по одну сторону
ребра как 'прямоугольную nJ^crftHKy, подверженную действию
касательных усилий 8ДрЛ1г одного Края (рис. 44, с), мы видим, что
сжимающие напряжения распределяк^тся неравномерно по ширине ^ шлки;
точный анализ показывает*), чтЬ эти напряжения распределены так.
■
■ . ,
^ i
ТГТШ
h^^l
... .■.■..,|
1
f
f
^f
^'
te^
\\щ
1—'^jT'
ITT
.'
<
1
г
1
<■
f
\/
1
1
/
.
CJ
JT
6J
Рис. 44.
как показано на рис. 44, с, наибольшее же напряжение в полке буд^т
таким, как в верхних волокнах ребра.'Изэтрй неравномерности
распределения напряжений момшо заключить, что, применяя к балке на
рис. 44, а простую формулу дл$ наибольшего напряжения от изгиба,
мы должны воспользоваться _уже«б1ие««оЙ шириной 2\j^, вместо
действительной ширины 2Ь двух полок, для того чтобы получить точное
значение наибольшего напряжения. Эта уменьшенная ширина, обычно
называемая полезной шириной, может быть вычислена, если известно
распределение сжимающих напряжений, показанное заштрихованной
площадью на рис. 44, с. Необходимо лишь сделать площадь
прямоугольника, указанного на рисунке пунктиром, равной заштрихованной
^) Рассмотрение точного решения, полученного Th. v. Кйгтап*ом, дано
в книге Т i m о S h en к о and G о о d i е г. Theory of Elasticity, стр. 171^ 1951.
См. также W. Ме tг е г, Luftfahrtforsch., т. 4, стр. I, 1929; К. Gi г к та пп,
Stahlbau, т. 6, стр.98, 1933; Н. Reissner, Z. angew. Math.-u. Mech., т. 14,
стр. 312, 1934: Е. R е i S sn е г, Stahlbau, т. 7, стр. 206, 1934; Е. С h w а 11 а,
Stahlbau, т. 9, стр. 73, 1936; L. BeschRine, Publ. Interhat. JlSsoc. Bridge and
Structural Engrg., T. 5, стр. 65, Ш7—1938.
m
62 ОСОБЫЕ ЗАДАЧИ ПРИ ИЗГИБЕ ВАЛОК 1ГЛ. Ш
площади. Величина 2Х^,. обычно изменяется по пролету балки, так
как она зависит от размеров балки, а также от формы эпюры
изгибающих моментов.
В частном случае, когда ширина полки весьма велика, скажем
2Ь ^ /, и эпюра изгибающих моментов представлена синусоидой
„ ii==^isin^, ^ (а)
уменьшенная ширина становится постоя1^ной и равной
где |А — коэффициент Пуассона. При ja = 0,3 мы получаем
2X^ = 0,363/. . " G1)
Следовательно, в этом частном случае действительная балка может
быть заменена эквивалентной тавровой балкой постоянного
поперечного сечения и с шириной двух полок, равной 0,363/. Применяя
к этой балке простую формулу, мы получаем такое же наибольшее
напряжение, как и для действительной балки.
В общем случае поперечной нагрузки эпюра изгибаюиХих моментов может
быть представлена синусоидальным рядом
Mx = ^MnSm^, (b)
где коэффициенты Л1„ могут быть вычислены в каждом частном случае по
известной формуле ^)
Mn = -f- \Мх sin -^ dx. (с)
6 "
В случае равномерной нагрузки, например, мы имеем Мл = -—^ ', и
формула (с) дает
^п = Ш, (d)
где гГ= 1, 3, 5, ...
Имея коэффициенты Мп адя ряда (Ь), мы получаем полезную ширину
из точного решения, которое в случае большой ширины полок дает
2Х^ Р
Ж. ' _^^
и= 1,3,6
Мп sin (mixll)
4 + (Л/Р)И7С
G2)
») См. п. 7.
11]
ПОЛЕЗНАЯ ШИРИНА ТОНКИХ ПОЛОК
63
Рис. 45.
рде ^z=tljdh есть отношение площади tl к площади поперечного сечения
ребра и *
fe==iL±iM=:J^ = 0,878 при ^ = 0Д
Взяв, например, случай балки с равномерно распределенной нагрузкой и
подставив уравнение (d) вместо Мп в формулу G2), мы нййдем, что для
различных значений отношения Р изменение полезной ширины по длине балки
такое, как показано на рис. 45. Видно, что в средней части пролета
полезная ширина изменяется очень мало и является приблизительно такой же, как
в синусоидальной эпюре изгибающих
моментов (см. формулу G1)). Если
полезная ширина найдена из формулы G2),
то наибольшее напряжение и
наибольший прогиб найдутся при помощи
простой формулы для эквивалентной
балки.
Мы рассмотрели случай, в котором
полки балки имеют очень большую
ширину. Имеются также точные решения
для случая, в котором полки не очень
широки, а также для случая, цлинной
прямоугольной плиты, усиленной
системой одинаковых и равноотстоящих друг
от друга ребер. Во всех этих случаях задача сводится к вычислению
напряжений и прогибов в эквивалентной балке*).
Задача такого же общего характера, как и разобранная выше, имеет
место лри ироектировани!! самолетов. Рассмотрим К(у)обчатую балку (рис. 46),
образованную двумя швеллерами, к полкам которых прикреплены
заклепками или сваркой два тонких
листа. Если такая балка заделана /? -С
на левом конце и нагружена, как '''
консоль, двумя силами,
приложенными к швеллерам на другом
конце, то элементарная теория изгиба
даст растягивающие напряжения
от изгиба в листе ABCD,
равномерно распределенные по любому
поперечному сечению,
параллельному /5С. Однако в
действительности лист воспринимает, как
указано на рис. 46, растягивающие
напряжения, вызываемые касатель- Рис. 46.
ными напряжениями, которые
передаются швеллерами его краям. При этом распределение растягивающих
напряжений по ширине листа не буцет равномерным; они будут большими
на краях, чем в средине. Это отклонение от равномерного распределений
*) Эти точные решения нашли применение в технических условиях для
бетонных плит, усиленных ребрами. При проектировании самолетов наличие
неравномерного распределения напряжений в широких полках учитывается
чутем применения приближенной теории, которая изложена в статьях
Р- Kuhn'a, Nat. Advisory Comm. Aeronaut, Repts, № 608, 1937 и К» 636,
1938. См. также Н. Е b п е г, Luftfahrtforsch., т. 14, стр. 93, 1937 и т. 15,
стр. 527, 1938.
64
ОСОБЫЕ ък1(кЧ1АтМ^Шгттв, вдлок
(ГЛ^^Ш
напряжений, п|]*дпядаг1аемого йо элеыеятариой теории, известно как зайоз^
далый сшайг, так как оно включает дефорыаиию сдвига в листах, - Задача
быда решена на основании рассмотрения энергии деформации йри некоторых
упрощающих допущениях *).
12. Ограничения метода иалощения
'При рассмотрени{Г |{згиба балок было показано, что вычисление
прогибов можно значительно уй]ростить с помощью метода наложения
(см. т. I, стр. 143). Этот метод может быть использован цри условие,
что изгиб балки не вносит каких-либо изменений в действие внешня^
сил. Например, малые прогиби балки от поперечных нагрузок не
изменяют эпюры изгибающих моментов от эти?с нагрузок, и метод
наложения может Й1лть успешно использован. Но если мы имеем изгиб
совместный с осевым "растяжением или сжатием', то прогиб,
производимы^^ поперечными нагрузками, изменяет действие осевых сия^^ и
последаие вызывают не только рсевое растяжение или сжатие, но тйкже
и некоторый дополнительный изгиб. В таких случаях, как мы уже
видели (п. 4), накладываются некоторые ограничения на метод налр-
женйя; мы можем использовать этот метод только в отношении
поперечных нагрузок, предполагая, что осевая сила всегда остается
пдзетоянной. Имеются другие случаи, ь которые малые прогибы балки
могут вносить з^1ачительные
изменения в действие сил. В таких
случаях метод наложения неприменим.
Некоторые примеры такого рода
будут теперь обсу-йсдены.
В качестве первого примера
рассмотрим такой изгиб консоли АВ
(рис. 47)j в процессе которого
происходит постепенное прикасание консоли с жесткой цилиндрической
опоро^й поверхности ЛС, имеющей постоянную кривизну IjR и гори-
зрнтальАую касательную в точке А. Очевидно, если кривизна балки
на конце Д даваемая формулой
Р*ис. 47.
г
М
Ж
EL
(а)
меньше, чем кривизна опоры }jR, консоль будет касаться
поверхности АС только в точке А, и прогиб /на конце В будет дан
известной формулой ^ ,
^) См. стать^ Е. Reissncr'a, Quart. Appl. Math. т. 4, стр. 268, 1946;
J. Hadji-Argyris, Aeronaut. Research Council (Brit) Rept«. and Mem.,
Ш 2038, 1944; J.-Hadii-Argyris and И. L; Cox, т^м же, № 1969, 1944.
В этих статьях даны ссылки на ранее опубликованные статьи.
12] ОГРАНИЧЕНИЯ МЕТОДА НАЛОЖЕНИЯ 65
Из уравнения
' " ' (е)
мы можем получить предельное значение груза Я, при котором балка
начинает приходить в соприкасание с цилиндрической опорной
поверхностью за точкой А. Пусть Pi^:^EJJIR будет таким
предельным значением груза; тогда при Я ^ Pi часть AD балки будет
опираться, как указано на рис. 47 пунктиром. Длина х неопертой части
консоли получается из условия, что в точке D кривизна 1/г балки
равна кривизне опорной поверхности; следовательно,
Рх 1
BJz R'
и мы получаем ' .
х^%. (d>
Полный прогиб на конце В консоли состоит из трех частей: 1) из
прогиба части DB балки как простой консоли, который равняется
f - ^^'' — J^JgY . {fX
2) из прогиба вследствие наклона касательной в точке Д который
равняется
«~ ^ —p/?4 РЯ)' ^^
и 3) из прогиба, представляющего расстояние точки D от
горизонтальной касательной в точке А, который равняется
Складывая эти три части, получаем полный прогиб:
f=fi +Л +/з = 2]^ — "б"Я*^' ' ^ ^^^
Это выражение для прогиба должно быть использовано вместо
уравнения (Ь), если Я больше предельного значения Я^ = EJ^/IR. Заметим,
что прогиб теперь уже не пропорционален Я. Если в дополнение ^ Р
имеется груз Q, приложенный на конце В консоли, то полный Йро-
гиб не будет равен сумме прогибов, вызываемых грузами Я и Q, если
оба груза рассматривать действующими отдельно. Следовательно,
метод наложения в этом случае неприменим.
В качестве второго примера рассмотрим случай равномерно
нагруженной балки с заделанными концами, как показано на рис. 48.
Предполагается, что при изгибе средний участок балки опирается на
3 с. п. Тимошенко, т.. II
ш
т
ОСОБЫЕ ЗАДАЧИ ПРИ- ИЗГИБЕ БАЛОК
[ГЛ. «I
жесткое горизонтальное основание так, что на этом участке прогиб
постояйен и равен /. Видно, что если прогиб э середине меньше чем/,
то мы имеем обычный случай изгиба балки с заделанными концам^.
Предельное значение qi интенсивности
нагрузки получается из известного
уравнения
т ЕЛ
==/.
О)
Рис. 48.
Для нагрузки интенсивности gi балка
точно касается горизонтального оснр^
вания в средней точке. С дальнейшим
увеличением нагрузки q появляется
реакция 2Х в точкеконтакта. Величина реакции может быть определена
т уравнения
ql* 2ХР
384ЯЛ 192£Л
=/.
0)
Это условие сохраняется до значения q^ нагрузки, когда изгибающий
момент и, кривизна посредине балки обращаются в нуль. Значение q^
можно найти из уравнения
gg/» 2X1
24
8
О,
(к)
которое дает
2Х:
Я^
3 •
Подставляя это значение в уравнение (j), мы получаем
3 384£/,
/.
A)
Сравнивая это с уравнением (i), мы находим, 4to^2==39i- При
интенсивности нагрузки, равной q^ элемент балки в середине становится
прямым и касается горизонтального основания. ••
При интенсивности нагрузки большей ч§м q^ участок CD балки
будет опираться на основание, как пойазанб на рис. 48. Эта часть
остается прямой, она не имеет изгибающих моментов, а её нагрузка
уравновешивается равномерно распределенной реакцией. Вместе с тем
на концах С и D сосредоточенные реакции Jt будут действовать на
непбдпертые основанием участки.и балки. Длена о этих участков
балки и величина АГ, сосредоточенных реакций могут быть получены
путем рассмотрения участка АС балки как консоли с равномерной
нагрузкой q и чс сосредоточенным грузом Л" н^ конце. Замечая, что.
поперечное сечение в С не поворачивается при изгибе, и пользуясь
W}
ОГРАНИЧЕНИЯ МЕТОДА ШЛ#КЁНИЙ
•■в^-
уравнениями (94) й A00) цв т. I (етр, 134 И: 136)i лолучабм
qu*
Ха^
откуда
(т>
Другое урйвненив получится из того условия, что прогиб в С
равняется /. Пользуясь известными формулами для прогиба консолей,.
получаем
ge* Ха*'
Рещяя уравнения (tn) и (п), мм находим
Отсюда непосредственно видно, что реакция* X непропорционйльна
нагрузке» Численно, наибольший^, изгибающий момент, который имеет
место в :баделанных концах,, получается из уравнения
а=-^ГШШ
Ма\ = \Мь
дат
АГо,
которое дает
M^^i^^Y2fEJ^ .
(Р>:
Мы сноба видим, что изгибающий момент не увеличивается в таком
же отношении, как нагрузка. Следовательно, метод наложения не
может быть применен.
ЗАДАЧИ
1. Найти прогиб консоли, показанный на рис. 47, если имеется равном^рно^
распределенная нагрузка (gi вместо силы Р.
2. Найти выражение для прогиба в центре балки, нагруженное посредине
силой Р (рис. 49) и опертой на две одинаковые цилиндрические поверхности
радиуса /?.
Решение. Когда груз Р
увеличивается, точки сопрйкасайия
балки с опорными поверхностями
перемещаются внутрь и пролет
уменьшае1ся; следовательно,
прогиб увеличивается в меньшей
степени, чем груз J^. Угол а,
определяющий пбложения точек
соприкасания, найдется из
того условия, что в этих точках
изогнутая ось касатедьна к
i-2%i
Рис. 49.
опорным поверхностям;} следовательно, дла.^ малых значений а имеем.
P(Z —2/?о)«
3«
Mr"
68
ОСОБЫЕ ЗАДАЧИ ПРИ ИЗГИБЕ ВАЛбК
1ГЛ. Ill
Имея о, МЫ получаем прогиб посредине пролета из уравнения
РA~2ЙаГ . ^а"
^"^ ASEJg "^ 2 •
3. Решить предыдущую задйгчу, предполагая, что балка заделана в
точках А к В.
4. Решить задачу 2, если груз приложен не посредине пропета АВ.
5. Длинная, равномерно нагруженная балка опирается на горизонтальное
' жесткое основание (рис. 50). Найти угол а
поворота конца А и длину л:, которая будет
изгибаться моментом Мо, приложенным на
конце.
Решение. Длина л: найдется из уравнения
дх'
Рис. 50.
2AEJ
Ш1-
-Угол поворота на койце А равняется
ЗЕ7 24EJ
дх^
6. Вертикальная сила Р приложена к концу А призматического стержня АВ,
опертого по BCieft длине на горизонтальную жесткую плоскость (рис. 51).
Исследовать изгиб бруса, предполагая, что Р меньше, чем половина веса gl
^руса.
^
'////////////////>^//////^Щв'^//. 7Ш.
I -
а)
шШ^^/м V////////////M
в
Ь)
Рис. 51.
Решение. Участок ВС бруса (рис. 51, Щ остается прямым и изгибающий
момент в селении С равняется нулю. Следовательно, длина х участка АС
бруса, подверженного изгибу, найдется из уравнения
откуда
В точке С будет действовать сосредоточенная вертикальная реакция, равная Р,
и участок АС бруса находится в тех же условиях, что и равномерио
нагруженная балка с пролетом х. Прогиб конца А бруса равняется
^ 24£/ •
ГЛАВА IV
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
13. Изгиб пластинки по цилиндрической поверхности
Предположим, что прямоугольная пластинка постоянной толщины h
изгибается по цилиндрической поверхности (рис. 52) *). В таком случае
достаточно рассмотреть лишь одну полоску шириной единица,
подобную АВ, как балку прямоугольного поперечного сечения длиной /.
Из условия непрерывности деформаций можно заключить, что при
Рис. 52.
Рис. 53.
изгибе в поперечном сечении полоски не будет такого искажения, как
показано на рис. 82, Ь-т. I, стр. 86. Следовательно, волокно, равное
по длине полоске, как, например, 55 (рис. 53), испытывает не только
продольное растягивающее напряжение Oj^ но также растягивающее
напряжение о^ в поперечном направлении, которое должно быть таким,
чтобы воспрепятствовать поперечному сокращению волокна. Мы
предполагаем,, как и прежде (см. т. I, стр. 85), что поперечные сечения
полоски остаются плоскими при изгибе. Следовательно, относительные
удлинения в направлении осей х а z соответственно будут равны
e^t=^i е^ = 0. Тогда соответствующие напряжения в направлении
') Такой изгиб имеет место в случае длинных прямоугольных пластинок,
если действующие силы не изменяются по длине пластинки и если
рассматривается участок пластинки, удаленный на достаточное расстояние от концов.
mm
70 . ТОНКИЕ ПЛАС1ГИНКИ и ОБрЛОЧКИ 1ГЛ. IV
Осей JIP.и f получатся, как в случае растяжения по двум взаимно.
перпе1|дйкулярным направлениям. При, помощи уравнений C8) т. I,
стр. 55, мы находим ,
i „}^ ^хЕ __ Еу . ^ Щ^^ ^ у£у
Теперь мы постгупим так же, как в с^лучае изгиба бруса, и вычислим
изгибающий момент в каком-либо поперечном сечении полоски, Тогда
+ А/2 -4-ft/2
С Е С Eh*
" _ -А/2 --ft/2
откуда^
где
' п Eh* ,-..
^ = 12A-,.») • (^4)
G3)
Эта величину называется ос^с/ийгостьк) щЛл изгибе пластинки vi
соответствует величине EJg, которая применялась при рассмотрении
тизгиба tiajioK. Сравнение выражения G3) для полоски с выражением E6)
1 ; , Т. I, стр. 88, для бруса показы-
///
вает, что жесткость полоски в пла-
G^' ———^jr и—J—4>| стинке больше, чем жесткость ^от-
'^ I ^ дельного бруса такого же допе-
\^ - i- речного сечения в отношении
^ *' l:(l--ti^).
Рис.54. Эксперименты показывают, что
в случае изгиба отдельной тонкой
иолрскй большой ширины Ь- имеет место искажение поперечного
сечения лйщь вблизи краев (рис. 54, Ij), а средний участок аа полоски
изгибается по поверхности цилиндра*); следовательно, у|)авнени€G3)
применимо при вычислении прогибов, и полоска будет обладать
большей жесткостью, чем следовало бы ожидать из простой формулы для
балок. ^
При малых прогибах полоски АВ (рис. 52) кривизна Iff может
быть заменена ее приближенным значением ^p/dx'^ и дифференциаль-*
ное уравнение изогнутой оси полоски будет
D-^^^-M, ■: G5)
*) Объяснение этого явления дано О. F. G Seaf.1«v Experimental Ela-
Bticity.Camhrldge, 1908. См. также Н. Lamb, London Ргос. Math. Soc, т. 21,
стр. 70, 1891 и статью am^pa Mech. Engrg., стр. 259, 1923.
141 ИЗГИБ ДЛИННОЙ ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ 71
Исследование пластинки, йзгйбак)щейся по цилиндрической поверхности,
заключается в интегрирований этого уравнения. Частный случай> в кото^
ром изгиб по цилиндрической поверхности вызывается равномерно
распределенной нагрузкой, рассматривается в следующей параграфе.*
14. Изгиб ДЛИННОЙ» равномерно нагружейиой
нрймругодьной пластинки
Если прямоугольна^ пластинка, длина которой велика по сравнению с ее
шириной, paBHOM«pHiO нагружена, то можно предположить, что вблизи центра,
где имеют место н^ибоЛьишй прогиб и напряжения, изогнутая поверхность
является приблизительно цилиндрической и для В1|1числения прогибов^) можно
воспользоваться уравнением G5). Рассмотрим эту важную задачу') для двух
крайних усло:ВИЙ: 1) края пластинки свободно оперты и могут свободно
поворачиватйя при изгибе и 2) края, заделаны. В обоих случаях 1тредпЬ>
лагается, что нет перемещений краев в плоскости пя;астишси. Тогда
элементарная nojiocKa, подобная АВ на рис. 52, находится в тех же условиях, что
и растянутый стержень с равномерной поперечной нагрузкой (см. п. 6) и
растягивающими усилиями S. Величина усилий S найдется из того условия,
что удлинение полоски равно разности между длиной изогнутой оси и дли*
ной / хорды ЛИ (рис. 52).
СбобаднЬ оперты£ края. В случае свободно опертых краев хорошее
приближенное значение для S получается при допущении, что изогнутая ось
представляет собой синусоиду . . _
ys=/sta^, ' (а)
где / означает лрогиб посредине. Тогда по выражению E6) стр. 48
удлинение осевой линии полоски будет
Взяв для прогиба посредине приближенное уравнение F1), мы имеем
(с)
где ■ ■ ": ■■
Подставляя в уравнение (Ь)| получаем
л
*) Если длина в три раза больше ширины для свободно опертой пластинки
и в два раза больше щирини для пластинки с заделанными краями, решение,
выведенное при этом предположении, достаточно точно.
') Решение задачи было дано И. Г. Бубновым. См. его книгу
«Строительная механика корабля». С.-Петербург, т. 2, стр. 545, 1914. Рассмотрение этой
задачи вместе с определением напряжений в обшивке корабля дано в книге
S. Timoshenko, Theocy of Plates and Shells, J^ew York, 1940; русский
перевод: Пластинки и оболочки, 1946, 1963.
mfi'
72 ТОНКИЕ ПЛАСТИНКИ и ОБОЛОЧКИ 1ГЛ. IV
Поперечное сужение полоски в плоскости пластинки при изгибе
предполагается равным нулю, следовательно, при помощи выражений G4) и G6)
удлинение осевой линии полоски, вызываемое усилиями S, определяется так:
._ - S/(l—fi") ^'аЛ'' '
Eh 12/
(е)
Приравнивая (d) и (е), получаем уравнение для определения а и,
следовательно, продольного усилия S в следующем виде:
а{1+аУ=Щ. G7)
Если даны нагрузка д и размеры пластинки, то правая часть ургГвнёния G7)
может быть легко вычислена. Решение уравнения G7) можно упростить,
положив
Л-\-а = х. (!)
>
Тогда »то уравнение обращается в
Л* '
т. е. величина л- такова, что разница между ее кубом и ее квадратом имеет
известное значение. Таким образом, л: можно определить при помощи
логарифмической линейки или соответствующей таблицы, а величина « найдется
из уравнения ({). Прогиб же и напряжения в полоске АВ можно затем
вычислить при помощи табл. 4, составленной для растянутых стержней
с поперечной нагрузкой (см: стр. 43). При пользовании этой таблицей н|еобт
ходимо помнить, что на основании формул B3) и G6) имеем
и.
Т 2
^V^- G8)
Возьмем, например, стальную пластинку, имеющую размеры /«»120 см и
Л = 1 tM и нагруженную равномерно распределенной нагрузкой
интенсивностью 9 = 0,7 кг/см'. Тогда уравнение G7) получится в таком виде:
аA+«J = 320, (g)
откуда
«1=6,19 и и = ~ 1^^ = 3,91.
Растягивающие напряжения, возникающие от продольной сипы S, равняются
а наибольший изгибающий момент посредине полоски на основании
уравнения'D5) равняется
Опять пользуясь табл. 4, мы находим путем интерполяции, что для и ic 3,91
4^1 (и) ^0,126. Это показывает, что благодаря действию продольной силы S
изгибающий момент значительно уменьшается и составляет лишь около 13«/о
момента, KOTopbrti возникает под действием одной только поперечной нагрузки.
Пользуясь формулой" (h), находим
И] ИЗГИБ длинной ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ 73
Соотве*ствующие наибольшие напряжения изгиба будут
„ бМвдах 6-159 ^_. , _
а* = —j^j—=———seS54 «гг/сж*.
Складывая напряжения от растяжения и от изгиба, получаем наибольшее
напряжение o^j^^^ == oj^ + oj|^ sa= 777 + 954 = 1731 кг}см*.
Можно видеть, что благодаря действию продольной силы наибольшие
напряжения возрастают непропорционально интенсивности нагрузки.
Например, если в вышеприведенном численном примере мы примем ^ = 1,4 лгг/сж*,
то из уравнения (g) получим
аA+«)* = 320.4==1280,
откуда « = 10,2 и « = 5,02.
Растягивающие напряжения, возникающие от продольной силы 5, рав->
S
няются oj^=c-— 3=1280 кг/см^, и иа таблицы при и«=5,09 находим ^^(м)=0,078.
Тогда наибольшее напряжение от изгиба будет
6Л1„„„ б • 1 4 • 120"
°; = -^= ЭР -0,078 = 1180 /сз/сж',
и полное наибольшее напряжение будет равняться
^тах = "х + ^^ = 1280 + 1180 = 2460 кг/см*.
Иными словами, благодаря действию продольных сил S напряжения
возрастают гораздо медленнее нагрузки. В том случае, когда нагрузка
удваивается, наибольшее напряжение увеличивается лишь на 42»/о.
Защемленные края. В случае защемленных краев уравнение (а)
заменяется уравнением ^)
y^{{\-cos^), * (i)
которое удовлетворяет условиям на защемленных краях, так как прогиб у и
угол наклона касательной dyjdx равняются нулю при х = 0 и л: = /.
Подставляя (i) в выражение (Ь), получаем удлинение оси полоски
о
Для определения прогиба посредине воспользуемся приб^пижен^ым
уравнением F2)
/=
/о
1+а/4 - -
и по формулам (]) и (е) находим следующее уравнение для определения а:
^) См. статью автора, цит. на стр. 45.
SSiW
74 tOHKHE ПЛАСТИНКИ и" ОБОЛОЧКИ
'l ■ ■■*
или, полагая 1 4- .(«/4) и» Ji, получаем
-— я f*
{ГЛ. IV
(к)
В пргедыдущем численном примере при л =^0,7 кг1см^ ypiaBHenne (к) дает
:,л(Г? — д:*г= 3,20, откуда л:=<в1,89 и «=s=3,5o. Следовательно» растягивающая
сила меньше, чем в рассмотренном вмще; сяучае пд1астйнкИ ,с опертыми
краями^ в отношении 3,66/6,19, в мы получаем
с; = ^ X 777 :»= 447 лгг/сж«.
При вычислений напряжений от изгиба пользуемся табл. 4 на стр. 43.
Замечая, что в нашем случае й = (я/2) ]/^а = 2,97, находим из таблицы путем
*/3
Рис.55.
интерполяиии ^,=10,678, ф, = 0,473. Изгибающий момейт в защемленных
концах будет ., ■'
'ЛГ==—0,6781^ = —568 fc^cjrf,
а соответствующее наибольшее напряжение cj^ = 3408 кг/смК Полное
наибольшее напряжение будет*) ^ '
«шах —'i + eJJ ^ 447 + 3408 = 3855 «:г/сл<».
^) Предполагается, что стадь имеет предел пропорциональности выше
вычисленного напряжения.-
14]
ИЗГИБ ДЛИННОЙ ПРЯМОУГОЛЬНОЙ Ш1АСТИНкИ
ш
Сравнивая это напряжение с полученным выше налряя1№нием для ^ой же
пластинки со свободно опертыми краями, мы »Шшм» что заделка краев
увеличивает яаиббльщёе напряжение. Это обстрят^льство можно объяснить
следующим образом: благодаря заделке 1ф1|ев арогибпластинкИ уменьшается,
вследствие чего уменьшается продольная с>|да S, а хакж)е и ё0 влияние tia
изгибающий момент. В случде свободно опертых краев наибольший!
изгибающий момент составляет лишь 0,131 ох момеИ-гй. вызываемого тЬлй-ift»
одной поперечной нагрузкой; В случае же защемленных краев изгибакнцщ
момент на этих краях составляет 0,686 от момента, вызываемого поперечной
нагрузкой, т. е, влияние продод{>ной силы в случае опертых краев
сказывается гораздо сильнее.
Этим приближенным методом можно пользоваться при вычислении
напряженке в обшивке судов, подверженной гидростатическому давлению.
Mi
-f/ /. .|У'.' ' Ич-|«||.|'^ lm,mi'—« jf Т. I . ,- I .f
ff 0J 42 ^ fffi 4^ ^S 0J Ц9 QS iff If
■.,,'■. . РЙС.-56. . -. ■ ■' . .
Наибольшее напряжение, очевидно, зависит от интенсивности нагрузки q
и от отношения //Л^ Величина этого напряжения для случая пластинки со
свободно опертыми краями и для различных значений отношения ЦЬ
представлена кривыми *) на рис. 55. Видно, что благодаря наличию растягивающих
сил 5, которые увеличиваются с увеличением нагрузки, наибольшее
напряжение непропорционально нагрузке q-
На рис. 56 даны кривые для наибольшего напряжения в случае
пластинок с защемленными краями. Видно, что для малых значений интенсивности
нагрузки 9, когда влияние осевой силы на прогибы полоски мало, наибольт
шее напряжение увеличивается приблизительно в том же отношении, в каком
увеличивается f.. Но для ^больших значений^ соотношение между нагрузкой
и наибольшим напряжением становится нелинейным.
*) Эти кривые взяты из статья S. Way, представленной на собрание
отдела прикладной механики А. S. М. Б», New Haven, июнь 1932.
sF^'^-i'T^^
76 ТОНКИЕ ПЛАСТИНКИ и ОБОЛОЧКИ |ГЛ. IV
16. Изгиб длинных прямоугольных пластинок,
имеющих первоначальную малую цилиндрическую кривизну ^)
В этой задаче мы можем воспользоваться результатами, уже
полученными для изгиба стержней с малой начальной кривизной (стр. 51). Края
пластинки предполагаются свободцо опертыми, а«координатные оси и
элементарная полоска взяты, как показано на рис 52. Пусть
Ув«=*8Шу. (а)
представляет малый начальный прогиб пластинки с наибольшим прогибом
посредине, равным Ь. Если приложена равномерная нагрузка q то вызывается
дополнительный прогиб, сопровойсдаемый растяжением срединной поверх^
иости 2) пластинки. Пусть S, как и прежде, означает растягивающие усилия
в полоске АВ шириной единица, а а — отношение этой силы к критической
силе 5кр я= n^Dtl*. Тогда дополнительный прогиб, возникающий от нагрузки q,
будет равняться
f^ . пх аЬ . пх ^.^
Первый член правой части представляет собой приближенное выражение для
прогиба прямолинейной полоски, которой ранее пользовались для плоских
пластинок; второй член выражает влияние начальной кривизны (см.
уравнение (d), стр. 52). Складывая уравнения (а) и (Ь)) получаем полный прогиб оси
. . пх . /- . ядг аЬ .тел Ь-\- ff. . лх
y = >'.H-y»-*sm-^+y^sm---j^^sin-^=-j:^8m-^. (с)
Величина а определяется из рассмотрения растяжения полоски АВ.
Пользуясь теми же рассуждениями, что и в п. 14. получаем следующее
выражение для ее удлинения:
-цт-'-цт
Подставляя (а) и (с) вместо у^ и у vi интегрируя, находим
Полагая эту величину равной удлинению, вызываемому продольной силой S
(выражение (е) й. 14, стр. 72), получаем:
иди
аA + «)« «3(^^")* - Зр A + а)«. (80)
При ^=sO это уравнение приводится к уравнению G7) для плоской пластинки.
В качестве примера возьмем стальную пластинку таких же размеров,
как в п. 14:
/ aos 120 см, А «а 1 смг, q » 0,7 кг/см* и Ьв=л\ см.
*) См. статью автора, цит. на стр. 51.
'^) Срелинная поверхность есть поверхность, делящая пополам
расстояние между верхней и нижней поверхностями пластинки.
16] чистый изгиб в ДВУХ ПЕРПЕНДИКУЛЯРНЫХ НАПРАВЛЕНИЯХ 77
Тогда
и из уравнеиия (80) получается
о A + о)* *= 377,4—3A+ а)«. (d)
Пусть по-прежнему
1 -)- а = л:;
тогда л:'+ 2л-* = 377,4, откуда л:==б,61, а = 5,61. Растягивающее
напряжение, возникающее от продольной силы S, будет
cJi. = -j7 = -rs~ = 704 кг/см'.
Это напряжение несколько меньше соответствующего напряжения для
плоской пластинки (см. стр. 72).
При вычислении напряжения от изгиба необходимо обратить внимание
на то, что прогиб, определяеА1ый уравнением (Ь), состоит из двух частей.
Первая часть представляет прогиб для плоской пластинки, а вторая часть
— -—-—sin-7- выражает влияние начальной кривизны. Наибольшее напряже-
ние от изгиба, cootвeтcтвyющee первой части прогиба, при а = 5,61; ы =
= -|-1/^^ = 3,72; 4^1 = 0,138 (из табл. 4, стр. 44) будет равно 1043 кг/смК
Изгибающий момент, соответствующий второй части прогиба, равняется
_ fif^ / ab . -кХХ an^bD . TzX , ^
\ — D -T-S — 7-1— sm -г- = — 7?—i—Tie sin -г-. (e)
£?л:*\^1+а /; (l+a)/« / ^'
Этот момент имеет отрицательный знак, и соответствующее ему наибольшее
сжимающее напряжение, которое необходимо вычесть из напряжения,
найденного для плоской пластинки, будет равняться
б а-кЧВ „„„ , ,
~F(T+^^~^^^ '''^'•^-
Складывая это напряжение с напряжением q'^ и напряжением от изгиба,
равным 1043 кгг/сж', вычисленным как для плоской пластинки, находим полное
напряжение
0^ = 704 + 1043 — 639 = 1108 лгг/сж».
Сравнивая эти результаты с результатами, полученными для плоской
пластинки, мы видим, что растягивающие силы S здесь несколько уменьшаются,
а напряжения от изгиба посредине будут гораздо меньше вследствие
отрицательного знака изгибающего момента (уравнение (е)). Влияние начальной
кривизны сводится к уменьшению результирующего напряжения с 1747 кг1см^
до 1108 кг/см^. Этот результат получается для пластинки, имеющей
первоначальный прогиб посредине, равный ее толщине. При увеличении
начального искривления наибольшее напряжение можно уменьшить значительнее.
.1
16, Чистый изгиб в двух перпендикулярных направлениях
Рассмотрим сначала прямоугольную пластинку, 140торая изгибается
моментами, равномерно распределенными по ее краям (рис. 57).
Обозначим через Ml изгибающий момент, приходящийся на единицу
длины края, параллельного оси у, и через М^ изгибающий момент»
кй?>та>'
м
,; /ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
{ГЛ. iv
-jr
Рис. 57.
р]риходящййсй йа единицу длины края, параллельного оси х.
Направления мо>1енто1з, по^сазйнныЕе на рисунке, будем Щщ?лъ Лоложнтельными.
ПлоскОрть, прох;одящую посредине между гранями )г|ластинки и
называемую г/^едш«ой /цослгос/ибю пластинки, прШещ щ плоскость ху,
■ и за ось jjf —лчнию,
перпендикулярную к этой плоскости и
направленную вниз. Из этой
пластинки двумя па|^ами
плоскостей, параллельных
плоскостям XZ uyz, выделим элемент
(рис. 58). Теория чистого
изгиба пластинки основана на
допущении, что при изгибе
боковые Грани этого элемента
О^аются ПЛОСКИМИ и поворачиваются около нейтральных осей п-—п.
При Указанных на рис. 57 направлениях коментов верхняя часть
элемента испытывает сжатие, нижняя часть — растяжение. Срединная
плоскость пп при этом изгибе пластинки не претерпевает деформаций
и поэтому является нейтральным слоем. Пусть 1/ri и J/rg означают
соответственно кривизны этой
нейтральной поверхности в сечениях,
параллельных плоскостямЧлг-г и з'-г;/ТОгда
относительные удлинения по направлениям х
и у элементарного слоя abed в
расстоянии > от нейтральной поверхности
оп1^еделяется так же, как и в случае
балки (т. I, стр. 86Х и будут равны
'х
г » >
г
г»'
(а)
Соответствующие им напряжения на основании уравнений C8) т. I,
стр.55.^^т ^^ fl , М
Ez fl , l\ , .
(с)
'-■T=V'\y,~^^yj'
Зги напряжения пропорциональны расстоянию z от нейтрального слоя.
Составляя моменты внутренних усилий, действующих по граням
элементе, и приравнивая их к моментам внешних пар, получаем сл^ую-
|Дие уравнения: ц1н/2 ^
\ tij(Zdydz^=Mxdyt (d)
—ft/2. ■ . .
+ft/2
J Cj)Zdx dz== Мч4х, (e)
-h/2 ' '■'" .
16] чистый ИЗГИБ в ДВУХ ПЕРПЕНДИКУЛЯРНЫХ НАП^^ 79
Подставляя вначения (Ь) и (с) вместо о^^ и «^ и замечая, чтЬ
+ АУ2
где D означает цилинЬрцчес^сую жесткость пластинки (фо(шулй
G4)), мы находим .
\ . ^G;+f^7r)=Af. ■ , (82)
которые соответствуют уравнению E6) т. I, стр. 88, для случая чистЪго
изгиба призматического бруса. Предполагая, что прогибы в
направлении оси г;, обозначаемые через да, малы, получаем для кривизны
приближеннее формулы \ ^
Тогда уравнения (81) и (82), выраженные через w, станут
0+^^)=Л.,. (84)
-•^(
Эти уравнения л соответствуют уравнению G9) т. I, стр. 124, для
изогнутой оси прямого бруса. В частном случае, когда, Afi = Ala=:Al,
кривизна изогнутой поверхности в двух перпендикулярных направлв'
ниях одинакова и поверхность является сферической. Кривизна сферы
из,уравнения (81) будет
T^DO + fx)- , / ^
По такой поверхности изогнется пластинка любой формы, если толькб
изгибающие моменты М равномерно распределены по ее контуру.
Выше предполагалось, что никакого изменения длины волокон
срединной поверхности не происходит, т. е. что эта поверхность
является нейтральным сло(»1 при изгибе пластинки. Это
предположение будет вполне точным лишь в том случае, если поверхность изо-*
Гнутой пластинки является развертываемой поверхностью, как,
например, цилиндрическая поверхность, рассмотренная в п. 15. Для нераз-
вертываемых поверхностей указанное предположение будет достаточно
точным лишь в том 1рлучае, когда прогиб w пластинки мал по
сравнению с ее толщиной h. Чтобы показать это, рассмотрим изгиб круглой
пластинки под действием моментов Л1, равномерно распределенных
80
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ.IV
ПО ее контуру. Из предыдущего^ изложения вытекает, что
пластинка будет изгибаться по сферической поверхности, радиус которой
определяется по формуле (85). Пусть
АОВ (рис. 59) представляет
диаметральное сечение изогнутой круглой
пластинки, а — ее внешний радиус и /—
прогиб посредине. Допустим сначала,
что размеры срединной плоскости
пластинки в меридиональном направлении,
например по АОВ, не меняются. Тогда
дуга 08 = а, (^^а/г и CB=^a^j=
= г sin 9- В таком случае, очевидно,
изгиб пластинки будет сопровождаться
сжатием в окружном направлении.
Величина этой относительной деформации контура пластинки будет
равнятьсй
а — fli г<р — г sin у
Рис. 59.
а
гср
При ы^лст прогибе / угол (р мал, и поэтому sin у
так что
:<р
6
(?V6).
(О
или, замечая что
получаем
f^r{\~cos^)^^^
'3r'
(g)
Это — величина наибольшего относительного сжатия по окружности
у края. Она получилась при том допущении, что деформация в
меридиональном направлении равна нулю. В действительности же
в меридиональном направлении возникает некоторая деформация,
вследствие чего истинное сжатие по окружности будет меньше
сжатия, определяемого уравнением (g)*).
Приближенная теория изгиба пластинок совершенно пренебрегает
деформацией срединной поверхности и рассматривает лишь
деформации, определяемые выражениями (а), наибольшее значение которых
^) Если прогибы не малы и деформация срединной поверхности принята
во внимание, то можно показать, что в случае чистого изгиба круглой
пластинки радиуса а==»23Л сжимающие напряжения срединной поверхности на
контуре в окружном направлении составляют около 18»/о от наибольшего
напряжения от изгиба, когда прогиб посредине равен 0,6 толщины пластинки.
См. статью автора в Сборнике Института инженеров путей сообщения,
С.-Петербург, 1915. См. также книгу автора «Theory of Plates and Shells»,
стр. 332, 1940; русский перевод: Пластинки и оболочки, 1946, 1963,
17] ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ПЛАСТИНКАХ , 81
В предыдущем примере равно А/2г. Следовательно, деформацией,
определяемой выражением (g), можно пренебречь, и срединную поверхность
можно считать не деформированной, когда //Зг мало по сравнению
с Л/2г, т. е. когда прогиб / мал по сравнению с толщиной: пластя"
нок А. Только при этом допущении можно с достаточной точностью
пользоваться результатами, полученными ниже для некоторых частных
случаев изгиба пластинок.
17. Температурные напряжения в пластинках
Соотношением (85) (п. 16), полученным для изгиба по
сферической поверхности, можно воспользоваться для вычисления
температурных напряжений, возникающих в пластинке вследствие
неравномерного нагревания. Пусть t означает разность, температур верхней
и нижней поверхностей пластинки, а а — коэффициент линейного
расширения материала. Предполагая, что изменение температуры п6
толщине пластинки происходит по линейному закону, мы найдем, что
по тому же закону будут изменяться и соответствующие удлинения;
если края пластинки свободны, то изгиб, обусловленный этими
удлинениями, будет прспгсходить по сфере*). Разность между
наибольшим удлинением на поверхности и удлинением в срединной
поверхности чравняется af/2, а кривизна, обусловленная этим неравномерным
at h
расширением, определится из уравнения -9" = о"' ^^^УД*
Такой изгиб пластинки не вызовет никаких напряжений при условии,
что ее края свободны и прогиб мал по сравнению с толщиной.
Однако если края пластинки защемлены, нагревание вызовет
изгибающие моменты по ее контуру. Величина^«тйх моментов должна
быть такова, чтобы они могли уничтожить кривизну, обусловленную
неравномерным нагреванием и определяемую уравнением (86), так как
только таким путем будет выполнено условие защемления края. Ив
уравнений (85) и {Ъ6) мы получаем следующее уравнение для
изгибающего момента, приходящегося на единицу длины защемленного края:
Так как М действует на площадь прямоугольника с шириной, равной
единице, и в1ЫСотой Л, находим соответствующее наибольшее
напряжение изгиба:
') Предполагается, что прогибы малы по сравнению с толщиной Л
пластинки.
imi'F
82 J ТОНКИЕ плАстийки Й о)БОлс);чки {rn.w
Это напряжение пропорционально коэффициенту линейного расшире*
нйя а,<разностй температур на обеих повержвбс^ях*) пластинки и
Модулю упругости. Разность температур ^ может воз]растать сувели'
. ^внн€^м толщины пластинки; поэтому бблыциё температурные напрЯг-
жёнйя следует ожидать в толстых пластинках, а не в тонких.
Интересно отметить, что уравнением ^87), выведенным Для плоских
пластинок, можно также пользоваться с достаточной точностью э случае
сферических или цилиндрических оболочек (см. стр. 192).
18» Изгиб круглых пластинок, нагруженийх симметрично
относительно центра *)
В этом случае изогнутая поверхность пластинки будет симметг
рична относительно оси, проходящей через центр пластинки перлен-
дикулйрно к ее плоскости; поэтому для вычисления прогибов и
напряжений достаточно рассмотреть диаметральное сечение, проходящее
через эту ось. Рис. 60 и^бражает
такое диаметральное сечение с осью
симметрии Ог^. Пусть W означает прогиб
пластинки в направлении оси z в какой-
либо точке Л, находящейся на
расстоянии JKT-OT оси. Для малых значений w мы
можем положить, что <р=—(dw/dx)
есть угол наклона касательной к
изогнутой поверхности в той же точке. Тогда
крийизна пластийки в диаметральном
сечений XZ будет равняться
Гу~~ dx'^'~йx' ^^f
При определении радиуса кривизны г^ в направлении,
перпендикулярном плоскости дгг^, нес^ходнмо заметить, что после деформации
пластинки ^сечения, подобные й/я, образуют коническую
поверхность с вершиной Б, находящейся в точке пересечения niw с осью О^:.
Тогда АВ будет представлять радиус г^, и из рис. 60 мы получаем
J-=i. ■ !'>;■ :. ■.,•.-. ;..(b)
*) Необходимо заметить, что t означает разность температур между
двумя поверхностями пластннйи, а не разность темц^атур между
жидкостями или газами, в месте соприкасания с платинной. Последняя вследствие
резкогОч изменения температуры на поверхности пластинки может €ыть
гораздо больше Y.
*)'^Этот случай изгиба был исследован Р о i as о-п'о м^ Mem, dc Г Acad.
(Paris), т. 8, 1829.
18] vs тгткруглтщАй7итк,м*^гркш Ш
Теперь мы преиб6ре^*аем влиянием Ывшл т ^лт^ЩЦ t^
гаем, что имеют место те ж^ сЬдтношения между Ш-<.
ментами и кривизнами, ^то и в случае/чистого изгиба пластинки (п. 1E^
поэтому можно врспольздааться уравнениям» (81) и (851); ИодставляяХа)
и (Ь) в эти уравнения, мы накодим
В этик уравне11йях Mi и М^ означают изгибающие MuMeHtbi, njRHXo-
дящиеся на "единицу длины, М^ — действующий по цилиндрическим
сечениям таким, как тп, и Ж»-г--действующий по диаметраяь1|ым
сечениям kz. "■■'-'■'- •;■ ■,_■
Уравнения (88) и (89) содержат f^i-^ffy, ф fi v
лишь оАну переменную <jp, которую ' ^ "-/Лштт -^ v ^-
можно определить из уравнения рав- *^ ' ( ^^^ш{~)г^'~'—'"^
г^
новесия, элемента al>£'rf (рис. .61), * г ^^ ^
вырезанного из пластинки двумя
цилиндрическими сечениями аЬ и cd ^ _ ^
и двумя диаметральными сечениями ^[""""^'-•^■С^ f
аО и ЬО, Момент, действующий по '--'^—^- I ^J- т"''^^
грани i7rf элемента, "равняется ^ —"V^""^""
AfiJc^^e. (с) Рис. 61.
Соответствующий момент, действующий по гр'ани иЪ^ равняется
Моменты, действующие по граням arf и Ы, равны каждый Mi^x
и имеют результирующую в плоскости лгг, равную .
ЩйхйЬ, ^ (е)
В дополйение к этим моментам имеются поперечные силы Q,
действующие по граням о^ ц €d% Если Q представляет поперечную
силу, приходящуюся на единицу длины, то полная* поперечная сила,
действуюЩ;ая по грани Ы элемента, равняется' Qxdb. Пренебрегая
малыми величинами высшего порядка, найдем, что по грани а^ дейст*
вует поперечная сила такой же величины. Эти две силы дают
момент в плоскости xti равный
QxdBdx. (f)
^) Из симметрии следует, что П9 граням i^c и ad элемента цоперечных
сил нет.
к^^ЖТЯ"'
84 ТОНКИЕ ПЛАСТИНКИ и ОБОЛОЧКИ 1ГЛ. IV
Складывая моменты (с), (d), (е) и (f), взятые с надлежащими знаками,
получаем следующе!? уравнение равновесия элемента abed
[Мх 4- ^ dx\{x + 4х)db — Mi^ db — M^dx db -f Qx dx dQ =s= 0,
из которого, пренебрегая малыми величинами высшего порядка^
находим
Л^1-1-^*^-Л^8 + С-^=в- (g)
После подстановки значений Ж, и Жа из уравнений (88) и (89)
в уравнение (g) получаем
dx'^xdx X' D- ^^^^
В любом частном случае симметрично нагруженной круглой пластинки
поперечная сила Q может быть~" определена из уравнений статики;
тогда уравнением (90) можно воспользоваться для опред|рлен;1я, угла
поворота ср и прогиба w пластинки.
Рассмотрим^ например, круглую пластинку, нагруженную
равномерно распределенной нагрузкой интенсивности q и сосредоточенным
грузом Я, приложенным в центре. Взяв сечение пластинки
цилиндрической поверхностью с осью Oz и радиусом х, найдем поперечную
силу Q, приходящуюся на единицу длины этого сечения, из условий
равновесия внутренней части пластинки, вырезанной цилиндрической
поверхностью. Нагрузка, действующая на эту часть пластинки,
равняется Р-\- Tzx^q, Эта нагрузка должна быть равна равнодействующей
поперечных усилий, распределенных по цилиндрической поверхности;
следовательно,
2'KxQ = P-\-'ax'^q
и
Подставляя это в уравнение (90), получаем
D V 2 "" 2пх)'
dx^ ' X dx~~^х^
или ^
откуда путем интегрирования находим
l^(^^)=-l(?j;+£in^)+c„ (h)
19] ИЗГИБ РАВНОМЕРНО НАГРУЖЕННОЙ КРУГЛОЙ ПЛАСТИНКИ 85-
где С| — постоянная интегрирования. Интегрирование уравнения (й>
дает
или '^
где Cj — вторая постоянная интегрирования. При малых прогибах
(рис. 60) имеем
dw
^ dx*
что дает следующее уравнение для прогиба:
<'«'__ 9-V' I ^^лг „, . Ctx Cs
откуда после интегрирования находим
Постоянные интегрирования Ct, Q и Q должны быть определены-
в каждом частном случае из условий на контуре пластинки.
В предыдущем изложении уравнения (81) и (82) былинспользо*
ваны при допущении, что срединная поверхность пластинки является
нейтральной поверхностькУ; т. е. что в этой плоскости нет никаких
деформаций. Это допущение, как мы видели (стр. 79), справедливр^^
лишь в том случае, когда края пластинки не испытывают никаких
напряжений в срединной плоскости пластинки и прогибы малы по»
сравнению с толщиной пластинки.
19. Изгиб равномерно нагруженной круглой пластинки
Пластинка с защемленным краем. Угол наклона касательной и
прогиб в этом случае определяются из уравнений (92) и (93) путем
подстановки в эти уравнения Я=0. Обозначая через а наружный,
радиус пластинки, мы имеем для защемленных краев 9 = 0 при х^а-
и при xs=sO. Эти условия дают следующие уравнения для вычисле-^
ния постоянных интегрирования Ci а d из уравнения (92):
U6£> 2 xh^a" *
ГЯ^ CjX Сл __„
.U6D 2 д:;х-.о~~ '
откуда
^==0 и С, = ^. (а>
mm
4i8 ^ ТОНКИЕ ЛЛАСТЙНКИ H ОБОЛОЧКИ 1ГЛ. IV
Подставляя эти Шченця в уравнение {92), Щлучлек
? = 1^(«*—^V (94)
16
Теперь прогибы можно вычислить по ур^нению (93). Полагая
;|1режде всего в ётом уравнении Р==0, а зйт(ей /лодставляя значения
ср(:тоянных Ct а С* из уравнений (а)/находим '
^==&--W+^- ; (Ь)
Постоянная Cj^ определится из того условия, что- на краю пластинки
тфогиб рарен л^лю. Следовательно,!
* /тА4
да* да
■ -^ ■■■ да* ■■■
откуда <:^с=:|^.
Подставляя это значение в уравнение (Ь), получаем
«'=6&(«'-^- > (95)
Шибольший прогиб будет в центре пластинки и равен
^ ^=^|£- I (96)
Этот прогиб составляет 3/8 прогиба полоски (рис. 62) с защемленными
концами и длиной, равной диаметру пластинки,
Изгибшошие моменты в. пластинке найдем из уравнений (88) ш
<89) путем подстановки в эти уравнения значения ^ из уравнения (94).
Т^аким путем получаем
- iMi==:|[a«(l4-tO--^C+|i)l, (с)
Л^a = ^[a«Cl+H^)~^(l + ЗF0^ (d)
На краю пластинки {х==а) моменты будут
г" Ж. = -^: >, = -!f!; ,(е)
■■■■■'■■■ *■•■■.'•■'"
4 В центре (л?=0) моменты равны
Mi = Mt=:^^qaK . , (f)
>!аибольшее напряжение будет на краю пластинки и равняется
191 , ИЗГИБ *>АВ11рмеРН0НАГРтЕЙН0Й круглой ПЛАС^Т^^^ ' %f:
Пластинка со свббаЬшз опёртым краем, Пр^ исследовании-
изгиба пластинки со свободно опертым краем воспользуемся методр1№
наложения. Было показано выше, что в случае защемленных: краей-
по контуру пластинки действуют
отрицательные изгибающие моменты
jWi = -^(^0^/8) (рис. 62; о). Если -
к этому случаю присоединить
случай чистого изгиба, йок$Занный на
рис 62, fc, таким об|разом, чтобы
уйичтожить изгибающие моменты ло
контуру, то мы получим изгиб
пластинки со свободно опертым краем.
Прогиб, при «iHCTOM изгибе пластинки определится из уравнения (85).^
Подставлйя в это уравнение M^^jga*/^^ мы находим
■ ' ■. 1 _ qa'f ■
r — SDil+i^r .
Соответствующий прогиб посредине для сферической поверхности^
будет (см. стр. 89 т, I) '
f л^ да*
^»~2r~::i6z>(n-fx)*
Чтобы получить прогиб пластинки со свободно опертым краеН^
нужно к полученному прогибу /i присоединить,прогиб, определя€М1ЛЙ
уравнением (96), Таким образом, для прогиба в центре пластинки
мы получим
f___ga* I да* ^ S + ft « (Ш
При {v = 0,3 этот прогиб приблизительно в четыре раза брльше
прогиба пластинки с защемленным краем.
Для определения изгибающих моментов нужно к постоянному из^
гибающему моменту qa^jB присоединить моменты, определяемые
уравнениями (с) и (d), найденные выше для случая пласти'нки с защемленныяк
краем. Отсюда
; Л==й(а+н)(а*-д:«),
М.=^| [«43+К)-^A Ч-3f01.
Наибольший изгибающий момент б^^дет в центре пластинки, где о»
равняется ' ^
Mi = Mi^^^qa*, ,,
ш
88 ТОНКИЕ ПЛАСТИНКИ и ОБОЛОЧКИ
i
Соответструющие ему наибольшие напряжения будут
[ГЛ. IV
(99)
Для сравнения напряжений с^. и в^, на нижних поверхностях
пластинок с/защемленным и со свободно опертым краем на рис. 63 представ-
-лены диаграммы, изображающие изменения этих напряжений по длине
радиуса пластинок. Измеряя ординаты от горизонтальной оси,
проходящей через точку О, мы получаем напряжения для пластинки с
защемленным краем. Прибавляя к этим напряжениям постоянную величину
Рис. 63.
Zqa^l4h\ т. е. измеряя ординаты от горизонтальной оси, прохйдящей
через точку Oi на рис. 63, мы получаем напряжения для свободно
-опертой пластинки. Отсюда можно видеть, что наиболее
благоприятное напряженное состояние получается при защемленном крае.
В предыдущих выводах пренебрегалось влиянием деформации
-сдвига на прогиб. Когда толщина пластинки не является малой по
•сравнению с ее радиусом, это влияние может быть значительным и
должно быть принято во внимание*). Дополнительный прогиб,
обусловленный сдвигом, найдется таким же способом, как и в случае
балок (см. т. I, стр. 150). В случае равномерной нагрузки поперечная
•сила на основании уравнения (91) будет
Если мы примем тот же закон. распределения касательных напряже-
^) Увеличение прогиба благодаря сдвигу было показано на опытах,
произведенных G. М. R U S S е 11'ом, Engineering, т. Г23, стр. 343, 1927. См. такж<
статью Н. Carrington'a там же, т. 125, стр. 31, 1928.
191 ИЗГИБ РАВНОМЕРНО НАГРУЖЕННОЙ КРУГЛОЙ ПЛАСТИНКИ В^
НИИ ПО толщине пластинки, как и в случае бруса прямоугольного
поперечного сечения, то наибольшие касательные напряжения будут
по срединной поверхности, и величина их в расстоянии х от центра'
пластинки определится по формуле
S Q Ъ вх
Та Тл* ^
Соответствующий этому напряжению относительный сдвиг срединной^
поверхности пластинки будет
,_^_i?-
4 бА'
а дополнительный прогиб, обусловленный перекосом какого-нибудь
элемента, например abed на рис. 61, равен
, S дх (jlx
Суммируя эти прогибы по длине радиуса пластинки и замечая, что>
на контуре пластинки прогиб равен нулю, мы находим
а
X
Присоединяя это к прогибу (уравнение @5)), обусловленному изгиг
, бающим моментом, получаем полный прогиб для пластинки с
защемленным краем
или, пользуясь выражением G4), можем написать :
^=-вЬ[<"'--^'>'+г^'^*(«'^-^')]- <1оо)
Прогиб в центре будет равен
в случае толстых пластинок второй член в скобках, Т1редставляю1Ций
собой влияние касательных напряжений, может иметь существенное
значение. ^
Изложенная теория изгиба круглых пластинок основана на
допущении, что, прогибы малы по сравнению с толщиной. При больших
прогибах необходимо принять во внимание деформацию срединной
поверхности пластинки. При этом можно показать, что при больших
прогибах пластинка получается более жесткой, чем это следует на осно- ^
m
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
!|ании изложенной тгеории *), и прогибы уже не йужут пропорциональны
-силам, в случае равн<шерйо нагруженной зкруг^Й пластинки с за-
■щемл^ннш краем прогиб можно вычислить из уравнения^):
A02)
/* 9в*
/+0,68 i, = g^
■которое хорошо согласуется с опытами.
Йа практике иногда применяет очень тонкие равномерно нагруг
зкенпые пл;астинкй. В таких случаях игапряжения от изгиба могут быть
малы по сравнению с напряжениями, обусловленными деформацией средйч,-
ной поверхности, и пластинка может рассматриваться как тонкая мем-
>брана, не имеющая сйвершенно изгибной жесткости ^). Прогиб посредине
равномерно нагруженной круглой мембраны определяется формулой
/=i: 0,662
"V
Eh'
A03)
Мы^толучим аналогичную формулу, если в уравнении A02) пренебрежем
величиной / по сравнению с членом, со/^ержащим/'* Опыты,
произведенные с тонкими мембранами, хорошо согласуются с формулой A03)*).
20. Изгиб круглых Пластинок переменной толщины
; В: случае равномерно нагруженной круглой пластинки переменной
толщины изменение толщины h с изменением радиального расстояния дг
можно представить с достаточной точностью зфавнением т-==tf~^**^^^
TrsSfl-s
*^S'
\A^^
Рис. 64.
в котором hjh^ есть отношение толщины на расстояний х к
толщине йо в центре и р—постоянная. Формы диаметральных сечений
пластинок для различных значений йосл-оянной ^показаны на рис. 64.
*) См. статью автора, цит. на стр. 80. См. также его «Theory of Plates
лпй Shells>, 1940 (русский перевод: Тимошенко СП., Пластинки и
оболочки, 1946, 1963).
*) Там же, стр. 336.
8) Н. Н еп ск у, Z. Math. и. Phys., т. 63, стр. 311, 1915.
*) В г U п о Е с к, Z. angew Math, u. Mech., т. 7, стр. 498, 1927. Сведения
о диафрагмах см. в Nat. Adviswy Сол»«- Aeronaut. Tech. Notes, № 738, 1939.
201
ИЗГИБ КРУГЛЫХ ПЛАСТИНОК пер1еменной толщины
^г
Наибольшее напряжение «л от цэагцбъ ь рйтл^^>ноы щпргв}\ет»
при радиальном рассхояний х от центра мож(^о выразить формулЬй
^ * AS V
где X есть коэфф1одиенТ| зависящий от расстояния х, Вйачешщ
эторо коэффициента*) ДЛЯ; пластинки с защемлённым контуром даны.
Рис. 65.
Ж
с^ е^ це (Iff W
Рис. 66,
а'
на рис 65. Для свободно опертой пластинки эти значения дани на рис.бв..
*) Эти значения дайы в диссертаций О. P'ichler'a, Die Biegung kreis-^
siihmetrischer Platten von veriinderUcher Dicke, Berlin, 1928. Позднейшие ие-
сяедования изгиба круглых пластинок переменной толщины были сделаны
H.Favre und Е. Chabloz, Z. angew. Math, u, Mech., т. 1,/Стр. 317»
1950 и Bull. tech. Suisse rOinande, № 1, 1952. См. также статью И. F а v г с;
представленную Международному конгрессу прикладной механики,
Стамбул, 1952.
SSiW
'92 ТОНКИЕ ПЛАСТИНКИ и ОБОЛОЧКИ (ГЛ. rv
21. Изгиб круглой пластинки* нагруженной в центре
Пластинка с защемленным краем. Подставляя ^3=0 в
уравнение (92), получаем в этом случае уравнение
Постоянные интегрирования d и Сд найдутся из условий, что <jp = 0
«а защемленном крае и в центре пластинки; отсюда
(Ь)
Так как (хЛпх)^^^=0^ то из уравнений (Ь) получаются следующие
значения произвольных постоянных:
С, '
а
■« уравнение (а) приводится к виду
0. J
Рх . а ...
Уравнение изогнутой поверхности пластинки получится путем
подстановки в уравнение (93) ^ = 0 и значений (с) произвольных по-
-стоянных, что дает
Постоянная Сз получится из того условия, что на закрепленном крае
прогиб равен нулю, следбвате^ьно, Сз==Рау16т:0. Подставляя это
в уравнение (е), получаем
Прогиб посредине пластинки будет
Этот прогиб в четыре раза больше того, который получается в слуг
чае равномерно распределенной нагрузки той же величины
(уравнение (96)).
21] ИЗГИБ КРУГЛОЙ ПЛАСТИНКИ. НАГРУЖЕННОЙ В ЦЕНТРЕ 93
Изгибающие моменты вычисляются из уравнений (88) и (89) путем
подстановки в них выражения (d), что дает
7W3=^[(l+l^)ln^-lx]. (h)
На контуре (х = а) эти моменты получают значения
Р
M,== —
4я'
а соответствующие значения наибольших напряжений будут
A06)
Сравнивая это с выражением (97) для равномерной нагрузки, видим,
что нагрузка; сосредоточенная в центре, вызывает на защемленных
краях пластинки напряжения вдвое ббльщие напряжений, возникающих
от нагрузки той же величины, но равномерно распределенной по
пластинке.
В центре пластинки уравнения (g) и (h) дают бесконечно
большие значения для изгибающих моментов и напряжений. Этот результат
получается вследствие допущения, что нагрузка сосредоточена в точке *)-
Если принять, что нагрузка распределена по малому кругу, то напря=
жения получаются конечного значения (см. стр. 96).
При определении безопасных размеров круглой пластинки,
нагруженной в центре, мы можем ограничить наши исследования вычисл^е-
нием наибольшего растягивающего напряжения от изгиба внизу
пластинки. Уже было упомянуто, что уравнения (g) и (h) не являются
подходящими для этой цели, и более подробное исследование ^)
указывает, что надлежащая формула для вычисления вышеупомянутого
растягивающего напряжения будет иметь вид
*) Местные напряжения в точке приложения сосредоточенного груза
рассмотрены в статье Н. Hen с к у, Der Spannungszustand in rechteckigen Plat-
ten, Darmstadt, стр. 54, 1913. См. также A. Nadal, Elastlsche Flatten,
стр. 97, 1925. -
*) Этот вопрос разобран в книге Timoshenko, Theory of Platess and
Shells, стр. 75, 1940;-русский перевод: Пластинки и оболочки, 1946, 1963.
к^^ЖТЯ"'
94 , '■ ТОНЙИВ ПЛАСТИНКИ и ОБОЛОЧКИ |ГЛ:;1У
Хо^'я сживающие напряжения по верху пластиши могут быть вошрго^.
раз (^йьше, yeie растягивающие напряжения внизу в случае резкой
сосредоточенной нагрузки, они не представляю^ непосредственной
ptt^CiiOCTHj потому что носят исключительно MectHHfl характер. Мест»
НАй текучесть, которая происходит в случае пластических материа-?
лрв, не влияет на общую деформацию пластинки, если растягиваю*
|цие нап|}яжения внизу пластинки остаются "в безопасных пределах-
Так как сопротивление сжатию хрупкого материала обычно во много
раз больше, чем его сопрот?*еление растяжению, то пластинка из
х;рупкого материала также будет находиться в чбезопасности, если
растягивающее напряжение внизу пластинки будет в пределах
безопасности.
Пластинка со своб'б^но рпермым краем. ПрОгиб пластинки со?
свободно опертым краем полечим, пользуясь,,методом наложения*
К прогибам по уравнению (f)j найденным выше для пластинки с ^зa-
деланным краем, мы присоединяем прогибы, вызванные в пластинке
моментами Ж1 = Р/4тг, равномерно распределенными по контуру, и
получаем решение- для пластинки со свободно опертым краем.
Кривизна, обусловленная действием моментов Mj = P/4ic, на основании
уравнения (85) будет
1 __ Р ■
S? г 4«A4-1*)£> *
а соответствующий прогиб посредине будет
/1 nZ
2г 8яA+(*)£)•
Прибавляя этот прогибу к прогибу по формуле A04), найдем прогиб
посредине пластинки со свободно опертым краем
>_ Ра» ■ Ра^ _ Ра»3 + ^^ ..г...
^';~ l&tD "Г 8я A + [х) D "" 1б7г£) 1 4- Р- * ^ ^
Этот прогиб приблизительно в 2,5 раза больше прогиба пластинки
с заделанным краем.
Прибавляя величину PjAtt к моментам, вьфаженным уравнениями (g)
и (h), полученными выше для Пластинки с заделанным краем, найдем
выражения для изгибающих моментов пластийки'со свободно опертым
краем. Наибольшее растягивающее напряжеййй получается путем до-
бййления F/Л')(Р/4те) к напряжению, вычиеленноцу по формуле A07).
22» Изгиб круглой пластинки, нагружёсгнбй кон1№итрически
Мы нйнем « трго случая, когда нагрузка равномерно распределфна по
кругу радиуса ft (рис. 67),. Рассмотрим отдельно участок пластинки 1иутри'
эТвго круга и участок вне его. Для каждого участка будем применять общее
уравнение (93), полагая 4=*= О для обоих участков и Р=0 для внутреннего
к^^ЖТЯ"'
©6
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
{ГЛ. IV
гружённой пластинки. Подставляя в уравнение A09) с = 0 и пс®д ==:/>, полу-
*1аем уравнение A04) для прогиба пластинки от сосредоточенной натрузки.
Чт0ы определить изгибающие моменты и напряжения в центре
пластинки, мы возьмем вторую производную выражения (а) по х. Подставляя
лг = О и Р = 2T.bq йЬ в эту производную, найдем 1фивиэну в центре,
обусловленную элементарной кольцевой нагрузкой (рис. ©8)
Х(_2.„:1 + ,_|!)*.». ,^
Кривизна в центре, вызываемая полной нагрузкой, равна
Соответствующий изгибающий момент в центре на основании уравнений (83)
и (84) будет
Mi^Mi=^ — D{\^]x)
1 +{Х
«''('"Т + 4У. <"')
их* 4
а наибольшие напряжения от изгиба в центре будут равны
Ытах = ("^'W = у <1 + f^) -^ (in ^ + ^2). A12)
Обозначав через Р полную нагрузку яс^^, получаем
Ытах = (')тах=-2-A+1^)^AПу4-:^2). (ИЗ)
Уменьшая радиус с круга, по которому распределена нагрузка, мы
приближаемся к условию сосредоточенного груза. Напряжения в"^ центре
увеличиваются с уменьшением с, но остаются конечными до тех пор, пока с
конечно.
23. Изгиб симметрично нагруженной круглой пластинки
с круглым отверстием в центре
Изгиб моментами. Обозначим соответственно через Мш и Л!,^
изгибающие моменты, приходящиеся на единицу длины пО внешнему и
внутреннему контурам пластинки (рис. 69, о). Для'^этого случая мы имеем Р=^=:0
и из уравнений (92) и (93) находим
^fa
jr-
"fia М,^ ».Ь М„
•~ ff
и
* 2 ^ л:'
(а)
.«'—%^~С,]п^4-Са. ' (Ь)
Произвольные постоянные Q, Cg и С,
определяются теперь из условий на краях.
Подставляя выражение (а) в уравнение (88),
получаем
Подставляя х = а к затем х = Ь, получаем следующие уравнения для опре-
28] ИЗГИБ ПЛАСТИНКИ Ск1*УГЛЬ|М ЬТВВ^СТИ)йм JB ЦЕНТШ
делёнияС^ и Cg: J
т'
откуда
в[^{1 +?-)-§A -^x)]-Лlш,
£> [§ A -f I*) - § A - [X)] =^M,b,
С.=
All»)
(d>
A—{x)D(a2--fc«) '
Постоянная Cg определится из рассмотрения прогиба пластинки. Положим^
например, что пластинка свободно оперта по внешнему контуру; тогда
прогиб на этом контуре будет равен нулю и С, найдется из уравнения (Ь), кот
торЪе при л: = в перепишется так: -'
так что
«--8 —ГТ *-'!'
Уравнение изогнутой ловерхности пластинки теперь можно полупить
подстановкой в уравнение (Ь) значений Cj, Cj и Cg. '
В качестве второго примере рассмотрим случай изгиба цластИнки под
действием моментов Мш, когда внутренний контур пластинки заделан
(рис. 69, Ь). Произвольные постоянные Сх и С^ в уравнении (а) в этом случае
определятся из условий <р = 0 при дгвей и д^лх^Мю при дг=^а. Тогда из
уравнейия (а) и (с) найдем
Сф , Ci
Сг
С,
2
и мы получаем
' b
= 0, :ii(l-|-^t)-^(l_^)=i!^,
в"
D
С.=
аЧШ
la
£>[«*A + »*) + **О-f*)r """" D[a«(l+Hb) + &«A-H4r
Пода:тавля(я эти значения в уравнение fa) и (с), находим
D[a^i\+li)-\-
аШ
ш
«'A+{х) + *'
Изги€{ Пластинки нагрузкой, равномерна распределенной по
внутреннему и внешнему контурам. Еспя изгиб пластинки происходит под
действием нагрузки, равномерно распределенной ^
вдоль ее контуров (рис. ?0, в), то (^ = О, а Р
рав]цяется всей нагруз!ке, приложенной ко
внутреннему контуру. Подставляем эти
значения в уравнения (92) и (93) и получаем из
уравнения (92)
Постоянные интегрирования Сх и Cg
определятся из условий на контурах. Например, если
пластинка защемлена на контурах (рис. 70, 6),
то произвольные постоянные определятся из
условий, что при лг = в и х^=Ь угол «psssO. Тогда из
4 . с, П, Тимошенко, т< II
Рис. 70.
уравнения
(g>
^^cTi^^f^F'
98
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
найдем
-^B1пв-1L
StcD
РЬ
StzD
Cttt ■ Cg
2 "^ а ■
О»
B1пб-1)+^ + ^=а
Определив значения С^ и Cg и вставив их в уравнение (g), получим
выражение для (р. После этого можно
вычислить изгибающие моменты из
уравнений (88) и (89).
Если вместо нагрузки,
распределенной вдоль контуров, будет действовать
нагрузка, равномерно распределенная
по пластинке, как пок1азано на рис. 71, в,
то поперечная сила Q в любой точке,
находящейся в расстоянии л" от uentpa,
будет равняться
2тел:
7^д{х'-Ь') = ^
2х
внения
получатся в
Эта величина должна
лена в уравнение (90),
следующем виде:
быть подстав-
и тогда ура-
= -^ + '#<='п..
1)
w =
qx^ ' b^qx^
64D
8D
Aпл:~1)
Сух^
2 "^Т'
-Cgln AT + Cg.
Для определения произвольных постоянных необходимо использовать
условия на^контурах. Например, если пластинка защемлена на краях, то для
определения Ci и Cfi получаются следующие уравнения:
-??'^??^B1„„_1) + ^ + :|1 = 0,
С,
16D т Ю
-'*'ь|^B1п*-1L
16D ' -SD
Cib ■ Сз
" 2 "^ &
:0.
Решения таких задач, как |1згиб поршней паровых машин и изгиб фланцев *)
цилиндров и труб, могут быть получены путем сочетания разобранных
в этом параграфе решений. Например, сочетая случаи, показанные на рис. 70,1>
и 71, а, можем получить приближенное решение задачи на изгиб поршня
(рис. 71, Ь) под давлением пара*).
^) См. статью Everett О. Waters and J. Hall Taylor, Trans..
A. S. M. E., 1927. ,
®) Несколько задач такого рода разобрано в статье
М.
En sslin, Ding-
lers Polytech. J., 1903 и 1904. См. также Pflei.de г er, Forschungsarb., № 97,
1911. Опыты с поршнями описаны в статье С. Codron, Revue de mecani-
que, т. 13, стр. 340, 1903; Круглые пластинки, усиленные ребрами, разобраны
М. Schilhansl, Z. angew. Math. u. Mech., т. 6, стр. 484, 1926 и Z. Ver.
deut. Ing., T. 71, стр. 1154, 1927. Более подробное изложение о круглых
пластинках дано S. Timoshenko, Theory of Plates and Shells, 1940 (русский,
перевод: Пластинки и оболочки, 1946, 1963).
23)
ИЗГИБ ПЛАСТИНКИ С КРУГЛЫМ ОТВЕРСТИЕМ В ЦЕНТРЕ
99
Несколько случаев, имеющих практическое значение, представлено на
рис. 72 ^). Во всех этих случаях наибольшее напряжение может быть
выражено формулой вида
'^ kP
A14)
^ьЛ^
"max — *" ^8
ИЛИ
max
(,2 >
В зависимости от того, равномерно ли распределена по поверхности
приложенная нагрузка или сосредоточена на контуре. Числовые значения
Сл/у'/аи f
iJ-Las^
w
Сл1/^ай JS
'/пах
^тах
C/7i/vau ff
С/т^гтй 7
^^и^Ф^
Щгкис
Ofjl/*^au8
\
%JZ^
%
max
Рис. 72.
коэффициента ft, вычисленные для некоторых значений отношения ajb и
для коэффициента Пуассона [х = 0,3, даны в табл. 5. Наибольшие прогибы
в тех же случаях определяются формулами типа
•W
max
■ k^
qa^
или
•w
= k.
Pa''
£/,8 """ "-max "-i Eh^'
Числовые коэффициенты ftj также даны в табл. 5^.
A15)
1) См. статью: А. М. Wahl and О. Lob о. Trans. А. S. М.Е., т. 52, 1929.
*) Более полные сведения относительно симметрично нагруженных
пластинок можно найти в статье: W. Е; Trumpler, J. Appl. Mech., т. 10,
стр. 173, 1943.
testTH"
100
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
■ - Т а б ji и ц а 5
Коэффициенты k и ft, в уравнениях A14) и <115) для восьми случаев,
показанных на рис. 72
■ ■ г . ..•
.■■■ а :.*«,''.
-Случай
1
2
3
4
5
6.
■ .7
8
о: Ь =.
Случай
1
' 2
3
4
5
6
7
8
«
1,10
0,66
0,135
0,122
0,090
0,115
0,592
0,227
k -
1,88
3,34 .
2,15
1,21
1,54
0,703
1,880
1,205
1,25
fti
0,841
0,202
0,00231
0,0034S
. 0,00077 .
0,00129
0,184
0,00510
3
ftl
'0,734
1,220
033
0,291
0,116
0,062
0,824
0,209
ft
1,26
1,19
0,410
0336
0,273'
0,220
0,976
0,428
ft
2,17
4,30
2,99
1,45
2.23
0,933
2,08
1,514
^
1.6
0,519
0,491
0,0183
0,0313
0,0062
0,0064
0,414
0,0249
4
ftl
0,724
1,300
0,448
0,417
0,179
0,092
0,830
033
\
ft
1,48
2,04
1,04
0,74
0,71
0,405
1,440
0,753
ft
2,34
5,10
3,69
1,59
2,80
1,13
2,19
1,745
2
ftl
0,672
0,902
0,0938
0,1250
W29
0,0237
0,664
0,0877 •
6
ftl
0,704
1,310
0,564
0,492
0,234
0,114
0,813
0,350
'' 24. Изгиб прямоугольных пластинок
Теория изгиба прямоугольных пластинок является более сложной, чем
теория круглых пластинок. Поэтому ниже приведены лишь окончательные
формулы для изгибающих моментов и прогибов. При выводе этих формул
лредполагалось, что прогибы малы по сравнению с толщиной пластинки и
—^а: что края пластинки при изгибе могут свободно
перемещаться в плоскости Шластинкщ т. е. в
срединной плоскости пластинки не действуют
никакие усилия.
Пластинка со свободно опертыми краями,
В случае равномерно распределенной нагрузки q
наибольший прогиб имеет место в центре
пластинки (рис. 73) и может быть представлен
уравнением
да*
Рис. 73.
PAi»
Eh
A16)
где a есть короткая сторона пластИНКИ| А — толщина «яаСтинки и а — число-
24] ИЗГИБ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК 101
. ' < ''■"'.■'■■-■'■. ■■"■■■■ ■ ■
ВОЙ коэффициент, зависящий от величины отношения bja. По-прежнему мы
обозначим через Mj и Мц изгибающие момейты,, приходящиеся на единицу
длины сечений, Соответственно параллельных осям у и х Наибольшие
изгибающие моменты имеют место' в центре пластинки и равны
(^fiW == PW«*; (Л^*)тах = Р«««
(П7)
где pj И Ра означают числовые коэффициенты, зависящие от отношения ft/o.
Некоторые значения ко$ф||)ИЦиентов в, Pj и. pg приведены fe табл. 6. Эти
значения вычислены в. предположении, что коэффициент {1уассона равен 0,3.
Та бли ца 6
Коэффициенты для расчета равномерно н)агружениых прямоугольных
пластинок со свободно опертыми краями
*/«=
ft/o'= ■
а =3 '
4.6
0,0443
0,0479
'0*0479
1.8
0,1017
0,0948
0,0479
1,1
0,0530
. 0,0553
0,0494
»'®
0,1064
0,0985
0,0471
1.2
0,0616
0,0626
0,0501
2,0^
0,1106
0,1017
0,0464
1.3
0,0697
0,0693^
0,0504
3.0
0,1336
0,1189
0,0404
1,4 * i.5
0,0770
0,0753
0,0506
0,0843
0,0812
0,0500
Л0 1 5.0
0,1400
0,1235
0,0384
0Л416
0Д246
0,0375
1.6
0,0906
0,0862
0,0493
1.7
0,0964
0,0908
0,0486
00..
- 0,1422
0,1250
0,0375
Из табл. 6 можно.видеть^ что при й/а>3 наибольший прогиб и
наибольший изгибающий момент существенно не отлича1ются от тех же величин,
вычисленных при fr/e=soo. Это значит, что для длинных прямоугольных
пластинок (fr/<i > 3) поддерживающим влиянием коротких сторон можно
пренебречь и с достаточной точностью можно" пользоваться формулами,
•выведенными в пп. 13—15 для изгиба по цилиндрической поверхности.
Пластинка с защемленными краями. Наибольший прогиб имеет место
в центре пластинки и может быть выражен тем же уравнением A16), что
и для глластйнки с опертыми краями. Численно наибольший изгибающий
момент имеет место в середине длинных сторон и определяется уравнеПием
A^iUi=P9«^-
A18)
Некоторые значения коэффициентов аир приведены в табл. 7.
Значения, приведе^^ные в табл. 7, указывают, что защемление краев
пластинки значительно у)м1еньшает ее наибольший прогиб. Влияние же
защемления на величину наибольших нормальных напряжений не так велико. Из
таблицы также видно, что в случае защемленных краев наибольший прогиб и
наибольший изгибающий момент при Ь/а^=2 почти совпадают с теми же
величинами, полученными при. &/а = оо. Это обстоятельство оправдывает
применение формул, полученных в п. 14 для изгиба по цилиндрической
поверхности, в случае расчета сравнительно длинных прямоугольных пластинок
(&/а>2) с защемленными краями. ,
102
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
Таблица?
Коаффициепты для равномерно нагруженных
прямоугольных пластинок с защемленными краями
г>/а =
р =
1,00
0,0138
0,0513
1,25
0,0199
0,6б65
1,50
0,0240
0,0757
1,75
0,0264
0,0806
2.00
0,0277
0,0829
00
0,0284
0,0833
Пластинка,у которой две гротивоположные стороны свободно оперты,
третья сторона защемлена и четвертая сторона свободна (рис. 74). В случае
равномерно распределенной нагрузки наибольший прогиб будет посредине
свободной стороны, т. е. в точке А. Этот прогиб
Уаде/7аишя можно представить уравнением
/=«
A19)
Значения числового коэффициента а. в этом
уравнении приведены в табл. 8. Наибольший
изгибающий момент Ml также имеет место в точке Л,
и его величина определяется уравнением
Рис. 74.
т^)ш^=ы<^'
A20)
Численно наибольший изгибающий момент Mg имеет место в точке В, т. е»
посредине заделанной стороны, и его величина определяется уравнением
Несколько значений коэффициентов Pj и Pg
приведено в табл. 8.
Таблица 8
Коэффициенты для равномерно нагруженной
прямоугольной пластинки, показанной на рис. 74
Ыа=Х 0
§2 =
1,37
0
0,500
1
3
1,03
0,0078
0,428
1
2
0,635
0,0293
0,319
2
3
0,366
0,0558
■Ч),227
1
0,123
0,0972
0,119
Из этой таблицы видно, что если а велико по
сравнению с&, то средняя полоска ЛБ приближается
, к условиям консоли, заделанной в точке В и равна-
мерно нагруженной.
Равномерно нагруженная пластинка, свободна
Рис. 75. лежащая на многих равно удаленных друг от
друга опорах (рис. 75). В этом случае мы можем
получить хорошее приближенно» значение наибольшего напряжения и закон.
распределения напряжений вблизи опоры следующим образом. Рассматриваем
часть пластинки вблизи опоры, ограниченную кругом радиуса а = 0,22 с
25]
ТОНКОСТЕННЫЕ СОСУДЫ ПОД ВНУТРЕННИМ ДАВЛЕНИЕМ
103
{где с есть расстояние между опорами), как круглую Пластинку, свободно
опертую по внешнему контуру и нагруженную в центре силой P=zqc^,
действующей вверх, и равномерно распределенной нагрузкой интенсивности q,
действующей вниз. Эти нагрузки показаны на рис. 75, b ^). Задача может
быть решена с помощью методов, изложенных в п. 23.
Изгиб прямоугольных пластинок на упругом основании в связи с
определением напряжений в бетонных дорогах был исследован Н, М. Wester-
gaard'oM *):
25. Тонкостенные сосуды, подверженные внутреннему давлению
Здесь мы ограничимся рассмотрением сосудов, имеющих форму
тел вращения и подверженных внутреннему ;^авлению интенсивности
р, не обязательно равномерному, но симметрично распределенному
относительно оси вращения О —О (рис. 76). Если толщина -стенок
мала по сравнению с радиусами кривизны и нет резких изменений-
Мз^б,
а) О
Ь)
Рис. 76.
в форме меридиональных кривых, то "■ напряжение можно вычислить
с достаточной точностью, пренебрегая изгибом стенок сосудов, т. е.
допуская, что растягивающие напряжения распределяются по толщине
стенки равномерно ^). В таком случае величина напряжений может
быть легко вычислена из уравнений статики.
Рассмотрим элемент mnsq, вырезанный из стенки сосуда двумя
меридиональными сечениями тп и sg' и дв)пу1я сечениями ms и nq^
*) См. статью: Н. М. Westergaard and А. Slater, Proc. Am,
Concrete Inst., T. 17, 1921. Cm. также V. Lewe, Die strenge L6sung des Pilzde-
ckenjproblems, Berlin, 1922.
*) Cm. его статью в Ingenioren, Copenhagen, стр. 513, 1923 и также в
Public Roads, т. 7, стр. 25, 1926. См. также S. Timoshenko, Theory of
Plates and Shells, 1940 (русский перевод, Пластинки и оболочки, 1946, 1963).
2 Оболочки, которые не сопротивляются изгибу, иногда называются
раидми, а напряжения, вычисленные без учета влияния изгиба,
называются мембранными напряжениями. Предполагается, что внешние силы,
равномерно распределенные по краю оболочки, направлены по касательным
к меридианам.
3^
104
•Тонкие пластинки и оболочки
[ГЛ. IV;
нормад1.й1^р1 к меридиану. Из условий симметрии можно заключить,
«<то йо граням 9toro элемента будут действовать только нормальные
напряжения. Примем следующие обозначений: = >
о,'—растягивающее напряжение в меридиональном направлении,
или меридиональное напряжение,
Оа—^растягивающее напряжение вдоль параллельного круга, или
окружное напряжение, .
h — посто!янная толщина стенки сосуда, ,
d$i — размер элемента в меридиональном направлении,
jcifSg — рйзЫер элемента по параллельному кругу, ^
Гу — |)ади;^с кривизны меридионального сечения,
Га— рад)яус кривизны сечения, перпендикулярного к меридиану.
Полные растягивающие усилия, действующие по граням элемента,
будут hoids^vi ho^Si. Растягивающие усилия ho^ds<^, действующие По
граням /»s и nq элемента, имеют составляющую в направлении
нормали к элементу, равную (рис.. 76, Ь)
ho,ds^,^^!^. (9)
."■,■■■■ ^ /'' ■ •
Точно таким же образом растягивающие усилия, действующие по;
граням тп и s^» имеют нормальную составляющую
ha^dsidst
ha^Sid% ■•
(b)
Сумма этих нормальных составляющих по условию равновесия
равняется нормальному давлению на элемент; следовательно,
или
ha,dS,ds, ,ho,ds,ds, ^pas,ds.
(c)
A22)
Рассмотрим теперь приложения этого уравнения-
Сферичесф1й^ сосуд под действием равномерного внутреннего
давления. В этом случае ri=r<i='r и
ai=:qij^:i=a. Из уравнения AS^2)
получаем' ' . ■''■■/■■■-.
■;'■-'-'-'юг
, , ■ ^ °—k-
Конический сосуд, Рассмотрим
открытый конический сосуд, наполненный
жидкостью (рис. 77). JS siroM случае кривизна
меридиана l/ri=p=.0'^ окружное
напряжение og, обусловленное давлением жид-
.. \кости, может быть вычислено из
уравнения A22). Внутреннее давление в точках /;ir.-^ л, на расстоянии d—у
25]^ ТОНКОСТЕННЫЕ еОСУДН rioi ВНУТРЕННИМ ДАВЛЕНИЕМ 105
от поверхности жидкости райняется jp = f (л?—j/), где 'у—^ вес
единицы обърема жидкости. Радиус кривизны Га в этих, точках равен
Га=^ ^° . Тогда уравйение A22) перепишется так:
cos о
cos а "ii^^-y)
о,.
откуда У ^^tid~y)ytga _
Наибольшее значей1?й ЭТОГО Напряжения имеет место в точках, где
произведение ,((/~-j/)j/ является щах1тцт'ом. Если »?ы положим
производную от, (rf—ji/)j/ равной нулю, то найдем j;=3:<i/2, я
напряжение в этой точке будет , , . ■
Напряжение Oj на уровне т-^п найдется из того условия, что
вертикальные составляющие меридиопальных растягивающих усилий
в стенках сосуда уравновешиваются весом объема tmOns жидкости
(рис. 77); следовательно, '.■■-■.
, . 2т:у (tg а) ft о, cos а = %у^ (tg^ а) ^Й _ j/ -[- у^) Т»
откуда / 2 \
°*'= 2ЛС08а • ^^>
3
Это напряжение достигает наибольшего значения при y=z-^d.
Подставляя это значение в уравнение (f), мы находим
(OlVax —Yg-;p^^^. (g)
Уравнения (d) и (f) представляют полное решение задачи в том
случае, когда напряжениями от изгиба в стенке сосуда можно,
пренебречь. __
В случае цилиндрического сосуда диаметром d, подверженного
равномерному давлению р, мы находим по-прежнему (см. т. I, стр. 46)
pd pd
°^ — ~Ш\ °2—2Л* , '
:< ЗАДАЧИ
1. Бак (рйс. 78) наполнен жидкостью до указанного на рисунке уровня.
Определить наибольщие напряжения о^ и Oj в цилиндрической и шаровой
поверхностях сосуда, а также сжимающее усилие в укрепляющем кольце тп.
Решение. Вес жидкости, содержащейся в сосуде, равняется
Q=:[«dr*-b«^~/?»-^«/ + |-]JY.
106
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ.IV
Для цилиндрической части бака имеем
; const
И
ы
— -^1Г_
max— fi
Для шаровой части наибольшее напряжение будет внизу на дне, где
гидростатическое давление жидкости равняется -^di и с^ = Og ж= ■^^1/?/2Л.
Растягивающие усилия в шаровой части сосуда»
приходящиеся на единицу длины кольца
тп, равняются С?/Bлг8т&). Радиальная
составляющая этого усилия, вызывающая
сжатие кольца (рис. 78,ft), равняется (Q/2nr) ctga,
а сжимающее усилие в кольце равно
{Qfill)ctga. Это является лишь
приближенным решением, полученным на основании
допущения, что цилиндрическая и шаровая
части представляют собой мембраны,
сопротивляющиеся только растяжению. При
вычислении сжимающих напряжений в
кольце необходимо к поперечному сечению самого кольца тп прибавить
сечения смежных участков цилиндрической и шаровой частей.
2. Определить напряжения в точках тп цилиндрического бака с полу-
шар'овым днищем, который наполнен до указанного на рис. 79 уровня.
т
О)
Ь)
Рис. 78.
Решение. Из уравнения A22) для какой-либо точки шаровой части,,
находящейся на расстоянии х от поверхности жидкости, имеем
TfAT
(h>
Так как меридиональные усилия, приложенные по сечению тп,
уравновешиваются весом объема smOnt жидкости, то второе уравнение будет
и из уравнения (h) получаем
7/? /d —/? , ^ 1
— sin' а \
COS^a /'
(i>
fR Id — R . R sin«a4-3sinacos^a —IV
Л \ 2 "•" 3 COS»ct J*
3. Для бака на рис. 80 определить зависимость между внешним
диаметром бака, диаметром опорного кольца тп и глубиной d жидкости по
■25]
ТОНКОСТЕННЫЕ СОСУДЫ ПОД ВНУТРЕННИМ ДАВЛЕНИЕМ
107
условию, чтобы опорное кольцо тп испытывало лишь вертикальное давление.
Средняя часть днища резервуара является . шаровой поверхностью с
центральным углом я/2. Тот же угол имеет и коническая часть тт^пщ.
Указание. Требуемая зависимость может быть получена из того условия,
что давления на кольцо со стороны шарового днища и со стороны
конической боковой поверхности, действующие под углом 45°, не должны давать
горизонтальной составляющей. Из этого следует, что объем жидкости,
ограниченный внутренней поверхностью mstn, должен быть равен объему
жидкости, ограниченной наружной поверхностью. V
4, Определить наибольшее напряжение в баке, представленном 'на
рис. 78, если ^ = 3 м, г = 2,4 м, rf = 6 м, if = 1 г/сж^ и Л = 0,6 см.
5. Определить напряжение oj и Og в стенках тора, подверженного
равномерному внутреннему давлению р (рис. 81).
Решение. Условие равновесия
для вертикальных сил в части
J7, ' тпт^п^, вырезанной из сосуда
"^^^z::^
Рис. 81.
О
Рис. 82.
вертикальной цилиндрической поверхностью радиуса а и конической
поверхностью тОт^, выразится так:
откуда
л (г^ — а^)р — tsiltl-ar sin а = О,
_р(г2_д2)
' 2гЛяпа "
Теперь напряжение Og можно вычислить из уравнения A22).
Рис. 84.
6. Определить наибольшее напряжение в стенках сосуда, представленного
на рис. 81, если а = 3 л, 6х=3,6 jw, Л = 0,6 см ар = 3,5 кг/ем^.
loa
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
7. Шаровой купол постоянной толщины h (pnt. 82) нагружён собственным
весом 4^1 приходящимся ни единицу площади. Найти' напряжения в мери-
AHonaJ^bHOM направлении, а также в перпендикулярном к меридиану.
qR „ ^Щ L
Ответ. Oi=-
cos^
)•
ЛA+со8хр) ' * А Vl4-cbS9
: ^Решить предыдущую задачу, если верхняя часть шарового купола уда-
4^йа (рис. 83) I к верхнему контуру приложена равномерно распределенная
Шгрузка Р, приходящаяся на единицу длины.
' Ответ.
__^ д R(cos(fo — ср&ф Явшув
h sin® (f
qjR /созуо — cos<p
sin*<p
hsln'<f '
cos^
л sin^ <p *
T . 9. Шзровой бак (рис. 84), опертый по параллельному кругу, полностью
^наполнен жидкостью удельного веса у. Найти о^ и вз-
Ответ. Если <р<а: _ , "
Of cs:
ХДЧ. 2cos4\ Т^/с ft , 2cos»«p\
6Л \ l-f-cos^j' 6Л \ ^ ' IH-cos^/
Если ф>о:
/^- , 2cos=«\ Ч Y^eVi Й 2cos»4)\
\ ' 1 — cos^/' 6я \ ^ 1 — cos<p/
^^*
26. Местные напряжения изгиба в тонкостенных сосудах
В предыдущем параграфе пренебрегалось изгибом стенок сосуда и
рассматривались только растягивающие, так называемые мембранные
напряжения. Перемещения, обусловленный мембранными напряжениями,
вызывают изгиб стенок, и результирующая напряжений изгиба может иметь
существенное значение. В особенности это относится к местам перелома
MepHjodHana^ Если меридиан состоит из кривых, которые не имеют в месте
сопряжения общей касательной, то для
того, чтобы воспрепятствовать
значительному изгибу стенок сосуда,
необходимо устроить <псрепляющее кольцо, как
показано на рис. 78. i
Напряжения могут достигать
значительной величины JB местах сопряжения
в меридиональном 5сечении, состоящем
из нескольких кривых, также и в том
случае, если ё-местах сочленения
имеются общие к?[Сательные.
Дополнительные напряжения» возникающие, в этих
Рис. 85. точках, называются напряжениями раз^
рыва непрерылнфтц напряжений.
Покажем теперь способ их определения в простом случае цилиндрического
сосуда с полушаровыми днищами, подверженного Действию равномерного
внутреннего давления (рис.85)- Сначала мы рассмотрим только мембранные
напряжения и для гщлиндрической части найдем '^
о <
OJ
6/
о. =
PL
2h^
X
(а)
26]
МЕСТНЫЕ НАПРЯЖЕНИЯ ИЗГИБА В ТОНКОСТЕННЫХ СОСУДАХ
Ш&
где г — радиус цилиндра и полушйра и Л — тодщяяа стенки. Для шаровой
части ]имеём. . .-■■■'■
. . • ■ •'■ рг ■: ■,'■■' • .•
■ , ■ 2л , ^ / ■
Соответствующие радиальные перемещения для цилиндрической и шаровой
частей будут равны '
Е
(«.-
^'^-ШЁ^^-^^ « Ш<^-^*>-
Если бы шаровая и адлиндрическая части были разъединены (рис. 85, Й),
то разность радиусов вследствие дефор<11ации, вызываемой мембранными
нап]ря»сениями, равнялась бы
ЗЛИСЬ)
М
А
iz
-з:
Ь)
В действительном же сосуде днище и цилиндр связаны взаимно на их
стыке усилиями сдвига Qo = Po и изгибающими моментами М^ (рис. 85,&),
отнесенными к единице длины окружности срединной поверхности сосуда, ^та
усилия вызывают изгиб смежных ча- * ,
стей сосуда. При изучении изгиба
цилиндрической части достаточно
рассмотреть изгиб элементарной полоски
(р1ис. 86), поскольку деформация
симметрична относительно оси и прогиб
этой полоски совершается в мери>
дионадьной плоскости. Для простоты
предположим, что полоска имеет ши-;,
рину, равную единице. Если у
означает радиальное перемещение в
каком-либо- поперечном сечении
полоски, то радиус цилиндра в этом
сечении укорачивается на величину у,
вследствие чего появляется
относительное сжатие в окружном
направлении величиной у\г.
Соответствующее сжимающее напряжение будет у
Ey\t. Следовательно, когда полоска прогибается в направлении оси цилиндра,
то возникают поперечные сжимающие усилия Т (рис. 8б, с), величина
которых на единицу длины полоски равна . , ''
Ю
> (
о
Рис. 86.
Еу
h.
(с)
TttK как угол в равен l/r, то эти усилия дают радиальную результирующую^
равную N
Eyh . Eyh
е
rS >
(d>
которая препятствует прогибу полоски. (Предполагается, что угол в мал.)
Эти р«активные силы распределяются по полоске пропорционально
прогибам у, так что при изгибе полоска находится в тех же условиях, что и
балка на упругом основании^) с коэффициентом постели k^=Ehjr^. Так к^к
^) Кажется, что этот метод анализа местного изгиба в цилиндрических
оболочках был Введен. Н. Schef fl ег'ом, см. Organ i Eisenbahnwesen, 1859.
imw
110 Тонкие пластинки и оболочки [гл. iv
любому изменению формы поперечного сечения полоски препятствуют
смежные полоски точно таким же образом, как в пластинках, то здесь для
расчета полоски также используется цилиндрическая жесткость (см. стр. 70)
£) = £Л'/12A—(х^). Тогда дифференциальное уравнение изогнутой оси
полоски будет (см. уравнение A) стр. 12)
^dy Eh ,
Вводя, как и прежде, обозначение
получим уравнение изогнутой оси полоски (см. уравнение (И), стр. 21)
y^-^j^iQoCos^-^ — ^oicos^x — sin^x)]. - (е)
Это волнообразная кривая с быстро з1атухающими амплитудами и длиной
волны
4 г ^2/j8
=^-f;
которая мала по сравнению с г, если Л мало. Из SToro можно видеть, что
изгиб в месте соединения цилиндра и днища имеет местный характер и
оказывает заметное влияние на напряжения лишь в узкой полоске в
непосредственной близости к соединению. Эта узкая полоска по краю днища
.является почти цилиндрической по форме, и следовательно, уравнением (е),
которое было выведено для цилиндрической части сосуда, также можно
пользоваться для приближенного вычисления прогибов и напряжений
в днище*).
В простейшем случае, когда цилиндрическая стенка и шаровое днище
имеют одну и ту же толщину, прогибы и углы наклона, вызываемые на
краях шаровой и цилиндрической частей силами Qq, равны. Тогда условия
непрерывности в месте соединения удовлетворятся, если AIq == О, а Оо = ^о
имеет такую величину, которая вызывает прогиб на краю цилиндра,
равный //5." Подставляя в уравнение (е) JWe = О и х =2= О, получаем для вычисле-
0 f
ния Qo уравнение ^^ = у, откуда
Зная Qo, мы можем вычислить из уравнения (е) прогиб и изгибающий
момент в любом поперечном сечении полоски. Соответствующие напряжения
разрыва непрерывности напряжений должны быть прибавлены к
мембранным напряжениям, определяемым уравнениями (а).
Если днище и цилиндрическая часть сосуда имеют разную толщину, то
в месте соединения будут существовать усилие сдвига Qg и момент Mq. Эти
две величины определяются из следующих условий: 1) сумма прогибов на
краю шаровой и цилиндрической частей должна равняться / (рис. 85,&);
2) углы поворота обоих краев должны быть равны между собой.
^) Доказательство того, что это является достаточно точным, было дано
Е. М е i S S п е г'ом, Schweiz. Bauzeitung, т. 86, стр. 1, 1925.
Щ МЕСТНЫЕ НАПРЯЖЕНИЯ ИЗГИБА |В ТОНКОСТЕННЫХ СОСУДАХ Щ
■ Указанный метод можно применить также в тех случаях, когда днища
ие являются полушаровыми *). Если толщина стенок сосудов, испытывающих
давления, не мала, то напряжения от изгиба в стенках могут иметь
первостепенное значение, и в этом случае становится необходимым более
подробное исследование закона распределения напряжений').
ЗАДАЧИ
1. Определить напряжения вследствие разрыва непрерывности в сосуде,
показанном на рис. 85, если ^==10 wг/cлt^ г = 60 сл<, А = 1,2 см, fA = 0,3.
Решение. Из уравнения A23) мы получаем рз= 0,151 и из выражения A24)
10
8-0,151
полоске равняется Ж = —D ~^. Пользуясь уравнением (е) и подставляя
мы находим Qo = Q а i к i ==8,3 кг/см. Изгибающий момент в элементарной
•
«г « f"" сие рл, пилу чаем
Ре
WI^
«■"Р-^сов^, получаем
М = —^g-p*sinpJC.
р
Численно наибольшее значение этого момента имеет место при Рл: = я/4,
когда -Мд,ах== 17,8 кг см. Соответствующее наибольшее напряжение от изгиба
в полоске будет равно 6M„,^/A^ == 74 кг/смК Это напряжение нужно сложить
с мембранным напряжением
рг 10 . 60 окп I «
«1 = §^ = 2 . 12 *" ^^ кг/см».
Изгиб полоски вызывает также окружные напряжения. Эти напряжения
состоят из двух частей: 1) напряжений, которые препятствуют искажению
поперечных сечений полоски (см. стр. 70) и наибольшее значение которых
в любом поперечном сечении полоски равно ±6{л.Л1/Л^ й й) напряжений
—у Б/г, обусловленных укорочением окружности. Подставляя вместо у и М
найденные выше выражения, получаем напряжение разрыва непрерывности,
которое надо добавить к мембранному напряжению og. По уравнению (И):
-^^-FcospA: + ^^e-P^sinpA:=^^»£-p^(sin§A:-l,83cosH-
*) Этот метод был применен при исследовании закона распределения
напряжений в различных формах днищ па'ровых котлов; см, Е. Н б h п and
А. Huggenberger, Ober die Festigkeit der gew6lbten Boden und der
Zylinderschale, Zurich, 1927 и W. M. Coates, The State o! Stress in Full
Heads of Pressure Vessels, Trans. A. S. M. E., Appl. Mech. Div., 1929. Метод
также был применен при исследовании местного изгиба в резервуарах,
содержащих жидкости; см, Т. P6schl и. К. Т е г z а g h i, Berechnung von Behal-
tern, Berlin, 1926. H. Reissner, Beton u. Eisen, т. 7, 1928; и С. Runge,
Z. Math u. Phys., т. 51, стр. 254, 1904. Цилиндрические оболочки с плоскими
днищами были рассмотрены Е. О. Н о 1 m b е г g'OM и К. Axelso п'ом, Trans.
А. S. Ml е., т. 54, стр. 13, 1932. Метод также был применен к толстостенным
цилиндрам и дал удовлетворительные результаты; см. статью: С. W. М а с-
Gregor and L. F. Coffin, J. Appl. Mech., т. 14, стр. A-301, 1947. Далее
о цилиндрических оболочках (;м. S. Т i m о s h е п к о, theory of Plates and
Shells, 1940; русский перевод: Пластинки и оболочки, 1946, 1963.
*) См. S. Timoshenko, там же.
mm
1^12
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
1Гл; rv
■.^'
Наибольшее значение этого напряжения можно л^гко найти обычным путем.
Оно мало ho сравнению с^ мембранным круговым напряжением prjh =зт
= 500 ic;&/cj»*,, так что. .напряжения разрыва непрерывности в этом случав
сущ,^ственно не влияют на наибольшее напряжение.
2, Тонкий цилиндрический барабан, прикре11|(енный к двум сплощны«с
дискам, вращается около оси О — О (рис. 87) с окружной скоростью v.
Определить местные напряжения от изгиба
в барабане, если он заделан по краям тп
и гПгЩ.
Решенае. Если бы барабан был отделен
от дисков, то увеличение радиуса бараба-.
на вследствие действия центробежной силы
равнялось бы -^v^rfg'E (см. т. I, уравнение
A5), стр. 36). Увеличение же радиуса
сплошных дисков (см. выводы,, на стр. 181 —
,/77 if^ ^i
jC- -
!'!«>%-у>УИ«'>'ХЛЯ/9Ми»иШ<К«9!в1%
т
г
_1.
■/7
Рис 87.
I
■■./■
^^^Л-У-У^^г
-т-^ i-=r. Разность этих двух
4 g£
183) равняется
(Предполагается, что 7. ~f* и ^ одинаковы как
величин равна .г.
. А gE
для барабана, так и для, дисков.) Применяя тот же метод, что и в
предыдущей задаче, и рассматривая полоску шириной, равной единице, найдем при
помощи уравнений A1) и-A2) величины поперечной силы Q,, и изгибающего
крмента AJp. Э^ими уравнениями можно воспользоваться, если рассматрива-^
«мая полоска является очень Длинной. В дополнение мы можем считать
диски весьма жесткими по сравнению с барабаном и пренебречь
деформациями, вызываемыми в них силами Qo и моментами М^^. Тогд1а уравнениями
для вычисления С?о и Af» будут
2Р^^(Оо-РЛ1о)==*Ь, .-|^((?„_2рЖо) = 0,
откуда
Оое=48р»Д Мо«=2Вр«£>.
При помощи этих величин прогибы и напряжения от изгиба в барабане
найдутся из уравнения, аналогичного уравнению A1).
. Зь Определить наибольшее напряжение от изгиба в барабане
предыдущей задачи, если гаа«;бр ем, йзся 1,2 см, v= 150 Mjceic и материалом является
<;тг^яь. ■■'■■''
4. Определить напряжения от изгиба, возникающие в трубе под'дей-
ствмём насаженного на нее узкого кольца (рис 88).
Решение. Рассмотрим продольную полоску шириной, равной единице, и
обозначим через Р давление между кольцом и трубой, приходящееся на
единицу длины окружности трубы. Эта
полоска будет изгибаться точно так же,
как длинный стержень на упругом
основании, который несет сосредоточенный груз Р
. (п. 1). Уменьшение радиуса трубы иод
действием силы Р на основании формулы (8)
равняется Р/8р*/). , Увеличение радиуса
.^ Рис. 88, кольца равно Pr^jFE, где F—площадь
поперечного сечения кольца. (Уменьшение
]^Ольца в радиальном направлении предполагается малым по сравнению
с радиусом г,) Если через В обозначить первоначальную разность между
внутренним радиусом кольца и наружным радиусом трубы, то для
вычисления Р получим следующее уравнение:
Р Рг^
Ь^»Р^ FE *
€»A-^J'J'^M'^At^M'^/y^MrMM'A^rj'^MM^^^fyyi'y^jf^i
1 ^'М'У'г/ж/гг^г^/ж^^/г/'жлгм'ГУл^лг^улг^ггуА/м-уум
■ <■ ■ ■■ ■ ■ ■■■■"■ •■ ■ ■■■■'■■■■■■' ' , ■' '^' ■
26] МЕСТНЫЙ НАПРЯЖЕНИЯ ИЗГИБА В ТОЩОСТЕННЫХСОС^^ 113
ИЛИ, пользуясь формулой A23) И принймгГя|Х=й: 0,3, получает
Р определяется из этогй-уравнения, и наибольший изгибающий мо]мент
в полоске найдется из выражение (9) ^). Наибольшее н;апряжение изгчуба
в полоске'будет '
А* У 8A—{Л»)*
Тот же метод Применяется также в случаях, когда цилиндрическая
труба с укрепляющими кольцами подвергается равномерному внутреннему
или равномерному ,наружному давлению. Если расстояние между кольцами
настолько велико, что влиянием любого из них на прогибы, вызываемые
другими, можно пренебречь, то Р можно получить из уравнения (g) путем
подстановки В=/>г^/£'Л. Это выражение представляет собой величину язле-
нения радиуса трубы под действием равномерного давления *).
б. Решить предыдущую задачу^ предполагая, что длина / трубы
невелика и что кольцо находится в середине длины. Материалом дрляется сталь
и да^ы следующие размеры: г^в=60,сж* Ла=Л,2 см, / = 120 см, F7t=: 25 см^ и
6 = 0,12 см.
Указание. При вычислении давления Р, приходящегося на единицу длины
кольца, воспользоваться {Результатами, полученными для балки, показанной
на рис. 13, стр, 25. Таким образом, прогиб,
вызываемый в трубе давлением Р, равняется иш -/
Р chpfH-cos^/-f2 , Y ■ ■ ■ '^
т
sh>/ + sinp/ • ГТТТТТТТ
I ' I
» / ! 7 I
if
Тогда уравнение для вычисления P будет
. Р chg/-|-cosP/ + 2 . Pr^ . u^l „i , I-^
WD shp/ + sinp/ '^ EF^ I ', J
6. Круглая цилиндрическая труба со свободно 1 } \ \ Л \ \ \ \
опертыми краями подвергается внутреннему равно- А' V А
мерному давлению р. Найти продольное
напряжение от изгиба и прогиб посредине трубы (рис. 89). Рис. 89,
Размеры трубы те же, что и в предыдущей задаче.
Указания. По результатам решения задачи, представленной на рис. 20,
стр. 29, прогиб и изгибакмций , момент, приходящийся на единицу длины
окружности, вг среднем поперечном сечении С — С будут
/ о wP' Р' \ ' иР' ■ Р'
^*"£Л\ chpZ-fcosp//' V^*"p^chp/ + cosp/* ,
7. Решить предыдущую задачу, предполагая, что края трубы жестко
заделаны.
Указание. Воспользоваться результатами задачи, представленной на
рис. 21, стр. 29.
*) Пример Таких вычислений дан в статье: G. С о^ к. Engineering, т. 116,
стр. 479, 1923. См; также R. Lorenz, Z. Ver. deuti Ing., т. 52, стр. 1706,
1908; М. W е S t р h а 1, там же, т. 41, стр. 1036, 1897.
?) Приложение этого метода к вычислению окружных напряжений
в подводных лодках, имеющих круговое поперечное' сечение, дано в статье
К. V. Sanden'a, «Werft u. Reederei», стр. 189, 1920.
ДКЖвГ"'
Щ
114
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
Т
11
-1^--^—#--~-п
I
I
и
8. Круглая стальная труба усилена кольцами, которые находятся на
расстоянии Л одно от другого (рис. 90, о), и подвергается внутреннему
давлению р. Найти давление Р, возникающее на единице длины внутренней
окружности кольца. Найти наибольшие напряжения изгиба трубы.
. ' Решение. Начнем с рассмотрения частл
трубы между двумя кольцами, находящейся
под действием поперечных сил Q^ (рис 90, Ь)
и изгибающих моментов Мо (рис. 90, с),
приходящихся^ на единицу длины окружности
трубы. (Предполагается, что шириной
кольца можно пренебречь по сравнению с
расстоянием I между кольцами.) Рассматривая
продольную полоску шириной, равной
единице, как балку на упругом основании, и
пользуясь результатами задач,
представленных на рис. 12, стр. 24, и ни рис. 18, стр. 28,,
мы находим прогиб и угол наклона
касательной к левому концу полоски по рис. 90,6:
(«'i).K-o = WT- .и о, 1 .;„ fi> , (n>
11
II
II
и
11
II
11
a)
Op
^o
У
0,
Zr
1
«-
Mo f^a.
Cr^
У
b}
Рис. 90.
Eh shp/ + sinp/ •
[dwA 2QopV« shp/ —sinp/
\dx]x^^'^ Eh shp/ + sinp/ •
(i>
Для левого конца полоски на рис. 90, с получаем
2AiopV shpf —апрг
(и'гЬ-о— £;^ shpZ + sinp/'
IdwA 4Mop»r^ сЬрг —cosp/
\dx }х^{Г^ Eh sh p/ -f sin U '
A>
Из нашего определения P следует, что Qo = о"' Подставляя это в
уравнение (i) и замечая, что в трубе (рис. 90, а) касательная к полоске должна
быть параллельна оси трубы, получаем
откуда
\dx}x=^ \dxjx=o
Р shp/ —sirip/
Мо =
а>
4pchp/—cosp/ •
При вычислении Р мы предполагаем сначала, что кольца абсолютно
жестки. В таком случае прогиб в трубе, вызываемый силами Р под кольцами,,
должен равняться радиальному расширению pr^jEh, которое труба должна
была бы иметь при отсутствии укрепляющих колец. Следовательно,
уравнением для вычисления Р будет
{^y)x-o'^{^i)x-iy=^,
или
Ррг» chp/ + co^p/ Р^г'^
(shp/ —sinPO'
_ Pr^
Eh sh p/ + sin p/ 2Eh (sh pZ -f sin pZ) (ch pz — cos pZ) Eh *
(m>
В каждом частной случае это уравнение можно легко решить относительно Р,.
Подставляя значение Р в уравнение A), мы получаем требуемое значение
изгибающего момента Мц.
-Br
Ш
•271 ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ЦИЛИНДРИЧЕСКИХ ОБОЛОЧКАХ 115
Чтобы принять в расчет расширение укрепляющих колец, мы замечаем,
что силы Р вызывают увеличение внутреннего радиуса кольца, равное Pr^/FE,'
где F—площадь поперечного сечения кольца. Прогиб трубы уменьшается
на ту же величину. Следовательно, чтобы
получить силу Р в этом случае; мы должны
подставить в правую часть уравнения (т) величину
^ _-^ вместо рН/Яй.
9. Найти изгибающий момент М^ и
поперечную силу Qf„ приходящиеся на единицу
длины окружности в днище цилиндрического /^^
стального резервуара, наполненного жидкостью ,
(рис. 91), если г = 9 ж, rf = 7,8 ж, Л = 35 см, ^
7 = 1 g/cj»*" и fA = 0,25. Рис. 91.
Отерт. Мо = ^^^Ь кг cmIcm,Qo = 225 кг1см.
10. Решить задачу 5, предполагая, что кольцо насажено на левый конец
трубы. Сопротивлением кольца кручению можно пренебречь.
Указание. Воспользоваться результатами, полученными в .задаче 6,
стр. 29.
27. Температурные напряжения в цилиндрических
оболочках
Если цилиндрическая оболочка со свободными краями испытывает
равномерное изменение температуры, то никаких температурных
напряжений не возникает. Но если края оперты или защемлены, это будет
препятствовать свободному расширению оболочки и на краях возник-
н)гг местные напряжения изгиба. Предположим, например, что края
длинной цилиндрической трубы защемлены; тогда поперечные силы и
изгибающие моменты на краях получатся такие же, как в задаче 2,
п. 26. Необходимо лишь подставить в уравнение этой задачи
величину b = ra.t, представляющую собой увеличение радиуса оболочки
вследствие температурного расширения. Если длина трубы невелика и
одновременно должны рассматриваться оба конца; то изгибающие
моменты и поперечные силы могут быть легко получены при помощи
результатов задачи 8 п. 26. Рассмотрим теперь слз^ай, когда
происходит изменение температуры в радиальном направлении.
Предположим, что ^1 и ^2 — постоянные температуры цилиндрической стенки
соответственно на вн)ггренней и наружной поверхностях и что
изменение температуры по толщине стенки происходит по линейному закону.
Тогда в точках, удаленных на большое расстояние от концов
оболочки, не будет изгиба, и напряжение можно вычислить при помощи
уравнения (87), стр. 81, выведенного для пластинки с заделанными
краями. Эта формула дает следующее наибольшее напряжение от изгиба:
(Предполагается, что t^^t^^ На.внешней поверхности оболочки будет
действовать растягивающее напряжение.
mm
116
ТОНКИб ПЛАСТИНКИ и ОБОЛОЧКИ
1ГЛ. ly
Вблизи концов оболочки будет некоторый ее изгиб, и полные тем-
перйтуриые нап^)яжения получатся путем наложения напряжений,
возникающих вследствие этого изгиба, на йвпряжеиия, определяемые
уравнением (а). Рассмотрим в качестве примера напряжения на
свободном конце дайнной цилиндрической
трубы. При вычислений! напряжений в этом
случае заметим, что напряжения на краю,
представленные уравнением (а),
складываются в равномерно распределенные
моменты Мо (рис 92, а) величиной
{f.
-л:
а)
Ж„ =
Рис. 92.
12A-fx) •
Чтобы иметь свободный край, нужно Ш"
ложить моменты той же величины, но
противоположного направления (рис. 92, ^)*
Следовательно, и температурные
напряжения на свободном крае получаются путем
наложения на напряжения, определяемые
уравнением (а), напряжений, вызываемых
показанными на рис. 92, ^ моментами. Эти
последние можно легко получить, рассматривая изгиб элементарной
полоски и затем пользуясь уравнением A1), стр. 21, которое дает
y = -^^e-^*{cos^x~sm^x\ (с)
где р определяется подформуле A23). Наибольший прогиб,
получаемый на свободаом конце (лг = 0), ра1вняется '
^ , (d)
Утях.'
2^Ю'
а соответствующие окружные напряжения
(«)
Изгибающий момент, Чдействующий на конце элементарной полоски»
определяется ПО'уравнению (Ь). Изгибающие мои^енты, препятствующие
искажению поперечных сечений полоски при Шцбе, будут равняться
Наибольшее температурное напряжение дей<^ует иа наружной
поверхности трубы в окружном" направлений и ц^Ь^стоит из трех частей:
1) напряжения, определяемого по выражению |if),^S) напряжения,
определяемого по выражению (е), и 3) напряжений, вызываемого моментами,
определяемыми по выражению (f). Следовательно
_ аЕ it, - Q f ^ , Vr=t' _ \ ^ A25)
^— 2A-fi) V^ уж '
""шад-
^ . л, , - . .
28] КРУдаНЙЕ КРУГЛОГО КОЛЬЦА ПОД ДЕЙСТВИЕМ МОМЕНТОВ 117
при jji, = 0,3 это напряже!ние приблизительно на 25*/о больше, чем
напряжение, определяемое по уравнению (а), вычисленное в точках на
большом расстояний от концов. Поэтому мы можем заключить, чта
если имеет место Tpeuipha в хрупком материале, как* например,
в стекле, вследствие р?зйости температур ti'—ti,: го она шацщгф
с края и будет проходить « осевом направлении. Подобным способом
можно также вычислить напряжения в случаях, когда края защемлены^
или оперты*). '
ЗАДАЧИ
' ■, • . .' ■ '^
1. Найти темйературные напряжения, возникающие в длинной стальной--
трубе с защемленными краями, если г == 60 см, h == 1,2 ел, ja = ОД
коэффициент температурного линейного расширения <х == 125 • 10"'' и увеличение
температуры трубы 55° С. ,
Решение. При данных размерах мы находим
р = 0,151 CJK-V D==^m^-W кгсм.
Свободное удлинение радиуса трубы вследствие повышения температуры
равно Ь s=-iir (t — tft) s= 125 • 10"' • ©О• 55 == 4125 • 10"^ ~сж. Подставляя в
формулы задачи 2 предыдущего параграфа, находим поперечную силу и
изгибающий Момент, приходящиеся йа единицу длины окружности, в заделанном
конце:
Мо^Щ^О = 577,^ кг cMlcM. .ч
По значениям Q,, и Mq можно легко вычислить напряжения в осевом и
круговом направлениях в защемленном конце. (Предполагается, что труба можег
свободно расширяться в осевом направлении.)
2. Решить предыдущую задачу, предполагая, что края свободно оперты.
.3,-Стальная труба тех же размеров, что и в задаче 1, имеет температуры
ti fi is соответственно на внутренней и наружной поа^рхности. Найти
наибольшее напряжение в трубе, если ti — /2 ===55* С и края свободны.
Omeetn. 0g,3jj«= 1250 лгг/сл^.
4^ Решить предыдущую задачу, предполагая, что края трубы были
защемлены, когда "Груба имела постоянную температуру, равную (^i+<a)/2.
. • ' > ■' . .
28. Кручение круглого кольца под действием моментов,
pa&HOMejpHO распределенных по его оси
Имеются случай, когда круглое кольцо постоянного поперечного
сечения подвергается действию .скручивающих моментов, равномерно
распределенных по его оси^). Рассматривая половину кольца (рис. 93, а)
как Сврбодное тело, мы заключаем, что из условия равновесия мо-
*) Несколько примеров такого рода разобрано С. Н. Kent'oM, Trans.
А. S. М. В., т. 53, стр. 167, 1931. Случай изменения температуры в осевом
направлении разобран в книге: S. timoshenko. Theory of Plates and
Shells, стр. 423, 1940 (русский перевод, 1946 и 1963).
2) Примерами таких задач является расчет напряжений в
удерживающих кольцах коммутаторов электрических машин и р1асчет напряжений во
фланцах труб.
118
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
тментов относительно диаметра Ох изгибающий момент, действующий
в поперечных сечениях тип, должен быть равен
М = М^а,
(а)
где а — радиус оси и Mk — скручивающая пара, приходящаяся на
«диницу длины оси.
Рассмотрим теперь деформацию кольца. Из условий симметрии можно
заключить, что при кручении каждое.поперечное сечение поворачивается
в своей плоскости на один и тот же угол б, который в последующем
изложении будем считать малым *). Пусть С
будет центр вращения (рис. 93, Ь) п В —
точка в поперечном сечении, находящаяся
на расстоянии р от С. Вследствие
поворота поперечного сечения точка В
описывает малую дугу BBi = pQ. Благодаря
этому перемещению радиус продольного
волокна кольца, которое перпендикулярно
сечению в точке В, увеличивается на B^Bi.
Если координатные оси приняты, как
указано Ifa рисунке, из подобия
треугольников ВВА и BDC имеем
Рис. 93.
ВгВ, = ВВгЩ-==:рЬ^ = Ьу.
(Ь)
Рассмотрим сначала случав, в котором размеры поперечного
сечения кольца малы по сравнению с радиусом а оси. Тогда радиус
любого волокна кольца можно без большой погрешности принять
[равным а, и относительное удлинение волокна В благодаря
перемещению, определяемому по уравнению (Ь), будет равно
^— а-
(С)
Если не имеется бокового давления между волокнами кольца, то на
пряжения, соответствующие этому удлинению е волокна, равняются
ЕЬу
а
(Ф
Теперь из условий .равновесия половины кольца следует, что сумма
всех нормальных усилий, действующих по поперечному сечению
*•) Общее решение задачи, когда угол в не мал, дано R. Gramme Гем,
Z. angew. Math. u. Mech., т. 3, стр. 429 и т. 7, стр. 198, 1927. См. также
книгу С. В. Biezeno and R. Grammel, Technische Dynamik, x. 1,
стр. 30, 1953.
28]
КРУЧЕНИЕ КРУГЛОГО КОЛЬЦА ПОД ДЕЙСТВИЕМ МОМЕНТОВ
119
кольца, должна равняться нулю, а момент этих усилий относительно
оси X должен равняться М (см. выражение (а)). Если через df
обозначить элементарную площадь поперечного сечения, то указанные
условия равновесия напишутся так:
{^dP = 0; {^dP = M.
^
(е)
где интегрирование распространяется на всю площадь р поперечного
сечения. Первое из этих уравнений показывает, что центр тяжести
поперечного сечения должен быть на оси лс; из второго уравнения
находим .-. .. .
где Jx — момент инерции площади поперечного - сечения кольца
относительно оси X. Подставляя это в уравнение (d), находим
A27)
т. е. закон распределения нормальных напряжений по поперечному
сечению кольца тот же, что и в случае изгиба призматических
стержней; напряжение пропорционально
расстойнию QT нейтральной оси х,
и - наибольшее напряжение имеет
место в точках, наиболее удаленных
от оси.
В качестве второго примера
рассмотрим кольцо прямоугольного
поперечного сечения (рис 94), ширина b
которого не мала по сравнению с
радиусом в оси. Пусть с VI d соответственно
означаю^ внутренний, и наружный
радиусы кольца, а г — радиус какого-либо
волокна кольца; предположим, как
выше, что деформация кольт1а заключается в повороте его поперечного
сечения *) на угол е. Относительное удлинение волокна при радиусе г и
соответствующее ему напряжение будут
Рис. 94.
.^JL. „-^
({)
Уравнение равновесия, аналогичное второму из уравнений (е), получится
в следующем виде:
+ Л/2 d
Л/2 с
*) При ЭТОМ рассмотрении возможность искажения поперечного сечения
исключается. Соответствующая погрешность мала при условии, еслий/с< 1,5.
См. А. М. W а h 1, цит» на стр. 99.
mw
;i2o
интегрируя, яаходйм ^
юткуда
■'■':■ ./
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
1ГЛ. IV
в
12М
ПМкЧ
£АЧп— ЕН'^Ы^'
A28)
с с
Подставляя это значение во второе из формул (f), получаем
12Л1у
ft»rln^
Наибольшее напряжение имеет место во внутренких углах кольца, где г = с
я-.j; яг: Л/2; ^ ■■-■.■■■■. ■
шах
ем
кЧ In
6Mftg
кЧ In -
с
A29)
Если 6 мало, то уравйениё A28) можно легко привести к виду урав-
йенйя A26). Таким образом, полагая d=^Q-\-{bj2) и с = а — (*/2),
находим
1„_Ц^1„^1+1^.
Ь
d-
fl-
При маЛых значениях отношения bfa этот логарифм
приблизительно равен Ь\й. Подставляя это в i^bipa-
женле A28), приходим к уравнению A26).
Этими выводами можно воспользоваться при
вычислении напряжений, возникающих в месте со^
пряжения трубы и фланца *) под действием сил /?
(рис. 95)i ^? есть сила, приходящаяся на единицу
длины внутренней окружности трубы. Cnjiaj
приходящаяся'на единицу длины внешней окружности
фланца, равняется Ricjd). Под действием этих сил
поперечное сечение фланца повернется на угол в, а
стенка трубы изогнется,' как показано на рис. 95, b
пунктиром. Пусть Мо и Qq =; pQ будут изгибающий
момент и поперечная срла в месте сопряжения,
приходящиеся на единицу длины внутренней
окружности трубы. Значения этих ;tJeflriv«H можно найти из
условий непрерывности в й€СТ€ сопряжения трубы!
и фланца. Так как обы'^но^фдавец бывает очень жест-'j
КИМ в плоскости, перпендикулярной к оси трубы, то?
радиальное перемещейй^^-: вызываемое во фланце
•силами Оо, ничтожйЬ, и прогиб на конце трубычмЬз1^но считать равным нулю.
Угол поворота конца трубы равняется в, т. е. угЛ^ поворота поперечного
Рис. 95.
*) Другой метод вычисления этих напряжений дан Е. О. Water s'om,
J. Appl. Mech., т. 59, стр. 161, 1937. См. также J. D. Mattimore,
N. О. Smith-Pete г sen and Н. С. Bell; trails. A. S. M. E., т. 60,
<:тр. 297, 1938. Этот метод был распространен на нецйлиндрические обОлочкл
G. Horvay and I. М. Clausen, см. статью №63'-А-43, представленную
\на годичное собрание Американского о-ва инженеров-механиков, декабрь 1963.
281 ' КРУЧЕНИЕ КРУГЛОГО КОЙЬЦА ЛОД ДБЙСТеИЕММОМЕНТОВ 1^;
■ - ■■■;■'■■ л • ■ •'. ^' ■■•.■..-■■,.■■ ; -!'
сечения фланца. Тогда уравнения A1) я A2) (см. стр. 21) превращашся в
следующие ypJaBHCHHH д^я определения М^ и 0^:
■■■.■■■-■ " ■ ■ ' l' ■■ ■'■■.■.
Первое из этих уравнений, даёт .;
: . :: Qo=mo- . (g>
Тогда
Мв = 2рЛв и (?o=2p«Z>e. (h>
Для трубы толщиной hi и внутренним радиусом с мы находим р по
формуле A23) - •.
(]рсли толщина трубы мала, то разницей между внутренним радиусом и
радиусом срединной поверхности можно пренебречь.) Скручивающий момент^
приходящийся на единицу длины фланц1а и вызываемый показанными на
рисунке силами, равняется
Подставляя это is выражение A28), получаем угол в, а затем из первой
формулы (h) находим
Л1в = 2р£> —i^^U(rf-c)-Mo-AIo'| р1.
£А'1п—^ *-
с
Заменяя D его.значением ЯА|/12A—{**), мы получаем
кл — Rjd — c) ; , „^
^« = §Л , l~^V*Vin,rf-" ^ ^
^ 2 ^ 2рй \ /ij
с
Если даны размеры tpyeH, коэффициент Пуассона и сила /?,.то из
формул A30) и (g) мы сможем вычислить величины Мд и Q,^ а затем, зная их,,
можем найти напряжения изгиба в трубе, как указано в п. 28.
ЗАДАЧИ
1. Определить изгибающий момент Mf, и поперечную силу (?„ в трубе^,
показанной на рис. 95, если й=15,5 см, с=8,5 см, Л=а=3,5 см, Л, = 2 сМ,.
f* = 0,3.
Решение. Из формулы (i) имеем
Р ~ 17^^ =0,313 слг*.
mw
122
ТОНКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
[ГЛ. IV
Кроме того, In — = 0,601;^ = 0,505, Подставляя эти'значения в выражение
A30), получаем
Мо = 0,467^? {d — с), Оо == РЛ1о = 0,145^? {d — с).
Ша
Наибольшее напряжение от изгиба в трубе получится из формулы 0 = -^.
'
2. Найти выражение для малого прогиба конического кольца,
показанного на рис. 96 и представляющего элемент пружины Белльвиля. R —
нагрузка на единицу длины внутреннего контура кольца.
Решение. Возьмем, как и прежде, координатные оси л: и _у с началом
координат в центре вращения С. Относительное удлинение и напряжение для
какого-либо волокна радиуса г
0\ ^ I определятся уравнениями (f). Из
условий равновесия половины
кольца мы получаем
ЕЬу
J?
dF = 0,
5^
£^//F = М = Л>/? Г//—
(к)
dF^M^Rc^d—c).
Положение центра вращения
можно определить по первому из этих
уравнений. Пусть а будет радиус в точке С, и допустим, что угол р конуса
настолько мал, что мы можем принять sinP:=P; cosp=l. Тогда, принимая
оси jCj и у^ параллельными сторонам прямоугольного поперечного сечения и
замечая, что y^=^yi-\-^Xi=yi-\-^{r — а), перепишем первое из
уравнений (к) в таком виде;
2 d
\ \^\yi + ^{r--a)\drdy, = Em
г — в In г
2
откуда
■ ЕЩк frf —с —fltln-^]=0.
в =
d — e
1п —
с
A)
Второе из уравнений (к) преобразуем так:
-J-A/2 d
J \y{yx + Hr--a)fdrdy,^
— л/2 с
Подставляя вместо а его значение A), получаем следующее выражение для
281 КРУЧЕНИЕ КРУГЛОГО КОЛЬЦА ПОД действием'МОМЕНТОВ 123
вертикального прогиба верхнего края конуса:
Rc{d~c)
f=Hd~c) =
Л» , d . .^. (d-\-c
[Щ7=7)'"Т + ?"*
2 , d
In —
с
(m>
Из этого уравнения мы можем определить /, если нам будут известны
размеры кольца, модуль упругости материала и нагрузка R. При этом выводе
влиянием изменения угла р всл|едствие поворота на угол 6 пренебрегалось *).
*) Для больших прогибов изменение угла р должно быть принято во
внимание. В таких случаях прогиб уже не пропорционален грузу. См. статью:
W. А. Brecht and А. М. Wahl, Trans. A.S. М. Е. Appl. Mech. Div., т. 52,
стр. 52, 1930. См. также статьи J. О. А1 m е п and А. L а s z 1 о, там же, т. 58^
стр. 305, 1936 и S. Gross, Z, Ver. deut. Ing., т. 79, стр. 865, 1935.
ГЛАВА V
ПОТЕРЯ УСТОЙЧИВОСТИ СТЕРЖНЕЙ. ПЛАСТИНОК
И ОБОЛОЧЕК»)
'29. Продольный изгиб призматических стержней
(простые случаи)
Рассмотрение одновременного действия изгиба и сжатия стержней
(т. Л,,стр. 223) показало, что существует определенное критическое
значение сжимающей силы, при котором можно незначительной
поперечной нагрузкой вызвать большие прогибы. Для призматического
стержня с шарнирно закрепленными концами и имеющего две пло*
скости симметрии*) эта критическая сжимающая сила равна
р —tei Ya\
где У—наименьший главный момент ирерции площади поперечного
сечения. Опыты показывают, что когда сжимающая сила, приложенная
к гибкому') стержню, приближается к этому значению, то начинается
боковое выпучивание и оно настолько быстро происходит с
возрастанием сжимающей силы, что величина нагрузки, равная критическому
/значению, обычно бывает достаточной для того, чтобы привести
к потере несущей способности конструкции,. Следовательно, эту
критическую нагрузку нужно принимать зй'^критерий прочности гибких
колонн и стержней.
Из выражения (а) видно, что эта критическая нагрузка не зависит
от предела прочности материала стержня, а зависит лишь от раз--
меров конструкции, и моДуЛя упругости .материала. Два одинаковых
гибких стержня, один из которых имеет материалом высокопрочную
*) Подробные сведения по вопросу б .продольном изгибе можно найти;
в книге S. Tinioshenko, Theory of Elastic Stability, New York, 1936;
русский перевод, 1946; 1955.
*) Более общий случай, в котором продол1ЬНый изщб сочетается с
кручением, рассмот{}ен ниже (стр. 231). Т"
*) Когда стержень недостаточно гибок, продольный изгиб происходи»
при сжимающих напряжениях, превосходящих йрёдел пропорциональности.
Этот случай разобран ниже (стр. 150).
29] ПРОДОЛЬНЫЙ ИЗГИБ ПРИЗМАТИЧЕСК. СТЕРШИВЙ (ПРОСТЫВ СЛУЧАИ) J 25
сталь, а другой ~ обыкновенную стрбительндгю сталь, будут
выпучиваться При одной и той же сжиматр1й,ёй си^, хотя прочиэсть
материала в этих двух случаях весьма различна. Уравнение (а)
показывает также, что несущая способность стержня может быть увеличена
п)пем увеличения момента инерции J. Это можно сделать без
изменения площади поперечного <сечени~я, путем размещения материала, воз»-
можно дальше от главных осей инер11ии Поперечного сечения. Следо*
вательно, трубчатые сечеййя более экономичны, чем сплошные сечения
для сжатых стержней. Уменьшая толщину стенки таких сечений и
увеличивая поперечные размеры, мы можем увеличить. их
устойчивость. Однако существует низший предел для толщины стенки, ниже
которого сама стенка становится неустойчивой, и вместо продольного
изгиба стержня как целого происходит местный продольный изгиб,
который коробит стенки.
Эти рассуждения тказывают, что устойчивость упругих систем
или боковое выпучивание сжатых элементов имеет большое
практическое значение. Это особенно cnpaBejD[4HBo во многих новейших
конструкциях, где размеры поперечного * сечения делаются все меньшими
и меньшими благодаря использованию прочных материалов Иг^ в целях
экономии веса. Вр многих случаях разрушение инженерных С(йоруже-
ний можно объяснить упругой неустойчивостью, а Hie недостаточной
прочностью материала.
В прежнем изложении (т. I, стр. 223) величина критической
нагрузки стержня была получена путем рассмотрения одновременного
действия сжимающих и изгибающих
сил. Тот же результат можно
получить, если допустить, что
стержень сжимается только одним
центрально приложенным грузом *).
Рассмотрим^ случай стержня в виде
гибкой вертикальной лризмы,
защемленной внизу и нагруженной по оси
вверху (рис. 97). Если груз Р
меньше, чем его критическое значение,
то стержень рстается прямым и ис'
пытыв«1ет лишь осевое сжатие. Эта
прямая форма упругого равновесия
устойчива, т. е. если приложить поперечную силу и вызвать малый
прогиб, то прогиб исчезает, когда поперечная сила будет удалена, и
^) Значения критических грузов для различных условий на концах
сжатого призматического стержня впервые были получены Л. Эйлером; см,
Additamentutn, «De curvis elasticis», в Methodus inveniendi lineacs curvas maximi
minimive proprietate gaudentes, Lausanne, 1744. см. также HIetoire de I'Aca-
demie, Berlin, т. 13, 1757. Английский перевод этой работы дан в Isis, № 58,
т. 20, 1938.
ш
126, ПОТЕРЯ УСТОЙЧИВОСТЛ [ГЛ. V
стержень снова становится прямым. Увеличивая Р постепенно, мы при-^
ходим к условию, при котором прямая форма равновесия становится
неустойчивой и незначительная поперечная сила нагрузки вызывает
поперечный прогиб, который не исчезает после удаления нагрузки.
Тогда критическая нагрузка определится как осевая нагрузка, которая
достаточна для того, чтобы удержать стержень в слегка изогнутом
виде (рис. 97, Ь). ' '
Эта нагрузка может быть вычислена с помощью дифференциаль'*:
ного уравнения изогнутой оси. Взяв оси, как указано на рис. 97, Ь^
изгибающий момент в произвольном поперечном сечении тп получи»!
равным Р(Ь—уУ, дифференциальное же уравнение изогнутой оса
будет *)
Очевидно, что при свободном верхнем конце выпучивание стержне
произойдет в плоскости наименьшей жесткости. Обозначая через EJ
наименьшую жесткость при изгибе и полагая
приводим уравнение (Ь) к виду
^+Р'У^Р'^. (d)
Общее решение этого уравнения будет
J/ s= 8 -j^ Ci cos /7л: -|- Cg sin px, (e)
в котором Ci и Ci — постоянные, которые должны быть подобраны
так, чтобы удовлетворить следующим условиям в заделанном конце:
Эти условия будут выполнены, если мы примем
Ci = — 8, Са == 0.
Тогда
V = 8 A — cos рх). (f)
Условием на верхнем конце будет
*) Для прогиба, показанного на j^nc. 97, b,d^yldx^ положительно,
следовательно, мы пользуемся положительным знаком в правой част»
уравнения (Ь).
Щ ПРОДОЛЬНЫЙ ИЗГИБ ПРИЗМАТИЧЕСК. СТЕРЖНЕЙ (ПРОСТЫЕ СЛУЧАИ) 127
которое удовлетворяется, если cos/;/= О или если
jp/=Bw-f-l)
п
(g)
где л —целое число. Наименьшее значение р1, а следовательно и Я,
которое удовлетворяет уравнению (g), получается, если положить й=«0.
Тогда, пользуясь уравнением (с), получим
р1:
Yts
откуда
A31)
Это и есть критическая нагрузка для стержня, представленного на
рис. 97, а,, т. е. наименьшая нагрузка, которая может удерживать
стержень в- слегка изогнутой форме.
При п==1, w==2, ... из уравнения (g) мы получаем
р==-
А1*
А1^
Соответствующие изогнутые оси показаны .на рис. 97, с и 97, d. Для
формы, показанной на рис. 97, с, необходима сила в девять раз
большая, чем критическая, а для формы, показанной на
рис. 97, d, сила должна быть в 25 раз больше. Эти
формы продольного изгиба являются неустойчивыми и
не имеют практического значения, потому что
конструкция теряет сопротивления, когда, нагрузка достигнет
значения, данного уравнением A31).
Критическая нагрузка для некоторых других
случаев может быть легко получена из решения для
предыдущего случая. Например, в случае стержня с
шарнирно закрепленными концами (рис. 98) по условиям
симметрии очевидно, что каждая половина стержня
находится в тех же условиях, что и стержень, показанный
на рис. 97, Ь. Следовательно, критическая нагрузка для
этого случая получится путем подстановки в уравнение A31) //2
вместо /, что дает
'"^^"^ A32)
р =
I'
Случай стержня с шарнирно закрепленными концами очень часто
встречается в практических приложениях и называется основным
случаем продольного изгиба призматического стержня.
В случае „стержня с защемленными концами (рис. 99) возникают
реактивные моменты, которые удерживают концы' от поворота при
продольном изгибе. Сочетание Сжимающей силы и концевых моментов
MW
128
ПОТЕРЯ УСТОЙЧИВОСТИ
Кгл. ^
эквивалейтйО с»Фма|ощей силе Р, приложенной эксцентрично {рис. 99).
Имеются точки перегиба, где линия действия Я пересекает изогнутую
ОС^ иоскольку изгибающий момент в этих точках равен нулю. Эти
точки и средняя точка пролеага разделяют стержень т
четыре равные части, каждая из которых находится в
тех же условиях, что и стерлкень,-представленный на
рис. 97, Ь. Следовательно, критическая нагрузка для'
'стержйя с заделанными концами найдётся Из уравнения
A31) путем подстановки //4 вместо Д.что дает
Р =-
4««£7
/Я
A33)
В . предыдущих рассуждениях предполагалось, "что
стержень весьма гибок и напряжения, которые/имеют
место при продольном изгибе, остаются в пределах прр-
порциональйости. Только при этом условии можно
применять уравнение (Ь). Для того чтобы установить прег
Дел применимости формулы, выведенной выше для
критических нагрузок, рассмотрим основной случай (рис. 98).
Разделив Ъбе части формулы A32) па площадь F поперечного сечет
нйяч:тержня и обозначив через i наименьший радиус инерции, мы получим
Рис. 991
'кр
=^=.^.щ.
A34)
гт
tm -
Это уравнение применимо до тех пор, пока напряжение djtp остается
ниже предела пропорциональности материала. Если этот предел и
модуль £■ для данного материала
известны, можно по формуле >( 134) легко
получить для каждого частного случая
предельное значение отношения ///,
которое называется гибкостью стержня.
На рис. 100 зависимость (формула A34))
между гибкостью /// и значением о^^
дается кривой ЛСВ для строительной
стали, имеющей 4i?=== 2 • 10® kzjcm^. Пред-^
полагая, что предел пропорционально-'
сти матери^алй равняется '2000 Kzjpji^i
мы заключаем,' что лишь участок Ci5'
кривой можно использовать для определения )<f^
Поступая точно таким же образом, как И выше, мы находим
следующие уравнения .для случаев, представлейчых на; рис. 97 и 99:
г/г
Рис im.\
'кр
■'кр"
A35)
A36)
29] ПРОДОЛЬНЫЙ ИЗГИБ ПРЙЗМАТИМЕСК. СТЕРЖНЕЙ (ПРОСТЫЕ СЛУЧАИ) 129
Формулу для основйого случая A34) можно применить и к этим слу:
чаям, если мы воспользуемся щ^иведенной длиной li вместо
действительной длины стержня. В случае призматического стержня с одним
защемленным и другим свободным концом приведенная длина
(формула A35)) в два раза больше действительной длины, так что/i = 2Л
В случае призматического стержня с обоими защемленными концами
приведенная длина (формула A36)) равняется половине действительной
длины или /, = //2. Выражения для критического напряжения в общем
случае можно, следовательно, представить в следующем виде:
%■
-'^Ш=^Ц^Г- ,037)
где а зависит от условий на концах стержня и .иногда называется
коэффициентом длины.
При |13ложении расчета колонн^ (т. I, стр. 227) был рассмотрев
основной случай колонны с шарнирно закрепленными концами.
Полученные в этом случае сведения теперь могут быть применены к
колоннам с другими условиями на концах, если вместо действительной
длины / воспользоваться приведенной длиной /j. Таким образом»
в каждом частном случае расчет колонны сводится к определению
надлежащего значения коэффициента длины.
При выводе уравнения (f) для изогнутой оси после продольнбго
изгиба наибольший прогиб 8 остается неопределенным, т. е. при
критической нагрузке стержень может иметь любой малый прогиб.
Приведенная выше теория может быть применена только к малым
прогибам, потому что только в этих случаях можно воспользоваться
п^ближеииым выражением d^yjdx^ для кривизны вместо точного
выражения rfs
1^
8 iVs
Решение точного дифференциального уравнения для изогнутой ос»
было найдено для некоторых случаев*); оно показывает, что в дей-.
Ствительности не существует такой неопределенности в прогибе, как
предполагалось выше. Например, для стержня с шарнирно закреплен-
ныв^и койцами наибольший прогиб можно представить выражением *)•
^) См. Saalschfitz, Der beiastete Stab, teipzig, 1880. См. также Н a 1-
phen, Traite des fonctions elliptiques, x. 2, стр. 192, 1888.
*) См. R. V. M i s es, Z. angew. Math. u. Mech., т. 4, стр. 435, 1924, см. также
О. Domke, Bautechnik, т, 4, стр.747, 192GhR. W. В urges, Phys. Rev. 1917.
Б С. П. Тимошенко, т, П .
mw
130 f ПОТЕРЯ УСТОЙЧИВОСТИ [ГЛ. V
которое показывает, что прогиб увеличивается очень быстро, когда
нагрузка будет выше критического значения. Предполагая, например,
что нагр|узка будет на IVo больше чем Р^р, мы находим из
выражения A38), что прогиб составляет приблизительно Эу^ длины / стержня.
{Предполагается, что деформации лежат в пределах
пропорциональности.)
Зависимость между нагрузкой и прогибом можно представить
графически (рис. 101) кривой ОАВ, в которой нагрузка представлена
•ординатами, а прогибы абсциссами. До тех пор, пока нагрузка меньше
чем Ркр. прогиб равен нулю. За этим
пределом прогиб увеличивается быстро
с возрастанием нагрузки. (Когда
начинается текучесть, кривая АВ уже
неприменима, и в дальнейшем
выпучивание происходит, как указано на рис. 101
пунктирной линией ВС.)
При опытных исследованиях
явления выпучивания сжатых,стержней
найдено, что связь между прогибом и на-
Рис. 101. ^ грузкой зависит в значительной степени
от точности, с какой центрирована
нагрузка, и от прямизны и однородности стержня. Кривая, изображающая
зависимость между нагрузкой и прогибом, обычно подобна кривой 0D
на рис. 101. Вследст-Бие неточностей различного рода искривление на-,
чинается при малых нагрузках, но прогибы возрастают очень медленно
до тех пор, пока нагрузка значительно ниже критического значения.
Как только нагрузка приближается к критическому значению,
прогибы растут очень быстро. Чем точнее выполнен и нагружен стержень,
тем ближе опытная кривая приближается к теоретической ОАВ^).
ЗАДАЧИ
1. Стальной стержень прямоугольного поперечного сечения 2,5 хЬ см
с шарнирно закрепленными концами сжимается вдоль оси. Определить
наименьшую длину, при которой можно применить формулу A32), если
£ = 2 • 10^ KijcM^ и предел пропорциональности равняется 2000 kzjcm^.
Определить величину критического напряжения, если длина стержня р^няетсв 1,5 jk.
Решение. Наименьший радиус инерции равен i = 2,5/2 ]/^ 3 см;
следовательно, наименьшая длина найдется из формулы A34)
2000 = л2.2.10«.^ .-J- ^
и 'min = 71,8 см.
Критическое напряжение при /=1,5 м из A34) будет акр = 457 kzjcm^.
^) Очень близкое совпадение опытных и вычисленных значений
критических нагрузок было получено Th. v. Кагтап'ом, Forschungsarb., № 81,.
1910. См. также К. Memmler, Ргос. 2d Internal. Congr. Appl. Mech., Zurich,
стр. 357, 1926.
801 ПРОДОЛЬНЫЙ ИЗГИБ ПРИЗМАТИЧЕСк. СТЕРЖНЕЙ (СЛОЖНЫЕ СЛУЧАИ) 131
2. Решить предыдущую задачу, полагая, что стержень имеет круглое
поперечное сечение диаметра, 2,5 см и концы его защемлены.
Отит. Наименьшая длина равняется 1,25ж.При/= 1,5жа^р= \Ъ1^кг\см^.
3. Определить критическую сжимающую нагрузку для стойки с шарнирна
закрепленными концами двутаврового сечения длиной 1,8 л^ при 7 = 64,4 сл^^.
Ответ.
Р.,=
Tt^fJ 9,87 . 2 • 10« • 64,4 „^„,„
• -^— =39360 кг.
/«
180»
30. продольный изгиб призматических стержней
(более сложные случаи)
В качестве примера более сложного случая продольного изгиба
стержней рассмотрим центрально сжатую стойку с заделанным'
нижним концом и с шарнирно закрепленным верхним
(рис. 102). К]ритическое значение сжимающей силы есть
такое значение Р , которое может удерживать стойку
в слегка изогнутой форме. Можно видеть, что в этом
случае при продольном изгибе возникает поперечная
реакция Q, и дифференциальное уравнение изогнутой
оси получается в виде
^=-Py^Q(l-x). (а)
EJ
Общим решением этого уравнения при обозначении (с)
из п. 29 является
y = Ci cos рх -\- Сз sin рх
|-(^--^).
(Ь)
Для определения постоянных Ci и Сд и неизвестной
реакции Q мы имеем следующие условия на концах:
Щ =0
(у)х^о = ^> Су)л-./ = 0,
Рис. 102.
Подставляя значение у из уравнения (Ь), получаем по этим условиям
С,
О
1=0, Ci COS р1-j-Ci sin р1= о, pd $- = ^- (с)
Определив постоянные Ci и С^ из первого и третьего уравнений, а
затем подставив во второе, приходим к следующему
трансцендентному уравнению для вычисления критической нагрузки:
tg р1==р1. (d)
Для решения этого уравнения полезен графический метод. На рис, 103
начерчены кривые, представляющие tgpl в функции от р1. Эти кривые
асимптотически приближаются к вертикальным линиям/?/=-у, -^, ...•
при этих значениях tgpl становится бесконечным. Теперь корни
уравнения (d) получатся как абсциссы точек пересечения вышеуказанных
3^
ItOtEPB УСТОЙЧИВОСТИ
[ГЛ.: ¥
кривых с прямой линией у=^р1. Наименьший корень, полученный
таким образом, равняетЬя j»/= 4,493. Тогда
P,,=^p'EJ:
20,19Е/ ««£/.
/* -
Эта критическая нагрузка является такой же, как для стойки с шар-
«ирно закрепленными конц£(ми, имеющей приведенную длину li = {y,7L
В качестве второго примера
рассмотрим Стержень, лежащий'на трех
опорах и центрально сжимаемый
силами Р (рис. 104). При вычислении
критического значения сжимающей
силы последуем нашему предыду-
.щему определению и предположим,
что Р™ есть сила, которая может
удержать стержень слегка
искривленной формы, В результате
искривления возникает изгибающий момент
Рис. 103.
Рис. 104.
Mi на средней опоре *), который может быть вычислен из уравнения
{38), стр. 39, выведенного для неразрезных стержней. Замечая, что
в нашем . случае концы стержня шарнирно закреплены, получаем
VW| == Д1з ====^ О, и уравнение C8) напишется в следующем, виде: .
.(Р,^ + Р5:^)Л., = 0.
(е)
Это уравяение удовлетворяется, и искривленная форма стержня
становится возможной, если , ' у ^
,/1 «/2 ■
Здесь приняты следующие обозначения (см. выражения C6) и B3)):
В — 3 f-i-——L-^
(О
(g)
*) Исключение составляет Тривиальный случай, когда два пролета
одинаковы и поперечное сечение постоянно по всей длине. В этом случае Mg = О
на промежуточной опоре и каждый пролет находится в тех же условиях,
что и стержень с шарнирно закрепленными концами^
SOI ПРО|1рЛЬНЫЙ ИЗГИБ nPH3JVLATM4ECKi СТЕРЖНЕЙ (СЛОЖНЫЕ СЛУЧАН^^ 133
Й
"»—Xf ЯГ,» "«=Т"ГШ;
(h)
Если размеры стержня даны, тр^из уравнений (h) известно отнЬше-
ние .Щ'.щ, а из уравнения ;(f) находим отношение ^i'.^ равное . - ,
Имея числовую таблицу функций р, мы можем легко решить это
уравнение при соответствующих значениях щ и «g. Тогда критические
значение Р получится из уравнения (h).
Возьмем, например, J{==J<j^=J и 4=2/1. Тогда П2=2н1 и
Pi:p,=r-2, (j)
Для того чтобы решить это уравнение, мы должны найти т1акое.зна-:
ченйе_Н1'(п,о табличному аргументу 2н), чтобы после удваивания
аргумента .^го функция Ра изменила знак и уменьшилась до половины
численного значения функции pj. Пользуясь таблицей *) числовых
значений р, мы легко найдем, что это условие удовлетворяется, если
2mi?=1,93.
Следовательно, из уравнений (h) находим
р _ 1,93« EJ _ t,12EJ __ 14.9Е7
Видно, что значение критической нагрузки лежит между двумя зна- ,
ч^ниямй Tz^EJjH и 7c^£J//i, вычаленными для отдельных пролетов, как
^ёСли бы каждый представлял с^гержень с шар-
нирйо закрепленными концами. Устойчивость
более короткого пролета уменьшается
благодаря действию более длинного пролета, в то,
время как устойчивость более длинного пролета
увеличивается.
ЗАДАЧИ"
1. Решить задачу 1 п. 29, предполагая, что один
конец стержня шарнйрно закреплен, а другой
защемлен, как показано на рис. 102.
2, Определить критическое значение сил Р,
которые сжимают вертикальные <;тержни прямоугольной
рамы, показанной на рис.- 105.
Решение. Симметричноб выпучивание, показанное
пунктиром на рис. 105, вызывает реактивные
изгибающие моменты vWq, которые сопротивляются свободному повороту
концов вертикальных стержней. Дифференциальное уравнение изогнутой оси
Рис. 105.
') Такая таблица функций р = ф по аргументу 2и дана в книге автора «Theory
of Elastic Stabilitx>, 1936 (русский перевод, 1946, 1955).
134 ПОТЕРЯ УСТОЙЧИВОСТИ " 1ГЛ. V
вертикального стержня будет
Общее решение этого уравнения таково:
' М
y = Ci cospA: + Cg siapx -\- -рг • (к)
Постоянные инте1:рирования и моменты Л1„ определятся из следующих
условий, основанных на симметричности формы искривленной рамы (рис. 105):
Подставляя значение у из уравнения (к), получаем
С^ + -рГ = 0, — CipsmY + ^sP cos-2' = 0, С^ = '2ЕГ'
Эти уравнения дают следующее трансцендентное уравнение для
определения р и критической нагрузки:
р1 Pli
или, пользуясь обозначением уравнения (с) п. 29, находим
р1 J 1, р1
Когда {JIJi){lill) велико, т. е. когда сопротивление горизонтальных стержней
рамы выпучиванию вертикальных стержней мало, Totgp//2 является большим
отрицательным числом и /?//2 приближается к я/2. Тогда критическая нагрузка
приближается к значению «*£///®, полученному прежде для стержня с шар-
нирно закрепленными концами (формула A32)).
Когда {J!Ji){ltJl) мало, т. е. сопротивление горизонтальных стержней рамы
выпучиванию вертикальных стержней очень велико, то tg (р//2) представля.ет
малое отрицательное число и р//2 приближается к я. Тогда критическая
нагрузка' приближается к критическому значению in^EJjl', полученному прежде
(формула A33)) для стержня с защемленными концами.
В случае квадратной рамы со всеми стержнями одинакового поперечного
сечения (/ = /i, Jf = Ji) уравнение для определения критической нагрузк!^
получается
откуда
р1
-^ = 2,029,
16,47£7 _ 7t^£/ "
Р^р— /2 — @,774/)» ; ^"^)
Следовательно, в этом случае приведенная длина равняется 0,774/. (Кривые,
подобные кривым, изображенным на рис. 103, можно использовать также
и в этом случае.)
3. Решить предыдущую задачу, предполагая, что в дополнение к
вертикальным силам Р имеются две пары горизонтальных сил Q, которые
вызывают сжатие горизонтальных стержней рамы.
30] ПРОДОЛЬНЫЙ ИЗГИБ ПРИЗМАТИЧЕСК. СТЕРЖНЕЙ (СЛОЖНЫЕ СЛУЧАИ) 135
f
Указание. Так как горизонтальные стержни сжаты, то угол поворота,
указанный на рис. 105, равняется *) 8== ^wf ~Т~~г ^^^ 'fpi' ^^Р^"^"^"
ние для вычисления критического значения Р получается путем подстановки
7i«/tg а вместо 7^ в уравнение A) задачи 2.
4. Стойка АВ с шарнирно закрепленными концами (рис. 106) сжимается
двумя силами Р^ и Pg. Найти критическое значение силы Pi+ ^2» если
(Pi + Ps)IPi = т, Jilh = « и /s//, = г.
Решение. Предполагая, что искривленная форма стойки будет такой,
как показано на рис. 106 пунктиром, найдем, что горизонтальные
реакции, вызываемые при выпучивании, будут равняться Q = bP^jl.
Дифференциальные уравнения верзсрего и нижнего участков
изогнутой оси будут, '
d^Vi SPg
ЕЛ
d'y.
SP,
'2 ^д.2 = —PtVi — -J- (i — x)-^ Pg (8 —3>s).
Пользуясь обозначениями
(n)
Pt + P,
2_
Рш
=Pl,
(o)
Рис. 106.
Eh ~'^'" EJi
мы получаем следующие решения уравнений (п):
В />|
Ух = С, sinpiAT + Cg cos/>ia: —~Y~^ il~x\
. Ь pi '
y^ = Cg sm Pa a: + C4 cospgA: + X p*~ •*^-
Постоянные интегрирования получаются из условий на концах обеих частей
искривленного стержня:
(>'i)x=o=0. (yi)x=fg = ^. Ыж=„ =
Из этих условий мы получаем
^ipll+рЦд
». 0'2);,=0=0.
Ci =
с« =
/?f/ (sinpi/g — tg/?,/ cosA/j) '
S(pf/-pi/2)
pll sin psl^ '
Подставляя в условие непрерывности
С2=—CitgA',
С4=0.
получаем следующее трансцендентное уравнение для вычисления
критических нагрузок:
Pi pti-bPVi _ Pi . рЫ-pIU
pl
PtXgPih
Pl
+
Ps^PbIs
(P)
*) Это получается из уравнения D8), стр. 43 подстановкой tg и вместо th и.
imw
136
ПОТЕРЯ УСТОЙЧИВОСТИ
1ГЛ. V
которое можно решить в каждом частуом случае путем последовательных
noACTaMOjBOK или построением графиков обеих частей уравнения и ьпределе-.
нием, точек пересечения двух кривых. Взйв, например,/, =/g, Ji = J^==J щ
/?1 issPj, получим
(Л + Pshp — @,87;)» •';
5. Найти критическую нагрузку для колонны,'заделанной внизу и
свободной наверху, состоящей из двух призматических участков с моментами инер-
i№H./i и У^ (рис. 107).
Решение. Если 5 — прогиб верха колонны, то дифференциальные
уравнения дл>^ двух участкор изогнутой'оси будут
Pi
Пользуясь обозначениями (о), получаем решение этих
уравнений в следующем' виде:
/ ' у 1 == Ь-}-С cos piX-\-D sin PiX,
^2
Рис. 107.
Постоянные интегрирования получатся из условий
которые дают
8-f-С со8/>|/+ Z) sin/>i/= 5,
Ь-\-С cospilg + D sin/?i/g = 5A — cos/?g/g),
откуда"
С=в—Dtgpi/, £) =
5 cospg/g cospj
Так как два участка изогнутой оси имеют одну и ту же касательную при
x = li, то и»еем уравнение
8pgSin/>2Zs = — CpiSinpiZg-l-/)/?! oos/Ji/g.
Подставляя вместо С к D найденные выше значения, окончательно получаем
следующее уравнение Для определения P,q,: -
tUPJitgpili
Pi
(q>
в частном случае, когда оба участка колонны будут одинаковы, мы имеем
и уравнение (q) получается
или
Ti^EJ
2 у EJ 4
и Ркр = Ats • Это — критическая нагрузка для колонны постоянного
поперечного сечения. '.
31] ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКИХ НАГРУЗОК 137
31. Энергетич^^ский метод определения
. критических сжимающих нагрузок*)
Формула, Эйлера, выведенная в п. 29, была получена путем
решения дифференциального уравнения изогнутой оси для сжатого
стержня с заданными условйян^й на концах. Имеются случаи, ё которых
это уравнение йолучается сложным и точное решение становится
затруднительным. Тогда можно пользоваться приближённым метадом,
основанным; на рассмотрений энергии системы;
В качестве простого примера рассмотрим колонну, заделанную
внизу и несущую нагрузку вверху (рис. 97, а и 97, Ьу
Прямолинейная форма равновесия сжатого стержня является устойчивой, если
сжимающая сила Р мала, но она неустойчива после того, как Р до^-
стигает своего критического значения, при котором нач1шается попе,-
речное выпучивание. Это критическое значение Р можно найти,
сравнивая энергию системы в двух случаях: 1) когда стержень просто
сжат и 2) когда он сжат и изогнут. Энергия деформации в
изогнутом стержне больше, чем энергия, деформации в прямом сжатом
стержне, так как энергия изгиба должна быть прибавлена к энергии
сжатия^ 1{0торую можно считать постоянной для малых поперечных
прогибов. Потенциальная энергия груза Р также должна быть
рассмотрена. Прогиб стержня сопровождается понижением точки
приложения груза- Р, так что потенциальная энергия груза уменьшается.
Пусть 77—энергия деффмации изгиба и U^ — уменьшение
потенциальной энергии груза. Если Ui меньше, чем U, то прогиб стержня
сопровождается увеличением потенциальной энергии системы. Это
значит, что нужно было бы приложить некоторую дополнительную
поперечную силу, чтобы произвести изгиб. В таком случае
прямолинейная форма равновесия является устойчивой. С другой стороны, если
Ui'>>Uy то прогиб стержня сопровождается уменьшением
потенциальной-энергии системы^ и изгиб будет происходить без'приложения
кйхой-либо поперечной силы, т. е, прямолинейная форма равновесия
будет неустойчивой. Иоэтощ критическое значение сжимающей силы
получится из условия
и=и^. _ A40)
Для того чтобы вычислить величину критической нагрузки из этого
уравнения, мы должны иметь выражения для С/ и Ui. Когда стержень
находится'под действием "сжимающей нагрузки, равной критической
нагрузке (р/==7с/2), то на основании уравнений (f) п. 29, стр. ,126
уравнение изогнутой оси стержня будет
д, = 8A_со8-^). (а)
■ \
•) См. ctaTbii автора в Известиях Киевского политехнического института»
1910 и Ann. ponts et chausseee, РагЦ I913w
ш
138 ПОТЕРЯ Устойчивости , 1ГЛ. V
при этом значении у выражение потенциальной энергии изгиба
получится равным
о
Понижение точки приложения нагрузки при изгибе равняется (см.
стр: 48)
о
и, следовательно,
Подставляя значение (Ь) и (d) в уравнение A40), получаем
р — ^
£ I
ЧТО совпадает с формулой A31), полученной ранее.
В этом примере изогнутая ось (уравнение (а)) была заранее
известна, и поэтому точное решение для критической нагрузки было
получено из уравнения A40). В случаях, когда изогнутая ось
неизвестна, приближенное значение критической нагрузки можно получить,
взяв подходящую кривую (т. je. кривую, удовлетворяющую условиям
на концах стержня) для изогнутой оси и поступая таким же образом,
как описано выше.
Для того чтобы показать точность, которую можно достигнуть при
помощи этого метода, рассмотрим снова предыдущую задачу.
Предположим, например, что в случае, показанном на рис. 97, Ь,
изогнутая ось является такой же, как для консоли, нагруженной на конце
поперечной силой Q. Тогда из уравнения (97) т. I, стр. 134, мы по-^
лучаем y=(Qx'^/6EJ)Cil — х). Это выражение нужно подставить
в уравнение (Ь) для энергии деформации U изгиба, а также в
уравнение ^(d) для Ui, и мы получим
^=fHI^^-=
6EJ
^j_/^A_-2-J to] ^■^-~Т5-(7р-
Подставляя в уравнение A40), получаем Р= 2,5£7/Д Сравнивая этот
результат с точной формулой (выражение A31)), мы видим, что ошибка;
происходящая от этого приближения, составляет лишь около И/о-
31] ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ КРИТИЧЕСКИХ НАГРУЗОК 139
Ошибка может быть значительно уменьшена и получится лучшее
приближение, если мы возьмем для энергии деформации изгиба
выражение
1С
о
Подставив в это выражение
мы найдем ,
2^/35 •
Уменьшение потенциальной энергии груза Р равняется
fj _ Р Q^'l^ _^ ЗР 8'
^^^~~ 15 (Е/)*~" 5 / •
Подставляя в уравнение A40), получаем
Р«62 17/ ЗР В^
откуда
Точное же значение
2£/ 35 ~~ 5 / •
р = ^^Ё£ = 2 4674 —
Следовательно, ошибка приближенного решения составляет лишь 0,1 ЗУ„.
Пользуясь уравнением (е) вместо уравнения (Ь) для энергии
деформации, мы вводим в вычисления прогиба у предполагаемую кривую
вместо производной cPy/dx'^. Так как у представляется с большей
точностью, .при помощи предполагаемой кривой, чем (Py/dx^, то
второй .метод вычисления дает лучшее приближенное Значение для Р^р.
Энергетический метод обычно дает весьма удовлетворительное
приближение при условии, что принятая кривая является надлежаще
выбранной. Иногда мы можем сделать весьма грубое допущение для
формы кривой и все же получим удовлетворительный результат.
Например, мы можем, принять в предыдущем примере изогнутую ось
как параболу, определя|емую уравнением д/ = -^. Тогда
II
С МЧх __Р^Ь^ С Л лг^« _^^^^А/
^^~~J 2EJ~2Ej][ v] °'^~EJ \Ъ^'
140 ПОТЕРЯ УСТОЙЧИВОСТИ - [ГЛ. V
' ■ ■ ' '~ ' "'. у ' '-. ■ •■■ ' :
Подставляя В уравнение A40), находим 2Ml5^*^"aT^ и /^кр =
==2^5-^g . Таким образом, получается удовлетворительное
приближение к критической нагрузке, хотя предполагаемая параболическая;
кривая не может рассматриваться как очень удачная. Она имеет приблй"-
зйтельно постоянную кривизну по/Длине, между тем как в действи-
'дельной кривой кривизна пррпорциональнад13гибающему моменту. Она
равняется нулю вверху стержня и имеет максимум внизу.
Применяя энергетический метод и пользуясь предполагаемой кривой,
которая удовлетворяет условиям на концах, мы всегда получаем зиа-
'чение для критической нагрузки выше, чем истинное значение. Это
следует из того факта, что действительная изогнутая ось
искривленного стержня является такой, которая соответствует наименьшему
сопротивлению стержня. Только по чистой случайности предполагаемая
кривая будет истинной кривой наименьшего сопротивления. Почти'
•в каждом случае предполагаемая кривая будет отличаться от этой
кривой наименьшего сопротивления, давая таким образом более высо-;.
кие значения для критических kajrpysoK *).
ЗАДАЧИ
1. Решить задачу, показанную на рис. 102, предполагая, что изогнутая
otb будет точно такой же, как дли равномерно нагруженной балки с одним
заделанным и другим шарнирно опертым концом^
2. Решить при помощи энергетического.метода задачу 4 п, 30 (стр. 135)^
допустив/л =/а =^.
Решение. Претолагая, что изогнутая кривая представляет синусоиду
■■'. ^ . пх
найдем, что изгибающие моменты для двух участков кривой будут
]Р
I
ЬР
М^^{Р\ + Р,)у-
Ьр^х
I
Потенциальная энергия изгиба равняется
/ 7/2
}_^ 2EJ,:^ } 2£Л 2EJi V^ 4 -+^^«24 + ^1^8 ^2] +
//2/ , О
*) Дальнейшее изложение энергетического метода см. S- Т i m о s h е п к о,
Theory (Л Elasti? Stability, стр. 120, 1936 (русский перевод, 1946, 1955).
821
ДЕЙСТВИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ ОСЕВЫХ СИЛ
Ш
Уменьшение потенциальной энергии вследствие понижения;тх)ч!ек
приложения грузов Я, и Ра равняется
Подставляя в уравнение (НО) и пользуясь предыдущими обозначениями
(стр. 135), получаем ---''■ -..-.'.
(Я, + Р8),£р=^
(««£72//*)(т+1)
, т /т~-\\^^ 8 > ... Г \ , т (т~ \\* ,s 8 т~\ \
т
нием
получаем
'==»(l —
еов^.)^
1
A41)
3. Решить задачу 5 п. ^ при помощи энергетического метода.
Ответ. Предполагая, что изогнутая кривая представится уравне-
A42)
32. Продольный изгиб призматических стержней
ПОД действием равномерно распределенных осевых сил
,> ^Предполагая, что под действием равномерной* осевой нагрузки имеет
место небольшое боковое выпучивание (рис. 10^),,мы можем получить
критическое значение «агрузки интегрированием дифферен- "■ >
цнальнОго ур1авнения изогнутой ocjh. В^ этом случае^
уравнение не является таким простым, как было paHcie,
и его точное решение требует применения функций Бёс-
селя'). Однако приближенное решение можно легко
получить с псйшэщью-Энергетического метода.
За приближенное выражение для изогнутой оси
примем л ял-\ , ,
^ :У^«^1—cos-^j, (а),
которое представляет истинную кривую для случая,
когда происходит продольный изгиб йод действием
сжимающей нагрузки, приложенной на конце.
Изгибающий момент в поперечном сечении mn, возникающий
От нагрузки, лежащей выше этого сечения, равняется
■'■•/.
i
Рис. 108.
') См. S. timoshenko. Theory of Elastic Stability, стр. 115, 1936;
русский перевод: Устойчивость упругих систем, 1946, 1955.
3^
142
ПОТЕРЯ устойчивости
[ГЛ. V
Подставляя выражение (а) вместо у и полагая
,^6(l-cos|).
получаем после интегрирования по 6
Al=6?|(/-^)cos^-H^(l
Подставляй это в выражение потенциальной энергии изгиба, получаем
I
7сл:>
s\n^)\
3 2EJ 2EJ V 6 ^ ^^ ^"У
(Ь)
При вычислений уменьшения потенциальной энергии распределенной
нагрузки вследствие бокового выпучивания заметим, что благодаря наклону
в поперечном сечении тп элемента ds изогнутой оси верхняя часть груза
испытывает перемещение вниз, равное
ds
dx^-L
Ш"-
и соответствующее уменьшение потенциальной энергии будет
Ш%<'
л:) dx.
Полным же уменьшением потенциальной энергии -"от нагрузки при
продольном изгибе станет
Подставляя (Ь) и (с) в уравнение A40), мы получаем
___^ кЧ^д ( I 1
"
7С^ 7С^
2EJ
8
л'
§ I »
"X
7,89£7 „
откуда (?/)кр = -^—. Точным решением для этого
случая является
(90кр =
7,83Е/ iz^EJ
1^
A,122/J-
A43)
Таким образом, ошибка в приближенном решении
меньше 1«/о-
ЗАДАЧИ
1. Призматический стержень с шарнирно закрепленные
ми концами (рис. 109) подвергается действию равномерно
распределенной осевой нагрузки интенсивности q и
осевой сжимающей силы Р. Найти критическое значение Р,
предполагая, что уравнение для изогнутой оси дается в следующем виде:
у = Ъвт~.
п-
•EJ ql
Ответ. Ркв = —?i
2*
33]
ПРОДОЛЬНЫЙ ИЗГИБ СТЕРЖНЕЙ ПЕРЕМЕННОГО СЕЧЕНИЯ
143
83. Продольный изгиб стержней переменного
поперечного сечения
На рис. ПО показан стержень переменного поперечного сечеяия,
симметричный относительйо середины длины и имеющий две осевые плоскости
симметрии. Средний участок имеет постоянное поперечное
сечение с наименьшим моментом инерции, равным У^.
К концам поперечное сечение изменяется, и наименьшие
моменты инерции сл^луют закону
У=У|
«(vf.
(а)
где X w а — расстояния от некоторой фиксированной точки
(рис. 110), т—число, зависящее от типа колонны. Когда
средний участок представляет собой сплошной цилиндр, а
концы — сплошные конусы, / изменяется пропорционально
четвертой степени ли т = 4 в уравнении (а). Когда ко^
лонна имеет постоянную толщину в направлении,
перпендикулярном плоскости рис. НО, моменты инерции J
относительно оси, параллельной плоскости рисунка,
пропорциональны л: и m=l в уравнении (а). (Когда колонна
состоит из четырех уголков, связанных решеткой, как
показано на рис. Ill,, площадь поперечного сечения остается
постоянной, и / можно принять пропорциональным л:^, так
что- от = 2 в уравнении (а).) Вычисления, сделанные для
т = \, 2, 3, 4, показывают •), что критическая нагрузка в пределах
упругости может быть представлена уравнением ',
Рис. ПО.
^кр — а —js^ ,
в котором а — числов(Эй коэффициент, зависяпдий от отношения h/l и
где Ji^=.J^{bla)"''—^ момент инерции площади концевого
поперечного сечения. В табл. 9 даны величины а для различных
отношений в предположении, что концы колонны шарнирно
закреплены. Можно видеть, что когда отношение hjl или отношение
У,//„ приближается к единице, то коэффициент а приближается
к 7с^, и значения по формуле A44) сближаются со значениями
по A32) для призматического стержня.
В качестве примера на применение этой таблицы рассмотрим
деревянную стойку прямоугольного поперечного сечения длиной
2 м. Толщина стойки остается постоянной и равной 2 слс.
Ширина изменяется по прямолинейному закону и равняется 10 см
в средине и 6 см на концах. Определить Ркр» ^сли Е=
= 80 000 KZJcM^. В этом случае hjl^O; т—\ и Л/Л = 6/10 = 0,6.
Из табл. 9 находим а = 8,60 и критическая нагрузка по
формуле A44) будет
80000-10.28
A44)
кр
8,60
12-200*
115 кг.
._^j
Для второго примера рассмотрим пирамидальную колонну Рис. 111-
(рис. 111), поперечное сечение которой состоит из четырех
уголков 90 X 90 X 10 мм. Наружная ншрина колонны на концаз^ равна 30 см.
') См. А. Н. Д и н н и к. Вестник инженеров, 1927. Таблица 9 взята из
этой статьи.
144
ПОТЕРЯ УСТОЙЧИВОСТИ
Коэффициент а в формуле A44)
{ГЛ. V
Таблица 9
Jl/Jo
• ■.'.'
ол
0,2
0,4
(
Ь,б
0,8
■ '-'l:'
А//=
т= 1
т = 2
т = 3
т = 4
7И = 1
т = 2
т = 3
т = 4
«1=1
й»^2
га = 3
/п = 4
ш = 1
т = 2
т = 3
тп = 4
ш = 1
m ==i2
; m?=-3-;i
.7И=4
0
6,48
5,40
5,01 '
4,81
7,01
^ 6,37
6,14
6,02
7,87
7,61
7,52
7,48
8Д)
8,51
8,50
8,47
9,27
9,24
9,23
9,23
^^
0.2
7,58
6,67
6,32
6,11
7,99
7,49
7,31
7,2Q
8,60
8,42
8,38
8,33
9,12
9,03
9,02
9,01
9,54
9,50
9,50
9,49
1С*
0.4
8,68
-8,08
7,84
7,68
8,91
8,61
8,49
8.42
9,ia
9,15
9,10
9,10
9J55.
fi.48
9,47
9,45
9,69
9,69
9,69
9,69
л"
OS
9,46
9,25.
9,14
9;08
9,63
9,44
9,39
9,38
9,70
9,63
9,63
9,62
■ 9,74
9;74
9,74
9,74.
9,83^
9,82
9,81
9,81
TtS
0,8
9,82
9,79
9,77
9,77
9,82
9,81
. 9,81
9,80
9.84
^,84
9.84
9,84
9,85
9,85
9,85
9,85
9,86
9,86
9,86
9,86
л»
1
„8
> .
>
>
»
: >
> .
»
>
. »
>
, > ■ .
>
>
>
>
...»
>
>
■ >
>
а в средине 50 слг. Длина колонны равняется 20 слг. Определить
критическую нагрузку для этой колонны, принимая для строительной
стали £t=2 X 19° кг]см^ и полагая, что peiueTKH из стержней настолько
жестки, что позволяют прил^енить формулу A44), выведенную для сплош-'^
ных стержней. Площадь и моменты инерции поперечного сечения /'=4х
X 17,2 = 68,8 см\ Л=4[128 +17,2A5 —2,59)*] t= II 075 еж*; У„ = 41128 +
4-17,2B5 —2,59)«1 = 35 035 еж*. Взяв 7,/7„ = 0,3, m«s2 и Л// = 0, найдем из
табл. 9 путем интерполирования а =«7. Тогда по формуле A44) получим
Ркр = 7
2а0«-35035
2000^
==122 623 лгг и
»кр'
122 623
68,8
= 1782 кг1см\
34] ' ВЛИЯНИЕ ПОПЕРЕЧНОЙ СИЛЫ НА КРИТИЧЕСКУЮ НАГРУЗКУ 145^
34. Влияние поперечной силы на величину
критической нагрузки: /
В предыдущих выводах формул для критических нагрузок мы
пользовались дифференциальным уравнением изогнутой оси (см. стр. 126),
в котором влиянием х^оперечнрй силы на прогиб прене-^ .
брегалось.. Но когда произойдет выпучивание, поперечные
сечения стержня уже не будут перпендикулярны сжимайэ-
щей силе ив этих сечениях будут действовать попереч- ^
ные силы. Влияние этих сил можно оценить с помощью
энергетического метоДа, изложенного в п. 31. При
использовании этого метода к энергии изгиба должна быть
добавлена энергия сдвига цри вычислении энергии деформации U (Hl.
вследствие продольного изгиба. - , -
Пусть АВ (рис. 112) — сплошного сечения стойка '"
с шарнирно закрепленными концами, изогнутая действием
сжимающих сил Р. Величины изгибающего момента и
поперечной силы в каком-либо поперечном сечении тп будут д
■Л ' Ж = Ру; Q = P^. (а)
По предыдущему (см. т. I, § 69) потенциальная энергия, иакоп.г{еннай
в элементе стержня, равняется
где F —площадь поперечного сечения,'а — числовой коэффициент,
зависящий от формы поперечного сечения (см. т. I, стр. 150).
Перемещение сечения тп относительно гпуП^ благодаря сдвигу здесь
принято равным {C.QIQP)dx, и второй член правой части уравнения (Ь)
представляет потенциальную энергию сдвига элемента. При помощи
уравнений (а) и (Ь),найдем, что пртенциальная энергия, накопленная
в стержне при продольном изгибе, райняется .
О О -
Уменьшение потенциальной энергии груза равняется
о
Допуская, что изогнутая ось искривленного стержня представляет
собой синусоиду
3; = 8sin^, (е)
146 ПОТЕРЯ УСТОЙЧИВОСТИ {ГЛ. V
и подставляя это значение в выражения (с) и (d), получаем
(f)
у=8»« , J.P''™'
Тогда уравнение A40) дает
4EJ ^ 4GF /8
п ^^"EJ 1 , .
•'Р /2 . . EJ aiz^ ' AgJ
1 +
GF /8
Сравнение с формулой Эйлера (уравнение A32)) показывает, что
благодаря действию сдвига критическая нагрузка уменьшается в отно-^
шении
I
^ EJ ап^ •
A45)
GF Z*
Если мы положим
ТО формула (g) примет вид
1
^кр==Р.-^р-. A46)
14-^
Для сплошных Стержней Я^ весьма велико по сравнению с Р^, , и
влиянием поперечной силы .можно пренебречь, В случае составных
стержней, особенно когда применяются соединяющие планки или
распорки (см. рис. 114, л), Р^ может получиться того же порядка, что и
Pf, и в этом случае уже нельз! пренебречь влиянием поперечной
силы. Эта задача рассматривается в следуюш.ем параграфе.
35. Продольный изгиб составных стержней ')
Составные стержни иногда применяются в стальных конструкциях.
Их способность сопротивляться нагрузкам всегда меньше, чем
сплошных колонн, имеющих ту же площадь поперечного сечения и ту же
гибкость, т. е. отношение ///, и зависит главным образом от
конструкции решетки составных стержней, от размещения распорок и планок.
Это уменьшение критических напряжений объясняется главным
образом тем обстоятельством, что в случае составных колонн поперечные
») См. F,Engesser, Zentr. Bauverwalt., стр. 483, 1891 и стр. 609, 1907;
L. Prandtl, Z. VeT. deut. Ing., 1907, a также статью автора в Известиях
Киевского политехнического института, 1908. Эти статьи рассматривают
вопрос о продольном изгибе составных стержней в связи с потерей
устойчивости сжатого стержня Квебекского моста.
щ
ПРОДОЛЬНЫЙ ИЗГИБ СОСТАВНЫХ СТЕРЖНЕЙ
147
I
силы оказывают значительно большее влияние на прогибы, чем в
случае сплошных стержней. Чтобы оценить влияние поперечной силы на
критическую нагрузку, мойсно применить к составным стержням
формулу A46), которая была выведена для
сплошных стержней. Пусть Pg, как и ра- t
нее, будет критическая нагрузка, опреде- ^
ляещя формулой A32). В случае
сплошных стержней Р^ в формуле A46) имеет
простой физический смысл, а именно
отношение Q/Pa представляет собой
дополнительный угол наклона -^ изогнутой
кривой, вызываемый поперечными силами. Р^
также имеет то же значение в случае
составных стержней при условии, что число
панелей велико. Чтобы определить Р^ в ка--
ком-либо частном случае, мы должны
исследовать боковые перемещения, вызванные ,,
поперечными силами.
Рассмотрим сначала панель составного
стержня, показанного на рис. ИЗ, й.
Перемещение сдвига зависит от удлинения и
укорочения диагоналей и распорок
каждой панели (рис. 113, Ь). Положим, что
узлы я1вляются шарнирными; удлинение
диагонали, вызываемое поперечной силой Q, равняется Qa (sin ср cos ср £"F^
где (f — угол между распоркой и'диагональю, Q/cos (р —
растягивающее усилие в диагонали, а/sin <f> — длина диагонали. Fa — площадь;
поперечного сечения двух диагоналей. Соответствующее боковое пере-"
мещение (рис. 113,^) будет '
fB
а';
Укорочение распорки
(рис. Ид, с) равно
sin <f cos® ^EJFd'
соответствующее
боковое
^2
"EFi,'
площадь
перемещение
(b)
поперечного сечения двух
где b — длина распорки, Ff,
распорок.
Из выражений (а) и (Ь) получаем угловое перемещение,
вызываемое поперечной силой Q:
Используя ранее введенное соотношение QjPa = '[, находим
1,6
Л)=е-
Ра siiKfcos^EFa ' aEFi,
3^
\4В ПОТЕРЯ УСТОЙЧИВОСТИ
' ■•.■■/■
Подставляя это в формулу A46), получаем
я^£/ ,1
Р =
1ГЛ. ¥
A47)
Если площади сёчейий Р^ и Ff, очень малы по сравнению с площадью*
иоперечного сечения швеллеров (рис. 113, а), критическая нагрузка
(выражение A47)) может быть
значительно меньше той, которая
получается по формуле Эйлера A3S0I.;/;
Выражение A47) можно также
применить в случае, представленном;
на рис. 113, d, если угол ср измерять!
как показано на рисунке, и
исключить при этом член, обусловленный
деформацией распорок.
у В случае стержня с
соединениями только из планок, как на рис. 114, ai,
для определения бокового nepeMei-j
щения от поперечной силы Q ыЩ
должны рассмотреть деформацик»
участка стержня, вырезанного попег-
д, речными сечениями тп к т^Пх-
Допустим, что изогнутые оси швеллеров имеют точки перегиба в этих
сечениях; условия изгиба будут отвечать - показанным на рис. 114, Ьм
(Растягивающие и сжимающие усилия^ч^действующие на* швеллеры, Щк
рисунке не показаны.) Прогиб состоит из двух частей; из перея^ещё^
ния 8, вследствие изгиба планки и перемещения 8^ вследствие изгиба
швеллеров. По концам планки действуют моменты Q а/2, и
соответствующий угол повората 9 (см. уравнения A03) и (МL) т. I, стр. 141)
равняется
ift__Qo ^ Од b __ Qab
2 6Е7а
2 ЗЕУа
l2Eys'
где Ь—длина планок и EJ<j, — их жесткость при изгибе. Боковое
перемещение Ь^, вызванное изгибом планок, равняется
К
а а Qa^b
"~4Е7, *
(С)
Перемещение V можно вычислить по формуле для консоли
о(т)"
Qa*
2 3£/j ~" 48E/J •
(d)
Щ ПРОДОЛЬНЫЙ ИЗГИБ СОСТАВНЫХ СТЕРЖНЕЙ 149^
Полное угловое перемещение, вызываемое поперечной силой Q,
равняется/
"~ ■ ^ ~ ^'^^•^» "т" 24ЯЛ»
' ■ 2 ,:.
но так как Q/P^ = ']f» полз^чаем
1 аЬ , в«
Ра ~\2EJi ' 24£7i »
и формула A46) для определения критической нагрузки становится'
^«р /8 ^sEj I ab ■, в' \ '
1
^ ' /« I 12£Л "^
12£/в ~^24EJJ
где по-прежнему tz^EJJP представлжот критическую нагрузку,
вычисленную для сплошной колонны по формуле Эйлера. Можно видеть,
что Korflia жесткость при изгибе планок мала, действительная
критическая нагрузка будет гораздо меньше, чем нагрузка, определяемая,
по формуле Эйлера.
Из выражений A47) и A48) вытекает, что при вычислении
критических нагрузок для составных колонн действительная длина
колонны заменяется приведенной длиной, которая определяется в случае
составной колонны (рис. ИЗ) формулой
/—/уЛ r^^Ejr 1. \ Ь \
H — t у ' -t- р \ sin <р cos^ <fEFa~^ aEFj'
^ в случае колонны, составленной с помощью планок, как показанр>
на рис. 114, формулой !";
Когда приведенная дл^ша составной колонны определена, допускаемое
напряжение получается, как для сплошной колонны с гибкостью,
равной отношению /,/i. ,
При проектировании составных колонн важное практическое
значение имеет выбор размеров составных стержней и планок. В основу
для определения напряжений в этих деталях при проектировании
коротких колонн предполагается, что ужимающие силы приложены
эксцентрично*). Если эксцентриситеты' на двух концах равны е и
^) Этот вопрос рассмотрен более подробно в статье D. Н У о и п g, Pfoc,
Am. Soc. Civil. Engrs, декабрь, 1934 и в другой статье того же автора в.РиЬ^
Internal. Assoc. Bridge and Structural Engrg., Zurich, т. 2, стр. 480, 19341 .См.
также S. Timoshenkt), Thepry of Elastic Stability, стр. 197, 19Э6; рудский
перевод, 1946, 1955 и F. Bleich, Buckling Strength of Metal Structures^
New York, стр. 167, 1952.
150
ПОТЕРЯ УСТОЙЧИВОСТИ
[ГЛ. V
Ф1ротивололожны по направлению, то сжимающие силы образуют пару
•сил с моментслй 2Ре, который вызывает на концах стержня попереч--
ные силы, равные
2Ре
Q-
I
A49)
Наибольшее значение Q получается путем подстановки в это урав-^
нение вместо Р наибольшей нагрузки Р^р, которую колонна может
выдержать. Эксцентриситет е обычно принимается как некоторая часть
радиуса г ядра сечения, скажем ejr = ^,^. Тогда детали должны быть
спроектированы таким образом, чтобы наибольшие напряжения, вызьь
ваемые в них силой Qmax» не превосходили предела текучести.
В случае сжатых составных элементов фермы с жесткими узлами
при нагружении фермы на концах элемента возникают некоторые-
изгибающие моменты. Если величины М^ )л М^ этих моментов вычис-
лец[ы из анализа вторичных напряжений, то соответствующие
эксцентриситеты et==MilP и е^ = М^/Р точек"приложения сжимающей силы
известны, и величина их алгебраической суммы должна быть
подставлена в уравнение A49) вместо 2е.
36. Неупругий продольный изгиб прямолинейных колонн
В предыдущем изложении вопросов устойчивости всегда
предполагалось, что материал колонны является совершенно упругим и
следует закону Гука. Предположим теперь, что материал, хотя и является
б
Рис. 115.
совершенно упругим, но не следует закону Гука, и что диаграмма
^^^атця подобна показанной на рис. 115, й. Если стержень из такого
материала находится под действием сжимающих напряжений,
соответствующих точке С на диаграмме, а затем вызывается некоторое малое
изменение в напряжении (положительное или отрицательное), то связь
56]
НЕУПРУГИЙ ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОЛИНЕЙНЫХ КОЛОНН
151
между изменением напряжения и изменением деформации будет
зависеть от величины начального напряжения. Эта связь определяется
наклоном опытной диаграммы сжатия в точке С или, как показана
на рисунке, наклоном жирного элемента диаграммы. Величина
отношения dajde может рассматриваться как переменный модуль упругости
материала, будет называться касательным модулем и обозначаться
через Ef.
Рассмотрим тейерь сжатый по оси призматический стержень с шар-
йирно закрепленными концами (рис. 116, а) и предположим, что упругие
свойства материала представлены диаграммой на рис. 115, а. При:
Р
(
р.
а)
Ь)
Рис. 116.
определении значения критической нагрузки для такого стержня мы
можем поступить, как и прежде, и предположить, что после
приложения сил Р возникает бесконечно малый, прогиб стержне- Тогда
критическая сила Ф^^ определится как сила, необходимая для того,
чтобы удержать стержень в этой слегка искривленной форме. Так как
предполагаемый прогиб бесконечно мал, то соответствующие
напряжения от изгиба малы по сравнению с начальным сжимающим
напряжением, и зависимость между напряжением и деформацией от изгиба
определится соответствующим значением касательного модуля Е^
В таком случае дифференциальное уравнение изогнутой оси будет
иметь тот же самый вид, что и для материала, следующего закону
Г)гка, но вместо Е появится касательный модуль Е^. Интегрирование
этого уравнения дает
кр
и
Vp — ^ ^t IS •
A50)
A51)
Разница между этими формулами и уравнениями A32) и A84) для
материалов, следующих закону Гука, заключается лишь в замене
к^^^^^^ТЖГ^
W
152 - ПОТЕРЯ УСГГОЙЧИВОСТИ {ГЛ. «
•постоянного модуля упругости Е касательным модулем Е^, который
-является функцией сжимающего напряжения о, /
Если диаграмма сжатия, подобная приведенной на рис. 116, а, изве-
•стна,, то значение f^ можно легко определить для любого значения*.
%обы установить зависимость между а^^ и гибкость^), равной отно?<
тению //i, мы возьмем ряд значений а^р с соотве^с^твующими значен
ниями Ef и подставим их в^уравнение A51), Тогда уравнение опрё-
_делит соответствую,щиё значения ///, /Пользуясь е^тими значениями^
можно представить зависимость между /// и о^р кривой, аналогичной
шолученной на рис. 100 для 1йатериала, следующего закону Гука.' р
Этот метод вычислений о^р для случая, когда материал не следуем
закону Гуна, был предложен Ф. Энгессером *), который подал также
мысль о пр)именении метода для металлических стержней, сжатых выше
11редела пропорциональности. ОднакЪ в этом случае задача становится
•более сложной. Если стержень сжат за предел упругости и возник
малый прогиб (рйс. 116, а), то дефор1«ацйя сжатия на вогнутой
стороне увеличивается, й зависимость между деформацией и напряжением
«определяется здесь; величиной касательного мбпуля Е^. В то же самоё
время деформация сжатия на выпуклой стороне уменьшается, и в тако!»
чслучае зависимость между напряжением и деформацией определяек^
там начальным значением Е модуля. Таким образом, здесь усло»|й|
'будут такие, как для материала, имеющего два различных модуля,
один при растяжениий другой при сжатии. Соответствующие наклоны
указаны на рис. 115,/> двумя короткими жирными элементами графика.
Предполагая, что поперечные Сечения стержня остаются плоскими при
изгибе, малые напряжения изгиба можем представить двумя треуголм
пиками, показанными на рис. 116, ft. Эти напряжения от изгиба накла?
.дываются на равномерно распределенные начальные сжимающие на-
тпряЖения. Если через г обозначить радиус кривизны изогнутой оси
в рассматриваемом поперечном сечении, через Ehi/r и EJi^/r — соот-^
ветственно наибольшие растягивающие и сжимающие напряжения от
'магиба, то положение нейтральной оси О (рис. 116, ft) найдется и!
условия, что результирующие растягивающих и сжимающих напряжен
1ЙИЙ изгиба должны быть равны и должны создать пару, которая
уравновесит изгибающий момент /ИГ. В случае прямоугольного попе-
речнЪго сечения высотой h и шириной ft эти условия требуют
^%| = Л. (Ь)
*) F. EngesFser, Z. Architect, u. Ingenieurw., стр. 455, Ш89. См. также
■С о п S i d ё г е, Congr. iiiternat. procedes de construction, Paris, т. 3, стр. 37t^
1889. , . ^ ,
Щ > НЕУПРУШЙ ПРОДО;1ЬНЫЙ ЙЗГИ5 П1>ЯМО?1ИНЕЙНЫХ КОЯОНН 163?
Замечая, что А, 4-^=='^j получаем из уравнения (а)
Тогда уравнение (Ь) дает
А« =
Кя+УЩ
I м*
AEEt
Вводя обозначение
г 12 (YE-^YTif
_\ 4EEt
ж.
получаем из уравнения (d)
Erf\^
М,
(G>
(d>
A62).
A53>
Уравнение A53) имеет тот же вил что и уравнение для упругой
кривой, когда материал следует закону Гука. Мы должны лишь
заменить модуль Е величиной ^"^ определяемой уравнением A52) и назы-
bu^uoVi приведённым модулем упругости. Пользуясь для l/r егсу
приближенным выражением d^yjdx^ и интегрируя- уравнение A53), мы
1Й)лучим для стержня с шарнирно закрепленными концами (рис 116, а>
n^ErJ
кр
'кр'
/«
■ Tz'^E.
р
Aб4>
A55>
&ffW
Сравнивая эти выражения с A5Q) и A51^ видим, что разница заклю-
Чйется лишь в замене касательного модуля £^, примененного в
первоначальных уравнениях Эн-
гессера, приведенным
модулем Ег' Так Как £"/ <^ £", из
формулы A52) видно, что
Er^Et^) и, следовательно,
аначения Р^^ иг основании
формулы A54) будут
большими, чем значения- по
формуле A50). Это
повышенное значение получается из
Toroi соображения, что при
предполагаемом изгибе (рис.
116, а) деформация на
выпуклой стороне стержня
^/^
представляет уменьшение начаЛьно^
1) Можно показать, что это справедливо не только для случая
прямоугольного сечения стержня, но также для стержня с любым симметричным,
поперечным сечением, который изгибается в плоскости симметрии.
^^crs^y^T^rF»
w
154
ПОТЕРЯ УСТОЙЧИВОСТИ
1ГЛ. V
деформации сжатия. Таким образом, деформация упрочнения материала
как бы имеет влияние на изгиб. На ]рис. 117 представлены кривые,
устанавливающие зависимость между о^р и l/i, вычисленные по
выражениям A51) и A55) для прямоугольных стержней из строительной
стали*).
В течение многих лет формула A55), основанная на приведенном
модуле Bf, применялась инженерами, которые имели -дело с такими
пластическими материалами, как алюминиевые сплавы и строительная
сталь, но некоторые эксперименты показали, что результаты
испытаний лучше согласуются с формулой A51). Рис. 118, например,
представляет результаты испытаний для сплошных круглых стержней из
алюминиевого сплава ^). Видно, что для больших значений гибкости
результаты совпадают с кривой Эйлера, для коротких же стержней
результаты удовлетворительно согласуются с кривой, отвечающей
теории касательного модуля. Таким образом, метод рассуждения,
примененный при вычислении о^р в упругой области, становится неудов-
-летворительным за пределом упругости, так как к-ривая, отвечающая
теории Ег, основанная на этом методе, не согласуется с результаталЙ!
Д4спытаний. '
«Ш7г
fW
1.
N
^Vrt
тео/тЕг
S^
■^
/T7eopai/£f
\
ч
\
>ч^
4
придай
'Эйлера
^М
20
40 Ш
l/i
Рис. 118.
во
aj
b)
Рис. 119.
Чтобы объяснить несостоятельность этого общепринятого мето/ia ^),
тйы должны помнить, что в случае, пластической деформации стержня
величина прогибов может зависеть не только от значений
действующих сил, но также от порядка, в каком эти силы приложены. Возьмем,
например, случай одновременного сжатия и изгиба (рис. 119, й). Если
*) Рис. 117 и 118 взяты из F. Bleich, Buckling Strength of Metal
Structures, !New Yotk, Mc Graw-Hill Book Company, Inc., 1952,
») Cm. статью R. L. T e m p 1 i n, R. G. S t u r m, E. С H a r t m a n n and
M. Holt, Aluminum Research Laboratories, Aluminum Company of America,
Pittsburgh, 1938.
') Объяснение было дано F.R.Shan ley, J. Aeronaut Sci., т. 14,
стр. 261. 1947.
361 НЕУПРУГИЙ ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОЛИНЕЙНЫХ колонн 1Ь^
деформации совершенно упруги, то прогибы стержня зависят только-
от величин Р и Ж и не зависят от порядка, в котором они были
приложены. Условия будут совершенно отличны, если при нагружении
возникнут пластические деформации. Предположим, например, что
сначала приложены осевые силы Р и их величина такова, что
возникает пластическая деформация. Если теперь будут приложены моменты Ж»
то на изгиб стержня под их действием будет оказывать влияние
наклёп материала силами Р. Этот накЛеп должен быть принят во
внимание, и при вычислении прогибов нужно применить приведенный
модуль Вг- Другой путь нагружения рассмотрим в случае, когда
одновременно приложены постепенно увеличивающиеся нагрузки Р и М.
Такое условие нагружения получается, например, если стержень сжат
силами Р, приложенными с некоторым эксцентриситетом, как
показано на рис. 119, ^f. В этом случае деформации в каждом продольном,
волокне непрерывно увеличиваются, и зависимость между напряжением
и деформацией определяется для каждого этапа нагружения
соответствующим значением касательного модуля Е^.
При экспериментальном исследовании поперечного выпучивания
колонн условия обычно подобны представленным на рис- 119,/?.
Благодаря неизбежным эксцентриситетам изгиб колонны начинается
немедленно после начала нагружения. Одна"ко так как эксцентриситеты
весьма малы, то прогибами пренебрегают до стадии, когда нагрузка
начинает приближаться к ее критическому значению. В этот период
деформации начинают увеличиваться быстро, и йх величина
определяется с помощью модуля Ef соответственно критическому значению
нагрузки. Следовательно, из этих соображений вытекает, что
Первоначальная формула A51) Энгессера будет давать критические
напряжения с большей точностью, чем формула A55), как об этом
свидетельствуют и результаты опытов.
Предыдущие рассуждения, изложенные для основного случая
продольного изгиба (рис. 98), можно также применить к другим случаям
продольного изгиба, как, например, показанным на рис. 99 и 102.
Критическое напряжение можно вычислить по формуле A37) путем
подстановки Ef вместо Е. Однако в общем задачи на продольный
изгиб в пластической области являются более сложными, так как
условия на концах и коэффициенты длины обыкновенно перестают
быть постоянными и изменяются с изменением Р^р. Возьмем, например,
случай, показанный на рис. 105. В пластической области коэффициент
длины для этого случая зависит лишь от отношения (см. уравнение A),.
стр. 134)
Л/'
(е>
которое не зависит от значения Р^^. Но в пластической области
должно быть применено Е^ вместо £"> и взамен отношения (е) мы
"^W
156
TtOTEPfl Ус:той*1и вости
[Tfl.-lf
долучиыг
Mi
EJil '
if)
я-д^ JS/ меньше E и зависит от величины Ря^,Следовательно^
отношение жесткости изгиба горизонтальных элементов рамы к жесткост|<
вертикальных элементов получается большим, в результате чего коэфи
^фициент длины получается меньше в пластической области,'чем дли
«случая совершенной упругости. Из этого мы заключаем, что если при
расчете вертикальных элементов -рамы в пластической области вос-г
пользуемся для приведенной длины тем же значением, какое вычйс^г
лено для совершенно упругих условий, io мы обеспечим-безопасность^
Подобные заключения получаются также для случаев, разобранных
> пп. 32, 33, 36. „-
37. Устойчивость круговых колец и труб
, ^ под действием внешнего давления
'..- Устойчивость кругового кольца. Хорошо известно, что круговое
кольцо или труба могут потерять устойчивость при действии лиш|^;
внешнEР0 давления. Если жесткость изгиба кольца недостаточнаг Щ
такая потеря устойчивости может произойти при напряжениях, значи*
т'ельно меньших предела упругости материала. Это явление нужно
принимать во внимание в таких задачах как расчет трубок паровых
котлов, подвергнутых внешнему давлению, и расчет укрепляющих
1солец подвсднцх лодо1Й
Давление, при котором круговая форма становится неустойчиво^
я происходит сплющивание, называется критическим давлением. Er<j
Рис. 120.
значение можно получить при помощи общего уравнения для
изогнутой оси (уравнение B35) т. I, стр. 339).' '
Предположим, что иод действием внешнего давления кольцо сплю*
ацивается в эллиптическую форму, как показано на рис. 120, а пункти*
37} УСТОЙЧИВОСТЬ КРУГОВЫХ КОЛВЦИ'ГРУВ 157
ром. Примем следующие обознамения: <?-т-внешнее давление,
приходящееся на единицу длины Оси, R-—радиус оси кольца; к-—радиальное
перемещение кольца при сплющивании, -и».— радиальное перемещение
поперечного сечения ^, Ж©^—изгибающий момент в поперечном
сечении, Л/^ = ^(/? — Мо) ~ продольная оцимающая сила в лоцеречно!*
сечении А.
Изгибающий моме1нт в каком-либо поперечном сечении ^
сплющенного кольца будет .
M~Mf,-}-qAd-'Ab — fA^. (а)
Тепфь в треугольнике АОВ имеем
OBl' = ASf*-j-AO^~^AO-AD
Vina
~j0'-.^JdAD=F=^JoS^--Ad^^
Так каг ч мало по сравнению с /?, vTO членами н* или «^ ^ожно
пренебречь, следовательно.
~ АЕ^~ АО' АО^Щщ — н).
2
Вставляя это значение в уравнение (аХ мы получаем ,
Ж = Ж о — 9^^? («о — к)- •
Уравнение B35) т. I, стр. 339, получается в таком виде:^
^8 + к == — g^ [Жо — ^/? («о — к)]
или ^
Общее решение этого уравнения будет
.^ u^Qsinp<? + C,cosp<? + -'^^^'*\ (с)
где С| и Се — постоянные, которые должны быть определены из
условий в поперечных сечениях Аир сплющенного кольца, и
Из условий симметрии следует, что
Ш,_»=«' Q _.- = <'• (е)
mw
158
ПОТЕРЯ УСТОЙЧИВОСТИ
1ГЛ. V
На основании первого из этих уравнений мы получаем Ci=i=Oi а из
второго
sm^ = 0. (f)
Наименьший корень этого уравнения будет ^ = ir, или р = 2.
Вставляя это в выражение (d), мы получаем значение для крити-:
ческого давления*)
A56)
3EJ
7кр DS
Друхие корни уравнения (f) такие, как />те/2 = 2те, ;ж/2 = 37с и т. д.,
соответствуют большему числу волн сплющенного кольца и дают боль?
шие значения для давления д. Рис,
120, b показывает, например, сплющей^
ную форму при /7те/2 = 2те. Эти вые»
шие формы сплюш.иваиия представля--
ют интерес при исследовании устой^
чивости коротких цилиндрических
трубок с закрепленными концами^
Устойчивость круговой арки.
Если круговая арка, имеюш,ая шарни]р^
но закрепленные концы,
подвергается действию равномерно
распределенного радиального давления, она может
выпучиваться, как показано на рис.
121 пунктиром. Критическое значение давления зависит от величины
угла а и может быть вычислено по следующей )формуле ^):
Рис. 121.
A57)
Задача об устойчивости кольца в направлении, перпендикулярном его
плоскости, также решена ^). .
Устойчивость круговых труб. Изложенная выше теория
устойчивости кругового кольца может быть применена также и в случае
длинной круговой трубы, подверженной равномерному внешнему
давлению. Рассмотрим элементарное кольцо, вырезанное из трубы двумя
поперечными сечениями на расстоянии одно от другого, равном еди-)
^) Эта задача была решена М. В г е s s'o м, Cours dc mechanique appliquee,
Paris, T. 1, стр. 334, 1866.
^) Cm. статью автора «Об устойчивости упругих систем». Известия
Киевского политехнического института, 1910; французский перевод Ann. ponts et
chaussees, 1913. См. также Е. Hurlbrink, Schiffbao, т. 9, стр. 640,-1907 —
1908; Е. Chwalla and С. F. Kollbrunner, Stahlbau, 1937 и 1938;
A. .H. Д и H H и к. Продольный изгиб стержней, Москва, 1939.
«) См. Е. L. Nicol а j, Z. angcw. Math. u. Mech.^ т. 3, стр. 227, 1923; см.
также статью автора там же, стр. 358.
371
УСТОЙЧИВОСТЬ КРУГОВЫХ КОЛЕЦ и ТРУБ
159
1Л'
нице. Момент инерции поперечного сечения этого кольца будет J=-^,
где h означает толщину стенки трубы. Так как при изгибе
поперечные сечения кольца не искажаются, то вместо Е нужно воспользо-
Е
. Формула A56) для вычисления критического
ваться величиной г
1—{А
давления получается в следующем виде:
Ркр =
4A—11^I^ •
A58)
Этим выражением можно пользоваться до тех пор, пока
соответствующее сжимающее напряжение в трубе будет меньше предела
пропорциональности материала. За пределом пропорциональности истинное
критическое давление будет меньше, чем получаемое из формулы A58),
и для материала с ясно выраженным пределом текучести можно
пользоваться формулой *):
Р.Р = |-^^.' A89)
В которой о обозначает предел текучести материала при сжатии.
Когда толщина уменьшается, критическое давление приближается
к предельному значению Eh^l^R^, которое несколько меньше
даваемого формулой A58), и во всех случаях его значение меньше чем
ho jRj т. е. меньше давления, соответствующего пределу текучести ^).
В области за пределом упругости мы
можем поступать так же, как в случае
сжатых стержней и воспользоваться Е^
вместо Е в уравнении A58). Таким путем
устанавливается зависимость между р^^ и
hjR в пластической области.
Трубы с начальной эллиптической
формой. Потеря устойчивости труб под
действием равномерного внешнего
давления в значительной степени зависит от
различного рода недостатков в них.
Наиболее важным недостатком является
начальная эллиптичность, предельная величина которой в каждом типе
трубы обычно хорошо известна по многочисленным измерениям
») См. R. V. Southwellj Phil. Mag., т. 29, стр. 67, 1915.
*) Опыты над потерей устойчивости коротких труб под действием
внешнего давления описаны G. Соок'ом, Phil. Mag., стр. 51, 1914. Библиография
по этому предмету того же автора см. Brit. Assoc. Adv. Sci. (Birmingham)
Repts., 1913.
mw
160 ,'пбТЕРЯ УСТОЙЧИВОСТИ 1ГЛ. "^
при осмотре. Поэтому желательно иметь расчетную формулу, в
которой эт15Ин(а<1альная эллиптичность явно выражена.. Чтобы вывести такую
^рщуяу% йредположим, что начальное отклонение формы трубы от
совершенно круглой формы, указанной nyHKTHjioM на рис. 122;
определяется уравнением
' Щ==ЩС08 2% (g)
в котором Ив — наибольшее начальное радиальное отклонение,
рассматриваемое малым по сравнению с^, а ср-^центральный угол^!
измеряемый, как показано на рисунке. Начальная форма трубы, пред^^
ставлена сплошной линией.
Если к такой некруглой трубе приложить внешнее давление, т<?
будет происходить дальнейшее сплющивание трубы. Обозначая рад|Й
альное перемещение, соответствующее дополнительному сплющиванию,
через щ и рассматривая элементарное кольцо с шириной, равной
единице, мы получаем ,из.уравнения B35) т. 1, стр. 339:
где
> , D ''''
12A-fx^)
—^ жесткость изгиба элементарного кольца. Что касается изгибающего
момента Л1» возникающего от давления р^ то мы видим, что уменьшение
кривизны имеет место на участках АВ и €D элементарного кольца;
следовательно, М является положительным в этих областях, в то
время как на Остальных участках кольца момен! отрицателен.
В точках Aj В, С и D изгибающий момент равняется нулю, и
взаимодействие между частями элементарного кольца представится лишь
силами 5, касательными к пунктирному кругу, представляющему
идеальную форму трубы. (Действие сил ^S на участок АВ кольца
показано на рисунке.) Этот круг можно рассматривать как веревочную
кривую. для внешнёГр равномерного давления р. Сжимающее усилие
вдоль этой кривой остается постоянным и равным S=pR. Таки»|
образом, изгибающий момент в каком-либо поперечном сечении
получается путем умножения 5 на полное радиальное отклонение «i-j-Kji
в 9toM поперечном сечении. Тогда
М=pR(щ-\-щ COS Щ,' (i)
и уравнение (h) получается в виде
-^ -f Щ = — -^pR^ («в + Ко cos 2(j>),
*) См. статью автора J. Appl. Mech., т. 1,^стр. 17^, 1933.
371 УСТОЙЧИВОСТЬ КРУГОВЫХ КОЛЕЦ И TPJi'B 161
ИЛИ
df
+ щ {l -\-р ^)'= — -^рН^Щ COS 2(р.
Решение этого уравнения, удовлетворяющее условиям непрерывности
в точках Л, Д С и Д будет '
«2=3-^cos2cp, A60)
В котором /7кр дается формулой A58). Видно, что в точках Д В, С
и D перемещение щ и его вторая производная обращаются в нуль.
Следовательно, изгибающие моменты- в этих точках равняются нулю»
как предполагалось ранее. Наибольший изгибающий момент имеет
место при <р = 0 и при ^ = ж, где
м^=рк[щ+^]^-е^. Aб1>
Ркр
Видно, что при малых значениях отношения pjp^^ изменением в
эллиптичности трубы вследствие давления р можно пренебречь и что
наибольигий изгибающий момент получается путем умножения сжй-'
мающего усилия S==pR на начальное отклонение щ. Если
отношение р/Рщ не мало, то изменение в начальной эллиптической форме
трубы до^^жно быть учтено и для вычисления Мтах нужно*
воспользоваться уравнением A61).
Наибольшее сжимающее напряжение получится тогда путем
добавления наибольшего сжимающего напряжения от изгибающего
момента Мтгх к напряжению, возникающему от см^имающего усилия
pR. Таким образом, находим
|о|шах— л + Л^ 1-р/Ркр* "^
С помощью этого выражения можно разработать для расчета труб
метод, подобный методу расчета колонн на основан^ш допускаемых
несовершенств.
Предельное значение давления р есть то значение, при котором
начинается текучесть материала. Обозначая это давление через рг и
подставляя в уравнение (j) а^ вместо Отах, получаем
PtR , ^Рт^Щ \
'^кр
откуда можно вычислить предельное добавление рт, если известны
От и начальное отклонение Кд. При помощи обозначений
-f ==/и и -§- = « A)
JR
6 с, П, Тимошенко, т. II
3^
162
ПОТЕРЯ УСТОЙЧИВОСТИ
уравнение (к) для вычисления Рг получается в таком виде:
Р?
^ + A+6/И«)Ркр]'
«Лр
0.
т
|гл, Ш
A62)
На основании этого уравнения можно построить кривые, дающи^
среднее сжимающее напряжение PrR/h как функцию R/h для различ«
«ых значений отношения u^/R и для различных значений а^. При
помощи таких кривых ' и при надлежащем коэффициенте безопас-;
ности можно легко подобр*ать подходящую толщину стенки трубы*
Необходимо заметить, что давление р^, определенное таким образом|
меньше, чем^ давление, при котором происходит полная потеря устО^*
чивости трубы; следовательно, пользуясь рт» как предельным зна^
чением давления, мы всегда сможем обеспечить устойчивость трубЦ
В предыд)одем изложении предполагалось, что длина трубы Л
велика по сравнению с ее радиусом, скажем, IjR ^ 20. Для коротки^
труб, если их края защемлены или просто оперты, значение р^^ больше
значения, даваемого формулой A58), и зависит от отношения l/R.
Теория устойчивости таких труб является более сложной *), так как
труба разбивается при выпучивании на несколько волн по окружно-^
сти и число.этих волн зависит от отношения l/R^). • ;i
Задача об устойчивости труб, закрытых на концах и подвержен-*
ных равномерному давлению на концах и с боков f), также решена *).
88. Устойчивость прямоугольных пластинок
Проблема выпучивания сжатых прямоугольных пластинок
представляет большой практический интерес при рассмотрении упругой
устойчивости сжатых элементоВ|
1
\
\
\
■
»
/
/
aj
Рис. 123,
1 г I . . • I \ М составленных из пластинок, кото-*
рые часто применяются в
стальных конструкциях (рис. 123).
Потеря устойчивости таких элементов
может быть вызвана выпучиванием;
стенки или боковых пластин, но
не выпучиванием элемента как
целого, Напр,имер, в случаях, показанных на'рис. 123, выпучивание
пластин, как указано пунктиром, имеет место, если толщина пластинки
*) Рассмотрение этой задачи см. S» Timoshenko, Theory of Elastic
Stability, стр. 445, 1936; см. русский перевод, 1946, 1955.
*) Некоторые кривые для вычисления критических давлений на короткие
трубы были предложены Комитетом исследования по сопротивлению сосудов,
находящихся под внешним давлением, A.S. М. Е., декабрь 1933.
, 8) Это условие возникает при исследовании устойчивости обшивки
корпуса подводной лодки между двумя укрепляющими кольцами.
*) См. статью R. V. М i s е s in Festschrift f. Prof. A. Stodola, Zflrich, 1929.
38} УСТОЙЧИВОСТЬ ПРЯМОУГОЛЬНЫХ йлАстинок , 163;
выбрана неудовлетворительно. Так как длинй сжитого элемента
Обычно велика по сравнению С размерами поперечного сечения, то
задача сводится к задаче о выпучивании длинной сжатой пластинки
(рис. 124). Короткие стороны пластинки можно рассматривать как
свободно опертые; условия для двух других сторон зависят от форлы
поперечного, сечения. Например, если
сечение колонны имеет квадратную
форму (рис. 123, с), и вСе боковые
пластинки имеют одну и ту же
толщину, то они стремятся выпучиться
одновременно. Каждую грань можно
тогда рассматривать как сжатую
прямоугольную пластинку со всеми Ри<:- 124.
четырьмя свободно опертыми сто-" ^
ронами. В случаях, показанных на рис. 123,^1 и 123, Ь, нижние кра»
вертикальных стенок свободны, а верхние края упруго защемлены *).
Имеется строгое решение задачи. об устойчивости для различных
условий вдоль длинных сторон пластинки, показанной на рис. 124^).
Здесь мы даем только некоторые окончательные результаты
и.значения Критических напряжений, полученные из этих решений.
Прямоугольная пластинка, свободно опертая на.четырех краях.
Свободно опертая пластинка под действ|йем равномерного сжатия в направлении
оси л: (рис. 124) выпучивается, разделяясь на квадраты или прямоугольники,,
близкие к квадратам. Критическое значение сжимающего напряжения ^laeTC»
формулой») - .
в~ которой
где Л—-толщина пластинки к b — ее ширина. Коэффициент ,
_____ |=(i^+^r ■ ■ >^>
») Первые опыты, в которых вопрос об устойчивости тонкостенных
конструкций был рассмотрен, были сделаны В. Фейрберном и описаны в его
книге «Britannia and Conway Tubular Bridges», London, 1849, См. также работу
В. Годкинсона, опубликованную. в качестве приложения к. Report of the
Commissioners Appointed to Inquire into the Application of Iron to Railway
Structures, London, 1849.
«) Cm. S. Timo,shenko, Theory of Elastic Stability, 1936; см. русский
перевод, 1944, 1956.' Ч, i л
«) Решение такой задачи принадлежит G. Н. Вгуап'у; см. Ргос. London
Math. Soc, т. 22, стр. 54, 1891. Другие случаи продольного изгиба
прямоугольных пластинок были рассмотрены автором. См. его статьи «Об
устойчивости сжатых пластинок». Известия Киевского политехниче:ского
института, 1907; Z. Math. и. Phys. т. 58, 1911; Eisenbau, т. 12^ 1921. Ргос. Am. Sos.
Civil. Engrs., т. 55, стр. 855, 1929; см. также Н. Reissner, Zentr. Bauverwalt.^
Berlin, стр. 93, 1909.
164
ПОТЕРЯ УСТОЙЧИВОСТИ
[ГЛ. V
зависит от величины отношения ajb, а целое число т представляет число
волн, на которые пластинка разбивается при выпучивании. Число т должно
быть выбрано так, чтобы р сделать mininjum'oM *). Некоторые значения
коэффициента р даны в табл. 10. Для более длинных плйстинок (с/6>-3)
хорошее приближенное значение дает § = 4.
Таблица 10
Коэффициенты для вычисления критического сжимающего напряжения
в прямоугольных пластинках со свободно опертыми краями
о/6 =
1=
0.4
8,41
1520
0.6
5,14
933
0.8
4,20
760
1.0
4,00
727
1.2
4,13
747
1.4
4,47
807
1,6
4,20
760
1.8
4,04
733
2.0
4,00
727
2,2
4,04
733
2.4
4,13
747
2,7
4,04
733
3
4,00
727
Значения о^р, данные" в табл. 10, вычислены в п'^)едположении, что
.Ё = 2 X 10^ KZjCM^, fx = 0,3 и h/b = Ofi]. Критическое напряжение для какого-
либо другого значения отношения h/b можно получить путем умножения
табличных значений на 10* (Л^^^*). Для пояснения сказанного рассмотрим
длинную стальную пластинку, имеющую предал текучести, равный 2800 кг/см'.
Предположил», что мы желаем определить значение отношения b/h, при
котором критическое напряжение равняется пределу текучести. Полагая
Л*
^ = 4 и пользуясь табл. 10, мы получаем Окр = 725 X 10* х р- = 2800 кг/см',
откуда ^ 1,
А = 50,8. (Ь)
При больших значениях отношения b/h выпучивание будет происходить
при сжимающих напряжениях, меньших предела текучести материала. При
таких условиях за основу определения рабочего напряжения нужно
принимать критическое напряжение, а не предел текучести материала.
Три края пластинки оперты, а четвертый свободен. Если один из
длинных краев, например у = Ь, свободен (см. рис. 124), то для вычисления
критических значений сжимающего напряжения можно воспользоваться
предыдущей формулой A63), взяв значения коэффициента р из
нижеследующей табл. П.
Таблица 11
Коэффициент р для вычисления критического сжимающего напряжения
в прямоугольной пластинке с тремя свободно опертыми краями
и четвертым (у=:Ь) свободным
а1Ь =
Р=
0.5
4,40
1.0
1,440
1.2
1,135
1.4
0,952
1.6
0,835
1,8
0,755
2.0
0,698
2.5
0,610
3.0
0,564
4.0
0,516
5,0
0,506
^) Можно видеть,' что это наименьшее значение р равняется 4 и имеет
место при а = тЬ, т. е. когда пластинка при изгибе разделяется на квадраты.
38]
УСТОЙЧИВОСТЬ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
165
Два противоположных края свободно оперты, третий защемлен, а
четвертый свободен. Края л: = 0, л: = с на рис. 124 будут
рассматриваться как свободно опертые, а край дг = О-^ как защемленный. Здесь можно
воспользоваться той же самой формулой A63), причем значение
коэффициента р брать в табл. 12. (Для^ больших значений отношения а/Ь хорошее
приближенное значение дает § = 1,33.)
Т а б л и ц а 12
Коэффициент Э для вычисления критического сжимающего
напряжения в прямоугольной пластинке с двумя
противополбжными краями, свободно опертыми,
третьим защемленным и четвертым (^ = {>) свободным
а/Ь =
■ ' Р==:.
а/Ь==
Р =
1.0
1,70
1.8
1,34 .
».»
1,56
1.9
1,36
1.2
1,47
2.0
1,38
1.3
. 1,41
2.2
1,45
1.4
1,36
2.4
1,47
1.5
1,34
2.6
1.41
1.6
1,33
2.8
1,36
1.7
1,33
3
1,34
Два противоположных края просто оперты, два других защемлены *).
Края л: = О и х = а рассматриваются свободно опертыми. Соответств^ующиё
значения коэффициента § формулы A63) даны в табл. 13.
Таблица 13
Коэффициент р для вычисления критического сжимающего напряжения
в прямоугольной пластинке с двумя противоположными свободно
опертыми краями и с защемленными двумя другими краями
а/Ь =
Р =
0.4
9,44
0,5
7,69
0.6
7,05
0.7
7,00
0.8
7,29
0,9
7,83
1.0
7,69
1.2
7,05
1.4
7,00
1.6
7,29
1.8
7,05
2.1
7,00
Прямоугольная пластинка, опертая по контуру и подвергающаяся
действию касательных напряжений, равномерно распределенных по
контуру (рис. 125). Критическое значение
касательного напряжения, при котором может
произойти выпучивание пластинки, равняется
V = K- ' A65)
Значения численного коэффициента р даны
в табл. 14.
Табл. 14 можно пользоваться при выборе
толщины стенки составной балки. У опор р ,ос
балки поперечная сила имеет наибольшее зна-
чение. Поэтому часть стенки между двумя ребрами жесткости можно
*) Мы имеем это условие, когда два противоположных края сжатого
элемента, показанного на рис. 123, с, очень жестки и только два других
края могут выпучиваться.
166
ПОТЕРЯ УСТОЙЧИВОСТИ
|ГЛ. у
Таблица 14
Коэффициент р для вычисления критического касательного напряження
в прямоугольной пластинке, опертой по контуру и подвергающейся
действию равномерно распределенных по ее контуру касательных
напряжений
о/й =
1
9,42
1.2
8,0
1.4
7,3
1.5"
7,1
1,6
7,0
1.8
6,8
2,0
6.6
2,6
6,3
3
^^
оо
5.4
рассматривать как прямоугольную пластинку со свободно опертыми краями,
подвергающу1бся лишь действию касательных напряжений. Например, если
расстояние между ребрами жесткости,равняется 1,5 ж, £ = 2 X Ю* wz/cj»*
и fJisi=G,3, то, пользуясь табл. 15*), получим следующие значения
критического напряжения в kzjcm^ для балок со стенкой высотой h и толщиной Ь*
Т аб л и ца 15
Критическое напряжение (кг/см^) в балке
со стенкой высотой b и толщиной Ь
Ь, см
150
210
300
Л = 0,95 см
683
530
478
h^\,\\CM
933
723
654
Л=1.27сж
1220
945
850.
Л= 1,43 еж
1550
1200
1086
При помощи табл. 10—15 можно получить необходимую толщину
стальных листов, применяемых в составных сжатых элементах, сечения которых
показаны на рис. 123. Если стороны трубчатого сечения рис. 123, с рас-
сматр%вать как длинные прямоугольные пластинки с опертыми краями, то
критинескре сжимающее напряжение будет '
_ л. — ^'^^ Е
(с)
Взяв, например, Л/й = 0,01, мы найдем Окр = 725 кг/см\ Это напряжение
значительно ниже предела пропорциональности для строительной стали.
Если длинные края той же пластинки рассматривать как защемленное, то
мы находим -
Окр = 7се =-I-. 725-= 1270 кг/cjM «.
В случаях, показанных на рис. 123, с и 123, Ь, сжатые вертикальные
стальные листы можно рассматривать как длинные пластинки, защемлен-
*) Дополнительные данные относительно выпучивания стенки и расчет
ребер жесткости даны в статьях автора, Ргос. Am. Soc. Civil Engrs., т. 55,
cTpi 855, 1929 и Engineering, т. 138, стр. 207, 1934. См. также Е. Chw all а,
Repts, 2d Congr. Internat Assoc. Bridge and Structural Engrg., Berlin, 1936;
Stahlbau, 1936. -
Щ- ВЫПУЧИВАНИЕ БДЛОК, НЕ ИМЕЮЩИХ БОКОВЫХ ОПОР 167
вые *) верхним краем и со ^:воб.одным нижним краем. Поэтому критическое
напряжение будет равняться .,
— 1^4 _ l>33it« Л" В ^ ...
Опять устойчивость пластинки зависит от величину отношения Ь/А.
Предполагая, что предел текучесия строительной стали равняется 2000 кг/см*,
значение b/h, при котором о,£р равняется этому напряжению, получится из
уравнения (d):
b -ш Г 1,ззя« гло*" ^^
~" г 12-200
h~~ Г 12.2000'ПбДГ
Следовательно, если 6/Л>35, то критическое напряжение получается
меньше предела текучести материала. Это обстоятельство должно быть
принято во внимание при выборе величины допускаемого напряжения.
УЬтойчивость пластинки можно увеличить путем усиления свободного края
йластинки. .
Во всех приведенных выше случаях предполагалось, что критическое
напряж:ение ниже предела пропорциональности. Для напряжений за пределом
пропо^щиональности приведенные выше формулы дают преувеличенные
значения критических напряжений ®).
39. Выпучивание балок, не имеющих боковых опор
Хорошо известно, что при отсутствии поперечных опор двутавровые
балки, нагруженные в плоскости стенки, оказываются недостаточно устой*?
чивыми в поперечном направлении. Если нагрузка увеличивается за
некоторый критический предел, то такие балки выпучиваются из плоскости
стенки, и дальнейшее нагружение вызывает в йих потерю устойчивости*).
Для определения этого предела можно воспользоваться энергетическим
м1етодом.
Для пояснения этого, рассмотрим бапку АВ (рис. 126^ с) узкого прямо^
угольного поперечного сечения, нагруженную в центре тяжести среднего
Поперечного сечения силой Р, действующей в продольной вертикальной
плоскости симметрии. Если эта сила мала, то изгиб балки происходит только
в вертикальной плоскости и эта форма изгиба будет устойчива. Это значит,
что если балка изгибается в боковом направлении поперечной силой, то
этот прогиб исчезает по удалении силы, и балка возвращается к своей
первоначальной форме. Однако если сила Р увеличивается, достигается ее
предельное значение, при котором изгиб вертикальной плоскости становится
_ '. ; • л - . .
^) Это предположение дает верхний предел для критического
напряжения. Истинное критическое напряжение будет несколько ниже, так как
закрепление верхнего края не абсолютно жестко.
*) Этот вопрос разобран в книге S. Tinioshenko, Theory of Elastic
Stability, стр. 384, 1936; русский перевод, 1946, 1955.
^) Потеря устойчивости! балок вследствие бокового выпучивания иллю-
i стрируется катастрофой с мостом вблизи Тарба, Франция; см. Revue technique,
ноябрь 15,~ 1897. Боковое выпучивание балок узкого прямоугольного
поперечного сечения было разобрано Л, Прандтлем, Диссертация, Нюренберг, 1899
И А. О. Mich ell, Phil. Mag., т. 48, 1899. Выпучивание двутавровых
балок было разобрано автором; см. Известия Петербургского
политехнического института, ТОМЫ 4 и 5, 1905 и 1906. См. также Ann. ponts et chaussees,
168
ПОТЕРЯ УСТОЙЧИВОСТИ
1ГЛ. V
неустойчивым. Тогда балка выпучивается в боковом направлении и могут
иметь меето большие поперечные прогибы при весьма малом увеличении
нагрузки. Это предельное значение Р называется критической нагрузкой.
Критическая нагрузка определяется путем рассмотрения потенциа[льной
энергии системы. Какой-либо боковой прогиб балки сопровождается
увеличением энергии деформации. После малого бокового выпучивания мы имеем
не только энергию деформации изгиба в вертикальной плоскости, которую
хожно рассматривать неизменной, но также энергию деформации изгиба
в поперечном направлении и энергию деформации кручения. В то же самое
время потенциальная энергия груза уменьшается, потому что боковое
выпучивание сопровождается понижением ее точки приложения. Пусть Ui
означает это уменьшение потенциальной энергии груза, U— энергию
деформации вследствие изгиба в поперечном направлении и f/j — энергию
деформации вследствие кручения. Тогда критическая нагрузка определится
по уравнению A40), стр. 137, которое получается в следующем виде:
и+и,^и,. (а)
Теперь мы должны вычислить величины,-входящие в это уравнение.
Изгибающий момент в вертикальной плоскости в каком-либо поперечном сечении
в расстоянии х от лезой опоры (рис. 126, Ь) равняется Рх/2. При
рассмотрении бокового выпучивания необходимо вычислить изгибающий момент
относительно оси z^ (рис. 126, с). ЭтЬт момент равняется (Рх/2)<р, где <f
означает малый угол закручивания, переменный по длине балки. Тогда при
малых поперечных прогибах^) мы имеем следующее дифференциальное
уравнение:
Соответс11вующая энергия деформации изгиба равняется
^=^^4E^Г'^"=4ё71"^^^^"'
(с)
1913 и Trans. Ann. Soc. Civil. Engrs., т. 87, стр. 1247, 1924. Практическое
приложе11ие теории разобрано Е. ChwaUa, Die Kipp-StabilitSt gerader
Trager mit doppeltsymmetrischem I-Querschnitt, Berlin, 1939. См..также книгу
Ф. Блейха,.цит. на стр. 149, гл. 4.
*) При малых прогибах мы можем принять для кривизны d^yjdx^ вместе
d^yJdxK
Щ ВЫПУЧИВАНИЕ БАЛОК, НЕ ИМЕЮЩИХ БОКОВЫХ ОПОР 169
-^im'"- «»
Энергия деформации кручения уравняется (см. т. I, уравнение A86))
и,
о"
где жесткость при кручении С для прямоугольного поперечного сечения
получается из уравнения A59) т. I, стр. 245.
Рассмотрим теперь понижение точки приложения груза Р вследствие
поперечного прогиба. Возьмем два симметрично расположенных элемента dx
балки (риС; 126, b и 126, с) и рассмотрим влияние изгиба только этих двух
элементов в плоскости xyi. Угловое перемещение вследствие этого изгиба
равно —i-~]dx. Так как этот изгиб происходит в плоскости xyi,
наклоненной под углом ср к горизонту (рис. 126, с), то он приводит к понижению
груза Р на —x<f(d^y/dx^)dx. Полное понижение Р в результате изгиба
С d^y
всех элементов балки при выпучивании поэтому будет 5 = — \ x<s-~^dx;.
.; ' dx
о
пользуясь уравнением (Ь), находим
Отсюда
о
U, = Pb=^^^x^fdx. (е)
Подставляя в уравнение (а) выражения (с), (d) и (е), находим
4£7.С \ D^V dx
о
"^ i Vdxj
^кр= г • <*)
\ ^*<Р^ dx ,
Взяв для угла закручивания «р удачно выбранную функцию х,
удовлетворяющую условиям на концах, получаем приближенное значение критической
нагрузки из уравнения (f). Предположим, например, что
. пх
<f = asm-^. (g)
Эта функция имеет нулевое значение на концах балки, где угол
закручивания равен нулю, и наибольшее значение в середине (л: = /). Подставляя
(g) в выражение (!), находим *)
17,2 yCEJz
"Р ~~ B1)
Р^.= '.,..'• A66)
*) Более подробное исследование показывает, что ошибка этого
приближенного решения составляет около 1,5"/о. Следовательно, формула A66)
достаточно точна для практических приложений.
mw
170 ПОТЕРЯ УСТОЙЧИВОСТИ 1ГЛ-,'^
Таким образом, критическое значение нагрузки зависит от произведени4
жесткости кручения и жесткости бокового изгиба балки.
Выше предполагалось, что груз Р приложен в центре тяжести среднего
поперечного сечения балки. Если точка приложения находится на расстояни!^
а выше центра тяжести,- то правая часть формулы A66) должна быт!?
умножена на
[1 —1,74@/2/)/ЕуС]»). ,
Если нагрузка равномерно распределена по центральной оси балки
(рис. 126), то ее критическое значение равно
_2S,sYCEJz
B?/)Kp=«^^^^-feS^^. ^m
Для консоли длиной/, нагруженной в центре тяжести свободного конца,,
критическая нагрузка равняется >
4,01 УСЮ,
Ркр»= ' V • ^^^^
л
в Случае двутавровой балки формулы для критических нагрузок имеют
вид, полученный выше для балки узкого прямоугольного поперечного
сечения, с той разницей, что числовой коэффициент в числителе правой части
не является постоянным, но зависит от величины выражения®)
С /2/\« „,
Например, если двутавровая балка опирается, как показано на рис. 126,
и равномерно нагружена по центральной оси, то критическое значение
полной распределенной нахрузки будет
B^0кр = ^^*^?^. A69)
Величины коэффициента р для различных значений отношения а
даны в табл. 16. Видно, что с увеличением а постоянная р приближается
к величине. Данной ранее для балки прямоугольного поперечного
сечения.
В третьей строке табл. 16 даны .величины соответствующих значений
критических напряжений изгиба, вычисленные в предположении, что
iD,)'_=o.oooi. , - т
7
'У
Здесь JjtIJy—отношение боковой и вертикальной жесткости изгиба и Л/2/-—
отношение высоты балки к ее пролету. Для любых других соотношений
размеров балки критические напряжения -получаются путем умножения
чисел третьей строки на Ю*^. Четвертая и пятая строки табл. 16 дают крйт
тическое напряжение, когда нагрузка соответственно приложена к верхней
*) См. статью автора в Ann. ponts et chaussees, 1913, См. также его
«Theory of Elastic StabiHty>, стр. 254, 1936; русский перевод, 1946, 1955.
*) Жесткость при кручении С для двутавровых балок рассмотрена
в п. 47, стр. 204.
щ
ВЫПУЧИВАНИЕ БАЛОК, НЕ ИМЕЮЩИХ БОКОВЫХ ОПОР
171
ИЛИ нижней полке балкИ. Все вычисления сделаны в предположении
совершенной упругости материала 1). '
/- Таблица 16
Критические напряжения (гсг1см') для двутавровых балок,
находящихся под действием равномерной нагрузки
при •r*==0,0001 и £=2.10« жг/с.»1»
а =•
Р =.
'кр^^™-
%==
°«р^^ 1
а =
% =
*кр
<р=
If "
°кр =
V-
0,1
143,0
568
367
880
16
30,5
1530
1290
1810
1
53,0
663
454
970
20
30,1
1780
1440
1960
2
42,6
753
538
1050
32
1
29,4
2080
1840
.2350
4
36,3
907
684
1200
60
29,0
2570
2330
2840
6
33,8
1040
813
1330
70
' 28,8
3020
2770
3280
8
32,6
1153
923
1430
90
28,6
3400
3160
3670
12
31,5
1353
U20
1630
100
28,6
3580
3330
3840
Рассмотрим в качестве примера строительную стальную двутавровую
балку следующих размеров: длина 2/=:б .^высота Л = 60 см\ ширина
полки ft = 18 см\ толщина стенки 8^ = 17 см\ средняя толщина полок 8 =
= 2,2 еж, площадь поперечного сечения /^= 175 см*\ главная жесткость
изгиба £/у = 910б0 Е KzjcM^; главная жесткость изгиба £'У;г=1840 Е KZJcM^.
Из уравнения B24), стр. 204 имеем
gAu8«+ ^
Й8»
:226G.
^ Тогда из уравнения (h), полагая Е
ния (i) получаем
1840
Т =
2,6G, находим а := 4,78 и из выраже-
= 202-10-».
91 060.100
Путем интерполяции из табл. 16 получаем при а=:4,78
Окр = 907+ A040—907)
0,78
i 959 кг/смК
*) Более подробное исследование этого предмета см. в статье автора
Trans. Am. Soc. Civil. Engrs., т. 87, стр. 1247, 1924 и его <Theory of Elastic
Stability», гл. 5, 1936; русский перевод, 1946, 1955; см. также Е. С h w а 11 а,
цит. на стр. 168.
к^^ЖИГ"'
Щ
172 ПОТЕРЯ УСТОЙЧИВОСТИ 1ГЛ. V
Это критическое напряжение при 7 = 0,0001. Критическое напряжение в
рассматриваемом примере будет равняться 959 • -у • Ю* = 1937 кг/см^. Нагрузка,
соответствующая этому напряжению, должна рассматриваться как
предельная нагрузка для балки.
Этот числовой результат показывает, что боковое выпучивание монсет
иметь место при напряжениях, меньших предела прочности материала при
непосредственном сжатии и даже меньших предела упругости. Это
обстоятельство следует учитывать, и для определения рабочих напряжений
нужно принимать за основу критическое напряжение, а не предел текучести.
В этом примере,, взяв коэффициент безопасности, равный 3, найдем, что
рабочее напряжение будет равняться 1937/3:= 646 кг/см^.
ГЛАВА VI
ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ
40. Толстостенный цилиндр
Если круглый цилиндр со стенкой постоянной толщины
подвергается действию равномерно распределенных внутреннего и
наружного давлений, то вызываемые ими деформации будут симметричными
относительно оси цилиндра и не будут меняться по его длине.
Рассмотрим кольцо, вырезанное из цилиндра двумя перпендикулярными
к его оси, плоскостями, отстоящими одна от другой на единицу
(рис. 127). Из условий симметрии следует, что по граням элемента
а)
Рис. 127.
тпшхЩ (рис. 127, Ь), выделенного из этого кольца двумя осевыми
плоскостями и двумя концентрическими цилиндрическими
поверхностями, не будут действовать касательные напряжения. Пусть о^
означает окружное напряжение, действующее по нормали к граням mnti
и пщ элемента, и а^ — радиальное напряжение, нормальное к грйни тп.
Это напряжение изменяется с изменением радиуса г, и величине этого
изменения в расстоянии dr равняется (dcSrldr)dr. Нормальное
радиальное напряжение по грани jriitii, следовательно, будет
'r + ^dr.
к^^ЖТЯ"'
174 - ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО оси 1ГЛ. Vf
^Проектируя усилия, приходящиеся на элемент, на йаправлени^
биссектрисы угла £^ср, получим следующее уравнение равновесия:.
a^rd(f-{-Ctdrd(^—^a^-\--^dr^(r-\-drjd(^ = 0, (а)
«ли, пренебрегая малыми величинами высшего порядка,
7--г-Г^ = 0. (Ь)
'О,
Это уравнение содержит два неизвестных: напряжения <j^ и о^.
Второе уравнение, необходимое для определения этих величин,
получится из рассмотрения деформации цилиндра.
. Деформация цилиндра симметрична относительно его оси я
состоит из радиального перемещения всех точек стенки цилиндра.
Это перемещение постоянно в окружном направлении, но меняется
по радиусу,- т. е. является только функцией радиуса. Если и
означает радиальное перемещение цилиндрической поверхности радиуса г,
то перемещение на поверхности радиуса r-\-dr равняется u-\~j-dr.
Следовательно, элемент тит^щ претерпевает полное удлинение в
радиальном направлении, равное {dujdr)dr, и относительное удлинение
в этом жЬ направлении будет
du , .
Относительное удлинение того же элемента в окружном направлении
равно относительно]^у удлинению соответствующего радиуса, т. е.
8^ = -. (d)
На^ основании формул C8) т. I, стр. 55, выражения для напряжений
в зависимости от деформаций будут
Е [du I и\
ius ) A™)
Е ( и , du\
Нормальные напряжения о^ и а^, очевидно, не независимы, поскольку
они могут быть выражены в функции Ъдного и. Подставляя
выражения A70) в уравнение (Ь), -получаем следующее уравнение для
определения н:
rf^ , J_dw ^t — f\ ( \
dr^'^ г dr~^ г^~ ^^'
*) Весом элементй здесь пренебрегается.
401 ТОЛСТОСТЕННЫЙ ЦИЛИНДР 175
Общее решение этого уравнения будет
и^С,г-]г^, (О
что можно проверить путем подстановки. Постоянные Q и Q
определяются из условий на внутренней и наружной поверхностях цилиндра,
где давления, т. е. нормальные напряжения о^, известны. Подставляя
решение (f) в выражения A70), получаем ,
'^ = Г:^['^1A + |^) + аЦ=^|. (h)
Если р^ и р^ означают соответственно внутреннее й наружное
давления, то условия на наружной и внутренней поверхностях цилиндра
будут
■{0,)г^Ь== — Р» и (Ог)г = а = —Рв- (i)
Знак правой части каждого условия отрицателен, потому что за
положительное нормальное напряжение принято растягивающее.
Подстановка выражения о^ (выражение (g)) в условия (i) дает два
уравнения для определения постоянных С^ и Сз, из которых получаем
Имея эти значения для произвольных постоянных, мы из выражений
(g) и (h) получим общие формулы *) для нормальных напряжений о^ и о^:
о<==
A71)
Интересно отметить, что сумма этих двух напряжений остается
постоянной; деформации же всех элементов в направлении оси цилиндра
одинаковы, и поперечные сечения цилиндра после деформации остаются
плоскими. Это оправдывает наше рассмотрение задачи как плоской.
Рассмотрим теперь частный случай, когда /?„ = О, т. е. цилиндр
подвергается только внутреннему давлению. Тогда формулы A71)
напишутся так:
",= »1^.A-^). A72)
*) Это решение появилось впервые в статье Ламе и Клапейрона «Memoire
sur I'equilibre interieur des corps solides homog6nes», Mem. divers savans,
T. 4, 1833.
к^^ЖТЯ"'
176 ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ [ГЛ. VI
Эти уравнения показывают, что о^ всегда является сжимающим
напряжением, а о^ — растягивающим напряжением. Последнее является
наибольшим на внутренней, поверхности цилиндра, где оно равняется
^ (а) —Р^(^^±П Г174^
Это уравнение показывает, что (а/)тах всегда численно больше
внутреннего давления и приближается к этой величине, когда b
увеличивается. Наименьшее значение о^ будет на наружной поверхности
цилиндра. Отношение
Ыт1ах_аЧ1*! -
(-/)min 2а^
увеличивается с увеличением толщины стенки цилиндра. При
сравнительно малой толщинне нет большой разницы между наибольшим и
наименьшим значениями а^. Взяв, например, Ь=1,\а, найдем, что
(о^)тах превосходит (o^)mjn на 10,5У(,. Поэтому ошибка будет малой,
если мы. предположим, что растягивающие напряжения о^ равномерно
распределяются по толщине стенки, и воспользуемся формулой
а
I
которая совпадает с выражением, приведенным на стр. 106,для
тонкостенных цилиндров. Касательное напряжение будет наибольшим на
внутренней поверхности цилиндра, где оно равно
2 1 62 —fl2 "Г" г,2_д2 J—г,2_д8- КЧ
2
Когда на цилиндр действует только наружное давление, мы имеем
^?з = 0, и формулы A71) дают
__ РнЬ
д — РХ^'
В этом случае а^ и о^ оба — сжимающие напряжения, и о^ всегда
численно больше, чем а^. Наибольшее сжимающее напряжение будет
на внутренней поверхности цилиндра, где
Ыг=« = -^^. A77)
Интересно отметить, что когда отношение bja радиусов цилиндра
увеличивается, то это наибольшее сжимающее напряжение
приближается к удвоенному' значению наружного давления, действующего
на цилиндр, а именно к — 2/?„.
41]
НАПРЯЖЕНИЯ, ВЫЗЫВАЕМЫЕ ГОРЯЧЕЙ ПОСАДКОЙ
177
Рассмотрим теперь деформацию цилиндра. Подставляя значения (j)
произвольных постоянных в уравнение (f), находим •
и
Ка'рв
Ь'Ри
. 62 —fls
A78)
Это дает радиальное перемещение для любой точки стенки цилиндра.
В частном случае цилиндра, подверженного только внутреннему
давлению (рц = 0), радиальное перемещение на внутренней поверхности
на основании выражения A78) будет
A79)
Когда цилиндр подвергается только наружному давлению (р^ = 0),
радиальное перемещение на наружной поверхности равно
A80)
Знак минус указывает на то, что перемещение направлено к оси
цилиндра.
41. Напряжения, вызываемые горячей посадкой
Если необхо;5имо вызвать контактное давление между втулкой и
валом или между двумя кольцами, собранными одно внутри другого,
то обычно на практике делают внутренний радиус наружной части
меньше наружного радиуса внутренней части и конструкцию
собирают после предварительного
подогревания наружной части. ^-.-.^/^^/^^
После охлаждения возникнет
контактное давление между
двумя частями, которое
называется давлением от горячей
посадки. Величину этого
давления и напряжение,
возникающее от него, легко можно
вычислить при помощи формул
предыдущего параграфа. .
Предположим, например, что
нар)окный радиус внутреннего
цилиндра в ненапряженном со- ^
стоянии больше внутреннего радиуса наружного цилиндра (рис. 128)
на величину 8. Тогда после сборки возникнет давление р между
двумя цилиндрами. Величина р найдется из того условия, что .
увеличение внутреннего радиуса, наружного цилиндра плюс уменьшение
наружного радиуса внутреннего цилиндра должно быть равно 8.
Г"р_ -S7ffl - -
а>
Ь)
Рис. 128.
ш
178 ДЁФХ)РМАЦИИ. СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО оси 1ГЛ. VI
Следовательно, на основании формул^A79)' и A80) запишем
Тогда формулы A72) и A73) дадут напряжения в наружном цилиндре
A81), а A75) и A76) —напряжения во внутреннем цилиндре. При
расчете обычно рассматриваются напряжения, возникающие на
внутренней поверхности наружного цилиндра. Эти напряжения будут
Наибольшее касательное напряжение на этой поверхности равное
((СМ. формулу (к), стр. 176) -
рс^ '
или, подставляя вместо р его значение из формулы A81), находим
В частном случае сплошного вала и втулки мы имеем а = 0, что
дает
d
(\ •^'nax^f, A84)
^^"'^'^'4 - т. е. наибольшее касательное напряжение будет
таким же, как в простом растянутом стержне»
Рис. 129. который претерпевает относительное удлинение,
'равное bjb.
В предыдущих рассуждениях предполагалось,, что оба цилиндра
имеют одинаковую длину. В случае вала и втулки (рис." 129)
выступающие части вала сопротивляются сжатию, в результате чего давле-^
ние вблизи концов втулки увеличивается, как показано
заштрихованной эпюрой *). 1 \ '
- ^) Экспериментальное исследования напряжений or горячей посадки
приведены в статье: А. Huggenberger, Technische Blatter, Schweiz. Loko-
motiv. und Maschinenfabrik, Winterthur, 1926. Дальнейшее рассмотрение
напряжений от горячей посадки даны в статье: W. J а п i с к i, Schweiz. Baiizei-
tung, т. 88, 93, 1926 и т. 90, стр. 127, 1927. См. также J. W. Baugher,
Trans. А' S. М. е., г. 52, 1930 и О. J. Horger and С. W. Nelson, J.Appl.
Mech., т. 4, стр. 183, 1937 и т. 5, стр. 32, 1938. Практические сведения
о напряжениях от горячей посадки см. О. J. Horger, изд., А. S. М. Е.
Handbook, New York, стр. 178, 1953. Точное решение задачи см. S. Timo-
S h е п к о and J. N. G о о d i е г, Theory ol Elasticity, стр. 388, 195K
41] НАПРЯЖЕНИЯ, ВЫЗЫВАЕМЫЕ ГОРЯЧЕЙ 1^0САДК0Й 179
Если составной цилиндр, как» например, представленный на рие. 128,
подвергается внутреннему давлению, то вызываемые этим давлением
напряжения будут такими же, как в цилиндре со сплошной стенкой
толщиной с — а. Эти напряжения накладываются на напряжения от
торячей посадки. Горячая посадка вызывает окр)окное сжимающее
напряжение ва внутренней поверхности цилиндра, которое уменьшает
наибольшее окружное растягивающее напряжение, вызываемое
внутренним давлением в этом месте, так что можно получить более
благоприятное распределение напряжений, чем в случае цельной трубы
{см. задачу 2, стр. 179). Поэтому цилиндры, составленные из несколь-
, ких труб, применяются в тех; случаях, где внутренние давления очень
высоки, как, например, в стволах орудий.
Расдределение начальных напряжений, аналогичное описанному
*ыше» в случае составных цилиндров можно также получить и в
цельной трубе, применяя высокое внутреннее давление, достаточное для
того, чтобы вызвать остаточную деформацию во внутренней части
трубы. После удаления этого внутреннего давления останутся
некоторые напряжения в трубе вследствие остаточной деформации, так
что тогда внутренняя часть будет находиться в состоянии сжатия, а
наружная часть в состоянии растяжения*).
ЗАДАЧИ
1. Определить окружные напряжения на внутренней и наружной
поверхностях и в середине толщины стенки цилиндра при внутреннем радиусе 10 cjf
я наружном радиусе 20 см, подверженного внутреннему давлению р„ =
«= 2000 лгг/сж ■.
Ответ. Из формулы A73) получаем (ог^)^ = ю ел = ^^^ кг/см^; (а^)^ ^ ,^ ^^ =ss
fc 1830 лгг/сж»; Ы^^зо сл= 1^^ '^^Z''^^-
2. Определить напряжение в составном цилиндре (риЬ. 128),
подверженном'внутреннему давлению /»в = 2000 lfг/cлf^ если а = 10 см, Ь = 1Ъ см,
€ = 20 см, Ь = 0,Ь\2 см, , -
Решение. Определим сначала первоначальные напряжения в цилиндре
всле^^ствие разности внутреннего радиуса наружной поверхности и
наружного радиуса внутренней поверхности. По формуле A81) получаем
р- 2-10''-0>012A5«-10'')B0''-15«) _ . ~
Р~^ 15.2* 15=» B0* —10=») —/оилгг/сл.
Окружные напряжения, вызываемые этим давлением во внутреннем цилиндре,
йа основании формулы A76) будут
/ ч 2/»*=» 2-260-15* „^ , g
i'^t)r^ 10 cjK = — ь^^-а' "^ i5»_iQa = 7" ^^ кфм^
(«у)г=15гж=-.^^=^^-700 KZJCM\
b^~cfi
^) Дальнейшее изложение этого вопроса дано в п. 70.
^сг«<?^тж'Гр'
w
180 ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ [ГЛ. VT
Напряжения для наружного цилиндра на основании формулы A73) будут
/,л _Р(Ь' + с^) „ 260AУ + 20^) _ р ,
(Ч)г== 15см — с^ — ь^ ~ 20^—152 ^ ~ кг\см ,
/ ч _ 2/?г>^ „2-260•15''^^^ 5,
(Of)r = 20 CJK -"^ (.2 1,2 — 20® — 15® ~ л:г/сл .
Распределение первоначальных напряжений о/ по толщине стенки показано
на рис. 128, & пунктирами тп и ittiW,. Напряжения, вызванные внутренним
давлением, такие же, как и в предыдущей задаче, представлены на рисунке
пунктиром SS. Наложение этих двух распределений напряжений дает эпюру
напряжений, представленную заштрихованной площадью. Можно видеть, что
благодаря перЁоначальным напряжениям, возникшим при сборке, наибольшее
напр)яжение в цилиндре, подверженном внутреннему давлению, уменьшается
с 3330 до 2800 л:г/cлf^
3. Пользуясь рис. 128, найти напряжение о^ от горячей посадки при
г,= 15 см и г = 25 см, если в = 10 см, ft = 20 см, с = 30 см. Воспользоватьсй
коэффициентом насадки bjb == 0,001 и принять £ = 2 • 10* tcejcM^.
Ответ. (<ц\^'^^^^ = — 900 кг/сж''; (о<)^^25сл~^^^ '^^/'^•***-
4. Для втулки и вала на рис. 129 найти равномерное давление р, если
радиус вала равен 15 см и наружный радиус втулки равен 30 см. Начальная
разность диаметров между втулкой и валом равняется 0,03 см. Принять
£ = 2-10« KZJcM^. ч
42. Вращающийся диск постоянной толщины
Когда круглый диск вращается вокруг оси симметрии, которая
перпендикулярна диску, то силы инерции вызывают напряжения,
которые могут получиться очень большими при высоких, скоростях. Эти
напряжения распределяются симметрично относительно оси вращения
и могут быть вычислены при помощи метода, указанного в п. 40.
Предполагается, что напряжения не изменяются по толщине диска, и
эта толщина принимается равной единице.
Уравнение равновесия такого элемента, как тпт^п^ на рис. 127,
выводится п)пгем добавления к силам, которые были рассмотрены
в п. 40, силы инерции, действующей на элемент:
"f^^drdb. (а)
В этом уравнении ^ есть вес единицы объема и ш—угловая скорость
диска. Остальные обозначения те же, что в п.' 40. Тогда уравнение
равновесия получится в следующем виде:
o,-",-r^-L_ = 0. (b)
Подставляя вместо напряжений о^ и о^ выражения их в зависимости
от перемещения и (выражение A7G), стр. 174), получаем след)гющее
уравнение:
rf^U , 1 rfW «1/1 Si^t^^^r rt /10КЛ
42] ВРАЩАЮЩИЙСЯ ДИСК ПОСТОЯННОЙ ТОЛЩИНЫ 181
Общее решение этого уравнения получается путем сложения частного
решения с решением соответствующего однородного уравнений^
{cjA. уравнения (е) и (f), стр. 175). Частное решение будет
Тогда, пользуясь обозначением
iV=(l-fx«)J^, (С>
получаем общее решение уравнения A85)
H = -iV^+Qr + ^% (d)
где так же, как и прежде, Q и Са — постоянные, которые нужно
определить таким путем, чтобы удовлетворить условиям на краях
диска. * '
Для диска с отверстием в центре (рис. 127) и при отсутствии
сил на его контуре эти условия выразятся так:
(оЛ-а==0. (о,),_, = 0. (е>
Общее выражение для о^. получится, если подставить выражение (d)-
в первое из уравнений A70), стр. 174, что дает
■ °.= r^[-^A^'-' + (l+f*)Ci-(l-fx)C«-i]. (f)
при г = а и г = Ь это выражение должно обратиться., в нуль, как та
следует из уравнений (е). Производя эту подстановку, мы получаем1
для определения Ci и С^ следующие уравнения:'
_3±ifyv«a_|_(i_|_j,)Q-(i-fx)a^,=o, *
„3_+^A/^.2_|_(i_|_j,)C',-(l-fx)a^ = 0,
откуда
C, = j^(a'+n« C,=^|i±£gaWW. (h>
Общее выражение для и получится, если эти значения подставить
в уравнение (d). Затем, подставив в уравнения A70) результирующее
выражение для м, мы найдем
°r=-^^)EN[a--\-b--r'^-^^)^ A86>
(g>
m
•182
ДЕФОРМАЦИИ. СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ
1ГЛ. Vl
Если теперь N заменить его значением, данн£|м формулой (с), и по-*
-ложить •
= а,
г
Т
:ЛГ, Й@ = г>,
то формулы A86) и A87) станут следующими:
Видно, что радиальное напряжение о^ обращается в нуль на краях,
где х==1 или х==а, и оно цоложительно для других значений х
Наибольшее же значение имеет место при
(i)
A88)
A89)
j, = lAa==|/"|
!ИЛИ
Пользуясь формулой (j) для г, получаем из -выражения A88)
ш
A90)
Окружное напряжение а^ достигает наибольшего значения на
внутреннем крае диска. Подставляя х = а.
в выражение A89Х получаем
A91)
Можно видеть, что (o^)max всегдя
больше, чем (ОгУтах-
На рис. 130 значения членов,
_ содержащихся в скобках
выражений A88) и A89), показаны как
ординаты в зависимости от
значений X, принятых абсциссгАйи.
Сплошные линии представляют
случаи а =1/4, т.е. внутренний
радиус "составляет 1/4 наружного
радиуса. Пунктиры представляют
значения члена, содержащегося в скобках выражения A89), для
других значений а. Формулой A91) устанавливается, что напряжение
{о/)тах на внутреннем крае изменяется в зависимости от а по
параболическому закону. Это показано кривой тп на рис. 130.
Рис. 130.
42] ВРАЩАЮЩИЙСЯ ДИСК ПОСТОЯННОЙ ТОЛЩИНЫ 1Ш
Интересно отметить, что когда внутренний радиус очень мал,
т. е. Ъ приближается к нулю, то наблюдается очень резкое изменение-
напряжения Of вблизи отверстия. Это показано кривой mpq, дл» KOTOjpofi.
(=,W=f'4^. 0'92>
Для другого крайнего случая, когда внутренний радиус приближается
к наружному радиусу Диска и а приближается к единице,
выражение A91) приводится к виду
Это совпадает с формулой A5) т. I, стр. 36, которая была получена-
для тонкого вращающегося кольца. Видно, что в случае диска с
отверстием в центре наибольшее напряжение незначительно меняется
с изменением радиуса отверстия; значение для очень тонкого кольца
лиш^> приблизительно на 20*%, выше значения для очень толстого-
кольца с малым отверстием.
В случае сплошного диска условие на конце будет м = 0 при
г :р= 0; следовательно, постоянную Cj в общем регйенйи (уравнение (d))-
нужно принять равной нулю. Постоянная Q найдется из условия, что
0^ = 0 на наружном крае диска. Пользуясь вторым из выражений (g),.
мы, таким образом, получаем
c.=g|^m ^ (к>
Рводя теперь значения постоянных Q и Са в общее выражение
(уравнение (d)) для перемещения и, подставляем затем результат в
формулы A70) стр. 174. Таким путем получаем
где X =: г/Ь. и радиальное, и окружное напряжения всегда
положительны и увеличиваются с уменьшением х. Другими словами,
напряжения увеличиваются с |1риближением их к центру. В центре (х=0}
напряжения будут
@/)шах==(б^)тах==^ ^. A95)
Сравнивая это с формулой A02), видим, что благодаря концентрации
напряжение на кр^ю малого центрального отверстия в два разд
больше, чем в центре сплошного диска. Закон изменения
напряжения Of по радиусу сплошного диска представлен на рис. 130
пунктиром pipg.
^t
mm
i 84 ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО оси 1ГЛ. V!
Формулы, выведенные выше для вращающихся дисков, применяются
чиногда для сравнительно длинных цилиндров *), например, для роторов
электрических машин. В больших машинах окружные скорости
бывают весьма велики. Вышеприведенные рассуждения показывают, что
'Напряжения, вызываемые силами инерции, пропорциональны квадрату
окружной скорости и поэтому они имеют первостепенное значение
« таких случаях. Следовательно, для материала данной прочности й
для данной угловой скорости ротора существует определенный предел
для диаметра ротора, за который опасно переходить.
При выборе рабочих напряжений для таких роторов необходимо
иметь в виду, что очень большие поковки могут, по всей вероятности,
ниметь дефекты материала у центра, где как раз достигают
наибольшего значения напрйжения, обусловленные силами инерции. Чтобы
■исключить неопределенность, на практике обычно просверливают
^центральное отверстие по оси ротора. Хотя наибольшие напряжения
вследствие наличия отверстия увеличиваются вдвое, однако это ком-
ттенсируётся возможностью исследования доброкачественности
материала внутри поковки. При предварительных испытаниях ротор
заставляют вращаться со скоростью, выше обычной % так что
напряжения Около отверстия могут превосходить предел текучести. После
-остановки ротора напряжения не исчезнут совершенно вследствие
•остаточной деформации материала у отверстия. Внутренняя часть
металла, претерпевшая текучесть, сжимается наружной, а наружная,
наоборот, растягивается внутренней ^). Это явление совершенно
аналогично тому, что происходит в толстостенном цилиндре, перенапряжен-
шом под действием внутреннего давления (см. стр. 179). Остаточные
напряжения, вызываемые у отверстия перенапряжением,
противоположны по знаку напряжениям, обусловленным силами инерции;
следовательно, перенапряжение оказывает благоприятное влияние на
окончательное распределение напряжения в роторе ^).
Необходимо также заметить, что полученные выше выражения для
напряжений (см. формулы A88) и A89)), кроме v и постоянных,
определяющих свойства материала, содержат лишь отношения а и х.
Следовательно, для данного материала и данной окружной скорости
напряжения равны в подобно расположенных точках геометрически
*) Распределение напряжений в толстых дисках рассмотрено в книге
Timoshenko and Goodier, Theory of Elasticity, стр. 352, 1951; русский
перевод, 1937, стр. 348.
*) В электрических машинах обычно на 2070 выше рабочей скорости.
^) Этот вопрос разобран С. Honegge г'ом. Brown Bowery С. Mitt.,
«оябрь 1919.
^) Остаточные напряжения во вращающихся дисках, вследствие
текучести металла, были исследованы А. N а d а i and L. Н. D о n n е 1 Гем; см.
Trails. А. S. М. е., Appl. Mech. Div., 1928. См. также Н. Н е п с к у, Z. angew.
Math. u. Mech., т. 4, стр. 331, 1924 и F. Laszlo, там же, т. 5, стр. 281,
i925.
42]
ВРАЩАЮЩИЙСЯ ДИСК постоянной ТОЛЩИНЫ
185-
подобных роторов. Это обстоятельство может упростить вычисления
напряжений геометрически подобных дисков, а также может быть
испол^ьзовано при установлении прочности больших дисков на
основании испытаний моделей. ' '
В предыдущем изложении предполагалось, что контуры дисков свободны
от внешних сил. Если же на диск действуют растягивающие или сжимающие
силы, равномерно распределенные по его контуру, то вызываемые ими
напряжения найдутся при помощи формул, выведенных для толстостенных
цилиндров (п. 40). Эти напряжения (см. формулы A71)) можно представить-
в виде /
с, = А ■
п
0^
A>
где k и п — постоянные, зависящие от размеров диска и от величины
внешних сил, действующих на контуре. Напряжения, определяемые по
формулам A), должны быть присоединены к напряжениям из формул A88) и A89),
и полные напряжения могут быть представлены так:
В
A96>
где
<^г = А + ~
■л В
<^1 = Л~-^-
Т 3 + fA
g 8 '
- h'^'r\
-pco^r».
s
1
l+3{ji
8
A97>
}
A98>
A99>
A и В — постоянные интегрирования, которые можно вычислить в каждом
частном случае при помощи выражений A71), A88) и A89). При
обозначениях „ „ „
W = ~s
выражения A96) становятся
s~A-\rBw; t=nA — Bw. B00>
Если S н t известны для какой-либо точки диска, то эти величины для
другой точки можно легко найти, пользуясь следующим графическим методом *)..
Пусть Sj и tt означают величины ей/ для какой-
либо точки, где w = Wx (рис. 131). Тогда
величины Ss и ti для какой-либо другой точки, где
W = tJWg, получатся как отрезки, отсекаемые на
вертикальной линии, проходящей через w^,
прямыми s^s^ и t{tz, которые между собой
пересекаются на оси ординат (t4; = 0) и одинаково
наклонены к этой оси. Эти линии представляют
графически уравнения B00). Они имеют общую
ординату А на оси mjoeO и имеют равные и
противоположные по знаку углы наклона (it В). Это
графическое построение является весьма
полезным при вычислении напряжений во вращающихся дисках переменной
толщины, как мы увидим в следующем параграфе.
/7
1
s.t
L,'^^
1
1^^
\
1
-!•%
-.1^^
О
и/
*^,
^
Рис. 131.
*) Этот метод .был разработан R. Gramme Гем, Dinglers Polytcch. J.^
т. 338, стр. 217, 1923. .
186
ДЕФОРМАЦИИ* СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ
ЗАДАЧИ
{ГЛ^ V;I
1, Определить напряжения, возникающие под действием центробежны|:
ц:ил в роторе; наружный его радиус равей 65 см и радиус внутреннего
отверстия —10 см. Наружная часть ротора имеет прорези глубиной 25 сщ
9 которые вкладывается обмотка (рис. 132). ?*отор стальной и делает 1800
оборотов в минуту. Вес обмотки в прорезях равен весу удаленного мате-*
риала. ' ' -
Решение. Часть ротора, заключенная между наружной поверхностью
й цилиндрической поверхностью радиуса 40 сие из-за наличия радиальных
прорезай не может испытывать окружные
растягивающие напряжения.' Центробежная сила,
возникающая в этом вращающемся кольце, передается
в виде радиальных растягивающих напряжений на
поверхность цилиндра радиусом 40 см. Величина этих
напряжений равняется
65
Ро
I
2те.40
i
I
'Ifco''
r=«40
g, 2«-40 g
2% \ r4r =
If CO*
g
• 1755.
Рис. 132.
При Y== 0,0078 кг!CM* и g = 98l см/сек* это дает
/>„ = 495 кг/смК
Наибольшее окружное напряжение, возникающее на внутреннем контуре от
р1а1стягивающих напряжений р^, по формуле (П7) равняется
2-495-40»
40*—10»
= 1056 кг/смК^
Наибольшее окружное напряжение на том же контуре, обусловленное влия-
яием массы ротора, расположенной между радиусами в" 10 см и 40 см, и
вычисленное, как для вращающегося диска, по формуле A91), равняется
0^ = 378 кг/см'. Тогда полное наибольшее окружное напряжение на
внутреннем контуре будет равно (fff)mg,jj = (a^4-a^')= 105б-{-378= 1434 KeJcM'.
2, Стальное кольцо насажено на чугунный диск (рис. 128). Определить
изменение давления по поверхности их соприкасания, вызванное силами
«нерции при 3600 об/мин, если- «( = 2,5 см, b = \2,5 см, с =25 см,
£с==2«10» лггМ*, Яч= I • 10* Ifг/сл**, Yc = 0,0078 лгг/слс» и ^ч = 0,0072 кг(см^.
Решение. Пусть ро будет увеличение давления между^жольцом и диском.
Произвольные постоянные в уравнении (f) для наружного кольца
определятся из уравнений
. |^_ £±ii yvc* + A -f ^) с, -A - ^)Q -^] = о,
^+ A+1^)С,-A-fi)C,-iJ=-Po.
8
(m)
Если мы применим уравнение (f) к внутреннему диску, для которого
произвольные постоянные обозначим через С[ к С^, & N" — постоянная,
определяемая формулой (с), то для определения С[ и С'^-иы получим следующие
491 ВРАЩАЮЩИЙСЯ диск ПЕРЕМЕННОЙ толщины 187
уравнения:
i^[-^A^v+(i+f^)ei-(i-,x)c;^]=o.
(п>
Из уравнений (га) и (п) можно найти четыре постоянные С„ С^, С[ и С^.
как функции 7>о. Величина-^ке Ро найдется из того условия, что на
поверхности соприкасания радиальные перемещения диска и кольца равны между
собой. В результате, пользуясь уравнением (d), получим для определения р^
следующее уравнение:
Числовые вычисления предоставляется произвести читателю.
3. Найти изменение давления р, вычисленного в задаче 4 п. 41, если
вал и втулка вращаются со скоростью 1800 оборотов в минуту, 7=^
==0,00.78 кг/сж» и £s=2»10« кг/сж«.
43. Вращающийся диск переменной толщины^
Вопрос об определении напряжений во вращающемся диске переменной
толщины является более сложным *). Мы разберем приближенный метод
решения этой задачи, основанный на замене действительного профиля
системой дисков постоянной толщины (рис. 133)''). Напряжения в отдельных
дисках вычисляются по формулам, выведенными в п. 42. В таком случае мьь
должны будем рассмотреть условия на границах между этими дисками,,
например, в сечениях 2, 3, 4 (рис. 133), где» имеет место резкое изменение
Хоящины jjHCKa. Если у и у-\-Лу означают толщины двух рассматриваемых
СМЕЖНЫХ дисков» то соответствующее изменение До^ величины радиального-
напряжения о^ найдется из уравнения ' ,
которое выведено в предположении, как и прежде, что напряжени»
равномерно распределяются по толщине диска. Решая это уравнение,.
^) Общее уравнение для этого случая вместе с решениями его
разными методами можно на^йти в книге: А. Stodqla, Dampf- und Gasturbi-
nen, 6 изд., стр. 312 — Й40, 1924. Вращающийся диск конического профиля
был рассмотрен Н. М. М а г t i п* о м. Engineering, т. 115, стр. 1, 1923, В. Н о d-
к i п S о п' о м, Engineermg, т. 116, стр. 274, 1923 и А. F i s с h е г' о м, Z, Osterr»
Ing. u. Architekt-Ver., т. 74, стр. 46, 19^2. См. также книгу: L. Malkin,:
Festigkeitsberechnung rotierender Scheiben, Berlin, 1935 и книгу: С. В. В i е-
гепо und R. Grammel, Technische Dynamik, т. 2, ст. 5, 1953.
^) Этот метод был разработан M.Don а th' ом. Die Berechnungrotierender
Scheiben und Ringe, Berlii^, 1912. Это описано на английском языке Н. Не а г 1 е
в Engineering, т. 106, стр. 131, 1918. Дальнейшая разработка метода при-
надлежит R. Grammel'ю, цит. на стр. 185, и числовой пример рис. 133
был взят из этой статьи. См. также статьи: М. G. Dr lessen. Trans.
А. S. М, е., Appl. Mech. Div., 1928; К. Grammel, Ing. Arch., т. 7, стр. 136,.
1936; R. G. Olsson, там же, т. 8, стр. 270 и 373, 1937; А. Held, там же,,
т. 10, стр. 339, 1939. Приближенный метод решения задачи был дан О. F. L а-
к е, J. Ар1. Mech., т. 12, стр. А-65, 1945. .
188
ДЕФОРМАЦИИ. СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ
[ГЛ. У1
получаем
Ну
^<^r=-yqf^V (а)
изменение Да^ окружного напряжения в том же сечении найдется из
условия, что относительное окружное удлинение будет одним и тем же на обеих
•сторонах сечения. Следовательно,
а; — р.а^ = (а/-|-Да^) — fx (а^-f ДаД
•откуда
Да^ = (лДо^.
Toriia из соотношений A98) найдем
B01)
Д8
Да. = -г г~- <Sr,
tit = До^ = {лДв.
I
Формулы A97), A98), A99) и B01) совместно с графическим решением,
данным на рис. 131, достаточны для расчета диска переменной толш.ины.
В качестве примера рассмотрим изображенный на рис. 133 диск,
вращающийся со скоростью 3000 оборотов в минуту. Размеры диска даны
/б^;,-^/ —z\~ --^:- 2^ж
Сйнптиме/пры
I
Рис. 133.
в табл. 17. В дополнение предположим, что центробежные силы,
приложенные на внешнем крае, как,^ например, центробежная сила лопаток турбины,
вызывают радиальное напряжение на внешнем контуре, равное (аД =
= 100 KZlcM^. Пусть {А = 0,3 и Y = 0,00785 кг1см^. Тогда из соотношений A97)
мы получим Р|Со2== 0,327 /сг/слг*, рсоа = 0,188 кг 1см*,
Первые восемь колонок табл. 17 составлены на основании приведенных
выше данных и рис. 133. \
Вычисление напряжений мы начнем с внешнего контура диска, где
известно напряжение (a^)i. Величина окружного напряжения (a^)i на
наружном контуре обычно бывает неизвестной, поэтому для начала расчета
необходимо ею задаться. Возьмем для простоты вычисления (a^)j так, чтобы s и
t были равны между собой (см. формулы A98)). Тогда
(^<I = Ы1 + Р1«^?-Ро>П
431
-т—I
о»
«
ВРАЩАЮЩИЙСЯ ДИСК ПЕРЕМЕННОЙ ТОЛЩИНЫ
189
»
s
S
eg
&
«e
o.
la
о
oa
« '
s
s
Ф
зе
R
O.
В
ctt
s
к
as
X
«
о
s
vr
2
TO
еч
«•^
о
at
00
^^
<o
tf3
■*
TO
(N
—
t5
CM
CI
C4
©1 .
Ч
< >-
est
>>
+
>1
u
1^
CO.»!
eg
1
is
;
8
(
oo
о
о
5:
»—t
oo
о
о
I
О
*—4
00
CM
CO
о
coco
сою
Ю
S7
8T
s
•-и
- +
) с
г —
00
со
CM
со
со
см
см
ю
о
г—1
о
00
1ПЮ
ог-
оо -^
оосм
1 +
оо «
о 1
со
со
00
t
1 «^
о
со
см
§
со
со"
см
ю
со
со
со
ю
со
см
CDOO
см см
СО'-'
1
осл
оосм
7+
осм
юг-
о 1
о
о
1
оо
■—(
см
о
о
с^
ю
см
со
ю
см
•*
о
со
со
ю
■*со
^00
Ю '—'
Sf+
юг^
О) см
т+
см •*
оос»
со 1
со
00
о
1
) 1Г
г се
ю
со
о
о
ю"
см
8
о .
см
ю
00
оо
со
ю?о
^см
CMC»
т+
ОС»
"*СМ
7+
О! с»
^5 о
со
со
1
00
ю
о
о
1—*
со
со
со
о
со
I
ю
со
8
о
00
см
QO
о^
ю ю
со -^
см •*
со
t
с
см
•*
t^
у
-^
-^
•^
-*
ю
см
см
ю
г-н
г-
со
со
со
см
ю
с» см
t^ о
coco
оою
00 ю
1 +
■«fCM
0H0
см»-"
о
о
со
t
00
о
г-о
00"-
г-00
'-см
1
> о
*—4
с»
см
1—*
ю
8
со
58
ю
см"
00
с»
со
со
о
о
о
о
1 "■
8
г-н
о
¥—1
О)
190
ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ
1ГЛ. Vt
ИЛИ, пользуясь числами 5-й и 6-й колонок таблицы, получаем
(а^Х = 100-f 817 — 470 = 447 /сг/сл*.
Теперь из формул A98) находим
Si = (a^)i + PitoV; = 100+ 817 == 917 кг1см\
/j = (a/)j-f pcoV? = 447 + 470te: 917 к:г/cж^
Так как s,s=/„ то при построении, указанном на рщ. 131, прямые 8 и f
совпадают. На рис. 134, где s и ^ приняты ординатами, а а» = 1/г*
—абсциссой, эти линии изобразятся линией а — а, параллельной оси щ.-^ Длина этой
кг/аа^
Рис. 134.
линии, соответствующая радиальному расстоянию / — 2 диска (рис. 134),
определится из чисел 4-й колонки таблицы. Таким образом, получим для
селения 2 (рис. 133)
' 8я = *, = 917 KZlCM^,
а пользуясь формула|Ми A98), найдем
("Л = Ss — РХг| = 917—662 6= 255 кг/сж«,
(о^)я = fa ^рсо«г| = 917-^381 =s536 кг/слс".
В сечении 2 имеет место резкое изменение толошны диска. Чтобы
принять это в расчет, мы воспользуемся формулами (^1) совместно с числами
в-й колонки таблицы 17. Тогда
(Д8),=^(До^)»= (--j:^o^^== 1,50-255=^383 1сг/сл«,
(Д/)д = (Да^)л = I* (As)s 3= 0,3.383 = 115 KZICM\
44] ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ПОЛОМ ЦИЛИНДРЕ 191
%обы получить ТОЧКИ'5 и с, мы должны п|шбавить эти величины к
ординате точки а на рис. 134; линии ЬЬ и ее тогда будут построены, как указано
на рис. 131. Таким же образом будут найдены Sj и t^ для сечения 3.
Повторяя указанный процесс, поаучрм все необходимые данные для сечения 3 и
т. д. Таким образом, мы можем вычислить все Значения верхних строчек
в колонках от 9-й до 12а* табл. 17.
Вследствие того, что «алря^вкение (o^)i на краю диска было взято произ-
вольно, условия на щнутренн^м контуре обычно не будут удовлетворены и
напряжение (оД, полученное указанньлм способом, не будет совпадать с
напряжением, которое в дей<^тви*ельности там имеется. Для того чтобы
удовлетворить условиям на внутреннем контуре, необходимо произвести дополни^
тельное вычисление. Положив (a,.)j=0, <.) = 0 и взяв для (а^)^ произвольное
значение (в расчете принято (ij/)i == 50.1с?/сл1*), получим rent же, что и ранее,
приемом соответствующее распределение напряже>1ий. В этом случае по
формулам A98) мы получаем &^=^<Sr и < === о/. Результаты этих вычислений
приведены в нижних строчках колонок от 9-й до 12-й, а соответствукшдае
построения представлены линиями f к s' на рис. 134. Решение, которое
удовлетворяет действительным условиям на внутреннем контуре диска,
получится путем сочетания двух найденных выше р1аспределений напряжений
Следующим образом. Пусть @^)9 и (в^)' будут радиальные напряжения на
внутреннем контуре диска, полученные соответственно при первом и втором
вычислениях, и пусть (ij^)g означает действительное напряжение на
внутреннем контуре. Тогда решение для действительных условий получится, если
напряжения, найденные во втором вычислении, умножить на величину
(«л
и присоединить их к напряжениям, найденным в первом вычислении.
Величина средних напряжений в сечениях, где толщина резко изменяется, может
быть вычислена из следую1Щ1х уравнений:
ы.=(„+^)+„{<+^),
ы''=(«(+у)+"(«;+^)..
Результаты этих вычислений в случае, когда радиальные напряжения на
внутреннем контуре равны нулю, приведены в двух последних колонках
таблицы и представлены двумя кривыми на рис. 133.
44. Температурные напрйжения в длинном полом цилиндре
Когда стенки цилиндра неравномерно нагреваются, то их элементы
расширяются неодинаково, вследствие чего возникают температурные
напряжения. В последующем изложении распределение температуры принимается
симметричным относительно оси цилиндра и постоянным вдоль этой оси.
В такбм случае деформации цилиндра будут симметричны относительно оси»
и мы можем воспользоваться методом, изложенным в п. 40. Вырежем из
цилиндра кольцо с двумя поперечными сечениями, перпендикулярными к оси
и находящимися одно от другого на: расстоянии, равном единице. Можно
допустить, что при деформации эти поперечные сечения остаются плоскими,
если взять их на достаточной расстоянии от концов цилиндра *); следова-
*) На концах напряжения в направлении оси цилиндра равны нулю, и
распределение напряжений получается более сложным.
w
192
ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ
'1ГЛ. VI
теяьно, относительные удлинения в осевом направлении будут постоянными.
Пусть 2 булет осью цилиндра, и> —осевое перемещение по z, остальные
обозначения будут теми же, что и в п. 40 и на рис. 127, Тогда oTHocHTeAjb"
ные удлинения в трех перпендикулярных направлениях будут
dw
Hz
const.
du __ и
(a)
Эти удлинения могут быть выражены в зависимости от' напряжений
"^1 V» °i и температурного расширения.> Пусть а — коэффициент линейного
расширения, at — прирост температуры -^ сверх равномерной начальной
температуры. Температурный прирост меняется только с изменением
радиального расстояния г. Из уравнений D3) (см. т. I, стр. 64) удлинения
определяются так;
(Ь)
tSi Ц. , . . . .
Обозначая через Д относительное объемное расширение, получаем
— Е
" Е
--^(«'r-f «'Л + яА
^ (огЧ-о^)Ч-«^
- р ("г+ «!/■) Ч-°^-
Из уравнений (Ь)-и (с) н^аходим
Е
("г Ч- «ir + «^/) Ч- 3af.
(С)
El. JA а\ "^^
2|л
(Ф
Уравнением равновесия элемента тп mirii (рис. 127) будет (см. уравнение (Ь),
стр. 174)
Подставляя уравнения (d) и (а) в уравнение (е), получаем
и
d^u 1 du
dr^ '^ г dr
1—II </r*
B02)
Это уравнение определяет перемещение и для какого-либо частного распре-
делЬния температуры. Оно.может быть переписано в следующем виде:
d Г1 d . Л \-\-\>. dt
dr\_r dr^ '\ 1—ji. rfr
Интегрирование no r дает
^ (ru)=1^ o^r -f 2C,r.
dr^ ' 1 — (i '
44] ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ПОЛОМ ЦИЛИНДРЕ
Второе интегрирование приводит к решению
и.
1 \+ii
\^^atrdr + C,r + C,
1
193
(П
где Ci и Са—постоянные интегрирования, которые дол?£ны быть
определены таким образом, чтобы удовлетворить условиям на внутренней и
наружной поверхностях цилиндра. Если эти поверхности считать свободными от
внешних сил, то условия для определения С, и Q выразятся так:
ы,
>=й-
0.
(а^)^_^, = 0.
(g)
Общее выражение для а^ получится, если подставить во второе из
уравнений (d) е^ = dujdr и е^ = «/г И затем взять вместо и его значение (i), что
дает
г
'г = гТ-Л~Т^' i '^r-'r + т^-^^+T^ '>).
(h)
Тогда из уравнений (g) находим
а
(i-ftx)(i—2^) 1 f ^ .
с.
а
0>
Подставляя эти значения в уравнение (h), получаем общее выражение для а^:
о, = ; 1 S I atr аг + ■^r::rz ^ I atr йг I. B03)
а а
а из уравнения равновесия (е) найдем общее выражение для о^:
г . ь
Г*-{-й(
1 • ^°/-
~l-jxLr«i
dtr dr
r^ip*
t^^^atrdr-at]^. B04)
a
Если закон распределения температуры по толщине стенки известен, то мы
можем раскрыть интегралы выражений B03) и B04) и получить о^ и а^ для
к)аждого частного случая.
Когда стенки цилиндра имеют температуру tf, на внутренней
поверхности и температуру, равную нулю, на наружной *), то закон распространения
температуры можно представить следующей функцией:
t =
'* In А
In —
а
B05)
*) Любое другое температурное состояние на поверхностях цилиндра
можно получить путем наложения на это состояние состояние равномерного
нагревания или охлаждения, что не вызывает каких-либо напряжений.
7 С, П, Тимошенко, т« 11
194
ДЕФОРМАЦИИ, СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ОСИ
1ГЛ. VI
При помощи этого выражения для t формулы B03) и B04) получаются в
следующем виде:
"/=
2A~{аIп
Eatb
а
2A
Ii)ln —
..fit
[•-•"l-^-^KI^)-!]-
B07)
Наибольшего значения <ц достигает на внутренней
стях цилиндра. Подставляя в последнее уравнение г
Eatb
■ а
или внешней поверхно-
5= в и r=ft, получаем
i!^t)r==.a~'
2A
(o/)r=ft = -
— fA)ln —
JEatb
2A
•|хIп —
' fit
B08)
B09)
Распределение температурных напряжений по толщине стенки для частного
случая, когда ajb равно 0,3 и tb отрицательно, показано на рис. 135.
Если толщина стенки мала по сравнению с наружным радиусом цилиндра,
то мы можем упростить формулы B08) и B09), полаг^ая
а '
In — = m
а
2
и рассматривая т как малую величину. Тогда
Eatb
О)
(к)
В случае очень тонких стенок вторым членом в скобках этих уравнений
можно пренебречь, и формулы совпадают с выведенными для неравномерно
нагретой пластинки (см. выражение
(87), стр. 81).,
В предыдущем
рассмотрели только
изложении мы
а^ и а/ и
показали, что эти величины не зависят
от удлинения е^ в направлении оси
цилиндра. Напряжения а^ могут быть
опредедены из первой формулы (d).
Подставляя ё, = dujdr, е/ = ujr и
пользуясь выражениями (f> для и и
(i) для произвольных постоянных, мы
в состоянии найти общее выражение
для 0^. Это выражение содержит постоянное удлинение, е^ в наггравленИи оси
цилиндра. Если мы допустим, что цйдщндр может свободно удлиняться, то
получим величину $^ из условия, что сумма нормальных усилий по
поперечному сечению, цилиндра, перпеидикуля]^ному к оси г, равняется нулю. В
результате этих вычислений получим следующее окончательное выражение для а/.
Рис. 135.
Eatb
2A—ii)ln
(•-
2 In
b^
2л» , b\
B10)
44] ТЕМПЕРАТУРНЫЕ НАПРЯЖЕНИЯ В ПОЛОМ ЦИЛИНДРЕ 105
Можно видеть, что на внутренней и наружной поверхностях цилиндра
напряжения ssg и 0^ равны между собЬй *).
В случае диска без отверстия в центре и имеющего постоянную
толщину, которую можно считать малой по сравнению с радиусом * диска, ра-
jpiaabHoe и окружное напряжения определяются следующими выражениями:
■ . * ■ г
а,>«а£ -53
аЕ
i^^jtrdr-lAtrdry, ' Bil>
в каждом частном случае, когда температура t известна как некоторая
функция г, интегралы в этих выражениях можно легко раскрыть и получить
температурные напря:)кения.
Температурные напряжения представляют большое практическое
значение, особенно для больших цилиндров, как, например, роторов паровых
турбин, тяжелых валов или больших турбинных jpckos. Во всех этих сл^учаях
нагревание или охлаждение должно быть постепенным для того, чтобы
понизить температурный градиент в радиальном направлении'). Температурные
напряжения имеют важное значение также и в дизельных двигателях").
В случае лгатериалов, которые слабо сопротивляются растяжению, как, на-'
пример, камень, кирпич и бетон, трещины, вероятно, начнутся ''на
наружной поверхности цилиндра, где ti, положительно.
ЗАДАЧИ
1. Определить температурное напряжения в цилиндре, имеющем 2а=э=1 см^
2Ьхж=3 см, Еа/{1—ft) = 35,7, если температура на внутренней его поверхно*
сти равняется ti, = —1°С, а на наружной поверхности равн1яется нулю.
Решение. По формулам B08) и B09) находим
(°/)г=а »= Ыг=а = 24 кг1см\
Ыг=ft = Ыг = ft =^ — 12 '^^^/СЖ».
Величина о^, на основании формулы B06),' достигает наибольшего значения
при г = 0,78 см и равняется 4,6 кг/смК Закон распределения напряжение
по толщине стенки показан на рис. 135.
*) Более подробное исследование темНературных напряжений в
цилиндрах было произведено С. Н. Lees, Proc. Roy. Soc. (London) A, т. 101, 1922.
Графики для быстрого расчета напряжений на основании уравнения B66)
B®7) и B10) были даны L. Н. В а г к е г'о м. Engineering, т. 124^ стр. 443,1927.
Численный пример, который приведен ниже, взят из этой статьи.
*) Рассмотрение вопроса о температурных напряжениях в цилиндрах,
В которых температура изменяется вдоль оси, дано А. S t о d о 1 а, цит. на
стр. .187, Приложение. Qm. также G. Eichelberg, Forschungsarb., № 220,
1923 и № 263. О температурных напряжениях в дискйх см. Н. Quednau,
Z. Ver. deut. Ing., т. 72, стр. 522, 1928. Та же задача рассмотрена в книге
Т i ш о S h е п к о and в о о d i е г. Theory of Elasticity, стр. 408, 1951; русский
перевод, 1937, стр. 401.
') См. Hi. Z ulz ё г. Temperature Variation and Heat Stresses in Diesel
Engines, T. 121, стр. 447, 1926; A. N5gel. Transfer qI Heat in Reciprocating
Engines, там же, T. 127, стр. 282, 1929; W. Nus,selt, Z. Ver, deut. Ing.„
T. 70, стр. 468, 1926; J. N. Goodier, J. Appl. Mech., т. 4, стр. A-33, 1937.
Щг'
ГЛАВА VII
КРУЧЕНИЕ
45. Валы некругового поперечного сечения
Вопрос о кручении круглых валов был рассмотрен в т. I (стр. 238),
Там же были даны формулы для наибольшего напряжения и для угла
закручивания прямоугольных валов. Имеется несколько других форм
поперечного сечения скручиваемого вала, для которых задача о распре^
делении напряжений и угле закручивания решена. На следующих
страницах дано несколько окончательных результатов, которые могут
представить практический интерес.
Рис. 137.
Эллиптическое поперечное сечение *). Наибольшее касательное
напряжение имеет место на концах малой оси mn (рис. 136) и равняется
_ 16Mfe
B13)
*) Решения задач на кручение для эллиптического поперечного сечений,
а также для равностороннего треугольника принадлежат St.-Ven ant'y,
Mem. des savants etrangers, т. 14, 1855. Вывод формул, данных здесь, можно
найти в книге Timoshenko and G о о d i е г. Theory of Elasticity, стр. 258,
1951; русский перевод, стр. 261, 1937.
45] ВАЛЫ НЕКРУГОВОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 197
Угол закручивания на единицу длины равен
е^^!^, B14)
где 7р = Gс/64) (&Л*-{-&'Л) — полярный момент инерции площади поперечного
сечения (см. т. 1,Приложение А, стр.352) и F = %bhl4 — площадь поперечного
сечения.
Равносторонний треугольник. Наибольшее касательно1е напряжение
имеет место в^ середине сторон (точки т на рис. 137) и может быть вычис^
лено по формуле
т -20Л4 .215)
Угол закручивания на единицу длины равняется
Правильный шестиугольник *). Для этого случая будут
max"" 0,217Frf '
B17)
, ^^ 0,133 Frf^O' ^^^^^
где d — диаметр вписанного круга и F—площадь поперечного сечения.
Правильный восьмиугольник. Для этого случая будут
'^тах= 0,223Frf ' ^^^"^
®^ 0,130 Fd^G' ^^^^^
где F п d имеют то же значение, что и в предыдущем случае.
Трапеция. В случае равнобочной трапеции приближенные значения
наибольшего напряжения и угла закручивания получаются при условии замены
тра]^еции эквивалентным прямоугольником, который получен, как указано
пунктирными линиями на рис. 138. Из центра
тяжести С трапеции чертим перпендикуляры ВС и CD
на боковые стороны и затем проводим вертикали
через точки В к D. Формулы A58) и A59), данные
ВТ. I, стр. 245, если применить к таким образом
полученному прямоугольному поперечному сечению,
дают приближенные значения х^^^ и в для трапеции,
показанной на рис. 138. г. ir^n
^ Рис. 138.
Для какого-либо сплошного (нетрубчатого)
вала приближенное значение угла закручивания получается путем
замены поперечного сечения эквивалентным эллиптическим сечением
той же площади Р и того же полярного момента инерции Jp. Тогда
приближенное значение для 6 будет дано формулой B14).
• *) Решения для правильного шестиугольника, восьмиугольника и
трапеции см. С. W е b е г, Die Lehre von der Verdrehungsfestigkeit, Berlin, 1921.
иг
Ш'
198 КРУЧЕНИЕ 1ГЛ. VU
46. Мембранная аналогия^).
Мембранная аналогия устанавливает определенные соотношения
между поверхностью провисания равномерно нагруженной мембраны!
и распределением напряжений в скручиваемом стержне. Вообразим
однородную мембрану с тем же очертанием, какое имеет поперечное
сечение скручиваемого "элемента, подверженную равномерному
растяжению на контуре и равномерному поперечному давлению. Можно
показать, что дифференциальное урав1уение провисания поверхности*);
этой мембраны имеет тот же вид, что и уравнение, которое
определяет распре;деление напряжений по поперечному сечению-
скручиваемого стержня. Если 5 — растягивающее усилие,
приходящееся на единицу длины контура мембраны, р — поперечное
давление, приходящееся на единицу^ площади, и - 6 — угол
закручивания на единицу длинМ стержня, то оба дифференциальных урав^
нения будут идентичны, когда ^
-f- = 209 (а).
Если это условие выполнено, то устанавливаются следующие
соотношения между поверхностью мембраны и распределением
касательных напряжений при кручении: 1) касательная к горизонтали
поверхности в любой точке провисшей мембраны дает направление
ка,сательн®го напряжения в Соответствующей точке поперечного
сечения скручиваемого стержня; 2) наибольший угол наклона мембраны
относительно контура в любой точке определяет величину
касательного напряжения в соотв€тств)пющей точке скручиваемого стержня;
Ъ) удвоенный объем, заключенный между поверхностью изогнутой
мембраны и плоскостью, проходящей через ее контур,
пропорционален крутящему моменту скручиваемого стержня.
Все эти положения можно легко доказать в случае кругового вала.
Пусть рис. 139 представляет соответствующу19 круговую мембрану,
равномерно растянутую усилиями »1? и нагруженную равномерным
давлением р, действующим вверх. Рассматривая центральный участок
/й« радиуса г мембраны (рис. 139, Ь), замечаем, что полное давление
*) Дналоги9 была разработана L. Р г а п d t Ге м, см. Phys. Z., т. 4, стр. 758,
1903; Jahresber. deut math. Ver., т. 13, стр. 31, 1904. О дальнейшем развитии
см. статьи: А. А. Griffith and G. I. Т ailor, PWc. Inst. Mech. Engrg.,
стр. 755, 1917и Advisory Comm. Aeronaut. (England)-Tech. Repts., т. 3, стр.920,
938 и 950, 1917—1918. См. также Timoshenko and Goodier, Theory of
Elasticity, стр. 289,^1951; русский перевод, стр. 267, 1937. '
*) Предполагается, что прогибы малы.
46}
MEMBIi^AHHAH AHAflOfH»
19^
на этот участок равняется пг^р. Это давление уравновешивается
растягивающими усилиям^ S, которые равномерно распределены по кругу
радиуса г и имеют направление
касательной к деформированйой мем-
бр1айе; Обозначая через w смещения
мембраны, получаем
dw
dr
dw pr < ^^^
tzr^p^—2icrS
и
dr
Подставляя в этл уравнение
значение pJS, данное формулой (а),
полу »*аем
-^=». (С)
Рис. 139.
В правой стороне этого уравнения мы имеем выражение для напря-^
жения кручения в скручиваемом круглом вале (см. уравнение (Ь), т. I,
стр; 239). Следовательно, угол наклона касательной к мембране
дает величину напряжения при кручении. Наибольший угол наклона
касательной к ме1М(бране в каждой точке направлен по меридиану;
следовательно, напряжение при кручении в валу в каждой точке имеет
най'рабление, перпендикулярное радиусу.
Это заключение снова согласуется с результатом элементарной
тпеории кручения.
''Чтобы определить крутящий момент, который, вызывает
напряжения, определяемые по уравнению (с), вычислим обЗ)ем, заключенный
между мембраной (рис. 139,\,а) и плоскостью контура АВ. Интег^и-
ро1ание уравнения (с) дает деформированную поверхность, мембраны
ее.«
г').
а требуемый объем будет равняться
V:
а
2i:rw dr = QB
тса*
■f G9-/p.
Сравнивая это выражение, с обычной формулой для крутящего
момента (см. уравнение A50) т. I, стр. 240), мы в мембранной аналогии
заключаем, что удвоенный обз;ем дает величину «рутящего. момента.
Следовательно, приведешще выше три положения относительно
мембранной аналогии легко доказываются в случае кругового
вала.
MW
200
КРУЧЕНИЕ
1ГЛ. VH
m --I —
В других случаях форму поверхности провисания мембраны надо
представить для заданного поперечного сечения, вала; следовательно,
качественные заключения относительно распределения напряжения при-
кручении легко получить. Например, для прямоугольного поперечногй*'
сечения поберхность изогнуто||
мембраны можно представить Т0^
ризонталями, как показано нд
рис. 140, а. Напряжение обратно
пропорционально расстоянию ме*'
жду этими линиями; следователь*
но, оно больше там, где линии
сближаются. Наибольшее нацряже-
ние имеет место в точках т — т^
где наклон поверхности мембраны
является наибольшим. В углах а,
Ь, с, d, где поверхность мембран»
совпадает с плоскостью контуре
abed, наклон этой поверхности
равен нулю; следовательно, каса*
тельное напряжение в этих точ*
ках равно нулю.
Рассмотрим теперь случай узкого прямоугольного поперечного
сечения (рис. 140, Ь). Изогнутую поверхность равномерно нагруженной
мембраны на некотором удалении от коротких сторон прямоугольника
можно считать цилиндрической. При этом допущении каждая полоска mni
поверхности ведет себя подобно равномерно нагруженной нити и ее
наибольший прогиб определяется выражением
гггттттк
О)
Ь/
-*
г—
/
/
р
"*
Рис. 140.
8S '
или, пользуясь соотношением (ia), находим
4
Наибольшее напряжение равно зтлу наклона поверхности в точках т—w.
Этот наклон поверхности равен 48/с для параболической кривой;
следовательно,
АЛ
max с
Срответствзтощий крутящий момент равен удвоенному объему, огра-^
ничейному мембраной и плоскостью контура. Пренебрегая влиянием
коротких сторон прямозтольника на деформацию мембраны и
вычисляя объем, принимая его за объем параболического цилиндра длиною Ь,
находим
2 ., 1
Mk = 2-^bbc
bc^m.
(#
46)
МЕМБРАННАЯ АНАЛОГИЯ
20i
откуда
6 =
Mt
ЪсЮ
B21)
Подставляя в выражение (d), получаем
max:
Mt
bc^
B22)
Эти формулы совпадают с формулами A58), A59), приведенными в т. I
(стр. 245), если прямоугольник предполагается очень узким.
Если вместо узкого прямоугольника мы имеем узкую трапецию, как
показано на рис. 141, то приближенное решение получается при допущении,
что поверхность изогнутой мембраны на достаточном удалении от коротких
сторон является конической. Удвоенный объем, соответствующий
элементу mm поперечного сечения, получается как в приведенном выше
уравнении (е). и равняется
-у ОЬсЧх, (f)
где с — переменная ширина поперечного сечения,
определяемая уравнением
c=»Ci+ % ^ -у- . (g)
Подставляя это в уравнение (f) и интегрируя результат,
получаем крутящий момент в следующем виде:
С 1 L. ' ЬОЬ
Mk=\-^ ОЬсЧх = -J2- (<=1 + Св) (cf + с|).
Тогда угол закручивания будет
6 =
1
B23)
Рис. 141.
Если Cj =5: Cfi :
моугольника.
с, эта формула совпадает с B21), полученной для узкого пря-
В более' сложных случаях, в которых форма изогнутой
поверхности мембраны не может быть легко определена аналитически, эту
поверхность можно исследовать экспериментально при помощи мыль-
'ной пленки для равномерно растянутой мембраны и путем H3MepeHHi»
наклона ее поверхности оптическим методом. Для этой цели
применяется аппарат, показанный на рис. 142*). Алюминиевая пластинка
с д)вумя Отверстиями — одним круглым и другим требуемой формы—
>) Gm. А. А. Griffith and О. I.Taylor, цит. на стр. 198.
MP
202 КРУЧЕНИЕ 1ГЛ. va
закрепляется между двумя половинами чугунного ящика А. Нижняя
часть ящика, имеющая форму неглубокого лотка, поддерживается
установочными винтами. Вследствие накачивания воздуха в эту часть ящика
мыльные пленки, покрывающие отверстие!, выгибаются вверх.
Горизонтали на поверхности мыльной пленки вычерчиваются прц
помощи винта В, который проходит через отверстие в листе плоского
! '
Рис. 142.
стекла. Стекло достаточно велико для того, чтобы покрыть ящик/
когда винт В находится в любом возможном положении. Нижний ко?
нец винта Несет закаленное стальное острие С, расстояние которого
от стеклянной пластинки фиксируется винтом. Острие приближаю*'
к пленке путем передвижения стеклянной пластинки до тех пор, пока
искажение вида пленки не покажет, что контакт достигнут. Запись
делается на листе бумаги, прикрепленном к доске' Е, которая может
вращаться вокруг горизонтальной оси, расположенной на том же уров^не,.
что и стальное записывающее острие D* Чтобы отметить какое-либо
положение винт», необходимо только наколоть точку на бумаге,
поворачивая доску вниз на записывающее острие. После того как острие
В заставили коснуться пленки в ряде мест, точки, записанные на бу-
461
меМБРАННАЯ АНАЛОГИЯ
203
Л^бмм Smm
^мм Jmm
маге, используются для вы«1ерчйвания горизонталей. ]^еняя установку
винта Д можно повторить э*у операцию для любого числа грризон-
талей. Когда эти линии наче^чен^и, объем и соответствующий
крутящий ^мент можно получить суммированием.
Углы наклона в мембране йч^оответСтвующие напряжения в стержне
получаются в результате измерения расстояний между соседними
горизонталями. Лучшую точность измерения наклонов можно получить,
направляя луч света на поверхность пленки и измеряя угол
отклонения отраженного луча. Чтобы установить соотношения между
измеренным наклоном и напряжением, пленки, покрывающие два отверстия в
алю^йиниевом листе, сравниваются при одном и том же давлении
воздуха. Так как обе пленки имеют одно и то же отношение jp/i", то
соответствующие два вала имеют
ОДНИ и те же значения C (см.
уравнение (а)). Следовательно, измеряя углы
наклонения двух мыльных пленок,
мы можем сравнить напряжения вала
данного поперечного сечения с
напряжениями круглого вала
известного диаметра при условии, что они
имеют один и тот же угол
закручивания 6 на единицу длины и один
и тот же модуль" сдвига. CooifBeT-
Ствующее отношение п крутящих
моментов определяется отношением
объемов, заключенных между
мыльными пленками и плоскостью
пластики. Это отношение дает
отношение жесткостей при кручении двух сопоставляемых валов. Что
касается напряжений круглого вала, то эти напряжения можно легко
вычислить в любой точке для любого заданного крутящего момента
JMft. Напряжение т, вызванное в какой-либо точке некруглого вала
крутящим моментом пМ^у получаетс^г п^гтем умножения напряжения т^
в выбранной точке круглого вала на экспериментально определяемое
отнйшение наибольшик наклонов в рассматриваемых точках двух
валов.
На рис. 143 изображены горизонтали, полученные для части
сечения двутавра, который был использован как лонжерон крыла
самолета. Вследствие близкой группировки горизонталей в выкружках
входящих углов и в середине верхней грани надо считать, что
касательные напряжения наибольшего значения достигают именно в этих местах.
Выступающие части полки очень мало напряжены. Наибольшее
напряжение в с[)еднем участке стенки практически постоянно вдоль граней
стенки и равно напряжению в узком прямоугольнике для того же
угла закручивания.
Рис. 143.
204
КРУЧЕНИЕ
1ГЛ. VU
1
а/
! а
Рис. 144.
3
ti3
г
С)
47. Кручение прокатных профилей
Формулы B21)^-и B22), выведенные для узкого прямоугольного
поперечного сечения, можно применить также для приближенных .ре-
щений в других случаях, в которых ширина поперечного сечения мала.
Например, в случае одинаковой толщины поперечных сечений, пока-.
занных на рис. 144, а и 144, Ь^
угол закручивания
получается из формулы B21)
путем подстановки .развернутой
длины осевой линии вместо i>.
Эта длина равняется Ь=^г ц
случае сечения, представлен^
ного на рис. 144, а, и Ь=^
== 2fl — с в случае
сечения, представленного на
рис. 144, fr. Наибольшее
напряжение для первого из этих двух сечений получается из формулы
B22). Для углового сечения (рис. 144, Ь) наибольшее напряжение имеет
место у входящего угла. Это наибольшее напряжение получается
путем умножения напряжения, даваемого формулой B22), на
коэффициент концентрации напряжений, ббльший единицы. Величина этого
коэффициента будет рассмотрена ниже (см. п. 68, стр. 258). -
'Приведенные здесь заключения следуют из мембранной аналогии,
Jм^мoтpeннoй в предыдущем параграфе. Из этого рассуждения чита-
т^ь мржет видеть, что если толщина с поперечного сечения,
показанного на рис. 144, а, мала по сравнению с радиусом г, то с
достаточной точностью все еще можно использовать параболическую кривукз!,
показанную на рис. 140, b и- определяющую провисание пленки *).
В таком случае наибольший наклон пленки и соответствующее
наибольшее напряжение для поперечного сечения на рис. 144, а будут
приблизительно такими же, как для узкого прямоугольника.
В случае швеллера, (рис. 144, с) угол закручивания получается
путем расчленения поперечного сечения на три прямоугольника, как
показано на ридгнке, с подстановкой в формулу B21) величины
"' ^1^1 ~Ь 2^2^! вместо Ьс^. Таким образом, мы получаем
6
гмк
(^c? + 2Vi)G-
B24)
Чтобы вычис>1ить напряжение, которое имеет место в середине
сторон Ьч полок, необходимо лишь, как видно из формул B21), B22)
■ ») Поверхность провисания здесь уже не цилиндрическая, но если с мало
1К) сравнению с г, то кривизна пленки в тангенциальном направлении мала
по сравнению с кривизной в радиальном направлении и ею можно пренебречь.
•47]
КРУЧЕНИЕ ПРОКАТНЫХ ПРОФИЛЕЙ
205
умножить 0 на с^О; тогда
SM^^
V? + 2Mr
B25)
Эти же приближенные формулы можно использовать также при
кручении двутавровых балок *) с полками постоянной толщины (рис. 145. а).
В случае двутавровой балки с наклонными полками (рис. 145,6)
мы обозначим через с^ толщину полок на к^аях и через Сд толщину
полок у стенки, так что
C3==C2 + Y^2tga-
^-
Т
i,^
1 L
^^ ^
/77
^г-
i
1 ГТ
4^^.^
/77
t)
Рис. 145.
Пользуясь выражением B23) для
полок, мы заключаем, что угол
закручивания б получается из фор- 1
мулы B24) путем подстановки в f—
него величины -^{c^-^-c^icl-^c"^ ^^
вместо с\.
Наибольшее напряжение
обычно имеет j^ecTO в выточках и носит
местный характер. Его величина будет рассмотрена в п. 58.
Значительное напряжение может также иметь место в точках /и (рис. 145, Щ
в середине наружных граней полок. Это последнее напряжение
получается по-прежнему путем умножения угла закручивания 6 на СдО, где
fg представляет наибольшую толщину полки.
Необходимо заметить, что при выводе формулы B24) была
использована формула для бесконечно узкого прямоугольника и что
влиянием коротких сторон прямоугольника на рис. 140 на величину
объема, ограниченного мыльной пленкой, совершенно пренебрегалось.
Благодаря наличию этих сторон объем, очевидно, будет несколько
уменьшен. В тс1 же самое время в углах швеллера (рис. 144, с\ где
сходятся вместе два прямоугольника, можно ожидать ббльшей
деформации мыльной пленки, чем в случае одного прямоугольника. Такое
дополнительное смещение вызывает увеличение объема. Эти два
фактора, которыми пренебрегалось при выводе формулы -B24),
противоположно действуя, в некоторой степени нейтрализуют друг
друга, так что формула B24) достаточно точна для тонкостенных
сечений \
^) Наибольшее напряжение имеет место во входящих углах, оно будет
рассмотрено ниже (см. п. 58, стр. 258).
^) Опыты с тонкостенными двутавровыми балками при кручении были
проделаны автором. Известия Петербургского политехнического института,
ъ 5, 1906. Эти испытания, показали удовлетворительное согласование с
формулой B24). Весьма обширный ряд испытаний на кручение прокатных балок
206
КРУЧЕНИЕ
1ГЛ. sftt
Для случаев кручения двутавровых балок и швеллеров, в которых
толщина полок не мала и изменяется по ширине полки, была выведеи1>1^
более сложная формула для жесткости кручения, которая wes^iiii
удовлетворительно согласуется с опытами.
ЗАДАЧИ
" 1. Найти отношение углов закручивания цельной и разрезанной кр}гг|(^Й
тонких труб одинаковы? геометрических размеров (рис. 146) и находяо^Йхся
под действием равных крутящих моментов.
Решение. Пользуясь формулами йЩ^
т. I, стр. 241 и B21), получаем для цеяьййА
и разрезанной труб соответственно
^>
\\
6 =
32Mk
Ttd
Oi
ЗМк
Рис. 146.
<Ч^){^)'о'
Отношение углов закручивания будет равняться
Ь _2id — d„f
Bi 3 8d« + dr
Для очень тонких труб (d* + <^в)'^ 2rf* и отношение получается в виде
6 4 /Л\«
___ ■fTg __ (—i 1
6^ ■ 3 U j •
2. Определить угол закручивания на сантиметр длины швеллера
= 25 CJW, &8=:9 см, Ci=cil СМ,
■■ 0,€0088 рад на см.
(рис. 144, с), если M„=0000 кг-см, Ь^
fg = 1,5 см, О =в 8 • 10* кз/см^
Решение. Ь
3-20000
B5-18+18.1,5») 8-10*
', 3. Определить отношение наибольших касательных напряжений Щ9Д
труб, рассмотренных в задаче 1, если крутящие моменты одинаковы дМ.
обеих труб.
4. Определить жесткость кручения С для Двутавровой балки, рассмотреи-
ной на стр. 205, если полки наклонены так, как пояснено на той же странице»
48. Кручение тонкостенных трубчатых: стержней
При рассмотрении кручения тонкостенных трубчатых стержней
опять удобно применить мембранную аналогию *). В этом случав
наружный и внутренний края поперечного сечения располагаются
был сделан А. F б р р Гем, Sitzungsber. Bayer. Akad. Wissensch., стр. 295, 1921
и Bauingenieur. т. 3, стр. 42, 19Й. Некоторые поправочные коэффициенты
ДЛЯ формулы B24) были получены на основании этих опытов.
^ Формула была выведена на основании опытов, проделанных Inge Lys*
and В. G. Johnston, Lehigh University Publ., т. 9. 1935.
*) Кручение трубчатых стержней было рассмотрено R. В г е dt'oM, Z. Ver,
deut. Ing., т. 40, стр. 815, 1896. См. также Т. Р г еscо11^ Phil. Mag., т. 60,1920.
48} КРУЧЕНИЕ ТОНКОСТЕННЫХ ТРУ0ЧАТЫХ СТЕРЖНЕЙ 207
В мембране на различных горизонтальных плоскостях, соединяющих
края, как показано линиями тп на рис, 147. Если толщина трубы
Щп% то кривизной мембраны можно пренебречь, т. е. линии m;i можно
считать прямыми. Угол наклона мембранной поверхности в таком
случае будет постоянным по толщине стенки и
равным //А, где/—разность уровней двух краев
и h — толщина трубы, которая может
изменяться вдоль контура поперечного сечения. Мем- .
бранная аналогия указывает на то, что в этом
случае касательные напряжения равномерно рас-'
прёделяются по толщине стенки и определяются . , п "^ \
наклоном поверхйо<1ти, равным Ц_' \Л У f 'nI" 7
•= = 1' (^> " Рис.147.
Следовательно, напряжение/ по контуру обратно пропорционально
толщине стенки. Объем, заключенный между поверхностями mm и пй,
вычисляется при помощи осевой линии кольцевого поперечного
сечения, показанной штриховой кривой на рисунке. Если F — площадь,
ограниченная этой линией, объем ттпп равен Ff, то из мембранной
аналогии мы получаем -
M^^Wf. (b)
?*
Тогда из выражений (а) и (Ь) мы находим
т=^, B26)
Эту формулу можно применить при вычислении напряжений в труб;
чатых стержнях при кручении, если толщина стенки мала, изменение
толщины не является резким и нет входящих углов.
Угол закручивания 6 на единицу длины трубчатого стержня можно
вычислить из рассмотрения энергии деформации кручения. Энергия
деформации, приходящаяся на единицу длины трубчатого стержня,
равняется
U-.
I
S
•z^hds
2G
где S — длина осевой линии кольцевого поперечного сечения,
показанная на рис. 147 штриховой линией.
Подставляя в это уравнение значение т из формулы B26) и
приравнивая энергию деформации работе, совершенной крутящим
моментом,, получаем
,Jf = T^.e. (с)
о
3. Р ds 1
208
КРУЧЕНИЕ
1ГЛ. vn
откуда
B27)
В случае трубы одинаковой толщины т — постоянно и-Быражение B27)
приводится к виду
« = 2^- B28)
По этой формуле можно легко вычислить угол закручивания, когда
даны размеры /^поперечного сечения, касательное же напряжение х
можно определить, используя формулу B26).
Выражение B27), выведенное из рассмотрения энергии деформации
скручиваемого трубчатого стержня, можно также получить из
мембранной аналогии. Рассматривая равновесие плоскости п — w на рис. 147;
мы заключаем, что давление pF *), действующее на эту плоскостц '
уравновешивается растягивающими усилцями S, действующими в
мембране. Растягивающее усилие Sds, действук^ее на элемент ds контура,
имеет малый наклон поверхности, равный т; следовательно, вертикаль-^
„ пая составляющая этого усилия равна xSds,
и условие равновесия плоскости п — п будет
^
С
I
/7
П
^
ГГ-А"г^^
У /77
r-js.
лк
pF^^^iSds.
(d)
3
^ f
Рис. 148.
Замечая, что растягивающее усилие 5 в
мембране постоянно и что p/S = 2Cfi (см.
уравнение (а), стр. 198), мы находим из
уравнения (d) ' S '■
О
р_
S
:2G9.
Решая это уравнение относительно 6, мы получаем формулу B27)
для угла закру'^ивания.
Иногда требуется вычислить напряжения кручения в трубчатом стержне,
имеющем промежуточные стенки, как на рис. 148, а. Границы поперечного
сечения в этом случае формируются ^из трех замкнутых кривых. Применяя
мембранную аналогию, заметим, что эти кривые будут размещены в трек
различных горизонтальных плоскостях пп, рр и mm, как показано на рис. 148, Ь.
Мыльная пленка, соединяющая эти три кривые, образует ограниченную
поверхность, поперечные сечения которой показаны^ линиями тп, пр и /?т.
Предполагая опять, что толщины стенки hi, Л, и hg малы, и пренебрегая
*) В случае тонкостенных стержней площадь F, ограниченную осевой
линией (показанной пунктиром), можно рассматривать вместо площади
плоскости п —п.
48} КРУЧЕНИЕ ТОНКОСТЕННЫХ ТРУБЧАТЫХ СТЕРЗкНЕЙ 209
кри№Зной мембраны в направлениях, нормальных к краям сечения,
заключаем, что ЛИНИЙ тп, пр и рт являются прямыми. В таком случае наклоны
мембраны, дайщие напряжения в стенках трубчатого стержня, будут
'"—лГ-^^—лГ— ^*^
Величина крутящего момента, вызывающего эти напряжения, получается
путем удваийания объема фигуры тппррт на рис. 148, Ь. Если мы
обозначим площади, ограниченные пунктирными линиями на рис. 148, а, через Fi
и Fj, то этот крутящий момент будет равняться
Мк = 2(ПЛ + ^^,), (g)
или, пользуясь формулами (е), получаем
^k==2FAti+2FAv - (h)
Другие уравнения для решения задачи получаются применением
уравнения B27) к двум замкнутым кривым, указанным штриховыми линиями на
рис. 148, q^ Предполагая, что участок BCD стенки имеет постоянную
толщину hi и что участки DEB и DB имеют постоянную толщину, соответственно
равную Ла и Л,, из уравнения B27) имеем
^iSi + T8S8 = 2Ge/="i, (i)
•t2Sa—T8S8= 206^2. (j)
В этих выражениях s^, Sg и Sg являются длинами осевой линии, измеренными
по пунктирным линиям соответственно BCD, DEB и DB. Применяя
интеграл B27) к замкнутым кривым BCDB и DEBD, мы проходим участок DB
длины Sg в двух противоположных направлениях; следовательно, вторые
члены левых частей уравнений A) и (]) появляются с противоположными
знаками. Угол закручивания 6 правых частей выражений (i) и (j), очевидно,
тот же, что и угол закручивания всего трубчатого стержня. Четыре
уравнения (f), (h), (i) и (J) содержат четыре неизвестных т^, х^, Тд и 6, которые
можно легко вычислить. Исключая 6, мы получаем для касательных
напряжений следующие формулы:
^ _М Ma/'> + M8(fi + /^g) .к,
^^'''«2[M8S*/='? + M8StFi + A,/i,S8(/^\ + F,)«]' ^""^
^ ^М : /tsSifa + /tiSg (Fi + Fs) .,.
' '"^[fiih,s,Ff + h,h,s,FI + h,h,s,(Fi + F,n' ^'
■"' ""/^^ 2 [h,hsS,Ff + hJJiFi + h,h,s, (F, ^ F,Y] • ^^l
Если стенка DB поперечного сечения на рис. 148, а есть плоскость сим-
метрии поперечного сечения, то мы имеем Si = Sj, hi=^ha и F^ = F^, и
уравнение; (m) дает Т8 = 0. Таким, образом^^ в этом случае крутящий момент
воспринимается полностью наружной стенкой трубы, а промежуточная
стенка является ненапряженной ^).
Чтобы получить угол закручивания 6 для трубчатого стержня, мы должны
подставить вычисленное значение напряжений в уравнение (i) или (j). Таким
*) В этом выводе малыми напряжениями, соответствующими изменению
наклона мембраны по толщине стенки, пренебрегается. ■ '
ш
210
КРУЧЕНИЕ
[fJl^-VII
образом^ задача О кручении трубчатого стержня, подобного показанному ;щ
рис. 148, может быть легко решена с достаточной точностью при усло$|№^
что толщина стенки мала по сравнению с общими размерами nonepe^abi^d
сечения.
, В предыдущем примере был рассмотрен трубчатый стержень; состоящие
трдько из двух ячеек. В практических приложениях мы часто встречав!!!
стержни с ^большим числом ячеек, в ко^
торых случай алгебраического решение
описанный выше, становится
громоздким. . Быстрый ответ можно получить
путем численного решения задачи в
каждом частном случае при помощи метода
последовательных приближение) *).
Чтобы пояснить численные Метод, мы
рассмотрим случай трубчатого стержнях
тремя ячейками (рис. 149). Следуя npe-i'
Д1;|1дущим обозначениям, мы обозначим через /i, /g и /, соответствующие
трем ячейкам уровни мембраны, s^, ..., Se — длины осевых линий стенЬк
сегментов и Л^, Лв — соответствующие толщины стенок. Тогда, поступая
•по-прежнему, мы получаем вместо уравнений (i) и (j) следующие:
Рис. 149.
Ч/.-Л)|+л(|+|)+№-/.)|
.2аьр^,
(/2-Л)|^+Л|^ = 2Gв^в.
(^
Здесь величины /j = '«iAi, fa = 4^t, /i—А = Ъ^»г •••» называемые касатель*
ными потоками, вводятся вместо касательных напряжений т^, Tg, -pg, ...
Вводя обозначение sj/Aj = r|, мы можем переписать эти уравнения в следую-»
щем простом виде:
{^r^fi^rJ,^2QbF„
(
rji + (S П) Л - г J, = 2QbF„
2
(о>
где У\г1, ^Г|, y^ff—суммы значений г^ соответственно для первой, вто-
1 2 3
рой и третьей, ячеек. Разделяя эти уравнения на коэффициенты
диагональных членов и вводя обозначения
2оел -,
===— «18»
2 3
2 2
(р)
^) См. статью F. М. Вагоп'а, J. Appl. Mech., т, 9, стр. А-72, 1942.
481
КРУЧЕНИЕ ТОНКОСТЕННЫХ ТРУБЧАТЫХ СТЕРЖНЕЙ
21!
ок([|ичательно напишем уравнения в следующем виде:
-d.
Катим уравнениям мы прибавляем уравнение для вычисления крутящеги
момента, подобное уравнению (g):
A—dstfi=^fs, \
dtufi+ft^f». J
(q)
Mk^2(F^, + F^, + F,/3).
<r)
К численному рещению уравнений (q) мы приступаем, назначив численное
значение для угл? закручивания на единицу длины 6. Величины f[, /, и /,
тогда определятся, и уравнения (q) можно решить. Для того чтобы найти
соответствующее значение М^, в уравнение (г) подставляем результирующие
значения fi, /g и /ji Для какого-либо другого желательного значения
крутящего момента Мк мы должны лишь изменить значение в, /j, /, и /g в
прямой пропорции. >
tim
Д/7/ Р^Ц^^
ff,7 /J^
4Й7
ГЦВ
ff/0
цоз
072
£iff/S &,Ш2
f=SSS
7Д/ S.S7
Vyiz. 150.
«Л^
Применяя метод последовательных приближений к решению
уравнений (q), мы замечаем, что все коэффициенты «?;у меньше единицы. Поэтому
как Первое приближение мы сохраним лишь диагональные члены в
уравнениях (q) и примем /[, /i и j^ за первое приближение для /i, /а и /g.
Подставляя эти первые приближения в недиагональные члены уравнений (q),
мы получаем первые поправки:
A7i = rfiE/,. A%==rf8tf; + rf«aJ^, Д'Л==^«8/8- (S)
Подставляя значения (s) в недиагональные члены уравнений (q), получаем
бторые поправки:
Поступая точно таким же образом, находим третьи поправки и т. д.
Вычисления нужно повторять до тех пор, пока дальнейшие пойравк1и станут весьма
212 КРУЧЕНИЕ 1ГЛ. VII
малыми. Тогда, прибавляя все поправки к первым приближениям f[, /^ и /^^
получаем приближенные значения fi, /а и /j. Уравнение (г) даст
соответствующее значение М^, а значения касательных напряжений впредейятся
из уравнений, подобных уравнениям (е) и (f).
Чтобы пояснить вычисления, на рис. 150 приведен численный пример*)
для четырехячеечного сечения крыла. Площадь/каждой ячейки дана числом,
ограниченным прямоугольником, а значения г проставлены около каждой
стенки сегмента. В таблице, приведенной под рисунком, значения ^О дли-
каждой ячейки даны в первой строке. Во второй строке д^ны
коэффициенты dij для стенок промежуточных ячеек. През^де чем начать вычисления,
нужно эти коэффициенты переставить, как показано, стрелками в третью
строку. В следующей строке написаны первые приближения/* для
касательных потоков, вычисленные при допущении, что G6 = l. Первые поправки
вычисляются путем умножения каждого из значений/' на коэффициенты d^
расположенные над ними с перестановкой результирующих значений в смеж-^
ные ячейки, как показано стрелками. Полная поправка для внутр1енней ячейки
состоит из двух чисел, написанных по обе\стороны вертикальной линии..
Эти числа мысленно складываются и умножаются на соответствующий мно-,
житель при вычислении вторых поправок. Вычисления повторяются до тех
пор, пока поправки станут незначительными. Окончательные значения
касательных потоков, полученные путем добавления (сложения) всех поправок
^ к первым приближениям /', даны в последней строке на рис. 150. Подставляя
эти значения в уравнение (г), получим крутящий момент, соответствующий
Ов=1.
49. Кручение тонкостенных стержней открытого
профиля, в которых предотвращено искажение некоторых
поперечных сечений
В предыдущем обсуждении задачи о кручении двутавровых балок
и швеллеров (стр. 204) предполагалось, что крутящие моменты
приложены к концам (Стержня и «^то все поперечные сечения могут
совершенно свободно искажаться (коробиться). Однако имеются случаи,
в которых одно или несколько поперечных сечений стержня
вынуждены оставаться плоскими, и возникает вопрос, как это препятствие
искажению влияет на угол закручивания и на распределение
напряжений. Для стержней сплошного поперечного сечения, как, например,
эллипсы или прямоугольники, сопротивление искажению оказывает
лишь незначительное влияние на угол закручивания ^) при условии,
что размеры поперечного сечения малы по сравнению с длиной
стержня, В случае двутавровых балок, швеллеров и других тонкостенных,
стержней открытого профиля препятствие искажению при кручении
сопровождается изгибом полок и может оказать значительное влияние
на угол закручивания.
Простой случай, в котором имеет место препятствие искажению,
представляет собой двутавровая балка, скручиваемая парой сил по-
*) Этот пример взят из статьи Stanley U. Benspoter'a, J.
Aeronaut. Sci., т. 13, стр. 438, 1946.
*) Обсуждение этого вопроса см. в Timoshenko and Goodie г,
Theory of Elasticity, стр. 302, 1951; русский перевод, стр; 303, 1937,
49]
КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ
2\д
средине и свободно лежащая *) на двух опорах (рис. 151).
Вследствие "симметрии поперечное сечение тп при кручении должно
оставаться плоским, а поворот этого поперечного сечения относительно
концевых поперечных сечений будет сопровождаться изгибом полок.
Концевой крутящий момент уравновешивается в любом поперечном
сечении частично касательными напряжениями, возникающими от
кручения, и частично касательными
напряжениями, возникающими у^ ] ___«_.:____ у ^^^
от изгиба полок ^). Рис. 152, а >г:—
1]|редставляет половину балки,
показанной на рис. 151.
Среднее поперечное сечение тп
остается плоским благодаря
симметрии, и мы можем рас- Рис, 151.
сматривать его как заделанное
с крутящим моментом, приложенным на другом конце. Пусть ^^ будет
угол закручивания в каком-либо поперечном сечении балки. Тогда
часть крутящего момента. Mi, который уравновешивается
касательными напряжениями, вызванными кручением, определится из уравнения
^
777
\П
5
^—^
m:=c
dx'
(а>
в котором с — жесткость кручения стержня (см. т. I, стр. 246).
Чтобы определить часть крутящего момента Жк, который
уравновешивается касательными напряжениями в полках, возникающих от
изгиба, мы должны
рассмотреть изгиб полки (рис. 152, с).
Обозначая через h расстояние
между центрами.тяжести
полок (рис. 152, Ь), найдем
прогиб в каком-либо
поперечном сечении верхней полки:
> = f, (Ь)
и путем дифференцирования
получим
5^^~Т5^' ^^^ Рис. 152.
*) Простые опоры таковы, что концы балки не могут nOBopaqHeaTbCir
вокруг продольной оси, но могут свободно искривляться (коробиться).
®) См. статью автора «Известия Петербургского политехнического
института», 1905—1906, Z. Math. и. Phys., т. 58, стр. 361, 1910. См. также К. Н и b е г.
Диссертация, Мюнхен, 1922 и С. Weber, Z. angew. Math. u. Mech., т. 6^
стр. 85, 1926. Дальнейшее рассмотрение вопроса о различных формах
тонкостенных стержней дано А. Oetenfel d'oM, Lab. Baustatik Techn. Hochschule,,
Kopenhagen, Mitt. № 6, 1931.
'214 КРУЧЕНИЕ 1ГЛ. Vli
■Обозначив' череа D жесткость при изгибе одной полки в плоскости гл?;?
и заметив, что г; положительно в направлении, показанном на рис. Id^ivc,
получим выражение для поперечной силы в полке от изгиба*)
п — ^—п^—^^ /А\
где М — изгибающий момент полки. Принимая за положительное
направление Q такое, как показано на рис. 152, с, имеем ^
И полный крзггящий момент равняется
M, = ML + M'. = c'^^-5^§^.- B28)
В рассматриваемой задаче (рис. 152, с) крутящий момент 711^
является постоянным по длине / балки. Концевые условия таковы*^
тл поэтому рещение уравнения B29) будет
■*" " \ ch — /
\ а /
где .
Так как жесткость при изгибе D и жесткость при кручении С
измеряются в одних и тех же единицах (кгсм^), то из выражения (g)
следует, что а имеет, линейнуюг'размерность и зайисит от размеров
^алки.
Благодаря наличию второго члена в уравнении (f) угол
закручивания на единицу длины изменяется по длине стержня, хотя крутящий
момент остается постоянным. Кручение стержня, которое зависит от
изгиба полок и определяется уравнением, подобным уравнению B29),
называется неравномерным кручением.
Когда dtf/dx определено,- то части Мк и Жк полного крутящего
момента М^ можно вычислить для любого пеперечного сечения из
^) Влиянием поперечной силы на кривизну изогнутой оси полки в этом
выводе пренебрегается.
^) Условия определяются из рассмотрения каждой полки как балки
с одним защемленным и другим свободным концами.
49j КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖН1ЕЙ ОТКРЫТОГО ПРОФИЛЯ 21$
урацнейий (а) и (о). Для заделанного сечения, где л?5=0 и d(j>/rf^ = 0,.
мы получаем из уравнения (а), что Жк = 0. Следовательно, в этой
течке полный момент уравновёщивается моментоз! от поперечных сил,
действующих в полках, и мы имеем Q=s;: — Mjh. На концах jc = 4
пользуясь уравнением (f), получаем
Если длина балки велика по сравнению с ее поперечными размерами,
/ велико по сравнению с а, и второй член в скобках выражения (h)-
становится ничтожным, то d(f/dx приближается к значению MjC.
Изгибающий момент в полках находится из уравнения (d):
подставляя же выражение (f) ъкесто dtf/dx и пользуясь обозначен
нием (g), получаем
sh
^ sh —
Изгибающий, момент в заделанном конце будет равняться
Mjaax^^-^M^tgb-^. (к>
Когда / в несколько раз больше а, то tgh(l/a) приближается к еди-
аще и мы можем применять формулу
т. е- наибольший изгибающий^ момент полки такой же, как и для
консоли длиной а, нагр)гженной на конце«силой MJh. Для очень
короткой балки / маЛо- по ^сравнению с а, tg h (//а) приближается ^
к l/a, и мы имеем из выражения (к)
Afmax==^. (Ш)
Возьмем в качестве примера двутавровую балку с площадью
поперечного сечения 61,2 см'. Поперечное сечение заменяется эквивалентным
поперечным сечением (рис. 153), {состоящим из трех прямоугольников, имеющих
те же площади поперечных сечений полок и стенки, что и действительное
сечение ^}. Пользуясь уравнением B24), мы находим-
С =ж B7,12.0,9« + 2.12,6.1,44')-^ = 81,7 О.
1>
*) Несколько лучшее приближение для С можно получить, если принять
в расчет наклон полок, как пояснено на стр. 205.
m
216
КРУЧЕНИЕ
|ГЛ. VH
Жесткость при изгибе полки D получится, если взять половину момента
!11нерции стандартного поперечного сечения относительно вертикальной
главной оси*) и умножить на Е. Тогда В = ~Л'Е*зк
= 200 Е, и мы получаем из уравнения (g)
■Шмм-^
_ ^'■Smm
.300мм
а
V 2С
: 2,8 л.
(о)
А.
J^.'tMM
т
Рис. 153.
Следовательно, если балка нагружена, как показано
на рис. 151, то наибольший изгибающий момент в
полке на 0С(Н0вании формулы A) приблизительно
в три раза больше крутящего момента Жк при
условии, что балка достаточно длинна, так что tgh (//а)
близок к единице. Например, если //в = 2, так что
/«а 5,6 Л, мы имеем tg h f—^j =0,96, и ошибка в
предыдущем вычислении составит 4 процента.
Для вычисления угла закручивания <р мы пользуемся уравнением (f).
Интегрируя это уравнение и подбирая постоянную интегрирования
так, чтобы 9 = 0 при л:х=0, получаем
/ — X
I П СП
ash-
<Р
•^ +
а
а
atgh-^
(Р)
Подставляя в это уравнение д; = /, получаем
@,_,=^(/-«tghi-)
(ч)
Второй член в скобках представляет влияние изгиба полок на угол
закручивания. Для длинных балок tgh(//a)?=%:# 1, и уравнение (q)
получается в следующем виде:
М«
{i)x^i^-^{l—a\
(О
'Следовательно, влияние изгиба полок на угол закручивэний
эквивалентно уменьшению длины / на величину а.
Описанный выше метод для постоянного крутящего момента М.^
можно также применить в том случае^ когда крутящий момент
изменяется по длине балки. Необходимо лишь в уравнение B29)
подставить точное выражение Ж^ в функции х.
В предыдущем анализе кручения двутавровой балки (рис. 152)
■предполагалось на основании симметрии, что каждое поперечное
сечение поворачивается относительно центральной оси балки. Поэтому
нужно было рассматривать только изгиб полок- Ви^но также, что
*) Момент инерции площади поперечного сечения стенки предполагается
личтожным.
49]
КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ
217
этот изгиб не препятствует простому кручению стенки, так как в
местах соединения стенки с ^ полками напряжения от изгиба в полках
обращаются в нуль. В случае несимметричных поцеречных сечений
или поперечных сечений только с одной осью симметрии задача
становится более сложной, так как не только изгиб полок, но также
1
й
u;3
а)
Рис. 154.
^)
и изгиб стенки будет возникать при кручении. В качестве пример»
рассмотрим кручение швеллера (рис. 154). В этом случае при
кручении каждое поперечное сечение поворачивается относительно центра
сдвига О, который находится на
горизонтальной оси симметрии
поперечного сечения, на расстоянии,
равном (см. т. I, стр. 203)
от срединной плоскости стенки.
Из этого следует, что прогибы
полок и стенки в их срединных
плоскостях соответственно будут
2 = ±-^(р и >/ = е<р, (t)
Q
гх'О
^.
Т"
А
^
-X
&
^
^
Рис. 155.
где <р есть угол закручивания, который предполагается малым. Также,
предполагается, что толщины полок и стенки малы, так что
напряжениями, вызванными изгибом их в направлениях, перпендикулярных
к их средним плоскостям, можно пренебречь.
Взаимодействие между верхней полкой и стенкой • представлено
касательными напряжениями (Tjjj^)o, показанными на рис, 155. Эти
Напряжения вызывают изгиб и сжатие полки. Если .^ есть величина
сжимающего усилия в полке на расстоянии х от заделанного конца,,
то мы имеем ^
N *('Сгл)л = 0 = —^ Н
;=<Jc
ZX.
.)q йХт.
218
КРУЧЕНИЕ
Itn/i^i
Величина усилия 5 теперь определится из того условия, что
Деформация Sjp в продольном направлении в месте сопряжения стештм
полки одинакова для обеих этих частей. Вычисляя кривизны изогн^г
тых осей из выражений (t), находим, что условие представится урав*
иением *)
®J^~^^rfA:8T*~ 2 dx» 2 ЫЕ-
(«)
Теперь, пользуясь выражением (s) и замечая, что JgZ=:--^^~\ s—
получаем
■ 4SJg dx^'
(V)
Имея это выражение для 5, мы можем легко определить касательные
напряжения в стенке и в полках, а также часть Жк крутящего
момента, уравновешиваемого этими напряжениями.
Начнем с расчета касательных напряжений в стенке. Взяв два
смежных поперечных сечения тп- и тпфх (рис. 166, а) и рассмотрев
обычным путем равновесие ^штрихованного элемента, получим
В этом уравнении Sg—^ статический момент относительно оси z
заштрихованного участка поперечного сечения стенки (рис. 156, Ь),
t,h*
Jg =3= -i^—. момент инерции площади поперечного сечения стенки
относительно оси Z и М — изгибающий момент в стенке. Изгибающий
момент М является
положительным, если он вызывает
растяжение в верхней грани стенки
и равняется
1. гч^щ
%
^Ч dS
\
bl
С)
Тогда выражение для
напряжений получится в виде
Рис. 156,
^ух'
dS (. Sgh\
hdxV J'gl'
Замечая, что изменение Sg по высоте поперечного сечения следует
параболическому закону, находим, что распределение касательных
напряжений Ху^. дается заштрихованной площадью на рис. 156, с и что
^) В этом вУводе влиянием поперечных сил на кривизну изогнутой оси
полки пренебрегается.
щ
КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ
21^
равнодействующая касательных усилий в стенке обращается в нуль.
Это последнее заключение можно было предвидеть, так как касатель-^
ные усилия в стенке и в двух полках должны ур^авновесить часть М^
крутящего момента, а это возмвжно лишь в том случае, если каса-^
тельное усилие в стенке обращается в нуль, а касательные усилия.
в двух полках образуют пару
сил.
При вычислении
касательных' напряжений т^ в полке
(рис. 157, а) замечаем, что в
поперечном сечении /wn действует
сжимающее усилие 5 и
изгибающий момент*)
Ж;
(W)
Рис. 157.
Рассматривая равновесие заштрихованного элемента между двумя;
смежными поперечными сечениями, получаем
V\f^VtiMJv
dS J Ь — г
ах
dx
dx ^^ Л '
где Sgx и Jy должны быть вычислены для полки таким же образом,,
как Sg и J'z для стенки. Подставляя вместо М его значение (w)^
находим XdSb-z i£ rfy/^S,,
t dx^ 2 '
"ZX"
t dx b
Два члена правбй части этого уравнения представлены на рис. 157, b
заштрихованными, площадями соответственно треугольника и
параболического сегмента. Сумма этих двух площадей, у1мноз|«нная' на t^
дает полную поперечную силу в полке, которая равняете»*)
Q^
b dS , htb'' 1/89
2 dx J 24 dx^ '
Тогда, подставляя из уравнения (v) значение «S, получаем крутящий
момент, уравновешиваемый касательными (поперечными) усилиями в.
полках, в следующем виде:
Полный крутящий момент равняется
2 И '^4Jg)dx^'
^^-^dx
(У>
Etb
') ^= ~То~ означает, как и ранее (стр. 214), жесткость при изгибе полки.
в ее 1;лоскости.
') Положительное направление для Q показано на рис. 152, с.
iir
220
КРУЧЕНИЕ
(ГЛ. VH
Следовательно, все заключения, полученные для двутавровой балки,
можно применить для швеллера, если величину а^, определяемую
выражением (g), заменить величиной
«'=^('+^)-
\~i,4
\«'
St,
П
Метод, примененный при изложении кручения симметричного
швеллера (рйс. 154), мокно приложить также к более общему случаю
несимметричного корытного сечения (рис. 158). Положение центра
сдвига О для этой формы было определено
ранее (см. т. I, стр. 204—206). Далее, поступая
по-прежнему (см. выражения (t)), выразим
уравнения изогнутых осей полок и стенки в завиг
симости от утла закручивания <р- Продольные
усилия «Si и ,Sa в полках теперь определятся
из того условия, что в местах сопряжения
продольная деформация г^. одинакова, как для
■ стенки, так и для полки. Когда усилия 5i и 5^
^ вычислены, то распределение касательных
напряжений можно найти, как и для
симметричного швеллера. Затем можно показать *), что
касательное усилие в стенке обращается в нуль
и что касательные усилия jR в двух полках
создают пару, уравновешиваемую частью Жк крутящего момента. Мы
опять получаем для полного крутящего момента уравнение, подобное
уравнениям B29) и (у^ а вообще можно установить, что в случае
неравномерного кручения уравнение имеет следующий вид:
ii.
Т
Рис. 158.
^^-^%
Су
B3Q)
Постоянная Q, называемая жесткостью при короблении^ должна
быть определена в каждом частном случае так, как пояснено на
предыдущих примерах.
Метод, изложенный выше для неравномерного кручения стержней
открытого профиля,' можно также применить в случае трубчатых
стержней полигонального поперечного сечения*), и мы опять найдеМ,
что полный крутящий момент состоит из двух частей: 1) части,
обусловленной чистым кручением, как было показано в п. 48, и 2) части,
обусловленной изгибом плоских граней трубы. Логично ожидать, что
*) Вычисления даны в статье А. Ostenfeld'a, цит. на стр. 213.
2) Эта задача была рассмотрена впервые Н. R е i s s п е г'ом, Z. Flugtech.
U. MotGfluftschiffahrt, т. 17,стр. 384, 1926. См. такжестатыбТЬ. v. КЗгтйп'а
и N. В. Chr istensen'a в J. Aeronaut. Sci., т. 11, стр. 110, 1944 и статью
F. Stiissi, Publ. Internaut. Assoc. Bridge and Structural Engrg., т. 11, стр-
375. 1951 и т. 12, стр. 25§, 1952.
щ
КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ
221
в случае трубчатых стержней вторая часть крутящего момента будет
иметь весьма ограниченный характер в защемленном поперечном
сечении. Вычисление соответствующих напряжений по формуле для простой
балки может оказаться неточным, так что желательно произвести более
тщательный анализ напряжений для этого попе1речного сечения *).
H-iJ
ЗАДАЧИ
1. Консоль зетового сечения (рис. 159) защемлена одним концом и скру-
чива€тся парой сил М^, приложенной на другом конце. Найти угол
закручивания и наибольший изгибающий
момент в полках.
Решение. В этом случае центр сдвига
совпадает с центром тяжести С
поперечного сечения (см. т. I, стр. 206) и
никакого изгиба в стенке не происходит.
Усилия S идентичны для обеих полок;
распределение касательных напряжений
показано на рис. 159,- Ь.
Равнодействующая касательных усилий в стенке
обращается в нуль, а равные и
противоположные касательные усилия Q в
полках будут равняться
^ — — 12 Г 2bt + hti j dx* • Рис. 159.
Крутящий момент, обусловленный действием усилий Q, равняется
. = -С,* = -Ш.B-,,-^H
где D — жесткость при изгибе одной полки. Угол закручивания и
наибольший изгибающий момент в полках вычисляются по формулам (h) и A),
в которых для этого случая
"^ С V 2bt^htJ'
2. Решить задачу I, предполагая, что поперечное сечение такое, как
показано на рис. 160.
Ответ. Касательные усилия в полках будут рав- .^' ^
няться
Q=.±Dd^
dx^
где
n-Et,bl
^^ 12
bU
d
^1_
2*2
h — d blti •
Крутящий момент, от изгиба полок равняется
W
4^
^
Рис. 160.
*) См. статью Th. von Ка г mй n 'а and Wei-Zang Сh i е п 'а, J. Aeronaut
Sci., Т. 13, стр. 503, 1946. "
к^^^^^^ТЖГ^
W
222
КРУЧ11НИЕ
[ГЛ. VH
Значение а, подставляемое в выражения (h) и (Ь), имеет вид
Ddh
?. Решить задачу 1 для поперечных сечений, показанных на рис. 16).
)твет. В обоих случаях центр сдвига О находится на пересечеда1|
полок. Вращение относительно этой точки не вызывает никакого из1гибС
Рис, 161,
полок в их плоскостях, поэтому полный крутящий момент передаетсл
напряжениями от кручения и Л1*=0,
50. Совместный изгиб и кручение тонкостенных
^ стержней открытого профиля ^)
Рассмотрим общий, случай тонкостенного стержня, находящегося
под действием каких-либо поперечных нагрузок. Каждую силу можно
заменить параллельной силой, проходящей через ось центров сдвига,
и крутящим моментом. Таким образом, мы получи»! стержень,
нагруженные по оси центров сдвига и подверженный действию крутящих
моментов, приложенных в некоторых поперечных сечениях.
Поперечные силы, приложенные к оси центров сдвига, вызывают только
изгиб (см. т. I, п. 52, стр. 206). При рассмотрении кручения мы
можем воспользоваться результатами п. 49. Возьмем начало координат
в конце стержня (л: = 0) и обозначим через Жк крутящий момент
на этом конце. Чтобы определить угол закручивания <р,
воспользуемся уравнением B30). Разделив это уравнение на Ci и введя
обозначение
С
получим
_w
А^=
k\'
с г
B31)
где штрихи означают производные по х. Общее решение этого
^) См. стать*) автора, J. Franklin Inst, т. 239, № 3,4 и 5, стр. 258, 1945;
:кий перевод: Устойчивость упругих систем, Гостехиздат, 1955^
русский перевод
стр. 502-561
SO] СОВМЕСТНЫЙ ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ 223
уравнения будет
<р —__£—l-A-^Aishkx-^AiChkx, B32)
мк как в этом случае Л1к = Жк. Подобное уравнение можно написать
цля каждого участка стержня, взятого между двумк
последовательными поперечными нагрузками. Необходимо лишь заменить Жк
значением крутящего момента в начале этого участка. Постоянные
интегрирования должны быть тогда определены из условий
непрерывности в точках приложения нагрузок.
Вычисления можно значительно упростить, есщ вместо постоянных
интегрирования А, Ai и Л^^ мы вводим величины,, определяющие
условия на конце лг=О стержня*). Дифференцируя уравнение B32)
и подставляя дг = О, мы получаем
где нуль указывает на то, что величины относятся к концу х = 0
ётержня. Решая эти уравнения относительно, постоянных Л, Ai и Л9
и подставляя эти значения в уравнение B3^, получаем
<p==(po+i<PoSh^Ar+i^¥«4ch^Ar-l)-f Щх-^). B33)
В этом выражении угол закручивания «р для 1^акого-либо поперечного
сечения на ,первом участке стержня выражен в зависимости от величин
fo. ?о. <ро и Жк на конце х = 0. Дифференцируя уравнение B33),
находим
<p' = <P(,ch ^Аг -j-^ sh kx-\--^(l — ch kx),
<fi" = ^tpj sh kx -f- <po ch kx ^ sh kx. '
/
B34)
Уравнения B33) и B34) применимы в пределах между x = Q
и х=а, где а определяет положение первой поперечной
нагрузки.
При рассмотрении второго участка стержня (л; ]>> а) мы должны
принять в расчет крутящий Moiwenr Жк, приложенный, в пореречном
сечении л: = а. Выражение для )пгла.закручивания во втором участке
бруса теперь получится путгем добавления угла закручивания, вызванного
*) Этот метод был раз])аботан А.^Н. Кр^лдорым в связи с
рассмотрением изгиба балок, лтащйк;;на,упругим ос4йРЗНЙи._ См. его книгу «Расчет
балок на упругом основакйи», АН CGOP,- Ленинград, 1931.
224 КРУЧЕНИЕ [ГЛ. VII
Ml, к уравнению B33). Таким образом, мы получим для л:]>а
<? == срв + ^ <Ро sh.*-v-f-р-То (ch A-V — 1)-f
Последний член правой части представляет собой угол, вызываемый
Ml, Он получается из последнего члена уравнения B33) путем под-,
становки Мк вместо Мк и лг -— а вместо х, так как расстояние М^ от
рассматриваемого поперечного сечения равняется х — а.
Подобным образом мы можем поступить с третьим участком
стержня и так далее до последнего участка. Выражения для (р во
всех участках стержня содержат одни и те же постоянные <ро, <ро»
9о и Жк. Все эти постоянные можно теперь определить из условий
на двух концах стержня.
Чтобы пояснить метод, рассмотрим несколько простых примеров. Мы^
начнем со случая, в котором стержень скручивается крутящими моментами,
приложенными на концах, и в то же самое время концы оперты т^к, что
они могут вращаться, но коробление их совершенно исключено. Так как
в пролете не приложены силы, то уравнение B33) можно применить по
всей длине стержня. Предполагая, что конец л: = 0 неподвижен, и замечая,
что коробление исключено, мы должны в уравнение B33) подставить <{>о = 0»
Уд = 0, что дает
1 ./ v^fc 14 1 ^к f shftATN ' :
1 К
«p' = ^^2^ shkx-\-—^A — chАл:).
B36)
Так как коробление на другом конце {х = 1) стержня также устранено, то
мы имеем ^^
«р; =-^ «Ро sh А/+-^ A — ch й/) = О,
откуда ^
"fo— с shkl '
Подставляя это в первое из уравнений B36), получаем угол закручивания
Взяв x = t, мы получим поворот конца х = 1 стержня
^^ С \ А//2 }•
Второй член в скобках оценивает влияние концевого сопротивления
короблению на величину угла закручивания.
В качестве второго примера рассмотрим случай, показанный на рис. 162»
Стержень, опертый на концах, эксцентрично нагружен на расстоянии а от
501
СОВМЕСТНЫЙ ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ 225-
левого конца. Обозначая через е расстояние груза от оси центров сдвига,
мы сводим задачу к задаче на простой изгиб стержня нагрузкой Р в
сочетании с кручением, вызываемым крутящим моментом Ре. Предположим
сначала, что концы стержня не могут поворачиваться Относительно оси л:,,
но могут свободно коробиться. В таком случае условия на концах будут
^=«р''=0 при л: = 0 и л: = /.
Для участка стержня от л: = 0 до _—-?
д: = о мы пользуемся уравнением
B33). Подставив в это уравнение
«Рр = у^=:0, получим
<р == -^ <ро sh kx -}-
, ^к / sh Лл: \
Рис. 162.
Для правого участка стержня (л: > с) воспользуемся уравнением B35),,
которое при <рд=^* = 0 и M^ = Pe дает
1
' ии > ^к/ sh.kx\ Ре \
sb.k{x—^"fl)
k ^" ' С
Дифференцируя, мы находим
]■
kMl
kPe
<р* = k<f'o sh kx -^r- sh kx jT- sh ft (л: — a).
Замечая, что на конце x = l условия будут щ = (^^ = О, получаем следующие
уравнения для вычисления постоянных уц и М^г.
К
Ре
<fo sh kl + ~ (kl — sh kl) = — -^ [kl — ka — sh ft (l — a)\,
Щ Pe
<f 0 sh kl yr- sh kl = -yr sh ft (/ — fl).
Решая эти уравнения, получаем
Ml = — Ре
I —а
I
Ъ
Per sh ft (/ — а), /
С
a
shft/
^ /
Подставляя ^ти значения в выражения для «р, мы получаем углы
закручивания для обоих участков стержня. ■
Если концы стержня на рис. 162 защемлены и не могут коробиться, то
условия на концах будут
9 = 9' = О при л:==0 и х = 1.
Подставляя <рд = ^^ = О в уравнение B35), получаем при л: > а
Л^о / shftA- \ .'РеГ shft(^: —а)
1 ^ '''^к /
¥ = ^?o(chftA;-l) + -^(^:
8 С. П, Тимошенко, т, II
-) + ?^-«
]■
*226 КРУЧЕНИЕ ГГЛ. Vtt
Применяя это уравнение для конца х = 1, получаем следующие уравнений
для вычисления постоянных «fS и М*: -
kM?, л kPe
tpj (ch W ^ 1) И—^ {kl — sh fe/) = ^ [kl — ka — shk{l — a)];
ftM« kPe
<Po'shft/H—^ (l^chft/) = — ^[1—chfe(/ —fl)].
Из этих уравнений можно' вычислить постоянные ^о и М^ в каждом частной
случае. Подставляя их в выразрения для у, мы опять находим полное
решение задачи. Имея решение для одной сосредоточенной силы, как показано
на рис. 162, мы можем найти решение для любого числа сосредоточенных
■сил, применяя метод наложения.
Случай распределенной нагрузки также решается без затруднения.
В «ачестве примера рассмотрим опять стержень, показанный iia^nc. 162, и
предположим, что вместо силы Й имеем распределенную нагрузку
постоянной интенсивности д, приложенную по линии, параллельной оси х на
расстоянии е от "оси центров сдвига. Тогда крутящим моментом в произврль-
JHOM поперечном сечении будет ' \
Надставляя это значение в уравнение B30) и решая по-прежнему, получаем
Если оба конца стержня жестко защемлены, то условия на концах будут
-^г=у' = 0 при х=0 и х = 1. Тогда, подставляя <рд = ^о = 0 в выше
приведенное выражение для 9, получаем
' ^^-^-^«(chftA:—1L- "c-v k~j'^-:
2C '
Применяя это уравнение для конца л: = / и замечая, что из условий сим-
;^етрии М^==--gel/2, получим следующее уравнение:
откуда ^
^ gekl shkl
<Ро=^
2С chkl—l
Подставляя это значение в выражение для f, находим
gel shkl ... ,. gel { ^ %hkx\ . дех^
Это выражение мажно упростить и привести к следующему виду:
^_gel
kx
^ Т ^k(l~x) kx(l — x)
^Ы 2 2/
3hy
Из этих примеров видно, что решение уравнения B30) можно легко
получить в любом частном, случае.
щ
КРУТИЛЬНАЯ ФОРМА ПОТЕРИ З^рТОЙЧИВОСТИ
5L Крутильная формк потери устойчивости тоикоетенных
стержней открытого профиля*)
Ийвестно, что тонкостенный стержень под действием равномер-
•ного осевого сжатия ийогДа может потерять устойчивость в
крутильной форме, в то время как его ось остается
прямой. Рис 163 показывает пример
такого чистого, выпучивания от кручения
в случае стержня, имеющего четыре
одинаковых полКй. Волокно, совпадающее
с осью, остается прямым при этом
выпучивание, и момент Mg сжимающих сил,
приложенных на конце, обращается в нуль
для каждого поперечного сечения стержня.
Чтобы определить крутя1ций момент,.
вызывающий кручение, указанное на рисунке,
нужно 'рассмотрёт^> перемещение полок
при выпучивании. ^ ; '
Метод, которой должен быть
применен в последующем расчете, сначала
поясним на простом случае выпучивания стержня
(рис. 164, а). Первоначально стержень яв-^
ляется прямым и на него дейс-пвует тодько
центрально приложенная сила Р.
Предположим теперь, 1|то'сила Р достигла своего
критического значения, так что стержень
/^1
/ I
/ I
-М-
Рис. 463.
имеет слегка изогнутую
\\
f I
1.1
•*л
dri P
&)
Рис: 164.
форму равновесия. Благодаря этому изгибу напряжения изгиба будут
») См. статью автора, J. Franklin Inst., т.239, ^6 3, 4 и 5, стр. 263, 1,945.
^^cTi^^f^F'
28 КРУЧЕНИЕ - [ГЛ. VII
накладываться на первоначально равномерно распределенные
сжимающие напряжения. В то же время начальные напряжения будут
действовать на слегка повернутые поперечные сечения, как показано
на рис. 164,^. Каждый элемент изогнутого стержня между двумя
смежными поперечными сечениями находится в равновесии, и мы
можем считать, что напряжения изгиба, возникающие при
выпучивании стержня, находятся в равновесии с первоначально
сжимающими напряжениями, дейс^-вующими на слегка повернутые поперечные
сечения. Угол между двумя последовательными поперечными сечени-
ями после изгиба (рис. 164,^) будет а = — -r-^dx, где w — прогиб
стержня в направлении z. Поэтому мы заключаем, что действие
сжимающих сил Р на повернутые поперечные сечения стержня
эквивалентны, действию на каждый элемент стержня поперечной нагрузки
(рис. 164, с), равной — P-j—^dx. Отсюда ясно, что изогнутую ось
стержня и соответствующие напряжения изгиба можно найти,
предполагая, что. стержень нагружен фиктивной • нагрузкой интенсивности
— Pd^wjdx^. Дифференциальное уравнение изогнутой оси'в этом
случае будет
FT ^*^ fyd^W
Из этого уравнения можно получить обычным путем известное
критическое значение сжимающей силы Р^р-
Возвращаясь теперь к задаче о крутильной форме потери
устойчивости, показанной на рис. 163, мы можем установить, что в
критическом состоянии выпученная форма равновесия поддерживается
продольными сжимаюхйими напряжениями, действующими на повернутые
поперечные сечения волокон. Предполагая, что толщина t полок мала,
и рассматривая полоску поперечного сечения tdp на расстоянии р от
оси, мы видим, что вследствие выпучивания прогиб ее равняется
w =^ р9- Взяв один элемент этой полоски между двумя
последовательными поперечными сечениями, находящимися на расстоянии dx одно
от другого, и рассмотрев действие первоначального сжимающего
усилия at dp на слегка повернутые поперечные сечения полоски (рис. 163),
мы получим поперечную силу
— iptdp)^dx = — {atdp)P'^^dx.
Момент этой силы относительно оси х будет равняться
— ^j^dxitp^dp).
Суммируя эти моменты и распространяя суммирование на все
поперечное сечение, мы получаем крутящий момент, действующий на эле-
Б11 КРУТИЛЬНАЯ ФОРМА ПЬтЁ1*И УСТОЙЧИВОСТИ '' 229
мент выпученного при кручении стержня, заключенный между двумя
последовательными поперечными сечениями. Пользуясь обозначением т^
для крутящего момента, приходящегося на единицу длины стержня,
получаем
о
где Jo— полярный момент инерции плбщади поперечного сечения
стержня относительно центра сдвига, совпадающего в этом случае
с центром тяжести площади поперечного сечения. Для того чтобы
вывести теперь уравнение для выпученного стержня, воспользуемся^
уравнением B30). Дифференцируя это уравнение по лг и замечая, что
тх = j^, находим
Ci<p""—С<р" = отд^ B37)
Подставляя вместо т^ его значение, даваемое уравнением (а),
получаем
С,(р"" —(С—oJo)/' = 0. B38>
Из этого уравнения теперь будет получено критическое значение
сжимающего напряжения о. ' " '
Для случая, показанного на рис. 163, средние линии всех полок
пересекаются в поперечном сечении в одной точке, и, следовательнЬ,
жесткость при короблении Су обращается в нуль; поэтому
уравнение B38) получается в следующем виде:
(G—oJo)<p" = 0.
Это уравнение удовлетворяется, если допустить, что величина в
скобках обращается в нуль, что дает
4
Формула B39) указывает на то, что критическое значение
сжимающего напряжения не зависит от длины стержня и от формы
выпучивания, определяемой углом (р. Такой результат получается потому, что
при выводе уравнения B30) пренебрегалось каким бы то ни было
сопротивлением полок изгибу в направлении, перпендикулярном
плоскости полки. Для того чтобы такой изгиб принять в расчет, мы
должны рассматривать каждую полку как равномерно сжатую
пластинку, свободно опертую тремя краями и могущую совершенно
свободно выпучиваться по четвертому краю. Такое более точное
к^^ЖТЯ"'
230 КРУЧЕНИЕ 1ГЛ. V«
исслецование показывает, что критическое напряжение будет
равняться*)
Второй член в скобках дает влияние длины стержня на критическое
напряжение. Для стержней значительной длины этим членом можно
пренебречь. Тогда мы пЬлучим
_ 0,75 G^
При A== 0,3 это значение больше значения, вычисленного выше
(уравнение B39)), приблизительно на тУо-
Выражение B38) сохраняет свою силу также в случаях, когда Ci
не обращается в нуль, оно справедливо и для несимметричных попе^
речных сечений при условии, что ось стержня остается прямой при
выпучивании. Это требует, как мы увидим в следующем параграфе,
чтобы ось центров сдвига и Ъсь центров тяжести совпадали, как
в случае зетового сечения. Во всех таких случаях критическое
сжимающее напряжение получается из решения уравнения B38). Вводя
обозначение
B==°J^^, (b)
мы находим, что этим решением будет
tf = Asmkx-\-Ax cos kx ~\- Дл: ~\- А^ B40)
Если концы сжатого стержня не могут поворачиваться, но могут
свободно крробиться, мы имеем следующие условия на концах: , -
^ = (р'' = 0 при x = Q и x=-U
откуда следует
4i=i=^a = ^3 = 0 и Ы=П'к.
Подставляя это значение k в выражение (Ь), получаем
Наименьшее значение о, удовлетворяющее этому условию, равняется *)
°кр=^;^(с + ^С,). V B41)
% *) Это решение было получено автором, см. Известия Киевского
политехнического института, 1907 и Z.^'Math. и. Phys., т. 58, стр. 337, 1910.
^) Это решение было получено Н. Wagner'oM, 25th Anniversary
Publication, Technische Hochscfiule, Danzig, стр. 329, 1929.
щ
ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ИЗГИБА И,КРУЧЕНИЯ
231
Если концы стержня заделаны и не могут коробиться, условия
на концах будут
(pz=(p'==0 при х=0 и при х=1.
Для того Чтобы удовлетворить этим условиям, мы должны npHHHtb
Ai = — Лз, Л = Ла = 0 и- kl=2mzy
Наименьшее критическое сжимающее напряжение в этом случае будет
°-р'=^{^~^1^^')'
52. Потеря устойчивости тонкостенных стержней
открытого профиля от одновременного действия изгиба
и кручения ^} ^
Рассмотрим теперь общий случай потери устойчивости, когда под
действием центрального сжатия имеет место не только кручение, но
также и изгиб оси сжатого стержня. Предположим, что у и z
являются главными центральными осями поперечного сечения стержня до
выпучивания (рис. 165), nj/©» ^е —
координаты центра сдвига О. Перемещения
оси центров сдвига jb направлениях
у_ч Z при выпучивании обозначим че- '^^^ д>
рез V V. W соответственно, а через
9— угол поворота произвольного
поперечного сечения относительно оси
центров сдвига. На рис. 165 точки С viO
представляют отклоненные положения
центра тяжести С и центра сдвига (X
Тогда перемещения центральной оси при
выпучивании будут равны
V -\- г'оф и
^—Jo?-
Рис. 165.
Предполагая, что сила Р действует на
концах стержня по оси х, в случае _
свободно опертого стержня находим, что нагибающие моменты
относительно главных осей в дроизвольном поперечном сечении будут
My = P{w~y^4i\ Л!г = —PCiJ + ^o?).
^) Продольны^1 изгиб при кручении был рассмотрен Н. W а g п е г'ом,
цит. на стр. 230. См.также Н. Wagner and Pretschner,Luftfahrtforsch.,
т. 11, стр. 174, 1934; R. Kappus, там же, т. 14, стр. 444, 137. Английский
перевод последней статьи дан в Nat. Advisory Comm. Aeronaut. Tech. Mem.,
J№ 851, 1938. Cm. также статью автора в J. Franklin Inst,, т. 239, ^f^ 3, 4, 5,
стр. 201, 1945. Русский перевод. Устойчивость упругих систем, стр. 502—^561,
iir
232 КРУЧЕНИЕ [ГЛ. VII
Дифференциальн!^.1ми уравнениями упругой кривой для оси цеятров
сдвига будут
B42)
В дополнение к изгибу стержня, описанному уравнениями B42),
будут иметь место деформации кручения. Чтобы написать уравнение
для угла закручивания ср, поступтл так, как в п. 51. Возьмем
полоску поперечного сечения ^fl?s*), определяемую координатами у и z
в плоскости поперечного сечения, (доставляющие ее смещения в
направлениях у }А Z при выпучивании будут
'it
V-{-{ZQ~Z)(f и W--{yQ~y)(^.
Взяв вторые производные этих выражений по jc и рассмотрев
элемент dx волокна, найдем ло-прежнему, что сжимающие усилия at ds,
действующие pa слегка повернутые концы элемента dx, дают
следующие усилия в. направлениях у а z:
— atds-^[v~\-(z,i~-z)(^]dx,
d^
-~otds^^\w-~{yft~-y)<^\dx.
Опять обозначая черточками производные по л: и взяв моменты
указанных выше усилий относительно оси центров сдвига, получим (как
долю одной полоски) следующий крутящий момент, приходящийся на
единицу длины стержня:
dmjc = — atds[v"-{-(Zo — ^)?"](^в — ^)-{-
^ ~\-atds [w" — (у о—у) ф"] (Уо —у)
Интегрируя по всей площади поперечного сечения и замечая, что
- a^tds = P, \ztds = 0, ^ytds = 0,
F F F
1955; J. N. G о о d i e r, Cornell Univ. Eng. Exp. Sta. Bull., >fe 27, 1941 и
JSfe 28, 1942; и книгу В. 3. Власова «Тонкостенные упругие стержни»,
Москва, 1940. Относительно экспериментов на выпучивание при кручении
см. статью А. S. N i 1 е s, Nat. Advisory Comm. Aeronaut. Tech. Notes,
№733, 1939.
^) Величина ds есть элемент длины по средней линии поперечного
сечения.
Ъ2] ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ИЗГИБА И КРУЧЕНИЯ 233
получаем
т^ = iy,w" — z^if) Р — rg/Xp". (а)
где
^6 у о -Г ^0 -+" -^^-р •
Здесь Го — полярный радиус инерции площади поперечного сечения
относительно центра сдвига. Подставляя вычисленное значение т_^
(уравнение (а)) в уравнение B37), получаем
Ci^""—iC--rlP)t/' — P(y,w'' ~Zov") = 0. B43)
Это уравнение совместно с уравнениями B42) используем теперь для
определения критического значения сжимающей силы Р*).
Видно, что угол поворота (р входит во все три уравнения,
указывая на.то, что в общем случае "выпучивание при кручении
сопровождается изгибом оси, и мы имеем сочетание крутильной и изгибной
форм потери устойчивости. В частном случае, когда j;oF=-2^0 == О, т.е.
когда ось центров сдвига совпадает с центральной осью, каждое из
уравнений B42) и B43) содержит только одну неизвестную и может
быть решено отдельно. Тогда уравнения B42) дают два значения
критической нагрузки, соответствующие потере устойчивости в двух
главных плоскостях, как дается теорией Эйлера, а уравнение B43) дает
критическую нагрузку для чисто крутильного выпучивания, уже
рассмотренного в п. 51. Из этих трех значений критической нагрузки
естественно принять в расчет для практических приложений
наименьшее значение.
Возвращаясь к общему случаю, предположим, что концы сжатого
стержня не могут поворачиваться относительно оси х (рис. 163), но
они свободно могут коробиться и поворачиваться относительно осей
у i( Z (свободно опертые концы). В таком случае условия на концах
будут ,
V ^^w =(f =0, \
' „ „ f, (^ \ при лг = 0 и х = 1.
Все эти условия будут удовлетворяться, если взять решения
уравнений B42) .,и B43) в виде
г;==Л18ш^, и; = Ла8ш^, ср = Лз51п'^. B44)
^) Система уравнений, эквивалентная уравнениям B42) и B43), была
впервые получена Robert'oM К а р р и s*om; см. Jahrb. deut. Luftfahrtforsch.,
1937 и Luftfahrtforsch., т. 14, стр. 444, 1938.
2U
КРУЧЕНИЕ
[ГЛ. VII
Подставляя эти в]ыражения в уравнения B42) и B43), получаем
уравнения для вычисления постоянных i4i, Лд и Лд-
ip~EJ,pjAy + Pz,A, = 0,
[Р - £7,^) Л - РуоАз == О,
B45)
Эти уравнения удовлетворяются, если взять Ai = Ai = As = 0, что
Соответствует прямолинейной форме равновесия сжатого стержня.
Чтобы иметь выпученную форму равно8есия,чурав1нения B45) должнц
Лать 'для Ai, Ai и Аз решения, отличные от нуля, что возможно лишь
в том случае, если детерминант уравнений B45) обращается в нуль.
Для Простоты записи введем здесь обозначения
Р.=
/^8=7^@+^^). B46)
в которых Р, и Ра — эйлеровы нагрузки для продольного изгиба
в двух главных плоскостях, а Р^ означает критическую нагрузку для
чисто крутильного выпучивания, определяемую формулой B41). Тогда
приравнивая нулю детерминант уравнений B45), получаем
Р—Pi. О, ^ ,z^P
О, P—Pi —ГоР =0,
ZoP, -1УоР: гЦР~Рз)
что после раскрытия дает следующее кубическое уравнение^для вы-'
числения критических значений силы Р:
{-г1Л-у1^г'^Р^^\{Р^-\-Р^-^Рз)г1-~у1Р,-г1Р^]Р'~
~rUPiPi~bPiPB~}-PiPb)P-\-PiPs,P3rl = 0. B47)
Это уравнение позволяет сделать одно важное заключение.
Предполагая, что Pi<^P<i, т. е. что меньшая эйлерова нагрузка
соответствует изгибу в плоскости ху, исследуем знак левой части
уравнения B47) для различных значений Р. Если Р весьма мало, то мы
можем пренебречь всеми членами, содержащими Р, и левая часть
уравнения сводится к PiPaPa^ot которое положительно. Если Р
принимает значение Pj, то левая часть уравнения B47) сводится к
ZoPtiPt — P'i), которое отрицательно, так как Pi<i[Pg. Это
указывает на то, что уравнение B47) имеет корень меньший чем Pj.
Поэтому мы заключаем, что когда рассматривается возможность
кручения при выпучивании^ мы всегда получаем критическую нагрузку
меньшую эйлеровой.
52] ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ИЗГИБА И КРУЧЕНИЯ 235
Чтобы найти критическую нагрузку в любом частном случае^ мы
вычисляем, используя обозначения B46), численные значения
коэффициентов в уравнении (;247) и решаем это кубическое уравнение *).
Таким образом, мы получаем три значения для Р, из которых будет
принято для практических приложений наименьшее. Подставляя
критические значения в у|)авнение B45), мы находим для каждой
возможной критической формы отношения A^iA^ и А^:А^. Эти
отношения, устанавливающие зависимость между вращением и переносом
поперечных сечений, определяют для каждой критической формы
положение оси центров сдвига и вращение вокруг этой оси.
Если стержень имеет весьма тонкие стенки" и малую длину /, Pg
может получиться меньшим, чем Pj и. Р^. В таком случае наименьший
корень уравнения B47) приближается к значению Pg. Подставляя это
значение в уравнения B45), находим, что Ai и А^. малы по сравне"
нию с перемещениями от вращения, что указывает на то» что форма
потери устойчивости приближается к чисто крутильной,
рассмотренной в п. 51. В случае толстой стенки и большой длины/ обычно Рз
больше, чем Pj и Pg, и наименьший корень уравнения B47)
приближается к значению Рх. Влияние кручения на критическую нагрузку
мало в этом случае, и обычная формула для расчета колонн дает-
удовлетворительные результаты. '
Если поперечное сечение имеет ось симметрии, вычисление Р^р
упрощается. Пусть ось у будет осью симметрии; тогда Zq = 0 к член,
содержащий <р в первом из уравнений B42), обращается в нуль.
Выпучивание стержня в плоскости симметрии не зависит от кручения, и
соответствующая критическая нагрузка дается формулой Эйлер1а. Мы
должны рассмотреть лишь изгиб, перпендикулярный плоскости
симметрии, и кручение. Соответствующие уравнения будут -.
EJyW"==^--P(w—yii'f),
C,f"-iC-~rlP)f:=Py^'ar.
Поступая по-прежнему и пользуясь уравнением B44), получаем для
вычисления критической нагрузки
Р—Р^, -rj/oP
что дает
гЦР-Р^ПР — Рг)--^^^^. B48)
Это квадратное уравнение дает два решения. Вместе с эйлеровой
нагрузкой для продольного изгиба в плоскости симметрии они
определяют три критических значения для Р, из которых для практических
приложений должно быть принято наименьшее. Рассматривая левую
= 0,
') Это решение можно значительно упростить при помощи номограммы,
показанной в статье Kappus'a, цит. на стр. 233.
imw
236 КРУЧЕНИЕ [ГЛ. VII
V
часть уравнения B48), мы видим, что для очень малых значений Р
эта часть сводится к значению rlP^Ps, которое является
положительным. Мы видим также, что она является отрицательной для Р=р<^и
Р=Р^, так как обращается в —уЬР^, Она отрицательна также для
всех значений Р между Р=Рч и р=р^, так как первый член
становится отрицательным, а второй — всегда отрицателен. Из этих
рассуждений мы заключаем, что один корень уравнения B48) меньше
чем Рч или Рз, в то время как другой — больше любого из них.
Меньший из этих корней, или эйлерова нагрузка, для продольного
изгиба в плоскости симметрии дает требуемую критическую нагрузку.
Все приведенные выводы основываются на уравнениях B44). Не
осложняя вопроса, мы можем принять решение в более общем виде
и предположить /
v=:AiSm -J-, w=A,iSin -J-, (р = Лз5ш—у-, B49)
что соответствует допущению, что при потере устойчивости стержень
разделяется на п полуволн. Наши предыдущие заключения будут
также справедливы и в этом случае; мы должны только подставить
в выражения B46) значения n^iz^ft^ вместо it^//^. Соответствующие
критические значения нагрузки, естественно, будут большими, чем
получаемые при выпучивании в одну полуволну, и будут представлять
практический интерес лишь в том случае, если стержень имеет промежу-
то»Л1ые равноотстоящие боковые опоры.
Еслр концы стержня защемлены, то условия на концах будут
, , ,~ г^ ) при х = 0 и х = 1.
Так как при выпучивании появятся моменты на концах, то мы будем
иметь вместо уравнений B42) следующие:
B50)
Эти уравнения совместно с уравнением B43) *) определяют формы
выпучивания стержня и соответствующие критические нагрузки. Все
вти уравнения и условия на концах будут удовлетворены, если принять
B51)
v = aA\ — cos-^j, 'w = aJ\ — cos-^j,
| = Лз^1 —cos-^j.
cp:
^) Уравнение B43) было выведено из рассмотрения элемента стержня
между двумя смежными поперечными сечениями и не учитывает влияния
изменения условий на концах.
53]
ПРОДОЛЬНЫЕ НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ
23Г
Подставляя эти выражения в уравнения B43) и B50), получим тоже
уравнение B47) для рычисления критических нагрузок; необходимо
лишь в обозначениях B46) воспользоваться величиной 4^*//^ вместо 'sz^jP,
53. Продольные нормальные напряжения
в скручиваемых стержнях
При рассмотрении кручения круглых валов (т. 1, стр. 238)
предполагалось, что расстояние между любыми двумя поперечными сечениями вала при
кручении остается неизменным. Теперь будет
показано, что это допущение весьма точно для
малых деформащ1й, как это наблюдается в стальных
валах. Но для таких материалов, как каучук,
наибольшая деформация сдвига при кручении может
быть значительной^ Тогда изменение расстояний
между поперечными сечениями вала при
кручении нужно принять во внимание, если мы
желаем найти точные значения напряжений.
Такое заключение справедливо также для
стальных скручиваемых стержней узкого
прямоугольного 'поперечного сечения или тонкостенных
поперечных сечений, какие показаны на рис. 144.
Начнем рассмотрение со случая сплошного круглого вала и предположим
сначала, 4fo расстояние между двумя последовательными поперечными
сечениями (рис. 166) остается неизменным при кручении. Если i—деформация
сдвига на поверхности вала, то удлинение продольного волокна ас получится
из треугольника асс^ в следующем виде:
Рис.- 166.
flC =
ас.
cos 7
«c,(l+|
Выражая 7 через угол закручивания на единицу длины, получим
относительное же удлинение волокна ас будет
ас-
ас.
max
aci
2 ^
~ 8 2 C?*
(a)
Соответствующее растягивающее напряжение равняется
max
^max-^ =
max
2 G^
Для любого другого волокна, находящегося' на расстоянии г от оси вала,
относительный сдвиг меньше ^ в отношении г: d/2, и растягивающее
напряжение равно
(Ь)
max
AГ=
max
-qT-
Предположение, что расстояние между поперечными сечениями остается
неизменным при кручении, приводит нас, следовательно, к заключению, что
к концам должна быть приложена продольная сила, вызывающая
растягивающие напряжения (уравнение (Ь)), чтобы сохранить длину неизменной.
Если такая сила не приложена, то скручивание при чистом кручении будет
S38 КРУЧЕНИЕ [ГЛ, VH
сопровождаться укорочением вала. Иусть e^ будет соответствующее
относительное укорочение. Тогда вместо формулы (Ь) получим
Величина £„ определится из того условия, что продольная сила,
соответствующая распределению нг^пряжений по уравнению (с), должна быть равйа
нулю. Разделив поперечное сечение на элементарные кольца и
просуммировав усилия, соответствующие напряжениям (с), получим ^)
d/2 rf/2
?e£!b_.FW^.^!i^r:!s
2nradr = 27c \ (ri__^|±i_e„E)rdr ••"^' "•"
G^ <>"'/' "• -^ 4 V4G'
8-
»)=o,
откуда
■с*
щах
1, " AG
2 )
И распределение лапряжений на основании уравнения (с) получится в виде
4G
(l^-l). B52)
Наибольшее напряжение имеет место на наружной поверхности, где r = rf/2,
и мы пояучаем
B53)
с,
max
- 4(Р
В центре поперечного сечения мы получаем сжимающее напряжение той же
величины.
Интересно отметить, что напряжение с пропорционально т^„;
следовательно, значение этого напряжения растет с ростом т:щах' ^* ^- ^ увеличе^ие!м
угла закручивания. Для такого материала, как сталь, t^^^^ всегда очень мало
по сравнению с G, и величина с^^ поэтому мала по сравнению с х^^^ и ею
можно пренебречь. Но дIя материала, подобного каучуку, т^^^^ может быть
того же порядка, что и G; следовательно, с^^д^^ уже не будет мало по
сравнению с t^jgjj и должно быть принято в расчет.
/' Первое исследование осевой деформации от кручения круглого вала
было сделано Томасом Юнгом^), Он показал, что благодаря растяжению
наклонных волокон, как, например, волокно ас на рис. 166, будет наблю*-
даться дополнительное сопротивление вала кручению, пропорциональное в^
Если вместо круглого поперечного сечения мы имеем узкое
прямоугольное сечение, то можно показать 8), что даже для таких материалов, как
сталь, напряжение о может получиться того же порядка величины, что t,nax-
Если длинная сторона b поперечного сечения велика по сравнению с корот-
^) Предполагается, что косинусы углов между волокнами и осью стержня
можно принят]^ равными единице. *
2) См. Thomas Y о и п g, А Course of Lectures on Natural Philosophy, etc.,
London, 1807:
s) Cm. статью Buckley, Phil. Mag., стр. 778, 1914; см. также С.
Weber, цит. на стр. 213, и также-его статью в Festschrift zum Geburtstage
August F6ppl, Berlin, 1924.
Щ ПРОДОЛЬНЫЕ НОРМАЛЬНЫЙ НАПРЯЖЕНИЯ 239!
кой стороной с, то наиб<^льшее удлинение наиболее удаленного волокна
вследствие только кручения нолучается из уравнения (а) путем подстановки
ft вместо d: ^
■ ■ ■ е ■ = — 62 ■■„■.■■.
Для любого волокна, нахрд^егося на расстоянии у от оси, удлинение
меньше чем е^^ в отношении (^у\Ъу. Складывая это удлинение
с'продольным относительным укорочением £«, получаем
-8"" \Т/ "'"-"
Соответствующее растягивающее напряжение будет равняться
= £(^
(d>.
Постоянная 8д определяется 1|о-прежнему из того условия, что
растягивающая продольная сила равна нулю; следовательно,
+ Ь/2 ^ +''/2
у cady — cE \ (уУ — Ео) rfy = «£| (у уз""^"* J""*^'
-ft/2 ^Ь/2' / ^
откуда
и мы получаем из выражения (d)
ЕЬЧ ^ ft«\ ■ .
■ . » . '
"Наибольшее растягивающее напряжение для наиболее удаленного волокна
(у = &/2) равняется
Наибольшее сжимающее напряжение в центре (у = 0) равно.
°inin 24 * '
Чтобы сравнить эти продольные напряжения с Xj^g^^, можно
воспользоваться формулами B21) и B22). Для узкого прямоугольного сечейия из них
мы получаем ■ ^
6=^. ■ (h)
Подставляя это значение в формулы (f) и (g), находим
_ ^"^тах ft" __?!«!5f.*l тд^
°гаах— 12C/V С» • ""min— 24<7« С» ' ^ '
Видно, что когда ft/c велико, напряжения а^^^ и с^^,^ могут быть не малы
по сравнению с "t^^^. Распределение напряжений (см; уравнение (е))
240
КРУЧЕНИЕ
[ГЛ. VII
доказано ^) на рис. 167. Эти напряжения имеют I^jlпpaвлeниe продольных
волокон скрученной полоски и наклонены к оси полоски под углом %у. Их
проекции на плоскость, перпендикулярную оси стержня, будут
Рис. 167.
ь=
£63
12 j
(i)
Составляющая (i) напряжения с для элемента cdy
поперечного сечения дает момент относительно оси стержня, равный
12
Следовательно, равнодействующий
напряжений равняется
~ £ev..« b^y
су ,dy.
крутящий момент этих
\
— Ь/2
т\-
12
су dy =
Ecb^
360
08.
-Складывая этот крутящий момент с крутящим моментом от
касательных напряжений (формула B21), стр. 201), получаем
следующее выражение- ддя полного крутящего момента:
м,=
ЬсЮЬ
Можно видеть,'что в случае узкого прямоугольного поперечного сечения и
сравнительно больших углов закручивания напряжение с может поглотить
значительную часть крутящего момента, так как эта часть, представленная
вторым членом в уравнении B55), пропорциональна 6^, в то время как часть
момента от касательных напряжений т пропорциональна 6. Когда величина
крутящего момента дана, соответствующий угол закручивания можно найти
из уравнения B55). Тогда наибольшее касательное напряжение х^^^
определится по формуле (h), а с,^^^ и c^^j^ — из формул B54).
В качестве примера возьмем стержень узкого прямоугольного
поперечного сечения со следующими размерами: Ь=10 см, с =0,125 см, £'/(?=2,6,
G = 7,7 • \0^ кг/см^ и М^ = Х/ЗЬс^ • 1000 = 52 лгг • см. Если нормальными
напряжениями с пренебречь, то формула B22) дает т^дх^^"^^^ KzfcM^, а B21) —
е =-^ = 0,0104 СЖ-».
си
принимая во внимание продольные напряжения, мы должны воспользоваться
уравнением B55). Из него после делеяия на 1/3 ЬсЮ получим
0,0104 = 6A + 13 870 62),
откуда 6 = 0,00656 см~^. Тогда из формул (h) и B54) имеем
Ь^
%ax = ^G6 = 620;cг/€Ж^ а =
max
12G2
= 700 кг/смК
^) Это распределение напряжений имеет место на некотором расстоянии
от концов стержйя. Вблизи концов имеется более сложное распределение
напряжений, чем даваемое уравнением (е). Оно таково, что исключает
совершенно нормальные напряжения на концах. Такого рода распределение
напряжений рассмотрено в книге:' Timoshenko and G о о d i е г. Theory of
Elasticity, стр. 167, 1951; в русском переводе, стр. 304, 1937.
64) ЦИЛИНДРИЧЕСКАЯ ПРУЖИНА С БОЛЬШИМ ШАГОМ ВИТКА 241
Можно видеть, что при большом угле закручивания тонкой мeтiaлличecкoй
полоски, как в этом примере, -нормальные напряжения, о будут того же
порядка, что и касательные напряжения т, и ими нельзя пренебречь при
. вычислении угла закручивания. Из проведенного обсун{дения можно также
заключить, что "равномерное продольное растяжение будет иметь известное
влияние на угол закручивания тонкой прямоугольной полоски. Предположим,
например, что равномерное продольное растягивающее напряжение о^,
приложено к полоске, которую только что мы рассматривали. В таком случйе
уравнение для вычисления е^ будет
'^^[Y Т2~^»* ) ="°о^'^'
и мы получаем
— ^ *1_^
"""" 2 12 Е •
Тогда Выражение для продольного напряжения ^^олучится в таком виде:
а соответствующий крутяир!й момент будет
+ Ь/2
— fc/2
Тогда вместо уравнения B55) для полного крутящего момента получим
M„=l»..oe(i+ig|^e»+i §-*-). B56)
Вицно, ЧТО когда bfc — большое число, т. е. в случае тонкой полоски,
растягивающее напряжение может значительно уменьшить угол закручивания в.
i ...
54. Цилиндрическая пружина с большим шагом витка
В предыдущем изложении задачи о винтовых пружинах (т, I, стр. 246)
предполагалось, что угол а между витками и плоскостью, перпендикулярной оси
цилиндра, был весьма мал. Пренебрегая влиянием угда, мы получили, что
деформация сводится лишь к кручению проволоки. В пружинах с большим
шагом витка угол а уже не является малым, и деформация, вызванная
осевыми грузами Р, состоит из деформаций кручения и изгиба (рис. 168). В
произвольной точке А касательная к винтовой осевой линии пружины не
перпендикулярна силе Р, и поэтому эха сила вызывает в поперечном сечении А
изгибающий момент относительно оси щ и крутящий момент. Силу Р
разлагаем на две составляющие: Pcosa, перпендикулярную к касательной
в точке Л, и Psina, параллельную касательной в точке А. В поперечном
сечении А составляющая Pcosa вызывает крутящий момент, равный
Л1к = PR cos а, (а)
где /? — радиус винтовой линии, составляющая Psina вызывает изгибающий
^°"^" М = Р/? sin а. (Ь)
Максимальное главное напряжение (см. т. I, стр. 252). равно
<'шах = ^(Л^+1^Л^МПИ|)==-^A + «Ь«), B57)
3^
.242
КРУЧЕНИЕ
|ГЛ. Vir
где d-^дааметр проволоки. Максимальным касательным напряжением
является*).
х_..=Л|Кмпрж^'«''«
"max ^^8
■лф '
B58>
.Рассмотрим теперь деформацию лружины & предположении, что она
закреплена верхним концом и нагружена осевой нагрузкой в нижнем конце.
Элемент ds между двумя С]^ежными попер,ечными сечениями в точке А
закручивается крутящим моментом Л1^ на угол, равный
, P^cosa .
(с>
Как результат этого кручения нижняя часть
пружины поворачивается вокруг касательной,^
проведанной у точки А, на угол rff, Этот ма-г
лый поворот представлен на рис. 168
вектором п, отложенным по касательной.
Положительное направление вектора таково, что между
направлением вектора и напрдвлением
вращения сГуществует та же зависимость, что и
между перемещением и вращением винта
с правой нарезкой. Малый поворот я может
быть разложен на две составляющие: 1)
поворот ncosa вокруг горизонтальной оси и
2) поворот л sin а вокруг вертикальной оси.
Последний не вызывает никакого понижения
конца пружины и поэтому здесь не
рассматривается. Снижение конца В вследствие
поворота на ncosa оценивается так же, как и
для пружины с малым шагом витка. В
результате этого точка В перемещается в i?, (рис. 168),^
и мы имеем BBi = АВпсо^а. Вертикальная
составляющая этого перемещения равна
Рис. 168.
ВВа = ВВ, -=^ = /?ncosa.
АВ
(d>
Полное опускание конца В вследствие кручения р;авно сумме элементарных
снижений, определенных выражением (й) или
Ь, ;s= ^ /?я cos а,
(е>
тде суммирование принято по всей длине пружины от нижнего конца В до
верхнего закрепленного конца С.
*) Если диаметр d проволоки не очень мал по сравнению с диаметром 2R
винтовой линии, то это значение нужно умножить нд поправочный
коэффициент, который при а < 20° можно принять таким же, как для пружин
с малым шагом Ьктка 1т. I, стр; 0,41). Дальнейшее изложение этого вопроса
дано О. G oh пег'ом, Z. Ver. deut. Ing., т. 76° стр. 269, 1932. См. также-
Timoshenko and G о о d i е г, Theory of Elasticity, стр. 391, 1951.
■6*1 ЦИЛИНДРИЧЕСКАЯ ПРУЖИНА С БОЛЬШИМ ШАГОМ ВИТКА 243
Ойускание вследствие изгиба можно вычислить таким же способом.
Угловое перемещение благодаря изгибу элемента efs моментом Af
(выражение (Ь)) равняется
J : PR sin а . ...
d^~—^j—ds. , (f)
Соответствующее вращение нижней части, пружины показано на рис. 168
вектором щ. Таким же ^образом, как и выше, можно показать, что только
■его горизонтальная составляющая njsina вызывает вертикальное перемещё^;-
иие конца В и что величина этого перемещения равна
■ ■ ' '.'■'-.- с '' ■
"- «8 = ?/?л, sin а. . (g)
Складывая выражения (е) и (g), получаем полное опускание конца В
8 = 8j-j-bg =/? \ (« cos а-f-«1 sin а).
В
Подставляя выражение (с) вместо и и выражение (f) вместо Пу, получаем
в V
или, замечая, что выражение 6 скобках постояйно, и o6o3HajiaH длину
проволоки пружины через s, имеем *
Если диаметр d проволоки не мал по сравнению с 2/?, то жесткость при
асруч|?нйи Ч?/р в уравнении B59) должна быть умножена на Поправочный
коэффициент
16
ь-т
Этот же коэффициент можно использовать для пружины с квадратным
поперечным сечением *).
Уравнения B57), B58) и B59) дают полное решение задачи о винтовой
пружине с большим шагом витка, подверженной действию осевой сил«11 *).
Растяжение пружины сопровождается поворотом конца В относительно
вертикальной оси винтовой линии. Для того^ чтобы определить этот поворот,
рассмотрим опять деформацию элемента ds на рис. 168, а. Благодаря
кручению этого элемента будет происходить вращение нижней части пружины на
и sin а = —^-,— sin а.
*) О, Gehner, цит. на стр. 242.
*) Теория винтовых пружин была разработана Сен-Венаном; см. Compt.
rend., т. 17, стр. 1020, 1843. Ряд частных случаев был разобран Th о
треб п'ом and Tait'oM, Nat. Phil., ч. 2, стр. 139; I. Perry, Applied. Mechanics,
New York, стр. 613, 1907; Q. W. S h e a r e r,' Engineering, т. 93, стр. 206,1912.
*) Предполагается круговое поперечное сечение проволоки.
imw
244
КРУЧЕНИЕ
1ГЛ. Vir
Изгиб элемента вызывает угловое перемещение п^ (рис. 168, а), и
результирующий поворот нижней части пружины относительно вертикальной оси
будет
— щ cosa = —
Mds
EJ
■ cos a.
Следовательно, полный поворот вокруг оси винтовой линии нижней части
пружины вследствие деформации элемента ds будет
' iM^ sin а
EJ
)■
(h>
Сумма этих -элементарных поворотов равняется полному углу вращения tp
конца В относительно закрепленного конца С пружины:
iMy^ sin а Л! COS а\
sPH sin а COS
о7р Ej]'
B60)
где s есть полная длина проволоки. В случае других форм поперечного
сечения проволоки в формулу B60) нужно подставить соответствующее
значение жесткости при кручении С вместо QJp.
Осевое кручение. Пусть вектор 'AD представляет крутящий момент М^^
приложенный на конце В пружины (рис. 169). Изгибающий и крутящий
моменты, действующие на элемент ds в точке А, будут
M = M2C0Sa, Mjj = Д!^ sin а.
Поворот конца В пружины вокруг оси z вследствие деформации элемента ds
равен
ds
^к . , М \ .. . /sin" а , cos' а \
^sm« + _cosa) = M,rfs(-^ + -^),
(i)
Полный поворот конца В относительно оси z, вызываемый крутящим
моментом Mz, равняется
«Pi
= ^Мг (■
+
cos^ а
~Ё7
)•
B61>
Так как растягивающая сила Р вызывает поворот «р
конца В пружины, то из теоремы о взаимности
перемещений (см. т. I, стр. 296) можно заключить, что крутящий
момент Мг будет вызывать удлинение пружины. Величина &
этого удлинения получается из уравнения
откуда J. / 1 1 \
6 = ^.p = M^sPsin«cos«(^^-—j. B62)
Изгиб в продольной плоскости. Иногда необходимо
рассмотреть чистый изгиб винтовой пружины в ее
продольной плоскости (рис. 170). Пусть М^,, представленный
вектором АВ (рис. 170, Ь), будет величина изгибающего
момента в плоскости yz. Рассматривая элемент ,ds
пружины в точке А, определяемой углом 6, разложим вектор
Рис. 169. АВ на две составляющие: ЛC = ^'И^,cose и AD ::;= М^ sin Ь,
Первая составляющая представляет пару сил, которая
находится в плоскости, касательной к цилиндрической поверхности радиуса
/?, и вызывает изгиб проволоки в этой плоскости. Вторая составляющая
Б4]
ЦИЛИНДРИЧЕСКАЯ ПРУЖИНА С БОЛЬШИМ ШАГОМ ВИТКА
245
представляет пару, действующую в продольной плоскости пружины, и
может быть разложена на крутящий момент М^ sin в cos а и изгибающий
момент в плоскости витка М^ sin 6 sin а. Следовательно, элемент rfs
испытывает изгиб под действием равнодействующего изгибающего момента, равного-
У Ml cos" е + Ml sin^ е sin^ а, (f >
и кручение под действием крутящего момента'^ равного Мь sin в cos а. Энергия.
Рис. 170.
деформации элемента, в предположении кругового поперечного сечения
проволоки, равняется
Г Ml (cos'' е + sin» е sin» а) Mi sin» 6 cos» а П
. dU=ds[-^ 2Е7 + 2GJ, J- ^*^>
Подставляя rfs = ^ d6/cos a и интегрируя от 6 =: О до 6 = 2т:п, где л — число
витков, получаем
_ тт^? Г М^ A + sin» а) _ Ml cos» а
cosaL 2£У
Щ cos» al
A>
Угловое перемещение одного конца пруж)шы относительно другого
равно //р, где / — длина пружины (рис. 170, а) и р — радиус кривизны
упругой кривой оси пружины. Длина / определяется из выражения
2п1^п .
/ = SSina=: sma.
COS а
Пpиpiaвнивaя работу, совершенную изгибающими моментами Mi„ энер^^ии
деформации (уравнение A)), получаем
Mbl
= и,
откуда
р sm а \
2 р
1 + sin» а
COS'
Следовательно, величина
В =
2EJ
sma
2G7,
^)-
1 + sin» а cos» а
B63>
(ту
2EJ
2GJ.
должна быть принята за жесткость изгиба в случае осевого изгиба винтовой
пружины с проволокой кругового поперечного сечения.. Если угол а мал, то
мы можем допустить с достаточной точностью, что sin»a = 0 и cos»a=l.
Но так как sina = //s, жесткость изгиба винтовой пружины можно-
•246
КРУЧЕНИВ
1ГЛ. VII
лредставить формулой
В =
2EJI
I
Е '■
14- —
B64)
При рассмотрений изгиба винтовой пружи1^ы поперечной нагрузкой,
(рис. 171) надо принять во лйтмание не только прогиб, вызываемый
изгибающим моментом, но также и прогиб, вызываемый Лтоперечной силой.
Предполагая, что конец О пружины заделан и что угол «мал, мы найдем
перемещение bji верхнего конца А пружины под действием изгибаю^цего момента
по обычной формуле для консоли, с подстановкой значения B64) вместо
жесткости изгиба. Следовательно,
\ =
Р1* 5
3 2EJI
{'+т)'
(п)
Для выяснения влияния поперечной силы на прогиб рассмотрим искажение
годного витка в его плоскости *), вызванное поперечной силой Q (рис. 172).
Рис. 171.
Мзгибак)щий момент, возникающий от Q в какой-либо точке А, равняется
43/? sin 6, а соответствующая энергия деформации одного витка будет равна
\~Mj~~ 2EJ •
О -.
Относительное перемещение е тогда будет
дСТ %Q/^
U--
е=.
Щ
EJ
Разделив это перемещение на шаг Л пружины, получаем дополнительный
угол наклона т изогнутой оси благодаря действию поперечной силы
ЕЛ
Формулы, выведенные ранее (см. т. 1, п. 39) для прогиба сплошных балок,'
производимого сдвигом, можно применить к расчету поперечного переме-
*) При этом рассмотрении предполагается, что угол а мал.
Wl ЦИЛИНДРИЧЕСКАЯ ПРУЖИНА с БОЛЬШИМ. ШАГОМ ВИТКА. 247"
щения винтовых пружин. Необходимо лишь подставить угол наклона, данный
выра^жецием вместо ранее принятого выражения aQlFG. В случае,
показанном'на рис. 171, поперечная Сила постоянна по длине I и равна J^
следовательно, прогиб вследствие сдвига равен
^ = T'==-gj-. (Р>;
Складывая выражения (п) и. (р) и принимая s = 2n/?n, получаем
»-S. + ^ = -3^p(l+2G+-7rj« B65),
Последний член в скобках представляет влияние сдвига. Им можно
пренебречь, если радиус Й пружины мал по сравнению с длиной /*). .
*) Поперечное выпучивание винтовых пружин под действием осевогосжатил
рассмотрено в книге: Timoshenko, Theory of Elastic Stability, стр. 165^
1936; русский перевод, 1946, 1955. Там же приведена библиография по этому
вопросу.
mm
ГЛАВА vm
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
55. Концентрация напряжений в растянутых или сжатых
элементах
При изучении простого растяжения или сжатия предполагалось,
•что стержень был призматической формы. Тогда для центрально
приложенных сил напряжения будут равномерно распределены по
поперечному сечению. Равномерное распределение напряжений предполагалось
также в случае стержня переменного поперечного сечения (см. рис. 14
т. I, стр. 24), но это есть приближение, которое дает
удовлетворительные результаты лишь в том случае, когда изменение ноперечного
сечения происходит постепенно. Резкие изменения поперечного
сечения вызывают большие неправильности в распределении напряжений.
Эти неправильности имеют особенно важное значение при проектиро-
:^ании машинных частей, подверженных действию переменных внешних
•сил и знакопеременных напряжений. Неправильности в распределении
яапряжений сводятся к тому, что в некоторых точках напряжение
значительно выше среднего значения и под действием
знакопеременных напряжений возможно образование все
возрастающих трещин. Большинство поломок
машинных частей во время работы можно прип»?
!^rjr.^_ сать таким прогрессирующим трещинам.
Для иллюстрации расгфеделения напряжений в
стержне переменного поперечного сечения, йаходя-
щегося под действием растягивающих сил,
рассмотрим симметричный клин постоянной толщины Л,
нагруженный, как показано^ на рис. 173. Точное
решение показывает (см. сноску 2) стр. 249), что
здесь будет простое радиальное распределение
напряжений. Элемент в радиальном направлении в
какой-либо точке А ' находится в условиях простого
радиального растяжения. Величина этого радиального растягивающего
напряжения дается уравнением
, Р cos е
hr
(а)
Б61 НАПРЯЖЕНИЯ В ПЛАСТИНКЕ С КРУГЛЫМ ОТВЕРСТИЕМ 249*
В котором 6 есть угол между осью л: и радиусом О А, г—расстояние точк№
А от О Hft = l/ (a + -K-sin2a] — коэффициент, зависящий от угла 2а клина.
Распределение нормальных напряжений Oj^ по какому-либо поперечному
сечению тп, перпендикулярному оси симметрии клина, является неравномер-
а
ным. Пользуясь уравнением A7) т. 1, стр. 41, и подставляя г = -—-^ в фор-
мулу (а), находим . ^^^^^^
oj,=Or cos2 е = —^^ (b>
Это показывает, что нормальное напряжение является наибольшим в центре-
поперечного сечения (в = 0) и наименьшим при в = а. Разность между
наибольшим и наименьшим напряжениями увеличивается с увеличением угла а.
При а = 10" эта разность составляет около бо/о оТ среднего напряжения,
полученного путем деления нагрузки Р на площадь поперечного се'чения тп.
Аналогичные заключения можно также вывести для ^конического стержня.
Можно показать, что распределение нормальных напряжений по поперечному
сечению приближается к равномерному, если угол конуса уменьшается.
Эти рассркдения показывают, что предположение о равномернолг
распределении нормальных напряжений по поперечному сечению
непризматического стержня дает удовлетворительные '^результаты, есл»
изменение поперечного сечения по длине стержня происходит не
резко. Однако условия будут совершенно отличны, когда имеются
резкие изменения в поперечном сечении. В таких местах
распределение напряжений весьма далеко от равномерного, и результаты,
полученные при допущении равномерного распределения напряжений,
совершенно неправильны. В следующих параграфах будет рассмотрена
несколько примеров резкого изменения поперечного сечения.
56. Напряжения в пластинке с круглым отверстием
Если в пластинке, подвергнутой действию равномерно растягивающих
напряжений о, сделано малое круглое отверстие*), то в точках пп (рис. 174, ау
имеет место высокая концентрация напряжений. Точная теория ^)
показывает, что растягивающее напряжение в этих точках равняется За. Теория
также показывает, что эта концентрация носит чисто местный характер и
ограничивается непосредственной близостью к отверстию. Если начертить
концентрический круг с отверстием и притом сравнительно большого
радиуса с, как показано на рис. 174, а пунктиром, можно предположить, что на
напряженное состояние по окружности этого круга наличие отверстия не^
оказывает существенного влияния. Пусть рис. 174, b представляет ^круглое
кольцо, вырезанное из пластинки круглой цилиндрической поверхностью-
радиуса с. В каждой точке наружной поверхности этого кольца мы
приложим вертикально направленные напряжения величиной o-sm<f, равные напря*-
жению на соответствующей элементарной площадке dF пластинки (см.
уравнение A6) т. I, стр. 40). Тогда напряжения в кольце будут приблизительно*
*) Диаметр отверстия меньше, скажем, 1/5 ширины пластинки.
^) Эта теория была предложена Kirsch'oM, Z. Ver. deut. Ing., 1898. См.
также Ti m osh enk о an^ Goodier, Theory of Elasticity, стр. 78, 1951;,
русский перевод, 1937, стр. 107,
1250
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
1ГЛ. VHI
такие же, как в части пластинки, ограниченной окружностью радиуса с
.(рис. 174, с). Таким образом, задача о распределении 'напряжений
вблизи отверстия в пластинке
сводится к задаче о круглом кольце
прямоугольного поперечного сечения,
' подверженном действии^ вертикаль-
. ной нагрузки интенсивности esin^,
непрерывно распределенной по его
' внешнему контуру *). Эта задача
может быть решена методом,
изложенным в т. 1, стр. 319. Рассматривая
один квадрант кольца, сводим напря- -
жения, действующие Ло поперечному
сечению тп, к продольной
растягивающей силе Л^о, приложенной в
центре тяжести поперечного сечения, и к
изгибающей паре Mq. Продольная сила
может быть определена из уравнения
статики и равняется
Nf, = ac, (а)
Момент Мо является суатически
неопределимой величиной и'^,
вычисляется при помощи теоремы о най^
меньшей работе, ^ля вычисления потенциальной энергии применяется
Фыраженце B28) т. I, стр. 322, для которого продольная сила и изгибающий
момент в произвольном поперечном сечении кольца, определяемом углом ip
(рис. 174, 6), будут Л^ = ос cos* ijp; ■
М = Mo-f- ос A — cos (р) I -g- (I — cos <j))-f- у cos у — ас (с — y) (I —cos <p). (b)
Здесь h — высота прямоугольного поперечного сечения. Тогда
-. ic/2 */2
dU _ С Md<f С Ndtf _ .
dMo"J FEe~'yFE "^'
0 0
Рис. 174.
откуда после Интегрирования получаем
Мо
2ос^Г г h [ 1 \
е%
^
4 "j-^ 4с +'2Г<"—2)J
(с)
Здесь по-прежнему ^>—радиус осевой линии и е—т расстояние нейтральной
оси от центра тяжести поперечного сечения.
Напряжение в точке я Поперечного сечения тп кольца состоит из двух
■частей: 1) растягивающего напряжения, вызываемого продольной силой N^
« равного
^ о,
N.
ос
т
(d)
я 2) напряжения, от изгиба, вызываемого Mq, Kotopoe на основании
формулы B12) т. 1, стр.308, равняется
^Ч 2 ~ ^) __ Л1в / _2е\
Fea ~~ 2ео \ , Л J •
(е)
где в—радиус отверстия.
*) Толщина пластинки предполагается равной единице.
56]
НАПРЯЖЕНИЯ В ПЛАСТИНКЕ С КРУГЛЫМ ОТВЕРСТИЕМ
25t:
|*асстояние е вычисляется (см. т. 1» п. 79, стр. 31 ly для различных
значений отношения с/в, и тогда величины Oj и Oj определяются из формул (d) »
(е). Шибольшее напряжение-равняется
-max
^ о, + Н-
1?£ёультаты этих вычислений приведены в табл. 18.
Таблица 18
Значения местных напряжений в пластинке у круглого
отверстия
с/а
2elh
aja
°ih
0 /а
max'
3
0,1796
1,50
2,33
3,83
4
0,2238
1,33
1,93 ,
3,26
5
0,2574
1,25
1,83
3,08
6
0,2838
1,20
1,83
3,03
k
0,3239
1,14
1,95
3,09
10
0,3536
1,11
2,19
3,30
Ср1авнение цифр последней строки табл. 18 с точным решением Ощах —З»'
для очень' малого отверстия показывает, что при 5 <: с/в <: 8 результаты прйг
ближенного вычисления хорошо согласуются с точным решением. Когда*
cja < 5, отверстие нельзя рассматривать очень малым, и оно имеет заметное
влияние, на распределение напряжений по кругу радиуса с (рис. 174, а)^
в котором наше допущение относительно распределения сил по внешнему
•контуру кольца (рис. 174, ^^ не является .вполне точным. Отклонение or
точной теории для cja^b объясняется недо-
CTaf очной точностью элементарной теории кри»
вых^ брусьев для случая, когда внутренний
радиус очень мал по сравнению с наружным.
Взяв какую-либо точку в поперечном
сечении тп (рис. 174, Ь) на расстоянии г оТ центра
отверстия, найдем из точной теории, что
нормальное, напряжение в этой точке равняется
*де о есть равномерное растягивающее
напряжение, приложенное к концам пластинки. Это
распределенТие напряжений показано на рис. 174,
а заштрихованными площадями. Видно, что
концентрация напряжений в этом случае
имеет сугубо местный характер. В точках п, т. е. при^г = ie, мы имеем
^'шах ^^ ^°- Напряжения быстро уменьшаются, когда расстояние от этой
перенапряженной точки увеличивается; на расстоянии от края отверстий,
равном радиусу отверстия, т. е. при г = 2в, мы получаем из уравнений (f) нор-
■ мальное напряжение, равное I'oo""'- Напряжение также быстро уменьшается
т
Phq. 175.
32
п
с увеличением угла у (рис. 174, &); и при tft^-^, т. е. для сечения, паралт
лельного приложенным растягивающим напряжениям, о, мы 41аходим на краю
отверстия сжимающее Напряжение в окружном направлении, равное
растягивающему напряжению а, приложенному на концах пластинки.
Если вместо растяжения мы имеем сжатие пластинки (рис. 175, в), то
должны лишь изменить знак напряжений, полученных в предыдущем
.изложении, и мы заключаем, что в точках п будет сжимающее напряжение
величиной Зо, а в точках т — растягивающее напряжение величиной о. В
случае хрупкого материала, как, например, стекло, которое очень прочно прл
3^
•252
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
[ГЛ. VIII
-сжатии и слабо при растяжении, трещины обычн© начинаются в точках т,
•«ак показано на рис. ПЬ,Ь.
Имея напряжения для простого растяжения и сжатия и пользуясь
методом наложения, мы легко получим концентрацию напряжений для случая
■сложного растяжения или сжатия в двух взаимно перпендикулярных
направлениях. Например, в случае, показанном на рис. 176, мы находим, что
тангенщ1альное напряжение в
ff I i точках п равняется Зо^ — Oj^, а
в точках т дапряжение рав-
у В частном слу-
сдвига мы имеем
Ш.
- .-С).
u
/7t
т
-а:
пттл
Рис. 176.
няется 3<jjf — а
чае чистого
Ojf=:—<3y = <3 И получаем для
точек п напряжение —4о, а
для точек т напряжение +4о;
таким образом, в этом случае
наибольшее напряжение в
четыре раза больше напряжений,
приложенных по краям
пластинки. Такое условие большой
концентрации напряжений
получается при кручении тонкостенной круглой трубы с малым круглым от-
шерстием (рис. 1.77). Если приложенный крутящий момент имеет направление,
указанное на рисунке, то наибольшее растягивающее напряжение, которое
в четыре раза больше касательных напряжений, приложенных на конце,
вызывается на краю отверстия в точках, отмеченных
знаком плюс. В точках, отмеченных знаком минус,
возникает сжимающее напряжение такой же величины.
Приближенный метод, описанный выше для
вычисления напряжений у круглого отверстия, можно также
применить для случая отверстия с ребордой (рис. 178).
' Ь ^. t
tx
max
11,-^=0,01
раз-
га
для
6
2,56
Результаты этого вычисления*) при
дают следующие значения отношения
личных значений 'с\а\
с1а = 4 5
/гаа>=2,56 2,53
В рассматриваемой области отношение o^^^Ja
изменяется, но незначительно, с изменением cja, так что
дальнейшие вычисления будут проделаны только для
случая с/а = 5. Влияние площади поперечного сечештя
реборды на а^^^^ можно изучить путем изменения
размера b реборды. Если Fi = 2tia означает уменьшение
поперечного сечения пластинки вследствие наличия
отверстия и F2 = {b — t^t означает площадь поперечного
•сечения реборды, то отношение o^j^Jo для некоторых значений отношения
.F^i дано ниже:
F,/F, = 0,10
='max/° = 2-53
0,20
2.17
0,30
1,90
0,40
1,69
0,50
1.53
*) Рассмотрение этой задачи дано в статье автора, J. Franklin Inst., т. 197,
■стр. 505, 1924. Предполагается, что все поперечное сечение реборды
является полезным. О дальнейшем исследовании задачи см. L. Beskin, J. Appl.
JVlech., т. И, стр. 140, 1944. См. также С. Gurney, Air Ministry Repts. and
-Mem. (London) Ka 1834, 1938.
Ъ7]
ДРУГИЕ СЛУЧАИ РАСТЯНУТЫХ ЭЛЕМЕНТОВ
253
приведенные числовые данные можно применить также в случае друг.их
форм поперечного сечения реборды при условии, что размер t реборды в
радиальном направлении можно рассматривать малым по сравнению с
радиусом а отверстия. Возьмем, например, широкую пластинку, подверженную
растяжению, толщиной 10 мм, с круглым отверстием диаметром 1 ж. Пусть
край отверстия усилен Двумя уголками 100 X 100 х 10 мм. В таком случае
FsjFi = 0,40, и вышеприведенная таблица дает "'„,3^/0 = 1,69.
57. Другие случаи концентрации напряжений
в растянутых элементах
Имеется лишь немного случаев, в которых,/ как в случае
круглого отверстия, задача о концентрации напряжений строго
теоретически решена *). В большинстве случаев сведения относительно
наибольших напряжений в точках резкого изменения поперечного сечения
получаются из опытов ^). В дальнейшем изложении представлены лишь
некоторые окончательные результаты теоретических и
экспериментальных исследований, которые могут
иметь практическое значение *).
В случае малого эллиптического
отверстия в пластинке *) (рис. 179, а)
наибольшее напряжение будет на
концах горизонтальной оси отверстия; оно
определяется формулой
max
0^-^^)'
(а)
* ^ * ^^[
L
""Щ
- а)
\ S ♦ Ki
Рис. 179.
где о — растягивающее напряжение,
приложенное на концах пластинки. Это
напряжение увеличивается с возрастанием
отношения alb, так что очень узкое
отверстие, перпендикулярное к направлению растяжения, вызывает
большую концентрацию напряжений. Этим объясняется, почему
трещины, перпендикулярные к направлению приложенных сил, имеют
тенденцию к распространению. Это распространение мож^т быть
остановлено путем высверливания отверстий на концах трещины для того,
чтобы устранить острые углы, которые вызывают высокую
концентрацию напряжений.
*) Теоретические решения задач о концентрации напряжений для отверстий
различной формы даны в книге Г. Н. Савина. «Концентрация напряжений
у отверстий», 1951.
^) Различные экспериментальные методы для определения наибольших
напряжений описаны в пп. 61 и 62. См. также Е. Lehr, Spannungsverteijung
in Konstruktionselementen, 1934.
^) Весьма полное собрание сведений относительно концентрации
напряжений дано в книге: R. Е. Peterson, Stress Concentration Design Factors, 1953.
*) См. Г. Колосов, Диссертация, 1910, Петербург; см. также С. Е. I п g-
1 i S, Engineering, т. 95, стр. 415, 1913 и Trans. Inst. Naval Architects, 1913.
ш
254
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
|ГЛ. Vlir
Малые пЬлукруглые выточки^) в пластинке, подверженной
растяжению (рис. 179, Ь), также вызывают" высокую концентрацию
напряжений. Опыты^) показывают, что в точках т vi п напряжения
4^
3.0
2Jff
а)
t
^|^ю>Ш
с)
^ ^
ZnHp^ewe отберапг/е Пол/г/нр^гль^ ^/точт
^1г
т^а^^
у^ш
Вь/нруМг/ш
ffi^ as ае.
Рис. 180.
IB r/d
приблизи1;ельно в три раза больше напряжений, приложенных по
концам пластинки, если радиус г выточки весьма мал по сравнению с
* Л
•г,о
12
t •
:' "
//у
ш
//^^
^
^ ■
..
,- ■
"^
^шт WM *
щ ■
-
— .•«—■,-
. -*-* "■""
—..■.—
^- •
—-—""^
м.
-JJ}
§=т ^
^Ц7
"^ ■*»
Ч
М2
Q2?
S 1 l£i
/ ^ ? 1 '
о
w
2/^
ДО
Рис. 181.
#/'
SjO
^)h/r
шириной rf наименьшего сечения, Вообще наибольшее напряжение
Е TOjiKax W и л является функцией отношения-r/rf. Отношение наиболь-
») О теорехи'ческом решении этой задачи см. статью F. G. Maun se 1Г а,
Phil. Mag,, т. 21, стр. 765, 1Э36.
«) См. М. М. Frocht, J. Appl. Mech., т. 2, стр. 67, 1935.
Ъ7\
ДРУГИЕ СЛУЧАЙ РАСТЯНУТЫХ ЭЛЕМЕНТОВ
255
шего напряжения к среднему напряжению в наименьшем сечении тп
о'^Шао называется коэффициентом концентрации напряжений vi
•обозначается через k. Значения k для различных значений отношений r/d
даны на рис. 180 кривой //*). На том же рисунке даны также
коэффициенты концентрации напряжений для случая круглого отверстия
выкружки (кривая /Я). На рис./181
приведены более подробные данные
{кривая /) и для случая
2,8
^*
2jff
/А
12
Iff
•
,
ZL
1 /
i §■//
'
/
//
'/
/>
^z.
M
/
•
■
'
^
к"
^^ -•
._
.
■
•
^^
— ''
_-—-
..—.—
0,0^
Mx
<l7fi
\^
Ш5
цгщ
•
относительно концентрации
напряжений б выкружках.
На рис. 182 коэффициенты k
даны для выточек различной
глубины, - имеющих круглую
форму на дне. Видно, что для
глубоких выточек коэффициен-
тц концентрации напряжений
больше, чем для полукруглых
с тем же отношением r\d.
Рис. 182.
Рис. 183.
Случай пдастинки весьма большой ширины с гиперболическими выточ-
|сами (рис. 183) можно исследовать теоретически *). Решение показывает, что
коэффициент концентрации напряжений, т. е. отношение наибольшего
напряжения.в точках W и п к среднему растягивающему напряжению по
поперечному сечению тп можно представить следующей приближенной формулой *);
^=|/0,8f
+ 1.2-0,1,
(b)
где d — ширина nanMeHbrncfro сечения и г — радиус кривизны дна выточки.
Интересно отметить, что значения ft, получаемые из этой формулы, весьма
хорошо согласуются с результатами опытов, полученных для глубоких вьн
точек (Л/г = 4), полукруглых на дне (рис. 182). -
*) Кривые, приведенные в последующем изложении, взяты из статьи
М. М. F г о с h t'a. там же (см. стр. 254). \
') Н. Ne uber, Z. angew. Math. u. Mech., т. 13, стр. 439, 1933. См. также
книгу: Neuber, Kerbspannungslehre, 1937. -
*) В выражениях (Ь), (с) и (d) коэффициент Пуассона взят равным 0,3.
m
256
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
|ГЛ. VIII
Предположим теперь, что рис. 183 представляет собой продольное
сечение круглого цилиндра большого диаметра с глубокой выточкой
гиперболическою профиля, находящегося под действием осевого pacтяжeнJия.
Наибольшее растягивающее напряжение опять имеет место на дне выточки,
и значение коэффициента концентриций -напряжений будет *)
=|^«.4
+ 0,85 + 0,08.
(с)
Сравнение этой формулы с формулой (Ь) показывает, что в случае цилиндра
с выточкой концентрация напряжений меньше, чем' в случае пластинки.
Дальнейшее обсуждение этого сравнения дано- ниже (см. п. 60).
В случае растянутого цилиндра с эллипсоидальной полостью на оси, для
KOTopioro рис. 179, а можно рассматривать как продольное сечение,
наибольшее растягивающее напряжение имеет место в точках т. Его значение дает
следующая приближенная формула:.
max
= « (|/0,8 у+ 0,05 + 0,78 ] .
(Ф
где с— равномерное растягивающее напряжение, приложенное по концам
цилиндра, и г — радиус кривизны эллипса в точках т.
Стайдартный образец для испытания на растяжение цемента (рис. 184)
представляет другой пример растянутого элемента с резким
изменением поперечного сечения. Опыты показывают^), что наибольшее
напряжение имеет место в точках типа что это напряжение
приблизительно в 1,75 раза больше среднего напряжения по
поперечному сечению тп.
Рис. 184.
Рис. 185.
Рис. 185 представляет соединение в виде ласточкиного хеоста,
которое часто применяется в электрических машинах для удержания
магнитных полюсов в ободе якоря. Центробежная сила, действующая
на полюс, вызывает, по поперечному сечению тп большие р1астягива-
юш,ие напряжения. Распределение этих напряжений показано на рис.
^) Н. N е U b е г, Z, angew. Math. u. Mech., см. сноску стр. 255.
*) См. Е. G. С о к е г, Ргос. Congr. Internal. Assoc. Testing Materials;
N. Y., 1913.
57] ' ДРУГИЕ СЛУЧАИ РАСТЯНУТЫХ ЭЛЕМЕНТОВ 257
185, ^*). Вследствие резкого изменения поперечного сечения в
точках тип имеет место высокая концентрация напряжений.
Растягивающие напряжения а^^ сопровождаются напряжениями Су в
поперечном направлении. Распределение этих напряжений по тп показана
на рис. 185, Ь, а распределение их по вертикальной плоскости
симметрии показано на рис. 185, а.
Все предыдущие выводы относительно распределения напряжени*^
сделаны в предположении, что наибольшие напряжения не
превосходят предела пропорциональности материала. За пределом
пропорциональности распределение напряжений зависит от пластичности
материала. ^Пластический материал может испытывать за пределом
текучести значительное удлинение без большого увеличения напряжения.
Благодаря этому обстоятельству при дальнейшем растяжении
материала за пределом текучести распределение напряжений получается
все более и более равномерным. Этим объясняется, почему при
статическом испытании образца из пластического материала отверстия
и выточки не понижают предела прочности. Более того, при
испытании образцов из мягкой стали с глубокими выточками обычно
получается некоторое увеличение предела прочности благодаря тому
обстоятельству, что выточки препятствуют образованию шейки образца
в месте разрыва (см. гл. X).
Однако в Случае хрупкого материала, как, например, стекло,
высокая концентрация напряжений сохраняется до момента
разрушения. Это оказывает существенно ослабляющее влияние на прочность,
что подтверждается уменьшением предела прочности б^^усков из
хрупких материалов с любыми надрезами. Интересно отметить, что очень
тонкие царапины на поверхности образца, изготовленного из стекла,,
не. вызывают уменьшения прочности, хотя на дне царапины должна
быть весьма большая концентрация напряжений^). Для объяснения
этого явления предполагают, что обыкновенное стекло в своем
естественном состоянии имеет множество внутренних микроскопических
трещин, и немного дополнительных трещин на поверхности не изме-
няе!т прочности образца.
Таким образом, предыдущие рассуждения показывают, что
применение выточек и входящих углов при проектировании требует
большой осмотрительности. В случае пластического материала, как,
например, строительной стали, большая концентрация напряжений не
опасна при условии, что нет переменных напряжений. Например, в
О См. статью Е. О. С о к е г, J. Franklin Inst., т. 199, стр. 289, 1925.
Т-образные головки, которые также имеют частное применение при
проектировании машин, были испытаны М. Н е t е п у i, J. Appl. Mech., т. 6, стр. 151,^
1989.
') Это явление было исследовано А. А. Griffith'oM, Phil. Trans. Roy.
Sec. (London), A, т. 221, стр. 163, 1920. См. также статью: 1. N. Sneddon,,
Proc. Roy. Soc. (London), A, т. ^87, стр. 229, 1946.
9 С. П, Тимошенко, т. II
258 КОЩШ11ТРАЦИЯ НАОДЯЖЕНИЙ {ГЛ. Virt
соединений ласточкиным хвостом, доказанном! на рис. 185, напряжения
очень часто бывают настолько высокими, что происходит текучесть
в точках ^ и и, но эта текучесть не считается опасно!!, • потОму что
конструкция подвергается действию постоянной силы. В случае хруп*
кого материала значительно, уменьшают прочность те точки, в котог
рых имеет место концентрация напряжений, и. такие места должны
быть устранены, или концентрация напряжений , должна быть )гмень-
щена при помощи соответствующих размеров выкружек.
В элементах, изготовленных даже^3 пластических материалов, но
подверженных действию повторных усилий,, необходимо принимать'
во внимание влияние концентрации напряжений, так как в леренапря-
женных точках появляются трещины, которые стремятся к
дальнейшему расширению (рм. п. 87).
л 68. Концентрация напряжений 41ри кручении
При рассмотрении кручения стержней переменных поперечных'
сечений {см. пп. 46 и 47) указывалось, что входящие углы или
другие резкие изменения в контуре поперечного сечения вызыйак|т
большую концентрацию напряжений. Продольные отверстия производят
подобный эффект.
В качестве первого примера рассмотрим случай наличия малого
круглого отверстия в скручиваемом круглом вале *) (рис. 186).
При исследовании этого вопроса весьма полезно
применить гидродинамическую аналогию *). Задача
кручения стержней постоянного поперечного
сечения математически идентична с задачей движения
совершенной жидкоеmUt пе|ремещающейся с
постоянной угловой скоростью внутри цилиндрической
оболочки, имеющей,такое же поперечное сечение»
как и стержень. Окружная скорость циркулирующей
Рис. 1S5. жидкости в какой-лдбо точке может быть принята
за изображение касательного напряжения в той же
точке поперечного сечения ' скручиваемого стержня. Влияние малого
отверстия в валу, кругового поперечного сечения подобно тому, какое
окажет сплошнрй цилиндр тех же размеров, введённый в поток
гидродинамической модели. Такой цилиндр значительно измейяет CKopocTiji
жидкости в непосредственной близости от себя. Скорости в передних
*) Этот случай был исследован J. Larmoiir'oM, Phil. Mag., т. 33,
стр. 76, 1892.
* ^) Эта аналогия была разработана Lord'oM Kelvin'oM and Tait'ow,
Natural Philosophy, т. 2; J, Boussiti esq't>M, J. math. (LiouviUe), т. 16, 1871;
A. G. OreenhliroM, статья 4Hydromechanics>, Encyclopaedia Britaonica,
изд. 9. Относительно приложения аналогии в опытах «м. статью: J. Р. Den
На г tog and J. G. McGivern, J. Appl. Mech., т. 2, стр. 46, 1935.
S81 КОНЦЁНГРАЦЙЯ ИАПШЖЕНИЙ ПРИ К»^^^^ ^ 2Ш
И задних точках об]ращаются В йуль, В то время как й'боковых точках
ni » п они удваиваются^, следовательно, отверстие такого рода
удваивает наибольшее напряжение! в toi! части вала, где оно р^цолои^ено.
Малая полукруглая канавка, на поверхности вала, паралл€ль1нУ1*: его
длине (рис. 186), оказывает то же влияние. Касательные напряжения
вблизи точки I» буду* почтой в два раза больше касательных напря-
жений, вычисленных для точек- на поверхности вала^ значительно
удаленнытс от К9навкй«
Та же гидродинамическая аналогия объясняет влияние отверстия
аллиптаческого поперечного сечения или канавки полуэллиптического
поперечного сеченця: Если одна из главных осей эллипса равна а и
расположена в радиальном иапра!влении, а другая равна. Ь, то
напряжения у краёв отверстия на концах оси а увеличиваются в отноше-
-нии [1-|-fl/fe]'1- ТГаким образом, наибольшие напряжения, возникаю-'
щие в это)м случае, зависят от величины отношения а/&. Влияние
эллиптического отверстия на Jвeличинy напряжений будет больше
в том случае, когда большая ось эллипса имеет радиальное
-направление, а не направление касательной к окружности. Этим объясняется,
почему радиальные трещины оказывают такое вредное влияние на
прочность вала. Подобные „рассуждения можно
применить также и в случае полуэллиптической
канавки на поверхности вала, параллельной его оси.
В случщ шпоночной канавки с острыми углами
(рис. 187) г1идродинамическай аналогия указывает
нд. то, что скорости диркулирующёй жидкости в
наружных углах (точки т — /и) равны нуЛю;
следовательно, касательные напряжения,
соответствующие задаче кручения, равны нулю в тех же углах. Рис. 187.
В Точках л — л, т. е.^'в вершинах входящих углов, ,
скорости циркулирующей жидкости теоретически равны бесконечности.
В соответствующей задаче круч(вния каса^тельные напряжения в точках
и — п также ра^вны бесконечности; это значит, что незначительный
крутящий момент будет вызывать в этих точках ьстаточяые
деформации. Такая концентрация напряжений может быть уменьшена путем
закругления утлоь/п-^п. . : / .
Опыты,= произведенные') йад полым валом, имеющим внешний
диаметр 25,4 см'^ ьщтретШ диаметр 14,73 см, глубину шпоночной
канавки 2,54 гж,'ширину; шпоночной канавки 6,35 смц радиус
закругления в вершинах углов канавки г, показали, что наибольшее
напряжение в закругйённых углах равняется наибольшему напряжению
в таком же валу без канавки, умноженному на коэффициент k,
значения которого даны в табл. 19. ',
*) См. сборник работ The Mechanical Properties of Fluids, New York^
D. Van Nostrand Company, Inc., стр. 245, 1924.
260
, КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
Таблица 19
Значения коэффициента к при выкружках
разных радиусов
1ГЛ. VIM
г (см) =
/^=
0,25
5,4 о
0,51
3,4
0,76
2,7
1,01
2,3
1,27
2,1
1,52
2,0
1,78
1,9
Эта таблица показывает, что концентрация напряжений может
^ыть значительно уменьшена путем увеличения радиуса в вершинах
углов п.
Ослабляющее влияние концентрации напряжения в валах вслед-
■ствие наличия отверстий и выточек зависит от того, пластичен ли
материал или нет, и выводы, сделанные в предыдущем параграфе,
применимы также и здесь.
Если трубчатый элемент, имеет входящие углы, то концентрация
напряжений будет иметь место в этих углах, и величина наибольшего напряжен
ния будет зависеть от радиуса углов. Приближенное значение этого наиболь-
щего напряжения можно получить по мембранной
аналогии. Рассмотрим простой npHJuep трубы постоянной
толщины и предположим, что угол ограничивается двумя
концентрическими окружностями (рис. 188) с центром
в точке О и радиусами г,- и г^. Поверхность мембраны
в поперечном сечении мож1но рассматривать *) как
поверхность вращения с осью, перпендикулярной
плоскости рисунка в точке О. Мы видели, что наклон
.мембранной поверхности в какой-либо точке М численно
равен касательному, напряжению т. Обращаясь к
рис. 189, который показывает меридиональное сечение,
проходящее через тп, находим, что главные кривизны
1 d^ dx
I т
Рис. 188.
мембраны в этой точке будут — = -i = ^ для меридионального сечения
{принимая элемент ds по меридиану равным dr) и
R^
— —для
сечения,
перпендикулярного меридиану. Тогда уравнение равновесия мембраны на
основании Уравнения A22) стр." 104 будет
dz х^ р
или на основании соотношения (а), стр. 198
^ + l. = 2Ge.
dr ' г
(а)
') Это предположение удовлетворяется при условии, что г,- не мало по
сравнению с Гд. ^
68)
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ПРИ КРУЧЕНИИ
261
Пусть То означает среднее касательное напряжение, полученное из
выражения B26). Тогда из выражения B27) найдем ч
-J- -f- — = 2С/" = -ёг ,
dr г г '
(Ь)
где S — длина осевой линии сечения трубчатого элемента. Общее решение
уравнения (Ь) будет
Постоянная интегрирования С получится из уело- >Л" ~\ ~^j<f
ВИЯ-О ' ^4 ь^-""
\ т:^г = ТоЛ.
Подставляя" выражение (с) вместо т, находим
С = хЛ
1 —4р('-а + ''*)
1п^
И из, решения (с) получаем
1п^
2F
B66)
Рис. 189.
%~
it44
''/•
Во входящих углах г = г,-, подставляя это значение в формулу B66), мы
можем вычислить наибольшее напряжение в этих углах®). Возьмем,
например, квадратную трубку (рис. 190) с
наружными размерами 10 х 10 см, толщиной стенок
h==\ см и радиусами в углах г^ = 0,5 см,
г^»==1,5 см. Тогда
. /='=9-9—РD —7с)==80,14 еж»,
8 = 4-9—1(8 —27с)==34,28 еж .
Среднее Напряжение То определяется по
формуле B26). Напряжение же во входящих углах
по формуле B66) равняется т= 1,54 tf^.
Коэффициент . концентрации напряжений в этом
случае равен, 1,54. Можно видеть, что этот
коэффициент увеличивается с уменьшением
внутреннего радиуса г^.
Формулой B26) можно пользоваться также
для приближенного вычисления напряжений
6 том случае, когда закруглен лишь входящий угол (рис. 190, ft). Так как
напря:№ения малы в выступающих угл^х, то мы можем принять г^»= к 4- г^,
как показано на рисунке пунктиром.
*) Это условие вытекает из гидродинамической аналогии (стр. 258). Если
жидкость движется в канале, имеющем форму поперечного сечения трубча-
toro стержня, то ее количество, протекающее через любое поперечное
сечение, канала, должно оставаться постоянным.
*) Такая формула дана С. W е b е г'ом, цит. на стр. 213.
262
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
ргд. vm
в случае прокатных фофилей, та^их, какие показаны на рис. 144, b и
Л44^с, jCtp. 204, наибольи1ее>на-
пряжение имеет место во
входящих углах. Его значение,
получается путем умножения напрям<:ё-
' нйя, вычисленного по формулам
B22) или B25) (см. стр. 201,
205), на коэффициент
концентрации, для которого можно
воспользоваться выра>1^нием^')
\
\А
1.
-
•
*
-
,
В
Ч
\
i
\
Рис. 191.
■' - S
к=.1,74-у^^,
B67)
напряжений значения, представленные
в котором f^-г-толщина полки
и ^ г —радиус выкружки. Более
сложные вычисления дают для
коэффициента концентрации
на рис. 191 кривой АВ%
" 69. Круглые в1Е1лц переменногб диаметра^)
Если диаметр вала постепенно изменяется по его длине, то
наибольшее напряжение можно получить с достаточной, точностью при
noMOiiJ№i формулы'A52) т.Л, стр. 241, вы1?еденной для
цилиндрического вала. Но если изменение диаметра происходит резко, как
показано на рис 192, ;То в точках т — от, т. е. у начала выкружек, имеет
мерто большая кощентрацйя напряжений. Величина наибольшего на-»
пряжения зависит от отношений p/d а Dj4, где р есть радиус
выкружки, а d! и D —диаметры двух цилиндрических участков вала.
*) Е. Trefftz, i. anjgew. Math. u. МесЬ-.т. 2, сТр. 263, 1922. Формула
B67) выведена для угла, для которого смежные час$и имеют одинаковую
толщ;ину, как на рис. Л44, й. В случае разной толщины Cj и Сд, как на
рис Л44, с, в формуле B67) нужно принять ббльшую толщину. Дальнейшее
обсуждение этого вопроса дано Н. М. Wester g^ard'osi and R. D. Mi.nd-
lin'oM, Proc. Am. Soc. Civil Engre./стр. 509, 1935,
:«) См. статью: J. Н. Hutft, J. Appl. Mech^ т. 17, стр. 388, 1Й50. Резуяъ*:.
fafH ёычиСлешй Hut h'a очень хорошо .согласуются с результйтами опытов
N. S; W*a п € г'а и W. W. So^.rbk'a, полученными путем проведения листовой
аналогии; см; Ргос. Зос Expi Stress Anal, т, 11, стр. 19, 1953.
*) Общее решение этой задачи принадлежит J. Н. Michell'y, Proc.
London Math. Soc, т. 31, 1899 и A. Foppl, SitztmgsbeT. Bayeh Akad. Wis-
senscfi, T. 35, cm 249, 19p5. Случай, показанный на ^йс. 192,-был
рассмотрен впервые А. гДррГем, см. Z. Ver. deut. Ing., стр. 1©32, 1906. Литература
по этому вопросу приводится в книге: Timoshenko and Goodie^,
Theory of Elasticity, стр. 310, 1951; русский перевод. Стр.- 305, 1937.
69]
КРУГЛШ ВДЛЫ ПЕРЕМВНШ^ГО ДИАМЕТРА
263
Эти высокие местные напряжения, хотя и не опасные для статического
нагружёния вала иэ пластического материала при постоянной нагрузке,
могут оказывать аначительное влияние на
понижение прочности в случае переменных усилий,
какие наблюдаются в пропеллерных и
коленчатых валах. Большинство,' поломок,
происшедших во время работы, можно объяснить этой
причиной. Тефетйческое 'Определ1ение
наибольшего напряжения в выкружке слишком сложно*)
для практических целей, и поэтому ниже
изложен экспериментальный мето/i определения
наибольшего напряжения. Этот метод основан на аналогии между
распределением 41апряжений в скручиваемом валу и распределением элёк»
трического тока в пластинке*).
Рассмотрим сначала круглый вал постоянного диаметра.
Представим себе такой вал разделенным на такие э/!бм»1тарные трубочки.
Рис. 192,
Ра&юиомеят-
угла c/ffi^dama
Рис. 193.
ЧТО каждая воспринимает одинаковую часть полного крутящего
момента Ж^.' Например, на рис. 193 вал разделен на пять частей, кажг
дая из которых несет 1/5 Ж^. Эти трубочки будем назьЛвать
трубочками равного момента, а соответствующие линии диаметрального
сечения вала — линиями равного момента. Обозначим через ДЖ^
крутящий момент, приходящийся на трубочку, и допустим, что тол-
ш^нна каждой трубочки мала. Тогда угол закручивания на единицу
длины, одинаковый для всех трубочек, будет равен
(а)
Q_.MfK
G/«
*) Такие вычисления были сделаны F. А. Wilier s'om при помощи
приближенного метода интегрирования; см. Z. Math. и. Mech., т. о5, стр; 225,
150'^ см. также R. S о п п t а g. Dissertation, Munich, 1926.
^) Эта аналогия была разработана L: S. Jacobsen'oM, см. Trans.
A.S.M. е., т. 47, стр. 610, Ш26.
264 КОНЦЕНТРАЦИЯ HAПPЯЖEHЙJЙ [ГЛ. VIII
где г — средний радиус трубочки и ft —его толщина. Так как АЖ^
и 6 *) одинаковы для всех трубочек, то толщина трубочек изменяется
обратно пропорционально кубу среднего радиуса. Среднее касательное
напряжение в трубочке по формуле B26) равно
На рис. 193 показана вторая система линии в диаметральном
сечении. Эти линии перпендикулярны линиям равного момента и
называются линиями равного угла закручивания. Они соответствуют
сечениям вала, которые называются поверхностями равного угла
закручивания и которые выбираются так, чтобы угол закручивания
между двумя такими последовательными поверхностями был
постоянным по длине вала. Пусть Д<р — этот угол. Для рассматриваемого
круглого вала поверхностями равного угла закручивания будут
равноудаленные друг от друга плоскости; пусть а — расстояние между ними.
Тргда на цилиндрической поверхности какого-либо радиуса г
относительный сдвиг будет Y = ~, а соответствующее напряжение
GAspr ', .
х=—i-* (с)
Обе взаимно перпендикулярные системы линий равного момента и
равного угла закручивания разделяют диаметральное сечение вала на
элементарные прямоугольники, как показано на рис. 193. Размерами
этих прямоугольников можно воспользоваться для сравнения
касательных напряжений в соответствующих точках вала. Пользуясь
формулой (Ь) и сравнивая касательные напряжения т^ и tg в точках,
находящихся соответственно на расстояниях гх rf Га от оси вала.
Находим
(d)
Из выражения (с) получаем
(е)
в рассматриваемом случае ai = a^ = a, но соотношение (е) в
дальнейшем будет применено и к более общему случаю. Очевидно, что
каждой системой линий можно пользоваться для определения
касательных напряжений. В одном случае (выражение (d)) отношение
напряжений зависит от отношения расстояний между линиями равного
момента h^/hi, между тем как в другом случа.е (выражение (е)) оно
зависит от отношения расстояний между линиями равного угла
закручивания aja^.'
*) е — угол закручивания для сплошного вала.
S91
КРУГЛЫЕ ВАЛЦ ПЕРЕМЕННОГО ДИАМЕТРА
265
Рассмотрим вал переменного диаметра, изображенный на рис. 192.
Неравномерность в распределении напряжений, происходящая у
выкружек, имеет местный характер. На достаточном расстоянии от места
сопряжения двух участков разных диаметров распределение
напряжений практически такое же, как и в вале постоянного поперечного
сечения, и две системы описанных выше линий могут быть построены
в диаметральном сечении (рис. 194). Вблизи переходного сечения
распределение напряжений
получается довольно "сложным, и
линии равного момента и равного
угла закручивания становятся
кривыми. Исследование этого вопроса
показывает*), что эти линии,
будучи кривыми, все же остаются
взаимно перпендикулярными и
разделяют диаметральное сечение на
криволинейные прямоугольнички,
подобные заштрихованным на
рисунке. Выражения (d) и (е),
выведенные для вала постоянного
поперечного сечения, сохраняются
также и здесь, нужно только за h и а
принимать расстояния, измеряемые
от середины каждого
криволинейного прямоугольника. Тогда линии
равного момента и равного угла
закручи]^ания дадут полную
картину распределения напряжения
в вале. Рассматривая, например,
линии равного момента и пользуясь выражением (d), видим, что
напряжения увеличиваются с уменьшением радиуса и толщины трубочек равного
момента. Из рис. 194 видно, что напряжения достигают наибольшего
значения у выкружек, где толщина h наружной трубочки равного
момента наименьшая. К тому же заключению мы придем также, если
будем рассматривать линии равного угла закручивания. Из рисунка
видно, что у выкружек расстояние а между этими линиями очень
мало; следовательно, по выражению (ё) напряжение будет большим.
Из выражений (d) или (е) мы можем определить отношение
наибольшего напряжения у выкружки к напряжению в какой-либо другой
точке при условии, что нам известны линии равного момента или
линии равного угла закручивайия.
Упомянутая на стр. 263 электрическая аналогия указывает способ
измерения расстояний а между линиями равного угла закручивания.
Рис. 194.
^) См. статью F. А. Willers'a, цит. на стр. 263.
imw
266
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ,
[ГЛ. VHI
Эти расстояния измеряются на поверхности вала меньшего диаметра d
сначала у точки, удаленной от переходного сечения, а затем у
выкружки.. Отнощение этих двух расстояний дает, как видно из соотно'-
тения (е), коэффициент, на который нужно умножить вычисленное
по обычной формуле напряжение для того, чтобы получить
наибольшее напряжение у выкружки- Рассмотрение электрической аналогии
Линии роЗмдао потенциала
\
\
~^ V
г-
ч
1
/
/
/
\1
/7и»1/и равного така
Рис. 195.
'■■ ■
\
г
\
Рис. 196.
Ь)
,мы начнем.со случая прямоугольной пластинки постоянной толщины
(рис 1^5).,^сли на концах йластинки поддерживается постоянная
разность -потенциалов, то по пластинке будет идти электрический
ток, равномерно распределенный по ее поперечному сечению.
Разделяя электрический ток на равные части, мы получим систему
равноудаленных линий тока.
Система этих линий будет
перпендикулярна системе Линий
равного потенциала. В однородной
1.
п
Рис. 197.
з^зг
гам.
"^о^ nd^
Рис 198.
пластинке пЪстоянного поперечного сечения падение потенциала
будет происходить равномерно по направлению тока, и поэтому линии
равного потенциала будут вертикальными разноудаленными друг от
друга линиями. Для того чтобы получить две системы линий,
аналогичных линиям на рис 193, нужно взять пластинку, толщина которой
изменяется прбпэрциональнр кубу расстояния г, как показано на рис. 196, Ь.
Тогда расстояние между линиями тока будет обратно пропорцио-
59]
КРУГЛЫЕ-ВАЛЫ ПЕРЕМЕННОГО ДиАМЕТ^^А
тт
нальна кубу г'), а расстояйие между вертикальными линиями равного
потенциала остается потйрежнему постоянным.. Таким образо1*, мы
можем получить такую же систему взаимно перпендикулярных линий»
как и на рис. 193. Край О — О пластинки соответствует оси вала.
Линии равного потенциала соответствуют линиям равного угла
закручивания, а лйййи тока—^линиям равного момента б задаче кручения.
^г
£Д
г^
2/J
16
^
т
Ofi
'
л •
^ '
J
у
'
^^Ш>
^1
кп
11/
fe^
'Д
я
■
..
-
Я^Т7П
^fe^£ '•'''
1^
&в
-
т ojiff Ш2 т 1Ш т ^p/^i
Рис. 199.
Исследование показывает ^), что эта аналогия сохраняется также в слу-,
чае пластинки; имеющей участки различной ширины при толщине,
изменяющейся пропорционально кубу расстояния г. (рис. 197). Это
дает возможность исследовать концентрацию напряжений у выкружки
скручиваемого вала при помощи^ электрической аналогии. Будем подг
держивать постоянную разность потенциалов на концах пластинки и
измерять^ падение потенциала по краю mnpq. Таким образом, мы
получим расстояния Ui и а^ между линиями равного потенциала
соответственно у удаленной тбчки тку выкружки п. Отношение ai/а^тйх
*) Предполагается, что ток, приходящийся на единицу площади
поперечного сечения, равномерно распределяется по сбчению.
^) См. статью L. S.. J а с о b s е п'а, цит. на стр^ !^8.
ш
268 КОНЦЕНТРАЦИЯ НАпРйжЕний [Гл. vni
расстояний дает ко^фициент концентрации напряжений для выкружки
у точки п. ■ \ '
Действительные измерения были произведены над стальной моделью
длиной 61 см, наибольшей шириной 15,2 си« и наибольшей толщиной
по краю рд 2,54 см. Падение потенциала вдоль края тпрд модели
было исследовано при помощи очень чувствительного гальванометра,
зажимы которого Ъыш соединены с двумя острыми иголками,
закрепленными в пластинке на расстоянии 2 мм одна от другой. Касаясь
этими иголками пластинки, можно определить по гальванометру
падение потенциала на расстоянии между остриями иголок. При движении
иголок вдоль выкружки можно найти место наибольшего градиента
вольтажа и измерить этот maximum. Отношение этого maximum'а
градиента вольтажа у удаленной точки т (рис. 197) дает величину
коэффициента концентрации напряжений k в уравнении
*^'- B68)
'•шах
71
Результаты таких испытаний в одном частном случае представлены
на рис. 198, где падение потенциала, измерейное в каждой точке,
показано длиной перпендикуляра к краю пластинки в этой .точке. Из
этого рисунка видно, что коэффициент концентрации напряжений
найден равным 1,54. Значения этого коэффициента, полученные при
разных соотношениях размеров валов, даны на рис. 199, где абсциссы
изображают отношения радиуса выкружки к наименьшему радиусу
вала 2j>/d, а'ординаты —^^коэффициент k для различных отношений D/d.
60. Концентрация напряжений при изгибе
Формулы для нормальных и касательных напряжений при изгибе,
выведенные для призматических балок, очень часто применяют также
в случае балок nepeivieHHoro поперечного сечения. Это будет давать
удовлетворительные резу/1ьтаты при условии, что изменение
поперечного сечения происходит не слишком, быстро (см. п. 9).
Если же поперечное сечение резко изменяется, то в переходном
сечении имеет место значительное Нарушение в распределении
напряжений. Наибольшее напряжение обычно гораздо больше, чем
напряжение, даваемое простой формулой изгиба балки, и оно может быть'
представлено формулой
<^max = ka, ^ (а)
где о — напряжение в рассматриваемой точке, полученной по формуле
для призматической балки, и Л — коэффициент концентрации
напряжений. Лишь в немногих случаях этот коэффициент получается при
помощи уравнений теории упругости').
^) Н. N е U b eV, Ingenieur-Ar^hiv, т. 5, стр. 238, 1934 и т. 6, стр. 133, 1935.
601 : КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ ПРИ ИЗГИБЕ 269^
Пластинка большой ширины с гиперболическими выточками (рис. 183),
представляет один из случаев, где мы имеем строгое решение при изгибе
для распределения напряжений в выточках. Это решение показывает, что-
в случае чистого изгиба пластинки парами сил, действующими в срединной
плоскости, наибольшее напряжение имеет место в точках m и я, и
коэффициент концентрации напряжений в формуле (а) можно представить
следующей приближенной формулой: .. '
^ft=|/o,355-^-f 0,85+ 0,08, (b'>
где d—наименьшая ширина пластинки и г — радиус кривизны дна выточки.
В случае круглого вал,а с гиперболической вытдчкой, для которого-
рис. 183 представляет продольное сечение, коэффициент концентрации
напряжений при чистом изгибе будет
*=J/(/24+>+')[i-<'T^>/l+'+^+'']. ,. <^^
. V.=3(|^+l)^(l+4.)-)/"|+T+^^'+^
По-прежнему d — диаметр наименьшего поперечного сечения и г —
наименьший радиус кривизны на дне выточки. Для больших значений отношения
dflr уравнение (с) можно заменить с достаточной точностью приближенной-
формулой
где
(d>
3 -,/"</
(е>
Большинство сведений относительно величины коэффициента k
в уравнении (а) получается опытным путем при помощи оптическога
метода '). Коэффициенты концентрации напряжений для чистого изгиба
пластинок с полукруглыми выточками и с выкружками в в^де ч1етверти1
окружности, и с диаметром D^d-\-2r даны кривыми на рис. 200,
На pnic. 201 даны коэффициенты концентрации напряжений для
выкружек с различными значениями отношения D/d. На рис. 202
даны коэффициенты концентрации напряжений для выточек разной
глубины при чистом изгибе.
Для сравнения коэффициентов концентрации напряжений при
растяжении и изгибе для пластинок и для круглых валов даны кривые
на рис. 203^). Кривые/ и 2, которые дают коэффициенты
концентрации напряжений для гиперболической выточки в пластинке и
в круглом вале при.растяжений, вычислены из уравнений (Ь) и (с)
стр. 255. Кривые 3 и 4, показывающие подобные значения для
выточек при чистом изгибе, вычислены из уравнений (Ь) и (с) стр. 269.
*) Кривые, данные в последующем изложении, взяты из статьи
М. М. Frocht'a, цит.~на стр.^ 254. См. также статью: М. М. Leven and
М. М. Frocht, L Appl. Mech., т. 19, стр. 560, 1952.
^) Этот рисунок и следующие взяты из статьи: R. Е. Peterson and
А. М. Wahl, J. Appl. Mech.> т. 3, стр. 15, 1936.
ш
270
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
{ГЛ. ViH
г,?
W
Iff
//7
■J
-
■ -■
^
-
-\
^
у
f
/7о
гг
'Л г
/
»^
,л>Л!И1/-;>п^г
'/l//J^rV/S>/7A/fi fi/.>/T7/U/M/J
' /7а/А'/7Л'Я|<"АУУ
-
/
\
1
..
^
/?Л
--ь..
^-^^хг- ^.
F^
3
^
г^2^^
Y
/
' •
-. ■
-^
/
■ .
-
- ;
^ ■
'
ff .а/ аг^ лу ofi as т' 0,7 сш т- iffr/d
' ■ , - ■ ■* - ■
Рис. 200.
Л
¥
is
/^
7Д
.-^^т
- Ч
■„- ,
«*"«-»
,
Ч
0^7
М.
т
\
-
\
■
-ff/
(
--
_-w:_
'
■o,z
,",
щ ^
Г i г.
. ■
1 \
''i feJL'
Tjo гл Ш ^.o
Рис.201.
SM 0 ff/r
601
К0НЦЕНТР4ЦЙЯ НМ№ЯЖЕЙИЙ ПРИ ИЙГИБВ
27.1
2,6-
Iff
ы
12
W
1 /
и/:
ФЧ
-*"'^
——
к
WS
1^ш^^^*
■■
:
щяшл «^
b*j ШЛ^
-т.
—oj
1;
^^V-^ 4j|:.
лг
T-f
Zr
az'
•\
:
Рис.'202.
4i7
Siff/rM
I
I
I
■I
A/i
^fi
^.ff
3fi
z§
г/f
2Д
jfi
и
i,
1 \
V
1 i^ ) \ X
J S-
■
- &>imo4Ku
З-шоснШ/ i-" » »» изгиб
^-На/гдыа ., . „. „ г,
5-/Шат обр.,/1Д^еаЛю^/7ю^т^к1дпяз11сей1й т
0' м „ „ , ,; изгиб
7- .. ' .■,j(pg&Uk№/hwp^/M:ffU »
—— lhpe$Bwmi6/ff подсчетом
V—
^
\
Ч л
/
J
• V
\3
vV
о
.4 1
7^
кривые ло NeaiKpy
ntmffVBffMbx из offi/тоб автгмеС'
мим Актовом /та Фрох/^
3~
■-
>х
^
'nS
'-
s
1^
:Jj"
^-~.
-'
i^
'
.•
^
>"
■^'
^
,
-..
fi Ф Ц2 GJ m MS mr/d
Рис. 26a
272
КОНЦЕНТРАЦИЯ НАПРЯЖЦЛИЙ
(ГЛ. VIII
По ЭТИМ кривым можно установить, что коэффициенты концентрации
напряжений выше для пластинок, чем для круглых валов; в случае
растяжения разница становится более заметной. В случае чистого
изгиба, что имеет большое практическое значение, разница между
двумя случаями мала, около 6—8Уо для "вытolieк практических
размеров. Пунктирные кривые 5 и б на рис. 203 получаются из кривых
на рис. 182 и 202 путем экстраполирования этих кривых к большим,
значениям отношения h/r, которое соответствует. глубокой выточке
полукруглой I на дне. Можно видеть, что к|эивы€ 5 и 6
удовлетворительно согласуются с кривыми 1 и 3 ддя гиперболических выточек
ч
\\
\\
\
'#■
ч
VV
V
Z'
:/
h
>^
A
[Е
dL
V
Ч
\
' " I J
Vm/j'/T/.///Лгтл г^M/fn//.7lirte /Атгг/А
Е^О
для а лра Л-а-1^
Олтт.ис^ы/патяЗля b при
ЛФ2 по Фрахту
—Олти¥.1/ст//ггашяд/юЬпра
П.^ 1Г rf. U.
±i-ii
-',v
f^ JW
V/j
'OMi
w
IS
. /^
/^
10
"O a? Ci2 ЦЗ ff.4 O^ Off 0,7 ^ Ц8 QSr/d
' Рис. 204.
для отношений r\d между 0,15 и 0,50. Это указ|1вает на то, что
в случае глубоких выточек величина коэффициента концентрации
иапряжений зависит главным образом от величины отношения rid и
не зависит от формы выточки. '' ^
Пунктирная к]ривая 7 получается из кривых, изображенных, на
рис. 2|01 и представляет коэффициенту концентрации напряжений
в выкружках пластинки при чидтом изгибе с отнош^ниен D/f/=:2.
Видно, ч?о для выкружек коэффициенты концентрации напряжений
несколько ниже, чем для глубоких выточек (кривые ^ и 6) с тем же
•отношением rid. *
Для того чтобы получить коэффициенты концентрации
напряжений для выкружек в круглых валах, были сделаны >в
исследовательской лаборатории Вестингауза испытания? ^больших ^стальных валов
с отношением диаметров Did = 1,5% Значения этих коэффициентов,
полученные путем непосредственного измерения деформаций в
выкружках, даны крз^жочками на рис. 204. Для сравнени! на том же рисунке
*) Westinghouse Research Laboratories.
61] ИССЛЕДОВАНИЯ С ПОМОЩЬЮ МОДЕЛЕЙ 273
кривыми / и 2 Даны *) результаты фотоупругих опытов над плоскими
моделями с Dld = 2 vi Dfd = l,6. Из этих опытов можно сделать
весьма важное заключение, что коэффициенты концентрации
напряжений для круглых валов очень хорошо -согласуются со значениями,
полученными при помощи фотоупругого метода испытания плоских
образцов.
61. Исследования концентрации напряжений с помощью моделей
Уже указывалось, что полное теоретическое решение вопроса
о распределении напряжений в местах резких изменений поперечных
сечений имеется лишь для немногих простейших случаев, как, напри-,
мер, для круглого или эллиптического отверстия й гиперболической
выточки. В большинстве случаев сведения относительно концентрации
напряжений получаются из опытов. С этой целью иногда удается
произвести измерения деформаций в местах резких изменений
поперечных сечений при помощи чувствительных экстензометров. Таким
путем, например, была исследована^) концентрация напряжений при
растяжении образцов с выточками. При пользовании этим методом
возникают большие затруднения из-за чисто локального характера,
распределения напряжений в указанном меСте, поскольку необходимо
получить удовлетворительные результаты ^) при очень малой длине
датчика и, следовательно, при очень большом увеличении.
Грубое значение коэффициентов концентрации напряжений можно
получить, если образец или модель конструкции нагружать до начала
текучести в наиболее напряженных точках. Эту текучесть можно ясно
видеть на полированных поверхностях образцов из мягкой стали.
Рис, 205'представляет фотографию линий текучести на полосе из
мягкой стали. Эти линии текучести (называемые линиями Людерса,
см. главу 10) впервые появляются в местах, соответствующих
наибольшим напряжениям. Распределение этих линий дает весьма ценные
указания относительно напряжений в местах резких изменений попе:
речных сечений *).
^) Эти кривые были построены на основании данных, приведенных на
рис. 201. / - .
^) См. Е. Preuss, Z. Ver. deut. Ing., т^ 56, стр. 1349,1912; т. 57, стр. 664^
1913 и Forschungsarb., № 134, 1913, см. также Th. W у s s, Ргос. Internat. Congr.
Appl. Mech., Delft, стр.'354, 1924 и его диссертацию, Цюрих, 1923. См. также
F. Rots Che г und J. Crumbiegel, Z. Ver. deut. Ing., т. 76, стр. 508, Ш32.
^) Для увеличения деформаций в местах резких изменений сечейий также
применялись в некоторых случаях резиновые модели: "см. А. Stodbla,
Z. Ver. deut. Ing., т. 51, стр. 1272, 1907; Hummel, Schweiz. Bauzeitung,
стр. 143^1^24; L. Chitt^ and A. J. S. Pippard, Proc. Roy. Soc. (London),
A, T. 156, стр. 518, 1936. Об улучшений техники измерения деформаций см.
статью: James А. Л\>111ег, Ргос. Soc. Exp. Stress. Anal., т. 10, стр. 29, 1952.
*) См. статью М. А. В о р о п а е в а, Известия Киевского политехнического
института, 1910 и статью автора в Ргос. Internat. Congr. Appl. Mech., Zfirich,
стр. 419, 1926.
m
S74 КОНЦЕНТРАЦИЯ нл[1РЯЖ15Н1^й [гдГущ
P>ic. 206 показывает линию Людерса у выкружки модели,
изготовленной из мягкой стали (рис. 181) при соотношении rjd ==0,16.7
и JD7<i3== 2,5. Линия начинается отстой точки иавыкружке, в которой»
согласно предварительным опытам, при п(})ирщи поляризованнрго света
следовало ожидать наибольшей концентраций напряжений. Коэффициент
концентрации напряжений по кривой, взятой из рис. 181, равняется 1,85.
Следовательно, текучесть должна начаться в ^наибо^^е-слабой части,
когда среднее растягивающее. напряжение в более узком участке
модели будет составлять, лишь 1/1,85 того напряжейия, которое
необходимо для появления 71ИНИЙ Людерса в призматическом стержне
Рис. 205. ^ Рис. 206.
(рис.^^05) из того же. материала. Опыт показал, что нагрузка, при
кот-ерой началась текучесть у выкружки, равнялась 1/1,8 нагрузки
призматического стержня. : .. ) -:. ^:
На рис. 207^ изображены линии Людерса у края круглого
отверстия в полосе из^йягкой стёЛй. Снова эти линий точно указывают
места наибольшей концен-^ации напряжений. Среднее напряжение' по
кемцевому поперечному сечению у пластинки, при котором произошла
•М^кучесть, равнялась 1/2,3, напряжения, необходи^^рго Для текучести
в призматическом стержне. ' - ;
В обои]^ предыдущих примерах текучесть в Л*1встах Наибольших
напряжен^]^ появлялась при среднем напряжениц,;;котррое выше
указываемого действительными коэффициентами кбткШрацитЭто мояшо
объяснить следующим обраакэм. Небольшая обласЙг перенапряженного
материала окружена участками, где напряжение нё%ревосходит предела
€i3 ИССЛЕДОВАНИЯ G ПОМОЩЬЮ МОДЙЛЕЙ 276
пройорциональности. Это препятствует* скольжению» показанному на
рШ 205, по плоскостям, перпендикулярным плоскости'. рисунка и
наклоненным под углом ^5° К' направлению растяжения, В случаях,
изображенных на рис. - ^06 й 207^ линии Людерса начйнаютсй'
на полированных поверхностях пластинок лвПвиде тонких лиц^
перпендикулярных , наибольшему растягивающему напряжению. Эт0;
указывает «а то, что в этих случаях скольжение происходит по
плоскостям, "прОхрдяШйм через эти линии й наклоненным под углом 45*
к плоскост'ям пластинок. В taKOM случае толщина пластинки играет
Рис 207. .
Важную роль. Эта толщина должна, быть очень мала по сравнению
с радиусом отверстия или выкружки для того, чтобы, поверхность
скольжения, полностью находилась в области сильно
перенапряженного материала. То обстоятельство, что поверхность скольжения,
начинающаяся в. точках наибольших напряжений, должна пересечь
область с меньшими Напряжениями, объясняет *) запаздывание в
появлении линий Людерса. В указанном, выше случае круглого отверстия
чширина пластинки была 15,24 еж, диаметр отверстия 2;54 ел, а
толщина пластинки — лишь 0,32 см.- При испытании моделей, у которых
толщина и диаметр отверстия были одного порядка, невозможно было
обнаружить какое-лй!&о существенное влияние концентрации
напряжений на величину ййгрузки, вызывающей .линии Людерса. Другой
причиной запаздывания в появлении лаяний Людерса может служить^ то
обстоятельство, что прежде чем линии Людерса станут заметными,
может иметь место некоторая остаточная Iеформация.
V *) Это объяснение было предложено автору L. Н. DonfieU'oM.
mw
276 КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ [ГЛ. VHI
. Метод определения слабых мест в конструкциях, основанный. на
изучении линий Людерса, не ограничивается каким-либо частным типом
задачи и имеет перед оптическим методом, описанным в следующем
параграфе, то преимущество, что он применим к пространственным
задачам, т. е. к таким, в которых рассматриваются напряжения- по
трем взаимно перпе;ндикулярным направлениям. Для того чтобы
сделать' текучесть металла цидимой на шероховатой поверхности, при
исследовании напряжений в днТ^щах котлов *) и в составных сжатых
стержнях ^) поверхность покрывают хрупким лаком. Делая после
испытаний разрезы образцов и моделей и применяя специальный
способ протравливания поверхностей разреза, можно обнаружить
внутренние области, в которых имела место текучесть, и таким образом
получить указание относительно текучести металла в наиболее
напряженных точках ^).
62. Оптический метод измерения напряжений
Имеется много задач 6 напряженном состоянии, когда деформация,
по существу, происходит в одной плоскости. Это так называемые
двумерные задачи. Примерами служат: изгиб балок узкого
прямоугольного поперечного сечения, изгиб ферм, арок, зубчатых колес или
вообще пластинок какой угодно формы, но постоянной толщины,
на которые действуют силы или моменты в плоскости пластинки. Форма
пластинок может быть такой, что становится весьма затруднительным
аналитическое определение закона распределения напряжений; для таких
случаев оказывается весьма полезным фотоупругий метод. В этом
методе применяются модели, вырезанные из пластинок изотропного
прозрачного материала, как, например, стекло, целлулоиД^или бакелит.
Хорошо известно, что под действием напряжений эти материалы
становятся двояколучепрёломляющими, к если луч поляризованного
света проходит через прозрачную модель, находящуюся в
напряженном состоянии, то при этом йожно получить окрашенное
изображение, по которому удается найти закон распределения напряжений*).
*) См. статью: F. КоегЬег und Е. S i е b е 1, Mitteil., Kaiser-Wilh. Inst.
Eiseniorsch. (Dusseldorf), т. 8, стр. 63, 1926 и т. 9, стр. 13, 1927.
, 2) R. S. Johnston, Iron and Steel Inst., т. 112, стр. 341, 1925. См. также
статью: William F. Stoke у, Proc. Soc. Exp. Stress Anal., т. lOj, стр. 179, 1952.
Метод-был применен к исследованию напряжений в машинных частях
Dietrich und Lehr, Z. Ver. deut. Ing., т. 76, 1932. См. также Н. К а у s е r,^
Bautechnik, 1936; А. V. de Forest and Greer Ellis, J. Aeronaut. Sci.,
T. 7, стр. 205, 1940 и М. Hetenyi, Handbook of Experimental Stress
Analysis, стр. 636, 1950. ' _
^) См. статью: A. Fry, Kruppsche Monatsh., июль 1921, также Stahl u,
Eisen, 1921.
*) Явление двойного лучепреломления под действием напряжений было
открыто D. В г е W s t ё г'ом, Phil. Trans. Roy. Soc. (London), 1816 и в
дальнейшем изучено F. Е. Neuman.n'oM, Berlin Abh., 1841 и J. С. Maxwell'oM»
62]
ОПТИЧЕСКИЙ МЕТОД ИЗМЕРЕНИЯ НАПРЯЖЕНИЙ
2^7
На ]рис. 208 abed представляет прозрачную пластинку постоянной
толщины, а О — точку пересечет1ия пластинки с лучом
поляризованного света, перпендикулярным к плоскости пластинки. Предположим,
что О А изображает плоскость световых колебаний, а, длина О А = а,
представляет амплитуду этих колебаний. Предположим, что свет
совершает простое гармоническое колебание; тогда
перемещение может быть представлено
уравнением
S == а cospt, . (а)
где р пропорционально частоте колебаний,
которая зависит от цвета светового луча.
Представим, что к краям пластинки
приложены разные по величине напряжения с^
и Оу. Вследствие разности напряжений
оптические свойства пластинки также получаются
различными Bi двух перпендикулкрных
направлениях. Пусть v^ и Vy соответственно
означают скорости распространения света
в плоскостях Ох и Оу. Разложим простое колебание в плоскости
О А на два компонента в плоскостях Ох и Оу с соответствующими
амплитудами ОБ = а cos а и 0С= а sin а.
перемещения будут
Тогда соответствующие
х = а cos а cos pt, у^=а sin а cos pt.
(b>
Если h — толщина пластинки, то промежутки времени, потребные для
прохождения сквозь пластинку двух указанных составляющих
колебаний, соответственно будут
h =
h
V
X
4=
h
V,
(с>
Trans. Roy. Soc. (Edinburgh), т. 20, 1853, см. также его научные статьи,,
т. I, стр. 30. Применение этого явления к решению технических задач было
начато С. Wi 1 son'oM, Phil. Mag. (сер. 5), т. 32, 1891 и в дальнейшем развито
А. Mesnager'oM, Ann. ponts et chaussees, 1901 и 1913; и E. G. С b к e г'ом.
General Electic Co. Mag., 1920 и J. Franklin Inst, 1925. О дальнейшем
развитии оптического метода см. статью: Henry F а v г е, Schweiz. Bauzeitung,
т. 20, стр. 291, 1927; см. также его диссертацию «Sur une nouvelle methode
optique de determination de tensions int€rieures>, Париж, 1929. Применение
монохроматического света (так называемый метод полос) было введено
7. Tuzi, Inst. Phys. Chem. Research (Tokyo), т. 8, стр. 247, 1928. Этот вопрос
очень подробно разобран в книге'Е. G. Сокег and L. N. G. F ilon, Photo-
Elasticity, 1931; и также в книге: М. М. Frocht, Photo-Elasticity, 1941.
Точность оптического метода исследования разобрана в статье М. М. F г о с h t'a
R. Guernsey and D. Landsberg'a, Proc. Soc. Exp. Stress Anal., т. il^,
стр. 105, 1953.
78; KOHliEHTPAUHR НАПРЯЖЕНИЙ ^ГЛ. Vlfr
Tt пб(}ем0щенйя ^равнения (b)) после! прохоз^сдения света сквозь пла-
•стйнку представятся уравнениями "
; JCi == а cos и cos я (^ — ^i), Уг=а sin а^ cos р (t — t^). (d)
Мргза разности скоросте)^ эти составляющие кблебания имеют разность
'фаз, равную/7(^2 —^i). Опыты показывает, что разность скоростей
распространения света • пропорццрнальна разности напряжений, т. е.
где V есть скорость распространения света при напряжении, равном
нулю, и k — Численный коэффициент, зависящий от физических свойств
материала пластинки. Мы видим, что разность двух главных напря-
гжений может быть найдена путем измерения разности фаз двух коле-
нбанйй. Эта может быть проделано, если колебания будут
интерферировать в одной и той же плоскости. С Этой целью за пластинкой
Помещают призму Николя (называемую анйлизатором) так, чтобы
она пропускала лишь колебания в плоскости тп, перпендикулярной-
плоскости О А. Составляющие колебания (d), которые пройдут сквозь
призму, будут иметь амплитуды, OiSj = 0^ sm а = f у J sin 2а и
ОС\^=^0Сcos а=г: f—I sin 2а. Следовательно, результирующее коле-
■бание в плЪскости тп будет . ^
4- sin 2аcosp{t — t^ — -J sin 2aCOSp(t~t,^^
=it-(a sin 2a sin/7,^i^«] sin p ( ^—Ц-^*], (f)
Т^им образом, получается простое гармоническое колебание, амплитуда
JKOtoporo пропорциональна sin p{{ti — ^а)У2]; "Следовательно, Интенсив-
H<9ct'b освещения является функцией разности фаз p{tx'~t^. Если
напряжения Ojt и .о_у равны между собой, toV^i и ^а также будут равны
и амплитуда результирующего колебания будет равна нулю, В этом
случае мы будем наблюдать затемнение. Это же Оудет и в том
случае, если разность напряжений такова, что
Р^-^^пж, , (g)
где п — целое число. Наибольшая интенсивность освещения получится
и в том хлучае, когда разность напряжений такова, что
sinD^^ = ztl.
Вообразим, что вместо элемента а&сс? (рис. 208) мы имеем
пластинку из прозрачного M^tepnafla, находящуюся в состоянии простого
62] ОПТИЧЫ^КШЙ МЙТ1ЭД ИЗМЕРЕНИЯ «М^ПРЯЖЕНИЙ 27&
расшкения. Путем постепенного увеличения растягивающего напряжения
мы ^получим темную картину 1К|б6ражения пластинки на экране каж>
дый раз, когда уравнение (g) выполняется. Таким образом, мы можем
установить опытным путе»! ДЛЯ данного материала данной толщины
напряжение, соответствуюц^еёйромежутку между двумя последоватеЛьнкг^.
ми темными иаображенйяма образца. Например, для одного рода феноли-^
товой пластинки толщиной 1 мм это напряжение было найдено
равным 108 кг(см\ Следовательно; для пластинки толщиной 6,36 мм
соответствующее напряжение *) будет равняться 108/6,36 = 17 кг/см\ Имея
эти сведения, мы можем получить напряжения в пластинке,
находящейся в состоянии. растяжения, считая число промежутков между
последовательными темными изображениями, имеющими место при
постепенном нагруженйи рбр'азцз;
Рис. 209.
Если мы возьмем пластинку, находящуюся в состоянии чистого из-^
гиба, то ползучим картину, подобную показанной на рис. 209. Пара л г
дельные темные полоски*указывают на то, что в части полосы, hsl-^
ходящейся на достаточном расстоянии от точек приложения грузов*
распределение напряжений • одинаково во всех вертикальных
поперечных сечениях. Считая число полосок, мы можем определить величины
напряжений^ поскольку напряжение между двумя последовательными
полосками такое же, как напряжение между ^вумя последовательными
темными изображениями при простом растяжении- Наблюдая за пласг-
тинкой при постепенном приложении нагрузки, мы можем видеть,
что число темных полосок увеличивается с возрастанием нагрузки.
Новые полоски всегда появляются вверху и внизу полосы, и ^посте-^
пенно двигаются-к нейтральной плоскости, так что полоски
становятся все более-близкими друг другу. Тогда напряжение в какой-либо
точке получится лутем отсчитывания числа полосок, которые
проходят через эту точку. >, ."
Метод подсчета числа темных полосок, проходящих через
выбранную точку, можно применить также.в любом случае плоского
распределения напряжений. Как видно из наших предыдущих
рассуждений, это число дает "разность между двумя главными напряжениями
в точке. Для полного определения напряжения в tOMKe остается
найти направления главных напряжений и их сумму. Уравнение _ (f)
*), Z: Т U Z i, ScH*apefs, Inst. Phys. Chem. Research (Tokyo), 1.12, стр. 247,1929.-
ш
■280
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
[ГЛ. vm
показывает, что интенсивность света, проходящего через анализатор,
пропорциональна sin 2а, где а — угол между плоскостью поляриза-
иии и плоскостью одного из, главных напряжений (рис. 208). Если
эти две плоскости совпадают, то sin 2а равен нулю, и мы получим
темное пятно на экране. Следовательно, при исследовании
напряженной прозрачной модели в
поляризованном свете мы
получаем не только темные полоски,
рассмотренные ранее, но также
темные линии, соединяющие
точки, в которых одно из
направлений главного напряжения
совпадает, с плоскостью
поляризации. Вращая обе призмы
Нйколя, поляризатор и
анализатор, и отмечая темные линии
на изображении напряженной
пластинки для различных
направлений плоскости
поляризации, мы находим систему
изоклинных линий, которые
соединяют вместе точки с оди-
на1(овыми направлениями
главных иуацряжений. Имея эти
линии, мы можем начертить линии,
которые будут касательными
в каждой точке к осям главных
напряжений. Эти последние ли-
- ^ НИИ называются траекториями
главных напряжений (см. т. I, стр. 115). Таким образом, направления
главных напряжений в каждой точке пластинки можно получить
опытным путем.
Сумма главных напряжений может быть также получена из опыта
измерением изменений Дй толщины h пластинки, происходящих под
действием напряжений о^ ш о^*), и применением известного
соотношения
Рис. 210, -^
Д/г
^{^'хЛ-Ь)'
(h)
Имея разность двух главных напряжений из оптического метода
испытаний и их сумму по выражению (h), мы мОжем легко вычислить
13еличины главных напряжений. Полоски,, полученные в пластинке
*) Этот метод был предложен А. М е s п а g е г' ощ цит. на стр. 277.
Необходимый боковой .экстензометр был разработан и успешно применен
А. М. W а h Гом.. См. статью: R. Е. Peterson and А. М. W а h 1, J. Appi.
.Mech., т. 2, стр. 1, 1935.
63]
НАПРЯЖЕНИЯ ПРИ КАСАНИИ ШАРОВ И ЦИЛИНДРОВ
281
с выкружками, подверженное действию чистого изгиба, показаны для
иллюстрации на рис. 210. Из-того обстоятельства, что полоски сгу-^
щены у выкр5^жек, можно заключить, что в этих точках имеет место
значительная концентрация напряжений. На рис. 211 показаны
полоски для центрально нагруженной балки, лежащей на двух опорах^
Рис.211.
В приведенном изложении оптического метода при анализе
напряжений предполагалось, что мы имели дело с плоскими задачами. В
последнее время были сделаны значительные усилия к тому, чтобы
распространить оптический метод на пространственные задачи, и уже
получены некоторые многообещающие результаты *).
63. Напряжения при касании шаров и цилиндров
Если два упругих тела, скажем два шара, давят один на другой, то-
образуется малая поверхность соприкасания как резуЛьтат местной
деформации. Давления, распределенные по этой
поверхности, называются контактными давлениями.
Величина этих давлений и напряжения,
возникающие в телах, могут быть вычислены
при помощи уравнений* теории упругости^).
Здесь мы, дадим лишь окончательные
результаты таких исследований.
В случае двух шаров, сжатых силами Р
(рис. 212), давления распределяются по малому
кругу контакта тп, радиус которого
определяется формулой
а = 0,88 |/-P(^i + £s)<?A /269)
В этом выражении Е^ и Es — модули
упругости двух шаров и «?1 и d^ — соответствующие
диаметры. Наибольшее давление имеет место в центре круга контакта и
дается формулой
Р
B70)
Ртах — ^»^
Ttfl*
*) См. статью: М. Н е t ё п у i, J. Appl. Mech., т. 5, стр. 149, 1938; см.
также R. Welle г, J. Appl. Phys., т. 10, стр. 266, 1939 и параграф D. С. D г и с-
кег'ав М. Не ten у г, ed.. Handbook of Experimental Stress Analysis,
New York, 1950.
^) Эта задача была решена Н. Н ertz'eM, Gesammelte Werke, т. 1, 1895.
Разбор задачи и библиография даны в книге: Tinioshenko and G о о d i е г
шШ
2§2
КОНЦЕНТРАЦИЯ НАПРЯЖВНИЙ
{ГЛ. vm
Вследствие местной деформации центры ш&ро^в приближаются один к дру-
грму на расстояние ',^ >
-ол.|/.Р.(|-+1Щ+±).
B71)
Когда диаметры шаров и модули упругости равны между собой, то
вышеприведенные формулы получаются в сяед^ющ^м виде:
«-0,88-j/g^ ^«ах-0.62|/;^, X==i^ B72)
Когда шар диаметром d прижимается ж упругому телу, имеющему плос^
кую поверхность, требуемые формулы получаются путем подстановки d^z^sd,
491=00 в формулы B69) — B71). Полагая Е1 = Е»^=>'Е,^иъх.0щнл для $того
случая: - ' ' ,
:=0,88-^-^ . /»«,«.= 0.62:у^^ , X = 1,54 -^^ •
B73)*
В случае шара в сферическом углублении {рпс. 213) знак d^ в выражениях
<269)--B71) должен быть изменен. Тогда для случая Ei=^£j=aE находим
B74)
)
Необходимо заметить, что в случаях, представленных формулами B72)
fi B73), наибольшие сжимающие напряжения 9 центре поверхности
соприкасания зависят от величины орошения P/d', т. е. ^наибольшее напряжение
остается постоянным, если это отношение не
меняемся. Так оправдывается обычная практика Оцре-
деления безопасного диаметра шара назндЧёняем
определенной величины нагрузки^^на квадратный
^сантиметр диаметрального сечения шара. Так как
материал в центредповерхноСти соприкасания удер^
живаетсяот поперечного расширения, он находится
в состоянии сжатия со всех сторон и может
выдерживать оченьвысокие давления без раггрушения(см. п.81).
В опытах *) С- закаленной тигельной сталью
допускаемая сжимающая сила Р в случае давления
шара на плоскую поверхность иногда принималась
по формуле
Рис. 213. Р1пи=49 d',
л1 которой d с сантиметрах и Р в килограмма^. Подставляя во второе
на выражений B73), находим />тах равным приблизительно 87 000 кг/см\
Theory of Elasticity, стр. 372, 1951; русский перевод, 1937, стр. 96. См, также
И. Я. Щ т а е р м ан, Контактные задачи, 1949; р. М. Б е л я е в,
Сопротивление материалов, 1945.
») См. S t г i b е с к, Z. Ver. deut. Ing., стр. 73, 1901. Schwinning,
там же, стр. 332 и А. BauscHlicher, там же, стр. 1185, 1908.
63]
НАПРЯЖЕНИЯ ПРИ КАСАНИИ ЩАРОа И ЦИЛИНДРОВ
283
Для общего случая сжатия двух тел, имеющих одинаковые /модули
упругости Я, пусть 1/г1 и l/rl явдйются главными кривизнами в точке
соприкасания-Одного из тел, а 1/г, и J/r, —кривизнами другого ^У, я пусть ^
означает угол между нормальными плоскостями, содержащими кривизны 1/Г| и
l/fj. Поверхность контакта и общем случае представл^яет-эллипс^ лодуоси:1
которого даются формудий!^
в которых Р—сжимающая сила, а
т
1
1
п
АЕ
3A-и*)*
Гх ^ Г\^ Г,^ Г',
Постоянные оуй р берутся из табл. 20 для каждого частного случая. Угой fr
в первой ко.лонке таблицы вычисляется из соотношения ;
cos^ 5==
В
(а>
2
In
в котором А
Выражение длй наибольшего давления в центре поверхности соприкасания
в этом случае буд^т.' . * ■
-. . ■ , V ' '
B76)
шах
1.5
'%аЬ
Таблица 2а
Постоянные для вычисления полуосей эллипса контакта
■■■• -Ь:
градусы
20
-30
35
40
45
... .-:_ ■ .
■О .'
• ■
3,778
2,731,..
Z397
2,136
1,926
.-•■р ■-.
0,408
0,493
■ 0,530
«,567
(Щ*4
■ '■- ■
"в
градусы
50 ^ .
. 55
• 60
65
70
/
:j,7S4.
1,611
1,486:
1,378
1,284
• ,• ■
^' f. ■■
0,641
0,678
0,717
0,759.
0,802
е
градусы .
1 ■■^■75 ','
«0
; 85
90 V
■■■■в
1,202
У 28
1,061
1,000
- ■. г
' . ■
- J '
0,846^
0,893
0,944-
1,000
->■ ■
В случае сжштия цилиндрических катков (рис. 214) площадь контакта
представляет собой узкий прямоугольник; ширина которого b дается ^);$t)pv
мулой
Ь^2
Ш^Ш^к^М
B77>
1) Главные кривцзны л1}едставляют собой наиббльщую и наименьшую
кривизны и находятся в перпендикулярных плоскостях. Кривизна тела
рассматривается положительной, если соответствующий центр, кривизны находится
внутри тела: - '^ ^
«) См. А. Foppl, Technische Mechanik, т. 5, стр. 351, 1907.
1284
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
[ГЛ. VIH
8 которой Р означает сжимающую силу, приходящуюся на единицу длины
катка. Наибольшее единичное давление в середине прямоугольника
соприкасания будет
B78)
В частном случае, в котором модули упругости для двух катков равны
между собой, имеем
Если один из диаметров взят бесконечно большим, как в случае касания
IHUt
ГТТПТ
Рис. 214.
цилиндра с плоскостью, то формулы B79) сводятся к следующим:
* = 2,15|/'^. Ртах = 0,59 |/"^.
B80)
Видно, что наибольшее. напряжение остается постоянным, если Р'
изменяется пропорционально d. Это оправдывает практику определения без-»
опасных размеров по диаметральной площади поперечного сечения катка.
Допускаемая с^симающая сила Р' в случае обычных стальных
цилиндрических катков,, в мостах например, получается по формуле
p'=49rf.
Подставляя в уравнение B80), мы находим, что наибольшее давление будет
приблизительно равняться боЫ) nejcM^ ^).
ЗАДАЧИ
1. Определить наибольшее давление на поверхности контакта С в
простом шариковом подшипнике, показанном ,на рис. 215. Диаметр шариков
d = 3,8 см, радиус поверхности канавки ==^ см, диаметр обойМы равен 20 см,
а наибольшая сжимающая шарик сила Р==2000 кг.
*) Об испытании стальных цилиндров см. W. М. W i 1 s о п, Univ. of
Illinois Eng. Exp. Sta. Bull., № 162, 1927; № 191, 1929; № 263, 1934. См.
также V. P. J e n s e ri, Iowa Eng. Exp. Sta. Bull., № 138, 1937. Испытания
на усталость катков рассмотрены в п. 89.
€3] НАПРЯЖЕНИЯ ПРИ КАСАНИИ ШАРОВ И ЦИЛИНДРОВ
Решение. Пользуясь обозначениями на стр. 283, получаем
38
Г1 = г;=-~ = 1,9 сл«, Г2 = —2,5сж, Га = —10 еж;
285
т
1
1
4 . 2 2 • 10^
= 7,^5, п= о пш =3,22.10«;
3 • 0,91
1.9
2Л
1,9 2,5
1 4
10
^ = 0,553, 2^ = 2j"TO = «'3-i
Подставляя в уравнение (а), получаем
cos«=g||g = 0,543, 6=57°
Тогда из таблицы 20 путем интерполирования найдем
«=1,561, р = 0,694.
Полуоси эллипса контакта вычисляем по формулам B75)
см.
» = 0,в94т/^^ = 0,115,«.
И из формулы B76) получим
_ I с 2000
Ртях 1»Э
max
nab
= 32 260 лгг/сж».
^Шмм
Такие высокие напряжения может выдерживать
закаленная сталь благодаря тому, что в центре эллипса контакта
'материал сжимается не только в направлении действия
сил Р, но также й в боковых направлениях, v
2. Определить поверхность^ контакта и наибт5льшее
давление между двумя кр^углыми цилиндрами, оси которых
взаимно перпендикулярны. Примером такой задачи может
служить контактное давление кол«са, имеющего
цилиндрический 0андаж, на рельс ^).
Решение. ^Обозначая через г^ и г^ радиусы цилиндров и пользуясь
обозначениями стр. 283, находим: '
4 АЕ
п =
Рис. 215.
1 ^ 1 ^ It . >, у
иг
3A-Ю'
*) Вопрос о давлении в месте соприкасания приобретает большое
значение, поскольку нагрузки на оси в новейших локомотивах увеличиваются.
О р(ешении этой задачи см. статью Н. Fromm'a, V. D. I.,т. 73, стр. 957,
1929 и статью Н. М. Б е л я е в а. Известия Ленинградского института
инженеров путей сообщения, 1929.
286 КОНЦЕНТРАЦИЯ НАПРЯЖЕ|!*ий [ГЛ. ущ
Знак ну^го выбрать так, чтобы £^ было положительным. Из уравнения (а)
находим
cos в = ±—ri
±+1
г, Га
Зная Ь, мы определит полуоси эллипса контакта^ по формуле B75) и
наибольшее давление по формуле B76).
В частном случае, когда цилиндры имеют одинаковое радиусы, cos 6?= О,
и на основании табл, ^, можно заключить, что поверхность соприкасания
имеет круговой контур/ -
3. Найти наибольшее давление менаду колесом с цилиндрическим банда^-
жом радиуса г=40 см и рельсом с радиусом головки Га = 30 см, если
Р == 400 Агг; и коэффициент Пуассона {х== 0^25.
^ ОШетУ Полуоси эллипса контакта равны а = 0B36 см, Ь=^0,1% см,
а наибольшее давление
"''■•"■■.■ 3 ■ " Р
: ртах=-ф^—^ я» 4000 кг1см\
ГЛАВА IX
ДЕ^РМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
<^г
о
1
64. Системы из идеально пластических материалов
В предыдущем, изложении всегда предполагалось, что материал
конструкции следует закону Тука. На основании этОго закона были
проанализированы деформации и распределения напряжений в
различных случаях. Однако имеются за^з^ачи, в которых необходимо ис-
Следевать деформацию сооружения за
пределом пропорциональности. Для выпЬл- . '
нения такого исследования нужно знать
механические свойства материалов за
пределом пропорциональности. Эти свойства
обычно определяются при помощи диа^
грамм растяжения и сжатия. _
Простейший вид диаграммы имеют в
случае идеально пластического жавг(?-
jptta^fl. Такой материал следует закону Тука
до дЬредела проггорциональности,' и затем
начинается текучесть^ при постоянном на-
прязкений. Соответствующие диаграммы
растяжения и сжатия даны на рис. 216Г
Строительные стали с резко выраженным
пределом текучести и значительным при этом удлинении гфиближаются в
известных границах по своим свойствам к идеально пластическим
материалам, а анализ напряженного состояния сооружений на
основании диаграммы на рис. 216 имеет большое практическое значение
во многих случаях. В этом и следующем параграфах мы
рассмотри* несколько зггдач такого рода>
Чистый изгиб. При рассмотрении чистого изгиба за пределом
пропорциональности мы буДем делать те же предположения, что -и в
случае упругого изгиба (см. т. I, п. 23, стр. 85). А именно,
предположим: 1) что поперечные сечения балки при изгибе остаются
плоскими и нормальными к изогнутой оси и 2) что продоль{1ые волокна
7
Рис. 2t6.
288
ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
[гл: IX
балки находятся в состоянии простого растяжения или сжатия и не давят
друг на друга в поперечном направлении *). Рассмотрим балку с
продольной плоскостью симметрии и предположим, что изгибающие моменты
действуют в той же плоскости; мы будем наблюдать, что изгиб
происходит в этой же плоскости и что при изгибе поперечные сечения
балки будут поворачиваться вокруг своих нейтральных осей,
перпендикулярных плоскости изгиба. Относительное удлинение волокна в
расстоянии у от нейтральной оси (См. j. I, стр. 86) при этом равно
_>'
(а)
Величина же изгибающего момента, при котором начнется текучесть,
должна быть вычислена по формуле (см. т. I, стр. 88)
М^ = о^
(Ь)
в,которой Jg — момент инерции площади поперечного сечения балки
относительно ее нейтральной оси, и с — расстояние от этой оси до
наиболее удаленного волокна балки. ,
/у
а)
Ь)
Рис. 217.
С}
d)
ej
Рассматривая в качестве простейшего примера прямоугольную
балку (рис. 217), получаем''^)
Л4т = 0т-«-; (с)
соответствующее распределение напряжений показано на рис. 217, с.
Все волокна балки находятся в упругом состоянии и наиболее
удаленные волокна как раз достигли напряжения, соответствующего
пределу текучести. Если мы несколько увеличим изгибающий момент
*) Эти предположения хорошо согласуются с опытами; см. статью G. Н. Мас-
CuHough'a, Trans. А. S. М. Е., т. 55, стр. 55, 1935.
2) Мы предполагаем, что Зт при растяжении и сжатии одинаковы. Наши
выводы можно легко обобщить, если о^ имеет различное значение при
растяжении и сжатии.
€41
СИСТЕМЫ ИЗ ИДЕАЛЬНО ПЛАСТИЧЕСКИХ МАТЕРИАЛОВ
28&
сверх вел'ичины М^, то волокна вблизи верхней и нижней
поверхностей балки начнут испытывать состояние текучести и распределение
напряжений будет таким, как показано на рис. 217, 4. Пластические
деформации проникают все глубже в балку с увеличением
изгибающего момента. Для каждого значения е глубины этого
распространения соответствующий , изгибающий момейт, определяемый с
помощью заштрихованной площади на рис. 217, d дается уравнением
М = о^Ье {h — e)-{- о^
b{h — 2ef
6
6
Ь+¥{^~Ш
(d)
Соответствующая кривизна изогнутой оси балки найдется
использованием уравнения (а). Применяя это уравнение к волокнам,
находящимся на расстоянии ft/2 — е от нейтральной оси, и замечая,..что
напряжение в этих волокнах достигает предела пропорциональности о^^
получаем
и — :
^A-^) ■
Пользуясь уравнениями (d) и (е), мы можем представить
зависимость между изгибающим моментом М и кривизной 1/г графически,
как показано на рис. 218. До значения ^
М = М^ деформация является упругой и
кривизна бэлки увеличивается
пропорционально изгибающему моменту. Когда М
увеличивается за М^, то зависимость между
Ж и 1/г становится нелинейной.
Соответствующая кривая (рис. 218) становится
круче по мере того, как глубина е
распространения пластической дефор^ции
приближается к значению ft/2, а
распределение напряжений — таким, как показано
на рис. 217, е. Подставляя e = hj2 в выражение (d), получаем
наивысшее значение изгибаю.щего момента, равное
^пред
Рис. 218.
м — М^
■'"пред ''т 4 *
Ф
На рис. 218 значение Жпред определяет положение вертикальной
асимптоты к кривой. Когда М приближается к Ж^ред, малое
увеличение М вызывает большое увеличение кривизны, так что Жпред
вызывает полное разрушение балки *).
*) Понятие о предельном моменте хорошо подтверждается опытными
исследованиями; см. 'статью J. F. В а к е г' а, J. Inst. Aeronaut. Engrs., т. 31,
стр. 188, 1949.
10 С. П. Тимошенко, т. II
290
ДЕФОРМАЦИЙ ЗА ПРЕДЕЛОМ УЦРУГОСТИ
{ГЛ. IX
ФoplMlyлia (с) И (!),были выведены для прямоугольных балок, и
мы можем заключить, чта при этой форме поперечного сечения для
полного разрушения балки требуется изгибающий момент. на 60Ve
больший того, при котором начинается пластическая деформация-
Подобные же формулы можно легко вывести для симметричных
поперечных сечений других форм. '
Рассмотрим, например, .двутавровую балку (]рис. 219). Изгибающий
момент, при котором начинается текучесть, получаетей путем умно-
,жения От на момент сопротивления (см. формулу (Ь)), и мы получаем
М^а(^^Ш1^ (а)
^У^—-°т[12 12 )h' ^8^
При вычислении Mщ^J^ учтем, что распределение
1-
I
Р
Л
Рис 219.
напряясений должно отвечать показанному на
рис. 217, £>. Момент внутренних растягивающих
усилий относительно нейтральной оси
получается умножением о^ на статический момент
половины поперечного сечения относительно
Этой же оси. Удваивая этот момент, находим
rbh^ bj h\\
4 4
М
(bh^ bt Л?\
(h)
Из выражений (g) и (h) теперь получим
"^пред
b,h\
IB
1
b,hr
(i)
M»
Мы видим, что для двутавровой балки отношение M„p^jM^ меньше
чем 3/2 и что его значение зависит от размеров попе](>ечного
сечения. ПрёдпЬлагая, например, /'i//!>=fti/A = 0,9,, мы найдем из
уравнения (i) Л1прец/Жт= 1,18. В 9T0&i случае M„p^J^ т ЛЪ% больше М^.
В х:лучае обычных прокатных двутавровых балок вычисления дают
значения для M^^^JM^, равные 1,15—1,17.
Из ^того обсуждения видно, что если прямоугольная и двутавро-
вай балки рассчитываются при одном и том ж6 коэффициенте
безопасности по отношению к пределу текучес1ги, то прямоугольная
балка будет прочнее двутавровой балки, если иметь в виду полное
разрушение. После начала текучести прямоугольная балка имеет
ббльшую способность дополнительного сопротивления, чем
двутавровая балка. В теоретическом случае двутавровой байки, у которой
весь материал сосредоточен в тонких полках, найдем Л1п^ед = Жт, и
начало текучести совпадет с полным разрушением балки.
В случае прямоугольного и двутаврового поперечных сечений
мы имеем две Qce симметрии и нейтральная ось совпадает с. одной
из этих осей при упругой и пластической деформации. Если же мы
64]
СИСТЕМЫ ИЗ ИДЕАЛЬНО ПЛАСТИЧЕСКИХ МАТЕРИАЛОВ
2^1
имеем только ©дну ось симметрии, например в случае таврового
сечения (рис. 220), положение будет.иным. При вычислении Жу все;
ъопокт балки находятся в . упругом состоянии, и нейтральная ось
проходит через центр тяжести поперечного сечения. При вычислений
УИдред примем распределев|»ё напряжений, как
на рис. 220,/», и поскольку С]$гмма внутренних-
растягивающих усилий доли^на равняться сумме
сжимающих y^unnttV заключаем, что
нейтральная ось делйт^ площадг поперечноко сечения
на две равные части. Когда положение ней--
тральной оси найД€!НО, величина Ждред вычи-
слится из выражеййя
М,
= ^a^Fa,
пред 2
?■
'
а
-
ff
<г 1 Щ
^
:
а)
Ь)
в котором Р — п.^ощадь поперечного
сечения и а — расстояние между центрами тяже- Рис. 220.
сти дв)^ частей поперечного сечения.
Яз2йб поперечными силами. Ра(:смотрим для примера случай
свободно опертой и центрально нагруженной прямоугольной балки
(рис. 221). Эпюра изгибающих моментощ представляет треугольник,
и если Л1т<С^^/4<С^пред» то длина среднего участка балки, в котОг
ром имеет место пластическая деформация, может б'йть определена^
Рис.'21.
как показано на рис. 221, Ь. Пренебрегая влиянием касательных
напряжений*), глубину е распространения пластической деформации
в каждом поперечном сечении можно вычислить из выражения (d) и
таким путем определить области"пластического течения, заштрихованные.
*) Опыты J. Р. Вакег'а and J. Roderick'a оправдывают этопредпо-,
ложение; см. Тгап§. Inst. Welding, т. 3, стр. 83, 1940.
1С»
w
292 ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ [ГЛ. IX
на рисунке. Когда наибольший изгибаюш,ий момент Р//4
приближается к 31^ачению Жпред, то области пластичности приближаются
к нейтральной оси среднего поперечного сечения балки.
Сопротивление изгибу в этом поперечном сечении определится наибольшим
значением момента, при котором балка начнёт разрушаться. Две
половины балки будут поворачиваться одна относительно другой вокруг
нейтральной оси среднего поперечного сечения, как вокруг шарнира.
Это сечение, называемое пластическим шарниром, противостоит
вращению при действии постоянного предельного момента Ж^ред.
Чтобы исследовать прогиб балки, имеюш,ей области пластической
деформации (рис. 221, а), пренебрежем влиянием поперечных сил
на прогиб и воспользуемся выражениями (d) и (е), выведенными для
чистого изгиба. Исключая о^ из этих уравнений, получаем
1 __ М
г kEJ. •
(J)
где
"Н'-Ч-Ь+Щ^-Ш *)
Величина k является функцией е и равна единице, когда е = 0, и
равна ну^^ю, когда e = h/2. Для поперечного сечения любой формы
в пластической области балки по рис. 221, а, е можно вычислить по
выражению (d), и k — найти из формулы (к).
Уравнение (j) для кривизны имеет такой же вид, как и в случае
упругого изгиба, при условии, что мы принимаем M/k вместо М.
Для применения графоаналитического метода (см. т^ I, стр. 131)
при вычислении прогибов мы должны воспользоваться
видоизмененной эпюрой изгибающих моментов, в которой ординаты равны M/k.
Когда М приближается к Жпред, k приближается к нулю; ординаты
видоизмененной эпюры увеличиваются неограниченно, и мы
приближаемся к условию, когда образуется пластический шарнир.
В предыдущем изложении была рассмотрена прямоугольная балка,
но подобные выводы можно сделать для других форм поперечных
сечений. Вообще прогиб балки в плоскости симметрии за пределом
пропорциональности можно вычислить, пользуяс!» графоаналитическим
методом при помощи видоизмененной эпюры изгибающих моментов.
Величина^ в уравнении (j) должна быть выведена для каждой
частной формы поперечного сечения.
ЗАДАЧИ
1, Определить отношения Л1пред/Л1т Для балок, имеющих поперечные
сечения, показанные на рис. 222.
Отит. .) -^= 1,70. .) -!|l ^. С) 2.
64]
СИСТЕМЫ ИЗ ИДЕАЛЬНО ПЛАСТИЧЕСКИХ МАТЕРИАЛОВ
293
2. Найти Мпред Для балки таврового поперечного сечения, показанного
на р1Ис. 223, если «=«=&.
Ответ. Жпрсд = °-
'-"*№)•
aj
8. Найти Мпред/Мт для поперечного сечения, представляющего
равносторонний треугольник.
Ответ. Мпред/Л^т — 2,343.
4. Найти прогиб / в середине прямоугольной
балки, показанной на рис. 224, если Рс =* 1,4 М^.
Р /2 Рс
1
А
л
1
■
а
' .
Ответ. /=
т^юг- *=«-«^-
8Г U ,VX.^^
б. Решить предыдущую задачу для тавровой
балки рис. 223, если Рс = 0,90 Мт»
/?
^
с
1
/7
1
/•
" f , "
/
1
/Я
\
с
Рис. 223.
Рис. 224.
6. Найти А'пред ДЛя равномерно нагруженной квадратного сечения
(рис. 225), если площадь поперечного сечения /^ = 56,25 еж*, /с=120
балки
см и
6^ = 2400 лгг/сж*.
. Ответ. «Упред^^^О ksJcm.
' ■' ' i
z.
ii
ill
'
i/г
»
/>
-
Рис 225.
Рис. 226.
7. Показать общий вид видоизмененной эпюрм изгибающих моментов
и найти приближенное значение прогибов посредине пролета равномерно
m
294 ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ {ГЛ. КС
нагруженной квадратного сечения бмки^рис. 225), если д1*1Ь==1Л М^, а
орочие данные те же, что и в предыдуще1й, задаче.
6. Найти прогиб посредине прямоугольной балки, показанной на рис. 226,
если Р/г= 8,6 Мпред- Показать контуры пластических областей балки.
65^ Предельное сопротивление систем
Обычная практика лроектированйя металлических конструкций,
воспринимающих статические нагрузки, сводится к выбору
безопасных размеров конструкции при том условии, чтобы рабочая нагрузка,
умноженная на коэффициент безопасности, вызывала наибольшее
напряжение, равное пределу текучести материала*). Однако в
большинстве случаев начало текучести не означает полного разрушения,
и сооружение обычно Оудет выдерживать нагрузку, ббльшую той,
при которой начинается текучесть. Чтобы использовать эту
дополнительную способность сопротивления, было предложено*) при выборе
надлежащих размеров сооружения вычислять предельное значение
нагрузки для предполагаемых размеров сооружения. Тогдй безопасная
нагрузка на сооружение может быть получена как некоторая
определенная часть того предельного значения, которое представляет
нагрузку, вызывающую л^олное разрушение сооружения. Коэффициент
безопасности в этом случае, естественно, будет выше, чем в случае,
если нагрузка при пределе текучести принята за основу расчета.
Процесс расчета, который принимает предельную нагрузку за основу
для выбора безопасных размеров сооружения, называетсй расчетом
по предельному состоянию. В последующем изложении будет
рассмотрено несколько приме]зов приложения такого расчета к
различным сооружениям.
Начиная со статически определимы^ систем, мы заключаем^ что
усилия, действующи* йа элементы таких сооружений^ определятся из
уравнения статики и не зависят от механических свойств материала
при ^условии, что деформации остаются малыми. Если такая система сос-
^) Случаи, в которых размеры выбираются на основании рассмотрения
упругой устойчивости, не изучаются в этом параг]рафе;
*)^Этот метод определения безопасных размеров стальных сооружений
был предложен N. С. Ki^t'oM, Eisenbau, т. 11, 1920. Опыты для
определения предельных нагрузок были проделаны М a_i е ГгЬ е i b п i t г'ем, Baute^hnjk,
1928 иК. Oirkmanh'ow, Bautechnik, 1932. Теоретическое изложение иэгиба
балок ^а пределом текучести было дано J. F г i t s с h е, Bauihgenieur, 1930
и 1981. Сочетание изгиба и сжатия бЫло рассмотрено К. Girkmann'oM,
Sitzungsber. Akad. Wissensch., Wien, ч. Па, т. 140, 1931. В последнее время
важная работа в этой области была выполнена в Кембриджском унив:ерси-
тете^ Англия, под руководством J. F. Clark'a, см. J. Inst. Civil Engrs., т. 31,
стр. Ш, 1949 И статью В. ОГ N е а 1'а and Р. S. S уда о п d s'a Proc. Inst.
Civil Engrs., 1952. В США вопрос расчета на оснований предельно^
нагрузки рассматривался J, А. van den В г о е с к'о м, Trans. Am. Soc. Civil
Engfs., т. 105, стр. 6^, 1940. См. также статью Н. J. Or е en b е г g'a and
W. Р г а g е г'а, Ргос. Am. Soc. Civil Engrs., т. 77, 1951.
651
ПРЕДЕЛЪНОВ СОПРОТИВЛЕНИЙ СИСТЕМ
29а
тойт из стержней, испытыэаюадх растяжение или ржатие, как в
случае фермы с шарнирными узлами, нагрузка, при которой начинается
текучесть, является также и предельной нагрузкой, так как при йдег,
ально пластичном материале (рйс 216) текучесть продолжается при
постоянном напряжении. В случае изгиба балок ofИошение
предельной нагрузки к нагрузке» при которой начинается текучесть, будет
равняться отноицению ^^Мдред/Жд, и ^удет 8ависеть> как мы вйдели> от
формы поперечного сечения балки.
0^преЭ
Рис. 227.
в статически неопределимых системах вопрос об анализе
напряженного состояния становится более сложным, так как усилия,
действующие на элементы системы, зависят в этом слу«1ае не только от
величины внешних сил, но также и от упругих и пластических
свойств элементов системы, и требуется рассмотрение дефор?аадий
ковструкции. Методы, применяемые при исследовании деформа1Ц1й в
пределах упругости, отличны от методов, применяемых при изучений
пластических деформаций. Разница в этих двух методах будет теперь
пояснена на нескольких примерах.
Перейдем к рассмотрению статически, неопределимых случаев
изгиба балок постоянного поперечного сечения. Возьмем, например,
балку с одним защемленным концом и другим свободно опертым
(рис. 227). Рассматривая сначала изгиб, происходящий в пределах
упругости, и учитывая, что конец Л балки защемлен, мы находим эпюру
изгибающих моментов, которая показана иа -рис. 227, а
заштрихованной площадью (см. т. I, стр. 158). Если мы возьмем за основу
296 ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ [ГЛ. IX
«< . ■ .
расчета нагрузку, при которой начинается текучесть, то установим, что
наибольший изгибающий момент имеет место в конце А балки, и
зна'^еыие Р, определяется условием
которое дает „
При вычислении Рщея "^ь! замечаем, что, когда нагрузка
увеличивается за Pj, текучесть начинается, в заш,емленном конце А. При
несколько большей нагрузке чем Р^, текучесть начинается в
поперечном сечении С, где имеется другая вершина в эпюре изгибающих
моментов. Продолжая увеличивать нагрузку, найдем, что условие
образования пластического шарнира достигается на конце А балки, но
это условие не вызывает полного разрушения балки. Сооружение
будет сопротивляться далее с увеличением нагрузки до тех пор,
пока изгибающий момент в поперечном сечении (^ также достигнет
значения Жпред. Тогда возникнут пластические шарниры в А и С рри
свободном повороте в Л. Это и есть предельное состояние,
соответствующее полному разрушению балки. Изгибающие моменты в Л и
С для этого Случая будут численно равны ТИдред, а эпюра
изгибающих мрментов станет такой, как на рис. 227, Ь. Отсюда видим, что
наибольшая ордината треугольника в точке С, соответствующая
нагрузке Рпрел» равняется 1,5 Ж^ред, и Рдред вычисляется по условию
которое дает
Р бМпред
^пред 1
Из условий (а) и (Ь) теперь получаем
пред ^ ^ .
(Ь)
£пр^ — ^ ^пред X ч
т. е. отношение нагрузок Рдред-^т больше в статически
неопределимом случае, чем значение отношения Жпред'.Жх, которое получается
в статически определимом случае. ■ .
Видно также, что путем введения пластических шарниров в А и
С (рис. 227, t) мы имеем задачу, которая может быть легко решена
уравнениями статики, что значительно проще, чем в статически,
неопределимой задаче на рис. 227, а. Таким образом, вычисление Рпред
по предельному состоянию проще, чем вычисление Р^ в расчете>
основанном на предположении упругого поведения сооружения. Это
более правдоподобно, тдк как результаты, получаемые на основании
65]
П1>ЕДЕЛЬНОЕ СОПРОТИВЛЕНИЕ СИСТЕМ
297
допущения о совершенной упругости, зависят от точности
предполагаемых условий на концах балки. Незначительное же вращение ^ш-
деланного конца А или небольшое понижение опоры В может
значительно изменить величину Р^, в то время как несовершенство такого
рода не оказывает влияния на значение Рпред» вычисленное для
статически определимой системы по рис 227, Ъ. Таковы два главных
преимущества метода предельного расчета.
в
V
f
1 , . - 1 - .• , 1 -.1 , „ . .
1к.и 1
"ццщ «■
. i Т
а)
/%
Ьред
В качестве второго примера рассмотрим случай равномерно
нагруженной балки с одним защемленным концом и с другим свободно
опертым (рис. 228). В упругой стадии эпюра изгибающих моментов
будет такой, как показано рис. 228, а. Численно наибольшее значение
изгибающего момента будет в защемленном конце, и величина нагрузки
q^ найдется из уравнения
= М.
т>
которое дает
8М,
/2
(d)
Если мы будем продолжать увеличивать нагрузку сверх значения q^
текучесть в защемленном конце А будет продолжаться, а
соответствующий изгибающий момент будет увеличиваться до значения Ждред,
когда в точке А образуется пластический шарнир. Чтобы довести
балку до полного разрушения, следует продолжать увеличение
нагрузки до значения ^пред» при котором образуется нластический шарнир
mw
ш
ДЕФОРМАЦИИ ЗА Т1Р^ДЕЛОМ УПРУГЪСТЙ
[ГЛ. IX
В некотором Промежуточном поперечном сечении С балки (рис. 228; Ь}.
Положение АЪперечвЬго сечения С и значение ^дред будут найдены из
условий, что изгибающий момент в С является наибольшим и что он раэен
М V Пользуясь заштрихованной эпюрой изгибающих моментов на
риа 228, fc, запишем эти условия в слёдз^щем виде:
М
«ред»
dM
их
2
9прек^ ~Г
М
sm.=s=o.
Из этих уравнений по^|учим
;С = 1{2^/2),
X:
Яп9
|ед
г=
2УИ
прея
(е)
(f)
(g)
(h)
/8C —2/2)*
а на основании выражений (d) и (g) заключаем, что
i?>M =: 1,46 ^«^.
При рассмотрении более общих случаев иластическОй деформации
конструкций замечаем, что за пределом упругости пришгип наложения
неприменим, и деформация сооружения зависит не только от окон-
^ , чательных значений нагрузок, но т^1кже
и от порядка, в котором нагрузки
приложены к сооруженидо. Возьмем,' на-
,/} с J? пример, случай, показанный на рис. 229, а.
Если обе силы приложены
одновременно, то соответствующая эпюра изги-
h -I" f« —-I бающих моментов будет иметь форму,
OJ: воказанную на рис. 229, Д и
наибольший изгибающий момент равен Р//9.
Мы видим, что деформация будет
совершенно упругой, если
Р
J
i/J
р
l/S
г/3
■/
^^
^
.— >^
р<».
0)
Рассмотрим теперь случай, когда
нагрузка Р сначала приложена в
поперечном сечении В, а нагрузка ъ С
приложена после. После того как нагрузка
С) приложена в В, соответствующая эпюра
Рис. 229. изгибающих моментов «меет вид,
показанный на рис. 229, г, наибольш^1Й
изгибающий момент будет в два раза больше, чем в предыдущем случае,
и может произвести пластическую деформацию, хотя условие, (i)
удовлетворяется. Эта пластическая деформация не будет устранена
65)
ПРЕДЕЛЬНОЕ СОЦРСГИВЛЕ11ЙЕ СИСТЕМ
299^
Ь
I
С
1/2
2Р
J) В
/А
■ ДВп
ТТТТтт
J±A
et)
^ *Ц^'1
^
Si-Л
■^
W
Г-~^J<^
I
-йс
1 Vii?
последующим приложением силы р в nonfejMJ4HOM сечении (>, и
окончательная деформация балки будет отлична от сдаая
одновременного приложения, сад в поперечных сечениях В и С,В,наших
дальнейших рассуждениях мы будем всегда п]редполагать, что Силы
приложены одновременнд й что в процессе нагружения отнощёйий
М(ежду силами остаютрй постоянными и
равными отношениям окончательных
значений сил. Все С1?лы будут
обозначены одним и тем же символом, умно-
жеиныл на числовые коэффициенты,
указывающие требуемые отношения
между величинами' сил.
В ранее разобранных- задачах,
например показанных на рис. 227 и 228,
была только одна возможность
размещения пластических шарниров, и
приходилось рассматривать только одну
форму разрушения балки. Но если на балку
действует несколько сил, то будет не-
(жолько различных возможных
положений пластических шарниров и
несколько возможных форм разрушения
балки. Естественно, проектировщик
должен выбрать из всех возможных форм
разрушения ту, которая отвечает
наименьшему значению нагрузок. Тогда эти
нагрузки будут рассматриваться как
предельные нагрузки для сооружения.
В качестве" примера выбора
надлежащих положений для пластических
шарниров рассмотрим балку на рис. 230,
которая заделана в Л, свободно оперта
в В и несет два груза Р и Чр. Эпюру
изгибающих моментов в этом случае будем изображать пунктиром,
вершины же, соответствующие наибольшим изгибающим моментам, будут
находиться на вертикалях, проходящих через поперечные сечения Л, Си D.
При. условии полного разрушения пластические шарниры будут
образовываться в двух из этих трех поперечных сечений. Все возмож-^
ные положения этих шарниров и соответствующие формы
разрушения показаны на рис. 230, Ъ — d. Замечая, что в каждом
пластическом шарнире моменты Ждред к^прввлены так, чтобы препятствовать
взаимному повороту частей балки, мы можем написать уравнение
равновесия для каждого участка балки и определить величину
Р, соответствующую предполэтаемой форме разрушения.
Например, для. формы, показанной на рис. 230, by соответствующие
щ
С)
г
4^
\2Р
I
X
Т-
d)
Рис. 230.
щ
300
ДЕФОРМАЦИИ ЗА П|РЕДЕЛОМ УПРУГОСТИ
[ГЛ. IX
СИЛЫ показаны на рис. 231, а, и уравнения равновесия будут
QI
2
2Л1„ред«=0,
2 Г^ •**^пред
О,
откуда мы находим
ЗМ
пред-
пред
Вместо того чтобы применять уравнения равновесия, подобные
приведенным выше, удобно при вычислении Рпред использовать
принцип виртуальных перемещений *). Рассматривая опять форму
разрушения, показанную на-рис. 230, Ь, мы видим, что путем введения
*%7pei
<
ш
1—
^пред
i
к
V
V
т
ZP
//«
с^
пластических шарниров в Л и С мы получаем механизм, состоящий
из двух шарнирных чёстей (рис. 231, Ь). Чтобы написать условие
равновесия этого механизма, рассмотрим виртуальное перемещение,
определяемое малым углом поворота 6. При этом повороте моменты
^пред в поперечных сечениях Л и С, препятствуя вращению, будут
производить рабоуу, равную — Шпред и — 26Л1пред- В то же самое
время грузы Р и 2Р произведут работу, равную Р0//2 и 2Р9//4, так
что уравнение виртуальных перемещений получается в следующем виде:
ре/ , 2Рд1
—ем
пред
2ВМ
пред
= 0,
*) Этот метод вычисления был рассмотрен J. F. Baker' ом, J. Inst
Strectural Engrs., т. 27, стр. 397, Ш49.
65]
откуда
ПРЕДЕЛЬНОЕ СОПРОТИВЛЕНИЕ СИСТЕМ
пред'
ЗМпред
3D1
(D
Поступая таким же путем и в случаях, показанных на-рис 230, с
и 230, (/, получаем следующие результаты:
р s= ^'^-^ПРЗД р
6Ж
пред
пред'
пред
(к)
Сравнивая результаты выражений (j) и (к), заключаем, что для балки,
представленной на рис. 230, а, предельная нагрузка равна Рпр^дгзп
= 2,5Жпред//, а соответствующая форма разрушения показана на
рис. 230,6-. ' '
Метод вычисления предельных нагрузок, который был прлменен
в предыд)Ш1их задачах о балках, можно использовать также при
рассмотрении предельного сопротивления рам. Рассмотрим раму^
показанную на рис. 232, <2, которая имеет три лишних неизвестных усилия.
Р А
А
С
V//////
1
£
\
Р
г
л
ш
в
Wf
1
а>
р
7
2 3
Г
/
777?
Р
<
't
Г
/^
VM77>
р г
I
^^
TiT^^TZ
X
гв
Г
с)
k
/
Р Z
Xr^
г
'/////л
^
Г--<П-
Рис. 232.
г
d)
S
Мы можем взять, например, за три лишние неизвестные изгибающий
момент и две составляющие реактивной силы е В. Если эти три
величины известны, то момент и две составляющие усилия в любом
поперечном сечении рамы можно легко найти из уравнений статики.
Мы можем сделать систему также статически определимой, если
наметим в ней три шарнира. Например, принимая шарниры в А, В vi Е,
получаем систему, которую можно легко рассчитать как трехшар-
нирную арку. Длч того чтобы сделать из рамы подвижную систему
mfi'
302 ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ [ГЛ. fX
(или механизм)^ мы Должны ввести четыре пластических шарнира.
Чтобы определить полоЯсения этих шарниров* замечаем» что эпюра
изгибающих моментов будет иметь вершины в поперечных
сечениях /, 2, 3, 4, 5 (рис. 232), где действувот сосредоточенные силы.
Пластические шарниры должны быть помешены в некоторых из этих
поперечных сечений, так как изгибающий момент достигает своих
наибольших численных значений в этих точках. Два возможных
способа помещения четырех пластических шарниров, которые
соответствуют двум различным формам разрушения рамы, показаны на
рис. 232,^ и 232,г»).
Н^ рис. 232,rf мы имеем особый случай разрушения. Вводя только
три пластических шарнира, мы, естественно, не получим механизма
такого же типа, как в двух предыдущих случаях. Когда образованы
пластические шарниры в поперечных сечениях 2,3 и 4, то не происходит
. неограниченнОгр относительного поворота в этих шарнирах при
дальнейшем увеличении нагрузки Р. Два стержня 2—3 и 3^-4 после
некоторого вращения будут в состоянии сопротивляться дальнейшему
увеличению нагрузки Р, работая на растяжение.--Но соответствующие
перемещения будут большими, и придется рассмотреть также и эту
деформацию, как представляющую полное разрушение рамы.
Чтобы вычислить значения Рпред» соответствующие трем
различным формам разрушения, показанные на рис.^ 232, используем
размеры, показанные на рисунке, и предположим, что поперечное сечение
горизонтального стержня CD больше поперечного сечения
вертикальных и что Жцред представляет предельный момент для вертикальных
Стержней, а 1,5Л^пред является предельным моментом для
горизонтального стержня*). Виртуальные перемещения будут определяться малым
углом 6. Тогда уравнение равновесия ^для случая, показанного на
рис. 232, ^, будет
' Р9/-4еЖ„ред = 0,
откуда
р 4/Ипред
пред / '
Для случая рйс. 232, с уравнение равновесия буде*
откуда
*) По вопросу о выборе всех возможных форм разрушения рамных
конструкций см. статью Р. S. Sy шоп de'a and В. G. NeaFa, J. Inst. Civil
Engrs., r. 35, стр. 21, Ш50.
*) Пластические шарниры в узлах будут образовываться в слабейших
стержнях, как показано кружками иа jinc. 232, fr, с и d.
щ
ПРЕДЕЛЬНОЕ е<>ПРОТЙВЛЕНИ? СИСТЕМ
303
для случая же на рис. 232> rf ЭДолучаем таким же путём
йред'
ПЪ ЭТИМ результатам, включаем, что действительной формой разруг-;,
шения будет показанная на рис. 232, си что предельная нагрузйа
равняется _ ЗЖ^ед
С ЗАДАЧИ
. 1. Найти значения Рдред ** ?пред для балок, показанных, на рис. 233.
Ответ. а) Рщев.
8Мпред ^ч _1Ё^ред г'к Р
7 » ''^ ¥пред— /2 t V/Л]
/2
_,6Mgge5
. \^г/г-^
пред V J
Р
\
itfuVitu
-^г/г-^л
\-^^ij&-
'ifi^
а)
б)
РиЬ. 233.
CJ
2. Двухпролетная балка постоянного поперечного сечения равномерно
нагружена (рис. 234). Найти (?пред» предполагаЯ| что /j > /,.
Ответ, ^пред =
2Л1,
пред
/f C — 2/2)*
шжШжшш
I
I I t т t ч т I т ? 1 f t 1 -
Рис. 234.
///-—
-//«^
г/»
K//f*
Рис. 236.
^П?//^!-
//?
I
•^jm4-si/4 -^Щ -//gX^g-l
Рис. 235,
Р
ш
1^М„ред
^—1
f'V>e9
Рис. 237.
3. Найти значение Яиред Для неразрезной балки постоянного поперечного
сечения, показанной на рис. 235. Показать форму разрушения,
Отбш. />„ред«:1^е|д;
30.4
ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
[ГЛ. !Х
4. Балка с защемленными концами подвергается действию двух сил Р к
2Р (рис. 2йв). Найти Рпр-д и показать соответствующую форму разрушения.
AM.
Ответ.
Ptipejs. —
/
(ред
5. Найти Рпред и соответствующую форму разрушения рамьг,
показанной на рис. 237.
66. Чистый Д1згиб балок, материал которых
не следует закону Гука
В предыдущих параграфах предполагалось, что материал балок
был идеально пластичным (рис. 216). Рассмотрим теперь более общий
случай, в котором механические свойства материала представлены
кривой АОВ диаграммы на рис. 238. При рассмотрении чистого
изгиба таких бал©к будем предполагать по-прежнему, что поперечные
сечения балки остаются плоскими при изгибе; следовательно,
удлинений и укорочения продольных волокон пропорциональны их
расстояниям от нейтрального слоя. Взяв это за основу дальнейших
выводов и предположив, что при изгибе существует такое же
соотношение между напряжением и деформацией, как и в случае простого
растяжения и сжатия, мы' сможем легко найти напряжения,
возникающие в балке от ■ изгибающего момента любой заданной величины *).
6
£г^
i
If
А
1
ill
)% -
г " 'Л
£,
е
Рис. 238.
Рис. 239.
Начнем с балки прямоугольного поперечного сечения (рис. 239) и
предположим, что радиус кривизны нейтрального слоя при действии
изгибающих моментов М равен г. В таком случае относительное
удлинение волокна, находящегося на расстоянии^ от нейтрального слоя,
равно
^=f. (а)
^) Эта теория была разработана Сен-Венаном в его примечаниях к
книге N а vie г, Resume des lemons, 3-е изд., стр. 173, 1864. См. также статью:
E.Mayer, Phys. Z., 1907 и Н. Н е г b е г t, Диссертация, Гёттинген, 1909.
€6] ЧИСТЫЙ ИЗГИБ ВАЛОК 305'
Обозначив- через hi и /?2 расстояния от нейтральной оси
соответственно до нижней и верхней поверхностей балки, находим, что
удлинения в крайних волокнах будут
Ч=^, е,=:-^. (Ь)
Видно, что удлинение или укорочение какого-либо волокна легко
получается при условии, что известны положение нейтральной оси и
радиус кривизны/Г. Эти две величины можно найти из двух уравнений
статики:
hi
^adF==b^ady = 0, (с)
^ -Ла
aydF=b^<3ydy~M. (d)
I
Первое из этих уравнений устанавливает, что сумма нормальных
усилий, действующих по любому поперечному сечению балки, обращ^-
€тся в нуль, так как эти усилия образуют пару сил. Вторым
уравнением устанавливается, что момент тех же сил относительно
нейтральной оси равен изгибающему моменту М.
Применим уравнение (с) для определения положения нейтральной
оси. Из выражения (а) имеем
д/ = ге, dy^=:rdz. (е)
Подставляя в уравнение (с), получаем
hi «1
5 cdy = r\od& = 0. (f)
— Л2 «2
Следовательно, положение нейтральной оси таково, что интеграл
«1
\ adz обращается в нуль. Чтобы определить это положение, восполь-
зуемся кривой АОВ на рис. 238, которая представляет собой диаграмму
испытания на растяжение и сжатие материала балки: обозначим через Д
сумму абсолютных значений наибольшего удлинения и наибольшего
укорочения, т. е.
Чтобы решить уравнение (f), мы должны так отметить длину Д на
горизонтальной оси (рис. 238), чтобы две заштрихованные на рисунке
площади стали равными. Таким образом, мы найдем деформации е, и
306 ДЕФОРМАЦИЙ ЗА ПРЕДЕЛОМ УПРУГОСТИ {ГЛ. tx
63 В Крайних волокнах. Выражения {b> тогда дадут
^
с
i
Ч
чйй и определится положение нейтральной оси. Замечая, что
удлинения в пропорциональны' расстояниям от нейтральной оси, заключаем»
что кривая АОВ также представляем распределение напряжений при
иагйбе по высоте балки, если вместо А подставить fe.
Для определения радиуса кривизны г воспользуемся уравн(ением (d).
Подстав ЛЯ!? вместо J/ и dy их вначёния из выражений (е), йредставим
уравнение (d) в форме «
■■ «1
Ьг'^\ 6&d&^M. (i>
Зг1мечая, что по формуле (g) г = А/А, можем уравнение (i) после
простого преобразовайия привести к виду , ^ -^
bh* 1 12 V . " ,, ' ' ,.ч
:■•■>.. ■..,.. . ■ /' ■■ ^ ■
Сравнивая атот результат с известным уравнением
EJ
^==Ж ' (к>
для изгиба балок, следующих закону Гука, заключаем, что за преде-
лом пропорциональности кривизна, вызываемая. моментом М, можег
быть вычислена из уравнения
■^^М, B81)
в котором i?,. — приведенный модуль упругости, определяемый
выражением
V=g^oerfe. (Ш>
«а
Интеграл этого выражения представляет собой момент относительно
вертикальной оси, проходящей через начало координат О
заштрихованной плЪщади, показанной на^ рис. 238. Так как ординаты кривой
на рисунке представляют напряжения, а абсциссы-—относительные
деформации, то интеграл, а также Е^ имеют размерность кг/см\ т. е.
ту же, что и модуль упругости Е.
Величина Я,, для. Данного Л1ате1)иала, соответствующая данной
на рис. 238 кривой, является функцией А или /г/г. Взяв ряд значе-
€6}
ЧИСТЫЙ ИвГИБ ВАЛОК
Ш
НИИ Д и воспользовавшись кривой* на рис. 238,.как ужй объяснено*
мы получим для каждого значения Д соответствующие крайние
значения ti и Bj, и по выражению B82) определим соответствующие
значения Ef. Таким образом, получается кривая, представляющая £",
как функцию Д =: Л/г. На рйс. 240 такая кривая показана для
строительной стали с £"=:2,Ы0* кг/сМ
f frg/cM* ^ пределом пропорциональности,
*" равным 2100 кг/см^.В этом слуг
£/ff'h>^ чае при Д<^ 0,002 Е^ остается
ISffJiff^
as7f^ •
о ШШ cm AP^s 020 (тз
4=р
Рис. 240.
0т iim
Р»Гс. 241. •
тз
постоянным и равным f. При помощи такой кривой момент,,
соответствующий любой предполагаемой кривизне, можно легко вычислить
из уравнения B81), и мы можем начертить кривую (рис. 241), считая
момент функцией Д. Лл.я малых значений Д материал следует закону
Гука, и кривизна пропорциональна изгибающему моменту Ж, как
показано на рис. 241 прямой линией ОС. За пределом
пропорциональности скорость изменения кривизны увеличивается с увеличением
момента. ■ , •
Если вместо прямоугольника мы имеем какую-либо дрз^ую сим-^
метричную форму поперечного сечения с переменной шириной Ь
поперечного сечения, то уравнения (с) и (d) должны быть написаны
в следующем виде: .
J г>ОЙ!)/==:г5^»ОА?е=:0,
-Ла eg
Д Ыу rfj/ = Г* \ Ьаг rfe ==
— Ло J бе
Ж.
(О
(ш)
Возьмем в качестве примера случай таврового сечения (рис. 242).
Если обозначить через е' продольную деформацию в месте сопря*
жения стенки и полки, то уравнения A) и (т) можно написать в
mfi'
308
следующем виде:
ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
е'
% о f^e -4- \ -^ в f/e = о,
sa t'
1ГЛ. IX
(п)
(о>
«2
Ви^но, ЧТО в ЭТОМ случае ординаты кривой растяжения АОВ
(рис. 243) в области, соответствующей полке поперечного сечения,
должны быть увеличены в отношении bi/b. Для определения
положения нейтральной оси поступим, как в предыд)пцем случае, пользуясь
диаграммой растяжения — сжатия (рис: 243), и так отметим на гори-,
зонтальной оси положение предполагаемой
длины Д = й/г, чтобы две заштрихованные
площади получились численно равными одна
другой. В результате найдутся деформации Sj
и Ёа крайних волокон. Деформация е' в месте
сопряжения стенки и цолки получится из
уравнения ,
с^г-с' с
1
Рис. 242. .
В котором с есть толщина полки (рис. 242). Определив
положение нейтральной оси и замечая, что выражение в скобках
уравнения (о) представляет собой момент
заштрихованных на рис. 243 площадей относительно вер-
тикальц/йй оси, проходящей через начало
координат О, мы можем легко вычислить по
уравнению (о) момент Ж, соответствующий принятому
значению Д = й/г. Таким образом, для балки
таврового сечения можно построить кривую,
подобную показанной на рис. 241. Аналогично
можно поступить и с двутавровой, балкой.
В предыдущих примерах для определения
положения нейтральной оси и величины радиуса
кривизны г была использована диаграмма испытания
на растяжение и сжатие. Если существует
аналитическое выражение для кривой АОВ^ то
приведенные выше величины можно получить только
вычислением, не применяя графического метода,
разъясненного на рис. 238 и 243. Наиболее общее урав-'
нение для кривых напряжение — деформация было
применено Сен-Венаном *). Он предположил, что для изгиба за пределом
пропорциональности распределение растягивающих и сжимающих напряжений
Рис. 243.
*) Цит. на стр. 304. См. также статью W. R. О s g о о d'a, J. Aeronaut,
Sci., т. 11, стр. 213, 1944.
66] чистый ИЗГИБ БАЛОК .
ПО высоте балки можно представить следующими уравнениями:
309
(р>
в которых оо и о\ а также а и b являются некоторыми постоянными,
которые вместе с показателями.''степени тип определяют кривые
распределения напряжений, показанные на рис. 244. Для
очень малых расстояний у п yi иы можем
допустить, что
!=» 1
И
ту
а
и уравнения (р) дают
а
о„ mrt , Oq nyi «о пгг
и о = —г— = —т—
а b о
Следовательно,
Of^mr
а
■El и
b
= £-,
31
(q)
где El и Е^ — модули упругости материала соответственно для очень м^-
лых растяжения и сжатия. Если эти два модуля упругости материала
равны между собой, то две кривые, определяемые уравн^иями (р), имеют
общую касательную на нейтральной оси, и мы имеем
ОоШ
ОоП
а
(г)
Используя уравнения (р) и уравнения равновесия (с) и (d), можно
вычислить в каждом частном случае положение нейтральной оси и радиус
кривизны. Взяв, например, m = л = 1 и воспользовавшись выражениями (q),
получим на основании у]|равнений (р)
Ejy
г
,ЕвУ1
(s>
Это случай, в котором материал балки следует закону Гуна, но имеет
разные модули упругости при растяжении и сжатии. Подставляя выражения (s)
в уравнение (с) и предполагая, что балка имеет прямоугольное- поперечное
сечение, получаем .
Eihl^E^hl
что совместно с равенством hi-{-h^ = h дает
Ai
кУЩ
VTi+VK'
Тогда из уравнения (d) найдем
_ Л У El
§ihibhi 2 u^bh*\ 4EiEi
r 2 З""- 12го75=>Ует
*зш
ДЕФОРМАЦИЙ ЗА ПРВ ДЕЛОМ УП1^УГ0СТИ
(ГЛ. 1Х
Видно, ЧТО 9 ЭТОМ ,случа<^ кривизна получается из уравленйя B81) при
следующем значении приведенного модуля упругости;
Этим модулем упругости иногда пользуются для
вычисления нагрузки, которая выпучивает колрнну,
сжатую за пределом пропорциональности материала
(см. стр. 153). ^^ '■'-:":■
В качестве другого примера предположим, что
кривые напряжение г— деформация при растяжении и
сжатии одинаковы. Тогда в уравнениях (р) w авй,
в»* и Оо=>а!о. Предполагая такйсе, что в=й1*=в=л/2,
находим из уравнения (d) для прямоугольной балки
bh^ 3ffl(/n-f3)
'«'max-g- 2(m + l)(w+2) •
Рис. 245.
Мл
B84)
растанием т момент приближается к значению
Нейтральная ось в этом случае проходит через ucjhtp
тяжести поперечного сечения. Кривые, дающие
распределение напряжений для рмличных значений
показателя степени да, показаны на рис. 245. С воз-
67. Изгиб балок поперечной нагрузкой
за пределом упругости
В случае изгиба балок поперечной нагрузкой мы пренебрегаем
действием сдвига на прогиб*) и предполагаем, что зависимость
между изгибающим моментом и кривизной представляется ур;авнением
B8IX выведе|гным для чистого изгиба. Тогда для вычисления проги-
бЬв за пределом пропорциональности мозкно применить
графоаналитический метод (см. т. I, стр. 131), Необходимо лишь заметить, что
жесткость при изгибе в этом случае.непостоянна, изменяясь с
величиной изгибающего момента. Чтобы установить зависимость между
этими двумя величинами для прямоугольных балок, воспользуемся
кривой на рис. 24 L Для любого значения Д=7г/г орд^ината i4i9 дает
соответствующее значение изгибающего момента, а ордината АС —
жомент при услбвии, что материал следует закону Гука. В результате
Таким путем ^мы получим для каждого предполагаемрго значения
изгибающего момента отношение f/.J/f'J. приведенной жесткости изгиба
к начальной жесткости изгиба балки. Обозначая это отношение
^) Влияние сдвига было рассмотрено А. Е i с h i п g е г'ом, Final Report,
2d Congr. latern. Assoc. Bridge Mid Struct. Engng., Berlin, 1938.
67] М^гив Бдлок поперЕчнрЙ НАГРУЗКОЙ ЗА Ш'ЕдвлоМ J'npyrocTH 81 it
через р, представим его в функций изгибающего момента М кривой,,
приведенной на рис 246; / "
Чтобы показать, как мржуо пользоваться этой кривой при
вычислении прогибов, расхмотрим случай свободно опертой бадаси»
««груженной посредине (рйе. 247). Эпюра изгибающие' моментов ц этом
случае йредставляёт треугольник АСВ. Пусть Ж^ будет величина из*
гибающего мощщщ до которого материал следует закону Гз^ка.:
В таком случае участок iwn балки будет напряжен за пределотл про-
порционйльностй, и /для вычисления прогиба вместо начальной жебт-
кости изгиба нужно воспользоваться приведенной жесткостьк),
которая меняется на 9Т0М участке балки. Поступая, как в случае балок
переменного nonefie4Horo сечения (см. т. I, стр. 188), разделим
ординаты эпюры изгибающих моментов на соответствующие значения р^
/f^i^
Рис. 246.
Рис. 247.
взятые 413 рис. 246. Таким образом, получится измененная эпюра ,
изгибающих моментов ADEFB, Рассматривая площадь измененной
эпюры изгибающих моментов как фиктивную "нагрузку и поступая
обычным путем, получаем прогиб в любом сечении балки делением
на EJ изгибающего момента, возникающего в этом сечении от
фиктивной нагрузкц.
Здесб'-мы рассматривали только случай прямоугольной балки, но
тот же метод применим и в других слзгчаях, при условии, что
получена кривая для коэффициента ^, подобная доказанной на рисунке 246.
Такую кривую можно построить с помощью метода,
иллюстрированного на рис. 243; ее ординаты можно вычислить, если дан1Е1 аналй*
тичёскай зависимость между напряжениями и деформациями за пре»
делом пропорциональности материала, подобная уравнениям (р) в п. 66.
В нашем обсуждении изгиба балок поперечными нагрузками
предполагалось, что задача была статически определимой, следовательно,
построение эпюры изгибающих моментов не требовало рассмотрения
изогнутой оси. В статически неопределимых случаях задала становится
более сложной, так как за пределом пропорциональности лишние
силы и моменты уже не пропорциональны действующим нагрузкам, и
»ш^
312
ДЕФОРМАЦИЙ ЗА ПРЕДЕЛОМ УПРУГОСТИ
[ГЛ. IX
принцип наложения неприменим. Однако иногда задачу можно
упростить на основании соображений о симметрии. Предполагая,
например, что концы балки на рис. 247 заделаны, мы заключаем из
-симметрии, что изгибающий момент обращается в нуль в точках,
соответствующих четвертям пролета и изогнутая ось состоит из четырех
одинаковых участков, которые можно получить таким же путем, как
и для консоли, нагруженной на конце. В случае равномерно нагру-
^кенной балки с защемленными концами мы на основании симметрии
заключаем, что моменты на концах равны между собой. Величину
этих моментов можно получить методом последовательных попыток.
Необходимо, принять некоторое значение для этих моментов и по-
"^ ч:троить измененную эпюру изгибающих моментов, как показано для
случай, изображенного на рис. 247. Точным значением моментов,
очевидно, будет то, при котором полная фиктивная нагрузка,,
представленная площадью измененной эпюры изгибающих моментов,
обращается в нуль.
Из предыдущих рассуждений можно видеть, что- в случае изгиба
за пределом пропорциональности вычисление лишних сил и лишних
моментов обычно требует более сложных исследований. Однако в
<:лучае материалов, которые имеют ясно выраженный предел
текучести, как, например, строительная сталь, расчет статически
неопределимых соорзокений можно значительно упростить, если ограничить
наши рассмотрения стадией нагрзокения, при которой сооружение
достигает предельной нагрузки и текучесть происходит без
дальнейшего увеличения нагрузки (см. п. 65).
68. Остаточные напряжения, вызываемые неупругим изгибом
Если балка изгибается за пределом упругости, возникает
некоторая непрерывная текучесть, и деформация не исчезает после
удаления нагрузки. Волокна,
которые претерпели текучесть,
препятствуют упруго напряженным
волокнам восстанавливать свою
-Ч ^г 1— б
/77
) ^
J -А
/7,.
»*
'Т
j£ziZZ
т^
У+
о ft
п
|1
\\
^
а)
первоначальную Длину после
/ разгрузки, и таким путем по-
/ являются некоторые остаточ-
S ные напряжения. Чтобы опре-
6) делить распределение этих
Рис. 248. напряжений по поперечному
сечению, начнем с простейшего
■случая прямоугольной балки, в которой распределение напряжений при
изгибе за пределом текучести можно представить двумя прямоугольниками
ОМт и Орт, показанными на рис. 248. Предположим также, что материал,
будучи растянут за предел текучести и затем разгружен, следует за-
68] . ОСТАТОЧНЫЕ НАПРЯЖЕНИЙ. ВЫЗЫВАЕМЫЕ НЕУПРУГИМ ИЗГИБОМ 313^
./
кону Гука при разгрузке, как показано на рис. 248, b пунктиром.
В результате этого предположения можно заключить, что напряжения
при изгибе, которые накладываются во время разгрузки балки,
следуют линейному закону, показанному на рис. 248, а линией ШхЩ.-
Наложение этих двух распределений напряжений — прямоугольного
во время нагрузки и треугольного во время разгрузки, показанное
заштрихованнцми площадями на рис. 248, а, представляет напряжения,
которые остаются в балке после разгрузки. Эти остаточные
напряжения вызываются в балке пластической деформацией''). Знаки этих
напряжений, как показано на рисунке, были получены при
допущении, что начальный изгиб вызывает кривизну выпуклостью вниз.
Так как прямоугольное и треугольное распределения напряжений
(рис. 248) оба представляют изгибающие, моменты той же величины,
можно заключить, что момент относительно оси pOk
треугольника От/Пх равен моменту прямоугольника Oklm относительно той же оси..
Следовательно, напряжение, представленное на рисунке длиной mnii
должно быть равно 1,5 а^, и наибольшие растягивающее и сжимающее
напряжения, которые остаются в наиболее удаленных волокнах после
разгрузки балки, равны 0,5 а^. Остаточные напряжения в волокнах
вблизи нейтрального слоя имеют величину а^. Можно видеть, что
распределение напряжений, представленное на рисунке заштрихованными
площадями, сводится к двум разным и противоположным парам сил
величиной a^bh^l27, которые находятся в равновесии. Существован*ие
этих остато»?ных напряжений можно показать экспериментальйо
путем распиливания балки вдоль нейтрального слоя. Тогда каждая
половина балки получает некоторую кривизну.
Если балка с остаточными напряжениями, как указано на рис. 248, а,,
вновь изгибается моментами той же величины и в том же
направлении, как и в предыдущем опыте, напряжения, вызываемые этими
моментами и представленные прямой линией miHi, будут накладываться
на остаточные напряжения, даваемые заштрихованными площадями,
так что результирующее распределение напряжений будет
представлено прямоугольниками Oklm и Опгр. Наибольшее результирующее
напряжение равно а^, и во время этого вторичного изгиба никакой
текучести не наблюдается. Следовательно, остаточные напряжения,:
вызываемые первым изгибом, таковы по природе, что увеличивают
изгибающий момент, который может выдерживаться брусом в
упругом состоянии, при условии, что направление изгиба неизменно. Это
явление улучшения упругой спбсобности сооружения путем
предварительного нагружения и создания подходящих остаточных напряжений
а.
^) Кажется, что А. Wohler был первым, который обратил внимание
инженеров на остаточные напряжения, вызываемые пластическим изгибом
балок; см. S. Т i m о S h е п к о, History of Strength of Materials, New York,
стр. 172, 1958; русский перевод, История науки о сопротивлении материалов^
Гостехивдат, 1957, стр. 2Й2.
3:14
ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
[ГЛ. IX
«НОГда применяется на практике* Некотс^ые ?^астные случаи будут
разобранй ниже (см. п. 78).
В более общем случае неупругого изгиба прямоугольной балки
распределение напряжений дается кривой, по^шбной «jO/Wi на рис. 249, а,
предполагая опять, что при разгрузке материал следует закону Тука,
мы находим, что остаточные напряжения, вызываемые пластическим
к--^ ^
/?7
/7
х-г
V • - ••" -•"•'•
ff
Т'
0Ьй
бЬй
Рис. 249.
течением, распределяются^ как показано на рисунке, заштрихованными
площадями. Если кривая ПхОгпу определена, как объяснено в п. ,66,
то величину остаточного напряжения можно легко получить для
каждого волокна. Если же кривая щОт\ неизвестна, то распределение
остаточных напряжений можно исследовать опытным путем, снимая
в бйлке один за другим тонкие слои, параллельные нейтральному
слою, и измеряя после каждого среза упругую деформацию, которая
происходит в балке.
Предположим, что остаточное напряжение на нижней поверхности баяки
растягивающее, величиной е. Тогда удаление тонкого слоя толщиной Д,
показанного на рис. 249,1^, очевидно, вызовет деформацию в остальной части
^алкй, как1ая была бы вызвана приложением двух равных И
противоположных сия oj)^, показанных стрелками BHHSj рис. 249, i^. Мы найдем, что после
срезывания тонкого слоя ось балки получит удлинение и кривизну,
согласно формулам ч
Отсюда яс1Ю, что ^сли кривизна йЩг) измерена, то величину остаточного
растягивающего напряжения « в наиболее удаленном волокне легко
вычислить по выражению (а).
Определение остаточного напряжения Од в волокне отя, находящемся
щ расстояний а от верхней грани балки (рис. 249, 6), оказывается более
трудным. Снимая один слой за другим, мы, наконец, достигнем слоя тп
68} оетАТочныЕ НАПРйжения, вьКзывАВмыЕ ту^рутмизтщьок 31&'
и мож^м определить напряжение в нем при noMiQuiH выра:жеиия, подобйога
выраШ<Е^«ию (а). Однако это напряжение будет иметь вел)ачину о^,^от,лйчную
от начального остаточного йапряжения Од, так как удалеид!? шедыдущих
слоев вызывало измен1ёние Hanj^KeHHti в остававшихся'частях шякй. Оче^г
видно, что только посл^ и1с;сл^ед<Увания этих изменений будет возможно рп*
ределение требуемого остаточного напряжения Од. Предположим, что *ytei*A
снятия одного слоя за другим ^ы достигнем волокна, поквзанногр
пунктиром на рис. 249, ^ на расстоянии 2г от верхней грани балки. Если мы теп^рь-
снимем тонкий слой ТРЯ1ДИН0Й Д, то напряжение <s'g в этом слое получился.
из .уравнения
ЛтУ-
где
a'gbzA
Ь BгУ
' 12
откуда
т
Удаление этого слоя вызовет в волокне /п« напряжение раст^яжения
W *>■
и напряжение изгиба
9'bzA(e — z)
■. J . (d>
Уравнения (с) и (d) дают изменения напряжения в волокне тп благедаря-
удалению одного лишь слоя. Принимая теперь во внимание все слои,
отвечающие измбнению^г: от А до а, получим полное изменение остаточного
напряжения в волокне тп в следующем виде:
где о'^ для каждого шага вычисляется по формуле (Ь) при помощи измерен-
пых значений d(ljr). Искомое остаточное напряжение Од в волокне тп
получится теперь путем вычитания величины (е) из напряжения о^, которое
определяется подстановкой а вместо 2z в формулу (Ь). Следовательно,
в =а' \°'^ ^c',bzA(e-z)
Этот метод экспериментального определения продольных остаточных
напряжений можно применять не только в случае изгиба," но также в других
случаях призматических стержней, претерпевающих продольную пяастиче-^
скую деформацию (см. п. 70). Он был, например, успешно применен при
измерении остатокчных деформаций в холоднотянутых латудных трубах^).
*) Этот метод б]Ь1Л разработан Н. Н. Даввденковым, дит. на стр. ,'325
и Z. Metallkunde, т. 24, стр. 25, 1982, См. также докторскую диссертацию:
С. G. А п d е г S о п, University of Michigan, 1935 и статью D. J. Demores t'a
and D. O. L e e 6 e r'a, Proc. Soc. Exp. Stress Anal., т. 11, стр. 45, 1953. Описание
^16
ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
[ГЛ. IX
Чтобы снимать тонкие слои металла, был применен в этой работе специальный
химический раствор. Изменения кривизны были замерены оптическим
методом. Таким путем можно было получить полные свецения относительно
остаточных напряжений в холоднотянутых трубах. Такие сведения имеют
большое практическое значение для разработки процесса надлежащей
горячей, обработки труб при их изготовлении. ^
69. Кручение за пределом упругости
Начнем с рассмотрения кручения круглых валов и предположим,
что 83 пределом упругости поперечные сечения скручиваемого
вала-продолжают оставаться плоскими, а "их радиусы остаются прямыми *).
В таком случае относительный сдвиг у, в paccToifiHHH г от оси вала
i определится той же формулой, что и в
случае кручения в пределах упругости (см. т. I,
стр. 239), Ti е.
t = rQ, (а)
где 6 есть угол закручивания на единицу
длины вала. Чтобы определить величину кру-»
тящего момента, который требуется для
закручивания вала на угол 6, необходимо знать
зависимость между относительным сдвигом f
и касательным напряжением т за пределом
Рис. 250. пропорциональности. Предположим, что
диаграмма на рис. 2^0 дает требуемую
зависимость*). Если а есть внешний радиус вала, то наибольшая, касательная
деформация сдвига равна аВ, а соответствующее наибольшее
касательное напряжение будет ординатой тп на диаграмме рис. 260.
Таким же путем можно легко получить из диаграммы касательное
напряжение на любом расстоянии ~г от оси.
Крутящий момент М^, который должен вызвать закручивание на
угол 6, будет найден из уравнения старики
\2%r\dr:^M„
(b)
Некоторых методов анализа остаточных напряжений дано в статье С. S, Ваг-'
rett'a, там же, т. 21, стр. 147, 1944; см. также статью О. J. Horger'a^
в издании М. Hetenyi, Handbook of Experimental Stress Analysis, New'
York, I960.
^) Эта теория была разработана Сен-Венаном, J. de math., т. 16, стр. 373,
1871. См. также I. Todhunter and К. Pearson, History о! the Theory of
Elasticity, т. 2, ч. 1, стр. 170. О дальнейшем рассмотрении этого вопроса см.
А. N ad аi. Theory of Flow and Fracture of Solids, New York, стр. 347, 1950.
^) Такую диаграмму можно получить опытным путем, если произвести
испытание на кручение тонкой трубы. Чтобы исключить возможность
выпучивания, толщину стенки можно довести местным утонением до малой
величины, сделав круговую выточку прямоугольной формы в толстой трубе.
€9) КРУЧЕНИЕ ЗА ПРЕДЕЛОМ УПРУГОСТИ 31?
Подставляя в это уравнение из выражения (а)
получаем
о
Интеграл левой части этого уравнения имеет простой геометрический
смысл: он представляет собой момент инерции относительно
вертикальной оси Ох площади ОтпО из рис. 250. После вычисления этого
момента 'инерции для любого принятого значения аВ соответствующий
крутящий момент легко получим по выражению (с). Следовательно,
можно начертить кривую, представляющую зависимость между М^
и 0, если дана диаграмма на рис 250. Так как абсциссы на рис. 250
пропорциональны радиальным расстояниям, то кривая От также
представляет в некотором масштабе распределение касательных
напряжений по радиусу вала. Если при кручении материал все время следует
закону Гука, то мы имеем т = 'у(}=г60, и выражение (Ь) дает
а
27:dQ^r4r = BQJp = M^, • (d)
о
|Что является известным уравнением для кручения круглых валов
в пределах упругости.
Если материал вала имеет ясно выраженный предел текучести,
то криволинейный участок диаграммы на рис. 250 можно заменить
горизонтальной линией с абсциссой т^. Следовательно, для большого
угла закручивания распределение касательных напряжений по
радиусу вала приближается к равномерному распределению.
Соответствующую величину крутящего момента обозначают через {М^)„р^^. Его
значение получается путем подстановки в уравнение (Ь)ту вместо т,
что дает
(^к)пред = -з-^ (е)
Когда крутящий момент достигает этого значения, дальнейшее
скручивание вала происходит без увеличения крутящего момента, пока
не станет заметным упрочнение материала. Для сравнения вычислим
также значение крутящего момента (М^^, при котором начинается
текучесть. Для этой цели воспользуемся формулой (d) и подставим
в нее то значение 0, при котором начинается текучесть. Это
последнее значение получается из формулы (а), если принять г = а и у = 7т»
что дает
о Jfr^ '''т
От—- д —аО'
ъш
ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
[ГЛ. tX
Следовательно, из формулы (d) найдем
яв?»
■T^V
(f)
Сопоставляя формулы (е) и (f), видим, что
^ ^ ^(Л1в)пред:(Л4к)т=^.:
Если после приложения крутящего момента (М^)„р^.^ мы раэд-ру-
8ИМ вал, то в нем останутся некоторые остаточные напряжения.
Величину этих напряжений можно получить, повторив те же
рассуждения, кото11ые были применены в случае изгиба (стр. 812). Пусть
ординаты горизонтальной линии тп т
рис. 251 представляют касательное на*
пряжение т,, вызываемое моментом
-Л^пред» равномерно распределенное по
радиусу, вала. При pasrpysKie в'ала
материал следует закону Гука, и
напряжения от кручения, которые; вследствие
разгрузки должны быть вычтены,
подчинены линейному закЬну, показанному
на рис. 261 линией ШхЩ. Разность между
двумя распределениями напряжений —
прямоугольного во время нагрзокения и"
треугольного во время разгрузки ^—представляет те, которые остаются
в вале после разгрузки. Распределение этих напряжений по радиусу
вала показано на рис. 251 заштрихованными площадями. Величине
ординаты й|р, обозначаемая,через tjnax, найдется из тех
соображений, что ^ прямоу?ольное и треугольное распределения напряжений
представляют крутящий моменг той ^е величины М^^^^. Для
прямоугольного распределения напряжений этот момент определяется
выражением (е). Фор|!ула для того же крутящего момента при
треугольном распределении напряжений получается путем подстановки
в выражение (f) Ттах-вместо т^:
Рис. 251.
2я«8 7t«*
ИЛИ
•-max-
i^-v
Видно, что остаточное напряжение от кручения на поверхности вала
равно 1/3 т^, а у центра — т^.
Распределение о^та'згочных напряжений при кручении можно также
исбледовать ©йытным путем. Для этой цели необходимо снимать
последовательно тонкие слои металла с вала и измерять после удалё-
.ния каждого слоя изменение угла закручивания вала.
щ
КРУЧЕНИЕ ЗА пределом уп^^кгости
aid
в случае идеально йяастйчёнских материале» (см. стр. 287) можно с
успехом применить мембраннук) аналогию для изучения кручения .за пределом
текучести. Когда величина крутящего момента несколько больше Ч1й* (Mg)^,
внешний участок йала находаи^С*^ в условиях текучести, Ь то времся как
внутренний участок продолжает деформироваться упруго. Чтобы распрострд-
нить мембранную аналогии на этот случай, необходимо применить oflHOBpef
мевво с мембраной жестНйй конус АСВ (рис. 252), наклон поверхности
KOTOpoi^o в надя|ежа1цем масштабе представляет напряжение при пределе
текучести т^. Есяй на «(ембрану действует небольшое давление/>, ее
перемещения будут тккже небольшими и коническая поверхность не
препятствует свободному дмещениК) мембраны. Следовательно, ее поверхность
определяет распределение; напряжений для случая упругого кручения, как было
разобрано, pfftee (см. tTp. 198). С увеличением Давления перемещения
мембраны также увеличиваются и, наконец, внешний участок мемб1^а5ы приходит
в сопр!йкасаниё с жестким конусом, как показано на рис. 252. ©то
состояние определяет кручение за пределом текучести. Внешний участо1(
мембраны, совпадающий с конусом, имеет постоянный нйсдон поверхности, соотг
ветствующий пределу текучести %. Внутренний участок тп мембраны
Рис. 252.
Рис.. 253.
соответствует внутренному участку/Вала, который находится в упругом
состоянии. Удвоенный объём, заключенный между мембраной и плоскостью
контура j4B, прододжает представлять крутящий момент. Из этого мы
заключаем, что удвоенный 1}бъем конуса должен дать нам значение Мпред- Так
как наклон конуса равняется t^, то его высота равна at^, а его удвоенный
объем равен -^ па*ат^, *4то совпадает с выражением (е).
Подобный метод может быть применен и в случае некруговых яопереч-
ных сс'^енйй валов; он весьма полезен при определении участков вала,
в которых начинается текучесть. Рассмотрим для примера прямоугольны й
вал. При исследовании кручения этого вала за пределом текучести нужно
воспользоваться мембраной совместно с жесткой поверхностью в виде
крыши (рис. 253)> которая во всех точках имеет постоянный наклон,
представляющий в некотором масштабе напряжение предела текучести т^. ©.невидно,
что мембрана, деформируемая под действием увеличивающегося paBHOiii^p-
ного давления, касается крыши сначала у с и d—срединных то^^^ дли|КДЫх
сторон прямоугольника. В этих точках начинается текучесть, а при Ufiiibt
Высоком давлении некоторые участки мембраны будут совпадать с крышей,
320 ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ [ГЛ. IX
как указано на рисунке заштрихованными площадями. Эти площади
определяют области, где материал течет. В остальном вале мы имеем только
упругую деформацию. Дальнейшее увеличение давления на мембрану
увеличивает участки соприкасания с крышей, гак,же как и области пластической
деформации. Двойной объем, заключенный между кровлей и плоскостью АВ,
очевидно, даст величину Л^пред Д^я прямоугольного вала.
Если прямоугольный стержень из сварочного железа закручивается за
пределом текучести, го области пластического течения можно выявить
надлежащим протравливанием «поперечного сечения." После травления в
пластических областях поперечного сечения появляются темные параллельные линии
с направлениями, показанными на рис. 253. Эти линии свидетельствуют
о скольжении металла вдоль слоев, параллельных оси вала, вызываемом
напряжениями, соответствующими пределу текучести'^).
70. Пластические деформации толстостенных цилиндров
под действием внутреннего давления ^)
При рассмотрении упругой деформации толстостенного цилиндра
под действием внутреннего давления р мы нашли (см. стр. 175), что
радиальное и окружное напряжения в радиальном расстоянии г от
оси цилиндра выражаются формулами
где avib — соответственно внутренний и наружный радиусы цилиндра.
Наибольшее окружное растяжение и наибольшее радиальное сжатие
имеют место на внутренней поверхности цилиндра. На этой
поверхности действует также наибольшее касательное напряжение; его
величина равна
рЬ^
'■max-
Постепенным увеличением внутреннего давления мы, наконец,
достигнем момента, когда материал на внутренней поверхности начинает
течь. Это произойдет, когда наибольшее касательное напряжение (Ь)
становится равным пределу текучести t^^). Подставляя это значение
в формулу (Ь), находим, что давление, при котором начинается теку-
*) Интересные фотографии этих линий, полученные для различных форм
скручиваемых стержней, показаны в статье А. Nadai, Trans. А. S. М. Е.,
■ц 53, стр. 29, 1931; см. также его книгу «Theory of Flow and Fracture of
Solids», стр. 494, 1950; русский перевод, и^д-во ИЛ, 1954, стр. 558.
*) Исследование пластического течения в толстостенных цилиндрах,
подверженных внутреннему давлению, было произведено Сен-Венаном; см.
Compt. rend., т. 74, стр. 1009, 1872; см. также I. Todhunter and
К. Pearson, History of Theory of Elasticity, т. 2, ч. 1, стр. 172 и статью
L. В. Turner'а, Cambridge Phil. Soc. Trans., т. 21, стр. 377, 1913.
•) Вопрос 6 текучести материала при различных напряженных состояниях
рассмотрен в п. 82. Mfj допускаем здесь, что т^ имеет то же значение, что
и в случае кручения. <см. стр. 317).
701 ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ 321
честь, равно
, и т
Ь^ — Ф - , .
Pt—'^-v—л1^ . (с)
Полагая, например, Ь=:=2а,^ы находим, что в этом частном случае
/7т==0,75 V Цри дальнейшем увеличении давления пластическая
деформация проникает все глубже и глубже в стенки цилиндра и,
наконец, при некотором давлении, которое вызовем Рщ^тр вся стенка
цилиндра придет в состояние текучести. Распределение напряжений
в стенке npi^ этом, состоянии текучести можно исследовать без
особого затруднения, если предположить, что материал является идеально
пластичным; это означает, что течение происходит под действием
постоянного касательного напряжения, равного т^. Тогда для каждой
точки в области пластической деформации справедливо ус^|овие
Ч—Jr
т^. , (d)
Второе условие для определения главных напряжений о^ и о^
получится рассмотрением равновесия элемента стенки, показанного на
рис. 127. На основании предыдущего изложения (см. стр. 174)
уравнением равновесия будет
о^ —о, —г^ = 0. - (е)
Подставляя, вместо разности главных напряжений его значение по
условию (d), получаем / ^
/ dQf. 2т.
dr г
^-—- (f)
Интегрирование этого уравнения дает
о,==2т^1пг + С -'^ . (g)
Постоянная интегрирования С найдется из условия, что на наружной
поверхности цилиндра, т. е. при г = Ь, радиальное напряжение
обращается в нуль. Это дает ,
0 = 2т^1п^ + <^. С== —2'c^In^.
Подставляя это значение постоянной С в уравнение (g), получаем
о, = 2'с^1п-|-. ^ B85)
Тогда для внутренней поверхности цилиндра находим
- Ч<';)л-а=^2х,1п-|-, B86)
1 с. П, Тимошенко, т^ II
mif^
322
ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ
1гл: IX
а давление, которое~^ребуется для тогх), чтобы привести всю стенку
цилиндра, в состояние пластической деформщии, равно
а
2т,1п^.
Рпред—■ (fr/r-a^^^
Ваяв опять Ь=:2а, найдем
Рпред = 2т,1п2=.0,б93B'у: ,
Имея уравнение B8Ь) для радиальных напряжений, мы получаем
окружные напряжения по выражению (d), что дает
o, = 2x,(l+ln-^). " B87)
Если^ = 2о, то отс^ода находим
Ыг-а = 2х, (l+1П 1) =:^ 0.307 Bх,),
' ' ^ (o?W=2v
Распределение напряжений о^ ri о^ raff толщине стенки для частного
случая Ь = 2й показано на рис. 254 ч соответственно кривыми mln^ и
st: Если после приаддения материала цилиндра к состоянию текучести
мы удалим внутреннее давление, то в Стенке цилиндра сохранятся
. ^ Рис. 254,
некоторые ^остаточные напряжения. Эти напряжения можно легко вы-
. числить, если предположить, ^ что при разгрузке материал цилиндра
следует закону Гука. В таком случае напряжения, которые должны
вы^чйтаться при разгрузке цилиндра, определятся формулами (а), если
мы подставим в, эти выражения /^^pg^ вместо р. Эти напряжения для
частного случая г> = 2а показаны «а рис^ 254 крив^наи fi^j и tnkn.
Тогда заштрихованные площади дадут остаточные напряжения в стен-
701 ПЛАСТИЧЕСКИЕ двфовмАций толетостщных цйлийдров 3^3
ке цилиндра. Видно, что благодаря пластической деформации в части
стенки цилиндра возникают значительные сжимающие окружные
напряжения*). Если цилиндр С такими остаточными напряжениями снова
нагружается внутренним давлением, равным Рщф то вызываемые-
этим давлением окружные напряжения, определяемые кривой вд^ц/
будут наложены на остаточные напряжения, определяемые saijiTpHXOf
ванными площадями, так что результирующее распределение
напряжений будет отйеч#Г|> кривой st. Наибольшее результирующее
напряжение равно 2t,, и никакой текучести при этом втором приложении
внутреннего давления не/происходит. Следовательно, остаточные
напряжения, вызьйваемые пластическим расьиирением цилиндра, по
природе таковы, что увеличивают давление, которое может выдержать
ййлиндр в упругом состоянии. Этим обстоятельством иногда пользуют-
^ся при изготовлении орудий, когда они должны выдерживать
высокое внутреннее давление газов *).
В нашем изложении ^ыло.допущено, что приложенное внутреннее
давление может привести * весь цилиндр * в состояние текучести, но
этот же метод можно применить без затруднения к случаям, в кото-
рнх только внутренняя часть ртенки цилиндра находится в состоянии
текучести, в то время как наружная часть находится, в упругом
состоянии. Допустим, что приложено давление р' большее, чем р^, но
меньшее, чем ,/>пред, и Пусть с будет радиусом цилиндрической
поверхности, Отделяющей пластическую область стенки От упругой области.
Между, этими двумя областями будет действовать радиальное
давление, которое мы назевем-^iV. Величина этого давления может быть
найдена из рассмотрения упругой наружной части стенки.
Наибольшее касательное напряжение х^щ в этой части найдется из
выражения ^Ь) подстановкой в него с йместо а и ЛГ вместо р, что дает
Так как цилиндрическая поверхность при г = с разделяет упругую
и пластическую зоны, то материал на этой поверхности как раз
достигает предела текучести. Следовательно, Хо1ах = '^т* Тогда уравнением
для определения давления X будет -
t,
ХЬ^
т ^8—<;«'
(h)
i
*) Пр^вдпвлагается, что это сжимающее напряжение мевыце, чем
напряжение,'соответствующее пределу текучести, и что при разгрузке не
происходит текучести. (Случай текучести при разгрузке (щл изучен L. 6. fur-
п е г'ом, цит, яа стр. 82в.
') Описание этого применения начальной пластической деформации
можно лайти в книге: L. Jacob, Resistance et construction des benches a feu:
Autofretage, Paris. См. также S. J.* Brown, u. S. Naval Inst. Proc, т, 46,
стр. 1941, 1920. >
If
mt'^
324 ДЕФОРМАЦИИ ЗА ПРЕДЕЛОМ УПРУГОСТИ [ГЛ. IX
^1 МЫ получим
^— ^5 • (и
Имея это давление, мы можем леУко вычислить напряжения в любой
точке в упругой области стенки, пользуясь формулами, подобными
формулам Ха) *).
Для вычисления напряжений в пластической области стенки
воспользуемся выражением (g). Постоянная интегрирования С найдется
из условия, что при г = с, о^ = — X; это дает
— Х = 2х^1пс-\-С, С= —X —2т^1пс.
Подставляя значение С в выра!жение (g) и пользуясь формулой (i),
получаем
а,= 2т,1п-^-^^-^^1=^. ' B88)
Приняв г равным внутреннему радиусу а цилиндра, мы получим
величину р' давления, которое должно быть приняте для того, чтобы
произвести пластическую текучесть в стенке до глубины,
соответствующей радиусу г = с. Это давление будет
;/ = -2..1nf + i^i^^^. B89)
Обратившись к нашему предыдущему примеру, где Ь = 2а и
положив сж=:1,5а, мы найдем из уравнения B89), что р' = 0,624 B т^).
Распределение окружных напряжений о^ получается из выражения (d),
которое дает
o, = 2T,-fOr = 2^1»f+ '^т.^'У . - B90)
При г = с первый член правой части ypaвнe^^ия обращается в нуль,
и значение о^ становится равным значению окр)гжного напряжения,
вызываемого давлением X в смежной упругой зоне стенки.
Выражения B89) и B90) дают напряжения, возникающие во внутренней части
стенки цилиндра, которая претерпевает пластическую
деформацию. Для наружной части, которая остается упругой, нужно
использовать формулы, подобные формулам (а). Таким путем задача о
распределении напряжений для случая цилиндра, который ^ претерпевает
лишь частичную пластическую деформацию, полностью решена.
Если после Частичной текучести стенки цилиндра удалить
внутреннее давление /?', то в стенке цилиндра удержатся некоторые
остаточные напряжения. Внутренняя часть стенки, в коТорой имела место
пластическая деформадия, не возвращается к ее первоначальному
О Нужно принять в этих уравнениях радиус с вместо an X вместо р.
70] ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ 325
диаметру и испытывает давление со стороны упругой наружной части
стенки. Распределение напряжений, возникающее в результате этого,
подобно распределению напряжений, вызываемых - горячей посадкой в
составных цилиндрах (см. п. 41). Чтобы вычислить эти напряжения,
мы поступаем точно так же, как пояснено ранее и показано на рис. 254.
Все эти вычисления основываются на допущении, что за пределом
текучести материал течет без увеличения напряжений. Ц противном
случае остаточные напряжения не могут быть вычислены так просто,
как пояснено выше, и нужно обратиться к опытному определению
остаточных напряжений. В таких случаях можно использовать метод,
подобный тому, который применяется при определении остаточных
напряжений при изгибе. Мы снимаем тонкие слои металла, начиная с
внутренней поверхности цилиндра*), и после каждого среза измеряем
деформацию, вызванную в осевом и окружном направлениях на
наружной поверхности цилиндра. Такие измерения дают достаточные
сведения Для вычисления остатрчных напряжений.
Остаточные напряжения в цилиндрах можно вызвать не только
пластической деформацией, описанной выше, но также и
неравномерным охлаждением и изменением объема металла при рекристаллизации
в различных процессах горячей/ обработки. Иногда эти напряжения
приобретают первостепенное значение, как, например, в v больших
поковках, и уже разработано несколько методов их определения ^).
^) Были проделаны некоторые опыты с отслаиванием с наружной
стороны: см. Н. В U h 1 е г und W. S с h г е i b е г, Metallwissensch. fi. Techn.,
сентябрь 1954, и статью Бюллера в книге «I^esidual Stresses in Metals and
Metal Constriiction», 1954. _
®) Первое исследование этого рода^было сделано Н. Калакуцким,
Петербург, 1887. См. также N. К а 1 а к о и t z к у. Investigation into the Internal Stress
in Cast Iron and Steel, London, 1888. Полное решение задачи было дано
G. Sachs'oM, Metallkunde, т. 19, стр. 352, 1927 и Z. Ver. deut. Ing., т. 71»
стр. 1511, 1927. Эти две статьи содержат полную библиографию предмета.
Дальнейщие улучшения методов измерения остаточных напряжений в трубах
были сделаны Н. Н. Давиденковым, Журнал технической физики
(Ленинград), т. 1, 1931. См. также G. Sachs, Trans. А. S. М. Е, стр. 821, ,1939.
Библиография по пластической деформации металлов и остаточным
напряжениям дйна в книге: G. Sachs, Handbuch der Metallphysik, Leipzig, т. 3, ч. 1,
1937. См. также статью О. J. Horger'a, цит. на стр. 316. Остаточные
напряжения в шатунах нефтяных насосов рассмотрены в статье R. Е. Н an s-
И'р'а, Proc. Soc. Exp. Stress Anal., т. IGi, стр. 97, 1952.
шм
ГЛАВА X
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
71. Общие соображения
В предыдутцизс^ главах излагались методы анализа распределения
напряжений, вызываемых различного рода силами в конструкциях.
Зная напряжения, проектировщик должен "^атем, выбрать материал и
размеры конструкции та15, чтобы в работе она безопасно
выдерживала различные сочетаний нагрузок. В этих целях необходимо иметь
сведения относительно упругих свойств и прочностных характеристик
строительных материалов при различных напряженных состояниях.
При анализе напряжений обычно предполагают, что материал следует
закону Гука, и тогда для решения задачи достаточно знать упругие
характеристики материала.. Но для выбора безопасных размеров
сооружения этих сведений недостаточно. Проектировщик должен не
только .знать пределы, при которых материал можно рассматривать
как совершенно упругий при различных напряженных состояниях, но
и изучить поведение материала за этими пределами. Сведения такого
рода мож1ю получить только в опытных - исследованиях. Лаборатории
для. испытания материалов должны быть снабжены машинами*) для
1выйолнения некоторых типичных деформаций опытных образцов, таких,
как растяжение, сжатие, кручение,и изгиб.
Чтобы сделать результаты испытаний сравнимыми, были
установлены определенные размеры испытуемых образцов, которые признаны
стандартными. Наиболее Широко применяемыми* механическими
испытаниями строительных матёриадЬв, несомненно, являются испытания
на растяжение. Стандартный обра^ц для испытания на растяжение
в США принимается круглым, диаметром Q,b дм и "расчетной
длиной 2 dMt так что . ^ '
-1=-=4 или /=4,51 VF;
1) Описания испытате'льных машин и библиографию по предмету см. в
статье J. Marin*a в издании М. Hetenyi, Handbook ol-Experimental
Stress Analysis, Ne^v York, 1950; см. также статью A. Eichinger'a в
издании E. S i e b e 1, Handbuch der Werkstoffprufung, Stuttgart, 1940.
7П
ОеиШВ'СООБРАЖЕНЙ?
327
где /^===^6/^/4 есть .площадь поперечного сечения образца*). В случае
прямоугольных образцов предпочтительно иметь то же соотношение
между длиной и площадак) поперечного сечения, как и для круглых
о^азцов. ,
а)
Рис. 255.
Длина цилиндрической части обраэда всегда несколько больше,
чем расчетная длина / и обычно равняется по меньшей мере l-\-d.
Концы образца вообще изготавливаются большего поперечного
сечения для того, чтобы предохранить образец от разрушения в зажимах
ис1штательной машины, где условия напряженности более сложные,
Так^ как здесь имеются местные неправильности в распределении
напряжений. На рис. 255, а показан
цилиндрический образец при /=±:10с^ здесь показаны также >^
сферические гнезда в зажимах машины,'
имеющие целью обеспечить центральное приложение
нагрузки. На рис. 5^55, ^ приведен плоский
прямоугольный .образец.
Испытательные машины на растяжение
обычно \снабжа19тся устройством, которое автоматиг
чески вычерчивает диаграмму растяжения,
представляющую зависимость между нагрузкой Я и
удлинением Д / = Вюбразца. Такой диаграммой
обнаруживаются важные характ^йстики, материала.
Например» рис1 256 приеодитч ряд кривых
растяжения Для углеродистой стали с различным
содержанием углерода. Можно видеть, что по
, Mi^e увеличения содержания углерода предел
прочности стали также увеличивается, но в то
же время удлинение при разрыве уменьшается, ' '
и материал имеет меньшую пластичность- ВысокОуглеродистая ст^ль
является относительно хрупкой. Она следует закону Тука до
высокого зиаченйя напряжения и затей* разрывается гфи очень малом
^) В Центральной Европе применяются двух разных размеров круглые
образцы: 1) длинные образцы, для которых 1^^\Ы^з=. 11,3 YР^ и 2) короткие
образцы, для которых/ = 5rf = 5,65 f^/^.
Рис. 256.
328
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
удлинении. С другой стрроны, мягкая сталь с малым Содержанием"
5Тлерода является пластичной и значительно вытягивается перед
разрывом. В последующем изложении мы сначала рассмотрим испытания
на растяжение хрупких материалов.
72. Испытания на растяжение хрупких материалов
Начнем с рассмотрения стекла, являк)ф,егося примером хрупкого '
материала. Стекло практически следует закону Гука до разрушения,
и диаграмма испытания может быть представлена приблизительно
прямой линией О А (рис. 257). Обычные испытания на растяжение
стекла дают очень низкие значения предела прочности, а
соответствующее количество работы, требуемое для того, чтобы произвести
разрушение (представлено на рис. 257 заштрихованной площадью ОАВ),
весьма мало по сравнению с количеством энергии, теоретически
требуемой для отделения молекул
друг от друга. Эта последняя
величина может быть получена
опытным путем — плавлением и затем
выпариванием стекла. Работа,
требуемая для того, чтобы отделить
молекулы, будет тогда того же
порядка величины, как количество
теплоты, требуемой для
выпаривания. Эксперименты показывают,
что эта величина в тысячи раз
больше, чем рйбо^-а, требуемая при
испытании на растяжение (рис. 257).
Чтобы объяснить это несоответ-
^ ■ ствие, Гриффис предложил
теорию *)j согласно которой энергия, требуемая для разрушения стеклянного
офазца, неравномерно распределяется по объему, и в образце
имеются области концентрации энергии, вызываемой микроскопическими
трещинами,, которые действуют как концентраторы напрязкений. Рас-,
сматривая одну из этих микроскопических трещин как узкое
эллиптическое отверстие в пластинке, которая равномерно растягивается,
(рис. 258), и пользуясь известными выр|^жениямн[ для. напряжений
вокруг эллиптического отверстия (см. п. 57), мы можещ показать,
что энергия деформации пластинку (на единицу толщины) умень1иает-
ся благодаря наличию отверстия на величину^^)
.'.'.'■. \ . пРа^ '
(а)
О S ^
Рис. 257.
4£
, *) А. А. Griffith, Trans. Roy. Soc. (London), A, т. 221, стр. 163^198,
1921. См. также Ргос. Interna^. Congr. Appl. Mech. Delft, стр. 55—63, 1924
^) Предполагается, что расстояния между трещинами сравнительно
^велики, так что нарушения в распределении напряжений из-за трещин можно
72] ИСПЫТАНИЯ НА РАСТЯЙ^ЕНИЕ ХРУПКИХ МАТЕРИАЛОВ 329
В ЭТОМ выражении / есть длина трещины, о — равномерно
распределенное растягивающее напряжение и Е — модуль упругости материала.
Рассмотрим теперь величину напряжения, при котором трещина
начнет распространяться поперек пластинки й вызовет разрушение.
Такое распространение трещины становится возможным без какой-либо
дополнительной работы только при условии, если увеличение
поверхностной энергии вследствие приращения dl длины трещины
компенсируется соответствующим уменьшением энергии деформации пластинки.
Обозначая-цоверхностное натяжение через S, мы получаем таким
путем следующее уравнение'для состояния на пределе прочности:
|-('-^)й=2ЭД (Ь),
или
. 4SE
пч
8 . (с)
Для того чтобы/ определить поверхностное натяжение 5, Гриффис
слелал ряд испытаний с расплавленным стеклом при различных
температурах. Температуры были таковы, что стекло вело себя, как
вязкая жидкость. Значение 5 при комнатной температуре при этом, было
■получено, экстраполированием в' предположении линейного изменения
5 с изменением температуры. Предел прочности о^^ стекла
находился из обычных испытаний на растяжение, и длина / трещины теперь
могла быть вычислена*) из уравнения (с). Из уравнения (с) вместе с
тем видно, что предел прочности при растяжении обратно
пропорционален квадратному корню из /.
Чтобы проверить теорию, Гриффис проделал опыты с тонкими
стеклянными трубками, подверженными внутреннему давлению. Делая
алмазом искусственные трещины, пapaл;^eльныe оси цилиндра,
различной при этом длины, он нашел предел прочности о^^ опытным путем.
Эти опыты удовлетворительно согласовались с теоретическими
выводами, вытeкaюш^^ми из уравнения (с). Гриффис провел далее опыты
с тонкими стеклянными волокнами и нашел предел прочности при
растяжении равным 3,5-10* k?Jcm^ для волокна 3,3-10"' мм в
диаметре. Это было приблизительно в двадцать раз выше, чем ранее
найденное значение для более толстых образцов. Такая значительная
прочность тонких волокон может быть объяснена также на
основании теории Гриффиса, если заметить, что в процессе вытягивания
тонких волокон исчезают любые трещины, которые были
первоначально перпендикулярны длине волокон. Гриффис отметил, что спустя
некоторое время волокна теряют часть своей прочности. Производя
рассматривать независим.о одно от другого. Тогда достаточно рассмотреть
лишь одну трещину, перпендикулярную напряжениям, как наиболее неблаго-
приятнук}. .
*) Опыты Гриффиса дали для / значение порядка 1 • 10~* см.
шт
330
МЕХАНИЧЕСКИЕ СВОЙСТВА Л^АТЕРИАЛОВ
[ГЛ. X:
ОПЫТЫ С волокнами немедленно-после того, как они были вытянуты,
он получил"t;poмaдный предел прочности, равйый 6,3 ■ 10* ifzjcA^ для
диам0^ра 0,5 мм: Это значение составляет приблизительно половину
теоретической прочности, определенной, путем рассмотрения
молекулярных сил. . . - "■'
Другие исследования прочности, при рйстяжении Хрупких
материалов были сделаны с образцами из монокристалла, вырезанными из
большого кубика кристаллической соли*). Эти опыты показывали, что
предел прочнос:^и этого материала равнялся только ^б кг/см^ в
испытаниях на воздухе при комнатной температуре. Когда -тот же образец
испытывался в процессе погружения в горячую воду, он достигал
предела текучести при напряжении 80 кг/см\
а затем растягивался пластически -до окончат
тельногр разрушения, происходившего при
напряжении, равном 16 000 кг/см^ Такое значение
предела прочности близко к теоретической проч-,
но^ти 20 000 л;г/сж', вычисленной Ф. Цвик^си^).
Эти опыты показалиг^ что' сглаживание
поверхности испытуемого. образце оказывает большое
влияние на прочность при растяжении образца.
Интересные опыты, относящиеся к прочности
при растяжении л1у;тов слюды, были проделаны
Е. Орованом *). Вместо применения стандартных
образцов на растяжение (рис. 255, Ь),
вырезанные из листов слюды, он пользовался листами
слюды, подвергавшимися растяжению на участке
тп с помощью захватов А (рис. 259). ff этом
случае предел прочности получался приблизительно tt десять раз
большим, чем для. стандартных образцов при испытании на растяжение. Это
указы)вает на то, что несовершенства, имеющиеся по краям стандартных
образцов (рис. 255, Ь\ значительно уменьшали прочность и что,
устраняя их влияние с помощью приспособление приведенного на рис. 259,
можно получ#ь высокие значения предела прочности. Все описанные
опыты подтверждают гипотезу Гриффиса, что низкие значения
прочности при растяжении хрупких материалов обусловлены такими
несовершенствами, как микроскопические трещины и царайины на
поверхности испытуемого образца.
Если на прочность хрупких материалов оказывает значительное
влияние наличие несовершенств, то кажется логичным ожидать, что
т-
■ ■'
¥
1
>J
.-
^
-/7
*'■
, т
Рис. 259.
*) См. статуо А. Иофф€, Z. Phys., т. 22, стр. 286, J924; см. также Ргос.
Interaat. Congr. Appli Medi., Delft, гтр. 64, 1924. Дальнейший разбор работы
Иоффе дан в книге: Ё. Schmid und W. чВоав, Kristallplastizitat, j^erlin,
стр. 271, 1935.
2) СМ. Z. Phvs., т.'24, стр. 131, 1928. '
•) См. Z. Phys., т. 82, стр. 235, 1933.*
72] ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ ХРУПКИХ МАТЕРИАЛОВ 331
предел прочности будет зависеть от размеров o6piasua и будет
становиться все меньшим с увеличением размеров, так как тогда воз-
Исркность наличия слабых мест увеличивается. Влияние размера было
замечено в случае xpyni^ofo р^азрушения, которое производатся
ударом*) или при испытаниях на усталость^). Объяснение на основе статй-.
стическвго метода было дано Вейбуллом^). Он показал, что для данного
материала в геометрически подобных образцах с объемами Vi и Vg
значения пределу прочности, определяемые испытанием н^ растяжение,
будут находиться, в отношении
где т — постоянная материала. После определения т из уравнения (d)
л«ожно найти значение о„^ для любого иного размера образца. Затем
'такие опыты_^ были ' проделаны Н. Давиденковым *), использовавшим
сталь с высоким содержанием фосфора. Производя опыты с
образцами двух разных диаметров (с^=10 мм и с? = 4 мм) и с двумя
разными длинами (/=50 мм и /.= 20 мм), он нащел-для o„^
соответственные значения E7,6 кг/мм^ и 65,0 kzjmm^). Величина m = 23,5
была затем определена из уравнения (d). Для этого; т предел
прочности образца с d=\ мм и /=5 мм найден равным 77,7 кг(мм\
Опыты же дали значение 75,0 kzjmm\ так что теория оказалась, в
хорошем согласии с опытами.
Пользуясь статистическилг методом, Вейбулл вычислил также ')
предел прочности для прямоугольного стержня при чистом изгибе и
нашел отношение '
-J^i5Ws6_.^B/«-}-2)V'». (е)
\*^пч/растяжение " ~~
Эта формула была также проверена опытами Давиденкрва. Его
испытания дали для этого'отношения значение 1,40, в то время как
теоретическая цифра была 1,41, вычисленная для w = 24.
Некоторые другие общие видьк распределения напряжений были
разобраны в статье Вейбулла. Он упрминает также различные
опытные исследования, которые показали удовлетворительное совпадение
со статистической т^еорией. Эта теория применима только к материалам,
имеющим хрупкое разрушение, ноне к тем, которые получают sHiah
*) М. С h а г р у, Assoc, intern at. essais materiaux, 6th Congr,, New York, m. 4,
стр. 5, 1912.
*) R.E. Peterson, J. Appl. Mech., т. 1, стр. 79, 1933. ,
*) W. Weibull, Proc. Roy. Swed. Inst. Engrs. Kesearch (Stockholm),
№ 151, 1939.
*) В английском переводе его статью смотри J. Appl. Mech., т. 14,
стр. 63, 1947.
**) W. W е i b U11, цит. здесь же.
332
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
чительную пластическую деформацию перед, разрушением^^ластическая
деформация будет смягчать местные концентрации напряжений в
местах несовершенств, и поэтому только средние напряжения становятся
важными при анализе состояния разрушения.
ч - . ■
73. Испытания на растяжение пластических материалов
Механические свойства пластических материалов, например стали
и других металлов, применя(ем^>1х в конструкциях, обйчно
определяются опыхами на растяжение. Рис. 260 представляет диаграмму
растяжения для мягкой строительной стали. Из этой диаграммы можно
получить такие важные характеристики, как предел текучести, пре-^
дел прочности и величина
пластического удлинения.
При определении предела
пропорциональности- нужны чувствительные
экстензометры для того, чтобы
обнаружить малейшее отклонение от прямой
линии на диаграмме растяжения.
Очевидно, положение этого предела на
диаграмме в значительной степени
зависит от чувствительности инструмента.
Чтобы получить большее однообразие
результатов, эа основу для определения
предела пропорциональности часто принимают определенную величину
остаточной деформации или определенную степень отклонения-от
пропорциональности. Международный конгресс по испытанию материалов
в Брюсселе A906 г.) определил предел пропорциональности как
растягивающее напряжение, при котором остаточная деформация
составляет 0,001%. Позднее' наметилась тенденция повысить это предельное
значение остаточной деформации до 0,01Уо*).
Предел текучести является весьма важной характеристикой для
таких материалов, как строительная^ сталь. При напряжении,
соответствующем пределу текучести, образец удлиняется на значительную
величину без какого-либо увеличения нагрузки. В случае мягкой стали
это удлинение может, быть больше двух процентов, Инорда текучесть
сопровождается, резким уменьшением нагрузки, и диаграмма раст5Лке-
ния имеет форму, показанную на рис. 260. В таком случае верхний
и нижний пределы нагрузки ъ а ш Ь, разделенные на-первоначальную
площадь поперечного сечения, называются соответственно верхним и
нижним пределами текучести. Положение верхнего предела текучести
зависит от скорости испытания, формы образца и формы поперечного
Рис. 260.
*) См. статью Р. L U d W i к' а, Bruchgefahr und Materialpriifung, Schweiz.
Verband i. Materialpruf. d. Technik (Zurich), Ber., № 13, 1928.
73] ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ ПЛАСТИЧЕСКИХ МАТЕРИАЛОВ ЗЗЗ
сечения (см. п. 77). Нижний предел текучести обычно рассматривается
как истинная характеристика материала и поэтому принимается за
основу для определения рабочих напряжений.
Благодаря относительно большому удлинению материала на
пределе текучести нет необходимости пользоваться чувств ителй>ными экс-
тензометрами для опреде'ления этой точки. Ее можно определить^ с
помощью простейших инструментов или можнсг взять непосредственно
из диаграммы растяжения. Для строительной углеродистой стали
напряжение, соответствующее пределу текучести, приблизительно
составляет 55-*-60Уо от предела прочности. Строительная сталь
приблизительно с 1Уо кремния имеет напряжение предела текучести, равное
до 70—80% предела прочности. Предел прочности для кремниевой
стали приблиз?ительно такой же, как и для углеродистой стали;
высокое же значение для пре21ела^ текучести оправдывает обычную
практику применения более высоких рабочих напряжений для кремниевой
стали.
Резко выраженный предел текучести является характеристикой не
только строительной стали; но также и таких материалов, как бронза
и латунь. Однако С)шлествуют другие материалы, которые не имеют
вполне определенного предела текучести. Для этих материалов за
предел текучести иногда принимается напряжение, при котором
остаточная деформация (пластическое удлинение) достигает значения 0,2%.
Нужно помнить, что предел текучести, определяемый таким образом,
не представляет определенной физической характеристики материала,
но зависит от произвольно выбранной ъеличины остаточной
деформации. В случае строительной стали с ясно выраженным пределом
текучести величина удлинения на пределе текучести обычно
значительно больше 0,2"Д, и в таком случае действительный предел текучести
совпадает с пределом текучести^ найденным пЪ величине 0,2У(,
остаточной деформации.
Предел прочности обычно определяется как напряжение,
получаемое путем деления наибольшей нагрузки, образца (точка с на рис. 260)
на первоначальную площад|> поперечного сечения. Эта величина
часто принимается за основу для определения рабочих напряжений.
Площадь, ограниченная диаграммой растяжения Oacde (рис. 260),
представляет работу, необходимую для того, чтобы произвести
разрушение. Этой величиной также пользуются как характеристикой
свойств материала, зависящей не только от прочности, но также и
от пластичности материала.
Пластичность металла обычно характеризуется, ^;длил^«к^ж
расчетной длины образца при испытании на растяжение и уменьшением
площади поперечного сечения, где происходит разрушение. В первой
стадии пластического удлинения от а до с на рис. 260 образец
удлиняется равномерно по своей длине. Это равномерное удлинение
сопровождается равномерным поперечным сокращением, так что объем
жг
334 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ' (ГЛ. X
образца остается практически постоянным ^). В точке с рйстягива-
ющая сила достигает наибольшего значения; дальнейшее растяжение
образца сопровождается уменьшением нагрузки. В этой стадии
пластического удлинения деформация становится местной, т. е. сосредоточи-
. . , вается в некотором месте, и начинается образование шейкщ
причем образец принимает форму, -показанную на рис 261.
Трудно определить точно момент, когда начинается
образование шейки, и поэтом^ трудно установить отдельно
величину равномерного удлинения и отдельно величину
удлинения, вызванного образованием шейки. Поэтому обычно
измеряют полное ^ увеличение расчетной длины после
разрыва образца. Тогда относительное удланение^опрет-
лйется как отношение этого полного удлинения ^^асчетной
Рис. 261. длины к ее первоначальной длине. На практике удлинение
при разрушении обычно дается в процентах. Если / есть
начальная расчетная длина и S — полное удлинение, то относительное
удлинение при разрушении в процентах будет < ■
-.100. (а)
Это удлинение обычно принимается за меру рластичности материала.
Относительное удлинение, полученное так^м образом, зависит от
размеров образца. Увеличение S расчетной длины вследствие образования
шейки представляет бодьшую часть полного увеличения и
практически 01J0 одно и то же как для короткой расчетной длины, так и для
дли!1ной расчетной Длины. Следовательно, о*носйтельное удлинение»
определяемое^ уравнением (а), оказывается ббЛьшим по мере
уменьшения расчетной длины. Для стали относительное удлинение образцоэ
при /ss=5rf приблизительно в 1,22 раз больше удлинения образца из
того^ же материала при /== 10^. Опыты также показывают, что форма
поперечного сечений влияет на местную деформацию в шейке и, сле-
jQ[OBiaT€JibHo, влияет на ухугинение образца. Из этого следует, что
сравнимые результаты в отношении удлинения можно получить, лишь
применяя геометрически подобные образцы.
Относительное сужение площади поперечного сечения при
разрыве определяется формулой
9=^^\ ^ " (Ь)
в которой Fo есть первоначальная площадь поперечного сечения и
Fj--^ конечная площадь поперечного сечения в месте разрыва.
Таблица, дающая результаты большого количества статических
испытаний на растяжение различных сталей, приведена в конце главы.
: . ^ i ■...-. у .
*) Малая упругая деформация изменения объема значительнр меньше
сравнительно большой пластической объемной деформации, и поэтому ее
можно не учитывать.
74] ИСПЫТАНИЯ ОБРАЗЦОВ ИЗ МОНОКРИСТАЛЛА В УПРУГОЙ ОБЛАСТИ 335
74. Испытания образй^ов из моАокр^юталла
6 уоругой области
Металлы, которые йоюльзуются в инженерной практике, х^ы^чно
имеют кристаллическую структуру. Кусок металла состоит из
большого числа мелкик кристаллов, и механические свойства материала
можно лунще пояйть, если изучить сначала сроЙСтва монокристалла»^,
Рентгенов1скйЙ ^налйЭ позволяет установить, что каждый кристалл
любого материала состоит из. большого числа атомов, расположенных
в харак^ернщ для него геометрическом порядке. Порядок атот
образуется повторением единичной ячейки^ два^ типа Kofopott показаны
на рис. 262. Рис. 262, й тображаегг обьемнецентрироЬанку10 ^чейУсу
кристаллической структуры железа при^ комнатной т«емйературе;
Я=Я1=7Т
, ^ а^ ^ , ■ 4^ J м г
\
т
^
7р=я
и ° И^ nuzy
5Е
а)
и
Рис. 262.
рис. же 262, ib показывает гранецентрированную ячейку, представляв
ющую кристаллическую структуру для алюминия,^^ меди и некоторых
других металлов. Размеры решетки, например длина а на рис 262,
постоянны для каждого материала и имеют порядок 1 • 10~* см.
Были разработаны *) различные методы для получения
металлических кристаллов больших размеров для то^^б, чтобы образцы для
механических испытаний можно было вырезать из одиночного кристалл
ла. Рис. 263 яоказывае* *) процесс получения образцов из одиночног
го кристалла алюминия путем рекристаллизации. Если мелкозернистый
йлюмйниевы!^ образец^- какой показан на фотографии вверху,
равномерно вытягивать на величину 1—т2% и затем отжечь медленным
увеличением температурь^ A1—28° С в день) с последовательным
медленным бхлаждением, мы обычно получаем образец, состоящий
только из немногих кристаллов, как показано на фотографии внизу.
») См. С. F. Elam, The Distortion of Metal Crystals, Oxford, 1936.
») Фотографии 263 и 264 взяты из Е. Schmid and W.Boas, Kri-
stallplastizitat, Berlin, 1935; английский перевод: V,. A. Hugher, London, 1950.
|}Ш|р^
336
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
|ГЛ. X
Тщательно отбирая материал с большим единообразием размеров зерна
и опытным путем устанавливая необходимую величину удлинения при
надлежащем режиме нагревания и охлаждения, можно послб ртжига
Рис. 263.
получить образцы из монокристаллов. Ориентировка кристалла
относительно оси образца не поддается контролю, и главные оси
кристалла (оси X, у, Z на рис. 262) будут обычно составлять различные
углы с осью образца для каждого
отдельного образца.
Испытания образцов из
монокристаллов в упругой стадии
обычно показывают значительное
-колебание его упругих характеристик,
зависящее от ориентировки
кристалла. Рис. 264 пояснен случай,
л когда модули упругости Е vi Q
Рис. 264. для кристалла железа могут ме-
пяться с изменением ориентировки.
При помощи опытных данных о поведении монокристалла были
в такой мере разработаны/) приемы определения средних значений
модулей упругости для полйкристаллических образцов, что стало
возможным предсказывать с известной точностью результаты опытов
Используя чувствительный экстензометр, можно показать, что
при испытании на растяжение образца из монокристалла даже в
упругой стадии существует некоторое отклонение от закона Гука.~На
показаниях экстензометра сказывается также влияние времени. Чтобы
объяснить это явление, нужно- рассмотреть термический эффект.
Если испытания на растяжение выполняются 2) с очень медленным
увеличением нагрузки, то температура образца остается равной тем-
») См. Boas and Schmid, Helv. phys. acta. т. 7, стр. 628, 1934.
) См, Lord Kelvin, Elasticity aod Heat, Edinburgh, стр. 18, 1880.
74]
ИСПЫТАНИЯ ОБРАЗЦОВ ИЗ МОНОКРИСТАЛЛА В УПРУГОЙ ОБЛАСТИ 337
пературе окружающей среды и зависимость между напряжением и
деформацией можно представить прямой линией О А (рис. 265, а).
Наклон этой линии дает величину модуля упругости Е при
изотермическом состоянии. Если же растягивающая нагрузка прикладьша-
•ется так быстро, что нет достаточного времени для теплообмена, то
получается прямая линия ОВ вместо О А и обычно модуль упругости
Е при адиабатическом состоянии больше модуля, получаемого
изотермически. Вследствие своего внезапного вытягивания образец
"охладится i) ниже комнатной температуры. Если образец остается под
постоянной нагрузкой в течение достаточного времени, он постепенно
ff С
С)
согревается до тех пор, пока не будет достигнута комнатная
температура, В результате возникнет дополнительное удлинение образца
(представленное на рисунке горизонтальной линией ВА\ Это есть
упругое ■ последействие, обнаруживаемое благодаря термоупругим
свойствам материалов. Если после пoлнo^;o. уравнивания температуры
образец будет внезапно разгружен, то его адиабатическое
сокращение будет представлено на рис. .265, а линией ЛС, параллельной ОВ.
Благодаря этому внезапному укорочению образец согреется, и
последующий процесс охлаждения до комнатной температуры будет
вызывать дальнейшее сокращение, представленное линией СО. Видно, что
деформированием образца адиабатически с последующим
предоставлением достаточного времени для температурного у|)авнивания
описывается полный цикл, прёдсравленный параллелограммом ОВАС.
Площадь этого параллелограмма представляет потерю механической
энергии за один цикл. В наших рассуждениях мы предполагали
адиабатическую деформацию, тогда как на практике всегда происходит в
течение цикла известный'теплообмен. Таким образом, вместр
параллелограмма получается петля, как показано на рис. 265,^.
*) Изменение температуры можно измерить путём присоедине1^ия
термопары к образцу. ,
338
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. t
Разн!йца между адаабатическим и изотермическим модулями упру-г
гости обычно мала*) , и потеря механической энергии за один цикл'
также весьма мала. Но если происходит последовательно много
цикле^ Шк, например, при колебаниях, то потери механической энергий
становятся значительными и должны быть приняты во внимание. Они
вызываются так называемым внутренмгм трением и являются при*
чиной затухания колебательного движения. Пе^У!^, подобная
показанной на рис. 265, Ь, называется пе/Нлей гистерезиса, н так как после
полного цикла образец возвращается к своему первоначальному
состоянию, то иногда употребляется jepuwa ущ>угпй гистерезис.
Выше предполагалось, что после внезапного удлинения образец
продолжает оставаться под действием постоянно приложенной нагрузки.
Теперь пр^едположим, что образец 15удет сохранять постоянную^ длину..
Тогда'согревание образца будет иметь результатом некоторое
уменьшение первоначально приложенной силы. Это процесс релаксации^ пред-^
ставленный на рис. 26б,г вертикальной линией BD. В таком случае после
внезапной разгрузки образца ^1аблюдается участок J9C, а позже,
вследствие охлаждения, получается замыкающая линия СО щтл&^ВРС.
В предыдущем изложении мы касались испытаний на растяжение,
однако в действительности большинство све^Ьний относительно от*
клонений от закон^Г Гука и влияния
времени в упругой стадии было получено при
испытаниях на изгиб полосок, вырезанных
из кристалла кварца. При этом было
показано, что все отклонения от
совершенной упругости можно вполне объяснить
путем рассмРотрения jepMoynpyrHX и ньезо-
электричесю^х свойств материала *).
т
I
^3
t
§
у
'^^'.
^
-^
—А-.
48S'€
ЮО'С
тгче
75. Пластическое растяжение образцов
из монокристалла
Путем увеличения нагрузки при испы-:
танни o6pa^j.a на растяжение, наконец,
достигается состояние, при Нотором образец
начинает течь и плаЬТически удлиняться.
^Диаграммы') для образдов из
монокристалла алюминия, испытанных на
растяжение при различных температурах, показаны
^ на рис. 266. Видно, что предел
пропорциональности очень низок и за этим
пределом образец вытягивается пластически. Вследствие пластической
2/7 ^ff Sff Ш
YSfttiHe/fite/^ %
' Рис. 266.
*) Для стали он составляет l/S»/©.
*) См., статью А*. И о ф ф е, Журнал физики (серия 4, т. 20, 1906).
«) Рис. 266 взят из Schmid ahd Boas, цит. на стр. 335.
щ
ПЛАСТИЧЕСКОЕ РАСТЯЖЕНИЙ ОБРАЗЦОВ ИЗ МОНОКРИСТАЛЛА
339
Рис. 267.
де^юрмации материал становитсй жестче, я с увелтентм растяжения
напряжения, необходимые длгя-продолжения деформаций, становятся все
6oiibiiiHMH. Это —явление наклепа; оно особенно ясно выражается при
низких температурах. С увеличением температуры влияние наклепа
уменьшается, при ЗОО'^ С кривая приближается к горизонтальной лини1|.
и удлинение об|5азаа продолжается при практи- .
чески постоянном.^й|11ряжении.
Наблюдение '^линиями (полосами
скольжения), которые появляются на поверхности
образцов i^ монокристалла во время njjacTH4ecKQft
дефор*{1ацйи, обнаруживает, что эта^ деформация
СВОДИТСЯ к скольжению материала по некотором
кристаллографическим плоскостям в опр^еделен-
ных направлениях. Например, лри/^ испытании /
образца' из монокристалла алюминия, который
имеет структуру гранецентрирова'нной
кубической решетки (рис. 267), скольжение будет происходить параллельно
одной'^ из октаэдральных плоскостей (как, например^ плоскости аЫ) и
направление скольжения будет параллельным одной из сторон тре-
yrojftiHHKa'fl^c. В" растянутом образце скольжение будет происходить
по наиболее неблагоприятно ориентированной
октаэдральной плоскости скорее, чем по плоскостям под
углом 45% по которым действуют наибольшие
касательные напряжения." Этим объясняется, почему-при
испытании образцов из монокристалла мы получаем
рассеивание результатов для значений растягивающей
нагрузки, при которой начинается текучесть. Эти
значения зависят не -'только от механических свойств
материала, но также и от ориентировки осей
кристалла относительно оси образца.
Предположи^, например, что в образце, из
монокристалла (J)HC 268), испытываемом на растяжение и-
имеющем площадь поперечного' сечения р,
направление наиболее неблагоприятно ориентированной Ъкта-
эдральной плоскости скольжения определяется нор-
м^алью п, а направление скольжения линией pq.
Касательное напряжение, которое действует по плоскости скольжения, равно
•crrr-gCtosa sinoi.
г >
' (а)
Опыты показывают, что начало скольжения происходит не при
напряжении t, а от действия составляющей xcosy этого напряжен/1я а
направлении скольжения /р^. Скольжение начинается, когда эта
составляющая достигает определенного значения Ч^р. Тогда из выражения
340
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
(а) мы получим
с^р= t COS <i> = -p COS a sin a cos cp.
(b)
Видно, что в то Время как т^р постоянно ^ для данного материала,^
нагрузка Р, при которой начинается текучесть образца, зац^исит от
значений углов а и ср.
Процесс, при котором образец удлиняется вследствие скольжения
по кристаллографическим плоскостям, иллюстрирован рис. 269.
Можно допустить, что растяжение выпол-
. няется в два этапа; Л)
поступательным движением по'плоскостям
скольжения (рис. 269, Ь) и 2) вращением
образца на угол р к его, начальному
направлению (рис. 269, с). Из такого
представления о механизме
растяжения следует, что угол между
направлением растягивающей силы Р и
плоскостями скольжения изменяется при
растяжении. Более того, цервоначаль-
^*но круговое поперечное сечение
образца становится эллиптическим с
отношением длин главных осей,
равным 1: cos р. Многочисленные опыты
с монокристаллами дали результаты,
которые подтверждают эти заключения. Например, рис. 270
представляет вытянутый образец из монокристалла*) меди—алюминия.
Опыты также показали, что величина t^p,npH^ которой начинается
скольжение, обычно очень мала*). Однако вычисления значения т^р»
ej
Рис.. 270.
основанные на рассмотрении молекулярных сил^), дают большие
значения — порядка G/30. Это указывает, на то, что процесс скольжения
не состоит только в жестком поступательном движении атомных
"Ж"
1) См. С. F. Е1 а т, Th€ Distortion of Metal Crystals, Oxford, стр. 182,1936.
^) Там же.
•) См. И. Френкель, Журнал физики, т. 37, стр. 572, 1926.
761 ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ МЯГКОЙ СТАЛИ . ,341
плоскостей одной относительно другой. Необходимо допустить
существование местных несовершенств, которые позволяют начать
скольжение под действием- малой силы и затем распространиться rio всей
плоскости скольжения. Модель, показывающая возможность скольже-^
ния, которая начинается в месте несовершенств, была описана Л. Пранд-
тлем *). Другая механическая модель была предложена Г. И. Тейлором ').
Допуская местную неправильность в распределении атомов,
называемую дислокацией, он показал, что эта неправильность,
распространяясь по плоскости скольжения в кристалле под влиянием малого
напряжения т^р," вызывает относи1гельное перемещение одной части
кристалла относительно другой. Пользуясь своей моделью, Тейлор был
в состоянии объяснить не только начало скольжения при очень малых
значениях т^р, но также и явления наклепа ^).
76. Испытания, на растяжение мягкой стали
в упругой области
Ограничившись приведенным в пп. 74 и 75 К1)атким описанием
механических свойств монокристаллов, перейдем ^теперь к
рассмотрению испытаний на растяжение поликристаллических образцов,
например образцов из строительной стали. На рис. 260, стр. 332, показана
типичная диаграмма испытания на растяжение с^али. Для области
низких напряжений соответствующий участок диаграммы можно
представить с удовлетворительной точностью прямой линией; наклОн этой
линии определяет значение модуля упругости Е. Как результат
различных ориентировок, модули упругости отдельйых кристаллов по
осевому направлению образца будут различными. Поскольку же
зерна весьма малы, мы можем игнорировать этот факт и рассматривать
материал как изотропный. 'Значение Е является, таким образом,
средним из полученных в испытаниях на растяжение
поликристаллического образца.
С помощью чувствительного экстензометра можно наблюдать
некоторое отклонение от закона Гука и обнаружить явление
последействия в упругой стадии испытания на растяжение. Объяснение
сводится к учету термоупругого влияния, как и в случае образца иа
м:ОНокристалла (см. стр. 336). Однако нужно заметить, что термоупру-
rife свойства кристалла зависят от ориентировки кристалла, и поэтому
^) Модель была рассмотрена 11рандтлем на семинаре по теории
упругости в Геттингенё в 1909 г., и ее описание было опубликовано в Z. angew.
Math. u. Mech., т. 8, стр. 85.-106, 1928.-
2) G. J. Taylor, Proc. Roy. Soc. (London), A, т. 145, стр. 362—404, 1934.
^) Работа Тейлора вызвала интерес у физиков, и в настоящее время
имеется большая литература по дислокациям. О новейшей библиографии
этого предмета см. А. Н. С о 11 г е 11, Dislocations and Plastic Flow in
Crystals, Oxford, 1953.
к^^^^^^ТЖГ^
W
342 МЕХАНИЧЕСКИЕ СВОЙСТВА ЛЦГЕРИАЛОВ'' [ГЛ. X
изменения температуры, вызываемые растяжением поликристалличе-
ского образца, колеблются от зерна к*^зерну. Это значит,' что мы
должны рассматривать не толькр (теплообмен между образцом, и
■окружающей средой, но также течение теплоты между отдельными
кристаллами. Так как теплота, образованная в зерне,
пропорциональна его объему, и теплообмен з1ависит от величины его поверхности,
то очевидно, что уравнивание температуры будет облегчено и потери
механической энергии увеличатся при уменьшении размеров зёрен.
Это лмеет большее практическое значение, так как имеются случаи,
в которых 5^атухание колебаний в упругой системе зависит главным
образом от внутреннего трения материала. Для того чтобы, увеличить
затзгхание в такой системе, должны применяться материалы с малым
размером зерна. ..
В проведенном анализе предполагалось, что деформация образца
идеально упруга, как и надо было ожидать при малых напряжениях.
Явление внутреннего трения при больших напряжениях становится
более" сложным, так как мы должны рассмотреть не только потери
механической энергии вследствие теплообмена, как описано выше,
но также и потери, вызванные пластической деформацией в отд:ель-
;«ых зернах*). >»^
Путем полирования и протравливания поверхности
поликристаллического образца можно увидеть кристаллическую структуру материала
и обнаружить, что при нагрузках меньших той, которая соответствует
пределу текучести, появятся полосы скольжения на поверхности
некоторых зерен. Полос^>1 указывают на скольжение по определеннык!
кристаллографическим плоскостям в этих зернах, причем, они того
же типа,, что, и рассмотренные ранее при испытаниях монокристаллов.
Так как упругие свойства монокристалла различны в разных
направлениях и так «как кристаллы ориентированы случайно, то напряжения'"
в растянутом образце распределяются неравномерно ^и скольжение
может произойти в наиболее неблагоприятно ориентированных
отдельных кристаллах прежде, чем среднее растягивающее напряжение
достигнет значения предела текучести. Если такой образец разгрузить,
то кристаллы, которые испытывали гкольжение, не могут свободно \
вернуться к своей первоначальной форме, и в результате этого в
разгруженном' образце будут оставаться некоторые остаточные
напряжения. Такая податливость отдельных . кристаллов содействует
*) Значительное количество исследовательской работы по измерьнию
демпфирующей-^способности различных материалов выполнено" Rowett'OM,
Ргос. Roy. Soc. (London), А, т. .89, стр. 528, 1913 и О. РбррГ(Вм него
сотрудниками по Wehler-Institut, Braunschweig; см. Z. Ver. deut. Ing., т. 70,
стр. 1291, 1926; т. 72,,стр. 1293, 1928; т. 73, стр. 766,1929.Важное значение
термоупругой причины внутреннего трения было показано исследованиями
С. Zener'a и его сотрудников; см. Phys. Rev., т. 52,. стр. 230, 1937; т. 53,
<^тр. 90, 1938; т. бр, стр. 455, 1941. Результаты эти? исследований
представлены в книге: С. Z е п е г. Elasticity and Inelasticity of Metals, 1948.
76]
ИСПЫТАНИЯ НА РАСТЯЖЁМИБ МЯИКОЙ СТАЛИ
•34»
также потерям энергии при нагрузке и разгрузке, и будет
увеличивать площадь петли гистерезиса (см. рис. 265, Ь, стр. 337).
\ • Если после разгрузки образец подвергнется испытанию на
растяжение во второй раз, то зерна, в которых происходило скольжение ^
при первом испытаний, ^е будут испытывать текучести до тех пбр^
пока растягивающая нагрузка не достигнет значения нагрузки,
приложенной при nepftor нагружении. Когда же нагрузка превзойдет
это значение^ снова начнется скольжение. Если образец подвергнется
сжатию после предыдущего нагружения при растяжении, то
приложенные сжимающие напряжения в сочетании с остаточными напряжениями,
созданными предыдущим испытанием на растяжение, будут вызывать
Рис. 271.
текучесть в наиболее неблагоприятно ориентированных кристаллах
прежде, чем среднее сжимающее напряжение достигнет значения, при
котором полосй скольжения вызывались в образце в его
первоначальном состоянии. Таким образом, цикл испытания на растяжение
вызывает возрастание предела упругости при растяжении, но понижает
предел упругости при сжатии. Это явление было изучено Баушинге-
ром*)и называется аффектом Баушингера. Мы видим, что эффект
Баушингера объясняется скольжением в отдельных кристаллах и
остаточными напряжениями, вызываемыми этим скольжением.
Появление остаточных напряжений, введенных в материал
текучестью наиболее неблагоприятно ориентированных зерен, а также
эффект Баушингера можно иллюстрировать с помощью модели,
изображенной на рис. 271. Модель состоит из трех стержней, сделанных
из одного и ^бго, же материала, с одной и той же площадью F
поперечного сечения. Материал имеет один и тот же предел теку-
сжатии. Если вертикальная нагрузка Р
чести о при растяжений и
») См. Mitt. Mech.-tech. Lab. Munchen, 1886; см. также Dipglers Polytech. J.,
т. 266, 1886.
44" МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ ^ГЛ. X
Приложена К модели, то будут появляться растягивающие усилия Si
и б'а соответственно в вертикальном и наклонных стержнях. В
упругой стадии эти усилия будут (см. т. I, стр. '27):
о Р ^j, Pcos^g ^ .
*^i— l+2cos««' "^а— i+2cos«a,* ^^^
Благодаря упругой деформации шарнир Н модели передвинется
вертикально вниз на величину
Р1
^~ FE{\+2 cos^ а)' - (^)
Зависимость между на1г,рузкой и перемеи^ением "представлена на
рис. 271, b линией О'А. Из выражений (а) следует, что усилие в
вертикальном стержне больше, чем усилие в каждом наклонном стержне.
Вертикальный стержень модели соответствует наиболее
неблагоприятно ориентированному кристаллу поликристаллического образца.
Постепенным увеличением нагрузки мы достигаем состояния, при
котором вертикальный стержень начинает течь, в то время как
наклонные стержни продолжают упруго деформироваться. Соответствующее
значение Pi груза и соответствующее перемещение 8i найдутся из
выражений
» т I + 2 COS» а •' ^/^/="£(!+ 2 cos" а)' '^^
■ЧТО дает
Pi = Fo^(l-}-2cos3a), Si = -^. (d)
Sto состояние соответствует точке А на рис. 271, Ь.
Если мы будем продолжать увеличивать нагрузку, то вертикальный
•стержень будет вытягиваться пластически *) при постоянном
напряжении о и дополнительная нагрузка Р^ будет восприняла упругими
наклонными стержнями. Дополнительные усилия S'^ в этих стержнях
и дополнительное вертикальное перемещение Ва будут
2 2.cosa ' ^ 2FEcos^a ' у'^
Зависимость между Pg и Sa показана на рис. 271, b наклонной
линией АВ. Если мы начнем разгружать модель после достижения
точки В на диаграмме, то все три стержня будут вест;и себя упруго,
и зависимость между снимаемой нагрузкой и перемещением узла Н
вверх будет определяться выражением (Ь). Поэтому на диаграмме
мы получим линию ВС, параллельную ОА, полное же вертикальное
^) ПрТГэтом рассмотрении наклепом пренебрегаем.
76| ' ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ МЯГКОЙ СТАЛИ 345-
перемещение вверх при разгрузке будет -
Мы видим, ЧТО вследствие Пластического вытягивания вертикального
стержня модель не возвращается в свое первоначальное положение,,
и создаётся остатЪчная деформация ОС. Величина остаточной
деформации находиться из формулы
Благодаря этой остаточной деформации в наклонных стержнях
возникают растягивающие усилия 6^', причем эти усилия будут
уравновешиваться сжимающим усилием 6^/ в вертикальном стержне. Таковы
усилия, которые остаются в системе после полной разгрузки модели
и которые иллюстрир)тот остаточные напряжения в
поликристаллическом образце после цикла испытания на растяжение.
Чтобы -найти значения остаточных усилий в модели, отметим
прежде всего, что наклонные стержни оставались в упругой стадии
на протяжении врего цикла нагружения. Поэтому' зависимость между
усилием ^2 в наклонных стержнях и перемещением 8 можно получить
путем использования выражений (а) и (Ь), что дает
б'а —^ . (h)
.' '' .^ ' ' ■ •
Подставляя вместо 8 значение oct»тoчн6й деформации' (уравнение (g)),
получаем остаточное растягивающее усилие S"^ р наклонных стержнях
.с "_ \ ^а (\\
^ • , . * ~" 2cosa(I + 2'cos«a) • v W
Уравновешивая вертикальные силы в шарнире //, найдем остаточное
сжимающее усилие 5,' в вертикальном стержне ■
4S;'==r25^c6sa= , . f^ , . (J)
^ °,1+2 cos^ а ^■''
■ ■ . ■ ' ',' '^
Ч^Обы. иллюстрировать эффект? Баушингера, рассмотрим второй цикл.
нагружения. При малых зна.чениях нагрузки все три стержня
деформируются упруго, и на рис.* 271, Ь график процесса второго
нагружения будет начат в точке Си пойдет по прямой СВ. Когда он
дойдет до -точки Д вертикальный стеркень будет освобожден от
остаточного"^ сжимающего усилия S'[ и в течение дальнейшего
нагружения будет испытывать растяжение. Соответствтенно точке В
растягивающее напряжение в этом' стержне достигнет значения о^, и
начнется пластическая; деформация стержйя. , Видно, что предел
imw
46 мЕХАн:йчЕСКив Свойства^ MjfiTEPH АЛ OB \ |гл. к
пропорциональности модели возрастает благодаря остаточным найря-
жениям. В первом цикле лредел пропорййонаяьности был при на-
|фу^е Pi, а ао втором цикле — при нагрузке Pj -|- Р^. Процесс
разгрузки во втором цикле полностью уттругий и следует линии ВС.
Теперь'изменим направление- силы на обратное,, приложив
нагрузку Р вверх. Тогда деформация будет прои|сходитъ в соответствии
с прямой СЕ графика, являющейся продолжением линии ВС. Сжимав
ющее усилие в вертикальном стержне создается нагруакоЙ^Р,
направленной вверх и остаточным сжимающим усилием 5['- Точке ё
отвечает направленная вверх полная сила Pj-^-Pe.' а сжимающее усилие
в вертикальном стержне будет вызывать напряжение, равное пределу
текучести. Если нагрузка увеличивается, процесс деформации
соответствует линии EF. Ерли модель разгружается после достижения на
-графике точки F, то она вернется в первоначальное положение,
представленное точкой О. Видно, что нагружение модели на растяжение
до точки В графика повышает ее предел пропорционЛгьности при
растяжении от Р, до Pi-j-Pa- В то же самое время предел
пропорциональности при сжатии уменьшается от Pi до Pi—^Pg. Это иллю-
стри15ует эффект Баушингера. -^
Если модель подвергается циклическим усилиям, изменяюи]иимся
от Pi-tJ-/^ при растяжении до Pi при сжатии, то мы получаем
петлю гистерезиса, представленную на рис, 2/1, ^
параллелограммом OABCEFO. Площадь этого параллелограмма дает величину
потери механической энергии за один цикл*).
В этом параграфе мы касались испытаний на растяжение о6]раз-
цов из мягкой стали, в которых Д(еформации малы и измеряются
' чувствительными экстензометрами. В следз^щем параграфе мы рас-
смотфим ббл1?шие унеформации, приводящие к riлactичecкoй дефррма-
дии не только отдельных- неблагоприятно бриентированных
кристаллов,'но и всего материала образца^:
«"
Д7. Предел текучести
Изучая прочность строительной стали цри растяжении, инженеры
особенно интересун/гся явлением внезапного удлинения образцов на^
пределе текучести. Хорошо известно, что при некотором значении
растягивающего напряжения имеет место внезапное падение
растягивающей нагрузки, сопровождаемое значительным удлинением металла
при несколько более низком напряжении. К. Бах ввёл') термины
верхнего и нижнего пределов текучести для этих двух значений на-
*) Др/гая модель для иллюстрации петель гистерезиса и эффекта
Баушингера была пред'^южена С. F. J е п к i nVoM, см. Engineering, т. 114, стр. 603,
1922. .
^VZ. Ver. deut. tag., т. 58, стр, .1040, 1904; т. 59, стр. 615, 1905. , .
771.
ПРЕДЕЛ ТЕКУЧЕСТИ
347
пряжения* обозначенных^на рис. 272 точками ,А и В*. Дальнейшие
опь11г|л показали, что на нижний предел текучести форма образца
оказывает меньшее влияние, чем на верхний предал текучести. Такимг
образом, большее npaKTis4ecKoe значение придается нижнему пределу
текучести. :—^-^ .
Форма диаграммы ншряжение —деформация" ^йс. 272) у предела
текучести зависит в Значительной степени от технических
особенностей испытательной машины: Если
растяжение обраада вызывается увеличением
расстояний между вахватами машины,
смещающимися с постоянной скоростью, то
внезапно^ - пластическое удлинение будет
несколько з^еньшать растягивающее
усилие в образце и на диаграмме-получится
острая вершина А, Если вставить упругую
пружину • между образцом и захватом, то
угол наклона кривой Лj9 диаграммы можно
умены11^ить, как показано пунктирной
линией АВх- С другой стороны, если растя-.
гивающая нагрузка приложена непосред-
ственнр 1к образцу, то растягивающее уси-^
лие при текучести будет зависеть от малого перемещения груза при
внезапном yjDUiHHeHHH и на диаграмме могут отразиться малые вибрации.
Чтобы изучить более подробно деформации, которые имеют место
на пределе ^екучес^'И, применяют образцы с полированными
поверхностями. Такие опыты показывают, что за время падения
растягивающего^ напряжения от точки А к точке В (рис 272) на поверхности
обрашха начинают появляться тонкие темные линии. Эти линии
наклонены приблизительно под углом 45° к направлению растяжения и
называк?тея линиями Людерса*) (см. рис. 205, стр. 274). При даль*
нейшем удлинепии линии увеличиваются по ши1у1не И по числу, и за
время удлинения от В до Bi (рас. 272) они покрывают всю
поверхность образца. Первые линии обычно начинаются в точках концев-,
трации напряжений. На рис; 266" (стр. 274) показана, например,
линия Людерса, которая начинается у точки наибольшей концентрации
напряжений в выкружке. Вместо полирования иногда примен|1ют
специальные краски (называемые покрытием для напряжений), чтобы вы-
яёдагь линии,Людерса. Краски эти хрупки и не могут выдержать
больших деформаций; они растрескиваются при нагруж€нни, причем^
образуется сетка линий Людерса.
Рис. 272.
*) Эти линии впервые были описаны Lued6rs'oM, Dinglers Polytech,
J., 1854. См. также L. Hajtmann, Disfributiwi des defermations, etc.,
Paris, 18&6 и A. N a d a i, Theory of Flow and Fracture of Solids, New York,
1950; русский перевод: Пластичность и разрушение твердых тел, Москва,.
1954.
348
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
Исследование с помощью микроскопа показывает, что линии Лю-
дерса образуют пересечения у боковой поверхности образца тонких
слоев материала, в которых имеет место пластическая деформация,
между тем как смежные участки материала остаются совершенно
упругими. Путем разрезания образца и применения специального
протравливания *) можно сделать видимыми тонкие пластические слои
внутри образца. Под микроскопом видно, что эти слои состоят из
. ' кристаллов^ которые были
^ разрушены скольжением, как
'^•^' ^ ^ ' ' ' описано р^нее (см. п. 75).
Опыты показывают, что
значения напряжений на
пределе текучести и
соответствующие -деформации зависят
'^ от скорости
деформирования^). Кривыми на рис. 27дг
показаны диаграммы
напряжение — деформация ]адягкой
стали для широкого
диапазона скоростей деформации
(rf=rfe/rf^=x=d,5-10-' в
секунду до и = 300 в
секунду). Видно, что не только
предел текучести, но и
предел прочности и полное
удлинение зависят в
значительной степени от скорости
деформации. Вообще эти
величины возрастают с
увеличением скорости деформации.
Для объяснения внезапного удлинения стали на пределе текучести
высказывалось мнение^), что поверхности зерен состоят из хрупкого
материала и "образуют жесткий скелет, который препятствует
пластической деформации зерен при низком напряжении. Без такого скелета
диаграмма растяжения была бы похожа на обозначенную пунктирной
линией на рис. 274 Благодаря наличию жесткого скелета материал
остается совершенно упругим и следует закону Гука до точки Af
где скелет разрушается. Тогда пластический материал зерен внезапно
2ff
Рис. 273.
») См. статью А. F г у, цит. на стр. 276. , .^,.
2) М. J. Manjoine, J. Appl. Mech., т. 11, стр. 211, 1944; см. также
К. G. Smith, Т. Е. Pardue arid L Vigness, U. S. Naval Research Lab.
Kept. 4468, 1954. , , , „
«) Cm. p. L u d w i к und S с he u, Werkstoffanschuss, Ver. deut. Ing. Ber.,
70, 1925; \У- Kfister, Arfhiv Eisenhfitfeiiw.,/47, 1929. См. также Н. Н. Дави-
денков, Нёткоторые проблемы механики материалов, Ленинград, 1943.
781 ^АС1"ЯЖЕНИЕ СТАЛИ ЗА ПРЕДЕЛОМ ТЕКУЧЕСТИ 349
получает остаточную деформацию АВ, после чего следует обычной
для пластического материала кривой ВС. Эта теория объясняет
состояние неустойчивости материала при верхнем пределе текучести.
Теория объясняет также тот факт, что материалы с малым размером
зерна обычно показывают более высокие значения напряжения на
пределе текучести. В результате такие материалы ''
претерпевают большее удлинение на пределе теку- &
чести, определяемое длиной горизонтальной линии
АВ на рис. 274. Кроме того, теория объясняет и
то явление^ что при высокой скорости испытаний
увеличение напряжения при пределе текучести
сопровождается увеличением пластического
удлинения ,текучести! что показано крищлми на рис. 273.
Линии Людерса появляются в стальных
образцах, испытываемых на сжатие так же л"очно, как
и в случае растяжен1^я. Кроме того, опыты на
изгиб и кручение показывают, что линии Людерса Рис. 274.
наблюдаются и в этих случаях, но при гораздо
более высоком значении напряжения, чем при однородном
распределении напряжений. На основании предположения, что текучесть
начинается, когда хрупкий скелет (образованный поверхностями зерен)
изламывается, была выдвинута *) теория, что напряжение на пределе
текучести зависит от размера образца. Опыты с малыми образцами
показали более высокие значения напряжения предела текучести, чем
было найдено для образцов обычного размера.
78. Растяжение с^-али за пределом текучести
Пр]№^астяжении стального образца за пределом текучести материал
упрочняется и напряжение, требуемое для вытягивания стержня, увели^
Читается, как показано участком ВС диаграммы напряжение —
деформация (рис. 275). Удлинение обраща с©провЬждается^]^вномерным
сужением площади поперечного сечения,"^ и объем образца остается
практически постоянным. Работа, произведенная при удлинении, пре^
вращается в большой степени в теплоту, образец становится горячим.
Однако калориметрические измерения показывают, что не вся
механическая энергия превращается в теплоту; часть ее остается в
образце в форме энергии деформации. Вследствие разницы в ориентировке
кристаллов напряжения неравномерно распределяются по поперечным
сечениям и после разгрузки в образце остается некоторое остаточное
напряжение и некоторое количество энергии деформации.
I*) С. W. Richards,. Статья, представленная 57-му Годичному
собранию Американского общества испытания дштериалрв, 1954.
350
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. Х
Если после^ разгрузки мы нагрузим образец во второй раз, то
найдем, что его предел текучести повысился. Это характерное явление
\
^от
2W0
/у
■ ■1
^
^
^—• "^
С
■
-
■"ч
ч
/7 fff ^ го J0
- Удлинение 0'Ув
Рис. 21Ь:
показано «а рис. 276, который представляет диаграмму испытания на
растяжение мягкой стали*). После растяжения стержня соответственно
3000
^вОО
О ^ /о. iS го
Рис. 276.
ydffuf/emie в *'/о
Рис. 277,
точке С он был разгружен. При разгрузке материал следовал
приблизительно прямолинейному закону, как показано линией CD на
диаграмме. Когда нагрузка была приложена к стержйю во второй
раз, материал снова следовал нриблизительно закону Гука и была
*) См. Е W i п g, Strength of Materials, стр. 35, 1914. , _
78]
РАСТЯЖЕНИЕ СТАЛИ ЗА ПРЕДЕЛОМ ТЕКУЧЕСТИ
361
ттолучена линия DF. В точке F, которая соответствует^ точке С пред^
вар|Нтельной нагрузки, кривая резко изменила характер и вычертила
участок РО, который можно рассматривать как продолжение кривой
ЛС Это указывает на повышение предела текуяести, вызванное
пр^вдварительным вытяшваниём образца. Если после первой разгрузки
пройдет несколько дней, то при повторной нагрузке можно получиарь
еще большее повыщевие предела текучести, как, это показано
пунктиром у т.7^ (pjtf^ 276). Рис. ;2lf7 показывает результаты испытания на
растяжение образца из литого алюминия*). Перройачальный предел
пропорциональности материала был равен 376 кг/см^. После
предварительного растяжения образца на 2% предел пропорциональности
при повторной нагрузке был найден равным
1330 kz/cm\ а предел текучести—-около
ХШ кг/см^
Более подробные исследования показы-v
BaipT, что Промежуток времени, протекающий
между разгрузкой и повторной нагрузкой,
значительно влияет на кривую напряжение —
деформация при новом нагружении. Если
повторное нагружение начинается немедленно
после разгрузки, то, как показывают точные
измерения, отклонение от прямолинейного
закона происходит при очень низком напряже-,
НИИ, т. е. предел пропорциональности
сильно понижается. Но если пройдет значительный
промеж)ггок времени между разгрузкой и повторной нагрузкой, то
материал полностью восстанавливает свои упругие свойства. Рис. 278
изображае!--кривые; полученные') при испытании образцов из мягкой
стали; »8 рассмотрения кривых видно, что если повторное нагружение
происходит через 10 минут после перегрузки за- предел упругости,
то материал не следует закону Гука, но через 5 дней он частично
восстанавливает свою упругость, а через 21 день—; почти полностью
восстанавливает ее-, \ -
Опыты также показывают, что если -материал после разгрузкц
подвергнуть слабой термической обработке, например в ванне при
100*^ С, то восстановление упругих свойств происходит в гораздо
бсмгее короткий промежуток времени. Рис. 279 показывает результаты
таких испытаний, произве^денных над стальным бруском^).
Первоначальное испытание на растяжение представлено кривой Д. Кривая
В вредетавляет растяжен]^ё при повторном нагружении того же
бруска через 10 минуг 1после ра&грузки и значительное отклонение
Рис. 278.
*) Исследовательская лабвратория фирмы «Westinghouse £1. Corp.».
*) См. Е W i п g. цит. на стр. 350.
*) 1. М U i г, Phil. Trans. Roy. Soc; (Ldndon), A, 1899.
ш
352
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
£46.
Ц2 • О.^ aj) Ц9
Рис. 279.
ifi ^
от закона Гука. Кривая С получена для того же бруска после
вторичной разгрузки и после нагревания его в продолжение 4 минут
при температуре 100° С. В этом
бнг/см' случае материал совершенно
восстановил свои упругие
свойства.
Явление наклепа в
результате пластической деформации
встречается во многих
технологических процессах, как,
например, прокатка стержней,
вытяжка труб и волочение
проволоки при низкой температуре,
резание листового металла и
протягивание, пробивание
отверстий. Во всех этих случаях
чдсть материала, которая
подвергается пластической
деформации, становится более жесткой и ее пластичность значительно
уменьшается *). Для устранения этого нежелательного влияния наклепа
, обычно материал отжигают, после чего восстанавливается его
пластичность^). . -
Иногда наклеп пластических материалов находит себе
практическое применение в производстве. Обычно на практике цепи и канаты
. подъемных машин предварительно растягивают на некоторую
остаточную величину для того, чтобы устранить нежелательное
вытягивание этих частей в работе. Цилиндры гидравлических прессов'' под-
йергают иногда предварительному внутреннему давлению,^ Достаточному
для того, чтобы произвести остаточную деформацию в стенках.
Деформация наклепа и остаточные напряжения, вызываемые этим
способом, препятствуют возникновению какой-либо остаточной
деформации во время службы. Предварительное вытягиваияе металла
производят и при изготовлении артиллерийских орудий (см. стр. 179, 323).
Растягивая металл в стенках орудия за первоначальный предел
текучести и затем подвергая его умеренной термической обработке, можно
улучшить упругие свойства материала; в то же само^е время
возникают первоначальные напряжения, которые в сочетании С
напряжениями, возникающими при выстреле, дают более благоприятное
распределение напряжений в стенках орудия. Турбинные диски и роторы
подвергают иногда аналогичной обработке. При вращении этих частей
*) Об общем анализе свойств холодно обработанных металлов см. статью;
Z. Jeffries and R, S. A г с h e r, Chem. and MeJallurg. Engrg., т. 27, стр. 747,
1922. См; jjaicafte G. M a si n g und M. P о 1 a n у i, Kaltreckung und Verfestigung,
Berlin, 1923. ■- ~ '
^) Cm. статью Rees*a, Iron and Steeil, Inst. J., 1923.
781
РАСТЯЖЕНИЕ СТАЛИ ЗА ПРЕДЕЛОМ ТЕКУЧЕСТИ
35а
СО скоростью, выше обычной, получают вокруг центрального
отверстия остаточную деформацию, которая повышает предел текучести
материала и вызывает первоначальные напряжения, действующие в
благоприятном направлений*). Литые алюминиевые лопасти
пропеллера иногда подвергаются перенапряжению у втулки, чтобы устранить
какую-нибудь возможность их ослабления на валу во время работы.
Значительное пластическое течение металла иногда вызывают при
насаживаний ступиц паровозных колес на оси и это, оказывается.
бг^зттг б^г^гОсмг
'§_0,Г/а
Рис. 280.
производит благоприятное действие. Медные стержни в коммутаторах
электрическ^1Х машин подвергают значительной холодной обработке
путем в,ытягивания, чтобы дать им требуемую прочность.
Применяя подобное предварительное перенапряжение для
повышения предела текучести и улучшения упругих свойств конструкции,
необходимо иметь в виду: 1) что влияние наклепа исчезает, если
конструкция подвергается отжигу и 2) что предварительное
вытягивание металла в некотором направлении делает его прочнее при
работе на растяжение в том же направлении, но не улучшает в такой
же степени его механические свойства при работе на сжатие в этом
же направлении. Это явление ясно показано на рис. 280, который
») См. А. N а d а i and L. Н. D о п п е 11, Trans. А. S. М. Е., т. 51, стр. 173, 1929.^
12 с. П. Тимошенко, т. II
ш
354 - МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
представляет результаты испытаний, произведенных над электроли?
тической медью*). Кривая а) изображает механичео^ие свойства меди
в отожженном состоянии. Предел пропорц^юнальности и предел
текучести*) в этом состоянии очень низкие. Такой материал не может
^ыть применен в КЪнструкциях, которые подвергаются действию
значительных напряжений. Кривая Ь) представляет результаты испытаний
на растяжение и скатие -того же материала после предварительной
пластической вытяжки на 15Vo- Предел пропорциональности и предел
текучести значительно возросли, особенно при растяжении. Кривые
с) VI д) изображают результаты испытаний после предварительной
вытяжки на 20 и 25Уо. Дополнительное вытягивание вызывает
дальнейшее улучшение механических свойств, особенно при растяжении.
В то же самое время предел пропорциональности при сжатии не-
<:колько уменьшается. Кривая е); представляет результаты испытаний
на растяжение и сжатие стержня, который протягивали сквозь
матрицу, уменьшая площйдь его поперечного сечения на 15Vo. ^
процессе волочения материал подвергается не только продольному
растяжению, но также поперечному сжатию, ^тому обстоятельству нужно
приписать разницу между кривыми Ь) vi е). Хотя в обоих случаях
брусок получил одно и то же уменьшение площади поперечного
сечения, тем не менее материал, протянутый сквозь матрицу, показал
лучшие механические свойства « отношении сжатия, чем материал,
подверженный равномерному продольному растяжению на
испытательной машине.
Jo обстоятельство, что предварительная вытяжка металла в
некотором направлении не улучшает механических свойств при сжатии в таком
же отношении, 1как при растяжении, нужно иметь в виду в тех случаях,
когда материал подвергается действию переменных напряжений (см.
п. 84). Необходимо также упомянуть имеющиеся указания*) йа то,
что материал, который имел текучесть в некоторой области,
является более чувствительным в этой области к химическому
воздействию, и что наблюдается тенденция к коррозии металла по поверхностям
скольжения. Это явление и^еёт важное значение для паровых котлов
и других сосудов, подверженных одновременно химическим и силовым
воздействиям. ' -
При построений диаграммы растяжения в виде, например, кривой ABC
на рис. 275, растягивающую нагрузку обычно делят"" на
первоначальную площадь поперечного сечения /^ образца для того, чтобы полу-
*) Исследовательская лаборатория фирмы «Westinghouse El. Corp. Research
Laboratory». ,
*) Предел текучести определялся как напряжение, при котором
относительное удлинение или относительное укорочение составляли &,2'>/о.
«> См. F. К б г b е г und А. Pomp, Mjtt. Kaiser-Wilh. Inst. Eisenforsch.
(Dusseldorf), т. 8, стр. 135, 1926; ч:м. также S. W. Parr and F. G. Stfaub,
Engineering, т. 124, стр. 216, 1927.
Щ '\ • РАСТЯЖЕНИЕ СТАЛИ ЗА ПРЕДЕЛОМ ТЕКУ4ECJH 355
■у
ЧИТБ условное напряжение. Однако при большом удлинении будет
jmetb место значительное уменьшение площади поперечного сечения;
по&тому,. чтобы получить истинное напряжение, необходимо
считаться с действительной " площадью F вместо />! Из условие дот*
стОянства объема обрада11аи11|еем
и истинным напряжением будет
Р Р
■ а = ^ = ^A4-е). (Ь>
Чтобы получить диаграмму истинных напряжений, нужно ординаты
условной диаграммы умножить на 1-f-е. На рис. 275 такая диаграмма
показана йунктиром. Она простирается до вертикали, проходящей-
через точку С, где нагрузка достигает своего-наибольшего значения.
При дальнейшем вытягивании образца начинается лйестное
уменьшение поперечного сечения (образование шейки), и е уже больше не
является постоянным по длине образца. Тогда выражение (Ь) более
уже неприменимо, так как напряжения по наименьшей площади
поперечного сечения распределяются неравномерно (см. стр. 360). В
таком случае выражение (Ь) дает среднее значение о. Среднее
Относительное удлинение е в наименьшем сечении можно найти из
выражения (ау которое^ дает
е = ^-1. (С)
Пользуясь, символом ^ для относительного сужения площади
поперечно!*© сечения (см. стр'. 334Х получаем -
р
из выражения (с) находим
==^, F=F^{\—q\
Г
Ъ.. ■ (Ч)
т. е. относи*ельиое удлинение в наименьшем сечении можно легко
вычислить, если измерить сужение площади^ этого сечения. Это s
называется*) эффективным удлинением; оно гораздо больше,\ чем
удлинение е = 8//, определяемое из полного, удлинения Ъ расчетной
длины. ^
Рассмотрим теперь более подробно понятие об относительном^
удлинений е. Для его вычисления обычно пользуются,
выражением е = (/ — 4)/4» так что приращение относительного удлинени»
^) См. Р. L U d W i к, Elemente der technologischen Mechanik, Berlin, 1909.
12*
356 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
определяется формулой
de = Y* * (е)
ъ которой приращение длины делится на первоначальную длину /о-
Кажется более логичным во многих случаях определять приращение
•относительного удлинения по уравнению
J г dl
d^j==j, (О
где / есть длина, к которой добавлено приращение dl. Тогда полное
•относительное удлинение получается в таком виде:
II
s'=^rfe'=^^ = ln^ = In(l+s) = ln^». (g)
Это удлинение называется естественной деформацией ^). Для малых
удлинений естественная деформация е' очень близка к е. Но для
больших деформаций, как в случае ка)гчука или пластического
удлинения стального образца, разница между е' и е становится
значительной и имеется некоторое преимущество в использовании понятия
естественной (истинной) деформации.
Рассмотрим в качестве примера изменение объема к)^а из
материала, имеющего первоначальный объем, равный 1 кубическому
сантиметру и претерпевающего равномерные удлинения Sj^., е^, е^ по
направлению его сторон. После деформации объем куба будет равен
A+е.)AЧ-^з')A->а
Если деформация такова, что объем не изменяется, как в случае
пластической деформации металлов, то услЬвие постоянства объема
будет V
A+е,)A+е,,)A+0=1- (h)
Если деформации е^,, е^, е^ не малы, так что их степенями пренебречь
нельзя, то условие в уравнении (h) будет очень сложно. Но ^если
мы восйользуемся понятием естественной деформации,^ то это же
условие принимает очень простой вид. Для этой цели мы возьмем
логарифм от обеих частей уравнения (h) и получим
ln(l+^.) + ln(l+e^) + In(l-be,) = 0.
Используя определение естественной деформации (формулу (g)),
получаем условие постоянства объема в простом виде
®л + 4 + 2г = 0. (i)
*) Это было впервые предложено М е sn а g е г'ом; см. Ргос. Congr. Internal.
Phys., Paris, т. 1, стр. 348, 1900.
78j
РАСТЯЖЕНИЕ' СТАЛИ ЗА ПРЕДЕЛОМ ТЕКУЧЕСТИ
357
Pij^/J^i^/Ш
Диаграммы испытания на растяжение для наименьшего сечения
в шейке растянутого^) образца можно строить,.откладывая истинное
напряжение (выражение (Ь)) в зависимости от естественной
деформации е'. Эти диаграммы (рис. 281) показывают, что за напряжением,
при котором начинается образование
шейки, зависимость между истинным, б=-"
напряжением неестественной
деформацией является практически линейной.
Рис. 282 иллюстрирует приемы^
измерения условной деформации е ,'
и истинной деформации е'. Экстен-
зометр на рис. 282, а прикреплен
к образцу в двух фиксированшлх
точках А и Б. Расстояние между
А И( В изменяется при растяжении
образца в пределах от начальной
длины /о до конечной, длины t. Экётензометр на рис. 282, Ь
(называемый экстензометром Баушингера) прикреплен к образцу в А
и иуеет каток в В, так что длина АВ остается равной /о. Если два
одинаковых образца (рис. 282) растян)пгы от /о до /, а затем к ним
приложены два .одинаковых^ приращения нагрузки, то изменения в
Рис. 281.
4-»
Рис. 282.
е
Ь)
показаниях дв)гх инструментов, являясь, очевидно, неравными, будут
находиться в отношении Ц1^=\-\-г. Но это отношение (на
основании выражений (е) и (f)) равно отношению dzjd&'. Следовательно,
инструмент на рис. 282, а дает условное относительное удлинение,
в то время как экстензометр Баушингера дает естественную
деформацию &'.
') Такие диаграммы были применены С. W. MacGrego г'ом, Ргос. Am.
Soc. Test. Mat., т. 40, стр. 508, 1940; см. также его статью в издании М. Н е-
t ё п у i, Handbook of Experimental Stress Analysis, 1950.
miw
358 MEXAHHHEiGKHE СВОЙСТВА ДЦТЕРИАЛОВ " 1ГЛ. X
79. Типы разрушений при растяжении *)
Имеются" два ' рода разрутиений, которые необходимо различать
при испытаниях на растяжение образцов из монокристалла. Для
таких материалов, как каменная соль, напримбр, мы имеем хр)Т1кое
разрушение без существенной пластической деформации, причем оно
наблюдается, когда величина нормального напряжения на одной из
главных плоскостей кристалла достигает критйческогоч. значения.
Такой вид разрыва называется растением отрывом.
Монокристаллические образцы метал;1а обычно показывают переде разрушением
большую пластическую деформацию, состоящую из скольжения по
определенным кристаллографическим плоскостям. Разрушени(е этого
типа называется разрушением сдвигом.
Зависимость между сопротивлением разьединению (при
разрушении отрывом) и сопротивлением скольжению (при разрушении
сдвигом) не остается постоянной для одного и того же материала.
Она зависит от температуры образца и от скорости, при которой
производилось испытание. Очевидно, что сопротивление скольжению
возрастает с по«ижением температуры и с повышением скорости
деформации. Однако сопротивление разъединению не зависит в одной
и той же степени от этих двух факторов. Этим объясняется, почему
каменная соль, которая является хрупкой п]ри комнатной температуре,
показывает разрушение вследствие сдвига, если испытывать''ее в
теплой воде, когда сопротивление скольжению уменьшается вследствие
более высокой температурш. Этим объясняется также} почему брусок
из такого металла, как цинк, может быть'согнут-при медленном
деформировании подобно бруску из пла^стического материала, между
тем как тот же самый брусок ,оказ]^вается хрупким й
разрушается без пластической деформации, если нагрузка приложена
внезапно^). .
В "случае поликристаллическйх материалов необхЬдимо
рассматривать опятьг два рода разрушения: 1) хрупкое разрушение^ как в
случае чугуна или хтеклц, и 2) разрушение сдвигом, как в случае
мягкой стали, ллюминия и других металлов. В первом случае
разрушение происходит практически без пластической деформации по
поперечному сечению, перпендикулярному оси образца. Во втором
случае разрушение происходит после значительной пластической вытяжки,
и место разрыва имеет приблизительно форму «чашки и конуса»
(рис. 283). При обсуждении этих двух типов разрушения была снова
выдвин)пга Теория, что прочность материала может быть описана двумя
характеристиками — сопротивлением материала разъединению и сопро-
^) Полная библиография по этому предмету дана в статье Р. L и d w i к'а,
Eidg. Materialprufuligsanstalt (Zurich) Ber., № 35, 1928. Gm. также Forschungs-
arb № 295 1927.
"«) P. Lu d wik, Stahl u. Eisen, f. 43, стр. 1427, 1923.
79|
ТИПЫ РАЗРУШЕНИЙ ПРИ РАСТЯЖЕНИИ
359
тАвлением скольжению. Если сопротивление cкo/fьжeнию "больше, чем
сопротивление разъединению, хо.диы имеем хрупкий материал, и
разрушение будет прод1схрдить в «результате преодоления сил сцепления
без какой-либо заметной дефррмации. Если сопротивление"^
разъединению больше, чем Сопротивление скольжению, то мы имеем пластй-,
ческий мaтepиa^f. Тогд;а сначала начинается скольжение по наклонным
плоскостям, и разрушение в форме «чашка и конус» происходит
лишь после! зиачительной равномерной вытяжки и последующего
местного уменьшения площади поперечного сечения ^образования
шейки) образца.
Рис. 283.
Распределение напряжений в наименьшем, сечении шейки*) для
типа разрушения «чашка и конус» было исследовано, и найдено,
что вблизи шейки -растягивающие усилия в продольных волокнах
имеют направления, указанные стрелками на рис '2%А,а.
Горизонтальные составляющие этих усилий в шейке вызывают радиальные и
окружные напря}кения, так что Каждый :бесконечно малый элемент,
выделяемый у плоскости наименьшего поперечного сечения, находится
в трехмерном напряженном состоянии, показанном на рис. 284, Ь.
Предполагая, что пластическое теч^ие требует постоянного
наибольшего касательного напряжения, мы заключаем, что осевые
растягивающие напряжения неравномерно распределяются по наименьшему
поперечному сечению образца, но имеют наибольшее значение в
центре поперечного сечения, где о^ и о^ являются также наибольшими.
Распределение осевых напряжений показано на рис. 284, а
заштрихованной площадью. Величины о^^ и а^^ зависят от радиуса а
наименьшего поперечного сечения и радиуса кривизны R шейки, и
*) См. статью Н. Н, Давиденкова, английский перевод, Ргос. Am.
Soc. Test Mat, 1946. См. также P. В г i d g m а n, Trans. Am. Soc. Metals, т. 32,
стр. 553, 1944. - -
§fi^
360 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
даются формулами
1ГЛ. X
1 +
max «
а
2R
1
а ' min « а *
где а^=Р/'ка^ есть среднее напряжение.
тт
^у
^ис. 284.
Вследствие трехмерного напряженного состояния материал вблизи
центра наименьшего поперечного сечения обладает настолько
пониженной способностью к пластической деформации,
что при растяжении в этой области *) начинается
образование трещины (рис. 285), между тем как
материал вблизи пов^рхнрсти продолжает
растягиваться пластически. Этим обстоятельством
объясняется, почему центральная часть области
разрушения по типу «чашка и конус» имеет
хр)шкйй характер, между тем как вблизи
поверхности наблюдается пластический тип
разрушения.
Вследствие неравномерного распределения
напряжений в области шейки в образде имеют
место остаточные напряжения, если он
разгружен до появления трещины. Эти напряжения были исследова-.
Рис. 285.
») См. Р. L U d W i к, 2. Ver. deut. Ing., т. 71, 1927.
79]
ТИПЫ РАЗРУШЕНИЙ ПРИ РАСТЯЖЕНИИ
361
ны*) методом, применяемым в случае толстостенных цилиндров (см.
стр. 322). Было вычислено распределение напряжений, имеющихся в
образце перед разгрузкой, и установлено, что оно удовлетворительно
согласуется с результатами теории Н. Н. Давиденкова (рис. 284). Кроме
того, изучение разрушений с помощью микроскопа показало, что они
происходили поперек зерен и были разрушениями сдвигом по типу
«чашка и конус» как во внутренней, так и во внешней частях шейки.
Предыд)тлие рассуждения относятся к. испытаниям на растяжение
стандартных круглых образцов цилиндрической формы. Результаты,
полученные с другими формами образцов, совершенно иные, что можно
показать на образце с выточкой ^), изображенном на рис. 286. При
испытании на растяжение наблюдается, что уменьшению площади
поперечного сечения у выточки частично препятствует наличие участков
Таблица 21
Предел прочности {кг/см^) цилиндрических образцов и образцов
с выточками "
5
ДЮЙМЫ ММ
1/32 = 0,8
1/16=1,6
1/8 =3,2-
Норм, образец
Углеродистая сталь
вычислен по
первоначальной
площади
11450
11550
10050
7 150
вычислен по
уменьшенной
площади
"^12 350
12 450
11 100
15 950
Хромоникелевая сталь
вычислен по
первоначальной площади
13550
12 950
10850
7 600
вычислен п6
уменьшенной
площади
16 650
16 300
14 000
24 450'
большего диаметра D. Естественно, что это действие должно
возрастать с уменьшением ширины 8 выточки, В табл. 21 даны результаты,
полученные в испытаниях образцов из двух различных материалов ^):
1) углеродистой стали при пределе пропорциональности 3950 кг/см^,
пределе текучести 4550 кг/см^, пределе прочности 7150 кг/см^,
удлинении 26,5%, сужении площади 55Уо и 2) хромоникелевой стали
>) См. статью Е. R. Р а г к е г' а, Н. Е. D а V i S' а и А. Е. F1 а п i g а п^ а,
Ргос. Am. Soc. Test. Mat.,.т. 46, стр. 1159, 1946.
^) Первые опыты с образцами с выточками были проделаны Д. Ки2кальди.
Таким путем он показал, что хрупкий тип разрушения можно произвести в
пластическом материале. См. его книгу Results of an Experimental Inquiry, etc.,
Glasgow, 1862.
3) > Эхи испытания были проведены в Исследовательской лаборатории
фирмы Вестингауза. См. также испытания, проделанные Р. L и d w i к 'ом и
R. Scheu, Stahl und Eisen, т. 43, стр. 999, 1923.
mw
362
МЕ^САЙЙЧЕСКИЕ CBOftCTiBA МАТЕРИАЛОВ
{ГЛ. X
при пределе пропорциональности 5600 кг1см\ пределе текучести
5900 KzjcM^y пределе прочности 7600 Й?г/сл*, удлинении 2 7У(„ суже-,
НИИ Площади'бЭУо- Эти цифры были получены из обычных испытаний
на растяжение нормальных цилиндрических образцов диаметра 0,5
дюйма и расчетной длины. 2 дюйма. При вычислении напряжений
была принята первоначальная площади, поперечного сечения. Образцы
с выточками типа, показанного на рис. 286, имели й== 0,5 дюйма
и D==l,^ дюйма.
Таблица показывает, что во всех случаях разрушающая нагрузка
для образцов с выточками была большей, чем для соответствующих
цилиндрических образцов, б образцах с выточками
имело место ^лйшь небольшое уменьшение площади,
и по внешн(ему виду разрушение было подобно
^ характерному для хрупких материалов. Истинный
црёдел прочности цилиндрических образцов был
^больше, чем для образцов с выточками, потому что
разрушение цилиндрических образцов происходило
после значительного пластического течения. В
результате этого появился наклеп и увеличилось не только
сопротивление скольжению, но также и
сопротивление разъединению.
Подобные условия иногда встречаются в
инженерной практике. Влияние, аналогичное влиянию
узкой вытопки по рйс. 286, моI^но вызвать
внутренними ракойинами в больших, поковках, цапример в
турбрроторах. Термические й остаточные напряжения
могут сочетаться с влиянием концентрации напряжений у раковины и
вызвать появление трещины. Последующее затем разрущение будет иметь
характер хрупкого разрыва без заметного пластического течения, хотя
материал'мог оказаться пластичным при обычных иtпытaнияx н^ растяжение.
Так как большинство образцов с выточками (рис. 286), оставаясь
упругим при испытании на растяжение до разрушения, будет иметь
малое удлинение, то только малое количество pa6ofibi потребуется,
чтобы произвести разрушение. Малая сила удара может легко
создать работуГ необходимую для разрушения. Образец оказывается
хрупким вследствие его формы, но «е вследствие каких-либо
механических свойств материала. В машинных частях, подверженных
удару, все резкие изменения в поперечных сечениях, опасны, и их нужно
избегать.
80. Испытания на сжатие
Испытания на сжатие произврдят обычно над хрупкими
материалами, как-то: камень, бетон и чугун. Образцы, применяемые при
испытаниях, обычно выполняются либо кубической, либо щ^лйндрй-
ческой формы. При сжатии образцов между плоскими поверхностями
80]
ИСПЫТАНИЯ НА СЖАТИЕ
363
Рис. 287.
испытательной машийц обычйо предполагается^ что сжимающее
усилие 'равномерно расцределяется по поперечному сечению.
Действительное же распределение напряжений
значительно сложнее, если даже
поверхности приходит в йолноё соприкасание,
а нагрузка приложена 'Центрально.
Благодаря трейик) На поверхностях
соприкасания между образцом и плитами
машины поперечное расширение,
которое сопровождает сжатие, устраняется
на этих поверхностях, и материал в этой
Области находится в более благоприятном
напряженном состоянии. В результате
получается тип разрушения при испытании на
сжатие кубического образца из бетона,
показанный яарие. 287 *). Материал,
находящийся в соприкасании с машиной," /
остается нетронутым, в то время как материал на гранях крошится.
Чтобы получить истинное сопротивление сжатию такого
материала, как бетон, нужно исключить или уменьшить влияние ,трения
на поверхностях соприкасания. Для ^тОй дели А. Фёпль покрывал
эти поверхности парафином *) и нашел, что предел прочности тог/|[а
значительно уменьшался. Тип разрушения был совершенно иным,' и
кубические образцы разрушались путем разделения на
пластинки, параллельные, одной из боковых граней.
Другой ыетол устранения, влияния сил трения заключается
в исп(ОЛьзовании образцов в форме призм, имеющих
длину э направлении сжатия в несколько раз большую,
чем поперечные размеры. Тогда средняя часть призмы
находится примерно в условиях равномерного сжатия^).
Очень интересный метод воспроизведения'равномерного
сжатия цилиндриче<;ких образцов, разработанный в Ин-'
ституте К; Вильгельма *), показан на рис. 288. Опорные
п^иты испытательной ^машины и концы цилиндрического
образца сделаны таким образом. Что образуют
конические поверхности с углом наклона „а, равным углу
трения. Таким- образом, влияние трения компенсируется
расклинивающим действием плит, и в результате наблюдается
равномерное сжатие.
») См. С. В а с h, Elastizitat und Festigkeit, 6-е изд., Berlin, стр. 160, 1911.
2) А. F б р р 1, Mitt. Mech.-tech. Lab., MOnchen, № 27, 1900.
8) См. Prandtl und Rinne, Neu. Jahrb. Mineral., 1907; см. также
W.^Gehler, Bauingeniem, т. 9, стр. 21, 1928. Шлиндрические образцы
высотой в два раза больше диаметра п]рименялись при испытании бетона.
^ *) Mitt. Kaiser-Wilh. Inst Eisenforsc^. (Dusseldorf), ^. 9, ст|з. 157, 1927.
mm
364
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
(ГЛ. X
Испытания на сжатие таких материалов, как бетон, камни и чугун,
показывают, что эти материалы имеют очень низкий предел
пропорциональности ^). За пределом пропорциюнальностй деформация
увеличивается быстрее, чем нагрузка, и диаграмма сжатия имеет форму,
показанную на рис. 289. Иногда желательно иметь ..аналитическое
выражение для такой диаграммы. В этих целях
Бах предложил*) показательный закон в форме
уравнения
пП
(а)
Рис. 289.
где п — число, зависящее от свойств материала.
Бах нашел значения и ==1,09 для чистого
цемента и Ах = ,1,13 для гранита. ^
Испытания на сжатие пластических материалов показывают, что форма
диаграммы зависит от размеров образца. Если размер в направлении-
сжатия уменьшается, то влияние трения на концах становится
более резко выраженным и диаграмма испытания на сжатие получается
круче. На рис. 290 для примера приведены результаты испытания
8000
6000
^ООО
гооо
ч
"/
Л-J
,/Э с
Г 'г
%ии
ffia
'7,50
-t,07
-0,75
yqso
.£
/О
JO so
Рис. 290.
70
%
на сжатие") медных цилиндров с различным отношением ЩН диаметра
к высоте образца. При испытаниях на сжатие таких пластических
материалов, как медь, разрушение наблюдается редко. Сжатие
сопровождается поперечным расширением, и сжатый цилиндр в конечном
^) Предел пропорциональности для чугуна при растяжении был
определен G г й п е i S е п'рм; см. Вег' deut physik. Ges., 1906.
2) С. Е-а с h, Elastizitat und Festigkeit, 5-е изд., Берлин, стр. 67, 1905.
**) См. G. Sachs, Grundbegriffe der mechanischjen Xechnologie der Me-
talle, Leipzig, стр. 36, 1925.
81]
ИСПЫТАНИЯ ПРИ СЛОЖНОМ нАпряжЕнн®м состЪянии
365
счете получает форму плоского диска. Чтобы уменьшить влияние
сил трения на поверхностях соприкасания и, следовательно, получить
удовлетворительную диаграмму испытания на сжатие, иногда
применяется метод проведения сжатия по стадиям ^). После того как образец
приобретает благодаря поперечному расширению форму боченка^
он подвергается обработке до своего первоначального диаметра.
Дальше прикладывается сжимающая сила, и процесс повторяется
в каждой стадии. Таким образом, испытание происходит при
непрерывном уменьшении высоты образца.
81. Испытания материалов при сложном напряженном состоянии
Закончив обсуждение вопросов об испытаниях на простое
растяжение и сжатие, рассмотрим теттерь случаи, когда материалы
находятся под действием сложных напряжений. Мы начнем с рассмотрения
материалов, испытываемых при всестороннем равномерном
гидростатическом давлении ^). Такие испытания показывают, что под Действием
равномерного давления однородные , материалы могут противостоять
громадным сжимающим напряжениям и оставаться упругими.
Испытания показываю^, что относи-
Таблица 22
Значения постоянных а и Ь
для оценки изменения объема
при всестороннем сжатии
тельное изменение объема при
наличии гидростатического
давления р можно представить
уравнением ^)
~—~ар-\- Ьр^.
о
Значения'постоянных а vi b для
некоторых материалов (р
измеряется в KzjcM^) даны в табл. 22.
Видно, что большие давления
вызывают лишь малое
изменение объема.
Было сделано несколько, попыток осуществить всестороннее /?аб-
номерное растяжение материалов, но до сих пор не было получено
удовлетворительного решения этой интересной задачи.
- Материал
о. 107
5,87
7,32
13,34
27,74
30,08
b ■ 1012
—2,10
—2,70
—3,50
+7,1^
4-4,86
*) См. G. J. Taylor and Н. Q и i п п е у, Ргос. Roy. Soc. (London), А. т. 143,
стр. 307, 1933—1934.
^) Обширные испытания такого рода были проведены П. В. Б р и д ж м е-
н о м, который разработал технику для получения огромных давлений; см. его
книги The Physics of High Pressure, New York, 1931 и Studies in Large
Plastig Flow and Fracture, New York," 1952; см. русский' перевод.
Исследования больших пластических деформаций и разрыва, 1955, ИЛ, Москва.
Новые испытательные машины для трехосного напряженного состояния
были описаны И. А. В. Wiseman'oM и Joseph, Marin'oM, Ргос. Am. Soc.
Test. Mat., т. 54, 1954. ^
*) В г i d g m a n. Studies in Large Plastic Flow and Fracture.
ш
366
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
Испытания на растяжение различных сталей в сочетании с
боковым давлением показали*), что это давление оказывает большое
влияние иа форму шейки и на уменьшение площади в наименьшем
поперечном сечении. На рис. 291 изображено приспособление из скоб,
воздающее рас^гягиваюихее усилие в образца;с, помещаемых внутрь
сосуда, в котором создается давление. Фотографии 292, а и 292, b
иллюстрируют разрушения среднеуглеродистой стали @,45Vo углеро-^
да) Соответственно при атмосферном давлении, и при поперечном
давлении 10 200 кг/см^. В первом случае естественное удлинение
было ргавно In FfijF = 0,92, а среднее истинное напряже-
iH»e 8000 кг/см^.. Во втором случае соответствующие
■ . значения были 2,37 и 33.300 кг/cif* Было найдено, что
I . I с увеличением поперечного давления относительный
размер плоской части на дне «чашки и конуса»
уменьшался; при определенном давлении плоское дно
совершенно исчезало и разрушение Полностью происходило
от сдвига. ,
Сочетание осевого сжатия и поперечного
давления было применено Т. Карманом^) в испытаниях на
сжатие мрамора. Эти испытания показали, что с
увеличением поперечного давления мрамор становится все
более и более пластичны1м, и первоначально
цилиндрические образцы могут получить форму боченка, как
показано на рис. 293.
^ри изучении плоскогр напряженного состояния
[ , были испытаны тонкостенные цилиндрические трубы.
Подвергая трубы осевому растяжению, в сочЬтании с
Рис. 291. внутренним давлением, исследователи установили®)
предел текучести для различных отношений двух главных
напряжений для некоторых материалов, включая железо, медь и никель.
Результаты, полученные таким путем, удовлетворительно
согласовались с теорией энергии формоизменения (см. стр. 376). Дальнейшие
опыты*) с тонкими трубами из мягкдй стали, подверженными внзггрен-
нему давлению в сочетании с растяжение!^, сжатием или кручением,
также дали результаты, согласующиеся с той же теорией. Испытания
на одновременное дейртвие растяжения и крз^ения тонких труб из
стали, меди и алюминия показали'), что начало текучести можно
J
^) В г i d g m а п,> там же; см. сноску »), стр. 365. Русский перевод, стр. 94.
8) Z. Ver. deut. Ing., стр. 1749, 1911. .
") Такие, опыты были проделаны В. Л о д е под руководством А. Н а д а и;
см. Forschungsarb., № 303, Ш28; см. так же Z, Phys., т. 36, стр. 913—939, 1926.
*) См. М. Ro§^ and А. Ei chinger, Ргос. Internal. Congr. Appl. Mech.,
Zurich, 1926.' '■
^) G. I. Taylor and H. Quinney, Phil. Trans; -Roy. See. (London),
A, T. 230, стр. 323^362, 1931. .
81]
ИСПЫТАНИЯ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ
867
Рис. 292.
• :>
Рис. 2Ш
к^^ЖИГ"'
Щ
368 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
предсказать с хорошей точностью уравнением
о2-|-Зт2 = а|,
в котором о есть осевое растягивающее напряжение, t — касательное
напряжение при кручении и о^ — напряжение на пределе текучести
при простом растяжении. Это уравнение также вытекает из теории
энергии формоизменения.
В практических приложениях не только напряжение на пределе
текучести, но свойства пластичности и наклеп также имеют важное
значение при сложном напряженном состоянии. Неожиданные случаи
разрушений, например взрывы больших сферических резервуаров ^)
и внезапные трещины в корпусах сварных грузовых судов, в
последнее время привлекли внимание к этим вопросам. В обоих из
указанных' типов разрушения были применены листы из
малоуглеродистой стали^ которые показывали удовлетворительную прочность
и пластичность при обыкновенных испытаниях на растяжение. Но
поверхности разрушения листов во взорванных ■ от давления
резервуарах и в поврежденных судах не показали пластической
деформации и носили хрупкий характер. Большинство из этих разрушений
произошло при низких внешних температурах в условиях двумерного
напряженного состояния.
Для оценки влияний температуры и плоского напряженного
состояния, на прочность и пластичность малоуглеродистой стали
в последнее время в различных лабораториях было проделано
значительное количество экспериментальных работ. Чтобы осуществить
плоское напряженное состояние, применялись тонкостенные трубы.
Эти трубы подвергались одновременно осевому растяжению и
внутреннему гидростатическому давлению, благодаря чему можно было
вызвать растягивающее напряжение о^ в окружном направлении и
Од в осевом направлении при любом желательном отношении « =
== о^/од. Пользуясь трубами из среднеуглеродистой стали @,23%
углерода) наружного диаметра 36,8 мм ^1,450 дюйма) и с толщиной
стенок 2,54. мм @,1 дюйма), Е. А. Девис проделал испытания ^)
для пяти различных значений отношения п. На рис. 294 показаны
полученные типы разрушений. Пр№, малых значениях отношения п
трещины были направлены по окружности, при больших' же они
были продольными. После ряда дополнительных испытаний было
установлено, что переход от одного типа разрушения к другому
имел место при значении и = 0,76. Было нййдено, что в случае
трещин по окружности разрушение происходило по плоскостям
наибольшего каса1ельного напряжения и при истинных напряжениях
приблизительно такой же величины, как и в случае плрских образцов, изго-
^) См. А. L. в f о W п and J. В. S m i t h, Mech. Engr., т. 66, стр. 392, '1944.
^) См.- E. A. Davis (Исследовательская лаборатория Westinghouse),
J. Appl. Mech., T. 12, стр. 13, 1945 и т. 15, стр. 216, 1948.
81]
ИСПЫТАНИЯ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ состоя'нии
369
товленных из того же материала, что и трубы. В случае*
продольных трещин тип разрушения оказывался более хрупким. Разрушение
обычно начиналось по плоскостям наибольшего касательного
напряжения, но благодаря высок'ой концентрации цапряжений у концов
грещины оно продолжалось как хрупкое в продольной плоскости,
без существенной пластической деформаций. Наибольшее касательное
Рис. 294.
напряжение, при котором на1»инались продольные трещины, было
всегда значительно меньшим, чем в случае трещин по окружности.
По-видимому, разница' в двух видах разрушения была обязана в
значительной ,степени форме образцов. В случае трещин по
окружности материал был более способен к образованию шейки, чем
в случае продольных трещин, и поэтому последние происходили
с меньшей местной деформацией и меньшим падением нагрузки за
пределом прочности. i
Опыты Калифорнийского университета *) над тонкостенными
трубами из малоуглеродистой, стали были проведены при двух
1) См. Н. Е.
стр. 201, 1948.
Davis and
*
E.R.
Parker, J. Appl. Mech., т. 15,
370 МЕХАНИЧЕСКИЕ хвойствл Материалов , 1гл, х
различных- температгурах. Диаметр труб был 133 мм E.1/4 дюйма)^
температуры- же равнялись 21,1,ЯС и —94,4° С. Испытания при
комнатной температуре всегда давали тип разрушения сдвигОм со'
значительной пластической деформацией. Испытания при. низкой
температуре (при и=1) показали'хрупкое; разрушение с очень малой
пластической деформацией. Эта хрупкость была приписана местным
напряжениям в местах сварки концов труб.
Кроме описанных ис^йытаний малых труб^ исследовались *)
больших размеров трубчатые образцы наружного диаметра 608 мм
B0 дюймов) и Длиной 3 м A0 футов), сделанные из корабельной
обшивки толщиной в 19 мм C/4 дюйма) при 21,1^ С и —40° С.
Исцыта>1ия при низкой температуре, особенно при отношении.п == 1»
показали хрупкое разруц]ение от напряжений значительно меньших,,
чем напряжения, полученные в испытаниях на раст1яжение обычных
цилиндрических образцов, сделанных из того же материала.
85^. Теории прочности^
, Механические свойства строительных 'материалов обычно
определяются опытами, которым подвергаются образцы при сравнительно
простых напряженных состояниях. Большинство наших сведений,
отйосительно прочности металлов было получено,-например, из
испытаний на растяжение. Подобным же образом испытания на сжатие
применялись для изучения хрупких материалов, в частности камня и
бетона. Кроме того, небольшое количество полезных сведений
относительно прочности материалов получено в испытаниях на сдвиг.^^
Однако прочность материалов при более сложных напряженных
состояниях была исследована лишь в фмногих частных случаях,
например таких, которые были рассмотрены в предыдущем параграфе,
* . Чтобы обоснованно определять допускаемые напряжения для
сложных напряженных состояний, которые имеют место при
практическом проектировании, были разработаны различные теорий
прочности. Цель этих теорий состоит в том, чтобы предугадать, когда
произойдет разрушение при сложных напряжениях, в предположении^
что поведение материала при простом растяжении или сжатии известна'
Под разрушением материала разумеют либо текучесть, либо
появление излома в зависимости от того, что наступит раньше.'
>1аиболее общее напряженное состояние, которое может иметь
место в теле, всегда вполне определяется величинами главных напря^
жений Oj, Ojj и og (рис. 295). В последующем изложении растяжение
») См. Welding J., т. 27, стр. 348, 1948.
®) Описание этих теорий можно найти в статьях; Н. М. W е s t е г g а а г d,
J. Franklin Inst., l^O; A. J. Becker, Univ. of Illinois Eng. Exp. Sta. Bull.,
Jvfe 85; F. Schleicher, Z. angew. Math. u. Mech., т. 5, стр. 199, 1925;
A. N a d tfi, J. Appl. Mech^, т. Ij стр. Ill, 1933.
82]
ТЕОРИИ ПРОЧНОСТИ
371
рассматривается положительным; а сжатие--отрицательным, прр^чем
оси на рис. 295 выбираюта}: тадс, что зависимость между
алгебраическими значениями/-ла^ййх напряже- ~
НИИ будет ; •
;><^
в^
(а)
Теория наибф1вших напряжений *)
принимает за ^критерий прочности
наибольшее или нйименьшее главное
напряжение. Для пластичных материалов
это означает, что текучесть в элементе
напряженного тела (рис. 295) начнется,
ког-да наибольшее напряжение достигг
нет величины, соответствующей пределу "^
текучести материала при простом растяжении, или когда наименьшее
напряжение достигнет предела текучести при простом сжатии. Таким
образом, условиями начала текучести будут
Рис. 295.
@1)т = ат ^ли |(оз).
'т»
B91)
где o^j. и От — соответственно напряжения предела Текучести при
простом растяжений и сжатии. Имеется много примеров, которые .
противоречат теории «наибольших напряжейий. Уже было указано
(см. стр: 339), что при простом растяжении скольжение происходит
по плоскостям, наклоненным на угол .45° к оси образца. Для этих
плоскостей ни растягивающие, ни сжимающие напряжения не являются
наибрльшими, и разрушение вызывается касательными напряжениями.
Также было указано (см. стр. 365), что однородный и йзотропнцй
матерйай, хотя бы и слабый при простом сжатии, может
противостоять очень большим гидростатическим давлениям без появления
текучести. Это указывает на то, что величина наибольшего
напряжения недостаточна для определения условий текучести материала или
его разрушения.
' Вторая теория прочности — теория, наибольших деформаций,
обычно приписываемая Сен-Венану. По ^той теории предполагается,
что пластичный материал начинает течь, если наибольшая
деформация ][удлинение) равна деформации на пределе текучести при
простом > растяжении или когда наименьшая деформация, (укорочение)
pai^Ha^ деформации на пределе текучести тгри простом сжатии.
Наибольшая 1^ 'наименьшая деформации (см. т. I, уравнение D3), стр. 64)
будут
1^--ёг(<'а-|-0з)=е1, -|.—9^C1-foO — Es.
Ренкина.
^) Это самая (уарая теория разрушения и иногда называется теорией
Mr''
372 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
Подставляя деформации предела текучести, равные а^Е при
растяжении и (Sj/E при сжатии, вместо Ej и eg, получим критерий
разрушения согласно теории^ наибольших деформаций в следующем виде:
oj — (Л, @2-|-оз) == °т и-'^и 1 °з "—fJ^ (°1 + °2) 1= °т- B92)
Имеется много случаев, когда тебрия наибольших деформаций
может также оказ1аться ^несостоятельной. Например, если пластину
подвергать равным растягивающим напряжениям в двух
перпендикулярных направлениях, то по теории наибольших деформаций следует,
что напряжение предела текучести будет выше, чем при* лростом
растяжении. Этот результат получается вследствие того, что
удлинение в каждом направлении уменьшается из-за растяжения в
перпендикулярном направлении. Однако это заключение не подтверждается
опытами *). Результаты испытаний материалов под действием
равномерного гидростатического давления также противоречат этой теории.
Для такого случая второе из выражений B92) дает
°т
1°з1т==131
2{л'
где оз'представляет гидpocfaтичecкoe давление. Опыты показывают,
что однородные материалы под действием равномерного
всестороннего сжатия могут выдерживать более высокие напряжения й
оставаться упругими (см. стр. 365).
Теория наибольших касательных напряжений дает лучшее
согласование с опытами, по крайней мере для пластических материалов,
для которых а^ = а'^. Эта теория предполагает, что текучесть
начинается, когда наибольшее касательное напряжение в материале
становится равным наибольшему касательному напряжению предела
текучести при испытании на простое растяжение. Так как наибольшее
касательное напряжение в материале равняется половине разности
между наибольшим и наименьшим гд^вными напряжениями ^), и так как
наибольшее касательное напряжение при испытании' на растяжение
равно половине нормального напряжения, то условием состояния
текучести -будет ,_._.
oi — 03 = 0^. B93)
При проектировании машин теория наибольших касательных
напряжений обычно применяется для пластических материалов ^). Эта
теория хорошо согласуется с опытами ^) и очены проста в применении.
*) См. W eh age, Mitt. Tech. Versuchsanstalt. (Berlin), стр. 89, 1888. "
^) Cm. t. I, стр. 64.
^) Сравнение различных теорий прочности, примененных при
проектировании машин, дано J. Marin'oM, Product Engrg., май, 1937.
*) Теория подтверждается опытами J. J. G и е s f а, Phil. Mag., г. 50,
стр. 69, 190а См. также L. В. Turner, Engineering, т. 86, стр. 169;
W. А. Scoble, Phil. Mag., декабрь 1906 и январь 1910; C.A.Smith,
Engineering, т. 88, сгр.^238. ' I ■
82] ТЕОРИИ ПРОЧНОСТИ 37S
В тебрии наибольшей энергии за основание для установления
критерия разрушения принимается количество энергии деформации,
накопленное в единице объема материала *). Пользуясь общим
выражением потенциальной энергии деформации ^выражение A95) т. I,.
стр. 277) и приравнивая энергию ^цля случая, показанного на рис. 295,
энергии на пределе текучести при простом рУйстяжении, находим
критерий для начала текучести
^T==2^(°' + <+°8^-|(^L°2 + °2°^ + °»°«> = S- ^294>
Для сравнения описанных теорий прочности рассмотрим случай
чистого сдвига. В этом особом случае двумерного напряженного
состояния наибольшее растягивающее, наибольшее сжимающее и
наибольшее касательное напряжения численно равны между собой
(см. формулу (а) т. I, стр. 57^ т. е.
01 = Од = X, 02= о.
Предполагая, что материал имеет один и тот ^же предел текучести
при растяжении и при сжатии, найдем, что условиями текучести,^
согласно теории наибольших напряжений, теории наибольших
деформаций и теории наибольших касательных напряжений, соответственно
будут
От От
Т ■■ П Т Z= Т 'Z= =-
Теория наибольшей потенциальной энергии дает зависимость
_af(l-f-t^)_°?
Е 2£'
откуда
X.
т
/2A 4-f^)-
Принимая для стали jx = 0,3, приходим к следующим результатам'
,по теории наибольших напряжений х^ = а^;
по теории наибольших деформаций х^ = 0,77 о/,
по теории наибольших касательных'напряжений Хт== 0,50 о^
по теории наибольшей энергии деформации Хт = 0,62о,
Видно, что разница между различными теориями в этом частном
случае получается значительной^). Например, при расчете на кручение
'т»
*) Эта теория впервые была предложена Бельтрами, Rendiconti,.
стр. 704,1885; Mat. Ann., стр. 94, 1903; см. также G i г 11 е г, Sitzungsber. Wiener
Akad.,T. 116, 11а, стр. 509, 1907; В. Р. Haigh, Engineering, т. 109, стр. 158,
1920 и Brit. Assoc. Adv. Sci. Repts. (Edinburgh), 1921.
^) Сравнения теорий прочности, примененных к различным задачам
проектирования, даны в статье Roth, Z. Math. u. Phys., т. 48, 1902.
374
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
>+ |б.
■круглого вала придется сначала установить допускаемую величину ра-
-бочего напряжения при сдвиге [т] = т^ад == «Ц./^. Тогда диаметр вала
может быть найден по формуле A52) т. I, cтp^ 241. Пользуясь
четырьмя теориями, разобранными выше, получаем следующие отноше-
лйя диаметров: ; ^ , ^
1:1,09М,26:1,17,
Другой способ сравнения рассмотренных выше четырех теорий
прочности приведен на рис. 296. Рисунок, начерчен для материала,
который имеет одинаковый предел
текучести при растяжении и сжатии и
находится в плоском напряженном
состоянии ^), следовательно, Од =^0. Линий
на рисунке определяют -значения 0| и од,
при которых начинается текучесть.
Теория наибольших напряжений
представлена квадратом 1'2 S 4, в котором
длины ОА и ОВ цредртавляют
напряжения на пределе текучести" при
простом растяжении в направлениях,
соответствующих главным напряжениям.
Таким же образом А' и Б' соответствуют
простому сжатию; Точкой /
представлены равные растягивающие напряжения
в двух перпендикулярных направлениях,
причем каждое равно пределу текучести при простом растяжении.
Согласно teopBH наибольших напряжений текучесть не имеет места
при напряжениях, представленных точками внутри- KsaApata 12 3 4,.
Теория . наибольших деформаций представлена ромбом 6 6 7 8
(рис. 296). Так как растяжение в одном направлении уменьшает
деформацию в перпендикулярном, эта теория указывает на то, что два
равных растягивающих напряжения вызовут текучесть при гораздо
больших зн^енйях напряжений (точка , 5), чем указано теорией
наибольших напряжений (точка /). Координаты точки 5 на основайии
-выражения B92) будут aj{\ — tf). Если два главных напряжения
равны по величине, но противоположны по знаку, то теория наибольших
деформаций указывает, что текучесть н1ачинается срответственно
точкам б й 8, которые имеют координаты, численно равные <J^/A-{-(*).
Знйчения напряжений в этих точках, следовательно, являются
меньшими указываемых теорией наибольших напряжений (точки 2 и 4),
Теория ^наибольших касательных напряжений представлена
неправильным шестиугольником А! BA'SffA, который построен на
Рис. 296.
>) См. статьи А. J. В е с к е г'а, цит. на стр. 370; В. Р. Н а i g h, цит. на
стр. 373:
^щ ' ^ ТЕОРИИ ПРОЧНОСТИ > 375>
У . " '■ ' ' ' ■■■ '"■ '■ - ч ■.. ■' ■ ■ ■ ■ '
основании выражения B93). Пользуясь уравнениеяг B93), нужно ~учи-^
тывать, что в данном случйе Оз^^О, и поэтому'Og должно быть
принято вместо оз, когда о^ отрицательно- Эта теория совпадает с
теорией наибольших напряжений^ когда оба главных, напряжения имеюг
один и тот же знак, но они значительно расходятся,' когда главные
напряжения имеют пp6tивoпoлDжныe знаки. '
Для плоской.Задачи условие B94) теории наибольшей
потенциальной энергий сводится к следующему:
'т-
графиком этого уравнения является эллипс, показанный на рис. 296.
Эллипс лишь незначительно отклоняется от шесаенугольника,
представляющего теорию наибольших-касательных напряжений.
Когда материал подвергается равномерному гидростатическому
давлению по всем направлениям (oj =а^ = а^ = — р), теория наи- •
большей пбтенциэльной энергии дает ,
■ ■ / ' ' ■ '
■ . ^ От
где рт — давление, при котором начинается текучесть материала.
Однако этот результат не согласуется с испытания&1И на всестороннее
равномерное сжатие. Как уже отмечалось (см. стр. 365), однородные
изотроцные материалы могут противостоять большим тидростати-
ческим давлениям, оставаясь упругими.
Чтобы получить лучшее-согласование между теорией и опытом,.
Губер'*) предложил разложить полную энергию деформации л-ела на
два компонента: 1) энергию деформации При всестороннем
равномерном растяжении или сжатии и 2) энергию деформации,
соответствующую изменению формы.^ Затем он предложил использовать только-
энергию формоизменения Для оценки состояния текучести и
разрушения, материала % Чтобы выполнить разделение энергии деформации
на две части, начнем опять с рассмотрения объемного напряженного
состояния, определяемого тремя главными, напряжениями Oj, og и а^.
(рис./295). Закон Гука дает
Н = Б Г Ё (^+ °з), ^2 = J — I (^1 + Ы Ч = ^ — I (oi + оз)-
*) М. т. Huber, Gzasopismo technizne, Львов (Лемберг), 1904; см. также
А. Foppl und L. Foppl, Drang und Zwang, Munchen, 2-е изд., т. 1,стр.50,
1924.
2) По-видимому, К. М а к с в ё л л был первым, который выразил мнение, что
«когда (энергия формоизменения) достигнет определенного- предела, тогда
элемент начнет разрушаться». Это было сформулировано в письме
Максвелла A856 г.) к Вильяму ToMcoHj и стало известным 'лишь после
опубликования писем Максвелла. ' *
1*1^
376 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Складывая эТи уравнения, получаем
^1 -f- ^2 + ^3 = £ (°1 + 02 + Оз).
[ГЛ. X
(С)
■чем устанавливается, что относительное изменение объема
пропорционально сумме трех главных напряжений. Если эта сумма равна
нулю, то изменение объема отсутствует, и материал подвергается
только деформации изменения формы.
Если 01 = 02 = 03=^, имеем
Eg Eg е р р.
(d)
В этом случае никакого искажения формы не будет и существует
только всестороннее равномерное растяжение или сжатие.
Для общего случая введем обозначение
Ol + «8 + 08
= Р
(е)
-и затем разложим каждое из трех главных напряжении на два
составляющих следующим образом:
■р-{-а[, 02=^4-^2'
■■Р-{-<-
(О
Складывая эти три выражения и пользуясь выражением (е), получаем
Так как сумма а[, Og и о^ обращается в нуль, то эти напряжения
вызывают лишь искажение формы, и выражения (f) обеспечивают
разделение данной системы напряжений а^, од и а^ на две: 1)
равномерно растягивающее или сжимающее р, вызывающее лишь
изменение объема, и 2) сиртему напряжений а[, о^ и а^, вызывающую лишь
искажение формы.
.4
'Л
I/
Z
f
26,
J
Рис. 297.
С)
.в качестве примера приложения выражений (f) рассмотрим случай
простого растяжения (рис. 297, а). Подставив аа==о£ = 0 в формулы
82] ТЕОРИИ ПРОЧНОСТИ 377
(е) и (f), получим
Таким образом, простое растяжение в направлении х можно
разложить на равномерное растяжение (рис. 297, Ь) и сочетание явлений
чистого сдвига по плоскостям ху 1л xz (рис. 297, с). Можно видеть,
что работа напряжений, вызывающая лишь искажение формы (рис.
297, с), на перемещениях, возникающих от равномерного растяжения
(рис. 297, Ь)у обращается в нуль. Энергии деформации случаев (Ь)-
и (с), таким образом, не зависят друг от друга, и полная энергия
деформации jnpn простом растяжении (рис. 297, а) получается пзггем
сложения энергии деформации при всестороннем равномерном
растяжении и энергии деформации изменения формы.
Это заключение также справедливо в общем случае, когда
действуют все три главных напряжения oi, og и Og. Из этого следует, что
энергия искажения формы получается путем вычитания энергии
деформации всестороннего равномерного растяжения из полной
энергии деформации. Подставив
01 = 02 = 03 = g
В выражение B94), получим для энергии деформации при
всестороннем равномерном растяжении выражение
^@1 + 02 + Оз)^.
Taj<HM образом, энергия деформации изменения формы в общем
случае будет
^» — 2Ё t°» + °2 + «^з — 2f^ (°1°2 + «^аоз + °10з)] ^^ (°1 +
4-°2 + 0з)' = ^1@1-02)' + (°2-08)'Ч-@1~0зЛ. B95)
Это выражение можно принять за основу для определения
разрушения пластичных материалов, имеющих ясно выраженный предел
текучести о^ при простом растяжении. Согласно этой теории в общем
случае действия напряжений Oj, og и од текучесть начинается, когда
энергия формоизменения (выражение B95)) достигает значения
энергии этого же вида на пределе текучести в случае простого
растяжения. Последняя величина получается из выражения B95)
подстановкой 01 = 0^, 05 = 0^=0, что дает
MW
^78
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТВРИАЛОВ
[ГЛ. X
Тогда условие для состояния текучести, основанное на теории энер-
хии изменения формы, будет „ ?
(Pt~o^-i-(c^-~-o^-^(p,~a^ = 2a,. B96)
Б; частном случае плоской задачи мы' подст;авим сюда о^ = 0, и
условием текучести будет
СЦОч
+°1^
B97)
Рассматривая, например, сочетание осевого растяжения и кручения
тонких труб (см. стр. 369) и обозначая через о и -с соответствующие
напряжения, находим главные напряжения (см. формулы C1) и C2)
т. I, стр, 61) в виде
:й условием текучести (формула B97)) становится
. о«4-Зт2==о|. ; B98)
Это выражение, рассмотренное и ранее (стр. 368), хорошо согласу-
•ется с опытами. В случае одного только кручэния мы имеем о = 0,
и выражение B98) дает • .
■Ст==у^ =-0.577 Ох,
B99)
■что опять хорошо согласуется с результатами опытов.
В настоящее время условие текучести B96) npHKHMaeirCR вообще
£ качестве пригодного для пластичных материалов, причем
предполагается, что материал начинает течь, когда
энергия деформации изменения формы
достигает определенного значения.
Эйхингером *) было показано, что
то же условие текучести, определяемое
теорией наибольшей энергии изменения
формы (выражение B96)), можно также
получить рассмотрением касательных
напряжений, де^^ствующих по октаэд-
^ - , ральной плоскости, например ABC на
^ рис. 298, Koitaa кубик подвергается
действию главных напряжений Oj, og и og.
Из рисунка видно, что косинус угла
между нормалью п к октаэдральной
плоскости и координатными осями X, у HZ равняется 1/к 3.
Разложив результирующее напряжение 5, действующее по октаэдральной
Рис. 298.
^) А, Eichiflger, Proc. 2d Internat. Congr. Appl. Mech., Zurich., стр.
525, 1926.
821 ТЕОРИИ ПРОЧНОСТИ 379*
плоскости, на три составляющие X, У, Z и написав три услов|»я
равновесия, найдем ^ %. .'- ,
-.4 '• ' v^^-fL-" ".-vC__?«-■■ ■ ' y:-^_?»I'
■■ -^.Кз' -. ■^у'з' ; '^'~■■^^r•.:
Peзyльтиpyющee лапр! жение ло октаэдральной плоскости равно
1
5=
Щ'¥У^г^=у^У<^<+^
Нормальнай ; составляющая N напряжений S может быть получен»
проектир(>ванием составляющих Х, Y, Z на направление нормали л^
что дает
Тогда, касательное напряжение т^^, "^ октаэдральной плоскости;
будет/ i^,,- "■ ;•. :., ' V,...■'■•■•;'.■ ^■■ "■ -.-^ " . ■ ./^
•^окт =- /5^^=-^^=т^^ (°^+^^+°«) - (^^+^« -Ь ^'^^"^ : '
' == -|-1/ (oi — о^)« -1- (оз — Оз)'> 4- (oi — Оз)«Г
Сравнивая этот результат с выргь^ейием B96), видим, что-ус^ювие-
текучести,"основанное на теории энергии искажения формы,
эквивалентно положению, что текучесть начинается, кс^гда октаэдральное
касательное; напряжение достигает критического значения, равного
':""> -7.
i-^tC
КкЛр=-V: °у "^ ^'"^^ '^т
г, Захс принял критическое значение t^p для мрнофйсталла'(см.
стр. 336) за основу д^я. вычисления напряжения на^- пределе
текучести дляЛюликристаллического образца *). По вы|р^жению {Ь),/стр. 340,.
мы знаем, что нагрузка на пределе текучести образца на
монокристалла зависит, от ориентировки кристалла. Рассматривая
поликристаллический элемент как систему кристаллов, размещенных
беспорядочно, Захс вычислил зависимость между о^ для образца при
рйстя?кейии и -с^р для образца из монокристалла методом
^приближенного осереднения. В вычислениях пренебрегалось влиянием граничнТух
поверхностей кристаллов и предполагалось, что на пределе текучести
все кристаллы потекут одновременно. Для кристалле с гранецентри-
рованной решеткой кубической структуры (например, алюминий, медь
: ») G. Sachs, Z. Ver. deut. Ing., т. 72, стр. 734, . 1928. См. также
Н. L. Сох and D. G. Sopwitn, Prec, Phys. Soc. (Londcn), т. 41),
стр. 134, 1937 и и. Dehlinger, Z. Metallkunde, т. 35, стр. 182, 1943.
1ШГ
-380
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
Л,никель) он нашел
о^ = 2,238 -с^р.
ТТовтрряя вычисления для кручения, он нашел напряжение,
соответствующее пределу текучести при сдвиге для поликристаллического
•образца, равное ^ •
• . -с^^ 1,293 т^р.
Из последних двух соотношений получаем
, 1,293
2,238 °т
0,577 а^.
что совпадает с результатами теории энергии искажения формы
(см. формулу B99)). ^ Захс предположил, что подобный результат
может быть '^получен и для кристаллов с зрбъемноцентрированной
решеткой кубической структуры (как для железа). Таким образом, мы
/ видим, что имеется некоторое физйческде обоснование для результата,
полученного ранее на основании предположения, что текучесть
кристаллического материала начинается, когда количество энергии фор-
мризме1^ния достигает определенного значения для каждрго материала.
^ В предыдущем изложении мы кас^ались установления критериев
для начала текучести пластичных материалов" в юбщем случае
напряженного^ состояния. В случае хрупких материалов, которые
разрушаются без пластической деформации, мы также нуждаемся в
критерии разрушения в общем случае действия
напряжений oj, og и Og. Такой критерий
представлен теорией прочности, разрабо-2
тхинной Мором *), в которой рассматривает-:;
ся не только текучесть, но также и
собственно разрушение. При разработке своей
теории Мор применил графическое изобра-*
жение напряженных состояний з элементе
тела с помощью кругов напряжений, как
пояснено в п. 18, т. I, стр. 64. В этом
изображении (круг Мора) нормальные и каса-;
тельные составляющие напряжения,
действующие по какой-либо площадке,
определяются координатами некоторой точки
в пределах заштрихованной площади (рис.
:299). Точки, лежащие на одной и той же вертикальной линии (как,
например, MN), представляют напряжения по площадкам с
одинаковым нормальным напряжением о и с различными касательным»
Рис. 299.
^) О. М a-h г, Z. Ver. deut. Ing., т. 44, стр. 1524, 1900. См. также его
Abhandlungen aus dem Gebiet der technischen Mechanik, 2-е изд., Берлин,
стр. 192, 1914.
«21
ТЕОРИИ ПРОЧНОСТИ
381"
напряжениями. Естественно предположить, что самая слабая из этих^
площадок — площадка с наибольшим касательным напряжением,
представленная точкой ЛА на внешнем круге. Повторяя те же
рассуждения с точками на какой-либо другой вертикальной линии, мы
окончательно приходим к заключению, что наиболее слабой площадкой
должна быть одна из площадок, напряженное состояние которой
представлено точками на внешнем круге ANC. Следовательно, один
лишь внешний круг достаточен для определения предельного
напряженного состояния, т. е. напряженного состояния, при котором
имеет место либо начало текучести, либо разрушение в зависимости
от того, пластичен ли материал или хрупок.
Начнем с v определения напряжений текучести. Пусть на рис 300
круг диаметром ОА представляет условие текучести при простом
растяжении. По тем же соображениям круг диаметром ОС представит
условие текучести при простом сжатии, а круг с. диаметром DB
представит условие текучести при чистом сдвиге. Если на основании
проделанных с данным материалом опытов 'получить ряд кругов
такого рода, то можно построить огибающие этих кругов (ММ и MiNi).
Мор далее допустил, что текучесть может" начаться только при
напряженных состояниях, представленных одним из кругов, касающихся
этих огибающих кривых.
м
г
><^
1
г
» •
^ ^
'о
^
Ч'^'Ч^
\/?\>«
/* /
^-^
^
Рис. 300.
Рис. 301.
Предположим, например, что огибающие кривые МН и M^N^
можно заменить прямыми линиями (рис. 301). Тогда, зная предельные
условия при простом растяжении (oi = o^) и при простом сжатии
(оз = — о'^), можно легко получить условия текучести при чистом
сдвиге. Необходимо лишь йайти радиус OF круга, построенного при
центре в точке О й касающегося прямой M.N. Из рис. 301 имеем
'0K^'0P — KF = x^ — a^l2 и Ш = НР — 1р=:.а^12--а^12, Тогда
из подобия треугольников QOK и QHL получим
2й-
Ш'
GO
GH
или
2хт
а;+ат'
382
откуда
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
О- о
/:■
\ТП. Х-
(g>
Когда о^ = От, уравнение (g) совпадает с теорией наибольших каса-
Т41Льных напряжений.
Теперь приложим теорию Мора к случаю хрупкого материала при
условии плоского напряженного состояния и предположим, что на
м
F
Я
nvpaan
Рис. 302.
рис. 30^ ОА представляет предел прочности материала при
растяжении бпч.^аст и ОС представляет предел прочности лри сжатии o^^ ^ж-
Тогда для любого отношения <3i„ax/''min^^^°»/°«- Крзйние значения этих
ч
напряжений получатся путем построения круга диаметром BD=<i{\—<ii^
касающегося линии MN% , Из рйс. 302^^ получим теперь следу1шцие
соотношения: . - , >
SK=SF — KF:
JiL — HP~LP:
■'пч.сж
"пч.раст .
2 »
^пч.рас'т .
о.
0Я== GO Н-0Я=== ^?5^^ + 2п!^.
из подобия же треугольйиков QSK и QHL находим
SK GS
И1 GH
или
■'пч.раст
■'пч.раст"
'пч-сж
'пч.раст
'пч.раст
-j^ о
пч.сж
откуда
'^пч.раст "пч.сж
(h)
- Ц Заметим, что, о, й Oj представляют алгебраические величины и,
следовательно, раСстояние_0/)=— о«.
«2]
ТЕОРИИ ПРОЧНОСТИ
383
Таким образом, для любого заданного значения отношения о,/аа
можно вычислить значения .0| и од при разрушении. .
В предыдущем параграфе предполагалось, что 0| представляет
наибольшее главное йапряженйе а^^^ и что og-^ наименьшее глайное
напря^кеиие Ojjjj^. Так как третье главное шапряжение равно нулю
в случае плоского, напрйженного состояния, то oj и о, должны
иметь противопдлбжные знаки, как и показано на рис. 302, и
отношение 0|/f3a должно быть отрицательным. Однако в случае
растяжения по двум взаимно перпендикулярным направлениям третье
главное напряжение Оз= О будет представлять a^^^, и соответствующий
круг Мора будет кругом диаметром ОА на рис. 302. Тогда разру-
тиёнче произойдет, когда большее из двух растягивающих
напряжений достигнет значения Опч.раст- Подобным же образом в случае
сжатия по двум взаимно перпендикулярным направлениям
напряжение Og==0 представляет о^^^, и на рис. 302 получается круг
диаметром ОС. В этом случае разрушение произойдет, когда большее
сжимающее напряжение достигнет значения Опч.сж* * » . •
„, Построив для теории Мора чертеж, подобный рис. 296, стр. 374,
мы получим для растяжения по двум взаимно перпендикулярным
направлениям граничные линии АВ и ВС (рис. 303), указывающие
на то, что в этом случае разру-
411ение произойдет, если большее
растягивающее напряжение
достигнет значения Опч.раст- Подобным
образом для сжатия по двум
взаимно перпендикулярным
направлениям мы получим линии DE и ЕР.
Если мы имее|и о, при
растяжении и Оз при, сжатии, то условия
для разрушения будут представ^'
лены уравнением (h), которое дает
линию AF на рис. 303. Линия CD
получается подобным же образом.
Никакого разрушения не будет
njSfpHCXOAHTb при напряженных
состояниях, определяемых точками,
лежащими внутри шестиугольника ABCDEF, предельные же
напряжения можно получить из этого шестиугольника для любого
значения отношений aila,i. Например, для того чтобы найти предел
прочности хрупкого материала при чистом сдвиге, мы заметим, что
в этом случае Oi = —Og, а соответствующаяч^ предельная точка
будет являться точкой пересечения Л^ линии ОМ (рис. 303) и
стороны AF шестиугольника. Значение ^ч.раст можно определить
из рисунка или вычислить из уравнения (h), которое для Oi==—о.
Рис. 303.
|ШР
384 ' МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
дает
„.— - . , — °ii4.pacT °пч.сж лч
— ^пч.раст"" „ ' _1 „ • М/
°пч.раст ~Г °пч. еж
Это уравнение имеет тот же вид, что и условие (g) для текучести.
Если применить выражение (i) к такому материалу, как чугун,
и допустить, что предел прочности при сжатии в четыре раза
больше предела прочности йри растяжении, то мы найдем предел
прочности при сдвиге равным
"пч.раст — "»"''пч.раст>
ЧТО удовлетворительно согласуется с опытами Баха*).
Квадрат BKBL, намеченный штриховыми линиями на рис. 303,
представляет усдария разрушения согласно теории наибольших
напряжений. Видно, что, пользуясь теорией Мора, проектировщик
обеспечит конструкции больший запас прочности, чем по теории
наибольших напряжений, когда главные напряжения имеют противоположные
знаки. Теория Мора может быть рекомендована в случае хрупких
материалов, хотя предположение, что должен быть рассмотрен только
внешний круг напряжений (рис, 299, стр. 380), не всегда
подтверждается опытами ^).
83. Испытания на удар
Испытания на удар применяются для изучения вязкости
материалов, т. е. способности материала поглощать энергию при
пластической деформации. При статических испытаниях на растяжение эта
энергия представляется площадью диаграммы кривой растяжения
и можно заключить, что для того, чтобы иметь высокую вязкость,
материал должен иметь высокую прочность ив то же время
большую пластичность. Хрупкие материалы имеют низкую вязкость, так
как они имеют лишь малую пластическую деформацию перед
разрушением. Применение таких материалов в конструкциях является
опасным, так как разрушение может произойти внезапно без
значительной деформации.
При обсуждении вопросов о различных видах разрушений (см. п. 79)
было указано, что один и тот же материал может верти себя как
хрупкий или как пластический материал в зависимости от внешних условий.
Испытание на растяжение образца из монокристалла каменной соли дает
хрупкое разрушение (раскалывание) по одной из главных
кристаллографических плоскостей при испытании в комнатной температуре.
Тот же образец при испытании в горячей воде деформируется пласти-
1) С. Bach, Elastizitat und Festigkeit, 7-ё изд., стр. 362.
^) Th. V. Karman, Forschungsarb., № 118 и Z. Ver. deut. Ing., т. 55, 1911.
См. также R. В б к e г, Forschungsarb., № 175/176.
83]
ИСПЫТАНИЯ НА УДАР
385
чески путем скольжения по октаэдральным плоскостям. Подобные
условия могут встретиться также в ответственных случаях
применения мягкой строительной стали. При обычных испытаниях на
растяжение сталь может иметь большую пластическую деформацию, в то
время как в испытаниях при некоторой пониженной температуре
разрушение может иметь вид, как у вполне хрупкого материала.
Примеры катастрофических случаев таких разрушений наблюдались
во время второй мировой войны в многочисл'енных разрушениях
сварных торговых судов ^). Последующие исследовательские работы
показали, что температура охрупчивания стальных пластин,
примененных в обшивках судов, была того же порядка, что и рабочая
температура.
Для того чтобы пояснить переход от хрупкого разрушения
к пластическому для образца из монокристалла каменной соли, испы-
тайного на растяжение, А. Ф. Иоффе ^) предложил различать два
рода растягивающих напряжений: 1) растягивающее напряжение а„,.
вызывающее хрупкое разрушение отрывом по одной из главных
кристаллографических плоскостей, и 2) растягивающее напряжение а^^
соответствующее началу скольжения по
одной из октаэдральных плоскостей
кристалла^). На рис. 304 эти две
величины представлены в функции
температуры t образца. В опытах Иоффе
сопротивление отрыву оставалось
практически независимым от температуры.
На рис. 304 диаграмма для а„ дана
горизонтальной линией. В то же самое
время сопротивление скольженикг
зависело в значительной степени от
температуры образца, и ординаты кривой
для Og уменьшались с увеличением
температуры. Точка - С пересечения двух
кривых определяет критическое
значение ^кр температуры. Если температура при испытании выше ^^р» то
сопротивление скольжению меньше, чем сопротивление отрыву, и
образец будет течь пластически. Для температур ниже, чем ^^р мы имеем
о„<|]о^, и образец будет разрушаться отрывом без пластической
деформации.
Имеются другие важные выводы, которые можно сделать на
основании диаграммы, представленной на рис. 304- Рассмотрим влияние
Рис. 304.
*) См. статью Finn J о п а s s е п'а в W. М. Murray (изд.). Fatigue and
Fracture-of Metals, 1952. '
2) г. Phys., т. 22, стр. 286, 1924.
^) Предполагается, что ось образца параллельна одной из
кристаллографических осей.
13 СП. Тимошенко, т, II
imw
ЪВб МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ {ГЛ. X
скорости нагружения на результаты испытания. Известно, что с
увеличением скорости сопротивление материала скольжению
увеличивается, В То время как его" сопротивление отрыву остается практически
постоянным. В результате этого ординаты Ъ^ кривой будут
увеличиваться и кривая будет смещаться в ловое положение AiBi (рис. 304),
в то время как линия °п остается стационйрной. Таким образом,
точка пересечения двух кривых смещается вправо, указывая на то,,
что с увеличением скЬрости нагружения критическая температура
растет. Это заключение подтверждается в испытаниях на удар,
которые дают хрупкое разрушение при более высоких температзфах, чем
в статических испытаниях. ч. !
Предположим теперь, что образец подвергается кручению и чхо
-ось образца принята перпендикулярной к одной из октаэдральных
плоскоетей. Текучесть образца при сдвиге начнется приблизительно
при том же значений касательного напряжения, как и при -
испытаниях на растяжение, но соответствующее значение наибольшего
нормального напряжения о„, равного в этом случае наибольшему
касательному напряжению, будет составлять приблизительно половину
значения Од при испытании на растяжение. Следовательно, при
построении диаграммы для испытания на кручение, подобной диаграмме
на рис. 304, мы должны принять значения ординат о^у кривой
приблизительно вдвое меньшими, чем значения для испытаний на растяжение.
В р^у^ьтате этого точка С пересечения кривых будет смещена влево,
и мы заключаем, что при испьаРганиях на кручение критическая
температура должна быть ниже, чем при испытаниях на растяжение. Это
заключение согласуется с опытами.
Рассматривая Далее влияние напряжен^10го состояния на значение
критической температуры, предположим, что равномерное растяжение
по всем трем направлениям накладывается на простое растяжение,
так что мы получаем пространственное напряженное состояние.
Известно (см. предыдущий параграф), что такое наложение не влияет
на значение иаиббльшего касательного напряжения, при котором
начинается текучесть. Однако значен?1е (Jg увеличивается, ординаты Og
кривой, представленной на рис,'/304> увеличиваются, а точка С
пересечения перемещается вправо. Таким образом, критическая таипера-!
тура для принятого пространственного напряженного состояния будет
выше, чем для простого растяжения. Подобное трехмерное
напряженное состояние возникает в над]^езе образца с вллточкой. Такие
образцы имеют более высокие значения t^^, чем гладкие'образцы *).
Фундаментальные идеи относительно критической температуры,
при которой происходит переход от хрупкого li^ пластическому раз-:
*) О более подробных сведениях о напряжениях в канавках см. статью
Е. Ого wan'а в изд. W. М. Murray, Fatigue and Fracture of Metals,
1952.
щ
ИСПЫТАНИЯ НА УДАР
387
руцйгнйю, были развиты Н. Н. Давиденковым и применены к
кристаллическим материалам, особенно к различного рода сталям, Прльзуясь
диаграммой, подобной йиаграмме, изображенной, на рис. 304, он
предусмотрел влияние различных факторов на значение критической
температуры. и показал своими экспериментальными работами, что
предвучисления удралетворительно согласовывались с опытными
фактами *). Для олредбления критической температуры были
использованы испытайй:^ на удар. Так как количество рафты, необходимой
для случая jcpyriKoro разрушения, во много раз меньше, чем для
пластического разрушения, опыты показали при критической темпе-
рату^ре |)е8кое изменение количества погло- ^
щечной энергии. Рис. 305 представляет
результаты испытаний на растяжение при ударе
гладких цилиндрических стальных образцов.
Можно видеть, что имеет место резкое
изменение поглощенной энергий в интбрвале от
—130° др —110°С. -
Изменением процесса тепловой обработки
может варьироваться в значительной степени
беличина зерна стали, и исследование влия- ^
чия размера зерна на величину критической
температуры представит практический
интерес. Ведь известно, ^что с увеличением
размера зерна сопротивление стали отрыву
, уменьшается* Следрвательно, для
крупнозернистых сталей горизонтальная линия для о„'
(рис. 304) будет понижаться, и критическая
температура будет выше, чем для
мелкозернистых сталей. Для того чтобы проверить это заключение, ^ образцы
из среднеуглеродистой стали @,23Уо углерода) были подвергнуты
двум различным температурн«м обработкам. В первом случае
температура была поднята до 1100° С в течение двух часов, а затем
образцы были медленно охлаждены в печи. Во втором случае после
пребывания образцов при; температуре 950° С в течение двадцати
минут, они были охлаждены на воздухе. В этом процессе в
перлам ! случае были получены ^ крупные зерна, во втором — мелкие
8i^Ha. Затем были испытаны на удар Гладкие цилиндрические
образцы, и результаты опытов представлены на рис. 306. Видно, что
критическая температура для крупнозернистой стали была
приблизительно равна —95° С, в то время как в случае мелкозернистой она
была равна — 160° С
-Ш7 -/^ -120 -faff
TeAi/iepamyfia, "С
Рис. 305.
*) См. в книге Н..Н. Д а в и д е н ков а «Динамические испытания металлов»,
1936 и «Вопросы удара при изучении металла*, йзд. Акад. наук, Москва,
1938. Результаты, приведенные в последующем изложении, если нет особых^
указаний, взяты из последней книги.
13*
w
388
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
I
I
I
I
/^
^
i".
/7
ж
.Л
зер/^ucmaff
-2O0-/ffS 420 -во -^О О
Темтрат^ра, "С
Рис. 306.
^О. 00
Было также исследовано влияние размера образца на значение
критической температуры. Но здесь простая диаграмма на рис. 304
не дает ясного представления о результатах опытов. С увеличением
размеров можно ожидать уменьшения сопротивления хрупкому
разрушению, так как вероятность
наличия решающих
несовершенств увеличивается с
увеличением объема*) (см. стр. 331).
Следовательно, при больших
объемах горизонтальная линия
о„ будет понижена на рис. 304,
вызывая смещение точки С
вправо. Но вместе с тем
оказывается, что увеличение ^
объема уменьшает значение а^ (см.
стр. 331), и соответствующее
понижение кривой Qg на рис. 304
повлечет за собой смещение С
в противоположном
направлении. Таким образом, окончательный результат зависит от
относительного значения этих двух факторов. Опыты с гладкими
цилиндрическими образцами показывают, что понижение линии о„ является более
важным, и точка С перемещается вправо, показывая, что критическая
температура увеличивается с увеличением объема образца. Этот
фактор нужно учитывать, кЬгда применяют результаты испытаний над
малыми образцами в процессе проектирования конструкций больших
размеров.
В предыдущем изложении мы рассмотрели только испытания на
растяжение цилиндрических образцов, в которых распределение
напряжений было равномерным. Однако на практике при испытаниях
на удар применяются образцы с надрезами и имеется налицо
концентрация напряжений. Чтобы исследовать влияние неравномерного
распределения напряжений на величину критической температуры,
начнем со случая изгиба гладкого цилиндрического образца. Опыты
на изгиб при статической нагрузке показывают, что текучесть стали
начинается при более высоких напряжениях, чем в случае
равномерного растяжения. Напряжение, соответствующее пределу текучести,
сначала достигается в тонких слоях волокон, находящихся на
наибольшем расстоянии от нейтральной оси, и образование участков
текучести у этих волокон задерживается наличием смежного материала
с более низким напряжением. Последующий затем рост величины предела
текучести кужно рассмотреть, используя диаграмму рис. 304 приме-
1) О распространен|1и критерия Гриффиса на пластические материалы
см. Е. О г о W а п, цит. на стр. 386.
83]
ИСПЫТАНИЯ НА УДАР
389
нительно к испытаниям на изгиб. Ординаты о^ кривой должны
увеличиться, в результате чего происходит смещение точки С вправо.
Критическая температура, полученная из испытаний на изгиб, будет
тогда выше, чем значение, полученное из испытании на растяжение.
Это заключение согласуется с результатами опытов.
Подобные рассуждения можно применить и к случаям
концентрации напряжений, вызываемых выточками и надрезами (см. стр. 254),
причем надо ожидать увеличения ^«р ^^^ стержней с надрезами.
На рис. 307 даны результаты испытаний на удар при изгибе для
тех же двух сталей (мелко- и крупнозернистых), рассмотренных
ранее *) (см. рис. 306). Примененный тип выточки показан на рис. 308.
Сравнивая рис. 306 и 307,
видим, что вследствие на-
?^ личия выточки критическая
t ^ '. ~ "^^^Z^ ^^ температура значительно уве-
^ °^/% /С "' личилась. Мы видим также,
|.
I
о
-2ff0 -ш -/го -т -^0 о HJ ео ш
Темлера/п^ра(°с/
Рис. 307. Рис. 308.
-*
■ ■
jefiffucma/f -^
О
о/^
о
ООр<
о/ ,
ч°
I
о j
1
1щ
-^^»
b/fpi^mo-
j^Hucmaa
■•
что интервал температуры, при котором происходит переход от
хрупкого к пластическому разрушению, гораздо больше в случае
образцов с надрезами, и критическая темйература не так четко
определяется, как для образцов без надрезов./ Статические испытания
образцов с надрезами в интервале ^) перехода показали, что характер
разрушения изменялся постепенно, и часть поверхности разрушения,
которая имела хрупкий характер, увеличивалась при понижении
температуры. В то же самое время количество работы, потребное
дяя того, чтобы произвести разрушение, уменьшалось. Рис. 309
представляет несколько диаграмм нагрузка — смещение, полученных при
статических испытаниях на изгиб образцов с надрезами при различных
температурах. Н. Н. Давиденков предложил принять за критическую
такую температуру, при которой поглощаемая работа при
испытаниях на удар составляет 40Уо наибольшей работы, получаемой
1) См. Н. Н. Д а в и д е н к о в и Ф. Ф. В и т м а н, Журнал технической
физики, Ленинград, т. 7, стр. 343, 1937.
2) Давиденков и Витман, там же.
w
390
МЕХАНИЧЕСКИЕ СВОЙСТВА ^МАТЕРИАЛОВ
1ГЛ. X
70%
-WB'C
при несколько более высокой температуре. Для того чтобы получить
диаграммы нагрузка —смещение при испытаниях на удар, были
сконструированы спещгальные пьезокварцевые динамометры.
После этих 'общих рассуждений рассмотрим теперь ,тип
испытаний на удар, который должен применяться на практике для
определения jf^p. Точное определение t^^ важно
для того, чтобы избежать опасного
положения, при котором критическая
температура материала является
такой же, как рабочая температура
конструкции. Очевидно, что
испытания, на удар при комнатной TeMnie-
ратуре недостаточны, и в
ответственных случаях должна быть проделана
серия испытаний -для ряда
температур. Должна быть построена
кривая перехода, подобная
изображенной на рис. 307, и по ней должно
быть определено ^кр« Испытания на
Ладй^лиир
О)
Смещение
Смещеше
i>)
*^ff''C
Смеще/^ие
Рис, 309.
изгиб стержней с надрезами пред-
пoчтитeль^^ы,v так как они дают
переходную "кривую при высоких
температурах и этим самым уменьшают
количество работы, затрачиваемой
на, проведение опытов при очень
низких температурах. Если
критическая температура определена и^ известна рабочая температура- ^о
конструкции, то за меру безопасности Н. Н. Давиденков рекомендует
принять отношение n
-^Ц%. (а)
где,7"о и Ткр являются абсолютными температуралии,
соответствующими ifo и ^кр« Это отношение уменьшается и Т1риближается к нулю;
когда Те приближается к Г^р. Результат говорит о весьма опасном
положении, при котором малый внешний импульс может вызвать
хрупкое разрушение конструкции. С другой стороны, отношение
приближается к единице, когда Т^р приближается к * абсолютно>4у нулю.
В этом случае хрупкие разрушения не будут иметь места, и
необходимо лишь -в1мбрать размеры конструкции так, чтобы она была
достаточно прочной для несения нагрузки без пластической
деформации.
При выборе .приемлемого значения отношения (а) для
использования при проектировании нужно рассмотреть условия, которые
действительно существуют б конструкции. Такие факторы, подни-
841 УСТАЛОСТЬ МЕТАЛЛОВ 391
мающие напряжение, как резкие входящие углы и несовершенства
при сварке, содействуют увеличению ^^р температуры. Увеличение
размеров конструкции имеет то же влияние. Для того чтобы иметь.
дост|аточную безопасность и сохранить отношение (а) по
возможности большим, нужйо использовать материалы с низким значением
^кр. KjiHTH4ecKajiTeMttepaTypa может быть понижена не только путём
изменения химичёекрго содержания материала, но тАкже надлежащей
тепловой d6j)i^iTK<^; Мелкозернистая cta^b имеет более низкое
значение i^i,.чем крупнозернистая сталь. В последнее время проявился
3Ha4RTeiiiJeMe интерес к хрупкому характеру металлов при низких
температурах, и мы можем ожидать усовершенствования наших
знаний пЪ этому важному преди^ту *).
84. Усталость металлов *)
Части машин часто подвергаются действию переменных усилий^
поэтому важно знать прочность материалов при таких условиях
работы '). Хорошо известно, что под действием повторной нагрузки и
разгрузки или под действием знакопеременных напряжений материалы
разрушаются п|ри напряжениях меньших, чем предел прочности
материала в условиях его ста'тическвго н^ружения. Величина ycилияi
необходимого для того, чтобы произвести разрушение, уменьшается с
увеличением числа циклов напряжений. Это явление уменьшения со- ,
противляемости материала повторным напряжениям называется уста-
лостьЮу а испытание материала путем приложения таких напряжений
называется испытанием на выносливость.
■Если о^^^ и а^}д представляют наибольшее и наименьшее зна-
чейий повторного напряжения, то алгебраическая разность
*) Библиографию ПО этому предмету можно найти в книге: Н. Н.
Дави д е нк о в, Вопросы уда1^а при изучении металлов, 193iS. См. также статью
С. W. М а с G ге g о г' а в издании W. М. Murray, Fatigue and Fracture
of Metals, стр.-229, 1952. ^
,*) Этот предмет разобран у Н. J- О о u gh. The Fatigue of Metals, London,
Ш4 и H, F. Moore and J, B. Komraers, Tht Fatigue of Metal, New
Yor^i, 1927. Эти книги содержат библиографии по предмету. О
дополнительных сведениях см. литографированное издание лекций Н, J. Opugh'a в Мас-
caiysetcKOM технологическом институте, ле^^о 1937. См. т^1кже R. Саха и d.
Fatigue qI Metals (английский перевод), London, 1953, Battelle Memorial
Institute, Prevention of the Failure of Metals under Repeated Stress, New York,
1941, M. Ro§ und Л. Eichinger, Die Bruchgefahr fe^er Кбгрег bei wie-
derholter Beanspruchung Ermiidung, Eidg. Materialpriifungsanstalt (Zfirich) Ber.,
№ 173, 1950. -
*) J. O. Roos нашел из испытаний большого количества разрушений
частей машин, что W^\^ можно приписать усталости; см. Ргос. Internat
Assoc. Test. Mat., 1912.
mfi'
392
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
называется диапазоном напряжения. Цикл вполне определяется,
если даны диапазон • и наибольшее напряжение. Среднее напряжение
равно
В частном случае симметричного цикла напряжений о =—о
(Ь)
max'
i^==2o^^^ И а„ = 0. Любой цикл переменных напряжений можно
получить путем наложения симметричного цикла напряжений на
постоянное среднее напряжение. Наибольшее и наименьшее значения
переменного напряжения тогда определятся следующими ^формулами:
2 •
max
'm
\ 9 »
mill'
'm
(С)
Существуют различные способы приложения нагрузки п'ри
испытании на выносливость. Образец может подвергаться осевому
растяжению и сжатию, изгибу, кручению или некоторым их сочетаниям.
Простейшим способом деформирования является знакопеременный
изгиб. На рис. 310 показан общепринятый для испытания на усталость
/тт
SFmm-
iJ77,^
7
фммрад
Шмм —-
1
1
Ц^ми £Z/mm
Рис. 310.
стержень *) в форме консоли. Поперечное сечение образца изменяется
по длине таким образом, что наибольшее напряжение имеет место
между сечениями w/г и тф^ и практически постоянно в этой
области. Влияние концентрации напряжений исключено с помощью
выкружки' большого радиуса и увеличением диаметра стержня вблизи
выкружки. Нагрузка JP^всегда направлена вниз, а образец вращается
с постоянной скоростью. Поэтому напряжение изменяет знак через
каждые полоборота, и число циклов напряжения равно числу
оборотов машины. Этот цикл напряжений является строго симметричным,
знакопеременным при среднем напряжении, равном нулю,'и диапазоне,
равном удвоенному о^^^^.
Взяв несколько образцов и испытав их при различных грузах Р,
можно получить кривую, подобную показанной на рис. 311. Здесь
*) См. McAdam, Chem. and Metallurg., Engrg. 1921.
84]
УСТАЛОСТЬ МЕТАЛЛОВ
893
а представлено как функция числа циклов п,- необходимого для
того, чтобы произвести излом образца. Изображенная кривая была
получена из опытов над образцами из мягкой стали. Вначале а^^^
уменьшается быстро с увеличением п, но после примерно четырех
\2Ш
I
Ч
%Ш7
^ff?ax
\
•
V
'
п
О
Рис. 311.
S
Ю
миллионов циклов нет уже какого-либо заметного изменения о^^^ и
кривая асимптотически приближается к" горизонтальной линии о^^^ =
= 1900 KzjcM^. Напряжение, соответствующее этой асимптоте,
называется Пределом выносливости материала. Теперь в обычной практике
I
II
=^1
й>
/пах
2ШО
Wff7
/SSJ
JffOO
^
10
Рис. 312.
70'
/О
/7
в
испытаний ^на выносливость вычерчивают о^^^ как функцию \gn. В
этом приеме величина предела выносливости обнаруживается
определенным надломом кривой *). Пример такой кривой показан на
рис. 312.
*) Результаты испытаний на усталость обычно весьма разрознены.
Чтобы улучшить их изложение и истолкование, некоторыми исследователями
было рекомендовано использование статистических методов. См. Симпозиум
по статистическим аспектам усталости, Американское общество испытания
материалов, 1951.
Щ¥
394, МЕХАНИЧЕСКИЕ СВОЙСТВА. МАТЕРИАЛОВ (ГЛ. X
Существует значительная разница меж^у разрушениями мягких
стааьиых ображов, испытанных статически, и тех же образцов, ис-
пытанйык при првторно переменных напряжениях. В Первом случае
значительное пластическое течение предшествует разрушению и по-
ве]рхности разрушенного сечения имеют вследствие большой шы-
тяжки кристаллов шелковистую волокнистую! структуру. Трещина
же усталрсти выглядит совершенно иначе. Она начинается в
некоторой точк^ материала из-за местного дефекта или концентрации
напряжений, вызванной резким изменением поперечного сечения. Раз
образовавшись, трещина распространяется вследствие концентрации
напряжений на ее концах. Это расп1Гостранение прогрессирует под
действием переменнь^х напряжений до тех пор; пока в поперечном
сечении площадь не уменьшится до такой степени, что оставшаяся
ее часть разрушится !^незапно под влиянием |1агрузки.
. Обычно можно различить две зоны в изломе усталости: одну,
возникшую при постепенном развитии трещины, и другую,
образовавшуюся при внезапном разрушении. Последняя зона походит на
излом при испытании на растяжение образца с глубокой узкой
выточкой (см. стр. 362), в которой форма Ъбразца препятствует сколь-
женинз, и поэтому разрушение происходит в результате преодоления
сил сгУепления. Это разрушение имеет вид хрупкого^ если даже
материал является пластичнйм. В сл)^ае испытания консольных
образцов (рис. 310) наибольшие напряжения будут is наружных волокнах.
/Следовательно, трещина усталости обычно начи1^ается на периферии
и распространяется к центру. Там^ где имеется концентрация
напряжений вследствие выточек, выкружек или отверстий, трещина обычно
начинается в наиболее высоко напряженном месте и распространяется
от него в , стороны. В таких случаях на поверхности излома видны
концентрические относительно этой начальной точки кольца. Это
Bepbitia общий тип разрушения в частях машин, которые
подвергаются действию переменных напряжений. Таким образом, очевидно, что
хрупкий тип усталостного разрушения обязан с]воеобразному
механизму разрушения, но не кристаллизации материала, как думали
' ранее. ■ '' - \
В. Фэрбэрн первый установил на основании опытов над балкой
из сварояного^ железа натуральных размеров*), что viuQeTOi
предельное напряжение, которое мокно прикладывать безопасно
бесконечное число раз. Хотя это нельзя доказать непосредствённ11м опытом,
все опытные данные ^) подтверждают это положение, и теперь
считается общепринятым, что для сталей и сплавов железа имеется
определенный ^пре/1ёльный диапазон напряжений, действию которого мож-
*) См. W. Fa it bairn, Phil. Trans. Roy. Soc. (London), 1864.
*) Бой>шбе число кривых испытан1^й на выносливость было построено
О. Н, Basquin, Proc. Am. Soc. Test. Mat., т. 10, 1910.
841
УСТАЛОСТЬ МЕТАЛЛОВ
395
но ссйтротивлятьсй в течение: бесконечно большого числа циклов без
разрушения. »
Практически очень важно знать, как быстро кривая о — п
приближается к асимптот©;^ так как это определит число циклов, необхо^
дймых для уртанбвленйй предела выносливости. Опыты пока^ыйают^
что для /черных металлов предел вцносливости можно усйнбвить
с достаточной^ т^^^ на основании 6—10 миллионов циклов.
Для цветных металлов, например алюминия, нет определенного предела
выносливости, и ординаты o-yw кривой уменьшаются беспредельно
с возрастанием числа циклов.
Из предыдущих рассуждений следует, что определение предела
вУН()Сливости для любого материала требует большого числа испы-
taHHfl и значительного вре-. „_„^ '
мени. Следовательно,
практический интерес заключается
в том, чтобы установить за-~
висимость между пределом
выносливос*и и другими
механическими свойствами,
которые можно определить при
помощи статических
испытаний. Но, хотя накоплено
большое количество
опытных данных, все- еще. нет
возможности установить
такую связь*). В грубом
приближении предел
выносливости для черных металлов
при симметричном цикле на- V .
пряжений может быть принят равным от 0,40 до 0,55 предела г^очно-
сти, полученного обычным испытанием на:растяжение. Когда имеёлС делЬ
с 1йатериалами, Механические характеристики которых очень хорошо
известны, например с углеродистыми сталями, оценки этого, типа мо*
гут считаться достоверными. В противном случае такие оценки могут
ввести в заблуждение, и необходимо пользоваться непосредственными
испытаниями на выносливость. Некоторые результаты испытаний на
выносливость сталей даны-на рис. 313, а также в табл. 26 в конце
главы. ^
В большинстве случаев испытания на выносливость выполняются
для симметричного цикла напряжений (отах = —a^min)» ^ то время
как во многих случаях расчета машин имеют дело с напряжениями,
изменяющимися не по симметричному циклу. Необходимо знать
пределы выносливости при этих переменных напряжениях. Вёлер — первый
ttuuu
1
1& г^ла
«s/j-w
/
'^-
.в
^ с ■
с**
о
. .>
вы*
о
л
в>
, ^
\
9у
о
.-„
,_с.^
-
-^
ff гб?о S3^ вт mew ~mff
npeffeff протеста пра /^ааттЖешиСкг/ем^)
- • Рис. 313. ,
*) См. книгу Н. J. G о U g h'a,. цит. на стр. 391; см. его лекции, там же.
IF
396
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
экспериментатор, систематически изучивший явление усталости *). Он
показал, что диапазон напряжений R, необходимый для^ого, чтобы
произвести разрушение, уменьшается с увеличением среднего
напряжения 0^. На основании этих опытов и работы Баушингера ^) Гербер
предложил ^) параболичес1^ий закон, свйзываюш,ий диапазон
напряжений R й среднее напряжение о^. Эта связь изображена
параболическими кривыми на рис. 314, где среднее напряжение и диапазон
напряжений выражены в долях предела прочности. Диапазон
напряжений оказывается наибольшим при симметричном цикле напряжений
Рис. 314.
(Ода = 0) и прибли^каетсй к нулю, когда среднее напряжение
приближается к пределу прочности. Если предел выносливости для
симметричного цикла напряжений и предел прочности известны, то предел
выносливости для любого несимметричного цикла напряжений можно
получить из приведенных кривых. Другие исследования показывают,
что не существует общего закона, связывающего . среднее
напряжение и диапазон напряжений*). Например, имеются материалы"),
для которых зависимость между R, и i^ представляется более
точно пунктирными линиями (закон ГуДмана) на рис. 314, а не
параболами. / -
Прямые О А и ОБ на рис. 314 имеют уклон, равный 2, и
определяют область АОВ^ в которой напряжение изменяет знак в
течение цикла. Вне этой области напряжение всегда' остается
растягивающим или сжимающим. Определенные опытным путем значения вну-
^) А. Wohler, Z. Bauwesen, тт. 8, 10, 13, 16 и 20, 1858—70. Оценка этой
работы на английском языке дана в Engineering, т. 11, 1871; см. также
Unwin, The Testing of Materials of Construction, 3-е изд., 1910.
^)J. Bauschinger, Mitt. Mech.-tech. Lab. Munchen, ^f^ 13 и 25.
^) W. G er b e г, Z. bayer. Architekt Ind.—Ver., 1874; см. также Unwin,
Elements of Machine Design, т. 1, гл. 2.
•*) Широкое обсуждение этого вопроса можно найти в книге Н. J. Gough'a,
цит. на стр. 391. См. также его лекции, там же.
») См. статью В. Р. Н а i g h, J. Inst. Metals., т. 18, 1927.
84]
УСТАЛОСТЬ МЕТАЛЛОВ
397
три области лов обычно лежат между параболами
и,соответствующими прямыми *). Если напряжение всегда растягивающее или всегда
сжимающее, значения диапазона напряжений R, как найдено опытом,
лежат иногда не только ниже парабол Гербера, но даже -ниже и
соответствующих прямых.
Вместо того чтобы представлять диапазон напряжений R как
функцию а„ (рис. 314), иногда вычерчивают а^ах и'Ощш в функции
о„ (рис. 315). Напряжения а^ах и а^щ получаются из уравнений (с)
А^лг. ^/77//7 (^<г/смг)
4^
Рис. 315.
И изображаются графиком путем добавления ± f?/2 к- ординатам
прямой линии А ОБ, наклоненной под углом 45°. Вертикальная линия,
проходящая через точку О (рис. 315), соответствует симметричному
циклу напряжений. Вертикаль, проходящая через точку Д
соответствует пульсирующему растягивающему напряжению, при котором
нагрузка изменяется от нуля до максимума и затем возвращается
к нулю.
Подобно этойТу, вертикальная линия, проходящая через Е,
соответствует пульсирующему сжимающему напряжению. Точка Л
представляет предел прочности материала при растяжении, а точка
*) Некоторые опыты с мягкой сталью указывают на то, что среднее
напряжение о^ имеет малое рлияние на величину диапазона напряжений R.
См. лекции Н. J. Gough'a, цит. на стр. 391, и его статью в J. Appl.
Mech., т. 17, стр. ИЗ, 1950.
Щ¥
398
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
{ГЛ. X
В — предел прочности при сжатии. Кривые для Отях и о^ш
Представляю^ предельные состояния для переменных напряжений. Если
точки, соответствующие некрторому .действительному переменному
напряжению, лежат внутри площади AEBDA, то материал может
п|)отивостоять этому напряжению бесконечное число циклов без
разрушения. Кривые.для Отах и а^ги (рис, 315) получены из
параболической кривой, представленной на рис.-314. Но, как упомянуто
ранее.^ парабола замещается во многих случаях Двумя наклонными
линиями, и область безопасности на рис. 315 тогда получается в
виде параллелограмма y4FfiGA.
O„^(,aemfS0a<i/CMi
Omt^^^ff^fff/eMi
Рис. 316.
Рис. 317.
В. предыдущем изложении предполагалось, что трафик диапазона
напряжений является симметричной кривой, например в виде
парабол рис. 314'^ однако многие опыты показывают,, что диапазон нап-
рязкений зависит не только от величины, но также и от знака
среднего напряжения-<j^. Когда'*^то напряжение является сжимйющим, то
материал |йожет противостоять большим значениям,- диапазона
напряжений, чем R том случае, когда оно является растягивающим. Кроме
того, часто предел прочности при сжатии Од;,^^ выше предела
прочности при растяжении Опч.раст. Тогда вмбсто симметричных
парабол (рис. 314) мы получаем несимметричные кривые*), и область
безопасности для пластического материала имеет форму, показанную
на' рис. 316. Разность между Опч.раст. и Опч.сж '1)собенно велика
для хрупких материалов, и график области безопасности имеет большую
выпуклость на стороне сжатия, как показано на рис. 317 для
чугуна*).
О Ом. статью R. Е. Peterson'ae Fatigue лпA Fracture of Metals, 1952.
^) A. Pomp und M, Hem pel. Mitt. Kaiser-Wilhelm Inst. Eisenforsch.
(Dfisseldorf), T. 22, стр. 169, 1940.
85]
УСТАЛОСТЬ МЕТАЛЛОВ ПРИ СЛОЖНОМ наТпряжбн, состоянии dQQ'
85. Усталость металлов при сложном напряженном состоянии
Большинство наших опытных сведений по усталостной прочности
материалов получено для случая одноосного напряженного состояния»
как, например, в. испытаниях на изгиб вращающихся образцов. Но
в практических задачах мы часто встречаем случаи действия сложнзах
напряжений, и весьма важно для Ьтпх условий также знать предед
выносливости. ;*1тобы получить данные об устал|остной прочности
♦Ш?
I
I
^ffTlff
i
4
I ffw
у
1,.
\ 0
теория J
- ^
/
J ■ 0
У' /^/сасстеммых
/ напря^етй
-
о Wff 2ff7ff ^OOff S330 еб70
Лреде/7 A/f^cffiz/focmu при useudef/ta/cM'J
Рис. 318. ,
различных пластичных материалов при чистом сдвиге, были
проделаны испытания на' кручение, в которых угол закручивания был
знакопеременным. Результаты некоторых из этих испытаний показаны i)
Й9 рис. 318. С целью сравнения предел'выносливости при изгибе
эдесь принят за абсциссу, а предел выносливости при сдвиге — за:
Ьрйинату. Видно, что отношение этих пределов для всех испытанных
материалов весьма близко к 1/^3. Это значение для отношения
пределов текучести при изгибе^- и сдвиге (см. выражение B99)) дает
теория наибо.льшей энергии изменения формы.
*) Этот рисунок взят из книги: I?. Е. Peterson, Stress Concentration
Dfesign Factors, New York, 1953. -
ш
400
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
(ГЛ. X
Испытания на усталость под действием сложных напряжений,
вызываемых одновременным действием переменных изгиба и кручения*),
были также проведены, и результаты показаны ^) на рис. 319. Здесь
снова результаты испытаний хорошо согласуются с теорией
наибольшей энергии формоизменения, что и можно было ожидать,
поскольку сдвиг обычно предшествует развитию трещины усталости ^).
I
Sf
I
I
• «r
■
о
— —--
^'^^
Эшрге/пшескш
теория
^формоизменения
о
Teapuff иаибо/я,ших \ *s
^
Напр/гженая лра изгибе
/7реде/г вьт^ю^ибости /три лзаий?
Рис. 319.
QS
W.
Для того чтобы получить уравнение для вычисления предела
выносливости при одновременном действии изгиба и кручения следует
лишь подставить в соответствующее условие текучести (см.
уравнение B98)) значение предела выносливости а^ для знакопеременного
изгиба вместо а_, что дает
a2-f-3T2=^a^.
(а)
Соответствующий эллипс показан на рйс. 319, из которого видно,
что результаты испытаний хорошо согласуются с уравнением.
Другие испытания*) на усталость при двухосном растяжении или
растяжении со сжатием для отношения oi/og, остающегося
постоянным в течении цикла, -также; удовлетворительно согласуются с тео-
1) См. Н. J. Go ugh and Н. V. Р oil аг d,% Engineering, т. 140, стр. 566,
1935. См. также Nisihara and Kawamoto, Trans. See. Mech. Engr.
(Japan), T. 6, стр. 2, 1940.
») См. R. E. Peterson, Proc. Soc. Exp. Stress Anal., т. И, стр.- 118, 1943.
3) Н. J. Go ugh, Proc. Am. Soc. Test. Mat. т. 32, стр. 3, 1933.
*) A. F. М a i e r, Stahl u. Eisen, т. 54, стр. 289,1934; С. W. М a с G г e g о г,
J. Appl. Mech., T. 16, стр. 269, 1949.
8Ъ] УСТАЛОСТЬ МЕТАЛЛОВ ПРИ СЛОЖНОМ НАПРЯЖЁН. СОСТОЯНИИ 401
рией наибольшей энергии формоизменения. Таким образом, мы
можем воспользоваться для определения предела выносливости в случае
симметричного цикла напряжений следующим уравнением (см. стр. 378):
of —OiOaH-o|=:o;, (b)
в котором о,. — предел выносливости для одноосных напряжевных
состояний. Предполагая, что Oi]>oa и пользуясь обозначением
<j2 = aoi, из уравнения _ (Ь) получаем
В случае пульсирующих напряжений, в которых напряжение
изменяется от нуля до некоторого наибольшего значения, соответствующее
одноосное пульсирующее напряжение а^^^ должно быть подставлено ^)
в уравнение (с) вместо а^
Чтобы установить предельные условия в случаях трехосного
напряженного состояния, воспользуемся уравнением B96). Подставляя
02 = aoi и 03 = aiOi, получаем следующее уравнение для симметрич-'
дого цикла напряжений:
<3i |/l—а — ai-{-ci.^-\-9,l — aai=a^. (d)
Из этого уравнения можно вычислить предельное значение oi для
любых данных значений а и а^.
Имеется лишь небольшое количество достоверных сведений,
которые можно приложить к пр^1мерам, в которых отношения ai/a^ и
oi/оз не остаются постоянными во время цикла нагружения. Гаф
исследовал *) случай, в котором статический изгиб и кручение были
наложены на симметричный цикл напряжений. Было найдено, что
влияние моментов статического нагружения на, предельные значения
переменных моментов было весьма мало') и что для вычисления
предельных значений переменных напряжений Ъсожно воспользоваться
эллипсом того же типа, что и на рис. 319. Оси эллипса равны диапаг
аонам переменных напряжений*) при изгибе и кручении. Диапазоны
находятся в соответствии с приложенными статическими
напряжениями, так как последние являются в этом случае средними
напряжениями. ■ ,
*) Если не имеется опытных данных, то для определения <з^^^^ можно
воспользоваться параболой Гербера или законом Гудмана.
2) Н. J. Go ugh, J. Appl. Mech., т. 17, стр. ИЗ, 1950.
') Использованным материалом был сплав стали при высоком значении
отношения 'зфпч-
*) Эти диапазоны можно взять из рис. 318, если пределы выносливости
для изгиба и кручения определяются порознь опытным путем.
m
402 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. Г
■ L . ' ■ ■ ■
Для хрупких материалов при вычислении предельных сложных
напряженийКот усталости применяется Теория Мора. Если эти напря-)
жения имеют один и тот же йнак, нужно рассматривать только
численно большее напряжение! Его предельное значение можно получить
Hg диаграммы одноосных напряжений, показанной на рис. 317 для
чугуна. Если напряжения имеют противоположный знак, то мы можем
воспользоваться уравнеиирм (h) стр. 382, выведен|шм для
статических нагрузок. Обозначая численно большее главное Напряжение
через Oj, а меньшее через 02 = —aoj, получаем
^'пч. еж
д —а "пч. еж
* '^'^• раст о ^ Л- по *
"пч. ьж Т^ ""пч.рает
Теперь можно допустить*), что для предельного значения о^ при пе-
ре11<енных напряжениях будет пригодно
Oi=:0 ^nSrSL . /еУ
^ г в -i- «а ' ^ '
V "вч.ежт^ ""^пч.рвает
где о^ — предел выносливости для одноосного напряженного
состояния. Применяя это уравнение к улучаю чистого сдвига (а;=1),
получаем
т. = о.
о,
ПЧ..СЖ
. '^ '' ''пч. ок "Г ®пч. рает
которое удовлетворительно со1'ласуетея с результатами испытаний ^)..
Имеются лишь скудные сведения относительно усталостной
прочности хрупких материалов для случаев, в которых статические
напряжения накладываются на переменные напряжения» Одноосные
испытания по пульЪ!рующему циклу, в которых напряжение меняется,
от нуля до максимума, были проделаны с чугуном®). Испытания
были, произведены как при растяжении, так и при сжатии и
показали, что предельные значения напряжений для этих двух случаев
(обо^значим их через Ор.рарт ** °п.сж) находятся в том же отношении,,
что и Ялч рас/*'пч. еж "Р^ сйтических йспытанйях. Таким образом, для
пульсирующего крутящего момента, применяя те же рассуждения,
что и :в предыд)щем случае, мы можем написать
•Сг
^яч.сж
'п ^прает о -1_ о
"пч.еж г "пч.раст
•Для чугуна Опч.еж/°пч.рает находится обычно В пределзх между 3 и 4,
*) Это равносильно предположению, что влияние Og на значение -о^
одинаково как при усталостном, так и статическом испытаниях.
^) Н. J. Go ugh and Н. V. Pollard, Proc. Inst. Mech. Engrs. (London),,
T. 131, стр. 1 и т.,132, стр. 549, 1935.
3) Ij. F. М о о г е, S. W. L у о п and N. Р. I п g 1 i s, Univ. of Illinois Eng,.
Exp. Sta. Bull, № 164,1927. Cm. также статью A. Pomp'a und M. Hempel'a,
ЦИТ. на стр. ^8.
«tej ФАКТОРЫ. ВЛИЯЮЩИЕ НА ПРЕДЕЛ выносливости 403
i
86. Факторы, влия|дщие на предел, выносливости
После общего обсуждения вопроса в предыдущих параграфах рас-
с1«сугрим теперь различные факторы, которые )влияют на результаты,
получаемые при испытании на выносливость. v
Влияние холодной обработки. При анализе поведения
пластичных металлов й процессе вытяжки, волочения и прокатки при
комнатной температуре было отмечено (см. п. 78), что благодаря
холодной обработке материал становится более жестким, предел текучести
повышщется> несколько увеличивается и предел прочности.
Следовательно, мы можем ожидать, что холодная обработка будет также
влиять и на предел выносливости материала. Опыты, проделанные
со стальными образцами, подвергнутыми холоднЬйгвытяжке *), показада,
что умеренная степень вытяжки вызывает некоторое увеличение
предела выносливости. При дальнейшем увеличении xofloj^noft обработки
можно достичь положения, при "котором имеет место падение пре--
дела вынослийости вследствие перегрузки *). Улучшение состояния хо-.
лодно обработанного материала можно получить, подвергнув материал
пйсяе холодной обработки слабой термической обработке, например,
оставив материал в кипящей воде на некоторое время.
'Влияние перенапряжения и недонапряжения. Ъыла лтроделацы
опыты, в которых циклы напряжений выше предела выносливости
■были приложены неоднократно, до начала обычного испыта[нйя на
выносливость. Это перенапряжение образцов показало, что имеется
предельное число циклов перенапряжения, зависящ|^ от величины
перенапряжения. Перенапряжение с числом циклов ниже предельного
не оказывает влияния^ на предел выносливости, в то время как
превышение этого числа влечет уменьшение предела выносливости.
Построив график з1ависимости перенапряжения от предельного числа
циклов, получим кривую ущерба^) для испытываийого vматериала.
В качестве примера на рис. 320 показана кривая*) для материала,
имеющего предел. выносливости, равный 2340 кг(см\ Площадь ниже
этой кривой определяет все те степени перенапряжения, которые не
причиняют ущерба (повреждения).
*) Н. F. М о о г е iand J. В. К о m m е г s, Univ. of Illinois Eng. Exp. Sta.
Butl,, № 124, 1921; O. J. Horger, Trans. A. S. M. E., т. 57, стр. A-128, 1935.
В опытах Мура углеродисто-стальные образцы @,18<»/о углерода) были
подвергнуты вытяжке на Во/о и \2f>lo. В ойытах Хорджера был применен тот же
процент вытяжки,/ но со сталью, содержащей 0,48<»/о углерода.,
*) См. Н. F. Moore and Т. М. Jasjper, Univ. of Illinois Eng. Ехр^ Sta.
Bull., № 136 и Rr;M. Brown, Trans. Inst. Engrs. Shipbuilders Scot, 1928.
84 H. J. French, Trans. Am. Soc. Steel Treat, т. 21, стр. 899, 1933 и
Н. W. R u s s e И and W. A. W e 1 с к e r, Proc. Am. Soc. Test Mat, т. 36, 1936.
\*) См. H. F. Moore, Metals and Alloys, т. 7, стр. 297, 1936. О
библиографии по этому предмету см. Battelle Memorial Institute, Prevention of the
Failure of Metals under Repeated Stress, New York, 1941.
ш
404
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
|ГЛ. X
Рис. 320.
Кривая ущерба имеет практическое значение для частей машин,
которые нормально действуют при циклах напряжения ниже предела
выносливости, но подвергаются время от времени циклам
перенапряжения. Если величина
перенапряжения известна, то
безопасное »^исло циклов
перенапряжения легко
получить из кривой ущерба *).
По кривой на рис. 320
можно видеть, например,
что циклы перенапряжения
it: 27@0 KzjcM^ не
производят повреждения, если числа
ЦИКЛОВ перенапряжения
меньше чем 100 000.
" В области
проектирования самолетов вопрос об
усталостной прочности становится более сложным, так как части в
работе аодвергаготся циклам напряжений различных интенсивностей^
При проведении необходимых испытаний на усталость применяются
статистические методы. На основании измерений напряжения и
ускорения, проделанных в полете, возможно установить вероятное число
циклов каждой интенсивности. Затем производятся испытания на
усталость, в которых интенсивность напряжения изменяется согласно
статистическим ^1анным ^).
Производя оЛыты на выносливость при нагрузке, несколько
меньшей предела выносливости, а затем увеличивая'^е малыми порциями,
можно повысить предел выносливости. Это явление называется
влиянием недонапряжения. Величина, на которую можно повысить
предел выносливости таким щт&л, зависит от материала^). Для мягкой
стали эта величина иногда превышает ЗО"/© первоначального предела
выносливости, в то время как на железо Армко и медь недонапряже-
ние практически не окайы^ает влияния. ^
Влияние частоты. Воздействие частоты циклов было также
изучено при испытаниях на выносливость, но заметного влияния не
наблюдалось^ до частоты около 5000 циклов в минуту. Для более
») В. F. Langer предложил формулу для вычисления числа циклов
перенапряжения, которому часть машины может противостоять до разру-
шенид. См. J. Appl. Mech., т. 4, стр.,А-160, 1937. См. также М. А. Miner,
там же, т. 12, 1945. „ ,, „ j j п. t^ i.
2) О библиографии см. статью: Н. L. D г у d е п^ F. V. Ro d е and Р. К и h п
в изд W. М. Murray, Fatigue and Fracture of Metals, 1952, см. также
A. М. Freudenthal, Proc. Am. Soc. Test. Mat., т. 53, стр. 896, 1953.
3) Н. F. М о о г e and Т. М. J a s p e r, Univ. of Illinois Eng. Exp. Sta. Bull.,
jsfe 142, 1924; J. B. К о m m e r s, Engrg, News Record, 1932.
86] ФАКТОРЫ, ВЛИЯЮЩИЕ НА ПРЕДЕЛ ВЫНОСЛИВОСТИ 405
ВЫСОКИХ частот было найдено некоторое увеличение наблюдаемого
предела выносливости. Очень интересные опыты такого рода были
проделаны К. Ф. Дженкином *). Увеличивая частоту свыше миллиона
циклов в минуту, он нашел увеличение предела выносливости более
чем на ЗО^/о для так^х материалов, как железо Армко и алюминий^
Чтобы получить эти высокие частоты, Дженкин применил
вынужденные колебания малых образцов. Машина, вращающая образец, была
использована Г. В. Кроусом ^) для высокоскоростных испытаиий при
30 000 циклов в минуту. Для алюминия и латуни он нашел при этой
скорости увеличение предела выносливости на 8у<).
Влияние температуры. Выше мы рассматривали испытания на
предел выносливости, сделанные при комнатной температуре. Однака
имеются случаи, когда материалы подвергаются действию циклических
напряжений при низкой температуре, как, например, некоторые части
самолетов. Наоборот, в паровых турбинах и двигателях внутреннего
сгорания, материалы подвергаются действию очень, высоких те^пера-^
тур. Следовательно, испытания на выносливость при низких и
высоких температурах имеют практическое значение. Сравнительные ис-^
лытания на выносливость, проделанные при -f~ 20° С и — 40° С ^) с
^монель-металлом, нержавеющей сталью, никелевой сталью и хромо-
молибденовой сталью показали во всех случаях увеличение предела
выносливости с уменьшением температуры. Подобные выводы были
также получены для других материалов*).
Испытания на выносливость при высоких температурах,
проделанные с различного рода сталями на машинах, вращающих образец %
а также на машинах, производящих знакопеременные осевые
напряжения ^), указывают, что вплоть до 300-5-400° С температура не окаг
зывает большого влияния на предел выносливости. Наибольший предел
выносливости обычно получается в промежутке от 300° С до 400° С,
между тем как от 100° С до 200° С предел выносливости обычно
несколько меньше, чем при комнатной температуре. Опыты также
показывают,, что кривые о—п не приближаются к своим асимптотам
так быстро, как при комнатной температуре, и что для определения
величины предела выносливости требуется более чём 10'циклов.
Усталость при коррозии. Явление усталости при коррозии также
имеет практическое значение. Этот термин применяется для обозна-
*) С. F. J en к in, Proc. Roy. Soc. (London), A, т. 109, стр. 119, 1925-и
С. F. Jen kin and O. D. Lehmann, там же, т. 125, 1929.
2) О. N. К г о u s e, Proc. Am. Soc. Test. Mat, т. 34, 1934.
3) H. W. Russel and W. A.Welcker, там же, г. 31, стр. 122, 1931. См.
также Nat. Advisory Cottim. Aeronaut. Tech. Notes, X» 381. 1931.
*) W. D. Boone and H. B. W i s h a r t, Proc. Am. Soc. Test. Mat., т. 35,1935.
^) H. F. Moore and T. M. Jasper, Univ. of Illinois Eng. Exp. Sta. Bull.,
№ 152, 1925 и H. F. Moore, S. W. Lyon and N. P. Inglis, там же,.
№ 164, 1927. '
«) Н. J. Т a p s e 11 and J. Bradley, J. Inst. Metals, т. 35, 1926.
шм
406 ' »1ЕХАНЙЧЕСкЙЕ fcBOftCtBA МАТЕРИАЛОВ , [ГЛ. X
"нения одновременного действия коррозии и усталости. В 1917 г. Хэг')
опубликовал результаты некоторых очень интересных испытаний на
выносливость латуни, в которых он нашел понижение предела Ьы»-
йосливости под де|1ствием переменных усилий, когда образец
подвергался действию соленой воды, аммиака или соляной кислоты. Он
также указал, что вредное действие аммиака на латунь не
проявляется, если не было ©дновременного воздействия разъедающих
веществ и переменных усилий.
Дальнейший прогресс в исследовании устйлости п^)и коррозии
^ыл достигнут Мак-Адамом *),^ который исследовал одновременное
действие коррозии и усталости на различные металлы и сплавы. Эти
испытания показали, что в большинстве случаев сильная коррозия;
предшествовавшая испытанию на выносливость, гораздо менее вредна,
^ем слабая коррозия, которая имеет меЬто одновременно с
испытанием. Испытания бЬли проведены на сталях с различным содержанием
углерода, имеющих пределы. выносливости ^) в симметричных циклах
цапряжений йт 1400 до 2800. iKzfcM\ Когда ббразцы при испытаниях
-были подвергнуты действию пресной воды, пределы выносливости
значительно уменьшились, варьируясь от 1120 до 1400 кг/смЬ Эти
пониженные пределы выносливЬсти называются пределами усталоетИг
при иоррозии. Испыташя йоказали, чт|0, в то^ремя как при испытаний;
на воздухе предел выносливости стали растет прирлизительно,
пропорционально росту предела прочности, результаты, полученные при
испытаниях в пресной воде, оказываются ийыми. Предел выносли-^
«ости при коррозии стали, имеющей углерода более 0,25Уо, не растер
после горячей обработки*), а может даже уменьшиться. Было та1$же
показано, что добавление хромй, достаточное для увеличения
сопротивления стали обычной коррозии, увеличивает и предел
выносливости при коррозии до значения большего предела выносливости
углеродистой или никелевой сталей'). -
Шиытания на ;в1ынocливocть^в^тмocфepe сухого пара*) показали,
что сухой пар не оказывает влияния на предел выносливости, но
в случае пара^ содержащего воздух или воду, наблюдалось
понижение предела выносливости. Опыты в вакууме') показали, что предел
выносливости стали приблизительно такой же, как в^ воздухе, в то
^) в. р. Н aigh, там же, т. 18, 1917. -
• s)D. J. МГс Adam, Pfoc. Am. Soc. Test. Mat., т. 26, 1926; j. 27, 1927;.
Trans. Am. Soc. Steel Treat, т. 2,1927; Pfoc. Internat. Congr. Test Mat, Amster-:
,dam, T. 1, ctp. 305, 1928. См. также Н. F. Moore в Metals-Handbook,
Американское общество мет., стр. 147—153, 1939.
-^ ") Определейные При помощи испытаний на воздухе.
4 МсА d ат, Ргос. Ititemat Cofigr. T^st Mat, Amsterdam, т. 1, стр. 308,
1928; \
») См. М с A d^a m. Trans. A. S. M. E., Appl. Mech. Div., 1928.
«) Cm. T. S. Fulle'r, Trans. Am. Soc. Steel Treat, т. 19, стр. 97, 1931.
') Н. J. Gough and D. O. Sopv^ith, J^lrjst Met, т. 49, стр. 93, 1932.
Щ ФАКТОРЫ, вЛИЯ1РЩИ6 НА ПРЕДЕЛ, выносливости 407
время как опыты с медью и латунью в вакуум[е. показали-увеличе-^
ниё вынбсливости по MeiitiiiielfJ мере на 14 и 16% соответственно.
Известно много случаев разрушений во время работы, которые-
можно приписать уст^4ос№ при коррозии. Эти случаи включают
поломки таких частей,, как валы судовых двигателей, охлаждаемые
водой поршневые Штоки судовых нефтяных двигателей внутреннего
сгорания, лоцатки турбин, рессоры локомотивов, штанги насосов
нефтяных скважин, паровые котлы, трубы пароперегревателей и т. д.
Во многих случаях разрушения от усталости при коррозии были
устранены введением материалов, сопротивляющихся коррозии. Опыты
Мак*Адв:ма со сталями, сопротивляющимися коррозии, показали, что
такие Ьтали дают весьма удовлетворительные результаты при испыта^
ВИЯХ на усталость йри коррозии. Более поздние опыты со специаль"
Яыми бронзами*) показали, что фосфористая бронза и алюминиеззая,
бронза, испытанные при крайне тяжелых коррозийных условн^^с, об-,
ладают значительным сопротивлением усталости при коррозии и
выдерживают сравнение с лучшими нержавеющими сталями.
Защитные покрытия^) и холодная обработка^) поверхности эле-
мштов, подверженных усталости при коррозии, также были успешна
применены для предупреждения разрушений, ' ^
Влияние остаточных напряжений. Остаточные напряэйения
обычно вызываются горячей обработкой частей машин н^ наблюдаются при
сварке конструкций, причем возникает вопрос о влиянии этих .
напряжений на предел выносливости/ Опыты с закаленными стальными
образцами, испытанными на машине для испытания на усталость
вращающихся образцов, показали *), что остаточные напряжения па-
даЬт до Значения, меньшего 1/4 их первоначальной величины в
результате приложения симметричного цикла напряжений; влиянием
остаточных напряжений На предел выносливости можно было
пренебречь. Подобные же заключения были получены из испытаний на
усталость сварных двутавровых балок*). Е- Е. Вейбель отметил
неблагоприятное влияние остаточных напряжений, возникающих в витках"
пружин ^).
Влияние обработки поверхности. Влияние рбработки
поверхности на предел выносливости также было изучено. Были
проведены испытания из стали, содержащей 0,49»/о углерода, имею1цей
^^v ,»> Н, J. Oough and D, G. So p with, J." Inst, Metals, т. 60, стр. 143, Ш37.
- *) D. О. S о p w i t h and Н. J. Oough, -J.' Iron and Steel Inst, 1937,
«) O. F б p p 1, O. В e h г e n s und T. D u s о 1 d, 2. Metallkunde, т. 25, 1933.
«) См. H. В fi h 1 e f und H. В u с h h о 11 z, Stahl u. Eisen, т. 53, стр. 1330,
1933 и Mitt. Forsch-Inst, Verein. Stahlwerke (Dortmund), т. 3, стр. 235, 1933.
^) E. H. S с h u 1 z und H. В u с h h о 11 z, Stahl u. Eisen,^. 53, стр. 545,1933.
*) Trans. A. S. M. E., T. 57, стр. 50t, 1935. См. также E.. Wever und
G. M a г t i n, Mitt, Kaiser-Wilh. InsL Eisenfofsch. (Dfisseldorf), т. 21, стр. 218,
1939 и С. W. MacGregor в изд. W. R. Osgood, Kesidval Stresses in
Metals and Metal Construction, New York, 1954.
|*|Г^'
408
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
тхредел прочности, равный 6700 кг^см^, и обычный предел выно-
•сливости 3400 KzjcM^. Е<;ли принять за 100 предел выносливости
для тщательно полированных образцов, то были получены
следующие результаты для^ образцов с различным качеством
обработки*): с обработкой шлифовкой — 89; с обработкой гладкой
обточкой—84, с обработкой грубой обточкой —81. Испытания стали,
содержащей 0,02»/о углерода (железо Армко), дали для последних
двух типов обработки соответственно 92 и 88. Подобные опыты
•были проделаны В. Н. Томасом ®) со сталью, содержащей 0,33»/о
углерода; он измерял величину царапин при различных
обработках с помощью микроскопа. Другие опыты были проведены
В. Цандером^).
Табл. 26, помещенная в конце этой главы, дает - результаты,
полученные при статических испытаниях и испытаниях на выносливость
некоторых сталей, применяемых в технике.
87. Усталость и концентрация напряжений
*
ripn обсуждении вопросов концентрации напряжений, вызываемой
резкими изменениями поперечных сечений стержней и валов (см. гл. VIII),
было указано, что такая
концентрация напряжений особенно
вредна в случае переменных
напряжений. В машинах концентрация
напряжений всегда имеет место из-за
выточек, выкружек, отверстий,
шпоночных канавок и т. д., и опыты
показывают, что большинство
трещин усталости начинается в
местах концентрации напряжений.
Несколько примеров таких
разрушений будет теперь кратко
разобрано.
Фото на рис. 321 дает*)
картину разрушений от усталости
круглых валов с поперечными
отверстиями, подверженных
действию знакопеременного кручения. Наибольшее напряжение в этом случае
имеет место по краю отверстия на площадке, наклоненной на 45°
Рис. 321.
^) См. Н. F. Moore and J. В, Kommers, Univ. of Illinois Eng. Exp.
Sta. Bull., № 124, стр. 683, 1921.
*) Engineering, т. 116, стр. 483, 1923. Более поздние исследования
шероховатости поверхности рассмотрены в статье S. W а у, цит. на стр. 423.
^) Диссертация, Техническая высшая школа, Брауншвейг, 1928.
*) См. статью А. Т h U m'a, Forschung, т. 9, сгр. 57, 1938.
87]
УСТАЛОСТЬ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
409'
к оси вала (см. стр. 252). В этих точках трещины начинаются и
постепенно развиваются по винтовой линии, следуя направлению одного
из главных напряжений.
Фото на рис. 322 показывает разрушение от усталости при
кручении вала большого мотора-генератора, который плохо работал
вблизи резонанса*). Трещина началась у шпоночной канавки, где
имела место высокая концентрация напряжений, и постепенно
развивалась по винтовой линии. Винтовую трещину, соответствующую
направлению главного
напряжения, можно видеть на фото. Фота
на рис. 323 дает картину
разрушения от кручения вала
генератора дизельмашины. Высокая
Рис. 322.
Рис. 323.
концентрация напряжений у малой выкружки вызвала появление
нескольких винтовых трещин, которые в целом придают трещине
пилообразную форму. На фото рис. 324 показанй трещины усталости,
которые развивались постепенно у корней зубьев зубчатой передачи.
Места пунктов высокой концентрации напряжений отвечают
характеру изгиба зубьев как консолей.
Наконец, фото hI рис. 325 дает представление о характерном
разрушении от усталости мощной винтовой пружины. Трещина
началась изнутри, как предписывает теория (см. т. 1, стр. 247),
и опять-таки следует направлению одного из главных напряжений.
Все эти фотоснимки ясно показывают вредное действие, вызываемое
*) Фоз;^оснимки 322—325 взяты из статьи R. Е. Peterso п'а,
представленной на конференцию Массачузетского технологического института по
проблемам сопротивления материалов в промышленности, июль 1937.
Механизм роста трещины также рассмотрен Петерсоном, J. Appl. Mech.,
т. 1, стр. 157, 1933. Многие примеры разрушений от усталости
двигателей описаны в статье L. W. Schuste г'а, Ргос. Inst. Mech. Engrs. (LondonX
апрель 1933.
mw
то
МЕХАНИЧЕСКИЕ CBOftCtlBA МАТЕРИАЛОВ
1ГЛ. X
т фактор должен быть
вании частей мащин*).
-концентрацией напряжений, и понятно, что этот
<:ёрьезнб принят во внимание при проектирбвании
Более ранние испытания на усталость, проделанные с образцами,
имеющими резкие изменения поперечного сечерия, показали,, что имело
место уменьшение прочности вследствие концентрации напряжений,
но это уменьшение было обычно меньше, ^м следовало ожидать,
исходя от величины В1>1численнргб коэффициента концентрации
напряжений. Например, в случае плоских стальных образцов с малыми
- ' круговыми отверс^'иями,
подверженных действию осевого
напряжения, теоретический
коэффициент концентрации
напряжений равен 3 (см. стр. 249).
Если величина наибольшего
напряжения является
определяющим фактором при. испытаниях
на выносливость, то следовало
бы ожидать, что г нагрузка рас-
Т>ис. 324.
Рис 325.
tяжeниe — сж^1тие, необходимая для разрущения от усталости образца
ч:. отверстием, должна составлять около одной трети нагрузки для
образца без отверстия. Однако опыты показали, что в этом случае умень-:
шение прочности от концентрации напряжений менее значительно
■сравнительно с вычисленны)у[^). " >
Чтобы объяснить это расхождение и дать необходимые указания
Для проектировщиков, Р. Е. Петерсрном была проделана весьма
<$ольшая серия испытаний в исследовательской лаборатории фирмы
*) Очень важно для практики иметь некоторые средства для обнаруже-
иия трещин, как только они появятся. Различные методы обнаружения тре^
щин описаны Charles Lipsоп'ом в его статье в изд. М. Hetenyi,
Handbook of Experimental Stress Analysis, 1951. "!
Ц B. P. Haigh and J. S. Wilson, Engineering, т. 115» стр. 44б, 1923.
«71
УСТАЛОСТЬ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
411
•«tBecfHHfауз» *). Геометрически; подобные конеоАьные опытные об-
ращы, изменявшиеся в диаметре от 2,54 мм jp 76,2 мм с
выкружкой или с поперечным круглым отверстием, из разных, материалов
(см. :габл. 23), были испытаны на усталость^) в специальных испыта-
.тельных машинах. Результаты этих испытаний для образцов с вы-^
кружками даны на риа 326. Наименьшие диаметры образцов приняты
за абсциссЫ; jnespiy тем как ординаты представляют отношения a^g;
нагрузок при;vlJC63wi*aHHH на выносливость гладких образцов к
нагрузкам при йспша1ниях на выносливость для соответствующих образцов,
с концентрацией напряжений. Подобные же результаты были
получены йля образцов с пбперечными отверстиями.
Таблица 25
Материал, использованный Петерсоио» при испытаниях на усталость
Сталь
Средаеуглеро-
дйстая *)
Молйбдено-ни-
ке левая*)
Хромо-никеле-
. вая")
Химический состав, %
С
0,45
0,52
0,45
Мп
0,79
0,68
0,65
Si
0,18
■0,19
—'■,
S
0,03
—
—
р
0,013
0,014
■- —
•
Ni
_
2,96
1,38
Сг
'
..—
0,64
-
Мб
,,,,.'
0,38
—
- Н
л, И —.
Снх
2300
3200
6390
Сих
5340
6800
8400
■в>.
g
в).
>»»*
32
26
24
^) Нормализованная: 849° С, охлажденная на воздухе.
^) Нормализованная и подвергнутая вытяжке: 954° С, охлажденная на
воздухе; 793° С, охлажденная на воздухе; 627" С, охлажденная в печи. .
*) Закаленная и подвергнутая вытяжке: 802° С, закаленная в масле;-649° G,.
охлажденная в печи. .
Горизонтальные линии на рис. 326 дают значения коэффициентов
концентрации напряжений, полученные для каждого параметра
выкружки при непосредственном измерении деформации в точках наи-
<Й)Льщей концентрации напряжений (см. стр. 254). Эти значения
обозначаются Через oi^T и называются в последующем изложении теоре-
тическими значениями коэффициентов концентрации напряжений,
Ё^сли бы усталостная прочность образца зависела только от
наибольшего напряжения, то о.^^, очевидно, было бы равно а^д.
») R. Е. Peterson,J.Appl.Mech., т. 1, стр. 79 и 157,1933и1?. Е. JPetcTson
and А. М. Wahl, там же, т. 3, стр. 15, .1936. См, также Отчеты Комитета
по исследованию усталости металлов, Ргос. Am. Sos. Test. Mat., т. 42, стр. 145^
1942 и т. 43, 1943.
^) Описание этих машин дано в статье Р. Е. Петерсона, Ргос. Am. Soc*
Test. Mat., т. 29, стр. 371, 1929.
412
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
На основании хвоих испытаний Петерсон пришел к следующим
выводам:
1) В некоторых случаях результаты испытаний на усталость очень
•близко согласуются с теоретическими значениями коэффициентов
концентрации напряжений. Этот вывод имеет огромное практическое
значение, так как существует общее представление, основанное на
некоторых ранних опытах, что данные об усталости для случаев
концентрации напряжений всегда ниже теоретических; значений, и,
значит, при проектировании это обеспечивает больший запас прочности.
2.J^ S,oe
Рис. 326.
7,62
2) Результаты испытаний на усталость для стальных сплавов и
закаленных углеродистых сталей рбычно ближе к теоретическим
значениям, чем соответствующие результаты на усталость для
углеродистых не закаленных .сталей. В этих испытаниях ожидалось, что
теоретические значения должны быть достигнуты для всех сталей
при том условии, что образцы сделаны достаточно большими, но
рис. 326 показывает, что ординаты кривой для нормализованной
стали, содержащей 0,45*/<> углерода, очевидно, приближаются
асимптотически к значению, лежащему гораздо ниже теоретического.
3) С уменьшением размера образца понижение усталостной
прочности при наличии выкружки или отверстия становится несколько
меньшим; для очень малых выкружек или отверстий уменьшение
«71
УСТАЛОСТЬ И КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
413
усталостной прочности относительно мало. Это можно ясно видеть
из кривых на рис. 326.
Другой путь представления результатов испытания на усталость,
имеющий целью показать степень, с которой достигаются
теоретические значения, состоит во введении параметра
Ч =
«кт — 1'
(а>
который назызается коэффициентом чувствительности. Когда а^д
лриближается к значению а^^» значение q приближается к единице.
О ЦГ 0,г Ц^ ff.9 О^ 0.ff^ 0.7 Off {i9 ^
Вь//(р^Жла a^ii o/nffepc/nue, г ff см ^
Рис. 327.
когда |же концентрация напряжений имеет лишь малое влияние на
усталостную прочность, а^д близко к единице и q приближается
к нулю; Значения q для некоторых видов концентрации напряжений
и для двух родов стали представлены *) на рис. 327, где радиус
^) См. книгу Р. Е. Петерсона, цит. на стр. 411.
iir
414
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ.Х
выкружки или отверстия принят ёа aOepHCCyv Видно, что коэффициент-
чувствительности непостоянен. Он зависит не только от рода мате*
риала, но также и от Ь^змеров образцов. В случае легированных сталей
и для ^больших образцов ^ приближаемся к единице; в то же время;,
для крупнозернистой стали, содержащей 0^45% углерода, q
приближается к несколько меньшему значению *). -
На основании приведенных рассузкдений можно рекомендовать
при проектировании частей,машин больших размеров применять
теоретическое значение а^т концентрации напряжений, как и в Случае
мелкозернистых сталей, легированных сталей, прошедших
термообработку углеродистых сталей. Для частей малых размеров и для
крупнозернистых материалов можно принять уменьшенное значение
Коэффициента концентрации напряжений. Это значение, основанное
на выракении (а), б^^дет
Значения q, полученные опытным путем для выкружек, отв^рстдй и
Рйдиус вь/ттяа f ff см
^ О mSllBS ОМ.Ф Qt2 ilfS 0J7 112 IjZS Q^ т (^ ЦЗЕ 105 07, Oj^ Щ €fi5
Й 10
Ф5 42^ Щ2
/Щ/^ бь//тЮ¥/ш г 3 ем
Рис. 328.
зыточек, представленные на рис 328,' можно применять как
руководящие при выборе надлежащих значений tt.^^ для других случаев
концентрации напряжений *).
. , *) Испытания чугуна показывают, что концентрация напряжений имеет
малое влияние на результаты испытаний на усталость; см. А. Thum und
Н. Ude, Z. Ус?г. deut Ing., т. 74, стр. 257, 1930.
*) См. книгу P. £. Петерсона, цит. на стр. 411, и С. Е. Phillips'a and
R. В. Н е у w о о d'a, Ргос. Inst. Mech, Engrs. (Lond6n)i Appl.Mech., т. 165, стр. 11^»
Щ УМЕНЬШЕНИЕ ЙЛИЯНИЙ КОНЦЕНТРАЦИИ НАПРЯШЕНИЙ 415
Изломы усталости имеют СХОДСТВО со статическими раа^ушениями
хрупких материалов в т0М отношений, что они происходят .практик-
чески без пластическо1* деформации. Трещина начинается ^^ некото-
pioro местного несоверй1е||Ства и прогрессирует в направлении, нор-"
"мальном к pacMrHB|iiQiHiitli напряженийм. Поэтому логично ожидать,
что при испытаниях на усталость *) можно также применять теорию
вероятностей^ рарййтуЬ при изучении разрушения хрупких материалов
<см. стр. 3^31^ gcirJiacHO этой идее нужно ожидать, что йредел
выносливости: .|*Шрйала (будет уменьшаться с увеличением размеров
испытуемого образца. Работая над испытаниями на усталость при изгибе,
некоторые экспериментаторы заметили уменьшение усталостной
прочности ^..с увеличением диаметра образцов*). Гораздо большее елия-
Нпё размера было найдено при"'испытании образцов с различного
рода концентрацией напряжений, но кажется, что йе было еще попытки
изучать это явление при помощи теории вероятностей^). Задача
становится весьма сло1Кной, потому. что объем высоко напряженного
материала в таких случаях обычно очень мал, и становится
необходимым рассмотреть размер зерн^ кристаллического материала. Хотя
мы говорим о геометрически подобных обраэдах из одного и того
2ке материала, но очевидно, что их металлографические структуры
не>являются теометрически подобными, и это обстоятельство имеет
влияние- на результаты усталостных испытаний. При рассмотрении
области наибольших X напряжений можно ожидать различных
результатов в зависимости от того, мало ли содержится зерен в этой
области или в ней их содержатся тысячи. Зависимость между
коэффициентом чувствительности q, полученным из испытания на усталость,
и размерами зерен материалов рассмотрена в статье Р. Е. Петерсона •*).
.■■■■■ "^ '
86. Уменьшение влияния концентрации напряжений
на усталость
Мбжно считать, что вопрос об уменьшении вредного влияния
концентраций напряжений- йвляется вопросом nepeocteiteHHoro
значения для проектировщиков, Некоторое понижение концентрации
1951. Испытания на усталость при кручении валов диаметром 247,7 жл, еде-
даиные Т. W.B и п у о п'ом and Н. Н. А11 la, Trans. Engrs. Shipbuilders Scot., 1953,
показаяи для коэффициента чувствительности меньшие значения (^==,2/3),
чем полученные при испытаниях на из^;и6 Р. Е. Петерсоном.
*) См. статью: W. W е i b и 11, Trans. Roy. Inst. TechnoL (Stockholm), № 27, Ш49.
8) RE. Peterson, Proc. Am. Soc. Test. Mat. т. 29^, стр. 371, 1929;
К. Faulhaber, Mitt. Forsch.-Inst. Verein.. Stahlwerke (Dortmund), т. 3,
стр. 153, 1Ш'иО. J. Horger and H.R. Neifert, ProcAm.SocTest Mat.,
T. 39, 723, 1939.
') Это явление было рассмотрено Р.Е. Петерсоном, Ргос. Am. Soc.
Metals, 1948. '
*) См. Contributi^s to the Mechanics of Solids, Dedicated to Stephen
Timoschenko by His Friends, New York, стр. 179, 1938.
шш
416
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
напряжений можно получить, внося подходящие видоизменения в
проект. Например, проект может быть значительно улучшен
устранением острых входящих углов и введением выкружек большого радиуса,
приданием выкружкам надлежащей формы', введением разгрз^ающих
выточек и т. д. На рис. 329 показаны приемы уменьшения
концентрации напряжений у уступа вала с сохранением при этом линии
I
у.
I
ф-
w//////^
4
L
А
а)
контура АА. Напряжение можно уменьшить, вырезая в уступе
выкружку возможно большего радиуса и не нарушая целостности
насаженного на вал элемента, как показано на рис. 329, Ь. Если же высота
уступа слишком мала, то может быть применена, как показано на
рис. 329, с разгружающая выточка.
.В)
Ь)
Рис. 330.
На рис. 330 показаны две различные конструкции соединения
болта с гайкой. На рис. 330, а гайка испытывает сжатие, в то время
как болт испытывает растяжение.. Высокая концентрация напряжений
имеет место в конце нарезки у поверхности гайки, и под действием
переменных усилий разрушение от усталости происходит в этой
88]
УМЕНЬШЕНИЕ ВЛИЯНИЯ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ
417
т
плоскости*). При наличии прокладки (рис. 83G, ^>) наибольшее
напряжение иногда ослабляется потому, что прокладка напряжена в
том же направлении, что й б^олт. Испытания на усталос*ь показывает ''j^
что конструкция с прокладкой прочнее .приблизительно на 30%.
Иногда эти меры рйзгруз- ■
ки недостэточны для того^ j
чтобы* исклк>Чй1> разру- _ 4
шения 9^ усЙлост». В каче- <f
с'гве важного примера
рассмотрим типйчнйе
разрушения, Тсрторые имеют место в
Подступичнкх частях
локомотивных и железно:^орожных
вагонных осей, на
поверхностях^ .попирания "колес цли
подшипников автомобильйых
осей, в напрессованных или
насаженных сверлах длинных буровых штанг, применяемых при
разработке нефтяных скважин. Во всех этих случаях насаженных
элементов, подверженных действию переменных усилий, имеется
а/
^
Рис. 331.
Рцс. 332.
тгостоянный источник разрушения от усталости. Рассматривйя,
например, случай ступицы колеса, напрессованной на ось (рис. 331, а),
мь? можем видеть, что высокая концентрация напряжений в сочетаннв^
*) J. Н. Ooodier, J. Appl. Mech., т. 62, стр. U, 1940. См. также
М. Hetenyi, Proc. Soc. Exp. Stress Anal., т. Ij, стр. 147, ШЗ.
*)\Н. W i e g a п d, Диссертация, Техническая высщая ииюл9, Parmetadt,
1933. См. также S.M, Arnold, Mech. Engrg., т. 65, стр. 497, 1943.
14 С. п. Тимошенко, т. 31
ES.eri'
щ
418
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
С трением*) возникает во входящих углах тип. При вращении
оси имеют место знакопеременные напряжения в точках тип, ив
конце концов разрушение от усталости по поперечному сечению
может произойти, как намечено на рис. 332. Концентрацию
напряжений можно несколько уменьшить утолщением места опирания
€/fa3//avefaiff-: а: место/:хгзр£^шег/г/^
/п: Hoaflff3/fa NO/fOffiie
п,р: место o/ropffbvrnoda/un/fUffoS
Рис. 333.
С устройством выкружек, как показано на рис. 331, Ъ, Дальнейшее
улучшение получается введением вспомогательной выточки (рис. 331,(&).
Хотя такие изменения и улучшают положение, в этом случае они
недостаточны. Опыт показывает; что при просто напрессованной на
ось ступице (рис. 331, а) усталостная прочность оси уменьшается
до значения, меньшего половины ее первоначальной прочности, в то
время как изменения, показанные на рис. 331, Ь, повышают
усталостную прочность оси, может быть, не более чем на 20о/о-
*) Относительно изнашивания от коррозии и усталости см. G. А. Т о m И п-
son, Р. L. Thorpe and H.J. Go ugh, Proc. Inst. Mech. Engrs. (London),
T. 141, стр. 233, 1939; см. также О. J. Horger, Symposium of Fretting
Corrosion, Американское общество по испытанию материалов, 1953.
SS)
УМЕНЬШЕНИЕ ВЛИЯНИЯ КОНЦЕНТРАЦИЙ НАПРЯЖЕНИЙ
419
Чтобы улучшить это положение и исключить разрушения от
усталости, была успешно применена холодная обкатка поверхности
оси в области концентрации напряжений. Первые опыты ^) при
условии холодной обработки ловерхностей были проведены на малых
образцах, поэтому для получения достаточных данных для
практических приложений, была выполнена обширная серия лабораторных
испытаний с большими образцами. Три типа испытаний на усталость,,
сделанных О. Д. -Хорджером в лаборатории Мичиганского
университета *), представлены на рис. 333. Свойства материалов, примененных
в этих испытаниях, приведен^! в табл. 24. Пределы выносливости,
полученные для стали S.A.E и для никелевой стали из обычных
испытаний на усталость консольных стержней, соответственно были
равны 2400 и 3400 кг/см'^. После прессовой посадки муфты в
испытаниях по типу А (рис. 333) предел выносливости для стали S.A.E..
уменьшился до 1050лгг/сл/^. В испытаниях по типам В и С пределы
Таблица 24
Материалы, примененные в испытаниях по рис. 333
Сталь
С
0,47
0,24
Химический состав, %
Мп
0,72
0,86
р
0,015
0,034
S
0,034
0,021
S1
0,23
0,24
Сг
0,03
-N1
0,05
2,79
к".
спи
3350
6050
6250
7800
S. A. E. ^) 1045
2,75% никеля *)
32
23
^) Нормализованная при 882° С и протянутая при 60Г С.
^) Закаленная при 802° С и отпущенная при 621° С.
выносливости были найдены соответственно равными 850 и 990
кг/см\ Это указывает на то, что благодаря прессовой посадке
усталостная прочность образцов уменьшилась до значения, меньшего
половины ее первоначального значения. Подобные результаты были
получены также и для образцов из никелевой стали. Для повышения'
^) Улучщение . усталостной прочности холодной обработкой
поверхности было предложено О. РбррГем, Stahlu. Eisen, т. 49, стр. 575, 1929.
Оно было применено в различных испытаниях на усталость в Институте
Вёлера. См. Mitt. W6hler-Inst., тт. 1—37, 1929—1940. См. также А. Т h и m und
F. W u n d е г 1 i с h,- Mitt. Materialpriifungsanstalt, Tech. Hochschule, Darmstadt,.
T. 5, 1934 и R. Kuhnel, Stahl u. Eisen, j. 110, стр. 39, 1932.
*) Описание этих опытов дано в статьях О. J. Н or ger'a, J. Appl. Mech.,^
т. 2, стр. A-128,1935 и О. J. Н о г g e r'a and J. L. Maulbetsc h'a, там же, т. 3,
стр. А-91, 1936. Работа, проделанная в исследовательской лабора*ории
Вестингауза, описана в статье Р, Е. Петерсона и А. М. Валя, там же, т. 2,
стр. А-1, 1935 -
14*
miw
ш
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ, Х
каш6ро§аянт
Л1/кетя
/6гт/(а
усталостной прочности поверхность образцо]& была пoдвepгнyta перед
посадкой муфт или ступиц колее холодной обработке при помощи
ТЕридпособления, >показанного на рис. 334.
Для операции обкатки был применен токйрный станок,
поддерживавший образец в своих центрах, поддерживавший и
приспособление для обкатки в поперечных
салазках, прикрепленных к
суппорту токарного станка. Чтобы
обеспечить в результате обкатки
достаточно гладкую
поверхность, были применены подачи,
дающие более 40 )содов винта
на 1 дюйм.
Результаты испытаний на
усталость по типу С (рис. 333),
проделанных с холоднообкатан-
ными образцами, приведены на
рис. 336. Видно, что усталостная
прочность образцов из стали
S.A.E. увеличивалась после
обкатки до значения, более чем
вдвое превосходящего их
первоначальную прочность.
Подобные результаты были получены
также ДJ^я образцов из
никелевой стали.
Дальнейший шаг в исследовании влия1^ия холодной обкатки нг»
усталостную прочность связан с появлением больших испытательных
машин на усталость, в которых могли испытываться локомотивные
оси в на!туральнбм виде. Фото на рис. 336 представляет одну из этих
машин ^). Устройство — подобно использованному в испытаниях типа
С по рис. S^Pi притом такое же, какое, было применено Вёлером
в его знаменитых испытаниях на усталость осей. Результаты
лабораторных испытаний с o6p^sttiaMH больших разМ^ов бы^и настолько
многообещающими, что некоторые железные jjoporn ввели
требование обкатки поверхностей осей и других локомотивных частей, как,
например, поршневых штоков, шатунов, кривошипов и бандажей ^).
Чтобы получить слой наклепанного (нагартованного) материала
достатбчной толщины, требовалось значительное давление катка при
поверхностной обкатке осей большого диаметра. В случае валов малого
Рис. 834.
*) Три машины 9Х0Г0 типа использовались в исследовательской
лаборатории Timken. Roller Bearing Company, Canton, Ohio. Рис.332 взят из
одного лз этих испытаний.
^) См. статью О. J. Н о г g е г'а, представленную к годовому собранию
Американского общества по испытанию металлов, февраль Ш4б.
Щ ;
УМЕНЬШЕНИЕ ВЛИЯНИЯ КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ
42Х
т
M0/fe//faff7o/f
УетамватиШ'
- ^Ш
диаметра и легких частей машин даже тонкий слой наклепанного
металла будет показывать значительное улучшение усталостной
прочности. Простым способом выполнения такого наклепа поверхности
^ J00O
I
I ^-
2 гооо
1670
% Ш0
mff
^ ^г г ^ б fffo г0 <^ sffmioo гор
Рис. 335.
I
Рис. 336.
является обЬувка струей дроби. Этот процесс нашел широкое
применение в автомобильной промышленности^).
^) См. о. J. Horger and Н. R. Neifert, Proc Soc. Exp.Stress Anal.,
T. 2i, стр. 178, 1944.
шт
422
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
89. Разрушение поверхности при усталости
Другой случай разрушения от усталости при действии высокой
концентрации напряжений представляет разрушение поверхности
катков и зубчаты-х колес под повторным действием контактных
давлений во время вращения. Рассматривая два вращающихся катка,
прижатых трут к другу силами Р (рис. 337), мы
можем вычислить наибольшее сжимающее напряжение
на поверхности контакта при помощи формул п. 63.
В случае идеально гладкой поверхности вычисленное
таким образом напряжение является истинным, и
поверхностная усталостная прочность катков данного
материала будет зависеть только от величины stofjo
напряжения. В действительности поверхность катка
имеет различного рода неровности, величина которых
зависит от рода обработки поверхности. Несколько
примеров обработки поверхности показано*) в
увеличенном виде на рис. 338. Естественно, шероховатая
поверхность будет влиять на распределение давления
на поверхности соприкасания катков (рис. 337). В
результате местного перенапряжения у вершин наиболее резких
неправильностей трещины усталости будут появляться раньше, чем в
случае гладких катков. Это указывает на то, что усталостная прочность
катков зависит от степени шероховатости их поверхности.
Рис. 337.
Рис. 338.
, Опыты показывают, что если испытания на поверхностную
усталость сделаны со смазанными катками, то трещины поверхностной
1) Этот фотоснимок и два последующих взяты из статьи С. Вэя,
представленной собранию Американской ассоциации производителей зубчатых
передач, май 1940. Различные методы исследования обработки поверхности
описанй С. Вэем в статье, опубликованной в Ргос. Special Summer
Conferences oii Friction and Surface Finish, Массачузетский технологический
институт, июнь 1940. Библиография по предмету дана в этой статье.
щ
РАЗРУШЕНИЕ ПОВЕРХНОСТИ ПРИ УСТАЛОСТИ
423
усталости принимают вид ямок (раковин). Ямкообразные трещины,
которые иногда развиваются в катках и зубчатых передачах в
условиях работы, весьма нежелательны, поэтому значительные усилия
были направлены на изучение причин этого явления*). Эти
исследования показали, что причины развития ямкообразных трещин имеют
гидродинамическую природу. Ямкообразные трещины принимают на-
правление,' уходящее наклонно внутрь металла и приобретают
примерно форму конической поверхности. ._
Трещины пересекаются с
поверхностью контакта по кривой, имеющей
форму параболы или буквы. V,
причем, верх V является частью,
которая первой приходит в контакт при
в1эащении. На рис. 339,
показывающем увеличенный вид поверхности
катка, начальная точка ямкообразной
трещины указана стрелкой. Понятно,
что смазка, попадающая в трещину,
будет стремиться удерживаться в ней,
когда трещина проходит по
нагруженной области. Высокое давление
масла в трещине будет вызывать
высокие растягивающие напряжения на
дне! трещины и трещина будет
проникать дальше в металл. Так теория
объясняет, почему наличие масла
сопровождает рост ямкообразных
трещин и почему рост трещин может
быть остановлен либо изменением
направления вращения, либо
уменьшением] давления масла в трещине.
Чтобы получить сравйительные значения сопротивления ямкообра-
зованию различных материалов, были произведены *) усталостные
испытания вращением пар катков (рис. 337). В этих испытаниях один
каток был диаметром 40 мм, другой диаметром 38,1 мм, ширина
испытанной поверхности была 12,? мм. Все катки имели чисто
отшлифованную поверхность, на которой наибольшая глубина
неправильностей была между 0,0025 мм и 0,0046 мм. Скорость
вращения лежала в пределах 300-5-500 оборотов в минуту, при смазке
из ванны машинным маслом, вязкость которого была 700 —
900 секунд по Сейболту при рабочей температуре. Наибольшее
Рис. 339.
^) Такие исследования были проделаны С. Вэем в исследовательской
лаборатории Westinghouse; см. его статью в J. Appl. Mech., т. 2, 1935.
- ") См. статью С. Вэя, там же.
w
424
МЕХАНИЧЕСКИЕ СВОЙСТ^ВА МАТЕРИАЛОВ
1ГЛ. X
сжимающее- напряжение, даваемое формулой B79), стр. 284,
вычислялось по сжимающей нагрузке, достаточной для того, чтобы вызвать
появление по меньшей мере одной ямки на квадратный дюйм
испытываемой поверхн<)Сти при 10 миллионах циклов; оно бУло принято
3$ предел усталости при ямкообразовании. Результаты таких"
испытаний образцов из стали, содержащей 0,45Ve углерода, для различных
ч
■ . '
V,
■^
Jf^
V
ч
Wi'
/А
/в
■ ' .
- ^
■Г
'
т яю W0
ffffff
Рис. 340. Сравнение приближенного сопротивления ямбо-
образованию зубчатых колес и катков.
Кривая А — сжимающее напряжение в зубце колеса в прлюсе зацепления
(вычисленное в предположении полированной поверхности зуба и^ри
отсутствии всяких отклонений в контуре, но с учетом выпуклости и
отклонений в шаге), достаточное для того, чтобы выввать шесть яыак,
т. е. одну ямку примерно на 6 слс^ площади, заключенной между
начальной окружностью и концом зацепления одного зуба. Исследуемый зуб
совершал 10? оборотов.
Кривая В ~ сжимающее напряжение при испытании катков дву^ разных
диаметров {Ъ&,\ мм. и 40 жл) с - полированной, поверхностью, вполне
достаточной, чтобы вызвать одно углубление примерно на 6 cлc^ плог
щади за 107 Циклов.
условий термообработки представлены на рис. 340 кривой В. Числа
твердости*) катков взяты за абсциссы, а соответствующие пределы
ямкообразования—^^-за ординаты. Для сравнения проведена прямая С,
которая соответствует пределам ямкообразования, в 32;|^ раза
превышающим числа твердости. Так как ямкообразование приводит к ра&ру-
шению от усталости, мы должны были ожидать, что сопротивление
ямкообразованию увеличивается пропорционально твердости. Опыты
показали,^что предположение о линейной зависимости между сопро-
^) Числа твердости можно считать пропорциональными пределу
прочности поверхностного слоя материала катка. . _
щ, ' ПРИЧИНЫ УСТАЛОСТИ 425
тавлейием ямкообразований и-твердостью является осторожным
подходом. " -■>>■■■■ '. ,-
Кривая А на рис. 340 дает значения пределов ямкообразования,
найденных из опытов с зубчатыми колесами, сделаннцми из того
же самого материалу, 'чтй и указанные только что катки! Условия
на поверхностях соприкасания зубцов зубчатой передачи несколько
отличаются от услЬ)вий в катках, причем главное отличие заключается
в том, что здесь качение соединяется со скольжением. Эта разница
условий влечет за собой увеличение предела ямкообразования.
90. Причины усталости
- Хотя собрано большое количество данных относительно прочности
при усталости материалов, но.до сих пор еще не установлена
обоснованная теория, объясняющая причины и механизм этого явления.
Разрушение от усталости раньше приписывали «кристаллиа^ации»;
металла, делающей eiro хрупким. Такая теория выдвигалась на
основании рассмотрения внешнего вида разрушения (см. стр. 394). Теперь
мы знаем, что^ отдельные кристаллы-остаются неизменными при
испытании на усталость, кроме тех, внутри которых произошла
деформация скольжения. ^
Баушингер первым начал исследование действия циклических,
напряжений. Он медленно нагружал и разгружал образцы и поIьзовался
чувогвительными экстензометрами для установления зависимости
между напряжениями и деформациями при этих условиях *). Таким путем
он показал, что пределы пропорциональности при растяжений и сжатии
не являются постоянными параметрами для данного материала и что
они могут изменяться, если образец подвергать воздействию
переменных, напряжений. Для объяснения того обстоятельства, что предел
выносливости для стали при CHMMefричных циклах напряжений иногда
бывает ниже предела пропорциональности, полученного из
статических испытаний, Баушингер выдвинул теорию, согласно которой
материал, полученный с завода, может иметь свои пределы
пропорциональности при растяжении и сжатии, повышенные благодаря холодной
обработке, а истинными или естественными пределами
пропорциональности будут те, которые установятся после того, как материал
будет подвергнут действию переменных напряжений. Эти
естественные пределы пропорциональности предполагаются определяющими
безопасный диапазон напряжений при испытаниях на усталость.
Идея Баушингера была развита далее Бэрстоу*). Пользуясь
медленно нагружающей и разгружающей машиной (два цикла в минуту)
с зеркальным экстензометром Мартенса, прикрепленным к образцу.
1) J. В а U S с h i п g е г. Mitt. Mech.-tech. Lab., Мюнхен, 1886. См. также Ding-
lers Polytech. J., т. 266, 1886.
*) L. В a i г s t о w, Phil! Trans. Roy. Soc. (London), A, т. 210, стр. 35, 1911.
ЕЖТЯ"'
426
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
ОН пол)гчил зависимость между напряжениями и деформациями для
циклов с различными диапазонами напряжений. Рис. 341 представляет
некоторые результаты, полученные Бэрстоу с осевой сталью (предел
^ текучести 3500 kzJcm^ и предел
i-6(f(a^M). прочности 5900 kzjcm^) при
симметричном цикле напряжений
(среднее напряжение равно нулю).
Линия А изображает ^тервоначальные
испытания на растяжение и сжатие
с амплитудой 2200 кг/см^. В этих
пределах зависимость между
напряжениями и деформациями
следует, как видно, точно
прямолинейному закону^).
После этого образец был
подвергнут действию
знакопеременных напряжений 2200 кг/см^, и
было обнаружено, что
первоначальная прямая линия А постепенно
развивалась в петлю определенной
формы. Такая петля, полученная
после 18 750 циклов, изображена
кривой В. Можно видеть, что в
этом случае первоначальные
пределы пропорциональности были выше так называемых естественных
пределов гГропорциональности, установившихся после многих циклов
знакопеременных напряжений. Так как эти пределы лежат ниже 2200 кг/см^
то появилась циклическая остаточная деформация, равная
ширине 'тп. Петли С, D vi Е были получены после действия
знакопеременных напряжений, соответственно равных 2350, 2650, 3300 кг/см\
Число циклов в каждом случае было достаточным для установления
постоянных размерив петель. Построив график изменения ширины
этих петель в зависимости от соответствующих наибольших
напряжений, Бэрстоу получил приблизительно прямую линию. Пересечение
этой линии с осью напряжений определяет диапазон напряжений,
который не Ьлияет на образование петель. Определенный таким образом
диапазон напряжений был принят Бэрстоу за безопасный диапазон
напряжений, и последующие испытания на выносливость пoдtвepдили
это предположение с достаточной точностью. С тех пор на этом
основании разрабатывались различные методы для быстрого
определения диапазонов напряжений при усталости 2).
Рис. 341.
^) Расчетная длина в этих испытаниях была лишь 0,6 дюйма, и малый
упругий гистерезис не мог быть обнаружен экстензометрами Мартенса.
2) См. книгу: Н. J. О о U g h, The Fatigue of Metals, London, гл. 10. 1924.
См. также E. Lehr, Die AbkOrzungsverfahren, диссертация, StuttgarT, 1925.
90} ПРИЩ1НЫ УСТАЛОСТИ 4S7
Измерение петель гистерезиса для Определения безопасного
диапазона напряжений может быть сделано другим путем, с
использованием калориметрических измерений. Площадь петли представляет
рассеянную в продолжение одного цикла энергию. Эта энергия
превращается в теплоту, количество которой может быть измерено.
Первые опыты этого рода были произведены Гопкинсоном и Виль-
ямсом ^), которые показали, что площади петель, определенные
калориметрическим методом, совпадают в пределах 6*Уо с площадями,
определенными измерениями при помощи экстензометров. При этих
испытаниях было показано также, что возмЪжно установить
определенную величину гистерезиса, которая никогда не вызовет
разрушения и может быть принята за истинный упругий гистерезис. На базе
таких калориметрических измерений было разработано также нес-
колькб быстрых способов определения пределов выносливости.
Первая попытка объяснить механизм разрушение при испытаниях
на выносливость была сделана Юингом и Хемфри*,). Они применяли
вращающийся образец из шведского железа с полированной
поверхностью и исследовали эту поверхность при помощи
металлографического микроскопа после приложения симметричных циклов напряжений.
Они нашли, что если были приложены напряжения выше
определенного- предела, то после достаточного числа циклов на поверхности
некоторых кристаллов появлялись полосы .скольжения. При
повторении циклов число полос скольжения увеличивалось, и некоторые
из прежних полос скольжения заметно расширялись. Этот процесс
расширения продолжался до окончательного образования трещины,
которая шла по расширенным полосам скольжения. Они нашли, что
знакопеременные напряжения в 850 кг/см^ можно приложить миллионы
раз, не вызывая каких-либо полос скольжения. Напряжение в
1100 кг/см^ вызывало- лишь одну изолированную полосу
скольжения после 3 миллионов циклов, и эта линия ограничивалась средним
участком кристалла. Из этих испытаний было выведено заключение,
чтб напряжение в 1100 кг/см'^ было пределом выносливости для
шведского железа. На основании таких испытаний была выдвинута
теория, утверждающая, что циклы напряжений, лежащих выше
безопасного предела, вызывают полосы скольжения в отдельных
кристаллах. Если продолжать прикладывать такие ц^1клы напряжений, то
будет происхадить беспрерывное скольжение по поверхностям.
Скольжение сопровождается трением, подобным наблюдаемому между
поверхностями скольжения твердых тел. В результате трения,^согласно
этой теории, материал постепенно истирается по поверхностям
скольжения и образуется трещина.
*) В. Hopkinson and О. Т. Williams, Ргос. Roy. Soc. (London), А,
т. 87, 1912.
*) J. А. Е W i п g and J. С. W. Н u m f г е у, Ph}l. Trans. Roy. Soc. (London),
A, T. 200, стр. 241, 1903.
tmw
428 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
Дальнейшие исследования ^) показали, что полосы скольжения
могут возникнуть прй"^ напряжениях, значительно меньших предела
выносливости материала. Они могут развиваться и расширяться,-не
вызывая образования трещины. Это указывает на то, что появление
полос скольжения не может быть принято эа осйование для
определения предела выносливости и не может объяснить механизм
появления трещины усталости. ,
Чтобы глубже проникн)ггь в механизм разрушения при-
испытаниях на усталость, Гаф применил^ новый метод исследования,
используя точную рещгеновскую технику *). Начав с образцов монокристалла,
он показал, что механизм дефорл1ации пластических ^^металлических
кристаллов под действием переменных напряжений остается там же,
что и в статических условиях^ т. е. скольжение происходит по
некоторым кристаллографическим плоскостям в определенных
направлениях и обусловливается величиной составляющей касательного
напряжения в направлении скольжения. Рентгеновский анализ показал,
что если цикли были вне безопасного диапазона напряжений,- то
«кристаллографические плоскости оказывались искаженными в такой
мере,, что, в то время как их кривизна в среднем была цезаметноЙ>
все же' существовали отдельные местные искривлейия. Следовало
предооло'жить, что большие местные деформации — также, вошиожно,
и действи^ельйые разрывы решетки — должны были произойти в таких
искривленных плоскостях, которые под приложением достаточно
большого диапазона внешних напряжений или деформаций мо1У1и
повести к образованию прогресси^>ующей трещины; при более
низком значении циклического деформирования состояние могло быть
устойчивым». . ' ;
При проведении опытов с кристаллическими материалами,
например с- мягкой сталью, нредварительиые статические испытания
показали, что не происходит постоянного изменения в зернах, если
сохраняется упругое состояние. На участке между пределом
упругости иупределом текучести нд поверхности некоторых
неблагоприятно ориентированных зерен появляются линии скольжения. Этими
линиями определяются плоскости' ск9льжен1^я кристаллов. Если
переменные напряжения, большие предела выносливости материала,
приложены к образцу, то слабейшее зерно начинает повреждаться
в плоскости Скольжения, и тонкая трещина развивается по этой'
плоскости. Трещина расширяется с числом циклов, распространяясь
на^ы^жные зерна, ив конце концов приводит к разрушению
образца. Это показывает, что повреждение от усталости начинается в
том месте, где происходит пластическое течение, между тем как
окружа1рщий материал остается совершенно упругим.
*) Н. J.GQu^h and D.Hanson, Ргос.Roy.Soc. (London), A, т. 1Ц 1923„
*) Выводы атой работы были представлены Королевскому аэронавти-
ческому обществу. См. J. Roy, Aeronaut. Soc, август 1936.
90}
ПРИЧИНЫ УСТАЛОСТИ
42&
Для - изучения деформации в месте, где начинается устало;:тное
поэреждение от действия знакопеременных напряжений, рассмотрим
снова модель, составленную из трех стержней (рис. 271,^ стр. 343),
которая была использована для пояснения эффекта Баушингера.
Предполагая, что действует симметрично знакопеременная сила Р^
которая больше предела упругости модели, и поступая, как"Ъбъясйвно
на стр. - 346, мы пол)гчаем петлю в виде параллелограмма abed
(рис. 342). В предыдущем, выводе наклепом материала вследствие
пластической деформации в
вертикальном стержне пренебрегалось и
предполагалось, что напряжение пре-'
дела текучести стержня остается
постоянным в течение циклов нагру-
^кения. При этом предположении
размер петли оставался постоянным и
независимым от числа, циклов. Если
же принять во внимание наклеп, мы
лолучим совершеннр иные
результаты. Начиная от точкч а, которая
определяет начало разгрузки модели,
получаем линию аЬ (рис. 342). Точка
b отвечает состоянию, когда
вертикальный стерж^ь еще не начаЛ Чечь,
так как его предел текучести несколь-
ко-повысился из-за предыдущей
пластической деформации (участок еа
диаграммы). Стержень будет
продолжать работать упруго до
некоторого более высокого значения
нагрузки, например соответственно тЪчке Ъ' диаграммы. Начиная с этого
значения нагрузки, вертикальный стержень течет, и мы получим
участок J>V диаграммы. Точка с' соответствует для модели силе Р,
действующей вверх. Разгружая теперь модель и затем вновь нагружая
ее в противоположном направлении, мы найдем, что на графике ход
упругой деформации продолжается до некоторой точки'1с?' вследствие
накл1впа вертикального стержня. Точка d' определяет начало текучести,
1» мы получаем участок d'e' на диаграмме.
Продолжая и дальше циклы нагружения и разгрузки, получим
точки/', ^, К, i\... Видно, что благодаря наклепу вертикального
стержня, который аналогичен слабому месту образца, испытываемого
на усталость, петли гистерезиса становятся все уже и уже с увел'иче-
нием числа циклов. Это указывает на то, что амплитуда пластической
деформации стержня уменьшается с каждым циклом, в то время как
/амплитуда внешней нагрузки остается постоянной (нк/')- В то же са-
^Ое время амплитуда напряжений в стержне растет с. числом циклов
rssStTH"'
[Щ"
430
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОЙ
[ГЛ. X
И приближается к значению, которое следовало бы получить при
действии нагрузки Р, приложенной к совершенно упругой модели.
Возвращаясь теперь к рассмотрению слабых мест в образцах,
испытываемых на усталость, мы должны разрешить главный вопрос, будет
ли зерно, которое пластически деформируется, безопасно
сопротивляться прогрессирующему наклепу или же будет начинаться и
развиваться трещина усталости. Для того чтобы ответить на этот вопрос,
Орован исследовал *) наклеп слабого места при переменных
напряжениях, используя кривую наклепа, выражающую предел текучести в
функции пластической деформации ^). Он рассмотрел два случая, как
показано на рис. 343, а и 343, Ь. В обоих случаях линия ОРА
а)
4/
Рис. 343.
представляет кривую наклепа материала. Ордината точки Я,
соответствующая точке а рис. 342, дает напряжение в слабом месте образца,
испытываемого на усталость, в начале первого ч^икла. Зигзагообразная
кривая р р' р"... отвечает последовательным переменным
пластическим деформациям слабого места при ходе циклов внешней нагрузки.
Предполагая, что наклеп не зависит от направления деформации, но
зависит только от суммы их абсолютных значений в течение циклов,
мы определяем наклеп слабого места по точкам р\ р"... на кривой ОРА
наклепа. Мы видим, .что в случае на рис. 343, а, где точка Z ниже
точки В, даже для неограниченного числа циклов наклеп всегда
остается меньше его предельного значения (точка А). Таким образом,
мы заключаем, что в этом случае переменная нагрузка является
безопасной.
.^) Е. О го wan, Proc. Roy. Soc. (London), A, т. 171, стр. 79, 1939.
®) Вследствие перемены направлейия пластической деформ&цйй эта
кривая будет несколько отлична от кривой, полученной при статическом
растяжении образца, но эта разница не является существенной в наших дальней*
ших рассуждениях^
91] МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ высоких ТЕМПЕРАТУРАХ 431
В случае, показанном на рис. 343, Ь, где точка Z выше точки В,
наклеп в слабом месте достигает своего крайнего значения в точке В.
С дальнейшим увеличением числа циклов трещина начнет развиваться,
и образец разрушится от усталости. Видно, что опасный и безопасный
циклы отличаются только положением точки Z. Поэтому предел вынос<
ливости будет соответствовать случаю, для которого точка Z
совпадает с точкой В. Ордината 0Z представит предельное напряжение,
к которому близка амплитуда напряжений в слабом месте, когда число
циклов возрастает *). Это местное напряжение, зависящее от
ориентировки слабого зерна, и оно может быть выше чем о^ред, вычисленное
как среднее напряжение по поперечному сечению образца.
Базируясь на диаграммах рис. 343, Орован сделал некоторые
выводы относительно усталостной прочности, которые
удовлетворительно согласуются с опытными данными.
1) Так как влияние переменных йапряжений зависит только от
относительного значения ординат 0Z и ОВу можно ожидать, что
предел выносливости материала связан с пределом прочности и не зависит
.от таких характеристик, как предел пропорциональности, предел
текучести и пластичность.
2) Предполагая, что участок РА (рис. 343) кривой наклепа может
быть заменен наклонной прямой, можно показать, что кривая о — п
(рис. 312) должна иметь характерную форму, состоящую из
наклонной и горизонтальной прямой линии. Может быть также сделана
грубая оценка числа циклов,, соответствующего точке пересечения этих
двух линий (предел выносливости).
3) Влияние среднего напряжения на величину диапазона
напряжений можно исследовать также, используя диаграмму, которая подобна
представленным на рис. 343.
91. Механические свойства металлов при высоких температурах
Во многих случаях части инженерных конструкций подвергаются
одновременному действию напряжений и высоких температур. Такие
условия имеют место, например, в силовых установках и в
химической промышленности. Вследствие тенденции к непрестанному
увеличению начальной температуры пара ^) в силовых установках и в связи
с развитием газовых турбин вопрос о прочности материалов при
высоких температурах стал важным и практически, и в этой области
было выполнено значительное количество исследовательских работ ^).
*) Это соответствует амплитуде напряжений в вертикальном стержне
ранее рассмотренной модели.
■*)Mellanby and Kerr, Proc. Inst. Mech. Engrs. (London), 1927;
H. L. Guy, там же, 1929 и Engineer,.т. 147, стр. 136, 1929.
8) О библиографии см. G. V. Smith, Properties of Metals at Elevated
Temperatures, New York, 1950. См. также Н. J. Т a p s e 11, Creep of Metals,
Oxsford, 1931.
imw
432
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
Опыты показывают, что пределы текучести и прочности металлов
«три растяжении зависят в значительной степени от температуры.
i^atumif
Рис. 344.
Несколько диаграмм, полученных при испытаниях, на растяжение
средне-угле]родйстой стали при^различных температурах, показано*)
/
VdffUffemie
Рис. 345.
на рис. 344. Приблизительно до 260° С предел прочности сталей
увеличивается, но с дальнейшим увеличейием температуры он быстро
*) См. доклад о работе, проделанной R. В. iVilhelra'oM в
исследовательской лаборатории Веб^ЙГЙГйуза, PfOC. Am. Sue. Tefit. Mat, т. 248, Щ. 151,1^24.
щ
МЕХАНИЧЕСКИЕ СВОЙСТВА ЙРИ БЫСОКИК ТЁЛШЬРАТУрАХ
433
падает. С убеличени«м температуры предел текучести становится
менее резко выраженным, и при 300° С его уже «ельЗя * различить на
диаграмме* На рис, 346 первые участки тех же диаграмм показаны
в увеличенном масштабе. Из рисунка видно, что при увеличении
^
^.^fi~i
о 20
700 . 200
Рис. 346.
^
soox
температуры предел пропорциональности стали уменьшается. В то же
самое время уменьшается угол наклона прямых участков диаграмм и,
€ледовател|^но, уменьшается модуль упругости. Результаты указанных
выше испытаний представлены на рис. 346, который показывает, что,
S то время как при возрастании температуры прочность материала
уменьшается, его пластичность, .хара1^теризуемая увеличением длины
й уменьшением площади сечения, увеличивается.
imtW
434
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
{ГЛ. X
Опыты при ВЫСОКИХ температурах показывают, что результаты
испытаний на'растяжение в значительной степени зг1висят от
продолжительности испытания. При увеличении времени испытания на
растяжение нагрузка, необходимая для доведения образца до разрушения,:
становится все меньше и меньше. На рис. 347 приведены диаграммы
испытаний на растяжение для ранее рассмотренной стали при 5©0°С
и при продолжительности испытания, соответственно равной 6
минутам, 70 минутам и 240 минутам. Очевидно, данные испытания на
растяжение, полученные из обычных кратковременных испытаний
(продолжающихся примерно 15 или 20 минут) и представленные на
1
1
1
-
\£
~мщ
t/m
/ .
V
V
/
"^
N
/
\
\
)
. 70минут
\
Г
/
/
'\e:2'fffMUfty/n
.
\
\
\
\
Д!еформация
Рис. 347.
рис. 346, полезны лишь для случаев, когда нагрузки действуют
только в течение корш-кого времени *).
В случае нагрузок, действующих в течение продолжительного
периода времени и при высокой температуре, например таких, как
вес конструкции или давление пара в силовых установках, мы
нуждаемся в дополнительных данных относительно влияния времени.
Опыты показывают, что при этих условиях может иметь место
непрерывная деформация, или ползучесть^ которую, как весьма важный
фактор, необходимо учитывать при проектировании. Хотя пО этой
проблеме значительное количество исследовательских работ*) было
*) Чтобы исключить влияние времени при определении модуля упру-
гести, были применены испытания на колебания. См. О. Verse, J. Appl.
Mech,, т. 2, 1935 и его докторскую диссертацию, Мичиганский университет.
") О библиографии см. книгу О. V. Smith'a, цит. на стр. 431.
911'
МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
435
выполнено и в еще большем числе в]Ь1ПОЛняется сейчас, все же
вопрос о поведении металлов при высокой температуре и
продолжительном действии нагрузки не может считаться вполне
выясненным. ,
В большинстве опытов, относящихся к пoлзyчetти, исследуют
постепенное удлинение материала при длительном растяжении.
Образцы, применяемые при испытании на растяжение при высокой
температуре, подвергают действию некоторой постоянной нагрузки и
температуры, и при этой нагруз>«е исследуют прогрессирующую
ползучесть. Результаты таких опытов для данной температуры и для
различных значений нагрузки можно
представить кривыми время —
удлинение, как показано на рис. 348 *).
К]ривая А представляет типичную
кривую ползучести для
сравнительно высокого напряжения. После
приложения нагрузки ползучесть
происходит при постепенно
уменьшающейся скорости. В точке а имеет
Mecfo перегиб, и скорость
ползучести начинает увеличиваться до тех
пор, пока испытуемый образец не
разорвется. Кривая 5,
соответствующая несколько меньшей нагрузке,
имеет подобную форму, но
вследствие более низких скоростей
ползучести для разрушения образца
требуется более продолжительное время.
Если нагрузку уменьшать дальше,
подобные же испытания над
различными образцами приводят к кривым С, D, Е, F и О. Если
напряжение уменьшается, то для достижения точки перегиба на
кривой ползучести требуется все больше и больше времени. Для
определения точек перегиба для таких кривых, как F и О, потребовалось
бы для испытаний чрезвычайно продолжительное время. Видно, что
с уменьшением напряжения кривая ползучести, по существу, является
прямой на все более продолжительном отрезке времени. Рабочие
напряжения, встречающиеся в практике, на графике располагаются
обычно ниже кривой С^ следовательно, предположение, что кривая
ползучести приближается к прямой линии, достаточно точно для
практических целей. Наклон этой линии дает наименьшую скорость
ползучести лля данного напряжения и данной температуры. Величина
■Время
Рис. 348.
1) Рис. 348—353 взяты из статей McVetty, Mechanical Engineering,
стр. 149, 1934 и Proc. Am. Soc. Test. Mat., т. 34, 1938.
436
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
|ГЛ. X
f-/^ : -.
Сплаб А
»тОй скорости ползучести уменьшается с уменьшением напряжения,
но нет убедительного доказательства, что она когда-либо : обратится
в нуль, т- е. что имеется предельное напряжение, при котором
образец может бесконечно сопротивляться напряжению при высокой
температуре. .
При изучении прогрессирующей ползучести, испытывая образцы
на растяжение под постоянной нагрузкой и при высокой температуре,
нужно иметь в виду двй явления:!) наклеп материала вследствие
пластической деформации и 2) устранение этого наклепа или
«смягчение» материала вследствие продолжительного действия высокой
температуры. Механизм пластического
течения при высокой температуре тот
же, что и при комнатной температуре.;
Пластическая деформация вызывается
скольжением металла. Это скольжение
сопровождается увеличением
сопротивления скольжению, котЪрое
представляет собой наклеп (стр. 362).
Скорость, с которой влияние
наклепа устраняется, зависит от
температуры. Ранее было упомянуто (стр. 333),
что влияние наклепа можно исключить-
в короткое время отркигом металла
при некоторой особой высокой
температуре, зависящей от рода металла. Тот
же эффект, можно получить при гораздо
более низкой температуре, если
температура действует в течение продолжи-
тельногб периода времени. Было
показано*), например, при исследовании
смягчения холоднообработанной меди, что смягчение, произведенное
в течение 12 минут nJ)H 300° С, потребовало бы 10,4 дня при 200° С
и что, видимо,, потребовалось "бы около 300 лет, чтобы произвести
то" же смягчение при 100° С.
Кривые время — удлинение (рис. 348) показывают, что в. течение
начального периода cKopoctb растяжения постепейно уменьшается.
Это, 1?роисхрдит благодаря накЬепу. В точке пер^егйба
устанавливается некоторая постоянная скорость растяжения, при которой
наклеп и смягчение нейтралиауют друг друга, т. е. наклеп, вызываемый
ползучестью, непрерывно уничтожается смягчающим эффектом
высокой, температуры. Затем ползучесть продолжается при постоянной
скорости, Зависящей от величины напряжения и температуры.
^
время, vocu
Рис. 349.
») См. Р i U i n.g and Н a 11 i w e 11, Prec. Am. Soc. Test. Mat., • т. 26,
1925. См. также R. W. Bailey, J. Inst Metals, i. 85, 1926.
m
МЕХАНИЧЕСКИЕ СВОЙСТВА ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
437
Так как мы всегда должны учитывать прогрессирующую ползу-
, честь» в элементах, подверженных одновременному действию высокой
температуры и напряжения, проектирование должно быть основана
на допущении некоторой продолжительности службы конструкции,,
а тйкже некоторой величины допустимой остаточной де^рмации.
Рабочие напряжения должны быть выбраны в кгшдом частном ;случае
так, чтобы ocTato4Hafl деформация констрзгкции в течение ее* срока.
т//7
Г7
1
.S
Л7
Iff
Щ -
Цй7
vr-^-gl'-Vo+ce
i'^B^vjjt-^e
■о
Mill
X
цр7,1ВЮ^
7330нг/СА»^
SOO TOOff
, Рис. 850.
£Ш7
службы не превосходила бы определенного предела, вависящего. от
>йпа конструкции. Целью испытаний при высоких температурах ю
течение длительного времени является предоставление
проектировщику достаточных сведений для удовлетворительного вычисления
остаточных деформаций, обусловленных ползучестью. ■
Наибольшая продолжительность лабораторных испытаний
составляет о(^чно несколько тысяч часов, и для того 4to6H предугадать
деформацию ползучести во время срока службы конструкции,
необходимо проделать экстраполяцию результатов Лабораторных
испытаний. Опыты с различными сталями показывают, что в первом участке
кривых ползучести на рис. 348 превышение скорости ползучести
над наименьшей скоростью ползучести уменьшается геометрически.
438
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
шри условии, ЧТО время нарастает арифметически. Следовательно,
обозначая через е неупругое относительное удлинение в некоторый
момент времени t, через v — соответствующую скорость ползучести
й через Vq наименьшую скорость ползучести, мы можем для
скорости ползучести принять
^/7M-
Сплад А
следующее выражение*):
V:
de.
i^ = ^o + ^^-^ (а)
где с, Vq и а — постоянные,
которые должны быть
определены из кривых
ползучести. Возьмем, например,
кривые ползучести, показанные
на рис 349. Эти кривые
были получены путем
испытания металла дтри
нескольких значениях напряжения
и при постоянной'
температуре 454*^ С. Измеряя
наклон в пяти точках на
каждой из этих кривых, мы
получаем значение скорости
ползучести при пяти
различных значениях t и скроим
кривые, показанные на рис. 350.
Горизонтальные асимптоты
этих кривых, очевидно, дают
значения v^ для
приложенных значений напряжения.
Теперь, построив значения
lg(T» —г»о) как функцию времени, мы получим систему наклонных
параллельных линий, указывающих, что предложенное выражение (а)
выбрано удовлетворительно. Значения постоянных с и cf в
уравнении (а) получаются из этих линий измерением при t = Q ординат
линий, а также их наклона.
Пластическое относительное удлинение теперь получится путем
интегрирования уравнения (а), чтр дает
Ц2 О,^ as QB W/o
Рис. 351.
£o-hV —7« "'»
(b)
где Sq — постоянная. Применяя это уравнение к тому значению t,
для которого пластическое удлинение известно из рис. 349, можем
*) См. сноску на стр. 435. Для сравнения методов экстраполяции данных
испытаний см. J. Маг Ml, Proc. Am. Soc. Test. Mat., т. 37, стр. 258, 1937.
91]
МЕХАНИЧЕСКИЕ СВОЙСТЙА ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
439^
вычислить значение е^. Следовательно, все постоянные, входящие в
уравнение (Ь), определяются при помощи кривых, представленных
на рис. 349 и 350. Мы можем "теперь применить это уравнение при-
вычислении s для любого данного промежутка времени. Этим путем
были получены кривые, показанные на рис. 351. Имея такую систему
кривых для определенного материала и для определенной
температуры, проектировщик может легко выбрать надлежащие значения
рабочего напряжения, если даны срок службы сооружения и допу*
стимая пластическая деформация.
Рис. 352.
штюЛ
fm
Ч2Т^
\
Рис. 353.
При вычислении е для больших значений t мы находим, что-
последний член в уравнении (Ь) весьма мал, и им можно пренебречь^
Это значит, что вместо кривой^ показанной на рис. 362, мы можем
воспользоватьсй пунктирной прямой. В результате значение е будет
определяться через величину отрезка ползучести ц и наименьшую
скорость ползучести v^. Опытные значения е^ можно представить
кривыми, подобными показанным на рис. 353, которые были
получены для 12у„-ной хромистой стали.
Что кйсается наименьшей скорости ползучести, то опыты
показывают, что Vq можно представить с удовлетворительной точностью'
степенной функцией напряжения
v^^kc^ (с>
где k и п—постоянные для> данных материала и температуры.
Значения этих постоянных*) для некоторых сталей, испытанных в
исследовательских лабораториях фирмы «Вестингаузл, приведены
в табл. 25.
*) См. М с V е 11 у, цит. на стр. 435.
mm
440
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ {ГЛ. X
Таблица 25
Значения постоянных Jiti и А
Материал
Кованая сталь 0,39% С. . *
Сталь 0,30% С f
Сталь №—Ст~Мо. .... .
Сталь 12%-иая Сг ..... .
Температура, *С
400
400
500
455
16.10^"
48.10-»в
91.10-««^
10-10-»'
0,6
0,19
0,31
Spesm
Рис. 354.
В этой таблице k — относительное удлинение в течение 24
часов и а —напряжение в .кг1см\ При помощи этих постоянных в
различных частных случаях для элементов конструкций можно
вычислить деформацию ползучести и рас)пределение напряжений.
В нашем предыдущем изложении предполагалось, что
пластическое течение сопровождается наклепом. Опыты показывают, что с
увеличением температуры наклеен
становится все менее и-менее резко
выраженным. Наибольшая температура, при кото-
]рой' наклеп наблюдается, различна для
разных А1атериалов и в случае стали
меняется В/ зависимости от состава стали.
Например, никакого наклепа не было
замечено *) в мягкой углеродистой стали@,17Уд
углерода) при напряжении 155 кг/слс* и
/ температуре 647° С При таких условиях
жривая время—удлинение имеет вид, представленный на рис. 354, т.е.
■скорость ползучести постояйно увеличивается с течением времени.
Интересно отметить, что два рода кривых время—удлинение^
показанных на рис. 348 и 354, соответствуют различным типам
разрушения. Ко1*да имеет место наклеп, текучесть в каком-либо месте о6-
•разцй увеличивает сопротивление в этом месте, и поэтому
следующее скольжение происходит по некоторому другому поперечному
сечению. В результате этого наблюдается равномерное удлинений, и
образец остается цилиндрическим до начала образования шейки.
Когда наклеп отсутствует, местная текучесть, коз'орая начинается в
слабейшем поперечном сечении, распространяется при уменьшающей-
^ -ся скорости к концам образца. В результате две части разорванного
образца .суживаются в виде конусов от концов к поперечному
сечению в месте разрыва.
При выполнений экстраполирования с помощью уравнения (Ь)
предполагается,' что величины %1 е и (v характеризующие материал,
остаются постоянными "в течение срока службы конструкции. Но при
*) См. Н. J. lapse 11, Creep of Metals, 1931-
92]
ИЗГИБ БАЛОК ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ
44Г
йродолжительном действии высоких температур сопротивление стал»
ползучести несколько уменьшается. Чтобы компенсировать это
термическое действие^ иногда рекомендуются лабораторные испытания
при температурах выше рабочей температуры *). Термическое действие
больше проявляется в случае высокоуглеродистых сталей. Для
того чтобы уменьшить структурное перерождение, необходи190
применить .подходшш,ую термическую обработку, которая обеспечит
структурную устой<1ивость *).
Прежде чем закон»Л!ть 'это\ рассмотрение, необхбдимо заметить,,
что^ прогрессирующая ползучесть может производить
перераспределение напряжений в частях, подвергнутых одновременному Действию
напряжений и высоких температур. В местах высокой кстцентраций
напряжений скорость ползучести больше, и, следовательно^ в ревуль-
тате ползучести будет более благоприятное распределй1не
напряжений. Это обстоятельство нужно учитывать при проектировании..
Несколько примеров этого рода разобрано Бэйли®).
92. Изгиб балок при высоких температурах
В этом параграфе мы рассмотрим изгиб призматических -балок
симметричного поперечного свечения и предположим, чФо. изгибающие
■ ч"
-- __
V Г ^
У
Рис. 355.
силы действуют в плоскости симметрии. Тогда из условий симметр!^
следует, чт© изгиб будет прсжсходить в той же плоскости. Наше
дальнейшее изложение мы начнем с чистого изгиба (рис. 355) и
») См. статью R. W. В alley, J. Appl. Mech., т. 21, стр. 309, 1954.
^) См. F. R. Hensel and Е. I. Lars en. Trans. Am. Inst. JMHn. Metal-
lufg. Engrs., T. 99, стр. 55, 1932. Влияние продолжительного действия
высоких- температур на свойства различных сталей разобрано в книге О. V.^
S m i t n' a, цит. на стр. 431. Случай внутрикристаллического разрушения сталей
с высоким сдпротив^еннем ползучести при высоких температурах разобран
R. W. Bailev, Ргос. Inst. Mech. Engrs. (Lofldon), т. 131, стр. 131 — 349, 1935..
*) R. W. В а i 1 в у, там же, 1927 и 19гЙ; Enguieering, т, 124, стр.
и т. \Щ 1930. См: также С. R. Sodefberg, J. Appl. Mechi., т. 1, стр. 131,.
1933; G. Н. М а с С u 1 J о u g h, там же, стр. о7; J. а г 1 п, Jr. Franklin Inst.^
Т. 226. стр. 645, 1938.
imw
442 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
шредположим, что при изгибе: 1) поперечные сечения остаются
плоскими*), 2) каждое продольное волок*^ находится в состоянии простого
растяжения или сжатия и 3) уравнение ползучести (уравнение (Ь) на
•стр. 438), установленное для растяжения, также сохраняет свою силу
и для сжатия. Обозначим через у расстояния волокон от нейтрально^*
-Ъси и через г — радиус кривизны изогнутой оси; относительным
удлинением или укорочением произвольного волокна будет
e = f. ■' (а)
При вычислении соответствующего напряжения предполагаем, что
ттротекло значительное время с момента приложения нагрузки. Пре-
«(ебрегая переходным периодом, представленным на рис. 352 кри-
«ой, можно для оценки ползучести воспользоваться выражением (с),
■стр. 439. В результате получим
e = ^ = ka'4 (b)
ЙИ ,
Обозначая через hi и h^ расстояния наиболее удаленных от
нейтральной оси волокон, для наибольшего растягивающего или сжимающего
напряжений находим значения
Растягивающее и сжимающее напряжения в расстоянии у от нeйtpaль-
1НОЙ.ОСИ будут ~
раст
= (°шах)раст(^) ". °сж = (Ошах)сж (^) " • (е)
Для определения положения нейтральной оси и расстояний Л^ и
.Аа применим условие статики, которое устанавливает, что сумма ра-
«стягивающих усилий по нижнему участку поперечного сечения (рис. 355)
должна равняться сумме сжимающих усилий по верхнему участку,
.йтим условием будет
(р.л>сг I (Й""''''=(%..и|'Ш"" -i^. (О
^) Это предположение удовлетворительно согласуется с опытами; см.
G, Н. М а с С U П о U g h> Trans. А. S. М. Е., т. 55, стр. 55, 1985; Н. J.
X а р S е 11, J. Inst. Metals, стр. 387, 1935.
92] ИЗГИБ БАЛОК ПРИ ВЫСОКИХ ТЕМПЕРАТУРАХ 443^
Если ширина поперечного сечения являемся известной функцией у^.
можно преобразовать указанные интегралы и получить уравнение дл№
вычисления отношения Л1/Й2.
Задача упрош.ается, если поперечное сечение имеет ось симметрии,,
перпендикулярную к плоскости изги0а. Тогда сразу же заключаем,
что эта ось является нейтральной осью поперечного сечения,
поскольку при этом условие (f) удовлетворяется. Получая в результате-
для растягивающего и сжимающего напряжений мы можем
пользоваться формулой
Для вычисления с^^^^ воспользуемся уравнением статики, которое
устанавливает, что момент внутренних сил, распределенных по
поперечному сечению, равняется внешнему изгибающему моменту М. Та-
ким] образом, имеем
А/2 - .
о
Рассмотрим теперь в качестве простого примера случай
прямоугольной^ балки шириной Ъ. В этом случае уравнение (i) дает
А/2
О
и мы получаем
__Mh 2п 4-1
о
max 2У Зп ' '
где J есть момент инерции площади поперечного сечения
относительно нейтральной оси. Подставляя в уравнение (h), для
напряжения в любом волокне находим
°~~ 2/ Зп А А / .
На рис. 356 показано распределение напряжений о для и =10 и_
/1 = 6. Видно, что при больших значениях д изменение п лишь в
незначительной степени влияет на напряжение. Для сравнения
распределение напряжений при упругом состоянии показано прямой,
линией ОА.
m
444
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
Зная величину о^д^, находим кривиану балки из выражения- (d).
Если нейтральной осью является ось симметрии площади поперечного
<:ечения, то кривизной «будет
2kt п
л шах
(J)
Когда балка испытывает поперечный изгиб, нормальные
напряжения и кривизна^ каком-либо поперечном сечении балки будут
вычислены путем подстановки значения изгибающего момента М в
формулы для чистого изгиба. Таким образом, если нейтральной осью будет
ось симметрии, напряжения должны вычисляться при помощи уравнений
(h) и (i), а кривизне найдется из
уравнения (j).
jr» - ^ «^ ' Для прямоугольной балки диф-
Ji ^1—Г"* ~ у ференцйальным уравнением
изогнутой оси будет >
^1
JtJC
чо
<5*
^^
■•
■ ■
^
/Wf J
l^^Ci
-Лв-Л^
^
d^y
^
ц$ ф Uf
2kt п
—-— а :
h шах
Рис. 356.
Это уравнение можно легко
проинтегрировать в каждом частном
случае распределения нагрузки, и постоянные интегрирования можно
определить из условий на концах балки. Подобным пзггем можно
исследовать изгиб прямоугольной балки при одновременном Действии
изгиба и растяжения или сжатия*).
93. Релаксация напряжений
В предыдущих параграфах была рассмотрена ползучесть при
постоянной нагрузке. Однако имеются случаи, когда ползучесть
происходит при постепенно уменьшающихся силах. Болтовое соединение,
подверженное высоким температурам, представляет важный случай
этого типа. Затяжкой болтов вызывается значительное первоначальное
растягивающее напряжение, но .вследствие ползучести напряжение
постепенно уменьшается с течением времени. Это явление
называется релаксацией. Уменьшение первоначальных напряжений в болтах
может о.казать нежелательное' действие, как, например, утечку пара
9 турбине Д1ЛИ в паропроводе при высокой температуре. В этой связи
^) Этог случай разобран R. W. В а i I е у, цит. на стр. 441.
9^1 РЕЛАКСАЦИЯ НАЙРЯЖВнШ ' ' 446
njpn изучении явления релаксаций *) была проделана большая
теоретическая и эксйериме^тальная работа. , -
-Начнем наше обсуждение этого вопроса с рассмотрения простого
-Случая, когда концы болта удерживаются на неизменном расстоянии
друг от друга. Щредпрложим, нто затяжкой болта были вызваны
первоначальное растягийающее напряжение о^ и соответствующая; упругая
деформация о^Е. С течением времени^ растягивающее напряжение и
упругое удлинение в болте постепенно "уменьшаются из-за ползучести.
В то же время будут иметь место пластические деформации. Так
как концы болта закреплены, то полное удлинение должно остаться
постоянным и ' равным начальному утщтощ удлинению. Обозначая
через о растягивающее напряжение в болте в какой-либо момент
времени t и через %^ пластическое удлинение вследствие ползучести,
1йы получаем уравнение
:Э этом уравнении е„ и о являются функциями времени ^.
Дифференцируя уравнение (а) по f, получаем
de„ I do
« ^ - (b)
При решении этого уравнения начнем с предположения, что
уравнение (с), стр. 439, для скорости ползучести достаточно точно для
нашей задачи. Тогда
1 da
и мы получаем
'^° Edt\
Интегрирование дает \
и зависимость напряжение—время для болта будет представлена
кривой'') на рис* 367. Опыт показывает, что напряжение в болте,
предсказываемое этой кривой, является слишком высоким. Болт теряет
свое первоначальное напряжение в значительно более короткий срок,
^) Несколько методов решения этой задачи разобрало Е. П. Поповым,
J. Appl; Mech., т, 14, стр. А-135, 1947; библиография по предмету дана в
этой статье. См. также <3. W. Н о и s п е г, *ам же, стр. 352. Об
экспериментальном исследовании релаксации напряжений см. А; Nadai and J. Boyd,
Proc. 5th Internal. Congr. Appl. Mech., стр. 245, 1039,
») См. J. Marin, Mechanical Properties of Materials and Design, стр. 241,1942.
mw
446
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
И прямая АВ на рис. 352 не может быть применена с достаточной
точностью при решении уравнения (Ь).
Чтобы получить более удовлетворительный рез^ьльтат, нужно
воспользоваться кривой ОСВ на рис. 352. Тогда скорость ползучести
надо задать более общим выражением *)
dt.
■-/{о, t).
dt
Подставив (d) в уравнение (Ь), получим
Л. 1 da
(d>
(е)
Это уравнение обычно решается последовательным числещшм ин--
тегрированием («шаг за шагом»). Положив t==0 к о = 0^, вычислим
левую часть )фавненияг (е). Это дает в некотором масштабе началь--
ный угол наклона кривой релаксации напряжений. Используя эту
величину, можно вычислить напряжение о в момент времени t = At.
Подставляя это новое напряжение в уравнение (е), получим зн«дение
11
11^/7%/: стагтб
-
п f^ п
г '^ 6 в
в/^емл fff. гадах)
Рис. 357.
W
Рис. 858.
угла наклона для момента времени t = Д^. Вычислением о для t = 2Af
можно сделать следуюш;ий шаг, и процесс продолжается. Вычисления,,
сделанные Поповым, показали, что, следуя этому приему, можно
получить KJDHByro релаксации напряжений, которая удовлетворительно
согласуется с опытами.
В предыдущем изложении предполагалось, что концы болта были
абсолютно неподвижны; но на практике обычно имеется некоторая
податливость в закреплениях концов, которая должна быть принята во
внимание при вычислении кривых релаксации напряжений. На рис. 358
^) Несколько видов функции /(о, t) разобрано в вышеупомянутой статье
Е. П. Попова. Необходимо заметить, что уравнение (а) стр. 438 для
ползучести при постоянном напряжении должно быть изменено при изучении
релаксации, в которой материал первоначально имеет высокие напряжения и
затем ползет при непрерывно уменьшающемся напряжении.
«4] ПОЛЗУЧЕСТЬ ПРИ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ 447
лоназано соединение труб при .помощи болтов, подверженное
высокой температуре. При затяжке фланцев п болтами w будет иметь
место упругая деформация. Ищ релаксации эта деформация
уменьшается и длина болта увеличивается. Пусть Po/f представляет
упругую деформацию двух фланцев (на единицу длины между фланцами),
вызванную напряжением а в болтах*). Тогда при релаксации мы по^
лучим вместо уравнения (а) следующее уравнение:
Последние два члена правой части этого уравнения представляют
относительное удлинение болта при релаксации вследствие упругого
и пластического изменения расстояния между фланцами^
Окончательно уравнение (f) можно написать в следующем виде:
®пб ~Т~ ®пф — g •
Дифференцируя по t, мы получаем
dt~^dt~' Е dt ' ^^'
Для скорости ползучести болта мы опять используем выражение (d).
Подобное же выражение можно применить и для скорости
ползучести фланцев. Тогда уравнение (g) будет иметь тот же вид, что и
уравнение (е), и его можно решить, пользуясь последовательным
численным интегрированием. Тогда, мы найдем, что благодаря упругости
закрепленных концов постепенное уменьшение напряжений в болте
происходит гораздо медленнее, чем в случае неподвижных концов.
94. Ползучесть при сложном напряженном состоянии
Было проведено лишь несколько опытов, касающихся ползучести
под действием сложных напряжений. Р. В. Бэйли*) при комнатной
температуре испытывал свинцовые трубы, подверженные внутреннему
давлению и сочетанию внутреннего давления с осевой нагрузкой.
Свинец имеет низкую точку плавления, и явление ползучести имеет
место при комнатной температуре. Он также исследовал свойства
стальных труб при 482° С и 549° С для сочетания осевого растяжения
*) Для вычисления р должна быть исследована упругая деформация
фланцев (см. стр. 120).
*) Всемирная конференция по энергетике, Токио, 1929; Engineering,
т. 129, стр. 265—266, 327—329 и 772, 1930. -
щщ
44в
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. Х
и кручения, Ф. Л. Эверет *) испытывал Стальные трубы, подвержен-
ные кручению при высоких температурах. Такого рода испытание
имеет некоторые преимущества по сравнению с обычными
испытаниями на растяжение, так как пластическое кручение не оказывает
влияния на размеры поперечного сечения образца, а небольшие
изменений объема из-за колебаний температуры и преобразования структуры,
не влияют на измеряемый угод. закручивания/ ^
При отсутствии дополнительных Щссперйментальных данных
относительно ползучести под действием сложных напряжений ^^необходимо
применять результаты испытаний на ползучесть при простом растяже-
цик к решению этих более слоз^ных задач. Такое р)ешение обычно
сопровождается допущениями: Д) при пластической деформации
направления главных напряжений Oj, og и Og
совпадают с направлениями главных
деформаций Ej, Ей и Sg; 2) объем материала остается
постоянным, ^ак что для малых деформаций
имеем -
- «1-1-69 4-68 = 0, (а)
и 3) наибольшие касательные напряжения
пропорциональны соответствующим
относительным сдвигам. Можно показать, что значения
относительного сдвига в плоскостях, делящих
пополам углы между главными плоскостями,
будут равны Ej — ц, ^ — вз и Ез — ej; Этот результат можно получить,
если рассмотреть куб (рис.^ 359), имеющий относительные Удлинения
Ej и 62 в направлениях J и 2. Относительный сдвиг i,
соответствующий плоскостям Oi» и Ос, найдется из треугольника ОаЬ, Полагая,
что Si ^ еа, получаем у
Рис. 359.
Ml-i)
1—;
^■^1
1-Fe,
l + e,
откуда
:6, —I
Подобно, этому можно найти относительные сдвиги для двух других
плоскостей, делящих пополам углы между главными плоскостями, и
тогда предположение 3) принимает следующую форму:
■ ■ ■ ' ■■'■.■ ■ с
О. Оо Оо О. О. О,
■■»,
(Ь)
где 6 есть функция oj, oj и og, котор.ая" должна быть определена из
») Trans. A.S.M.E.," т.. 53, 1931; Ргос. Am. Soc. Test. Mat., т. 89, стр. 215—224,
1939. См. также Н. J. Т а р s е U and А. Е. J о h п s о п. Engineering, т. 150,1940.
Э41
ПОЛЗУЧЕСТЬ ПРИ сложном НАПРЯЖЕННОМ СОСТОЯНИИ
449
ОПЫТОВ *). Из выражений (а) и (Ь) следует, что
^з = -з [°з—2'(°i4-°a)J- J
Эти выражения подобны зависимостям между напряжениями и
деформациями в законе Гука (см. т. I, стр. 64), нр они отличаются в двух
отношениях. Величина 26/3 появляется вместо постоянной 1/f и
множитель 1/2 заменяет коэффициент Пуассона.
Чтобы применить уравнения (с) к задаче о ползучести при
постоянной скорости, разделим эти уравнения на время i. Пользуясь
обозначениями v^, v<i и т^з Для главных скоростей ползучести и
обозначая множитель, стоящий перед скобками, через т, ты приходим
к следующим уравнениям: ,
г»1=:/и|^0, — ^(Oj-f Оз)],
TJ:2 = ot[o2— ^(Oi-f Оз)],
г'з = W [оз — 2" (oi + «'а)].
(d)
Применяя эти уравнения к простому растяжению, где oi = o и
-32 = 03 = 0, получаем
v = ma. (е)
Мы уже установили (см* стр. 439), что в результате опытов
скорость ползучести в случае простого растяжения при постоянной
температуре можно представить удовлетворительно степенной функцией
- - t> = yfeo«, (f)
где^ и W — две постоянные материала. Чтобы привести уравнения (е)
и (f) ic согласованию, мы должны принять
/й==Ло"->.
(g)
Чтобы установить вид функции т для общег»^ случая ползучести,
представленного уравнениями (d), воспользуемга уравнением B96)
стр. 378, которое дает зависимость между условием текучести для
пространственного напряженного состояния системы и для простого
^ Указанные выше три предположения являются в сущности теми же,
что были приняты пионерами теории пластичности Барре де-Сен-Венаном,
Compt. rend., т. 70, стр. 473, 1870 и М. Леви, там же, стр. 1323.
15 С. П^ Тимошенко, т. II
m
450 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ (ГЛ. X
растяжения: Вводя значение эквивалентного напряжения
1
°9 =
yfViPt~o^f-\-ioi~~o^-\-{o,~~o^ C00)
в уравнение (g) вместо а, получаем'
9 •
C01)
Тогда уравнения (d) получаются в следующем виде:
г>1 = Ло^'"'* l^oi—у (оа ^ a8)J,
^2 = Ао" ~ * [^Оа — Y (оз 4-ai)J,
Для простого растяжения (ai==::o== а^, а^ = Од = 0) эти уравнения дают
v^ = ka^, гг2 = г»8 = -^. ' ^ (h)
В общем случае выражения C01) позволяю; вычислить скорости
ползучести г>,, ©2 и щ путём использования значений кип, пол)гчен-
ных из испытаний на растяжение. Подобные формулы были
применены различными авторами *) при решений задач на ползучесть в
случаях сложных напряженных состояний.
96. Частные случаи двумерной ползучести
Применим теперь^ уравнения C01) к исследованию плосконапря-
жепного состояния и предположим, что
^Оз = О, Oi ]> oj, oa/oi = а.
Из выражения C00) получаем
<^в-
,==:oi/l—a-f а*.
и уравнения C01) принимают вид
\ .!p»=Jfeof(l—a-j-o?)^"-*^''^(a--l/2),
C02)
^)K К. G. G d q V i S t, Plasticitetsteori, Proc. Roy. Swed. Inst. Engrj
Research, 1934; R. W. Bailey, J. Inst. Mech. Engrs., т. 131, стр. 131, iM
С. R. S о d e r b « r g, Trans. A, S. M. E., т. 58, стр. 733—744, 1936.
Щ ЧАСТ1ед1 СЛУЧАЙ ДВУЙШРНОЙ ПОЛЗУЧЕ^^^ 451
В]^дйр, что выражения для скоростей подзуч^сти в главных
направлениях отличаются от, выражений для простого растяжения
(уравнения (h) п. 94) лишь числовыми коэффицие;н^амй. Величина этих
коэффициентов может быть легко вычислена, если известны постоянная п
Материала и отношение а. - •
Тонкие трубы. Если даны допускаемые дефор^мации в главных
направлениях до время срока службы конструкции^ то допускаемое
напряжение <?1 Найдется из уравнений C02). Этим путем можно решить
такие'задачи* как выбор надлежащей толщины тойкой трубы,
подверженной внутреннему давлению совместно с осевой силой или кру-
тяшлм моментом при высоких температурах. Приняв Vi в йаправле-
ний по окружности и v^ в осевом направлении и предположив, что
действует только одно внутреннее давление, мы получим <х=; Г/2 И
%=:0. Тогда не будет ползучести в осевом направлении, но будет
только в направлении по 01фу.жности. /
Это заключение согласуется с результатами опытов со
свинцовыми трубами, hpojaleлaнныx Р. В. Бейли *).
В случае, когда действует только крутящий момент, главные
напряжения численно равны и'направлены под углом 45° к оси трубы.
В этом случае а=—1, и для оценки ползучести по главным
направлениям мы получаем
т;, = -г»а=|Ао«C)«-»Д
Здесь мы имеем деформацию чистого сдвига без ползучести трубы
в OC0OM: направлении. Таким образом, неосевая' ползучесть вызывает-
сй либо отдельно действующим крутящим моментом, либо отдельно
действз^ющим внутренним давлением. Однако когда действук^т
одновременно давление и крутящий момент, возникает осевая ползучесть.
Чтобы оценить ползучесть для этого случая, мы должны определить
в каждой частной задаче величины и направления главных
напряжений. Тогда уравнения C02) дадзгг скорости ползучести в главных
направлениях. Осевая и окружная скорости ползучести получатся затем
из простых геометрических соображений. Для любого направления,
взятого под углом tf к. направлению""-»!, скорость ползучести будет
^ г> = ф, cos^<p-|-i>2 sin*<p. ( "^
-Вычисленные таким образом значения скоростей ползучест»
удовлетворительно согласуются с опытами. ^ " .
Толстые трубы. Ранее мы изучили случаи однородного
распределения ндпр)шений. В качестве примера действия , неоднородных
напряжений рассмотри^ толстую трубу под действием внутреннего
*),Цйт. на стр. 447.
16*
452
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
давления р (рис. 360). Предполагая, что труба находится в
плоском деформированном состоянии, получаем, что. осевая деформация в^
обращается в нуль, и уравнения C01) дают:
а из последнего уравнения мы заключаем,
что I
По условию равновесия элемента,
показанного на рис. 360, имеем (см. стр. 174)
Рис.360. r-^=^''t-^r' (с)
Чтобы определить а^ и а^, мы должны рассмотреть деформацию
трубы. Обозначая через и радиальные перемещения при расширении
трубы, заключаем, что (см. стр. 174)
и
du
и
de-t
dr
Ь==Г'
1 du
г dr
'г dr
и . 1
ЬГ
Предполагая, что состояние ползучести установившееся, получаем путем
деления на время dv* I
Подставляя выражения (а) вместо iJ^ и v^, получаем дополнительное
уравнение для оп5редедения главных напряжений. Это уравнение можно
значительно упростить при помощи выражения (Ь). Toi[7ia эквивалентное
растягивающее напряжение получается в виде
V^f \ '
w из выражений (а) мы находим
^гТ-
(е)
Гогда уравнение (d) принимает тшгой вид;
d_
dr
^ (о,_.,)«^_?-(о,-о,)«,
951 ЧАСТНЫЕ СЛУЧАИ ДВУМЕРНОЙ ПОЛЗУЧЕСТИ 453
и МЫ заключаем, что
(°^~<^.Г = ^, . /(f)
f де С — постоянная интегрирования. Теперь уравнение (с) переходит в
dr~'r\r^] ''
после 'иятегрирования получаем
п
-B/я)
где С, = С^''".
Постоянные Q и Cj теперь будут определены из условий на
внутренней и наружной поверхностях трубы, откуда
iPr) г-а = - р = - |- С, а-B/«> + Q
м ..ft=О=-1- С, ^-(з/") -f а.
ъ
Из этих уравнений находим
2р
С,=
„ (ft-B//i) _ а-B//1)) '
и уравнение (g) дает
а=
pb-(Vn)
b-B/n)—a-(Vn) '
^r = ~P
В результату из уравнения (f) получаем
(h)
з^=р
6\2//1
AГ-
0)
Уравнения (Ь), (h) и (i) дают напряжения в трубе при условиях
установившихся скоростей ползучестл. Величины скоростей ползучести
получаются ho уравнению (е), которое приводит к
f/
T;, = i-C)^«+>.V2yfe-^(lj''
Л4Г-
При'выводе предполагалось, что температура трубы не изменяется
с изменением радиуса. В случае теплопередачи через стенки трубы
можно "поступить подобным же образом*).
*) См. Р. В. Б е й л и, дит. на стр. 447.
.454
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
1ГЛ. X
В предыдущем изложении было получено простое ^решение в
предположении установившегося состояния ползучести, дающее
удовлетворительные результаты при ползучести, которая имеет место после
длинного периода действия сил. Если бы мь*. захотели выяснить, какова
ползучесть в результате лишь краткого'действия нагрузки, то рледует
признать, что формулы, выведенные в предположении
установившейся ползучес1и, оказываются здесь неудовлетворительными; мы
должны 15ыли бы прибегнуть тбгда к кривой ползучести по рис. 352»
стр. 439. Задача становятся сложной, и; ползучесть может быть
вычислена лишь в процессе последовательных приближений («шаг за
шагом») *). Такие вычисления показывают^ что с увеличением /
продолжительности действия сил
получаемые результаты
приближаются^ результатам,
найденным при установившейся
ползучести. При
продолжительности действия, равной, может
быть, году илй^ более, оба
метода вычислений дают
приблизительно одни и те же
результаты.
Вращающийся диск. В^
заключение дадим краткое изложение
метода расчета на ползучесть
последовательными . приближениями,
для случая вращающегося диска ^>
(рис. 361), Предпод^г-ается, что
переменная толщина z диска мала по сравнению с его радиусом, что на-'
пряжения О/и а^ равномерно распределены по толщине, а о^ обращается
в нуль. Таким образом, мы имеем плосконапряженное состояние, и для
скоростей ползучести можно воспользоваться уравнениями C02), В этих урав-
нейиях о = а^/о; теперь является функцией г, т. е, о = <р (г). Предполагая,
что ползучесть устйновивщаяся и опять обозначая радиальные перемещения
через/Г, мы-получаем
,(/?.-1)/2
^J
b)
Рис. 361.
e, = ^ = ^<=:ft^^(l-a+«^)^ (^-1)'
(J>
.Условием равновесия элемента, заштрихованного на рис. 361, а (см. стр. 180),
будет
^гго^)—го^-|-
лЗ^а-
^) Примеры таких вычислений даны в статье С. Я. Soderberg'a,
цит. на стр. 441. См. также статью L. F. Coffin'а, Jr., Р. R. Shepler'a
and G. S. Chern'iak'a, J. Appl. Mech., т. 16, стр. 229, 1949.
*) См. P. В. Б e й л и, цит. на стр. 447. См. также Е. П. П о п о в, доктор-^
екая диссертация, Стенфордский университет, 1946.
^j : ЧАСТНЫЕ СЛУЧАЙ ДВУМЕРНОЙ ПОЛЗУЧЕСТИ 455
н интегрированием мы получим ^
а о
Вилно что если известно распределение напряжений в^ то значение о>. для
лЖго значения г можно вычислить по уравнению <к) при ус1йовии, что
тякже даны (в,.)г-я и z как функция г.
Поименяя^етой последовательных приближений, мы начнем с
предположения что а. равномерно распределены по диаметральному сечению
Sa показанному штриховкой на рис. 361. Ь. Это среднее значение ^по-
5уча1тся из уравнения (к) интегрированием от г = а до г = & и Дает в hep-
BOM приближении i г -уазут
{Ci)i=-p\(rzar)r^l,^(rz<Sr)r^+—j, (i)
где 6 *
F= t zdr,/==\ r'zrfr..
Крл«чяны (rzoX'h и (rzo^V^ можно получить легко в каждом частном
случае; Заккгйс силы, действующие на внутренней и наружной поверхностях
^^**My^fl"?or"*3 уравнения A), мы вычисляем о^ как функцию г из
уравнения (к) и получаем первое приближение для отношения
По бтим значениям о^ первое приближение для оценки ползучести
получится из первого из уравнений (J), которое дает
Чтобы пО|1учить ^чш^е приближение, возьмем отношение двух
уравнений 0) Hi, г 9а —1
. аГ и ^ — «1
Значение Ф1 (г) можно легко вычислить, так как ai=(pi(r) уже известно.
Тогд^ из уравнения (п) мы получим
и
и интегрированием находим /•
и_ __^ (»)r-g в« .
Подставляя в уравйение (т) это значение вместо (tt/r)i, получим второе
приближение для о^ ^
Jr-i4<i(r)dr
а
, ч (tt)r-o -J- — • Го)
SSiW
456 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
Постоянная (и)г^а найдется из уравнения статики, подобного уравнению A)»
что дает
b
0
Когда (u)r^a найдется из этого уравнения, величина (а^)^ будет вполне
определена, и, поступая по-прежнему, мы. найдем вторые приближения (аД, «g,
$2 (г) и (u/r)s и т. Д.
Практика показывает, что процесс быстро сходится, и второе
приближение дает удовлетворительные результаты для напряжений и деформаций
ползучести. Все вычисления удобно выполнять в табличной форме. После
вычисления (а^)| По уравнению A), мы разделим расстояние от г = йдо
г = Ь, скажем, на десять равных частей. Пользуясь уравнением (к) и
интегрированием «шаг за шагом», можно составить таблицу значений (a^)i. Имея
эти значения, можно вычислить величины «^ и ^^ для каждого значения г,
и Приготовить таблицу значений к/г. По этим значениям и при помощи
уравнения (о) можно для таблицы вычислить значения (а^)^ и т. д.
96. Рабочие напряжения
Общие соображения. .Вопрос о выборе йадлежащего
коэффициента безопасности при проектировании сооружений и частей машины
имеет первостепенное практическое значение. Если этот коэффициент
принят слишком низким, и рабочие напряжения слишком высоки, то
конструкция в условиях службы может оказаться слабой. С другой
стороны, если рабочие напряжения слишком низки, то конструкция
получается излишне тяжелой и неэкономичной.
Для выявления различных факторов, учитываемых при выборе
рабочих напряжений, возьмем простой пример растяжения
призматического стержня.* Допустим, что за основание для определения
рабочего напряжения принят предел текучести материала; тогда
безопасная площадь F поперечного сечения" получится из уравнения
Мы видим, что плош,адь поперечного сечения зависит от величины
внешней нагрузки, от предела текучести материала а^ и от
коэффициента безопасности k. Очевидно, величина этого коэффициента,
который иногда называется коэффициентом незнания, зависит от
точности, с которой мы знаем внешнюю нагрузку и механические
свойства материала, и от точности, с которой это уравнение
определяет наибольшее напряжение.
Есть случаи, когда внешние усилия известинце большой
точностью. Например, мы знаем точно гидростатическое давление*
действующее на плотину, если известна глубина воды. Мы знаем точно
центробежные силы, действующие в роторе, имеющем определенную
угловую скорость. Но в большинстве случаев силы известны лишь
приблизительно, и наиболее неблагоприятное условие нагружения
96] РАБОЧИЕ НАПРЯЖЕНИЯ 457
ДЛЯ конструкции мржет быть установлено лишь на основании
длительного опыта. Рассмотрим, например, расчет моста. Вес самого
моста и вес движущегося по мосту поезда могут быть известны
с достаточной точностью. Но' при проектировании моста необходимо
принять во внимание динамические влияния. Из-за наличия
противовесов давление колеса паровоза на рельс непостоянно, и наибольшее
давление больше статического. Под действием движущихся и
меняющихся по величине нагрузок мост будет приведен в состояние
колебаний, а np1h таких условиях задача определения усилий в
отдельных стержнях моста становится чрезвычайно сложной. Другой тип
действующих на мост сил, которых мьь не знаем точно, это —
давление ветра. Величина этих сил обычно устанавливается на основании
наблюдений над существующими сооружениями. ,Из этих
рассуждений ясно видно, что если выражение (а) и представляет условие
безопасности элемента моста, то неизвестная точно сила Р может быть
определена лишь-ч; некоторым приближением. Естественно, точность,
с кбторой может быть сделано это определение, будет влиять на
величину коэффициента безопасности.
Величина предела текучести а^ также неизвестна точно. Она
может меняться в некоторых пределах для разных образцов из одного
и того же материала, а эти изменения зависят от степени
однородности материала. Поэтому совершенно естественно, что в случае
таких однородных материалов, как сталь, коэффициент безопасности
может быть взят более низким, чем в случае таких материалов, как
дерево или камень. ^ . "*
При выборе коэффициента безопасности необходимо также
учитывать точность самой формульь Уравнение (а) можно считать очень
точным дЛя вычисления напряжений 6 образце при испытании на *
растяжение (см. рис. 255, стр. 327), поскольку особые меры пре^
досторожности принимаются для того, чтобы приложить нагрузку
центрально и распределить ее равномерно по наиболее слабому
поперечному сечению. Но, взяв одять в качестве иллюстрации расчет
элемента мостовой фермы моста, можем сказать, что уравнение (а)
ecTi> лишь грубое приближение, связанное обычно с допущением^ что
в узлах имеются идеальные, шарниры. Действительное напряженное
состояние в таком стержне очень далеко от простого растяжения.
Благол^аря жестким узловым соединениям стержни мостовой феушы
испытывают не только напряжения растяжения или сжатия, но и
напряжения изгиба. Соответствующие напряжения" от изгиба достигают
иногда значител^.ной величинв|, и если их не принимают во
внимание, а для определения площади поперечного сечения пользуются <
уравнением (а), то неточность уравнения (а) в этом случае обычно
компенсируется увеличением коэффициента безопасности.
Из этих рассуждений можно видеть, насколько трудно дать
какие-либо определенные указания отноеительно величины коэффициента
458 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. Х
безопасности. Выбор коэффициента всегда зависит от опыта, и
суждения конструктора. *
В последующем изложении будем предполагать, что величины
действующих сил установлены' опытом «'* что механические свойства
материала известны. Следовательно, дополнительно надо изучить
методы оценки влияния различного' рода напряж^нйых состояний на
выбор рабочих напряжений. Будем считать, что инженер должен так
проектировать конструкцию, чтобы во всех ее частях был равный'
коэффициент безопасности. Очевидно, это требование необходимо
всегда выполнять, чтобы проект был экономичным, поскольку
несущая способность конструкций' определяется сопротивлением её
наиболее слабого места. _
Рабочие напряжения' для статических условий. Начнем с рас»/
смотрения ]ра!бочих напряжений для статических условий, например^
для случая, когда конструкцияг подвергается действию - постоянной
. (или почти постоянной) нагргузки. Будем разли,чать, Д(ва рода
материалов: пластичные материалы^ ттьпыы образом ))азличн6го рода
строительные стали, и хрупкие материалы, 1такие, как цугун, камня
и бетон. : ;
В случае пластичных материалов за основание для выбора pa6of
,чих напряжений обычно принимается предел текучести <т^ так как:
большие деформации, которые имеют место при текучести,
недопустимы в инженерных конструкциях. Если известен у материала предел
текучести о^, коэффициент безопасности при простом растяжении или
сжатии будет*). "^
А=у[4 (Ь>
Дойускаемое напряжение |о],. принимаемое за номинальное, вычи<:^
ляется при помощи выражения (а). Концентрация напряжений, вызьь
ваемая_отверстиями или выточками, об)ь1чно не учитывается Nwa том
основании, что, благодаря пластической' деформации напряжения
стремятсй выравниваться в местах наибольших напряжений. Такое
предположение справедливо лишь до тех пор, пока нагрузки
приложен^ статически. В случае ударногб действия нужно учитывать
Свойства хрупкости стержней, имеющих глубокие выточки и резк^
изменения поперечного сечения (см. стр. 362). • / ^
Для общего случая однородного распределения напряжений
воспользуемся эквивалентным напряжением, определяемым по
формуле C00), Стр.^450, а коэффициент безопасности найдем из условия
*) Здесь предпрлагается, что с^ один и тот же при растяжении и
сжатии. Для материалов, которые не имеют ясно выраженного предела
текучести, растягивающее напряжение, 11ри котором остаточная деформация до-
ст1|гает значения 0,2''/Ь» Обычно принимается за о^.
Щ РАБОЧИЕ НАПРЯЖЕНИЯ 459
Для плосконаггряженного состояния, используя обозначение оаМ = а.
получим
в частном случае чистого сдвига ai===--a^=x, аЪ=—1 находим
КЗ [т]'
(е)
В/'случае неЬдпородного распределения напряжений, как, например,
лри изгибе или кручении, мы должны принять во внимание то
обстоятельстбо, что начало текучести в области наибольших
напряжений не влечет за собой большой деформации всей конструкции.
Чтобы получить большую деформацию, эквивалентную деф<^мации
призматического стержня при растягивающем напряжений, равном о^,
мы должны принять более высокие нагрузки, чем те, при которых
о^д^ достигает значения о^. Возьмем, например, изгиб, прямоугольной
балки. При нагруж^нии балки, если наибольшее напряжение в
волокнах, наиболее удаленных от нейтральной оси, достигает значения а^,
опасной пластической деформации балки , не происходит. Чтобы
получить'условия, эквивалентные наблюдаемым в стержне, .растян)ггым
напряжением' а^, мы долАны приложить изгибающий момент, на бОу^
больший того, при котором о^^^ только достигает знйчения( а^ (см.
стр. 290). Принимая во внимание этот факт, запишем уравнение для
вычисления коэффициента безопасности .при изгибе в таком виде:
где р — коэффициент, зависящий от формы поперечного х:ечения.
Он равен. 1,5 для прямоугольник балок,/" 1,3—для тонкостенных
круглых труб'(^в„/^„ар = 0,95) и зависит от размеров поперечного
сечения в случае двутавровых балок (см. стр. 290).
Подобные соображения применимы также в случае^ ■крушения;
уравнение для коэффициента безопасности в этом случае будет
Для сплошных круглых валов р,=:1,33 (см. стр. 318). Для тонких
круглых труб р1 приближается к значению единица; й формула (g)
совпадает с формулой (е).
Для случая совместного действия однородных нормальных и
касательных напряжений иногда вместо формулы (d)"" применяется
формула B98), стр. 378. Это дает ^
SSiW
460 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. X
При выводе формулы для k в случае одновременного действия изгиба
и кручения мы должны видоизменить формулу (h) 'таким же образом^
как это сделано при выводе формул (f) и (g). Тогда получим
Если т обращается в нуль, то эта формула совпадает с формулой (f);
если же нормальное напряжение обращается в нуль, то оно
совпадает с формулой (g).
В вышеприведенных рассуждениях предполагалось, что принцип^на-
ложения сохраняет свою силу; это означает, v что наибольшее
напряжение пропорционально нагрузке. Следовательно, коэффициент k^
который применялся при определении рабочего напряжения, должен
быть также связан и с внешней нагрузкой. Тогда мы можем
утверждать, что текучесть в конструкции начинается под действием
нагрузки, которая в k раз больше действительно безопасной нагрузки.
Если принцип наложения несправедлив, то необходимо отнести
коэффициент безопасности лишь к нагрузке и определить размеры
конструкции из условия, что текучесть начинается, если только действующая
нагрузка увеличится в k раз. Применение этого приема к случаю
одновременного действия изгиба и растяжения — сжатия было
рассмотрено 5 п. 4 (см. стр. 33). Этот метод -рекомендуется также для
расчета колонн на основе предполагаемых неточностей (т. I, стр.232).
В случае хрупких материалов за основание для выбора
рабочих напряжений берется предел прочности при растяжении и сжатии.
При этом должны быть приняты,- во внимание местные наибольшие
напряжения, которые имеют место у выточек и отверстий.
Номинальные напряжения, полученные из элементарных формул,'должны быть
умножены на теоретический коэффициент концентрации напряжений *).
Опыты с чугуном не показывают ослабляющего влияния выточек
и отверстий ' так. резко, как указывает теоретический коэффициент.
Причина этого кроется в неоднородном характере чугуна. Различные
включения и трещины, которые всегда имеют место в чугуне,
увеличивают напряжения, но дополнительные наибольшие напряжения,
обусловленные выточками и отверстиями, не понижают существенно
прочности материала.; Введение коэффициентов концентрации
напряжений при проектировании чугунных конструкций оправдывается как
компенсация понижения сопротивления материала незначительным
толчкам, так как возможность возникновения напряжений от удара при
перевозке и установке всегда должна быть предусмотрена. Тогда
формулы для вычисления коэффициентов безопасности при растяжении и
^) о ко^фициентах концентрации напряжений в различных случаях, см.
гл. 8. См. также книгу, Р. Е. и е тер со на, цит. на стр. 253.
961 РАБОЧИЕ НАПРЯЖЕНИЯ 461
сжатии будут
°пч.раст А "пч.сж
«ft И раст «ft I'^J еж
(J)
В которых Опч.раст " ''пч.сж — пределы прочности соответственно при
растяжении и сжатии. Эти формулы можно также применять и для
изгиба. •
Для случая сложного напряженного состояния в хрупких
материалах воспользуемся теорией Mopai (см. стр. 380). Если о^^^ и а^^^
оба одного и того же знака, то при вычислении k мы должны
применять формулы (j). Если а^^^ и o^j^ противоположных знаков,
применим формулу (h) стр. 382. Обозначая <^^ха1°т&л '^^Р^^ а, получим
{„ \ . '^пч-раст
V°max^n4 „
1 „ '^пч.раст
/ \, «°пч.раст
ч ^Omin^n4 ;,
^ 1 "пч.раст
(к)
Для чистого сдвига о ==—о , =т, а = —1 и формулы (к) дают
_ °пч.раст
^пч
1 _|_ пч.раст
''пч.сж
Тогда коэффициент безопасности для кручения будет
у —— °пч.раст
\ "пч.сж '
(I)
где а.}ц есть теоретический коэффициент концентрации напряжений
при кручении.
Когда действуют одновременно нормальное и касательное
напряжения, как в случае сочетания изгиба и кручения, мы имеем (см. т. I,
стр. 251)
°ш1„ =\{Ч<^- Vi4 ^f -f 4(%,'^f , tx =
°mifl
''max
где a^ и a^ —теоретические коэффициенты концентрации
напряжений для изгиба и кручения. Теперь, пользуясь предельными
значениями (формулы (к)) лля тех же напряжений, получаем
коэффициенты безопасности для главных растягивающего и сжимающего
EstTa"'
462 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ 1ГД. X
/ ■
напряжений
4 . '
L ^пч.сж J
L , 2aqp4.pacf
L . <»пч.сж J
(m)
Если t = О, то эти формулы совпадают с формулами (j), а . если
0 = 0, то мы получаем формулу A). / ' .
Рабочие "напряжения для переменных нагрузок. В случае
переменных нагрузок за основание для определения коэффициента
безопасности принимают значение предела выносливости о^ материала.
Начиная с рассмотрения пластичных материалов, примем для
одноосных напряженных состояний формулу
«кдМ *
(п)
Так' как концентрация напряжений имеет большое влияние на
усталостную прочность пластичных материалов, то в формулу (ft)
вводится коэффициент а^д. Этот коэффициент* несколько меньше, чем
теоретический коэффициент концентрации напряжений (см, стр. 413),
и может быть noj^y4eH из результатов ишытаний на усталость,
приведенных на рис. 327» или может быть вычислен при помощи
кривых, представленных на рис. 328.
В случае плбсконапряженногр состояния предельное значение
наибольшего напряжения будет (см. стр. 401). /
(о)
Пользуясь этим выражением, находим для кручения (а = —1).
k^ '>: ' (Р)
У3акд[т1
где а'кд получается из испытаний на усталость при кручении или из
кривых, представленных на рис.' 328i В случае одновременного дейт
ствия изгиба и кручения получаем
K(fi^«<^)^+3(aV)'"
@)
Для 0 = 0 эта формула совпадает с формулой (р), а для т = 0 она
совпадает с формулой (п).
Для хрупких материалов существуют лишь скудные
экспериментальные сведения. Для того чтобы конструкция была в безопасном
состоянии, обычно в формула^с для вычисления коэффициента без-
96}
РАБОЧИе НАПРЯЖЕНИЯ
463
опасности применяются полные теоретические коэффициент^л
концентрации напряжений. Для одноосных напряженных состояний мы в этом
случае юлеем . ' -■ _
(г)
Г=
«аМ
Для кручения, пользуясь теорией Мора, получаем
^ , °ПЧ. СЖ /
(S)
Для одновременного действия изгиба и кручения мы имеем
k=
(t)
где а есть отношение наименьшей амплитуды двух главных
напряжений к наибольшей. . *<
Сочетание перелцгнных и постоянных напряжений. Предельнее
напряженные состояния в таких случаях определяются кривыми,
показанными на рис. 315 и- 31,6.
В дальнейшем обсуждении мы
ограничим наше внимание слу-:
чаем, в котором циклы
напряжений накладываются на rto-
стбянное растягивающее
напряжение. Этот случай, вероятно,
.один ий чаще всего
встречающихся в практических
приложениях, и в йашем 'ряспоряже-
нии; имеется достаточное
количество экспериментальных све- /
дений.
Начнем со слу"^ая илас/теик-
ных материалов', предельные
состояния для~образцов из
стали, содержащей 0,7"/о
углерода, без концентрации
напряжений представлены кривыми ВС А -
vi DFA на рис. 362. Точкой А
определенб напряжение Опч.раст.
Кривые BiCiA и DiFiA полу- '
чены для образцов с надрезами. Видно, что благодаря
концентрации напряжений диапазон напряжений несколько 5^меньшается, в то
время как среднее напря)к€ние остается неизменным^ На основе
Рис. .362.
464
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
[ГЛ. X
таких экспериментальных данйых в практике проектирования
машин установлено применение коэффициента концентрации напряжений
к переменным составляющим напряжений, но не к постоянным.
Также обычно заменяют на практике кривые ВС А и В^С^А
прямыми, 'показанными пунктиром на рис. 362. Для дальнейшего
обсуждения мы можем тогда воспользоваться треугольниками. ОВА и ОВ^А
по рис. 363, в котором абсциссы дают постоянные составляющие
напряжения о^, а ординаты дают переменные составляющие о„. Так
"/ткраст
Рис. 363.
как для постоянного напряжения и пластичных материалов
напряжение о^ было ранее принято за основание для выбора допускаемых
напряжений, заменяем-точку Л точкой Л,, имеющей абсциссой о^.
Линией ВуАх пользуются, чтобы определить предельное напряженное
|:остояние для образца с концентрацией, напряжений *). Если
постоянное напряжение на образце задано абсциссой 0D (рис. 363), то
предельная амплитуда для переменного напряжения дается ординатой DC,
и точка С будет представлять предельное напряженное состояние.
Соответствующее безопасное состояние будет представлено точкой F
с. коорди^натами о^ и o„. Эти координаты получаются путем деления
координат точки С на коэффициент безопасности k. Из подобия
треугольников ОВуАу и DCA^ мы имеей
или
CD ^DA Or—OP
CD ■ 0D__.
<^/-/«кд "т
^) Эта поправка ведет к увеличению безопасности.
96] РАБОЧИЕ НАПРЯЖЕНИЯ 465
I
Разделив это уравнение на k, получим для безопасного
напряженного состояния (точка Р)
°а _4- — = —
или
Это ^—выражение для коэффициента безопасности в случае
одноосных напряженных состояний с концентрацией напряжений •).
В случае сложного напряженного состояния в формулу (и) вместо
Од и а^ нужно подставить ^) эквивалентные напряжения. Тогда для
плоского напряженного состояния получим
'■ ' •' (V)
[«КД— + —J ]/!-« + «
Применяя это выражение к случаю кручения, имеем Oi = •:, а = — 1,
и пользуясь авд вместо а^д, получаем
, > 1
■>^^(«-?+v:)'
\
(W)
Для одновременного действия изгиба и кручения коэффициент
безопасности получится из формулы
-. - , , •
• 1 -
^ KKi+W+^t<^^¥+¥'
(X)
Если действует только один изгиб, то т„ и i^ обращаются в нуль,
и формула чзовпадает с (и). Когда о^'и о^ обращаются в нуль, и
формула совпадает с (w). Когда а^ и z„ обращаются в нуль, шь1 имеем
симметричный цикл напряжений, и формула совпадает с формулой (q)-).
Для хрупких материалов имеется немного экспериментальных
сведений относительно совместного действия сложных переменных и
*),,Так как мы рассматриваем здесь разрушения от усталости, которые
происходят без пластической деформации, то можем также пользоваться
формулой (и) для изгиба, не вводя коэффициента р, который был применен
в формуле (f). Вид формулы (и) для k был предложен С. R. Sdderberg'oM,
Trans. A.S.M.E., т. 52, АРМ 52-2, 1930.
^) Предполагается, что отношении о,: Og: 03 остаются постоянными при
действии переменных напряжений,
') Формула (х) применяется также в случаях, где отношение главных
напряжений o,/og изменяется на протяжении цикла.
mm
466 МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ [ГЛ. К
постоянных напряжений. Вводя o„^ р^^^ вместо с^ и пользуясь
теоретическими коэффициентами концентрации aj^ и a^i, вместо
уменьшенных коэффициентов а^д и а'^, для одноосного напряженного
состояния получим
' ' (у)
^''г . 'пч.раст /
»пч.раст
Для кручения, пользуясь теорией Мора, находим
i\°r *^йч.раст-/* 'пч.сж /
(Z)
В предыдущем изложении предполагалось, что размеры
конструкции определяются только из ус^довйй прочнрсти. Иногда имеютсй
ДQfloлниt€льныe требования,--кртррые должны учитываться лри
проектировании. Встречаются задачи, >для решения которых заранее
предписывается "предельная деформация, принимаемая за основу при,
определении'размеров. Деформация имеет' большое; значение в тЬ»!
случае,- когда надо' учитывать колебания системы. Валы должны^
икогда удовлетворять требованиям относительно величины угла -ёа-г
круяибания на единицу длиAы.
Проектирование- конструкций, подверженных действию высоких^
температур. Должно основываться на предположении об определенной^:
продолжительности срока чгл)гжбы конструкции и определенной
величине деформации, которую можно считать допустимой: Рабочие
напряжения 1вц0ираются так, чтобы-деформация констгрукции в'течение
срока ее службы не превосходййа ^определенного предела, зависящего;
от типа 1(сш€трукции (см.-П. 91). ^
При Проектировании гибких стержней и тонкостенных жонструк-
ций, выбирая. р!абочие напряжения, нужно рассматривать вопрос об
упругой устОйчвв!рсти (см. гл. V). . '
Проведенное здесь обсуждение .позволяет видеть, что выбор
рабочих напряжений представляет очень .важную и в то же время
очень сложную задачу. При установлении коэффициента безопасности k;
проектировщик должен всегда' руководствоваться опытом прошлого.
Приведенный анализ, дйющий., сравнение рабочих напряжений для:
различных напряженных состояний, не имеет целью заменить
использование имеющегося опыта, но он может быть полезным при истолко"
вании этого опыта и при подходе :к такому способу проектирования,
когда все части конструкции будут одинаково прочными. Полезным
может он быть также при сравнении различных проектов и cohoctjib-
лении прочности существующих конструкций. Исследование на это*|
же теоретической основе действительных случаев разрушений яв-*
ляется весьма полезным для получения более глубоких знаний о
»—*
й s «^
«11
w ДОЗ
я и- о 2 S g
«-Й рЧ (S » -) »
QlQO Q» о
O^ Dis о
N fc О
О
и n ,
о -,
ja О
■ О? Со Со Со
Ъ» ел ел "о
ел со >С^ Ф).
*». - со JO iO
■— Т|^ to ю
->| о> -д ->1
iл . j» irt со
to о -^ сд
to кэ to to
со СП to >-*
ел Фь Фь »f^
о> 00 со to
|+- 1+ 1+ 1+
со > со со to
j3J i» J-* i»
*k to о -^
. я
■ сл'ч
"oo,^
X
en
и-*
о
X 1
' КЗ
СЯ
^ ^
о S о
•Я za S
vj p5 ra
о £ й
>tx-J ra
CO« Д
CO
о
» n
о
. й
rt
ел со
со 4-^
о- ►?>. ,
ел <us
ел со
"*^ "о
со di'^.
О) Со
со
^ "
''' ел ick..
— о
1+ 1+
Jt" io
oo ■—
о
^ о 2
2 •-» в ~
,« о сг
п
Is
V-
W X о*
о S о >н
а U S S
VJ pj. га -ч
'^^ i i
ad-
^ 00
Ш g
о
Ю о
о
tJ
n
>i^ to to
<Р» vP» P"
ел ел СЛ
*>^ to N3
00 50 05
"o 0 Ъ»
--J ел >i^
CO СЛ CO
СЛ --1 0
■ J
>
/ •
СЛ >^ Ф>.
CJ? с» CO
1+ 1+1+
CO Ю Ю
СЛ о о
. -vj ,СЛ >-*
о
0>13
СЛ 2
to
i
■
Источник
S
к
е
„
к
1
■в
■ S
Предел
пропорциональности
Предел текучести
Предел ирочности
Относительное
удлинение в %
на длине
/ = 60.8 лгж
Относительное
сужение в %
Предел
выносливости
^
я ',
к
т
■ S
а
/ . '
• ;
■
-at
*
я -. "
№
HI
0
ааг
уМ^
я
ре
' Я'
га
1
S
1
0:
is
■ >.<■
... •-?
03
я
■■■^
I9f
ЬИHЗЖHdUVH aHhOaVd
ы
^Mk^^St
s
X
s
u
S
2
3
1
Химич. состав
в %
С = 0,24
Мп = 0,37
Ni = 3,3
Cr = 0,87
С = 0,30
Мп = 0,56'
Ni = 4,3
Cr=l,4
С = 0,32
Мп = 0,74
Si = 0,32
Термообработка
Отжиг 780° С , >
Закалка 830° С в масле '
Воздушная закалка 800° С
Воздушная закалка 800° С;
отпуск 600°С
Литье
Отжиг 925° С
Нормализация 925° С
•
1
1
е
о
ч
■ а> *
« S
40,0
80,5
31,5
64,5
14,0
26,0
28,5
S
н
и
ы
4)
ч
«
в)
о.
с
42,2
90,0
424
99,8
23,6
29,0
32,8
S •
о
X
V
о
о.
в
ч
0)
fcf
4)
О.
с
61,2
97,0
171
по
53,0
56,0
59,5
- ■
о
Ч в) V
к 0) s -
Й * so.
5 Id
33
18
10,8
17,5
26
27
28
'Таблица 26 (продолжение)
в)
аз 5^
4 в
о
^ <и
5 я
и аз
о о
£*
67
62
Р
55
34
40
46
■1
II
±34,3
±47,5
±71,5
±56,0
±21,3
±24,5
±24,5
^ Примечания
S
Образец
50,8x25,4 мм
Образец
диаметром 28,6 мм
Образец
57,2x31,8 мм
'''
4^
(Si
00
Источники: 1—Исследовательская лаборатория фирмы «Westinghouse». См. С. Ти м о,ш е н к о и Дж. М.
Лессе л л с. Прикладная теория упругости; русский перевод, стр. 342, 1924.
2 — Н. F. Moore and Т. Jasper, Технический бюллетень Иллинойского университета, № 136, стр.
3 — L, Aitchison, Технические стали, стр. 209, 1921.
33.
2
>
S
j:
гя
о
X
S
са
Ci
га
%
о
н
га
>
3
>
-i
ся
■в
S
>
о
га
-1
чг^шт^^^^щт^я^тт
96] РАБОЧИЕ НАПРЯЖЕНИЯ 46^
сопротивлении конструкций *). Сочетая анализ разрушений с
теоретическими исследованиями распределения напряжений и с лабораторными
исследованиями прочности материалов при различных напряженных
состояниях, мы получаем возможность накопить более достоверные
знания о действительной прочности конструкций. При наличии таких
знаний мы смбжем'значительно улучшить существующие технические
нормы для рабочих напряжений в различных отраслях инженерного
дела. Это, без сомнения, повлечет за собой экономию материала и
большую надежность сооружений и машин.
^) в этом отношении такие опубликованные труды, как Technical Reports,.
British Engine, Boiler, El. Insurance Co. представляют большое практическое
значение.
mm
ОБОЗНАЧЕНИЯ
a — угол, коэффициент линейного температурного
расширения, числовой коэффициент,
Р'-—угол, числовой коэффициент,
Y—относительный сдвиг, все единицы объема,
А—относительное объемное расширение, расстояние,
8 — полное удлинение, полный прогиб, расстояние,
е — относительное удлинение или укорочение,
^jc» S' ®« — относительные удлинения по направлениям осей лг, j/ и z,
6 — угол, угол закручивдния ни единицу длины вала,
{А — коэффициент Пуассона,
Р'—расстояние, радиус,
о—нормальное напряжение, . -
<li'°i>°a — главные напряжения,
"j^» °у> °г — нормальные напряжения по плоскостям,
перпендикулярным осям Ху у vi Z,
о -^—нормальное напряжение на пределе выносливости.
Од, — предел прочности,
^'пч.сж» °пч.раст — предел прочности при сжатии и растяжении,
\а\—^^допускаемое (рабочее) напряжение,^
о^—^^ напряжение на пределе текучести,
^ т — касательное напряжение,
''^jcv» Sz» "^ггл-~: касательные напряжения по плоскостям,
перпендикулярным осям X, у Vi Z и параллельным осям у^ z и л:,.
х^ — предел выносливости при сдвиге,
•"^окт •"-касательное напряжение по октаэдральной плош.адк€^
"^пч — предел прочности при сдвиге,
[■с] — допускаемое (рабочее) напряжение при сдвиге,
Тт ^ предел текучести при сдвиге,
ф—^угол,-угол закручивания вала,.
(О — угловая Скорость,
л, Ь, с, d, е — расстояния, -
С—жесткость при кручении, постоянная интегрирования,
Ci — жесткость при депланации (короблении),
D — жесткость при изгибе, постоянная интегрирования,
d — диаметр,
ОБОЗНАЧЕНИЯ 471
Ey Efy Ef. — модуль упругости, касательный модуль, приведенный
модуль упругости, ' ,
F — площадь поперечного сечения,
О — модуль упругости при сдвиге,
' h — высота, толщина, \ ^
Jp, Jq —полярные моменты инерции площади относительно
центра тяжести и центра сдвига,
Jj^ J^ Jg — моменты инерции площади относительно осей х, у и z,.
i — радиус инерции площади,
' k — коэффициент постели, коэффициент концен1рраций
напряжений, коэффициент безопасности, числово]^
коэффициент,-
/ — длина, пролет;
М — изгибающий момент,
iW^-^предельный^изгибающий момент,
vV^f—изгибающий момент, при котором начинаёт<ся текучесть,,
Д1к "~ крутящий момент,
{М^1^ — предельный, крутящий момент,
{M^j:— крутящий момент, при котором начинается teKy4eCTb,.
Р — сосредоточенная сила,
Q—поперечная сила? груз, собственный вес,
** р — давление на единицу площади, частота колебаний,
Я'—распределенная нагрузка на единицу длины
(интенсивность нагрузки), коэффициент уменьшения площади,.
' коэффициент чувствительности,
Ji?—'реакция, сила, радиус, амплитуда напряжений,
г-—радиус, радиус кривизны,
5"—^^ Осевая сила*, поверхность натяжения, .
S — длина, ;'
Т—осевая сила, абсолютная температура,
^ — температура, толщина, ,
.6/—энергия деформации.
If— энергия деформации, приходящаяся на единицу объема,
и" — энергия деформации, прихбдящаяся на единицу веса,
, и—перемещение в направлении оси J*;, , '
1^—объем, "
V — скорость, скорость ползучести, перемещение в
направлении оси у,
W—момент сопротивления,
•гг» *—перемещение в направлении оси -г,
Хуу, -г—-прямоугольные координаты.
m
ИМЕННОЙ УКАЗАТЕЛЬ
-Айтчисон Л. (Aitchison L.) 468
Аксельсон К. (Axelson К.) Ш
Ллмен (Alnjen J. О.) 123
Алфен (Halphen) 129
Андерсон (Anderson С. G.) 315
Арнольд С. (Arnold S. М.) 417
Арчер Р. (Archer R. S.) 352
Базгунн (Basguin О. Н.) 394
Байрли (ВуеПу W. Е.) 46
Бакли (Buckley) 238
Баркер Л. (Barker L. Н.) 195
Барон Ф. (Вагона F. М.) 210
Баррет (Barrett С. S.) 316
Баугер (Baugher J. W.) 178
Баушингер (Bauschinger I.) 343, 345, 346. 357,
396, 425 .
Баушлихер (Bauschlicher A.) 282
Бах К. (Bach С.) 384
Беккер (Becker А. J.) 370, 374
Бёкер (Вбкег R.) 384
. Белл (Bell Н. С.) 120 '
Бельтрами (Beltrami) 373 ~^
Беляев Н. М. 282, 285
Бенскотер С. У. (Benscoter S. U.) 212
Беренс (Behrens О.) 407
Бескин Л. (Beskin Ь) 252
Бешкин Л. (Beschkine L.) 61
Био М. (Biot М. А.) 11
Бицено (Biezeno С. В.) 118, 187
Блеих Ф. (Bleich F.) 149. 168
Боас (Boas W.) 330, 335,-336, 338
Брайэн (Bryan G. А.) 163
Бредт (Bredt R.) 206
Брехт (Brecht VV: А.) 123
Бриджмен (Bridgman Р.) 359
Броун Р. (Brown R. М.) 403
Броун С. (Brown S. J.T 323
Брьюстер (Brewster) 276
Брэдли (Bradley) 405
Бубнов И. Г. 27. 42, 71
Буч (Воопе W. D.) 405 -
Бурджес Р. (Burges R.,W.) 129
Буссинеск (Bousslnesq J.) 258
Бухгольц (Buchholz Н.) 407
Бэйли Р. (Bailey R. W.) 436, 441, 446, 450, 454
Бэкер (Векег J. F.) 289. 300
Бэньон Т. (Bunyon Т. W.) 415
Бэрстоу Л. (BairstowJ 425
Бюлер (Bfihler Н.) 325, 407
Вагнер (Wagner Н.) 230, 231
8аль (Wahl А. М.) 99, 119, 123, 269. 280, 281,
411. 419
Ван ден Брук (Van den Broecfe) 294
Банер Н. (Waner N. S.) 262
Вебер (Weber С.) 197, 213, 238, 26J
Вевер Э. (Wever Е.) 407
Вейбель Е. Е. (Weibel) 407
Вейбулл (Weibull W.) 331, 415
Вей-Цанг (Wei-Zang) 221
Веллер Р. (Weller R.) 281
Вёлер (WShler А.) 313, 395. 396, 419
Велькер (Welcker W. А.) 403,.405
Вестергор (Westwgaard Н. М.) 45, ЮЗ, 262,
370
Вестфаль (Westphal М.) ИЗ >
• Вехаге (Wehage) 372
Виганд (Wiegand Н.) 417
Вигнесс (Vigness I.) 348
Виллерс (Wiilers А.) 263. 265
Вилльямс (Williams G. Т.) 427
Вильгельм (Wilhelm R. В.) 432
Вильсон К. (Wilson С. W.) 277 '
Вильсон И. (Wilson J. S.) 410
Вильсон В. (Wilson W. М.) 284
Винклер (Wtnkler Е.) 11 . i
Висе (Wyss Th.) 273
Висхарт (Wishart Н. В.) 405
Витман Ф. Ф. 389 ^
Власов В. 3. 232 , »
Воропаев М. А. 273
Вундерлих Ф. (Wunderlich F.) 419
Вэй (Way S.) 75, 408. 422, 423 '
Вэрсе (Vers6 G.) 434
Гарабедян (Garabedian G. А.) 95
Гарии (Gurney G.) 252
ДГартман Е. (Hartmann Е. С.) 154
Гартманн Л. (Hartmann L.) 347 "*"
Гаузиер (Hausner G. W.) 445
Гаф (Gough H.-J.) 391, 395, 396, 397, 400. 401,
•402, 406, 418. 428 .
Гелер (Oehler W.) 363 ^
Гёнер (Gohner О.) 242. 243
Гензель.Т. (Hensel Т. R;) 441- /
Гербер (Gerber'W.) 396, 401
Герберт (Herbert И.) 304
Герц (Herz Н.) 281
Гест (Quest J. J.) 372
Гир (Gier) 9 -: .
Гиркман (Girkmann К.) 61, 294
Гиртлер (Girtler) 373
Годкинсон В. (Hodkinson) 169, 187
Гопкинсон Б. (Hopkinson В.) 427
Граммель Р. (Grammel R.) 118. 185, 187
Гринберг (Greenberg Н. J.) 294
Гринхилл (Greenhill А. G.) 258
Гриффис (Griffith А. А.) 198. 201, 257, 328,
388
Гросс (Gross S.) 123
Грумбигель Г. (Grumblegel О.) 273
ИМЕННОЙ УКАЗАТЕЛЬ
47$
Губер К. (Huber К.) 213
Губер М. (Huber М. Т.) 375
Гудир (Goodier J. К.) 54, 57, 61, 178, 184, 195,
196, 198, 212. 232. 240, 242, 249, 262. 281, 417
Гудман 401
Гук Г. (Gook G.) ИЗ
Гук Р. (Hook R-) 151. 152. 287, 328
Гуммель (Hummel) 273
Гюи (Guy Н. L.) 431
Давиденков Н. Н. 315. 325, 331, 348, 359, 387,
389, 391
Дайдн (Dyden) 404
Ден Гартог (Den Hartog J. P.) 258
Джаспер Т. (Jasper Т. М.) 403. 404, 405. 468
Дженкин (Jenkin С. F.) 346, 405
' Джеффрис (Jeffries Z.) 352
ДжОнсон (Johnson А. Е.) 448
Джонстон Г. (Johnston В. G.) 206
Джонстон^ Б. (Johnston R. S.) 276
Динник А. Н. 143, 158
Дитрих (Dietrich) 276
Домке О. (Domke О.) 129
Донат М. (Donath М.) 187
Донелл Л. (Donnell L. Н.) 184. 275, 353
Дриссен М. (Driessen М. G.) 187
Дусольд Т. (Dusold Т.) 407
Дэвис (Davis Н. Е.) 369
Жакоб Л. (Jacob L.) 323
Заальдиутц (Saalschutz) 129
Завриев К. С. 37
Закс (Sachs G.) 325. 379
Занден {Sanden К. V.) И. ИЗ
Зибель (Siebel Е.) 276. 326
Зонтаг (Sonntag R.) 263
Зульцер (Sulzer R.) 195
Иенсен (Jensen W. Р.) 284
Илэм (Elam) 335, 340
Инглис (Inglis С. Е.) 402, 405
Иоффе А. Ф. 330, 338. 385
Кавамото (Kawamoto) 400 ,
Казо Р. (Cazaud) 391
Кайзер (Kayser Н.) 276
Калакуцкий Н. 325 '
Каппус Р. (Каррий' R.) 231, 233, 235
Карман Т. Шгхойп Th.) 61, 130, 220, 221, 384
Кеднау (Quednau Н.) 195 .
Кельвин (Kelvin lord) 258, 387
Кент (Kent С Н.) 117
Керр (Kerr) 431 --
Кёрбер Ф. (КбгЬег F.) 276. 354
Кестер (K6ster W.) 348
Киркальди (Kirkaldi D.) 361
Кирш (Kirsch) 249 -'
Кист (Kist N. С.) 294
Клапейрон (Clapeyron) 175
Клаузен (Clausen I. М.) 120
Клебш (Clebsch) 95
Клерк (Clark J. F.) 294
Кодрон (Codron С.) 98
Кокер ((Joker Е. G.) 256, 257, 277
Кокс ((Jojc Н. L.) 64. 879
Коллбруннер (Kollbrunner G. F.) 158
Колосов Г. 253
Коммерс (Kommers J. В.) 391, 403, 404, 408
Консидер (Considire) 152
Коте (Coates W. М.) Ill
Коттрелл (Cottrell А. И.) 841
Коффин (Coffin L. Р.) Ill 454
Кристенсен Н. (Christensen N. В.) 220
Круз (Krouse G. N.) 405
Крылов А. Н. И, 223
Куинии (Kuinney) 356, 366
Кук (Cook G.) 159
Кун П. (Kuhn Р.) 63, 404
Кэрриигтои (Carrington) 89
Кюлер Р. (Kflhler.R.) 419
Лазло (Laszlo А.) 123, 184
Лайон (Lyon S. W.) 402, 405
Ламб (Lamb Н.). 70
Ламе (Lame) 175
Лангер Б. (Langer В. F.) И, 404
Ландсберг Д. (Landsberg D.) 277
Лармор (Larmor L.) 258
Ларсен (Larsen Е. I.) 441
Леве (Lewe V.) 103
Леезер Д. (Leeser D. О.) 315
Леман (Lehman G. D.) 405
Л ер (Lehr Е.) 253, 276, 428
Лессельс М. (Lessels М.) 468
Ливн М. (Leven М. М.) 269, 449
Лиз (Lyse I.) 206
Линч Т. (Lynch Т. D.) 410
Липсон Ч. (Lipson Ch.) 195
Лобо (Lobo G.) 99
Лоде (Lode W.) 366
Лоренц P. (Lorenz) ИЗ
Лэйк (Lake G. F.) 187
Людвик П. (Ludwik P.) 332, 348. !355, 858
Людерс (Luders) 273, 275, 347
Мазинг (Masing G.) 352
Майер A. (Maier A. F.) 400
Майер—Лейбниц (Maier-Leibnitz) 294
Майиер М. (Miner М. A.) 404
Майсснер (Meissner E.) 110
Мак-Адам (Mac Adam) 392, 406
Мак Бетти (Mac Vetty) 435i 439
Мак Грегор (Mac Gregor C. W.) 11, 357. 39f^
400, 407
Мак Дживерн (MaciGivern J.) 258
Мак Каллоу (Mac Cullough Q. H.) 288, 442
Максвелл Дж. (Maxwell J. C.) 276, 277
Максвелл К. (Maxwell К.) 375
Малкин (Malkin I.) 187
Марин (Marin J.) 872, 438
Мартин Г. (Martin G.) 407
Мартий Г. М. (Martin Н. М.) 187, 326
Маттнмор (Mattimorl J. D.) 120
Маульбетч (ZV\^ulbetch) 419
Маунзелл Ф. (Maunsell F. G.) 254
Мелланби (Mellanby)*'431
Меммлер К. (Memmler К.) 130
Менаже (Mesnager А.) 277, 280, 356
Менджойн М. (Manjoine М. J.) 348
Метцер (Metzer W.) 61
Мизес Р. (Mises R.) 129, 162
Миллер (Miller А.) 273
Миндлин Р. (Mindlin R. D.) 262
Мичелл (Michell А. G. М.) 167
Мичелл (Michell J. Н.) 262
Мор О. (Mohr О.) 380, 381, 383, 384
Мур (Мооге Н. F.) 391, 402. 403, 404, 405, 406,
Муссе'льт (Musselt W.) 195
Мюир (Mujr I.) 351
Иавье (Navier L. М.) 304
Надяи (Nadai) 93. 184, 316, 320, 347, 353, 370
Найлс (Niles) 40, 232
474
ИМЕННОЙ УКАЗАТЕЛЬ
Нег«ль (NSgei А.) 196
Нейбер (Neuber Н.) 255, 256, 268
Нейман Ф. (Neumienn F. Е.) 276 ■
Нейферт (Neifert Н. R.) 415, 421
Нельсон (Nelson С, W.) 178
Низихара (Nlsihara) 400
Николаи Б. Л. 158
Ни7(Кеа1 В. G.) 294, 302
Нуссельт (Nusselt W. I.) 196
Ньюмл (Newell J. S.) 40 /
Одквнст (Odqulst F. К. О.) 480
Олссон Р. (Olsson R. О.) 187
Онеггер (Honegger С.) 184
Оро^ваяг Е, (Orowan В.) 330, 386, 388. 430
Осгуд (Osgood W. R.) 46, 308, 407
•Остенфельд (Ostenfeld А.) 213. 220
Папкович П. Ф. 27
Паркер (Parker Е. R.) 369
Парус (Parkes Е. W.J 54
Парр (Parr S. W.) *4-
Перяью (Pardue Т. Е.) 348
Перри (Perry J.) 243
Петерсон Р. (Peterson R. Е.} 263, 269, 280.331,
398. 399. 400. 4Q9. 411, 413, 415, 460
Пёщль Т. (РбвсЫ Т.) 111
Пиллинг (Pilling) 486 »
Пнппард (Pippard А. J. S.) 273
Пирсон К. (Bearspn К.) 316, 320
Пйхлер (Plcfiler О.) 92
Шлаки М. (Polanyl М.) 352
По^лард ,<PoHard Н. V.) 400
Помп (Pomp А.) 364, 3^. 402
Пбпов (Popoff Е. Р.) 446, 446. 464
Прагер (Prager W.) 11. 294
Прандтль Л. (Prandtl L.) 146, 167. 198. 341
Прейсс (Preuss Е.) 273
Прескотт Т. (Prescott Т.) 206
Прет«вёр (Pretschner) 231
Пуассон (PoiSson) 32, 121
П^лайдерер (Pfteiderer) 98'
Рассел Г. М. (Russel О. М.) 89 .-
Рассел. (Russel Н. W.) 403 .
Рейснер Е. (Reissner Е.) 61. 64
Рейснер Г. (Reiesnet Н.) 61, 111, 163, 213
Реякин (Rankin) 371
Рётчер Ф. (Ratscher F.) 273
Рис-(Кеев) 862 '
Ричарде" (Richards С. W.) 349
Роветт (Rowett) 342
Роде Р. (Rode R. V.) 404
Родерик (Roderick J.) 291
Рой (Роу J.) 428
Рот (Roth) 373 ,
Рош М. (I^es М.) 891
Рунге (Runge С.) Ш
Рус (Roos Т. О.) 391
Савин Г. Н. 253
Саймондс (Symonds Р. S.) 294, 302
Саусвелл Р. (Southwell) 169
€ен-Венан Б. (Salnt-Venant В.) 96, 1%, 248,
304. 316. 320, 87Г, 449
Сиэрл (Searle О. F. СЛ70
Скобл (Scoble W. А.) 372
Слэйтер (Slater А.) 103
Смит К. А. (Smith С. А.) 372
Смит Р. ISmith R. С.) 348
Смит.Г. В, (Smith О. V.) 431. 434
Смит-Петерс^ц (Smlth-Petersen N. О.) 120
Снеддои (Sneddon 1. N.) 257
Содерберг, (Soderberg) 441, 450, 454
Сопвис Д. (Sopwith Б. G.) 379. 406. 407
Сорока (Soroka W.) 262
Стодола А. (Stodola А.) 162. 187. 195. 273
Стоки Ф. (Stokey.F.) 276
Такемур'а К. (Takeinura) 4(Ю
Тапседл (Tapsell Н. i.) 405, 431^ 440
Тейлор Дж. Дж. (Taylor О. 1.) 198.' 201, 341
Тейлор Дж. (Taylor J. Н.) 98
Темп ЛИН (Templin R. L.) 154
Те^ер Л. (Turner L. В.) 320. 323. 372
Терцаги К. (Terzaghi К.) Ill
Тимошенко С. П. 11. 12. 18. 40. 45, 46, 51. 64,
57. 61, 71. 80. 90. 93. 98. 103. 111. 117. 124,
133. 137, 140, 141. 149. 158. 160, 162, 163, 167.
170.. 178, 184. 195. 196. 198, 2(». 212.213,222.
227, 2Ж). 231, 240, 242. 247. 249. 252. 262,281,
313. 415. 468 -
Тодхентер Л. (todhunter L.) 316. 320
Томас (ТЬощаз W. N.) 408
Томливсои (Tomiinson Q. А.) 418
Томпсон (Thompson W.) 243
Тонассеп Ф. (Tohassen Р.) 386
Торпе П. (Thorpe Р. L.) 418 /^.
Tpeффtц (Trefffz Е.) 262
ТЪумплер (Trumpler W. Е.) 99
Тум (Thum А.) 408. 414, 419 _
Туци (Tuzi г.) 277
Тэт (Tait) 243. Й8
Уде (Ude Н.) 414
Уввин (Unwin) 396
Уотерс (Waters Е. D.) 98, 120
Фавр А. (Favre Н.) 92, 277
Файлон Л. (Fllon.L. N. G.) 277
Фан-дер-Флит А, П. 35, 42
Фаульхабер Р. (Fatilhaber R.) 416
Фейрберн В. iFalrb&irn W.) 163. 394
Фёппль А. (F6ppl А.) 206, 262. 275. Й83
Фёппль Л. (Flippl L.) зге
Фёппль О. (F6ppf О.) 342, 407, 419
Филлипс (Phillips С. S.) 414
Фншер (Fischer А.) 187 -
Форест (Forest А. V.) 276
Фрай (Fry А.) 276, 3*В
Фрейдеяталь OPreudenthal А.) 404
Френкель 1Л.Щ
<^ё&ч (French Н. J.) 403
Фриче (Fritsche JO 294
Фромм (Fromm Н.) 285
Фрохт (Frocht М. Д1.) Ж4, 265, 269, 277
^ллер Т. (Fuller Т. S.)-406
Фусс Н. И. 11 ■ -—
Хаджи-Аргйрис (Hadji-Argyris J.) 64
Халливзлл (HalUwell) 436
Ханслнп Р. (Hanslip R.) 325
Хавсои (Hanson В.) 428
Хат (Huth J. Н.) 262
Хаяши (Hayasbi) 11
Хвалла Э. (Chwalla Е.) 61, 168, 168, 170
Хейвуд-(Heywood R, В.) 414
Хейг Б. (Halgh Б. РЛ 373, 374. 396, 406, 410
Хельд (Held А.) 187
Хемпель М. (Нёшре! М.) 898. 402
ИМЕННОЙ УКАЗАТЕЛЬ
476
эй (Hurafrey J. С. W.) 427
XeH'(H6hii Е.) Ill
Х^дри А. (Hendry А. W.) 67
Хеяки (Hencky Н.) 90, 93
ХетениЙ (Hefenyi). 11, 23, 60. 257. 276, 281.
316. 326, 357. 410. 417
Хирл (Hearl Н.) 187
Ходт М. (Holt М.) 164
Холъмберг (Holmberg) 111
Хорвай (Horway G.) 120
Хорджер (Horger О. J.) 178. 316. 325. 403,418.
419, 420,421
Хуггенб^гер (Huggenbefger А.) HI. 178
Хюрльбринк (Hurloilak) 158
Цайдер (Zander W.) 408
Ценер (Zener С.) 342
Циммермана (Zimmermanh) И, 38
■. *
Чершгк (Cherhiak О. S.) 454
Читти Л. (Chitty L.) 273
Шабло Э. (Chabloz Е.) 92
Шарпи М. (Charny М.) 331
Швиннииг (Schwlnning) 282
Шеплер П. (Schepler Р, R.) 454
Шер^ (Schearer О. W.) 243
Шеу Р. (Scheu Щ 3i8 *
•Шеффер (Scheffer Н.) 109
- Шидьхансль М. (Scbiihansl М.) 98
Шлейхер Ф. (Schleicher F.) И, 370
ШниА (Schmid Б.) 330. 335, 336, 338
Шрайбф В. (Schreiber W^ 3^
Штаерная И. Я. 282
' Штрауб Ф. (Straub F. G.) Ж4
Штрнбек (Strlbeck) 282
Штурм Р, (Sturm R. О.) 154
Штюсси Ф. (Stflesi F.) 220
Шульц (Schulz Е. Н.) 407
Шустер Л. (Schuster L. W.) 409
Шэили Ф. (Sl^anley F. R.) 154
Эбнер {Ebner Н.) ,63 , '
Эверег Ф. Л. (Evierett F. L.) 448
Эйлер Л. (Euler L.) 125; 146
Эйхельберг (Eichelberg G.) 1S6 '
ЭйхингеР (Eichlnger А.) 810. 326, 378, 391
Экк Б. (Еск В.) 90 -
Эллис К- (Eilis С.) 276
Энгессер Ф. (Engesser F.^ 146, 152
Энслвн М. (Enssiin М.) ~
Эттле (AtUa Н. Н.) 415
Юинг (Ewinfe J. А,> 350, 351, 427
Юнг Д. (Joung D. Н.) 46. 149
Юнг Т. (Joung Т.) 238
Якобсеи (Jacobden L. S.) 263
Яниакий (Janickl W.) 178
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аварии в сооружениях, взрывы резервуаров
368
— , внезапные трещины 368
, выпучивание 167
, поломки 263, 407
—, , разрушения 299, 302
. — в сварных судах 385
Алюминий см. Испытания
Анализатор см. Призма Николя
Аналогия гидродинамическая 258. 261
~ мембранная 198. 206, 260, 319
— Электрическая 263, 266
Арка круговая, устойчивость 158
Бак (сосуд) конический 104
— сферический 104, 108
— цилиндрический 105, 106
Балка И, 54
— абсолютно жесткая 26
—' бесконечно длинная 12, 17
— двутавровая 56, 60
— длинная 26
— конечной длины 23
, классификация типов 26
— коробчатая 63
— короткая 26, 56
— на упругом основании И, 23, 109^
— неограниченной, длины И
— неразрезная 38
— переменного поп^ечного сечения 50, 58
— переменной высоты 59
— под осевой и поперечной нагрузками 30
— полубесконечная 20
— с защемленными концами 27
— с шарнирными концами 27
— со свободными концами 23
— статически неопределимая 34
— узкого поперечного сечения 55
— эквивалентная 62, 63
Барабан цилиндрический тонкий 112
Бетон, см. Испытания
Болт с гайкой 416
£рус кривой 51
Вал 195
— восьмиугольного сечения 197
— коленчатый 263
— круглого сечения 196
переменного диаметра 262
— правильного шестиугольного сеЬения 197
— пропеллерный 263
— равносторонне-треугольного сечения 196
— трапецеидального сечения 197
I— эквивалентного- эллиптического сечения 197
— эллиптического сечения 196
Волочение проволоки 352
Время, влияние ва деформации, 336
— , — на результаты испытания 434
Выкружка 255. 260. 347. 418
Выносливость см. Предел выносливости
Выпучивание боковое 124, 130, 141, 167
— винтовых пружин 247
Выточка 254. 255, 361, 362, 389
Вытягивание пластическое 345
Вытяжка 352. 359, 403
Вязкость 384
Гибкость 128, 146
Гистерезис упругий 338
^ — истинный 427
Давление внешнее (наружное) ИЗ. 156
— внутреннее 103, ИЗ, 175
— гидростатическое 365
— контактное 28, 64, 281. 422
— критическое 156 -^
— от горячей посадки 177
— поперечное 366 .
Деформация допустимая 439
— естественная 356
— за пределом упругости 287
— истинная 357
— местная 334
— на пределе текучести 347
— непрерывная (ползучесть) 434
— осевая при кручении 238
— остаточная 332, 352. 428, 437
— пластическая J54, 320, 323. 436
— — допустимая 439
толстостенных цилиндров 320
— сдвига 88
— симметричная относительно оси 173
— срединной поверхности пластинки 80
— условная 357
— циклическая остаточная 428
Диаграмма изгиба 304
— истинных напряжений 355
— напряжение — -деформация 347
— растяжения и сжатия 150, 287, 327, 332,
36* -■
— условная 355
Диапазон напряжения 392
безопасный 425
Динамометры пьезокварцевые 390
Диск 112, 186
— вращающийся 180, 454
, моделирование 185
— — переменной толщины 187
, подобие 185 '
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
477
Диск вращающийся с отверстием 181
— турбинный 195, 352
Дислокация 341
Длина приведенная 129. 149
Жесткость изгиба 27. 156, 160, 214
пластинки 70, 90
— коробления 220 ^
— кручения 170, 214
— цилиндрической пластинки 79, НО
Задача двумерная 276
Закон Гука 150, 153, 287, 304. 310. 326. 338,
375, 449 , .
— — , отклонения от и^го 304, 336, 352
Затухание колебаний 338. 342
Затяжка фланцев 447
Изгиб балки И, 54
, не следующей закону Гука 304
— — под осевой и поперечной нагрузками 30
— — поперечными силами за пределом
упругости 287, 291, 310
— — при высоких температурах 441
— — статически неопределимой 34
— бруса 51, 70
— — знакопеременный 392
чистый 79, 287
— клина'57
— консоли 58, 64, 392
— неупругий 312
— пластинки 69
— — круглой 79
—, нагруженной в центре 92
, — концентрически 94
переменной толщины 90
по сферической поверхности 81
— — — под симметричной нагрузкой 82
— — 'прямоугольной длинной 71
по цилиндрической поверхности 69
с малой начальной кривизной 75
— - чистый 77, 83 ,
— полок балки 212. 216
— продольный 124, 127, 128. 143
— — местный 125
— — неупругий ISO
при защемленных концах 127
— — при переменном сечении 143
при шарнирно закрепленных концах 127
— — равномерно распределенными осевыми
силами 141
совместно с кручением 231
, сложные случаи 131
— — составно1'о стержня 146
— рельса 18 ^ '
— стенки 217 -
Излом 370
— усталости 394, 415
Изоклины 280
Искажение сечения 212
Испцгание алюминия 338, 340
— бетона 362
— больших образцов 419
— бронзы 333
— в вакууме 406
Испытания высокоскоростные 405
— , их продолжительность 434
-^ , их скорость 358
— камня 362
— меди 340, 354
— Ча выно<у1ивость (усталость) 391, 4W -.
на растяжение 328, 332. 338,
Испытания
341. 349
— на сжатие 362
— на удар 384
— образцов из монокристалла 335, 338, 358,
-г пластических материалов 332
— поликристаллических материалов 341, 358
— при сложном напряженном состоянии 365 .
— свинца 447
— слюды 330 " '
— соли 330. 385
— стали 327. 331. 332, 349, 352, 361, 385
мягкой 341
углеродистой 327, 361
фосфорной 331
— — хромоиикелевой 361
— Стекла 328
— тонкостенных труб 368
— хрупких материалов 362
— чугуна 364
Камень см. Испытания
Канавка, см. Концентрация напряжений
Касание консоли и опорной поверхности
— шаров и цилиндров 281
Катки цилиндрические 283, 422
Клин 57. 58
Колебания 338, 466
Колонна 37, 136
— гибкая 124
— , защемленная внизу 136, 137
— короткая 149
— неупругая 150
— переменного сечения 143
— пирамидальная 143
— составная 149
Кольцо коническое 122
— круговое 156 ,
— опорное 106
Консоль 58, 64. 66. 67
Конструкции металлические 146, 294
., продолжительность службы 437
Концентрация напряжений ьЬ, 183, 248, 268.
394 ■ , .
в растянутых или сжатых элементах .248
, исследование на моделях 273
— — при изгибе 268
при кручении 258
— — при повторных нагрузках 258, 408
у входящих углов 257, 260
у выкружек 255, 260 347, 408
у выточек 254, 255, 408
-у канавок 259, 408 ^^
— ^ у надрезов 388, 389, 390
— — у острых углов 253
— — у отверстий 249
у отверстий с ребордами 252
—: — у отверстий эллиптических 253
— — у резких изменений сечения 256
У трещин 258, 328
Коррозия 405
Коэффициент безопасности 36, 294, 456
для переменной нагрузки 462
для статических условий 458
при изгибе 459
при концентрации напряжений 465
при кручений 459, 461
при сложном напряженном состоянии 461
— длины 125
— концентрации напряжений 255, 268, 273, 4il, f
461
теоретический 411, 461
MW
478
ПРЕДМЕТНЫЙ ifnm&tmb
Коэффициент незнания 486
— основания 11. 18
—'постеЛи 11, 109-
— формы сечения 459 '
-г- чувствительности 413 -
Кривая изгиба 45
— нагрузка—прогиб 130 ^.
'- ползучести 435^ 438
— релаксации 446
— ущерба 403
Кривизна иаогаутой поверхности пластинкн
.79-., ;. - ■■■.
— малая начальная 51, 75
— оси балки 12 ■
Критерии текучести 380
Критерий щючнрсги 371
— разрушения 380
Круг контакта 281
— Мфа 380 '
Кручение 196
— вала^ см. Вал ■. ■ \
— двутач^а 205. 316 ■ ' '
— коледа круглого Ш
— неравномерное 214 v
— прокатных профилей' 204
— пружины 241, 244
— с изгибом 231 ^
-^ стержней открытого.профиля 212. 223-
— — Переменного сечения ^
Полигонального профиля 220 '
— трубчатого стержня 20G, 208
— усталостное 409
— швеллера 197, 204, 217 -
Купол ш^ювой 108
Линии изрклиняые 280
— равного момента 263
Потенциала 266
■^ — угла закручивания 264
— скольжения 339
— текучести (Людерса) 273, 278, 347
— тока 266 « ^
Материал идеально пластический 287
-^ неоднородный 460
— однородный 457
— пластический 257, iMTv 332, 458, 463
— хрупкий ^7. 362. ЗЙ, 402, 458, 462
Материалы, свойст|1а мех1йвические ЗИб
— , с~ пьезоэлектрические 338 ~
— . — те1»1йупруги§ 337, 338^
Медв-см. Испытания
Мембрана ,90. 103, 106, 108
Металлы, механические свойства при яькоких
тёмаературах 431
Метод графоаналитический 292
— лаковых покрытий 276
— модел1фовани^ в исследовании
концентрации напряжений 268, 273
— мыльной пленки 201
— наложения 14, 19, 20, 55, 64, 152
— оптич($ский измерения напряжений 276
— последовательных приблии^евий 211, 455
— предельных нагрузок 296, 301
— статистический 404
— тригонометрических рядов 45, ВО -
— фотоуп|>угий 276
— численного ивтегрнр«ващ|я 446
— виергетическнй 64'
• определения критических нагрузок
Модель механическая 341
Модуль упругости а;дйабати»}ескиа 337
изотермический 337 ,
— ^ касательный 161
•i; приведенный 153, 306 -
Момент изгибающий балки 13
— 1футящна 198
— предельный 289
Монокристалл 330
Нагрузка безопасная 36
■— вна^ентревная (»ксцентрическая) 128. 149
— критическая 127. 131, 133, 137, 148, 168 \
— овевая равномерно распределевн{Е1я 141
и поперечная 30
— парой сил 17 '
— пшгорвая 391 . ^ ■''
— равномерно распределенная 12,17. 33
— растягивающая 41
— сжимающая 30, 38, 137,
— симметричная и асимметричная 12, %, 82
-^ сосредоточенная 12, 18, 33-
— трапецеидальная 39
— треугольная 40 .
— циклическая 346
— эйлерова 37, 127, 146
Надрез 388. 389. 463
Наклеп 339, 341, 352. ^3. 362. 368, 429. 436
На1фяжёние истинное 365
— критическое 129, 358
, — предельное 394
— пульсирующее ЗУ7
— рабочее 439
— среднее (цикла) 392
Нахфяжёния вторичные 150
V—горячей посадки 177
— знакопеременные 20, 248, 391
^ — касательные в балках переменного сечение
68
в стержнях от1фытого профиля 218
— критические 129, 164
— мембранные 103,J08
'— местные 54, 108, 261, 263
^ на опорах 57 ,
— окружные 111, 182
— остг5очные 312. 343, 352, 407
— переменные 394
, — рабочие 456
— радиальные 64, 58. 182 ~ -
— разрыва непрерывности напряжений.!^
— растягивающие Ш> -
г-^ температурш>ге в пластинках 81
в оболочках цилиндрических 115
— — в цилиндрах полых 191
Насадка 353. 419
Натяжение поверхностное 329
Недовалряжение 403. 404
Обдувка струей дроби 421
Оболочка 69, 124 ^
— цилиндрическая 116 . ч.
Обработка термическая 391, 403 )
— холодная 403, 420
. Образцы для испытания материалов 326,
363
— т вращающиеся 427
цемента iS6
— из 11онокристалла 330
— поликристаллические 336
Обшивка судов 76
Осадка основания 26 .
Основание жесткое 68
— упругое 11. 103 ,
Ось изогнутая балки 12, 13, 137'
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
479
Ось нейтральная 305, 308
— цеитроз сдвига 222
Отверстия, см. Нонцентраиия напряокенай
Отжиг 352, 353
Отрыв 358, 387
11ер(№апряжение %8^ З&З, 403
Летля гистерезиса 338, 342, 427 г
И лайки составных ст^жней 146. 143
Пластинка 50. 69, 124
— бесконечно большая 64 ^
— длинная пpямoy^oльнaя 69, 75
— круглая 79
, нагруженная в центре 92
— —, — концентрически 94
переменной тблщины 90
под симметричной нагрузкой 89
равиомерно нагруженная £5
— -^ с круглым отверстием в центре 96, У7
— 1ф'ямоугольная 100 ^
-на упругом основании 103
Пластичность 2Ы, 333. 384
Плнта ребристая железобетонная 63
Плоскость наименьшей жесткости. 126
— октаэдральная 339
— срединная пластинки 78
Поверхности равного угла закручивания
Поверхность контакта 283 Ч^
— пластинки изогнутая 71
-г- неразвертываемая 79
— развертыааемая 79
срединная 76
сферическая 79, 81
Поков|са большая 325, 362
Ползучесть 434
— , скорость 435, 438, ^
— йри сложном вапряженном состоянии 447
— прогрессирующая 435
— установившаяся 453
Полки балок 60
noJ^Cbi в оптическом методе 278
— скольжения 339, 428
Посадка горячая 177, 325
Последействие упругое 337
Пот)фя устойчивости 124, 137, см. также
Устотивость
— -f, крутильная форма 2*27
— •—•, сочетание крутильной н изгибной форм
- 231
Лоток касательный 210
Предел выносливости 393. 395, 403, 427 '
, его повышейиб 404
— пропорциональности 128, 152. 257, 287, 332,
— «^ естественный (истинный) 425
— прочности 124, 257, 325, 332. 361, З^Й, 432
— -^ истинный^62
— Текучести 36, 159. 257, 287, 294, 332, 3«,
846, 349. 432. 456 -
—г -^ . его повышение 350, 351
— усталости 424
Прщна Николя 278. 230
Прввцмп виртуальных перемещений 300
— вложения 14, 21, 23, 33, 466, см. также
Метод наложена»
Прогиб 11, 13
г- фльшой 89, 124
— малый 129
— н^ибольхЬий 50, 129
— 1шчальный о1
Пршолжительность испытания 434, 437
Прокатка металла 352
ПроЬеллер, обработка 353
Протравливание пов^хностн 348
Протягивание металла 352
Прочность, 1фвтерии 371
— теоретическая 330
— , теории 370 ^
— усталостйая v404, 412, 462 '■
-Пружина Белльвиля 122
— винтовая 241
-^ цилиндрическая 241
Путь желеЗНбдоро^кный, расчет И
1>авновесие, убтойчивая и неустбйчивая фор-:
мы 124. 137
Размеры образцов 349, 3S8
— поперечного сечения безопасные 36 ,''
Разрушение 299. 302, 358
— .отрывом (хрупкое) 358
— пластическое (сдвигом) 358
— поверхности 1фи усталости 4Й
— сдвигом 358
— типа «чашки и конуса> 358
— , типы его при рабТ1|жевин 858
— хрупкое 331, 358, 370, 386, 389
Раковины (ЯМКИ1362. 423
Рамы 133, 134* 301
Распорки 146. 147 .
Растяжение 41, 327, .332, 338. 341, 849. 358
— всесторошГёе 365
— длителыюе 435
— до разрушения 358 ' , >
^. его механизм 340 s
— за пределом текучести 349
— пластическое моиокристадла 338^
— пружины 243
— хрупких материалов 328 -.■
Рдсчет по предельным состояниям 294 *
Резервуар цилиндрический МЬ.}
Резонанс 469
Рекристаллизация 325
Релаксация вапряжений 338, 444
Рельс, изгиб 18
Решетка кристаллог1^афическвя 339
— соста№ых стержней 147
Ротор Щ, 186
Ряд тригоиометрический, представление кри*
' вой изгиба 45, 51
Самолетостроение 404
Сварка 385, 39t -^
Свинец см. Йспмтаная ~
Сдвиг щпозвАЖхк 61
— чистый 373i 451 -
Сечение гео1«етрически подобное 19
>-эквивадейтное 197, 216
Сжатие 30, 137, 368 _^
'— всестороннее 365
-^ иера^езного стержня 38
— пластических материалов 364
— равномерное 363
— сверх предела пропорциональности 152
Сила инерции 180
•^ Критическая 124* 131. 133. 137, 145, см. т^к-
жё Нагрузка
— молекулярная 340
— поперечная, влияние на критическую на-
Грузку 145
Симметрия и а$:имметрия нагрузки 12, 25
Система статически неопределимая 295
определимая 294 \
Скорость деформирования 348
— испытания да8
Слой нейтральный пластинки 78, 304
Смягчение материала 43б
>
480
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Сопротивление отрыву 387
— предельное рамы 301
систем 294
— разъединению 358
— сжатию истинное 363
— скольжению 358
Состояние ' напряженное предельное 381,
464
сложное 365, 399. 447, 461
Сосуд толстостенный 111
— тонкостенный 103, 108
Сталь, механические свойства =467—468,
также Испытания
Ствол орудия 79, 352
Стекло 257, 328, см. также Испытания
Стенки' балок 56
Стержень (стойка, колон^1а) гибкий 124
— короткий 154
— открытого профиля 212
, потеря устойчивости 227, 231
— переменного сечения 143
-^ призматический 124
— растянутый и поперечно нагру>кенный 41
— сжатый и попёре<шо нагруженный 30, 38
— составной 146
— сплошной 147
— трубчатый (кручение) 206
Структура кристаллическая 335, 342
Ступица колеса 353
Сужение попереч&ого сечения (шейки) 334,
355, 359
Текучесть 130
Температура 81, 115, 191, 336, 385
— , в^lияниe на предел выносливости 405
— высокая, влияние на механические свойства
материалов 431
— критическая 385 _
— охрупчивания стали 385
Теории прочности 370
Теория Давиденкова 361
— концентрации напряжений Гриффиса 328
— Мора 380. 461, 463, 466
— цаибольшей энергии формоизменения 366,
373, 399
'- наибольших деформаций 371
касательных напряжений 372
главных-напряжений 371
— приближенная изгиба плаСтинок 80
Траектория главных напряжений 280
Трение внутреннее 338
Трещины 117, 258, 328.368
— винтовые 409
— усталости 20, 394, 408, 422
— ямкообразные 423
Труба 98, 158.
— короткая W2
— круговая 158
— с насаженным кольцом. 112
— толстая 451
— тонкая 451
— тонкостенная 566
— .усиленная кольцами 114
Труй, устойчивость 156, 158, 162
— эллиптическая 159
Уголок прокатный (прбфиль) 143
Удар 331, 362, 384
, Удлинение внезапное 348
'—.относительное 334
— пластическое 332
— эффективное 355
463, Уравнение трех моментов для сжатого
стержня 39
■ Усталость 20, 331, 391
—, влияние концентрации напряжений 408,
415
см. —, — обработки 403, 407
— , — остаточных напряжений 407
— , — темпч)атуры 4(fe
, — при коррозии 405
—г при сложном напряженном состоянии 399
— , причины ее 425
Устойчивость арки круговой 158
— кругового кольца 156
— пластинки 162
— стержня 137 <й
— тонкостенных конструкций 163
— — стержней открытого профиля 227, 231
— упругих систем 125
Формула Эйлера 37, 127, 146, 148, 149
Функции Бесселя 141
Центр сдвига 217
Цепь подъемника 352
Цикл напряжений 391,. 392
Цилиндр длинный 184
— полый, температурные напряжения < 191
— составной 179
— толстостенный 173, 184, 320, 361
.пластическая деформация 320
Частоты циклов нагружеиия 404
Число предельное циклов 403
Чувствительность к концентрации
напряжений 413
Чугун, см. Испытания
Шар в сферическом углублении 282
Шарикоподшипник 284
Шарнир пластический .292, 299
Швеллер (кручение) 197, 204
Шейка, см. Сужение шейки
Ширина полок в балке 60, 61
Штанга буровая 417
Экстензометр 332, 336 '
— Баушингера 357
— Мартенса 428
Эксцентриситет 128, 149, 159
Эллипс контакта 283
Эллиптичность трубы 15Э "^
Энергия деформации 46, 137, 168, 207
— поверхностная 329
Эффект Баушингера 343, 345, 429
— термический 336
Угол закручивания 196, 207. 216
зн^акопеременцый 399
Ямкообразование 423
Ячейка кристаллографической структуры 83&