Автор: Калинин Э.В.
Теги: подземное строительство земляные работы фундаменты строительство тоннелей общая методология научные и технические методы исследований, изучения, поисков и дискуссий научный анализ и синтез строительство строительное проектирование строительная механика
ISBN: 5-211-04961-6
Год: 2006
Э.В.Калинин
ИНЖЕНЕРНО-
ГЕОЛОГИЧЕСКИЕ
РАСЧЕТЫ
И МОДЕЛИРОВАНИЕ
допущено учебно-методическим советом
по геологии УМО по классическому университетскому образованию
в качестве учебника для студентов университетов,
обучающихся по направлению 511000 «Геологияж
и специальности 011400 «Гидрогеология и инженерная геология»
Издательство Московского университета
2006
УДК 624.131.3:001.8
ББК 38.58
К17
Р е ц ' • н । е н т ы:
кафедра инженерной геологии Москивскогударстьснного
геологоразведочного университета (зав. кафедройЬессор В,В, ПенЯинУ,
доктор геозого-минералогических наук ирор р,Э. Дашко
1Санкт-Петербсргский государственный юрный иуг им. ГВ. Плеханова
Горный университета
Калинин Э.В.
К17 Инжеиерно-кологические расчеты и моделирование:
Учебник. — М.: Изд-во МП’, 2006. — 256 с
ISBN 5-2П-04961-6
В учебнике рассмотрены методы математическою моделирования,
применяемые для решения инженерно-геологических задач и основанные
на использовании математической модели наиряженно-деформированно-
го состояния массива горных пород. Изложены основы теории подобия и
дано описание области применения и возможностей экспериментального
моделирования методов эквивалентных материалов. поляризационно-
оптических способов и аналоговою моделирования, используемых при
инженерно-геологическом изучении природных процессов. Приведена
методика инженерно-геологических расчетов оснований сооружений, ус-
тойчивости склонов, переработки берегов водохранилищ. деформаций
массивов юрных пород вокруг подземных полостей, аеформаиии поверх-
ности при разработке полезных ископаемых и откачках подземных вод
или нефти и др.
ДЛЯ студентов и аспирантов ),ниверситетов и вузов, общающихся по
специальности инженерная геология и гидрогеология, и специалистов,
занимающихся инженерно-геологическими изысканиями для обоснова-
ния проектирования и строительства инженерных сооружений.
УДК 624.131.3:00 1.8
ББК 38.58
ISBN 5-211-04961-6 С’ Издательство Московского университета, 2006
ВВЕДЕНИЕ
Одной из основных задач инженерной геологии является
изучение современных геологических и инженерно-геологиче-
ских процессов. При инженерно-геологических исследованиях
оценка интенсивности проявления и прогноз развития процессов
должны быть выражены в каличественной форме. Получение ко-
личественных характеристик возможно различными способами,
среди которых одно из ведущих месит занимают лабораторное и
натурное моделирование и инженерно-геологические расчеты.
Расчетные методы и моделирование с успехом применя-
ются при оценке устойчивости природных склонов и откосов
котлованов и насыпей, для определения осадки оснований
различных сооружений, с целью прогноза переработки берегов
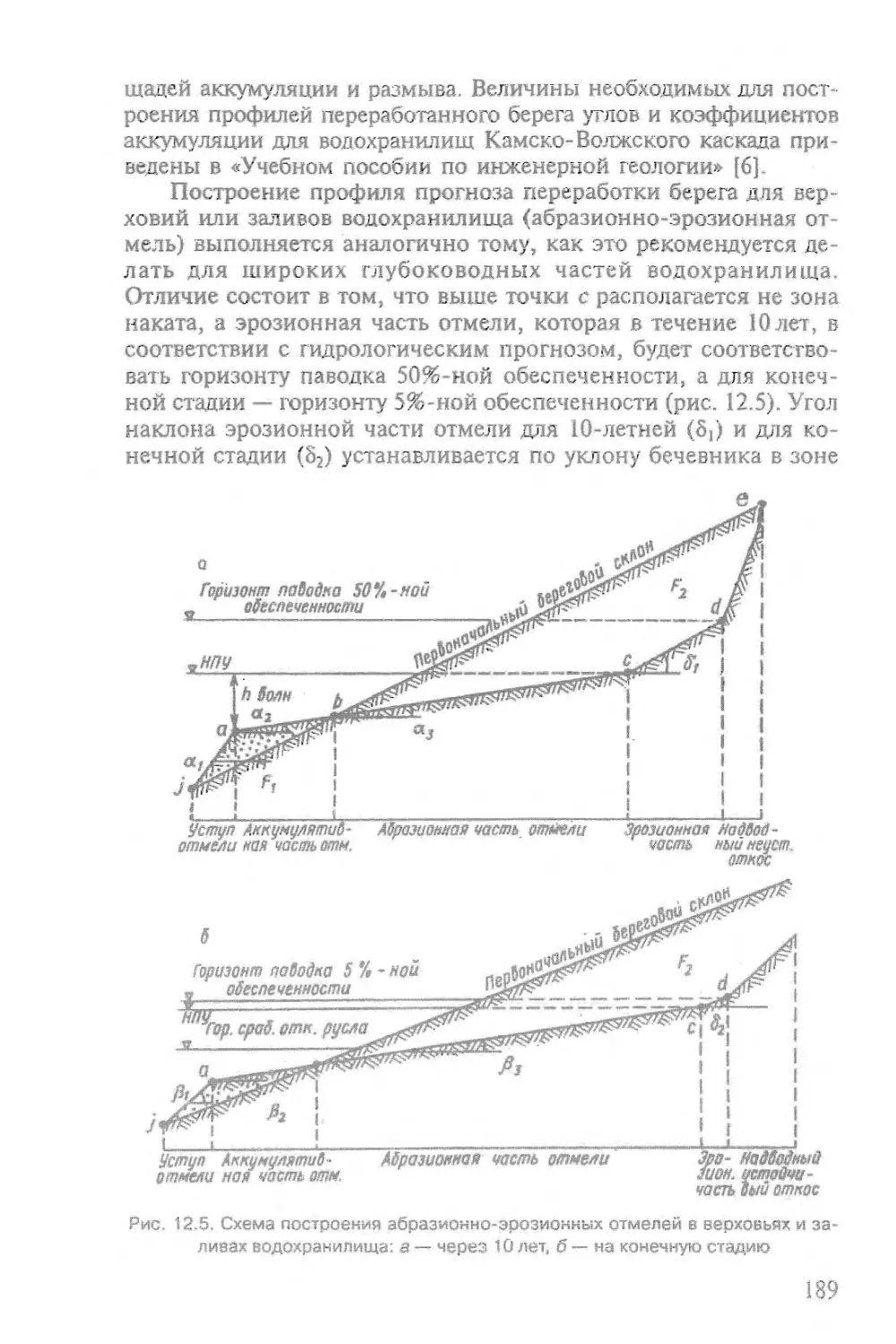
водохранилищ, для оценки деформаций в результате проходки
подземных горных выработок И тоннелей и в других случаях.
В Последние десятилетия в связи с бурным развитием вычисли-
тельных методов и технических средств для их реализации су-
щественно возросли возможности математического моделиро*
вания, что отразилось на более широком его использовании по
сравнению с физическим моделированием. Однако последнее
остается основным способом при необходимости изучения ме
ханизма процессов.
В настоящем учебнике предпринята попытка отразить воз-
можности различных методов моделирования и способов расче-
та, применяемых при инженерно-геологических исследованиях.
В первой части учебника рассматриваются методы матема-
тического и экспериментального моделирования. Применение
математического моделирования для решения инженерно-геоло-
гических задач рассмотрено на примере использования матема-
тической модели напряженно-деформированного состояния мас-
сива горных пород. Выбор этой модели обусловлен тем, что она
широко применяется при расчетах осадок оснований, оценки
устойчивости склонов и откосов, прогнозе деформаций при под-
земных разработках ит.д.
Описание экспериментального моделирования содержит крат-
кое изложение основ теории подобия и характеристику' области
применения и возможностей методов эквивалентных материа-
лов, поляризационно-оптических способов и аналогового моде-
лирования, применяемых для инженерно-геологического изуче-
ния природных процессов.
Во второй части изложена методика традиционных инженер-
но-геологические расчетов оснований сооружений, устойчиво-
сти склонов, переработки берегов водохранилищ, деформаций
массивов горных пород вокруг подземных полостей, деформа-
ции поверхности при откачках подземных вод или нефти и др
При выполнении расчетов и моделирования важным являет-
ся назначение показателей свойств горных пород. Поэтому в за-
ключении приводится краткое описание статистических методов
обработки данных для выбора расчетных показателей.
Курс инженерно-геологических расчетов и моделирования
читается на кафедре инженерной и экологической геологии гео-
логического факультета МГУ им, МВ. Ломоносова с 1954 г. Чте-
ние его было связано с введением на кафедре специальности
«инженерная геология» и впервые было проведено М.Н. Троиц-
кой. Наряду с традиционными приемами инженерно-геологиче-
ских расчетов ею рассматривались возможности применения ме-
тодов теории математической статистики при обработке данных
полевого и лабораторного изучения свойств горных пород. С
1963 г. курс читал ОН. Максимов, который включил большой
раздел, посвященный методам физического моделирования (эк-
вивалентных материалов, фотоупругоста и др.), которые могут
быть применены при решении инженерно-геологических задач,
It курс тогда получил название «Инженерно-геологические рас-
четы и моделирование».
В настоящее время изучаемая дисциплина существенно рас-
ширена за счет изложения основ математического моделирования,
которое в наступившем столетии несомненно станет основным
способом количественного изучения геологических и инженер*
но-геологических процессов
В основу учебника положен курс лекций9 который читают
студентам отделения гидрогеологии, инженерной геологии и гео-
криологии геологического факультета МГУ по специальностям
инженерная геология, грунтоведение и искусственный литоге-
нез, охрана геологической среды, общая геокриология и др.
Учебник «Инженерно-геологические расчеты и моделиро-
вание» предназначен для студентов геологических факультетов
университетов и кафедр инженерной геологии строительных,
горных, автодорожных и других вузов, обучающихся по специ-
альности инженерная геология И гидрогеология. Учебник также
полезен широкому кругу специалистов, занимающихся инже-
нерно-геологическими изысканиями для обоснования проекти-
рования и строительства различных инженерных сооружений.
Раздел «Имитационное компьютерное моделирование» на-
писан профессором, доктором геолого-минерапогических наук
Е Н. Коломенским, а раздел «Расчет суффозионных и карсто-
вых провалов на закарстованных территориях» - старшим на-
учным сотрудником, кандидатом геолого-минералогических наук
А.В. Аникеевым.
Автор выражает глубокую благодарность старшему научному
сотруднику, кандидату геолого-минералогических наук ЛЛ. Па-
насьян за помощь в подготовке учебника к изданию.
Автор будет признателен за все замечания и пожелания, ко-
торые просит присылать по адресу: 119992, Москва, ГСП-2, Во-
робьевы горы, МГУ, Геологический факультет, кафедра инже-
нерной и экологической геологии.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Gy — нормальные напряжения, МПа
Ху — касательные напряжения, МПа
ег — относительные деформации удлинения (укорочения)
Уу - относительные сдвиговые деформации
и, V, w — компоненты перемещений вдоль осей соответствен-
но х, у, Z, М
Р г этнос гь, г/см3
Е — модуль упругости, МПа
ц — коэффициент поперечной деформации (коэффици-
ент Пуассона)
G — модуль сдвига, МПа
g — ускорение свободного падения, м/с2
- пористость, %
— объемный вес породы, г/см?
ув — объемный вес воды, г/см"
Увзи “ объемный вес породы, взвешенной в воде, г/см3
— сцепление, МПа
ф — угол внутреннего трения, град.
ф ......- угол сопротивления сдвигу» град.
X — коэффициент устойчивости (запаса)
~ оползневое давление, Н
— удельный вес минеральной части скелета, г/см3
Размерности удельного и объемного веса даны в системе
МКГСС
ЧАСТЬ I. МАТЕМАТИЧЕСКОЕ И ФИЗИЧЕСКОЕ
МОДЕЛИРОВАНИЕ
ГЛАВА 1. МЕТОДЫ МОДЕЛИРОВАНИЯ ГЕОЛОГИЧЕСКИХ
И ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИХ ПРОЦЕССОВ
Одной из основных задач инженерной геологии является
прогноз развития современных геологических и возникновения
новых инженерно-геологических процессов как в естественных
условиях, так и в результате строительства различных сооруже-
ний и освоения территорий. При этом в большинстве случаев
прогноз должен быть количественным Поэтому при решении
прогнозных задач необходимо применение расчетных методов и
моделирования, которое начали использовать с 50-х годов. Сна-
чала для решения возникающих задач применяли различные мето-
ды физического моделирования, в дальнейшем в связи с бурным
развитием вычислительной техники И методики программирова-
ния при решении инженерно-геологических вопросов более ши-
рокие возможности раскрылись и перед математическим моде-
лированием.
1.1. Основы инженерно-геологической схематизации
Применение методов математического и физического моде-
лирования при изучении геологических и инженерно-геологи-
ческих процессов требует схематизации природных условий. Схе-
матизация играет важную роль в инженерно-геологических
исследованиях и позволяет выбрать и обосновать расчетные схе-
мы или схемы моделирования природных процессов
Схематизация осуществляется в несколько этапов. Основным
результатом первого этапа являются инженерно-геологические
карты и разрезы, где дается общая характеристика природной
обстановки изученного объекта. На втором этапе составляются
специализированные |16] карты и разрезы исследуемого объек-
та, где по возможности более подробно показываются те черты
природной обстановки, от которых будет зависеть развитие изу-
чаемых современных процессов. В зависимости от сложности
природных условий и решаемой задачи специализированных карт
и разрезов (инженерно-геологических моделей) может быть не-
сколько На последнем этапе составляются расчетные схемы или
схемы для моделирования (геомеханические схемы), в которых
учитываются требования выбранного метода расчета или спосо-
ба моделирования.
Например, для оценки инженерно-геологических условий
участка возведения плотины по данным полевых наблюдений,
разведочных и опытных работ составляется инженерно-геологи-
ческий разрез створа. В зависимости от того, какую предстоит
решать задачу — оценивать деформируемость основания плоти-
ны или изучать его проницаемость, — составляются инженерно-
геологические модели, отличающиеся представленной на них
информацией. Для оценки деформируемости основания на раз-
резе показываются литологические пачки, характеризующиеся
рахпичными деформационными свойствами. Для изучения фильт-
рации под плотиной и в обход ее плечевых примыканий при
выделении пачек основным признаком служит проницаемость
пород. Очевидно, что эти разрезы будут отличаться не только
информацией, но и положением границ, так как одинаковыми
свойствами могут обладать литологически различные породы, а
различия в свойствах одних и тех же пород могут определяться
степенью их раздробленности или другими причинами.
Выбор метода расчета или моделирования осуществляется
исходя из особенностей геологического строения изучаемого
объекта. С другой стороны, расчетная схема, или схема для моде-
лирования, зависит от выбранного способа, так как нет необхо-
димости отражать на схеме те черты строения или свойств изуча-
емого объекта, которые не учитываются выбранным способом
расчета или моделирования Поэтому на расчетной схеме могут
отсутствовать слои, показанные на инженерно-геологическом
разрезе, или наоборот, дается более подробное их расчленение,
например, в зависимости от степени их влияния на развитие изу-
чаемого процесса или оценку условий строительства.
Выбранную таким образом для расчета иди моделирования
Схему необходимо предварительно опробовать, чтобы убедиться
в справедливости принятых упрощений исследуемого объекта и
правильности выбора метода. Критерием такой проверки долж-
ны служить удовлетворяющие практику результаты расчета или
моделирования. В противном случае исходную схему следует уточ-
нить или подобрать другой метод исследования. При анализе
полученных расчетом или в результате моделирования данных
следует иметь в виду, что их точность не может быть выше точ-
ности заложенных в расчет или принятых при моделировании
исходных параметров.
Моделируемые При инженерно-геологических исследованиях
объекты обладают сложным строением и поэтому при их схема-
тизации необходимы упрощения, которые осуществляются в ре-
8
зультате решения следующих вопросов: 1) оценки характера из-
менения процесса во времени; 2) установления пространствен-
ной структуры процесса; 3) выбора способа задания расчетных
параметров.
Геологические и инженерно-геологические процессы явля-
ются нестационарными, поэтому их изучение должно осуществ-
ляться в динамической постановке Однако многие процессы
развиваются во времени очень медленно, что позволяет нестаци-
онарный процесс рассматривать как серию сменяющих друг дру-
га стационарных состояний Если изменение свойств пород при
выветривании происходит относительно медленно, то такая ха-
рактеристика, как мощность коры выветривания, для некоторого
временного периода является константой. Медленное изменение
свойств пород позволяет также считать эти свойства неизменны-
ми в течение времени, соизмеримого со сроком возведения или
эксплуатации сооружения. Поэтому массивы горных пород в та-
ких случаях условно могут рассматриваться как статические сис-
темы с неизменными в течение некоторого времени свойствами,
внутренними и внешними границами, уровнем действующих на
них сил ИТД Это позволяет, например, решать задачу устойчи-
вости склона на определенный момент времени в статической
постановке. Кроме того, решение статической задачи возможно,
когда интересукпсм конечным результатом процесса. а не разви-
тием его во времени. Во многих случаях необходимо оценить
только конечную осадку основания сооружения, но не исследо-
ван» ее изменение в период строительства.
СяедуйГ иметь в виду, что всегда рассматриваются динами-
ческие задачи, и решение их в статической постановке возможно
потому, что получаемые при этом результаты описывают изучен-
ное явление с точностью, достаточной для практических целей.
В некоторых случаях при исследовании поведения массива
горных пород под воздействием быстро и значительно, вплоть до
перемены знака, меняющихся во времени нагрузок, в частности,
сейсмических илй взрывных, необходим учет инерционных сил
и, следовательно, соответствующие задачи следует решать как
динамические
Рассматривая решение задач в статической постановке, пред-
полагают неизменность во времени свойств массива пород, его
формы, внешних факторов, действующих на него, итл Но это
далеко не так. В процессе деформирования основания под по-
стоянной нагрузкой могут изменяться механические свойства
пород основания, что повлияет на окончательный результат Тогда
прибегают к решению задачи в квазистатической постановке, а
инерционные силы не учитываются, но массив горных пород
рассматривается в качестве реологической системы»
Геологические и инженерно-геологические процессы разви-
ваются не только во времени, но и происходят в трехмерном
пространстве. Во многих случаях допустимо предполагать, что
траектории перемещения частей массива горных пород при раз-
витии какого-либо процесса лежат в одной плоскости, и рас-
сматривать не объемную, а плоскую (двумерную) задачу. Это воз-
можно тогда, когда исследуется поведение массива пород, который
в определенном направлении имеет одно и то же геологическое
строение, неизменную форму и геологические границы, обла-
дает одинаковыми свойствами, испытывает не изменяющиеся
внешние воздействия. Тогда сечения массива пород, перпенди-
кулярные этому направлению, не будут отличаться друг от друга
и, следовательно, если изучить поведение одного из сечений, то
тем самым будет известно поведение всего объема пород, Так,
если вдоль геологической структуры или в однородном массиве
пород пройдена горизонтальная горная выработка неизменного
сечения, то вызываемое ею перераспределение напряжений мо-
жет быть изучено в сечении, перпендикулярном этой выработке
(рис. 1.1). Таким образом, фактически решается объемная задача
путем изучения только одного из характерных сечений
Рис. 1 1» Сечение горной выработки для расчета напряженного состояния
Возможно рассматривать процесс одномерным, как, напри-
мер, в случае уплотнения толщи горных пород под равномерно
приложенной вертикальной нагрузкой, если размеры площади
нагружения значительно превышают мощность сжимаемой тол-
щи. В таком случае вертикальная деформация толщи во всех точ-
ках нагруженной площади, кроме точек лежащих вдоль ее конту-
ра, будет одинаковой.
Геологические объекты, как правило, отличаются простран-
ственной изменчивостью свойств слагающих их горных пород,
что обусловлено условиями их образования, историей развития,
тектоническими движениями, климатическими факторами и др.
Неоднородность свойств горных пород может быть упорядочен-
ной (закономерной) или хаотической (незакономерной), или ста-
ционарной и нестационарной [2|.
10
Закономерное распределение свойств горных пород может
иметь характер постепенного изменения в определенном направ-
лении по какому-либо закону. С глубиной монотонно может воз-
растать плотность горных пород, уменьшаться трещиноватость
и т.д. Другой тип закономерного изменения свойств горных по-
род обусловлен особенностями строения массива, состоящего из
слоев с различными свойствами, прорванного интрузиями, ослож-
ненного тектоническими нарушениями, неравномерно изменен-
ного процессами выветривания. В этом случае массив горных
пород состоит из отдельных частей, в каждой из которых свой-
ства постоянны, но параметры соседних частей существенно раз-
личаются. Такие массивы могут быть представлены в виде кусоч-
но-однородной модели. Следует иметь в виду, что массивы могут
быть неоднородными по отношению к одним свойствам, но од-
нородными — к другим.
При хаотической неоднородности свойства в массиве гор-
ных пород незакономерно изменяются от точки к точке. Разброс
в значениях показателя свойств зависит от неоднородности по-
род, слагающих массив, условий отбора проб для исследования,
методики экспериментальных работ, точности лабораторных или
полевых определений и др. Характер изменчивости показателей
свойств при хаотическом их распределении исследуется с помо-
щью методов математической статистики, так как: данные опро-
бования в этом случае можно рассматривать как выборку слу-
чайных показателей свойств из генеральной совокупности.
Понятие неоднородности массива горных пород является
относительным. Участок массива можно рассматривать как од-
нородный, если его размеры существенно больше, л.м размер
испытуемого образца или элементарного объема, по отношению
к которому производится исследование массива, а размеры пос-
ледних, в свою очередь, существенно больше размеров элемен-
тов, которые обусловливают неоднородность массива. Чтобы
массив пород, можно было считать однородным, необходимо чтобы
размер элементарного блока или испытуемого образца, по оцен-
кам разных авторов, был в 20-100 раз больше характерных раз-
меров элементов неоднородностей [15]. Если размеры образцов
соизмеримы с элементами неоднородности массива, го опреде-
ленные на этих образцах свойства будут различными.
1.2. Классификация методов моделирования
Методы моделирования можно классифицировать по раз-
личным признакам. Например, по сферам приложения (.моде-
лирование в физике, общественных науках, в технике и др.), по
11
характеру моделируемых объектов (моделирование геологичес-
ких процессов, механическим мркшессов и др )5 по характеру
самих моделей и другим признакам. Единая и всеобъемлющая
классификация методов моделирования затруднительна И, сле-
довательно, любая их классификация не может претендовать на
полноту. Рассмотрим кратко классификацию методов моделиро-
вания по средствам моделирования, обратив при этом внимание
нате» которые используются при моделировании талогических
и инженерно-геологических процессов
Общая схема классификации методов моделирования по ха-
рактеру моделей представлена ниже:
Виды моделирования
" Мыслен ное
Идеальное (теоретическое)
"^“Знаковое
Кибернетическое
__► Предметно-математическое
Материальное (экспериментальное)
-Фит т^скце
Все способы .-моделирования могут быть разделены на две
группы: методы., которые не используют материальные средства
(идеальное моделирование^ и моделирование с помощью физк
четких моделей (материальное моделирование).
Идеальное, или теоретическое, моделирование представляет
собой умственный эксперимент. Оно подразделяется, на мыслен-
ное, или интуитивное моделирование и знаковое.
Интуитивное моделирование протекает на уровне «модель-
ных представлений», состоит в построении образов, отражаю-
щих реальную действительность, и является непременным усло-
вием любого познавательного процесса на его начальной стадии.
При знак€)вом моделировании моделями служат знаковые
образования какого-либо вида: разнообразные схемы, графики,
чертежи, формулы, графы, слова и предложения в некотором
алфавите естественного или искусственного языка и т.д. Хорошо
известны геологам знаковые модели — геологические и инженер-
но-геологические карты и разрезы. Очень важным и широко при-
меняемым видом знакового моделирования является логико-ма-
тематическое, или математическое, моделирование, включающее
формулы, уравнения, системы уравнений и операций над, ними,
с помощью которых решается множество научных и практичес-
ких задач. Отличительная черта логико-математического моде-
лирования состоит в том, что знаковые образования и их эле-
менты всегда рассматриваются вместе с определенными преоо
разованиями или операциями над ними, которые выполняются
человеком или машиной.
Современной формой материальной реализации логико-ма
тематического моделирования, получившей в последние годы
широкое распространение, является моделирование на ЭВМ,
или кибернетическое моде лирование. Этот вид моделирования —
знаковое по содержанию, но требует материальный носитель в
виде электронной вычислительной машины, что роднит его с
предметным моделированием. С помощью ЭВМ можно зафик-
сировать описание любого процесса (явления) в виде програм-
мы, же. закодированной на машинном языке системы правил,
следуя которым машина может воспроизвести ход моделируе*
ж то процесса.
Материальным, или экспериментальным, называется модели-
рование, в ходе которого исследование ведется на модели, вос-
производящей основные геометрические, физические, динами-
ческие и функциональные характеристики исследуемого объекта.
Оно подразделяется на предметно-математическое и физическое
м с де л иро в а н и е.
Предметно-математическим называется такой вид модели^
рования, когда явление (система или процесс) исследуются пу-
тем опытного изучения какого-лиоо явления иной физической
природы, но если Оно описывается теми же математическими зс-~
отношениями, что и моделируемое явление. Наиболее распрост-
раненным и важным видом предметно-математического модели
рования является аналоеовое моделирование, основанное на
аналогии (более точно — изоморфизме) процессов различной фи-
зической природы, но описываемых одинаковыми математичео
кими (дифференциальными, алгебраическими или какими-либо
другими) уравнениями. Это уравнение служит теоретической
моделью обоих аналогичных явлений (процессов, систем), лю-
бое же из них — экспериментальной моделью этого уравнения и
аналоговой моделью друг друга. Предметно-математическое мо
делирование широко применяется для замены изучения одних
явлений изучением других, более удобных для лабораторного
исследования, в частности потому, что они допускают измере-
ние неизвестных величин. В практике гидрогеологических ис-
следований широко применяется так называемый метод ЭГДА,
когда исследование движения подземных вод в пористой среде
производится с помощью аналогии движения электрического тока
в электропроводной бумаге. Этот вид моделирования возможен
лютому, что закон Дарси, описывающий движение подземных
вод, имеет такой же вид, как и закон Ома, характеризующий
движения электрического тока в проводнике
Физическое моделирование состоит в замене объекта или яв-
ления экспериментальным исследованием его модели, имеющей
ту же физическую природу. В основе моделирования лежит ‘тео-
рия подобия и анализ размерностей. Среди методов можно на-
звать метод эквивалентных материалов, центробежное моделиро-
вание и др.
По характеру той стороны объекта, которая подвергается ис-
следованию на моделях, различают моделирование структуры
объекта и моделирование его поведения (функционирования про-
текающих в нем процессов). Так, можно говорить о двух основ-
ных инженерно-геологических моделях: условий и процессов,
первая из которых отражает строение, свойства, состояние мае
сива пород ИЛИ территории, а вторая - характеристику развития
в них геологических и инженерно*геологичес|СмК процессов.
Для исследования сложных процессов пользуются стохасти-
ческим моделированием, основанным на установлении вероят-
ностей изучаемых событий. Такие модели не отражают весь ход
отдельных процессов в данном явлении, носящих случайный ха^-
рактер, а определяют некоторый средний суммарный результат.
При решении инженерно-геологических вопросов все пере*
численные методы моделирования применяются в разнообра:
ных областях С различной частотой использования»
1.3. Методы моделирования в инженерной геологии
Для изучения современных геологических и инженерно-гео-
логических процессов широко применяется как физическое* так
и математическое моделирование: склоновые (обвалы, оползни,
сели, солифлюкция, снежные лавины и др ); процессы, обуслов-
ленные деятельностью поверхностных вод (абразия, эрозия, с :
рагообразование); процессы, вызванные деятельностью подзем*
ных вод (карст, суффозия).
Процессы абразии и эрозии изучаются на искусственно со-
зданных моделях для оценки условий проектирования и строи-
тельства гидротехнических и портовых сооружений. Главными
задачами этого моделирования являются изучение изменения
волнового режима водоемов и перемещения наносов и течений.
С другой стороны, этот вид моделирования является необходи-
мым этапом исследования абразионных и эрозионных процес-
сов, гак как основным фактором их развития служит волновое
воздействие на берег, которое может существенно изменяться в
резул тате с гр и г ел ьст ва
Лабораторное моделирование применяют при изучении про-
цессов выветривания [17, 18], для выявления степени влияния
различных факторов на развитие и скорость процесса, а также
при изучении условий и факторов формирования просадочных
свойств лёссовых пород [12].
Большую роль в исследовании суффозионных процессов
играет физическое моделирование. Например, с помощью фи-
зических моделей изучаются условия и характер перемещения
песчаных частиц через окна’М подстилающих экранирующих от-
ложениях в полости и пустоты ниже залегающих пород под дей-
ствием фильтрационного потока [1, 13]. Этот вид моделирования
также позволяет изучить* закономерности образования проваль-
ных явлений на поверхности, сложенной песчаными породами.
Суффозионный размыв заполнителя трещин изучался при про-
ектировании плотины Иркутской ГЭС натурными эксперимен-
тами, которые моделировали предполагаемый фильтрационный
поток под будущей плотиной.
Карстовые процессы представляют собой очень сложную
проблему. Для ее решения используется как физическое модели-
рование, которое применяется для исследования химической де-
нудации карбонатных пород [7]3 так и математическое — для про-
п-хп.~ образования карстовый гэронок на поверхности [6].
Для изучения движения снежных лавин разработана матема-
тическая модель, которая может быть применена для оценки ско-
рХП. - ДхИ-ДХИ '1 ; СПИЛ?? -п-тхохсп Ф, 2] ГАТ
годами физического моделирования изуч-гасэ ударная сила
тххньт лгдлэ, дгп ЧПГС ?*£??/ ' ’Эзсипд была сбору--
дована специальная экспериментальная установка.
Перераспредежние напряжений и деформаций в массиве
пород в результате проходки горных выработок изучалось в гор-
ном деле с помощью математического моделирования [И] и ме-
тодом эквивалентных материалов, разработанным I . Н. Кузнецо-
вым [5]. В строительной механике для изучения распределения
напряжений в сооружениях и конструкциях использовались по-
ляризационно-оптические методы моделирования [9, 10. 14]. В
дальнейшем эти виды моделирования нашли применение при
решении некоторых инженерно-геологических задач. Одной из
них является изучение напряженно деформированного состоя-
ния (НДС) массивов горных пород, при решении которой ис-
пользуются разнообразные методы моделирования Наибольшее
развитие эти методы получили в случаях, когда инженерно-гео-
логические исследования стали проводиться для проектирования
крупных гидротехнических сооружений в горно-складчатых об-
ластях и для оценки устойчивости оснований сооружений и
склонов. Математическое моделирование также применялось
при исследовании НДС естественных массивов горных пород на
территориях предполагаемой разработки месторождений полез-
ных ископаемых.
В связи с важностью исследования НДС массивов горных
пород для решения ряда инженерно-геологических проблем ма-
тематическое моделирование целесообразно рассмотреть на при-
мере изучения НДС массивов горных пород и связанных с ним
процессов деформирования и разрушения.
Контрольные вопросы
1. Цель и основные этапы проведения схематизации при
родных условий.
2 Вопросы, решаемые при схематизации.
3. Случаи решения задачи в двухмерной и одномерной по-
становке.
4, Условия рассмотрена г . родных процессов в качестве
5. Способы задания расчетных параметров.
6. Методы математического и экспериментального Модели-
рования, применяемые при инженерно-теологических ис
следованиях.
7. Задачи инженерной геологии, решаемые^ помощью мо-
делирования.
ГЛАВА 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Методы математического моделирования, приводящие изу-
чение явлений внешнего мира к математическим задачам, зани~
мают большое место среди других методов исследований, что
особенно проявилось в связи с появлением ЭВМ.
Изучение геологических и инженерно-геологических процес-
сов- с помощью 'математических, методов встречает значительные
трудности. Это обусловлено тем. что исследуемые объект^- отли-
чаются сложным строением, обладают изменяющимися во вре-
мени свойствами, подвержены воздействию различных факто-
ров, степень влияния которых не всегда может быть оценена
полностью Кроме того, никогда в полной мере не известны свой-
ства изучаемого объекта, а точность их определения невысокая.
Наконец, не для всех геологических и инженерно-геологических
процессов разработаны описывающие их математические моде-
ли. Следует добавить, что математические модели природных и
техногенных процессов отличаются очень большой сложностью,
а их создание может быть осуществлено специалистами высокой
квалификации, подготовка которых на теологических факуль-
тетах вузов не производится. Тем не менее разработка и ис-
пользование математического моделирования для исследования
инженерн а го с логических и геологических процессов являются
чрезвычайно важной задачей на современном этапе развития
инженерной геодинамики.
Рассмотрим применение методов математического модели-
рования на примере изучения напряженно-деформированного
состояния массивов горных пород. Выбор примера обусловлен
важностью решения данной задачи, так как оценка распределе-
ния напряжений в массивах пород необходима при изучении оса-
док сооружений, при прогнозе деформации пород в результате
проходки горных выработок, откачках подземных вод, нефти или
газа. при оценке устойчивости природных склонов и бортов ка-
рьеров и др. Кроме того, решение этой задачи наиболее разрабо-
тано и широко применяется на практике
2.1. Математическая модель
напряженно-деформированного состояния
массивов горных пород
Под математическим моделированием понимается матема-
тическое описание изучаемого процесса, т е. построение его ма-
тематической модели и исследование этой модели с помощью
17
математических методов. Математической моделью называется
приближенное описание какого-либо класса явлений внешнего
мира, выраженного с помощью математической символики. Ма-
тематическая модель является методом познания внешнего мира,
а также метолом прогнозирования и управления.
Процесс математического моделирования включает четыре
этапа. На первом необходимо сформулировать законы, связыва-
ющие основные объекты модели. Этот этап требует знания мно-
жества фактов, относящихся к изучаемым явлениям, и глубокого
проникновения в их взаимосвязи. Результатом этой стадия явля-
ется запись е математических терминах сформулированных ка-
чественных представлений о связях между объектами модели. Эта
связь может быть выражена одним уравнением или системой.
На втором этапе производится исследование математичес-
кой задачи» к которой приводит математическое моделирование*
Основным здесь является решение прямой задачи, в результате
чего получаются данные, которые в дальнейшем сопоставляются
с результатами наблюдений изучаемых явлений. На этом этапе»
как правило, абстрагируются от изучаемых явлений, и важную
роль приобретают математический аппарат, необходимый для
анализа математической модели, и вычислительная техника, по-
зволяющая получить количественную выходную информацию.
На третьем этапе янясняют, насколько согласуются резуль-
таты наблюдений с теоретическими следствиями модели. Если
отклонение расчетных данных от наблюденных не выходит за
пределы точности наблюдений, то модель считается удовлетво-
рительной. В случае, когда модель была определенной, те. все ее
параметры были заданы, го полученные теоретические результа-
ты являются решением прямой задачи Если некоторые характе-
ристики при построении модели остаются неопределенными, то
они могут быть установлены путем решения обратной задачи,
т.е. таким образом, чтобы выходная информация была сопоста-
вима в пределах точности наблюдений с результатами наблюде-
ний изучаемых явлений. Если ни при каком выборе характерис-
тик этим условиям нельзя удовлетворить, то модель непригодна
для i< следования рассматриваемых явлений. Применение кри-
терия практики к оценке математической модели позволяет де-
лать вывод о правильности представлений, лежащих в основе
изучаемой модели.
Четвертый этап заключается в анализе модели в связи с на-
коплением данных об изучаемых явлениях и модернизации мо-
дели. В процессе развития науки и техники данные об изучаемых
явлениях все более и более уточняются и наступает момент, ког-
да выводы, полученные на основании принятой математической
модели, не соответствуют новым знаниям о явлении, и тогда воз-
18
ни кает необходимоеть построения новой, более совершенной
м аге м атическо й моде л и.
Любая математическая модель представляет собой совокуп-
ность уравнений движения, совместности и состояния при за-
данных начальных и граничных условиях. Наиболее просто вы-
вод всех названных уравнений может быть осуществлен на
примере построения математической модели для исследования
напряженно- деформированного состояния любых материальных
объектов, включая массивы горных пород, находящихся под воз-
действием внешних сил.
Внешние силы, воздействующие на массивы горных пород,
подразделяются на объемные и поверхностные. Первые действу-
ют на каждый элементарный объем горных пород... К ним отно-
сятся, прежде всего, силы гравитации, а также инерционные силы,
возникающие например, пол :е;ядетрлссниях или взрывах, кос*
мические силы (силы приливного действия Луны и Солнца), сипы
гидродинамического давления и гидростатического взвешивания
и гд. К поверхностным силам, которые приложены ко всей или
части поверхности массива пород, могут быть отнесены тектони-
ческие силы сжатия, растяжения или сдвига, нагрузки от зданий,
плоткп насыпей, водохранилищ л др.
В результате действия внешних сил в 'Массиве пород, в каж-
дой егс- зтчтс, возникают тнутрениие силы, мерой т вторых яздт-
:отся напряжения. стяикающие напряжения, г стон очередь,
вызывают деформации. Чтобы описать напряжения в каждой точке
массива, введем прямоугольную систему координат и вы-
делим вокруг произвольной точки М этого массива (рис.. 2.1)
Рис 2,1. Компоненты напряжений В лОЧКВ М
19
элементарный прямоугольный параллелепипед с бесконечно ма-
лыми ребрами dx. dymdzn гранями, параллельными координат-
ным плоскостям. Через каждую грань параллелепипеда одна часть
массива действует на другую с некоторой силой, встречая рав-
ную по величине и противоположную по направлению. Если от-
нести эту силу к площади грани, получим напряжение, которое
можно разложить в соответствии с выбранной системой коорди-
нат на компоненты: нормальную к грани и параллельную коор-
динатной оси, направленной перпендикулярно этой грани, и две
касательные, действующие вдоль грани и параллельные двум дру-
гим координатным осям (см. рис. 21). Аналогично можно опре-
делить компоненты напряжений на других гранях параллелепи-
педа В теории механики сплошных сред доказывается, что
напряженное состояние в точке определено, если известны ком-
поненты напряжений, действующих на трех взаимно перпенди-
кулярных площадках — гранях параллелепипеда, проходящих
через эту точку. Это значит, что тогда могут быть определены
напряжения, действующие на любой площадке, проходящей че-
рез данную точку, по формулам аналитической геометрии. Та-
ким образом, напряженное состояние в произвольной точке бу-
дет известно только тогда, когда оно известно на всех площадках,
проходящих через эту точку.
Нормальные напряжения обозначаются а>у, касатель-
ные — Тух, при этом первый индекс показывает,
параллельно какой координатной оси действует напряжение, а
второй указывает на то, какой оси перпендикулярна площадка,
на которой действуют эти напряжения [1]. Обычно в обозначе-
нии нормальных напряжений один из двух одинаковых индексов
опускается: ох, о,,, <т,. Исходя из изложенного, напряженное со-
стояние в точке можно записать так:
(2.1.1)
Графическим изображением напряженного состояния в лю-
бой точке массива пород служит диаграмма Мора (рис. 2.2).
Все тела могут быть подразделены на абсолютно жесткие и
деформируемые. Массивы горных пород относятся к деформи-
руемым телам, и в дальнейшем будут рассматриваться только
деформируемые тела Возникшие под воздействием внешних сил
напряжения вызывают в них деформации, которые могут быть
двух видов. Нормальные напряжения вызываю! удлинение или
укорочение ребер параллелепипеда, приводя к изменению его
' n; V-.
W= a3
Рис. 2.2. Диаграмма Мора — графическое отображение напря-
женного состояния в точке
объема; касательные напряжения приводят к увеличению или
уменьшению утла между ребрами, изменяя форму параллелепи-
педа (рис. 2.31 Если обозначить относительные удлинения (уко-
рочения) ребер параллелепипеда через еЛ, 8Г а относительные
изменения углов через у^, yXZi у‘ух, уи, у^, to деформи-
рованное состояние в точке можно описать следующим образом:
У zx У zy^z .
Под воздействием внешних сид каждая точка деформируе-
мого тела изменяет свое положение в пространстве или переме-
Рис. 2.3, Схемы расчета деформаций при действии напря-
жений: а — нормальных, б — касательных
щается. Проекции вектора перемещения произвольной точки М
на координатные оси Ох, Оу, Oz обычно обозначаются через и, у»
Ж Тогда относительные деформации удлинения (укорочения) по
осям х, у, z ребер элементарного параллелепипеда .длиной dx, dy
и dz (рис. 2.3.6/) могут быть представлены в дифференциальной
форме:
Относительные деформации сдвига в дифференциальной форме
можно записать в виде:
tn . & + £., - ~^ + ^, „ 3»+^, (2.1.4)
Ду dx' 1 - - dz dy а dx dz ' '
ди
где —----тангенс угла, равный, в связи с его малостью, самому
dV
••
углу (в радианах), на который отклоняется ребро деформируемо-
го параллелепипеда от оси Оу по направлению, совпадающему с
осью Ох (рис. 2.3,6). Эти уравнения называются геометрически-
ми, или по имени их автора — уравнениями Коши.
Напряженно-деформированное состояние массива пород бу-
дет установлено в том случае, если известны компоненты напря-
жений и деформаций в каждой его точке. Напряженно-дефор-
мированное состояние называется однородным, если в каждой
точке напряжения и деформации одинаковы. Если напряжения
и деформации изменяются от точки к точке, то такое напряжен-
но-деформированное состояние называется неоднородным. На-
пример, неоднородным будет поле напряжений в основании со-
оружения, где дополнительные напряжения максимальны под
фундаментом и уменьшаются при удалении от него.
2.2. Вывод основных уравнений математической
модели НДС массива горных пород
Математическая модель включает уравнения движения, не-
разрывности и состояния, а также начальные и граничные усло-
вия [3].
Уравнения движения и равновесия. Уравнения движения вы-
ражают связь кинематических элементов с динамическими. Они,
как и уравнения совместности, применимы для описания напря-
женно-деформированного состояния любых тел, в том числе и
массивов горных пород, включая и абсолютно твердые, недефор-
мируемые тела. Уравнения состояния, напротив, зависят от фи-
зических особенностей массивов горных пород, о чем подробнее
будет сказано ниже.
Если тело находится в равновесии, то в статических услови-
ях, как известно из теоретической механики, дай элементарного
прямоугольного параллелепипеда. описанного около произволь-
ной точки, должны удовлетворяться шесть условий равновесия;
Ек-0, Е^-0, Е^х-0, ^Му-О, ЕМ-° (2.2.1)
Эти условия показывают, что для находящегося в равновесии тела
суммы проекций действующих на него сил на координатные оси
должны равняться нулю, и суммы моментов тех же сил относи-
тельно координатных осей должны также равняться нулю.
Для тела, находящегося в движении или при динамическом
воздействии, правые части условий равновесия (2,2.1) не будут
равны нулю. В этих уравнениях вместо нулей будут проекции
инерционных сил, которые по второму закону Ньютона равны
произведению массы т элементарного объема на соответствую-
щие проекции его ускорения, равные вторым производным со-
ответствующих перемещений по времени
Аналогично в правых частях уравнений моментов вместо нулей
должны быть проекции моментов тех же инерционных сил. Пусть
на трех гранях элементарного прямоугольного параллелепипеда
действуют напряжения <ух, ол Ofp та, как это показано на
рис. 2.1. Тогда на параллельных гранях, отстоящих от граней,
проходящих через точку М, на расстояниях dx, dy и dz будут дей-
ствовать другие напряжения, которые могут быть определены
следующим образом. Так, на грани, перпендикулярной оси Ох и
отстоящей ол точки М на расстоянии dx, нормальное напряже-
ние получит некоторое приращение, пропорциональное измене-
нию интенсивности напряжения вдоль оси Ох -?*- и расстоянию
ох
dx, и будет равно ох — dx (рис. 2.4). Аналогичными рассуж-
дениями можно определить все напряжения, действующие на всех
гранях элементарного прямоугольного параллелепипеда. Напря-
жения определяют поверхностные силы , приложенные к граням
параллелепипеда извне, величина которых определяется умноже-
нием напряжения на площадь грани, к которой оно приложено.
Например, сила на грани, где действует напряжение ох, будет рав-
на vydydz, а на грани, отстоящей от нее на расстояние dx, равна:
А й
Рис. 2.4. Схема к определению напряжений, действующих
на противоположных гранях параллелепипеда
Кроме того, элементарный параллелепипед испытывает Дей-
ствие объемной силы.. Величины проекций этой силы определи
югся как произведение плотности пород массива на объем эле-
ментарного параллелепипеда и на соответствующие проекции Л-
У, Z приложенных объемных сил, отнесенных к единичной плс,
ности. Например, проекция объемной силы на ось Ок будет равна:
р Х dxdydz^
(2.2.4)
Раскроем одно из уравнений динамического равновесия (движе-
~~т—(рис. 2.4):
dt~
—— dx dydz — о xdydz + т
-^-dy dxdf—x^dxdy + pXdxdydz = pdxdydz
дГ
Сделав необходимые сокращения и раскрыв аналогичным
образом два других уравнения динамического равновесия
dt
движения:
&w ..
—г-, окончательно получим уравнения
дг
Эти уравнения могут применяться для изучения динамических
процессов, например, при исследовании напряженно-деформи-
рованного состояния массивов горных пород при землетрясени-
ях, взрывах и в других случаях, когда условия нагружения меня-
ются очень быстро. Однако в большинстве случаев изменение
свойств массивов горных пород, их геометрии, условий нагруже-
ния и т.д. происходит в геологическое время, т.е. очень медлен-
но, что позволяет исследовать их напряженно-деформированное
состояние в статической постановке, что существенно упрошдет
решение задачи. В этом случае в уравнениях движения правая
часть обращается в нуль, и уравнения (2.2.5) принимают вид;
(2.26)
(?т„. дх, да, _
4 4- pZ = 0.
дх у;-
В таком виде эти уравнения получили название уравнений рав-
но весия
В случае стационарного процесса в уравнениях моментов пра-
вые части также равны нулю, откуда следует закон парности каса-
тельных напряжений: на любых двух взаимно перпендикулярных
площадках касательные напряжения равны между собой и проти-
воположно направлены, т.е. хуг = х^, х& = т^.Таким
образом, напряженное состояние в точке полностью определяет-
ся шестью компонентами напряжений: тремя нормальными и
гремя касательными. Отсюда также вытекает равенство дефор-
маций; =Уух, уп =Угу, Уа ; Следовательно, деформи-
рованное состояние в точке полностью определяется шестью ком-
понентами: тремя относительными деформациями по трем
координатным осям и тремя относительными деформациями сдви-
га. Таким образом, чтобы изучить напряженно-деформирован-
ное состояние любого тела, в том числе и массива горных пород,
25
необходимо в каждой его точке определить Шесть компонент на-
пряжений и шесть компонент деформаций.
Уравнения равновесия (2 2.6) позволяют исследовать объем-
ные (трехмерные) задачи. Однако при изучении напряженно-де-
формированного состояния массивов горных пород нередки слу-
чаи, когда решение объемной задачи может быть полнено в
результате рассмотрения плоской (двухмерной) или даже одно-
мерной задачи Подчеркиваем, что всегда рассматривается объем-
ный случай, но для упрощения вычислений решение объемной
задачи может быть осуществлено в двухмерной или одномерной
постановке.
При решении плоской задачи уравнения равновесия приник
LK ВИД-
(2.2.7)
и число неизвестных сокращается до грех компонент напряже-
ний ох. ог, и трех компонент деформаций Однако
для их определения пока есть только два уравнения равновесия,
что недостаточно, и следовательно, для решения задачи о на-
пряженно-деформированном состоянии массива пород необхо-
димы дополнительные условия, к которым относятся условия
совместности.
Уравнения совместности для случая описания деформацион-
ного процесса получили название условия неразрывности дефор-
маций. Необходимость введения этих уравнений вытекает из ус-
ловия, что при деформировании под влиянием внешних нагрузок
вплоть до разрушения деформируемое тело должно оставаться
сплошным. В процессе деформации каждая точка тела изменяет
свое положение в пространстве, и величина этого перемещения
определяется тремя функциями и, v, w, представляющими собой
проекции векторов перемещений на координатные оси Ох, Оу, Oz.
Деформация каждой точки деформируемого тела описывается
шестью компонентами е,, ez,..., у^, которые могут быть однознач-
но определены по заданным перемещениям согласно геометри-
ческим уравнениям (2.1,3, 2.1.4). Однако задать произвольным
образом компоненты деформаций нельзя, так как в соответствии
с геометрическими уравнениями однозначно определить компо-
ненты перемещений невозможно, так как уравнений больше, чем
неизвестных, и следовательно, между компонентами деформа-
ций должна существовать зависимость. Эта зависимость выража-
ется уравнениями неразрывности деформаций, которые можно
получить из геометрических уравнений. Для объемной задачи
таких уравнений шесть. Они получили название по имени авто-
ра — уравнения Сен-Венана — и выражают зависимость между
удлинениями (укорочениями) и углами сдвига. В случае плоской
задачи остается только одно уравнение неразрывности, которое
может быть получено из геометрических уравнений и в компо-
нентах деформаций имеет вид:
Уравнения состояния. Для определения напряженно-дефор-
мированного состояния массивов горных пород под воздействи-
ем объемных и поверхностных сил к уравнениям равновесия,
геометрическим соотношениям и уравнениям неразрывности
необходимо добавить физические уравнения, определяющие зако-
номерности деформирования горных пород под действием напря-
жений. Боли первые три группы уравнений могут быТь выведены
логически, то физические, уравнения или уравнений состояния
строят на основании экспериментальных данных. Необходимо
подчеркнуть, что уравнения равновесия, геометрические соотно-
шения и уравнения неразрывности справедливы для любого вида
деформирования сплошной среды, включая упругое, пластичес-
кое и ползучее.
При составлении физических уравнений состояния масси-
вов горных пород необходимо учитывать многообразие факто-
ров, оказывающих влияние на механические свойств#- В настоя-
щее время при решении задач прикладной геомеЯники для
сплошных тел (включая и горные породы) используются физи-
ческие уравнения теории упругости (линейной и нелинейной),
теории пластичности, теории ползучести и теории пластично-
вязких течений. Для несплошных тел при составлений физичес-
ких уравнений необходимо учитывать их физические особеннос-
ти, обусловленные в первую очередь их несплошносУью.
Уравнения состояния связывают изменение объема и формы
тела с изменением силового фактора. Для того чтобМ получить
уравнения состояния, необходимо иметь закон, вьфюкающий
связь между напряженным состоянием тела и вызвайн°й им ДО-
формацией. Для тел, обладающих различными реологическими
свойствами, зависимость между напряжениями и деф°рмациями
выражается по-разному, но наиболее просто, когда Тело прояв-
ляет упругие свойства. Для упругого тела связь междУ напряже-
ниями и деформациями выражается законом Гука. Этот закон
был опубликован Гуком (Robert Hooke, 1615-1703) в 1678 г., как
«Деформация упругого тела пропорциональна действующему на
него усилию». Сформулированный закон подтверждается экспе-
риментально, но при условии достаточно малых деформаций.
Следует подчеркнуть, что упругие свойства проявляют практи-
чески все тела, в том числе и массивы горных пород. Поэтому
достаточно рассмотреть вывод уравнений состояния для упруго-
го тела, как наиболее простого в реологическом отношении, и в
связи с тем, что свойство упругости является универсальным
Предложенный Гуком закон выражает связь между напряже-
ниями и деформациями для условий одномерного сжатия или
растяжения В трехмерном случае напряженное и деформиро-
ванное состояние любого тела в произвольной точке характери-
зуется шестью величинами каждое, и поэтому связь между на-
пряжениями и деформациями выражается более сложным
образом. В начале XIX в, Коши и Пуассоном был сформулиро*
ван обобщенный; закон Гуки «Компоненты напряжений т дгя-
ной точке тела суть линейные и однородные функции компо-
нент деформаций в той же точке и обратно». Таким образом,
обобщенный закон Гука утверждает, что в каждую компоненту
деформаций определенный вклад вносят все компоненты напри
жений, действующих в данной точке.
Величины, характеризующие упругие свойства тела в-данной
точке, не зависят от значений измпонент на пряжений z соответ-
.ствующих деформаций Они могут иметь различные значения в
разных точках тела, и тогда тело будет неоднородно по упругим
свойства*/ Если упзщие постоянные одни и те же во всех точках
тела, то тело однородно.
Для анизотропного тела уравнения обобщенного закона Гука,
выраженные в декартовой системе координат йптс Имеют вид:
^х ‘ ^11 Дх ^12^у ” И ' > 14 " 5 '* ?'< ~г :;
yZx У -Л-я6бЪг
В этих уравнениях а„ — упругие постоянные. Если при деформа-
ции не происходит изменения температуры тела, то симметрич-
ные относительно диагонали упругие постоянные одинаковы, и
следовательно, число упругих постоянных в самом общем случае
анизотропии равно 2L
Упругие постоянные ау занимают неодинаковое положение
в уравнениях обобщенного закона Гука и имеют различный фи-
зический смысл [2]. Можно показать, что если тело обладает уп-
ругой симметрией, то уравнения обобщенного закона Гужа для
него упрощаются, т.е. у тел, обладающих упругой симметрией,
1:
число независимых упругих постоянных не 21, в значительно
меньше.
Например* если через каждую точку тела проходит три орто-
гональные плоскости упругой симметрии, то число упругих кон-
стант уменьшается до 9 — это главные упругие постоянные. Они
могут быть выражены через «технические упругие постоянные^
к которым относятся модули упругости и сдвига и коэффициен-
ты поперечной деформации. Такие тела, у которых в каждой точ-
ке имеются три ортогональные плоскости упругой симметрии,
называются ортотропными Примерами таких тел являются дре*
веси на и фанера.
Если через каждую точку тела промыт ось упругой симмет-
рии вращения, то все направления в шюскостях, нормальных к
этой оси, эквивалентны в отношении упругих свойств, и тело
является изотропным в этих плоскостях. Тогда число независи-
мых упругих постоянных сократится до 5, и уравнения состоя-
ния примут вид:
(2,2 10)
1
I}’? QJ ’я*
1
Tjlt " ~Q!
где Е, Ег —- модули упругости Для растяжения-сжатия по напра
пениям, лежащим в плоскости изотропии и перпендикулярно к
ней; ц — коэффициент поперечной деформации, характеризую-
щий поперечное сжатие в плоскости изотропии при растяжении
В той же плоскости: ц' — коэффициент поперечной деформации,
характеризующий поперечное сжатие в плоскости изогропии при
растяжении в направлении, нормальном к ней; G, G' — модули
сдвига соответственно для плоскостей параллельных и нормаль-
ных плоскости изотропии Такое тело получило название транс-
версально-изотропного, примером которого являются слоистые
горные породы
Наконец, в изотропном теле все направления эквивалентны
в отношении упругих свойств и любая плоскость является плос-
кое тью упругой симметрии. В этом случае число независимых
упругих постоянных сокращается до двух. Если Е — модуль Юнга,
модуль сдвига, и — коэ
ПИП
ициент Пуассона, тс уравнения
обобщенного закона Гука принимают вид:
Т =ук- - - >
1 f ..Л. VI
g '1®л “ Kvb + <b)p
(2
Д'";?:
’ /г = -< ’>'€ ’
а упругие постоянные связаны зависимостью G =
2.3. Математическая модель НДС массива горных
пород для двухмерного случая
Решение большинства задач о напряженно-деформирован-
НОМ состоянии массива горных пос с г с двухмер-
ной постановке. Возможны два варианта решения плоской зада-
чи: во-первых, можно рассматривать деформирование гонкой
пластинки» и во-вторых, изучать напряженное состояние в плос-
ком сечении При изучения поведения массивов горных пород
естественно рассматривать его деформацию в одном из равно-
правных плоских сечений. Но тогда в каждом ИЗ таких прилега-
ющих друг к другу сечений траектории перемещения частиц мае*
сива горных пород в процессе его деформирования будут лежать
в одной плоскости, ке. деформация в направлении перпендику*
лярном сечению будет отсутствовать. Если оси & и Оу лежат
изученном сечении, а ось Oz. направлена перпендикулярно ему
(рис. 2.5), то высказанное предположение равносильно тому, что
деформация вдоль оси z равна нулю: Тогда из уравнений
30
Рис. 2.5. Сечение оползневого склона вертикальной плоскостью XOY
состояния (2 2 11) следует, что между сечениями возникает на-
пряжение:
О 7 = Ц I О -г ‘ J v I, (х, Э.. 11
с сами уравнения состояния при решении плоской задачи будут
иметь вид:
Если в уравнение неразрывности (2.2.8) подставить значения
компонент деформаций из уравнений {2Л.2) и сделать необходи-
мые преобразования с уметом уравнений равновесия (2.2.7). то
уравнение неразрывности может быть записано относительно
компонент напряжений:
\ 1 I CCA , (J 1 \ . ! • Ч
V (от т о~ — -----1——jr ”7“ L (2.3.3)
l-p\dx dy f
~ с?
где V = —у ч - оператор Лапласа.
д:^ д'_-'
При изучении НДС массивов горных пород основной объем-
ной силой, действующей на него, является сила гравитации, ком-
поненты которой выражаются следующим образом.
У “ X “О, (2.3.4)
где g — ускорение свободного падения, ось Ок — горизонтальна,
а Оу направлена вертикально вверх. Тогда уравнение (2.3.3) упро-
щается
V(Од. ~ оv) — 0. (2.3.5)
Окончательно объединив уравнения (2>Х7^В (23.2)и (2.3 5) с уче-
том (2.3 4) и добавив к ним зависимые только от х и у соотноше-
ния из (2.1.3) и (2.1.4), получим математическую модель для изу-
чения напряженно-деформированного состояния массива пород
в двухмерном случае:
(2.3.6)
Ог =н(о.х +<Ъ-)’
Эта система уравнений представляет собой стационарную
математическую модель, позволяющую исследовать НДС масси-
ва пород в вертикальном плоском сечении, когда действующая
объемная сила является гравитационной, а массив горных по-
род — сплошным, упругим и изотропным.
В распространенных случаях, когда массивы горных пород
находятся ниже уровня подземных вод, уравнения равновесия
ид |4):
(2.3.7)
32
где о* и <гг эффективные напряжения, у» — объемный вес воды,
7Bgrad/i —фильтрационная сила, увзв =(А - ув)(1 -л) — объем-
ный вес породы, взвешенной в воде, где Д — удельный вес мине-
ральной части, л пористость.
Система уравнений (2.3.6) может быть также записана в ком-
понентах смещения. Тогда для плоского случая уравнения рав-
новесия будут следующими:
(2.3.8)
я- я з2 э2
где 0 = ~~ + = ег + г v, V = —₽ + —-г- — оператор Лапласа,
сбс ду ' дх2 у-‘
X и
М -
Y— компоненты объемной силы, 1 - —------—ж-^Х
(1 + р)(1-2ц)*
' = G — постоянные Ляме, характеризующие упру-
гие свойства исследуемого массива пород.
2.4. Способы задания граничных условий
Для Того чтобы решение поставленной задачи было одно-
значным, кроме уравнений равновесия, неразрывности и состо-
яния математическая модель должна включать начальные и гра-
ничные условия. В случае решения динамической задачи к
граничным условиям должны быть добавлены начальные усло-
вия, т.е. следует задать напряжения, смещения, скорости или ус-
корения точек тела в начальный момент времени. При решении
статической задачи граничные условия могут быть заданы следу-
ющими тремя способами. Во-первых, на границе задаются толь-
ко напряжения (статические граничные условия), во-вторых, на
границе задаются только смещения (кинематические граничные
условия) и, наконец, на части границы могут быть заданы на-
пряжения, а на другой части — смещения (смешанные гранич-
ные условия).
Необходимость задании граничных условий возникает из того,
что дифференциальные уравнения (2.3.6) справедливы для лю-
бой точки внутри тела. Для точек тела на ею внешних границах
следует установить соотношения между компонентами приложен-
ной на границе тела внешней нагрузки и компонентами напря-
жений внутри тела рис. 2.6):
33
¥
Рис, 2,6. Схема для определения статических гршшмшж условий
X
п ~~
<УХ О
Г------5£---
- sin 2а ь t rv cos 2а
(24.1)
Изучение НДС массивов горных пород при решении плос-
кой задачи производится либо в полуплоскости, либо в области,
вырезанной из полуплоскости. Рассмотрим задание граничных
условий 8 -области, показанной на рис. 2.7. При ее выделении
следует отнести от участка действия фактора, изменяющего НДС
изучаемого массива, нижнюю и боковые границы на такое рас-
стояние, чтобы они не нянями на результаты решения задачи о
перераспределении напряжений. С другой стороны, вырезанная
область должна иметь минимальные размеры, что позволяет со-
кратить затраты на подготовку исходных данных и обработку
по лученных результатов.
Граничные условия в выделенной области задаются следую-
щим образом. Верхняя граница. которая может быть неровной,
свободна от напряжений или в какой-то ее части действуют на-
пряжения от приложенной к этой поверхности нагрузки, напри-
мер, от инженерного сооружения (см. рис. 2.7). Поскольку ниж-
няя граница удалена так, что не оказывает влияния на решение
задачи, то она должна быть неподвижной, и поэтому на ней за-
даются нулевые значения перемещений (u = 0, v = 0) Такой спо-
соб задания граничного условия называется жестким закрепле-
нием. Боковые границы также не испытывают влияния факторов,
вызывающих перераспределения напряжений. Поэтому точки,
расположенные на боковых гранях, не будут перемещаться в го-
ризонтальном направлении (« = 0). В связи с тем, что исследуе-
34
Рис. 2.7. Способы задания граничных условий в расчетной об-
ласти, расположенной в верхней части полуплоскости
мая область находится под действием гравитационной силы, она
должна иметь возможность свободно деформироваться в верти-
кальном направлении. Следовательно, вдоль боковой границы
области ничто не должно препятствовать вертикальному переме-
щению или должно отсутствовать трение, по боковой поверхнос-
ти, что равносглгкл стд"::::г нулевого касательного напрд^ения
(тж»0). В случае, когда исследуемая область подвержена дей-
ствию дополнительных боковых сид, например, тектонических,
граничные условия на боковых поверхностях задаются в соответ-
ствии с известными величинами приложенных сбоку сил.
При изучении НДС в области 5, расположенной внутри полу-
плоскости у<0 (рис. 2.8), например, в случае, когда необходимо
Рис. 2 8. Способы задания граничных условий в расчетной об-
ласти, расположенной внутри полуплоскости
исследовать перераспределение напряжений вокруг подземной
полости или горной выработки, граничные условия задаются сле-
дующим образом. Если размеры этой области 5 невелики, то
можно считать, что напряжения, обусловленные собственным
весом пород, изменяются незначительно. Следовательно, изуча-
емая область «У находится под действием равномерно распреде-
ленных напряжений: вертикальных, в среднем равных весу вы-
шележащих пород oy=pgA? и горизонтальных, составляющих
часть от вертикальных, = tpgh. Тогда область S будет нахо-
диться в однородном поле напряжений, и поэтому граничные
условия могут быть заданы в виде постоянных напряжений, дей-
ствующих на бесконечности.
2.5. Типы расчетных моделей для изучения
геомеханических процессов
При изучении НДС массивов горных пород принимаются
две основные модели: модель линейно деформируемой среды и
модель предельного напряженного состояния.
Модель лине±<з дед’з-уиируерхй среды предполагает; :т: во
всех точках деформируемого массива, сохраняется линейная связь
между деформациями и напряжениями, и полностью отсутству-
ют предельные зоны. Эта модель позволяет исследовать НДС
массива горных пород заданной неизменной конфигурации под
влиянием Заданных контурных и объемных сил при неизменных
механических свойствах горных пород.
Модель предельного напряженного состояния предполага-
ет 5 что ВО всех точках массива пород, чего практически никогд
не бывает, или только в некоторой его части наблюдаются пре-
дельные соотношения между напряжениями и прочностными
показателями пород. С помощью этой модели исследуется ус-
тойчивость массива горных пород» В эюм случае / уравнениям,
составляющим математическую модель напряженного состоя-
ния массива, необходимо добавить предельные соотношения,
при которых произойдут необратимые деформации, приводя-
щие к разрушению массива горных пород. Основными видами
разрушения массива горных пород являются отрыв и сдвиг.
Отрыв произойдет в том случае, когда одно из нормальных на-
пряжений (ол), действующих в точке., станет больше сопротив-
ления горных пород растяжению (Rp) в направлении этого на-
пряжения:
(25Л)
36
Рис. 2.9. Круг мора» позволяюш.ий определить условие предель-
ного равновесия вдоль площадки сдвига
т . .' нормаль к площадке. по отношению к которой действует
разрывающее напряжение и которая является поверхностью отрыва
Во втором случае предельное соотношение связывает нор-
мальные (оя) и гдсателъкые (tj напряжения, действующие на
наиболее неблагоприятной площадке с нормалью л с показате-
лями прочности горных пород (с, ф) вдоль той же площадки. Эта
связь определяется законом Кулона: т* = <jfftg(p + c, которая че-
рез компоненты напряжений, зтнтссиндл к д-тгс:те координат
Оху в той же точке, выражается следующим образом:
+ т/;: -= .... + ~у + дгд (2.5.2)
Это соотношение может быть л ыко получено из Мора
(рис 2.9).
Контрольные вопросы
1. Какие уравнения содержит математическая модель?
2. Под действием каких внешних сил может находиться мас-
сив горных пород?
3. Что такое напряжение?
4. Какие деформации возникают в телах, подверженных дей-
ствию внешних сил?
5. В каком случае можно утверждать, что напряженное со-
стояние в точке известноО
6. Графическое изображение напряженного состояния в
точке.
7. Какая связь существует между деформациями и переме-
щениями?
8 Как определяются напряжения, действующие на парал-
лельных гранях?
37
9. Из каких соображений вытекает закон парности касатель-
ных напряжений?
10 Какой смысл имеют уравнения неразрывности (совмест-
ности)'!
11. Для чего необходимы граничные условия?
12. Физический смысл обобщенного закона Гука.
13, Ортотропные., трансверсально-изотропные и изотропные
тела, их отличия.
14. Чем отличается деформирование плоского сечения от де-
формирования тонкой пластинки?
15. Способы задания граничных условий.
16. Какие расчетные модели используются при изучении гео-
! . ехан- . 2 х I . те хов?
ГЛАВА 3. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
ПРИ МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ
Математическое моделирование находит широкое примене-
ние при решении различных инженерно-геологических задач.
Применение ЭВМ и расширение математического образования
резко увеличило возможности построения и исследования мате-
матических моделей Все чаще результаты расчетов позволяют
обнаруживать и предсказывать ранее никогда не наблюдавшиеся
явления, что дает основание говорить о своеобразном математи-
ческом эксперименте. Одной из наиболее важных задач, которая
возникает при решении многих инженерно-геологических воп-
росов, является оценка современного напряженного состояния
массива горных пород и его изменения в результате воздействия
разнообразных внешних факторов. Решение этой задачи может
быть осуществлено с помощью сформулированной математичес-
кой модели (Х3.6), представляющей собой систему дифферен-
циальных уравнений.
Система дифференциальных уравнений может быть разре-
шена аналитическими и численными методами. В последнее время
роль численных методов при решении прикладных задач суще-
ственно возросла, что в значительной степени связано с созда-
нием и развитием средств вычислительной техники. Это объяс-
няется тем, что в результате появления ЭВМ с программным
управлением менее чем за 50 лет скорость выполнения арифме-
тических операций возросла с 0,1 операции в 1 секунду при руч-
ном счете до 1070 операций на современных ЭВМ, т.е. стала быст-
рее в 1018раз. Однако при решении задач это не исключает
возможности использования аналитических способов.
Аналитические методы решения дифференциальных уравне-
ний (2.3.6) разнообразны и хорошо разработаны в работе [4], но
их применение рационально только при решении простых задач.
Для большинства сложных задач, к которым относятся задачи о
НДС массива горных пород, точное их решение оказывается тру-
доемким, а в отдельных случаях просто невозможным. Тогда не -
обходимо применять различные приближенные методы решения
исходных дифференциальных уравнений.
Численные методы решения дифференциальных уравнений
(2.3.6) можно объединить в две группы. Во-первых, это методы,
требующие использования аппроксимации во всей исследуемой
области. К этой группе относятся методы конечных разностей,
или сеточные методы, в том числе основанные на использовании
вариационного принципа, а также метод конечных элементов
(МКЭ). Во-вторых, это методы, требующие использования ашь
роксимации TWIbKn на границе исследуемой области* К этой груп-
пе относятся различные модификации метода граничных элемен-
тов (МГЭ) или метод граничных интегральных уравнений (I
3.1. Аналитические способы
Точное решение системы дифференциальных уравнений
(2.3.6). описывающих напряженно-деформированное состояние
изотропного упругого тела, может быть осуществлено путем ин-
тегрирования этих уравнений. Однако этот путь связан с боль-
шими трудностями, и решение задачи аналитическими методами
может быть получено только для ограниченного числа случаев
Точное аналитическое решение применимо в основном для опи-
сания напряженно-деформированного состояния однородных
массивов горных пород, ограниченных гладкими границами, ко-
торые. редко встречаются в природе. Но если получено решение в
виде формул, то это дает возможность легко исследовать влия-
ние. различных факторов, которые учтены данной схематизацией,
на напряженно-деформированное состояние изучаемого масси-
ва горных пород.
В наиболее простом случае решение поставленной задачи
может быть получено простым подбором. Например, в соответ
СТВНИ с гипотезой А.Н. Динника (рис 3.1), распределение напря-
жений в однородном изотропном массиве горных пород с гори-
зонтальной поверхностью, который находится под действием силы
тяжести, описывается следующими соотношениями:
с , xij = 0> (3.1.1)
где Ъ, — коэффициент бокового распора, i, J принимают значения
х, у, z и / #/ Подстановкой формул (3,1.1) в дифференциальные
уравнения (2.3.6) можно убедиться в том, что они являются ре-
шением этой системы уравнений Коэффициент бокового рас-
пора легко определить из уравнения состояния (2.2.11), положив
в одном из уравнений либо е г -0, либо et = 0 , так как в гори-
зонтальном направлении в гаком массиве горных пород дефор-
мация должна отсутствовать.
Имея в виду формулы (3.1.1), получим;
Ър£У - ц(р£У +&gy) -0 ,
ъ т-^- • '3.
i - ц '
Это решение справедливо, когда массив горных пород является
однородным и изотропным.
40
Рис. 3.1. Распределение напряжений в однородном изотропном упру-
гом массиве горных пород с горизонтальной поверхностью
Для примера рассмотрим, как распределены напряжения в
слоистом горизонтально залегающем массиве горных пород с
горизонтальной поверхностью, который находится в поле тяго-
тения. Такая среда является неоднородной, так как горизонталь-
но залегающие слои облапаю! различными деформационными
свойствами и плотностью. Ее напряженно-деформированное со-
стояние может быть изучено двумя способами. Во-первых, рас
пределение напряжений в л-ом слое (рис. 3.2) определяется сле-
дующим образом:
Слой 1
г
Слой к
Рис. 3.2. Определение напряжений в горизонталь-
но слоистом неоднородном массиве пород
41
Л= )
.У ~ 5
(3.1.3)
где hk, p* — мощности горизонтально залегающих слоев и плот-
ности пород, р„, р„ — плотность и коэффициент поперечной де-
формации пород «-го слоя.
В некоторых случаях при частой смене различных по дефор-
мационным свойствам слоев изучаемая среда может быть рас-
смотрена как однородная, но трансверсально-изотропная, когда
плоскости изотропии совпадают с напластованием пород. Для
горизонтально залегающего однородного трансверсально-изотроп-
ного упругого массива пород его напряженное состояние в каж-
дой точке определяется формулами:
Е \х!
~ Р£У, а, = = jr j~ pgr, И. (3.1.4)
где Е, ц — модуль упругости и коэффициент Пуассона в плоек -
сти изотропии, а Е', ц' — то же, но в плоскости перпендикуляр-
ной плоскости изотропии
При изучении напряженно-деформированного состояния
массива горных пород, когда оно зависит от нескольких факто-
ров, используется прием приведения решения системы диффе-
ренциальных уравнений (2.2.6 или 2.2.7) к случаю отсутствия
объемных сил, что существенно упрощает решение задачи. Не-
редко верхние горизонты земной коры подвергаются совместно-
му воздействию гравитационных и тектонических, например сжи-
мающих сил, направленных горизонтально В этом случае
достаточно определить величины и характер распределения на-
пряжений в массиве пород, обусловленных действием каждого
фактора в отдельности, а затем сложить полученные результаты,
что возможно, потому что напряжения относятся к аддитивным
величинам. Если сжимающая тектоническая сила интенсивнос-
тью Т действует в упругом однородном изотропном массиве гор-
ных пород с горизонтальной поверхностью вдоль оси Ох (рис. 3.3),
то в точке М возникну] следующие дополнительные (обуслов-
ленные только тектонической силой) напряжения:
о, = Т, о, - 0, о. =117’, = 0 , (3.1.5)
где ц — коэффициент поперечной деформации, i,j=x, у, z, i* J.
Напряжение ог, действующее перпендикулярно направлению
приложения сжимающей тектонической силы, возникает из-за
невозможности расширения в этом направлении массива пород,
42
Рис. 3.3. Напряжения, возникающие в массиве горных пород, под воздей-
ствием горизонтальной сжимающей тектонической силы
так как каждый элемент, стремящийся расшириться, встречает
аналогичное сопротивление со стороны соседних элементов. Для
определения величины напряжения о,. следует в одном из урав-
нений состояния (2.2.11) положить = 0, так как в этом направ-
лении деформации не будет. Напряжение в вертикальном на-
правлении должно отсутствовать из-за того, что массив пород
имеет свободную от напряжений поверхность и может деформи-
роваться в этом направлении. Равенство нулю касательных напря-
жений возникает из закона парности касательных напряжений.
Компоненты напряжений (3.1.5) являются решением дифферен-
циальных уравнений (2.3.6), но только при условии, если массив
пород не подвержен действию объемных сил. Общее решение для
случая совместного действия гравитационных и тектонических сил
получится в результате сложения уравнений (3.1.1) и (3.1.5).
При оценке перераспределения напряжений вблизи неров-
ностей рельефа, например, в окрестности речных долин или в
бортах котлованов или карьеров, начальное напряженное состоя-
ние, когда поверхность принимается горизонтальной, выражается
соотношениями (3.1.1) или (3.1.3 и 3.1.4). Тогда напряжения, обус-
ловленные неровным рельефом, можно найти аналитическим
способом, решая систему уравнений (2.2.6) или (2.2,7), но при
отсутствии объемной гравитационной силы и при вынесенных
на поверхность соответствующих граничных условиях.
При изучении напряженного состояния массива горных по-
род вокруг карстовой полости или горной выработки сначала
43
определяются обусловленные гравитацией начальные напряже-
ния, действующие на глубине, на которой находится полость или
выработка. Если их размеры существенно меньше гой глубины,
где они расположены, то можно считать, что напряжения, вы-
званные собственным весом массива пород, на уровне: полости
или выработки практически не изменяются с глубиной. Тогда
перераспределение напряжений в породах под влиянием любой
полости изучается в бесконечной плоскости с отверстием в ре-
зультате действия приложенных на бесконечности сил, создаю-
щих начальное напряженное состояние. Решение такой задачи
может быть осуществлено аналитическими методами, поскольку
определяемое заранее начальное состояние массива пород при-
водит ее решение к системе уравнений, но уже при отсутствии
объемной силы. Искомое поле напряжений в массиве пород в
окрестности полости получается в результате суммирования на-
пряжений, обусловленных действием гравитационных сил* с на-
пряжениями, з- .орые возникают в том же маез пород под
влиянием отверстия (рис. 3 4).
Рис. 3.4. Перераспределение напряжений ох и ау в массиве горных пород в окрест-
ности : пости
Таким образом, задача о напряженно-деформированном со-
стоянии массивов горных пород обычно решается в три этапа:
1) постулируется начальное напряженное состояние; 2) ставится
и решается краевая задача в дополнительных напряжениях; 3) пол-
ные напряжения в горной породе находятся сложением допол-
нительных и начальных напряжений.
Гак, при решении задач Инженерной геологии или горной
геомеханики необходимо, прежде всего, постулировать началь-
ное напряженное состояние горных пород. Это начальное на-
пряженное состояние нарушается в результате влияния других
причин: наличием неровностей рельефа и подземных полостей,
действием дополнительных сил, проходкой горных выработок и
др. Тогда полные напряжения а у в любой точке массива горных
пород можно представить жж сумму начальных напряжений ;
обусловленных гравитацией, и изменения напряжений , выз-
ванных влиянием других факторов:
° у >? + оф . (3.1 6)
Начальные напряжения должны удовлетворять уравнениям (2.2.6)
или (2.2.7) и представляют собой частное решение этой системы.
Изменения напряжений называются дополнительными напряже-
ниями, которые удовлетворяют тем же уравнениям, но уже при
отсутствии объемных сил У-0.
3.2. Конечно-разностные
и вариационно-разностные методы
К решению задач прикладной механики, которые возникают
при исследовании напряженно-деформированного состояния мас-
сивов горных пород, существует два подхода. При первом исполь-
зуются дифференциальные уравнения, описывающие поведение
некоторой произвольной бесконечно малой области. Второй под-
ход основан на использовании вариационного экстремального
принципа, справедливого во всей изучаемой области.
С математической точки зрения оба подхода эквивалентны,
т.е. приводят к одному и тому же решению. Различие между этими
подходами состоит в способах получения приближенного реше-
ния. Конечно-разностные методы аппроксимируют дифференци-
альные уравнения разностными соотношениями. При использо-
вании вариационного принципа решение получается путем
минимизации некоторой величины, которая определяется как
интеграл от неизвестных величин по всей области и называется
функционалом. Метод конечных элементов, который будет рас-
смотрен в следующем разделе, связан с приближенной миними-
зацией функционала.
Метод конечных разностей, или метод сеток является уни-
версальным вычислительным методом, применяемым для реше-
ния широкого крута задач. Различные его модификации могут
45
быть использованы для изучения НДС неоднородных массивов
горных пород, при решении нестационарных и нелинейных за -
дач и др. Методы конечных разностей представляют собой мето-
ды приближенного решения дифференциальных уравнений, ос-
нованные на замене этих уравнений соотношениями относительно
дискретного аргумента [3]. Метод конечных разностей состоит в
следующем |5]. Область непрерывного изменения аргументов
исходной задачи заменяется дискретным множеством точек (уз-
лов), называемым сеткой, и вместо функции непрерывного аргу-
мента рассматриваются функции дискретного аргумента, опре-
деленные в узлах сетки. Эти функции называются сеточными
Производные, входящие в дифференциальное уравнение, и гра-
ничные условия аппроксимируют разностными соотношениями,
содержащими значения сеточной функции в нескольких узлах
сетки. При этом краевая задача для дифференциального урав-
нения заменяется системой алгебраических уравнений или раз-
ностной схемой Если полученная таким образом разностная
краевая задача разрешим» и ее решение при безграничном и:
мельчен-I? -зеткн Приближается 'ходится) к ретрндю исходной
задачи дифференциального уравнения, то полученное на любой
фиксированной сетке решение разностной задачи и принимает-
ся за ее приближенное решение Близость решения, к истинному
определяется шагом сетки и порядком аппроксимации, исполь-
зуемой для решения разностной схемы.
Одним из этапов применения численных методов для иссле-
дования НДС массивов пород является разбиение непрерывной
области на элементы Используемые при дискретизации сетки в
случае применения разностных методов могут быть квадратными
(с одинаковым шагом по координатным осям), прямоугольными
(с разными шагами), криволинейными (с одинаковыми и разны-
ми шагами), с изменяющимся шагом в определенном направле-
нии ит.д. (рис, 3.5). С помощью таких сеток может быть выпол-
нена дискретизация сложных в геометрическом отношении
областей путем разделения их на четырехугольники (можно кри-
волинейные) и последующего сшивания полученных частей
Сшиваемые стороны четырехугольников должны иметь одина-
ковое число узлов (рис. 3.6). При выборе способа разбиения не-
однородных областей возникают дополнительные трудности. Ис-
пользуемые в этом случае сетки должны обладать тем свойством,
чтобы расстояния между узлами не превышали размеров тех не-
однородностей, влияние которых на НДС необходимо учесть рас-
четом. Немаловажное значение имеет также расположение узлов
по отношению к внутренним границам, разделяющим различ-
ные по физическим свойствам участки. Когда граница проходит
между узлами, то это приводит к значительным градиентам на-
Рис. 3.5. Сетки, применяемые для дискретизации исследуемых областей с шага-
ми по координатным осям: а — равными, б — неравными, в — неравномерными
г -- криволинейн ьми
пряжений. Если по смыслу задачи переход из одной части обла-
сти к другой должен быть плавным, то точки сетки следует со-
вмещать с границей, что не всегда возможно из-за использова-
ния регулярных сеток. Это особенно важно иметь в виду при
исследовании НДС неоднородных массивов горных пород.
Дискретное представление изучаемых областей предполагает
задание параметров, характеризующих упругие и другие свойства
среды, в отдельных точ-
ках, исходя из опреде-
ленных представлений
о строении массива
пород и изменениях его
свойств. Чтобы задать
Рис. 3.6. Сшивка четырех-
угольников при дискретиза-
ции сложных областей
Рис. 3.7. Определение сред-
н е в з е е ш е н н о г о показателя
свойств неоднородного мае
сива пород в узловой точке
расчетные параметры используются статистические подходы; при
известном закономерном изменении свойств пород характеризу-
ющие их показатели могут быть определены как функции коор-
динат точек разбиения исследуемой области; наиболее приемле-
мым способом задания расчетных параметров следует считать
случай представления массива пород в виде кусочно-однородной
среды
Если разбиение осуществляется с помощью сеток, то показа-
тель, присвоенный одной точке, характеризует свойство массива
на некотором участке вокруг этой гоч*
ки, который имеет форму четыреху-
гопьнима со сторонами равными ша-
гам разбиения Когда точка находится
на расстоянии от внугренней границы
большем шага, четырехугольный уча >
ток однородный и характеризующие его
свойства присваиваются расположенной
в его середине точке.
Если точка находится на границе
или вблизи нее, когда граница пересе-
кает четырехугольный участок, и раз
личные его части отличаются свойства-
ми, то присваиваемое центральной точке данного участка свойство
может быть определено как средневзвешенное:
t
sm cboj ствс зсегт
где Я — показатель
участка площадью 5; Rr— свойство /-й части участка площадью
5; (рис. 3.7).
В качестве примера рассмотрим решение задачи об одномер-
ной консолидации с помощью конечно-разностного метода. Из
менение напряжений о во времени в водонасыщенных, грунтах
под постоянным давлением р описывается уравнением фильтра-
ционной консолидации:
д~с 1 д<з
dh2 &
(3.2.2)
где ск — коэффициент консолидации грунта.
Аналитическое решение этого уравнения очень сложная зада-
ча, поэтому предпочтительнее решать его численным способом.
Для решения дифференциального уравнения, в котором функ-
ция зависит одновременно от координаты у и времени г, с помо-
щью конечно-разностного метода необходимо ввести двухмер-
7
ную сетку, узлы которой будут иметь координаты /, h (рис. 3.8).
Расстояния между узлами по координатным осям могут быть как
одинаковыми, так и переменными Во втором случае расстоя-
ния. например, могут уменьшаться по оси h при приближении К
точке приложения нагрузки, а по оси г при стремлении к началу
процесса. Значение искомой функции в каждой точке сетки рав-
но. о = о/ j = , где Аномера шагов соответственно по
ОСЯМ t И Л.
Рис. 3.8. Двухмерная сетка для численного решения урав-
нения фильтрационной консолидации
Аппроксимация производных в дифференциальном уравне-
нии разностными соотношениями:
ст Аг
и подстановка их в дифференциальное уравнение (3.2,2)
приводят к выражению:
которое позволяет определить значение функции в одной точке,
если известны ее значения в грех соседних (рис. 3.8).
Для определения значений функции во всех точках сетки,
необходимо знать начальные и граничные условия. Начальное
условие о0у = р, показывающее, что в момент времени f=0 при-
ложенная нагрузка р вызывает во всех точках одномерной области
(Л = 0,1,...,т) одинаковые напряжения, позволяет вычислить
напряжения в последующие моменты времени Для |ж| можно
определить значения напряжений Оц..., ot z, ; для/ = 2 —
напряжения от о2> до - и т.д.
Чтобы определить напряжения в остальных точках сетки, не-
обходимо воспользоваться граничными условиями; о,о = Р,
Вычисления по описанной разностной схеме производятся явно,
т.е. Gi+i.j по формуле (3.2.4) выражается через ога, ;+1 .
Она крайне проста в реализации, но обладает недостатком —’ она
устойчива не при всех Дг и Дй. Это означает, что при некоторых
значениях этих параметров будет происходить накопление оши-
бок округления, что приведет к неправильному решению и воз-
можному сбою при работе на ЭВМ. Такие схемы относятся к
условно устойчивым. Для данной схемы условие устойчивости
«аи *. А"
имеет вид: дг < -=—,
“ 2с„
которое существенно ограничивает вели-
чину шага по времени и тем самым замедляет время расчета до
фиксированного момента г.
Рассмотренный вариант решения реализует так. называемую
явную схему, основным недостатком которой является возмож-
ность накопления ошибок. Поэтому предпочтение отдается не-
явным схемам, когда не производится прямое вычисление функ-
ций, а путем последовательного выражения функций через другие
и с учетом начальных и граничных условий приходят к системе
линейных алгебраических уравнений* позволяющих решить по-
ставленную задачу с большей точностью.
Для преодоления недостатка явных схем можно использо-
вать неявную схему
которая абсолютно устойчива (при любых Д/ и Дй), но не
находится явно через о,, , где ;=1,., т. Для ее определения,
нужно решать систему линейных уравнений:
i
<рд/
- -7П
(J(. Q — р
^1,14 ~ О
(3.2.6)
Эта система решается эффективно методом прогонки, опи-
санным во многих учебниках по численным методам.
3.3. Метод конечных элементов
Метод конечных элементов явдяется одним из наиболее эф-
фективных современных способов численного решения инже-
нерных, физических, и математических задач с использованием
вычислительной техники [1, 6]. Метод конечных элементов на-
ходит применение при исследовании тектонических процессов,
протекающих в земной коре, при решении различных задач ин-
женерной геологии и механики грунтов, гидродинамики, тепло-
проводности» Строительной механики, горного дела и др. [7, 8].
Метод конечных элементов является методом, основанным
на использовании вариационного принципа Лагранжа Идея по-
строения вариационно-разностной схемы состоит в том, чтобы
при специальном выборе координатных функций получить систе-
му линейных алгебраических уравнений, совпадающую по струк-
туре с системой разностных уравнений. Для составления сеточных
уравнений на основе вариационного принципа осуществляется
минимизация функционала, который представляет собой потен-
циальную энергию деформируемого тела. Такая потенциальная
энергия системы является разностью энергии деформирования и
работы внешних сил:
- f XjUjdv - J RjUids, (3.3.1)
'' :* S
где — компоненты напряжений и деформаций; Х;, R,—
проекции массовых и поверхностных сил; и, — компоненты пе-
ремещений; v} s — объем и площадь поверхности тела; /,/» Г, 2.
Если рассмотреть все возможные перемещения данной системы,
то действительными, т.е. соответствующими условию равнове-
сия и принципам неразрывности деформаций в упругом теле,
будут те перемещения, при которых полная потенциальная энер-
гия будет минимальной. Отсюда следует равенство первой про-
изводной функционала нулю, что служит основой составления
сеточных уравнений.
Для построения разностной схемы по методу конечных эле-
ментов исследуемая область заменяется набором дискретных эле-
ментов. Метод конечных элементов отличается от конечно-раз-
ностных методов способом дискретизации. В случае решения
одномерной залами элементами являются прямолинейные отрез-
ки произвольной длины. При решении плоской задачи изучае-
мая область заменяется системой плоских элементов различного
51
размера и формы: треугольниками, прямоугольниками или дру-
гими геометрическими фигурами. Наиболее часто выбираются
треугольные элементы, причем наилучшие результаты получают-
ся, когда треугольники равносторонние. Решение объемных за-
дач выполняется путем представления исследуемого массива с
помощью тетраэдров, кубов, параллелепипедов или других объем-
ных фигур
Обычно узлы располагаются в вершинах элементов. Возмож-
но применение сложных криволинейных элементов и произвольно
расположенных узлов, например на стороне элемента.
Способ дискретизации, когда используются элементы раз-
ного размера, позволяет сгущать сетку в той части изучаемой
области, где необходимо уточнить исследования, и уменьшить
число элементов за счет увеличения их размеров там, где реше-
ние задачи не имеет практического Значения Произвольность
формы и размеров элементов дает возможность аппроксимиро-
вать как угодно сложные внешние и внутренние границы изуча-
емых областей, что выгодно отличает этот метод от других.
Так как вершины элементов размещаются на границах раз-
дела сред с разными свойствами, то в пределах каждого элемента
среда является однородной, а в целом система элементов будет
представлять неоднородную среду. В каждом элементе задаются
параметры, характеризующие свойства изучаемой области.
Поверхностные силы, действующие на изучаемую область,
представленную системой, состоящей из конечного числа эле-
ментов, прикладываются только к узлам, расположенным на внеш-
нем контуре этой области. Объемные силы вычисляются, исходя
из размеров и плотности элементов, и в виде сосредоточенных
сил прикладываются к их вершинам. Например, если изучаемая
плоская область представлена системой треугольных элементов,
то к вершинам каждого треугольника прикладываются сосредо-
точенные силы, составляющие треть его веса. Таким образом, к
каждому узлу будет приложена сосредоточенная сила представ-
ляющая собой сумму третей весов всех треугольников, вершины
которых сходятся в этом узле.
Предполагается, что в процессе деформации среда остается
сплошной (условие совместности), т е. элементы ведут себя не
как отдельные части, а деформируются вместе и вьщеляются толь-
ко для рассмотрения в них напряженно-деформированного со-
стояния.
Приложенные к каждой узловой точке внешние силы долж-
ны уравновешиваться силами, действующими внутри элемента
(условие равновесия). Под действием внешних сил происходит
перемещение узловых точек. Связь между перемещениями внут-
ри каждого элемента и перемещениями его узлов задается с по-
мощью функций формы. При этом должно быть реализовано
соотношение силы перемещения, согласно которому внутренние
силы и перемещения должны соответствовать геометрии и свой-
ствам данного элемента» Эго соотношение представляется мат-
рицей жесткосШ.
В результате замен! : СПЛОШНОЙ среды дискретной схемой С
конечным числом параметров приходят к математическому ап-
парату линейной алгебры^ минуя стадию составления дифферен-
циальных уравнений Для построения разностной схемы в каж-
дом узле исследуемой области определяются значения исходных
функций. Сеточный аналог исходного функционала Z поддает-
ся путем подстановки интегралов в виде конечных сумм, завися-
щих от значений функций в узлах сеточной области, Система
разрешающих Конечно-разностных уравнений получается диф-
ференцированием компонент сеточного аналога по всем узло-
вым значениям неизвестных функций. Приравнивая производ-
ную функционала нулю, получается система алгебраических
уравнений относительно значений узловых перемещений. По вы-
численным из итерационного процесса значениям узловых пере -
мещений определяют компоненты деформаций и напряжений.
Таким образом, задача сводится к решению системы 2N ал-
гебраических уравнений.
И} = (3.3.2)
где [А] — матрица жесткости, связывающая вектор обобщенных
сил F, приложенных в узлах, с вектором обобщенных перемеще-
ний узлов U, a N — число узлов. Коэффициентами этих уравне-
ний служат матрицы жесткости элементов, которые зависят от
деформационных показателей и координат.
Решение поставленной задачи осуществляется в перемеще-
ниях, по которым можно рассчитать и деформации, и напряже-
ния. Перемещения ищутся только в узловых точках, т.е. предпо-
лагается, что непрерывное поле перемещений в исследуемой
области определяется перемещениями вершин элементов, состав-
ляющих область.
Рассмотрим применение метода конечных элементов на примере оценки
одномерной деформации сжатия под нагрузкой. Пусть к поверхности полупро-
странства приложена нагрузка Р с помощью фундаментной плиты большой
площади. В этом случае можно считать, что деформация, по крайней мере под
центральной частью плиты, будет одномерной. Поэтому можно изучить осадку
основания, рассматривая деформацию только одного «столбика» площадью по-
перечного сечения у (рис. 3.9,а). Решение этой задачи осуществляется в несколько
этапов.
Во-первых, строится функционал, определяющий потенциальную энергию
деформирования. В рассматриваемом случае он запишется:
53
Рис. 3.9. Одномерная деформация полупространства в пределах «столбика» пло-
щадью S под нагрузкой Р (а) и его разбиение на элементы (б|
с
Ф(» = ~ fasdy -Ри(0),
~ А
(333)
где € = ~ — относительная деформация; о = £е = Е — напряжение; Ры(0) -
работа силы Г по перемещению точки 0 на величину i/(0); s — площадь поперек*
ного сечения. На глубине Л предполагается, что деформация отсутствует: u(h) - 0.
Исходя из вариационного принципа потенциальная энергия, заграчинаемая на
деформирование выделенного столбика, должна быть минимальной.
Во-вторых, производится разбивка столбика на элементы (рис. 3.9, б), тог-
да: функционал (3.3.3) можно записать:
(33.4)
В-третьих. осуществляется интерполирование искомой величины (переме-
щения) по элементу, с целью выражения перемещения любой точки элемента
через перемещения его концов. Рассмотрим £й элемент длиной 4 (рис. 3.10, я),
в котором узловые точки i и i + 1 получают перемещения соответственно и, и дй1.
Выразим перемещение произвольной точки у /-го элемента, лежащей в интерва-
ле от / до / + 1, следующим образом: ц^(у) = a + by . Тогда перемещения узловых
точек / и i'+ 1 можно записать:
и, = a + by{
«ж “ « + ьУм •
откуда
...
Рис. 3.10. Перемещения: а — узловых точек /-го
элемента, б— всей сжимаемой области, представ-
ленной в виде одного элемента
Окончательно перемещение внутренней точки у /-го элемента будет равно
«<0(у) = л/л+
(3.3.5)
у — ). - / — Р
где - -—^-i±L, Я|Х| - ‘у—, которые получили название функции фор-
ч ч
мы. В матричной форме формула (3.3.5) записывается следующим образом:
««(П=(.V, л/+|)
или о'"(>) = [ЛЦ'<).
(3.3.6)
В-четвертых, строится дискретный аналог функционала, т.ё. строится функ-
ционал только через узловые значения перемещений. В рассматриваемом при-
мере, если сжимаемую область представить в виде одного элемента, функционал
(3.3.4) может быть выражен через перемещение д(0) в одной точке 0, так как
перемещение в другой точке д(Л) = 0 (рис. 3.10, б):
1 ГЕ^
iJ Ш
Л
Ф(»
dy - Pu(Q).
(337)
В соответствии с (3.3.5) перемещение в любой внутренней точке у элемента
длиной Л будет равно:
w(y) == iV(A) • и(Л) i Л(0) i/(0) (3.3.8)
и
Ж = u(h. = _“W (3.3.9)
dy d/\ h ' ‘ h < ay t - h h v
Подставив (3.3.9) в фуюсционал (3.3 7) получим:
0 2/лх
ф(и) = | J£jL^dy “
Л
и окончательно
*5 / - . ш •’О „. ..
Ф(и(0)) = 4f d)! - Ри(0) -Ри(01 (3.3.10»
l h ч л
Наконец, ищутся узловые зн&ченмж перемещений, исходя из принципа
минимума потенциальной энергии. Поэтому, если подсчитать производную
55
функционала (3.3,10) и приравнять се иулю, то получится выражение ДЛЯ опре
деления искомого перемещения (осадки). В рассматриваемом случае
^0» = 4 иед _ р =о
ткудь
В промежуточной точке у отрезка h перемещение вычисляется по формуле
(33Л) и равно t/(y) = JWO) ц(0); = .
A SjD
В более сложном случае, когда количество элементов бол ьше одного, реше
ние задачи приводится к системе 2N алгебраических уравнений с постоянными
коэффициентам^ зависящими от свойств среды и координат, где # — число
УЗЛОВ.
Метод конечных элементов обладает наглядностью, что по*
служило причиной его огромной популярности среди инженеров.
МКЭ наиболее удобен в случае необходимости изучения не:
инородных областей со сложными внутренними и внешними гра-
ницами, что очень важно при исследовании напряженно-дефор-
мированного состояния массивов горных пород. Метод конечных
элементов может быть применим для решения широкого круга
задач, включая нестационарные., что обусловлено возможностью
улучшения элементов путем увеличения числа параметров, опи-
сывающих данный элемент.
3.4. Метод граничных элементов
Метод граничных элементов (МГЭ), называемый также ме-
тодом граничных интегральных уравнений (ГИУ), используется
для приближенного решения задач о распределении напряжений
и деформаций в бесконечных и полубесконечных областях с не-
ровными границами, отверстиями произвольной формы, трещи-
нами и др. Этот метод нашел широкое применение при решении
задач строительной механики, горного дела и других научных и
прикладных направлений [2].
В методе граничных элементов разбиению на отдельные эле-
менты подвергается только граница исследуемой области, что
отличает МГЭ от других численных методов, таких, как вариаци-
онно-разностные, метод конечных элементов, применение кото-
рых требует представления в виде элементов или точек всей изу-
чаемой области. На рис. 3.11 показано разбиение одной и той же
области R при использовании МКЭ и МГЭ. В первом случае вся
область R представляется в виде сетки элементов треугольной
или другой формы. Решение задач ищется в узловых точках сет-
56
Рис. 3.11 Разбиение: а — области R на конечные элементы (МКЭ);
б — границы S области R на граничные элементы (МГЭ)
км, а между узлами решение выражается в простой приближен-
ной форме через значения в узлах. В конечном итоге нахождение
решения осуществляется С помощью системы линейных алгебра-
ических уравнений, в которых неизвестные параметры во внут-
ренних узловых точках выражаются через известные величины в
узлах сетки, расположенных на границе области. Во втором слу-
чае разбиению на элементы подвергается только граница 5 обла-
сти R Численное решение строится на основе полученных пред-
варительно аналитических решений для простых случаев точечных
возмущений в бесконечной однородной среде таким образом,
чтобы удовлетворить приближенно граничным условиям, задан-
ным на каждом элементе контура 5. Так как каждое аналитичес-
кое решение удовлетворяет в области R определяющим диффе-
ренциальным уравнениям, го нет необходимости делить саму
область на сетку элементов. Поэтому в методе граничных эле-
ментов система уравнений, подлежащая решению, оказывается
существенно меньшей, чем система, которую нужно решить в
той же краевой задаче, если использовать метод конечных разнос-
тей или конечных элементов.
В случае применения метода граничных элементов для изу-
чения напряженно-деформированного состояния массивов гор-
ных пород используются аналитические решения от сосредото-
ченной силы в некоторой точке бесконечной или полубесконечной
области, например, при приложении сосредоточенной силы к
границе полуплоскости. Для реализации МГЭ контур делится на
конечное число элементов и принимается, что приближенное-
решение будет достаточным, если оно отвечает заданным усло-
виям на границе только в данных, например, центральных, точках
57
этих элементов. Если контур разделен на У элементов, необхо-
димо иметь такое же число аналитических решений, которые будут
удовлетворять требуемым условиям в центре каждого элемента
на границе. Возможность суммирования отделыашений воз-
никает из предположения о линейности ди
иТн
еренниальныл урав-
нений. Точки приложения сосредоточенных сил размещаются по
одной в центре каждого элемента, и тогда суммарное воздей-
ствие всех N приложенных точечных сил на произвольный эле-
мент легко выражается через их интенсивности. Значения этих
интенсивностей не известны, но так как из граничных условий
известно их совместное влияние, то можно записать систему N
линейных алгебраических уравнений относительно У неизвест-
ных значений интенсивностей сосредоточенных сип. Решение этих
уравнений позволяет определить искомые характеристики напря-
женно-деформированного состояния в любой точке исследуемой
области R. Поскольку в методе граничных элементов использу-
ется аналитическое решение, которое справедливо всюду в ис-
следуемой области, он потенциально более точен, чем, напри-
мер, метод конечных элементов, в котором аппроксимация
производится в каждой подобласти исследуемой области.
Существует несколько вариантов метода граничных элемен-
тов. В прямых вариантах МГЭ неизвестные функции, входящие
в интегральные уравнения, являются реальными, имеющими
определенный физический смысл. Непрямые варианты МГЭ ос-
нованы на использовании фундаментальных решений исходных
дифференциальных уравнений. Примером непрямых методов
может служить метод фиктивных нагрузок. Существующий ме-
тод разрывных смещений обладает чертами прямого и непрямо-
го вариантов МГЭ Определяемые в этом методе «разрывы сме-
щений» при изучении сплошных областей представляют собой
некоторые фиктивные разрывы. С другой стороны, в задачах о
трещинах разности смещений берегов трещин перестают быть
фиктивными и приобретают реальный физический смысл, что
роднит метод разрывных смещений с прямыми вариантами МГЭ
Преимущества метода граничных элементов перед другими
численными методами выражается в том, что, во-первых, при
его применении сокращается на единицу геометрическая размер-
ность задачи, что приводит к значительному упрощению разбив-
ки на элементы, снижению объема входной информации, сокра-
щению времени вычислений. Кроме того, снижение размерности
задачи делает МГЭ незаменимым при решении объемных задач.
Во-вторых, благодаря использованию аналитических решений,
можно легко определить искомые параметры в любом месте ис-
следуемой области и, следовательно, можно произвольно выби-
рать точки, в которых желательно получить решение, вместо ав-
тематической привязки результатов к раду фиксированных то-
чек — узлам сетки, как это происходит при использовании се-
точных методов. Применение аналитических решений позволяет
также легко изучать полубесконечные области, что существенно
при исследовании НДС массивов горных пород. В-третьих, МГЭ
позволяет естественным образом определить сложные условия
взаимодействия на соприкасающихся границах тел, что делает
этот метод перспективным для исследования НДС массивов по-
род с трещинами и блочного строения
Контрольные вопросы
Способы аналитического решения задач о напряженно-
деформированном состоянии массивов горных пород.
Прием решения системы дифференциальных уравнений в
случае действия объемных сил.
Виды сеток, используемых при решении задач конечно-
разш . и v -• щами.
4. Различие разбиения исследуемых областей на элементы в
конечно-разностных методах и в МКЭ.
5. Чем отличаются явная и неявная схемы решения задачи о
НДС областей конечно-разностными схемами?
6. Метод конечных элементов, его отличие от других чис-
ленных методов.
7 В чем отличие МКЭ от метода граничных элементов?
8 Преимущества и недостатки численных методов решения
здач о НДС массивов горных пород.
ГЛАВА 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ЭКСПЕРИМЕНТАЛЬНОГО МОДЕЛИРОВАНИЯ
В большинстве случаев исследование геологических объек-
тов с помощью математического моделирования встречается с
непреодолимыми математическими трудностями. В этих случаях
главную роль играют экспериментальные методы исследования,
которые дают возможность установить, простейшие опытные фак-
ты. Больше того, чтобы описать какое-либо природное явление С
помощью математических соотношений, необходимы опытные
данные, только на основе которых можно формулировать зако-
ны, управляющие исследуемыми явлениями
При экспериментальном моделировании необходимо обосно-
вать возможность:
• отображения основных черт оригинала на его модель,
• переноса результатов, полуденных на модели, на оригинал .
Возможность моделирования, т.е. переноса результатов, по-
лученных на модели, на оригинал, основана на том, что модель
в определенном смысле воспроизводит его черты. Для успеш-
ного моделирования необходимы теорий, указывающие предель-
но допустимые при построении моделей упрощения и позволя-
ющие перенос результатов с модели на оригинал. Отображение
и перенос основаны на точных понятиях подобия между изуча-
емым объектом (моделью) и оригиналом. Для явлений одной и
той же физической природы применяется теория подобия, ос-
нованная на использовании понятия размерности физических
величин.
4.1. Размерность физических величин
Измерить какую-либо величину Q — значит сравнить ее с
другой величиной q той же физической природы, т.е. определить
во сколько раз Q больше (или меньше) q. Для однообразия уста-
навливают определенное значение величины q и называют ее
единицей измерения. Например, за единицу времени (секунда)
принимается определенная часть года и т.д.
Единицы измерения различных физических величин, объе-
диненные на основе их непротиворечивости друг другу, образу-
ют систему единиц.
В 1960 г. 11-й Генеральной конференцией по мерам и весам
была принята Международная система физических величин
(Systeme International d’Unites), которая в СССР была введена с
1982 г. [1]. Сокращенное обозначение системы — Si, а в русской
транскрипции — СИ. Эта система разработана для замены слож-
ной совокупности систем единиц и отдельных внесистемных еди-
ниц, сложившейся на основе метрической системы мер, и упро-
щения пользования единицами. Достоинствами системы СИ
являются ее универсальность, так как она охватывает все отрасли
науки и техники, и согласованность производных единиц, кото-
рые образуются по уравнениям, не содержащим коэффициентов
пропорциональности. Благодаря этому при расчетах, если выра-
жать значения всех величин в единицах СИ, в формулы не тре-
буется вводить коэффициенты., зависимые от выбора единиц.
Любая система единиц измерения включает основные и произ-
водные единицы измерения, причем за основные могут быть при-
няты любые единицы. Выбор числа физических величин, прини-
маемых за основные, и самих этих величин, в принципе произволен,
но практические соображения приводят к некоторому ограниче-
нию свободы выбора основных величин и их единиц.
Так, в системе СИ за основные приняты единицы измерения
длины (.wen?/»), массы (килограмм) и времени (секунда), которые
позволяют образовывать согласованные производные единицы
для всех величин, имеющих механическую природу. Для образо-
вания производных единиц величин, не сводимых к механичес-
ким, добавлены следующие основные единицы: ампер — для элект-
рических и магнитных, кельвин — для тепловых, кандела — для
световых, моль — для величин в области молекулярной физики и
химии. Другой системой единиц, которая используется в науч-
ных исследованиях, является система СГС, в которой за основ-
ные приняты единицы длины (сантиметр), массы (грамм) и вре-
мени (секунда). До 1982 г. в СССР действовала система МКГСС,
в которой основными были единицы длины (метр), силы (кило-
грамм-сила) и времени (секунда). Единицы этой системы до сих
пор используются в практических целях и встречаются в научной
литературе (3J. Между одинаковыми физическими величинами
различных систем единиц измерения существуют определенные
зависимости. Например, связь между единицами давления при-
ведена табл. 4.1
Среди физических величин различают размерные или име-
нованные и безразмерные или отвлеченные величины.
Размерностью называется выражение производной единицы
измерения через основные единицы. Формула размерности фи-
зических величин имеет вид степенного одночлена, что может
быть строго доказано: [0] = или dim Q- L'MmT', где dim,
от английского слова dimension, означает размер, размерность;
[Q] — символ размерности производной величины, введенный
л
3
X
е*
-
со
Дж.К. Максвеллом; I, М,Т — сим?
волы величин соответственно дли-
ны, массы, времени, принятых за
основные; /, m, t — целые или дроб-
ные, положительные или отрица-
тслькые вещественные числа гч
зываемые показателями размерности
производной величины Q
Размерность производной ве-
личины находится при помощи
уравнения, служащего определени-
ем этой величины в математичес-
кой форме. Так, формула размер-
Мости для ускорения a-dl/dt2
записывается в виде: [д] = LT~\ для
силы F&ma IF]- LMT~\ для на-
пряжений [of | = L~XMT~2 и т.д. Поня-
тие размерности распространяется
и на основные величины, Прини-
мают, что размерность основной
величины в отношении самой себя
равна единице и что от других вели*
чин она не зависит; тоща формула
размерности основной величины
совпадает с ее символом. Если еди-
ница производной величины не
меняется при изменении какой-
либо из основных единиц, то такая
величина обладает нулевой размер-
ностью по отношению к соответству-
ющей основной. Например, ускоре-
ние обладает нулевой размерностью
по отношению к массе.
Величины, в размерности ко-
торых все основные величины вхо-
дят в нулевой степени, называют-
ся безразмерными. Таким образом,
для безразмерных величин едини-
цы измерения одинаковы во всех
принятых системах единиц измере-
ния. Примером безразмерных вели-
чин служит число л, коэффициент
поперечной деформации и др.
Наименования десятичных
кратных и дольных единиц обра-
зуются при помощи специальных приставок, приведенных в
таб- 4.2.
Таблица 4.2
Множители и приставки для образования кратных и дольных единиц
- — — -““I Множитель i Приставка
нанмено- ванне L. обозначение
международное
1 000 000 000 000 000 000 = го1* экса э Е
1 000 000 000 000 000 - ю15 пэта 1
1 1 000 000 000 000 = 10“ тера т т
1 000 000 000 = 10’ гига т G
1 000 000 106 нега м М
1 000 - 10’ кило к к
100 = ю2 гекто I h
10 = 10' дека да da
:> .к деци д d
0,01 = ю 2 санти dft С?
0,001« мг> милли м m
0s000 001 = АО'6 микро мк И
0,000 000 001 • иг* нано н
€.000 000 000 001 = 10- ’ ПИКО D
0,000 000 000 000 001 = 10“” фемто ф f
|[в,000 000 000 000 ОТО 001 = 10-18 а’гто а а
4-2, Понятие об анализе размерностей
Анализ размерностей это метод установления связи между
физическими величинами, существенными для изучаемого явле-
ния, основанный на рассмотрении размерностей этих величин
[4J. В основе анализа размерностей лежит требование, согласно
которому уравнение, выражающее исходную связь между физи-
ческими величинами, должно оставаться справедливым при лю-
бом изменении единиц измерения, входящих в него величин. Это
требование совпадает с требованием равенства размерностей ве-
личин в левой и правой частях уравнения.
Если для исследуемого явления установлено, с какими вели-
чинами может быть связана искомая величина, но вид этой свя-
зи неизвестен, для ее нахождения составляют уравнение размер-
ностей. В этом уравнении в левой части будет стоять символ
искомой величины со своим показателем размерности, а в пра-
вой — произведение символов величин, от которых искомая ве-
личина зависит, но с неизвестными показателями размерности.
Задача нахождения связи между физическими величинами в
этом случае сводится к нахождению значений соответствующих
63
показателей размерности. Если, например, требуется найти вы-
соту Л вертикального уступа, сложенного связными породами,
обладающими прочностью с (ср = 0) и плотностью р, и находяще-
гося в Доле действия гравитационных сил у = pg, то можно соста-
вить уравнение размерности, имеющее вид:
Х=(МГ’Т*2)Х(ЛЛ V (LT 2)1, (4.11)
где х, у, z — неизвестны. Требование равенства показателей раз-
мерности левой и правой частей в уравнении (4.2.1) приводит к
системе уравнений:
решение которой дает х = 1, у »t й» —1.. Отсюда связь высоты
вертикального уступа с прочностью и плотностью выражается с
помощью формулы:
h = к(с / pg) = к(с / у), (4.2.3)
где к — безразмерный коэффициент, определяемый из уравне-
ний обобщенного закона Гука и равный 2, но который с помо-
щью анализа размерностей определить нельзя.
Таким образом, устанавливаемая с помощью анализа размер-
ностей зависимость искомой величины от величин, определяю-
щих исследуемое явление, находится с точностью до постоянно-
го коэффициента. Для получения точных количественных
соотношений нужны дополнительные данные, что не позволяет
рассматривать анализ размерностей универсальным методом.
Однако идеи, развитые в анализе размерностей, находят приме-
нение в теории подобия, которая положена в основу исследова-
ния многочисленных физических явлений [2].
4.3. Основы теории подобия
Любой физический процесс характеризуется набором физи-
ческих величин или параметров, описывающих его элементы и
воздействующие на него внешние объекты, т.е. таких величин,
которые выделяют данный физический процесс из множества
других той же физической природы. Среди них можно выделить
основные или определяющие, и производные, или зависимые,
параметры. Так, механические процессы зависят от геометрии
физических объектов, свойств материала, величин и направле-
ния приложенных внешних сил, они описываются перемещения-
ми. скоростями и ускорениями. Внутреннее состояние механи-
ческих систем характеризуется действующими в них напряжения-
ми и соответствующими им деформациями итщ. Линейные раз-
меры механической системы, свойства материала, из которого она
состоит, например плотность, модуль упругости, коэффициент
поперечной деформации, внешние силы, приложенные к повер-
хности этой системы, время — будут определяющими параметра-
ми. Любые перемещения точек тела представляют собой измене-
ния линейных размеров, скорости и ускорения и могут быть
выражены как отношения перемещений ко времени; объемные
силы представляются в виде произведения плотности на ускоре-
ние свободного падения; напряжение — это отношение силы к
площади, на которую эта сила действует; относительные дефор-
мации являются отношениями двух линейных размеров и туи
Следовательно, все эти параметры являются производными или
зависимыми от определяющих параметров. Для описания меха-
нического процесса достаточно знать только определяющие па-
раметры Таким образом* из множества параметров, характера
зующих состояние данной системы, можно всегда выделить
минимально возможное количество параметров, достаточное для
однозначного определения состояния системы; эти параметры
Между тс эой независимы и называются основными, или опреда*
ляющими.
Подобие двух физических явлений определяется следующим
образом. Физические явления, процессы или системы подобны,
если в сходственные моменты времени в сходственных точках
пространства значения переменных величин, характеризующих
состояние одной системы, пропорциональны соответственным ве-
личинам другой системы. Таким образом, физическое подобие
достигается в случае, когда поля соответствующих физических
параметров двух систем пропорциональны между собой в про-
странстве и времени*
Коэффициенты пропорциональности для каждой из величин,
характеризующих состояние двух подобных систем, называются
коэффициентами подобия.
Рассмотрим две подобные системы одной и той же физичес-
кой природы, состоящие из одинакового числа аналогичных эле-
ментов, которые играют в обеих системах одинаковую роль. Одну
систему назовем природной и все параметры, характеризующие
ее, будем записывать с индексом «н» (натура), другую систему
назовем моделью и характеризующие ее параметры будем отме-
чать индексом «м* (модель) Отношение соответствующих пара-
метров. характеризующих натуру и модель, т.е. коэффициенты
подобия, будем обозначать символом а с индексом параметра.
65
Гак, при геометрическом подобии все линейные размеры двух
систем, а также изменения этих размеров пропорциональны:
/^м =<Х/. Кинематическое подобие предполагает пропорцио-
нальность полей скоростей и ускорений:
Ук = _ уч
vm
(43.1)
При динамическом подобии между точкамж двух систем суще-
ствует материальное подобие и, следовательно, имеет место по-
добие силовых полей:
(43.2)
Механическое подобие предполагает наличие геометрического,
кинематического и динамического подобия. При этом коэффи-
циенты подобия различных величин выражаются через исходные
коэффициенты подобия ар, аь а, при помощи формул размерно-
сти этих величин, например:
M ==[Z]/[TL
а? [Л
(4.3.3)
Любой физический процесс может быть охарактеризован
набором независимых между собой определяющих параметров
размерных и безразмерных. Связь между размерными парамет-
рами (переменными или постоянными) может быть выражена в
виде зависимости, в которой размерная величина а является функ-
цией независимых между собой размерных величин аи ап :
а„). (43.4)
Пусть среди размерных величин аь. ап первые к величин (к £ и)
имеют независимые размерности. Независимость размерностей
означает, что формула, выражающая размерность одной из вели-
чин, не может быть представлена как комбинация в виде степен-
ного одночлена из формул размерности для других величин При
66
этом число основных единиц измерения должно быть больше
или равно к. Для простоты примем, что число величин с незави-
симыми размерностями равно числу основных единиц измере -
ния. Среди механических величин обычно имеется не более трех
с независимыми размерностями. Такими величинами могуз быть,
например, масса, длина и время* Тогда размерности (Л) величин
. ty*-1?ап могут быть выражены через размерности параметров
? ' , ак-
J Пь^Пп_к).
Таким образом, связь между п 4 1 размерными величинами а, аи
a2^..s дл, независимая от выбора системы единиц измерения,
принимает вид соотношения между nt 1 - к величинами /7, /7Ь...,
Пп„к, представляющими собой безразмерные комбинации из
n + 1 размерных величин. Это положение составляет суть я-теоре-
мы или центральной теоремы теории подобия, которая формулиру-
ется следующим образом: из п независимых параметров аш
среди которых имеется не более к параметров с независимыми
размерностями нельзя составить больше п ~к независимых без-
размерных степенных комбинаций. Безразмерные комбинации,
составленные ИЗ определяющих параметров, получили название
критериев подобия. Всякое физическое соотношение между раз-
мерными величинами можно сформулировать как соотношение
между безразмерными величинами. В частном случае, если число
основных единиц измерения равно числу определяющих парамет-
ров, которые имеют независимые размерности, то с помощью тео-
рии размерности эта зависимость полностью определяется с точ-
ностью до постоянного множителя. Если п - к, т.е. все размерности
независимы., то из параметров , ап нельзя образовать без-
размерной комбинации, и поэтому функциональная зависимость
может быть представлена в виде: а — cat 1 -а,2 •... • а„ ", где с — без-
размерная константа, а показатели степени легко определяются
с помощью формулы размерности для а.
Среди критериев подобия различают тривиальные и нетри-
виальные критерии подобия. К тривиальным критериям подо-
бия относятся, во-первых, отношения двух параметров, характе-
ризующих состояние системы, которые имеют одинаковую
размерность, и, во-вторых, все безразмерные параметры. Все ос-
тальные безразмерные комбинации, составленные из парамет-
ров, характеризующих состояние системы, представляют собой
нетривиальные критерии подобия. Любая комбинация из крите-
риев подобия также является критерием подобия. Среди множе-
ства критериев подобия число независимых критериев определя-
ется согласно центральной теореме теории подобия. Независимые
критерии подобия образуют базу процесса.
67
Рассмотрим применение теории подобия для случая модели-
рования механического процесса. Основными параметрами, ха-
рактеризующими состояние механической лш'тмы, являются
параметры, огчсываюшие свойстве материала (з itltt случае • -
-ЭТО горные породы^ годулз ултугсотт (Е). коэффициент попе*
речной деформации (и) и плотность (р); параметры, характера*
зующие внтштте создейотвий: поззухт’сстные силы (Р) и
объемные силы, которые могут быть определены через ускоре-
ние свободного пад-зинн V; линейные размелн объекта (1)2 на*
пряжения, возникающие под воздействием внешних сип в гор-
ных породах (о, т) и соответствующие им деформации (е, у),
перемещения и др. Определяющими, или независимыми, пара-
метра!.: л В: зтом случае будут только следующие шеста: Е, щ р, Р,
у, Е, размерности которых в системе СИ запишутся так:
i£, лО/*7’2
[ц] = безразмерная
IС« = < 'К
!-С -
Безразмерный параметр уже сам является критерием подобия»
но тривиальным. Среди остальных размерны/ определяющих
параметров три (напримеу, поверхностная сила, ускорение сво-
бодного паления и линейный размер) имеют независимые раз
мерности. Следовательно, согласно- центральной теореме теории
подобия, число независимых критериев подобия равно разности
общего числа размерных -определяющих параметров (л) и 'числа
независимых размерностей (к). В рассматриваемом случае Л«5л
£ = 3 и шишя образом, при моделировании механических
процессов нетривиальных- критериев подобия будет два: P/EL',
E/pgL. Первый критерий подобия применяется, в том случае, когда
механический процесс происходит в результате действия только
поверхностной силы Р, второй критерий подобия применяется
тогда, когда механический процесс обусловлен действием толы з
объемной силы р&
Первый критерий подобия используется, например, при мо-
делирований механических процессов, происходящих в строи-
тельных конструкциях или в деталях машин, когда объемными
силами можно пренебречь Если модель изготавливается из того
ЖС ПОТОЧНЫЙ. ЧТО ЕЗУНТСИЬШ 2 _П ТИТ, TH. Д.: "
необходимо приложить новерхностные силы, которые будут во
столько же раз меньше су ту приложенных к изучаемому объекту^
во сколько раз квадрат его линейных размеров больше квацрата
линейных размеров модели.
68
Второй критерий подобия применяется при моделировании
механических процессов,, протекающих в массиве горных пород
и обусловленных главным образом объемными (гравитационны-
ми) силами.
Критерии подобия используются, во-первых, для создания,
модели и, во-вторых, для пересчета результатов, полученных при
исследовании модели, на моделируемый объект. Так, подбор ма-
териала модели Для исследования распределения напряжений в
массиве пород, находящегося в поле гравитации, осуществляется
z помощью критерия подобия: E/pgL. Если моделирование про-
изводится на поверхности земли, т.е. в условиях действия уско-
рения свободного падения, н материал модели имеет плотность,
близкую к плотности горных пород, то модуль упругости материала
модели должен быть во столько же раз меньше модуля упругости
пород, во сколько размер моделируемого-объекта больше размен-
ров модели. Для шздзсчета определенных на модели напряжений
пользуются критерием подобия. o/pg£, так как модуль упругости
Е и напряжение имеют одинаковые размерности. Действитель-
но, отношение двух характеризующих механический процесс па- •
рэ метров с одинаковыми размерностями есть тривиальный кри-
терий подобия о/£ и, следовательно, произведение двух критериев
дает искомый критерий подооия:
(E/pgL)(s>/E) = o/pgL.
При моделировании природных процессов, отличающихся
сложностью, не всегда удается удовлетворить одновременно всем
критериям подобия. В таком случае прибегают к частичному по-
добию. Например, при моделировании массивов горных пород
обязательно добиваются выполнения критерия подобия £/pgZ, а
равенством коэффициентов Пуассона пород и материала моде-
ли, так как безразмерные параметры сами являются критериями
п од об ия, п ре н ебре га ют „
Введение критериев подобия облегчает процесс моделирова-
ния, так как происходит сокращение числа независимых пере-
менных, которые необходимо учесть при построении модели адек-
ватной изучаемому объекту, и зависимость между шзмерными
параметрами представляется в безразмерной форме. Таким обра-
зом, теория размерностей и подобия позволяет рассматривать
закономерности в безразмерной форме с уменьшением числа
переменных.
контрольные
Основные системы единиц измерения и понятие размер-
ности физических величин.
2 qT0 такое анализ размерностей и алгоритм его приме-
нения?
X Определяющие параметры физического процесса.
4 Чем отличаются критерии подобия от коэффициентов
подобия?
5. Как определяется число независимых критериев подобия?
6. Критерии подобия при моделировании механического про-
цесса и случаи их применения.
7. Какие преимущества использования критериев подобия
при моделировании?
ГЛАВА 5. ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ
К физическим относятся методы моделирования, которые осу-
ществляются на моделях, состоящих из материалов с той же физи-
ческой природой, что И моделируемый объект. Среди этих мето-
дов наибольшее распространение получили методы эквивалентных
материальных объектов, центробежного моделирования, тензосет-
ки, разнообразные поляризационно-оптические методы и др. [3].
Методы физического моделирования используются .для ре-
шения широкого спектра исследований поведения материальных
объектов как в пределах упругого и пластического деформирова-
ния, так и в состоянии предельного равновесия и разрушения. В
связи с развитием численных методов решения различных задач
с использованием вычислительной техники математическое мо-
делирование во многих случаях стало предпочтительнее, чем экс-
периментальное моделирование. Однако последнее незаменимо,
когда исследуют механизм изучаемых процессов — без них не-
возможно построение математического описания.
5.1. Теоретические основы методов
эквивалентных материалов
Метод эквивалентных материалов был предложен Г.Н. Куз-
нецовым (1968) для изучения устойчивости целиков в горных
выработках и решения ряда задач, возникающих при разработки
месторождений полезных ископаемых. Начиная с 60-х годов, этот
метод стал применяться для исследования напряженного состоя-
ния и оценки устойчивости склонов и бортов карьеров в научно-
исследовательских и учебных институтах (ВИОГЕМ, МГИ. МГУ,
ОГУ и др ).
Метод эквивалентных материалов применяется для исследо-
вания напряженно-деформированного состояния и устойчивос-
ти неоднородных трещиноватых массивов горных пород в зави-
симости от их формы, строения, физико-механических свойств
и приложенных к ним внешних сил Этот метод основывается на
общих законах механики и теории подобия При использовании
этого метода нет необходимости делать допущения о законах де-
формирования изучаемой среды, например, о линейной связи
между напряжениями и деформациями.
Для проведения моделирования основная зависимость меж-
ду параметрами модели и изучаемого объекта получается из вто-
рого зак ЮТО!
Р= МА — для изучаемого объекта,
р ~ та — для модели,
где Р, р — силы, действующие на элемент соответственно изуча-
емого объекта и модели; М, т — массы элементов изучаемого
объекта и модели; Л, а — ускорения соответствующих элементов.
Для того, чтобы процессы, протекающие в исследуемом объек-
те и модели были подобны необходимо, чтобы соответствующие
параметры, характеризующие два подобных процесса, были лро-
п-?рц сальны:
Р _ МА
Р та
или
А-
= О
т а
(5.1.1)
Заменим в отношении (5.1.1):
A V/Т\ a—v/t ,
где L, I— линейные размеры изучаемого объекта и модели; Т,
t— время протекания процессов в изучаемом объекте И мотели;
)/ у _ скорости равноускоренного движения элементов изучае-
мого процесса» его модели; — плотности элементов соот-
ветственно изучаемого объекта и модели.
Тогда отношение (5.1 1) примет вид;
Р _ ZV/pH
т Г-.т^
Учитывая, что // 7 = Ии ///= v, получим:
—г = —Д—г ® const - Ne (5.1.2)
рД2Г2 рДМ
закон динамического подобия И. Ньютона, который использует-
ся для вывода основного соотношения, применяемого в методах
эквивалентных материалов
Если в формуле динамического подобия Ньютона (5.1.2) про-
извести замены:
И2= AL - gL, v2 = al=gl,
что возможно, когда моделирование осуществляется на поверхно-
сти земли и на массив пород и модель действует сила тяжести, и
P/L^NK, р/1г = ^
где N„ и NM — некоторые параметры соответственно изучаемого
объекта и модели, имеющие размерность напряжения, то получим:
-^ 7 = —^7 ~ К = idem или aN = алх-Cti. (5.1.3)
Рн^ Рм^ Р
Здесь NH и NM или значения напряжений в изучаемом объек-
те и модели, или некоторые показатели механических свойств
материала изучаемого объекта и модели, отражающие их поведе-
ние в условиях изучаемого типа деформирования или разруше,
ния, например, модули упругости, прочность на одноосное сжа-
тие, сцепление и др.
Безразмерное число
К = N /pgL, или 1« о N / араgd, (5.1.4)
представляет собой «определяющий критерий подобия» процессов
деформации и разрушения пород под действием сил тяжести и
напряжений, вызванных этими силами. Выведенный из закона
динамического подобия Ньютона критерий подобия полностью
совпадает с критерием подобия, полученным на основе исполь-
зования теории подобия. Таким образом, для того чтобы все ме-
ханические процессы, вызываемые внутренними напряжениями
под действием сил тяжести, были подобны во всех элементах
двух сравниваемых систем необходимо, чтобы во всех сходствен-
ных точках этих систем значение К, вычисленное по данным изу-
чаемой природной системы, было равно значению К, вычислен-
ному по параметрам модели.
Рассмотрим возможные варианты моделирования с использо-
ванием полученного критерия подобия. При этом будем считать,
что N является показателем некоторого свойства материала моде-
ли и изучаемого объекта, имеющим размерность напряжения.
1. Предположим, что модель создается из того же материала,
из которого состоит исследуемый объект. Тогда NH = рн = рм
(аЛ,= 1, ар -1) и следовательно, если моделирование производит-
ся в обычных условиях, т е. когда на модель так же как на изуча-
емый объект действует сила тяжести (а^ = 1), модель должна иметь
те же размеры, что и изучаемый объект: L = l (at = 1). Но это не-
возможно, так как заранее предполагается, что моделирование
геологических объектов имеет смысл выполнять на моделях мень-
шего размера. Следовательно, либо Nu, либо рн*р».
2. Предположим сначала, что jVh = tVm. Тогда, если то
должно быть рм g > pHg. Последнее возможно в двух случаях: во-
первых, для модели можно подобрать материал, плотность кото-
рого больше плотности горных пород, например, моделировать с
помощью свинцовой дроби, что не всегда удобно, во-вторых,
придать модели ускорение с помощью дополнительно приложен-
ной инерционной силы, которая так же, как и гравитационная,
является объемной (gM>gH) Приложить инерционную силу мож-
но путем вращения модели в центрифуге, и такой способ моде-
лирования подучил название центробежного.
3. Пусть N** Лгм. Это предположение составляет основу ме-
тода эквивалентных материалов. В этом случае модель строится
из материала, свойства которого отличаются от свойств изучае-
мого объекта. Механические характеристики материала модели
подбираютс - по формуле:
Lo £ н
' Н ”н
или, если моделирование производится в обычных условиях
(аг=0:
* £Рн "
5.2. Метод эквивалентных материалов
С помощью метода эквивалентных материалов [2] изучаются
процессы разрушения массивов горных пород и деформирования.
При моделировании разрушения массивов горных пород не-
обходимо выполнить требование подобия в отношении механи-
ческих констант прочности, определяющих предельное состоя-
ние породы перед разрушением. В качестве характеристик
прочности при подборе материалов-эквивалентов для сыпучих и
пластичных пород пользуются совокупностью значений сцепле-
ния (с> и угла внутреннего трения (tg ср):
см ® -;у" с» ’ tg<рм = tg<р„ • (5.2.1)
Подбор материалов-эквивалентов для скальных пород осуществ-
ляется по сопротивлению одноосному сжатию R:
Лм=^-Лн. (5 2.2)
Дня подобия процессов упругого деформирования подбор
материалов-эквивалентов производится по деформационным ха-
рактеристикам:
£м=-^-£в;рм=Ин (5.2.3)
ьРн
Если изучаемый объект состоит из нескольких различных по
механическим свойствам материалов, то при изучении его де-
формирования или разрушения на моделях механическое подо-
бие может быть соблюдено только в том случае, если дополни-
тельно будет удовлетворено:
Рм| _ _ Рм,
Рн. Ри,
(5.2.4)
Для моделирова-
ния применяются ма-
териал ы5 представ-
ляющие собой смеси
инертных и вяжущих
(цементирующих) ве-
ществ. Инертными за-
полнителями служат
кварцевый песок, мо-
лотая слюда, тальк,
мел, глина и др. В ка-
честве вяжущих ис-
пользуются машинное
м ас л о, с ил и катн ы й
клей, парафин, гипс,
цемент, канифоль, ва-
зелин и др. Наиболее
распространенным эк-
вивалентным материа-
лом является смесь
кварцевого песка с ма-
шинным маслом, На
фотографиях показан
пример моделирования
с помощью эквивалент-
ного материала (смесь
кварцевого песка с
солидолом) процесса
формирования и раз-
вития трещин в скло-
не при увеличении его
крутизны (рис. 5.1).
Варьирование ко-
личества различных
компонентов в смеси
обеспечивает получе-
ние эквивалентных ма-
териалов с заданными
физико-механи s к и
ми свойствами. Если,
Рис. 5.1. Последователь-
ность образования трещин в
модели склона при увеличе-
н о крут
например, у горных пород сопротивление одноосному сжатию
Я* изменяется в пределах 15-120 МПа, а модуль упругости Е* **
в пределах 15 000 40 000 МПа, и если принять, что отношение
ри/рн- 0/7, го при масштабах моделирования от 1:10 до 1:200 эк-
вивалентные материалы должны обладать следующими свойства-
ми: сопротивление одноосному сжатию ~ 0,05-8,40 МПа, мо
дуль упругости £м - 500-2800 МПа.
Для получения эквивалентных материалов с особыми свой-
ствами используются специфические вещества. Так, для получе-
ния тяжелых материалов применяется свинцовая дробь, для полу-
чения материалов с низкими значениями модуля упругости (Е"=~ 0,5-2 МПа)
применяется резиновая крошка, древесные опилки, керамзите*
бетон, в качестве материалов с низким сопротивлением сдвигу
используются стеклянные шарики или палочки и др.
Моделирование с помощью эквивалентных материалов об-
ладает рядом прц/иущестг.
из эквивалентных материалов можно создавать сложно по-
строенные неоднородные модели;
модели могут быть как плоскими, так и объемными;
при моделировании на эквивалентных материалах получает-
ся наглядная картина деформирования и разрушения.
С другой стороны этот метод моделирования не лишен су-
щественных недостатков:
большие трудности возникают при подборе материалов-эк-
вивалентов из-за невозможности получения в некоторых случаях
материалов с заданными свойствами, из-за малого диапазона
изменения свойств, применяемых для моделирования материа-
лов, и невозможности изготовления однородных смесей;
подбор материалов, создание модели, проведение экспери-
мента занимает много времени и требует значительных матери-
альны/ затрат;
модели из эквивалентных материалов, как правило, очень
громоздкие, а используются однократно.
5.3. Метод термопластических материалов
Моделирование с применением термопластических материа-
лов является разновидностью метода эквивалентных материалов
и используется для изучения деформаций массивов горных по-
род в том случае, когда изменение их механических свойств про-
исходит во времени. Такие деформации наблюдаются, например,
при развитии оползневого процесса на склоне, в результате увлаж-
нения оползающих масс пород подземными или поверхностны-
ми водами П].
76
Определяющими параметрами процесса деформирования
указанием их размерностей) в этом случае будут:
геометрический размер [/] ~ С
показатели прочностных свойств ту лд5“1 Г'-2
динамическая вязкость пород
ПЛ от н о сть
ускорение свободного падения
[tg ф] = безразмерная
h] = Ml-'l ’
[р] - МЕ~3
Т
ь с тле
Число нетривиальных критериев подобия определяется на
основании теории подобия: размерных определяющих парамет-
ров шесть, число параметров с независимыми размерностями три,
независимых критериев подобия три:
c/pgl=idem, q/p/Vg/ -idem} tjgfi =^idem. (5.3.1)
К этим критериям необходимо добавить тривиальный крите-
рий: tg<pM^tg(pH.
Термопластический тстериал представляет собой с; сеть швар-
цввого песка с машинным маслом. При моделировании исполь*
суется его свойство изменять прочность и вязкость при измене-
нии температуры. Подбор материала-эквивалента производится
по прочностным показателям с и tg ф в соответствии с приведен-
ными критериями подобия путем смешивания инертного и вя-
жущего веществ в нужных пропорциях. Зависимость изменения
вязкости ст температуры используется г .кт леделирстанил при-
родного процесса, в котором изменение вязкости горных пород
происходит, например, в результате изменения сложности, но
имеет ту же закономерность. Эксперимент Позволяет изучить
изменение напряжений и развитие деформаций в модели во вре-
мени и пересчитать полученные величины на изучаемый при*
родный : ъект в соответствии с критериями подобия (5.3.1):
н
Моделирование с применением термопластических материа-
лов проводят. как правило, на объемных моделях на специаль-
ных столах, позволяющих дифференцированно подогревать Ма-
териал модели и выполнять необходимые измерения. При этом
нагревание .возможно- осуществи.™ двумя стозобами: снизу с
помощью специальных пластин, разогрев которых происходит
независимо по заранее разработанной программе, причем сте-
пень нагрева пластин должна, например, соответствовать харак*
теру увлажнения пород подземными водами; и с помощью ламп
сверху. Режим нагрева во втором случае может отвечать про-
цессу увлажнения пород выпадающими атмосферными осадками.
Контроль степени нагрева материала модели ведется с помощью
термопар, деформации модели определяются по перемещению
реперов простыми измерениями или при повторном фотографи-
ровании, для измерения давления движущихся масс пород уста-
навливаются тензодатчики.
Преимуществом этой разновидности метода эквивалентных
материалов является возможное^ изучения процесса во време-
ни. С помощью такого моделирования можно не только прогно-
зировать развитие процесса, но и разрабатывать мероприятия по
стабилизации оползневого склона.
5.4. Центробежное моделирование
Метод центробежного моделирования, разработанный Г.И. По-
кровским и Н.И. Давиденковым (1932) и одновременно с ними
П.Б, Баки (США), основан на общих положениях теории подо-
бия (4]. При моделировании процессов, протекающих в масси-
вах горных пород, поведение которых, прежде всего, зависит от
действия гравитационной силы, определяющими параметрами
[ц] = безразмерная величина
[р 1« ML 3
являются:
геометрический Л <м-.
деформационные свойства:
модуль упругости
коэффициент Пуассона
плотность
ускорение свободного падения [g] = LT~'
В соответствии с теорией подобия критериями подобия бу-
дут: тривиальный ц = idem и нетривиальный E>'pgl = idem Если
модель создается из того же материала, из которого состоит изу-
чаемый объект, т.е. Е„ = Ея, рм = рн, то должно быть gl = idem Но в
случае, когда моделирование производится в обычных условиях,
Т.е., если gM = gH, модель, должна иметь те же размеры, что и при-
родный объект. Следовательно, если модель меньше природного
объекта, то необходимо, чтобы все элементы модели испытыва-
ли ускорения во столько же раз большие ускорения свободного
падения, во сколько раз модель меньше изучаемого объекта.
Идея центробежного моделирования заключается в замене
гравитационных сил другими объемными силами, величина ко-
торых подбирается в зависимости от соотношения размеров изу-
чаемого объекта и модели (L/I), т.е. от масштаба моделирования.
Такими силами могут быть центробежные инерционные силы,
создаваемые вращением модели в центрифуге. При этом разме-
ры модели должны быть во столько раз меньше натурных, во
сколько раз создаваемые центрифугой объемные силы превыша-
ют силу тяжести.
Использовать при построении модели только идею центро-
бежного моделирования не всегда достаточно, из-за невозмож-
ности соблюдения требуемого масштаба. Поэтому целесообраз*
но сочетать центробежное моделирование с моделированием на
эквивалентных материалах или на оптически активных, причем
последнее в сочетании с замораживанием напряжений. Такой
подход, когда одновременно изменяют ускорение и свойства ма-
териала модели, позволит расширить возможности моделирова-
ния. В этом случае масштаб моделирования определяется крите-
рием подобия:
£й#мРм ’ ' ~ «<«0 '
(5.4.1)
Для центробежного моделирования требуется громоздкое обору-
дование, что в значительной степени осложняет применение этого
метода для решения инженерно-геологических задач.
Контрольные вопросы
1. Что является теоретической основой метода эквивалент-
ных материалов?
2. Какие процессы изучаются с помощью метода эквивалент-
ных материалов?
3. Разновидности метода эквивалентных материалов.
4. Какой состав имеют эквивалентные материалы?
5. Какие критерии подобия используются в методе термо-
пластических материалов?
6 Область применения, достоинства и недостатки методов
эквивалентных материалов.
ГЛАВА 6. ПОЛЯРИЗАЦИОННО-ОПТИЧЕСКИЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ
11оляризационно*Ш1Тические методы широко применяются
для изучения распределения напряжений в строительных конст-
рукциях, в деталях машин и механизмов, в массивах горных по-
род. Изучение напряженною состояния может осуществляться
как при условии пропорииональносги между напряжениями и
деформациями (метод фотсупругости), так и в случае, когда воз-
никают пластические деформации (метод фотопластичности), как
при решении статических задач, так и при исследовании дина-
мических процессов.
6-1. Метод фотоупругости
Первоначально методы фотоупрутости для изучения распре-
деления напряжений в массивах горных пород были применены
при решении задач горного дела [6, 8]. Широкое применение
метод фотоупругости как в нашей стране, так и за рубежом полу-
чил при исследовании напряженного состояния оснований тя-
желых сооружений [3, 4]. Позднее методом фотоупругости были
начаты исследования распределения' напряжений- в массивах по
род земной коры, в склонах речных долин, в бортах карьеров и
искусственных..откосах |1, 5, 7],.
В основе поляризационно-оптического метода исследования
Напряжений [9] лежит способность некоторых оптически про-
зрачных изотропных материалов (стекло, целлулоид, искусст*
венные Смолы и дрД приобретать под дейстыыл: ыыынической
нагрузки временную оптическую анизотропию (становиться дву-
лучепреломляющими). Степень анизотропий зависит от напря-
женного состояния материала. Такие материалы называются оп-
тически чувствительными,
В изотропной среде свет распространяется во всех направле
ниях с одинаковой скоростью. При входе в анизотропную или
кристаллическую среду луз света разлагается в общем случае на
две плоскополяризованные составляющие, распространяющиеся
с различными скоростями во взаимно перпендикулярных плос-
костях. Это явление названо двойным лучепреломлением, кото-
рое является Оптическим свойством кристаллических тел.
Д. Брюстером в 1816 г. было открыто явление искусственно-
го двойного лучепреломления, или пьезооптический эффект. Оно
состоит в том, что В некоторых прозрачных телах при их дефор-
мировании внешней нагрузкой, не превышающей предела упру-
гости, возникает временное двойное лучепреломление, исчезая^
шее при снятии нагрузки. Если через пластинку из пъезсюоти-
ческоп) материала толщиной d, в которой под действием внешней
нагрузки имеет место плоское напряженное состояние (бу^О^ось £
направлена перпендикулярно пластинке), пропустить по норма-
ли к ее поверхности луз плюскополяризованного света, то этот
луч разложится на две плоскополяризованные волны или на два
луча* обыкновенный и необыкновенный,
При этом, во-первых, плоскости колебаний этих волн вза-
имно перпендикулярны и совпадают с направлениями главных
напряжений (деформаций); во-вторых, скорости распространен
ния этих волн различны, и поэтому при выходе из пластинки
возникнет разность хода Л, которая пропорциональна не только
разности показателей преломления обыкновенного (п0) и нео-
быкновенного (де) лучей, но и разности главных нормальных
Д = d(n0 -пе) = dcipy -03) = 2сЛтах
(6 11)
Где Oj и оу — соответственно максимальное и минимальное глав-
ные напряжения, ттах — максимальное касательное напряжение^
с — относительный оптический коэффициент напряжений Это
соотношение является основным законом поляризационно-оп-
тического метода (уравнение Бергтайма) > который выражает ЙН
личественную связь между оптическим эффектом и разностью
главных напряжений (деформаций) в упругом механически изо
тро П Э’ С 3.
При моделировании возникает интерференционная картина
(рис. бД) со светлыми и темными или цветными полосами (изо-
хромами). Точки, лежащие на одной полосе, имеют одинаковую
разность хода и на основании уравнения (6.1.1) — одну и ту же
разность главных напряжений или одинаковые максимальные
касательные напряжения. Определение величин разности хода
выполняется методом компенсации с помощью координатно-
синхронных поляриметров (КСП). Зная относительный оптичес-
кий коэффициент напряжения с для материала модели и ее тол-
щину по формуле (6.1.1) можно вычислить максимальные
касательные напряжения в любой произвольной точке модели:
О*| — О1 /\
““ 5 2 c d (6.1.2)
Кроме того, просвечивая модель, можно определить положе-
ние изоклин, которые представляю! собой геометрическое место
точек, где оси оптической анизотропии имеют одинаковый на-
клон относительно выбранной системы координат. По изоклинам
о
Рис. 6.1. Изолинии равных максимальных касательных
напряжений при оптическом моделировании: а —. в по-
луплоскости под сосредоточенной нагрузкой; б — во-
круг отверстия при растяжении. в — в бортах выемки
определяются направления действия главных напряжений, так
как они совпадают с осями -оптической анизотропии. Зная раз-
ность (о, - о3) и направление главных напряжений, можно спе-
циальными графоаналитическими методами с помощью урав-
нений механики сплошной среды ВЫЧИСЛИТЬ главные напряжения
(аь сгз) и затем компоненты напряжений относительно выбран-
ной системы координат хОу .
Решение плоских задач поляризационно-оптическим мето-
дом возможно потому, что Для плоского напряженного состоя-
ния односвязного и в отдельных случаях многосвязного тела, при
граничных условиях, заданных в напряжениях, распределение
напряжений не зависит от упругих постоянных материала Е и ц
(теорема Митчела-Певи). Если модель и натура имеют подобные
формы и размеры, а нагрузки имеют одинаковое отношение и
прикладываются в соответственных точках то в соответствии с
теорией подобия для каждой из компонент напряжений будет
верно соотношение:
hlP
°H HLp A ’
(6.1.3)
где crM— напряжение в модели и натуре, кг/см2; А, Н— тол-
щина пластинки или плоского сечения, CM; I, L — линейный раз-
мер в плоскости модели и натуры, см; р, Р — сила, действующая
в модели и натуре, кг. Соотношение (6,1.3) может быть представ-
лено в форме:
K — P/^HL или 1 —
(6.1.4)
откуда следует:
Р
= idem
или
—- idem,
EL
(6.1.5)
(6.1.6)
т.е. соотношение (6.1.3) приводится к критериям подобия, кото-
рые используются при моделировании механических процессов,
протекающих только под действием поверхностных сил Крите-
рий подобия (6.1.6) используется для подбора материала при со-
здании модели в соответствии С модулем упругости, а (6.1.5) —
для пересчета определяемого с помощью модели напряжения на
исследуемый объект.
Следует обратить внимание на то, что метод фотоупругости
создан и развивался главным образом в связи с изучением рас-
пределения напряжений в конструкциях или деталях, возника-
ющих в результате действия поверхностных сил. Массивы гор-
ных пород деформируются в основном под действием сил
гравитации. Поэтому для решения вопроса о напряженно-де-
формированном состоянии массивов пород методом фотоупру-
гости было предложено |5] использовать особые низкомодуль-
ные оптически чувствительные материалы, способные заметно
деформироваться под собственным весом. Тогда при подборе
материала модели и для пересчета напряжений, определяемых
при моделировании, на природный объект используется другой
критерий подобия:
—г = idem или
idem,
(6.1.7)
где у — обт емный вес, г/см'.
Основная трудность, возникающая при моделировании с
помощью низкомодульных материалов, состоит в том, что суще-
ствует большая разница в значениях модулей упругости природ-
ного объекта и модели. Поэтому приходится соглашаться с выте-
кающим из критерия подобия масштабом моделирования. Это
вынуждает создавать очень маленькие по размерам модели, на
которых трудно производить необходимые измерения.
Моделирование методом фотоупрутости проводится на од-
нородных прозрачных материалах, в основном аморфных поли-
мерах, для которых зависимость между деформациями и напря-
жениями подчиняется линейному закону. Среди них выделяются
высокомодульные и низкомодульные материалы. К первым от-
носятся различные пластмассы: целлулоид, плексиглас, полисти-
рол и др. Эти материалы применяются для создания моделей,
когда напряжения в них вызываются поверхностными силами.
Низкомодульные материалы (игдантин, агарин, эпоксигель) спо-
собны деформироваться под собственным весом, и поэтому при-
меняются при изучении поведения тел, например массивов гор-
ных пород, находящихся в поле гравитационных сил.
Наибольшее применение получил игдантин, разработанный
в институте Горного дела и представляющий собой желатино-
глицериновый студень (30% желатина, 30% глицерина и 40%
воды). В зависимости от соотношения составляющих компо-
нентов можно получить материал, модуль упругости которого
изменяется от 0,3 до 3 кг/см2. Коэффициент поперечной дефор-
мации игдантина равен примерно 0,5. Недостатком игдантина
является его быстрое «старение », в результате чегоон становит-
ся непрозрачным.
Методика создания плоских моделей из низкомодульных
материалов состоит в следующем. Проваренный игдантин зали-
вается в горизонтально расположенную плоскую прямоугольную
раму. Модели придают форму, аналогичную форме изучаемого
природного объекта. Приведение модели в вертикальное поло-
жение вызывает в; ней напряжение от собственного веса и соот-
ветствующие им деформации. Измерение напряжений в любой
точке модели и направление их действия производятся с помо-
щью поляриметров (КСП).
Метод фотоупругости обладает рядом достоинств, основны-
ми из которых являются следующие. Во-первых, этот метод иде-
ален с теоретических позиций и, следовательно, полученные им
результаты отличаются высокой точностью. Во-вторых, с помо-
щью метода фотоупрутости получается непрерывная картина рас-
пределения напряжений в модели, так как разность хода может
быть определена в любой точке. В-третьих, это простой метод,
позволяющий быстро изготовить модель и легко производить
необходимые измерения,
К недостаткам метода фотоупрутости следует отнести невоз-
можность многократного использования одной и той же модели,
так как она быстро стареет. Наилучшие результаты получаются
при исследовании методом фотоупругости однородных, изотроп-
ных объектов, чему никогда не отвечают массивы горных пород
Недостатком этот© вида моделирования также является малый
диапазон изменения модуля упругости игдантиИЯ и высокий ко-
эффициент поперечной деформации, что затрудняет использо-
вание этого материала при изучении напряженно-деформирован-
ного состояния скальных пород.
Поляризационно-оптические методы моделирования посто-
янно совершенствуются. Развиваются методы фотопластичности
и фототекучести, позволяющие исследовать изменение напря-
женно-деформированного состояния объектов, проявляющих
пластические свойства, что очень важно при изучении массивов
горных пород. Методы фотоупрутости нашли применение при
решении динамических задач, например при изучении перерас-
пределения напряжений в горных породах и сооружениях в ре-
зультате прохождения сейсмических волн [3|.
6.2. Метод замораживания деформаций
Разновидностью поляризационно-оптически.' изтодов мо-
делирования является метод замораживания деформаций. Не-
которые оптически чувствительные материалы (например, от-
вержденные эпоксидные смолы) обладают способностью после
охлаждения запоминать то напряженное сос тояние, в котором
они находились, будучи нагретыми.
Моделирование с помощью материалов, способных «замора-
живать» полученные при нагреве деформации, осуществляется
следующим образом. Модель нагревают до температуры 80-120 °C.
К нагретой модели прикладывается нагрузка, соответствующая
моделируемому усилию. Затем модель, находящуюся под нагруз -
кой, охлаждая» до комнатной температуры. После снятия на-
грузки деформация, возникшая в модели, когда она находилась в
эластичном состоянии, и сопровождающая ее оптическая ани-
зотропия, фиксируются. Наглядно это явление описывается при
помощи условной двухфазной модели. При нагреве одна часть
материала размягчается, другая остается упругой. Под нагрузкой
деформируется не размягченный скелет. При охлаждении раз*
мягченная часть застывает или «замораживается» и фиксирует
деформацию, возникшую в скелете, Таким образом, модель со-
храняет информацию о том напряженно-деформированном состо-
янии, которое она приобрела в результате приложения нагрузки.
Изучение распределения напряжений в охлажденной модели
выполняется так же как и в методе фотоупрутости.
Метод замораживания деформаций наиболее эффективен
при изучении объемных моделей. Деформации, полученные под
нагрузкой, сохраняются в охлажденной объемной модели, и по-
этому их можно использовать для изучения распределения на-
пряжений. Из указанной модели в интересующих исследовате-
лей частях выпиливаются тонкие (толщиной 0,2-2 мм) пластинки,
которые исследуются как и в предыдущих случаях.
Напряженное состояние массивов горных пород обусловле-
но в основном действием гравитационной силы. Поэтому изуче-
ние распределения напряжений в горных породах можно прове-
сти с помощью объемных моделей и при сочетании методов
замораживания и центробежного моделирования Несмотря на
принципиальные возможности осуществления такого способа
моделирования, оно, в связи с громоздкостью необходимой при
этом аппаратуры, не нашло практического применения.
Таким образом, преимущество метода замораживания за-
ключается в возможности изучения напряженно-деформирован-
ного состояния массивов горных пород на объемных моделях.
Главным недостатком этого метода является необходимость ис-
пользования сложного оборудования, что затрудняет его широ-
кое применение.
6.3. Метод тензометрической сетки
Метод тензометрической сетки, разработанный для решения
задач теории упругости и строительной механики [4], основан на
пропорциональности деформаций, замеряемых в элементах мо-
дели, величинам действующих напряжений. Исследования этим
методом проводятся главным образом на плоских моделях, но в
отдельных случаях могут быть использованы и объемные модели.
Если на поверхность плоской модели из эквивалентного ма-
териала нанести тонкими линиями тензометрическую сетку, т.е.
сетку с точными расстояниями между этими линиями, и прило-
жить к модели нагрузку, то произойдет деформация модели, ко-
торая выразится в изменении расстояний между линиями. Изме-
ряя в отдельных элементах модели величины деформаций ячеек
тензометрической сетки, и получая значения вертикальных, го-
ризонтальных и диагональных смешений линий, ограничиваю-
щих ячейки сетки, и предполагая, что произошедшая деформа-
ция сетки пропори ио -.ярил . ого напряжения,
можно рассчитать действующие в модели напряжения, используя
методы теории упругости. Первоначально ячейки тензометричес-
кой сетки могут быть строго квадратными или иметь какую-либо
другую форму, например, круглую (рис. 6.2). Произошедшие в
модели деформации либо измеряются с высокой точностью не-
86
Рис» 6.2. Типы клише для нанесения тензометрической сетки
посредственно на модели, либо определяются при повторном
фотографировании на стереоавтографе [2].
Испытание методом тензометрической сетки сводится к сле-
дующим операциям:
изготовление модели нужного масштаба с соблюдением гео-
метрического подобия формы и динамического подобия свойств
и действующих сил;
нанесение на поверхность ненапряженной модели тензомет-
рической сетки в виде, квадратов или окружностей и снятие конт-
рольного отпечатка с недеформированной сетки;
создание в модели напряженного состояния путем приложе-
ния нагрузки или приведением ее в вертикальное положение;
снятие отпечатков с деформированной тензометрической
сетки;
измерение деформаций по ячейкам сетки с определением
относительных деформаций по сторонам и диагоналям или диа-
метрам ячеек;
расчет напряжений по формулам теории упругости, связыва-
ющим напряжения с деформациями.
В качестве эквивалентного обычно выступает оптически чувстви-
тельный материал, и тогда появляется возможность совместить
метод тензометрической сетки с поляризационно- оптическим ме-
тодом моделирования, особенно в случае использования низко-
модульных материалов.
Контрольные вопросы
1. Что служит теоретической основой метода фотоупрутости?
2. Какая связь существует между оптическими и механичес-
кими эффектами?
3. Что и как изучается при поляризационно-оптическом мо-
делировании/
4. Какие материалы используются при изучении напряжен*
но-де,формированного состояния массивов пород метода-
ми фотоупрутости7
5. Что лежит в основе метода замораживания деформаций?
6. Область применения поляризационно-оптических мето-
дов, их преимущества и недостатки.
7. Каковы основные отличия метода тензометрической сетки?
ГЛАВА 7. АНАЛОГОВОЕ И ИМИТАЦИОННОЕ
МОДЕЛИРОВАНИЕ
Исследование напряженно-деформированного состояния
массивов горных пород может быть выполнено с помощью ана-
логового моделирования. Для решения задач механики грунтов
метод электрогидродинамических аналогий был впервые приме-
нен В.А. Флориным [9]. Изучение распределения напряжений в
гравитационных плотинах этим методом производилось Л.И. Дят-
ловицким (1 ]. Для исследования напряженно-деформированного
состояния массивов горных пород, слагающих природные скло-
ны, метод элекгрогеодинамических аналогий широко применял-
ся для оценки устойчивости склонов Одесского побережья Чер-
ного моря |5J.
7.1. Метод элекгрогеодинамических аналогий
Метод элекгрогеодинамических аналогий (ЭГДА) входит в
группу аналогового моделирования )5]. Под аналоговым пони-
мается такой вид моделирования, при котором процесс одной
физической природы изучается с помощью процесса другой фи-
зической природы, но при условии, что оба процесса описыва-
ются однотипными математическими выражениями. Метод ЭГДА
основан на том, что и распределение напряжений в массиве гор-
ных пород, и электрическое поле описываются одними и теми
же дифференциальными уравнениями. Действительно, при от-
сутствии объемных сил напряженное состояние тел характеризу-
ется системой однородных уравнений равновесия и уравнения
совместности:
(7.1.1)
(7.1.2)
где принято (сд- •+• ау) == © .
Условия в электрическом проводнике описываются уравне-
нием равновесия
5.Х. 'у
(7.1.3)
и уравнением совместности
у
где ix и , проекции векторов плотности тока на координатные
оси Ох и Оу, U— функция электрического потенциала. Из сопо-
ставления этих уравнений легко сделать вывод об их аналогич-
ности. В качестве уравнения совместности как для напряжений в
массиве горных пород, так и для электрических потенциалов,
используют уравнение Лапласа.
Связь между напряжениями и деформациями в случае плос-
кого напряженного состояния (ог = 0) выражается обобщенным
законом Гука:
(7.1.5)
Если сложить компоненты относительных деформаций, по-
лучится выражение:
1 — и 1 —и „ .
£ « tjj + £у = —~(ах + Оу) = —~ в, (7.1.6)
где величина г характеризует плоскую относительную деформа-
цию в результате действия суммы нормальных напряжений
0 = а х 4оу, а ~ — представляет собой коэффициент пл ос-
кой деформации, зависящий от упругих параметров, деформиру-
емого тела: модуля упругости Е и коэффициента поперечной де-
формации ц.
Связь между силой тока и напряжением выражается законом
Ома
1 = \и, (ТЛТ)
1\
где 7— сила тока. U— напряжение. Я— сопротивление.
Сопоставление формул (7.1.6) и (7.1.7) показывает аналогич-
ность законов Гука и Ома. Для доказательства условий подобия
заменим характеристики поля напряжений на аналогичные харак-
теристики электрического поля через масштабные коэффициенты
или коэффициенты подобия. Так как t = a,/, —^- = аг4г»
£ п К
0 = aeU , то из (7.16) получим:
(7.1.8)
Если выбрать масштаб таким, чтобы удовлетворялось соотно-
шение
Ct g - ОС д (X Q,
(7.L9)
то выражение (7.1.8) тождественно перейдет в закон Ома (7.1.7),
что доказывает подобие процессов, причем соотношение (7.1.9)
представляет собой критерий подобия. Таким образом, исходя из
аналогии уравнений, описывающих движение электрического тока
в проводнике и распределение напряжений в массиве горных
пород, можно изучать последнее, например, с помощью моделей
из электропроводной бумаги. Модель необходимо построить гео-
метрически подобной моделируемому объекту и задать сопро*
тивление модели обратно пропорциональным коэффициенту
плоской деформации К —
, который зависит от деформа-
циоиных свойств из .? бъекта.
Для определения электрического потенциала вводится отно-
сительный электрический по ген пиал 0 < U < 1:
(7.1.10)
где Д(7тах - утах &U --V Из подобия этих двух
рассматриваемых процессов следует пропорциональность элект-
рического потенциала U и суммы главных напряжений 0;
ДО max
Д max
откуда
ле
/1
ИЛИ и = а
А
.- .
(7.1.11)
В результате приложения к контуру модели электрического по-
тенциала, соответствующего по величине поверхностной на-
грузке, которую испытывает массив горных пород, в модели
возникает электрический ток. Линии равных напряжений на
электропроводной бумаге отвечают линиям равных сумм нор-
мальных напряжений. Измерив на модели электрический потен-
циал U, можно рассчитать величину функции 0 = ах + , по
которой с помощью численных методов и используя уравнения
равновесия, можно определить напряжения.
Метод ЭГДА наиболее успешно может быть применен для
изучения распределения напряжений в линейно деформируемой
среде при отсутствии объемных сил. Изучение напряженного
состояния массивов горных пород, деформация которых про-
исходит, прежде всего, под действием собственного веса, с по-
мощью ЭГДА затруднено. Оно может быть осуществлено, если
91
собственный вес заменить эквивалентными поверхностными си-
лами, используя, например, метод отрицательных ИДИ компенса-
ционных нагрузок.
Преимущество метода ЭГДА состоит в простоте изготовле-
ния моделей (они просто вырезаются из электропроводной бу-
маги). Недостатками метода являются малый диапазон измене-
ния сопротивления электропроводной бумаги, что затрудняет ее
подбор для проведения моделирования: нестабильность резуль-
татов определения напряжений, что вызвано зависимостью со-
противления бумаги от ее неоднородности и качества, влажно-
сти, температуры и других факторов; невозможность в ряде случаев
повторять эксперимент на одной и той же модели.
Кроме сплошных моделей ЭГДА применяются сеточные элект-
рические модели, основу которых составляет сетка электричес-
ких сопротивлений, соединяемых в узловых точках. С помощью
таких моделей возможно решение пространственных задач. Тео-
ретической основой сеточных моделей является метод конечных
разностей. Следует признать, что ЭГДА и сеточные электричес-
кие модели не нашли широкого применения при исследовании
напряженно деформированного состояния массивов горных по-
род, так как это успешнее производится с помощью численных
методов решения дифференциальных уравнений и современной
вычислительной техника.
7.2. Имитационное компьютерное моделирование
Имитационное компьютерное моделирование — относительно
молодое и новое направление в исследовании сложных динами-
ческих систем, которое в настоящее время интенсивно развива-
ется и используется во многих областях науки и техники [12s 14]
Идея Имитационного моделирования первоначально была
сформулирована и реализована в биологии |2] для исследования
поведения сложных самоорганизующихся систем, состоящих из
множества элементов (особей). Типичными примерами таких
систем являются популяции и сообщества живых организмов Как
правило, динамика их развития характеризуется стохастичнос-
тью, нелинейностью и нестационарностью, а функционирова-
ние происходит под воздействием факторов разнообразной и
малоизученной природы. В связи с этим моделирование такого
рода систем традиционными эмпирическими и аналитическими
методами связано с большими сложностями как теоретического,
так и технического характера, а иногда просто невозможно. В
этих условиях имитационное компьютерное моделирование по
существу является единственным методом исследования и про-
92
гнозирования их поведения. Суть имитационного моделирова-
ния заключается в том. что все известные сведения о системе
записываются в любом доступном для ЭВМ формализованном
виде, а затем на компьютере прорабатываются все возможные
варианты и сценарии того, что может дать совокупность этих
знаний в плане прогнозирования ее развития.
В инженерной геологии получил развитие другой, вероятно-
стный, подход к имитационному моделированию, в основу кото-
рого положены клеточные автоматы и дискретные модели. Под
клеточными автоматами понимается фиктивная среда, в которой
на микроуровне моделируется взаимодействие большого числа
движущихся и неподвижных элементарных частиц (газа, жидко-
сти, сыпучей среды и др ) для установления закономерностей
макроскопического поведения системы в среднем. Клеточные
автоматы и дискретные модели в большей степени, чем другие
средства приспособлены для описания процессов, протекающих
в грунтах и грунтовых массивах
Возможность использования клеточных автоматов для моде-
лирования инженерно-реологических процессов базируется на
положении статистической физики о том, что макроскопичекое
поведение системы, состоящей из большого количества элемен-
тов (частиц) определяется не микроскопическими свойствами
каждого элемента в отдельности, а главным образом характером
их взаимодействия между собой. Поэтому поведение любой жид-
кости, газа или твердого тела, независимо от химического состава
И строения их молекул, на макроскопическом уровне подчиняется
одним и тем же законам. Природа подобия в макрокопическом
поведении различных по своему составу материалов кроется в
том, что даже в самом малом объеме любого твердого тела, жид-
кости или газа насчитывается огромное количество молекул, а
макроскопическое поведение всей системы в целом определяет-
ся особенностями их взаимодействия между собой.
При использовании клеточных автоматов существенным яв-
ляется требование, чтобы внешние воздействия реализовались
во времени и пространстве в масштабе несопоставимо большем,
по сравнению с масштабом взаимодействия на микроскопичес-
ком уровне. Отсюда следует, что локальное равновесие на мик-
роуровне будет определяться только характером взаимодействия
между элементарными частицами. В итоге эволюцию развития
системы на макроуровне можно установить, если существует воз-
можность количественно описать взаимодействие элементарных
частиц на микроуровне за достаточно длительный промежуток
времени.
Методика построения дискретных моделей с помощью клеточ-
ных автоматов чрезвычайно проста. Жидкость, газ или сыпучая
динамическая среда представляется в виде множества «виртуаль
ных* частиц (дискретных математических точек), которые могут
передвигаться между узлами сетки под. влиянием внешних и внут -
ренних сии. Если две или несколько частиц одновременно при-
ходят в один и тот же узел. они взаимодействуют друг с другом, В
зависимости от типа моделируемого процесса характер взаимо-
действия может быть разнообразным (упругое отталкивание, при-
липание, разрушение, реакция и др ) но всегда в соответствии с
фундаментальными законами сохранения вещества и энергии.
таким образом, что масса и количество движения частиц,
участвующих во взаимодействии, остаются неизменными до и
после столкновения.
Наиболее важным моментом методики моделирования явля-
ется составление для каждого процесса собственного набора пра-
вил, описывающих взаимодействие виртуапьных частиц динами-
ческой среды для всех возможных ситуаций при столкновении.
Такие правила программируются и сводятся в таблицу матрицу
коллизий, Воспроизведение динамики развития того или иного
процесс сводится по сухдству к выбору соответствующего на-
бора правил взаимодействия.
Построение модели осущестзлястод с помощью программы •
графического редактора, организованного по модульному типу,
Т.е. таким образом, что для описания каждого компонента (слоя
модели) предусмотрен отдельный блок СО своими специфичес-
кими функциями и свойствами. Всего таких компонентов пять:
движущиеся частицы (динамические узлы модели), препятствия
или неподвижные частицы (статические узлы), источники час-
тиц (дрены) и внешнее силовое поле.
Каждый едой модели прорисовывается индивидуально в виде
контура, занимающего определенную часть в поле модели, а за-
тем в автоматическом режиме слои накладываются друг на друга.
В случае пересечения контуров изображений различных слоев
между ними реализуются отношения приоритетности. С помо-
щью редактора задаются параметры модели, ее геометрические
размеры и форма, определяются необходимые граничные усло-
вия, описывается характер внешних воздействий и механизмы
взаимодействия частиц динамической среды. Процесс построе-
ния модели в зависимости от ее Сложности занимает 5-10 минут.
Описанная технология позволяет практически одними сред-
ствами создать широкий спектр моделей разнообразных процес-
сов. К их числу прежде всего относятся процессы течения жид-
ких и газообразных сред, которые изучаются классической
гидродинамикой и аэрохтинамикой, фильтрационные процессы
как в естественных условиях, так и под влиянием техногенных
факторов, процессы конвективного и диффузионного массопе-
94
реноса в горных породах, процессы речной эрозии и переработ-
ки берегов, суффозионные и карстовые процессы и многочис
ленные склоновые процессы, такие, как оползни-потоки» сели,
снежные лавины и осыпи.
Собственно моделирование осуществляете» с помощью дру-
гой программы, в результате работы которой .динамику развития
процесса можно наблюдать на экране компьютера в режиме ре-
ального времени и получать запись серии количественных ха-
рактеристик, таких, как скорость перемещения моделируемой
среды, давление, плотность, дивергенция и механическая энер-
гия по всему полю модели.
На современном этапе уже имеется опыт моделирования с
помощью клеточных автоматов некоторых инженерно-геологи-
ческих процессов [2, 10].
7.3. Типы моделей массивов горных пород,
применяемые при их исследовании методами
математического и экспериментального
моделирования
Все рассматриваемые методы математического и физическо-
го моделирования применяются при исследовании напряженно-
деформированною ссстсяния массивов горных город. Ктюды
обладают разными возможностями, и поэтому в каждом конк-
ретном случае необходим правильный выбор соответствующего
способа решения поставленной задачи. Невозможно указать уни-
версальный способ решения указанных задач для различных
объектов, Конкретные из рассмотренных выше методов имеют
свою область применения, и поэтому важно, используя возмож-
ности каждого метода, умело их комплексировать. При Изучении
распределения напряжений в неоднородных массивах горных
пород с неровными внешними и внутренними границами наибо-
лее рационально использовать численное математическое моде-
лирование. В настоящее время численное моделирование вытес-
нило физические методы моделирования. Однако не следует
полностью отказываться от предметного моделирования^ так как
только с его помощью возможно выявить механизм процесса и
получить наглядное представление о деформировании и разру-
шении массивов горных пород под влиянием внешних усилий и
в зависимости от их внутреннего строения Большая роль принад-
лежит лабораторному моделированию при создании постоянно
действующих моделей (ПДМ), которые призваны решать задачи
изучения» прогноза и управления геологическими и инженерно-
геопогическм м процесса* ги.
Большинство методов математического моделирования ис-
ходят из представления о линейной деформируемости и сплош-
ности изучаемых массивов горных пород. Но реальные массивы
никогда не бывают сплошными, так как они осложнены пусто-
тами разного размера и формы, разбиты трещинами, раздробле-
ны и т.д При математическом моделировании существуют под-
ходы , позволяющие рассматривать влияние пустот, трещин,
выработок и других типов полостей на распределение напряж е
ний в массиве горных пород, сохраняя предположение об их
сплошности. Например, сильно трещиноватые раздробленные
породы можно рассматривать в качестве сплошных сред, но об-
ладающих существенно большей деформируемостью. С другой
стороны, возможен и принципиально иной подход, когда масси-
вы раздробленных горных пород, в том числе скальные и полу-
скальные, могут рассматриваться в качестве дискретных, сыпу-
чим, сред. Но в таком случае необходимо использовать другой
математический аппарат. Следовательно, один и тот же массив
Горных пород можно изучать, применяя различные математичес-
кие модели.
Более сложные математические модели необходимо исполь-
зовать для изучения напряженно-деформированного состояния
двухфазных сред. Такие задачи возникают при изучении уплот-
нения водонасыщенных Пород под нагрузкой, при откачках жид-
кости из подземных полостей и слоев и в других -случаях.
При изучении напряженного состояния массива водона-
сыщенных горных пород большое значение приобретает у- ;
влияния давления флюидов, для чего используются различные
математические модели, Отражающие взаимодействие жидкой
и твердой составляющих породы. Первой была модель К. Тер-
цаги [8], согласно которой полные главные напряжения в гор-
ной породе включают две части. Напряжения, действующие на
воду и твердую составляющую в любом направлении с одина-
ковой силой, называются нейтральными или поровым давле-
нием. Разность между полными главными напряжениями и по-
ровым давлением называется эффективным напряжением^
которое действует только в твердой фазе. Изменение объема
породы, условия разрушения определяются исключительно ве-
личиной эффективного напряжения. Эта модель позволяет ре-
шать одномерную задачу
Модель М Био [13] создана дня решения задачи о напряже-
ниях в трехмерной модели флюидонасыщенной среды. Эта мо-
дель объединяет уравнения, характеризующие деформирование
твердой фазы по закону Гука, с уравнениями, описывающими
движение жидкости в горных породах согласно линейному зако-
ну фильтрации Дарси, и учи*ывает СГЖИМЗвМОСТЬ минеральных
зьтон. 'Л? товременном зтато теория гтроупругости М. Био яв-
ляется наиболее полной и. достаточно строгой для математичес-
кого моделирования напряженного состояния флюидонасыщен-
ных массивов пород.
Усложнение тоттотодтотоэй модели необходимо л з случае
исследования нторяженно-дефсщтодтоаннэто тостслнто масси-
ве .в горных пород., проявляющих платотототое свойстог. что ха-
рактерно для многих типов осадочных пород. Решение задачи о
распределении напряжений и деформировании пластических
пород в окрестности подземных выработок приобретает большое
значение при создании резервуаров в слоях, каменной соли для
хранения различных видов жидких и газообразны/ продуктов в
связи С необходимостью оценки их устойчивости |7|.
Реповое инженерно-геологл'ческих задач не исчерпывается
только исследованием напряженно-деформированного состояния
массивов горных пород. Остро стоят вопросы оценки условий
разрушения горных пород, которые будут рассмотрены во вто-
рой части настоящего учебника Ж примере оценки устойчивос-
ти оползнеопасных склотое.. Столетовым процессы отличаются
большим разнообразием. Поэтому для оценки степени устойчи-
вости склонов к зтоезлия движения оползневых масс применя-
ются различные математические модели. Например, в склонах
или откосах* сложенных однородными горными породами* на-
руттолто устойчивости происходит при несоответствии прочнос-
ти пород их напряженному состоянию. В этом случае возможно
прштотоние модели предельного лапряжтотото ссотолния, ко-
торая толючает как уравнения (2. то}, ток 7>дд~л^ то тотото-
шение (2 5.2).
Широ ким распространением в природе толкуются про-
цессы, предстогтоющие собой перемещение г.тоо тодтото. раз-
личной прирсто и состава be з по склону. К таким процессам
относятся снежные лавины, селевые потоки, солифлюкция, ополз-
ни-потоки и сплывы и др. Эти я.вления отличаются не только
Природ?/' о юставом поток-/ то, что очень гущзтовенно, вязко-
стью смещающегося вещества. Крайними случаями являются
водные потоки с низшей вязкостью и абсолютно твердые блоки
или глыбы, медленно ползущие вниз по склону„ Главным вопро-
сом является установление характера движения смещающихся
вниз по склону масс вещества Следует подчеркнуть, что при
описании рассматриваемого процесса не решается задача потери
устойчивости находящегося на склоне вещества. Для выявления
условий, приводящих к началу его смещения вниз по склону,
требуется разработка других инженерно-геологических моделей.
97
Модель, описывающая движение вещества вниз по склону,
предполагает внезапную потерю им устойчивости, как в случае
плотины, удерживающей водохранилище^ в одно мгновение пе-
рестающей выполнять возложенную на нее функцию. Основной
моделью, которая описывает смешение снежных лавин, селей,
оползней-потоков и им подобных, пока еще является гидрав-
лическая модель, представляющая собой частный случай
уравнений Навье-Стокса Гидравлическая модель при описания
движения оползней-потоков учитывает вязкость материала, из
которого он состоит, трение потока по дну и стенкам русла, по
которому происходит смещение, возможность захвата нового
материала при движении или его потери. При этом считается,
что вязкость постоянна по длине и мощности потока, а трение
по поверхности смешения подчиняется закону Кулона или тому
же закону с уточнением С.С. Григоряна [4], и предполагается,
что движение потока осуществляется в русле постоянного сече-
ния. Эта модель позволяет изучить движение оползня-потока по
склону с изменяющейся крутизной. Основными результатами
применения этой модели являются изменение во времени ско-
рости движения и мощности потока дифференцированно по его
длине, и, кам следствие, общее расстояние, которое пробегает
поток
Методы физического моделирования применяются для ис-
следования выноса песчаного материала в искусственные и есте-
ственные подземные полости под влиянием движущегося потока
подземных вод, нередко приводящие к образованию провалов на
поверхности земли. Суффозионные и провальные процессы раз-
виваются на территориях покрытого карста и, как правило
условиях изменяющегося режима движения подземных вод, выз-
ванного техногенными причинами. В геологическом строении
участков, где развиваются эти процессы, принимают участие за-
карстованные породы (известняки, доломиты, гипсы), которые
перекрываются слабопроницаемым слоем незначительной мощ-
ности (глины, доломитовая мука и др.), выше которого залегают
песчаные породы. В гидрогеологическом отношении эти участки
характеризуются вертикальной фильтрацией подземных вод из
вышезалегающих песков в закарстованные отложения.
Наиболее типичной инженерно-геологической моделью уча-
стков с проявлением суффозионных и провальных процессов
является трехслойная модель. Нижний слой представлен раство-
римыми горными породами, в которых обязательно должны при-
сутствовать открытые полости, причем, последние должны рас-
полагаться в кровле закарстованных пород. Породы нижнего слоя
могут быть либо сухими, либо содержать безнапорный водонос-
Г
ный горизонт. Средний спой сложен слабопроницаемыми пре-
имущественно глинистыми породами незначительной мощнос-
ти, возможно ослабленными повышенной трещиноватостью.
Верхний слой представляет собой сухую или водонасышенную
песчаную толщу.
Существенной чертой этой модели является предположение
О возможности вертикальной фильтрации из выше залегающих
песков в закарстованные породы нижнего слоя через слабопро-
ницаемый глинистый экран Если толща сухая, то фильтрация
может возникнуть при техногенном обводнении песчаной тол-
щи, например, в результате утечек из водопроводных сетей. Если
пески и закарстованные породы обводнены, То фильтрация бу-
дет происходить при соответствующей разнице напоров. Не ме-
нее важной особенностью этой модели является возможность
возрастания проницаемости экранирующего слоя при возникно-
вении условий дня вертикальной фильтрации, что может про-
изойти в результате разрушения слабопроницаемого слоя.
Таким образом, с помощью рассмотренной модели может быть
решена задача об условиях, при которых возможно нарушение
сплошности экранирующего слоя в результате суффозии и под-
земной эрозии, причем возможны различные механизмы разви-
тия этого процесса в —з умости ст особенностей 'то? ногинс-
кой обстановки и гидрогеологического режима.
Разрушение в результате суффозии и эрозионного размыва
экранирующего слоя создает условия для свободного истечения
сухих или водонасыщенных песчаных пород верхнего слоя в об-
разовавшуюся полость. Процесс развивается снизу вверх, зах-
ватывает выше расположенные горизонты и может выйти на
поверхность с образованием провальной воронки. Сложность раз-
вития рассмотренного процесса приводит к необходимости при-
влечения к его описанию и изучению нескольких расчетных мо-
делей и способов физического моделирования.
Широко применяются математические модели, основанные
на использовании уравнения теплопроводности, для исследова-
ния движения жидкости в пористых средах, а также промерзания
и протаивания горных пород (в районах распространения много-
летней мерзлоты) и связанных с ними криогенных процессов.
Наконец, среди новейших подходов к изучению различных
геологических и инженерно-геологических процессов следует
назвать использование синергетических моделей и образы ком-
плексных динамических систем (фракталы) для описания и про-
гноза развития современных процессов. Первый из них позво-
ляет проводить оценку нарушения равновесного состояния
динамических систем на основании знания закономерностей
99
саморегуляций процессов [11]. Второй предполагает знание за-
кона управляющего динамикой процесса, связей масштабных пре-
образований с изменениями структуры исследуемых объектов,
выявление периодичности наблюдаемых процессов и их класси-
фикацию [6]. Это становится возможным только при проведе-
нии продолжительного мониторинга и использовании его дан-
ных для составления уравнения процесса, учитывающего его
периодичность, устойчивость и равновесие.
Контрольные вопросы
1. Что такое аналоговое моделирование?
2, Сущность метода электро-теодинамических аналогий.
3. Область применения и сущность имитационного компью-
терного моделирования,
< Основные модели массивов горных пород и применяемые
для изучения их поведения методы математического и экс-
периментального моделирования.
ЧАСТЫ1. ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИЕ
РАСЧЕТЫ
ГЛАВА 8. РАСЧЕТЫ ОСНОВАНИЙ СООРУЖЕНИЙ
Расчеты оснований проводятся с целью прогноза поведения
массива горных пород в результате воздействия на него инже-
нерных сооружений При проектировании зданий и сооружений
необходимо учитывать, что деформации их оснований не долж-
ны превышать предельно допустимые величины, а несущая спо-
собность должна быть достаточной, чтобы не произошло потери
устойчивости или разрушения основания. Поэтому основания
рассчитываются по двум группам предельных состояний: дефор-
мациям и несущей способности. Полученные в результате расче-
тов деформации и несущая способность основания сопоставля-
ются с предельно допустимыми деформациями и минимально
необходимой несущей способностью, которые учитывают осо-
бенности конструкций инженерных сооружений, методы их воз-
ведения и условия эксплуатации.
8.1. Виды нагрузок, учитываемых при расчетах
оснований сооружений
Основания инженерных сооружений могут испытывать раз
личные виды нагрузок (статических и динамических, направлен-
на вертикально и горизонтально и т.да часто и сложные их
сочетания. Эти нагрузки передаются сооружениями на основа-
ния и обусловлены действием приложенных к сооружению раз-
нообразных сил. Так, плотина одновременно испытывает дей-
ствие как горизонтальных, так и вертикальных сил (рис. 8.1),
Горизонтальные силы обусловлены давлением воды и льда со
Рис. 8.1. Силы, действую^
щие на плотину: Р — вес
плотины (1) вместе с пону-
ром (2) и зубом (3). шпун-
товой ряд (4); Q — эпюра
давления воды и наносов:
F — давление фильтраци-
онного потока: W — взве-
шивающая сила
10 i
стороны верхнего бьефа, давлением наносов, накапливающихся
за ачитияой, давлением фильтрующейся через основание воды
на зуб плотины и шпунты. Вертикальные силы, действующие вниз,
это вес плотины и понура, давление воды на тело плотины и
понур, а направленные вертикально вверх возникают благодаря
взвешивающему давлению воды и давлению восходящего фильт-
рационного потока. Высокие здания, башни, трубы, опоры для
высоковольтных линий передают на основание не только верти-
кальное давление, но и горизонтальное усилие, возникающее
благодаря ветровой нагрузке Мосты передают на основание не
только вертикальные и горизонтальные усилия, но и динамичес-
кие нагрузки, которые возникают ст проходящею транспорта и
от движущейся воды и льда. В результате воздействия перечис-
ленных нагрузок основания деформируются, а иногда, и разру-
шаются При строительстве плотины, например, возможны сле-
дующие «иды нарушения равновесия, разрушение основания под
действием веса плотины и воды; сдвиг плотины по основанию
горизонтальной силой Q; опрокидывание плотины в результате
совместного действия горизонтальной Q и взвешивающей ИИ сил
вокруг низового ребра; «всплывание» сооружения в результате
действия взвешивающей силы Ж
Расчеты деформаций и несущей способности оснований дол-
жны проводиться исходя из рассмотрения совместной работы
инженерного сооружения и основания. Расчетная схема системы
сооружение — основание должна выбираться с учетом наиболее
существенных факторов, определяющих напряженное состояние
и деформации основания и самого сооружения, таких, как ха-
рактер напластования и свойства грунтов основания, конструк*
ции и технологии возведения сооружения и г д. В необходимых
случаях должны учитываться анизотропия, пластические и рео-
логические свойства грунтов и материалов, а также возможность
их изменения.
8.2. Расчеты оснований по деформациям
Расчеты основан; зданий и сооружений по деформациям
проводятся для ограничения деформаций такими величинами,
при которых будет невозможно достижение состояния, затруд-
няющего нормальную эксплуатацию зданий и сооружений в це-
лом или их отдельных частей. Как правило, расчет деформаций
производится исходя из условия совместной работы здания и
основания.
Основания могут испытывать разнообразные деформации:
вертикальные и горизонтальные, равномерные и неравномерные,
К
быстрые и длительные и др. В зависимости от причин их возник-
новения выделяются деформации грунтов от нагрузок, передава-
емых на основание зданием или сооружением (осадки и просад-
ки). и деформации, не связанные с нагрузкой от зданий или
сооружений, такие, как набухание, усадка, оседание и др. Верти-
кальные деформации подразделяются на:
осадки — деформации, происходящие в результате уплотне-
ния грунта под воздействием внешних нагрузок и в отдельных
случаях собственного веса грунта;
просадки — деформации уплотнения грунта в результате сов-
местного действия внешних нагрузок и собственного веса грунта
и дополнительно с ними действующих факторов, таких, как за-
мачивание просадочного грунта, оттаивание ледовых прослоек в
замерзшем грунте, и др.;
набухания и усадки — деформации, связанные с изменением
объема некоторых типов глинистых грунтов при изменения их
влажности, температуры (например, морозное пучение, прогрев
от промышленных сооружений) или воздействия химических
веществ;
оседания — деформации земной поверхности над природны-
ми, например, карстовыми полостями или искусственными под-
земными выработками, создающимися при разработке полезных
ископаемых, откачками подземных вод, нефти и газа или др.
Совместная деформация основания и здания (сооружения)
характеризуется различными показателями, основными из кото-
рых являются следующие:
1) абсолютная осадка основания отдельного фундамента —
2) средняя осадка основания здания или сооружения — 5ср;
3) относительная неравномерность осадок двух фундамен-
тов — где Д5 — разность их вертикальных перемещений,
I— расстояние между ними;
4) крен фундамента или сооружения — /, т.е. отношение раз-
ности осадок крайних точек фундамента к его ширине или длине;
5) относительный прогиб или выгиб — у , где f — стрела
прогиба, I — длина однозначно изгибаемого участка здания или
сооружения;
6) горизонтальное перемещение фундамента здания (соору-
жения) — U.
Расчет оснований по деформациям производится исходя из
условий 5 < 5пр, где 5 — величина совместной деформации основа-
ния и здания (любая из выше названных), полученная расчетом,
5™ - предельно допустимая величина совместной деформации,
103
устанавливаемая в зависимости от характера взаимодействия
сооружения с основанием и конструкционных особенностей
сооружения [1].
Расчет деформаций основания сооружений производится по
разным схемам, которые выбираются в зависимости от механи-
ческих свойств грунтов, характера ж залегания и конструктивных
•особенностей сооружения. Такими расчетными схемами могут бы ш
линейно и нелинейно деформируемое полупространство, дефор-
мируемый слой конечной толщины, основание, характеризуемое
коэффициентом постели, илр, На практике для расчета деформа-
ций основания применяются две основные расчетные схемы.
1. Линейно деформируемое полупространство с условным
ограничением глубины сжимаемой толщи основания.
2. Линейно деформируемый слой конечной толщины. Такая
схема используется в двух случаях: кого.? з пределах сжимаемой
толщи основания, которая устанавливается так же как .для ли-
нейно деформируемого полупространства, расположен грунт с
модулем деформации Е> 100 МПа. и корца ширина (диаметр)
фундамента более 10 ми грунты обладают модулем Е> 10 МПа
независимо от глубины залегания мало -сжимаемого грунта.
Результаты расчета деформаций основания по этим схемам
злдтаются удовлетворительными, еели среднее дав-
ление на грунт под подошвой фундаменте не превышает расчет-
ноге давления на сснозание. б„од расчетным понимается д.аыш-
ние, не вызывающее в Основании таких деформаций. при которых
основание перестает быть линейно деформируемым. Расчетное
давление определяется в зависимости от платности грунта осно-
вания, его сопротивления сдвигу, размеров и глубины заложения
фундамент^
8.3. Расчет осадки основания
Одним из основных видов расчета оснований зданий или
сооружений по деформациям является расчет осадки основания.
Осадка основания фундамента при использовании расчетной схе-
мы основания в виде линейно деформируемого полупростран-
ства Определяется методом послойного суммирования осадок от-
дельных слоев в пределах сжимаемой толщи основания.
В случае, ксмьа ширина или диаметр фундамента менее Юм,
принимается, что-осадка вызывается дополнительным давлением ,
равным разности среднего давления, передаваемого фундаментом.,
и природного давления от веса грунта выемки котлована.
Таким образом, чтобы рассчитать осадку с тховаНИя, необхо-
димо знать распределение вертикальной составляющей природ-
ных напряжении, произвести расчет вертикальной составляющей
дополнительных напряжений, возникающих в результате действия
на основание нагрузки от сооружения, и оценить мощность сжи-
маемой толщи или глубину активной зоны.
Распределение вертикальной составляющей природных напря-
жений в основании при. горизонтальном залегании слагающих
его слоев определяется по формуле
1=1
где р/ —- плотность пород, слоя, й(- — мощность >*го слоя, g —
ускорение свободного падения, п — число слоев»
Таким образом, эпюра распределения вертикальной состав-
ляющей природных напряжений, обусловленных собственным
весом пород, представляет собой ломаную линию, наклон отрез?*
ков которой зависит от плотности слагающих основание пород и
их обводненности (рис. 8.2).
Рис. 8.2. Эпюры распределения вертикальных природных эффективных напря-
жений в зависимости от плотности пород и их обводненности: а — в однородных
породах: б — в однородных обводненных породах: в —* в двухслойной толще с
грунтовым водоносным горизонтом
Дополнительные напряжения определяются исходя из пред-
положения, что основание представляет собой линейно дефор-
мируемое полупространство. Вертикальная составляющая допол-
нительных напряжений рассчитывается для вертикального сечения
сжимаемой толщи основания вдоль вертикали, проходящей че-
рез центр подошвы фундамента, так как именно вдоль этой ли-
нии напряжения имеют максимальную величину.
105
Расчет напряжений осуществляется с помощью математичес-
кой модели (2.3.6).
Обычно в плане фундамент имеет форму вытянутого прямо-
угольника с различным соотношением сторон (при отношении
сторон больше 10 фундамент называется ленточным), либо пред-
ставляет собой изометричную плиту (круглой или близкой к квад-
рату формы). Для большинства случаев существует аналитичес*
кое решение задачи о распределении напряжений в полулиюскости
в зависимости от величины и характера распределения прило-
женной к ее поверхности нагрузки. Такие задачи решены и ре-
зультаты решения приведены в табл. 8.1 в виде коэффициента а.
Таблица 8.1
Значения коэффициента для определения дополнительных напряжений
в основании различных фундаментов
1 < 1 i 1 Коэффициент а для фундаментов Левточ.' (П>Ю)
круглых прямоугольных с соотношением сторон т)=1/Ъ равным
1,0 1.4 1,8 2,4 3,2 j 5
I
0 1,000 1,000 1,000 1,000 /000 1,000 • J ,000 1,000
0,949 1 0,960 i 0,972 0,97$ 0,976 : 0,977 0,977 0,97?
0.8 0,756 0,800 0,848 0,866 0,876 0,879 ; 0,881
0,547 о?боб i 0,682 0,739 / : j 0,754 0,755
i ,t> 0,390 0,449 />-. f 6,578 0>6I2 | 0,639 0,642
2,0 0,285 0,336 0,414 0,463 0,505 0,530 ! 0,545 0,550
0,214 0,257 0,325 0,374 0,419 0.449 0,470
| 2,8 0,165 0,201 0,260 03,4 0,34$ 0,383 0,410 0,420
3,2 0,130 0,160 0,210 0,251 0,294 j 0,329 0,360 0,374
0 106 0,131 0173 0,209 0,250 0,285 0,319 0,337
4,0 0,087 0/108 0,145 ... 0,214 0,248 0/285 0,306
4,4 0,073 0,091 0,123 0,150 0,185 0,218 0,255 0,280
4,8 0,062 I 0,077 0,105 0,130 0,161 0,192 0,258
5,2 0,053 0,067 1 0,091 0,113 0,141 0,170 0,208 0,239
5,6 0,046 0,058 0,079 0,099 0,124 ’ 0,152 0,189 1 0,223
6,0 0,040 0,051 0,070 0,087’ 0,110 0,136 0,173 0,208
6,4 0,036 0,045 0,062 0,077 0,099 0,122 0,158 0,196
6,8 0,031 0,040 0,055 0,064 i),O88 0,110 0,145 0,185
7,2 0,028 0,036 -0,049 0,062 0,080 0,100 /133 j 0,175
7,6 0,024 0,032 ' 0,044 0,056 0,072 0,091 ; 0,123 i ., у -
8,0 0,022 0,029 0,040 0,051 0,066 0,084 0 133 0,158 .1
/ /
Окончание табл. 8.1
fylzlb Коэффициент а для фундаментов Леиточ. (П>Ю)
круглых прямоугольных с соотношением сторон т|=1/Ь равным
1,0 1,4 1,8 1 2,4 3,2 5
м 0,021 0,026 0,037 0,046 0,060 0,077 0,105 0,150
8,8 0,019 0,024 д! 'Л Г 0,042 0,055 0.071 ! 0,098 0.143
9.2 0,017 0,022 0,031 0,039 0,051 0,063 0,091 0Л 37
9,6 0,016 0,020 0,028 0,036 0,047 0,060 0,085 0.132
10,0 0,015 0,019 0,026 j 0,033 0,043 0,056 0,079 0,126
104 0,014 0,017 i 0Д24 0,031 0,040 0,052 0,074 0,122
10,8 0,013 0,016 0,022 0,029 0,037 0,049 0,069 0,117
11,2 0,012 0,015 ' ' jj 0,035 0,045 0,065 0,111
11,6 0,011 0,014 0,020 :, 0,033 0042 0,061 0,109
12,0 0,010 0,013 0,018 0,023 0,031 0,040 0,058 0,106
Примечания*
I. В таблице обозначено. Ь — ширина или диаметр фундамента, / - длина
фундамента.
2. Для фундаментов, имеющих подошву в форме правильного многоуголь-
ника с площадью А. значения а принимаются как для круглых фундаментов
радиусом г — Ja/tl .
3. Для промежуточных значений п коэффициент а определяется по
интерполяции.
Величина напряжения на глубине z определяется умноже-
нием разности между средним давлением под подошвой фунда^
мента и природным давлением в грунте на уровне подошвы фун-
дамента на величину коэффициента а, который зависит от
глубины расположения рассматриваемой точки, размеров и фор-
мы фундамента. На рис, 8.3 приведена схема распределения вер-
тикальных напряжений в толще основания, где приняты следую-
щие обозначения:
h — глубина заложения фундамента от поверхности природ-
к го рельефа;
Р — среднее фактическое давление (напряжение) под подо*
швой фундамента;
— природное вертикальное напряжение от веса вышеле-
жащих пород на уровне подошвы фундамента:
о, — природное вертикальное напряжение в породах на глу-
бине z ниже подошвы фундамента (или на глубине h + z от по-
верхности природного рельефа);
Р$~Р- ch— дополнительное (к природному) вертикальное
давление на породы по подошве фундамента;
107
I
Рис. 8.3. Схема для расчета осадки методом послой-
ного суммирования
Рг — дополнительной вертикальное давление в породах на
глубине < от подошвы фундамента, вычисленное по формуле:
гдл с коэффициент, учитывающий изменение по глубине до-
полнительного вертикального давления в породах.
Как видит табл 8.L есгичина коэффициенту <х зависит от
формы подошвы фундамента, отношения ширины фундамента и
Глубины, принимаемой для прямоугольных фундаментов шири-
ной b равной а .для крултдх фундаментов радиусом г
равной и соотношения сторон прямоугольного фундамента
т] ~ 1/Ь. где / — зге .глина.
Распределение дополнительных вертикальных давлений за-
висит от площади загрузки (рис. 8.4), На любой заданной глуби-
не сжимающие вертикальные напряжения тем больше, чем боль-
ше размер фундамента, при прочих равных условиях. Если на
некоторой глубине расположен слабый прослой, то при одной и
той же средней нагрузке его влияние на величину осадки также
будет зависеть от размера фундамент3
Если на осадку фундамента могут повлиять нагрузки от со-
седних фундаментов необходимо их учесть, используя метод уг-
ловых точек |1|. В этом случае дополнительно определяется рас*
пределение нормальных давлений по вертикалям, проходящим
108
Рис. 8.4. Зависимость распределения вертикальных напряжений
от ширины фундамента
под углами «фиктивных фундаментов» (рис. 8.5). Распределение
по глубина нормальных давлений, обусловленных нагрузкой от
соседнего фундамента, передающего на породы дополнительное
давление в любой точке С в пределах или за пределами рассчи-
тываемого фундамента, находится алгебраическим суммированием
Рассчитываемый фундаме,.
Рис. 8.5. Взаимное расположение рассчитываемого и влияющего фундаментов
(а) и схема расположения «фиктивных фундаментов» (5) для расчета распреде-
ления по глубине дополнительных вертикальных давлений в центре С рассчиты-
ваемого фундамента по формуле 8.3.3, учитывающей влияние соседнего фунда-
мента (к- 1)
давлений в угловых точках Р' нескольких фиктивных фундамен-
тов, равномерно загруженных тем же дополнительным давлением
Ро. Тогда вертикальное давление на любой глубине z по вер-
тикали, проходящей через центр рассчитываемого фундамента, с
учетом нагрузки от соседних к фундаментов, будет равно:
к п
где Р/ — дополнительные давления вдоль вертикальной линии,
проходящей через центр рассматриваемого фундамента, передавае-
мые соседними фундаментами; Р/ — дополнительные давления под
угловыми точками необходимого числа п фиктивных фундаментов.
Для определения глубины активной зоны должны быть извест-
ны модули деформации и в отдельных случаях коэффициенты
поперечной деформации всех горизонтально залегающих в осно-
вании сооружения слоев пород.
Глубина сжимаемой толщи основания Я ограничивается ис-
ходя из соотношения величин дополнительного давления от фун-
дамента Рн или с учетом влияния соседних фундаментов P# (г
вертикали» проходящей через его центр) и природного давления
на той же глубине ан • При наличии грунтовых вод природное
давление вычисляется с учетом взвешивающего действия воды.
Для песчаных и глинистых грунтов это соотношение допус-
кается принимать равным: Pff=0,2otf.
Если найденная нижняя граница сжимаемой толщи закан-
чивается в слое грунта с модулем деформации £45 МПа или если
такой слой залегает ниже этой границы, он должен быть вклю-
чен в состав сжимаемой толщи. В этих случаях граница сжимае-
мой толщи определяется соотношением Рй-0,1оя.
Для расчета осадки основание разбивается на слои одинако-
вой мощности. При этом необходимо, чтобы новые границы со-
впали с природными (геологическими) границами, разделяющи-
ми слои с различными деформационными свойствами Осадка
основания фундамента рассчитывается методом послойного сум
миро ван ия и определяется (с учетом: и без учета влияния сосед-
них фундаментов) по формуле:
" рр
(8,3.4)
i=l
где 5— конечная (стабилизированная) осадка фундамента; п —
число слоев, на которое разделена по глубине сжимаемая толща
основания; Д — толщина /-го слоя грунта; Д— модуль деформа-
ции /-го слоя грунта: Р, — среднее дополнительное (к природно-
му) давление в /-м слое грунта, равное полусумме дополнительных
давлений Рг на верхней и нижней границах этого слоя, определяе-
мо
мых по формуле (8.3.2) для случая, когда не учитывается влияние
соседних фундаментов, и по формуле (8.3.3) при учете этого влия-
ния; Р — безразмерный коэффициент, принимаемый равным 0,8.
Коэффициент р вводится, чтобы учесть отсутствие бокового
расширения пород при их осадке Он зависит от коэффициента
Пуассона, и его величина может быть получена из уравнений
совместности. Если в уравнениях (2.2.11) принять сх = 0 или ег = 0,
гак как в горизонтальных направлениях деформация отсутству-
ет, то деформация в вертикальном направлении при учете равен-
ства горизонтальных напряжений может быть определена следу-
ющим образом:
, (1+ ц)0 - 2g) с.
* 1 - ц Е
Формула послойного суммирования (8.3.4), когда деформируе-
мое основание можно рассматривать как один слой мощностью
Н. представляется в виде:
Н р Е 1
.. д, - (1 т ц)(1 - 2ц)
Из формул (8.3.5) и (8.3 б) видно, что р = ' *7 ——
при р. = 0,27. ц
(8.3.6)
и 0 = 0,8
Если рассматривается случай расчета основания в соответ-
ствии со схемой 2, то принимается, что осадка вызывается пол-
ным средним давлением, действующим по подошве фундамента
без вычета природного давления. Расчетная величина толщины
линейно деформируемого слоя берется до кровли грунтов с мо-
дулем деформации Е> 100 МПа, а для фундаментов больших раз-
меров при модуле деформации £>10 МПа по формуле:
#раСЧ = (#0 + ЦЬ)Кр,
(8.3.7)
где Hon v — принимаются соответственно равными для основа-
ний, сложенных глинистыми грунтами, 9м и 0,15, песчаными
грунтами — 6 м и 0,1; b — ширина фундамента. Коэффициент Кр
принимается равным 0,8 при среднем давлении под подошвой
фундамента р - 100 кПа; Кр~ J,2 при р = 500 кПа, а при промежу-
точных значениях — по интерполяции. Расчетная величина (НрЛСЧ)
толщины линейно деформируемого слоя увеличивается на тол-
щину слоя грунта с модулем деформации £<10 МПа, если этот
слой расположен ниже, Ярасч и его толщина меньше 5 м. При боль-
шей мощности слоя такого грунта, а также если вышележащие слои
грунта имеют модуль деформации £<10 МПа, осадка вычисляет-
ся по расчетной схеме линейно деформируемого полупространства
методом послойного суммирования. Осадка основания отдель-
ного фундамента по расчетной схеме основания в виде линейно
111
деформируемого слоя конечной толщины определяется в соответ-
ствии с указанием СНиП [2] = Расчет по этой схеме производится
для определения осадки жестких фундаментов, с равномерно рас -
пределенной нагрузкой по ограниченной плошадм*
При расчете деформаций основания используются расчет-
ные схемы, основанные на предположении о линейной дефор-
мируемости полупространства. Следовательно, среднее давление
на основание под подошвой фундамента не должно быть больше
некоторой величины, называемой расчетным давлением, превы-
шение которой может вызвать необратимые деформации в поро-
дах основания» проявляющиеся в виде сдвигов. Расчетное давле-
ние определяется по формуле, приведенной в СНиП [2], в
зависимости ОТ прочностных характеристик (утла внутреннего
трения и сцепления) пород основания.
8.4, Расчет оснований по несущей способности
Расчет оснований по несущей способности осуществляется
для обеспечения прочности и устойчивости оснований, а также
предотвращения сдвига фундамента по подошве или его опроки-
дывания, что может привести к невозможности эксплуатации
сооружения.
Расчет оснований по несущей способности производят исхо-
дя из условия:
Лг<^-, (8.4.1)
Л н
где N — расчетная нагрузка на основание, Ф — несущая способ-
ность основания, Кн — коэффициент надежности, устанавливае-
мый в зависимости от ответственности здания или сооружения и
степени изученности грунтовых условий и принимаемый равным
не менее 1,2.
Несущая способность (прочность) оснований, сложенных
скальными грунтами, независимо от глубины заложения фунда-
ментов вычисляется по формуле:
Ф - КСЫ ,
где /?£-* расчетное значение временного сопротивления образ-
цов скального грунта сжатию в водонасыщенном состоянии; b и
/ — приведенные ширина и .длина фундамента: Ь — Ь — 2еь и
1=1- 2е,, где е, и е, — соответственно эксцентриситеты прило-
жения равнодействующей всех нагрузок в направлении продоль-
ной и поперечной осей фундамента.
Если основание сложено нескальными грунтами, то его не-
сущая способность определяется из условия, что в грунте образу-
112
ется поверхность скольжения, охватывающая всю подошву фун-
дамента или сооружения. При этом предполагается, что соотно*
шение между нормальным о и касательным т напряжениями по
всей поверхности скольжения, соответствующее предельному
состоянию основания, подчиняется зависимости Кулона
T~atgip + c,
где ф и с —- расчетные значения утла внутреннего трения и удельно-
го сцепления грунта. В случае, когда основание сложено медленно
уплотняющимися водонасыщенными глинистыми в заторфован-
ными грунтами, его несущая способность должна определяться с
учетом уменьшения касательного напряжения т по поверхности
скольжения за сжег образования избыточного давления в поро-
вой воде и. Тогда соотношение между нормальными и касатель-
ными напряжениями примет вид:
г = (о - fc)tg (р + с.
Несущая способность оснований из нескальных грунтов оп-
ределяется на основе теории предельного равновесия пород осно-
вания путем решения системы уравнений (2.3.6) совместно с ус-
ловием предельного равновесия (2.5.2). Приложение нагрузки
приводит к уплотнению пород основания. Начальной критичес-
кой нагрузкой называется нагрузка такой интенсивности, при ко-
торой заканчивается уплотнение грунта, начинается формирова-
ние упругого ядра и появляются площадки сдвига в зоне смежной
с упругим ядром (рис. 8.6) При начальной критической нагрузке
нормальные и касательные напряжения для появляющихся пло-
щадок сдвига связаны условней предельного равновесия. Расчет-
ное давление, определяемое при расчете основания по деформа*
циям? не должно превышать начальной критической нагрузки
Предельной критической нагрузкой является такая нагрузка,
когда полностью заканчивается развитие областей предельного
равновесия и образуется поверхность сдвига При расчетах несу-
щей способности допускается образование зон пластических де-
формаций на глубину z (см. рис, 8,6).
Если основание сложено однородными грунтами и фунда-
мент имеет плоскую подошву, то его несущая способность Ф для
вертикальной нагрузки
определяется с примене-
нием аналитических ре-
шений по формуле:
Рис 8,6. Уплотнение основа-
ния под фундаментом: z— глу-
бина, на которую допускается
развитие пластических дефор-
маций
113
Ф — bl (Ab у 4- Bhy' + De), (8.4.2)
где b Я I — ширина и длина фундамента; Л — глубина заложе-
ния фундамента; у и у' — расчетные значения объемного веса
грунтов, находящихся в пределах возможной призмы выпирания
ниже и выше подошвы фундамента, определяемые для песчаных
грунтов с учетом взвешивающего действия грунтовых вод; с —
расчетное значение удельного сцепления грунта; А, В, D — безраз-
мерные коэффициенты, зависящие от угла внутреннего трения <р
грунтов основания, углов наклона к вертикали равнодействую-
щей всех нагрузок и соотношения сторон подошвы прямоуголь-
ного фундамента.
Несущая способность основания определяется графоаналити-
ческим методом с построением круглоцилиндрических поверхнос-
тей скольжения в том случае, когда основание сложено неоднород-
ными грунтами или водонасыщенными глинами и затор^юванными
грунтами, фундаменты расположены на откосе, под откосом или
на крутопадающих пластах и др. Для определения несущей спо-
собности основания этим методом находится положение центра и
величина радиуса наиболее опасной окружности, выделяющей
сдвигаемую часть грунта основания. Несущая способность осно-
вания считается обеспеченной, если отношение моментов сил,
препятствующих сдвигу по выбранной поверхности скольжения и
сил сдвигающих, составляет величину не менее 1,2. Несущая спо-
собность оснований, сложенных водонасыщенными грунтами, оп-
ределяется без учета их утла внутреннего трения (<р = 0)
При действии на фундамент значительных горизонтальных
усилий обязательно производится расчет фундамента на сдвиг
по его подошве. В этом случае коэффициент надежности должен
быть не менее 1,2 и определяется по формуле:
(8.4.3)
где ГТуд и £ГСДВ — суммы проекций расчетных удерживаю-
щих и сдвигающих сил на плоскость скольжения.
8.5. Особые случаи расчета несущей способности
и деформаций оснований
Методика расчетов деформаций и несущей способности, при-
веденная в предыдущих разделах, может быть использована в
самых простых случаях приложения нагрузки и строения и свойств
пород основания В более сложных случаях необходимо приме-
114
нять нестандартные подходы и производить расчеты по несколь-
ким видам деформаций. Если, например, фундамент передает на
основание внецентренную нагрузку, то необходимо определять
крен фундамента, при неоднородном строении основания оце-
нивают неравномерность осадки. При проектировании опор воз-
душных линий электропередачи необходимо производить расчет
основания с учетом возможного действия выдергивающих сил.
При проектировании мостов и водопропускных труб необходи-
мо учитывать возможность размыва пути и др.
Если основание сложено просадочными грунтами, то при
расчетах их деформирования необходимо учитывать, что при за-
мачивании водой в этих грунтах могут возникнуть дополнитель-
ные деформации — просадки. Замачивание пород основания
может происходить как в результате искусственного обводнения
производственными водами, так и при подъеме уровня грунто-
вых вод или при повышении влажности просадочного грунта,
вызванном нарушением природных условий испарения грунто-
вой влаги, например, при асфальтировании территории.
Просадочные деформации учитываются при величине отно-
сительной просааочности гр унтов 6пр > 0,01. Дополнительные вер-
тикальные деформации (просадки) возникают, во-первых, в пре-
делах деформируемой зоны основания от подошвы фундамента
до глубины, на которой суммарные вертикальные напряжения от
нагрузки фундамента и собственного веса пород равны началь-
ному просадочному давлению рр. Во-вторых, просадки происхо-
дят в нижней части просадочной толщи, начиная с глубины, на
которой вертикальные напряжения от собственного веса пород
равны начальному просадочному давлению рП|„ и до нижней гра-
ницы просадочной толщи. Наконец, горизонтальные деформа-
ции возникают при просадке грунтов от их собственного веса в
пределах криволинейной части просадочной воронки. Суммар-
ная величина вертикальной деформации основания из просадоч-
ных грунтов складывается из осадок от нагрузки, передаваемой
фундаментом, и просадок от нагрузки фундаментов и собствен-
ного веса грунта.
При расчетах оснований, сложенных набухающими грунта-
ми, необходимо учитывать дополнительные деформации: увели-
чение этих грунтов в объеме при замачивании, а при последую-
щем снижении влажности способность их давать усадку. Величина
набухания грунтов основания зависит от действующего давления
по подошве фундамента, вида и состояния грунта, площади за-
мачивания, физических и химических свойств жидкости, зама-
чивающей основание.
Основания, сложенные заторфованными грунтами или ила-
ми, отличаются значительной водопроницаемостью, большой
115
сжимаемостью, медленным протеканием осадок во времени, из-
менчивостью И анизотропией прочностных, деформационных,
фильтрационных' м реологических свойств, а также возможнос-
тью проявления ютами тиксотропных свойств при динамических
воздействиях Расчет оснований по несущей способности и по
деформациям в этом случае должен производиться с учетом ско-
рости приложения нагрузки; возникновения гидродинамических
сил, изменения напряжений в скелете грунта вследствие процес-
са консолидаций и анизотропии прочностных свойств водона-
сыщенных пород и илов.
При расчетах оснований, сложенных элювиальными грунта-
ми, необходимо учитывать высокую неоднородность этих грун-
тов по прочностным и деформационным свойствам и их способ-
ность снижать прочностные свойства при вскрытии котлованов.
Если основание сложено засоленными грунтами, то при его
длительном замачивании и фильтрации через него воды возмож-
на суффозионная осадка, зависящая от свойств грунта, длигел?
ности фильтрационного замачивания и действующего давленияэ
которую необходимо учитывать при расчетах деформирования
основания. Суффозионная осадка определяется суммированием
осадок отдельных слоев основания, которые находятся по значе-
ниям относительных величин суффозионной осадки.
При строительстве на насыпных грунтах расчет деформаций
основания необходимо производить е учетом возможности само-
уплотнения от собственного веса насыпного грунта, особенно в
случае действия вибрационной нагрузки от сооружения юти транс-
порта, Кроме того следует иметь в виду, что насыпные грунты
обладают большой и неравномерной сжимаемостью.
Расчет устойчивости фундаментов при действии сил мороз-
ного пучения фунтов основания производится, если грунты со-
прикасающиеся с боковой поверхностью фундаментов или рас-
положенные под их подошвой, являются пучинистыми и
возможно их промерзание.
Виды и методика расчетов оснований зависят не только от
строения, свойств и состояния слагающих их пород, но могут
определяться и расположением района строительства Так, в сей-
смических районах с сейсмичностью 7, 8 и 9 баллов расчеты ос-
нований зданий и сооружений должны производиться с учетом
требований СНиП [3]. Расчеты оснований по несущей способ-
ности выполняются, как правило, только от действия вертикаль-
ной составляющей нагрузки, передаваемой фундаментом, исхо-
дя из условия:
т
N <—
кн ’
116
где ТУверт — вертикальная составляющая нагрузки5 Ф — несущая
способность основания, Ан = 1,5 — коэффициент надежности, mQ -
сейсмический коэффициент, принимаемый для скальных, круп-
нообломочных и песчаных грунтов равным 1,2, насыщенных мо-
дой и глинистых грунтов— 0,7, для остальных, грунтов— 1,0.
Горизонтальная составляющая нагрузки учитывается при про-
верке устойящвости зданий на опрокидывание и сдвиг по подо-
шве фундамент#.
При строительстве на подрабатываемых территориях расчет
оснований зданий и сооружений необходимо производить с уче-
том возможности неравномерного оседания земной поверхнос-
ти, сопровождаемою горизонтальными деформациями сдвигаю-
щегося грунта, происходящего в результате производства горных
работ и перемещения грунта в выработанное пространство.
Выполнение всех расчетов необходимо производить в соот-
ветствии с рекомендациями, которые приводятся в соответству-
ющих приложениях СНиП [2].
Контрольные вопросы
1. Какие нагрузки испытывают основания сооружений?
2. Виды деформаций оснований.
3. Какими показателями характеризуется деформация осно-
вания сооружения?
4 Какие схемы используются для расчета осадки основания
сооружений?
5. Какие факторы влияют на характер распределения напря-
жений в породах под фундаментом?
6. Какое влияние на характер распределения напряжений в
породах основания оказывают грунтовые воды?
7. Исходя из каких условий и с какой целью определяется
глубина активной зоны
8. Как учитывается влияние на осадку сооружения соседних
фундаментов?
9. Сущность метода послойного суммирования.
10. Как определяется несущая способность основания в зави-
симости от состава и строения слагающих его пород?
II. Что такое начальная и предельная критическая нагрузка?
12. Особые случаи расчета несущей способности и деформа-
, оснований.
ГЛАВА 9. МЕТОДЫ РАСЧЕТА УСТОЙЧИВОСТИ СКЛОНОВ,
ОСНОВАННЫЕ НА АНАЛИЗЕ НАПРЯЖЕННОГО СОСТОЯНИЯ
ПОРОД В ПРЕДЕЛАХ ВСЕГО СКЛОНА
Расчеты устойчивости склонов и откосов производятся при
решении следующих практических задач:
при оценке устойчивости обвало- и оползнеопасных склонов;
для определения оползневого давления в связи с проектиро-
ванием подпорных сооружений;
при проектировании откосов плотин, дамб, насыпей и бор -
тов карьеров и котлованов;
с целью прогноза изменения устойчивости склонов и ополз-
невого давления при различных видах внешних естественных и
искусственных воздействий.
Для расчета устойчивости склонов и откосов разработано боль-
шое число методов, которые можно разделить на две группы: ме-
тоды, основанные на анализе напряженного состояния массива
горных пород (1) — в пределах всего склона; (2) — только вдоль
известной ИЛИ предполагаемой поверхности скольжения.
К первой группе относятся, во-первых, методы, основанные
на построении профиля склона или откоса предельного равнове-
сия, во-вторых, методы, использующие сравнение напряженно-
го состояния массива горных пород, слагающих склон или от-
кос, с их прочностными характеристиками.
Ко второй группе относятся методы расчета устойчивости
оползневых тел, когда их поверхность скольжения может быть
аппроксимирована, во-первых, системой плоских поверхностей
скольжения, во-вторых, кр}тло-цилиндрической поверхностью
скольжения
Расчеты с помощью методов второй группы могут быть вы-
полнены как Для оползней, когда поверхность их скольжения
известна или ее положение определяется геологическим строе-
нием склона, так и для склонов и откосов, когда поверхность, по
которой происходит нарушение их устойчивости, неизвестна (по-
верочные расчеты).
9.1. Понятие о коэффициенте устойчивости
Оценка устойчивости склонов и откосов производится путем
расчета коэффициента устойчивости или запаса, а также может
быть установлена с помощью дефицита устойчивости. На вели-
чину коэффициента или дефицита устойчивости оказывают вли-
118
яние: 1) неточность определения исходных параметров; 2) непол-
ное соответствие принятой расчетной схемы природному объек-
ту; 3) погрешность метода расчета
Поэтому величина коэффициента или дефицита устойчивос-
ти всегда является приближенной.
Потеря устойчивости оползня происходит либо в результате
возрастания действующих на оползневое тело сдвигающих уси-
лий, либо при уменьшении прочности пород вдоль поверхности
скольжения. Поэтому возможны, по крайней мере, два подхода к
определению коэффициента запаса. Если нарушение устойчиво-
сти оползневого тела будет происходить при возрастании сдвига-
ющих усилий до значений равных по величине удерживающим
силам или, что то же. самое, до критических или предельно допу-
стимых значений, то коэффициент запаса может быть определен
как отношение:
удер
уст ~ _
1СДВИГ
^крит
”дейст
где тдейст и ткрит— соответственно действующее и критическое
значения сдвигающего усилия Аналогично коэффициент запаса
может быть определен как отношение моментов этих сил!
м М
. , удер _ J 1 крик
Луст ~ 1/ I/
' СДВИГ ' деЙСТ
Если принять, что нарушение устойчивости оползневого тела
будет происходить в результате снижения прочности пород вдоль
поверхности скольжения, то в этом случае коэффициент устой-
чивости может быть определен как отношение действующих вдоль
поверхности скольжения прочностных характеристик к тем по-
казателям прочностных свойств, при которых оползневое тело
придет в состояние предельного равновесия, т.е. к критическим
значениям прочностных характеристик:
> tCT _ ст
Уст (О С
ткрит ъкрит
Определение коэффициента запаса может осуществляться как
аналитическими способами, так и с помощью графических по-
строений. В большинстве случаев расчет устойчивости склонов и
откосов и определение коэффициента устойчивости производит-
ся для плоских сечений, построенных по линиям, совпадающим
с наиболее вероятным направлением смещения оползневого тела.
Кроме приведенных вариантов определения коэффициентов за-
паса, возможны другие способы их введения, например, как от-
ношение среднего утла профиля откоса, который находится в
состоянии предельного равновесия, к среднему углу профиля
оцени! е> . го скг она.
9.2 Методы, основанные на построении профиля
склона предельного равновесия
Метод В.В. Соколовского
Этот метод предполагает построение откоса предельного рав-
новесия в Том случае, когда он формируется в среде, обладаю-
щей внутренним фением и сцеплением.
Основными уравнениями, определяющими плоское дефор-
мированное состояние любой среды находящейся в состоянии
предельного равновесия, в системе прямолинейных прямоуголь-
ных координат хОу являются дифференциальные уравнения рав-
новесия в сочетании с условием предельного равновесия:
(9.2.1)
л
+ . -н 2с • ctgqf д
(9.2.2)
где р-" плотность, ф- угол внутреннего трения. : - удельное
сцепление пород, слагающих откос.
Система трех уравнений (9.2ЛХ (9.2.2) содержит три неизве-
стные компоненты напряжений оЛ, о>: и и поэтому задача о
нахождении этих компонент при статических контурных данных
(граничных условиях) является статически определимой.
В.В. Соколовским был предложен [3] метод приближенного
решения системы уравнений (9.2.1), (9.2.2), который позволяет
определить форму свободного от давления криволинейного кон-
гура, при котором откос находится в предельном равновесии. На
рис. 9.1 приведен профиль откоса предельного равновесия, кото-
рый имеет горизонтальную поверхность, вертикальный уступ
высотой h и криволинейный контур 0/?, наклоненный к горизон-
ту под углом р, а в точке 0 имеющий вертикальную касательную
или наклоненный к горизонту под углом = тс/2. В этом откосе
можно выделить две области: непредельную, занимающую слой
над положительной полуосью Ох, мощностью Л, и предельную,
расположенную ниже полуоси Ох Предельная область делится
Рис. 9.1. Криволинейный профиль откоса предельного
равновесия
на зону ДОЛ, где действуют условия невозможности расширения
пород * горизонтальном направлении,, и зону AQB, гае напряже-
ния распределены сложным образом.
Поле напряжений в непредельной части откоса вблизи вер-
тикального уступа может быть определено следующим образом:
-<у = • :х = ' . = ' С
Нормальное напряжение на вертикальных площадках равно
нулю так как наличие вертикального уступа дает воз
можность породам, расположенным в этой области свободно де-
формироваться в горизонтальном направлении. Касательные на-
пряжения равны нулю ) г закона парности
касательных напряжений и их отсутствия на горизонтальной по-
верхности откоса. Следовательно, ол и az являются главными на-
пряжениями. Однако такое распределение напряжений в этой
области может наблюдаться только до некоторой предельной глу-
бины, зависящей от прочности слагающих вертикальный уступ
пород. В предельном состоянии соотношение между главными
напряжениями может быть определено по кругу Мора:
(9 2 4)
или в рассматриваемом случае, когда
а2 = ох = 0 :
п v .... 2с cosq
------ L ~ SIH m откуда 03, = -7- Г.. .
т 2с • '-----------------------------------si -«ф
Поскольку предельное напряженное состояние имеет место уже
на положительной полуоси Ox, го из условия непрерывности
121
компоненты ov можно установить максимальную высоту’ верти-
кального уступа, которая называется критической высотой, или
мощность слоя, занимающего непредельную область:
Р£(А + у)~
2с cos ф
1 - sin ф
а при у = 0:
Л - — • COS<P ... (9.2.5)
sin ф
Таким образом, в непредельной области компоненты напряже-
ния имеют вид
2с * COS Ср л л /л
о» = =---s—Ь + Р£У, = 0, тп, = 0. (9.2.6)
у 1 srncp ’
В зоне ЯоОЛ предельной области компоненты напряжений будут:
2с-cosф
- - ,-~ + Р8У
1 - sin ф
1 - sin <р
r+sincp ’
0
Величина нормального напряжения сх, действующего на верти-
кальных площадках, устанавливается из условия невозможности
расширения пород, слагающих склон, в горизонтальном направ-
лении из (9 2.4). принимая О, ~ ау, так k8ktv.= 0. Напряже-
ния в переходной зоне (Л05) распределены сложно и изменяются
от напряжений в зоне ДОЛ, гае их распределение описывается
формулами (9.2.7), до нулевых значений нормальных и касатель-
ных напряжений на криволинейной поверхности откоса 05.
На рис 9.2 приведены формы криволинейных контуров от-
косов для различных углов внутреннего трения ф от 5 до 40° (с
шагом 5°), которые получены в результате предложенного В, В Со-
коловским численного решения системы уравнений (9.2.1), (9.2.2).
Результаты даны в безразмерных переменных х и у с характерной
длиной / = — .
PS
Метод Н.Н. Маслова
Метод равнопрочного откоса, или метод Fp [2] является при-
ближенным способом построения профиля предельного равно-
весия (равнопрочного откоса), сложенного песчано-глинистыми
породами. Этот метод может быть применен для оценки устой-
чивости склонов, имеющих однородное строение или сложен-
ных горизонтально залегающими породами с различными проч-
ностными свойствами, а также для проектирования откосов с
заданным коэффициентом устойчивости.
122
Оценка устойчивости, природного склона производится срав-
нением его крутизны с построенным профилем предельного рав-
новесия. Если профиль предельного равновесия имеет большую
крутизну. чем естественный склон, то последний является устой-
чивым, а степень его устойчивости определяется как отношение
угла откоса предельного равновесия к углу естественного склона.
При этом отношение углов профиля предельного равновесия и
естественного склона определяется для всех горизонтов по высоте
откоса и за коэффициент устойчивости всего оцениваемого скло-
на принимается минимальное значение этого отношения.
Если профиль равнопрочного откоса совпадает с профилем
оцениваемого склона, то естественный склон находится в состоя-
нии предельного равновесия (т.е. имеет коэффициент устойчи-
вости близкий к единице).
Природный склон с крутизной, превышающей уклон про-
филя предельного равновесия хотя бы в одной точке, является
неустойчивым.
Рассмотрим случай, когда склон образован в идеально сыпу-
чих породах (с= 0) и имеет крутизну а. Известно, что профиль
склона предельного равновесия, сложенного песками, будет иметь
крутизну, равную углу внутреннего трения гр. Тогда, если а><р,
склон неустойчив, при а = ф достигается состояние предельного
равновесия, если и<ф, склон является устойчивым с некоторым
запасом, который может быть выражен с помощью коэффициен-
та устойчивости:
Используя выражение (9 2.8) .row несвязного грунта, можно
построить устойчивый откос с заранее заданным коэффициен-
том запаса, что и осуществляется при проектировании насыпных
сооружений: плотик, дамб и др.
В случае, когда склон сформирован в связных, например,
глинистых породах (с*0), оценка его устойчивости может быть
выполнена следующим образом. Рассмотрим условие устойчиво-
сти некоторого объема грунта весом Q, лежащего на откосе кру-
тизной а (рис. 9.3,а). Нормальная составляющая веса Р- Q cos а,
а сдвигающая T-Q sin а. Сопротивление сдвигу т этого объема
грунта в соответствии с законом Кулона будет складываться из
силы трения я силы сцепления! С.
С = Р tg ф +
(9.2.9)
Рис. 9.3. Схема для расчета профиля предельного равнове-
сия по методу Н.Н. Маслова, а — условие равновесия эле-
ментарного объема на склоне; б — схема для определения
угла устойчивого откоса
1,
Если выражение (9.2.9) разделить на Р, то получится:
-р = W + у- = Ш ¥ > - ?р
и сопротивление сдвигу будет равно:
t = Р tgу р, (9 210)
где у р — угол сопротивления сдвигу, a Л, = tg vР представляет
собой коэффициент сопротивления сдвигу [2| При равновесии
сопротивление сдвигу t должно быть равно сдвигающей силе Г:
Т или Р tg Tt откуда
Q cos а • tg у р Q sin а,
tg¥ =liH«=tga. (9.2.11)
cosa
w p — a.
i JT
Таким образом, для определенной точки откоса угол устойчиво-
го откоса а для связного грунта равняется углу сопротивления
сдвигу породы Если склон устойчив, то коэффициент запаса
для некоторой его точки опреде ляется из уравнения;
Угол сопротивления сдвигу' является величиной перемен-
ной и зависит от нормальной нагрузки Р. Если нагрузка Р возра-
стает, л» угол V? стремится к углу внутреннего трения <р (рис. 9.3,6),
при уменьшении нагрузки Р угол Vr увеличивается и при Р = 0
угол уг= 90°.
Поскольку угол устойчивого откоса равен углу сопротивле-
ния сдвигу’, то его величина так же будет зависеть от нагрузки Р
и, следовательно, для определения угла устойчивого откоса не-
обходимо знать, как изменяется величина Р по всему откосу.
Основным предположением, на котором основывается опреде-
ление величины Р и построение профиля устойчивого откоса,
является гипотеза о гидростатическом распределении напряже-
ний в откосах, сложенных глинистыми породами. Следователь-
но, величина напряжения в любой точке откоса, сложенного изот-
ропными глинистыми породами, не зависит от ориентации
площадки, а определяется только ее глубиной: P=yz, или если
откос состоит из различных по плотности горизонтально залега-
ющих слоев глинистых пород:
(9.2,13)
%
где п — число слоев, расположенных выше рассматриваемой точ-
ки, Y<=P<g— объемный вес пород /-го слоя, й, — его мощность
(рис. 9.4).
п Рп с„
1 Pi Ct <pi
Рис. 9.4. Криволинейный профиль откоса предельного равновесия
Отсюда следует, что профиль устойчивого откоса будет иметь
вогнутую форму: в верхней части склон будет очень крутым, близ-
ким к вертикальном)', ниже он выполаживается и при очень вы-
соком склоне его угол а в нижней части приближается к углу
внутреннего трения пород ф
Для построения профиля устойчивого откоса необходимо
иметь инженерно-геологический разрез природного склона, ус-
тойчивость которого следует определить, или профиль проекти-
руемого откоса и располагать данными о плотности (р) и проч-
ностных свойствах, характеризующих сопротивление пород сдвигу
(с и <р), для каждого слоя, которыми сложен склон.
Построение профиля устойчивого откоса может быть выпол-
нено как аналитическим способом, так и графическим. При по-
строении профиля с помощью аналитического метода необходи-
мо определить абсциссу х точки на поверхности откоса,
отвечающую глубине z: x=f(z)- Производная f'(z) = tg 0, где 0 —
угол наклона касательной, проведенной к линии поверхности
откоса, к оси z и 0 = п/2 -у (рис. 9.4). Следовательно /'(z) = ctg у,
а так как tg у = tg ф + —, о = у?, то f'(z) = 1 /tg у = -——-.
о tg ф • yz + с
Проинтегрировав это выражение и определив постоянную ин-
тегрирования из условия, что при z=0 и х-0, получим формулу.
х = —-г— [tg ф • yz + с In с - с -In(tgф yz н-с)], (9.2.14)
ytg ф
по которой легко построить кривую, отвечающую профилю пре-
дельного равновесия в случае, если откос сложен однородными
породами.
Аналитический способ построения профиля предельного рав-
новесия является более точным по сравнению с графическим
способом, но применяется тогда, когда склон имеет однородное
строение. Если склон сложен различными по механическим свой-
ствам породами, то аналитический прием становится неоправ-
данно громоздким, и поэтому в таком случае построение профи-
ля предельного равновесия предпочтительнее осуществлять
графически.
Построение профиля устойчивого откоса графическим спо-
собом выполняется в следующей последовательности
1. Природный склон или проектируемый откос делится на я
горизонтальных слоев, желательно одинаковой мощности (см.
рис. 9.4). Если природный склон сложен горизонтально залегаю-
щими породами, то деление склона на слои производится таким
образом, чтобы границы раздела совпали с геологическими гра-
ницами При уменьшении мощности слоев точность построения
профиля предельного равновесия повышается.
2. Вычисляется среднее напряжение в слое:
затем определяется у, по графику сопротивления сдвигу (рис. 9.3,6)
или рассчитывается по формуле: у, •- arctg tgср, +
/ /
3. Для каждого слоя, начиная снизу, строится равновесный
откос крутизной а, = у, или откос с заранее заданным коэффи-
циентом запаса к: tga,- - tg хр* / к Для этого, начиная с нижней
точки откоса z = H, где Н— общая высота откоса, проводится
линия под утлом а„ = в пределах всего самого нижнего слоя п
до пересечения с границей выше расположенного слоя п - 1. Да-
лее в пределах слоя п - 1 от полученной точки пересечения про-
водится линия поп углом an_] = v«-i Д° пересечения с границей
следующего выше расположенного слоя л - 2 и так до выхода
откоса на поверхность.
Таким образом, этим методом можно решить две основные
задачи: найти коэффициент устойчивости природного склона
путем сопоставления его углов с установленными углами откоса
предельного равновесия или спроектировать устойчивый откос с
любым заданным коэффициентом запаса.
127
За коэффициент устойчивости природного склона принима-
ется минимальное значение из отношений углов оцениваемого
(а,*) и предельного (а#) склонов, определяемых для всех слоев.
tga*
tga
Метод равнопрочного откоса страдает недостатком, так как
крутизна склона предельного равновесия, построенного по это-
му методу, зависит от числа прослоев, на которые разбивается
склон. Чем больше слоев, тем круче линия построенного откоса.
Этот недостаток устранен в методе, предложенном М.Н. Троиц-
кой [1, 4].
Контрольные вопросы
1. Какие существуют методы оценки устойчивости склонов?
2. Способы определения коэффициента устойчивости.
Ь. Как осуществляется построение профиля предельного рав -
новесия по методу В В. Соколовского?
4, На каких предположениях основаЯ метод равнопрочное о
откоса Н JL Маслова?
5. Какие сведения необходимы для построения профиля ус-
тойчивого откоса?
6. В чем заключается графический способ построения про-
филя устойчивого откоса?
ГЛАВА 10. МЕТОДЫ РАСЧЕТА УСТОЙЧИВОСТИ
СКЛОНОВ ПО ИЗВЕСТНОЙ ПОВЕРХНОСТИ
СКОЛЬЖЕНИЯ
Ко второй группе относятся методы расчета устойчивости
оползневых тел, которые применяются, когда поверхность сколь-
жения оползня известна или ее положение может быть установ-
лено предположительно по геологическим признакам, или, на-
пример. в случае анализа устойчивости однородных склонов или
искусственных откосов, когда рассматривается серия возможных
поверхностей скольжения с целью выбора наиболее опасной по
верхности.
Существует множество натурных и теоретических методов
определения поверхности скольжения. Во-первых, положение
поверхности скольжения может быть установлено в результате
визуального наблюдения за породами при бурении скважин и
проходке шурфов — по зеркалам и штрихам скольжения: по по-
вышенной влажности и низкой плотности и т.д : по данным ди-
намического и статического зондирования, с помощью которых
могут быть выявлены области пониженного сопротивления пе-
ремещению зонда; по поведению установленных глубинных ре-
перов. по длительным йаблюдениям за искривлением обсадки
скважин и т.д. Во-вторых, положение поверхности может быть
определено предположительно на основании анализа геологичес-
кого строения, например, по приуроченности этой поверхности
К слабым прослоям, границам раздела слоев различного состава,
свойств и происхождения, зонам повышенной трещиноватости
или отдельным трещинам и т.д. В-третьих, положение поверхно-
сти скольжения может быть установлено теоретическими мето-
дами, например методами Б М Ломизе, И В. Федорова, Г.М Ша-
хупянца [6] и
Установленную или предполагаемую поверхность скольже-
ния наиболее естественным способом аппроксимируют системой
плоских поверхностей, так как любая поверхность может быть
представлена в гаком виде. В отдельных случаях поверхности
скольжения могут быть аппроксимированы кривыми второго
порядка, например, круглоцилиндрической, параболической и др.
Если поверхность скольжения не известна, и нельзя высказать
никаких предположений о ее возможном положении в склоне,
то поверхность скольжения предполагается кругло-цилиндричес-
кой, что используется главным образом при оценке устойчивое*
ти искусственных откосов или склонов однородного строения.
129
10.1. Основные положения метода фрагментов
Основными предположениями, которые используются при
расчетах- устойчивости склонов, когда оползание происходит по
определенной поверхности скольжения, являются следующие.
1. Как правило, все расчеты устойчивости склонов произво-
дятся дня плоского сечения оползневого тела единичной шири-
ны, т.е решается плоская задача. Выбор сечения для расчета пред-
ставляет собой важный этап оценки устойчивости оползневого
гела. Обычно выбирается сечение, совпадающее с наиболее ве-
роятным направлением смещения оползня, которое может опре-
деляться максимальными значениями углов наклона поверхнос-
тей скольжения. Возможно для одного и того же оползневого
тела производить расчет его устойчивости по нескольким сече*
ничм. Поскольку оползневое тело имеет ограниченную ширину,
ТО сопротивление его смещению будут также оказывать и боко-
вые поверхности. Расчетами устойчивости это сопротивление, как
правило, не учитывается, а идет в запас устойчивости оползня.
2. Практически все расчетные методы оценки степени ус-
тойчивости склонов основаны на применении теории предель-
ного равновесия и предположения о том, что формирование на
склоне оползня происходит в результате сдвига по поверхности
скольжения в соответствии с теорией прочности Кулона-Мора,
т.е. в момент предельного равновесия вдоль поверхности смеше-
ния действует зависимость: т-гЛяфэс. В этом выражении
нормальное напряжение а является величиной, изменяющейся
вдоль поверхности скольжения и зависящей ст ряда факторов,
что вызывает затруднение при его определении. Для установле-
ния: величины и характера распределения нормального напряже-
ния на поверхности смещения используются различные подхо-
ды, что определяет разнообразие методов расчета устойчивости
оползневых тел.
3. Оползневое тело разбивается на части (блоки, фрагменты
и др.) вертикальными плоскостями с таким расчетом, чтобы каж-
дый выделенный блок опирался на одну плоскую поверхность
скольжения (рис. 10.1), с помощью которых аппроксимируют
установленную или предполагаемую поверхность смещения. При
разбиении оползня на блоки необходимо также следить за тем,
чтобы каждый блок по возможности был однородным по составу
и свойствам слагающих его пород. Каждая часть оползня пред-
ставляется абсолютно твердым телом и, следовательно, может
рассматриваться в качестве материальной точки. При смещении
оползня его части взаимодействуют между собой (действуют друг
на друга), и относительно характера этого взаимодействия могут
Г
Рис. 10.1 Разбиение оползневого тела на блоки и силы, действующие на каждый
блок
быть высказаны различные предположения, что также предопре-
деляет различие существующих методов расчета устойчивости
оползней.
Каждый из блоков, на которые разбивается оползневое зело,
испытывает действие шести внешних сил
1. На каждый блок действует собственный вес (?, величина
которого определяется исходя из плотности горных пород, слага-
ющих блок, и его объема (в плоском случае — площади):
G= pgS* (1 м),
где р — средняя плотность пород, слагающих блок, S — площадь
блока, g — ускорение свободного падения. Эта сила приложена к
центру масс оползневого тела и направлена вертикально вниз.
Если на оползне располагаются инженерные сооружения, то вес
блоков определяется с учетом величины И Направления: действия
сил, которые эти сооружения оказывают на оползневое тело.
2. Возникает реакция опоры N, направленная перпендику-
лярно плоской поверхности, на которую опирается оползневой
блок, но величина которой неизвестна.
3. Вдоль плоской поверхности скольжения действует сила тре-
ния Т, направленная в сторону’ противоположную смещению опол-
зня, и равная: Т- Ntg <р, где N— нормальная реакция опоры, tg <р —
коэффициент трения. Величина силы трения неизвестна, поскольку
неизвестной является нормальная реакция опоры.
4. Вдоль плоской поверхности скольжения возникает сила
сцепления С, направленная так же, как и сила грения, в сторону,
131
противоположную смещению оползня, И равная; С = cl., где с —
удельное сцепление, / — длина плоской поверхности скольжения.
Во многих методах удобнее пользоваться геометрическими
суммами нормальной реакции опоры /V и силами, действующи-
ми вдоль поверхности скольжения Т и С. Тогда RNT представляет
собой реакцию опоры, учитывающую нор-
Рис. 10.2. Равнодейству-
ющие нормальной реак-
ции опоры (N) и сил тре-
мапьную реакцию опоры и силу трения,
R^tc— это реакция опоры, гредс^гляю-
щая собой равнодействующую нормальной
реакции опоры И сил трения и сцепления.
В состоянии предельного равновесия рав-
недействующая RNT отклоняется от норма-
ли к поверхности скольжения на угол внут-
реннего трения ф, з равнодействующая
Rjvtc — на Угол сдвига w (рис. ГО ..2ц
5. Каждый блок оползневого тела мо-
жет испытывать давление со стороны выше
расположенного блока Е-^ и встречает zz-
ния (7) и сцепления (Q противление со стороны ниже расположен-
ного Стога Д. Обычно эти две силы взаи-
модействия блока с -эседними представляются м виде
геометрической суммы АД- = Е^ + Д-. Их величины и направ-
ление действия неизвестны.
Первые четыре СИЛЫ’ собственный вес, нормальная реакция
опоры, сцепление и трение — - пересекаются в одной точке. От-
носительно направления действия и точек приложения сил взаи-
модействия блоков высказываются различные соображения.
Золи предлогожтть, что о моме-т 7-тч^л- смещения силы
трения и сцепления действуют только вдоль поверхности скольже-
ния и полностью отсутствуют вдоль вертикальных поверхностей,
которые делят оползневое тело на части, ТО силы взаимодействия
между соседними блоками будут направлены строго горизонталь-
но. Все способы расчета устойчивости оползневых тел, исполь-
зующие это предположение, могут быть объединены в группу
методов горизонтальных сил (рис. 10.3, <ц G-0).
Если вдоль вертикальных поверхностей в момент начала сме-
шения трение и сцепление присутствуют, то силы взаимодей-
ствия между соседними блоками будут направлены наклонно, и
способы, учитывающие действие сил трения и сцепления, объе-
диняются в группу методов наклонных сил. Возникает вопрос,
под каким углом направлены силы, с которыми один блок дей-
ствует на другой. В том случае, когда вдоль вертикальных п лос-
кое гей действуют только силы трения, силы взаимодействия между
соседними блоками будут наклонены к горизонту под углом внут-
реннего трения (рис. 10.3, 8 = tp),
132
г
Рис. П). . Направления сия взаимодействия соседних блоков. Силы
направлены: а — горизонтально: J— под углом (р: в — под углом у; г —
параллельно поверхности скольжения
Если вдоль вертикальных плоскостей будут действовать не
только силы тренько /_ сцепления, :.т силы взаимодействия
между соседними блоками будут наклонены к горизонту пол уг-
лом сдвига (рис. 102, т, 0 Сдт-ко можно высказать предпо-
ложение, что углы наклона к горизонту сил взаимодействия между
соседними блоками не осязательно должны соответствовать уг-
лам внутреннего трения или сдвига, а могут быть и другими.
Например, угол наклона сильц С которой один блок действует на
другой, -может быть принят равным или какой-либо дру-
гой величине.
Наконец, существует и иной подход к установлению угла
наклона сиг взаимодействия между соседними блоками. Напри-
мер, угол наклона силы, с которой выше расположенный блок
действует на ниже расположенный, может соответствовать углу
наклона плоскости смещения, на которую опирается верхний
блок, т.е. угол наклона сил взаимодействия соседних блоков из-
меняется в соответствии с изменением углов наклона плоских
поверхностей скольжения (рис. 10.3, г, 9 = а).
В момент предельного равновесия должно выполняться ос-
новное условие статики, которым утверждается, что тело нахо-
дится в равновесии в том и только в том случае, если суммй про-
екций всех действующих на него сил на любую ось и сумма
моментов этих же сил относительно центра вращения равны нулю.
Для двухмерного случая и произвольно выбранной системы ко-
ординат лОу должно быть выполнено:
ЕУ=0: 1М=0
.» 1_Г
(10 1.1)
Однако следует заметить, что практически ни в одном из
существующих методов расчета устойчивости удовлетворить од-
новременно всем трем условиям но удаетсл, ?• выводе урав-
нений предельного равновесия чаще используется только одно
из условий (10.L1). В большинстве существующих методов для
вывода уравнения предельного равновесия проектирование дей-
ствующих на оползневое тело сил осуществляется на горизон-
тальную ось, иж на -ось, совпадающую с одной из наклонных
поверхностей скольжения, либо используется условие: равенства
нулю моментов этих сил относительно выбранного центра вра-
щения В некоторых методах используется условие равенства нулю
внутренних сил, действующих в оползневом теле, находящемся в
условиях предельного равновесия.
10.2. Методы плоских поверхностей скольжения
Методы этой группы применяются в том случае, когда по-
верхность оползания имеет сложную конфигурацию и может быть
представлена системой плоских поверхностей скольжения К этой
группе относится большое число методов, среди которых широ-
кое распространение получили методы, предложенные Р Р. Чу-
гаевым [5] и ЕМ. Шахунянцем [6].
Метод Чугаева
Этот метод применяется в том случае, когда оползневое тело
опирается на поверхность скольжения, состоящую из отдельных
плоских' участков. Оползневое тело разбивается вертикальными
плоскостями на части таким образом, чтобы каждая опиралась на
прямолинейную поверхность. Расчету подвергается так называемая
предельная схема данного оползневоготела, когда вдоль поверх-
ности скольжения действуют критические значения нормально-
го (ак) и касательного (тк) напряжений, т.е. такие величины, ко-
торые появляются в момент предельного равновесия, а свойства
грунта характеризуются критическими значениями угла внутрен-
него трения (фк) и сцеплением (ск), т.е. такими величинами, ксг-
торые надо придать грунту, чтобы рассматриваемое оползневое
тело пришло в состояние предельного равновесия. Тогда в ре-
зультате расчета в соответствии с условием тк = о’к СёФк
можно составить для оползневого тела уравнение предельного
равновесия в виде:
Ск = /<Ш-фЛ ИЛИ С,, = /(фД
(10.2.1)
Графически это уравнение выражается кривой АВ (рис. 10.4),
называемой кривой связи. Каждая точка линии АВ соответству-
ет паре критических значений угла внутреннего трения и сцеп-
ления ф*, ск. при которых рассматриваемое оползневое тело я а
ходится в состоянии предельного равновесия. Для тоге чтобы
построить линию АВ из уравнения (10.2.1), сначала определяют
значение сцепления при Фк-0г а затем значение угла внут-
реннего трения при сцеплении сс J. Полученные таким обр2
зом точки А и В соединяют прямой исходя из линейности урав-
нения (10 2.1).
Чтобы оценить устойчивость оползневого тела, необходимо
знать действительные значения угла внутреннего трения (фД и
сцепления (Сд), которыми характеризуется порода в зоне сколь-
жения в направлении смещения. Если жочка т. соответствующая
действительным значениям угла внутреннего грения и сцепления,
лежит ниже кривой связи АВ. то рассматриваемое оползневое тело
является неустойчивым, так как порода в зоне скольжения имеет
характеристики сопротивления сдвигу менее критических значе-
ний. Если в соответствии с величинами фд и сд точка т занимает
положение выше кривой связи АВ. то рассматриваемое оползне-
вое тело находится в устойчивом состоянии, при этом, чем даль*
ше точка т отстоит от кривой АВ. тем больший запас устойчиво
сти имеет оползень.
Для определения коэффициента устойчивости необходимо
через точку т провести линию АВ- параллельную линии связи
АВ, Линия АВ1 выражает связь действительных значений сцеп-
ления и угла внутреннего грения для рассматриваемого оползне-
вого тела, имеющего запас устойчивости. Искомый коэффициент
устойчивости Kv должен в аналитической форме отражать пере-
нос линии АВ в положение Af№ (см. рис. 10.4) и может быть,
исходя из подобия треугольников A0B и AQB', выражен следую-
щим образом:
_ Ш Фд Сд __ /4/0
^"'У ВФК ” 40
При выводе условия предельного равновесия используется
условие равенства нулю суммы проекций всех внутренних сил,
действующих в оползневом теле, на любую ось. Внутренними
силами в рассматриваемом случае будут силы взаимодействия
между соседними блоками, на которые делится оползневое тело.
Если геометрическая сумма сил взаимодействия какого-либо блока
с двумя соседними 4- Ёч, то условие предельного рав-
новесия для всего оползневого тела выразится уравнением:
Х(дД) = 0; (10.2 2)
из которого возможно получить связь между сцеплением и утлом
внутреннего трения в виде (10.2.1).
Направление сил4 с которыми соседние блоки действуют друг
на друга, может быть различным, в зависимости от принятой
Гипотезы их взаимодействия
; । Рассмотрим наиболее про-
I стой случай, когда эти силы
а ч натравлены горизонтально,
л что соответствует предполо-
жению отсутствия трения и
m сцепления по вертикальным
поверхностям, которые делят
________| _____г оползневое тело на части.
Г Фа в В1 ф ДлЯ каждого блока строится
Рис. 10.4. График для определения коэф- МНОГОУГОЛЬНИК действующих
фициента устойчивости на него сил, когорые пока-
заны на рис. 10.5, направляя
силу ДД горизонтально. Также необходимо отметить, что испод
зуемое предположение о том, что сила ДД проходит через точку
пересечения всех остальных сил, не соответствует действитель-
ности, но может быть условно принято, особенно торца, когда
оползневое тело имеет протяженность вдоль поверхности сколь-
жения существенно большую, чем мощность.
Последовательность посгроения многоугольников сил легко
увидеть из чертежа (см. рис. 10.5). Во-первых, через точку а, ле-
жащую на плоскости скольжения, на которую опирается один
блок, проводится вектор G, соответствующий весу этого блока,
направленный вертикально вниз и известный по величине. Во-
вторых, от нормали к плоскости скольжения, которая соответ-
ствует направлению нормальной реакции опоры, откладывается
известный угол внутреннего трения <р, определяя направление
действия реакции опоры RNT с учетом силы трения. В-третьих,
' —
X
Рис. 10.5. Построение многоугольников сил по методу РР. Чугаева
известная по величине и направлению сила сцепления С перено-
сится параллельно самой себе вдоль направления реакции опоры
7?Лгдо ее пересечения с горизонтальной линией, проведенной из
конца вектора G, которая соответствует направлению силы взаи-
модействия Л£, данного блока с двумя соседними. В результате
определяются все действующие на блок силы: сила трения Т, как
продолжение силы сцепления до точки ее пересечения с линией
действия нормальной реакции опоры; нормальная реакция опо-
ры N; равнодействующая нормальной реакции опоры и суммы
сил трения и сцепления Луге? И» наконец, геометрическая сумма
сил взаимодействия данного блока с двумя соседними Д£;. Сила
д£ может быть направлена вдоль склона, в глубь склона или
равна 0. В первом случае рассматриваемый блок является неус-
тойчивым и требует поддержки снизу, во втором — блок имеет
запас устойчивости и способен поддержать выше расположен-
ные блоки, в третьем — блок находится в состоянии равновесия.
Для равновесия оползня необходимо, чтобы геометрическая
сумма всех внутренних сил ДД = 0. Если эта сумма имеет избыток,
действующий от склона, т.е. положительна, то все оползневое тело
является неустойчивым. Если сумма сил д£ дает величину, дей-
ствующую в глубь склона, т.е. отрицательна, то оползневое тело
имеет запас устойчивости.
Силы взаимодействия, возникающие между соседними бло-
ками, можно рассматривать в качестве величин, характеризующих
ЛЕ,
Рис. 10.6. Схема для расчета
величины силы (Л£$ взаимо
действия данного блока с
двумя соседними блоками
оползневое давление. Для его определения в каком-либо верти-
кальном сечении достаточно просуммировать величины дей-
ствующие на все блоки, расположенные выше этого сечения.
Полученный результат будет характери-
зовать оползневое давление, направлен-
ное перпендикулярно вертикальной по-
верхности, разделяющей оползневое тело
на блоки, т.е. имеющее горизонтальное
направление.
Решение задачи об устойчивости
оползневого тела, опирающегося на сис-
тему плоских поверхностей смещения,
может быть осуществлено и аналитичес-
ки. Уравнение связи между сцеплением
и углом внутреннего трения получается
для случая предельного равновесия из
условия равенства нулю проекций сил
взаимодействия между блоками на го-
ризонтальную ось (10.2.2) или, посколь-
ку силы взаимодействия между соседни-
ми блоками направлены горизонтально,
из условия £(Д£/) =0< Сила АД, представляющая собой алгебра-
ическую сумму сил взаимодействия данного блока с двумя со-
седними, определяется следующим образом (рис. 10.6):
ЛЕ = |Д_:| - |Д1 = G tg (а - ч0
(10 2.3;
Если угол наклона плоскости скольжения, на которую опирается
блок, больше угла сдвига (а > у), ТО сила АД положительна и,
следовательно, блок является неустойчивым. Чтобы удержать его
в равновесии, необходимо приложить удерживающую силу, рав-
ную по величине, но противоположно направленную. В случаях,
когда а<у, а = 0 или при обратном уклоне поверхности сколь-
жения а = -а, сила Л£) отрицательна и блок будет иметь запас
устойчивости.
Для вывода соотношения между критическими значениями
ск и <рк производятся следующие тригонометрические преобразо-
вания. Необходимо подчеркнуть, что во всех формулах значения
нормального и касательного напряжений и величины сцепления
и угла внутреннего трения являются критическими, но для со-
кращения записи их обозначения даются без индексов (Лг, Т, с, <р).
Для каждого блока имеем:
д£, =G tg(a-у) =
tga-tgy
+ tg a • tg v
(10.2.4)
., iz С 4- N • tg <p C
Из закона Кулона tg ш -------- t v ~ ~ + tg to, где C
N bl '
как G = N • cos a + (T -t C)sin a, 7 ~ Л' tg <p, to
Gf sina 6 • tg <p + e/ cc" a
cosa + tg<p • sin a G - cl sin a
Подставив (10.2.5) в (10.2.4), получим:
Д£, - G tg(a - <p) - c(l + tga tg(a - ф)} • be,
где b = Г cos a,
Для всего оползневого тела сумма сил взаимодействия между
соседними блоками в состоянии предельного равновесия равна
нулю и, следовательно, можно выразить связь между с и <р.
jb cl, а так
(10.2.5)
(10.2.6)
п п и
52д£, = 52Gj tg(a, - ф) - - c£bi - Ф) = 0 >
1=1. f=l 1=1
n
VG, tg(a, -Фх)
/ = |
МС- Л
я+52 6,tga/ tg,a* '
i=l
(10.27)
n
где ~ длина оползневого тела, л ~ число блоков, на
f=i
которые оно разделено, ск и фк- критические значения прочно-
стных свойств, те. при которых оползневое тело находится в со-
стоянии предельного равновесия.
Определив из (10 2 7) ск при фк = 0 и <рк при ск = 0? получим на
графике в координатах с, (р прямую линию, представляющую со-
бой геометрическое место пар критических значений cY. фк, при
которых оползневое тело находится в предельном равновесии
(рис. 10.4).
Уравнение связи (10 2 7) выведено для случая, когда вдоль
поверхности скольжения прочностные свойства пород одинако-
вы и силы трения и сцепления действуют одновременно.
Если склон сложен однородными сухими песками (ск = 0), то
уравнение (10. 7) упростится:
52G, tgtrt, - Ф„) - 0 (10.2.8)
1=1 .. _ t
» Г .. zr t»- ' 1
и коэффициент устойчивости будет равен; Лу ~ ’
139
Если склон сложен однородными связными сухими грунта-
ми (фк *0), то уравнение (10.2.7) примет вид:
В + ^Ь' tg?a(
(10.2.9)
з ::: s с; ф ятя яд" ' х::е : з:: . Ту = .
В случае, когда склон сложен различными по свойствам гор-
ными породами, необходимо рассчитывать коэффициент устой-
чивости с учетом неоднородности, Учет неоднородности в отно-
шения обдеиксгс теса перед. слтпщещия сяплэгШеся --ercy
осуществляется просто. Если какой-либо из блоков, на которые
разбивается оползень, состоит из частей, образованных грунтами
разного объемного веса, величина которых известна, то необхо-
димо подсчитать вес каждой части и определить их общую сум-
му. Можно также рассчитать вес блока через средневзвешенное
значение объемного веса слагающих его грунтов.
Учет неоднородности грунта в отношений прочностных
свойств может быть осуществлен следующим образом. Когда склон
сложен неоднородными грунтами и вдоль поверхности скольже-
ния изменяются прочностные свойства, те оползневое теле нс
обходимо разделить на блоки таким образен, чтобы каждый блок
опирался на плоскую поверхность скольжения, вдоль которой
прочностные свойства постоянны. Для построения кривой связи
ИЗ системы плоских поверхностей скольжения, на которые опи-
рается сшолзневое тело, выбирают так называемую «основную»
поверхность В качестве нее обычно выбирается наиболее протя-
женная поверхность или та, нт которую опирается- самый тяже-
лый блок оползневого тела. Тогда действующие вдоль основной
поверх пзето угол внутреннего трения к зцспл°,-же ~акже прини-
маются основными (фд и г °). Прочностные свойства пород вдоль
остальных поверхностей скольжения выражаются через основ-
ные показатели следующим образом:
И с ,
= Ф = Т. Лд
гтк;па
(10.2.10)
Для основной поверхности скольжения коэффициенты €, и ц.сбудут
равнЫ единице, для остальных поверхностей скольжения будут
140
отличагься oi единицы о зависимости oi соотношения соответ-
ствующих прочностных показателей.
Если ввести допущение, что соотношения критических ве
личин ск и фк для разных участков поверхности сдвига являются
такими же. как и соотношения действительных величин са и (рд
для тех же участков поверхности сдвига:
Фк
Фк
to кривая связи может быть выражена через соотношение крити-
ческих значений «основных* прочностных характеристик:
, (10.2 11)
где фх и с* относятся к той же плоской поверхности скольжения,
для которой были введены «основные» действительные значения
Аналогичные соотношения связи между прочностными ха-
рактеристиками могут быть получены в том случае, когда силы
взаимодействия между соседними блокаых будут те горизонтали
ними (0-0), а наклонными (0 = ф, 0-О,5ш, 0 = у и т.п.). Расчета-
ми установлено, что пдафициент устойчивости, рассчитанный
ПО способу гоо.-нодаальных гоняется наименьшим, дей-
ствительный коэффициент запаса? по видимому, занимает про-
межуточное положение между коэффициентами, вычислен-
ными по методам горизонтальных и наклонных сил.
^уст|е
Метод Г.М. Шахунянид
Этот метод применяется в том случае, кода поверхность
оползания имеет сложную конфигурацию и может быть пред-
ставлена системой плоских поверхностей скольжения. Дня рас-
чета оползневое тело с учетом его неоднородности и в соответ-
ствии с формой поверхности скольжения делится вертикальными
плоскостями на блоки таким образом, чтобы каждый блок опи -
рался на соответствующую плоскую поверхность.
Рассмотрим условие равновесия произвольно выбранного
/-го блока (рис. 10 7). Все внешние силы, действующие на блок
Рис. 10.7. Схема к расчету устойчивости оползня по методу
ГМ Шахунянца
(его вес, внешние нагрузки и др.), приводятся к равнодействую-
щей силе Gr Для простоты будем считать, W> сила (Я вертикаль-
на, и тогда, если ее разложить на нормальную М и касательную
Т.. к плоской поверхности скольжения* на которую опирается блок,
составляющие, получим:
/V^C^cosa/; 7)» sin а<. (10.2.12)
При падении поверхностей скольжения в пределах каждого
блока в сторону возможного его смещения значения а, положи-
тельны, при падении поверхностей скольжения в противополож-
ную сторону значения а, — отрицательны.
Рассматриваемый f-й блок находится во взаимодействии с
двумя соседними. Пусть расположенный выше по склону блок
действует на r-Й блок с силой Е^ь а ниже расположенный блок с
силой Е/. В общем случае сила Ef.j направлена под некоторым
углом 0z_j к горизонту, а сила Д под углом 0/ к горизонту. Для
простоты допустим, что сипы Ei и направлены перпендику-
лярно к вертикальным поверхностям, делящим оползневое тело
на блоки. Поэтому все силы Е- будут ориентированы горизон-
тально и ~ 0,
Вдоль поверхности скольжения, наклоненной под углом а, к
горизонту и длиной /,, действует сила сцепления с/, и сила трения
5, tg Ф/, где 5^— нормальная реакция основания, величий кото-
рой неизвестна.
142
Величина определяется из расчета, который выполняет-
ся для выше расположенного блока, ^ (м:гзегся неизвестной. Для
нахождения неизвестных сил 5, и Е;достаточно использовать два
уравнения <гики? проектируя все силы на нормаль к основа-
нию блока и на направление самого основания и приравнивая
суммы проекций нулю.
5/ - Nj - Еч sin 4-sin а, = О,
7* ^5. tg<p, -с,/, - Еч cosa, + Е,^ cosa, = 0. (10.2.13)
Подставив найденное из первого уравнения значение S, во вто-
рое, получим уравнение для определения Е,:
Ti = iVs tgVi +С.А -f-(£, -^„aCcosce +tg(p,- -sinaj. (10.214)
При необходимости обеспечить каждому блоку некоторый запас
устойчивости против сдвига по своему основанию следует значе-
ние Tj увеличить в Кураз, где Ку — заранее запанный коэффици-
ент устойчивости. В этом случае все оползневое тело будет иметь
В целом тот же коэффициент устойчивости.
Касательная составляющая 7] внешних активных сил G= обыч-
но дьправленэ а сторону возможного смешения сползи',
вето тела, и тогда она обозначал, из Если та же касательная
составляющая 7} будет направлена в сторону, противоположи у- э
направлению возможного смещения Оползневого тела, что будет
иметь место при обратном уклоне поверхности скольжения., на
которую опирается блок^ то она будет уже силой, удерживающей
его от возможного смещения и ее не следует увеличивать в Ку
раз. В этом случае обозначим Т’ через TivJl. '3^ в уравнении
(10.2.14) выполнить преобразования:
cos a., cos<р. + sm ф. • sin a, costa, - ф,)
cos a, + tg w. sin a, =-----------—-------~------- =------1—-
СОБф| СО$ф,
то в общем виде ложно записать:
Для блоков, основание которых направлено в сторону возмож-
ного смещения оползневого тела, следует принимать 7}ya = 0. Если
блок опирается на основание с падением в сторону противопо-
ложную направлению возможного смешения, следует принимать
Так как в большинстве практических случаев направле-
ние возможного смещения каждого оползневого блока совпадает
с направлением падения поверхности скольжения по всей про-
тяженности оползневого тела, в дальнейших формулах будут
фигурировать лишь значения под которыми следует подразу*
мевать 7* = 7}ед, а будут приниматься равными нулю. Однако
при выполнении расчетов в каждом конкретном случае следует
помнить о возможности появле* "я сил 7,¥11. Тогда формула
(10.2.15) примет вид:
(ЛЛ.
Tt~N. tg ф, - с,/,) cos ф,
cos(a4 * Ф,)
(10.2.16)
Для первого блока Ej. = 0:
' z.. Г, -N} Ш<₽1 -Ci/j)cos<p|
£ ---Д.-----------------------.
COS< X -ф|)
Оползневое давление в любом сечении определяется как алгеб-
раическая сумма сил взаимодействия всех п блоков, расположен-
ных выше этого сечения:
(10.2.17)
Величины сил Eh с которыми каждый ..-к действует на
ниже расположенный, можно определить последовательными
расчетами, идя от первого блока, для которого = 0, к после-
днему.. Последовательное определение сил Д наиболее целесооб -
разно. когда без расчета невозможно заранее отделить на инже-
нерно-геологическом разрезе устойчивые части склона от
неустойчивых. Первый из блоков, для которого сила Д получи-
лась равной нулю или отрицательной, отделяет вышележащую
часть оползня, включая и /-й блок, от нижележащей части. По-
скольку на растяжение грунт практически не работает, нижерас-
положенная часть оползня должна рассматриваться отдельно. Аг г
лизируя последовательно значения Е>9 нетрудно установить места
перехода от неустойчивых частей к устойчивым частям оползня,
где возможен разрыв оползневого тела, места целесообразного
расположения удерживающих конструкций, например, где сила
Д имеет наименьшее значение и мощность смещающегося слоя
минимальна. ит.д.
Очевидно, что у природного устойчивого склона сила Еоп, под-
держивающая последний блок, должна быть равна нулю. Исходя из
этого, для природного склона можно определить значение коэффи-
циента устойчивости, приняв £Оп = 0. Тогда из (10.2.17) получим:
(10.2.18)
Рис. 10.8, Построение мнегт.
угольника сип для расчета устой-
ч В Q ст и о ПОЛ 3 'Л я
Определение коэффициента устойчивости может быть'Вы-
полнено графически путем ооследователъного построения мно-
гоугольников сил для всего оползневого.тела, как это показано
на рис. 10.8. Если при введенном при построении коэффициен-
те устойчивости сила, которую надо приложи гы в конце послед-
него блока, будет равна нулю» то склон имеет запас устойчиво-
сти 5 соответствующей заданному коэффициенту. Если в конце
последнего блока необходимо при-
ложить силу на поддержание ополз-
ня, то он имеет запас устойчивости
меньше заданного. Если сила направ-
лена в CtnpoEy .зеддожногэ смеще-
ния, то оползень имеет больший за-
пас. у сто й ч ивосгй*
Таким образом, этот метод по-
ЗВОЛ ГТ’Г:
1) определить коэффициент ус-
тойчивости природного склона:
2) спроектировать защитные ме-
роприятия так., чтобы оползневой
склгч ил: откос имел заданный
пас устойчивости,
3) определить активное давление
грунта. кз. удзр/ллзл:
или оползневое давление;
4) определить пассивное давление
или отпор-реакцию удерживающей
конструкции. Так как при отпоре сдвигающая сила Тстановится
силой, сопротивляющейся сдвигу, то при этом следует принять
Полученные расчетные формулы могут быть использованы
также для схемы, учитывающей, что силы, .д отклонены от гори-
зонтали на угол О, постоянный для всех блоков Так как этот угол
ограничен величинами 0 <в < у, где цг — угол сдвига, то его можно
принять равным 0,5 ц/. Для этой схемы в расчетных формулах вы-
COS(p .
ражение-------—-—г, отвечающее условию 0 = 0. необходимо за-
cos(oc — ф;
менить на г (где 9 = const)..
COSH -6-ф) '
При выводе формулы для определения оползневого давле-
ния и коэффициента устойчивости были использованы два урав-
нения статики: ЕХ=0и £У’=0. Третье условие статики (уравне-
ние моментов 1 Л/о = 0) дает возможность определить точку
45
приложения силы Ддля любого /-го блока или реакции удержи -
вающего сооружения. Это решение является точным при кругло-
цилиндрической поверхности скольжения и приблизительным в
других случаях.
Графическая реализация этого метода состоит в следующем
[2L На рис. 10 7 оползневое тело В соответствии с формой поверх-
ности скольжения разделено вертикальными плоскостями на п
блоков Как было показано в предыдущих случаях, на каждый из
этих блоков действуют следующие силы: 1)вес блока с учетом
построенных на нем сооружений Gb который может быть разло-
жен на нормальную Лг, и касательную 7} составляющие по отно-
шению к поверхности скольжения; 2) по поверхности смещения
В условиях предельного равновесия действуют реакции со сторо-
ны этой поверхности: нормальная реакция Sb сила трения
Д = Sf tg ф.- и сипа сцепления 3) со стороны соседних бло-
ков действуют сипы Д н Е^ которые для простоты будем счи-
тать направленными горизонтально.
Заменим силу трения Д и нормальную реакцию поверхности
скольжения Д равнодействующей:
R. = Jf? +У2 - Д2 ц>. + 5/ - 5, (10.2.19)
наклон которой к нормали поверхности скольжения будет равен
углу внутреннего трения ф,- грунта вдоль этой поверхности.
Силами, сдвигающими весь массив по поверхности скольже-
ния, будут касательные составляющие 7} сил G., если они на-
правлены в сторону возможного смешения массива. Все осталь-
ные силы являются силами либо непосредственно не влияющими
на устойчивость, как, например, нормальная составляющая N,
силы Gj, либо сопротивляющимися возможному смещению.
Будем считать, что все оползневое тело будет иметь задан-
ный коэффициент устойчивости Ау, если каждый блок, на кото-
рые это тело разбито, будет иметь тот же коэффициент устойчи-
вости. Если А,, в отношении возможного смещения каждого блока
по плоской поверхности скольжения рассматривать как отноше-
ние всех касательных сил, удерживающих массив (Ауа), ко всем
касательным силам, стремящимся вызвать его смещение (F^),
А'у = Fya/Гсд, то для обеспечения заданного коэффициента устой-
чивости необходимо, чтобы
Еуд - АуЕ^Д, ИЛИ F;a АуЕдд 0.
(10.2.20)
Таким образом, задача обеспечения заданного коэффициента
устойчивости сводится к обычным условиям равновесия, если
при рассмотрении действия сил вместо сдвигающих касательных
146
сил брать силы в Ку раз больше по величине и действующие в
том же направлении.
Для определения коэффициента устойчивости природного
оползневого тела задача сводится к определению Ау. при кото*
ром наступит состояние предельного равновесия В этом случае
определение коэффициента устойчивости йсуществляетея под-
бором, и если его величина удовлетворяет соотношению (10.2/20)»
то он принимается за искомый коэффициент
При решении задачи для каждого блока будут известны силы
Т,: С- и Е^. При составлении условий равновесия вместо каса-
тельной составляющей 7} силы G, примем величину . если
сила 7} стремится сдвинуть массив, когда она направлена в сто-
рону возможного смешения, и значение силы 7} принимается без
изменения, если она сопротивляется смещению. Сила Е^ известна
в результате решения задачи для предыдущего блока, если при-
нять во внимание, что в первом блоке такая сила отсутствует^
Направление силы принимается горизонтальным, хотя оно
может быть и иным, что реализуется в других способах оценки
устойчивости оползневых тел.
Неизвестными силами являются нормальная реакция опоры
S,-, и сила £г. Найти эти силы можно аналитически, как было
рассмотрено выше, и графически, путем построения многоуголь-
ников сил. .Для оценки устойчивости всего оползневого тела за-
дача решается последовательным построением многоугольников
сил от одного блока к другому, начиная с верхнего На рис 10,8
приведено построение многоугольника сил для л блоков (в рас
сматриваемом случае л ® 3). Сначала из произвольной точки А
строится вектор Xy7i4- С/Ч по направлению повер-
хности скольжения. Из конца этого вектора перпендикулярно
ему проводится нормальная составляющая Л^силы G(}. Неиз*
вестные силы Т^и Е^.\ заданы своими направлениями: равно
действующая. Д„| силы трения tgcpT^n нормальной реакции
опоры 5^| расположена под углом фздК нормали, проведенной к
поверхности скольжения, а сила Е,+горизонтальна. Эти данные
позволяют дострюить многоугольник сил для первого блока, прф*
ведя из конца вектора горизонталь, а из точки А под углом
Ф1 = Ф;..|К нормали вектора КуТ^-С^др пересечения с горизон-
талью в точке Б. Таким образом, определяются и величины сил
Лми Последняя представляет собой силу, с которой первый
блок действует на второй, и направлена в сторону возможного
смещения Второй блок оказывает сопротивление первому < си-
лой равной Ef.„h ж> направленной в противоположном направле-
нии. поэтому в многоугольнике сил второго блока ее необходимо
учесть. Эта сила одновременно является оползневым давлением^
147
которое действует в сечении оползневого тела, совпадаюшем с
вертикальной плоскостью, отделяющей первый блок от второго*
но только при Ку ~ 1,
Для построения многоугольника сил второго блока из точ-
ки В необходимо провести вектор K/I}- С, где в на-
правлении, совпадающем с плоской поверхностью скольжения,
на которую опирается этот блок. Из конца вектора КУТ(- Ct и
перпендикулярно ему строится вектор Nh из конца которого
проводится горизонталь, соответствующая направлению неиз-
вестного по величине вектора лд. Дроведя из точки Б под углом
Ф, к нормали вектора КуТ,- Q до пересечений С горизонталью в
точке Б', получим величины вектора Rh представляющего собой
рсщпдействующутз г;Ж’ трен мл J;. rg<p. и нормальнее ± такции
опоры Д, и вектор.? Л- аким образом, переходя от блока к
блоку, строится многоугольник сил для всего оползневого тела.
У многоугольников сил Двух соседних блоков есть общая сторо-
на — вектор Eh направление которого при переходе от одного
блока к дру.гщ/д следует ; менять на обратное, так как для /-го
блока Ej есть сила, которая передается от данного блока на пос-
ледующий, а для поеждяошего блока сна является реакцией на
данный блок.
Сила Еп, определенная для последнего л-го блока, может быть
направлена в сторону возможного смещения, иметь противопо-
ложное направление и может быть равна 0. Если построение
многоугольников сил выполнялось при Ку - }., а определенная
для последнего блока сила Е„ направлена в сторону Возможного
смещения, то оползневое тело находится в неустойчивом состо-
янии. и сила £Л будет представлять собой оползневое давление
£оп=£„. Если при условии Av=l* определенная для последнего
блока сила Ег1 направлена в сторону, противоположную направ-
лению возможного смешения, то оползневое тело находится в
устойчивом состоянии. В последнем случае можно подобрать та-
кой коэффициент устойчивости больший единицы (К, > 1), что-
бы установленная для последнего блока сила Еп обратилась в нуль
(£л--0). Полученный таким образом £у и будет характеризовать
степень устойчивости всего оползневого тела,
При построении многоугольников сил необходимо следить
за гем чтобы сила, препятствующая смещению /-то блока (Е-
не обращалась в нуль или не меняла знак на противоположный,
т.е. не исчезала и не становилась вместо силы поддерживающей
силой сдвигающей. Эта сила не может быть сдвигающей, так
как обычно принимается условие, что грунтовый массив не ра-
ботает на растяжение и, следовательно, растягивающие силы в
оползневом теле возникать не должны Если при расчете на-
' С
правление силы £; совпадет с направлением возможного сме-
шения- и, следовательно, сила ^ станет препятствовать смеще-
нию, это будет означать, что часть оползневого тела от егс та-
чала и до некоторой границы внутри / го блока является не
только устойчивым, но и обладает избыткам устойчивости. Та-
ким образом, при построении многоугольников сип иепосред-
ственно определяете..; границы устойчив/ участков опеле г ый
вого тела.
Если в результате того же построения в z-м блоке получи-
лось, что сила Д- направлена в сторону смешения оползневого
тела, то при построении многоугольников сил для последующего
/+ 1-го блока сила Е,- (г зледовгтзгзно, т д') е этот i слоге;’''зле
ник не включается, что соответствует условию недопущения ра-
стягивающих напряжений. В случае, когда растягивающие на-
пряжения допускают5 л, следует учитывать лишь ту часть силы
Е„ при которой растягивающие .напряжения не превосходят пре*
дельно допустимых напряжений.
Для определения изменения оползневого давления вдоль
оползневого тела достаточно построить эпюру этих сил (см.
рис, 10.7). Многоугольники сил и эпюра оползневого давления
позволят зт определить место наиболее версятных разрывов о пел
зневого тела, места, где возможно возникновение бугров- И тер-
рас выпирания при оползают:. (лу< 1), а также установить^ ка-
кую нагрузку должно воспринять удерживающее сооружение^
чтобы обеспечить заданный коэффициент устойчивости, и наи-
и/чиюз месте- его расположения.
Точку приложения реакции удерживающего сооружения
которая известно по величине и направлению (в рассматриваем
мом случае направление горизонтальное), можно приблизитель-
но найти, йсподазуя третье условие равновесия — равенство нулю
моментов всех действующих на оползневое тело сил относитель-
но некоторого центра вращения .Для этого необходимо подо-
брать круговую кривую радиусом г с центром О, которая наибо-
лее близко совпадает с фактической кривой скольжения, и
выписать уравнение моментов:
оз куда.
где z — плечо от центра Одо направления силы £оп — реакции
удерживающего сооружения
1Д
10.3. Методы круглоцилиндрических поверхностей
обрушения
На склонах, сформированных в однородных массивах гор-
ных пород, образуются оползни* Поверхность скольжения кото-
рых может быть аппроксимирована круглым цилиндром. Кро
того, при оценке устойчивости искусственных сооружений (пло-
тин, насыпей, дамб и др.) используется гипотеза об их разруше-
нии по круглоцилиндрической поверхности. Такие методы ши-
роко применяются в поверочных расчетах, когда из всевозможных
поверхностей обрушения производится выбор наиболее опасной.
Следует заметить, что поверхность вероятного оползания можно
аппроксимировать криволинейными поверхностями другой фор-
мы, например, логарифмической, но круглоцилиндрическая яв-
ляется наиболее простой.
Существует две группы способов расчета, когда поверхность
скольжения оползня принимается круглоцилиндрической. К пер-
вой относятся методы, когда оползневое тело разбивается верти-
кальными плоскостями на отдельные столбики, каждый из кото-
рых считается абсолютно твердым телом и опирается на дугу,
которую аппроксимируют прямой линией. Эти методы, по сути,
аналогичны методам, использующим представление о том, что
оползневое тело опирается на систему плоских поверхностей
смещения. Вторую группу образуют методы, когда оползень рас-
сматривается как монолитное твердое тело, и тогда нет необхо-
димости высказывать какие-либо предположения относительно
сил, действующих внутри оползневого тела. В качестве примера
можно привести метод К. Терцаги [3], который является пред-
ставителем первой группы методов, и метод весового давления
[4], относящийся ко второй группе.
Среди методов, использующих предположение о том, что
оползание происходит по круглоцилиндрической поверхности,
существует много разновидностей, получивших различные на-
звания. Принципиально все эти методы объединяет гипотеза о
том, что нарушение устойчивости склона или откоса происходит
в результате вращения оползневого массива вокруг центра О
(рис. 10.9), а поверхность скольжения представляется дугой кру-
га радиусом г, очерченного из этого центра.
Для оценки устойчивости склона методами круглоцилинд-
рической поверхности скольжения используется уравнение мо-
ментов. Коэффициент устойчивости определяется как отноше-
ние момента удерживающих сил к моменту сдвигающих сил
относительно центра вращения 0. Удерживающие силы трения и
сцепления всегда действуют вдоль поверхности скольжения и,
G;
Рис. 10.9. Схема к расчету устойчивости оползневого
тела, опирающегося на круглоци линдрическую поверх-
ность, если оно делится на столбики вертикальными
плоскостями
следовательно, имеют плечо, равное радиусу г. Относительно то-
чек приложения и направления действия других сил необходимо
высказывать дополнительные предположения, что обуславлива-
ет разнообразие методов расчета.
Метод К. Терцаги
В этом методе предполагается, что оползневое тело разбива-
ется вертикальными плоскостями на столбики, а равнодейству-
ющая сил взаимодействия каждого столбика с двумя соседними
направлена по касательной к круглоцилиндрической поверхнос-
ти скольжения. Построение многоугольника сил осуществляется
так же, как и в предыдущих случаях (рис. 10.10), так как извест-
ны вес i-ro столбика оползневого тела G„ сила сцепления e,/f,
угол внутреннего трения вдоль поверхности скольжения <р,. На-
правление равнодействующей сил взаимодействия i-го столбика
с соседними Д£, совпадает с направлением действия сил трения
и сцепления.
Нормальная реакция основания проходит через центр вра-
щения, и поэтому ее момент равен нулю. Тогда моменты сдвига-
ющих и удерживающих сил для каждого столбика:
** (Ni Ш Ф, + cili + АД к, (10.3 I)
где а,— плечо силы б,; Л*— нормальная реакция опоры;
длина поверхности скольжения, на которую опирается столбик и
аппроксимируемая прямой линией. Чтобы определить моменты
151
Рис. 10.10. Построение многоугольника сил
по методу К. Терцаги
сдвигающих и удерживающих сил для всего оползневого тела,
необходимо суммировать вычисленные моменты по всем п стол-
бикам:
(10.3.2)
по отношению к оползневому телу. Коэффициент устойчивости
определяется как отношение моментов удерживающих и сдвига-
ющих СИЛ!
/=.;
Разделив числитель и знаменатель на г и заметив, что #/r=sin а.,
а /Ч=(г cosаг, где а,— угол наклона поверхности скольжения,
на которую опирается |-й столбик, получим формулу:
л п
УЖ tg ф, + 52с‘1‘
1 = 1 i—1
if
sin ci ,
(10.33)
При однородном строении склона положение центра враще-
ния 0 неизвестно» Поэтому прибегают к так называемому пове=
речному расчету, когда положение центра вращения устанавли-
вается путем определения коэффициентов устойчивости для
нескольких возможных поверхностей скольжения. Та поверхность,
для которой получится минимальное значение коэффициента
устойчивости; принимается за наиболее опасную, а минималь-
ный коэффициент запаса характеризует степень устойчивости
в(»его слзнай
Оползневое давление может быть установлено графически
путем построения многоугольников сил или рассчитано как раз-
ность между знаменателем и числителе/ в формуле JO.3.3) ’От-
дельно для каждого столбика.
Методы круглоцилиндрических г озерхностей скольжения
мяло пригодны для оценки /стсйчизост:?. склоеоз, слеженных
переслаивающимися породами с различной прочность о.
Метод весового давления
Вторую группу составляют методы круглоцилиндрических
поверхностей смещения, ехгт? оползневое тело цжлмгт^ивается
единым блоком. Эти методы применяются для оценки устойчи-
вости склонов, сложенных рыклыт и однородными горными по-
родами, искусственных откосов, например, камненабросных или
намывных плотин, дамб, насыпей и других сооружений, а также
в случае выполнения поверочных расчетов.
Во всех методах этой группы оползень рассматривается как
единое твердое тело, опирающееся на поверхность, которую ап-
проксимируют круглым цилиндром с центром вращения в точ-
ке О (рис. 10.11). Поэтому нет необходимости учитывать внутрен-
ние силы и, следовательно, вводить какие-либо допущения о
направлении их действия. Основные силы, действующие на ополз-
невое тело, приведены ниже.
1. Внешние объемные и поверхностные силы, к которым от-
носятся вес оползневого тела, сейсмическая сила, гидродинами-
ческое давление, силы, приложенные к поверхности, например,
нагрузки от сооружений и др. Все эти силы могут быть приведе-
ны к одной равнодействующей силе G. Если на оползневое тело
действует только вес,
тогда G направлена вер-
тикадьно вниз и прохо-
дит через центр тяжести
оползня. Ее величина оп-
Рис. 10.11. Схема к расчету ус-
тойчивости оползневого тела,
опирающегося на круглоцилим-
дрическую поверхность, когда
оно рассматривается единым
блоком
ределяется как произведение объемного веса у горных пород, сла-
гающих оползень, на его площадь 5 и единичную толщину: G= yS,
так как рассматривается плоский случай.
2. Сила сцепления, действующая вдоль поверхности смеще-
ния, равная произведению ее длины L на удельное сцепление С и
единичную толщину: С = cL.
3. Силы реакции опоры, действующие перпендикулярно по-
верхности смещения, которые определяются как сумма произве-
дений нормальных напряжений о На соответствующие части I
длины поверхности L и единичную ширину: 87V= el и N= IxsI.
4. Силы трения, действующие вдоль поверхности смещения
и равные: T=Ntg <p
Все способы расчета устойчивости склонов и откосов, ис-
пользующие представление о смешении оползня как единого тела
по круглоцилиндрической поверхности, основаны на примене-
нии уравнения моментов относительно центра 0 поверхности
обрушения:
Л/а; =Мпас. (10.3.4)
Активный момент создается равнодействующей всех объемных и
поверхностных сил, действующих на оползень, и в случае, когда
такой силой является его вес, Л/ак = aG, где а — плечо действия
силы G относительно центра вращения 0. Пассивный момент
обусловлен действием сил трения и сцепления вдоль поверхнос-
ти смещения: Afnacc - г(Т + С), где г — радиус круглоцилиндри-
ческой поверхности. Нормальная реакция опоры не создает мо-
мента, гак как проходит через центр вращения.
Подставив в уравнение (10.3.4) все входящие в него величи-
ны, окончательно получим:
aG=r(Ntgy + cL). (10.3.5)
В этом уравнении все величины за исключением нормальной
реакции опоры N могут быть легко определены. Нормальная реак-
154
ция опоры неизвестна, так как неизвестным является распреде
ление нормальных напряжений о вдоль поверхности скольже*
ния. С другой стороны, очевидно, что нормальная реакция опо-
ры зависит от веса оползня G, и поэтому может быть представлена
в виде:
N^G, (10.3.6)
где р — некоторая величина, которая выбирается в зависимости
от предположения относительно величин
пряжений, действующих нормально повер-
хности скольжения, что определяет разно-
образие расчетных способов.
Таким образом, при расчетах устойчив
вости оползня необходимо определить, как
вдоль дуги обрушения L распределяются
нормальные напряжения о и какова их ве-
личина. Если известна эпюра этих напря-
жений, то легко подсчитать все элементар-
ные силы 67V и получить их алгебраическую
сумму N. Затем в рамках закона Кулона
можно определить и момент силы трения,
действующей вдоль поверхности смещения.
Однако определение величин и распреде-
ления нормальных напряжений вдоль по-
верхности скольжения представляют собой
сложную задачу, и поэтому прибегают к
ее приближенному решению. Так, если
и распределения на-
Рис. 10.12. Схема для рас-
чета нормального напря-
жения, действующего на
рассмотреть элемент оползневого тела поверхности скольжения
(рис. 10.12), который вырезан в виде вер-
тикального столбика шириной Ь и средней высотой h единичной
толщины, опирающийся на наклонную под углом а элементар-
ную часть длиной / дуги обрушения Z, то нормальное напряже-
ние о, которое передает этот столбик весом 5G на наклонную
поверхность опоры, будет:
о SO сому f но bG-ybhy I- b/cos а
I
и окончательно:
ybhcos2a
л--------= yh cos а ’
Этот закон распределения нормальных напряжений вдоль по-
верхности скольжения принят, например, в методе К. Терцаги.
Но в расчетах могут быть приняты и другие способы распределе-
ния нормальных напряжений.
155
В большинстве расчетных методов величина р <Л, те. нор-
мальное напряжение, действующее на поверхности скольжения,
составляет некоторую часть от веса оползневого тела. Однако
анализ значений р показывает, что их отклонение от единицы
невелико. Поэтому был предложен метод [4], в котором велиЧМ*
на р принята равной единице (Ц» 1), — способ весового давле-
ния. Следовательно, элементарная нормальная сила SA*, соответ-
ствующая любому элементу 7 дуги скольжений £, равна внешней
силе 56, т.е. весу той части оползня, которая опирается на дугу /.
и приложенной по линии ее действия. Алгебраическая сумма N
элементарных сил 82Vравна весу всего оползневого тела (7 вместе
с расположенными на нем сооружениями, Таким образом, в каж-
дой точке поверхности скольжения действует нормальное по от-
ношению к этой поверхности напряжение:
ybh
b/cosa
= yftcosa,
(10.3.8)
где обозначения те же, что и в формуле (10.3.7). Формула (10.3.8)
справедлива для случая, когда объемная сила G является силой
тяжести, направленной вертикально вниз.
Но если известны действующие на поверхности скольжения
нормальные силы Д то легко определить момент сил трения вдоль
этой поверхности:
Мт ® г tg фА У <7, = г tg фА(?
/=1
и тогда уравнение предельного равновесия будет:
л л п
£ (afii) = г tg £ 6, + rck V /,,
/=1 1-1 1=1
где <р* и сА— критические показатели прочности горных пород
вдоль поверхности скольжения радиуса г, а, — плечо силы тяже-
сти, приложенной к каждому /-му элементу оползневого тела (см.
рис 10.9).
Разделив обе части уравнения (10.3.9) на г и подставив
tg Ф* = tg Ф/*у. ск = с/Ку, где ф и с прочностные показатели пород
вдоль поверхности скольжения, установленные опытным путем,
Ку — коэффициент запаса, получим:
156
Д;
sin а,
i=i
(10.3.10)
Сравнивая последнюю формулу с формулой (10.3.3), легко
увидеть, что при расчете коэффициента запаса по способу ве-
сового давления его величина будет больше, чем в методе
К. Терцаги.
Способ весового давления может быть применен и в случае,
когда склон сложен неоднородными породами или подвержен
воздействию фильтрационных или сейсмических сил.
10.4. Определение дефицита устойчивости
Коэффициент устойчивости или запаса характеризует сте-
пень устойчивости склона или откоса применительно к опреде-
ленной расчетной схеме или по отношению к определенному
воздействию, которое может вывести склон из равновесия. По-
этому коэффициент запаса в основном может использоваться для
сопоставления различных решений, получаемых для одного и того
же склона [1]. Более корректным показателем устойчивости склона
является непосредственно определяемая величина запаса устой-
чивости (или прочности) или обратная ей по знаку величина де-
фицита устойчивости:
Лда ~ Ля, (10.4.1)
где Ffgn Fva — соответственно сдвигающие и удерживающие силы.
Если смещение тела происходит по полигональной поверх-
ности, то для определения дефицита устойчивости этого тела оно
повно разбивается на отсеки вертикальными плоскостями, ко-
торые опираются на соответствующие участки полигональной
поверхности смещения (рис. 10.13).
Для каждого из отсеков, начиная с верхнего, вычисляются
дефициты устойчивости, которые представляют собой внутрен-
ние силы взаимодействия между отсеками. Например, для /-то
отсека дефицит устойчивости без учета действия сейсмической
силы АсСг,, равен:
Sj -- Gjisinai -tg<pcosaf) + ft - Р. tg<p-+
+ 5,_l[cos(a,_1 - a,) - tgq>sin(a,_i - ix,)J,
(10,4.2)
Рис . 10.13 Схема для расчета дефицита устойчивости Аго блока
где Gj - вес г-го отсека, — дефицит устойчивости выше рас-
положенного отсека, передаваемый на рассматриваемый отсек,
Р, и Qi — нормальная и касательная по отношению к поверхно-
сти смещения составляющие приложенных к отсеку внешних сил.
Направление сил S-, предполагается совпадающим с линией па-
дения соответствующей плоскости смешения. В случае, если вы-
численная по формуле (10.4.2) величина получится отрица-
тельной, в расчет расположенных ниже блоков вводится значение
S{ = 0. Общий дефицит устойчивости определяется дефицитом
устойчивости самого нижнего блока. Если дефицит устойчивос-
ти отрицательный, то оползень имеет запас устойчивости, если
дефицит равен нулю — оползень находится в состоянии предель-
ного равновесия, при положительном дефиците — оползень не-
устойчивый. Величина дефицита устойчивости позволяет наибо-
лее точно охарактеризовать оползневое давление, что необходимо
при проектировании оползневых мероприятий.
Контрольные вопросы
1. Как устанавливается положение поверхности скольжения?
2. Основные положения метода фрагментов.
3. Силы, действующие на оползневое тело.
4. Как взаимодействуют между собой отдельные блоки ополз-
невого тела?
5. Как определяются коэффициенты устойчивости по мето-
ду Р.Р. Чугаева?
6. Как строится многоугольник сил в методах Р.Р. Чугаева,
Г.М. Шахун: н г К. Тери.аги?
158
7. Как определяются коэффициенты устойчивости в случае
неоднородного строения оползневого склона?
8. Какие задачи решаются методом Г.М. Шахунянца?
9 В каких случаях применяются методы круглоцилиндрй-
ческих поверхностей обрушения?
10. Какие основные положения используются в методе
К. Терцаги?
11. В чем отличие методов К. Терцаги и весового давления?
12. Как определяется оползневое давление?
13. Что такое дефицит устойчивости и способы его расчета?
14. Как учитывается сейсмическая сила при определении де-
фицита устойчивости?
ГЛАВА 11. РАСЧЕТЫ УСТОЙЧИВОСТИ СКЛОНОВ
В СЛОЖНЫХ СЛУЧАЯХ
Методы оценки устойчивости оползневых склонов рассмот-
рены для случаев, когда основной силой, вызывающей смещение
оползня, является сила тяжести. Однако устойчивость склонов
может быть нарушена в результате дополнительного воздействия
на массив пород, слагающих склон, сил другой природы. Движу-
щиеся в горных породах подземные воды оказывают на массив
пород как взвешивающее воздействие, так и гидродинамическое
давление, что может стать причиной оползневого смещения. При
землетрясениях возникают инерционные силы, способные нару-
шить устойчивость находящихся на склонах оползневых тел. Тех-
ногенное воздействие в виде дашлнительных нагрузок, подрез-
ки склонов, обводнения пород, взрывных работ также может
вызвать Изменение устойчивости склонов. Рассмотрим влияние
на формирование оползней в пределах склона действия подзем-
ных вод и сейсмичности.
11.1. Учет действия подземных вод
Действие подземных вод на устойчивость оползневого скло-
на проявляется различными путями.
1. Подземные воды, насыщая породы, изменяют их физико-
механические свойства и, в частности, прочностные показатели.,
уменьшая сопротивление горных пород сдвигу. Кроме того, под-
земные воды; смачивая возможные поверхности скольжения,
играют роль смазки и также влияют на уменьшение сил трения.
2. Подземные воды взвешивают минеральный скелет горных
пород, что вызывает уменьшение нормальных напряжений в плос-
кости скольжения и может привести почти к полному снятию
трения вдоль этой поверхности. Действительно, если сопротив-
ление сдвигу определяется уравнением:
i - (о- w)tg<p ч с 9 (11.1.1)
то при возрастании порового давления величина (о - и) может
оказаться равной нулю, и тогда сопротивление породы сдвигу т
будет зависеть только от сцепления.
3. Подземные воды при своем движении оказывают фильт-
рационное или гидродинамическое давление. Если поток под-
земных вод направлен в сторону поверхности склона, то возни-
кающее при этом фильтрационное давление может стать причиной
развития на склоне оползневых деформаций.
160
Действие фильтрационного давления можно рассмотреть дая
случая, когда через наклонный пласт горных пород, залегающий
на водоупоре, параллельном поверхности, фильтруется водный
поток, целиком заполняющий пласт, и линии тока воды парал-
лельны поверхности откоса (рис. 11.1). Этот случай является наи-
более простым, но позволяет наглядно представить сущность
рассматриваемого процесса и, кроме того, имеет практическое
значение, так как используется при решении задач об устойчи-
вости оползневых склонов в качестве одного из допущений [3].
Рис. 11.1. Схема для определения гидродинамического давления
Если вода полностью насыщает поры наклонного пласта, то
верхняя линия тока совпадает С поверхностью склона, а ниж-
няя — с плоскостью скольжения. Линии, перпендикулярные ли-
ниям тока, являются эквипотенциальными, т.е. во всех точках
каждой такой линии пьезометрические напоры одинаковы. Тог-
да разность напоров h между двумя эквипотенциальными лини-
ями равна разности отметок точек, расположенных на какой-
либо линии тока ДА = г) - z2. Соответствующая д лина линии тока
будет равна
Д/ = ДА /snip» (Z| - 22)/sinP,
где р — угол наклона линии тока, а гидравлический градиент бу-
дет равен:
i = ДА/Д/= sin р. (11.1.2)
Так как наклон поверхности скольжения и наклон линии тока
совпадают, т.е. а = р, то градиент будет:: i=sin cl
Гидродинамическое (фильтрационное) давление на единицу
объема горных пород равно градиенту умноженному на объем-
ный вес воды уь:
161
f не m Y, sin a,
(11.1.3)
а обшее давление на ске лет горной породы объемом И будет равно:
Ф = Иув$та. (11.1.4)
Это давление направлено вдоль линии тока, а в нашем случае и
вдоль поверхности откоса и скольжения, и является сдвигающей
силой.
Рассмотрим условие равновесия некоторого объема К наклон-
ного пласта водонасыщенных горных пород. Пусть поверхность
скольжения является кровлей водоупора. Вес горной породы в
объеме Ис учетом взвешивания будет равен V, где у —
объемный вес водонасыщенной породы. Тогда сдвигающая сос-
тавляющая 5 этого веса направлена параллельно поверхности
скольжения вниз и равна: 5= Р sin а = (у - ув) Ksin а. Нормальная к
поверхности скольжения составляющая N= Pros а- (у- y,)Kcosa.
Общая сдвигающая сила складывается из сдвигающей составля-
ющей веса и гидродинамического давления (S+Ф), а удержива-
ющая сила равна сипе трения Т- .Vtg<p = (y-yb)Tcosa- tg<p, но
при условии отсутствия сцепления. В противном случае следует
добавить силу сцепления С= cl, где / — длина поверхности сколь-
жения, на которую опирается блок. Коэффициент устойчивости
пласта объемом V будет равен отношению удерживающих сил к
С? . л:
(y-yB)(zcosa' tg<p
у (y-yB)Tsina-rlzyBsina
(Y-YB)cosa tg<p (у-у„) tg<p
ysina у tga
(11.1.5)
При отсутствии фильтрационного и взвешивающего давления этот
коэффициент равен-
к e tgq> yKcosa tgq> = tgu< „, I
< S у sin a tga'
Следовательно, при насыщении водой горных пород, слагающих
склон, коэффициент устойчивости снижается в у/(у ™ув) раз, т.е.
во столько раз, во сколько вес скелета грунта в воздухе больше
веса скелета взвешенного в воде
Формулу (11.1.5) для определения коэффициента устойчиво-
сти можно получить, не рассматривая отдельно гидродинамичес-
кого давления. Определяя сдвигающую силу S\ исходя из объем-
ного веса полностью водонасыщенного грунта, а удерживающую
силу трения — из веса того же фунта, но с учетом взвешивания,
получим:
162
к в ~ (Г -ув)^ cosg tg<p __ (у —YB) tgcp (j j j 7
5* < И sin a у tga
Этот способ оценки устойчивости склона получил название
«метода взвешивания». Физический смысл этого метода заклю-
чается в том, что напор грунтовых вод оказывает на сползающую
толщу пород взвешивающее противодействие и тем самым сни-
жает нормальное давление вдоль поверхности скольжения, а сле-
довательно и силу грения, что ведет к уменьшению сопротивле-
ния сдвигу в контактной зоне.
При расчетах устойчивости склонов с учетом движущихся в
породах подземных вод приходится определять объемный вес
горных пород с различной степенью водо насыщения. Если Д —
это удельный вес минеральной части скелета, ай — пористость
горной породы, то объемный вес:
сухого грунта (скелета) усух = уск =Д(1-я); (11.1.8)
влажного грунта Увл = Д(1 ~«)+Д(1 - лКЦЛИ7 = уск(1 +0,01И');
(11.1.9)
водонасыщенного грунта у^ = Д(1 - л) + пуя
~ У СК Т ЯУв •>
(11.1.10)
взвешенного в воде уВ1В = Д(1 - л)-ув(1 - л) - (Д-ув)(1 -и),
(11.1.11)
где у, — объемный вес воды, IK— естественная влажность грун-
та, %.
Оценка влияния гидростатического взвешивания и гидроди-
намического давления может быть осуществлена, по крайней мере,
двумя различными, но равнозначными способами. В первом гид-
ростатические и гидродинамические силы учитываются непос-
редственно. Во втором указанные силы заменяются эквивалент-
ными контурными силами, приложенными вдоль поверхности
скольжения оползневого тела.
Во всех способах сдвиговые характеристики горных пород
вдоль поверхности скольжения принимаются для их полного во-
донасыщения
В первом способе учет гидростатического взвешивания и гид-
родинамической силы производится раздельно. Подчеркнем, что
и гидродинамическая и взвешивающая силы являются объемны-
ми, и поэтому могут складываться с собственным весом горных
пород. Гидростатические и гидродинамические силы определяются
по величине и направлению и суммируются по всему оползневому
телу исходя из их удельной (объемной) интенсивности. Гидро-
статическое взвешивание учитывается при определении объем-
ного веса пород, слагающих оползневое тело: выше уровня под-
земных вод собственный вес оползня устанавливается на основе
использования объемного веса пород при естественной влажно-
сти (11.1.9). а вес части оползня, расположенного между кривой
депрессии и поверхностью скольжения, определяется с учетом
взвешивания (B i ll)
Интенсивность и направление гидродинамических сил уста-
навливается по сетке фильтрации, которая может быть построена
в результате аналитических или численных расчетов или методом
моделирования. Полученные таким образом гидродинамические
силы раскладываются на две составляющие в зависимости от
применяемого метода расчета устойчивости оползня. Например,
если используется метод горизонтальных сип. то гидродинами-
ческая сила раскладывается на горизонтальную и вертикальную
составляющие. Вертикальные составляющие гидродинамической
силы складываются с соответствующим знаком с весом частей
оползневого тела, на которые оно делится, а горизонтальные со-
ставляющие прибавляются к силам взаимодействия частей ополз-
ня, действующих горизонтально. Тогда формула (10 2.7) для оцен-
ки устойчивости оползневого тела по методу горизонтальных сил
С учетом влияния движущихся подземных вод примет вид:
tg(a, -<₽К) + Фг(]
___.
л
V {[1 + tg(а, - фк) tg а, ] Ь,}
(11.1.12)
где Фг горизонтальная составляющая гидродинамических сил.
В некоторых других методах разложение гидродинамической
силы осуществляется на составляющие, расположенные парал-
лельно и перпендикулярно поверхности скольжения, что неред-
ко приводит к усложнению расчета.
Этот способ учета фильтрационных и взвешивающих сил
является наиболее общим и при известной сетке движения под-
земных вод позволяет полностью оценить влияние силового воз-
действия движущейся воды на напряженно-деформированное
состояние пород склона и устойчивость оползня. Этот способ
применяется преимущественно в таких методах расчета устойчи-
вости склона и величины оползневого давления, в конечных
формулах которых нет явно выраженных отдельных величин
удерживающей и сдвигающей сил.
Второй способ учета гидродинамических и взвешивающих сил
основан на их замене эквивалентными контурными сипами и при
164
практических оценках устойчивости склона наиболее удобен [2L
Этот способ применяется, когда удерживающие и сдвигающие сипы
оказываются явно выраженными На рис. 112 представлен опод*
зень, разделенный вертикальными плоскостями на отсеки. На него
Рис. 11.2. Схема действия фильтрационной и взвешивающей сил на единичный
объ ем
оказывает воздействие фильтрационный поток, движущийся в сто -
рону склона. Для простоты будем считать, что депрессионная кри-
вая совпадает с ’поверхностью оползневого тела. Рассмотрим один
из отсеков, ограниченный потенциальной поверхностью скольже-
ния АВ, депрессионной кривой CD идвумя боковыми вертикаль-
ными гранями AD и ВС. На единицу объема в пределах выделен-
ного отсека действуют: вертикально вниз направленная сила, равная
объемному весу пород с учетом взвешивания а также горизон-
тальная и вертикальная составляющие удельной фильтрацион-
ной силы, величины которых определяются:
где Н— гидростатический напор, Н + он — давление
Yb
воды или нейтральное напряжение в некоторой точке, г™ орди-
ната той же точки относительно поверхности сравнения. Для оп-
ределения величин гидростатической и гидродинамической сип,
действующих на весь отсек, необходимо суммировать все еди-
ничные силы по его объему И= 5 * 1 м (или площади 5 в случае
плоской задачи). В результате интегрирования получим общий
вес пород, слагающих отсек, с учетом взвешивания G* = увзв • 5 .
а также горизонтальную (Фх) и вертикальную (Фг) составляющие
гидродинамической силы. Их равнодействующая:
Ф* = ув f f =ув f f grad H ds (11.113)
г
165
направлена по касательной к линии тока или, что то же, — по
нормали п к поверхности равных напоров (эквипотенциали) в
данной точке. По теореме Остроградского-Гаусса:
f [gradff ds = ftfdl, (11.1.14)
5 t
где dl — элемент контура L, ограничивающего площадь S. Так
как Н — —
Ив
т.е. силу Ф’ можно заменить двумя силами. Нейтральное напря-
жение он ориентировано по нормали к контуру L области S в
каждой его точке, сила ув5 ориентирована по направлению силы
тяжести. В итоге три действующие силы G\ j GHdl, ув5 могут
L
быть сведены к геометрической сумме только двух сил;
G = G' + ув5 = уюв5 + ys5 » ТжиФ
Ф = /он Л, (11.1.16)
где увоа — объемный вес водонасыщенной породы.
Таким образом, если в расчет вводить вес пород блока вмес-
те с заключенной в них водой, то совместное действие гидроста-
тических и гидродинамических сил в пределах расчетного блока
может быть условно сведено к расчетной контурной силе Ф. Для
ее определения необходимо геометрически суммировать силы
нейтрального давления он вдоль контура L, перпендикулярно ко-
торому они ориентированы Такой способ замены фильтрацион-
ных объемных сил контурными является точным.
Если расчет устойчивости склона осуществляется методом,
когда оползневое тело делится вертикальными плоскостями на
отдельные блоки (рис. 11.3), то при суммировании сил Ф( по всем
блокам (i — номер блока) контурные интегралы вдоль вертикаль-
ных граней, подсчитываемые для каждых двух смежных блоков
дважды, но в разных направлениях, взаимно уничтожаются. В
сумме сохранится лишь контурный интеграл вдоль поверхности
скольжения АВ, так как нейтральное давление вдоль кривой деп-
рессии СБ равно 0. Поэтому формула К. Терцаги (10.3.4) для рас-
чета устойчивости неподтопленного откоса, т.е. когда он вдоль
поверхности склона равно 0, с учетом гидростатических и гидро-
динамических сил примет вид:
166
(11.1.17)
где силы Nj и 7, подсчитываются как составляющие веса пород в
пределах блока вместе, с заключенной в них водой, а силы Ф„
перпендикулярные поверхности скольжения, определяются по
формуле Ф, = (Я,, где (Я,-г,) — пьезометрическая
высота, определенная вдоль участка контура (см. рис. 11.3).
Рис. 11.3. Схема для расчета устойчивости оползня с учетом действия гидро ди-
ких сил и езвешивани)
Для подтопленного склона в формулу (11.1*17) должны до-
полнительно вводиться силы гидростатического давления, нор-
мальные затопленной поверхности склона АС.
11.2. Учет сейсмических воздействий
Расчет устойчивости склонов и откосов в сейсмических рай-
онах должен проводиться с учетом силы возможных землетрясе-
ний. Расчеты устойчивости с учетом сейсмичности производятся
в районах, для которых сила землетрясений оценивается в 7 бал-
лов и выше по принятой в России 12-балльной шкале. При этом
необходимо учитывать, что на отдельных участках одного и
того же по балльности района фактическая сила землетрясений
может отличаться от средней в зависимости от геологических ус-
ловий. Балльность следует увеличивать^ если в оползневые про-
цессы вовлекаются насыщенные водой гравийные, песчаные и
лёссовидные грунты* мягкспластичные и текучие глины, вывез
релые и сильно трещиноватые породы или оползни происходят
на участках с близким расположением тектонических разрывов,
с сильно расчлененным рельефом и т.д. Повышение балльности
территории следует оценивать на основе анализа карт сейсми-
ческого микрорайонирования
Учет сейсмического воздействия при расчете устойчивости
склонов и откосов или определении оползневого давления осу-
ществляется добавлением к расчетным усилиям так называемой
сейсмической силы. Последняя является объемной силой и по-
этому ее величина, отнесенная к единице объема, определяется
как некоторая часть объемного веса грунта и может геометричес-
ки складываться с гравитационной силой. Учет сейсмического
воздействия осуществляется двумя способами: в первом величи-
на сейсо'зжт<ой силы непосредственно 'учитывается при расче-
те, во втором — используется прием, известный как метод фик-
тивного откоса.
Первый способ. Величина сейсмической силы отнесенной к
единице объема ус определяется; ус = Асу, где у объемный вес
грунта, 7^ —1 коэффициент сейсмичности, значение которого
принимается в соответствии с табл 111 [4]:
Таблица 111
Коэффициенты сейсмичности
j Сейсмическая балльность района 1-6 * 0 10 и 12
Коэффициент | сейсмичности, Кс 0,0 0,025 0,05 о,1 —1—1 0.5 б 1
При расчете устойчивости оползневых тел и особенно при
оценке устойчивости искусственных откосов (плотин, насыпей,
дорог и др.) значение коэффициента рекомендуется увеличи-
вать в 1,5 раза, как это делается при проектировании инженер-
ных сооружений, где этим коэффициентом учитывается высота
сооружения:
(11.2 1)
В расчетах обычно рассматривается наиболее неблагоприят-
ное направление сейсмической силы, т.е. предполагается, что она
направлена горизонтально и в сторону склона. В методе гори-
зонтальных сил сейсмическая сила, определяемая как интеграль-
’ 58
ная по каждому блоку, на которые делится оползневое тело, скла-
дывается с силами взаимодействия между блоками, направлен-
ными так же горизонтально, откуда следует:
.=
V{|U tg(af - <pK)tga,J^z}
(11.2.2)
коэффициент сейсмичности
В других методах горизонтально направленную
сейсмичес-
кую силу раскладывают на составляющие: параллельную и пер-
пендикулярную поверхности скольжения. Первую прибавляют к
силам, сдвигающим оползневые блоки, вторую учитывают с со-
ответствующим знаком при определении нормальной составля-
ющей веса блоков. Учет сейсмической силы при определении
дефицита устойчивости изменяет формулу (10.4,2) следующим
образом:
5) » {[sin<Х| ч £rcos(az - 6)| - tg(p[cos az — Kc sin(af -- S)]} 4
(11.23)
где 5 — угол наклона сейсмической силы к горизонту, взятый с
соответствующим знаком (см рис. 10,13).
Направление сейсмической силы может быть выбрано и дру-
гим. В некоторых случаях рекомендуется выбирать направление
сейсмической силы параллельно поверхности скольжения, что
принципиально не верно, но упрощает расчет.
Если склон омывается водой, то сила гидростатического дав-
ления, действующая на наклонный откос, уменьшается на неко-
торую величину, определяемую в соответствии со СНиП |4].
Второй способ. Пусть на откос, сложенный породами с объем-
ным весом у, действует горизонтальная сила ус = 1,5А^у, направ-
ленная горизонтально и в сторону склона (рис 114). Тогда рав-
нодействующая гравитационной и сейсмической сил будет;
: у.
(11.2.4)
т.е. даже при сейсмичности территории в 10 баллов величина
(1.5 Al)2 мала по сравнению с единицей и сейсмическая сила прак-
тически не изменяет вес оползневого тела. С другой стороны,
(11.2.5)
ГО:
Рис. 11.4. Схема расчета устойчи-
вости склонов по методу «фиктив-
но г . гг
и если откос повернуть на угол 0С,
то объемные силы уо. которые дей-
ствуют на откос, займут вертикаль-
ное положение, и тогда все методы,
описанные ранее, можно применить
для расчета его устойчивости. Рас-
считанный для фиктивного откоса
коэффициент устойчивости и будет
определять степень устойчивости
действительного откоса с учетом
воздействия на него сейсмической
силы.
Углы поворота действительного
откоса для различных по силе- зем-
летрясений приведены в табл. 112.
Таблица 11.2
Углы поворота откоса
Сейсмическая балльность района | 7 8 Г””- 9 10
Угол поворота откоса, | 2° 30' 4О46 9°29' - J 22°5О' —
11.3. Методы расчета устойчивости склонов
в породах с жесткими связями
Расчеты устойчивости скальных откосов основываются на
идеях, аналогичных тем, которые используются при расчетах ус-
тойчивости оползневых склонов в рыхлых породах. Однако су-
ществуют и некоторые отличия, которые связаны с особенностя-
ми геологического строения склонов в прочных массивах. Одной
из основных причин нарушения устойчивости скальных склонов
является наличие В слагающих их породах плоскостей ослабле-
ния, обусловленных напластованием или трещинами. Поэтому
оползневые тела чаще имеют блоковое строение и опираются на
одну или несколько плоскостей. Среди них различают плоскости
скольжения, по которым происходит смещение оползневого тела,
и плоскости отрыва, которые отчленяют его от склона. При рас-
четах устойчивости скальных склонов решается плоская задача,
в отдельных случаях возможна оценка устойчивости оползневого
тела в объемном варианте.
Во многих методах предполагается, что оползневое тело опи-
рается на поверхность, образованную двумя плоскостями
(рис. 11.5). Существуют различные подходы к оценке устойчиво-
сти такого оползневого тела. Во-первых, оползневой блок может
170
быть мысленно разделен вертикальной плоскостью на два отсека
таким образом, чтобы каждый из них опирался на одну из двух
плоскостей скольжения, а сами отсеки рассматриваются как аб-
солютно твердые тела. В результате приходят к методам, которые
были рассмотрены в предыдущей главе. Если принять, что между
отсеками силы взаимодействия Д= £^= Е горизонтальны, то при
построении алгоритма расчета можно использовать методы го-
ризонтальных сил
Рис. 11.5. Схема к расчету устойчивости оползневого
блока, опирающегося на две поверхности
Однако деление оползневого тела, сложенного скальными
породами, на отдельные блоки трудно считать правомерным.
Естественнее рассматривать оползневое тело в скальных поро-
дах, тем более в момент смещения, единым блоком. В качестве
примера рассмотрим способ расчета устойчивости трещиновато-
го скального охкоса, йрсдаоженный Н.Н; Куваевым (1958). В этом
расчете предполагается, что поверхность, на которую опирается
оползневой блок, состоит из двух плоскостей: крутопадающей и
пологопадающей. Основное положение расчета состоит в том,
что сначала рассматривается случай, когда собственный вес
оползневого блока целиком передается на крутопадающую плос*
кость. Из условия предельного равновесия по крутопадающей
плоскости определяется дефицит удерживающих сил. Затем из
условия предельного равновесия того же блока, но вдоль полого-
падающей плоскости, загруженной дефицитом с обратным зна-
ком, определяется коэффициент устойчивости Кг
Возможны два варианта расчета. В первом устойчивость ополз-
невого тела определяется коэффициентом устойчивости, одина-
ковым для обеих плоскостей сдвига: А'| - А2 - А',
Пусть к оползневому телу кроме собственного веса приложе-
на инерционная сила от сейсмического воздействия, направлен-
ная горизонтально, в сторону склона (см рис. 115) и равная
171
F= KCG Тогда сдвигающая и нормальная составляющие сил, дей-
ствующих на оползневое тело, относительно крутопадающей по-
верхности скольжения будут:
У — G(cos а1 - Кс sin оц ),
Т — Gfsinaj + ATccosat).
(11.3.1)
Чтобы обеспечить устойчивость оползневого тела по этой
плоскости с коэффициентом запаса Кь необходимо приложить
гак называемый дефицит удерживающих сил Д:
Т
(11.3.2)
откуда
Д=К1Т-ЛЧвф1 - с,/,. (11.3.3)
Определенный таким образом дефицит Д должен быть ком-
пенсирован удерживающими силами вдоль пологопадающей по-
верхности. Коэффициент запаса К7по этой поверхности может
быть определен из условия устойчивости оползневого тела, на
которое действует сила, равная дефициту удерживающих сил Д,
но приложенная с противоположным знаком:
ДепКоц - a2)tgcp2 +с2/2
^cos(.ai -a2)
Подставив в (11.3.4) выражение для Дно формуле (11.3.3) и
учитывая, что « Ку, получим квадратное уравнение отно-
сительно Ку:
К} - Ку {А +В) +АВ -С =$,
ГДе а = ; в = tg(ai -a2)tg<p2, С
Т cos (а, -а2)
При втором варианте расчета принимается, что по крутопа-
дающей плоскости имеет место предельное равновесие, т.е. А, = 1.
а устойчивость всего оползневого тела определяется коэффици-
ентом запаса по пологопадающей плоскости: А'у= А2. Тогда из
формулы (11.3.3) получим:
~cih
(11.3.5)
и коэффициент устойчивости оползневого тела определяется из
-a2)tg<p2 +с2/2
Д'со8(а] -а2)
(11.3.6)
Наиболее просто коэффициент устойчивости может быть
определен, если его понимать как отношение удерживающих сил
к сдвигающим, действующим одновременно по обеим поверхно-
стям сдвига — крутопадающей и пологопадающей. Если ополз-
невое тело разбить на два блока вертикальной плоскостью (см.
рис. 115), то при проектировании действующих на оползневое
тело сил на наклонную поверхность /2 коэффициент устойчивос-
ти определится по формуле.
(Nj tg<p| +Ci/i)cos(ott -ct2) -biVztgtp; +c2li
7} cos(a! - a2) +T2
(11.3.7)
где
Ni — G|(cosai -Icsina|),
#2 = </2(cosa2 - Kc sinotj),
Tj ~ Gf (sin a! + Ac cos сц ),
~ G2(sina2 -I- Kc cosa2).
tg ф|, и tg 4>j, c2 — значения величин коэффициентов трения и
сцепления по крутопадающей и пологопадающей плоскости сдви-
га, Ас — коэффициент сейсмичности, а сейсмическая сила на-
правлена горизонтально и в сторону склона.
11.4. Пространственные методы расчета
устойчивости склонов
При оценке устойчивости оползневых тел в скальных и по-
лускальных породах иногда целесообразнее решать не плоскую,
а объемную задачу. Оползневые тела в этом случае имеют блоко-
вое строение, так как их формирование происходит благодаря
наличию в массиве пород поверхностей ослабления, обусловлен-
ных напластованием пород, литогенетическими и тектонически-
ми трещинами ит.д. По поверхностям ослабления образуются
поверхности скольжения либо поверхности отрыва. По поверх-
ностям скольжения происходит смещение оползневых тел. Вдоль
поверхности отрыва в начале смещения оползневое тело полно-
стью отчленено от массива или происходит разрыв еще сохра-
нившихся связей. При расчетах влияние на устойчивость ополз-
невых тел поверхностей отрыва обычно не учитывается, так как
установить его чаще всего не представляется возможным.
Смещение оползневых тел в скальных и полускальных поро-
дах может происходить по одной или нескольким поверхностям
скольжения Если поверхность скольжения одна, то коэффициент
устойчивости определяется исходя из модели поведения тела на
наклонной плоскости:
173
Gcosa- tg<p+ c5
O sin a
(11.4.1)
где G— вес оползневого тела; 5— площадь поверхности сколь-
жения; a — угол наклона поверхности скольжения; <р — угол внут-
реннего трения; с. — сцепление.
Если смещение оползневого тела возможно по нескольким
плоскостям скольжения, то задача по определению коэффици-
ента усложняется. Рассмотрим случай, когда смещение оползне-
вого тела может произойти одновременно по двум плоскостям
скольжения, падающим навстречу друг другу [1]. В этом случае
движение оползневого тела происходит в направлении, совпада-
ющем с линией пересечения поверхностей скольжения (рис. 11.6).
Тогда коэффициент устойчивости определяется по формуле:
к ~ Gi cosot, tg(p| +С2со5аг tg<p2 4 e,S, 4-с252 (пдэ)
у G sinp ’ ' • • '
где G= G^ + Gj — вес оползневого тела и его частей, опирающих-
ся на соответствующие поверхности скольжения, если оползне-
вое тело разделить вертикальной плоскостью, проходящей через
линию их пересечения; 5,, S2 — площади поверхностей скольже-
ния; a,, a2 — углы наклона поверхностей скольжения; р — угол
наклона к горизонту линии пересечения поверхностей скольже-
ния; ф(, с,, ф2, с2, —« углы внутреннего трения и сцепления по
соответствующим поверхностям скольжения.
Существуют и другие, но немногочисленные способы оцен-
ки устойчивости объемных оползневых тел. При решении таких
Рис. 11.6. Схема для расчета устойчивости
оползневого тела, которое смещается по двум
падающим навстречу друг другу поверхностям
скольжения. Fy и — силы сопротивления
сдвигу, обусловленные трением и сцеплением
174
задач обычно рассматривается блок скального или полускально-
го массива, ограниченный несколькими поверхностями сколь-
жения, принимаемыми за плоскости, и дневной поверхностью
склона- Задача сводится к определению условия равновесия это-
го блока при заданных действующих силах и принятых прочнос-
тях на сдвиг по рассматриваемым плоскостям ослабления.
Оползневой блок представляется геометрически внутренни-
ми нормалями к плоскостям ослабления. Эти нормали, восста-
новленные из одного центра, образуют на поверхности единич-
ной сферы криволинейную зону, треугольную, четырехугольную
и т.д., в зависимости от количества отделяющих оползневое тело
плоскостей ослабления. Вокруг каждой из нормалей строится
конус с углом при вершине, равным 9, = 2 arctg б„ где б, пред-
ставляет собой параметр прочности на сдвиг (например, угол внут-
реннего трения) по соответствующей плоскости ослабления. Сле-
ды этих конусов на поверхности сферы единичного радиуса
представляют собой окружности, описанные относительно углов
криволинейной зоны. Соединив эти окружности внешними ка-
сательными, получим криволинейную зону, названную зоной
устойчивости.
Затем определяются величина и направление равнодейству-
ющей /? всех сил, действующих на оползневое тело:
1) собственный вес G оползневого блока;
2) внешние нагрузки Р, приложенные к блоку;
3) фильтрационное давление воды в плоскостях ослабления
(4,,
4) инерционная сила Р, вызванная сейсмическим ускорени-
ем, приложенная в наиболее неблагоприятном направлении.
После определения положения этой равнодействующей в
пространстве точка приложения ее переносится в центр единич-
ной сферы и устанавливается точка пересечения равнодействую-
щей R с поверхностью сферы. Если эта точка попадает в пределы
зоны устойчивости, то устойчивость скального оползневого бло-
ка считается обеспеченной. В противном случае оползневое тело
является неустойчивым.
Контрольные вопросы
1, Какова роль подземных вод в формировании оползней?
2. Каким образом оценивается воздействие движущихся под-
земных вод на устойчивость склона?
. Как определяется объемный вес взвешенного в воде фунта?
4. Какие существуют способы оценки гидростатических и гид-
родинамических сил при расчетах устойчивости склонов?
. ..
5. Способ замены фильтрационных (объемных) сил поверх-
ностными.
б. Способы учета сейсмических сил при расчетах устойчиво-
сти СКЛОНОВ.
7. Какова сущность метода «фиктивного откоса»?
8. Какие существуют варианты расчета устойчивости ополз-
невых тел в скальных массивах?
9. Пространственные методы расчета устойчивости склонов
в скальных массивах.
ГЛАВА 12. РАСЧЕТЫ ПЕРЕРАБОТКИ БЕРЕГОВ
ВОДОХРАНИЛИЩ
Задача прогноза переработки берегов водохранилищ возник-
ла в 50-е годы в связи с развернувшимся строительством плотин
на реках Русской платформы. Для ее решения было разработано
несколько десятков методов и предложений по прогнозам пере-
формирования берегов, основанных на разных схемах взаимо-
действия геологической среды и водохранилищ, каждый из ко-
торых имеет свои пределы применения..^ отражаетусхповия района
строительства. Большинство методов создавалось для прогноза
переработки берегов равнинных водохранилищ, широких, С ВЫ
сокой волной, малой сработкой и относительно простым геоло-
гическим строением. В зависимости от исходных методических
позиций имеющиеся методы можно объединить в группы.
1. Расчетные методы, основанные на предпможении, что
объемы переработки пропорциональны общей энергии волн, или
«энергетические» методы.
2. :. Сравнительно-геологические, или методы анапогий»
3. Статистические, ил л в-зроятностныг-етоды.
Группа «энергетических» методов включаетметоды: Н.Е. Конд-
ратьева (Государственный гидрологический институт^ 1953, 1976),
Е.Г. Калугина (ВСЕГИНГЕО, 1959)., Е.К. Гречищева (институт
Земной коры СО АН СССР, 1961), Б.А. Пышкина (институт Гид-
ротехники АН УССР, 1954, 1963).
К сравнительно-геологическим методам; относятся «графоа-
налитический» метод ЕС. Золотарева (Геологический факультет
МГУ, 1955), .метод «природных аналогов» Л.Б. Розовского (Одес-
ский Государственный университет, 1962), получивший дальней*
шее развитие в работе В.М. Воскобойникова и О.Г. Лиходеевой
(1984), и аналого-расчетный, предложенный Н.Е Варазашвили
(1983) применительно к небольшим горным водохранилищам.
Статистические (вероятностные) методы разработаны на
основании наблюдений за размывами низких берегов простого
геологического строения Волжских водохранилищ (М/М. Адас,
В.И Экзарьян, 1975, 1979).
Перечисленные способы могут быть применены для расчета
переработки береговых склонов с относительно простым геоло-
гическим строением. Для расчетов в более сложных случаях усо-
вершенствовались старые или были разработаны новые методы.
На основе графоаналитического метода ГС. Золотарева разра-
ботаны; способ прогноза переработки берегов водохранилищ
Средней Азии и других районов распространения лёссовых
легкоразмокаемых пород (3. Халматов, 1969) и метод прогноза
формирования высоких берегов водохранилища сложного геоло-
гического строения с развитыми оползневыми и другими про-
цессами при нестационарном уровенном режиме (ГС. Золота-
рев, А.Л. Рагозин, 1979). На основе наблюдений за процессами
на закарстованных территориях Камского, Братского и других
водохранилищ получены эмпирические зависимости и предложе-
ны оригинальные методы прогноза переработки берегов в карстую-
щихся породах (И.А. Печеркин, 1981). Метода прогноза специфи-
ческих процессов формирования ложа и берегов водохранилищ в
районах распространения многолетней мерзлоты практически не
разработаны Имеются данные ограниченных наблюдений на су-
ществующих водохранилищах (Хаитайское, Вилюйское и др.) и
отдельные предложения по прогнозу переработки берегов север-
ных водохранилищ (Ф.Э. Аре, Я.А. Кроник и др.).
Выбор метода прогноза формирования берегов на конкрет-
ном участке должен основываться на знании неодинаковых в раз-
ных районах закономерностей взаимодействия берегов и водохра-
нилища, выявленных при наблюдениях на существующих водоемах
По гидрологическим факторам, влияющим на величины и
интенсивность переработки берегов, водохранилища подразде-
ляются:
1) по уровенному режиму на водохранилища многолетнего,
сезонного и ежедневного регулирования с величинами сработок
от первых метров до многих десятков метров и со скоростями сни-
жения уровня до 0,5-1 м/сут в зависимости от водопотребления;
2) по волновому воздействию, обусловленному преобладаю-
щими ветрами, шириной и рельефом дна водоема,
3) по образованию и перемещению наносов, связанных с
воздействием волн и течений;
4) по характеру и скоростям течений в паводковые периоды,
особенно в заливах и верховьях водохранилищ.
Для водохранилищ равнинно-платформенных областей (на
Волге, Каме, Днепре и др.) типична сработка 2-4 м и площадь
3200-5500 км2 (Волгоградское, Братское и др ), а для горно-склад-
чатых областей сработка достигает в маловодные годы 55-70 м и
более при ширине водоема до 1-2 км (Чарвакское, Токтогульское
и др.). Особым режимом обладают водохранилища ГАЭС, на ко-
торых ежедневная сработка и подъем уровней достигают 8-10 м.
С инженерно-геологических позиций берега водохранилищ
для прогноза их формирования обособляются по следующим
признакам:
• по характеру пород, слагающих склон, выделяются шесть
основных комплексов, определяющих качественно различные про-
цессы переработки: 1) легкоразмываемые (пески, суглинки рых-
лые); 2) легкоразмокаемые (лёссы и др.); 3) средней прочности,
178
преимущественно морские осадочные, интенсивно выветриваю-
щиеся (глины, мергели, песчаники полимиктовые глинистые
и т.п.); 4) легкорастворимые (гипсы, соли); 5) прочные слабо вы
ветривающиеся и практически не размываемые (интрузивные,
массивные известняки, метаморфические); 6) многолетнемерзлые
породы предыдущих групп, нередко содержащие льды, при отта-
ивании которых будут возникать различные деформации;
• по наличию на берегах активных оползней, осыпей, обва-
лов разного объема, карста, селевых потоков, просадок и других
процессов различной интенсивности;
• по гидрогеологическим условиям: наличию и развитию под-
пора подземных вод и увеличению общей обводненности массива
пород берега, по возникновению и величинам взвешивающего и
гидродинамического давлений, особенно при быстрых сработках
уровня водохранилища ,
• по высоте и крутизне склонов;
* по образованию на отмелях и в заливах водохранилищ ак-
кумулятивных форм за счет выноса селевыми потоками и ополз-
нями обломочных масс прочных трудноразмываемых пород.
Побережья водохранилищ нередко Являются территориями
строительства и хозяйственного испомьзования, в связи с чем на
них неизбежно возникают подрезки склонов, отвалы. возводятся
здания, склады, осуществляются защитные мероприятия, что
влияет на процессы переформирования берегов, перемещение
наносов и общую устойчивость. Эти техногенные факторы необ-
ходимо учитывать в прогнозах.
При прогнозах следует составить инженерно-геологическую
модель строения склона и модель предполагаемых процессов пере-
формирования берега по типичным стадиям их развития, для каж-
дой из которых методы и исходные данные могут быть разными в
реальных условиях гидрологического режима водохранилища.
12.1. Энергетические методы
В основе энергетических методов прогноза переработки бе-
регов водохранилищ лежит представление о том, что объем раз-
мытых пород в некоторой точке размываемого берега пропорци-
онален энергии волнения в той же точке.
Метод Н.Е. Кондратьева
Этот метод [8] применяется для расчета ширины зоны ко-
нечной переработки берега. Он используется для случая разру-
шения волновым воздействием устойчивых берегов, сложенных
L ...!
песчаными, супесчаными и суглинистыми породами. Расчет ве-
личины Переработки оереговых склонов по этому методу произ-
водится в следующем порядке.
1. По периметру водохранилища намечается ряд створов, рас-
положенных перпендикулярно линии уреза, для которых произ-
водится расчет переформирования берега. Для проведения вол-
новых расчетов на намеченном створе выбирается точка, лежащая
на некотором расстоянии от берега. Эта точка должна распола-
гаться на внешнем крае будущей береговой отмели. Вез расчета
определить положение этой границы невозможно и первоначально
расчетная точка намечается на глубине, которая в 3*4 раза пре-
вышает высоту ожидаемой волны.
2. Выбирается расчетная скорость ветра, так как расчет волн,
перерабатывающих береговые склоны, ведется исхода из наиболь-
шей скорости ветра, которая наблюдается в районе водохрани-
лища в течение безледного периода. Для учета влияния защи-
щенности метеостанции вводят поправочный коэффициент 1,5 на
расчетную скорость ветра. В предварительных расчетах рекомен-
дуется для европейской части России принимать расчетную ско-
рость ветра 20 м/с.
X Для определения расчетной высоты волны hP через точку,
выбранную на расчетном створе, проводится рад лучей (в п на-
ветренных румбах) до противоположного берега водоема. При-
нимая эти лучи за направление разгона волн, по номограммам
А.П. Браславского [1], определяются в выбранной точке высоты
волн /к. Значения высот волн* полученные по разным направле-
ниям разгона, исправляются на угол подхода волны:
й A„>/cosc,7 .
где ал - угол, образованный направлением разгона волны и рас-
четным створом, расположенным нормально к береговой линии.
Наибольшее из полученных значений высот волн пересчитыва-
ется на 15% обеспеченность умножением на коэффициент 0,7
(Л «к 0,7йтах ), которое и принимается за расчетную высоту вол-
ны. Для определения расчетной высоты волны можно пользо-
ваться СНиП 2 06.04-82 «Нагрузка и воздействия на гидротехни-
ческие сооружения *.
4. Расчет размеров вновь образуемой береговой отмели про-
водится для ее предельного (динамически устойчивого) состоя-
ния и для стадии формирования на срок 10, 25, 50 лет ит.д. На
рис. 12.1 приводится схема береговой абразионно-аккумулятив-
ной отмели, образованной в Легкоразмываемых породах. Для ее
построения необходимы следующие данные: первоначальный
профиль берегового склона с характеристиками гранулометри-
ческого состава пород, их плотности и размываемое™; глубина
размывающего действия волны z5 определяемая в зависимости от
расчетной высоты волны hp и коэффициента устойчивости грун-
тов отмели на ее внешнем крае т, по графику на рис. 12.2; уклоны
отмели — аккумулятивной ix между точками а И Ьа.верхней абра-
зионной /2 между точками b и с (см рис. 12.1); коэффициент ак-
кумуляции наносов 5 - отношение объема аккумулятивной час-
ти отмели к полному объему разрушения; уровни наивысшего
подпорного горизонта (НПГ) и горизонта сработки (ГС|-
Рис. 12.1. Схема построения береговой отмели
По кумулятивной кривой, предварительно исключив части-
цы диаметром менее 0,05 мм, узс-ц .мые в виде взвеси,
ют средний диаметр 30% наибе лле шшгких частиц и средний дед
метр 10% наиболее Крупных частиц. По табл. 12 1? исходя из
средне--:- диаметр: мелких
частиц, определяется уклон
аккумулятивной прей муже-
ственно прямолинейной ча-
сти отмели 4? а по среднему
диаметру крупных фрак-
ций — уклон абразионной,
как правило, криволинейной
части отмели ъ, а также оп-
ределяется коэффициент Т).
Если фракции диаметром
менее 0,05 мм отсутствуют, то
коэффициент аккумуляции 3
принимается равным едини-
це (8-1). В том случае, когда
Рис. 12.2. График для определения глуби-
ны z размывающего действия волны
эти частицы составляют большую
часть грунта размываемого берега, расчет производится без исклю-
чения указанных фракций и коэффициент 3 следует принимать
равным нулю Угол склона аккумулятивной части отмели i соот-
ветствует углу естественного откоса слагающих ее пород под во-
дой. Размеры прямолинейного В„ и криволинейного Вк отрезков
предельной береговой отмели определяются по эмпирическим
формулам:
Вк --az2 + Pz,
В„ = z(2a Ч-
(12.1.1)
где a = ; I =
20,7*1 Л
Форма надводного уступа определяется по аналогии с су-
ществующими природными склонами сходного геологического
строения.
Таблица 12 1
Уклоны устойчивости береговой отмели (по Н.Е. Кондратьеву)
Грунт d, ММ h '1 п
Пыль 0э01—ОД 0,005 0,001 100
Песок
мелкий 0,1-0,25 0,03 0,005 70
средний 0,25-03 0,07 001 70
крупный 0,5“ 1 0,14 0,02 U 70
Гравий мелкий 1-2 0,19 0,03 45
средний 2-5 0,21 0,05 45
крупный 5-10 0,25 0,08 25
мелкий 10—20 03 0,1 11
средний 20-50 0,36 0,15 6
крупный 50-100 0,4 0,' 4
Построение профиля береговой отмели производится по у. -
тановленным уклонам ее поверхности ij и /2 и размерам прямоли-
нейного и криволинейного отрезков Вп и Вк (см. рис. 12.1) с уче-
том уровней НПГ и ГС. Положение береговой отмели
относительно первоначального берега определяется подбором
местоположения точки а так, чтобы отношение площади акку-
мулятивной призмы к площади размываемой призмы было рав-
но коэффициенту 5. Расстояние L характеризует величину ко-
нечной переработки берега водохранилища. Для расчетов
параметров отмели во времени необходимо определить удельную
мощность потока волновой энергии Е на единицу береговой ли-
нии и в единицу времени и коэффициент сопротивляемости по-
род волновому размыву е. Для каждого направления волн вычис-
ляете энергия по формуле:
Е = 795й '3 cos a,
где h — высота волны, а — угол между направлением разгона
волн и нормалью к береговой линии Энергия волн всех направ-
лений определяется как средневзвешенная величина. Коэффи-
циент е устанавливается натурными опытами Пример расчета
предельного положения береговой отмели приведен в «Учебном
пособии по инженерной геологии» [6].
Метод Е.Г. Качу<
Этот метод расчета [7] переработки берегов водохранилищ
основан на следующих предположениях:
• в переработке берега участвуют волны всех высот и общий
объем размытых пород пропорционален суммарной энергии волн
в данном месте;
• интенсивность процесса переработки зависит от сопротив-
ления пород размыву и высоты берега;
• процесс переработки затухает во времени и его изменение
характеризуется кривой параболического вида.
Исходя из приведенных предположений, общий объем раз-
мытых пород может быть определен по формуле:
Q = Ek^t', (12.1.2)
где Q— объем размытых пород на 1 м берега, и1; Е— суммарная
энергия волн, тм; t— время размыва (число сезонов); в — пока-
затель степени (меньше 1), зависящий от скорости затухания
процесса; к^ — коэффициент, учитывающий высот}' берега: кР —
коэффициент размываемости пород.
Коэффициент, учитывающий высоту берега, вычисляется по
формуле: к6 = h$c , где А6 — средняя высота берега, с — изменя-
ется от 0,03 для легкоразмываемых, до 0,05 — для трудноразмы-
ваемых пород. При высоте берега более 30 м значение к$ прини-
мается равным единице.
В первый год заполнения водохранилища (/= 1), когда сфор-
мировалась отмель, количество размытых пород в основном за-
висит от энергии волнения, размываемости пород и высоты бе-
рега. У крупных высоких берегов (более 30 м) в первый год почти
вся энергия расходуется на размыв уступа. Отношение объема
размытых пород высоких берегов за первый год Q. к энергии вол-
нения £гза тот же период был назван Е.Г. Калугиным коэффи-
циентом размываемости пород [6]:
*0=->м3/тм. (12.1.2)
Для расчета энергии волнения сначала по методу А.П. Брас-
лавского в зависимости от скорости ветра определяются высоты
183
волн. Зная высоту волны и продолжительность действия ветра в
сутках, по графикам [6] можно установить ее энергию. По каж-
дому выбранному направлению подсчитывается сумма энергий
всех волн, которая затем умножается на синус угла между ли-
нией берега и направлением их подхода. Суммарная энергия волн
по всем направлениям принимается за характеристику средне-
многолетней энергии в данной точке берега
Показатель степени в представляет собой отношение шири-
ны абразионной части отмели к ширине всей отмели. Если от-
мель абразионная, то показатель степени в достигает 0,95, в слу-
чае большой ширины аккумулятивной части отмели он снижается
до 0,45 (в среднем в = 0,7). При определении показателя в необ-
ходимо учитывать перемещение наносов вдоль берега.
Расчет объема берегового размыва производится для 10, 20,
50 и 100 лет эксплуатации водохранилища. Возможно решение
обратной задачи — определение времени переработки берега при
заданном объеме размытых пород.
Для построения профиля переработки берега необходимо
определить размеры зоны, в пределах которой происходит его
размыв. Зона размыва зависит от амплитуды колебания уровней
воды водохранилища. Верхний уровень — нормальный подпор-
ный горизонт (НПГ) — соответствует уровню 2-4% обеспечен-
ности при высоком положении уровня воды. Нижний уровень —
горизонт сработки (ГС) — уровню 96—98% обеспеченности при
низких сработках безледного периода. Для определения верхнего
горизонта размыва к НПГ прибавляют 1/3 высоты рабочей вол-
ны, нижний горизонт размыва получают, откладывая от ГС вниз
высоту рабочей волны (рис. 12.3), высота которой рассчитывает*
ся по формуле:
= 0,7 Лс,
Рис. 12.3. Построение профиля переработки берега
где hc — средняя высота волны 0,1%-ной обеспеченности из высот
волн для наибольших значений энергий по всем направлениям, а
0,7 — переходный коэффициент на 15%-ную обеспеченность.
Построение зоны размыва начинается от точки а, соответ-
ствующем началу абразионной части отмели (см. рис. 12 3), от
которой под утлом р проводится прямая, отвечающая ровной
поверхности абразионной отмели, до пересечения с продолже-
нием верхнего горизонта размыва (точка Ь). Угол р подбирается
таким образом, чтобы площадь зоны размыва на профиле чис-
ленно равнялась вычисленному объему размытых пород Q
В надводной части профиль склона строится по аналогии с
существующими в таких же геологических условиях наиболее
крутыми склонами или с применением расчетных методов. Рас-
стояние от уреза НПГ до границы зоны разрушения (точка с)
представляет собой искомую величину переработки берега водо-
хранилищем.
12.2. Сравнительно-геологические методы
прогноза переработки берегов водохранилищ
Графоаналитический метод Г. С. Золотарева
Метод был разработан для прогноза переработки берегов во-
дохранилищ Волго-Камского каскада. Прогноз переработки бе-
рега предполагает определение величины отступания берега в
результате его размыва волнами водохранилища. Для расчета ве-
личины отступания берега производится построение профиля
переработанного берега. Графоаналитический метод позволяет
решать эту задачу для множества случаев. Во-первых, расчет пе-
реработки может быть выполнен для берегов водохранАищ, по-
строенных как на равнинных реках, так и в горно-складчатых
областях, отличающихся режимом и величиной сработки уров-
ней водохранилищ. Во-вторых, этот метод предполагает различ-
ные способы прогноза переработки берегов, сложенных отлича-
ющимися комплексами пород, имеющих разную морфологию и
происхождение, В-третьих, графоаналитический метод может быть
применен для прогноза переработки берегов, как в широких глу-
боководных частях водохранилища, так и в его верховьях и зали-
вах. В-четвертых, прогноз переработки берегов водохранилища
может быть выполнен для одного сечения или в пределах боль-
шого отрезка берега, т.е. возможно решение не только профиль-
ной, но и пространственной задачи. В-пятых, прогноз возможен
для первых 10 лет после создания водохранилища и для конеч-
ной стадии переработки берега
185
Для построения профиля прогноза переработки берегов не-
обходимы следующие данные.
1. Параметры волн — высота, длина, угол подхода К берегу в
зависимости от силы везра и при разной обеспеченности, что
можно получить в результате фактических наблюдений за ветром
и волнами или расчетами по СНиП 2.06.04-82.
2. Прогнозный или фактический уровенный режим водохра-
нилища для лет разной водообеспеченности.
3. Инженерно-геологические разрезы склона в масштабе от
1:1000 до 1:2000 с подробным микрорельефом, характеристикой
состава, неоднородности, выветрелости, трещиноватости и об-
водненности пород и с данными о величинах сопротивления сдви-
гу, размыву и размоканию пород в разных состояниях.
4. Гидрогеологические данные — количество И приурочен-
ность водоносных горизонтов, уровни и режим подземных вод, а
также сведения, необходимые для оценки влияния подземных
вод на прочность пород, для расчета подпора во времени и опре-
деления гидравлических градиентов при сработках уровня водо-
хранилища.
5. Для прогноза переработки берега в широкой части водохра-
нилища необходимо иметь расчетные значения величин углов аб-
разионных (аз и р3) и аккумулятивных (а2 и |3-.) отмелей и зон на-
ката (а4и р4) в разных породах, коэффициенты аккумуляции
наносов на подводном склоне и углы эрозионных частей отмели
(5! и 62), определяемые на основе изучения бечевников рек.
6. Данные о форме и крутизне устойчивых откосов и скло-
нов разных генетических типов, выработанных в различных по-
родах, имеющих разную высоту, экспозицию и состояние.
7. Сведения о состоянии и поведении различных генетичес-
ких типов пород в аналогичных условиях на берегах крупных
озер, водохранилищ и на отмелях морей.
Перечисленное выше необходимо для оценки переработки
берега в плоском сечении (профильная задача). Для прогноза
переработки берега на значительном протяжении (пространствен-
ная задача) дополнительно надо иметь:
1) топографическую, геолого-литологичекую, геоморфологи-
ческую и гидрогеологическую карты оцениваемого участка бере-
га водохранилища в масштабе от 1:2000 до 1:100 000 в зависимос-
ти от его размера, сложности строения и стадии исследования;
2) данные о возможном направлении и силе течений, очагах
формирования, перемещения и аккумуляции наносов в пределах
рассматриваемого участка берега.
Графоаналитический метод рекомендуется применять для
расчета переработки берегов водохранилищ значительной шири-
ны с небольшими сработками уровня, когда берега имеют от-
186
носительно простое геологическое строение и отличаются мало-
активными склоновыми процессами.
Построение профиля прогноза переработки берега для широ-
ких частей водохранилища выполняется в последовательности,
приведенной на рис 12.4. Сначала определяется тип прибрежной
отмели, которая может быть абразионной, аккумулятивно-абра-
зионной или абразионно-эрозионной. Если склон сложен тон-
кими легкоразмываемыми глинистыми породами, коэффициент
аккумуляции которых близок к нулю, или, когда с участка дан-
ного профиля наносы будут полностью удаляться волнами или
течением, образуется абразионная отмель. Тогда в отсутствие
аккумулятивной части отмели точку а, от которой начинается
построение профиля переработки, следует расположить на ли-
нии первоначального склона. Если отмель аккумулятивно-абра-
зионная, то глубина бровки уступа аккумулятивной части отме-
ли (положение точки а) определяется подбором. В зависимости
от того, для какой стадии (10-летней или конечной) дается про-
гноз, точка а располагается на различных глубинах.
'•
Уступ Аккимилятибная Абразионная часть отмели Зона немодный
отмели часть отмели наката неуст откос
откос
Рис, 12.4. Схема построения береговых отмелей в широкой глубоководной части
водохранилища: а — через 10 ЛЗД б — для конечной стадии
1
При построении профиля переработки берега, сложенного
легкоразмываемыми песчаными и суглинистыми породами, для
10-летней стадии прогноза рекомендуется брать глубину бровки
отмели, равную 1,5 высоты волны 20%-ной обеспеченности. Для
окончательной стадии переработки глубину бровки отмели для
легкоразмываемых пород следует принимать равной 3-3,5 высо-
ты волны 5% ной обеспеченности, а для плотных глинистых или
мергелистых пород, размываемых при выветривании, 2,5-3,0 вы-
соты волны с повторяемостью один раз в 100 лет. Для водохра-
нилища с малой сработкой уровня указанное расстояние откла-
дывается для 10-летней стадии от наивысшего подпорного уровня
(НПУ), а для конечной — от горизонта сработки (ГС) безледного
периода в маловодный год.
От бровки уступа аккумулятивной части отмели (точка а) под
углом <Х| или Pi в зависимости от стадии переработки проводится
линия уступа отмели, а под углом <х2или р2 поверхность.
Величины углов <|М Pi зависят от состава наносов и колеблются
от 10 до 20°. Углы а2и также зависят от состава материала, об-
разующего аккумулятивную часть отмели, а их величины анало-
гичны углам отмели в тех же породах и колеблются от 0°30? до
10°. Линия под углом а2или р2проводится до пересечения е пер-
воначальной поверхностью склона (точка Ь) и далее проводится
под углом а3или ргДО пересечения с продолжением горизонта
НПУ (точка с). Отмель между точками b и е абразионная, выше
точки с располагается зона наката волны с углом наклона или
р4. Высота зоны наката равна 0,3-0.4 высоты волны, а ее ширина
для 10-летней стадии переработки примерно в два раза меньше,
чем конечной стадии.
Над зоной наката располагается надводный уступ, контур
которого зависит от свойств слагающих его пород. В 10 летнюю
стадию, когда уступ формируется^ он является неустойчивым и
имеет предельную крутизну подмываемого Обрушивающегося
откоса, а для конечной стадии переработки его профиль долже
соответствовать устойчивому состоянию и устанавливается по
аналогии с такими же природными склонами данного района. В
сложных случаях профиль надводного уступа определяется рас-
четными методами.
После выполнения первого построения прогноза переработ-
ки для 10 лет или конечной стадии производится проверка, на-
сколько соотношение объема аккумулятивной части отмели (пло-
щадь F|, ограниченная точками /, а, Ь) и объема размытых пород
(площадь заключенная между точками bt с, dt е) соответствует
принятому коэффициенту аккумуляции. Если совпадения нет,
необходимо произвести повторное построение, перемещая точку
а вправо или влево, чтобы добиться нужного соотношения пло-
188
шадей аккумуляции и размыва, Величины необходимых для пост-
роения профилей переработанного берега углов и коэффициентов
аккумуляции для водохранилищ Камеко-Волжского каскада при-
ведены в «Учебном пособии по инженерной геологии» |6]
Построение профиля прогноза переработки берега для вер-
ховий или заливов водохранилища (абразионно-эрозионная от-
мель) выполняется аналогично тому, как это рекомендуется де-
лать для широких глубоководных частей водохранилища
Отличие состоит в том, что выше точки с располагается не зона
наката, а эрозионная часть отмели, которая в течение 10 лет, в
соответствии с гидрологическим прогнозом, будет соответствен
вать горизонту паводка 50%-ной обеспеченности, а для конеч-
ной стадии — горизонту 5%-ной обеспеченности (рис. 1Х5КУгол
наклона эрозионной части отмели для 10-летней (80 и для ко-
нечной стадии (82) устанавливается по уклону бечевника в зоне
о
Гэризонт лабодка 50 %-ной
обеспеченности
нпу
6 Лют
; !
It! I !
।___t «. ........ ...... . - . - -i... - - t-1
Уступ Аккумулятио- Абразионная часть отмени Эрозионная Надбоб’-
отмели нал часть отм. часть ный неуст
лкос
1
Эр о- Надбобный
зион. устойчи-
чаегь оый откос
Горизонт
„ обеспеченности
у ...... - ----------
гор. сраб отк. русла
I 1 .............J---------------------------------
Уступ Аккунулятиб Абразионная часть отмели
отмели нал часть отм.
;
Рис. 12.5. Схема построения абразионно-эрозионных отмелей а верховьях и за-
ливах водохранилища: a — через 10 пет, б — на конечную стадию
Г
осенних паводков. Это связано с тем, ЧТО паводок в водохрани-
лище по величине скорости течения более сходен с осенним,
чем с весенним.
Учет перемещения наносов вдоль берега при прогнозе пере-
работки берегов для отдельных районов водохранилища прибли-
зительно может быть выполнен путем изменения коэффициента
аккумуляция. Очевидно, что его величина находится в зависи-
мости от скорости и направления течений при разных уровнях
водохранилища, изрезанное™ береговой линии и микрорельефа
затопленной части территории, наличия возможных очагов фор-
мирования наносов, т.е. участков берега, сложенных легкораз-
мываемыми породами.
Метод природных аналогов Л. Б. Розовского
Прогноз переработки берегов водохранилища методом при-
родных аналогов [11] выполняется с помощью переноса резуль-
татов изучения переформирования берега на натурной модели,
которая подбирается по качественным оценкам и количествен-
ным критериям подобия. Чтобы применить этот метод, необходи-
мо иметь широкий набор натурных моделей процесса формирова-
ния берегов водохранилищ, полученных в результате проведения
комплексных инженерно-геологических исследований и много-
летних натурных режимных наблюдений на водохранилищах в
различных регионально-геологических, зонально-климатических
и техногенных условиях. Метод природных аналогов разработан
для прогноза переработки неоползневых берегов построенных или
проектируемых водохранилищ, сложенных преимущественно
пылеватыми суглинками и супесями. Для его применения Л.Б. Р
зовским был создан альбом природных аналогов [10] на основа-
нии изучения побережья одного из водохранилищ Днепровского
каскада. Каждый аналог представляет собой инженерно-геоло-
гическую карту, на которой приведены результаты режимных
наблюдений за развитием размыва берегов в течение пяти лет
эксплуатации водохранилища.
Метод природных аналогов представляет собой разновидность
физического моделирования, когда в качестве модели выступает
природный обьекг. Подбор аналога вначале осуществляется по
качественным признакам, т.е. оцениваемый объект и его аналог
должен обладать рядом общих свойств и характеристик. 1)они
должны отличаться общностью механизма переработки берегов;
2) объект и аналог должны иметь одинаковые геологические ус-
ловия формирования прибрежной отмели, которая, например,
может вырабатываться в рыхлых отложениях, представленных
только лёссами; 3) должна быть общность гидрологического ре-
190
жима, т.е. прогноз может выполняться для нижней или средней
зоны водохранилища; 4) на исследуемом объекте и его аналоге
формируются берега одного и того же динамического типа, на-
пример, только абразионные или абразионно-аккумулятивные;
5) методика получения параметров, входящих в критерии подо-
бия и расчётные формулы, для объекта и аналога должна быть
одинаковой. Единообразие оцениваемого объекта и аналога уста-
навливается сравнением имеющихся инженерно-геологических
материалов (карт, разрезов и др.).
Точный выбор аналога на изучаемом объекте производится
по количественным критериям подобия. Для расчета критериев
подобия вводится система определяющих параметров, характе-
ризующих основные факторы, от которых зависит форма и вели-
чина переработки берега (табл. 12.2).
Таблица 12.2
Определяющие параметры для оценки переработки берегов водохранилищ
Факторы Определяющий параметр Обозначение Размерность
Энергия прибойного волнения энергия волн на внешнем крае отмели - 5 * , V2 ML:T 2
Гидродинамические условия преобразова - ния волн на отмели ширина отмели / 1
Сопротивляемость пород размыву коэффициент лзйга tg V б/р
Объем пород в одном цикле обрушения высота берега h L
Профиль склона угол склона i б/р
Извилистость берего- вой линии коэффициент извилистости J б/р
Режим наносов у бе- рега [ коэффициент аккумуляции б/р
Вес пород плотность Р ML"3
Ускорение силы тяже - сти .. g h LT2 j
Из приведенной таблицы видно, что число независимых оп-
ределяющих параметров равно восьми (ширина отмели и высота
берега имеют одну и ту же размерность). Так как число размер-
ных независимых определяющих параметров равно четырем, а
чисто независимых размерностей трем, то согласно центральной
теореме теории подобия число нетривиальных критериев подо-
бия равно единице.
101
7 -.
Этим критерием подобия будет безразмерная комбинация:
Е
pgh* ML 'LT^L*
(12.2.1)
Число безразмерных параметров равно четырем, и, следова-
тельно, к полученному критерию подобия следует добавить че-
тыре тривиальных критерия подобия, так как каждый безразмер-
ный определяющий параметр одновременно является критерием
подобия
Для определения критериев подобия необходимо выполнить
следующие расчеты.
Энергия волнения устанавливается по общепринятой мето-
дике в зависимости от продолжительности действия ветра, высо-
ты волны и С учетом угла подхода волны к берегу.
Приведенная высота берега определяется в зависимости
от его морфологического типа. Для берегов первого типа — акку-
мулятивных террас или плато с вертикальными и крутыми усту-
пами, приведенная высота равна высоте бровки уступа а над НПГ
(рис. 12.6, в), т.е, = Л,,, где Ag — высота берега. Для берегов
второго типа — слабонаклонных поверхностей с углом менее 10° —
Afi определяется по графикам. По величине расчетной энергии
волнения Е и крутизне склона находится ориентировочная вели-
чина размыва 5 (рис. 12.7). По графику (рис. 12.8) в зависимости
от величины размыва 5 и крутизны склона определяется приве-
денная высота берега Пл.
Рис. . ,!.6. Мс. гические типы берегов:
а — уступы, б — склоны
100 300 500 L тыс.
У
Рис. 12.7 График зависимости величины размыва
(S) обеспеченностью 10% от энергии волн (tj и
крутизны склона
Рис. 12.8. Номограмма связи приведенной высоты берега (Лб) и
величины размыва (S) для пологих склонов
Средняя величина плотности толщи пород р вычисляется как
средневзвешенное значение плотности слоев, залегающих в зоне
193
переработки от бровки внешнего края отмели до верха надвод-
ного уступа.
Средний угол сдвига у вычисляется как средневзвешенное
для всех литологических разностей пород в зоне переработки.
Коэффициент аккумуляции z, представляющий собой отно-
шение объема наносов на отмели к объему’ размытых пород на
данном участке берега, определяется с учетом возможного вдоль-
берегового перемещения наносов и принимается равным содер-
жанию фракции крупнее 0,05 мм, выраженному в долях единицы.
Глубина размывающего действия волн Н, равная глубине водо-
хранилища на внешнем крае отмели, устанавливается аналогично
тому, как она определяется в методе Н.Е. Кондратьева [8]. Ширина
склона в зоне волнового воздействия d вычисляется по формуле:
d = /7 ctg 5, где 5 — угол склона в пределах зоны размыва.
Средняя глубина открытого водоема Нт определяется по трем-
четырем топографическим профилям разного направления как
средняя величина.
Вычисление критериев геологического подобия производит-
ся следующим образом.
Критерий гидродинамического подобия вычисляется по фор-
>
критерий литологического подобия равен коэффициенту сдви-
га Кг = tgw;
критерий подобия аккумулятивных процессов равен коэф-
фициенту аккумуляции — z
критерий геометрического подобия профилей склонов для
берегов первого типа А‘4 =
а для второго типа — он равен
среднему уклону склона до начала переработки Кд - i,
критерий геометрического подобия береговой линии в плане
К5 = J, где j — коэффициент извилистости, равный отношению
дайны береговой линии изучаемого участка к ее проекции.
Выбор аналога производится в два этапа. Предварительный
выбор аналога осуществляется по качественным оценкам мор-
фологических и динамических типов берегов, приведенных в аль-
боме [ 10]. Второй этап предусматривает выбор одного из несколь-
ких предварительно намеченных аналогов по сходству критериев
геологического подобия. Последние делятся на обязательные и
дополнительные. На абразионных берегах к обязательным отно-
сятся критерии А( и Кд, на абразионно-аккумулятивных берегах
Аь А) и Кд. Остальные критерии относятся к дополнительным
критериям.
Вычисленные для изучаемого объекта критерии сравнивают-
ся с критериями, приведенными для аналогов. Так как геологи-
ческое подобие является приближенным, то потребовать точного
совпадения критериев подобия для объекта и аналога не пред-
ставляется возможным. Допустимы следующие отклонения кри-
териев подобия; — ± 50%, Кг ± 3%, К3 ± 30%, Л* от ±30% до ±40%,
А5 ±50%. Приведенная высота берега у объекта и аналога может
отличаться не более чем на 1 м.
Прогноз величины размыва производится с использованием
альбома аналогов Л. Б. Розовского, где приведены карты, на ко-
торых указан фактический размыв лёссовых берегов за пять лет
эксплуатации водохранилища. На картах-аналогах величины раз-
мывов даются в виде кривых обеспеченности, которые позволя-
ют выбрать величину размыва в зависимости от экономической
ценноста участка. При наличии ценных строений следует брать
величину размыва с обеспеченностью 10%, для менее ценных
строений или при их отсутствии — с обеспеченностью 25%. Выб-
рав на карте аналога величину размыва, ее пересчитывают для
объекта в следующем порядке:
1) определяют ширину отмели у аналога la - Sa + da , где. Sa —
величина размыва на аналоге за пять лет или иной срок, снятая с
кривой обеспеченности; da — ширина склона в зоне волнового
воздействия у аналога (которая приводится на картах);
h —
2) вычисляют величину отмели у объекта /0 = 1в , где
Аба
и йб4 — приведенные высоты берегов соответственно объекта и
аналога;
3) определяют величину размыва за выбранный срок у объекта
5О = /0 - d0 , где d0 — ширина склона в зоне волнового воздей-
ствия на объекте.
При необходимости оценки переработки на более длитель-
ные сроки или при другом геологическом строении требуются
новые карты аналогов. Для оползневых берегов в четвертичных
отложениях приближенно можно определить ширину зоны раз-
мыва путем увеличения значений переработки за пять лет в 1,3-
1,5 раза для 10-летнего срока и в 2,0-2,2 раза для 20-летней ста-
дии переработки, в зависимости от особенностей геологического
строения берега и гидрологической обстановки.
12.3. Расчеты переработки берегов водохранилищ
в особых условиях
Рассмотренные выше методы прогноза переработки бере-
гов водохранилищ применимы тогда, когда водохранилище
195
расположено на равнинной территории, а его берега имеют про-
стое геологическое строение. В более сложных условиях, напри-
мер, при прогнозе переработки берегов горных водохранилищ
или берегов, осложненных оползневыми процессами, необходи-
мо разрабатывать новые или использовать усовершенствованные
методы Например, прогноз переработки в зоне распростране-
ния многолетнемерзлых пород представляет собой сложную за-
дачу, решение которой требует неординарных подходов.
Прогноз переработки берегов, сложенных лёссовыми породами
Создание водохранилищ в районах распространения лёссо-
вых пород приводит к развитию своеобразных процессов перера-
ботки берегов Так, в горно-складчатых областях Средней Азии
при больших сработках уровней (за период открытого русла) и
относительно небольших размерах водохранилищ волновое воз-
действие на лёссовые берега играет малую роль. Основное значе-
ние имеют уровенный режим и обусловленное им обводнение
лёссов, распад структурных связей в породе, возникновение гид-
родинамического давления при сработке уровня и, как следствие,
разрушение берегов Выявлено, что объем переработки такого
берега находится в зависимости от длительности стояния высо-
ких уровней водохранилища
Для прогноза переработки сложенных лёссовыми породами
берегов водохранилищ с большой сработкой можно применять
графоаналитический метод ГХ. Золотарева с некоторыми до-
полнениями [12]. Если первоначальная крутизна склона боль-
ше, чем предполагаемый наклон отмели в зоне сработки, то
начальную точку прогнозного профиля следует брать на линии
горизонта сработки в месте ее пересечения со склоном. Если
горизонт сработки приходится на пологую часть склона или
поверхность затопленных террас, то начальная точка берется
гам, где крутизна первоначального склона становится больше
крутизны отмели. От выбранной начальной точки проводится
линия поверхности абразионной отмели до пересечения с про-
должением линии НПГ. Если прогноз составляется на 10 лет,
то она проводится под углом 10-12°, при прогнозе завершения
активной стадии разрушения лёссового берега — 4-6°, при про-
гнозе устойчивого профиля по окончании процесса — 2-3°.
Надводный уступ в сухих лёссовых породах высотой 10-30 м
оо чно имеет крутизну 70-80°
На интенсивность переработки лёссовых берегов существен-
но влияют гранулометрический состав и исходная плотность лёс-
сов. Если они представлены легкими пылеватыми суглинками с
легко разрушаемыми связями, то объемы переработки возрастут
196
в 5-10 раз (около 300 м3/м берега в год) по сравнению с тем объе-
мом, когда воздействию подвергаются лёссы в виде тяжелых пы-
леватых суглинков.
Прогноз переработки оползневых берегов
Прогноз формирования берегов сложного геологического
строения, например, осложненных оползневыми процессами,
может быть выполнен с помощью существующих методов, но
при условии внесения в эти методы необходимых дополнений.
При прогнозе переработки берегов водохранилищ, представляю-
щих собой склоны с оползневыми накоплениями, могут быть
применены методы природных аналогов или графоаналитичес-
кий [5]. Для этого, прежде всего, необходимо установить меха-
низм переработки берега и построить модель процесса формиро-
вания береговой отме ли в результате воздействия водохранилища,
который может проходить в несколько стадий. На первой стадии
возможна переработка оползневых накоплений, залегающих на
склоне в зоне сработки водохранилища и в уступе над НПГ. Для
построения профиля переработки можно использовать графо-
аналитический метод, если будут известны необходимые для его
построения данные, полученные по результатам наблюдений на
водохранилищах в аналогичных геологических условиях. Однако
необходимо иметь в виду, что в результате обводнения оползне-
вых накоплений, которое приводит к снижению прочности по-
род, и сработки уровня водохранилища, которое вызывает в опол-
зневых накоплениях гидродинамическое давление, возможно
смещение оползня в сторону водохранилища и его размыв. По-
этому на этой стадии необходимо проверить устойчивость опол-
зневых тел моделированием или расчетами и выявить условия
возможного их смещения в результате размыва оползневых на-
коплений водохранилищем.
Если смещение оползневых масс произойдет, то необходимо
продолжить прогноз переработки освободившегося от оползне-
вых накоплений склона. Для построения нового профиля бере-
говой отмели на второй стадии также может быть применен гра-
фоаналитический метод. Но тогда существует реальная опасность,
что формирующийся в результате подмыва водохранилищем кру-
той склон может потерять устойчивость с образованием новых
оползневых смещений. На этой стадии большое значение приоб-
ретает прогноз не только переформирования профиля берега, но
и оценка его устойчивости, которая может быть выполнена рас-
четными методами или моделированием. При оценке устойчиво-
сти необходимо учитывать не только изменившийся профиль
склона, но и снижение во времени показателей прочности пород
197
и возникающего при сработке уровня гидродинамического дав-
ления. При потере склоном устойчивости в зону воздействия
водохранилища вновь могут попасть оползневые накопления, и
следовательно, придется повторить построение, которое было
сделано на первой стадии.
Таким образом, при прогнозе переформирования берегов
водохранилищ, осложненных оползнями, необходимо сочетание,
прогноза процесса переработки берега с оценкой устойчивости
оползневых склонов.
Существующие методы прогноза переработки берегов водо-
хранилищ не являются универсальными и не могут быть приме-
нены во всевозможных случаях развития этого процесса Поэтому
постоянно возникает необходимость усовершенствовать имею-
щиеся и разрабатывать новые методы. Так, для прогноза форми-
рования берегов водохранилищ, сложенных карбонатными по-
родами различной степени литификации, была разработана
методика построения профилей вновь образующихся отмелей
на примере изучения переработки берегов на Камском водохра-
нилище [9]. ПНИИИСом были изданы рекомендации по оценке
и прогнозу размыва берегов равнинных рек и водохранилищ при
строительстве в с лучаях, если берега сложены несвязными и связ-
ными породами. Практически неразработанным является про-
гноз переработки берегов водохранилищами, построенными в зоне
распространения многолетнемерзлых пород.
12.4. Стохастические методы прогноза переработки
берегов водохранилищ
Энергетические и сравнительно-геологические методы раз-
рабатывались в основном в 50-е годы. С помощью таких методов
прогнозировались размеры переработки берегов водохранилищ.
Многочисленные проверки выполненных прогнозов на водохра-
нилищах Волжского и Днепровского каскадов показали невысо-
кую точность примененных методов. За прошедшие годы выпол-
нены комплексные инженерно-геологические исследования и
многолетние натурные режимные наблюдения на водохранили-
щах в различных регионально-геологических, зонально-клима-
тических И техногенных условиях. Эти исследования позволили
установить, что многофакторный процесс формирования бере-
гов водохранилищ является неоднородным в пространстве и не-
стационарным во времени. Было также установлено, что процесс
формирования берегов водохранилищ имеет стохастическую (слу-
чайную или вероятностную) природу, и следовательно, для его
изучения и прогноза могут быть применены методы математи-
198
ческой статистики. Так, статистический анализ эмпирических
кривых процесса формирования берегов горных водохранилищ с
целью выявления развития процесса во времени был выполнен
Н.Е Варазашвили [2]. Наиболее перспективным методом прогноза
переработки берегов водохранилищ, основанном на применении
вефоятностных подходов, является метод стохастических моде-
лей, разработанный В ТС Епишиным и В.Н. Экзарьяном [4].
Разработка метода стохастических моделей была вызвана не-
обходимостью повышения точности прогноза и учета в прогноз-
ной модели вероятностной природы процесса переформирова-
ния берегов водохранилищ, потребностью в комплексных И
перманентных прогнозах и необходимостью автоматизации их
производства. Возможность использования стохастического под-
хода была обусловлена накоплением данных многолетних натур-
ных режимных наблюдений за факторами и процессом форми-
рования берегов и внедрением вычислительной техники, что
позволило строить многомерные прогнозные модели процесса.
В геологической модели процесса формирования берегов
водохранилищ было принято следующее: значения характерно*
тик процесса в любой период эксплуатации водохранилищ опре*
деляются суммарным воздействием энергии волн и экзогенных
геодинамических факторов в данных региональных геологичес-
ких, зоналызо-климатических и гидротехнических условиях. В
этой геологической модели есть факторы — процессы, имеющие
стохастическую природу, и факторы — условия, которые всегда
детерминированы. В соответствии с выбранной геологической
моделью процесса формирования берегов водохранилищ была
построена общая прогнозная математическая модель, которая
может быть представлена в виде системы линейных алгебраичес-
ки: /равнений:
/з(хз), Ф1(Я), (12.4 1)
где у ~ (у1э у2, — упорядоченный набор прогнозируемых
характеристик процесса; хн х2, х3 — векторы характеристик
геолого-литологических, геоморфологических, геодинамических
факторов переработки, Н — вектор характеристик уровневого
режима; Е— вектор характеристик волнового энергетического
режима; / — время, /2, /3 — детерминированные функции;
Фь Ф2 — стохастические функции.
Однако для решения задачи прогноза формирования берега
конкретного водохранилища, как правило, достаточно выбрать
некоторую частную математическую модель. Она представляет
собой многомерную регрессионную модель:
хо=Дким.
(12.4.2)
199
где у— вектор характеристик процесса; х — вектор характерис-
тик факторов процесса; г — время; Р, — функция в виде полино-
ма i-ro порядка. Выражение (12.4.2) есть система уравнений:
У1V) = (*)
у„(0-Л»(х). (12.4.3)
В условиях конкретного водохранилища при построении про-
гнозной модели для фиксированного периода прогноза, во-пер-
вых, всегда удается сократить количество учитываемых факторов
процесса и, во-вторых, можно ограничиться прогнозом только
одной характеристики процесса формирования берегов, напри-
мер, линейным отступлением бровки уступа, так как другие ха-
рактеристики процесса зависят от нее. Тогда вместо системы урав-
нений остается одно:
y(t).-= 7»(х). (12.4.4)
Для прогнозов процесса формирования берегов водохрани-
лищ методом стохастических моделей необходимо произвести
предварительную оценку значений характеристик факгоров, вхо-
дящих в выбранную частную модель, на прогнозируемый период.
Исходя из принятой геологической модели процесса формиро-
вания берегов, все факторы процесса можно условно разделить
на две группы. В первую входят факторы, характеристики которых
постоянны или детерминированы во времени. Значения характери-
стик этих факторов могут быть прогнозированы с высокой точно-
стью, которая зависит от детальности геологоразведочных работ.,
точности геодезических замеров и др. К ним относятся, напри-
мер, высота абразионного уступа, ширина и крутизна подводной
отмели, коэффициент размываемости пород и др. Вторую группу
составляют факторы, стохастические характеристики которых
изменяются во времени и требуют вероятностной оценки на весь
заданный период прогноза. Эти факторы переработки определя-
ют доверительную вероятность прогноза процесса в целом. В про-
стейших случаях в прогнозные модели можно вводить средне-
многолетние значения характеристик факторов второй группы.
Изменяющимися во времени факторами являются функции уро-
венного и волно-энергетического режимов.
Прогнозные стохастические модели процесса формирования
берегов водохранилищ строятся на основе применения много-
мерного регрессионного анализа. Предварительно точность про-
гнозной стохастической модели может быть оценена методом
ретроспективной проверки.
Метод стохастических моделей носит универсальный характер.
Он может быть использован для прогноза процесса формирования
берегов эксплуатируемых равнинных и горных водохранилищ в
любых регионально-геологических, зонально-климатических и
техногенных ситуациях при условии построения моделей на эм-
пирическом режимном материале того же водохранилища.
Контрольные вопросы
1 Какие группы методов переработки берегов водохрани-
лищ могут быть использованы в практике инженерно-гео-
логических изысканий?
2. Какие факторы определяют развитие процессов перера-
ботки берегов водохранилищ на равнинах и в горно-склад-
чатых областях?
3. Что лежит в основе энергетических методов расчета пере-
работки берегов водохранилищ?
4. Как определяются параметры, необходимые для оценки
величины переработки?
5. Что такое коэффициент размываемости пород?
6. Какова методика построения профиля береговых отмелей
в различных методах?
. На каких принципах основаны сравнительно-геологичес-
кие методы переработки берегов водохранилищ?
8. Как подбираются природные модели-аналоги для прогно-
за величины переработки на проектируемых водохрани-
лищах?
9. Какие критерии подобия используются для выбора моде-
ли-аналога''
10. Особые случаи оценки переработки берегов водохранилищ.
11. Стохастические подходы, используемые для оценки вели-
чины переработки берегов водохранилищ.
ГЛАВА 13. РАСЧЕТЫ ДЕФОРМАЦИЙ МАССИВОВ
ГОРНЫХ ПОРОД
Деформации массивов горных пород отличаются разнообра-
зием и происходят как в естественных условиях, так и под влия-
нием техногенных причин. Широко распространены деформа-
ции земной поверхности» к которым относятся провалы над
карстовыми пустотами, суффозионные воронки, проседание по-
верхности над выработанными пространствами и в результате
откачек подземных вод, нефти или газа. Разрушение горных по-
род наблюдается вокруг подземных полостей как природных, так
и образовавшихся при проходке подземных горных выработок. В
результате эрозионных врезов или разработки карьеров и строи-
тельных котлованов на склонах и в бортах таких выемок проис-
ходит обрушение, осыпание ft Оползание, а в днищах этих соору-
жений возможно выпирание пород. Расчет большинства из
перечисленных деформаций — сложная задача. Поэтому во мно-
гих случаях оценка наблюдаемых деформаций производится на
основе использования эмпирических зависимостей.
13.1. Расчет перераспределения напряжений
(и деформаций) в массиве пород вокруг
подземных полостей
Подземные полости как естественные, так и искусственные,
являются существенным фактором, влияющим на изменение ес-
тественного поля напряжений массива горных пород. В свою
очередь изменение напряжений и их концентрация в породах
вокруг подземной полости может вызвать деформации в виде
выпора горных пород в сторону пустого пространства, обруше-
ния или горного удара. Поэтому оценка перераспределения на-
пряжений в массиве горных пород под влиянием полости явля-
ется важным этапом на пути изучения инженерно-геологических
условий, и в частности условий, которые вызывают деформиро-
вание и разрушение пор
Исследование распределения напряжений вокруг подземных
полостей может быть выполнено с помощью математического или
физического моделирования. При математическом моделировании
используется система уравнений (2.3.6), приведенная в гл. 2.
В общем случае характер формирующегося вокруг подзем-
ных полостей поля напряжений зависит от совокупного дей-
ствия нескольких групп факторов Во-первых, на напряженное
состояние пород вблизи полостей влияют величины и соотно-
шение напряжений, обусловленных собственным весом мас-
сива горных пород, действием тектонических сил и другими
причинами. Во-вторых, распределение напряжений зависит от
строения и деформационных свойств пород, расположенных в
непосредственной близости от контура подземной полости В--
третьих, большую роль в формировании поля напряжений иг-
рают форма поперечного сечения, соотношение геометричес-
ких размеров самой подземной выработки или полости и наличие
вблизи соседних полостей
Полный учет всех факторов, влияющих на перераспределе-
ние напряжений в массиве пород в окрестности подземных: по-
лостей, с помощью математического моделирования не представ-
ляется возможным. Однако для практических оценочных целей
бывает достаточно знать приближенную картину распределения
напряжений. Тогда вместо реального сечения подземной полос-
ти можно рассматривать окружность и массив пород считать од-
нородным, изотропным и упругим [91. В этом случае величины и
распределение нормальных радиальных (о,) и тангенциальных (ов)
напряжений выражаются простыми формулами, представляющи-
ми собой решение уравнений математической модели (2.3.6). Они
зависят главным образом от соотношения нормальных напряже-
ний, действующих в массиве без полости (нетронутом) — и ст3,
и от координат точек, в которых определяются напряжения
(рис. 13.1).
Рис. 13.1 Радиальные и тангенциальные напряжения в стенках подземной полос-
ти кругового поперечного сечения при гидростатическом распределении напря-
жений в нетронутом массиве
203
Оценка перераспределения напряжений может быть сделана
с помощью коэффициента концентрации, который представляет
собой отношение максимального нормального напряжения в рас-
сматриваемой точке о, к нормальному напряжению в той же точ-
ке, действующему на горизонтальной площадке, но в массиве
полости
<ъ
Рис 13.2. Радиальные и тангенциальные на-
пряжения в стенках подземной полости круго-
вого поперечного сечения при геостатическом
распределении напряжений (о1 = 0,25а3) [9]
/области влияния подземной полости.
Х = (13.1.1)
Если в нетронутом массиве горизонтальные напряжения
<зj равны вертикальным о, (гидростатическое распределение на-
пряжений: <51 = <Тз), то величины к характер распределения на-
пряжений в массиве с полостью круглого сечения определяются
только расстоянием данной точки от полости и не зависят от
направления (рис. 13.1). В любой точке контура коэффициент
концентрации К=2, а все напряжения являются сжимающими.
Если вертикальные и горизонтальные напряжения в нетро-
нутом массиве не равны (ст, х о3), то напряжения в кровле и стен-
ках подземной полости существенно отличаются. На части кон-
тура со стороны большей
нагрузки появляется об-
ласть растягивающих на-
пряжений, которая тем
обширнее, чем больше
разница между 0)И
Сжимающие напряже-
ния имеют большие зна-
чения со стороны дей-
ствия меньших нагрузок.
Так, при ot = 0,25о3 (если
коэффициент Пуассона
|i= 0.2) максимальный
коэффициент концентра*
ции тангенциальных на-
пряжений наблюдается на
стенках полости и состав-
ляет Х=2,75 (рис. 13.2), а
при ст, = IO03 (если дей-
ствует горизонтальная
тектоническая сила) — в
кровле и составляв! при-
мерно К = 30 (рис. 13.3).
1 шлется и раз: 1
Для условий гидростати-
ческого напряженного состояния нетронутого массива уже на
расстоянии /= 1,65с* значения тангенциальных и радиальных со-
ставляющих отличаются от соответствующих компонент напря-
жений в нетронутом массиве не более, чем на 5%. Для других
условий нагружения различия в скорости затухания компонент
напряжений о, и ав по мере удаления от контура полости суще-
ственны. При этом, как правило, быстрее затухают те компонен-
ты, которые имеют большие коэффициенты концентрации на
контуре, Так, при с, = 0,25о3 наиболее быстро затухает тангенци-
альное напряжение оя в стенке полости, уже на расстоянии I = 1,35с/
от контура оно практически не отличается от такового в нетро-
нутом массиве. Остальные компоненты уменьшаются медленнее,
и отмеченный уровень достигается только на расстоянии I = 2,75rf.
Рис. 13.3. Радиальные и тангенциальные напряжения в
стенках подземной полости кругового поперечного сече-
ния в условиях действия горизонтальпых тектоническихсил
(с, = о.з3)[91
При О] = 10о'3так же очень быстро затухают тангенциальные
составляющие в кровле (/=2,75d), и здесь же очень медленно
уменьшаются радиальные составляющие (1=1d).
Таким образом, размер зоны влияния подземной полости
зависит от степени равномерности начального поля напряжений
и, в наиболее благоприятном случае, для круговой формы сече-
ния составляет около 1,5 диаметров. В действительности формы
подземных полостей разнообразны и отличаются от круговой В
общем случае коэффициент концентрации возрастает на конту-
рах с большой кривизной, а в угловых точках напряжения могут
достигать очень больших значений.
205
Кроме того, на характер распределения напряжений вблизи
подземной полости оказывают влияние сложность геологическо-
го строения массива, неоднородность и анизотропия упругих
свойств горных пород.
13-2- Оценка деформаций пород над подземными
полостями, выработанными пространствами и при
откачках подземных вод, нефти или газа
Присутствие в массиве горных пород подземных полостей
приводит к развитию таких процессов, как обрушение кровли,
возникновение провалов, проседание поверхности. Наиболее ча-
сто происходит образование мульд проседания над выработан-
ным пространством или при откачках подземных вод, нефти
или газа.
Образование подземных полостей или проходка горных вы-
работок вызывает в массиве горных пород перераспределение
напряжений [7]. Непосредственно к полости прилегает область,
характеризующаяся пониженными значениями или отсутствием
напряжений. Ее окружает зона повышенных напряжений, кото-
рая, в свою очередь, постепенно переходит в зону, где напряже-
ния соответствуют естественному состоянию массива пород при
отсутствии полости. В соответствии с этим вокруг выработки
может сформироваться область разрушения пород, которая про-
двигается в глубь массива и сначала переходи! в область неупру-
гих, а затем и упругих деформаций.
Обрушение кровли подземных полостей протекает по-разному
в зависимости от геологического строения массива горных по-
род При возникновении карстовых пустот в слоистых карбонат-
ных породах деформирование кровли может происходить в виде
прогиба и последующего обрушения выше залегающих слоев. Для
оценки условий возникновения этого процесса применяется ме-
тод, основанный на аналогии механизма деформирования слои-
стой кровли карстовой полости и прогиба плоской плиты или
балки и хорошо разработанный в теории сопротивления материа-
лов. Известно, что при соотношении h/l < I/4- где h — мощность
перекрывающего слоя, а I — полуширина полости, применение
формул сопротивления материалов обеспечивает достаточную для
практики точность.
В практических целях для оценки условий обрушения кров-
ли подземной полости, перекрытой слоистой толщей, могут так-
же использоваться эмпирические зависимости. Например, мак-
симальная величина пролета L = 2/, когда прогибание залегающего
206
над полостью слоя происходит без нарушения сплошности, оп
ределяется по формуле:
ж /
(13 2.1)
где Лр — предел прочности горной породы на растяжение, кг/см2;
у — объемный вес породы, кг/см , Л — мощность слоя, м;
К — V3— эмпирический коэффициент.
Другая группа гипотез, используемых для оценки условий
обрушения кровли подземных пустот, исходит из предположе-
ния, что над пустотами или горными выработками образуется
свод естественного равновесия За пределами этого свода поро-
ды не испытывают изменений и влияние пустоты здесь практи-
чески не сказывается. Внутри свода происходит’ разрушение гор-
ных пород, в результате чего породы в зависимости от их свойств и
строения либо обрушаются в пустоту', либо только деформируются в
сторону пустого простран-
ства. При этом, если имеет-
ся в виду полость горной вы-
работки, то максимальная
нагрузка на ее крепь (горное
давление) определяется ве-
сом пород внутри свода, па-
раметры которого связаны с
размерами поперечного се-
чения полости, и практичес-
ки не зависит от глубины ее
расположения. Наиболее
разработанной является рас-
четная схема М.М. Про-
тодьяконова (1907), в основе
которой лежит представле-
ние о массиве горных по-
род как о некоторой услов-
Рис. 13.4. Распределение напряжений вдоль
контура прямоугольной полости
ной сыпучей среде. Распределение напряжений вдоль контура
полости показано на рис. 13.4. Согласно гипотезе М.М. Прото-
дьяконова высота разрушающего свода Лсв может быть определе-
на в зависимости от коэффициента крепости пород f^:
(13.2.2)
/кр
где /— полуширина полости. Коэффициент крепости зависит от
прочностных свойств породы и приближенно может быть оце-
нен следующим образом:
для рыхлых пород /кр tg <р,
для связных пород
tg<po„ 4-С
для скальных пород ,
р 100
где ал — нормальное напряжение на площадке сдвига, — со-
противление пород одноосному сжатию. Отсюда величина ко-
ициента крепости для рыхлых пород находится в пределах
0,1—1, для связных — 1—5, для скальных — 5—20
Максимальное напряжение в кровле полости действует по
оси разрушающего свода и равно;
uTi»
о «Ж
Jmax г5 *св г -
1ф
(13.2.3)
где р — плотность пород.
Горизонтальные напряжения, действующие в боковых стен-
ках полости в верхней и нижней точках, будут соответственно
равны:
Подошва полости также испытывает давление, которое нередко
приводит к деформации, получившей название «выпор пород»
(рис 13.4).
Широко распространен процесс сдвижения горных пород и
земной поверхности, под которым понимается деформирование
и перемещение пород в результате потери ими равновесия. Сдви-
жение пород может происходить под влиянием тектонических
процессов, изменения механических свойств пород, выщелачи-
вания, водопонижения, а также в результате горных разработок.
Если образование полостей происходи! глубоко на большой
площади, то деформация перекрывающих пород распространя-
ется на значительные расстояния, образуя область сдвижения
горных пород, и может достигать поверхности, где будет форми-
роваться мульда сдвижения или мульда проседания, Иногда на
земной поверхности формируются провалы.
Непосредственно над подземными полостями образуется зона
обрушения, в пределах которой породы наиболее деформирова-
ны и разделены на отдельные блоки (рис. 13.5) Для определения
высоты этой зоны используются эмпирические зависимости, на-
пример, в случае разработки пластовой залежи [1] она составит:
Л- З-п—тт-----, где А — высота зоны обрушения, т— мош-
(x-l)cosa
> -
ность разрабатываемого пласта, к — коэффициент разрыхления
пород, определяемый экспериментально и равный 1,1-1,4, а —
угол падения пласта. Мощность зоны обрушения обычно (3—6) W
Выше расположена зона, которая характеризуется появлением в
прогибающихся слоях большого количества секущих трещин, Зона
трещин развивается вверх на расстояние (30-60)т.
Рис. 13.5. Схема сдвижения горных пород над выработанным про-
странством. Плюс означает растяжение, минус — сжатие
Изд зоной трещин наблюдается плавный прогиб пород, ко-
торый распространяется до поверхности земли, где образуется
мульда сдвижения. Нередко на ее границе появляются трещины
разрывов, быстро затухающа с глубиной.
Деформация поверхности земли возможна и при откачках
подземных вод, нефти или газа. Известны случаи проседания
поверхности на территориях крупных городов, эксплуатирую-
щих водоносные горизонты. Наиболее ярко этот процесс про-
является, например, в г. Мехико, где осадка поверхности СО-
ставила более 8 м
Если в горных породах, слагающих верхние горизонты зем*
ной коры, содержится гидравлически связанная вода, то она воз-
действует на минеральный скелет горной породы двояким обра-
зом. Во-первых» каждая частица горной породы испытывает
всестороннее гидростатическое давление, и, во-вторых, прояв-
ляется эффект взвешивания породы, расположенной ниже уров-
ня подземных вод. Гидравлическое давление вызывает очень ма-
лые деформации, соответствующие сжимаемости минеральных
зерен, которая на два—три порядка ниже сжимаемости самой поро-
ды. Снижение уровня подземных вод устраняет эффект взвешива-
ния для осушенных пород, в результате чего возникает дополни-
тельная нагрузка, что приводит к сжатию их минеральнО|ГО скелета
Для оценки перераспределения напряжений в во^юсодержа-
щих породах при снижении уровня подземных вод рассмотрим
полное (общее) давление оп, оказываемое столбом породы мощ-
ностью Н на горизонтальную площадку As единичной площади
(рис. 13.6).
оп ~ f 7(У)^У> (13.2.5)
о
где у(у) — объемный вес породы на глубине у (выше уровня грун-
товых вод — влажной породы, ниже уровня — вместе и заключен-
ной в ней водой). Давление оп уравновешивается двумя силами:
реакцией минерального скелета породы оэ и гидростатическим
давлением он, направленным по нормали к площадке •
Рис. 13.6. Схема для расчета осадки поверхности земли ПРИ
водопонижении
Изменение гидростатического давления не влияет на СИЛУ взаи-
модействия минеральных частиц. Поэтому напряжения он в по-
ровой (свободной) жидкости получили название нейтральных.
Реакция минерального скелета оэ уравновешивает ту часть веса
вышележащих пород оп, которая обусловливает силу взаимодей-
ствия частиц минерального скелета. В отличие от нейтральных
напряжений он напряжения аэ получили название эффективных:
= «и ~ он
(13.2.7)
210
При изменении напора подземных вод (при снижении уров-
ня подземных вод) полное напряжение оп, если пренебречь из-
менением общего веса вышележащих пород, остается неизмен-
ным, и тогда из равенства (13.2.7) можно получить:
de = -deK (132.8)
Следовательно, снижение напоров приводи! к росту эффек-
тивных напряжений и сжатию минерального скелета, что, в свою
очередь, вызывает осадку толщи горных пород под влиянием во-
допонижения.
Равенство (13.2.7) справедливо, если пренебречь сжимаемос-
тью минеральных зерен по сравнению со сжимаемостью горной
породы, что допустимо при невысоких давлениях. В противном
случае необходимо пользоваться формулой
а =<тп-аан, (13.2.9)
где коэффициент а отвечает отношению показателей сжимаемо-
сти минеральных зерен и горной породы.
Изменение нейтральных напряжений пропорционально
объемному весу жидкости у„ и понижению уровня подземных
вох 5:
JaH=r»5. (13.2.10)
Величина общей деформации толщи пород при водопониже-
нии определяется по формуле:
ДЛ=—^ = У.^, (13.2.11)
где Е*• модуль общей деформации пород. Вычисленное по фор-
муле (13.2.11) изменение мощности слоя вызывают осадку по-
верхности земли на ту же величину Дй.
13.3. Расчет деформаций в котлованах и карьерах
При сооружении карьеров и котлованов могут происходить
деформации бортов как под влиянием сил гравитации, так и в
результате оплывания и суффозии, разгрузка пород в бортах и
днище и выпор дна котлована или карьера. Явление выпора так-
же возможно в подземных горных выработках, в результате чего
происходит разрушение подошвы выработки с последующим
прорывом в нее подземных вод.
Расчеты устойчивости и деформаций бортов котлованов и ка-
рьеров производятся с использованием методики, разработанной
для оценки устойчивости склонов. В случае, когда борта карьера
211
сложены слоистыми скальными породами, предельная высота
вертикального услутта йп/2 может быть определена по формуле
где с — сцепление горной породы. Эта формула справедлива при
любом залегании горных пород за исключением случаев, когда
слои, грещины или другие поверхности ослабления падают в сто-
рону выемки под углом большим, чем угол внутреннего трения
по контактам слоев или поверхностям ослабления.
Водонасыщенные песчаные откосы деформируются благодаря
действию гидродинамических сил фильтрационного и стекаю-
щего по поверхности откоса потоков. Для учета воздействия на
устойчивость песчаных откосов фильтрационных сил необходи-
мо составить условие равновесия единичного объема породы,
расположенного на поверхности откоса (рис. 13.7). На единич-
ный объем породы действует сила его веса, равная объемному
весу взвешенной в воде породы увзв, и фильтрационная сипа Ф,
Рис. L7, Схе г яки воздействия фил
ционных сил на устойчивость песчаных откосов
равная произведению объемного веса воды ув на градиент напора
на участке высачивания (выхода на поверхность) подземных вод.
На участке, где поток направлен вдоль поверхности откоса кру-
тизной а, градиент напора /= sin а. Так как фильтрационная сила
и сила веса уравновешиваются силой фения Fo то можно запи-
сать условие предельной устойчивости:
0 4(?sina = jF или ув sin a 4 sin a = уюв cos tg ф, (13 3.2)
tga = —Хвз»— tgф O,5tgcp,
v -4- V '
3 * i B3B
(13.3.3)
т е. уклон устойчивого водонасыщенного откоса в точке высачи-
вания вдвое меньше естественного уклона песчаного откоса. Влия-
ние гидродинамических сил стекающей по откосу воды нередко
212
приводит к значительному (в несколько раз) его выполажиьа-
нию, причем известны случаи, когда размеры «языка» оплыва-
ния достигают нескольких десятков метров |5], и имеющего ук-
лон значительно меньший, чем вычисленный по формуле (13.3.3).
Фильтрационный выпор происходит в днищах карьеров и кот-
лованов, в горных выработках, особенно при наличии в их осно-
вании слабопроницаемого слоя, экранирующего выход фильтра-
ционного потока, имеющего избыточный напор (рис. 13.8).
Рис 13.8. Схема для оценки расчета возможного фильтраци-
онного выпора в днище карьера или котлована
Разрушение слабопроницаемого экранирующего, слоя происхо-
дит различно в зависимости от соотношения глубины и ширины
горной выработки. Если ширина карьера или котлована суще-
ственно больше глубины, то можно предположить, что экрани-
рующий слой начнет разрушаться («всплывать») при напоре, рав-
ном его весу. В этом случае условие равновесия элемента породы
единичной площади и мощностью т запишется в виде:
. (13.3.4)
н-н0 л
где I =----» — градиент напора, у„ — объемный вес влажно-
ш
го грунта, у, = 1 — объемный вес воды. Отсюда
yMm = Я - Яо.
(13.3.5)
Обычно возможность разрушения (всплывания) экранирующего
слоя выражается с помощью коэффициента устойчивости на
всплывание:
= я7-Яо ' (1316)
Если карьер узкий и ею ширина значительно меньше глуби-
ны или в случае разрушения подошвы горной выработки, необхо-
димо при оценке выпора блока экранирующего слоя учитывать
сопротивление вдоль возможных поверхностей среза. При со-
ставлении условия равновесия необходимо к силе веса приба-
вить силы, препятствующие перемещению по боковым поверх-
ностям взвешиваемого блока шириной b Если упитывать только
сцепление, то уравнение равновесия примет вид:
4 2ст =• у\(Н - Н{У)Ь, (133.7)
а взвешивающий градиент будет равен:
/=1вл. + _2^_ (13.3.8)
Ув Ув*
Эти соотношения позволяют оценить условия разрушения дни-
ща карьера или основания горной выработки, если известны проч-
ностные свойства экранирующего слоя и градиент напора восхо-
дящего фильтрационного потока.
13.4. Расчет суффозионных и карстовых провалов
на закарстованных территориях
Устойчивость закарстованных территорий и в первую оче-
редь районов покрытого карста может оцениваться двумя прин-
ципиально различными способами. Первый реализует вероятно-
стный подход к Прогнозу карстового процесса и позволяет
рассчитать его скорость и пораженность территории, если извест-
ны частота и площадь (объем) провали : зоронок оседания. Он
широко применяется в тех районах, где наземные формы прояв-
ления процесса хорошо выражены и поддаются визуальному' изу-
чению. Второй подход к анализу деформирования и разрушения
покровной толщи закарстованных массивов детерминированный
и рассматривается ниже.
Несмотря на большое разнообразие вербальных моделей об-
разования карстовых и суффозионных провалов и блюдец оседа-
ния, практически все существующие методы расчета устойчиво-
сти грунтовой толщи базируются на схеме смещения «столба»
грунта — среза по цилиндрической поверхности над ослаблен-
ным участком растворимых пород (рис. 13.9). Впервые она была
предложена немецким ученым А. Бирбаумером в 1913 г. [8] для
определения давления пород на плоскую крепь горизонтальной
горной выработки. Очевидно, что в соответствии с этой схемой
сдвигающей силой, вызывающей перемещение грунтов в полость-
приемник, будет вес пород в объеме цилиндра (рис. 13.9, а):
F=oynR2 = у hnR2, (13.4.1)
214
Рис. 13.9. К расчету устойчивости покровной толщи по схеме смещения грунто -
вого цилиндра диаметром D: F, N— сдвигающая и удерживающая силы, Е— сила
бокового давления призмы, сползающей под углом р - п/4 + ф/2 к горизонту; ах—
эпюра горизонтальных напряжений; ре—давление связности; — мощность эк-
вивалентного слоя; аг — вертикальное давление в подошве слоя (а. б) и его зави
СИМОСТЬ от мсщности (в)
Ей противостоят удерживающие силы в результате действия го-
ризонтального давления ох = (< — коэффициент бокового рас-
пора) на боковую поверхность этого цилиндра. Для песчаной
толщи при ф * О, с = 0, £ = tg2(%/4 - ф/2) они равны:
й
N — 2лЯJ<тх tgipJy — y/rjtJ’itgq» tg2(n/4 ф/2). (13.4.2,0)
о
В слое связных грунтов согласно закону Кулона (т - o tg <р + с)
наряду с трением вдоль сдвиговой поверхности «работает» и сцеп-
л ;i ис:
tg ф + с) dy = nHh(yh tg ф tg 2 (я / 4 - <p / 2) у 2c).
(13.4.2,6)
Правда, есть предложение [4] учитывать сцепление через всесто-
роннее давление связности (ре=с^ф), приложенное к кровле
глинистого слоя, примерно так, как это делается в теории под-
порных стен. Тогда, заменяя это давление действием эквивалент-
ного слоя (Лс = c/ytg<p), получим несколько меньшее значение N
(рис. 13.9, 6).
N = 2nR tgф f у(Л + hc)tdy = nRhtg2(n/ 4 - ф/2)(уйtgф +2с).
° (13.4.2,в)
Для многослойной покровной толщи закарстованных масси-
вов строятся эпюры вертикального и горизонтального давлений,
и рассчитываются суммарные значения LF и 1AL В состоянии
предельного равновесия F= Л'(EF= E7V) Приравнивая выраже-
ния (13.4.1) и (13 4 2) и решая полученное уравнение относи-
тельно R3 h и N/Ft находим значения предельно допустимого
радиуса карстовой полости, а следовательно, и диаметра возмож-
ного провала» критической глубины залегания участка ослабле-
ния массива и коэффициента устойчивости покровной толщи:
ЛКр| = (/? - 2с,/у)Д tg <р,
£*(ЧШф + 2c/y)/R.
(13.4.3)
(13.4.4)
При выводе этих формул использовалось выражение (13.4.2,6),
поскольку правомерность (13.4.2,в) вызывает некоторые сомне-
ния. Однако небольшое: численное различие значений удержива-
ющих сил, которое дают формулы (13.4,2,6) и (13 4,2,в), не имеет
пришлипиального значения.
Намного важнее понять и оценить достоверность предполо-
жений, на которых построена расчетная схема, д на основании
этого определить границы применения расчетного метода Допу-
щения формулируются следующим образом: 1) провал реализу-
ется в форме вертикального смещения фунтового столба: 2) диа-
метр провала соответствует диаметру ослабленного участка;
3) перемещающийся блок не деформируется; 4) сдвигающей си-
лой служит вес грунтов в объеме цилиндрического блока, высота
которого равна мощности нерастворимых пород; 5) сопротивле-
ние сдвигу мобилизуется на боковой поверхности цилиндра.
Последние два допущения следствие первых трех, а потому не
являются самостоятельными.
Первое предположение носит формальный характер — нет
препятствий для решения, например, плоской задачи, если ос-
лабленная зона вытянута перпендикулярно плоскости рис. 13.9
Второе и особенно третье допущения не совсем корректны Дей-
ствительно, иногда после деформирования земной поверхности
диаметр провала внутри массива, или воронки обрушения по
другой терминологии, оказывается равным диаметру карстовой
полости. Но это результат последовательного развития процесса
деформирования и разрушения покровной толщи от ее подошвы
к кровле. Для каждой стадии этого процесса характерны свои
поверхности скольжения и своя форма области деформирования,
В общем случае не цилиндрические. Иными словами, априорное
216
признание жесткости грунтового столба по всей мощности пере-
крываюших порол заставляет игнорировать истинный механизм
образования провала Поэтому отмечавшаяся популярность рас-
смотренной схемы объясняется не ее адекватностью, а просто*
той. Благодаря последней в расчетах относительно легко учесть
не только разнообразные свойства и строение массивов водона-
сыщенных пород, но и техногенные воздействия Например, вес
наземных сооружений нетрудно представить 8 виде давления эк-
вивалентного слоя пород, а снижение уровня подземных вод —
выразить через изменение эффективных напряжений, как это
показано в разделе 13 2, Остается ответить на вопрос, существу-
ют ли частные случаи оправданного использования расчетного
метода А. Бирбаумера, детально разработанного к настоящему
времени
Для примера рассмотрим слой несвязных грунтов, высоту
которого можно увеличивать по своему желанию. Давление пес-
ков на податливую крепь горной выработки или разделяющий
глинистый пласт, мощностью которых пренебрегаем, определя-
ется разностью выражений (13.4.1) и (13.4.2, a): W/itR1.
Так как F пропорциональна й. a N пропорциональна й2, функция
<sy=f(h) имеет максимум (рис. 13ЛМ). Взяв производную d<syfdh
и приравняв ее < нулю, найдем то значение й. выше которого
вертикальное давление уменьшается, становится нулевым и даже
отрицательным:
day /dh - (у - у й2Е, tg ф/ЛУ = О,
h^ = R/2k tg<p. (1146)
При сравнении выражений (13.4.4) и (13.4,6) видна, что.для
несвязных грунтов (с = 0) йкр5 = 2йкр2. Причем первое значение h
более чем удивительно (рис. 13.9, в): в засыпках меньшей высоты
столб грунтов смещаегся вниз (су> 0), а большей — вверх (ov< 0).
Ожидать уменьшения давления с увеличением мощности слоя,
очевидно, не приходится. Опыты показывают, что начиная с неко-
торой мощности вертикальное давление сыпучих тел стабили-
зируется и дальше определяется их весом внутри свода равнове-
сия, стрела подъема которого, по М.М. Протодъякоиову (см.
раздел 13.2), равняется й = 7?/tg <р. В широком диапазоне «проч-
ности» песков (20° < ф < 40*) с точностью до второго знака
^12 Ф = 0?19. Подставляя это значение в (13.4.6), находим тот
верхний предел, ниже которого допущения 1-5 достаточно кор-
ректны: 1.3D. Для грунтов мощностью больше 1,3jD
лучше отвечает действительности, хотя также носит частный ха-
рактер. схема последовательного развития сводов обрушения.
2 И
Но поскольку, как отмечалось в разделе 13.2, аналитическое ре-
шение имеется лишь для первичного устойчивого свода, то эта
схема в настоящее время остается вербальной, а при расчетах
решение М.М. Протодьяконова комбинируется с Тем, что рас-
смотрено выше.
Перспективен подход К определению устойчивости районов
покрытого карста с помощью анализа напряженного состояния
пород вблизи полости (см. раздел 13,1). Однако при использова-
нии методов механики сплошной среды не рассматриваются по-
ведение несвязных грунтов и влияние подземных вод. А расчеты,
основанные на гипотезе Гейма-Динника, не учитывают большой
вклад ослабленных зон в формирование общего поля напряжений.
Метод, предложенный в работе |2], позволяет легко устранить эти
недостатки, но оставляет открытым вопрос об изменении напря-
женного состояния массива пород в ходе его деформирования —
разрушения.
Оптимальным способом локального прогнозирования устой-
чивости покровной толщи закарстованных массивов представля-
ется последовательный расчет возможного деформирования и
разрушения слоев связных и несвязных дисперсных пород, сла-
гающих разрез. При этом для оценки устойчивости глинистых
пластов в зависимости от их мощности удобно воспользоваться
имеющимися решениями для балок, плит, продавливания слоя
по цилиндрической поверхности, но с учетом уменьшения дав-
ления на его кровлю, сводов обрушения и другими корректными
и хорошо разработанными моделями.
Проблема образования провалов в песчаном слое гораздо
сложнее, но в то же время проще. Сложнее потому, что сам по
себе процесс деформирования даже воздушно-сухой сыпучей сре-
ды над отверстием, как ни странно, вызывает много вопросов.
Если же необходимо учитывать влияние подземных вод, то их
становится еще больше. Проще — поскольку истечение водона-
сыщенных песков в полость-приемник происходит как при вер-
тикальной фильтрации (нисходящей и восходящей), так и в гид-
ростатических условиях при равенстве уровней грунтовых и
трещинно-карстовых вод. Более того, можно показать, что и ка-
пиллярно-влажные пески не могут противостоять обрушению в
виде серии сводообразных вывалов над полостями с пролетом
больше 1 м. Иначе говоря, локальное прогнозирование устойчи-
вости песчаной толщи сводится не столько к выявлению законо-
мерностей ее деформирования, сколько к определению аккуму-
ляционной емкости подстилающих отложений (Ра). В первом
приближении она равна произведению объема того массива ра-
створимых пород, который способен принимать и накапливать
несвязные грунты (4'м), на коэффициент трещинно-карстовой
пустотност и (А'п):
Общим результатом выноса песка из толщи среднего и плот-
ного сложения является ее разуплотнение в пределах области
деформирования Поэтому из уравнения баланса массы сыпу*--
чего грунта (рис. 13.10) р(1 - п0) = р(1 - п)( + V), где р — плот-
ность минеральной части песка, «о и п — средняя пористость грун-
тов в объеме до и после деформирования, легко получается
выражение для объема материала, удаленного из толщи:
К«=- Ко (п - Яв)/(1 - п) = V^k. (13.4.8)
Экспериментально установлено, что оседание дневной по-
верхности возможно только после того, как высота зоны разуп-
лотнения становится равной мощности песчаной толщи. Поэто-
му для областей деформирования, аппроксимированных конусом,
цилиндром и эллипсоидом (рис. 13.10), выражение (13,4.8) пере-
писывается соответственно в виде:
far/f-й/З: (13.4.8,а)
V=kn^h, (13.4.8,6)
К=4АпА2й/3. (13.4.8)
Таким образом, если объем вынесенного материала, рассчи-
танный по (13.4.8), больше аккумуляционной емкости, опреде-
ленной по (13.4.7) в ходе инженерно-геологического изучения
массива закарстованных пород, то деформации песков внутри
толщи практически не отразятся на ее поверхности. И наоборот,
если V< Рд, провалы и оседа-
ние земной поверхности неиз-
бежны, независимо от того,
какие техногенные нагрузки
(изменение уровней подземных
вод, давление сооружений и
др.) испытывает толща песков.
Рис. 13,10. Схема к расчету критичес-
кого объема (V) несвязного грунта, вы-
несена ; из о i< л . деформи|
ния (Уо). которую аппроксимируют
круговым конусом (а)8 цилиндром (6) и
элг 4ГК >дом(е) вращения
219
Отметим, что рис. 13.10, а отражает стадию подготовки сдви-
жения покровной толщи, аналогичного тому, что показано на
рис. 13.5. Такой механизм нарушения устойчивости реализуется
при небольшой мощности перекрывающих грунтов, величину ко-
торой для несцементированных и раздробленных горных пород
можно оценить примерно как h = (1,3 - 2,6) D (рис. 13.9, в). Этот
случай представляет наименьший интерес для расчетов устой-
чивости районов покрытого карста, поскольку столь крупные
полости, во-первых, легко фиксируются в ходе инженерно-гео-
логических и геофизических работ, во-вторых, a priori чрезвы-
чайно опасны, в-третьих, встречаются крайне редко. Намного
важнее выяснить, когда истечение, или массовая суффозия пес-
ков развивается внутри «трубы» течения (рис 13.10, б), а ког-
да — в пределах эллипсоида или цилиндра со сходящимися в
нижней части стенками (рис. 13.10, е). Для этого можно вос-
пользоваться критерием устойчивости трубообразной области,
разработанным применительно к выпуску сухих сыпучих тел из
бункеров и силосов [3]:
б.'кЦоу. (13 4 9)
в котором а/ — горизонтальные напряжения на внутреннем кон-
туре стен «трубы» вблизи выпускного отверстия, исходные
вертикальные напряжения на днище емкости, определяемые по
известной формуле Яншина [41, Кк — коэффициент концентра-
ции вертикальных напряжений по периметру выпускного от-
верстия. В осесимметричных емкостях большой высоты (Л > 3D*.
D* — ширина или диаметр хранилища) с центральным донным
отверстием критический диаметр последнего в соответствии с
(13.4.9) равен
/)кр = 4Х/^>.//,
(13.4.10)
где у1 — объемный вес материала в канале тече-
ния,/=tg(<pl/+vmip), фр'— угол контактного тре-
ния, vnun — наименьший угол дилатансии, харак-
терный для достаточно разуплотненного грунта.
(Исходной плотности засыпки соответствует угол
внутреннего грения ф = ф/ + v, < v < vmax, пес-
ку в канале течения— ф = ф/.) Если вычислен-
ный по (13.4.10) больше диаметра выпускного
Рис. 13.11. Схема расчета диаметра «трубы» течения -
Пунктиром показаны формы канала течения на ранних стадиях
деформирования
220
отверстия D, то независимо от начальной плотности материа-
ла, «эффект трубы» может реализоваться лишь на высоте
hm = (£)кр - P)/2tg [3 от днища (рис. 13 11), где Р'ж/4 + ср/2, со-
гласно традиционным представлениям механики грунтов, м
p = n/4 + arcsin[tg(q)HM v)J в трактовке [6]. Результаты расчетов
критического диаметра и данные физического моделирования о
ширине канала течения в целом совпадают. Однако в массиве
пород, не ограниченном стенками емкости, решение Яншина
для вертикальных напряжений» очевидно, не «работает». При
подстановке <ту= у А в (13.4.10) величина становится больше
мощности песчаной толщи. Это требует дальнейшего изучения,
тем не менее подход к решению, выраженный критерием (13.4.9),
представляется перспективным.
Таким образом, локальное прогнозирование провалыю~суф-
фозионного процесса в районах покрытого карста является слож-
ной и далеко не решенной проблемой, тесно связанной с задача-
ми напряженно-деформированного состояния массивов пород,
механики грунтов, динамики подземных вод, шзурного выделе-
ния и описания ослабленных зон, участков и аккумуляционной
емкости закарстованных отложений в целом, лабораторного изу-
чения закономерностей процесса и рядом других задач. Рассмот-
ренные методы и приемы оценки устойчивости закарстованных
территорий показывают, что правильный выбор расчетной схе-
мы, сходимость вычисленных и измеренных показателей про-
цесса, а следовательно, и точность его прогноза определяются в
первую очередь адекватностью модельного» реального механиз-
мов деформирования и разрушения покровной толщи
Контрольные вопросы
1, Какое влияние на перераспределение напряжений в мас-
сиве пород оказывают подземные полости?
2. Как зависит распределение напряжений в массиве пород
вокруг полости от типа напряженного состояния?
3, Расчетные схемы для исследования условий обрушения
кровли подземных полостей.
4. Какие зоны по условиям деформирования и разрушения
образуются в массиве пород при сдвижении?
5. Что является причиной деформации поверхности земли
при откачках?
6. Виды деформаций откосов и бортов котлованов и ка-
рьеров.
7. При каких условиях возможен выпор днища котлованов,
карьеров или подземных выработок?
8. Модели, используемые для расчета суффо знойных и кар-
стовых провалов.
9. Какими параметрами характеризуются условия устойчи-
вости покровной толщи?
10. Какие предположения положены в основу построения
расчетных схем для изучения провальных явлений?
11. Условия образования провалов и способы расчета дефор-
мирования и разрушения в песчаном перекрывающем слое.
ГЛАВА 14. ВЫБОР РАСЧЕТНЫХ ПОКАЗАТЕЛЕЙ
Выбор расчетных показателей является необходимым этапом
применения математического или физического моделирования
для решения инженерно-геологических задач. Расчетные пока-
затели устанавливаются в результате экспериментального изу-
чения свойств горных пород. Основными вопросами, которые
решаются при обработке данных инженерно-геологических ис-
следований.. является оценка уровня, около которого осуществ-
ляется колебание показателей, характеризующих инженерно-гео-
логические условия или физико-механические свойства горных
пород и установление характера колебания, а также оценка точ-
ности и надежности полученных результатов и определение ко-
личества наблюдений, необходимых для получения конечных
результатов с требуемой точностью (3].
14.1, Показатели свойств горных пород
и случайные величины
С целью определения показателей физико-механических
свойств горных пород производится их опробование и лабора-
торные испытания образцов Данные лабораторных определений
называются частными показателями физико-механических
свойств горных пород. При массовом опробовании возникает
необходимость выбора из многочисленных результатов лабора-
торных исследований одного значения, которое является наибо-
лее типичным для данной породы. Это значение получило назва-
ние обобщенного показателя физико-механических свойств
горных пород. Обобщенный показатель является лишь статисти-
ческой характеристикой выборочной группы измерений, гак как
измеряемая величина не имеет постоянного значения. Поэтому в
инженерно-геологических расчетах к обобщенным показателям
применяются специальные поправочные коэффициенты, учиты-
вающие возможную ошибку определений среднего значения и
особенности работы сооружения. Исправленный обобщенный
показатель получил название расчетного.
Данные лабораторных испытаний образцов заметно отлича-
ются друг от друга даже в том случае, когда образцы отобраны из
внешне вполне однородной породы. Такой разброс значений
показателей свойств является результатом ряда причин. Первая
группа причин связана с неоднородностью горных пород. Вторая
группа — с нарушением естественной структуры и физического
состояния образцов при их отборе, транспортировке и хранении
и с погрешностями лабораторных определений. Так как в даль-
нейшем ЭТИ ошибки влияют на конечный результат, то возника-
ет необходимость, с одной стороны, сведения их к минимуму
путем усовершенствования методики отбора образцов и лабора-
торных исследований и, с другой — количественно® оценке уровня
допускаемой ошибки. Такая оценка возможна путем проведения
специально поставленных экспериментальных исследований.
Вычисление обобщенного показателя основывается на резуль-
татах лабораторных и полевых исследований. Данные лаборатор-
ных определений являются независимыми друг от друга. Если
опробуемый геологический объект предварительно расчленен на
инженерно-геологические элементы, отличающиеся однородно-
стью состава (минерально-петрографического), сложения (струк-
турно-текстурными особенностями, пористостью) и состояния
(влажностью, трещиноватостью и др.), и частные показатели фи-
зико-механических свойств отнесеян к этим элементам, то ре-
зультаты лабораторных иссждований образуют качественно одно-
родные совокупности. Изменение величин частных показателей в
пределах единого инженерно-геологического элемента при неболь-
шом интервале опробования незакономерно, так как в противном
случае, если величина частного показателя является функцией
положения точки опробования в пространстве, следует прибег-
нуть к более дробному расчленению отдельных элементов
Все это позволяет рассматривать частные показатели, харак-
теризующие какое-либо свойство единого инженерно-геологи-
ческого элемента и отличающиеся случайным характером изме-
нений, как случайные величины и дает право использовать для
их обработки методы математической статистики.
Установление характера изменчивости частных показателей
помогает более обоснованно производить выбор расчетных по-
казателей. Действительно, зная распределение данных лабора-
торных определений, можно с большей уверенностью судить о
возможных величинах отклонений показателей от среднего зна-
чения и выбирать величину расчетного показателя с заранее за-
данной надежностью.
При изучении физико-механических свойств горных пород
отбираются образцы и выполняются необходимые лабораторные
исследования, т.е. производятся испытания. Испытанием назы-
вается осуществление какого-либо определенного комплекса ус-
ловий, который может быть воспроизведен сколько угодно боль-
шое число раз. Результат одного эксперимента (испытания)
назовем событием, или исходом. Если бы имелась возможность
опробовать массив во всех точках и выполнить бесконечное мно-
224
жество экспериментов, тогда мы получили бы исчерпывающую
характеристику изучаемого свойства горной породы, а результа-
ты всех экспериментов составили бы полную систему событий,
или генеральную совокупность- Генеральной совокупностью на-
зывается все множество возможных исходов при данном испыта-
нии. Однако на практике мы имеем дело с ограниченным чис-
лом лабораторных определений, которые составляют выборочную
совокупность, или выборку. При этом количество и места отбора
образцов должны быть такими, чтобы выборка быта представи-
тельной (репрезентативной), т.е. правильно отражала действи-
тельные свойства пород.
В рассматриваемом примере событие состоит в получении кон-
кретных числовых величин, характеризующих определенное свой-
ство изучаемого объекта. Величина, принимающая при повторении
эксперимента те или иные- заранее неизвестные значения, называ-
ется случайной. Отдельное значение случайной величины называет-
ся вариантой, а совокупность случайных величин, расположенных
в порядке возрастания (убывания), — вариационным рядом.
Случайные величины могут быть непрерывными и дискрет-
ными. Дискретной называется случайная величина, которая мо-
жет принимать счетное множество значений, т.е. такое множество,
элементы которого могут быть пронумерованы в каком-нибудь
порядке. Непрерывной случайной называется такая величина, ко-
торая может принимать любое значение в одном или нескольких
заданных интервалах.
Результаты экспериментов являются непрерывными случай-
ными величинами. Отдельные результаты эксперимента — част-
ные показатели — являются вариантами, их совокупность (вы-
борка) — первоначальным рядом наблюдений.
14.2. Статистическая характеристика показателей
при обработке результатов полевого
и лабораторного изучения свойств пород
Анализ выборочной совокупности заключается в установле-
нии характера распределения единиц совокупности по интерва-
лам значений признака [1]. Такой анализ возможен, так как хотя
отдельные варианты, составляющие совокупность, не равны между
собой (варьируют), они могут принимать равные значения или
значения, лежащие в одном и том же интервале.
Обработка лабораторных данных начинается с построения
графика рассеяния, разбиения вариационного ряда на классы и
подсчета частот и частостей.
225
График рассеяния имеет одну вертикальную ось, на которую
наносятся значения изучаемого показателя в виде точек, поло-
жение которых фиксируется только по ординате. По оси абсцисс
точки могуч размещаться произвольно Для разбиения вариаци-
онного ряда на классы ось ординат графика рассеяния делится
на несколько равных интервалов, что зависит от размаха зна-
чений показателя и точности его определения. На практике
число таких интервалов колеблется от 6 до 12. Величина каж-
дого интервала Д( определяется из соотношения Д. ~ , где
т
R - Хтах “ хтт — размах варьирования, равный разности между
наибольшей и наименьшей вариантами статистической совокуп-
ности, т — число интервалов. Число вариант, попавших в один
класс, названо частотой (л,), отношение частоты к общему числу
испытаний (числу вариант) в выборке (N), называется относи-
тельной частотой, или частостью:
wt=^- (14.2.1)
Частость может быть выражена в процентах.
Плотностью частоты Ри (или частости ) называется от-
ношение частоты п, (или частости w,) к величине классового ин-
тервала Д,:
Накопленной частотой (или частостостью ) для
/-го интервала называется сумма частот (частостей) всех интер-
валов от первого до /-го. Для наглядности эмпирическое распре-
деление можно изобразить графически в виде гистограмм (поли-
гонов распределения) и кумулятивных кривых.
Гистограммой называется ступенчатый график, построенный
по плотности частот (частостей). На графике по оси абсцисс от-
кладываются классовые интервалы, а по оси ординат — плотно-
сти частот соответствующих классов. Площадь всей гистограммы
частот равна объему N статистической совокупности, площадь
всей гистограммы частостей равна единице, или 100%.
Для построения кумулятивной кривой по оси абсцисс откла-
дывают величины середин классовых интервалов, а по оси орди-
нат — накопленные частоты (или частости), соответствующие
интервалам. Рассмотренные графики отражают функциональную
зав между частотами из-.....
ми величин, которые он может принимать. Такие зависимости
называются законами распределения. Для установления закона
распределения, что является одной из наиболее важных задач
226
математической статистики, необходимо изучение статистичес-
ких характеристик совокупности случайных величин
Основными свойствами любой статистической совокупнос-
ти являются: 1) положение распределения относительно начала
координат, определяемое средним значением; 2) степень рассея-
ния отдельных значений величин относительно среднего значе-
ния, характеризуемая дисперсией; 3) степень асимметричности
распределения относительно среднего значения, определяемая
асимметрией; 4) степень крутизны кривой распределения, харак-
теризуемая эксцессом.
Характеристиками положения распределения являются раз-
личные средние, медиана и мода. Средняя величина характери-
зует тот центр, вокруг которого группируются отдельные част-
ные значения. Основное назначение средней — представлять в
расчетах, сопоставлениях и выводах индивидуальные особеннос-
ти признаков, из которых она выведена. Обобщенные показате-
ли физико-механических и других свойств горных пород, как
правило, являются средними арифметическими значениями, вы-
численными по результатам лабораторных определений.
Из всех видов средних чаще всего используется средняя ариф-
метическая, определяемая из уравнения;
или средняя арифметическая, взвешенная по частотам значений
величин: _
М = /-^..2 , (14.2.4)
где Xj— среднее значение каждого классового интервала, л,—
частота, N = — число вариант в выборке или объем иссле-
дуемой совокупности.
Медианой (Me) называется варианта, делящая вариационный
ряд на две равные по числу вариант части. Если число вариант
равно 2k+ 1, то медианой будет k + 1 варианта, а при числе вари-
ант, равном 2k:
Me = , (14.2.5)
где хк и х^-1 — варианты, стоящие на соответствующих местах
Геометрически медиана — это абсцисса вертикальной прямой,
которая делит гистограмму на две равные по площади части.
Модой (Мо) называется значение признака, имеющее наи-
большую частоту. В случае непрерывной случайной величины по
таблице распределения может быть указан модальный интервал,
такой интервал, которому соответствует наибольшая частота.
227
Мера рассеяния, или вариация ряда распределения, имеет
несколько видов. Наиболее простыми характеристиками рассея-
ния являются размах варьирования R и вероятное отклонение. Раз-
мах варьирования равен разности между наибольшей и наимень-
шей вариантами статистической совокупности. Вероятное
отклонение определяется по квартилям, которые делят весь ва-
риационный ряд на четыре равные по количеству вариант части.
Они обозначаются 02и Q3 Первая квартиль — это варианта,
меньше которой в данной статистической совокупности имеется
четверть ВССХ вариант. Вторая квартиль совпадает с медианой.
Третья квартиль представляет собой варианту, меньше которой в
данной статистической совокупности находится три четверти всех
вариант. Вероятным отклонением называется половина разно-
сти между третьей и первой квартилями. Размах и вероятное от-
клонение являются грубыми характеристиками рассеяния.
Средним абсолютным отклонением (o') называется средняя
арифметическая абсолютных величин отклонений отдельных ва-
V(x - х|
риант х, от их среднего арифметического значения gr — • —-
или, если оно вычислено с учетом средней арифметической, взве-
шенной по частотам,
Наиболее объективной характеристикой рассеяния является
дисперсия. Чем больше дисперсия^ тем более рассеяны величины
около своего среднего значения. Дисперсией называется среднее
арифметическое ИЗ квадратов отклонений вариант х, от средней
арифметической;
о2 - ——— или о2 = ——'—г?.——(14.2.7)
А А
Среднее квадратичное отклонение рассчитывается по средним
значениям и частоте каждого классового интервала й равно кор-
ню квадратному из дисперсии:
(14.2.8)
Коэффициент вариации — это отношение среднего квадратич-
ного отклонения и средней арифметической, выраженное в про-
центах:
(14.2 9)
228
Для вычисления средней арифметической и дисперсии, а
также асимметрии и эксцесса по ряду распределения можно ис-
пользовать моменты ряда распределения. Моментом l-ю поряд-
ка М называется среднее значение степеней отклонений от -
дельных вариант от некоторой постоянной величины с:
V (X : ~ С)‘ П.
М i = 1 J . (14.2.10)
/V
Если постоянная величина, от которой исчисляются отклоне-
ния вариант, является началом отсчета (например нулем), то мо-
менты называются начальными. Если постоянная есть среднее
значение вариант, то моменты называются центральными. Началь-
ный момент первого порядка есть среднее значение вариант:
У'(х,-0)л, У'хщ,
Vj = --<• -- = М . (14.2.11)
ZV .(V
Центральный момент первого порядка равен нулю:
У(х,— М}п
—— * 0 • (14.2.12)
Л
Центральный момент второго порядка равен дисперсии ряда рас-
пределения:
(14.2.13)
Центральные моменты третьего и четвертого порядков вычисли
ются аналогичным образом и используются для определения сим-
метрии и эксцесса.
14.3. Нормальный закон распределения
случайной величины
Из практики известно, что если наблюдения над массовым
случайным явлением производятся несколько раз в одинаковых
условиях, то частости одних и тех же событий во всех сериях на-
блюдений колеблются около некоторых определенных чисел Ча-
стость характеризует степень возможности события, с которым она
связана. Очевидно, что в одинаковых условиях из двух событий
более возможно то, которому соответствует большая частость. Ве-
личина, характеризующая степень объективной возможности слу-
чайного события, называется вероятностью Р. Частость служит
проявлением вероятности события в результате наблюдения.
Законом распределения случайной величины называется всякая
функция, устанавливающая связь между возможными значениями
229
/учайной величины и соответствующими им вероятностями. В
случае непрерывной случайной величины нельзя заранее указать
все возможные определенные ее значения й соответствующие им
вероятности, а можно говорить лишь о вероятности попадания слу-
чайной величины в определенный интервал ее изменения.
Пусть вероятность того, что случайная величина х примет
значение, лежащее в определенном интервале Ах ее изменения,
равна Pi, тогда функция
характеризует плотность непрерывного распределения вероятно-
стей случайной величины х и называется законом распределения
случайной величины Графически дифференциальный закон рас-
пределения может быть изображен в виде графика плотности
вероятности.
Одним из основных вопросов, который приходится решать
при обработке статистического материала, является вопрос о том,
какому теоретическому закону соответствует распределение, по-
лученное опытным путем. При обработке данных определения
физико-механических или любых других свойств горных пород
наиболее часто приходится иметь дело с нормальным распреде-
лением случайных величин.
Случайная величина подчинена нормальному закону распре-
деления, если плотность вероятности случайной величины выра-
жается функцией:
<х-М)'
/(х)- —2”2 . (14.3.2.)
оУ2л
Величины М и о называются параметрами распределения и пред-
ставляют собой среднеарифметическое значение вариант (М) и
среднеквадратичное отклонение (а) теоретического распределе-
ния. Изменение параметра М влечет за собой смещение всей
кривой вдоль оси абсцисс (рис. 14.1, а), изменение параметра о
приводит к изменению степени сжатия кривой (рис. 14.1, ф.
Для проверки гипотезы о нормальности эмпирического рас-
пределения необходимо произвести сравнение эмпирического
и теоретического распределений. Для оценки степени близос-
ти фактического распределения к нормальному используются
две характеристики: асимметрия и эксцесс. Коэффициент асим-
метрии (as) и показатель эксцесса (es) определяются из соот-
ношений:
= , ех--1--3.
о о
(14 2.16)
Отрицательная асимметрия указывает на то, что восходящая ветвь
кривой положе, чем нисходящая, а положительная — об обрат-
ном (рис. 14.2, а). При |os| < 0,1 распределение практически сим -
метрично, при |дз| > 0,5 распределение резко асимметрично Эк -
сцесс показывает, насколько эмпирическая кривая является более
плоской и растянутой (ез < 0) или более сжатой и заостренной в
центре (ез > 0) по сравнению с теоретической кривой нормаль-
ного распределения (рис. 14.2, б). В первом случае вершина кри-
вой ниже кривой нормального распределения, во втором — выше.
Для нормального распределения аз = 0, es = 0 a средняя арифме-
тическая. медиана и мода совпадают.
-
Рис. 14.1. Изменение положения и фор-
мы кривой нормального распределе-
ния: a -- при М3 > М2 > M1f б — при
' 'J > СТ ।
Рис. 14.2. Изменение формы кривой
нормального распределения в зависи-
мости от коэффициента асимметрии (а)
и показателя эксцесса (б)
Современные пакеты программ, вычисляющие статистиче
кие характеристики, рассматривают различные законы распре-
деления: логнормальный, экспоненциальный, полиномиальный
и др. 14].
14.4. Оценка выборочных статистических
характеристик
Выше были рассмотрены задачи вычисления основных ста-
тистических характеристик совокупности, определяющие цент-
ральное значение ряда и степень рассеяния частных значений
около среднего, выяснения характера распределения случайной
231
величины и установления теоретического распределения, наибо-
лее близко отвечающего эмпирическому. Перечисленные задачи
могут считаться решенными только в том случае, если обследо-
ванию были подвергнуты все без исключения варианты статис-
тической совокупности, т.е. когда при анализе данных мы имели
дело с генеральной совокупностью. Однако на практике изуче-
ние свойств осуществляется на основе анализа ограниченного
числа данных, составляющих выборочную совокупность, или
выборку. Возникает вопрос: всегда ли статистические характери-
стики; вычисленные поданной выборочной совокупности, отра-
жают свойства генеральной совокупности и насколько точно?
Иными словами, всегда возникает необходимость оценки истин-
ности полученных характеристик. При увеличении объемов вы-
борки (согласно закону больших чисел) рассеяние выборочных
характеристик около истинных уменьшается, а надежность оценки
истинной характеристики по данным выборки возрастает. Если
объем выборки Л достаточно велик (например, N > 20), то с ве-
роятностью сколько угодно близкой к единице можно утверж-
Да’_'_'-, ЧП'О*
М( (14.4.1)
где Мт и Л/в —~ средние величины, ну я частости некоторого
признака в генеральной и выборочной совокупности, о и <у| —
соответствующие дисперсии.
Вероятность, связанная с величиной ошибки (так называемая
гарантийная вероятность Д), характеризует надежность определе -
ния численного значения ошибки. Связь между гарантийной ве-
роятностью и величиной ошибки осуществляется посредством
гарантийного коэффициента Л который определяет собой веро-
ятность получения фактической ошибки, не выходящей за пре-
делы вычисленных границ, и вводится в формулы для определе-
ния ошибок. Значения t зависят от уровня вероятности, с которой
необходимо определить величину возможной ошибки, и от объе-
ма выборки, и приводятся в табл. 14 1. Гарантийная вероятность
показывает долю тех случаев, когда оправдывается предположи -
14. •
Значения гарантийного коэффициента в зависимости
от гарантийной вероятности и объема выборки
р N 3 4 6 8 10 12 14 16 20 оо
0,682 0,954 1,32 <3 1,3 3,3 ALL 2,6 L08 2,4 1,06 2,3 1,04 2,3 1.02 2,2 .01 1,01 Л1 1,00 Z.0 1
232
ние о том, что фактическое отклонение выборочной характерис-
тики от генеральной не выйдет за пределы установленных гра-
ниц интервала. Например, при /V) = 0.954 выборочная характе-
ристика в 954 случаях из 1000 не будет отличаться от генеральной
на величину большую вычисленной возможной ошибки.
Приближенная величина возможной абсолютной ошибки
определения выборочной средней арифметической вычисляется
по формуле:
- -fc—или ем =- ±- ^== , если выборка малая. (14.4.2)
v# </V - I
Если полученная величина возможной ошибки оказывается боль-
ше допустимой и требуемая точность не обеспечивается, то уве-
личивается объем наблюдений, что должно привести к увеличе-
нию точности определения средней. Относительная ошибка
определения средней арифметической вычисляется:
(14.4.3)
С учетом (14.4.2) и (14.4.3) получим;
ей " ±-=-% и для малых выборок ем — ± — % , (14.4.4)
где И7 - —у-100% — коэффициент вариации. Ошибка выборочно-
го среднеквадратичного отклонения для большой выборки равна:
(14.4.5)
Величиной гарантийной вероятности обычно задаются зара-
нее в зависимости от требуемой точности определения статисти-
ческих характеристик, что обусловлено стадией проектирования,
капитальностью сооружения, инженерно-геологическими усло-
виями его возведения и др.
Например, средняя плотность молодых базальтов, измерен-
ная в лабораторных условиях, равна 2,55 г/см3, среднее квадра-
тичное отклонение ов= 0,6. Гарантийной вероятности 0,954 при
объеме выборки N = 50 соответствует гарантийный коэффициент 2
(см. табл. 14.1). Тогда абсолютные ошибки определения выбо-
рочных средней арифметической и среднеквадратичного откло-
нения б
51
233
£о = =- - ±0,12.
V2W V100
Относительная ошибка определения выборочной средней ариф-
метической вычисляется по (14.4,3):
«Ж ~ « ±А11100% - ±6,67%.
М 2,55
Не менее важным является решение обратной задачи, кото-
рая заключается в определении необходимого объема выборки
N, обеспечивающего с гарантированной вероятностью P(t) вели-
чину фактической ошибки £., не выходящую за пределы задан-
ных границ. Для этого следует воспользоваться формулами (14.4.2)
и (14.4.3). Предположим, следует определить объем выборки, до-
статочный для того, чтобы относительная ошибка определения
выборочной средней арифметической не превышала 5% с гаран-
тийной вероятностью 0,954. Значения с, можно определить по
выборке малого объема (N < 10), или в рассматриваемом случае
принять равным 0,6. Тогда объем выборки должен быть:
4 0,36
0,0162
14.5. Определение расчетных показателей
Вычисленные обобщенные показатели не всегда могут рас-
сматриваться как расчетные, так как они вычисляются: 1) по срав-
нительно небольшому числу определений, что ставит под сомне-
ние их типичность для всей породы; 2) на основании данных того
состояния породы, в котором она находится в момент изыска-
ний, без учета тех изменений, которые могут произойти в ее со-
стоянии и свойствах в процессе строительства и эксплуатации
сооружения.
Поэтому расчетные показатели могут быть использованы как
расчетные только в тех случаях, когда анализ показывает, что
указанные причины не могут изменить их величину. Например,
величины показателей сжимаемости, сопротивления сдвигу, про-
садочности пород и другие могут существенно меняться. Поэто-
му в обобщенные значения таких показателей приходится вно-
сить специальные поправки, гарантирующие от опасных для
проектируемых сооружений ошибок, т.е. практически заменять
их другими, более надежными значениями. Рассмотрим наибо-
лее часто применяющиеся в этом случае приемы [2].
Среднее максимальное или среднее минимальное значения, вы-
численные после отброса 10% значений как расчетные показатели.
Из числа всех полученных в лаборатории данных отбрасывают
10% наиболее высоких и наиболее низких величин показателя, а
затем вычисляют среднее максимальное и среднее минимальное
значения. Проще всего это может быть сделано по графику рас-
сеяния, на котором нетрудно отсчитать 10% точек, расположен-
ных в самой верхней и самой нижней частях графика. Величины
средних минимальных и максимальных значений вычисляются
по формулам:
М + х М + х
— r mm s ' ^шах Л 4 S П
•*cp min “ 2 ’ *cp.max /
В расчет принимается то из них, которое является менее благо-
приятным, максимальное и минимальное значения берут из чис-
ла оставшихся на графике. Этот прием используется главным
образом для предварительных расчетов на первых стадиях проек-
тирования или для неответственных сооружений.
Среднемаксимальное и среднеминимальное взвешенные значения
как расчетный показатель. В этом случае расчетный показатель
принимается равным верхней или нижней квартилям. Опреде-
лить эти значения с достаточным для практических целей при-
ближением можно по графику рассеяния. Для этого в верхней и
нижней частях графика достаточно отсчитать по 25% точек и от-
делить их горизонтальными прямыми, которые отсекут на орди-
нате интересующие нас значения, соответствующие нижней и
верхней квартилям. В программном статистическом пакете мож-
но воспользоваться так Называемыми «усатыми» графиками, ко-
торые строятся по значениям, попадающим в указанные интер-
валы. Как и в предыдущем случае, в расчет принимается менее
благоприятное значение, обычно расположенное в нижней квар-
тили. Изложенный прием используется наиболее широко на всех
:та щях проектирования.
Метод доверительных пределов исходит из положения, дока-
занного в математической статистике, что генеральное значение
среднего арифметического, характеризующего всю изучаемую
породу, находит .. е, ’ -
<М. <Mt +'л (14.5.2)
где Мъ — выборочное среднее арифметическое, Mt — генераль-
ное среднее арифметическое, е м — абсолютная ошибка опреде-
ления средней арифметической. Разность и сумма Л/„ ± е w в
математической статистике называются гарантированным или
доверительным пределами.
235
В расчет принимается значение одного из доверительных
пределов, которое является менее благоприятным. Оно получило
название гарантированного значения расчетного показателя. Из-
меняя величину гарантийного коэффициента, можно увеличить
или уменьшить надежность определения расчетного показателя.
Метод доверительных пределов является наиболее обосно-
ванным и обычно используется на заключительных стадиях изыс-
каний при проектировании инженерных сооружений.
Контрольные вопросы
1. Обобщенные и расчетные показатели свойств горных
пород.
2. На каком основании показатели свойств горных пород
можно рассматривать в качестве случайных величин?
3. Основные статистические характеристики, определяемые
при обработке данных экспериментального определения
свойств пород
4. Нормальный закон распределения случайной величины.
5. Способы оценки истинности характеристик свойств гор-
ных пород, определенных экспериментально.
6. Способы определения расчетных показателей, метод до-
верительных пределов.
ЛИТЕРАТУРА
Литература к гл. 1
1. Аникеев А.В. Современные методы изучения карста// ЦПНТТО.
Совет по карсту и спелеологии. М., 1987. С. 35.
2. Вондарик ГК. Основы теории изменчивости инженерно-геологи-
ческих свойств горных пород. М , 1971. С. 271.
3. Григорян С. С. и др. Количественная теория геокриологического
прогноза. М., 1987.
4. Задачи механики: в гляциологии и геокриологии / Под ред. С.С. Гри-
горяна. И., 1984.
5. Кузнецов ГН. и др. Изучение проявления горного давления на
моделях. ML* 1959.
6. Кутепов В.М. Оценка устойчивости закарстованных территорий.
М., 1986
7. Лехов А.В. Математическое моделирование карстового процесса
в совокупности трещин// Инженерная геология. 1985. № 5. С 61-67.
8, Механика ледников / Под ред. С.С. Григоряна. М.? 1977.
9- Моделирование задач динамики термоупругости и статики поля-
ризационно-оптическим методом / Под ред. Г.Л Хесина М.» 1970.
10. Проблемы термомеханики грунтов / Под ред. С.С. Григоряна.
М , 1986.
1L Савин ГН. Распределение напряжений вокруг отверстий. Киев,
1968.
12. Трофимов В Т. Генезис просадочности лёссовых пород. М... 1999.
13. Хоменко Б.П. Карстово-суффозионные процессы и их прогноз.
М., 1986.
14. Трумбачев В Ф, Молодцова Л. С Применение оптического мето-
да для исследования напряженного состояния пород вокруг горных
выработок. М., 1963.
15. Ухов С.Б. Скальные основания гидротехнических сооружений
М., 1975
16 Фишман Ю.А , Мирошникова Л. СОпыт разработки и примене-
ния инженерно-геологических моделей в практике гидротехнического
строительства // Инженерная геология. 1984. № 5. (X 24-37.
17. ЯргЛ.Я. Инженерно-геологическое изучение процессов вывет-
ривания. М., 1987.
18. ЯргЛ.Я. Методика инженерно-геологических исследований про-
цесса и кор выветривания. М., 1991.
237
Литература к гл. 2
1. Безухов НИ. Основы теории упругости, пластичности и ползуче-
сти. М., 1988
2- Лехницкий С.Г. Теория упругости анизотропного тела, М , 1977.
3. Мусхелишвили НИ. Некоторые основные задачи математической
теории у ругос 1966
4. Харр М.Е. Основы теоретической механики грунтов, М., 1971.
Литература к гл. 3
Г Зенкевич В. С Метод конечных элементов в технике. М., 1975.
2. Крауч С, Старфилд А. Методы граничных элементов в механике
твердого тела. М. , 1987я
3. Математическая энциклопедия. Т. 4. М.? 1984, Стб. 843-847.
4. Мусхелишвили НИ. Некоторые основные задачи математической
теории упругости. М , 1966.
5. Самарский А.А. Введение в численные методы. М.» 1982.
6. Сегерлинд Л. Применение метода конечных элементов. М.? 1979.
7. Ухов С.Б. Расчет сооружений и оснований методом конечных эле-
л нто М . 1973
8. Фадеев А .Б. Метод конечных элементов в геомеханике. М.» 1989.
Литература к гл. 4
L ГОСТ 8.417-81.
2. Гу хм ан А.А. Введение в теорию подобия. М., 1973.
3, Кирпичев М. В. Теория подобия. М., 1957.
4. Седов Л.И Методы подобия и размерностей в механике. М.? 1987.
5. Сена Л. А. Единицы измерения физических величин и их размер-
ности. М , 1977.
Литература к гл. а
1. Гулакян К.А., Осиюк В.А. Физическое моделирование в инженер-
ной геологии (применительно к проблеме прогнозирования оползней //
Гидрогеология, инженерная геология. М1993.
2. Кузнецов ГН и др. Моделирование проявления горного давле-
ния. Л., 1968.
3. Методика инженерно-геологических исследований высоких об-
вальных и оползневых склонов/ Под ред. Г.С. Золотарева, М. Янича.
М., 1980.
4. Покровский Г И., Федоров Л. С. Центробежное моделирование в
горном деле, М.7 1969.
Литература к гл. б
I. Каменева Ю. А. 7 Шарий А А Изучение напряженного состояния
массива порол высоких склонов методами лабораторного моделирова-
ния / Вопросы инженерной геологии и грунтоведения. Вьш. 2. М., 1968.
С 300-316.
2. Махорин А.А., Фаминцын Б.М. Применение стереотензометричес-
кого метода моделирования /7 Вопросы формирования и устойчивости
склонов. М., 1970.
3. Метод фотоупру гости / Под ред. ГЛ. Хесина. М,, 1975.
4. Розанов Н С. Метод гензосетки и его приложение к исследова-
нию напряженного состояния гидросооружений. М ;Л., 1958.
5. Осокина Д Н Пластичные и упругие низкомодульные оптически
активные материалы для исследования напряжений в земной коре ме-
тодом моделирования. М.5 1963.
6. Трумбачев В.Ф., Молодцова Л. С. Применение оптического метода
для исследования напряженного состояния пород вокруг горных выра-
боток. М., 1963.
7 Федоров И. В. Методы расчета устойчивости склонов и откосов.
MU 1962.
8. Фисенко Г, Л. Устойчивость бортов карьеров и отвалов. М., 1965.
9. Хаимова-Малькова Р,И. Методика исследований напряжений по-
ляризационно-оптическим методом. М1970
Литература к гл. 7
1. Дятловицкий ЛИ Напряжения в гравитационных плотинах на не-
скальных основаниях. Киев, 1959.
2. Коломенский Е.Н., Харитонов Д.Д’Имитационное компьютерное
моделирование в инженерной геологии (проблемы и перспективы)//
Геоэкология. Инженерная геология. Гидрогеология, Геокриология. 1999.
№ 4. С. 374-378.
3. Ляпунов А.А. О кибернетических вопросах биологии // Проблемы
кибернетики. Вып. 25. М., 1972. С. 5-41
4. Методика инженерно-геологических исследований высоких об-
вальных и оползневых склонов/ Под. ред. Г.С. Золотарева и. М. Янича.
Мм 1980.
5. Розовский Л. Б, Зелинский И, П , Воскобойников В. М Инженерно-
, 14 кл но и е. рован
6. Рогозин А.Л. Синергетические модели развития и трансформации
опасных геологических процессов в процедуре риск-анализа / Сергеев-
ские чтения. Вып. 2 М., 2000 С. 103-109.
Сохранений В Б и др. Метод прогнозной оценки экранирующей
способности каменной соли в приконтурной зоне подземного резервуа-
ра// Геоэкология. Инженерная геология. Гидрогеология. Геокриоло-
гия. 2000. № 5. С. 474-478
239
8. Терцаги Л. Теория механики грунтов. М.. 1961.
9. Флорин В.А. Основы механики грунтов. Л.5 1959—1961 Т. 1—2*
10* Хоменко ВЛЕ, Коломенский Е.Н. Влияние подземных полостей на
состояние вышележащих дисперсных пород// Пром и гражд. строи-
тельство 2000 № 8. С. 39—41.
11. Федер Е Фракталы М, 1991.
12. BaudetC^ Hulin J-P., Lallemand Р (THumieresD. «Lattice-gas
automata: a model for the simulation of dispersion phenomena // Phys, Fluids
A. L (3), March 1989= P. 507-512.
13. Biot ML A. Mechanics of deformation and acoustic propagation in porous
media// J. of Applied Physics. 1962. Vol. 31 N 4. P. 1482-1498.
14. R. Bremond et D. Jeulin. Random Media and lattice gas simulations.
Geostatistical Simulations Workshop / fedite par M Armstrong et P.A. Dowd,
Kluwer Academic Publishers — Dordrecht, 1994. P. 89—105
Литература к гл. 8
1. СНиП IL15-74. Основания зданий и сооружений. Госстрой СССР.
М , 1975.
2. СНиП 2.02.01-85. Основания зданий и сооружений. Госстрой
СССР. М.? 1985.
3 СНиП 2-7-81*. Строительство в сейсмических районах. Госстрой
СССР М.? 1990.
Литература к гл, 9
L Золотарев Г.С., Калинин ЭВ., Минервин А.В. Учебное пособие по
инженерной геологии. М.: Изд-во МГУ9 1970.
2 Маслов Н.Н. Прикладная механика грунтов. М.: Машстройиздат
1949=
3. Соколовский В.В. Статика сыпучей среды. М.г Наука, 1990.
4. Троицкая М.Н. Новый способ расчета откосов и склонов. Мл
Дориздат, 1951.
Литература г 10
1. Газиев Э. Г. и др. Современное состояние инженерной оценки ус-
тойчивости скальных откосов //Инженерная геология. 1984. № 2. G3-16
2. Золотарев Г. С. у Калинин Э В Минервин АВ. учебное пособие по
инженерной геологии. М., 1970.
3. Терцаги К Теория механики грунтов. М., 1961.
4 чугаевр р Расчет устойчивости земляных откосов и бетонных
плотин на нескальном основании по методу круглоцилиндрических
поверхностей обрушения. М.;Л., 1963=
5. Чугаев Р.Р. Расчет устойчивости земляных откосов по методу плос-
ких поверхностей сдвига грунта. М ;Л , 1964
6. Шаху няни Г.М Железнодорожный путь М., 1969.
Литература к ДО 11
1. Методическое пособие по инженерно-геологическому изучению
горных порол Т. I. Полевые методы. М., 1984. С 408-415.
2, Мироненко В.4., Шестаков ВМ. Основы гидрогеомеханики М.,
1974.
3 Рекомендации по выбору методов расчета коэффициента устой-
чивости склона и оползневого давления. М , 1986.
4. СНиП 2-7-81* Строительство в сейсмических районах. Госстрой
СССР. М., 1990.
Литература к гл. 12
1 Браславский АЛ. Расчет ветровых волн / Тр. ГГИ Л., 1962 Вып 35
(89). С 82-97.
2. Варазашвили НЕ Особенности формирования берегов водохра-
нилищ в условиях нестационарности уровенного режима на примере
горных водохранилищ Закавказья / Тр. Гидропроекта М., 1983. №96.
С. 75-84
3. Воскобойников В.М., Лиходеева О.Е Изучение и прогнозирование
геологических процессов на основе метода обобщенных переменных
(на примере переработки берегов водохранилищ) // Инженерная геоло-
гия. 1984 № 1. С. 23-36.
4. Епишин В. К. Экзаръян В.Н. Прогноз процесса формирования бе-
регов водохранилищ. М., 1979.
Ж Золотарев Г.С у Рогозин А.Л. Закономерности формирования скло-
нов Днестра и методика прогноза их переработки при нестационарном
уровенном режиме водохранилищ// Инженерная геология. 1979. №6
С 47-63.
6. Золотарев Г С, Калинин Э.В., Минервин Л.& Учебное пособие по
инженерной геологии. М., 1970.
7. Качугин Е.Г. Геологическое изучение динамики берегов водохра-
нилищ. М.» 1975 С 145.
8. Кондратьев НЕ. Расчеты ветрового волнения и переформирова-
ния берегов водохранилищ. Л., 1953.
9. Печеркин M.A.t Печеркин берегов
водохранилищ// Гидротехническое строительство. 1981 № 3. С. 38-43.
10. Розовский Л. Б Альбом аналогов для прогноза переработки бере-
гов водохранилищ. Одесса, 1962. Т 152.
11. Розовский Л. Б. Введение в теорию геологического подобия и мо-
делирования. М., 1969
241
12. Халма тов 3. Методика изучения инженерно-теологических явле-
ний в период наполнения и эксплуатации водохранилищ // Инженерные
изыскания для водохозяйственного строительства в Таджикистане. Ду-
шанбе, 1969. С. 89-96.
Литература к 13
1 Аверишн CJ Сдвижение горных пород при подземных разработ-
ках. М.» 1947.
2. Аникеев А В.. Калинин Э.В,, Тараканов СИ Определение напря-
женного состояния грунтовой толщи нал карстовой полостью// Инже
мерная геология. 1991. №5. С 64-70.
3 Крамаджян АА, Линдквист ПА, Мансон А. и др. О формах обла-
стей течения в сыпучих материалах при выпуске // ФТПРПИ. 1994. № 2.
G 34-46.
4 Кутепов В. М.9 Кожевникова В. НУУстойчивость закарстованных
территорий. М., 1989
5. Мироненко ВА. Шестаков В.Л/. Основы гидрогеомеханики. М.,
1974.
6. РевуженкоА.Ф., Стажевский СБ. Об учете дилатансии в основ-
ных справочных формулах механики сыпучих сред// ФТПРПИ. 1986.
№4 С. 1116
7 Слесарев ВД. Механика горных пород. М., 1948,
8. Терцаги К Строительная механика грунта на основе его физичес-
ких свойств / Пер. е нем под ред. НМ. Герсеванова. М.;Я., 1933.
9. Турчанинов ИА, Иофис МА* Каспарьян Э.В. Основы механики
горных пород. Л.. 1977.
10. Фисенко ГЛ. Предельные состояния горных пород вокруг выра-
боток М.» 1976.
Литература к ЭД 14
L Дементьев Л.Ф Статистические методы обработки и анализа про-
мыслово-геологических данных. М., 1966
2. Коломенский НВ. Общая методика инженерно-геологических ис-
следований. М. 1968
3. Миллер P.s Кан Дж. Статистический анализ в геологических на-
уках. М., 1965.
4. StatSoft. 2000
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ ................... . ... . . . . . .... ......... . 3
Основные обозначения .................................... ........................ 6
ЧАСТЬ I. МАТЕМАТИЧЕСКОЕ И ФИЗИЧЕСКОЕ
МОДЕЛИРОВАНИЕ ..... ...................................... 7
ГЛАВА 1 МЕТОДЫ МОДЕЛИРОВАНИЯ ГЕОЛОГИЧЕСКИХ
И ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИХ ПРОЦЕССОВ ...... 7
1.L Основы инженерно-геологической схематизации................... 7
1.2. Классификация методов моделирования....... ......... 11
1.3. Методы моделирования в инженерной геологии. . .. 14
ГЛАВАХ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ...................... 17
2.1. Математическая модель напряженно-деформированного
состояния массивов горных пород ... .... . ..... ................ .... 17
2.2. Вывод основных уравнений математической модели НДС
массива горных пород.................................... .... Z
XX Математическая модель НДС массива горных пород
для двухмерного случая ................ ............................... 30
2.4. Способы задания граничных условий............................. 33
2.5. Типы расчетных моделей для изучения геомеханических
процессов........................................... ........ . i
ГЛАВА 3. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
ПРИ МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ............................ . 39
3.1. Аналитические способы .......................... ....... 40
3.2. Конечно-разностные и вариационно-разностные
методы........................... .................... . 45
3.3. Метод конечных элементов........................................ 51
3.4. Метод граничных элементов ........................... . . ...
ГЛАВА 4. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ЭКСПЕРИМЕНТАЛЬНОГО МОДЕЛИРОВАНИЯ ...................... 60
4.1 Размерность физических величин ............. „ ..... 60
4.2. Понятие об анализе размерностей = ................................... 63
43. Основы теории подобия.. . .. .. . .... . . .. .. .. ... .. ..... 64
243
ГЛАВА 5. ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ.................... 71
5.1. Теоретические основы методов
эквивалентных материалов...... .. ........ . 71
5.2. Метод эквивалентных материалов ........... 74
5.3. Метод термопластических материалов........... 76
5.4. Центробежное моделирование................... 78
ГЛАВА 6. ПОЛЯРИЗАЦИОННО-ОПТИЧЕСКИЕ МЕТОДЫ
МОДЕЛИРОВАНИЯ. ................................... 80
6.1, Метод фотоупругости_. . ...._.... . . .. 80
6.2. Метод замораживания деформаций................ 85
6.3. Метод тензометрической сетки.................. 86
ГЛАВА 7 АНАЛОГОВОЕ И ИМИТАЦИОННОЕ
МОДЕЛИРОВАНИЕ .................................. 89
7.1. Метод электрогеодинамических аналогий __ .... 89
7.2. Имитационное компьютерное моделирование. .... 92
7.3. Типы моделей массивов горных пород, применяемые
при их исследовании методами математического
и экспериментального моделирования .............. 95
ЧАСТЬ II. ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИЕ РАСЧЕТЫ.... 101
ГЛАВА 8. РАСЧЕТЫ ОСНОВАНИЙ СООРУЖЕНИЙ .. . . .. . .... 101
8 1. Виды нагрузок учитываемых при расчетах оснований
сооружений...—.. ............. 101
8.2. Расчеты оснований по деформациям............. 102
8.3. Расчет осадки основания...................... 104
8.4. Расчет оснований по несущей способности .. 112
8.5. Особые случаи расчета несущей способности
и деформаций оснований ........................ 114
ГЛАВА 9, МЕТОДЫ РАСЧЕТА УСТОЙЧИВОСТИ СКЛОНОВ,
ОСНОВАННЫЕ НА АНАЛИЗЕ НАПРЯЖЕННОГО
СОСТОЯНИЯ ПОРОД В ПРЕДЕЛАХ ВСЕГО СКЛОНА........... 118
9.1. Понятие о коэффициенте устойчивости ......... 118
9.2. Методы, основанные на построении профиля склона
предельного равновесия............................ 120
Метод В В Соколовского.... . ............... 120
Метод НН. Маслова .122
244
ГЛАВА 10. МЕТОДЫ РАСЧЕТА УСТОЙЧИВОСТИ СКЛОНОВ
ПО ИЗВЕСТНОЙ ПОВЕРХНОСТИ СКОЛЬЖЕНИЯ................................. 129
10 1 Основные положения метода фрагментов................. . _ 130
10 2 Методы плоских поверхностей скольжения ................ 134
10 3 Методы круглоцилиндрических поверхностей
обрушения .................................... . .......... . 150
10.4. Определение дефицита устойчивости ............................ 157
ГЛАВА 11. РАСЧЕТЫ УСТОЙЧИВОСТИ СКЛОНОВ
В СЛОЖНЫХ СЛУЧАЯХ............. ........................ .......... 160
ILL Учет действия подземных вод............... .. . . . .. .. ...... 160
1L2 Учет сейсмических воздействий .................... 1й7
11.3. Методы расчета устойчивости склонов
в породах с жесткими связями....................................... 170
114, Пространственные методы расчета устойчивости
склонов ..............................1?3
ГЛАВА 12. РАСЧЕТЫ ПЕРЕРАБОТКИ БЕРЕГОВ
ВОДОХРАНИЛИЩ..............................♦........................ 177
12 1. Энергетические методы..............................179
12.2 = Сравнительно-геологические методы прогноза
переработки берегов водохранилищ................. ............... 185
12.3 . Расчеты переработки берегов водохранилищ
в особых условиях ........................................ 195
12.4 . Стохастические методы прогноза переработки берегов
водохранилищ ........................................................................... 198
ГЛАВА 13 РАСЧЕТЫ ДЕФОРМАЦИЙ МАССИВОВ
ГОРНЫХ ПОРОД.................................................... 202
13.1. Расчет перераспределения напряжений (и деформаций)
в массиве пород вокруг подземных полостей..................... 202
13 2 Оценка деформаций пород над, подземными полостями,
выработанными пространствами и при откачках
подземных вод, нефти или газа ................... 206
13.3. Расчет деформаций в котлованах и карьерах................ . 211
13.4. Расчет суффозионных и карстовых провалов
на закарстованных территориях......................=..=.. ....... 214
ГЛАВА 14. ВЫБОР РАСЧЕТНЫХ ПОКАЗАТЕЛЕЙ ...... 223
14.1. Показатели свойств горных пород и случайные
величины ......... .........* ............................... 223
245
14.2. Статистическая характеристика показателей
при обработке результатов полевого и лабораторного
изучения свойств пород. . . .. .. .. . ........ 225
143. Нормальный закон распределения случайной величины 229
14.4. Оценка выборочных статистических характеристик .......... 231
14.5. Определение расчетных показателей....................... 234
ЛИТЕРАТУРА...................................................... 237
Учебное издание
Калинин Эрнест Валентинович
ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКИЕ РАСЧЕТЫ
И МОДЕЛИРОВАНИЕ
Редактор
/'С Савель ева
Художественный редактор
ГД, Колоскова
Переплет художника
АЛ Умуркулова
Технический редактор
ГД. Колоскова, НИ. Матюшина
Корректоры
ВЛ Ветров, В.В. Конкина
Подписано в печать 27.02.2006 г. Формат 60x90 1/л.
Бумага офсетная М 1. Гарнитура Таймс.
Печать офсетная. Уел -печ. л. 16,0. Уч.-изд. л. 15,7.
Тираж 1000 экз. Заказ 421 ;^Изд. N& 7725.
Ордена «Знак Почета»
Издательство Московского университета.
125009, Москва, ул, Б. Никитская, 5/7,
Тел.: 629 jO-Sl Факс: 203 66-71,
939-33-23 (отдел реализации)
E-mail: kdjTigu@rambler.ru
В Издательстве МГУ
работает служба «КНИГА — ПОЧТОЙ»
Тел.: 629-75-41
Типография ордена «Знак Почета»
Издательства МГУ.
119899, Москва, Воробьевы горы.
В Издательстве Московского
университета имеется в продаже:
Жариков В.А. Основы физической геохимии: учебник. —
2-е изд., испр. и доп. — Мл Изд-во МТУ, 2005. — 654 с. -
(Классический университетский учебник). -
В учебнике представлен полный курс основ
физической геохимии. Рассмотрены предмет и методы
физической геохимии как науки о физико-химических
закономерностях образования минералов, горных пород и
руд. Даны общие положения термодинамики равновесных
природных систем» являющихся особым типом систем с
вполне подвижными компонентами. Выведены главные
термодинамические соотношения, характеризующие
природные процессы, показано их применение.
Подробно изложены вопросы теории, топологии, методы
построения диаграмм, используемых в геохимии, петрологии,
учении о минеральных месторождениях.
Для студентов, аспирантов и всех специалистов,
занимающихся изучением физико-химических
закономерностей природных процессов.
По всем вопросам, связанным с приобретением книг,
обращайтесь в Издательство МГУ по адресу:
125009, Москва, ул. Б. Никитская, 5/7.
Га./Рахс: (095) 939 33 23, 629 75 41.
E-mail kd~ jyygi^a)rambler. ru
www.msu ru/depts/MSUPubl2Q05
В Издател ьстве МГУ работает
,:лужба «Книга—почтой».
Дорогие читатели!
В Издательстве МГУ им. М.В. Ломоносова работает
служба "КНИГА—ПОЧТОЙ". Вы можете заказать любые
книги по действующему прайс-листу, и мы вышлем их Вам
заказной бандеролью.
Закажите книги:
• по почте: 125009, Москва, ул Б. Никитская, д 5/7,
Издательство МГУ,
• по телефону или факсу: (095)629 75 41;
• по электронной почте: E-mail: kd_mgu@rambler.ru
Заявка заполняется в произвольной форме и считается
действительной при наличии: ФИО, почтового адрес
номера телефона (с кодом города).
Мы выпишем Вам счет и отошлем по указанному Вами
адресу
Перечислите указанную в счете сумму на р/с
Издательства МГУ.
В течение 15 рабочих дней после поступления средств
на счет Издательства МГУ книги будут высланы по Вашему
адресу.
Примечания
1. Счет включает в себя стоимость заказанных книг и почтовые
расходы (ориентировочно 50% от стоимости книг + НДС).
2. Заказчик имеет право исключить из счета любое название (или
уменьшить количество экземпляров) без согласования с
Издательством.
3. После оплаты счета необходимо сообщить письменно, по
телефону, факсу или электронной почте номер платежного
поручения и номер счета.
4. Заказ сохраняется в течение одного месяца со дня выписки
счета.
5. При несвоевременной оплате счета Издательство
оставляет за собой право изменить отпускные цены на книги
без дополнительного объявления.
В Издательстве Московского
университета работает
Ассортиментный кабинет вузовской
литературы
Здесь Вы найдете весь спектр учебной литературы для
студентов и абитуриентов от Издательства Московского
государственного университета и различных
факультетов и подразделений МГУ, Издательства
СПбГУ, а также других университетских и вузовских
издательств. Представлена литература издательств
"Высшая школа", "Инфра-М", "Наука", "Аспект Пресс",
"Дрофа", "ЧеРо", "Юридическая литература" и многих
других.
Книги продаются по минимальной розничной цене.
Москва, Центр, ул. Б.Никитская, д. 5/7.
Тел.: 629-47-02. Факс: 629-75-41,203 66 71
E-mail: kd_mgu@r ambler. ru
Москва, ул. Хохлова, 11 (Воробьевы горы, МГУ).
Тел./Факс: 939-33-23.
E-mail: izd-mgu@yandex.ru
Сайт Издательства МГУ: www.msu.ru/depts/MSUPubl2005
Для заметок
Для заметок
Для заметок
Для заметок
Я»
Для заметок