Автор: Ободовский Б.А. Ханин С.Е.
Теги: испытания материалов товароведение силовые станции общая энергетика сопротивление материалов
Год: 1982
Текст
Б. А. ОБ ОДО ВС КИИ
С. Е. ХАН ИН
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
в примерах
и задачах
*
Издание четвертое,
переработанное и дополненное
Допущено
Министерством высшего и среднего
специального образования УССР
в качестве учебного пособия
для студентов технических вузов
Харьков
Издательство при Харьковском
государственном университете
издательского объединения «Вища школа»
1982
30.121Я73
0-21
УДК 620.1(076)
Сопротивление материалов в примерах и задачах. Обо-
довскнй Б. А.. Хании С. Е.— 4-е перераб. и доп.
изд. Харьков: Внща школа. Изд-во при Харьк. ун-те,
1981.— 344 с.
В учебном пособии на большом количестве примеров
показаны приемы и методы решения типовых задач
курса «Сопротивление материалов». Даиы расчетные
формулы и краткие указания по методике расчетов,
задачи для самостоятельного решения. Пособиедопол-
иено главой «Учебио-исследовательские работы сту»
деитов», включены материалы о применении ЭВМ, рас.
смотрен метод конечных элементов в'сопротивлении
материалов.-
Для студентов технических вузов.
Табл 19. Ил. 411. Список лит.:’71 назв.
Рецензецт: кафедра сопротивления материалов
Киевского политехнического института
Редакция научно-технической литературы
Зав,{гедф.кцюей Л. АГ Гаврилова
ОТЕКА
.ського ф1л1
ДП1
Борис Ари ч
Соломе ।
|оаич Ободоаский
|шммйч Хании
СОПРОТИВЛЕНИЕ
МАТЕРИАЛОВ
в примерах
и задачах
Редактор. Е. П. Иващенко. Переплет художника В. А. Рияка.
Художественный редактор В. Б. Мартыняк. Технический редактор
Л. Т. Момот. Корректоры А. А. Федоренко, В. В. Николаева
Ииформ. бланк № 5193
Сдано в набор 29.12.80. Подп. в печать 21.10.81. БЦ 09314. Формат 60x90*/,,. Бумага
газетная. Лит. сари. Выс. печать. 21.5 усл. печ. л. 21,75 усй.кр.-отт. 24. уч.-изд. л.
Допечатка тиража 1000 экз. Изд. № 846. Зак. 1-10. Цена 95 к.
Издательство при Харьковском государственном университете издательского объедн*
нения «Внща школа». 310003, Харьков-3, ул. Университетская, 16
Отпечатано с матриц Книжной фабрики им. М. В. Фрунзе РПО «Полиграфкнига»
в Харьковской городской типографии № 16. Харьков-3, ул. Университетская, 16. Зак. 271.
° 159—81 2105000000
№226(04)—82
Издательское объединение
«Вища школа», 1981
ПРЕДИСЛОВИЕ
Преподавателям курса «Сопротивление материалов» хорошо
известны трудности, которые возникают у студентов, и в первую
очередь у студентов, обучающихся по вечерней и заочной формам,
в процессе изучения этого курса. В основном трудности связаны
с овладением практическими методами и приемами выполнения ин-
женерных расчетов элементов конструкций на прочность, жесткость
и устойчивость.
Помочь студентам овладеть методами решения типовых задач
сопротивления материалоз, заменив в известной мере личное обще-
ние с преподавателем, должна, по замыслу авторов, данная книга.
Это обусловило ее структуру и характер изложения материала.
Пособие охватывает материал всей программы по сопротивлению
материалов. Книга не может служить учебником по курсу, и ее при-
менение будет наиболее эффективным в сочетании, например, с «Кур-
сом сопротивления материалов» Г. С. Писаренко и др.
По каждой теме курса приведены краткие сведения из теории,
которые должны помочь студенту с минимальной затратой времени
освоить ранее изученный материал по учебнику этого курса.
Основная часть пособия отведена примерам решения типовых за-
дач, причем их разбор проводится довольно подробно, чтобы студент
мог понять метод решения, не прибегая к помощи преподавателя.
Задачи для самостоятельного решения в каждой из глав пособия
дают студенту возможность проверить степень усвоения им методов
решения задач по данной теме курса.
Примеры решенных задач и задачи для самостоятельного ре-
шения в основном составлен^ авторами настоящего-пособия, некото-
рые из них заимствованы нз учебной литературы. В большинстве
случаев, заимствуя расчетные схемы к задачам, авторы подвергали
их определенной переработке с целью обеспечить единство методи-
ческих принципов и приемов, принятых в пособии.
В приложении к пособию даны некоторые справочные материалы,
в частности новая таблица ГОСТов на профили прокатной стали.
В книге принята двойная нумерация: первая цифра — номер
главы, вторая — порядковый номер примера, задачи и рисунка
в данной главе.
При подготовке четвертого издания пособия учтены замечания,
высказанные преподавателями и студентами.
В книге нашло отражение постановление Центрального Комитета
КПСС и Совета Министров СССР «О дальнейшем развитии высшей
школы и повышении качества подготовки специалистов».
3
Настоящее издание подготовлено Б. А. Ободовским, которым
написаны главы 6—9, 14—16, сделаны дополнения по отдельным
главам, в частности приведены элементы научных исследований,
составлены новые задачи для самостоятельного решения, а также
внесены коррективы в примеры и задачи в соответствии с новым
ГОСТом на.профили прокатной стали; главы 1, 3—5 и 12 написаны
С. Е. Ханиным (умер в 1971 г.)*. Кроме того, в подготовке пособия
приняли участие О. П. Оржеховская, автор глав 10—12, и Г. М. Иц-
кович, написавший главу 2, совместно с Б. А. Ободовским — главу
13 и совместно с С. Е. Ханиным — главу 18, а также составивший
ряд примеров (5.5, 7.4, 7.5,8.8, 12.4, 15.5—15.7, 15.9, 15.10,17.1).
Дополнительно написана глава 19: § 19.1—19.5 — Б. А. Обо-
довским и В. М. Львовским, § 19.6—19.8 — Б. А. Ободовским.
Глава посвящена современным методам расчета элементов инженер-
ных конструкций. В ней содержатся примеры и задачи исследова-
тельского характера (УЙРС) и метод конечных элементов (МКЭ)
б сопротивлении материалов.
Считаю своим приятным долгом выразить глубокую благодар.-
ность рецензентам книги проф. А. В. Даркову и коллективу сотруд-
ников кафедры сопротивления материалов и строительной меха-
ники Всесоюзного заочного политехнического института, проф.
Э. С. Уманскому и коллективу сотрудников Киевского политех-
нического института, возглавляемой акад. АН УССР Г. С. Писа-
ренко, чл.-кор. АН УССР А. С. Космодамианскому за полезные
советы, использованные при подготовке четвертого издания посо-
бия, а также ассист. Ждановского металлургического института
В. И. Коссе за существенную помощь б подготовке данной книги.
Критические замечания и предложения просим направлять по
адресу- 341000, г. Жданов, Металлургический институт.
МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ И ЕЕ ПРИМЕНЕНИЕ
* В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
В октябре 1960 г. в Париже XI Генеральная конференция по мерам и
весам приняла Международную систему единиц. Комитет стандартов, мер
и измерительных приборов при Совете Министров СССР утвердил Между-
народную систему единиц для предпочтительного применения во всех отрас-
лях техники и промышленности и при преподавании (ГОСТ 9867—61).
Сокращенное обозначение этой системы русскими буквами — СИ и латин-
скими — SI, что означает: система иитериациоиальиая.
СИ, как и любая другая система единиц, состоит из двух групп
единиц: основных и производных. Производные единицы устанавли-
ваются на основании формул, выражающих физические закономер-
ности.
Одно из принципиальных отличий СИ от системы МКГСС, широко при-
меняемой для измерения механических величии, состоит в том, что в системе
МКГСС единица силы является основной, а единица массы — произ-
водной. В СИ основной является единица массы, а единица силы — произ-
водной.
Рассмотрим некоторые основные и производные единицы системы СИ,
применяемые в сопротивлении материалов.
Величина Единица Обозначение
русское международ- ное
Длина Основные единицы метр М гй
Масса килограмм КГ kg
Время секунда с s
Плоский угол Дополнительные единицы радиан рад rad
Площадь Производные единицы квадратный метр м» m’
Объем, вместимость кубический метр м3 m3
Статический момент и мо- кубический метр м3 . m3
мент сопротивления плоского сечения Момент инерции плоского метр в четвертой сте- м4 m*
сечения Плотность Скорость пени килограмм на кубиче- ский метр кг/м3 kg/m’
, метр в секунду м/с m/s
Угловая скорость радиан в секунду рад/с rad/s
5
*
Продолжение таблицы
Величина Единица Обозначение
русское международ- ное
Ускорение метр иа секунду в квад- рате м/с2 m/s2
Угловое ускорение радиан на секунду в квадрате я рад/с2 rad /s2
Сила ньютон Н N
Момент силы ньютон-метр Н • м N • tn
Давление (механическое напряжение) паскаль (ньютон иа квадратный метр) Па(Н/м2) Pa (N/m2)
Работа, энергия джоуль л Дж ' J
Мощность ватт Вт W
Удельный вес ньютон иа кубический
Момент инерции (дина- мический) метр Н/м® N/m®
килограмм *метр в квад* рате кг • м2 kg • m2
Частота герц Гц Hz
Более крупные или мелкие (кратные или дольные) единицы образуются
умножением основной или производной единицы на десять в положительной
или отрицательной степени.
Наименования кратных и дольных единиц образуются прибавлением
приставок к' наименованиям исходных единиц. Наиболее употребительны
следующие приставки:
Приставка Обозначение Множитель Приставка Обозначение Множитель
Гига г 10® Децн д 10-1
Мега м 10» Санти с 10"2
Кило к 10® Милли м 10-®
Гекто г Ю2 Микро мк 10-е
Д- ка да 10
Не допускается применение двух приставок к простому наименованию
единицы (например, мёгакнлоиьютон). Нельзя применять приставки к наи-
менованиям таких единиц, которые обозначают кратную или дольную еди-
ницу (например, к тонне, к центнеру).
В отдельных случаях можно относить десятичную приставку к наимено-
ванию единицы, стоящей в знаменателе производной единицы. Так, для изме-
рения напряжений допустимо применять единицу Н/мм2. Заметим, что
1 Н/мм2 = 1 МН/м2.
Зависимости между механическими единицами СИ, единицами системы
МКГСС, СГС и внесистемными единицами даны в следующей таблице.
Единицы систем
МКГСС и СГС
и внесистемные
единицы
Единицы СИ
Единицы систем
МКГСС и СГС
и внесистемные
единицы
Единицы СИ
Площадь
1 см1 2 I 10~4 м2
Момент сопротивления и статический
момент плоского сечения
1 см3 | 10"? м8
Момент инерция плоского сечения
1 см4 | ю-8 м*
Масса
1 тоииа (т) [ 103 кг
1 грамм (г) I 10 ~» кг
Угловая скорость
Объем
1 см*
10~« м3
Момент силы; пары сил
1 килограмм-сила-
метр (кгс • м)
1 килограмм-сила-
сантиметр (кгс • см)
9,81 Н • м =
= ЮН • м
0,0981 Н • ms
= 10-1 н - м
Удельный вес
1 тс/м3; 1 гс/см3
1 кгс/см3
9,81.10» Н/м3»
= 104 Н/м»
9,81-10» Н/м3»
» 10’ Н/м»
1 оборот в минуту
(об/мин)
£ рад/с
Мощность
1 об/с 2л рад/с ,
1 тонна-сила (тс) 19,81 -ID’alO* Н
1 килограмм-сила (кгс) 9,81 » 10 Н
1 дина (дин) | 10"’ Н
1 килограмма ила-
метр в секунду
(кгс • м/с)
1 лошадиная сила
(л. с.)
1 эрг/с
9,81 « 10 Вт
735,5 Вт
10-’ Вт
Работа и энергия
Давление (механическое
напряжение)
1 килограмм-сила-метр
(кгс • м) 9,81 » 10 Дж
1 кВт • ч 3,6 • 10» Дж
1 эрг 10"’ Дж
1 бар (бар)
1 кгс/см2 = 1 ат
1 кгс/м2
10’ Па
9,81 • 104»
» 10’Па
9,81» 10 Па
ЧАСТЬ
первая
ГЛАВА 1. РАСТЯЖЕНИЕ И СЖАТИЕ
§ 1.1. Основные понятия и зависимости
|—|а р’ис. 1.1 показан простейший частный случай рас-
тяжения, а на рис. 1.2—сжатия бруса. При рас-
тяжении — сжатии внутренние силы упругости, возникающие
в поперечном сечении бруса, приводятся к одному внутреннему си-
ловому фактору — продольной (нормальной). силе, обозначаемой
Nx (или N).
Рис. 1.1.
Продольная сила Nx определяется с помощью метода сечений:
она численно равна алгебраической сумме проекций на продоль-
ную ось (Ох) бруса всех внешних сил, расположенных по одну сто-
рону от мысленно проведенного сечения (рис. 1.3). При растяжении
принято считать, что Nx> 0, а при сжатии — Nx< 0.
В поперечном сечении бруса при растяжении — сжатии возни-
кают только нормальные напряжения, вычисляемые по формуле
о = где F —• площадь поперечного сечения бруса.
Правило знаков для о принимается то же, что и для Nx. Размер-
ность напряжения: сила!длина?, соответственно единицы физиче-
ских величин кгс/см2 или кгс/мм2.
При использовании Международной системы единиц основная
единица Н/м2, а также соответствующие кратные и дольные еди-
ницы, например, кН/м2, МН/м2, Н/мм2, Н/см2.
8
Относительное удлинение при растяжении (или относительное
укорочение при сжатии) бруса по рис. 1.1 (или 1.2) е = Д//(, где ДI =
= (1г— I) — абсолютное удлинение (или абсолютное укорочение)
бруса; I — первоначальная длина бруса.
Относительное изменение поперечного размера бруса е' = Да/а.
Здесь Да = ах— а.
При растяжении считают, что е > 0, следовательно, О,
а при сжатии — наоборот.
Величины е и е' называют также линейными дефор-
РИС. 1.3
маниями.
Абсолютная величина отношения е' к е называется коэффи-
циентом поперечной де-
формации или коэффи-
циентом Пуассон а: р = |8-|.
Коэффициент Пуассона для всех изо-
тропных материалов 0 р. 0,5.
Между относительным удлинением
и нормальным напряжением сущест-
вует зависимость: а = Ее. Эта зави-
симость является аналитическим вы-
ражением закона Гука при линейном
напряженном состоянии.
Здесь Е — модуль продольной упругости или модуль упругости
первого рода; размерность Е та же, что и напряжения.
Абсолютное удлинение (укорочение) бруса (при F = const
и const)'определяется по формуле Д/ = NxllEF.
При .переменных Мх и F (или одной из этих величин) Л/ = J
i
В наиболее общем случае, когда законы изменения Nx и Р
- Л/ V ^Nxdx
для отдельных участков бруса различны, Д( — \ ) -gy •
Отсюда как частный случай следует формула Д/ — ,
i=k
применимая при условии, что продольная сила и площадь сечения
в пределах отдельных участков бруса постоянны (см. пример 1.1).
Взаимное перемещение каких-либо двух поперечных сечений
бруса равно удлинению (укорочению) той его части, которая заклю-
чена между этими сечениями.
Условие прочности:^ = ~[а],
где а, Nx— нормальное напряжение и продольная сила в опасном
поперечном сечении (т. е. сечении, в котором возникают наибольшие
напряжения)? F — площадь опасного сечения; [о] — допускаемое
напряжение.
9
Требуемая площадь поперечного сечения F^Nxl]p\.
Величина допускаемой (безопасной) продольной силы [Л/Д =
= F[aJ.
По найденному значению [2VJ на основе метода сечений (для
статически неопределимых систем дополнительно составляют урав-
нения перемещений) определяют допускаемую величину внешних
сил".
§ 1.2- Статически определимые случаи
растяжения — сжатия
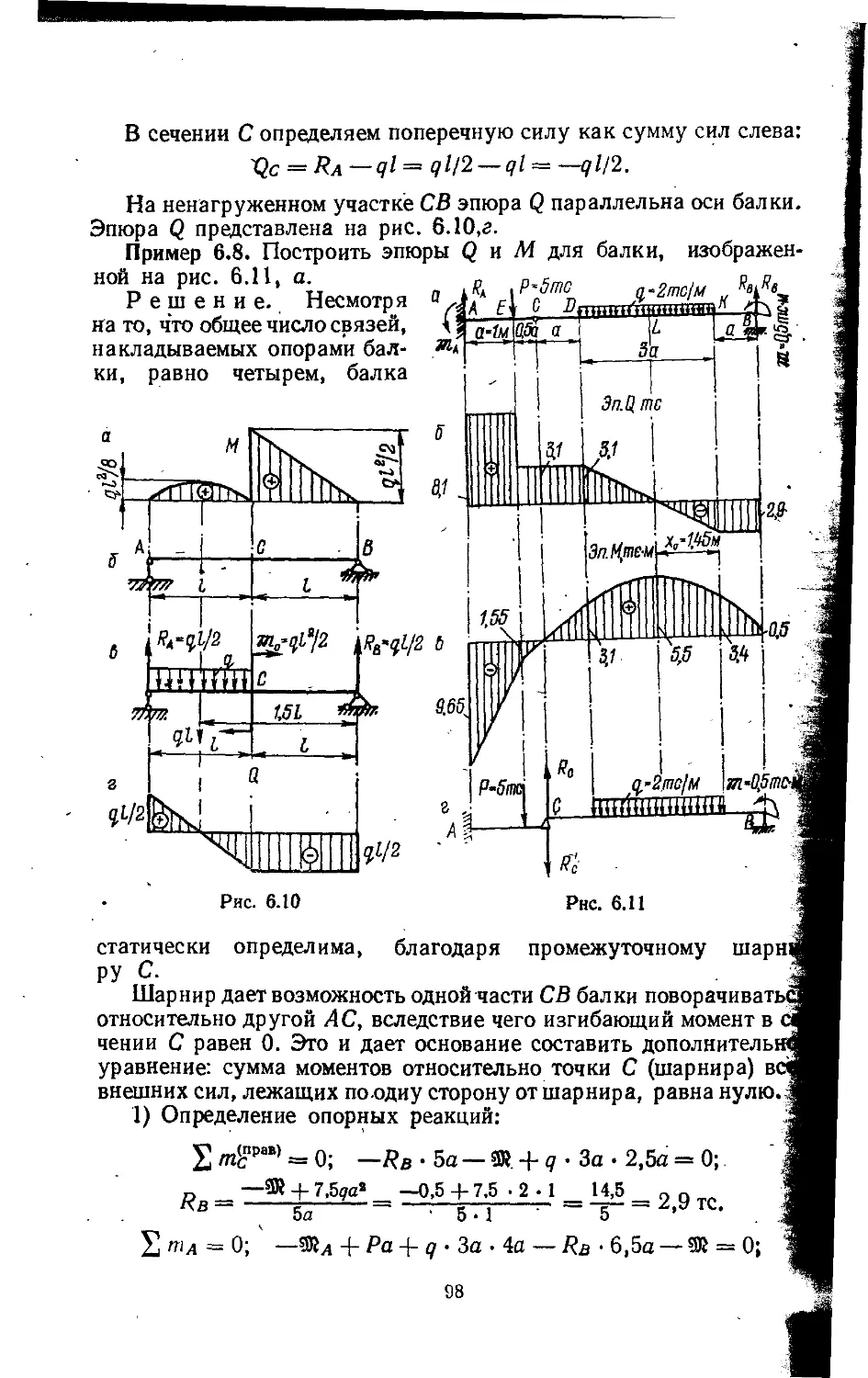
Пример 1.1. Для заданного бруса (рис. 1.4,а) построить эпюры
продольных сил и нормальных напряжений.
Решение. Разобьем брус на пять отдельных участков, начи-
ная от его свободного конца; границами участков служат сечения,
где приложены внешние силы, а также места изменения размеров
поперечного сечения (на рис. 1.4,а эти участки отмечены римскими
цифрами). Проведем произвольное сечение 1—1 на участке I и,
отбросив верхнюю часть бруса, рассмотрим условие равновесия ос-
тавленной (нижней) части, изображенной отдельно на рис. 1.4,6.
На'оставленную часть действуют сила Pt и искомое усилие Nx.
Проектируя на ось х силы, действующие на оставленную часть,
получаем Nx— Pi= 0, Nlx— Pt~ 10 • 10s кгс.
Рис. 1.4
Продольная сила Nx получилась со знаком плюс, т. е. она дей-
ствительно направлена от сечения, как и было принято предвари-
тельно (рис. 1.4,6). Таким образом, первый участок бруса испыты-
вает растяжение.
Сопоставляя рис. 1.4,6 и 1.4,в, заключаем, что Nx= Nlx= Р,—
= 10 - 10s кгс.
Проведем произвольное сечение 3—3 на участке III, отбросим
верхнюю часть бруса и рассмотрим равновесие оставленной нижней
его части, изображенной отдельно на рис. 1.4,г. На оставленную
10
часть действуют силы Plt Ря и искомое усилие Nxl}. Проектируя эти
силы на ось х, получаем Nxl— Pt -)- Ря— О, №жи= —^2+ ^i=
= —16 . 10®+ 10 . 10®= —6 • 10® кгс.
Знак минус указывает, что в действительности сила Л/”1 на-
правлена к сечению, а не от сечения, как было предположено (см.
рис. 1.4,а). Следовательно, участок III испытывает сжатие.
Аналогично найдены значения продольных сил в сечениях 4—4
(рис. 1 А,д) и 5—5 (рис. 1.4,а).
Рис. 1.5 Рис. 1.6
Построим график (эпюру), показывающий, как меняется про-
дольная сила по длине бруса. Проведя ось абсцисс графика парал-.
лельно оси бруса, откладываем в произвольно выбранном масштабе
найденные значения продольных сил по оси ординат.
Положительные значения продольных сил откладываем вправо
от оси эпюры, а отрицательные — влево (рис. 1 А,ж). Эпюру нормаль-
ных напряжений получим,разделив значения Nx на величины соот-
ветствующих площадей поперечных сечений бруса (рис. 1.4,з).
Пример 1.2. Для стального бруса (рис. 1.5,а) построить эпюру
перемещений поперечных сечений. Е — 2 • 106 кгс/см2. Собственный
вес бруса не учитывать.
(S Решение. Эпюру перемещений следует строить, начиная от
закрепленного конца. Перемещение произвольного сечения 1—1,
принадлежащего нижней части бруса, &x=PxlEF, т. е. перемещения
возрастают (по мере удаления сечения от заделки) по линейному
закону.
Перемещение сечения С—С равно нулю, так как оно закреплено,
п * Pit 40.10» - 10» п „„
11еремещение сечения а — а Да_а — = 2 = см в=
= 0,8 мм.
Перемещения поперечных сечений верхней части бруса (выше
сечения а—а) одинаковый равны Да_а (так как эта часть бруса не
деформируется). Эпюра перемещений показана на рис. 1.5,6.
Пример 1.3. Для стального бруса (рис. 1.6,а) , имеющего форму
усеченного конуса, построить эпюру нормальных напряжений
и вычислить перемещение свободного конца. Собственный вес бруса
не учитывать. Е — 2 • 10е кгс/см2.
Решение. Продольная сила в любом поперечном сечении
одинакова: Nx = Р = 4 • ГО3 кгс.
Площадь произвольного поперечного сечения (см. рис. 1.6,а)
Нормальное напряжение (в произвольном поперечном сечении)
„ _ N_x Р
т. е. по длине бруса ох изменяется по гиперболическому закону.
Для построения эпюры 0Х вычисляем три частных значения:
Р 4000 1О_Л . „
о,_0 =-------=-------?= 1270 кгс/см2;
2Ld2
4 0 4
Р 4000 сс- . 9
о 1 =--------------гг =---------г» = 567 кгс/см2;
+ я /2 + 4?
4 \ 2 . / 4 \ 2 /
Р 4000 0,0 ^., а
-------------- = 318 кгс/см2.
— d*--------— 4s-’
4 “ 4
0
Эпюра о представлена на рис. 1.6,6. В рассматриваемом примере
площадь поперечного сечения бруса изменяется по его высоте не-
прерывно, и хотя продольная сила постоянна, для определения уд-
линения бруса нужно применить общую формулу:
i i
А/ _ Р Nxdx __ Р Р dx _
= = -
о о '
4Р1 (I 1\ 4.4 - 103.400 / 1' П^П197 '
~ En(d — da) \ do d] ~ 2- 1О’я(4 — 2) \ 2 4/ v,lZ/CM.
Пример 1.4. Для стального бруса (рис. 1.7,а) построить эпюры
продольных сил, нормальных напряжений и определить его абсо-
лютное удлинение, если Е = 2 • 105 МН/м2. Верхняя часть бруса
находится под действием равномерно распределенной по ее длине
осевой нагрузки интенсивностью// = 10 кН/м.
Решение. Применяя метод сечений, устанавливаем законы
изменения продольных сил по длине каждого из участков бруса.
На первом участке (рис. 1.7,6) Л/] = Р = 20 кН.
На втором участке (рис. 1.7,в) Nx = Р -f- qx.
На этом участке продольная сила изменяется по линейному зако-
ну. В начале участка A/*L0 = Р = 20 кН, в конце — Л/*=о.5/ =
12
— Р 4- q-^ — 20 4- 10 • 1 = 30 кН. Эпюра продольных сил пока-
зана на рис. 1.7,а.
{Определяем нормальные напряжения.
На первом участке и в начале второго участка (при х — 0)
о1 = = 10 • 107 Н/м2 = 100 МН/м2.
В конце второго участка о11 = -у = § , jp^ — 150 МН/м2.
Эпюра о представлена на рис. 1.7,5.
Абсолютное удлинение бруса
J _L
2 - 2
”2 . I Nxdx _ Pl I (Р + qx) dx __ Pl qls
EF + J EF 2EF + J EF ~ EF ' 8EF
о о
20 • 10» • 2 , 10 • 10» • 2»
~ 2 • 10» • 2 • 10-4 + 8 • 2 • 104.2 • 10“4 ~
’ => 1,125- IO'3 м « 0,113 cm.
Пример 1.5. Определить перемещение узла А стержневой си-
стемы (рис. 1.8,а), если = 2 • 10* кгс7см2; Ем= 1 • 10* кгс/см2.
Решение. Рассматривая условие равновесия узла А под
действием заданной нагрузки Р и искомых усилий в стержнях
и М2, строим силовой треугольник (рис. 1.8,6). По теореме синусов
находим
3000.0,707
0,966
= 2200 кгс;
Р sin 60° __ 3000 • 0,866
ып 75° 0,966
= 2690 кгс.
., _ Р sin 45°
771 sin 75°
N2=^
13
Абсолютные удлинения стержней:
*, 2200.10b „ Лоо п пп
А11 = = 2- -д,- 5 = 0,022 см = 0,22 мм;
\ л / Л^2/о 2690 • 200 л10лс 1 охс
Д/2 = --Р?Р* = т—т- = 0,1345 см — 1,345 мм.
2 ЕКЕ% 1 • 10е • 4 ’ ’
Для нахождения положения шарнира А после деформации (точ-
ка A J следовало бы провести из точек В и С дуговые засечки ради-
усами /х+ Д/х и /а+ Д/2, но в силу малости деформаций можно
отложить на продолжении каждого стержня величину его удлинения
и вместо дуговой засечки провести из полученной точки перпенди-
куляр к направлению стержня.
Полученное таким образом геометрическое построение (рис.
1.8,в) называют диаграммой перемещений. Из этой
диаграммы следует, что Д/х равно алгебраической сумме проекций
горизонтального Дж и вертикального Ду перемещений шарнира А
на направление 1-го стержня, а Л/2 равно сумме проекций Дж и Ду
на направление 2-го стержня, т. е.
Д= Ду sin 30’ — Дж cos 30°; Д /2 = Ду sin 45° + Дж Cos 45°;
или 0,5Ду— 0,866Дж =, 0,22 мм; 0,707+ 0,707&ж = 1,345 мм,
откуда Дж = 0,53мм; Ду= 1,36 мм.
Пример 1.6. В стержневой системе (рис. 1.9,а) определить из
условия прочности требуемые диаметры (di и dg) поперечных сече-
ний стержней. Материал стержней сталь Ст. 3, [о] = 1600 кгс/см2.
Решение. Рассекая стержни ВС и EF и заменяя действие
отброшенных частей системы на оставленныеЗпродольными силами
Nt и Nt, получаем расчетную схему, показанную на рис. 1.9,6. Со-
ставим уравнение равновесия для балки АВ 2гпа — 0; • 3,75 —
— Р • 3 = 0, откуда = ЗР/3,75 = 3 • 4 • 103/3,75 = 3,2 • 103кгс.
. Необходимая площадь сечения стержня ВС
Fi > Л\/[а] - 3200/1600 = 2 см2,
14
требуемый диаметр стержня ВС
di = ]/”= 1Л1,6 см.
* г я т 3,14 ’
Составим уравнение равновесия для балки CD:
ZmD — Q, Nt • 3,8 — N2 • 3,2 sin 30° = 0,
., /V, • 3,8 3,2- 103 - 3,8 _
откуда N2 = = -3.2:o~- = 7>6 ' 108 ис-
1 Р-1200кг1
Рис. 1.10
требуемая площадь сечения стержня EF
F2>2V2/[<j] = 7600/1600 = 4,75 см2, требуемый диаметр стержня
EF d2 = УИ\/л = Vb -4,75/3,14 « 2,5 см.
Пример 1.7. Определить с учетом собственного веса напряжения
в опасных сечениях каждого нз участков двухступенчатого бруса
(рис. 1.10) и его полное удлинение, если у =
= 7,85 гс/см®, Е — 2 • 10е кгс/см2.
Решение. Опасными являются сечения
/—I и II—II. Продольная сила в сечении I—I
max Nlx = Р + уМ = 1200 + 7,85 • 10“®- 2 •
• 80 • 102— 1326 кгс. Нормальные напряжения
з сечении I — I
maxoy — max Nx/Ft — 1326/2 = 663 кгс/см2.
Продольная сила в сечении II — II
max/V" = Р + yFx/j + yF2/2 = 1200 4-
+ 7,85 • 10“s • 2 • 80 • 102 + 7,85 • 10“® • 4 • 40 •
• Ю2 = 1452 кгс.
Нормальное напряжение в сечении II — II
max о„ = max Nx/F2 = 1452/4 = 363 кгс/см2.
Полное удлинение бруса
д / 81, , Р1г । y^iI1I2 ,
EFi'1' 2£f! EF2 “T EF2 2EFt
15
где PlfjEFi — удлинение нижней части бруса от силы Р;
ТЛЛЛ/2£Г1== —удлинение нижней Части бруса от соб-
ственного веса этой части *; Р/2/РР2— удлинение верхней части
бруса от силы Р; yPi/i^/PPa— удлинение верхней части бруса
от действия веса нижней части, которая для верхней части явля-
ется сосредоточенной силой; уР2/2/2/2£Р2 = у/|/2£ — удлинение
верхней части бруса от собственного веса этой части.
Подставив числовые значения, получим Д/ = 3,22 см.
Пример 1.8. Для устоя из каменной кладки в форме бруса рав-
ного сопротивления сжатию (рис. 1.11) определить: 1) площадь
верхнего сечения Ро; 2) площадь нижнего сече-
ния Ртах! 3) вес Q кладки..'Допускаемое напря-
жение на сжатие кладки [ис1 = Ю кгс/см2, объ-
емный вес кладки у = 2,5 тс/м3.
Решение. 1) Требуемая площадь верх-
него сечения
Ро = Р/[О] = 300 ООО/10 = 30 000 см2 = 3 м2.
' 2) Требуемую площадь нижнего сечения
Ртах определяем по формуле
2,5-15
Ртах = Р^0? = з - 2,72 '°0 = 4,37 м2, .
где [о] = 10 кгс/см2 = 100 тс/м2.
3) Вес кладки
Q = Ртах [CTj — Р = 4,37 • 100 — 300 = 137 тс.
Объем кладки V = Q/y = 137/2,5 = 53,8 м3.
Задачи для самостоятельного решения
1.1. Построить эпюры продольных.сил, нормальных напряжений
и определить полное изменение длины бруса (рис. 1.12), если Е —
= 2 • 105 МН/м2.
Ответ. | max Nx | = 20 кН, | шах а | = 10О МН/ма, Д1 = 0,015 см.
1.2. Для ступенчатого бруса (рис. 1.13) построить эпюры про-
дольных сил, нормальных напряжений и определить его полное
удлинение. При решении принять Еаа— 0,7 • 106 МН/м2, £м= 1 х
X Ю5 МН/м2, £ст = 2 • 10» МН/м2.
Ответ. Ы = 0,318 см.
1.3. Стальная тяга АВ площадью сечения Р = 5 см2 поддержи-
вает балку CD (рис. 1.14). Определить напряжение в тяге, а также
* Напомним, что удлинение бруса (участка бруса) постоянного попереч-
ного сечения от действия собственного веса вдвое меньше, чем удлинение от
сосредоточенной силы, равной собственному весу н приложенной к свобод-
ному концу бруса,
1G
ее абсолютное удлинение и построить эпюру продольных сил для
балки CD.
Ответ. аАВ — 1540 кгс/сма; МАВ = 0,148 см.
1.4. Определить удлинение стальной полосы постоянной тол
щинщ и переменной ширины (рис. 1.15), если Е ~ 2 • 10е кгс/см3
Собственный вес не учитывать.
Ответ. 'Ы = 0,87 мм.
1.5. Вычислить полное пере-
мещение шарнира А (рис. 1.16),
если Е = 2,1 • 10е кгс7см2.
Рис. 1.15
Указание. Рекомендуется решить задачу графическим методом,
т. е., построив диаграмму перемещений, определить искомую величину путем
измерения соответствующего отрезка диаграммы.
Ответ. Лл = 0,295 см.
1-6. Определить перемещение точки D стержневой системы
(рис. 1.17), если £ст= 2 • 10е кгс/см2, Ем= 1 • 10е кгс/см1.
Ответ. bD = 0,126 см.
1.7. Определить требуемую толщину стенки трубы (рис. 1.18),
если [о.] = 900 кгс7см2.
Рис. 1.16 Рис. 1.17
1.8. Затяжка арки диаметром d = 30 мм растягивается силой
ъ сторону а квадратной шайбы из
чтобы давление ее на арку не
ло 80 кгс/см2.
г. а = 12,5 см.
Р = 12 тс
ic. 1.19).
Р'вОтс
условия,
I д-з/ю!
7777777
Рис. 1.18
(}*2,5тс/мГТ
В
5м
/о|
, , 25
Рис. 1.21
А
[
1
1.9. Определить требуемый диаметр тяг (рис. 1.20), если предел
текучести их материала от= 30 кгс/мма, заданный (требуемый)
коэффициент запаса [пт1 = 2.
Ответ, d = 2,35 см.
18
1.10. Грузовая пластинчатая цепь испытывает растягивающее
усилие Р = 600 кгс. Каждое звено цепи состоит из двух пластин
(рис. 1.21). Определить напряжения в опасном сечении пластины.
Ответ. 1250 кгс/см8.
1.11. Подобрать по ГОСТ 8509—72 два равнобоких уголка для
стержня металлической фермы, растягиваемого усилием 32 тс,
Рис. 1.22
при допускаемом напряжении [о] = 1800 кгс7см2. Следует учесть,
что сечение стержня будет ослаблено заклепочными отверстиями
диаметром 20 мм (рис. 1.22).
Ответ. 75 X 75 X 7 (при перенапряжении « 2,2%).
1.12. Определить требуемые размеры поперечных сечений стерж-
ней кронштейна (рис. 1.23), если для стали [о]ст = 1400 кгс7см2,
для дерева [о]дер= 50 кгс/см2.
Ответ, d = 3,6 см; а = 17 см.
1.13. Определить , растяги-
вающее усилие S в тросе АВ
башенного крана (рис. 1.24)
и количество стальных прово-
лок диаметром d — 2 мМ, из ко-
торых должен быть свит трос.
Расчетный предел прочности
проволоки каната 120 кгс/мм2.
Канат должен работать с семи-
кратным запасом прочности.
Ответ. S = 12 400 кгс; 240 про-
волок.
1-14. Для измерения глубины
моря опускают на проволоке
Диаметром d — 1,5 мм в море приборы, объем которых V — 2400 см3,
вес G = 17 кгс. Определить предельную глубину h опускания,
при которой произойдет разрыв проволоки, если ее предел проч-
ности ав= 6500 кгс/см2 и объемный вес у == 7,8 гс/см®. Принять
объемный вес морской воды равную 1 гс/см®.
Ответ, h я* 9550 м.
19
1.15. Определить напряжения, возни кающие'В сечениях I—I,
II—II, III—III ступенчатого фундамента квадратного сечения
(рис. 1.25), если у = 2,4 тс/м3. Влияние грунта, окружающего фун-
дамент, не учитывать.
Ответ. a7_z= 7,09; = 2,75; = 2,51кгс/сма.
1.16. Сравнить площади основания и кубатуры трех колонн
(рис. 126), если [ос] ~ 10 кгс/см2, у = 2,5 тс/м3.
Ответ. F{ = 4,8 ма; V, = 144 м3; Г// = 2,82ма; Уц~ 65,5 м3; =
= 2,54 м2; = 53,6 м3.
Рис. 1.25 Рис. 1.26
1.17. Рогатка, сделанная из двух резинок круглого сечения диа-
метром 8 мм и длиной 12 см, растягивается для метания камня так,
что резинки удлиняются на 10 см каждая. Вес камня 0,1 кгс. Опреде-
лить начальную скорость полета, если к. и. д. рогатки, т. е. доля
использованной энергии упругой деформации, составляет 0,5.
Модуль продольной упругости резины Е = 10 кгс7см2. (Сужением
сечения пренебречь).
Ответ, v & 6,4 м/с.
§ 1.3. Статически неопределимые случаи
растяжения — сжатия
Пример 1.9. Для бруса, жестко закрепленного обоими концами
(рис. 1.27,а), определить реакции заделок, построить эпюры про-
дольных сил и нормальных напряжений, если Ест — 2 • 10е кгс/см2;
Ем = !’• 10е кгс/см2.
Решение. Рассматриваемая задача относится к категории
статически неопределимых — внутренние усилия не могут быть
определены с помощью лишь одних уравнений статики, дополни-
тельно должны быть составлены уравнения (в данном случае одно)
перемещений.
20
Под действием внешней силы возникают опорные реакции Ra
и Rb-
Статика дает одно уравнение с двумя неизвестными: Ra 4- Rb=P*
Из условия деформации бруса очевидно, что перемещения се-
чений А п В равны нулю (так как они закреплены). Отбросим нижнее
закрепление и заменим действие нижнего закрепления неизвестной
пока реакцией Rb. Таким образом, получим статически определи-
мый брус, нагруженный силами Р и Rb (рис. 1.27,6).
Перемещение сечения В от известной внешней силы Р Авр=Р1ст!'
/ В СТ X Р ст.
Составим выражение для перемещения сечения В от неизвестной
силы Rb-
А Рв1м РВ1 ст
р р Е F '
м ^ст ст
Перемещение сечения В от совместного действия сил Р, Rb рав-
но (на основании принципа независимости действия сил) алгебраи-
ческой сумме перемещений от известной и искомой сил:
Afl = Авр + Abrb.
Но перемещение сечения В равно нулю: Авр + ABrb — 0, или
Р^ст Рв^м^ Рв^ст П ___________г> Р
Ер ер е Р ~ 0’ огкУДа Кв / , f
стгст ^мгм ^ст'ст
______ст
^ст^м^м
Подставляя числовые значения, получаем
12 • Ю» .ппп
Кв— 40.2 • 10» • 15 — 4000 КГС'
1 + 60 . 10’ • 10
Из уравнения равновесия имеем
Р — Рв— 12 000 — 4 000 = 8 000 кгс.
Эпюра продольных сил представлена на рис. 1.27, в, а эпюра
Нормальных напряжений — на рис. 1.27, г.
21
Приведенные записи значительно упрощаются после введения коэффи-
циента жесткости (кгс/см) с/ = EtFiflt. Удлинение бруса записывается
в виде Д//= Pilcj. Уравнение совместности деформации здесь RAlc1 —
— RB!ct = 0, а условие равновесия — RA + RB = Р. Решая совместно эти
уравнения, находят
RA =* PciHci + сг); RB = + с»)-
Поскольку Ni= Ra, Nt= RB, из полученных соотношений следует, что
усилия в стержнях пропорциональны их жесткостям.
вую трубку (рис.
______I Р'бОта
Пример 1.10. Короткий чугунный брус свободно вставлен
в стальную трубку, которая в свою очередь вставлена в алюминие-
1.28). Определить напряжения в поперечных сече-
ниях бруса и трубок, если £Ст == 2 • 10® кгс/смЕ 2;
Еч= 1,2 • 10® кгс/см2; Еал = 0,7 • 10® кгс/см2.
Решение. Под действием силы Р в труб-
ках и брусе возникают усилия N4yr;
/Уал- Статика дает одно уравнение с тремя
неизвестными А/чуг + А/ст + — Р. Следо-..
вательно, задача дважды статически неопре-
делима. Поскольку нужно определить напря-
жения, а не усилия, то удобно выразить
последние через площади поперечных сече-
ний и напряжения:
А/чуг = ЛугОчуг’, ст “ Ест^ст} /Уал “ 7**алОал.
Алюминий
Сталь
Чугун
Рис. 1.28 Вычислим площади поперечных сечений
бруса и трубок:
^F4yr = ZL-ll* = 78,5 см2; FCT = ~ (152 — 102) = 98,2 см2;
Аал = Л. (202 — 152) = 137,2 см2.
Тогда 78,5очуг + 98,2аст + 137,2аал = 60 • 103. Очевидно, что все
элементы системы укорачиваются одинаково, т. е. Д/чуг — Д/ст ==
= Д/ал., или, учитывая, ЧТО let ~ /чуг — /ал.
СЧуг — бет ~ ®ал*
Выразив продольные деформации по закону Гука через о и Е,
получим Очуг/^ч = OctlEст == OenlEan- Выразим 'ост, Оал через очуг:
Е Е
----- ст , -- дал
Ост ___________________ Очуг • ~р1 Оал _ Oqyr • дГ" •
СЧ СЧ
Е Е
Тогда 78,5ачуг + 98,2очуг + 137,2очуг ~ = 60 • 10s.
22
Подставив числовые значения, получим
стчуг = 186 кгс/см2; стст = 186 • = 310 кгс/см2;
Стал = 186 • “ 109 кгс/см2-
Пример 1.11. Определить усилия в стержнях, имеющих одина-
ковые площади поперечных сечений (рис. 1.29, а), если Е„~ 2ЕМ =
== 2 • 10е кгс/см2.
Решение. Применяя метод сечений и рассматривая равно-
весие узла А под действием заданной нагрузки Р и искомых уси-
лий в стержнях /Vi, /V2, /V3 и т. д. (рис. 1.29,5), имеем
2/V2 cosp + 2/Vj cos a + N3 = P. (1)
Рис. 1.29
При составлении уравнения равновесия учтено равенство уси-
лий в симметрично расположенных боковых стержрях — N4,
= У6).
Равенство указанных усилий является следствием симметрии
системы. Боковые стержни одинаково наклонены к оси симметрии
системы и, кроме того, жесткости симметрично расположенных
стержней одинаковы. Вообще говоря, заданная система трижды"
статически неопределима: пять неизвестных и два уравнения ста-
тики (плоская система сходящихся сил), но одно уравнение ста-
тики и одно уравнение перемещений решаются устно (они даже
не написаны) и дают Л/1 = Л/4, ЛГ2==ЛГБ. Устное решение уравне-
ний является использованием симметрии заданной констру^ции.-
Таким образом, остается составить два уравнения перемещений.
Из диаграммы перемещений (рис. 1.29, в) находим
а , * 1 » Nil Nsl
Mi — Д/, COS а, Или ------- = р-Ч; cos a.
cos a ECTF
Учитывая, что £CT == 2£м, получаем = /V3cos2a/2. (2)
Также из диаграммы перемещений следует, что Д/2 = AZsCOsji,
или — Nil___~ - cos я
£CIFcosP £CTFCOSP’
ОТкУДа /V2 =/V3cos2p. ’ (3)
23
Подставив значения Nlt N2 из уравнений (2), (3) в (1), по- 1
лучим
* N3 = Р/( 1 4- cos3 а + 2 cos3 0).
Подставив значение N3 в выражения (2), (3), найдем
Pcos2a N3 ,
Mi = отг-i---5—ft;—тот = cos2 a;
1 2 (1-|-cos3 a-|-2 cos3 Р) 2
N2 = г-г ~ —ай = М3 cos2 р.
2 14- cos3 a 4- 2 cos? 0 3 r
Подставляя числовые Значения, получаем
30 • 103
= 1 + 0,744 + 0,376 = 14,1 ' 103 КГС’
Nt = Ц’1'-1-03 cos2 25° = 5,81 • 10s кгс; j
М2 = 14,1 • 103 cos2 55° = 4,66- 103 кгс.
Обращает на себя внимание неравномерность нагружения j
стержней в заданной системе: наиболее напряжен средний стер- i
жень и наименее напряжены крайние стержни. Растягивающее |
усилие в крайнем стержне состав- |
ляет всего 33% усилия, возникаю- 1
щего в среднем стержне.
Пример 1.12. Определить реак-
цию Ла шарнирной опоры А и уси-
лия в стержнях, . поддерживающих
Р=4отс
1
абсолютно жесткую балку (рис.
1.30, а). Материал стержней оди-
наков.
Решение. Система сил, дейст-
вующих на балку, показана на
рис. 1.30, б. Для такой системы сил
статика дает два уравнения равно-
весия, а неизвестных три: Mr, N2,
Ла- Следовательно, система* один раз статически неопределима. 1
Составим уравнения' равновесия: ।
1
1м ’•*>0.5
< с
t P=4mc
ff
Рис. 1.30
£У=0; -4-М14-Мл4-М2 = 0; (1)1
£тл = 0; 4 • 0,8 —М2 • 0,5 —Mi • 1—0,8 = 0. (2) |
]
На рис. 1.30,6 схематически показана система в деформиро- i
ванном состоянии. Из чертежа следует: Д/2/Д/2 = CA/AD, или -
Д/г/Д/2 = 1/0,5 = 2. ?
Абсолютные удлинения стержней по формуле Гука Д/л =»
= Nih/EFf, Д/2 = N2h!EF2. Тогда — 2. Подставив чис-
ловые значения /4 и F2, получим
МГ = 1,25М2. (3)д|
24
Подставив соотношение (3) в уравнение (2), найдем
/Vj = 1,41, М2 = 1,7 тс.
Из выражения (1) найдем
Ял = 4 + Л\ — У2 = 4+1,41 —1,7 = 3,71 тс.
Температурные напряжения
Рис. 1.31
Пример 1.13. Стальной брус, жестко закрепленный обоими
концами в неподвижных опорах (рис. 1.31), нагревается на 40е"
по сравнению с температурой, при которой брус был закреплен.
Вычислить напряжения, возникающие в поперечных сечейиях
бруса в результате его нагрева, если Е = 2 • 10® кгс/см2; аСт =
= 12 • 10"®.
Решение. При нагреве
бруса в его закреплениях воз-
никают реакции Ra и Rd (на
рисунке они не показаны), для
определения которых статика
дзет лишь одно уравнение:
S X = 0; Ra — Rd ~ 0, Ra —
= Rd. Следовательно, задача
статически неопределима.
Дальнейший ход решения аналогичен решению примера 1.9:
отбрасываем, правую заделку и заменяем ее действие на брус
искомой реактивной силой Rd.
Перемещение сечения D от нагрева (при отброшенной заделке>
А/, = аст (2а + й) А/. Укорочение бруса от действия силы Rd:
Тогда о„Д<(2а + 6)-^ + ^. От-
«стД/ (2а + b) EFJt 12 • 10-’40(2 • 40 + 30)2 • 10« • 4-6
сюда Rd =-------------------=---------Лб^ЗО-б--------------=
= 5080 кгс.
Напряжения в поперечных -сечениях средней части стержня
Rd 5080 1О-7А I 2
°вс = — X =-------г = ~1270 кгс/см •
Напряжения в поперечных сечениях крайних частей стержня
Rd 5080 о._ ' 2
. = °СП = - -F- = — -А- = —847 кгс/см2.
Минусы поставлены потому, что напряжения сжимающие.
Пример 1.14. Определить напряжения, возникающие в попе-
речных сечениях стержней, поддерживающих абсолютно жесткую
балку (рис. 1.32, а), при нагреве среднего (медного) стержня на
А/ = 50°. Принять ам — 16,5 • 10_®, Ест = 2£м = 2-10® кгс/см2.
25
Решение. Нагревание среднего стержня вызовет его удли-
нение, которому препятствуют оба крайних стержня. Поэтому
в среднем стержне появится сжимающее усилие N2, а в край-
них стержнях—растягивающие усилия Nlt N3 (рис. 1.32, б).
Ввиду симметрии конструкции = N3. Составляя уравне-
ние равновесия ХУ = 0, получаем 2Л/Х—N2— 0; Л/2=2Л/Г
Система один раз статически неопределима — три неизвест-
ных и два уравнения статики (одно из них решено устно).
Очевидно, что балка опус-
Рис. 1.32
б
тится, оставаясь горизонталь-
ной, т. е. уравнение перемеще-
ний имеет вид Д/х = Д/2 == Д'3,
где А/^^-; Д/2 = ам/Д/-
СТ
AU J А. 2VJ ~
Тогда
Nil/EctFct = cc»J At — 2N1l/EuF№
(знак минус перед вторым сла-
гаемым поставлен потому, что
усилие во втором стержне при-
нято сжимающим),
Ni = а„ At I 1-р-р-
I Х^ст* ст
+ _2_\
I
Подставив числовые значения, найдем
16,5 • 10-в • 50 Nv 330 onn г
Nt —------j-2--------5---= 330 кгс; Ост = = -т- =330 кгс/см2;
2,0-10’-1 1,0-10«-1
JV2 = 2Nt = 660 кгс; ом = ~ — 660 кгс/см2.
Положительные значения усилий (напряжений) указывают,
что предварительно .принятые их направления (см. рис. 1.32,6)
совпадают с действительными.
Начальные и монтажные напряжения
Пример 1.15. В представленной на рис. 1.33,а системе стальных
стержней средний стержень был изготовлен короче, чем требуется,
на 6 — 0,6 мм. Определить напряжения, возникающие в попереч-
ных сечениях стержней после сборки системы, если £ст= 2 • 10е
кгс/см2.
Решение. После сборки в стержнях возникнут в среднем рас-
тягивающее, в крайних — сжимающие усилия.
На рис. 1.33,6 показаны усилия, действующие на узел А. Для
такой системы сил статика дает два уравнения равновесия. Следо-
26
вательно, задача статически неопределима. Составим уравнения
равновесия для узла A: SX = 0; sin а — N3 sin а — 0;
SF = 0; —cos а + ?V2—/Vscosa = 0;
/V2 = 2/Vi cos а = 2/Vi cos 30°, или /V2 = 1.73Л4.
Площади сечений одинаковы, следовательно,
(У2==: 1,73(Т^.
Третье уравнение можно получить из условия деформации
системы. После сборки шарнир А займет некоторое положение А1Г
промежуточное между
А и Ао.
Как видно из рис.
1.33, а, в, 6 = Д/2 +
+ Aij/cos а, где Д/2 =
= а2/*2/£; Д/j = aJilE.
Но 1г = Z2/cos а, тогда
6=o2l2/EA-o1l2/E cos2a.
Учитывая, что ст2 =
— 1,73a!, получаем
6= 1,730x4/£ +
4- o^fE cos2 a,
откуда
Г / 1 VI
“ '-73+
a2 = 1,73a! = 1,73 • 130= 225 кгс/см2.
Задачи для самостоятельного решения
1.18. Определить требуемые площади поперечных сечений стерж-
ней, поддерживающих абсолютно жесткую балку (рис. 1.34). Все
стержни изготовлены из одинакового материала и имеют равные
сечения. Принять [а] — 1600 кгс/см2.
Рис. 1.34
Ответ, F = 5,30 см2.
1.19. Вычислить напряжения, возни-
кающие в стержнях системы, изображен-
ной на рис. 1.35, если после сборки
стержни были нагреты на Д/ = 40°. При-
нять аст= 125 • 10“’; ам= 165 • 10“’.
Ответ. аст = -{-354 кгс/см2; ам —
— 122 кгс/см2.
• По закону Гука Д/ = Nl/EF = N/F X
X 1/Е = al/E.
27
1.20. Вычислить напряжения, возникающие в стальных стерж- s
нях (рис. 1.36) после сборки системы. Стержень 2 изготовлен коро-
че, чем требуется, на 6 = 0,4 мм.
Ответ. аг = —57; ая=258; а>= —171 кгс/см1. •;
1.21. Подобрать из расчета на прочность площади поперечных |
сечений стержней при условии, что/г1= f2= F; Fa= 2F (рис. 1.37).
Принять [ст] = 140 МН/м2.
Ответ. Ft = Ft = F = 3,46 см1;
Рис. 1.35
1.22. Для заданного бруса (рие. 1.38) необходимо:
1) вычислить напряжения при нагреве его иа Д/, если модуль
упругости материала бруса Е, коэффициент линейного расшире-
ния а;
2) на основании полученного общего решения определить темпе- !
ратурные напряжения в рельсах сварного железнодорожного пути, |
если температура изменяется от —20 до + 30°. )
Принять Е = 2 • 10вкгс/см2, а = 125 • 10~7. ]
Ответ, а --------а ; а.. -----------а А^.--; а = —1250 кгс/см1 ]
1 n-4-k—" 11 п(4-1) + Г i
k 1
(fe = 1). -
1.23. В системе стальных стержней (рис.. 1.39) средний стержень j
оказался длиннее номинального значения на 6 =» 7 • 10-4/. Опреде-
лить напряжения в стержнях после сборки узла А при условии, что
сечения всех стержней одинаковы,
Ест = 2 10® кгс/см2; а = 30°.
Ответ. at = аа = 456,4 кгс/см2; а2 = —896 кгс/см2.
Для расчета статически неопределимых задач типа 1.18—1.20 может
быть применена программа дли ЭВМ МИР-2 (приложение V).
Задаваясь различными отношениями kF = Fi/Fj и различными углами
наклона стержней, поддерживающих абсолютно жесткий брус, можно опре-
делить то отношение kF, при котором вес конструкции минимальный. Таким
образом решается задача оптимизации статически неопределимой конструк-
ции при ее расчете на прочность.
ГЛАВА 2. ТЕОРИЯ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО
СОСТОЯНИЯ
§ 2.1. Основные сведения из теории
Напряжения, возникающие на различно ориентированных пло-
щадках, проходящих через данную точку тела, в общем случае на-
гружения тела не одинаковы. Совокупность нормальных и каса-
тельных напряжений, возникающих на всем бесчисленном множе-
стве площадок, которые можно провести через данную точку, харак-
теризует напряженное состояние в этой точке.
В окрестности данной точки всегда можно выделить элементар-
ный параллелепипед таким образом, чтобы на его гранях не было
касательных напряжений. Иными словами, через точку можно про-
вести три взаимно перпендикулярные площадки, на которых не
возникает касательных напряжений (в некоторых частных случаях
таких площадок можно провести бесчисленное множество). Ука-
занные площадки называют главными. Возникающие на них
нормальные напряжения называют главными напря-
жениями; их обозначают о,, <т2, о3. Индексы расставляют так,
чтобы выполнялись неравенства <з^ о3 (неравенства алгебраи-
ческие, напряжения сжатия считают отрицательными), т. е. сначала
надо определить все главные напряжения, а потом расставить ин-
дексы. Для данной точки Oj— наибольшее, а о3— наименьшее на-
пряжение.
Если все три главных напряжения отличны от нуля, напряжен-
ное состояние называют объемным, или трехосным
(рис. 2.1,а). Если только два главных напряжения не равны нулю,
напряженное состояние плоское, или двухосное (рис.
21,6). Если лишь одно из главных напряжений отлично от нуля,
напряженное состояние линейное, или одноосное (рис.
2-1, в).
29
Семейством, или серией, площадок называют совокуп-
ность бесчисленного множества площадок, параллельных одной
и той же прямой (перпендикулярных одной и той же грани эле-
ментарного параллелепипеда). Напряжения на площадках, принад-
лежащих серии площадок, параллельных какому-либо из главных
напряжений, не зависят от этого последнего. Например, нормаль-
ное и касательное напряжения на площадке, параллельной о3 и рас-
положенной так, что нормаль к ней составляет угол а с направле-
нием ffj (рис. 2.2), определяются по формулам
Рис. 2.2
Для рассматриваемой серии площадок наибольшее касательное
напряжение возникает на площадке, биссекторной по отношению
к главным площадкам; оно определяется, по формуле
Xia = (<Т1 — <та)/2. ' (2.3)
Это касательное напряжение не максимально для данной точки.
Максимальное касательное напряжение возникает на площадке,
параллельной о2 и биссекторной к площадкам действия ffj и <т3;
его величина определяется по формуле
Тщах — Т13 = (CFj. <т3)/2. (2-4)
Взамен аналитического определения ва и та могут быть най-
дены графоаналитически при помощи круга Мора, построенного
30
для данной серии площадок. Круг Мора — это геометрическое
место точек, абсциссы и ординаты которых равны соответственно
нормальным и касательным напряжениям, возникающим на пло-
щадках данной серии. Применение круга Мора для определения
сга и та показано в примере 2.2.
Из формул (2.1), (2.2) как частный случай получаются зависимо-
сти для одноосного растяжения (^> 0; о2= о3= 0)
0а ~ — (1 + cos 2а) = Ojcos2 а; (2.5) Ta=yO1sin2a. (2.6)
В случае одноосного сжатия (04= о2= 0; о3< 0) в формулы
(2.5) и (2.6) взамен следует подставить о3 и при вычислениях
учесть, что величина о3 отрицательна.
Приведенные сведения об исследо-
вании напряженного состояния относи-
лись к случаям, когда заданными (ис-
ходными) были главные напряжения.
Кроме того, исследование ограничива-
лось сериями площадок, параллельных
главным напряжениям; определение на-
пряжений на площадках, ие принадле-
жащих указанным сериям, выходит за
рамки программы.
При плоском напряжением состоя-
нии в окрестности исследуемой точки
можно выделить элементарный параллелепипед таким обра-
зом, чтобы две его противолежащих грани были свободны от
напряжений (рис. 2.3). Ограничиваясь исследованием напряжений
для серии площадок, перпендикулярных свободной от напряжений
грани элемента; имеем следующие зависимости (рис. 2.4):
Ста = — + — g- ^cos 2а — хху sin 2а; (2.7)
та = ^sin 2а + хху cos 2а. (2.8)
Среди площадок исследуемой серии имеются две взаимно пер-
пендикулярных главных площадки; их положение определяется
углами а0’ и а", значения которых находят из выражения
tg2a0 = — 2тхг//(стх — Су). (2.9)
Величины главных напряжений
Огл = 2^ ± 4 У(ах-ау)* + 4х*у. (2.10)
Индексы у главных напряжений устанавливают после вычисления
этих напряжений. При пользовании формулами (2.7)—(2.9) знак
касательного напряжения принимают в соответствии с рис. 2,5.
Характерны частные случаи плоского напряженного состояния:
31
а) Так называемое упрощенное плоское напряженное состояние, |
для которого 04 > 0; ст2= 0; о3< 0. При этом элементарный паралле-|
лепипед может быть выделен так, что одно из исходных нормальных 1
напряжений окажется равным нулю (рис. 2.6). Взамен формул-1
(2.9), (2.10), для этого случая Получается j
tg2d0 = -^; ' (2.11)1
+ = ¥ + |^ + 4t^ O2 = 0; = + (2J2M
’7777777777/ 7777777777/ tgx
Рис. 2.5
Рис. 2.6
б) Чистый сдвиг, для которого 0!= —п3; п2= 0. В этом слу-'
чае есть возможность выделить’ элементарный параллелепипед
так, что на четырех его гранях будут только равные по модулю^
касательные напряжения, а две грани будут от напряжений сво-
бодны (рис. 2.7). При этом.у казанные касательные напряжения экс- 1
У
' Рис. 2.7
тремальны и связаны с главными
напряжениями зависимостью
04 = Од — ^щах = Тху. (2.13) ;
Главные площадки составляют 1
углы 45° с площадками действия
. экстремальных касательных на- I
пряжений. 1
Исследование плоского напря- 1
женного состояния с помощью 1
кругов Мора для случаев, когда исходные площадки не главные, i
показано в примерах 2.4, 2.5. 1
Через данную точку тела можно провести три взаимно перпен-I
дикулярных оси, углы между которыми и после деформации оста-1
нутся прямыми. Это так называемые главные оси дефор-1
м а ц и и; их направления совпадают с направлениями главных 1
напряжений. Линейные деформации в направлениях главных осей* |
называют главными деформациям и; их величины свя- ’
заны с соответствующими главными напряжениями обобщенным
законом Гука-.
81 = К — 1* (а2 + сг3)]; е2 = [04 — ц (04 + ст3)];
£3 = 4*[огз — H(<h + o4)b (2 14)
i
32
Если выделить в окрестности точки элемент не главными пло-
щадками (на гранях элемента будут как нормальные, так и каса-
тельные напряжения), то формулы (2.14) для линейных деформаций
в направлениях каждого из нормальных напряжений (не главных!)
остаются в силе, следует лишь изменить индексы;
е* *= 4~ + стх)В е, = 4 1°* ~ Н (°* + СТ*)Ь 14 а)
Относительное изменение объема в окрестности дайной точки
тела определяется по формуле
© = ех + еу + ех = (ах + ау + вх). (2.15)
Удельная потенциальная энергия деформации для данной точки
тела связана с главными напряжениями зависимостью
ы в ~ 2,х (CTi°a + Ста°» + °з®1)]- (2-16)
Полная удельная потенциальная энергия деформации может
быть разложена на удельную энергию, связанную с изменением
объема элемента
и°б а ~Qg2~ (°i + ст» + °з)2> (2-17)
и на удельную энергию, связанную с изменением формы элемента
“♦=1 —а»>2+(°а ~~а^2+~~ <2 18>
§ 2.2. Аналитическое и графоаналитическое исследование
напряженного состояния
Пример 2.1. Определить аналитически и с помощью кругов Мо-
* ра нормальные и касательные напряжения в точке А сечения 1—1
и в точке В сечения 2—2 бруса по
рис. 2.8,а. Вычислить максимальные
касательные напряжения, возникаю-
щие в указанных точках.
Решение. Для поперечного
сечения, проходящего через точку А,
Na — Pi = 3 • 103 кгс,
и соответственно нормальное напря-
жение в указанном поперечном сече-
йии, являющееся главным напряже-
нием для точки А,
(°jc)a — (&1)а — Na/F =
*= 3 • 10®/2 1 = 1500 кгс/см2.
е
1-10
33
Аналогично для точки В
Л^=/>2= 3 • Ю3—5,5 • 103 == —2,5 • Ю3 кгс.
Эпюра продольных сил показана на рис. 2.8, б. Напряжение
в поперечном сечении, проходящем через точку В,
(ах)в = (ст3)в _ NB/F= — 2,5 • 10®/2 • 1 = —1250 кгс/см .
На рис. 2.9, а показан (в проекции на плоскость чертежа) эле-
мент, выделенный в окрестности точки А поперечными и продоль-
Рис. 2.10
ными сечениями; там же показана площадка, параллельная сече-
нию 1—1, напряжения на которой подлежат определению.
По формулам (2.5), (2.6) находим
(Оа,)л = (Pi)a cos2 = 1500 cos2 155° = 1230 кгс/см2;
(та,)л = у (01)л sin 2ах = у 1500 sin 310° = —575 кгс/см2.
Максимальное касательное напряжение в точке А
. . (О1)л 1500 _ел , ,
(Тщах)л = —2~ = — = 75Q КГС/СМ2.
Строим круг Мора (рис. 2.9, б) для серии площадок, перпенди-
кулярных плоскости чертежа. По оси абсцисс откладываем от на-
34
чала координат отрезок ОК, равный в выбранном масштабе (О1)л-
Точка К изображает площадку действия главного напряжения
(о1)л> точка О — площадку, перпендикулярную предыдущей (ну-
левую главную площадку). Разделив пополам расстояние ОК,
получим центр круга Мора точку О± и проведем окружность. Через
точки О и К проводим линии, параллельные нормалям к площадкам,
изображаемым этими точками. Эти линии (лучи) пересекаются в точ-
ке К, которая, следовательно, является полюсом (главной или
особой точкой) круга Мора. Напоминаем что полюс обладает тем
свойством, что в нем пересекаются.лучи, параллельные нормалям
ко всем площадкам данной серии.
Для нахождения точки, изображающей сечение 1—1, проводим
из точки К луч, параллельный нормали к сечению 1—1, и в пересе-
чении этого луча с окружностью получаем искомую точку С. Ее абс-
цисса и ордината в принятом масштабе дают соответственно величи-
ны нормального и касательного напряжений, возникающих по
сечению 1 — 1. Очевидно, площадка действия максимального
касательного напряжения изображается точкой D, получаемой в
пересечении окружности с ее вертикальным диаметром. Для опре-
деления положения указанной площадки соединяем точку D с полю-
сом — линия DK параллельна нормали к площадке действия
(тщах)л. Величина нормального напряжения на этой площадке опре-
деляется абсциссой точки D. Напряжения на площадках, изобра-
жаемых точками К, С, D, показаны на рис." 2.9,6. Все нормальные
напряжения положительны (напряжения растяжения). Касательное
напряжение на площадке, изображаемой точкой С, отрицательно
(точка под осью абсцисс), поэтому для получения направления
(т«1)л поворачиваем внешнюю нормаль к площадке на 90° в направ-
лении, противоположном движению часовой стрелки (рис. 2.9,6).
Для точки В сечения 2— 2 элемент показан на рис. 2.10, а.
Нормальное и касательное напряжения получаем по формулам
(2.5), (2.6), учитывая, что (о1)л заменяется на (ст3)в, и это напряже-
ние отрицательно:
(оа2)в = (о3)в cos2 а2 = —1250 cos2 215° = —837 кгс/см2;
(т<х?в ~ у (стз)в sin 2а2 = 0,5 (— 1250sin 430°) = —587 кгс/см2.
Максимальное касательное напряжение для точки В
, \ —(аз)в 1250 сос , 2
(Гтах)в=---§-- = — = 625 КГС/СМ2.
Круг Мора для точки В построен на рис. 2.10, 5. Так как по-
строение его принципиально не отличается от выполненного для
точки Л, то пояснений не приводим, подчеркнем лишь, что круг
Расположен влево от начала координат [(а3)в< 0], и, следовательно,
на любой площадке, проходящей через точку В, нормальное напря-
жение отрицательно (напряжение сжатия).
2"
35
Пример 2.2. Для заданного напряженного состояния (рис. 2.11) -
построить круги Мора для серий площадок, параллельных каждому !
из главных, напряжений. Определить максимальное касательное;
напряжение. Определить нормальное и касательное напряжения •
на площадке, нормаль к которой составляет угол а = 30° с направ-
лением н перпендикулярна к вектору а3.
Решение. Исходными являются главные напряжения; все
они отличны от нуля, т. е. заданное напряженное состояние объем- ]
иое (трехосное). Наибольшим (в алгебраическом смысле) является 1
напряжение, равное 800 кгс/см2, следовательно, его надо обозиа- j
чить ах. Наименьшее напряжение равно— 1000 кгс/см2 (напряже-1
нне сжатия), его следует обозначить |
&3. Итак, ах = 800 кгс/см2,
а2 = —600 кгс/см2, а3 =
= —1000 кгс/см2.
Для построения кругов Мора откладываем вправо от началу |
координат отрезок OL, соответствующий olt и влево от начала коор-
динат — отрезки 0/С и ОМ, соответствующие а3 и о3 (рис. 2.12)s
Разделив пополам отрезки KL, К.М, LM, получим точки 0ъ О2,
03— центры кругов Мора, каждый нз которых построен для серии
площадок, параллельных одному из главных напряжений.
Максимальное касательное напряжение равно (с учетом масштаб
ба) радиусу наибольшего (иногда его называют главным или опреде-
ляющим) круга*Мора, т. е. того круга, который построен для серии
площадок, параллельных а2. Итак, ;
а, — <т3 800—(—1000) ППЛ , 2 а
•Стах = --2 - = -----5------ = 900 КГС/СМ2. J
Площадка, на которой по условию задачи требуется определите
нормальное и касательное напряжения, принадлежит к серии
площадок, параллельных а3. Эта площадка показана на рис. 2.13,а!
где заданный элемент изображен в проекции на плоскость, перпен!
дикулярную а3. Круг Мора для рассматриваемой серии плошадоя
еще раз изображен отдельно (рис. 2.13,6). Проведя через точку Й
луч, параллельный Oj, а через точку К — параллельный а2, уста-й
36
навливаем, что точка К — полюс данного круга Мора. Из точки К
проводим луч, параллельный нормали к интересующей нас наклон-
ной площадке. Измерив абсциссу и ординату точки С, соответствую-
щей указанной площадке, найдем
<1а=зо° = 450 КГС/СМ2; Ta_30« = 606 кгс/см2.
Этот же результат может быть получен по формулам (2.1), (2.2).
Рис. 2.13
Пример 2.?. Построить круги Мора для заданного напряженного
состояния (рис. 2.14).
Решен’Н е. Заданными, как и в предыдущей задаче, являются
главные напряжения aj= ст2= 1200 кгс/см®, ст3= —900 кгс/см®.
Особенность рассматриваемого
напряженного состояния состоит
Рис. 2.14
в том, что два главных напряжения равны между собой. При построе-
нии кругов Мора (рис. 2.15) устанавливаем, что один из них, а имен-
но соответствующий серии площадок, параллельных а3, вырожда-
ется в точку (имеет нулевой радиус). Это значит, что на любой пло-
щадке, параллельной а3, касательное напряжение бтсутствует,
т- е. все эти площадки главные (случай, когди главных площадок
бесчисленное множество). Круги, соответствующие сериям площа-
док, параллельных cij и а2, сливаются в один круг; на рис. 2.15,
37
чтобы подчеркнуть указанное обстоятельство, один из этих кругов
чуть уменьшен и изображен штриховой линией.
Пример 2.4. Определить главные напряжения и максимальное
касательное напряжение для заданного напряженного состояния
(рис. 2.16, а).
Решение. Одна из исходных площадок свободна от напряже-
ний, поэтому заданный элемент изображен не в аксонометрии,
а в проекции на плоскость, параллельную упомянутой площадке.
Наличие свободной от напряжений площадки указывает на то, что
заданное напряженное состояние не трехосное. Круг Мора для слу-
чая, когда исходными являются неглавные площадки, строим сле-
дующим образом: от выбранного начала координат откладываем
вправо отрезок Ос, рарный (в принятом масштабе) о*, из точки с
восстанавливаем перпендикуляр к оси абсцисс и на нем отклады-
ваем вверх отрезок, соответствующий тЖу (рис. 2.16, б). Полученная
таким образом точка С изображает вертикальную исходную пло-
щадку; подчеркиваем, что и ох и хху положительны. Аналогично
находим точку D, изображающую горизонтальную исходную пло-
щадку (здесь oj и хуХ отрицательны). Соединив точки С и D, полу-
чаем в пересечении прямой CD с осью абсцисс центр круга Мора.
.Оказалось, что центр круга Мора в данном частном случае
совпал с началом координат. Проводим окружность из полученного
центра через точки С и D. Из этих точек проводим лучи, параллель-
ные нормалям к площадкам, которым эти точки соответствуют.
Пересечение этих лучей дает полюс круга Мора (точку К). Очевид-
но, точки L и М круга, находящиеся на оси абсцисс, соответствуют
главным площадкам. Абсциссы этих точек равны по величине
и противоположны по знаку, то же относится к главным напря-
жениям.
Известно, что такой частный случай плоского напряженного,
состояния, для которого отличные от нуля главные напряжения рав-
ны по модулю и прогивоположны по знаку, называется чистым
сдвигом. Пэ чертежу, измерив отрезок 0L (или ОМ), находим
38
ai= — ст3= 400 кгс7см2. Равное нулю главное напряжение должно
быть обозначено сг2, так как оно является промежуточным между
неравными нулю главными напряжениями. Точка W изображает
площадку, на которой возникает максимальное касательное напря-
жение; величина этого напряжения ттах= Oj— —о3= 400 кгс/см2.
Положение главных площадок и площадки, на которой возникает
ттах> показано на рис. 2.16, б.
Решим эту же задачу аналитически. По формуле (2.10) имеем
Огл = ^4^ ± 4 ^(Ох -оу)2 + 4т2, =
= 265- 265 ± ^(2б5 265)2 + 4 3002 = +400 кгс/см2.
Рис. 2.17
Для определения наклона главных площадок к исходным приме-
няем формулу (2.9):
ta9n._______2xxj<_______2 • 300 ____. .3
ig^a0— ах_а#— 265—(—265) — ld’
откуда получаем два угла: а„=—24°15' и а„ =—114°15'. Мень-
ший из этих углов дает направление нормали к первой главной
площадке (см. рис. 2.16, б).
Пример 2.5. Для заданного напряжённого состояния (рис. 2.17,а)
определить главные напряжения и максимальное касательное на-
пряжение.
Решение. Построение круга Мора (рис. 2.17,6) аналогич-
но показанному в предыдущей задаче. По заданным напряжениям
наносим точки С (с абсциссой ах и ординатой xXJ/) и D (с абсциссой
и ординатой хух). Соединив эти точки, получаем центр круга
(точка Oj); из этого центра проводим окружность через точки С
и D. Эта окружность проходит через начало координат, следова-
тельно, одно из главных напряжений (для серии площадок, перпен-
дикулярных плоскости чертежа, рис. 2.17,а) равно нулю. Итак, для
заданного напряженного состояния лишь одно из главных напряже-
ии отлично от нуля; это напряжение отрицательно, следовательно,
39
имеем одноосное сжатие а,*- 0, а,— —600, кгс/см* (величина
а8 определена по чертежу).
Тот же результат получим, применив формулу (2.10):
_ -W- IM ± у-(_445+ 155)1 + 4-263* _ —300 ± зад
» 0;
а, а* —600 кгс/см*.
По формуле (2.4) находим максимальное касательное напряжо-.
ине (см. также рис. 2.17,6): . 1
Ттах = °- «ж 300 КГС/СМ».
Задачи для самостоятельного решения |
2.1. Определить величину Р, если в точке А сечения 1 — Ц
бруса по рис. 2.18 нормальное напряжение равно 650 кгс/см». 1
Ответ: 735 кгс. 1
1
Рис. 2.18 Рис. 2.19 Рис. 2.20
2.2. В сжатом брусе (рис. 2.19) напряжения по одной из наклон,*
ных площадок ста=75МН/м2, т«= 43 МН/м2. Определить максималь^
ные нормальные и касательные напряжения, возникающие в брусе
и силу Р. I
Ответ. оа = —99,4 МН/м2; ттах « 49,7 МН/м2; Р = 9940 Н. I
2.3. Для заданного напряженного состояния (рис. 2.20) опредв
лить аналитически и графоаналитически (с помощью круга Мора
нормальное и касательное напряжения на площадке, отмеченной я
чертеже. ’
Ответ- оа == 675 кгс/см2; та = 217 кгс/см*. J
40
2.4. Для заданных напряженных состояний (рис. 2.21, а, б,
в, г) построить круги Мора для серий площадок, параллельных
каждому из главных напряжений, н определить максимальные ка-
еательные напряжения.
Ответ. а) 1200 кгс/см*; б) 0; в) 250 кгс/см*; г) 1100 кгс/см*.
2.5. Построить круг Мора для серии площадок, перпендику-
лярных к свободной от напряжений грани параллелепипеда (рно.
2.22). Определить главные напряжения и максимальное касатель-
ное напряжение.
Ответ. Ot » 240 кгс/см*; о. » 0;ff. « —1040 кгс/см*; т_,_ = 640 кгс/см*.
* * • 9 а швл
Рис. 2.23
Рис. 2.22
2.6. Определить главные Напряжения для заданного напряжен*
ног о состояния (рис. 2.23). Построить три круга Мора и найти мак-
симальное касательное напряжение.
У Казани е. Для серии площадок, параллельных аг, напряжения
не зависят от аг, т. е. исследование для указанной серии ведется как дл»
плоского напряженного состояния.
Ответ, а, = 1200 кгс/см®; а3 = 722 кгс/см®; а. — —222 кгс/см®; т «
~ 'И кгс/см®.
Для исследования плоского напряженного состояния и оценки проч-
ности по различным теориям может быть использована программа для ЭВМ
«МИР» (приложение V).
41
В программе используются следующие идентификаторы: аа = ЕЛ,
= SB; главные напряжения: aj = Q 1, аа = Q 2, а3 = Q 3; эквивалент» '
ные напряжения по III н IV теориям прочности SE3 и SE4. Программа пре»
дусматривает вычисление относительной объемной деформации EVи удель-
ной потенциальной энергии упругой деформации ЭНЕРГ/'-
$ 2.3. Применение обобщенного закона Гука
Пример 2.6. Алюминиевый кубик свободно, но без зазоров встав-
лен в прорезь массивной (недеформируемой) детали (рис. 2.24)
и сжат силой Р = 180кН. Определить главные напряжения и глав-
ные ' деформации для произвольной точки кубика. Вычислить
относительное и абсолютное изме»
\У нения объема кубика. Определить
Рис. 2.24
удельную потенциальную энергию де-
формации (полную, изменения объема
и изменения формы). Принять Е —
= 0,7 • 105 МН/м*; и = 0,36.
Решение. Кубик находится
в однородном (одинаковом для всех
его точек) напряженном состоянии,
и, следовательно, обобщенный закон
Гука можно применять к кубику в це-
лом. Торцовая грань кубика (на рис.
2.24 заштрихована) от напряжений
свободна, т. е. 0. Напряжения
на верхней и нижней гранях кубика
(предполагается, что сила Р равномерно распределена по верх-
ней грани):
= -7,2-10’ Н/м2.
Напряжение ох определим, использовав условие, что в направле- ;
нии оси х деформация равна нулю (ех = 0), так как принято, что де- ;
таль, в которую вставлен кубик, абсолютно жесткая. Применив ,
обобщенный закон Гука, получим J
ех = -^-[ах —14(0,+ ог)] = 0, J
откуда
ох == щгу = 0,36 (—7,2 • 10’) = —259 • 10» Н/м*.
Окончательно имеем Oj = аг = 0; at = ах = —259 • 10®.Н/м2 == ?
= — 25,9 МН/м2; а3 = ау = —720 • 10® Н /м2 = —72 МН/м2. \
Вычисляем величины главных деформаций: е2 = ех = 0
«з = е, = 4- - Н (°* + *«)] = Ь,7 ! 10® (-72 + °’36 25’9) =
42
/
= —8,96 -IO4; ex = ег = ~[crz — ц(ax + ст^)] = [—0,36X
X (—25,9 — 72)] = 5,03 , IO-4.
Относительнее изменение объема
0 = еж + еу ег = —8,96 • 10"4 + 5,03 • 10"4 = —3,93 • 10’4.
Абсолютное изменение объема
AJZ = 6 У = 0 а®= —3,93 • 10’4 • 5®= —0,0491 см3=
= —4,91 • IO’8 м«.
Полная удельная потенциальная энергия деформации
ц = ф + = -720 . io; (-£96 . £0-4) = 322 . 102 н • М/М”.
Удельная потенциальная энергия деформации, связанная с из-
менением объема,
(<71 + *2 + *з)2 = 6.0,7; 10U К—259 . 10®) +
+ (—720 10е)]2 = 64 • 102 Н • м/м®.
Удельная потенциальная энергия деформации, связанная с из-
менением формы,
“Ф = Чт f((J1 ~ + (СТг — а®)2 +
+ (as-oi)2] = бЧтЧЧ^2592 +
+ (—259 + 720)2 + 7202] 1010 =
= 258 • 10® Н • м/м®.
Пример 2.7. Жесткая обойма состоит
из двух половин, стянутых восьмью бол-
тами (рис. 2.25). В обойме сжимают
призму из пластмассы, коэффициент
Пуассона для которой и = 0,4 . Сила,
сжимающая пластмассовую призму вдоль
оси обоймы, Р' — 10 10® кгс. Определить требуемый диаметр бол-
тов, пренебрегая их деформацией и не учитывая влияния кручения
при затяжке. Принять для болтов [ор] = 1000 кгс/см2.
Решение. При сжатии пластмассового бруса размеры его по-
перечного сечения должны увеличиваться, но этому увеличению
препятствуют'стенки обоймы. В результате возникают силы взаи-
модействия между поверхностями пластмассового бруса и стенками
обоймы. Брус находится в однородном напряженном состоянии.
43
Учитывая, что по условию задачи обойма абсолютно жесткая *
и деформации болтов ие принимаются во внимание, заключаем, что j
деформации бруса в направлениях осей х и у равны нулю. Учитывая :
далее, что по условию симметрии сгх= оу, и применяя обобщенный j
закон Гу«а, получаем ех~еу — -^-[ах—р.(ах + сгу)] = 0, откуда :
р —10 • 1(Я
<гх(1 — И) = 1^2. — И). W р* д • эдг- — -:
=‘—=2,78 кгс/см2; • -
= ~?’4 'Л" = —J»85 кгс/см«.
Полное усилие, действующее на болты.
/ ’ . j
Q = flL|ax| == 60 • 100 • 1,85 = 11 100 кго.
9
__ г
а
Усилие, приходящееся на один болт,
Qe = Q/i = п ЮО/8 1390 кто, -
J
Требуемое по условию прочности сечение болта (по внутреннему
диаметру резьбы) '
Цif 4.TS90' _ „
4 ^[ар1 ’ у л [<тр| К 3,14 • 1000 1,33 СМ‘ j
По ГОСТ 9150-59 принимаем болты с резьбой Ml 6 х 2, имеющей ;
внутренний диаметр dx=» 13,83 мм.
Пример 2.8. На растягиваемом образце установлен тензометр 1
АВ, как изображено на рис. 2.26,а. База тензометра с = 20 мм, |
коэффициент увеличения тензометра k « 1000, показание тензо-. j
метра при заданной нагрузке Де = 6,5 мм. Определить коэффициент |
Пуассона для материала образца, если известно, что Е — 2,1 • 10* |
кгс/см2. з
44
Решение. Выделим из бруса элемент плоскостями, параллель-
ными базе тензометра и ей перпендикулярными (рис. 2.26, б). Зная
напряжения в поперечном сечении бруса
= CTj == == Ю00 кгс/см2,
найдем нормальные напряжения, возникающие на гранях выделен-
ного элемента: <та= агсо$2а = 1000 cos2 30°= 750 кгс/см2;
о» 4- чо° =* <*1 cos2(a -|-99°) = oj sin3 а = 1000 sin2 30°= 250 кгс/см2.
Составим выражение для определения линейной деформации в на-
правлении базы тензометра: 8a = g-(oe— рпа+эо»).
По условию задачи можно определить численное значение ука-
занной деформации sa = ^ = Оп-6’,ъЛп — 3,25 • 10~*.
Таким образом,
еа = -~ (aa - Р<т3 + 90»)'= 2jTio«(750 - 250fi) = 3’25 ’ 1 °’4-
Отсюда 750 — 682 = 250р;
_ 750 — 682 q 2у2
" 250
Задачи для самостоятельного решения
2.7. Кубик с ребром а — 20 мм вставлен в гнездо, ^сделанное
в массивной плите, которую можно считать недеформируемой.
К верхней грани кубика приложена сжимающая сила Р = 5 х
X 10® кгс, равномерно распределенная по пло- у.
щади грани. До приложения силы Р ребра гнез- . п сппп
да в плане больше ребер кубика на 26j= 1Р-5000кгс
= 4 • 10"® мм, 26,= 3 • 10~® мм (рис. 2.27).
Определить главные напряжения и главные де-
формации для произвольной точки кубика. При-
нять Е = 0,7 • 10е кгс/см2; р = 0,36.
Ответ. а± = аг= —498 кгс/см2; а2 = ах =
= —524 кгс/см2; а. = = —1250 кгс/см2; «з = еу =
= —126 • 10"5.
2.8. Стальной брус квадратного поперечно-
го сечения, жестко закрепленный обоими кон-
цами (рис. 2.28), на участке длиной b подвер-
гается действию равномерно распределенно-
го давления р = 1500 кгс/см2. Определить пере-
мещение сечения 1 — 1. Принять Е = 2 х
X 10е кгс/см2, р = 0,30.
Ответ. 3,86 • 10“‘ см.
2.9. Нижняя часть ступенчатого стального бруса находится под
Действием всестороннего давления р (рис. 2.29). Определить
45
опорные реакции, напряжения в поперечных сечениях бруса и пере-
мещение сечения 1 — 1. Принять Е ~ 2 • 105 Н/мм2; р ~ 0,30.
Рис. 2.28
Ответ. RA = RB = 174,5 кН; сА = 109 Н/мм21
ав = 27,3 Н/мм2; Г.64 • 10"2 мм.
2.10. На стальной брус (рио. 2.30) нак-
леен тензодатчик А, направление базы ко-
торогосоставляет угол 45° с осью бруса. При
нагружении бруса силой Р в направлении
базы датчика возникает деформация еа=
= 1,05 • 10-4. Определить величину силы Р,
если для материала бруса Е = 2 • 10е кгс7см,
р ='0,3.
Ответ. 6300 кгс.
2.11. Бетонный куб АВСД (рис. 2.31)
сжимается с помощью шарнирного механи-
зма усилиями, равномерно распределенны-
ми по четырем боковым граням. Опреде-
лить относительное упругое уменьшение 0
объема куба, если длина его ребра равна
20 см, модуль упругости материала Е ~
= 0,17 • 10®кгс/см2, р = 0,16,
= 100 кгс/см2, Р = 28 тс.
Ответ. О = —0,792 • 10-3.
предел пропорциональности сгпц=»
46
ГЛАВА 3. ПРАКТИЧЕСКИЕ РАСЧЕТЫ НА СРЕЗ И СМЯТИЕ
§ 3.1. Основные понятия и расчетные формулы
Возникающие в сечении тп (рио. 3.1) касательные напряжения
(напряжения сдвига или среза) вычисляют по формуле тср— Q/Fcv.
Здесь Q — внутренний силовой фактор, называемый поперечной
силой. В данном случае Q = Р.
Условие прочности при срезе тср =
=.Q/FсР [Т'срЬ При статической на-
Рис. 3.2
грузке [тСр] = (0,6 -н 0,8) [сгр], где [ор] — допускаемое напряже-
ние на растяжение для того же материала.
Напряжения смятия осм возникают по площадкам контакта
между поверхностями отверстий и соединительных элементов.
Условие прочности на смятие- crCM = P/iFCM [<тсм], где P/i —
нагрузка, приходящаяся на одну
соединительную деталь; [осм]— р
— допускаемое напряжение на —
смятие; [осм] = (1,7 -ь 2) [ор];
Fcm—расчетная площадь смя-
тия.
При контакте по цилиндри-
ческой поверхности (по поверх- ис- 3 3
ности полуцилиндра) FCM услов-
норавна площади-проекции цилиндрической поверхности контакта
на диаметральную нлоскость(рис. 3.2): FCM = d6.
При контакте по плоскости (рис. 3.3) FCM = tb.
Здесь b — размер шпонки в направлении, перпендикулярном плос-
кости чертежа.
При различной толщине соединяемых, деталей в формулу под-
ставляется 6min ИЛИ (mln.
47
$ 3.2. Расчет заклепочных соединений
Пример 3.1. Проверить прочность заклепочного соединения
(рис. 3.4), если [Стр] =- 1400 кгс/см*, [тср1 > 1000 кгс/см*, [стсм1 =*
— 2400 кгс/см®.
Решение. 1. Вычисляем напряжение в листах по ослаблен-
ному сечеиию 1 — 1. Предварительно определяем площадь нетто
сечения:
26.-1,2—-2,3.3.1,2 «22,9 см®;
ор = = 1400 кгс/см® = (Ор).
Рис. 3.4
2. Проверяем прочность заклепок на срез, учитывая, что заклеп-
ки двухсрезные (А = 2):
тер = р/а^2 = “ 640 кгс/см2 <
Здесь i — число заклепок по одну сторону стыка.
3. Проверяем прочность заклепочного соединения на смятие;
(учитываем, что 26, > 61):
Р 32-10® 1АОА , 2 г 1
= idSl= -672,-371,7 = 1930 кгс/см® < [a«J.
Следовательно, прочность соединения обеспечена.
Пример 3.2. Стержень из двух равнобоких уголков (рис. 3.5),
растянутый силой Р = 30 тс, прикреплен к фасонному листу тол-
щиной 6 — 12 мм заклепками диаметром d = 20 мм. Материал —
сталь Ст. 2.
48
Подобрать профиль уголков и определить необходимое число за-
клепок в соединении, если [ор] = 1400 кгс/см2, £тср1 — 1000 кгс/см2,
[асм1 = 2800 кгс/см2.
Решение. 1. Подбор сечения стержня. В опасном сечении
/—/ уголки Ослаблены отверстиями. Поэтому расчет ведем по ГНетто-
Необходимая рабочая (нетто) площадь сечения уголков
FMno = Р/[стр] = 30 • 10*/1400= 21,4 см2.
Площадь сечення /^брутто уголков будет несколько больше. Поль-
зуясь таблицей сортамента, выбираем уголок 80 х 80 х 8. Тогда
F6p « 12,3 • 2 - 24,6 см2.
Проверяем напряжения в сечении
/—/ стержня:
_ Р
24,6 — 2 • 2,0 • 0,8
*= 1400 кгс/см2.
2. Определение числа заклепок из ус-
ловий прочности на срез и смятие:
а) допускаемое усилие на одну заклеп-
ку из условия прочности на срез (заклеп-
ки двухсрезные k — 2)
[QcpT = (TcpJ k = 1000 • =
= 6280 кгс;
б) допускаемое усилие на одну заклеп-
ку из условия прочности на смятие
[Qcm] = [OcmJ Fck = 2800 - 2,4 = 6730 кгс,
где FCM= bd = 1,2 2 — 2,4 см2 (толщина
косынки меньше удвоенной толщины полки уголка, поэтому рас-
четная площадь смятия определяется по толщине косынки).
Необходимое число заклепок определяем из условия прочно-
сти на срез, так как [Qcp] < [QCM], i =. =, » 4,78; при-
нимаем / = 5.
30 • 10»
Задачи для самостоятельного решения
3.1. Определить необходимое число заклепок в соединении
(рис. 3.6), если [тсг1 = 1000 кгс/см2 н [стсм] — 2800 кгс/см2.
Ответ: Трн заклепки.
3.2. Подобрать сечение стержня из двух иеравнобоких уголков,
прикрепленных к фасонке и растягиваемых силой Р — Збтс, и опре-
делить необходимое число заклепок, если [Стр] = 1400 кгс/см2,
49
диаметр заклепки d = 20 мм; [тср] ~ 1000 кгс7см2; [<тсм1 =
== 2800 кгс7см2; толщина фасонного лцста (косынки) 6 ='12 мм.
§ 3.3. Расчет сварных соединений *
Сварное соединение прямым стыковым швом, нагруженное рас- <
тягйвающей hjjh сжимающей силой, независимо от способа подго- .
товки кромок соединяемых листов (рис. 3.7), рассчитывают на рас- ?
тяжение (или сжатие) по формуле аэ= Р/Ь8< [аэ] .
Допускаемое напряжение [аэ1 (при растяжении [сгэ]Р и при ежа- 1
тин [оэ]с)для сварного шва зависит от допускаемого напряжения
для свариваемых деталей, способа
сварки и марки электродов.
РГ жч I р
Рис. 3.7 Рис. 3.8*
Соединения валиковыми (угловыми) швами рассчитывают на?
срез. Например, для соединения лобовыми валиковыми швами
р '
по рис. 3.8, а условие прочности имеет вид тэ = л- а С [Ы- -
Расчетная толщина шва для всех валиковых швов т = 0,7А;
(рис. 3.8,6) в предположении опасности разрушения шва по,;
биссекторному сечению. Допускаемое напряжение на срез для
сварного шва [тэ] зависит от тех же факторов, что и [стэ]. •
* Фундаментальное изложение этого вопроса можно найтн в учебнике!
Г. А. Николаева «Расчет сварных соединений и прочность сварных кон-а
струкций».—М.: Высш, школа, 1965. ' :>
50
(рис. 3.10) условие прочности тэ=
Для фланговых швов (рис. 3.9) условие прочности
Тэ = 2 • 0,7Л/ф^^э^'
Для комбинированного соединения валиковыми лобовыми, флан-
говыми и косыми швами
= P/0,7feL^[T3], где
£ — общий периметр ва-
ликовых швов.
Пример 3.3. Опреде-
лить требуемые длины
фланговых швов, соеди-
няющих уголок с фасон-
ным листом (рис. 3.11).
Толщина (катет) шва
одинакова со стороны
обушка и пера и равна
толщине полки уголка: k = 10 мм, допускаемое напряжение для
шва на срез [тэ] = 100 МН7м2.
Решение. В рассматриваемой задаче швы со стороны обушка
и со стороны пера нагружены неодинаково, очевидно, сильнее на-
гружен шов со стороны обушка.
Из условия равновесия легко получить величины сил, действую-
щих на шов у пера Рп и у
обушка Ров:
Р =P-^i-' Р . — р °2
t'n—r а , /'ов — г а .
При одинаковой толщине
швов их длины относятся так
же, как и передаваемые эти-
ми швами усилия, т. е.
/n = L^-; /o6 = L^,
гДе L — суммарная длина обоих
Из условия прочности
Р 160 • 10»
0,7к [тэ] ~ 0,7 • 1,0 10-2 • 100 • 10е
1П = 230 •
швов.
L
® 230 • 10“3 м = 230 мм;
64 мм; /об = 230 • ~ 167 мм.
120
Размер at— расстояние от обушка до центра тяжести профиля,
взято по таблице ГОСТ 8509—72; там это расстояние обозначено г0.
Пример 3.4. Стальная полоса А приварена к листу В фланго-
выми швами и прорезным швом (рис. 3.12). Определить длину про-
резного шва, если [тэ1 = 1000 кгс/см2; Z = 100 мм.
' 51
Решение. Определяем усилие, которое воспринимают флан-
говые швы: -
Рфл = 2/. 0,7/с[тэ] = 2 - 10 - 0,7 - I - 1000 = 14000 кгс.
Усилие, воспринимаемое прорезным швом,
Л,р = Р — РфЛ = 24 000—14000= 10000 кгс.
Длина прорезного шва
. _ Рпр юооо
- д[тэ| — 2 • 1000 е
= 5 см = 50 мм.
Рис. 3.12.
Задачи для самостоятельного решения
3.3. Стык листов перекрыт двумя
периметру к листам сварными швами
накладками, приваренными по1
толщиной k =* 10 мм (рис. 3.13).1
Определить длины /ф флан-1
говых .швов при [тэ] «J
= 800 кгс/см2. I
Ответ. = 170 мм j
3.4. Труба А плотно встав»!
лена одним концом в трубу!
В и приварена к ией по п«4
Рис з ]3 риметру сварным швом толе
щиной k — 8 мм (рис. 3.14)3
Определить расчетные напряжения в сварном шве. 1
Ответ. Тэ = 410 кгс/сма.
52
3.5. Швеллер приварен к листу двумя фланговыми и одним
прорезным швом (рис. 3.15). Толщина фланговых швов равна тол-
щине 6 стенки швеллера.
Определить длины фланговых швов (/ф) н прорези (/пр), если
[тэ] = 960 кгс/см2 и допускаемое напряжение на растяжение для
швеллера [а] = 1600 кгс/см2.
Р-7,2Ю*кес
Рис. 3.14
Рис. 3.16
Указания. Расчет выполнить из условия равиопрочиости сварных
швов и привариваемого швеллера. Начать с определения силы Р, допускае-
мой из условия прочности швеллера иа растяжение. Затем найти величину
/ф — /пр, исходя из условия, что в сечеиии 1—1 швеллера действует усилие,
допускаемое по прочности этого ослабленного, сечения.
Ответ. “ 388 мм; = 369 мм.
Ф пр
ГЛАВА 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ *
§ 4.1. Основные понятия и зависимости
ч
К геометрическим характеристикам поперечного* сечения бруса
относятся: площадь, осевыё и полярный моменты инерции, осевые
и полярный моменты сопротивления, а также статические моменты
и центробежные моменты инерции сечения.
1) Статические моменты плоских сечений.
Статическими моментами сечения относительно
координатных осей г, у называют интегралы вида (рис. 4.1)
5г = [ydF — Fyc, Sy =\zdF = Fzz,
*См. об этом также учебное пособие Б, А. Ободовского, В. В. Сушева,
1972МеТ75ЧвСКИе хаРактеРистикк плоских сечеиий».— М.: Высш, школа.
53
где гс, у, — расстояния от центра тяжести сечения соответственно 1
до осей Оу и Oz. 1
Статический момент плоского сечения относительно любой цент- I
ральной оси равен нулю. ' |
2) Моменты инерции: осевые (экваториальные), полярный и цен- |
тробежщяй. 1
а) Интегралы вида Jz=\y2dF, Jy=\z2dF называют осе- j
F F I
вы ми, или экваториальными моментами инерции 1
сечения относительно оси г'или у (см. рис. 4.1). j
б) Интеграл вида Jр ~ § р2dF называют полярным мо- j
F
ментом инерции сечения отно-
сительно точки О (см. рисунок 4.1).
в) Интеграл вида Jzy = § zydF
F
называют центробежным момен-
том инерции сечения относитель-
но осей г и у.
3) Некоторые свойства моментов
инерции.
а) Сумма осевых моментов инерции
сечения относительно двух координат-
ных осей равна полярному моменту
инерции относительно начала коорди-
нат J„ = Jz 4- Jу.
б) Момент инерции сложного (составного) сечения равен алгебра-
ической сумме моментов инерции составляющих сечения частей.
в) Осевые и полярный моменты инерции сечения — величины су-
щественно положительные; центробежный момент инерции может
быть положительным, отрицательным и, для некоторых осей, рав-
ным нулю. ' j
г) Если сечение имеет ось симметрии, то центробежный момент-
инерции относительно этой оси и ей перпендикулярной равен;
нулю. 4
4) Параллельный перенос осей. з
Момент инерции сечения относительно любой оси, проведенном
параллельно центральной, равен моменту инерции относительно!
этой центральной оси плюс произведение площади сечения на „квад-4
рат расстояния между осями (рис. 4.2): JZl = Jz-\- a2F. Аналоя|
гично JUi = Jy + b2F. |
Для центробежных моментов инерции — Jzy + abF. 1
Величины a, b должны быть подставлены со своими знаками,1
•определяемыми из условия, что они представляют собой коор'динатьп
начала новой системы осей в старой системе координат. |
5) Поворот координатных осей. 4
54
Если известны моменты инерции сечения Jz, Jy, Jzy относитель-
но осей Ог, Оу, то моменты инерции относительно осей Ozlt 0ylt
повернутых иа угол а по отношению к исходным осям (рис. 4.3),
определяются по формулам = Jzcos2a 4-JySin2a —J^sin 2а;
Jyi == Jzsin2 a + Jy cos2 a + Jzy sin 2a; Jz,y, = -2 2 — sin 2a +
4- Jzy cos 2a.
6) Главные оси инерции. Главные моменты инерции.
Главными осями инерции (или чаще просто глав-
ными осями) называют две взаимно перпендикулярные оси, относи-
тельно которых центробежный момент инерции равен нулю, а осе-
вые моменты приобретают экстремальные значения (max, min).
Если главные оси проходят через центр тяжести фигуры, они на-
зываются главными центральными осями
и н е р ц и и.
Главные моменты инерции вычисляют по формуле
А. 2 = Jmax = J-±+h ± |К(^-^)2 + 4^.
min ч z z
Положение главных осей инерции находят из следующих зави-
симостей:
tg al = J zylij У ^max); tg CCj = J zyl(J у — J min).
Можно также пользоваться формулой tg2ali 2.= 2</XF/(JF— Jz).
Углы a1( a2 отсчитывают от положительного направления оси Z,
причем при a1(S > 0 угол откладывают против часовой стрелки, и по
часовой стрелке при а£,2< 0.
Заметим, что |aj— а2|=90°.
Приводим таблицу значений моментов инерции некоторых часто
встречающихся сечений. у • '
бб
Таблица 4.1. Значения моментов инерции наиболее употребительных
сечений относительно центральных осей
56
окончание табл. 4.1
$ 4.2. Вычисление геометрических характеристик
. плоских сечений
Пример 4.1. Определить положение главных центральных осей
и вычислить главные центральные моменты инерции сечения
(рис. 4.4).
Решение. Найдем положение центральной оси г—г сечения-
Отсчет координаты у0 ведем от вспомогательной Оси z3—z8
_ nR*R —яг* (R —с) R3 — r*(R — с)
F — — = R’ —г* в
20»-10*. 15. .rf. ?
20»— 10» — СМ‘
Моменты инерции фигуры относительно осей z — г и у—у
найдем как разность моментов инерции большого и малого круга.
Момент инерции большого круга относительно своей центральной
оси — Zx Jzt = л£>4/64 = п/?4/4, относительно оси г — z Jx=*
Аналогично момент ииерцин малого круга относительно оср
z — Z
•Jz = Ji-j" = -5-.20* + «-20«(21,7 —20)8— : •;
_Л . Ю4 — п102 (5 + 21,7 —20)2 = 107,4 - 103 см4;
= JL#‘~--lr4 ^ — (го4 — 104)-~ 117,8- Wcm4.
Пример 4.2. Вычислить момент
инерции сечения (рис. 4.5) относи-
тельно главной центральной оси г.
Р’е ш е н и е. Сначала находим
момент инерции Jбрутто, т. е. без
учета ослабления сечения закле-
почными отверстиями.
Рис. 4.4
По таблице сортамента находим: площадь уголка 80 х 80 х
X 8 мм Fyr = 12,3 см2; момент инерции этого уголка относитель-
но оси г0—г0, проходящей через его центр тяжести параллельно
полке (см. верхнюю часть рисунка), JZ(= 73,4 см4; расстояние центра
тяжести уголка от грани полки ус = 2,27 см. Расстояние центра
„ „ 105
тяжести уголка от горизонтальной главной оси г — г а = ------
— 2,27 = 50,23 см.
Момент инерции вертикальной стенкн относительно оси г — г
J 1 • 1053 Г\С С IA3 4
"Z стенки — |7) — 96,5 • 10 СМ .
58
Момент инерции четырех поясных уголков относительно той
же оси Луголков = 4 [73,4 -J- 12,3 • 50,232] = 124,4 • 103 см4.
Момент инерции двух пар поясных листов относительно той же
оси (каждую пару листов рассматриваем как один прямоугольник)
Глистов = 2^^ + 18 • 2 . 53,52] = 206 • 1С3см4;
Лбрутто = (96,5 + 124,4 + 206) 103 = 426,9 • 103 см4.
Чтобы получить ^гнетто, надо из Jбрутто вычесть момент инер-
ции прямоугольников, изображающих заклепочные отверстия.
Момент инерции четырех прямоугольников (вертикальных отверстий
в листах и горизонтальных полках уголков)
отверстий - 4(Щ^ + 2 2,8.53,12) = 63,2 • 103 см4;
Jг нетто = «7в брутто г отверстий = (426,9 ' 63,2) 103 =
= 363,7 • 103см4.
Цример 4.3. Найти положение главных центральных осей и вы-
числить главные центральные моменты инерции сечения (рис. 4.6).
Решение. По таблице сор-
тамента находим площадь, момен-
ты инерции и координаты центра
тяжести каждого элемента. Для
швеллера № 22а: Fm = 28,8 см2;
z0 = 2,46 см; JZt = 2330 см4; Jy =
= 187 см4.
Для уголка 100 X 100 X ‘10 :
Fyr =19,2 см2; у0 = 2,83 см (по
сортаменту — г0); 7max = =
= 284 см4; Jmin = Jу = 74,1 см4;
Л2 = Jyi = 179 см4.
Для нахождения положения
центра тяжести фигуры в качестве
вспомогательных выбираем цент-
ральные оси ?! и уг швеллера.
Относительно этих осей статичес-
кие моменты швеллера равны ну-
лю, и вычисление координат цент- Рис. 4.6
Ра тяжести сечения упрощается.
Статические моменты сечения относительно осей гг и уг
S2l = Fyrz/2 = 19,2^—у0) = 19,2^11—2,83) = 157 см3;
5,, = Fyrz2 = 19,2 (z0 + уп) = 19,2 (2,46 + 2,83) = 102 см3.
Площадь составного сечения F = Fyr + Рш = 19,2 + 28,8 =
= 48 см2.
59
Координаты центра тяжести составного сечения относительно
осей г1( У!
3,28 <м-, zc~ ^‘ = ^-2,13 см:
Определяем осевой и центробежный моменты инерции состав*
кого сечения относительно центральных осей tc, ус. Определим коор-
динаты центров тяжести частей сечения в осях гс, уе.
Для швеллера ai~ —2,13 см; Ьг= ус=°—3,28 см. Для
уголка а^— 3,17 см; Ь2— 4,89 см.
Осевые моменты инерции относительно оси гс; для швеллера
З1^ = Jltt + Ь[РШ ° 2330 + 3,28» • 28,8 «= 2628 см*;
для уголка 3"с = 3{[ + bjFyr = 179 4- 4,89* • 19,2 = 640 см*;
для всего сечения Jtc = J[c + 3"е ~ 2628 4- 640 = 3268 см*.
Осевые моменты инерции относительно оси ус:
для швеллера Зус = Зу, 4- d%Fm = 187 + 2,13* • 28,8--= 316 см*|
для уголка Jyc 3* + a^Fyr = 179 4- 3,17* • 19,2 = 371 см*;
для всего сечения 3Ус = 31Ус 4- Jyc ~ 316 + 371 = 687 см*.
Вычислим центробежный момент инерции относительно осей
Zc, Ус-
для швеллера = ахЬгРт = (—2,13) • (—3,28) • 28, = 200 см*;
для уголка 3^с = = 7?1а1С 2 — • + аА^уг =*
= + 3,17 <4,89 • 19,2 = 40"’,5 см«;
для всего сечения Зг^с = 31г^с +-3^с = 200 + 402,5 = 602,5 см*,
Примечание. Приведем некоторые дополнительные пояснения/;
касающиеся определения .центробежного момента инерции. 1
Для уголка оси zs и у3, параллельные его полкам, ие являются главными,.^
Для нахождения J2>yt> использована формула изменения центробежного мо-j
мента инерции при повороте осей (см. § 4.1), при этом в качестве исходны»!
приняты главные центральные оси уголка (оси и, о — см. рис. 4.6). Кроме]
того, учтено, что угол, составляемый осями и, г, равен 45 , /«„ = 0. При*
вычислении центробежного момента инерции нередко допускают ошибку]
в знаке, поэтому наряду с внимательным отношением к примеиеиню правила;
знаков следует контролировать знак центробежного момента ииерпии, ори-|
еитируясь на расположение сечения относительно осей. I
Так, в рассматриваемом случае вполне очевидно, что Jz,y> > 0. Дей-]
ствительно, существенно большая часть сечения расположена в / и III ква-i
дрантах, для точек (площадок), находящихся в этих квадрантах, произвел
деиия координат (z3y3) положительны. Таким образом, при суммирование
величин г3Уг<№ по всей площади сечеиия положительные слагаемые в сумм!
дают ббльшую по модулю величину, чем отрицательные. ’
Определим положение главных центральных осей инерции се-
чения:
tg2“i 2 = = -°>465;
2аг = —25°; а\ = — 12° 30', а2 = —102° 30'.
Главные центральные оси 1, 2 показаны на рис. 4.6.
Вычисляем главные центральные моменты инерции:
Л. 2 = ^4^ ± + ;
Л «= Лп« = 3268 + 687 + у /(3268 — 687)2 + 4 (602,5)2=3407,5 см4;
Jt - Jmin « 3268. t887 — -L/(3268 — 687)2 + 4 (602,5)2 = 547,5 см4.
Задачи для самостоятельного решения
4.1. Вычислить моменты инерции сечения (рис. 4.7) относи-
тельно осей х — х и — хи f
Ответ. J. = 832 см4, J, = 5632 см4.
Рис. 4.7 Рис. 4.8
4.2. Определить положение центра тяжести сечения (рис. 4.8)
н вычислить главные центральные моменты инерции.
Ответ. Jmax = 3915 см4; Jmin = 2341 см4.
4.3. Найти положение главных центральных осей и вычислить
главные центральные моменты инерции сечения (рис. 4.9).
Ответ, а = —ЗГ 30'; «=’1224 см4; J . = 288 см4.
шаЛ 111111
4.4. Найти положение главных центральных осей и вычислить
главные центральные моменты инерции сечения (рис. 4.10).
Ответ. ах = —33° 15'; Jmax = 4071 см4; Jmin = 1634 см4.
61
4.5. Найти положение главных центральных осей и вычислить
главные центральные моменты инерции сечения (рис. 4.11).
Ответ, а, = 17°; = 3735 см4; Jmln = 854 см4.
Hid Л ' ИЦ И
4.6. Для поперечного сечения элемента литой станины (рис. 4.12)
определить положение главных центральных осей и вычислить глав-
ные центральные моменты инерции.
Указание. Расчленить заданное сечение иа ряд простых фигур, прене-
брегая тем, что вершина треугольника несколько срезаиа.
Ответ. ах = —34° 22'; Jmax = 1000 см4; Jmin = 292 см4.
Рис. 4.12
Рис. 4.13
4.7. Определить -центробежный момент инерции относительно
осей zy площади сектора, представляющего собой четверть круглого
сечения радиусом 7? (рис. 4.13).
Ответ. ]гд = 7?4/8.
Для определения геометрических характеристик плоских сечений мо-
жет быть использована программа, приведенная в приложении V.
В программе использованы следующие идентификаторы: площади сече-
ний Fl, F2 ... , осевые и центробежные моменты инерции этих сечений 1X1,
1У1, 1ХУ1, 1X2, 1У2, 1ХУ2 и т. д., координаты центров тяжести по отно-
С2
шеиию к вспомогательной системе отсчета Х[1], У [11, координаты центра
тяжести всего сечения ХС, УС, моменты инерции сеченяя относительно цен-
тральных осей IXC, 1УС, 1ХУС, главные центральные моменты инерции
1И, IV, угол наклона главных центральных осей АЬФА.
Все необходимые данные выводятся на печать.
ГЛАВА S. КРУЧЕНИЕ
§ 5.1. Основные понятия и зависимости
При работе бруса на кручение в его поперечных сечениях воз-
никает только один внутренний силовой фактор — крутящий
момент Мк.
В любом поперечном сечении бруса крутящий момент численно
равен алгебраической сумме внешних скручивающих моментов,
приложенных по одну сторону от рассматриваемого сечения.
Условие прочности при кручении бруса" круглого (сплошного
Мк
или кольцевого) поперечного сечения имеет вид ттах = =- [т],
где Ттах — наибольшее касательное напряжение, возникающее
в опасном сечении бруса; Мк — крутящий момейт в опасном сече-
нии бруса; [т] — допускаемое напряжение при кручении; Wp—
полярный момент сопротивления сечения; *WP = ~ 0,2d3 для
круглого сплошного сечения и Fp = ^-(1—с4) « 0,2£>3(1—с4)
для кольцевого сечения. Здесь d — диаметр сплошного сечения;
D и d0 — соответственно наружный и внутренний диаметры коль-
ца; c = dnlD.
Угол поворота одного сечения относительно другого называется
углом закручивания участка бруса между этими сечениями.
Угол закручивания бруса (участка бруса) определяется по фор-
Г
муле (рад) <р = } .
о р
Здесь GJp— жесткость сечения при кручении; G — модуль сдвига;
Jp— полярный момент инерции сечения.
Для круга Jp = ~^ 0,Id4.
Для кольца
При Мк = const, Jp — const угол закручивания участка дли-
ной I определяется по формуле <р = MKllGJp.
Условие жесткости при кручении имеет внд max <p0 = MK[GJP
г , 180" мк • 100
['I о] ИЛИ max Фо = — • — «С [<Ро1 •
63
В первой из приведенных формул максимальный относительный
угол закручивания max <р0 и допускаемый относительный угол за-
кручивания [<р0] в рад/м; Мк в Н • м; G в Н/м2 и Jp в м4.
Во второй формуле: тах<р0 и [<р01 в град7м, Мк в кгс • см; G в
кгс/см2 и Jp в см4.
При определении диаметра вала из условий прочности и жестко-
сти из иайдейиых двух значений диаметра выбирается большее.
Указание: Полученные по расчету значения диаметров следует округлять
до чисел, оканчивающихся на 0, 2, 5 или 8 (в мм);
При расчете валов зачастую бывают заданы передаваемая мощ-
ность N (в Вт или кВт или л. с.) н угловая скорость ® (рад/с) или п
(об/мин). При этом передаваемый валом вращающий момент опреде-
ляется по одной из следующих формул: SR — N/a>, где SR в Н • л»
N в Вт, &> в рад/с; или SR = 71620 N/n, гДеЯЙ в кгс «см, N в л. с.»
п в об/мин; или SR =» 97380 N/n, где SR в кгс • см, N в
кВт, п в об7мии.
, § 5.2. Расчеты не прочность и жесткость
при кручении бруса круглого поперечного сечения
Пример 5.1. Построить эпюры крутящих моментов и углов пово-
рота поперечных сечений (Мк, <р) для бруса, схема нагружения кото-
рого показана на рис. 5.1, а.
Решение. 1. Построение
эпюры Мк.
Разбиваем брус на два участ-
ка: СВ и ВА.
Участок СВ (0
1,50. Начало координат по-
мещаем в точке С.
Определяем ЛТК как сумму
Рис, 5.1
внешних моментов, приложен-
ных слева от произвольного по-
= 2ml — уравнение прямой, па-^
раллельной оси эпюры. ;
Участок ВА (0 /),’
Начало координат помещаем в|
точке В. 4
Выражаем крутящий момент как сумму моментов, приложен-^
ных слева от сечения: м"^т(1 — х3) — уравнение прямой. На-,
ходим две точки прямой: мУх,-о e nil', =* 0, ’
Эпюра ЛГК изображена иа рис. 5,1,6,. i
2. Построение эпюры <р.
а
А
S
64
Участок СВ. Определяем угол поворота произвольного се-
чения с координатой ф7 = M^/GJ р = Imlxi/GJ р — уравнение
прямой.
В крайних сечениях участка <рс = <р* 0 =* 0 (в защемлении);
<РВ= <=1.5/= 3m/Wp.
Участок В А. Угол поворота любого сечения второго участка
определится как сумма угла поворота фв сечения В и угла поворота
рассматриваемого сечения относительно сечения В.
f тх2
= ф + I тх*^ _ ф 4 (эпюра — квадратная парабола).
* J GJ р ° 6\JJ р
г, г п 3ml2 г г
В крайних сечениях участка <рв = ф"=0 = ; фл = Ф“=/ =
, ml2- 3,5ml*
+ 2дГр ~
Эпюра у представлена на рис. 5.1,в.
IV
Й0 п^’260оВ/ии
М^12лс.
//
А I
-
/
______ n,‘1W об/мин
N^Zdne.
in vi
n^ZW) об/мин
п5-ЗбО об/мин
Рис. 5.2
Пример 5.2. Вал I (рис. 5.2) , соединенный муфтой А с валом II
и получающий от двигателя мощность 40 л. с., передает валу
III мощность Ns= 28 л. с. и валу IV — 12 л. с.
Вал Шв свою очередь передаетвалу V — А/а= 14 л. с.; осталь-
ная мощность, полученная этим валом, передается через муфту
В валу, который на рисунке не показан.
Определить диаметры валов из расчета на прочность и жесткость,
если [т1 = 600 кгс./см2. [ф01 ~ 0,3 град/м, модуль сдвига G = 8х
X 105 кгс/см2.
Потери в ременных передачах и подшипниках не учитывать.
Решение. Вал /. Nj.— 40 л. с.; nt— 140 об/мин. •
МО
G5
Крутящий момент в поперечных сечениях этого вала, равный
передаваемому валом вращающему моменту,
Мк, = = 71620 — = 71620= 20400 кгс см.
’ 1 tit 140
Требуемый диаметр вала (на участке между шкивами) из ус-
ловия прочности находим, применив формулу Wp, ~ 0,2dJI>-~,
, >/ Л4К1 з/ 20400 к
о.куда У |/ о^Гббб = 5’53 см-
т Л i о 180 ^к!100
Го же из условия жесткости Jpi 0,1^^— ~q >
*/ 180Л4к1100 if iso . 20400 • 100 о о
откуда У 01п6(фо| - У од.3,14-8 • 105-0,3~ 8,3сМ>
Принимаем d4 — 85 мм.
Вал II. N2 = 12 л. с.; п2 = 140 об/мин; /Ик2 = 71620-jp =•
-= 71620-^ =6110кгс • см.
140
гл л - -,3/ 6110 о _
Из условия прочности d2 > у оТТбОО ~ 3’' см’
Из условия жесткости
У 0>1 - ЗЛ4 - 8 • 10ч .„0,3 ~ 6,18 Ш'
Принимаем d2 = 62 мм.
В поперечных сечениях вала III (на участке между шкивами)
возникают крутящие моменты, соответствующие мощности =«
== 14 л. с., п3 = 240об/мин. При этом
Мкз = 71620 ~ = 4170 кгс • см.
Из условия прочности d3> у 02. ббо = 3’^8 см-
Из условия жесткости d3 > у б~1 ~ 3~14 ~ 8 0.16s - 03 = 5,62 СМф
Принимаем d3 = 58 мм. Вал IV. N4 = 12 л. с.; п4 =
12
— 260 об/мин; /ИК4 = 71620= 3300 кгс - см.
По результатам расчетов на прочность и жесткость, выполняе-
мых аналогично предыдущему, принимаем d4= 55 мм.
Вал V. Л(5=14л. с.; п& = 340об/мин; Л4кз = 71620^- =
~ 2950 кгс • см..
Не приводя расчетов, указываем окончательный результат d6=
= 52 мм.
Расчеты для валов IV и V рекомендуем выполнить самостоя-
тотьно.
66
Задачи для самостоятельного решения
5.1. Построить эпюры крутящих моментов и углов поворота по-
перечных сечений для бруса, нагруженного распределенными скру-
чивающими моментами (рис. 5.3).
3ml 28 ml*
Ответ, a) max Мк = ; <ртах = — .
„ 39 ml*
б) max Л1к = 5ml; <ртах = — •
5.2. Сплошной вал диаметром 90 мм заменяют валом кольцевого
сечения, у которого внутренний диаметр на 10 % меньше наружного.
Определить наружный d и ткН-м/м 2ткН-м/м
внутренний d0 диаметры труб-
чатого вала при условии
сохранения прежнего коэф-
фициента запаса прочности.
Сравнить' веса сплошного н
трубчатого валов.
Ответ, d = 128 мм; <4 =
= 115 мм; отношение весов 2,58.
5.3. Два участка вала сое-
динены втулочной муфтой
(рис. 5.4). Не учитывая ос-
лабления вала и муфты шпо-
ночными канавками, опреде-
лить из условия равнопроч-
ности на кручение отношение наружного диаметра (£))» муфты
к диаметру (d) вала, если для материала вала тт — 200 Н/мм2, а для
материала муфты тт= 172 Н7мм2. Величину [п] для вала и муфты
принять одинаковой.
Ответ, 1,25.
Рис. 5.4
5.4. Три вала I, II, III, имеющие равновеликие площади по-
перечных сечений (рис. 5.5), [скручиваются .моментами ®/,
Определить величины SR/z, ®//z, если наибольшие
касательные напряжения, возникающие в поперечных сечениях
каждого из валов, одинаковы. Построить эпюры касательных
67
напряжений для всех сечений. Определить касательные напряже-
ния в точках внутреннего контура кольцевых сечений.
Ответ. = 1,12; й = 1,41.
= 0,2</S; Wpfr = 0,27«Р: Wpl[l = 0,43</s;
= т • 0.2rf3: =т .0,27d3; = т . 0,43</з.
Рис. 5.5
5.5. На вал передается ведущим шкивом от электродвигателя
мощность N = 60 л. с., при угловой скорости п — 300 об7мии.
Остальные четыре шкива передают рабочим машинам мощности
Nt, равные 20, 18, 12, 10 л. с. (рис-. 5.6). Где следует расположить
ведущий шкив (указать номер) и распределить потребляемые стан-
ками мощности по шкивам, чтобы требуемый диаметр вала был цаи-
М3*8кВт
М^ЗкВт
Рис. 5.7
3
Ведущий шкиб
меньшим? Построить эпюру крутящих моментов. Определить тре-
буемый диаметр d вала, считая его по всей длине постоянным, если
М = 300 кгс/см®.
Ответ, d — 50 мм.
68
5.6. Пройерить прочность и жесткость вала постоянного сече-
ния (рис. 5.7), если [т] = 200 кгс/см2, [<р01 = 0,4 град/м, G = 8 х
X Ю5 кгс/см2.
Ответ. ттах= 153 кгс/см2; <р0 — 0,35 град/м.
§ 5.3. Статически неопределимые задачи при кручении
Пример 5.3. Определить требуемый диаметр бруса (рис. 5.8,а)
из условий прочности и жесткости, если [т] = 400 кгс/см2, [<р0] =
- 0.25 град/м, G = 8 • 105 кгс/см2.
Решение. Отбрасываем заделку В и заменяем ее моментом
50?в (рис. 5,8, б). Сечение в заделке В не поворачивается, по-
. 0,5 , ®2 • 1,25 ®в • 2,5 п
этому Фв = --^—4- —----------------^ = 0,
откуда Жв = кф— ’25 = 22 кгс • м;
+ Жв — = 40 4- 22 —60 = 2 кгс • м.
Строим эпюру крутящих моментов (рис. 5.8,в). Из эпюры видно,
что максимальный крутящий момент возникает в поперечных се-
чениях среднего участка: Л4тах = 3800 кгс «.см.
Определяем диаметр из условия прочности
я -> 1/ Мт™ - 3800 -
d 2 -0,2 [т] ~ V 0,2 • 400 ~ 3,62 СМ-
Определяем диаметр из условия жесткости
«/ 180 • Мк • 100 у 3800 • 100 • 180 VTmn к тк
' G [фо] • л • 0,1 ~ V 8 • 105 • 0,25 • л 0,1 ~ и Ю90 — 5,75 см.
69
Принимаем наибольшее значение диаметра (с округлением)
d = 58 мм.
Пример 5,4. Определить реактивные моменты и построить
эпюру крутящих моментов для бруса постоянного сечения
(рис. 5.9,а).
Решение. Статика дает нам одно уравнение равновесия
0; ®л-|-®в= Ж +ml.
Для составления второго уравнения (уравнения перемещений)
мысленно отбросим одну заделку, например правую, и заменим
ее действие моментом ®в, равным искомому реактивному моменту
(рис. 5.9, б):
<ГВ = фд(ЭД) + <РВ(т1 > + (Рв(ЭДв) = 0,
Рис. 5.10
Л Ж/j Т mxdx mil ЯЯв^
где фв (®) - gy- ; фВ(т0 — J - 20/р ; Ф^Жв) - — Qjr-.
о
~ Ж/j ml2 ' ЯНв^ л
Тогда g77 + 2gT;-g77 = 0’ .
_ ml .. ЯМ,, 100 - 3 , 500 - 1
откуда Жв : у + — = —2-------1---— = 317 кгс • м.
Из уравнения равновесия находим = 483 кгс • м. Строим
эпюру Л4К.
На левом участке (0^х^/2) Мк=Жл— tnx\ /Икх=о = Жд —
= 483 кгс • м; Moli, = Жд — tnli — 383 кгс • м.
На правом участке (1г х /) /Ик — Жд — тх — Ж; М"px‘~it =»
= —117 кгс • м. = —317 кгс • м = —Жв.
Эпюра крутящих моментов приведена на рис. 5.9, в.
Пример 5.5, Дюралюминиевая трубка и стальной валик жестко
заделаны одним концом, а на другом конце соединены между собой
диском А (рис. 5.10). Определить допускаемое значение момента SR,
приложенного посередине трубки. Принять для стали [т]ст=
= 900 кгс/см2; для дюралюминия [т!д = 600 кгс/см2; Ост= ЗСЯ —
- 8,1 • 10’’ кгс'см2.
70
Решение. Силы взаимодействия между диском А и валиком
приводятся к скручивающему моменту X; такой же по величине,
но противоположно направленный момент действует на правый
торец трубки. Схемы нагружения валика и трубки показаны на рис.
5.11, а, б. Величина момента X определится из уравнения переме-
щений, выражающего условие равенства углов поворота правых
торцовых сечений валика и трубки:
_ - Х2а __ ®а Х2а
вал <₽Л тр’ G J G J G J
ист'/рвал ’-*д',ртр ид',ртр
1 — —— I
\ 2d !
Здесь J - ™*4 • / - n <2d>4
J р вал - , J р тр---------
175
16 -
После подстановки получаем
2X ,
З^рвал G 275
Д KJ "р вал
2Х ,
s
«1
J -512ЯЙ ’ 7рвал-
------------
G
иц jg Jр вал
Отсюда X = = 0,1075®.
Эпюры крутящих моментов для
валика и трубки представлены на
рис. 5.11, в, г.
Условие прочности валика твал =
вал _ 0,1075® ,
IF “ лЯЗ 1Т1СТе
w р вал 31(1
16
Огсюда |Я|в., = г£ . _ |3 120 кгс . см.
Для трубки опасными являются поперечные сечения ее левого
участка; условие прочности ^при
_ max Мк тр
ТтР
WO тр
И7 _ dPTp _ 175 ,а
кК₽тр~ d ~ 512ЯЙ,
0,8925® г ,
w— <Мд-
512 ndS
Отгтппа ГЯВ1 — 175~_^ 1Т|Д _ 175 • 3,14 • 23 - 600 С„СА
Д 1®1]тр 512 о,8925 512 .0,8925 5760 кгс • СМ.
Таким образ&м, допускаемый внешний момент [®] = [®]тр=
— 5760 кгс см определяется прочностью трубки. При нагружении
конструкции моментом, равным допускаемому, валик будет недо-
гРужен — наибольшие напряжения в его поперечных сечениях
71
, 13120 — 5760 , ллп, г с а, г\
будут на 13420— ’ 56 % ниже допускаемых. Отсюда не
следует, что диаметр валика может бйть уменьшен. Действительно,
если уменьшить d (жесткость валика), то трубка будет восприни-
мать большую долю внешнего момента (X будет меньше) и в резуль-
тате величина [SR1 станет меньше.
Задачи для самостоятельного решения
5.7. Определить угол поворота сечения I —I стального бруса
(рис. 5.12), если G = 8 • 105 кгс/см2.
Ответ. ф1_1 « 36 • 10“’ рад.
5.8. Концы двух трубок, стальной и медной, жестко соединены
между собой. Трубки нагружены скручивающими моментами,
как показано на рис. 5.13. Опре-
делить наибольшие касательные
напряжения, возникающие в попе-
речных сечениях трубок. Принять
GCT = 2GM.
Ответ. тм = 60 кгс/с^м2; тст ==
= 131 кгс/см2.
5.9. Определить потенциаль-
ную энергию деформаций бруса,
Рис. 5.12
жестко закрепленного обоими концами и нагруженного скручиваю-
Щи'м моментом ® (рис. 5.14).
Рис. 5.13
Рис. 5.14
5.10. Найти максимально допустимый момент SR, приложенный;?
к брусу в сечении С (рис. 5.15), если М = 900 кгс/см2. |
Ответ. [®] ~ 52 • 103 кгс • см. ।
5.11. Брус, закрепленный одним концом и удерживаемый двумя 4
1 ',п ими в виде полос, прикрепленных шарнирно по концам, скручи-1
72
вается двумя моментами 9R (рис. 5.16). Определить напряжения о
в поперечных сечениях тяг и наибольшие напряжения тшах в попе-
речных сечениях бруса. Тяги прикреплены к абсолютно жесткой
поперечине DE, жестко скрепленной с брусом. Принять Е = 2,5G,
I =* 10d.
Рис. 5.15 Рис. 5.16
§ 5.4. Кручение прямого бруса некруглого
поперечного сечения *
При кручении брусьев прямоугольного сечения угол закручива-
ния и наибольшие касательные напряжения вычисляются по форму-
лам <р = MKl/GJK; Tmax = MK/WK, где ттах—напряжение посере-
дине большей стороны прямоугольника.
Значения JK, IFK определяются по формулам JK = аб3й; IFK =
= ₽62/i.
Здесь b — размер меньшей, a h большей стороны прямоугольника.
Касательные1напряжения посередине меньшей стороны прямоуголь-
ника Определяются ПО формуле Ту = уТтах-
Коэффициенты а, р, у зависят от соотношения сторон и имеют
значения, приведенные в табл. 5.1.
Таблица5.1. Коэффициенты для расчета бруса прямоугольного
поперечного сечения
h Ъ 1 1.5 2 3 4 5 8 10 00
а 0,141 0,196 0,229 0,263 0,281 0,291 0,307 0,313 0,333
р 0,208 0,231 0,246 0,267 0,282j 0,291 0,307 0,313 0,333
У 1,0 0,859 0,795 0,753 0,745 0,743 0,742 0,742 0,740
* Подробно этот вопрос изложен, например, в таких книгах: Арутюнян
Н. X., Абрамян Б. Л. Кручение упругих тел.— М.: Физматгиз, 1963.—
686 с. Ободовский Б. А., Урбанская В. С., Урбанский Р. Е. Кручение не-
круглых валов.— М.: Высш, школа, 1974.— 228 с.
- 73
Брусья, имеющие поперечные сечения в виде уголков, тавров,
двутавров, швеллеров и т. п., рассчитываются на кручение по тем же
формулам, что и брусья прямоугольного поперечного сечения. При
этом геометрическая характеристика жесткости JK определяется ив
выражения Л — Л где 6, h — соответственно малая и
большая стороны каждого из прямоугольников, из которых со-
стоит сечение. Коэффициент т] зависит от формы сечения и равен
для уголкового сечения т] = 1; для двутаврового — т] = 1,2; для
таврового — т] = 1,15; для швеллерного — т] — 1,12.
Геометрическая характеристика прочности (момент сопротивле-
у2Л63
ния крученую) IFK определяется по формуле WK = —т----------=»
°тах
JK
= —т----, где 6тах—наибольшая из толщин прямоугольников, об-
^Ощах
разующих сечение.
При расчете на кручение брусьев с тонкостенными замкнутыми
профилями предполагается, что по толщине стенок касательные
напряжения распределены равномерно. Максимальное касательное
1 Мк
напряжение определяется по формуле ттах = -^р-ё— ,
2r0°tnin
где Fo— площадь, ограниченная средней линией профиля; 6min —
минимальная толщина
Угол закручивания
моменте определяется
стенки.
при постоянном по длине бруса жрутящем
, f ds
по формуле ф= I-g-,
s
где ds — элемент средней линии профиля. Интегрирование ведется
по всей длине средней линии профиля. В частном случае профиля
с постоянной толщиной стенки из предыдущей формулы следует
<р= Mk/s/4GF^6, где s — длина средней линии профиля.
Для тонкостенного кругового кольца (при отношении толщины
С1енки 6 к среднему диаметру Dcp кольца Fo = —
$ = лОср.
Методами сопротивления материалов можно рассчитать на проч-
ность и жесткость лишь валы, поперечные сечения которых имеют
форму круга или кругового концентрического кольца.
Теоретический расчет других поперечных сечений валов можно
осуществить только путем привлечения методов математической
теории упругости.
Большой вклад в создание эффективных методов решения задач
кручения валов произвольного поперечного сечения внесли совет-
ские ученые Н. И. Мусхелишвили, Д. И. Шерман, А. С. Космода-
мианский, А. Г. Угодчиков, Б. Л. Абрамян, Н. X. Арутюнян,
74
Ю. А. Амензаде, И. А. Бахтияров и др. В качестве примера приведем
результаты решения задачи кручения вала, поперечное сечение ко-
торого является эллиптическим с двумя круговыми отверстиями
(рис. 5.17, а). Полуоси эллипса обозначены соответственно а, Ь,
радиусы круговых отверстий — Rlt R2, расстояние между их
центрами равно 21. Крутящий момент в поперечном сечении вала —
Мк.
Задача об определении напряженного состояния такого вала
была рассмотрена ранее [221. Для одного из вариантов численного
расчета принято, что Ri= R2= R = 1; 21 = 3R; а = 3,5 R\ b =
= 2R.
Значения искомых напряжений хгх, хух приведены в табл. 5.2,
Таблица 5.2. Значения касательных напряжений в характерных точках
Сечение • Напряжения в долях т/К
А 1 в с о Е
Эллиптическое с двумя кру- говыми отверстиями т2х/Л1 0 —1,799 0 0 —2,54
1,126 0,017 1,593 1.847 0
Эллиптическое tzx/K% 0 • —1,508 0 0 —3,015
Хух/Кц 0,246 0,738 1,231 1,723 0
75
в которой также показаны аналогичные данные для вала без круго-
вых полостей, т. е. для эллиптического бруса без полостей; Klt
Ki— некоторые постоянные.
На основании анализа численных значений для касательных на-
пряжений (см. табл. 5.2) можно заключить, что в случае круговых
полостей в брусе имеет место некоторая концентрация напряжений
в точках А, В, С, Д. Наибольшее напряжение отмечается в точке Е.
Для вала с полостями напряжение в этой точке понизилось по срав-
нению со сплошным валом. Как установлено в данной задаче, на-
личие круговых отверстий, облегчающих конструкцию, оказывает
также разгружающее действие.
На рис. 5.17, б—д показаны поперечные сечения некруглых ва-
лов, часто встречающиеся в металлургическом машиностроении. Ре-
шения, такого класса задач кручения валов сложного поперечного
сечения приведены в упомянутом выше нашем учебном пособии.
Результаты решения представлены в виде эпюр напряжений,
графиков и таблиц, что удобно для практического пользования.
При решении задач широко применима ЭВМ.
Пример 5.6. Стальной стержень длиною I — 1 м прямоугольного
поперечного сечения размерами 2 х 6см нагружен по концам скру-
чивающими моментами 5R = 30 кгс • м.
Определить: 1) величину касательных напряжений посередине
длинной стороны (ттзх); 2) величину касательных напряжений
посередине короткой стороны (тх) и 3) угол закручивания стержня.
Решение. Отношение сторон прямоугольника -у = ^- = 3.
Выписываем' из таблицы значения коэффициентов а = 0,263;
₽ = 0,267; у == 0,753 и определяем геометрические характеристики
жесткости и прочности:
JK = abah = 0,263 • 23 • 6 = 12,64 см4;
WK = 0&2Л = 0,267 • 22 • 6 = 6,41 см3.
Максимальное касательное напряжение (посередине длинной
стороны) ттах = MK/WK = 3000/6,41 = 468 кгс/см2, где Мк =
Касательное напряжение посередине короткой стороны тг =
= УТтах = 0,753 • 468 = 352 кгс/см2.
Угол закручивания стержня
МК1 3000 . 100 _ поп_ . _0
JKG 12,64 • 8 • 10^ ~ 0,0295 рад 1,7 •
Пример 5.7. Стержень из швеллера № 22а скручивается момента-
ми 600 Н м, приложенными в его торцовых поперечных се-
чениях. Определить наибольшее касательное напряжение, возни-
кающее в поперечном сечении стержня.
Р е ш е н и е. По таблице сортамента (ГОСТ 8240—72) устанав-
ливаем размеры сечения (рис. 5.18,а). Стенки йс= 220 мм, 6С=
= 5,4 мм; полки hn= 81,6 мм (из полной ширины полки вычитаем
76
толщину стенки), бп = 10,2 мм. Определяем геометрическую харак-
теристику жесткости при кручении (принимая т] = 1,12 поданным,
приведенным в этом параграфе):
Л = Н | J /i63 = 1,12 • 1 (220 • 5,43 + 2 • 81,6 • 10,23) =
= 77,4 103 мм4 = 77,4 • 10~9 м4.
Геометрическая характеристика прочности
= J* _j_ 77,4 • 10~9___6 7Q . 1 0"® м3
пбщах “ !’12 • 10-2 • 10-3 ~ 6,7У 10 •
Максимальное касательное напряжение (возникает в точках,
находящихся посередине длинных сторон наиболее толстых прямо-
угольников, т. е. в данном
случае полок)
_ мк 600
Ттах — 6 79 . 10_6 —
= 88,4 • 10е Н/м2 =
= 88,4 МН/м2.
Ь'п*8?см
Рис. 5.18
Здесь учтено, что Мк = ®.
Пример 5.8. В поперечных
сечениях тонкостенной тру-
бы, имеющей средний диаметр
DCp— 15 см (рис. 5.18,6), воз-
никает крутящий момент
/Ик= 50 • 10® кгс • см. Како-
ва должна быть толщина б
стенки трубы, чтобы касательные напряжения в ее поперечном се-
чении не превышали [т] = 600 кгс/см2?
Найти угол закручивания на длине I — 1 м, если G = 8 • 10е
кгс/см2.
Решение. Из условия прочности
Ттах = Мк/2Г06< [т]
определяем искомую толщину стенки трубы
6>Мк/2Г0[т],
где Fo = лОср/4 — площадь круга, имеющего средний диаметр Dcp.
.Следовательно, б = 2 jy'. ббб = см.
Округляя, принимаем б = 2,5 mnL
Угол закручивания можно определить по формуле, приведенной
в этом параграфе:
M-Js
m = ----— =
4GF26
50 • 103 • 100 • 3,14 • 15 n nnQ.„
-------------------------- 0,00942 рад.
154 • 0,25
4 . 8 • 108
77
Задачи для самостоятельного решения
5.12. Концевая часть вала имеет квадратное поперечное сечение
(рис. 5.19). На сколько (в процентах) прочность этой части вала
ниже левой части, имеющей круглое сечение?
Ответ. 62,4%.
Рис. 5.19
5.13. Построить график зависимости площади прямоугольного
поперечного сечения скручиваемого бруса от отношения сторон
прямоугольника h ; b при постоянной величине допускаемого по
Рис. 5.20
условию прочности кру-
тящего момента.
Указание. График-
строить, давая значения
h : b (1; 1,5; 2; 3; 4; 6; 8;
10). Площадь квадратного
сечения принять за единицу
Отчет. Fmax:Fmln=~
= 1,63.
5.14. Построить гра-
фик, указанный в пре-
дыдущей задаче, исхо-
дя из условия равной
жесткости брусьев при
тех же отношениях
h : b. Смотрите указа-
ние к предыдущей за-
даче.
Ответ. fmax : fmin = 2,12.
5.15. Определить требуемый по условиям прочности и жестко-
сти размер стороны квадратного поперечного сечения бруса, если
в поперечных сечениях бруса возникает крутящий момент Мк =
= 120 кгс • м. Допускаемое напряжение [т] = 600 кгс/см2; допус-
каемый угол закручивания [<р01 = 1,0 град/м; G = 8,0 • 106 кгс/см2.
Ответ. 50 мм.
78
5.16. Определить наибольшее касательное напряжение в пред-
ставленном на рис. 5.20 поперечном сечении скручиваемого бруса
и его относительный угол закручивания, если Мк— 11 кгс • м,
G = 2,7 • 108 кгс/см2. Принять т) == 1.
Ответ. ттах = 435 кгс/см2; <р0 = 2,68 • Ю-3 рад/см.
5.17. Брус, жестко заделанный обоими концами, имеет на поло-
вине длины квадратное, а на другой половине — круглое попереч-
ное сечение (рис. 5.21). Определить расстояние х0 из условия, что-
реактивные моменты, возникающие в заделках, должны быть оди-
наковыми.
§ 5.5. Расчет Цилиндрических винтовых пружин
с малым шагом при осевом нагружении
Условие прочности пружины растяЯсения или сжатия, свитой из
,8PD^,r .
проволоки круглого сечения, имеет вид ттах = k М>
где Р — нагрузка, действующая по оси пружины; D — средний
диаметр пружины; d — диаметр витка пружины; k — поправочный
коэффициент, отражающий влияние кривизны витков и поперечной
‘, D
силы. Его величина зависит в основном от индекса пружины сп=
и ее можно принимать по следующим данным:
сп 4 5 6 8 10 12
k . 1,37 1,29 1,24 1,17 1.14 1,11
Изменение высоты пружины X (удлинение при растяжении или
осадку при сжатии) определяют по формуле X = ^PD^fi/Gd*,
где п —’рабочее число витков пружины; G — модуль сдвига.
Условие прочности пружины, свитой из прутка квадратного
сечения:
- _ , PD .
Тщах — "l 2fift3
73
где kt— поправочный коэффициент, принимаемый в зависимости
от отношения среднего диаметра (D) пружины к стороне (&) сечения
витка по следующим данным:
D Ь 4 5 6 8 10 12
fei 1,33 1,26 1,21 1,16 1,13 1,10
коэффициент § = 0,208 (см. табл. 5.1).
Изменение высоты пружины X = PDsnn/AGab*, где а = 0,141
(см. табл. 5.1).
Пример 5.9. Две цилиндрические винтовые пружины одинако-
вого среднего диаметра D отличаются одна от другой тем, что пер-
вая изготовлена из проволоки круглого сечения, а вторая — квад-
ратного сечения. Максимальные касательные напряжения, возни-
кающие в пружинах, одинаковы,. О игь веса этих двух пружин
и их удлинения. Коэффициент'k ечитагь одинаковым для обеих
пружин.
Решение. Веса пружин будут пропорциональны площадям
поперечных сечений проволок. Поэтому надо определить площади
поперечных сечений проволоки каждой из пружин.
гг <, 8pD
Для пружины из проволоки круглого сечения ттах= я .
Для пружины из проволоки квадратногб сечения
ь PD h PD
Tmax — Л 2р*з — « 2 • 0,208*3 '
как левые части уравнений (ттах) по условию равны, то
16 • 0,208 = °>981d-
- 5^7 — 0,9812d2 =
4 1 4 /
л
Так
= 2 • 0,208&3, откуда b = d у
Отношение площадей сечений р------
# *"квадр
= 0,816.
. Пружина с круглым сечением проволоки легче пружины с
квадратным сечением примерно на 19%.
Удлинение
. 8Р£Яп
пружины с круглым сечением проволоки .
Удлинение пружины с квадратным сечением проволоки
. PD3m
~ 4Ga.b*
Отношение удлинений
М 32а6* 32 • 0,1416* 32 • 0,14 (0,981)* _ . о,
, Х2“ nd* ~ nd* 3,14 Ь Ь
Пример 5.10. Жесткий рычаг AD подвешен на трех пружинах
с одинаковым числом витков и нагружен силой Q = 400 кгс (рис.
80
5.22). Подобрать диаметр проволоки для каждой пружины так.
чтобы напряжения в них были одинаковы и равны [т! = 5000 кгс/см2.
Средние диаметры витков пружин: D{— 6; D2= 8, D3= 10 см. По-
правочный коэффициент k для всех пружин принять равным еди-
нице.
Решение. Задача дважды статически неопределима — в шар-
нире, очевидно, возникает только вертикальная реакция; кроме
того, на балку действуют со стороны пружин три вертикальных ре-
активных силы, т. е. общее число неизвестных равно четырем,
а для плоской системы параллельных сил статика дает два уравне-
ния равновесия.
Используем лишь одно из
них, так как реакцию шарни-
ра определять не нужно:
S/ил — 0; Q • За = F\a +
+ Р22а 4- Р З3а
или Pi+ 2Ра+ ЗР3=
= 3Q = 1200 кгс. (1)
Два уравнения перемеще-
ний удобно записать совмест-
но в виде ।
Xj: Xj: Х3 = а : 2а: За =
= 1:2:3,
Рис. 5.22
или
ЗР^п
Gd*
8P2Da2n . 8Pgo|n
' Gd*2 ' Gd*
8 3
= 1:2:3, откуда
27P2 ___ 64Pa == 125P3
dj 2d*2 3d*a ' (2)
\ '
Используем также условие равенства напряжений, возникаю-
щих В Пружинах *: Т1 гаах = Т2 max = Тз max = М, ИЛИ
откуда
8Pj£\___8P2D2____8Р
nd| nd| ’
3Pj___4Pa___5P g
df ~ df~ df'
. (3)
Решая систему уравнений (1), (2), (3), получаем
Р,= 1,9Ра= 2,1Р3; Р,= 345 кгс.
* Для определения усилий в пружинах должно быть известно соотно-
шение жесткостей пружин. Своеобразие рассматриваемой задачи состоит
в том, что в явной форме указанное соотношение не задано (неязвестны диа-
метры проволоки, из которой свиты пружины), ио его заменяет условие рав-
непрочности пружин.
81
Тогда
. ,3/8PiOi ,/"345 -8.6 , ло
d> = F ж = К ТТ50М = 1 -02 см;
<^2 = §• = 0,907 см; d3 = || dr = 0,944 см.
a S
Рис. 5.23.
Следует отметить, что если округлить диаметры пружин (по .
существу говоря, из технологических соображений это необходимо), ।
то условие равнопрочности пружин выполняться не будет; возни- -
ка ощие в них усилия, естественно, будут отличны от найденных |
вы те. Интересно выяснить, насколько существенны будут изменения. J
в усилиях и расчетных напряжениях !
(при k = 1), если принять d = 10 мм; а
d2= 9 мм; d3= 9,5 мм. Рекомендуем |
читателю произвести - соответствую- |
щий расчет. 1
Пример 5.11. Цилиндрическая вин- 1
товая пружина, закрепленная обоими «
концами, диаметром D = 200 мм, из |
круглого прутка диаметром d = 20 мм fl
нагружена силой Р = 400 кгс в точ- 1
ке С (рис. 5.23,а). Определить наи-J
большее касательное напряжение в I
пружине и перемещение точки С, Я
если G ~ 8 • 105 кгс/см2. Я
Решение. Для решения задачи Я
необходимо определить реактивныеЯ
силы, возникающие в закреплениях Я
А и В. Статика позволяет написать Я
лишь одно уравнение равновесия: Я
Ra + Rb = Р. я
Задача, таким образом, однажды статически неопределима. j
Для составления второго (недостающего) уравнения рассмотрим|
условия деформации. 1
Освободив пружину от одной из заделок (например, от нижней)!
и заменив действие заделки на пружину силой Rb, получим схему!
действия сил, изображенную на рис. 5.23, б. ]
Нижний конец пружины под действием силы Р должен получить!
перемещение вниз (кр), а под действием силы Rb— перемещение!
вверх (Xrs). В действительности же вследствие закрепления конец 2М
не может перемещаться ни вверх, ни вниз, а следовательно, |ХР| =|
=|Xrs | (уравнение перемещений), 1
. 8РО®Я1. . 8^SD» (Я14-n2) I
где Лр — G(p , Л«й — Gdi I
После подстановки получим |
8PD3n, S^bD8 (»i + пг)
Gd* ~ Gd*
82
откуда Rb^P = 400 J = 160 кгс;
Ra = Р — Rb = 400 — 160 = 240 кгс.
Таким образом, пружина на участке С А растянута силой Ra =
= 240 кгс, а на участке СВ — сжата силой Rb= 160 кгс.
Следовательно, наибольшие напряжения имеют место в попереч-
ных сечениях пружины на участке СА. Определим этим напряжения
,SrAD . , , 8 • 240 . 20 „
Ттах — k —1,14 я . 23 , — КГС/СМ ,
где при сп= = у = 10 по данным, приведенным в § 5.5, k —
= 1,14.
Перемещение (Хс) точки С пружины вниз равно удлинению верх-
ней части С А пружины:
8RADsni 8.240.203.8 Q(.
^=~53Г-= -8.-i6S— =9,6 см.
Очевидно, тот же результат можно получить, учитывая, что пере-
мещение равно укорочению нижней части СВ пружины.
Задачи для самостоятельного решения
5.18. Цилиндрическая винтовая пружина, свитая из проволоки
круглого сечения, имеет средний диаметр D = 40 мм. Найти диа-
метр проволоки d и число витков п, если наиболь-
шая сжимающая сила Р ~ 100 кгс и при этом
осадка X = 30 мм. Допускаемое напряже-
ние [т] = 4800 кгс/см2. Модуль сдвига G =
= 8.10s кгс/см2. Принять k = 1.
Ответ, d = 6 мм; п = 6.
5.19. Винтовая стальная пружина из прутка
квадратного сечения 15 х 15 мм имеет 16 вит-
ков и средний диаметр D = 12 см. Определить
допускаемое значение осерой нагрузки [Р], если
1т] = 3000 кгс/см2. Вычислить осадку, пружины
при нагрузке, равной допускаемой. G — 8 х
X 10s кгс/см2.
Ответ. [Р] = 303 кгс; А = 11,6 см.
5.20. Две пружины, имеющие одинаковую
высоту и одинаковое число витков пг= пг= 10,
I Р‘90нгс
к
Л-5Ц
Ht-50
вставлены одна в другую (так называемая кон- рис. 5.24
Центрическая пружина) и сжимаются силами
Р = 90 кгс, как показано на рис. 5.24. Проверить прочность пру-
жин, если [т] = 5000 кгс/см2. Определить осадку пружины, прини-
мая G = 8,1 х Ю5 кгс/см2. .
Ответ. т1гаах = 5480 кгс/сма (пружина перегружена на 9,6%); т2гаах
1420 кгс/смг; А = 30,9 мм.
83
ГЛАВА 6. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ
ДЛЯ БАЛОК И РАМ
§ 6.1. Общие понятия. Аналитическое построение эпюр
поперечных сил Q и изгибающих моментов М ?
для статически определимых балок
Балка испытывает прямой поперечный изгиб, если действующие J
на нее нагрузки (сосредоточенные силы, распределенные нагрузки,
пары сил) расположены в одной из главных плоскостей инерции j
и при этом силы перпендикулярны к продольной оси балки (рис. |
6. 1). В поперечных сечениях балки возникает два внутренних сило- |
вых фактора: изгибающий момент и поперечная сила. л
В частном случае поперечная сила может быть равна нулю, |
такой изгиб называется чистым. Поперечная или перерезырающая 3
сила Q в любом поперечном сечении численно равна алгебраической
сумме всех внешних сил*, действующих по одну сторону от прове- 1
денного сечения. Определяя поперечную силу в данном сечении, ,
внешние силы, лежащие слева от сечения, берем со знаком плюс, |
если они направлены вверх, и со знаком минус, если — вниз (для |
правой отсеченной части — наоборот). s
Изгибающий момент М в произвольном поперечном сечении бал- |
ки численно равен алгебраической сумме моментов всех внешних |
сил, действующих по одну сторону от сечення, относительно той из!
главных центральных осей этого сечения, которая перпендикуляр-J
на плоскости нагружения. Моменты внешних сил, лежащих слева|
от сечения, считаем положительными, если они стремятся повернуть|
отсеченную часть балки относительно данного сечения по часовой!
стрелке (для правой отсеченной части — наоборот). I
Можно связать знак М с характером деформации отсеченной^
части балки:-изгибающий момент в сечении считается положитель-я
ным, если отсеченная часть балки изгибается выпуклостью вниз,!
т. е. сжатые волокна находятся вверху (при этом мысленно защем-1
ляем отсеченную часть балки в рассматриваемом сечении). 1
Ординаты эпюры М обычно откладывают в сторону вогнутости
упругой линии, т. е. в сторону сжатых волокон, поэтому такое праЯ
вило знаков для М называют правилом сжатого волокна (рис. 6. 2). я
• Подчеркиваем, что внешние силы перпендикулярны продольной ос>Я
балки. В более общем случае надо брать алгебраическую .сумму п р о е к<Я
ц и й указанных сил на главную центральную ось, расположенную в плосЧ
кости действия внешних сил. ' 1
84
Между изгибающим моментом, поперечной силой и интенсивно-
стью распределенной моментной нагрузки, приложенной к балке,
существует следующая дифференциальная зависимость: dM/dx =
= Q -J- т, где т(кг • м/м) — интенсивность внешних распределенных
моментов (моментно-распределенной нагрузки, см. рис. 6. 1). При
т = 0 dM/dx = Q.
Вторая производная от изгибающего момента по координате
х равна интенсивности распределенной нагрузки с обратным знаком
(распределенную нагрузку, направленную вниз, считаем положи-
dQ d2M / t
тельной) = —q (при т — const; или пг = 0).
Из дифференциальной зависимости между М и Q следует:
1) на участках, где М возрастает, Q имеет знак плюс, там, где М
убывает, Q — минус;
2) там, где М имеет максимальное или минимальное значение,
Q переходит через нуль, меняя знак.
Эпюры Q и М — это графики, показывающие законы изменения
данных величин по длине балки.
Для построения эпюр Q и 'М существует несколько способов:
1) аналитический (по уравнениям); 2) построение по характерным
точкам; 3) способ сложения действия сил'.
При построении эпюр условимся положительные значения Q и М
откладывать вверх от оси (базиса) эпюры, которая параллельна
оси балки.
Построение эпюр для двухопорной балки нужно начинать с оп-
ределения опорных реакций.
Для консоли (балки, защемленной одним концом) это необяза-
тельно — построение эпюр можно начинать от свободного конца
балки.
Погтроение'эпюр Q и М аналитическим способом (по уравнениям).
По этому способу балка разбивается на участии, в пределах кото-
рых выражение для изгибающего момента и поперечной силы ос-
тается постоянным; иными словами, функции, дающие законы из-
менения Q и М, не имеют разрывов.
Границами участков служат точки приложения сил, пар сил,
а также места изменения интенсивности распределенной на-
грузки.
На каждом участке берется какое-либо произвольное сечение
на расстоянии х от начала координат, и для этого сечения составля-
Ю/Тся выражения для Q и М. Получаем Q =» fx(x) и М =« fa(x). На-
чало координат можно брать на левом либо на правом концах балки,
в начале или в конце любого участка. Придавая х несколько значе-
ний на каждом участке, получаем соответствующие значения Q и М,
пэ которым строятся эпюры.
Приведем примеры построения эпюр Q и М по уравнениям.
Пример 6.1. Построить эпюры Q и М для заданной балки (рис.
ь-3, а).
85
Рис. б.З
'Решение.
1) Определение опорных реакций.
Равнодействующая всей нагрузки, приложенной к балке, рав-
на произведению ql и проходит посередине пролета. В силу симмет-
рии нагружения очевидно, что /?л= Rb~ ql/2.
2) Построение эпюры поперечных сил Q.
Мысленно проведем сечение на расстоянии х от левого конца
балки. Рассмотрим левую часть балки длиною х с приложенными
к ней внешними силами (рис. 6.3, б).
Согласно определению, поперечная сила в проведенном сече-
нии равна сумме проекций на вертикальную ось всех сил, располо-
женных слева от сечения. Слева
от сечения действует направлен-
ная вверх сила= и рав-
номерно распределенная нагруз-
ка, равнодействующая которой
направлена вниз и равна про-
изведению qx, следовательно,
Q = Ra— qx= ql/2 — qx.
Отсюда видно, что попереч-
ная сила изменяется по закону
прямой линии: Q*=o = Ra =
= ql/2 и Qx=i = ql/2 — ql =
= -ql/2.
^пюра Q показана на рис. 6.3, в.
3) Построение эпюры изги-
бающих моментов М.
Обращаясь к рисунку 6.3,6, составим выражение изгибающего
момента в проведенном сечении, взяв сумму моментов относительно
центра тяжести сечения всех внешних сил, приложенных к оставлен-
ной части (слева от сечения).
Слева от сечения приложена реакция Ra, плечо которой равно
х, и равнодействующая распределенной нагрузки qx с плечом х/2.
Таким образом, М == Rax— qx • х/2 = qlx/2 — qx*/2.
Изгибающий момент изменяется по закону квадратной параболы.
Для построения кривой определим три ее точки.
Дадим х следующие значения: 1) х — 0; 2) х = I; 3) х = 1 .
11
2 / ql*
Получаем Мх=о = 0; Mx=i — 0; М* _L 2 "2
Очевидно, что посередине пролета изгибающий момент максима-
лен — в этом сечении поперечная сила равна нулю: Л4тах= ql2/8.
Эпюра изгибающих моментов показана на рис. 6.3,г.
86
Пример 6.2. Построить эпюры Q и М для заданной балки (рис.
6.4, а).
Решение.,
1) Определение опорных реакций.
Направим опорные реакции вертикально вверх и запишем урав-
нения статики:
2/пл = 0; -RBl + ®i = 0,
откуда Rb = SR//;
£/nB = 0; RAl + $t = 0, откуда RA = —SR//.
Знак минус указывает на то,
что реакция Ra направлена
вниз, т. е. противоположно ра-
нее принятому.
Для удобства дальнейшего
решения задачи показываем на
схеме (рис. 6.4,а) действитель-
ное направление реакции,а ре-
акцию, направленную вверх,
зачеркиваем.
2) Построение эпюры попе-
речных сил Q. .
Поперечная сила в сечении
на расстоянии хг от левого
конца, т. е. для первого участ-
ка (О С XiC a) Qi = — Ra =
SB
= —j- ; на второй участке
(О х2^С Ь): Qn= — Rb =
SB ,
= —j (справа).
Рис. 6.4
Отсюда заключаем, что эпюра Q представляет собой прямую,
параллельную оси абсцисс (рис. 6.4, б).
3) Построение эпюры /И.
Изгибающий момент в сечении Ох, выраженный через силы, при-
SB
ложенные слева от сечения, М/ = —RaXi — —j-x{.
Определим Mj в двух сечениях:
^t=o=°; MlXi=a = -RAa = -®l±.
Изгибающий момент в сечении О2, выраженный через силы,
ЭД
приложенные справа от сечения, Мл = /?йх2 = —х2.
Вычислим Мл в начале и в конце II участка:
«//..-о-»;
87
Эпюра М представлена на рис. 6.4, в.
Обращаем внимание, что на эпюре М имеет место скачкообразное
изменение ординат («скачок») там, где приложен внешний сосредото-
ченный момент.
Пример 6.3. Построить эпюры Q и М для балки, подверженной
на участках, примыкающих к опорам, действию равномерно распре-
деленной моментной нагрузки интенсивностью т (рис. 6.5,а).
Решение. 1) Определение опорных реакций.
Взяв сумму моментов относительно точек А и В, получим
тА ~ 0; —/?в • 4а — та + та — 0; RB = 0;
S тв = 0; RA • 4а + та — та — 0, т. е. RA ~ 0.
‘ Рис. 6.5
2) Построение эпюры Q.
Определяя Q как сумму
внешних сил, приложенных
слева от произвольного сече-
ния, получаем, что Q = 0,
т. е. Qi — Qu = Qin — Q — 0.
3) Построение эпюры М-
На первом участке (0
^Xi^a) имеем
Mi = тхг (линейный закон);
М/Х1=о = °; Mlxi=a = ma.
Для II участка (0 х2 а)
М1Г = тх2; МцХг=0 = 0; Мцх^а = та.
На III участке нагрузка отсутствует, следовательно, эпюра, изги- |
бающих моментов на этом участке — прямая линия, но значение- 3
моментов в крайних сечениях участка, как было установлено, оди- |
яаково. Итак, изгибающий момент в пределах рассматриваемого |
участка постоянен: 1
М/п = та. 1
Эпюра М представлена на рцс. 6.5,в. 1
Пример 6.4. Построить эпюры поперечных сил Q и изгибающих 1
моментов М для заданной балки (рис. 6. 6,а). Я
Решение. 1) Определение опорных реакций. Я
Составляем уравнения равновесия: Я
Утд-0; -4g + p“+qa^-RB.3a + ® = 0,
+',.4+4««,+®
откуда RB =-----5----— >=•
88
0,8 • 22 2 , 3
2 +d2 + 2
3 • 2
= 1,2 тс;
2 тв = 0; —да • 3,5а + RA 'За — Рг • 2,5а — да • 1,5а + SR = 0,
откуда
/?л =
3,5да2 + 2,5а • Pv + 1,5<?а2 — SR
За '
3,5 • 0,8.22 + 2,5 • 2.3 + 1,5 - 0,8.22 — 1
3 • 2
= 5 тс.
Проверка:
S Y = —да —ga — P1 + RA'+ Rb
=—0,8 • 2 — 0,8 • 2 —3 + 5+1,2 = 0.
Реакции определейы
верно.
2) Построение эпюры Q.
Балка имеет шесть
участков нагружения.
Участок / (СЛ)О^
+ хг +2 а. Начало коорди-
нат в точке С. Находим Q/
как сумму сил слева:
Q/ = — дхг — уравне-
ние прямой.
Определяем два значе-
ния Q,:
Qix _0 = 0 и Q, =
= —qa = —0,8 • 2 =
= —1,6 тс.
Участок II (AD) 0
x2<J-^. Начало коорди-
нат в точке А. Определяем
Qu как сумму сил слева:
Qn= —да + Ra = — 0,8 х
X 2 + 5 = 3,4 тс — уравне-
ние прямой, параллель-
ной оси абсцисс.
Рис. 6.6
Участок III (DE) 0 х3 у. Начало координат в точке D.
Определяем Qm как сумму сил слева:
QUI = —qa + Ra—Pi = —0,8 -2 + 5 — 3 = 0,4 тс — уравне-
ние прямой, параллельной оси балки.
Участок I V (КВ) 0^х4 < а (справа). Начало координат
в точке К. Определяем Q,v как сумму сил справа: Qiv = 0.
8!)
Участок V (BF)Q^. хь^.а (справа). Начало координат
в точке В. Определяем Qv как сумму сил справа:
Qv = —Rb = —1,2 тс — уравнение прямой, параллельной оси
абсцисс.
Участок VI (FЕ) 0 хв а (справа). Начало координат
в точке F. Определяем Qvi как сумму сил справа:
Qvi = —Rb + qxe = —1,2 + 0,8xe — уравнение прямой.
Определяем два значения Qvi' Qvix=0 =—1,2 тс; QivXe=a~
=—1,2 + 0,8 • 2 = 0,4 тс.
По полученным значениям строим эпюру Q (рис. 6.6, б).
Найдем дополнительно значение х° — абсциссу точки, в кото
рой эпюра Q пересекает ось абсцисс (т. е. QVI = 0).
Для этого приравняем QVi нулю (Qvi =—1,2 4-0,8x2=0);
х«= 1,2/0,8= 1,5 м.
3) Построение эпюры М. L O^Xj^a.
Определяем М1 как сумму моментов сил слева:
.. 4*? ,
М, =---g-----уравнение параболы.
Находим три значения М,: М'с = Л4,Ж1=0 = 0;
/ а)2
,, ’И/ 0,8.1» А.
ЛГ, а =------=-----------— = —0,4 тс • м;
” Т
ч оа» 0,8 • 2» , ~
МА = М,х _а = — у -------— = — 1,6 тс • м.
II. 0^х2^а2.
Определяем Мп как сумму моментов сил слева:
Мп — —(у + х*} + RaX% = —0>8 -2(14- х2) 4~
4- 5х, — уравнение прямой.
Находим два значения МГ1:
Ма = М„х_0 = ~°’8 • 2 = —1,6 тс • м;
MD = Ми а =2—0,8 • 2 (1 4- 1) 4- 5 • 1 = 1,8 тс • м.
х. = т
III. 0<х3<|.
Определяем Мш как сумму моментов сил слева:
Мщ = qa (х3 4~ а) 4~ Ra (х3 4~ g’j — Р1X3 = —0,8 • 2 (х3 4~ 2) 4~
4- 5 (х3 4~ 1) — Зх3 — уравнение прямой.
ч()
Находим два значения Мш:
MD = М111х^0 — —0,8 • 2 • 2.4- 5 • 1 = 1,8 тс • м;
МЕ = МП1 а = —0,8 • 2 (1 4- 2) 4- 5 (1 4- 1) — 3 • 1 = 2,2 тс • м,
IV. 0^х4^а (справа).
Определяем MIV как сумму моментов сил справа:
M/v = —® = —1 тс • м— уравнение прямой, параллельной ос»
абсцисс. V. 0 х5 а (справа).
Определяем Му как сумму моментов сил справа:
Му = —® 4- RbX^ = —1 -j- 1,2*5 — уравнение прямой.
Определяем два значения Му: Мв = МуХ)=0 = —1 тс • м;
Ме = Мух_а = —1 4- 1,2 • 2 = 1,4 тс • м. VI. 0^х6 а (справа).
Определяем Myi как сумму моментов сил справа:
Му! = — ® 4-/?в (а 4-*в) —-у-= —1 4- 1,2(2 4-*«)-
0,8 •
----2-----уравнение квадратной параболы.
Найдем три значения Mv/—на кс^нцах участка EF и в точке
с координатой х® = 1,5 м, где Mvt = Л4тах (так как здесь Qv/ = 0),
MF = Afv/Xe=0 = —14- 1,2 • 2 = 1,4 тс • м.
МЕ = Mylx = -1 4- 1,2 (2 + 2) -°Д^- = 2,2 тс м;
A4max = Mv/x_lr5H = — 1 4-’1,2(2 4- 1,5)-= 2,3 тс • м.
Строим эпюру М по полученным значениям (рис. 6.6,в).
Пример 6.5. Построить эпюры Q и М для балки, нагруженной
распределенной нагрузкой, интенсивность которой меняется по ли-
нейному закону (рис. 6. 7,а).
Решение. 1) Определение опорных реакций.
Нетрудно сообразить, что равнодействующая распределенной
нагрузки (обозначим эту равнодействующую Ро) равна Ро= .
Иными словами, она вдвое меньше, чем равнодействующая равно-
мерно распределенной нйгрузки интенсивностью qm3K. -Сила Pt>.
приложена в центре тяжести треугольника, представляющего собой
эпюру нагрузки, т. е. приложена на расстоянии 1/3 от правой опоры.
Составляя суммы моментов всех сил относительно центров шарни-
ров (опор), имеем = 0; —RBl 4- Ро~ I = 0, откуда RB =
~ р ~ ^max^ . V т___П- R /___• Р —__0 Р = — Р — —® —
3 3 ’ з — и, 3 ГО (j
91
2) Построение эпюры поперечных сил.
Проведем произвольное сечение на расстоянии х от левой опоры;
ордината эпюры нагрузки, соответствующая этому сечению, опреде-
лится из подобия треугольников i,-~ = ; q(x) ~ qmax~.
Равнодействующая той части распределенной нагрузки, которая
расположена слева от сечения,
Р0(х) = ~q(x)x =
Утахх2
21
Таким образом, получаем следующее выражение для попе-
речной силы:
е = т?л-р0(х)=^
gmax*2
21
Поперечная сила изменяется по закону квадратной параболы.
Давая абсциссе х ряд частных значений, получаем соответствующие
ординаты эпюры Q. Кроме того,
1/2
Рис. 6.7
приравнивая поперечную силу ну-
лю, находим абсциссу Хо того’ сече-
ния, в котором эпюра Q пересекает
свою ось:
./1 „
9тах*1;§- 2/«/ ~ U’
откуда
х0= 0,577/.
Эпюра Q представлена на рис.
6; 7,6.
3) Построение эпюры изгибаю-
щих моментов.
Выражая момент в произволь-
ном сечении, находящемся на рас-
стоянии х от левой опоры, через
левые силы, получаем
М = Rax — Ро (х) 4 =
О
Утах/ Утах*3
~ 6 . 6/ •
Таким образом, изгибающий момент изменяется по закону куби-
ческой параболы. В сечениях, проходящих через опоры (т. е. при ;
х = 0 и х = /), изгибающий момент равен нулю. Максимальное зна-
чение изгибающий момент имеет в сечении с абсциссой х0~
У 3
~ 0,577/:
ДД ___ УтахР УтахР ^тах Р УтахР . ,;
таХ “ 6/3 “ 18/3 9/3 ~ 15'6
92
4*1,5 тс/м
1,5 a 1,5 a Д
тп-ЗОкНм Р,-50кН P^IOkH
c
3a
Ш’ЮкН-м Д-ЮнН/м
4a f
(^•бкН/м
Р-30кН
^20кН1м т'50кН^
Шт
ЙТи’”.
1»
Рис. 6.8
93
Для более точного построения кубической параболы, помимо
трёх найденных частных значений изгибающего момента, следует
вычислить еще три-четыре значения. Эпюра М изображена на
рис. 6,7Л
Задачи для самостоятельного решения
6.1. Построить эпюры Q и М аналитически (по уравнениям)
для балок, показанных на рис. 6.8.
Уч а з а н н е. В ответах даны значения Q н М, наибольшие по абсо»
лютной величине. Значения х0 отсчитываются от левого конца балки.
Ответы.
а) Q = Р* “max — г » ^max = 4PZ ПрИ %0 = 4-
б) <? ’‘max 1 ’ Л1тах = 2®о ПРИ хо = 0.
в) Qmax = 8 тс; Л4тах = 8 тс • м (хд = 2 м и в заделке).
г) Qmax = 9’1 тс’ Afmax = 8 тс •’м (иа правой опоре).
V Qmax = 3 Мтах = 3,25 тс • м (при хд = 0,5 м).
е) Qmax = 2,25 тс; . Afmax = 2 тс • м (справа на длине балки, равной а).
<2max = -4 A1max = -jTjV2 (при х0 = 0.5Z).
3) Qmax = 4.5 тс; Мтах = 4 тс • М(при х0 = -g- 1 •
«) Qmax = 2 т> ^тах = ml (при х0 = /).
к) Qmax = 5-2 ТС! Л4тах = 7,67 тс • м (при х0 = 7,25 м).
Л) Qmax = 3-1 ТС! Л4тах = 5,4 тс • м (на средней опоре).
л) Qmax = 48 кН; Л4тах = 6 кН • м (на левой опоре).
«) Qmax =15 «И; Л4тах = 27 кН • м (прн хд — 6м н хо1 = 9 м).
0) Qmax = ® ’ Мтах = 12 кН • м (в заделке).
«) Qmax = Ю КН; Л4тах = 12,5 кН • м (при хд = 2,5 м).
₽)] Qmax = 30 кН; МтаХ = 60 кН • м (при х0 = 3,5 м).
с) Qmax = 4 кН; ^тах = 6,32 кН • м (при хд = 2,3 м).
Щ) Qmax = 22 кН; Мтах = 24>2 кН • м (при хд — 2,8 м).
У) Qmax = 3 кН; Мтах = 1,5 кН • м (в заделке).
Ф) Qmax = 30 КН; Л4тах = 50 кН • м (на правой опоре).
§ 6.2. Построение эпюр Q, М для балок
по характерным точкам
Построение эпюр Q и М можно упростить, если воспользоваться!
дифференциальными зависимостями между М, Q и q. Применяя этой
способ, вычисляют значения Q и М в характерных точках, т. е. на
94
границах участков, а также там, где данный внутренний силовой
фактор имеет экстремальное значение. В пределах между ордина-
тами, соответствующими указанным характерным точкам, очертание
эпюры устанавливается иа основе дифференциальных зависи-
мостей.
При построении эпюр по характерным точкам надлежит руковод-
ствоваться следующими правилами.
1. В концевом сечении балки поперечная сила и изгибающий
момент численно равны соответственно приложенным в этом сечении
внешней силе и моменту внешней пары сил (имеются в виду как ак-
тивные, так и реактивные силы и пары сил).
2. На ненагруженном участке балки эпюра поперечных сил —
прямая, параллельная оси балки; эпюра моментов — наклонная
прямая.
3. На участке балки, несущем равномерно распределенную
нагрузку, эпюра Q — наклонная прямая, а эпюра М — квадрат-
ная парабола.
4. На участке балки, несущем нагрузку, распределенную по ли-
нейному закону, эпюра Q — квадратная парабола, а эпюра М —
кубическая парабола.
5. В сечении, где эпюра Q, изменяясь непрерывно, проходит
через нуль (пересекает ось), изгибающий момент экстремален —
касательная к эпюре М параллельна оси абсцисс. Если эпюра Q
линейна, положение указанного сечения проще всего найти из по-
добия треугольников, образуемых эпюрой Q и осью абсцисс. Если
эпюра Q — парабола, приходится составлять уравнение, дающее
закон изменения Q на данном участке , и, приравнивая Q к нулю,
находить абсциссу сечения, где изгибающий момент экстремален.
6. В том месте, где к балке приложена сосредоточенная сила, на
эпюре Q получается скачкообразное изменение ордцнаты на вели-
чину приложенной силы. На эпюре М в этом месте возникает излом,
т. е. соседние участки эпюры не имеют плавного сопряжения.
7. В том месте, где к балке приложена сосредоточенная пара сил,
на эпюре М происходит скачкообразное изменение ординаты
на величину момента приложенной пары. На эпюре Q это не
отражается.
8. Если на некотором участке балки поперечная сила равна ну-
лю, то изгибающий момент постоянен и изображается на эпюре пря-
мой, параллельной оси балки.
Все указанные выше правила могут быть объединены в графиче-
скую таблицу.
Применение табл. 6.1 значительно облегчает построение эпюр
внутренних силовых факторов по характерным точкам.
Пример 6.6. Построить эпюры Q и М для балки по рис. 6. 9,а.
Решение. 1) Построение эпюры Q.
Построение эпюры начинаем от левого (свободного) конца, при
этом нет необходимости в определении опорных реакций. Сила Рг~
Та'блипа 6.1. Зависимости между нагрузкой, поперечной силой и изги-
бающим моментом
\ ко г ——5 |Р VI г~к U J а=0 i* const g~const nmni Jimpi
I а Р q ШЩп ffi ! щ 1 ТЕШ ШШЯ । ।
i nil ЖЙ Ди
= 2qa направлена вниз, следовательно, поперечная сила на участ-
ках АВ и ВС отрицательна. Согласно изложенным выше правилам
в сечении А поперечная сила численно равна внешней силе На
участках, не несущих распре-
деленной нагрузки, поперечная
сила постоянна. Наличие пары
сил не влияет на эпюру Q. Итак,
Рис. 6.9
Qi = Qn = —2qa.
В точке С приложена си-
ла Р%== qa, направленная вверх;
в этом сечении на эпюре будет
скачок вверх от прежнего зна-
чения Q на величину Р2 —
= qa, т. е. QcP = 0сев + qa =
= —2qa + qa — —qa.
Следующая характерная точ-
ка (сечение)—D. Определяем
значение Q в этом сечении как
сумму проекций на ось Оу сил,
приложенных слева от точ-
ки D: ]
Q.D = —Pi + Р^ — q%a = |
= —2qa + qa — 2qa = —3qi. |
Откладываем это значение Qo на эпюре под точкой D и соеди-
няемс предыдущим значением (под точкой С) прямой линией. Орди-
ната эпюры Q в сечении заделки дает значение опорной реакции,
Эпюра Q показана на рис. 6.9,6. f
2) Построение эпюры М.
’ 96
В сечении А момент равен нулю (на свободном конце консоли).
В следующей характерной точке В определяем М как сумму момен-
тов сил слева: Л4дев = —Р^а— —2qa2.
На участке АВ проводим прямую линию от 0 до —2qa2 (иенагру-
женный участок). В точке В приложена пара сил; в этом сечении
в эпюре М будет скачок вверх на величину qa2, т. е.
Мвр = МТ + SR = — 2qa2 + qa2 = —qa2.
В характерной точке С определяем М как сумму моментов
сил слева: Мс — —Pi 2а + Ж = —4qa2 + qa2 — —3qa2.
На иенагруженном участке ВС также проводим прямую ли-
нию от —qa2 до —3qa2.
В характерной точке D определяем М как сумму моментов
сил слева: Md — —Pi • 4а + SR 4- Р2 • 2а — q2a • а = —2qa • 4а +
+ qa2 4- qa2a — 2qa2 == —7qa2.
Значение M в точках С и D соединяем ветвью параболы, обращен-
ной выпуклостью вверх.
Эпюра М представлена на рис. 6. 9,«.
Пример 6.7. По заданной эпюре М (рис. 6. 10, а) для балки
(рис. 6.10,6) определить действующие нагрузки и построить эпюру Q.
Решение. 1) Определение нагрузок, действующих на балку.
Участок Л С несет равномерно распределенную нагрузку, так как
эпюра М на этом участке — квадратная парабола. Заметим, что для
определения интенсивности этой нагрузки требуются некоторые до-
полнительные расчеты, которые выполнены ниже.
В сечении С к балке приложена пара сил с моментом qP/2,
действующая по часовой стрелке, так как эпюра М имеет скачок
вверх на величину ql2l2.
Очевидно, на участке СВ балка не нагружена, так как эпюра М
на этом участке прямолинейна.
Определим реакцию опоры В, использовав известное значение
изгибающего момента в сечении С:
Мср ~-^-ql2 = RBl,' откуда RB = qll2.
Для определения интенсивности (q^> распределенной нагрузки
составим выражение для изгибающего момента в сечении А через
правые силы и при этом учтем, что по заданной эпюре Мд = 0,
МА = RB2l — SRo — = — —-^- = 0, откуда qx = q.
Реакция Ra определяется обычным порядком из уравнения рав-
новесия. Нагруженная балка показана на рис. 6.10, в.
2) Построение эпюры Q.
Начиная от левого конца балки, откладываем в точке А вверх
ординату, равную Ra = ql/2.
4
1-19
97
В сечении С определяем поперечную силу как сумму сил слева:
Qc = Ra —ql=ql!2 — ql = —ql/Z.
На ненагруженном участке СВ эпюра Q параллельна оси балки.
Эпюра Q представлена на рис. 6.10,г.
Пример 6.8. Построить эпюры Q и М для балки, изображен-
ной на рис. 6.11, а.
Решение. Несмотря
на то, что общее число связей,
накладываемых опорами бал-
ки, равно четырем, балка
Я'
За
Эп.Ц ms
6
а
8,1 .
3
!ишш«»йпипп:п1
RSaitom
d-ZM
»г*
Р'Зтс а-2 тс/м
0 Д '* ——
0.5а а
a
Н111Ш11
шиннипнии
Рис. 6.11
^442
С____
1.5L
___С
Рис. 6.10
статически определима, благодаря промежуточному шарн
РУ с.
Шарнир дает возможность одной части СВ балки поворачивать!
относительно другой АС, вследствие чего изгибающий момент в а
чении С равен 0. Это и дает основание составить дополнитель
уравнение: сумма моментов относительно точки С (шарнира) вс<
внешних сил, лежащих по одиу сторону от шарнира, равна нулю.
1) Определение опорных реакций:
J т£рав) = 0; — Ив • 5а — SR. + <? • За • 2,5а = 0;
= -Ж+ 7^ _ rOA+ZiS-lJ = 1« _ 2.9 тс.
Ьа ' о • 1 о
S ша = 0; —ЗЛд + Ра q • За • 4а — Rb • 6,5а — SR = 0;
98
Яйл = 5. 1 4-2.3.4 — 2,9.6,5—0,5 = 9,65 тс-м.
Sr=.O, RA-P-q-За +RB^0’,
Ra = 5 + 6 — 2,9 = 8,1 тс.
2) Построение эпюры поперечных сил Q.
Строим эпюру Q по характерным точкам. В сечении на левой
опоре поперечная сила равна опорной реакции (/?л = 8,1 тс). До се-
чения Е поперечная сила остается постоянной. В сечении Е на эпюре
получается скачок вниз на величину силы Р = 5 тс. Полученное
значение поперечной силы, равное 3,1 тс, сохраняется'до сечения
D. На участке DK поперечная сила изменяется по линейному за-
кону.
Для построения эпюры на этом участке вычисляем значение по-
перечной силы в сечении К- Удобно это значение вычислить как
сумму сил справа: Qu— —Rb~ —2,9 тс.
Это значение остается постоянным на участке КВ. Эпюра Q по-
казана на рис. 6.11,6.
3) Построение эпюры изгибающих моментов.
В сечении А МА — —9,65 тс • м.
В сечеиии Е находим изгибающий момент как сумму моментов
слева: Me = —®л 4- Ra • а = —9,65 4- 8,1 • 1 = —1,55 тс • м.
На участке АЕ изгибающий момент изменяется по линейному
закону.
В сечении D:
Md~ —®л 4- /?л*2,5 - а — Р • 1,5 • а = —9,65 4- 8,1 • 2,5 х
X 1 — 5 • 1,5 • 1 = 3,1 тс-м.
На участке ED эпюра изгибающих моментов также прямая ли-
ния, пересекающая ось в точке С.
На участке DK изгибающий момент изменяется по закону квад-
ратной параболы.
В сечении L, где эпюра Q пересекает ось (проходит через нуль),
М достигает максимума. Для определения Л4тах находим абсциссу
сечения, где Q = 0:
Ql = — Rb 4- qx0 = 0; х0 = = 1,45 м;
- ч £
Afmax = ® 4- Rb (а 4- х0) — q-£- = 0,5 4- 2,9 • 2,45 —
2 • 1,45» . - с
-----jf— = 5,5 тс • м.
В ..числяем изгибающий момент в сечении К:
Мк = ® 4- RB • а = 0,5 4- 2,9 • 1 = 3,4 тс • м.
По трем значениям М на участке DK строим параболу. '
В сечении, проходящем через опору В, Мв— 5R = 0,5 тс • м.
-1
99
Эпюра М представлена на рис. 6.11, в.
Заметим, что эту задачу можно было решить по схеме, пред-
ставленной на рис. 6.11,г.
Определив реакции подвесной балки СВ, можно перейти к ос-
новной балке ЯС, нагрузив ее дополнительно силой Rc, являющей-
ся силой давления подвески СВ на балку АС.
Задачи для самостоятельного решения
6. 2. Построить эпюры Q и М (по характерным точкам) для балок,
показанных на рис. 6.12.
Указание. В ртветах даны значения Q н М, наибольшие по абсо-
лютной величине, х0 отсчитывается от левого конца балки.
Ответы.
“) <2гпах = р;
6)
«) Отах = 5тс;
«) Qmax = 4TCf
*) <2™х = 2Р;
е) Отах = 1.8 тс;
^1 Отах = ’
^тах ~ Рс (ПРИ *0 = С- « ПР» *о1 = е + Л-
.. Я1* ( 1 3 .
Мтах = \П₽И *о = Г " ПР" *01 = Т 1
Мтах = 16,5 то • м (в заделке).
,, л ( II.
Мтах = 4 тс • м I на участке — < х < -g- слева I •
Л4тах = Ра (на опорах и посередине, пролета).
Afmax = 2 тс • м (на участке длиной а справа),
g
Л1тах = ок?1* (посередине пролета).
°) Отах = ?«=20кН;
«) Опшх = 2<?а = 24 кН;
«) Отах = = 20 кН;
Отах = 4?“ = 16 кН;
*) Отах = 156 кН;
«) Отах = 90 кН;
<» Отах = Р = 60 кН;
я) Отах = = 50 кН;
Р) 0тах=10кН;
4 Отах = ¥ = 6 КН;
«) 0тах = ^ = 5кН;
У) Отах = 4 кН,
Ф) Отах *= ЮО кН;
Л4тах — 2,5qa* — 50 кН • и (в заделке).
Мтах = Sqa* = 28,8 кН • м (в заделке).
Л4тах = 1>5?а* = 60 кН-м (посередине пролета).
Л4тах = 7.5<7а2 = 30 кН-м (посередине пролета).
Л4тах 345,6 кН • м (при *о = 4,8 м).
^тах = 61.25 кН • м (при х0 = 3,25 м).
Мщах = Ра = 90 кН • м
Л4тах = Т=25кН.м
•Wmax = 5R = 60 кН • М
^max = V=4KH,M
(иа правой опоре).
(на правой опоре).
(на участке длиной о’
(в заделке).
Л4тах = о- = 6>67 кН • м (из правой опоре).
О
Л4тах =4 кН • м (при = а и при х01 = За)
Л1тах = 150 кН • м (на участке длиной а сле|
и на правой опоре).
100
ТО!
г го
НЬЛПЩШПГГ
H/HHOS-1)
О
6.3. По заданной эпюре Q (рис. 6.13) восстановить нагрузку
и построить эпюру М. Смотрите указание к предыдущей задаче.
Ответ, a) Afmax = <?а2 (при х0 = а);
б) Л4тах = 2Ра (при = а и при х01 = За).
6.4. По заданной эпюре М (рис. 6.14) восстановить нагрузку
и построить эпюру Q.
2
Ответ, a) Qmax ~ у qa (иа левой опоре);
б) Qm.x — 2Р (на участке длиной а слева).
2Ра
Ра
Рис. 6.14
§ 6.3. Построение эпюр Q, М, N для статически
определимых плоских рам *
Рамой называют систему брусьев, жёстко соединенных между!
собой в узлах. В некоторых частных случаях возможно, что рама!
наряду с жесткими узлами имеет часть узлов шарнирных. Брусын
рамы в основном работают на изгиб; при их деформации углы между!
ними не изменяются (в жестких узлах). Рама называется плоской,I
если оси всех составляющих ее брусьев лежат в одной плоскости и щ
той же плоскости расположена действующая на раму нагрузка^
Пример плоской рамы приведен на рис. 6. 15, там же показано, чти
при деформации рамы угол между ее горизонтальным и вертикалы!
ным элементами остался прямым. На рис. 6. 16 изображена рама!
брусья которой расположены в горизонтальной плоскости, а нагруЯ
ка {(сила Р) — в вертикальной. Такого типа рамы обычйЯ
называют плоскопространственным и. “Я
102
Рама является статически определимой, если внутренние силовые
факторы, возникающие в поперечных сечениях составляющих ее
брусьев, могут быть определены с помощью метода сечений без рас-
смотрения условий деформации рамы*. В частности, для статиче-
ской определимости рамы необходимо, чтобы опорные реакции могли
быть найдены из уравнений статики. На рис. 6. 17, а, б приведены
примеры статически неоп-
ределимых рам; первая из
них, как принято говорить,
один раз статически неоп-
ределима (опорные закреп-
ления дают четыре связи,
а уравнений статики для
плоской системы сил мож-
но составить лишь три);
вторая из представленных
рам трижды статически
Рис. 6.15
неопределима.
В общем случае в поперечных сечениях брусьев плоских рам
возникают три внутренних силовых фактора: поперечная сила Q,
изгибающий момент М и продольная (нормальная) сила N. Опреде-
ление внутренних- силовых факторов производится с помощью ме-
тода сечений. Для определения Q и М следует руководствоваться
указаниями, которые были даны применительно к балкам. Продоль-
ная сила в произвольном поперечном сечении какого-либо из стерж-
ней рамы численно равна алгебраической сумме проекций на про-
дольную ось этого стержня всех внешних сил, приложенных к раме
по одну сторону от проведенного сечения.
Построение эпюр для рам также нужно начинать с определе-
ния опорных реакций за исключением рам, имеющих жесткую
* Встречаются рамы, опорные реакции которых могут быть определены
ИЗ уравнений статики, и все же рама является статически неопределимой.
Рамы такого типа содержат замкнутые контуры. Эти рамы иногда называют
внутренне статически неопределимыми.
103
заделку на одном конце, а другой конец свободный. В этих рамах
можно определить внутренние силовые факторы, двигаясь от сво-
бодного конца, тогда опорные реакции получаются «автоматически».
При построении эпюр условимся считать, что наблюдатель на-
ходится внутри контура рамы.
Пример 6.9. Построить эпюры Q, М, W для рамы (рис. 6. 18, а).
Решение. 1) В рассматриваемой П-образной раме прежде
всего необходимо определить опорные реакции.
Рис. 6.18
Шарнирно-неподвижная опора А дает две составляющих опор-
ной реакции: Ra и На’, шарнирно-подвижная опора В дает лиШ1
одну вертикальную реакцию Rb (предварительно принимаем, чтс
она направлена вверх). 1
Составляем уравнение равновесия: 1
У тА = 0; — Рв • 4 — #2 • т = °> откуда RB = —Р2. |
Знак минус указывает на то, что направление опорной реакци|
было выбрано неверно,— реакция Rb направлена верти калым
вниз. Наносим на чертеж реакцию Rb, учитывая ее действительна
направление, а реакцию, направленную вверх, зачеркиваем (сМ
104
рис. ,6.18,а). Составляем сумму моментов всех сил относительно
точки В: ^mB = 0; RA • ~ — Рг • у = 0, откуда Ra = Р2 =
= 5 тс.
Горизонтальную составляющую полной реакции шарнира А,
т. е. На, определим из условия, что сумма проекций всех сил
на горизонтальную ось х равна нулю: 2-^ = 0; На— Pi — Р2=
=* 0, откуда На — Pi + Р2 = 8 тс.
Проверка.
Для проверки используем уравнение £ Y = 0; Ra — Rb=*
= 5 — 5 = 0.
Таким образом, опорные реакции найдены правильно.
2) Построение эпюры Q.
Рама имеет четыре участка: AC, CD, DK, КВ.
Рассмотрим / участок АС (0 С ft), взяв начало координат
в точке А. Находим поперечную силу как сумму проекций на ось,
перпендикулярную стержню АС сил слева от сечения:
Qi = — На = — 8 тс.
Значение Q,, очевидно, остается неизменным на всем участке ЯС.
На // участке* (о^х3^4) Qu — Ra — Ьтс.
Третий и четвертый участки рамы рассмотрим, двигаясь со
стороны ее правого конца (В):
III, 0<х3<4;
QHl = Рх = 3 тс — на всем участке ВК',
IV. о<х4<4-; ;
Qiv = Pi + Р2 = 3 + 5 — 8 тс — на всем участке KD.
По полученным значениям строим эпюру Q (рис. 6.18, б).
3) Построение эпюры М..
/ участок (0^ Хх Л). Определяем М. как сумму моментов
сил слева от сечения: М.! = —На • xt.
Давая хг значения, соответствующие границам участка, по-
лучаем
М1х _0 = Ма = 0; MiXi^h = Мс = —На • h=*—8 • 6 = —48 тс- м.
// участок (о^х3^ 4). Находим Ми также как сумму мо-
ментов сил слева от сечения: Ми = Ra • xa — На • ft.
Определяем два значения Мц — в сечениях С и D:
Мцх = Л4с = —На • ft = —48 те • м
и Mllx = MD = Ra^ — На - h = b • ^ — 3 & ~ —33 тс • м.
* Перекладину П-образной рамы называют ригелем.
105
Ill участок ^0<x3s^-£-j. Определяем Мш как сумму момен-
тов сил справа от сечения: М1П = —Рг х3.
Определяем два значения Мт-.
Мш 0 == Мд — 0; M/ц h — Мк = —~ =»
Х' = Т 2
= —3 • = —9 тс м.
IV участок ^0х4Определяем Мп как сумму момен-
тов оил справа от сечения: Мп = —+ — Ргх4.
Находим два значения Мп' MnXt=0 = Мк « —Pi =*
= —9 тс • м и Мп h = MD = ~Pih~P2 —3-6 —5-3=«
X.
4 2
= —33 тс • м, что совпадает с ранее полученным значением из-
гибающего момента в узле D.
Строим эпюру М, откладывая, как было условлено, ординаты
в сторону сжатых волокон (см. рис. 6. 18,в).
4) Построение эпюры N.
На первом участке находим М.как сумму проекций на ось АС
всех сил слева от сечения: N/— —Ra— —5 тс.
Знак минус указывает, что стойка АС сжата. Проектируя все
силы слева от сечения II на направление ригеля CD, получаем-
АГ„ — —На — —8 тс (ригель сжат).
На III и IV участках определяем продольную силу как сумму
проекций на ось DB всех сил справа от сечения:
Nln = Riv = Ra ~ Rb — 5 тс (правая стойка растянута).
Строим эпюру М, откладывая положительные ординаты снару-
жи, а отрицательные — внутри контура рамы (см.рис.6. 18, а).
Пример 6.10. Построить эпюры Q, М, N для рамы (рис. 6.19,а).
Решение. 1) Определение опорных реакций.
Для определения четырех опорных реакций (RA, Ra, НА, Нв)
составляем три уравнения равновесия для рамы в целом и дополни-
тельно используем условие, что изгибающий момент в сечении, про-
ходящем через шарнир С, равен нулю:
S тв = 0; Ra • 4а — q • 2а • а = 0;
„ 2аа 2 • 2 • 1 ,
= -Т = —— = 1 тс;
£m^ = 0; Ra а-Нл- ft = 0; НА = = 0,333 тс;
106
^X = O-,Ha—Hb^Q;Hb = Ha = 0,333 тс;
SK = 0; Ra + Rb — q- 2a = 0;
Rb = 2qa — Ra = 4 — 1 = 3 тс.
Проверка: £ тпср = —3 -3 + 0,333 • 3 + 2 2 • 2 = 0.
2) Построение эпюры поперечных сил.
Эпюру Q строим по характерным точкам.
Рис. 6.19
Участок AD — левая стойка. В сечении А:
Qa = —На = —0,333 тс.
Это значение поперечной силы на участке AD не меняется.
Участок DK —ригель. В сечениях D и Е находим Q как сумму
проекций на ось, - перпендикулярную ригелю, внешних сил слева:
Qd = Ra = 1 тс; Qe = Ra =** 1 тс.
В сечении К проще определить Q, рассматривая правую часть
рамы: Qk = —Rb = —3 тс.
Участок КВ— стойка. В сечении К' 0,к1=Нв = 0,333 тс.
Это значение Q остается постоянным на участке КВ.
Эпюра поперечных сил показана на рис. 6. 19, б.
3) Построение эпюры М.
107
Участок AD. В сечении А (на шарнирной опоре) Ма = 0. В се-
чении D MD= —На h = —0,333 • 3 — —1 тс-м. На участке
AD эпюра М — прямая линия.
Участок DK- В сечении О, принадлежащем ригелю, изгибающий
момент имеет то же значение, что и в сечении D, принадлежащем ле-
вой стойке.
В шарнире С изгибающий момент равен нулю.
На участке ЕК изгибающий момент изменяется по закону квад-
ратной параболы. Для построения эпюры на этом участке найдем
три значения изгибающего момента:
М е = Ra %а — На h —2 — 0,333 -3= 1 тс-м (сумма мо-
ментов слева);
Мк = —Нв h — — 0,333 • 3 — — 1 тс• м (сумма моментов справа).
Третье значение — Л1тах. Положение этого сечения найдем,
приравняв Q нулю:
Q = —Rb + qx0 — 0; Xq = — = -х- = 1,5 м.
» ч
M^^Rb- Хо — Нв-h--------Ч-£=тЗ- 1,5- 0,333-3 —
— 2~i~~ ~ тс • м-
Участок КВ. В сечении К сохраняется найденное значение
Мк = —1 тс-м.
На шарнирной опоре В момент равен нулю. На участке КВ из-
гибающий момент изменяется по линейному закону.
Эпюра изгибающих моментов показана на рис. 6. 19, е.
4) Построение эпюры У. _
Продольная сила в стойке AD постоянна:
NA = Nd == — Ra = —1 тс.
В ригеле DK
Nd = Rk= —На = —0,333 тс.
В стойке КВ
К к ~ Nb ~ —Rb = —3 тс.
Эпюра продольных сил показана на рис. 6.19, г.
*
Задачи для самостоятельного решения
6.5. Построить эпюры поперечных сил Q, изгибающих моментов
М и продольных сил N для плоских рам (рис. 6. 20).
Ответы.
Указание.
В ответах даны наибольшие по абсолютной величине значении Q, М, Nt
а) ^тах ~ ^шах = У щах ~
108
б) Стах = 2тс:
в) Стах = 4 тс;
г) Стах = 2’25 тс;
8) Стах = 3 тс;
е1 Стах = 1 тс;
^тах = 4 ТС • м; Ытгл = 1,3 ТС.
^тах = 4 ТС • м; Nmax = 4 ТС.
Чпах = 20 ТС • м; Nmax = 2,25 ТС.
^тах = 6 ТС • м; Nmax = 5 ТС.
^тах = I ТС • М, ^тах 1 ТС‘
Рис. 6.20
6.6. Для указанных плоских рам (рис. 6.21) построить эпюры
(?, М, N (см. указание к предыдущей задаче).
Ответы.
°) Стах - 4’5 тс; Чпах = ’О-1 тс ’ м; Л'тах = 2’7 тс-
б) Стах = 3 тс; ^тах^ 10’5 -м; ^тах = 3 ТС.
е) Стах == 2 ТС! ^тах == 6 ТС •М, Мпах ~ 2 Тс’
г) Стах = 2 тс; Мтах = 2 ТС • М; Л%ах = 4тс-
8) Стах = 2 ТС’ ^тах “ 3 ТС • М; ^тах ~ 2 ТС‘
е) , Стах ~ 2,3 ТС’ ^тах ~ ^>2^ тс ' м’ ^тах = 2,3 ТС'
ж> Стах = 3 тс; Мтах = 8,5 ТС • м;.. Nmix = 5 ТС.
6.7. Построить эпюры Q, М, N по характерным точкам для
плоских рам (рис. 6.22),
Ответы.
«) Стах = 20 кН: ^тах = 4® кН • м; Nmax = 20 кН.
б) Стах = Ю кН; Л4тах = 30 кН • м; /Vmax = 10 кН.
109
Mjomi. -i
Рис. 6.21
в) Стах = 6 кН; Л4тах = 15 кН • М; 1Утах = 6кН.
г) Стах-40 кН; Мтах = 84 кН • м; /Vmax = 40 кН.
Я) Сп?ах = 20кН; Л4таХ = 60 кН • м; /Vmax = 20 кН.
*) Стах = 50 кН; Л1тах = 100 кН . м; /Vmax = 50 кН.
ГЛАВА 7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ПРЯМОМ ИЗГИБЕ
§ 7.1. Расчет на прочность по нормальным напряжениям
При прямом чистом изгибе балки в поперечных сечениях ее воз-
никают нормальные напряжения, которые зависят от изгибающего
момента в соответствующем сечении. При прямом поперечном изгибе,
кроме того, возникают касательные напряжения, связанные с попе-
речной силой.
Нормальное напряжение в любой точке поперечного4сечения оп-
. м <
ределяется по формуле ах= ~гУ,
*2
где М — изгибающий момент в данном сечении; Jz— момент инер-
ции сечения относительно нейтральной оси; у — расстояние от точ-
ки, где определяется напряжение, до нейтральной оси.
Максимальные нормальные напряжения возникают в точках,
наиболее удаленных от нейтральной -оси (рис. 7.1): атах =
= Мутах//г, или, вводя, обозначение Wz = Jz/ymax, получаем
Отах M/Wz.
Ill
При этом возможны два случая:
а) сечение симметрично относительно нейтральной оси (рис. 7. 2).
В этом случае расстояния крайних растянутых и сжатых волокон
до нейтральной оси одинаковы, т. е.
б) сечение несимметрично относительно нейтральной оси.
В этом случае вычисляют два значения IF — для крайних растяну-
тых и сжатых волокон (рис. 7.3): = J2/t/i max; IF2 = Jjyt max.
Напряжения в крайних растянутых и сжатых волокнах раз-
личны: maxop = Af/IFj; |maxoc| = M/W2.
Для балок с сечениями, несимметричными относительно нейт-
ральной оси, нет необходимости вводить в расчетные зависимости
Рис. 7.3
моменты сопротивления. Формулы для определения наибольших
напряжений растяжения и сжатия можно записывать в таком виде
виде (см. ниже пример. ,7.3): тахар = у ук\ тахос = ~Уи
где ^к=</1тах, У[.~ У2тах — расстояния от нейтральной оси
соответственно до наиболее удаленных точек растянутой и' ежа"
той зон сечения.
Условия прочности при прямом изгибе ffmax = Afmax/IFz^ [а].
Замечания.
а) Для сечений, симметричных относительно нейтральной оси, расчет на
прочность ведут по допускаемому напряжению на растяжение или сжатие,
смотря по тому, какое из них меньше.
б) Для сечений, несимметричных относительно нейтральной оси, при ма-
териале, неодинаково сопротивляющемся’ растяжению и сжатию (например,
112
чугун), нужно вести расчет на прочность отдельно для растянутых л сжатых
волокон.
в) Для сечений, несимметричных относительно нейтральной оси, при
материале, одинаково сопротивляющемся растяжению и сжатию (сталь),
расчет на прочность нужно вести по меньшему значению W, т. е. для воло-
кон, в которых нормальные напряжения достигают наибольшей величины
по абсолютному значению.
Подбор сечения при изгибе производится по формуле Wz > Л4тах/[о].
При этом укажем следующие случаи:
а) При подборе прокатных профилей нужный номер балки выбирается
по сортаменту по вычисленному Wz.
б) Если сечение круглое, его диаметр определяется по формуле
d > V32Fz/« = /32Мтах/л [о].
в) Для кольцевого сечения наружный диаметр
..................................^х_.(
' л[о](1 —с4)
где с = dfD.
г) Для прямоугольного сечения W2 =
Если материал балки неодинаково сопротивляется растяжению и сжа-
тию, то балку лучше выбрать несимметричного относительно нейтральной
оси сечения. Например, для чугуна рационально выбирать тавровую форму
сечения (см. рис. 7.3), причем большую часть материала расположить в рас-
тянутой зоне, так как чугун лучше сопротивляется сжатию, чем растяжению.
Если эпюра М дли данной балки имеет участки разных знаков, то ска-
занное выше (о рациональном расположении профилей балок из хрупкого
материала) относится к сечению, где М максимален по абсолютной величине.
Дополнительно следует провести расчет иа ^прочность для сечения, где име-
ется наибольший момент противоположного знака — по максимальным рас-
тягивающим напряжениям.
Р-Цблтс
inmunmm
I' 0,8м
------г-
Рис. 7.4
б
Пример 7.1. Вычислить наибольшие нормальные напряжения,
возникающие в поперечном сечении балки (рис. 7. 4,а), рассмотрев
варианты сечений, указанные на рис. 7.4, б — г\
Сравнить экономичность указанных профилей.
Решение. Для определения нормальных напряжений поль-
зуемся формулой
. [ Оглах = Aftnax/^z.
Очевидно, что Л4шах при указанном нагружении балки будет
в сечении заделки
Мпах = Р14- ч-£ = 0,6 • 0,8 + ,20,8> = 0,64 тс-м = 64- 10s кгс см.
113
Находим моменты сопротивления приведенных сечений:
Гб = ^-2 = = 32 см3; We = = 4-~ = 96 см3;
= Ц113 + 2 4- 2 12 3 • 7,5е = 4536 см4;
= 554 см3.
Определяем натряжения:
06 = = Щг~ = 2000 кгс^см2«
а. = = 666,7 кгс/см3;
Мтах 64-10® 1О7 , . »
аг — — 504 — 127 кгс/см .
г »
з
Оценим экономичность сечений отношением Wz: F 2 ,
Сечение по рис. 7.4,6: 32/Р 483 — 0,0955;
Сечение по рис. 7.4, в-. 96/]/483 = 0,287;
Сечение по рис. 7.4,'г: 504/]/1083=> 0,446.
Выгодны при изгибе те формы сечений, у которых основные час-
ти площади максимально удалены от нейтральной линии.
Пример 7.2. Деревянная плотина состоит из ряда вертикальных
столбов квадратного сечения, обшитых досками (рис. .7.5, а, 6).
Какого размера должны быть поперечное сечение столбов и толщина
досок, если глубина реки в этом месте h = 3 м, расстояние между
осями столбов I = 1,5 м и допускаемое напряжение на изгиб для
дерева [аи] = 50 кгс/см2.
При расчете досок считать их свободно лежащими на двух опо-
рах, а расстояние между опорами принять равным 1,5 м.
Решение. Столбы плотины представляют собой балки, ра-
ботающие на изгиб. Нагрузка, действующая иа один столб,
114
равна силе давления воды на вертикальную стенку высотой h
и длиной I.
Сила давления воды на .1 см длины стенки представляет собой
распределенную нагрузку, изменяющуюся по закону треугольника
от 0 (на поверхности воды) до значения yh (на глубине h). Равнодей-
ствующая этой нагрузки равна площади треугольника ууЛЛ и при-
ложена на расстоянии h/З от основания. На стенку шириной I при-
ходится нагрузка Р = ~yh2l.
Рассматривая столб как консольную балку, найдем максималь-
ный изгибающий момент в сечении заделки (рис. 7.5, в):
= = ~yh2l. = 1 • 30^‘п150 = 67,5 • 10* кгс см.
О Z О О 1 иии
Требуемый момент сопротивления сечеиия столба
Wz> Afmax/M. Wz = 67,5 • 10*/50 = 13500см3.
Для квадрата Wz = а3/6.
Получаем а 6IFZ = |/б • 13500 = 43,5 см.
Доски обшивки находятся . в разных условиях, так как на-
грузка изменяется по высоте плотины; Найдем толщину нижне-
го ряда досок как наиболее напряженных, выделив полоску вы-
сотой в 1 см у основания плотины и ведя расчет по наибольшей
интенсивности нагрузки: q = yh • 1 = 1 • 300/1000 = 0,3 кгс/см.
Рассматривая доску как балку на двухч опорах (рис. 7.5, г),
найдем Мпах .= ^- = °’Э — 845 кгс см.
Находим UZz> ^-х = = 16,9 см3.
[о] оО —
Определяем толщину доски, учитывая, что (рис. 7.5, д):
Г2 = ^ = Ц^; === /6 • 16,9 « 10 см.
Пример 7.3. Проверить прочность чугунной балки П-образ-
ного сечения (рис. 7.6, а, б), предварительно выбрав рациональ-
ное расположение сечения. Принять [ар] = 400 кгс/см2 и [сгс] =
= 1200 кгс/см2.
Решение. Определим реакции опор
£тд = 0; —1,7. 1 + 0,5 • 1 — 1,*+Яв • 3—1 • 4 = 0; .
£ms = 0; —1,7'4+ /?л. 3 — 0,5-2 — 1,5 —1 • 1 = 0.
Отсюда Ра = 3,43 тс; Rb = 2,23 тс.
Эпюры Q, М показаны на рис. 7.6, в, г. Наибольший (по абсо-
лютной величине) изгибающий момент возникает в сечении А. В этом
сечении сжатые волокна балки находятся внизу, поэтому сечение
балки нужно расположить так, как указано на рис. 7.6, б,— боль-
шая часть материала находится в зоне растяжения.
115
Положение центра тяжести сечения
, - 25г, 2.20 • 2 • 10 + 2 • 8- 19 ,1С '
Ус SF 2-20 «2 + 2 «8 —11,5 СМ.
Момент инерции сечения относительно нейтральной оси
А = 2 + 2 2 • 20 • 1,52 + + 8-2.7,52 = 3750 см«.
Расстояния от нейтральной оси до наиболее удаленных точек
в зонах растяжения и сжатия (для сечения А):
Ук = 8,5 см; Уг.= 11,5 см.
— У к 8,5 п _. [°р1 400 п пп „ Ук 1°р1
4 Так как yL ~ 11,5 ~ °’74’ а |о£] — 1200 ~ 0,33 И yL > 1ас] ’
опасными являются точки растянутой зоны, наиболее удаленные
от нейтральной оси.
Производим проверку прочности по наибольшим растягивающим
напряжениям в сечении А (для точки К):
тахор = —— ук =’«—3750— • 8,5 = 386 кгс/см2 < [ор].
Необходимо проверить прочность балки в сечении С. Хотя
|Л4с|<|Ма\, но в сечении С профиль балки расположен нера-
ционально. Опасной точкой здесь будет точка L:
шахор = ~ у. = 1,2XU°- 11,5 = 385 кгс/см2.
Сечения А, С оказались равноопасными.
Прочность балки обеспечена.
116
Задачи для самостоятельного решения
7.1. Чугунная труба (наружный диаметр D = 30 см и толщина
стенки б = 0,3 см) наполнена водой и свободно опирается по концам.
При каком расстоянии между опорами наибольшие напряжения
в трубе будут а = 250 кгс/см2? Собственный вес трубы принять во
внимание,'считая объемный вес чугуна у = 7,5 гс/см8.
Ответ. 667 см.
Рис. 7.7
Рис. 7.8
7.2. Построить эпюры Q, М и вычислить нормальное напряжение
в точке В опасного сечения балки (рис. 7.7).
Ответ. 206 кгс/см*.
7.3. Определить из расчетов на прочность размеры сечения бал-
ки, изображенной на рис. 7.8, при трех показанных на рисунке ва-
Рис. 7.9
Рис. 7.10
риантах форм сечений. Принять [ст] — 1600 кгс/см2. Сравнить
рациональность сечений.
Ответ, a) D — 16 см; б) D = 18 см; в) а = 13,4 см.
7.4. Определить из условия ’ прочности значение допусти-
мой нагрузки [<?] для заданной балки (рис. 7.9). Принять [ст] =
= 1600 кгс/см2. Собственным весом балки пренебречь.
Ответ. [<?] = 0,85 те/м.
7.5. Полагая, что напряжения от собственного веса в сечениях
Л, В, С двутавровой балки, изображёинрй на рис. 7.10, одинаковы
и достигают сттах, определить расстояния от точек опоры балки
117
до ее концов, а также значение допускаемой длины Ш балки, если
1а] = 1600 кгс/см2.
Ответ, а «= 0,209/; [/] = 9,28 м.
7.6. Определить из расчета чугунной балки (рис. 7.11) на проч-
ность требуемую величину 6. Предварительно выбрать рациональ-
ное расположение сечения. Принять
[ор] = 300 кгс/см2; [ас] = 900 кгс/см2.
Ответ. S = 16,7 мм.
2 тс/м
иинажкижн;
К „« I
1 а
Рис. 7.11
§ 7.2. Проверка прочности по касательным напряжениям
Помимо проверки прочности балки по нормальным напряжениям
иногда приходится делать проверку по касательным напряжениям,
вычисляемым по формуле Д. И. Журавского: т = QSzlbJz, гдет —
— касательное напряжение в любой точке
поперечного сечения; Q — поперечная сила %
В данном сечении балки; S2— статический |
момент относительно нейтральной оси час- 1
ти площади поперечного сечения от уров-й
ня, на котором определяются касательные!
напряжения, до края балки; b — ширина!
сечения в том месте, где определяется на-3
пряжение т; Jz— момент инерции попереч-Я
иого сечения балки относительно нейтраль-!
ной оси. J
Наибольшие касательные напряжения для сечений типа прямоЯ
угольник, двутавр, круг возникают на нейтральной оси. УсловиеЯ
прочности в этом случае имеет вид , Я
Тщах = Qma*Szmax/bJz [т], . Я
где SImax — статический момент полусечения относительно нейЯ
тральной оси. Я
а) Прямоугольное сечение. Касательные напряжения на расстояЯ
иии у от нейтральной оси вычисляются по формуле . Я
г = _ 3Q[i _ 4рЛ2] Я
118
Наибольшие касательные напряжения возникают в точках ней-
з* 7’ 3 Q 3 Q
тральной осн (у = 0): ттах= -j = -j 7? .
где F — площадь поперечного сечения балки.
На рис. 7.12 изображен^ эпюра касательных напряжений
для прямоугольного сечения. Касательные напряжения в любой
точке сечения параллельны плоскости нагрузки.
б) Круглое сечение. Максимальные касательные напряжения воз-
4 Q
никают в точках нейтральной оси (рнс. 7.13, а): тшах =
в) Двутавровое сечение. Максимальные касательные напряжения
QS
возникают в точках нейтральной оси (рис. 7.13, б): ттах = у-
а В
Рис. 7.13
где &ст — толщина стенкн; S2max— статический момент полусече-
ния относительно нейтральной оси.
г) Круговое кольцо. Вопрос о критерии применимости формулы
Д. И. Журавского к полым брусьям исследован Д. И. Шерманом.
Формула Д. И. Журавского является приближенной, точные ре-
зультаты могут быть получены лишь методами математической тео-
рии упругости.
Сопоставляя точные расчеты с приближенными,' можно для каж-
дой частной задачи установить критерий применимости формулы
Д. И. Журавского, т. е. определить, при каких соотношениях отно-
сительных размеров параметров полых сечений приближенная
формула дает результаты, близкие к точным, и в каких случаях
резко от них отличается.
Приведем результаты, полученные нами для кругового коль-
ца (рис. 7.14,а).
Установлено, что при Rt, очень малом по сравнению с напря-
жения у внешнего контура не зависят от наличия отверстия, а в ок-
рестности самого отверстия они вдвое больше, чем для поперечного'
сечения, не ослабленного отверстием.
Следовательно, в случае отверстия малого диаметра формула
Д. И. Журавского неприменима.
Касательные напряжения, определяемые на основании точной
формулы, монотонно возрастают с увеличением относительных раз-
меров радиуса отверстия. Наиболее напряженными являются точки»
119
расположенные на нейтральной оси г. Напряжения в них убы-
вают в направлении от внутренней границы к наружной, т. е. от
точки А к точке В.
Эти напряжения в точках нейтральной оси можно записать
в виде т — Km(PRl/Jz), где Кт —некоторые постоянные (/п=1,
2, 3); Jz — экваториальный момент инерции поперечного сечения
бруса относительно'нейтральной оси.
Аналогично для тех же точек получим по формуле Д. И. Жу
равского т* = Х-^, где X = [1 + а + а2]; а — (табл. 7.1).
Таблица 7.1. Значения коэффициентов Кт и X (ц=0,3)
а Л, . к. К, X
0 - 0,6923 0,3363 0,3076 0,3333
0,01 0,6923 0,3363 0,3077 • 0,3366
0,05 0,6930 0,3393 0,3094 0,3508
0,1 0,6953 0,3494 0,3146 0,3699
0,2 0,7046 0,3846 0,3353 0,4133
0,3 0,7199 0,4347 0,3700 0,4633
0,4 0,7415 0,4957 0,4184 0,5199
0,5 0,7692 0,5649 0,4807 0,5833
0,6 0,8030 0,6408 0,5569 0,6533
• 0,7 0,8430 0,7227 0,6469 0,7299
0,8 0,8892 0,8100 0,7507 0,8133
0,9 0,9415 0,9025 0,8684 0,9033
0,95 0,9699 0,9506 0,9325 0,9508
0,97 0,9818 0,9702 0,9590 0,9702
Касательные напряжения т*, вычисленные по формуле Д. И. Жу-
равского, удовлетворяют СЛеДуЮЩИМ УСЛОВИЯМ: Tmin < Т* < Ттая^
т* ~ Ту- где т т , тг—соответственно минимальное, макси-!
О ’ liiifl П13Х О
120
мальное и значение напряжения посередине толщины стенки тру-
бы— в точке С (см. рис. 7.14, а).
На рис. 7. 14,6 приведены графики изменения касательных на-
пряжений т, т* в зависимости от параметра а.
Как следует из графиков, в тех случаях, когда внутренняя гра-
ница близка к наружной, искомый результат может быть получен
без громоздких вычислений с помощью формулы Д. И. Журавского.
Пример 7.4. Проверить прочность клееной деревянной балки
(рис. 7. 15, а, г), если допускаемое напряжение на изгиб для мате-
риала балки [о] =100 кгс/см2 и допускаемое напряжение на сдвиг
для слоя клея [т] = 8 кгс/см2.
Т* а=0,6тс/м 4
|ншишпнншинншн.|
Рис. 7.15
Решение. Определив опорные реакции, строим эпюры по-
перечных сил и изгибающих моментов (рис. 7. 15, б, в).
Для проверки балки на прочность по нормальным напряжениям
определяем момент инерции и момент сопротивления ее поперечного
сечения относительно нейтральной оси:
, 123 - 24 63 . 10 . т 3276 клс
J, — —гх------пт— = 3276 см4; W, = = 546 см3.
2 12 12 2 6
Максимальные нормальные напряжения, возникающие в опасном
поперечном сечении (посредине пролета) балки,
<т£2
Мтах 8 0,6 • 2,52 • 105 ого . » „ ' , .
Отах — — ~Wz — 8 • 546---- 85,8 КГС/СМ , Отах < [О].
Касательные напряжения, возникающие в продольных (парал-
лельных нейтральному слою) сечениях балки, равны касательным
напряжениям в соответствующих точках ее поперечных сечений.
Наибольшие касательные напряжения в слое клея возникают возле
опор балки, где поперечная сила достигает наибольшего значения.
Эти напряжения определяем по формуле Журавского:
Tmax ~ QmaxSzmax/^
121
где SZ[nax— статический момент полусечения относительно ней-
тральной оси; SZmax = 24-6-3 — 10 • 3 • 1,5 = 387 см3; Qmax ==
== <///2 = (0,6 • 2,5 • 103)/2 — 750 кгс; b = 24 —10 = 14 см — шири-
на сечения на уровне нейтрального слоя.
После подстановки числовых данных получаем
Ттах = (750 • 387)/(3276 • -14) = 6,33 кгс/см2; ттах < [т].
Пример 7.5. Построить эпюру распределения касательных на-
пряжений по высоте стенки несимметричного двутаврового сече-
ния (рис. 7. 16), в котором возникает поперечная сила Q = 160 кН.
Рис. 7.16
Определить расчетные напряжения в сварных швах, прикрепляю-
щих верхнюю и нижнюю полки к стенке. Катет швов k — 6 мм.
Решение. Для использования формулы Журавского надо
знать величину момента инерции сечения относительно главной
центральной оси, перпендикулярной плоскости нагрузки.Находим
расстояние центра тяжести сечения от его нижней кромки — оси
, _ sz. 300 - 6 - 3 + 400.6.206<+100.8.410
Z1 (рис. 7.17): Ус = -^=--------.збо". 6 + 400.6+ 1'00 .-8-=
= 165,7 мм.
Момент инерции сечения относительно оси г (см. рис. 7.17)
J2 = + ю • 0,8 (41 — 16,57)2 + + 40-0,6 (20,6 —
— 16,57)2 + + 30 • 0,6 (16,57 — 0,3)2 = 13 120 см4.
В пределах стенки сечения эпюра т очерчена по квадратной
параболе. Ограничимся вычислением т в трех отмеченных на рис.
122
7. 17 точках стенки. Для этого определяем статические моменты
относительно нейтральной оси соответствующих частей сечения:
Зг верхи, полки = 10-0/ (41 — 16,57) = 195,5 см3;
SZmax ~ верхи, полки 4* ОД (40 — 15,97)2 • -g- = 368 СМ3;
Згиижв. полки = 30 • 0,6 • 16,27 = 292,5 см3.
Вычисляем касательные напряжения в точках А, С, В:
QS
г верхи, полки _ 160 • 103 • 195,5 • 10-«
-------7^-------= i 3120-1о~8'-б~^То~4~ ~ 397 • 10 Н/м ;
Ъ - - Ъ s—S,m" '' - 397 •105 W - 727 ,0‘ Н/м’;
г верхи, полки * ’
= нижи, полки 397 . 105.2|2Д> = 594 . 105 Н/М2
верхи, полки ’
Эпюра т представлена на рис. 7. 17.
Из сварных швов более нагруженным является шов, прикреп-
ляющий нижнюю полку, статический момент которой относительно
оси г больше, чем статический момент
верхней полки/
Сила, сдвигающая нижнюю полку
(на единицу длины балки), Т = тв х
X йст . 1= 594 • 105 • 0,6 • 10-2= 356,4 х
х.Ю’Н/м, Эта сила воспринимается
двумя сварными швами с расчетной тол-
щиной 0,7k и длиной, равной единице.
Напряжения в этих швах
Т 356,4 • 10» .
Тшв — 2 • 0,7k ~ 2 • 0,7 • 6 . 10-3 ~
= 426 • 108 Н/м2 = 434 кгс/см2.
Пример 7.6Л Определить положение центра изгиба для швеллера
№ 36. Закруглениями углов и уклоном полок пренебречь (рис.
7. 18).
Решение. Центром изгиба сечения называется точка прило-
жения равнодействующей касательных снл упругости, возникаю-
щих в данном сечении. Практическое значение определения поло-
жения центра изгиба состоит в том, что при изгибе швеллера в глав-
ной плоскости, не являющейся плоскостью симметрии, он, помимо
изгиба, испытывает и кручение, а если силовая плоскость, будучи
параллельной главной центральной оси у, проходит через линию
Центров изгиба поперечных сечений, то кручения не будет.
Расстояние е ot центра изгиба (точка К) до стенки
123
где по ГОСТ 8240—72 />==11 см; h = 36 см; d = 0,75 см; t =
= 1,26 см; J г~ 10 820 см4.
Подставив в приведенную формулу числовые данные, получим
(11 — 0,75)’ (36— 1,26)’ ,
е = 2----ГЛУ820------ • 1 -26 = 3’67 СМ‘
Задачи для самостоятельного решения
7.7. Подобрать сечение двутавровой балки (рис. 7.19), если [а] =
— 1600 кгс/см2, 1т1 = 1000 кгс7сма.
Р
Р=25тс
1=^м
Рис. 7.19
Ответ. № 36.
7.8. В поперечном сечении (рис.
7. 20) балки возникает направленная
по оси симметрии поперечная сила
Q = 7 тс. Вычислить касательные на-
пряжения в точках А и В стенки.
Ответ. iA = 408 кгс/см’, тв = 241 кгс/см’.
7.9. Определить наибольшее касательное напряжение, возни-
кающее в поперечном сечении балки, изображенйой на рис. 7.21.
Ответ. 12 Н/мм’.
Рис. 7.20
Ш=30кН-м
г-*- ф°24«///м
4а
Рис. 7.21
ГЛАВА 8. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ
ПРИ ПРЯМОМ ИЗГИБЕ
§ 8.1. Основные положения
При действии на балку внешних сил, расположенных в одной из
главных плоскостей инерции и действующих по нормали к ее оси,
имеет место прямой изгиб: искривление оси балки происходит в си-
124
ловой плоскости. Ось деформированной балки называют упругой
линией.
Деформация балки характеризуется двумя величинами: 1) про-
гибом, т. е. перемещением точки оси балки перпендикулярно к ее
недеформированной оси, и 2) углом поворота, т. е. углом, на который
поворачивается каждое поперечное сечение вокруг нейтральной
оси по отношению к своему первоначальному положению*.
Рис. 8.2
Прогибы будем обозначать буквой у, углы поворота 0 (рис. 8.1).
Наибольший прогиб, называемый стрелой прогиба,— /* **.
Заметим, что углы поворота сечений 0 равны (как углы со вза-
имно перпендикулярными сторонами) углам наклона к оси х каса-
тельной к упругой линии.
Уравнение у = f(x), выражающее зависимость между прогибом
у при заданной нагрузке и координатой х, называется
уравнением у п ругой линии.
Рис. 8.3
На основании известного положения о геометрическом смысле
производной tg 0 = dy/dx.
На практике обычно углы поворота поперечных сечений 0^С 1°,
поэтому можно принять, что tg 0 0. Тогда 0 — dy/dx.
Между кривизной упругой линии, изгибающим моментом и жест-
костью поперечного сечения балки при прямом изгибе существует
♦ Перемещением поперечного сечеиия балки вдоль ее оси пренебре-
гают как величиной высшего порядка малости по сравнению с прогибам.
** Стрела прогиба стальных балок ие должна превышать для балок
перекрытий: //400 — //250, для подкрановых балок и крановых мостов:
//700 — //1000, где / — пролет балки.
125
следующая зависимость: 1/р(х) = M.{x)lEJfy где р(х)— радиус
кривизны упругой линии балки в точке, отстоящей на расстоянии
х от начала координат (рис. 8.2); М(х) — изгибающий момент
в том же сечении балки; EJZ— жесткость поперечного сечения
балки.
Из приведенной зависимости вытекает приближенное дифферен-
циальное уравнение упругой линии балки: EJzy"=^ М(х).
При оси у, направленной вверх (рис. 8.3), левая и правая части
уравнения имеют всегда один и тот же знак. Путем интегрирования
приближенного дифференциального уравнения упругой линии по-
лучают выражения для определения углов поворота и прогибов се-
чений балок. ,
§ 8.2. Определение перемещений методом
непосредственного интегрирования
В результате двукратного интегрирования приближенного диф-
ференциального уравнения упругой линии появляются постоянные
интегрирования, ^подлежащие в дальнейшем определению. Если
балка имеет одни участок нагружения, то таких постоянных будет
2, при п участках — 2л постоянных. Чтобы их найти, необходимо
воспользоваться условиями закрепления концов балки, а также
свойствами плавности и непрерывности упругой линии на границах
Рис. 8.4
участков.
Напомним, что из условий
плавности и непрерывности
осн изогнутой балки (упру-
гой линии) следует, что в каж-
дом поперечном сечении бал-
ки значение прогиба и значе-
ние угла поворота будут един- j
ственными. Таким образом, всегда имеется возможносткопределить 1
постоянные из 2п уравнений. Эта задача при нескольких участках |
нагружения балки связана с громоздкими вычислениями. Однако, 1
применяя специальные приемы при интегрировании приближенного 1
дифференциального уравнения упругой линии, можно добиться pa- J
венств а постоянных на участках и свести задачу при любом количе- 3
стве участков к нахождению лишь двух постоянных. Указанные Я
приемы сводятся к следующему: 1
1) интегрирование уравнения вести без раскрытия скобок; 1
2) влагаемое от сосредоточенного момента SR в выражении 3
для изгибающего момента М (х) записывать в виде ®(х — а)0, гДе З
а — абсцисса сечения, где приложен момент SR; начало координат —-3
левый либо правый конец балки; |
3) если на каком лнэо участке балки действует равномерно^
распределенная нагрузка, не доходящая до сечения, где определяла
ется прогиб (или угол поворота), то ее следует продолжить до этого 1
126
сечения, приложив в виде компенсации нагрузку той же интенсив-
ности, но противоположного направления.
Пример 8.1. Найти углы поворота опорных сечений и прогиб
посередине балки (рис. 8. 4).
Решение. Совершенно очевидно, что опорные реакции равны
нулю. Балка имеет одни участок. Приближенное дифференциальное
уравнение упругой линии запишется в виде
EJ2y" = М(х) = &. (1)
Проинтегрируем его дважды:
EJj/'==Мх + С-, (2) EJj/ = ~ + Сх + D. (3)
Постоянные интегрирования С, D найдем из условий закрепле-
ния концов балки.
Поскольку на опорах А, В прогибы равны нулю, можно записать
у0— Уа — 0, yi~ ув— 0. Рассматривая поочередно эти два условия
совместно с уравнением (3), заключаем, что/) — 0, SR/2/2 -|- С1 = 0,
откуда С = —SR//2.
Полученные значения С, D подставим в уравнения (2), (3).
~ ' П , 1 /ем ^1\ 1 /®?%2
Тогда получим 0 = у -----------------------jj.
По этам уравнениям можно вычислить угол поворота 0 и прогиб
у в произвольном сечении заданной балки.
Практический ин-терес представляют наибольшие значения (по
абсолютной величине) перемещений, т. е. 0тах, t/max-
Угол поворота опорного сечения Л 0д= 0О= —SR//2£JZ, а на
правой опоре 0В = 0; = SR//2£J2.
Углы поворота 0д, 0в отличаются друг от друга лишь знаком,-
сечение А поворачивается Tjo часовой стрелке, а сечение В — про-
тив нее. В силу симметрии приходим к выводу, что наибольший
прогиб (стрела прогиба) будет посередине балки (в этом сечении
0 = 0): f = yL = — MP&EJ,.
2
Знак минус здесь указывает на то, что балка прогибается вниз,
т, е. в сторону отрицательных значений у. Постоянные С, D, делен-
ные на жёсткость сечения Е]г, представляют собой соответственно
угол поворота и прогиб сечения в начале координат.
Пример 8.2. Найти прогибы посередине и иа свободном конце
консоли (рис. 8.5,а).
Решение. Определим опорные реакции в защемлении S Y =
= 0; Ra — q j — q~^ — 0, откуда == g//2; ^/пл== 0; —®д +
+ т‘4’ + '^_’т^ = 0, 0ТКУда = ^2/4-
Для определения прогибов ув, у к воспользуемся интегрировани-
ем дифференциального уравнения упругой линии. При этом приме-
ним те приемы, которыерекомендованы выше для уменьшения числа
127
постоянных интегрирования при нескольких участках нагруже-
ния балки.
Начало координат поместим на левом конце консоли (в защемле-
нии), ось у направим вверх, ось х — вправо. Запишем и дважды
проинтегрируем дифференциальное уравнение упругой линии для
первого участка: /. EJzy^ — Mi(x); —Яйл +
+ R,,x-f = -ф + ^-£.
Рис. 8.5
Тогда EJzy" —
= -^ + 4*-^ О)
EJzy^~^x +
+ (2)
с 1 аРх* , д/х3
+ Сгх + Dx'.
24
(3)
Постоянные интегрирования
С, D найдем из начальных усло-
вий: а) уи=о = 0Л = 0;
б) t/u=o = Ул = 0.
Рассматривая условие а) совместно с уравнением (2), а условие
б) совместно с уравнением (3), получаем Сх— 0, 0.
Переходя ко второму и третьему участкам, необходимо продол-
жить равномерно распределенную нагрузку до конца консоли, а для з
компенсации приложить такую же нагрузку, но противоположного |
направления (рис. 8. 5,6). На втором участке получим 3
и I 3 , J
' 4 4 l' 1
I____£\2 J
EJzy^= М2(х); M2(x) = — y+4-x— ?+ ~—2~~~ ’ |
Дифференциальное уравнение упругой линии для второгоя
учйстка ' -я
/ _ М2 JI
z? / ’ . ql qx2 . 4/ ,
EJzUi — 4 + 2 Х Т + 2 '
Интегрируем это .уравнение дважды, не раскрывая скобок: fl
ад - - «г+т - т+'ДД+с>-
Е1Л + ’-VI + + D.
(1
и
128
Проверим, добились ли мы равенства постоянных интегриро-
вания на участках, TJa границе первого и второго участков со-
гласно условиям плавности и непрерывности упругой линии за-
пишем в) у i = у i , откуда Сг = Са = 0;
!* = Т 2* = т
г) У. _ i = У. _ i , отсюда Di = Da = 0.
2Х- —
Уравнение прогибов (6) запишем в виде
____ 1 I д/’х* . g/х3 дх4
У* ~ EJt L ~8~ 12 24
i ' Y1
ф-т/
24 .
Из этого уравнения найдем прогиб сечения /С:
_ 1 Г <?/* , ____<?/* । 1______143 q&_
Ук=*Угх = ±-~ EJZ[ 32 'г 96 384 6144 | 6144 EJZ '
(7)
(8)
Далее на третьем участке будем иметь
III. I; EJ^ = М3(х), где
/ _£\*
.. . . ql* . ql „ qx*- . У\Х 4/
Мя (х) — 4 + j х 2^ 2
I 3 ' ’
9(х —- Л
2
откуда
и после двукратного интегрирования
+ + + (10)
( _L? ( _з A4
___+ , JL__4 / ? \ 4 /
^гУз — 8 "Г i2 24 + 24 24
+ C3x+Da. (11)
На границе второго и третьего участков, аналогично изложен-
ному выше, имеем:
з , з ,
х — ~г1 х=т1
Д) Уз = Уз [см. уравнения (5), (10)], откуда после
соответствующих подстановок найдем, что С2 =* С3 =• 0;
Я =~1 X = ~1
е) У2 =у3 , откуда £>2 = D3 = 0.
Таким образом, мы убедились в том, что при соблюдении ряда
Условий можно добиться равенства соответствующих постоянных
1 -10
129
интегрирования на участках и при любом их количестве свести
задачу к определению лишь двух постоянных: С, D.
В рассматриваемом случае
Cg33 Сд— С ~ 0; D±~ Dg== D^~ D ~ 0.
Подставляя в уравнение (11) значение х = I, находим прогиб
вечения В, т. е. на конце консоли
if ql* , Igl* gl* . 81?/* ql* 1
. yix=i ~ EJzL 8 -12 24 +614? 6144]
t ! i 9 ql*
или окончательно [в ~ ] ув ] = pgg .
432 ql*
6144 EJZ’
12
(12)
Задачи для самостоятельного решения
8.1. Найти прогиб свободного конца А консоли (рис. 8. 6) из
двутавра № 30, изгибаемого в плоскости
Принять Е = 2 • 10* кгс7сма.
Qpieem. \уА \ = fA — 0,371 см.
наибольшей жесткости.
8.2. Определить 0л, в, 0с, ус
для балок, схемы которых представ-
лены на рис. 8.7.
I
a
1/2
А’
U
Р=3тс
с
_____ъ
L
|С
-Я
р/2
Рис. 8.6
Рис. 8.7
Р1й
Ответ, а) 0В = —0Л = ; 0С = 0;
- - е -о-и
iSEJj l&EJt' ”с~0’ Ус
Ы п
12EZ,’ *Св°*
рр
Ус----48ЁГг • 0А =
qhP
192£/г 48Е/г
• ®) 0А “ 0В =
J
24Е/г i
х К
А
В
а
А
В
1
&
В
а
а
к
I
в
в
130
§ 8.3. Определение перемещений методом начальных
параметров *
Метод начальных параметров позволяет записать одно уравнение
прогибов (или углов поворота сечений), пригодное для всех участков
балки, поэтому это уравнение называется универсальным, или обоб-
щенным.
Универсальное уравнение упругой линии (в форме, предложен-
ной профессором А. П. Коробовым), учитывающее все основные
типы нагрузок — сосредоточенный момент, сосредоточенную силу,
распределенную нагрузку переменной интенсивности,— имеет для
Рис. 8.8
балки постоянного сечения при указанных направлениях нагрузок
и осей (рис. 8. 8) следующий вид:
. , А , мох» , а)2 I
fp — Ро + 0о* + 2EJz + &EJz + 2j 2EJz I
x>a
SP(*-t>P II _ у f
6EJX И J *
z>b Ct
Здесь y0, 0O, Mo, Qo— начальные параметры; y0— прогиб в нача-
ле координат; 0О— угол поворота начального сечения; Мо— изги-
бающий момент в начальном сеченин; Qo— поперечная сила в том Же
сечении. Отметим, что у0, 0О— геометрические факторы, а Мо и Qo—
силовые.
Начальные параметры у0, Qo, Af0, Qo могут принимать какие
угодно значения: положительные, отрицательные и равные нулю.
Определяют эти четыре величины, исходя из условия закрепления
j* Подробнее этот вопрос освещен в учебном пособии Б. А. Ободовского
«Определение перемещений в балках методом начальных параметров».—
М.: Высш, школа, 1971,— 87 с
5*
131
балки, а также нагружения левого конца, который принят за на-
чало координат. На рис. 8. 8, а все начальные параметры положи-
тельны: у0 отложен вверх от оси х\ 0О— поворот сечения предпола-
гается против часовой стрелки; /Ио направлен по часовой стрелке;
Qo— вверх. Что касается других слагаемых в уравнении метода
начальных параметров, то их знак определяется в зависимости от
того, создает ли данная нагрузка положительный или отрицатель-
ный изгибающий момент в сечении с абсциссой х.
Последнее слагаемое, входящее в уравнение, отражает влияние
распределенной нагрузки переменной, интенсивности q(E), где
с с3 фиксирует положение этой нагрузки на балке.
Знак \}х>а (прерыватель) показывает, что соответствующее слагае-
мое нужно учитывать только при х > а. Этоозначает, что при опре-
делении прогиба в каком-либо сечении с координатой х в уравнение
входят лишь нагрузки, лежащие слева от этого сечения. Если вместо
нагрузки, распределенной по произвольному закону, будет прило-
жена нагрузка, распределенная по линейному закону (по закону
трапеции), то универсальное уравнение прогибов упрощается и при-
нимает вид (рис. 8. 8,6)
, - , Л4пх2 ,
У ~ Уй + + 2ЁГг +
Qo*3 , V ~ а>а Ц
&EJ* Т 2EJZ ||
х>а
V Р Ч — b)3 | _ VI (х — е,)4 I yi ?8 (х — с2)4 ||
Zu 6ZV2 I Zu 24£/z I ’’’Zu 24Е/г ||
Х>Ь Х>С1 х>сг
— V fe(*~gi)b || । Vk (~х~с^ъ II
U- 120£/2 || ^ Zu 120£7г II ’
X>Ci • X>Ct
где k = ——— = tg а.
ca — ci
Итак, универсальное уравнение прогибов содержит следующие
слагаемые: а) четыре — Для начальных параметров, б) одно — для
внешних моментов, в) одно — для сосредоточенных сил, г) четыре —
для нагрузки, распределенной по линейному закону. Поскольку
трапециевидная нагрузка представляет собой сочетание равномерно
распределенной и треугольной, в этом случае из четырех слагаемых
два соответствуют равномерно распределенной, а два — треуголь-
ной нагрузке. Заметим, что все слагаемые, кроме начальных параме-
тров, находятся под знаком суммы, распространяемой на все нагруз-
ки данного вида. В таком виде универсальное уравнение прогибов ;
рекомендуется к практическому использованию (и к запоминанию). J
Уравнение углов поворота может быть легко получено из урав-
нения прогибов путем вычисления производной по координате;:.
Если кроме указанных выше нагрузок к балке приложена
распределенная моментная нагрузка интенсивности т (т]), то уни-
версальное уравнение упругой линии примет вид (рис. 8.9)
132
4-fir ' . V ^(x-d)2 II __ V |[ __
у Уо + o0X + 2EJx + 6£/г + £j 2EJz I 2j 6£7г ||
x>a *>b
Ci ds
_ У f - eMs I V I' rn W (jf-T))a
~ Zj J 6ЁГ2 + Zj J 2£Л •
e, rft
Рис. 8.9
Если принять начало координат на правом конце балки и напра-
вить ось абсцисс справа налево, то для углов поворота сечений
должно быть принято правило знаков, противоположное тому, кото-
рое применяется при начале координат
на левом конце балки. 4 у
Пример 8.3. Определить прогиб и
угол поворота свободного конца консо- ________
ли (рис. 8. 10). Ч
Решение. Обращаясь к универ- |< —r/^-Zl /в
сальному уравнению, запишем для за-
данной коисоли уравнение упругой ли- Рис. 8.10
нии в виде
, МоХ* , Q„x3
' 2EJ2 6EJ2
У = Уо + %х
Р\х 2/ ЯЛ(х—/)«
&EJ2 + 2EJ2
I х>1
х>~
(1)
Начальные параметры найдем из условий закрепления левого
конца консоли АВ и уравнений равновесия у0= 0; 0о= 0; Мо=/= 0;
0 (так как левый конец защемлен):
^тл = о; -®гл + р| + ж = о,
133
откуда 8R4 = ®1 + у; ’J] Y = 0; Ra — Р = 0; Ra =* Р, т. в. Мо »
= = - («Я + ^) •, Q0 = ^ = p.
Учитывая значения начальных параметров, перепишем уравне-
ние (1) в виде
/ I V
«Их» Plx* Рх3 P\~~2J , .
У 2EJZ Шг + QEJZ 6EJZ Т 2ЕЛ ’ W
I х>1
Замечанне. Очевидно, последнее слагаемое не следует учитывать,
так как оно имеет смысл лишь при х> I, т, е. относится к воображаемому
участку, расположенному вне балки. Поэтому в последующих примерам
аналогичные слагаемые будем опускать.
Искомый прогиб найдем, подставив в уравнение (2) х « U ,
(4)
рр рр рр
Ув—У*^" 2EJZ 4EJZ' &EJZ 48EJZ'
После приведения подобных членов будем иметь
ув~ — «де/а/2ЕЛ — 5Pl3/4&EJt. J
Уравнение углов поворота сечений найдем, взяв производную ]
по координате х от уравнения прогибов (2):
р/х-Д’Й
Я1х. Plx . Рх* \х 2 / И
ЕЛ 2Е/г + 2ЕЛ 2EJZ || ’
’>4
Угол поворота концевого сечения В получим, подставив в уравнение
(4)х =/:
о а ЯП Р1* . Pl* Pl*
«в = —§4 “2ЁЛ +
или окончательно
0 = У
“ ЕЛ 8ЕЛ ’
I у
Х~~2)
24 EJ,
(О
Пример 8.4. Для балки постоянной жесткости (рис. 8. 11,а) ;
построить эпюры углов поворота сечений и прогибов. з
Р е ш е и и е. Для данной балки уравнение упругой линии имеет J
вид
,, । о v 1 М$х* , Qpx3__^х* ,
У У о + 00* + 2Е/г + &Е/г 24ЕЛ^
Здесь последнее слагаемое учитывает распределенную нагрузку, |
направленную вверх и приложенную на правой части балки для!
компенсации пр?йления заданной нагрузки до конца балки. 1
Продленная и компенсирующая нагрузки на чертеже не показаны.!
134
Начальные параметры:
г/о= 0; Qqt6 0; 2И0= 0; Qo¥= 0-
Найдем опорную реакцию Ra из условия равновесия
IX =0;
откуда Ra = ql, (Rb = ql = -^ qty .
3
Отсюда получаем, что Qo = RA = -g- ql.
С учетом значения Qo уравнение (1) запишется так:
= fi г 4- — _£l_
* 0 + 16£J2 24£7.
24 EJ?
(2)
J 2
Найдем 0O из условия, что
прогиб правого конца балки
равен нулю: ух=4 = ув = 0,
т е е I I f Ql*
т. е.* + 24Ё^ +
+ 38&=0- 0ТКУда
0о = 0а^ — з^^-. (3)
Рис. 8.11
Уравнение изогнутой оси балки имеет вид
( — —V
9qPx ) qbfl qx* , \ 2 /
384EJ2 1627, 24£/, + 24£J2
(4)
Отсюда легко получим уравнение углов поворота, сечений
/ _£\*
д_..> , Ч\*. 2/
у ~ 384£J, 16EJZ 6EJ2 "Г 6£J2
(5)
~2
Давая абсциссе х различные значения, постррим эпюру 0. По-
лучаем согласно уравнению* (5)
д ___ д _а____________.
0О — 0Л — Их=0 — 3S4£JZ >
135
в I SqF qP '
x - “ 384£/2 + UEJZ ~ 48EJ2 ~ 384£72 ’
a a _ fy/8 . 3qF_____________________qP , qlA 7qP
од o*=; =« 384£72 ' 16£72 6£72 48£7, 38?£Л ’
Замечаем, что на первом участке ^O^x^yj эпюра должна
пересечь ось абсцисс, так как согласно (6) 0 меняет знак с ми-
нуса (при х = 0) на плюс (при х = 1/2).
Как известно, в тех сечениях, где 0 = 0, прогиб будет наиболь-
шим (либо наименьшим). Положение этого сечения найдем, прирав-
няв нулю правую часть уравнения (5), предварительно отбросив
в
нем последнее слагаемое.
Тогда будем иметь 0 =*
9<?/3 , 3<7/хо <7*о
= — 384 £72 + 16£У2 6Ё72
=• 0, или 64х®—721x1 +
-|-9/3 = 0, откуда-х0 = 0,46/.
По полученным значениям
углов поворота сечеиий стро-
им эпюру 0 (рис. 8. 11,6).
Для построения эпюры прогибов вычисляем по уравнению (4)
их значения для некоторых характерных сечений
_ 9 - 0,46^/“ , (0,46)3 ql* (0,46)“ ql*
Ух=о,АЫ = 384£у2 т I6£/t 24£J2 “
’-------^(4,14-0,0973.24 + 0,0448. 16)--^;
‘/-.S<--5Sfel9.0.5-(0.5)'.24 + (0,5)-. 16J-----
Эпюра прогибов представлена на рис. 8. 11, в.
Существенно отметить, что в рассмотренном примере прогиб
посередине пролета крайне незначительно отличается от макси-
мального (примерно на 1,2 %). Этот результат является в значитель-
ной мере общим — максимальный прогиб двухопорной балки без
консолей при нагрузках, вызывающих однозначные прогибы, мало
отличается от прогиба посередине пролета. Поэтому в указанных
Случаях для упрощения расчетов на жесткость прогиб посередине
пролета принимают за максимальный.
Пример 8.5. Подобрать сечение двутавровой балки (рис. 8. 12)
из условия прочности, если lol = 1600 кгс/см2. При найденном
профиле вычислить наибольший прогиб и углы поворота опорных
сечений.
Решение. Требуемый момент сопротивления сечения IF2^
> /Итах/[®], где в рассматриваемом случае (см. пример 6.5)
/Umax ~ 7о/2/15,6 (при х =» 0,577/). После подс!ановки численных
136
вначений имеем И?2 = jg-g- = 200 см3, чему соответствует по
ГОСТ 8239—72 двутавр’№ 20а (W2 = 203 см3; J2 = 2030 см4).
Уравнение изогнутой оси запишется в виде
У Уо + щх + 4- 6EJz 120£j2» (j)
где k = q0/l.
Начальные параметры: y0 = yA = 0; Л40 — 0; 0о=#О; Q0=#0.
Опорную реакцию Ra найдем из условия равновесия
£^ = 0; RAl-"4-Xi = o,
откуда = <7<Ж и тогда Qo = RA = qol/Q.
Принимая во внимание значения известных начальных пара-
метров,- получаем
!'“9»«+Ж-етэ;- (2)
Угол поворота 0О найдем из граничного условия yx==t = 0 (про-
гиб на правой опоре В равен нулю):
Q 1 I ffo^4__Яр1* _л
°Z + 36&/2 12077 2 ’
откуда 0О = 0л =-^7<7о/3/36О£Т2. (3)
После*подстановки значения 0О в уравнение (2)-окончательно
будем иметь
______7qol»x дох* .
у ~ 360Е/2 'г 36Е72 , 120Е72/' * 1
Затем, взяв производную по координате х, получим уравнение.
углов поворота сечений
ft . 7<Ма I Яо1х* Чо*
» ” 360£V2 ~ \2EJZ 24EJJ ’ ’ ' ,
Из уравнения (5) найдем угол поворота опорного сечения В;
eB = Qx=l = q0l3/45EJz. (6)
Максимальный прогиб будет в том сечении, в котором угол пово-
рота 0 = 0. Согласно уравнению (5) определим положение этого се-
чения:
-36&<7'‘-зо^+'5<> = °'
откуда найдем х0=^ 0,52/.
137
Наибольший прогиб (стрела прогиба) равен на основании урав»
иения (4)
Утах = №=0,52/ = —0,0065 . (7)
Итак, окончательно получаем
д 7?0/з 7.2.53.10’ П^.1О
°Л — 360£72 ~ 360 • 2 • 10» • 2030 ~ рЭД5
a <7oz’ 2 • 53 • 10’ а 0.07 „„ .
0В 45EJZ 45 • 2 • 10» • 2030 ~ °»0137 РаД>
_ 0,0065до1» _ 0,0065 • 2.5» • 10» _ „
Утах — EJz — 2 • 10» • 2030 — Z СМ'
Задачи для самостоятельного решения
8.3. Найти прогиб и угол поворота концевого сечения В консоли
(рис. 8. 13).
Од = —7qa?!&EJ2.
Ответ. ув = —41 qa4/24EJZ-
Рис. 8.13
2a
а^О&п'с/м ’
Bffnra in»#
IZZzESS
НИИ
Рис, 8.14
8.4. Вычислить прогиб сечения С балки (рис. 8.14).
Ответ: yc = 3qa*J2EJz'= 1,2 см.
Указание. Дли упрощения решения сЛедует отбросить коисол^
заменив действие консольной нагрузки соответствующими силами и момен-
тами, а затем рассмотреть деформа*
цию балки АВ, приняв за начало
координат точку А.
8.5. Определить прогиб ус се-
чения С и угол поворота 0р се-
чения D балок, изображенных
иа рис. 8. 16.
£Л
л ШТП/
1ННЙ1
да
с
Рис. 8.15
a
2 a
п ' 1 Яа* а о <№* Л IStya4 „ qa3
Ответ, а) ус-------7 — ^ = 2-^. б) ус ==
8.6. Определить прогиб ус сечения С и угол поворота 0D сече-
ния D балки (рис. 8. 15).;"
7qa* „ 2qa*
'Ответ. ус----
8.7. Определить прогибы посередине пролета и на свободном
конце консоли (рис. 8.17).
Ответ. yD — ~97qa4/24EJz, ус = 35ga4/liEJz.
138
8.8. Найти углы поворота опорных сечений, стрелу прогиба,
а также прогиб посередине балки (рис. 8.18).
о~. |/c|=|/D| = -g; ,K = 0.
Рис. 8.17
а
[ШПШззпн!
шиш;
Рис. 8.18
Рис. 8.16
8.9. Определить прогиб сечения В консоли, подверженной •дей-
ствию моментной нагрузки, распределенной по закону треугольника
(рис. 8.1§).
Ответ. ув — 11,6^^ <
Рис. 8.19 Рис. 8.20
8.10. Определить прогибы и углы поворота сечений А, В, С бал-
ки (рис. 8.20).
. 32?а4 10?а4. п _ б^а» п„ 8<?а’ п
Ответ. уА = ; ус 3EJ* , 0Л EJ* ; 0л 3EJ*; 0В -
4<?дЗ _ Зда3
= EJz 5 °с “ EJz'
§ 8.4. Определение перемещений энергетическим методом
(с помощью интеграла Мора)
Потенциальная энергия деформации упругой системы
В общем случае работа внешних сил
где Рп— обобщенные силы; 6П— обобщенные перемещения.
139
Напомним, что действию пары (момента) соответствует угловое
перемещение (угол поворота), а действию сосредоточенной силы —
линейное перемещение (прогиб или удлинение).
Формула для определения потенциальной энергии деформации
при поперечном изгибе с учетом изгибающих моментов М и попереч-
ных сил Q имеет вид
j. V ftfdx V f AQ2 dx
и ~ 2—’ J 2EJz + Д J 2Gf ’
l I
где k — коэффициент, зависящий от формы поперечного сечения
балки (например, для прямоугольника k => 1,2). Второе слагаемое
в большинстве случаев мало по сравнению с первым, им пренебре-
гают и пользуются следующим приближенным выражением потен-
циальной энергии:
—« J Ze. J г
О
Интеграл Мора для определения перемещений при изгибе
Интеграл Мора позволяет определять перемещения (угловые
и линейные) для балок, рам, а также для кривых брусьев. При из-
гибе прямого бруса или бруса малой кривизны интеграл Мора запи-
сывается в виде (влияние поперечных сил не учитывается)
S
Здесь 6 — искомое перемещение (угловое или линейное); М — вы-
ражение изгибающего момента от заданных сил в произвольном
сечении бруса (рамы); Мг— выражение изгибающего момента в про-
извольном поперечном сечении от единичной нагрузки Р^= 1
(или = 1), приложенной в сечении, где отыскивается переме-
щение 6; EJ — жесткость сечения бруса; ds — элемент длины
бруса.
Для прямолинейных элементов интеграл Мора принимает вид
с VI Г М!Лл dx
s = 2J-w
i
С учетом поперечных сил
_ уч ММ± dx j уч J kQQ± dx
l ' l
no
Вычисление интеграла Мора по способу Верещагина
Для прямолинейных элементов бруса интеграл Мора можно вы-
числить графоаналитически по способу Верещагина. По этому спо-
собу перемещение в направлении приложенной единичной силы
определяется по формуле
б = ^t\c/EJz,
где со — площадь нелинейной эпюры изгибающих моментов; т]с—
ордината линейной эпюры изгибающих момёнтов под центром тя-
жести площади со; EJZ — жесткость сечения рассматриваемого уча-
стка при изгибе.
Если имеется несколько участков.нагружения, то
s = V
X- EJZ •
При применении способа Верещагина надо иметь в виду следую-
щее: 1) эпюры изгибающих моментов должны быть разбиты на
такие участки, в пределах каждого из которых хотя бы одна из эпюр
линейна и жесткость сечения бруса постоянна; 2) при перемножении
эпюр ставим знак минус, если эпюры находятся по разные стороны
от оси отсчета.
Таблица 8.1. Площади эпюр и положения их центров тяжести
Эпюра изгибающего * момента Координата центра тяжести Площадь Эпюра- изгибающего момента Координата центра тяжести Площадь
Рис. 8.23, а *ц. т = =!«+•> Рис. 8.23, д *ц. т = f со = -5- lh
Рис. 8.23, б II Рис. 8.23, е ХЦТ=-Р, со = ~ lh 4
Рис. 8.23,в X =~1 Ц. т 2 со = lh Рис. 8.23, ж х Ц. т 2 (^ = ~lh □
Рис. 8.23, г со |оо II 2 Н. °> = ~3lh Рис. 8.23, з хцт =0,533/ со = 0,65/ft
Пример 8.6. Найти прогиб и угол поворота сечения А балки
(см. рис. 8.21, а).
Решение. Изгибающий момент в произвольном сечении балки
« .г ЧаХ2 , ах X
от заданной нагрузки = + у •
При составлении этого выражения «треугольная» нагрузка допол-
нена до «прямоугольной» и приложена компенсирующая «треуголь-
ная» нагрузка, направленная вверх (рис. 8.21, а).
Замечая, что из подобия треугольников q/q0 — х[1, нли q =s
= q^x/l, получаем М = —q0x2/2 + q0x3fi>l.
141
Для определения прогиба прикладываем в сечении А единич-
ную силу Р(1> = 1 (рис. 8.21, б); — —1 • х.
Теперь получаем бл = dx = (—х) dx.
о 2 • о
Отсюда искомый прогиб
Л — *М4 11 Ы*
л &EJZ 3OEJZ 120 EJ, '
Знак плюс указывает, что направление прогиба совпадает с на-
правлением силы
Угол поворота найдем аналогично, имея при этом в виду, что
в этом случае 9R(1)— 1(рис, 8.21, в),
0 0
т. е.
0 . — _ ?о.Г .1. __ fy.?_
л 6EJZ 24£JZ 8£JZ ’
Знак минус здесь указывает
на то, что сечение-Л поворачи-
Рис. 8.22
вается от заданной нагрузки в сторону, противоположную еди*
ничному моменту, т. е. против хода часовой стрелки.
Пример 8^7. Определить наибольший прогиб балки (рис. 8.22, а).
Решение. Эпюра изгибающих моментов М от заданной на-
грузки представлена на рис. 8.22, б. Очевидно, что наибольший про-
гиб имеет сечение посередине пролета балки. Прикладываем в этом
сечении единичную сосредоточенную силу (рис. 8.22, в) и, определив
опорные реакции, строим эпюру изгибающих моментов Мх (рис.
142
8.22, в). Эта эпюра имеет два линейных участка, поэтому эпюру М
также разбиваем на две части. Выражение, определяющее величину
искомого прогиба, имеет два слагаемых б = f = 4- где
CJ2 2
2 ql3 I ql3 ' <
Qi = соа = -у • • у = -^----площадь параболического треуголь-
5
ника (рис. 8.23, г табл. 8.1); тц = I — ординаты на эпюре
143
Л41э под центрами тяжести площадей coj, и2; эти ординаты находим
из подобия треугольников abc и ade (рис. 8.22, г):
f „ о ______о 5 <__ 5?/4
‘‘ EJZ 24EJZ ' 32 384EJZ'
Пример 8.8. Определить прогиб посередине Пролета заданной
балки (рис. 8.24, а).
Решение. Определив опорные реакции, строим эпюру из-
гибающих моментов от заданной нагрузки (рис. 8.24, б). К балке,
освобожденной от заданной нагрузки, прикладываем посередине
пролета единичную силу (рис. 8.24, в) и, определив опорные реак- .
ции, строим эпюру моментов от действия указанной силы (рис.
8.24, г). В рассматриваемой задаче эпюра изгибающих моментов от
заданной нагрузки линейна на всем протяжении балки, а эпюра от
единичной силы ломаная (нелинейная), поэтому, применяя правило
Верещагина, берем площадь эпюры М1( а ординату на эпюре М:
EJ^o где со — 2 4 / 8 , 2 ’ S 16ЕЛ •
Приведенный пример заслуживает особого внимания, так как
нередко у изучающего сопротивление материалов складывается
ошибочное представление, что при пользовании правилом Вереща-
гина надо всегда брать площадь эпюры моментов от заданной нагруз-
ки, а ординату — из эпюры моментов от единичной силы. На самом
144
деле происхождение эпюры не играет роли — важно лишь, какая из
эпюр линейна и какая нелинейна.
Пример 8.9. Определить прогиб свободного конца заданной бал-
ки (рис. 8.25, а).
Решение. Строим эпюру изгибающих моментов М от задан-
ной нагрузки (рис. 8.25, б). В том сечении, где отыскивается прогиб,
прикладываем единичную силу (рис. 8.25,в) и строим от нее эпюру
изгибающих моментов (рис. 8.25, г). Так как моменты инерции
по длине консоли различны J2), то, применяя способ Вереща-
гина, необходимо отдельно рассмотреть два участка перемножения
эпюр, хотя на всем протяжении балки обе эпюры моментов линейны.
Обращаясь к рисункам 8.25, б, г, получаем (трапецию в эпюре М
разбиваем на прямоугольник и треугольник): бд = fB = +
, WjTlcj WjTlcs __ 1 p
5 n 3
Ti = у a; co2 = Paa; T]fa = ~2
Ре» 2
®з ; r]f3 = -g-a.
Окончательный результат:
f _ 5Pa? 3Pa3 , Pa3 _
~ 6EJ1 “* ZEJ^ 3EJ2 ~
__ 14Pa3 , Pa3
" 6ЕЛ ' 3£Ja ’
Пример 8.10. Определить
прогиб посередине пролета за-
данной балки (рис. 8. 26, а).
Решение. В данном при-
мере, как и во многих других
случаях, удобно строить эпюру
изгибающих моментов от задан-
Рис. 8.26
ной нагрузки (грузовую эпюру) в так называемом. «расслоенном»
виде. Сущность метода расслоения эпюр состоит в следующем: если
уравнение изгибающего момента от заданной нагрузки представляет
собой многочлен, то вместо того, чтобы строить график этого много-
члена, для применения способа Верещагина целесообразно строить
отдельные графйки (эпюры), каждый из которых соответствует од-
ному из слагаемых. Так, для участка балки, нагруженного рав-
номерно распределенной нагрузкой,
Mj = Rax —
Эпюры, соответствующие каждому из слагаемых для этого уча-
стка, показаны на рис. 8. 26, б (их площади обозначены Wj и wa).
145
Эти эпюры построены до сечения С, которому соответствует место
излома единичной эпюры, показанной на рис. 8, 26, г. Для части
балки, расположенной правее сечения С, расслоенные грузовые эпю-
ры моментов (их площади обозначены (о3 и <о4) построены при «движе-
нии» по балке справа налево. Применив способ Верещагина, получим
6с = («iflci + ®2Т1С2 + СОзПсЗ + ®4П«),
1 15 л л 15 о _______________ 1 2 п 2
где (Oj = -g • qa • 2a •2a = qa3-, т]е, = у 2a = у a;
w2 = — -3 2a • 2qa1 = — у qa3; = у • у • 2a = у a;
1 9 no 9 s 1 2 o 2
“» = у • У ’ 2q ' 2a = y?as; = - • у • 2a = ya;
1 qa?____ qa? 17 7.
C04 -у у a -j у 1 ~ У ’ T a ~ "8 U‘
После подстановки су, т)<г получим
- = 9^/15 2__± i.l 2____________L П 137 go*
с ~ EJZ Ц ' 3 3 • 4 + 4 ’ 3 б ' 8/ “ 48 EJt'
Задачи для самостоятельного решения*
8. 7. Найти прогиб и угол поворота свободного конца А консоли,
изображенной на рис. 8; 27. _ - .
-Рис. 8.27
р/8 Р/2
/л = Шг; ел = 2ЁГг.
8. 8. Определить прогиб и угол пово>
рота свободного конца В консоли (рие.
8. 28).
О'/4 о/8
Ответ, — =
Рис. 8.28
Рис. 8.29
♦ В ответах к задачам 8,7—8.11 даиы абсолютные значения прогибов
•и углов поворота,
146
8. 9. Определить прогиб посередине пролета и угол поворота
опорного сечения В балки, изображенной иа рис. 8. 29.
Рис. 8.30
Рис. 8.31
8. 10. Определить прогиб fc сечения С и' углы поворота Од,,
0о„ сечений слева и справа от шарнира D балки (рис. 8. 30).
л . 7Ра» „ Ра* _ Ра*
Ответ. fc- , бО1 = 2£7г: 0D>“ 4£}г'
8. 11. Найти прогиб посередине пролета балки (рис. 8.31).
n . 13РЯ
Omeem</
ЧАСТЬ
вторая
ГЛАВА 9. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫХ СИСТЕМ *
§ 9.1. Статически неопределимые балки. Основные понятия
в ряде случаев для определения опорных реакций балок
® уравнений статики недостаточно, т. е. число опорных реак-
ций больше числа уравнений статики, которые можно составить
для данной балки. Такие балки называют статически неопредели-
^Рис. 9.1
мыми. Так, для балок, изображенных на рис. 9.1,9.2, имеем че-
тыре и шесть опорных реакций.
Недостающие уравнения, так называемые уравнения переме-
щений, число которых соответствует числу «лишних» неизвестных,
составляются по ’условиям деформации.
Рис. 9.2
Термин «лишние» неизвестные, широко применяемый в теории
статически неопределимых систем, в значительной степени условен.
Дополнительные опорные закрепления балок и рам (т. е. не являю-
щиеся необходимыми для обеспечения геометрической неизменяе-
мости системы) дают повышение прочности и жесткости конструк-
* См. работу [35]. В этой книге изложены элементы теории моментов
высоких порядков.
148
ций и, естественно, с этой точки зрения отнюдь нелишни. Следова-
тельно, «лишними» они оказываются только с позиций минимально
необходимого числа связей, которые должна иметь балка (рама)
и которые могут быть найдены из уравнений статики. Вопрос о том,
какие из связей, наложенных на систему, считать .«лишними», в лю-
бом случае имеет бесчисленное множество решений. Из этих реше-
ний надо выбрать то, которое приводит наиболее коротким путем
к нахождению «лишних» неизвестных. Во многих простейших зада-
чах различные варианты выбора «лишних» неизвестных оказы-
ваются практически равноценными.
Рис. 9.3
Ход решения (раскрытия статической неопределимости) показа»
на примерах.
Пример 9.1. Определить размеры поперечного сечения (номер
двутавра) балки (рис. 9.3, а) из условия прочности, если [о] ==.
= 1600 кгс7сма.
Решение. Составляем уравнения статики: SX = 0; На = 0;
2К = 0; Ra + Rb — Р = 0; - 0; ®iA ~RBl + Ра = Ь.
Таким образом, мы имеем два уравнения с Тремя неизвестными,,
т. е. балка один раз статически неопределима. Одна из трех неизве-
стных реакций , Rb, Ra является «лишней» неизвестной. Какую
именно принять за «лишнюю» неизвестную, практически .безразлич-
но — ход и трудоемкость решения задачи (раскрытие статической
неопределимости) при разных выборах «лишней» неизвестной отли-
чаются в данном случае незначительно.
Применим метод решения, обычно называемый способом сравне
ния перемещений. За «лишнюю» неизвестную примем реакцию
опоры В. Отбросим мысленно эту опору и заменим ее действие не-
известной пока реакцией Rb '(рис. 9.3, б). В результате получена
статически определимая балка, нагруженная заданной силой Р
149
и искомой реакцией Рв. Основная система* при, таком нагружении
должна быть полностью эквивалентна заданной системе.
Следовательно, вертикальное перемещение сечения В балки
по рис. 9. 3, б должно быть равно нулю (ув~ 0), так как в заданной
<5алке в этом месте имеется опора.
Применив принцип независимости действия сил, найдем про-
гиб сечения В отдельно От силы Р и от Рв, полученные результаты
алгебраически сложим: ув= уВР+ Уврв~ О*
.Из этого условия найдем Рв. Прогиб сечения В от силы Р най-
дем на основании известных формул и элементарных геометриче-
ских построений (рис. 9. 3, в):
Увр ~ Увр "Ь Увр'
ГД? у$р — уСр — -т- ; у^р = Qcpb —
(ра2 \
угол поворота 0с₽ = 0в₽ =—2£J~J‘ Окончательно получаем
Ра» Г. . 3 Я
Увр “ 3£/л [ + 2 a J ’
Прогиб селения В от силы Рв (рис. 9.3, г) уВРв = RB?l3EJг.
~ Ра» Г, . 3 Я . Кв1* п
Т»Г» —ЗЁГ, I1 + -2 7] + W = °’ °гкуда
г, п а» Г, , 3 Я с 3» . 3 2\ О1с
+ 2 -у] — 5 • 5» (! + 2 з) 2,16 тс.
Рис. 9.4
После определения силы Рв возвращаемся к рис. 9.3, б и строим
эпюры Q, М, как для обычной статически определимой белки, на-
груженной двумя известными силами (Р, Рв). Эпюры Q, М пред-
ставлены на рис. 9. 3, д, е.
Опасным оказалось сечение С балки i Требуемый момент со- -
противления. Wz Afmax/M = 4,32 • Ю5/1600 — 270 см8.
Ближайший профиль двутавра — № 24, имеющий ~ 289 см3.
Пример 9. 2. Балка АВ (рис. 9. 4, а) концом А защемлена, а кон-
цом В опирается на середину пролета шарнирно опертой по концам.;
• Основная сястема получается из заданной при удалении лишней связ»^
и нагрузки.
150
балки CD (рис. 9. 4, б), имеющей такое же сечение, как балка АВ.
Определить реакций опор балки CD.
Решение. Предварительно надо определить силу давления
Rb Ца балку CD или, что то же, опорную реакцию Rb балки АВ.
Валка АВ однажды статически неопределима. Принимая за «лиш-
нюю» неизвестную реакцию Rb опоры В и учитывая, что сила, об-
ратная и равная реакции Rb, является ндгрузкой, действующей по-
середине статически определимой балки CD, можем записать урав-
нение, выражающее равенство прогиба на конце консоли АВ (от
Силы Р и реакции RB) и прогиба посередине балки CD от силы RbI
Увр Увр.в Увв.в' |ЯВ| = [ЯВ!,
или (см. решение предыдущего примера)
(Ра? , Pa*(l — a)V RB19.' RB13
2EJZ / ZEJz ~ 48EJZ '
Отсюда RB - £*$.—> . = 2.98тс
и Re = Rd = -g- Rb = 1,49 тс.
Задачи для самостоятельного решения
9. 1. Построить эпюры Q, М для балки по рис. 9. 5.
Ответ. QA »=> ql/2>, МА=МВ = —?/2/12; Мх=4/2 ~ ЯМЫ.
Рис. 9.6
Рис. 9.7
9.2. Раскрыть статическую неопределимость и построить эпюры.
Q, М для балки, изображенной на рис. 9. 6.
Ответ. | Мтах | = Ра.
9.3. Определить силу давления R между перекрещивающимися,
балками (рис. 9.^7). Жесткость сечений балок одинакова.
‘ 5
Ответ. R — R>
4 *
151
§ 9.2. Неразрезные (многопролетные) бапки
Балки, опирающиеся более чем на три шарнирные опоры, или
• балки, имеющие жесткую заделку, и, кроме того, более одной шар-
нирной опоры, являются дважды и более статически неопредели-
мыми. Для таких балок метод раскрытия статической неопределимо-
сти, показанный в предыдущем параграфе, обычно оказывается
более трудоемким, чем применение специального метода расчета,
приводящего к так называемым уравнениям трех моментов. Эти
уравнения являются соответствующим образом преобразованными
уравнениями перемещений, получаемыми при выборе основной
системы в виде многоопорной бал-
ки, над всеми промежуточными
опорами которой врезаны шарни-
ры, а в качестве «лишних» неизве-
стных приняты изгибающие момен-
ты в надопорных сечениях. Каж-
дое из уравнений перемещений
выражает ту мысль, что взаимный
угол поворота крайних (примы -
кающих к данной опоре) сечений
двух смежных пролетов равен
нулю.
пролетов уравнение трех моментов
Для любых двух смежных
имеет вид
Мп.г1п + 2Мп (1п 4- /п+1) + = -6 •
Здесь %, a»n+i— площади эпюр моментов от заданных нагрузок i
соответственно в п и п + 1 пролетах, рассматриваемых как двух- |
опорные шарнирно-опертые балки; ап—расстояние от центра тяжести J
«грузовой» площади <о„ до левой опоры п— 1; —расстояние от 1
центра тяжести «грузовой» площади <оп+1 до правой опоры п. -|- 1 1
(рис. 9.8). _ 1
Уравнение трех моментов устанавливает связь между тремя J
последовательными опорными моментам» в двух смежных проле- |
тах неразрезной бал^и. Таких уравнений можно составить столько, J
сколько имеется промежуточных опор (в предположении, что все
опоры шарнирные), т. е. количество уравнений равно числу «лиш- 1
них» неизвестных. • Я
Решая совместно уравнения трех моментов, составленные для Я
неразрезной балки, находят все опорные моменты, а затем опорные Я
реакции заданной балки. Я
Расчеты неразрезной балки ведут в следующем порядке: я
1) строят эпюры изгибающих моментов от заданной внешней®
нагрузки для каждого пролета неразрезной балки, рассматривая-®
его как отдельную двухопорную -балку; Я
152
2) вычисляют «грузовые» площади (со) эпюр на каждом пролете
и находят положения их центров тяжести;
3) составляют уравнения трех моментов и определяют опор-
ные моменты, т. е. изгибающие моменты в надопорных сечениях;
4) рассматривая ряд шарнирно-закрепленных балок, нагру-
женных уже известными опорными моментами и заданной нагруз-
кой, определяют опорные реакции для каждой из указанных
балок;
5) определяют опорные реакции заданной неразрезной балки; 6 7
Рис. 9.9
6) пользуясь обычнымй приемами (известными из предыдущего),
строят эпюры Q, М для заданной неразрезной балки;
7) проверяют правильность решения задачи.
Пример9. 3. Построить эпюрц поперечных сил/? и изгибающих
моментов М для нерйзрезной балки, изображенной на рис, 9.9, а.
Определить из расчета на прочность требуемый номер двутавра,
если [ст] = 1600 кгс7см2.
Решение. 1) В случае жесткого защемления конца нераз-
резной балки следует заменить это защемление фиктивным допол-
нительным пролетом длиной /0 н написать уравнение трех моментов
обычным порядком, положив затем /0->- 0 (рис. 9. 9, б).
2) Строим эпюры изгибающих моментов для первого и второго
пролетов неразрезной балки, как для самостоятельных шарнирно-
опертых балок (рис. 9. 9, в). При этом для удобства определения пло-
щадей и координат центров тяжести этих эпюр строим эпюру для
второго пролета в расслоенном виде (см. также пример 8. 10). Отдель-
но построение указанных эпюр показано на рис. 9. 10, 9. 11.
153
3) Определяем площади грузовых эпюр и находим положение их
центров тяжести. На основании рис. 9. 10 имеем
~ • б • 5,83 = 14,58 тс • м2;
а>; = ~ 2,5 • 5,83 = 7,29 тс • м2;
01 = 4 • у/1 = 4 • 7,5 = 3,33 м;
+ = f-7.5-4.17 «I
1/31,'ЗЁу
U, о,
Рис. 9.10
Рис. 9.11
с
- 41 4 4 - i-1 --7’4 5 -5-83
,,х'-Гт'>=1'>-4-7>5“1-67“-
На основании рис. 9.11 имеем
®2=I • Iр*1*'1*=4р*1*=I •3 •61 в 18 тс •м2;.'
402 = -Т • ТР^ • '2 = -Г2Р^ = ~12 ’ 3'62 = ~9ТС • м2;
aj = 1/2 = 1 • 6 = 2 м; Ь;=_4/2 = 4-6=4м;
О О О О
а;=1/а =1.6= 1,2 м; &;=1/2 = 1-6 = 4,8м.
* о о о о
4) Составляем уравнения трех моментов и определяем опор-
ные моменты. На основании рис. 9.9, б имеем
M9l9 + 2Мг (/0+ /х) + Мг1. = -6 j;
М,1г + 2М2 (1г + /2) 4- М312 = -6 4*й1 •
к *1) *2 J
154
Учитывая, что Мо— 0, /0-> 0, со0= О, после подстановки задан-
ных и найденных выше величин получаем
17Ш „14,58 • 4,17 4-7,29 • 1,67 « оо „.
15/Vli 4- 7,5Л1, = —6—1--------------— =» —58,33 тс • м;
/ (О
„ e,t , п Р ₽ 114,58 • 3,33 + 7,29 • 5,83 ,
7,5М1 -4- 27М« — 2,75 • 6 — —6 —--------- ’---------h
4- 18 ,‘_4 • 4Л ) « —101,72 тс м,
или 7,5^!-)- 27Л14= —85,22 тс • м.
Решив полученную систему уравнений, найдем
5) Определяем опорные реакции неразрезной балки и строим
эпюру поперечных сил Q. Рассмотрим первый пролет (рис. 9. 12, а).
Реакции определим обычным порядком:
1Х = 0; Ah + P^-RA-M^O,
п Ml— Ма . 2 п —2,68 4-2,41 .2-35 о Q
откуда Т?2 = х[4 -8-4- з-Р1 == - 7J- - 4- — =• 2,3 тс;
£/nfl = 0; Л11 + /?1/1-Р1-^-Л12 = 0,
п Мг—М1 . 1 п -2,414-2,68 . 3,5
откуда ^«-1—1 + -Р1=—i-g--------+т,
или . ='1,2 тс.
Для первого пролета эпюра Q представлена на рис. 9.12,6.
Рассмотрим далее второй пролет — балку* с консолью (рис.
9.13, а): ^тв^0- М2 + |р2/2 + Ж-/?з'2 = 0,
откуда
, Ms + ®1 1 р _—2,414-2,75 , 3
3 — 13 + 3 6 ’’’ 3 ’
155
т. е. R3 — 1,06 тс.
Взяв сумму моментов всех сил относительно точки С, найдем
£/яс = 0; M2 + Rn2l2-~P2l2 + $l = Q,
Л12 + ?К . 2 п —2,41+2,75 .2-3
откуда R, = - +-т Р2 -----------g----+ — ,
т. е. R2 = 1,94 тс.
Для второго пролета эпюра поперечных сил Q показана на
рис. 9. 13, б. Точку пересечения графика Q с осью х найдем из уело-
2
вия: Q = 0, или —/?3+ у—° = 0 (см. рис. 9. 13, б), решив это урав-
нение относительно координаты х. Так найдено расстояние
= 3,56 м.
Полные опорные реакции неразрезной балкш Рг~ 1,2 тс, R2=>
= 2,3 + 1,94 = 4,24 тс, R3^ 1,06 тс.
На рис. 9.9, г изображена эпюра Q для неразрезной балки; эта
эпюра получилась путем присоединения эпюр Q для первого и вто-
рого пролетов (см. рис. 9. 12, б, 9. 13, б).
6) Строим эпюру изгибающих моментов для неразрезной балки.
Зная полные опорные реакции, можно построит^ эпюру М, как
изложено в гл. 6. В рассматриваемом примере поступим несколько
иначе: сначала построим эпюру М от опорных моментов (эта эпюра
представлена на рис. 9.9, д), затем построим эпюры изгибающих
моментов ot заданных сил для каждого пролета неразрезной балки,
рассматривая при $том каждый пролет как простую балку на двух
опорах (эти эпюры даны на рис. 9. 9, е). Сложив алгебраически эпю-
ры от опорных моментов и указанные эпюры от заданной нагрузки,
получим суммарную эпюру М (рнс. 9. 9, ж). Из этой эпюры видно,
что нулевой линией для отсчета ординат результирующей (суммар-
ной) эпюры моментов является ломаная линия опорных моментов.
Целесообразно привести эпюру М к горизонтальной оси, что
представлено на рис. 9. 9, з.
7) Проверяем полученные результаты.
Сначала проведем статическую проверку, спроектировав все
действующие на балку активные и рёактивные силы на вертикаль-
ную ось: S У— 0, т. е. Rj + R2+ R3— Pi— Рз~ 0> или после под-
становки численных значений 1,2 + 4,24 + 1,06 — 3,5 — 3 = 0.
Далее вычислим «прогиб» у2 на средней опоре, зная заведомо,
что он равен нулю.
Поместим начале координат в центре тяжести левого опорного
сечения балки и запишем уравнение упругой линии балки для пер-
вого пролета:
. , , Q . М0х3 . Q0x3
У1 (х) - У о + во* + 2ЁТ; +
156
Учитывая, что в рассматриваемой задаче г/0= 0, Оо= О, Мо—
= —2,68 тс • м, Qo— 1,2 тс, и подставляя численные значения
в уравнение упругой линии, будем иметь
, . 1,34х2 0,2х3 3,5 (х — 5)3 II
Ух (х) => - -Ё7Г +-£77-----6£ТТ~ II •
х>5
Отсюда найдем у2 = ух (/J = (—75,38 + 84,38 — 9,11) ~0,
что подтверждает правильность расчета.
Аналогично можно проверить, что прогиб на правой опоре
также равен нулю.
8) Определяем из условия прочности требуемый момент сопро-
цг ^шах 3,33 -10s _________________________________________
тивления поперечного сечения балки W ---
= 208 см3, чему соответствует двутавр № 22.
Задачи для самостоятельного решения
9. 4. Построить эпюры поперечных сил и изгибающих момен-
тов и определить наибольшие нормальные напряжения, возникаю-
щие в поперечном сечении бал-
ки по рис. 9. 14.
Ответ. атах = 1087 кгс/см2.
0= 1500кгс/м
ГПТП- ..
I I i J№22
9.5. Определить размеры
поперечного сечения (требуе- Рис. 9.14
мый номер двутавра) балки
(рис. 9. 15, а, б) из условия прочности, если [о] = 1600 кгс/см2.
Указание. При построении грузовых эпюр для балки по рис. 9.15, б
момент ЯВ, приложенный в опорном, сечении, целесообразно отнести пол
ностью к первому или ко второму пролетам, т. е. мысленно сместить его иа
бесконечно малое расстояние влево или вправо.
Ответ, а) № 24а, б) № 16.
.т,^тс-м
ти/шинн-пт
а
д,=2тс!м
Р^Зтс
l+|toc
'а*1,5м
р„2т т*2тс-м ^=0,5 тс/и
инн:
/ -я н-2 И *3
а а д а
В
Рис. 9.15
Для определения опорных реакций многопролетных статически неопре-
делимых балок и балок, приводимых к ним путем добавления фиктивных
пролетов, может быть применена программа, приведенная в приложении V.
Для расчета в программу вводится массив длин пролетов и абсцисс точек
приложения нагрузок на^каждом пролете.
157
§ 9.3. Простейшие статически неопределимые плоские рамы
Рама является статически неопределимой, если внутренние си-
ловые факторы в поперечных сечениях составляющих ее стержней
не могут быть найдены на основе применения только уравнений
статики.
Расчет статически неопределимой рамы ведут в следующем по-
рядке.
1. Устанавливают степень статической неопределимости рамы,
т. е. число «лишних» неизвестных. Например, рама, изображенная
на рис. 9.16, а, трижды статически неопределима. Общее число не-
известных реактивных сил равно шести: в каждой из заделок (А
и В) возникает три реактивных фактора —горизонтальная, верти-
шйпи
а
(ШЛИ
С
Р
D
л
С
р'
S
Рнс. 9.16
Хз
Л
в
6
а
реактивный момент. Уравнений статики для
сил можно составить три.
и
кальная реакции
плоской системы
Таким образом, число неизвестных на три превышает число
уравнений статики (6—3 =» 3), и, значит, данная рама имеет три
«лишних» неизвестных.
2. Выбирают основную статически определимую систему» кото-
рая получается .из заданной системы путем отбрасывания] «лишних»
связей. В приведенной раме можно, в частности41отбросить правую
заделку, и рама превращается в ломаную коисоль, которая и будет
основной статически определимой системой для данной рамы (рис.
9. 16, б).
Основная система должна быть геометрически неизменяемой. •
Отброшенные связи заменяют силами, которые и являются
искомыми «лишними» неизвестными. В данной раме таковыми яв-
ляются три реакции опоры В, их обозначают Х3, Х3, Х9 (рис. <
9.16, в). Основная система, нагруженная заданными силами и иско- ч
мыми лишними неизвестными, должна быть эквивалентна заданной]
системе.
3. Для определения лишних неизвестных составляют канони*
ческие уравнения метода сил. Для рамы с тремя «лишними,» неизвест-
ными канонические уравнения имеют вид А3= Х^ц-]- Ха61а
+ Х3613-[- Aip= 0; Аа— Xj6ai4- Хг6аг4- Ха6аа-|- Аар= 0; А»
= Xi63i4“ Ха6аа-]- X3633-f- АЗР = 0.
15R
Первое уравнение выражает ту мысль, что суммарное переме-
щение сечения В по направлению Xi от заданной нагрузки и от
сил Х1т Х2, Х3 равно нулю; второе уравнение показывает, что
суммарное перемещение точки В по направлению Х2 от нагрузки и от
сил Xi, Х2, Х3 равно нулю; третье — угол поворота сечения В
от заданных нагрузок и искомых реакций равен нулю.
Если в раме два «лишних» неизвестных, пишутся два канониче-
ских уравнения Ai= Х^ц-f X26i2+ &ip= О, Д2= Xi621+ Х2622 +
4- Д2р= 0.
При одном «лишнем» неизвестном имеем одно каноническое
уравнение Ai= Х^ц-f- Д)Р= 0.
В этих уравнениях перемещения имеют два индекса: первый
указывает направление перемещения, второй — причину, вызвав-
шую это перемещение. Итак, 6ц— перемещение сечения В по на-
правлению Хг от единичной силы, приложенной в том же направ-
лении; 612— перемещение того же сечения по направлению силы Xj
от единичной силы, приложенной взамен Х2; 613— перемещение то-
го же сечения по направлению Xi от единичной силы (в рассматри
ваемом примере момента), приложенной взамен Х3; 621— переме-
щение сечения В по направлению Х2 от единичной силы* Х2= 1;
622— перемещение того же сечения по направлению Х2 от единичной
силы Х2= 1; 623— перемещение того же сечения по направлению
Х2 от единичной силы (момента) Х3= 1; 631 — перемещена^ сече-
ния В по направлению силы (момента) Х3 от единичной силы X j = 1;
632— то же от единичной силы Х2— Г, 633— то же от единичной силы
(момента) Х3= 1; Д1Р— перемещение сечения В от заданной нагруз-
ки в направлении силы Xi; ДгР— перемещение того же сечения от
заданной нагрузки в направлении силы Х2; ДзР— перемещение се-
чения В от этой же нагрузки в направлении силы (момента) Х3.
По теореме о взаимности перемещений 612= 621; 613= б31;
623= 632. Эти перемещения (оба индекса у них различные) назы-
ваются побочными перемещениями. Они могут иметь величину по-
ложительную, отрицательную или равную нулю. •
Перемещения 6ц, 622, 633 (с одинаковыми обоими индексами)
называются главными перемещениями. Они всегда имеют поло*
жительное значение.
Перемещения Д1Р, ДаР, ДзР называют грузовыми перемещения-
ми, каждое из них может быть положительно, отрицательно или
равно нулю.
4. Определяют перемещения, входящие в канонические урав-
нения. При этом пользуются интегралом Мора, который на
прямолинейных участках рамы вычисляют по способу Вереща-
гина.
* Единичные силы (моменты), прикладываемые взамен лишних неиз-
вестных Xj, Х2 в т. д., здесь н в дальнейшем будем обозначать Х±, Х2 в т. д.
159
5. Решают канонические уравнения и находят значения «лиш-
них» неизвестных. Рассматривая затем основную систему, нахо-
дящуюся под действием заданной нагрузки и «лишних» неизвестных
(которые на этой стадии расчета перестали быть неизвестными),
строят как для обычной статически определимой рамы эпюры ЛГ,
Q, М.
6. Проверяют решение, перемножая окончательную эпюру
моментов на одну из единичных эпюр моментов (целесообразно
умножать на единичную эпюру, взятую не из той основной систе-
мы, с помощью которой решалась задача — следует помнить, что для
любой заданной системы существует множество основных систем).
Это указание не распространяется на системы с одцой лишней не-
известной.
Дополнительно укажем, что встречаются случаи, когда в каче-
стве «лишних» неизвестных должны быть приняты внутренние си-
ловые факторы, возникающие в том или ином поперечном сечении
какого-либо из стержней рамы. Тайие системы принято называть
внутренне статически неопределимыми. Один из примеров подобной
системы приведен на рис. 9.17. Всякий жесткий замкнутый контур
трижды статически неопределим. Рама (см. рис. 9.17) внешне стати-
чески определима — опорные реакции находятся из уравнений ста-
тики, но внутренне она трижды статически неопределима. Основную ,
систему получают путем разреза одного из стержней рамы (целесооб-
разно резать по оси симметрии). Для рамы основная система с задан-
ной нагрузкой и искомыми «лишними» неизвестными показана на i
рис. 9. 18. Форма записи канонических уравнений, естественно, 1
остается прежней, но физико-геометрический смысл их изменяется.^
В частности, в этом случае Ai= О обозначает, что торцы сечения
образовавшиеся после проведения разреза, не имеют взаимного сме=Ц
щения по вертикали, ибо фактически здесь одно сечение. Аналогич-ж
но истолковываются и остальные два канонических уравнения. jB
Пример 9.4. Построить эпюры N, Q, М для рамы, изображенндяИ
на рис. 9. 19, а. Жесткость сечений стержней рамы одинакова. Я
И>()
Решение. На раму наложены четыре связи — жесткая за-
делка и шарнирно-подвижная опора; статика дает три уравнения
равновесия, следовательно, система один раз статически неопре-
делима.
Выбираем основную систему, отбрасывая шарнирно-подвиж-
ную опору. Основная система с заданной нагрузкой и искомой
Рис.. 9.19
«лишней» неизвестной показана на рис. 9.19, б. Каноническое урав-
нение для системы с одной «лишней» неизвестной имеет вид
^1^11+ ^iP— 0.
Прикладываем взамен единичную силу Л\= 1 (рис.9.19, в)
и строим соответствующую эпюру изгибающих моментов (рис.
9.19, г). Затем рассматриваем основную систему под действием толь-
ко заданной нагрузки (рис. 9. 19, д) и строим эпюру изгибающих
моментов от этой нагрузки (рис. 9. 19, е).
6 ыо 161
Вычисляем главное перемещение 6^ и грузовое перемещение
Для определения умножаем по правилу Верещагина эпюру
12 4
саму, на себя EJ,8n — аа а + ааа = -х- а8.
А о о
Для определения Д1Р умножаем эпюру М? на эпюру Mi; при
этом разбиваем первую из них на вертикальном стержне на пря-
моугольник и параболический треугольник:
ЕJг \\р — —
qa2 а 3 да2 1 qa2
Т-2Та-Таа-зТаа =
Подставляя полученные величины в каноническое уравнение,
vz 4 о 53 л "/ч v 53 53 - -
получаем Хл у а3 — qa4 = 0, откуда Хх = qa = • 1 • 5=
= 1,665 тс.
Положительный результат указывает на то, что сила Хх дейст-
вительно направлена вверх, как предполагалось (см. рис, 9. 19, б).
Эпюры N, Q, М (рис. 9. 19, ж, з, и) строим, ориентируясь на
рис. 9. 19, б, как для обычной статически определимой рамы.
Для проверки решения выбираем новую основную систему,
заменяя жесткую заделку шарнирно-неподвижной опорой. Эта
основная система с заданной нагрузкой и «лишней» неизвестной
(моментом показана на рис. 9. 20, а. Рассматривая основную
систему, нагруженную единичным моментом Хх = 1 (рис. 9.20, б),
строим эпюру изгибающих моментов от этой нагрузки (рис. 9.20, в).
Произведение (по правилу Верещагина) окончательной эпюры
изгибающих моментов для заданной рамы (рис. 9. 19, и) на эпюру
по рис. 9.20, в должно дать нуль, так как указанное произведение
дает величину угла поворота сечения А основной системы от дей-
ствия заданной нагрузки и лишней неизвестной. Очевидно, что этот
угол поворота равен нулю, так как в заданной системе сечение 4 v
защемлено. Перемножение эпюр предлагаем выполнить читателю;
самостоятельно.
162
h-26-бм
Рис. 9.21
Заметим, что в данном случае не было необходимости в использо-
вании для проверки решения другой основной системы, так как еди-
ничные эпюры для старой и новой основных систем отличаются лишь
знаком (см. рис. 9. 19, г, 9. 20, в).
Пример 9. 5. Для заданной рамы (рис. 9. 21, а) построить эпюры
М, Q, N.
Решение. В данной раме пять реактивных усилий: три в же-
сткой заделке и две в шарнирно-неподвижной опоре. Следовательно,
рама дважды статически неопределима. Основную статически
определимую систему получаем, отбрасывая шарнирно-неподвиж-
ную опору. Заменяем ее действие на раму неизвестными реакциями
Xi, Х2; получаем эквивалентную систему (рис. 9; 21, б).
Система канонических уравнений для статически неопредели-
мой рамы с двумя л’ишними неизвестными имеет вид Хх^ii + Х2612+
4* &ip— 0; Ххб21+ Х2б22 + Д2р= 0.
Определяем перемещения (коэффициенты и свободные члены)
канонических 'уравнений. Для этого, нагружая основную систему
последовательно силами Xv= 1 (рис, 9.21, в), Х2= 1 (рис. 9.21, д)
и заданной нагрузкой (рис. 9.21, ж), строим соответствующие эпю-
ры изгибающих моментов (рис. 9.21, г, е, з):
л 1 I 1 чЬ2 L 4 «Л
Д‘₽=-ЁГДТ2ЬЬ + -3 =
А 1 1 , , 9ft4 .
Е1г 3 *ГЬЬ ~ 6EJ2 ’
«..-«и —^,1»» = -®;;
« = 0;(34“тд + “6) = <- ]
После подстановки имеем ?
7ft® у ft® у 9<7ft* _ п. ft® у , 2ft® у , <?&* _ п j
SEJz1 2EJz2 8£V2~U’ 2Е72 1 + 2 + 6£72 |
После упрощения получим 56X1—12Х2— 27qb—0;—3Xi + J
+ 12Х2 + qb = 0. ' Э
n v 26 , 26 , о ~ I
Решая уравнения, получаем Хх = — 90 = — • 1 • 3 = 1,47 тс; 4
Х,-Й»0-Й-1.3 = 0,118Ю. j
Положительные значения Xi и Х2 указывают на то, что направ- I
ления этих реакций были выбраны правильно. Ч
Теперь, рассматривая данную раму как статически определи- 1
мую, можно построить суммарную эпюру М изгибающих момен- я
тов (рис. 9. 21, и), а также эпюры поперечных Q (рис. 9. 21, к) и npojl
дольных N (рис. 9.21, л) сил. Я
1G4
Для проверки правильности построения суммарной эпюры
изгибающих моментов следует «умножить» ее на одну из единич-
ных эпюр, не использованных в решении задачи. Например, можно
заменить заделку шарнирно-подвижной опорой (рис. 9.22, а) и по-
етроить эпюру изгибающих моментов, соответствующих единич-
ной силе, приложенной взамен Х2 (рис. 9. 22, б, в). В результате
перемножения должен получиться нуль, так как перемещение се-
чения А в любом направлении отсутствует.
Эпюру М по левой стойке можно представить как сумму двух
Треугольных эпюр, построенных по всей длине стойки; одна с мак-
имальной ординатой в точке В, другая — в точке А.
Эпюру изгибающих моментов на ригеле представим как соче-
тание трапеции, лежащей под осью (ее разобьем на прямоугольник
и треугольник), и симметричного параболического сегмента, лежа-
щего над осью, со стрелкой qb^/S. Таким образом, = 1 х
X 0,354 • 3 • 4 • 3 + 0,354 * 3 -%. * 3 + 1 * 0,09 • 3 * 4 • 3 — 4 х
О Z 2 0*0
X • 3 • ~ . 3 + ~ . 0,444 • 6 • 4*6-1 . 0,264*6*1*6 =
= 11,85—11,7, т. е. погрешность составляет
0,15 • 100%
11,85+ 11,70
2
= 1,27%, что обусловлено приближенностью вычислений.
Пример 9. 6. Для заданной рамы (рис. 9. 23, а) построить эпюры
М, Q, N.
Решение. Замкнутая плоская рама — трижды внутренне
статически неопределимая система, так как в произвольном попе-
речном сечении любого стержня рамы в общем случае возникает три
внутренних силовых фактора/И, Q, N, которые невозможно опреде-
лить из уравнений статики.
Разрежем раму по вертикальной оси симметрии. Тогда на каждую
половину будут действовать силы Р/2 и моментыХ{. Основная систе-
ма (точнее, ее половина), нагруженная заданными силами и иско-
мыми лишними неизвестными, показана на рис. 9.23, б. Очевидно,
что продольных и поперечных сил в разрезе быть не может, значит,
хотя рама трижды статически неопределима, для раскрытия стати-
ческой неопределенности нужно составить лишь одно каноническое
уравнение: бцХх-f- Ai₽= 0.
Рис. 9.23
Таким образом, & данном случае рациональный выбор основной
системы позволяет свести решение трижды статически неопредели-
мой системы к отысканию только одной «лишней» неизвестной.
Чтобы найти'перемещение, строим эпюры изгибающих момен-
тов от заданной нагрузки (рис. 9.23, в) и единичного момента
Хх = 1 (рис. 9.23, г). Перемножив их по правилу Верещагина,
имеем би = -Д- 2 • 1 • + 1 • о) = ;
11 EJz - 2 ) EJz
л 1 (п 1 1 в а , . 1 D ЗРа*
Л’₽ “ EJZ 1 2 ‘ 2 4 Ра 2 ’ + 4 Раа ‘ 1 / “ 8EJt '
После подстановки полученных значений в каноническое ура:
v 2а v ЗРа2 л v 3 п 3 0 п
нение находим X,: лгет- = 0; Хх = г^Ра = • 8 • 2 <
CJz OC.J2 10 10
= 3 тс • м.
Теперь, имея статически определимую раму, обычными сп
собами строим эпюры изгибающих моментов, поперечных и пр
дольных сил (рис. 9. 23, д, е, ж).
166
Задачи для самостоятельного решения
9.6.*. Для изображенных на рис. 9. 24 ломаных брусьев опреде-
лить вертикальные перемещения и углы поворота сечений С.
Ответ.
. А _ 7 ph3 д 5 Ph» . а 7 qh»
} с 24 24£7г ’ 6<? 8 EJ2 ' “ 128£Л ’ °C ~ 48 ЕЗг ‘
Рис. 9.26
* Задачи иа определение перемещений в статически определимых плос-
ких рамах (ломаных брусьях) включены в этот параграф как материал способ-
ствующий приобретению навыков применения метода Мора и правила Вере-
щагина к рамам. Эти навыки необходимы для успешного использования кано-
нических уравнений.
167
9. 7. В плоской раме, показанной на рис. 9. 25, определить, на
какое расстояние приблизятся точки А под действием сил Р; EJZ=*
— const.
Ответ. бл = Рс?1Е1г.
9.8. Для заданных рам (рис. 9. 26) построить эпюры Д', Q, М.'
«) Мтах = з тс • м. б) мтак = 2,94 тс . м. в) Л4шах = МА = Мв =
= 6,63 тс • м. г) Л1тах = A qa*. д) Л1тах = j- ?в».
ГЛАВА 10. КОСОЙ ИЗГИБ
§ 10.1. Основные понятия и расчетные формулы
Брус испытывает косой изгиб, если плоскость действия внешних
еил не совпадает ни с одной из его главных плоскостей (рис. 10. 1).
Различают плоский косой изгиб (все внешние силы лежат в од-
ной плоскости, упругая линия бруса — плоская кривая) и про-
странственный изгиб (внешние силы действуют в различных плоско-
стях, упругая линия — пространственная кривая).
Плоский косой изгиб
Разложив внешнюю силу на составляющие по главным осям по-
перечного сечения, можем рассматривать косой изгиб как совокуп-
ность двух прямых изгибов, происходящих во взаимно перпендику-
лярных главных плоскостях.
Расчет на прочность при косом изгибе ведется, как правило,
только по нормальным напряжениям.
Нормальное напряжение в любой точке поперечного сечения
бруса определяют на основе принципа независимости действия сил;
, ми , мг
по формуле a = -^г + Т^у,
W.f-
где /И2, Му— изгибающие моменты относительно главных цен-
тральных осей (г, у) поперечного сечения;
J2, Jy— моменты инерции поперечного сечения бруса относи-
тельно главных центральных осей г, у;
z, у •— координаты точки, где отыскивается напряжение.
Изгибающие моменты Мг, Му берутся со знаком плюс в формуле,
если в точках первой четверти им соответствуют растягивающие
нормальные напряжения, и со знаком минус, если — сжимающие.
Координаты точки (z, у) берутся со своими знаками.
Уравнение нулевой (илщ нейтральной) линии получим, рассмат-
ривая ее как геометрическое место точек сечения, в которых нормаль-
Му , Мг п Mz Jy
ные напряжения равны нулю: y^z 4- ~у = 0, или г = —-f-y.
J у J z Wly J 2
Это уравнение прямой с угловым коэффициентом
Здесь <р — угол- наклона силы к оси Oz (см. рис. 10.1).
Нейтральная линия в случае косого изгиба — прямая, не пер-
пендикулярная к силовой линии.
Для определения прогибов при косом изгибе также применяют
принцип независимости действия сил. Полный прогиб равен геомет-
рической сумме прогибов, происходящих в направлении главных
осей: f = ]/Fy+f;-
При плоском косом изгибе направление полного прогиба перпен-
дикулярно к нейтральной линии и не совпадает с силовой линией
(поэтому изгиб и называется косым).
Расчет иа прочность ведется по напряжению в опасной точке
опасного сечеиия. При постоянном поперечном сечении бруса опас-
ным является сечение, где изгибающие моменты достигают наиболь-
шего значения. Опасной точкой в этом сечении для бруса из плас-
тичного материала является точка, наиболее удаленная от нулевой
линии. Условие прочности для бруса из пластичного материала
max. Ми , maxAfj ,
omax = —J----------j ГДе У A' 2 А ~ КООрДИНЭТЫ ОПЗС-
НОЙ ТОЧКИ.
Для бруса из хрупкого материала в опасном сечении следует
сделать проверку на прочность для точек с наибольшим растяги-
вающим и наибольшим сжимающим напряжением, если
| max стс | > шах ар. Условия прочности в этом случае шах ар [ор];
j max ос [<?с].
Если max стр> |max стс j, проверка на прочность производится толь-
ко для точки с наибольшим растягивающим напряжением.
Для сечений, имеющих две оси симметрии и точки, наиболее
удаленные одновременно от обеих главных осей (например, прямо-
угольник, двутавр), опасную точку можно найти, не определяя
положения нулевой линии.
169
Опасной будет угловая точка, наиболее удаленная от обеих
главных осей (для пластичного материала — точка А либо В, для
хрупкого опаснее точка В, так как предполагается, что в ней возни-
кают растягивающие напряжения (рис. 10.1, б)).
Условие прочности в этом случае сттах = max My/Wy +
+ max Mz/Wz[ст].
Пространственный косой изгиб '
Расчет на прочность ведется так же, как и в случае плоского
косого Изгиба. Осложняется лишь нахождение опасного сеченйя из-
за того, что Му, Мг могут достигать максимума в различных сече-
ниях. Обычно выполняют расчет на прочность для двух сечений
с max Му и max Mt.
§ 10.2. Примеры расчетов на косой изгиб
Пример 10.1. Определить размеры поперечного сечения балки
(рис. 10.2, а), если [ст] = 1600 кгс/см2. При найденном профиле се-
чения определить величину и направление максимального прогиба
балки.
Рис. 10.2
моменты возникают
max Mz = (Psin <p) I = (200 sin 30°) 3 = 300 кгс • м
Решение. Наибольшие изгибающие
в заделке:
max Му = ч~ + (Р cos <p) I = 4- (200cos 30°) 3 = 2770 кгс • м.;
Момент М2 действует в горизонтальной плоскости, момент Му—•
в вертикальной. Условие прочности имеет вид сттах = 4-
»т у
, тахМ,____ ,
В этом уравнении два неизвестных: Wy,
170
Рассматривая таблицы сортамента, замечаем, что для средних
размеров двутавровых балок отношение находится в пределах от
6 до 8 (в таблицах сортамента
Для подбора сечения предварительно задаемся отношением
wz /пт/ о -г max Ми , тахЛ12.8 max Ми + 8 (max Мг)
Wy/W, = 8. Тогда отах = + -----Ч
max Ми + 8 (max Мг) 277 • 103 + 8 • 3 • 104
<[о], откуда =----------------------------------—---------=
= 324 см3.
По сортаменту подходит двутавр № 24а, имеющий Wy = 317 см3,
Г2=41,6см3.
Проверка прочности балки:
Отах = 3)7---1—= 1594 кгс/см2 < [ст] = 1600 кгс/см2.
Эпюра нормальных напряжений дана на рис. 10.2, б. Положение
нейтральной линии предлагаем определить самостоятельно.
Максимальный прогиб будет на свободном конце балки. В плос-
кости хОг
Pl3 COS <р'|
3 /
1 /5 • 3* • 108
~ 2 • 10е • 3800 8
, 200 • 3’ • 0,866 • 10«\ п 0-„
-----------~---------1 = 0,876 см
Прогиб в плоскости хОу
1 Pl3 sin <р 1
И-"ЁГг 3 — 2-106. 260
200 • З3 .'10е -0,5
3
1,73 см.
Полный прогиб свободного конца балки
f = //F+7I = /0,8762 + 1,732 = 1,94 см.
Прогиб будет направлен под углом а к оси у:
[ga = fylfz=-- 1,73/0,876 = 1,975; а = 63° 10'.
Пример 10.2. Проверить прочность чугунного бруса (рис. 10.3, а),
если [ор] == 350 кгс/см2; [ос1 = 1300 кгс/см2.
Построить эпюру напряжений для опасного поперечного се-
чения бруса.
Решение. Брус работает на плоский косой изгиб. Разло-
жив нагрузку на составляющие по главным осям у, г (рис. 10.3, б),
получим сочетание двух прямых изгибов. Опасным является сечение
заделки:
max Л», =4’ = ~ =935.10, кгс.см.
max М, = 54,1 - 103 кгс см.
171
Не вычисляя значений нормальных напряжений, соответствую-
щих каждому изгибающему моменту (Ми, Мг), покажем характер
эпюр этих напряжений — , оМг (рис. 10.3, в).
Для определения опасной точки сечения найдем положение ну-
левой линии. Угловой коэффициент k нулевой линии
k = tg а ~ ~ yL = —tg <р • ,
S Му Jz S Jz'
где моменты инерции поперечного сечения бруса
. nd4 bh3 Л • 164 7 • И3 ПОЛА -7ОА ОЛЛА 4
J у = "6Г ~ = “64------12~ = 3220 — 780 =,2440 см4;
j — М = = 3220 — 312 =« 2910см4.
2 64 12 64 12
Тогда k = tga = —0,577 • = —0,485; а = —25е 52'.
Отрицательный угол а откладываем от оси у по часовой стрелке
и проводим нулевую линию.
Для построения суммарной эпюры напряжений отыскиваем
точки сечения, максимально удаленные от нулевой линии. Эти
точки получаем, проведя две касательные к сечению, параллельные
нулевой линии. На-рис. 10.3, в это точки Л, В. Из них опаснее точка
А (в ней возникают растягивающие напряжения).
Ось эпюры о перпендикулярна нулевой линии. Для построения
эпюры о достаточно вычислить ординату одной ее точки, так как ну-
тах Ми , тах Мг
левая точка определена: ал = —,—-*а 4--—Уа-
Jy J2
Координаты точки А найдем, используя перпендикулярность
отрезка ОА к нулевой линии: уА ~ ysin а = 8 • 0,436 = 3,49 см;
172
г. = £cosa = 8 • 0,900 = 7,2 см. Тогда о. = 93’05.' *°3 7,2 +
54 1 . 103
Н—^9io— ‘ 3.49 = 276 + 65 = 341 кгс/см2 < [ор], т. прочность
балки обеспечена.
Пример 10.3. Определить допускаемую нагрузку для бруса,
изображенного на рис. 10.4, а, если [о] = 1000 кгс/см2.
Решение. Брус испытывает пространственный косой изгиб.
Разложим силу Р{ по координатным осям Оу, Ог (рис. 10.4, б),
Рис. 10.4
изобразим расчетные схемы бруса с нагрузкой в вертикальной
плоскости (рис. 10.4, в) и в горизонтальной (рис. 10.4, г) и построим
эпюры Му, Мг от действия этих нагрузок (рис. 10.4, в, г).
Для расчета на прочность определяем главные центральные
моменты инерции заданного составного сечения (рис. 10.4, д):
/, = 24 + 2^- + 2Г2а2 = 2.1290-Ь2-^-3 +
+ 2 • 12 • 1 • 9,52 = 4748 см4,
Л = 27', + 2FX • al + 2 = 2 • 82,6 + 2 • 23,4 • 4,52 +
+ 2Ц^-3 = 1401 см4.
(В сортаменте Jly, j\t обозначены соответственно J х, Jy).
173
Расчет на прочность выполним для двух сечений балки о
наибольшим Му и наибольшим Мг. Это — сечения В, С. В каж-
дом из них расчет будем вести для двух предположительно опас-
ных точек К, L (или равноопасных им точек К', L'). Подчеркнем,
что заданное сечение не имеет точек, которые одновременно были бы
максимально удалены от обеих главных центральных осей.
Для
точки К сечения В
, . МуВ , МгВ 0,766? • I2 • 10- .
(°Л)в = -^-гк + ~^=--------------4748------ 10 +
, 0,643? • I2 • 10* 1С, , о-г
+ —1401----------6 = 161<7 + 275<? = 436?.
точки L сечения В
МуВ^ \МгВ 0,766? . I2 • 105 о ,
(ffL>B = 7/ + ~77 --------4748----- 8 +
+ ,40,-----9 = 145? + 413? = 558?.
точки К сечения С
ч МуС_ , МгС .. . 0,232? • I2 • 10® 1П ,
<аЛ = 77 гК + -JTy* =------------4748----- 10 +
, 1,29? • I2 • Юь6 = 48 9? + 552(? = 601(?
Для
Для
1401
Для'точки L сечения С
i \ Мус। Мгс
(°ь)с — ZL + Jz УL ~
0,232? • Р • 10® п , .
3620 9 +
+ -°-9 = 44? + 828,7? = 872,7?.
Опасной является точка L сечения С. Окончательно условие
прочности (oL)c^[oJ; 872,7 [?J= 1000; [?J = — 1.146 тс/м.
Задачи для самостоятельного решения
10. 1. Проверить прочность деревянного бруса (рис. 10. 5),
если [о] = 100 кгс/см2; tg <р = 1/3.
Ответ. атах = 94,2 кгс/см2.
?=600нес/м
шлйшшл
L-Зм
Рис. Ю.Ь
10. 2. Проверить прочность чугунного бруса (рис. 10. 6),
если [Ор] = 400 кга7см2, [о0] = 1300 кгс7см2. Построить в опасном
сечении бруса эпюры нормальных напряжений, соответствующих
изгибающим моментам Му, Мг.
Ответ, шах ар = 388 кгс/см2 < [ар].
10. 3. Определить требуемый размер b поперечного сечения
балки, показанной на рис. 10. 7, если [о] — 1600 кгс/см2.
Ответ. Ь =• 6 см.
ГЛАВА 11. СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И РАСТЯЖЕНИЯ
(СЖАТИЯ)
§ 11.1. Изгиб с растяжением (сжатием)
При сочетании изгиба и осевого нагружения бруса (рис. 11. 1)
расчет на прочность ведется только по нормальным напряжениям,
т. е. учитывается влияние продольной силы Nx и изгибающих
моментов Му, Мг (в общем случае изгиба).
Будем рассматривать только брусья большой жесткости, при
расчете которых на совместное действие изгиба и растяжения или
сжатия можно применять принцип независимости действия сил.
Для определения опасного сечения строят эпюры Nxt Му, Мг.
Расчет на прочность ведут для сечения, где Nx, Му, Мг одновре-
менно достигают максимума, либо для нескольких сечений, если
наибольшие значения внутренних силовых факторов соответствуют
разным сечениям.
175
Нормальное напряжение в произвольной точке поперечного
сечения бруса о = -? + -у*- г + -у— у.
При определении напряжений будем применять правила зна-
ков, установленные в главе 1 (растяжение — сжатие) и в главе 10
(косой изгиб).
На рис: 11. 2 показаны эпюры нормальных напряжений, со-
ответствующих каждому из внутренних силовых факторов, и сум-
марная эпюра напряжений. Уравнение нулевой линии получим,
приравнивая нулю правую часть выражения, определяющего о
в произвольной точке сечения:
Нулевая линия — прямая,
не проходящая через начало ко-
ординат.
Рис. 11.2
Уравнение нейтральной линии можно представить в виде урав-
нения прямой в отрезках z/a2 + ylau= 1.
о 4 Nx 4 Nx hiN*
Здесь аг = —/ ау = -или а, =----------------;
hNx
аУ~ Мг • ___ __________
Величины iy = -у-» называются главными
радиусами инерции поперечного сечения бруса; az, ау —
длины отрезков, отсекаемых нейтральной линией на осях г, у.
Для бруса из пластичного материала опасной будет макси-
мально удаленная от нейтральной линии точка А (см. рис. 11. 2).
Условие прочности Отах = у5 + 7^ < [OJ.
Для бруса из хрупкого материала расчет на прочность ведут,
для точек с наибольшими сжимающими и растягивающими напря-
жениями (если |fnax oe|> max ор).
Для бруса с сечением, имеющим две оси симметрии и точки,
максимально удаленные одновременно от обеих главных осей (пря-
моугольник, двутавр), опасной при пластичном материале будет
176
угловая точка, в которой знаки напряжений, соответствующих
каждому из силовых факторов (Nx, Му, Мг), совпадают. Усло-
вие прочности в этом случае отах= — + 1°1-
Для бруса из хрупкого материала при сжимающей продольной
силе надо выполнить расчет для двух угловых точек — с наиболь-
шими растягивающими и сжимающими напряжениями. Подбор се-
чений производится вначале без учета влияния продольной силы.
Для бруса круглого поперечного сечения Wy = Wz =
Для бруса прямоугольного или двутаврового сечения формула
для проектного расчета имеет вид Wy у 4- Мг) [о].
Задавшись отношением сторон прямоугольника, получим от-
ношение Wy/Wz = h/b.
Для двутаврового сечения задают среднее значение отношения
а затем находят нужный-номер способом последовательных
приближений. После определения размеров сечения производят
окончательную проверку с учетом влияния продольной силы и при
необходимости корректируют размеры.
Пример 11. 1. Определить размеры поперечного сечения (номер
швеллера) бруса (рис. 11.3, а) из условия прочности, если [о] =
= 1600 кгс/см2; Pt, Р2, SR расположены в плоскости хг, Р3— в плос-
кости ху.
Решение. Разложим силу Рг на составляющие по осям х,
г, а силу Р3— по осям х, у. Расчетная схема бруса показана на рис.
11.3, б. Брус испытывает изгиб в вертикальной плоскости (от силы
Р2» составляющей Pj sin а и пары сил SR), изгиб в горизонтальной
плоскости (от составляющей P3sin0) и растяжение (составляющие
Pi cos а, Р3 cos Р).
На рис. 11.3, в показаны эпюру продольных сил (Nx) и изгибаю-
щих моментов (Му, Мг). Опасным является сечение заделки.
Первую пробу для определения размеров сечения берем из рас-
чета на прямой изгиб от момента Му:
„7 Му 800 • 10® елл « .
Юр — [а] 1600 ~ 5°0 см3 (для двух швеллеров).
По сортаменту ближайший больший момент сопротивления имеет
швеллер № 24а (W^— 265 см3). В сортаменте этот момент сопротив-
ления обозначен Wx.
Учитывая, что кроме Му в поперечном сечении балки возникают
изгибающий момент Мг — 0,40 тс • м и продольная сила Nх —-
— 4,16 тс, для проверки берем швеллер № 27.
Определим геометрические характеристики сечения:
Wy = 2Wy^2 -308 = 616 см8,
177
где Wy— момент сопротивления одного швеллера (в таблице сорта-
мента Wx)‘, F = 2Fx— 2 • 35,2 — 70,4 см2 — площадь сечения;
j'z— 262 см4— момент инерции одного швеллера (в таблице сорта-
мента это Jy); уй= 2,47 см (в сортаменте z0); Ь = 9,5 см.
Момент инерции всего сечения (рис. 11.3, г) = 2721 + 2F jt/n —
= 2 • 262 + 2 • 35,2 • 2,472= 956 см4;
= 4 = 5? = 100,5 см3.
г о У,о
Эпюры нормальных напряжений, соответствующих каждому
из силовых факторов, имеют вид, показанный на рис. 11.3, г. Опас-
Рис. 11.3
ной точкой сечения будет точка А, где знаки всех напряжений со-
впадают. Напряжение в точке А находим по формуле
_ Nx , мг , Му 4160 , 0,4 - 10ь , 8 • 105
Отах р "Г й7г "Г — 704 + 1005 + 61ц —
= 59,5 + 397 -|- 1300 = 1757 кгс/см2 > 1600 кгс/см2.
178
Перенапряжение составляет почти 10%, поэтому проверим сле-
дующий номер швеллера (№ 30). Для него Wy — 2Wy — 2 • 387 =
= 774 см3; F = 2Fr— 2 • 40,5 — 81 см2; J'Zi — 327 см4; у0 = 2,52 см;
6= 10см; J, = 2 • 3274-2 • 40,5 • 2,522 = 1168см4; = =
1168 ,
= -jy »» 117 см3.
Вычисляем напряжения в точке А:
„ Nx , Мг , Му _ 4160 , 0,4 • 105 8 . 105
«max F + Wz + Wy 81 ‘ 117 + 774
= 51,4 + 341 + 1030 = 1422 кгс/см= < [о].
Недогрузка составляет 11%. Останавливаемся на швеллере № 30.
§ 11.2. Внецентренное растяжение (сжатие)
Внецентренное растяжение (сжатие)' имеет место при нагруже-
нии бруса силой, параллельной его продольной оси (рис. 11.4).
Расстояние е называется эксцентриситетом, точка приложения
силы — полюсом. Приведя силу к оси бруса, можно представить
внецентренное растяжение (сжатие) как соче-
тание центрального растяжения (сжатия) с чис-
тым косым изгибом. Расчеты на прочность произ-
водят по формулам, приведенным для случая
изгиба с растяжением (сжатием), но необходи-
мость в построении эпюр внутренних силовых
факторов отпадает: все сечения равноопасны.
Огрёзкн, отсекаемые нулевой линией на главных центральных
осях, в рассматриваемом случае можцо определить по формулам
аг = — 1%/ег; ау =
где е2, еи — проекции эксцентриситета на главные центральные
оси или, что то же, координаты полюса.
В частных случаях, когда приложенная внецентренносила лежш
в плоскости одной из главных осей сечения, а также для сечений,
179
у которых все центральные оси — главные, имеет место сочетание
прямого изгиба с растяжением (сжатием). Для материалов, плохо
сопротивляющихся растяжению при работе бруса на внецентренное
сжатие, нежелательно возникновение растягивающих напряжений.
Однозначные напряжения во вуе.м сечении будут в том случае,
если нулевая линия не пересекает сечения. Положение нулевой ли-
нии связано с положением полюса. Геометрическое место полюсов,
которым соответствуют нейтральные линии, касательные к сечению,
образуют контур ядра сечения.
Если внецентренная сила приложена в любой точке ядра сече-
ния, она вызывает во всем сечении напряжения одного знака, Ядро
сечения для некоторых фигур показано на рис. 11.5 (заштрихован-
ная часть).
Пример 11.2. Определить напряжения в сечении т — п детали
(рис. 11.6, а).
Решение. Внецентренное сжатие в этом случае можно свести
к центральному сжатию и чистому прямому изгибу в плоскости
гОх.
Определим положение центра тяжести сечения и вычислим
момент инерции сечения относительно главной центральной оси у
(рис. 11.6, б):
FjZi + Faz2 __ 9 • 2 1 + 8 • 2 6 _ о ок
гс- Fl + F3 9 • 2 + 8 • 2 СМ*
Jy-J'y + Jy-,
J'y = 4 4- Fia2i = 9-^ + 9 • '2 • (3,35 — I)2 = 105 cm4;
J" = Jy' + M = + 2 • 8 • (6 - 3,35)2 = 197 cm4;
Jy = Ю5 + 197 = 302 cm4.
Площадь F — Fl 4- F2 = 18 4- 16 = 34 cm2.
180
В сечении возникают два внутренних силовых фактора: про-
дольная сила Nx = —Р и изгибающий момент Му= —Ре, где е =•
= 9,3 + 3,35 = 12,7 см.
Нормальные напряжения от центрального сжатия (соответствую-
щие продольной силе) одинаковы во всех точках сечения:
Nx р 14 • 103 411 IM и / !
°NX — Р — Р — 30 . ю-4 ~ 411-10 Н/м .
Нормальные напряжения от изгиба достигают максимума в край-
них точках сечения: Л(гА = —6,65 см), B(zB= zc~-^ 3,35 см):
i \ Ре 14 - 103 - 12,7 - 10-2 , с сс
- =* - -v z* ----------зоГЛ^-------(-6-65 • 10 “> =
= 385 • 105Н/м2 (растяжение);
, , Ре 14 - 103 . 12,7 - 10-2 0
(стмх/)в ' jyzB- 302 • IO-8 3,35 ' 0 ' ~
= —194 • 105 Н/м2 (сжатие).
Эпюры нормальных напряжений, соответствующие Nx, Му,
и суммарная эпюра напряжений показаны на рис. 11.6, в.
Крайние ординаты суммарной эпюры напряжений
° а = (°м )а + = 38,5 — 4,11 = 34,4 МН/м2;
У X
°в = (°м )в + ^ =-19,4-4,11 =-23,5 МН/м2.
у х
Пример 11.3. Короткая стойка двутаврового сечения № 30 на-
гружена внецентреннб приложенной сжимающей силой (рис. 11.7, а).
Определить допускаемую нагрузку, если [о] = 1400 кгс/см2.
Решение. Стойка подвергается внецентренному сжатию,
которое можно представить как сочетание центрального сжатия
181
и чистого косого изгиба (полюс не лежит ни на одной из главных
осей сечения).
Геометрические характеристики сечения берем из таблицы сор-
тамента: h = 30 см; b — 13,5 см; F = 46,5 см2; Jy = 7080 см4; Jz =»
= 337 см4; iy == 12,3 см; i2 = 2,69 см; Wy = 472 см8; Wz = 49,9 см8.
Координаты полюса ей = 6,75 см; ег = 15 см.
Внутренние силовые факторы во всех сечениях одинаковы:
^х— —Р', Му = —Рег', Мг — —Реу.
Рис. 11.Ь
Эпюры нормальных напряжений, соответствующие каждому
из внутренних силовых факторов, показаны на-рис. 11. 7,6.
Опасной является точка А.
Условие прочности
| max стс [ | стл | — | -р + + jpr | [о],
|тахас[ = |-^5-^-^^| = 0,0215Р+0,0318? +
’ 4-0,135? = 0,188?СМ,
-откуда [?] = М = “ . 7450 кгс; |
Пример 11.4. Проверить прочность короткой чугунной стойки
•(рис. 11.8, а), если [стр1 = 400 кгс/см2; [стс1 = 1000 кгс/см2. J
Решение. Стойка испытывает внецентренное сжатие силой Р, |
которое можно представить как сочетание осевого сжатия и чистого |
косого изгиба.
182
Определим вначале геометрические характеристики сечения.
Главную ось z сечения проведем, вычислив расстояние у0 центра
тяжести сечения от его стенки (рис. 11.8, б).
Сечение разбиваем на три прямоугольника:
2Г 1(/1 + F2у2 2 • 24 • 6 + 32 • 1 320 .
Ус 2Ft + 2 • 24 + 32 80
Главные центральные моменты инерции сечения
Jу = 2 (+ 24 • 9I 2 * * *) + = 4580 см*;
J2 = 2 + 24 22) + + 32 - 32 = 1070 см*.
Квадраты радиусов инерции сечения
/2 __ Jy _ 4580 __ 4580 __ -- „ . .2 _ Jz __ 1070 _ jg и 2
1У F 2-24+ 32 80 о< ,-э СМ , l2 f 80 10,4 СМ .
Внутренние силовые факторы, возникающие в любом попереч-
ном сечении, Nx = — Р\ Му = —Р |et|; Mz = — Р | еу |. Здесь-
еу = —2 см, ег = 8 см— координаты полюса.
Для нахождения опасных точек сечения определим положение
нулевой линии, вычислив отрезки ау, аг, отсекаемые ею на коорди-
натных осях (главных централь-
ных осях):
.2
‘2 13,4 С 7
= = 6,7 см;
.2
iy 57,3
ег ' 8 “
= —7,17 см.
Нанося на чертеж нулевую
линию (рис. 11.8, б), видим, что
наиболее удаленными от нее точ-
ками сечения будут точки А(уА~
— —4 см, гл= 10 см), в которой возникают напряжения сжатия,
и В(ув~ 8 см, zB= —10 см), в которой возникают напряжения
растяжения. Поскольку [стл] > og, т. е. [max стс] > max стр, про-
верку прочности производим для. обеих точек.
Наибольшие сжимающие напряжения
I I I I , Мг I
ImaxcrJ = |<тл) = [— +—+ —
, , I 20 000 20 000 - 8 , „ 20 000-2 ,
lmaXCT‘l = |-"во--------4580-- 10-------(ОТО"
= | —250 — 350 — 1501 = 750 кгс/см2 < [<тс ].
183
Наибольшие растягивающие напряжения
Nx . Му , Мг
max о„ = Од = ~ z„ + уя;
Р о F J у В Jг а В
20 000 20 000-8 . 20 000 - 2 о
тахор =-----вд-------4580— ' (“10) + ~Т070“ ‘ 8 =
= —250 + 350 + 300 = 400 кгс/см2 = [стр].
Прочность стойки обеспечена.
Задачи для самостоятельного решения
ПЛ Определить максимальные растягивающие напряжения,
возникающие в балке (см. рис. 11.9).
Рис. 11.10
Ответ. сттах = 79,2 МН/м2.
11.2. Найти наибольшие рас-
тягивающие и снимающие на-
пряжения в опасном поперечном
сечении балки с учетом ее соб-
ственного веса (рис. 11.10).
Ответ. оА — 81,9 кгс/см2; ав =
= —73,1 кгс/см2.
11.3. На боковой грани сталь-
ного внецентренно растянутого
•бруса (рис. 11.11) наклеен тейзодатчик А, деформация в направле-
нии его базы (продольная деформация ребра CD), определенная
с помощью электротензометричес-
кой установки, равна 3,2 х Ю~4.
Определить величину силы Р, если
для материала бруса Е = 2 х
X 10е кгс/см2.
Ответ. 5760 кгс.
11.4. Для бруса, показанного на рис. 11.12, требуется опреде-
лить допустимое значение силы Р, если [ст] = 1600 кгс/см2.
Ответ. 230 • 103 кгс.
184
ГЛАВА 12. ПРИМЕНЕНИЕ ТЕОРИИ ПРОЧНОСТИ К РАСЧЕТУ
ПРЯМОГО БРУСА
§ 12.1. Теории прочности
Теории прочности — это гипотезы об основной причине перехода
материала в предельное напряженное состояние (состояние теку-
чести или хрупкого разрушения). Они позволяют оценить прочность
при любом напряженном состоянии путем замены его равноойасным
одноосным растяжением. Напряжение такого одноосного растяже-
ния называется эквивалентным напряжением (величина условная).
Теории прочности устанавливают признаки равноопасности двух
напряженных состояний — сложного н одноосного растяжения.
Условие прочности для любого сложного напряженного состояния
может быть записано в виде аэкв^ [егР1.
где. стэкв— для данного напряженного состояния зависит не только
от характеризующих его величин (главных напряжений), но и от
принятой теории прочности.
Приведем основные сведения о тех теориях прочности, кото-
рые применяются в расчетной практике.
По теории наибольших касательных напряжений (она назы-
вается третьей теорией прочности) критерием равноопасностн
двух напряженных состояний является равенство наибольших
касательных напряжений.
Условие прочности по этой теории оХв^^г— «ГзСГ^рЬ
Здесь стх, о3— наибольшее и наименьшее главные напряжения.
По теории удельной потенциальной энергии формоизменения два
напряженных состояния равноопасны, если количество потенци-
альной энергии изменения формы, накопленной в единице объема,
для них одинаково.
По этой теории (будем называть ее четвертой) условие прочности
ст'кв = ~ — аз)2 + (ai — [0Гр1‘
Указанные теории прочности применимы лишь к пластичным
материалам: Для хрупких и хрупко-пластичных материалов при
меняется теория прочности Мора (условно будем называть ее пятой
теорией прочности).
Условие прочности: аХв = —vos [стр], где v == [стр]/[стс].
§ 12.2. Совместное действие кручения и изгиба.
Кручение с растяжением или сжатием
При совместном действии кручения и растяжения (сжатия)
в поперечных сечениях бруса возникает крутящий момент Мх— Мн
и продольная сила -Ух; при кручении с изгибом — крутящий
185
момент и изгибающие моменты Му, Mz (действием поперечных сил
Qy, Qz, возникающих при изгибе, пренебрегают)*.
Для отыскания опасного сечения бруса следует построить
эпюры внутренних силовых факторов. В некоторых случаях ука-
зать сразу опасное сечение нельзя, приходится производить про-
верку прочности для нескольких сечений.
Расчет на прочность ведут по эквивалентному напряжению
для опасной точки. Опасной является точка, для которой эквива-
лентное напряжение имеет наибольшее значение.
В опасных точках при указанном сочетании деформаций имеет
место упрощенное плоское напряженное состояние (см. гл. 2). Экви-
валентное напряжение можно вычислить в зависимости от принятой
теории прочности по одной из следующих формул: Стэ”в = V ст24-4т2;
ст'Ув = У О2 + Зт2;- аХв = + Цр’ Vо* + 4т2-
В этих формулах т — касательное напряжение в опасной точке по-
перечного сечения; ст — нормальное напряжение в этой же точке.
При расчете брусьев круглого поперечного сечения на изгиб
•с кручением вычисляют так называемый эквивалентный момент
для опасного сечения.
По теории прочности наибольших касательных напряжений
= к Ml 4- М®4- М®.
По теории удельной потенциальной энергии формоизменения
м£ = /0,75М: + М1 + М1.
Опасным будет то сечение, для которого Л4ЭКВ имеет наибольшее
значение (предполагается, что поперечное сечение бруса по его дли-
не постоянно). В этом сечении опасными явдяются точки пересече-
ния силовой линии ст контурной окружностью сечения.
Условие прочности имеет, вид стэкв= Мэкв/^и С [оР1-
Примзр 12.1. Определить диаметр вала ременной передачи
(рис. 12.1, а), пользуясь третьей теорией прочности. Весом шкивов
пренебречь; [ст] = 500 кгс/см2. Принять Т = 2/.
Решение. На рис. 12.1, б показано приведение сил, действую-
щих на шкив I, к ори вала. При переносе сил 7\ и получаем силу.
Л-h приложенную в центре шкнва (на оси вала), и пару сил,
скручивающую вал, с моментом — (Т1— /х)
Аналогично для // и /// шкивов
S01K2 = (Т2 - ; Жк3 = (Т3-t3) .
* В частных случаях может возникать лишь один из изгибающих момен-
тов Му или Мг.
1 об
Вычислим вращающие моменты, передаваемые каждым шкивом:
s0?Ki = 71620 = 5740 кгс см; Wk2 = 71620 • =
OUU OUv
= 12 900 кгс • см;
Эгк3 = 71620 • = 7162 кгс • см.
□мм
N„=90 л.с.
II
Н„‘50л.с.
:JTi]/// Л
N^Wjic.
§
/
z
400
о
S
б
~\_\п= 500 об/мин
200
539кгс
\Т,<г1077кгс
30'
У
932ка^
5740
Tiso
V 200, |
30
К Tr2t,
Т1*б3’:975кгс
ТгЧг=1935кгс
ЗпМцкгс-см
%1ц^5740кгс-см 'М-цf12900кгс.
ягнз*7160кгс-см
7160
Ra=880hsc Верт. пл.
1 1932 кгс
-----
20см
-о------
“40см !
,Е 1б
! _20cmJ^15cm
75500 И *
। 375кгс
RB^923 кгс
Ъ-14600
§
It '
№
г
д «
1935иге | Rg *15В5кгс
е
20см Лг15см
20см
40см
Гор. пл.
Rg-ввВкгс 539кгс
31700
Рис. 12.1
Определим натяжения ветвей ремня Т, t на каждом шкиве, поль-
зуясь ранее данным соотношением между силами и моментами и учи-
тывая, что Т = 2t-. = 2SRKi/Z)i = (2 • 574Э)/32 = 359 кгс; 7\ =
= 2/х — 718 кгс; Л + ^ = Ю77 кгс; t2 = 2Жк2//?2 = (2 • 12 900)/40 -
187
₽= 645 кгс; Т2 = 2/а = 1290 кгс; Т2 + t2 — 1935 кгс; t3 — 2Жкз/£>3 =»
₽= (2 х 7160)/44 = 325 кгс; Т3 — 2t3 = 650 кгс; Т3 -|- t3 = 975 кго»
Расчетная схема вала показана на рис. 12.1, в.
Вал испытывает кручение от действия моментов ЖК1,
изгиб в вертикальной плоскости силами ('7’1+Z1)cos30°=1077-
• 0,866=932 кгс — вертикальная составляющая силы /7’1-]-/1)
и Т'з + /з= 975 кгс и изгиб в горизонтальной плоскости
силами (Т1 -|- ZjJsin 30°= 1077 • 0,5 = 539 кгс, 7’2-]- t2— 1935 кгс.
Эпюра крутящих моментов Мх показана на рис. 12.1, г.
Расчетные схемы и эпюры изгибающих моментов в вертикаль-
ной и горизонтальной плоскостях представлены на рис. 12.1, д, е.
При построении эпюр изгибающих моментов вал рассматривается
как шарнирно опертая балка. На определении "опорных реакций
и построении эпюр не останавливаемся, так как эти вопросы по-
дробно освещены в главе 6.
Опасным является сечение Е, для которого, как нетрудно убе-
диться, эквивалентный момент имеет наибольшее значение:
= МЭКв = VM* + M* + М* = У 71602 + 15 5002 + 31 7002 =.
— 36 000 кгс • см.
т, Мэкв Л1
Из условия прочности Оэкв = = л^/32 1а1 определяем
32МЭКВ 3/ 36000.32 п
диаметр вала у —г-т- = у О1. спп = 9,04 см.
г ’ я [ ст] т о, 14 • оии
Принимаем d = 90 мм._
Пример 12.2. Определить требуемый диаметр вала червячного
колеса (рис. 12.2, а), передающего мощность /V = 12 кВт при угло-
вой скорости п = 80 об/мин; [а] = 400 кгс/см2.
При расчете пользоваться четвертой теорией прочности.
Решение. Определим момент, передаваемый валом:
= 97380— = 97380 = 14600 кгс • см.
п 80
Выразим этот момент через, окружное усилие Р 3RK = P^-»
п 2®к 2-14 600 сос
откуда Р = —= —^6— = 635 кгс.
Найдем радиальное усилие Т и осевое Q, пользуясь соотношени-
ями, приведенными на рис. 12 2, а: Т = 0,36Р =0,36 • 635 =
= 228 кгс; Q = 0,28Р = 0,28 - 635 = 178 кгс.
Для составления расчетной схемы приведем все силы к точке
геометрической оси вала (рис. 12.2, б). При переносе силы Р добав-
ляется пара сил с моментом Э1к= Ру = 14 600 кгс • см, скручи-
вающая вал. При переносе силы Q добавляется пара сил с момен-
том = Q ~ = 178 = 4С94 кгс • см, действующая в плоскости
188
xOz и вызывающая изгиб вала в этой плоскости. Сила = Q. вы-
зывающая сжатие правой половины вала, при расчете не учиты-
вается.
Расчетная схема вала показана на рис. 12.2, в. Вал испыты-
вает кручение (скручивается часть вала от правого конца до се-
редины колеса), изгиб в вертикальной плоскости парой сил Жи =
= Qj и силой Т, изгиб в горизонтальной плоскости силой Р.
Эпюра крутящих моментов изображена на рис. 12.2, г.
Для построения эпюр изгибающих моментов определяем опор-
ные реакции.
В плоскости zOx (рис. 12.2, д) у тА = 4094 + 228 • 10 —
— RB 20 = 0, откуда RB = (4094 4* 2280)/20 = 319 кгс; у тв =
189
== —Ra 20 + 4094 — 228 • 10 = 0, откуда Ra — (—2280 +
+ 4G94)/20 « 91 кгс.
Эпюра My представлена на рис. 12.2, е.
Схема нагружения силой Р данй на рис. 12.2, ж и соответ-
ствующая эпюра изгибающих моментов (Мг)— на рис. 12.2, з.
Схема нагружения и эпюра Мг совмещены .с плоскостью чертежа.
Очевидно, опасным является сечение С, расположенное бес-
конечно близко справа от середины колеса. Эквивалентный
момент для этого сечения Мэкв — V 0.75Л42 + М2У + Ml —
= V 0,75 • 146002 + 31942 + 31752 « 13 300 кгс - см. Из условия
Рис. 12.3
прочности Оэкв “ -tiino и находим диаметр вала d~ I/ —=
ЛЛ у Л [<JI
__ гЛ ' 13300____fi до см
~ Г 3,14.400 6,99 См’
Принимаем d = 70 мм.
Пример 12.3. Подобрать размеры поперечного сечения бруса
АВ (рис. 12.3, а), если [а] ~ 1400 кгс/см2. Расчет вести по теории
прочности наибольших касательных напряжений.
Решение. Брус испытывает кручение и изгиб. Опасным
будет сечение заделки, где возникает наибольший изгибающий мо-
мент шахЛ4и = Р1 — 800 • 90 = 72 000 кгс • см, а также крутящий
момент Мк = Р1Х = 800 • 120 = 96000 кгс • см.
Наибольшие нормальные напряжения возникают в точках верх-
ней и нижней кромок поперечного сечения (см. эпюру на рис.
12.3, б)
max Мя 72 000 • 6 432 000 108 000
omax — - bhi - b (2b)t = ft8
Наибольшие касательные напряжения возникают в точках
(рис. 12.3, б). Не учитывая влияния поперечной силы, имеем ттах » i
= МкЖ, где = ^b2h = 0,246b22b = 0,492ft3; i
ттах = 96 000/0,492b3 = 195 000/b3.
190
Касательное напряжение в точке Ki
n „ПС 195000 155000
Ti = уттах = 0,795 —
В точке /<1 имеет место упрощенное плоское напряженное со-
, in V 1/1-----------ГТа ]/ (108 000.2 , ./155000 2
стояние (оэквМ1 = Qmax + 4т‘= \ ) + 4 [ b3 ) =
330 000
Ь3
1400,
. з/ЗЗОООО „ „ , ,о .
откуда у 140Q- = 6,2 см; h = 2b = 12,4 см.
В точке К2 напряженное состояние — чистый сдвиг (см. гл. 2)
. Ш \ 1/п । л 2 о 390 000 ____ .
(Оэкв)к2 ~ ' 0 И- 4ттах = 2Ттах = // 1400,
откуда b 3^4от~> = 6,5 см; h — 2b = 13 см.
Окончательно принимаем большие из найденных размеров.
Опасной оказалась точка /(2.
Пример 12.4. Определить допускаемое значение нагрузки для
чугунного бруса (рис. 12.4), если пределу прочности его материала
на растяжение оПчр == 210 Н/мм2 и
требуемый коэффициент запаса
прочности [п]= 4,5.
Решение. Брус работает на
кручение и сжатие; при заданной
схеме нагружения все его попереч-
ные сечения равноопасны. В каж-
на сжатие опчс = 840 Н/мм2,
J’hc. 12.4
дом из поперечных сечений опас-
ны точки контура, так как в них
возникают наибольшие напряжения от кручения; нормальные
напряжения распределены по поперечному сечению равномерно.
Выразим напряжения в опасной точке через искомую величину Р:
4Р _ м* _ 2pd _ 32Р
nd2 ' Т W„ ~ nd3/16 ~ nd2 •
Применив теорию прочности Мора, получим следующее условие
прочности:
„V 1 — V 1 + v .г-- . „ 1 — 0,251 4Р .
о9кв=— а + — И о +, 4т2 = —у— +
+ И42 + 4"-'322<^,
2 nd2 1 [«1
где v = Опчр/Оичс — 210/840 = 0,25.
191
После дальнейших преобразований получим
(_4.0,375 + 0,625 • 64,2) тт .
Допускаемое значение нагрузки
= ЙГЙ7-1.5) = 3Jb-^8T6 - = 6080 н = 6’08 кН-
Задачи для самостоятельного решения
12.1. Определить требуемый диаметр вала ременной передачи
(рис. 12.5), применив третью теорию прочности; принять [о] =
= 700 кгс/см2. Учесть вес шкивов Gt и G2.
Ответ, d = 93 мм.
1,0 м
s
Н=30л.с.
n WM
Ол.с. *--
n=200 од!мин
сСг-15'
1-3J5M
б1=250нгс^8^200нгс
' “ cCf^lO
" Рис. 12.5
12.2. Проверить прочность стального бруса малой кривизны
(рис. 12.6), применив третью теорию прочности; принять [о] =«
— 1000 кгс/см?.
12.3. Определить допускаемое значение силы Р для бруса (рис.
12.7), если [ор] = 1200 кгс/см2; расчет вести по теории наибольших
касательных напряжений. ' J
Ответ. [Р] = 22,8 • 10s кгс.
192
12.4. Пружинная шайба (рис. 12.8) при затягивании болта на-
гружается силами Р = 12 кгс. Определить эквивалентное напряже-
ние для опасной точки, применив третью теорию прочности. Расстоя-
ние между силами пренебрежимо мало по сравнению с диаметром
шайбы.
Ответ, = 3970 кгс/см4.
12.5. Определить допустимую величину силы [Р] для пружинной
шайбы (рис. 12.9), если [о] = 400 Н/мм2. Расчет вести по теории
наибольших касательных напряжений. Разрез шайбы считать бес-
конечно узким.
г Ответ. [Р] = 154 Н.
12.6^ Определить коэффициенты запаса прочности для обоих
стержней (рис. 12.10). Материал стержней—Ст. 3. с пределом
текучести ат= 2400 кгс/см2. При расчете использовать четвертую
теорию прочности. Силы трения между стержнями не учитывать.
Ответ, гц = 1,69; 2,43.
§ 12.3. Общий случай действия сил на брус
_ В ,общем случае действия сил на прямой брус в его поперечных
сечениях возникают шесть внутренних силовых факторов (рис.
12.11): Nx — продольная (нормальная) сила; Qy, Qz—поперечные
силы; Му, Mz—изгибающие моменты; Мх — Мк—крутящий мо-
мент.
Для отыскания опасного сечения или выявления нескольких
предположительно опасных сечений, как правило, нужно построить
эпюры внутренних силовых факторов. При их построении исполь-
зуют для каждого элемента ломаного бруса'скользящую систему
координат, показанную на рис. 12.11: х — продольная ось бруса;
У, г — главные центральные оси его поперечного сечения.
7 1-ю
193
Для нахождения опасной точки сечения строят эпюры нор-
мальных и касательных напряжений, соответствующих каждому
из внутренних силовых факторов; при этом влиянием^поперечных
сил в большинстве случаев пренебрегают. Опасной является та точ-
ка, для которой эквивалентное напряжение имеет наибольшую ве-
личину. В опасной точке в общем случае имеет место, у прощен ное
плоское напряженное состояние, в частных случаях — чистый сдвиг
или одноосное растяжение (сжатие).
Пример 12.5. Проверить прочность чугунного бруса (рис.12.12,а),
если [стр] — 300 кгс/см2, [Сте] == 1000 кгс/см2.
Решение. Брус испытывает кручение, сжатие и изгиб. В по-
перечных сечениях его возникают внутренние силовые факторы Nx,
Мх, Му (поперечную силу Qy
не учитываем).
.Эпюры Мх, Nx, Му пока-
заны на рис. 12.12, б.
Проверим прочность бру-
са в сечении NiL^.
Максимальное
ние. от кручения
max Мх
шахт^-^—* =
Напряжения от сжатия
напряже-
30000 =
тИ
= 153 кгс/см2.
. Mt . Мс•4
NXI ~ F, ~ nd* ~
5000 «4 л . о
- ,лг = —63,7 кгс/см2.
л • 10а
Максимальные напряжения от изгиба
max Al у max Al« 18 750 • 32 . , л, , »
max oMyi ~ ± = ± = ± - ± 191 кгс/см2.
32 “
Эпюры напряжений в поперечном сечении показаны на
рис. 12.12, в.
Какая из точек (D или Е) рассматриваемого сечения является
опасной, не очевидно, так как по абсолютной величине ст в точке Е
больше, чем в точке/?, но материал бруса — чугун, который лучше
сопротивляется сжат'ию, чем растяжению. Поэтому проведем расчет
для обеих указанных точек.
Определяем нормальные напряжения в этих точках:
сто = Од, 4- (тахСТд! )D = —63,7 + 191 =s 127 кгс/см2 (растяжение);
оЕ = ол + (max Од, )Е = —63,7 — 191 » —255 кгс/см2 (сжатие).
194
Определяем эквивалентные напряжения для точекD и Е, приме-
няя теорию прочности Мора (пятую теорию прочности) и учитывая,
[Ор1 300 Л „
чт0 v = == Тбоо == °’3-
Рис. 12.12
Для точки D
(аУкв)о = 127 + 1±А?/1272 + 4- 1532 = 260 кгс/см2 < [ор].
л
Для точки Е
{^ъ)е = (-255) + Г2552 + 4 • 1532
= 170 кгс/см2 < [ор].
7*
195
Опасной оказалась точка D. Прочность бруса на первом участке
обеспечена.
Проверим прочность бруса в сечении У2Г2. Геометрические
характеристики этого сечения F — а2 — (d/ ]^2)2 = 102/2 = 50см2;
г a* 2) _ d* ___ 10*______________ /у __ 208_к
Jj, — — — 12 — 48 — 48 — 208см , Wy 5 —41,6см .
Эпюры нормальных и касательных напряжений представлены
на рис. 12.12, г. Сопоставив эти эпюры с эпюрами для сечения
A убеждаемся, что любая точка сечения N2L2 менее опас-
на, чем точка D, и, следовательно, прочность II участка обес-
печена.
Пример 12.6. Найти размеры поперечных сечений участков
пространственного бруса (рис. 12.13, а). Участок ED квадратного
сечения, участок CD — прямоугольного (ft = 26), участки СВ
. и АВ — круглого сечения (рис. 12.13, б).
Расчет выполнить по теории наибольших касательных напря-
жений. Допускаемое напряжение [ст] = 1000 кгс/см2.
Решение. Построим эпюры внутренних силовых факторов,
для чего будем пользоваться скользящей системой координат,
. показанной на рис. 12.13, а. При построении эпюр будем двигаться
от свободного конца бруса.
Эпюры Nx, Qg, Qz изображены' на рис. 12.13, в, г, д — спе-
циальных пояснений по построению этих эпюр не приводим.
Построение эпюры крутящих моментов Мх.
Участок СВ Мхс — <7^/2 = (100 • 352)/2 = 6 1 250 кгс • см.
Участок ВА Мх ~ Мх = РЛ, — 500 • 60 = 30 • 10s кгс • см.
в л 18
Эпюра Мх представлена на рис. 12. 13, е.
Построение эпюры изгибающих моментов МЙ.
Участок DC Му — Ми => —1000 кгс • см.
Участок СВ (Му)с = —1000 кгс • см;
> = —5R — ql1la = —1000— 100 - 35'-60 = —211 • 10®кгс-см.
Участок ВА Ми =—211 • 10s кгс - см;
МуА = —5R — д1г13 + Р2/4 = —1000— 100 • 35 • 60 + 200 • 90 =
= —193 • 10s кгс • см.
Эпюра Му, построенная на каждом участке со стороны его сжа-
тых волокон, представлена на рис. 12.13, ж.
Построение эпюры изгибающих моментов Мг.
Участок .ED. /Иг£ = 0; Л4гд = — ^/2/2 = — (100 • 352)/2 =
= —61 250кгс-см.
Участок DC Мг = Мг„ = —61,25 • 10s кгс см.
D С
Участок СВ Мг — 0; Мг = Р2/3 = 500 • 60 — 30 • 10s кгс -см.
196
Z6I
00g|i 11 i 111 I ГТ ГТ1ТГТТП
щи 11111 i.i 11111 m
0092
9‘Si9
(ззх)3Ц
Участок BA MZB =—<7/2/2 =—61,25 • 103 кгс • см; Mz^ =
= —7^/2 + = —61,25 • 103 + 500 • 90 = —16,25 • 103 кгс см.
Эпюра Мг представлена на рис. 12.13, з, ее ординаты отложены
со стороны сжатых волокон.
Переходим к определению размеров поперечных сечений
участков.
1) Участок ED испытывает прямой поперечный изгиб.
Опасным является сечение О, где изгибающий момент Mzd —
= 61 250 кгс • см. Пользуясь условием прочности при прямом
изгибе Ощах = max Mz/Wz^ [о], находим Wz== max.Мг/[а].
Отсюда а 6 max /И2/[о] = >/б • 61,25 • 10я/1000 = 7,16 см.
Принимаем а = 72 мм.
2) Участок CD, как видно из эпюр, испытывает чистый
косой изгиб и растяжение (все сечения этого участка равноопасны).
Внутренние силовые факторы на этом участке:
Nx = 3500 кгс; Му = 1000 кгс • см; Мг = 61 250 кгс • см.
Подбор сечения производим предварительно из расчета, на
косой изгиб с последующим учетом Nx.
Расчетная формула для опасной точки (угловой) amax = My/Wy+
+ Mz/Wz^[<j],
где wz — 6 — 12 , 6 24 , w z.
м । г м
„ TV7 . TV7 ^У и Л3 61,4 • 103 Н- 2 • 10®
Определяем Wz: Wx >-------—— =»
= 63,4 см3; 12 • 63,4 = 9,14 см.
Принимаем h = 9,4 см и производим проверку с учетом влия-
ния продольной силы: F = bh = 9,4 • 4,7 = 44,2 см2;' Wz — +/12=
= 9,4s/12 ==69,2 см3; W„ = 34,6 см3;
Nx . Му Mz 3500 . 1000 . 61 400 , оо[-
max а= + + = 79 + 29 + 885 =
= 993 кгс/см2 < [о].
3) Участок ВС.’ Здесь имеет место общий случай действия
сил. Опасное сечение вблизи точки В. Внутренние силовые фак-
торы в этом сечении следующие: Nx — —200 кгс; Мх = Мк ~
=.61,25 • 103 кгс • см; Му = 211 • 103 кгс • см; Mz ~ 30 • 10s кгс-см.
Влиянием поперечных сил пренебрегаем.
Подбираем диаметр сечения из расчета'на кручение и изгиб.
Эквивалентный момент по третьей теории прочности /Иэ”в —
= /М2 + М2 + М2 = К(61,252 + 2112+ 302) • 10е =
= 222 103 кгс • см;
W. « 0,М3> ЛО[о] = (222 103)/103; |^2220 « 13 см.
198
Проверяем достаточность размеров сечения, учитывая продоль-
ную силу: Ги = = 216 см3; Wp = 2№и = 432 см3; F =
м2 ОЛ,
nd3 п • 13а 1QQ „.,2
= т = —4— = 133 см2.
Изгибающий момент
Ми = ЮИ2 + /И2 = /(211 • 10s)2 + (30 • 103)2 = 213 103 кгс • см.
Максимальное нормальное напряжение
° = Т “ F ~ = —1,5 — 986 « -988 кгс/см2.
г м<и loo 210
Касательное напряжение т — MgjWp = 61 400/432 =. 142 кгс/см2.
Эквивалентное напряжение по третьей теории прочности
а’” = /а2 + 4т2 = У 9882 + 4 • 1422 = 1027 кгс/см2.
Перегрузка °эк”ау1<Т- • 100% = -°^^(р00 100% = 2,7%, что до-
пустимо.
4) Участок АВ.
Опасное сечение рблизи точки В: Nx — —3500 кгс; Мк = 30 х
X 103 кгс • см; Мг = 61,25 • 10s кгс - см; Мй = 211 • 10s кгс • см.
Подбираем диаметр сечения из расчета на кручение и изгиб.
Эквивалентный момент по третьей теории прочности
М"кв ~ /Af’ + AfJ + AfJ = /(3022112 + 61,252) 10е =
- 222 • 10s кгс • см.
Основываясь на расчете участка ВС, берем d0 — 13 см и про-
веряем достаточность размеров сечения, учитывая продольную
силу: Ги = 216 см3; Wp = 432 см3, F = 133 см2.
Изгибающий момент
Мя = //И2 + Ml = /(61,252 + 211®) • 10е = 218 • 10» кгс • см.
Нормальное напряжение а = Nx/F — Ma/WB = —3500/133 —
— 218 000/216 = —26,3 — 1006 « —1032 кгс/см2.
Касательное’напряжение т = AfK/lFp = 30000/432 = 69,5 кгс/см2.
Эквивалентное напряжение по третьей теории прочности
а"Кв = /о2 -f- 4т2 = У 10322 + 4 • 69,52 = 1040 кгс/см2.
Перегрузка составляет 4%, что допустимо.
Пример 12.7. Проверить прочность детали (рис. 12.14, а) в се-
чениях т — т, п — п, s — s. Расчет вести по третьей теории проч-
ности при [а] = 750 кгс/см2.
199
Рис. 12.14
Решение.
Сечение т—т (см. рис. 12,. 14, а). Участок 0—1 испыты-
вает прямой изгиб от действия силы Р. Изгибающий момент в се-
чении т — т Ми Р • 3 = 350 • 3 => 1050 кгс • см.
Наибольшие нормальные напряжения отах = M„/Wa— 1050/0,1 X
X З3 = 389 кгс/см2 < [ст].
Сечение п — п (рис. 12.14,6). Сечение примыкает к участку
1—2, Внутренние силовые факторы в сечении п — п найдем, рас-
сматривая все внешние силы, лежащие слева от п — п (т. е. на
участках 0 — 1, 1 — 2).
Продольная сила Nx = —Pu——Pcos45Q =—350 • 0,707 =
= —247 кгс.
Поперечные силы Qz = PZ = Р sin 45° = 350 • 0,707 = 247 кгс.
Qu °0.
Крутящий момент Мк = Мх = Р/ = 247 • 4,5 = 1110 кгс • см.
Изгибающие моменты Mz — РуГ = 247 • 4,5 == 1110 кгс • ем;
Му = Рг1 = 247 • 22 = 5440 кгс • см. Участок 1 — 2 испытывает
изгиб с кручением и сжатие.
Для определения опасной точки строим эпюры напряжений
в этом сечении (см. рис. 12.14, б).
Проверим прочность бруса в точках А и В:
> |_| ЛЬ Му Мг1 I 247 5440 - 6 1110-61
I | р Wj/ —I 3-4,5 3-4,5* 4,5 • З2| ~
720 кгс/см2 < [ст].
В точке В возникают нормальные и касательные напряжения.
Нормальное напряжение в точке В
а _ _ 247 111(ь6 , 183 кгс/см2
GB р jrz 3-4,5“4,5.3* 183 кгс/см .
Касательное напряжение в этой точке
т -Д-1 3 1110 -I 3 - - 146 кгс/см2
в 2 F 0,231 • 3*4,5 ‘ 2 3^Z§ 1™КГС/СН'
Эквивалентное напряжение по третьей теории прочности
Л)д = /о» + 4т» = /183*4-4 • 1462 = 335'кгс/см2 < [ст].
Сечение s—s. Внутренние силовые факторы в этом сечении:
крутящий момент (рис. 12.14, в)
Мк = Ра = Р22 cos 45° = 350 • 22 • 0,707 = 5450 кгс • см;
изгибающий момент
Мл = Р (г 4- с) “ 350 • 9,5 = -3320 кгс • см;
г 4- с — расстояние между плоскостью действия силы и сечением
з — з.
201
*
Пренебрегая влиянием поперечных сил, ведем расчет по экви-
валентному моменту:
Мэ’кв = + = К54502 + 33202 = 6370 кгс • см.
Эквивалентное напряжение
III ^экв 6370 ещ ___г 1
Оэкъ = = ОД .58 = 510 кгс/см2 < [о].
Таким образом, прочность бруса в указанных сечениях обес-
печена.
Задачи для самостоятельного решения
12.7. Определить требуемый диаметр поперечного сечения •
ломаного стержня (рис. 12.15), если [а] = 16С0 кгс/см2 Расчет
выполнить по третьей теории прочности.
Ответ, d - 5 см.
12.8. Определить допускаемую на-
грузку Р на вертикальную стойку (рис.
12.16), если la] = 1600 кгс/См2. Расчет выполнить по третьей
теории прочности.
Ответ. [Р] = 19,7 • 103 кгс.
Рис. 12.17
202
12.9. Определить допускаемую нагрузку [Р] для ломаного
бруса, изображенного на рис. 12.17. Применить третью теорию
прочности; принять [<г] — 1200 кгс/см2.
Ответ. [Р] = 171 кгс.
12.10. Определить требуемый диаметр поперечного сечения
ломаного бруса, изображенного на рис. 12.18. Принять 1а] =
= 1000 кгс/см2. Расчет вести по четвертой теории прочности.
Ответ. d = 39 мм.
ГЛАВА 13. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ
И ТОНКОСТЕННЫХ СОСУДОВ
§ 13.1. Расчет толстостенных цилиндров, находящихся
под действием внутреннего и внешнего давления
Исследование вопроса о напряжениях и деформациях толсто-
стенных цилиндров (закрытых, т. е. цилиндров с днищами, и.от-
крытых), подверженных действию внутреннего и наружного давле-
ния, представляет собой одну из осесимметричных задач теории
упругости и сопротивления материалов; ее называют задача
Ляме.
Рис. 13.1
Результаты решения задачи применяют к расчету цилиндров
компрессоров, орудийных стволов, трубопроводов и сосудов вы-
сокого давления, многослойных составных оболочек, прессовых по-
садок втулок на валы и т. д.
Если выделить из закрытого цилиндра, нагруженного внутрен-
ним давлением и наружным р2 (рис. 13.1), элемент, ограничен-
ный цилиндрическими поверхностями радиусов г и г -j- dr, двумя
бесконечно близкими поперечными сечениями (расстояние между
ними dz) и двумя радиальными сечениями, составляющими между
собой угол dQ, то нетрудно убедиться, что на гранях элемента
отсутствуют касательные напряжения. Такой элемент изображен
203
на рис. 13.2, там же показаны возникающие на его гранях нормаль-
ные напряжения, которые согласно сказанному являются глав-
ными напряжениями. Напряжение 0г называют осе-
вым,^ — радиальным, О/ — окружным или коль-
цевым (иногда встречается наименование — тангенциаль-
н о е). Для определения этих напряжений служат формулы:
Z Z
Р1Г1- Pzrz
= 2 2
z 2 , z a
Piri — Рггз (Pi — Рг) rira
a.
2 2 / 2 2Ч « »
2— Г1 (Г3~ Г1)Га
Как видно из приведенных формул, напряжения ог равномерно
распределены по поперечному сечению цилиндра, а напряжения •
а„ ot изменяются по толщине его стенки по гиперболическим за-
конам. Соответствующие эпюры напряжений показаны на рис. 13.3.
Если цилиндр открытый (без днищ), то о2 — 0; формулы, для
определения ar, <Jt остаются в силе.
Для расчета двух- и многослойных цилиндров, а также при рас-
чете посадок с гарантированным натягом используется формула,
определяющая величину радиального перемещения и произволь-
ной точки цилиндра. Для открытого цилиндра эта формула имеет
Z Z ..22
1 — Ц Р1Г1 — Рзг2 1 4- Ц (Р1 — Рз) Г1Г2
ВИД U = —=-£ 5----5— Г----5-1- J--j-- .
£ rs2-4 . (гз—г\)г
В частном случае, когда цилиндр находится под действием
только внутреннего давления pi — р (р2 = 0), формулы для глав-
2 ,2 /
Г1 ri .
ных напряжении имеют вид аг = р —---р; а, = р—-----р I1 —
a
гз
.a
a
z
204
В этом случае окружные напряжения ot растягивающие, а
радиальные а, — сжимающие. Эпюры напряжений приведены на
рис. 13.4.
Напряжения ot, ог достигают наибольших по модулю значе-
ний в точках внутренней поверхности цилиндра. Эти точки явля-
ются опасными. Соответствующие величины главных напряжений
/ Z । 2
z . р(Гъ + Г1) рГ1
(Jj -- 2 2 » ^2--- -- 2 2 » СТ3 р*
гг — Г1 гг—Г1
Эквивалентное напряжение для опасной точки вычисляют по
одной из следующих формул:
Рис. 13.4 Рис. 13.5
по гипотезе наибольших касательных напряжений
Нэкв — Hi — ffg — 2р J j-;
га — ri
По гипотезе энергии формоизменения
2
Пив = 4= V (П1 — П2)2 + (<h — <*з)2 + (стз — <h)2 = Р /3 ——-2-;
у 2 'а—Г1
по теории прочности Мора
v (v+1)г1 —(V—l)rj
Оэкв — <4 — W3 — Р г а •
ГГ~ГЪ
Приравнивая эквивалентное напряжение для опасной точки
допускаемому напряжению на растяжение Юр] для материала ци-
линдра, нетрудно получить из этого условия прочности выражение
для требуемой толщины стенки цилиндра при заданном радиусе rt.
205
Так, по гипотезе энергии формоизменения требуемая толщина
стенки цилиндра определяется по формуле
Из этой формулы следует, что при давлении в цилиндре
[Op] lV3 невозможно обеспечить выполнение условия прочности
при сколь угодно большой толщине стенки.
Интересно отметить, что при безгранично большом увеличении
толщины стенки цилиндра (при г2 -► °°) можно полагать ог — О
и для любой точки стенки at = —аг = .
Таким образом, в рассматриваемом случае напряженное со-
( стояние в любой точке стенки представляет собой чистый сдвиг
(oi = —а3). Практически указанный результат достаточно точен
при г2/гг >4.
Эквивалентные напряжения для точек внутренней поверхности
цилиндра определяются по формулам oBkb — 2р; п|Ув = р ]/3.
Остановимся также на частном случае нагружения цилиндра
только внешним давлением (рг — 0). В этом случае формулы для
главных напряжений имеют вид
а , а . 2 , а .
г3 /1 Г1 ) г2 / \
°г Ра 2 \' г» ’ Ра • v г*/'
Га — ri ' г > гг — г1 \ г /
а
г2
Oz-----р а .
га — гх
Эпюры напряжений по толщине цилиндра показаны на рис. 13.5.
Опасными являются точки внутренней поверхности. Главные
а
, . А. Га
напряжения в этих точках: ох = (Or)r-r, == 0? о2 = аг = —р —-г‘»
га —G
. . 2rl
Оз — (Oi)r=Ti--Р ~а- а" •
га — ri
При отношении толщины 6 стенки цилиндра к его внутреннему
радиусу rlt меньшем 0,1 (6 : гх < 0,1) с погрешностью, не превы-
шающей 5%, взамен формул Ляме можно пользоваться более
простыми выражениями, приведенными в § 13.2.
Из изложенного выше следует, что повышение рабочего (внут-
реннего) давления в цилиндре ограничено требованием соблюдения
условия прочности аэкв ЮР1 для внутренних точек цилиндра.
Для повышения допускаемого давления применяют составные ци- .
линдры, состоящие из двух или большего числа труб, искаженных
одна на другую с натягом. В дальнейшем ограничимся сведениями
о расчете двухслойного цилиндра.
206
При посадке с натягом на поверхности контакта цилиндров
возникает контактное давление рк, вызывающее во внутреннем
цилиндре сжимающие, а в наружном — растягивающие окруж-
ные напряжения. Эпюры напряжений, обусловленных посадкой
с натягом, показаны на рис. 13.6.
При нагружении составного цилиндра внутренним давлением
р он будет работать как одно целое. Напряжений, вызванные рабо-
чим давлением р, алгебраически суммируются с напряжениями от
контактного давления рк. Во внутренних, наиболее напряженных
точках рабочие напряжения и напряжения от посадки имеют раз-
ные знаки. Поэтому суммарное напряжение в этих точках снижа-
ется и составной цилиндр может выдержать большее давление, чем
Рис. 13.6
обычный. Эпюры распределения напряжений в составном цилиндре,
нагруженном внутренним давлением, показаны на рис. 13.7. Штри-
ховыми линиями изображены эпюры, соответствующие нулевому
контактному давлению.
Связь между натягом\натяг А — это разность наружного диа-
метра внутреннего цилиндра и,, внутреннего диаметра наружного
цилиндра до сборки) и контактным давлением выражается формулой
/I С С \
2га1 -gA 4- /, где для сокращения записи введены обо-
1 2 , V 2,2
Гц-|-Га
значения Са = -----j- 4- ра; Сг = —---j- — fo;
г3 — Г 2
Е±, р,! и Е2, ра — модули продольной упругости и коэффициенты
Пуассона соответственно для материалов внутреннего и наружного
цилиндров.
При расчете составного цилиндра стремятся обеспечить условие
равнопрочности внутреннего и наружного цилиндров, т. е. условие
(^экв)л = (Оэкв)а (см. рис. 13.7). Это условие будет выполнено при
назначении величин га, г3, А по формулам (для пластичных мате-
риалов при = £а = Е и рх = ра)
гз = [СТр]Р_дГ1‘> г2 = Vvs, А = 2 ^г4 .
207
Пример 13.1. Определить коэффициенты запаса прочности
для опасных точек закрытого и открытого цилиндров при рабо-
чем давлении внутри цилиндров рг — р = 900 кгс/см4. Радиусы
цилиндров г, = 80 мм; г3 = 180 мм. Условный предел текучести
материала цилиндров а0,а = 3100 кгс/см2. Расчет выполнить по
гипотезам наибольших касательных напряжений и энергии формо-
изменения.
Решение. Определим величины главных напряжений для
точек внутренней поверхности закрытого цилиндра (см. § 13.1):
s . »
== (tff)r=r, = Р = 900 [fajZfo = 1340 кгс/см2; 7
с2 = ог = р 2 — 2-%= 900 = 220 кгс/см2;
' а3 — (ar)r=rt = —р = —900 кгс/см2.
Эквивалентное напряжение по гипотезе “ наибольших касатель-
ных напряжений <4^ = — ст8 = 1340 —(—900) = 2240 кгс/см2.
Соответствующий коэффициент запаса
„ __ °0.2 3100 , OQ
Д1П — III “ 2240“
V9KB
Эквивалентное напряжение по гипотезе энергии формоизмене-
ния (см. формулу в § 13.1)
IV 900 • 182 • /3 1Олп м 2
Стэкв = -2_ i = -—82_-82 -- = 1940 кгс/см2.
Соответствующий коэффициент запаса^
п - °0-2 г3100 _ 1 R
"iv— -IV 1940 — *’ •
Для точек внутренней поверхности открытого цилиндра значе-
ния Hi, о3 остаются теми же, что и для закрытого, а а, = 0. По
гипотезе наибольших касательных напряжений величина а2 не
влияет на условие прочности и, следовательно, величины аЭкв и
/ini получаются такие же, как и для закрытого цилиндра.
Определим эквивалентное напряжение по гипотезе энергии
формоизменения
Оэкв = Y= V(ffi — Оа)4 + (<Та — стз)а 4" (СТ3 — а1)2 =
= у= /13402 + 9002 + (—900— 1340)® = 1950 кгс/см4.
Коэффициент запаса njv = 00,2/Оэкв = 3100/1950= 1,59.
208
Пример 13.2. Определить требуемую толщину стенки цилиндра
гидравлического пресса при Р = 30 тс (рис. 13.8). Материал
цилиндра сталь Ст. 3 с пределом текучести ат == 2400 кгс/см8.
Требуемый коэффициент запаса щ] = 2,5. Расчет выполнить по
гипотезе наибольших касательных напряжений.
Решение. Определим рабочее давление в цилиндре
Р 30000-4 ,„„2
р - ~ я - 15* - 170 КГС/ •
•Условие прочности-для опасных точек цилиндра
СГэкв = сгх — сг3 = 2рг8/(г8 — г8) [ст].
Допускаемое напряжение
[al = от/[п] — 2400/2,5 = 960 кгс/см8-.
Из условия прочности определяем тре-
буемую величину наружного радиуса ци-
линдра: '
Рис. 13.8
г - г V М - 7 5 V 960 -
r2 —Г1 Г [о( —2р~'»° V 960 — 2-170 ~
= 9,35 см.
Принимаем га — 9,5 см.
Требуемая толщина стенки цилиндра 6 = 9,5 — 7,5=^ 2 см.
Пример 13.3. Определить внешний диаметр da, диаметр da
контактной поверхности и величину натяга Д для составного ору-
дийного “Ствола, внутренний диаметр которого dt = 122 мм. Опре-
делить контактное давление между цилиндрами при принятом
натяге. Максимальное давление в момент выстрела р — 2000 кгс/см8.
Материал ствола — сталь с условным пределом текучести а012 —
= 6000 кгс/см8. Требуемый коэффициент запаса щ] = 2. Принять
Е = 2 • 10* кгс/см8;, р, = 0,3.
Решени е. Допускаемое напряжение
[сгр] = ао.2/[«] = 6000/2 = 3000 кгс/см8.
По формулам, приведенным в § 13.1, определяем оптимальные
значения внешнего радиуса г3 и радиуса г2 контактной поверх-
ности:
• _ .1°р1 _ 6,1-3000 1й„
Г1[ор1 — Р 3000 - 2000*" 16,d СМ’
г2 = Vt\r3 = У 6,1 • 18,3 = 10,6 см.
Итак, da — 2г3 = 2 • 183 = 366 мм; d2 = 2г2 = 2 • 106 = 212 мм.
Требуемая величина натяга
Д = 2 ф = 2 2°°° '-5”’» = 2,12 - 10-2 см = 0,212 мм.
Е 2 • 10§ ’ ’
209
Для определения контактного давления вычисляем вспомога-
тельные величины:
Г - 4- и - 18’3* + 10-6* । О 3 - 9 Я
ь2 — 2 2 + Р 18,32— 10,62~
„ >г + 4 . 10,62 4-6,1а nQ , сс
— 2 2 Р 10,62— 6,12 1.68.
'2'1 , ’ ’
Определяем величину контактного давления:
Л ЛЕ _ 2,12 • 10-2.2-10’ __
Рк^о |СХ С2\ ~ 2га (Сг + С2) ~ 2 • 10,6(2,3 4- 1,68)“
= 502'кгс/см2.
Задачи для самостоятельного решения
13-1. Определить коэффициент запаса для латунной трубки
(рис. 13.9) маслопровода, находящейся под внутренним давле-
нием р — 150 бар. Условны^ предел текучести для материала трубки
о0,2 = 200 Н/мм2. Расчет выполнить по
гипотезе наибольших касательных на-
пряжений.
Ответ. 1,93.
Рис. 13.9 13.2. Определить величину контакт-
ного давления на поверхностях сопри-
косновения стальных втулки и вала (рис. 13.10), если натяг-
А — 0,25 мм. Принять Е = 2 • 10е кгс/см2, у. — 0,3.
Ответ. 1980 кгс/см2.
4-1
Рис. 13.10
13.3. Построить эпюры радиальных и окружных напряжений /
по толщине стенки двухслойного стального цилиндра, находя-
210
щегося под действием, внутреннего давления р = 1500 кгс/см2.
Радиусы цилиндра: гх = 120 мм;>2 = 160 мм; г3 = 200 мм.
Натяг Д= 0,26 мм.
Ответ. См. рис. 13,11.
§ 13.2. Расчет тонкостенных сосудов
Резервуары для жидкостей и газов в. большинстве случаев
представляют собой тонкостенные осесимметричные оболочки. Гео-
метрическое место точек, равноотстоящих от внешних поверхностей
оболочки, называют ее срединной
поверхностью. В сопротивлении
материалов рассматривают расчет оболо-
чек, срединная поверхность которых явля-
ется поверхностью вращения (рис. 13.12, а)
и нагрузка (внутреннее давление жидкости
или газа) симметрична относительно оси
оболочки.
Оболочки принято считать тонкостен-
ными, если отношение толщины их сте-
нок к наименьшему главному радиусу
кривизны срединной поверхности не более
одной десятой (в случае точности расчетов
иногда считают рассматриваемую ниже
теорию расчета применимой при указан-
ном отношении, не превышающем одной
двадцатой).
Для тонкостенных осесимметричных
оболочек при отсутствии нагрузок в виде
сосредоточенных сил или моментов и постоянной или изменяю-
щейся без скачков кривизне меридианов можно считать, что на- '
пряжения по толщине стенки оболочки распределены равномерно.
Грани элемента, выделенного из оболочки двумя бесконечно
близкими меридиональными сечениями и двумя бесконечно близ-
кими коническими сечениями (перпендикулярными к меридиональ-
ным), являются главными площадками. Соответствующие главные
напряжения — от — меридиональное и crt — окружное или коль-
цевое (рис. 13.12, б) — связаны между собой уравнением Лапласа:
Стт/Рт + С//Рг = Р/Д где рт, р,— радиусы кривизны соответст-
венно меридионального и нормального к нему сечений для данной
точки оболочки (главные радиусы кривизны); р—давление в этой
точке; 6 — толщина стенки.
Таким образом, в точках стенки сосуда возникает двухосное
напряженное состояние. Точнее, для внутренней точки напряжен-
ное состояние трехосное — одно из главных напряжений —
численно равно р. Но р мало по сравнению с ат, сгг и упомянутым
211
главным напряжением пренебрегают, т. е. полагают, что и в ука-
занных .точках напряженное состояние тоже двухосное.
Для определения напряжения ат (в-тех случаях, когда р< «Л °°)
используют уравнение равновесия всех сил, действующих на отде-
ленную коническим сечением часть оболочки (см. рис. 13.12, б):
ат2лгд cos а =
где г — радиус кривизны параллели в плоскости, перпендикуляр-
ной оси оболочки; SP£z — сумма проекций на ось оболочки всех
Внешних сил, действующих на оставленную часть (собственный
вес оболочки обычно не учитывают): SPiz = уУи 4- рлг*.
Здесь у — удельный вес жидкости, заполняющей сосуд; VH —
объем нижней части сосуда; р — давление на уровне проведен-
ного сечения, определяемое высотой столба жидкости, располо-
женного выше; сечения. При наличии в сосуде помимо жидкости
газа под давлением р0 эта величина должна быть учтена при опре-
делении р. :
Если опора сосуда расположена ниже проведенного сечения,
то в величину должна дополнительно войти реакция этой
опоры.
Для частного случая цилиндрического сосуда внутренним диа-
метром D, содержащего газ под давлением р, меридиональное
и окружное напряжения определяются по формулам <rm — pD[4§t
Gt = pD/26.
Учитывая, что в тонкостенных сосудах радиальное напряжение
принимают равным нулю, из приведенных формул Oj = о2 =
= ст, °з — 0 и условия прочности по гипотезам наибольших
касательных и энергии формоизменения о^в = [ср]', Сэкв =
Для сферической тонкостенной оболочки диаметром D, нахо-
дящейся под действием газового давления р, am = at^= pD^b,
главные напряжения ох = оа = ат = о<; условие прочности
Сэкв = <4кв = pD№ < [Ор].
Пример 13.4. Определить требуемую толщину стенки сфери-
ческого сосуда (рис. 13.13) при р = 12 бар и 1<тр] = 120 Н/мм2.
Решение. Из условия прочности а^в = Оэкв — рВЦЪ[а^
получаем (1 бар = 10® Н/м2 = 10-1 Н/мм2)
«, pD 1,2 2000 г
6>41^]=-4Й20- = 5мм-
Пример 13.5. Определить из условия прочности допускаемую
величину 1р) внутреннего давления в сосуде (рис. 13. 14). Принят!
Юр] = 1200 кгс/см2; применить гипотезу энергии формоизменения-.
212
Решение. Из условия прочности цилиндрической части со-
суда а'кв =~ 0,433 < [Ор] имеем =
1,0 • 1200 ос , 8
~ 0,433 • 160 — 17,25 кгс/см .
Из условия прочности сферической части сосуда
Сэкв »^у < [Ср]
получаем' [р]' = 48 jM =« IjJ’P/J200 = зо кгс/сма.
Таким образом, окончательно принимаем меньшее из двух
найденных значений: [р] = [р]' = 17,25 кгс/см2.
, Пример 13.6*. Построить эпюры o/t от, <т9кв для тонкостенных
сосудов, изображенных на рис. 13.15, а, б, если Н, D, 6, у заданы.
Решение. Очевидно, что при закреплении сосуда по схеме,
показанной на рис. 13.15, а, в верхней части АВ и в нижней части
ВС меридиональные напряжения от равны нулю.
В верхней части АВ окружные напряжения at = 0, так как
она не нагружена.
Нижняя часть ВС испытывает гидростатическое давление.
Окружные напряжения найдем из уравнения Лапласа: сг</р< +
+ 0т/рт = р/6, в которое следует подставить р< = D/2, 0п = 0>
р^ = оо, р = yz — давление жидкости в любой точке на расстоя-
нии z от свободной поверхности (см. рис. 13.15, а).
После подстановки получаем = (yD/26)z,
т. е. в данном случае окружные напряжения по высоте сосуда из-
меняются по линейному закону от 0 до 0,4 ^у^.
Эпюра 0t показана на рис. 13.15, в. На рис. 13.15, е показан
элемент, вырезанный в районе точки К (см. рис. 13.15, а), с возни-
кающими на его гранях напряжениями.
♦-Примеры 13.6, 13.7 составил ииж. А. И. Винокуров.
213
Очевидно, что Oj = at, а2 = ат = 0, а3 = —р = —yz.
Пренебрегая величиной а3 по сравнению с <т1( получаем
in vD _
Оэкв — О'! — ОТ; — 2g
т. е. эпюра а”1 совпадает с эпюрой <г(.
Построим эпюры для сосуда, показанного на рис. 13.15, б.
Верхняя часть АВ не испытывает ни газового, ни гидравличе-
ского давления и, следовательно, для нее <г* = 0.
Рис. 13.15
Уравнение равновесия 2Р(г = 0 дает (рис. 13.15, ас) amn,D8 =»
= ^-0,8Яу, откуда ит = 0,2 = const.
Нижняя часть ВС испытывает гидравлическое давление.
Окружное напряжение найдем Из уравнения Лапласа =»
= •£.== 3^, откуда ct = (y£>/26)z. /
. Составляя уравнение равновесия = 0 для нижней части
сосуда (рис. 13.15,яс), отл£>6 = ^-(0,8Я— z)у4-yz, нахо-
дим ат = 0,2 (yDH/8).
Эпюры ат, st показаны на рис. 13.15, з.
В любой точке верхней части АВ сосуда возникает линейное
напряженное состояние = 0,2 ; ст2 = ст3 = 0.
214
• Следовательно, для точек верхней части Стэйв = ат = 0,2^^.
Как видно из эпюр стт, ст, (см. рис. 13.15, з) для точки М.
меридиональное и окружное напряжения равны. Для точек, лежа-
щих выше точки Л1, CTj = стт = 0,2; ст2 = ст, = z < стт; ст3—
= —р = —yz (этой величиной пренебрегаем).
6 в
Рис. 13.16
Таким образом, для точек, лежащих выше точки М, ст’кв **
= 0,2 (yDH/b), т. е. с небольшо i погрешностью, обусловлен-
ной Пренебрежением ст3, эквивалентное напряжение постоянно.
Для точек, лежащих ниже точки М, окружное напряжение
больше меридионального: CTj = ct, = -^z; ст2 = стт = 0,2 ;
о3 = _ р = —yZ.
На рнс. 13.15, д показан элемент, вырезанный в районе точ-
ки L (произвольной точки, расположенной ниже точки М). Для
215
этой точки Оэкв = 01 — аз = ("gy + l)?2 или, пренебрегая, как
« ранее, а3, получаем Оэкв = (?£>/2б) г.
Эпюра Оэкв показана на рис. 13.15, и.
Пример 13.7. Определить требуемую толщину стенки б резерв
вуара, показанного на рис. 13.16, а, если (0Р1 = 600 кгс/см2, у =
= 1 гс/см3. Расчет выполнить по гипотезе наибольших касательных
«апряжений.
При найденном значении б построить эпюры а^в.
Решение. Так как верхняя часть АВ резервуара не испы-
тывает ни газового, ни гидростатического давлений, то в точках
этой части резервуара crt — 0.
Составив уравнение равновесия SPl2 = 0 для оставленной части
1 л£>о
резервуара (рис. 13.16,6), найдем ат: атяО2б cos а = у — Ну,
где £>0=2#tga; Dt~ 2ztga; tga = ~ 0,312, a ~
17° 20'; cos 17° 20' = 0,955.
Подставив в уравнение равновесия значения Do, Dz, найдем
величину am в точках стенки, расположенных выше уровня свобод-
ной поверхности жидкости: a = уН* tg a/6z6 cos a.
Нижняя часть ВС резервуара испытывает гидростатическое
давление.
Окружные напряжения найдем из уравнения Лапласа: о#/р#-f-
+ °т/рт = р/&, где рт = °°; р< = 2&с = г^с <рис- 13-16-в);
—г)у.
Подставляя в уравнение Лапласа значения pb рт, р, получаем
<Jt = yz(H — z)tga/6cosa.
Окружные напряжения на участке ВС изменяются по пара-
бслическому закону. Исследовав функцию = /(г) на экстремум, J
находим, ,что max at возникает в точках, отстоящих от вершины
конуса на расстояние Н/2.
Составим уравнение равновесия ЕР£2 = Одля оставленной части
/ Г \ л
резервуара (см. рис. 13.16, в): атяОгбcos а = —j-1 р + у zy I. От-
сюда стт = X2tga (ЗН— 2z).
т 6о cos а' '
Исследовав функцию = f(z) на экстремум, находим, что ?
шах ат возникает в точках, соответствующих z = 3/4/7. J
По полученным уравнениям строим эпюры оДсгтб (рис. 13.16, г),|
На рис. 13.16, д показан элемент (в двух проекциях), выре-,
занный в районе произвольной точки на внутренней поверхности-
резервуара. ' ' |
Так как р значительно меньше crt, от, т. е. сг3 много меньше
Пр а2, можно принять а3 = 0 и считать, что во всех точках стеной
резервуара возникает двухосное растяжение. При этом по эпюраь
216
изображенным на рис. 13.16, г, видно,* что опасной является
точка К, для которой условие прочности имеет вид Оэйв = тахо, —
29,4 & 29,4 29,4 п
= ~у < Естр]. откуда 6 = = 0,049 см.
Принимаем 6 = 0,5 мм.
- При построении эпюры о1"в учтем, что ранее было решено
пренебречь величиной ст3 = —р и, следовательно, о'кв = <4.
Для точки A Oskb = om/6 = 14,7/0,05 = 294 кгс/см2.
Для ТОЧКИ 1 о!кв = Ощ/б = 16,8/0,05 = 36 кгс/см2.
Для точки 2 а1экв — от/8 = 19,6/0,05= 392 кгс/см2.
Для точки 3 о”Кв = о,/б = 21,8/0,05 = 436 кгс/см2.
Для точки 4 Оэкв = <4/6 = 24/0,05 =' 480 кгс/см .
Для точки 5 Стэкв = <4/6 = 26,2/0,05 = 524 кгс/см2.
Для точки ft Оэкв = о,/б = 29,4/0,05 = 588 кгс/см2.
Для точки 6 Стэ’кв = о,/б = 26,2/0,05 = 524 кгс/см2.
Для точки 7 ctVkb — <4/6 = 16,3/0,05 = 326 кгс/см2.
\ Эпюра Ствкв показана на рис. 13.16, е. Строим эпюру <4кв- Как
известно, ai™ = -Ly (ai — ст2)2 4- (о2 — о3)2 + (ст3 — <4)2.
В рассматриваемой задаче принято ст3 = 0, тогда
<4кв = У О2 4- СТ2 — 0404.
Для точки A 04 = om, о2 = 0,
Сэкв = <4 = от — 14,7/0,05 = 294 кгс/см2.
Для точки 1 04 = ат, о2 — 0,
о’Лв = О1 — от = 16,8/0,05 = 336 кгс/см2.
Для точки 2 ?! = от, ст2 = 0,
04кв = о1 — ат — 19,6/0,05 = 392 кгс/см2.
Для точки 3 04 = от, о2 = <4,
„IV 1//21,8\2 , Л16,3\® 21,8 16,3 19,6 опо , 2
°-в= У W + W —г—=oj5 =392 кгс/см -
Для ТОЧКИ 4 <?! = 04, 04 = стт,
IV 1//24,0\2 /22,1\2 24j) 22,1 23,1 лсо , „2
0экв= У (-у) ---у -у = 0^ = 462 кгс/см2..
* При двухосном растяжении для любой- точки стенки эквивалентное
напряжение а*"в равно либо am, либо at большему из этих напряжений
(при а2 = 0 получается, Что а^в = <4).
217
Для точки 5 aj = ао а2 == ат,
IV 1//2б,2\г /21,8\а 26,2 21,8 26,0 соп ‘ „
пэкв = Пт) + Ы -т Т = о^= 520 кгс/см •
Для точки К. Oj = ар ст2 = ат,
IV 1/(29,4\а . /19,61® 29,4 19,6 25,8 К1с , 2
аэкв = У (-§-) + (-J-)--------g. = — = 516 КГС/СМ8.
Для точки 6 Oj = аь а2 — ит,
IV -1//26,2\2 /15312 26,2 15,3 22,8 .сс . ,
Пэкв = И (-§-)+ W-----------Г “Г = 0^5 = 456 КГС/СМ •
Для точки 7 Oj = ао ст2 = стт,
iv 16,3\® . /8,7V 16,3 8,7 14,1 осо , 2
Оэкв г \ 6 ) "Н 6 ) 6 Т 0,05 ~ 1 2®2 кгс/см •
Эпюра Оэкв показана на рис. 13.16, ж.
Задачи для самостоятельного решения
13.4. Определить требуемую толщину стенки цилиндрического
резервуара диаметром D = 2 м, находящегося под действием
внутреннего газового давления р = 15 бар.
Расчет выполнить по гипотезе энергии фор-
моизменения, принять Юр] = 100 Н/мм2.
, Ответ. 12 мм.
13.5. Для конического резервуара с полу-
сферической крышкой (рис) 13.17) опреде-
лить коэффициент запаса прочности, если
в резервуаре находится газ под давлением
р = 24 кгс/см2. Материал резервуара — сталь
с пределом текучести ат = 28 кгс/мм2. Рас-
чет выполнить по гипотезе наибольших
касательных напряжений. Построить эпюры
меридиональных и окружных напряжений для стенки резер
вуара.
Ответ, п = 1,99.
ГЛАВА 14. ПЛОСКИЕ КРИВЫЕ БРУСЬЯ
§ 14.1. Построение эпюр внутренних силовых факторов.
Перемещения в кривых брусьях
1. Будем рассматривать кривые брусья, у которых: поперечное
сечение имеет ось симметрии; геометрическая ось — плоская кри-
вая, лежащая в плоскости, симметрии;действующие силы лежат.
218
в той же плоскости; жесткость достаточна для того, чтобы можно
было применять принцип независимости действия сил.
2. Внутренние усилия в поперечном сечении кривого бруса
определяются так же, как в балках и рамах, методом сечений.
В данном случае они приводятся к трем силовым факторам: к изги-
бающему моменту Л1; к продольной силе М; к поперечной силе Q.
Изгибающий момент положителен, если ему соответствует
увеличение кривизны оси бруса, продольная сила положительна,
если она соответствует растяжению, а поперечная сила положи-
тельна, если ее направление получается из положительного на-
правления продольной силы поворотом на 90° по часовой стрелке.
Условимся откладывать значения М, N, Q на эпюрах по нор-
мали к геометрической оси кривого бруса, т. е. по радиусу кривизны
положительные в сторону от центра его кривизны, а отрицатель-
ные значения — к центру кривизны. Если брус имеет криволиней-
ные и прямолинейные участки, соответствующие эпюры на прямо-
линейных участках следует располагать в те же стороны от гео-
метрической оси, что и на. криволинейных участках, т. е. строить
эпюру М со стороны растянутых волокон.
Перемещения (линейные и угловые) в плоских кривых брусьях
малой кривизны в общем случае, т. е. с учетом изгибающего мо-
мента М, продольной силы N и поперечной силы Q, могут быть
определены с помощью интеграла Мора:
я V f MMi ds V^ f jV.Vf ds VI (* £QQi ds
dlp = 2j J —ЁГ~ + 2j J ~ёГ + 2j J ~gf~ ’
S ~ s s
где M, N, Q — указанные выше силовые факторы сгг заданной
нагрузки в произвольном сечении кривого бруса; Mi, N{, Qi —
аналогичные силовые факторы в том же сечении от единичной силы
(момента), приложенной по направлению искомого перемещения;.
k — коэффициент, зависящий от формы сечения (в частности,
k = 1,2—для прямоугольника, £ = у—для кРУгаХ — эле-
мент дуги; s — длина дуги.
Влияние N, Q на величину перемещений обычно незначительно*
по сравнению с влиянием М, поэтому практически последними двумя
слагаемыми интеграла Мора в большинстве случаев можно прене-
бречь. '
При решении задач будем пользоваться таблицей 14.1.
Пример 14.1. Построить эпюры М, N, Q для бруса, изображен-,
ного на рис. 14.1, а.
• Решение. Очевидно, что от действия сосредоточенного мо-
мента SK не возникает ни продольных, ни поперечных сил, и его
влияние отразится лишь на эпюре М. Поэтому рассмотрим, какие
силовые факторы возникают в поперечных сечениях криволиней-
ного участка бруса от распределенной нагрузки -интенсивностью q.
219
Таблица 14.1. Таблица интегралов, часю встречающихся в расчетах
, кривого бруса *
Интеграл Значения в пределах
0— а -г 0— я
J sin ф йф 1 —cos а 1 2
J COS ф </ф sin а 1 0
У sin2 ф dtp ^-1 Sin 2а я V Л 2
а , 1 . „ я л
§ COS2 ф </ф -s- + — sin 2а 2 4 т ~2
1 . . 1
У sin2 ф cos ф dtp -g- sin’ а 3 0
1 — cos’ а 1 2 "
J cos2 <р sin ф г/ф 3 3 3
У sin 2ф </ф sin2 а 1 0
§ cos 2ф dtp 1 . „ •g- sm 2а 0 0
1 . . 1
J sin ф cos ф йф -sin’a 2 0
J Ф sin ф dtp sin а— а cos а 1 л
У Ф cos ф dtp а sin а + cos а — 1 Я | т —2
1 . „ а cos 2а я ‘ л
У Ф sin ф cos ф dtp 8Sln2“. 4 "8~ г
1 . л2 , 1 л2
§ Ф sin2 ф dtp (а2 — a sin 2а + sin2 а) Тб+Т 7
1 , . л2 1 л2 "
У фС032ф</ф “ (as + a sin 2а — sin8 а) 16 ~ 7 4
J Ф sin 2ф dtp 1 (1 . „ „ \ -g-1 -g- sin 2а — a cos 2а 1 Я 4 Л . . “ 2/1
У фсоз2фйф у (a sin 2а — sin2 а) 2 ° 1
1 л • J
У sin (а — ф) sin ф йф у (sin a —a cos а) 2
* Таблица заимствована из учебника Е. Н. Тихомирова «Курс сопротивч
ления материалов», ОНТИ, 1934.— 583 с. *
220
В произвольном поперечном .сечении, положение которого фикси-
руем отсчитываемым от вертикали углом <р, от элементарной сосре-
доточенной силы dP = qds = qRoda, найдем (рис. 14.1, б) dM(q) =
== dPR0 (sin <р — sin а) = qR* (sin <p — sin a) da; dN — —dP sin <p =
== —qRa sin (p da; dQ = dP cos <p = qRQ cos <pda.
Рис. 14.1 Рис. 14.2
221
9
Тогда М (q) == qR% j (sin ср — sin a) da = qR%(4) sin <p + cos <p — 1);
о
<p
N — —qR0 sin ф j da——qRoq>sin <p; Q = qR0cos фjda = qRoq> cos <p.
о о
На прямолинейном участке BD, как указано выше, продоль-
ная и поперечная силы равны нулю; изгибающий момент на этом
участке постоянен: М = ЭД = qR%.
На криволинейном участке АВ выражение для изгибающего
момента найдем согласно принципу сложения действия сил:
М = ЭД + M(q) = qR%(ф sin ф + cos ф).
Вычисляя значения М, N, Q в четырех сечениях (ф = 0, ф =
Л Л Л \ . . . .
= -у, ф = у , ф = у!, строим соответствующие эпюры (рис. 14.1,
в, г, д): M<f=o = ЭД — qRf, Л4т=зо» = sin -у + cos ---
= 1,128^; Mf=60» = qR* (у- sin у- + cos 1,409^; MT=90°=
== sin-=- +cos-=-) = 1,571^; (VT=o = O; tfT=3o° =
= — <7^0-^sin у = —0,262qR0; JVT=60= = ~qR0~ sip у =--
= —Q,9Q9qR0; N4^o: = —qRo у sin у => —1,571 qR0', Qv==0 = 0;
Qf=30« = qR0 у cos у = O,455^/?o; Q!p=45» = qRD у cos у = O,555q7?o;
Q<P=6o» = qR0 у cos у = 0,525qRo; Q¥=90» = qR0 у cos = 0.
Пример 14.2. Определить горизонтальное перемещение и
поворота сечения А бруса малой кривизны (рис. 14.2, а).
угол
Решение. Для определения искомых перемещений следует
найти опорные реакции, составить уравнения изгибающего мо-;
мента на участках бруса от заданной нагрузки (Л49). Далее по-на-
правлению искомого перемещения приложить в сеченнн А еди^
ничную силу (в данном случае единичную силу и единичный мс ‘
мент, ибо отыскиваются два перемещения) и составить для обои:
участков бруса уравнения изгибающего момента (Mlt ;W2); зате!
по формуле Мора найти искомые перемещения.
Определяем опорные реакции: Хтв = 0; —RAa 4- ЭД + Ph
откуда Ra = ^ ~ 4 ^g3’73 = тс* так как h = a(\-
4-sin60°) = 3,73 м; 2Х=0; — Нв + Р cos 30° = 0; Нв=>
= Р cos 30° - 0,866 тс; 2У = 0; RB — Ra — Р sin 30° = 0; RB *
— Ra + P sin 30° — 4,37 тс.
222
Выражение изгибающего момента от заданной нагрузки в про-
извольном сечении первого участка кривого бруса имеет вид (рис.
14.2, б) О С «Pi С 120°; Л4И = Дд (а — a cos <рг) = 7,74 (1 —
— cos tpj.
На втором участке 0 <р2 150° Л4<р2 = Два sin <р2 + Нв(а —
— a cos <р2) = 8,74 sin <р2 — 1,732 Cos <р2 4- 1,732.
Для определения горизонтального перемещения приложим в се-
чении А горизонтально направленную единичную силу (рис.
14.2, в).
Определим соответствующие опорные реакции 2тв = 0;
—Raci + 1 • а = 0, откуда Ra = 1.
Проектируя все силы на вертикальное и горизонтальное на-
правления, находим Rb — 1; Нв = 1. Выражение единичного изги-
бающего момента для первого участка (0 С Ф1 С 120°) М} =
— la sin <р£ + Ra (а —- a cos ф^ = 2 (sin фх — cos <px + 1); для
второго (0 < <p2 < 150°)
Л41 = Reasin <р2 + Нв (а — а cos ф2) = 2 (sin ф2 — cos ф2 + 1).
По формуле Мора определим горизонтальное перемещение опор-
ного сечения А:
2 5
зя Т"
бдр = ^[[ J Мр,Л41а<1ф2] =
L о о
2
Г*
J 7,74(1—cos фх) 2 (sin ф! —со8ф! + 1) 2^фг+
о ,
+ j (8,74 sin ф2 — 1,732 cos ф2 +1,732) 2 (sin ф2 — cos<p2 + 1) 2tftp2j.
Окончательно получаем 6дор =
Определим угол поворота сечения А.
Следуя общей методике определения перемещений по формуле
Мора, приложим в сечении А единичный момент (рис. 14.2, г).
Опорные реакции показаны на рис. 14.3, д; их значения
Яд « Д" = 1 = 0,5 1/м; Нв = 0.
Составим выражения изгибающего момента. Для первого уча-
стка (0СФ1С 120°)
Л42 = 1 — Ra (а — a cos фх) = 1 —0,5 • 2 (1 — cos ф1) = совфх,
для второго — (0 ф2 150°)
/И2 = Ява sin <р2 = —0,5 • 2 sin ф2 = —sin ф2.
223
Применив формулу Мора, получим
. \i С M M2ds iff . (* .1
«Г = L J -ТТ- = Ezl J MVtM,adV1 + j M,aM”ad<p2\ -
so о
[J 7,74(1 — cos <Pi) cos фх 2ЙФ! + J (8,74 sin <p2—
о о
-г- 1,732 cos <p2 + 1,73 ) (—sin <p2) 2d<p2]
и окончательно 8%я « —32,14/£V.
Рис. 14.3
Знак минус указывает
на то, что опорное сечение А поворачи-
вается не по направлению единичного момента, а в противоположную:
сторону, т. е. по ходу часовой стрелки. *
Пример 14.3. Определить вертикальное, горизонтальное и
полное линейные перемещения свободного конца бруса малой кри-
- визны, нагруженного распределенными силами постоянной интен-’
сивности q, направленными по касательным к оси бруса (см. рис.
14.3, а). . .
Решение. Для определения вертикального и горизонтал:
ного перемещений надо будет рассмотреть нагружение бруса ве]
тикальной и горизонтальной единичными силами, приложенных
в сечении, перемещение которого требуется найти. Полное линейж
перемещение определяется как геометрическая сумма вертикал
ного и горизонтального перемещений.
Влияние продольных и поперечных сил не будем учитыват
Составим выражение для изгибающего момента от заданной в
грузки. Элементарная сила, приходящаяся на элемент бруса дли
224
ной ds (рис. 14.3, б), dP — qds = qRoda. Изгибающий момент, ко-
торый вызывает эта сила в произвольном поперечном сечении бруса
(сечении, составляющем угол <р с горизонталью), dM = dP [/?0 —
— Ro cos (<p — а)1 = qRo [1 — cos (ф — а)1 da.
Полный изгибающий момент в указанном сечении определится
9 9
как сумма элементарные моментов, т. е. М = <;/?*[ J da — § cos(q>—
о о
— a) da] = qR* (ф — sin ф).
Рассматривая брус нагруженным в сечении В вертикальной еди-
ничной силой (рис. 14.3, в), получаем выражение изгибающего мо-
мента от этой силы = 1 (Ro — Ro cos ф) = Ro (1 — cos ф).
Применяя интеграл Мора, находим вертикальное перемещение
сечения В (используем табл. 14.1):
Я 4
сверт С AfAfj , QPq С . . . .. . , Я® QPo
Ofi = J-^ds =-gy-J (ф—Sin ф)(1 — СОЗфНф = J -gy-.
4 e
Выражение изгибающего, момента от горизонтальной единичной
силы, приложенной в сечении В (рис. 14.3, г): Л42 = 1 • Ro sin ф.
Горизонтальное перемещение сечения В
4Я 4
crop f ММ* , - 4^9 f , . . . ' , я ЧРо
°в ~ J~EJds= EJ ' (Ф—slnф)slnфdф = у rgy-.
Полное линейное перемещение сечения В
- 6В = /(^ерт)2 + (fiBop)2 = 'Ж К4^4 = 5’18 -Z7 •
Задачи для самостоятельного решений
14.1. Построить эпюры М, N, Q для кривого бруса (рис. 14.4).
Ответ. |Мтах | = 0,125qRt- | Л/тах | = | | = 0,5qRo> I Стах I = I Св I =
= 0,5qRQ.
р 1-10
225
14.2. Определить вертикальное, горизонтальное и полное пере-
мещение сечения В стального бруса (рис. 14.5). Принять Е =
— 2 • 10е кгс/см2.
л PR3
Ответ. Вертикальное перемещение 6“рт = — яа 0,4 см. Горизон-
тальное перемещение 6^op = PRl I2EJ — 0,25 см. Полное перемещение
Sfi = 0,472 см.
14.3. Определить вертикальное перемещение и угол поворота
сечения А бруса малой кривизны (рис. 14.6).
14.4. Построить эпюры Q, М, N для эллиптической двухшар-
нирной арки (рис. 14.7).
Ответ. Qmax = 7,5 тс; Л1тах = 18 тс? м; ^ах = 7,5 тс.
§ 14.2. Расчет на прочность кривых брусьев
большой кривизны
В поперечных сечениях плоских кривых брусьев возникают
нормальные и касательные напряжения,
большой кривизны (крюки, кольца и др.),
Для кривых брусьев
у которых отношение
радиуса кривизны геометрической оси к размеру поперечного се-
чения вдоль этого радиуса удовлетворяет неравенству 7?0/й С 5, вы-
числение нормальных напряжений по формуле, выведенной для
расчета на изгиб прямых брусьев, дает недопустимо большую по-
грешность.
Нормальные напряжения, соответствующие изгибающему мо-
ДЛ z
менту, должны определяться по формуле сгм = где М —
изгибающий момент в данном сечении; S — статический момент
поперечного сечения относительно нейтральной оси; г — радиус
кривизны нейтрального слоя; z — расстояние от нейтральной оси до
волокна, где требуется определить напряжение.
226
На рис. 14.8 даны обозначения, соответствующие приведенной
формуле, и изображена эпюра нормальных напряжений, построен-
ная по этой формуле. Эпюра представляет собой гиперболу.
Напряжения, соответствующие продольной силе, вычисляют
как при осевом растяжении — сжатии прямого бруса: сг^ = N/F,
где F — площадь поперечного сечения.
Касательные напряжения, • возникающие в поперечных сече-
ниях кривого бруса при его изгибе, могут быть приближенно опре-
делены по формуле Журавского как для прямого бруса.
В зависимости от направлений изгибающего момента и про-
дольной силы, формы поперечного сечения и материала кривого
2
Рис. 14.8
бруса опасными могут оказаться как внутренние (ближайшие
к центру кривизны), так и наружные точки поперечного сечения.
В наиболее общем случае расчет следует выполнить для тех и
других точек. Нормальные’ напряжения в этих точках определя-
ла М 2
ются .по формуле tn, 2 = у ± -у г < [о].
Значение продольной силы N следует подставлять с учетом
ее знака; во втором слагаемом изгибающий момент подставляют
по абсолютной величине, а знак плюс или минус ставят в зависи-
мости от того, вызывает ли изгиб бруса растяжение или сжатие
в рассматриваемой точке; В знаменателе этого же слагаемого знак
плюс относится к наружным волокнам, а знак минус — к внут-
ренним. Знак,-стоящий перед вторым слагаемым, и знак в знамена-
теле этого слагаемого между собой не связаны.
Нейтральная ось поперечного сечения кривого бруса смещена
в сторону центра кривизны от главной центральной оси поперечного
сечения.
Радиус кривизны г нейтрального слоя определяем из выраже-
ния I dF — 0.
J г +?
F
8 *
227
Приводим формулы, полученные из этого выражения для не-
которых форм поперечных сечений.
Для круга (рис. 14.9) г = —=---— -т.
4 [27?О — И47?’—
. bj 6а
п 2
Для трапеции (рис. 14.10) г=---------------—-----------.
(h + RiЬл^) In ~ fci)
Для прямоугольника г = , •
miKl/Kt)
Для сечений других форм значения г и е = Ro — г приведены
в справочниках и в некоторых учебниках (см., например, [2, 311).
Величину смещения нейтральной оси можно также определить j
J у
по приближенной формуле Н. Н. Давиденкова: е « -?-£,
Г А® -4
где Jyi — момент инерции сечейня отнЪсительно главной централь- -»
ной оси, перпендикулярной силовой плоскости, т. е. параллельной
нейтральной оси (см. рис. 14.9, 14.10). г ]
Пример 14.4. Построить эпюру нормальных напряжений для I
опасного поперечного сечения крюка (рис. 14.11, а). I
Решение. Опасным будет сечение А—А, так как там изги- 4
бающий момент М = РР0 и продольная сила N — Р имеют наи- ]
большие значения. Напряжения в опасных точках указанного се- |
М М ^12 N М ^12
чеиия таковы: Ш. 2 = ₽- ± -з- • т-т2?—, или О[ 2 =4- ± -о- 1
Г о г ± Л^ 2 • Г_ s 2 3
Положение центра тяжести трапеции определим, разбив ее на
два треугольника: 1
hb2 h,hbi
, _ 5гл> _ 2 ’ 3 + 2 3 h (2*! + йа) 15 • (2 • 5 + 10)
c F hb, . hbt 3(*!4-*a) 3(5 4-10) ~
hbt , hbj
2'2
= 6,66 см (рис. 14.11лб).
228
Радиус кривизны нейтрального слоя
, fej +
2
+ щ _ (ьа - м
\ П / Mg
(5 + 25- -^-5) Ing— (10 —5)
\ U / IV
112,5
“ 13,35 - 2,303.0,3979 —5
= 15,62 см.
Найдем величины, необходимые
для вычисления напряжений: f *=
15 = 112,5см2;
/?0= /?2 + = 10+ 6,66 =16,66см;
е = £0 _ г = 16,66 — 15,62 =
«= 1,04 см; S = Fe = 112,5 • 1,04 =
= 116,9 см3; hx = h — zc + е =
= 15 — 6,66 + 1,04 = 9,38 см;
h2 = 2c — е = 6,66 — 1,04 = 5,62 см.
Нормальные напряжения в точ-
ках большего основания трапеции
— 15000 15 000 . 16,66 • 5,62 _
°2 ~ 112,5 + 116,9-Ю ~
= 133 + 1200 = 1333 кгс/см2;
то же в точках меньшего осно-
вания
_ 15000 15 000 . 16,66.9,38
01 “ 112,5 “ 116,9 • 25 “
= 133 — 803 — —670 кгс/см2.
Эпюра о представлена на рис.
14.11, в.
Пример 14. В. Определить допус-
каемую величину нагрузки на крон-
штейн (рис. 14.12, а), если [а] =
«= 1600 кгс/см2.
Решение. Радиус кривизны
Р
Рис. 14.11
геометрической оси бруса
Ro .= #2 + 4 = 17 см.
п
Отношение -°
h
17
16
229
т. е. при расчете следует применять формулы для кривого бруса
большой кривизны. По рис. 14.12, а выражаем изгибающий момент
и продольную силу в опасном сечении (у заделки) через заданные
размеры и искомую силу Р:
М = Р(а + Ro) = Р(15 + 17) = 32Р кгс • см; N = — Р.
Наибольшие (по абсолютной величине) напряжения возникают
во внутренних (ближайших к центру кривизны) точках сечения:
Рис. 14.12
N М h2
maXCTc = a2 = __T _L_,
или
. . I Р 32Р Л2 | . . .
1^2 I - I F — s Ri | М-
Радиус кривизны нейтраль-
ного слоя
h _ 10 _
Т~ . /?! ~ . 22 ~
lnFi л12
= 3,09104 — 2,48490 = 16,498 см-
Смещение нейтральной оси
от центра тяжести сечения
е = Ro _ г = 17 — 16,498 =
= 0,502 см.
Для сравнения найдем е по
приближенной формуле Давиден-
bh3 _ hi =
кова: е ~ t2/?0
= 12^7 = 0,4412 см.
Таким образом, в данном частном случае формула Давиденкова
дает в определении величины е погрешность примерно 12%.
Определив е, находим значения S и й2: S = Fe — bhe = 5Х
ХЮ • 0,502 = 25,1 см3; й2 = h!2 — е = 5,00 — 0,502 = 4,498 см.
Подставив эти величины в условие прочности, получим +
+ < 1600, 0ТКУда == ОДГРШ = 32,1 • Ю2 кгс.
Если выполнить расчет, использовав значение е, полученное
по формуле Давиденкова, то [Р] = 28,1 • Ю2 кгс, т. е. погреш-
ность составляет 9,37%, что несколько меньше погрешности в ве-
личине смещения нейтрального слоя.
На рис. 14.12, б представлена эпюра ст для опасного сечения
бруса при значении нагрузки, равном допускаемому. Рекомендуем
проверить вычисление CTt.
230 '
Задачи для самостоятельного решения
14.5. Определить грузоподъемность крюка (рис. 14.13), если
[а] = 1400 кгс/см2.
Ответ. [Р] я* 2 тс.
14.6. В брусе АВС, со-
стоящем из прямолинейной
части АВ и криволинейной
Рис. 14.14
ВС (рис. 14.14), определить величину наибольших и наименьших
нормальных напряжений в опасном поперечном сечении.
Ответ. атлх = 1246 Krc/cM2,, amin = —1284 кгс/см2.
14.7. Определить допускаемую величину сил Р для серьги,
изображенной на рис. 14.15. Принять [ст] = 12 кгс/мм2.
J ртвет. Р = 8,2 10э кгс.
231
L
14.8. Проверить прочность чугунного бруса, имеющего форму
полукольца (рис. 14.16). Принять [ст!р = 600 кгс/см2; [ст1с =
= 1800 кгс/см2.
Ответ. атвх — 564 кгс/см2; Gmin — —285 кгс/см2.
ГЛАВА 15. ПРОДОЛЬНЫЙ И ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ
§ 15.1. Расчет сжатых стержней на устойчиаость
Критическая сила (при потере устойчивости в упругой стадии)
вычисляется по формуле Эйлера Ркр — n2EJmin/(pl)2, где р, —
коэффициент приведения длины, зависящий от способов закрепле-
ния концов стержня; Jmln — минимальный момент инерции попе-
речного сечения стержня.
Допускаемая величина сжимающэй силы [Р] = РКр/[Пу],
где [ну] — требуемый (допускаемый) коэффициент запаса устой-
чивости.
Напряжения, возникающие в поперечном сечении стержня при
Р — Ркр, называются критическими: окр = P^IF^rfE/W;
где A=p//imin — гибкость стержня; imin = К-Лпш/Р — минималь-
ны ' радиус инерции поперечного сечения стержня.
Формула Эйлера применима при условии, что критическое на-
пряжение не превышает предела пропорциональности материала
стержня: акр апя'
Таблица 15.1. Значения коэффициентов приветения длины и критических
сил для некоторых случаев закрепления сжатых стоек
Оба конца шарнирно за> реплены, р. « 1 Один конец жестко защемлен, другой—, свободен. Один конец жестко защемлен, другой — шарнирно закреплен. Оба конца защемле- ны, р. = О,5
р 1 К \ \ \ и г* 1 1 1 1 у 1 1
1 я * к < • »
Л
Обычно условие применимости формулы Эйлера выражают через
гибкость стержня: Х>Хпред, где Л,пред = л КД/^пц.
Для стали Ст. 3 &пред « 100; для стали Ст. 5 Хпред =» 90, для
чугуна Хпред« 80, для сосны %пред НО; для дюралюминия Д16Т
^пред 60,
232
Расчет на устойчивость по формуле Ясинского
Если потеря устойчивости наступает в пластической стадии
(формула Эйлера неприменима), то критическое напряжение вы-
числяют по эмпирической формуле Ясинского: акр = а — ЬК +
+ сА2,
где а, Ь, с — опытные коэффициенты, зависящие от материала и
имеющие размерность напряжения.
Для стальных и дюралюминиевых стержней формула Ясинского
Применима При ГИбкОСТЯХ Ао С А Апред,
где А^ — значение гибкости, при котором критическое напряже-
ние равно пределу текучести материала стержня. При гибкости,
меньшей Ао, критическое Ч1апряжение принимают постоянным и
равным пределу текучести.
Для стали Ст. 3 а = 3100 кгс/см2; b = 11,4 кгс/см2; с = 0; А^ = 61.
Для стали Ст. 5 а = 3500 кгс/см2; b = 11,5 кгс/см2; с = 0; Ао = 57.
Для дюралюминия Д16Т а = 4060 кгс/см2; Ь = 28,3 кгс/см2; с =
= 0;.А0 = 30.
Для чугуна <г= 7760 гкс/см2; Ь = 120 кгс/см2; с = 0,53 кгс/см2.
Для сосны и ели а = 293 кгс/см2; b = 1,94 кгс/см2; ,с = 0.
Критическая сила вычисляется по формуле Ркр = aKpF. *
Расчет на устойчивость по коэффициентам <р продольного изгиба
Этот расчет применяется для элементов строительных конструк-
ций и для стальных конструкций подъемно-транспортных сооруже-
ний. Расчет производится как на простое сжатие, но с уменьшением
основных допускаемых напряжений. р
Расчетная формула имеет вид
— а = Р/F С <Р [и],
N>14 <£
где <р — коэффициент уменьшения основного допус- и V
каемого напряжения на сжатие с учетом опасности
продольного изгиба или коэффициент продольного __________
изгиба. Его величина зависит от гибкости А и от
материала стержня; коэффициент <р выбирают по Рнс 151
табл. 15.2. .
Пример 15.1. Определить допускаемую нагрузку иа стержень
(рис. 15.1), если требуемый коэффициент запаса устойчивости
[Пу] — 3; материал стержня сталь Ст. 3; Е = 2,1 • 10е кгс/см2.
Решение. Гибкость стержня А = /привЛ’т1п == pZ/imin = 1 X
X 180/1,55 = 116, где радиус инерции imin взят по таблице сорта-
мента. Так как А > Апред = 100, критическую силу вычисляем по
формуле Эйлера:
_ П^1П з,142 • 2,1 • 10» . 41,9 , 2д 8 10» ,;гс
~ (р/)2 - (1 • 180)* Z0’° КГС'
Допускаемая нагрузка [Р] = />кр/[,ту] ~ 26 800/3 = 8933 кгс.
23’
Таблица 15.2. Значения коэффициентов 7 продольного изгиба
Гибкость X Дерево Чугун СЧ12-28, СЧ16-32, СЧ18-36, СЧ21-40 Сталь Ст. 3, Ст. 4 Сталь Ст. 5 Сталь 14Г2, 15ГС, 10Г2С, 15ХСНД
0 1,00 1,00 1,00 1,00 1,00
10 0,99 0,97 0,99 .0,98 0,98
20 0,97 0,91 • 0,97 0,96 0,95
30 0,93 0,81 0,95 0,93 0,92
•40 0,87 0,69 0,92 0,90 0,89
50 0,80 0,57 0,89 0,85 0,84
60 0,71 0,44 0,86 0,80 0,78
70 . 0,61 0,34 0,81 0,74 0,71
80 0,49 0,26 <0,75 0,67 0,63
90 0,38 0,20 0,69 0,59 0,54
100 0,31 0,16 0,60 0,50 0,46
НО 0,25 0,52 0,43 0,39
120 0,22 — 0,45 0,37 0,33
'130 0,18 0,40 0,32 ✓ 0,29
140 0,16 0,36 0,28 0,25
150 0,14 0,32 0,25 0,23
160 0,12 0,29 0,23 0,21
170 .0,11 — 0,26 0,21 0,19
180 0,10 0,23 0,19 0,17
190 0,09 0,21 0,17 0,15
200 0,08 — 0,19 0,15 0,13
е ш е н и е. в этом
р 0,7 (см. табл. 15.1) и
Пример 15.2. Решить предыдущий пример для случая, когда
нижний конец стержня защемлен, а верхний шарнирно оперт.
" ” 1учае коэффициент приведения длины
гибкость стержня А = р///щ|п = 0,7 х
X 180/1,55 = 81.
Таким образом А < Апред и фор-
мула Эйлера неприменима. Опреде-
ляем критическую силу, пользуясь
эмпирической, формулой Ясинского:
РкР = ^Окр = F (а — ЛА) =
= 18,9(3100 — 11,4 • 81) = 41138 кгс.
Допускаемая нагрузка [Р] =
= Ркр/hy] = 41138/3 = 13713 кгс.
Пример 15.3. Определить допус-'
каемую величину сжимающей силы
для стойки (рис. 15.2, а), если (7гу1 =
= 2; материал стойки сталь Ст. 3. Уголки жестко соединены меж-
ду собой.
Решение.
• Вычислим момент, инерции сечения (рис. 15.2, б)
= Jy = 4(Jn + а2Рх) = 4 [16 + (0,6 + 1,57)2 X
X 5,41] = 166 см4,
где а -- г0 0,56.
Рис. 15.2
2 31
Радиус инерции
Imin — Гтах —- lz — ly —
166
4.5,41
= 2,77 см.
Гибкость стойки % = = (2 • 100)/2,77 = 72.
Так как % < Хпред, формула Эйлера неприменима.
Определим критическую силу по формуле Ясинского:
Php = CTKpF = (a — bX)F = (3100— 11,4-72) • 4 • 5,41 =
— 49,6 103 кгс.
Допускаемая нагрузка на стойку
[Р] = Ркр/[лу] = (49,6 • 103)/2 = 24,8 • 103 кгс.
Рис. 15.3
Пример 15.4. Определить требуемый номер профиля дву-
тавровой стойки, один конец которой жестко защемлен, а другой
шарнирно оперт. Сжимающая нагрузка Р — 120 кН, высота стой-
ки I = 3 м. Требуемый коэффи-
циент запаса устойчивости шу]=
— 2,7. Материал стойки сталь
'Ст. 3, Е = 2 • 105 МН/м2.
Решение. Выполним расчет
по формуле Эйлера. Записав усло-
вие устойчивости стержня в виде
Z’< /’крЛПу] = n2£Jmin/((p/)2 [пу]),
найдем отсюда требуемый мини-
мальный момент инерции попереч-
ного сечения стойки:
, Р [лу] (р/)2
п2£ —
120 - 103.2,7 (0,7 • 3)«
“ 3,14» -2. 1011 ~
= 72,5 • IO”8 м4.
Момент инерции (минимальный),
несколько больший требуемого,
имеет двутавр № 18, для которого Jy = Jmin = 82,6 см4, iy = imin =
= 1,88 см.
Проверим применимость формулы Эйлера к стойке принятого
профиля. Найдем гибкость стоики Л = у— =—j-gg— = 112.
Для стали Ст. 3 %Пред = 100, следовательно, X > Хпрёд, и фор-
мула Эйлера была использована в области ее применимости.
Пример 15.5. Определить из условия устойчивости допускае-
мое понижение температуры стержней, поддерживающих весьма
жесткую балку, шарнирно закрепленную одним концом (рис.
15.3, а). Требуемый коэффициент запаса устойчивости (пу] =2,5.
Материал стержней сталь Ст. 5; Е = 2,1 • 10е кгс/см2; а = 12 • 10^.
235
Решение. Заданная конструкция один раз статически не-
определима, вертикальная реакция шарнира А и усилия в стержнях
образуют плоскую систему параллельных сил (рис. 15.3, б). Таким
образом, неизвестных три, а уравнений статики можно составить
лишь два.
Для выяснения вопроса об усилиях, возникающих в стержнях,
будем рассуждать следующим образом: при одинаковом охлажде-
нии стержней они получили бы одинаковые укорочения, если бы
температурным деформациям ничего не препятствовало. Из гео-
метрических соображений ясно, что укорочение второго стержня
должно быть больше, чем первого (см. рис. 15.3, б), следовательно,
на свободные температурные деформации накладываются упругие
деформации, и в стержнях возникают усилия. Стержень 1 испыты-
вает растяжение, а стержень 2 — сжатие.
В качестве дополнительного пояснения к приведенным рассуж-
дениям на рис. 15.3, в показаны три положения балки: линия 1
соответствует свободной' температурной деформации стержня 1
(т. е. такой деформации, которая имела бы место при отсутствии
стержня 2); аналогично, линия 2 соответствует свободной темпера-
турной деформации стержня 2 и, наконец, линия 3 дает положение
балки при стесненных температурных деформациях.
Для установления связи между усилиями и температурой со-
ставляем уравнение статики и уравнение перемещений: X тА = °;
-400#, + 1000^ = 0, откуда N, == ~ N2. = S = | • Под-
ставив Д/1 = а/Д/ — Д/j = а/Д/4-получим (аД<4-
+ -^•)|(а Д/ — = 5/2, откуда 2а Д/4--ут’= 5а Д/—,
За Д/Д/7 = 2^4-5^.
5 I 25\
Учитывая, что = получаем За MEF = 12 -f-
откуда JVa = 6а Д/ EF/23.
Допускаемое значение Д/ определяется из условия устойчивости
второго стержня: [Х2] = А^кр/Р^у]. Гибкость стержня Л=4-=«
_ JL = J00_=120
- d/4 20/4 1ZU"
Для стали Ст.5 %пРед« 90, следовательно, %>XnpeA и фор-
мула Эйлера применима: [А^2] = л2£?т1п/^[Лу]-
Допускаемое понижение температуры найдем, приравняв вы-
ражение для Nt, полученное при раскрытии статической неопреде-
лимости системы, к допускаемому по условию устойчивости значе-
нию этого усилия: (6а [ Д/ ] £Д)/29 = n2£/min/(/2 [лу]), откуда
«, 29jt* Д dl
[Д/1 _ 29 ” 'ml" 64, 29 • 3,14» • 2» . „о
1 J 6аЯ»[ЯуГй nd»-,lr , - 6 • 12 • 10-» • 16 • 60» • 2,5 ~ 11,5 *
у 6a-j-/*[«y]
236
Пример 15.6. Проверить на устойчивость сосновую стойку
(рис. 15.4), если основное допускаемое напряжение [ст] = ЮМН/м’.
Решение. При заданном основном (т. е. без учета опасности
продольного изгиба) допускаемом напряжении расчет на устойчи-
вость выполняют по коэффициентам продольного изгиба. Опреде-
ляем радиус инерции поперечного сечения стойки и ее гибкость:
Imin — I
J Л/ b* b 12 „
-p — V 775TS = -7=- = -7= = 3,46 CM J
F Г 12/А- /12 J/J2
1 _ И/ _ ' 4 _ кя
А — i ~ 3,4 • 10-» ~ °0,
Напряжение, возникающее в поперечном сечении стойки при
заданной нагрузке,
Р 100 • 10» _
а ~ F ~ 12» • 10-4
= 6,95 • 10е Н/м2.
По табл. 15.2 находим
коэффициент продольного
изгиба ф = 0,73; понижен-
ное допускаемое напря-
жение
ф[ст] = 0,73 • 10 • 10е =
Рис. 15.4
Рис. 15.5
= 7,3 • 10е Н/м2.
Таким образом, условие ст < ф [ст] соблюдено. Стойка недогру-
жена на 4,8%.
Пример 15.7. Определить допускаемую величину сжимающего
усилия в стержне фермы, состоящем из двух жестко соединенных
между собой неравнобоких уголков (рис. 15.5). Длина стержня
i = 3,4 м; материал низколегированная сталь 15ХСНД, основное
допускаемое напряжение [ст] = 1900 кгс/см2. Концы стержня счи-
тать закрепленными шарнирно.
Решение. Допускаемое усилие определяем по формуле
[ЛГ] == Гф [ст].
Для нахождения величины коэффициента ф следует определить
гибкость стержня, а это в свою очередь требует вычисления мини-
мального главного радиуса инерции поперечного сечения стержня.
Определяем главные центральные моменты инерции сечения, поль-
зуясь таблицей ГОСТ 8510—72 (здесь обозначения осей приняты
по таблице сортамента),
Л = 2Jxyr = 2 • 172 = 344 см4;
Jy =? 2 [Jp, yr + (х0 + 0,5б)2 Fyr] = 2 [54,6 +
4- (1,64 + 0,6)2 13,9] =. 249 см4.
' 237
Таким образом, Jy< Jx и минимальный радиус инерции
imin = iy = = 2,99 см.
Гибкость стержня Л = p//imin = (1 • 340)/2,99 = 114.
По табл. 15.2, интерполируя, находим ф = 0,366.
Допускаемое значение сжимающей силы
1ЛГ] = 2 • 13,9 - 0,366 • 1900 = 19332 кгс.
сительио оси
Р 420 тс
Рис. 15.6
Пример 15.8. Подобрать номер двутавра для стойки (рис. 15.6),
если [er] = 180Q кгс/см2 (материал стойки сталь Ст. 3).
Решение. Выпучивание стержня может происходить отно-
у, так как относительно этой оси момент инерции зна-
чительно меньше, чем относительно оси г.
Требуемая площадь поперечного сечеиия опреде-
ляется ПО формуле Гтреб Р/ф [о]. -
. В этой формуле два неизвестных (F, ф), поэтому
задаемся значением одного из них. Примем предва-
рительно значение ср = 0,6.
Тогда Гтреб = (J20 • 10®)/(0,6 • 1800) = 111 см2.
По таблице сортамента берем ближайший иомер
двутавра — № 60, площадь которого F = 138 см2,
и проверяем стойку йа устойчивость по формуле а =
= Р/Г<ф[(Т].
Найдем значение ср, соответствующее двутавру № 60. По таб-
лице ГОСТ 8239—72 находим минимальный радиус инерции сече-
ния Imin = iy — 3,54 CM.
. Гибкость стойки Л = = °’о‘Л°0 43; ф = 0,49; ф (а) =
lmin
= 0,49 • 1800 — 882 кгс/см2. Тогда о = —= 870 кгс/см2 <
< 882 кгс/см2. „ . . .
Таким образом, условие о ф [а] соблюдено. Стойка недогру-
жена на 1,4%.
Пример 15.9. Стержень прямоугольного поперечного сечения
(рис. 15.7, а) сжат силами Р. Определить требуемые размеры попе-
речного сечения стержня. Стержень должен быть равиоустойчив в
главных плоскостях инерции. Расчетная схема стержня показана на
рис. 15.7, б. Материал стержня — сталь Ст. 3. [ас] = 160 Н/мм2.
Решение. При равноустойчивостй стержня в главных плос-
костях инерции гибкости относительно главных центральных осей
поперечного сечения стержня равны между собой: кх — ку, где
= цх1/1х; Ьу = цу1/1у.
Подставляя в эти выражения = 1, рр = 0,5, получаем
l/ix = 0,57/i^, откуда ix = 2iy,
238
где I = = 1/ _JL. ; - 1/ Ll = l/'^L = _±_
где ix у F у l2bh — y—, lu— у F у l2bh .
Следовательно, -£= = 2 —A= ; h — 2b.
/12 /12
Требуемые размеры поперечного сечения определим из расчета
на устойчивость по коэффициенту продольного изгиба.
Условие устойчивости а = Р/F ф [егс]-
Зададимся значением фх = 0,5. Тогда
F = ^/Ф1[огс] = (400 • 10®)/(0,5 • 160) = 50 • 102 мм2. .
Рис. 15.7
Определяем размеры поперечного сечения стержня
F — bh— Ь2Ь; b = /F/2 = /50 • 102/2 = 50 мм;
h — 2b = 50 - 2 = 100 мм.
Гибкость стержня кх = ку = // 12/й = 3750 /12/100 = 130.
Го табл. 15.2 находим ф = 0,4. Зададимся теперь новым значе-
нием ф: ф2 = (ф1 + ф)/2 = (0,5 4- 0,4)/2 = 0,45; • F = Р/ф2 [ос] =
= (400 • 10®)/(0,45 • 160) = 55,6 • 102 мм2; b = /Р/2 = /55,60/2 =
= 52,7 мм; h = 105,4 мм. __
Гибкость стержня Кх = = l]/~l2/h = 3750/12/105,4 = 123.
Этому значению гибкости для стали Ст. 3 соответствует
Ф = 0,44.
При принятых размерах поперечного сечения имеем
а = Р/F = (400 • 103)/(55,6 • 102) = 72 Н/мм2;
Ф [стс] = 0,44 • 160 = 70,5 Н/мм2.
Стержень перегружен на —~^^’5 • 100% =2,12%, что допус-
тимо.
Пример 15.10. Определить допускаемое значение сил Р из
условия прочности рамы и устойчивости распорного бруса CD
(рис. 15.8, а). Материал — сталь Ст. 5; [а] — 1700 кгс/см .
При раскрытии статической неопределимости деформацией
бруса CD пренебречь. Сечения всех стержней рамы одинаковы.
Решение. Заданная система один раз статически неопреде-
лима. Основную систему получаем, разрезая брус CD. Этот брус
Рис, 15,8 I
прикреплен к раме шарнирно и в промежутке между концевыми |
шарнирами не нагружен. Следовательно, в любом его поперечной^
сечении возникает лишь продольная сила, которую и принимаем!
за лишнюю неизвестную. Основная система с заданной нагрузкой
и искомой лишней, неизвестной представлена на рис. 15.8, б. 3
Каноническое, уравнение для системы с одной лишней неизвесж|
ной имеет вид
AiP = 0. -Ц
Строим эпюру изгибающих моментов для основной системы»»
• нагруженной заданными силами (рис. 15.8, в) и единичными си-
240
лами (рис. 15.8, г). Применяя метод Мора и правило Верещагина,
находим 6П = ^2 • • 2а • 2а • -у • 2а + 2а • а • 2а) = Цу ;
. Д1Р = — ± (2 • 4 • 2а • 2а • 4 Ра + 2а • а • ЗР • а} = —.
С4 \ 2 О • /
После подстановки найденных величин в каноническое уравне-
„ 28а8 А&Ра» п v 23 п
ние имеем Хх -------— 0, откуда Хх = Р.
Окончательная эпюра изгибающих моментов, полученная в ре-
зультате суммирования эпюр Мр, Mi с ординатами, увеличенными
в Xi раз, представлена на рйс. 15.8, д (для большей наглядности
масштаб этой эпюры несколько крупнее, чем эпюры МР, см. рис.
15.8, в).
Для определения допускаемого значения сжимающего усилия
в стержне CD находим его гибкость Л = = 75.
По табл. 15.2 находим ф = 0,73. Допускаемое значение силы Хх
' [Хх] = <р [ст] = 0,73 • 1700 = 9960 кгс.'
Находим допускаемое значение силы Р:
[Хх] = к [Р]\ откуда [Pf = [Хх] = И . 9960 = 6060 кгс.
Наибольший изгибающий момент, возникающий в поперечных
сечениях стержней рамы, Л?тах = Ра; соответствующее условие
прочности <Апах = ^7 =Й^6<[СТ], ОТКуДЭ [Р]’ = ^-' =
1700.8 . 16»
= —г—ёп-----= 9690 кгс.
о > 60
Итак, [Pf < [Pf и, следовательно, допускаемая нагрузка кон-
струкции [Р] = [Pf = 6060 кгс ограничивается условием устойчи-
вости бруса CD.
Задачи для самостоятельного решения
15.1., Определить значения критической и допускаемой сил
для трубчатой стойки (рис. 15.9). Материал стойки легированная
сталь, для которой предел пропорциональности стпц = 5700 кгс/см8
£ = 2,2 10е кгс/сма.
Требуемый коэффициент запаса устойчивости [яу] = 3,2.
Указание. Решение начать с выяснения применимости формулы
Эйлера.
Ответ. Ркр = 2,86 • 10* кгс:
15.2. Определить требуемый диаметр d контрштока компрессора.
Длина контрштока 900 мм, сжимающее усилие Р = 800 кгс, тре-
241
буемый коэффициент запаса устойчивости 1яу] = 3. Полагать, что
шток работает как стержень с одним шарнириоопертым, а другим
защемленным концом. Материал сталь Ст. 5; Е — 2 • 10е кгс/см2.
Указание. Расчет выполнить по формуле Эйлера с проверкой ее
применимости. Если окажется, что при найденном d формула Эйлера непри-
менима, пересчитать, использовав формулу Ясинского.
Ответ, d = 18 мм.
15.3. Определить допускаемую нагрузку для сжатой чугунной
колонны высотой / = 6 м. Сечение колонны — кольцо наружным
диаметром D — 250 мм и толщиной стенок б = 20 мм. Концы ко-
Рис. 15.9
Рнс. 15.11
лонны шарнирно закреплены. Основное допускаемое напряжеиш
на сжатие [о] = 100 МН/м2.
Ответ. 448 кН.
15.4.,Определить допускаемую нагрузку для стойки (рис. 15.10),
состоящей из двух- жестко соединенных между собой швеллеров.
Материал стойки сталь Ст. 3, основное допускаемое напряжение
на сжатие [а] = 1600 кгс/см2;
Ответ. 31 - 103 кгс.
15.5. Определить требуемые размеры профилей равнобоких
уголков для стойки по рис. 15.11. Материал стойки сталь Ст. 3,
основное допускаемое напряжение на сжатие [ст] = 1600 кгс/см2.
Ответ. Уголки 75 X 75 X 8.
§ 15.2. Продольно-поперечный изгиб
При продольно-поперечном изгибе бруса .(рис. 15.12) прогибы
определяют по приближенной формуле
у°
У~Г=^р3-
Здесь у° — прогиб от поперечной нагрузки; у — полный прогиб,
вызванный действием не только поперечных, но и осевых сил S;
242
Р9 — jr£J/(p./)2 — эйлерова сила, при ьычислении которой момент
ннерцни сечення J определяется относительно главной осн, перпен
днкулярной плоскости действия поперечной нагрузки.
Приведенная формула для прогиба дает удовлетворительные
результаты при условии, что кривизна упругой линии, соответ-
ствующей действию поперечной нагрузки, однозначна.
Для брусьев с обоими шарнирно закрепленными концами
(ц = 1) формула точнее, чем прн других видах закреплений.
Наибольшие (по абсолютной велнчнне)^ормальные^напряжения
в поперечном сеченнн бруса анаИб = NxiF + M/W = SIF +
+ M°/W + Sy/W,
Рис. 15.12
где М = ЛГ + Sy — суммарный изгибающий момент в произволь-
ном поперечном сечении бруса; М° — изгибающий момент в том же
сечении от поперечной нагрузки.
Прн продольно-поперечном изгибе принцип независимости дей-
ствия сил неприменим, так как зависимость между напряжением
н нагрузкой нелинейна. Напряжения возрастают быстрее, чем на-
грузка.
В случае продольно-поперечного изгиба бруса расчет следует
вести не по допускаемым напряжениям, а по предельным нагрузкам.
Формула расчета по предельным нагрузкам для бруса нз плас-
тичного материала может быть записана в виде
' 1 I [п1у° • 1 ] I [”1Л1°<а
р + w 1—[n]S/P9|+ № ^ т’
где [nJ — требуемый коэффициент запаса прочности; стт—предел
текучести.
Пример 15.11. Деревянная стойка нагружена, как изображено
на рнс. 15.13. С помощью тензометров определено нормальное на-
пряжение в точке А: од'= 70 кгс/см2. Определить величину силы
Р, выполнив расчет в двух вариантах: а) по принципу независимо-
сти действия сил; б) на продольно-поперечный изгиб. Модуль упру-*
гости Е = 105 кгс/см2.
Решение. При расчете, основанном на принципе независи-
мости действия сил, нормальное напряжение (по абсолютной вели-
чине) в точке А связано с действующей нагрузкой выражением
243
S , M P cos 45° , (P cos 45°)/ „ aAnd*
° Л = T + > = + ad>/32- • 0TKУДа P ---------1---Й’
4 cos45°( l+8-j)
70 • 3,14 • 20» Anc
_-----------------— 426 Krc
4.0,707(1+8^
При расчете на продольно-поперечный изгиб связь между на-
пряжением и нагрузкой определяется выражением
S , Hl , Sy° Р cos 45° , (Р cos 45°) I ,
стД-/г4-^4-^(1_ S/P9) - то/1/4 + ^3/32 +
0.707Р
(Р cos 45°) у'
"г (жР/32)[1 — (Pcos45°)/PJ •
Эйлерова сила для рассматриваемой
3,14». 10» М? 20*
р — п &_____________64_________ко? .
9 ~ (fi/)» ~ (2 • 180)» ~
Прогиб свободного конца от действия силы Н (см)
У° = 5g = = (1750 • 10-в)Р.
3 • 10» • 4|? 20*
о4 • .
После подстановки найденных величин 'в фор-
мулу для напряжения получаем
СТОЙКИ
102 кгс.
0,707Р • 180
У? go»
32 '
0.707Р» • 1750 • 10-« . 2
3,14 9Пв/. 0.707Р \ ~ 70 КГС^СМ '
•32--2ОТ~597-По5
0.707Р \ “
597 • 10»J
Отсюда Р == 422 кгс. '
Данный результат весьма мало отличается от полученного
на основе принципа независимости действия сил, что вполне есте-
ственно, так как рассчитываемый брус имеет довольно высокую
жесткость.
Пример 15.12. Для бруса (рис. 15.14) определить фактический
коэффициент запаса прочности п, если материал — сталь Ст.З;
ат — 2400 кгс/см2; Е = 2 • 10* кгс/см2.
Решение. Наибольшие напряжения (сжимающие) в опасном
S Sf° . Л4°
поперечном сечении о = -р- + w _ s/p > + .
Определяем геометрические характеристики сечения:
F =-J (D2 — d2) = j (102 — 82) = 28,3 см2;
J « 0,05 (D4 — dj) = 0,05 (10* — 84) - 295 см4;
W = —— = — = 59 см8
W 0.5D 5 СЛГ’
244
Определяем максимальный прогиб от поперечной нагрузки й ве-
личину эйлеровой силы: /° - = 2,2 см; Р3 =
л!£/ л». 2- 10е. 295 . 1ПЯ . ..
~ (jx/)1 (500)1 — 2.3,4- 10 кгс (р. — 1).
Максимальный изгибающий момент от поперечной нагрузки
М° == Р//4 = (500 • 500)/4 = 6,25 • 10* кгс • см.
Отношение осевой силы к эйлеровой S/P3 = (6 • 103)/(23,4 X
X 10s) = 0,26.
Подставив эти значения в формулу для наибольшего напряже-
6-10» , 6-103.2,2 , 6,25-10* ,с_о , ,
ния, получим о = + 59(j-_o>26) + = 1573 кгс/см3.
При линейной зависимости между напряжениями и внешними
силами коэффициент запаса прочности па = стт/ст = 2400/1573 = 1,53.
В действительности при продольно-поперечном изгибе п будет
меньше, так как напряжения возрастают быстрее нагрузок. Иско-
мую величину п найдем из формулы
„е [_L ।______nf° | , пМ° _
+ W(l—nS/P3) | + _даг~СТт- х
После подстановки числовых значений и упрощений получим
уравнение 106,5л2 — 1897л + 2400 = 0, откуда найдем лх = 1,4,
и2 = 16,4. Очевидно, что значение ла не будет решением задачи:
при п — 3,85 выражение 1 — tis/P3 рдвно нулю, а напряжение
неограниченно возрастает. Таким образом, окончательно л =- 1,4,
следовательно, при расчете по линейной зависимости погреш-
ность составила бы ~ • 100% « 9,3%.
1,4
Задачи для самостоятельного решения
15.6. Найти наиболь-
шие сжимающие нормаль-
ные напряжения в по-
перечном сечении сталь-
ной балки из швеллера
ЗЧитс
“Ж , 4 о №30 J тг
j
Рис. 15.15
245
№ 30, изгибаемой в плоскости наименьшей жесткости (рис.
15.15).
Принять Е = 2 • 10е кгс/см2.
Ответ. 975 кгс/см1.
ГЛАВА 16. ЗАДАЧИ ДИНАМИКИ В СОПРОТИВЛЕНИИ МАТЕРИАЛОВ
§ 16.1. Учет сил Инерции
Как известно из теоретической механики, задача динамики
может быть на основании принципа Даламбера приведена к задаче
статики. Напомним, что этот принцип состоит в том, что движущуюся
систему (или точку) можно в любой момент времени рассматривать
как находящуюся в равновесии, если к действующим на систему
(или точку) заданным силам и динамическим реакциям связей при-
соединить силы инерции. Сила инерции материальной точки равна
произведению массы точки на ее ускорение и направлена в сторону,
противоположную ускорению.
Рис.
16.1
В общем случае неравномерного кри-
волинейного движения точки силу инерции
раскладывают на две составляющие: каса-
тельную (или тангенциальную) силу инер-
ции и нормальную (или центробежную)
силу инерции. Первая из указанных со-
ставляющих направлена в каждый дан-
ный момент времени по касательной к
траектории движения в сторону, противо-
положную направлению касательного уско-*
рения at. Вторая направлена по нормали*,
к траектории противоположно направлен
нию нормального ускорения которой
как известно, всегда направлено к центр?;
кривизны траектории. J
Таки и образом, величины касательной Pat и центробежной Ряп сидй
инерции точки массы т определяются по формулам ги/ — tnat = тж
п У2
Ря„ = тап — т—, где о — скорость точки; р—радиус кривизн!®
ее траектории. J
Пример 16.1. Определить требуемую площадь поперечной
сечения стального троса (рис. 16.1, а), при помощи которого грЯ
Q — 2500 кгс поднимают на высоту I = Юме постоянным ускоря
нием а = 3 м/с2. Допускаемое напряжение для троса [ст] — 180Й
кгс/см2, объемный вес материала троса у == 7,2 тс/м8. 1!
Решение. Согласно принципу Даламбера, рассмотрим равйв|
весие системы с учетом заданных сил и возникающих при равн<Й
ускоренном подъеме сил инерции груза и троса. Применив метЦ
246
сечений, определим продольную силу в произвольном поперечном
сечении троса (рис. 16.1, б): SX = 0; — yFx — Q — Ри = 0,
где Ри — сила инерции груза и троса, Ри = a; g —9,81 м/с2—
ускорение силы тяжести.
Выражение для продольной силы будет иметь вид
• ЛГд=(0+уГх) + ^±^а = (0 + уГх)(1 + |).
Вводя обозначение 1гя = 1 + a/g (динамический коэффициент)
и учитывая, что Q 4* yFx = NCT — продольная сила при статичес-
ком- (без учета сил инерции) нагружении, получаем &A/VCT.
Динамическое напряжение в поперечном сече-
нии троса Од — Мд/Р — &даст.
Условие
max Од
прочности троса примет вид
(Q + yFl) 1 + 4)
-----------------F-----
требуемую площадь попе-
при этом с некоторым при-
max Л'д
F
определяем
Отсюда
речного сечения троса;
ближением принимаем, что длина троса от места
его набегания на барабан лебедки до места под-
Z7^ Q
веса груза равна высоте подъема: —у/-
После подстановки численных значений F
2500 t оо а
|олл — 1,82 см . .
__1800 —72- 10~3 • 10 • 10а
1 + 3/9,81 *
При длине троса Z = 10 м учет его собственного
Рис. 16.2
веса практи-
чески не отражается на результате расчета.
Пример 16.2. Цилиндрическая винтовая пружина с малым
шагом вращается в вертикальной плоскости вокруг неподвиж-
ного шарнира О с угловой скоростью п = 300 об/мин; на свобод-
ном конце к ней приложен груз Q = 2 кгс (рис. 16.2).
Найти максимальное касательное (динамическое) напряжение
в поперечном сечении проволоки пружины, а также максимальное
перемещение груза Q при следующих данных: длина пружины в не-
нагруженном состоянии I = 15 см, диаметр витка D = 6 см, диа-
метр сечения проволоки d = 0,6 см, число витков = 5; модуль
сдвига материала пружины G = 8 • 105 кгс/см2. Массу пружины
в расчете не учитывать.
Решение. Максимальным значение динамической силы, рас-
тягивающей пружину, будет тогда, когда груз Q займет крайнее
п гкнее положение. Эта сила будет равна сумме силы тяжести груза
и центробежной силы инерции груза:
Ра - Q + Ри == Q + ~ an = Q+ и2+.ах -= Q (1 +
247
, Т. е.
Здесь <о — лл/30 = (3,14 • 300)/30 = 31,4 рад/с— угловая скорость
пружины; гтах = / 4- Хд — максимальное расстояние от осн враще-
ния до центра груза; Хд — искомое максимальное (динамическое) -
перемещение груза Q, равное удлинению пружины.
Как известно (см. § 5.5), Хд = 8PfP3nxlGd*. Тогда Рл =
, (й2 (, , 8рвР3"1\ п ОГ, . 31,4*/. с .
+ g Gd* / ’ ИЛИ 981 V®
Рд = 2 [1 4- 1,006 (15 4- 0,0833РД) , откуда Рд = 38,4 кгс.
х Удлинение пружины (динамическое перемещение груза)
0,
8РД • 6» • &
8 • 106 • 0.6V
1/2
1/2
-Оа
Рис. 16.3
dx
. 8 • 38,4.6s • 5 о о „ .
д ~ 8 • 10* • 0,64 ~ СМ#
Максимальное касательное напряже
ние, возникающее в пружине,
.8РдР 1,14-8 • 38,4 • 6
тахтД = k-^- = ---=
— 3100 кгс/см2,
где k — 1,14, по данным § 5.5.
Пример 16.3. Стальной стержень
круглого поперечного сечения равн
мерно вращается вокруг оси (рис
16.3). Определить наибольшую допус
мую по прочности длину стержня I
.при скорости его вращениям = 1400 об/мин, если [ст] = 800 кгс/см
7 = 7,85 гс/см3.
Решение. Элементарная сила инерции (центробежная сил
действующая на элемент dx, масса которого dm (см. рис. 16.3
определяется по формуле dPB = dman = ^dxcosx.
Максимальное значение продольной силы равно сумме элем
тарных сил инёрции, действующих на одну из половин стержН
</2
тпахА/д = f a>2x dx = ^ ш2 .
д J g g 8
По условию прочности, тахстд= тахЛ/д/Р^[ст], или таход
— T®2lJP/8g = [ст], откуда /пр = У 8g [о]/уш2.
Учитывая, что и = ”" = ——— = 146,5 рад/с, получаем 1^
„_1 1/Щ__________L 1/8 •981 •800юА см
“ «О’ V v ~ 146,5 V 7,85- 10“3 1УдСМ‘
Пример 16.4. Регулятор (рис, 16.4) равномерно вращается
круг оси ОО с угловой скоростью (D = 30 рад/с. Определить г
зонтальное перемещение точки С, а также величину иаиболь
нормальных напряжений в стальном Стержне ВС. Элемент
94Я
считать абсолютно жестким. Массой стержня ВС при расчете прене-
бречь. Принять Е — 2 • 10* кгс/см2.
Решение. Стержень ВС можно рассматривать как консоль,,
нагруженную на свободном конце центробежной силой:
Р. = |<»‘гв|со2(а + /я) = ^-*(10 + /д) = 9,17(10 + /д). (а>
Здесь через /д обозначено искомое горизонтальное перемещение
точки С — прогиб свободного конца стержня ВС, возникающий
при его вращении. Связь между силой инер-
ции и перемещением получается из извест-
ного (§ 8.2, 8.3) выражения для максималь-
ного прогиба консоли, нагруженной иа
свободном конце сосредоточенной силой,
= где 4 = M3/12:
Таким образом, Рн = =
= 192/д. ’ (б)
Сопоставляя равенства (а) и (б), по-
лучаем /д = 0,50 см. Прн этом Ря = 0,5 х
х 192 = 96 кгс.
Наибольшие нормальные напряжения
возникают в сечении В стержня: таход =
|гях P„l Qfi . 40 . О
=~w~=w=VH=1200 кгс'см-2-
Пример 16.5. Ломаный брус (рис. 16.5,а)
круглого поперечного сечеиия (d «= 18 мм)
равномерно вращается вокруг оси АВ.
Определить наибольшую допустимую
Рис. 16.4
угловую скорость, если
у = 7,8 rc/cM’/fo] = 1000 кгс/см2.
Влияние деформации бруса на величину центробежных сил не
учитывать.
Решение. Находим силы инерции, действующие иа части
CD hDE ломаного бруса. При равномерном вращении бруса с угло-
вой скоростью о нормальные (центробежные) силы инерции по-
стоянны во времени. Для участка DE центробежные силы представ-
ляют собой равномерно распределенную нагрузку. На элемент
ds стержня DE приходится сила инерции dPB = dmafr,
где масса этого элемента dm = ds/g = yrtd2ds/4g, г = /—'рас-
стояние элемента от оси вращения; dPB — -^-g ds = qBds, где:
qB = V — интенсивность сил инерции на участке DE,
930 • Л • 1,8* • 7,8 с ш-4 2 „ л/л .
9й 4 - 981- 1000" = 6’06 • 10 “ КГС/СМ-
219
Участок CD нагружен силами инерции, которые изменяются
от нуля в точке С до максимума в точке D по длине участка по
линейному закону (рис. 16.5, б). Наибольшая интенсивность силы
инерции (в точке D) равна найденной величине qK.
Пользуясь схемой нагружения, представленной на рис. 16.5, б,
определяем опорные реакции. Заметим, что равнодействующая сил
инерции участка CD равна половине произведения максимальной
интенсивности ди на длину участка: ^тв = 0; —q„l-^ — 0,5q,tlx
Рис. 16.5
, П О/ A D 6,06. 10-!. 30 „ п пп у
Xl+RA2l=Q, откуда RA = — = ---------------%----<о2 = 9,09 X
X 10-3й2 кгс; тА — 0; —RB2l + Q,5qul • I + qItl • 1,5/ =0, от-
куда Rb = q»l = %Ra = 18,18 • 10-3<d2 кгс. j
Пользуясь схемой по рис. 16.5, в, строим эпюру изгибающих
моментов как для обычной плоской статически определимой рамы |
(см. § 6.3).
Эпюра изгибающих моментов показана на рис. 16.5, г.
Наибольшую допустимую угловую скорость определим, соста-
М
вив условие прочности для участка АВ: ст = ^ах^[о]; [/Итах] =*
*= W [о] = [о]; [7Итах] = в’-зз’"- ' Ю00 = 572 кгс • см.
250
Согласно эпюре, /Umax = 0,5454w3 • 0,5454 [со]2 = 572, откуда
1“) = КоЙ? == 32,4 раД/'С'
Задачи для самостоятельного решения
16.1. Тонкое кольцо площадью поперечного сечения F и сред
ним диаметром D равномерно вращается вокруг оси О, перпенди-
кулярной плоскости кольца (рис. 16.6). Определить окружную
скорость v, при которой кольцо разорвется от действия центробеж-
ных сил, если оно изготовлено: 1) из стали опч = 8000 кгс/см2,
уст = 7,85 гс/см3; 2) из чугуна опч = 1200 кгс/см2, учуг = 7,2 гс/см3.
Ответ. Для стали: 316 м/с, для чугуна: 128 м/с.
Рис. 16.7
16.2. С помощью лебедки С, установленной на двух двутавро-
вых балках № 22 а, поднимают груз, масса которого т? — 4500 кгс
(рис. 16.7). В начале подъема груз движется с постоянным ускоре-
нием и за первые три секунды проходит расстояние 12 м. Проверить-
прочность балок при ю| = 160 Н мм2. Учесть собственный вест
лебедки; масса которой тл — 700 кг.
Ответ, max = 110 Н/мм2.
16.3. Стальной стержень АВ равномерно вращается вокруг
оси А, перпендикулярной плоскости чертежа (рис. 16.8). Опреде-
лить угловую скорость со стержня, при которой наибольшее ног-
251
мальное напряжение, возникающее в его поперечном сечеиии, до-
стигнет предела пропорциональности апц = 2000 кгс/см2. Вычи-
слить абсолютное удлинение стержня Д/ при указанной величине
напряжения. Принять у = 7,85 гс/см3, Е — 2 • 10е кгс/см2.
Ответ. а> = 281 рад/с; Д/ = 0,053 см.
16.4. Рама равномерно вращается вокруг оси ОхОа (рис. 16.9).
Определить допускаемую угловую скорбеть вращения рамы, если
ее стержни имеют квадратное поперечное сечение 1,5 X 1,5 см;
1а] = 780 кгс/сма; у = 7,8 гс/см8.
Ответ. [<*>1 = 148 рад/с.
16.5. Маховик с моментом инерции 1т= 50 кг • м2, вращаю-
щийся с угловой скоростью п — 800 об/мии, насажен на вал диа-
метром d = 80 мм. При торможении маховик останавливается,
сделав 12 оборотов; Найти максимальное касательное напряжение,
возникающее в поперечном сечении вала при торможении, считая
силу торможения постоянной.
Ответ. 231 • 10» Н/м2 = 23,1 МН/м2 = 23,1 Н/мм2.
§ 16.2. Напряжения и перемещения при ударе
Напряжения и перемещения при ударном действии нагрузки
определяют по следующим формулам:
Од == Лдбст! 6д == ^д6ст«
Здесь ад, 6Д — соответственно динамическое напряжение и
перемещение при ударе; аст, 6СТ — напряжение и перемещение,
вызванные статическим действием'силы, равной весу падающего
груза.
Динамический коэффициент при ударе (&д) без учета собствен-
ной массы конструкции, подвергающейся удару, определяют по
формуле йд = 1 + И1 + 2/i/6CT,
где h — высота падения ударяющего груза.
В частном случае при мгновенном безударном приложении си-
лы, т. е. при h = 0, ka = 2.
С учетом массы упругой системы, испытывающей удар, вел!Р
чина йд определяется по формуле &д = 1 + 1 / 1 Н---—-----»
V W+₽£l
В этой формуле Р — вес упругой системы, подвергающейся
удару; Q —.вес падающего груза; h — высота его падения; 6СТ —<
перемещение в точке удара при статическом приложении груза Q1
Р — коэффициент приведения массы ударяемой системы к точке
удара (Р < 1).
252
Коэффициент приведения определяют по следующей формуле:
₽ = J (6хст)МР/6с2тР.
i
можно принять
Рис. 16.10
Здесь бхст — уравнение эпюры перемещений, вызванных стати-
ческим действием силы, равной весу падающего груза и приложен
ной в точке удара.
Если отношение Л/6СТ велико (больше 100),
приближенные выражения для &д: kA = V2h/8cr-
Или при учете собственной массы системы
}Gft/6eT(l + ₽ £).
Пример 16.6. На стальной ступенчатый стер-
жень падает груз Q (рис. 16.10). Считая, что
устойчивость стержня обеспечена, определить
наибольшие сжимающие напряжения, возни-
кающие в поперечном сеченни стержня.
Задачу решить в двух вариантах: а) без уче-
та массы стержня; б) с учетом массы стержня
(у — 7,85 гс/см3).
Решение. Максимальные статические
(сжимающие) напряжения возникают в сече-
ниях верхней части стержня аст = N/F2 —
= QlFa~ 40/5 = 8 кгс/см2.
Статическое перемещение в месте удара равно, очевидно, уко-
рочению стержня при статическом приложении груза Q: 6СТ =
Sa/ Qh , Qi» 40 /70 , ioo\ 1Л,
Д/°т — EFi + EFt~ 2 • Ю«\10 + 5 / — 54 • 10 см. .
Отношение /г/6ст = 10/(54 • 10~5) = 185 • 103, следовательно,
применим приближенную' формулу для динамического коэффици-
ента. Без учета собственной массы стержня получим &д =
« К2/г/бст = К(2 • 10)/(54 • 10-6) = 193.
Динамическое напряжение ад — ЛдСГст *“ 193 • 8 — 1542 кгс/см2.
Полученный результат имеет смысл лишь при условии, что
предел пропорциональности материала стержня выше найденного
динамического напряжения..
Для выполнения расчета с учетом собственной массы стержня
определим коэффициент приведения массы к точке удара.
Статическое перемещение произвольного поперечного сечения
нижнего участка стержня 6*от = (0^хг С 4)- .
То же для верхнего участка: б!'ст = 4)>
Статическое перемещение верхнего сечения стержня было опре-
делено/ выше.
253
Вес бесконечно малого элемента нижнего участка стержня
dPx = yFidx,; то же верхнего участка dP2 = yF2dx2. После под-
становки данных в формулу для р получаем
2
О
₽ =+----—
62СТР
(?2/з
о
\-12
Н UF111+FM
2/ J
_ 3 (£F1)2 VF1 + (EFi)‘ V?2 2 + £’F1F2 yFs + 3 (£F2)2
— Гл/; F \12
чим ₽ =
[£" \77 + 77/1 v(F1/*+ F>/2)
Подставив F1 — 2F<S: /, = 0,7/2 и произведя сокращения, полу-
0,7а , 0,7» , 0,7 , 1
------—---------- -= 0,197.
(v + 0 (M + D
Вес стержня
Р = yF^ + yF2l2 = 7,85 • 10~3(10 • 70 + 5 • 100) = 9,42 кгс.
Динамический коэффициент с учетом собственного веса стержня
2 • 10
- ---- = 188.
V 54 • Ю?5(1+0,197^
Динамическое напряжение с учетом массы стержня
ад =. /гдоСт — 188 8 = 1504 кгс/см2.
Тормоз
tea
f=>
1=2и
Рис. 16.11
В рассмотренном примере влия-’
ние собственной массы конструк-
ции незначительно.
Пример 16.7. Шкив весом Q —
= 60 кгс насажен на стальной
вал (рис. 16.11), вращающийся с уг*
ловой скоростью п = 300 об/ми
Вычислить величину максималв^
пых касательных напряжений, возникающих в поперечном сечени
вала в момент внезапного торможения (крутящий удар). Масео
вала пренебречь.
Решение. Считая, что кинетическая энергия шкива равн
потенциальной энергии деформации (при крутящем ударе), имее*
lm w2/2 = M\l/2GJV.
Момент инерпии» массы шкива* 1т =--- QD2/8g — (60 • 242)/(8
х 981) = 4,40 кгс • см • с2.
* Шкив усгосно рассматривается как сплошной цилиндр.
2'1
Угловая скорость w = — Юл рад/с.
* QV UV
Динамический крутящий момент Мл = lmGJр/1.
Максимальные динамические касательные напряжения в попе-
Мд ш if/„find* 10л-1/8.4,4-8-105л
речном сечении вала тд = ^ =_ у = _ I/ - ----------------------
16
200
= 833 кгс/см2.
Пример 16.8. На стальной ломаный брус, изображенный на
рис. 16.12, а, падает груз Q.
Рис. 16.12
Определить максимальные расчетные напряжения в 'конструк-
ции (без учета ее массы), а также вертикальное перемещение се-
чения А.
Элемент АВ считать абсолютно жестким.
Решение. Брус В КС испытывает изгиб силой Q и круче-
ние моментом Qa — схема нагружения приведена на рис. 16.12, б.
Для определения опасного сечения бруса ВКС построим эпюры
изгибающих моментов Ми и крутящих моментов Л4К. Эпюра Мк,
согласно схеме нагружения по рис. 16.12, в, представлена на рис.
16.12, г, а эпюра Мк по схеме нагружения, данной на рис. 16.12, ж,
з. Из рассмотрения этих эпюр заключаем, что опасным может быть
либо сетение С, либо К. Хотя для второго Ми меньше, чем для пер-
вого, но и диаметр его тоже меньше. То сечение, для которого ста-
тические эквивалентные напряжения окажутся большими, явля-
ется опасным.
С' пение С: МИ = Q (lt + /2) — 25 180 = 4500 кгс • см; -
= Qu = 25 • 50= 1250 кгс см.
215-
Статические эквивалентные напряжения вычислим по гипотезе
наибольших касательных напряжений (см. § 12.1, 12.2):
оГкв = йг + = -oj7grK(45OO)2 + (125O)2 = 91,2 кгс/см2.
Сечение К: М„ = Qlt = 25 • 120 = 3000 кгс • см; Мк = Qa —
— 1250 кгс • см;
+ = g— И(3000)2 + (1250)2 = 508 кгс/см2.
Итак, опасным является сечение К-
Определим статическое вертикальное перемещение сечения А.
Полное перемещение можно рассматривать как сумму перемещения
обусловленного изгибом бруса В КС и перемещения Д, обус-
ловленного закручиванием того же бруса (см. рис. 16.12, б).
Перемещение равно прогибу fB сечения В от силы Q (напом-
ним, что по условию задачи брус АВ — абсолютно жесткий):
где <pfl — угол поворота сечения В бруса ВКС в результате его
закручивания.
Величину Д определим методом Мора с применением правила
Верещагина (рис. 16.12, в — е): [в = fi = > гДе
= + a>2 = Ql2-l1 ть = /2 + £;
®3=yQ/22; Tb3 = 4z**’ Л = ^«0.05Р‘; J2 = ^«0,05d\
После подстановки численных значений получим Л = 0,644 см
„ МК11 МК1»
Находим угол поворота сечения В-. <рн = ~г-,-Н-ттт—; Jp,~
UJPt ujp,
= ^-«0,lD4; 4, = 5-0, Id4.
Подставив численные значения, найдем <рв = 0,756 • 10-2 рад;
/2 = aq>B = 0,378 см.
Статическое вертикальное перемещение сечения А
бст = fA = Д + f2 = 0,644 + 0,378 = 1,022 см.
Определяем динамический коэффициент:
*. _ 1 + /i+=1 + у 77g - 3,62.
Для опасного сечения К максимальные эквивалентные дина-
мические напряжения ад = /гдстэ’.в = 3,62 • 508 = 1840 кгс/см2. Ди-
намическое вертикальное перемещение сечения А 6Д == /гд60Т «
= 3,62 • 1,022 = 3,70 см.
256
Задачи для самостоятельного решения
16.6. Сравнить напряжения, возникающие в поперечном се-
чении стального стержня, при статическом действии силы Q =
= 40 кгс при внезапном ее приложении и при падении груза ве-
сом Q с высоты h = 10 см на жесткий диск, неподвижно прикреп-
ленный к концу стержня — продоль-
ный растягивающий удар (рис. 16.13).
Массой стержня пренебречь.
Ответ. аст = 5,65 кгс/см2; <тд"
= 11,3 кгс/см2; (Тд — 1944 кгс/см2.
иши
с
1/Z X
Рис, 16.14
16.7. -На двутавровую балку № 18а пролетом I = 6 м падает
груз Q = 100 кгс с высоты h = 5 см (рис. 16.14).
Вычислить максимальные нормальные напряжения в опасном
поперечном сечении балки, а также величину стрелы прогиба, пре-
небрегая массой балки.
Ответ. (Тд ~ 349 кгс/см2; 6Д = / = 0,581 см.
Рис. 16.15
16.8. Для балки из предыдущей задачи определить коэффициент
приведения ф) ее массы к середине пролета. Решить задачу с уче-
том массы балки.
17
Ответ. ₽ = 55 : <т„ = 304 кгс/см2: 6 == f = 0,506 см.
ОО Л АД
16.9. На середину двутавровой балки, опирающейся на две
пружины (рис. 16.15), с высоты 1г падает груз Q. Размеры первой
пружины = 140 мм; = 16 мм; п = 12. Размеры второй
9-1-Ю 257
пружины D2 — 85 мм; d2 — 8 мм; п — 9. Модуль сдвига для мате-
риала пружин G = 8 • 106 кгс/см2. Определить наибольшие напря-
жения в балке в момент удара. Показать амортизирующее действие
пружины. При решении задачи учесть массу балки.
Ответ. — 1140 кгс/см2 (с пружинами); а. — 1635 кгс/см2 (без пру-
жин).
16.10. На стальной вал диаметром d = 100 мм, вращающийся
с угловой скоростью п = 50 об/мин, насажен маховик, момент
инерции которого Jm — 1800 кгс • см • с2 (рис. 16.16). Опреде-
лить наибольшие динамические
Тормоз
Рис. 16.16
напряжения, возникающие при
внезапной остановке вала. Мас-
су вала не учитывать. Задачу
решить в двух вариантах:
а) тормозное устройство уста-
новлено на левой опоре,
б) тормозное устройство уста-
новлено на правой опоре.
Ответ. тд = 4060 кгс/см2 (тор-
моз на левой опоре); тд =
= 1820 кгс/см2.
§ 16.3. Колебания систем с одной степенью свободы
Колебания упругой Системы, вызванные однократньш воздей-
ствием силового импульса и в дальнейшем происходящие под влия-
нием сил упругости самой системы, называют свободными
или собственными колебаниями. Такие колебания не могут быть
опасны для прочности конструкции, так как практически всегда
есть силы внешних и внутренних сопротивлений, вызывающие зату-
хание собственных колебаний. Вместе с тем определение частот
собственных колебаний имеет весьма большое практическое зна-
чение, так как знание их необходимо для расчета на вынужденные
колебания. Последние возникают под действием так называемых
возмущающих сил, величина или направление которых периодиче-
ски изменяются во времени. При вынужденных колебаниях в кон-
струкции возникают переменные во времени напряжения, что свя-
зано с опасностью усталостного разрушения (см. гл. 17). При сов-
падении частоты собственных колебаний с частотой возмущающей
силы возникает явление резонанса колебаний. При резонансе ампли-
туды колебаний достигают недопустимо больших значений (теоре-
тически — без учета затухания колебаний — получается, что они
бесконечно велики), и, следовательно, упругая система Должна
быть рассчитана таким образом, чтобы бна работала в области час-
тот, достаточно далеких от резонансных.
Частота возмущающей силы <о, как правило, является величиной
заданной, изменить которую при проектировании конструкции нет
гозможности поэтому для «отстройки» от резонанса надо обеспе-
258
чить соответствующую частоту <оо собственных колебаний. Обычно
считают, что «отстройка» от резонанса обеспечена, если <оо отлича-
ется от со не менее чем на 30%. Частота собственных колебаний
упругой системы зависит от ее жесткости. Таким образом, для
«отстройки» от резонанса выполняется расчет конструкции на
жесткость, т. е. определяется такая жесткость системы, при кото-
рой соо лежит в указанных выше пределах. Обеспечив расчетом на
жесткость «отстройку» системы от резонанса, все же надо проверить
ее на прочность с учетом переменности напряжений во времени
(как говорят, рассчитать на усталостную прочность).
Упругая система имеет бесчисленное количество степеней сво-
боды, т. е. независимых координат, определяющих положение
всех точек системы. При расчете конструкции на колебания выби-
рают ее расчетную схему, которая должна отражать все основ-
ные особенности работы конструкции и в то же время давать воз-
можность выполнения расчета конструкции наиболее простыми
путями. Число степеней свободы рассчитываемой системы опреде-
ляется выбором ее расчетной схемы. Так, балка с сосредоточенным
грузом при колебаниях, перпендикулярных оси балки, является
системой с одной степенью свободы при условии, что собственная
масса балки не принимается во внимание. В приведенном примере
положение любой точки балки определяется только одной коорди-
натой — перемещением (прогибом) точки приложения груза.
Здесь рассматриваются только колебания систем с одной сте-
пенью свободы. Круговая частота собственных (свободных) коле-
баний системы с одной степенью свободы соо — Vg/бст = VС/т,
где g « 981 см/с3 — ускорение земного притяжения; 6СТ — переме-
щение в направлении колебаний' от статически приложенной силы,
равной весу тела, совершающего колебания; С — коэффициент
жесткости упругой системы, равный силе, вызывающей перемеще-
ние, равное единице; т— масса колеблющегося груза.
В случае крутильных колебаний, например колебаний диска,
насаженного на невесомый вал, = VС/1т.
В этом случае коэффициент жесткости представляет собой вели-
чину момента, вызывающего в месте насадки диска (шкива и т. п.)
угол поворота сечения упругой системы (вала), равный единице;
1т — момент инерции массы диска.
Круговая частота представляет собой число колебаний, совер-
шающихся за 2л секунд. Единицей измерения круговой частоты
является с-1.
Из определения понятия круговой частоты колебаний следует,
что период свободных колебаний То находятся по формуле То =
= 2л/соо = 2л У бет/g = 2л ) т/С.
Для системы с одной степенью свободы, испытывающей вынуж-
денные колебания под действием возмущающей силы, изменяю-
щейся во времени по гармоническому заксну Р — Ро sin u>t,
9*
259
где Ро — максимальное (амплитудное) значение возмущающей
силы; о — круговая частота ее изменения, амплитуда колебаний
Pp^ll__________
ш2\2 4п2<о2
2 1 “
о>0' <1>0
В приведенной формуле Р0Ьц = 6СТ — перемещение, которое
получила бы масса т при статическом приложении к ней силы Ро.
Величину
называют динамическим коэффициентом при колебаниях (иногда —
коэффициентом нарастания колебаний). Влияние затухания коле-
баний учтено так называемым параметром (или коэффициентом)
затухания, обозначенным здесь п (с-1). При силах сопротивления,
пропорциональных скорости колебательного движения (системы
с линейным затуханием),— именно к таким системам и относятся
приведенные формулы п = где а — коэффициент пропорцио-
нальности между силой сопротивления и скоростью. Для осталь-
ных конструкций ориентировочно можно принимать п 0,012<о0.
При отсутствии затухания (точнее, если пренебречь МЙю влия-
нием) формула для динамического коэффициента принимает вид
Ад = ----L—
Д I . (О2 •
1 2
I
Амплитудное значение напряжений, вызванных действием воз-
мущающей силы, определяется по формуле од = где стСт —
напряжение, которое было бы вызвано в системе при. статиче-
ском приложении силы, равной амплитудному значение" возму-
щающей силы. При расчете на прочность зачастую/помимо
напряжений от возмущающей силы надо учесть постоянные во вре-
мени напряжения, вызванные в системе весом приложенного к ней
груза (например, весом электродвигателя, установленного на балке
или раме).
Пример 16.9. Определить частоту собственных крутильных коле-
баний стального диска, закрепленного на стальном валу ступен-
чато-переменного поперечного сечения (рис. 16.17). Влияние соб-
ственной массы вала не учитывать.
Решение. Определим момент инерции массы диска, не учи-
тывая центрального отверстия, т. е. рассматривая диск как сплош-
ной цилиндр. По известному из курса теоретической механики
, 1 о2 1 лО2 , О2 лрО‘Л
выражению - т ~ ~ h Т ,
2f>f)
32
где р = 7,85 • 103 кг/м3 — плотность материала диска. Подставив
Л , 3.J4 -7,85 • Юз .0,6*. 0,08
числовые значения, получим 1т = —*------------------’— —
= 7,98 кг • м2.
Определим коэффициент жесткости вала, составив выражение
для угла поворота сечения на свободном конце от приложенного
в этом сечении закручивающего момента Жк (величина этого мо-
Жк2а 32Жка/ 321
л / 3 \4 ~ Gnd4 V +81/
мента произвольна):
<Р = —— +~
О
3616Жка
81Grtd4 '
Рис. 16.17
2а
Рис. 16.18
/
(Коэффициент жесткости
г 81Gnd4 81 8 • 1010 • 3,14 • 44 • IO-8 оо о 1ЛЯ „
“ ‘3616а’ =----------ЗбТбТад-------= 28’8 • 103 Н • М.
Круговая частота собственных крутильных колебаний диска
1/"С 1/28,8 • Юз
<°о= V ГпГ V -^98- = 60с\
Пример 16.10. Определить частоту собственных колебаний
балки, на конце консоли которой находится груз массой т (рис.
16.18). Задачу решить как без учета, так и с учетом собственной
массы ms балки.
Решение. Для определения частоты собственных колебаний
балки находим прогиб конца консоли от статической нагрузки
Q = mg. Определив опорные реакции балки (показаны на рис.
16.18), составим уравнения упругой линии для / и II участков.
1 X3
Для I участка EJy1 — GJQox—Q-&-.
При составлении этого уравнения учтено, что прогиб в начале
координат (на левой опоре) равен нулю. Для нахождения угла
поворота сечения в начале координат используем граничное усло-
вие 1/1=20 = 0 (прогиб на правой опоре равен нулю) 0 = EJua2a—
— 1 , откуда EJB0 = Qa2/3.
261
Окончательно уравнение упругой линии для / участка имеет
вил EJu1___г
вид Ct и у —- л 12 *
Для II участка
EJy" = EJ%x — + 4 - (^72"~ = Т х ~ + °--72^ •
Подставив в последнее уравнение х = За, получим величину
прогиба на конце консоли EJy^za = Qa8 (4------+ т) =
Частота собственных колебаний без учета массы балки Ио3
«= Kg/бет, где 6СТ = |g”=3a| = Qa3/£J = gma3/EJ. Таким образом,
<в0 = V EJ/tna3.
Приведение собственной массы балки к точке, в которой на-
ходится масса груза, осуществляется так же, как при расчетах
на удар. Точечная (приведенная) масса должна обладать такой
же кинетической энергией, как распределенная масса всей балки.
Обычно предполагают, что эпюра динамических перемещений по-
добна эпюре статических перемещений, и в результате получают
для коэффициента приведения формулу (см. также § 16.2)
У (fixcT)’dff!6
В — L_________
Н fi2 >
6СТ«б
где dm.6 = pFdx: р — плотность материала балки; F— площадь се-
чения балки, m6 = pFl« pF3a.
При вычислении р оказывается целесообразным составить урав-
нение упругой линии для второго участка балки, расположив
начало координат на ее правом конце (см. рис. 16.18).
Для составления этого уравнения должны быть известны про-
гиб (определен выше) и угол поворота сечения на конце консоли.
Продифференцировав ранее составленное уравнение для у11, найдем
£J0n ---------QL + 4Q(x — 2a)2. Подставив х = За, получим
т'=за+Qa2 (j - 4+4 V --J Q«2.
Уравнение упругой линии для II участка*
EJy" =. —Qa3 + 4 Qa2u - Q-у ,
где и — абсцисса сечения, отсчитываемая от правого конца балки.
* При начале координат иа правом конце балки и оси абсцисс, направ-
ленной влево, знак угла поворота должен быть изменен иа противоположный
по сравнению с полученным при оси абсцисс, направленной слева направо.
262
Выражение для коэффициента приведения после некоторых оче-
видных сокращений будет иметь вид
7а2и и2 2
а63а
64 3318
945 11340 ~ о 12 j
3
Частоту свободных колебаний с учетом собственной массы балки
определим из выражения со0 =
где 6СТ—стати-
ческий прогиб от веса груза.
г Пример 16.11. На конце консольной балки из двух двутав-
ров № 30а установлен двигатель весом Q — 3 тс (рис. 16.19). Найти
период свободных колебаний си-
стемы и угловую скорость вала
двигателя, при которой наступит
резонанс. Собственный вес балок
не учитывать.
Решение. Период свобод-
ных (собственных) колебаний уп-
ругой системы определим по фор-
муле
То =.- 2л КЬст/g,
где бст = / = Ql3/3EJ — стрела прогиба консоли при статическом
приложении груза Q. Подставив числовые значения, найдем 8
8 == f _ Q/3 _ 3000-(1,2)»-10» _ .
°ст ' ~ 3EJ~ 3 • 2 • 10е • 2 • 7780 СМ’
где на основании ГОСТ 8239—72 принято J = 2Jlx = 2 • 7780 см\
Тогда получим То = 2л j/” -|-т = 2л ]/ ^’55g^j1 ~~ = 0,0472 с.
Определим (критическую) угловую скорость вала двигателя,
учитывая, что если ротор двигателя из-за неуравновешенности
создает возмущающую силу, то резонанс колебаний наступит при
равенстве о>0 = юкр.
2G.3
Применим формулу для круговой частоты свободных коле-
баний
Шкр=®0 = »j/ 5|5!8/о-» = 13315 Рад/С’
или пкр ~ 30о?кр/л = (30 • 133,5)/3,14 = 1273 об/мин.
Рис. 16.20
Пример 16.12. Определить амплитуду вынужденных колебаний
рамы (рис. 16.20, а) и наибольшие нормальные напряжения, воз-
никающие в ее опасном поперечном сечении от действия веса дви-
264
гателя и вращающейся с ротором двигателя массы т = 5 кг. Плечо
(эксцентриситет) вращающейся массы г = 5 см. Угловая скорость
вала двигателя п — 940 об/мин. Сечение рамы — квадрат со сто-
роной b = 8 см; Е = 2 • 106 кгс/см2.
Собственный вес рамы не учитывать.
Решение. Заданная система один раз статически неопреде-
лима. Предполагая, что сила Q приложена статически, раскроем
статическую неопределимость. В этом случае каноническое урав-
нение метода сил имеет вид (см. § 9.3). бцХ] + = 0.
Величины бц и Ахр вычислим по методу Мора, применив пра-
вило Верещагина.
На рис. 16.20, б дана основная система с заданной нагрузкой
и искомой лишней неизвестной. Грузовая и единичная эпюры пред-
ставлены на рис. 16.20, в, г\
» ___ 1 /а • а 2 , а • 2а 2 \___о3 .
011 — EJ ’ 3 а 2~ ’ 3"а/ ~ EJ ’
д L12. Qa — 02-
А1Р EJ,2 ' 2 ’ 2й ' 2/ ~ 4EJ'
- v Д1Р Qa3 Q 400 ]ПГ. „
Теперь Хл = —-g- = -^5- = T= — = 100 кгс.
Окончательная эпюра изгибающих моментов для Заданной
системы дана на рис. 16.20, д. Определим перемещение (прогиб)
6q в заданной системе под силой Q.
В сечении D приложим к основной системе единичную силу
по направлению искомого перемещения (рис. 16.20, е). На том же
рисунке показана соответствующая эпюра изгибающих моментов.
Перемножив ее по правилу Верещагина на эпюру по рис. 16.20,5,
„ s 1 Г 1 3 а 5 2 а . 1 3 « 2 а 10а
найдем — £/ [у ’ д' ' 3 ' ~2 + ~2 ' ' ~3 ' ~2 2 4 аХ
1 _а 1 Qa8 И _1_______ _5 Qa«
Х 3 2] ~ EJ \16+ 16 48 / 48 £7 ’
Подставив числовые данные, имеем
<, х 5Qa» 5-400. lOe.12 с 1Л_2 ,
Ост — OQ - 48£7 43.2. 10е . 84 — 6,11 • 10 СМ.
Круговая частота собственных колебаний рамы
“«= /J=V6-jr?V-=i27r«-
Центробежная сила, возникающая при вращении неуравнове-
шенной массы т, Ро — та-г.
. Вертикальная составляющая этой силы является гармонической
возмущающей силой (рис. 16.20, з): P = P0sinco/.
Вынужденные колебания от силы Р совершаются с круговой
„ пп л940 с
частотой со = -хк- == = 98,6 рад/с.
265
Максимальное значение возмущающей силы
Ро = т®2г = 5 • 98,62 • 5 10"2 = 2430 Н « 248 кгс.
Прогиб посередине ригеля при статическом приложении этой
с 5Р0аз 5-248 - 106-12 о _о 1п_2
СИЛЫ бет — ^EJ ~ 48 . 2 . Ю6 • 84 ~ ^’7® ' 0 СМ‘
Динамический коэффициент без учета затухания колебаний
ь — 1________1 _ 1_____о 51
д ~ со2 ~ 98,б2 ~ 1 -0,602 ~
о>2 1272
Амплитуда вынужденных колебаний рамы
Авын = Мст = 2,51 3,78 • IO’2 = 9,49 • 10“2 см.
Наибольшие нормальные напряжения, возникающие ет веса
двигателя в опасном поперечном сечении рамы (см. рис. 16.20, д)
maxMQ /3 А \/ £3 18.400-100 ,„с , ,
°Q = ~уТ~ Ч Т =---------------8TF~ = 176 кгс/с№.
Наибольшие нормальные напряжения в том же сечении от дей-
ствия возмущающей силы
- Рол
max Од = йд (шах ост) = — = 2,51 = 278 кгс/см2.
Динамические напряжения изменяются во времени по симме-
тричному циклу (см. гл. 17). Суммарные напряжения в опасных
точках опасного сечения изменяются по асимметричному циклу.
При этом максимальные напряжения
Стах — с<5 + таХ °Д = 176 + 278 ~ 454 кгс/см2,
минимальные
amin — °q — max °д = 176 — 278 = —102 кгс/см2.
Учет затухания колебаний в данном случае практически не ска-
жется на результате расчета. Действительно, приняв параметр
затухания п = 0,012 ®0 (см. § 16.3), получим значение динамиче-
ского коэффициента
98,62\2 , 0.0122 • 98,62 /0,16+ 3,456 • 10'3
Т272/ + 4 1272
отличающееся от вычисленного без учета затухания всего лишь
на 1,6%.
266
Задачи для самостоятельного решения
16.11* . Определить момент инерции массы ротора электро-
двигателя на основании данных следующего эксперимента. Ротор
Подвешен на стальной калиброванной првволоке (рис. 16.21),
затем он повернут на некоторый угол (проволока закручена) и от-
пущен; за 1 мин ротор совершил 40 полных колебаний. При рас-
чете принять модуль сдвига материала проволоки G = 7,8 X
X 10®. кгс/см2.
Ответ. 1т = 1,39 • 10-2 кг • м2.
Рис. 16.21
Рис. 16.23
16.12. Электродвигатель массой т — 3200 кг установлен на
двутавровой балке (рис. 1.6.22). Вал электродвигателя вращается
с угловой скоростью 970 об/мин. Определить требуемый номер
профиля двутавра, исходя из условия, чтобы частота собственных
колебаний балки была на 30% выше частоты возмущающей силы,
возникающей от неуравновешенности ротора двигателя. Массой
балки пренебречь.
Ответ. Ns 50.
16.13. Определить частоту собственных поперечных и крутиль-
ных колебаний вала диаметром d = 65 мм, несущего диск диамет-
ром D = 500 мм, весом Q = 125 кгс (рис. 16.23).
Ответ. ®0nonep = 125 1/с; ®0 крут = 200 1/с. *
* Заимствована из книги А. А. Лапина «Колебания и вибрации в маши-
нах». Машгиз, 1953.— 95 с.
267
ГЛАВА 17. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ *
§ 17.1. Основные понятия об усталостной прочности
1. Общие понятия
Части машин или сооружений, в которых возникают напряже-
ния, переменные по величине и повторяющиеся большое число
раз, разрушаются при напряжениях значительно меньших, чем при
постоянных во. времени напряжениях. В наиболее напряженном
месте детали появляются микротрещины, которые, развиваясь, ос-
лабляют сечение и приводят к разрушению детали. Это явление
разрушения материала при переменных напряжениях называется
Рис. 17.1
усталостью материала. Способность материала вос-
принимать многократное действие переменных напряжений без раз-
рушения называется выносливостью или цикличе-
ской прочностью.
Наибольшее (предельное) максимальное напряжение цикла,
при действии которого не происходит усталостного разрушения об-
разца из данного материала после произвольно большого числа
циклов, называется пределом выносливости.
Эту характеристику материала обозначают а %.
Расчет детали на прочность при действии переменных по вели-
чине напряжений называется расчетом на выносливость или расче-
том на усталостную прочность.
Различают 1) симметричный цикл изменения напряжений, когда
наибольшие и наименьшие напряжения (о или т) одинаковы по ве-
личине и противоположны пО знаку (рис. 17.1), и 2) несимметрич-
ный (или асимметричный) цикл (рис. 17.2)—при неодинаковых
по величине наибольшем и наименьшем напряжениях (о или т).
Основными параметрами цикла напряжений являются макси-
мальное и минимальное напряжения отах и omin (или ттах и Тщщ),
* Современное состояние вопроса освещено в монографии. В. П. Ко-
гаева «Расчеты иа прочность при напряжениях, переменных во времени».—
М.: Машиностроение, 1977.— 232 с.
268
а также амплитуда напряжений оа = -тах 2—— (или та =
__ Tmax Tmin \
“ 2 )
и среднее напряжение цикла * ис — тах^~ т1П (или тс = max^~
Отношение минимального напряжения цикла к максимальному
называется коэффициентом асимметрии цикла
n ainin / n ^minj '
Ro = -— ИЛИ Rx =------- .
CTmax \ Tmax'
Индекс при R зачастую опускают.
Характеристикой цикла называют отношение о — — шли р =
tel '
Циклы, у которых максимальное или минимальное напряжения
равны нулю, называют отнулевыми или пульсирую-
щими (рис. 17.3).
При симметричном цикле (см. рис. 17.1)
Отах — —Ominj (Tmax = —^min)j &с О, R — —lj &R — О-х-
При знакопеременном асимметричном цикле (см. рис. 17.2)
Отах > 0 (Тщах > 0)i Omin < 0 (^min < 0)j —1 <С R < 0.
При отнулевом цикле с' положительными средними напряже-
ниями (см. рис. 17.3, б) Отах (ИЛИ Ттах) > 0; Orain (ИЛИ Tmin) = 0;
_ — ^max / „ ^max inn
<Ja = oc = -g- ^или та = тс = -Tj-j; R = 0; oR = o0.
2. Опытное определение предела выносливости материала
Как уже было указано, предел выносливости обозначают uR
или xR, где индекс R — коэффициент асимметрии цикла, например,
о_! — предел выносливости при симметричном цикле изменения
нормальных напряжений; т0 — предел выносливости при отнулевом
цикле изменения касательных напряжений.
* Для среднего напряжения никла часто применяют обозначениезт,
269
Предел выносливости является основной характеристикой уста-
лостной прочности материалов. При симметричном цикле предел
выносливости имеет самое низкое значение, и поэтому этот цикл
является наиболее опасным.
Величина предела выносливости при симметричном цикле
(o_i или определяется на основании опытных данных.
Подвергая испытанию серию одинаковых образцов при различ-
ных величинах напряжений и строя график результатов испытаний,
получают кривую, показанную на рис. 17.4, называемую кри-
вой выносливости. Здесь
1 Отах (или ттах) представлено в функ-
*3|\ ции числа циклов N, необходи-
« \ мых, чтобы вызвать излом. Вна-
* 'К - чале атах (илитщах) быстро умень-
| шается с увеличением числа N,
"° ______ а затем это уменьшение замедля-
---------— ется, и кривая асимптотически при-
__ ближается к горизонтальной пря-
q - , /У мой. Напряжение, соответствую-
щее ординате такой асимптоты, при-
Рис. 17.4 нимают за предел выносливости. '
3. Зависимость между пределами выносливости и пределом
прочности
Многочисленными опытами установлены следующие приближен-
ные соотношения между пределами выносливости при симметрич-
ном изгибе (о_1), симметричном осевом растяжении — сжатии
(о_1р), симметричном кручении (т_х) и пределом прочности (вре-
менным сопротивлением) апч. Для углеродистой стали « (0,4-г-
-ьО,45)оПч. Для легированной стали о_г = 0,35сгпч 4-(7-н
н- 12) кгс/мм2. Для чугуна о_х 0,4опчр. Для стали о_)р « (0,7-ь
-£-0,9)0^; т_! « (0,5-f-0,6)o_I.
4. Влияние различных факторов на величину предела
выносливости
Предел выносливости зависит не только от свойств материала,
из которого изготовлена деталь машины или сооружения, но и от вели-
чины, формы, способа изготовления и условий эксплуатации детали.
Концентрация напряжений. В местах резкого изменения попе-
речных размеров детали, у отверстий, надрезов, выточек и т. п.
возникает местное повышение напряжений, называемое концентра-
цией‘Напряжений, а сами конструктивные элементы (отверстия, вы-
точки, галтели и т. д.), вызывающие концентрацию напряжений,
называют концентраторами напряжений.
270
Отношение максимального местного напряжения (оНаиб или
тНаиб) к номинальному напряжению (о или т) в ослабленном кон-
центратором сечении при статической нагрузке называют т е о р е-
- тическим коэффициентом концентрации на-
пряжений и обозначают ао (или ат). При переменных напряжениях
вводится понятие эффективного коэффициента концентрации
напряжений ka (или fex): Z>3 =-2=1 или
°_1к
Эффективный коэффициент концен-
трации напряжений представляет собой
отношение предела выносливости при
симметричном цикле гладкого образ-
ца (о_! или t_j) к пределу. вынос-
ливости образца тех же размеров, но
с концентратором напряжений
или T_lfe). Коэффициент ka(kx) отражает
влияние на предел выносливости не
только геометрии концентратора, но
и материала образца. Зависимость меж-
ду теоретическим и эффективным коэф-
фициентами концентрации напряжений
выражается формулой
ka = 1 + <7 («а — 1),
k-
Т1
т-1к '
Рис. 17.5 -
где q представляет собой так называемый коэффициент
чувствительности материала к концентрации напряжений.
На рис. 17.5. приведен график приближенных значений q для
стали различных марок в зависимости от коэффициента ао концен-
трации напряжений и предела прочности опч стали.
Рис. 17.6
Рис. 17.7
На рис. 17.6. дан график теоретического коэффициента концен-
трации для валов с выточкой при изгибе t/г = 1; d =» 30 -+- 50 мм.
Величину эффективного коэффициента концентрации опреде-
ляют по графикам или таблицам, составленным на основании ре-
зультатов опытов. .
271
На рис. 17.7—17.10 приведены графики эффективных коэффи-
циентов концентрации напряжений для различных валов*.
На рис. 17.11 даны графики значений поправочных коэффи-
циентов на отношение Did (к рнс. 17.9, 17.10), где / — изгиб;
2— кручение. Если Did <2, то ka(kx) надо определить по фор-
муле ka—l + l,(kao—1), где k„o — коэффициент, найденный из
графиков рис. 17.9 или 17.10.
Масштабный эффект. Предел выносливости зависит также
и от абсолютных размеров детали. С увеличением размеров детали
предел выносливости уменьшается.
Уменьшение предела выносливости с увеличением размеров
детали оценивается масштабным фактором или коэффициентом
(ем < 1), представляющим отношение предела выносливости
а_1<г(т_1(г) образца данного диаметра d к пределу выносливости
ОЦ1 (t_x) стандартного образца диаметром 7 мм.
°— id т—Id
ем = —— или е„ = —— .
°-1 Т-1
* Обширный справочный материал по величинам эффективных коэффи-
циентов концентрации напряжений для различиях видов концентраторов
приведен в «Вестнике машиностроения» Ns 10, 11, 12 за 1949 г. и Ns 3, 4, 6, 7,
8, 9 за 1950 г. См. также С. В. Сервисен, В. П. Когаев, Р. М. Шнейдерович.
Несущая способность и расчеты деталей машин на прочность, Машгиз.
1963.— 421 с.
272
На рис. 17.12 приведен график значений ем для углеродистой
(1) и легированной (2) стали. Этим графиком можно пользоваться
для приближенного определения ем как при изгибе, так и при кру-
чении.
Состояние и качество поверхности. Влияние состояния и каче-
ства поверхности детали на величину предела выносливости учиты-
вается коэффициентом качества поверхности еп, который представ-
ляет собой отношение предела выносливости при симметричном
цикле образца с заданным состоянием поверхности о_1п или т_1п
к пределу выносливости такого же образца с полированной поверх-
ностью:
Грубая обработка поверхности детали значительно снижает
предел выносливости. Поражение коррозией поверхности металла
способствует образованию трещин усталости, что также влечет за
собой значительное снижение предела еы юсливости.
На рис. 17.13 приведен график зависимости еп от от для дета- ,
лей с различным состоянием поверхности. Здесь 1 — полирование;
2 — шлифование; 3 — тонкое точение; 4 — грубое точение; 5 —
наличие окалины.
Термохимическая обработка, например азотирование, а также
поверхностный наклеп путем обкатки поверхности роликами или
обдувки дробью приводят к повышению предела выносливости
и в этих случаях коэффициент еп > 1.
Общий коэффициент снижения предела выносливости при сим-
метричном цикле, при учете всех перечисленных факторов, связан
с указанными коэффициентами зависимостью
• ВМВ|
Таким образом, предел выносливости детали при симметричном
цикле связан с пределом выносливости малого лабораторного
образца, имеющего полированную поверхность, соотношением
а_, т_,
ог_|д = ^А Или т_1д = -р-.
ЛоО лтО
ИЛИ KzD = —
емеп
м‘п
273
§ 17.2. Расчет на прочность при переменных напряжениях
Расчеты на прочность при переменных напряжениях в боль-
шинстве случаев выполняют как проверочные, по размерам, взя-
тым с чертежа детали. Для предположительно Опасных сечений
детали определяют фактические коэффициенты запаса прочности,
которые сопоставляются с коэффициентом запаса, требуемым для
данной конструкции.
Условие прочности: п^[п]. В случае неудовлетворительного
результата расчета приходится изменять те или иные размеры де-
тали (а -иногда и материал) и вновь производить проверку проч-
ности.
Расчеты на прочность при линейном напряженном
состоянии и при кручении
При постоянных во времени напряжениях условия прочности
для детали из пластичного материала могут быть записаны в виде
ат Тт
Пат = — >[nj, или птт = — [пт].
Здесь ZIgt, Zl-tT — коэффициенты запаса соответственно по нормаль-
ным и касательным напряжениям для проверяемого сечения де-
тали; (nJ, [пх]— требуемые (допускаемые) значения коэффициентов
запаса; стт, хт — пределы текучести соответственно при одноосном
напряженном состоянии и при чистом сдвиге; ст, т — наибольшие
напряжения, возникающие в проверяемом сечении детали.
При симметричном цикле изменения напряжений условия проч-
ности при линейном напряженном состоянии и при чистом сдвиге
кручении) имеют вид '
п, = к,- - > [nJ; пг = у - 1 - > Гцх1.
'Сортах . /WmaX^tXj
Первая из этих формул относится к детали, работающей на
изгиб; при симметричном цикле растяжения — сжатия ст_! должно
быть заменено на ст_1р .
Расчеты при асимметричном цикле напряжений осложняются
из-за отсутствия экспериментальных данных о соответствующих
пределах выносливости. Формулы для определения коэффициен-
тов запаса прочности получают на основании схематизированных
диаграмм предельных амплитуд или диаграмм пределов выносли-
вости. Существует ряд способов схематизации этих диаграмм.
Здесь приведены формулы для нахождения коэффициентов
запасов прочности, основанные на схематизации диаграмм по спо-
собу Серенсена — Кинасошвили и предположении о подобии ра-
бочих и предельных циклов напряжений*.
* Напоминаем, что подобными называют циклы, имеющие одинаковые
коэффициенты асимметрии, а следовательно, и характеристики.
274
При изгибе
п - °~1
° KaDoa+^Oc’
при растяжении — сжатии
п = °-1Р •
° ЛаОоа + %ое’
при кручении
п T-i
т V«+V('
В этих формулах фа(фт) — коэффициент чувствительности мате-
риала к асимметрии цикла. Его ориентировочные значения для
стали: = 0,1 н- 0,3; = 0,05 -4-0,15; большие значения отно-
сятся к стали с более высоким содержанием углерода и к легиро-
ванной стали.
Первые две из приведенных формул относятся к циклам с по-
ложительными (растягивающими) средними напряжениями (ое >
> 0). При отрицательных средних напряжениях в указанных
формулах следует полагать фо = 0.
Для деталей из пластичных материалов помимо коэффициентов
запасов по усталостной прочности обычно определяют коэффици-
енты запаса по сопротивлению малым пластическим деформациям,
т. е. коэффициенты Пат(Птт), по отношению к пределам текучести
(см. § 17.2). При этом, если оказывается, что п„ < па (или лтг <
< пт), то коэффициент п„ (nxrj иногда считают решающим для
оценки надежности детали. В других случаях принимают допус кае-
мый коэффициент запаса [пот1 или [птт] несколько меньше, чем
[по] (или [nJ), тогда проверки по обоим коэффициентам запаса
выполняют независимо одну от другой.
Расчет на прочность при сложном напряженном состоянии
При расчете бруса на изгиб с кручением, кручение с растяже-
нием (или сжатием), а также при сочетании изгиба с кручением и
растяжением (или сжатием), т. е. в тех случаях, когда в опасной
точке возникает так называемое упрощенное плоское напряженное
состояние, коэффициент запаса п определяется из выражения
1/п2 = 1/п? + 1/п2.
Здесь па, пт — коэффициенты запаса соответственно по нор-
мальным и по касательным напряжениям, определяемые как ука-
зано выше. Следует определять общий коэффициент запаса по уста-
лостной прочности и по текучести.
Пример 17.1. Построить для образцов из стали 35Х схемати-
зированную диаграмму предельных амплитуд, если предел проч-
ности стт = 95 кгс/мм2; условный предел текучести = ст0,2 =
= 75 кгс/мм2.
275
Пользуясь построенной диаграммой, установить, при каких
коэффициентах асимметрии цикла решающим будет расчет по те-
кучести, а не по выносливости. Найти пределы выносливости для
циклов с коэффициентами асимметрии = —0,4 и = +0,4.
Решение. Пользуясь приближенной зависимостью, приве-
денной в § 17.1, находим предел выносливости при симметричном
цикле изгиба: = 0,35опч + (7 -н 12) кгс/мм2.
Взяв среднее значение второго слагаемого, найдем
= 0,35 • 95 + 10 = 43 кгс/мм2.
Отложив по оси ординат в принятом масштабе отрезок, соот-
ветствующий найденному значению о_1( получим точку А, «изо-
бражающую» симметрич-
ный цикл (рис. 17.14). При-
няв по справочным данным
У, = 0,30, откладываем по
оси абсцисс отрезок ОВ,
равный (в масштабе диаг-
раммы)
а_, _ 43
S“ фо ”0,30-
= 143 кгс/мм2.
Рис. 17.14 Точки А и В соединяем
прямой линией. Из точки С,
абсцисса которой равна пределу текучести, проводим прямую CD под
углом 45° коси абсцисс. Все точки, лежащие выше этой прямой, соот-
ветствуют циклам, для которых максимальные напряжения выше
предела текучести. Таким образом, часть OALC диаграммы пред-
ставляет собой область безопасных циклов, для которых макси-
мальные напряжения ниже предела выносливости и предела теку-
чести. Для любого луча, проведенного из начала координат, тан-
генс его наклона к оси абсцисс равен характеристике цикла tg 0=
= Р = (1 - Я)/(1 + /?).
Луч 0L, проведенный в точку пересечения линий АВ и CD,
отделяет область циклов, для которых предел текучести меньше
предела выносливости (область OLC), от области, для которой
между указанными характеристиками существует противополож-
ное соотношение (область OAL). Координаты точки L найдем,
сосгавив уравнения прямых АВ и CD.
Уравнение прямой АВ oa = a_i-у ас = 43—]^ос.
Уравнение прямой CD оа = от— = 75— ос.
Абсцисса и ордината точки L пересечения прямых АВ и CD
43 — — (ос)ь = 75 — (ac)iA (<jc)l«45,8 кгс/мм2; (оа)ьг«29,2 кгс/мм2.
1^0
' 276
Характеристика циклов, соответствующих лучу OL,
х д 29,2 д
tg0o = Po = (^=4^ = °>64-
Коэффициент асимметрии указанных циклов
Ро = 7ъ? = 0,640, откуда /?0 = 0,2195.
1 "t"
Таким образом, для циклов, у которых коэффициент асиммет-
рии больше 0,2195, коэффициент запаса по пределу текучести мень-
ше коэффициента запаса по пределу выносливости.
Для определения пределов выносливости при заданных коэффи-
циентах асимметрии найдем предварительно соответствующие ха-
рактеристики циклов: pi = ! ~ о1 = 1 7 = 2,33; р2 = г7-б-2 =
I I — 1 "Т“ ^2
= 1°’* = 0 428
1 + 0,4 и’ °’
Проведя из начала координат лучи под углами 0£ — arc tg рх
и 02 = arc tg р2 к оси абсцисс, получим точки и К2 (см. рис
17.14), «изображающие» предельные циклы с коэффициентами
асимметрии соответственно = —0,4 и = +0,4. Сумма абс-
циссы и ординаты точки Ki дает предел выносливости соответствую-
щего цикла. Непосредственно по диаграмме находим <т_ол =
= 55 кге/мм2. Аналогично для точки К2 <тоЛ = 84,5 кге/мм2.
Естественно, что второй из определяемых пределов выносливости
оказался выше предела текучести.
Пример 17.2. Определить коэффициент запаса прочности для
оси диаметром d = 36 мм, изготовленной из стали 45, для кото-
рой апч — 60 кге/мм2, о_1 = 24 кге/мм2, если изгибающий момент,
возникающий в поперечном сечении оси, изменяется в пределах
А1тах = —Л1пип = 350 кгс • м. Поверхность оси чисто обточена.
Форма оси строго .цилиндрическая (концентраторы напряжений
отсутствуют).
Решение. Определяем максимальное напряжение цикла
Птах = cP = (350 • 102)/^ 3,63 = 765 кгс/см2.
Общий коэффициент снижения предела выносливости при сим-
метричном цикле /Сад = &а/е„еп.
В данном случае ka= 1. Значения 8„, еп определяем по гра-
фикам, приведенным на рис. 17.12 и 17.13: е„=0,87; еп = 0,89.
Предел
выносливости
детали о—1 д — — 24/Q . 0,89 —
= 18,6 кге/мм2. Коэффициент запаса прочности п = —— = =
amax
= 2,44.
277
Пример 17.3. Ступенчатый стержень (рис. 17.15) из стали
50Г2 (опч = 75 кгс/мм2) нагружен ссевой силой, изменяющейся
по симметричному циклу. Поверхность стержня шлифованная.
Определить допускаемую величину амплитуды осевой силы
[Ртах] при требуемом коэффициенте запаса прочности [п] = 2.
Решение. Условие прочности стержня п = ^~1р” = ст~1р
^шах т, 'max
nd2
°-1р Т
г-8
• Р
Р
> [п], откуда [Ртах] = [п ] .
По графику рис. 17.7 эффективный коэффициент концентрации
напряжений ka « 1,62. Масштабный коэффициент (по рис. 17.12)
ем = 0,81. Коэффициент поверхностной чувствительности (по рис.
17.13) еп = 0,93.
Общий коэффициент снижения
предела выносливости при сим-
метричном цикле доо =---------=
емеп
__ __lj62_____„ IE
— 0,81 • 0,93 ~
Предел выносливости при симметричном цикле растяжения —
сжатия определяем по эмпирическим зависимостям, приведенным
в § 17.1: а_х к* 0,43оПч; o-iP « 0,8o_i = 0,8 • 0,43оПч = 0,8 • 0,43 х
X 75 = 25,8 кгс/мм2.
Рис. 17.15
Окончательно имеем [Ртах] = 25,8 3,1 / 2,15 2 — 12 х
X 10s кгс.
Пример 17.4. Ступенчатый брус круглого поперечного сечения
(D — 100 мм, d = 50 мм), изготовленный из стали 30ХГС.(опч =
— ПО кгс/мм2, стт = о012 = 85 кгс/см2), работает на изгиб при
напряжениях, изменяющихся по циклу с коэффициентом асимме-
трии Р = —0,6.
Максимальный изгибающий момент, возникающий в переход-
ном сечении от меньшего диаметра к большему Л4тах = 1000 Н • м.
Радиус галтели переходного сечения г = 5 мм. Поверхность бруса
подвергнута обкатке роликами, в результате чего коэффициент
поверхностной чувствительности имеет значение еп = 1,15.
Определить коэффициент запаса прочности для переходного
сечения. ;
Решен не. Определяем предел выносливости при симметрич-
ном цикле изгиба по эмпирической формуле, приведенной в § 17.1:
-О-i = 0,35опч + 12 = 0,35 • ПО + 12 = 50,5 кгс/мм2.
Эффективный коэффициент концентрации напряжений опреде-
ляем по рис. 17.9: /га = 1,7. Масштабный коэффициент (см. рис.
17.12) е„ = 0,81. Общий коэффициент снижения предела вынос-
278
Tr ч 1,7 ion
ливости при симметричном цикле = оУРТиГ =
Коэффициент чувствительности к асимметрии цикла по спра-
вочным данным = 0,3.
Максимальное нормальное напряжение, возникающее в прове-
ряемом сечении детали,
отах = Мтах^3 = Ю001 ^503 = 81,5 Н/мм2 = 8,3 кгс/мм2.
Амплитуда цикла нормальных напряжений
+nax CTmin 1 — R о о 1 — (—®,6) сел , 9
а0 -----------_ Qniax __— _ 8;з----'2—~~ = 6,64 кгс/мм-.
Среднее напряжение цикла нормальных напряжений
сттах "1“ ^min 1 + R о о 1 4~ (—®>6) , сс / 2
+ ----g------~ атах —Г" — °>3 -Л-1—~ = 1,66 кгс/мм -
Коэффициент запаса прочности
„ — a-i —______________52^_________ — 4 о 1
KoDaa 4- ++ 1,82 - 6,64 + 0,3. 1,66 ~ 1 •
Коэффициент запаса по отношению к пределу текучести
Пример 17.5. Определить коэффициент запаса прочности для
опасного поперечного сечения вала, в котором возникают пере-
менные изгибающий и крутящий моменты: Мта* = 48 кгс • м,
Almtn = —24 кгс • м, max Л4К = 76 кгс • м и min Л4К = 38 кгс X
Хм. Опасное сечение совпадает с переходом от D = 60 мм к d =
40 мм. Радиус галтели г = 2 мм.
/Материал вала сталь 45, улучшенная, с механическими харак-
теристиками апч =* 75 кгс/мм2, <тт = 45 кгс/мм2, тт = 26 кгс/мм2,.
a.i = 34 кгс/мм2 и тч = 19 кгс/мм2. Коэффициенты чувствитель-
ности материала к асимметрии цикла фо = 0,22; фт = 0,12.
Поверхность вала шлифованная.
Решение. По графикам на рис. 17.9, 17.10, применяя ли-
нейную интерполяцию, определяем эффективные коэффициенты
г 0 2
концентрации напряжений при = -у = 0,05 и сгпч = 75 кгс/мм2
(на графиках радиус галтели обозначен р) /гао = 2,1; /гТо=1,60.
Так как отношение диаметров ~ = 1,5 < 2, то в величины
k„, k-, принятые на рис. 17.9, 17.10, надо внести поправки.
По графикам рис. 17,11 уточняем значения
1 + МЧ- 1) = 1 + 0,95(2,1 - 1) = 2,05;
= 1+МЧ- 1)= 1 +'0,85(1,60- 1)= 1,51.
279
По кривой 2 рис. 17.13 при опч — 75 кгс/мм2 определяем ко-
эффициент поверхностной чувствительности еп = 0,93, масштабный
коэффициент находим по кривой рис. 17.12: ем = 0,84.
Общие коэффициенты снижения пределов выносливости при
„ k~ 2,05 „ „ k-
симметричных циклах К<>d =------— а ял поч = 2,63; К-о =--------=•
емеп и>°4 • U>yJ емеп
= —_______ — 1 94
0,84 • 0,93 1 ’
Наибольшие и наименьшие нормальные и касательные напря-
жения имеют следующие значения:
4800
_ max max _ чоии __ _ Krf,/r^.2.
Umax — o,lds ~ 0,1 . 43 ~ КГС/СМ ,
/Wmin 2400 „
Omin — — — 0 1 • 4s------375 кгс/см2;
max Л4К max Л4К 7600 „
Ттах 0,24s 0 2 • 4s 594 кгс/см ,
min 38ОО
Tmin = = -Q 2- 43 = 297 кгс/см2.
Амплитуды и средние напряжения циклов нормальных и каса-
тельных напряжений (кгс/см2):
а,
Ga ^fma^ CTmin^ Тб®------Ь£5) = 5б2)5;
gmax + CTmin _ 750 4- (—375) _ Jg7 5.
Tmax Tmin
2
^max 4" ^min
2
,48.5.
У4+-И7 = 445.5.
а —
Коэффициент запаса усталостной прочности по нормальным
напряжениям
_________CT-i_______________3400__________ л оз
’ AaDaa+ 2.63 • 562,5 + 0,22 - 187,5 ’
по касательным напряжениям —
n — T-i =__________________1900_______, _. 5 57
AxDta+1рхтс 1,94-148,5 + 0,12.445,5
Из выражения —= = -4- + -V находим общий коэффициент за-
". ", "т
паса по усталостной прочности
z2’23-5’57 - 9 ПЯ.
)/„2 + „2 V 2,233 + 5,57’
280
Коэффициенты запаса по текучести
°т 4500 „ тт . 2600 .
“ а ~ 750 — М — _ — 594 ~~ 4,37.
’’max 'ои ттах эа’
Общий коэффициент запаса по текучести
пт = - = Д 4-37 = 3,52.
К«;т + 4 1/ба + 5,372
Таким образом, решающую роль в данном случае играет уста-
лостная прочность, так как соответствующий коэффициент запаса
оказался меньше, чем коэффициент запаса по текучести.
Задачи для самостоятельного решения
17.1. Определить коэффициент запаса прочности стержня круг-
лого поперечного сечения d = 40 мм. Материал стержня углеро-
дистая сталь (стПч = 50 кгс/мм2; ст_х = — 20 кгс/мм2). Стержень
работает на изгиб при симметричном цикле напряжений. Макси-
мальный изгибающий момент Л4тах = 2560 кгс см. Поверхность
стержня шлифованная. Форма строго цилиндрическая без концен-
траторов напряжений.
Ответ, п ж 4.
17.2. Ступенчатый стержень из углеродистой стали с стп, =
= 50 кгс/мм2 и стт = 25 кгс/мм2 работающий на изгиб, имеет d —
= 3 см, D — 6 см и радиус галтели р = 1,5 мм. Коэффициент
асимметрии цикла R = 0,4; коэффициент поверхностной чувстви-
тельности с учетом упрочнения еп = 1,3. Коэф-
фициент чувствительности к асимметрии цик-
ла фз = 0,15.
Определить допускаемое напряжение для
стержня при коэффициенте запаса прочности
[п] = 1,4.
оз
II
Ответ. [ст0,41 29 кгс/мм3.
МО
Рис. 17.16
17.3. Вал с кольцевой выточкой (рис. 17.16)
работает на изгиб с кручением, при этом изгибающие и крутящие
моменты переменны во времени: Мтй* = 500 кгс • м; TMmin =
= 100 кгс • м; max Мк = 500 кгс • м; min Мк = 200 кгс • м.
Материал вала сталь 45 с механическими характеристиками:
оПч = 60 кгс/мм2; от = 30 кгс/мм2; ст_х = 26 кгс/мм2; тт =
18 кгс/мм2 т_г = 14 кгс/мм2; фа = 0,20; <pt = 0,1. Поверхность
вала шлифованная.
Определить коэффициенты запаса по усталостной прочности
и по текучести для сечения по кольцевой выточке.
Указание. Теоретический коэффициент концентрации нормальных
напряжении определить по графику рис 17.6; затем найти коэффициент чув-
281
ствительностн материала к концентрации напряжений (см. рис. 17.5) и вы-
числить эффективный коэффициент напряжений. Для кручения эффективный
коэффициент концентрации напряжений принять равным 0,65 от эффектив-
ного коэффициента концентрации нормальных напряжений.
Ответ. По усталостной прочности п «г 3,8; по текучести п 3,5.
ГЛАВА 18. РАСЧЕТ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ
НАГРУЗКАМ *
§ 18.1, Основные понятия
Расчеты на прочность элементов конструкций при статическом '
нагружении, рассмотренные в предыдущих главах пособия, вы-
полнялись по методу допускаемых напряжений. При этом методе
расчета прочность элемента конструкции считается нарушенной,
если хотя бы в одной точке элемента напряжение достигает пре-
дельного зиачеиия. В общем случае имеется в виду эквивалентное
(приведенное) напряжение, вычисленное по принятой для расчета
теории прочности. Наряду с названием «расчет по допускаемым
напряжениям» такой метод может быть назван расчетом по
опасной точке.
Для конструкций из пластичных материалов при статическом
нагружении возможен принципиально иной подход, к оценке их
прочности. Возникновение текучести в отдельной точке (или точ-
ках) конструкции не приводит к ее выходу из строя и поэтому
соответствующее состояние конструкции не считается предельным.
Несущая способность конструкции будет исчерпана при условии,
что она обратится в геометрически изменяемую систему, не способ-
ную оказывать сопротивление возрастающей нагрузке и неогра-
ниченно деформирующуюся при постоянной нагрузке. Указанное
состояние конструкции называется предельным, а соответ-
ствующая нагрузка (сила, момент) называется предельной
нагрузкой.
При таком подходе к расчету коэффициентом запаса прочности
конструкции является отношение предельной нагрузки к рабочей
(эксплуатационной) нагрузке, действующей на конструкцию. Этот
коэффициент запаса должен быть не меньше требуемого (заданного,
допускаемого) коэффициента запаса для данной конструкции. Ме-
тод расчета на прочность, основанный на изложенных представле-
ниях, называют расчетом по предельным нагрузкам. Встречаются
и другие названия, в частности, «расчет по допускаемым нагрузкам»,
«расчет по несущей способности», «расчет по предельному равно-
весию».
* См. учебное пособие (38].
282
^т°^пц(^т~^-пц)
к .
е(Т)
Рис. 18.x
Условие прочности при расчете по предельным нагрузкам за-
р М
писывается в виде п ~ или п = — [и]> где
/’пред (Л/пред) — предельное значение нагрузки (силы или момента),
при котором несущая способность конструкции оказывается ис-
черпанной; Р (М)—рабочая нагрузка конструкции; п — действи-
тельный коэффициент запаса прочности; [п] — требуемый (задан-
ный) коэффициент запаса прочности.
Рассматриваемые ниже расчеты по предельным нагрузкам бази-
руются на допущении о том, что материал конструкции является
идеально упруго-пластическим..Диаграмма деформирования такого
материала состоит из двух прямолинейных участков (рис. 18.1) —
при напряжениях ниже предела пропорциональности (стпц или тпц)-
соблюдается закон Гука, затем возни-
кает текучесть. При этом принимается,
что пределы пропорциональности равны
пределам текучести, т. е. стПц = сгт,
тПц = тт, и, кроме того, считается, что
площадка текучести имеет неограничен-
ную протяженность.
Применение такой схематизирован-
ной диаграммы деформирования мате-
риала (она называется диаграммой
Прандтля) существенно упрощает расчеты по предельным нагруз-
кам. Из диаграммы Прандтля следует, что при возникновении те-
кучести в какой-либо точке конструкции (либо во всех точках
элемента конструкции или некоторого его сечения) рост напряже-
ний в этой точке прекращается независимо от возрастания нагруз-
ки, действующей на конструкцию.
В статически определимых системах, элементы которых рабо-
тают на растяжение или сжатие, результат расчета по предельной
нагрузке, очевидно, совпадает с результатом расчета по опасной
точке. Действительно, при возрастании нагрузки текучесть возни-
кает одновременно во всех точках наиболее напряженного элемента
конструкции, а переход в состояние текучести одного элемента
превращает систему в геометрически изменяемую. В статически
неопределимой системе, элементы которой в упругой стадии работы
системы нагружены различно, возникновение текучести в каком-
либо одном элементе (а при системах многократно статически не-
определимых и в нескольких элементах) не приводит к исчерпанию
несущей способности, так как остальные элементы системы, находя-
щиеся в упругом состоянии, еще способны оказывать сопротивление
возрастанию нагрузки. В этих случаях предельная нагрузка РПред
будет больше нагрузки Рт, при которой текучесть возникает лишь в
одном элементе. При расчете по опасной точке нагрузка Рт рассмат-
ривается как опасная, и допускаемая нагрузка определяется как
частное от деления нагрузки Рт на требуемый коэффициент запаса.
283
Отсюда следует, что допускаемая нагрузка для статически
неопределимой системы, рассчитанной По предельным нагрузкам,
будет больше, чем в случае расчета этой же системы по опасной
точке, если в обоих методах расчета требуемые коэффициенты
запаса будут приняты одинаковыми. Практически коэффициенты
запаса при расчете по предельным нагрузкам принимают несколько
выше, чем при расчете по опасной точке, как следствие, различие
в результатах расчета несколько уменьшается по сравнению с полу-
чающимся при одинаковых коэффициентах запаса.
В тех случаях, когда в упругой стадии работы системы напря-
жения в поперечных сечениях ее элементов распределены неравно-
мерно (например, при кручении или при изгибе), расчет по пре-
дельным нагрузкам также дает результат, отличный от получаю-
щегося при расчете по опасной точке, даже если система стати-
чески определима. Подробнее об этом сказано в § 18.3, 18.4.
Рис. 18.2
§ 18.2. Расчет статически неопределимых систем
с элементами, работающими на растяжение или сжатие
Пример 18.1. Определить по способу предельных нагрузок
допускаемую величину силы Р для бруса (рис. 18.2). Материал
бруса сталь Ст.З с стт = 2400 кгс/см2; требуемый коэффициент
запаса [nl = 2.
Решение. Обозначив реакции опор соответ-
ственно Ра и Rb, составим уравнение равновесия
Ra + Rb = Р. (а)
Очевидно, что верхняя часть стержня испытывает
растягивающее усилие, равное Rb, а нижняя —
сжимающее усилие, равное Ra.
В предельном состоянии конструкции напряже-
ния в обеих частях стержня достигнут предела теку-
чести от сначала в верхней, а затем в нижней части,
поскольку нижняя часть стержня длиннее верхней*.
Выражая усилия Ra и Rb через от, уравнение
(а) можно представить в следующем виде; oTF -J-
СТТР = Рпред, или 2отР = Рпред-
Подставив числовые данные, получим Рпред = 2 • 2400 15 =
= 72 • 103 кгс.
Допускаемая нагрузка [Р] — = 72 2108 = 36 • 108 кгс.
Пример 18.2. Определить значения предельной и допускаемой
нагрузок для системы, изображенной на рис. 18.3, а. Балку АВ
считать абсолютной жесткой. Материал стержней сталь с пределом
* Верхняя часть стержня жестче, чем нижняя, н в упругой стадии рабо-
ты стержня усилие в.верхней части больше, чем в нижней.
281
текучести crT = 3000 кгс/см2. Площади поперечных сечений одина-
ковы /4 = F2 = F = 3 см2. Требуемый коэффициент запаса
[п] = 1,8.
Решение. Можно было бы рассмотреть упругую стадию
работы системы и убедиться, что усилие в первом стержне в этой
стадии больше, чем во втором. Следовательно, при возрастании
силы Р текучесть возникает раньше в стержне /; при дальнейшем
увеличении нагрузки напряжения в этом стержне будут оставаться
постоянными (это следует из диаграммы растяжения идеального
упруго-пластического материала, имеющего площадку текучести
неограниченной протяженности). Усилие в стержне 2 будет воз-
растать, пока напряжения в нем не достигнут предела текучести.
В этот момент несущая способность кон-
струкции будет исчерпана — она прев-
ратится в геометрически изменяемую
систему, свободно поворачивающуюся
вокруг шарнира А. В рассмотрении
упругой стадии работы нет необходимос-
ти — проще сразу рассмотреть предель-
ное состояние системы (состояние пре-
дельного равновесия), при котором оба
стержня находятся в состоянии текучес-
ти, применить метод сечений (рис.
18.3,5) и составить уравнение равновесия у тА = —Л/2преда—
~Nl пред2® + Рпред3а = °’ ИЛИ —OfFd—iOiFa + ЗРпредй = 0. Та-
КИМ образом, Рпред — OyF-
Допускаемое значение силы Р;
* го, ЗООО-з кллл
[Р] = ЙТ = “17“ = 5000 кгс-
Пример 18.3. Определить требуемые площади поперечных сече-
ний стержней, поддерживающих абсолютно жесткую балку (рис
18.4, а). Расчет выполнить по предельной нагрузке. Предел текуче
сти материала стержней стт = 2 600 кгс/см2; требуемый коэффи
циент запаса прочности [п] = 1,8.
Решение. Несущая способность системы будет исчерпана,
когда в каких-либо трех стержнях возникнет текучесть* Для
того чтобы установить, в какой последовательности стержни будут
переходить в состояние текучести, следовало бы раскрыть статиче
скую неопределимость системы в упругой стадии ее работы.Дакое
а 2 а 1 I _ а !
«т* 2 пред ^тред D р
л я Рпред ’
Рис. 18.3
* Исключением является случай возникновения текучести в стержнях
1, 2, 4, так как соответствующее состояние системы не является предельным.
Действительно, равнодействующая нагрузки совпадает с осью стержня 3, и
если он находится в упругой стадии, то при росте нагрузки усилие в нем
продолжает возрастать и несущая способность конструкции окажется исчер-
панной лишь тогда, когда текучесть возникнет и в этом стержне.
285
решение довольно громоздко, тем более, что заданная система дваж-
ды статически неопределима. Быстрее приводит к цели метод, назы-
ваемый иногда кинематическим. Сущность его заключается в том,
что последовательно рассматриваются все возможные варианты
исчерпания несущей способности системы, для каждого из них со-
ставляется уравнение предельного равновесия и определяется соот-
ветствующее значение предельной нагрузки. Очевидно, что истин-
ной предельной нагрузкой^будет меньшая из соответствующих раз-
личным вариантам перехода системы в предельное состояние.
Применим этот
заданной
метод к
системе.
F 6
6r2F 6TF
f 4
6TF
4 „ ii „4
7- 2-
Ди ...АВ
6T2F 6TF
5 Г
J—to
6TF
нгс[м
' 6T2F
"г
♦
шп
Рис.
6TF 6TF
4
д
6j-F 6tF 6TF
18.4
3
4-
a C
а П
г
Вариант 1 (рис. 18.4,6) — предполагаем, что текучесть воз- j
никла в стержнях 1, 2, 3. Тогда уравнение предельного равнове- 1
сия запишется в виде % то = О', or2F3aoTF2a + oTFa1
-~^преД2аа =. О, откуда ^пред = Эстт^/га. *
Вариант 2 (рис. 18.4, в) — предполагаем, что текучесть воз- ]
никла во всех четырех стержнях (случай, когда стержень 3 нахо- J
дится в упругой стадии при текучести остальных стержней, це явля- а
ется состоянием предельного равновесия — см., вторую сноску |
в § 18.2). J
Проектируя все силы на вертикальную ось, получаем oT2F + j
+ cttF + crTF + aTF — 2дпреЛа = 0, откуда = 5oTF/2a. j
Вариант 3 (рис. 18.4, г)—предполагаем, что текучесть возни- *
кает во всех стержнях, кроме второго, т. е. в предельном состоя-J
нии балка поворачивается вокруг точки В. При этом стержень 13
сжат*, а стержни Зи 4 растянуты. Уравнение предельного равно-3
весия: £ тв = 0; —aT2Fa — oTFa — oTF2a -|- q"^ejfi.aa = 0, откуда!
Уиред = бСТт/7 l^d. J3
* Для сжатых стержней принимаем, что опасность потери ими устой»у
чивости исключена.
2S6
Вариант 4 (рис. 18.4,5) — предполагаем, что текучесть возни-
кает во всех стержнях, кроме первого. Уравнение предельного
равновесия; У тд = 0; —oTFa— t^Fla— a-J'За + (Дред • 2а • 2а=
n iv 6aTF . -<rTF
= 0, откуда <7пред = = 1,5 — .
Итак, наименьшей оказалась предельная нагрузка, соответст-
вующая четвертому варианту, следовательно, <?преД является ис-
тинным значением предельной нагрузки.
УсЛОВИе ПрОЧНОСТИ КОНСТРУКЦИИ П = <7пред/<?^ [п], или п =
in а - Гт а 50.1,8-100 о о ,,г
= l,^F/aq^[n], откуда F>~^ = —f/s . 26ОО~ = 2’3 см '
Задачи для самостоятельного решения
18.1. Стальной стержень защемлен верхним концом и нагру-
жен, как показано на рис. 18.5. Между торцом стержня и неподат-
ливой 'плоскостью до нагружения имеется зазор 6 = 0,03 мм.
Найти по способу предельных нагрузок допускаемое значение
силы Р при стт = 2800 кгс/см2; In] = 2.
Ртвет, [Р] = 22,4 • 103 кгс.
Рис. 18.5
• Рис. 18.6
18.2. Для конструкции по рис. 18.6 определить по способу пре-
дельных нагрузок требуемое значение площади F. Пределы текучести
для материалов стержней: (стт)ал = 2000 кгс/см2; (стт)м = 1600
кгс/см2; (Стт)ст = 2800 кгс/см2. Требуемый коэффициент запаса
in] = 2.
Ответ. F = 8,5 сма.
§ 18.3. Расчет на кручение бруса круглого поперечного
сечения
При кручении бруса круглого поперечного сечения касатель-
ные напряжения в его поперечных сечениях распределяются по
линейному закону (рис. 18.7); максимального значения эти напря-
287
жения достигают в точках контура: ттах = MJWP. Следовательно,
материал внутри бруса остается недонапряженным.
При возрастании крутящего момента до величины /Икт напря-
жения в точках контура сечения достигнут предела текучести т„
а внутри брус будет находиться в упругом состоянии; при дальней-
шем возрастании крутящего момента напряжения во внутренних
точках бруса также достигнут предела текучести. На рис. 18.8
Пластическая область
Рис. 18.8 Рис. 18.9
касательных напряжений для случая, когда
представлена эпюра
часть поперечного сечения охвачена текучестью, а внутренняя об-
ласть находится в упругом состоянии.
При дальнейшем увеличении крутящего момента будет достигнуто
такое состояние, когда упругая зона исчезнет и по всему сечению
напряжения будут равны пределу текучести (рис. 18.9). Это будет
предельное состояние, соответствующее полному
исчерпанию несущей способности бруса.
Предельный крутящий момент, соответствую-
щий этому состоянию, /Ипред = WpTXT, где WPT —
пластический полярный момент сопротивления по-
перечного сечения.
Для сплошного кругового сечения WpT = nd3/12;
для кольцевого поперечного сечения (рис. 18.10)
lFpT = g(D3-d3) = ^-3(l-C3),
Рис. 18.10
где с — d/D.
При расчете
является опасным при возникновении текучести в точках контура J
поперечного сечения. Соответствующий крутящий момент /Икт= i
= Wpt„
Предельный
нию текучести
= Готтт.
по опасной точке считают, что состояние бруса
крутящий момент, соответствующий возникновв'
во всех точках поперечного сечения, Мк Пред =
М W
Таким образом, - “ пред = яр
^КТ " о
лО3
-12-
288
Это отношение стремится к единице по мере уменьшения тол-
щины стенки кольца. Максимальным оно получается для сплош-
М . пред лО3 InD3 __ 4
Л4КТ 12 j 16 3 '
ного сечения:
Пример 18.4. Определить по способу предельных нагрузок
требуемый диаметр бруса (рис. 18.11, а), если для материала бруса
предел текучести тт = 1600 кгс/см2; требуемый коэффициент за-
паса [п] = 2.
Решение. В предельном состоянии во всех поперечных
сечениях обоих участков бруса крутящие моменты достигают пре-
дельного значения Мк пред- Двумя се-
чениями а—а и b—Ь выделим часть
бруса (рис. 18.11, б). В состоянии пре-
дельного равновесия на отсеченную часть
действует внешний момент 9КпРед и кру-
тящие моменты Л1к пред, заменяющие
действие отброшенных частей бруса на
оставленную.
Условие равновесия оставленной час-
ти бруса: 2Мк пред — ^пред— 0; ®1пред =
__ о ля — О — _nd3
— бМк пред — |2 — g Тт.
т-г „ .л*, *-“‘пред пи- ли-
Допускаемый момент равен [ж] = Тт ~ Тт’ от'
3 12 [SR]
куда |/ —.
По условию прочности момент 9R, приложенный к брусу, ра-
вен допускаемому моменту, т. е. [9R] = 9R = 8 • 108 кгс • см, еле-
3 /” 12 • 8 • 16*
довательно, d— у 3 . 16QQ = 12,4 см.
При решении этой задачи по способу предельных нагрузок
отношение длин участков : /2 не имеет значения. При применении
способа допускаемых напряжений величина этого отношения имеет
существенное значение,— допускаемая величина момента будет
наибольшей при = /2.
Пример 18.5. Стальной валик и дуралюминиевая трубка за-
креплены одним концом в неподвижной опоре, а на другом конце
жестко соединены диском А, к которому приложен скручивающие
момент 9R (рис. 18.12, а). Определить из расчета по методу пре-
дельных нагрузок допускаемое значение скручивающего момента,
если пределы текучести материалов валика и трубки: (тг)ст =
= 170 Н/мм2; (тт)д = 130 Н/мм2 и требуемый коэффициент запаса
прочности [п] = 2,2.
Решение. Независимо от того, возникнет ли текучесть
раньше во всех точках поперечного сечения трубки или валика,
несущая способность конструкции будет исчерпана лишь при пере-
1 10 । j о
289
ходе в состояние текучести обеих деталей. Для состояния предель-
ного равновесия получим (рис. 18.12,6) ®пред — Мпред + Мпред,
где Мред = (Тт)ст = 170--14^25а = 695 • 103 Н • мм = 695 Н • м;
^ред = (тт)д [1 - (А)3] = 130^АВ8 [1 - (g Л = 950 X
X 103 Н • мм = 950 Н • м.
Таким образом ЭДпред = 695 + 950 = 1645 Н • м.
Рис. 18.12
Допускаемый момент [9R] = ~~р^ед = уу = 750 Н • м.
Рекомендуем для сравнения определить (при той же величине
коэффициента запаса)' значение допускаемого момента из расчета
по допускаемым напряжениям.
Задачи для самостоятельного решения
18.3. Для бруса кольцевого поперечного сечения найти отноше-
ние предельного крутящего момента Мк пред к крутящему моменту
Мкт, при котором теку-
честь возникает в точках
внешнего контура попереч-
ного сечения. Рассмотреть
два случая: а) отношение
внутреннего диаметра коль-
ца к наружному с = dlD =
= 0,5; б) с = d/D =- 0,8.
Ответ, а) 1,24; б) 1,1.
18.4. Определить допускаемую величину 9R для бруса по рис
18.13, если тт = 18 кгс/мм2 и in] = 2.
Ответ. 23,4 • 10® кгс • см.
§ 18.4. Расчет статически определимых балок
При расчете на изгиб по допускаемым напряжениям (по опасной
точке) балки из пластичного материала опасным считается состоя-
ние конструкции, при котором в крайних точках опасного попереч-
290
ного сечения нормальные напряжения достигают предела текуче
сти. Для симметричного поперечного сечения (рис. 18.14, а) соот-
ветствующая эпюра нормальных напряжений представлена на рис.
18.14, б. При возрастании действующей на балку нагрузки, а сле-
довательно, и изгибающего момента, возникающего в опасном
поперечном сечении, текучесть будет охватывать все большую часть
сечения; для некоторой стадии нагружения эпюра нормальных на-
пряжений будет иметь вид по рис. 18.14, в. Во всех точках той зоны
сечения, которая охвачена текучестью, напряжения равны ат
(предполагается, что диаграммы Прандтля для сжатия и растяже-
ния одинаковы); для части сечения, работающей упруго, напряже-
ния распределены нели-
нейному закону.
Несущая способность
балки будет исчерпана,
когда во всех точках
опасного поперечного се-
чения нормальные на-
пряжения достигают
предела текучести (рис. Рис 18 д4
18.14, г). Соответствую-
щий изгибающий момент является предельным (МпРед)- Если хотя бы
в одном поперечном сечении статически определимой балки изги-
бающий момент достиг предельного значения, то балка обращается
в механизм и теряет способность сопротивляться дальнейшему воз-
растанию нагрузки.
Возникновение полной текучести в некотором поперечном сече-
нии балки можно уподобить образованию в этом сечении шарнира
(так называемый пластический шарнир или шарнир текучести),
который позволяет при постоянной нагрузке (предельной) частям
балки, разделенным этим шарниром, свободно поворачиваться
относительно друг друга. Пластический шарнир является одно-
сторонним, т. е. он допускает взаимный поворот частей балки
лишь в направлении, соответствующем предельному изгибающему
моменту. При разгрузке балки (или, что то же самое,— приложе-
нии к балке дополнительной нагрузки противоположного направ-
ления) поворот становится невозможным.
Предельный изгибающий момент определяется по формуле
Л1Пред = Стт^т, где Г т — так называемый пластический момент со-
противления поперечного сечения балки.
При симметричном поперечном сечении (см., в частности,
рис. 18.14) ff’'T~2SmsJ. Здесь Sma3t — статический момент поло-
вины сечения относительно нейтральной оси. Например, для пря-
моугольного сечения шириной b и высотой Л W? = 2 =»
bh*
4 *
*/» Ю1
291
Рис. 18.15
А
шпшшшшп
* 400см я
При несимметричном поперечном сечении (рис. 18.15) нейтраль-
ная ось при охвате текучестью всего сечения делит его на две рав-
новеликие части (положения нейтральной оси в упругой и плас--
тической стадиях работы не совпадают). Пластический момент со-
противления определяется по формуле 1FT = + S2, где и
S2 — статические моменты полусечений относительно нейтральной
оси (Si S2). Значения Sj и S2 принимаются по модулю (по абсо-
лютной величине).
Строго говоря, сказанное выше относится к чистому изгибу ба-
лок, но практически влияние поперечных сил очень мало и приве-
денные зависимости дают вполне достаточную точность и при попе-
речном изгибе.
Изгибающий момент, при котором- напря-
жения, равные пределу текучести, возникают
только в крайних точках опасного попереч-
ного сечения (см. рис. 18.14, б), обозначают
Мт; его величина определяется из выражения
Мт = отГ.
С позиций расчета по опасной точке мо-
мент Мт является опасным. Из приведенных
формул следует, что отношение предельного
изгибающего момента к моменту Мт равно
отношению пластического момента сопротивления к моменту со-
противления при изгибе (так сказать, обычному): а = МпРед/Мт —
= WT/W.
Величина этого отношения, очевидно, всецело определяется
формой поперечного сечения. Так, для прямоугольного попереч-
ного сечения а = 1,5; для прокатных двутавров при изгибе в плос-
кости наибольшей жесткости в среднем а — 1,15.
Отношение допускаемых изгибающих моментов, определенных
из расчета по предельной нагрузке и по опасной точке, несколько
меньше а, так как, ведя расчет
но предельной нагрузке, обычно
принимают более высокий коэффи-
циент запаса, чем при расчете по
допускаемым напряжениям.
Пример 18.6. Определить до-
пускаемую величину интенсивности
равномерно распределенной нагрузки для двухопорной балки по
рис. 18.16. Поперечное сечение балки изображено на рис. 18.17.
Предел текучести материала балки от = 2300 кгс/см2, требуемый
коэффициент запаса [п! =1,6.
Решение. Определим положение нейтральной оси попереч-
ного сечения из условия, что оиа делит поперечное сечение на две
равновеликие части (в предельном состоянии). Площадь стенки
больше площади полки, и, следовательно, нейтральная ось пере-
секает стенку. Обозначив у0 расстояние нейтральной оси от внутрен-
292
ней грани полки и учитывая, что F1 — Ft (см. рис. 18.17), получим
10 • 1 + 1 • у0 = 1 • (20 — уа), откуда у0 = 5 см.
Статические моменты полусечений Относительно нейтральной оси
= 1 . 15 . ^ = 112,5 см3;
S2 = 10 • 1 . 5,5 + 1 • 5 • 2,5 = 67,5 см3;
Пластический Момент сопротивления поперечного сечения
WT = Sj + S2 = 112,5 + 67,5 = 180 см3.
Предельный изгибающий момент
Л1ПреД= oTlFT= 2300 • 180 = 414 • КРкгс • см.
Допускаемый изгибающий момент
[М] = = 414 ‘ 108 = 258,8 • 103 кгс • см.
[л| 1,6
Наибольший изгибающий момент возни-
кает в сечении посередине пролета: /Итах =
= qF!8.
Приравняв максимальный изгибающий мо-
мент допускаемому, получим [</] z2/8 =
ГЛЛ1 8 [Af] 8 - 258,8-103
= [Л4], откуда [</] = =-------pj----=
= 12,94 кгс/см.
Пример 18.7. Определить из расчета по предельным нагрузкам
требуемый номер профиля прокатной двутавровой балки длиной
I = 8 м, лежащей на двух опорах, при действии постоянной на-
грузки интенсивностью q = 800 кгс/м и сосредоточенной силы
Р = 2000 кгс, приложенной посередине пролета. Предел текучести
от = 2400 кгс/см2. Коэффициент запаса прочности [п] = 1,6. Ка-
кой номер двутавра нужно взять, если подбор сечения вести по до-
пускаемым напряжениям при том же коэффициенте запаса?
Решение. Наибольший изгибающий момент (в сечении по-
Л . .. ql2 , Pl 800-8® . 2000 -8 1Л/|ПП
середине пролета) Afmax = V + Y =—$— --------4—— Ю400 кгс-м.
Для симметричного сечения условие прочности по предельным
2<S_g,.(Jp
нагрузкам выражается формулой п = [п], где
"''max '"max
Зтах — статический момент половины сечения отнрсительно ней-
тральной оси.
- , со ^тах, , 10400- 10«- 1,6
Требуемая величина Smax: Smax = [п] ----2 >2400— ==
= 347 см3.
По сортаменту (ГОСТ 8239—72 — см. приложение) подходит
двутавр № 33, у которого Sx — 339 см3 (перегрузка 2,36%).
293
При расчете по допускаемым напряжениям
ту/ ^max ^тах f . 10400 • 10* • 1,6 спп з
W = M” = -Vfnl = —2400-----------= 692 СМ =
подходит двутавр № 36, у которого W = Wx = 743 см3.
Пример 18.8. Определить сжимающее усилие, по которому
надо вести расчет винта пресса, предназначенного для гибки дву-
тавровых балок (рис. 18.18). Наибольший двутавровый профиль
№ 22. Максимальный предел текучести материала изгибаемых на
прессе балок ат = 26 кгс/мм2.
Решение. Расчетное усилие для винта пресса определяется
из условия, что в среднем сечении двутавра должен возникнуть
8.6
220
Рис. 18.19
пластический шарнир, т. е. изгибающий момент в этом сечении дол-
жен быть равен предёльному. Для двухопорной балки, нагружен-
ной силой, приложенной посередине пролета Mmax = РИ$-
Учитывая, что Л4тах = Л4пред, получаем Р — 4Мпред//.
Для определения Л4прад вычислим статический момент полусе-
чения относительно нейтральной оси. Воспользуемся упрощенным ;
изображением сечения (закруглениями и уклонами полок прене- '
брегаем), представленным на рис. 18.19:
• Smax ^ 2 -5,5- 0,86-^- + (22-2 • 0,86) ^^ = 26,8 см3.
Пластический момент сопротивления №т = 25ТОах =• 2 • 26,8 =
= 53,6 см3. Предельный момент Л4пРед = = 2600 ; 53,6 я»
* 4Л1 4 13 9 • 10*
~ 13,9 • 10*кгс • см. Расчетное усилие Р = ———
= 7950 кгс.
Задачи для самостоятельного решения
18.5. Балка длиной I = 1,2 м, шарнирно опертая по концам,
несет равномерно распределенную по всей длине нагрузку. Попе-
речное сечение балки показано на рис. 18.20. Определить допускае-
мую интенсивность нагрузки, если от = 250 Н/мм2 и (nJ — 1,7,
Ответ. 17,85 кН/м.
294
18.6. Для балки двутаврового поперечного сечения (двутавр
№ 40) определить отношение величины предельного изгибающего
момента МпРед к величине изгибающего момента Мт, соответству-
ющего возникновению текучести в крайних точках поперечного
сечения. Рассмотреть случаи изгиба балки в плоскости наибольшей
и наименьшей жесткости.
Ответ а) При изгибе в плоскости наибольшей жесткости а = 1,14;
б) при изгибе в плоскости наименьшей жесткости а = 1,89.
Рис. 18.20 Рис. 18.21
18.7. Выполнить то же, что и в предыдущей задаче, для балки
коробчатого сечения по рис. 18.21. Изгиб балки происходит в плос-
кости наибольшей жесткости.
Ответ, а — 1,28.
§ 18.5. Расчет простейших статически неопределимых балок
В -статически неопределимых балках за редким исключением
возникновение одного пластического шарнира не приводит к исчер-
панию несущей способности балки.'В частности, один раз стати-
чески неопределимая балка без консолей превращается в геометри-
чески изменяемую систему при возникновении двух пластических
шарниров (см. примеры 18.9, 18.10). Несущая способность дважды
статически неопределимой балки обычно оказывается исчерпанной
при возникновении трех пластических шарниров. В результате для
статически неопределимой балки величина нагрузки, соответствую-
щей возникновению текучести в крайних точках лишь одного попе-
речного сечения, отличается от предельной существенно больше,
чем для статически определимой балки, имеющей поперечное сече-
ние той. же формы.
Количество пластических шарниров, которые необходимы для
перехода балки в предельное состояние (превращение ее в геоме-
трически изменяемую систему), далеко не всегда должно быть на
единицу выше степени статической неопределимости балки. Много-
пролетная статически неопределимая балка (неразрезная балка)
теряет несущую способность, если хотя бы один из ее пролетов об-
ращается в геометрически изменяемую систему.
295
Для определения предельной нагрузки можно рассмотреть упру-
гую стадию работы балки и установить последовательность возник-
новения пластических шарниров, необходимых для превращения
балки в механизм .(см. пример 18.9). Значительно проще, минуя
рассмотрение упругой стадии работы системы (не раскрывая ста-
тическую неопределимость), установить возможные варианты исчер-
пания несущей способности балки и вычислить для каждого из
них предельную нагрузку. Действительной предельной на-
грузкой будет меньшая
из определенных
указанным
Ы‘-2Ц
\32-103кгсм
Мпред
В
“пред
д
^преа‘7,81-1О3кгсм
'1,81'Ю3кгс-м
е
Рис. 18.22
Этот прием расчета применяется в примерах данного параграфа, ’
кроме примера 18.9.
Пример 18.9. Для балки по рис. 18.22, а, определить коэффи- -
циенты запаса из. расчетакпо опасной точке и по предельной на-
грузке. Для материала балки от 2400 кгс/см2. ;
Решение. Для расчета по упругой стадии работы материала '
балки следует раскрыть статическую неопределимость одним из ]
методов, рассмотренных ранее. В частности, можно применить метод J
сил, выбрав в качестве основной системы балку с отброшенной шар-
нирной опорой. В этом случае лишней неизвестной (XJ является J
реакция .отброшенной опоры. В результате решения канонического 3
54 Ч
уравнения получается Хх = Р. Соответствующая эпюра изги- j
бающих моментов представлена на рис. 18.22, б. Максимальное 1
нормальное напряжение, возникающее в сечении под силой, оШах = 1
= = 4,328‘910 = 1490 кгс/см2, где 1Гг — 289 см® (в таблице |
ГОСТ 8239—72 обозначено Ц7Х). 1
Коэффициент запаса по напряжениям п = ат/отг,х = 2400/1490 = ч|
= 1,61. /
296
При возрастании действующей на балку нагрузки до некоторой
величины Рг в сечении С возникает пластический шарнир (рис.
18.22, в). Таким образом, балка становится_статически определимой,
но ее несущая способность еще не исчерпана. Эпюра изгибающих
моментов, соответствующая возникновению пластического шарнира
в сечении С, представлена на рис. 18.22, г. Величина предельного
момента определяется из выражения
Мпред = 25тах<Тт = 2 • 163 • 2400 = 7,81 • 105 кгс • см,
где Smax = 163 см2 (по ГОСТ 8239—72) — статический момент по-
лусечения относительно нейтральной оси.
При дальнейшем возрастании нагрузки балка работает как
статически определимая, нагруженная в промежуточном шарнире
сосредоточенной силой (которая возрастает) и постоянными мо-
мёнтами Л4Пред- Исчерпание несущей способности балки наступает
при возникновении второго пластического шарнира. Очевидно, он
возникает в сечении Л. Балка обращается в механизм (рис. 18.22, д).
Эпюра изгибающих моментов, соответствующая состоянию пре-
дельного равновесия, представлена на рис. 18.22, е.
Величину предельной нагрузки определим, составив выраже-
ния для изгибающих моментов в сечениях С и А: Мс = Л4пред=
= RBb, откуда RB = Мпред/6; МА = — Мпред = Rb (а + Ь) —
- РпРедй = ^-л(а + Ь) - Рпреда, откуда Рпред =
Чред , 2ЧРед 7,81-106 , 2 • 7,81 • 106
b ‘ а — 200 ‘ 300
9110 кгс.
Коэффициент запаса из расчета по предельной нагрузке
i _ Чред _ 9110
Р ~ 5000
1,82.
Интересно отметить, что в рассмотренном примере статическая
неопределимость балки, почти не сказывается на отношении коэф-
фициентов запаса, определенных двумя методами. Действительно,
если условно принять, что предельное состояние соответствует
возникновению первого пластического шарнира, то коэффициент
запаса будет равен 1,81, т. е. почти не будет отличаться от най-
денного по истинному предельному состоянию, соответствующему
возникновению двух пластических шарниров. Причина такого
результата состоит в том, что оба пластических шарнира возникают
почти одновременно — изгибающие моменты в сечениях А и С
в упругой стадии работы балки (см. рис. 18.22, б) близки по абсо-
лютной величине.
Последовательность возникновения пластических шарниров не
влияет на величину предельной нагрузки. Можно было не рассма-
тривать упругую стадию работы балки, а сразу рассмотреть пре-
дельное состояние, и зная, что изгибающие моменты в сечениях
И 1-ю
297
а=2м
С д,
Ъ
А
а Л
N-22
Рис. 18.23
А и С равны Мпред, найти Рпред, как это было сделано в конце
приведенного решения.
Пример 18.10. Для балки по рис. 18.23, а определить допус-
каемую нагрузку из расчета по предельной нагрузке. Для мате-
риала балки ит = 2300 кгс/см2. Требуемый коэффициент запаса
щ] = 1,6.
Решение. Несущая способность балки будет исчерпана при
возникновении двух пластических шарниров. Совершенно очевидно,
что наибольшие изгибающие моменты возникают в сечениях, где
приложены силы Р, и над средней опорой. Какие из указанных
моментов больше,..для расче-
та по предельной нагрузке
не играет роли. В общем слу-
чае, если бы силы, прило-
1 женные в пролетах, были раз-
личны, следовало бы рассмот-
реть возможные варианты
возникновения двух пласти-
ческих шарниров и опреде-
лить соответствующие пре-
дельные нагрузки. Скажем,
можно принять, что пласти-
ческие шарниры возникают .
над средней опорой и в пра-
вом пролете в месте прило-
жения силы; затем принять,
что пластические шарниры
возникают над средней опо-
рой и в сечении под силой
в левом пролете. В заданной j
балке силы в пролетах равны и расположены симметрично отно-
сительно опор, следовательно, наибольшие моменты в пролетах \
(в сечениях под силами) одинаковы. Таким образом, здесь в ripe-
дельном состоянии возникают сразу три пластических шарнира
(хотя, повторяем, для перехода в предельное состояние было бы ’
достаточно и двух), как показано иа схеме механизма разрушения
балки (рис. 18.23, б).
• Соответствующая эпюра изгибающих моментов дана на рис. .
18.23, в
Для определения предельного значения сил Р составим выра-
жения для изгибающих моментов в сечениях D и В: Md ~
= МПред = Яла, откуда Ra = Мпрел/а-, Мв = —МпРед = Ra - 2а —
М 37Й
— Рпред • а = 2а — Рпред • а, откуда Рпред = —.
Вычисляем значение предельного момента Л4пред = 2SmaxaT =
= 2 • 131 • 2300 =и= 602 • 10® кгс • см, где Smajt = 131 см® принято по
ГОСТу 8239—72.
298
Предельная сила Рпр^л = ~-ред'= 3 ’ -3 = 9030 кгс.
Допускаемая сила [Р] = = 5644 кгс.
Пример 18.Ц*. Определить из расчета по предельной нагрузке
требуемый номер двутаврового профиля для балки по рис. 18.24, а.
ат — 2400 кгс/см2; [п] = 1,6.
Решение. При возрастании действующей на балку нагрузки
первый пластический шарнир возникает либо в заделке, либо
в каком-то сечении в пределах пролета; где именно — можно уста-
новить, выполнив расчет (раскрыв статическую неопределимость)
для упругой стадии работы балки, но
в этом нет надобности. Несущая способ-
ность балки будет .исчерпана при воз-
никновении двух пластических шарни-
ров — в заделке и в пролете. Соответст-
вующая схема балки представлена на
рис. 18.24,6, а на рис. 18.24,в дана эпю-
ра изгибающих моментов. Положение
сечения (в пролете), в котором возни-
кает пластический шарнир, заранее не-
известно; на рис. 18.24, б, расстояние
этого сечения от левой опоры обозначе-
но х0. Для составления зависимости меж-
ду предельной нагрузкой и величиной
предельного момента, что даст затем
возможность составить условие прочнос-
ти, выразим изгибающие моменты (предельные) в сечениях, где об-
разовались пластические шарниры, чер^з внешние силы, прило-
женные слева от этих сечений:
Мс = МПред= Рлх0-^-°;
а I*
Мв^~Мпрел=ЯА1--^-.
Этих двух уравнений недостаточно для установления зависи-
мости между Л4Пред и ^пРед. Так как момент в сечении С макси-
мален, то, следовательно, поперечная сила в этом сечении равна
нулю. Это условие и дает недостающее уравнение Qc — 0 = Ra —
— 9предХ0. Решив совместно приведенные* уравнения, найдем х0 =
9М _ М
= (/2-1)/=0,414/; <7пред-=-7г^(1 + /2)= Н.66
q = 3500 кгс/м
a Ш
£1=4м Л
Ъ
Р'пред
Рис. 18.24
* Составлен по материалам учебного пособия: С. М. Жда нов. Расчет
конструкций с учетом пластических свойств материала.— М.: Изд. Моск,
энерг. ин-та, 1952.— 80 с.
11*
299
а М W о
Условие прочности п = = 11,66 —^ед [п], или 11,66 /3=
, ,vz /2<7[п] 4002 . 35 .1,6 „„„ „
[и], откуда WTii^gg - 11,66 - 2400 3 20 см, т. е. требуе-
мый статический момент полусечения относительно нейтральной
ОСИ Sx = Smax = Wr/2 = 320/2 = 160 см3.
По ГОСТ 8239—72 принимаем двутавр № 24, у которого Sx =
= 163 см3.
Пластический шарнир в пролете возникает не в том сечении, в котором
в упругой стадии работы балки изгибающий момент максимален,— место
возникновения пластического шарнира несколько ближе к середине пролета.
Объясняется это тем, что первый пластический шарнир возникает в сечении
заделки (таким образом, говоря о максимальном моменте в пролете, имеют
ввиду наибольший момент в пределах пролета, исключая сечение заделки);
при дальнейшем возрастаниищагрузки балка работает как шариирио опертая.
Для такой балки изгибающий момент, обусловленный дальнейшим прирос-
том нагрузки, максимален в сечеиии посередине пролета. В итоге в упруго-
пластической стадии работы балки сечение с максимальным изгибающим
моментом смещается к середине пролета и при потере балкой несущей спо-
собности занимает найденное выше положение.
Если для упрощения расчета принять, что пластический шарнир (второй)
образуется посередине пролета, то ?ПЕед будет определяться из выражения
q = 12 —?р..еД ,
‘'пред /2
т. е. погрешность такого приближенного расчета составит 2,9%>
Задачи для самостоятельного решения
18.8. Для балки по рис. 18.23 найти отношение предельной на-
грузки Рпред к нагрузке Р<т, при которой текучесть возникает
в крайних точках опасного поперечного сечения.
Ответ. 1 27.
Рис. 18.25
а=2м
Р-6000кгс
Рис. 18.26
Р
18.9. Определить допускаемую величину интенсивности рас-
пределенной нагрузки для балки по рис. 18.25. Принять от =
= 240 Н/мм2, in] = 1,7.
Ответ. [<?] = 9,32 кН/м.
18.10. Определить требуемый номер двутаврового попереч-
ного сечения для балки по рис. 18.26. Принять от = 2500 кгс/см2;
[nl = 1,6.
300
Указание. Рассмотреть возможные варианты возникновения двух
пластических шарниров; найти предельное значение сил Р, соответствующих
каждому из этих вариантов.
Ответ. ЗОа.
ГЛАВА 19. УЧЕБНО-ИССЛЕДОВАТЕЛЬСКИЕ РАБОТЫ СТУДЕНТОВ
Одним из эффективных путей повышения качества подготовки специа-
листов с учетом требований иаучио-технической революции является все-
мерное развитие научно-исследовательской работы студентов, включенной
в учебный процесс.
• Начиная со II курса студенты привлекаются к учебно-исследовательской
работе (УИРС) по сопротивлению материалов. Они ведут теоретические и
экспериментальные исследования, имеющие непосредственное отношение
к их дальнейшей специализации, а также к научно-исследовательским рабо-
там, проводимым кафедрой.
На основе теоретических .сведений о напряжениях в поперечных сече-
ниях брусьев, в цилиндрах и дисках, вычисленных в зависимости от меха-
нических и температурных воздействий, предложены задачи для научно-
исследовательских работ студентов,-рассмотрен метод конечных элементов
(МКЭ) применительно к расчету балок и рам. Задачи снабжены методиче*
скими указаниями, облегчающими поиск решения. Большинство задач не
содержит ответов, что дает возможность руководителю УИРС и студенту
варьировать исходные данные задачи и конечную цель исследования.
Для выполнения расчетной части УИРС предполагается использование
ЭВМ. Некоторые программы для ЭВМ МИР представлены в приложений.
При исследовании других задач студент может составить программу само-
стоятельно, что само по себе также является элементом исследования. Приве-
денный набор задач может обеспечить учебно-исследовательской работой
значительную часть студентов. Некоторым студентам по усмотрению ка-
федры могут быть выданы экспериментальные или реферативные работы,
а также расчетно-проектировочные задания с элементами исследования.
Учебно-исследовательские работы, в том числе и реферативные, должны
способствовать более глубокому закреплению теоретических знаний по со-
противлению материалов, развивать умение самостоятельно разбираться
в рекомендованной литературе, развивать требовательность к себе, точность
при изложении полученных результатов, расширять возможность приобре-
тения уже в стенах института навыков научного исследования каждым сту-
дентом.
Отчет по УИРС включает: задание; исследование состояния вопроса
по литературным источникам; задачи исследования; описание мёТ&днки ис-
следования (для экспериментальных работ); решение поставленной задачи
(для теоретических работ); результаты исследования с графиками, табли-
цами, программами для ЭВМ; обсуждение (защиту) результатов исследова-
ния с выводами; список использованной литературы.
§ 19.1. Определение нормальных напряжений в поперечных
сечениях стержня с учетом механических
и температурных воздействий
Рассмотрим прямой неоднородный стержень с переменным по сечению мог
дулем упругости (рис. 19.1. а). Внутренние силовые факторы Nx, Ми, М
и их положительные направления показаны на рис. 19.1,6. Под действием
продольной силы Nx сечеиие параллельно перемещается на расстояние ш0,
под действием изгибающих моментов Мг и Му оно поворачивается относитель-
но осей соответственно на углы <р и ф.
301
С учетом гипотезы плоских сечеиий произвольная точка А сечения имеет
перемещение
w (у, г) = а>о + <РУ + Ф2- (1)
Деформация волокна, на котором находится точка А, определяется произ-
водной перемещения w по координате х:
где ем—деформация от механических воздействий;
в/ — температурная деформация;
Т = М— приращение температуры.
Из уравнений (2), (3) получаем
a=£(e-a7’)»£(e,+ {/^- + z-g.-arj) (4)
где £ — модуль упругости, зависящий от координат и температуры.
Внутренние силовые факторы определяются выражениями
Nx — ^odF, Mz=^oydF, Mu=\ozdF. (5)
f f 'f
Подставляя уравнение (4) в формулу (5), имеем
Nx = ^EdF + ^x j Ег dF — J EaT dF-,
F F F F
Л12 = е0 + Ezy dF — J EayT dF;
F F F F
Mv = e0 EzdF 1 Ez2dF—\ Ea.zT dF. (6)
F F F F
302
Выберем оси гну так, чтобы
J Ег dF = Еу dF = Eyz dF = 0.
F F F
(7)
Первые два интеграла называются упруго-статическими моментами
(обобщенными статическими моментами). Равенство их нулю обозначает,
что оси г и у проходят через приведенный центр тяжести сечения. Послед-
ний интеграл называют упруго-геометрическим центробежным моментом
инерции. Оси координат, удовлетворяющие условиям (7), называются глав-
ными обобщенными центральными осями инерции.
Из уравнений (6) с учетом (7) получаем
е0 = Nx ] $ EdF + j EaT dF / j EdF;
F F F
Ег2 dF.
(8)
(9)
(10)
F F
Выражения, стоящие в знаменателях зависимостей (8)—(10), называются
упруго-геометрическими характеристиками сечения.
, Подставляя выражения (8)—(10) в (4), находим
(J EaT dF
\ EdF \ Ey2dF I Ег2 dF I EdF
F F F F
j EaTydF § EaTzdF \
+ У :---И г А;----------аТ I
I Еу2 dF 1 Ег2 dF у
F F
(И)
Это общая формула для определения нормальных напряжений в произ-
вольном сеченни неоднородного стержня от механических и температурных
воздействий, когда температура и модуль упругости изменяются по сечению.
При постоянном модуле упругости первые три члена формулы (11) соот-
ветствуют напряжениям при растяжении с косым изгибом,остальные члены —
термонапряжениям. Температурные деформации в обшем случае температур-
ного воздействия записываются в виде ~
^EaTdF ^EaTydF § EaTzdF
Ч = ------1- у ----------1- z . (12)
I EdF . \ Ey2dF I Ez2 dF
F F F
§ 19.2. Температурные напряжения
. Пример 19.1, Найти температурные напряжения в прямом однородном
стержне с закрепленными торцами при постоянной температуре по длине
и сечению стержня (рис. 19.2).
303
Решение. Деформацию растяжения — сжатия находим по формуле
(8). Удлинение Д/о определяем интегрированием:
При Е = const условие совместности деформации имеет вид
Получена известная формула сопротивления материалов.
Пример 19.2. Определить температурные напряжения в защемленном
с двух сторон стержне постоянной жесткости (рис. 19.3), если температура
у ___________________________________________________j”
изменяется по параболическому закону Т'(х) = Го—-хп.
Решение. Условие совместности деформаций имеет вид уравнении (14).
Nx Г-п
Интегрируя с учетом изменения температуры Т (х), получаем —7ть+ « 'ох4"
Сг I
7\ — 7\ I
+ —— = 0.
I « + !](
о
Отсюда находим продольную силу и напряжения:
Nx=EFa^ + T^\, а^ = £а(то + ^о). (1б)
При n = 0, Т (х) = 7\ -= const Nx = EaT1F, а — ЕаЛ\. (17),
При п=1, Т(х) = 7’о + (Г1-Го)-1 /Vx^Ea^±^F, о = ЕаЩ-Ьр8)
Напряжения в этом случае равны термонапряжениям от температуры, '
равной средней температуре стержня.
При п = 2, Т (х) = То + хг
Nx^Ea(Tl) + '!-^^F,
q=a(r8+b- (I9>
304
Пример 19.3. Определить температурные напряжения в однородном пря-
моугольном стержне, если температура, оставаясь постоянной по его длине,
изменяется по закону Г («/) = Tm!ix по высоте сечения (рис. 19.4). Па-
раметры упругости постоянны.
Решение. Торцы стержня свободны, следовательно, Nx = 0. Темпе-
ратурная деформация По уравнению (8) равна
Рнс. 19.4
Рис. 19.5
Рассмотрим частные случаи.
а) п = 0: = eTnwx’ Т= Гп>ах-
Температурные напряжения Ot = Е (et — аТ) = Е (аТтах — аТтах) = 0.
Таким образом, если температура постоянна по высоте сечения одно-
родного стержня, температурные напряжения не возникают, хотя темпера-
турная деформация не равна нулю.
б) п=1: Т(^) = Ттах|.
вГтах
По формуле (20) при п — 1 имеем в/ =
Таким образом, относительная
равна нулю. По уравнению (9)
Л/2
( aTЕу dF aTmax § y2b dy
_ _________________— Л/2______
= Г « JO */2
\ Еу2 dF f
£ j by2 dy
л» LU/ к т/]~и-
продольная деформация стержня также
относительный угол понорота =
2 — ^^tnax
’ h ~ h
—Л/2
Температурные напряжения определяются с помощью формулы (11): =
= £(во/+^1/-а7') = £((Н-^^»/_вТтах^ =0.
305
Отсюда следует, что при линейном законе изменения температуры па
высоте сечения температурные напряжения равны нулю.
в) » = 2; Т(г/) = Ттах(|У .
ft/2
С
«Гтах J ^ЬаУ
Осевая температурная деформация е< = ------------------
a^max
3
* d(p If*
Изменение кривизны стержня -г-= »------- I ЕаТт 4 -£5- yb dy=0.
М Ey*dF \ h
F —h/2
Температурные напряжения
<jt = E(et-aT) (21)
- о L \ п / J
. Графики изменения температуры и термонапряженнй представлены
на рис. 19.5.
§ 19.3. Учебно-исследовательские работы
и методические указания к их самостоятельному выполнению
19.1. Вывести формулу для определения касательных напряжений в по»
перечных сечениях неоднородного стержня с учетом механических и темпе-
ратурных воздействий (рис. 19.6).
Указание. При выводе формулы предположить, что в сечении
стержня действуют внутренние силовые факторы и сечение имеет ось сим-
метрии у,которая является главной приведенной центральной осью инерции
(т. е. распределение модуля упругости н температуры симметрично относи-
тельно осн у). Рассмотреть равновесие элемента, выделенного из стержня
двумя сечениями, перпендикулярными осн х, и одним сечением, параллель-
ным плоскости xz на расстоянии у от нее. Спроектировать все силы на ось х.
Продольную силу, действующую на отсеченную часть сечения Fj, обо-
значить NPi = Вместо а подставить ее значение нз уравнения (11)
по § 19.1. Рассмотреть случай постоянного модуля упругости и постоянной
температуры по оси стержня, случай стержня переменного сечения,
306
В пределе при Е = const и Т = 0 должна получиться формула Журав-
ского для касательных напряжений при изгибе.
19.2. Вывести формулу для определения нормальных напряжений при
изгибе кривого неоднородного бруса с учетом механических и температур-
ных воздействий, если брус имеет продольную плоскость симметрии, в кото-
рой действуют внешние силы. Брус нагревается (охлаждается) по произ-
вольному закону в направлении радиуса кривизны (рис. 19.7).
Указание. При выводе формулы рассмотреть деформацию волокна
на расстоянии у от нейтрального слоя, записать выражение для относитель-
ной деформации. Выразить продольную силу Nx и изгибающий момент
через нормальные напряжения аналогично тому, как это сделано в задаче
19.1 и в § 19.1. Учесть, что свободное температурное удлинение устанавли-
вается так же, как и для прямого бруса. Тогда из условия = О выведем
уравнение, которое позволит определить положение нейтральной оси бруса
и радиуса нейтрального слоя. Преобразовывая выражение для Мг, получаем
формулу для нахождения относительного угла поворота сечения и затем фор-
мулу для нормальных напряжений.
В случае постоянного модуля упругости и отсутствия температурного
воздействия получается известная формула для напряжений в кривом брусе
(см. § 14.2 гл. 14).
Общая формула для напряжений в криволинейном брусе с учетом меха-
нических и температурных воздействий может быть применена для расчета
распорно-подвесных сводов металлургических нагревательных печей. Для
этого следует задаться реальным законом изменения температуры в зависи-
мости от толщины свода и по нему определить закон измеиеиия модуля упру-
гости кладки.
19.3. Исследовать температурные напряжения в биметаллическом (двух-
слойном) стержне (рис. 19.8, а).
Указание. Вследствие различия коэффициентов линейного расши-
рения слоев и их модулей упругости биметаллический стержень при нагре-
вании искривляется (рис. 19.8, б). Это свойство позволяет использовать его
в качестве чувствительного элемента терморегуляторов.
Для решения задачи нужно выразить напряжения через модули упру-
гости и расстояния до нейтральной оси. Из условия равенства нулю про-
дольной силы установить расстояние а до нейтрального слоя. Далее составить
выражение для Мг по формуле (5) из §19.1 и найти радиус кривизны р. Это
даст возможность определить прогиб бруса. По уравнению (11) отыскать
нормальные напряжения. При вычислении интегралов считать температуру
постоянной посечеиию, а модули упругости — постоянными в пределах каж-
дого слоя.
„ (а, — а2) t Г 1 (hi + Л2) 1
Ответ: Oj = —ДД--------- — + у О/с. , - , [ 5
/1 1 । Лт 2 (£p/i£Ws)J
(«1 — «2) t [ 1
<т2 =
7Г2Л2
(/?i + ha) £2. 1 , = (At + o)3 — дз
У 2 (E^ + Б2/2) I ’ ГД 1
3
307
(h2 — g)3 + g3
3
J 2 —
о — расстояние от линий сцепления слоев до нейтраль-
ного слоя.
19.4. Определить температурные напряжения в неоднородном стержне
(рис. 19.9) с постоянной температурой по длине и изменяющейся по закону
по высоте.
Указание. Модули упругости и коэффициенты линейного расшире-
ния слоев считать постоянными. Решение задачи • начинается с изучения
§ 19.1, 19.2. Поскольку стержень не имеет опорных закреплений, температур-
ные напряжения определяются по уравнению (11) при Nx, Му, Мг, равных
нулю. Рассмотреть решение задачи при п = 0, 1, 2, 3. Исследовать влияние
толщины слоев на возникающие температурные напряжения для выбранных
материалов. Найти отношение толщины слоев hxih2, при котором напряжения
Рис. 19.9
Рис. 19.10
минимальны. Представляет интерес исследование термонапряжеинй пр:
законе изменения температуры по высоте сечения Т (у) —Т1 I ,т. <
при симметричном законе распределения температуры н нечетных значения
показателя п. Построить эпюры термонапряжений по высоте сечения дл
каждого случая изменения температуры.
19.5. Исследовать температурные напряжения и деформации в равис
мерно нагретом по высоте биметаллическом стержне, концы которого не имею
осевых смещений, т. е. шарнирно оперты или защемлены (рис. 19.10
Размеры сечения b X ft, модули упругости Elt £а, коэффициенты лииейиог
расширения ап а2 и не зависят-от t.
Указание. При решении задачи изучить .§ 19.1, 19.2. Температур
Е < 250° С, следовательно, параметры упругости можно считать постоя!
иыми. Поскольку концевые сечения закреплены, Д/ — 0.
Удлинение определяют из выражения (13), а затем находят продольну
силу Nx. Напряжения устанавливают по формуле (И), деформацию — !
(9). Рассмотреть оба случая, представленные на рис. 19.10. Следует иайт
отношение высот слоев, прн котором для заданной пары материалов отмеч
ется наибольшая деформация, так как биметаллические стержни использ
ются в качестве чувствительных элементов терморегуляторов и чем болы
изгибная деформация, тем выше чувствительность регулятора.
19.6. Исследовать температурные напряжения в прямом стержне прям
угольного сечения с учетом зависимости модуля упругости и коэффициен'
линейного расширения от температуры, которая изменяется по параболич
скому закону Т(у) = т(^\ , н = 0, 1, 2, 3.
308
Указание. При решении задачи изучить § 19.1 и 19.2. Найти модуль
упругости Е н коэффициент линейного расширения а в зависимости от тем-
пературы i. Графики их изменения для стали представлены на рис. 19.11.
Модуль упругости и коэффициент линейного расширения с помощью ме-
т
тода наименьших квадратов можно записать в виде £(/) —У Eit1, а (/) —
т
== V- Ait1 (т -- 4 пли 5).
/=о
Напряжения определяют по формуле (11). При вычислении интегралов
пределы интегрирования должны совпадать с пределами изменения а. Зная
законы изменения Е и а, выражают все величины через у и интегрируют по
dF = bdy.
-Коэффициенты Ei и At вычисляют с помощью ЭВМ (например, МИР или
МИР-2). Программы приведены в приложении 5. Необходимые данные для
различных сталей можно найти в работе (21).
Задача представляет особый интерес при высоких температурах нагрева
(до 1000° С), перепад температур можно выбрать произвольно. При расчетах
следует под интегралами (11) учитывать приращение температур Т = А/,
а упругие константы брать для температуры Г С. Построить эпюры напря-
жений по высоте сечения для всех рассмотренных значений п в формуле из-
менения Т (у),
§ 19.4. Исследование напряжений в цилиндрах и дисках
1. Уравнение равновесия толстостенного цилиндра. Элемент цилиндра
показан на рнс. 19.12. Взяв сумму проекций всех сил на направление радиу-
са, при осесимметричном напряженном состоянии для dx = 1 получим урав-
нение, (<тг + doг) (г + dr) dG — orr dG — ot dr <49 = 0.
Пренебрегая бесконечно малыми второго порядка, имеем
^7 (гог) — ot = 0. (22)
Остальные уравнения равновесия удовлетворяются тождественно.
Радиальные н окружные деформации таковы:
где w—радиальное перемещение точки цилиндра.
309
Из выражений (23) получают уравнение совместимости деформаций
d
-^(etr) — er=O.
(24)
Выразим деформации через напряжения по обобщенному закону Гука
с учетом температурной деформации:
ег = [о, — р, (Of -f- oA-)J + аТ;
е/ = ~ [о/ — р (ох + ог)] + аТ,
[Ох — р (аг + a/)j + аТ.
(25)
r dt°r _1_ Я dar
Модуль упругости, коэффициент линейного
расширения и коэффициент Пуассона являются
функциями температуры t. При t < 300° С их мож-
но считать постоянными.
По длине цилиндра ех = const, поэтому
dex „ - „
= 0 и ех не зависит от радиуса. Подставив
выражение (25) в (24), получаем уравнение
d / \ ЕаГ dT (Г)
которог после подстановки а/ из равенства (22)
принимает вид
d2ar ,^}dar_ Е а ОТ (г) .
dr*r г dr 1 — р. г dr ' 11
нение.
Это н есть искомое дифференциальное урав-
2. Графический способ определения напря-
жений. При отсутствии неравномерного нагрева
уравнение (27) превращается
ненне. Используя тождества
в однородное
урав-
~ -^-(orr2)j > ar -bty == 2Л = const, (28)
можно записать решение однородного уравнения в виде
°г=А-~, Ot = A+-^. (29)
Постоянные интегрирования А и В определяются по граничным усло-
виям (см. § 13.1 гл. 13). Для составных труб аналитический способ становится
громоздким. Приведем графический способ определения напряжений, позво-
ляющий наглядно исследовать многослойные (составные) трубы. Введем но-
. 1 „
вую переменную х =’ -g- . Тогда t
г3
ог = А — Вх, О/ = А + Вх. (30)
После введения новой переменной формулы Ламе (29) выражаются урав-
нениями прямых, отличающихся знаком углового коэффициента. Расположим
системы координат, как показано на рис. 19.13. Прямые, построенные по
уравнениям (30) в указанных осях, будут продолжением друг друга. Справа
от начала координат расположены напряжения О/, слева — ог. Считая задан-
310
ными радиусы внутренней н наружной поверхностей гх, г2 и давления на них
Pi, р2> вычисляют , х2 = —j- и откладывают их вправо и влево от
Г1 ’’г
начала координат. Радиальные напряжения на внутренней и наружной поверх-
ностях равны соответственно =—Pi. °г2~—Pf ОтлоЖИМ эти величины
по оси ординат и соединим полученные точки прямой лилией. Продолжив ее
в правую область, получим эпюру Ot между абсциссами хг и х2.
3. Напряжения в дисках. Рассмотрим диски рабочих колес турбин или
турбокомпрессоров переменной толщины h (г) (рис. 19.14). У наружной по-
верхности они нагружены напряжениями агн, создаваемыми' центробежными
силами рабочих лопаток, по внутренней поверхности действуют контактные
давления Pj от напряженной посадки на вал. Интенсивность сил инерции
Рис. 19.14
у
ди = ~ <о2г, где со— угловая скорость вращения; у— объемный вес. Термо-
напряжения в диске зависят от поля температур Т (г).
Инженерная теория расчета дисков основана на таких допущениях:
нормальные напряжения в плоскостях, параллельных срединной поверх-
ности, равны нулю, т. е. напряженное состояние двухосное; температура
и напряжения <тг, <Т/ постоянны по толщине диска.
Величины <тг, <Jt находим нз формул (25), уравнение совместности де-
формаций имеет вид (24). Из этих уравнений получаем
r 17 [т— Мг)]+ ‘Чг(<7/ — °г) +17 = °’
(31)
Второе недостающее уравнение составляется на основании условия р 4в-
новесия элемента аналогично уравнению (22):
^7 (^rhr) ~ ath + Pnrh = 0. (32)
Решая совместно уравнения (31) и (32), определяем напряжения.
Могут быть рассмотрены случаи постоянных (при t < 300° С) и перемен-
ных (при /> 300° С) параметров упругости.
4. Температурные напряжения в кольцах, шайбах и цилиндрах.
4.1. Рассмотрим неоднородную тонкую квадратную пластинку, растя-
гиваемую равномерно-распределенной нагрузкой по двум направлениям
и нагреваемую в поперечном направлении по любому симметричному закону
311
(рис. 19.15). Для плоского напряженного состояния при одинаковых дефор-
мациях в направлении х и у
(33)
ст - ст - е^ + ^£- Ее
Стх — (Ju-:----5- с — -
У 1 — Ц2 1 — р
По сравнению с законом Гука для одноосного напряженного состояния
при одинаковой продольной деформации напряжения для рассматриваемого
, 1
случая будут в ---- раз больше.
Следовательно, чтобы получить формулы напряжений при симметричном
двухосном состоянии достаточно
z
Рис. 19.15
в формулы напряжений для одноосного
состояния ввести приведенный модуль
4.2. Определим температурные напряжения в кольце и шайбе, соблюдая
-неравенства /к 0,2/? , р = -5^>0,7, где h — толщина кольца, /?в, /?н—
“в
внутренний и наружный радиусы. Кольцо свободно от внешних нагрузок, по-
этому на поверхности нормальные иаприжеиия равны нулю: аг — <зх lr=R
|г=«н =
Эксперимент показывает, что с достаточной точностью можно считать осевые
и радиальные наприжеиии равными нулю. Окружные термонаприжения можно
приближенно определять по формуле (11) при отсутствии внешних нагрузок
и изгибиых напряжений:
4.3. Рассмотрим термонапряжения в длинном неоднородном тонкостенном
цилиндре (рис. 19.16). Если развернуть цилиндр по образующей, будем иметь
тонкую пластинку, для которой наприжения <тг = 0. Из условия симметрия
ст/ = о» Получаем двухосное симметричное состояние, поэтому термонапряже-
ния определяются по формуле одноосного с заменой модуля Е на приведенный
модуль £/(1 — ц):
*н Rb
<3x = <3t = aTdF I I dF — aT). (35)
1 — it'.’ 1 — [i / ,) 1 — u. /
Rb Rp
312
Элементарная площадь dF = 2лг dr. Тогда
Rn
Е [ Е I F
°х = О/ = i-- I \ i-- uTr dr \ --г dr —аТ
1—Ц / 1 — р
(36)
Если считать р = const, формула упрощается. Данной формулой мож-
но пользоваться при постоянных и переменных параметрах упругости,
когда температура переменна по толщине стенки.
§ 19.5. Учебно-исследовательские работы и методические
указания к их самостоятельному выполнению
19.7. Определить графическим способом напряжения при соединении
двух цилиндров с помощью прессовой посадки, если контактное давление
рк, радиусы — rt, г2, гк (рис. 19.17).
Указание. Изучить п. 1 § 19.4. Задаваясь различными отношениями
к , Г1
радиусов — при выбранном отношении — , исследовать напряжения и по-
r2 г-2
строить график зависимости напряжений от г. Проследить за изменением
радиальных и окружных напряжений в зависимости от контактного давле-
ния рК'
19.8. Определить графическим способом по-
садочные напряжения в трехслойиом цилиндре
при следующих параметрах: Гц = 4; ri2 = 8;
Гг! = 8; г22 = И; г32 = 14 см, рк] = 4000; рк2 =
= 4000 Н/см2. Исследовать оптимальные значе-
ния радиусов и иатягов.
Указание. Первую часть задачи решать
путем построения, описанного в п. 2 § 19.4. Для
определения оптимальных радиусов и иатягов
целесообразно построить график, соответствую-
щий рабочему внутреннему давлению р для
сплошной трубы. Затем, задавшись значениями
контактных радиусов гк1, гк2 и контактных
давлений рк1, рк2, отложить в соответствую-
щих точках хк1 и хко контактные давления, соединить эти точки прямыми
линиями до пересечения с ординатами, соответствующими абсциссам хк1,
хк2 и х2 на правой стороне графика. Построение дает наглядное представление
о том, насколько удачно выбраны радиусы контактных поверхностен и кон-
тактные давления. Изменяя контактные радиусы, т. е. расположение точек хк1
и х.(2, можно изменять характер распределения напряжений <st. Контактные
напряжения между внутренней и средней трубой следует принять большими,
чем между средней и наружной.
19.9. При стационарном тепловом режиме температура распределяется по
толщине стенки цилиндра по логарифмическому закону t (г) = 7 In — 1п ~-
[ределить термонапряжения в цилиндрической трубе со свободными торцами.
Рассмотреть численный пример: r2 = 2,5r1, Т = 60° С.
Указание Изучить п. 4 § 19.4. Для интегрирования уравнения (27)
при заданном законе изменения температур воспользоваться тождеством (28).
Для определения произвольных постоянных использовать условия, что поверх-
12
1-19
ЗВ
ности цилиндра свободны от радиальных напряжений. Зная ог н Of, найти ох
из условия равенства нулю продольной силы Nx~ \ oxdF = 0.
F
EaT 11 — 2 In г2/г
2(1 — р) [ 1п гг:гг
Ответ:
2/-1 ]
2 2
ъ — -I
19.10. Вывести дифференциальное уравнение для определения напряже-
ний в диске переменной толщины при нагреве и равномерном вращении.
Рассмотреть случаи, когда h — const, Е = Const, а = const, р = const.
Найти напряжения в случае отсутствия иагрева для диска без отверстия
и с отверстием. Построить эпюры напряжений для обоих случаев.
Ответ: Для диска с отверстием
2
3 -р В 9 ( 2 . 2
О/ = V<B2 ^,2 Д- —
19.11. Исследовать деформации в однородном толстостенном цилиндре
при действии внутреннего и внешнего давления. Вывести формулы для опре- 1
деления радиального перемещения произвольной точки сечения цилиндра. 1
Указание. Использовать формулу (23) и выражение обобщенного 1
закона Гука. Подставив выражения для напряжений в формулу е/, получим |
формулу для w. Вывести формулы для частных случаев: ра = 0,
Построить эпюры изменения
= °- 1
w по толщине стенки. Исследовать влияние Л
различных материалов на полученные резуль-
таты. Я
19.12. Исследовать посадки с гарантиро-
ванным натягом при оптимальных парамет- S
рах. Цель работы — определение напряжений, Я
возникающих при посадке одного цилиндра Я
на другой. Я
Указание. Натягом А называется раз- Я
иость диаметров посадочных поверхностей .Я
наружного dy и внутреннего d2 цилиндров И
(рис. 19.18). Для решения задачи следует, Я
основываясь на формуле (23), получить выра-
жеиие для w. Затем записать условие совмес- Я
тности деформаций, состоящее в том, что сум- Я
ма перемещений точек контакта цилиндров
равна А/2. :Из этого условия определить кон- W
тактное давление рк. Распределение напря-
женин исследовать графическим путем (см. £
значение рк получается из условия равнопроч-
dl
Рис. 19.18
de
§ 19.4 п. 2). Оптимальное
ности внутреннего и наружного цилиндров, а оптимальное значение гк — Л
из условия наибольшего снижения эквивалентного напряжения в опасной '
точке.
Ответ: гк = рк = ~ ’ Л = 2Ргк/Ь'
19.13. Исследовать напряжения в неравномерно нагретом вращающемся;
диске с радиусами rlt г2 при t (г) = Т —----- I .
— г1!
Указание. Для решения задачи изучить § 19.4. В результате должны
быть построены эпюры ог и о; по радиусу диска при п — 0, 1,2. Решение
задачи провести для случая постоянных и переменных параметров упругости.
— ) , п = 0, 1, 2, 3; И = 800, t2 —
гг /
Для переменных параметров ознакомиться с указанием к задаче 19.8 из
§ 19.3.
19.14. Найти в условиях отсутствия неравномерного нагрева закон
изменения толщины диска равного сопротивления.
Указание. Диском равного сопротивления называется диск, в ко-
тором ог и Of одинаковы по величине и постоянны по радиусу: or = °: =
= Ио — const. Часто диск равного сопротивления изготавливается с наруж-
ным ободом. Рассматривая обод как кольцо, нагруженное силами инерпии,
а также радиальными напряжениями иа наружной и внутренней поверхнос-
тях огн и о0, вычислить окружные напряжения. Приравнивая радиальные
перемещения обода и диска, получают уравнение для определения h(r).
А(г~2—г2)
Ответ: h (г) = h2e , А = y<u2/2ga0.
19.15. Исследовать термонапряжения в тонкостенном цилиндре при изме-
нении температуры t (г) = Н + (t2 — Н)
= 1000° С.
Указани е. Изучить § 19.4 п. 4, обратив внимание на формулы (35),
(36). Параметры упругости зависят от температуры, поэтому закон их изме-
нения определяется так же, как в задаче 19.6 и в указании к ней. Прн реше-
нии задачи использовать программы, приведенные в приложении 5 к насто-
ящей главе.
§ 19.6. Основные понятия и зависимости метода
конечных элементов
В последние годы в инженерную практику внедряются довольно слож-
ные конструктивные элементы: стержни переменного сечения, работающие
на поперечный и продольно-поперечный изгибы, валы некруглого сечения,
трехмерные элементы и детали. В связи с этим развит ряд методов, позволя-
ющих решать указанные более сложные задачи с использованием современ-
ных методов и ЭВМ. Большая часть методов выходит за рамки вопроса о со-
противлении материалов и относится к теории упругости и пластичности.
Это справедливо и по отношению к наиболее универсальному методу реше-
ния задач — методу конечных элементов (МКЭ). Однако данный метод можно
использовать и в рамках сопротивления материалов, например, в сочетании
с традиционной для сопротивления материалов теорией изгиба балок. При-
водимый ниже вариант изложения МКЭ отличается в определенной мере от
принятого в литературе*. Он ограничивается задачами сопротивления мате-
риалов, сохраняет обычные гипотезы теории изгиба балок. Примеры носят
методический характер, так как решение практических задач с помощью
МКЭ неизбежно связано с использованием ЭВМ и весьма сложных программ.
Однако и рассмотренные простые примеры, которые отличает небольшое
число конечных элементов, дают представление о возможностях использо-
вания метода в задачах сопротивления материалов.
Разобьем стержни системы по длине на прямолинейные участки (конеч-
ные элементы) так, чтобы сосредоточенные силы действовали только на гра-
ницах участков (или, как мы будем их называть, в узлах). Количество эле-
ментов т, на которые разбивается конструкция, зависит от желаемой точ-
ности расчета и от возможностей применяемой вычислительной техники.
Но оно должно быть достаточным для того, чтобы ни одна сосредоточенная
* Более полное представление о методе и его возможностях можно
получить, например, из книг О. Зенкевич. Метод конечных элементов в тех-
нике.— М.: Мир, 1975— 541 с. Справочник по теории упругости 1 Под ред,
П. М. Варвака и А. Ф. Рябова.— Киев: Буд1вельник, 197!.— 4 In с.
12*
315
сила не оказалась внутри конечного элемента — сосредоточенные силы могут
действовать только в узлах*. Если на конструкцию действуют распределен-
ные нагрузки, их также следует представить в виде сосредоточенных сил.
Изгибные перемещения в пределах каждого конечного элемента с номе-
ром i зададим в виде некоторой функции координаты xit отсчитываемой
вдоль оси конечного элемента от одного из его концов (обычно от левого или
от верхнего конца). Удобно выражать эти перемещения в локальной системе
координат (рис. 19.19) так, чтобы в начале координат перемещение у, равня-
лось нулю. Пусть перемещение выражается через локальную координату
функцией
W--=<PiU«. «if- a2i, ... , ani), (37)
где он-, a-2i, . .. , ani — параметры, которые следует отыскать. Число этих
параметров также определяется требуемой точностью — можно принять боль-
шое т при малом п или наоборот.
Таким образом, задача расчета кон-
струкции сводится к нахождению не-
известных параметров а-с для каж-
дого конечного элемента общим чис-
лом т X п.
Для определения указанных па-
раметров удобно использовать прин-
цип минимума полной потенциаль-
ной энергии системы.
Как известно, полная потенциальная энергия системы П представляй»
собой разность работы внутренних сил U, совершаемой при деформировании
конструкции, и работы внешних сил А:
П = U — А.
(38)
Эти величины можно виразить через перемещения изгибаемой системы
в виде
т л,
tn I
t;=4S J E]^dx-
М о
где di — длина конечного элемента под номером i, и
тх
Л = £ Рцуи, (40)
А=1
где mi — количество узлов; k — номер узла; yk — перемещение узла, выражен-
ное в какой-то общей для всей конструкции (глобальной) системе координат;
Ph — сосредоточенная сила, действующая в k-м узле.
Требование минимума полной потенциальной энергии системы приводит
к необходимым условиям минимальности, которые используютси в различных
приближенных методах решения задач *. * **
* Можно допустить действие сосредоточенных сил внутри элементов,
но это усложнило бы выражение для работы внешних сил.
** Требование минимума полной потенциальной энергии системы выте-
кает из принципа Лагранжа, принципа минимума потенциальной энергии
деформирования (см. например, Г. С. Писаренко и др. Сопротивление мате-
риалов.— Киев: Вища школа, Головное изд-во, 1979.— 696 с. Подробное;;
обоснование этого требования и классические примеры его использования
см. в книге С. П. Тимошенко и Дж. Гере. Механика материалов.— М.: Мир, J
1976.— 669 с.
,".16
Глобальные перемещения yt можно выразить через локальные перемещения
yk с помощью простых уравнений, вид которых зависит от конфигурации кон-
струкции. Тогда U, А станут функциями параметров а^. Следовательно, па-
раметры позволяют определять глобальные перемещения узлов yk, связан-
ные с действующими иа узлы силами линейными зависимостями
*11У1 + *12'/2 +
*21.71 + *22^2 +
• • + Ь\т1Ут1 ~ Р1’
• + b2miymt = Р2-
Ьт,У1 1 Ьт2У% “Ь * - • Ь/г^гпУУ/п, Pmt<
которые получаются в результате дифференцирования квадратичного выра-
жения полной потенциальной энергии поочередно по всем переменным.
Пользуясь матрично-векторной записью, эту систему уравнений можно пе-
реписать проще в виде
[В] ;у} = {в?,
(41)
[</1 1
гДе {У}, {Р}— векторы перемещений и усилий {у} = М2 !• , {В} = <
1 Ут, J I Ргг
а квадратная матрица
[В] =
'*и
blmt
• • ’ bm1m1
называется матрицей жесткости (чем выше жесткость конструкции, тем меньше
перемещения под действием заданных нагрузок).
Разрешая уравнение (41) относительно {у}, получаем {у} = [В]-1 {В}, где
fS;—1 — является обратной матрицей по отношению к матрице [В]. Она носит
название матрицы податливости.
После того как получено выражение полной потенциальной энергии кон-
струкции П через неизвестные параметры ati, а2ь . . . , ати> Для отыскания
этих параметров достаточно приравнять к нулю производные
= 0 (1 = 1, 2, . . . , m; j — 1, 2, .... п) (42)
и получить систему алгебраических уравнений. Поскольку потенциальная
энергия системы будет квадратичной функцией этих параметров, после при-
равнивания к нулю производных получается система линейных алгебраиче-
ских уравнений.
В частном случае, когда число конечных элементов равно единице (т. е.
конечным элементом служит вся конструкция), метод конечных элементов
сводится к классическому методу Ритца. И наоборот, МКЭ можно считать
обобщением метода Ритца в случае, когда конструкция разбита иа подобласти
(конечные элементы), в каждой из которых неизвестные поля имеют разные
аналитические описания.
Когда распределение изгибающих моментов в стержневой системе из-
вестно (его легко найти, например, для статически определимых систем),
удобно использовать выражение для потенциальной энергии системы в виде
п - f [y у'2 - ~ Sy* - Л4у] dx, (43)
где интегрирование производится вдоль всех стержней системы, Л4(х) — вы-
ражение для изгибающих моментов, S -- продольная сила.
317
Это выражение соответствует уравнению изгиба балки второго порядка
типа (38) § 8.2, в то время как более общие зависимости (39)—(40) соответ-
ствуют уравнению изгиба четвертого порядка вида EJy™ — q, которое
следует применять для статически неопределимых систем. Отметим, что вы-
ражение (43) имеет иную размерность чем (39)—(40), и, следовательно, опре-
деляет потенциальную энергию системы лишь с точностью до размерного
множителя, но мы тем не менее будем называть в дальнейшем эту величину
потенциальной энергией. При использовании МКЭ в одинх случаях мы бу-
дем пользоваться уравнениями (39)—(40), в других — выражением (43),
которое позволяет упростить зависимости и повысить точность.
В справедливости формулы (43) нетрудно убедиться с помощью вариа-
ционного исчисления. Действительно, необходимым условием минимума
функционала
Z = ) F (х, у, у') dx min
служит уравнение Эйлера
dF d dF _
dy dx dy’
(a)
(6)
Применяя (б) к (а), получаем хорошо известное уравнение изгиба*.
§ 19.7. Примеры расчетов с помощью метода конечных
элементов
Пример 19.4. Определить с помощью МКЭ максимальный прогиб кон-
соли под действием сосредоточенной силы (см. рис. 19.20, а).
Решение. Разобьем консоль'
по длине на три конечных элемен-
та, каждый длиной d = //3 (на
рис. 19.20, б пронумерованы рим-‘
скими цифрами), Для каждого ко-1
нечного элемента с номером i при-,
мем локальную систему координат,-;
начало которой поместим на левом:
конце (рис. 19.20, в). Предположим,
что в пределах Z-го конечного эле-;
меита локальные перемещения вы-
ражаются параболической зависи--
мостью )
yi = aixi bix] (1=1, 2, 3) (44)
(в начале координат при х( = 0 име-
ем у( = 0). Таким образом, задача-
сводится к определению шести пара»®
метров ai, ftj, tz2, bit аг, b3, череЭ^
которые можно выразить прогибы«£
Запишем выражения для проиЗ*?*
водн ых:
yt = ai + ibixe, (45) у, — 2bt. (46)г|
* Вывод уравнения (б) имеется в любом курсе вариационного исчисле-й
ния (см. напр., В. И. Смирнов. Курс высшей математики, т. 4 — М.: Наука,|£
1975,— 336 с.).
318
Теперь воспользуемся граничными условиями задачи:
угол поворота сечения на левом конце в узле 1 должен равняться нулю,
откуда _
У1 = «1 = 0- (47)
На правом конце должен равняться нулю изгибающий момент, но момент
пропорционален у", т. е. 63, откуда
= 0. (48)
Поскольку согласно (44) в пределах конечного элемента кривизна счи-
тается постоянной, мы одновременно полагаем кривизну равной нулю иа
всем конечном элементе III, чем, разумеется, вносится некоторая погрешность.
Используем условия совместности деформаций в узлах 2 и 3, где сопря-
гаются конечные элементы. Потребуем, чтобы углы поворота в узлах сопря-
жения оставались непрерывными (соблюдалось условие плавности). Для
узла 2 согласно уравнению (45) это приведет к условию
а1 + 2bid = а*. (49)
Для узла 3 аналогичное условие имеет вид
а2 + 2b2d = as. (50)
Четыре условия (47)—(50) позволяют исключить четыре неизвестных
из шести. Удобно выразить все неизвестные через blt b2, так как именно
вти неизвестные входят в выражение для потенциальной энергии деформа-
ции. Из уравнения (49) получаем (с учетом = 0)
а2 = 2btd, (51)
а из (50) следует
= 2d (Й1 + Ь2). (52
Потенциальная энергия внутренних сил согласно формуле (39) состав
Ляет
d d
U = ~^ (2bt)2 dx^\ (2b2)2 dx = 2EJd (bi + b}), (53)
0 0
а работа внешних сил
л = Pyi = Plyi(d) + y2(d) + y3(d)]. (54)
Здесь i/4 — глобальное перемещение сечения на свободном конце стержня
в узле 4. Локальные перемещения всех трех узлов, сумма которых равва
глобальному перемещению узла 4, можно с помощью формул (51), (52), вы-
разить через параметры
bi, b2:
А = Р £ (acd + Ь^) = Р [М2 + 2М2 + М2 + 2d2 (Ь± + *2)| =
/=1
= Pd2 (5b1 + 3/>2). (55)
Отсюда окончательное выражение для потенциальной энергии конструкции
(полной)
П = U — А = 2EJd (bi + bl) — Pd2 (5bt + 3/>2). (56)
Дифференцируя уравнения (56) по bif b2 и приравнивая к нулю произ*
водные, находим дП/д&г = 0; 4EJdbr — 5Р(Р = 0; 6П/д&2; 4EJdb2 —
— 3Pd2 -= 0.
.419
Отсюда получаем
bi = SPdltEJ, b2 = SPdHEJ. (57)
Теперь, используя уравнения (51) , (52), можно найти остальные пара-
метры
а2 = 5Pd2/2£J, а3 = 4Pd?IEJ, (58)
pd3
а затем по формуле (54) с учетом (44) найти перемещение Ю +
17Р/3
+ 3+ 16) = 54£Т’ нли
Р13
lh = 0,944 (59)
Точное значение перемещения равно P13I3EJ.
г 1 /3 17/54
Погрешность МКЭ составляет Л =--------- • 100% ~ 6%.
Во многих случаях такая погрешность приемлема. Однако ее можно
значительно снизить, если увеличить число конечных элементов. Обратим
внимание на то, что МКЭ дал заниженное значение прогиба: задавшись фор-
мой деформирования внутри конечных элементов, мы тем самым наложили
на систему дополнительные связи, увеличив ее жесткость по сравнению
с истинной. Но это справедливо лишь в интегральном смысле, в отдельных
точках прогибы могут оказаться завышенными.
Замечание. Известно, что выражение для прогибов балки дается в на-
шем случае полиномом третьей степени (см. пример 8.3). В МКЭ мы факти-
чески заменили приближенно кубическую параболу на трех участках отрез-
ками квадратных парабол (точнее двумя отрезками парабол и одним отрезком
прямой). Получающиеся при этом преимущества можно оценить лишь при
проведении счета на ЭВМ для систем высокого порядка. Для этого служат
специально разработанные программы. Особенно МКЭ эффективен, когда
участки имеют разные жесткости.
Пример 19,5. Построить с помощью МКЭ эпюру изгибающих моментов
для рамы, изображенной на рис. 19.21, а.
Решение. Прежде всего следует подсчитать потенциальную энергию
деформации. Это можно сделать, как и в первой задаче, интегрируя вдоль
стержней, однако в данном случае удобнее другой путь. Допустим, конец
защемленного по концам стержня длиной I с жесткостью EJ поворачивается
на единичный угол вместе с защемлением. Тогда в поворачиваемом узле
появится изгибающий момент bEJll, а в противоположном конце того же
стержня — момент ЧЕРИ. Эти формулы позволяют нам выразить потенциаль-
ную энергию деформации через углы поворота узлов. Действительно, если ‘
единичный поворот вызывает моменты 4EJU и ЧЕЛ1, то поворот на угол 9 j
вызовет моменты в 0 раз большие*.
В качестве основных неизвестных выберем углы поворота узлов 0j, 02 j
(см. рис. 19.21, а), под действием внешней нагрузки.
Найдем сначала моменты, возникающие от единичного поворота 1-го
узла (рис. 19.21, б) в стержнях рамы (тс • м):
= ^==V-3=-2; = ^ = 0;
ь(з1’ = -ь(41’ = о- (во) J
* Г. С. Писаренко и др., Сопротивление материалов.— Киев; Вища
школа. Головное изд-во, 1979.— 696 с.
320
Здесь первый индекс внизу у переменной означает номер узла, в котором
определяется изгибающий момент, второй индекс — номер узла на противо-
положном конце того же стержня. Таким образом, оба индекса определяют
сечение рамы вблизи узла. Верхний индекс указывает номер узла, в котором
производится единичный поворот. Аналогичные действия производим и при
повороте второго узла (рис. 19.21, в):
Для дальнейшего нужно сделать предположение относительно распре-
деления моментов и перемещений внутри каждого конечного элемента-
Примем в качестве конечного элемента стержень рамы, а распределение мо-
ментов по длине этого стержня будем считать линейным.Поскольку это соот-
ветствует истине, получающееся таким образом решение не будет отличаться
от точного, если в раме нет внеузловых нагрузок. Умножая моменты на угло-
вые перемещения у лов О-j и 92, находим с учетом (38)—(39) потенциальную
энергию внутренне сил:
и = ~ + &<’2>02 + Ь'^ + 6(2>922 + 6<22>92 + Ь%^2) =
,ь2)
Внешние силы совершают работу только в узле 1:
А = - 2f'r (63)
Отсюда можно найти потенциальную энергию системы
п = :/-л = 1(зе1 + з91 + 2ех92)-2е1. (64)
Приравнивая последовательно производные от П по 9f, 02 к нулю,
получаем систему уравнений
30х + 02 = 2; 91 + 392 = 0. (63)
Решение этой системы имеет вид I
9Х = 3/4, 92 = — 1/4. (66) Я
Умножая на эти значения моменты от единичных поворотов узлов (9Х, Я
92 — истинные повороты), находим изгибающие моменты в сечениях рамы Я
(тс.м): Я
'4-°-4-4; л,--°-4+|-т-4: I
л|>.-'4-2-4=4; «.-«-4-4—4- ,И) I
На рис. 19.21, г построена соответствующая эпюра изгибающих момен- Я
тов. Можно убедиться, что все узлы рамы находятся в равновесии: в данном Я
случае уравнения равновесия в расчете отсутствуют, но требование минимума Я
полной потенциальной энергии системы предполагает их выполнение. Ника- Я
кой погрешности МКЭ не вносит, так как принятые предположения не рас- Я
ходится с истиной. Я
Использованные выше зависимости можно представить в матричной Я
форме. Матрица жесткости для рассматриваемой задачи согласно уравнению Я
(65) вмеет вид Я
[В] = [3 (68) Я
Вектор перемещений узлов, как и вектор внешних сил, включает две ком- Л
поненты, соответствующие названным перемещениям: Я
{9} = Щ, (69) = (70) J
Это позволяет перепвсать уравнения (41) в виде X
[B]{O} = {SR}, (71) откуда {9} = [В]-1 W- (72) j
Зависимость моментов от перемещений (67) также может быть представлена J|
в матричной форме: Я
{М} - [С] {0}, (73)
где (А4} = {МХЗ, AfX2. М2Х 1 и 7ИЗХ, /И<2); (С]т=
-— 1 —2 1 0 1 __ 0 1 (индекс т обозначает транспонирование 1
маа 0 —1 рицы). 2 -4 Подставляя 0 -т уравнение ( ’2) в (73). получаем i
(ЛП = [С] [В]-1 W- (74)
Пример 19.6. Найти максимальный прогиб в балке под действием про- i
дольной и поперечной нагрузок (рис. 19.22, а). Участки балки / и // имеют
разные жесткости (тс • м2): EJt = 1/2; EJ2 = 1-
322
Решение. Аналитические методы позволяют решать аналогичные
задачи лишь при постоянных по длине жесткостях. В данном случае исполь-
зуем МКЭ. Разобьем балку по длине на четыре элемента. В каждом эле-
менте прогибы зададим в виде линейной функции локальной координаты х.
У = У1 +
У1+1 — У1
d
(75)
Отсюда производная у' равна
У' = (yt+i —yi)/d-
(76)
Основными неизвестными
граничного условия на опоре .
формуле (43) составит
2 • 1 Г f 1 ,
2 b 2 d* dx +
О
d
f (Уз — #а)2 л J _
J d* "
о J
_ 1 /3 2 , 2 . \
— (ду Уг + Уз — ЪугУъ j =
= -р 2г/з — 4у2у3. (77)
являются прогибы в трех точках: ylt у2, у3. Из
у1 = 0. Работа внутренних сил в балке согласно
S=0,5 тс I
d
Р = 0,1тс „ пс.
_________ о =0,5 то
I - 2м
Множитель 2 перед инте-
гралами учитывает здесь сим-
метрию (без него приведеииое
выражение составило бы энер-
гию лишь половины балки).
Работа продольной нагрузки
Рис. 19.22
согласно той же формуле (43)
d d
О О
U =
a
. / 1 2 1 2 . 1
=:d^ Уг + у Уг + ’6 УгУз
(78)
Работа поперечной нагрузки выразится в форме интеграла от выражения
изгибающего момента
.. 0,1 1 ,7Г,
М = ~2~ Х ~ 20Х (7,)
на функцию прогибов
d d
А* = 2 [ j Ч • 20 *dx ь .1A{d + Х) + dx\=
о о
(ЙОГ
Здесь интегрирование в каждом случае производится по длине соответ-
ствующего конечного элемента. Потенциальная энергия системы принимает
'( . 2 1\
вид (при </= — = —)
[П=6/- А-А- (81)
Дифференцируя выражение (81) по у2, у3, получаем два уравнения-
5yV2 —4—z/з =7q , — 4j2 Уг + 3— у3 = jg • (82)
Решение системы (82) дает
Уз ~ 0,0299 м. (83)
Проверить этот результат по точной теории невозможно, так как точное
решение для данного случая отсутствует.
Для сопоставления рассмотрим случай бруса постоянного сечения при
EJ = 1. Выражения для работ внешних сил останутся прежними, а выраже-
ние потенциальной энергии деформирования примет вид
U = ~(2yl + y3-2y2y3), (84)
отличаясь от прежнего лишь первым членом. Отсюда получаем уравнения
4^-4r2^=i: <85)
Решая систему (85), имеем
Уз = 0,0223 м. (86)
р / 1
Это значение можно сравнить с точным* (а = l/S/fj) у* = —= I tg-_ —
--у-)., или а — 0,707, у* = 0,0208 м.
В то же время по приближенной формуле из § 15.2 f° = 0,0167 м; Рэ =
= 2,47 тс: f = 0,0187 = 0,0209 м.
1-
2,47
Как видим, МКЭ в данном случае дает большее значение прогиба, чем
точный метод и другой приближенный. Это объясняется тем, что в МКЭ
эпюра прогибов в точке 3 имеет излом, в то время как она должна повсюду
быть гладкой. Как мы уже отмечали, в отдельных точках перемещения, по-
лученные с помощью МКЭ, могут и превышать точные значения.
В матричной форме уравнения (85) можно переписать в виде одного
уравнения
[В] {У} = {М}, (87)
где [5J — матрица жесткости
[BJ =
‘4
~4
412
41
(88)
* См., например, М. М. Филоненко-Бородич н др. Курс сопротивления
материалов, т. 1.—М.: Гостехтеоретпздат, 1956.— 644 с.
324
г
Кроме нее, в уравнении фигурируют заданный вектор внешней нагрузки
и вектор узловых перемещений
{Af} =
_1_-
4
5
• 24,
(уз/
(89)
Поскольку матрица жесткости симметрична, численное решение задач
упрощается. Формально решение системы (87) можно записать через обрат-
ную матрицу
= (90)
Однако в большинстве случаев (исключая случаи большого числа на-
гружений) удобнее решать н^росредственно систему уравнений (87), так как
на ее решение уходит значительно меньше времени, чем на обращение мат-
рицы.
§ 19.8. Учебно-исследовательские работы и методические
указания к их самостоятельному выполнению
19.16. Определить с помощью МКЭ максимальный прогиб консольной
балки длиной / и нзгибной жесткостью EJ под действием сосредоточенной
силы на конце (см. рис. 19.20, а) с разбиением на два и на четыре конечных
элемента.
У казаки е. Изучить § 19.6, 19.7, тщательно провести все выкладки
в примере 19.4. Локальные перемещения в пределах каждого из двух конеч-
ных элементов принять в виде кубических парабол, что даст более высокую
точность, чем квадратные параболы. В случае четырех конечных элементов
перемещение можно принять один раз в виде квадратных парабол, а вто-
рой раз — в виде кубических. Постоянные определить аналогично тому,
как это сделано в примере 19.4. Потенциальную энергию и работу внешних
сил вычислить по уравнениям, аналогичным (53)—(55). Получить систему
алгебраических уравнений и по формулам примера 19.4 установить макси-
мальный прогиб. Оценить погрешности решения по МКЭ с точным решением
и приведенным в примере 19.4 для следующих случаев:
1) для двух конечных элементов с параболической зависимостью у от х;
2) для двух конечных элементов с кубической зависимостью у от х;
3) для четырех конечных элементов с квадратичной зависимостью у
от х;
4) для четырех конечных элементов с кубической зависимостью у от х.
При двух конечных элементах с параболической зависимостью у от х дол-
жен быть получен ответ утах = ЗР/3/16Е/.
19.17. Определить прогиб двухопорной балки, нагруженной силой посе-
редине пролета, представив балку в виде совокупности двух конечных эле-
ментов.
Указание. Изучить § 19.6, 19.7 и пример 19.4. Локальные перемеще-
ния принять: а) в виде зависимости (44); б) в виде нескольких членов типа
. . inxi , inxt
yin = А£ sin^-j— для левого элемента и yin = Л( cos — для правого, где
4СЦ £ui
di = I/2—длина конечного элемента; х/ — текущая координата по длине ко-
нечного элемента.
Дополнительный узел выбрать в точке приложения нагрузки. При реше-
нии принять один раз по одному члену yin и у1п, второй раз — в виде суммы
двух членов. При выборе одного члена элемент будет иметь одну степень
свободы: перемещение левого у£л и правого yin концов i-ro элемента; при
двух членах — две степени свободы: вертикальное перемещение у н угол пово-
рота сечения у'.
Потенциальную энергию и работу внешних сил вычислить аналогично
тому, как это сделано в примере 19.4. В случае представления прогиба в виде
тригонометрической функции с одним членом матрица жесткости элемента
будет иметь один элемент. Перемещение в точке приложения нагрузки будет
2Р13 Р1а
У\п = У<1л = ~ °’983 48£j •
19.18. Найти изгибающие моменты в неразрезной балке, изображенной
на рис. 19.23. Жесткость балки постоянна.
Указавие. Изучить § 19.6, 19.7 и пример 19.5. Подсчет потенци-
альной энергии можно провести, интегрируя вдоль стержней выражения
(53)—(55), задавшись параболическим законом изменения прогиба от теку-
щей координаты конечного элемента.
Но можно, как в примере 19.5, рассмотреть стержень, защемленный
с одной стороны и шарнирно-опертый с другой, и стержень с двумя защем-
ленными концами. Если в левом стержне повернуть защемление на единич-
ный угол, то в поворачиваемом узле появится изгибающий момент ZEJll,
а на другом шарнирно-опертом конце изгибающий момент будет равен нулю.
Для стержня с двумя защемленны ми
Ш=2тс-м ~ концами формулы приведены в при-
; 3 мере 19.5. Эти формулы дают воз-
fl" V можность выразить потенциальную
1-kM д’ I энергию через углы поворота узлов.
------------*4-«----------*- Неразрезную балку следует раз-
бить на два конечных элемента, так
Рнс. 19.23 как заданная нагрузка приложена
на средней опоре.
В результате решения задачи должен быть получен ответ: Л11? = 0;
Af2i = —10/7 тс • м; Л123 = 4/7 тс • м; Л132 = —4/7 тс • м.
19.19. Конечный элемент представлен в виде стержня с защемленными
концами и заданной жесткостью. Получить матрицу жесткости конечного
элемента.
Указание. Изучить § 19.6, 19.7. Продольную силу Л/, поперечную
силу Q и изгибающий момент в левом сечении стержня обозначить цифрами
1, 2, 3, те же усилия в правом защемленном сечении обозначить 4, 5, 6.
Сообщить левому сечению А линейное перемещение = 1 вдоль стержня
и определить усилия в стержне (по закону Гука), которые обозначаются
Сц, ctl. Здесь cik означает усилие в направлении перемещения 6( = 1, вы-
званное вынужденным единичным перемещением 5* = 1.
Далее сообщают левому сечению А линейное перемещение 5а — 1 по
направлению поперечной силы, чтобы угол наклона балки в нем ие изме-
нился, и определяют с22, с52, с32, св2. Наконец, сообщают сечеиию А вынуж-
денное угловое единичное перемещение б3 = 1 и находят соответствующие
ему усилия <г33, с23, сез, с53.
Совокупность всех усилий представляет квадратную матрицу, назы-
ваемую матрицей жесткости конечного элемента [В].
Если через [Р] обозначить матрицу-столбец нагрузки, а через [6J —
матрицу-столбец перемещений, то разрешающее уравнение метода конечных
элементов примет вид
[В] {6} --= {Р}. (91)
Используя это векторное равенство и имея матрицу жесткости, можно
решать задачи, ие прибегая к методике, изложенной в § 19.7.
Таблица 1. Сталь прокатная угловая равнополочная Ого ГОСТ 8509—72)
ПРИЛОЖЕНИЕ 1
У^У,
СО
to
Обозначения:
Ъ —ширина полки;
d — толщина полки;
J — момент инерции;
i — радиус инерции;
г0—расстояние от центра тяжести до наружной грани полки
Номер Размеры, мм Площадь J х СМ* см хй макс См* макс см мин см Jх см4 Масса 1 м, кг
про- филя b 1 d сечения F, см2 СМ* Z0 см
5 50 3 4 5 2,96 3,89 4,80 7,11 9,21 11,20 1,55 1,54 1,53 11,3 14,6 17,8 1,95 1,94 1,92 2,95 3,80 4,63 1,00 0,99 0,98 12,4 16,6 20,9 1,33 1,38 1,42 2,32 3,05 3,77
5,6 56 4 5 4,38 5,41 13,10 16,00 1,73 1,72 20,8 25,4 2,18 2,16 5,41 6,59 1,Н 1,10 23,3 29,2 1,52 1,57 3,44 4,25
6,3 63 4 5 6 4,96 6,13 7,28 18,90 23,10 27,10 1,95 1,94 1,93 29,9 36,6 42,9 2,45 2,44 2,43 7,81 9,52 11,20 1,25 1,25 1,24 33,1 41,5 50,0 1,69 1,74 1,78 3,90 4,81 5,72
328
Продолжение табл. 1
Номер Размеры, мм Площадь Jх СМ* см гх0 макс ел Jy0 мин см* 1Уо МИН СМ Масса
про- филя b d сечения F, см2 см*
7 70 4,5 5 6 7 8 6,20 6,86 8J5 9,42 10,70 29,00 31,90 37,60 43,00 48,20 2,16 2,16 2,15 2,14 2,13 46,0 50,7 59,6 68,2 76,4 2,72 2,72 2,71 2,69 2,68 12,00 13,20 15,50 17,80 20,00 1,39 1,39 1,38 1,37 1,37 51,0 56,7 68,4 80,1 91,9 1,88 1,90 1,94 1,99 2,02 4,87 5,38 6,39 7,39 8,37
7,5 75 5 6 7 8 9 7,39 8,78* 10,10 11,50 12,80 39,5 46,6 53,3 59,8 66,1 2,31 2,30 2,29 2,28 2,27 62,6 73,9 84,6 94,6 105,0 2,91 2,90 2,89 2,87 2,86 16,4 19,3 22,1 24,8 27,5 1,49 1,48 1,48 1,47 1,46 69,6 83,9 98,3 113,0 127,0 2,02 2,06 2,10 2,15 2,18 5,80 6,89 7,96 9,02 10,10
8 80 5,5 6 7 8 8,63 9,38 10,80 12,30 52,7 57 65,3 73,4 2,47 2,47 2,45 2,44 83,6 90,4 104,0 116,0 3,11 3,11 3,0 > 3,0» 21,8 23,5 27,0 30,3 1,59 1,58 1,58 1,57 93,2 102 1 19 137 2,17 2,19 2,27 6,78 7,36 8,51 9,65
9 90 6 7 8 9 10,60 12,30 13,90 15,60 82,1 94,3 106 118 2,78 2,77 2,76 2,75 130 150 168 186 3,50 3,49 3,48 3,46 34,0 38,9 43,8 48,6 1,79 1,78 1,77 1,77 145 169 194 219 2,43 2,47 2,51 2,55 8,33 9,64 10,90 12,20
10 100 6,5 7 8 Ю 12 14 16 12,80 13,80 15,60 19,20 22,80 26,30 29,70 122 131 147 179 209 237 264 3,09 3,08 3,07 3,05 3,03 3,00 2,98 193 207 233 284 331 375 416 3,88 3,88 3,87 3,84 3,81 3,78 3,74 50,7 54,2 60,9 74,1 86,9 99,3 112,0 1,99 1,98 1,98 1,96 1,95 1,94 1,94 214 231 265 333 402 472 542 2,68 2,71 2,75 2,83 2,91 2,99 3,06 10,1 10,8 12,2 15,1 17,9 20,6 23,3
11 110 7 8 15,20 17,20 176 193 3,40 3,39 279 _315 _ 4,29 4,28 72,7 81,8 2,19 2,18 308 353 2,96 3,00 И,9 13,5
12,5 125 8 19,70 294 3,87 467 4,87 122 2,49 516 3,36 15,5
9 22,00 327 3,86 520 4,86 135 2,48 582 3,40 17,3
10 24,30 360 3,85 571 4,84 149 2,47 649 3,45 19,1
12 28,90 422 3,82 670 4,82 174 2,46 782 3,53 22,7
14 33,40 482 3,80 764 4,78 200 2,45 916 3,61 26,2
16 37,80 539 3,78 853 4,75 224 2,44 1051 3,68 29,6
14 140 9 24,70 466 4,34 739 5,47 192 2,79 818 3,78 19,4
10 27,30 512 4,33 814 5,46 211 2,78 911 3,82 21,5
12 32,50 602 4,31 957 5,43 248 2,76 1097 3,90 25,5
16 160 10 31,40 774 4,96 1229 6,25 319 3,19 1356 4,30 24,7
11 34,40 844 4,95 1341 6,24 348 3,18 1494 4,35 27,0
12 37,40 913 4,94 1450 6,23 376 3,17 1633 4,39 29,4
14 43,30 1046 4,92 1662 6,20 431 3,16 1911 4,47 34,0
16 49,10 1175 4,89 1866 6,17 485 3,14 2191 4,55 38,5
18 54,80 1299 4,87 2061 6,13 537 3,13 2472 4,63 43,0
20 60,40 1419 4,85 2248 6,10 589 3,12 2756 4,70 47,4
18 180 11 38,80 1216 5,60 1933 7,06 500 3,59 2128 4,85 30,5
12 42,20 1317 5,59 2093 7,04 540 3,58 2324 4,89 33,1
20 200 12 47,10 1823 6,22 2896 7,84 749 3,99 3182 5,37 37,0
13 50,90 1961 6,21 3116 7,83 805 3,98 3452 5,42 39,9
14 54,60 2097 6,20 3333 7,81 861 3,97 3722 5,46 42,8
16 62 00 2363 6,17 3755 7,78 970 3,96 4264 5,54 48,7
20 76,50 2871 6,12 4560 7,72 1182 3,93 5355 5,70 60,1
25 94,30 3466 6,06 5494 7,63 1438 3,91 6.733 5,89 74,0
30 11 1,50 4020 6.00 6351 7,55 1688 3,89 8130 6.07 87.6
22 220 14 60,40 2814 6,83 4470 8,60 1159 4,38 4941 5.93 47,4
16 68,60 3175 6,81 5045 8,58 1306 4,36 5С61 6,02 53,8
25 250 16 78,40 4717 7,/6 7492 9,78 1942 4,98 8286 6,75 61,5
18 87,70 5247 7,73 8337 9,75 2158 4,96 9342 6,83 68,‘>
20 97,00 5765 7,71 9160 9 72 2370 4/4 10 401 6.91 76,1
22 106,10 6270 7,69 9961 9,69 2579 4,93 11 464 7,00 83, >
25 119,70 G06 7,65 11 125 9,64 2887 4.91 13 064 7,Н 94,0
28 133,10 7717 7,61 12 244 9,59 3190 4,89 1 I 674 7,23 104,5
Г") И2,')0 J 177 7,59 12 965 9,56 3389 4,89 13 . 53 7,31 111,4
Таблица 2. Сталь прокатная угловая неравнополочная (по ГОСТ 8510— 72)
Обозначения:
В— ширина большей полки;
Ь — ширина меньшей полки;
d— толщина полки;
J — момент инерции;
i—радиус инерции;
хо> Уй — расстояние от центра тяжести до наружных граней полок
330
Номер профиля Размеры, мм Площадь сечения F, см8 Jx СМ4 1х СМ Jy СМ* ‘у СМ J и МИН см 1и мин см Угол на- клона оси У. tg а Х1 см* см* Хц см Уй см Масса 1 м.
в ь d
5,673,6 56 36 4 5 3,58 4,41 11,4 13,8 1,78 1,77 3,7 4,48 1,02 1,01 2,19 2,66 0,78 0,78 0,406 0,404 23,2 29,2 6,25 7,91 0,84 0,88 1,82 1,86 2,81 3,46
6,3/4 7/4,5 63 70 40 4 5 6 8 4,04 4,98 5,90 7,68 16,3 19,9 23,3 29,6 2,01 2,00 1,99 1,96 5,16 6,26 7,28 9,15 1,13 1,12 1,11 1,09 3,07 3,72 4,36 5,58 0,87 0,86 0,86 0,85 0,397 0,396 0,393 0,386 33,0 41,4 49,9 66,9 8,51 10,8 13,1 17,9 0,91 0,95 0,99 1,07 2,03 2,08 2,12 2,20 3,17 3,91 4,63 6,03
45 5 5,59 27,8 2,23 9,05 1,27 5,34 0,98 0,406 56,7 15,2 1,05 2,28 4,39
7,5/5 75 50 5 6 8 6,П 7,25 9,47 34,8 40,9 52,4 2,39 2,38 2,35 12,5 14,6 18,5 1,43 1,42 1,40 7,24 8,48 10,90 1,09 1,08 1,07 0,436 0,435 0,430 69,7 83,9 112,0 20,8 25,2 34,2 1,17 1,21 1,29 2,39 2,44 2,52 4,79 5,69 7,43
1
/5 80 50 5 6 6,36 7,55 41,6 49,0 2,56 2,55 12,7 14,8 1,41 1,40 7,58 8,88 1,09 1,08 0,387 0,386 84,6 102,0 20,8 25,2 1,13 1,17 2,60 2,65 4,99 5,92
9,о. э 90 56 5,5 7,86 65,3 2,88 19,7 1,58 11,8 1,22 0,384 132 32,2 1,26 2,92 6,17
6 8,54 70,6 2,88 21,2 1,58 12,7 1,22 0,384 145 35,2 1,28 2,95 6,70
8 11,18 90,9 2,85 27,1 1,56 16,3 1,21 0,380 194 47,8 1,36 3,04 8,77
Ю/6,3 100 63 6 9,59 98,3 3,20 30,6 1,79 18,2 1,38 0,393 198 49,9 1,42 3,23 7,53
7 11,10 113,0 3,19 35,0 1,78 20,8 1,37 0,392 232 58,7 1,46 3,28 8,70
8 12,60 127,0 3,18 39,2 1,77 23,4 1,36 0,391 266 67,6 1,50 3,32 9,87
10 15,50 154,0 3,15 47,1 1,75 28,3 1,35 0,387 333 85,8 1,58 3,40 12,10
11/7 НО 79 6,5 11,4 142 3,53 45,6 2,00 26,9 1,53 0,402 286 74,3 1,58 3,55 8,98
8 13,9 172 3,51 54,6 1,98 32,3 1,52 0,400 353 92,3 1,64 3,61 10,90
12,5/8 125 8 : 7 14,1 227 4,01 73,7 2,29 43,4 1,76 0,407 452 119 1,8 4,01 11,0
8 16,0 256 4,00 83,0 2,28 48,8 1,75 0,406 518 137 1,84 4,05 12,5
10 19,7 312 3,98 100,0 2,26 59,3 1,74 0,404 649 173 1,92 4,14 15,5
12 23,4 365 3,95 117,0 2,24 69,5 1,72 0,400 781 210 2,00 4,22 18,3
11/9 140 90 8 18,0 364 4,49 120 2,58 70,3 1,98 0,411 727 194 2,03 4,49 14,1
10 22,2 444 4,47 146 2,56 85,5 1,96 0,409 911 245 2,12 4,58 17,5
16/10 160 100 9 22,9 606 5,15 186 2,85 110 2,20 0,391 1221 300 о 93 5,19 18,0
10 25,3 667 5,13 204 2,84 121 2,19 0,390 1359 335 2,28 5,23 19,8
12 30,0 784 5,11 239 2,82 142 2,18 0,388 1634 405 2,36 5,.32 23,6
14 34,7 89/ 5,08 272 2,80 162 2,16 0,385 1910 477 2,43 5,40 27,3
18/11 180 ПО 10 28,3 952 5,80 276 3,12 165 2,42 0,375 1933 444 2,44 5,88 22,2
12 33,7 1123 5,77 324 3,10 194 2,40 0,374 2324 537 9 52 5,97 26,4
20/12,5 200 125 11 34,9 1449 6,45 446 3,58 264 2,75 0,392 2'120 718 2,79 6,50 27,4
12 •37,9 1568 6,43 482 3,57 285 2,74 0,392 3189 785 2,83 6,54 29,7
14 43,9 1801 6,41 551 3,54 327 2,73 0,390 •3726 922 2,91 6,62 34,4
16 49,8 2026 6,38 617 3,52 367 2,72 0,388 1264 1061 2,99 6,71 39,1
_'3 16 250 160 12 48,3 3147 8,07 1032 4,62 604 3,54 0,410 6.-3? 1631 3,53 7,97 37,9
16 63,6 4091 8,02 1333 4,58 781 3,50 0,408 3.69 8,14 49,9
18 71,1 4545 7,99 1475 4,56 866 3,49 0,107 9338 1 187 3,77 8,23 55,8
20 78,0» 4 981 7,97 1613 4,53 949 3,48 0,405 10 -НО , ’/ь 8,31 61,7
Таблица 3, Сталь горячекатаная. Балки двутавровые (ио ГОСТ 8239 -72)
Обозначения:
332
h — высота балки;
Ь — ши рина полки;
d — толщина стенки;
t — средняя толщина полки;
J — момент инерции;
U7—момент сопротивления;
i — радиус инерции;
S—статический момент полусечения
Номер профиля Размеры, мм Площадь сечения Г, см8 см‘ Wx см3 i см Sx сма Jy см* Wy Смэ ‘у см Масса 1 м, кг
Л b d | t
10 100 55 4,5 7,2 12 198 39,7 4,06 23 17,9 6,49 1,22 9,46
12 12) 64 4,8 7,3 14,7 350 58,4 4,88 33,7 27,9 8,72 1,38 11,5
14 140 73 4,9 7,5 17,4 572 51,7 5,73 46,8 41,9 11,5 1,55 13,7
16 160 81 5 7,8 20,2 873 109 6,57 62,3 58,6 14,5 1,7 15,9
18 180 90 5,1 8,1 23,4 1290 143 7,42 81,4 82,6 18,4 1,88 18,4
18а 180 100 5,1 8,3 25,4 1430 159 7,51 89,8 114 22,8 2,12 19,9
20 200 100 5,2 8,4 26.8 1840 184 8,28 104 115 23,1 2,07 21,0
20а 200 ПО 5,2 8,6 28,9 2030 203 8,37 114 155 28,2 2,32 22,7
22 220 ПО 5,4 8,7 30,6 2550 232 9,13 131 157 28,6 2,27 24,0
22а 220 120 5,4 8,9 32,8 2790 254 9,22 143 206 34,3 2,5 25,8
24 240 115 5,6 9,5 34,8 3460 289 9,97 163 198 34,5 2,37 27,3
24а 240 125 5,6 9,8 37,5 3800 317 10,1 178 260 41,6 2,63 29,4
27 270 125 6 9,8 40,2 5010 371 11,2 210 260 41,5 2,54 31',5
333
27а
30
30а
33
36
40
45
50
55
60
270 135 6 10,2 43,2 5500 407 11,3 229 337 50 2,8
300 135 6,5 10,2 46,5 7080 472 12,3 268 337 49,9 2,69
300 145 6,5 10,7 49,9 7780 518 12,5 292 436 60,1 2,95
330 140 7 11,2 53,8 9840 597 13,5 339 419 59,9 2,79
360 145 7,5 12,3 61,9 13 380 Z43 14,7 423 516 71,1 2,89
400 155 8,3 13 72,6 19062 953 16,2 545 667 86,1 3,03
450 160 9 14,2 84,7 27 696 1231 18,1 708 808 101 3,09
500 170 10 15,2 100 39 727 1589 19,9 919 1043 123 3,23
550 180 11 16,5 118 55 962 2035 21,8 1181 1356 151 3,39
600 190 12 17,8 138 76 806 2560 23,6 1491 1725 182 3,54
Таблица 4. Сталь горячекатаная. Швеллеры (по ГОСТ 8240—72)
Обозначения:
h — высота швеллера;
Ь — ширина полки;
d — толщина стенки;
t — средняя толщина полки;
J — момент инерции;
W — момент сопротивления;
i—радиус инерции;
S — статический момент полусечения;
z0 — расстояние от оси у до наруж-
ной грани стенки
33,9
36,5
39,2
42,2
48,6
57,0
66,5
78,5
92,6
108,0
Номер про- филя Размеры, мм Площадь сечения F. см* J см* \VX см3 ix см S*. См3 Ju см‘ U7/y смз ' ,м см Масс 1 м, к;
1 6 1 “ 1 t
5 50 32 4,4 7 6,16 22,8 9,1 1,92 5,59 5,61 2,75 0,954 1,16 4,84
6,5 65 36 4,4 7,2 7,51 48,6 15 2,54 9 8,7 3,68 1,08 1,24 | 4,9
Продолжение табл. 4
Номер профиля Размеры, мм Площадь сечения см> 7* см* wx см’ 1х см S% См3 см* Wy см’ | ‘у см г0 см Масса 1 м, кг
Л b 1 d t
8 80 40 4,5 7,4 8,98 89,4 22,4 3,16 13,3 12,8 4,75 1,19 1,31 7,05
10 100 46 4,5 7,6 10,9 174 34,8 3,99 20,4 20,4 6,46 1,37 1,44 8,59
12 120 52 4,8 7,8 13,3 304 50,6 4,78 29,6 31,2 8,52 1,53 1,54 10,4
14 140 58 4,9 8,1 15,6 491 70,2 5,6 40,8 45,4 11 1,7 1,67 12,3
14а 140 62 4,9 8,7 17 545 77,8 5,66 45,1 57,5 13,3 1,84 1,87 13,3
16 160 64 5 8,4 18,1 747 93,4 6,42 54,1 63,6 13,8 1,87 1,8 14,2
16а 160 68 5 9 19,5 823 103 6,49 59,4 78,8 16,4 2,01 2 15,3
18 180 70 5,1 8,7 20,7 1090 121 7,24 69,8 86 17 2,04 1,94 16,3
18а 180 74 5,1 9,3 20,2 1190 132 7,32 76,1 105 20 2,18 2,13 17,4
20 200 76 5,2 9 23,4 1520 152 8,07 87,8 ИЗ 20,5 2,2 2,07 18,4
20 а 200 80 5,2 9,7 25,2 1670 167 8,15 95,9 139 24,2 2,35 2,28 19,8
22 220 82 5,4 9,5 26,7 2110 192 8,89 НО 151 25,1 2,37 2,21 21
22а 220 87 5,4 10,2 28,8 2330 212 8,99 121 187 30 2,55 2,46 22,6
24 240 90 5,6 10 30,6 2900 242 9,73 139 208 31,6 2,6 2,42 24
24а 240 95 5,6 10,7 32,9 3180 265 9,84 151 254 37,2 2,78 2,67 25,8
27 270 95 6 10,5 35(2 4160 308 10,9 7 178 262 37,3 2,73 2,47 27,7
30 300 100 6,5 11 40,5 5810 387 12 224 327 43,6 2,84 2,52 31,8
33 330 105 7 Н,7 46,5 7980 484 13,1 281 410 51,8 2,97 2,59 36,5
36 369 НО 7,5 12,6 53,4 10 820 601 14,2 350 513 61,7 3,1 2,68 41,9
40 40 0 115 8 13,5 61,5 152 20 761 15,7 444 642 73,4 3,23 • 2,75 48,3
ПРИЛОЖЕНИЕ 2
Модули упругости и коэффициенты Пуассона
Матери ал Модуль упругости Е МПа Модуль упругости G. МПа Коэффициент Пуассона •!
Чугун серый, белый (1,15—1,60) • 10® 4,5 • 104 0,23-0.27
Ковкий чугун 1.55 • 10® — —
Углеродистые стали (2,0—2,1) • 10® (8,0—8,1) • 104 0.24—0,28
Легированные сталн (2,1—2,2) 10® (8,0—8,1) 104 0.25—0,30
Me дь прокатанная 1.1- 10® 4,0 • 104 0.31—0,34
Медь холоднотянутая 1,3 • 10® 4,9 - 104 —
Медь, литье 0,84 • 10® — —
Фосфористая бронза ка- таная 1,15 • 10® 4,2 • 104 0,32—0,35
Латунь холоднотянутая (0,91—0,99) • 10® (3,5—3,7) • 104 0,32—0,42
Корабельная латунь ка- таная 1,0 • 10® 0,36
Марганцовистая бронза катаная 1,1 • Ю5 4,0 • 104 0,35
Алюминий катаный 0,69 • 10® (2,6—2,7) • 1О4 0,32—0,36
Алюминиевая проволока тянутая 0,7 • 10^ г —
Алюминиевая бронза, ли- тье 1,05 • 105 4,2 • 104
Цюралюминий катаный 0,71 • 10® 3,7 • 104 —
Динк катаный 0,84 . 10® 2,2 • 104 0,27
Свинец 0,17 • 10® 0,70 • 104 0,42
Лед 0,1 • 10® (0,28—0,3) • 104 —
Стекло 0,56 • 105 2,2 • Ю4 0,25
Гранит 0,49 • 10® — —
Известняк 0,42 • 10® — —
Мрамор 0,56 • 105 — —
Песчаник 0,18 • 105 —. —
Каменная кладка: из гранита (0,09—0,1) • 105 — —
из известняка 0,06 • 10® —- —
из кирпича (0,027—0,030) • 10® — —
Бетон прн пределе проч- ности, кг/см2: 100 (0,146—0,196) • 105 . 0,16—0,18-
150 (0,164—0,214) • 105 — 0,16—0,18
200 (0,182—0,232) • 105 — 0,16-0,18
Дерево: вдоль волокон (0,1—0,12) • 105 0,055 • 104 —
поперек волокон (0,005—0,01) • 10® —• —
Каучук 0,00008- Ю5 — 0,47
Текстолит (0,06—0,1) • 10® — —
Гетинакс (0,1—0,17) - 10® — —
Бакелит 43 • 102 — 0,36
Висхомлит «ИМ—44» (40—42) • 102 — 0,37
Целлулоид (14,3—27,5) • 102 0,33—0,38
335
ПРИЛОЖЕНИЕ 3
Величины основных допускаемых напряжений на растяжение и сжатие
Материал Допускаемые напряжения, МПа
на растяжение н а сжатие
Чугун серый в отливках 28—80 120—150
Сталь ОС и Ст. 2 14 0
Сталь Ст. 3 16 0
Сталь Ст. 3 (в мостах) 140
Сталь углеродистая конструкционная
(в машиностроении) 60- -250
Сталь легированная конструкционная
(в машиностроении) 100— 400 и выше
Медь 30— 120
Латунь 70— 140
Бронза 60— 120
Алюминий 30— 80
Алюминиевая бронза 80— 120
Дюралюминий 80— 150
Текстолит 30— 40
Гетинакс 50— 70
Бакелизированная фанера 40— 50
Сосна вдоль волокон 7—10 10—12
Сосна поперек волокон — 1,5—2
Дуб вдоль волокон 9—13 13—15
Дуб поперек волокон — 2—3,5
Каменная кладка до 0,3 0,4—4
Кирпичная кладка до 0 ,2 0,6—2,5
Бетон 0,3—1,5 1—2
ПРИЛОЖЕНИЕ 4
Коэффициенты линейного расширении а (на Г С)
Материал а Материал а
Алюминий Магний Медь Бронта и латунь Бетон 255 • 10-’ 255 • 10-’ 167 • 10-’ (170—220) -10-’ (100—140) • 10-’ Лед Сталь Каменная кладка Дерево Целлулоид 507 • 10-- (100—130) • ю-7 (40—70) • 10-’ (20—50) • И)*7 (16—20) • Ю-5
ПРИЛОЖЕНИЕ 5
Программы для ЭВМ «МИР»
1. К расчету статически неопределимой системы при растяжении и сжатии
”3 "ВЫВ”[УРАВНЕНИЕ..РАВНОВЕСИЯ...AlxX'l+BlxN2=Cl],”CTP”;”BbIB”
[УРАВНЕНИЕ. .ПЕРЕМЕЩЕНИЙ...A2xNl+B2xN2=0].”CTP»;Al=XlxSlN(A
Ll);Bl=X2\SlN(AL2);Cl=PxXPJ-Qx(XQ2—XQl)X(XQ2-)-XQl)/2; ”ДЛЯ”КР
= КЕО”Ш”Т”ДО”КЕ1”ВЫП”(А2=Х2хSIN(AL2) X L1/L2;B2=— XI xSlN(ALl)X
КР;ДС=А1хВ2-А2хВ1;ДН1=С1хВ2;ДН2=-А2хС1;ХЧ=ДН1/ДС;К2=ДН
2/nC;FlT=Nl^Oni;FlTl=N2xKF/SflOn2;»E’’FlT>FlTl”TO”(Fl=FlT;F2=
F1T/KF)”HH»(F1=F1T1;F2=F1T1/KF);V=F1xL1+F2xL2;S1=N1/F1;S2= N2/
Р2;”ВЫВ””ТАБЛ” 1 ,KF,N1 ,F1 ,S1 ,N2,F2,S2,V)”EflE”
2. К исследованию плоского напряженного состояния
””5.A=SA+SB;B=V((SA—SB) f 2+(2xTA) f 2);S10=.5x(A+B);S20=.5x(A-
B);S30=0;C=—2xTA/(SA—5В);А1ФА=АКСТС(С)/2;А1ФА=А1ФАх i^0/3.1416;”E
”S10<S20’’TO”(S3=S10;S4=S20)’’HHA”(S3=S20;S4=S10);”E”0 <S3”TO"(Q3 = S3
0;02=S3;Ql ==S4)”HHA”(”E’’S30 > S4”TO”(Q1 =S30;Q2 = S4;Q3=S3)”HHA”(Q1 =
S4;Q2=S3O;Q3=S3));E1=(Q1—Mx(Q2+Q3))/E;L2 = (Q2—MX(Q3+Q1))/E;E3=
(Q3-MX (Ql+Q2))/E;EV=E 14-Е2+ЕЗ;ЭНЕРГ=.5x (Ql XEl+Q2zX E2+Q3X E3);
SE3=Ql-Q3;SE4=V(0.5x((Ql— Q2) f 2+(Q2—Q3) f 2+(Q3—Ql) f 2));”ВЫВя01
,”nP”2,Q2,”nP’’2,Q3,’’nP’’2,А1ФА,”ПРОБ”2,ЕУ,”ПР”2.ЭНЕРГ,”ПР”2,5ЕЗ, ”ПР
’’2,5Е4;’’ВЫВОД”’СТРОКА’’;"Е"5ЕЗ<5ДОП”ТО’’(’’ВЫВ’’[ЭЛЕМЕНТ..УДОВДЕ
ТВОРЯЕТ..УСЛОВИЮ..ПРОЧНОСТИ..ПО..3..ТЕОРИИ]) "ИНА’’(”ВЫВ”[ЭЛЕМ
ЕНТ..НЕ..УДОВЛЕТВОРЯЕТ..УСЛОВИЮ..ПРОЧНОСТИ..ПО..3..ТЕОРИИ]);”
ВЫВ””СТР”;”Е”5Е4<5ДОП”ТО”("ВЫВ”[ЭЛЕМЕНТ УДОВЛЕТВОРЯЕТ УС
ЛОВИЮ ПРОЧНОСТИ ПО 4 ТЕОРИИ])”ИНА”(”ВЫВ”[ЭЛЕМЕНТ НЕ УДОВ
ЛЕТВОРЯЕТ УСЛОВИЮ ПРОЧНОСТИ ПО 4 ТЕОРИИ])”ГДЕ”
337
3. К определению геометрических характеристик плоских сечений
’”6.O=l(I=l,K,F[Il):Sy=l(I=l>K,F[I]xX[I]);XC=Sy/O;SX=v(i==itK>F[i]Xyr
1]);УС=5Х/Ф;”ДЛ"1=1"Ш’1"ДО"К"ВЫП"(А[1]=У[1]—УС;В[1]=Х[1]—ХС);1ХС
=1(1=1, К,1Х[1Ц-А[1] t 2xF[I]);iyC=X(I=l ,К,1У[1]+В[1] f 2хР[1]);1ХУС=1(
1=1,К,1ХУ[1]+А[1] B[I]XF[I]);C=IXC+iyC;D=/((IXC-iyC)t 2-(2х1ХУС
) f 2);IU=(C+D)/2;IV=(C—D)/2;AIOA=.5xARCTG(—2Х1ХУС/(1ХС—1УС))х
57.3;”ВЫВ’’ХС,[ ].УС.[ ],1ХС,[ ],1УС,[ ],IU,[ ], А1ФА,[ J ЛХУС,[ ]
4. К расчету неразрезной балки
””5.0.”ДЛЯ”1 —1”ШАГ”1”ДО”Х”ВЫП”Р[1]=1;”ДЛЯ”К=1”ШАГ” 1”ДО”М—1”В
ЫП”(Е=0;”ДЛЯ”1=К”ШАГ”1”ДО”Д”ВЫП””ДЛЯ”4 =К”ШАГ” 1”ДО’’Х”ВЫП”’
ЕСЛИ"АВ5(Е)—ABS(A[I, J]) <0”TO”(E=A[I ,J];B= 1 ,С=Л);”ЕСЛИ,!К=В”ТО”(’’Н
А’’Л);’ДЛЯ’’Л=К”ШАГ”РДО’’Д+1”ВЫИ”(5==А[КЛ];А[КД]=А[В,Л];А1ВД]=3
);Л."ЕСЛИ”К=С"ТО”(”НА"Е); «ДЛЯ’1=1’ШАГ’1’ДО«№ВЫП’<(5=А[1,К];А[1,
K]=A[I,CJ;A[I,C]=S);D=P[K1; P[K1=P[CJ;P[C]=D;L. "ДЛЯ’1=К-Е 1’ШАГ"1”
ДО”№ВЫП’’(Ц-.Л|1.К]/А1К,К|;”ДЛЯ”Л=К”ШАГ’’1’’ДО’’Х+1”ВЫГГ’А|1Д1=.А
[LJ]—МхА[КЛ));”ДЛЯ"1=№ШАГ"— 1"ДО"1’'ВЫП"(5=0;"ДЛЯ ”К=0’’ШАГ"
1”ДО’’М— I— l»Bbin»S=S+A[N—К, N+HxA[I, N—K];A[I,N+1J=(—S+AJI-N
-F11) /А[1,11) ;”ДЛЯ"1= 1’ШАГ” 1”ДОЯМ—1”ВЫП"(”ДЛЯ"К= 1”ШАГ’1"ДО" N»B
ЫПЯЯЕСЛИ«Р[К]=1ЯТОЯ(ЯЕСЛИЯК=1ПО’’(’’НА’’О)’’ИНАЧЕ” (S=A|I,N+1];A]I
,N+1J=A[K,N+11;A[K,N+1J=S;D=P[IJ;P[I]=P[K1;P[K]=D;’HA>’G));G.);^
Я”1 = 1”ШАГ”1”ДО”Х”ВЫП”Р[1]=А[1,М+Ц;”ВЫВОД””МАССИВА”Р"ГДЕ”
N=4;A[4,5]=I2,3,0,0,0,3112,3,0,0,0,3,I2,3,0,0,0,3,12,— 32;Р[4]’’КОН”
5. К определению напряжений при переменных параметрах упругости
’”’5.H11=S(Z=A>B,2O,F1(Z));H12=S (Z=A,B,2O,F2(Z));H1=M11/H12;M21=$ (Z=
А,В,20, F3(Z));H22=$(Z= A,B,20,E(Z));H2=H21 /И22;"ДЛ”К=1 Ю”Ш’2”ДО’ 146’
ВЫП"(Р5=Е(Ю/(1—MIO);F6=—AL(R)XT(R);SZ=F5X(F6+H1);ST=F5X(F6+H Л
2);STEK=41.110—4.0142710—2Х T(R)+.386761O—3XT(R) f 2—.82737l0—6XT(R)
f 3+.42794lo—9xT(R) f 4;"BbIB””TAB"l,R,SZ.ST,STEK,F5,F6.Hl.H2) «ГДЕ’A M
= 110;B=146;M10 = .28;AO=4.602391(I4;A1 = —4.571741U2;A2=—.54130wl;A3-=.8
338
1О451о—1;А4=—2.5553010—4;T(X)=AO+A1XX4-A2XX f2+A3XX t3-f-A4XX
f4;E(Xl)=2.10lo4—9.2862хТ(Х1)+1.80771в—2sT(Xl) f2—,1836210—4ХТ(Х1)
j 3—.8243210—8хТ(Х1) f 4;AL(X2) = 1.10310—5+2.8841710—9ХТ(Х2) —1.8985610
—11; Т(Х2) f 2+1.090621()—13хТ(Х2) f3—1.02887I0—16ХТ (Х2) f 4;F1(X3)=A
L(X3)XT(X3)XE(X3)XX3;F2(X4)=E(X4)xX4;F3(X5)=AL(X5)XE(X5) X Т(Х5)”
КОН”
6. Способ наименьших квадратов для аппроксимации функции полиномом
””9.1.”ВЫВ””СТР”, {ПОЛИНОМ], ”СТР”;”ДЛЯ”1=1”Ш”1”ДО”ЗХК-|-2”ВЫП”О[
1]=0;”ДЛЯ”Л=1”Ш”1”ДО”КяВЫП”(1 = 1 ;R1 = 1;D[I]=D[I]+R1 ;Q.R2=R1 ХУ [J
];D|I+2xN+l]=D[I+2xN+l]+ R2; P1.R1= R1 x X[J]]=D[I+ 1 Ц-Rl;I
= I4-1;”E”I<N4-2”TO”(”HA”Q);”E”I <2 хНД-1’ТО”(лНА”Р1));”ДЛЯ”1=
ДО”Ь1+ 1»ВЫП””ДЛЯ”3 = 1”Ш”1”ДО”М-|- l”Bbin”A[I,J]=D[I—1+Л];”ДЛЯ”1
= 1”Ш”1”ДО’Н+1”ВЫП”В[1]=О[2хН+1 + 1];’ДЛЯ”Ж=1”Ш”1”ДО”Н+1”ВЫП
ДТ=0;”ДЛЯ"1=Ж”Ш”1”ДО”Н+1”ВЫП”((О=2(Р=1,Ж— 1 ,А[1,Р]хА[Р,Ж]);А[
КЖ]=А[1,Ж]—О);”Е”АВ5(А[1,Ж])> Т”ТО”(Т=АВ5(А[1,Ж]);М=1));”Е”М=Ж”Т
О”(”НА”КП;”ДЛЯ”3=1”Ш”1”ДО”Н+1”ВЫП”(Т=А[ЖД];А[Ж,Л=А[МД];А[М,
Л]=Т);Т=В[Ж];В[Ж]=В[М];В[^]=Т;К1.”Е”АВ5(А[Ж,Ж])<ЕР5"ТО”(5=1;”НА”Ь
1);”ДЛЯ”1=Ж+1’Ш”1’ДО’Н+1”ВЬ!П”А[1,Ж]=А[1,Ж]/Л[Ж,?К]:”ДЛЯ”1=Ж
+ 1”Ш”1”ДО”Н+1”ВЫП”(О=2(Р=1,Ж—1,А[Ж,Р]ХА[Р,Л);А[Ж,Л| = А]Ж,Л
—D):D=S(P=1 ,Ж—1 ,А[Ж,Р]ХВ[Р]); В|Ж]=В[Ж]—0);”ДЛЯ”Ж=Н+1”Ш”-
1”ДО”1”ВЫП”(О=2(Р=ЖД-1,Н+1,А[Ж,Р|ХВ[Р]);В[Ж]=(В[Ж1-О)/А|Ж,Ж1)
;РЗ=0;Е2=0;”ДЛЯ”1=1”Ш”1”ДО”К”ВЫП”(3=Н;Р1=В[3+1|; L.R1=R1 хХП]
+BfJ];J=J—1; ”E”J>0”TO”(”HA”L); R2=ABS(R1—y[I]);L2=L2+R2 f 2,”E”R?
>R3”TO”(R3=R2;R4=y[I|));”E”R4=O”TO”(Rl =O)"HH’(Rl=R3/R4):L2=r (L
2/K);”BbIB”R3,”nPOB”5,Rl.”nPOB”5,L2;Ll.”BbIB””CTP”,S;”BbIB””MACC”B:”
СТОП”Т;”ДЛЯ”\У=1”Ш”1”ДО”К”ВЫП”(У=В[11:”ДЛЯ”У= 1”Ш”1”ДО”1\’ВЫП
»y=y4-B[V + l]xX[W] f У;”ВЫВ””ТАБЛ”1 ,У,Х№])’ГДЕ"
Список литературы
1. Айнберг В. Д. Основы 1фограммирования на алгоритмическом языке
«АЛГОЛ-60».— М.: Машиностроение, 1978.— 152 с.
2. Арутюнян И. X., Абрамян Б. Л. Кручение упругих тел.— М.: Физмат-
гиз, 1963.— 686 с.
3. Амензаде КБ А. Теория упругости.— М.: Высш, школа, 1971.— 287 с.
4. Безухов И. И. Сборник задач по теории упругости и пластичности.—
М.: Гостехтеоретнздат, 1957.— 286 с.
5. Беляев И. М. Сопротивление материалов.— М.: Наука, 1976.— 608 с.
6. Беляев И. М. Сборник задач по сопротивлению материалов.— М.: Наука,
1063.— 348 с.
7, Бернштейн С. А. Сопротивление материалов.— М.: Высш, школа,
1961.— 464 с.
8. Варвак П. М. Новые методы решения задач сопротивления материа-
лов.— Киев: Вища школа. Головное изд-во, 1977.— 160 с.
9. Дарков А. В., Шпиро Г. С. Сопротивление материалов.— М.: Высш,
шк-'ла, 1975.— 654 с.
10. Дарков А. В., Кутуков Б. И. Сопротивление материалов. Методически
указания и контрольные задания для студентов-заочников всех техни-
ческих специальностей высших учебных заведений.— М.: Высш, шко-
ла, 1976.—56 с.
11. Жданов С. М. Расчет конструкций с учетом пластических свойств.—
М.: Изд. Моск, энергет. ии-та, 1952,— 144 с.
12. Зенкевич О. Метод конечных элементов в технике.— Мл Мир, 1975.—
541 с.
13. Иванов И. И. Сборник задач по сопротивлению материалов.— М.: Гос-
техиздат, 1956.— 275 с.
14. Изюмов С. М., Кудрявцев И. И., Олисов В. А. Сборник задач по сопро-
тивлению материалов.— М.: Стройиздат, 1940.— 248 с.
1 • Ильюшин А. А., Ленский В. С. Сопротивление материалов.— М.: Физ-
матгиз, 1959.— 371 с.
16. Ицкович Г. М. Сопротивление материалов.— М.: Высш, школа, 1966.—
512 с.
17. Ицкович Г. М., Винокуров А. И., Барановский И. В. Сборник задач по
сопротивлению материалов.— Л.: Судостроение, 1965.— 287 с.
18. Ицкович Г. М., Винокуров А. И., Минин А. С. Руководство к решению
задач по сопротивлению материалов.— М.: Высш, школа, 1970.— 544 с.
19. Кинасошвили Р. С. Сопротивление материалов.— М.: Физматгиз, 1963.—
387 с.
20. Когаев В. П. Расчеты на прочность при напряжениях, переменных во
времени.— М.: Машиностроение, 1977.— 232 с.
21. Конструкционные стали. Справочник. Под ред. Гудцова Н. Т. М.:
Металлургиздат, 1947.— 481 с.
22. Космодамианский А. С. Кручение эллиптического стержня с двумя
круговыми полостями.— Инж. сб. т. XXL—М.: Изд. АН СССР, 1961,
с. 76—79.
23. Космодамианский А. С. Плоская задача теории упругости для пластин
с отверстиями, вырезами и выступами.— Киев: 1975.— 228 с.
24. Курс лекций по сопротивлению материалов/С. С. Крюковский, С. П. Ни-
китин, А. А. Ойхер, С. В. Рабинович.— М.: Изд. Моск, энергет. ин-та,
1959, ч. 1—248 с.; ч. 2—309 с.
3W
25. Курс сопротивления материалов / М. М. Филоненко-Бородич, С. М.
Изюмов, Б. А. Олисов и др.— М.: Гостехиздат, 1956, т. I—644 с.; т.
Л — 539 с.
26. Лапин А. А. Колебания и вибрации в машинах.— М.: Машгиз, 1953. —
95 с.
27. Лившиц Я. Д_, Скатынский В. О. Сборник задач по сопротивлению мате-
риалов.— Киев—Львов: Гостехиздат Украины, 1949.— 444 с.
28. Любошиц Af. И., Ицкович Г.' М. Справочник по сопротивлению мате-
риалов.— Минск: Вышэйш. школа, 1969.— 464 с.
29. Малинин И. И. Прикладная теория пластичности и ползучести.— М.:
Машиностроение, 1968.— 400 с.
30. Методические указания по курсу сопротивления материалов.— М.:
Изд. Всесоюз. заоч. энерг. ин-та, 1955, ч. 1 •— 146 с.; ч. 2 — 92 с.
31. Метод конечных элементов в механике сплошной среды / П. М. Варвак,
И. М. Бузун, А. С. Городецкий и др.— Киев: Изд. Киев, автомоб.-дор.
пи-та, 1976.— 115 с.
32. Николаев Г. А. Расчет сварных соединений и прочность сварных кон-
струкций.— М.: Высш, школа, 1965.— 451 с.
33. Ободовский Б. А. О применимости формулы Д. И. Журавского к рас-
чету цилиндрической трубы, изгибаемой поперечной силой.— Расчеты
на прочность, 1958, вып. 2, с. 182—188.
34. Ободовский Б. А. Изгиб полого бруса эллиптического сечения.— Расчеты
иа прочность. 1960, вып. 5, с. 182—190.
35. Ободовский Б. А. Расчет статически неопределимых балок.— Харьков:
Изд-во Харьк. ун-та, 1960.— 47 с.
36. Ободовский Б. А. Определение перемещений в балках методом началь-
ных параметров.— М.: Высш, школа, 1971.— 87 с.
37. Ободовский 'Б. А., Сушев В. В. Геометрические характеристики плоских
сечений.— М.: Высш, школа, 1972.— 75 с.
38. Ободовский Б. А., Сушев В. В. Расчет элементов конструкций по пре-
дельным нагрузкам.— М.: Высш, школа, 1972.— 80 с.
39. Ободовский Б. А., Урбанская В. С., Урбанский Р. Е. Кручение некруг-
лых валов.— М.: Высш, школа, 1974.— 228 с.
40. Оржеховская О. П. Изгиб поперечной силой круглого бруса, несимме-
трично ослабленного двумя продольными цилиндрическими круговыми
полостями.— Изв. вузов. Машиностроение, 1967, № 12, с. 21—30.
41. Писаренко Г. С., Яковлев А. П., Матвеев В. В. Справочник по сопро-
тивлению материалов.— Киев: Наук, думка, 1975.— 704 с.
42. Пономарев В. А. Программирова ие для ЭЦВМ «Мир-1».— М.: Сов.
радио, 1975.— 216 с.
43. Пономарев С. Д., Телепнева Г. Г. Исследование геометрических харак-
теристик поперечных сечений брусьев.— М.: изд. МВТУ, 1978.— 28 с.
44. Попов А. А. Сопротивление материалов.— М.: Машгиз, 1958.— 511 с.
45. Пособие к решению задач по сопротивлению материалов/ И. Н. Миро-
любов, С. А. Енгалычев, Н. Д. Сергиевский и др.— М.: Высш, школа,
1967,— 482 с.
46. Рабинович С. В. Расчеты на прочность при переменных напряжениях.—
М.: Изд. Моск, энерг. ин-та, 1951.— 43 с.
47. Работное Ю. Н. Сопротивление материалов.— М.: Физматгиз, 1962.—
455 с.
48. Расчеты на прочность в машиностроении. С. Д. Пономарев, В. Л. Бидер-
ман, К. К- Лихрев и др.— М.: Машгиз, т. 1, 1956.— 884 с.; т. II, 1958.—
974 с.; т. III — 1959,— 1118 с.
49. Рубинин М. В. Руководство к практическим занятиям по сопротивлению
материалов.— М.: Росвузиздат, 1963.— 488 с.
50. Сборник задач по сопротивлению материалов / А. В. Александров,
Б. П. Державин, Б. Я. Лащеников и др.— М.: Стройиздат, 1977.— 335 с.
51. Сборник задач по сопротивлению материалов / А. А. Уманский,
А. М. Афанасьев, А. С. Вольмир и др.— М.: Наука, 1964.— 550 с.
341
6
С2. Свегн.шцкий В. АСтасенко И. В. Сборник задач по теории колебаний.—
М.: Высш, школа, 1973,— 454 с.
53. Сервисен С. В., Когаев В. П., Шнейдерович Р. М. Несущая способность
и расчеты деталей машин на прочность.— М.: Машгиз, 1963.— 451 с.
54. Синяговский И. С. Сопротивление материалов.— М.: Сельхозгиз, 1958.—
432 с.
55. Смирнов В. И. Курс высшей математики,— М.: Наука, т. 4, 1975.— 336 с.
56. Сопротивление материалов, вып. II. Метод указания и задания по кур-
су — Харьков: изд-во Харьк. ун-та, 1961.— 64 с.
57. Сопротивление материалов / Г. С. Писаренко, В. А. Агарев, А. Л. Квит-
ка и др.— Киев: Вища школа. Головное изд-во, 1979.— 696 с.
58. Сопротивление материалов / А. Ф. Смирнов, А. В. Александров,
Н. И. Монахов и др.— М.: Высш, школа, 1969.— 600 с.
59. Справочник по теории упругости / П. М. Варвак, А. Ф. Рябов, Н. П. Абов-
ский и др.— Киев: Будгвельник, 1971.— 418с.
60. Тимошенко С. П. Сопротивление материалов.— М.: Наука, т. I, 1965.—
363 с.; т. II. 1965.—480 с.
61. Тимошенко С. П., Гере Дж. Механика материалов.— М.: Мир, 1976.—
669 с.
62, Тихомиров Е. Н. Курс сопротивления материалов.— М.-Л.: Гостех-
издат, 1934,— 583 с.
63. Уманский А. А., Вольмир А. С., Коданев А. И. Курс сопротивления
материалов.— М.: изд. ВВИА им. Н. Е. Жуковского, ч. 1, 1954.— 552 с.
64. Филин А. П. Прикладная механика твердого деформируемого тела.—
М.: Наука, т. 1, 1975,— 832 с.; т. II, 1978.— 616 с.
65. Феодосьев В. И. Десять лекций — бесед по сопротивлению материалов.—
М.: Наука, 1962,— 173 с.
66. Феодосьев В. И. Избранные задачи и вопросы по сопротивлению мате-
риалов.— М.: Наука, 1973.— 400 с.
67. Феодосьев В. И. Сопротивление материалов.— М.: Наука, 1979.— 560 с.
68. Ходж Ф. Г. Расчет конструкций с учетом пластических деформаций.—
М.: Машгиз, 1963.— 380 с.
69. Чиченев Н. А., Свистунов Е. А. Руководстве к решению задач по при-
кладной механике,— М.: Машиностроение, 1979.— 80 с.
70. Шерман Д. И. Об одной задаче кручения.— Докл. АН СССР, т. XIII,
1948, № 5, с. 499—502.
71. Шерман Д. И. Изгиб поперечной силой эллиптического бруса, ослаб-
ленного продольно круговой цилиндрической полостью. Ииж. сборник,
т. XVI].—М.: Изд. АН СССР, 1953, с. 75—82.
ОГЛАВЛЕНИЕ
Предисловие........................................................3
Международная система единиц и ее применение в сопротивлении мате-
риалов ........................................................5
Часть первая
Глава 1. Растяжение и сжатие
§ 1.1. Основные понятия и зависимости . . . . . . . . 8
§ 1.2. Статически определимые случаи растяжения — сжатия . . 10
§ 1.3. Статически неопределимые случаи растяжения — сжатия 20
Г лава 2. Теория напряженного и деформированного состояния
§ 2.1. Основные сведения из теории............................29
§ 2.2. Аналитическое и графоаналитическое исследование напряжен-
ного состояния...............................................3.3
§ 2.3. Применение обобщенного закона Гука................... 42
Глава 3. Практические расчеты на срез и смятие
§ 3.1. Основные понятия и расчетные формулы ....... 47
§ 3.2. Расчет заклепочных соединений .......... 48
§ 3.3. Расчет сварных соединений............................ 39
Г лава 4. Геометрические характеристики плоских сечений
§ 4.1. Основные понятия и зависимости.........................53
§ 4.2. Вычисление геометрических характеристик плоских сечений 57
Глава .5. Кручение
§ 5.1. Основные понятия и зависимости.........................63
§ 5.2. Расчеты на прочность и жесткость при кручении бруса круг-
лого поперечного сечения .................................... 64
§ 5.3. Статически неопределимые задачи прн кручении...........69
§ 5.4. Кручение прямого бруса некруглого поперечного сечения . . 73
§ 5.5. Расчет цилиндрических винтовых пружин с малым шагом
при осевом нагружении....................................... 79
Глава 6. Построение эпюр внутренних силовых факторов для балок
и рам
§ 6.1. Общие понятия. Аналитическое построение эпюр поперечных
сил Q и изгибающих моментов М для статически определи-
мых балок.....................................................84
§ 6.2. Построение эпюр Q, М для балок по характерным точкам 94
§ 6.3. Построение эпюр Q, М, .V для статически определимых
плоских рам .................................................102
Глава 7. Расчеты на проч 'ость при прямом изгибе
§ 7.1. Расчет на прочность по нормальным напряжениям . . . .111
§ 7.2. Проверка прочности по касательным напряжениям . • .118
Г лава 8. Определение перемещений в балках при прямом изгибе
§ 8.1. Основные положения................................. . 12J
§ 8.2. Определение перемещений методом непосредственного инте-
грирования ..................................................126
§ 8.3. Определение перемещений методом начальных параметров . 131
§ 8.4. Определение перемещений энергетическим методом (с помо-
щью интеграла Мора)..........................................139
Часть вторая
Г лава 9. Расчет простейших статически неопределимых систем
§ 9.1. Статически неопределимые балки. Основные понятия . . . 148
§ 9.2. Неразрезные (многопролетные) балки.................. 152
§ 9.3. Простейшие статически неопределимые плоские рамы . . . 158
343
Глава 10. Косой изгиб
§"10.1. Основные понятия и расчетные формулы..................168
§ 10.2. Примеры расчетов на косой изгиб..................... 170
Глав1 11. Совместное действие изгиба и растяжении (сжатия)
§ 11.1. Изгиб с растяжением (сжатием).........................175
§ 11.2. Внецентренное растяжение (сжатие).....................179
Глава 12. Применение теорий прочности к расчету прямого бруса
§ 12.1. Теории прочности.................................. . 185
§ 12.2. Совместное действие кручения и изгиба. Кручение с растя-
жением или сжатием............................................185
§ 12.3. Общий случай действия сил на брус ................... . 193
Глава 13. Расчет толстостенных цилиндров и тонкостенных сосудов
§ 13.1. Расчет толстостенных цилиндров, находящихся под действи-
ем внутреннего и внешнего давления . .........................203
§ 13.2. Расчет тонкостенных сосудов ........... 211
Глава 14. Плоские кривые брусьи
§ 14.1. Построение эпюр внутренних силовых факторов. Перемеще-
ния в кривых брусьях..........................................218
§ 14.2. Расчет на прочность кривых брусьев большой кривизны . .226
Глава 15. Продольный и продольно-поперечный изгиб
§ 15.1. Расчет сжатых стержней на устойчивость................232
§ 15.2. Продольно-поперечный изгиб ...........................242
Глава 13. Задачи динамики в сопротивлении материалов
§ 16.1. Учет сил инерции .....................................246
§ 16.2. Напряжения и перемещения при ударе....................252
§ 16.3. Колебания систем с одной степенью свободы ...... 258
Глава 17. Переменные напряжения
§ 17.1. Основные понятия об усталостной прочности ..... 268
§ 17.2. Расчет на прочность при переменных напряжениях . . . 274
Глава 18. Расчет элементов конструкций по предельным нагрузкам
§ 18.1. Основные понятия................................... . 282
§ 18.2. Расчет статически неопределимых систем с элементами, рабо-
тающими на растяжение или сжатие..............................284
§ 18.3. Расчет на кручение бруса круглого поперечного сечения 287
§ 18.4. Расчет статически определимых балок................... 290
§ 18.5. Расчет простейших статически неопределимых балок . . 295
Глава 19. Учебно-исследовательские работы студентов
§ 19.1. Определение нормальных напряжений в поперечных сече-
ниях стержня с учетом механических и температурных воз-
z действий . ............................................... 301
§ 19.2. Температурные напряжения .............................303
§ 19.3. Учебно-исследовательские работы и методические указа-
ния к их самостоятельному выполнению ....... 306
§ 19.4. Исследование напряжений в цилиндрах и дисках . . . 309
§ 19.5. Учебно-исследовательские работы и методические указания
к их самостоятельному выполнению..............................313
§ 19.6. Основные понятия и завнснмостн метода конечных элементов 3[5
§ 19.7. Примеры расчетов с помощью метода конечных элементов 318
§ 19.8. Учебно-исследовательские работы и методические указания
к их самостоятельному выполнению..............................325
Приложения ................................................. ..... 327
Список литературы.................................................340
314