Текст
ВЫХОДИТ РАЗ В ДВЕ НЕДЕЛИ Рекомендуемая розничная цена: 279 руб.
Розничная цена: 49,90 грн, 990 тенге
занимательные
ГОЛОВОЛОМКИ
КОЛЛЕКЦИЯ ЛОГИЧЕСКИХ ИГР ОТ D^AGOSTINI
4
Шестигранная «колючка»
9 тггъ 178772 111 » А г•
занимательные
«ЗАНИМАТЕЛЬНЫЕ ГОЛОВОЛОМКИ» Издание выходит раз в две недели Выпуск №4,2012 РОССИЯ
ГОЛОВОЛОМКИ
КОЛЛЕКЦИЯ ЛОГИЧЕСКИХ ИГР ОТ bWMSTINI
В этом выпуске:
ИЗДАТЕЛЬ. УЧРЕДИТЕЛЬ, РЕДАКЦИЯ;
ООО «Де Агостини^ Россия ЮРИДИЧЕСКИЙ АДРЕС: 105 066. г Москва, ул. Александра Лукьянова, д.З. стр.1 Письма читателей по данному адресу не принимаются.
ГЕНЕРАЛЬНЫЙ ДИРЕКТОР; Николае* Скмгакис ГЛАВНЫЙ РЕДАКТОР: Анастасия Жаркова ФИНАНСОВЫЙ ДИРЕКТОР: Наталия Василенко КОММЕРЧ ЕС КИИ ДИРЕКТОР: Александр Якутов МЕНЕДЖЕР ПО МАРКЕТИНГУ: Михаил Ткачук МЛАДШИЙ МЕНЕДЖЕР ПО ПРОДУКТУ: Любовь Мартынова
Свидетельство о регистрации средства массовой информации в Федеральной службе го надзору в сфере связи, информационных технологии и массовых коммуникаций. [Роскомнадзор] ЛИ №ФС77-43310 от 28,12.2010 г.
Для мказа пропущенных номеров и по всем вопросам, касающимся информации о коллекции, «ходите на сайт www.deagostmi.ru
по остальным вопросам обращайтесь по телефону бесплатной «горячей линии)* в России:
С 8-800-200-02-01
Телефон ^горячей линии» для читателей Москвы: С 8-495-660-02-02
АДРЕС ДЛЯ ПИСЕМ ЧИТАТЕЛЕЙ; Россия, 170100» г» Тверь, Почтамт, а/я 245, «Де Агистикио, «Занимательные головоломки»
РАСПРОСГРАНЕНИЕ:ЗАО «ИД Бурда*
УКРАИНА
ИЗДАТЕЛЬ И УЧРЕДИТЕЛЬ: ООО «Де Агостини Паблишинг, Украина ЮРИДИЧЕСКИМ АДРЕС; 01032, Украина, г. Киев, ул. С аксага некого. А-119 ГЕНЕРАЛЬНЫЙ ДИРЕКТОР: Екатерина Клименко
Свидетельство о государственной регистрации печатного СМИ Министерства юстиции Украины КВ V 17502-6252Р от 01.03.2011
АДРЕС ДЛЯ ПИСЕМ ЧИТАТЕЛЕЙ:
Украина. 01033, г. Киев, a/я Де Агостини», Занимательные головоломки»
УкраГна, 01033, м, Кшв, а/с «Де АгоспнЫ
Для заказа пропущенных номеров и по всем вопросам, касающимся информации о коллекции, «ходите на сайт www.deago5tini.ua
по остальным вопросам обращайтесь по телефону бесплатной лгорячей пинии в Украине: £0-800-500-8-40
БЕЛАРУСЬ
Импортер и дистрибьютор в РБ ООО РЭМ-ИНФО*, г. Минск, пер. Козлова, д. 7г, тел,: (017) 297-92-75 АДРЕС ДЛЯ ПИСЕМ ЧИТАТЕЛЕЙ:
Республика Беларусь, 220037, г. Минск а/я 221. 000 РЭМ ИНФО . «Де Агостини , Занимательные головоломки»
КАЗАХСТАН
РАСПРОСТРАНЕНИЕ: ТОО -КГП а Бурда-Алатау-Прессс
РЕКОМЕНДУЕМАЯ РОЗНИЧНАЯ ЦЕНА. 279 руб. РОЗНИЧНАЯ ЦЕНА: 49,90 грн, 990 тенге
ОТПЕЧАТАНО В ТИПОГРАФИИ. 6. Canale & С. S.p.A 5cs.Cemica47. Bururesti, Pantehmcn - tlfov Romania.
ТИРАЖ: 240 000 эм.
Издатель оставляет та собой право изменять последовательность номеров и их содержание.
Издатель оставляет за собой право увеличить рекомендуемую цену выпусков.
Неотъемлемой частью каждого выпуска является приложение.
U ООО вДе Агостиник*, 2012 6 RBA CdeCcionables, 2011 ISSN 2225 1782
ДАТА ВЫХОДА В РОССИИ: 27.03.2012
Математическая вселенная
Атомы арифметики Многие из нас знаки алгебру или у влекались геометрией, а кто-то наверное еще помнит тригонометрические функции или знаком с началами математического анализа. Но что мы можем сказать об обычных числах? Да, да, о тех самых, которые так и называются — «простые числа» ? А ведь это основа основ математики! А кто из нас знает, сколько существует простых чисел? И для чего они нужны я нашей жизни, я эпоху сложнейших математических вы числений и расчетон? Хотите узнать, как обороноспособность гос у дарства зависит от арифметики? Значит этот раздел — для вас!
Блистательные умы
Вездесущий мудрец Любому человеку знакомо имя одного из величай ших ученых-математиков — имя Леонарда Эйлера. Пожалуй, в классическом математике невозможно назвать ни одной области, к которой не относились бы сто труды. Но Эйлер был чрезвычайно одаренным чело веком И занимался нс только своей любимой математикой. Жизнь великого швейцарца многие годы была связана с Россией.
Математика на каждый день
Пропорции прекрасного Некоторые уверены в том, что музыка — искусство, нс поддающееся логическому осмыслению. Однако ученые уже давно дика тали обратное. Оказывается, еще философы Античности знали о том, что ритмы, паузы, тона и гармонию можно выразить в числах. Пифагор утверждал, что музыка хьный гений есть всего лишь правильное понимание правил и соразмерностей, формирующих гаммы. А великий композитор Вольф! анг Амадей Моцарт изобрел необычную игру, позволяющую даже далекому от мира искусства челове-
ку сочинять музыку.
Математически* задачки
fyvtuei гн Генри Дьюдени Подарок для любителей математических задачек! Предлагаем вашему вниманию задачи, составленные настоящим гением математических головоломок. Казалось бы, что сложного в определении родственных связей? У каждого из нас есть родители, братья или сестры и много других родственников, и мы в них не путаемся. А теперь попробуйте разобраться и задачках господина Дьюдени. У\ачи!
Головоломки
Шести, ранная «колючка» Уникальная новая головоломка! Она не только развивает пространственное мышление и сообразительность, но и очень хороша для тренировки силы воли Ваши упоре тво и терпение будут вознаграждены, когда наконец из отдельных шестигранных брусочков сложится объемная деревянная «снежинка». Успешно
преодолевшим трудности в освоении этой головоломки предлагаем бонус! Это еще одна удивительная голов >ломка — «Прекрасные октаэдры» ! Попробуйте свои силы!
Простые числа — основные элементы, из которых состоят положительные целые числа. Для нахождения непредсказуемых простых чисел математики ПОЛЬЗУЮТСЯ МОЩНЫМИ КОМПЬЮТЕРАМИ.
Простые числа
Атомы арифметики
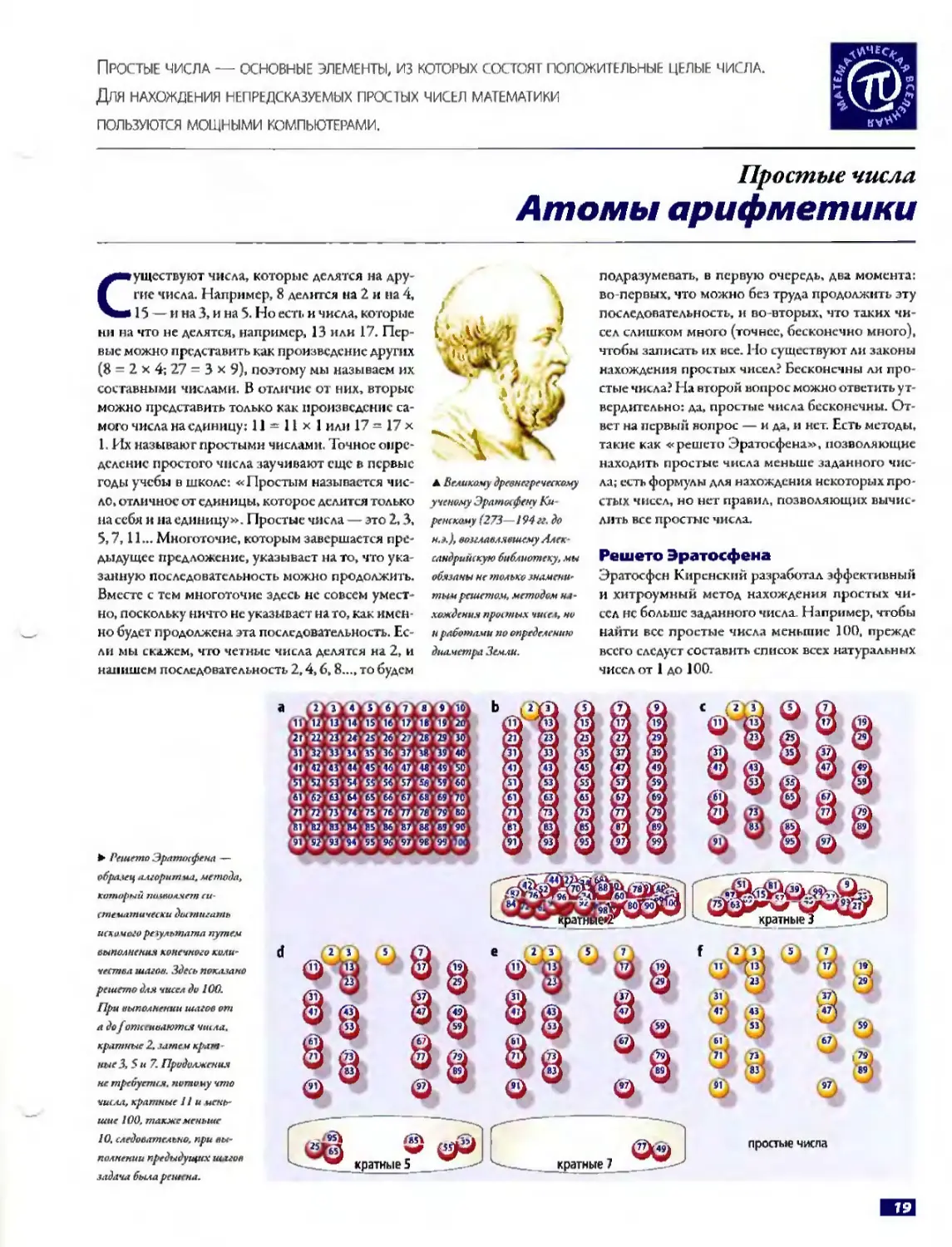
Существуют числа, которые делятся на другие числа. Например, 8 делится на 2 и на 4, 15 — и на 3, и на 5. Но есть и числа, которые ни на что не делятся, например, 13 или 17. Первые можно представить как произведение других (8 - 2 х 4; 27 - 3 х 9), поэтому мы называем их составными чис ламй. В отличие от них, вторые можно представить только как произведение самого числа на единицу: 11 = 11x1 или 17 = 17 х 1. Их называют простыми числами. Точное определение простого числа заучивают еще в г.ервьк годы учебы в школе: *.Простым называется число, отличное от единицы, которое делится только на себя и на единицу». Простые числа — это 2,3, 5,7,11... Многоточие, которым завершается предыдущее предложение, указывает на то, что указанную последовательность можно продолжить. Вместе с тем многоточие здесь не совсем уместно, поскольку ничто не указывает на то, как именно будет продолжена эта последовательность. Если мы скажем, что четные числа делятся на 2, и напишем последовательность 2,4, 6, 8..., то будем
л Великому древнегреческому ученому Эратосфену Кя ренскому (273—194гг. до н.з.), возглавлявшему Алек сандрийскую библиотеку, мы обязаны не только знамени-кт решетом, методом нахождения простых часе«, но n pavomoMti по определению диаметра Земли.
подразумевать, в первую очередь, два момента: во-первых, что можно без труда продолжить эту последовательность, и во-вторых, что таких чисел слишком много (точнее, бесконечно много), чтобы записать их все. Но существуют ли законы нахождения простых чисел? Бесконечны ли простые числа? На второй вопрос можно ответить утвердительно: да, простые числа бесконечны. Ответ на первый вопрос — и да, и нет. Есть методы, такие как «решето Эратосфена», позволяющие находить простые числа меньше заданного числа; есть формулы для нахождения некоторых простых чисел, но нет правил, позволяющих вычислить все простые числа.
Решето Эратосфена
Эратосфен Киренский разработал эффективный и хитроумный метод нахождения простых чисел НС больше заданного числа. Например, чтобы найти все простые числа меньшие 100, прежде всего следует составить список всех натуральных чисел от 1 до 100.
To’oVo’G’oVo’al < И Ф<1 ii tl’ iL <L ф’
Ф д ф’@ Ф Ф '•£ Ф 'й 2- Ф ФФ Ф ‘.Ь Ф Ф’Сь-'ф ф Q)'Q) ф ф ф с ф’ф’ 'Ф ф ФФФФФФФ' ‘Фф ф ф ф ф Ф ФФ'Ф' 'Ф ф ф й ф ф ф fi.' ф ’ф ф ф ф фф ф Ф фф' *ф ф'ф ф ф ф’ф ф‘ф >£
► Решето Эратосфена образец алгорит на, метода, который пшволнет систематически dot шагать иски чего раультдп/д путем выполнения конечного колш чествд шагов. Здесь показано решето для чисел до 100. При выполнении шагов от а до fотсеиваются Числа, кратные 2, заме и кратные 3, 5 и 7. Продолжения не требуется, нити иу что числа, кратные Пи меньшие 100, также меньше 10. следовательно, при выполнении предыдущих шагов задача была решена.
а
Определяется первое про
стое число, отличное от единицы (то есть 2), затем зачеркиваются все числа, После
▲ ВИобаьок ко всем клучным
кратные ему. этого нахо-
первое не-
дится зачеркнутое число (это 3). отличное от 2, н зачеркиваются все числа, кратные ему. Этот процесс повторяется столько раз, сколько это возможно. Наконец незачеркнутыми останутся только простые числа от 1 до 100. Как правило, для нахождения всех простых чисел, меньших числа N, не обяза-
тельно повторять весь трудо< мкий про-
цесс для всех целых чисел до N. Можно доказать,
что достаточно выполнить вычеркивание для целых чисел, которые меньше или равны квадратному корню из N. В нашем примере достаточно вычеркивания для чисел, меньших квадратного корчя из 100, то есть меньших 10.
Решето Эратосфена — один из методов, которые эффективны для нахождения малых простых чисел, не превышающих 10 миллиардов. Разумеется, незачем пользоваться им вручную, с бумагой и ручкой. Мы живем в век информатики, существуют различные алгоритмы, которые позволяют применить тот же метод в компьютерной программе и выполнить необходимые действия максимально быстро, избежав необходимости
.ы&ртис увековечившим его достижения* новым подтверждением признания Эратосфена, как великого математика* стало присвоение его имени лунному кратеру
составлять длинные списки простых чисел, поскольку программа находит такие числа гораздо быстрее, чем компьютер, считывающий информацию с жесткого диска.
Бесконечны ли простые числи?
Существуют десятки способов доказательства бесконечности множества простых чисел, в гом числе чрезвычайно сложные, которые предложил Фюрстенберг в 1955 г., пользуясь топологическим пространством. Ни, вероятно, самое элегантное и наиболее простое доказательство выдвинуто Ев клидом. Оно выглядит так: предположим, что су ществует конечное число простых чисел. В »том случае одно из них будет больше всех остальных — обозначим его Р. Перемножая все простые числа до Р и обозначив результат как N, получим 2 х 3 х 5 х 7 х 11 х... х Р = N. Посмотрим, что в этом случае происходит с числом N + 1. Ясно, что это число не делится на 2, так как это один из множителей N, поэтому мы получим в остатке 1. По той же причине это число нельзя разделить на 3, так как это тоже множитель, содержащийся в N, и у нас снова получится остаток 1. Поэтому мы приходим к вывод], что N + 1 не делится ни на одно простое число до Р, и это означает, что либо оно само является простым, либо делится на простое число, большее Р. Поскольку мы предположили, что не существует таких простых чисел — больше Р, значит, N + 1 простое число, а это противоречит предположению о том, что Р — самое большое простое число. Мы пришли к противоречию, и это означает, что наше изначальное нредполо жение было неверным.
Современное «решето»
Гениальным ученым удается заметить необычную взаимосвязь м< жду, казалось бы, совершенно разными вещами. Что общего у простых чисел и параболы? В XX в. русские математики Юрий Матиясевич и Борис Стечкин открыли следующее примечательное свойство этой кривой: ее можно представить в виде последовательности целых чисел, расположенных между двумя ее ветвями таким образом, чтобы точка пересечения линии между какими-нибудь двумя из этих чисел и осью параболы в точности соответствовала их произведению. Методично отсеивая участки оси с такими сегментами, мы «вычеркиваем»
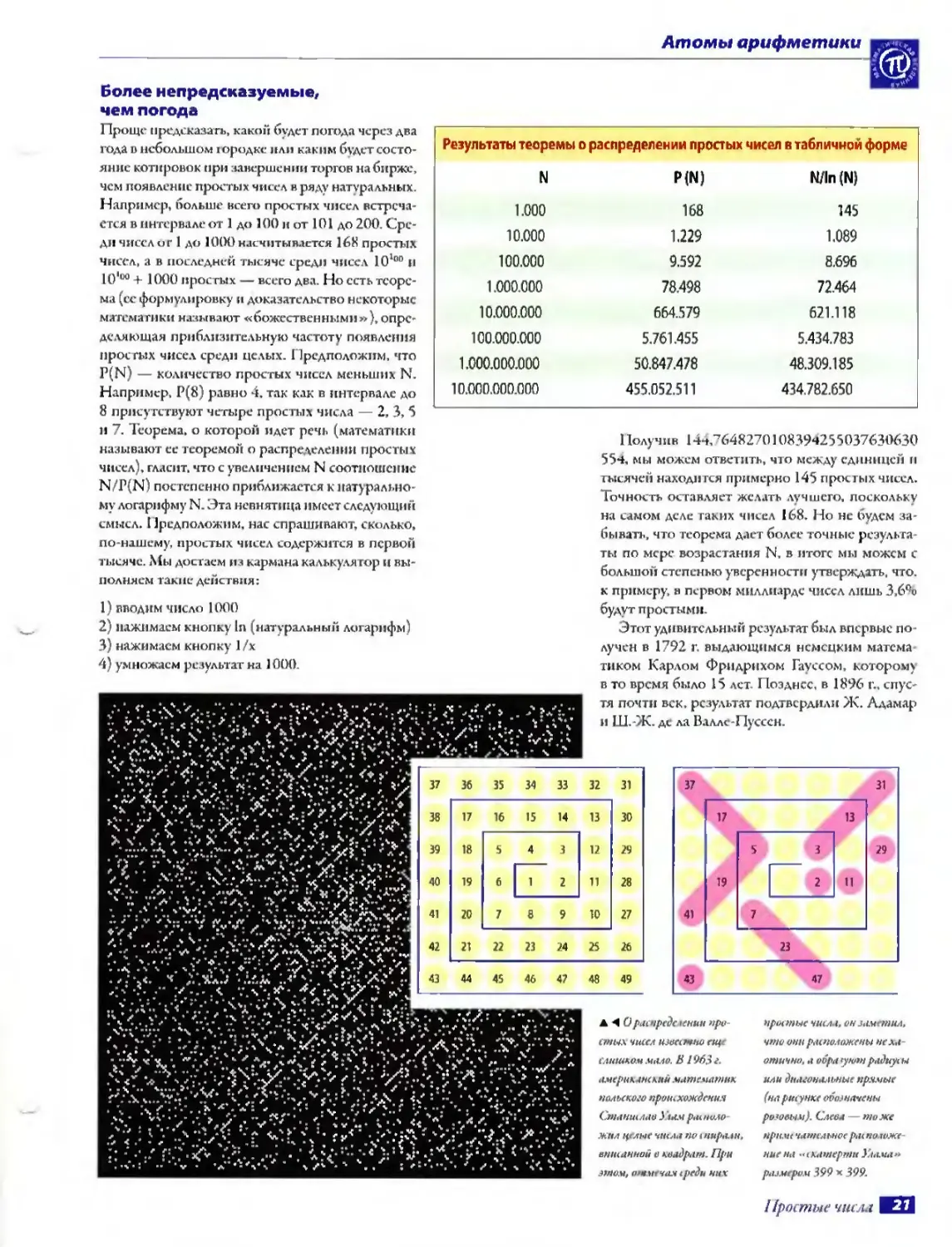
Более непредсказуемые, чем погода
Проще предсказать, какой будет погода через два года в небольшом юродке или каким б\дет состояние котировок при завершении торгов на бирже, чем появл. апе простых чисел в ряду натуральных. Например, больше всего простых чисел встречается в интервале от 1 до 100 и от 101 до 200. Среди чисел о г 1 до 1000 насчитывается 168 простых Чисел, а в последней тысяче среди чисел 101ьл и 10'°°+ 1000 простых — всего два. Но есть теорема (се. формулировку и доказательство некоторые математики называют «божественными»), определяющая приблизительную частоту появления простых чисел среди целых. Предположим, что P(N — количество прсч гых чисел меньших N. Например, Р(8) равно 4, так как а интервале до 8 присутствуют четыре простых числа — 2, 3, 5
и 7. Теорема, о которой идет речь (математики называют се теоремой о распределении простых чисел), гласит, что с увеличением N соотношение N/P(N1 постепенно приближается к натуральному логарифму N. Эта невнятица имеет следующий смысл. 11редположим, нас спрашивают, сколько, по-вашему, простыл чисел содержится в первой тысяче. Мы достаем из кармана калькулятор и выполняем такие действия:
1) вводим число 1000
2) нажимаем кнопку In (натуральный логарифм)
3) нажимаем кнопку 1/х
4) умножаем результат на 1000
Л Ч Ораоереда lenuu простых чисел известно еще слишком .ч<ма. В 1963 г ,ыерик снстч'г математик польского происхождения СтаниЛигв 1 t гм р,и положил целые чиг ><> по г пирали, вписанной е кеадраш При зтом, anew чаи среди них
Результаты теоремы о распределении простых чисел в табличной форме
N P(N) N/ln (N)
1.000 168 145
10.000 1.229 1.089
100.000 9.592 8.696
1.000.000 78.498 72.464
10.000.000 664.579 621.118
100.000.000 5.761.455 5.434.783
1,000,000,000 50.847.478 48309.185
10.000.000.000 455.052.511 434.782.650
Получив 1 •+‘+,"’648270108394255037630630 55ч, мы можем ответить, что между единицей и тысячей находи гея примерно 145 простых чисел. Точность оставляет желать лучшего, поскольку на самом деле таких чисел 168, Но не будем за бывать, что теорема дает более точные результаты по мере возрастания N, в итоге мы можем с большой степенью уверенности утверждать, что, к примеру, в первом миллиарде чисел лишь 3,6% будут простыми.
Этот удивительный результат был впервые получен в 1792 г, выдающимся немецким мегома тиком Карлом Фридрихом Гауссом, которому в то время было 15 лет. Позднее, в 1896 г„ спустя почти век, результат подтвердизн Ж. Адамар и Ш.-Ж. дс ла Валле-Пуссен.
простые числа, он заметил, что они расположены нс хаотично, а оврлгуЛтрадиусы или диагональные прямые (на рисунке обозначены роговым). Слева — тоже npumt нательное рас по тже-ние на ••скагиерти Уломал риале ром 399 ж 399.
Мир гипотез
Неуловимые простые числа позволили сделать немало наблюдений и i области сложных математических гипотез. К примеру, замечено:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 5 + 5 12 = 5+7 14 = 7 + 7
При некотором терпении можно получить более примечательные результаты, например, 37ч = = 151 + 223. Кристиан Гольдбах, состоявший в переписке с Эйлером, выдвинул гипотезу, согласно которой любое число, большее двух, можно представить как сумму двух простых чисел. Доказать это пока никому не удалось. В 193? г Н.М. Виноградов доказал, что любое «достаточно большое» число можно представить в виде суммы трех простых. В дальнейшем он увидел, что это «достаточно большое» число содержит около 7 000 000 знаков, и тем не менее его достижение имело большое значение. Благодаря ком пьютерам было доказано, что гипотеза Гольдбаха верна для всех четных чисел меньше 2 х 10е. В 2000 —200? гг. была назначена премия в размере миллиона долларов тому, кто докажет эту гипотезу- Премию не получил никто, но нс потому, что желающих оказалось недостаточно.
Еще одна до сих пор нс доказанная гипотеза — гипотеза простых чисел-близнецов: существует бесконечное множество пар простых чи-
► Письмо, отправленное Гольдбахом .дилеру 7 июня 17-^2 г. В этом письме впервые была высказана гипотеза о простых числах. Кристиан Гольдбах (1690— 1764 гг.) был высокопоставленным русским VUHDBHUKOM. наставником царя Петра //, .1этыклмг выдающимся математиком.
Основная теорема арифметики
Числа, которые не являются простыми, называются составными и могут быть представлены разными способами. Например, 12 —составное число, которое можно предс гавить как 3 х 4,2 х б, 3 х 2 х 2. В отличие от него, число 11 нельзя представить ни в какой другой форме, кроме 1 х 11. Из трех видов, в которых можно представить число 12, только последний состоит из простых чисел и обладает важным свойством: это единственная форма числа 12 как произведения простых чисел, и то же свойство распространяется на любые числа. Например, 18 = 2x3x3 — единственная возможная форма числа 18 как произведения простых чисел Это следствие, одно из самых важных в арифметике, было доказано Евклидом и получило известность как основная теорема арифметики. Согласно ее формулировке, каждое положительное число, большее единицы, можно представить как произведение простых чисел.
► Почтовые штемпе ш C11L4 в честь открытия очередного простого числа Мерсенна.
Увмк. гтельные иктеллек-UCKlhU3 — один из элементов^ чм то встречающихся в произведениях художественной литератур ы. В этом романе с!посто.юса Доксиаднса ^Дядюшка Пе-тр&еи проблема Гольдбаха» герои тратит немалую часть лшзни, тщетно пытаясь доказать гипотезу Гольдбаха.
сел, разность которых равна двум — например, 17 и 19, 41 и 43, 59 и 61 (самые большие известные пары — 835335”ОМ и 835335”014 + 2). Но в других случаях два ближайших простых числа могут быть разделены сотнями тысяч миллионов целых чисел, нс являющихся простыми (в сущности, доказано, что для любого заданного целого числа к можно найти последовательность целых чисел протяженностью к, которая ие содержит ни одного простого числа).
Колоссальные числа
Р 164+ г. известный ученый Марен Мсрсенн, состоявший в переписке с Декартом, Галилеем и Ферма, изучал числа, впоследствии названные в сю честь. Числа Мсрсснна (МР) — числа вида 2Р - 1, где р — простое число. Например. М2 =
= 22-1 = , - 1 = 3; М, = 23 - 1 = = 8-1-7. £сли продолжать в том же роде, М, = = 31 и М7 = 127, то есть простые числа.
Но 211 - 1 - 2047 = 23 х 89, значит, М11 уже нс простое. Мсрсенн предположил, что в промежутке до р = 257 число 2Р - 1 простое, только если р = 2,3,7,13,17,19,31,67,127 и 257, Доказ шо, что этот список содержит ошибки и упущения. Например, в промежутке до 5000 число 2₽ - 1 простое для р = 2, 3, 5,7, 13, 17, 19, 31, 61, 89, 107,127, 521, 607,1279, 2203,2281,3217.4253 и 4423.
Можно задаться вопросом, зачем нужно уметь находить числа таким сложным способом. Ответ будет таким: мы живем в эпоху мощных компьютеров, а числа Мсрсенна позволяют проводить тест, идеально подходящий для компьютеров. Этот тест, называемый «тест простоты Люка-Ле-мера», показывает, является ли число Мерсей на простым или нет. Существует организация, которая руководит посредством интернета широ комасштабным проектом поиска чисел Мерсен-на, и называется она GIMPS (the Great Internet Mcrsennc Prime Search). Среди ее достижений — найденные числа M6seWJ, MjqWMJ7 и
Мз25»2637, последнее из которых — простое число с почти десятью миллионами знаков. Последнее число Мсрсенна в таблице справа — самое большое из известных к началу XXI в.
VNIVERSjE
GEOMETRIC Ш MIXT/F-QVE^
M ATHEMATICjE SYNOPSIS, FT EINI REFRACTIONVM
1 I MUMl RAI ARV.M TRACTATVi.
Stkdit Of ra F. At At ERSENNl сЯС
parish*.
Aped A * t о * I •» Bi.TitR.valm». hit, 1,(00 Fornins.
ic'DC . LI
UM tttflUtlt it tit.
МерсенН был человеком помет мне энцмклонеди ческих помыннк. Зл я которого в науке нс было неинтересных областей. В члтеиатике его привлекала теория чисел, и в геометрии — исследование циклоид.
Долгое ожидание
Представим себе гигантский склад красок, где хранятся сотни тысяч банок с краской самых разных цветов. Возьмем две банки и с.' ешаем их содержимое. До сих пор процесс был прост. Но если теперь мы покажем кому-нибудь результат и попросим объяснить, каким образом была по лучена эта смесь, то поставим человека в тупик. Речь идет о функциях, ко
торые называются «ловушками» или «односторонними функциями», их легко прос седить в одном направлении и почти невозможно в обратном. А теперь предположим, что вместо банок с краской мы взяли простые
Л Страница mj трактата Марена Л/срсенни ^Всеоб-щ. гя гармония » (1 588— /6-48гг.), Этот священник, математик, физик и фило-соф также мшишмя «г-i ледования чи музыкальных феноменов* анализу которых посвятил не менее шести трудов.
числа. Возьмем любые два из них, например, 7 и 13, и перемножим, воспроизводя перемешивание краски и получив результат? х 13 = 91. После чего возникает вопрос: можно ли определить, какие два числа были перемножены, если они дали результат 91 ? Для этого надо взять список простых чисел и заняться кропотливым подбором. Задача казалась бы простой, как и ее аналог с крацкамн, образовавшими смесь, если бы на складе имелось не более дюжины разных красок. Но с простыми числами дело обстоит иначе К примеру, дока
Число Мерсенна Кол-во знаков Год Компьютер
М521 157 1952 SWAC
Мда 183 1952 SWAC
Мц79 386 1952 SWAC
^2203 664 1952 SWAC
М3021377 909.526 1998 Pentium (200 .Ylhz)
^6972593 2.098.960 1999 Pentium (350 Mhz)
М30402457 9.152.052 2005 Itanium 2 (1,5 Ghz)
М32582657 9.808.358 20J6 Itanium 2 (1.6 Ghz)
зательство, что число 14()93О5б8ч859 — резуль* тат перемножения двух простых чисел, 705967 и 1996277, в некоторых случаях может с 1 агь серьезным испытанием терпения, особенно если принять во внимание, что эти \ва простых числа входят в список, где значатся все простые числа от 1 до 2 000 000, которых насчитывается 250 000. Но мы живем в эпоху' информатики, когда с такой задачей мощный компьютер и хорошая программа могут справиться очень быстро. Тем не менее все зависит от размеров нашего «склада», а «склад» простых чисел не просто велик — он бесконечен.
В предыдущем примере речь идет о сравнптель но небольших числах. Если же мы возьмем простые числа с сотнями знаков каждое, ждать, когда компьютерная программа закончит работу и наконец методом простого перебора найдет нужные числа, придется очень долго — время ожидания превысит продолжительность сущео вования Земли. Ьолес того. Оно превысит даже время существования Вселенной, которое по последним подсчетам составляет около 14 миллиардов лет.
Торговля простыми числами
На трудностях поиска простых чисел, произве
дение которых дает другое число, построена сов-
ременная криптография. Переводы в электронных банковских системах, кредитные карты и переговоры по мобильным телефонам защищены криптографическим способом, в основе которого лежит этот затрудненный поиск. Поэтому, как ни странно, простые числа занимают важное место в нашей повседневной жизни, они имеют отношение и к нашей кредитной карте, и к персональному компьютеру, который стоит у нас на столе. Отсюда следует, что на рынке имеется уст ойчивый спрос на простые числа, так как они необходимы для составления секретных шифров. Такой рынок деист вительн о существует, «промышленное прочзводство» больших простых чисел продолжается. Разумеется, ire каждый нашедший пару простых чисел мо-
жет положить их к себе в бумажник и выставить на аукцион. Мы уже видели, что искать большие простые числа непрог го. Кроме того, найденные числа должны пройти официальную проверку, подтверждающую, что они действительно простые.
х*(х-|)’(хг-1>Чх’-1)
-xl‘(x-i)*(x’--)W-n(x’-0 xl’(x-l)*(x4)(x’- ОЧх’-i)
-х" (x-rt’OMftxMrx’-i)
xl’(x-l)J(x1-l)1(x3-i)
Л Простые числ.1 превратились в ценный товар, в итоге возник рынок со специфическим спросе и и предложением.
Intrigued?
nri г i LrtS м иЯдигь
eh» r* 9 >* * Wwr «wtя-hs-ertMtrS
bnl prfkr-i я mniLi^r mj.mj
** tinwca&rwtfdwi Птч
<< ’hr vvhmJ
Iht ftrtnhlr k lh aitati 4 a ,**?*’ p *
Ew EwrltM
firm, it1 .Чрйт. PrirfiJ».-
Wih> hu&a- » a Ltr оятжА,
скЬжчВД йая! *41 «Г* I 1ЬеЬ«гтт4—юй n» partvcpceTi—m'fxaiitn
Iwr'mr цтгФНтнпМж гт-ri h гЙЧШ й‘1иг wl
h* < Ы k riui auU ртЫнт isi W W
у*1«г*к9гаМг™Мч
\al..xiai ми nr VC
Uta, muuni. FL Mca^c ЧтШ 9Г»4М»
IK Opr'rtmakn rt I ,Jrtm
)T0 Ш1ТШО10
i Число 313 (кстати, это номерной знак машины, на которой ездил Дональд Дак) имеет любопытное свойство: это палиндром (читается одинаково слева направо и справа налево) как в десятичной, так и в двоичной системе счисления и, кроме того, единственное трехзначное простое число, обладающее подобным свойством:
313 (в десятичной системе) = 100111001 (в двоичной системе), и, кроме того, число 100111001 в десятичной системе тог:е простое.
г Число 91 составное191=7x13. Если вс гавить между его цифрами 9 и 0, попучится простое число 9901, если проделать то же самое еще раз, число снова станет составным.
И так далее:
9901 — простое
999001 — составное
99990001 — простое 9999900001 — составное 999Г990СЗС01 — простое 99999990000001 —составное 9999999900000001 — простое 999999999000000001 — составное 99999999990000000001
К сожалению, последнее число составное нарушающее удивительную последовательность Нахождение подобных чисел в настоящее время остается преимущественно развлечением, но когда-нибудь эти незначительные результаты могут стать объяснением какой-нибудь важной теоремы, которую еще только предстоит открыть.
©
Требуются математики Одна из сфер математики, которой занимаются в органах безопасности, — поиск больших простых чисел, пригодных для использования в криптографии. Например, стоит принять к сведению, что один фонд предложил 100 тысяч долларов тому, кто найдет простое число, в котором десять миллионов знаков
Один ИЗ НАИБОЛЕЕ ПЛОДОТВОРНО РАБОТАВШИХ МАТЕМАТИКОВ, ВЕЛИКИЙ УЧИТЕЛЬ, МНОГОЛЕТНИМ ТРУДОМ СНИСКАВШИЙ УВАЖЕНИЕ У ИЗВЕСТНЫХ И РЯДОВЫХ МАТЕМАТИКОВ, СЧИТАЮЩИХ СЕБЯ ЕГО УЧЕНИКАМИ.
Формулы Эйлера, полиномы Эйлера, постоянная Эйлера, интегралы Эйлера, числа Эйлера...
Тот, кто изучает математику, не может не знать имени Эйлера: оно постоянно встречается в математической литературе начиная с XVIII в. и до наших дней.
В классической математике от вычислений, дифференциальных уравнений, аналитической и дифференциальной геометрии до теории чисел, рядов и вариационного исчисления нет области, к которой не относились бы его труды.
Вездесущи/ мудрец
Леонард Эйлер
пенсионных сбережений, в России возглавлял департамент картографии и службу мер и весов. Мы говорим о Леонарде Эйлерс, одной из самых значительных фигур в истории математики.
Многогоанность гения
В возрасте 20 лет Эйлер возглавил Петербургскую Академию наук, куда его пригласили на
Плодотворная деягельн* >сть
Леонард Эйлер родился в Базеле в 1707 г.
Сын пастора-кальвиниста, некогда учившегося математике у Якоба Бернулли, он уже в раннем возрасте демонстрировал блестящие способности к этой науке. Эйлер изучал ее под руководством Иоганна Бернулли вместе с его сыновьями Николаем и Даниилом, с которыми его на про-
должность преподавателя физиологии на медицинский факультет. Речь идет о все том же Эйле-
ре? Да, о том, который двумя годами ранее получил премию французской Академии наук за научную работу по строительству и оснастке судов, создал аналитическую механику твердых тел, изучал работу балки на изгиб и допустимую нагрузку на опоры, эффект смещения небесных тел на планетарных орбитах, теорию графов, баллистику и приливы. И кроме того, он занимался
прикладными вопросами чеканки монет, водоснабжения, судоходных кантлов. страхованием
Греко-латинские квадраты
Предположим, что мы расположили в квадрате предметы, характеризующиеся двумя свойствами (на рисунке — формой и цветом). Это греко-латинский квадрат (он называется так, потому что изначально форму и цвет обозначали греческими и
В А А А
А А 1 L&# а А А А.
В А А 1
* . /еонард Эйлер (1Ю7— I7S3 гг.). Жизнь зтого великого швейцарского
матемлтика — наглядный при мер досадной пропасти
«ли п; повседневной леи мню и наукой: научные труды обеспечили ему в мире математики такую же славу, как Иоганну Себастьяну Баху — в мире музыки, но за пределами узкого круга специалистов Эйлер был почти
неизвестен.
А А В А А А^'Й'В А & В А А^ А А*# В
тяжении всей жизни связывала крепкая дружба. В 1727 г. он переселился в Россию, чтобы занять пост преподавателя на медицинском факультете
Петербургской Академии наук, где уже преподавали математику Николай и Даниил. Нико хай не
выдержал суровой русской зимы и вскоре умер. Его брат Даниил вернулся в Швейцарию, оставив свой пост, в итоге Эйлер в 27 лет оказался наиболее выдающимся математиком Академии, поглощенным в том числе работой над многочисленными статьями для недавно основанного журнала Comentarii Academiae Scientiarum Impel satis Petropolitane.
В А А ©
латинскими буквами), если в каждой строке и в каждом столбце представлены все формы и все цвета (например, вверху показано два греко-латинских квадрата пятого и седьмого порядков). Эйлер предположил, хоть и не доказал, что греко-латинских квадратов шестого порядка не существует. Строгое доказательство было получено лишь в 1900 г.
Эй пер (1707— 1783 гг.)
7
Прямая Эйлера
ется прямой Эйлера.
Одним из наиболее элегантных в геометрии стало доказательство Эйлера, согласно которому в треугольнике ортоцентр Н, центр тяжести G и центр описанной окружности М лежат на одной линии. Эта линия называ-
В 1733 г. Эйлер, который уже обрел достаток, женился на Катарине Гзель, дочери швейцарского художника. Через два года из-за катаракты он перестал виде гь правым глазом, что не помешало ему продолжать свой титанический труд и добиться международного признания. В 17ч1 г. он принял приглашение прусского короля Фридриха II и приступил к работе в Берлинской Академии наук. Во время пребывания в Германии двадцатипятилет-
ний Эйлер сторонился светского общества. По харак теру он был сдержанным и необщительным, вдобавок
Фридрих болег тяготел к обществу философов, оживляющих научными беседами пышные дворцовые приемы, к чему Эйлер, по его собственному признанию, был не способен. Уязвленный пренебрежением монарха и вместе довольный тем, как сложились обстоятельства, Эйлер осуществил поразительное множество исследований, о которых часто сообщал в Петербургскую Академию, по-прежнему выплачивавшую ему жалованье.
Л Обложка «Анали м бесконечно малых» (1748г.), главного вклада Эйлера в дш/мреренцнлльное исчисление, основы которого заложили Ньютон и Аейбющ
20
DDR
LEONHARD EULER 1707 1783
в
Второй период деятельности в России
По предложению императрицы Екатерины II в 1766 г. Эйлер вернулся в Санкт-Петербург и занял в Академии новый пост. В этот период он много писал на больших досках и диктовал формулы своим помощникам, так как из-за катаракты постепенно переставал ви-
)Т0 гоо
Математические способности и фотографическая память Эйлера общеизвестны. Он читал и писал на ла тыни и греческом, по-французски, по-немецки и пс русски. Мог перечислит^ по памяти шесть первых степеней первой сотни чисел, знал наизусть такие тексты, как «Энеида», и даже мог назвать первые и последние стоок 1 поэмы на каждой странице в любом ее издании, названном собеседником.
Научная деятельность Эйлера была невероя । но плодотворной. Он сам говорил, что его карандаш обгоняет разум — с легкост* с которой давало» ему написание трудов. Петербур. скал Академия продолжала издавать прежде не публиковавшиеся работы и после его смерти. Полное собрание трудов Эйлера издинное швейцарской Академией наук, составило 90 увесистых томов.
В неимоверно широкую сферу интересоь Эйлера входила и теория музыки. !1м написаны в том числе т рактаты о гармонии; извес гчо, что за советом к нему обращались такие выдающиеся музыканты той эпохи, как итальянский скрипач Дж.Тартини.
деть и другим i лазом. В 1771 г. он окончательно
потерял зрение и последние 12 лет прожил еле-пыы. Тем не менее в этот период его труды публиковались чаще, чем когда-либо прежде. У Эйлера было 13 дет ей (восемь из которых умерли в младенчестве) и 26 внуков. Он умел писать математические труды и одновременно играть с детьми, и в последние годы жизни находил время, чтобы придумывать развивающие игры для внуков. Эйлер скоропостижно скончался в возрасте 76 лет У во время чаепития. Знаменитая фраза
Кондорсе: «Ои перестал вычислять и жить» — пожалуй, лучшая эпитафия для великого ученого.
•К -К Памятная ыркп с портретом Эйлера и один из его трудов по алгебре. На марке шобраяеени знаменитая формула, связывающая количество вершин (е), гранен (k) и ребер (f) любого выпуклого многогранника.
Философы Античности утверждали, что числа лежат в основе всех вещей, ОБОЗНАЧАЮТ РИТМЫ, ПАУЗЫ, ТОНА И ГАРМОНИЮ, ТАКЖЕ МАТЕМАТИКА — НЕЗАМЕТНАЯ И МОЛЧАЛИВАЯ — ПРИСУТСТВУЕТ В МУЗЫКЕ.
Музыка и математика
Пропорции прекрасного
Музыкальные инструменты генерируют звуковое давление, которое заставляет вибрировать барабанную перепонку человеческого уха. Частота этих вибрации определяет тона — от низких до высоких, а измеряется она в герцах 'Гц) по числу колебаний в секунду. Камертон — специальное приспособление, имеющее форму латинской буквы U — используется для настройки инструментов. При небольшом ударе он издаст звук с частотой 440 Гц. что соответствует музыкальной ноге Ля.
мире, — очень долгая исте-
рия, главные персонажи которой — теория музы-
ки и математика.
659.26 622.25 587.33 554 37 523 25 493.88 466.16
440.00 415 30 392 00 369.99 349.23 329.63
311.13 293.66 277 18 261 63
246.94 233 08 220 00 207.65 196.00 185.00
Mi5
Re #Mi5 1, Re5
Do. #(Res t Do.
Я» La 1
La4
5ola F4<3, 1 Sol, Fa. «(Sol, b
Mi.
Re. №, Л
Re, Do, ttffie, b
Do,
L3j J,
LaJ л
SqIj flu,1 5ol3
Fa3 ttSol, b
рисунке показан фрагмент фортепианных клавши (справа) и частоты (слевл) и их соответствие нотам (в середине), что позволяет увидеть непосредственную связь между числами и нотами. В музыке принято обозначать ноты нижним индексом, как видно на рисунке. Путь к такому обозначению и распределения} частот, используемому почти во всем музыкальном
Пифагорова музыка
Одновременное звучание двух или более нот называется аккордом. Звуки могут быть приятными или неприятными (или не очень приятными). Хотя эта оценка и нс является объективной, все- таки большинство людей, независимо от степени их музыкального образования, единодушно различают эти два типа звуков. Один из многих существующих вариантов воспроизведения
звука — вибрация струны. Нота зависит от длины издающей ее струны. Так как длину можно выразить в цифрах, Пифагор решил изучать взаимосвязь между размером струны и гармонией издаваемых ею звуков. Для этого он изобрел монохорд — натянутую на дощечке струну, длина которой менялась с помощью деревянной планки (процесс, аналогичный настройке гитарной струны). Ученый разделил струну на 12 частей и, передвигая планку, искал приятные слуху звуки.
12
I 4---1--1--1--1--1--1--t--1--1--1--1
9
।—।—1—।—।—।—।—।—।—Т—।—।—।
8
I--1--1--1--1--1--1--1—?---1--1--1--1
6
J--1--1--1--1--1--?--1--1--1--1--1--1
Оказалось» что самые гармоничные звуки издавались струной на участках 9» 8 и 6. Пифагор назвал звуки» издаваемые полной струной» тоном, а трем отрезкам дал имена диатессарон, диапенте и диаплсон, которым в современном музыкальном мире аналогичны названия октава» квинта и кварта. Таким образом на свет появилась первая музыкальная гамма, или «Пифагорейский строй».
4 Гений, кынирыимь: Приписываем Му.ЫК IHfHUU, нл саме.м деле есть лишь набор правил и сорлхиерншлгяй» формирующих силены. Осно-ввпологлникач mioR науки ст ели греческий филогиф Пифагор и его последователи, придумавшие монохорд (см. рисунок .лева).
Соэтиошг‘НИЯ
4 Пифагор , читал, что в основе музыки лежат числа 1, 2, 3 и 4, которые символизируют совершенство числа 10(1+2 + 3 + 4 = 10) чьи части дают начале точке, линии, плоскости и про стрлнству (см. рисунок внизу слева) Таким обрЛЗСНА, по мнению ученого, выстрди* едется въшшзсаязъ чежду кр,и от ой музыки и числами. И люстрация к работе Лтантиуса Кирхсри Mufurgia muveis.t&j (о звуке и музыке, 1650г,).
1 X 12= 12
3/4 х 12 = 9
2/3 х 12 = 8
1/2 х 12 = 6
показывают нам соотношение с длиной струны:
1 = тон
3/4 = кварта
2/3 = квинта
1/2 = октава
Гармоничные комбинации дрожащей струны соотносятся с целыми числами и длиной агон струны, как и показано на следующей таблице. Она резюмирует музыкальную систему, созданную великим греческим философом 11ифагором.
До Ре Ми Фа Соль Ля Си До
1 9/8 81/64 4/3 3/2 27/16 243/128 2
Пентатоника
Чистая квинта — что второй интервал по важности звукового восприятия. [ервый и самый простой — октава, которую можно было бы назвать естественным удвоением Вс время парного исполнения самое очевидное и неинтересное, что могут делать два человека, — петь в унисон. Затем следует пение с интервалом в одну октаву. После — так уж исторически сложилось — пятый интервал. Это означает, что мы перемещаемся в музыкальном интервале между двумя ногами. где отношение частот составляет 2:3. Если за основную ноту мы возьмем фортепианную Ая., (центральная фортепианная клавиша на 4ч0 Гц) и начнем искать две квинты выше нее и две ни же, то у нас получится следующий набор час тот.
л Пентатоническ к. шкала очень распространена во воем мире, особенно в фольклорной музыке, например такой как чумака индейцев, живущие в Андах.
Две квинты выше:
440 X 3/2 = 660; 660 X 3/2 = 990;
Две квинты ниже:
440 X 2/3 = 293,3333:293,3333 X 2/3 = 195.5556;
Серия и» пяти частот:
195,5556 / 293,3333 / 440 / 660 ! 990.
Ноты, наиболее близко подходящие к этим час готам' Соль, — Ре4 — Ля4 — Сй4 — Ре,.
Если мы поместим все эти ноты внутри одной октавы, в нашем случае 4а,то нам необходимо умножить или разделить на два каждую частоту, и тогда в конце мы получим следующий набор частот:
293,33 330,00 391.11 440,00 495,00 586,67
Ре Ми Соль Ля Си До
Это гак называемая «пентатоническая шкала». Такой вид шкал имеет широкое распространение во всем мире, особенно в фольклорной музыке (скажем, в национальной музыке индейцев, живущих в Андах). Любой, кто будет играть на инструменте по этой системе, получит приятную мелодию, нс затрачивая никаких сил — например, используя черные клавиши фортепиано начиная с фа-дисз.
Тона и полутона
При создании своих шкал пифагорейцы применяли гармонический строй, начиная его с определенной ноты и каждый раз поднимаясь на квинту выше, следовательно, затронутые в процессе
а Партитуры Баха (Ток-ката и фуги Л1и шенор. слева) и Дебюсси (Прелюдия, справа) покоряют нс только красотой звучания. но и гармоничны» расположением нот на бумаге.
этого струны сохраняли соотношения длин которые в числовом выражении выглядят так:
= 1.-----,-----.-----,----,------
2 4 8 16 32
причем некоторые из этих нот имеют соотношение 2/1, то есть нс принадлежат к одной и той же октаве. Эту проблему можно решить, разделив ноты на два и поменяв их порядок, что в числовом выражении будет вьплядсть следующим образом:
9 81 3 27 243
1,---,-------,---,----
8 64 2 16 128
что приблизительно соответствует нотам До, Рс, Ми, Фа, Соль, Ля, Си. Добавив квинту 2/3 и умножив сс на два (дабы она уложилась в октаву): 2 X X 2/3 = (4/3), мы получим недостающую ноту Фа, в результате чего ткала приобретет тот вид, о котором говорилось ранее:
До Ре Ми Фа Соль Ля Си До
1 9/8 81/64 4/3 3/2 27/16 243/128 2
A Zf.i схеме показанорасстояние.межд- садами гктнары, настроенными на самые высокие нвтьк выраженные о гео метрической прогрессии в соотношении 1/г, где г = V? в соотеет, те ->я
I равномерно те итерированным строем.
формулой До выше Ре на один гон, а Ре выше Ми на полтона. Казалось бы, чтобы дополнить шка-
лу перемежающимися между собой диезами и бемолями (т.е. чтобы прибавить к белым клавишам фортепиано черные и получить так называемую цветовую шкалу), логичнее всего постепенно добавлять полутона. Но дело в том, что в интерва-
ле двух полутонов находится соотношение длин,
которое можно выразить следующим уравнением: (256/243)* = 65.536/59.049 = 1,1098579... результат которого можно с легкостью округлить до 1,11. Однако тон равен 9/8 = 1,125, из чего следует, что два полутона не могут равняться одному тону. Вот тут-то и начинаются грудности — особенно у тех, кто занимается изготовлением музыкальных инструментов.
Равномерно темперирован иый строй
Настраивая струнный инструмент по чистым квинтам, изготовитель обнаруживает, что Си диез слишком приближается по звучанию к До. С другой стороны, они не совсем тождественны, ведь Си диез немного выше До, и они находятся в интервале, называемом пифагоровой коммой. Следовател! но, для каждой из этих нот потребуется отдельная струна. Это в свою очередь приведет к возникновению неразрешимых проблем, та-
Расположение нот в этой шкале приблизительно соотвстс.вугт расположению белых клавиш на фортепиано. Интервалы между располагающимися друг за другом нотами равны 9/8 и 256/243-Например, 9/8 X 9/8 = 8/164, а 8/164 X 256/243 = 4/3, где соотношение 9/8 выступает как тон, а 256/243 — как полутон. В соответствии с этой
ких как появление чрезмерного количества струн
Ч Наравне с философией, ариф.м такой и геометрией, музыка входила в священную vt тверку наук. Это символически июбраяа но на сраеюре-ил тстйацгш к книге Грегора Рейша «Философская жемчужина», выпущенной в 1503 г.
же
и расстояний, которые нево (можно охватить пальцами рук. К тому
Ч Бах поспособствовал по-нуляри.,ацииравномерно тем-перироваънт , -троя, напшае «Хорошо пн мт рированный клавире, состоящий из 24 прелюдий и руг, содержащих все тональности. Можно было сыграть любое из згяих произведений, не менял музыкальных инструментов в ходе исполнения.
при смене тональности
последовательность интервалов также меняется. Необходимость решения этой проблемы возникла, когда композиторы перестали пользоваться модальными ладами (такими как квинты, идеальные аккорды и т.д,), заменив их на тональные. Необходимо было наити среди полутонов величину, способную акустически уравновесить ноты, получившие название энгармонических. Так появился равномерно темперированный строй.
Л?улык.1 и штсмагника
11
ЛОГОО .
Пифагорейский строй никогда не был совершенным — ни в музыкальном плане, ни в математическом. Совершенным он был бы при следующих значениях:
1 г г2 г3 г4..............г" = 2
Но все встречающиеся в пифагорейском строе значения включают в себя только лишь числа 2 и 3, то есть все они соответствуют образу 2" X X 3'. Например:
9/8 = З2 X 2 Э 243/128 = 3s X 2'7
Если одно из этих значений г = 2* х зу, как
г12 = 2, получается, что 212" X З121' = 2, благодаря чему 212""1 = З"121', что невозможно, потому что сила 2 никогда не может быть равна силе 3, так как она не соответствует уникальности деления простых чисел. Это не означает, что нельзя найти другой тип интервала для строя, если и не совершенного, то почти совершенного. Ведь можно просто взять г - -1,04946...
что приближенно равно значению, взятому для построения равномерно темперированного строя. Греки не могли этого сделать, потому что не знали о существовании иррациональных чисел, таких как 'Vl
Фрактальная музыка
Когда в хаотичной системе появляется аттрактор, становится возможным написать компьютерную программу, которая свяжет координату л: с музыкальной нотой, а координату у — с длительностью этой ноты. По этому принципу создается фрактальная музыка. Изобретение нс предназначено для того, чтобы непосредственно писать музыку, но оно может подтолкнуть автора к ес созданию. Одна из самых известных программ — The Vtell Tcm Fractal (TWTF), позволяющая проектировать до 10 аттракторов на 21 шкале. Результат действительно впечатляет.
В «Музыке сфер» самой сильной нотой была Гипатия происходившая из центра Земли которая сейчас соответствовала бы основной ноте или ot новному тону нашего строя Примерно в 370 г. директор Александрийского музея Геон назвал свою дочь именем Гипатия. Это была первая женщина-математик в истории и, к сожалению, первая жертва религиозной нетерпимости в отношении науки.
▲ Бгрмоничные интервалы пифагорейского строя были использованы Зля установления связи чежЗу инопланетянами и землянами в фильме Стивена Спилберга «Близкие контакты третьей степени».
В187б г., в подлинном стремлении к пуризму в музыке Бланше удалось создать «фисгармонию с генерализованной клавиатурой», которая имела 53 клавиши на октаву Конечно же, речь не шла о темперированном строе.
Известные последовательное!л Фиооначчи 1,2 3,5,8, были использованы композитором Бела Барток для создания музыкальной шкалы, названной им шкалой Фибоначчи.
Случайная музыка В возрасте 21 года Вольфганг Амадей Моцарт написал вальс, состоящий из 16 тактов (номер каталога К. 294). Он сделал это, следуя инструкциям придуманной им же музыкальной игры в кости, которая помогала писать музыку даже не будучи композитором. Игра состояла из двух костей и двух таблиц с разными номерами. Первая должна была использоваться для начальной части вальса, вторая —для окончания. Чтобы написать первую часть вальса, которая состояла из
восьми тактов, надо было кинуть две кости и сложить выпавшие числа. Первая колонка таблицы содержала только 11 возможных результатов. Если, например, выходило после первого броска 9, то выбирался такт из колонки 1 и строчки 9, и так далее, пока не складывалось восемь тактов первой части. То же самое — со второй таблицей во второй части. Таким образом Моцарт составил из обеих таблиц 176 тактов. Будем надеяться, что никто не решит записать все возможные вальсы, так как количество вариантов равно 750 триллионам.
Лучшее из Генри Э. Дьюдени
Задачи о возрасте и родственных связях
< Сколько лет маме, Томми и паке?
«Дней лет наших семьдесят лет».
Псалтирь, 89:10
На протяжении веков математические задачи нередко пред» тавляли в виде вопросов, касающихся возраста того или иного человека. Как правило, решение алгебраическими методами оказывалось несложным, зачастую трудность представляли корректные формулировки. Условия таких задач могли быть доволььо запутанными, для их решения требовался талант, общие правила для них были неприменимы. Читателю приходилось призывать на помощь свою сообразительность.
Что касается задач о родственных связях между людьми, их способность ставить в тупик удивительна, Даже в повседневных разговорах некоторые замечания, касающиеся родственных связей и совершенно очевидные с точки зрения говорящего, порой озадачивают его слушателей. Выражения вроде «сестра зятя дяди» кажутся бессмысленными без подробных и утомительных объяснений, В таких случаях удобнее всего наскоро набросать генеалогическую схему, чтобы внимательный взгляд пришел на помощь уму. Поскольку в настоящее время семьи стали менее разветвленными, большинство людей не имеют навыка рисования подобных схем, и это печально, потому что в некоторых случаях они могут сэкономить время и вместе с тем избавить слушателей от необходимости ломать голову.
1. Возраст мамы
Томми: «Сколько тебе лет, мама?»
Мама: «Дай-ка подумать, Томми... Общий возраст нас троих — ровно 70 лет».
Томми: «Так много! Сколько же лет тебе, папа?»
Папа: «Всего лишь в шесть раз больше, чем тебе, сынок».
Томми: « А мне когда-нибудь будет вдвое меньше лет, чем тебе, папа?»
Папа: «Конечно, Томми, и тогда сумма возрастов нас троих ровно вдвое превысит тсп ерешнюю ».
Томми: «А если бы я родился раньше тебя, папа, а мама забыла бы об этом, и если бы ее не было дома, когда я родился, тогда...»
Мама: «Тогда тебе давно пора в кровать, Томми. Идем, детка, а то головка разболится».
Будь Томми постарше, он сумел бы вычислить точный возраст родителей на основании полученной от них информации. А вы сможете точно определить, сколько лет маме?
2. Задача для переписчики
В семье Джоркинс 15 детей, все они рождались с разницей в полтора года. Самая старшая дочь, Ада Джоркинс, постеснялась во время переписи назвать свой точный возраст, но призналась, что он вей о в семь раз больше возраста ее младшего брата Джонни. Сколько лет Аде? Решая эту задачу, не спешите, иначе наверняка ошибетесь!
3. Пакет орехов
Трое детей получили в подарок на Рождество пакет орехов и договорились ра лде лить их между собой пропоргдюнально возрасту, который в сумме составлял 17 с половиной лет.
В пакете было 770 орехов, и если Герберт брал четыре, то Роберт брал три, а если Герберт брал шесть, Кристофер брал семь. Требуется найти сколько орехов досталось каждому ребенку и сколько ему было лет.
4. Запутанное родство
— Кстати, о родственных связях, — сказал за ужином священник, — наши власти устроили страшную путаницу с брачными законами. Возьмем к примеру, один невероятный случай, который привлек мое внимание. Два брата женились на двух сестрах. Муж одной умер, жена другого брага гоже умерла. После этого оставшиеся в живых поженились.
— Муж женился на сестре своей умершей супруги, что ра 1решено новыми законами? — вмешался адьокат
— Вог именно. Следовательно, согласно граждан скому законодательству, он состоит в законном браке, и его ребенок законнорожденный. Но дело в том, что этот мужчина — брат покойного супруга своей жены, и по тем же законам она не считается замужней, а ее ребенок — законнорожденным. — Получается, что он женился на ней, а она не вы шла за него? — воскликнул врач.
— В некотором роде. А ребенок — законный для отца, но не законный для матери.
— Безусловно, этот закон — бессмыслица, — зая-вил Художник, — если вы не против подобных выражений, — добавил он, повернувшись к адвокату. — Конечно, — последовал ответ — Мы, адвокаты, стремимся укротить это чудовище и заста-
4 hfapu и МармаЗьюк с удовольствием гуляют по парку.
вить его служить человеку. Во всем виноваты наши >аконодатсли.
— Мне, кстати, — продолжал священник, — вспомнился один мужчина из моего прихода, который обвенчался с сестрой его вдовы. Так вот, у этого человека...
— Минутку, будьте любезны, — прервал профессор. — «Обвенчался с сестрой у го вдовы »? Вы венчаете усопших?
— Нет, но я потом объясню, в чем дело. Итак,
у этого человека есть родная сестра. Их зовут Стивен Браун и Джейн Браун. На прошлой недс ле Стивен представил мне одного молодого человека, своего племянника.
Разумеется, в разговоре я назвал Джейн его теткой, однако, к mocnv удивлению, молодой человек поправил меня, пояснив, что хотя он и приходится племянником Стивену, но Джейн, сестре Стивена, он нс племянник. Поначалу я растерялся, однако понял, что он совершенно прав.
Адвокат первым добрался до сути этой загадки. А какую ра >гадку предложили бы вы?
5. Мэри и Мармадьюк
Мармадьюк: « Представь, дорогая через семь лет нам на двоих будет 63 года!»
Мэри: « Правда? А когда тебе было столько же лет, сколько мне сейчас, тебе было вдвое больше, чем мне тогда. Я вчера подсчитала».
Итак, сколько лет Мэри и сколько Мармадьюку?
Решения
1 Малле 29 лет и 2 месяца, папе 35 лет, а Томми 5 лет и 10 месяцев. В сумме получается ровно 70 лет. Отцу в шесть раз больше лет, чем сыну, а когда пройдет 23 года и 4 месяца, их общий возраст составит 140 лет, и Томми будет вдвое меньше лет, чем его отцу.
2. Аде Джоркинс 24 года, ее младшему брату Джонни 3 года, 13 братьев и сестер по возрасту занимают промежуточные положения между ними. Подвох заключен в словах о возрасте, который «в семь раз больше» возраста Джонни. Как правило, при этом забывают учесть сам больший возраст. По сути дела, это различие не в семь, а в восемь раз. Подобная досадная ошиб
ка встречается даже у лучших авторов задач. Правы те читатели, которые подсчитали, что возраст сестры и брата — 24 с половиной и 3 с половиной года соответственно.
3. Когда Герберт взял 12 орехов, а Роберт и Кристофер — 9 и 14 орехов соответственно, всего за один раз было взято 35 орехов. Поскольку 35 содержится в 770 всего 22 раза, от нас требуется умножить 12,9 и 14 на 22, чтобы узнать, что Герберту досталось 264 ореха, Роберту — 198, а Кристоферу — 308. Далее, поскольку их общий возраст — 17с половиной лет, или половина суммы 12, 9 и 14, соответственно возраст детей — 6 4с половиной и 7 лет.
4. Если мужчина женился на женщине, которая затем умерла, а потом женился на сестре своей умершей супруги и тоже умер, значит, правильным будет сказать, что раньше он был женат на сестре его вдовы.
Молодей человек не приходится Джейн Браун племянником, потому что он ее сын. Она но'эт ту же фамилию, что и ее брат Хотя Браун — ее фамилия в браке, она могла выйти за однофамильца.
5, Возраст Мармадьюка — 29 лет и 2/5, возраст Мэри —19 лет и 3/5. Когда Мармадьюку было 19 лет и 3/5, Мэри было
9 лет и 4/5, то есть Мармадьюк был вдвое старше Мэри.
Шестигранная «колючка» — разновидность новой головоломки, получившей название «хекстикс» («ШЕСТИГРАННЫЕ БРУСОЧКИ»). ГЛАВНАЯ ЗАДАЧА — СОБРАТЬ ПРОЧНУЮ КОНСТРУКЦИЮ ИЗ 12 ОТДЕЛЬНЫХ ДЕТАЛЕЙ. ЭТО НЕПРОСТО, НО ТЕРПЕНИЕ, ЗДРАВЫЙ СМЫСЛ И ЛОВКОСТЬ НЕПРЕМЕННО ПРИВЕДУТ К ПОБЕДЕ.
Детали, соединенные звездообразно
Шестигранная «колючка»
Шестигранники» придумал один из самых плодовитых изобретателей головоломок современности Стюарт Коффин, он же запатентовал их в 1970 г. Одновременно, но независимо от него, такую же головоломку изобрел Билл Катлер в 1964 г. Шестигранная «колюч
ка» — одна из разновидностей «шестигранников».
Предшественники соединяющихся деталей
В удивительном мире механических головоломок есть одно разветвленное семейство, представляющее особый интерес — головоломки-«колючки». Они состоят из трех и более частей, сцепляющихся между собой и образлющих одно эффектное целое. Самый известный представитель этого семейства — сложный крест из шести деталей, который появился предположительно еще до 1803 г., когда он впервые был внесен в каталоги игр и игрушек Beitermeier
Форма деталей
Детали большинства подобных головоломок продет авляют собой призмы квадратного сечения с пазами, позволяющими соединять их между собой. Детали шестигранной «колючки», как видно из названия, в сечении имеют вид шестиугольников. У шести деталей по два фигурных паза, у трех — по одному, у грех оставшихся — по три.
к. Шестигранная «дю-лючка» — головоломка из 12 деревянных деталей, шестиугольных в сечении. Все детали имеют свои размеры, каждая снабжена одни w ил и более пазами, которые позволяют собирать из них крмнвую фигуру, показанную выше.
Прекрасные октаэдры
Эти головоломки состоят из четырех наборов по три детали в каждом, оси которых параллельны «руг другу. Если соединить центры оснований этих призм, получится равносторонний треугольник. Обращенные друг к другу стороны деталей и этот треугольник дают четвертый шестигранник точно такого же размера, как остальные.
Каждая из этих четырех групп деталей образует тройную ось воображаемого октаэдра, как можно увидеть на иллюстрациях в следующем столбце.
Октаэдр — одна из самых распространенных форм природных кристаллов. Такую форму особенно часто имеют алмазы. Во время огранки обычно срезают верхнюю вершину октаэдр?, получая грань, которая называется «площадкой» или «табличкой». Ее окружают новыми гранями, в том числе сложными и многочисленными, как в случае огранки способом Перуцци, насчитывающей 57 граней.
1. Сначала сложите подобие пирамиды из трех деталей с двумя пазами, как показано на рисунке.
2. Чтобы получившаяся конструкция не развалилась, приставьте к ней по бокам три детали с одним пазом.
3. Теперь из оставшихся трех деталей с двумя пазами сложите треугольник так, как показано на рисунке.
4. Наденьте получившийся треугольник на три подпирающие (темные) детали так, чтобы он сцепился со всей конструкцией.
I*
6. После этого поверните группу деталей так, чтобы она сцепилась с уже собранной конструкцией.
7. Головоломка собрана.
Невидимый додекаэдр
В этой красивой головоломке скрыта правильная геометрическая фигура, хотя разглядеть ее непросто.
Внутренняя полость этой головоломки имеет форму ромбического додекаэдра.
В следующем выпуске через 2 недели
Число «пи»
Очарование трансцендентного числа
Основатель современной информатики
Алан Тьюринг
Исследование операций
Математика эффективности
Льюис Кэрролл
История с узелками
Спрашивайте в киосках!