Автор: Нестеренко Ю.В. Олехник С.Н. Потапов М.К.
Теги: математика задачи занимательные задачи
ISBN: 5-02-013759-6
Год: 1988
Текст
СН.Олехник
Ю. В. Нестере н ко
М.К.Потапов
шганные
ЗДНИМАТ6ДЫШ6
ЗАДАЧИ
СИ. Огіехник
Ю. В. Нестеренко
М.К. Потапов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1988
22.1
0-53
УДК 51 (023)
Олехник С. Н., Нестеренко Ю. В., Потапов М. К.
О -53 Старинные занимательные задачи.— 2-е изд.,
• испр.— М.: Наука. Главная редакция
физико-математической литературы, 1988.— 160 с.
ISBN 5-02-013759-6
В книге собрано 170 занимательных задач из руеских рукописей
и книг, опубликованных до 1800 года.
Как правило, задачи решаются с привлечением минимальных
сведений из арифметики, алгебры в геометрии, но требуют
сообразительности и умения логически мыслить. В книге содержатся как
задачи, доступные детям, так и задачи, представляющие интерес для
взрослых. Книга будет интересна также любителям истории
математики.
Первое издание вышло в 1985 г.
Табл. 7. Ил. 97. Библиогр. 32 назв.
1702010000-065
° 053(02)-88 56"88
ББК 22.1
51 (023)
ISBN 5-02-013759-6
Издательство «Наука».
Главная редакция
физико-математической
литературы, 1985; с
исправлениями, 1988
Предисловие
В книге собраны занимательные задачи из русских
рукописей и книг, опубликованных в России до 1800 года.
В русской математической литературе, в учебниках
всегда уделялось, большое внимание занимательным
задачам, так как считалось, что элемент занимательности
облегчает обучение. К занимательным задачам мы
относим задачи с интересным содержанием или интересными
способами решения, математические игры, задачи,
касающиеся интересных свойств чисел и геометрических тел.
Книга разделена на три части. В первую часть вошли
задачи из рукописей и из книги Л. Ф. Магницкого
«Арифметика». Во вторую часть — задачи из учебников,
опубликованных в России после издания книги Магницкого,
но до 1800 года. В третью часть — задачи из книг
(последнего десятилетия XVIII века), целиком либо в
значительной степени посвященных занимательным задачам.
Каждая часть состоит из разделов. Разделы внутри
части расположены в порядке возрастания трудности.
Многие задачи подверглись стилистической обработке.
В оглавлении после названия каждой задачи в скобках
указаны два числа: первое из них — номер страницы
книги, на которой приведен текст задачи, второе — номер
страницы, на которой приведено ее решение.
При подготовке второго издания были внесены
некоторые исправления.
С. Н. Олехник,
Ю. В. Нестеренко,
М. К. Потапов
ИЛИ Д'БАТМНАА .
Что (чть мідліітікд ;
ДрТАЛггікд или чнслнтыннцд , рсть ^дожктво
ЧЕСТНОі , НЕЗДВИСТНОі , Н вНіЛІХ ОуДСВОПОАТНОЕ ,
ліногололезн'БЙшк , и жного^вл'лн'Ьйсше , ffi дре-
кн4йшн)р я» и нбв+йшн^я , вх рд'зндд нре,ишд
ЙВЛШН^СА ІОД^ДІОЕЙШН^Ж jSp'bMuViKWX , HgiUBfE-
тенноі , и изложенное .
КОДИКОгввД НТЬ 4р'іАДІ(Ѵі'КД ІірЛКТІКД j
^еть с^гЗвд .
і ДоіА/НІтікд полЬжд , или гмждднскдд .
2 Д^ІАМГПКД ДОГІСТНКД , Н« КО Г^ДЖДДНСТК^
т6к-мш,н6 йкдкнжшТм нвны^х к^гооі п^индлѳкдіидА.
Введение
Из первых известных письменных источников узнаем
мы о том, что математические знания на Руси были
распространены уже в X—XI веках.
Они были связаны, естественно, с практическими
нуждами людей: летоисчислением, вычислением поголовья и
стоимости стада, определением прибыли от сбора урожая
и т. д. ч
«А полбы немолоченые 15 копен,
а на то прибытка на одно лето 7 копен,
а на всю 12 лет в той полбе прибытка
1000, 700 и 50 копен»*).
Эти строки взяты из статьи «О полбе немолоченой» одного
из ранних рукописных исторических документов —
«Русской Правды»— первого из дошедших до нашего времени
сборника русских законов.
Судя по всему, подсчет «прибытка» в этой статье
основан на предположении, что каждый год в течение 12 лет
вся собранная в предыдущий год полба высевается, что
каждый раз полученный урожай составляет несколько
меньше, чем 3/2 посеянной полбы, и что все вычисления
ведутся в целых числах.
Другое дошедшее до нас наиболее древнее русское
математическое произведение «Учение им же ведати
человеку числа всех лет» принадлежит новгородскому монаху
Кирику и посвящено календарным расчетам. Как известно,
даты ряда церковных праздников непостоянны. От года
к году они определяются по довольно сложным правилам,
связанным с движением солнца и луны. Вычисление дня
*) Полба — злак, разновидность пшеницы.
5
пасхи (с этим церковным праздником жестко связаны
даты других праздников церковного календаря)
представляет поэтому непростую математическую задачу
В начале «Учения» указывается, что написано оно в 6644 г
от «сотворения мира» (в 1136 г. по принятому сейчас у нас
летоисчислению) и что от «сотворения мира» прошло
79 728 месяцев или 346 673 недели или 2 426 721 день или
29 120 652 дневных часа и столько же ночных. После этого
сообщается, как вычислить так называемые «солнечный»,
«лунный» и «великий» круги и, наконец, указывается, на
какой из дней приходится праздник пасхи в текущем году
В XVI—XVII веках в России начинает появляться и
распространяться рукописная математическая
литература (этого требуют межевание и измерение земель,
система податного обложения, градостроительство и военное
дело, развивающиеся торговые отношения внутри страны
и торговля с другими государствами). В настоящее время
известно значительное количество математических
рукописей XVII века. В основном они предназначались для
купцов, торговцев, чиновников, ремесленников, землемеров
и носили сугубо практический характер. Материал их рас
пределялся по «статьям», содержащим указания, как надо
поступать при решении тех или иных задач. Правила
пояснялись разнообразными примерами и задачами.
Некоторые из этих задач интересны либо своей формулировкой,
либо способом решения. Многие из них перешли в
учебники по арифметике и алгебре XVIII века, некоторые
сохранились и до нашего времени.
Рукописи XVI—XVII веков сыграли большую роль в
распространении математических и практических знаний.
Они явились той основой, на которой создавалась
учебная литература XVIII века.
Перестройка государственной, общественной и
культурной жизни страны, начатая Петром 1, подняла и
вопросы образования. Требовались специалисты для создания
новой регулярной армии, для постройки торгового и
военного флота, для развития промышленности и т. д. Для
подготовки таких кадров, для распространения в стране
математических знаний нужны были учебники. В 1703 году
такой учебник был издан типографским способом
необычайно большим по тем временам тиражом — в количестве
2400 экземпляров. Назывался он «Арифметика, сиречь
наука числительная...». Автором его был выдающийся
6
педагог-математик — Леонтий Филиппович Магницкий
(краткие биографические сведения о нем содержатся в
приложении). Взяв за основу имевшуюся рукописную
математическую литературу, Магницкий создал книгу,
которая на протяжении 50 лет была основным учебником по
математике для почти всех учебных заведений России. Она
сыграла большую роль в распространении
математических знаний, в подготовке кадров для государственных
учреждений страны.
«Арифметика»— одна из самых замечательных
русских книг — являлась энциклопедией математических
знаний того времени. Понимая роль заинтересованности
в обучении, Магницкий приводит много задач с
остроумным содержанием, занятными формулировками,
интересными способами решения. К некоторым задачам
приводятся рисунки. Занимательным задачам он посвящает целый
раздел «Об утешных некиих действах чрез арифметику
употребляемых».
Первая часть настоящей книги посвящена
занимательным задачам из рукописной литературы и «Арифметики»
Магницкого. Рукописи и «Арифметика» написаны на
старославянском языке, поэтому в первой части в
основном приводятся тексты задач, подвергшиеся
стилистической обработке; для любознательных читателей в ряде
случаев приведены и их подлинные формулировки на
старославянском языке. Сделано это также и для некоторых
решений задач.
В основном мы сохранили в задачах и старые меры
(веса, длины и денег).
В 1725 году в Петербурге открылась Академия наук
с университетом и гимназией. Вначале для работы в
Академии были приглашены ученые из-за границы. Среди них
приехал в Россию двадцатилетний швейцарец Леонард
Эйлер, будущий великий математик. Его неустанная
педагогическая деятельность во многом способствовала
формированию русских национальных научных кадров
(подробнее жизнь и деятельность Л. Эйлера описаны в
приложении) . Отметим здесь только учебники Эйлера по
элементарной математике: «Руководство к арифметике, для
употребления в гимназии при Императорской Академии
наук» (1738—1740 гг.) и «Универсальная арифметика»
(1768—1769 гг.). Материал в этих книгах изложен очень
ясно, доходчиво, сопровождается большим количеством
различных увлекательных задач и примеров.
7
Книги Магницкого и Эйлера послужили основой для
многих учебников других авторов: Н. Г. Курганова,
Д. С. Аничкова, С. К. Котельникова, С. Я. Румовского и др.
Многие из этих руководств были написаны для тех или
иных учебных заведений, отличавшихся спецификой
подготовки своих учеников. Кроме отдельных учебников,
появляются и целые курсы математики. Так, например, в 1787—
1790 гг. вышел «Курс чистой математики» Е. Д. Войтяхов-
ского, состоящий из пяти книг (Арифметика, Алгебра,
Геометрия, Тригонометрия и Фортификация),
предназначенный для учеников основанной им в Москве
Математической школы. Книги эти пользовались большой
популярностью и неоднократно переиздавались.
В учебниках того времени можно найти множество
занимательных задач. Некоторые из них по своим идеям
восходят к рукописям XVII века и к книге Магницкого, но
также появляется и ряд новых задач. Эти задачи
составляют содержание второй части настоящей книги. Кроме
них во вторую часть включены некоторые задачи из
учебников Эйлера и сохранившейся обширной переписки
Эйлера с учеными.
Если в русской рукописной литературе XVII века и в
книгах начала и середины XVIII века занимательные
задачи были рассеяны среди учебных задач, то уже в конце
ХѴШ века этим задачам посвящаются отдельные
издания. Такой, например, является книга «Детский гостинец,
или четыреста девяносто девять загадок с ответами в
стихах и прозе, взятых как из древней, так и новейшей истории
и из всех царств природы и собранных одним другом детей
для их употребления и приятного препровождения
времени». Эта небольшая книжка вышла в Москве в 1794 году
и содержала различные занимательные вопросы, загадки,
пословицы и небольшие истории. В предисловии к ней
сказано, что «книга, сей источник просвещения и истинного
удовольствия, не должна быть для детей источником скуки
и горести». Надо, чтобы учение было привлекательным,
и обучение малолетних детей необходимо представлять как
«забаву, а не как скучную должность». При обучении детей
«надо знать их склонности и способности и надобно уметь
делать в упражнениях радость, которая для них весьма
приятна». В книге говорится далее, что написана она для
того, чтобы давать ее читать детям «вместо награды за
успехи в учении».
8
Аналогичным вопросам посвящена и «Библиотека
учения, экономическая, нравоучительная, историческая и
увеселительная в пользу и удовольствие всякого звания
читателей», изданная в 12 томах в 1793—1794 гг. в
Тобольске. В каждом томе этой «Библиотеки» несколько
страничек посвящено занимательным вопросам: здесь и
задачи об угадывании задуманных чисел, и
математические фокусы, угадывание числа предметов, угадывание
зачеркнутой цифры и некоторые другие.
Особо среди книг, изданных в это время, следует
отметить книгу «Гадательная математика для забавы и
удовольствий». В этой книге собрано более 40 занимательных
задач: на отгадывание задуманных чисел, на переправы,
переливания жидкостей, угадывание числа лет и т. п.
Включенные в третью часть задачи взяты из этих трех
книг.
Часть первая
ЗАДАЧИ
ИЗ СТАРИННЫХ РУКОПИСЕЙ
И «АРИФМЕТИКИ» Л. Ф. МАГНИЦКОГО
1. Житейские истории
1. Бочонок кваса.
бДИНЪ ЧЛКЪ ВЫПЬЕТЪ КАДЬ ПИТІА В 14 ДНЕЙ, А СО ЖЕНОЮ
ВЫПЬЕТЪ ТОІ ЖЕ КАДЬ В 10 ДНЕЙ, И В*ВДДТЕЛН» ЕСТЬ В КОЛИКѴѴ
ДНЕЙ ЖЕНА ЕПѴ ОСОБНО ВЫПЬЕТЪ TOE ЖЕ КАДЬ-
Один человек выпивает бочонок кваса за 14 дней, а
вместе с женой выпивает такой же бочонок кваса за 10
дней. Нужно узнать, за сколько дней жена одна выпивает
такой же бочонок кваса.
2. В жаркий день.
В жаркий день 6 косцов выпили бочонок кваса за 8
часов. Нужно узнать, сколько косцов за 3 часа выпьют такой
же бочонок кваса.
3. На охоте.
Пошел охотник на охоту с собакой. Идут они лесом,
и вдруг собака увидала зайца. За сколько скачков собака
догонит зайца, если расстояние от собаки до зайца равно
40 скачкам собаки и расстояние, которое пробегает собака
за 5 скачков, заяц пробегает за б скачков? (В задаче
подразумевается, что скачки делаются одновременно и
зайцем и собакой.)
4. Собака и заяц.
Собака усмотрела зайца в 150 саженях от себя. Заяц
пробегает за 2 минуты 500 саженей, а собака — за 5 минут
1300 саженей.
За какое время собака догонит зайца?
10
5. Как разделить орехи?
Говорит дед внукам: «Вот вам 130 орехов. Разделите
их на 2 части так, чтобы меньшая часть, увеличенная
в 4 раза, равнялась бы большей части, уменьшенной в 3
раза».
Как разделить орехи?
6. На мельнице.
На мельнице имеется три жернова. На первом из них
за сутки можно смолоть 60 четвертей зерна, на втором 54
четверти, а на третьем 48 четвертей. Некто хочет смолоть
81 четверть зерна за наименьшее время на этих трех
жерновах.
За какое наименьшее время можно смолоть зерно
и сколько для этого на каждый жернов надо зерна
насыпать?
7. Воз сена.
Лошадь съедает воз сена за месяц, коза — за два
месяца, овца — за три месяца.
За какое время лошадь, коза и овца вместе съедят
такой же воз сена?
8. Двенадцать человек.
Двенадцать человек несут 12 хлебов: каждый мужчина
несет по 2 хлеба, женщина — по половине хлеба, а
ребенок по четверти хлеба.
Сколько было мужчин, женщин и детей?
п
9. Постройка дгма.
Четыре человека х»тать дворъ стр&ити, ідйнъ и% пихт»
мбжетъ лостр«ити въ 1 г&дъ: дрвгій мбжетъ въ 2 года,
трётій въ 3 годд, л четвертый въ 4 года: и в4ддт£лно есть,
ВЪ КОЛИКѴѴ ГОДѴѴВЪ ОНИ ВСЙ ОВЦІ6 ТОЙ ДВОрЪ ПОСТрОАТЪ-
Четыре плотника хотят строить дом. Первый плотник
один может построить дом за год, второй плотник может
построить дом за 2 года, третий плотник может построить
дом за 3 года, а четвертый — за 4 года. Однако строили
дом четыре плотника вместе.
За какое время они выстроили дом?
10. Скворцы.
Летели скворцы и встретились им деревья. Когда сели
они по одному на дерево, то одному скворцу не хватило
дерева, а когда на каждое дерево сели по два скворца, то
одно дерево осталось не занятым.
Сколько было скворцов и сколько было деревьев?
11. Сливы.
Двое ели сливы. Один сказал другому. «Дай мне свои
две сливы, тогда будет у нас слив поровну»,— на что
другой ответил: «Нет, лучше ты дай мне свои две
сливы,^— тогда у меня будет в два раза больше, чем
у тебя».
Сколько слив было у каждого?
12. Мальчики и яблоки.
Трое мальчиков имеют по некоторому количеству
яблок. Первый из мальчиков дает другим столько яблок,
сколько каждый из них имеет. Затем второй мальчик дает
двум другим столько яблок, сколько каждый из них теперь
имеет; в свою очередь и третий дает каждому из двух
других столько, сколько есть у каждого в этот момент.
После этого у каждого из мальчиков оказывается по
8 яблок.
Сколько яблок было вначале у каждого мальчика?
13. Кому пасти овец?
У пятерых крестьян — Ивана, Петра, Якова, Михаила
и Герасима — было 10 овец. Не могли они найти пастуха,
чтобы пасти овец, и говорит Иван остальным: «Будем,
12
братцы, пасти овец по
очереди — по столько дней,
сколько каждый из нас имеет
овец». По сколько дней
должен каждый крестьянин
пасти овец, если известно, что у
Ивана в два раза меньше
овец, чем у Петра, у Якова в
два раза меньше, чем у
Ивана; Михаил имеет овец в два
раза больше, чем Яков, а
Герасим — вчетверо меньше,
чем Петр?
14. Сколько яиц в
лукошке?
Пришел крестьянин на
базар и принес лукошко яиц.
Торговцы его спросили:
«Много ли у тебя в том
лукошке яиц?» Крестьянин
молвил им так: «Я всего не
помню на перечень, сколько в
том лукошке яиц. Только
помню: перекладывал я те
яйца в лукошко по 2 яйца, то
одно яйцо лишнее осталось
на земле; и я клал в лукошко
по 3 яйца, то одно же яйцо
осталось; и я клал по 4 яйца,
то одно же яйцо осталось; и я клал по 5 яиц, то одно же
яйцо осталось; и я их клал по 6 яиц, то одно же яйцо
осталось; и я клал их по 7 яиц, то ни одного не осталось. Сочти
мне, сколько в том лукошке яиц было»?
II. Путешествия
15. Из Москвы в Вологду.
Послан человек из Москвы в Вологду, и велено ему в
хождении своем совершать во всякий день по 40 верст. На
следующий день вслед ему послан второй человек, и
приказано ему проходить в день по 45 верст.
На какой день второй человек догонит первого?
16. Через сколько дней встретятся путники?
Идет один человек в другой город и проходит в день по
40 верст, а другой человек идет навстречу ему из другого
города и в день проходит по 30 верст. Расстояние между
городами 700 верст.
Через сколько дней путники встретятся?
17. Путешественники.
Путешественник идет из одного города в другой 10
дней, а второй путешественник тот же путь проходит за
15 дней.
Через сколько дней встретятся путешественники, если
выйдут одновременно навстречу друг другу из этих
городов?
18. Вокруг города.
Два члкд пондбшд с ідйндгѵи дѵ&стд окрктъ грддд, и едйнъ
<Ю нй^ъ йдаіш по 4 версты нд чдеь, д дрЗгій по 3 — версты,
3
окрктъ же того грддд 15 вірстъ, и в-бддтЕлнѵѵ есть в коликѵѵ
члеѵѵвъ пдки сошаиса, и колйкожды кійждо Лвшелъ той
грддъ*
Два человека пошли одновременно друг за другом из
одного места вокруг города. Один из них идет по 4 версты
в час, а второй по 3= версты в час. Путь вокруг же того
города составляет 15 верст.
Через сколько часов они сошлись и сколько раз каждый
из них обошел город?
19. Два -воина.
Один воин вышел из города и проходил по 12 верст в
день, а другой вышел одновременно и шел так: в первый
день прошел 1 версту, во второй день 2 версты, в
третий день 3 версты, в четвертый 4 версты, в пятый 5 верст
и так прибавлял каждый день по одной версте, пока не
настиг первого.
Через сколько дней второй воин настигнет первого?
20. Далеко ли до деревни?
Прохожий, догнавший другого, спросил: «Как далеко
до деревни, которая у нас впереди?». Ответил другой
прохожий: «Расстояние от той деревни, от которой ты идешь,
15
равно третьей части всего расстояния между деревьями,
а если еще пройдешь 2 версты, тогда будешь ровно
посередине между деревнями».
Сколько верст осталось еще идти первому прохожему?
III. Денежные расчеты
В дальнейшем в некоторых задачах употребляются
следующие денежные единицы:
рубль— 100 копеек,
гривна — 10 копеек,
алтын — 3 копейки,
полушка — - копейки.
21. Покупка сукна.
К&пйлъ — дршйнд, дллъ 3 длтынл; что достоитъ длти ^д
100 дршинъ-
Некто купил - аршина сукна и заплатил за них 3
алтына. Сколько надо заплатить за 100 аршин такого же
сукна?
22. Сколько стоят гуси?
Некто купил 96 гусей. Половину гусей он купил,
заплатив по 2 алтына и 7 полушек за каждого гуся. За
каждого из остальных гусей он заплатил по 2 алтына без
полушки.
Сколько стоит покупка?
23. Сколько куплено баранов?
Один человек купил 112 баранов старых и молодых,
заплатив за них 49 рублей и 20 алтын. За старого барана
он платил по 15 алтын и по 4 полушки, а за молодого
барана по 10 алтын.
Сколько каких баранов было куплено?
24. За какое время окупятся куры?
Один человек купил три курицы и заплатил за них 46
копеек. Первая курица несла по 3 яйца через 4 дня,
вторая — по 2 яйца через 3 дня, а третья — по 1 яйцу через
2 дня.
Продавал он яйца по 5 штук за полкопейки.
За какое время окупятся куры?
16
25. Покупка масла.
Некий человек покупал масло. Когда он давал деньги
за 8 бочек масла, то у него оставалось 20 алтын. Когда же
стал давать за девять бочек, то не хватило денег полтора
рубля с гривною.
Сколько денег было у этого человека?
26. Сколько стоит кафтан?
Хозяин нанял работника на год и обещал ему дать 12
рублей и кафтан. Но тот, проработав только 7 месяцев,
захотел уйти. При расчете он получил кафтан и 5 рублей.
Сколько стоит кафтан?
27. Хозяин и работник.
Хозяин нанял работника с таким условием: за каждый
рабочий день будет ему платить по 20 копеек, а за каждый
17
нерабочий день — вычитать 30 копеек. По прошествии 60
дней работник ничего не заработал.
Сколько было рабочих дней?
28. Замысловатый ответ.
Принес крестьянин на рынок продавать яйца.
Подходит к нему торговец и спрашивает: «Сколько стоит десяток
яиц?». Крестьянин ответил замысловато: «Двадцать
пять яиц без полушки стоят пять полушек без пяти
яиц».
Сосчитайте, по какой цене продавал крестьянин
десяток яиц.
29. «Полторажды полтора».
К$пйлъ полторажды полтора аршина, далъ полтрстьджды
полтрггкй гривны: koahkw дати т,л полаебатажды нолдевата
аршина-
В этой задаче «полторажды полтора» означнет
з з_9
2*2 4'
«полтретьяжды полтретьи» означает
2І.2І = 25
2 2 4'
«полдевятажды полдевята» —
8І-8І = ^.
2 2 4
Текст задачи следует понимать так:
ѵ 9 25
Куплено J аршина сукна и за них уплачено -j-
289
гривны. Сколько надо уплатить за —т- аршина
сукна?
30. Четыре купца.
Четверо купцов имеют некоторую сумму денег.
Известно, что, сложившись без первого, они соберут 90 рублей,
сложившись без второго — 85 рублей, сложившись без
третьего — 80 рублей, сложившись без четвертого —-
75 рублей.
Сколько у кого денег?
18
31. Покупка птиц.
Хозяин послал работника на базар купить 20 птиц:
гусей, уток и малых чирков. Он дал работнику 16 алтын.
Гусей велел покупать по 3 копейки за штуку, уток по копейке,
а малых чирков по два на копейку.
Сколько гусей, сколько уток и сколько чирков купил
работник?
32. Проторговался ли купец?
Некто продавал коня и просил за него 1000 рублей.
Купец сказал, что за коня запрошена слишком большая
цена. «Хорошо,— ответил продавец,— если ты говоришь,
что конь дорого стоит, то возьми его себе даром, а заплати
только за одни гвозди в его подковах. А гвоздей во всякой
поднове по б штук. И будешь ты мне за них платить таким
19
IV. СЭ ©ѵткшныхт» ігнкТихъ Д'Ьйствдх'ь чре^
АрѴдлѵетикй оѵпотревлАелѵых-ь («об утешных не-
киих действах через арифметику употребляемых»)
33. Как узнать день недели?
Пронумеровав дни недели, начиная с понедельника,
по порядку с 1 до 7, предложите кому-нибудь загадать
некоторый день недели. Затем предложите порядковый номер
задуманного дня увеличить в 2 раза и к этому
произведению прибавить 5. Полученную сумму предложите
умножить на 5, а затем то, что получится, умножить на 10. По
объявленному результату вы называете загаданный день.
Как узнать загаданный день недели?
34. У кого кольцо?
Перенумеровав присутствующих и! отвернувшись от
них, предложите кому-либо взять кольцо и одеть его на
какую-нибудь руку на какой-нибудь палец. Затем
попросите удвоить порядковый номер того, кто взял кольцо, и к
полученному результату прибавить 5. Полученную сумму
попросите умножить на 5 и к ней прибавить номер пальца,
считая с мизинца. Полученную сумму попросите опять
умножить на 10, к результату прибавить число 1, если
кольцо надето на левую руку, и число 2, если кольцо
надето на правую руку. После объявления результата
предложенных вами арифметических действий вы отгадываете,
кто из присутствующих взял кольцо и на какой палец
какой руки надел его.
Как по объявленному результату это определить?
35. Отгадать несколько чисел.
Предложите кому-либо задумать несколько (вам
известное количество) однозначных чисел. Затем
предложите первое из задуманных чисел умножить на 2 и к
полученному произведению прибавить 5. Получившееся
число попросите умножить на 5 и к тому, что получится,
попросите прибавить 10 и второе задуманное число. Затем
надо столько раз, сколько осталось неиспользованных
задуманных чисел, проводить такие операции: умножать
полученное от предыдущих действий число на 10 и к
произведению прибавлять очередное задуманное число. После
объявления результата предложенных вами действий вы
объявляете, какие числа были задуманы.
Как узнать загаданные числа?
20
36. Какое число задумано-? <
Предложите кому-нибудь задумать двузначное число
и объявить вам остатки от деления этого числа на 3, 5
и 7. После этого вы говорите, какое число было
задумано.
Как отгадать задуманное число?
37. У кого какая вещь?
Троим из присутствующих, отвернувшись, предложите
взять какие-нибудь три вещи, например, монету, часы,
пуговицу.
Предварительно положите на стол 7 одинаковых
предметов, например, орехов. Все еще отвернувшись,
попросите проделать следующее. Если первый человек взял
монету, то пусть он орехов не берет, если же он взял часы, то
пусть возьмет 1 орех, а если взял пуговицу, то пусть
возьмет 2 ореха. Если второй человек взял монету, то пусть
он возьмет 1 орех, если взял часы, то пусть орехов не берет,
а если взял пуговицу, то пусть возьмет 2 ореха. Если третий
человек взял монету, то пусть он возьмет 3 ореха, если он
взял часы, то пусть возьмет 1 орех, а если взял пуговицу,
то пусть орехов не берет. Обернувшись и посмотрев,
сколько орехов осталось на столе, вы объявляете, кто какую
вещь взял.
Как узнать, кто какую вещь взял?
V. Любопытные свойства чисел
38. Умножение на пальцах («Способ к твержению
таблицы по перстам ручным...»).
Каждый вспомнит, как трудно заучивать наизусть
таблицу умножения. Между тем эту работу можно
существенно облегчить, если воспользоваться одним старым
способом вычисления на пальцах.
Вот как описывает его Магницкий на примере
вычисления умножения семь на семь:
*
йціе ^офЕши в4ддти коаикѵѵ бЗдетъ 7-7, и ты причти
къ пЕрстшлѵъ лѢвыа р8кй, Ш прдвыл 2, и стлнетъ 7:
такожде и к перстѵѵлѵъ прдвыл р8кй ГО л*квыд что вы стало
7 же: и сложи причтЕныА оньіа пірсты овойхъ р8къ по 2, и
в8д8тъ ^ндчити 40: достдлныл же овойхъ ріЗкъ, сйр*вчъ 05
провыл 3, и ГО л-квыд 3: оѵлшожи й^ъ междЗ совою й б$детъ
9, йд-ъ же приложи к 40, й вЗдетъ 7• 7:49. Тдклѵ й w прочить•
21
Загнем на левой руке столько пальцев, на сколько
первый сомножитель превышает 5, а на правой руке столько
пальцев, на сколько второй сомножитель превышает 5.
В рассмотренном примере на каждой из рук будет загнуто
по 2 пальца. Если сложить количества загнутых пальцев
и перемножить количества не загнутых, то получатся
соответственно числа десятков и единиц искомого
произведения (в данном примере 4 десятка и 9 единиц).
Если этим способом вычислять произведение 6X7, то
получим 3 десятка и 12 единиц, т. е.
30-1-12 = 42.
Так можно вычислить произведение любых однозначных
чисел, больших чем 5.
Найдите объяснение этого способа умножения чисел.
39. Движение пальца. (
А вот еще один из способов помочь памяти с помощью
пальцев рук запомнить таблицу умножения на 9. Положив
обе руки рядом на стол, по порядку занумеруем пальцы
обеих рук следующим образом:
Первый палец слева обозначим 1, второй за ним
обозначим цифрой 2, затем 3, 4,... до десятого пальца, который
означает 10. Если надо умножить на 9 любое из первых
девяти чисел, то для этого, не двигая рук со стола, надо
приподнять вверх тот палец, номер которого означает
число, на которое умножается девять; тогда число иальцев,
лежащих налево от поднятого пальца, определяет число
десятков, а число пальцев, лежащих справа от аоднятого
22
пальца, обозначает число единиц полученного
произведения.
Пример. Пусть надо найти произведение
4X9.
Положив обе руки на стол, приподнимем четвертый палец,
считая слева направо. Тогда до поднятого пальца
находятся три пальца, а после поднятого — 6 пальцев.
Результат произведения 4 на 9, значит, равен 36.
Найдите объяснение этого способа умножения чисел.
40. Одинаковые цифры.
Если умножить число 777 на число 143, то получится
шестизначное число, записываемое одними единицами:
777ХНЗ = ПІ 111.
Если же число 777 умножить на 429, то получится число
333 333, записываемое шестью тройками.
Найдите, на какие числа надо умножить число 777,
чтобы получить шестизначные числа, записываемые
одними двойками, одними четверками, одними пятерками и т. д.
41. Свойство числа 481.
Возьмем какое-нибудь двузначное число, например,
12. Удвоим его и припишем справа 0. К результату (240)
прибавим исходное число. Получится 252. Умножим это
число на 481.
В записи произведения трижды повторяется число 12:
252X481 = 121 212.
Возьмем другое двузначное число, например, 23.
Проделаем с ним те же операции:
23X2 = 46; 460 + 23=483; 483X481=232 323.
Опять результат есть шестизначное число, в записи
которого трижды повторяется исходное двузначное число 23.
Можете проделать еще несколько экспериментов, взяв,
например, числа 34,19, 70 и т. д. Опять в записи результата
будет трижды повторено исходное двузначное число.
Попытайтесь объяснить этот удивительный факт.
42. «Проверка» сложения.
Торговая практика требовала умения правильно
выполнять вычисления с большими числами. Для
уверенности в надежности вычислений в старину употреблялись
23
некоторые методы «поверения» (проверки). Один из
методов проверки правильности сложения был таков.
Допустим, что, найдя сумму нескольких чисел, мы хотим
убедиться в правильности сделанных вычислений. Прибавим
друг к другу все цифры слагаемых и получившееся число
разделим с остатком на 9. Остаток запомним. После этого
сложим цифры вычисленной суммы и результат разделим
на 9. Если получившийся при этом остаток отличен от
остатка, найденного ранее, то вычисления выполнены
неверно; в них вкралась ошибка.
Пример. Предположим, что в результате
сложения чисел 9873, 9837, 17 976 была получена сумма 38 686.
Нет ли ошибки в вычислении? Сумма цифр слагаемых
равна, как легко видеть, 27 + 27 + 30 = 84. Остаток от
деления этого числа на 9 равен 3. Складывая цифры
вычисленной суммы, найдем 31. Это число при делении на 9 дает
в остатке 4. Так как 3=^4, то сумма найдена с ошибкой.
И действительно, правильная сумма равна 37 686.
На каком свойстве чисел основан такой способ
проверки сложения?
43. «Проверка» умножения.
Так же, как в предыдущей задаче проверялось
сложение, можно проверять и умножение. Допустим, что,
перемножив два числа, мы хотим проверить правильность
вычислений. Для этого найдем суммы цифр сомножителей,
затем разделим полученные суммы на 9 с остатком.
Найденные остатки перемножим, и получившееся число опять
разделим на 9. Остаток после этого деления запомним.
Затем найдем сумму цифр вычисленного произведения
и разделим ее с остатком на 9. Если получившийся при
этом остаток не равен остатку, запомненному ранее, то
произведение вычислено неверно.
Пример. Допустим, что после умножения числа
7373 на 4521 получилось произведение 33 334 333. Сумма
цифр первого сомножителя равна 20, а второго—12. Эти
числа при делении на 9 имеют остатки 2 и 3. Произведение
остатков равно 6, остаток от деления 6 на 9 также равен 6.
Вычислим теперь сумму цифр найденного произведения.
Она равна 25. Разделив это число на 9, получим в
остатке 7. Так как 6=5^7, то произведение вычислено с
ошибкой.
Авторы старинных рукописей предлагают для удобства
располагать результаты вычислений в вершинах креста
(рис. 1). У концов вертикальной черты ставятся остатки
24
от деления на 9 сумм цифр сомно- 2
жителей. У левого конца
горизонтальной черты ставится остаток от деления
на 9 произведения чисел, стоящих у е
концов вертикальной черты, а у правого
конца горизонтальной черты — остаток
от деления на 9 суммы цифр
вычисленного произведения. Если у горизон- Рис- 1
тальной черты стоят разные числа, то
произведение найдено с ошибкой. На рис. 1 показано, как
будут стоять числа в разобранном выше примере.
Как обосновать этот способ проверки умножения?
VI. Старинный способ решения задач
на смешение веществ
44. Как смешать масла?
У некоторого человека были продажные масла: одно
ценою 10 гривен за ведро, другое же 6 гривен за ведро.
Захотелось ему сделать из этих двух масел, смешав их,
масло ценою 7 гривен за ведро. Какие части этих двух
масел нужно взять, чтобы получить ведро масла
стоимостью 7 гривен?
Приводим старинный способ решения этой задачи.
Друг под другом пишутся стоимости имеющихся масел,
слева от них и примерно посередине — стоимость масла,
которое должно получиться после смешения. Соединив
написанные числа черточками, получим такую картину:
^"•10
Меньшую цену вычтем из цены смешанного масла и
результат поставим справа от большей цены. Затем из
большей цены вычтем цену смешанного масла, а то, что
останется, напишем справа от меньшей цены. Получится
такая картина:
<х
Из нее делается заключение, что дешевого масла
нужно взять втрое больше, чем дорогого, т. е. для получе-
25
ния 1 ведра масла ценою 7 гривен нужно взять дорогого
масла і ведра, а дешевого - ведра.
4 4
Верно ли найден ответ задачи?
45. О сплаве серебра.
Имеется серебро: одно одиннадцатой пробы, а другое
четырнадцатой пробы. Сколько какого серебра надо взять,
чтобы получить 1 фунт серебра двенадцатой пробы?
(В России существовала золотниковая система
обозначения пробы на основе русского фунта, содержащего
96 золотников, по которой проба выражалась весовым
количеством благородного металла в 96 единицах сплава,
например, слова «серебро одиннадцатой пробы» означают,
что в 96 частях сплава содержится 11 частей серебра.
В наше время проба обозначает число частей благородного
металла в 1000 частях (по массе) сплава.)
Решите эту задачу тем же способом, что приведен при
решении задачи 44.
46. Верен ли старинный способ?
Всегда ли при решении задач на смешение двух
веществ способ, приведенный в задаче 44, дает
правильный ответ?
47. Как смешать чай?
Имеет некто чай трех сортов — цейлонский по 5 гривен
за фунт, индийский по 8 гривен за фунт и китайский по
12 гривен за фунт. В каких долях нужно смешать эти три
сорта, чтобы получить чай стоимостью 6 гривен за фунт?
Вот решение из «Арифметики» Л. Ф. Магницкого:
«А когда случится мешати три товара из них же
зделати четвертый по желаемой цене и тогда един перечень
малейший дважды в правиле полагается. Яко же зде
видимо есть:
^5\ /* 6
^•ИГ ^І 2
^8^ ^-1 1
26
10»
Здесь предлагается взять 6 + 2=8 частей чая ценой по
5 гривен и по одной части чая ценой 8 гривен и 12
гривен за один фунт. Указанный Л. Ф. Магницким способ
состоит в следующем. Надо метод, изложенный при
решении задачи 44, применить два раза: первый раз, взяв
вещества с наименьшей и наибольшей стоимостью, а во
второй раз с наименьшей и средней стоимостью. При этом
будут найдены доли, в которых нужно смешивать вещества
наибольшей и средней стоимости (в приведенном
примере 1 и 1). Сложив затем доли дешевого вещества»
найденные в первый и во второй раз (6 + 2 = 8), получим долю
дешевого вещества в общей смеси. Верно ли найден ответ
задачи?
48. Серебро трех сортов.
Некто имеет серебро разных проб: одно — двенадцатой
пробы, другое — десятой пробы, третье — шестой пробы
Сколько какого серебра надо взять, чтобы получить 1 фунт
серебра девятой пробы? Решите эту задачу способом
приведенным в задаче 47.
49. Единственный ли ответ?
Имеют ли задачи на смешение трех веществ
единственное решение?
VII. О правилах «фальшивых»
или «гадательных»
50. Найти число.
Найти число такое, что если к нему добавить его третью
часть и от полученной суммы отнять ее шестую часть, то
будет 100.
По правилу, которое носило название
«фальшивое», или «гадательное», эту задачу следует решать
так:
1. Предположим, что неизвестное число есть 144.
Проделав с ним описанные в задаче операции, получим
ІХІ44 = 48, 144 + 48=192,
ІХІ92 = 32, 192-32=160.
о
Так как получилось не 100, то не угадали.
п
2. Предположим теперь, что неизвестное число есть
108. Имеем последовательно:
ІХЮ8 = 36, 108 + 36=144,
ІХ 144 = 24, 144-24 = 120.
О
Опять не угадали.
3. Оказывается, что по результатам двух неверных
попыток можно найти искомое число. Это делается
следующим образом. Вычисляем, насколько мы ошиблись:
В первом случае Во втором случае
160-100 = 60 120-100 = 20
Затем рисуем таблицу:
Перемножим числа, стоящие накрест:
108X60 = 6480, 144X20=2880. .
Разность произведений (6480 — 2880 = 3600) разделим на
разность ошибок (60 — 20=40):
3600:40=90.
Полученное число и дает ответ к задаче, т. е. искомое
число равно 90.
Правилен ли этот ответ?
Числа 144 и 108 мы взяли наугад, но оба раза
результат вычислений оказался больше, чем 100.
Правило гласит, что так же нужно поступать и в
случае, если оба результата окажутся меньше данного числа.
Если же один из результатов окажется меньше данного
числа, а другой больше, то искомое число можно найти,
разделив сумму произведений на сумму разностей.
51. Ответ учителя.
Вопроси н4кто оѵчйтелА некоего глагола: повтскдь мм
колйклѵ ймдши оѵченикѵѵвъ оѵ севе во 8чйлиціи, понеже
йлшнъ сына Фдати во Зчйлицк: и х*ф£ оѵв-Ьддти w числ-fc
оѵченик&въ твой^ь- оѵчйтель же (Юв-кціівъ ртчс ім&: дф<
прйдггь ми оѵченикѵѵвъ толйко же, ілйко ймдмъ, и
28
ПОЛТОЛЙКД, Н ЧСТВЁрТАА ЧАСТЬ, ІЦК ЖЕ И ТВОЙ СЫНЪ, И
тогда видеть оѵ мене еѵчЕиик&въ 100: вопроснвый же
«ѴДИВЛСА Фв4тв ЕПМ ФЙДЕ, И НАЧАТЬ Й^МВр-КТАТИ*
Спросил некто учителя: «Скажи, сколько у тебя в
классе учеников, так как хочу отдать к тебе в учение своего
сына». Учитель ответил: «Если придет еще учеников
столько же, сколько имею, и полстолько и четверть столько
и твой сын, тогда будет у меня учеников 100».
Спрашивается, сколько учеников в классе?
Решение с помощью «фальшивого»
правила. Предположим, что в классе было 24 ученика.
Если еще придет столько же учеников и затем полстолько,
затем четверть столько и, наконец, еще один ученик, то
всего получится
24 + 24+ 12+6 + 1=67
учеников. Не угадали.
Если предположить, что в классе 32 ученика, то,
проделав такие же выкладки, получим
32+32+16 + 8+1=89
учеников. Опять не угадали.
Действуя согласно «фальшивому» правилу, находим
24\ ^33 100-67 = 33, 100-89=11
><Г 24X11=264, 33X32 = 1056
32^ ^МІ 1056-264=792, 33-11=22
Следовательно, в классе было 792:22 = 36 учеников.
Правилен ли этот ответ?
52. Сколько куплено сукна?
Купил некто сукно трех сортов, а всего 106 аршин.
Первого купил на 12 аршин больше, чем второго, а второго
на 9 аршин больше, чем третьего.
Сколько же сукна каждого сорта было куплено?
Решение с помощью «фальшивого»
правила. Предположим, что сукна первого сорта куплено
32 аршина, тогда второго сорта куплено 20 аршин, а
третьего сорта куплено 11 аршин. Всего, следовательно, куплено
32 + 20+11=63 аршина, что на 43 аршина меньше, чем
дано в условии задачи. Если сукна первого сорта куплено
50 аршин, то второго — 38 аршин и третьего — 29 аршин.
Всего же в этом случае куплено 50 + 38 + 29= 117 аршин,
29
что на 11 аршин больше, чем было куплено в
действительности. Применяя «фальшивое» правило, имеем
32\ ^43 32X11=352, 50X43 = 2150
^>С 2150 + 352 = 2502, 43+11=54.
Значит, сукна первого сорта было куплено 2502:54 =
= 46- аршина, сукна второго сорта 46^—12 = 34-
аршина, сукна третьего сорта 34І—9 = 25- аршина.
О О
Отметим, что полученные в результате предположений
числа (63 и 117) одно меньше, чем 106, а другое больше,
чем 106. Поэтому для нахождения ответа задачи по
«фальшивому» правилу следует сумму произведений разделить
на сумму разностей.
Верен ли ответ задачи?
Решите с помощью «фальшивого» правила
задачи 53—56.
53. Покупка коровы.
Два человека хотят купить корову. Говорит первый
второму: «Если ты дашь мне - твоих денег, то я один смогу
О
заплатить ее цену». А второй отвечает первому: «Дай
з
мне - твоих денег, тогда и я заплачу ее цену».
Сколько у каждого из них денег, если корова стоит
24 рубля?
54. Беседа.
Три человека беседуют. Первый, обращаясь к двум
другим, говорил: «Если бы я взял из ваших денег по
половине, то у меня было бы 17 рублей». Второй же,
обращаясь к первому и третьему, сказал, что если бы
они дали ему по - своих денег, то у него стало бы также
О
17 рублей. На что и третий ответил, что если бы
собеседники дали ему - своих денег, то также и у него стало бы
17 рублей.
Сколько денег имеет каждый из собеседников?
зѳ
55. Сколько у кого денег?
Три человека собрались покупать товару на 54 рубля.
И говорит первый второму: «Дай мне из своих денег
- часть, и я один заплачу за товар». А второй обращается
к третьему: «Дай мне - часть твоих денег, тогда и я
один смогу заплатить за товар». Также и третий человек
обратился к первому, но попросил ^ часть его денег.
Сколько у кого денег?
56. Какова цена сукна?
Некто купил 64 рулона сукна. Из них 20 рулонов
белого сукна, 13 рулонов черного, 5 красного, 19 зеленого,
7 лазоревого и уплатил за них 486 рублей. Цена же их
была неравная: за черный рулон он платил на четыре
рубля больше, чем за белый, за красный — на три рубля
меньше, чем за черный, за зеленый на два рубля меньше,
чем за красный, а за лазоревый на один рубль больше,
чем за зеленый.
Сколько денег он платил за каждый рулон?
57. Верно ли «фальшивое» правило?
Попробуйте выяснить, в применении к каким задачам
«фальшивое» правило дает верный ответ?
Часть вторая
ЗАДАЧИ ИЗ КНИГ,
ИЗДАННЫХ В XVIII ВЕКЕ
(ПОСЛЕ «АРИФМЕТИКИ»
Л. Ф. МАГНИЦКОГО)
I. Забавные истории
58. Смекалистый слуга.
Постоялец гостиницы обвинил слугу в краже всех его >
денег. Смекалистый слуга сказал так: «Это — правда,
я украл все, что он имел». Тогда слугу спросили о сумме
украденных денег, и он отвечал: «Если к украденной мною
сумме прибавить еще 10 рублей, то получится мое годовое
жалованье, а если к сумме его денег прибавить 20 рублей,
получится вдвое больше моего жалованья».
Сколько денег имел постоялец и сколько рублей в год
получал слуга?
59. «Богатство».
У приезжего молодца оценили «богатство»: модный
жилет с поношенным фраком в три алтына без полушки,
но фрак вполтретья дороже жилета. Спрашивается
каждой вещи цена.
(«Вполтретья» — в 2- раза. Подобные названия
сохранились и в современном языке. На вопрос «Который
час?» мы отвечаем «Половина двенадцатого», имея в виду
11- часов.)
60. «С чем иностранка к россам привезена?»
Нововыезжей в Россию иностранной мадаме
Вздумалось оценить свое богатство в чемодане:
Новой выдумки нарядное фуро
И праздничный чепец а ля фигаро.
Оценщик был русак,
Сказал мадаме так:
32
«Богатства твоего первая вещь фуро
Вполчетверта дороже чепца фигаро;
Вообще же стоят не с половиною четыре алтына,
Но настоящая им цена только сего половина».
Спрашивается каждой вещи цена,
С чем иностранка к россам привезена.
(«Вполчетверта»— в 3- раза.)
61. Веселый человек.
Веселый человек пришел в трактир с некоторой суммой
денег и занял у содержателя трактира столько денег,
сколько у себя имел. Из этой суммы истратил 1 рубль.
С остатком пришел в другой трактир, где опять занял
столько денег, сколько имел. В этом трактире также
истратил 1 рубль. Потом пришел в третий и четвертый
трактиры и повторил то же самое. Наконец, когда вышел
из четвертого трактира, не имел ничего. Сколько денег
имел первоначально веселый человек?
II. Дележ и размен денег
62. Сколько у кого денег?
Двое крестьян поделили между собой 7 рублей, причем
один получил на 3 рубля больше другого.
Сколько денег досталось каждому из них?
63. В 49 раз больше.
Разделить 25 рублей на две части так, чтобы одна часть
была в 49 раз больше другой.
64. Сколько было полтинников?
Некто купил вещь, заплатив за нее 157 рублей 50
копеек, причем платил одинаковым числом рублевых монет
и полтинников.
Сколько было полтинников? (Полтинник — монета
в 50 копеек.)
65. Размен по 2 и 3 копейки.
Каким количеством способов можно разменять 25
копеек монетами по 2 и 3 копейки?
66. Размен по 3 и 5 копеек.
Как разменять 59 копеек пятнадцатью монетами по 3
и 5 копеек?
33
67. Разделить на 8 частей.
Разделить 46 рублей на 8 частей так, чтобы каждая
часть была больше предыдущей на полтинник.
68. 22 монеты.
Как составить сумму в 99 копеек из 22 монет по 2, 3
и 5 копеек?
III. Сколько кому лет?
69. Сколько лет сыну?
«Сколько лет твоему сыну?»— спросил один человек
у своего приятеля. Приятель ответил: «Если к возрасту
моего сына прибавить столько же да еще половину, то
будет 10 лет».
Сколько же лет сыну?
70. Каков возраст братьев?
Средний из трех братьев старше младшего на два года,
а возраст старшего брата превышает сумму лет двух
остальных братьев четырьмя годами.
Найти возраст каждого брата, если вместе им 96 лет.
71. «Сколь он стар?»
Некто будучи вопрошен, сколь он стар, ответствовал:
«Когда я проживу еще половину да треть, да четверть
моих лет, тогда мне будет сто лет».
Сколько лет этому человеку?
72. Сколько лет каждому сыну?
Некто имеет 6 сыновей, один другого старше 4 годами,
а самый старший сын втрое старше младшего.
Каков возраст сыновей?
73. Лета каждого.
Дочь спрашивала отца о числе своих лет; ей ответ-
ствовано: «Теперь твои лета составляют ■= моих лет, а
Э
за 4 года перед сим лета твои равнялись - настоящих
моих лет». Спрашиваются лета каждого.
74. Сколько им лет?
Мне теперь вдвое больше лет, чем было вам тогда,
когда мне было столько лет, сколько вам теперь; а когда
34
вам будет столько лет, сколько мне теперь, то нам будет
обоим вместе 63 года.
Сколько лет каждому?
75. Возраст сыновей.
Отец имеет семь сыновей. Сумма возрастов первого
и четвертого сына равна 9 годам, первого и шестого — 8
годам, второго и пятого — 8 годам, второго и третьего —
9 годам, третьего и шестого — 6 годам, четвертого и
седьмого — 4 годам, а седьмого и пятого — также
4 годам.
Сколько лет каждому сыну?
76. Замысловатый ответ.
У отца спросили, сколько лет его двум сыновьям.
Отец ответил, что если к произведению чисел, означающих
их года, прибавить сумму этих чисел, то будет 14.
Сколько лет сыновьям?
IV. Часы
77. Сколько раз бьют часы?
Часы бьют каждый час и отбивают столько ударов,
сколько показывает часовая стрелка. Сколько ударов
отобьют часы в течение 12 часов?
78. Который час?
На вопрос «Который час?» был дан ответ: «Половина
времени, прошедшего после полуночи, равна | времени,
оставшегося до полудня».
Сколько было времени?
79. Две стрелки.
Две стрелки насажены на одну ось и в некоторый
момент времени совмещены. Одна из стрелок описывает
круг за 12 часов, а другая за 16 часов.
Через какое время стрелки совместятся опять?
80. Сколько раз совместятся стрелки?
Часы пробили полночь. Сколько раз и в какие
моменты времени до следующей полуночи часовая и минутная
стрелки будут совмещаться?
.35
81. Сколько было времени?
Один человек спросил: «Который час?» Ему ответили,
что часовая и минутная стрелки совмещены и находятся
на одной линии между 9 и 10 часами.
Сколько было времени?
V. Денежные расчеты
82. Продажа двух коней.
Некто продает двух коней с седлами, из коих цена
одного седла 120 рублей, а другого — 25 рублей. Первый
конь с хорошим седлом втрое дороже другого с дешевым
седлом, а другой конь с хорошим седлом вдвое дешевле
первого коня с дешевым седлом.
Какова цена каждого коня?
83. Сколько стоят кони?
Некто имеет трех коней да богатое седло за 55 рублей.
Оседланный первый конь стоит столько, сколько стоят
вместе неоседланные второй и третий кони. Оседланный
же второй конь стоит столько, сколько стоят вместе
неоседланные первый и третий кони, а оседланный третий
конь стоит столько же, сколько стоят вместе
неоседланные первый и второй кони.
Найти цену каждого коня.
84. Обмен зайцев на кур.
Крестьянин менял зайцев
на кур: брал за всяких
двух зайцев по три курицы.
Каждая курица снесла
яйца — третью часть от числа
всех куриц. Крестьянин,
продавая яйца, брал за каждые
9 яиц по столько копеек,
сколько каждая курица
снесла яиц, и выручил 72 копейки.
Сколько было кур и
сколько зайцев?
Две крестьянки продали 100 яиц. Они продавали яйца
по разной цене, но денег они выручили поровну. Первая
85. Две крестьянки.
36
сказала второй: «Если бы твои яйца были у меня, то
я бы получила за них 45 копеек». На что вторая ответила:
«А я бы за твои выручила 20 копеек».
Сколько яиц было у каждой крестьянки?
86. Полтабуна и пол-лошади.
К табунщику пришли три казака покупать лошадей.
«Хорошо, я вам продам лошадей,— сказал табунщик,—
первому продам я полтабуна и еще половину лошади,
второму — половину оставшихся лошадей и еще
поллошади, третий также получит половину оставшихся
лошадей с полулошадью. Себе же оставлю только 5
лошадей». Удивились казаки, как это табунщик будет делить
лошадей на части. Но после некоторых размышлений они
> успокоились, и сделка состоялась.
:37
Сколько же лошадей продал табунщик каждому из
казаков?
87. Покупка товаров.
Крестьянин, покупая товары, сначала уплатил первому
купцу половину своих денег и еще 1 рубль; потом уплатил
второму купцу половину оставшихся денег да еще 2 рубля
и, наконец, уплатил третьему купцу половину оставшихся
денег да еще 1 рубль. После этого денег у крестьянина
совсем не осталось.
Сколько денег было у крестьянина первоначально?
88. Обмен деньгами.
Двое, Андрей и Федор, обмениваются деньгами.
Сначала Андрей отдал часть своих денег Федору, потом
"Федор Андрею, затем опять Андрей Федору и, наконец,
Федор отдал Андрею деньги в последний раз, и после этой
передачи у каждого стало по 160 рублей. Количество
передаваемых денег всякий раз было равно количеству
денег у получающего их.
Сколько денег было у Андрея и Федора первоначально?
89. Раздел наследства.
Деньги, оставшиеся после смерти купца, были
разделены, по завещанию между его сыновьями. Старший сын
получил 100 рублей и ^ часть остатка. Вслед за ним
второй сын получил 200 рублей и - остатка. Затем третий
сын получил 300 рублей и - остатка и так далее до
последнего сына, который получил все, что осталось после
старших братьев. В результате оказалось, что все сыновья
получили денег поровну.
Сколько было сыновей и какова сумма наследства?
VI. Задачи на переливание
90. Три бочки.
Хозяин имеет три бочки А, В, и С. Бочка А наполнена
квасом, бочки В и С — пустые. Если квасом из бочки
о
А наполнить бочку В, то в бочке А останется = ее
содержимого. Если же квасом из бочки А наполнить бочку
38
С, то в бочке А останется - ее содержимого. Чтобы
наполнить обе бочки В и С, надо взять содержимое бочки А
и еще добавить 4 ведра кваса.
Сколько ведер кваса вмещает каждая бочка?
91. Четыре бочки.
Хозяин имеет четыре бочки А, В, С и D, причем
бочки С и D одинаковой вместимости.
Пусть бочки А и В наполнены квасом; если
содержимым бочки А наполнить бочку С, то в бочке А останется
- ее содержимого; если же содержимым бочки В напол-
нить бочку D, то в бочке В останется - ее содержимого.
Пусть бочки С и D наполнены квасом; чтобы наполнить
бочки А и В, надо взять содержимое бочек С и D а
добавить еще 9 ведер кваса.
Сколько ведер кваса вмещает каждая бочка?
92. Сколько останется воды?
Из ведра, содержащего 5 литров воды, отливают
1 литр, а затем в ведро вливают 1 литр сока.' Перемешав
все это, из ведра отливают 1 литр смеси, затем в ведро
опять вливают 1 литр сока. Опять перемешивают,
отливают I литр смеси и вливают 1 литр сока.
Сколько в ведре после этого останется воды?
93. Можно ли отлить половину сока?
Из бочки, содержащей 100 литров сока, отливают
1 литр и вливают в нее затем 1 литр воды. Перемешав
полученную смесь,- из бочки отливают один литр смеси и
опять вливают в нее 1 литр воды. Перемешав полученную
смесь, опять отливают один литр смеси и вливают 1 литр
воды, и так делают неоднократно.
Можно ли в результате таких операций получить
смесь, содержащую 50 литров воды и 50 литров сока?
VII. Латинские квадраты
94. Квадрат 3X3.
В квадрате, состоящем из 9 клеток, расставить три
единицы, три двойки и три тройки так, чтобы в каждом
горизонтальном ряду (строке) и в каждом вертикальном
39
ряду (столбце) любая из цифр I, 2, 3 встречалась только
раз. Сколько существует различных расстановок цифр?
95. Квадрат 4X4.
В квадрате.состоящем из 16 клеток, расставить четыре
буквы а, четыре буквы Ь, четыре буквы с, четыре буквы
d так, чтобы в каждом горизонтальном ряду и в каждом
вертикальном ряду любая из букв а, Ь, с, d встречалась
только один раз. Сколько существует различных
расстановок букв?
96. Квадрат пХп.
Квадрат, в котором каждая строка является
перестановкой некоторого набора различных букв или чисел,
причем в каждом столбце буквы или числа различны,
называется латинским квадратом. Это название
связано с тем, что Эйлер,
изучавший такие квадраты,
расставлял в их клетках
латинские буквы.
Задачи, подобные двум
последним, можно решать и
для квадрата, состоящего из
25, 36, 49 и т. д. клеток.
Придумайте
какой-нибудь способ построения
латинского квадрата размером
rtX'rt клеток.-
97. Шестнадцать
офицеров.
Собрались вместе 16
офицеров четырех полков. Из
каждого полка прибыло по
четыре офицера разных
званий (полковник, майор,
капитан, лейтенант). В зале стоит
16 кресел, расположенных в
виде квадрата размером.
4X4. Как рассадить этих
офицеров, чтобы в любом
ряду, параллельном стороне
квадрата, был офицер
каждого звания и представитель
каждого полка?
40
VIII. Обход мостов
98. Мосты в Кенигсберге.
Вот перевод латинского текста, который взят из письма
Эйлера к итальянскому математику и инженеру Маринони,
отправленного из Петербурга 13 марта 1736 года:
«Некогда мне была предложена задача об острове,
расположенном в городе Кенигсберге и окруженном рекой,
через которую перекинуто семь мостов. Спрашивается,
может ли кто-нибудь непрерывно обойти их, проходя
только однажды через каждый мост. И тут же мне было
сообщено, что никто еще до сих пор не смог это проделать,
но никто и не доказал, что это невозможно. Вопрос этот,
хотя и банальный, показался мне, однако, достойным
внимания тем, что для его решения недостаточны ни
геометрия, ни алгебра, ни комбинаторное искусство...
После долгих размышлений я нашел легкое правило,
основанное на вполне убедительном доказательстве,
с помощью которого можно во всех задачах такого рода
тотчас же определить, может ли быть совершен такой
обход через какое угодно число и как угодно расположенных
мостов или не может. Кенигсбергские же мосты
расположены так, что их можно представить на следующем
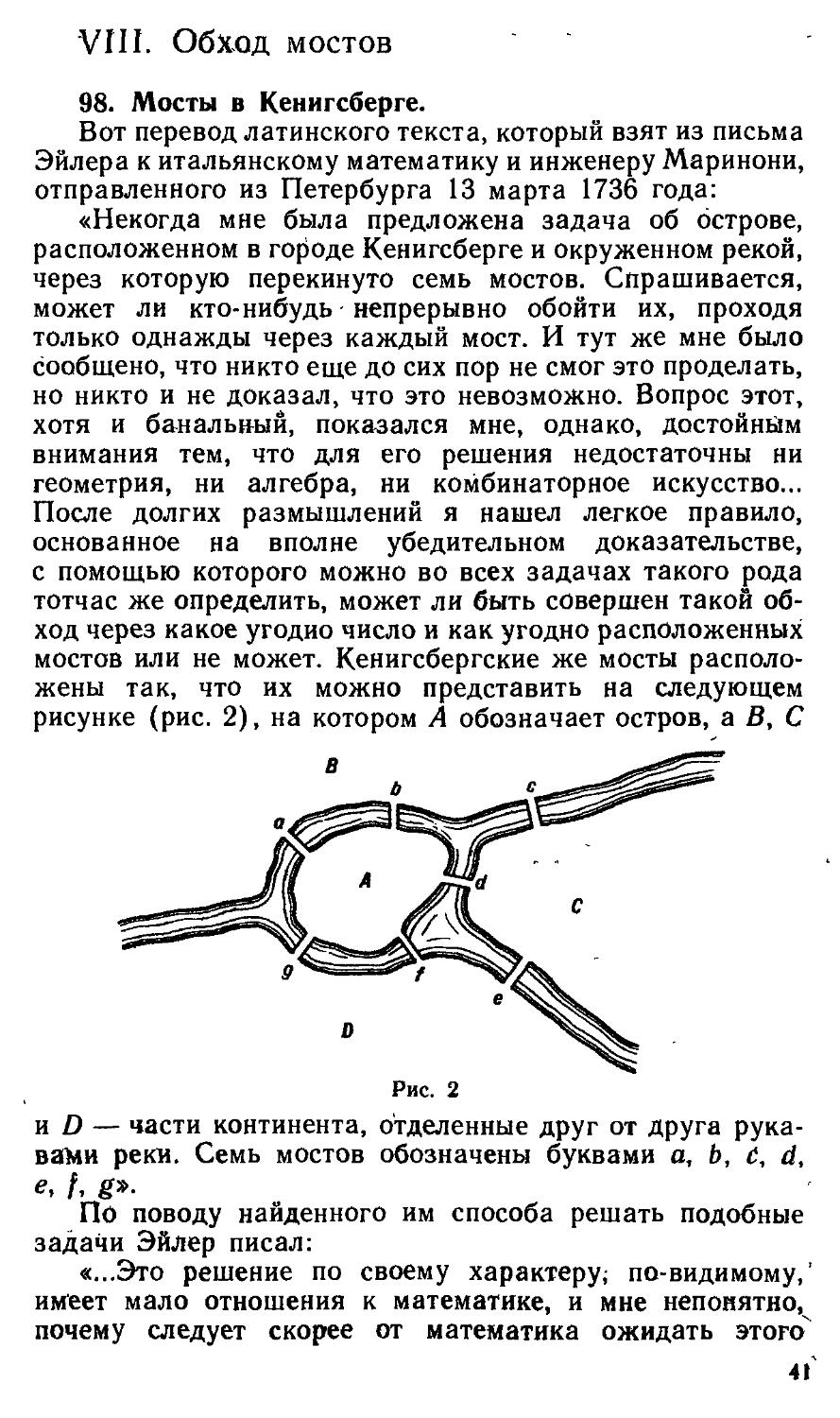
рисунке (рис. 2), на котором А обозначает остров, а В, С
Рис. 2
и D — части континента, отделенные друг от друга
рукавами реки. Семь мостов обозначены буквами а, Ь, С, d,
е, f, g».
По поводу найденного им способа решать подобные
задачи Эйлер писал:
«...Это решение по своему характеру; по-видимому,'
имеет мало отношения к математике, и мне непонятно,
почему следует скорее от математика ожидать этого^
41
решения, нежели от какого-нибудь другого человека, ибо
это решение подкрепляется одним только рассуждением
и нет необходимости привлекать для нахождения этого
решения какие-либо законы, свойственные математике.
Итак, я не знаю, каким образом получается, что вопросы,
имеющие совсем мало отношения к математике, скорее
разрешаются математиками, чем другими.»
Можно ли обойти Кенигсбергские мосты, проходя
только однажды через каждый мост?
99. Пятнадцать мостов.
В некоторой местности через протоки переброшено
15 мостов (см. рис. 3).
Можно ли обойти все мосты, пройдя по каждому из
них только один раз?
IX. Шахматы
100. Путешествие коня по шахматной доске.
Для понимания этой задачи не обязательно уметь
играть в шахматы. Важно лишь знать, как ходит
шахматный конь. Эта фигура скачет по доске с клетки на клетку,
всякий раз прыгая по диагонали прямоугольника,
состоящего из 6 клеток и имеющего размеры 2X3. На рис. 4
показан путь коня, состоящий из 5 ходов.
Поставьте теперь коня на некоторую клетку и
попробуйте обойти им все 64 клетки шахматной доски так, чтобы
на каждой из клеток конь побывал только один раз. Для
того чтобы не нарушить условия, надо отмечать каким-
42
либо способом клетки, уже пройденные ранее. Л. Эйлер,
упомянувший эту задачу в письме к петербургскому
академику X. Гольдбаху от 26 апреля 1757 года и посвятивший
ей впоследствии большую статью, отмечал пройденные
клетки, помещая в них некоторые предметы. Для этой цели
можно воспользоваться монетами, пуговицами,
горошинами и т. п. Еще лучше сделать маленькие карточки,
помещающиеся внутри одной клетки, нанести на них
номера от 1 до 64 и, поместив в начальную клетку
карточку с номером 1, раскладывать карточки на
проходимые поля в порядке возрастания номеров. Тогда, попав
в тупик, т. е. на клетку, из которой ходы возможны только
на клетки, уже пройденные ранее, можно будет попытаться
исправить путь, изменив предыдущие ходы с тем, чтобы
избежать тупиковой ситуации.
После некоторых усилий требуемый путь будет,
вероятно, обнаружен.
Попытайтесь теперь ответить на следующие вопросы:
1) Со всякой ли начальной клетки можно обойти
конем все клетки шахматной доски, посетив каждую из
них ровно один раз?
2) Если ответ на первый вопрос положителен, то как
указать путь коня для каждой из начальных клеток?
/
4S
•?
/
1
А
"ѵ
«•
V
^
ж
1
ч ■ ■ я
Рис. 4 Рис. 5
101. Задача о 8 ладьях.
Шахматная фигура ладья ходит, как известно, по
горизонталям и вертикалям шахматной доски. Если две
ладьи стоят на одной горизонтали или вертикали и между
ними нет других шахматных фигур, то говорят, что эти
ладьи угрожают друг другу.
Если поставить 8 ладей на черной диагонали обычной
шахматной доски (рис. 5), то ни одна из них не будет
43
44
угрожать остальным. Существуют и другие расположения
л-адей с этим условием.
Определите число размещений 8 ладей на шахматной
доске, не угрожающих друг другу.
102. Задача с запретом.
Обозначим Qn, п~^2, количество размещений п ладей
на шахматной доске размером пХп клеток с условием,
что каждые две ладьи не угрожают друг другу и ни одна
ладья не стоит на главной диагонали (так будем называть
Рис. 6
диагональ, идущую из левого нижнего угла в правый
верхний). Тогда Q2=l, Qz — 2 (рис. 6).
Л. Эйлер, занимаясь этой задачей, установил
соотношение
Q„=(n-1) (Q„_, + Qn_2), и>4.
Из него, в частности, следует, что
Q4 = 9, Q5=44, Q6 = 265, Q7=1854, Q8=14 833.
Докажите соотношение Эйлера.
Задача о подсчете числа Q„ стала классической в
разделе математики, называемом комбинаторикой. Для нее
существует множество эквивалентных формулировок.
103. Задача о шляпах.
Предположим, что п мужчин оставили свои п шляп
в гардеробе. Затем шляпы были перепутаны и возвращены
собравшимся в произвольном порядке. Чему равна
вероятность того, что ни один мужчина не получит своей
шляпы?
Уточним, что мы понимаем под вероятностью. Шляпы
между мужчинами можно распределить многими
способами. При некоторых из них каждый мужчина получит
чужую шляпу. Отношение количества таких
распределений к общему числу распределения шляп между
мужчинами и есть искомая вероятность.
,45
X. Биллиард
104. Отражение от одного борта.
На биллиардной столе находятся два шара А к В.
Каким образом надо ударить кием по шару А, чтобы он,
отразившись от заданного борта, попал в шар В? Считать,
что при ударе о борт под углом а шар отражается
также под углом а (рис. 7).
Рис. 7
105. Отражение от двух параллельных бортов.
На биллиардной столе находятся два шара А и В.
Каким образом надо ударить кием по шару А, чтобы он,
отразившись от двух заданных параллельных бортов,
попал в шар В? Считать, что при ударе о борт под
углом а шар отражается также под углом а (рис. 7).
106. Отражение от двух перпендикулярных бортов.
На биллиардной столе находятся два шара А и В.
Каким образом надо ударить кием по шару А, чтобы он,
отразившись от двух заданных перпендикулярных бортов,
попал в шар В? Считать, что при ударе о борт под углом а
шар отражается также под углом а (рис. 7).
107. Отражение от трех бортов.
На биллиардной столе находятся два шара А и В.
Каким образом надо ударить кием по шару А, чтобы
он, отразившись от трех заданных бортов, попал в шар В?
Считать, что при ударе о борт под углом а шар отражает-
ея также под углом а (рис. 7).
108. Отражение от четырех бортов.
На биллиардной столе находятся два шара А и В.
Каким образом надо ударить кием по шару А, чтобы он,
отразившись по одному разу от всех четырех бортов,
попал в шар В? Считать, что при ударе о борт под углом а
шар отражается также под углом а (рис. 7).
46
XI. Фигурные числа
109. Квадратные и треугольные числа.
Натуральное число называется квадратным, если оно
является квадратом некоторого натурального числа.
Например, квадратными будут числа 1, 4, 9, 16 и т. д.
Возьмем лист бумаги, разграфленный сеткой прямых
линий на маленькие квадратики. Нарисуем квадрат,
стороны которого идут по линиям сетки, а вершины
находятся в ее узлах. Количество узлов сетки, лежащих на
сторонах квадрата и внутри него, и будет квадратным числом
(рис. 8).
U
4* •
• • •
• • •
9. • •
о • е •
• • • •
• • • •
16 • • • •
Рис. 8
6. •
Рис. 9
10
• • •
• • • •
36
Рис. 10
• • •
0 • •
47
По аналогии число назовем треугольным, если оно
равно количеству узлов сетки, лежащих на сторонах и внутри
равнобедренного прямоугольного треугольника с
катетами, идущими по линиям сетки, и вершинами в
узлах сетки (рис. 9). Будем также считать треугольным
число 1.
Число 36, как легко проверить, является
одновременно треугольным и квадратным (рис. 10).
Существуют ли еще числа, одновременно являющиеся
квадратными и треугольными?
ПО. m-угольные числа.
Нарисуем правильные т-угольники с одной общей
вершиной О и со сторонами 1 см, 2 см, 3 см как показано на
рис. 11. Отметим в каждом многоугольнике все вершины,
о
Рис. 11
а также точки, разделяющие его стороны на отрезки
единичной длины.
По определению первое m-угольное число равно 1,
второе /n-угольное число равно т, третье т-угольное число
равно количеству отмеченных точек, лежащих внутри и на
границе второго правильного т-угольника. т-угольное
число с номером п равно количеству отмеченных точек,
лежащих внутри и на границе правильного m-угольника с
номером п — 1.
Треугольные и квадратные числа получаются из этой
конструкции при т = 3 и т = 4.
Докажите, что m-угольное число с номером п
равно
(го-2) га2 — (т — 4) п
2
111. Сколько стоит дом?
Некто купил дом. На вопрос, дорого ли он за него
заплатил, он ответил, что число рублей, которое он за него от-
48
дал, есть 365-угольное число
с номером 12.
112. Треугольные и
шестиугольные числа.
Доказать, что каждое
шестиугольное число будет и
треугольным.
ИЗ. Пирамида из ядер.
У пушки сложены
приготовленные для стрельбы
ядра.
Ядра, образующие
первый слой, составляют
правильный треугольник, на
стороне которого лежит п ядер.
Ядра второго слоя положены
в выемки, образованные
ядрами первого слоя. Точно
так же образуются третий,
четвертый и последующие
слои. Последний слой состоит
из одного ядра. Таким
образом, ядра сложены в виде
треугольной пирамиды.
Сосчитайте количество
ядер в этой пирамиде.
XII. С помощью линейки, циркуля и ножниц
114. Правильный шестиугольник.
Из листа бумаги вырезать правильный шестиугольник
со стороной, равной данному отрезку.
115. Правильный восьмиугольник.
Из листа бумаги вырезать правильный
восьмиугольник со стороной, равной данному отрезку.
116. Правильный двенадцатиугольник.
Из листа бумаги вырезать правильный
двенадцатиугольник со стороной, равной данному отрезку.
49
117. Правильный шестнадцатиугольник.
Из листа бумаги вырезать правильный
шестнадцатиугольник со стороной, равной данному отрезку.
118. «Правильный» семиугольник.
Нарисуем окружность и впишем в нее правильный
треугольник ABC. Затем от точки А последовательно сделаем
на окружности 6 засечек радиусом, равным - \АВ\, и
вырежем семиугольник с вершинами в построенных 6 точках
и точке А. Является ли этот семиугольник правильным?
119. Из прямоугольника — треугольник.
Разрезать прямоугольник по прямой линии на две
части, из которых можно сложить треугольник. -
120. Из треугольника — прямоугольник.
Разрезать треугольник по двум прямым на три части,
из которых можно сложить прямоугольник.
121. На части равной площади.
Выпуклый четырехугольник разрезать по прямой,
проходящей через его вершину,-на две части равной площади.
XIII. Построения на местности
122. Как измерить расстояние от дома до башни?
Вы находитесь на берегу реки. На другом, недоступном
для вас берегу стоит дом. Как измерить расстояние от него
до стоящей на вашем берегу башни? .
123. Как измерить расстояние между деревом и
крепостью?
Дерево и крепость расположены на недоступном для
вас берегу реки. Как найти расстояние между ними?
XIV. Геометрические задачи Эйлера
Содержащиеся в этом разделе задачи широко
известны, их можно встретить во многих сборниках
нестандартных задач. Традиционно эти задачи связываются с именем
Эйлера, который заметил лежащие в их основе интересные
геометрические факты и нашел им обоснование.
50
124. Прямая Эйлера.
Докажите, что в произвольном треугольнике точка
пересечения высот, точка пересечения медиан и центр
описанной окружности лежат на одной прямой.
Эта прямая называется прямой Эйлера.
125. Окружность Эйлера.
Докажите, что в произвольном треугольнике основания
медиан, основания высот, а также середины отрезков,
соединяющих точку пересечения высот треугольника с его
вершинами, лежат на одной окружности.
Эту замечательную окружность иногда называют
окружностью Эйлера.
126. Формула Эйлера.
Пусть R и г — радиусы окружностей — описанной
вокруг некоторого треугольника и вписанной в него, ad —
расстояние между центрами этих окружностей. Докажите,
что треугольник, длины сторон которого равны id, r, R — г,
прямоугольный. Иначе говоря, величины R, г и d связаны
следующей формулой Эйлера:
й?2 = Я2-2/?г.
127. Свойство диагоналей и сторон выпуклого
четырехугольника.
Докажите, что в произвольном выпуклом
четырехугольнике сумма квадратов длин сторон превышает сумму
квадратов длин диагоналей на величину, равную
учетверенному квадрату расстояния между серединами
диагоналей.
Заметим, что в параллелограмме диагонали точкой
пересечения делятся пополам, и сумма квадратов длин
сторон равна сумме квадратов длин диагоналей.
128. Интересное свойство выпуклого многогранника.
В любом выпуклом многоугольнике число вершин
всегда равняется числу сторон. Обозначив буквой В число
вершин, а буквой С — число сторон многоугольника, это
утверждение можно записать в виде равенства В — С = 0.
Доказательство его очевидно.
Рассмотрим теперь какой-нибудь выпуклый
многогранник. Число его вершин обозначим буквой В, число ребер —
буквой Р, а число граней буквой Г.
Существует ли соотношение между величинами В, Р и
Г, аналогичное соотношению между числом вершин
многоугольника и числом его сторон?
51
Вычислим выражение В — Р + Г для нескольких типов
многогранников — см. табл. 1.
Таблица 1
Тип многогранника
1. Куб
2. л-угольная пирамида
3. л-угольная призма
В
8
п + \
2л
Р
12
2л
Зл
Г
6
л + 1
л + 2
В-Р + Г
2
2
2
Обратите внимание, что в последней колонке табл. 1
все числа равны 2. Если вы продолжите эту таблицу,
вычисляя значение В—Р-\-Г для каких-нибудь других
выпуклых многогранников, то всегда будете получать в
последней колонке число 2.
Докажите, что для любого выпуклого многогранника
имеет место равенство
В-Р + Г = 2.
Утверждение этой задачи есть один из начальных
фактов большого и важного раздела современной математики,
называемого топологией. На языке этой науки
приведенное выше равенство может быть переформулировано так:
эйлерова характеристика выпуклого многогранника в
трехмерном пространстве равна 2.
Часть третья
ЗАДАЧИ ИЗ СБОРНИКОВ
ЗАНИМАТЕЛЬНЫХ ЗАДАЧ
КОНЦА XVIII ВЕКА
I. Задачи — шутки, задачи — загадки
129. Коза.
Один человек купил трех коз и заплатил 3 рубля.
Спрашивается: по чему каждая коза пошла?
130. Много ли ног?
Мельник пришел на мельницу. В каждом из четырех
углов он увидел по 3 мешка, на каждом мешке сидело по 3
кошки, а каждая кошка имела при себе троих котят.
Спрашивается, много ли ног было на мельнице?
131. Одним мешком — два мешка.
Как можно одним мешком пшеницы, смоловши ее,
наполнить 2 мешка, которые столь же велики, как и мешок,
в котором находится пшеница?
132. Много ли гвоздей найдут?
Двое пошли
— 3 гвоздя нашли.
Следом четверо пойдут
— много ли гвоздей найдут?
133. Сколько уток?
Летели утки: одна впереди и две позади, одна позади
и две впереди, одна между двумя и три в ряд. Сколько
всего летело уток?
134. Что это такое?
Что это такое: две ноги сидели на трех, а когда пришли
четыре и утащили одну, то две ноги, схватив три, бросили
их в четыре, чтобы четыре оставили одну?
53
54
135. Возможно ли такое?
Что это может быть: две головы, две руки и шесть ног,
а в ходьбе только четыре?
136. За сколько минут?
Ребята пилят бревна на метровые куски. Отпиливание
одного такого куска занимает одну минуту. За сколько
минут они распилят бревно длиной 5 метров?
137. Землекопы.
Два землекопа выкапывают 2 м канавы за 2
часа. Сколько землекопов за 5 часов выкопают 5 м
канавы?
138. Два отца и два сына.
Два отца и два сына поймали трех зайцев, а досталось
каждому по одному зайцу. Спрашивается, как это могло
случиться?
139. Как это могло быть?
У одного старика спросили, сколько ему лет. Он
ответил, что ему сто лет и несколько месяцев, но дней рождения
у него было всего 25.
Как это могло быть?
140. Как разделить?
Разделить полтину на половину.
141. Написать число.
Написать цифрами число, состоящее из одиннадцати
тысяч, одиннадцати сотен и одиннадцати единиц.
II. Затруднительные ситуации
142. Волк, коза и капуста.
Крестьянину надо через речку перевезти волка, козу
и капусту. В лодке может поместиться только один
человек, а с ним или волк, или коза, или капуста. Если
оставить волка с козой без человека, то волк съест козу; если
оставить козу с капустой, то коза съест капусту. В
присутствии же человека" коза не может съесть капусту,
волк — козу.
Человек все-таки перевез свой груз через речку. Как
он это сделал?
55
143. Рыцари и оруженосцы.
Три рыцаря, каждый в сопровождении оруженосца,
съехались на берегу реки и хотят переправиться на другой
берег. Есть лодка, которая может вместить только двух
человек. Могут ли переправиться рыцари и их оруженосцы
на другой берег при условии, что оказавшись отдельно от
своего рыцаря, ни один оруженосец не находился бы при
этом в обществе других рыцарей?
144. Разделить квас поровну.
Восьмиведерный бочонок заполнен доверху квасом.
Двое должны разделить квас поровну. Но у них есть
только два пустых бочонка, в один из которых входит 5
ведер, а в другой 3 ведра. Спрашивается, как они могут
разделить квас, пользуясь только этими тремя
бочонками?
145. Разделить бочки и мед.
Три человека должны разделить между собой 21
бочонок, среди которых 7 бочонков полных медом, 7 йолных
медом наполовину и 7 пустых. Могут ли они разделить
бочонки и мед так, чтобы каждый из них имел одина:
ковое количество меда и одинаковое количество
бочонков? (Предполагается, что все бочонки одинаковые
и переливать мед из одного бочонка в другой не
разрешается.)
146. Девичья хитрость.
Золотошвея, взяв 20 девушек в учение, разместила их
в 8 комнатах своего дома так, как показано на рисунке
бв
(рис. 12). По вечерам золотошвея
обходила дом и проверяла, чтобы в комнатах
на каждой стороне его было по 7
девушек. Однажды к девушкам в гости
приехали 4 подружки и, заговорившись,
остались у них ночевать, причем все 24
девушки разместились в комнатах так,
что вечером золотошвея насчитала
в комнатах на каждой стороне дома
опять по 7 девушек. На следующий день 4 девушки пошли
провожать своих четырех подруг и дома не ночевали.
Оставшиеся 16 девушек разместились так, что опять вечером
золотошвея насчитала в комнатах с каждой стороны дома
по 7 девушек. Как размещались девушки по комнатам в
двух последних случаях?
147. Во время шторма.
Во время шторма капитан корабля приказал выбросить
за борт половину из 30 тюков с товарами, которые везли
два купца. Купцы были в нерешительности: каждому было
жаль выбрасывать свой груз. Видя это, капитан сказал:
«Сделаем так: матросы расставят 30 тюков по. кругу, а мы
будем ходить по кругу и выбрасывать каждый девятый
тюк, пока не выбросим половину тюков*. Один из купцов
подкупил матросов, и они сумели расставить тюки так, что
15 оставшихся на палубе тюков оказались с товарами
этого купца.
Как были расставлены тюки?
III. Угадывание чисел
148. Как найти задуманное четное число?
Предложите кому-нибудь задумать четное число, затем
это число утроить, полученное произведение разделить
на 2 и частное опять утроить. После объявления
результата предложенных арифметических действий вы
называете задуманное число.
Как это сделать?
149. Как найти задуманное нечетное число?
Предложите кому-нибудь задумать нечетное число.
Затем попросите этб число утроить и к полученному
произведению прибавить число 3; этот результат предложите
разделить на 2 и частное опять утроить. После объявления
2 3 2
3 3
2 3 2
57
результата предложенных арифметических действий вы
называете задуманное число.
Как это сделать?
150. Как найти задуманное число?
Предложите кому-нибудь задумать некоторое число и
утроить его. Затем спросите, является ли полученное
произведение числом четным или нечетным. Если
произведение окажется числом четным, то предложите это
произведение разделить на 2; если же это произведение окажется
числом нечетным, то, прежде чем делить его на 2, к этому
произведению предложите добавить 3, а уже потом
разделять на 2. Частное, полученное от деления на 2,
предложите утроить. После объявления результата указанных
арифметических действий вы можете назвать задуманное число.
Как это сделать?
151. Как отгадать два числа?
Предложите кому-нибудь задумать два числа, из
которых одно превышает другое на единицу и каждое из
которых не более девяти. Затем попросите перемножить два
этих числа, из произведения вычесть меньшее из чисел, и
результат опять умножить на меньшее из задуманных
чисел.
По объявленной последней цифре полученного
результата вы можете назвать задуманные числа.
Как их найти?
152. Угадывание числа.
Предложите кому-нибудь задумать не очень большое
число и умножить его само на себя. К полученному
результату попросите прибавить удвоенное задуманное число и
еще 1. По объявленному результату предложенных
арифметических действий вы можете назвать задуманное число.
Как найти задуманное число?
153. Как найти цифру?
Записав число, сумма цифр которого делится на 9, и
отвернувшись, предложите кому-нибудь это число умножить
на любое число. В полученном произведении предложите
зачеркнуть любую из цифр, кроме нуля, а оставшиеся
цифры переставить в произвольном порядке. После
объявления результатов указанных действий вы можете указать,
какая цифра была зачеркнута.
Как найти зачеркнутую цифру?
S8
154. Отгадать зачеркнутую цифру.
Предложите кому-либо написать некоторое число.
Приписав к нему спереди или сзади некоторую цифру так,
чтобы сумма цифр вновь полученного числа делилась на 9, вы,
отвернувшись, предлагаете умножить вновь полученное
число на любое натуральное число, зачеркнуть в
полученном произведении любую из цифр, отличную от нуля, и
найти сумму оставшихся цифр.
После объявления результата предложенных
действий, вы можете угадать, какая цифра была
зачеркнута.
Как найти зачеркнутую цифру?
155. Найти зачеркнутую цифру.
Отвернувшись, попросите кого-либо написать любое
многозначное число, не все цифры которого
одинаковы. Затем попросите в этом числе произвольным образом
переставить цифры так, чтобы получилось число,
отличное от уже написанного, и также его записать. Меньшее
из двух таким образом написанных чисел попросите
вычесть из большего. В полученной разности попросите
зачеркнуть любую цифру, отличную от нуля, найти сумму
оставшихся цифр и объявить ее. После этого вы можете
назвать зачеркнутую цифру.
Как найти зачеркнутую цифру?
156. Какая цифра зачеркнута?
Предложите кому-либо задумать некоторое
многозначное число, найти сумму цифр этого числа и отнять ее от
задуманного числа. В полученной разности предложите
зачеркнуть любую из цифр, отличную от нуля, и сообщить
вам сумму остальных цифр (либо сообщить цифры этого
числа). По объявленному результату вы можете назвать
зачеркнутую цифру.
Как найти зачеркнутую цифру?
157. На сколько одни человек старше другого?
Пригласите двоих из присутствующих и объявите, что
вы сейчас узнаете разницу в их возрасте. Пусть младший
из них число своих лет вычтет из 99, а затем старший к этой
разности прибавит число своих лет и вам объявит
результат. После этого вы можете сказать, на сколько лет один
человек старше другого.
Как это узнать? (В задаче предполагается, что
возрасты каждого из присутствующих меньше 100 лет.)
89
158. Как узнать день рождения?
Предложите кому-нибудь утроить число, являющееся
его днем рождения. Затем предложите разделить
полученное произведение на 9, частное умножить на 3, а остаток
разделить на 3. Попросив, чтобы было объявлено это
произведение и это частное, вы можете сказать, какого числа
был день рождения этого человека.
Как найти день рождения?
159. Сколько лет человеку?
Предложите кому-нибудь умножить число его лет на 2
и к произведению прибавить 4, затем полученную сумму
умножить на 5, к этому произведению прибавить 12 и
полученную сумму умножить на 10. После объявления
результата предложенных арифметических действий вы
можете объявить число лет.
Как это сделать?
160. Быстрое сложение.
Предложите кому-нибудь написать несколько чисел,
состоящих из одинакового количества цифр. К этим
числам вы приписываете несколько чисел- Затем вы
предлагаете сложить все написанные числа, объявляя сразу же
ответ. Какие числа надо дописать и как найти сумму всех
чисел?
161. Чему равна сумма ненаписанных чисел?
Предложите кому-нибудь из присутствующих написать
на листе бумаги три пятизначных числа. Затем на другом
листе бумаги напишите некоторое число и скажите, что
сейчас вы напишете на первом листе еще два числа, сумма
которых с уже написанными, ранее на этом листе числами
будет, равна числу, написанному вами на втором листе
бумаги.
Какие числа нужно дописать? Как узнать сумму всех
чисел?
Эту задачу можно усложнить, предложив написать на
первом листе бумаги не три, а несколько, но не более
десяти, и не менее двух чисел-, состоящих из одинакового
количества цифр.
Для большего эффекта число на второй лист можно
записать сразу же после того, как на первом листе будет
написано хотя бы одно число.
60
IV. Игры с предметами
162. У кого монета?
Положите на стол монету. Каждому из
присутствующих определите некоторый порядковый номер: 1, 2, 3,...
Затем предложите, чтобы кто-либо из них взял монету,
когда вы отвернетесь. Обращаясь к собравшимся, скажите,
что тот, кто взял монету, должен свой порядковый номер
удвоить и к произведению прибавить число 5, полученную
сумму он должен опять умножить на 5. После этого вы
просите кого-нибудь из присутствующих объявить вам
результат предложенных действий и указываете на человека,
взявшего монету.
Как определить порядковый номер человека, взявшего
монету?
163. У кого кубик?
Для этой игры нужны три кубика разных цветов,
например красный, синий и желтый, и еще 24 каких-либо
одинаковых предмета. Можно взять орехи, кости домино
и т. п. Если разноцветных кубиков у вас нет, возьмите
вместо них три других не очень больших предмету. В игре,
кроме вас, участвуют еще три человека.
Положите на стол кубики и 18 орехов, а остальные 6
орехов распределите между участниками, дав одному из
них 1 орех, другому 2 ореха, а третьему 3 ореха.
Отвернувшись, предложите каждому из участников взять один из
кубиков, а затем пусть тот, кто взял красный кубик,
возьмет со стола столько же орехов, сколько ему было
дано, тот, у кого синий кубик, пусть возьмет вдвое больше
орехов, чем ему было дано, имеющий желтый кубик пусть
возьмет со стола в 4 раза больше орехов, чем ему было
дано. Взглянув после этого на стол, вы можете отгадать,
кто из участников игры взял какой кубик.
Как это узнать?
164. Кто что взял?
Выберите среди присутствующих трех человек.
Назовите их первым, вторым и третьим и предложите им три
предмета, которым также присвойте номера 1, 2 и 3. Пусть
каждый из выбранных после того, как вы отвернетесь,
возьмет один из предметов и спрячет его. Далее
предложите первому человеку порядковый номер взятого им
предмета умножить на 3, второму человеку — порядковый номер
61
62
его предмета умножить на 10, а третий пусть умножит
порядковый номер своего предмета на 12. Сложив
полученные произведения, пусть кто-либо из троих участников
игры объявит сумму. Зная сумму, вы можете узнать, кто из
троих человек взял какой предмет.
Как это сделать?
165. У кого какой предмет?
Покажите четверым участникам игры четыре предмета,
присвоив этим предметам номера 1, 2, 3 и 4. Пусть каждый
из участников после того, как вы отвернетесь, возьмет один
из предметов и спрячет его. Затем пусть первый человек
умножит номер своего предмета на два, второй — на 21,
третий — на 25, а четвертый, пусть умножит номер своего
предмета на 26. Далее попросите их сложить,
получившиеся произведения и объявить результат. После этого вы
можете узнать, кто из четверых человек взял какой
предмет.
Как это сделать?
166. Сколько выпало очков?
Отвернувшись, предложите кому-нибудь подбросить
два кубика, на каждой из шести граней которых написано
по одной цифре от 1 до 6. Затем попросите к двойному
числу очков верхней грани одного из кубиков прибавить 5.
Полученную сумму попросите умножить на 5 и к
произведению прибавить число очков верхней грани второго кубика.
По объявленному результату вы сразу же можете назвать
число очков, находящихся на верхней грани каждого из
кубиков.
Как определить число очков, выпавших на верхних
гранях каждого кубика?
167. Кто сколько взял кубиков?
Пусть имеется ящик с достаточным количеством
кубиков или каких-нибудь других предметов. Предложите
некоторому числу людей взять из ящика по несколько
кубиков, но каждому не более девяти. Присвоив каждому из
игроков, бравших кубики, номер, предложите первому из них
удвоить число, означающее количество взятых им кубиков.
Из получившегося числа пусть он вычтет 1, разность
умножит на 5 и сообщит результат человеку, порядковый
номер которого два. Этому человеку предложите к числу,
сообщенному ему первым человеком, прибавить число
взятых им кубиков, увеличенное на 5, и полученный результат
63
удвоить, затем пусть он из этого произведения вычтет 1,
полученное число умножит на 5 и сообщит результат
третьему человеку. Третьему человеку предложите проделать
аналогичные арифметические выкладки и сообщить
результат четвертому человеку. Все следующие, кроме
последнего, пусть проделают такие же арифметические
операции. Последний же человек, после того как ему
предыдущий человек сообщит свой результат, пусть к
этому результату добавит число взятых им кубиков,
увеличенное на 5, и назовет получившееся число. Вы тотчас
скажете, кто из присутствующих сколько взял кубиков.
Как узнать, кто сколько кубиков взял?
168. В какой руке нечетное число предметов?
Вы даете кому-нибудь нечетное число предметов, и
пусть он некоторое число предметов.возьмет в левую руку,
а остальные предметы возьмет в правую руку. Затем вы
предлагаете количество предметов в левой руке умножить
на 2, а количество предметов в* правой руке умножить
на 3 и полученные произведения сложить. После того, как
вам скажут, какое число получилось — четное или
нечетное,— вы сможете сказать, в какой руке четное число
предметов, а в какой руке — нечетное число.
Как это узнать?
Если вместо нечетного числа предметов предложить
играющему две монетки с нечетной суммой их стоимостей,
например, в 1 и 2 копейки, то таким способом можно
угадать, в какой руке лежит какая монета.
169. Перекладывание карточек.
Напишите на 16 одинаковых карточках числа от 1 до 16.
Предложите одному из присутствующих загадать какое-
нибудь из написанных чисел. Соберите карточки в стопку
цифрами вниз, а затем, раскрывая карточки по одной,
складывайте их цифрами вверх попеременно в две стопки
А и Б. Спросите у человека, задумавшего число, в какой
стопке оно находится. Предположим, вам ответят, что
задуманное число находится в стопке А. Наложите тогда
стопку Б на стопку А и, перевернув получившуюся стопку
из 16 карточек числами вниз, разложите опять карточки
на две стопки, как указывалось выше. Эту процедуру с
разложением карточек следует проделать всего четыре раза.
После четвертого ответа легко найти карточку с
задуманным числом.
Как это сделать?
64
170. Фокус с 16 буквами.
Написав по кругу 16 букв, как показано на рис. 13,
предложите своему товарищу загадать некоторую букву.
Потом предложите ему считать буквы «про себя» от
задуманной буквы (включая и ее) по часовой стрелке до тех
пор, пока он не дойдет в счете до 40. Затем пусть он скажет
вам букву, на которую пришелся счет 40.
Как узнать загаданную букву по букве, объявленной
вашим товарищем?
о.
н*
м»
•
л
р
•
•
н
А
•
•
И
Рис. 13
Б
•
•
3
.в
•г
•д
•£
•
Ж
м
•
л.
к*
и#
•
3
-
1 в
•
•в
• г
•д
•
• Е
Ж
Рис. 14
171. Фокус с 12 буквами.
Написав по кругу 12 букв, как показано на рис. 14,
предложите кому-нибудь из присутствующих загадать
одну из написанных букв. Затем скажите, чтобы он считал
«про себя» буквы, начиная от буквы М, в направлении
против часовой стрелки до тех пор, пока не дойдет до
загаданной буквы. После этого пусть он продолжит счет, начав его
с буквы Л, но уже в направлении по часовой стрелке, и
объявит букву с номером 19.
По объявленной букве легко отгадать задуманную.
Как это сделать?
ОТВЕТЫ И РЕШЕНИЯ ЗАДАЧ
Часть первая
I. Житейские истории
1. За 140 дней человек выпьет 10 бочонков кваса, а вдвоем с женой
за 140 дней они выпьют 14 бочонков кваса. Значит, за 140 дней жена
выпьет 14—10 = 4 бочонка кваса, а тогда один бочонок она выпьет за
140:4=35 дней.
2. Поскольку за 8 часов 6 человек выпивают бочонок кваса, то за
один час такой же бочонок кваса выпьют 48 человек, а тогда за 3 часа
этот бочонок кваса выпьют 16 человек.
3. Если заяц сделает 6 скачков, то и собака сделает 6 скачков, но
собака за 5 скачков из 6 пробежит то же расстояние, что заяц за 6
скачков. Следовательно, за 6 скачков собака приблизится к зайцу на
расстояние, равное одному своему скачку. Поскольку в начальный момент
расстояние между зайцем и собакой было равно 40 скачкам собаки, то
собака догонит зайца через 40X6=240 скачков.
4. За одну минуту заяц пробегает 250 саженей, а собака 260 саженей.
Следовательно, за одну минуту расстояние между собакой и зайцем
уменьшится на 10 саженей. Поскольку между собакой и зайцем, когда
собака увидала зайца, было 150 саженей, то собака догонит зайца через
150:10=15 минут.
5. Уменьшив втрое количество орехов в большей части, мы получим
их столько же, как в четырех меньших частях. Значит, большая часть
должна содержать в 3X4= 12 раз больше орехов, чем меньшая, а общее
число орехов должно быть в 13 раз больше, чем в меньшей части.
Поэтому меньшая часть должна содержать 130:13=10 орехов, а большая
130 — 10 = 120 орехов.
6. Ясно, что все три жернова должны работать одинаковое время,
потому что простой любого из 3-х жерновов увеличивает время помола
зерна. Поскольку за сутки все 3 жернова вместе могут смолоть 60+54 +
+ 48 = 162 четверти зерна, а надо смолоть 81 четверть, то жернова
должны работать 12 часов и за это время на первом жернове надо смолоть
30 четвертей, на втором 27 четвертей, а на-третьем 24 четверти зерна.
7. Поскольку лошадь съедает воз сена за месяц, то за год (12
месяцев) она съест 12 возов сена. Так как коза съедает воз сена за 2 месяца,
то за год она съест 6 возов сена. И, наконец, поскольку овца съедает воз
сена за 3 месяца, то за год она съест 4 воза сена. Вместе же они за год
съедят 12+6+4=22 воза сена. Тогда один воз сена они все вместе съедят
за 12:22=-г- месяца.
8. Давайте подумаем, как могут распределиться 12 хлебов между
мужчинами, женщинами и детьми. Попробуем мысленно распределить
хлеба между ними. Сначала дадим всем по половине хлеба. При этом
будет роздано 6 хлебов. Чтобы удовлетворить условию задачи, нужно
раздать оставшиеся 6 хлебов мужчинам, а затем взять у каждого из детей
по четверти хлеба и также распределить этот хлеб среди мужчин.
Каждому мужчине до его нормы не хватает полтора хлеба. Шесть хлебов
по полтора хлеба можно распределить между четырьмя мужчинами,
после чего каждый из них будет нести по два хлеба. Отсюда следует, что
мужчин не менее пяти. Иначе излишки хлеба, имеющиеся у детей, некому
было бы нести. Но если бы мужчин было шесть, то они сами несли бы
весь хлеб, а женщинам и детям ничего бы не осталось. Итак, имеется
всего пять мужчин. Пятому мужчине до его нормы не хватает полтора
хлеба, и именно эти полтора хлеба нужно собрать по четверти у каждого
из детей. Так как полтора хлеба состоят из шести четвертей, то детей
имеется всего шестеро и, значит, количество женщин равно 12—5—6=1.
Следовательно, хлеба несли 5 мужчин, одна женщина и 6 детей.
9. Приводим решение из рукописи: «... Возьми число первому
плотнику 12, а другому вполы 6, а третьему -г—4, а четвертому -т—3. Сочти
же все те перечни как 12 да 6 да 4 да 3, станет 25. То стал деловой
67
перечень. Разочти же те 12 годов — первое число на дни; умножи
с 365-ю дни, придет 4380 дней. Дели же те дни на 25, придет 175=- дни,
4 *>
столько они вместе делали. Станет 25 недель 4^ часа».
Таким образом, в рукописи задача решается с помощью
приведения количества работы каждого плотника к одному и тому же времени,
именно, к 12 годам. За 12 лет первый плотник может построить 12 домов,
второй — 6 домов, третий — 4 дома, а четвертый — 3 дома. Всего же
они вместе могут построить 12+6+4+3 = 25 домов. Принимая, что
в году 365 дней, автор рукописи
умножает 365 на 12 и получает 4380
дней. Поделив это число на 25,
узнаем, за какое время четыре
плотника вместе построят дом, получаем
4380:25 = 175^ дней или 25 недель
4= часа.
10. Эта задача встречается в
современной литературе в такой
формулировке.
Прилетели галки,
Сели на палки.
Если на каждой палке
Сядет по одной галке,
То для-одной галки
Не хватит палки.
Если же на каждой палке
Сядет по две галки,
То одна из палок
Будет без галок.
Сколько было галок?
Сколько было палок?
Предположим, что после того
как скворцы сели на деревья по два,
с каждого дерева взлетело по одному
скворцу. Один из взлетевших
скворцов может сесть на незанятое дерево,
тогда на каждом дереве будет сидеть
по одному скворцу. По условию,
если на каждое дерево сядет по
одному скворцу, то один скворец останется в воздухе. Значит, взлетело 2
скворца. Тогда общее число скворцов равно 4, а число деревьев 3.
Другое решение.
Поскольку в первом случае для одного скворца не хватило дерева,
а во втором случае сидели все скворцы и одно дерево осталось без сквор-
68
ца, то, чтобы занять все деревья, во втором случае нужно скворцов на три
больше, чем в первом. Во втором случае на каждое дерево садится на
одного скворца больше. Следовательно, деревьев было три, а тогда
скворцов было четыре.
11. Так как передача двух слив уравнивает число слив у
собеседников, то у одного из них на четыре сливы больше, чем у другого. Если же
человек, у которого слив меньше, две сливы отдаст человеку, у которого
их больше, то разница увеличится до 8 слив. Поскольку второй человек
тогда будет иметь слив в два раза больше, то ясно, что у одного из них
после передачи будет 8 слив, а у другого 16 слив. Следовательно, до
передачи двух слив у одного было 10 слив, а у другого было 14 слив.
12. Так как в конце у каждого из мальчиков оказывается по 8 яблок, а
непосредственно перед тем третий дал первому и второму столько,
сколько они имели, то перед последней передачей яблок первый и второй
мальчики имели по 4 яблока, а третий — 16 яблок. Но тогда перед второй
передачей первый мальчик имел 2 яблока, третий 8 яблок, а следовательно,
второй мальчик 4 + 2+8=14 яблок.
Таким образом, сначала у второго мальчика было 7 яблок, у
третьего 4 яблока, а у первого 2+7+4=13 яблок.
13. Из условия следует, что и у Ивана и у Михаила вдвое больше
овец, чем у Якова, у Петра вдвое больше, чем у Ивана, и, значит,
вчетверо больше, чем у Якова. Но тогда у Герасима столько же овец, сколько
имеет их Яков. Общее число овец поэтому в (2+4+1+2+1) = 10 раз
больше, чем число овец у Якова. Отсюда следует, что у Якова 1 овца,
тогда и у Ивана и у Михаила по 2 овцы, у Петра 4 и у Герасима 1 овца.
Соответственно столько же дней должен пасти овец каждый из них.
Эту задачу можно решить иначе.
Поскольку Герасим имеет вчетверо меньше овец, чем Петр, то у
Петра либо 4 овцы, либо 8 овец. Если у Петра 8 овец, то у Герасима 2 овцы.
Поскольку 8 + 2= 10 и так как еще овец имеют Иван, Яков и Михаил, то
общее число овец уже будет больше 10. Следовательно, у Петра 4 овцы,
а тогда у Герасима одна овца, у Ивана в два раза меньше, чем у Петра,
т. е. 2 овцы, у Якова в два раза меньше, чем у Ивана, т. е. одна овца,
а у Михаила две овцы, поскольку у него в два раза больше, чем у Якова.
14. Задача сводится к нахождению такого числа, которое делится
нацело на 7, а-при делении на 2, 3, 4, 5 и 6 дает в остатке 1. Если искомое
число уменьшить на 1, то получится число, делящееся на 2, 3, 4, 5 и 6.
Наименьшее число, которое делится без остатка на числа 2, 3,4, 5 и 6,
есть 60. Нужно, значит, найти такое число, которое делилось бы на 7
нацело и было бы вместе с тем на 1 больше числа, делящегося на 60.
Рассмотрим числа 61, 121, 181, 241, 301 и т. д. Первое из выписанных
чисел, делящееся на 7, есть 301. Кроме этого числа, условию задачи
удовлетворяют 721, 1141, 1561 и т. д. Ряд чисел, удовлетворяющих условию
задачи, бесконечен. Каждое из них получается прибавлением к
предыдущему 420 — наименьшего числа, делящегося на 4, 5, 6, 7.
69
II. Путешествия
15. За день первый человек пройдет по направлению к Вологде
40 верст и, значит, к началу следующего дня будет опережать второго
человека на 40 верст. В каждый следующий день первый человек будет
проходить по 40 верст, второй по 45 верст, а расстояние между ними
будет сокращаться на 5 верст. На 40 верст оно сократится за 8 дней.
Поэтому второй человек настигнет первого к исходу 8-го дня своего
путешествия.
Приводим решение из рукописи:
«... Придет в восьмой д«нь на един ночлег сошлися. А считай сяце:
выни 40 из 45, останется 5. Дели ж 40 на 5 придет 8, в столько дней
настиг другой юноша прежняго юношу».
16. За один день путники сближаются на 70 верст. Поскольку
расстояние между городами равно 700 верст, то встретятся они через
700:70=10 дней.
17. За тридцать дней путешественники проходят 30:10+30:15=
= 5 расстояний между городами. Следовательно, они сойдутся через
30:5=6 дней.
18. За первый час второй путник отстанет от первого на 4 — 3^=
2 2 2
=- версты, за второй час еще на ^ версты, за третий час еще на ^ версты
о о о
я т. д. Путники сойдутся вместе опять, когда отставание сравняется
с длиной пути вокруг города, т. е. станет равным 15 верстам. На это
понадобится
., 2 15-3 „„1
15:3 =— =222 ЧаСЭ-
Первый путник за это время пройдет
4-22- = 90 верст
и обойдет 90:15=6 раз вокруг города. Второй путник пройдет на
15 верст меньше и, значит, сделает на один обход меньше. Следовательно,
путники сойдутся опять через 22^ часа, первый из них обойдет вокруг
города 6 раз, а второй 5 раз.
Приводим решение из рукописи.
3- верст из 4 верст, и „
о о
1 2
«Преж выни З^ верст из 4 верст, останется ^ версты. Дели ж 15 верст
2 1
на -, придет 22-часа, в столько часов настиг резвый юноша тихаго. По-
стави же на строку и молви: 1 час дает 4 версты, что даст 22^ часа,
придет 90 верст. Дели ж ту 90 на 15 верст, придет 6: столкижды обошел
70
град резвый юноша. Да опять молви: 1 час дает З^ версты, что даст
1
22^ часа, придет 75 верст. Дели ж ту 75 на 15 верст придет 5; стод-
киждЫ обошел град тихий юноша».
19. В первый день второй воин отстанет на 12—1 = 11 верст, во
второй еще на 12 — 2=10 верст, в третий еще на 12 — 3=9 верст и так
далее. На 12-й день отставание составит (II + 10+9-+.. +2+ 1 +
+ 0) верст.
А затем расстояние между ними начнет сокращаться. В 13-й день
на 13—12=1 версту, в 14-й день еще на 14—12 = 2 версты, в 15-й
день еще на 15—12 = 3 версты и, наконец, в 23-й день на 23—12 =
= 11 верст. На 23-й день расстояние между ними уменьшится на (1 + 2 +
+ 3+ +Ю+11) верст. Это значит, что второй воин по прошествии
23 дней догонит первого.
20. До середины расстояния между деревнями первому прохожему
нужно идти 2 версты, и это составляет
1 1 1
2~3=6 ЧаСТЬ
всего расстояния между деревнями Поэтому расстояние между
деревнями равно 12 верстам, к моменту встречи первый прохожий прошел
"12 = 4 версты и осталось ему идти еще 8 верст.
о
III. Денежные расчеты
з
21. Поскольку - аршина стоят 3 алтына, то 3 аршина стоят 12 алтын
и 1 аршин стоит 4 алтына. Следовательно, 100 аршин стоят 400 алтын,
что составляет 1200 копеек или 12 рублей.
22. Так как алтын состоит из 12 полушек, то 2 алтына и 7 полушек
составляют 2Xf2 + 7=31 полушки. Следовательно, за половину гусей
уплачено 48X31 = 1488 полушек. За вторую половину гусей уплачено
48 X (24— 1) =48X23= 1104 полушки, т. е. за всех гусей уплачено
1488+И04 = 2592 полушек, что составляет 2592:4=648 копеек
или 6 рублей 48 копеек, или 6 рублей 1:6 алтын.
23. Поскольку в одном алтыне 3 копейки, а в одной копейке 4
полушки, то старый баран стоит 15X3+ 1 =46 копеек. Так как молодой баран
стоит 10 алтын, т. е. 30 копеек, то он на 16 копеек стоит дешевле старого
барана. Если бы были куплены только молодые бараны, то за них
заплатили бы 3360 копеек. Поскольку за всех баранов уплатили 49 рублей и
20 алтын, или 4960 копеек, то излишек в 1600=4960—3360 копеек
пошел на оплату старых баранов. Тогда старых баранов куплено 1600:
: 16= 100. Значит, молодых куплено 112—100, т. е. 12 баранов.
71
Приводим решение из «Арифметики» Л. Ф. Магницкого:
А ИЗОДРАН СНШ ;
4 б КОПІІКЪ 34 tTAfATO ,
3 О 3* молоддго:
I б рь'знрдо
I і г
з_2.
ЗЗбо
fflCA If&IA
4 9 б о
3 3 б о
X б О О
*■*ah ѵ{»з* f&**60 j У я
У £ £, ф Гі О О чго/ufew vriyup,-
24. Три курицы стоят 46 копеек. Для того чтобы возместить эту
сумму, необходимо продать (4б:„-) Х5=460 яиц. За 12 дней первая курица
снесла 9 яиц, вторая — 8 яиц, а третья — 6 яиц. Вместе же они снесли
23 яйца. Так как 460=23X20, то за 12X20=240 дней курицы снесут
23X20=460 яиц. Значит, куры окупятся за 240 дней.
25. Девять бочек с маслом стоят на полтора рубля с гривною (т. е.
на 16 гривен) больше суммы денег, имеющейся у покупателя, а эта
сумма, в свою очередь, на 20 алтын (6 гривен) больше стоимости восьми
бочек. Значит, одна бочка масла стоит 16 + 6=22 гривны. Когда
человек давал деньги за 8 бочек масла, у него оставалось 6 гривен. Значит,
до покупки у него было 8X22+6=182 гривны, или 18 рублей и
2 гривны.
26. Работник не доработал у хозяина 5 месяцев и недополучил 7
рублей. Значит, месячная его плата в деньгах составляет ■= рубля или
7 4
1 рубль и 40 копеек. Плата за 7 месяцев составит 7X^=9= рубля или
9 рублей 80 копеек.
Но работник за это время получил 5 рублей и кафтан.
Значит, кафтан стоит 4 рубля 80 копеек.
72
27. Если бы работник работал без прогулов, то за 60 дней он
заработал бы 20X60= 1200 копеек. За каждый нерабочий день у него вычитают
30 копеек и он не зарабатывает 20 копеек, т. е. за каждый прогул он теряет
20+30=50 копеек. Поскольку за 60 дней работник ничего не заработал,
то потеря за все нерабочие дни составила 1200 копеек, т. е. число
нерабочих дней равно 1200:50=24 дня. Количество рабочих дней поэтому
равно 60—24=36 дням.
28. Так как 25 яиц без полушки стоят пять полушек без пяти яиц,
то 30 яиц без полушки стоят пять полушек. Следовательно, 30 яиц стоят
6 полушек, откуда получаем, что один десяток яиц стоит две полушки или
полкопейки.
Приведем текст решения этой задачи из рукописи: «А считай сице:
складывай яйца с яйцы да деньги с деньгами. Как 25 яиц да 5 яиц станет
30 яиц. Сложив деньгами 2^ деньги да ^ деньги — 3 деньги. Дели ж 30
яиц на 3 деньги, придет 10 яиц за деньгу». (Деньга — 2 полушки.)
9 25
29. Поскольку за j аршина уплачено — гривны, то 9 аршин стоят
25 289
25 гривен, а, значит, один аршин стоит -^- гривны. Поэтому ■ аршина
289 25 ...25
сукна стоят •-5-=200^g гривны.
4 У ОО
30. Второй, третий и четвертый купцы, сложив свои деньги вместе.
соберут, как сказано в условии, 90 рублей. Если от этой суммы отнять
деньги второго купца и добавить деньги первого, то получится по
условию 85 рублей. Поэтому у первого купца на 5 рублей меньше, чем
у второго. Но точно так же легко увидеть, что у третьего купца на 5 рублей
больше, чем у второго. Значит, первый, второй и третий купцы, сложив
свои деньги вместе, соберут втрое больше денег, чем имеется у второго
купца. В условии сказано, что эта сумма составляет 75 рублей, и мы
73
находим, что у второго купца было 25 рублей, у первого — 20 рублей,
у третьего — 30 рублей. Но тогда у четвертого купца было 35 рублей.
Второе решение Предположим, что первый, второй и третий
купцы положат на стол третью часть имеющихся у каждого из них денег
По условию на столе окажется третья часть от 75 рублей, т. е. 25 рублей.
Затем пусть первый, второй и четвертый добавят к этой сумме еще третью
часть от первоначально имевшихся у каждого денег. Тогда прибавится
80 2
третья часть от 80 рублей и на столе станет 25-f--5"=51- рублей.
о о
После этого пусть к имеющейся сумме добавят третью часть первый,
третий и четвертый купцы и, наконец, добавят третью часть второй, третий и
четвертый купцы. На столе окажется
рублей, а каждый из купцов окажется без денег. Мы установили, таким
образом, что общая сумма денег у всех купцов равна 110 рублей. Но
тогда у первого купца имеется 110 — 90=20 рублей, у второго 110—
—85 = 25 рублей, у третьего 110 — 80 = 30 рублей и у четвертого
110—75 = 35 рублей.
31. Работник, отправившись на базар, имел 16 алтын, что составляет
48 копеек. Так как за гуся велено платить по 3 копейки, то взятых денег
хватит на 16 гусей Но тогда нельзя будет купить ни уток, ни чирков. Итак,
работник купил не более 15 гусей.
Допустим, что работник уже купил чирков и уток. Если бы гуси
стоили по 1 копейке, то за все покупки работник заплатил бы менее 20 копеек
и у него осталось бы более 28 копеек. Эти оставшиеся копейки работник
должен фактически потратить на гусей, доплатив за каждого гуся по 2
копейки По условию работник израсходовал все деньги. Значит, он купил
74
более 14 гусей. Из всего сказанного выше следует, что работник купил в
точности 15 гусей, потратив на них 45 копеек.
Итак, работник потратил 3 копейки на покупку 5 птиц — уток и
чирков. Если бы чирки стоили по 1 копейке за штуку, то покупка обошлась бы
в 5 копеек. Лишние 2 копейки возникли потому, что пришлось бы
переплатить за каждого чирка по половине копейки. Поэтому было куплено 4
чирка и, значит, 1 утка.
Таким образом, работник купил 15 гусей, 1 утку и 4 чирка.
32. Всего гвоздей 24. За все гвозди купец должен заплатить
1+2 + 22 + 23 + -|_223 полушек. Обозначим эту сумму буквой А.
Имеем
Л=АХ(2—1)=2 + 22 + 23 + +224-(1+2 + 22 + 23 + ...+223) =
= 224- 1 =210 Х210 Х24— 1 = 1024Х 1'024Х 16- 1 = 16777215
полушек или 41 943 рубля и 15 полушек. Следовательно, купец должен
заплатить 41 943 рубля 15 полушек вместо тысячи рублей. На таких
условиях не обидно и лошадь дать впридачу!
IV. Q ©ѵтѣшны^ъ {Плоить д'Ьйствдхъ чре^
ДрТ&Л>ѴЕТИК§ ОѴПОТрЕБЛАЕМЫХЪ («Об утешных некиих
действах через арифметику употребляемых»)
33. Надо из первой цифры объявленного результата вычесть 2.
Остаток укажет номер задуманного дня недели.
Пример. Пусть задуман четверг. Порядковый номер этого дня
есть 4 (начинается счет с понедельника). После удвоения этого числа
получим 8, прибавляя к восьми число пять, получаем 1.3. Умножив это
число на пять, а затем полученный результат — число 65 — умножив на
10, имеем число 650. Отняв от числа 6 — числа сотен — число 2,
получаем 4 — порядковый номер задуманного дня недели, т. е. четверга.
Обоснование. Пусть кто-то задумал некоторый день недели,
порядковый номер которого т удовлетворяет условию 1 ^ т <; 7 После
умножения этого числа на два и прибавления к результату 2т числа 5
получим число 2т + 5 Умножая это число на 5, а затем умножая
полученный результат на 10, имеем
[(2т + 5)Х5]ХЮ=100ш + 250=(2 + т)ХІ00 + 50
Поскольку 1^от^7, то 3^т-)-2^9. Если от числа т-\-2,
означающего число сотен числа (2 + т) X 100 + 50, отнять 2, то получим число т,
т. е. как раз то число, которое означает порядковый номер задуманного
дня недели.
34. Надо из объявленного числа вычесть 250. Тогда последняя цифра
полученной разности укажет, на какую руку надето кольцо (если 1, то
на левую, а если 2, то на правую). Предпоследняя цифра укажет номер
75
пальца, считая с мизинца, на который кольцо надето, а оставшиеся
цифры в порядке следования слева направо означают число,
определяющее номер того человека, который взял кольцо.
Пример. Пусть шестой человек взял кольцо и надел его на
третий палец, считая с мизинца, на левую руку. В результате
предложенных вами действий получится число
[(2X6+5) X5+3JX 10+1=881.
Вычитая из этого числа 250, получим 631. Здесь 1 означает, что
кольцо надето на левую руку, цифра 3 означает, что надето оно на
третий палец, считая с мизинца, и цифра 6 означает, что надел его
шестой человек.
Обоснование: Обозначим через ft порядковый номер человека,
взявшего кольцо, и пусть он надел его на палец с номером /, считая
с мизинца, на руку с номером т(т= I, если рука левая, и т = 2, если —
правая).
В результате предложенных арифметических действий получится
число [(2ft + 5)X5+/] X10 + m=100ft+10/+m + 250. Если от этого
числа отнять 250, то получим число 100ft +10/+ m, которое можно
записать в виде Mm. Последняя цифра этого числа т совпадает с
номером руки, на которую надето кольцо, предпоследняя цифра / совпадает
с номером пальца, считая с мизинца, на который надето кольцо, а число ft
совпадает с порядковым номером человека, взявшего кольцо.
35. Надо из объявленного результата вычесть 35, если было
загадано два числа, вычесть 350, если было загадано три числа, вычесть
3500, если было загадано 4 числа, и вообще вычесть 35ХІ0"-2, если
было загадано п чисел. У полученного таким образом числа первая
слева цифра является первым из задуманных чисел, вторая за ней —
вторым задуманным числом, следующая за ней — третьим задуманным
числом и т. п. Последняя цифра является последним из задуманных чисел.
Пример. Предположим, что кто-либо задумал числа 8, 6, 4 и 2.
Последовательно выполняя предложенные действия, получим число
([(8Х2 + 5)Х5+10+6]ХЮ+4]ХІ0+2=12 142.
Поскольку было задумано четыре числа, то, вычитая из 12 142
число 3500, получим 8642, откуда видно, что первая слева цифра есть
первое из задуманных чисел, вторая за ней — второе задуманное
число и т. д.
Обоснование. Пусть было задумано п чисел он, а2, ..., а„.
Проводя последовательно предложенные действия, получим число
(...((((2a,+5)X5+10 + a2)XlO+a3)X
X10+a4)X10+ ...)+an_,)Xl0+a„ =
= (...(10a,+35+a2)XlO+o3)X10+...+a„_,)XlO + a„ =
= 10"-'fll + 10"-2a2+.., +100an-2+10on_,+a„ + 35X10"-' =
= a,a2a3...on+35X10"-2.
76
Вычитая из этого числа 35Х10"-2, получим число щаіаз.-.а* Цифры
этого числа в порядке следования слева направо как раз и являются
задуманными числами.
36. Остаток от деления задуманного числа на три умножьте
на 70, остаток от деления задуманного числа на пять умножьте на
21, остаток от деления задуманного числа на 7 умножьте на 15.
Полученные таким образом три числа сложите и сумму разделите на 105.
Частное и будет являться задуманным числом.
Пример. Пусть задумано число 97, тогда остатки от деления,
этого числа соответственно на 3, 5 и 7 равны 1, 2 и 6. Умножая эти числа
соответственно на 70, 21 и 15 и складывая эти произведения, получим
число 202. Остаток от деления этого числа на 105 есть 97. Это и есть
задуманное число.
Обоснование. Пусть А — задуманное число и р, д, г —
остатки от деления этого числа на 3, 5 и 7. Разность (70p-\-2\q-\- \Ъг) —
—А делится на 3, на 5 и на 7. Это легко следует из равенств
( 3(23p + 7q + 5r)-(A~p),
(70р + 21<7 + 15г)-Л= \ 5 (Up + 4q + 3r)-(A-q),
{ 7 (10р + 3? + 2г) - (А-г).
Значит, эта разность делится на произведение 3X5X7, т. е. на число
105. Так как по условию 0<М < 105, то А есть остаток от деления
суммы 70р + 21<7+15г на 105. Вместо чисел 3, 5 и 7 можно взять другие
числа. В табл. 2 указан способ нахождения задуманного числа по
остаткам от деления этого числа либо на 5, 7 и 9, либо на 15, 19 и 28, либо на
19 и 28.
Таблица 2
Операция
Деление
задуманного числа на
Умножение
соответствующих остатков на
Деление
соответствующей суммы на
1-й
способ
3
70
5
21
7
15
105
2-й
способ
5
126
7
225
9
280
315
3-й
способ
15
6916
19
4200
28
4845
7980
4-й
способ
19
476
28
57
532
37. Правило угадывания дается в табл. 3, взятой из старинной
рукописи. Таблица состоит из двух частей. В верхней строке левой части
таблицы указаны номера играющих. Под каждым из номеров записано
77
Таблица 3
Предмет
Монета
Часы
Пуговица
1
0
1
2
2
1
0
2
3
3
1
0
1
3
1
2
2
3
2
1
3
2
3
1
4
1
3
2
5
2
1
3
7
1
2
3
количество орехов, которое играющий с этим номером должен взять со
стола, если у него находится предмет, указанный в крайнем левом
столбце таблицы.
В первой строке правой части таблицы указаны количества
орехов, остающиеся на столе в конце игры. Под каждым из них в
первой строке указан номер игрока, взявшего монету, во второй строке —
номер игрока, взявшего часы, а в последней строке — номер игрока,
взявшего пуговицу.
Например, если осталось 5 орехов, то цифры, стоящие в правой
части таблицы в столбце под номером пять, покажут, что монету взял
второй, часы взял первый, а пуговицу взял третий человек.
Столбик с номеров 6 отсутствует. Это означает, что шесть орехов
не может остаться, как бы монета, часы и пуговица ни распределялись
между участниками игры.
Обоснование. Весь секрет, конечно же, заключается в левой
части таблицы. В ней указано, сколько орехов должен брать каждый
из трех участников игры в зависимости от того, какой предмет он
возьмет. Легііо видеть, что предметы между тремя людьми можно
распределить шестью способами и каждому распределению
соответствует своя, отличная от других, сумма взятых орехов.
Это соображение вытекает из того, что можно шестью способами
пометить три клетки в левой части вышеприведенной таблицы 3X3 так,
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
Рис. 15
чтобы в каждой строке и каждом столбце находилось по одной
отмеченной клетке. Суммы чисел, стоящих в помеченных клетках (рис. 15),
при этом будут различны между собой.
Можно переставить в этой таблице строки — это будет
соответствовать переименованию вещей, или столбцы — это будет соответ-
78
ствовать изменению нумерации людей, но описанное свойство
таблицы сохранится.
Существуют и другие таблицы 3X3, обладающие тем свойством,
что суммы чисел, стоящих в помеченных клетках, все различны.
0
О
3
1
О
2
О
2
О
О
1
3
1
О
3
О
2
О
Рис. 16
О
1
1
2
О
1
О
3
О
Например, приведенные на рис. 16. Каждая из них может быть
использована в описанной игре.
Возникают вопросы:
Можно ли перестановкой строк и столбцов получить какую-нибудь
из этих таблиц из таблицы, взятой из рукописи, или из другой
приведенной на рис. 16 таблицы?
Можно ли в таблице 3X3 расставить числа так, чтобы остающиеся
количества орехов равнялись 1, 2, 3, 4, 5, 6?
Ответим на эти вопросы.
При перестановках строк и столбцов не меняетея количество
нулей, единиц, двоек и троек в таблицах. Перенумеруем таблицы
на рис. 16 цифрами 1, 2, 3. Таблице из рукописи присвоим номер 0.
Подсчитав количества чисел в таблицах, получим табл. 4. Никакие
Таблица 4
Числа
0
1
2
3
Таблицы
0
3
3
2
1
1
4
3
1
1
2
4
2
1
2
3
5
1
2
1
два столбика цифр здесь не совпадают. Значит, ни одна из таблиц не
может быть переведена в другую перестановкой строк и столбцов.
Предположим, что в таблице 3X3 можно расставить числа так,
что остающиеся количества орехов равны 1, 2, 3, 4, 5, 6. Обозначим
количество орехов через а (в разобранном случае а = 7). Тогда
количества взятых орехов будут равны а—\, а —2, а—3, а —4, а—5, а—6.
Так как каждая клеточка таблицы участвует ровно в двух взятиях,
то имеем
(о-1) + (а-2)+ ... +(а_6)=26,
79
где 6— сумма всех чисел в таблице Упростив, получим 6а —26 = 21.
Но это равенство при целых а и 6 невозможно. Ответ на второй вопрос
отрицательный.
V. Любопытные свойства чисел
38. Представим сомножители в виде 5 + а и 5 + 6, где а и b —
количества пальцев, отогнутых на левой и правой руках. Тогда количества
загнутых пальцев будут равны 5 —а и 5 — 6. Объяснение описанного
способа умножения чисел заключено в тождестве
(5 + а) X (5 + 6) = 10Х (а + 6) + (5-а) (5-6).
39. Проще всего убедиться в справедливости этого правила,
поднимая по очереди пальцы от первого до десятого и сравнивая
результат «ручного умножения» с таблицей умножения. "А вот
доказательство. Если поднимаемый палец имеет номер п, то слева от него
лежит (п — 1) палец, а справа (10—п). Тождество
10(п-1) + (10—я)=9п
подтвержает правило умножения на пальцах.
40. Для того чтобы получить шестизначное число, записываемое
двойками, надо 777 умножить на 286. Если же мы число 777 умножим
соответственно на числа 572, 715, 858, 1001, 1144, 1287, то получим числа,
записываемые одними четверками, пятерками, шестерками, семерками,
восьмерками и девятками. Это видно из следующего. Поскольку
777X143=111 111
и .
143X2 = 286, 143X3 = 429 143X9=1287.
то, например,
777X858 = 777X143X6 = 111 111X6 = 666 666,
777X1001=777X143X7=111 111X7 = 777 777.
Можно найти и два четырехзначных числа, произведение которых
записывается восемью единицами.
Требуемое свойство имеют числа 7373 и 1507. Для того чтобы
найти их, надо разложить на множители число 11 111 111. Легко
видеть, что
И 111 111 = 1111X10001 = 11X101X10001.
Числа 11 и 101 далее на множители не раскладываются. Это так
называемые простые числа. Последний множитель 10 001 простым не является,
но найти его разложение на простые множители не легко. Путем
деления этого числа на 3, 5, 7, 11, 13, 17 и другие простые числа можно,
в конце концов, найти делители числа 10 001 и разложить его.
Можно значительно сократить число проб, если заметить, что каждый
80
простой делитель обязательно должен иметь вид 8ft +1. Это связано
с тем, что 10 001 = 10*+1. Остается проверить только делимость на
17, 41, 73, 89, 97. Оказывается, что 10 001 не делится на 17, 41 и делится
на 73. Так получается разложение 10 001=73X137 и
11 111 111 = 11Х101Х73Х137=(101Х73)Х(ИХ137)=7373Х1507.
41. Если взять двузначное число а, удвоить его и приписать
справа нуль, то получится число 20а. Добавив к нему исходное число а,
получим число 21а. Секрет загадочного умножения скрыт в равенстве
21X481 = 10 101. Имеем 21аХ481 =аХ 10 101. Это, как легко видеть,
есть число, в записи которого участвует три раза повторенное
двузначное число а.
42. Указанное правило проверки объясняется довольно просто.
Заметим, что разность между числом и суммой его цифр всегда
делится на 9. Это легко понять хотя бы на примере трехзначных
чисел. Если abc=aX 100+6ХЮ + С — трехзначное число, то сумма его
цифр равна а+Ь + с и разность аЬс— (а + Ь + с) = 99а+96 делится
на 9.
Пусть А, В, С, ... — целые числа, которые нам необходимо
сложить, и Ді, В|, С — суммы их цифр. Обозначим буквой р
остаток от деления на 9 суммы цифр числа (А+В + С+ ...). Из
сказанного выше следует, что разность (А + В + С+ ...)—р делится на 9.
Но эту же разность можно представить в виде (А— А\) + (В — В\) +
+ (С-С,)+ ... +(Лі+В, + Сі+ ...—р). Все числа А-Аи В — Ви
С—С делятся на 9, а потому на 9 будет делиться и число А\ +
+В\ + С\ ... —р. Это означает, что остаток от деления на 9 числа
і4і + Ві + Сі+ ... также равен р. Итак; если сложение выполнено
правильно, то остатки должны совпадать.
Этот способ проверки в случае совпадения остатков, конечно,
не дает полной уверенности в том, что сумма найдена правильно.
Если, например, ошибка состояла в том, что мы случайно поменяли
местами в сумме цифры десятков и единиц,
то остатки совпадут, а результат будет
ошибочным Вместе с тем указанный способ проверки
иногда довольно быстро позволяет установить
наличие ошибки.
43. Пусть Р и Q — перемножаемые числа,
р и а — остатки от их деления на 9. Разность
между числом и суммой его цифр делится на 9,
поэтому, если разделить на 9 суммы цифр Рис. 17
чисел Р и Q, в остатках получатся числа р
и q. Эти числа по условию должны быть записаны у концов вертикальной
черты (рис. 17). Так как разности Р—р и Q — q делятся на 9, то из
равенства
PQ-pq=(P-p) Q+p (Q-q)
81
следует, что числа PQ и pq имеют одинаковые остатки при делении
на девять Значит, у концов горизонтальной черты должны стоять
одинаковые числа. Если же это условие не выполнено, то произведение
PQ вычислено неправильно.
Конечно, совпадение чисел у концов горизонтальной черты не
означает, что результат найден верно.
VI. Старинный способ решения задач
на смешение веществ
44. Ответ задачи найден верно. В самом деле, если взять - часть
3 4
ведра масла стоимостью 10 гривен и j части ведра масла
стоимостью 6 гривен за ведро, то получим одно ведро масла стоимостью
1 3 28
10X7+6Xt=x = ^ гРивен> чт0 и требовалось в задаче.
45. Следуя способу, изложенному при решении задачи 44, имеем
<"х2
Значит, для получения серебра 12-й пробы надо брать 2 части серебра
11-й пробы и 1 часть серебра 14-й пробы. Поэтому для получения
2
одного фунта серебра 12-й пробы надо взять - фунта серебра 11-й
1 6
пробы и - фунта серебра 14-й пробы.
46. Старинный способ решения задач на смешение двух веществ
всегда позволяет получить правильный ответ.
В самом деле, предположим, что смешиваются два вещества —
первое стоимостью а гривен за фунт и второе стоимостью Ъ гривен за
фунт. Желательно же получить вещество стоимостью с гривен за фунт.
Будем считать, что а<Ь. Ясно, что если о Ь или е<а, то задача
неразрешима (смешивая дешевые вещества, дорогое не получишь)
Поэтому можно считать, что а<.с<Ь. Смешаем 1 фунт первого
вещества и q фунтов второго. В результате получится 1 + q фунтов
вещества стоимостью a-\-bq гривен. Один фунт смеси должен стоить
с гривен. Значит, должно выполняться равенство a + bq = c(l -\-q).
Отсюда находим q — (с—а): (Ь—с). Вещества нужно мешать в соотно-
шении 1: —или (Ь — с): (с —а). Но именно это отношение и дает
старинный способ
82
Замечание. Предложенный способ позволяет легче запомнить
последовательность действий при решении задач на смешение и
добиться автоматизма при выполнении самих действий. В условиях,
когда приходится решать много подобных задач (а купцы в старые
времена часто занимались их решением), этот способ экономит время.
Вот одна из современных задач на смешение:
Имеется два раствора шестидесятивосьмипроцентной и
семидесятивосьмипроцентной серной кислоты. Сколько надо взять каждого раствора
серной кислоты, чтобы получить 100 граммов семидесятипроцентного
раствора серной кислоты.
Решение. По изложенному выше способу имеем
70 \
Таким образом, надо взять 80 г шестидесятивосьмипроцентного и 20 г
семидесятивосьмипроцентного растворов серной кислоты.
47. Полученные числа являются одним из ответов к задаче:
в самом деле, если возьмем -г= фунта чая ценой по 5 гривен за фунт и
по — фунта чая ценой 8 и 12 гривен за фунт, то получим 1 фунт чая
8 1 1
ценой -^X5+-jqX8 + -^X12=6 гривен.
48. Следуя способу, изложенному при решении задачи 46, мы
должны написать схему:
-3+1-4
10
4 3
Отсюда следует, что надо взять j= фунта серебра шестой пробы, -rjr
фунта серебра двенадцатой пробы и у- фунта серебра десятой
пробы.
49. Ясно, что задачи на смешение трех веществ могут иметь не
единственное решение. В задаче 47 чай стоимостью 6 гривен за фунт
можно получить, смешивая цейлонский и китайский чай в отношении
6:1(1 смесь) или цейлонский и индийский чай в отношении 2:1 (II смесь).
Способ решения, приведенный в условии задачи 47, также приводит к
цели. Ведь соединив две смеси стоимостью в 6 гривен за фунт (в
первой — 6 частей цейлонского и I часть китайского чая, во второй —
83
2 части цейлонского и 1 часть индийского чая), мы также получим
смесь стоимостью в 6 гривен за фунт (в ней будет 8 частей цейлонского,
1 часть китайского и 1 часть индийского чая). Соединяя смеси I и II в
любой пропорции, мы будем получать различные смеси ценой по 6 гривен
за фунт. Причем любая смесь, отвечающая условию задачи, может быть
так получена. Действительно, предположим, что смесь, составленная из
а фунтов цейлонского, Ь фунтов индийского и с фунтов китайского чая,
имеет цену 6 гривен за фунт. Тогда
5а + 86+12с
a+b+c ~
или а=6с + 26. Значит, эта смесь может быть получена соединением
с фунтов смеси I и Ь фунтов смеси II, другими словами, смешением
их в отношении с:Ь.
Таким способом можно решать задачи на смешение любого числа
веществ.
VII. О правилах «фальшивых»
или «гадательных»
50. Ответ найден верно. В самом деле,
^Х90=30, 90+30=120, 120X^=20, 120-20=100.
о о
51. Ответ найден верно. Действительно,
36 + 36+ix36+|x36+ 1 = 100.
84
Приводим решение из «Арифметики» Л. Ф. Магницкого:
П/fsof аолоп'тЧ : gTOfo'r mA0*?tnt t
z 4
1_ ^^ KuWh,/Z % t_
6 7—:—3 3 3 a^.X^ ,.■''' g 9—*—11
99 *4 nf*W;
I О у 6 z б 4
г б 4 *
7 9 * Г у
Ъ % І. iJ) 3 бтслііп»(с-ш<вто«*
і
Эта задача встречается в старинных рукописях в различных
формулировках: как задача «о стаде гусей», «о матросах на корабле»,
«о продаже гусей» и т. д.
52. Так как
4б|—34^=12, 34І—2б|=9. 46 і+34 ^+25^=106,
то ответ найден верно.
53. Предположим, что у первого человека 12 рублей. Тогда второй
2
должен дать ему 24—12=12 рублей, что составляет по условию ^ от
3 d
денег второго человека. Значит, второй имеет 12Хк=18 рублей.
3
После того как первый даст второму - своих денег, у второго станет
3
18+^X12 = 27 рублей, что на 3 рубля больше стоимости коровы.
Предположим, что у первого человека 20 рублей. Тогда у второго
3 3
5 (24 — 20) =6 рублей. После того как первый даст ему - своих
3
денег, у второго человека станет 6+^X20 = 21 рубль, что на 3 рубля
85
меньше стоимости коровы. Применяя «фальшивое» правило, имеем
12
20
12X3 = 36,
20X3 = 60,
60 + 36 = 96, 3 + 3 = 6
Значит, у первого человека было 96:6 = 16 рублей, а у второго ^Х
Х(24 —16) = 12 рублей.
54. Предположим, что у первого из беседующих 8 рублей. Тогда
половина суммы денег второго и третьего равна 17 — 8 = 9 рублей, т. е. у
второго и третьего человека вместе 18 рублей, а всего денег у них 8+18 =
= 26 рублей. После того как первый и третий собеседники дадут вто-
1 1 оа 2
рому q имеющихся у них денег, у второго станет , от 26 да еще ^ своих
о о о
т
3 / 26\ 25
денег. Таким образом, у второго человека -X 17—— )=— рублей
25 11
Но тогда у третьего 26 — 8—9~ = ~5~ РУ°лей. Если теперь первый и второй
1
дадут третьему человеку по — имеющихся у них денег, то у того станет
-y+jX(8+-^-)=-^- рублей, что на -^- рублей меньше, чем должно
быть.
Предположим теперь, что у первого из беседующих 6 рублей.
Повторяя выкладки, найдем, что при этом у второго должно быть
23 21
-х- рублей, а у третьего — рублей. После того как первый и второй
дадут деньги третьему человеку, у него станет
21 , ІѴЛ,23\ 119 , „
что на — рублей меньше, чем должно быть.
о
Пользуясь теперь «фальшивым» правилом, находим:
51 51 17 17 . 51 0 17 85
Т Т-Т=Т 6Х8~ 8Х1Г=Т'
^J7 «5.17
6 8 ТТ-5-
Значит, у первого из беседующих было 5 рублей. Повторяя все
вычисления еще раз, теперь уже с числом 5 вместо 8 и 6, находим, что
у второго человека было 11 рублей, а у третьего 13 рублей.
55. Допустим, что у первого человека 50 рублей. Тогда четвертая
часть денег второго равна 4 рублям и, значит, у второго 16 рублей.
Но тогда третья часть денег третьего человека равна 54— 16 = 38 рублей
и, значит, у третьего человека 38X3=114 рублей. Если он получит
половину денег первого человека, то у него станет П4 + 25= 139 рублей,
что на 139 — 54 = 85 рублей больше стоимости покупки.
Положим теперь, что у первого человека 46 рублей. Тогда у второго
человека 4Х (54—46) =32 рубля, у третьего Зх (54 — 32) =66 рублей.
После того как третий получит половину денег первого человека, у него
станет 66 + 23 = 89 рублей, что на 89 — 54 = 35 рублей больше стоимости
покупки.
С помощью «фальшивого» правила находим:
50^ ^85 85-35 = 50, 85X46-50X35 = 2160,
87
46^ ^35 2160:50 = 43І
Таким образом, у первого человека было 43 рубля и 20 копеек. Тогда у
1 2
второго также будет 43= рублей, а у третьего 32= рублей.
56. Положим, что за каждый белый рулон было уплачено по 5
рублей. Тогда за каждый черный уплачено по 9 рублей, за красный по
6 рублей, за зеленый по 4 рубля и за лазоревый по 5 рублей. Вся покупка
стоила бы тогда
20X5+13X9 + 5X6+19X4 + 7X5 = 358
рублей, что на 486—358 = 128 рублей меньше, чем было заплачено в
действительности.
Положим, что за каждый белый рулон было уплачено по 6 рублей.
Тогда за каждый черный уплачено по 10 рублей, за красный по 7 рублей,
за зеленый — по 5 рублей и за лазоревый — по 6 рублей. А за всю покупку
20X6+13X10 + 5X7+19X5 + 7X6=422
рубля, что на 486 — 422 = 64 рубля меньше данной суммы. С помощью
«фальшивого» правила находим ответ:
5\^ ^128 128-64=64, 6X128-5X64 = 448,
б-^ ^^64 448:64 = 7.
Значит, за каждый рулон белого сукна было уплачено по 7 рублей,
черного — по 11 рублей, красного — по 8 рублей, зеленого — по 6 рублей,
лазоревого — по 7 рублей.
Заметим, что задачи, решаемые с помощью «фальшивого» правила,
могут быть решены и другими способами. Приведем, например,
Второе решение задачи 56. Легко видеть, что самое
дешевое сукно — зеленое: лазоревое стоит дороже его на 1 рубль, красное —
на 2 рубля, черное — на 5 рублей, белое — на 1 рубль. Если бы за каждый
вид сукна было уплачено столько же, сколько за зеленое, то при этом
было бы уплачено меньше на
20X1 + 13X5+5X2 + 7X1 = 102
рубля. Вся покупка стоила бы 486—102=384 рубля. А так как куплено
64 рулона сукна, то рулон зеленого сукна стоит 384:64=6 рублей.
Зная это, легко находим стоимость остальных рулонов.
57. Если внимательно просмотреть решения задач на применение
«фальшивого» правила, то можно заметить, что в их решениях всегда
отыскивается какое-то одно неизвестное число. Если в задаче есть и
другие неизвестные, то они с помощью условий задачи могут быть
выражены через это единственное неизвестное число. Это неизвестное число,
обозначим его х, всегда удовлетворяет уравнению ах+Ь = с, где а,
Ь и с — некоторые числа. Число с известно, числа же а, Ь, вообще
говоря, можно вычислить по условию задачи. Они не даны явно в
88
условии, но представлены в нем с помощью некоторой
последовательности операций (см., например, задачу 51). Будем считать, что они нам
неизвестны.
Взяв некоторое число х\ и проделав с ним положенные операции,
мы находим некоторое число с\. Повторив те же операции с числом хг,
получим новое число — сг. Как же, зная х\, дг2, с\, сг, с, найти решение
задачи, т. е. неизвестное число х") Из равенств
ах\-\-Ь — с\, ах2 + Ь = с2
С\ —С2 ул
выводим а— . В то же время известно, что ах+Ь = с. Это дает
Х\ —хг
нам
а (х—Хі) =с — Сг,
С — Сг (С — С2)(Х\—Хі) Хі(С\ — с)—Х\{Сі — с)
Х = Х2-\ = Х2-\ =
а с\—сг С\—С2
Если оба числа с\, сг больше, чем с, то имеем
Х2(С\—С)—Х\ (С2 — С)
(сі — с) — (с2 — с)
если сі<с, С2<с, то
Х2(С — С\)—Х\ (С — Сі)
(с-с,)-(с — с2)
если же Сі> с и С2<с, то
хг(с\ — с)+хі {с—сг)
(с\—с) + (с—сг)
В каждом случае получаем именно ту последовательность
вычислений, которая предписывается «фальшивым» правилом.
Часть вторая
I. Забавные истории
58. Из условия задачи следует, что удвоенное жалованье слуги
на 10 рублей превышает его же жалованье. Значит, годовое жалованье
слуги составляет 10 рублей, а постоялец, заявивший, что его обокрали,
вообще не имел денег.
59. Три алтына без полушки составляют 35 полушек и такова
стоимость фрака вместе с жилетом. Фрак по условию в 2-т раза дороже
1 г
жилета, поэтому жилет в З^ раза дешевле, чем фрак и жилет вместе.
89
Так что жилет стоит 35:3^=10 полушек или 2^ копейки, а фрак стоит
10X2^ = 25 полушек или б^ копейки.
60. Все имущество мадам было оценено в
Jx(.+J)
27 tI . ,1
что составляет — копеек. «Чепец фигаро» по условию в З^ раза дешевле
«фуро», и, следовательно, в 4^=^ раза дешевле всего имущества.
27 9 3
Поэтому чепец стоит -j":9==o копеики. а стоимость «фуро» равна
Зѵ,1 21 . 4 2 1
2Х32=Т копейки.
61. Так как после выхода из четвертого трактира у человека не
осталось денег, то после ухода из третьего трактира он имел 50 копеек.
В третьем трактире он истратил 1 рубль, а перед этим одолжил столько
денег, сколько имел, поэтому после ухода из второго трактира он имел
половину от 1 рубля 50 копеек, т. е. 75 копеек. Аналогично, после выхода
из первого трактира у человека имелось 175:2=87,5 копеек. Значит,
3
он пришел в первый трактир, имея (87,5+100):2=93^ копейки, т. е.
93 копейки и 3 полушки.
II. Дележ и размен денег
62. Возьмем 3 рубля у того из крестьян, который получил большую
часть денег. Тогда сумма в 4 рубля распределится между крестьянами
поровну. Значит, меньшая часть разделенных денег составляет два
рубля, а тогда большая часть равна 5 рублям.
63. Из условия задачи следует, что меньшая часть денег в
50 раз меньше всей суммы, т. е. 25 рублей. Поэтому она составляет
;г рубля, или полтинник. Но тогда большая часть равна 24^ рубля.
64. Сумма в 157,5 рублей равна 315 полтинникам. Если бы
покупатель вместо каждой рублевой монеты давал по 2 полтинника, то по
условию задачи ему пришлось бы дать продавцу втрое больше
полтинников, чем он дал их в действительности. Значит, количество
полтинников, отданных покупателем, равняется 315:3=105. Столько же
было отдано и рублевых монет.
65. Ясно, что монет по 3 копейки должно быть нечетное число.
Значит, для размена' 25 копеек можно взять I монету в 3 копейки
и 11 монет по 2 копейки, или 3 монеты по 3 копейки и 8 монет
по 2 копейки, или 5 монет по 3 копейки и 5 монет по 2 копейки, или
7 монет по 3 копейки и 2 монеты по 2 копейки. Взять 9 или больше
монет по 3 копейки нельзя, так как их сумма будет больше 25 копеек.
Следовательно, размен можно осуществить 4 способами.
90
66. Если бы все 15 монет были по 3 копейки, то сумма составила
бы 45 копеек, что на 14 копеек меньше, чем сумма, указанная в условии
задачи. Так как замена каждой трехкопеечной монеты пятикопеечной
приводит к увеличению суммы на 2 копейки, то заменить необходимо
14:2=7 монет. Итак, необходимо взять 7 монет по 5 копеек и 8 монет
по 3 копейки.
67. Вторая часть больше первой на 1 полтинник, третья больше
первой на 2 полтинника, четвертая — на 3 полтинника и т. д., восьмая
часть больше первой на 7 полтинников. Сложив числа 1, 2, 3 7,
получим 28. Это число полтинников равняется 14 рублям. Значит, если
бы все части равнялись первой, то сумма их составила бы 46—14 =
= 32 рубля. Поэтому первая часть равна 32:8 = 4 рубля, вторая часть
составляет 4,5 рубля, третья — 5 рублей и т. д., восьмая часть составляет
7,5 рублей.
68. Двадцать две монеты по 5 копеек составляют сумму в ПО
копеек, что на 11 копеек превышает сумму, данную в условии задачи.
При замене каждой монеты в 5 копеек на монету в 2 копейки сумма
уменьшается на три копейки, поэтому монет по две копейки можно взять
не более чем три. Число двухкопеечных монет четным быть не может,
иначе сумма четного числа трехкопеечных и пятикопеечных монет была
бы нечетной, а это невозможно. Значит, можно взять или одну, или три
двухкопеечных монеты. Количества трехкопеечных монет теперь легко
находятся, если воспользоваться тем, что при замене каждой
пятикопеечной монеты на трехкопеечную сумма уменьшается на две копейки.
Получаем 2 способа:
1-й способ 2-й способ
2 копейки
1 3
3 копейки ' ,
4 1
5 копеек 17 18
III. Сколько кому лет?
69. По условию задачи 10 лет составляют 5 половинок возраста
сына. Значит, половина возраста сына равна 2 годам, а возраст сына
равен 4 годам.
70. Удвоенный возраст старшего брата на 4 года больше суммы лет
всех троих братьев и равен поэтому 96 + 4 = 100 годам. Значит, возраст
старшего брата равен 50 годам. Удвоенный возраст среднего брата на
2 года больше суммы его лет и лет младшего брата и равен поэтому
(96—50) +2=48 годам. Значит, возраст среднего брата равен 24 годам.
Теперь находим возраст младшего брата: 22 года.
71. Предположим, что у этого человека есть внук, который в 12 раз
младше его. Тогда 12 возрастов внука, да еще 6 возрастов внука,
да еще 4 возраста внука, да 3 возраста внука составляют, по условию
задачи, 100 лет. Другими словами, возраст внука в 25 раз меньше, чем
91
100 лет, и равен поэтому 4 годам. Но тогда возраст человека, которому
был задан вопрос, равен 48 годам.
72. Так как каждый из сыновей на 4 пода старше
последующего, то старший брат на 20 лет старше младшего. Значит, удвоенный
возраст младшего сына равен 20 годам. Поэтому младшему сыну 10 лет,
а возраста остальных его братьев равны 14, 18, 22, 26 и 30 годам.
73. Поскольку в настоящий момент возраст дочери составляет
- от возраста отца, а 4 года тому назад он составлял ■% настоящего
2 11
возраста отца, то эти 4 года равны F—-=^-=- возраста отца. Поэтому
. 5 3 15
возраст отца равен 4:у==60 лет и, следовательно, возраст дочери
2
60Хе=24 г°Да-
о
74. Обозначим возраст старшего из беседующих буквой х, а возраст
младшего — буквой у. По условию задачи, когда старшему было у лет
92
(а было это х—у лет тому назад) и, следовательно, младшему у—
— (х—у) =2у—х лет, возраст младшего был вдвое меньше, чем
нынешний возраст старшего. Поэтому х—2(2у—х) или Зх=4у. С другой
стороны, когда младшему будет х лет, т. е. через (х—у) лет, сумма
возрастов составит 63 года, следовательно,
х+{х-у)+х=63
или Здс=г/ + 63. Из полученных равенств следует, что 4і/=</ + 63 и
у=2\. Но тогда х=28. Старшему из беседующих 28 лет, а младшему
21 год.
75. Сложив числа 9, 8, 8, 9, 6, 4 и 4, получим удвоенную
сумму возрастов всех детей:
9+8 + 8+9+6+4 + 4 = 48.
Значит, сумма возрастов всех детей равна 24 годам. Поскольку
сумма возрастов первого и шестого, второго и третьего, четвертого
и седьмого сыновей равна 8+9+4=21 году, а сумма возрастов всех
детей равна 24 годам, т о пятому сыну 3 года, а тогда второму сыну
5 лет. Поскольку .сумма возрастов второго и третьего сыновей равна
9 годам, то возраст третьего сына равен 4 годам. Поскольку сумма
возрастов третьего и шестого сыновей равна 6 годам, то возраст шестого
сына равен 2 годам. Далее находим, что возраст первого сына равен
6 годам, четвертого 3 годам и седьмого — одному году.
76. Пусть одному сыну п лет, а другому m лет. Тогда из условия
задачи имеем
тп + т + п = 14,
откуда
Поскольку т — натуральное число, а 15=5X3X1, то: а) либо «+1=5,
б) либо п + 1=3, в) либо п+1 = 1.
В случае а) я=4, тогда т=2, в случае б) п—2, тогда т=4,
в случае в) п=0, чего не может быть, так как п — натуральное число.
Следовательно, одному сыну 2 года, а другому 4 года.
IV. Часы
77. Количество ударов равняется 1+2+3+. ..+ 12 и, как легко
сосчитать, равно 78. Эту сумму можно вычислить очень просто, если
заметить, что суммы членов, равноотстоящих от концов (1 + 12, 2+11,
3+10,...), все равны между собой и равны 13. Таких пар
равноотстоящих от концов чисел имеется 6. Значит,
1+2+3+... + 12=6X13 = 78.
93
78. По условию время, оставшееся до полудня, в І^ раза меньше
1 г
времени, прошедшего от полуночи и, значит, в 2^ раза меньше
промежутка времени между полуночью и полуднем, т. е. 12 часов. Таким
1 24 4
образом, до полудня осталось 12:2-=—=4= часа, и время в момент,
когда был задан вопрос, равнялось 12 —4-=7= часа, т. е 7 часов
А „1
і задан вопрос, равнялось ѵг —
12 минут.
79. За один час первая стрелка совершит у^ полного оборота,
а вторая стрелка — у^ часть полного оборота, и отставание второй
стрелки составит т,-7с=7о часть оборота. За каждый час вторая
стрелка будет отставать на jz часть оборота, и через 48 часов
отставание составит 1 оборот, т. е. стрелки совместятся.
80. За один час минутная стрелка совершает 1 оборот, а часовая
і ,
■рт оборота, и, значит, отставание часовой стрелки от минутной равня-
1 И
ется 1 —Т5=Т9 оборота. Отставание станет равным 1 обороту в момент
1:-г5=тт часа после полуночи. В этот момент часовая и минутная
12
стрелки на циферблате часов совместятся. Еще через уу часа они
совместятся вновь и так далее. Моменты времени, когда будут
происходить совмещения стрелок, можно определить по формуле.
/ 12
'=ттл-
где л — номер совмещения, л = 1, 2, 3... Так как в сутках 24 часа, то до
следующей полуночи произойдут совмещения, номера которых удовлет-
12
воряют неравенству уу п<24 или п<22. Итак, до следующей
полуночи произойдет 21 совмещение часовой и минутной стрелок и происхо-
12 12 12
дить они будут в моменты времени —, 2Хтт 21 Хгт часов.
8!. Воспользуемся решением предыдущей задачи. В момент времени,
о котором идет речь в условии, часовая и минутная стрелки совмещены,
12
значит, этот момент равен уу п, где п — целое число, равное номеру
совмещения стрелок. Если вопрос был задан до полудня, то, ввиду
условия, имеем неравенство
12
9<^п<10
«4
99 НО _ 99 .1 110 А п
или-—</;<-—-; Так как тк=8т и -тн-^9?. т0 " = 9, и время в
12 12 12 4 12 о
12чхп 108 .9
момент, когда был задан вопрос, равняется — Х9= . = 9-гу часа,
т. е. примерно 9 часов и 49 минут.
Если же вопрос был задан после полудня, то
21<|?п<22
231 242 „ 231 ,„І 242 „„I
или -^-<л<-ц-. Поскольку -fg-^19^ и "Т2~=206' то " = 20>
и время в момент, о котором идет речь в условии задачи, равно
12 240 9
—Х20=—ту-=21-рг часа, т. е примерно 21 час и 49 минут.
V. Денежные расчеты
82. Стоимость двух коней с седлами по условию в 4 раза больше
стоимости второго коня с дещевым седлом и в 3 раза больше стоимости
второго коня с хорошим седлом. Значит, разность в стоимости хорошего и
дешевого седла, равная 120 — 25 = 95 рублей, составляет ,—t=Tq
чаеть стоимости двух коней с седлами. Кони вместе с седлами стоят
поэтому 12X95= 1140 рублей, а второй конь с дешевым седлом - X 1140=
= 285 рублей. Итак, стоимость второго коня равна 285—25 =
= 260 рублей, а стоимость первого коня равна 1140 — 260—120 — 25 =
= 1140 — 405=735 рублей.
83. Очевидно, что стоимость всех трех оседланных коней равна
удвоенной стоимости всех трех неоседланных коней. Поэтому стоимость
всех трех неоседланных коней равна утроенной стоимости седла, т. е.
равна 3X55=165 рублей. Так как оседланный первый конь стоит
столько же, сколько стоят вместе второй и третий неоседланные кони,
то удвоенная стоимость первого коня равна 165 рублям без стоимости
седла Значит, первый конь стоит (165 — 55) :2 = 55 рублей. Точно так же
получаем, что второй и третий кони стоят по 55 рублей.
84. Обозначим буквой т количество кур, которое выменял
крестьянин. Каждая курица снесла, как сказано в условии, -^-яиц, и общее число
о
., т т2
яиц у крестьянина составило шХ-г=т штук. Каждые 9 яиц крестья-
т . "і,1
нин продал по —копенки, т. е. одно яйцо за -^-Xq, и выручил поэтому
о ЗУ
-о-Х-5"Хй=о7 копеек, что по условию равно 72 копейкам. Из
j о У о!
95
равенства — = 72 находим m3 = 72X81 и m=9X2=18. Итак, крестья-
81 2
нин выменял 18 кур, а зайцев у него было ^Х 18=12 штук.
85. Пусть вторая крестьянка имела в п раз больше яиц, чем первая.
Тогда выручка второй крестьянки составила 20п копеек, а выручка
первой крестьянки копеек. Поскольку денег крестьянки выручили
оп 45 г 45 9 3 ,.
поровну, то 20л =— или /г=—=-т и «=g. Итак, первая крестьянка
имела в 1- раза меньше яиц, чем вторая, и потому в 2- раза меньше
яиц, чем они обе вместе имели. Значит, у первой крестьянки было
100:2^=40 яиц, а у второй 100—40=60 яиц.
86. По условию количество лошадей, купленных третьим казаком,
без полулошади равно числу лошадей, оставшихся у табунщика, с
полулошадью, т. е. 5^ лошадей. Значит, третий казак купил 6 лошадей,
и после продажи лошадей второму казаку у табунщика осталось 6 +
+ 5=11 лошадей.
Количество лошадей, купленных вторым казаком, без полулошади
равно числу лошадей, оставшихся у табунщика, с полулошадью, т. е.
11- лошадей. Значит, второй казак купил 12 лошадей, и после продажи
лошадей первому казаку у табунщика осталось 23 лошади.
Точно так же находим, что первый казак купил 24 лошади.
87. Третий купец получил, как легко видеть, 2 рубля, и, значит, эта
сумма была у крестьянина, когда он уходил от второго купца. Сумма,
заплаченная второму купцу, без двух рублей составляет поэтому 4 рубля,
и крестьянин, уходя от первого купца, имел 8 рублей. Деньги,
заплаченные первому купцу, без одного рубля составляют 9 рублей,
и, значит, первоначально крестьянин имел вдвое больше, т. е.
18 рублей.
88. Всего состоялось 4 передачи денег. После каждой передачи
сумма денег, имеющихся у Андрея и Федора, остается неизменной и
равной 160+160 = 320 рублей.
После четвертой передачи деньги у Андрея удвоились. Значит,
после третьей передачи у Андрея было 80 рублей, а у Федора 320 —
—80=240 рублей.
После третьей передачи удвоились деньги у Федора. Поэтому
после второй передачи у него было 120 рублей, а у Андрея —320—
— 120 = 200 рублей.
После второй передачи удвоились деньги у Андрея. Поэтому перед
ней, т. е. после первой передачи, у него было 100 рублей, а значит,
у Федора 320—100 = 220 рублей.
96
После первой передачи деньги удвоились у Федора.
Следовательно, первоначально у него было 110 рублей, а у Андрея — 320—110 =
=210 рублей.
Чтобы удобнее было проследить, как передавались деньги, а также
для проверки ответа составим таблицу, указывающую, как изменялись
суммы денег у Андрея и Федора при каждой передаче (см. табл. 5).
Таблица 5
Передачи
Первоначально
После 1-й передачи
После 2-й передачи
После 3-й передачи
После 4-й передачи
А
210
100
200
80
160
Ф
110
220
120
240
160
89. Обозначим буквой о сумму денег, полученную каждым из
сыновей. Так как старший сын получил 100 рублей и ^ часть того, что
осталось после вычитания 100 рублей из суммы наследства, то сумма
наследства равна 100 + 6 (а— 100) = 6а —500 рублей. Второй брат
получил 200 рублей и - часть от того, что осталось после вычитания из всей
суммы доли старшего брата и 200 рублей, т. е. доля второго брата равна
200+іх (6а-500-а-200) = 5а + 500.
о 6
рублей. Так как братья получили денег поровну, то
5а+ 500
откуда находим, что а=500 рублей, а сумма наследства равна 6X500 —
— 500=2500 рублей. Чтобы определить число братьев, необходимо
разделить сумму наследства на долю каждого из братьев. Поэтому число
братьев равно 2500:500=5.
Проверим, что при сумме наследства в 2500 рублей и в соответствии
с завещанием все пять братьев действительно получили денег поровну:
1-й брат: 100+^Х (2500- 100) =500 рублей;
2-й брат: 200+gX (2000—200) =500 рублей.
3-й брат: 300+|х (1500—300) =500 рублей;
4-й брат: 400+gX (ЮОО—400) =500 рублей;
5-й брат: остаток в 500 рублей.
97
VI. Задачи на переливание
90. Так как после наполнения бочки В в бочке А остается
2 3
■= ее содержимого, то вместимость бочки В равна - вместимости А. Так
5 о
5
как после наполнения бочки С в бочке А остается ^ ее содержимого, то
4
вместимость бочки С равна - вместимости бочки А. Значит, вмести-
3 4 47 2
мость бочек В и С равна — c"I"q==te==' "т~7с вместимости бочки А Из
условия задачи тогда следует, что j^ вместимости бочки А составляют
4 ведра, откуда получаем, что вместимость бочки А равна 90 ведер, а тогда
3
вместимость бочки В равна 90Xf—54 ведра, а вместимость бочки С рав-
о
4
на 90X^=40 ведер.
1
91. Так как после наполнения бочки С в бочке А останется = ее со-
5
держимого, то вместимость бочки А равна - вместимости бочки С.
4 1
Так как после наполнения бочки D в бочке В останется - ее содержимого,
9 °
то вместимость бочки В равна s вместимости бочки D. Так как вмести-
о
мость бочек С и D одинакова, то вместимость бочек А к В равна
5 9 19 3
■j + z = -5" =2+jr вместимости бочки С.
4 8 8 8 о
Из условия задачи следует, что -^ вместимости бочки С составляют
о
3
9 ведер, откуда получаем, что вместимость бочки С равна 9:^=24 ведрам.
5
Но тогда вместимость бочки А равна jX24 = 30 ведрам, а вместимость
9
бочки В равна ^Х24 = 27 ведрам.
о
92. После первого переливания в ведре останется 4 литра воды.
Отливая из ведра 1 литр смеси, мы каждый раз отливаем -=- часть со-
5
держащейся в смеси воды. Поэтому после второго переливания в ведре
1 16
останется 4—^-Х4=-р- литра воды. После третьего переливания в
16 I 16 64
ведре останется ~—^Х-^-=^ литров воды
93. После первого переливания в бочке останется 99 литров сока.
Отливая из бочки 1 литр смеси, мы каждый раз отливаем часть
содержащегося в смеси сока. Поэтому после второго переливания в
бочке останется 99—^-Х99=99х( 1—rhr) литров сока. После
третьего переливания в ведре останется
"Ч1 -таг) - wx99x(' —1J0) =99х(' ~ -ш)
литров сока. Продолжая так действовать, получим, что после п
переливаний в бочке останется 99х(і — —г)"-1 литров сока. Если бы после'
этого в бочке осталось 50 литров сока, то выполнялось бы равенство
"хО-гагГ'-6*
это равенство можно переписать так:
99" = 50ХЮ0"-'.
Поскольку для любого натурального п левая часть равенства нечетна,
а правая часть четна, получаем противоречие, доказывающее, что
требуемое переливание невозможно.
Заметим, что 99х( 1 —-^)70 <50<99х(і--щ-)69. Поэтому
после 69 переливаний в бочке будет несколько больше 50 литров сока,
а после 70 переливания — несколько меньше 50 литров. Эти неравенства
можно проверить, например, с помощью таблицы логарифмов.
VII. Латинские квадраты
94. Предположим, что цифры в клетках квадрата уже расставлены
так, как это требуется в условии задачи. Если поменять местами любые
2 столбца или любые 2 строки, то получится новое расположение
цифр, также удовлетворяющее условию задачи. Переставим теперь
столбцы так, чтобы цифры в первой строке расположились в порядке
возрастания (рис. 18). Перестановкой второй и третьей строки можно
добиться, чтобы в первом столбце цифры стояли так, как указано на
рис. 19. На пересечении второй строки и третьего столбца, а также
на пересечении третьей строки и второго столбца не могут стоять ни 2,
ни 3 Значит, на пересечении этих строк и столбцов стоят цифры 1.
После этого однозначно заполняются остальные клетки таблицы
1
2
3
1
2
3
2
3
1
2
3
2
3
1
3
1
2
Рис. 18 Рис. 19 Рис. 20
(рис. 20). Итак, каждое расположение цифр, отвечающее условию
задачи, получается из расположения, изображенного на рис. 20
перестановкой строк и столбцов. Из расположения на рис. 20
перестановкой столбцов получаются 6 расположений цифр. А при каждой
99
расстановке столбцов перестановкой второй и третьей строк — еще
2 новых расположения. Итак, существует всего 6-2=12 расположений
цифр, отвечающих условию задачи.
95. Предположим, что мы расставили буквы так, как это требуется
в задаче. Поменяем местами какие-либо два столбца или две строки.
При этом получится новое расположение букв, также удовлетворяющее
условию задачи. Очевидно, столбцы и строки
можно переставить так, что в верхней строке и
крайнем левом столбце буквы разместятся в таком
порядке, как показано на рис. 21. Легко видеть,
что во второй строке буквы а, с, d можно
разместить только тремя способами: (с, d. a), (d, а, с)
и (a, d, с). Первым двум соответствуют един-
Рис. 21 ственные расположения букв в третьей и четвертой
строках, третьему соответствуют два расположения. Таким образом,
получаем четыре размещения букв, представленных на рис. 22.
Четыре столбца можно переставить между собой 4-3-2-1=24
способами, а при фиксированном расположении столбцов вторую, третью и
четвертую строки можно переставлять 3-2-1 =6 способами. Поэтому из
каждого размещения букв, показанного на рис. 22, перестановками
abed
Ь
с
d
abed abed abed abed
b с d a b d а с bade bade
e d a b e a d b e d a b с d b a
d a b e d с b a d с b a d с a b
Рис. 22
столбцов и строк можно получить еще 24-6=144 латинских квадрата.
Общее же число латинских квадратов из 4 элементов равно 4 • 144=576.
96. Опишем некоторые способы построения латинских квадратов
произвольного размера. Элементы таких квадратов размера пХп будем
обозначать числами 1,..., п.
1. Пусть р — простое число и п=р—\. Перенумеруем строки
квадрата сверху вниз и столбцы слева направо числами от 1 до п. На
пересечении строки с номером а и столбца с номером Ь поместим остаток
от деления на р числа а-Ь. Так как номера строк и столбцов есть
положительные целые числа, не делящиеся на р, то в каждой клетке
квадрата будет стоять одно из чисел 1,2, .. , л. Докажем, что в каждой
строке стоят различные числа. Если в строке с номером а стоят два
равных числа, скажем, в столбцах с номерами Ь и с, то это означает,
что числа ab и ас имеют одинаковые остатки при делении на р и, значит,
их разность а (Ь—с) делится на р. Но оба сомножителя abb—с отличны
от нуля и по абсолютной величине меньше р. Следовательно, делимость
100
не может иметь места, числа ab и ас имеют разные остатки при делении
на р. Точно так же доказывается, что и в любом столбце квадрата
стоят различные числа. Поскольку строки и столбцы содержат по п
клеток, а всевозможных ненулевых остатков от деления на р тоже
имеется га, то каждая строка и каждый столбец будут представлять собой
некоторую перестановку чисел 1, 2 п.
Если построить таким способом латинский квадрат при р=5, а затем
заменить числа 1, 2, 3, 4 буквами а, Ь, с, d соответственно, то получится
второй из квадратов на рис. 22.
2. Пусть п — произвольное целое положительное число и ft —
целое число, не имеющее общих с га делителей, больших единицы.
Поместим на пересечении строки с номером а и столбца с номером Ь
остаток от деления на п числа ak + b. Если остаток равен 0, то в
соответствующую клетку поместим число п. Докажем, что таким
способом будет построен латинский квадрат.
Если на пересечении столбцов с номерами Ь, с и строки с номером
а стоят равные числа, то разность ak + b— (ak + c) =b —с должна
делиться на п. Но это невозможно, так как Ь, с — различные целые числа,
лежащие в пределах от 1 до га.
Предположим, что в некотором столбце, скажем, с номером Ь,
будут стоять одинаковые числа. Если соответствующие строки имеют
номера и, ѵ, то разность uk + b — (vk + b) = (и — v) ft должна делиться
на га. Ввиду того, что числа ft и га не имеют общих делителей, на га должно
делиться число и — ѵ. Но это невозможно.
Итак, в каждой строке и в каждом столбце будут стоять разные
числа. Это означает, как и ранее, что столбцы и строки квадрата будут
некоторыми перестановками чисел 1, 2,..., п.
ч Взяв, например, fc=l, получим латинский квадрат, каждая строка
которого получается из предыдущей циклической перестановкой, т. е.
сдвигом всех цифр влево на одно место и перестановкой первой цифры
на последнее место.
Количество различных латинских квадратов очень быстро растет
е увеличением п. Условимся обозначать через ft! произведение всех
целых чисел от 1 до ft:
ft! = l-2-3 ... ft.
Известно, что существует не менее л! ■ (я — 1)! ... 2! • 1! латинских
квадратов размером гаХга. Точное значение этого количества известно
только при маленьких л.
97. Возьмем латинский квадрат размером 4X4, у которого на
диагонали, идущей из левого верхнего угла в правый нижний, стоят
различные элементы. Такой квадрат можно получить из третьего
латинского квадрата, изображенного на рис. 22 перестановкой второй,
третьей и четвертой строк. Он изображен на рис. 23, причем буквы о,
Ь, с, d заменены соответственно цифрами 1, 2, 3, 4. Построим еще один
101
латинский квадрат (рис. 24), элементы которого симметричны элементам
квадрата, изображенного на рис 23, относительно диагонали, идущей
из левого верхнего угла в правый нижний. Обозначим для краткости
звания офицеров буквами 77, М, К, Л. Заменим теперь в квадрате на
рис. 23 числа 1 буквой П, числа 2 — буквой М, числа 3 — буквой К
(Л,1НМ.^(Н,2)(Л,3)
(Л,2) (Н,3) (М, 1) (П,4)
(М,3)(П,2)|
(Н,4)
(Л,1)'
(-Л.4)
(HI)
(П,ЗІ(М,2)
П
Л
М
К
М
Н
П
Л
К
м
л
п
л
п
н
м
1
4
2
3
2
3
1
4 '
3
2
4
1
4
1
3
2
Рис. 23 Рис. 24 - Рис. 25 Рис. 26
и числа 4 — буквой Л. Получится квадрат, изображенный на рис. 25.
В клетку квадрата нужно поместить офицера, звание которого
указано в этой клетке на рис. 25, а номер полка — на рис. 24. В результате
найдем расположение офицеров, изображенное на рис. 26 и отвечающее,
как легко проверить, условию задачи.
VIII. Обход мостов
98. Продолжим письмо Эйлера к Маринани:
«Итак, вопрос состоит в том, чтобы определить, можно ли обойти
все эти семь мостов, прохода через каждый только однажды, или нельзя.
.Мое правило лриводит к следующему решению этого вопроса. Прежде
всего нужно смотреть, сколько ест.ь участков, разделенных водой,—
таких, у которых нет другого перехода с одного на другой, кроме как
через мост. В данном примере таких участков четыре, А, В, С, D. Далее
нужно различать, является ли число мостов, ведущих к этим1 отдельным
участкам, четным или нечетным. Так, в нашем случае к участку А ведут
пять мостов, а к остальным — по три моста, т. е. число мостов, ведущих
к отдельным участкам, нечетное, а этого одного уже достаточно для
решения задачи. Когда это определено, применяем следующее правило:
если бы число мостов, ведущих к каждому отдельному участку, было
четным, то тогда обход, о котором идет речь, был бы возможен, и в то же
время можно было бы начать этот обход с любого участка. Если же
из этих чисел два были бы нечетные, ибо только одно быть нечетным не
может, то и тогда мог бы совершиться переход, как это предписано,
но только начало обхода непременно должно быть взято от одного из
тех двух участков, к которым ведет нечетное число мостов. Если бы,
наконец, было больше двух участков, к которым ведет нечетное число
мостов, то тогда такое движение вообще невозможно. Итак, поскольку в
предложенном примере к четырем участкам число мостов нечетное, мы
тщетно искали бы такой обход. А вот если бы [Через рукав, разъеди-
102
няющий части В и D на рис 2. — Примечание авторов] прибавить
еще восьмой мост, то тогда было бы только два участка, а именно А и С,
к которым ведет нечетное число мостов, и поэтому требуемый обход мог
бы совершиться, если бы только начало обхода было взято от А или С.
Если бы можно было привести здесь другие, более серьезные задачи,
этот метод мог бы принести еще большую пользу и им не следовало бы
пренебрегать».
Обоснование правила можно найти в письме Эйлера к своему другу
Элеру от 3 апреля 1736 года. Мы перескажем ниже отрывок из этого
письма.
Рассмотрим произвольный участок разветвления реки, а также
мосты а, Ь, с, d, e, f, как это указано на рис. 27. Области, отделенные
Рис. 27
друг от друга водой, назовем буквами А, В и С. Каждый путь,
пролегающий по участку, удобно обозначить последовательностью букв
А, В и С, указывающих области, последовательно проходимые на этом
пути. Так, АВСАСАВ будет обозначать некоторый переход,
начинающийся в области А (рис. 27), заканчивающийся в области В и,
как легко видеть, совершаемый через все мосты по одному разу. Число
букв всегда должно быть на единицу больше числа пересекаемых мостов.
Теперь рассмотрим, сколько раз в указанном ряде букв А, В, С, А,
С, А, В встречается каждая из букв А, В, С. Об этом можно судить
по числу мостов, ведущих в каждую из областей. Если буква А стоит
внутри последовательности букв, обозначающих переход, то при
прохождении через область А на этой части пути нужно пересечь два моста,
ведущих в А, один для того, чтобы войти в область А, и другой для
того, чтобы из нее выйти Итак, если какая-то область не является
начальной или конечной, то количество появлений соответствующей
буквы в последовательности, обозначающей путь, проходящий через
все мосты па одному разу, вдвое меньше числа мостов, ведущих в эту
область Так, в область С на рис. 27 ведет 4 моста, и в указанной
выше последовательности букв буква С встречается два раза. Отсюда
следует, что в область, не являющуюся начальной или конечной для
103
пути, проходящего через все мосты по одному разу, ведет четное число
мостов, значит:
1) если имеется более двух областей, в которые ведет нечетное
число мостов, то указанный переход невозможен;
2) если число мостов, ведущих в некоторую область А, нечетно,
то переход через все мосты не может совершиться иначе, чем таким
образом, чтобы он или начинался в области А или заканчивался в
области А;
3) если число мостов, ведущих во все области, четно и указанный
переход начинается в области Л, то в этой же области А он должен и
закончиться.
В случае, если на участке разветвления реки имеется не более
двух областей, в которые ведет нечетное число мостов, то требуемый
переход возможен. Для того чтобы проще представить себе это, будем
стирать на рисунке уже пройденные мосты. Легко проверить, что если
мы начнем двигаться в соответствии с правилами Эйлера, пересечем
один мост и сотрем его, то на рисунке будет изображен участок, где
опять имеется не более двух областей, в которые ведет нечетное число
мостов, а при наличии областей с нечетным числом мостов мы будем
располагаться в одной из них. Продолжая двигаться так далее, мы
лройдем через все мосты по одному разу.
99. Подсчитаем, сколько мостов ведет в каждую из областей на
рис. 3: в А — 8 мостов, в В — 4 моста, в С — 4 моста, в D — 3 моста,
в Е — 5 мостов.
Итак, имеется только две области D и Е, в которые ведет нечетное
число мостов. Обход должен начинаться с одной из них. Вот один из
возможных обходов, начинающийся в области Е:
а, Ь, с, d, e, f, g. ft, i, fe, m, n, p, q, I
(здесь последовательно указаны проходимые мосты).
В заключение отметим, что подобные задачи вместе с совокупностью
методов их исследования составляют очень важный в практическом
отношении раздел современной математики, называемый теорией графов.
IX. Шахматы
100. Эйлер дал ответ на оба вопроса, предложив замкнутый путь
коня по всем 64 клеткам шахматной доски. Замкнутость означает, что
с последней из клеток конь за один ход может перескочить на первую.
Если поместить коня в какую-нибудь клетку шахматной доски и
провести его по этому замкнутому маршруту, то конь побывает на каждой
из 64 клеток и только по одному разу. Путь, предложенный Эйлером,
указан на рис. 28.
Если поставить коня в левую нижнюю клетку шахматной доски
и провести его по указанному замкнутому пути, то клетки, последо-
104
54
39
50
37
28
11
14
1
49
36
53
12
51
64
27
10
40
55
38
29
26
13
2
15
35
48
57
52
63
30
9
24
56
41
62
31
20
25
№
3
47
34
45
58
61
6
23
8
42
59
32
19
44
21
4
17
33
46
43
60
5
18
7
22
Рис. 28 Рис. 29
Рис. 30 Рис. 31
вательно проходимые конем, можно занумеровать так, как это сделано
на рис. 29. Легко заметить, что путь, изображенный на рис. 28,
симметричен относительно центра доски. На рис. 29 это проявляется в том,
что разность номеров любых двух симметричных клеток постоянна и
равна 32.
В настоящее время известно множество различных замкнутых путей
коня по шахматной доске. Еще два примера изображены на рис. 30, 31
101. Будем решать задачу сразу для доски размером пХп клеток.
Обозначим Рп количество размещений п ладей на доске размером «Хп,
не угрожающих друг другу. Мы установим сейчас соотношение между
числами Рп и Р„_,, которое позволит вычислить Р8 и тем самым найти
искомое количество размещений ладей на обычной шахматной доске
Итак, рассмотрим доску размером пХп клеток. Поставим ладью
на какую-либо клетку первого столбца доски. Уничтожим теперь первый
столбец и строку шахматной доски, в которой стоит ладья. Оставшиеся
строки сдвинем так, чтобы получилась доска размером (л— 1) X (п— 1).
105
ft
^
^
В ее клетках можно расставить п—\ ладью, так чтобы они попарно не
угрожали друг другу, Р„-і способами. Следовательно, каждому
положению ладьи в первом столбце соответствует Рп-\ расположений
остальных п — I ладей, удовлетворяющих условию. Поэтому
Р„ = П-Р„-,.
Так как Рі = 1, имеем
р8 = 8-Р7 = 8-7-Рб = 8-7-6.Я5 = .. .=8-7-6 ... 2-1=40 320.
Точно так же в общем случае находим
Я„ = 1 -2■ 3 ... {п — \)-п = п\
102. Приведем рассуждения Эйлера. В каждом столбце из клеток
доски должна стоять и притом только одна ладья. В первом столбце
ладья может занимать только п — 1 позицию, ведь самая нижняя клетка
этого столбца принадлежит главной диагонали, и ставить на нее ладью
запрещено условием.
Поставим ладью на некоторую, скажем, на г-ю, клетку первого
столбца. Все расположения ладей, удовлетворяющие условию задачи и
такие, что в первом столбце ладья занимает г-ю клетку, разобьем на две
группы. Рассмотрим клетку, симметричную л-й клетке первого столбца
относительно главной
диагонали. Если
рассматриваемая клетка не занята
ладьей, то размещение
ладей отнесем в первую
группу, если же в
рассматриваемой клетке стоит
ладья, то размещение
отнесем во вторую группу.
Так, например, на рис. 32 при п = 4 и г = 2 указаны два
размещения ладей. Одно из них относится к первой группе, а другое — ко
второй.
Подсчитаем теперь количество размещений в первой группе. Если
удалить из доски г-ю строку, заменив ее первой, а затем отбросить
первый столбец, то получится доска размером (п—1)Х(і—1) клеток.
Каждое размещение ладей из первой группы дает после этих
преобразований некоторое размещение ладей на новой доске размером (п — 1) X
Х(я—I) клеток, удовлетворяющее условию задачи. Верно и обратное,
по каждому размещению ладей на новой доске, удовлетворяющему
условиям задачи, однозначно восстанавливается размещение ладей из
первой группы. Следовательно, первая группа размещений ладей
содержит в точности Q„_i размещений
Подсчитаем теперь количество размещений во второй группе. Если
удалить из доски первый столбец и г-ю строку, а также r-й столбец
и первую строку, а оставшиеся строки и столбцы сдвинуть, не меняя их
106
Рис. 32
порядка, так чтобы получилась доска размером (/г — 2) X (я — 2) клетки,
то каждое размещение ладей из второй группы даст при этом некоторое
размещение ладей на новой доске размером (п — 2)Х(я—2) клетки,
удовлетворяющее условию задачи. Отсюда следует, что вторая группа
содержит Qn-2 размещения ладей.
Итак, имеется Q„_! + Qn-2 размещений ладей на доске размером
пХп, которые отвечают условиям задачи и у которых ладья стоит на
пересечении первого столбца и г-й строки. Поскольку г может принимать
п—1 значение (2, 3, ..., п), находим, что
Q»=(n-l)(Qn-i + Q»-2).
103. Каждому мужчине, пришедшему на собрание, присвоим номер
от 1 до я и такой ж« номер присвоим его шляпе. Предположим,
что fe-й мужчина, уходя, получил шляпу с номером at, k = \, 2 п.
Поставим в первом столбце шахматной доски ладью на клетку,
имеющую номер аі при нумерации снизу вверх, во втором столбце поставим
ладью на клетку с номером аг и т. д. Так как все числа а\, аз а„
различны (каждая шляпа досталась только одному мужчине), то ни на
одной горизонтали не будет стоять двух ладей. Следовательно,
получившаяся расстановка п ладей удовлетворяет условию задачи 101.
Верно и обратное, каждой расстановке не угрожающих друг другу п
ладей на доске размером nXt клеток соответствует некоторое
распределение шляп между мужчинами. Значит, общее число распределений
шляп между мужчинами равно Рп=п\ (см. решение задачи 101).
То, что каждый мужчина получил чужую шляпу, означает, что
а\ ф 1, а2 Ф 2, ..., а„ ф п. Но эти же неравенства означают, что ни одна из
ладей, помещенных на доску в соответствии с указанным выше правилом,
не стоит на главной диагонали. Поэтому количество распределений шляп
между мужчинами, при которых каждый мужчина получает чужую
шляпу, равно Qn (см. задачу 102), а искомая вероятность равна Qn/Pn.
Пользуясь соотношением Эйлера из задачи 102, находим
Q„-nQ„_, = (rt-l)(Q„_,-f-Q„_2)-«Q„-i=-(Q„-]-(4-l) Q„-2).
Продолжая выполнять эти преобразования, получим
Q„-nQ„-., = -(Q„_,-(/!-l) Q„_2) =
= (-1)2(<Э„_г- (n-2) Q„-3) =... = ( —I)"-3 (Q3-3Q2) = ( —1)".
Итак,
Q» Qn Qn-i , (-1)" Qn-2 , (-I)""' , (-1)"
— ~~ H Ti = ,7 ^, + "7^ ІТТ + - ~~
Pn n\ (rt-1)! ' n\ (я-2)! ' (n-1)! ' n\
_Q* , (-P3 , , (-I-)""' , (-1)"
2! ' 3! ' "' ' (n-1) f ' n!
=J L+JL_ i (-')"
2! 3!T4! •"■"r n! "
Интересно, что с ростом п это число приближается к некоторой
постоянной, равной
е~'« 0,367 879 441 171 442 321 60,
где е«2,718 281 828 459 045 235 36—постоянная, играющая столь же
важную роль в математике, как и число п.
X. Биллиард
104. Решение задачи равносильно отысканию на заданном борту
биллиарда MN (рис. 33) точки С такой, что углы ACN и ВСМ имеют
равные величины.
Отразим точку А симметрично относительно прямой MN. Пусть
это будет точка Аі. Точку пересечения прямых MN и ВА\ обозначим
буквой С. В эту точку и нужно направить кием шар А. Действительно,
108
так как точки А и А\ симметричны, то /LACN= Z.A\CN, а ввиду того, что
С есть точка пересечения прямых ВА\ и MN, имеем *LBCM = ^.A\CN.
Следовательно, /LACN= /LBCM.
Задача не имеет решения, если шар В лежит на перпендикуляре,
опущенном из А на борт MN.
М
в\
ѵг
С\ і
\
N 1
Рис. 33
%
Рис. 34
105. Отразим точку Л симметрично относительно прямой MN, а
точку В симметрично относительно прямой PQ (рис. 34). Получим точки
А\ и В\. Обозначим буквами С и D точки, в которых прямая А\В\
пересекает параллельные борта биллиарда MN и PQ. Шар А необходимо
направить кием в точку С, тогда его траектория будет состоять из
трех отрезков AC, CD и DB. Действительно, как и в решении предыдущей
задачи, имеем равенства
<LACN=Z.DCM и Z.CDQ=APDB.
Задача не имеет решения, если прямая АВ перпендикулярна
заданным параллельным бортам.
106. Отразим точку А симметрично относительно прямой MN, а
точку В симметрично относительно прямой MP (рис. 35). Получим точки А\
и В\. Если прямая А\В\ пересекает борта MN и MP в точках С и D, то
Рис. 35 А,
шар нужно направить в точку С. Это доказывается так же, как и в
решении предыдущей задачи. В рассмотренном случае шар В лежит выше
луча МА.
Если шар В лежит на луче МА, то, как легко видеть, прямая АіВі
проходит через точку М. Если же шар В лежит ниже луча МА, то
прямая АіВ\ вообще не пересекает отрезок MN. Но в этом случае шар А
лежит выше луча MB, и если Bs — точка, симметричная точке В
относительно прямой MN, и Аг — точка, симметричная точке А
относительно прямой MP (рис. 36), то прямая АзВз пересечет отрезки MN и MP в
109
точках Е и F соответственно. Шар А нужно направить в точку F. Тогда
он, отразившись от борта MP, а затем от борта MN в точке Е, попадет
в шар В.
Итак, задача неразрешима только в случае, когда шары и точка,
общая двум заданным бортам, лежат на одной прямой.
107. Рассмотрим шесть равных прямоугольников, изображенных
на рис. 37. Будем считать, что правый нижний из них изображает
биллиард MPQN и заданные борта есть MN, MP и PQ.
Отразим точку В симметрично относительно прямой PQ, точку В\,
которая при этом получится, отразим симметрично относительно прямой
РМі, и, наконец, точку В2, получившуюся после второго отражения,
отразим симметрично относительно прямой N\Ni В результате получим
точку, которую обозначим В3. Легко
видеть, что если точку В\ отразить
относительно прямой M\N\ и
получившуюся точку отразить
относительно прямой МіРі, то получится та
же самая точка В3, что и ранее.
Точно так же, если сначала точку В
отразить относительно прямой MP, a
затем последовательно выполнять
отражения относительно прямых
Q2P и NiM\, то в результате опять
получится точка В3.
Точки, в которых прямая АВ3
пересечет стороны прямоугольников,
обозначим буквами С, D и Е (рис. 37). Шар А нужно направить кием
в точку Е. Так как /_AEQ= /LPED= Z.PED\, где Di — точка,
симметричная точке D относительно прямой PQ, то отразившись'от борта PQ в
точке Е, шар ударится о борт MP в точке D\. Пусть G — точка,
симметричная точке С относительно прямой М\Р\, и С2 — точка, симметричная
точке С\ относительно прямой PQ. Ввиду симметрии /CC2D\M =
= ACiDMi = /LCDMl, но, с другой стороны, /.CDM\ — /LPDE =
= Z.PDiE. Доказанное равенство Z.C2£iM= /LPDiE означает, что,
отразившись от борта MP в точке Di, шар ударится в борт MN в точке
Сг- Опять в силу симметрии имеем
Z-BCiN^/LBMiNy = /LB2CN3= Z.B3CN3= ADCM, ^^LDdMt =
= Z.DxdM.
Равенство величин углов BC2N и DiC2M означает, что шар А,
отразившись от борта MN в точке С2, пойдет по лучу С2В и, следовательно,
ударит шар В.
В зависимости от расположения шаров А я В в прямоугольнике
MPQN возможны различные чередования бортов при ударах. Наряду с
указанным выше порядком шар может ударяться о борта в порядке PQ,
MN, MP (рис. 38), что соответствует случаю, когда прямая АВ3 пересе-
110
Рис. 37
кает отрезки PQ, M1N1 и Mi Pi, а также в порядке MP, PQ, MN (рис. 39)
в соответствии со случаем, когда прямая АВз пересекает отрезки MP,
Q2P и Л/зМі.
В случае, если прямая АВз проходит через точки Р и М\, указанный
способ не дает решения задачи.
Рис. 38
Рис. 39
Начнем сначала. Рассмотрим опять шесть равных прямоугольников
таких же, как и на рис. 37, но будем теперь считать, что биллиард
MPQN изображает правый верхний р
из них (рис. 40). Отражая точку fi
симметрично относительно сторон
прямоугольников, получим точку Вз,
принадлежащую прямоугольнику
M\PiQiNz. Если прямая АВз
пересекает стороны прямоугольников в
точках С, D и Е (рис. 40), то шар
нужно направить в точку Е. Как и
ранее, доказывается, что при этом он
после трех отражений попадает в
шар В. В соответствии с тем, как
прямая АВз пересекает стороны
прямоугольников, возможны, как и
выше, три способа чередования бортов: (MN, MP, PQ), (MN, PQ, MP) и
(MP, MN, PQ). Вместе с тремя способами, указанными выше, они
дают все 6 возможных способов чередования трех бортов.
Для «почти всех» расположений шаров А и В возможны два решения
задачи, получающиеся с помощью рис. 37 и 40. Пример показан на
рис. 41.
N,
^ѵ
в/
р,
Рис. 40
N
Q,
%
Рис. 41
Рис. 42
В некоторых случаях задача имеет только одно решение (например,
если прямая АВз на рис. 37 проходит через точку Р, а соответствующая
111
прямая на рис. 40 не проходит через точки М и Рі). Иногда (если
прямые АВз на обоих рисунках проходят через вершины
прямоугольников) задача неразрешима. Например, если шары А и В лежат на
средней линии прямоугольника MPQN на расстояниях -т|МЛМ от бортов MP
и QN (рис. 42).
108. Рассмотрим 25 равных прямоугольников, изображенных на
рис. 43. Будем считать, что центральный прямоугольник MPQN
изображает биллиард, угловые прямоугольники обозначим так, как показано на
0г Рз_
Ms
Р,
М,
вг
V
в,/
Ъ
N.
/
р
м с;--
м3
Q.^
%
N
\
>
^,*»*^*
Р*
N3
N,
Мл
Q<
N<
Рис. 43
рис. 43. Обозначим через В\, Вг, Вг и Bt точки, получающиеся из точки В
при наложении прямоугольника MPQN на прямоугольники
MiPiQiN\, .... MiPtQiNi. Прямые ABu АВ2, АВз, ABt пересекают
стороны прямоугольника MPQN в четырех точках G, Сг, Сз, С*. Если
шар А направить в одну из этих точек, то отразившись от всех четырех
бортов он попадет в шар В. Доказать это можно точно так же, как
и в решении предыдущей задачи. Количество решений может
сократиться, если некоторые из прямых проходят через вершины
прямоугольников.
XI. Фигурные числа
109. Всякое треугольное число равняется, как легко видеть, сумме
последовательных целых чисел 1+2 + 3+ ... +п при некотором п,
т. е. имеет вид л(«+1)/2. Поэтому если N одновременно является
квадратным и треугольным числом, то с некоторыми целыми числами
х и у должны выполняться равенства
Х 2 •
Задача сводится к поиску целых чисел х и у, удовлетворяющих
уравнению о 2
2*2=і/(</+!)•
(1)
112
Числа х=\, у=\ и х=6, у=ѣ, соответствующие приведенным в
условии квадратно-треугольным числам 1 и 36, будут решениями этого
уравнения. Есть ли у него другие решения? Оказывается, есть, и
бесконечное множество.
Легко проверить, что выполняется тождество
2 (Злг + 2у+1)2—(4лг + 3г/+1) (4х+Зу + 2) = 2х*-у*-у.
Обозначив
x, = 3x+2t/ + l, ух=іх + Зу + \, (2)
это тождество можно переписать в виде
2*Т-*і (y> + \)=2x2-y(y+l).
Следовательно, если числа х и у удовлетворяют уравнению (1),
то числа *і и у\, найденные по формулам (2), также являются решениями
этого уравнения.
Подставляя в формулы (2) числа х=\, у—\, найдем *і=6, у\=ѣ,
что дает квадратно-треугольное число 36. Если в формулы (2)
подставить х=6, у=8, получим Хі=35 и у\=А% что дает еще одно число
1225 = 352, удовлетворяющее условию задачи. Действуя так далее,
получим и другие квадратно-треугольные числа. Выпишем, следуя Эйлеру,
первые несколько значений х:
1, 6, 35, 204, 1189, ... (3)
Можно доказать, что так получаются все числа, являющиеся как
квадратными, так и треугольными. Эйлер приводит интересную формулу
для последовательности чисел (3), позволяющую сразу вычислять их по
номеру п:
(3 + 2Ѵ2)"-(3-2Ѵ2)"
Хп~ 4~У2 ' п-1-2'---
Кроме того, каждые три последовательных числа в ряду (3) связаны
соотношением
хп+,=бх„ — х„-и п= 2, 3, ...
ПО. Обозначим т-угольное число с номером п символом р (я).
Тогда р(1)=1,р(2)=ти разность р (л) — р (л— 1) равна количеству
точек, лежащих на т — 2 сторонах правильного многоугольника с
номером л —1, т. е. равна 1 + (т—2) (л — 1) (на 1 больше суммы дл-ин
сторон). Итак,
р(я)=р(я-1) + [1 + (т-2) (я-1)] =
=р(л-2) + [1 + (т-2) (я-2)] + [1 + (т-2) (я-1)]= ...
-Ml) + [l + (m-2)-lJ + [l + (m-2).2]+ •••
. . +[і + (т_2) (л-1)] =
-1 + (я-1) + (т-2) (1+2 + 3+ ... +(я-1)).
113
Так как
a(tt — l)
1+2+3+.••+ («-!)=-
р (я) =п+ (т — 2)
.2
п (-я— 1) '(т—2) п1— (т — 4) п
Из приведенных выше рассуждений следует еще один способ
построения последовательности /га-угольных чисел. Напишем подряд члены
арифметической прогрессии с первым членом 1 ,и разностью (т — 2),
Например, при т = 6 получаем последовательность
1, 5, 9, 13, 17, 21, 25, 29, ...
Складывая первые два, первые три, первые четыре, первые пять и т. д.
членов написанной последовательности, получим последовательность
т-утольных чисел. При т=6 имеем
1, 6, 15, 28, 45, £6, 91, 120, ...
— последовательность 6-угольных чисел.
111. Подставляя в формулу из предыдущей задачи вместо т число
365, а вместо п — число 12, получаем, что дом стоит '23 970 рублей.
112. Из формулы, указанной в задаче 1 ГО, следует, что все
треугольные числа имеют вид
"' + " , «=1,2,3
2 '
а шестиугольные числа получаются с помощью формулы
An2 — In
—2~—, n = l, 2, 3, ..
Нужное утверждение следует теперь из тождества
Апг — 2п (2к-1)2+(2п—1)
Следовательно, шестиугольное число с номером п является треугольным
числом с номером 2л — 1.
113. Количество ядер, лежащих в первом слое, равно треугольному
числу с номером я, во втором слое — равно треугольному числу с
номером (п — 1) и т. д. В последнем слое с номером п лежит одно ядро,
и первое треугольное число также равно 1. Значит, количество ядер
в пирамиде равно сумме первых п треугольных чисел, т. е. сумме
чисел вида
k*+k ,. , „
о ■ А=1, 2 п.
114
Для того чтобы найти эту сумму, воспользуемся тождеством
кг+к k3 + 3k2 + 2k (fe-l)3 + 3(fe_i)2 + 2(fe-l)
2 = 6 6
п2 + п _ n3 + 3/i2 + 2n (п-1)3 + 3(п-1)2 + 2(/г-1)
2 6 6 "
Подставляя в него последовательно fe = l, 2, 3,..., п, получим равенства
1 = 1-0
3=4—1
6=10—4
10=20-10
п2 + п и« + 3п2 + 2п (п-1)3 + 3(и—1)2+2(п-1)
Сложим теперь почленно левые и правые части написанных равенств.
Слева получится сумма всех треугольных чисел от первого до га-го, т. е.
количество ядер в пирамиде. При сложении же выражений в правой
п3 + 3я2 + 2п _
части уничтожатся все слагаемые, кроме ■—^—■ .
Следовательно, пирамида сложена из
п3 + 3п2 + 2п п(п + 1){п + 2)
6 6
ядер. Например, если выкладывать основание пирамиды в виде
равностороннего треугольника со стороной в 8 ядер, то пирамида будет состоять
из 120 ядер.
XII. С помощью линейки, циркуля и ножниц
114. Раствором циркуля, равным данному отрезку, опишем
окружность (рис. 44), Взяв на окружности произвольную точку А, тем же
раствором циркуля сделаем из нее засечку на окружности в точке В.
Затем тем же раствором циркуля из точки В делаем засечку на
окружности в точке С. Точно так же, сделав еще три
засечки, получим точки D. Е и F. Соединим
последовательно точки A, В, С, D, Е. F и А
отрезками, получим правильный шестиугольник.
Действительно, соединив точки А, В, С, D, Е
и F с центром окружности точкой О, получим
пять равносторонних треугольников АОВ, ВОС,
COD, DOE и EOF. В равнобедренном
треугольнике FOA угол FOA равен 360°-5-60° =60°,
откуда следует, что полученный шестиугольник
правильный.
115
US. Из середины С данного отрезка АВ (рис. 45) восставим
перпендикуляр и отложим на нем отрезок CD, равный -х\АВ\. Затем
на его продолжении отложим отрезок DE, длина которого равна
длине отрезка AD. Тогда длина отрезка АЕ является радиусом
окружности, описанной около правильного восьмиугольника со
стороной АВ.
В самом деле, найдем величину угла ЛЕС. Так как \АС\ = \CD\, то
треугольник ACD — равнобедренный, и так как он прямоугольный, то
величина угла ADC равна 45°. Поскольку \AD\ = \DE\, то
треугольник ADE — равнобедренный и величина угла AED равна 45°/2 и,
следовательно, величина угла ЛЕВ равна 45°, т. е. дуга АД есть 1/8 часть
окружности.
Теперь надо на листе бумаги нарисовать окружность радиуса АЕ
и так же, как в задаче 114, от любой точки последовательно отложить
8 хорд, каждая из которых равна длине отрезка АВ. Получим
правильный восьмиугольник, что можно доказать так же, как в задаче 114.
D
А ѣ
Рис. 45 Рис. 46
11в. Построим равносторонний треугольник ЛЕВ со стороной,
равной данному отрезку АВ (рис. 46). Через точку Е проведем прямую,
перпендикулярную отрезку АВ. Отложим на этой прямой отрезок ED,
равный отрезку АЕ. Тогда длина отрезка AD является радиусом
окружности, описанной около правильного двенадцатиугольника со
стороной АВ. Для подтверждения этого достаточно доказать, что величина
угла ADB равна 30°. Точка Е равноудалена от точек А, В и D, т. е.
является центром окружности, описанной около треугольника ABD. Поэтому
Z.ADB = \^-AEB = ZQ". Построение правильного двенадцатиугольника
выполняется аналогично построениям в предыдущих задачах.
117. Из середины С данного отрезка АВ восставим
перпендикуляр (рис. 47) и на нем отложим отрезок CD, равный к\АВ\, затем
отрезок DE, равный отрезку AD, и отрезок EF, равный отрезку АЕ.
Тогда длина отрезка AF является радиусом окружности, описанной
около правильного шестнадцатиугольника со стороной АВ.
116
Так же как и в предыдущих задачах, находим, что
/,АЕВ=4г AADB=45°
1 45° 4fif)°
/.AFB=±Z.AEB=^-, т. е. ±AFB=~.
Построение правильного шестнадцатиугольника выполняется
аналогично построению в предыдущих задачах.
118. Вырезанный семиугольник не является правильным. В самом
деле, пусть О — центр окружности, точка D — середина отрезка АВ,
а точка Е — первая из засечек, сделанных на окружности радиусом
|Л£>| =ъ\АВ\ (рис. 48). Найдем величину угла АОЕ. Пусть R — радиус
Я
окружности, тогда |<4£| = \AD\ =-tj— R- Из равнобедренного
треугольника АОЕ находим
\AE\=2Rs\n(/z^£E\
откуда
Z.AOE\ \АЕ\ ѴЗ
. / Z.AOE\
2R
По таблицам синусов находим, что
51°19'< Z.АОЕ<5Г 20'.
Величина центрального угла а, опирающегося на сторону правильного
семиугольника, равна 360°/7, т. е.
51°25'<а<51°26'.
Следовательно, вырезанный семиугольник не является правильным.
117
Из этих неравенств следует, что центральный угол, опирающийся на
дугу АЕ, отличается от центрального угла правильного
семиугольника не более чем на Т. Поэтому величины дуг окружности между
вершинами построенного семиугольника и соответствующими вершинами
правильного семиугольника с вершиной в точке А не превосходят
6-7' = 42'<1°. Столь малые отклонения позволяют утверждать, что
предложенный способ дает возможность строить «практически
правильный» семиугольник.
119. Пусть Е — середина стороны CD прямоугольника ABCD
(рис. 49). Разрез нужно провести по отрезку BE, а затем треугольник
ВЕС переложить так, чтобы вершина его Е осталась на месте, а
вершина С совпала с точкой D (треугольник DEF на рис. 49). Так как
AADE = /LEDF — n/2, то точки A, D и F лежат на одной прямой.
Из равенства /_ВЕС= Z.DEF следует, что
Z. BED + Z. DEF = Z. BED + Z ВЕС = л,
т. е. точки В, Е и F также лежат на одной прямой. Следовательно,
многоугольник ABEFD есть треугольник.
Рис. 50
120. Пусть Е, F — середины сторон АВ и ВС треугольника ABC
и BD.LEF (рис. 50). Отрезки EF и BD — искомые разрезы. Переложим
треугольники BED и BDF так, чтобы отрезки ЕВ и BF совпали
соответственно с отрезками ЕА я CF (треугольники AEG и CFH на рис. 50)
Так же, как и в решении предыдущей задачи, доказывается, что точки
G, Е, F, Н лежат на одной прямой. Кроме того,
Z. GAC=jL GAE + /LEAC= /LEBD+ /.BED==n/2
и аналогично Z.ACtf=n/2 Итак, AGEFttC—прямоугольник.
Может случиться, что точка D не лежит на отрезке EF (рис. 51)
В этом случае
/LACB=Z.EFB> Z.FDB=n/2
и, значит, Z.ACB — самый большой по величине угол треугольника ABC.
Чтобы исключить случай, когда точка D не лежит на отрезке EF,
точки £ и F нужно брать в серединах сторон, заключающих между
118
собой угол наибольшей величины. Тогда /САВС^ Z-ACB и неравенство
/LACB> л/2 невозможно (сумма величин углов в треугольнике равна к).
Аналогично невозможно неравенство Z.BAC> я/2 и, следовательно,
точка D лежит на отрезке EF.
Правило выбора точек Е и F, указанное выше, позволяет
разрезать данный треугольник на три части (рис. 50), из которых можно
сложить прямоугольник. Одна из сторон этого прямоугольника
совпадает с одной из сторон треугольника.
В В
Рис. 51 Рис. 52
Усложним задачу и потребуем, чтобы у прямоугольника одна из
сторон совпадала с основанием АС треугольника ABC. Если точка D
лежит на отрезке EF, то нужные разрезы уже найдены. Допустим
теперь, что точка D лежит на продолжении отрезка EF за точку F.
Проведем разрез по отрезку EF и второй разрез по отрезку СК такому,
что CK±EF.
Переложим треугольник EBF так, чтобы точка Е осталась на месте,
а точка В совпала с точкой А (треугольник АМЕ на рис. 52). Затем
приложим треугольник CKF к треугольнику АМЕ так, чтобы совпали
вершины С и A, F и М (треугольник ALM на рис. 52). Это возможно,
так как \АМ\ = \BF\ = \CF\. Докажем, что многоугольник ALMEK.C —
прямоугольник. Поскольку
/LEKC=<LACK = n/2 и /.ALM = ZCKF = ji/2,
достаточно доказать, что точки L, М, Е и К лежат на одной прямой.
Имеем
г. LMA + /. А М Е = Z. KF С + Z. BFE = л,
/-AEM+/-AEK=^-BEF+ /-АЕК=к,
откуда следует требуемое утверждение.
Высота полученного прямоугольника равна половине высоты
треугольника. Это следует из того, что EF—средняя линия
треугольника
Заметим, что из решения этой задачи следует, что два треугольника,
имеющие одно основание и равные высоты, проведенные к этому
основанию, имеют равнГше площади.
119
121. Проведем через вершину В четырехугольника ABCD (см.
рис. 53) прямую параллельно диагонали АС. Пусть Е — точка
пересечения этой прямой с продолжением стороны AD и F — середина
отрезка ED.
1. Если точка F принадлежит отрезку AD, то CF — искомый
разрез. Докажем это. Так как ВЕ\\СА, то по замечанию, сделанному
в конце решения предыдущей задачи, SAEC=SABC и, значит, SABCF =
=S£cf. Поскольку F — середина отрезка ED, то SFCD=SECF = SABCF.
Рис. 53 Рис. 54
2. Если точка F лежит вне отрезка AD (см. рис. 54), то проведем
через точку F прямую параллельно Л С до пересечения ее с отрезком АВ
в точке G. Отрезок CG — искомый разрез. Действительно, так как
FGWAC, то SAoc=SAFC и SAGCD=SFCD. Аналогично
^овс=^лвс ~ $а ас=$аес ~ $afc=*«с*
Так как F— середина отрезка ED, то SfCD=^FEC и> значит, SAGco—
= Sobc-
Заметим, что в случае 2 прямую, параллельную диагонали АС,
можно провести через вершину D, и если Н — точка пересечения этой
прямой с прямой АВ, то G — середина отрезка ВН. Другими словами,
если построение пункта 1 провести не удается, то нужно выполнить
это же построение для вершины D и стороны АВ.
XIII. Построения на местности
122. Можно поступить так. Обозначим буквой А недоступный для
нас дом, а башню обозначим буквой В (рис. 55).
Вобьем на нашем берегу колышек в некоторой точке А\, такой,
что отрезок А\В не задевает реку. В середине отрезка А\В вобьем
колышек С. На доступной для нас части отрезка АВ поместим колышек D,
а на отрезке АіВ — колышки Е, F на равных расстояниях от В и А|.
Вобьем теперь колышек в такую точку G, что \FG\ = \ED\ и \А% G\ =
= \BD\, а точки G и А лежат по разные стороны относительно
прямой А\В. Это можно сделать, воспользовавшись, например, двумя
веревками. Найдем теперь на прямой A\G точку В\, лежащую на одной
прямой с Л и С, тогда искомое расстояние будет равно расстоянию
между колышками А\ и В\.
120
Действительно, треугольники DBE и GA\ F равны по трем сторонам.
Поэтому равны величины углов ABC и СА\Вь В треугольниках ABC
и А\В\С кроме этих углов равны также величины углов АСВ, А\СВ\
и стороны ВС и А] С. Значит, треугольники ABC и А\ В\ С равны, а
потому равны и длины сторон АВ и А\В\, т. е. расстояние между
колышками А\, В\ равно искомому расстоянию между домом и башней.
Если расстояние между домом и башней весьма велико, то
приведенный способ будет не очень удобен. На нашем берегу придется
откладывать и измерять очень большие отрезки, а построения и измерения
будут, возможно, не очень точны из-за имеющихся препятствий на
местности. Можно усовершенствовать предложенный способ так, чтобы
все измерения и построения проводить на ограниченном участке
местности.
Выполним все построения и измерения так же, как это указано
выше, за одним исключением: колышек С вобьем не в середине
отрезка А\В, а сместим его ближе к точке А\. Для определенности будем
считать, что отрезок ВС в 100 раз больше отрезка А\ С. Теперь
треугольники ABC и А\В\С будут не равны, а подобны, и коэффициент подобия
будет равен отношению |ВС|/|ЛіС| =100. е * т &
Следовательно, расстояние \АВ\ между домом
и башней будет в 100 раз больше длины
отрезка А\В\.
Рис. 55
Рис. 56
123. Поступим следующим образом (через Л и В на рис. 56
обозначены крепость и дерево). Вобьем на нашем берегу колышек С, а затем
колышки D, Е на продолжениях прямых линий ВС и АС. Найдем теперь
точку Fтакую, что |£>F| =\DC\ и \EF\ =|C£|, и вобьем в ней колышек.
На отрезке BE поместим колышек G, а затем найдем точку И такую, что
|£tf| = |£G| и \FH\ = \CG\.
Поместим теперь колышек на прямой DF в точку В\, из которой
колышек Н закрывает колышек Е. На отрезке AD поместим колышек К в
121
точку, из которой колышек G закрывается колышком С, а на прямой
FH за точкой F вобьем колышек L так, что \FL\ = \CK\. Теперь на
прямой DL найдем точку А\, из которой колышек Е закрывается
колышком F. Искомое расстояние от дерева до крепости равно
расстоянию между колышками А\ и В\. Действительно, треугольники DCE
и DFE равны по трем сторонам. Значит, Z.C£>£ = /LFDE и прямые DB
и DBi симметричны относительно прямой DE. Треугольники CGE и
FHE равны по трем сторонам. Поэтому Z.CEG = /.FEH и
Z-DEB= /-DEC+ Z.CEG = Z.DEF+ /LFEH=^DEH.
Следовательно, прямые ЕВ и ЕВ\ также симметричны относительно
прямой DE. Точки пересечения пар симметричных прямых также
симметричны. Поэтому точки В и В\ симметричны относительно
прямой DE.
По построению \CK\ = \FL\, \DC\ = \DF\ и
^.DCK = n— /LDCE — /LECG = n— /LDFE— Z-EFH= /.DFL.
Следовательно, треугольники DCK и DFL равны. Теперь точно так же,
как и для точек В, В\, доказывается, что точки А и А,
симметричны относительно прямой DE. Из симметрии отрезков АВ и А\Ві
следует, что
\АВ\ = \А1ВЛ.
С помощью соображений подобия можно, как и в решении
предыдущей задачи, все построения и измерения провести на ограниченном
участке местности.
XIV. Геометрические задачи Эйлера
124. Пусть Я— точка пересечения высот треугольника ABC,
М — точка пересечения его медиан и О — центр описанной окружности
(рис. 57). Построим треугольник А\В\С\, симметричный
треугольнику ABC относительно точки М. Пусть Н\ — точка пересечения высот
треугольника А\В\С\, симметричная точке Я. Точки Я, М и Яі лежат
на одной прямой. Рассмотрим треугольник АгЯгСг, гомотетичный
треугольнику А\В\С\ с центром в точке М и коэффициентом гомотетии,
равным 1/2. Тогда \МА2\ =^|AL4i| =-\AM\ Значит, точка Л2 является
основанием медианы, проведенной из вершины А, и лежит в середине
отрезка ВС. Аналогично В2 и Сі являются серединами отрезков АС и АВ.
Следовательно, точка пересечения высот треугольника Л2В2С2,
гомотетичная точке Яі, совпадает с точкой пересечения серединных
перпендикуляров к сторонам треугольника ABC, т. е. с точкой О. Так как
122
точки Н\ и О гомотетичны с центром М, то точки М, Н\, О лежат ла
одной прямой. Точка Н лежит на прямой МНі, следовательно, точки Н,
М, О лежат на одной прямой. Более того, \НМ\/\ОМ\ =\Н\М\/\ОМ\=2.
125. Пусть Н — точка пересечения высот треугольника ABC; К, L и
М — середины отрезков ВН, АН, СН и £ — середина отрезка AC; D —
основание высоты треугольника ABC, опущенной из вершины В (рис. 58).
Опишем окружность на отрезке КЕ как на диаметре. Так как KDJ-DE,
то точка D лежит на окружности. Отрезки KL и LE являются средними
линиями в треугольниках АВН и АНС. Значит, КЦАВ, LE\\CH.
Прямые АВ и СН перпендикулярны, поэтому Z.KLE=я/2 и точка L также
лежит на построенной окружности. Аналогично доказывается, что на этой
окружности лежит и точка М.
Таким образом, окружность, описанная вокруг треугольника KLM,
пересекает сторону АС в точках, одна из которых будет основанием
высоты, а другая основанием медианы. Если произвести аналогичное
построение для другой стороны треугольника, то получим ту же самую
окружность, описанную вокруг треугольника KLM. Это доказывает,
что все 9 указанных в условии задачи точек лежат на одной
окружности.
Если треугольник ABC — равнобедренный, скажем, \АВ\ = \ВС\,
то точки D и Е совпадают, а окружность девяти точек касается
стороны АС.
126. Пусть О — центр описанной окружности треугольника ABC
и К — центр вписанной окружности (рис. 59). Продолжим отрезок ВК
до пересечения с описанной окружностью в точке L. Вычислим двумя
способами произведение \ВК\-\КЦ.
Во-первых, проведем диаметр описанной окружности LM и опустим
из точки К перпендикуляр DK на сторону АВ (рис. 59). Прямоугольные
треугольники BDK и MAL подобны (углы ABL и AML опираются
на одну дугу окружности и потому имеют равную величину). Значит,
123
|0^|/|В/СІ = |;4І|/|ЛШ или
\BK\-\AL\ = \DK\-\ML\=2Rr.
Докажем теперь, что \AL\ = \KL\. Поскольку точка К лежит на
биссектрисах углов ВАС и ABC, а углы LAC и LBC опираются на одну дугу, то
/.KAL= <LKAC+ ALAC= /LKAC+ <LLBC=*^ (/.A+/.B),
/LAKL = '<LKAB+ /,KBA=y (/L.A+ Z.B).
Итак, треугольник AKL — равнобедренный, \AL\ = \KL\ и | В КI X
X\KL\—2Rr. Проведем теперь через точку К диаметр EF (рис. 60).
Треугольники ВЕК и LFK подобны потрем углам. Значит, \ВК\/\ЕК\ =
= \KF\/\KL\ или
\ВК\ -\КЦ = \ЕК\ • \KF\ = (R-d) • (R+d) =R2-d2.
Сравнивая найденные выражения для \BK\-\KL\, получим формулу
Эйлера.
127. Пусть A BCD — выпуклый
четырехугольник, точки Н и G —
середины диагоналей АС и BD
(рис. 61). На продолжении отрезка
Л О за точку G отложим точку Е
такую, что I AG I = | GE\. Аналогично
на продолжении отрезка CG за
точку G отложим точку F такую, что
\CG\=\GF\. В четырехугольниках
ABED, ACEF и BCDF диагонали
' в точке их пересечения G делятся
пополам. Следовательно, эти четырехугольники — параллелограммы.
Так как в параллелограмме сумма квадратов длин сторон равна
124
Рис. 61
сумме квадратов длин диагоналей, находим равенства
|Л£|2+|В£>|2=2|ЛВ|2-|-2|АО|2,
|В/>|2+|СЛ2=2|ВС|2+2|СО|2,
|Л£|2+ІСЛ2=2|ЛС|2+2|С£|2.
Заметим, что для некоторых четырехугольников ABCD
параллелограмм ACEF может выродиться в отрезок. Последнее из трех написанных
выше равенств, тем не менее, сохранится.
Складывая первые два равенства и вычитая из суммы третье
равенство, найдем
2|ВЯ|2=2|ЛВ|2 + 2|ВС|2 + 2|С£>|2 + 2|Л£>|2-2|ЛС|2-2|С£|2
или \AB\2+\BC\2+\CD\2+\AD\2-\AC\2-\BD\'=\CE\2. В
треугольнике АСЕ отрезок GH — средняя линия. Значит, |C£|=2|G#|,
откуда и следует нужное равенство.
128. Существует много замкнутых путей по ребрам многогранника.
Например, обойдя все ребра, принадлежащие одной его грани, мы
вернемся в исходную точку.
Будем последовательно окрашивать ребра многогранника в красный
цвет, пользуясь следующими правилами:
а) сначала возьмем любой замкнутый путь по ребрам
многогранника и окрасим какое-нибудь ребро, входящее в этот путь;
б) если существует замкнутый путь, проходящий по неокрашенным
ребрам многогранника, то окрасим какое-нибудь его ребро;
в) окраску прекратим, как только не станет замкнутых путей,
проходящих по неокрашенным ребрам.
На рис. 62 показана раскраска куба, выполненная в соответствии
с нашими условиями. Порядок раскраски ребер отмечен номерами;
ребра, окрашенные в красный цвет, выделены на рисунке жирными
линиями.
Докажем теперь, что всегда число неокрашенных ребер равняется
В —1, число окрашенных ребер равняется Г—1 и, следовательно,
/>=(В-Г) + (Г-1), т. е. В-Р+Г=2.
Установим для этого два утверждения.
1. Из любой вершины многогранника в
любую другую можно пройти по незакрашенным
ребрам единственным способом.
Перед началом окраски ребер из любой
вершины многогранника в любую другую можно
было пройти по неокрашенным ребрам. Это
свойство будет сохраняться и после окраски каждого Рис. 62
очередного ребра. Действительно, пусть С и О — две вершины
многогранника. Если соединяющий их путь по незакрашенным ребрам не
содержит очередное раскрашиваемое ребро, то утверждение очевидно.
В противном случае можно изменить путь так, как это указано на
125
у—
рис. 63. Итак, по окончании раскраски любые две вершины
многогранника будут соединены путем, проходящим по незакрашенным ребрам.
Если бы между какими-то вершинами многогранника существовали
два различных пути, проходящих по незакрашенным ребрам, то нашелся
бы замкнутый путь, все ребра
которого были бы неокрашены, а это в
соответствии с нашими правилами
окраски невозможно. Утверждение
под номером 1) доказано.
Фиксируем некоторую вершину
А многогранника и пройдем по всем
незакрашенным путям, ведущим из
вершины А в остальные вершины.
Если какое-то ребро CD лежит на
С*—"—-^ двух таких путях и проходится в
р go разных направлениях, то в вершины
С и D из вершимы А ведут два пути
по незакрашенным ребрам, не содержащие ребро С£>, и, значит,
существует замкнутый путь по незакрашенным ребрам. Поскольку это
невозможно, то на каждом незакрашенном ребре можно указать стрелочкой
единственное направление движения из вершины А. Поставим теперь в
соответствие каждому незакрашенному ребру вершину многогранника,
на которую указывает стрелочка, присвоенная этому ребру. Из
утверждения, сформулированного выше под номером 1), следует, что это
соответствие между незакрашенными ребрами и отличными от А
вершинами взаимно однозначно, и потому количество незакрашенных ребер
многогранника равняется В—1.
Для доказательства того, что число закрашенных ребер равняется
Г—\, будем двигаться по поверхности многогранника, переходя с грани
на грань только через закрашенные ребра.
2. Из. любой грани многогранника в любую другую грань можно
пройти по поверхности многогранника, пересекая только закрашенные
ребра. Последовательность пересекаемых при этом ребер определяется
единственным способом.
Предположим, что существуют две грани с и d такие, что из с в d
нельзя пройти, пересекая только окрашенные ребра. Покрасим в синий
цвет внутренность всех граней многогранника, которых можно достичь,
выходя из грани с и пересекая окрашенные ребра. В синий цвет при
этом окрасится только часть граней многогранника, и, как легко видеть,
граница синей области будет состоять только из неокрашенных ребер.
Двигаясь по границе, мы получим замкнутый путь, состоящий из
неокрашенных ребер. А это противоречит правилам раскраски. Первое
из утверждений под номером 2) доказано.
Предположим, что существуют две грани, скажем, / и g, такие,
что из / в g можно пройти двумя способами, пересекая только окра-
(26
XJ
шенные ребра. Сотрем окраску с одного из пересекаемых при этом
ребер. Тогда, как легко видеть, по-прежнему из любой грани
многогранника в любую другую грань можно будет пройти через окрашенные
ребра. Выше доказано, что из справедливости утверждения под
номером 1) следует, что количество неокрашенных
ребер равно В—1. Так как количество
неокрашенных ребер изменилось, то утверждение 1)
нарушилось и, значит, появился замкнутый путь
по неокрашенным ребрам многогранника. Но
этот путь разбивает поверхность многогранника
на две части. Из граней, входящих в одну часть,
можно пройти в грани другой части, только
пересекая ребра указанного замкнутого пути, которые рИСі §4
не окрашены {см. рис. 64, где они обозначены
волнистой линией), и, значит, невозможно пройти, пересекая только
окрашенные ребра. П-олученное противоречие завершает
доказательство утверждений под номером 2).
Вычисление количества окрашенных ребер проводится теперь точно
так же, как и вычисление числа веокрашенных ребер с помощью
утверждения 1).
Второе решение Рассмотрим сферу с центров внутри
многогранника и с таким большим радиусом, что она содержит внутри
весь многогранник. Спроектируем все вершины и ребра многогранника
из центра сферы на ее поверхность. Тогда на поверхности возникнет
некоторая сеть точек и дуг, соответствующих вершинам и ребрам
многогранника. Эти точки и дуги мы по-прежнему будем именовать
вершинами и ребрами сети «а сфере. Ребрами сети сфера разобьется на
некоторое число кусков, равное числу Г граней многогранника.
Докажем теперь более общее, чем нужно нам, утверждение: для
любой совокупности точек на сфере и соединяющих их
непересекающихся ребер, при условии, что сеть связна, т. е. из любой вершины
в любую другую можно пройти по
ребрам сети, справедливо равенство
В-Р + Г = 2, (*)
где В — число вершин, Р — число
ребер, Г — число кусков, на которые
сеть разбивает сферу.
Предположим, что это
утверждение неверно, и рассмотрим сеть S
с наименьшим числом ребер, для которой равенство (*) не имеет
места. В этой сети должно быть не менее двух ребер, так как для сети
с одним ребром имеем или В = 2, Р=\, Г=1 (рис. 65) или В = 1, Я=1,
Г = 2 (рис. 66), и в любом случае равенство (*) выполняется. Итак,
в сети S имеется по крайней мере два ребра.
127
\
Назовем длиной пути, проходящего по линиям сети 5 на сфере,
количество ребер сети, составляющих этот путь, а расстоянием между двумя
вершинами — наименьшую длину пути, соединяющего по ребрам сети эти
вершины. Пусть А и С — наиболее удаленные друг от друга в только что
указанном смысле вершины сети S. Если у сети есть только одна
вершина А, то С=А. Выбросим из сети какое-либо ребро, выходящее из
вершины С, а в случае, если такое ребро единственно, то выбросим
и саму вершину С. Получится новая сеть Si, для которой число ребер
Р\ равно Р— 1.
Докажем, что в новой сети Si из вершины А можно пройти
в любую из вершин по ребрам сети Si, отсюда будет следовать, что
сеть Si связна. Допустим противное, что есть в сети Si вершина D,
в которую невозможно пройти из вершины А. Тогда в сети S все
пути из вершины А в вершину D идут через выброшенное ребро,
а потому и через вершину С. Значит, расстояние между вершинами А
и D больше, чем между вершинами А и С, что противоречит выбору
вершин А и С. Итак, сеть Si связна.
Поскольку в сети Si меньше ребер, чем в сети S, то числа вершин
В\, ребер Р\ и кусков Ги на которые сеть Si разбивает сферу, связаны
равенством В\ — Яі+Л = 2. В случае, если из вершины С выходит
единственное ребро, для чисел В\ и Г\ имеем В\=В — 1, Гі=/\ так что
В-Р+Г=(В, + 1)-(/>, +О+Л=В,-Р,-т-Л=2.
Если же в сети S из вершины С выходит более одного ребра, то
В\ — В, и поскольку выброшенное ребро разделяет разные куски сферы,
то Гі=Г— 1 (это следует из того, что куски лежат по разные стороны
замкнутого пути в сети S, содержащего выброшенное ребро). Значит,
в этом случае
В-Я+Г = В,-(Р, + 1) + (Г1 + 1)=В1-Р,+Г,=2.
Получаем, что сеть S, вопреки ее выбору, удовлетворяет
равенству (♦). Значит, исходное предположение неверно и равенство (*)
выполняется для всех связных сетей на сфере. Этим доказано также и
равенство, утверждаемое в условии задачи для каждого выпуклого
многогранника.
Часть третья
I. Задачи — шутки, задачи — загадки
129. По земле.
130. Две ноги мельника, ибо у кошек и котят не ноги, а лапы.
131. Надо один из пустых мешков вложить в другой такой же, а
затем в него насыпать смолотую пшеницу.
132. Скорее всего ничего не найдут.
128
133. Всего летело три утки, одна
за другой.
134. Повар сидел на стуле,
имеющем три ножки, пришла собака
и утащила куриную ногу. Повар
бросил стул в собаку, чтобы она
оставила куриную ногу.
У Корнея Чуковского на этот
счет есть стихотворение-загадка-
Две ноги на трех ногах,
А четвертая в зубах.
Вдруг четыре прибежали
И с одною убежали.
Подскочили две ноги,
Ухватили три ноги,
Закричали на весь дом —
Да тремя по четырем!
Но четыре завизжали
И с одною убежали.
135. Всадник на лошади.
136. За 4 минуты.
137. 2 землекопа.
138. Это были дедушка, его сын
и внук. Из этих троих человек двое
являются отцами и двое являются
сыновьями.
139. Этот человек родился
29 февраля, т. е. день рождения у
него бывает один раз в четыре года.
140. Так как полтина — это 50 копеек, то надо разделить 50
на ^. Выполнив деление, получим: 50:^=100 копеек=1 рубль.
141. Конечно, многие считают, что это будет число 111 111. На самом
деле это число равно 12 111, так как если к И тысячам, т. е. к 11 000,
прибавить И сотен, т. е. 1100, и 11 единиц, то будет 12 111.
II. Затруднительные ситуации
142. Человек вначале перевозит на другой берег козу, оставляя
волка с капустой; затем возвращается, забирает волка и перевозит его
на другой берег, а козу увозит с собой обратно. Оставляя козу на берегу,
человек перевозит к волку капусту, затем возвращается и перевозит
козу. Таким образом, на другом берегу оказываются вместе с человеком
волк, коза и капуста.
129
143. Вначале переправляются два оруженосца. Затем один из
оруженосцев возвращается и перевозит на другой берег третьего
оруженосца. После этого один из трех оруженосцев возвращается к своему
рыцарю и с ним остается на первом берегу, два других рыцаря
отправляются к своим оруженосцам. Затем один из рыцарей возвращается со
своим оруженосцем, оставляет его, а с собой забирает рыцаря,
оставшегося на этом берегу. Теперь остававшийся на другом берегу
оруженосец переезжает и забирает с собой одного из двух оруженосцев,
а следующим рейсом забирает последнего оруженосца.
Приведем таблицу, иллюстрирующую переправу рыцарей и их
оруженосцев. Обозначим рыцарей большими буквами А, Б, В, а их
оруженосцев соответственно малыми буквами а, б, в.
Первый берег Второй берег
А
а
А
•
А
•
•
•
•
•
в
•
в
•
Б В
б в
Б В
Р в
Б В
• •
• В
• в
• •
б в
• •
• в
• в
• •
а
б
б
I А Б
\а б
і А Б
\ а •
А Б
а б
^ \ А Б В
\ а б в
144. Приводим два решения этой задачи в виде таблиц, которые
показывают, сколько кваса остается в каждом бочонке после каждого
переливания.
Решение 1.
До переливания
После 1-го переливания
После 2-го переливания
После 3-го переливания
После 4-го переливания
После 5-го переливания
После 6-го переливания
После 7-го переливания
Бочонки
8 ведер 5 ведер 3 ведра
8
3
3
6
6
1
1
4
0
5
2
2
0
5
4
4
0
0
3
0
2
2
3
0
130
Решение 2.
До переливания
После 1-го переливания
После 2-го переливания
После 3-го переливания
После 4-го переливания
После 5-го переливания
После 6-го переливания
После 7-го переливания
После 8-го переливания
8 веде[
8
5
5
2
2
7
7
4
4
Бочонки
5
ведер 3 ведра
0
0
3
3
5
0
1
1
4
0
3
0
3
1
1
0
3
0
145. Приводим два решения этой задачи.
I человек
II человек
III человек
I человек
II человек
III человек
Полные
бочонки
2
2
3
3
3
1
Полные
наполовину
бочонки
3
3
1
1
1
5
Пустые
бочонки
2
2
3
3
3
1
146. Двадцать четыре девушки можно разместить так, как показано
на рис. 67, а шестнадцать девушек, как показано на рис. 68.
1
5
1
5
5
1
5
1
3
1
3
1
1
3
1
3
Рис 67
Рис 68
147. Начертим круг и, отметив на нем 30 палочек, поставим у каждой
из них номер от 1 до 30. Теперь, начиная счет с цифры 1, перечеркиваем
девятую палочку, затем восемнадцатую, затем двадцать седьмую и
продолжаем этот процесс, вычеркивая каждую девятую из незачеркнутых
ранее палочек. Таким образом будут перечеркнуты палочки с номерами
5, 6, 7, 8, 9, 12, 16, 18, 19, 22, 23, 24, 26, 27, 30.
131
Значит, купец просил матросов расставить тюки следующим
образом: 4 своих, 5 чужих, 2 своих, 1 чужой, 3 своих, 1 чужой, 1 свой, 2 чужих,
2 своих, 3 чужих, 1 свой, 2 чужих, 2 своих, 1 чужой.
Существует старинный способ, запоминания этой
последовательности. Необходимо помнить следующие 6 мужских имен:
Полуект, Аника, Павел, Елизар, Евтех, Влас
Если под каждой буквой а, встречающейся в этих именах, поставить
цифру I, под каждой буквой е — цифру 2, под каждой буквой и —
цифру 3, под каждой буквой о — цифру 4 и под буквой у — цифру 5, то
получим
Полуект, Аника, Павел, Елизар, Евтех, Влас.
452 131 12 231 2 2 1
Первая цифра 4 означает число своих тюков, а затем в этой
последовательности цифр чередуются количества чужих и своих тюков.
III. Угадывание чисел
148. Для нахождения задуманного числа надо разделить
объявленный результат на 9 и затем умножить частное на 2.
Пример. Предположим, что задумано число 12. После утроения
этого числа получим число 36, половина этого числа равна 18; утроив
ее, получаем 54. Если теперь 54 разделить на 9, то получится 6, т. е.
половина задуманного числа.
Обоснование. Пусть кто-то задумал четное число, которое
обозначим через 2ft. Тогда в результате предложенных арифметических
действий получится число
( ( (2ft)X3):2)X3 = 9ft.
Разделив его после объявления на 9 и удвоив результат, найдем
задуманное число 2ft.
149. Для нахождения задуманного числа надо разделить
объявленный результат на 9, затем то, что получится, удвоить и, наконец, отнять 1.
Пример. Предположим, что задумано число 7; после его утроения
получаем число 21, прибавляя к нему число 3, получим 24; разделив 24
на 2 и опять результат утроив, получим число 36. Если теперь это число
разделить на 9, то в частном получим 4, удвоив число 4 и отняв единицу,
получим задуманное число 7.
Обоснование. Пусть кто-то задумал нечетное число, которое
обозначим через 2ft+1. После утроения и прибавления числа 3
получим число 6ft+6. Разделив это число на 2, получим число 3ft+ 3. Далее
(3ft + 3)X3 = 9ft + 9.
132
Частное от деления числа 9fe+9 на число 9 равно fe+І; удваивая это
число и отнимая 1, находим задуманное число 2£+1-
150. Для нахождения задуманного числа надо разделить
объявленный результат на 9, затем умножить частное на 2, если при нахождении
его не прибавлялось число 3. Если же в результате предложенных
вами действий прибавлялось число 3, то объявленный результат надо
разделить на 9, полученное частное умножить на 2 и затем отнять 1.
Пример. Предположим, что задумано число 9. Утраивая его,
получаем 27. Прибавляя к числу 27 число 3, получим 30. Половина от 30
равна 15. Утроив 15, получаем 45. Частное от деления этого числа на 9
равно 5. Умножая 5 на 2 и отнимая 1, получаем задуманное число 9.
Обоснование. Пусть задумано некоторое число k. После его
утроения получим 3k. Если число 3k — четное, то оно имеет вид 6т,
где k = 2m, после деления на 2 имеем число Зт, утраивая его,
получаем 9га, и для нахождения числа k надо объявленный результат 9т
разделить на 9 и умножить на 2, тогда получим задуманное число
k = 2m.
Если после утроения числа k получим нечетное число 3k, то это
означает, что k нечетно, т. е. fe=2m+l, и после прибавления к числу
3£ = 3 (2т + 1) числа 3 получим число 6т+ 6. Разделив это число на 2,
получаем Зт + 3, умножая на 3, имеем
(Зт + 3)ХЗ = 9т + 9.
Для нахождения числа k надо объявленный результат 9т+ 9
разделить на 9, полученное частное умножить на 2 и от этого числа отнять 1,
получим задуманное число 2т + 1 = k.
Замечание. Для угадывания задуманного числа необходимо
знать, прибавлялось ли число 3 в процессе вычислений. Это можно
сделать, не вызывая подозрений у человека, задумавшего число.
Действительно, если было задумано нечетное число, то после предложения
разделить на 2 ваш товарищ сам скажет, что число не делится. Тогда
ему нужно предложить прибавить число 3, а затем разделить на 2.
151. Для нахождения задуманных чисел надо запомнить табл. 6,
которая по объявленной последней цифре определяет задуманные числа.
Таблица 6
Последняя цифра
результата
Задуманные
числа
1
1; 2
2
8; 9
3
7; 8
4
4; 5
5
5; 6
6
6; 7
7
3; 4
8
2; 3
Пример. Пусть задуманы числа 3 и 4. Перемножая их,
получаем 12, вычитая из этого числа наименьшее из загаданных чисел,
133
имеем 9, после умножения чисел 9 и 3 получаем число 27. Последняя
цифра результата 7, поэтому из табл. 6 видно, что были загаданы
числа 3 и 4.
Обоснование. Пусть задуманы числа к и £+1, где l<Ife<8.
Тогда произведение этих чисел равно k (k + 1) = к*-\-к. Если из
последнего числа вычесть меньшее из чисел к, то получим кг. После
умножения этого числа на к получим к3.
Возводя последовательно числа от 1 до 8 в куб, получаем:
13=1, 3' = 27, 53=125, 7» = 343,
23 = 8, 43 = 64, 6Э = 216, 83 = 512. (*)
Каждое из полученных чисел оканчивается на одну из цифр от 1
до 8 и никакие два числа не оканчиваются на одну и ту же цифру.
Поэтому, если помнить таблицу кубов чисел от 1 до 8, то по
последней цифре куба некоторого числа можно сказать, какое число
возводилось в куб. Так, например, если вам объявляют, что после проведенных
операций получилось число, последняя цифра которого есть 3, то вы
говорите, что были загаданы числа 7 и 8, поскольку только одно число 7
после возведения в куб имеет последнюю цифру 3.
Замечание. Можно запомнить только меньшие из чисел второй
строки таблицы Если объявленная цифра равняется 1, 4, 5 или 6
(на эти цифры оканчиваются квадраты целых чисел), то она
совпадает с меньшим из задуманных чисел. В остальных случаях меньшее
из задуманных чисел равно дополнению объявленной цифры до 10.
152. Для нахождения задуманного числа надо из объявленного
числа извлечь корень квадратный, а затем вычесть число 1.
Пример. Пусть кто-либо задумал 13. В результате предложенных
действий над этим, числом вам будет объявлено число
13X13 + 2X13+1 = 196
Извлекая из него корень квадратный и вычитая 1, имеем
7196=14, 14-1 = 13,
т е. получим задуманное число.
Обоснование. Пусть кто-либо задумал некоторое число к.
После предложенных арифметических действий получится число
k-k + 2-k+\ = (k + \)2.
Это число будет объявлено. Для нахождения задуманного числа нужно
из числа (k+ 1)2 извлечь корень квадратный, получится число fe+ 1.
Вычитая из него 1, получим число к, которое и было загадано.
153. Зачеркнутая цифра есть то наименьшее натуральное число,
которое надо добавить к сумме цифр объявленного числа, чтобы
получить число, делящееся на 9.
134
Заметим, что если сумма цифр объявленного числа уже делится на 9,
то, значит, была вычеркнута цифра 9
Пример Предположим, что вы написали число
-132354 (1+3 + 2+3 + 5 + 4 = 18).
Пусть кто-либо, умножив это число, например, на 7, в полученном
произведении 926 478 зачеркнул цифру 6 и, переставив цифры, объявил
результат 79 482. Находя сумму цифр результата, вы получаете 30.
Ближайшее число, большее 30 и делящееся на 9, есть 36 Следовательно, как
раз цифра 6 и есть зачеркнутая цифра.
Обоснование. Способ угадывания опирается на то, что разность
между любым числом и суммой его цифр всегда делится на 9. Этот
факт уже использовался ранее при решении задач 42 и 43. Докажем
его. Пусть
Л=а„а„_і ... аіао=10"а„+10"_,а„_і+ ... +10аі+а0 —
натуральное число, записываемое п+1 цифрой. Разность между этим
числом и суммой его цифр равна
А — (а„ + а„_і+ ... +а,+ао) =
= а„ (10"-1)+а„_, (Ю"-'-1)+ . . +а, (10-1) =
= а„-99 ... 9 + а„_,-99 ... 9+ ... +а,-9
га га—1
и, следовательно, делится на 9.
Перейдем теперь к обоснованию способа угадывания. Пусть
В — нацисанное вами число, сумма цифр которого делится на 9. Из
сказанного выше следует, что и само число В делится на 9. После
того как это число было умножено на некоторое целое число,
получилось число С, также делящееся на 9. Значит, сумма цифр числа С
делится на 9. Если зачеркнуть любую цифру а числа С, получившееся
в результате число D будет иметь сумму цифр, на а меньшую, чем сумма
цифр числа С.
Так как при перестановке цифр их сумма не меняется, то
зачеркнутая цифра всегда будет равна наименьшему натуральному числу
(0 по условию не зачеркивается), которое необходимо добавить к
сумме цифр объявленного результата, чтобы получить число,
делящееся на 9.
154. Зачеркнутая цифра есть то число, которое надо добавить
к объявленному числу, чтобы получить ближайшее число, большее, чем
объявленное, и делящееся на 9
Заметим, что если объявленное число уже делится на 9, то, значит,
была зачеркнута цифра 9.
Пример. Пусть кто-либо написал число, например, 13456789.
Поскольку сумма цифр этого числа равна 43, то приписываем спереди
его или, сзади цифру 2, пусть цифру 2 приписали спереди, тогда
135
получим число 213 456 789. Пусть это число умножили на 5 и в
полученном произведении 1 067 283 945 зачеркнули, например, цифру 6.
Вам будет объявлен результат
1+7+2 + 8 + 3+9 + 4 + 5 = 39.
Ближайшее число, большее 39 и делящееся на 9, есть 45. Значит,
6 (45 — 39=6) —как раз та цифра, которая была зачеркнута.
Обоснование то же, что и в задаче 153.
155. Зачеркнутая цифра есть то число, которое надо добавить к
объявленному числу, чтобы получить ближайшее число, большее, чем
объявленное, и делящееся на 9.
Заметим, что если объявленное число уже делится на 9, то, значит,
была зачеркнута цифра 9.
Пример. Пусть кто-либо написал число 121 314 152 782, а
переставив в нем цифры, написал число 812 213 154 712. Разность этих чисел
равна
812 213 154 712—121 314 152 782 = 690 899 001 930.
Пусть в этом числе зачеркнули, например, цифру 3. Сумма
оставшихся цифр равна 51. Ближайшее число, большее 51 и делящееся на 9,
есть число 54. Значит, 3 (54 — 51=3)—как раз та цифра, которая
была зачеркнута.
Обоснование. Числа А и В имеют одинаковую сумму цифр S.
Так как разности A — S и В — S делятся на 9 (см. решение задачи
153), то и число С=А— В= (A — S) — (В — $) делится на 9. Значит, и
сумма цифр числа С делится на 9. Далее доказательство проводится
так же, как и в решении задачи 153.
Т56. Зачеркнутая цифра есть то число, которое надо добавить к
объявленному числу, чтобы получить ближайшее число, большее, чем
объявленное, и делящееся на 9.
Заметим, что если объявленное число уже делится на 9, то, значит,
была зачеркнута цифра 9.
Пример. Пусть кто-либо написал число 782 345. Сумма цифр
этого числа равна 29. Разность этих чисел есть число 782 316. Если
зачеркнуть в нем некоторую цифру, например, 8, то сумма оставшихся
цифр равна 19. Ближайшим числом, большим 19 и делящимся на 9,
является число 27. Разность 27—19 = 8 как раз и есть зачеркнутая
цифра.
Обоснование. Справедливость предложенного способа
угадывания зачеркнутой цифры следует из того, что разность между числом
и суммой его цифр делится на 9, и из рассуждений, приведенных
в решении задачи 153.
157. Приводим ответ из старинной книги:
«...После чего [после проделанных арифметических действий]
спрося его [старшего] о сумме, отбросить первую от левой руки цифру
136
и приложить оную к первой же от правой руки цифре. Сумма будет
искомая между двумя человеками разность лет старости».
Это надо понимать так: из объявленного числа нужно отнять 100
и к полученному числу прибавить 1.
Пример. Пусть возраст младшего равен 23 годам, а старшего
37 годам. Тогда, вычитая из числа 99 число 23, получим число 76.
Старший, прибавив к этому числу число, равное своему возрасту,
т. е. 37, объявит результат 113. Отбросив крайнюю слева цифру этого
числа и добавив к 13 единицу, вы объявляете, что возраст старшего1
на 14 лет больше возраста младшего: 37 — 23=14.
Обоснование. Пусть возраст старшего равен х, а младшего у.
Тогда после выполнения предложенных вами арифметических действий
будет объявлено число
(99-(/)+*=99+(*-0).
Отсюда искомая разность х—у равна
99+(*—у)— 99.
т. е. из объявленного результата надо отнять число 99 или, что то же
самое, отнять число 100 и прибавить 1.
158. Для угадывания дня рождения надо сложить два объявленных
результата. Это число и дает ответ.
Пример. Пусть у кого-либо день рождения 23-го числа некоторого
месяца. Для угадывания этого числа надо последовательно выполнить
следующие действия:
23X3 = 69, 69=9X7 + 6, 7X3 = 21, 6:3=2, 21+2=23.
Мы получили, что 23 — день рождения.
Обоснование. Пусть днем рождения будет т-е число некоторого
' месяца. После умножения числа т на 3 получим число 3/и, после
деления числа Зт на 9 получим частное k и остаток р такие, что
Зт = 9й + р, (*)
где или р = 0, или р = 3, или р = 6. Из равенства (*) следует, что
т = 3& + /, где или /=0, или /=1, или /=2. После умножения
частного k на 3 будет объявлено число 3/г, а после деления остатка р на
3 будет объявлено число /, т. е., действительно, для угадывания дня
рождения необходимо сложить объявленные числа': т = 3& + /.
159. Надо от объявленного числа отнять 320, затем полученный
результат разделить на 100.
Пример. Пусть число лет некоторого человека равно 37. Умножая
это число на 2 и прибавляя 4, получим 78. Умножая это число на 5,
имеем 390; прибавив 12, находим 402; умножая на 10, получаем 4020.
Вычитая из этого числа 320, имеем 3700. Если это число разделить
на 100, то получим число 37.
137
Обоснование. Пусть число лет некоторого человека равно т
После выполнения всех предложенных арифметических действий
получится число
((2т + 4)Х5+12)ХЮ
Это число можно записать в виде 100т+ 320. Если от него отнять 320,
то получится число 100т. Разделив последнее число на 100, будем
знать искомое число лет т.
160. Для каждого написанного числа А допишем число, цифры
которого получаются как дополнение до 9 соответствующих цифр числа А.
Если было написано т чисел, состоящих из Я цифр, то сумма
этих т чисел и m чисел, написанных вами по выше объявленному
правилу, равна 10"т — т.
Пример 1. Пусть написаны числа 327 564, 289 173 и 451027
Вы пишете числа 672 435, 710 826, 548 972 и объявляете сумму всех
шести чисел, равную
106-3 —3 = 3 000 000 —3 = 2 999 997.
Пример 2. Пусть написаны числа 932 и 127. Вы приписываете
числа 67 и 872 и объявляете сумму всех четырех чисел, равную
103-2 —2= 1998
Пример 3. Пусть написаны числа 9999, 1235, 9872. Вы пишете
числа 8764 и 127 и объявляете сумму
104.3-3 = 29 997.
Обоснование. 1. Если написано (п+ 1)-значное число
а„а„-і .. ао, а„Ф0,
то вы пишете число 6„6„_і ... Ьц, где 6, = 9 —а,, г'=0, I п Ясно,
что сумма чисел
а„а„-и. а0 и ЬпЬп-\-- йо
равна
99 ... 9=10"+' — 1
л +1 раз
Если было написано т. чисел, то сумма этих т чисел и т чисел,
написанных вами, равна
(10" + 1-1) m = 10"+1m-m
(см. пример 1).
2. Если а„ = 9, а„_і=^=9, то вы пишете число
138
6«-іЬ»-2... bo.
где 6, = 9 —а,, і = 0, I п— 1 Сумма чисел
а„а„-і ... ао и &„_|6„_г .. Ьа
равна
99 ... 9=10"+'-і.
п+\
Дальше рассуждаем аналогично случаю 1 (см. пример 2).
3. Если среди т написанных чисел есть число, записываемое
одними девятками, то для него не нужно писать никакого дополнительного
числа (см. пример 3).
161. Выбрав одно из трех написанных чисел, вы вычитаете из него
число 2 и к полученному числу приписываете спереди цифру 2. Это
число вы записываете на втором листе бумаги, а затем пишете на первом
листе два числа, получающиеся из оставшихся двух чисел первого листа,
следующим образом, каждая цифра числа, написанного вами,
является дополнением до цифры 9 цифры соответствующего разряда ранее
написанного на первом листе числа.
Пример. Пусть кто-либо написал числа 12541, 72953 и 84623.
Вычтем 2 из числа 72 953 и к получившейся разности 72 951 припишем
слева цифру 2. Результат этих операций — число 272 951 — запишем
на втором листе бумаги На первый лист допишем числа 87 458 и
15 376, равные соответственно 99 999—12 541 и 99 999—84 623 Сумма
пяти чисел, написанных на первом листе, равна, как легко проверить,
272 951, т. е числу, записанному на втором листе бумаги.
Вместо числа 272 951 можно было бы на втором листе написать
число 212 539, а на первый лист дописать числа 27 046 и 15 376. Или
на второй лист можно было бы написать число 284 621, а на первый
лист числа 87 458 и 27 046.
Обоснование. Пусть А — то из написанных на первом листе
чисел, из которого вычитается 2, а к результату слева приписывается
цифра 2 Оставшиеся числа обозначим В и С. В соответствии с
указанным выше правилом на первый лист будут дописаны числа
99 999 —В и 99 999 —С.
Тогда сумма всех пяти чисел, написанных на первом листе, будет равна
Л+2-99 999 = 2-10б + Л— 2.
Для того чтобы получить ее, необходимо из числа А вычесть 2 и слева
к результату приписать цифру 2 (число А записывается пятью цифрами).
Но именно это число должно быть записано на второй лист.
Если на первом листе первоначально были записаны не 3, а т чисел,
2<т^10, то вместо 2 вычитать и приписывать слева нужно будет
цифру m — 1. На первый лист нужно будет дописать не два, a m — 1 число,
образованные по правилу, которое указано в начале решения.
139
IV. Игры с предметами
162. Для того чтобы узнать, кто из присутствующих взял монету,
нужно после объявления результата вычесть из него число 25 и
полученную разность разделить на 10.
П р и м.е р. Пусть монету взял тот человек, порядковый номер
которого равен 7. Тогда имеем (7X2 + 5) Х5=95. Если из этого числа
вычтем 25 и полученный результат — число 70 — разделим на 10, то
получим 7, т. е. порядковый номер человека, взявшего монету.
Обоснование. Пусть порядковый номер человека, взявшего
монету, есть т. После умножения т на 2 получим 2т, прибавив 5 и
умножив полученную сумму на 5, имеем (2т+ 5) -5= Ют+ 25. Если
теперь от числа 10т + 25 отнять число 25 и полученную разность Ют
разделить на 1-0, то получится число т, т. е. как раз число, являющееся
порядковым номером человека, взявшего монету.
163. Все возможные случаи взятия кубиков, орехов и остатков
орехов видны из табл. 7 (здесь и далее играющим присвоены номера,
равные числу орехов, данных им первоначально).
Таблица 7
I человек
II человек
III человек
Взято всего орехов
Остаток
орехов
Дано
1 оре*
2 ореха
3 ореха
6
18
Возьмут кубики
Красный
Красный
Синий
Синий
Желтый
Желтый
Синий
Желтый
Красный
Желтый
Красный
Синий
Желтый
Синий
Желтый
Красный
Синий
Красный
2 + 6+15 = 23
2+10 + 9 = 21
3 + 4+15 = 22
3+10 + 6=19
5 + 4 + 9 =18
5+6 + 6 = 17
1
3
2
5
6
7
Из таблицы видно, что в каждом из шести возможных случаев
распределения кубиков у играющих остатки однозначно решают вопрос
о том, кто какой кубик взял. Имея под рукой таблицу и зная остаток
орехов, вы сразу же можете сказать, какой кубик взял первый человек,
какой второй человек и какой кубик взял третий человек.
Есть старинный способ запоминания этой таблицы.
Напишем шесть слов в следующем порядке:
I II III V
Валентин Герасим Тащите Екима
VI VII (*)
Приставьте Пимена
140
А теперь надо запомнить правило:
1) смотрим, сколько орехов на столе осталось, и берем то слово
из (*), которое находится под цифрой, равной числу оставшихся
орехов;
2) номер слога с буквой «а» указывает номер человека, взявшего
красный кубик;
3) номер слога с буквой «е» указывает номер человека, взявшего
синий кубик.
Если, например, на столе осталось 2 ореха, то вы берете второе;
слово: «Герасим». В нем буква «а» находится во втором слоге. Следова'-
тельно, красный кубик взял второй человек; буква «е» находится в первом
слоге, значит, синий кубик взял первый человек.
Если остаток равен 7, то берем слово «Пимена». В нем буква «а»
находится в третьем слоге. Следовательно, красный кубик в этом случае
взял третий человек.
Буква «е» находится во втором слоге, значит, синий кубик взял
второй человек.
Есть и другой способ угадывания. Прибавим к количеству
оставшихся кубиков наименьшее положительное число такое, чтобы сумма
делилась на 3. Это число равно номеру игрока, взявшего синий кубик.
Если теперь сумму разделить на 3 и частное вычесть из 4, то получится
номер игрока, взявшего желтый кубик. Оставшийся игрок взял красный
кубик.
В первом из разобранных выше примеров наименьшее
положительное число, которое нужно добавить к количеству оставшихся кубиков,
чтобы получить число, делящееся на 3, равно 1. Значит, синий кубик
взял первый из. играющих. Частное от деления суммы (2+1) на 3
равно 1. Поэтому желтый кубик взял игрок, номер которого есть 4— 1=3.
В справедливости этого правила легко убедиться, сверившись с
таблицей, но можно обосновать его и непосредственно. Обозначим номер
игрока, взявшего красный кубик, буквой х, номер взявшего синий
кубик — буквой у, номер взявшего желтый кубик — буквой г. Игрок,
взявший красный кубик, возьмет со стола х орехов, взявший синий
кубик — возьмет со стола 2у орехов, а тот, у которого желтый кубик,
возьмет со стола 4г орехов. Значит, на столе останется
18 — х — 2у — 4г
орехов. Так как сумма номеров играющих равна шести, т. е.
x+y + z=6,
то на столе останется 12 — у — Зг орехов. Из неравенства 1^(/<3
следует, что у есть наименьшее положительное число, которое нужно
прибавить к количеству оставшихся орехов, чтобы получить число,
делящееся на' три. Если сумму, равную 12 —Зг, разделить на 3, получится
4 —z, откуда и следует справедливость правила.
141
164. Для того чтобы узнать, кто из участников игры взял какой
предмет, нужно вычесть из 72 объявленное число, затем разность
разделить на 9 с остатком Частное покажет номер предмета, взятого первым
человеком, а половина остатка даст номер предмета, взятого вторым
человеком. Зная, какие предметы взяли первый и второй человек, легко
определить, какой предмет взял третий человек
Пример. Пусть первый человек взял третий предмет, второй
человек взял второй предмет, а третий человек взял первый предмет Тогда
3X3+10X2+12X1=41, 72-41=31, 31=9X3 + 4.
Частное 3, действительно, есть номер предмета, взятого первым
человеком, а половина остатка 4, равная 2, совпадает с номером
предмета, взятого вторым человеком.
Обоснование. Пусть первый человек взял предмет с порядковым
номером х, второй человек взял предмет с порядковым номером у, а тре-
142
тий — с порядковым номером г. После выполнения предложенных
арифметических операций получится число Ъх-\- 10</+ 12г.
Так как x-\-y-\-z — 6, то г = 6 —л: — у и результат вычислений с
номерами равен
Зх+ \0у+ 12 (6-х-у) = 72-9х-2у.
Если этот результат вычесть из 72, то разность будет равна 9х + 2у.
Частное от деления этого числа на 9, ввиду неравенства І^і/г^З,
будет равно х, а остаток 2у. Половина числа 2у равна у, откуда
и следует утверждение.
165. Чтобы определить, кто взял какой предмет, надо из 260 вычесть
объявленное число и разность разделить с остатком на 24, тогда частное
покажет номер предмета, взятого первым человеком. Если остаток
разделить на 5 с остатком, то частное от второго деления покажет номер
предмета, взятого вторым человеком, а остаток — номер предмета,
взятого третьим человеком. После этого ясно, какой предмет взял четвертый
человек.
Пример. Предположим, что первый человек взял третий предмет,
второй человек взял первый предмет, третий человек взял четвертый
предмет, а четвертый человек взял второй предмет. В результате
предложенных арифметических операций получится число
3X2+1X21+4X25 + 2X26=179.
Вычитая эту сумму из числа 260, получим число 81. Если это число
разделить на 24, то частное покажет, какой предмет взял первый человек
(81=3X24+9), т. е. первый человек взял третий предмет.
Остаток от деления 81 на 24 равен 9. Если этот остаток
разделить на 5, то частное покажет; какой предмет взял второй человек,
а остаток — какой предмет взял третий человек. Так как 9=1X5 + 4, то
второй человек взял первый предмет, а третий человек взял четвертый
предмет. Следовательно, четвертый человек взял первый предмет.
Обоснование. Предположим, что первый человек взял предмет,
порядковый номер которого х, второй человек взял предмет, порядковый
номер которого равен у, третий взял предмет с порядковым номером г,
а четвертый — с порядковым номером и. После выполнения
предложенных арифметических действий получится число
2* + 21г/ + 252 + 26«.
Так как x-\-y-{-z + u = 10, то
и = Ю-(х+у + г),
и результат вычислений равен
2x + 21</ + 25z + 26 (IQ-x-y — z) =260 — 24х-Ъу — г.
Если этот результат вычесть из числа 260, получится число 24* +
143
+5t/ + z. Частное от деления его на 24 (ввиду неравенства 1 ^.Ьу + г^.
^5-4+ 3 = 23) равно х, а остаток 5у-\-г Частное от деления числа
5{/ + г на пять (ввиду неравенства 1 ^г^4) равно у, а остаток г, откуда
следует утверждение.
166. Надо из объявленного числа вычесть 25, тогда первая цифра
полученной разности будет числом очков, выпавшим на первом кубике,
а вторая — числом очков, выпавшим на втором кубике.
П р"и м е р. Пусть при бросании двух кубиков выпали очки 2 и 4.
Проделывая последовательно предложенные арифметические действия,
в результате мы получим (2X2 + 5) Х5 + 4 —25=24. откуда видно, что
первая цифра числа 24 есть число очков, выпавших на одном кубике,
а вторая цифра — цифра 4 — число очков, выпавших на другом кубике
Обоснование Пусть в результате бросания двух кубиков числа
выпавших на кубиках очков соответственно равны а и Ь. Умножая
число а на 2 и прибавляя 5, получим число 2а+ 5, умножая это число
на 5, имеем число 10а+ 25, прибавив к нему число Ь и вычитая 25,
имеем число \0a + b — ab, откуда следует, что первая цифра есть число
очков, выпавших на первом кубике, а вторая цифра есть число очков,
выпавших на втором кубике.
167. Первая слева цифра результата предложенных вами
арифметических действий равна числу кубиков, взятых первым человеком, вторая
за ней цифра равна числу кубиков, взятых вторым человеком, третья
цифра — числу кубиков, взятых третьим человеком, четвёртая —
четвертым и т. д.
Пример. Предположим, что четверо из присутствующих
вынимают кубики, причем первый взял 5 кубиков, второй — 7 кубиков,
третий — 8 кубиков, четвертый — 9 кубиков.
В результате предложенных арифметических действий первый
человек получит число (5X2—1)Х5 = 45 и сообщит это число второму по
порядку человеку.
Второй человек проделывает следующие действия:
(((45 + 7)+5)Х2-1)Х5;
он получит число 565, которое сообщит третьему человеку. Третий
человек проделает аналогичные действия
(((565 + 8)+5)Х2-1)Х5
и получит число 5775.
Четвертый человек после сообщения ему числа 5775 добавит к
этому числу число вынутых им кубиков да еще прибавит число 5 и
объявит результат 5789. Первая цифра этого числа равна числу
кубиков, взятых первым человеком; вторая за ней цифра равна числу
кубиков, взятых вторым человеком, третья цифра — числу кубиков, взятых
третьим, и четвертая — четвертым.
144
Обоснование. Пусть имеется k человек, каждый из которых
имеет свой порядковый номер от 1 до ft, и количества кубиков, взятых
каждым, соответственно равны аь а2,..., ак.
После того как первый человек выполнит предложенные ему
арифметические действия, он получит число
Л, = (2аі — 1)-5=10аі — 5,
которое объявит второму по порядку человеку. Этот второй человек
в результате предложенных ему арифметических действий получит число
Л2= ((/1,+а2 + 5) -2—1) ■5=100а1 + 10а2 —5,
которое сообщит третьему человеку. Третий человек проделает
аналогичные арифметические действия и получит число
/1з=((Л2 + аз + 5)-2-1).5=103а, + 102а2+10аз-5,
которое сообщит четвертому человеку. Все аналогично будет
повторяться до человека с порядковым номером ft — 1. Этот человек получит
сумму
Л4-1 = ((Л*_2 + а»_, + 5)-2-1)-5 = 10Л*-2 + 10а*-1 + 45 =
= Ю(10*-*ві + 10*-9в2+ ... +10а*_2-5) + 10а*_І+45 =
. =10*-'аі + 10*-*а2+ ... +10а*_і —5
и объявит ее человеку, порядковый номер которого ft. Последний
человек к числу Ak-\ добавит число своих кубиков, увеличенное на
5, и объявит вам число, равное
Л*_І+а* + 5=10*-,а, + 10*-2а2+ ... +10а*-,+а*.
Это число можно записать в виде а\аг ... о*, откуда следует наше
утверждение.
168. Если после предложенных операций получится нечетное число,
то в правой руке было нечетное число предметов, если же получится
четное число, то в правой руке было четное число предметов.
Обоснование. Поскольку общее число предметов выражается
нечетным числом, то в одной из рук будет нечетное число предметов,
а в другой — четное число предметов. Очевидно, что если некоторое число
умножить на 2, то получится четное число. Так как число, выражающее
количество предметов в левой руке, умножается на 2 и это произведение
складывается с произведением количества предметов в правой руке на 3,
то сумма будет четной, если в правой руке было четное число предметов,
и будет нечетной, если в правой руке было нечетное число предметов.
169. Карточка с задуманным числом будет нижней в стопке из
8 карточек, указанных в последний раз. Это легко понять, если
представить, куда будет попадать карточка с задуманным числом при
каждом раскладывании карточек.
В момент после того, как карточки были разложены на две стопки
в первый раз, затем опять сложены в одну стопку, как указано в условии
145
задачи, карточка с задуманным числом находится среди восьми
нижних карточек. Эти восемь карточек при следующем раскладывании'
распределятся между двумя стопками поровну. Значит, после того, как
карточки будут собраны в одну стопку второй раз, карточка с
задуманным числом будет находиться среди четырех нижних карточек. В третий
раз она будет среди двух нижних карточек, и наконец, после четвертого
раскладывания карточек загаданная карточка будет нижней в одной из
стопок Именно это и утверждалось вначале.
170. После того как будет указана буква, на которую пришелся
счет 40, вы должны, начиная с нее, считать против часовой стрелки
до 8. Загаданной будет буква, на которую пришелся счет 8.
Пример. Пусть ваш товарищ загадал букву Л. Тогда, начав
считать с нее по часовой стрелке, при счете 40 он попадет на букву Б.
Считая от нее против часовой стрелки, при счете восемь попадем на
букву Л.
Объяснение. Буква с номером 40 при счете по часовой стрелке
будет первой при счете против часовой стрелки, буква с номером 39 будет
второй при счете против часовой стрелки и т. д. Номер 8 при счете
против часовой стрелки будет иметь буква, которая при счете па часовой
стрелке получила номер 33. По кругу написано 1'6 букв. Значит, буквы
с номерами I, 17, 33 будут совпадать и буква с номером 33 при счете
по часовой стрелке будет задуманной.
171. Для угадывания нужно считать буквы в направлении против
часовой стрелки, начиная с объявленной буквы. Буква с номером
5 будет загаданной.
Пример. Предположим, что была загадана буква Г. При счете от
буквы М против часовой стрелки буква Г получит номер девять.
Продолжая счет, присвоим букве Л номер 10, букве М — номер 11 и т. д.
Номер 19 придется на букву 3. Считая от нее против часовой стрелки,
при счете 5 попадем на букву Г.
Объяснение; Будем ставить рядом с каждой считаемой буквой
крестик. Сосчитав от буквы М до загаданной! буквы, мы расставим
крестики рядом со всеми буквами вдоль.дуги окружности от буквы М до
задуманной. Если бы продолжение счета после задуманной буквьі
начиналось не с буквы Л, а с буквы А, то нам пришлось, бы последовательно
заполнять крестиками вторую дугу окружности между буквами М. и
загаданной. При счете 12 рядом с каждой из написанных букв стоял бы;
крестик, а при счете 13 мы попали бы на загаданную букву. Так как
продолжение счета начинается не с буквы А, а с буквы Л, т. е. на 2 буквы
раньше, то на загаданную букву мы попадем не при счете 13, а при
счете 15.
Отгадывание сводится к тому, чтобы, зная букву с номером 19, найти*
букву с номером 15. Это делается именно так, как указано в условии,
задачи.
ПРИЛОЖЕНИЯ
I. О старинной русской нумерации
В одной из русских рукописей XVII века читаем мы следующее:
«. .знай же то, что есть сто и что есть тысяща, и что есть тма, и что
есть легион, и что есть леодр...», «...сто есть десятью десять, а тысяща
есть десять сот, а тма есть десять тысящ, а легион есть десять тем,
а леодр есть десять легионов.. ».
В старину на Руси цифры обозначались буквами. Для указания
того, что знак является не буквой, а цифрой, сверху над ним ставился
специальный знак« ^^ », называемый «титло». Вот, например, как
записывались первые девять чисел:
1
а
2
Ь
3
f
4
X
5
f
6
3
7
%
8
И
9
ЯЬ
Десятки обозначались так:
10
т
20
і<
30
л
40
1\\
50
н
60
3
70
0
80
п
90
ч
а сотни так:
100
т
200
т
300
'т
400
ч
500
^
600
X
700
f
800
/ '
900
ц
147
Тысячи обозначались теми же буквами с «титлами», что и
первые девять цифр, но у них слева внизу ставился знак « jf »,
например,
t А-1000, Б-2000, Jj-'i
_ -7000.
Десятки тысяч назывались «тьмы», их обозначали, обводя знаки
единиц кружками, например, числа 10 000, 20 000, 50 000
соответственно записывались следующим образом:
®. ®. ©•
Отсюда и произошло название «Тьма народу», т. е. очень много
народу.
Сотни тысяч назывались «легионами», их обозначали, обводя знаки
единиц кружками из точек. Например, числа 100 000, 200 000
соответственно имели обозначение
Л), (Б).
Миллионы назывались «леодрами». Их обозначали, обводя знаки
единиц кружками из лучей или запятых. Так, числа 10е и 2-106
обозначались соответственно
;,ЛЧ5 m *,Л."> \ Ь,с или ' U С«
''/lux* '»«'ѵ '''ПК4" ''<хѵ
Десятки миллионов назывались «воронами» или «вранами» и их
обозначали, обводя знаки единиц кружками из крестиков или ставя по
обе стороны буквы букву К, например, числа 107, 2-Ю7, обозначались
соответственно
{Л) ИЛИ КАК, (Б) ИЛИ КВК .
Сотни миллионов назывались «колодами».
«Колода» имела специальное обозначение: над буквой и под буквой
ставились квадратные скобки. Например, число 108 записывалось
в виде
А.
148
Числа от 11 до 19 обозначались так:
11
^т
12
Si
13
14
Ш
16
пТи ^ВТ
17
Я
18
m
19
, '
-И
Остальные числа записывались буквами слева направо, например,
числа 544 и 1135 имели соответственно обозначения
фмд, Шь.
При записи больших чисел, чем тысячи, в практической
деятельности (счете, торговле и т. д.) часто вместо «кружков» знак «jf»
ставили перед буквами, обозначавшими десятки и сотни, например, запись
,<)>мд. ,<р\д
означает числа соответственно 500 044 и 540 004.
В приведенной системе обозначения чисел не шли дальше ты,сяч
миллионов. Такой счет назывался «малый счет». В некоторых рукописях
авторами рассматривался и «великий счет», доходивший до числа 1050.
Далее говорилось: «И более сего несть человеческому уму разумети».
II. Старинные русские меры длины
Что это такое:
«Поутру с сажень, в полдень — с пядень,
а к вечеру через поле хватает»?
(Тень )
Малые старинные русские меры длины — пядь и локоть.
Пядь — это расстояние между вытянутыми большим и указательным
пальцами руки при их наибольшем удалении (размер пяди колебался
от 19 см до 23 см). До настоящего времени говорят «Не отдать ни пяди
земли», подразумевая не отдать, не уступить даже самой малой части
своей земли. Об очень умном человеке часто говорят: «Семи пядей
во лбу».
Локоть — это расстояние от конца вытянутого среднего пальца руки
до локтевого сгиба (размер локтя колебался в пределах от 38 см до
46 см и соответствовал двум пядям). Сохранилась поговорка: «Сам с
ноготок, а борода с локоток».
149
Большими единицами измерения были простая сажень — расстояние
между большими пальцами вытянутых в противоположные стороны рук
человека (равнялась примерно 152 см и состояла из 4 локтей или
8 пядей); маховая сажень — расстояние между кончиками средних
пальцев вытянутых в противоположные стороны рук человека среднего
роста (равнялась примерно 176 см); косая сажень — расстояние от
пальцев правой (левой) ноги стоящего человека до конца пальцев
вытянутой по диагонали левой (правой) руки (равнялась примерно 216 см).
И сейчас говорят: «Видеть на сажень сквозь землю» (отличаться
большой проницательностью), «косая сажень в плечах» (так говорят о
рослом, плечистом человеке), «ты от дела на пяденьку, а уж оно от тебя
на саженьку».
Большие расстояния в старину измерялись верстами (другое
название поприще) — отсюда и выражения «мерить версты», т. е. ходить
пешком на большие расстояния.
В XVI—XVII вв. наравне со старыми мерами длины появляются
новые: аршин, четверть и вершок. К концу XVII века система мер
длины представляла следующую картину: верста межевая равнялась
двум верстам путевым и составляла 1000 саженей, сажень делилась
на три аршина; аршин составлял 4 четверти или 16 вершков.
В переводе на современную систему мер верста межевая равна
примерно 2,16 км, сажень — 216 см, аршин — 72 см, а вершок — 4,5 см.
До сих пор бытуют выражения.
«От горшка три вершка», «мерить на свой аршин», «как аршин
проглотил», «семь аршин говядины да три фунта лент» (так говорят
о бессмыслице), «аршин на кафтан, два на заплаты» (т. е. починка
дороже вещи), «пять верст до небес и все лесом», «эка верста
выросла!» (так говорят о человеке большого роста).
III. Леонтий Филиппович Магницкий
(1669—1739)
«. .для чего не быть у нас Лейбницам,
Вольфам, для чего не быть Невтонам?
Российски ли головы к тому не способны?
Путь ли нам к достижению сего
неизвестен?»...
(Русский писатель С А. Порошин
[1741-1796 гг })
Сведения о жизни и деятельности Л Ф. Магницкого немногочислен*-
ны. Известно, что родился он 9 июня 1669 года в Тверской губернии
(ныне Калининская область).
Достоверных сведений о том, где и как он получил образование,
нет. Его сын по этому поводу написал так:
« наукам изучался дивным и неудобовероятным способом...»
150
В конце XVII века Магницкий живет в Москве и является широко
известным своей образованностью человеком. За «остроумие в науках»
в 1700 году Петром I он был «..именован прозванием Магницкий
и учинен российскому благородному юношеству учителем математики ..».
Реформы, начатые Петром I в конце XVII — начале XVIII веков,
коснулись и образования. Как писал М. В. Ломоносов, Петр I «усмотрел
тогда ясно, что ни полков, ни городов надежно укрепить, ни кораблей
построить и безопасно пустить в море, не употребляя математики;
ни оружия, ни огнедышущих махин, ни лекарств поврежденным в
сражении воинам без физики приготовить; ни законов, ни судов правости,
ни честности нравов без учения философии и красноречия ввести,
и словом ни во время войны государству надлежащего защищения, ни
во время мира украшения без воспоможения наук приобрести
невозможно».
14 января 1701 года Петр I подписал указ об учреждении в
Москве Математико-навигацкой школы. В школу принимались дети из
различных сословий. После окончания школы они направлялись на
военную, морскую и государственную службу. 22 февраля 1701 года
учителем школы по приказу Петра I был назначен Магницкий, который
был известен как лучший математик Москвы. Ему было поручено
создать для школы учебник по математике и навигации В короткий
срок Магницкий написал учебник — 21 ноября 1701 года он представил
его рукопись.
В 1703 году «Арифметика» была напечатана Выход книги являлся
знаменательным событием для всей отечественной науки и культуры.
Книга использовалась не только в учебных заведениях, но и широко
служила для самообразования Один из экземпляров «Арифметики»
в 1725 году попал к юному М. В. Ломоносову, который хранил эту книгу
до конца своих дней Позже М В Ломоносов назвал «Грамматику»
Смотрицкого и «Арифметику» Магницкого «вратами учености».
Из предисловия книги видно, что отпечатана она по распоряжению
Петра I «ради обучения мудролюбивых российских отроков и всякого чина
и возраста людей». Магницкий проделал огромную работу, чтобы
излагаемый в книге материал был доступным и интересным для читателя.
Многие параграфы заканчиваются стихотворениями, подытоживающими
изученное Стихотворения, в которых даются советы и назидания,
разбросаны по всей книге
Вот, например, пожелание из предисловия к книге.
«И желаем да будет сей труд
Добре пользовать русский весь люд».
А о приложениях математики, о пользе науки говорится в таких строках:
«Прими, юне, премудрости цветы, ...
Арифметике любезно учися,
В ней разных правил и штук придержися.
151
Ибо в гражданстве к делам есть потребно,
Лечити твой ум аще числит вредно.
Та пути в небе решит и на мори,
Еще на войне полезна и в поли.
Обще всем людям образ дает знати,
Дабы исправно в размерах ступати».
В 1715 году была открыта в Петербурге Морская академия, куда
было перенесено обучение военным наукам, а в московской Навигацкой
школе стали учить только арифметике, геометрии и тригонометрии. С
этого момента Магницкий становится старшим учителем Математико-
навигацкой школы и руководит ее учебной частью. Наравне с
преподавательской работой ему поручается также набор учителей для
открывавшихся в то время в России цифирных школ.
С 1732 года и до последних дней своей жизни Л. Ф. Магницкий
являлся руководителем Навигацкой школы. Скончался он 30 октября
1739 года.
Высокую оценку деятельности Магницкого давали его современники
и потомки. П. В. Чичагов, сын выдающегося боевого адмирала
В. Я. Чичагова (1726—1809), учившегося в свое время в Навигацкой
школе, вспоминает по рассказам отца: «Один из учителей, Магницкий,
слыл за великого математика. Он издал ... сочинение, бывшее у меня
в руках, в котором заключались арифметика, геометрия,
тригонометрия и начатки алгебры. Впоследствии эту книгу признавали за образец
учености. Тут-то отец мой почерпнул свои познания».
В. К. Тредиаковский (1703—1769) — русский поэт, ученый-филолог,
писал: «Магницкий Леонтий муж, сведущий славянского языка,...
добросовестный и нельстивый человек, первый Российский арифметик и
геометр; первый издатель и учитель в России арифметики и геометрии».
IV. Леонард Эйлер
(1707—1783)
«Вместе с Петром I и Ломоносовым Эйлер
стал добрым гением нашей Академии,
определившим ее славу, ее крепость, ее
продуктивность».
(С. И. Вавилов (1891 — 1951),
Президент Академии наук СССР)
Леонард Эйлер родился 4 апреля 1707 года в Швейцарии в
селении Рихен вблизи города Базеля. Начальное образование получил дома
под руководством отца. Затем обучение его продолжилось в гимназии
г. Базеля. Одновременно он стал посещать лекции по математике
в университете. Работавший там профессором известный математик
152
Иоганн Бернулли обратил внимание на способного ученика. Как писал
сам Эйлер, И. Бернулли «...высказал чрезвычайно полезный для меня
•совет, состоявший в том, чтобы я сам принялся за некоторые труднейшие
математические книги и прочитывал их с особенным вниманием; в случае
же (несомненно, что это лучший способ делать счастливые успехи
в математических науках) какого-либо недоразумения или трудности...
он... разъяснял мне встреченные затруднения».
В 1723 году Эйлер получил степень магистра искусств, а в 1727 году
защитил диссертацию о распространении звука.
В 1727 году Эйлер, а ему тогда едва исполнилось 20 лет,
принимает приглашение только что созданной Петербургской академии наук
и приезжает в Петербург, где он был назначен адъюнктом по
математике. В 1730 году Л. Эйлер получил место профессора (академика)
кафедры физики, а в 1733 — кафедру математики.
В этот период Эйлер ведет кипучую деятельность. Он постоянно
делает научные доклады на академических конференциях, выступает
с публичными лекциями, с лекциями по физике и математике в
университете и гимназии при Академии наук, принимает активное участие в
работе комиссий по обследованию различных машин и многочисленных
технических проектов, в составлении полного географического атласа
России, публикует в каждом томе «Комментариев Петербургской
академии наук» по несколько своих научных трудов и т. д.
В 1741 году Л. Эйлер переезжает в Берлин. Хотя Эйлер и оставил
Петербург, он поддерживал непрерывную связь с Петербургской
академией: оставался почетным членом Академии, продолжал печататься
в изданиях Академии наук, по ее запросам сообщал о новых
изобретениях и открытиях, исполнял разнообразные поручения. Кроме того,
Л. Эйлер руководил занятиями молодых русских людей, которых
Академия отправляла на учебу за границу, например, в 50-х годах
XVIII века у Эйлера в Берлине жили и обучались адъюнкты
Петербургской академии наук С. К- Котельников, С. Я. Румовский и М. Софронов.
Эйлер считал необходимым готовить русских ученых для замещения
профессорских должностей в России. Так, например, на просьбу
Петербургской академии наук рекомендовать ученого для занятия в ней
кафедры механики он писал: «...лучше всего будет заместить это место
способным русским...». Эйлер очень высоко ценил русских ученых
С. К. Котельникова и М. В. Ломоносова. Так, он предлагал С. К. Котель-
никова на должность профессора высшей математики Петербургской
академии наук, отдавая ему предпочтение перед рядом иностранных
ученых: «...по сравнению с ними я могу с полным правом считать
Котельникова Архимедом или Ньютоном...». О работах по физике и химии
М. В. Ломоносова Эйлер пишет: «Все сии диссертации не токмо хороши,
но и весьма превосходны...». Предлагая Петербургской академии наук
рекомендовать М. В. Ломоносову участвовать в конкурсе на тему
«О селитре», он писал: «Я сомневаюсь, чтобы мог кто-нибудь кроме
153
Ломоносова написать об этом лучше, почему и прошу убедить его
приняться за работу».
В 1766 году Л. Эйлер со своей семьей возвращается в Петербург
и приступает к активной деятельности в Академии наук. Он продолжает
вести обширные научные исследования и заниматься большой научно-
организационной работой.
В этот период он справедливо считался первым математиком
в мире и пользовался всеобщим уважением и почетом.
Умер Л. Эйлер 18 сентября 1783 года в Петербурге.
Необычайно велико научное наследие Л. Эйлера. Полное собрание
его сочинений насчитывает более 70 томов, а в списках его трудов более
850 названий. Эйлеру принадлежит первое систематическое изложение
математического анализа («Введение в анализ» — 2 тома,
«Дифференциальное исчисление»— 1 том, «Интегральное исчисление» — 3 тома),
он автор книг по механике, теории движения Луны и планет, по
географии, по теории кораблестроения, теории музыки и т д. «Творчество
Эйлера изумительно и в науке беспримерно» (академик А. Н. Крылов,
1863—1945). Л. Эйлер является основателем русской научной
математической школы. Его учениками считали себя семь петербургских
академиков.
Приведем в заключение выдержку из одного письма Л. Эйлера:
«Его королевское величество (Фридрих II) недавно меня спрашивал,
где я изучил то, что знаю? Я согласно истине ответил, что всем обязан
моему пребыванию в Петербургской академии наук».
Список основной использованной
литературы
1. Аничков Д С. Теоретическая и практическая арифметика в пользу
и употребление юношества, собранная из разных авторов и вновь
дополненная профессором экстраординарным ... Дмитрием Аничковым — М.,
1775.
2. Библиотека ученая, экономическая, нравоучительная, историческая и
увеселительная в пользу и удовольствие всякого звания читателей.
В. 1 — 12,—Тобольск, 1793—1794
3. Б о б ы н и н В. В. Очерки истории развития физико-математических
знаний в России XVII века. В. 1 — М, 1886, В. 2.—М, 1893.
4. БобынинВ В Состояние математических знаний в России до XVI
века- Журнал Министерства народного просвещения — 1884.—Ч 232, № 4.
5. Войтяховский Е. Д Полный курс чистой математики, сочиненный
артиллерии штык-юнкером и математики партикулярным учителем
Ефимом Войтяховским в пользу и употребление юношества и
упражняющихся в математике. Т 1—4 — М., 1794—1798.
6. Гадательная арифметика для забавы и удовольствия — Сиб., 1789.
7. Гнеденко Б. В. Очерки по истории математики в России.— М; Л,
1946.
8 Даль В. Толковый словарь живого великорусского языка. Т. 1—4.—
М, 1981 — 1982.
9. Д е н и с о в А. П. Леонтий Филиппович Магницкий, 1669—1739 — М , 1967.
10. Детский гостинец или Четыреста девяносто девять загадок с ответами
в стихах и прозе, взятых как из древней, так и новейшей истории и из
всех царств природы и собранных одним другом детей для их употребления
и приятного препровождения времени — М, 1794.
11. История отечественной математики. Т. 1 — Киев, 1966.
12 Каменцева Е И.Устюгов Н В. Русская метрология.—М , 1965.
13. Козельский Я П. Арифметические предложения для употребления
обучающегося в Артиллерийском и инженерном шляхетском кадетском
корпусе благородного юношества, сочиненные артиллерии капит. Яковом
Козельским.— СПб., 1764.
14 Котельников С. К. Первых оснований математических наук часть
первая, содержащая в себе арифметику, в пользу учащегося в Морском
шляхетском кадетском корпусе благородного юношества, сочиненная
профессором мафиматики и членом Спб. Имп. академии наук Семеном Ко-
тельниковым. — СПб., 1766.
155
15 Курганов Н. Г. Универсальная арифметика, содержащая
основательное учение, как легчайшим способом разные в обществе случающиеся,
математике принадлежащие арифметические, геометрические и
алгебраические выкладки производить, сочинена Николаем Кургановым,
Морского шляхетского кадетского корпуса математических и навигацких
наук подмастерьем рангу подпорутческого. — СПб., 1757.
16. Курганов Н. Г. Арифметика или числовник, содержащий в себе все
правила числовой выкладки, случающейся в общежитии. В пользу
всякого учащегося, воинского, статского и купеческого юношества. Изд.
4-е вновь поправил и пополнил проф. подполк. и кавалер Николай
Курганов. Ч. I — II. — СПб., 1791.
17. Леонард Эйлер. Сборник статей и материалов к 150-летию со дня смерти.
Сер. II, в. 1.—М.; Л.: Изд-во АН СССР, 1935.
18. Леонард Эйлер. Сборник статей в честь 250-летия со дня рождения —
М : Изд-во АН СССР, 1958.
19 Магницкий Л Ф Арифметика, сиречь наука числительная .. — М,
1703 г.
20 Меморский М. Ф Краткая арифметика, служащая к легчайшему
обучению малолетнего юношества, в вопросах и ответах Ч. I—II.—
М, 1794.
21 М у р а в ь е в Н. Е. Начальное основание математики, сочиненное
Николаем Муравьевым, капитан-порутчиком от инженеров. Ч. I.— Спб , 1752.
22. Руководство к арифметике, для употребления в народных училищах
Российской империи, изданное по вые. повелению царствующей Имп.
Екатерины Вторыя. Ч. 1,2. — СПб., 1786.
23. Прудников В. Е. Русские педагоги-математики XVIII—XIX веков.—
М, 1956.
24. Рукописи *):
1) Арифметика — ОР ВГБИЛ, ф 310, № 681, XVII в.
2) Арифметика — ОР ВГБИЛ, ф. 310, № 682, XVII—XVIII вв.
3) Книга глаголемая арифметика, сиречь цифирная мудрость счетная —
ОР ВГБИЛ, ф. 726, № 4, 1667.
4) Сборник руководств по математике и по навигации.— ОР ВГБИЛ,
ф. 726, № 23, XVIII в.
5) Сборник смешанного содержания — ОР ВГБИЛ, ф. 726, № 29, XVIII в.
6) Сборник задач по геометрии.— ОР ВГБИЛ, ф. 726. № 17, XVIII в.
7) Счетная мудрость — Труды общества любителей древней
письменности. Т. 43 —СПб., 1879.
25 РумовскийС. Я. Сокращения математики. Часть первая,
содержащая начальный основания арифметики, геометрии и тригонометрии,
сочиненная Академии наук адъюнктом Степаном Румовским.— СПб., 1760.
26. Р ы б н и к о в К. А История математики. Т. 1, 2.—М., 1960, 1963
27. С и м о н о в Р. А. Математическая мысль Древней Руси — М • Наука,
1977.
28. С и м о и о в Р. А Кирик Новгородец — М.: Наука, 1982.
29 Тихомиров М. Н. Пособие для изучения Русской правды.— М.' МГУ,
1944.
30. Эйлер Л. Руководство к арифметике для употребления в гимназии при
Императорской Академии наук. Ч. 1. —СПб., 1740; Ч. 2.—СПб., 1760.
31. Эйлер Л Универсальная арифметика ... Т. 1, 2. — СПб., 1787—1788.
32. Юшкевич А. История математики в России до 1917 г — М.: Наука,
1968.
*> ОР ВГБИЛ — Отдел рукописей Всесоюзной государственной
библиотеки им. В. И. Ленина.
Оглавление
Предисловие 3
Введение 5
Часть первая. Задачи из старинных рукописей и «Арифметики»
Л. Ф. Магницкого 10
I. Житейские истории 10
1. Бочонок кваса (10, 66). 2 В жаркий день (10, 66). 3 На охоте (10, 66).
4. Собака и заяц (10, 67). 5. Как разделить орехи? (11, 67). 6. На мельнице
(11, 67). 7. Воз сена (11, 67). 8. Двенадцать человек (11, 67). 9. Постройка
дома (12, 67). 10. Скворцы (12,68). 11. Сливы (12,69). 12. Мальчики и
яблоки (12, 69). 13. Кому пасти овец? (12, 69) 14. Сколько яиц в лукошке?
(13,69).
II Путешествия 13
15. Из Москвы в Вологду (13, 70). 16 Через сколько дней встретятся
путники' (15,70). 17. Путешественники (15,70). 18. Вокруг города (15,70).
19. Два воина (15, 71). 20. Далеко ли до деревни? (15, 71).
III. Денежные расчеты 16
21. Покупка сукна (16, 71). 22. Сколько стоят гуси? (16, 71). 23. Сколько
куплено баранов? (16, 71). 24. За какое время окупятся куры? (16, 72).
25 Покупка масла (17, 72). 26 Сколько стоит кафтан? (17, 72). 27. Хозяин и
работник (17, 73). 28. Замысловатый ответ (18, 73). 29. «Полторажды
полтора» (18, 73). 30. Четыре купца (18, 73) 31. Покупка птиц (19, 74).
32. Проторговался ли купец? (19, 75),
IV. 6 оѵтішных-ъ н4кТнхъ д4йств«хъ чре^ дрідоЁттсв «ѵпФтрсшмкмыхъ
(«Об утешных некиих действах: через арифметику употребляемых») . .20
33. Как узнать день недели? (20, 71). 34. У кого кольцо? (20, 75). 35
Отгадать несколько чисел (20, 75). 36. Какое число задумано? (21, 77). 37. У кого
какая вещь? (21, 77).
V. Любопытные свойства чисел 21
38. Умножение на пальцах («Способ к твержению таблицы по перстам
ручным»)- (21, 80). 39. Движение пальца (22, 80).40. Одинаковые цифры
(23, 80). 41. Свойство числа 481 (23, 81). 42. «Проверка» сложения (23, 81).
43. «Проверка» умножения (24, 81).
157
VI. Старинный способ решения задач на смешение веществ .... 25
44. Как смешать масла' (25, 82) 45. О сплаве серебра (26, 82) 46 Верен
ли старинный способ' (26, 82). 47. Как смешать чай' (26, 83) 48 Серебро
трех сортов (27, 83) 49. Единственный ли ответ' (27, 83).
VII О правилах «фальшивых» или «гадательных» 27
50 Найти число (27, 84). 51 Ответ учителя (28, 84) 52. Сколько куплено
сукна'(29, 85). 53 Покупка коровы (30,85) 54 Беседа (30, 86) 55 Сколько
у кого денег? (31, 87). 56. Какова цена сукна? (31, 88) 57. Верно ли
«фальшивое» правило? (31, 88).
Часть вторая. Задачи из книг, изданных в XVIII веке (после
«Арифметики» Л. Ф. Магницкого) 32
I Забавные истории 32
58. Смекалистый слуга (32, 89). 59. «Богатство» (32, 89) 60 «С чем
иностранка к россам привезена» (32, 90). 61. Веселый человек (33, 90).
II Дележ и размен денег 33
62 Сколько у кого денег' (33, 90). 63 В 49 раз больше (33/90) 64. Сколько
было полтинников' (33, 90). 65. Размен по 2 и 3 копейки (33, 90). 66. Размен
по 3 и 5 копеек (33, 91) 67 Разделить на 8 частей (34, 91) 68 22 монеты
(34, 91).
III. Сколько кому лет? 34
69. Сколько лет сыну? (34, 91) 70 Каков возраст братьев' (34,91)
71 Сколь он стар' (34, 91) 72 Сколько лет каждому сыну? (34,92).
73. Лета каждого (34,92) 74 Сколько им лет? (34, 92). 75 Возраст сыновей
(35, 93). 76 Замысловатый ответ (35, 93).
IV Часы 35
77. Сколько раз бьют часы' (35, 93) 78. Который час' (35, 94). 79 Две
стрелки (35, 94). 80. Сколько раз совместятся стрелки? (35,94) 81 Сколько
было времени' (36, 94).
V. Денежные расчеты 36
82. Продажа двух коней (36, 95). 83. Сколько стоят кони' (36, 95)
84. Обмен зайцев на кур (36, 95). 85 Две крестьянки (36, 96) 86
Полтабуна и пол лошади (37, 96) 87. Покупка товаров (38, 96) 88 Обмен
деньгами (38, 96) 89. Раздел наследства (38, 97).
VI Задачи на переливание . . 38
90. Три бочки (38, 98) 91 Четыре бочки (39, 98) 92 Сколько останется
воды' (39, 98) 93. Можно ли отлить половину сока? (39, 98)
VII Латинские квадраты 39
94. Квадрат 3X3 (39, 99). 95. Квадрат 4X4 (40, 100). 96 Квадрат
пХп (40, 100) 97. Шестнадцать офицеров (40, 101).
VIII. Обход мостов 41
98. Мосты в Кенигсберге (41, 102) 99. Пятнадцать мостов (42, 104)
158
IX Шахматы 42
100 Путешествие коня по шахматной доске (42, 104) 101 Задача о 8
іадьях (43, 105) 102 Задача с запретом (45, 106) 103 Задача о шляпах
(45, 107)
X. Биллиард 46
104. Отражение от одного борта (46, 108) 105. Отражение от двух
параллельных бортов (46, 109). 106 Отражение от двух перпендикулярных
бортов (46, 109). 107. Отражение от трех бортов (46, ПО) 108 Отражение
от четырех бортов (46, 112).
XI. Фигурные числа 47
109 Квадратные и треугольные числа (47, 112). ПО. m-угольные числа
(48, ИЗ) 111. Сколько стоит дом' (48, 114). 112 Треугольные и
шестиугольные числа (49, 114). 113. Пирамида из ядер (49, 114).
XII. С помощью линейки, циркуля и ножниц 49
114 Правильный шестиугольник (49, 115) 115 Правильный
восьмиугольник (49, 116). 116. Правильный двенадцатиугольник (49, 116).
117 Правильный шестнадцатиугольник (50, 116) 118 «Правильный»
семиугольник (50, 117) 119. Из прямоугольника — треугольник (50, 118).
120 Из треугольника — прямоугольник (50, 118) 121 На части равной
площади (50, 120).
XIII Построения на местности 50
122 Как измерить расстояние от дома до башни' (50, 120). 123 Как
измерить расстояние между деревом и крепостью? (50, 121)
XIV Геометрические задачи Эйлера ... 50
124 Прямая Эйлера (51, 122) 125. Окружность Эйлера (51, 123). 126.
Формула Эйлера (51, 123). 127. Свойство диагоналей и сторон выпуклого
четырехугольника (51, 124). 128 Интересное свойство выпуклого
многогранника (51, 125).
Часть третья. Задачи из сборников занимательных задач конца
XVIII века 53
I. Задачи-шутки, задачи-загадки 53
129. Коза (53, 128) 130. Много ли ног' (53, 128) 131. Одним мешком —
два мешка (53, 128). 132. Много ли гвоздей найдут' (53, 128) 133. Сколько
уток' (53, 129). 134 Что это такое? (53, 129). 135. Возможно ли такое?
(55, 129) 136. За сколько минут? (55, 129). 137 Землекопы (55, 129)
138 Два отца и два сына (55, 129) 39 Как это могло быть' (55, 129).
140 Как разделить' (55, 129). 141. Написать число (55, 129).
II Затруднительные ситуации 55
142 Волк, коза и капуста (55, 129). 143 Рыцари и оруженосцы (56, 130).
144 Разделить квас поровну (56, 130). 145 Разделить бочки и мед
(56, 131). 146 Девичья хитрость (56, 131). 147. Во время шторма (57, 131).
III. Угадывание чисел 57
148. Как найти задуманное четное число' (57, 132). 149. Как найти
задуманное нечетное число' (57, 132). 150. Как найти задуманное число?
159
(58, 133). 151 Как отгадать два числа? (58, 133). 152, Угадывание числа
(58, 134). 153 Как найти цифру' (58, 134). 154. Отгадать зачеркнутую
цифру (59, 135). 155 Найти зачеркнутую цифру (59, 136). 156. Какая
цифра зачеркнута? (59, 136). 157. На сколько один человек старше другого
(59, 136). 158 Как узнать день рождения? (60, 137). 159. Сколько
лет человеку' (60, 137). 160 Быстрое сложение (60, 138). 161. Чему равна
сумма ненаписанных чисел? (60, 139).
IV. Игры с предметами .... 61
162. У кого монета? (61, 140). 163. У кого кубик (61, 140) 164. Кто
что взял? (61, 142). 165. У кого какой предмет? (63, 143). 166. Сколько
выпало очков? (63, 144). 167. Кто сколько взял кубиков? (66, 144).
168 В какой руке нечетное число предметов' (64, 145). 169
Перекладывание карточек (64, 145). 170 Фокус с 16 буквами (65, 146). 171. Фокус с
12 буквами (65, 146).
Приложения ... 147
I О старинной русской нумерации . ... 147
П. Старинные русские меры длины 149
III. Леонтий Филиппович Магницкий (1669—1739) 150
IV Леонард Эйлер (1707—1783) . 152
Список основной использованной литературы 155
Олехник Слав Николаевич
Нестеренко Юрий Валентинович
Потапов Михаил Константинович
СТАРИННЫЕ ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
Редактор М. М. Горячая
Оформление худ. П. И. Чернуского, И. И. Нирижного
Художественный редактор Т. Н. Кольченко
Технический редактор Л. В. Лихачева
Корректор О. М Березина
ИБ № 32654
Сдано в набор 25 02.87. Подписано к печати 25.01.88. Формат 84X108/32.
Бумага книжно-журнальная. Гарнитура литературная. Печать высокая.
Усл. печ. л. 8,4. Усл. кр.-отт. 9,58. Уч.-изд. л. 9,16. Тираж 700 000 экз.
(1-й завод 1—200 000 экз.). Заказ № 481. Цена 55 коп.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15.
Ленинградская типография № 2 головное предприятие ордена Трудового
Красного Знамени Ленинградского объединения «Техническая книга» им.
Евгении Соколовой Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли. 198052, г. Ленинград,
Л-52, Измайловский проспект, 29.