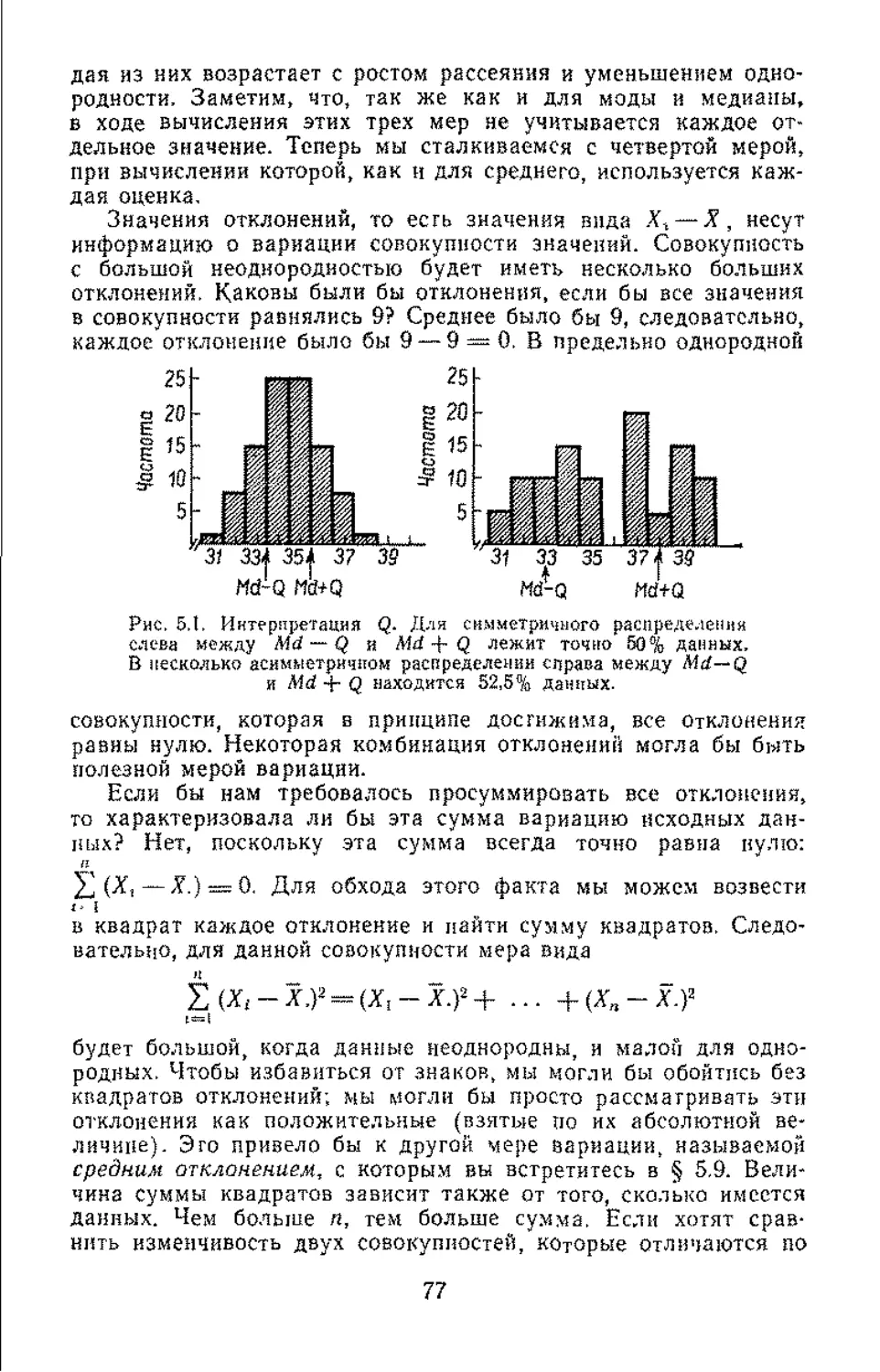
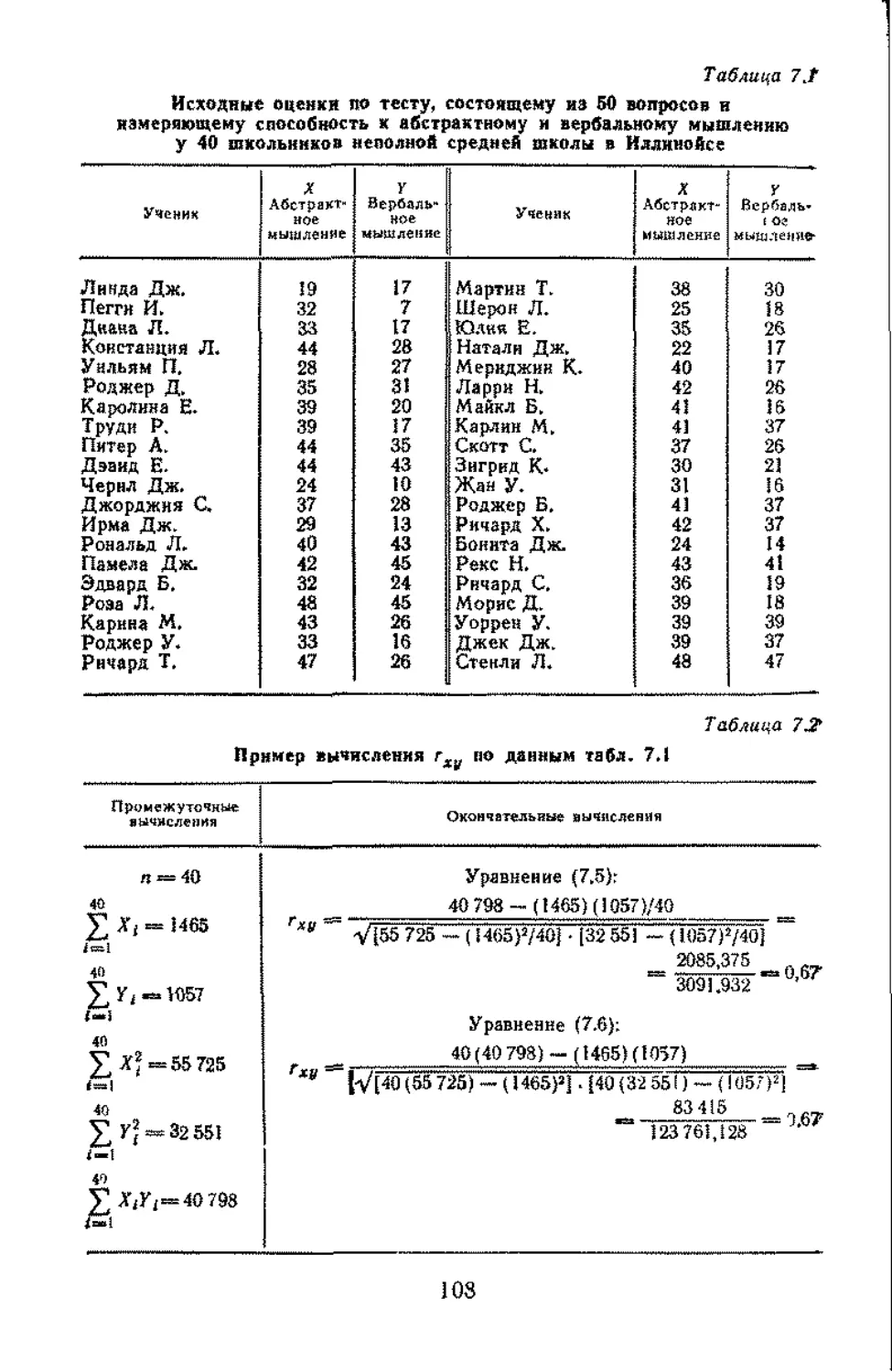
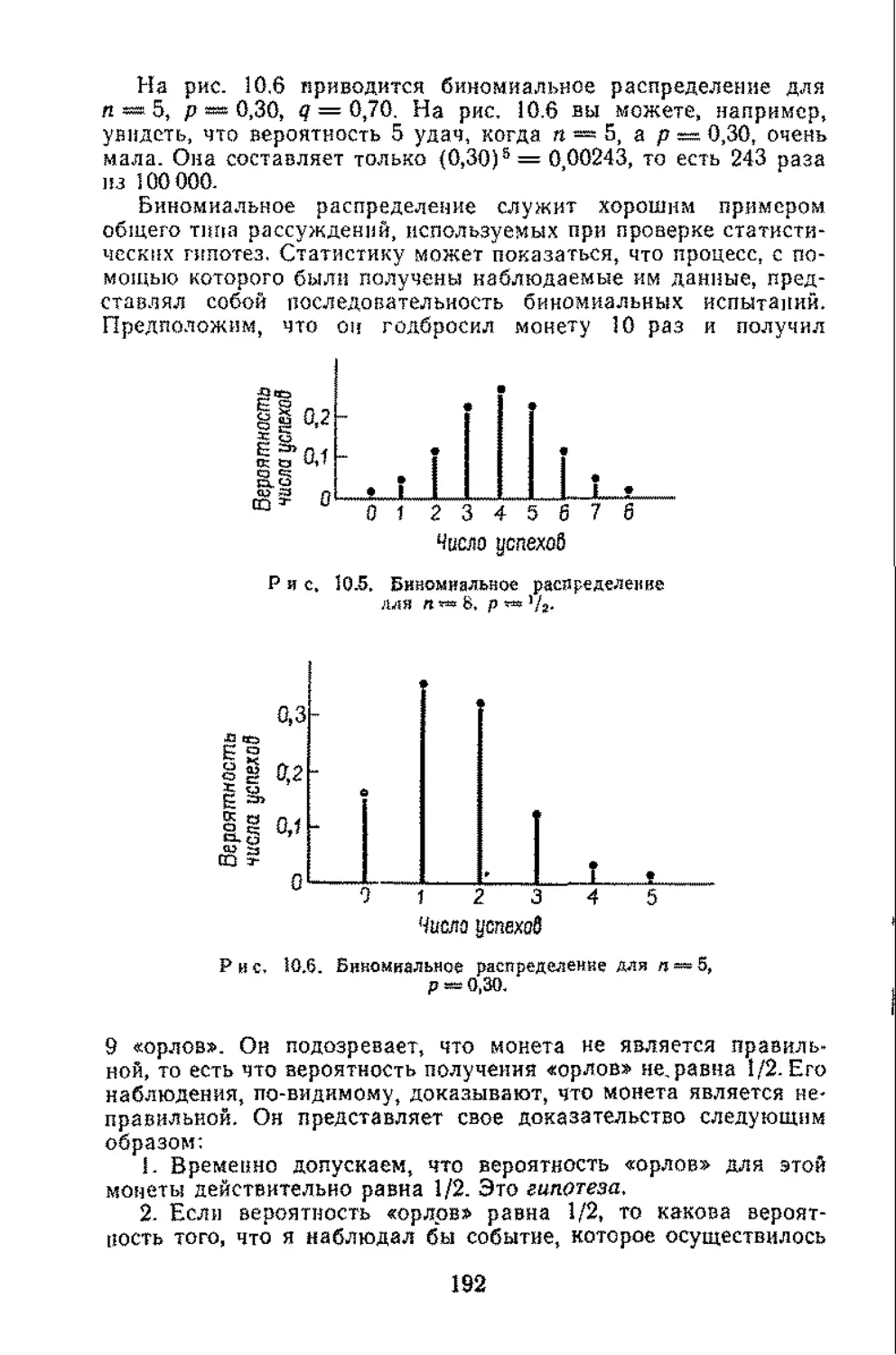
Текст
От издательства
В последние десятилетия происходит интенсивный про-
цесс внедрения количественных методов, основанных
на использовании математического аппарата, практи-
чески во все отрасли науки. Не составляют исключе-
ния и такие науки, как педагогика и психология. Ко-
личественные методы в практике научно-исследова-
тельской работы в этих областях используются все
более широко и эффективно.
На русском языке издан ряд работ как советских,
так и зарубежных авторов, в которых излагаются
различные аспекты применения количественных мето-
дов в различных областях науки, в том числе и в пе-
дагогике и психологии.
Однако имеющаяся литература не в состоянии удо-
влетворить бурно растущие потребности науки и прак-
тики в нашей стране, и в частности разнообразные
запросы широкого круга педагогов и психологов.
Этот пробел в известной мере должен восполнить
предлагаемый вниманию советского читателя перевод
книги известных американских ученых Дж. Стэнли
и Дж. Гласса. Книга представляет собой учебник по
статистическим методам, предназначенный специаль-
но для психологов и педагогов. По замыслу авторов
она должна служить, во-первых, учебником для пер-
вого знакомства с предметом, во-вторых, справочни-
ком но статистическойтехнике для людей, которые уже
владеют соответствующими идеями и методами, и,
в-третьих, руководством по планированию эксперимен-
тов и квалифицированной интерпретации их результа-
тов в реальных исследовательских задачах. В целом
авторам удалось решить все поставленные перед со-
бой задачи Книга учит читателя понимать литературу
по теории вероятностей и математической статистике.
5
Основным достоинством книги является простота
изложения, умение авторов доходчивыми средствами
донести до читателя, не имеющего специальной
математической подготовки, методологию того или
иного математического инструмента.
По содержанию книгу, состоящую из 19 глав,
можно разбить на три части. Первая из них
(главы со 2 по 9) посвящена вопросам так называемой
описательной статистики, вторая (главы с 10 по 14)
содержит основы теории вероятностей и третья (гла-
вы с 15 до 19) посвящена дисперсионному анализу
и основам планирования эксперимента.
Книга имеет четкую направленность на определен-
ный круг читателей: психологов, педагогов и социо-
логов.
Более подробный анализ основных идей книги
дан в послесловии Ю. П. Адлера и А. И. Ковалева
к настоящему изданию.
© «Првгркс». 1Ив г.
1
ВВЕДЕНИЕ
Распространенное отношение к статистике — смесь благоговения
с цинизмом, подозрением и презрением. Статистиков поместили
в нелестную для них компанию лгунов и обвинили в «статисти-
куляции»— искусстве обмана с помощью статистики, сохраняю-
щего видимость объективности и разумности. Однажды кто-то
заметил, что, «если бы всех статистиков мира скрутили одной
цепью, это принесло бы только пользу». Статистика насмеш-
ливо сравнивают с человеком, который тонет, переходя вброд
реку со средней глубиной 90 см, или сидит, держа голову
в холодильнике, а ноги в печи, и говорит: «В среднем я чувст-
вую себя прекрасно». В одном еженедельнике автор очерка
«Йаука и ловушки статистики» заключает, что «возможно,
наступит такое время, когда общество станет меньше разбирать-
ся в цифрах, а потому и меньше руководствоваться стати-
стикой»
Лицам, начинающим изучение статистики, полезно отказаться
от широко распространенного представления о статистике и
статистиках, Они должны понимать, что абсурд может найти
свое выражение как в словесной, так и в цифровой форме.
Одиако знание логики является надежной гарантией от некри-
тичного принятия словесного абсурда, а знание статистики пред-
ставляет собой лучшую защиту от абсурда цифрового.
Первый шаг к замене привычных представлений о статистике
на более реальные — это изучение структуры дисциплины «ста-
тистические методы» и ее исторических предшественниц.
На первоначальное развитие статистических методов ока-
зало влияние их происхождение. У статистики были «мать»,
которой нужно было предоставлять регулярные отчеты прави-
тельственных подразделений (штат и статистика происходят
от одного латинского корня — status), и «отец» — честный
1 «Time», 8. IX, 1967. р. 29.
7
карточный игрок, который полагался на математику, усили-
вавшую его ловкость — умение брать решающие взятки в азарт-
ных играх. От матери ведут свое происхождение счет, измерение,
описание, табулирование, упорядочение и проведение пере-
писей, то есть все то, что привело к современной описательной
статистике. От предприимчивого интеллектуала — отца возникла
в конечном счете современная теория статистического вывода,
непосредственно базирующаяся на теории вероятностей. Недав-
нее дополнение, называемое планированием экспериментов, опи-
рается в основном на сочетание теории вероя)ностей с несколь-
ко элементарной, но удивительной логикой. Данная работа
является введением в описательную статистику, теорию стати-
стического вывода и планирование экспериментов. Главы 2—9'
охватывают значительную часть описательной статистики.
В главах 10—14 рассматриваются некоторые разделы теории
статистического вывода. А в главах 15—19 обсуждаются мето-
дики статистических выводов, важные для планирования и ана-
лиза экспериментов.
Описательная статистика включает в себя табулирование,
представление и описание совокупностей данных. Эти данные
могут быть либо количественными, как, например, измерения
роста и веса, либо качественными, как, например, пол и тип
личности. Огромные массивы данных, как правило, должны
обобщаться или свертываться, прежде чем они будут интерпре-
тироваться человеком. Обезьяна беспомощна в своей неуклюжей
попытке развязать простой узел, так как сложность этой задачи
превосходит разрешающую способность бедного в творческом
отношении интеллекта. Безуспешная попытка рыбака разобрать-
ся в причинах люфта спиннинга аналогична попытке обезьяны.
Для рыбака этот люфт — гордиев узел; он дает слишком слож-
ную задачу для его ограниченного интеллекта. Точно так же,
но на ином уровне человеческий разум не может извлечь полной
информации из массы данных (Как варьируют данные? И как
велики эти вариации? Нельзя ли уменьшить неопределенность
в этих вариациях?) без помощи специальных методов (мечей,
разрубающих гордиев узел). Таким образом, описательная ста-
тистика служит инструментом, описывающим, обобщающим или
сводящим к желаемому виду свойства массивов данных.
Теория статистического вывода — это формализованная си-
стема методов решения задач другого рода, создающих значи-
тельные трудности для невооруженного человеческого разума.
Этот общий класс задач, как правило, характеризуется попыт-
ками вывести свойства большого массива данных путем обсле-
дования выборки. Например, школьная медсестра хочет опре-
делить долю учеников пятых классов в большой школе, которые
никогда не болели ветрянкой. Излишне было бы опрашивать
каждого ребенка, если бы можно было надежно определить
такую долю по выборке минимальным объемом, скажем в 100
детей. Но какова доля тех детей, которые никогда не болели
8
ветрянкой, в этой выборке по отношению к доле во всей сово-
купности пятиклассников? Ответ можно получить благодаря
теории статистического вывода. Итак, задача статистического
вывода состоит в том, чтобы предсказать свойства всей совокуп-
ности, зная свойства только выборки из этой совокупности.
Статистические выводы строятся на описательной статистике.
Они делаются от частных свойств выборок к частным свойствам
совокупности; описания свойств как выборок, так и совокупно-
стей производятся с помощью методов описательной статистики.
Планирование и анализ экспериментов представляет собой
третью важную ветвь статистических методов, разработанную
для обнаружения и проверки причинных связей между перемен-
ными. Исследователи в области общественных наук имеют дело
с причинностью—-очень сложным философским понятием. План
эксперимента настолько важен при изучении причинных свя-
зей, что в некоторых философских системах эксперимент пред-
ставляет собой их операциональное определение. Люди делают
заключения о причинах на протяжении всей своей жизни. Час-
тота употребления слов «потому что» подтверждает это;
«Школьная лотерея потерпела неудачу, потому что она не была
достаточно разрекламирована» или «Он получил мало очков
при выполнении интеллектуального теста, потому что очень
беспокоился о своих результатах».
Предложение «Лекарство А снимает боль быстрее лекарства
В» не содержит слов «потому что», но подразумевает, что «Боль-
шая часть пациентов одной группы по сравнению с пациентами
другой группы гораздо скорее избавилась от боли, потому что
первым было прописано лекарс!во А, а последним—лекарст-
во В». Недостаточность объяснения посредством «потому что» —
в его потенциальном неопределенности. Эта неопределенность
служит любимой отговоркой маленьких детей, когда на доло-
гических ступенях мышления им предъявляют свидетельства их
дурного поведения. Если их спрашивают: «Почему ты сделал
это?», они отвечают: «Потому что». Очевидно, эти слова
имеют множество оттенков и сопутствующих значений.
Статистические методы помогают исследователям описывать
данные, делать выводы в отношении больших массивов
данных и изучать причинные зависимости. Они могут оказаться
полезными при ответе на вопросы типа: Каков средний возраст
учащегося колледжа к моменту получения степени бакалавра
искусств? Какой процент этих новых выпускников имеет голубые
глаза? Какой процент из них в этот момент женат? Сколько
из них уже имеют 0, 1, 2. ... детей? Составляют ли те, кто
добился значительных успехов, будучи студентами, большин-
ство в аспирантуре по сравнению с теми, кто получал по-
средственные оценки? Влияет ли международная обстановка на
посещаемость студентов в высших школах? Будут ли студенты
колледжа, принятые группой доброжелательно, больше приспо-
сабливаться к суждениям этой группы, чем студенты, которых
9
группа отвергает? Зависит ли такая различная реакция (если
она будет установлена) от пола студента? Например, подвер-
жены ли женщины влиянию группы в большей степени, чем
мужчины?
Овладение статистическими методами требует некоторой
математической подготовки. Статистика — это ветвь прикладной
математики. Ее неправильно определяют в словаре как «науку
сбора данных». Если бы статистика была столь элементарной,
эта книга была бы меньше. Более строго статистику обычно
называют математической статистикой. Для специалистов в об-
ласти общественных наук и других нематематиков она опре-
деляется как «прикладная статистика» и предполагает ис-
пользование интуиции, элементарной арифметики и элементар-
ной алгебры. Для более серьезного изучения математической
статистики требуется известная подготовка, включающая по
крайней мере вычислительные методы и теорию матриц; однако
логическую сторону прикладной статистики и многие ее ме-
тоды можно изучить и без такой математической подготовки,
хотя и не столь глубоко. Возможно, в этом отчасти и кроется
причина тенденции различных общественных наук к технизации.
В крупных университетах отдельные курсы по «педагогической
и психологической статистике», «социологической статистике»,
«экономической статистике» и т. п. обычно далеки от статистики
как области знания. К счастью, однако, большинство основных
принципов применимо почти ко всем дисциплинам — от сельско-
хозяйственной науки до зоологии. Знание статистики становится
необходимым для успешной деятельности в любой эмпирической
области. Во многих высших школах недавно признали ее важ-
ность. Все большее признание статистики как элемента эруди-
ции вызывает в памяти описание образования детей в утопиче-
ском обществе Скиннера «Второй Уолден»: «Мы помогаем им
в любой сфере, за исключением обучения. Мы вооружаем их
новыми методами овладения знаниями и мышления... Мы даем
им прекрасный обзор методов и средств мышления, взятых из
логики, статистики, научного метода, психологии и математики.
Это и составляет то «обучение в колледже», в котором они нуж-
даются. Остальное они приобретают в наших библиотеках и
лабораториях» ’.
Слово «статистика» определяется Кендаллом и Баклендом-
(1957) 1 2 как «итоговое значение, вычисленное по выборке на-
блюдений, обычно (но необязательно) как оценка некоторого
параметра генеральной совокупности, функция объема выборки».
Альтернативный термин «параметр» мы определим позже. Таким
1 Skinner В. F. Walden Two New York, 1962, p. 121. В развитие из-
вестной книги: Thoreau Н. D. Walden, or life in ihe Woods, 1854. См. рус-
ский перевод: Г. Д Торо. Уолден, или Жизнь в лесу М, Изд «Наука».
1962. — Прим. ред.
2 Для полной информации об этой я следующих ссылках см библиогра-
фию в конце книги.
10
образом, среднее арифметическое чисел 1, 4 и 4, равное трем,
представляет собой статистику. А тот факт, что некто имеет
двоих детей, — это исходные данные, тогда как среднее число
детей в городе есть статистика (в действительности вы можете
видеть этих двух детей, но не среднего ребенка). Однако это
различие между «статистикой» и «данными» не всегда сохра-
няется. Некоторые специалисты по прикладной статистике и
исследователи пользуются термином «статистика» и в том,
и в другом случае, утверждая даже, что имя человека или цвет
его волос тоже имеет отношение к статистике.
В основе отдельных статистических методик лежит единый
главный принцип. Мы попытаемся продемонстрировать это един-
ство и взаимосвязи как можно яснее, пользуясь только элемен-
тарной математикой, которую читатель изучил в средней школе.
По мере надобности будут введены некоторые специальные обо-
значения; они будут сопровождаться подробным объяснением.
Их нужно усвоить с самого начала, поскольку подобные обозна-
чения облегчают изучение статистики.
Данный учебник преследует две цели:
1) Научить читать отчеты об обследованиях, научных ра-
ботах, исследованиях и экспериментах на среднем уровне ком-
петентности (при условии понимания тех реальных проблем,
которые изучаются) и
2) научить технике планирования собственных исследова-
ний и анализа полученных в результате этих исследований
данных.
В процессе работы над этой книгой мы стремились к тому,
чтобы она выполнила три функции: служила эффективны» учеб-
ным пособием при изучении статистики и надежным справоч-
ником, когда материал уже усвоен, и наконец, способствовала
более углубленному изучению статистики. Очевидно, что первая
функция основная, ибо нет никакого смысла в ссылках па го,
что неизвестно, так же как н в том, чтобы браться за чтение
более сложного материала до овладения основами.
2
ИЗМЕРЕНИЕ, ШКАЛЫ И СТАТИСТИКА
2.1. Измерение
Существует множество определений «измерения», несколько от-
личающихся друг от друга в зависимости от точки зрения ис-
следователя- Общим во всех определениях является, по-види-
мому, следующее: измерение есть приписывание чисел вещам
в соответствии с определенными правилами. Измерить рост че-
ловека— значит приписать число расстоянию между макушкой
человека и подошвой его пог, найденному с помощью линейки.
Измерение коэффициента интеллектуальности (/Q) ребенка —
эго присвоение числа характеру ответной реакции, возникающей
у него на группу типовых задач. Измерение преобразует опре-
деленные свойства наших восприятий в известные, легко под-
дающиеся обработке вещи, называемое «числами». Каким не-
выносимым был бы мир, если бы мы не измеряли! Разве не
полезно физику знать, что сталь плавится при высокой темпе-
ратуре, а путешественнику, — что Чикаго — это «город, вытя-
нутый вдоль спускающегося вниз шоссе»? Известно, какую
важную роль играет измерение в педагогике и почти в каждом
социальном предприятии.
2.2. Измерительные шкалы
Представления о «шкалах измерений» образуют полезную
группу понятий, Этими проблемами интересовались бихевиори-
сты и некоторые другие ученые. Теперь мы кратко рассмотрим
различные шкалы и их применение в статистике.
Измерения в шкале наименований (номинальные измерения)*
Номинальное измерение (присвоение обозначения или обо-
значений) едва ли заслуживает того, чтобы называться «изме-
• Использованные здесь названия шкал измерений и многие понятия
принадлежат С. С. Стивенсу (I960).
12
рением». Это процесс группирования предметов в классы, ког-
да объекты, принадлежащие к одному классу, идентичны (или
почти идентичны) в отношении некоторого признака или
свойства. Далее классам даются обозначения; вместо обо-
значений классы могут также принимать и часто принимают
для идентификации числа, которые могут служить объяснением
заголовка «.номинальное измерение». Схемы классификации ви-
дов в биологии—примеры номинальных измерений. Пси-
хологи часто кодируют «пол», обозначая «особей женского
рода» нулем, а «особей мужского рода» — единицей; это
также номинальное измерение. Мы выполнили бы номинальное
измерение, если бы присвоили 1 англичанам, 2—немцам, а 3—•
французам. Равна ли одному французу сумма одного англича-
нина и одного немца (1 4-2 = 3)? Конечно, нет. Числа, которые
мы присваиваем в номинальном измерении, обладают всеми
свойствами любых других чисел. Мы можем складывать их,
вычитать, делить или просто сравнивать. Но если процесс при-
своения чисел предметам представлял собой номинальное изме-
рение, то наши действия с величиной, порядком и прочими
свойствами чисел вообще не будут иметь никакого смысла но
отношению к самим предметам, поскольку мы не интересовались
величиной, порядком ц другими свойствами чисел, когда при-
сваивали их. При номинальных измерениях используется исклю-
чительно та особенность чисел, что I отличается от 2 или 4 и что
если предмет А имеет 1, а предмет В — 4, то Л и В различаются
в отношении измеряемого свойства. Отсюда вовсе де следует,
что в «В» содержится больше свойства, чем в «А». Три осталь-
ные шкалы, с которыми мы будем иметь дело, используют три
следующих свойства чисел: числа можно упорядочивать по ве-
личине, их можно складывать и делить.
Порядковые измерения
Порядковое измерение возможно тогда, когда измеряющий
может обнаружить в предметах различие степеней признака или
свойства. В этом случае используется свойство «упорядочен-
ности» чисел и числа приписываются предметам таким образом,
что если число, присвоенное предмету А, больше числа, при-
своенного В, то это значит, что в А содержится больше дан-
ного свойства, чем в В.
Допустим, мы просим кого-то прораижировать Мери,
Джейн, Алису и Бетти с точки зрения красоты. Мы можем рас-
положить их следующим образом: Бетти, Джейн, Мери, Алиса.
Порядковое измерение имеет место в том случае, когда мы
присваиваем Бетти, Джейн, Мери и Алисе соответственно но-
мера 1, 2, 3 и 4. Заметим, что номера 0, 23, 49 и 50 тоже подо-
шли бы, поскольку расстояние между двумя соседними номе-
рами не имеет значения. Мы не можем себе представить, что
измеритель в состоянии распознать, например, будет ли
13
различие между «количеством» красоты Бетти и Джейн больше
или меньше разницы между красотой Джейн и Мери. Поэтому
не стоит придавать большого значения тому, что разница в
оценках Бетти и Джейн такая же, как и дистанция между
Мери и Алисой.
Посмотрим теперь, как числа занимают места предметов.
Числа —это частичные представители предметов; мы обращаем-
ся к ним. когда важны как различия между ними, так и их
порядок. При порядковых измерениях числа обеспечивают неко-
торую экономию при передаче информации. Вместо сообщения
о том, что «Бетти признана наименее красивой, Джейн — следу-
ющей за ней, Мери — второй после самой красивой, а Алиса —
самой красивой», мы можем сказать-.
Имя
Мерн
Джейн
Алиса
Бетти
Шкала твердости минералов — тоже порядковая шкала. Если
минерал А может оставить царапины на минерале В, то он
тверже, следовательно, он получает более высокий номер. Пред-
положим, что минералам А, В, С и D подобным способом при-
писаны соответственно номера 12, 10, 8 и 6. Нам известен самый
твердый и самый мягкий минерал. Разность твердостей А и В
является такой же, как и разность твердостей С н В, илн нет?
Мы не имеем об этом никакого представления, потому что
номера были присвоены так, что учитывались только признаки
однозначности и порядка — измерение было порядковым.
Другой известной порядковой шкалой является «ранг в клас-
се средней школы». Номера устанавливаются от «1» для «мак-
симального среднего значения отметок» до п для «минималь-
ного среднего значения отметок» в группе из п учеников.
(Если бы, например, три первых ученика имели максимально
возможные средние, то каждый из них должен был бы получить
ранг «2», представляющий собой среднее первых трех рангов
1, 2 и 3. Этот способ присвоения чисел основан на соглашении,
потому что сохраняется постоянной сумма связанных и несвя-
занных рангов, например: 1-+-2-|-3 = 2-|-2-+-2.)
Не существует закона, запрещающего кому-либо складывать,
вычитать, умножать и производить другие операции над чис-
лами, которые присвоены предметам в ходе порядкового изме-
рения. Однако результаты этих операций могут и ничего не
говорить о количествах анализируемого свойства, которым обла-
дают предметы, соответствующие этим числам. Например, раз-
личие между «рангами красоты» Алисы и Бетти равно трем;
14
Senders
Virginia L.
Siegel S.
Стивенс С. C.
(редактор)
собой убедительный вывод против такого
представления, будто шкала измерения
указывает, какую статистику можно ис-
пользовать.
Measurement and Statistics, Oxford Univer-
sity Press, New York, 1958.
Этот учебник построен на основе понятий
Стивенса, позиция автора — одна из край-
них позиций, занимаемых психологами.
Nonparametric Statistics, McGraw-Hill,
New York, 1956. Позиция Зигеля идентична
позиции Стивенса. Книга Зигеля сосредото-
чивает внимание на том, какие статистиче-
ские методы свойственны тем или иным
шкалам. Несмотря на полезный во многих
отношениях материал, подчеркивание «до-
пустимости» и «пригодности» статистики,
вероятно, неуместно.
«Математика, измерение и психофизика» в
«Экспериментальной психологии», т. I, М.»
ИЛ, i960, стр. 19—89. Эта ранняя статья
пробудила интерес к проблеме измеритель-
ных шкал и вызвала горячую полемику.
Эти работы могут создать впечатление, что «шкала» некото-
рым образом задает определенные свойства. Некий набор чисел,
присвоенных группе объектов, вполне определенно относит их к
той или иной категории: шкала является либо номинальной, либо
порядковой, либо интервальной, либо шкалой отношений; и ни-
чего другого нет. Эта позиция может привести к хаосу при
недостатке понимания со стороны тех, кто реально осуществляет
психологические и педагогические измерения. Сторонники Сти-
венса утверждают, например, что шкалы IQ (коэффициента
интеллектуальности) порядковые, а не интервальные. Некритич-
ное принятие этого утверждения вынуждает совершенно игнори-
ровать величину разницы между оценками 1Q. Предположим,
Джо имеет по шкале IQ оценку 50, Сэм — ПО, а Боб—112.
Если IQ — в самом деле порядковая шкала, то можно сказать
лишь, что Боб умнее Сэма, который умнее Джо. Утверждение,
что Боб и Сэм более похожи с точки зрения IQ, чем Сэм и Джо,
было бы неоправданно. Сказать, что последнее утверждение
необоснованно, потому что шкалы IQ — только порядковые шка-
лы, было бы произволом. Спросите человека, проводившего
испытания IQ, и он скажет вам до проверки детей, что Джо
горазда менее умен, чем Сэм и Боб, которые более близки
друг к другу. Попытайтесь внушить этому исследователю, что
ему не следует обращать внимания на величины различий
между оценками, и он попросит вас заняться вашим собствен-
18
ным делом и будет прав. Даже несмотря на то, что единица
1Q не совсем эквивалентна единице измерения при различных
значениях /Q, шкалы IQ находятся не на одном уровне
с более низкими порядковыми шкалами. Шкала IQ производит
как строго порядковую, так и интервальную категоризацию:
может быть, лучше говорить о ней как о «квазиинтервальной».
Часто для исследователя важно классифицировать шкалы из-
мерений по категориям. Если числа, которые измеритель припи-
сывает п различным объектам, представляют собой ряд не
более чем в п рангов, то есть 1, 2, ..., п (порядковая шкала),
то некоторые операции с числами бессмысленны по отношению
к свойствам объектов. Исследователя следует предупредить об
этом. Он должен понимать также, что если он произвольно
присвоил 3 мужчинам, а 2 женщинам (номинальное измерение),
то тот-факт, что 3 больше 2, ничего не говорит об измеряе-
мом признаке, называемом «пол». Таким образом, различия
между шкалами могут оказаться полезными. Однако, за
исключением крайне редко используемых мер (таких, как
время, длина, масса), педагогические и психологические изме-
рения, особенно клинические, не поддаются какой-либо про-
стой классификации, вроде «порядковой» или «интервальной».
Больше мы не будем делать замечаний по шкалам. Лишь не-
многие статистические методы, обсуждаемые в этой книге, строи-
лись с учетом связи мер с объектами измерения. Характер этой
связи представляет интерес для специалиста по измерениям.
Статистические методы — это средства анализа чисел, как тако-
вых, а не как истинных значений некоторого признака. Всякий
статистический метод можно применить к любой совокупности
чисел (с некоторыми ограничениями, разумеется), но мы не
знаем метода, который был бы неэффективным, потому что ис-
пользуемые в нем числа являются «неподходящими». Статисти-
ческие методы (вероятно, кроме некоторых психометрических
методов шкалирования.) ничего не добавляют и ничего не отни-
мают от значимости чисел, к которым они применяются. Эта
точка зрения, сформулированная с юмором и проницательно-
стью, принадлежит Каплану (1964, р. 205—206):
«Математика может избавить нас от мучительной необходимости раз-
мышлять, но мы должны платить за эту привилегию, испытывая муки раз-
думий как до того как математика вступает в действие, так и после
Я вспоминаю детскую загадку, где обнаруживается эта необходимость.
Трое мужчин зарегистрировались в отеле, уплатив по 10 долларов каждый
за комнату. Служащий, чуть позже сообразивший, что три комнаты соста-
вили комплект, стоимость которого только 25 долларов, дал 5 долларов
коридорному для возврата гостям. Так как 5 долларов не делятся на
три, а также и по другим, менее деликатным причинам коридорный оста-
вил 2 доллара у себя и вернул только 3. На обратном пути он подсчитал-
«Каждый из них заплатил 10 долларов Я вернул 3 доллара или по од-
ному доллару каждому, поэтому каждый из них в действительности за-
платил 9. Далее, трижды девять —27, плюс 2 доллара, которые и оставил
у себя, получим 29 Где же тридцатый доллар?» Конечно, если его 2 дол-
лара вычесть из 27, а не прибавить, то остаток равен 25 —сумме оплаты
19
отеля. Мы вольны складывать числа, если хотим, но не должны рассчитывать
на то, чтобы сумма играла какую-нибудь роль в данной ситуации. В махина-
циях коридорного отсутствует не доллар, а здравый смысл, его логика была
2.3. Переменные и нх измерение
Переменными являются характеристики людей или вещей,
например, вес, возраст, время реакции, беглость чтения, количе-
ство детей, число студентов. Интуиция и опыт подсказывают
нам, что некоторые из этих переменных непрерывны (то есть
измерения их могут дать любое значение внутри некоторой об-
ласти). таковы вес, возраст и время реакции. Мы твердо знаем,
что некоторые переменные дискретны (то есть их измерения
могут давать только отдельные значения), например количество
детей. Наиболее известны те дискретные переменные, которые
измеряются в результате счета. «Количество детей» может
быть 0, 1, 2, 3 ... Естественно, эта переменная не может при-
нимать промежуточные значения, скажем 1,75,
С другой стороны, мы уверены, что если бы только у нас
были соответствующие приборы, средства и время, то можно
было бы измерять непрерывные переменные с желаемой точ-
ностью. Измеряя время в состязаниях по бегу, мы предпочитаем
останавливаться на определении десятых секунты Но хотя со-
общается, что расстояние SO м было преодолено за 10,4 сек,
более точные хронометры могли бы показать, что рекордное
время равно 10.416 сек. Но даже это время не точно; просто
оно верно до тысячных долей секунды. Настоящего, или точного,
измерения переменной никогда нельзя достигнуть, так как изме-
рение всегда должно где-то оборвать точное значение'. В силу
этого точное значение переменной — это косвенное значение Оно
является результатом процесса измерения. Мы не рассчитываем
на совпадение косвенного и фактического значений переменной,
но первое задает пределы для последнего Например, если рост
человека, измеренный с точностью до сантиметра, составляет
157 см, то его действительный рост в это время и в этих усло-
виях находится между 156,5 и 157,5 см.
Измерение любой непрерывной переменной должно сопро-
вождаться определением точности процесса измерения. Скоро-
сти хронометрируются с точностью до десятой доли секунды;
рост может быть измерен с точностью до сантиметра; возраст —
с точностью до дня. Чувствительность процесса измерения за-
дается минимальной единицей цифровой шкалы, которая фик-
сируется. Таким образом, чувствительностью в трех вышеприве-
денных примерах были соответственно десятые доли секунды,
сантиметры н дни.
1 Под точным значением, или меткой, не надо понимать «истинную» или
совершенно устойчивую метку, которой не бывает. Реальная метка может
быть нестабильной во времени
20
Часто мы хотим задать те границы любого найденного зна-
чения, в которых находится точное значение. Например, каковы
минимальные и максимальные действительные значения роста,
которые соответствуют установленному росту 147 см, если изме-
рение осуществляется с точностью до сантиметра? Пределы для
точного значения в окрестности любого найденного значения
устанавливаются путем прибавления и вычитания половины чув-
ствительности измерительного процесса от найденного значения.
Таким образом, человек с установленным ростом 147 см
имеет действительный рост в шиервале между 147 см —
— (1 см/2) = 146,5 см и 147 см + (1 см/2) = 147,5 см.
Следующие примеры должны внести ясность в эту про-
цедуру
Переменная Чувстви- тельность измерения измерения Пределы точного
Вес Возраст Время реакции Время пробега КГ ГОД 1/100 сек 2/10 сек 59 КГ 25 лет 0,53 сек 5,5 сек 58,5—59,5 кг 24 года 6 мсс— 25 лет 6 мес 0,525-0,535 сек 5,5—5,7 сек
Оценки в педагогических и психологических тестах часто
получаются в результате подсчета числа правильных ответов,
которые дает испытуемый. Джон ответил правильно на 45 из
90 вопросов по разделу речи школьного теста на определение
способностей. Поэтому соответствующая цифровая метка для
переменной «речевые способности школьника» составляет 45.
Поскольку мы вообще рассматриваем переменные, лежащие
в основе педагогических и психологических тестов, чаще всего
как непрерывные, чувствительностью этих измеряющих средств
является единица или одна точка шкалы (если тесты составлены
из отдельных пунктов). Таким образом, точная метка Джона
в тесте лежит между метками 44,5 и 45,5 Если сначала это
покажется вам странным, вспомните, что измеряется непрерыв-
ная переменная «речевые способности школьника», а не дискрет-
ная «число точных ответов».
Практический вопрос, который чуть позже возникнет, ка-
сается отношения к результатам измерений при выполнении
вычислений. Если 10 измерений IQ имеют одинаковое значение
105, а пределы точного значения образуют диапазон от 104,5 до
105,5, то 10 меток обычно считаются равномерно распределен-
ными в интервале, ограниченном пределами точного значения.
Если кому-нибудь для какой-либо цели нужно узнать, сколько
1 Определение пределов для точного значения в такой форме требует
многих оговорок и может рассматриваться лишь как сугубо ориентировоч-
ное — Прим. ред.
21
меток превышает 105,2, надо учесть 3 метки из 10 в интервале
от 104,5 до 105,5 (см. рис. 2.1). Это удобное допущение прини-
мается при определении средних величин и расчете меток,
ниже которых лежат заданные проценты испытуемых.
Приходится, к сожалению, признать, что понятие пределов
точных значений дискретных измерений является одним из ра-
123456789 fO
104,5 105,0 105,2 105,5
Рис. 2.1.
бочих орудий статистика. Хотя и бессмысленно говорить, что
точное число студентов, которых обучает данный преподаватель,
лежит между 33,5 и 34,5 — очевидно, что их 34, — это все же
иногда делается при выполнении расчетов.
2.4. Символы, данные и операции
Если мы хотим указать на множество чисел вообще, не запи-
сывая конкретно каждое из них, мы выбираем любую произ-
вольную величину, например X, (читается «.¥ с индексом t»).
X заменяет число; i, называемое подстрочным индексом, указы-
вает, какое число имеет i-й номер. Когда индекс зафиксирован,
скажем, на значении 4, то X* означает определенное число: чет-
вертый член некоторой группы. Х\ обозначает одно число, Х2—
другое, причем 1 и 2 являются только обозначениями или наи-
менованиями: мы не можем заключить на основе индекса, что
больше — или Xi- Мы можем обозначить 4,3; 2,1; 6,7 и 3,5
через Xi, Xi, Х3 и X*. Конечно, мы могли бы обозначить 4,3
через Х2 вместо Хи как мы сделали. Х\— просто первое число
в нашей последовательности из п чисел, а Хг_— последнее.
Если мы имеем группу из п чисел (числом п может быть 2,
3, 100 или любое другое число), то можем обозначить ее элемен-
ты с помощью символов Xi, ..., Хп. Вообще т-е измерение
(X) есть Х„ где i может быть каким-нибудь одним из индексов
1,2,..., п.
Данные могли бы быть расположены в таблице со строками
и столбцами. Каждый элемент такого расположения можно опи-
сать, если мы знаем группу (столбец), в которой он находится,
и его положение в этой группе (строку):
Порядок внутри гр уппы Номер группы
I 2 з
Первый (I) Хи =4,0 Х12 = 6,5 Хи = 4,4
Второй (2) Х21 =2,3 Х22 =2,1 Хгз = 5,3
22
Когда мы пишем Хи, то имеем в виду первый элемент вто-
рой группы, 6,5. Хгз заменяет второе число в третьей группе,
5,3. Когда же мы пишем Х,3-, то мы можем обозначать каждое
из этих 6 чисел, придавая i значение 1 или 2, а /—1, 2 или 3.
Допустим, вы собирались провести эксперимент, в котором
12 человек читали бы одну брошюру, а 10 человек — другую.
Вполне возможно, что вам захочется говорить о числах, кото-
рые получатся в результате этого эксперимента, раньше, чем
они будут получены. Вместо того чтобы сказать: «Я собираюсь
сравнить третий номер в первой группе со вторым номером
во второй группе», вы можете сказать: «Я думаю сравнить
Хз| с X22». Символы должны стать полезным и стенографиче-
ски экономным средством.
Данные можно классифицировать применительно к любому
количеству характеристик.
2. 5. Обозначение сигма (2)
Анализ большинства данных включает, между прочим, сло-
жение, вычитание, умножение и деление чисел. Поскольку мы
хотим поговорить о выполнении этих операций над группой
чисел вообще, произведем операции на символах вместо чисел.
Последовательность Х1( Х2, Хп представляет собой группу
из п чисел, каждое число которой можно записать как X,-.
Xj 4- Х2 заменяет сумму первого и второго чисел Порядок
индексов обычно совершенно произволен. С тем же успехом
можно было бы использовать Xj-f-Xj. X, 4- Х24- Хю представ-
ляет собой сумму первого, второго и десятого номеров.
Часто мы хотим сложить все числа группы. Если в группе
имеется 5 чисел, то п = 5, а сумма всех чисел равна Х|4~
4-Хз4- ••• 4-Xs. Xi4-X24- ... + Х„ обозначает сумму всех п
чисел в группе, когда точное значение п не оговорено.
Сокращение записи для Х)4-Х24- - 4--^п, которое часто-
употребляется, выглядит так: У. X;.
У. X; обозначает X, 4~ Х2 4~ 4~ Х„.
S X, = Х) 4-Х2 4-Х> У^Х; = Х3 4-Х4 4~ Xs.
5
S — это греческая прописная буква «сигма». У. X, читается
как «сумма Х„ когда i пробегает значения от 1 до 5». У Хг
читается как «сумма X,-, где I изменяется от 1 до п».
Общепризнано, что краткое обозначение S является эко-
номным. Статистики извлекают из этого большую пользу.
23
Сложение чисел, умноженных, например, на 6 или возве-
денных в квадрат (это значит умноженных на самих себя),
осуществляется, как обычно. Допустим, мы хотим умножить
каждое из п чисел на 2 и сложить результаты. Искомая сумма
есть
2Xi+2X3+... +2Хп.
Но вы наверняка заметите, что эта сумма—то же самое, что и
2(Х1+Х2+ ... 4-Хя).
Используя S-обозначение, мы можем заменить (Xi Ц-
-НХ2-+-... 4-Хп) на У Х(. Результат можно записать так:
2Х, + 2Хг + ... + 2Х.= £ 2Х, = 2 j X,-
Этот результат возник не вследствие какого-либо магиче-
ского свойства числа 2: с числами 4, 60 или 131,4 результат
будет тот же. В самом деле, если с представляет собой какое-
либо постоянное число (то есть число, которое не зависит от
i). то
сХ|-+-сХ24- ... 4-СХЯ == У сХ, = с У X,, (Правило!)
Если постоянное число (константу) с прибавить к каждому
из /г чисел, то получим
Xi + c, Х2 + с. ---, Хга+с,
Сумма этих значений
(X, +с) + (Х, + С) + ... +(Х„+<Г)-Ё(Х,+г).
При сложении мы всегда можем перегруппировать числа
л любом порядке до того, как складывать
У (X; 4- с) = (Х| 4* Хг 4- ... 4* Хя) 4* (с 4~с + 4*с).
Первая сумма в круглых скобках справа дает У X,.
Какова же вторая сумма в круглых скобках? Сколько с сло-
жено5 Ответ: п. Поэтому вторая сумма равна пс. Следова-
тельно,
У (X/ 4- с) = У Х; 4- У с = У Xt 4- пс. (Правило 2)
24
Если с — одна постоянная, a d — другая, то как иначе можно
записать £(сХ; 4~d)? (Используйте правила 1 и 2)
Другое важное выражение — сумма квадратов п чисел
(Xi-Xi)4-(X2-X2)4- ... 4-(ХЛ • Xn) = X, 4-Xi 4- ... Ч-Хп,
которое символически изображается как 22 X2i.
Аналогично
х?+й+ +/.= ёй
1=1
хотя в элементарной статистике это выражение встречается
редко.
Заметим, что £ Xt символически изображает единственное
число: число, которое получается в результате сложения п чисел.
'E.Xi может быть 10, 13 или 1300. с£хг —это произведе-
ние двух чисел сн£х(. ^£х/)^22х^ является произведе-
нием числа (некоторой суммы), умноженного на самого себя.
Мы также запишем это следующим образом:
(ЁхОСЁхО-ЩхУ.
Если Х, = 3. 1,-6, а Х,= 1,то j Х,— 10. а ( j X,) — 100.
Всегда ли У X] идентично (У X j ? (Указание, когда
а2 4- Ь! = (а 4- Ь)2?). Вычислите каждое выражение при Xs = 2,
Х2 = 1, Х3 = 4, Х4=1.
Обычным в статистическом анализе является выражение
2^ (X/4~ (Х| 4~ с)2 4~ (Х2 4~ с)г 4~ 4~(Х„4~С)“-
(Х,4-с)2, равное (X, 4-е) (X,-4-с), иначе можно записать
так:
Xi+c
Xj + c
cXf 4-е
X^+cXt
X/4-2cXf4-c2
25
Испытание (опыт)
! 2 ... J
12
Эти данные могли быть взяты из эксперимента, в котором п
испытуемым был дан 1-й вариант испытания (уровень), другим
п испытуемым — 2-й вариант и т. д. до варианта J. В подобном
эксперименте должно быть nJ различных испытуемых. Или
иначе —каждому человеку можно было бы задать все J испы-
таний. Эти две ситуации являются совершенно различными, как
мы увидим в следующих главах.
Сумма всех чисел на уровне 1 (то есть столбец I) равна
Хи 4-Х214- 4-^ni- Заметим, что первый номер в индексе
говорит о том, в какой строке находится данное наблюдение,
а второй — в каком столбце. Для определения суммы первого
столбца, которая представляет собой Хп4-^2»4- 4-^яь мы
суммируем i от I до п, в то время как / сохраняет значение 1.
Мы записываем это как У, Х(1. Выражение У, Х12 обозначает
сумму по i от 1 до л, тогда как / остается равным 2.
У, Xtl равна X|)4-Xi24- ... 4-Xu (читаем: «сумма по j от
I до 1 при I— 1>). Это выражение представляет собой сумму
наблюдений в первой строке таблицы (плана). У, Xtl есть-
сумма п чисел в столбце j; У, Хц — сумма J — чисел в/-и строке.
Как мы могли бы обозначить общую сумму всех nJ чисел?
Один путь заключался бы в сложении чисел в каждом столбце
отдельно и последующем сложении сумм 1 столбцов:
Общая сумма = У Х(| 4-У Xi2 4- ... 4-Ух</- ^У сумму-
J чисел можно обозначить проще. Общая сумма— У, ( У Хц} =
==У У %i/- Квадрат общей суммы имеет вид Cssm-
Символом суммы всех nJ чисел, которая получается в резуль-
тате возведения в квадрат каждого исходного наблюдения и
последующего сложения квадратов чисел, является ^У Ух|/.
27
Это выражение читается следующим образом: «Двойная сумма
по ij X, возведенного в квадрат, при /, изменяющемся от 1 до
/, и i — от 1 до п». Сначала j принимает значение i, когда
। пробегает значения от 1 до п, затем / присваивается значе-
ние 2 при 1, изменяющемся от I допит, д.
Сумма по столбцам квадратов сумм каждого столбца обоз-
начается при помощи
I / п \2
Придет время, когда мы будем говорить о сложении одной
константы со всеми числами первого столбца массива и дру-
гой константы со всеми числами второго столбца. Так как
величина константы зависит только от столбца, а не от поло-
жения в столбце, индекса i не требуется для ее идентифика-
ции. Поэтому достаточно говорить о и с2. Мы можем обоз-
начить константу для /-го столбца через с,. Таким образом,
если мы хотим говорить об Хг1 плюс константа, своя для
каждого столбца, то мы можем обозначить эту величину как
Хи + с,. Последовательность таких величин для /-го столбца
представляет собой
Х./Н-с,
Х,/+С/
+ с1-
Итак
£(Х!/ + с/)= ^Хц+nc/. (Правило 4)
поскольку «с} является константой при суммировании по I».
Для двойного суммирования
S (X,/ +^)= £ (Е X,j + пс^ = ^ Е Хи +п £с,.
Если бы константу d прибавили ко всем nJ наблюдениям,
то никаких индексов для d не потребовалось бы Величина
d одинакова независимо от того, в какой строке и каком
столбце она находится. Вы должны проверить, что
Д S (Хц + </)= £ £ Xlt +«/ d. (Правило 5)
Так как d прибавляется к наблюдениям п раз в каждом
из J столбцов, то в итоге она фигурирует в общей сумме
nJ раз.
28
Если вы все еще не убеждены в этом, то перечислите сим-
волы для каждого из nJ наблюдений или измерений, как ука-
зано ниже, и просуммируйте их:
S 2 ... /
Xl2-±d ... X17 + rf
Х,!2 + d ... XnJ-\-d
Очевидно, в каждый столбец константа d входит п раз, а всего
] столбцов, поэтому в целом имееюя nJ констант d.
Задачи и упражнения
1. Отнесите каждое из следующих измерений к одному из
классов: классу наименований, порядка, интервалов или отно-
шений:
а. Числа, кодирующие темпераменты.
б. Академический ранг (ассистент, доцент, профессор) как
мера продвижения по службе.
в. Метрическая система измерения расстояний.
г. Телефонные номера.
2. Разверните следующие выражения:
a.ix?- 6. в. (Ь,)’==
3. Переведите следующие выражения а сигма-обозначения;
а. ЗХ)-j-ЗХ2 + ЗХ3 == б. (Х,+ ... -(-Хю)2 —
в. (Х,+ ... +Х„) + 7п =
г. (х? + х,) + (х, + х,) + ... + Cti + xs)-
3
ТАБУЛИРОВАНИЕ И ПРЕДСТАВЛЕНИЕ ДАННЫХ
3.1. Табулирование данных
До анализа и интерпретации количественных данных обычно
необходимо их обобщить. В табл. 3.1 приводятся результаты
контрольной по чтению, проведенной в начале учебного года.
Таблица 3.1
Результаты контрольной по чтению в классе
(38 учеников)
Ученик
Дэвид А.
Барбара Б.
Чарльз Б.
Роберт Б.
Милдред С.
Роббнв С.
Роберт С.
Динни Д.
Джун Д.
Джон Д.
Роберт Д.
Дан Ф.
Ларри ф.
Ричард Дж.
Гровер X.
Робер? X.
Сильвия X.
Уоррен X.
Кларенс К.
Дэвид К.
Джером Л.
Роза М.
Билли Н.
Нэнси О.
I Кэрри П.
Ральф Р.
Джордж С.
Гретта С.
Джек С.
Мери С.
Поль С.
Ричард С.
Роберт С.
Уильям С.
Джин Т.
Адольфо У.
Долорес У.
I Ричард У.
75
75
51
Оценки проставлялись в алфавитном порядке так, как запи-
саны ученики в классном журнале. Однако в подобной форме
оценки не слишком удобны, и мы можем лишь с трудом судить,
30
например, о том, будет ли первый по списку ученик (Дэвид А.)
с оценкой 90 очков из 128 возможных преуспевающим или
только средним в чтении по сравнению со своими однокласс-
никами.
Ранговый порядок
Первый этап представления данных — это обычно упорядо-
чивание оценок по величине от максимальной до минимальной.
Такое представление называют несгруппированным рядом.
В небольшом классе этого часто вполне достаточно.
В таблице 3.2 рассматриваются те же 38 оценок, что и
в таблице 3.1, но упорядоченные по убыванию от 112 до 44.
Таблица иллюстрирует также ранговый порядок учеников (1-й,
2-й....38-й) и оценки, табулированные без последующего груп-
пирования. Теперь нетрудно заметить, что опенка 90 очков
Дэвида А. обеспечивает ему 13-й ранг в классе из 38 учеников,
или можно сказать, что он замыкает верхнюю треть списка.
Аналогичным образом можно легко интерпретировать каждую
оценку в терминах рангов. Но, вероятно, могут иметь место и
равные оценки, особенно в классах из 20 и более учеников.
Так, в нашем примере два ученика получили по 97 очков.
Поскольку в данном случае нельзя утверждать, что один ранг
выше другого, мы обязаны приписать нм одинаковые ранги.
Так как существуют 6 учеников, ранг которых выше (1,2. 3,4,
5,6), то следующие два ранга, 7 и 8, усреднены, что дало 7,5.
Точно так же среднее рангов 9 и 10 составляет 9,5 и т. д.
Имеется 3 ученика с оценкой 75 и 21 ученик, ранг которых
выше; среднее следующих трех рангов (22, 23 и 24) равно 23,
что дает ранг для каждой оценки 75. Кроме того, что для опре-
деления рангов требуется много времени и снл. список является
длинным, громоздким и неудобным для сравнения с другими
классами, большими или меньшими; ранг 19-й в классе из
38 учеников хуже, чем ранг 19-й в аналогичном классе из
70 учеников.
Распределение частот
Этот список можно сократить, классифицируя оценки по
распределению частот, иногда называемому просто распределе-
нием. Третий и четвертый столбцы таблицы 3.2 показывают
простейший вид распределения. Различные оценки размещаются
по величине в данном случае от 112 до 44, а справа от каждой
оценки указывается число ее повторений. Каждое число справа
называется частотой и обозначается /, а сумма частот обозна-
чается п.
Распределение сгруппированных частот
Для большого числа оценок — скажем, 100 или более — на
следующем этапе может иметь смысл обобщение данных. Как
31
Таблица 3.2
Оценки контрольной по чтению
из таблицы 3.1, упорядоченные по величине,
прораижироваввые и лротабулироаанные
Опенка
112
109
106
105
104
100
97
97
112
109
106
105
104
100
97
95
93
91
90
89
84
сумма= 19
середина
частот
сумма — 19
правило, существует настолько широкий диапазон оценок, что
целесообразнее сгруппировать их по величинам, например,
в группы, объединяющие все оценки от 105 до 109 включи-
тельно, от 110 до 114 включительно и т. д. Каждая такая
группа называется разрядом оценок. В случае полного разме-
щения по группам обычно говорят о распределении сгруппиро-
ванных частот. Хотя и не существует четкого правила выбора
32
1- Определение общего размаха внутри всей выборки, кото-
рый равен разности между максимальной и минимальной
оценками плюс единица. Из имеющихся оценок максималь-
ная равна 112, а минимальная — 44, что дает размах
(112 — 44)4-1=69. Фактически считают, что 112 покрывается
единичным интервалом оценок 112,5—111,5, а 44 — интервалом
44,5—43,5. Заметим, далее, что размах равен 69 [(112—44) 4- 1,
или 112,5—43,5]. Однако реальные границы оценок не всегда
являются дробными. Если возраст исчисляется ог последнего
(самого недавнего) дня рождения, то лица, объявившие себя
44-летними (то есть еще не 45-летними), находятся в интер-
вале 44,00 — 44,99... (почти, но не совсем 45,00), середина кото-
рого — 44,5. Если они называют возраст относительно ближай-
шего дня рождения, интервал составляет 43,5—44,5 со сред-
ним 44. Аналогично, если они представляют себя «приближаю-
щимися к 44», то интервал равен 43,00—43,99... со средним 43,5.
Между самым «юным» из «приближающихся к 44», который
только что достиг возраста 43 лет, и самым «старым» пред-
ставителем «44-го последнего дня рождения», которому почти 45,
будет наблюдаться разница приблизительно в два года. Спра-
шивая просто о «возрасте» без точного определения системы
счета, мы не в состоянии точно интерпретировать наши резуль-
таты.
2. Выбор интервала группирования разрядов, представляю-
щего собой шприцу разрядов, по которым должны быть клас-
сифицированы оценки, должен производиться таким образом,
чтобы разрядов было не менее 12, но и не более 15. Для этого
разделим диапазон на 12 и найдем наибольший возможный
класс или интервал разряда оценок. Разделим диапазон на 15
и найдем наименьший возможный интервал разряда. В нашем
случае 69:12= 5,75, а 69: 15 = 4,60. Так как использовать
любой нецелый интервал неудобно, то наибольшее число 5,75
округляется с уменьшением до 5, а 4,60 — с увеличением до 5,
хотя и интервал 6 обеспечил бы 12 разрядов для этих 38 оце-
нок. Интервал с шириной, определяемой нечетным числом, на-
пример 5, с целочисленным средним значением, если границы
разряда дробные (оканчивающиеся на 0,5), обычно предпочи-
тают интервалу с четной шириной, по дробными средними, когда
границы разряда дробные. Середина разряда 110—114, содер-
жащего 5 опенок: 110, 111 112, 113 и 114, равна 112, (то есть
110-Н(114—U0) :2] = 110+ (4/2) = 110+2= 112). (Другой
способ определения середины интервала состоит просто в усред-
нении зафиксированных границ интервала: (110+П4):2 =
= 112). Если бы использовался разряд шириной 6 с границами
оценок 108— ИЗ, например, то середина этой группы, опреде-
ляющейся четным числом, составила бы 110,5, что могло бы
привести в итоге к более сложному счету. Следовательно, интер-
вал 5 предиошнтельпее интервала 6, когда границы разряда
дробные.
31
3. Определение границ разрядов. Разумеется, надо образо-
вать достаточное количество разрядов для включения самой
высокой и самой низкой оценок. Для этого начинайте табули-
рование всегда с величины, кратной разрядному интервалу.
Если самый низкий разряд начать с 40, кратного 5, он включит
самую низкую оценку 44. А если начать с 45, то он не вклю-
чит 44. Следующий разряд будет начинаться с 45. затем с 50
и т. д. до тех пор, пока самая высокая опенка 112 не попадет
в разряд 110—114.
4. Табулирование. Подсчет ведется для каждой оценки про-
тив разряда, в который она попадает. Для табулирования нет
необходимости в упорядочении оценок, так как последнее мо-
жет потребовать больше времени, чем само табулирование.
В первоначальном алфавитном списке первая оценка 90.
В столбце таблицы против разряда, начинающегося с 90, для
регистрации оценки делается черточка. Следующая оценка —
66. Она попадает в разряд, который начинается с 65, так что
черточка делается гам. Аналогично результаты подсчета поме-
щаются в столбце против соответствующего разряда для всех
прочих оценок-
Таблица 3 -I
Распределение опенок контрольной по чтению
для всех шести школ в одном городе
35
В итоговой таблице не приводятся этапы, в результате ко-
торых она была получена. В простейшей форме распределения
частот есть только два столбца. В первом приводятся разряды,
обычно расположенные в убывающем порядке сверху вниз,
а второй содержит частоты — число оценок в каждом раз-
ряде.
Чтобы убедиться в том, что вы поняли вышеприведенные
этапы 3 и 4, остановитесь на этом месте и постройте групповое
распределение частот 38 оценок, пользуясь интервалом разря-
дов (сгруппированных) шириной 6. Удовлетворяет ли количе-
ство разрядов в этом случае критерию 12—15, введенному па
2-м этапе?
Когда нужно сравнить две или более выборок, обычно хо-
рошо поместить все данные в такую же таблицу. В этом слу-
чае будет один столбец для разрядов, в который сгруппированы
оценки, и по одному для каждой из сравниваемых, скажем,
школ или классов. В таблице 3.4 приведены распределения
частот, обобщающие отчеты шести школ. Количество интерва-
лов группирования меняется от 9 для школы Е до 17 для школ
А и Г, хотя для некоторых интервалов нет данных.
Уоллис и Робертс (1965, гл. 9) написали отличную главу
об искусстве интерпретации статистических таблиц. Они напо-
минают читателю о тех очевидных предосторожностях, которые
необходимо принимать, например о внимательном чтении за-
головков и «шапок» таблиц, и демонстрируют некоторые искус-
ные и утонченные методы извлечения скрытой в таблицах ин-
формации. Им удалось хорошо справиться со своей задачей,
придав вместе с тем этой главе занимательную форму.
3.2. Квантили
Одним из наиболее эффективных и полезных методов опи-
сания группы наблюдений является описание с помощью кван-
тилей. Квантиль — общее понятие, а процентили, децили и
квартили — три его примера. Квантиль — это точка на число-
вой шкале, по предположению, основанная па группе на-
блюдений; квантиль делит совокупность наблюдений на две
группы с известными пропорциями в каждой из них. Суще-
ствуют, например, три квартиля (Qi, Q2, Q3); они делят группу
наблюдений на четыре равные части (кварты). Четвертая
часть наблюдений лежит ниже Q,, половина наблюдений лежит
ниже Q2. а три четверти наблюдений — ниже Q3. Таким обра-
зом, три квартиля делят совокупность наблюдений на четыре
части, которые равны в смысле пропорциональности наблюде-
ний 99 возможных процентилей (Р......,Рю) делят множество
наблюдений на 100 частей с равным числом наблюдений в каж-
дой. Девять децилей делят множество наблюдений
на десять равных частей.
36
Если 25% всех наблюдений находится ниже Р^, 25-го про-
центиля, и то же справедливо для Q,, первого квартиля, то Р&
должно равняться Qj.
На рисунке 3.1 представлены взаимосвязи между различ-
ными квантилями, определенными раньше, и кроме того, так
называемые квинтили (квинта — пять). Четыре квинтиля делят
множество на 5 частей. Мы будем обозначать их К}, Кз, Кз, Kv
Квантили очень удобны для обобщения данных. Простое
сообщение, что Р5 есть 10,75, а PIS—16,80, сразу же говорит
нам о том, что 5% наблюдений меньше 10,75, а 10% из них
лежит между 10,75 и 16,80. В случае некоторых больших групп
данных, с которыми обычно приходится иметь дело, читатель
Gt 0з
Df D2
||Ш|П||1|»|1|||||.»
Р0 По Р20
04 о5 о6 d7 d8 ds
^0 Р40 Р50 Р8в P7Q P8Q Р90
Рис. 3.1. Связь между квантилями.
может представить себе общую совокупность наблюдений, если
ему известны, к примеру, только величины трех или четырех
процентилей. Однако чаще для описания данных используются
более сложные обобщающие меры, о которых мы вскоре будем
говорить, тогда как некоторые квантили проще вычислить и
легче интерпретировать. К сожалению, квантили еще не нашли
достаточно широкого применения, и исследователи пытаются
просто описывать совокупность данных.
3.3. Определение процентилей
Так как между различными квантилями существуют опре-
деленные взаимосвязи, приведенные на рис. 3,1, достаточно
знать только, как найти процентили, чтобы определить любые
требующиеся квантили (как правило, никто никогда не желает
разделить группу наблюдений более чем на 100 квантилей).
Определение процентиля является простым: Р-й процентиль
представляет собой точку, ниже которой лежит Р процентов
оценок. Вычисление процентиля немногим сложнее, чем опре-
деление, которым мы должны руководствоваться
Перед началом вычисления любого процентиля в группе оце-
нок цадо упорядочить эти оценки по возрастанию. Для больших
групп оценок это непроизводшельно и удобнее использовать
сгруппированные данные. Метод, который мы предлагаем
37
для нахождения точки процентиля, общий и пригоден как
для ранжированных, так и для сгруппированных оценок.
Преподаватель предложил 125 учащимся контрольное зада-
ние, состоящее из 40 вопросов. В качестве оценки теста выби-
ралось количество вопросов, на которые были получены пра-
вильные ответы. Негрупповое распределение частот 125 оценок
теста приводится в таблице 3.5. Каков 25-й процентиль в группе
125 оценок теста, то есть чему равна величина Р25? Ртя— это
точка, ниже которой лежат 25% 125 оценок.
Таблица 3.5
Определение Р25. 25-го процентиля, в распределении частот,
когда интервал оценок—единица
Оценка ц тесте Частота Накопленпан Вычисления
38 । 125 _ п 125 „.
37 1 124 Шаг 1. 0,25 п = — = —— — 31,2о
35 5 120 Шаг 2, Найти фактическую нижнюю
34 115 границу разряда оценок, содержа-
33 8 106 щего опенку 31,25
32 17 98 Z. = 28,5
3] 23 81 Шаг 3. Вычесть накопленную к L
30 24 58 частоту из 31,2.5
29 18 34 31,25 - 16= 15,25
28 10 16 Шаг 4. Разделить результат 3-го шага
27 3 6 на частоту f в интервале, содер-
26 1 3 жащем оценку 31,25
25 0 2 *5;? - о.®
24 2 « = 125 2 18 Шаг 5. Прибавить результат 4-го шага к L p2i = 28,5 + 0,85 = 29,35
Вычисление любого процентиля упростится, если построить
распределение накопленных частот. Накопленные частоты к лю-
бой заданной опенке представляют собой суммарное количество
частот на этой оценке или ниже ее. В третьем столбце таблицы
3 5 вы найдете накопленные частоты для 125 оценок контроль-
ного задания. Обратите внимание, например, что существует
106 лиц с (естовыми оценками 33 или меньше. Накопленные
частоты для тестовой оценки 33— 106.
Вычисление можно выполнить за 5 шагов:
Шаг I. Найти (0,25) п делением п на 4:
ту = 31,25.
Шаг 2. Определить фактическую нижнюю границу L раз-
ряда оценок, содержащего лицо с оценкой 31,25 снизу.
38
Так как 16 человек имеют оценки 28 или меньше, а 34 —
оценки 29 или меньше, то частота 31,25 лежит в интервале раз-
рядов оценок 28,5—29,5.
Допустим, что 18 частот на оценке 29 равномерно распре-
делены по интервалу 28,5—29,5. Тогда каждая частота займет
’/is часть интервала. Определить, на какие части рассекает
интервал оценка 31,25, — значит решить задачу интерполяции
внутри интервала. Шаги 3 и 4 реализуют такую интерполяцию.
Шаг 3. Вычесть накопленную к L частоту (cum. f) из 0,25 п.
L —• это 28,5, а к L накоплено 16 частот. Следовательно,
0,25 п — (cum. f) — 31,25 •- 16 — 15,25 На 3-м шаге определяет-
ся, сколько частот в интервале 28,5—29,5 лежит ниже 0,25 п.
Шаг 4. Разделить результат 3-го шага на частоту f в ин-
тервале, содержащем частоту 0,25 п.
15,25 ПйК
~ТГ=0.85.
4-й шаг — это определение той доли интервала разрядов,
которая лежит под частотой 0,25 п. В интервале 28,5 — 29,5 на-
ходится 18 частот, а 15,25/18 = 0,85-ю часть интервала зани-
мают первые 15 ’/< частот.
Шаг 5. Прибавить результат 4-ю шага к L Сумма равна
рк = 28,5 + 0,85 = 29,35-
В соответствии с условиями, которые мы приняли для пред-
ставления оценок, P2i — 29,35, то есть 25% из 125 оценок ле-
жит ниже 29,35 (Аналогично 75% из 125 оценок лежит выше
29,35 ) Шаги с 1-го по 5-й можно выразить одной формулой
+ , (3.1)
где L—фактическая нижняя граница единичного интервала
оценок, содержащего частоту 0,25 п снизу распределения;
cum. f— накопленная к L частота, a f—частота интервала оце-
нок, содержащего частоту 0,25 п.
Для определения любого процентиля распределения частот
в случае, когда интервал разряда оценок равен 1, применяется
более общий вид уравнения (3 1). Предположим, нам требуется
найти точку, превосходящую некоторую долю р частот Рр пред-
ставляет собой р-н процентиль.
Рр^1.+ , (3 2)
где /. — фактическая нижняя граница интервала оценок, со-
держащего частоту рп; cuin.f — накопленная к L частота; f —
частота оценок в интервале, содержащем оценку рп.
Мы проиллюстрируем использование уравнения (3.2) на при-
мере вычисления Р.;9. ио данным таблицы 3 5:
Д,,-30,5+ -—21= 31,24.
39
Вычисление любой точки процентиля группового распреде-
ления частот совершенно идентично вычислениям для несгруп-
пированного распределения. Действительно, формула группо-
вого распределения частот, которая будет рассматриваться,
включает уравнение (3.2) как особый случай, когда интервал
оценок имеет единичную ширину.
Данные таблицы 3.6 представляют собой возраст, округлен-
ный до года, 1982 преподавателей, принимавших участие в спе-
циальных летних мероприятиях по улучшению преподавания
ряда предметов в школе
Общая формула определения процентиля р в группе п
оценок выглядит так:
= (3.3)
где L — фактическая нижняя граница интервала, содержащего
pn-ю частоту снизу, cum. f — накопленная к L частота; f — ча-
стота интервала, содержащего частоту рп- W — ширина любого
интервала оценок.
Заметим, что уравнение (3.3) совпадает с уравнением (3.2)
при №=1, то есть когда интервал оценок имеет единичную
ширину и подразумевается, что оценки сгруппированы по разря-
дам не меньшей ширины, чем первоначально при построении
распределения частот.
Покажем теперь применение уравнения (3.3) на примере
определения Р20 по данным таблицы 3.6. Оценка рп — 396-я
оценка — лежит в интервале 24—27, который имеет фактиче-
скую нижнюю границу 23,5 Разность между рп и накопленной
к 23,5 частотой составляет 396,4— 135. Учитывая, что частота
в интервале, включающем 396-ю оценку, равна 295, а ширина
интервала равна 4, получаем
Р„ = 23,5 + -4-27,04.
В условиях, принятых для вычисления процентилей, мы мо-
жем сказать, что 20% преподавателей оказались моложе
27,04 лет. Мы не считаем это утверждение абсолютно верным.
В процедуру определения процентилей ошибки вошли по двум
причинам.
Во-первых, возраст определялся с точностью до года, а не
месяца, дня, часа или минуты. Во-вторых, предполагалось, что
частоты внутри каждого интервала оценок были равномерно
распределены по всему интервалу. Это предположение, не-
сомненно, было ложным: для молодых возрастов частоты, ве-
роятно. группировались у верхней границы каждого интервала
оценок, для более пожилых — наоборот, у нижней границы
интервала. При выдвижении гипотезы о равномерно распре-
деленных частотах был найден компромисс между вычисли-
тельными трудностями и ошибками аппроксимации. Ошибка,
40
Таблица 3.6
Иллюстрация вычисления Р50 по сгруппированным данным
Интервал возрастов Частота Накопленная частота Вычисления
64-67 4 1982 Шаг 1, 0,50л = 0,50-(1982) = 991
60-63 38 1978 Шаг 2. Найти фактическую нижнюю
56-59 82 1940 границу разряда оценок, содержа-
52-55 120 1858 щего 991-ю оценку:
48-51 125 1738 6 = 31,50
44-47 160 1613 Шаг 3. Вычесть накопленную к 6
40-43 221 1453 частоту cum. f из 991:
36-39 204 1232 991 —721 =270
32-35 307 1028 Шаг 4. Разделить результат 3-го шагг
28-31 291 721 на частоту f в интервале, содер-
24-27 295 430 жащем 991-ю оценку:
20-23 135 л = 1982 135 270 -0 88 Зб7~°188 Шаг 5. Умножить результат 4-го шага на ширину W разряда оценок: (0,88)-(4) =3,52 Шаг 6. Прибавить резулы ат 5-го шага к L: Р50 = 31,50+ 3,52 = 35,02
полученная при аппроксимации Р2П или любого другого процен-
тиля, вероятно, несущественна по сравнению с трудностями,
которые могли бы возникнуть, если бы мы исходили из не-
равномерного распределения частот по каждому интервалу
оценок.
То, что процентили при оценке возраста являются дробными
(например 27,04), приемлемо. Нам нетрудно представить себе,
что кому-то точно 27,04 года. Что же будет, если измеряемая
переменная дискретна? Предположим, что мы строим частот-
ное распределение объемов групп детских садов в системе боль-
шого города. Эта переменная, «объем группы», может прини-
мать только такие значения, как 25, 26, 27, 28 и т. д. Абсурдно
говорить о группе с 27,31 детьми. Однако, если бы нам потре-
бовалось построить частотное распределение объемов групп и
вычислить точки процентилей методами, изложенными в этой
главе, мы почти наверняка получили бы дробные величины.
Могут ли подобные точки дробных процентилей восприниматься
всерьез? Разве не абсурдно, что 81% групп имеет объем 32,41,
а 89% — 32,78? Конечно, это бессмысленно. Один и тот же про-
цент групп, содержащих не более 32,41 или 32,78 детей, точно
характеризует количество групп с не более чем 32 детьми.
Хотя дробные процентили для дискретных переменных и не
вяжутся с общепринятым смыслом, они все же полезны и
находят широкое применение. Отказавшись от такого удобного
и полезного процесса преобразования оценок в процентили.
41
пришлось бы принять какую-то другую, более трудоемкую про-
цедуру. Вряд ли кто-нибудь пойдет на это только потому, что
группа с 32,50 детей кажется несколько смешной.
3.4 Наглядное представление данных
Нет сомнений в том, чю графическое представление педа-
гогических данных является ценным дополнением к статисти-
ческому анализу и обобщению. График или диаграмма имеет
КАКУЮ ДИАГРАММУ
ИСПОЛЬЗОВАТЬ?
ДАННЫЕ
aSmoSi/coS в США
КРИВОЛИНЕЙНАЯ ДИАГРАММА
МЕЖДУГО-
РОДНИЕ
ЗАКАЗНЫЕ И
ЭКСКУРСИ-
ОННЫЕ
СКОЛЬЗЯЩАЯ ПОЛОСА
Ряс. 3.2. Одни и тс же данные, изображенные 15 различными
целью привлечь внимание читателя. Вероятно, внимание рядо-
вого читателя не привлечет обычным образом напечатанное
научное исследование и на него не произведет впечатления
масса таблиц, часто нагроможденных в конце. Однако не исклю-
чено, что его глаз задержится на каком-нибудь рисунке или
диаграмме, если они случайно подвернутся, и это, возможно,
пробудит его интерес ко всему исследованию.
График часто служит эффективным средством выявления
точки зрения. Один маленький график порой больше прояснит
РАЗДЕЛЕННЫЕ СТОЛБЦЫ
.....ИЛЛ.и IWC
СТОЛБЦЫ И КРИВАЯ
AJmoJjcw, 6 ток
ПЛАКАТ
г^ждзгароднл двгоезсы.в гзс
способами (Из М. Е. Spear. Charting Stdiisins. New York, 1952.J
суть дела, чем дюжина таблиц или параграфов. Утверждают,
что факты говорят сами за себя. Действительно, статистики
часто немы, таблицы нередко молчаливы, и только график
громко заявляет о своей миссии. Обычные количественные
данные совершенно абстрактны. Рисунок или график — более
конкретное представление.
Большое разнообразие графиков и диаграмм представлено
на рис. 3.2. Здесь вся основная информация, относящаяся
к эксплуатации автобусов в США, приведена в табличной
форме, которая сопровождается 15 различными графиками.
Каждый график наглядно интерпретирует конкретный вопрос.
Описание функций графиков, данное Мери Спир, — подхо-
дящее резюме к этому введению:
«Сейчас, когда наглядное обучение во всех его аспектах
рассматривается не только как помощь преподаванию, цо и как
его важнейшая основа, наше внимание, как никогда прежде,
обращено на почти абсолютную безграничность возможностей
в этой области. Глаз поглощает письменные «статистики», но
насколько медленно получает мозг сообщения, скрытые в напи-
санных словах и числах. Хороший график, однако, быстро и
ясно выявляет эту информацию. Цели, которые он преследует,
сводятся к следующему:
1 Лучшее понимание данных, чем это возможно при одном
голом тексте.
2. Более глубокий анализ предмета по сравнению с текстом.
3. Контроль точности.
Эта троякая цель графика может быть достигнута при осто-
рожном обращении с ним и знании функций графиков и всех
способов их построения. Следующие 6 этапов лежат в основе
разработки графиков, позволяя описывать статистические дан-
ные ясно и с требуемыми акцентами:
1. Определить существенную информацию в данных.
2. Ознакомиться со всеми типами представлений и сделать
правильный выбор.
3. Удовлетворить аудиторию на ее уровне: знать и исполь-
зовать все подходящие наглядные средства.
4. Разработать подробные и четкие инструкции для чертеж-
ника.
5. Знать оборудование чертежного кабинета и приемы обра-
щения с ним.
6. Осмыслить полученные результаты» 1.
3.5. Графическое представление распределения частот
Обычное распределение частот не дает вполне ясной кар-
тины. Существуют 3 общих метода графического представления
распределения оценок: гистограмма, или столбиковая диа-
грамма, полигон распределения и сглаженная кривая.
। Mary Е. Spear, Charting Statistics, New York, (952, p. 3—4,
44
Гистограмма, или столбиковая диаграмма
Гистограмма — это последовательность столбцов, каждый из
которых опирается на один разрядный интервал, а высота его
отражает число случаев, или частоту, в этом разряде.
На рис. 3.3 показана гистограмма распределения процентов,
присвоенных бумаге в клетку 42 оценщиками. Поскольку наи-
большая частота равна 9, в разряде 59,5—64,5, нет необходи-
мости тянуть вертикаль или шкалу частот слева выше 9. И так
как диапазон оценок распространяется от разряда 29,5—34,5 до
Присвоенные проценты
Рис. 3.3. Гистограмма, или столбиковая диаграмма про-
центов, присвоенных бумаге в клетку 42 оценщиками.
72 77 82 87 92 97 102107112 117122127 132137142147
Коэффициент интеллекта
Рис. 3.4. Гистограмма, или столбиковая диаграмма, предста-
вляющая распределение 83 IQ учащихся небольшого коллед» а.
разряда 74,5—79,5, нужно изображать горизонтальную шкалу
только в этом диапазоне. Для ясности, однако, приняю рас-
пространять шкалу на один разрядный интервал вправо и влево
от этого диапазона. Чтобы фигура не получилась слишком при-
плюснутой или слишком вытянутой, обычно выбирают шкалы
так, чтобы ширина гистограммы составляла около одной и двух
45
третей ее высоты, то есть чтобы отношение высоты к ширине
было приблизительно 3:5. Середина столбца совмещается
с серединой интервала разряда. На практике принято изобра-
жать гистограмму скорее в форме контура, чем отдельными
столбцами. Рис. 3.4 показывает заштрихованную контурную
форму гистограммы.
Полигон распределения
Построение полигона распределения во многом напоминает
построение гистограммы. В гистограмме каждый столбец закан-
чивается горизонтальной линией, причем на высоте, соответ-
ствующей частоте в этом разряде. А в полигоне он заканчи-
вается точкой над серединой своего разрядного интервала на
той же высоте. Далее точки соединяются отрезками прямых.
Присбоекные проценты
Р и с. 3.5 Полигон распределения, предстаяляю-
Ш1ш процентные значения, присвоенные бумаге
в клетку 42 оценщиками.
Так как на разрядах справа и слева от разрядов распределе-
ния частота имеет нулевое значение, полигон заканчивается
соединением точек, представляющих наивысший и наннизший
разряды, с координатной осью на серединах следующих интер-
валов. Рис. 3.5 изображает полигон для данных гистограммы
рис. 3.3.
Сглаженная кривая
Иногда вместо гистограммы или полигона строят сглажен-
ную кривую. Единственная разница состоит в том, что сглажен-
ная линия проводится по точкам настолько близко, насколько
это возможно, а для других двух фигур используются линии
с острыми углами или зубцами.
Гладкая кривая, широко применяемая при представлении
оценок, называется кривой процентилей, или огивой. На рис. 3 6
приведена кривая процентилей для тех же данных, по которым
ранее строили гистограмму и полигон. Точки, определяющие
кривую процентилей, расположены на горизонталях у верхней
46
изображается не более одного распределения. Но если нужно
сравнить два или более распределений, то для этой цели лучше
подходят полигоны частот (или полигоны относительных час-
тот), поскольку, когда гистограммы накладываются друг на
друга, множество линий совпадает, что, понятно, создает до-
вольно запутанную картину. Кривые процентилей имеют много
преимуществ, которыми не обладают другие представления.
Одно из важнейших преимуществ — возможность оценить с вы-
сокой степенью точности квартили, медианы и другие анало-
гичные точки. Как мы увидим ниже, с помощью процентиль-
ных кривых удобно сравнивать несколько групп данных на
одном графике. Главное достоинство ступенчатых диаграмм,
круговых графиков и рисунков, вероятно, в их наглядности
и стимулировании интереса учащихся. «Удачный график», как
уже давно сказал выдающийся педагог Дуглас Скейтз, «зависит
гораздо больше от тщательного обдумывания и суждения, чем
от методики» (Scales, 1942).
Графическое представление двух и более распределений
Часто требуется сравнить два или более распределений.
Например, администрация школы может пожелать сравнить
полное распределение оценок теста речевых способностей учени-
ков одной школы с подобным распределением учеников другой
школы Аналогично частичное перекрытие оценок различных
классов в одном учебном заведении служит надежным спосо-
бом убедить в необходимости индивидуального руководства и
варьирования материала внутри одного и того же класса.
П редставление полных распределений
Когда важно сравнить два и более полных распределения,
например при обследоваиии состояния школы или школьной
системы, придется сделать выбор между полигоном распреде-
ления и кривой процентилей. Мы уже сталкивались с пробле-
мой наложения двух или более гистограмм. На одном листе
бумаги можно изобразить несколько полигонов один иад дру-
гим или рядом. На рис. 3.8 показан метод сопоставления,
использующий ступенчатые диаграммы, выполненные машино-
писным способом. (Возможно, эти оценки сгруппированы слиш-
ком грубо. Согласно известному правилу, лучше было бы иметь
12—15 разрядов оценок вместо 7,9 и 7, использованных на
рис. 3 8.)
Использование полигонов
Существенное преимущество полигонов перед гистограммами
в представлении группы распределений заключается в том, что
полигоны можно наложить друг на друга при меньшем пере-
сечении линий. При этом легче сравнивать распределения.
49
Рис- 3.9 показывает это на примере распределения оценок
понимания прочшанного учеников 7-го, 8-го и 9-го классов
некоторой школы (по 100 учеников каждого класса) Изобра-
жение для этой цели пересекающихся полигонов могло бы при-
вести к полному искажению результатов из-за различных объ-
емов групп В подобных примерах частоты должны прообразо-
вываться в относительные частоты — пропорции Отчетливо
видно значшельное сходство в навыках чтения у трех классов
Но даже в случае только трех распределений линии скрещи-
Р и с. 3.9. Полигоны распределения оценок в тесте на понима-
ние прочитанного для седьмого, восьмого и девятого классов
rcKoTopofi школы (100 учащихся в каждом классе).
ваются и перекрещиваются столько раз, что трудно произведи
точное сравнение одного класса с другим. На одном графике,
пользуясь полигонами распределений, едва ли можно изобра-
зить без существенных затруднении более трех классов
Использование процентильных, кривых
Для графического сопоставления двух и более распределе-
ний некоторые существенные преимущества имеет кривая про-
центилей Так как частоты выражены в процентах, можно
сравнивать группы неравного объема. Другая важная особен-
ность состоит в том, что можно без труда и путаницы предста-
вить несколько распределений. Рис. 3,10 показывает распреде-
ление оценок понимания прочитанного для тех же классов, что
и на рис. 3.8—3.9, но в форме процентильных кривых.
50
По этим процентильным кривым мы можем установить не-
сколько закономерностей, которые не были обнаружены в поли-
гонах. Ясно, что, хотя седьмые и восьмые классы имеют почти
одинаковые средние оценки, восьмому присуща большая измен-
чивость. Это очевидно, поскольку верхняя половина оценок
восьмого класса выше верхней половины оценок седьмого
класса, а нижняя половина для восьмого класса, напротив,
выходит за нижнюю половину для седьмо, 0-
Кроме того, хотя девятый класс систематически превосхо-
дит два других, около 15% девятиклассников располагается
ниже медианы для седьмых и восьмых классов.
3.6. Запутанные графики
В этой главе мы обращали внимание только на корректные
процедуры построения графиков и привели много примеров
хороших графиков. Однако неопытный исследователь или про
пагандист может построить такие графики, которые сильно
запутают читателя Быть может, лучшая зашита от таких оши-
бок— изучение нескольких примеров неудачных графиков.
Рис. 311 показывает процент учеников, исключенных из
школы по окончании учебного года за период с 1960 до 1964 г.
в некотором районе. Процент исключенных постепенно растет
от 9 в 1960 г. до 14 в 1964 г., но отнюдь не удваивается за
пятилетку. Однако, из-за того, что вертикальная шкала графика
начинается не с 0%, как это следовало бы сделать, создается
впечатление, что процент исключенных в 1964 г в 6 раз выше,
чем в I960 г. Действительные отношения прокси юл исключен-
ных по годам выясняются лишь тогда, когда шкала начинается
от 0 и идет до 14%.
51
На рис. 3.12 изображены суммы школьных лотерей для трех
воображаемых школьных районов. Диаметр каждого круга
соответствует сумме лотереи в районе.
Сумма для района Б вдвое превышает сумму района А,
как это следует из сравнения диаметров двух кругов. Однако
глаз любого человека охватывает площади кругов рис. 3.12.
И хотя диаметр круга Б равен двум диаметрам круга А, пло-
щадь круга Б в 4 раза больше плошали круга А. Площадь
Р н с. 311, Процент исключенных после окончания
11-класса за 19€0—1964 гг.
круга района В в 16 раз больше площади круга района А, не-
смотря на то, что он должен представлять школьную лотерею,
сумма которой больше только в 4 раза. Геометрические фигуры
могут внести путаницу при использовании их для изображения
величин, особенно если их площади измеряются квадратами
или более высокими степенями изображаемой величины.
Район В
oloolod о 100200300 6 юи/иозЪи«ииоообЬо
Доллары, 6 тыс
Рис. 3 12. Школьные лотереи для районов А. Б и В
Наиболее серьезной ошибкой при построении рисунков и
графиков является некорректное описание осей координат.
Несмотря на то что обезличенные оси редки в публикациях,
они все же слишком часто попадаются в предварительных ва-
риантах неопубликованных научных работ. Можно значительно
сэкономить время и улучшить качество информации, если не
строить графиков без подробного и исчерпывающего описания
осей. Обратите внимание, как график рис. 3.13 не удобен без
разметки горизонтальной оси. Невозможно поверить, что «воз-
раст» растет слева направо.
52
Смысл, который можно приписать убывающей кривой
рис. 3.13, сильно изменился бы, если бы возраст хронологи-
чески распределялся, скажем, от 6 до 60 лег (самый молодой
и самый старый) вместо 4 и 6.
Рис. 3.14 показывает процент детей в группе в возрасте
3, 4, 5 и 6 лет, которые могли правильно ответить на вопрос:
«Кто открыл Америку?» Рис. 3.14 может показаться ясным и
верным, однако внимательный осмотр обнаруживает анома-
лию. У пятилстних оказался больший процент знающих, кто
открыл Америку, чем у шестилетних. Это в самом деле яв-
ляется неожиданным. Однако из графика выпал один важный
элемент информации: число'случаев, по которым вычислялись
Возраст
Рис. 3.13. Средний
IQ (Стенфорд—Бине)
в выборке из 1000 Лиц
в зависимости от воз-
раста.
проценты. Если вам говорят, что проценты по каждому возрасту
рис. 3.14 основывались на четырех детях, то вы видите, что
ответ знали двое 5-летних и один 6-летний Мы не рассчиты-
ваем, что этот результат будет стабильным, ибо пропеты
вычислены при весьма малом числе случаев. Вероятно, боль-
шие группы 5- и 6-летних дали бы больший процент верных
ответов среди 6-летних, а не среди 5-летних.
Объем главы не позволяет нам более перечислять все воз-
можные промахи при построении графиков и рисунков. Вы про-
чтете о них в забавной, поучительной и достойной вашего вни-
мания книге Даррелла Хаффа (1954) «Как лгать при помощи
статистики».
53
3.7. Общие советы при построении графиков
Построение графиков, используемых в психологии и педаго-
гике, должно опираться на множество практических навыков.
Заглавие иногда располагается выше рисунка, хотя, как пра-
вило, оно бывает под ним. Почти во всех книгах и журналах
наименование помещается внизу, а в диаграммах, не предназна-
ченных для печати, например в настенных диаграммах, целе-
сообразнее писать заголовок сверху.
Предлагаемые правила
В 1915 г. комитет представителей групп, интересующихся
графическими методами, представил отчет1, рекомендующий
правила построения графиков. За прошедшие годы проблемы
графического представления претерпели некоторые изменения,
но этот отчет по-прежнему охватывает множество моментов,
требующихся для правильного представления данных. Из него
извлечены следующие правила;
1. Общая структура графиков должна предполагать чтение
слева направо.
2. Когда используется возможность изображать количества
линейных величин с помощью, например площадей или объе-
мов. вероятнее всего, что их не удастся верно истолковать.
3. Вертикальную шкалу для кривой независимо от ее назна-
чения следует выбрать так, чтобы на рисунке оказалась нулевая
отметка.
4. Если нулевая линия вертикальной шкалы окажется не
перпендикулярной по отношению к графику, то нулевая линия
должна быть показана с помощью горизонтальной оси.
5 Нулевые линии шкал для кривой следует резко отграни-
чивать от других координатных линий.
Г> Для кривых, которые имеют шкалу, изображающую про-
центы, как правило, желательно выделить каким-то образом
линию 100% или другие линии, используемые в качестве основы
для сравнения.
7. Когда шкала относится к датам, а представляемый период
является неполным, лучше не выделять первые и последние
ординаты, так как подобная диаграмма не отмечает начало
или конец времени.
8. Когда кривые рисуются в логарифмических координатах,
ограничительные линии должны находиться на том же уров-
не— кратном десяти — на логарифмических шкалах,
9. Рекомендуется показывать не больше координатных ли-
ний, чем это необходимо, чтобы облегчить чтение диаграммы.
1 С Brinton Chairman, Preliminary Report, Joint Committee on
Star,' nis oi Graphic Representation. «Quarterly Publications oi the Ameri-
can Staiisiicai Association», 14, 1915, 790--797.
51
10. Кривые линии диаграммы должны резко отличаться от
прямых.
11. Для кривых, характеризующих труппы наблюдении, реко-
мендуется по возможности ясно указывать на диаграмме все
кривые, представляющие отдельные наблюдения.
12. Горизонтальную шкалу для кривых следует читать, как
правило, слева направо, а вертикальную — снизу вверх.
13. Цифры на шкалах следует располагать слева и снизу и ш
вдоль соответствующих осей
14. Часто желательно включать в график цифровые данные
или изображаемые формулы.
15. Если цифровые данные не попали па график, желате тьпо
привести данные в таблице, сопровождающей график.
16. Вес обозначения и цифры для удобства чтения следует
располагать от основания как начала или с правого края как
начала.
17. Наименования следует делать возможно яснее si полисе.
Если это требуется, необходимо дополнительно вводить подзаго-
ловки или пояснения.
По графическому представлению и табулированию данных
см. также Аркина и Колтона (1936), Уолкер п Дароста (193<:)
и Келли (19-17).
Задачи и упражнения
1. Эта задача на построение группового распределения ча-
стот. Следующие данные представляют собой оценки 75 взрос-
лых людей в тесте на определение коэффициента интеллекту-
альности Стенфорда — Бине:
141 104 101
92 87 1’5
100 133 124
132 118 98
97 124 118
НО 111 138
I0R 135 97
107 НО 101
105 ПО 116
83 127 112
127 114 113
95 105 95
109 102 102
108 92 131
104 91 121
148
96
123
107
107
129
123
105
139
106
89
134
103
а Определите включающий размах приведенной группы
оценок.
б. Разделите включающий размах (найденный в (а)) соот-
ветственно на 12 и 15.
55
в Выберите величину разряда, являющуюся целым числом,
которое находится между двумя значениями, найденными
и пункте (б).
г. Пользуясь величиной разряда, найденной выше, в (в),
постройте сгруппированные частоты для 75 оценок:
дачи № 1,
3. Закончите полигон распределения, построение которого
начато ниже, для группового распределения частот в задаче № 1.
Обязательно разметьте горизонтальную ось на серединах 14
интервалов оценок.
4. Изобразите 2 полигона относительных частот на одном
графике по следующим групповым распределениям частот оце-
S6
нок речевых способностей для 903 мужчин и 547 женщин —
студентов первого курса большого восточного университета:
750—800
700-749
650-699
600—649
550-599
500-549
450-499
400-449
350-399
300-349
250-299
200-249
27
63
138
174
202
171
96
25
0,059
0,016
0,002
0,002
0,000
л№=547
1,000
4
МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ
4.1. Введение
В 3-й главе мы видели, как свойства совокупности данных можно
представить в форме графиков или таблиц. Часто график или
таблица говорят больше, чем мы хотим или должны знать, а пе-
редаваемая информация может оцениваться временем, потреб-
ным на сообщение. Поэтому обычно мы используем для описа-
ния совокупности данных только два-три свойства. Эти свойства
(например, «значение», наиболее часто встречающееся среди
результатов (типичное) или разброс значений) могут быть опи-
саны показателями, известными как «статистики свертки».
Эти описательные индексы можно использовать для ответа
на вопрос вроде «каков рост типичного выпускника в этом уни-
верситете?». Если предположить, что множество результатов
расположено на числовой прямой, то свойство описываемой
совокупности проявляется в ориентации результатов относитель-
но этой прямой. Группируются ли они около значения 71 или
же центром служит 67? Различные меры центральной тенден-
ции совокупности данных предполагают разные определения
«центрального положения». Существует сравнительно неболь-
шое число таких мер, и ниже мы рассмотрим их подробно
4.2. Мода
Наиболее просто получаемой мерой центральной тенденции
является мода. Мода — это такое значение в множестве наблю-
дений, которое встречается наиболее часто. Однако не всякая
совокупность значений имеет единственную моду в строгом по-
нимании этого определения, поэтому рабочее определение моды
содержит особенности н соглашения, которые обсуждаются по-
сле примера.
В совокупности значений (2, 6, 6, 8, 9, 9, 9, 10) модой яв-
ляется 9, потому что оно встречается чаще любого другого зла-
58
чения. Обратите внимание, что мода представляет собой наи-
более частое значение (в данном примере 9), а не частоту этого
значения (в примере равную 3).
4.3. Соглашения об использовании моды
1. В случае, когда все значения в группе встречаются
одинаково часто, принято считать, что группа оценок не имеет
моды. Таким образом, в группе (0,5; 0,5; 1,6; 1,6; 3.9; 3,9)
моды нет.
2. Когда два соседних значения имеют одинаковую частоту
и они больше частоты любого другого значения, мода есть сред-
нее этих двух значений. Итак, мода группы значений (0,1, 1, 2,
2, 2, 3, 3, 3, 4) равна 2.5.
0 123456789 10 11
ТестоЭая оценка
Рис. 4.1. Распределение частот тестовых оценок с наибольшей
модой 6 и меньшими модами 3,5 и 10.
3. Если два несмежных значения в группе имеют равные
частоты и они больше частот любого значения, то существуют
две моды. В группе значений (10, 11, II, 11, 12, 13, 14, 14, 14,
17) модами являются и 11 и 14; в таком случае говорят, что
группа оценок является бимодальной.
Большие множества данных часто рассматриваются как би-
модальные, когда они образуют полигон частот, похожий на
спину бактриана — верблюда (двугорбого), даже если частоты
на двух вершинах не строго равны. Это незначительное искаже-
ние определения вполне оправдано, ибо термин бимодальный
допустим и удобен для описания. Можно условиться различать
большие и меньшие моды.
Наибольшей модой в группе называется единственное значе-
ние, которое удовлетворяет определению моды. Однако во всей
группе может быть и несколько меньших мод. Эти меньшие
моды представляют собой, в сущности, локальные вершины рас-
пределения частот. Например, на рис. 4.1 наибольшая мода
наблюдается при значении 6, а меньшие — при 3,5 и 10.
59
4.4. Медиана
Вы уже сталкивались с медианой, хотя она и не называлась
этим именем, и научились определять ее в разделе 3.2, посвя-
щенном квантилям.
Определение: Медиана, Md, представляет собой 50-й процен-
тиль в группе данных. Это значение, которое
делит упорядоченное множество данных пополам,
так что одна половина значений оказывается
больше медианы, а другая — меньше.
4.5. Вычисление медианы
1. Если данные содержат нечетное число различных зна-
чений, например 11, 13, 18, 19, 20, то медиана есть среднее
значение для случая, когда они упорядочены, то есть Ма == 18.
2. Если данные содержат четное число различных значе-
ний, например 4, 9, 13, 14, то медиана есть точка, лежащая
посредине между двумя центральными значениями, когда они
упорядочены: Md = (9 4- 13)/2 = 11.
3. Если в данных есть объединенные классы, особенно в окре-
стности медианы, возможно, потребуется табулирование частот.
В таких случаях придется интерполировать внутри разряда
значений. Пусть, например, 36 значений, упорядоченных от 7,0
до 10,5, имеют следующее распределение:
Оценкой медианы будет величина п/2 = 18-му значению
снизу. Мы видим, однако, что 18-е значение лежит в интервале
8,25—8,75. Так как к нижней границе интервала накоплено
13 значений, мы хотим пропустить еще 18—13 = 5 частот в ин-
тервале. А всего в интервале 10 частот, поэтому медиана лежит
на полпути через интервал (0,50 = 5/10). Интервал содержит
60
значения от 8,25 до 8,75, а его ширина равна 0,5; половина
этого расстояния — 0,25. Следовательно, медиана равна
8,25 4-0,25 = 8,50.
Вы могли заметить, что вышеописанный процесс не что
иное, как частный случай метода определения процентилей в
групповом распределении частот. Если мы назовем значение
интервала, содержащего и/2, наивысшим в упорядоченном ряду
значением интервала медианы, то получим следующую фор-
мулу:
(фактическая -
нижняя граница
интервала
медианы
«частота, на-,
копленная к
интервалу
медианы '
'ширина '
интервала
.медианы .
частота в интервале
медианы
(4.1)
Эта формула позволяет найти медиану для любого как сгруп-
пированного, так и несгруппироваиного распределения частот.
4,6. Среднее
Мы имеем п объектов, у которых измеряем некоторую ха-
рактеристику, и получаем значения Xt, X2, . ., Хп. Для таких
множеств уже были определены две меры центральной тенден-
ции. называемые модой (наиболее часто встречающееся значе-
ние) и медианой (значение, которое делит множество значений
на две половины равной частоты). Теперь определим третью
меру—-выборочное среднее (называемое иногда «средним» или
«арифметическим средним»).
Определение; Среднее совокупности п значений обозначается
через X. и определяется как
г (Х(+Хг+ ... +Х„)
Л.--------------
Или:
(4.2)
Вы можете спросить, зачем нужны все эти меры централь-
ной тенденции. Каждая мера обладает характеристиками, кото-
рые делают ее ценной в определенных условиях.
Мода наиболее просто вычисляется — ее можно определить
на глаз. Кроме того, для очень больших групп данных это до-
статочно стабильная мера центра распределения. Во многих
распределениях значительного числа измерений, используемых
в педагогике и психологии, мода близка к двум другим мерам —
медиане и среднему.
61
Медиана занимает промежуточное положение между модой
и средним с точки зрения ее вычисления, если последнее осуще-
ствляется вручную. Эта мера получается почти прямым счетом
и особенно легко в случае ранжированных данных. В больших
массивах данные сначала можно сгруппировать (что значитель-
но проще ранжирования), а затем можно легко наши медиану.
Среднее множества данных предполагает в основном ариф-
метические операции. На величину среднего влияют значения
всех результатов. Медиана и мода не требуют для определения
всех значении. Посмотрим, что произойдет, например, со сред-
ним, медианой и модой, когда удвоится максимальное значение
в следующем множестве:
Среднее Медиана Мода
Множество 1 : 1, 3, 3, 5, 6, 7, 8 -у- 5 3
Множество 2: 1,3.3,5, 6,7, 16 5 3
На величину среднего особенно влияют результаты, кото-
рые можно назвать «выбросами», то есть данные, находящиеся
далеко от центра группы оценок. Преимущество это или нет —
зависит от конкретных вопросов, которые вы решаете.
4.7. Вычисление среднего
Определение среднего настолько хорошо известно, а вычис-
ления, в результате которых оно находится, настолько просты,
что вы можете удивиться, почему эти вычисления заслуживают
специального внимания. Причина отчасти заключается в том,
что традиционно статистические вычисления делались вручную,
без помощи машин. Поэтому были необходимы или по крайней
мере полезны различные методы упрощения действий яри
определении X. Эти процедуры, называемые «методами коди-
рования», перестали быть полезными и сохранились в неко-
торых современных книгах лишь как следы ранней истории
статистики.
Среднее определяют совсем просто — суммированием всех
данных и делением на их число. Этот процесс может быть легко
реализован на любой суммирующей машине или настольном
арифмометре. Можно добшься некоторого упрощения, если от-
дельные результаты повторяются. Рассмотрим группу данных
в первых трех столбцах табл. 4.1.
Здесь записана группа из 21 результата, причем только 10 из
них различаются между собой. В четвертом столбце приведены
все различные результаты (X,) и в пятом — число их повторений
в группе (Л). Теперь сумма всех результатов определяется умно-
жением каждой величины X, на ее частоту f, для получения
62
и суммированием этих произведений (XX,/,). В табл. 4.1 сумма
10 произведений Xtfi равна 166; чтобы убедиться в том, что их
сумма действительно 166, мож-
но сложить все 21 значение
Последний этап получения
X'. — деление SxJ, на п (в
табл. 4 1: 166/21 = 7.90).
Принцип, который только
чю был изложен, иногда при-
меняется и для оценки сред-
него некоторой совокупности,
когда задано лишь групповое
распределение частот. Пусть
вся информация о данных —
это их групповое частотное
распределение, представлен-
ное в левой части табл. 4 2.
Из-за отсутствия большей
информации и простоты ради
допустим, чю результаты рав-
номерно распределены по каж-
дому интервалу. Обычно это
допущение ошибочно, и ве-
личина, которую нам пред-
стоит вычислить, — только
аппроксимация (то есть при- ----------------------------
блнзительное значение) среднего несгрупяированных дан-
ных [порядок ошибки, вносимой в процесс вычисления многих
Таблица 4 2
Пример вычисления среднего
по данным сгруппированного
частотного распределения
Интервал значений ft
70-74 1 72
65-64 0 67 0
60—64 ч Г,‘> 186
55-59 2 57 П4
50-54 6 52 312
4">-49 10 47 470
43 44 8 42 336
35—39 37 296
30-34 4 32 128
25—29 27 54
20-24 4 22 88
15-19 ) 17 17
10-14 1 12 12
= 50 У fi • середину = — 2085
63
статистических характеристик при этом предположении, был
предметом одной теоретической разработки Шеппарда (см., на-
пример, Keeping, 1962, р. 107), с которой вы можете познако-
м)[1ься на определенном этапе изучения статистики]. При таком
допущении сумма f, данных в любом интервале значений равна
ft, умноженному на значение в середине интервала. Эти произ-
ведения даны в последнем столбце табл. 4.2. Общая сумма всех
значений приблизительно равна сумме этих произведений. Та-
ким образом, среднее несгруппированных оценок приблизитель-
но равно общей сумме, деленной на п, то есть
„ . X'i. (середину)
Л~---------"-----
(4-3)
а суммирование осуществляется по всем интервалам.
Для табл. 42 в результате аппроксимации получаем
4.8. Свойства среднего
Рассмотрим теперь несколько интересных свойств среднего.
Вспомним, что
X. =— (Д'; 4- + ... + Хп) ~ — %!
Что произойдет, если мы вычтем X. из значения X,? Эта раз-
ность есть отклонение значения, оно может быть отрицательным
или положительным. Если бы мы нашли отклонения для каж-
дого значения и сложили их, то сумма всех п отклонений должна
быть точно равна нулю. Проиллюстрируем это свойство.
Данные: (0. 1, 1, 3, 5); л == 5; Д’. — 2.
64
Доказательство этого в общем виде состоит в следующем:
Сумма отклонений = У (Х{ — Х.)= У Xt — У Х.=
п п У X, п п
Что произошло бы с величиной среднего, если бы к каждому
результату наблюдений прибавили некоторое число (констан-
ту)? Возьмем, например, вышеупомянутые 5 значений и при-
бавим к каждому 3. Получим числа 3, 4, 4, 6, 8, среднее которых
составляет (3 4- 4 4- 4 4- 6 4-8)/5 = 5. Среднее на 3 единицы
больше, и это не случайное совпадение.
Если константу с прибавить к каждому значению, то среднее
X. превратится в среднее, равное X. 4- с.
Докажем это:
I i »+*>=I £ х<+4 d =+ (I) ™+°-
Если каждое значение множества со средним X. умножить
на константу с, то среднее станет сХ., поскольку
У сХ,/п = С У Л\/п « сХ.
Четвертое свойство среднего касается всех п отклонений.
Сумма квадратов отклонений значений от их арифметического
среднего меньше суммы квадратов отклонений от любой другой
точки.
То есть (Xj — ^.)2 4-(Х2 — Я.)24- ... 4-(Хп — X.)2 меньше,
чем (%!—й)24-(Х2 —Ь)24- ... + (Хп — Ь)2, где Ь —любое
число, отличное от среднего Я*. Например, сумма квадратов
" Доказательство:
£ (X, - (X. + <•)) - X «X, - X.) - е). -
” £(Х, - Х.)> - 2е £ (X, - X.) + пс‘ -
f-l i=l
- EfXi-X.)" 4- пс2, поскольку
У (Xj — X.) = 0. Так как с2 2г 0. то
X (Х< - X.)" < £ (X, - (X. + _ 0.
3 Зак. 44®
65
отклонений 0, 1, I, 3, 5 по отношению к 2, их среднему, состав-
ляет (0-2)4(1 -2)4(1 -2)4(3-2)4(5-2)2=(—• 2)2+
+ ( —1)2 + (—1 )2 4(1)2 4(З)2 = 16. А сумма квадратов от-
клонений О, I, 1, 3, 5 относительно I равна 21, что больше 16.
4.9. Среднее, медиана и мода объединенных групп
Мы можем знать средние, медианы и моды для трех разных
классов школы и желать найти те же характеристики для объ-
единения всех трех классов.
В отношении среднего все просто, но для определения ме-
дианы и моды приходится вернуться к исходным данным и вы-
полнить новые вычисления.
Пусть средние и числа учащихся для трех классов, А. В и С,
б>дут:
4 = Н,9 пл = 24
4 = 14,2 па=39
Хс =10.8 пс = 28
па=35
пс = 28
Общий итог п но всем трем классам п = п\ 4 пв 4- Пс —
= 82. Среднее объединенной группы есть просто сумма всех
82 значений, деленная на 82. Сумма 24 значений класса А равна
лЛ Яд = 24(11,9) = 285.6, ибо среднее —это сумма, деленная
на число значений, то есть 2Х = пХ. Аналогично для групп В
и С суммы составляют соответственно 30(14,2) = 426.0 и
28(10.8) = 302,4. 285,6 4426,0 + 302,4 = 1014.0, Если мы объ-
единим все 82 значения и просуммируем их, то также получим
1014,0. Таким образом, общее среднее всех трех классов равно
(1014,0)/82= 12,4. Символически среднее объединенной группы
есть
-4 пв Хв + псХс
(4.4)
Теперь вы должны вывести формулу для среднего 4 групп,
когда известны только 4 средних и число элементов в группах.
Обратите внимание на то, что если каждая группа имеет
одно и то же число элементов пд = пв = пс = п, то уравне-
ние (4.4) примет вид
i(xa + xs + xA ХлШа + Хс
Зп 'А
(4.5)
Разумеется, это справедливо в случае объединения любого
числа средних для групп равного объема.
Однако попытка определения медианы или моды комбинации
групп выдвигает несколько иные вопросы. Допустим, нам из-
вестно, что в группе/? есть 6 значений, мода равна 17,а в группе
66
В также 6 значений с модой 19. Какова мода общей группы,
объединяющей Л и В? Может быть, вы думаете, что она равна
18 = (17 4-19)/2? Если так, то вы можете ошибиться, по-
скольку группы А и В, возможно, имеют следующий вид:
17
Когда мы объединим <4 и В, оценка 15 попадется 4 раза
и станет модой общей группы. Тем не менее неизвестно, что
могло бы быть в том случае, когда нам известны только моды А
и В в отдельности. Как для моды, так и для медианы, чтобы
оценить эти меры, необходимо иметь исходные данные.
4.10. Интерпретация моды, медианы и среднего
Каждая мера центральной тенденции имеет интересную ин-
терпретацию в терминах ошибок, возникающих из-за того, что
единственная статистическая характеристика заменяет все
значения в группе. Смысл, в котором мода является наиболее
представительным значением или значением, которое наилуч-
шим образом «заменяет все значения», вполне ясен. Если мы
вынуждены выбрать одно число для замены любого из значений,
то совпадение было бы максимальное число раз, если бы вы-
бранное число было модой группы. Интерпретация медианы
группы не столь очевидна. Предположим, что оценки группы (1,
3, 6 ,7, 8) расположены на числовой оси, представленной ниже:
Md
0 О ООО
I I I I I I 1 I
012345 6 78
Md обозначает медиану группы, 6. Разность между 6 и 1 со-
ставляет 5; между 6 и 3 — 3; между 6 и 6 — 0; между 6 и 7 — 1;
между 6 и 8—2. Сумма этих разностей, 54-34-0+1+2 = 11,
меньше суммы разностей относительно любой другой точки
(можете убедиться в этом сами). Медиана представляет собой
такую гонку на числовой оси, для которой сумма абсолютных
(то есть без учета знака) разностей всех значений меньше
суммы разностей для любой другой точки.
Если вместо каждого значения выбрать медиану, то дости-
гается минимальная ошибка—при условии, чго «ошибка» опре-
деляется как сумма абсолютного отличия каждого значения от
оценки.
67
Интерпретация среднего уже была выполнена. Если взамен
каждого значения берется среднее, обеспечивается минимальная
ошибка—при условии, что «ошибка» определяется как сумма
квадратов разностей каждого значения с оценкой.
4.11. Выбор меры центральной тенденции
Вычисление моды, медианы или среднего — чисто механиче-
ская процедура. Машины выполняют ее с гораздо большей
точностью и скоростью, чем люди. Однако выбор из этих трех
мер и их интерпретация иногда могут потребовать некоторых
размышлений. Здесь приводятся полезные соображения, кото-
рые следует учитывать в процессе выбора:
1. В малых группах мода может быть совершенно нестабиль-
ной. Мода группы (I, I, 1, 3, 5, 7, 7, 8) равна 1; но если одна
из единиц превратится в нуль, а другая — в два, то мода станет
равной 7
Оценка
Рис. 4.2. Гистограмма оценок в тесте из 10 вопросов
на сложение двузначных чисел (zt==53).
2. На медиану не влияют величины «больших» и «малых»
значений. Например, в группе из 50 данных медиана не изме-
нится, если наибольшее значение утроится.
3. На величину среднего влияет каждое значение. Если одно
какое-нибудь значение меняется ра с единиц, изменится в том
же направлении на с/п единиц.
4. Некоторые множества данных просто «не имеют централь-
ной тенденции», что часто вводит в заблуждение при вычислении
только одной меры центральной тенденции. Особенно это спра-
ведливо для групп, имеющих более чем одну моду. Например,
один из авторов — исследователь в области педагогики утверж-
дает, что может построить тесты успеваемости, состоящие из
восьми разнообразных пунктов, которые делят группу учащихся
на тех, кто усвоил понятие сложения двузначных чисел, и тех,
кто не усвоил. «Усвоившие» получат оценки 6, 7, 8; «неусвоив-
шие»— 0, 1 и 2. Допустим, типичная группа учащихся получила
оценки, образующие гистограмму, показанную на рис. 4.2.
68
Среднее оценок, изображенных на рис. 4.2, приблизительно
равно 3,85, несмотря на то, что даже не существует лица с
оценкой 3,85.
Медиана этой группы равна приблизительно 2,17, несмотря
на то, что значение двумя разрядами выше средней равно 6'
Ни среднее, ни медиана не дают правильного представления об
этой группе. Возможно, наиболее простой характеристикой бу-
дет утверждение, что «гистограмма бимодальна и имеет U-образ-
ную форму с одной модой при 0, а другой --- при 8».
5. Центральная тенденция групп данных, содержащих край-
ние значения, возможно, наилучшим образом измеряется ме-
дианой, когда гистограмма унимодальна. Одно крайнее значение
может сместить среднее группы гораздо дальше того места, кото-
рое вообще стоит рассматривать как центральную область. На-
пример, если 9 человек имеют доходы от 4500 до 5200 долларов
со средним 4900 долларов, а доход десятого составляет 20000
долларов, то средний доход для 10 лиц будет 6410 долларов. Эта
цифра не позволяет судить о всей группе, хотя она выглядела
Рис. 4,3. Симметричная унимодальная группа дан-
бы внушительно для президента маленькой компании (чье жа-
лованье составляет 20 000 долларов), который хочет охарактери-
зовать среднюю зарплату по платежной ведомости. В этом
примере в качестве меры центральной тенденции следовало бы
избрать медиану. Демографы, экономисты и журналисты часто
выбирают для отчетов «доход по медиане», поскольку стремятся
избежать только что описанной ситуации.
6. В унимодальных выборках, которые симметричны (то есть
половина гистограммы, расположенная ниже моды, есть зеркаль-
ное отражение другой половины), среднее, медиана и мода
совпадают. Например, см. рис. 4.3. Полигон частот показывает,
что среднее, медиана и мода равны 40.
Отсутствие полной симметрии в полигоне частот или гисто-
грамме обычно оказывает определенное влияние на соотношения
между средним, медианой и модой. Предположим, что преобла-
69
дающее большинство данных некоторой группы расположено
выше вершины полигона частот, как, например, на рис. 4.4.
На рис. 4.4 мода (ЛТо) равна 100, медиана (Md) составляет
104,6, а среднее (Я.) 105,98, Если большинство оценок окажется
ниже вершины полигона частот, то среднее станет минималь-
ным, медиана больше, а мода максимальной,
7, Дальнейшие соображения, имеющие отношение к выбору
меры центральной тенденции, можно обсуждать только поверх-
ностно, если использовать понятия, рассмотренные до сих пор.
Когда считают, что группа данных является выборкой из боль-
шей симметричной группы, среднее выборки, вероятно, ближе
к центру большой группы, чем медиана или мода. Мы вернемся
к этому важному моменту в § 11.4.
Оценка
Рис. 4.4, Несимметричный полигон частот, иллю-
стрирующий соотношения между средним, медианой
и модой.
Приведенный ниже анекдот обобщает множество проблем»
возникающих в процессе применения разных мер центральной,
тенденции.
Однажды пятеро мужчин сидели рядом на скамейке парка Двое были
бродягами, имущество которых выражалось в 25 центах Третий был ра-
бочим, чей счет в банке и другое имущество составляли 2000 долларов
Четвертый владел 15 000 долларов в различных формах. Пятый же был
мультимиллионером с чистым доходом 5 000 000 долларов. Поэтому мо-
дальный актив группы составил 25 центов Эта цифра точно характери-
зует двоих, ио является чрезвычайно некорректной для трех других Ме-
диана, составляющая 2000 долларов, несколько меняет дело для всех, кро-
ме рабочего. Среднее, 1003 400,10 долларов, не является вполне удовле-
творительным даже для мультимиллионера. Если мы должны выбрать
одну меру центральной тенденции, возможно, это была бы мода, которая
точно описывает 40 процентов группы Однако, если сказать, что «модаль-
ный актив пяти лиц, сидящих на скамье парка, равен 25 центам», то нам
пришлось бы сделать вывод о том. что общий актив группы приблизи-
тельно составляет 1.25 доллара, что меньше фактического более чем на
пять миллионов долларов Очевидно, нет меры, адекватной этим «стран-
ным соседям по скамейке», которые просто не имеют «центральной тен-
денции» *.
1 Цит. по; Julian С. Stanley, Measurement in Today’s Schools, 1964,
p, 73,
70
Другой вывод из анализа противоречий этого анекдота со-
стоит в том, что для группы с пятью значениями не требуется
никакая обобщающая статистика.
4.12. Другие меры центральной тенденции
Существует много других способов определения «централь-
ного значения» в группе данных. Здесь будет представлено не-
сколько таких мер, хотя они редко встречаются в литературе
по педагогике.
Среднее геометрическое
Определение: Геометрическое среднее п положительных чисел
Xi ... Хп определяется выражением
gfn=VXi-X2- -Хп, (4.6)
то есть геометрическое среднее Х} ... Хп есть корень п-й степени
из произведения всех п X. Формула определения gm не удобна
для вычислений. Если нужно вычислить gm для 4, 5 и более зна-
чений, обратитесь к работе Сендерс (1958, р. 316).
Необходимо ограничить определение gm положительными
числами: если одно любое Хг было нулевым, то произведение
Xs ... Хп также будет нулем и, следовательно, gm будет равно
нулю, даже если нуль далек (по какому-нибудь другому опре-
делению) от центрального значения группы.
Геометрическое среднее полезно для описания положения
центра при переменных разрядах (см. Ferguson, 1959, р. 50).
Среднее гармоническое
Эта мера используется иногда для усреднения группы от-
ношений.
Определение: Гармоническое среднее п положительных значений
Xi ... Хп определяется выражением
Ц1/ХЧ) + (№) + ... +(11Хп)]/п
Таким образом, мы имеем взаимообратные величины (где
1/Х, обратно Xt). Для определения hm берется обратная вели-
чина каждого значения, эти обратные величины суммируются,
н на эту сумму делится п.
Гармоническое среднее имеет очень ограниченное примене-
ние. Нринято считать, что более широкое применение по сравне-
нию с геометрическим или гармоническим средним имеет обрат-
ное гармоническое среднее (см Senders, 1958, р. 317—318).
71
Отношение средних и среднее отношений
Оценка 1Q при вычислении самых ранних интеллектуальных
тестов содержит 100 отношений умственного возраста (Л1Л) к
хронологическому возрасту (C/1): /Q= 100 (МА/СА). На первый
взгляд, может показаться, что среднее IQ группы лиц можно
найти в результате деления среднего умственного возраста груп-
пы на средний хронологический возраст и умножения на 100,
то есть IQ — Ю0(МА/СА). Однако, вообще говоря, это неверно.
Это будет справедливо только при определенных условиях,
когда
то есть когда среднее отношений есть отношение средних (см.
Stanley, 1957 b). Это кажется само собой разумеющимся, однако
ошибка, что среднее отношений есть отношение средних в не-
сколько более завуалированной форме, проникает в статистиче-
скую литературу (см., например, Winer, 1962, р. 61, 119; Fergu-
son, 1959, р. 258).
Задачи и упражнения
1. Найдите среднее, медиану и моду следующего множества:
1,2; 1,5; 1,6; 2,1; 2,4; 2,4; 2,7; 2,8; 3,0; 3,0; 3,0; 3,1; 3,1; 3,1; 3,4.
2. Пусть к каждому из 15 значений предыдущего примера
прибавлено 0,5. Чему будут равны среднее и медиана этих уве-
личенных значений?
3. Определить среднее и медиану 100 данных в следующем
сгруппированном распределении частот:
Интервал I Частота
п= 100
4. Предположим, что каждое из 100 значений в сгруппиро-
ванном распределении частот 3-го примера умножено на 3. Ка-
ковы будут значения среднего и медианы?
5. В группе А содержится 10 значений, среднее и медиана
которых равны соответственно 14,5 и 13. В группе Б — 20 значе-
ний, среднее и медиана которых 12,7 и 10 соответственно. Чему
72
равны среднее и медиана 30 значений, полученных в результате
объединения групп А и Б?
6. Семь членов Общества Воскресных послеполуденных пик-
ников (ОВПП) обитают на Хайвей —101. Их дома располо-
жены следующим образом:
* . 8.5 , В . 8. f .4
8км 3,2 км 8км 3,2 км 1,6км Мкм
Цена бензина —2,2 цента за километр — за путешествие всех
членов к воскресному сбору оплачивается из казны клуба. По-
скольку любой пункт на Хайвей—101—прекрасное место для
пикника, то где по дороге должны провести свой пикник участ-
ники, чтобы израсходовать на путешествие минимальное коли-
чество денег?
5
МЕРЫ ИЗМЕНЧИВОСТИ
5.1. Введение
Меры центральной тенденции говорят нам о концентрации груп-
пы значений на числовой шкале. Каждая мера дает такое значе-
ние, которое «представляет» в каком-то смысле все оценки,
группы. В этом случае пренебрегают различиями, существую-
щими между отдельными значениями. Для измерения вариации
оценок внутри группы требуются другие описательные статисти-
ки. В этой главе будет введено и обсуждено несколько статисти-
ческих характеристик, которые по-разному служат мерами
изменчивости (неоднородность, дисперсия, разброс) в группе
данных.
Далее в этой книге вы увидите, что некоторые из наиболее
важных функций статистики связаны с процедурами, позволяю-
щими уменьшить, объяснить или интерпретировать изменчи-
вость, которая в известном смысле есть неопределенность.
Всякая научная деятельность связана с понятием изменчиво-
сти. Когда есть много необъяснимых причин вариабельности,
прогнозы не будут очень точными. Зато когда объяснения
причин различий люден и вещей представлены в виде не-
которой модели, неопределенность можно уменьшить, а часть
вариации устранять. Например, если бы было совсем неизвестно,
почему люди различаются между собой по умственному разви-
тию, то попытка прогнозировать интеллект наталкивалась бы
на большую неопределенность; некоторые люди выглядели бы
«смышлеными», а другие — «глупыми», и никто не знал бы.
почему. Однако если известно, что наследственность и окружаю-
щая среда оказывают количественное влияние на IQ, то инфор-
мация о происхождении ребенка и его воспитании в раннем
детстве позволила бы дать более точный прогноз его умствен-
ного развития в зрелости. Другими словами, вариабельность IQ
у лиц со сходной наследственностью и окружающей средой:
74
меньше, чем у людей вообще. Но прежде чем рассуждать о вы-
соких материях, следует ознакомиться с принятыми показате-
лями изменчивости.
5.2. Размах
Размах просто измеряет на числовой шкале расстояние,
в пределах которого изменяются оценки. Поскольку сущест-
вуют несколько иные определения размаха, то надо разграни-
чить два его типа: включающий и исключающий.
Определение: Исключающий размах—это разность максималь-
ного и минимального значении в группе.
Например, исключающий размах значений 0, 2, 3, 5, 8 равен
5 — 0 = 8. Значения: —-0,2; 0,4; 0.8; 1,6 имеют исключающий
размах, равный 1,6— (—0,2) = 1,8.
Определение: Включающий размах — это разность между естест-
венной верхней границей интервала, содержащего
максимальное значение, и естественной нижней
границей интервала, включающего минимальное
значение.
Например, рост пяти мальчиков измеряется с точностью
до ближайшего см. Получены следующие значения: 150, 155,
157, 165, 168 см. Фактический рост самого низкого мальчика
находится где-то между 149,5 и 150 см и действительная нижняя
граница равна 149.5 см. Верхняя граница интервала, содержа-
щего максимальное значение, составляет 168,5 см Таким обра-
зом, включающий размах равен разности 168,5—149,5=19,
которая ла единицу больше, чем 168—150.
Исключающим размахом является расстояние между мини-
мальным и максимальным имеющимися значениями группы, что
позволяет исключить возможное значение, находящееся выше
максимального или ниже минимального (см. в § 2.3 определения
точного и косвенного значений оценок).
Включающий размах достаточно велик, чтобы наряду с кос-
венными включить все возможные значения.
В дальнейшем если мы будем ссылаться на «размах» без
указания, включающий он или исключающий, то выводы будут
одинаково применимы для обоих. Поскольку размах опреде-
ляется только двумя значениями в группе, он не учитывает
распределения всех значений, помимо максимального и мини-
мального. Например, если 100 значений равномерно распреде-
лены от 1 до 10, то включающий размах равен 10,5 — 0,5= 10.
Но если одно значение приходится на 1, одно — на 10, а осталь-
ные 98 расположены на уровне 5, то включающий размах все еще
равен 10. В разных случаях эти два типа неоднородности имеют
различный смысл; но их нельзя различить, пользуясь только
размахом. Размах является довольно грубой, но общераспро-
страненной мерой изменчивости.
75
5.3. Размах от 90-го до 10-го процентиля
Второй мерой изменчивости является D, размах между 10-м
и 90-м процентилями в группе значений. Как установил специа-
лист в области педагогической статистики Т. Келли (1921),
IWM-PIO, (5.1)
D более стабилен, чем размах, так как па него непосредст-
венно влияет множество значений. Он вычисляется проще других,
мер изменчивости, с которыми нам придется иметь дело в даль-
нейшем. Ни одно из этих преимуществ не оказалось настолько
веским, чтобы превратить D в распространенную меру изменчи-
вости. Он используется редко.
5,4. Полу-междуквартильный размах
В § 3.2 мы рассматривали три квартиля распределения: Qi,
точку на оси, до которой лежит 25% данных, Q2 (медиану)
и Сз, точку, за которой лежит 25% данных. Разность между
первым и третьим квартилями группы, то есть Qs—Q,, назы-
вается междуквартилъным размахом. Полу-междуквартильный
размах равен половине этого расстояния.
Используя Q для обозначения полу-междуквартильного раз-
маха, имеем следующее.
Определение: Полу-междуквартильный размах Q равен поло-
вине расстояния между третьим и первым квар-
тилями, то есть
Q= —~ gl . (5.2) '
Q—легко получаемая и полезная мера изменчивости. Она бо-
лее пригодна для описательных целей, чем размах, но труднее
вычисляется. Если две выборки имеют одинаковое Q, то намного
вероятнее, что они имеют аналогичные структуры неоднородно-
сти, чем в случае двух групп с одинаковым размахом.
В распределениях, которые примерно симметричны в окрест-
ности среднего или медианы, Q можно использовать для кор-
ректировки границ, в которых находится 50% данных.
Если распределение данных в окрестности медианы крайне
несимметрично, то около 70% оценок может заключаться в пре-
делах от Md—Q до Md-{-Q. Симметричный и слегка несим-
метричный случай, а также применение Q показаны на рис. 5.1.
5.5. Дисперсия
Размах, полу-междуквартильный размах Q и D = Р&—Рщ
представляют собой три меры рассеяния, разброса, неоднород-
ности или изменчивости, которые встречались до сих пор. Каж-
76
дая из них возрастает с ростом рассеяния и уменьшением одно-
родности. Заметим, что, так же как и для моды и медианы,
в ходе вычисления этих трех мер не учитывается каждое от-
дельное значение. Теперь мы сталкиваемся с четвертой мерой,
при вычислении которой, как и для среднего, используется каж-
дая оценка.
Значения отклонений, то есть значения вида X, — X, несут
информацию о вариации совокупности значений. Совокупность
с большой неоднородностью будет иметь несколько больших
отклонений. Каковы были бы отклонения, если бы все значения
в совокупности равнялись 9? Среднее было бы 9, следовательно,
каждое отклонение было бы 9 — 9 = 0. В предельно однородной
Рис. 5.1. Интерпретация Q. Для симметричного распределения
слева между Md —- Q и ЛМ + Q лежит точно 50% данных.
В несколько асимметричном распределении справа между Md— Q
и Md + Q находится 52,5% данных.
совокупности, которая в принципе достижима, все отклонения
равны нулю. Некоторая комбинация отклонений могла бы быть
полезной мерой вариации.
Если бы нам требовалось просуммировать все отклонения,
то характеризовала ли бы эта сумма вариацию исходных дан-
ных? Нет, поскольку эта сумма всегда точно равна нулю:
У' (X,—Х.) = 0. Для обхода этого факта мы можем возвести
в квадрат каждое отклонение и найти сумму квадратов. Следо-
вательно, для данной совокупности мера вида
E(X,-J.)! = (X,-J.)!+ ... +(X, -
будет большой, когда данные неоднородны, и малой для одно-
родных. Чтобы избавиться от знаков, мы могли бы обойтись без
квадратов отклонений; мы могли бы просто рассматривать эти
отклонения как положительные (взятые по их абсолютной ве-
личине). Эго привело бы к другой мере вариации, называемой
средним отклонением, с которым вы встретитесь в § 5.9. Вели-
чина суммы квадратов зависит также от того, сколько имеется
данных. Чем больше п, тем больше сумма. Если хотят срав-
нить изменчивость двух совокупностей, которые отличаются по
77
объему, то возникает ограничение. Оно снимается после деле-
ния суммы на п—1. Такая мера изменчивости называется
дисперсией (обозначается з'-) и имеет вид
(5.3)
Почему мы делим на п— 1, а не на п? Об этом вы узнаете
в § 12.4.
Для иллюстрации вычислений дисперсии используем следую-
щие данные:
В примере s’вычислялась просто, так как каждое значение
и среднее были целыми числами. Однако вычисление s- было
бы крайне утомительным, если бы среднее, например, выража-
лось величиной 17,697. Поэтому мы ищем путем алгебраических
преобразований такое выражение для s‘‘x, которое в подобных
случаях проще для вычислений:
-2 __ 2=2__________ ____________________
• П -1 п — 1 ”
Если мы вспомним, что SX = пХ., то можем записать это
выражение так:
X*-W*+ пХ.г 2^-пХ3.
п — 1 п — 1
78
Так как квадрат среднего является квадратом суммы всех
значений, деленным на квадрат п, имеем:
(5.4)
Мы можем еще умножить числитель и знаменатель ур. (5.4)
на п/п (то есть на единицу) и получим другую формулу з2,
в которую не входит среднее:
»g 4
4(4-i)
5.6. Вычисление дисперсии s2x
Вычисление sj из ур, (5.4) покажем иа данных вышепри-
веденного примера: 1, 3, 3, 0. 4, 1.
X X’ 3 ihтючительные вы'шс.чеишг
3 0 4 6 1 9 9 0 А 16 г,|„ 1 ” । 1 s' i 4 S, II
Когда одно или более значений в выборке встречается чаще
одного раза, возможно упрощение s^, как это было и при вы-
числении X. (см, § 4.7), В примере число 3 встретилось дважды.
Вклад, вносимый в сумму (£ X) двумя тройками, составил
3 4- 3 = 2(3). Вклад, вносимый в сумму квадратов (£ X2) двумя
тройками, 9 4-9 — 2(9). Если величина X, имеет частоту
то эта величина внесет f,X, в сумму значений и f Xj в сумму
квадратов, Следовательно, при определении ^Х2, например, вег
необходимости возводить в квадрат X, всякий раз, когда он
попадется, Вместо этого сразу находим X2 и умножаем на
число повторений X, в группе.
79
Пользуясь теми же данными, для которых в § 4.7 было пока-
зано вычисление X., найдем $2 сокращенным способом, где
М И'/"]
k — количество разных значений, а £Ь = п.
Таблица 5.1
Пример вычисления дисперсии, когда некоторые значения
встречаются несколько раз
Исходные дачные Подсчет частот xi Х1 f Промежуточные вычисления Заключительные вычисления
2 0 10 3 6 10 3 6 11 5 8 11 5 8 11 5 9 15 5 9 18 2 4 1 3 9 2 5 25 4 6 35 3 8 64 2 9 81 2 10 100 2 11 121 3 15 225 1 18 324_1_ 2 4 6 18 20 100 18 108 16 128 18 162 20 200 33 363 15 225 18 324 £//г-=166 £/Х=1632 21 !0 fx?-SW>_|632 =1632-1312,19=319,81. 4.®1.15,995,
5.7. Стандартное отклонение s
Мерой изменчивости, тесно связанной с дисперсией, является
стандартное отклонение. Стандартное отклонение, обозначаемое
s, определяется как положительное значение квадратного корня
из дисперсии. Для определения s надо сначала найти $2, а затем
вычислить квадратный корень из з2
Стандартное отклонение часто является полезной мерой ва-
риации, так как для многих распределений мы приблизительно
знаем, какой процент данных лежит внутри одного, двух, трех
и более стандартных отклонений среднего. Например, мы можем
знать, что 70% значений лежит между X. — и X. 4- sx.
5.8. Некоторые свойства дисперсии
Предположим, что мы прибавили постоянное число к каж-
дому значению в совокупности. Как это повлияло бы на дис-
персию? В § 5.6 мы нашли, что данные 1, 3, 3, 0, 4, 1 имеют
80
дисперсию, равную 2,4. Прибавим 2 к каждому значению и вы-
числим s£:
з
5
2
6
3
Сумма =24
Среднее = 4
Сумма отклонений == О
8
Прибавление 2 к каждому значению не изменило величину
Вообще прибавление константы с к каждому значению не
будет изменять дисперсию (но не стандартное отклонение):
£ | <*<+<о - [ £ (*< + «>/»] j ]
Улх‘+с-*--с?
Что произошло бы с з*, если бы каждое значение умножили
на константу, скажем на 2?
(Исходное
л<аче„иеХ2)
— Среднее
2
6
6
О
8
2
Сумма =24
Среднее = 4
81
Отметим также, что 9,6 = (22) • (2,4). Вообще, умножение на
константу с дает дисперсию, равную c2s2:
-------------------------------5-------------------------------- —-----------------С----------i-------------------
В главе 4 было найдено, что среднее совокупности, образо-
ванной объединением двух разных групп, есть просто взвешенное
среднее значение средних этих групп (см. § 4-9). Для дисперсий
дело обстоит сложнее Покажем, что дисперсия совокуп-
ности. образованной объединением групп а и Ь. зависит как от
дисперсий, так и от средних двух групп. Кроме того, если груп-
па а содержит значения 3, 3, 3, 3, а группа b — 6, 6, 6. 6, то
общая дисперсия групп а и b (3. 3, 3, 3, 6, 6, 6, 6) не равна
нулю, хотя
^ = sft2 = 0.
Пусть а и Ь обозначают две различные группы:
Группа а | Группа Ь
Объем группы
Среднее
Дисперсия
Дисперсия группы па-{-п/„ образованной в результате соеди-
нения групп а и Ь, равна
0 4 Н"» - Ч 4 + - )г + ">(*-»-* -)Р
па + Пв — I
у _____НаХ а 4- П}>Х ,ь
ГДС Л ~ па + пь
(5.6)
5.9. Среднее отклонение
Еще одна мера изменчивости — среднее отклонение — вы-
числяется легче, чем стандартное отклонение, ио используется
реже. Отклонение каждого значения от среднего обозначается
как X,—Я.. Совокупность всех п отклонений характеризуй! из-
менчивость в исходных данных. Однако, как мы видели в § 48,
сумма положительных и отрицательных отклонений вовсе не
является мерой общей изменчивости в группе данных, ибо она
всегда точно равна нулю. Если рассматривать отклонения как
82
расстояния от X. без учета знака, то сумма этих расстояний бу-
дет характеризовать изменчивость данных.
Расстояние каждого от X. определяется с помощью взятия
числа по модулю. Оно равно /X,— X.j. Среднее значение п рас-
стояний оценок от их среднего называется средним отклоне-
нием, MD. (Не путайте MD, среднее отклонение, с Md, ме-
дианой )
Л1Л = —-----------.
Для среднего отклонения нет более простого выражения,
которое можно было бы использовать при вычислениях, Пример
вычисления MD приведен в таблице 5.2. Среднее отклонение не
часто используется как мера изменчивости, лаже несмотря
на легкость вычисления и логическую простоту. Одна из причин
этого состоит в том, что среднее отклонение не имеет теорети-
ческого обоснования в отличие, например, от дисперсии.
5.10. Стандартизированные данные
Часто желательно описать место некоторого значения в сово-
купности, измеряя его отклонение от среднего всех значений
в единицах стандартного отклонения. Например, данная сово-
купность 100 значений имеет среднее 18,75, а стандартное от-
клонение 2,60. Если вам известно лишь, что среди этих 100 зна-
чений есть одно, равное 20, то его относительное положение
в множестве 100 значений видно пе сразу.
Можно вычислить, что 20 находится на 1,25 единицы
(20—18,75 — 1,25) выше среднего и что это расстояние состав-
ляет 1,25/2,60 = 0,48 единицы стандартного отклонения.
Для произвольного Xi в совокупности 100 значений отклоне-
ние от среднего, измеренное в единицах стандартного отклоне-
ния, задается выражением
Xt - 18,75
2.60
Чему были бы равны среднее и стандартное отклонение
100 преобразованных значений?
Среднее 100 значений X—-18,75 равно среднему 100 исход-
ных значений минус 18,75, так как вычитание константы из
каждого значения отнимает ту же константу из среднего. Но
поскольку среднее X. ~ 18,75, то среднее X — 18.75 будет нулем.
Если X—18,75 имеет среднее, равное нулю, то (.¥—18,75)/2,60
также должно иметь нулевое среднее.
83
Таблица 5.2
Пример вычисления среднего отклонения
Дачные Xi-X. Иг--*. 1 Заключительное вычисление
10 12 10 У = 60 X. = 12 10—12=—2 12-12= 0 13-12= 1 10—12=— 2 15-12= 3 0 1 2 3 J !Х(-Х.| = 8 ЛГО = = |= 1,60
Для определения стандартного отклонения (Х4—18,75)/2,60
удобно сначала записать такую нормированную величину:
1 у 18.75
2,60 Л‘ 2,60 '
Хорошо известно, что прибавление константы—18,75/2,60 не
меняет стандартного отклонения X. Однако умножение на кон-
станту 1/2,60 влияет на стандартное отклонение. Умножение
каждого значения множества со стандартным отклонением sx
на константу с дает в результате новое множество cXi со стан-
дартным отклонением [фх.
Поскольку 100 исходных значений имели стандартное откло-
нение 2,60, то стандартное отклонение Х/2,60 составит
(1/2,60)2,60 = 1. Значит, и 100 значений
X 18.75 _ X — 18,75
2,60 2,60 2,60
имеют стандартное отклонение, равное 1. В итоге 100 значе-
ний X со средним 18,75 и стандартным отклонением 2,60 получат
среднее и стандартное отклонение 0 и 1 соответственно если
преобразовать значения с помощью выражения (X — 18,75^/2,65,
Любое множество п данных со средним X. и стандартным
отклонением sx можно преобразовать в другое множество со
средним 0 и стандартным отклонением 1 таким образом, что
преобразованные значения будут непосредственно выражаться
в отклонениях исходных значений от среднего, измеренных в еди-
ницах стандартного отклонения. Новые значения называют зна-
чениями Z:
84
Мы можем доказать, что эти значения z имеют среднее О,
а дисперсию (так же как и стандартное отклонение) 1:
£(г,-7.с £г;
<а _ _>____________ _J_____ _J___________
** П — 1 л — I п — 1
Г У (Xi - х. )*]
Значение г не только удобное средство информации о по-
ложении некоторого значения, связанного со средним и измерен-
ного в единицах стандартного отклонения, но и шаг вперед
к преобразованию множества X в произвольную шкалу с удоб-
ными характеристиками среднего и стандартного отклонения.
Сами оценки г могут не подходить для некоторых целей. Отри-
цательные оценки, например, могут оказаться неудобными, а
множество z будет, конечно, содержать дроби. Преобразование
самих z позволяет устранить эти несущественные трудности.
Известно, что значения cz, полученные умножением каж-
дого z на константу с, будут иметь стандартное отклонение |с|,
а для ez 4- d среднее равно
С2. 4- d = с (0) 4- d = d.
Существует множество шкал измерения (произвольные сред-
ние и стандартные отклонения), которые распространены в пе-
дагогике я общественных науках. Множество данных можно
расположить на любой шкале, то есть им можно приписать
желаемые среднее (е/) и стандартное отклонение (с), пользуясь
выражением cz-(-d. Оценки интеллектуального теста часто пре-
образуются в шкалу со средним 100 и стандартным отклонением
15 или 16. Значения 7', полученные с помощью Юг 4- 50, находят
широкое применение. Эти и другие распространенные шкалы
представлены на рис. 6.5 в 6-й главе.
5.11. Асимметрия
Одно из наиболее важных свойств распределения частот —
степень асимметрии. Практически точно симметричные полиго-
ны частот и гистограммы почти никогда не встречаются. Степень
асимметрии распределения частот для выборки называется про-
сто его асимметрией. Легко выявить н распознать асимметрию,
85
если рассматривать полигон частот или гистограмму, но это не
всегда возможно или удобно. Поэтому изобретены различные
обобщенные статистические характеристики, оценивающие вид
и степень асимметрии группы наблюдений.
Наилучшая мера асимметрии для группы данных выра-
жается формулой
асимметрия = —-----. (5.7)
Как было показано в § 5.10, принято обозначать непосредствен-
ное расстояние, на котором лежит оценка от среднего группы,
Рис. 5.2. Два асимметричных распределения частот.
в единицах стандартного отклонения этой группы с помощью
гх, то есть
Если
t-v, -X.)3 Г (X/ - X.) ~|3 з
s3 L sx J *
то мера асимметрии в (5.7) принимает вид
асимметрия =
(5.8)
Таким образом, наша мера асимметрии есть просто среднее
значение г, возведенных в куб. (В работах по математической
статистике эта мера обозначается как V₽i- Она обязана своим
существованием Карлу Пирсону, а свойства ее хорошо изучены.)
Пусть измеряется асим.метрия двух распределений (рис. 5.2).
Среднее данных распределения А на рис. 5.2 равно приблизи-
тельно 16. Когда для случая А строятся значения г, получается
86
значительно больше положительных значений (поскольку мак-
симальная оценка X = 22 и расположена на 6 единиц выше
среднего), которые по абсолютной величине существенно пре-
взойдут любые отрицательные (минимальное значение X — 13
лежит на 3 единицы ниже среднего). Для асимметрии алгебраи-
ческий знак сохраняется, так как находится куб числа
(—-2)э ——8. Поэтому для распределения А вклад отрицатель-
ных значений г, возведенных в куб, Х,г^п будет меньше вклада
«кубов» больших положительных значений. Следовательно, ве-
личина в ур. (5.8) будет положительной и большой. Мы
говорим, что распределение А имеет положительную асиммет-
рию, так как его мера асимметрии положительна.
Распределение В на рис. 5.2 имеет отрицательную асиммет-
рию Величина ЯгЦп для распределения В отрицательна. По-
пытайтесь сами убедиться в этом. Положительная асимметрия
распределения А более отчетливо выражена, чем отрицательная
для распределения В,
В симметричном распределении мера асимметрии в уравне-
нии (5.8) равна нулю. Это естественно, поскольку точная сим-
метрия означает, что каждое отрицательное значение г уравно-
вешивается положительным значением равной величины.
К сожалению, вычисление Ег’/n очень утомительно, даже
на настольном арифмометре, для любой выборки порядочного
размера. Из того факта, что на величину среднего крайние зна-
чения оказывают большее влияние, чем на медиану, следует
ускоренный метод измерения асимметрии распределения. В гла-
ве 4 мы показали, что в унимодальных положительно асиммет-
ричных распределениях среднее больше медианы, которая в
свою очередь больше моды. В отрицательно асимметричных
распределениях, наоборот — среднее меньше медианы, которая
в свою очередь меньше моды. Это значит, что положение сред-
него по отношению к медиане информирует нас в какой-то сте-
пени об асимметрии распределения, Это верно для умеренно
больших выборок, например объемом 50 пли более Простейшая
мера асимметрии, основанная на этих фактах, определяется
следующим образом:
3(Х. — Mil} ..
асимметрия =------------. (о.9)
Иными словами, асимметрию распределения можно изме-
рив, разделив утроенную разность среднего и медианы на стан-
дартное отклонение. Асимметрия из уравнения (5.9). вообше
говоря, может принимать значения в диапазоне от —3 до + 3.
Когда распределение симметрично, уравнение (5.9) даст нуль.
Такую меру асимметрии можно использовать для сравнения
различных распределений, так как деление на сделало эту
меру независимой от изменчивости распределения.
87
5.12. Эксцесс
Мы видели, как статистики описывают три свойства или осо-
бенности выборок: центральную тенденцию, изменчивость и сим-
метрию.
Четвертое свойство завершает набор особенностей распреде-
лений, представляющих интерес при анализе данных. Иногда
важно получить представление о том, являются ли полигон
частот или гистограмма островершинными или плоскими. Экс-
цесс— греческое слово, обозначающее свойство «остроконечно-
сти» кривой. (Карл Пирсон формализовал понятие «эксцесс»
в статистике и предложил метод его оценки.)
На рис. 5.3 изображены 3 кривые, отличающиеся по «остро-
конечности», или эксцессу. Первая (А) является совсем острой:
подобная кривая называется островершинной. Вторая (£>)—
сравнительно плоская: такие кривые называются плосковершин-
ными. «Островершинность», или степень эксцесса, третьей кривой
Рис. 5.3. «Островер-
шинная». «плоская»
и «промежуточная»
кривые (А, Б, В, со-
ответственно).
{В} представляет собой норму, по отношению к которой изме-
ряется эксцесс других кривых. Третья кривая на рис. 5.3 —
нормальная кривая, которая будет обсуждаться в 6-й главе;
принято говорить, что она является средневершинной.
Теперь мы рассмотрим способ измерения эксцесса кривой.
Однако сначала необходимо подчеркнуть, что понятие «эксцесс»
применимо лишь к унимодальным распределениям и относится
к крутизне кривой в окрестности единственной моды. (Если
распределение имеет две моды, то принято говорить об эксцессе
кривой в окрестности каждой моды.)
Обычная мера эксцесса определяется следующей формулой:
X IX, - £)•/»
эксцесс =—------j. (5.10)
sx
Если (Х( — X.y/s’ есть просто ==гх> то меРа
эксцесса задается формулой
эксцесс =-~— = г4. (5.11)
То есть эксцесс измеряется путем усреднения значений г,
возведенных в четвертую степень. Соотношения между величи-
88
ной статистики асимметрии и «островершинностью» распределе-
ния. для которого она вычислялась, показаны в табл. 5.3.
Таблица 5.3
Соотношение величины статистики эксцесса
с «островершинностью» распределения частот
Нормальное, напри-
мер кривая В на
рис. 5.3
Островершинное, на-
пример кривая А
на рис. 5.3
Плоское, например
кривая 5 на рис.
Средневершинное
Островершинное
Плосковершииное
Больше 3 (может
быть очень
большой)
Менее 3 (должна
быть не меньше
нуля)
3
Задачи и упражнения
!. Вычислите включающий размах, дисперсию, стандартное
отклонение и среднее отклонение следующей группы значений:
102 112 пн
106 114 119
111 115 120
112 1)5 122
(Рекомендация: для упрощения вычислений сначала отнимите
100 от всех данных; это не изменит никаких мер изменчивости.)
2. Определите полу-междуквартильный размах для оценок
/Q в следующем выборочном распределении частот:
Интервал значений Частота Накопленная частота
150-159 5 100
140-149 7 95
130-139 9 88
120-129 12 79
110-119 17 67
100-109 21 50
90-99 12 29
80-89 8 17
70-79 6 9
60-69 * 3
50-59 2 2
Медианой этой группы значений является 109,5. Найти
долю значений, лежащих в области, полученной в результате
89
прибавления Q к медиане и вычитания из нее, иначе говоря,
часть значений, попадающих в область 109,5 ±Q,
Дисперсии каждой из групп А и В равны 5. Будет ли диспер-
сия 10 значений, полученных путем объединения групп, меньше,
больше или равна 5?
6
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
6.1. Введение
Эта глава прерывает изложение, но она крайне необходима. Она
должна быть самостоятельной, не связанной со статистическими
характеристиками, которые мы излагали до сих пор, поскольку
здесь мы пытаемся познакомить вас с методикой, основанной на
понятиях, которые нс рассматриваются подробно из-за их слож-
ности. Такова цена, которую каждый из нас платит за попытку
поверхностного изучения статистики без усвоения ее основ
6.2. История нормального распределения
Краткая история открытия и изучения нормального распре-
деления, приведенная здесь, не соответствует той роля, которую
играет это распределение. Даже математически неподготовлен-
ный студент найдет изложение Э. Уолкер истории нормального
распределения содержательным и полезным (1929, гл. II).
В XVII в. в Европе горстка математиков проводила неболь-
шие частные исследования, которые впоследствии оформились
в теорию вероятностей (см. гл. 10) Эти исследования, проведен-
ные, в частности, Блезом Паскалем (1623—1662) и Пьером
Ферма (1601 —1665), выполнялись по просьбе Шевалье де Мере,
азартного игрока, которому было особенно важно понять при-
роду удачи.
Одним из наиболее значительных событий в ранней истории
теории вероятностей было издание в 1713 г. книги «Ars Conjectan-
di» швейцарского математика Я. Бернулли (1654—1705). В на-
чальный период развития основной проблемой теории вероят-
ностей было определение вероятности появления события неко-
торое число раз, если бы ему представилось несколько независи-
мых возможностей появления. Например, если правильная мо-
нета подбрасывается 20 раз, то какова вероятность выпадения
15 «орлов»? Или если игральная кость бросается 10 раз, та
91
какова вероятность того, что 6 очков выпадут точно дважды?
Ко времени опубликования «Ars Conjectandi» решения этих за-
дач были известны (мы рассмотрим их в гл. 10), и формула
свойств таких решений определила основное содержание этой
знаменитой работы. Однако такие вычисления для больших
задач слишком громоздки. Ни один разумный человек не станет
непосредственно вычислять вероятность того, что при 10000 под-
брасываний монеты, например, выпадут 8000 или более «орлов».
Хотя такие вычисления могут быть необходимы, трудоемкость
их все же слишком велика.
В начале XV111 столетия были предприняты некоторые уси-
лия для поиска удобных приближенных методов вычислений в
задачах теории вероятностей R 1730 г. Дж. Стирлинг опублико-
Рис. G1. График распределения вероятностей получения опре-
деленного числа «орлов» при 10 бросаниях правильной монеты.
вал формулу, аппроксимирующую произведение первых п целых
чисел, то есть (1) • (2) - (3) - ...•(« — 1)-(н), которое часто встре-
чается в задачах теории вероятностен. (То, что Стирлинг дейст-
вительно сам вывел формулу, постоянно оспаривалось матема-
тиками.) С появлением формулы Стирлинга удалось решить
в целом важнейшую проблему. Как оценить вероятность того,
что п независимых испытаний события с вероятностью Р получе-
ния одного («удача») из двух исходов обеспечат г «удач»? Че-
ловеком, способным решить эту задачу, оказался в то время де
Муавр (1667—1754).
Прежде чем обратиться к работе де Муавра, рассмотрим
подробнее ту задачу, которую он пытался решить. Предположим,
что монета подбрасывается 10 раз. Допустим, что она может
с равным успехом выпасть как «орлом», так и «решкой». Можно
спросить, какова вероятность того, что в результате получится
0 «орлов» или что выпадет 1 «орел»... или что в результате
10 бросаний мы получим 10 «орлов»? Можно дать точные ответы
на все 11 вопросов, несмотря на то, что для 10 бросаний вычис-
ления становятся уже трудными. (Если бросаний около 1000,
вычисления находятся на грани возможностей.) Вероятности
92
появления 0, 1, 2, ..., 9 или !0 «орлов» в результате 10 броса-
ний монеты графически представлены на рис. 6.1.
Задача, которую пытался решить де Муавр, состояла в том,
чтобы найти уравнение кривой, которая бы хорошо аппроксими-
ровала кривую, полученную соединением концов отрезков на
рис. 6.1. Если бы такую кривую удалось найти, то почти нереа-
лизуемые проблемы вычисления вероятностей можно было бы
заменить простым считыванием точек с кривых или просмотром
чисел в математической таблице.
Де Муавру удалось показать, что уравнение кривой, прохо-
дящей совсем близко от кривой, соединяющей концы отрезков
на рис. 6.1 (и кривой для любой другой подобной задачи), имеет
следующую формулу:
u = —X-e-tx-iow (6.1>
72л а '
где и — высота кривой прямо над всяким заданным значением X
на графике распределения частот; л —отношение длины окруж-
ности к диаметру круга, приблизительно равное 3,142; е — осно-
вание системы натуральных логарифмов, приблизительно рав-
ное 2,718, а и и о—числа, которые определяют положение кри-
вой относительно числовой оси и регулируют ее размах.
Уравнение (6-1) — формула для нормального распределения.
Конечно, оно имеет угрожающий вид, но пусть вас это не
пугает. С формулами подобного типа мы будем иметь дело не-
часто.
6.3. Нормальная кривая
График уравнения (6.1) —обычная, симметричная, колоко-
лообразная кривая, известная под названием нормальной кривой.
Мы говорим о некоторой нормальной кривой, ибо уравнение
(6.1) задает лишь некоторую типичную форму графика. Меняя
значения ц и о, мы можем сдвигать конкретную нормальную
кривую по числовой оси вверх и вниз и менять ее размах. Вели-
чина ц соответствует среднему распределения частот большой
выборки, похожего на нормальную кривую, а о — стандартному
отклонению этого распределения.
На рис. 6.2 построен график нормального распределения для
ц = 0и о=1. Мы будем пользоваться буквой г для обозначе-
ния нормально распределенной переменной с ц = 0 и о=1.
Кривая на рис. 6.2 не пересекает ось г в точках 3 и —3;
действительно, хотя она и приближается к оси z по мере того,
как X становится больше трех, но никогда не касается ее. Самая
высокая точка кривой расположена над нулевым значением г;
в этой точке «=*0,3989. Заметьте, что кривая симметрична отно-
сительно вертикали, проведенной через г = ц=-0 Нормальная
кривая всегда будет симметричной относительно ц. Площадь
93
между кривой и осью г точно равна !. Асимметрия нормальной
кривой равна нулю, так как кривая абсолютно симметрична.
Эксцесс нормальной кривой, то есть среднее значение г, возве-
денных в четвертую степень, равен 3. Как мы заметили ранее,
распределения с эксцессом выше трех более острые, чем нор-
мальное распределение, и их называют островершинными. Рас-
пределения более плоские, чем нормальное, имеют эксцесс мень-
ше трех и называются плосковершинными. Нормальное распре-
деление называют средневершинным (см. 5.11).
Другая особенность нормальной кривой —ее характерный
изгиб. По обе стороны от |л, равного нулю на рис. 6.2, кривизна
сначала уменьшается по мере удаления от оси симметрии, а за-
тем снова увеличивается, то есть кривая имеет точку перегиба,
лежащую точно на расстоянии в одну о от р. Оно равно единице
на рис. 6.2.
Нормальная кривая на рис. 6.2 — особая кривая, так как ее
выбрали как стандарт. Она называется единичной нормальной
кривой, ибо площадь под ней равна 1. Ее среднее и стандартное
отклонение (ц — 0, о—I) очень удобны, а всякую другую
нормальную кривую можно совместить со стандартной простым
преобразованием (то есть вычитанием и и делением на о)
Часто бывает необходимо найти ординату и (высоту кривой
над осью г) для какого-нибудь значения единичной нормальной
кривой или площадь под кривой между какими-нибудь двумя
значениями г. Решение уравнения (6.1) для и, когда z задано,
очень неудобно, хотя мы знаем, что площадь под кривой от
z =— оо до г=+°° равна 1, площадь между любыми дру-
гими двумя значениями определить трудно. Здесь необходимы
статистические таблицы. В таблицах дается площадь под еди-
ничной нормальной кривой влево от любой точки на оси z
между —3,00 и +3,00. Там приводятся также ординаты «м»
единичного нормального распределения для значений z от
—3,00 до 4-3,00.
94
Применение таблиц покажем на примерах. Пусть требуется
найти площадь под единичной нормальной кривой слева от
z = —2,50 Значение —2,50 находится в первом столбцетаблицы.
Справа, во втором столбце, озаглавленном «Площадь», нахо-
дится число 0,0062. Таким образом, слева от г = —2,50 содер-
жится только 62 десятитысячных площади под единичной нор-
мальной кривой. Высота единичной нормальной кривой в точке
г = —2,50 определяется в столбце «Ордината» справа от столб-
ца «Площадь». Для г == -—2,50, и == 0,0175.
Проверьте и посмотрите, можете ли вы правильно находить
эти площади и ординаты в таблицах.
Ордината
Рис. 6.3. Определение площади под
единичной нормальной кривой между
двумя значениями z-
Так как общая площадь под кривой равна 1, то площади
(только не ординаты) можно рассматривать как доли или про-
центы целого. 97,5% площади под единичной нормальной кри-
вой лежит слева от 1,96.
Таблица используется также для определения площади под
единичной нормальной кривой между двумя произвольными зна-
чениями г. Например, площадь слева от г = — 1,27 составляет
0.1020, а площадь слева от г = 0,50 равна 0,6915. Следовательно,
площадь между — 1,27 и 0,50 определяется разностью 0,6915-—
— 0,1020 = 0,5895. Иными словами, около 59% площади лежит
между этими двумя точками. Это показано на рис. 6.3.
6.4. Семейство нормальных кривых
Фактически существует бесконечное множество нормальных
кривых, отличающихся друг от друга парой значений ц и а. Кри-
вая на ряс. 6.4 имеет среднее ц — 20, а стандартное отклонение
о=5, по тем не менее это нормальная кривая.
Что же общего у всех этих нормальных кривых? Для наших
целей их наиболее важное общее свойство заключается в доле
площади под кривой между любыми двумя точками, выражен-
ными в стандартных отклонениях. Например, в любом нормаль-
ном распределении приблизительно:
95
i. 68% площади под кривой лежит в пределах одной а от
среднего в любом направлении (то есть ц ± 1 а),
2. 95% площади под кривой лежит в пределах двух о от
среднего у.,
3. 99,7% площади под кривой лежит в пределах трех а от
среднего ц.
к
5 W 15 20 25 30 35 X
Рис. 6.4. Нормаль-
ная кривая для
ц = 20 и а = 5.
Вы можете проверить эти соотношения и получить точные
площади, определяя площади под единичной нормальной кривой
между —I и +1, —2 и +2, —3 и +3 по таблицам.
Нормальная кривая и ее связь с различными преобразован-
ными шкалами, которые широко используются в педагогических
и психологических измерениях, показаны на рис. 6.5.
6.5. Единичное нормальное распределение как стандарт
Для единичного нормального распределения значение X
указывает, что точка отстоит от среднего на Хединяц.Эюбудет
крайне полезным в дальнейшем, если все значения в нормальных
распределениях давать в терминах отклонений от среднего у,
в единицах стандартного отклонения о. Почти при каждом
применении нормальной кривой мы хотим знать, на сколько
стандартных отклонений выше или ниже среднего лежит неко-
торое значение. Зная это, можно с помощью единичной нормаль-
ной кривой ответить на вопросы о площади между точками на
какой-либо нормальной кривой или высоте кривой над любой
точкой. Отклонение значения от его среднего есть X — у; число
стандартных отклонений, которое отделяет X от среднего, равно
(X — ц) /а, Величина (X—р)/а называется единичным нормаль-
ным отклонением. Если X имеет нормальное распределение со
средним ц и стандартным отклонением о, то (X — ц)/о обладает
единичным нормальным распределением, но не наоборот.
Форма нормальной кривой не изменяется при вычитании ц
и делении на о. Если бы нам захотелось выяснить, какая часть
площади лежит слева от значения 20 в нормальном распределе-
нии со средним 25 и стандартным отклонением 5, мы могли бы
заменить этот вопрос следующим: «Какая часть площади лежит
слева от (20 —25)/5 = — 1 в единичном нормальном распре-
делении?»
Эти вопросы обобщаются в следующем утверждении:
Если X имеет нормальное распределение со средним ц и
стандартным отклонением с, тог - (X — |х)/ст характеризуется
96
Нормальная кривая, процентили н стандартные оценки
Распределение оценок многих стандартизированных педагоги-
ческих и психологических тестов аппроксимируется формой НОР-
МАЛЬНОЙ КРИВОЙ, показанной в верхней части этой диаграммы.
Ниже представлены некоторые системы, разработанные для упро-
щения интерпретации оценок путем преобразования их в числа, кото-
рые указывают относительное положение экзаменующихся л группе.
Нуль (0) в центре базовой линии показывает положение средней
необработанной оценки теста, а символ о (сигма) размечает шкалу
необработанных оценок в единицах СТАНДАРТНОГО ОТКЛО-
НЕНИЯ.
Накопленные проценты являются основой шкалы «ПРОЦЕН-
ТИЛЬНЫЙ ЭКВИВАЛЕНТ:».
Некоторые системы осиованы на единице стандартного откло-
не ня. Среди этих шкал СТАНДАРТНОЙ ОЦЕНКИ z-оценка,
Г-оценка н девятнбалльная представляют собой общие системы,
применяющиеся во множестве тестов. Другие являются специфиче-
скими вариантами, используемыми в связи с тестами Экзаменацион-
ной комиссии по приему в колледж (СЕЕВ), основным армейским
тестом на определение «профессиональной ориентации», составленным
во время второй мировой войны, (AGCT) и шкалами интеллекта
Векслера.
Таблицы НОРМ, либо в виде процентилей, либо в форме стан-
дартной оценки, имеют значение только для конкретного теста, при-
мененною к определенной выборке. Диаграмма не позволяет сде-
лать вывод о том, например, что процентильный ранг 84 по одному
тесту обязательно эквивалентен z-оценке + 1,0 для другого теста,
это справедливо лишь в том случае, когда каждый тест непременно
имеет нормальное распределение оценок и когда обе шкалы осно-
ваны на идентичных или очень похожих группах людей.
Более подробно эти шкалы обсуждаются в «Test Service Bulle-
tin», X? 48, который включает также и эту диаграмму.
Рис. 6.5, Нормальная кривая, процентили ,• < тандартные оценки.
(Из «Test Service Bulletin», Xs 48,)
нормальным распределением со средним 0 и стандартным откло-
нением 1. то есть г= (X — р,)/а имеет единичное нормальное
распределение.
Площадь между и Х2 з нормальном распределении со
средним р. и стандартным отклонением о равна площади между
Zi = (A'i — ц)/с и г2 = (Х2— р.)/о в единичном нормальном рас-
пределении.
6.6. Применение нормальной кривой
Де Муавр изобрел нормальную кривую для частного приме-
нения, то есть для получения простого приближенного решения
в приложениях теории вероятностей. Конечно, он никогда не
Р н с. 6.6. Полигон частот для роста 8 585 взрослых людей, ро-
дившихся в Англии в XIX в.
представлял себе, что его открытие найдет применение практи-
чески в каждом разделе современной науки. Действительно,
нормальное распределение получило удивительно широкое рас-
пространение.
Нормальное распределение играет важную роль как в опи-
сательной статистике, так и в теории статистического вывода
(см. последующие главы).
Нормальная кривая является отличной аппроксимацией рас-
пределений частот большого числа наблюдений при множестве
переменных. Полигоны частот роста взрослых мужчин и женщин
подобны нормальной кривой. Полигон частот на рис. 6.6 пока-
зывает распределение роста 8585 взрослых людей, родившихся
в Англии в XIX в.
Полигон частот на рис. 6.6 основан на распределении частот,
приведенном в табл. 6.1 (см. Rugg, 1917).
98
Распределение частот для рнс. 6.6
Таблица 6.t
Ча-
стота
147 см
150 СМ
152 см
155 см
157 см
160 см
163 см
165 см
168 см
170 см
173 см
1230
1067
178 см
180 см
183 см
185 см
188 см
189 см
193 см
646
392
202
79
32
16
5
Психометрические тесты общих и специальных умственных
способностей часто дают распределения оценок, удовлетвори-
тельно согласующиеся с нормальным распределением. Довольно
хорошо известно, что значения IQ интеллектуального теста
Стенфорда — Бине распределены приблизительно нормально со
Коэффициент интеллекта (IQ)
Рис. 6.7. Распределение оценок IQ Стенфорда—Бине.
(Из L. М. Т е г т а п, М. A. Merrill. Measuring Intel-
ligence, 1937.)
средним (и) 100 и стандартным отклонением (о) 16 для обыч-
ных люден (см. рис. 6.7). Тесты образовательной подготовки,
строящиеся в соответствии с такими же психометрическими
принципами, что и тесты способностей, обычно имеют полигоны
частот, напоминающие нормальную кривую.
У многих учащихся иногда складывается неправильное пред-
ставление, что существует необходимая связь между нормаль-
ным распределением — идеальным описанием некоторых распре-
делений частот — и практически любыми данными. Нормальная
кривая — это изобретение математика, довольно хорошо описы-
вающее полигон частот измерений нескольких различных пере-
менных. Никогда не была — да и не будет — получена совокуп-
ность данных, которые были бы точно нормально распределены.
Но иногда полезно, допуская незначительную ошибку, у^верж-
* Неравномерность шага по росту связана с пересчетом дюймов в см.-—
Прим. ред.
99
дать, что значения переменной «нормально распределены» (по
этому вопросу см. Boring, 1920, н Kelley, 1923).
Множество различных уравнений кривых достаточно хорошо
сгладило бы эмпирические полигоны частот, но возникают из-
вестные математические преимущества, когда принимается, что
«данные сглаживаются» нормальной кривой. Известные матема-
тические свойства нормальной кривой, ур. (6.1), обеспечивают
простые и изящные доказательства во многих задачах теории
статистического вывода. Отказавшись от нормальной кривой,
специалисты по математической статистике столкнулись бы с
трудностями, возникающими в случае использования для пред-
ставления данных других кривых,
6.7. Двумерное нормальное распределение
Теория корреляции, которая будет предметом гл. 7, истори-
чески тесно связана с нормальным распределением и двумерным
нормальным распределением. Одной из задач статистики с мо-
мента ее зарождения как самостоятельной дисциплины было
описание характера связи переменных. Наблюдается ли у высо-
ких отаов тенденция иметь высоких сыновей? Даст ли участок
земли более высокий урожай зерна, если мы увеличим количе-
ство удобрений в почве? Являются ли сообразительные дети
менее развитыми физически, чем дети с более скромными интел-
лектуальными задатками, или нет? Каждый такой вопрос можно
изучать отвлеченно как проблему описания характера связи
значений переменной X со значениями второй переменной У для
тех же объектов. Таким образом, появляются вопросы о двумер-
ных связях, то есть связях между двумя переменными.
Если мы измеряем по две характеристики у большой группы
объектов, например, IQ (X) и физическую силу (У), то данные
можно представить двумерным распределением частот. Для каж-
дого липа существует пара значений — X и У. Двумерное
распределение частот задает частоты, с которыми различные
пары значений X и У встречаются в группе лиц. На рис. 6.8
представлено двумерное распределение частот для группы лиц,
у которых измерялся /Q (X) и физическая сила (У).
На рис 6.8 мы можем увидеть, что приблизительно 20 че-
ловек получили оценку 125 по переменной X, характери-
зующей IQ, и оценку 30 по переменной, оценивающей физиче-
скую силу У.
Многие двумерные распределения, построенные по данным,
накопленным в педагогических и психологических исследова-
ниях, имеют характерную форму. Поверхность, проведенная че-
рез концы отрезков, представляющих частоты в двумерном рас-
пределении, как правило, напоминает колокол —в трех измере-
ниях,— который можно вытягивать в направлениях X и У и
вращать вокруг центра в плоскости X—У. Было бы прекрасно,
100
если бы специалист по математической статистике мог найти
множество кривых, удовлетворительно описывающих множество
двумерных распределений частот. Уравнение поверхности, зада-
ваемое для этой цели, называется двумерным нормальным рас-
пределением. Гладкая, непрерывная, колоколообразная поверх-
X
Рис. 6.8. Двумерное распределение частот для большой группы
лиц. у которых производились измерения ZQ(X) и физической
силы (У).
ность обеспечивает математически удобное и практически удо-
влетворительное представление многочисленных двумерных нор-
мальных распределений.
Частота
Рис. 6.9. Пример двумерных нормальных распре-
делений (поперечные сечения).
Подобно обычному нормальному распределению, двумер-
ное нормальное распределение задается семейством трехмерных
поверхностей. Один пример этого семейства представлен на
рис. 6.9. Все двумерные нормальные распределения имеют
следующие характеристики:
1. Распределение значений X без учета значений У, которым
они соответствуют, есть нормальное распределение.
101
2. Распределение значений У без учета значений X, который
они соответствуют, есть нормальное распределение.
3. Для каждого фиксированного значения X, скажем Хь
значения У для объектов, имеющих Хьдаютнормальноераспре-
деление с дисперсией а' х.
4. Для каждого фиксированного значения У) переменной У
значения X для объектов, имеющих Уь дают нормальное рас-
пределение с дисперсией а’
5. Средние значения У для каждого отдельного значения X
ложатся на прямую.
(Для более детального обсуждения см.: Waiker, Lev, 1953,
р. 248—249).
Задачи и упражнения
I. Пусть г единичная нормальная переменная, то есть нор-
мально распределенная переменная со средним 0 и стан-
дартным отклонением 1. Определите площадь под единичной
нормальной кривой, которая лежит:
а) выше z— 1,00
б) ниже г ==2,00
в) выше г = 1,64
г) ниже z— — 1,96
д) между г = 0 и 2 = 3,00
е) выше z= —0,50
ж) между г = — 1,50 и г = 1,50.
2. Найдите ординаты единичного нормального распределе-
ния над каждой из следующих г-оценок:
а) 2= 1,00
б) 2==- 1,00
в) z = 2,25
г) z=-0,15
3. В обшей выборке детей значения IQ Стенфорда — Вице
имеют приближенно нормальное распределение со средним 100
и стандартным отклонением 16; найдите процентильный экви-
валент каждой оценки Для следующих /Q:
Процентильный
эквивалент
/<2
а 100
б 120
в 75
г 95
д 140
7
МЕРЫ СВЯЗИ
7.1. Введение
В этой главе мы приступим к изучению связей между перемен-
ными. Изложение этой важной темы закончится в 9-й главе.
Для полного анализа измерения связей, или корреляции, кото,-
рое было предметом почти столетних систематических исследова-
ний. потребовалась бы книга, в десять раз большая, чем эта
глава.
7.2. Коэффициент корреляции Пирсона,
равный произведению моментов
Исследователей часто интересует, как связаны между собой
две переменные в данной группе лиц (классы, школы, нации
и т. д.). Например, имеют ли
ученики, научившиеся чи-
тать раньше других, тенден-
цию к более высокой успе-
ваемости в шестом классе?
Наблюдаются ли в больших
классах .меньшие успехи в
приобретении знаний за се-
местр, чем в небольших
классах3 Связана ли сред-
няя продолжительность ра-
боты педагогов в школе не-
посредственно со средней за-
рабошоп платой? Очевидно,
для ответа на такие вопро-
сы мы должны провести на-
блюдения ио каждой пере-
менной для группы объектов
(типичных представителей, которыми могут быть классы, школы,
районы и т. д.). Данные, собранные для ответа на один из подоб-
ных вопросов, могут выглядеть, как на приведенной выше таблице.
№ учащегося Оценка IQ (Xi Стенфорда — Бине Необработан- но химия (У)
г 120 31
2 112 ‘Ж
ч НО 10
4 120 21
5 103 17
6 126 28
7 113 18
8 114 20
q 10(> 16
10 108 15
j । 128 27
12 109 19
103
В этом примере переменными, которые изучались у 12 школь-
ников, были оценки 1Q, определенные с помощью Шкалы ин-
теллекта Стенфорда —- Бине в шестом классе, и успеваемость по
химии в средней школе, оцененная на основе теста, состоящего
из 35 вопросов.
Связь между двумя переменными можно выразить графи-
чески диаграммой рассеивания. Диаграмма рассеивания для
данных примера показана на рис. 7.1.
На диаграмме рассеивания каждый ученик изображается
точкой. Точка, или метка, располагается в месте пересечения
прямых линий, проведенных через оценку IQ перпендикулярно
оси X и через оценку теста по химии перпендикулярно оси V
для каждого ученика. Диаграмма на рис. 7.1 показывает сла-
бую положительную связь X и У. Однако мы пока не имеем
обобщенной меры этой связи.
15. - * •
Ъц________।_______।____t--------1-------1------
100 105 110 115 120 125 X
Рис. 7.1. Диаграмма рассеивания, показывающая
связь IQ(X) с успеваемостью по химии (F) для
12 школьников
Надо поставить общий вопрос о более точном смысле термина:
«связь». Существует ли соответствие большого значения X боль-
шим или малым значениям тех же объектов по У или система-
тического распределения по парам с большими и малыми значе-
ниями не наблюдается?
Положение объекта относительно остальных в выборке по X
и У, определяемое средними двух распределений, проявляется
в величинах и знаках отклонений (X, — л.) и (У,— У.) соответ-
ственно. Если объект имеет высокий уровень по обеим перемен-
ным, как, например, учащийся Ц в вышеприведенном примере,
то произведение (%,• — ^.)-(У,— У) будет большим и положи-
тельным Аналогично, если он относительно низок как по X, так
и по У, то (X,-—,?.) (У,—У.) для него также будет большим
и положительным (поскольку произведение двух отрицательных
чисел положительно). Если X и У в основном связаны прямо’
104
(большие значения с большими, а малые — с малыми), то боль-
шинство произведений —Х.)-(У<—У.) будет положительным:
следовательно, сумма этих произведений для всех объектов [то
есть X (X, — X.)(У, —У.)] будет большой и положительной.
Если X и У имеют обратную связь (большое X встречается
с малым У и наоборот), то многие объекты с положительными
значениями (X,- — X.) будут тяготеть к отрицательным значе-
ниям (_У(—У.), а отрицательные (Х(—-X.) — к положительным
(У,—-У.). В этом случае произведения (Л< —X.)• (У< — У.) бу-
дут, как правило, отрицательными. Следовательно,
t{X,-X.){Y,~Y.)
будет отрицательной, когда X и У связаны обратной зависимо-
стью.
Если X и У не имеют систематической связи (большие X
сочетаются с малыми У столь же часто, как и с большими У,
и то же самое справедливо для малых X), то среди объектов
с большими положительными значениями (Х<—X.) у некоторых
(У, — У.) будут положительные, а у других — отрицательные.
При образовании произведений (X, — X.) • (У{—У.) одни сомно-
жители станут положительными, а другие — отрицательными.
Сумма произведений
£(.Х,-Х
должна приблизительно балансировать положительные и отри-
цательные члены и поэтому должна быть довольно близкой
к нулю.
Таким образом, мы имеем величину £ (X,Х.)(У\ — У.),
которая велика и положительна, когда X и У сильно связаны
прямой зависимостью, близка к нулю в случае отсутствия связи
между X и У и велика и отрицательна, когда X и У сильно свя-
заны обратной зависимостью. Однако эта сумма произведений
•отклонений все еще не является адекватной обобщенной мерой
связи. Прежде всего ее величина зависит от числа пар значе-
ний. участвующих в подсчете. Так как мы можем пожелать
сравнить степень связи между X и У в двух выборках разного
объема, то надо уметь измерять связь независимо от объема
групп. Простое усреднение позволяет достигнуть этого. Два
средних значения для выборок разного объема сравниваются
в терминах центров группирования данных, а простые суммы
для двух выборок не сопоставляются. Вот почему мы берем
среднее, если хотим, чтобы статистика не зависела от объема
выборки. Однако по той же причине, по которой s2x получилась
105
в результате деления суммы квадратов отклонений на п—1„
а не на п, нам следует разделить
£ (Х< - X.)(YI - Г.) на п- 1.
Величина J} (Л) — X.) (Yt — Y -)/(п— 1) является мерой связи X
и У и называется ковариацией X и Y. Ковариация X и Y обозна-
чается через sxv'.
£ (^-х.НЛ-Г.)
-------• (М)-
Заметим, что ковариация X с самим собой — это просто дис-
персия Л:
£(Л;-х.)(хг-х.) fjXi-х.у
е - — ±32______________________—
Ковариация является вполне удовлетворительной мерой связи)
во многих задачах физики и техники. (Действительно, физик»
называют пресловутый бихевиористский «коэффициент кор-
реляции», с которым мы вскоре встретимся, «безразмерной
ковариацией»). И она представляет собой адекватную меру
в той же степени, в какой шкала (среднее и дисперсия) пере-
менных не является произвольной и имеет некоторый смысл.
Многие переменные, с которыми мы имеем дело, измеряются
в произвольных шкалах: среднее и дисперсию можно сделать-
любыми, какими вздумается, поскольку нас обычно интересует
только взаимоположение объектов в группе. Это, в частности,
верно для обработки психологических и педагогических данных.
Вычитание значений X и Y из соответствующих средних сде-
лало s4!/ независимым от средних. Чтобы избавить меру связ»
от влияния стандартных отклонений двух групп значений, надо
только разделить sxy на sx и sy. В результате получим искомую
меру связи X и Y. Она называется коэффициентом корреляции —
произведением моментов — Пирсона и обозначается гху:
Обозначение г происходит or слова регрессия. На первона-
чальном этапе применения этого коэффициента Фрэнсисом Галь-
юном и Карлом Пирсоном (1857-—1936) он играл важную роль,
в исследовании связей физических характеристик людей, иссле-
довании. которое сначала было направлено на изучение регрес-
сии физических измерений от одного поколения к другому.
105
7.3. Формула для вычисления тху
Уравнение (7.2) определяет гх„, но неудобно для вычислений.
Теперь мы найдем выражение, более удобное для вычисления
гха на настольном арифмометре. Начнем с
zy/jlX.-X,)>/(«-!) д/ £ (П-г.-ецп - 1)
(7.3)
Заметьте, что 1/(п— 1) можно выделить в качестве сомножителя
из двух членов знаменателя уравнения (7.3) (ll-y/n— 1 из
каждого члена) и сократить с Щп—1) в числителе. Напоми-
наем также, что члены знаменателя уравнения (7.3) можно
объединить под знаком радикала.
(7.4)
Простые преобразования приводят к следующей формуле
г SwHZMtW
которую можно еще более упростить, образуя расчетную фор-
мулу
г „»Xw,--Q»(X>-<) ,7
7.4. Пример вычисления гху
Для иллюстрации вычисления гху по уравнениям (7.5) и
•(7.6) здесь будут использованы некоторые данные теста на опре-
деление общих и специальных способностей Исследователь изу.
чает связь двух типов умственных способностей учеников непол-
ной средней школы: абстрактное мышление и вербальное мыш-
ление. Разработаны два теста: для измерения склонности к аб-
страктному мышлению (X) и к вербальному мышлению (У).
Оба теста были предложены 40 школьникам младшего класса
неполной средней школы в одном городе штата Иллинойс с
.30 000 жителей. Результаты 40 учащихся представлены
в табл. 7.1. В каждом тесте было 50 вопросов, а результатом
107
Таблица 7.t
Исходные оценки по тесту, состоящему из 50 вопросов н
измеряющему способность к абстрактному и вербальному мышлению
у 40 школьников неполной средней школы в Иллинойсе
Ученик Абстракт- мышление Вербаль- мышленис Ученик X Абстракт- мышление Вербаль- мышленне-
Лннда Дж. 19 17 Мартин Т. 38 30
Пегги И. 32 у Шерон Л. 25 18
Диана Л. 33 17 Юлия Е. 26
Констанция Л. 44 28 Наталн Дж. 22 17
Уильям П. 28 27 Меркджии К. 40 17
Роджер Д. 35 31 Ларри Н. 42 26
Каролина Е. 39 20 Майкл Б. 41 16
Труди Р. 39 17 Карлин М. 41 37
Питер А. 44 35 Скотт С. 37 26
Дэаид Е. 44 43 Знгрид К- 30 21
Чернл Дж. 24 10 Жан У. 31 16
Джорджия С. 37 28 Роджер Б. 41 37
Ирма Дж. 29 13 Ричард X. 42 37
Рональд Л. 40 43 Боинга Дж. 24 14
Памела Дж. 42 45 Рекс Н. 43 41
Эдвард Б. 32 24 Ричард С. 36 19
Роза Л. 48 45 Морис Д. 39 18
Карина М. 43 26 Уоррен У. 39 39
Роджер У. 33 16 Джек Дж. 39 37
Рнчард Т. 47 26 Стенли Л. 48 47
Таблица 7J1
Пример вычисления гху по данным табл. 7.1
Промежуточные вычисления Окончательные вычисления
П —40 40 7 X,-1465 40 £ Г,-™» 40 £х*-55 725 Уравнение (7.5): 40 798 — (1465) (1057)/40 V [55 725 - (1465)2/40j - [32 55] - (1057)2/40] 2085,375 - SWw Уравнение (7.6): e 40(40 798) — (1465) (1057) __ |V[40 (55 725) - (1465)’]. [40 (32 551) — (I057)2!
40 7 У] = 32 551 123761,128
40
7X^,-40798
103
служило число правильных ответов. Диаграмма рассеивания
двумерных данных (поле корреляции) табл. 7.1 представлена
на рис. 7.2.
В табл. 7.2 приводятся промежуточные и окончательные вы-
числения rxv по формулам (7.5) и (7.6). Все расчеты выполнены
на настольном арифмометре. Возможно, единственной величи-
АЬстрактиое мышление
Рис. 72. Диаграмма рассеивания 40 пар резуль-
татов теста из табл. 7.1.
40
ной, происхождение которой не ясно, является £ Эта ве-
личина представляет собой сумму произведений X и Y по всем
ученикам. Для первой в табл. 7.1, Линды Дж., Х\ = 19, а
У] = 17; для второй — Пегги И., Хц — 32, а Уг = 7. Величина
40
£х,Г, — (19- 17) + (32-7)+ ... +(48 - 47) —40798.
Окончательные вычисления в правой части табл. 7.2 приво-
дят к rxv = 0,67 и по уравнению (7.5) и по уравнению (7.6).
В пределах ошибки округления обе формулы всегда дадут
в результате ту же величину. Таким образом, оказывается, что
существует сильная прямая связь между способностями к абст-
рактному н вербальному мышлению, измеренная по двум
тестам.
109
7.5. Область изменения гху
Хотя это и затруднительно доказать, но г1у никогда не может
принять значение ни меньше —1, ни больше -j-! (Если вы
обеспокоены кажущейся трудностью доказательства, предла-
гаемого в сноске, то можете по крайней мере утешиться тем,
что более простое доказательство, часто приводимое в элемен-
тарных учебниках, является ошибочным.)
Таблица 7Л
Интерпретация значений гху
Величина гХу Описание линейной связи ДиаЕрамма рассеивания
+ J.00 Строгая прямая связь У
Около +0,50 Слабая прямая связь У X
0,00 Нет связи (то есть ковариация X и У = 0) У
Около —0,50 Слабая обратная связь У
-1,00 Строгая обратная связь у X
В табл. 7.3 перечислены различные значения гху с иллюст-
рациями типа линейной связи, которая существует между X и У
для данных значений гху1 2.
1 Для доказательства тою, что величина r*v не может превышать + !,
раскроем £ ~ гУ)2. К0Т0Рая всегда больше или равна нулю, и исполь-
уп Z Z
зуем тот факт, что £ гх ~ S 2У = п ~ 1 к fxg — —• Чтобы
показать, что гх„ не может быть меньше —1. используйте £ (2* + 2у)2-
2 Тип связи rxv будет обсуждаться в главе 8 Еще по этому поводу см.
§ 7.7 этой главы, где рассматриваются нелинейные связи между X и У.
ПО
Таблица 7.4
Типичные значения
Описание переменных Характеристика испытуемых значение 'ху
X У
Результаты экзамена Ранг но успеваемо- Свыше 600 сту- 0,58
за 9-й класс в шко- лах штата Айова коэффициент интел- лекта (1Q) Стен- форда — Бине Способность к вер- бальному мышле- сти первокурсник ков колледжа То же через неделю Способность к не' вербальному деитов кол- леджа Учащиеся на- чальной шко- Учеяики непол- ной средней 0,00 0,65
нию (измеренная с помощью диффе- ренциального теста для определения специальных спо- собностей) мышлению Успеваемость по физике в кол- ледже школы Юноши — стар- шекурсники колледжа 0,00
В табл. 7.4 представлены некоторые типичные коэффициенты
корреляции. После приобретения опыта работы с реальными
данными у вас начнет развиваться «чувство» степени связи,
характеризующейся любым частным значением г. Возможно, вы
научитесь мысленно связывать диаграмму рассеивания точек
и соответствующую ей приблизительную величину г. Мы не ре-
шаемся применить описательные прилагательные к значениям г,
такие, например, как «высокие» для г = 0,80 или «низкие» для
г = 0,20. Зачем использовать неясные и двусмысленные описа-
тельные прилагательные для величины г, когда так просто со-
общить ее значение?
7.6. Влияние преобразования данных на rXJI
Часто среднее и дисперсия X и У произвольны. Кажется, что
мы можем изменять их по желанию без всяких последствии. Но
зависит ли от средних и дисперсий X и У величина глу? Нет.
Такой ответ подразумевался при выводе формулы гху; теперь
мы хотим показать это более наглядно.
Среднее и дисперсию X (или У) можно заменить на любую
желаемую величину, умножая X на константу b 0 н прибав-
ляя константу а к произведению, то есть образуя Это
называется «процессом линейного преобразования X». Пусть мы
проводим другое (или аналогичное) линейное преобразование У,
! 11
dY 4- с, где d =£ 0. Одинаков ли коэффициент корреляции между
X и Y и между ЬХ 4- а и dY 4- с?
Корреляция ЬХ + а и dY 4- с представляет собой их кова-
риацию, деленную на произведение стандартных отклонений.
Известно, что прибавление к переменной константы не изменяет
ее стандартного отклонения, а умножение ее на константу умно-
жает стандартное отклонение на абсолютную величину констан-
ты. Таким образом, стандартное отклонение ЬХ + а есть [&JsIr
a dY + с имеет стандартное отклонение, равное [d]sP.
a SdF+c = Hlstf. (7.7)
Ковариация ЬХ 4- а и dY 4- с равна
[bXt 4- а - (ЬХ. + а)] [dYt 4- с - (dY. 4- с))
s(*Y+-a) (йГ+с> ~ п -
Это выражение можно упростить:
п _ _ п _ _
£ (bXi - bX.)(dYt — dY.) bd£ (Xt -X.)(Yi — Y.)
_L-----------------------------!------------------- b dx.a. (7.8)
n — ! n — 1 xy \ >
Объединим результаты уравнений (7.7) и (7.8) в выражение
для корреляции Ьх 4- и dY 4- с.
& dsxy bd
гьхл a. dY+c = “ I b 11 di' Г^- <7-9>
Предположим, например, что X преобразовано в ЗХ 4- 5,
a Y— в 2Y 4- 8. Тогда
_ 3-2 __
тЗХ + 5. 2K+8 — | 3 | • | 2 | Гх!/ ’
Данное преобразование X и Y не повлияло на корреляцию
гху. Действительно, отношение bd к Ibl'jdl в уравнении (7.9)
никогда не может быть ничем иным, кроме 4-1 или —1. Следо-
вательно. никакое линейное преобразование X или Y (при ус-
ловии, что Ь или d—не нули) не изменит величину корреляции
между X и Y, хотя оно, возможно, приведет к изменению знака
корреляции. Это видно из табл. 7.6.
Таблица 7£
Влияние линейных преобразований X н Y на величину гху (особые случаи уравнения (7.14))
ЬХ + а dr+c Величина ЗУ + с
Ь — положительно d — положительно
Ь — отрицательно d — положительно
b — положитель; о d — отрицательно ~гхц
Ь — отрицательно d — отрицательно Г*И
112
7.7. Интерпретация коэффициентов корреляции
А. Причинность и корреляция
Наличие корреляции двух переменных отнюдь не означает,
что между ннмн существует причинная связь. Несмотря на то
что сосуществование (корреляцию) событий можно использовать
для выявления причинных связей наряду с другими методологи-
ческими подходами, монопольное применение корреляции к ана-
лизу причинности рискованно и может вводить в заблуждение.
Во-первых, даже в тех случаях, когда можно предположить
существование причинной связи между двумя переменными, ко-
торые коррелированы, гху сам по себе ничего не говорит о том,
вызывает ли X появление У или У вызывает появление X. Во-
вторых, часто наблюдаемая связь существует благодаря другим
переменным, а не двум рассматриваемым. В-третьих, взаимо-
связи переменных в педагогике и общественных науках почти
всегда слишком сложны, чтобы их объяснением могла служить
единственная причина. Успеваемость в школе — результат
многочисленных влияний, да и сама по себе она является
сложным понятием, которое нельзя описать адекватно при по-
мощи какого бы то ни было одного измерения.
Мы рассмотрим некоторые проблемы, возникающие при по-
пытке выявить причинные связи с помощью корреляции. Веро-
ятно, справедливо, что в США существует положительная кор-
реляция между средним заработком преподавателей в школах и
процентом выпускников, поступивших в колледж Значит ли эго.
что высокооплачиваемое школьное преподавание вызывает по-
явление лучше подготовленных абитуриентов колледжа? Уве-
личится ли процент выпускников, поступивших в колледж, если
повысить плату преподавателям? Конечно, утвердительные от-
веты на эти вопросы не объяснить одной ассоциативной связью.
Связь между двумя факторами не проста, кроме того, еще не
упоминалась одна существенная переменная, которая характе-
ризует финансовые и экономические условия жизни общества
и определяет его возможность нести расходы как по оплате
преподавателей, так и по обучению в колледжах. Наряду с этим,
экономическая и финансовая обстановка отчасти зависит от
интеллектуальных возможностей населения, другой переменной,
вносящей вклад и в более высокую оплату педагогов и в повы-
шенную посещаемость колледжей молодежью.
Установлено, что процент «исключенных» из школ отрица-
тельно коррелирует с числом учебников, приходящихся на уче-
ника в библиотеках этих школ. Но здравый смысл подсказывает
нам, что нагромождение книг в библиотеке не больше повлияет
на число исключенных, чем наем ленивого служащего па магиче-
ское увеличение школьной библиотеки. Если бы только здравый
смысл всегда служил нам так хорошо!
113
Многие исследователи не останавливаются на том ложном
выводе, что корреляция свидетельствует на первый взгляд о при-
чинной зависимости, а выводят также и другое заключение. Он»
приписывают причинной связи определенное направление. Рас-
смотрим более внимательно правдоподобный пример. Предпо-
ложим, что в большой группе учащихся коэффициент корреляции
между тревожностью (X) и результатом теста /Q (Y) равен
— 0,60. Означает ли это, что большое волнение привело к тому,
что учащиеся плохо выдержали испытание, а более спокойные
ученики, не травмированные страхом, оказались в состоянии
успешно проявить свои способности? Этот вывод склонны делать
некоторые исследователи. Но разве не столь же правдоподобно
считать, что сам этот тест есть фактор, вызывающий беспокой-
ство? Не могли ли тупые ученики бояться испытания их интел-
лекта, а способные найти эксперимент приятным и не вызываю-
щим беспокойства? В данном случае вопрос в том, можно ли
сказать, что X вызывает Y или что У вызывает X5 Обычный
коэффициент корреляции между X и У не может дать ответ на
этот вопрос. Без экспериментальной проверки связи сами по
себе часто трудно интерпретировать. Искусный эксперименталь-
ный подход к той же самой задаче предполагал бы формирова-
ние группы тревожных учеников и сравнение их оценок с оцен-
ками контрольной группы.
Хотя корреляция прямо не указывает на причинную связь,,
она может служить ключом к разгадке причин. При благоприят-
ных условиях на ее основе можно сформулировать гипотезы,
проверяемые экспериментально, когда возможен контроль дру-
гих влияний, помимо тех немногочисленных, которые подлежат
исследованию. Существуют также хорошо разработанные про-
цедуры. в частности в социологии, для вывода причин из связан-
ных данных.
Иногда отсутствие корреляции может иметь более глубокое
воздействие на нашу гипотезу о причинной связи, чем наличие
сильной корреляции. Нулевая корреляция двух переменных мо-
жет свидетельствовать о том, что никакого влияния одной пере-
менной па другую не существует, при условии, что мы доверяем
результатам измерений и что произведение моментов г Пирсона,
измеряющее только частный тип связи, подходит для измерения
более общего типа связи, называемой «причинной». Но все это
мало помогает: требуются методы обнаружения причинных
связей, а не методы иллюстрации беспричинных явлений. Для
более глубокого обсуждения этого вопроса см. Blalock, 1961,
Campbell, Stanley, 1963.
Б. Идентичные группы с различными средними
Существенная корреляция между двумя переменными — это
факт, который в разных ситуациях можно объяснить по-разному.
Некоторые корреляции — результат измерения причины и ее
действия, например когда X— пища, съеденная за месяц, a Y —
114
вес, приобретенный за то же время. Другие корреляции возни-
кают при измерениях двух переменных с общей причиной или
влиянием, например когда X— успеваемость во английскому
языку, а У — по общественным наукам. Иногда возникают иные
корреляции, когда объединяются две различные группы, в каж-
дой из которых X и У не имеют связи.
Предположим, что девочки проявляют большую тревожность,
чем мальчики, при проверке, например, цо шкале выраженной
тревожности Тейлор. Хорошо известно, что девочки, как правило,
имеют более высокие оценки по английскому языку по сравне-
нию с мальчиками, особенно в средних классах. Диаграмма
рассеивания тревоги и успеваемости по английскому для 15
мальчиков и 15 девочек могла быть подобна той, которая пред-
ставлена на рис. 7.3.
Рис. 7.3. Диаграм-
ма рассеипания
оценок тревоги и
успеваемости по
английскому языку
для 15 мальчи-
ков (S) и 15 дево-
чек (G).
5 8 г.
Тревожность
На рис. 7.3 видна довольно сильная положительная связь
между тревогой и успехами в английском, когда объединяются
оценки мальчиков и девочек. Свидетельствует ли это о том, что
тревожность (напряжение) заставляет учащегося усерднее тру-
диться и тем самым стимулирует большие достижения? Вовсе
нет. Если бы это было так, то почему никому не удалось уста-
новить какую-либо связь между двумя переменными отдельно
для мальчиков и девочек?
На рис. 7.3 видно, что ненулевые корреляции могут получить-
ся в тех случаях, когда объединяются отдельные группы, напри-
мер мальчики и девочки с различными средними. В результате
такого объединения могут наблюдаться либо положительные,
либо отрицательные связи.
Идентификация подгрупп с различными средними по X и У
не исключает возможности корреляции X и У. Однако она до-
пускает более рациональное объяснение того, почему гху суще-
ственно отличается от нуля.
13 Нелинейность и формы маргинальных распределений
переменных
Из всех способов, которыми могут быть связаны измерения
двух переменных, rxv оценивает только один. Величина rxv пред-
ставляет собой меру степени линейной связи X и У. Если X и У
115
жестко линейно связаны, то точки диаграммы рассеивания будут
расположены на одной прямой, как это показано в табл. 7.3.
Если мы разбросаем точки на таком графике над и под прямой
случайным образом и приблизительно на одинаковые расстоя-
ния, то получим различные степени линейных в своей основе
связей между X и У. Если точки на диаграмме рассеивания
ориентируются — хотя и отклоняются случайным образом — от-
носительно кривой, связь X и У может быть существенно криво-
линейной. Из того, что измеряет только линейную связь
между X и У, следует, что различные виды нелинейных связей
X и Y могут дать такие значения rXS(, которые подозрительно
близки к нулю, если интерпретировать их без учета диаграммы
А
2 о°0°
X
Сильная нелинейная сйязь
Рнс. 7.4. Два примера близкой к нулю корреляции, определяемой
произведением моментов.
рассеивания. Если известно, что X и У в общем тесно связаны
линейно, то смысл rxv совершенно ясен. Однако если X и У
имеют некую нелинейную связь, то близкие к нулю значения
rIV могут быть получены даже несмотря на то, что X и У сильно
связаны. Рис. 7.4 содержит две разные диаграммы рассеивания,
каждая из которых имеет близкие к нулю коэффициенты кор-
реляции.
Хотя обе диаграммы рассеивания А и В на рис. 7.4 имеют
нулевые коэффициенты корреляции, в В есть существенная
связь между X и У, а в Л нет никакой систематической связи меж-
ду ними. Одной иллюстрации на рис. 7.4, по-видимому, достаточно
для предупреждения против опрометчивого вывода о том, что-
две переменные не связаны только потому, что гху = 0. Опенки
педагогических и психологических тестов часто дают «потолоч-
ные» или «подвальные» эффекты у нетипичных групп, то есть
испытания могут быть слишком легкими или слишком труд-
ными, ибо многие получают максимальную или минимальную
оценку. Диаграмма рассеивания оценок теста А. который ха-
рактеризуется «потолочным эффектом», и теста В с «подваль-
ным эффектом» могла бы быть подобна диаграмме рис. 7.5.
116
Величина глв для данных рис. 7.5 невелика; вероятно, она
приблизительно равна 0,30. Оказывается, что в области, для
которой оба теста эквивалентны по трудности, они связаны бо-
лее сильно. Считают, что если бы тест А был более трудным, а
тест В — более легким без радикального изменения их содержа-
ния, то величина глв увеличилась бы. Диаграмма рассеивания
для подобных измененных тестов, возможно, обладала бы мень-
шей нелинейностью, чем имеющаяся. (Этот пример показывает
другой важный момент: степень связи между любыми двумя пере-
менными — независимо от того, как эта связь выражена, — за-
висит от характера измерения переменных. Например, мы обыч-
но считаем, что характеристики веса и роста довольно сильно
Рис. 7.5. Диаграмма
рассеивания оценок
для теста А (слишком g
простого) и теста В g
(слишком трудного *—
для испытываемой
группы).
Тест 5
связаны между собой у взрослых людей; но нетрудно предста-
вить себе весьма плохие способы измерения этих переменных —
например, измерение с помощью субъективных суждений четы-
рехлетних детей, оценки веса и роста которых не показали бы
почти никакой корреляции.)
7.8. Дополнительные замечания об интерпретации r*v
Кэрролл (1961) представил интересный доклад о том, как
интерпретация гХ11 зависит от формы распределений X и У и их
совместного распределения. Его статья содержит отличное изло-
жение многих вопросов, затрагиваемых здесь лишь бегло, и от-
части будет понятна учащемуся, чье ознакомление с корреля-
цией не выходит за рамки этой и двух последующих глав. Он
приводит следующее наблюдение одновременно над интерпре-
тацией гху и обучением студентов статистике:
«Студентам недостаточно точно объясняют, что пределы (от —I до +1] и
выражения («сильно связанный», «умеренно связанный», «не связанный»!
непосредственно относятся к определенным статистическим моделям Две
наиболее часто применяемые модели — нормальная двумерная поверхность
(см раздел 6.6) и модель линейной регрессии (см. главу 8)... Для вычис-
ления коэффициента Пирсона ие требуется никаких предположений, но ин-
терпретация его смысла определенно зависит от области, в пределах кото-
рой данные приводятся в соответствие с подходящей статистической мо-
делью для выполнения этой интерпретации. Поскольку реальные данные
отклоняются от модели, под которую их подгоняют (например, двумер-
ной нормальной поверхности), то пределы коэффициента корреляции мо-
гут сужаться, а предлагаемая интерпретация терять смысл».
117
В качестве примера того, как максимальное значение гху
может ограничиваться величиной менее 4* 1, когда частотные
распределения X и У асимметричны (скошены) в различных на-
правлениях, рассмотрим 99 оценок X и У со следующими распре-
делениями частот:
Оценка для X: О 1 2 3 4 5 6 7 8 9 10
Частота: 21 12 14 14 13 10 7 4 2 I 1
Оценка для К: О I 2 3 4 5678910
Частота: 00 1 1 2 24567 71
X скошен сильно положительно, а У — сильно отрицательно.
Максимальная возможная величина гхи приблизительно 0,60.
Другими словами, даже если между X и У существует макси-
мально возможная линейная связь, будет только 0,60. Это
вовсе не говорит о слабости гху как описательной меры; нельзя
упрекать в нарушении тех функций, которые не предусматри-
вались Тот факт, чго гХц нс может превышать 0,60 в данном при-
мере, надо рассматривать скорее как утешительный. Когда X
имеет так много значений ниже среднего, а У характеризуется
множеством значений, превышающих среднее, то невозможно,
чтобы все положительные отклонения У( относительно У. были
связаны с положительными отклонениями X, относительно X.. На
самом деле гху не может достигнуть крайних значений 4- 1 или
- i, пока распределения X и У не имеют идентичной формы.
Эта зависимость максимальной величины гху от распределе-
ний .¥ и У создает известные трудности. Предположим, что полу-
чено гчу = 0,60. Что это характеризует? Умеренную связь двух
переменных, совместное распределение частот которых подобно
двумерной нормальной поверхности, или максимально возмож-
ную связь между положительно скошенным X и отрицательно
скошенным У? Ранее мы видели, как подобные сомнения каса-
лись нулевого значения г1у. Действительно ли X и У не связаны
или связь между ними нелинейная? Наиболее удовлетворитель-
ное разрешение всех этих сомнений достигается анализом диа-
граммы рассеивания значений X и У. На такой диаграмме
можно сразу увидеть, имеют ли X и У выраженную криволиней-
ную связь и значительно лн они скошены.
7.9. Дисперсия суммы и разности переменных
В педагогике и психологии довольно часто требуется опреде-
лить дисперсию нескольких сложенных значений X и У. Кроме
того, простой анализ формулы, связывающей s2x+v, дисперсию
суммируемых значений X и У, с s2, з2 и гху1 может прояснить
путь, которым влияния комбинируются в общие эффекты. В исто-
рии теории интеллектуальных тестов общее выражение для дис-
персии суммы переменных играло важную роль (общий резуль-
тат теста равен сумме значений по отдельным вопросам),
118
Дисперсия X + У, где каждая из п сумм равна Х(4-Уг>
имеет следующее определение:
XtHi + l'J-fX. + r.»’
4t, = ----------------------- P.W
Члены в квадратных скобках уравнения (7.10) можно пере-
ставить:
Ё «*<“?)+ ~ г. >1"
Й« = -----------. (7.11)
Если раскрыть выражение в квадратных скобках в числи-
теле уравнения (7.11), то получим
f^Xi-X.r 2£(X<-X.>(7.-г.) Jir.-r.)*
S«+I“J H----'-------jrn------+J—^771------• <7-l2>
Вы сразу узнаете, что первый и последний члены правой
части уравнения (7.12) представляют собой соответственно
s’ и s’. Средний член просто равен двум ковариациям $м/.
Таким образом,
sx+b — s* + su 4" 2sx9- (7.13)
Очевидно, что sxy ~ rxysxsy. Поэтому замена sxy на экви-
валентное выражение дает
Sx+y= Sx + Sy -f- 2rxysxSy- (7-14)
Уравнения (7.13) и (7.14) связывают дисперсию суммы двух
множеств значений с дисперсией каждого множества и их ко-
вариацией.
Важен особый случай уравнения (7.14), когда X и У некор-
релированы, то есть rxv = 0. Если это справедливо, то
Sx+a = sx -f- Sy- (7.15)
Что же представляет собой выражение, эквивалентное s’_ff?
£ [(Х1 - У/) - (X.-У.)]2
-------------------------
+Ё(Х,-У.С-2 Ё(.7,-Х.1(7, -г.)
— St 4* $0 — 2$х^ = sx 4" Sy — 2гxySxSy.
119
Это соотношение весьма интересно. Дисперсия разности
между значениями X и У равна дисперсии X плюс диспер-
сия У минус удвоенная ковариация X и У (или удвоенное
произведение гху на и s^). Далее, если X и У не коррели-
рованье то
= Зх + Зу.
(7.16)
Рассмотренные результаты полезны не только в дальнейшем
процессе изучения статистики, они могут также кое-что прояс-
нить. Например, мы знаем, что
$х + у — Зх — Sy — Зх + Sy -f- 2rxySxSy — Sx — S2y — 2rXySxSy.
Поэтому, если мы разделим это соотношение на 2sxsv. то
найдем,что
Предположим, что существуют три переменные — X, У и Z.
Чему была бы равна дисперсия сумм, полученных при сложе-
нии значений этих трех переменных?
^((х, + г;+г()-”(х- +г- +z-)p
Sx + y±z п — 1
(7.17)
Члены в квадратных скобках уравнения (7.17) можно сгруп-
пировать иначе
Числитель уравнения (7.18) представляет собой квадратич-
ный трехчлен. Вспомните из школьной алгебры, что (д + b -j-
Н-с)2 — а2 + № + с2 + 2 ab + 2 ас + 2 Ьс. Отсюда
-г £(Х,-Х.С Sir,-г.)’ £(Z,-Z.).
Зх+ь+г— + n_5 + п-1
2 j; — У. )(Zj — Z.)
120
Все члены справа в этом уравнении — дисперсии или кова-
риации. Полное уравнение можно свернуть к виду
8*+у+г = S* + Зц 4~ sz 4~ -f- 2&хг 4~ 23аг,
что аналогично следующему:
S2x+y+z = 4 + $у 4- S* 4- 2rxuSxSu 4- 2rxiSxSx 4- 2r„xSySz.
(Дополнительные пояснения можно найти в книге: Edwards,
1964, р. 15—23.)
В этой главе не содержится полного описания корреляции.
Предметом 8-й главы является проблема оценивания по методу
наименьших квадратов, которая тесно связана с корреляцией
(см. раздел 8.4). В главе 9 приведены коэффициенты корреля-
ции для коррелированных данных, заданных в шкалах наи-
менований и порядка. Эти три главы никоим образом не исчер-
пывают вопроса об измерении взаимосвязей. Те аспекты темы,
которые здесь вскользь затронуты, можно усвоить более полно,
обратившись к другим книгам. (См. Езикиель, Фокс, 1968, Du
Bois 1957; Kruskal, 1958.)
Задачи и упражнения
1. Браун вычислил ковариацию роста в дюймах, X, и ско-
рости бега в секундах, У. Он получил значение 27,60 в выборке
из 50 учащихся. Смит вычислил ковариацию роста в футах,
Х^5у,5^ит. д.) и скорости бега У по тем же исходным
данным, что собрал Браун, и получил величину 2,30. Браун или
Смит получит более высокое значение корреляции между X н У,
пользуясь только этими данными?
2. Для некоторой совокупности данных sx = 5, s„ — 4.
Какова наибольшая величина sxs? [Указание: гху не может быть
больше 4- 1; rxt, = sxy!sxsy.]
3. а. Определите величину коэффициента корреляции г для
следующих данных:
121
6. Постройте диаграмму рассеивания для приведенных
данных.
в. Является ли связь между X и У—если она существует —
линейной или криволинейной?
4. Верно ли, что
£x,(r,-r.)=£r,(x,-Tj?
Указание: убедитесь, что
ПРЕДСКАЗАНИЕ И ОЦЕНИВАНИЕ
8
8.1. Введение
Идеи и методы, составляющие простейшую форму статистиче-
ского предсказания, можно лучше всего проиллюстрировать
с помощью нескольких элементарных представлений из анали-
тической геометрии. Мы изложим только идею двумерной ко-
ординатной системы и уравнения прямой в этой системе.
Декартова5 система координат представлена на рис. 8.1.
Оси этой системы — взаимно перпендикулярные линии X и У —
делят плоскость (плоскую, двумерную поверхность, имеющую
длину и ширину, но не глубину) на 4 квадранта: I, II, III и IV.
Эта координатная система есть такой способ деления плоскости,
что каждую точку в ней можно задать парой чисел (%, У),
Точка (0,0) называется началом системы и образуется пересе-
чением линий X и У. Первое число для любой пары — это рас-
стояние по горизонтали от начала (расстояние X) до данной
точки, а второе число — расстояние от начала координат по вер-
тикали. Точке А на рис. 8.1 соответствует пара чисел (2,2).
Первое число называется координатой X, а второе — координа-
той У. Точке В соответствует пара чисел (—2,1); она распо-
ложена на две единицы слева от начала по оси X и на единицу
выше начала по оси У. Точкам в I квадранте соответствуют
пары положительных чисел; точкам но II квадранте соответ-
ствуют пары чисел, в которых первое отрицательно, а второе —
положительно.
Какие знаки имеют числа, описывающие точки в третьем
квадранте? В четвертом квадранте? Какая пара чисел опреде-
ляет положение точки С на рис. 8 1?
Вы должны представлять себе, что любая точка на плоско-
сти соответствует паре действительных чисел, а всякая пара
действительных чисел определяет точку. Таким образом, пара
1 Названная по имени французского философа и математика Рене Де-
карта.
123
(—100; 3,67) определяет некую точку, так же как и пара
(—41,65; 214,6).
В конце концов мы приходим к методу предсказания мно-
жества точек, который для описания совокупности предсказы-
ваемых точек использует прямую на плоскости. Полезно узнать
способ полного описания любой прямой в плоскости простым
уравнением.
На рис. 8.2 прямая L пересекает ось Y в точке (0,1), а ось X
в точке (—0,5; 0). При смещении на единицу по оси X направо
линия поднимается на две единицы по оси Y. Следующие точки
Рис. 8.2. График прямой линии
Р и с. 8.5. Декартова двумерная (X и
Y) система координат.
лежат на линии L: (—2, —4); (—1, —1); (0,1); (1,3) и т. д.
Значение Y в описании точки (Л, У) систематически связано
со значением X. Для линии L на рис. 8.2 значение У для любой
точки равно двум значениям X плюс 1, то есть У = 2Х-Н.
Уравнение У = 2Х 1 и есть уравнение прямой на рис. 8.2.
Число 1 называется отрезком, по осн У, поскольку оно опреде-
ляет расстояние от оси X точки пересечения линии с осью У.
Число 2 — это наклон прямой. Наклон определяется числом
единиц, на которое поднимается линия на каждую единицу пе-
ремещения вправо по оси X, в данном случае 2 : 1.
Уравнение У — Ь\Х называется «общим уравнением
.прямой». Оно просто свидетельствует о том, что пары точек
(А', У), лежащих на некоторой прямой, связаны так, что для
любого значения X величину У, находящуюся с ним в паре,
можно найти, умножая X на некоторое число и прибавляя
второе число Ьо к этому произв ’‘шию.
124
8.2. Задача оценивания У по Л (или X по У)
Если задана конкретная оценка для характеристики (пере-
менной) X, то какую информацию можно получить относи-
тельно его опенки по характеристике (переменной) У? Вот не-
которые примеры задачи оценивания1:
1. Как и насколько хорошо мы можем предсказывать
отметки по английскому языку в колледже, зная отметки
в школе? (Школьные отметки предшествуют отметкам в кол-
ледже, поэтому мы можем предсказывать последние.)
2 Насколько правильно можем мы определить оценки IQ
Стенфорда — Бине по оценкам IQ Калифорнийского теста ин-
теллектуальной зрелости? (Никакой обязательной последова-
тельности этих тестов не предполагается, поэтому оценивание
необходимо лишь для определения того, насколько близко рас-
положены эквивалентные значения г каждого экзаменующегося
по двум тестам.)
3. Насколько правильно можем мы предсказывать зарабо-
ток в 35 лет по рангу в выпускном классе школы?
4. Насколько хорошо мы можем оценивать успеваемость по
интеллекту?
Чтобы вывести способ оценивания объекта по одной пере-
менной (мы будем обозначать ее У) на основе другой перемен-
ной (X), мы должны знать, как связаны между собой X и У.
Переменная, которую мы хотим оценить, называется зависимой
переменной (откликом) (У), а переменная, используемая для
ее оценки, — независимой переменной (фактором) (X). Напри-
мер, нам захотелось предсказать успеваемость по математике
в девятом классе (зависимая переменная У) по результатам
группового интеллектуального теста, проведенного в конце вось-
мого класса (независимая переменная X). Результатами изме-
рения У могут быть отметки за контрольную по математике для
девятого класса, включающую 50 вопросов. Сначала мы дол-
жны собрать данные для некоторого количества учащихся п,
интеллект которых мы проверяем в восьмом классе, а успевае-
мость по математике—в девятом. Далее выводим уравнение,
связывающее X и У в этой группе; мы хотели бы использовать
это уравнение в будущем для учащихся, значения X которых
известны, а У нам хотелось бы оценить.
Иллюстративные данные можно табулировать, как, напри-
мер, это сделано в табл. 8.1, и представить графически, как на
рис. 8.3. Из табл. 81 видно, что для определения bt требуется
5 сумм повеем парам (здесь и = 20', причем Л, представляет
собой наклон линии регрессии, необходимой для оценки. У
(оценки по математике в 9-м классе) по ¥ (/<? в восьмом
классе). Пять статистик в верхнем правом углу табл. 8.1 есть
1 Когда X предшествует Y. мы предсказываем Y по X, если нам известна
связь X и Y, основанная на предыдущей выборке.
125
Таблица 8.1
Данные для определения линии предсказания
103
100
102
103
105
106
106
106
109
£Х=2165 £У = 824
£.№ = 235 091 £У’ — 34 442
£№ = 89 715
п = 20
t п£ХУ - £Х£У
1 п£№ - CLX)1 “
20(89715) — (2165X824) _ 10340
20(235091) —(2165)2 14595
44
40
45
48
45
49
47
43
48
. =»~ - 0.708 (—р-) = -35.441.
Линия предсказания по методу
квадратов:
У = 0,708Х -35,441
Другие описательные статистики:
s^ = 6.198
зХу = 27,211 Sy = 5,095
гху~ 0.861
наименьших
сумма 20 значений X — то есть Xi + X2-f- Ч-Хп — 2165;
сумма 20 значений Y (824); сумма квадратов X, которая равна
Х'1 + Х2 + • • • + Хп = 235 091; сумма 20 квадратов У (34 442) и
сумма 20 произведений X на соответствующие значения У, пред-
ставляющая собой
+ + -V\ =
= 95 (33) + 100(31) + ... + i 18 (48) = 89715.
С помощью этих пяти статистик находим, что bi — 0,708 и
t>0 = —35,441. Таким образом, уравнение для оценивания У
по X выглядит так: 0,708л + (— 35,441) = 0.708Х —35,441. Пря-
мая, соответствующая этой формуле, изображена на рис. 8.3.
Какой же критерий привел нас к формулам для bt и Ьа,
использованным в табл. 8.1? Это важный вопрос, который за-
служивает подробного ответа.
Предположим, мы нашли уравнение для предсказания У
по X, которое обладает удовлетворительными свойствами. Мы
126
имели бы тогда две константы, &i и Ь», которые дали бы оцени-
ваемую величину У. Это означает, что
У i — b^Xt + &о,
предсказанное значение У для i-го объекта, обозначенное Л,
равно произведению bt на !-е значение X плюс Ьо- Очевидно,
У, не всегда будет равно У„ то есть даже при «наилучшем»
Рис. 8.3. Диаграм-
ма рассеивания X
(fQ а 8-м классе)
и У (успеваемость
по математике в
9-м классе) для
20 учащихся (см.
табл. 8.1) с по-
строенной по прин-
ципу наименьших
квадратов линией
предсказания.
линейном уравнении предсказания мы, как правило, будем оши-
баться в предсказании У по X. Мы говорим тогда, что
У i=== Ь^ X t с,,
где <?, характеризует ошибку оценивания У по У для Лго
объекта:
ег — У; — У г.
(8.1)
Другое название для et — ошибка оценки. Происхождение
ошибки оценки в задаче прогнозирования показано на рис. 8.4
для ученика, фактическое значение У которого на 4,36 единицы
ниже оцениваемого У, лежащего на линии регрессии.
Как нам следовало бы выбирать Ь\ и &0? Обычно Ь\ и Ьо
определяются таким образом, чтобы
Sej=-€]4-e2 + ••• +ея
была как можно меньше, то есть чтобы сумма квадратов оши-
бок оценки была минимальна.
Выбор критерия для подбора Ьо и является до некоторой
степени произвольным. Он обусловлен исторически и удобен
с вычислительной точки зрения, Кроме того, он предпочтителен
с точки зрения теории статистического вывода по причинам, ко-
торые лежат за границами этой книги. Однако критерий наи-
меньших квадратов (то есть минимум суммы квадратов ошибок
127
оценок) не единственно возможный. Хотя на роль критерия для
подбора линии регрессии и нет серьезного конкурента, тем не
менее существует и другой критерий. Он состоит в том, что Ьц
и Ь\ выбираются так, чтобы сумма абсолютных величин оши-
бок, полученных в процессе предсказания, была как можно
меньше, то есть минимизируется /ei/+ ... -\-1еп1- Этот крите-
рий приводит к «медианной линии регрессии». (Вспомните, что
медиана группы данных—это точка, относительно которой
сумма абсолютных отклонений минимальна.) Несмотря на про-
стоту вычислений медианной линии регрессии, для нее не суще-
ствует выводимого теоретического обоснования, какое имеет
линия регрессии метода наименьших квадратов.
Применению критерия наименьших квадратов для установле-
ния линии предсказания свыше 150 лет. Изобретение этого кри-
терня принадлежит известному немецкому математику, фи-
алку и астроному К- Гауссу (1777—1855). В той или иной форме
этот критерии лежит в основе большинства теоретических и
прикладных статистических работ.
Мы отметили ранее, чю е, есть разность между фактиче-
ским значением Y объекта и значением У, которое мы предска-
зываем для него:
е, = Yt - Гг = Гг - (6,Х; + Йо). (8.2)
Мы выбираем 6, и Ьо так, чтобы
ir,-(6,xi+6«)l! + li'!-(s,xi +W+ ... +ir„-«-Л + ад1
было как можно меньше. Точный способ, по которому опреде-
ляются величины 6, и Ьо. минимизирующие это выражение,
слишком сложен для нас в подробном изложении (см. McNemar.
1962, р. 119—124). Здесь мы просто приведем результаты,
а в § 8.5 рассмотрим проверку указанных решений.
bi задается следующим выражением:
(Д
(8.3)
bf> задается уравнением:
b^Y.-biX. (8.4)
Значения 6, и Ьо, определяемые таким образом, обеспечи-
вают «наилучшее» уравнение предсказания в том смысле, что
сумма квадратов разностей между У, и Y, = bjXi+bo для рас-
сматриваемых данных настолько мала, насколько это возможно.
В последнем разделе этой главы приведена простая алгебраиче-
ская проверка истинности этого утверждения.
Предположим, что мы осуществляем поиск «лаилучшего»
уравнения для оценивания У по X. используя прямую, наиболее
128
хорошо подобранную (в смысле принципа наименьших квадра-
тов) по точкам диаграммы рассеивания, и что у нас есть
оценки Хи У для 20 учащихся, например, из табл. 8.1.
На данном этапе ничего нельзя сказать относительно того,
будут ли зависимая и независимая переменные нормально рас-
пределенными или распределенными каким-нибудь другим обра-
зом. Чтобы вывести коэффициенты регрессии Ьо и bi методом
наименьших квадратов, не требовалось никакого представления
о форме кривых распределений X и У. Уравнения (8.3) и (8.4)
для Ьо и Ь\ дают прямую линию, которая минимизирует сумму
квадратов остатков независимо от характера диаграммы рас-
сеивания Хи У.
Рис. 8.4. Пример ошибки оценки для ученика, имею-
щего оценку 100 по X и 31 по У.
Если мы делаем некоторые правдоподобные предположения
относительно распределений большого числа значений X и У, то,
вероятно, мы должны быть вознаграждены возможностью бо-
лее тщательного исследования предсказания. Действительно,
наше исследование оказывается очень результативным, если мы
предполагаем, что X и У имеют двумерное нормальное распреде-
ление (см. § 6.7). Тогда можно полагать, что рассматриваемые
п пар значений X и У образуют случайную выборку из очень
большой совокупности X и У с двумерным нормальным распре-
делением.
Теперь важны следующие свойства двумерного нормального
распределения:
1. Выборочные средние У для каждого значения X лежат
на прямой.
2. Для любого значения X соответствующие значения У нор-
мально распределены.
5 Зак. М8 ]29
3. Для любого значения X соответствующие значения Y
имеют дисперсию одинаковую для всех X.
Если бы мы могли быть уверенными в том, что п пар значе-
ний X п У исходят из двумерного нормального распределения,
то свойство 1 из вышеприведенных говорило бы о том, что
использование прямой для прогнозирования У по X разумно
и никакая кривая не может дать лучших результатов. Свойства
2 и 3 можно было бы объединить в очень полезную методику,
которая вносит значительный вклад в предсказание У по X
и проблемы оценивания. Эта методика будет рассматриваться
далее.
8.3. Постоянство дисперсий
и стандартная ошибка оценки
Свойство 3 двумерного нормального распределения убеждает
«ас в том, что если мы имеем, например, 19 учеников с X = 75 и
21 ученика с X = 80, то дисперсии двух групп связанных значе-
ний У должны быть приблизительно одинаковыми. Это условие
аждого значения X известно как
гомоскедактичность (происхож-
дение этого слова связано с по-
нятием равнораспределенности].
Диаграмма рассеивания на
рис. 8.5 должна помочь вам ра-
зобраться в этом условии.
Важно отметить, что гомо-
скедактичность — это свойство
очень больших совокупностей
двумерных данных. Не следует
ожидать равенства дисперсий У
для любых двух значений X,
когда п мало, например порядка
100 или меньше. В случае л—19
и и = 21 дисперсии У для
Х = 75 и Х = 80 на рис. 8.5
равны $*.75 = 5,54 и $*.80= 6,85.
Эти две дисперсии не равны, но
они довольно близки. При таком
мы не можем строго установить,
выполняется ли условие постоянства, но, по крайней мере, оно
кажется до некоторой степени правдоподобным для X — 75
и X — 80 после анализа данных рис. 8.5.
Очевидно, величины ошибок, полученных в процессе оценки
У по X, характеризуют точность оценивания. Для рассматривае-
мых данных, то есть п пар значений X и У, разности между
фактическими значениями У и предсказанными значениями У
являются мерами ошибок, которые появились бы при использо-
130
равенства дисперсий У для
Рис. 8.5. Диаграмма рассеивания
для 19 учеников с X == 75 и 21 уче-
ника с X = 80, которые имеют
приблизительно постоянную дис-
персию значений Y для обоих зна-
чений X.
малом количестве объектов
вании X для оценки У. Эти ошибки называются ошибками
оценки. Формула для ошибки i-ro объекта есть:
ei==yi-yi = y(-Z>!X(-&0. (8.5)
Является ли среднее п ошибок оценки, ё., подходящей мерой
качества прогнозирования У по X?
Нет, поскольку, когда все в порядке, точно равно нулю:
= пУ. -nbtX- — nblj = nY. -nbiX. -n(Y. -b1X.) = O. (8.6)
(Вспомните, что b0 = Y. — btX.).
Поэтому средняя ошибка оценки всегда равна нулю, если
она рассчитывается во тем же парам значений, что и &а и Ь\-
Стало быть, она не является подходящей мерой точности пред-
сказания У по X.
Вспомните, что выборочное среднее обладало таким свой-
ством: £(T,-X.) = 0. Прин цип оценивания, дающий линию
регрессии метода наименьших квадратов, — оненивателя значе-
ний У с минимальной дисперсией, — подобен принципу, который
обеспечивает X. роль обшей меры склонности к центрированию
с минимальной дисперсией. Если бы требовалось использовать
одно значение вместо всей группы, то выборочное среднее X.
дало бы при этом минимальную сумму квадратичных ошибок
оценивания
Один из нескольких возможных способов измерения точ-
ности предсказания У по X—применение дисперсии п ошибок
оценки Она не будет зависеть от среднего значения, всегда
равного нулю, и от количества остатков, потому что исполь-
зуется операция деления на п—1. Дисперсия п опенок е, —
= У; — У> называется дисперсией ошибки оценки и обозна-
чается символом s*.
= — -----:---=» ——г- • (8-7)
е п — 1 п — 1 ' '
Формально (Xj — (X- +Р}]2 > J} (X, - X.)2. когда Р * 0. Убе-
дитесь в этом сами, возводя в квадрат левый член неравенства и выполняя
алгебраические упрощения
Указание: Х< - (X. 4- Р) == (Х> X ) - Р.
131
Существует способ выражения $• в терминах и корреля-
ции X и У, rxv, который выявляет некоторые связи между кор-
реляцией и предсказанием. Мы можем записать
Ё'.! £<Л~»Л-М! Ё (Л-‘A-T+ »,<)’
,! — ____= _!_______________ _!_________________
'• п ™ I п — I п - 1
Ё КГ, - Г.)-S, №-?.)) Ё(г«—7->’
““---------”-~Нг71-----------------+
»!Ё(а-а)! Ь.ЁСа-аКл-т)]
+ -------2Н-----------------J“
А/,— 26,5,,. (8.8)
Мы знаем, однако, что Ь> = ,,/sxf ~ rx„sx/sx. Поэтому
уравнение (8.8) можно переписать
Se = Sy -f- ГxySy 2t>tSxu.
Рассмотрим подробнее 2 £>isxs:
Так как гхв = sxv/(stsB), то sxvlsx должно быть равно
rxvSy. Поэтому
26|SXB =» 2г xySy.
В конечном счете
а’-з‘ + гМ-2« = 4(1-тУ. (8.9)
Уравнение (8.9) дает дисперсию ошибки оценки в терминах
дисперсии У и гх11.
Положительное значение квадратного корня из дисперсии
ошибки оценки называется стандартной ошибкой оценки:
= (8-10)
Стандартную ошибку оценки можно применить для опреде-
ления пределов в окрестности предсказанного значения У,
в которые, вероятно, попадает фактическое значение для
объекта. Если можно предположить, что объекты взяты из сово-
купности, приблизительно описываемой двумерным нормальным
распределением (см. § 6,7), то можно сформулировать следую-
щие утверждения. В большой группе объектов, для которых
используется уравнение предсказания:
I. Около 69% объектов будут иметь фактические значения,
лежащие в пределах одной se от их предсказанного значения Г;
!32
2. Около 95% будут иметь фактические значения, лежащие
в пределах двух se от их У;
3. Примерно 99,7% будут иметь фактические значения, ле-
жащие в пределах трех se от У.
Эти утверждения обоснованны, так как если справедливо
допущение о двумерной нормальности, то распределение факти-
ческих значений У нормальное относительно среднего Z>o-4-Z>iX
со стандартным отклонением se для любого X *. (Обратите вни-
Рис. 8.6. Пример стандартной ошибки оценки, se, па четырех
уровнях X, когда можно предположить двумерное нормальное
расаределение X и Y.
мание, что, хотя среднее нормального распределения У меняется
от одного значения X к другому, стандартное отклонение $е не
зависит от X). Эти соотношения показаны на рис. 8.6.
8.4. Связи & о и &1 с другими
описательными статистиками
Как задачи подбора «наилучшей» линии предсказания, так
и измерения корреляции двух переменных касаются пары пере-
менных для группы объектов. В обоих случаях данные можно
представить на диаграмме рассеивания. В этом параграфе мы
увидим, что есть несколько интересных соотношений между
rxy, sx, $у и коэффициентами bQ и &i для прямой метода наи-
меньших квадратов. Одни связи позволят прояснить природу
проблем линейного оценивания и измерения корреляции; другие
же относятся только к вычислениям Ьо, и rxv.
* О методах точного оценивания, устраняющих слово «около» из утвер-
ждений I—3, см. в: Dixon, .Massey, 1969. р 199—200.
133
Во-первых, посмотрим на формулу для bs при оценивании
У по Л':
01 м2Л2-(2Л]2 ’
Если мы умножим верхнее уравнение на тождество
1/п (л — 1) 1/п (л — 1)
\/п\п — }) = —
где п 7> 1 (операция, эквивалентная умножению на 1»1, что»
разумеется, ничего не меняет), то в результате получим сле-
Числитель уравнения (8.Н) —это sxy, ковариация X и Y.
Знаменатель уравнения (8.11)—это sj, дисперсия X. Поэтому
6,-^. (8.12)
то есть &| равен ковариации X и У, деленной на дисперсию X.
Ковариация X и Y для данных табл. 8.1 составляет 27. 211»
а $*= 38,408. Отношение sxy] s} = Q,7№>, значению bit найден-
ному из уравнения (8.3).
Вспомните, что rxy — sxv/{sxsy). Таким образом, если мы1
просто умножим это уравнение на
su __ sn
sx SK ’
то получим
Sy Sxy
r^“=~^=&r. (8.I3>
Пусть X и У имеют одинаковую дисперсию. Если это спра-
ведливо, TO Sy/5X = 1 и
= ~Ь,. (8.14>
Одним словом, если X и У имеют одинаковую дисперсию, то
bj равен гху.
Уравнения (8.13) и (8.14) будут полезны при изучении
области допустимых значений, которые может принимать bt.
Мы убедимся, что наибольшие и наименьшие возможные значе-
ния bi зависят от величин sy и sx. Нам известно, конечно, что
гху имеет максимальное значение 4-1, а минимальное —I1.
1 Но 'in = —I указывает на ту же степень обратной связи, о которой
говорит Гх» = 1 для прямой связи.
134
Поскольку гху не зависит от s* и зи, b, примет максимальное
значение при гху — 4-1, а минимальное — при гху = —I. Под-
ставляя эти два значения в уравнение (8.14), видим, что наи-
большее допустимое значение bi есть
<+>)”. а
наименьшее — (—1) — . Отсюда bi никогда не может быть
больше, чем sy/sx. Например, данные табл. 8.1 дают sy = 5,095
и sx = 6,198. Поэтому наибольшее возможное значение bt для
оценивания Y по X составляет 5,095/6,198 = 0,822. Наименьшим
возможным значением будет —0,822.
Если между X и Y не существует линейной связи, то гху
равен нулю. В этом случае
Следовательно, если X и У линейно не связаны, то прямая
«наилучшей» оценки имеет нулевой наклон. Это прямая, парал-
лельная оси X. Значением Ьо будет У., как можно убедиться,
подставляя Ь1 = 0 в уравнении (8.4). Таким образом,
У, = ьа 4- М, = У. -М- -ЬМ( = У- - 0 (X.) 4- 0 (Xt) = У.;
все предсказанные значения одинаковы.
Уравнение прямой наименьших квадратов для значений г
представляет особый интерес. Так как и zx и zy —
— имеют дисперсию, равную 1, то коэффициент при г,
для предсказания гу равен
Мы знаем, конечно, что zy=zz = 0. Поэтому константа Ьо
при оценивании zv по zx равна:
bo — Zy — b\Zx = 0 — 6)0— 0.
Следовательно, наилучшей оценкой гУг по гХ{ является гхугХ(.
Иначе говоря, расстояние, на котором Р находится or Р, в еди-
ницах стандартного отклонения определяется произведением
(8.15)
Является ли (Pi— Y.)lsv в уравнении (8.15) значением z?
Нет. Его среднее равно нулю, но его дисперсия скорее ггху>
135
чем единица. По уравнению (8.15) вы это можете легко дока-
зать. Заметим, что
sy ~ SrXyzx = г~ Гху’
Это значит, что величины У, когда они предсказываются по-
X в духе ур. (8.15), менее изменчивы, чем сами оценки zy,
пока не выполняется условие г^ = 1. Подобная «регрессия» по
отношению к среднему (Р.) характеризует методику оценки У
по X, которая описывается ниже уравнением (8.16).
Уравнение (8.15) легко запоминается. Из него вы можете
быстро определить формулу предсказания У по X, умножая
каждую его часть на sv и прибавляя Р. к обеим частям.
Существует явная связь между дисперсиями Р и У и коэф-
фициентом корреляции. Разумеется, дисперсия У обозначается
как s*; дисперсия У — kik s;j. Исследуем выражение для
.Yj = bv + blXl, то есть Р есть линейное преобразование X.
Мы можем определить другую форму для S;, используя все,
что известно о влиянии линейного преобразования на диспер-
сию X. Прибавление к X константы не изменяет его дисперсии;
умножение X на константу (например, bt) приводит к умноже-
нию на квадрат константы (например. Ь]). Это можно»
обобщить следующим образом:
Sy = St>,+btf = biSx.
Мы видели, что b^ — rxy(sF/$x); поэтому
4 = ®.ie>
Дисперсия предсказываемых значений, то есть значений Р,
равна квадрату коэффициента корреляции X и Y, умноженному
на дисперсию У. Например, гху для данных табл. 8.1 равен
0,861; s^ = 25,958. Поэтому дисперсия 20 предсказанных значе-
ний У равна:
$’= (0,861)’• 25,958 = 19,243.
Если rxv = 0, то дисперсия 7 = 0: фактически каждое пред-
сказанное значение У равно 7. Если rxv принимает значения ф-1
или —I, то У и Р имеют одинаковую дисперсию, s^.
Если мы разделим обе части уравнения (8.16) на s2 полу-
чим следующее:
Одним словом, отношение дисперсии предсказанных значе-
ний У, Р, к дисперсии фактических значений У равно квадрату
136
коэффициента корреляции между X и Y. Обратите внимание на
то, что это отношение ничего не говорит о направлении связи;
оно никогда не бывает отрицательным. Для данных табл. 8.1
-s* = 25,958, а $^=19,243. Отношение 19,243/25,958 равно 0,741,
что соответствует г2 для тех же данных. Пытаясь объяс-
нить смысл гху, часто говорят, что г2— это «доля дис-
персии У, объясняемая дисперсией X». Это сомнительное н
почти бессмысленное утверждение, если не определить ясно,
какой смысл имеет «дисперсия, объясняемая» переменной.
Наиболее важной формулой для «понимания» вопроса
о коэффициенте корреляции служит уравнение (8.17). Мы по-
пытаемся объяснить смысл г2 несколько иначе.
Допустим, мы хотим предсказать каждое значение перемен-
ной У, но в наличии не оказалось переменной X. Предсказывае-
мое значение, минимизирующее сумму квадратов ошибок пред-
сказания, при прогнозировании У оказываегся равным У. для
каждого объекта. То есть, если никакой переменной X нет и
о том, каковы индивидуальные значения У, ничего неизвестно,
то можно добиться наилучшего прогноза, предсказывая для
каждого объекта среднее У.. Оценка качества такого вредска-
зання характеризуется величиной ———
вается равной s2.
Теперь предположим, что в нашем распоряжении имеется
информация о значениях X для предсказания У. Сумма квадра-
тов ошибок предсказания, полученных при прогнозировании У
по X с помощью линии регрессии, задается выражением
^£(У/-~Л)2],’(Л“-1), которое есть s2e.
Теперь мы знаем, что s| + s’ — з-. Величина з---это
ошибка, возникающая при прогнозе без X; $2 — ошибка, полу-
ченная с учетом информации о переменной X. Доля ошибки, ис-
ключаемая из информацией об X, должна равняться sj. Вспом-
ним, что
, которая оказы-
Заметив, что ^15гу—г2, можно переписать уравнение так;
(8.18)
На основании уравнения (8.18) можно дать следующую
интерпретацию г%. .
137
Величина г2 равна отношению дисперсии квадратов ошибок,
в2, образующейся в процессе предсказания У без учета инфор-
мации об X, и дисперсии, которая исключается при прогнозе У
методом наименьших квадратов с учетом X.
8.5. Проверка выполнимости критерия
наименьших квадратов для 6 s и 6 о
Ранее мы утверждали без доказательства и проверки, что
уравнения (8.3) и (8.4) дают значения bt и Ьо, которые мини-
мизируют У, [У, —(60 + fejX,)]2, сумму квадратов ошибок оценки.
Это можно относительно просто проверить, мы, однако, не бу-
дем делать такой проверки.
8.6. Измерение нелинейных связей
между переменными, корреляционное отношение п2
Этот параграф приведен здесь ради полноты и логической
последовательности. Вы поймете его лучше после прочтения
главы 15 об однофакторном дисперсионном анализе.
Возраст
Рис. 8.7. Связь между возрастом и характе-
ристикой 28 людей по вспомогательному тесту
цифра-знак (S7A/S).
Мы уже говорили, что произведение моментов Пирсона г
измеряет лишь степень линейной связи между X и У, теперь
укажем еще описательную меру, применяемую в том случае,
когда связь между X и У преимущественно нелинейна. В каче-
стве примера нелинейной связи рассмотрим данные рис. 8.7, по-
казывающие связь возраста X с результатами У вспомогатель-
ного теста цифра-знак шкалы интеллекта взрослых Векслера
(WA1S). Данные рис. 8.7 представлены в табл. 8.2.
Из рис. 8.7 видно, что результаты растут линейно от 10 до
22 лет, достигают пика и затем довольно быстро уменьшаются.
138
Таблица 8.2
WAIS — Вспомогательные тест цифра-знак,
располагающий по шкале оценки 28 лиц в восьми
возрастных группах с равным шагом
Мера линейной или, нелинейной связи X и У обозначается
т|2 (читается «эта в квадрате») и называется корреляционным
•отношением. Корреляционное отношение определяется так:
где SSuomaa — X W i ~ У -)2, то есть сумма квадратов отклонений
каждого значения У от среднего всех п значений У, a SSDii>tph
получена следующим образом.
Для первого значения X находим отклонения соответст-
вующих значений относительно их среднего и вычисляем сумму
квадратов этих отклонений. Например, первая сумма квадра-
тов в табл. 8.2 есть (7 — 8,60)2 + (8 — 8,60)2+(9— 8,60)2 +
+ (9 — 8,60)2+ (10 — 8,60)2. Этот процесс повторяется для каж-
дого значения X. Так, для X = 14 имеем: (8 — 9,50)2 +
+ (9 — 9,50)2 + (10 — 9,50)2+ (11 —9.50)2. Для последней
группы. Х = 38, сумма квадратичных отклонений значений У
относительно их среднего равна (8—8)2 = 0, поскольку есть
только одно значение. Наконец, складываем эти суммы квадра-
тов отклонений для всех значений X. В результате имеем 55Впу-гРи.
(Если вы читаете этот раздел после главы 15, то обратите вни-
мание, что SSbhvtph есть «внутригрупповая сумма квадратов»
в однофакторном дисперсионном анализе с неравными п.)
139
Для данных табл. 8.2 величина SSo6ujaiI равна 54,68. а
55Ю1у1Ри — 24,87. Отсюда значение rfy х есть
<.«=1 - W “1 “ °'455 ” °’545-
Последующие соображения касаются интерпретации г)2 .
Коэффициент — заметьте, что Y предшествует запятой,
а X следует за ней,— является мерой степени предсказания
У по X с помощью «наилучшим образом подобранной» линии,
либо прямой, либо кривой.
Важно отметить, что rf и у обычно будут иметь разные
значения. Это противоречит известным нам случаям, когда
rxv = rvx. Мы можем смириться с фактом, что гц у может не
быть равным г;2 х, интуитивно обратившись к данным табл. 8.2.
Если человеку 10 лет, то можно довольно уверенно предсказать»
что его оценка по шкале цифра-знак равна «8,60. Однако
если известно, что оценка У равна 8, то возраст X может быть
как малым, около 10, так и большим, около 38 лет. Значит,
можно довольно хорошо предсказать У по X; но нельзя хорошо-
прогнозировать X по У. Эти обстоятельства отражаются на ве-
личинах т|2 х = 0,545 и т|2 которою мы не вычисляли, но ко-
торая близка к нулю.
Величину ту'у х надо сравнивать с г2&, а не с г Мы знаем»
что г2 — 1 — (s’ (s’), или
£<><-Л)1
-----Г~- (8.20>
L (>-< - г.>-
Уравнение (8.20) показывает, что r2xy (1 минус сумма квад-
ратов отклонений У относительно прямой предсказания) де-
лится на (л—-l)s2. Уравнение (8.19) показывает, что г\2у х
(1 минус сумма квадратов отклонений У относительно кривой
предсказания, проходящей через средние значения У для каж-
дого значения X) разделен на (n —-l)s2. Кривая предсказания
У по X показана на рис. 8.7.
Как и в случае г2у, ц’ х должна быть меньше или равна
единице и больше или равна нулю. Кроме того, т]2_ х^> г* . Раз-
ность т|2 х — гху является мерой степени нелинейности линии
наилучшего сглаживания для предсказания У по X. Glass,
Hakstian, 1969).
Отличным исчерпывающим учебником для студента, желаю-
щего продолжить изучение статистического предсказания, яв-
ляется книга У. Розебума «Основы теории предсказания»
140
r(Y. Rozeboom, 1966). Изучение корреляционного отношения и
вопросов связей можно найти в учебнике Э. Хаггарда «Внутри-
классовая корреляция и дисперсионный анализ» (Е. Haggard,
1958).
Задачи и упражнения
1. Постройте графики для следующих уравнений:
а.Г- -2+ЗХ,
«. У-1+ 1/ЗЛ'.
в. 2У = 4 + 2Х (Указание: разделить обе части на 2);
г. У = 2 (1 4- 2Х) (Указание: выполните умножение в пра-
вой части).
2. Частная школа определила уравнение предсказания для
прогноза среднего балла учащихся колледжа в университете
штата по среднему баллу учащихся школы. Уравнение выгля-
дит так; Р == 0,76 + 0,62Х. Назовите средний балл в колледже,
который получил бы ученик со следующими средними баллами
в школе:
а. 3,50 б. 1,68 в. 2,10 г. 4,00.
3. Для данных табл. 8.1 вычислите ошибку оценки У —Р,
для ученика, имеющего X — 100, а У — 35.
4. Верно ли, что чем больше величина Ь%, тем выше коэффи-
циент корреляции Пирсона между X и У?
5. В главе 7 было показано, что линейное преобразование
X и/или У не меняет гху. Каково влияние преобразования
сХ d на значения bj и f>0?
9
ДРУГИЕ МЕРЫ СВЯЗИ
9.1. Введение
В главе 7, где обсуждался коэффициент корреляции Пирсона, мы
видели, что применение и интерпретация гху зависит от харак-
тера данных, которые находятся в корреляционной связи: будут
ли данные соответствовать двумерному нормальному распреде-
лению, могут ли как X, так и Y принимать непрерывные значе-
ния, будут ли два распределения иметь идентичную форму. Те-
перь мы хотим исследовать меры связи, применимые к перемен-
ным, не столь хорошо оцениваемым количественно, как вес, воз-
раст, интеллект и др , для которых использовать гХ11 легко В част-
ности, мы рассмотрим коэффициенты корреляции, применяемые
для дихотомических (0, 1) данных, данных ранжирования
(1, 2, ... п) и прочих. Некоторые коэффициенты появятся в ре-
зультате применения формулы гху непосредственно к новым ви-
дам данных. Другие будут использоваться при попытках оце-
нить, каким было бы значение rxv, если бы данные не были
представлены в необработанном виде. Кроме того, будут рас-
смотрены новые коэффициенты, которые создают новые пред-
ставления о том, что такое «связь» и как ее следует измерять.
В последних разделах этой главы будут кратко рассмотрены
частная, частичная и множественная корреляции
9.2- Обзор главы
Различают четыре типа измерений переменных:
1 Измерения в дихотомической шкале наименований. Фик-
сируется просто наличие или отсутствие чего-либо. Данные пред-
ставляют собой пули и единицы. Порядок оценивания является,
как правило, произвольным. Примеры: республиканец (I) —де-
мократ—(0); учащийся школы (1)—не учащийся школы (0);
мужчина (1) —женщина (0); женат (1)—холост (0).
2 Измерения в дихотомической шкале наименований в пред-
положении нормального распределения. Предполагается, что бо-
142
лее утонченные, более полные н более совершенные методы
измерения могли бы обеспечить приблизительно нормальное
распределение результатов, но рассматриваемые данные говорят
лишь о том, будет ли объект занимать положение выше (1)
или ниже (0) некоторой точки в этом нормальном распределе-
нии, Если в отношении большой группы учащихся было извест-
но только, превышает ли коэффициент интеллекта отметку' 120
(обозначим этот факт единицей) или нет (обозначим это 0), то
единицы и нули представляли бы собой дихотомические данные»
основанные на нормальном распределении. Конечно, было бы
неэффективным пренебрегать исходными данными и записывать
вместо них единицы и нули, и это, как правило, не делается
(несмотря на то, что в рацией истории факторного анализа это
было удобным с точки зрения вычисления).
3 . Измерения в шкале порядка. Данные представляют собой
последовательные несвязанные ранги 1, 2, ..., п. Эти ранги
можно присвоить измерениям другой шкалы (например, когда
исходные данные 136, 124, 97 ранжируются номерами 1, 2, 3),
или они могут быть прямым переводом восприятий в числа
(например, когда судья ранжирует 10 конкурентов от наиболее
опытного—I до наименее опытного—10). Пример: 94 ученика
выпускного класса ранжируются от 1 до 94 по средним баллам.
4 . Измерения в шкалах интервалов или отношений. Суще-
ствует единица измерения, например дюйм, день и т. д., а (в
случае шкалы отношении) нулевая точка на шкале соответствует
отсутствию (то есть пулю) измеряемой переменной. Результа-
том может быть любое действительное число, а разности между
отметками отражают разности значений характеристики. В этой
главе мы, как правило, будем считать, что интервальные
и относительные измерения приблизительно нормально рас-
пределены, хотя, конечно, в некоторых случаях этого может
и не быть.
Если измерение можно произвести на уровне шкал интерва-
лов или отношений, то результаты можно преобразовать в лю-
бую из трех других названных шкал, Например, предположим,
что 10 студентов получили отметки в ходе испытания вербаль-
ного мышления, которые, как принято считать, характеризуются,
хотя и грубо, приближенным нормальным распределением по
шкале интервалов: см, табл, 9,1.
Первый столбец задает порядковый номер студента. Исход-
ные отметки, которые, по предположению, основаны на распреде-
лении, близком к нормальному, приведены во втором столбце.
Эти 16 оценок проранжированы в третьем столбце. В четвертом
столбце 5 наибольших исходных значений были заменены 1,
а 5 наименьших — 0.
Там, где присутствуют два множества значений X, и У, для
п объектов, X и У можно измерить любым из четырех описанных-
способов. Таким образом, существуют 4X4 — 16 возможных
пар измерений для двух переменных, которые могут коррели-
143
Таблица 9.1
Преобразование 10 оценок шкалы интервалов
в ранги (шкалу порядка) и в 0,1
(шкалу наименований)
ровать. Эти 16 возможных пар условий по X и Y можно предста-
вить так, как это сделано в табл. 9.2.
Достаточно рассмотреть только 10 из 16 возможных пар,
поскольку обе переменные обозначены X или У абсолютно про-
извольно (потому что rKif — Гцх.). В терминах теории корреля-
Габдица 9.2
Десять различных ситуаций, подучившихся в результате
сочетаний четырех шкал для двух переменных
Дихотомия
Дихотомия, осно-
ванная на нор-
мальном рас-
пределении
Шкала порядка
Шкала интерва-
лов или отно-
шений
А
В
ции 6 ячеек с буквами в круглых скобках табл. 9.2 подобны
ячейкам с аналогичными буквами без круглых скобок. Табл. 9.2
будет основой, на которой построено дальнейшее обсуждение не-
144
скольких специальных мер связи. Одна подходящая мера корре-
ляции для двух переменных в шкалах интервалов или отношений
(/) была предметом предыдущей главы. Это случай, когда ис-
пользуется коэффициент Пирсона rxv. Ниже мы рассмотрим
оставшиеся 9 случаев (А — I).
9.3. Меры связи
Случай А
Обе переменные измеряются в дихотомических шкалах наи-
менований: мера связи — коэффициент «фи», <р. Данные можно
представить расположенными в два столбца нулей п единиц,
где каждая строка соответствует каким-то двум отметкам неко-
торого объекта. Например, наблюдения за 12 студентами вто-
рого курса колледжа по переменным «семейное положение» и
«исключение из колледжа» приведены в табл, 9.3. Совершенно
произвольно 1 обозначает состоящих в браке и исключенных из
колледжа, а нуль — холостых и оставшихся в учебном заведении.
Одной из мер связи между X и У является просто гху. Коэффи-
циент Пирсона, вычисленный по номинально-дихотомическим
данным, называется коэффициентом «фи» и обозначается ср.
Значение ip для данных табл. 9.3 составляет 0, 507; но его нельзя
найти с помощью обычной формулы вычисления гху. Эту фор-
мулу можно в данном случае заменить на еще более простую,
чо алгебраически эквивалентную ей.
'Гав ища 9.3
Пример вычисления коэффициента фи, <р
<1у = 0,5000
= 0.3333—(0,4167) (0,5000)
Ф = V (М 167)(0,5833)(0,5000)(0,5000) “
= 0,507
Пусть рх будет доля людей, имеющих единицу no Л; qx—
доля людей, имеющих нуль по X, будет равна / — рх. Доля тех,
кто имеет единицу по У, обозначается pv, a qy = I — ру. Нужно
145
еще одно определение: pxv— доля людей, которые имеют еди-
ницу как по Л', так и по Y. Если бы мы оперировали формулой
для гху в соответствии с новыми определениями, то мы обна-
ружили бы, что она алгебраически упрощается до
Рху РхРу
-'JpxQxPy'ly
'9.1}
Уравнение (9 I) дает удобный способ вычисления коэффи-
циента фи. Дальнейший вывод показывает, что ф является коэф-
фициентом корреляции Пирсона между двумя переменными,
каждая из которых имеет оценки 0 и 1.
Если числитель и знаменатель уравнения (7.10) на странице
119 одновременно разделить на и, то образуется выражение для
гху-
(9.2}
Если X и У измеряются дихотомически, то X. и Р. будут про-
сто доли единиц по каждой переменной. Например, в примере из
таблицы 9.3
(0+1+0 + +0 4- О _ 5
12 — 12 ’
Таким образом, мы можем заменить X. и V. соответственно
на рх и ри, Далее X,Y, будет отличаться от нуля только тогда,
когда бй объект имеет 1 для всех переменных, причем
¥iy(«=|-|=s|. Понятно, что 1Х(У, — просто число объемов,
имеющих единицу и для X и для У; отсюда (1/п)2ХУ = ргу.
А так как X нуль или единица и поскольку О2 = 0, а 12^= 1,
Ух2 (02 + 12 + ... + 02 + 12)
___ =-------------------= рх.
Поэтому подстановка найденных выражений в уравнение
(9.2) приводит к следуюшему:
Рху - РхРу
Pty — РхРу
Рху — РхРу
'J'PxQxPyVy '
(9-3)
Когда нет особого интереса к долям рх н рч и считают бо-
лее удобным располагать дихотомические двумерные данные
в таблице сопряженности признаков (таблице, показывающей
совместные появления пар значений по двум переменным (прн-
146
знакам) в группе), <р можно вычислить по удобной исходной
формуле- Данные табл. 9,3 также можно представить на рис. 9.1.
Рис. 9,1 содержит частоты объектов, исчерпывающие 4 воз-
можных пары из табл. 9.3, Например, 5 человек в табл, 9,3 не
состояли в браке и остались в учебном заведении на втором
курсе. Итоги строк дают число лиц на обоих уровнях «признака»
независимо от их семейного положения, Какова же интерпре-
тация итогов столбцов?
Предположим, что в каждой ячейке таблицы сопряженности
мы заменяем фактические частоты на буквы. Тогда можно об-
общить вычисление <р. Смотрите рис. 9.2.
Число объектов, имеющих нуль по X и единицу по У, обо-
значается через а. Общее число объектов, имеющих нуль по Л,
признаков Семейное положение M-roi
S'
Исключенные 2 4 6
(Ч Оставшиеся 5 1 6
(0)
Итог 7 5 12
Pin. 9,1. Таблица сопряженности
для данных табл, 9.3.
Призрак X Итог
0 | ।
Признак У I ° 1 6 а + b
0 с | d | с 4- d
Итог O+£|l,+j| ,,
Рис. 9.2. Общая форма таблицы
сопряженности 2X2.
составляет а-j-с. Общее число объектов, представленных в таб-
лице, равно п. Сколько объектов имеет нуль по У и по Л?
Делая подстановки рх = {Ь -f- d)/n, Рц~ (а-\-Ь)/п и
Pxy — bln в уравнение (9.1), можно показать, что коэффициент
фи для данных, представленных в таблице сопряженности типа
таблицы на рис. 9,2, равен:
be — ad <п ,.
ф = ,... ..:.....:. . , (9.4)
+ с} - (b + d} (а -У Ъ)- (с + d)
Уравнение (9,4) было выведено впервые Карлом Пирсоном
в 1901 г в статье, опубликованной в «Философских трудах
Лондонского королевского общества» и посвященной корреляции
между переменными, которые невозможно измерить количествен-
но. Для примера вычисления <р по уравнению (9.4) воспользуем-
ся данными рис. 9.1
20-2 18 _ 3 Л-Л7
* V(7)(5)(6)(b) 6 V35 V35
Это значение ср равно значению из табл. 9.3 для тех же дан-
ных. Такое равенство имеет место всегда, ибо уравнения (9.1)
и (9,4) алгебраически эквивалентны.
147
т Кендалла со связанными рангами
Когда в рангах X или У встречаются связи, Р и Q все же
определяются так, как указывается в табл. 9.7. Единственное
изменение в формуле для т появляется в знаменателе. Поправка
знаменателя т содержит Кх и Ку (которые являются функциями
числа объектов, связанных на различных рангах у X и У).
Когда в рангах X и У имеются связи, то применяется следую-
щая формула:
^[п(п-Ы2]-ку' ' ‘ ’
me K, = (l/2)Sf,(f,-l)
(ft — число связанных наблюдений в каждой группе связей
по X), а Ку = (l/2)Sfi(/t—1) (ft— число связанных наблюде-
ний в каждой группе связей по У).
Пример применения уравнения (9.20) приведен у Зигеля
(1956, р. 218—219) или в более новых учебниках по непарамет-
рической статистике.
Случай 1
X измеряется в шкале порядка, а У — в шкале интервалов
или отношений. Для этого частного случая не было разработано
и исследовано никакого коэффициента. Если вы имеете дело
с переменными, измеренными таким образом, можно посовето-
вать преобразовать опенки У в ранги и найти коэффициенты
ранговой корреляции Спирмена пли Кендалла.
Возврат к случаю С
Бисериальная ранговая корреляция. В этом месте целесооб-
разно обсудить коэффициент, впервые упомянутый в разделе
«случай С». Один заслуживающий внимания коэффициент для
корреляции дихотомической переменной X и порядковой пере-
менной У был исследован Кертеном (1956) н Глассом (1966/?).
Этот коэффициент тесно связан с т Кендалла и использует
в своем определении понятия совпадения и инверсии. Мы будем
обозначать этот коэффициент как ггъ. рангово-бисериальныЙ г.
Пусть X дихотомическая переменная, а У —- переменная, име-
ющая п несвязанных рангов 1, 2, ..., п. Кёртен искал такой
коэффициент, описывающий связь между X и У, чтобы (а) при
любых условиях он мог достигнуть границы +К (6) был бы
равен + К когда все п наивысших рангов являются единицами
по дихотомии, и (в) был бы строго непараметричным, то есть
полностью определимым в терминах инверсий и совпадений без
использования таких понятий, как среднее, дисперсия, регрес-
сия и т. д.
165
Предположим, что для 10 объектов собраны следующие дан-
ные по А’ и Y:
Для вычисления ггь данные располагаются следующим об-
разом:
Совпадение для любого данного ранга равно числу объектов-
под столбцом 1 для каждого низшего ранга под столбцом 0.
Инверсия возникает при любом заданном ранге под столбцом G
для каждого низшего ранга под столбцом 1.
Таким образом, существуют 3 совпадения, соответствующие
рангу 4 под столбцом 1, поскольку имеются 3 низших ранга»
3, 2 и 1, под столбцом 0. Р представляет собой сумму всех
совпадений, a Q—сумма всех инверсий.
Кёртен определил гръ следующим образом:
трЪ
(9.21}
Когда связей не существует, Pmax = nBni, где п0 — числа
объектов при 0 дихотомии, a ni — число объектов при 1 дихото-
мии. Следовательно,
(9.22}.
166
Для предыдущих данных
г .20-4 .16 2 п
рЬ~~ (4)-(6) —‘ 24 “ 3 и>°' ‘
Гласс (1966Z?) показал, что гРь алгебраически эквивалентен
коэффициенту, аналогичному гы, для порядковых переменных.
Практическое значение этого факта заключается в том, что
появляется простой способ вычисления г-гь без подсчета совпаде-
ний и инверсий. Для получения того же результата, что был
получен по уравнению (9.22), можно воспользоваться следую-
щей формулой:
(9.23)
где Р.1 —средний ранг объектов, имеющих 1 по X; а Р.о —сред-
ний ранг объектов с 0 по X.
Для иллюстрации применения уравнения (9.23) используем
данные, на которых было показано вычисление гг& по ур. (9.22).
Ра™ у. Вычисления
10 8 П1 = 4 га0 = 6
9 6
7 5 30 25
4 2 Y. 1=—- = 7,500; у.0 = ^. = 4,167;
7.J - <7,300 - 4,167) _ AS1 _ 0.67.
Когда в Y нет связей, вместо уравнения (9.22) всегда ис-
•пользуется уравнение (9.23). В случае связей у У см. Cureton,
1968
Уайтфилд (1947) вывел коэффициент корреляции одной ди-
хотомической и одной порядковой переменной. Его подход сво-
дился к тому, чтобы рассматривать дихотомическую переменную
как ранжируемую переменную, связанную на двух рангах. Далее
он применил формулу т Кендалла для связанных рангов. Полу-
чившийся коэффициент имеет тот же числитель, что и rrb, но
другой знаменатель. В качестве меры корреляции предпочтитель-
нее рангово-бисериальиый коэффициент, поскольку коэффициент
Уайтфилда не достигает -{-1, когда между X и У существуют
некоторые строгие взаимосвязи. Например, когда п = 5, гц = 2,
по — 3, а четвертый и пятый ранжируемые по У объекты имеют
две единицы по X, то гг6 = 1, но коэффициент Уайтфилда равен
только 0,77.
9.4. Часть корреляции и частная корреляция
Мы начнем этот раздел с рассмотрения части корреляции,
поскольку частная корреляция представляет собой ее обобще-
ние, по крайней мере в статистическом смысле.
167
Если исследователь хочет определить корреляцию меры ин-
теллекта X с характеристикой усвоенных знаний в период обуче-
ния общественным наукам, он выбирает для оценки X интеллек-
туальный тест Кульмана—Андерсона. Однако он сталкивается
с некоторыми важными проблемами, касающимися оценки зна-
ний. Он может разработать приличный тест на усвоение содер-
жания изучаемого материала. Но применить тест н подсчитав
«число правильных ответов» — еще не значит определить «ре-
зультаты обучения». Сильная корреляция X с успеваемостью
может проявиться даже в том случае, если в учебный период
не было вовсе никаких занятии, поскольку вариабельность успе-
ваемости могла возникнуть благодаря разнице в интеллектах
Рис. 9.6. Пример определения оценки остаточного
прирйтеиия.
и погрешностям проверки, а вовсе не из-за различий в усвоении
знаний во время обучения. Организация проверки, успеваемости
как до, так и после обучения п вычитание исходной оценки
каждого учащегося из его оценки после обучения образуют
меру, довольно близкую к понятию «результаты обучения».
Остается одна несущественная трудность. Меры знаний типа
«итоговый тест минус предварительный тест» обладали бы
ожидаемой отрицательной корреляцией с интеллектом в част-
ности благодаря тому, что при вычитании одной меры, подвер-
женной ошибкам, из другой объединяются ошибки измерения.
В самом деле, почти наверняка эти «разностные оценки» будут
иметь отрицательную корреляцию с оценками предварительной
проверки, на которых они основываются. Когда у нас есть
основания считать, что объем знаний, как правило, не должен
иметь отрицательную связь со знаниями до испытаний, преды-
168
дущее обстоятельств рассматривается как дефект подобных
«разностных оценок». Альтернативным методом является изме-
рение знаний или их изменения путем подбора прямой регрес-
сии в данных предварительного и итогового теста и опреде-
лением отклонений от линии регрессии (ошибки оценки),
измеренных во оси итогового теста. Такое отклонение,
называемое остаточным изменением оценки, показано на рис. 9.6,
где У и Z обозначают соответственно результаты предвари-
тельной и вторичной проверки. (Здесь Z не надо путать с ранее
упомянутой стандартной оценкой г.)
Оценка остаточного приращения обозначается е|Л.2, потому
что эго та же самая величина, что и ошибка, полученная в про-
цессе предсказания У по Z по линии регрессии наименьших
квадратов. Из предыдущего опыта обращения к регрессионной
модели мы знаем, что корреляция е9.г с Z всегда равна нулю.
Как мера знаний ev-L обладает тем свойством, что измерение
усвоенного не связано (г = 0) с первоначальным уровнем. Ис-
следователь может цайти это свойство желательным*.
Корреляция X с еу-г называется частью корреляции, в том
смысле, что она представляет собой корреляцию X с У после
того, как часть У, которую можно предсказать no Z с помощью
линейной модели, была удалена из У. Однако подобное неодно-
значное словесное определение не заменит однозначного опреде-
ления, выражающегося символом гхеу^г-
Разумеется, коэффициент части корреляции гХе нельзя
было бы найти, фактически вычисляя значение по линии
регрессии У от Z и связывая эти значения с X. Однако сейчас
мы увидим, как можно преодолеть эту вычислительную труд-
ность.
По определению, гхе _ задается выражением
то есть отношением ковариации X с еи_г к произведению двух
стандартных отклонений.
Из § 8.3 нам известно, что s<, = sy I -- . Остается
оценить числитель уравнения (9 24)
= Sxjjr—ь0—— еХ11 -— 0 — b>sxx. (9.25)
(Нуль появляется потому, что ковариация X с константой
равна 0)
’Свойства оценок остаточного приращения всесторонне исследованы,
см. Bereiter (1963), Lord (1963), Tucker, Damarin, Messick (1966).
169
Наклон линии регрессии bt в уравнении (9.25) известен из-
уравнения для предсказания У по Z; он равен fvtsvISi. Объ-
единение этого уравнения с (9.25) дает:
gxy ~~ ryz(sy/sz)Szz
(9.26)
Деление числителя и знаменателя уравнения (9.26) на sxsv,
дает 1
(Szy/S^Sy) — гцг (s^/sxsz)
(9.27)
Итак, мы видим, что гхеу__г можно вычислить прямо по гха,
rxz и гу2. Например, пусть X будет мерой интеллекта по резуль-
татам теста Кульмана — Андерсона, a Z и У—мерами знаний до
и после обучения, соответственно. Предположим, что тха = 0,70;
гхг = 0,50, a rvz — 0,80.
Значение rxe _z равно:
_ °'70 ~ <0'5°) (0-80) „ °’70 — °>40
хе«~г УГ^- (0,80? “ адо
Таким образом, хотя корреляция гху между Л’ и У составляет
0,70, когда исключается линейная связь У с Z, остаточная связь-
X с еу_г равна только 0,50.
В некотором смысле частная корреляция — простое распро-
странение часть—корреляции. Для определения частной корре-
ляции X и У с Z, «поддерживаемым постоянным» или «частично
исключенным», мы просто вычисляем два множества ошибок
оценки для предсказания X по Z и Z по У и устанавливаем их
связь. Символически частная корреляция X и У с Z, «частично'
псключенним», представляется так:
еж_г = Х-(&0 + М) и
еу-г —У -(Й + ^Z).
Обратите внимание, что существуют две различные линии
регрессии, участвующие в процессе вычисления двух групп оши-
бок оценки (или «остатков»): линия для предсказания X по Z,
приводит к следующему:
V 1 - Ъз
170
•имеющая константы Ьц к Ь\, и линия для предсказания Y по Z,
жонстанты которой обозначены символами Ь$ и Ь*.
Как и в случае части корреляции, при вычислении гяу-2 фак-
тический расчет ошибок оценки для всех п объектов не обяза-
телен. Частный коэффициент корреляции можно вычислить пря-
мо ИЗ Гху, Гх2 и гу!.
Аналогично выводу уравнения (9.27) для коэффициента
часть—корреляции можно показать, что гху-г имеет следующую
формулу:
гд^д = .1 (9.28)
V1 - Гхг У 1 -
Далее мы увидим, какую интерпретацию можно дать расчет-
ному значению гху-2. Можно было предположить, что существует
положительная корреляция между навыками чтения X и пер-
цептивными способностями У (подтверждаемыми координацией
глаз, скоростью сканирования и т. д.). Пусть выборка из 30 де-
тей, прорацжированная по возрасту (Z) от 6 до 15 лет, дает
корреляцию X с У, гду = 0,64. Вывод о том, что некоторые дет
читают лучше вследствие больших перцептивных способностей,
весьма соблазнителен, но осторожный исследователь должен его
остерегаться. Очевидно, что с возрастом у детей сильнее разви-
вается координация глаз и другие перцептивные способности
в результате естественного созревания. Кроме того, дети прохо-
дят курс обучения в школе, что помогает им с каждым годом
читать все лучше. Разве не может быть так, что значения как
X, так и У увеличиваются (улучшаются) с возрастом, в одном
-случае вследствие физического созревания, а в другом—умст-
венного и возрастающей роли обучения? Это вполне возможно.
Если бы корреляция X и Г была нулевой на любом каком-то воз-
растном уровне (вместо всего диапазона от 6 до 15 лет), то гх„,
равный 0,64 для выборки из 30 детей, имел бы весьма различные
толкования. Действительно, даже осторожный исследователь
склонен был бы сделать вывод, что наблюдаемый гху = 0,64
объясняется общей зависимостью навыка чтения X и перцеп-
тивной визуальной способности У от возраста Z, а не только
прямой связью X и У. Как узнать, чему должно быть равно
значение гху для фиксированного значения возраста—перемен-
ной Z? При соответствующих допущениях искомая корреляция
есть частная корреляция X и У при Z, сохраняющем постоянное
значение: rViZ_;.
При условии, что Z имеет линейную связь и с X н с У и что
эта линейная связь X » У не зависит от уровня Z, гх„-г равен
гху, который получили бы в случае корреляции X и У для группы
' Глк-! называется частным коэффициентом корреляции первого порядка.
поскольку исключается доля линейного влияния одной переменпоп. Z
является коэффициентом корреляции нулевого порядка, так как при этом
ничто не исключается,
171
объектов, имеющих одинаковые значения Z. Например, предпо-
ложим, что в нашем примере гЛЙ = 0,64, = 0,80, a rvt = 0,80.
Тогда величина rsy_t из уравнения (9.28) равна
г — 0,64 — (0,80) (0,80) __ 0,64 — 0,64 __ -
Гха-г~ Vi--0,80’ д/! --0,80’ “ (0,60)(0,60) ~~
Таким образом, мы оценили бы, что величина rxv для детей
одного и того же возраста равна 0. Если бы в нашем распоряже-
нии было достаточно детей одного возраста, можно было бы
вычислить rxv только для них и проверить этот результат. Од-
нако в пашем примере не было достаточного числа детей одина-
кового возраста; было 30 ребят в возрасте от 6 до 15 лет.
Пользуясь методом множественной регрессии, обсуждаемой
в следующем параграфе, можно «частично исключить» более
одной переменной. Формулы и пояснения смотрите в работе Ези-
киеля и Фокса (1968), В случае частной корреляции нужно
особенно хорошо помнить, что корреляция нс обязательно пред-
полагает причинность.
(Обсуждение возможных в связи с этим «ловушек» см. в:
Lerner, 1965.)
9.5. Множественная корреляция и предсказание
Последний метод корреляции, представленный в этой главе,
извещен как метод множественной корреляции Тлк же кяк
н н случае обычного корреляционного метода Пирсона, множест-
венная корреляция имеет вторую сторону, известную как множе-
ственное предсказание. Вообще говоря, цель множественного
предсказания — оценивание зависимой переменной Уно линей-
ной комбинации in независимых переменных У,, X?, .... Хт.
Вспомните из главы 8, что когда одна переменная X исполь-
зовалась для оценки второй переменной У, то критерий оцени-
вания по «наименьшим квадратам» приводил к выбору таких
значении Ьо и bt, чтобы
t’.-b.xy
была наименьшей. Уравнение &o+&iA'i обеспечивает опенку У
для i-го обьекта по переменной У методом наименьших квадра-
тов. Этот вид оценивания иноща называется одномерным оцени-
ванием или предсказанием, поскольку существует только отца
«предсказывающая переменная». Многомерное предсказание пе-
ременной У по значениям пг независимых переменных пред-
с [авляет собой
У = Ьо + ЙЛ + + ... 4- bmXm. (9.29)
Уравнение (9 29)—это уравнение множественного предска-
зания или множественной регрессии. Иногда его называют уран-
172
пением линейной регрессии, поскольку Ь-коэффициепты входят
только в первой степени и никогда не фигурируют в квадра-
тичных, кубичных и т. д. членах. Разумеется, уравнение (9,29)
само по себе не представляет особой ценности; должна быть
установлена процедура, посредством которой для b выбираются
«хорошие» значения. Снова применяется критерий наименьших
квадратов, и значения br„ bi, ..., b,„ выбираются так, чтобы ми-
нимизировать величину
g (Г, -1>0 - м.! - М<2 - ... - W (Э.30)
для заданных множеств значений К и X.
Минимизирующие значения Ьо........Ьт дают нам при
bo + bjXs 4- ... 4- ЬтХт хорошую оценку У:
Pi = ba -j- b]X,i 4- ... 4“ bmXim.
Корреляция Пирсона между У и У является мерой того, как
«наилучшее» линейное взвешивание независимых переменных
X,, ..., Хт предсказывает или коррелирует с простой зависимой
переменной Y. Этот особый случай г Пирсона называется коэф-
фициентом множественной корреляции и обозначается как
... щ. Другой смысл, в котором значения &о......bm, мини-
мизирующие уравнение (9 30), являются «наилучтими», это
достижение максимально возможной положительной корреляции
между У н некоторой линейной комбинацией Xit Х,„, koi-ди
псе X объединяются в
b0 + btXt + ... +bmX,„.
причем b— те же значения, которые минимизируют уравнение
(9.30). Вследствие способа образования весов для переменных Y
коэффициент множественной корреляции всегда б}дсг либо по-
ложительным числом, либо нулем.
Теория и метолы множественного предсказания ц корреляции
запутаны и сложны. Исчерпывающий анализ этих вопросов за-
нял бы много страниц. К счастью, в педагогической литературе
по прикладной статистике нет недостатка в прекрасных руко-
водствах по этим темам.
Вы найдете теоретические и прикладные аспекты множест-
венной регрессии, наиболее полно изложенные в таких трудах,
как книги Дюбуа (1957), Розебума (1966), Дрейпера и Смита
(1973) и Эктона (1959). Наиболее сжатое изложение этих воп-
росов содержится в работе Вильямса (1968).
В оставшейся част» этого параграфа мы продемонстрируем
множественное предсказание и корреляцию для случая, когда
.тля предсказания У используются 2 переменные X, и Хг. Пред-
положим, что У — средний балл для первокурсников колледж? в
конце второго семестра Требуется предсказать У ио Xt, среднему
баллу в школе, и Xs. вербальным способностям, измеренным с
173
помощью теста на определение способности к обучению (SAT).
Многие детали последующего обсуждения упростятся, если пред-
положить, что У, и Х2 преобразованы в стандартные значе-
ния с нулевым средним и дисперсией, равной 1. Таким образом,
У, X! и Х2 переходят в zv, zt и г2. Мы ищем такие значения Ьо,
и &2, которые минимизируют У, (г? Ьо—- &>?! —- b2z2)2 для
группы из п учащихся, для которых известны средний балл
первокурсников. У, средний балл в школе, Х5, и значения SAT
Не приводя здесь доказательств, мы утверждаем, что оценки
наименьших квадратов Ьд, и Ь2 имеют вид:
£1132^1
1 ~~ г'12
h — rs2~r»ir12
°2— : г
1 “ г12
(9.31)
То, что Ьд = 0, следствие преобразования У, Xt и Х2 в стан-
дартные опенки; этого не было бы, если бы переменные не были
стандартизованы. Величины гу!, гу2 и г>2—-это просто коэффи-
циенты корреляции между У и Х1( У и Х2, Xt и Х2, вычисленные
по данным п учащихся.
Наилучшей (в смысле наименьших квадратов) оценкой стаи-
дар!нон отметки «-го учащегося по У на основе его стандартных
значений X) и Х2 будет
zy~ btzt 4- b2z2.
(9.32)
где b\ 11 b2 опенки, определенные в уравнении (9.31). Обратное
преобразование уравнения (9.32) в шкалу исходных переменных
дает \ равнение множественной регрессии для оценивания Y по
Xt и Х2:
?<=(«,4)х„+(б,4)х,а+(у.^б,^х.,-б^х.2).
(9.33)
Коэффициент корреляции между п фактическими средними
баллами первокурсников (У) и п предсказанными средними
баллами (У), полученными из уравнения (9 33), и есть коэффи-
циент множественной корреляции Ru-i,2 между средним баллом
первокурсника и наилучшей линейной комбинацией среднего
балла в школе и результатов SAT. Можно было бы вычислить
Ry-i,2 прямо на основании п пар значений У, и У,- Однако по-
скольку г!;|, г,,2 и Г12 известны, коэффициент множественной кор-
реляции удобно задать в виде
Ru-i, 2 = Vbiryi 4- b2ry2
(9.34)
174
Разумеется, значения b\ и Ь2 получены из формул (9.31)'.
Обратите внимание, что берется положительное значение квад-
ратного корня, потому что R никогда не бывает отрицательным.
Для иллюстрации множественного предсказания и корреля-
ции в случае двух независимых переменных будут использованы
данные исследования, проведенного Дизнее.м и Гроу.меном (1967).
Таблица 9.8
Результаты исследования множественного предсказания
(Dizney и Gromen, 1967 *)
Корреляции между X|, X; и У Средние Стаиларг- отхлопе-
Х| х3 У
Л; (МДЛ — чтение) Лг (MLA — письмо) Y (Ранг по немецкому языку) 1,00 0,58 1,00 0,33 0,45 1.00 25,55 63,22 2,61 10,20 11,91 0,50
* Дизией н Проучен представляют свои статистические дан-
ные со слишком малым количеством значащих цифр для тре-
буемого уровня точности вычислений. Значения г. например,
должны быть представлены скорее с четырьмя десятичными
знаками, чем с двумя. Вероятно, в своих вычислениях они
использовали больше цифр, чем сообщили читателю.
Дизней и Гроумен изучали связь умения читать X, с навы-
ками письма Х2 (измерения производились с помощью итогового
теста по иностранному языку Ассоциации новых языков) для
ранжирования студентов колледжа после второй четверти по
немецкому языку. В этом эксперименте участвовало п = 111 сту
дентов.
Значения Ъ-, и bz для предсказания стандартных значений У
по стандартным значениям X, и Х2 определяются из уравнений
(9.31) следующим образом:
1-г{2 l — (0.58)-
t!=^=^w>
1-4 I - (0,58>!
Следовательно, ианлучшей оценкой стандартных значений У
по г, и гг является
^ = 0,1042,4-0,39022.
На основе уравнения (9.33) и данных табл. 9.8 мы можем по-
строить уравнение множественного предсказания для исходных
данных.
175
su f 0,50 \
»,-X = 0,104 (ад) = 0,006,
sB / 0,50 \
=0,390 (w)=o, 0(6,
Y = 0,005Xs + 0,016X2 4- [2,61 - (0,005) 25,55 - (0,016) 63,22] =
= 0,005^4- 0,016X2 +1,47,
Коэффициент множественной корреляции Ry-t.2, представляю-
щий собой корреляцию произведения моментов между У и опти-
мально взвешенной смесью Х-, и Х2. можно вычислять либо непо-
средственно, либо по более удобной формуле (9.34):
К,,-!. 2 =х4- 62гв2 = V(0,l04) • 0,334-(0,390) • 0,45 = 0,46.
Заметим, что оптимальная комбинация X} и Х2 едва ли
сколько-нибудь лучше с точки зрения предсказания У, чем
просто Х2 Сочетание X, с Х2 оптимальным образом увеличивает
корреляцию Х2 с Y от 0,45 до 0,46. Эта особенность X) объяс-
няется тем, что Xi и Х2 коррелируют с Y приблизительно одина-
ково (корреляция с Х2 незначительно сильнее), а Х| и Х2 сами
имеют существенную корреляционную связь (гц = 0,58). Чистый
эффект объединения двух переменных X! и Х2 возрастает, когда
и X1, и Х2 заметно коррелированы с Y, но имеют слабую корреля-
цию друг с другом. Обратите внимание далее, как величина Ry-i.i
зависит от величины r,2-
Случай 1
Случай 2
1,0 0 0,50
1,0 0,50
’,0
1,0 0,5 0,5
1,0 0.5
1,0
Z>i = 0,33 Лг = 0,33
R„_t .,= V0,50M 0.502=0,71 й ( ? = <0,3310,50)+6,33(0.50) =057
Множественный R существенно больше в том случае, когда
г;2 = 0. Когда вы исследуете соотношения между корреляциями
X) и Х2 с У, корреляцию X, с Х2 и величину Ry~\,2, вам может
понадобиться неравенство, связывающее rBi и ry2 с г12:
r!liryi Vo '{VO r!2 ry\ru2 +
+ V(‘-^)('-4Д 0-35)
176
Этот результат получается после алгебраического преобразо-
вания неравенства — 1 rl2_y 1, где Гзг-и есть гхи,г из уравне-
ния (9.28). Обычно корреляция двух переменных 1 н 2 не может
выходить за пределы
'Л ± -VO-rMO-ry-
Для г!3 == гп = 0 пределы, которых может достигнуть г12,
традиционно равны ±1. Для г13 — ra = i или г23 =—1 у
должен быть равен 1- Для т и г23 — 1 г,2 = — 1. Подробности
смотрите в работах Стэнли и Вонг (1969) и Гласса и Коллинза
(1969).
Интерпретация результатов множественной регрессии с пози-
ций причинности чревата опасностями. Вероятно, социологи би-
лись над этой проблемой больше психологов или педагогов
(например, см.: Coleman и др., 1966; Weris, 1968; Pugh, 1968).
Задачи и упражнения
1. Приведенные данные — характеристики людей и методы
их измерения — таковы:
Характеристика Измерение
А. Пол 3. Возраст 3. Рост Г. Политическая принад- лежность Д< Тревожность Е. Интеллект Дихотомическое, мужчины —1, женщины — 0 Измеренный в месяцах с точностью ло ближай шего месяца Измеренный до ближайшего см Дихотомическое, демократ—1, республиканец—С Оцениваемая по мнению клинических психоло- гов в рангах от 1 до п для группы из п че ловек Измеренный путем преобразования оценок /Q в ранги от 1 до п для группы из п человек
В каждом из следующих примеров определите один или бо-
лее коэффициентов корреляции, пригодных для описания связи
между двумя переменными:
а. Пол и рост
б. Тревожность н интеллект
в. Пол и тревожность
г. Возраст и рост
д. Пол и политическая принадлежность
е. Политическая принадлежность и интеллект
2. Уравнение (9.11) показывает, что отношение ri,is к Уь
HMeei вид:
гь^ _ Уу»й
Г₽4 ич
177
Известно, что п\ = 25, п — 50 и грь = 0,60 Найдите вели-
чину п,„.
3. Клинический психолог и логопед совместно проранжнро-
вали п = 20 детей по двум переменным:
X— эмоциональная устойчивость (1 — наибольшая, 20 —
наименьшая);
У— степень заикания (1 — наименьшее, 20 — наибольшее).
Существуют С?= 190 различных пар детей в этой группе.
В 80% пар ребенок, обладающий более высоким рангом по X,
имел также более высокий ранг по У; в оставшихся 20% пар
ребенок с более высоким рангом по X имел более низкий ранг
по У. Какова величина т Кендалла для этих данных?
4. Ниже приводятся исходные оценки 12 учащихся школы
но тесту абстрактного и вербального мышления:
а. Преобразуйте исходные опенки в ранги (1 — 12) для каж-
дой переменной н вычислите гв.
б. Используя те же ранги, что и в (а), вычислите т.
5. Корреляция У с Х| составляет 0,91: корреляция г с А'-,
равна 0,87. Может ли корреляция с Х^ бьиь меньше 0,10?
10
ВЕРОЯТНОСТЬ
10.1. Введение
Ученый всегда стремится выйти за пределы своих данных. Даже
когда он максимально объективен и меньше всего склонен к об-
общениям, он делает молчаливое предположение о том, что
совокупность его данных обладает некоторым постоянством;
если бы завтра он накопил больше данных, они отражали бы
приблизительно, но не точно, аналогичную тенденцию. Будучи
же недостаточно объективным, он выводит обобщения из того,
что наблюдает сегодня, распространяя их на то, что увидит в
других местах и в других условиях aaeipa.
Каждый вывод обладает некоторой неопределенностью.
Правдоподобие вывода, как правило, не принимается нами
слишком всерьез, когда мы, например, слышим: «..Янки” одер-
жат победу над „Соксом” завтра, так как я видел, как они по-
бедили „Сокса" сегодня ». Другие выводы могут быть более
убедительны; «Я заметил, что солнце в течение последних20лет
восходило ежедневно, следовательно, оно взойдет и завтра ут-
ром». Выводы отличаются по правдоподобию от «маловероят-
ных» до «почти достоверных». По своей природе ни один вывод
не является абсолютно надежным, хотя некоторые из них при-
ближаю!ся к этому.
Большая часть работы специалиста л области статистики
состоит в создании методов приписывания вероятностей выво-
дам. Это в самом деле является важным делом. Вывод умоза-
ключения— метод науки: каким грубым был бы метод, если бы
ученые не имели объективных и систематических способов при-
своения вероятностей тем выводам, которые они делают. Обы-
денная речь, с помощью которой люди относят выводы к «мало-
вероятным» или к «почти достоверным», неадекватно служит
науке. Эти субъективные оценки варьируют от лица к лицу
в зависимости от слов, выбранных для определения правдоподо-
Речь идет о названиях спортивных команд —{Прим, ред)
179
бия, и от их смысла. Для общения ученых гораздо лучше, когда
они могут независимо прийти к одной и той же формулировке
вероятности верности вывода и когда эту формулировку можно
изложить в недвусмысленных терминах, имеющих одинаковый
смысл для всех ученых.
Мы несколько идеализировали действия ученых в предыду-
щих абзацах, чтобы подчеркнуть этот момент. Ученые и стати-
стики не единодушны в том, как присваивать вероятности
утверждениям и каким утверждениям следует их присваивать.
Теперь мы рассмотрим методы, разработанные статистиками,
которые позволяют утверждать, что, например, «Связь между
IQ и средним баллом детей 11 лет не случайна и что это верно
с вероятностью 0,99».
10.2. Вероятность как математическая система
Мы начнем изложение совершенно абстрактно. Вероятность
будет рассмотрена как система определений и операций, при-
надлежащих выборочному пространству. Понятие выборочного
пространства является фундаментальным. Мы никогда не сде-
лаем вероятностного утверждения, которое не было бы связано
с выборочным пространством некоторого типа. Фактически
утверждения о вероятностях есть просто утверждения о выбо-
рочно'! пространстве и его характеристиках5
Выборочное пространство — это множество точек. Эти точки
могут соответствовать людям, числам, шарам и т. д. Событие —
это наблюдаемый случай, подобный появлению «орлов» при под-
брасывании монеты. В выборочном пространстве может быть
несколько точек, каждая из которых есть пример события.
Так, выборочным пространством может быть множество из
6 белых и 3 черных шаров в урне. Это выборочное пространство
имеет 9 точек. Событие может состоять в том, что «вынут белый
шар». Этому событию соответствуют шесть точек. Сколько
точек имеет событие «Вынут черный шар»? Событие «Шар,
находящийся в этой урне, — красный» не имеет точек. «Шар
в этой урне либо белый, либо черный» также дает пример со-
бытия.
Формулировка вероятности производится относительно появ-
ления события, которое связано с выборочным пространством.
На последующих страницах мы будем обозначать события за-
главными буквами А, В, С, ...; вероятность события А будем
обозначать Р(А).
Определение: Вероятность события А, Р(А), представляет собой
отношение числа точек, приводящих к А, к обще-
1 Понятие выборочного пространства является сравнительно новым в
теории вероятностей, ведущим начало лишь от 20-х гг. XX в. и работы Ми-
зеса (1931).
180
му числу точек при условии, что все точки в вы-
борочном пространстве равновероятны.
Пусть А будет событием «Шар — белый», а выборочное про-
странство— множеством из 9 шаров (6 белых, 3 черных) в урне.
Сколько точек приводят к событию 4? Очевидно, ответ 6. Следо-
вательно, вероятность события А («Шар — белый») равна:
р, .. число появлений А 6 2_
' ' общее число точек 9 3 ‘
Если в нашем примере В представляет событие «Шар — чер-
ный», найдите Р(й). Сложите Р(А) и Р(В'). Чему равно Р(С)
в нашем примере, если С является событием «Шар —- красный»?
О —событие «Шар либо белый, либо черный». Каково Р(£>)?
Е— характеризует событие «Шар является как белым, так и
черным». Найдите Р(Е).
Предположим, у вас есть вторая урна, в которой находятся
4 белых шара и неизвестное число черных. Какова вероятность
события, что шар — белый? В пределах разработанной нами
системы на этот вопрос ответить нельзя. Вероятность можно
определить, если известны все характеристики выборочного про-
странства, а в этом примере они не известны.
Существует альтернативный путь, с помощью которого мы
можем определить вероятность события. Рассмотрим выборочное
пространство, содержащее конечное число элементарных собы-
тий Элементарное событие есть точка. Обозначим каждую та-
кую точку строчной буквой «о»: ai, а2, .. , а,,. Каждое собы:пе,
определенное в выборочном пространстве, состоит из множества
элементарных событий
Определение: Функцией вероятности называется правило соот-
ветствия, которое связывает с каждым событием
А в выборочном пространстве число Р{А) так, что-
бы (/) Р(А) 5s 0 для любого события А\ (2) сум-
ма вероятностей всех различных событий была
равна 1: (3) если А и В — взаимно исключающие
события которые не имеют общих ючек то
Р(А или В) = Р{А) +Р(В).
Если мы полагаем, что вероятность элементарного события
о, равна 1/п, где п — общее число точек, то вероятность собы-
тия А, состоящего из П| точек, равна:
PM)==1+1+... +l=i.
Отношение л,/п — это отношение числа точек, приводящих
к А, к общему числу точек.
Оба пути приводят нас к одному определению Р(А). Хотя
последний путь может иметь предпочтение для математика, пер-
вый, возможно, покажется вам более ясным.
181
10.3. Комбинирование вероятностей
Предположим, у нас есть урна, содержащая 4 красных, 3 бе-
лых и 3 черных шара. Для нас интересны три события: (1) А,
шар—красный; (2) В, шар — белый; (3) С, шар — черный. Эти
три события являются взаимоисключающими: каждая точка
ведет к одному и только одному событию.
Возникает вопрос: «Какова вероятность того, что шар будет
красным или белым?» Мы обозначим это событие символом
/HJfi, а его вероятность — символом P(AUB).
Первое правило сложения вероятностей
Когда события А и В взаимоисключающие, P(AUB), вероят-
ность либо А, либо В равна Р(А) 4- Р(В).
В нашем примере
р (л и В) = Р И) + Р (В) = TJ-+ 4-- 4.
Определите P(4U0) == Р(А) 4- Р(С). Чему равно значение
Р(виС)?
В некоторых выборочных пространствах 2 события могут не
быть взаимоисключающими, то есть одна точка может приводить
к обоим событиям А и В. Рассмотрим возможные исходы («ор-
лы» (О) или «решки» (Р)) подбрасывания монеты три раза
подряд. Мы рассмотрим эти исходы абстрактно: пока мы не
хотим обсуждать физическое действие подбрасывания монеты.
Восемь возможных исходов образуют выборочное пространство:
1. 000
2. OOP
3. ОРО
4. ОРР
5. РРР
6. РРО
7. POP
8. POO
Полагая, что все 8 исходов равновероятны, то есть имеют
вероятность //8, найти, какова вероятность «орлов» при первом
бросании? Чему равна вероятность «орлов» при первом и вто-
ром бросаниях?
Теперь мы определяем 2 события А и В в этом выборочном
пространстве:
А: «орлы» при первом и втором бросаниях;
в: «орлы» при втором и третьем бросаниях.
Точки, которые приводят к событию А, соответствуют первым
двум исходам (числа ( и 2 выше). Каковы же 2 точки, приводя-
щие к событию В?
Мы будем обозначать символом А П В новое событие, «Л
и В» В нашем примере ЛПВ— это следующее событие: «.орлы»
при 1 н 2 и «орлы» при 2 и 3 бросаниях. Если мы предположим,
182
если бы мы просто сложили Р(А) и Р(й) для определения
Р(Лив), то область, общая для Л п В, P(At]B), входила бы
р сумму дважды.
Хотя мы привели два разных правила сложения вероятностей,
первое правило является только особым случаем второго, когда
Р(ЛПВ) =0.
Если А и В — взаимоисключающие события в S, то они не
пересекаются. Смотрите рис. 10.2; здесь нет общей площади А
и В, так что Р(ЛПВ) = 0.
Вообще, P(^UB) =*Р(А)+Р(В)-Р(А(]В). Если А и В-
взанмоисключающие события, то Р(АПй)=0. Поэтому, если
А и В-взаимио исключают друг друга, то Р(ЛиВ)=--Р(Л) +
+Р(В)—0 = Р(Л)4-Р(В).
До сих пор мы рассматривали вероятность скорее абстрактно.
Аналогично математическим системам геометрии и алгебры тео-
рию вероятностей можно
представить как ряд аксиом
и определений. Но так же,
как геометрия и алгебра,
теория вероятностей может
служить моделью там, где
в окружающем нас мире
Рис. 10.2. Диаграмма Венца взаимо-
исключающих событий Л и В в выбо-
рочном пространстве S.
она отражает некоторые
классы событий.
Принципом, который
устанавливает связь вероят-
ностных положений с физическими событиями, мы обязаны
Якобу Бернулли (1654—1705).
Пусть мы имеем урну, содержащую 4 белых и 6 черных ша-
ров. Шары идентичны по величине, форме и весу и тщательно
перемешаны, так что если бы нам нужно было вытащить один,
то существовала бы одинаковая вероятность выбрать любой из
10 шаров: каждый шар имеет один шанс из 10 быть выбранным.
Мы опускаем руку в урну, вынимаем шар и отмечаем его цвет.
Шар возвращается в урну, шары в урне тщательно перемеши-
ваются, и действие повторяется в аналогичных условиях. Мы
повторяем это действие очень много раз, скажем 10000. После
10000 выниманий шаров мы подсчитываем число случаев по-
явления белого шара. Интуиция должна подсказать вам, что от-
ношение числа таких случаев к 10000 будет очень близким
к 4/10 (хотя, по всей вероятности, не точно равным этой вели-
чине).
Если мы рассматриваем 10 шаров в качестве выборочного
пространства и говорим, что А —событие «шар белый», то Р(А)
точно равно 4/10. Возникает вопрос, будет ли формальная ве-
роятность события, рассчитанная теоретически, хорошо соответ-
ствовать относительной частоте появления события? Ответ на
этот вопрос является ключом к связи теории вероятностей и ее
приложений, и этот ответ утвердителен.
184
Попытаемся дать формальное определение этой связи. Пред-
положим, что событие л либо встречается, либо нет при каж-
дом испытании. Вероятность того, что Л будет иметь место,
одинакова для всех испытаний и равна Р(А). Например,
Действием может быть подбрасывание симметричной монеты,
событие А может состоять в появлении «орлов», и предпола-
гается, что вероятность «орлов», 1/2, одинакова при каждом
бросании. Предполагается также, что каждое испытание неза-
висимо от всех других. Теперь после п испытаний доля появле-
ний А равна р. Можно доказать (доказательство является на-
столько трудным, что приводить его здесь нет смысла), что р
становится все ближе и ближе к Р(А) по мере того, как п ста-
новится все больше и больше. Мы можем сделать эту долю на-
столько близкой к Р(А), насколько захотим, производя испыта-
ния достаточное число раз. Таким образом, Р(А) свидетель-
ствует о том, что произойдет в длительном цикле, если мы дей-
ствительно произведем действия в описанных условиях.
Это буквальная формулировка закона больших чисел, Закон
больших чисел важен в приложениях теории вероятности, а так
как статистика — одно из таких приложений, то он представ-
ляется важным и для теории статистического вывода.
Правило умножения вероятностей
Существует правило умножения вероятностей, которое будет
иметь очень важное значение для нашей последующей работы.
Пусть мы подбрасываем монету 5 раз подряд, Допустим, что
вероятность «орлов» равна 1/2 при каждом бросании и что под-
брасывания независимы. Правило умножения вероятностей гла-
сит, что вероятность получения 5 «орлов» подряд составляет:
1/2-1/2-1/2-1/2-1/2 = 1/32. Общая формулировка правила та-
кова:
Правило умножения вероятностей: Вероятность того, что А,
имеющее вероятность Р(А) при любом единичном испытании,
встретится п раз при п независимых испытаниях равна:
Р(А) Р{А)- - • Р{А) = Р(А)”.
Пусть некто бросает игральную кость (играя в кости с са-
мим собой), вероятность появления любой из 6 граней равна
1/6, Каково выборочное пространство для одного бросания? —
Выборочное пространство в этом случае содержит множество
из возможностей — 1, 2, 3, 4, 5, 6. Какова вероятность того, что
на игральной кости выпадет 2? Чему равна вероятность того,
что при одном бросании кости выпадет четное число?
Р (четного числа) = Р(2) 4. р(4) 4. р (6) = | + | | —
Какова вероятность четного или нечетного числа при одном
бросании?
185
Предположим, что мы рассматриваем 2 бросания игральной
кости. Выборочное пространство разных возможностей испыта-
ний содержит 36 точек, представленных на рис. 10.3.
Пусть событием А будет «I при первом подбрасывании»,
а событием В — «2 при втором подбрасывании». Найдите
Р(4Л8) путем деления числа точек приводящих к 408
(иЛи8), на 36. Проверьте, что Р(ЛПВ) равно Р(А)-Р(В).
Найдите P(A\JB), вероятность события А или события В,
1,4
1.5
2,1
2,2
3,2
5,2
5,3
5,4
5,5
5,6
Рис. 10.3, Выборочное пространство исхо-
дов двухкратного бросания игральной кости.
помня, что Р(A U В) = Р(А) + Р(В~) — Р(А Г) В). Здесь мы имеем
6/36 4-6/36—1/36 = 11/36; точка 1, 2 является общей для А
и В.
Мы примем в качестве определения утверждение, что два
события независимы, если и только если Р(А 0 В)= Р(Л) -Р(В).
Независимость является важным понятием в статистике и тео-
рии вероятностей, и мы будем много говорить о нем позже.
10.4. Перестановки и сочетания
Еще двумя понятиями, которые неоднократно встречаются
при исследовании всевозможных результатов экспериментов, яв-
ляются перестановки и сочетания.
Перестановка группы объектов (букв Л, В, С и D, например)
представляет собой такое их размещение, в котором учитывается
их порядок. Различное упорядочение объектов дает различ-
ные перестановки. Сколько различных перестановок (упорядоче-
ний) существует для букв Л, В, С и D? Для ответа мы можем
записать и подсчитать их, как показано в табл. 10.1.
Первой буквой может быть либо Л, либо В, либо С, либо D.
Пусть этой буквой будет А (это приводит к четырем ступеням
табл. 10.1). Если первая буква — Л, то второй буквой может
быть либо В, либо С, либо D. Если второй буквой является В,
то третья буква — С или D. Если третья буква — С, то четвер-
той буквой должна быть D. Таким образом, ABCD — первая
возможная перестановка. Для первого положения существуют 4
возможных буквы; далее одна буква приписывается первому
положению; для второго положения существуют 3 возможных
буквы и т. д. Следовательно, число возможных перестановок из
4 букв Л, В, С н Ь равно 4-3-2' 1 = 24,
186
Таблица 10.1
24 перестановки из 4 букв.
Буква Буква Буква Буква Переста- Буква Буква Буква 3 Бу квв Переста- новка
А В С D ABCD С Л В D САВВ
D С ABDC D В CADB
с В D ACBD в А D CBAD
D В ACDB D А CBDA
D В С ADBC о А В CDAB
С В ADCB В А CDBA
В А С D BACD D а В С DABC
D С BADC С В DAC.B
с А D BCAD В А С DBAC
D А BQDA С А DBCA
о А С BDAC С А В DCAB
С А В DC А В А DCBA
Если мы имеем п различных предметов, можем получить-
п(п— 1) (п — 2) ... ?• 1 различных перестановок. Вместо записи
п(п—1)(л— 2) ... 2-1 мы можем обозначить эго произведение
как л!; читается «п факториал», н! есть произведение чисел от
1 до п и равно числу перестановок п различных объектов (Мы
согласимся считать О' равным 1.)
Величина nl возрастает с ростом п чрезвычайно быстро. На
первый взгляд, 10! = 10-9-8-7 ... 2 • 1 выглядит безобидным чис-
лом, но при вычислении его вы нашли бы, что 10! = 3 628 800.
Чтобы описать величину 52!, вообразите, что у вас есть дю-
жина яиц в картонке и вы хотите образовать все их возможные-
перестановки (расположения). Допустим, что вы можете созда-
вать новое размещение каждую секунду в течение восьмичасо-
вого рабочего дня. Если вы продержитесь па этой работе 5 дней
в неделю, 52 недели в год, то вам потребуется более 2 769 лет
для выполнения всех возможных размещений!
Понятие сочетания возникает в том случае, когда выбирается
некоторое число объектов из большего или равного множества
объектов. Сочетания — это различные множества объектов, в ко-
торых не учитывается порядок. Когда выбирается п объектов-
587
из п объектов, то есть выбраны все объекты, возможно только
одно сочетание. Если из п объектов выбран только один объект,
то имеется п сочетаний. Задача состоит в том, чтобы найти об-
щее выражение для числа сочетаний, существующих при выборе
rat объектов из п.
Рассмотрим 4 объекта А, В, С и D. Сколько различных со-
четаний можно получить, выбирая из этих 4 букв по две? Ответ:
6 — АВ, AC, AD, ВС, BD, CD. Обратите внимание, что порядок
сочетаний не учитывается. АВ—одно сочетание, а В А—то же
самое сочетание. Запишите 4 возможных сочетания, которые мо-
жно образовать, выбирая 3 буквы одновременно из А, В, С, D.
(Первым является АВС.)
Предположим, что из п объектов выбираются га, объектов.
Сколько существует различных сочетаний? Пока будем рассмат-
ривать порядок как важное обстоятельство, а несколько позже
объединим все те выборы, которые отличаются только порядком.
Если из п выбирается га5 объектов, то существует п выборов
для первого, п—1 для второго, п— 2 для третьего, п —3 для
четвертого и т. д. до тех пор, пока не останется п — Hi 4- 1 вы-
боров для П|-го объекта. Итак, общее число различных выборов
(то есть перестановок) nt из п, если важен порядок, равно:
п(п — 1)(га — 2) ... [n — thA-I)-
В этом произведении, соответствующем п\ объектам, суще-
ствует га1 членов. Однако каждому отдельному сочетанию
объектов соответствует П|! перестановок этих объектов. От-
сюда число сочетаний га( объектов, выбранных из п без учета
порядка, равно:
Символ^” ^обозначает «число сочетаний nt объектов, взя-
тых из и».
Довольно легко показать, и вам в этом следует убедиться,
что п(п — 1) (га — 2) ... (п — nt 4- 1) = га!/(га — га,)!; просто за-
пишите п! как п(п —1)(га — 2) ... ((л.— nt)1J(и. — nJX
Х((л —«О—1J ... 1.
Перепишите п\ в числителе и (га — гч)- в знаменателе н со-
кратите члены, общие для числителя и знаменателя, далее пред-
ставьте (п —П|)((га—-л;) — I] ... I как (га —П|)! Затем вы-
полните деление.
/га \ п!
Следовательно, \ га Л ^ («-«,)! '
Обобщая, получим, что число перестановок п объектов есть п\
Число перестановок га объектов, взятых по nt, равно п(п— 1) ...
• . (га — rij 1).
188
Число сочетаний п объектов, взятых nt раз, дается выраже-
нием:
(п — п|
\П|/ Л!Ця-П1Н
Сколько различных сочетаний существует для 3 объектов,
взятых из 5? В этой задаче п = 5, а П) = 3.
/5\_ 5! 51 5-4-3-2-1 5 - 4 20
1^3) 31(5 — 3)! “ 31 2! = (3-2- 1)(2-1) 2- 1 ~ 2 “ Ш
Обратите внимание, что существует 5-4-3 = 60 перестановок
из 5 объектов по 3. поскольку каждое из 50 сочетаний 5-тн объ-
ектов, взятых по 3, имеет 3-2-1 перестановок.
Для работы в некотором комитете есть 10 кандидатов. Ко-
митет должен состоять только из 7 человек. Сколько различных
комитетов можно было бы создать из 10 имеющихся в наличии
/ 10\
людей? Пусть п = 10, щ = 7; оцените I I.
10.5. Биномиальное распределение
Практически каждая тема, обсуждаемая до сих пор в этой
главе, может быть использована для решения задач в статисти-
ке. Следующая задача касается многократных независимых дей-
ствий, которые могут привести либо к «успеху», либо к «неудаче»
с постоянной вероятностью. Мы будем изучать биномиальное
распределение, которое опишет один аспект этой задачи — оценку
вероятности заданного числа успехов.
Предположим, что правильная монета, то есть симметричный
и однородный предмет, подбрасывается 5 раз подряд. Каждое
подбрасывание независимо от другого в том смысле, что, если
в результате первого бросания выпадает «орел», то «орел» при
втором бросании не более, но и не менее вероятен, чем в случае,
если бы первое бросание привело к появлению «решки». Допу-
стим далее, что вероятность «орлов» является постоянной ог
первого до пятого бросания. Пять бросков образуют 5 «испыта-
ний»; независимые испытания, которые могут выражаться в
одной из двух возможностей с постоянной вероятностью, назы-
ваются испытаниями Бернулли или биномиальными испыта-
ниями, (Якоб Бернулли —математик XVII века, чей «Ars Соп-
lectandi» был одним из первых трудов по теории вероятностей.)
Пять подбрасываний монеты представляют собой 5 биномиаль-
ных испытаний. Каким образом определяют вероятность того,
что в результате 5 испытаний выпадут 3 «орла»?
Одним из возможных результатов 5 подбрасываний, приво-
дящих к появлению 3 «орлов» и 2 «решек», является: О, О, О, Р, Р.
189
Из правила умножения вероятностей мы знаем, что вероят-
ность события О, О, О, Р, Р равна 1/2-1/2-1/2-1/2-1/2 = 1/32, по-
скольку и вероятность «орлов», и вероятность «решек» состав-
ляет 1/2. Однако выборочное пространство результатов 5 бро-
саний имеет 32 точки (2'2-2-2'2), а некоторые из этих резуль-
татов ведут к событиям 3 «орла» и 2 «решки». Мы можем опре-
делить число различных точек, приводящих к событию, о кото-
ром идет речь, пользуясь понятием сочетаний. Такими, на-
пример, являются события: О, О, Р, Р, О и О, Р, Р, О, О. Общее
число различных возможностей с 3 «орлами» и 2 «решками^,
представляет собой число сочетаний из 5 объектов по 3.
UJ 312! 2.1 Ш-
Существует 10 точек, которые приводят к событию, н каж-
дая из них имеет вероятность 1/32. Следовательно, используя
правило сложения вероятностей, найдем, что вероятность полу-
чения 3 «орлов» в 5 бросаниях правильной монеты равна
10(1/32)= 10/32.
Итак, 10/32 получено в результате умножения
(Ж
Следовательно, вероятность получения п «удач» в п бино-
миальных испытаниях равна
(л
где р— вероятность «удачи» при одном испытании; q—вероят-
ность «неудачи», равная 1—р, а П\ = 0, 1, 2 ... п.
Заметьте, что «биномиальные испытания» — это только испы-
тания с двумя возможными результатами: да или нет, удача или,
неудача, орлы пли решки, красный пли не красный и т. д. Вы-,
раженнс:
вероятность (П|) = ^я
есть формула биномиального распределения. Это распределение,
имеет множество важных приложений в теоретической и при-,
хладной статистике.
(п
Существует интересная связь между I j в биномиальном,
распределении и таблицей, известной как треугольник Паскаля,
[по имени французского математика и философа Блеза Паскаля,
(1623—1662)}. Каждая строка в треугольнике Паскаля (см.
рис. 10.4) образована сложением некоторых чисел верхней
190
строки, Каждое число есть сумма 2 чисел, расположенных выше
него по диагонали. Таким образом, 6 в 4-й строке является сум-
мой двух троек выше. Вы могли бы легко получить восьмую,
девятую, десятую и последующие строки сами.
строки
2
3
4
5
6
•7
Рис. 10.4. Треугольник Паскаля.
Можно доказать, что J равно nt 1-му числу в п-й строке
треугольника Паскаля, Например равно второму числу в
3-й строке:
1 есть первое число в 5-й строке; это число сочетаний
нуля объектов, взятых из 5. Обратите внимание па то, что пер-
вое и последнее число в каждой строке равно I, поскольку
Со)=С)“’
Вычисление, например, вероятности 14 удач в 30 испытаниях,
когда р = 3/8, a q = 5/8. представляло бы трудоемкую задачу.
К счастью, существуют отличные таблицы для биномиального
распределения. Краткая таблица биномиального распределения
приводится в работе Пирсона и Хартли (1966), Опубликованы
также более обширные таблицы Вычислительной лаборатории
Гарвардского университета (1956) и «Таблицы кумулятивных
биномиальных вероятностей» (1953). («Кумулятивные биноми-
альные вероятности» представляют собой просто сумму после-
довательных членов в биномиальном распределении и дают ве-
роятность по крайней мере п, удач в п испытаниях )
Рис. 10,5 иллюстрирует дискретное биномиальное распреде-
ление для 8 испытаний, когда р — q = 1/2, Обратите внимание,
что, когда р = q, распределение симметрично. Для р> q оно
будет скошенным влево, так как будут преобладать большие
значения, Как оно будет скошено для р < q?
191
На рис. 10.6 приводится биномиальное распределение для
л = 5, р — 0,30, <7 = 0,70. На рис. 10.6 вы можете, например,
увидеть, что вероятность 5 удач, когда п — 5, а р = 0,30, очень
мала. Она составляет только (0,30)5 = 0 00243, то есть 243 раза
из 100000.
Биномиальное распределение служит хорошим примером
общего типа рассуждений, используемых при проверке статисти-
ческих гипотез. Статистику может показаться, что процесс, с по-
мощью которого были получены наблюдаемые им данные, пред-
ставлял собой последовательность биномиальных испытаний.
Предположим, что он подбросил монету 10 раз и получил
0 1 2345676
Число успехоб
Рис. 10.5. Биномиальное распределение
для л™ 8. р ™ ’/2.
0,3
9 «орлов». Он подозревает, что монета не является правиль-
ной, то есть что вероятность получения «орлов» не. равна 1/2. Его
наблюдения, по-видимому, доказывают, что монета является не-
правильной. Он представляет свое доказательство следующим
образом:
1. Временно допускаем, что вероятность «орлов» для этой
монеты действительно равна 1/2. Это гипотеза.
2. Если вероятность «орлов» равна 1/2, то какова вероят-
ность того, что я наблюдал бы событие, которое осуществилось
192
(9 «орлов»), или когда достигается предел возможного
(10 «орлов»)?
3. Эта вероятность равна:
('9°)G)eG)'+(w)G),e(l)“-o—
(Вспомните, что всякое число в нулевой степени равно 1.)
4. Если эта монета — правильная, то я наблюдал событие,
которое чрезвычайно неправдоподобно.
5. Если эта монета имеет склонность к «орлам», то событие,
которое я наблюдал, оказалось бы более вероятным. Например,
если вероятность «орлов» для этой конкретной монеты действи-
тельно составляла 8/10, то вероятность получения 9 или
10 «орлов» в 10 подбрасываниях была бы
/ 10\/8 У / 2 V /10\/8 \!°/2 V
(9)(^) U) +(>о)(то) (го) =ода8-
6. По моим наблюдениям оказывается, что очень неправдо-
подобно, чтобы эта монета была правильной. Поэтому гипотеза
в (1) отвергается: признается, что монета имеет склонность
к «орлам».
Обратите внимание, что, конечно, отнюдь не невозможно по-
лучить 9 «орлов» при 10 подбрасываниях монеты; в действи-
тельности мы должны ожидать появление такого события при-
близительно один раз (1,07) в каждых 100 группах по 10 под-
брасываний. Существует возможность того, что монета, давшая
9 «орлов», является правильной, но вероятность того, что это
так, мала.
Логика экспериментатора часто следует этому образцу. Он
выдвигает гипотезу о том, что определенные черты модели его
эксперимента (биномиальное распределение является одной из
таких моделей) характеризуются определенными величинами
(например, вероятность «орлов» равна 1/2), Он не нуждается в
проверке этой гипотезы, он только временно принимает ее для
того, чтобы узнать, к чему она его приведет. Затем эксперимен-
татор производит наблюдения (например, подбрасывает монету
10 или 20 раз), после чего вычисляет вероятность получения на-
блюденного или более неожиданного результата, если его пер-
воначальная гипотеза была справедливой. Если эта вероятность
очень мала (скажем, 0,05 или 0,01), он подвергает сомнению
справедливость гипотезы. Если первоначальная гипотеза оказа-
лась ложной, а некоторая альтернативная гипотеза — спра-
ведливой (например, монета имеет смещение), его результант
могли быть более правдоподобными. Этот процесс, называемый
«проверкой гипотезы», есть отклонение или отказ от некоторого
объяснения (гипотезы) на основе вероятности получения имею-
щихся результатов в случае, если бы гипотеза была верной.
Если вероятность полученных результатов (или более неожи-
7 Зак. «8 193
данных) велика (например, 0,30 или более) при расчете вероят-
ности для некоторой гипотезы, ю гипотеза в данный момент не
отвергается. Если же вероятность полученных результатов мала
(0,05 пли менее) при расчете вероятности для другой гипотезы,
то гипотеза отклоняется. Нельзя доказать, что гипотеза является
ложной; существует некоторая малая вероятность (0,05 или ме-
нее), что она верна. Однако основания для ее отклонения ве-
лико.
Исследование вероятностей может быть интересным и зани-
мательным. Исторически концепции вероятности возникли в связи
с определением шансов на выигрыш в играх.
10.6. Случайность и случайный выбор
Понятие случайного выбора тесно связано с вероятностью;
наступил подходящий момент коснуться этой темы. Вывод —
это процесс рассуждения от «нечто» ко «всему». Обоснован-
ность вывода будет зависеть от того, при какой представитель-
ности «нечто» характеризует «все». Если бы вас интересовало
распределение голосов избирателей в Соединенных Штатах, то
здравый смысл подсказал бы вам брать интервью не только
у президентов корпораций. В этом примере «некоторые» (пре-
зиденты корпорации) не характеризуют «всех» (всех избирате-
лей в США). Как же обстоит дело с получением представитель-
ной выборки3
Существует несколько различных методов, но мы подробно
рассмотрим только один: простой случайный выбор. Часто при-
лагательное «простой» опускается, если нет необходимости раз-
граничивать различные методы испытаний Когда здесь упоми-
нается «случайный выбор», подразумевается «простой случай-
ный выбор».
Простой случайный выбор — это процесс отбора наблюдений
из большой группы таким образом, чтобы каждое наблюдение
имело равную и независимую вероятность быть выбранным. Мно-
гочисленная группа называется совокупностью-, меньшая — вы-
боркой. Если выбор случайный, то процесс отбора наблюдений
будет обеспечивать каждому наблюдению в совокупности оди-
наковый шанс попасть в выборку. Кроме того, если выбор дей-
ствительно является случайным, то результат одного выбора
не зависит от результата любого другого
Условие независимости выборов является очень важным, хотя
ему часто не уделяют должного внимания. Отсутствие незави-
симости между выборочными наблюдениями представляет собой
одну из наиболее распространенных ошибок в педагогических
и психологических исследованиях.
Условие равновероятности в определении случайного выбора
предполагает, что на каждой стадии процесса выбора все остав-
шиеся элементы имеют одинаковую вероятность быть выбран-
194
яыми. Допустим, что из 52-х карт колоды должны быть слу-
чайно выбраны 2 карты. Если первый выбор будет случай-
ным, то вес 52 карты будут иметь одинаковый шанс быть вы-
бранными, то есть 1/52. Если второй выбор должен быть слу-
чайным, то оставшиеся 51 карта должны снова иметь одинако-
вую вероятность быть выбранными, то есть 1/51. Как же прак-
тически достигается такая равновероятность? Существуют мно-
гочисленные способы приблизительного обеспечения равнове-
роятности; некоторые из них значительно лучше других Наи-
лучшим методом получения случайных выборок, подходящим
профессиональному статистику, является применение таблицы
случайных чисел.
Таблица случайных чисел — это таблица цифр от 0 до 9, рас-
положенных по порядку, определенному механическим процес-
сом, который аппроксимирует равную вероятность появления
каждой из цифр настолько близко, насколько позволяет тех-
ника. Рандомизированный выбор предотвращает любые систе-
матические смещения.
Независимость
Пример выбора, при котором наблюдения не являются неза-
висимыми,, показывает, чего следует избегать при случайном вы-
бора. Предположим, исследователь хочет оценить средний IQ
детей, имеющих близнеца—брата или сестру. Допустим, что
100 детей (50 пар близнецов) образуют соответствующую сово-
купность, а исследователь может назначить испытания интел-
лекта для 30 детей. Он решает, что его работа упростится, если
всякий раз он случайно выберет одного ребенка, а одновременно
также и его близнеца. Ему кажется, что так он получит случай-
ную выборку из 30 детей. Нет, не получит. 30 наблюдений не
были выбраны независимо. Если бы это было так, то выбор од-
ного ребенка не сделал бы более вероятным выбор его близнеца,
чем другого ребенка. Здесь же выбор ребенка обеспечил вероят-
ность выбора его близнеца, равную 1, с гарантией. У исследова-
теля нет простой случайной выборки 30 детей из совокупно-
сти 100. Он оправдывается, говоря, что получил простую слу-
чайную выборку 15 нар близнецов из совокупности 50 пар; и
он мог усреднить два IQ в группе близнецов для получения на-
блюдения, соответствующего его методике испытаний. Выбор пар
близнецов представляет собой пример группового выбора.
Отсутствие независимости наблюдений в случайной, по пред-
положению, выборке является весьма распространенным недо-
статком экспериментирования.
Частая ошибка недостаточно подготовленных исследователей
в педагогике заключается в случайном выборе «классов» для
участия и эксперименте и последующем анализе данных так,
словно «учащиеся» были выбраны случайно. Если класс А вы-
бран для проверки метода преподавания А, а класс В—для
195
метода В, то, несомненно, выбор «учащихся» не является
независимым. Если Джон и Джордж находятся в клас-
се А, то оба должны воспринимать метод А. Любой анализ, при
котором рассматриваются 30 учащихся в каждом классе и пред-
полагается, что они составили 60 отдельных наблюдений, ве-
роятно, неправилен, поскольку два класса представляют собой
именно две «группы» учащихся.
В заключение этого параграфа приведем другую формули-
ровку определения простого случайного выбора. Попытайтесь
убедиться в том, что эта формулировка эквивалентна определе-
нию, приведенному выше.
Если выборка из п наблюдений является случайной, то неза-
висимо от того, какими были первые выборов, вероятность
выбора любого возможного наблюдения при (п, + /) равна
Щп. — «0-
10,7. Случайные переменные
Случайная переменная определяется через два понятия, одно
из которых уже вводилось: выборочного пространства и функ-
ции. Мы уже обсуждали смысл выборочного пространства. Оно
представляет собой совокупность (конечную или бесконечную)
предметов или событий. Функцией называется любое множество
упорядоченных пар элементов, причем не существует 2 пар, имею-
щих одинаковый первый элемент. Как вы можете заметить, рпре-
деление функции является совсем общим: если {(а, 1), (Ь-, 2},
(с, 3)} — функция, то функция и {(Джон, Алиса), (Джо, Мэри),
(Тэд, Шерон), (Джим, Джойс)}. Функция возникает тогда, ко-
гда мы устанавливаем правило, связывающее первый эле-
мент с каждым элементом некоторого множества. Мы получаем
функцию, когда устанавливаем связь каждого лида с его возра-
стом: (Мистер Джонс, 37), (Марк Смит, 5)..........Случайная пе-
ременная есть такая функция, что все первые элементы являются
точками выборочного пространства. Предыдущий пример дает
случайную переменную. Выборочное пространство — все люди;
каждый человек связан со своим возрастом.
Ниже приводятся примеры случайных переменных (наиболее
интересными для статистиков и для нас являются те, у которых
элементы выборочного пространства связаны с числами):
1. Выборочное пространство: бросание монеты («орлы», «решки»).
Случайная переменная X
I-й элемент
2-й элемент
«орлы»
«решки»
196
2. Выборочное пространство- 6 различных исходов бросания играль-
ной кости.
Случайная переменная Y
/-й элемент 2-й элемент
грань с одной точкой 1
грань с двумя точками 2
грань с шестью точками 6
3 Выборочное пространство, бушель апельсинов,
Случайная переменная Z
1-й элемент 2-й элемент (sec апельсина в унциях)
Апельсин # 5 3
Апельсин #2 5
Апельсин # 3 2
Позже мы будем говорить о «значении случайной перемен-
ной Z». Если Z— случайная переменная, как определено выше
в (3), то Z подразумевает величину, вес в унциях для каждого
элемента выборочного пространства, каждого апельсина. Для
первого апельсина значение Z == 3.
В этой главе вы уже встречались со случайной переменной, но
не делали попыток обратить на нее внимание. Биномиальное
распределение — это распределение случайной переменной, Вы-
борочное пространство — совокупность точек, являющихся раз-
личными исходами п биномиальных испытаний. Случайная пе-
ременная X принимает значения 0, 1,2.......ггв соответствии
с числом «удач», которые имеют место в п испытаниях. Если мо-
нета подбрасывается 4 раза и появление «орлов» называется
«удачей», то X имеет значение 3 для события 0. Р, 0, 0, так как
наблюдались 3 «удачи».
Выборочное пространство может представляться концепту-
ально сложным. Например, ребенок должен прочитать заданную
страницу хрестоматии. Ему следует сделать это много раз;
каждое отдельное чтение страницы представляет собой точку
в выборочном пространстве всех чтений. Случайную перемен-
ную X можно определить на этом пространстве, связывая с каж-
дым актом чтения необходимое для него время.
197
10.8. Виды случайных переменных
Статистик считает полезным различать дискретные и непре-
рывные случайные переменные. Пока мы не испытывали необ-
ходимости в использовании этого различия; оно становится по-
лезным, когда определяются и совершаются некоторыеонерации
над случайными переменными.
Различие между дискретным и непрерывным относится к при-
роде чисел, которые являются вторыми элементами функции
случайной переменной с точками из выборочного пространства.
Дискретная случайная переменная такова, что может принимать
только определенные значения на оси действительных чисел. Мы
можем рассматривать все действительные числа как точки на
осн, которая простирается от —со до -f-oo, как на рис. 10.7. Ди-
*- -2-1012 +со->
Рис. 10.7. Ось действительных чисел.
скретная случайная переменная может принимать только неко-
торые значения между двумя точка,ми такой оси Примером ди-
скретной случайной переменной служит X в (1) предыдущего
§ 10.7. Она может принимать значения только 0 и 1. X не может
быть равным 1/2. Непрерывной случайной переменной назы-
вается переменная, которая может принимать любые значения
между двумя точками на оси действительных чисел. Примером
непрерывной переменной является возраст. Значением случай-
ной переменной «возраст» может быть 5 лет, 6 месяцев, 4 дня,
1! часов, 14 минут, 6,132... секунды. Человек, которому только
что исполнилось 10 лет. имел возраст, равный любому возмож-
ному числу на осн от 0 до 10 лет.
Какие из перечисленных случайных переменных являются
дискретными, а какие — непрерывными?
1. Число «орлон» при 6 бросаниях монеты.
2. Время, требующееся для решения задачи формирования'
понятия.
3. Высота столбика ртути в барометре.
4. Максимальная дневная температура воздуха.
5. Число зубов у младенца.
6. Количество денег в кармане президента корпорации.
Переменные 1.5 и 6 дискретны; другие — непрерывны.
Необходимо различать значения, которые случайная пере-
менная может принимать теоретически, и значения, которые-
обеспечиваются измерительными средствами. Такая, например,
переменная, как длина, теоретически может быть любым воз-
можным действительным числом, скажем, между 0 см и 5 см.
Так. из аналитической геометрии известно, что гипотенуза пра-
вильного треугольника, обе стороны которого равны 1 см. имеет
длину -\/2см. Число д/2 представляет собой бесконечное число,.
198
первые несколько цифр которого есть 1,414... Никакое физиче-
ское измерение не обеспечит величину, точно равную л/2 . Хотя
«длина» теоретически является непрерывной случайной перемен-
ной, любое ее измерение дает дискретные значения. Тем не ме-
нее целесообразно сохранять различие между дискретным и не-
прерывным, помня в то же время, что физическое измерение
обеспечивает получение дискретных величин.
10.9. Вероятность как плошадь
Вероятности наблюдаемых значений непрерывных перемен-
ных, например роста, удобно изображать с помощью математи-
ческих кривых, известных как распределения вероятностей.
Пусть мы имеем непрерывную случайную переменную X, кото-
рая может принимать значения от 0 до 10. Например, X может
быть временем, требующимся людям для решения некоторой
головоломки. Они могут решить ее сразу или в течение 10 мин,
по не более. Пусть промежуток времени, необходимый для ре-
Рис. 10.8. Функция плотности вероятности переменной X — времени,
требующегося для решения головоломки.
9 10 X
шения задачи, известен для огромного числа разных людей.
Тогда можно построить график, где «время решения» изобра-
жено в зависимости от доли людей, для которых необходимо
это время (см. рис. 10.8).
Доля людей, которым для решения головоломки требуется
время от 2 до 4 мин, может рассматриваться как вероятность
того, что человеку, случайно выбранному из совокупности, для
решения головоломки потребуется от 2 до 4 мин. Площадь под
кривой рис. 10.8 равна 1, так что площадь под кривой между
любыми двумя точками Xi и Х2 представляет собой вероятность
того, что случайно выбранному человеку для решения голово-
ломки потребуется время между Xt и Хц мин. Вероятность того,
что случайно выбранный человек решает головоломку более
5,3 мин, равна заштрихованной площади на рис. 10.8. Какая же
площадь соответствует вероятности того, что для случайно вы-
бранного человека потребуется меньше чем 0,5 мин? (Теоре-
тически вероятность времени, равного точно, скажем, 4 мин,
равна нулю, поскольку не существует площади 4 с самим со-
199
бой.) Если бы площадь под кривой рис. 10.8 между значениями
6 и 10 составила 0,07, то в группе из 100 случайно выбранных
людей мы могли бы ожидать появления приблизительно 7 чело-
век, которым для решения головоломки требуется от 6 до 10 мин.
Статистик часто изображает значения, которые может при-
нимать непрерывная случайная переменная таким образом,что
площадь между любыми двумя значениями переменной равна
вероятности того, что переменная будет принимать значение, ле-
жащее между этими двумя величинами. Результирующий гра-
фик называется функцией плотности вероятности. График часто
изображают как математическую функцию таким образом, что
Рас. 10.9. Функция плот-
ности вероятности пере-
менной X, принимающей
все возможные значешя
между 0 )! 2 с равной
вероятностью.
ординату Р(Х) можно определить путем подстановки любого-
значения случайной переменной X. Например, допустим, что X—
случайная переменная, которая может с равной вероятностью
иметь любое значение между 0 и 2- Если мы принимаем, что
Р(Х)= 1/2 для всех X, то график (рис. 10.9) будет представлять
функцию плотности вероятности X.
Площадь под кривой, например, прямоугольника на рис. 10.9,
точно равна 1(0,5-2,0). Заштрихованная площадь—вероят-
ность того, что X принимает значение между 0 и 1. Чему же
равна эта вероятность?
10.10. Ожидания и моменты
Моменты — это характеристики распределений в терминах
ожидании. Сначала мы рассмотрим определение математиче-
ского ожидания случайной переменной X.
Определение: Если X—дискретная случайная переменная, при-
нимающая значения Xlt Х3, .... %п с вероятно-
стями pi,Pz, ..., рп, то математическое ожида-
ние X, обозначаемое Е(Х), определяется как
Е (X) = ptXf + р2Х2 + ... + РпХп = PjXj,
где pt + р3 + ... + рп ~ 1 -
Обратите внимание, как это напоминает формулу для вычис-
ления среднего по сгруппированным данным:
х-=(Ж + (т)*>+ ••• +(#)*-
200
Однако ожидания определены только для бесконечных гене-
ральных совокупностей, а не для выборок.
Другим символом, обозначающим ожидание X, является р,
греческая буква «мю». р = Е(Х), среднему бесконечной гене-
ральной совокупности X.
Термины «ожидание» и «ожидаемое значение» — синонимы.
Ниже приведены примеры математических ожиданий:
1. Пусть X — случайная переменная, имеющая 6 возможных
значений, 1, 2...6. События в выборочном пространстве мо-
х ио представить как 6 граней игральной кости.
Будем считать, что с каждым значением X связана вероят-
ность 1/6. Какова величина Е(Х)?
= ' +|-2 + |-3 + |.4+4.5 + |-6 =
= у(1+2+ . +6) = -Д = 3,5,
середина между минимальным значением, 1, и максимальным
значением, 6:
Т=-3,5.
В этом примере Е(Х) — р = 21/6 ~ 3,5.
2 У специального монетного автомата имеются пазы: 0,00,
0,50. 1.00 и 2,00 доллара. Вероятности, связанные с каждым из
этих вариантов, составляют соответственно 0,80, 0,15, 0,04 и 0,01.
Определите случайную переменную X, которая принимает 4 зна-
чения: 0; 50; 100 и 200 центов с вероятностями 0,80, 0,15, 0,04 и
0,01 Какова величина Е(Х)?
д = Е(Х) = 0,80(0) 4- 0,15 (50) + 0,04 (100) +
4- 0,01 (200) = О 4- 7,5 4- 4,0 4~ 2,0 = 13,5.
Если каждое испытание монетного автомата стоит 0,25 дол-
лара. хотелось бы вам сыграть?
3. Пусть X будет случайной переменной, соответствующей
числу «орлов» в 4 бросаниях правильной монеты. X может при-
нимать значения 0, 1, 2, 3 и 4.
Найдите Е(Х).
Сначала мы должны вычислить вероятности того, что X при-
мет каждое из значений от 0 до 4, то есть вероятности того, что
яри 4 бросаниях будет наблюдаться: 0 «орлов», .... 4 «орла».
Вероятность (X _ 0) = Q (1)" (±)' = . Л - -Д
Вероятность (X = 1) = ( । ) (1)' (1)’ = А- = ^ _ 1.
201
Если вы забыли, как вычислить оставшиеся 3 вероятности,
вернитесь к соответствующим разделам этой главы. Затем по-
кажите, что Е(Х) = ц — 2.
Фактически нет необходимости вычислять среднее бино-
миального распределения так длинно, ибо оно равно просто пр,
где п — число испытаний, а р— вероятность в каждом испыта-
нии. Здесь пр 4(1/2)== 2, что соответствует результату, вы-
численному по формуле
S Р/Х/-
Если X — непрерывная переменная, то форма ее распределе-
ния описывается алгебраической функцией. Как мы видели ра-
нее, если X—непрерывна, то мы не можем приписать вероят-
ность одному значению X Вместо этого мы делаем утверждения
Рис. 10.10. Распределение вероятностей X.
относительно вероятности того, что X лежит в каком-то интер-
вале. По этим причинам определение, данное выше для Е(Х),
нельзя применить к непрерывной случайной переменной- К сожа-
лению для тех, кто не знает вычислительных методов, оказы-
вается, что не существует разумного способа определения ожи-
дания непрерывной переменной без обращения к интегрирова-
нию. Мы попытаемся эвристически описать понятие Е(Х) для
случая, когда X — непрерывен, поэтому те, кто незнаком с вы-
числительными методами, не будут испытывать затруднений в.
дальнейшем.
Пусть X — непрерывная случайная переменная, а распреде-
ление вероятностей X подобно распределению рис. 10.10. Суще-
ствует алгебраическое правило, которое дает ординату кривой’
рис. 10.10 для любого значения X. Площадь под кривой равна 1.
Вероятность того, что X примет значение, например, между 2
и 3, равна площади под кривой между этими 2 точками.
Определение; Математическое ожидание непрерывной случай-
ной переменной X есть сумма произведений, обра-
зованных путем умножения каждого значения, ко-
торое может принимать X, на ординату кривой
функции плотности вероятности над этим значе-
нием.
Поскольку X может принимать бесконечное множество зна-
чений, вас может удивить, как практически возможно умножить
каждое отдельное значение X иа ординату кривой при данном
X для определения ожидания. Это задача, которая возвращает
202
нас к вычислениям интегралов. Мы просим принять на веру то,
что это можно выполнить точным, но несколько окольным спо-
собом, путем «интегрирования».
Ожидание непрерывной случайной переменной X обозначается
Е(Х) или ц, так же как и ожидание дискретной переменной.
Моменты
Моменты — это величины, описывающие распределения пе-
ременных.
Определение: Первый момент случайной переменной X есть ц,
ожидание X.
Первый момент называется также «генеральным средним».
Первый момент X, и, описывает общее положение распределения
вдоль осн. Для некоторых распределений (наиболее часто встре-
чающихся на практике) Е(Х), или ц, является надежным указа-
телем центральной точки, вокруг которой имеют тенденцию груп-
пироваться значения X. Предположим, что X и У представляют
Рис. 10.11. Распределения X и Y, где 5(Х)= 10,
а Е (У) = 5.
собой нормально распределенные случайные переменные, но
Е(Х) — = 10, а Е(У) == = 5. Тогда мы знаем, что распре-
деление X находится на числовой оси правее распределения У,
как показано на рис. 10.11.
Определение: Второй момент случайной переменной X есть Е (X2).
Ет = р,Х‘ + р,Х‘+ ... +pJi,
если X — дискретен.
Мы немного получаем непосредственно от второго момента.
Однако представление о «втором моменте» используется для
определения очень важного понятия.
Определение: Дисперсия, или второй момент относительно сред-
него, случайной переменной X есть Е(Х— ц)2.
Если X — дискретная переменная, то
£и-и)2 = р](Х1-р)г+рг(Хэ-р}2+ ... + Рп(Ха - И)2.
Величина Е(Х— ц)2 обозначается как о2 (читается «сигма
в квадрате»).
Положительное значение квадратного корня из дисперсии,
•а, называется стандартным отклонением, о2 описывает рассея-
ние, размах, неоднородность или разброс случайной перемен-
ной X.
203
Пусть X и У — две нормально распределенные случайные пе-
ременные с одинаковым средним, р = 0, но с о2, равной 1 для X
и 4 для У. На рис. 10.12 показаны эти 2 распределения- Обра-
тите внимание на то, что оба распределения рис, 10.11 имели
одинаковые дисперсии.
Рис. 10.12. Распределения X и У при р «О для
обеих переменных, аа! = | для X и ст2 = 4 для У.
Всякое распределение имеет гораздо больше моментов, ко мы
будем пользоваться только первым, р, и вторым моментом отно-
сительно среднего, а2. Если вы хотите расширить свои знания
по этой теме, смотрите работу Эдвардса (1964).
Задачи и упражнения
I, Пусть колода из 52 игральных карт задает выборочное
пространство S. Определите вероятности каждого из следующих
событий:
а. А—событие, состоящее в том, что «вынутая карта — пи-
ковой маст|1». Найдите Р(А).
б. А —событие «вынутая карта — туз треф».
Найдите Р(4).
в. А — событие «карта бубновая», а В — событие «карта пи-
ковая». Найдите P(Af}B).
2. Университетская баскетбольная команда состоит из
13 игроков. Сколько возможных «стартовых пятерок» — пяти
игроков, начинающих игру, — мог бы создать тренер такой
команды?
3. Убедитесь в том, что
Вообще, Д(") = 2"'.
4. Постройте ожидаемое распределение результатов испыта-
ний X, которое было бы получено для 256 абсолютно невеже-
ственных экзаменующихся, которые случайно угадывают ответы
на 4 вопроса с 4 возможными ответами.
204
5, В генеральной -совокупности значения IQ Стенфорда —
Бине распределены приблизительно нормально со средним 100
и стандартным отклонением 16. С помощью таблиц определите
следующие вероятности с точностью до двух десятых:
а. Вероятность того, что случайно выбранный человек будет
иметь IQ между 80 и 120.
б. Вероятность того, что случайно выбранный человек будет
иметь IQ выше 140,
в. Вероятность того, что 3 независимо н случайно выбранных
человека будут иметь значения IQ выше 92.
6. Переменная X принимает значения О, I, 2, 3 и 4 с вероят-
ностями 0, 2/5, 1/5, l/5 и 1/5 соответственно. Каково значение
Е (X), ожидания X?
и
ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ,
ИСПОЛЬЗУЕМЫЕ
В СТАТИСТИЧЕСКИХ ВЫВОДАХ
11.1 Введение
Часть «рабочих инструментов» статистического вывода обра-
зует группа теоретических распределений некоторых спе-
циальных переменных. В этом разделе мы исследуем 4 таких
распределения: нормальное, которое было описано в главе 6;
распределение xu-квадрат; /-распределение и F-распределение.
11.2. Нормальное распределение
В главе 6 мы узнали, что нормальное распределение — это
математическая кривая специального вида. График нормаль-
ного распределения симметричен относительно среднего, ц, рас-
пределение является унимодальным, имеет эксцесс 3,0 н т. д.
Нормальное распределение—в действительности их суще-
ствует множество, для каждого сочетания значений ц и а—-
имеет большое значение в теории статистического вывода. Мно-
гие из приемов статистического вывода основаны на предполо-
жении о том, что распределение частот значений переменной в
генеральной совокупности адекватно описывается нормальным
распределением с некоторыми значениями среднего и стандарт-
ного отклонения. В этом параграфе будет показано, что другие
теоретические распределения также опираются на нормальное
распределение.
Примат нормального распределения можно отнести за счет
трех фактов, одного эмпирического и двух математических. Во-
первых, оказывается, что нормальное распределение является
довольно точным представлением частот распределения значе-
ний при действии большого числа различных переменных.
В § 6.G мы видели, что нормальное распределение было хорошим
представлением полигона частот роста 8585 взрослых людей,
родившихся в Англии в XIX в., и распределения результатов
теста IQ Стенфорда — Вине.
205
Во-вторых, имеется обстоятельство математического порядка:
благодаря усреднению отдельных значений, которые распреде-
лены не нормально, во многих случаях распределение в среднем
оказывается приблизительно нормальным. Это обстоятельство,
сформулированное и доказанное как «центральная предельная
теорема» математической статистики, находит большое приме-
нение в приемах современного статистического вывода, хотя и
не играет той решающей роли, которую сыграло однажды
(см § 12.3).
В-третьих, нормальное распределение удобно в математиче-
ском отношении. Его наиболее удобной особенностью является
то, что при получении выборок, в которых и и а оцениваются
известным путем, две оценки, полученные для повторных выбо-
рок, независимы.
11.3. Распределение хи-квадрат
Представьте себе огромную генеральную совокупность нор-
мально распределенных значений со средним 0 и стандартным
отклонением I. Предположим, что из этой совокупности случай-
но выбрано одно значение Xi и построено стандартизованное
значение z = (Xl — 0)/1. Для повторных выборов значений X z
будет иметь нормальное распределение с нулевым средним и
единичным стандартным отклонением. Обозначим квадрат z
следующим образом:
х! = г2, (11.1)
то есть квадрат стандартизованной оценки, выбранной из нор-
мального распределения, символически изображается посред-
ством Хр где верхний показатель 2 говорит о том, что имеет
место возведение в квадрат, а нижний индекс 1 свидетельствует
о том, что для получения хг «комбинировалась» только одна
оценка. Мы можем представить себе неограниченное число по-
вторений процесса получения величины х2- Каждый раз новое
значение X будет случайно выбранным, стандартизованным н
квадратичным. Мы можем построить полигон частот значении
X2, полученных таким образом. Если после регистрации многих
тысяч значений х? выполнить сглаживание полигона частот и по-
добрать такой масштаб ординаты, чтобы площадь под кривой
была равна 1, то получится график распределения хи-квад-
рат с одной степенью свободы. График этого распределения при-
веден на рис. 11.1.
Математическая кривая, изображенная на рис. 11.1 и опи-
сывающая распределение xj. имеет сложную формулу, которую
мы не будем изучать. (Если вас интересует эта формула, см.
Graybill, 1961, р. 31.) Мы обозначим кривую на рис. Ill —
207
у}. Кривая называется по греческой букве у, используемой для
ее обозначения. (Она была выведена Пирсоном в 1900 г.)
Площадь под кривой для х? положена равной 1, так что х,
является распределением вероятностей; например, вероятность
получения значения между 0,5 и 2,5 равна площади под кри-
вой между 0,5 и 2,5. Из рис. 11.1 мы видим, что 0,30, или 30%,
площади под кривой лежит справа от 1,07. Таким образом, нам
известно, что вероятность получения значения гг=Хр превы-
шающего 1,07, составляет 0,30. Другими словами, 30% значе-
ний z, случайно выбранных из нормального распределения, бу-
Рис. 11.1. Кривая распределения хи-ква1рат
с одной степенью свободы. (Заштрихованная пло-
щадь охватывает 30% площади под кривой.)
дет иметь квадраты, превосходящие 1,07. Это эквивалентно
утверждению, что 70-й процентиль в распределении хи-квадрат
с одной степенью свободы равен 1,07. Мы запишем так:
где у? обозначает распределение хи-квадрат с одной степенью
свободы, а 0,70 указывает на 70-й процентиль этого распреде-
ления.
Теперь мы рассмотрим распределение хи-квадрат с двумя
степенями свободы, xf. Вернемся к исходному нормальному
распределению Л'. Вместо выбора только одного значения X
выбираем случайно и независимо два значения. Нормализуйте
каждое из этих значений, вычитая из них ц и деля разность на о.
Назовите первое (в порядке выбора, а не по величине) норма-
лизованное значение гь а второе — z2. Теперь возведите в квад-
рат н сложите оба г для получения величины
x, = (i^y + (izJiy = 2. + 4 (11.2)
20Я
Процесс построения х® можно повторять тысячи раз с но-
выми парами значений г. Полигон частот этих значений х! мо-
жно представить, сгладить и преобразовать так, чтобы площадь
под кривой равнялась I. В итоге получилась бы кривая х? рзс-
пределения хи-квадрат с двумя
степенями свободы. На рис. 11.2
представлена кривая х?-
Распределение хи-квадрат
с п степенями свободы, хл
Переменная хи-квадрат с п
степенями свободы, х^,образуется
в результате сложения квадратов
п независимых значений из нор-
мального распределения:
X* = z* + z* + +гп- Ш-3)
При большом числе этих зна-
чений Хп< полученных по отдель-
ным группам п значений z, поли-
гон их частот будет иметь форму,
аналогичную форме математиче-
ской кривой х’. На рис. 11.3 по-
казаны кривые х1 и Хю-
Площадь под каждой кривой
площади под Хщ лежит за точно?
вест но, что вероятность того, что с
рис. 11.3 равна I. Половина
9,34. Следовательно, нам 113-
умма квадратов 10 значений г,
Заштрихованная площаЭь
поЗ кривой составляет
0,50, а под кривой xl
приблизительно 0,15
Рис. 11.3. Кривые Хз » Xio-
случайно выбранных из нормального распределения, превысит
9,34, равна 0,50. Аналогично 0ЮХю = 9,34, медиане распределе-
ния хн-квадрат с 10 степенями свободы.
Для любого целого п (1, 2, 3, ...) существует свое распреде-
ление хи-квадрат. Свойства кривой х£ зависят от п.
209
Следующие факты дают неполное описание семейства рас-
пределений хи-квадрат:
1. Среднее значение распределения хи-квадрат с п степе-
нями свободы равно п.
2. Мода находится в точке л —2 для п = 2 или больше.
3. Стандартное отклонение х„ равно -х/2п.
4. Асимметрия у* равна д/8/й. Следовательно, любое распре-
деление хи-квадрат имеет положительный скос, но для боль-
шого п асимметрия незначительна.
5. С ростом п х* стремится к нормальному распределению со
средним п и стандартным отклонением д/2«-
Важную теорему, касающуюся комбинирования переменных
с хи-квадрат распределением, можно сформулировать так:
Если хгп, имеет распределение хи-квадрат с числом сте-
пеней свободы п, и если %д, имеет хи-квадрат распреде-
ление с числом степеней свободы и не зависит от $.
то х^-Ь'Хд, имеет распределение хи-квадрат с числом
степеней свободы 4- «...
р-й процентиль в распределении хи-квадрат с п степенями
свободы обозначается Рх,- Процентили хи-квадрат распределе-
ния играют решающую роль в методах статистического вывода,
особенно в приложении к данным в шкале наименований Раз-
личные процентили распределений хи-квадрат от п = 1 до
п — 30 приводятся в таблицах. Рассмотрим пример использо-
вания таблиц.
Предположим, требуется найти 50-й процентиль распределе-
ния хи-квадрат с 4 степенями свободы, то есть о150х|- Во-первых,
находим строку, помеченную цифрой 4. Во-вторых, находим
столбец, озаглавленный «50-й процентиль», он расположен
близко к центру таблицы. На пересечении этих строки и столб-
ца видим число 3,36. Это и есть величина 0i50x|, медиана рас-
пределения хи-квадрат с 4 степенями свободы,
11.4. F — распределение
Представьте себе, что переменная хи-квадрат с 5 степенями
свободы Xs образуется из zj 4- ... 4--Ф Теперь предположим,
что вторая независимая переменная хи-квадрат с 10 степенями
свободы xfn образуется из выборочных значений нормирован-
ного нормального распределения путем возведения в квадрат и
сложения 10 квадратов. Случайная величина, называемая F-oi-
ношением, с 5 и 10 степенями свободы получается следующим
образом;
210
При многократном определении значений и х^0, делении
каждого на соответствующие степени свободы и образовании
отношения F5, io можно было бы получить распределение F3. (0.
Из математической статистики известно, что распределение F3, ю
есть F-распределевие с 5 степенями свободы для числителя и
10 степенями свободы для знаменателя, ^-распределение
с 5 и 10 степенями свободы имеет положительный эксцесс, сред-
нее (10)/(10 — 2) = 1,25 и медиану меньше 1. Вследствие воз-
ведения в квадрат возможны только положительные значения
Fs.ioJ следовательно, вся площадь под кривой распределения F5,)0
располагается справа от нуля. Площадь между любыми 2 зна-
чениями F3. ю равна вероятности получения F-отношения между
этими 2 значениями. Позже нам будут полезны некоторые про-
центили F-распределений. Простоты ради они уже давно табу-
лированы. Нам известно, например, что 90-й процентиль F-pac-
пределения с 5 и 10 степенями свободы, равен 2,52,
то есть вероятность получить значение F3, i0 между 0 и 2,52
равна 0,90. 0.95^5, ю = 3,35, а 0.99F5, ю = 5,64.
Существуют разные F-распределения для каждого F-отноше-
ння с заданным сочетанием степеней свободы в числителе и
знаменателе. Вообще, если две независимые переменные хи-
квадрат, одна из которых с п> степенями свободы, а дру-
гая — х2п с п2 степенями свободы, комбинируются в
то Fn,. п, имеют F-распределенне с числом степеней свободы
/11 и «2- Такое F-раснределенне с щ степенями свободы для
числителя и п2 степенями свободы для знаменателя обладает
следующими свойствами:
1. Положительной асимметрией.
2. Унимодальностью.
211
3. Имеет медиану, равную 1 или меньше.
4. Имеет среднее, равное п2/{п2— 2) для п2 3.
F-распределения с 4 и 4 степенями свободы и 4 и 25 сте-
пеням» свободы приводятся на рис. 11.4.
Процентили выше 50-го в распределении Fn„ п, связаны с про-
центилями ниже 50-го следующим образом:
Ш-6)
Например, пятый процентиль распределения Fjo.s равен
Верхние нроиеигвльные точки в F-распределениях прота-
булировавы для многих значений п, и п2. Столбцы таблиц соот-
ветствуют значениям /ь; строки — значениям п2.
11.5. /-распределение
Представьте себе, что у вас под рукой есть нормированное
нормальное распределение и распределение хи-квадрат с 10 сте-
пенями свободы. Из каждою распределения случайно выбрано
одно наблюдение: г и х^. Затем получено отношение:
V*Wi0
Ш-7)
Величина /щ в уравнении (Ц.7)— это наблюдение из /-рас-
пределения с 10 степенями свободы. Другими словами, если
процесс случайного выбора одного наблюдения из нормирован-
ного нормального распределения и из х2о и образования /10 =
“z/д/Хю/Ю повторялся бы бесконечно, то значения /10 дали
бы /-распределение с 10 степенями свободы.
/•распределение с 10 степенями свободы описывается сим-
метричной унимодальной кривой. Среднее распределения равно
нулю: стандартное отклонение несколько больше единицы, стре-
мится к единице с ростом числа степеней свободы. Распределе-
ние имеет эксцесс, несколько превышающий эксцесс нормаль-
ного распределения, то есть больше трех; следовательно, оно
более островершинно и имеет большую площадь на крайних
«хвостах» распределения по сравнению с нормальным распре-
делением.
Как и в случаях х2' и ^-распределений, существует се-
мейство /-распределений. Для каждого числа степеней сво-
боды хи-квадрат переменной в знаменателе ур. (Н.7) получает-
212
ся свое /-распределение. Если хи-квадраг переменная входят в
знаменатель с 5 степенями свободы, то
имеет /-распределение с 5 степенями свободы. Вообще, если г
имеет нормированное нормальное распределение, а х,— хи*
квадрат переменная с п степенями свободы, не зависящая от г,
то
Vxn/n
(11.8)
имеет /-распределение с п степенями свободы.
Все /-распределения описываются симметричными, унимо-
дальными кривыми со средним 0. Дисперсия /-распределения
с п степенями свободы равна п/(п — 2). Все они имеют не-
сколько увеличенный эксцесс. С ростом п распределение /п на-
чинает во многом напоминать нормальное распределение. Ко-
гда п бесконечно велико, что теоретически возможно, но прак-
тически неосуществимо, /-распределение совпадет с нормаль-
ным. /-распределения со степенями свободы 1, 5 и 25 приво-
дятся вместе с нормальным распределением на рис. 11.5. В ходе
последующих обсуждений статистических выводов будут исполь-
зоваться некоторые процентильные точки /-распределения,
р-й процентиль /-распределения с 10 степенями свободы будет
обозначаться р/щ. Наиболее часто применяемые процентили
/•распределений приводятся в таблицах. Там мы увидим, на-
пример, что 95-й процентиль /-распределения с 10 степенями
свободы, то есть равен 1,812.
В таблицах обычно рассматриваются только верхние процен-
тильные точки /-распределений. Из-за простоты связи нет не-
213
обходимости табулировать еще и нижние точки. Из симметрии
всех /-распределений следует, что
!-А = -Л. Ш-9)
то есть отрицательный р-й процентиль /-распределения с п
степенями свободы равен (!— р) процентилю Этого же рас-
пределения
11.6. Соотношения между нормальным,
хи-квадрат и F-распределениями
/-, х2 и ^-распределения основаны на нормальном, В каж-
дом случае используется выборка из нормального распре-
деления. Например, переменная хи-квадрат образуется путем
суммирования квадратов нормированных нормальных перемен-
ных; в свою очередь, для получения F-переменцых произво-
дится комбинирование хи-квадрат переменных, В этом парагра-
фе нам предстоит выяснить связи между различными семейства-
ми распределений.
Мы уже видели, что /-распределение с бесконечным числом
степеней свободы совпадает с нормальным. Взглянем на квад-
рат /-переменной с п степенями свободы:
(ИЛО)
В числителе уравнения (11.10) мы находим квадрат нормиро-
ванной нормальной переменной, деленной на 1; в знаменателе—
независимую переменную хи-квадрат, деленную на соответствен-
ное число степеней свободы. Пользуясь несколько иной формой
записи, имеем:
Мы узнали, однако, что выражение (11,11) задает F-перемен-
ную с 1 и л степенями свободы. Поэтому квадрат t-переменной
с п степенями свободы — это F-переменная clan степенями
свободы.
Несколько труднее доказать другой интересный факт, кото-
рый мы просто сформулируем так: всякое F-распределение с п
степенями свободы для числителя и числом степеней свободы,
равным бесконечности, для знаменателя эквивалентно распреде-
лению £, деленному на константу п, то есть
1 Доказательство опирается на то, что
214
Все эти результаты представлены на рис. 11.6. Рис. 116 —
перекрестная классификация семейства F-распределений по
степеням свободы (от 1 до оо) числителя и знаменателя. Каж-
дая ячейка рис. 11.6 соответствует /’распределению. Когда
оказывается, что F в ячейке совпадает со специальным случаем
нормального, t или ^-распределений, то символ F-распределе-
ния не пишется.
р-й процентиль ^-распределения аналогичен р-му про-
центилю распределения n(Fn.oo). Однако, если вы возводите в
Степени сЗобоЭы,^, Зля числителя
г.пг
Рис. 11.6. Семейство ^-распределений и их связь
с нормальным, t- и ^-распределениями.
квадрат р-й процентиль в /-распределении с п степенями сво-
боды, то получите 2р—1-процеитиль в распределении Fsn.
Например, 95-й процентиль /„-распределения равен 2(0,95) —
— 1 = 0.90 = 90-му процентилю /„ = Ft. „-распределения. (Это
справедливо, поскольку 5% случаев превышают 95-й про-
центиль в /„-распределении и 5% расположены ниже 5-го про-
центиля. Когда возводится в квадрат величина /. то как верхние
5°/о, так и нижние 5% становятся положительными; отсюда 10%
значений в Fi n переходят границы квадрата o.es/n-).
Задачи и упражнения
1. Заполните следующую таблицу, определяя величину ука-
занного процентиля но таблицам:
215
Распределение Степени свободы Пропен 1 Величина тиль 1 процентиля
а) Нормальное 54-й
б) t 20 97,5
в) Нормальное 90-й
г) 1 120 90-й
д) Хи-квадрат 6 1-й
е) F 4 и 60 99-й
ж} Хи-квадрат 15 99.9
2 Сравните 95-й процентиль F-распределення с числом
степеней свободы 8 и оо с 95-м процентилем распределения
хи-квадрат с 8 степенями свободы, деленным иа 8.
3 Какова вероятность того, что наблюдение, случайно вы-
бранное из распределения хи-квадрат с числом степеней сво-
боды 21, будет превосходить 36. 34?
4. Доказать, что дисперсия ^-распределения с п степенями
свободы составляет п/(п— 2).
12
СТАТИСТИЧЕСКИЙ ВЫВОД: ОЦЕНИВАНИЕ
12.1. Генеральные совокупности и выборки;
параметры и статистики
Задача статистического вывода, существующая в большинстве
научных и технологических исследований, — это прирост знания
о больших классах предметов, лиц или событий по их сравни-
тельно малым классам. Короче, статистический вывод — это рас-
суждение от частного к общему, от явного к неявному. (Вывод
дополняет дедукцию — рассуждение от общего к частному, как,
например, в силлогистическом рассуждении.) Рассуждения ста-
тистического вывода помогают ответить на такие вопросы, как:
«Что мне известно о средней скорости чтения десятилетних де-
тей (большой класс) после того, как было обнаружено, что эго
среднее у 100 таких детей (маленький класс) составляет
84,8 слова в минуту?» Всякая большая (конечная или бесконеч-
ная) коллекция или совокупность предметов, которые мы хотим
исследовать или относительно которых мы собираемся делать
выводы, называется генеральной совокупностью. Термин гене-
ральная совокупность приобретает подлинный смысл в сочета-
нии с определением выборки из совокупности. Выборка — это
часть или подмножество совокупности. Вообще, выборка из со-
вокупности производится специально, чтобы иметь возможность
изучить свойства совокупности. Теоретически совокупности мо-
гут быть как бесконечно большими, так и конечными. Истинные
бесконечные генеральные совокупности, которые нетрудно вооб-
разить,— нечто искусственное или умозрительное: собрание всех
положительных чисел, всех положительных значений длины
стержня, совокупность подбрасываний двух игральных костей,
которые можно бросать до бесконечности. Почти каждая пред-
ставляющая интерес генеральная совокупность физических
предметов—по сравнению с умозрительными возможностями —
конечна: все люди Западного полушария, холодильники, произ-
веденные в Канаде в последней декаде, школьные районы в США.
Конечная генеральная совокупность может быть чрезвычайно
большой, например, пресловутое «число песчинок на земле», то
217
есть 1501; но если процесс подсчета элементов совокупности мыс-
лится осуществимым, то совокупность конечна. Иногда, по не
как правило, в статистическом выводе важно провести границу
между конечными и бесконечными генеральными совокупно-
стями. Однако в статистическом выводе вообще не стоит беспо-
коиться о различии между конечными и бесконечными совокуп-
ностями, когда объем совокупности более чем в 100 раз превы-
шает объем выборки. Если отношение объема генеральной сово-
купности к объему выборки больше 100, методы вывода для ко-
нечных и бесконечных совокупностей дают в сущности одина-
ковые результаты. Принято применять статистические методы,
основанные на бесконечных совокупностях, всякий раз, когда
совокупность разумно велика (содержит несколько сотен или
более элементов), а выборка не составляет ее существенной
доли. Обычно говорят, что генеральная совокупность «факти-
чески бесконечна», когда она велика, но конечна, и для нее
можно использовать статистические методы, предполагающие
бесконечные совокупности. Мы не собираемся обсуждать ме-
тоды статистического вывода, разработанные для «конечных
совокупностей», то есть для небольших совокупностей, или для
случая, когда исследуемая выборка составляет, скажем, 1/100 со-
вокупности. Отличное изложение этих «конечных методов» мо-
жно найти в книге: W. Cochran, Sampling Techniques, 1963.
Измерения, полученные для совокупности объектов, можно
описать способами, которые мы обсуждали в предыдущих гла-
вах. Мы можем вычислить средние, медианы, дисперсии и про-
центили по данным, собранным из совокупности. Значения раз-
личных описательных мер, вычисленных для генеральных сово-
купностей, называются параметрами. Для выборок те же опи-
сательные меры называются статистиками. Параметр описывает
совокупность так же, как статистика — выборку. Принято обо-
значать статистики латинскими буквами, а параметры — грече-
скими, Символ X. принят для выборочного среднего, а греческая
буква р обозначает генеральное среднее. Выборочная дисперсия
обозначается s2; а генеральная о2.
Статистику, вычисленную по выборке, можно рассматривать
как оценку параметра совокупности. Оцениватель— некоторая
функция от значений в выборке, дающая величину, называемую
оценкой-, оценка же дает некоторую информацию о параметре.
Например, выборочное среднее Я. — оцениватель среднего или
среднего значения совокупности.
12.2. Случайный выбор
Выборки и оценки, вычисляемые по ним, дают нам некоторое
представление о характеристиках совокупности- Существует мно-
жество способов извлечения выборки из совокупности. Простой
случайный выбор, который обсуждался в § 10,6, — только один
218
из многих способов, хотя он, оказывается, получил наиболее
широкое применение. Другие разновидности планов выборки мо-
гут быть слишком сложными и приводить к трудоемким мето-
дам оценивания. В нашей книге мы ограничимся простым слу-
чайным выбором. В элементарной статистике настолько принято
говорить только о простых случайных выборках, что мы будем
иногда пользоваться словом «выборка», подразумевая «простую
случайную выборку». Более усложненные плацы выборок, та-
кие, как стратифицированная, групповая и двухстуценча1ая вы-
борка, рассматриваются в статистических учебниках повышен-
ной трудности (Cochran, 1963).
Чтобы служить основой для получения оценок параметров
совокупности, выборка должна быть представительной, репре-
зентативной. Однако требование представительности выдвигает
новую проблему. Как получить представление о том, будет ли
выборка описывать совокупность, пока неизвестны характери-
стики совокупности? А если характеристик» совокупности из-
вестны, то зачем нужна выборка, с помощью которой они дол-
жны быть оценены? Возникает недоумение. Оно рассеивается,
если случайные выборки из совокупности будут реализовывать-
ся многократно, так что в большой серии они представят сово-
купность. Бывает, что некоторые случайные выборки из сово-
купности характеризуют ее не очень полно. Случайный выбор 20
из совокупности всех школьных учителей Калифорнии мог при-
вести— хотя это неправдоподобно — к выявлению 20 препода-
вательниц французского языка. Некоторые случайные выборки
це будут служить хорошим представлением совокупности, дру-
гие— будут. Никто не знает, будет ли извлеченная выборка
представительной. Если она случайна, то можно сказать лишь,
что она представляет совокупность во всех отношениях слу-
чайно.
Важная особенность случайной выборки состоит в том, что
можно определить, каких типов нспредставнтельносгн следует
ожидать в большой серии или в большой группе случайных вы-
борок.
Ход рассуждений в статистическом выводе таков: нахожде-
ние оценки параметра по выборке н последующее определение
того, насколько представительной может быть подобная выборка
для оценивания параметра. Неудивительно, что теория статисти-
ческого вывода основана на предположениях о случайном вы-
боре из совокупностей.
12.3. Идея выборочного распределения
Статистик оценивает представительность, которую следует
ожидать по случайным выборкам, путем исследования выбороч-
ных распределений. Понятие выборочного распределения — осно-
ва целого раздела теории статистического вывода. Говорят, что-
219
статистика или оценка, вычисленная по выборке, обладает не-
которым выборочным распределением. Можете представить себе
процесс извлечения из некоторой генеральной совокупности вы-
борок объема п одной за другой и записи для каждой из них
некоторой оценки, например выборочного среднего X.. Если бы
этот процесс извлечения выборки из совокупности повторялся
тысячи раз, то можно было бы построить распределение частот
тысяч полученных выборочных средних. Построенное распреде-
ление частот имело бы вид выборочного распределения среднего
выборок объема п для совокупности, из которой извлекались
выборки. Если бы полигон частот для данных был представлен
в таком масштабе, чтобы площадь под кривой равнялась 1, то
кривая оказалась бы почти идентичной выборочному распреде-
лению выборочного среднего-
I
Е
0,40
0,30
0,20
....1111.J.IJ
0123456789
Рис. 12.1. Распределение вероятностей в генеральной
совокупности.
Предположим, например, что в некоторой генеральной сово-
купности содержится несколько тысяч элементов и что измерение
любого одного элемента будет обеспечивать число 0, 1, 2, .... 9
с равной вероятностью. Следовательно, случайная переменная X
принимает любое значение из 0, 1, 2, ...,9 с вероятностью 0,|0.
Распределение вероятностей для совокупности имеет форму, по-
казанную на рис. 12.1.
Из этой же генеральной совокупности извлекалось 100 слу-
чайных выборок объемом га = 2. Для каждой выборки вычисля-
лось среднее. Б первой выборке оказались цифры (3, 2), что
дает среднее, равное (3 Ц- 2)/2 = 2,5. Определялись другие99 вы-
борочных средних и все 100 средних были представлены графи-
чески.
Распределение частот 100 выборочных средних приводится
на рис. 12.2. Рис. 12.2 дает нам некоторое представление о том,
каково фактическое выборочное распределение X. для выборок
объема 2 из генеральной совокупности рис. 12.1. График
рис. 12.2 — эмпирическая аппроксимация выборочного распре-
деления X. в этой ситуации.
Вообще, статистик не может полагаться на эмпирические
процедуры (подобные рис. 12.2) при определении выборочного
220
распределения статистической характеристики для ответа на
вопросы типа: «Каково распределение среднего выборок объемам
из нормального распределения?» или «Каково распределение ко-
эффициента корреляции Пирсона для X и У в выборках объе-
ма п из генеральной совокупности, в которой корреляция X и У
равна 0?» Из-за математических трудностей, связанных с выво-
дами большинства выборочных распределений, которыми нам
предстоит пользоваться, мы просто будем приводить результаты
без доказательств.
Одна из основных теорем теории статистического вывода ка-
сается распределения выборочного среднего X. Эта теорема на-
зывается центральной предельной теоремой. Предположим, что
Рис. 12.2. Распределение частот 100 выборочных
средних (п = 2) из генеральной совокупности
рис. 12.1,
выборки извлекаются из бесконечно большой совокупности. Сред-
нее этой совокупности — ц, а дисперсия о2. Из генеральной со-
вокупности берутся случайные выборки объема п. каково рас-
пределение выборочного среднего А*.? Если п «достаточно ве-
лико» (и невозможно внести большую ясность в вопрос об объе-
ме п), то выборочное среднее будет описываться законом, близ-
ким к нормальному. Кроме того, среднее всех выборочных сред-
них будет равно р, среднему генеральной совокупности; а дис-
персия выборочных средних составит величину а2/л, где о2 —
дисперсия совокупности.
Для пояснения центральной предельной теоремы восполь-
зуемся следующим примером. Предположим, что среднее ц со-
вокупности рис. 12.3 равно 15, а дисперсия а2 = 100. Из совокуп-
ности рис, 12.3 извлекаются случайные выборки объемом 100.
Центральная предельная теорема говорит нам, что распределе-
ние средних X. этих выборок будет приблизительно нормальным
со средним 15 и дисперсией о2*/п = 100/100 — 1. Выборочное рас-
пределение X. в этом случае изображено на рис. 12.4.
Сначала может показаться неправдоподобным, что незави-
симо от формы исследуемой совокупности средние «достаточно
221
Поэтому
Каждая переменная Х{ (1=1,2, .... п) имеет дисперсию ог
и не коррелирует с другими п—1 переменными. Поэтому дис-
персия суммы п некоррелированных переменных — сумма дис-
персий переменных, поскольку каждая из п(п —- 1)/2 ковариа-
ций равна 0. Итак,
(4)4, +»У- <12-7’
Поскольку каждая переменная имеет одинаковую диспер-
сию о2, выражение (12.7) можно упростить:
(“)г(о3'{-о2+ ... 4-^)==(1у (па’)=-^.. (12.8)
Дисперсия средних случайных выборок объема п из совокуп-
ности с дисперсией о2 равна о2/п.
Выражение а2/п получило традиционное название дисперсии
ошибки среднего. Положительное значение квадратного корня
из выражения (12.8) дает другое важное понятие — стандарт-
ную ошибку среднего.
ог =а!\'п. (12.9)
Стандартная ошибка среднего, выражение (12.9), представ-
ляет собой стандартное отклонение выборочного распределения
средних бесконечного числа выборок объема п из совокупности
с дисперсией о2. Заметьте, что на рис. 12.3 и 12.4 стандартное
отклонение совокупности, из которой берутся выборки, равною,
а стандартное отклонение выборочного распределения средних
случайных выборок объема 100 из генеральной совокупности
равно 1. Это согласуется с выражением (12.9):
10 .
Or — " == I •
Vioo
Оценивание коэффициента корреляции совокупности служит
другим примером выборочного распределения. Вероятно, в сово-
купности двенадцатилетних детей США переменные «интеллект»
X и «время реакции» Y фактически не коррелированы. Пред-
ставьте себе, что некто предложил всем двенадцатилетним детям
Шкалу интеллекта Векслера для измерения X и проверил время
реакции Y. Для этих измерений можно было бы построить диа-
грамму рассеивания значений X и У и вычислить корреляцию.
Предположим далее, что нормальная двумерная поверхность
(см. § 6.6) оказалась адекватным описанием диаграммы рас-
сеивания X и У. Предположим также, что значение коэффици-
ента корреляции Йирсона, который мы обозначим греческой
буквой р, оказалось 0, то есть р1у = 0. (Поскольку коэффициент
8 Зак. 448 225
корреляции описывает всю совокупность, он является парамет-
ром, а не выборочной статистикой. Следовательно, р — коэффи-
циент корреляции в совокупности, а г — коэффициент корреля-
ции выборки. Из совокупности можно случайно извлечь выборку,
в которую входят 80 детей, и узнать значения X и У- Для этой
выборки можно найти значение rxv, выборочной корреляции
«интеллекта» и «времени реакции». Затем выборку объемом
80 детей можно вернуть в совокупность, Далее, можно извлечь
вторую выборку аналогичного объема, вычислить гху и вернуть
выборку в совокупность. Этот процесс можно повторять беско-
нечно; таким образом могло накопиться большое количество
значений гху для выборок объема, равного 80, из двумерной нор-
/ \ Е(г)=0
! \ о'^»о.я
-f.oo -0,80 -0,60-0,40 -ОД) 0 0,20 0,40 ОфО ОД) 1,00 Г
Рис. !2.6. Теоретическое выборочное распределение г для
случайных выборок объема 8Э из двумеркой нормальной
совокупности, в которой р=0-
мальпой совокупности, в которой = 0. Каким было бы рас-
пределение частот большого массива выборочных коэффициентов
корреляции? Статистик может ответить на этот вопрос, минуя
процесс извлечения тысяч выборок и не вычисляя каждый раз г.
Математически он может показать, что распределение этих зна-
чений г для случайных выборок объема 80 из двумерной нор-
мальной совокупности при р == 0 близко к нормальному распре-
делению с нулевым средним и дисперсией, равной 1/(н—1 ) =
= 1/79. Теоретическое выборочное распределение г для случай-
ных выборок объемом 80 из совокупности с р = 0 приводится
на рис. 12.6.
Стандартное отклонение выборочного распределения г назы-
вается стандартной ошибкой коэффициента корреляции. Оказы-
вается, что только в этом частном случае он равен 0,11. Стан-
дартная ошибка г обозначается <зг.
Приблизительно 68% выборок будут давать значения г ме-
жду -—0,11 и -f-0,11. Около 95% выборок будут иметь значенияг
между —0,22 и +0,22. В большинстве случаев выборки будут
давать величину г от —0,33 до +0,33. Если бы вы исследовали
связь X и У и получили величину г, равную 0,08, по выборке из
80 детей, когда значение р вам неизвестно, то стали бы вы. ка-
тегорически утверждать, что неизвестная величина р не равна
нулю? Вероятно, нет. Если вы захотите измерить часть пло-
щади под кривой рис. 12.6, находящуюся справа от значения
226
г = 0,08, то обнаружите, что около 23% выборок объема 80 из
совокупности, для которой р = 0, будут иметь значения г боль-
шие, чем 0,08. Заметим также, что 23% выборок этого же объе-
ма дадут значения г меньшие, чем —0,08, — иначе говоря, 46%
выборок будут иметь значения г, более отличающиеся от нуля
в том или ином направлении, чем ваше, когда действительно
р = 0; таким образом, вы видите, что ие существует веской при-
чины считать, что г — 0,08 по выборке из 80 делает генеральное
значение р, равное нулю, неправдоподобным. Этот ход рассуж-
дений хорошо соответствует одной теории статистического вы-
вода, которая более подробно будет изучаться несколько позднее.
12.4. Свойства оценок
Несмотря на большую важность статистического оценивания,
до начала XX в. не предпринимались сколько-нибудь серьезные
попытки формализации свойств оценок. Единственной удачной
попыткой была работа сэра Р. Фишера. Именно Фишеру мы
обязаны понятиями состоятельности и относительной эффектив-
ности, с которыми мы встретимся в этом параграфе.
Ранее подчеркивалось, что оценка—это значение статистик!!
для выборки, которая содержит информацию о параметре сово-
купности. Например, выборочное среднее Я. —оценка генераль-
ного среднего ц. Существует аналогия между способами вычис-
ления выборочного среднего и генерального среднего. Логично
считать, что Я. оценивает ц. Однако известны и другие методы
обработки выборочных данных для получения величины, оцени-
вающей ц. Почему же не используется медиана выборки или ее
мода для оценки ц? Разумеется, это принципиально осуществи-
мо; однако мы увидим ниже, что с точки зрения требуемых
свойств оценка X лучше описывает р, чем выборочная медиана
или мода выборки.
В этом разделе мы коснемся также свойств оценок медианы
совокупности, дисперсии (а2), стандартного отклонения (ст) и
коэффициента корреляции (р). Какие методы оценки этих па-
раметров существуют? Можно ли при оценивании некоторого
параметра предпочесть одну оценку всем другим и почему? Мы
подробно проанализируем три свойства оценок.
Несмещенность
Говорят, что оценка при оценивании параметра является
несмещенной, если среднее выборочного распределения оценки
равно величине оцениваемого параметра.
Независимо от характера совокупности, выборочное сред-
нее X. представляет собой несмещенную оценку генерального
среднего р. Заметьте на рис. 12.3 и 12.4, что генеральное среднее
совокупности р= S5 и среднее выборочного распределения так-
227
же равно 15. Это свидетельствует о несмещенности X. как
оценки ц. Если выборки извлекаются из нормального или лю-
бого другого симметричного распределения случайным образом,
то выборочная медиана — также несмещенная оценка генераль-
ного среднего р. Иными словами, среднее медиан бесконечного
числа случайных выборок из нормального распределения рав-
но и, среднему нормального распределения (которое есть, разу-
меется, также его медиана и мода).
Известно много примеров смещенных оценок. Предположим,
мы хотим оценить р, корреляцию между 2 переменными, имею-
щими двумерное нормальное распределение. Допустим, что для
конкретной совокупности р = 0,75. Среднее выборочного распре-
деления коэффициента корреляции выборки г будет меньше 0,75
для любого конечного объема выборки. Таким образом, г, как
правило, является смещенной оценкой р. Но на рис. 12.6 мы ви-
дели, что среднее выборочного распределения г было равно 0
для выборок объема 80 из совокупности, в которой р — 0. Сле-
довательно, г — несмещенная оценка р. Оказывается, г оцени-
вает р несмещенно только тогда, когда р = 0. Если р — любое
значение от —1,00 до +1,00, то в г как оценке р будет наблю-
даться смещение. (Олкин и Пратт, 1958, вывели несмещенную
оценку р. Ее вычисление по выборке довольно трудоемко. Они
построили таблицы для несмещенной оценки коэффициента кор-
реляции генеральной совокупности.)
Хотя в этой книге мы только в первый раз касаемся свой-
ства несмещенности оценок, оно все же оказало влияние на ме-
тоды, использованные для описания вариации в главе 5. В § 5.5
мы выбрали для измерения вариации выборки величину $,=
= S(X/-X.)2/(n- 1).
Более естественным было бы измерение изменчивости путем
простого усреднения квадратов отклонений относительно выбо-
рочного среднего, но вместо этого было решено взять (п—1),
а не п в знаменателе s2. Здесь необходимо тщательно разобрать-
ся в причине подобного выбора. Величина s2 называется не-
смещенной оценкой генеральной дисперсии о2, а2(Хг —Х.)2/я
представляет собой отрицательно смещенную оценку о2. То есть
и приближается к равенству только при п-*-оо.
Предположим, что мы производим случайные выборки из не-
которой совокупности с дисперсией а2 и все время вычисляем $2.
Среднее значительного числа этих выборочных дисперсий точно
определялось бы величиной о2. Следовательно, s2 — несмещен-
ная оценка о2. Если бы S(X, — Х.)2/п определялась для каждой
выборки, то среднее этих величин оказалось бы меньше о2,
а именно [(и—1)/и]а2. Конечно, если бы п был совсем боль-
шим— 100 или больше, — то разность между $2 и S(X<— Х.)2/л
228
была бы незначительной, поскольку величина (п—1)/га прибли-
жалась бы к I. Тем не менее последняя имела бы некоторое не-
большое смешение. Иногда говорят, что — Х.)г1п является
«асимптотически несмещенной» оценкой о2, так как смещение
уменьшается с ростом п.
Предположим, имеется нормальное распределение со средним
р—0 и дисперсией о2 = 100. Если бы из совокупности извлека-
лось бесконечное число случайных выборок объемом п = 6 и
для каждой выборки определялись з2 н 2(Хг— Х.)2/б,то было
бы получено 2 выборочных распределения (рис. 12.7).
Заметьте, что среднее выборочного распределения s2 со-
ставляет 100, величину 6s. В данном случае этим характеризуется
несмещенность з». Среднее выборочного распределения
Рис. 12.7. Выборочные распределения s’kI (Xt—Х.)2/6
для случайных выборок объема 6 из нормального рас-
пределения с дисперсией а8= 100.
-Я.)2/6 равно 83,33. В этом примере смещение в оценку а2
вносилось использованием п вместо п—I в знаменателе выбо-
рочной дисперсии. В данном случае оно довольно велико,
а именно
(п- 1)/л = 5/6.
Вы, вероятно, недоумеваете, каким образом определялось, что
знаменатель выборочной дисперсии должен иметь п — 1, а не
п — 2 или п—3 или п •— -j. Эмпирически не было установлено,
что п— 1 дает несмещенную оценку. Существует несколько спо-
собов математического доказательства того, что — несме-
щенная оценка о2. Алгебраическое доказательство громоздко,
хотя в нем нетрудно разобраться. Мы не будем его здесь приво-
дить. Его можно найти в книге Эдвардса (1964, р. 29—36).
Величина $'с — несмещенная оценка о2. Означает ли это, что
выборочное стандартное отклонение, является несмещенной
оценкой а, стандартного отклонения совокупности? Нет, не озна-
чает. Нелинейное преобразование несмещенной оценки само по
себе не дает несмещенную оценку, так что стандартное откло-
нение выборки — смещенная оценка стандартного отклонения
229
борки s будет приближаться к ст; чем больше выборка, тем s
ближе к а. Менее строго условие состоятельности означает, что
состоятельная оценка параметра вычисляется по выборке так,
что если бы аналогичный расчет выполнялся для всей совокуп-
ности, он дал бы значение параметра. Выборочное среднее — со-
стоятельная оценка р, поскольку если бы выборка превратилась
в совокупность, то X. оказалось бы равным р. (Выборочное сред-
нее-—также несмещенная оценка р.) Требование состоятель-
ности не противоречит здравому смыслу. Трудно найти какие-
либо важные оценки, которые не были бы состоятельны.
Относительная эффективность
Третьим свойством оценок будем считать их эффективность.
«Эффективность» относится к точности оценки параметра; она
имеет отношение к изменчивости оценки от выборки к выборке.
В нескольких предыдущих примерах мы измеряли эту изменчи-
вость (или эффективность), выбирая дисперсию или стандарт-
ное отклонение выборочного распределения статистики. Диспер-
сия ошибки выборочного среднего, о?_ — мера эффективности X.
как оценки р. Дисперсия ошибки выборочного коэффициента
корреляции, ст’ — мера эффективности г как оценки р.
Дисперсия ошибки оценки — одно из наиболее важных ее
свойств. Дисперсия ошибки любой статистики—дисперсия вы-
борочного распределения статистики.
Предположим, мы хотим оценить величину генерального сред-
него какого-нибудь конкретного нормального распределения.
Один из способов оценивания р состоит в определении сред-
него X. для выборки объема п. Однако выборочная медиана Md
также является несмещенной оценкой р. Обе они — состоятель-
ные оценки р. Какую же следует предпочесть? На этот вопрос
можно ответить, рассматривая относительную эффективность
двух оценок. Какая из оценок р — выборочное среднее или вы-
борочная медиана — варьирует меньше от выборки к выборке?
У какой из оценок меньше дисперсия ошибки?
Если дисперсия о2 исследуемой нормальной совокупности рав-
на 50, а объем выборки п — 10, то дисперсия X. для всех пов-
торных случайных выборок будет о2/п = 50/10 == 5. Какова дис-
персия ошибки медианы выборки, ст’^й? Если из нормальной
совокупности со средним р и дисперсией о2 извлекаются одна за
другой тысячи случайных выборок, и для каждой выборки вычис-
ляется медиана Md, то распределение частот этих выборочных
медиан будет нормальным со средним р и дисперсией (1,57) о2/п.
На рис. 12.8 показаны выборочные распределения X. и Md для
выборок объема 10 из нормального распределения с диспер-
сией 50.
Дисперсия ошибки выборочной медианы на рис. 12.8 равна
(!,57)а2/ч = (1,57) • (5) = 7,85. Этот рисунок свидетельствует
231
о том, что выборочная медиана будет изменяться в повторных
выборках больше, чем выборочное среднее. X. — более эффек-
тивная оценка ц, чем Md. В поисках большей точности описания
статистик определяет эффективность Я. по сравнению с Md как
отношение дисперсий их ошибок. В этом примере
относительная эффективность = = pg? = 0,637 = 63,7%,
это значит, что для нормально распределенных измерений неза-
висимо от величины п эффективность медианы на -j меньше
эффективности среднего.
Наша интерпретация коэффициента относительной эффектив-
ности заключается в том, что если для опенки ц используется
Выборочное—/Выборочное
распределение —«Л / распределение
Я j # Md
(бх= 2,24Hz/ \^C*Hd=2’80)
'PS15,'i ' ’ 2o' ' ' ' 25^
P нс. 12.8. Выборочные распределения среднего X.
и медианы Md для случайных выборок объема 10
из нормальной совокупности со средним ц —20
и дисперсией аг = 50-
медиана 100 выборочных наблюдений, то топ же самой степени
точности оценивания можно добиться, извлекая выборку из 64 на-
блюдений и вычисляя X..
Вообще статистики объединяют критерии несмещенности и
эффективности при выборе «нзилучшей» оценки параметра. На-
пример, па роль «паилучшей» оценки ц в нормальной совокуп-
ности могли с полным правом претендовать и выборочное сред-
нее, п медиана, и мода. Статистик прежде всего задал бы сле-
дующий вопрос: «Какие оценки являются несмещенными?»
Этому критерию удовлетворяют все три оценки. Следующим во-
просом, вероя!но, был бы такой: «Какая из опенок наиболее
эффективна?», то есть «Капая оценка обладает минимальной
дисперсией ошибки?» Выборочная мода наименее эффективна,
и мы видели, что медиана менее эффективна, чем выборочное
среднее. Выборочное среднее выигрывает. Действительно, выбо-
рочное среднее выигрывает во всех отношениях. Основная при-
чина того, что для оценки генерального среднего р любой сово-
купности применяется исключительно X., заключается в том, чго
по сравнению с любой другой несмещенной оценкой н оно имеет
наименьшую дисперсию ошибки. Отсюда видно, что свойства не-
смещенности и эффективности одинаково важны.
232
12.5. Интервальное оценивание
Вопросы, которые мы обсуждали до сих пор в этой главе,
относятся к одной области теории оценивания параметров- Эта
•область называется точечным оцениванием, поскольку в ка-
честве оценки параметра мы рассматривали одно значение или
число — точку на оси. Например, из совокупности всех учитель-
ниц младших классов страны для оценивания средней продолжи-
тельности работы можно было бы взять выборку, включающую
100 человек. Для этой выборки X. могло равняться 3,47 лет.
Число 3,47 — единственная точка на числовой оси: таким обра-
зом, получается точечная оценка ц, генерального среднего.
Другой распространенный вид оценивания, основанный на
понятии точечной оценки, называется интервальной оценкой.
Интервальное оценивание — крайне полезный метод теории ста-
тистического вывода. Мы будем постоянно встречаться с ним
в дальнейшем.
Интервальная оценка парамет ра —- это интервал числовой
оси, причем предполагается, что значение параметра лежит
где-то в этом интервале. Например, при извлечении выборки для
•оценки р можно получить интервал (25,91 —38,65), который ме-
жду границами — нижней, 25,91, и верхней,-38,65— содержит,
вероятно, значение р. Вместо вычисления одной точки как оценки
параметра теперь мы определили целую группу смежных точек,
интервал, и одна из этих точек, вероятно, является значением
параметра. Остальную часть этого параграфа мы посвятим из-
ложению механизма построения интервальной оценки парамет-
ра, для которой известна вероятность заключения значения па-
раметра в границах интервала.
Для первого примера интервального оценивания обратимся
к X. как оценке р и вспомним, что говорит нам центральная пре-
дельная теорема о выборочном распределении X. .Мы видели, что
если из совокупности со средним ц и дисперсией о2 берутся слу-
чайные выборки объемом п, то выборочное распределение X. бу-
дет иметь среднее р и дисперсию ог/п и приблизительно описы-
ваться нормальным законом, когда п достаточно велико. Выбо-
рочное распределение X- представлено на рис. 12.9.
11а рис. 12.9 стандартное отклонение выборочного распреде-
ления X., стандартная ошибка среднего, равно ст/Vя - Поскольку
распределение нормально, 68% наблюдений лежит в пределах
одного стандартного отклонения р, то есть 68% выборочных
средних, которые были бы получены при повторных случайных
выборках, находились бы в интервале от р —(o/Vn.) до р+
Ц-(а/д/п).Примерно 95% средних расположено в интервале от
1л — (2ст/д/п) до р + (2ст/Уп), поскольку около 95% площади
под нормальной кривой лежит в пределах двух стандартных от-
клонений среднего. С помощью таблицы нормированного нор-
мального распределения мы можем точно определить, сколько
233
стандартных отклонений надо отложить от ц в каждом направ-
лении, чтобы установить интервал, включающий 80, 90, 99 или-
любой другой процент площади под кривой. Например, из таб-
лиц можно увидеть, что 5% площади под нормальной кривой:
расположено выше оценки z = 1,64, а 5% — ниже опенки г —
— —1,64. Иными словами, 90% площади под нормальной кривой
лежит в пределах 1,64 стандартных отклонений по обе стороны
от среднего ц, то есть внутри диапазона ц± 1,64о. Для рис. 12.9-
это означает, что 90% выборочных средних, полученных при:
повторяющемся случайном выборе, было_бы расположено в ин-
тервале ц —(l,64o’/V'O и ц 4-(1,64а / д/л ). В терминах теории
Рис. 52.9. Выборочное распределение X. для случай-
ных выборок объема п.
вероятностей вероятность того, что случайно извлеченная выбор-
ка будет иметь среднее X., большее, чем ц — (1,64о/д/п), и мень-
шее, чем ц 4-(1,64а/д/л)> составляет 0,90.
Известно, что 90% случайных выборок, которые можно-
извлечь из нормально распределенной совокупности, будут да-
вать выборочные средние на расстоянии 1,64а/д/л или меньше
от ц. Теперь наступает важный этап в рассуждениях, состав-
ляющих основу интервального оценивания. Если 90% значе-
ний X. расположено внутри диапазона 1,64а/л/И от И, то при-
бавление и выч^танне__1,64а/д/а к любому X. дает интервал от
X. — (1,64а/д/п) до X. 4- (1,64а/ Vя). который в 90% случаев
заключает ц в своих границах. Рис. 12.10—попытка описать
соответствующий пример.
Выборочное среднее, полученное в результате извлечена
случайной выборки объема п, находится на расстоянии одного
стандартного отклонения, а/\'п, выше ц. Это не представляется
невероятным, так как перед извлечением выборки вероятность.
234
того, что среднее выборки находилось бы в пределах расстояния
1,64a/V« от И- составляла 0,90. Поскольку конкретное X. на-
ходится в пределах <з1-^п от ц, когда мы прибавляем и отни-
маем 1,64а/Ул от X., получается интервал, в который входит^.
Как велик или мал должен быть X., чтобы р попало внутрь
•области, составляющей 1,64а/Vя единиц от X.? Очевидно, если
X. лежит выше ц + (1,64а/Vя) или ниже р — (1,64а/V'D» то X.
расположено немного дальше от р, чем на расстоянии 1,64а/Vя*
Рис. 12.10. Иллюстрация_случая, когда интервал, уста-
новленный относительно X., содержит р в своих граня-
Рис. 1211. Иллюстрация случая, когда интервал, построен-
ный в окрестности Х^ не содержит ц.
Какова вероятность того, что выборочное среднее будет отстоять
•от р на расстоянии, большем 1,64а/Vя ? Вероятность этого собы-
тия равна 0,10. Это означает, что в 10% случайных выборок, ко-
торые можно взять из совокупности, прибавление 1,64с/л/п. к X.
и вычитание l,64a/V« из X. приведут к образованию интервала,
ле содержащего ц в своих границах. Такой интервал изображен
на рис. 12.11.
Предположим, что теперь мы рассматриваем всю совокуп-
ность средних значений случайных выборок объема п из выше-
235
Если мы хотим найти Z-преобразование величины р, ми
просто подставляем р вместо г в выражение (12.15):
/р=log, Vn^O/fi — Р).
Фактически никто не вычисляет Zr по формуле (12.15),
а пользуется вместо этого таблицей. В таблице величина Zr
дается для значений г от 0 до 4-1,000 с шагом 0,001. Если г
отрицательно, то просто меняем знак. Проверьте, что Zr=0,418
соответствует г = 6,395 и г ——0,775 дает Z, = —1,033 /-пре-
образование г графически представлено на рис. 12.13.
Допустим, мы решаем задачу: построить выборочное рас-
пределение г, извлекая тысячи случайных выборок объема п
Рис. 12.13. Связь г с /-преобразованием Фишера.
каждая из двумерной нормальной совокупности с корреляцией
р и рассчитывая г для каждой. Пусть, однако, вместо построе-
ния распределения частот значений г было построено распреде-
ление частот значений Zr. Как выглядело бы подобное распре-
деление? Выборочное распределение Zr было бы приближенно
нормальным со средним Zp и дисперсией \1(п — 3). Выборочное
распределение имело бы вид распределения рис. 12.14.
/-преобразование Фишера обеспечивает все необходимое
для решения задачу определения доверительных интервалов для
г. Стандартное отклонение Zr всех повторяющихся случайных
выборок равно 1/Vn —3, независимо от значения р, Следова-
тельно, 96% значений Zr, полученных по случайным выборкам,
будет лежать в пределах 1,64 стандартных отклонений — на рас-
стоянии 1,64(1/Vn-_ 3) от Ze, 95% Zr — в пределах
1,96(1 /-у/п — 3) от ZpH т. д. Распределение ZT приблизительно нор-
мально независимо от п. Следовательно, если прибавить и от-
нять некоторую величину, пропорциональную 1/V«“3, от /г,
то будем иметь определенную вероятность попадания 20 в эти
242
•интервалы. Далее описывается другая постановка проблемы.
Поскольку Zr нормально распределена со средним ZB и стан-
дартным отклонением 1/Vre —3. то выражение • _________= рас-
пределено по нормальному закону с нулевым средним и еди-
ничным стандартным отклонением. Следовательно,
или
вероятность 1,96 < -™т====- < 1,96^ = 0,95,
[zT — za т
— 2,58 < , ,.< 2,58 I = 0,99.
l/V/Г^з J
Поэтому интервал
Z,- 1,96-7»!==-. z,+ 1,96^=!= (12.16)
Vn — 3 Vп—3
накрывает ZB с вероятностью 0,95, а интервал
Zr-2,582,4-2,58-7=^ (12.17)
' Vn-з r 1 V«-3 ' ’
накрывает ZB с вероятностью 0,99.
Рис. 12.14. Выборочное распределение Z-преобразова-
ния Фишера для случайных выборок объема п из дву-
мерного нормального распределения с коэффициентом
корреляции р.
В качестве примера использования выражений (12.16)
и (12.17) возьмем выборку из 84 наблюдений, извлеченную слу-
чайно из воображаемой двумерной нормальной совокупности
и давшую г = 0,245. Требуется найти доверительный интервал
с доверительной вероятностью 0,95.
Во-первых, г преобразуем в Zr по таблице Z-преобразоваиия
Zo.245 0.250.
Во-вторых, находим произведение стандартной ошибки ZT
на 1,96:
1,96 - у = -^- = 0,218.
^84-3 9
243
95%-й доверительный интервал для 2Р получается после
подстановки данных в выражение (12.16). Нижними и верхними
границами интервала служат
Zt - 1,96 ;=- = 0,250 -0,218 = 0,032
— а
и
Zr + 1,96 ~~Л= = 0,250 + 0,218 = 0,468
—з
соответственно.
Л1ы лохе-и проще интерпретировать доверительный интер-
вал, если выполним обратное преобразование значений Z Фи-
шера в коэффициенты корреляции. Таким образом, мы снова
обращаемся к таблице и находим значения г, соответствую-
щие Z, равным 0,032 и 0,468. Величина г = 0.032 соответствует
2=0,032, а г = 0,436—2 = 0.468. Поэтому 95%-й довери-
тельный интервал относительно г = 0,245 простирается от 0032
до 0,436,
12.6. Заключение
Цель этой главы состояла в том, чтобы изложить теорию
и дать некоторые примеры практического применения интер-
вального оценивания. Мы выполнили эту задачу достаточно
подробно, поскольку важно, чтобы вы осознали большую по-
лезность теории статистического вывода. В последующих гла-
вах вы встретитесь с различными примерами построения дове-
рительных интервалов. В этих примерах некоторые приемы
вычисления доверительных интервалов будут отличаться от тех,
которые описаны в этой главе. Будет дано описание новых тео'
ретических распределений для выборочных распределений не-
которых важнейших статистик. Нам предстоит ознакомиться
с решением проблемы построения доверительного интервала
в окрестности X.. когда с2 неизвестна. Мы узнаем также, как
можно установить доверительный интервал для разности двух
выборочных оценок, например Х.^ и Х.% (средних двух отдельных
групп наблюдений одной переменной), с целью оценивания раз-
ности двух параметров, например щ и р-2-
В главе 13 мы введем второй важный аспект теории стати-
стического вывода: «проверку гипотез», методологию статисти-
ческого вывода, которая широко применяется в педагогических
исследованиях и других науках о поведении. Мы обнаружим
его тесную связь с интервальным оцениванием. Действительно,
интервальное оценивание и проверка гипотез — это две стороны
одной медали.
244
Задачи и упражнения
1. Требуется извлечь выборку объема п из совокупности со
средним 220 и дисперсией 50. Заполните следующую таблицу,
вычисляя дисперсии и стандартные ошибки Я. для различных
объемов выборки:
п crL а—
2. Когда из нормальной совокупности со средним р и дис-
персией о2 извлекаются выборки объема п, то дисперсия Я.
определяется величиной а2/п, а дисперсия выборочной медианы
Md составляет 1,57о2/л. Предположим, что для конкретной за-
дачи ц ~ 100, а2 — 25, а л = 25, Я. используется для оценки ц;
дисперсия Я. равна а2/п — 25/25 = 1. Если некто выбирает Md
для оценки р, то какого объема должна быть выборка, чтобы
дисперсия ошибки Md, cs24d также равнялась бы 1?
3. Случайным образом была получена выборка в 100 чело-
век из совокупности с дисперсией 16 и неизвестным средним р.
Величина Я. составила 106,75. Постройте 95%-н доверительный
интервал для р в окрестности Я.
4. Постройте 95%-й и 99%-й доверительные интервалы по р
для следующих данных:
а)п = 28, г== + 0,36
б)п=|2, т = — 0,65
в) п = 300, г = +0,14.
13
СТАТИСТИЧЕСКИЙ ВЫВОД:
ПРОВЕРКА ГИПОТЕЗ
13.1. Введение
В главе 12 была подробно рассмотрена на нескольких приме-
рах техника статистического вывода, известная как интерваль-
ное оценивание. Интервальное оценивание — только один (ве-
роятно, на данном этапе наиболее полезный и важный) эле-
мент структуры методов статистического вывода. В этой главе
мы познакомимся со вторым элементом статистического вы-
вода: проверкой гипотез. Проверка гипотез становится преобла-
дающей чертой эмпирического исследования в педаюгике
и науках о поведении. Без подготовки в области теории и ме-
тодов проверки статистических гипотез теперь нельзя читать
научных отчетов и понимать их достаточно полно- Эмпириче-
ские исследования в педагогике и науках о поведении редко
осуществляются без использования либо интервального оцени-
вания, либо проверки гипотез.
Ряд новых понятий, которые предстоит ввести и осмыслить
в связи с проверкой, гипотез, вызовет дополнительное обсужде-
ние. К счастью, основная роль при проверке гипотез отводится
интервальному оцениванию. Мы увидим, что понятия случайных
выборок, выборочных распределений статистик и значений
вероятностей, соответствующих гипотезам, образуют фун-
дамент проверки гипотез, как и интервального оценивания. Про-
верка гипотез и интервальное оценивание реализуются различ-
ными путями, но обычно они приводят к идентичным результа-
там или к результатам, допускающим несложное преобразование
одного в другое. Основной по-прежнему остается задача: «Ка-
кие выводы можно сделать о свойствах генеральной совокуп-
ности по выборочным наблюдениям?»
13.2. Научная н статистическая гипотезы
История проверки статистических гипотез ведет начало
с XVHI в. Самый первый пример испытания статистической
гипотезы появился в работе, датированной 1710 г. и написанной
246
Дж. Арбутнотом (1667—1735); она озаглавлена «Доводы
в пользу божественных пророчеств. Выведенные на основе по-
стоянных и систематических наблюдений над рождением обоих
полов». Отметив, что записи на протяжении 82 лег свидетель-
ствуют о большем числе родившихся мальчиков, Арбутнот по-
казал, что эти данные опровергают гипотезу отом, что рождения
мужчин и женщин равновероятны (с вероятностью 1/2); ибо,
если вероятность рождения мужчины точно равна 1/2, то ве-
роятность того, что за 82 года родилось больше мужчин, чем
женщин, была бы бесконечно мала. Более точной величиной
будет (1/2)82. Арбутнот пришел к выводу, что ббльшая доля
рождения мужчин — результат вмешательства Провидения; под-
держивался священный закон моногамии, поскольку более ве-
роятно, что мужчину могут убить на войне или он умрет от
непосильной работы, не достигнув зрелости. Статистические ха-
рактеристики Арбутнота были безупречны, но теология оказа-
лась несостоятельной для полигамных обществ. Современный
исследователь, подобно Арбутноту, часто имеет дело с вероят-
ностными выводами различных гипотез.
Одного исследователя интересует связь между творчеством
и тревожностью у пяти- и шестиклассников (пример основан на
результатах исследования Онмаха, 1966). Изучая литературу,
он обнаружил одну группу ученых, считающую, что творчески
мыслящий ребенок должен быть менее тревожным, другую —
полагающую, что эти две характеристики никак не связаны.
Наш исследователь пока не примкнул ни к какому лагерю. Он
не принял решения и думает удовлетворить свое любопытство,
проведя собственное небольшое экспериментальное исследова-
ние, Сначала он должен решить, как измерять творчество
и тревожность. Оказывается, существуют 2 теста, имеющие
определенную ценность для измерения этих двух характеристик:
тест «Назначение вещей» Гетцелза и Джексона принят как мера
творчества, а для оценки тревожности подходит «Шкала
выраженной тревожности у детей» Кастенады, Мак-Кендлесса
и Палермо. Исследованию подлежат 20000 пяти- и шестикласс-
ников, но наши возможности ограничены только 200 учащи-
мися. Прекрасно разбираясь в статистике, наш исследователь
планирует взять случайную выборку, состоящую из 200 детей,
из совокупности объемом 20000 учащихся так, чтобы можно
было сделать статистические выводы относительно всей сово-
купности по данным выборочных наблюдений Каждому из
200 учащихся выборки будут предложены оба геста. Надо вы-
числить коэффициент корреляции между их результатами. Наш
исследователь мог приступить к построению доверительного ин-
тервала относительно выборочного г по методике, описанной
в § 12.5. Однако он воспитан « несколько другой манере стати-
стического мышления, когда преобладают решения-, поэтому он
поступает иначе.
247
Решение, которое требуется принять исследователю, ка-
сается истинности или ложности статистической гипотезы. Су-
ществует по крайней мере 2 вида гипотез, которые стоило бы
распознавать и различать.- научные гипотезы и статистические
гипотезы. Научная гипотеза —это предполагаемое решение про-
блемы. Это разумное, обоснованное и развитое предположение.
Научная гипотеза, вообще говоря, формулируется как теорема.
«Опа является эмпирической теоремой в том смысле, что прове-
ряется по результатам эксперимента; опыт отвечает на вопрос,
будет гипотеза истинной или пег...» (Braithwaite, 1953). Форму-
лировка хорошей научной гипотезы — подлинно творческий акт.
Статистическая же гипотеза — просто утверждение относи-
тельно неизвестного параметра. В дальнейшем статистическую
гипотезу мы будем обозначать буквой Н-. (утверждение)
«Н ; р- = 125» — статистическая гипотеза; она гласит, что неиз-
вестное среднее конкретной совокупности равно 125. Очевидно,
такое утверждение либо справедливо, либо ошибочно. Решение
«Н: ц = 125 ошибочно» пример решения того типа, к которому
отмоется проверка статистической гипотезы. «/7:р==0, где р —
коэффициент корреляции в двумерном нормальном распределе-
нии»— другой пример статистической гипотезы. <Н-.о’ = —
статистическая гипотеза, утверждающая, что дисперсии 1-й и
2-й совокупностей равны. Как бы вы описали гипотезу, состоя-
щую в том, что средине значения трех совокупностей равны?
Важно различать' научную и статистическую гипотезы.
Можно проверять статистические гипотезы относительно любых
мелких проблем, обладающих ограниченной применимостью
и не имеющих научной значимости. Сразу же ясно, чго многие
исследователи находятся иод влиянием того, что, поскольку
главная задача науки — формулирование и опытная проверка
гипотез (научных), то они заняты научной деятельностью
только потому, что проверяют гипотезы (статистические). Это
не всегда справедливо. Не все научные гипотезы требуется про-
верять статистически; далеко не все статистические гипотезы
представляют научный интерес.
Психолог, изучающий связь тревожности и творчества у де-
тей, мог на основе опыта и предыдущих исследований прийти
к выводу, что между мерами тревожности и творчества должна
существовать отрицательная связь, то есть высоким оценкам по
тесту творчества должны соответствовать низкие оценки тре-
вожности и наоборот. Он может охарактеризовать творчество
как способность или, может быть, наклонность, котЪрая находит
выражение в работе или игре. Всякое подавление проявления
детского творчества, вероятно, огорчает ребенка, а такая фру-
страция может проявиться в тревожности, что мог предвидеть
психолог.
248
13.3. Проверка статистической гипотезы
Исследователь взял случайную выборку с целью изучения
связи между двумя переменными в совокупности. Сознавая не-
обходимость математического обоснования, он предполагает
(обратите внимание: мы не сказали, что он выдвигает
гипотезу), что его выборка — случайная выборка объемом 200
из гипотетической бесконечной совокупности, в которой данные,
касающиеся тревожности и склонности к творчеству, характе-
ризуются двумерным нормальным распределением. Это — допу-
щение, которое он, вероятнее всего, не будет проверять, даже
если бы у него была такая возможность. Интерес исследователя
сосредоточивается на р, корреляции между испытаниями тре-
вожности и творчества в совокупности, которую он выбрал. Как
закоренелый испытатель гипотез, он рассматривает задачу ста-
тистического вывода, рассуждая на основе выборочных данных
иго совокупности и р, и принимает решение для гипотезы о том,
что р — какое-то конкретное число. Отчасти по привычке,
отчасти в силу традиции или благодаря сознательному
выбору исследователь выдвигает гипотезу, которую тре-
буется оценить, Н : р = 0, то есть, что корреляция между твор-
чеством и тревожностью в совокупности равна 0. Это статисти-
ческая гипотеза. На основе наблюдений он возьмет из совокуп-
ности случайную выборку объемом 200 учащихся, а затем
будет решать, принять ли эту гипотезу как истинную или от-
вергнуть ее как ошибочную. Метод, которым он будет пользо-
ваться для принятия решения относительно справедливости
статистической гипотезы, называется проверкой гипотезы.
Что же такое правильная и разумная проверка гипотезы
Д:р = 0 в данной ситуации? Должен ли исследователь вычис-
лить г для выборки, состоящей из 200 детей, и решить, что Н
верна, если г — 0, и Н ошибочна, если г отличен от пуля? Оче-
видно, нет; нам слишком много известно о неустойчивом пове-
дении выборочных оценок, чтобы согласиться с таким планом.
Вполне возможно, что р = 0 в совокупности, а г будет суще-
ственно отличаться от нуля в выборке. Действительно, не <зк
уж невозможно, что выборка из 200 детей из совокупности
с р = 0 даст г = -f-1 или —1! Это маловероятно, но вполне воз-
можно. Это сложный вопрос. Даже если р = 0 в совокупности,
любое значение г от —I до -f-1—«возможно» в случайной вы-
борке 200 детей. Следовательно, независимо от величины г вы-
борки, исследователь не может с уверенностью заключить, что
р равно или не равно нулю. Мы пришли к важнейшему прин-
ципу, лежащему в основе всех проверок статистических гипо1ез,
и мы констатируем: При проверке любой статистической гипо-
тезы решение исследователя никогда не принимается с уверен-
ностью; он всегда допускает риск принятия неправильного
решения. Сущность проверки статистической гипотезы и со-
стоит в том, что она является средством контроля и оценки
249
этого риска. Мы изучим на примере приемы контроля и оценки
риска некорректного решения относительно истинности ги-
потезы.
Следующий этап после выдвижения гипотезы, которую пред-
стоит проверить, состоит в том, чтобы извлечь выборку из со-
вокупности! и провести наблюдения. Исследователь взял слу-
чайную выборку из 200 учеников, оценил учащихся по тестам
тревожности и склонности к творчеству и установил связь
между этими оценками. Значение г для этой выборки соста-
вило +0,09.
Неопределенность в принятии решения относительно Я:р==0
возникает из-за флуктуации выборки, обычно называемой
ошибкой выборки. Это не ново для нас. Все наше обсуждение
характеристик, используемых в статистическом выводе, имеет
отношение к тому, как про-
водить оценивание парамет-
ра с помощью выборочного
значения, которое почти на-
верняка содержит большую
или меньшую ошибку. Как
и прежде, мы связываем за-
дачи проверки гипотез с по-
Среднее=0
< бг=0,071
Найденное г
-0,20 - 0,10 0 0,10 0,20 г
Рис. н.1. Распределение г для выбо- нятием выборочного распре-
рок обьемом 200 из двумерной нор- деления.
малыой совокупности ср = 0.
После выдвижения гипо-
тезы надо найти выборочное
распределение оценки параметра, относительно которого де-
лается предположение. Кроме того, определим, какое выбороч-
ное распределение получилось бы, если бы проверяемая гипо-
теза была истинной. В нашем примере мы должны построить
выборочное распределение г для случайных выборок объемом
200 из двумерной нормальной совокупности, в которой р = 0.
К счастью, это было выполнено раньше. Это распределение г
для выборок объемом 200 оказывается приблизительно нор-
мальным, с нулевым средним и стандартным отклонением
1 / д/200 -- 1 = 0,071.
Рис. 13.1 показывает выборочное распределение г, когда
справедлива гипотеза Я:р = 0. Выборочное распределение,
учитывающее найденное фактическое выборочное г(г = 0,090).
способствует проверке справедливости гипотезы.
Мы отказываемся от всякой надежды принять с уверен-
ностью одно из решений: — верна» либо «Я — ошибочна».
Такая уверенность невозможна без знания свойств полной
двумерной совокупности. Вместо этого мы должны спросить:
«Вероятно ли, что «Н — истинна», после получения г—0,09?»
Или аналогично: «Разумно ли ожидать появления величины г,
отличающейся от нуля на 0,09, в случае, когда Н— справед-
лива?» Если ответ утвердителен, то исследователь решит при-
нять проверяемую гипотезу; в противном случае гипотеза от-
250
(НО
1,05 был произвольным.
Среднее=0,20
0 0,10 0,20 0,30 0,40 г
Рис. 13.2. Распределение г для выбо-
рок объемом 200 из двумерной нор-
мальной совокупности, в которой р =
на
вертается. Но каково точное значение слов «вероятно» и «ра-
зумно»? Толкование их весьма произвольно. Предположим, что
где-то дождь идет 90% времени. «Разумно» проснуться од-
нажды утром и заявить, что сегодня по всем признакам дождя
не ожидается? Да, это вполне вероятно. С другой стороны, если
на дождливую погоду приходится только 10% общего времени,
то неразумно повторять, будто дождь идет ежедневно, 90% —
залог постоянной дождливой погоды; 10% делают подобное
утверждение маловероятным.
Предположим, мы согласны с тем, что если событие обла-
дает вероятностью случайного появления, равной 0,05. то было
бы бессмысленно или невероятно ожидать его появления при
одном единственном испытании события, которое вы наблю-
даете. Мы могли бы выбрать значения вероятностей: 0,10; 0,01
или 0,001. Выбор величины
ожидать появления события
при одном испытании в том
случае, когда вероятность
его превышает, скажем, зна-
чение 0,10.
Если проверяемая гипо-
теза, /7:р==0, ошибочна, то
р либо больше, либо мень-
ше нуля. Если р — не нуль,
следует ожидать получения
выборочного г, которое рас-
положено несколько выше
или ниже главной части
пример, для р = 0,20 выборочное распределение приведено на
рис. 13.2.
Следовательно, если Н : р — 0 справедлива, то выборочное
распределение на рис. 13,1 сохранится. Если /7:р —0 оши-
бочна, то распределение г передвинется по шкале выше, если р
выше нуля, или же ниже в случае, когда р меньше нуля, по
сравнению с распределением рис, 13.1. Отсюда очень большое
значение г, например, г = 0,50, представляет собой невероятное
событие, если гипотеза Н : р = 0 верна, но оно становится более
правдоподобным, если р больше нуля, например если р = 0,40
или 0.59. Точно так же невероятно, что имеет место очень ма-
лая величина г, например г~ — 0,60, если р — 0, и наблю-
дается большая вероятность такого события, если р ниже нуля.
По этим причинам невероятно или неправдоподобно, что зна-
чения г, обеспечивающие истинность Н : р — 0, располагаются
справа от некоторой точки выше нуля и слева от некоторой
точки ниже нуля на рис. 13.1. Теперь мы хотим определить
некоторые из таких точек более точно.
Стандартное отклонение ог распределения на рис. 13 I со-
ставляет 0,071; таким образом, вероятность того, что величина
р превышает (1,96)ог = 0,140. равна 0,025. Вероятность того.
251
что она лежит ниже —0Д40, также равна 0,025. Поэтому ве-
роятность, что значение, выбранное из распределения на
рис. 13.1, будет лежать выше 0,140 или ниже —0,140, составляет
0,05. Менее точно говорят, что невероятно ожидать значений г
больших 0,140 или меньших —0,140.
В повторных случайных выборках объемом 200 из совокуп-
ности, в которой р = 0, значение г больше 0,140 или меньше,
чем —0,140, будет встречаться в среднем один раз в 20 выбор-
ках, то есть вероятность того, что случайная выборка будет
обеспечивать получение г большего, чем 0,140, или меньшего, чем
Рис. 13.3. Выборочное распределение рис. 13.1
с заштрихованными участками на краях пло-
щадью 5% (по 2,5% на каждом хвосте).
—0,140, равна 0,05. Когда мы учитываем одновременно реше-
ния, которые может принять наш исследователь относительно
гипотезы и возможных исходов извлечения выборки и вычис-
ления г, то обнаруживаем, что существуют четыре возможности.
Два возможных решения (после анализа данных) реальны,
а два других — неприемлемы, как и показано в соответствую-
щей таблице,
Выборка, обеспечившая г, которое находилось
между—0,140 н 0,140 выше 0,140 или
ниже —0,140
Н была
верной
Исследо-
ватель
решил, что
Н была
ошибочной
Решение исследователя приемлемо Решение исследователя неприемлемо
Решение исследователя Решение исследователя
неприемлемо приемлемо
Посмотрим, что подразумевается, когда исследователь при-
нимает решение об истинности Я:р = 0 после изучения г, ко-
торое по выборке объемом 200 лежит либо выше 0.140, либо
ниже —0,140. В таблице подобное решение мы назвали в свете
наших рассуждений «неприемлемым». Почему оно «неприем-
252
лемо»? Потому что нельзя ожидать значений г, отклоняющихся
от нуля более чем на 0,140, — они будут попадаться только в 5%
из всех возможных случайных выборок, если Я:р = 0 верна.
Если продолжают утверждать, что гипотеза Н : р = 0 верна, по
результатам анализа г, равного 0,30, для выборки объемом 200,
придется согласиться с тем, что наблюдаемое событие, то есть
г = 0,30 или еще больше, появляется сравнительно редко. Есте-
ственно, что мы надеемся наблюдать вероятные события, хотя
встречаются и невероятные. Следовательно, когда мы вынуж-
дены признать событие невероятным, чтобы принять решение
о справедливости Я:р = 0, то считается более приемлемым из-
менить наше решение. Более разумное решение состоит в том,
что Н: р = 0 ошибочна.
Ряс. 1зл. Представление площади в выборочном
распределении, когда г лежит на расстоянии более
1,26 единицы стандартного отклонения от среднего
дли выборок объемом 200, при р = 0,
Следовательно, разумно принять решение о верности гипо-
тезы Н: р = 0, если г для выборки объемом 200 лежит в ин-
тервале —0,140 4-0,140, и решить, что она ошибочна, если г
лежит ниже —0,140 или выше 0,140. Назовем это правило пра-
вилом принятия решений.
Не вводит ли нас в заблуждение это правило? Действительно,
возможность принятия неправильного решения по этому пра-
вилу существует. Сущность проблемы проверки гипотез — фор-
мулирование таких правил принятия решений и оценка вероят-
ности того, что они приведут нас к ошибочным заключениям,
Предположим, что фактически, хотя это нам и неизвестно, р
точно равно 0. Мы готовы принять решение о том, что гипотеза
H:p—Q ошибочна, всякий раз, когда г выходит за пределы
интервала —0,140 4-0,140. Какой процент из бесконечного
числа случайных выборок объемом 200 будет давать значения
г, отклоняющиеся от 0 по крайней мере на 0,140, когда фак-
тическая величина р — 0? 5% выборок Следовательно, если
Н : р = 0 верна, то правило принятия решений, которое мы при-
няли, заставило бы нас решить, что Н; р = 0 ошибочна в 5%
выборок — или с вероятностью 0,05 — когда в действительности
гипотеза была верной
Исследователь, изучающий связь склонностей к творчеству
с тревожностью, нашел корреляцию порядка 0,090 на основе
253
случайной выборки нз 200 учеников. Это значение г лежит на
расстоянии 1,26 единицы стандартного отклонения (0,090/0,071 =
= 1,26) выше нуля. Если гипотеза Н:р — 0 верна, то наш ис-
следователь выбрал г, которое находится на расстоянии 1,26
стандартных отклонений от среднего значения выборочного рас-
пределения г (см. рис. 13.4). Как часто следовало бы ожидать
получения г для выборки объемом 200, находящегося на 1,26
стандартных отклонений выше или ниже среднего этого нор-
мального распределения? Из таблицы мы видим, что 20,8%
площади под нормальной кривой лежит дальше, чем на 1,26
единицы стандартного отклонения от среднего. Поэтому сле-
дует ожидать, что значение г, отклоняющееся от 0 по край-
ней мере на 0,090, присутствует более чем в 20% выборок объ-
емом 200 из совокупности, в которой £ = 0. Нет ничего неве-
роятного в том, чтобы получить из совокупности с р = 0 г —
= 0,090. Следовательно, нет смысла делать вывод об ошибоч-
ности /7:р = 0 на основе г = 0,090 в выборке 200 детей.
13.4. Ошибка I рода, уровень значимости
и критическая область
В данном параграфе мы подведем итог основным моментам
предыдущего и введем некоторые условные обозначения для
многих излагаемых здесь понятий.
По результатам § 13.3 мы восстановим 4 Этапа:
1 этап: Формулируется проверяемая гипотеза. В нашем примере
эта гипотеза состояла в том, что /7:р = 0. Принято
называть проверяемую гипотезу нуль-гипотезой, Это
обозначение объясняется тем, что процедуры проверки
статистических гипотез возникли в области филосо-
фии—науки, которая считала своей задачей собира-
ние доказательств для аннулирования гипотез. В этой
главе мы не будем пользоваться термином «нуль-гипо-
теза», пока не возникнет необходимость сравнивать
разные гипотезы.
2 этап: Высказываются предположения, необходимые для опре-
деления выборочного распределения статистики, оце-
нивающей параметр, относительно которого высказы-
вается гипотеза. Выборочное распределение этой стати-
стики определяется для случая, в котором гипотеза
1-го этапа верна.
3 этап: Принимается степень риска для неправильного вывода
на основе выборочных показаний об ошибочности ги-
потезы Н. Риск, представленный как вероятность, обо-
значается а и называется уровнем значимости про-
верки гипотезы (или иногда «объемом» теста). Этот
обычай сделал «проверку значимости» синонимом «про-
верки гипотезы». Исходя из принятого риска, опреде-
254
ляется группа значений выборочной статистики, поз-
воляющих принять решение об ошибочности гипотезы
Н, если выборка приносит подобное значение. Группа
таких значений называется критической областью.
Например, в примере § 13.3 было решено, что приемлем
риск 0,05. Уровень значимости а при проверке гипотезы был,
таким образом, принят равным 0,05.
Определяя точки (0,140—0,140), выше которой и ниже ко-
торой попали бы 2,5% значений г для повторных выборок объе-
мом 200 из совокупности с р — 0, мы нашли бы 2 области «не-
вероятных г, характеризующих верную гипотезу Н:р — 0», Эти
две области, образующие наиболее невероятные 5% выбороч-
ных г, которые можно получить выборочным способом из сово-
купности с р = 0, называются критическими. Критические об-
ласти для примера из § 13.3 указаны на рис. 13.3. Одна часть
критической области располагается от 0,140 до 4-1,00, а дру-
гая от —0,140 до —1,00. Критическая область иногда назы-
вается областью отбрасывания, поскольку появление выбороч-
ного значения, находящегося в критической области, приводит
к отклонению гипотезы Н: р = 0.
4 этап: Из совокупности извлекается одна выборка, рассматри-
вается значение статистики и принимается решение от-
носительно истинности Н. Это — заключительный этап
в проверке гипотезы, сформулированной на 1 этапе.
Выборочные данные должны привести нас к принятию од-
ного из двух решений относительно Н: «Н — верна» или «Я —
ошибочна». Говорят, что первое решение «принимает Я», по-
следнее— «отклоняет Я». По данным любой выборки невоз-
можно сделать определенный вывод, что H:p — Q справедлива
или ошибочна; лучше всего принять такое решение относительно
Н, которое обладает большой вероятностью.
Если Н верна и свойства выборки позволяют принять Н, то
правильное решение обеспечено, Если И верна, а нам прихо-
дится отклонить Н, решение оказывается неверным. Подобное
неверное решение называется ошибкой / типа или ошибкой
первого рода (Позднее мы встретимся с ошибкой II рода.)
Ошибка I рода возникает тогда, когда отвергается истинная
гипотеза И. Разумеется, нельзя знать заранее, будет ли реше-
ние отклонить Н верным или в данном случае наблюдается
ошибка I рода. Для получения этой информации необходимо
знать, будет ли Н верной или ошибочной, но если известна ис-
тина относительно Н, то нет необходимости в теории статисти-
ческого вывода. В оптимальном варианте известна вероят-
ность— частота появления в длинном ряду — принятия пра-
вильного решения или ошибки 1 рода.
Величиной вероятности ошибки I рода можно управлять. Мы
будем обозначать вероятность ошибки I рода для любой произ-
вольной процедуры проверки гипотезы символом «. При испы-
тании H'.p — Q а было положено равным 0,05. Мы можем при-
255
давать символу а такие значения, как 0,20, 0,10, 0,0!, 0,00! или
даже 0,125, ибо мы их выбираем.
Так как а устанавливает вероятность принятия неправиль-
ного решения некоторого типа, мы предпочли бы сохранить ее
малой. Принято выбирать а равным 0,05, 0,01 или 0,001. Теперь
мы посмотрим, как можно было проверить Н : р = 0 при а=0.01.
Если р = 0, то распределение г для выборок объемом 200
является приблизительно нормальным с нулевым средним
и стандартным отклонением 0,071, как мы заметили ранее. Как
«большие», так и «малые» значения г вызовут у нас сомнение
в правильности утверждения, что р = 0. Поэтому мы допустим
величину риска порядка 0,01 для отклонения гипотезы Z/:p==O,
если она верна; нам необходимо определить 2 числа между —!
и -j-1, которые превосходят только 1% значений выборочного
-0,184 0,184
Рис. 13.5, Критическая область для проверки ги-
потезы о том, что р = 0 при а = 0,01 (л = 200).
распределения г, когда р = 0. Эти 2 половины критической об-
ласти представлены на рис. 13.5.
По таблице единичного нормального распределения можно
определить, что, когда нормально распределенная переменная ле-
жит выше среднего на расстоянии более чем 2,58 стандартных
отклонений, вероятность равна 0,005. Аналогично событие, со-
стоящее в том, что нормально распределенная переменная будет
находиться на расстоянии большем, чем 2,58 стандартных от-
клонений, ниже среднего, оценивается вероятностью 0,005. От-
сюда если мы установим критическую область от (2,58) •
.(0,071) = 0,184 до 1,00 и от —1,00 до (—2,58) • (0,071) =
= —0,184, то вероятность отклонения гипотезы Н: р = 0 в слу-
чае если она верна, равна 0,01.
Полезно проследить предыдущее рассуждение в математи-
ческой форме. Если гипотеза Н : р — 0 справедлива, то
где «--'A'(OJ)» означает: «распределено нормально, с генераль-
ным средним 0 и дисперсией 1». Поэтому
вероятность 2,58 < Q д7< 2,58^ = 0,99.
256
Умножение неравенства в круглых скобках на 0,071 дает
следующее выражение:
вероятность (-— 0,184 < г < 0,184) = 0,99.
Следовательно, если коэффициент корреляции для выборки
объемом 200 из двумерного нормального распределения лежит
выше 0,184 или ниже —0,184, то нуль — гипотезу Д:р = 0
можно отклонить на уровне значимости 0,01. Предположим, что
для выборки объемом 200 значение г составляет 0,340. Оче-
видно, решение можно представить несколькими идентичными
способами:
1. «Отклонить Н:р = 0 на уровне значимости 0,01».
2. «Отклонить // : р = 0 при а = 0,01».
3. «Отклонить II : р — 0 при 1% уровне значимости».
4. «Отклонить Н : р — 0 с вероятностью ошибки 1 рода
0,01».
13.5. Ошибка II рода, ₽, и мощность
Строго говоря, до сих пор мы рассмотрели только половину
вопросов, связанных с проверкой статистических гипотез. В этом
параграфе мы предложим вашему вниманию остальные.
Обычный метод проверки гипотезы H:p — Q состоит в том,
чтобы выбрать уровень значимости а, найти критические значе-
ния г или г = (г — 0)/ог (по вашему усмотрению), извлечь вы-
борку и вычислить г, а затем принять или отклонить Н. В пре-
дыдущем разделе мы показали, как оценить вероятность откло-
нения Н, когда фактически она была верной, то есть вероят-
ность ошибки I рода. Было показано, что решение «.Н оши-
бочна» могло оказаться неправильным. Теперь мы говорим, что
решение принять Н, то есть заключить, что «И справедлива»,
также могло быть неверным. Иными словами, мы могли ложно
принять Н, например считать, будто р = 0, когда на самом
деле р = 0,20. Ошибка принятия ложной Н называется ошиб-
кой второго типа или ошибкой II рода. Допуская возможность
учета ошибки типа П, мы теперь приступаем к обсуждению
методов оценки вероятности ошибки второго рода.
Если гипотеза Н: р = 0 ошибочна, то должна быть верной
какая-то другая альтернативная гипотеза — относительно значе-
ния р. Теперь мы будем пользоваться термином нуль-гипотеза
для исходной гипотезы р = 0, а термином альтернативная ги-
потеза для описания другой гипотезы, которую можно сформу-
лировать относительно значения р, например, что р — 0,20.
В дальнейшем нуль-гипотезу будем обозначать символом Но,
а альтернативную гипотезу — Н\. Мы редко можем выдвинуть
единственное альтернативное значение параметра. Вообще (но
не всегда) альтернативная гипотеза сложна, то есть предпола-
гает множество значений параметра, по сравнению с простой,
9 Зак. «в 257
как нуль-гипотеза, в которой делается предположение относи-
тельно одного значения. Рассмотрим пример простой нуль-ги-
потезы и сложной альтернативной:
Нуль-гипотеза: //0:р —0;
Альтернативная гипотеза: Н, 0.
В теории проверки гипотез утверждается, что может наблю-
даться одно из двух «состояний природы»: верна либо Н01 либо
Hit и это согласуется с тем, что после анализа выборки будет
принято одно из двух решений: либо будет принята Но (следо-
вательно, отклоняется Нх), либо принимается Нх (тогда Но от-
вергается). Ниже представлены 4 возможных сочетания этих
состояний природы и решений с описанием обоснования ре-
шения.
Состояние природы
На верна верна
Отклонить Но (Принять Нх) Решение Отклонить Н, (Принять На) Ошибка f рода (Вероятность = а) Правильное решение (Вероятность = 1 —0)
Правильное решение (Вероятность= 1 —а) Ошибка II рода (Вероятность = 0)
Мы условились обозначать вероятность ошибки I рода сим-
волом а. Вероятность ошибки II рода, то есть принятия Но,
когда верна Нх, будем обозначать символом р. Рассмотрим при-
мер вычисления р.
Предположим, исследователь хочет проверить нуль-гипотезу
Но: р = 0. Допустим также, что у него нет особой причины счи-
тать, что для р более вероятным является какое-либо одно не-
нулевое значение. Он предпринимает попытку извлечь выборку
п—200 лиц., после чего естественно принять, что наблюдаемые
переменные обладают двумерным нормальным распределением.
Кроме того, он учитывает риск отклонения Н0:р — б, когда она
верна, только в 5 случаях из 100; следовательно, а = 0,05.
Исследователь должен установить критические области г,
позволяющие отклонить Но, как это было сделано на рис. 13.3.
В качестве доказательства ложности Но следует взять выборку
со значением г — 0,140 и больше или г = —0,140 и меньше.
Далее, мы знаем, что, если фактически р — —0,140, то суще-
ствует 1 шанс из 20 (а = 0,05), что исследователь отвергнет Но-
Однако что будет, если р действительно равно 0,20? В этом
случае гипотезу Но: р — 0 следует отклонить в пользу утверж-
дения, что р отличается от нуля. Но какова вероятность того,
что Но будет отвергнута? Эта вероятность— мощность критерия
р — 0,20, и ее графическая характеристика представлена за-
штрихованной областью рис. 13 6.
258
Верхняя критическая область для г занята всеми значениями
от 0,140 до 1,00. Следовательно, мощность проверки гипотезы,
позволяющая отклонить в случае, когда р = 0,20, описы-
вается площадью за 0,140 под кривой, представляющей эмпи-
рическое распределение г для выборок объемом 200 при
р == 0,20. Эта площадь составляет приблизительно 82% общей
площади под кривой в правой части на рис. 13.6. Таким обра-
зом, мощность приблизительно равна 0,Й2. (Фактически суще-
ствует также бесконечно малая вероятность, что будет отверг-
нута в пользу Н\ при р = 0,20, что обусловлено значением вы-
борочного г ниже —0,140! В данном случае мы пренебрегаем
этой невероятностью, см. Kaiser (I960).] Площадь под кривой
Рис. 13.6. Пример мощности критерия для Яо: р = 0
против в случае, когда р«= 0,20 (га —200 и а *=0.05).
справа на рис. 13.6 (эмпирическое распределение г при
р = 0,20) до 0,140 — мера вероятности того, что г не будет пре-
вышать критического значения даже тогда, когда Но ошибочна;
данная площадь оценивает р, вероятность ошибки II рода. Пло-
щадь, о которой идет речь, занимает около 18% общей площади
под кривой. Следовательно, р приблизительно равна 0,18. По-
скольку, если р фактически оценивается величиной 0,20, мы
должны либо предусмотреть, либо нет ошибку II рода, вероят-
ность не совершить ошибку, то есть мощность проверки, за-
дается выражением 1—(5 = 0,82. Теперь попытайтесь сами убе-
диться в том, что если бы р было равно —0,20, то аналогичная
процедура проверки гипотезы привела бы к такому же риску
ошибки II рода и оценивалась бы той же мощностью (0,82),
как и при р — 0,20.
Повторим предыдущие рассуждения при определении
мощности критерия Н0:р~() для а — 0,05 и п — 200, когда
р = 0,10, а не 0,20. Критические области проверки остаются
прежними: от —1,00 до —0,140 и от 0,140 до 1,00. Эмпирическое
распределение г для выборок объемом 200 не претерпело ни-
каких изменений по сравнению с предыдущими обсуждениями
и рассматривается параллельно с эмпирическим распределе-
нием г для п = 200, когда р = 0,10, на рис. 13.7.
Предположим, что для проверки выбрана гипотеза Но:р — О
против Н} : р =#= 0 при а — 0,10 и с выборкой из 200 пар наблю-
дений. Обращаясь к рис. 13.6, попытайтесь определить, будет
9’ 259
ли мощность критерия больше или меньше критерия при
а — 0,05 в случае, когда р = 0,20.
В результате точного измерения площади под кривой в пра-
вой части за критическим значением 0,140 на рис. 13.7 можно
показать, что мощность критерия Н : р = 0 при р = 0,10 состав-
ляет 0,29. Разумеется, отсюда следует, что Р == 0,71.
Оказывается, в педагогике и психологии почти никогда не
бывает, что мощность критерия гипотезы для одного или двух
-альтернативных значений параметра обеспечивает достаточ-
ную информацию. Вообще было бы интересно определить
мощность критерия для нескольких альтернативных значений
параметра, изобразить эти значения мощности в сравнении
с величинами параметра, а затем соединить точки плавной ли-
нией. Полученная кривая обеспечивает адекватное определение
мощности в зависимости от альтернативных значений пара-
Рис. 13,7. Пример мощности критерия для /70: р -= 0 против Н, :
о случае, когда р <= 0,(0 (п —200 и п — 0.05).
метра. Кривая мощности для критерия Нд: р = 0 против
7/1 0 при « = 200 и а = 0,05 приведена на рис. 13.8.
На рис. 13.8 обратите внимание на то, что для р = ±0,20
н р = ±0,10 значения мощности равны соответственно 0,82
и 0,29. как подсчитано на рис. 13.6—13.7. Заметим также, что
когда р — 0, «мощность» определяется величиной 0,05; то есть
если Но верна, то имеет место вероятность, равная уровню зна-
чимости отклонения Но в пользу Нь
Из рис. 13.8 ясно, что мощность критерия стремится к 1,
когда величина р отклоняется от 0. Это утешительный факт, но
исследователь не может управлять случайностью, так как он
не «устанавливает» истинное значение р. Однако объем вы-
борки п и уровень значимости а. находятся под его контролем,
хотя это н имеет относительное значение. Для любого задан-
ного значения р, отличного от нуля, мощность критерия.
Яо:р==О возрастает с увеличением п (например, от 10 до 100)
и а (скажем, от 0,01 до 0,05).
В целом о процедурах проверки гипотез можно сказать сле-
дующее:
1, Для данного значения проверяемого параметра, например
р = 0,40, мощность критерия Нд увеличивается с ростом объема
выборки п.
260
2. Для данного значения проверяемого параметра, напри-
мер р <= 0,40, мощность критерия Но увеличивается, когда
возрастает, например, от 0,01 до 0,05, а, вероятность отклоне-
ния верной нуль-гипотезы.
Во многих случаях могло быть желательным установление
уровня риска ошибки I рода порядка 0,10, то есть а = 0,10,
чтобы гарантировать приемлемую мощность критерия. Третье
соотношение, которое мы сформулируем, в меньшей степени за-
висит от воли исследователя.
3. Для фиксированных значений аил мощность критерия
Но увеличивается, когда истинное значение проверяемого пара-
метра сильнее отклоняется от значения, предполагаемого в На.
Рис. 13.8. Кривая мощности для критерия Яо:р = О
против //[tp-yfeO при я = 200 и а = 0,05.
Например, если п = 100, а а = 0,01, мощность критерия
Д:р = 0 больше при р, фактически равном 0,60, чем в случае,
когда р равно 0,40 или —0,40.
В среде экспериментаторов распространено мнение, что ста-
тистик—-это человек, говорящий им, «каким должен быть
объем выборки». По-видимому, он принимает решение об объ-
еме выборки, исходя из затрат на наблюдение, издержек, свя-
занных с учетом ошибок I н И рода, и мощности критерия для
различных объемов выборки и конкретных альтернативных
значений параметра, относительно которых необходимо прове-
рить гипотезу. Теория — известная под названием теории про-
верки гипотез Неймана — Пирсона,—дающая нам представле-
ния об ошибках II рода и мощности, становится целесообразной,
когда можно определить эти затраты и конкретные альтернатив-
ные значения параметра. Однако при исследовании в области
педагогики и социальных наук определение их с какой бы то ни
было гарантией большая редкость. Мы подозреваем, что боль-
шинство статистиков, консультирующих исследователей по этим
вопросам, накопило опыт, подобный нашему. Мы, как правило,
сами советуем извлекать максимальную выборку, а потом опре-
деляем, не будет ли объем выборки неоправданно большим!
261
Если они могут взять выборку настолько большую, что мощ-
ность критерия Но определяется, скажем, величиной 0,97, даже-
когда истинное значение параметра лишь незначительно отли-
чается от величины, установленной в Но, им вполне можно по-
советовать сократить подобную излишне объемную выборку.
Вполне возможно, что мощность критерия снизилась бы только
до 0,90, если бы объем выборки составил половину максималь-
ного. В этом случае мы могли бы без всяких колебаний посове-
товать уменьшить объем выборки. Таким образом, когда наши
исследования в педагогике и социальных науках соответствую-
щим образом обоснованы, понятие мощности критерия стано-
вится более полезным как сигнал о том, что можно нечаянно
извлечь большую выборку, чем это фактически требуется для
«определителя объема выборки».
13,6, Направленные и ненаправленные альтернативы:
«двусторонние и односторонние» критерии
Альтернативная гипотеза Н\ может быть либо ненаправлен-
ной, либо направленной. Альтернативная гипотеза /7, :р по-
является ненаправленной, поскольку она утверждает только-
факт неравенства параметра нулю и не указывает, в каком на-
правлении (выше или ниже) возможно отклонение от 0. Рас-
смотрим две гипотезы Нд:р = 0 и Hi: р > 0. В этом примере
альтернативная гипотеза обладает направленностью; исследова-
тель при этом утверждает, что р или равно нулю, или, воз-
можно, больше нуля. Исследователь считает, что, по-видимому,
р не могло быть меньше нуля; он займется сбором доказа-
тельств, которые либо подтвердят, что р положительно, либо ои
по-прежнему будет считать, что р = 0.
Одно из следствий выдвижения направленной альтернатив-
ной гипотезы Н]-.р>0 для нуль-гилотезы состоит в том, что-
теперь критическая область для отклонения Нд в пользу Hi—
это значение г, превышающее величину 100(a) % площади
в эмпирическом распределении г, когда р = 0. Иначе говоря,,
только большие положительные значения г будут вызывать
необходимость принять решение в пользу Н{, а не Нд; следова-
тельно, критическая область отклонения Но лежит в правом
конце эмпирического распределения г для р = 0, как показано
на рис. 13.9. На рис. 13.9 критическая область простирается от
0,117 до 1,00. Очень малая величина г, скажем, —0,40, не спо-
собствует принятию гипотезы о том, что р > 0 по сравнению-
с гипотезой о равенстве параметра р нулю. Так как условиями
гипотез предусматриваются только 2 соотношения вида р = 0
или р > 0, то г == —0,40 подразумевало бы скорее истинность
Нд, а не Hlt даже если бы его появление в выборке п==200 было-
бы крайне невероятным при р = 0. Но подобные факты — свое-
образие проверок направленных гипотез.
262
' То, что критическая область «лежит а одном хвосте» выбо-
рочного распределения статистики в соответствии с нуль-гипо-
тезой, способствовало популярности выражения односторонний
критерий при оценке значимости направленной гипотезы. Этот
•оборот речи не совсем ясен и нередко вводит в заблуждение.
Между ненаправленной и направленной альтернативными гипо-
тезами имеется существенное различие; будет ли проверяемая
•статистика оцениваться таким способом, что один или два конца
выборочного распределения, лежат выше критических значений
статистики, — чистая условность. В главе 15 мы увидим, на-
пример, что ненаправленная гипотеза относительно группы
средних совокупности проверяется с учетом одной стороны
F-распределения.
Иногда думают, что проверяемые направленные гипоте-
зы представляются в виде Но. Р С О против альтернативной
'4s^/a'
-020-0,10 о о,яС^аа адо г
Рис. 13.9. Пример критической области для проверки Н:р”=0
против • р > 0 при п = 200 и a = 0,05
Ну-. р >0. Далее утверждается, что достаточно большие значе-
ния выборочного г склоняют нас к принятию Ну, а малые или
большие отрицательные значения г — До. На самом деле, в та-
«их утверждениях Но и Ну нет логики. Но призвана доказать,
что р = 0, а не что р 0. Кроме того, здесь кроется некоторое
противоречие. Обратите внимание на то, что Но'р >0 и
Л,Ф<0 так же приемлемы, как и HQ. р 0 и Н\: р > 0. Од-
нако для фиксированных п и а вероятность принятия решения
в пользу Но'.р^О, когда фактически р —0,10, гораздо больше
вероятности решения в пользу Ну : р > 0. Разумеется, совсем не
приемлемо, когда мощность критерия, позволяющего сделать
выводы о том, что р больше 0, когда р = 0,10, в основном зави-
сит от произвольного выбора между Н0-р > 0, Я|:р<0 или
Но'.р С 0, Ну-.р > 0. (См. Rozeboom, i960.)
Споры о достоинствах проверки направленных гипотез по
сравнению с ненаправленными при исследованиях в поведен-
ческих науках возникали неоднократно в период 1950—1960 гг.
(Основной материал вы найдете в- Burke, 1953, 1954; Goldfried,
1959; Hick, 1952; Jones, 1952, 1954; Kimmel, 1957, Marks, 1951,
1953, Peizer, 1967.)
За дальнейшей информацией целесообразно обратиться
к наиболее удачной, по нашему мнению,статье W. Kruskal.Tests
of Significance.— In: International Encyclopedia of the Social
263
Sciences (1968). Вероятно, с ней вам лучше познакомиться
после изучения этой главы и гл. 14 (см. также Nunnally, 1960;
Grant, 1962; Wilson, Miller, 1964).
Задачи и упражнения
1. Дайте определения следующим понятиям:
а) Нуль-гипотеза, Но.
б) Альтернативная гипотеза, Н\.
в) Ошибка I рода.
г) Ошибка И рода.
д) Уровень значимости, а.
е) Мощность критерия, I — р.
ж) Критическая область.
2. Исследователь берет выборку с п = 200 пар наблюдений
из двумерного нормального распределения. Он правильно рас-
суждает, что если р = 0, то г будет распределено приблизи-
тельно нормально с нулевым средним и стандартным отклоне-
нием 0,071. Кроме того, он принимает решение отвергнуть
//о:р = О, если г выше 0.10 или ниже —0,10. Какова вероят-
ность того, что он допустит ошибку I рода?
3. По рис. 13.8 оцените мощность критерия /70 т р == 0 по
сравнению с гр^О для п=200 и а=0,05, когда а) р—0,05,
б) р 0,25, в) р = —0,25, г) р — 0,40.
14
ИЗБРАННЫЕ МЕТОДЫ ВЫВОДА
14.1. Введение
Представьте себе, что к какому-то моменту времени изучены
свойства вывода почти всех известных статистик. Пользуясь
либо строгими математическими методами, либо иногда эмпи-
рическими методами, статистики получили выборочные распре-
деления для большинства практических целей, В этой главе
будут представлены свойства выводов только наиболее распро-
страненных статистик; таким образом, слово «избранные» в на-
звании главы оправдано. Будет описана методика проверки
значимости статистик и построения доверительных интервалов
во всех возможных случаях. Статистические характеристики,
с которыми нам придется иметь дело, относятся к четырем груп-
пам’ средние, дисперсии, коэффициенты корреляции и частот-
ные данные.
Обсуждение свойств вывода каждой статистики будет осу-
ществляться в такой последовательности: (а) формулирование
луль-гипотезы Но и альтернативной гипотезы nit альтернатив-
ная гипотеза будет «ненаправленной», так что возникает необ-
ходимость в изменении критических значений в том случае,
когда требуется «односторонняя» проверка; (6) формулирование
допущений, сделанных в процессе проверки; (в) определение
выборочной статистики, используемой при испытании Но и Ht;
(г) образование выборочного распределения проверяемой ста-
тистики для Но и Н\\ (д) определение критических значений
критерия; (е) построение доверительных интервалов в окрестно-
сти выборочной статистики; (ж) пример; (з) конкретный ана-
лиз в случае необходимости.
Первая группа гипотез, которую мы рассмотрим, имеет от-
ношение к средним значениям генеральной совокупности.
14.2. Выводы о среднем значении совокупности, И
а) Проверяемая гипотеза состоит в том, что среднее ц гене-
ральной совокупности равно некоторому действительному чис-
лу а. Альтернативная гипотеза, разумеется, выражается в том,
265
что р отличается от а:
Но'. р == а
Н} ц^а.
б) Принимается, что переменная X в рассматриваемой со-
вокупности обладает нормальным распределением. Величина
неизвестна.
в) Но проверяется с помощью статистики:
г) Если Но-.р.~ а верна, то i в выражении (14.1) имеет t-
распределение Стыодента с п—1 степенями свободы. Когда
Ряс. 14.1. Выборочные распределения J=(X.—0)/(з1/\'п)
для случая, когда верна гипотеза = и случая,
когда верна гипотеза Нг: и = 2. Значения п и иден-
тичны и равны 30 (а=«0,05).
верна Н|, то есть когда р действительно равно некоторой вели-
чине Ь, отличающейся от а, выборочное распределение t в выра-
жении (14.1) имеет вид н разброс /-распределения Стыодента
с п—1 степенями свободы, но среднее этого распределения
равно величине {Ь~а)1(ах/'\/п). Например, распределение /=»
= W. -0)/(sJV?) представлено на рис. 14.1 для ц = 0 и
ц = 2; п и а; равны 30.
д) Критические значения для проверки Но на уровне значи-
мости а при критерии / = (X. — а)/(sx / V") есть точка про-
центиля 100(1 — (а/2)] из распределения Стыодента с п—1 сте-
пенями свободы и та же точка, но с отрицательным значением
процентиля:
— I—(а/2)/«—1 и 1-(ал|/я_1.
Значение / = (Х. — а)/($х/д/п)> попавшее ниже отрицатель-
ного или выше положительного критического значения, служит
основанием для отклонения Но: ц = а в пользу Нс.ц^а.
266
е) 100(1 —а)% доверительный интервал для р строится сле-
дующим образом:
X. ±1-^/2,
(14.2)
ж) В 30-х гг. было проведено исследование влияния на ин-
теллект незаконнорожденных детей, у которых были нормальные
матери, условий воспитания в детских домах. Средний IQ, изме-
ренный по методике Кульмана, усовершенствовавшего тесты
Бине, у 175 детей в возрасте от 6 месяцев до года равнялся при-
близительно 115. Критики подняли вопрос, будет ли средняя
оценка совокупности всех таких детей действительно опреде-
ляться цифрой 100, как предполагалось. (Исследования позво-
лили показать, что генеральное среднее р значительно выше
100 )
Мы хотим проверить гипотезу Но о том, что средний IQ Куль-
мана в совокупности всех детей США равен 100 против альтер-
нативной гипотезы, утверждающей, что он не равен 100.
Но I р = 100 Hi : р ф 100.
Вероятность ошибочного отклонения 77 0 установим на уров-
не 0,01.
По случайной выборке 25 детей были получены значения 7Q
Кульмана при X. — 113,64 н sx = 12,40, Таким образом,
Критические значения t-. -0.995*24 = —2,797 и 0.995*24 = 2,797.
Отсюда мы видим, что Нй можно отклонить в пользу Hi на
уровне значимости 0,01. Пользуясь выражением (14.2), мы най-
дем 99% доверительный интервал для р:
113,64 ± 2,797 = 113,64 ± 6,94 -(106,70; 120,58).
з) Хотя при проверке гипотез относительно р, когда не-
известна, принимается допущение о нормальности генеральной
совокупности, нарушения этого допущения влияют либо на уро-
вень значимости, либо на мощность двустороннего /-критерия
(см, Srivastava, 1959). Однако ненормальность рассматриваемой
совокупности может существенно влиять на односторонние /-кри-
терии направленных гипотез.
Удобные в обращении таблицы для оценки мощности /-кри-
терия можно найти у Вайна (1964, р. 254—260).
267
14.3. Использование независимых выборок
для выводов относительно &—щ
а) Проверяемая гипотеза состоит в том. что разность ме-
жду средними значениями двух совокупностей, pi — равна
нулю против альтернативной гипотезы о том, что эта разность
отлична от нуля:
Но: Pi — Р2 = 0
Hl : Pl — Р2?Ь0.
б) Принимается, что Л, имеет нормальное распределение со
средним pi и дисперсией <%, а Хг — нормальное распределение
со средним pj и той эее дисперсией о*. Допущение о равных,
дисперсиях в двух совокупностях связано с понятием однород-
ности дисперсий, или гомоскедактичности (буквально «равно-
распределенности»). Кроме того, предполагается, что выборка
объемом П| случайным образом извлекается из совокупности 1,
а независимая выборка объема п2 случайно берется из совокуп-
ности 2.
Основное следствие допущения независимых выборок заклю-
чается в том, что 2 выборочных средних значения, ^.jh^.2, будут
совершенно некоррелированными для бесконечного множества
пар выборок. Гипотеза независимости нарушилась бы, например,
если бы 1 выборка была случайной группой 10-летних мальчи-
ков, а 2 — группой их сестер. Два средних значения парных вы-
борок «брат — сестра» имели бы корреляционные связи для
большинства переменных.
в) Проверяется Но против Н с помощью следующего кри-
терия: _ _
== —......(14.з>
(*,-iHi + (^-i)4 (± П
Я] + пг — 2 \ п, щ )
где и Х.2—выборочные средние из совокупностей 1 и 2 со-
ответственно,
и несмещенные оценки из выборок I и 2 с общей гене-
ральной дисперсией (^, ал, и п2— объемы выборок.
г) Когда верна Но, распределение t в выражении (14.3) для
пар выборок идентично / распределению Стыодента с nt 4-
4-п2 —2 степенями свободы. Когда верна Н. и. следовательно.
Mi — р.2 отлична от нуля, распределение / в уравнении (14.3)
имеет вид и разброс /-распределения Стыодента, но среднее
отличается от 0 — величина разности зависит от значений щ—р2,
о*, hi и п2.
д) Для проверки Но как альтернативы Ht на уровне значи-
мости а определяются и сравниваются с полученным по фор-
муле (14.3) значением / следующие критические значения:
— 1—<а/2)/Я| + Л;-2 И 1-(а/2^п, + п,~2-
268
' е) 100(1—а) % доверительный интервал для щ — цг отно-
сительно Х.1 —Х.2 строится следующим образом:
(X.i — X .2)±1-(а/2)/П|+л2-25г.1-х2, (14-4)
где S;.-х. —величина, равная знаменателю выражения (14.3).
ж) Скандура и Уэллс (1967) провели эксперимент по иссле-
дованию влияния «усовершенствованных пособий» (вводный ма-
териал, подготавливающий к восприятию изучаемого предмета)
на успеваемость по абстрактной математике. 50 учащихся кол-
леджа были случайно распределены по двум группам: 25 уча-
щихся !-й группы изучали очерк по топологии (1000 слов) после
предварительного знакомства с усовершенствованным пособием;
25 учащихся 2-й группы читали аналогичный труд по топологии
после изучения исторического очерка (1000 слов) двух извест-
ных математиков, Эйлера и Римана. В конце эксперимента каж-
дой группе был предложен тест на усвоение топологических по-
нятий. Зависимая переменная X—«количество правильных от-
ветов». Были получены следующие результаты:
Группа 1 (усовершенствованное пособие) Группа 2 (исторический очерк)
,ti = 25 «2 = 25
X. 1 = 7,65 X.г = 6,00
s? =6,50 = 5,00
Можно проверить гипотезу о том, что 2 группы — это случай-
ные выборки из нормальных совокупностей с равными средними.
Мы проверим эту гипотезу на уровне значимости 0,05. Из урав-
нения (14.3)
Х.1-Х.г_____________7,65 - 6,00____________2
siri2 / 2Т(6,50)+ 24(5,90) / 1 , ” 1 \ ~ '
Л/ 25 + 25-2 \ 25 + 25j
Критическими значениями, которые сравниваются с величи-
ной t ~ 2,34, являются:
- - 2.01 и 0®Л« = 2,01.
Следовательно, мы видим, что гипотезу /7о: pii— рг = 0 мо-
жно отклонить на уровне значимости 0,05. Действительно, вели-
чина t, отклоняющаяся от нуля более чем на 2,34, имеет вероят-
ность, что Но верна р, равную 0.03. 95%-ный доверительный ин-
тервал для ц! — ц2 можно построить по уравнению (14.4):
(X.I - Х.2) ± o.W«Sx. ,_«.2 = 1,65 ± 2,01 (0,705) = (0,23; 3,07).
з) Было показано, что нарушение допущения о нормальности
/-критерия Но: ц, — Ц2 = 0 имеет лишь незначительное влия-
269
ние на уровень значимости и мощность критерия, и поэтому им
можно пренебречь (Boneau, I960; Шеффе, 1962, гл. 10).
Нарушение предположения об однородности дисперсий во
многом зависит от nf и «2. Если п, и п2 равны, то нарушение ги-
потезы об однородности дисперсий несущественно и нас не ка-
сается (Box, 1954, а, b; Шеффе, 1962, гл. 10). Это наводит на
мысль об извлечении выборок равного объема во всех возмож-
ных случаях. Когда же дисперсии обеих совокупностей отли-
чаются и »| и П1 не равны, то вероятности ошибок 1 и 11 рода
могут существенно отличаться от предполагаемых значений (см.
§ 15.3). Когда исследование, в котором оценивается — ц2, не-
возможно спланировать так, чтобы П| = п2, и есть подозрение,
что две совокупности имеют существенно различные дисперсии,
следует обратиться к методам, разработанным Уэлчем (1937)
или Гронау (1951). Задача проверки значимости различия ме-
жду двумя средними, когда генеральные дисперсии не равны,
относится к классу задач Беренса — Фишера (см. Fisher, 1959,
р. 93-97).
14.4. Выводы относительно м1-~мг
при использовании зависимых выборок
а) Совокупность 1 имеет среднее ю, а совокупность 2 —ц2.
Проверяемая нуль-гипотеза аналогична предположению § 14.3:
Яо: th — Р2 = 0
Я| • Hi — Ц2#=0.
б) Принимается, что выборки i и 2 случайно извлекаются
из нормальных совокупностей с одинаковой дисперсией
В этом примере требующиеся выборки не являются независи-
мыми, то есть может существовать корреляция Jf.i и для
повторяющихся пар выборок. Примеры зависимых выборок:
1-я выборка представлена годовалыми детьми, а 2-я состоит
из близнецов детей 1-й выборки; 1-я выборка — совокупность зна-
чений теста на время реакции, полученных группой испытуемых
перед назначением лекарства, а 2-я — совокупность значений,
полученных теми же лицами после приема лекарства.
в) Всегда есть возможность «объединить в пары» данные из
двух различных выборок. Пары можно описать наименованиями
типа «брат —сестра», «до —после», «близнец 1, близнец 2»,
«первый партнер, второй партнер» и т. д. Следовательно, дан-
ные, собранные по различным выборкам, будут представлены
в виде п пар наблюдений Xit и Xt, для i — i, ..., п. Группиро-
вание данных по зависимым выборкам предстоит использовать
для проверки гипотезы о том, что pi — ц? = 0- Гипотеза, состоя-
щая в том, что и Х2 имеют одинаковое среднее, то есть pi =
= р.2, эквивалентна гипотезе о том, что Xj — Х2 обладает нуле-
270
вым средним в генеральной совокупности. Разность — Хг ме-
жду нормально распределенными переменными X) и Ха — сама
нормально распределенная величина; таким образом, методы
§ 14.2 можно применить для проверки гипотезы о том, что п
разностей Xi, — Xi, есть случайная выборка из нормально рас-
пределенной совокупности со средним щ — цг, равным нулю.
Обозначим разность пар наблюдений из выборок 1 и 2,
Xt,— Xi, символом di. Имеем критерий:
где
d.^^Xn-X^/n^tdiln,
среднее п значений разностей, а
стандартное отклонение п значений разностей Xi,— Х(,; п —
число пар наблюдений.
г) Если верна гипотеза Hq : ц, — ц2 — 0, то t в выраже-
нии (14.5) будет подчиняться /-распределению Стьюдента с
п—1 степенями свободы. Если правильной оказывается гипо-
теза Н\ : pi — то t в выражении (14.5) будет описываться
распределением, по форме идентичным (-распределению Стью-
дента сп—1 степенями свободы, однако со средним, отличным
от нуля по величине и направлению в зависимости от значения
pi — Иг-
fl) Критические значения для проверки Но против альтерна-
тивной гипотезы Н) на уровне значимости а с помощью /-стати-
стики по выражению (14.5) есть:
— l-la,'2>/n-l и
е) 100(1—а)% доверительный интервал для — р2 отно-
сительно встроится следующим образом:
J. ± I-(a/2i tn_s Jd,
(14.6)
ж) Вебстер и Берейтер (1963) представили данные по инди-
видуальным изменениям у 100 студенток с первого до послед-
него курса. Первокурсницам (100 человек) и им же — выпускни-
цам колледжа (100 человек) была предложена индивидуальная
программа из 60 вопросов. Первая группа, содержащая 100 зна-
чений, образует выборку 1; 100 значений выпускниц — выборку 2.
Имеется 100 пар значений типа «до — после». На основе 100 дан-
271
пых находятся значения разностей: di^Xi,— Xi,- Среднее и
стандартное отклонение 100 оценок d таковы:
|(Ю
Vioo
-----£9-------=8,02.
Мы будем проверять Но : jii — Цг = 0 на уровне значимости
0,01. Значение t в выражении (14.5) вычисляется так:
f _ d.________-7,02_____й --
s d/Vn 8,02/Vl00 ’ '
причем это значение лежит ниже минимального критического
значения -0.995^99 = —2,64. В самом деле, вероятность р получе-
ния t = —8,75 или меньше, обеспечивающая истинность нуль-
гнпотезы, значительно меньше 0,001. Таким образом, мы можем
уверенно отклонить нуль-гипотезу о том, что две зависимые вы-
борки по 100 наблюдений в каждой могли быть случайно взя-
тыми из двух нормальных совокупностей с одинаковым сред-
ним. Есть неопровержимое доказательство того, что в индиви-
дуальной ведомости учащихся от первого до последнего курса
наблюдается «прирост».
По уравнению (14.6) можно определить 99% доверительный
интервал для pj — у.3-.
1. ±».«l»^ = -7,02±(2,S4)-£|==(-9,14; -4,90).
з) У исследователей часто имеются зависимые выборки, они
отказываются от признания этого факта и некорректно приме-
няют ^-критерий для независимых групп с целью проверки ги-
потезы щ — р-2 — 0. Различие между ^-критерием зависимых
и независимых групп становится явным, когда рассматриваются
стандартные ошибки разности между некоррелированными и
коррелированными средними. Если Х.[ и Х.г не коррелированы
(оцениваются по независимым группам), то стандартная ошибка
разности двух средних есть
V «« «а
которая равна
ом
272
при nt = п2. Когда X, и Х2 имеют ненулевой коэффициент кор-
реляции pi2 (в случае 2 зависимых выборок), стандартная ошиб-
ка Я.1 — Х.2 представляет собой:
<•«>
Статистика t для проверки щ — цг = 0 с независимыми груп-
пами содержит X.i —Х.2 в числителе и оценку уравнения (14.7)
в знаменателе. Статистика t для зависимых групп имеет в чис-
лителе 3. = X.t — Х-2 и оценку уравнения (14.8) в знаменателе;
обратите внимание, что
Vs-
-Ул УП ’ п * л п п
Если в задаче с зависимыми группами, в которых Xi и Х2
имеют существенную положительную корреляционную связь, ис-
пользуется несоответствующая схема проверки по /-критерию
для независимых групп, то стандартная ошибка X.j — Х.2 будет
значительно переоцениваться, а существенные различия между
двумя средними будут признаны «незначимыми», Противопо-
ложная ошибка, принимающая несущественные разности за су-
щественные, была бы допущена в том случае, если бы /-кри-
терий для независимых групп применялся к зависимым груп-
пам, в которых X! и Хг обладают значительной отрицательной
корреляцией. Таким образом, мы видим, как важно уметь рас-
познавать и'различать независимые и зависимые выборки при
применении некоторых методов статистического вывода. Выбор
той или иной проверки обусловлен знанием исследуемых явле-
ний, а также чувствительности статистических задач к зависи-
мым выборкам.
14.5. Выводы относительно дисперсии совокупности, о*
Начиная с этого параграфа, мы займемся проверкой гипотез
относительно генеральных дисперсий.
а) Проверяемая гипотеза состоит в том, что генеральная со-
вокупность имеет дисперсию сгх» равную некоторому числу а,
в противоположность гипотезе о том, что <т; отличается от а:
Нл-.а\=а
б) Следует принять, что переменная X обладает нормальным
распределением в совокупности и что взята случайная выборка
из п наблюдений, по которой следует оценить о;.
273
в) Для проверки Но в противовес Ht используется стати-—
стика:
<' .9)
(» - 1) -------------- £ (X, - X
I
г) Когда верна На. выборочное распределение х2 в уравне-
нии (14.9) будет распределением хи-квадрат с п—1 степенями
свободы; когда справедлива Ht, а о’ фактически равна некото-
рому числу Ь, отличному от нуля, то выборочное распределение
Рис. 14.2. Выборочные распределения (n — IJs^/lO для
первого случая, когда верна гипотеза Zf0:ct* = lO, н вто-
рого случая, когда справедлива гипотеза Hi •.<% = 20 (л = 9),
(п — 1)з^а будет b/а раз повторять х2-]- Например, на рис. 14.2
представлены кривые (п— l)s2/10 для случая 0^=10, то есть
когда верна Но, и о’= 20 при истинности Ht; л = 9.
Если бы из выборки объемом 9 было найдено з® =21,40,то
значение критерия по уравнению (14.9) было бы следующим;
=
X ю ю
На рис. 14.2 мы видим, что значение критерия, равное 17,12
или больше, сравнительно маловероятно, когда ст; =10, но
вполне приемлемо, когда справедливо о; = 20. На основе на-
блюдения мы склоняемся отвергнуть HQ и принять Н{.
д) Для проверки Но против Ht на уровне значимости а уста-
навливаются критические значения — процентильные точки а/2
и 1 —(а/2) хи-квадрат распределения с числом степеней сво-
боды, равным п — 1, то есть х2_р
1-(вй)Хп-1-
274
е) 100(1 —а) % доверительный интервал для неизвестной о£
строится следующим образом:
------~2— и t <.-------j---. учли,
а/2Хп-1
ж) В течение нескольких лет инспектор, контролирующий
состояние учебных программ и проводимых исследований в круп-
ной школьной системе, наблюдал типичное стандартное откло-
нение, равное 0,80, измеренное в отметках с помощью обычного
теста проверки успеваемости по арифметике в конце учебного
года у учеников третьего класса. В отличие от предыдущих лет
в текущем году обучение арифметике в третьем классе проводи-
лось по программированному учебнику. Одна из наиболее раз-
рекламированных особенностей программированного обучения
состоит в том, что оно обеспечивает наиболее благоприятные
возможности сгладить индивидуальные различия в скорости обу-
чения по сравнению с традиционными методами. Следовательно,
в копие этого года у третьеклассников должна наблюдаться не-
сколько иная дисперсия при контроле успеваемости по арифме-
тике, чем в прошлые годы. Инспектор формирует случайную вы-
борку объемом 25 учащихся, которым предстоит принять уча-
стие в проверке успеваемости по арифметике. Данные будут ис-
пользованы для проверки следующих гипотез на уровне значи-
мости 0,10:
Яо:<^ = (О,8О)г = О,64
Н..: о’ #= 0,64.
Выборочная дисперсия, найденная по 25 контрольным оценкам,
равна 1,14,
Величина
_ 24(1,14)
'• 0,64
==42,75
сравнивается с критическими значениями
»,«A=-13.SS „^,-36.42.
и оказывается, что различие значимо на уровне 0,10. Вероят-
ность р того, что величина х2 будет равна 42,75 или большему
значению, при истинности 7/0 приблизительно равна 0,01.
90% доверительный интервал для определяется путем под-
становки выборочных данных в уравнение (14.10):
<• а2 <- JULlfZ 0 75 < ог < 1 98
36,42 <Ох< 13,85 < 1,УЙ.
Напрашивается вывод, что совокупность третьеклассников,
которых коснулось программированное обучение, обладает боль-
шей дисперсией в процессе проверки успеваемости по арифме-
275
тике по сравнению с предыдущим периодом- Обратите внима-
ние, что методы статистического вывода были реализованы в
случае, когда нет необходимости назначить проверку более чем
25 ученикам.
з) В отличие от проверки гипотез относительно средних по
/-распределению Стыодента предположение об извлечении вы-
борок из нормальной совокупности нельзя принять необдуманно
в случае гипотез о генеральных дисперсиях (см. Шеффе 1962,
гл. 10).
14.6. Выводы относительно
по независимым выборкам
а) Рассматриваемая задача намного важнее для практики, •
чем задача проверки того, будет ли генеральная дисперсия рав-
на некоторой предполагаемой величине а или нет.
Здесь мы имеем две совокупности (1 и 2) и хотим проверить,
равны ли их дисперсии а; и или нет:
б) Предполагается, что выборка объемом п, случайно извле-
кается из нормальной совокупности со средним pj и дисперсией
c'J; независимая случайная выборка объемом п2 извлекается из
второй нормальной совокупности со средним ц2 и дисперсией
При проверке На значения щ и ц2 несущественны и не представ-
ляют интереса.
в) Для проверки Но против Н{ используется критерий отно-
шения двух выборочных дисперсий:
S?
F-^. (14.11)
г) Когда верна гипотеза Н,.: о] = о^, выборочное распреде-
ление F = s^/s2 представляет собой F-распределение с п, —- 1
и п2— 1 степенями свободы. Когда имеет место Ht: о® сг»
распределение повторяет о’/сг; раз F-распределение с и, — 1
и п2 — I степенями свободы.
Таким образом, если фактически а]/о] = 2, распределение
будет иметь вид F-распределения, преобразованного умно-
жением на 2.
д) Критические значения, с которыми сравнивается F в урав-
нении (14.11) при проверке Но против Hi на уровне значимо-
сти а, есть:
a/2Fni~|,n,-l И
276
то есть это точки процентилей 100(а/2) и 100(1—(а/2)] a F-
распределении с rii — 1 и —1 степенями свободы. Верхние
процентильные точки в f-распределениях можно определить
непосредственно по таблицам. Нижние процентильные точки
связаны с верхними следующим образом;
(14.12)
е) 100(1—а) % доверительный интервал для
а’ к строится так:
sf 4
aflF»|-1. Л1—I < "^5" < l~(al2)Fп,—1, п,—I •
отношения
(14.13)
ж) В исследовании Сиэре (1940) детям давались обычные
арифметические задачи, а затем одной случайно выбранной по-
ловине учащихся сообщалось, что они не выдержали испытания,
а остальным—обратное. Затем у каждого ребенка спрашивали,
сколько секунд ему потребовалось бы для решения новой задачи.
Экспериментатор вычислял разность между ожидаемым време-
нем решения задачи (в сек), которое называл ребенок, и резуль-
татами ранее выполненного задания. Полагали, что провалив-
шиеся на предыдущем испытании могли проявить некоторую
неуверенность при оценке своих намерений.
Проверяемая на уровне значимости 0,05 гипотеза состоит
в том, что дисперсия совокупности детских оценок, имеющих от-
ношение к оценке их возможностей, постоянна независимо от
того, сообщалось детям о плохих результатах испытаний или об
удачном решении первой задачи. Сиэре получила следующие
данные:
Группа 1
{учащиеся, которым
«общалось
«1 = 12
s* «=8,16
мг = 12
sj = 90,45
Критерий проверки ур. (14.11) имеет следующее значение:
р — AIL л лол
Г 90,45 U’UyU-
Оно сравнивается с критическими значениями, которые опре-
деляются по таблице:
0.975^11.11— 3,47 И 0.025^11.11— !(
3,47 ” °’29-
277
Так как F = 0,09 оказывается меньше нижнего критического
значения, то гипотеза Яо: aj — a’ отклоняется на уровне значи-
мости 0,05.
95% доверительный интервал для а’^о’построенпоур. (14.13) г
8,16 а? 8,16 а?
(0,29) —г < -1 < (3,47) -2— — 0,03 < Ц < 0,31.
90,45 <з2 ’ 90,45 с’
з) Вопрос о том, какую выборку обозначать первым или вто-
рым номером, обычно решается произвольно, но его не следует
решать по результатам наблюдения, позволяющего определить <
большую дисперсию. Для определения, какую выборочную дис-
персию следует обозначить символом s,, можно прибегнуть
к подбрасыванию монеты. Если необходимо построить лишь ин-
тервальную оценку отношения генеральных дисперсий, то пре-
дыдущие соображения относительно обозначений и si ли-
шены смысла.
Допущение о том, что з, и $? найдены по независимым вы-
боркам из нормальных совокупностей, нельзя принять без обос-
нования— в отличие от гипотезы нормальности, лежащей в осно-
ве /-критерия для средних. Если ожидается значительное от-
клонение от нормальности, то следует применять проверку зна-
чимости в соответствии с § 15.14.
В прошлом было принято проверять гипотезу Но: = до
проверки по /-критерию гипотезы Но •. ц, — ц2 — 0. Первая ги-
потеза— это предположение об однородности дисперсий, сде-
ланное в процессе проверки последней гипотезы. В свое время
в учебниках советовали не приступать к простейшему испыта-
нию по /-критерию в случае, если привело к отклонению
Яу: o’= о’. Хотя подобный совет удержал бы от повышен-
ного интереса к допущениям в используемых критериях, оказа-
лось, что вообще он очень плох. В частности, предварительная
проверка предположения об однородности дисперсий может ока-
заться необоснованной при отсутствии нормальности совокуп-
ностей, но та же самая ненормальность не увеличивает обосно-
ванности /-критерия pi — р.2 = 0- Действительно, при п1=л2
нет оснований говорить о нарушении допущения об однородных
дисперсиях. Единственный случай, при котором стоит специально
проверять Но: ст’==а’ до проверки Но: = 0, возникает,
когда точно установлено, что совокупности описываются нор-
мальным законом, а щ и п2 не равны, Тут может понадобиться
простое преобразование наблюдений, которое позволит аппрок-
симировать данные распределением, близким к нормальному.
«Нормализующие преобразования» подробно рассматриваются
в книге П. Джонсона «Статистические методы исследования»
(1949, гл. 7).
278
14.7. Выводы о по зависимым выборкам
а) Как и в § 14.6, проверяемая нуль-гипотеза состоит в том,,
что 2 совокупности характеризуются одинаковой дисперсией:
Я,: а? ¥= <4
6) Предполагается, что берутся 2 возможно( зависимые вы-
борки, одна объема п из нормальной совокупности с дисперсией
а|, а другая того же объема п из нормальной совокупности
с дисперсией о". Значения Ц| и цз нас не интересуют.
Происхождение зависимых выборок обсуждалось в § 14.4
при оценке различий между средними.
в) При проверке На против Ht используется критерий
где si и si— дисперсии 1-й и 2-й выборок соответственно; п —
число пар наблюдений, объединяющих каждое наблюдение 1-й
выборки с одним наблюдением 2-й выборки, a г12— коэффи-
циент корреляции, найденный по парам наблюдений.
Как подчеркивалось в § 14.4, вообще допускается «образо-
вание пар» наблюдений по двум зависимым выборкам («до —
после», «брат—сестра», «муж-—жена»).
г) Когда верна Но'. — выборочное распределение i
в ур. (14.14) представляет собой /-распределение Стьюдента с
п— 2 степенями свободы.
д) Для проверки Но против Ht на уровне значимости а бе-
рутся следующие критические значения:
afztn-2 !-(a/2)fn-2.
е) Построение доверительного интервала для = или-
когда оценки дисперсий получены по зависимым выбор-
кам. 'слишком трудно для этой книги.
ж) Лорд (19636) описал данные, собранные У. Кофменом
по характеристикам выборки объема 95 учащихся седьмых
и восьмых классов при оценке успеваемости по Стенфордскому
тесту. Интересно было выяснить, будут ли характеристики уча-
щихся более постоянными (менее изменчивыми) в седьмом или
в восьмом классе. !-я выборка — группа оценок Стенфордского
теста успеваемости, полученных 95 семиклассниками, а 2-я вы-
борка представлена оценками тех же 95 учащихся в восьмом
классе. Таким образом, две выборки не являются независимыми.
279
верки нуль-гнпотезы о том, что рХ1? = а, используется следую-
щая статистика:
где ZT— Z-преобразованное значение, соответствующее выбо-
рочному rxy; Za — Z-прсобразованное значение, соответствую-
щее а, предполагаемому значению рху в До. а п — объем вы-
борки.
г) Когда верна Нй, то есть рхр = а, то г в уравнении (14.15)
имеет нормальное распределение со средним 0 и стандартным
отклонением 1, то есть г имеет единичное нормальное распре-
деление. Если, с другой стороны, верна а рху = 6, которое
отличается от а, то г в уравнении (14.15) описывается нормаль-
ным распределением с единичным стандартным отклонением,
причем распределение группируется вокруг среднего /ь— /а.
Рис. И.З. Выборочные распределения z = (Zr — O)/(1/Vn—3)
для выборок объема 12 при рЖ(,==0 и pXj, = O,bO.
Например, если правильной оказывается гипотеза До:рху = О,
то распределение z = (Zr — 0)/(l l^n — 3 ) для выборок объ-
ема 12 представлено кривой в левой части рис. 14.3. Если под-
тверждается Ht :рхц = 0.60, а п = 12, то выборочное распределе-
ние г ~(Zr — 0)/(l Iд/n — 3) — кривая в правой части рис. 14.3.
д) Критические значения, с которыми при проверке Но на
уровне значимости а сравнивается г в уравнении (14.15), пред-
ставляют собой процентили вида 100(а/2) и 100(1 —(а/2)] в еди-
ничном нормальном распределении:
a/2Z И |-(a/2)Z.
Например, если Па проверяется на уровне значимости 0,05, то
критические значения; —1,96 и 4-1,96.
е) Доверительные интервалы для рху строятся путем опреде-
ления доверительного интервала для /р относительно Zr и по-
следующего преобразования верхних и нижних пределов имею-
щегося интервала в исходную шкалу г, с повторным обраще-
нием к таблицам.
Первый этап построения 100(1—и)% доверительного ин-
тервала для рху — вычисление
Z,± (14,16)
281
где Zr и п определены ранее в уравнении (14.15), a про-
центиль вида 100(1 —(<х/2)1 в единичном нормальном распреде-
лении.
Уравнение (14.16) будет определять положение 2 точек на
шкале /-преобразования. С этими двумя значениями мы обра-
щаемся к таблице и находим 2 соответствующих значения гху.
Эти значения гху образуют 100(1 — а) % доверительный интер-
вал ДЛЯ Рху*
ж) Форхенд и Либби (1962) обобщили данные относительно
корреляции между «инспекторскими оценками новаторства», Д’,
и результатами испытаний рассеянности («гибкость» и «увлечен-
ность»— известные под названием критериев «творчества»}, У,
по п = 60 (группа правительственных администраторов). Был
найден гху — 0,30.
При а = 0,05 мы будем проверять нуль-гипотезу о том, что
— 0:
: рху — 0
Я] • Рхц^О.
По таблице находим /-преобразование г =0,310, то есть
/0,30 = 0,310. Разумеется, /в — 0.
Таким образом, значение г в уравнении (14.15) равно:
z=T7^=4-0-3,(,(VS5)“2M
Полученное значение z сравнивается с
0,025г ~— 1,96 И 0,975^ с= 1,96,
Поскольку 2,34 превышает 1,96, то Нц можно отклонить и
на уровне значимости 0,05 принять Н\. 95%-й доверительный
интервал для рху строится следующим образом:
ZM, ± (1,96)-^Д—— 0,310 ± 0,259 = (0,051; 0,569).
По таблице определяются значения гху, соответствующие
/, равным 0,051 и 0,569. Эти значения — 0,05 и 0,51 соот-
ветственно. Таким образом, 95%-ным доверительным интерва-
лом для рлу является (0,05; 0,51).
3) В большинстве случаев на практике значение рх», относи-
тельно которого выдвигается гипотеза, равно 0. Следовательно,
</г-— 0)/(l/Vn — 3) = /f(Vn — 3) относится к таблице единич-
ного нормального распределения. Существует альтернативная
статистика, точно описывающая выборочное распределение гху
при рхУ=0. (Приведенная проверка гипотезы является прибли-
женной, однако она почти не отличается от точной даже для
очень малых п, так что об аппроксимации можно не говорить.)
282
При Рхр = О
/ = —
имеет f-распределение Стыодента с числом степеней свободы
п — 2. Это обстоятельство было использовано для построения
таблицы критических значений гху с целью упрощения проверки
Но-. pxil = Q. В таблицах даны значения, которые должен пре-
вышать гху по абсолютной величине, чтобы стало необходимо
отклонить До: р1(, — 0. О влиянии нарушения предположения
о двумерной нормальности см.: Norris, Hjelm, 1961;Carroll, 1961.
14.9. Выводы о P| — Р2 по независимым выборкам
а) В данном случае выводы касаются возможной разности
между корреляцией р5 X и У в 1-й совокупности и корреляцией
тех же двух переменных во 2-й совокупности. Например, силь-
нее ли коррелированы способности X и успеваемость У у маль-
чиков (1-я совокупность), чем у девочек (2-я совокупность)?
Нуль-гипотеза, как обычно, утверждает, что р; — р2, альтерна-
тивная гипотеза — обратное:
Pi = Рг
Ht: Pi ^Pi-
б) Полагается, что из двумерной нормальной совокупности 1
с коэффициентом корреляции pi извлекается случайная выборка
объема «1, а независимая случайная выборка объема п2 берется
из двумерной нормальной совокупности 2 с корреляцией р2.
в) Проблемы статистического вывода решаются методами
Z-преобразования Фишера. Выборки 1 и 2 берутся соответс! вея-
но из совокупностей 1 и 2. Вычисляются 2 выборочных коэффи-
циента корреляции, Г| и г2, а затем их преобразуют в Zr, и Zr,
с помощью таблицы. Для проверки До'-pi — рг используется
статистика:
Д/ «I — 3 + пг — 3
г) Если фактически pi = р2, то г в уравнении (14.17) имеет
нормальное распределение с нулевым средним и единичным
стандартным отклонением по повторяющимся парам независи-
мых случайных выборок Если па самом деле pt и р2 отличаются,
то среднее выборочного распределения г в уравнении (14.17)
будет удаляться от нуля — оно станет определяться разностью
ZP1 —ZPt, однако стандартное отклонение сохранится прежним.
д) Для проверки Д0:р( = р2 против Hiipt^pz на уровне
значимости а единственное значение г ъ уравнении (14.17) срав-
283
нивается с процентилями вида 100(а/2) и 100(1 — (а/2)1 в еди-
ничном нормальном распределении:
аПг И
е) Доверительные интервалы для р1 — р2 построены по ме-
тоду определения доверительных интервалов для /-преобразо-
вания pi и ра. Для определения 100(1—а)% доверительного
интервала для pt — р2 вычисляется
(Zfi — Zrs) ± t-fa^z aJ7^~z'3‘+ (14.18)
Два значения на шкале Z, полученные из уравнения (14.га), па-
том преобразуются в шкалу г с помощью таблицы. Получен-
ные значения г образуют 100(1—а) % доверительный интервал
ДЛЯ pt — р2.
ж) Методы, излагаемые в этом параграфе, показаны на дан-
ных, построенных на основе исследований Хинтона (1939) и Дис-
пенсы (1938). В выборке из 200 детей в возрасте от 6 до 15 лет
корреляция между интеллектом (Стенфорд — Бине) X и ско-
ростью основного обмена веществ Y определялась величиной
Г] ==0,71. В выборке, включающей 78 взрослых людей в воз-
расте от 18 до 25 лет, интеллект и скорость обмена веществ
имеют корреляционную связь, оцениваемую коэффициентом
г2 =з 0,28. Мы будем проверять До: pi = р2 на уровне значимо-
сти 0,61. Следовательно, критические значения для г из уравне-
ния (14.17) представляются величинами —2,58 и 2,58
Z0.7i~0,887 /о.й = 0,288.
Zori~Zo,„ 0,887-0,288 0,599
г = ~т.....j.., I’" “ ..., = = от» - ‘‘•40-
Д/ Я| — з + па - 3 Л/ 200 — 3 + 78 — 3
Мы видим, что До’.pi = ps можно отклонить на уровне зна-
чимости 0,61. 99% доверительный интервал для pj и р2 опреде-
ляется по уравнению (14.18) следующим образом:
0,887 - 0,288 ± 2,58 д/ + jjiy -
= 0,599±0,350 = (0,249; 0,949).
Преобразование этих двух Z-велнчин снова в r-шкалу дает
99% доверительный интервал для pt—р3:0,24; 0,74.
з) В то время как нуль-гипотеза, утверждающая, что pt=p2,
имеет вполне определенный смысл, простое оценивание разности
двух коэффициентов п — г2 и определение доверительного
интервала относительно выборочной разности может не иметь
смысла. Предположим, например, что р,—-р2 = 0,20. Должно
выполняться какое-то из следующих условий для pt и р2: (1)
pt ==0,90, a pj = 0,70; (2) pt=0,20, а р2 = 0,00; (3) Pi=0,10,
284
a p2 = —0,10 и т. п. Хотя в каждом случае разность р! и р2 оди-
накова и равна 0,20, смысл, который придается 3 условиям, со-
вершенно различен. В (1) разность 0,20 характеризует более
существенное различие в возможности предсказания одной пе-
ременной по другой по сравнению с разностью 0,20 в (2). Кроме
того, разность 6,20 между 0,10 и —0,10 не описывает различий
в способности предсказать одну переменную по другой.
14.10, Выводы о Рху — рх. при зависимых выборках
а) Проверяемая нуль-гипотеза состоит в том, что перемен-
ная X имеет одинаковую корреляцию с двумя другими перемен-
ными, У и Z, против утверждения альтернативной гипотезы, что
рху Н р« не равны:
РхУ=Рхг
Н,- Px^P«.
Такая ситуация возникает, например, тогда, когда надо пред-
сказать «академическую успеваемость» (измеренную по сред-
нему баллу) с помощью двух предсказателей, У и Z. Если по
финансовым соображениям можно воспользоваться толькоодним
из них (У или Z), то полезно было бы собрать данные, оценить
гху и гх1, а затем проверить гипотезу о том, что наблюдаемая
разность между двумя выборочными г описывает действитель-
ное различие между рху и рхг.
б) Предполагается, что существуют 3 двумерные нормальные
совокупности для каждой пары переменных X и У, X и Z, У и Z.
Извлекается простая случайная выборка объема п, по которой
определяются 3 коэффициента корреляции гху, глг и гуг, Оче-
видно, эти 3 оценки не независимы.
в) Статистикой для проверки Но против утверждения Hi
служит:
_ Vn (г1у — гхг)
* ~ V0 - =w„ - w
(14.19)
где n — объем выборки; rxy— выборочная корреляция X и У;
гхг— выборочная корреляция X и Z; гуг— выборочная корреля-
ция У и Z.
г) Если подтверждается Но, то есть рху — рхс, то z в уравне-
нии (14.19) имеет выборочное распределение для всех выборок
объема д, которое аппроксимируется нормальным распределе-
нием с нулевым средним и единичным стандартным отклонением
(см. Olkin, Siotani, 1964; Olkin, 1967), Когда верна Hit среднее
выборочного распределения z в уравнении (14.19) уходит от
нуля, а стандартное отклонение остается неизменным.
285
д) Как следовало ожидать, нуль-гипотеза На: pxv — р« про-
веряется на уровне значимости а путем сравнения наблюдае-
мого значения г по уравнению (14.19) с точками процентилей
вида 100(а/2) и 100(1 —(се/2)] в единичном нормальном распре-
делении; двумя критическими значениями для проверки гипо-
тезы являются
а/22 и |-(а/2)2’
е) Интервальную оценку разности pIV — рХ! трудно объяс-
нить по тем же причинам, которые обсуждались в конце § 14.9,
но методы ее получения существуют (см. Olkin, 1967, р. 113).
ж) Предположим, что успех обучения в колледже X (изме-
ренный по среднему баллу в конце первого курса можно) пред-
сказать либо по комплексу тестов У, либо по комплексу тестовZ.
Из-за недостатка времени можно провести испытание только п<?
одному комплексу. Требуется проверить гипотезу Нй : pxv = pXI
при уровне значимости 0,05.
Для случайной выборки объема 100 первокурсников, которым
были предложены оба комплекса тестов, возможны следующие
коэффициенты корреляции X, У и Z;
rXJ,= 0,56; гхг —0,43; r^=0,52.
Величина г, согласно уравнению (14.19), равна:
_________________________УТоб (0,56-0,43)____________________
г V(1 - 0,56’j2 + (I -0.432)2 - 2 ( 0,52)’-__________________‘
- [2 (0,52) - (0,56) (0,43)] (1 - 0,56’ - 0,43’ - 0.52’)
= 1°<о.13) = 1,300 60
“ V^6597 0,8122 ’ '
Полученная величина z оказывается значительно ниже тре-
буемого критического значения 1,96. Таким образом, гипотезу
о том, что комплексы У и Z эквивалентны по точности предска-
зания X, нельзя отклонять,
14.11. Выводы о других коэффициентах корреляции
В этом параграфе будут обсуждаться процедуры проверки
значимости для коэффициентов корреляции, описанных в главе 9.
Характеристика методов вывода будет значительно упрощена,
поскольку ограниченность места не позволяет приводить под-
робности. Будут описаны приемы, с помощью которых можно
проверить нуль-гипотезу об отсутствии корреляции между пере-
менными X и У против утверждения ненаправленной альтерна-
тивной гипотезы для большинства коэффициентов 9 главы. При
любой возможности мы будем определять критерий как вели-
чину, имеющую известное или приблизительно известное выбо-
286
рочное распределение, когда известно, что коррелируемые пере-
менные— независимо от того, измеряются ли они дихотомически,
ранжированием или как-то иначе, — не связаны, то есть имеют
нулевой коэффициент в совокупности. Во всех примерах про-
верка значимости будет показана на гипотетических данных.
Коэффициент фи, ф
Предположим, что из совокупности, в которой две дихотоми-
ческие переменные X и У имеют нулевой коэффициент фи, извле-
кается случайная выборка объема п. Для больших значений п
(скажем, 20 или больше) выборочное распределение д/^Ф-
где ф—выборочный коэффициент фи, приближенно описывается
нормальным законом с нулевым средним и единичным стандарт-
ным отклонением. (Когда коэффициент фи совокупности отли-
чается от нуля, выборочное распределение д/” Ф становится
скошенным, группируясь около среднего, отклоняющегося от
нулевого значения па величину, которая увеличивается при уда-
лении коэффициента ф совокупности от 0.)
Случайная выборка при п — 25 изучается по двум дихотоми-
ческим переменным: X— «пол», имеющей два уровня: 0—жен-
щина, 1—мужчина; У—«адаптация», принимающей значения:
0 — «исключенные из школы», 1 — «оставшиеся в школе». Выбо-
рочное значение ф равно —0,41. Статистика критерия опреде-
ляется так:
г — VI ф = 725 (—0,41) = 5 (—0,41) = -2,05.
В единичном нормальном распределении величина г лежит
ниже 2,5 процентиля (0.0252=—1,96). Следовательно, гипотезу,
будто пол и адаптация в процессе обучения в школе не связаны
в рассматриваемой совокупности, можно отклонить на уровне
значимости 0,05- (Интересно отметить, что выборочное ф, от-
стоящее от нуля на —0,30, не привело бы к отклонению нуль-
гипотезы на уровне0,05 для 25 человек: д/n ф = — 1,50 > —1,96.)
Коэффициент ранговой корреляции Спирмена, rs
Выборочное распределение г8, характеризующее нулевую кор-
реляцию между двумя группами рангов X и У в совокупности,
нельзя описать в терминах любых хорошо известных распреде-
лений для п меньше 10. При га >10 выборочное распределе-
ние rs, когда коэффициент ранговой корреляции Спирмена равен
нулю, некоторым образом связано с i-распределением Стьюден-
та. Фактически для п > 10
/ = —?.................. (14.20)
287
имеет распределение, идентичное (-распределению Стъюдента
с числом степеней свободы п — 2, в случае, когда значение га
совокупности равно 0.
Предположим, например, что в выборке при п = 22, rs= 0,38-
Значение ( равно:
Для проверки гипотезы об отсутствии корреляции в совокуп-
ности на уровне 0,01 величина / = 1,84 сравнивается с
±0,995(20 = ±2,845. Так как г ва,ходится между 0,5 и 99,5 про-
центилями (-распределения с 20 степенями свободы, то нуль-
гипотезу об отсутствии корреляции в совокупности нельзя от-
клонить на уровне 0,01.
Для малых п в случае проверки нуль-гипотезы об отсут-
ствии связи между двумя ранговыми переменными находится
точное выборочное распределение rs (см. Кендалл, 1974). Вы-
бранные процентили в эмпирических распределениях rs для раз-
личных значений п табулированы.
т Кендалла
Значимость выборочного значения т Кендалла очень легко
проверяется с помощью одной из компонент, вычисляемой по-
путно. Как было показано в § 9.3, для выборки объема пт опре-
деляется по формуле:
_______S
Т п(п — \)/2 ’
где 8 — P — Q. —-разность между общим числом «совпадений»
Р и числом «инверсий» Q в двух множествах рангов,
Выборочное распределение 8 более удобно для исследования,
чем т, когда п больше или равно 10, выборочное распределе-
ние 8 является приближенно нормальным, если X и У в сово-
купности не коррелнрованы; стандартное отклонение S прибли-
зительно равно
— 1)(2п 4- 5)/18.
Выборочное распределение S можно приблизить к нормаль-
ному простой «поправкой на непрерывность», которая преобра-
зует 8 в величину, обозначаемую символом S*:
Если 8 отрицательно, 8* = 8 -f-1.
Если 8 положительно, 8* = 8 — 1.
Отсюда видно, что
г— fj{2n TsVis (14.21)
288
Тетрахорический коэффициент корреляции, rtet
Когда подтверждается нуль-гипотеза об отсутствии связи X
и У (две нормально распределенные дихотомические перемен-
ные) , эмпирическое распределение выборочного тетрахорического
коэффициента корреляции, rttl, аналогично нормальному для
п > 20 с нулевым средним и стандартным отклонением
(14.23)
где п—-объем выборки, рх = пх(п, доля объектов, имеющих еди-
ницу по дихотомической переменной X,
Pv — oy/nt доля объектов с единицами по дихотомической
переменной У,
их—-ордината над точкой z на единичной нормальной кри-
вой, выше которой находится доля рх площади, а ич — орди-
X
0
4 19
23
25 25 п = 50
Рис. 14.4, Таблица сопряженности, пока-
зывающая связь между полом и полити-
ческой Принадлежностью.
ната точки z на единичной нормальной кривой, выше которой
находится доля ру площади.
Итак, для умеренно больших и больших п для проверки ги-
потезы о том, что тетрахорический коэффициент корреляции со-
вокупности равен нулю,
можно отнести к единичному нормальному распределению.
Пусть данные рис. 14.4 накоплены при исследовании связи
двух переменных X и У, которые считаются нормально распре-
деленными и дихотомными.
Величина (bc)l(ad) равна (21) (19)/(4) (6) = 399/24 »
= 16,625. По таблицам можно найти, что 16,625 соответствует
rtet == 0,81.
Стандартная ошибка r«t оценивается по следующим данным:
0,50 ?,-0,50
/>.= >- 0.46 «, = 0,54.
290
По таблицам ордината на единичной нормальной кривой в
точке, выше которой находится доля = 0,50 площади, равна
их — 0,3989; ордината кривой в точке, выше которой лежит
доля ру = 0,46, равна uv — 0,3970. Таким образом, значение г
есть:
(0,50) (0,46) (0,50) (0,54)_________1________
50 ’ (0,3989)(0,3970)
В единичном нормальном распределении г — 3,64 намного
превосходит даже 99,5 процеитнль. Мы должны заключить, что
тетрахорический коэффициент корреляции отличен от 0.
Бисериальный коэффициент корреляции гы3
Точное выборочное распределение n,it неизвестно. Пирсон ни-
когда не занимался этим вопросом, и только Соупер (1914) вы-
вел формулу стандартного отклонения п,,» для больших выбо-
рок, Макнамара и Данлеп (1934) доказали, что в случае, когда
бисериальный коэффициент корреляции совокупности равен
нулю, для больших выборок Tbfs должен иметь распределение,
близкое к нормальному, с нулевым средним и стандартным от-
клонением ____
УЯ|«0
ипл[п
(14.24)
где п — объем выборки; nt — число объектов, имеющих 1 по ди-
хотомической переменной, а и—ордината единичной нормаль-
ной кривой в точке, выше которой находится доля nj/n площади
под кривой.
Когда бисериальный коэффициент корреляции совокупности
отдаляется от нуля, величина уменьшается на 1 /л/п —
часть от величины квадрата совокупности. При гы», не рав-
ном нулю, выборочное распределение гь^ становится ненор-
мальным, скошенным в сторону 0.
Экспериментальные исследования Лорда (1963а) п Бейкера
(1965) показали, что ранее приведенная оценка стандартной
ошибки гьч по большим выборкам является довольно точной;
в исследовании Бейкера подтвердилась точность оценивания
даже для выборок объема 15.
Пусть для выборки объема 36, в которой nt — 16, а пэ = 20,
величина г„.„ составляет —0,145. В случае, когда бисериальный
коэффициент совокупности равен 0, для значения сгг имеем:
Если rt,ts совокупности равен 0, то rbls/or будет иметь нор-
мальное распределение с пулевым средним и единичным стан-
10*
291
дартпым отклонением по всем случайным выборкам объема п.
rbls
Нет оснований отклонить нуль-гипотезу о том, что бисериаль-
ный коэффициент корреляции совокупности равен нулю.
Рангово-бисериальный коэффициент корреляции, гтъ
По вопросу проверки значимости рангово-бисериального ко-
эффициента корреляции гть см. работы Кертена (1956) и Глас-
са (1966 6),
Коэффициент частной корреляции, гху^г
Коэффициент частной корреляции между X и Y при постоян-
ном значении Z был описан в § 9.4.
Генеральный коэффициент частной корреляции X и ¥ при Z,
влияние которой «частично исключено», можно представить так:
Рху — PxzPyz
V0-«(>-<£)'
Когда рху-г = 0, статистика
имеет /-распределение Стыодента с числом степеней свободы
п — 3. Предположим, что в выборке с п = 12 величина гху_: рав-
на 0,60. Тогда
t = 0,80 . = 4,00.
V(1-0,80г)/(Т2-3)
99,5-й процентиль /-распределения с 9 степенями свободы ра-
вен 3,250. Нуль-гипотезу о нулевом значении коэффициента ча-
стной корреляции генеральной совокупности можно отклонить
на уровне значимости 0,01.
14.12. Выводы относительно Р, доли в совокупности
а) Теперь мы будем анализировать долю «элементов» (лю-
дей, семей, школ, округов и т. д.) в совокупности, обладающих
некоторой характеристикой (голубые глаза, автомобиль послед-
ней модели, программа «современной математики», центр дет-
ской диагностики и т. д.). Долю элементов совокупности, обла-
дающих рассматриваемой характеристикой, будем обозначать
Символом Р, соответствующим числу элементов, обладающих на-
292
званной характеристикой, деленному на общее число элементов
совокупности- Например, из 60 000 учащихся в системе частных
школ 3000 детей имеют испано-американское происхождение:
следовательно, Р = 3000/60 000 = 0,05, когда в качестве наблю-
даемой характеристики рассматривается «испано-американское
происхождение в сравнении с прочими национальностями».
Проверяемая гипотеза заключается в том, что в сравнитель-
но большой совокупности доля Р равна некоторому числу а, ко-
торое заключено между 0 и 1,0:
б) Для проверки Но против /fj необходимо только предполо-
жить, что из совокупности извлекается случайная выборка объ-
ема п.
в) Внутри выборки с п элементами находится число f эле-
ментов, имеющих рассматриваемую характеристику. Выбороч-
ная доля р— отношение f к п:
Статистика р— оценка Р. Действительно, если мы оцениваем
дихотомическую переменную X, равную 1, когда изучаемый эле-
мент обладает рассматриваемой характеристикой, и равную 0,
когда не обладает, то р соответствует Р так же, как X.— ц. На-
пример. пусть измеряемой характеристикой будет «пол?. Ха-
рактеристику ребенка обозначим X, со значениями 1 для маль-
чиков и 0 — для девочек. Если в выборке п детей присутствует
/ мальчиков, то
Ёх, = х,+ ... +x. = t.
Следовательно,
Генеральным средним X будет Р. Итак, р как оценка Р обла-
дает-всеми свойствами, присущими X. как оценке ц.
В данном контексте интересно также отметить, что дихото-
мическая переменная X имеет генеральную дисперсию, равную
о2^Е(Х-Р)2 = Р(1-Р),
где Р — доля в совокупности.
г) Предположим, что верна нуль-гипотеза, утверждающая,
что Р равна а. Вероятно, вы помните, что выборочное распреде-
ление X. имеет среднее ц и стандартное отклонение ох/л/п. То
же самое справедливо для р. Для выборок объема п среднее
293
выборочного распределения р равно а —доле в совокупности,
а стандартное отклонение есть Ох/'у/п — л/а(\ — а)[п'-
Е(р) — а
На вопрос о форме выборочного распределения р можно от-
ветить, обращаясь к центральной предельной теореме. Когда п
достаточно велико, выборочное распределение р является нор-
мальным со средним Р и стандартным отклонением (1 — Р)[п.
Выражение «достаточно велико» подразумевает, что для рас-
смотрения р как нормально распределенной величины значе-
ние пР или п(1 —Р), как бы мало оно ни было, должно быть-
больше 5. Это строгое правило зависит от объема выборки п и
неизвестной доли в совокупности Р. Предположим, например,
что антрополог хочет сделать вывод относительно доли «левшей»
в африканском племени. (У некоторых африканских племен
Р — 0,02, однако в Соединенных Штатах Р > 0,10.) Антропологу
следовало бы взять выборку объемом до 500 человек с тем,
чтобы обеспечить возможность оценки Р вплоть до 0,01 — пР =
= 500(0,01)— 5.
Если значение Р равно а, то есть если справедлива Но и
если па больше пяти, то
распределена приблизительно нормально для случайных выбо-
рок объема п с нулевым средним и единичным стандартным от-
клонением.
Если Р—некоторая величина Ь, не равная а, то Р, конечно,
останется приближенно нормально распределенным, но со сред-
ним b и стандартным отклонением -x/b(l — Ь)/п, при условии, что
nb или п(1 — Ь) больше 5.
д) Для проверки Но против Д’, на уровне значимости а ве-
личина z цз ур. (14.26) сравнивается с процентилями вида
1О0(а/2) и 100(1 —(а/2)] в единичном нормальном распределе-
нии:
о/2г I- (а/2)г-
е) 95 и 99% доверительные интервалы для Р относительно р
можно легко определить, обращаясь к таблицам. Предположим,
например, что в выборке п == 100 величина р = 0,60. 95% дове-
рительный интервал для Р простирается приблизительно от 0,51
до 0,71. Для больших выборок вероятность того, что интервал
р± i-(a/2)Z-\/p(l ~р)/л будет накрывать?, равна 1 — а.
ж) Инспектор школьного района хочет за месяц до город-
ских выборов провести голосование для оценки того, может ли
предложение о школьной лотерее получить большинство голо-
294
•сов. Проверяемая на уровне значимости 0,01 гипотеза утвер-
ждает, что Р, доля зарегистрированных избирателей, одобряю-
щих школьные лотереи, равна 0,50; альтернативная гипотеза
состоит в том, что Р =/= 0,50. Извлекается случайная выборка
п ==100 избирателей: по результатам анализа f ~ 42, то есть
42 избирателя указали, что они одобряют школьную лотерею.
Величина р составляет fin = 0,42. Значение г по ур. (14.26)
есть:
р — а 0,42 — 0,50 . сп
Z — ----------= т=- -- = 1,60.
у/а(1—а)/п <0,50(0,50)7100
z = —1,60 сравнивается с критическими значениями
0.0052==— 2>58 И 0.0952 = 2,58.
Нельзя сделать вывод о том, что р = 0,42 существенно отли-
чается от 0,50 на уровне 0,01. Действительно, даже если бы был
принят уровень значимости 0,05, не было бы оснований откло-
нить Но'. Р~ 0,50, так как критические значения были бы то-
гда — 1,64 и 1,64.
14.13. Выводы относительно Pi — Рг
при независимых выборках
а) Существуют две большие совокупности 1 и 2, в которых
доли лиц (или вообще «элементов»), обладающих некоторой ха-
рактеристикой, представлены символами Pt и Р2- Проверяемая
гипотеза утверждает, что = Pj, тогда как альтернативная ги-
потеза — что Р} =?= Р2-
H$'-Pt~ Р2
НГ-Р^ Рг-
Например, можно проверить нулъ-пшотезу о том, что доля Р(
учащихся, получивших профессиональную рекомендацию, из тех.
кто собирается посещать колледж, равна доле Р2 учащихся, не
получивших такой рекомендации, из той же группы.
б) Необходимо условиться, что из 1-й совокупности извле-
кается случайная выборка объема nt, а из 2-й — независимая
случайная выборка объема п2.
в) Число элементов в выборке из 1-й совокупности, облада-
ющих исследуемой характеристикой, равно f!k а доля — величина
р{ = ип\. В выборке из 2-й совокупности рассматриваемой ха-
рактеристикой обладают f2 (скажем, собирающиеся поступить
в колледж), и доля равна р2 = f2ln2. Определяется следующая
статистика:
д/йгНй (' “ "ЙУ (тг +
295
Величина (ft 4- fa)/(Ai + пг) —доля а обеих выборках. Если нуль-
гипотеза справедлива, то Р\ и Рг равны одной и той же вели-
чине Р, которая оценивается отношением (Л + f2)/(ni + ^г)-
A (fi + h)l{n\ + п?), умноженное на 1 минус то же отношение —
оценка дисперсии X, дихотомической переменной со средним Р.
Отсюда z в ур. (14.27) сходен с
'=<*• + ~).
которое используется для проверки гипотезы pi — ц2-
г) Если подтверждается гипотеза Яо'.Р^Ро и для обеих
СОВОКуПНОСТеЙ П\Р\ (или п( (1 — PQ] и п2Р2 (или пг(1 — Р2)£боль-
ше 5, то z в ур. (14.27) имеет нормальное распределение с пу-
левым средним и единичным стандартным отклонением для пар
независимых выборок.
д) Для проверки Нй против Я[ на уровне значимости а одно
расчетное значение г из уравнения (14.27) сравнивается с Q/2z
и (a/2;Z, процентилями вида 100(а/2) и 100(1—(a/2)j единич-
ного нормального распределения.
е) Для больших значений п1 и п2 (порядка 100 или более)
100 (1 — а) % доверительный интервал для Р\ — Р% определяется
пр^лизнтельно следующим выражением:
(л - л) ± V( «,'+«’)(1 “ »' + «, + А (14-28)
ж) Группа из 200 учащихся случайно делится па две группы
по 100 человек. Учащиеся 1-й выборки изучают пособия, в ко-
торых сначала дается определение относительного понятия
«выше, чем», а затем оно рассматривается на нескольких при-
мерах. В пособиях, предлагаемых учащимся 2-й выборки, сна-
чала приводятся примеры, а потом следует формулировка поня-
тия. После изучения пособий учащимся обеих выборок дается
один и тот же тест для определения, усвоено ли ими относитель-
ное понятие. Мы хотим проверить, будут ли доли Pt и Рг уча-
щихся в гипотетических совокупностях, усвоивших это понятие
(что подтверждается правильными ответами), равны.
Предположим, мы выбрали a = 0,05 и после эксперимента в
1-й выборке число усвоивших понятие fi = 68; во второй f г =
= 54. Значение г в уравнении (14.27) равно:
Z« (68/100)-(54/100) 2 3
// 68-54 W 68 +54 W ! _1_\
'V\ 100+ 100A 100+ 100 А 100 т 1007
Величина г = 2,03 превышает критическое значение =
= 1,96 и таким образом убеждает нас в необходимости откло-
нить Но'. Р\ — Р2-
В данном гипотетическом примере мы можем прийти к вы-
воду, что лучше сначала дать определение понятия, а потом при-
водить примеры.
296
з) Для выводов, относящихся к множеству J долей в сово-
купности (в этом параграфе 7 = 2), разработаны соответствую-
щие методы. О данных методах читайте сначала работу Мара-
скайло (1966), а затем Гудмена (1964).
14.14. Выводы о Pi-Рг при зависимых выборках
а) Проверяемые гипотезы те же, что и в § 14.13, а именно
//0 р} = р2 против Я, Р, =/= Р2.
б) Из совокупностей 1 и 2 извлекаются две случайные вы-
борки объема п. В отличие от § 14.13 мы не требуем выполнения
условия независимости двух выборок. Итак, выборки 1-я и
2-я могут состоять из супружеских пар, близнецов, наблюдений
типа «до — после» и т. д.
в) Как и во всех методах, связанных с зависимыми выбор-
ками, можно составить «пары» наблюдений, один элемент кото-
рых принадлежит 1-й выборке, а второй входит во 2-ю выборку.
Выборка 1
Выборка 2
О
h
n—ft
П — fl h n
Рис. 14.5.
Мы будем рассматривать 1-ю и 2-ю выборки как наблюдения п
объектов соответственно в 1-й и 2-й моменты времени. Число
объектов с 1 по дихотомии, то есть имеющих анализируемую ха-
рактеристику, в 1-й выборке определяется величиной a pt =
= ftln. В выборке 2-й соответственно f2 и р2 = f2/n. Следует
также найти число пар наблюдений, в которых оба члена (из
1-й и 2-й выборок) имеют единицу, то есть обладают наблюдае-
мым свойством. Подобные данные можно представить в виде
таблицы сопряженности 2X2, как видно из рис. 14.5.
Например, & —-число объектов из группы п, имеющих харак-
теристику в оба момента времени.
Для проверки Но против альтернативы Д’, можно применять
следующую статистику:
г) Когда справедлива гипотеза Но: Р] = Р2, z из ур. (14.29)
распределен приближенно нормально с пулевым средним и еди-
ничным стандартным отклонением при. условии, что d-j-a по-
рядка 10.
297
д) Критическими значениями, с которыми при проверке Но
на уровне значимости а сравнивается г из уравнения (14.29),
служат a/2z и i-^z.
е) Построение доверительного интервала для Pi — Р2 мы ие-
будсм рассматривать.
ж) Людям в выборке с п = 60 предлагается указать до и
после прослушивания убедительной лекции об отмене смертной
Выборка !
До лекции
Неодобрение Одобрение Неодобрение
а = 26 6 = 8 34
Одобрение с = 16 d= 10 26
42 18 п =
Рис. 14.6.
казни одобряют они ее или нет. Выборка 1-я образована 60 до-
лекционными ответами на вопрос о смертной казни; во 2-ю вы-
борку входят 60 ответов после лекции. Полученные данные све-
дены в табл. рис. 14.6.
Время
Согласие Несогласие
Несогласие 40 20 60 а» /2
Время
Согласие 0 40 40
40 60 = /, ]00 = п
Рис. 14.7.
Например, по табл. рис. 14.6 видим, что 26 человек одобрили-
смертную казнь до лекции и не одобрили после.
Нуль-гипотезу Pt = Р2 будем проверять на уровне значи-
мости 0,05. Величина г в ур. (14.29) равна:
d — а 10 — 26 16 п ст
z — — = —т==г —-------= —2.67.
у/d + a V Ю + 26 6
Значение z — —2,67 лежит значительно ниже критического
6,025z = —1,96. (Обратите внимание, что </Ц-а намного боль-
ше 10.) Следовательно, гипотезу о том, что в рассматриваемых
298
совокупностях доли людей, одобряющих смертную казнь, равны,
можно отклонить на уровне значимости 0,05.
з) Описанный выше критерий не эквивалентен критерию зна-
чимости «изменения». Заметьте, что в табл. рис. 14.7 наблю-
даются явные изменения, хотя статистика ур. (14.29) равна 0.
Проверка значимости этого раздела — оценка значимости
разности между р}—Щп и p2=f2!n, а не проверка гипотезы
об «изменении», которое оценивается в результате проверки зна-
чимости только в том случае, когда оно отражается на различии
Pi и Р2.
Методы, описанные в этом разделе, разработаны Мак-Нима-
ром (1947).
14.15. Выводы о независимости классификаций
в таблице сопряженности признаков
Часто производятся наблюдения, допускающие измерение
каждого элемента (человека, группы и т. д.) в соответствии с
двумя видами классификации. Например, учащихся можно клас-
сифицировать как по полу (мужской — женский), так и по спе-
циальности (гуманитарные, общественные, физические науки,
техника или педагогика)
Предположим, производилась классификация 120 людей по
политической принадлежности и полу.
Политическая принадлежность —
Демократ Республиканец Независимый
Мужчина 29 36 80
Женщина 14 24 2 40
43 60 17 120
Рис. 14.8
Частоты различных сочетаний свойств можно сгруппировать
в таблицу сопряженности, как показано на рис. 14.8.
Обратите внимание что на рис, 14.8 значение ftl = 29, Дг ==
= 36, ft. = 80, f.a = 17, a f. = п=* 120,
а) Проверяемая нуль-гипотеза состоит в том, что 2 вида
классификации, на которых построена таблица сопряженности,
независимы. Понятие независимости требует некоторого уточне-
ния
Рассмотрим снова исследование связи между полом н поли-
тической принадлежностью всех взрослых людей некоторого об-
щества. Обозначим долю мужчин в совокупности символом
299
а долю женщин — Р.2- Доли демократов, республиканцев и не-
зависимых в совокупности будут обозначаться соответственно
символами Pt, Рц, Pi. Если выборка п извлекается из совокупно-
сти строго случайно, то доли можно интерпретировать как ве-
роятности появления мужчин, женщин или любого типа полити-
ческой принадлежности.
В главе 10 было показано, что вероятность совместного по-
явления двух независимых событий — произведение их индиви-
дуальных вероятностей. Например, если пол и политическая
принадлежность независимы, то вероятность того, что слу-
мократом женского рода, равна Р2Р}.'. вероятность случайного
появления республиканца-мужчины определяется выражением
P.iP2 . Проверка нуль-гипотезы о независимости эквивалентна
проверке гипотезы о том, что вероятность появления представи-
теля, который попадает в ячейку Ц таблицы сопряженности,
равна произведению вероятности того, что элемент принадлежит
любой ячейке в строке i, и вероятности того, что он принадлежит
любой ячейке в столбце /:
t Рц = Р(. p.j для всех значений t и j.
Альтернативная гипотеза, Hi, заключается в том, что Р^ =
Pi.P.i не подтверждается по крайней мере для одной из ячеек
U в таблице сопряженности.
б) Предполагается, что из рассматриваемой совокупности
извлекается случайная выборка объема п.
в) Для проверки Яо против Ht используется следующая ста-
тистика:
(14-30>
300
где fij — число наблюдений в ячейке (ij) таблицы сопряженно-
сти; ft —число наблюдений в i-й строке таблицы; f.j— число на-
блюдений в /-ом столбце таблицы, a n = f,. — общее число на-
блюдений. i;
г) Когда нуль-гипотеза о независимости двух классификаций
подтверждается, статистика хг в ур. (14.30) имеет распределение
хи-квадрат с числом степеней свободы, равным (/ — 1) (J — 1)
для случайных выборок объема п. Например, если в совокупно-
сти, из которой бралась выборка рис. 14.8, пол и политическая
принадлежность независимы, то х2 для данных этого рисунка
должно быть, по-видимому, типичным наблюдением из распре-
деления хи-квадрат с числом степеней свободы (/ — 1) (J — 1) =
= (2 — 1) (3 — 1) = 2.
Если Но ошибочна, то х2 в уравнении (14.30) стремится к пре-
вышениюх2/_))(/_р — распределения. Иначе говоря, можно ожи-
дать, что отсутствие независимости приводит к появлению боль-
ших значений х2 в УР- (14.30).
д) Для проверки Но на уровне значимости а одно расчетное
значение х2 в УР- (14.30) сравнивается с точкой процентиля
100(1—а) в хи-квадрат распределении с (J—1)(/—1) степе-
нями свободы, то есть в распределении x2/-i)(/-d- Данная про-
центильная точка обозначается символом |_оХи_щ/_п> В табли-
цах представлены некоторые процентильные точки распреде-
лений хи-квадрат.
е) Проверяемая гипотеза содержит несколько параметров
(долей в совокупности), и вопрос об интервальном оценивании
некоторой функции этих параметров не возникает.
ж) Для примера будут использованы данные рис. 14,8. Из
совокупности взрослых людей в некоторой группе берется
случайная выборка с п= 120. Каждый человек классифици-
руется по полу и политической принадлежности. Гипотеза о не-
зависимости двух видов классификации проверяется на уровне
значимости 0,01.
Подстановка данных рис. 14.8 в формулу для х2 по ур. (14.30)
дает следующий результат:
2 292 , 36г , 15г . 14* ,
Х — 120 ^ 80 - 43 + 80 - 60 + 80- 17 + 40 - 43 +
+ tc+«?I7-1)“4-776-
Полученное значение хг = 4,776 сравнивается с критическим
С99Хг = 9,210. Нуль-гипотезу о независимости нельзя отклонить
на уровне 0,01. Однако вероятность получения величины у* =»
= 4,776 или больше в случае подтверждения нуль-гипотезы не-
сколько меньше 0,10. Доказательство связи между полом и по-
литической принадлежностью довольно слабое.
Мы рассмотрим второй пример, в котором / = J = 2. В со-
вокупности аспирантов первого года в нескольких крупных
301
университетах Комитетом по разработке программы математи-
ческого образования, входящим в Американскую математиче-
скую ассоциацию, исследовалась случайная выборка- 259 аспи-
рантов, специализирующихся либо в области психологии, либо
в социологии, классифицировались по признакам «нет зачета» и
«условный зачет» при изучении математики в аспирантуре.
Была получена таблица сопряженности, изображенная на
рис. 14.10.
Проверяемая нуль-гипотеза состоит в том, что не существует
связи между специализацией и математической подготовкой
Математика
в аспирантуре
Специализация
Психология Социология
Нет зачета /,1 = 25 /12 —34 Л, =59
Условный зачет = 151 /м = 49 /г. “200
/,f = 176 / .2-S3 /,.=259
Рис. 14.10.
аспирантов. В таблице 2X2 формулу для х2 из ур. (14.30) мож-
но значительно упростить:
(14.31)
Величину х2 со степенями свободы, равными (/ — 1) (/ — 1) =
= (2—1)(2—1)= I, для данных по математической подго-
товке определяем по выражению (14.31):
у2 - 259(25-49-34.151? _ 2„ qfi
Л 59 • 200 • 176 83 ,Э0,
Из таблицы видно, что вероятность получения х2 — 22,96
меньше 0.001, если специализация и обучение математике в
аспирантуре независимы. Мы можем прийти к выводу, что у
аспирантов психологического факультета наблюдается тенден-
ция к приобретению больших знаний по математике, чем у аспи-
рантов-социологов.
з) Обсуждение проверки независимости классификаций в
таблице сопряженности по критерию хи-квадрат в данном пара-
графе весьма поверхностно. Здесь мы можем указать лишь не-
которые важные аспекты применения этих методов и назвать
книги, где они рассматриваются.
Когда число наблюдений в любой ячейке таблицы сопряжен-
ности 2X2 мало (меньше 10), рекомендуется ввести поправку
302
в формулу х2 из ур. (14.31) по Йетсу (1934). Цель поправки на
непрерывность Йетса — улучшение соответствия выборочного
распределения х2 распределению хи-квадрат с одной степенью
свободы. (Обсуждение в учебниках прикладной статистики, на-
пример, McNemar, 1962; Ferguson, 1966; Hays, 1963.)
Существует другая интерпретация проверки по критерию
хи-квадрат, которая уместна, когда элементы разных строк (или
столбцов) таблицы сопряженности можно считать выбранными
из отдельных и различных совокупностей. Ранее приведенную
проверку по критерию хи-квадрат с помощью таблицы сопря-
женности можно тогда рассматривать как оценку однородности
совокупностей. (См. Keeping, 1962; Guenther, 1965.)
Есть методы проверки гипотезы о независимости трех видов
классификации в таблице сопряженности с тремя входами. (См.
Tate, Clelland, 1957.)
Вопрос об определении такого подмножества ячеек таблицы
сопряженности, которое дает значимую статистику х2. рассма-
тривался в работе Мараскайло (1966).
Ряд статей, касающихся пользы и вреда проверок по крите-
рию хи-квадрат для таблиц сопряженности, приводится в жур-
нале «Psychological Bulletin». (См. Lewis, Burke, 1949; Edwards,
1950; Lewis, Burke, 1950; Pastore, 1950; Peters, 1950; Burke,
1951.)
14.16. Связь интервального оценивания
с проверкой гипотез
В большинстве случаев существует связь методов интерваль-
ного оценивания с проверкой гипотез, позволяющая из анализа
100(1—а)% доверительного интервала определить, каковы ре-
зультаты проверки гипотезы на уровне значимости а. Например,
если 95% доверительный интервал относительно X. для ц содер-
жит 0, то гипотезу /?о: ц = 0 нельзя отклонить на уровне 0,05.
Вообще все значения из заданного 100(1— а)% доверитель-
ного интервала привели бы к принятию на уровне а нуль-гипо-
тезы о том, что оцениваемый параметр равен одному из этих
значений. Напротив, любое значение за пределами доверитель-
ного интервала привело бы к отклонению гипотезы.
Предположим, что 95% доверительный интервал для ц уста-
навливается относительно Я. с помощью уравнения (14.2). До-
пустим далее, что доверительный интервал целиком лежит выше
нуля. Следовательно, нижний предел доверительного интервала,
а именно Я. — o,9756>-jSx/Vn> больше нуля:
%- ~ > о.
303
Отсюда следует, что
X- > 0,975^t-i
у п
И ЧТО
s,/vr
Последнее неравенство означает, что критерий [см. ур.(14.!)]
для проверки гипотезы: р — 0 превышает 97,5 процентиль /-рас-
пределения с числом степеней свободы п—1. Следовательно,
гипотезу о том, что ц — О, можно опровергнуть на уровне зна-
чимости 1 —0,95 — 0,05. Таким образом, в доверительном ин-
тервале содержится информация, необходимая также для про-
верки гипотез.
Задачи и упражнения
1. Стеннет (1967) выбрал воспитанников детских садов из
сельских районов Миннесоты. В случайной выборке 873 мальчи-
ков (fij), которые в течение всего года отсутствовали 20 или
больше дней, Pi = 0,28. Доля девочек, отсутствовавших 20 или
более дней, в выборке с «2 = 837 определялась величиной pi =
= 0,27. На уровне значимости 0,01 проверить нуль-гипотезу о
том, что в совокупностях мальчиков и девочек доли детей, про-
пустивших 20 и более дней, равны (см. § 14.13).
2. Эшер и Шуслер (1967) накопили данные о /Q и отноше-
нии к автомобилям по выборке 190 старшекурсниц в пригород-
ном высшем учебном заведении. Имеются следующие данные:
Отношение к автомобилям
нет умеренное большое интерес итоги
111 и выше 20 25 2 47
IQ 101-110 14 47 16 77
Ниже 101 22 37 7 66
Итоги: 56 109 25 190
Пользуясь критерием хи-квадрат для проверки независимо-
сти классификаций в таблице сопряженности с двумя входами
(§ 14.15), проверьте на уровне значимости 0,01 нуль-гипотезу
о том, что /Q и отношение к автомобилям независимы в сово-
купности девушек.
15
ОДНОФАКТОРНЫЙ
ДИСПЕРСИОННЫЙ АНАЛИЗ —
ПОСТОЯННЫЕ ЭФФЕКТЫ
15.1. Структура данных
В качестве примера однофакторного эксперимента представим,
что исследователь хочет выяснить, отличаются ли по эффектив-
ности 4 метода изучения некоторой темы. Он планирует предло-
жить 10 студентам изучить денежную систему в Англии по крат-
кому конспекту. 10 других учащихся будут конспектировать
книгу; еще 10 ознакомятся с программированным учебником по
данному вопросу; наконец,
оставшиеся 10 человек будут
изучать материал на обучаю-
щей машине. Четыре варианта
условий (обработок) предпола-
гают различную активность со
стороны учащихся, которая
служит предметом наблюдения,
Один фактор в этом экспери-
менте — «активность учащего-
ся»; этот фактор — понятие,
относящееся к четырем усло-
виям. Условия эксперимента
образуются различными вида-
ми или количеством некоторо-
го предмета, называемого фак-
Услойия опыта
2 3 4
Х1,4
*2,1 Х2,2 *2,3 *2,4
*ю, г *10,3 *10,4
Рис. 15,1. Структура данных для
эксперимента по сравнению четырех
уровней активности учащегося.
тором. Исследователь хочет знать, будут ли по крайней мере
2 варианта условий изучения определять различную успевае-
мость (измеренную тестом с многовариантным выбором).
Данные результаты теста с многовариантными ответами 40
учащихся можно представить в виде таблицы, как показано на
рис. 15.1.
Вас может удивить, почему исследователь не посмотрит про-
сто на суммы по четырем условиям и не установит, есть ли раз-
личия в каких-нибудь двух из анализируемых сумм. Он не де-
лает этого потому, что его интересуют не только результаты,
305
полученные в отношении этих конкретных людей в данное вре-
мя. Какая польза была бы от его результатов, если бы он мог
сказать только, что какая-то группа из 10 учащихся была лучше
какой-то другой группы П сентября в этом месте? Хотя полу-
ченные данные относятся к 40 учащимся в определенное время,
для того чтобы его эксперимент внес какой-то вклад в науку,
интерес исследователя должен быть направлен на совокупности
учащихся, из которых эти 40 человек образуют некую выборку,
и на совокупность экспериментов, из которых он провел только
один. Исследователь стремится ответить на вопрос: «Могу ли я
ожидать того же самого результата, если выберу 40 разных
студентов и проведу эксперимент в разное время и при слегка
измененных условиях?»
15.2. Модель для данных
Для ответа на этот вопрос нужен вывод для совокупности
учащихся и совокупности результатов эксперимента. В таком
случае исследователь применяет методы теории статистического
вывода. Методы, представленные в этой главе, предназначены
для формирования статистических выводов применительно к ги-
потетической совокупности опытов, если совокупность данных, в
качестве которых выступают 40 выборочных результатов, имеет
определенный вид, а выборка производится определенным обра-
зом. Для выполнения тех требований, которые приводят к мето-
дам статистического вывода, исследователь должен предполо-
жить, что он извлек 40 полученных результатов случайно (то
есть с равными и независимыми вероятностями выбора) из че-
тырех (одно для каждого уровня фактора) нормальных рас-
пределений с равными дисперсиями о2. Эти предположения мо-
гут показаться слишком жесткими; позднее (§ 15.13) будет
отмечено, что некоторые нарушения этих предположений имеют
незначительное влияние на результаты статистического анализа.
Тем не менее эти предположения следует запомнить:
1. Результаты выбирались случайно
2. из нормальных совокупностей
3. с равными дисперсиями о2,
4. а различные выборки (в нашем примере их 4) незави-
симы.
Обратите внимание, что относительно р, среднего нормаль-
ных совокупностей, не делается никаких предположений. Будет
показано, что вопрос исследователя об эффективности четырех
методов приводит к вопросу о четырех средних, щ, ... , щ, для
четырех нормальных совокупностей.
Теперь мы должны поставить вопрос об эффективности четы-
рех методов в более точных терминах. С этой целью мы пред-
полагаем, что любой из 40 результатов может быть представлен
линейной моделью, суммой компонент (ни одна из которых не
306
должна быть квадратичной, кубичной и т. д.). Линейная мо-
дель— это разложение значения Хг} на сумму членов, имеющих
для статистика определенный смысл. Мы примем «иа пробу»
следующую линейную модель для Х1}:
X,/ == + «/ + <?//, (15.1)
где Xi, — i-e значение в /-ой группе; ц — член (равный сред-
нему 4 средних значений совокупностей), постоянный для всех
40 данных н отражающий общий уровень результатов; а,— кон-
станта для всех 10 значений в группе /, оценивающая прирост
(или уменьшение) этих 10 значений, полученных в одинаковых
условиях; ег;— «ошибка» линейной модели. Она представляет
собой остаток, образующийся после вычитания ц и а> из ре-
зультата опыта.
Вы должны помнить, чго ц, а, и ег!— числа. Если в опыте
ц — 12, а2 = —2, а £12 == 1, то Х)2 — 12 —2 4- 1 == И.
Можно ожидать, что интерес сосредоточится на а?. Член ц
мало интересен, относительно elt также нет особой информации;
а а; показывает, какое влияние имел уровень / условий опыта
на полученные результаты. Исходный вопрос исследователя:
«Отличаются ли 4 метода?» — теперь можно сформулировать точ-
нее: «Верно ли, что (Х| — аг = аз — ач?» Он хочет знать, можно
ли уверенно сказать, что 4 уровня условий не имеют одинако-
ных эффектов. Рассматриваемые методы предназначены для
проверки гипотезы, называемой нуль-гипотезой (поскольку в
ней не предполагается различий), о том, что а, = аг = аз — а«.
Необходимость в методе проверки гипотезы возникает пото-
му, что существуют ошибки вида ец. Если бы в линейной мо-
дели не содержалась ошибка, то исследователь просто мог бы
посмотреть на суммы оценок в 4 группах, чтобы убедиться в их
сходстве или различии, и проверить таким образом нуль-гипо-
тезу. Но ошибки eZj существуют, и мы должны их учитывать.
Как же возникают ег>? Они появляются по различным причинам.
Во-первых, люди или другие объекты измерения отличаются друг
от друга по существу даже в идентичных условиях испытаний.
Из 10 учащихся, собирающих сведения об английских деньгах,
некоторые в процессе испытания будут получать более высокие
оценки просто потому, что они умнее. Ни один метод контроля
условйй исследования не обеспечил бы 10 учащимся одинаковых
знаний. Во-вторых, ошибки возникают, когда предпринимается
попытка оценить учащихся. Подобные ошибки — следствие не-
надежности измерительного прибора, в данном случае теста с
многовариантными ответами. Сегодняшние оценки группы лю-
дей не будут идентичны завтрашним, даже если испытуемые
ничего не забыли. В-третьих, ошибки возникают вследствие не-
контролируемых случайностей во время эксперимента. Ученик
может сломать карандаш н должен получить другой, кто-нибудь
может заболеть и неудовлетворительно отвечать на вопросы;
другому может не понрввиться взгляд преподавателя и его дей-
307
ствия будут несогласованными. Дополнительные ошибки появ-
ляются в том случае, если постулируемая линейная модель не-
верна; возможно, что линейная модель не обеспечивает точного
описания данных.
Все эти источники ошибки в совокупности приводят к тому,
что результаты эксперимента, проведенного с различными груп-
пами в составе 40 учащихся сегодня, отличаются от прошлых ’
и будущих данных.
Вернемся к исходным данным и посмотрим, как можно про-
верить нуль-гипотезу о том, что ai = а2 = аа =• си. Во-первых,
нам нужно разработать некоторый аппарат.
Сумма значений для первого уровня обозначается так:
ю
X Хц-
Сумма значений, деленная на 10, число суммируемых значе-
ний, есть среднее арифметическое первой группы. Среднее бу-
дет обозначаться следующим образом:
- ^iX‘S
X-1 =^o~-
Как вы, должно быть, помните, черта над X обозначает сред-
нее-, точка вместо i означает, что среднее было найдено в ре-
зультате суммирования по i. Как вы определите J?,2?
Мы должны также иметь общее среднее, среднее значение
всех 40 данных. Для определения общего среднего находим
сумму всех 40 значений и делим ее на 40. Общее среднее обо-
значается
4 ю
i i хч
x..«2=Ls—
40
Напомним, что две точки вместо I н / указывают на то, что
суммирование осуществляется по i и /.
Если берется разность между каждой оценкой первой груп-
пы и ее средним л.(, возводится в квадрат и квадраты разностей
суммируются, то сумма имеет вид:
Sun-x.i)<
Сумма, деленная на 9=(п —1), называется выборочной
дисперсией первой группы и обозначается символом а*:
И — несмещенная оценка дисперсии совокупности, образую-
щей первую группу. Так как ст2 — также дисперсия трех других
308
совокупностей, то s“ — несмещенная оценка общей дисперсии
о2, st S3 и s2 — несмещенные оценки ст2. Теперь мы распола-
гаем необходимым аппаратом, Помните, что мы хотим знать,
можно ли твердо заявить, что утверждение, будто сц = аг ==
= а3 = а4, неправильно.
15.3. Оценки членов модели
В ходе эксперимента фактически рассматривается 40 значе-
ний Хц. Числовые характеристики ц, а; и еи неизвестны и нена-
блюдаемы; однако возможны некоторые оценки. Статистик на-
шел способ оценки компонент линейной модели, обладающий
очень полезными и желанными свойствами. Он получает так на-
зываемые опенки метода наименьших квадратов для ц, а> и е1Г.
Обозначим их символами |i, и соответственно. В процессе
получения этих опенок предполагается, что сумма наиболее
важных параметров, ai, ..., aj, равна 0, то есть, ai+ ... +«j=
== 0. Это довольно разумный вид ограничения, поскольку мы
представляем себе aj как «превышение» или «снижение» от об-
щего уровня, выражающегося в параметре ц. Устанавливая это
ограничение на а}, статистик почти предопределяет, что значе-
ния а,; будут обладать свойствами отклонений от среднего ц,
так как сумма отклонений относительно среднего равна 0. Ста-
тистик установил,что
ц ==» X..,
ftz=X.z-X..,
ё^Х,,-*.,.
Оценки разрабатываются для приспособления к результатам
наблюдений в том смысле, что Хц = £ + бу -{- ёц.
Обратите внимание, что
xt! = х.. + (X., - X..) + {Хц - Х.г). (15.2)
Первый член в правой части — ц, второй — ftj, а послед-
ний — ёц,
15.4. Суммы квадратов
Обоснование последующих этапов до некоторых пор пока-
жется не вполне ясным; продолжим преобразование уравнения
(15,2), которое выглядит как нечто произвольное.
Во-первых, вычтем общее среднее Я„ из каждой части урав-
нения (15.2); Xtj —- Х„ — (Х,3— Х.,) + (Хц— X.,-). Во-вторых,
809
возведем в квадрат и просуммируем обе части уравнения по }
н i:
;g gKx.^x.o + ix.^x.,)!*. (15.3)
Величина в левой части уравнения (15.3) называется полной
суммой квадратов. Для полного множества чисел, полученных
в эксперименте, сумма квадратов отклонений каждого числа от
общего среднего образует полную сумму квадратов.
Рассмотрим правую часть ур. (15.3). Обратите внимание,
что если мы вместо (X,— X,.) записываем й, а вместо
(Х13 — X 3) — Ь, то в правую часть входит величина (д + Ь)2. По-
скольку (а Ь)2 = а2 2а& -f- Ьг, нетрудно увидеть, что
j?£((X./-х..)* +
+ 2 (Х.; - X..) (Х17 - X./) + (Хц - Х./Я.
Правая часть уравнения равна следующему:
i f W •: - х • • )* + 2 i X (X . i - X..) (X „ - X.,) +
+ ХХ(Х„-Х.,)’. (15.4)
Рассмотрим теперь только средний член уравнения (15.4).
Так как величина Х} — X. не содержит индекса i, знак S для i
можно опустить; таким образом, мы можем записать второй член
иначе:
гХй-,-х..)2(Х„-х.,). (15.5)
Допустим, мы хотим определить по данным первой группы
f(X(!-x.,
Для этой группы Х.| — константа; пользуясь правилом 2 из
§ 2.5, можно показать, что
ю ю ю 10 У, Х1{
£(Хи-Х.,) = Xх»- (0Х.,= ХХп---------=0.
Возвращаясь к уравнению (15.5), видим, что
2£ (Х./-Х..)У (Х(,-Х.,) =
== 2[(Х.) — X..) - 0 4- +(Х.4-Х..)-01 = 0,
310
Так как средний член уравнения (15.4) точно равен нулю—
это не предположение, мы доказали это, и это справедливо для
любой группы чисел,— мы показали, что
4 10 4 10 _ 4 10
£ Е (xz, ~ х.. )2=jg Е (X. t - X.. )2 + £ Е, (Xlt - X ;)г.
(15.6)
Обратите внимание, что в первом члене правой части урав-
нения (15.6) нет индекса I. Величина (X,— X )2 одинакова для
всех i от 1 до 10 при фиксированном /.
Например, для первой, второй, .... десятой оценок первой
группы (X1 — X..)2 одна и та же. Поэтому
4 10 4
/ansi fas!
В итоге мы разбили полную сумму квадратов на 2 части:
4 10 _ 4 _ 4 10
2<х"~х")!=й10(Х-'"х">!+2
SSnMB.= £5межлу SSBHyTpH.
Полная сумма квадратов (SSno,iH) расчленена (разложена)
на 2 аддитивные компоненты, сумму квадратов между группами
(ЗЗмежду) и сумму квадратов внутри групп ($$внутрв). 55полн
отражает вариацию полученных данных. Полная вариация раз-
ложена на 2 компоненты, 55„СЯ(ду и SSBByTpi,. Отсюда наимено-
вание «дисперсионный анализ» (сокращенно ANOVA). Скоро
вы увидите, как используется этот анализ для проверки нуль-
гипотеэы си = «2 = аз = а-ь-
15.5. Новое определение нуль-гипотезы
в терминах генеральных средних
Прежде всего представим нуль-гипотезу о том, что а, =
= а2 = аз = а4 в эквивалентном, но несколько ином виде. В ка-
честве оценки at можно взять а, == X. । — X. .. Так как а( — не-
смещенная оценка а|( ожиданием Е&1 будет ai:
E(6,)-E(X.!-X..)-£(X.i)~£(X..)-pl-p = ai.
Аналогично, а2 = р2—р, аз = р3— р, а а4 = щ—р.
Нуль-гипотезу можно записать следующим образом: (щ — р) =
= (р2 — и) = (Рз “ и) = (р4 — р).
Прибавьте р к каждому из 4 членов, и вы увидите, что по-
лучится равенство р, == р2 = р3 = р4. Следовательно, нуль-гипоте-
за о том, что Qj =а2 = а3 = а4 в линейной модели —
311
аналогична гипотезе о том, что все средние нормальных совокуп-
ностей, из которых извлекаются выборки, равны, то есть
И| = g2 = Цз = щ.
Мы можем сформулировать нуль-гипотезу в любой форме.
Третья эквивалентная форма при nt — Пг = п-з = nt выглядит
так:
Но • Е(Н/ — Й-)г = 0.
/=1
где р. —среднее рь pj и равно р.
15.6. Степени свободы
Для демонстрации метода проверки нуль-гипотезы нужен не-
который дополнительный аппарат.
При расчленении полной суммы квадратов (55Полн, 55м0жду,
53впутря) мы должны связать с каждой суммой целые числа,
называемые степенями свободы.
«Степени свободы» —выражение, заимствованное из области
физических наук, где оно характеризует движение объекта. Если
объект имеет возможность двигаться только прямолинейно, он
обладает одной степенью свободы; объект, который может пере-
мещаться в любую точку плоскости, например катящийся по
аллее мяч, имеет две степени свободы; мяч на корте для игры
в гандбол обладает тремя степенями свободы; он может пере-
мещаться вперед и назад, из стороны в сторону, от пола до
потолка. Вас может удивить, что методы, которые мы объеди-
няем под рубрикой «дисперсионный анализ», или ANOVA (рас-
членение ЗЗиоли и проверка нуль-гипотезы), имеют геометриче-
скую интерпретацию. Однако, понятие «степени свободы» входит
в дисперсионный анализ (4JVOV4) с помощью геометрической
интерпретации.
Во-первых, рассмотрим степени свободы, связанные с
ЗЗмсжду- Вернемся к определению 55мсждУ:
С величиной X связаны уравнением 4 групповых средних,
.....X.S
Л|+2^±Л»±.*..:..< _Х.. (15.7)
Если Я.. = 6, — 3, J.2 = 4, ^з = 8, то каким должно
бЫТЬ Х,4?
Я 4 должно быть равно 9, Если Я.. задало, то мы вольны при-
своить любые значения 3 групповым средним так, чтобы можно
312
было определить последнее групповое среднее —оно должно
иметь величину, удовлетворяющую ур. (15.7). Для 55МеждУ
имеем 3 степени свободы {4— ]), на единицу меньше, чем число
групповых средних, то есть J — 1. Сокращенно будем обозна-
чать «Степени СВобОДЫ ДЛЯ 55Между» СИМВОЛОМ df.между-
Рассмотрим теперь степени свободы, связанные с 55вяутри.
ЗЗвнутри --X ./)'.
Для первой группы расчет 55ш,утри включает:
(х„ - x.j2+(х2! - хч)г+ ... + (х!0.1-х.[)2.
Как связаны между собой Хц, Х21, ..., X|W и Я;?
Если бы X.i было некоторым определенным числом, скажем
12,40, то какому множеству чисел из 10 от Хи до Xioi могли бы
вы присвоить любое желаемое число, прежде чем приписать
значение или значения, образующие X.i — 12,40? Ответ: 9 чис-
лам. Аналогично, при вычислении 5£енутрИ используется
(X12~X.2)z + (Xj2— Х.2)г + ... + (Х10.2 — Х.^.
При вычислении 55ВнУтрИ имеем девять степеней свободы для
каждой из четырех групп; следовательно, степени свободы для
SSaHyTpa равны (10—1) + (10—1) + (10—1) + (10—1) =
= 40— 4 = 36, общему числу наблюдений без числа групп, то
есть 7п —7 = 7(и—1). Целесообразно вместо «степени свобо-
ды для 55В11Утри» пользоваться обозначением ^внутри-
SSno3B. равна (Хп - X-)2+(Х21 - Х..)2+...+(Х)0.4 - X. р;
причем в выражении содержится 41 член, и между ними суще-
ствует следующая связь:
Из 40 величин в левой части уравнения 39 можно без огра-
ничений приписать числа до определения сороковой величины,
которая дает ранее заданное Х„. Число степеней свободы для
55Воли. равно 40 — 1 = 39, общему числу наблюдений минус 1,
то есть Jn — 1.
15.7. Средние квадраты
Сумма квадратов (SS), деленная на число степеней свободы
(df), называется средним квадратом (X1S). В однофакторном
дисперсионном анализе ANOVA будут представлять интерес
только 2 средних квадрата: средний квадрат между, MSb, кото-
313
рый равен отношению вида SSb/dfb, и средний квадрат внутри,
MSW, равный SSw/dfu,*. «Полный средний квадрат» не будет
определяться, так как он оказался непригодным для проверки
нуль-гипотезы. Однако следует запомнить важные соотношения:
SS*+
dfb + dfw = dft = Jn-- 1.
15.8. Ожидания средних квадратов MS6 и MSW
Здесь мы постараемся ответить на ряд вопросов, которые
должны были возникнуть при чтении нескольких последних
страниц- Почему SSt расчленяется на SSf, и 55ш? Для чего
определяются степени свободы и средние квадраты? Разумеется,
для проверки нуль-гипотезы Яо; но при анализе ожиданий MSb
и MSW вы начнете понимать, каким образом рассматриваемый
до сих пор аппарат связан с Н$.
Ожидание MSa подразумевает среднее по большой выборке
MS№ для многих экспериментов. Ожидание MSW будет обозна-
чаться E(MSa). Если бы наш эксперимент, исследующий актив-
ность учащихся, пришлось повторять бесконечно и каждый раз
при этом рассчитывать MSa, то среднее всех MSW определялось
бы величиной E(MSa). Мы легко можем представить себе этот
процесс, хотя он не реализуем. E(MS„)—среднее всех AfSu> в
совокупности опытов, относительно которой мы хотим сделать
выводы по полученным данным.
Мы можем записать E(MSa) в терминах характеристики
нормальных совокупностей, из которых полученные в результате
эксперимента оценки образуют случайную выборку.
Во-первых, взглянем на MSa несколько иначе:
. Г £XPc-s.,)1
* I 2=1-1_ 2=J_
• В дальнейшем «между» будет сокращенно обозначаться «Ъ», «вну-
три» — <w», а «полный» — «Ь (по начальным буквам соответствующих англий-
ских слов. — Прим. ред.). Итак мы будем иметь SSj>, SSB, SSi, dU. df„.
MSe и MS„.
314
io _
He является ли У (Хл — X. i)2/9 выборочной дисперсией пер-
вой группы? Мы будем обозначать ее символом «1, а выбороч-
ные дисперсии второй, третьей и четвертой групп — соответ-
ственно 4. 4 и
Поэтому MSW = (si + «г4- S3 + s1)> то есть МЗЮ—-сред-
нее выборочных дисперсий всех групп. Ранее мы утверждали,
что £($?) = в), дисперсии нормальной совокупности, из которой
были выбраны оценки первой группы. Так как все нормальные
совокупности имели одинаковую дисперсию, о2, то можно дока-
зать, что
£’^S№)=4£(s')+ + s’)~
= ... +£(S2)] = X(o2WW + (T2)-a2-
Ожидание М5Ш есть о2.
Величина MSW не зависит от средних значений совокупно-
стей, из которых извлекаются группы при проведении экспери-
мента. AfSu,— «свободное от среднего», отражающее изменчи-
вость только внутри групп. Подобная изменчивость существует
скорее относительно каждого среднего группы, чем для общего
среднего всех групп. Независимо от того, будут ли все группы
являться выборками из одной нормальной совокупности или все
нормальные совокупности имеют разные средние, £(MSW) будет
равно о2 *.
Однако этого нельзя сказать относительно Е(М8ь}- Мы пока-
жем, что если все нормальные совокупности имеют одинаковые
средние (мы уже предполагали, что они имеют одинаковую дис-
персию), то E(MSb) = ст2. Если же, по крайней мере две из
генеральных средних различны, то Е(М5ь) будет превышать ст2.
Если все генеральные средние равны, то нуль-гипотеза о том,
что pi == (12 = Цз = щ, подтверждается. Если но крайней мере
2 генеральных средних различны, например (it — рг, а
или [ij Ц2 =# Цз =# щ (2 из множества примеров), то нуль-ги-
потеза ошибочна.
Мы утверждаем без доказательства, что
"£(»/-»)’
Е(Л13,) = ог+ , (15.8>
где ст2 — дисперсия каждой совокупности; п — число элементов
в каждой группе (10 в нашем примере); J — число групп (4 в
• Убедитесь сами, что это действительно так. Начните с
E(MSa^E [(SSat + SS№i+ ... +55ш7)//(п~1)].
315
нашем примере); щ — генеральное среднее /-й совокупности, а
р — среднее / генеральных средних.
Скажем, например, что все 4 генеральных средних были рав-
ны 6,45. (Случай, когда Но верна). Тогда ц определялось бы
величиной 6,45, а
Возьмите пример, в котором Но не верна, и убедитесь, что
E(MSb) больше о2.
В итоге:
1. Если Но верна, то E{MSW)!= о2, и £(М5&)= о2.
2. Если Но ошибочна, то
E(MS,) = «’, а Е(Л15,) = <г' + -Игг1-------,
что больше о2.
В любом эксперименте MSW и М5ь известны, а значения их
ожиданий — нет. Сравнивая М5ь с М5Ю, можно определить, до-
стоверна ли Но- Если AfSj> очень велик по отношению к MSv. то
вероятно, что Но ошибочна. Но проверка нуль-гипотезы далеко
не так проста. Можно показать, что MSb и М5И не зависят друг
от друга (одно из следствий исходного предположения о нор-
мальных совокупностях).
Предположим теперь, что вы случайно извлекаете четыре
выборки по 10 оценок в каждой из нормальной совокупности.
Это было бы так, если бы в нашем примере четыре условия
эксперимента были одинаково эффективны (по средним, кото-
рые они дали). 40 выборочных значений можно представить в
таблице, подобной табл 15 1, и вычислить MS№ и MS;,. Помните,
что это случай, когда верна Но. Были бы равны MSU, и MSb?
Нет Нх ожидания могли бы оказаться равными, но от выборки
к выборке AfSl(, мог быть то немного больше MSf,, то немного
меньше. Исследователя волнуют те случаи, когда MSd значи-
тельно больше М5«,. Ему бы хотелось считать такой факт дока-
зательством ошибочности Но- (Если Но ошибочна, то он ожидал
бы, что MSb будет больше MSV). Но как можно быть уверен-
ным в том. что большое значение MSs по сравнению с MSw не
является просто результатом случайной флуктуации оценок, вы-
бранных из одной нормальной совокупности? Исследователь
никогда не может знать этого наверняка, но в следующем пара-
графе мы увидим, как он может контролировать долю случаев,
когда делается ошибочный вывод о ложности Но.
316
15.9. Некоторые сведения из теории распределений
В главе II мы видели, что переменная хи-квадрат с одной
степенью свободы имеет вид
(Х-м-У* . ..л
а* *1’
то есть квадрат нормального отклонения распределен как хи-
квадрат с 1-й степенью свободы.
Вспомним, что X — это нормально распределенная перемен-
ная с генеральным средним р и дисперсией о2.
Предположим, что из нормального распределения со сред-
ним ц и дисперсией о2 случайно выбираются п значений. Так
как переменные хи-квадрат обладают свойством аддитивности,
описанным в II главе, величина
<Ь—и)8. . + . +
а1 Т О2 f • • т An-
Сумма квадратов z имеет распределение хи-квадрат с п сте-
пенями свободы, то есть эта сумма, найденная по выборкам объ-
ема п, имеет известное распределение частот х2.
Мы не будем доказывать это утверждение, однако справед-
ливо (см., например, Уилкс, 1969), что если Х2, .... Хп — п
независимых наблюдений из нормального распределения с дис-
персией о2, то
(Х,-Х.у (Хг-Х-У (Х„-Х.Р ,
02 Т 02 -Г ... -Г ог Лп_г
Поэтому £ (X/— X.)2/o-~x2..i. Кроме того,
Обратите внимание, что X,—-выборочное среднее п наблю-
дений— заменило ц, среднее совокупности, из которой были
выбраны наблюдения. Кроме того, переменная хи-квадрат вме-
сто п степеней свободы имеет п — I.
В начале главы мы приводили определение 55ш для экспе-
римента:
10 _ 10 _ ” _
зз. = £(хп-х.,)!+£^.ги-.г.,,)=+ ... + £ (Х„-х.,)’.
Если бы мы разделили первую величину в правой части
этого уравнения на о2, то получили бы распределение (хи-
квадрат с 9 степенями свободы), поскольку мы предположили,
что данные первой группы были получены случайно из нормаль-
ной совокупности с дисперсией аг. То же самое можно сказать
317
о трех других величинах в правой части уравнения. Поскольку
все четыре величины распределены как X2, то их сумма, делен-
ная на <т2, распределена как х^+9+9+д), или х^ (хи-квадрат
с 36 степенями свободы). Отсюда, для нашего примера
<j2 A»-
Мы можем разделить 55ш на 36, чтобы получить AfS^; тогда
Хзб
ст2 36 ‘
Вообще как распределено среднее J. группы? Иначе говоря,
каким было бы распределение частот, если бы мы выбрали слу-
чайно п данных из совокупности, вычислили X, и потом записали
только одну эту оценку, X ? Как выглядело бы распределение
этих оценок, если бы этот процесс продолжался бесконечно? Ка-
кими были бы среднее, дисперсия и вид распределения?
Если средние значения X. основаны на я-значениях, случай-
но выбранных из нормальной совокупности, то они будут:
1. Нормально распределенными,
2. со средним ц и
3. дисперсией о2/л.
_ Пользуясь____этими фактами, мы можем заметить, что
(X. ~ц)1-у/о'1пнмеет нулевое среднее и единичную дисперсию,
то есть что это — значение г. Следовательно,
(X--u)g n(J. -н)2 ,
аг/п с2 Л'-
Если нуль-гипотеза верна, то
£ 10(Х.,-Т.)>
2=1-----р----------XI, (15.9>
потому что тогда
Это означает, что каждое из четырех Х.} — случайная вы-
борка из нормально распределенной бесконечной совокупности
Х.3-ов, среднее которой равно р. Наше исходное предположение,
что четыре совокупности, исследуемые в эксперименте, имели
одинаковую дисперсию о2, позволяет сделать это утверждение.
Разделив обе части ур. (15.9) на 3, мы видим, что
5* “ о2 3 >
при условии, что Нд справедлива.
318
Вспомните, что отношение двух переменных хи-квадрат,
каждая из которых разделена на свое число степеней свободы,
имеет F-распределение.
Ю(Х./-Х,.)ф'за» jjr Ю(Х-! - X. ,)’]/з
Гб 1 ~ 1 г 4 io Т~ ~ ^зм-
2 «<< - х -/>’]/зв,= [2 £ - х .,>]/Зв
Заметьте, что поскольку о2 появляется и в числителе и в зна-
менателе, то она сокращается.
Вы видите, что числитель — MSb, а знаменатель — MSm.
В результате, если нуль-гипотеза верна, то
то есть отношение среднего квадрата между, MSb, к среднему
квадрату внутри, MS№, имеет F-распределение с 3 и 36 степенями
свободы при pf = Ц2 = цз — Щ.
Отношение MSb/MSw называется F-отношением. F-отноше-
ние—статистика, которая будет использоваться на последних
этайах проверки Но-
15,10. F-критерий для нуль-гипотез: идея и метод
В соответствии с теорией распределения, которая была раз-
работана, рассмотрим повторяющуюся процедуру случайного
выбора четырех групп по 10 значений в каждой из одного нор-
мального распределения (обратите внимание, что при этом
нуль-гипотеза справедлива). Если бы к тому же всякий раз вы-
числялось F-отношение, равное MSb/MSw, и фиксировалось его
значение, то распределение частот этих F-отношений (их мно-
жества) соответствовало бы математической кривой F3,36. Это
очень важно, так как статистик может определить процент
F-отношений, превышающих 11,35 или 6,12; или он может найти
число, выше которого лежит 5%, либо 1% F-отношеиий, При
этом предполагается, что Нй верна. F-отношения, полученные
в процессе повторного выбора, были бы больше нуля, а их мак-
симальные значения теоретически равны бесконечности.
А что, если четыре группы по 10 значений в каждой были
выбраны не из одной нормальной совокупности, то есть если
испытание было проведено в условиях ложности нуль-гипотезы?
Ранее мы видели, что при этом ожидается появление MSb боль-
шей величины, чем могло быть в случае верности нуль-гипотезы.
Однако MSW обладало бы тем же ожиданием, о2. Когда нуль-
гипотеза не подтверждается, MSb не имеет х2-распределения, а
отношения вида MSb/MS№, полученные по выборке, не подчи-
няются F-распределеиию. Мы знаем, однако, какое влияние на
319
распределение F-отношений оказывает выборка в случае оши-
бочности нуль-гипотезы. В среднем они будут больше F-отноше-
ний, полученных в результате случайного выбора из одной нор-
мальной совокупности.
Предположим, что мы случайно выбрали 4 группы с 10 зна-
чениями в каждой из одной нормальной совокупности и опреде-
лили F-отношение. Характеристика полученных F-отношеннй
имела бы вид кривой Fj.se на рис. 15,2. Теперь допустим, что мы
неоднократно берем по 2 группы с 10 значениями из нормальной
совокупности со средним Ц), а еще 2 такие же группы из нор-
мальной совокупности с другим средним, р2. Нуль-гипотеза оши-
бочна. ио практически нам это было бы неизвестно, поскольку
pi и Ц2 — неизвестные характеристики совокупностей. Распреде-
ление полученных F-отношений имело бы вид кривой F*
Рис. 15,2 Выборочные распределения F = MS^IMSa, когда
На верна (кривая Fs,se) и когда Нй ошибочна (кривая F*).
(рис. 15.2). Обратите внимание, что в целом F-отношения сме-
щены вправо (увеличиваются) в случае, когда выборка произво-
дится в условиях ложной нуль-гипотезы.
Когда более вероятно появление F-отношения, превосходя-
щего 3,25, в случае верной или ложной нуль-гипотезы? Срав-
ните площади под 2 кривыми справа от точки 3,25 и посмотрите,
какая площадь больше (то есть дает большую вероятность по-
лучения величины F, превосходящей 3,25).
Статистик может найти 95-й и 99-й процентили кривой Fs.se-
95-й процентиль кривой Рз,зз = 2,86; 99-й процентиль равен 4,38.
В таблицах обычно указываются 75, 90, 95, 97,5, 99, 99,5 и 99,9
процентили для различных F-распределений. Как мы уже ви-
дели в 11 главе, F-распределение зависит от 2 величин: числа
степеней свободы числителя и числа степеней свободы знамена-
теля F-отнощения. Для определения 95 процентиля кривой Fz,io
найдите ячейку на пересечении 2 столбца и 40 строки в гра-
фе таблицы, озаглавленной «95 процентиль». Величина o.aso.w
есть 3,23.
Исследователю приходится рассуждать так: если величина
найденного F-отношення могла бы появиться менее 5 раз из 100
320
в случае верности нуль-гипотезы, то я приду к выводу о том,
что нуль-гипотеза ошибочна. По-видимому, более вероятно, что
это указывает на ложность нуль-гипотезы.
Выбор 95 процентиля кривой F3i3ti как точки, от которой за-
висит решение относительно Но, является произвольным. Можно
было выбрать следующие процентильные точки: 90,99 или 99,9.
А если выбрана точка 50 процентиля? Иначе говоря, что полу-
чилось бы, если бы кто-то согласился отвергнуть нуль-гипотезу
в случае Е-отношения, превосходящего 50 процентиль? Если бы
нуль-гипотеза была верна, вероятность отклонения На (считая
ее ложной) определялась бы величиной 0,5. Если бы исследо-
ватели для принятия решений выбрали точку 50 процентиля, то
половина из них пришла бы к выводу, что один метод лучше
другого, когда фактически они одинаковы. Ученые хотят убе-
речь себя от этих погрешностей, ошибок 1 рода, поэтому они
согласны сделать вывод о ложности нуль-гипотезы в том случае,
когда значения, равные F или превосходящие полученное его
значение, имеют малую вероятность появления в условиях вер-
ности нуль-гипотезы. Под выражением «малая вероятность»
подразумеваются значения 0,10, 0,05 или 0,01. Эти значения со-
ответствуют 90, 95 и 99 процентильным точкам.
Не следует думать, что если бы полученное в нашем экспе-
рименте Е-отношение было бы равно 6,51, нуль-гипотеза была
бы явно ошибочна. Подобные утверждения в нашем положении
невозможны. Исследователь делает вывод типа «Я отклоняю На
как истинное утверждение относительно средних значений со-
вокупностей, которые я выбрал» или «Я отказался отклонить На
как ...». Он никогда не уверен в истинности своего заключения.
Он знает, однако, что его выводы окажутся верными до неко-
торой степени (90%, 95%, 99% и т. д.) истинности или лож-
ности Но.
Предположим, что четыре уровня активности учащихся были
сходны по отношению к достигнутым успехам. Допустим также,
что наш исследователь поставил аналогичный эксперимент с
40 учащимися в 4 группах много раз. Каждый раз он должен
был найти Е-отношение и сделать вывод относительно Но- Он не
имел представления о том, что Но верпа. Кривая Рз.зе, которой
подчинялись бы полученные F-отпошения, известна, Й известно,
что 5% площади под кривой лежит справа от точки 2,86: следо-
вательно, ожидаемая ошибка отклонения Яо, когда она факти-
чески верна, — только 5% случаев.
Обратите внимание, что величина (2,86), которую выбирает
исследователь, полагая, что любое /’•отношение, превышающее
ее, рассматривается как доказательство ложности На, сама про-
извольна Если он выбрал 4,38 — точку 99 процентиля в распре-
делении F3>se и если Но верна, то в среднем один раз из 100 он
получит Е-отношение, превосходящее 4.38, и придет к непра-
вильному выводу о ложности Но. Вероятность, что исследова-
тель отвергнет Н6 как истину в случае, когда Не в действитель-
11 Зак. «в 32J
ности верна, называется а (альфа). Величина а зависит от ис-
следователя; он может установить ее по своему усмотрению,
выбирая число из таблицы F, определяющее его решение.
Принято считать (как мы видели в § 13,5), что существуют
2 состояния природы, имеющие отношение к модели ANOVA:
Но может быть истинной или ложной. Исследователь согла-
шается в результате анализа данных принять одно из двух ре-
шений: отклонить Но как объяснение сложившегося положения
или не отклонять (продолжая придерживаться) Но. Возможны
4 исхода эксперимента, как показывает следующая таблица.
Состояние природы
Но верна Нй ошибочна
Отклонить Но Ошибка I рода Верное решение
Не отклонять Но Верное решение Ошибка II рода
Если исследователь не находит доказательств ложности Но
и Но верна (положение соответствует нижней левой ячейке таб-
лицы), то его рассуждения будут в согласии с истинным состоя-
нием природы: в выводе ошибки не содержится. Если же иссле-
дователь отклоняет Но, когда фактически Но ложна (верхняя
правая ячейка), то он тоже не совершает ошибку. Однако, если
он отклоняет Но, когда она верна, мы говорим, что он совершил
«ошибку 1 рода» или «ошибку первого типа». Если фактически
Но ошибочна, и исследователь отказывается отвергнуть Но, мы
утверждаем, что он допустил «ошибку 2 типа» или «ошибку
второго рода».
Вероятность ошибки 1 рода равна а. Исследователь может
контролировать величину а, регулируя вероятность неправиль-
ного отклонения Но от очень большой (а = 0,25 или 0,30) до
очень малой (а = 0,01 или 0,00]). Принято брать величину а
равной 0,05 или 0,01; хотя 0,05 и 0,01 характерны для промыш-
ленных и сельскохозяйственных исследований, в которых метод
ANOVA впервые нашел применение, это недостаточное основа-
ние для их исключительного использования в педагогических и
психологических исследованиях. Величина а, которую исследо-
ватель собирается использовать, должна зависеть от некоторых
особенностей конкретного анализа. Величина а = 0,15 или 0,10
могли бы быть оправданы в том случае, если в эксперименте
участвует небольшое число объектов. Как будет показано да-
лее, величина а непосредственно связана с вероятностью ошиб-
ки П рода (отказ отклонить ложную нуль-гипотезу). Вероят-
ность отказа отклонить ложную нуль-гипотезу определяется до
некоторой степени исследователем, р зависит от числа испытуе-
мых в эксперименте и выбранной величины а. Обозначим веро-
322
ятность правильного отбрасывания Нв, когда она является лож-
ной, 1 — р. Отсюда вероятностью ошибки 77 рода будет р.
I — р — вероятность отбрасывания На в случае, когда она оши-
бочна; она называется «мощностью» критерия. Чем больше а,
тем больше 1 — р. Величина 1 — ₽ очень важна для исследова-
теля. Тем не менее довольно часто полностью пренебрегают
«мощностью». Много времени и средств тратится на экспери-
ментальные исследования, которые характеризуются вероятно-
стью появления различий между испытаниями, скажем, равной
только величине 0,2. То есть, даже если различия данной вели-
чины и существуют, исследователь имеет 2 возможности из 10
0 2,86 F
Рис. 15.3. Пример вероятностей ошибок I и II рода для / =
л =10 и частной альтернативной гипотезы.
отбросить Но («обнаружить», что различия существуют). Есть
большая вероятность, что ему ничего не удастся обнаружить
даже там, где предмет поисков существует.
Может оказаться, что если исследователь устанавливает а
на уровне 0,05, то соответствующая величина 1 — Р составит
0,20; но если а было бы равно 0,10, то 1 — р определялось бы
числом 0,50. Очевидно, целесообразно для увеличения вероят-
ности 1 — р определения различий между опытами принять
больший риск совершения ошибки 1 рода.
Определения а и р и их связь представлены на рис. 15.3.
Вычисление мощности f-критерия для На будет описанр в
§ 15.15.
15.11. Однофакторный дисперсионный анализ (ANOVA)
с л наблюдениями в каждой ячейке (резюме)
Проводится эксперимент с одним исследуемым фактором, ко-
торый имеет / уровней. На каждом из / уровней берется п неза-
висимых наблюдений. Исследователь предполагает, что п на-
блюдений на каждом уровне независимы и взяты из нормальной
совокупности с дисперсией о2. Предполагается, что дисперсия ст2
одинакова на всех I уровнях. (Данное допущение часто на-
зывается гипотезой однородности — гомоскедактичностщ слово
323
«гомоскедактичность» происходит от двух греческих слов, озна-
чающих «одинаковый» и «рассеяние» или «дисперсия»).
ANOVA включает в себя 5 этапов:
1. Для объяснения данных постулируется линейная модель.
Xi} = И + «} + где <11 + ... + <xj = 0, а все ец независимы.
2. Формулируются нуль-гипотеза Но и альтернативная Hi.
Но: at ~ аг = ... ~ aj; Ht: «По крайней мере 2aj различны».
Или иначе Но: pt = ... = ju ^t'- S (и/— Й-)1 2 ¥= О-
3. Выбирается уровень а, то есть исследователь решает, ка-
кую вероятность он присвоит отбрасыванию Но, когда она вер-
на. Уровень а обычно выбирается равным 0,16, 0,05, 0,01 или
0,001. Значения а, превышающие 0,10, вероятно, допускают
слишком большой риск неверного отбрасывания Но, а значе-
ния а, которые меньше 0,001, вероятно, выбраны слишком осто-
рожно.
4. Производятся вычисления сумм квадратов [(а) и (б) ниже},
степеней свободы [(в) и (г)] и средних квадратов (д).
Результаты эксперимента можно расположить следующим
образом:
Условия опытов
1_______2 ...__________/
Хп Х|2 ... Х„
Хи Хц
ХП\ ... xnJ
a- SS.=^
В результате алгебраических преобразований SSW можно за-
писать в виде, более удобном для вычисления:
1 шаг. Вычислить SSW, возводя в квадрат каждое наблюде-
ние и суммируя квадраты. Тогда вы имеете: У У Х2ц.
2 шаг. Найти сумму исходных наблюдений для каждого из
! столбцов. Сумма /-го столбца равна: S Х(/.
324
Возвести в квадрат каждую из / сумм столбцов. Разделить
эту сумму на п. Получите величину
кы
п
3 шаг. Найти SSW, вычитая результат 2 шага из результата
1 шага.
б. SSb — £n(X.j — Снова в результате алгебраиче-
ских упрощений можно показать, что
ss ЙЫ
------п------------п----
1 шаг. Взять величину ~которая была вычис-
лена на 2 шаге в пункте (а).
2 шаг. Сложить все Jn исходных наблюдений и возвести в
квадрат эту сумму. Разделить сумму квадратов на Jn.
Теперь вы получите величину У, xu"j /jn.
3 шаг. Найти SSt>, вычитая результат 2 шага из результата
1 шага.
в. Число степеней свободы, связанное с SSW,
равно J(n— 1).
г. Число степеней свободы, связанное с SS&,
равно J — 1.
д. Вычислить ТИБа, и MSb следующим образом:
5. Рассчитывается F-отношение MSb!MSw и сравнивается с
точкой процентиля 100(1 —а) в распределении Fj-i.J(n-i)-
Проверка нуль-гипотезы осуществляется путем сравнения
отношения MSb/MSw, F-отношения с J — 1 и J(n — 1) степенями
свободы с величиной, полученной из F-таблицы, которая пре-
вышает а процентов F-отношений, найденных в случае правиль-
ной нуль-гипотезы. Если MSi>/MSw превышает эту величину (обо-
значаемую символом i-aFj-t, то исследователь отбрасы-
вает Но-
Для иллюстрации предыдущих вычислений вернемся теперь
к примеру § 15.1, в котором экспериментатор пытался опреде-
325
лить относительную эффективность 4 различных уровней актив-
ности учащегося в процессе изучения английской денежной си-
стемы. 40 испытуемых были случайно распределены по 4 уров-
ням (10 на каждом уровне) активности. Результаты приводятся
в табл. 15.1.
Вычисления для SSt,, SSW, MSb и MS„ выполнены в табл. 15.2.
В верхней части табл. 15.2 данные табл. 15.1 суммируются тре-
буемым образом.
Нуль-гипотеза Но о том, что pi = цг = цз — щ, проверяется
сравнением F — MSb/MSw с /^-распределениями в таблицах.
Таблица 15.1 Полученная величина Р
сопоставляется с различ-
ными процентильными
точками /^-распределения
с 3 и 36 степенями свобо-
Результаты теста, содержащего
100 вопросов по английской
денежной системе, 40 испытуемых
с 4 уровнями активности
Сокращен- ная програм 2 Конспекти- рование 3 Пособие Обучающая нашит
26 51 52 41
34 50 64 49
46 33 39 S6
48 28 54 64
42 47 58 72
49 50 53 65
74 48 77 63
61 60 56 87
51 71 63 77
53 42 59 62
ды.
Величина /^-отношения
для данных табл. 15.1—
15.2 есть F = 570,69/
149,93 = 3,81. В табли-
цах мы найдем процен-
тильные точки Гз.зо и Fs,io,
но не Fs.36, поскольку
там табулированы не все
/^-распределения. Мы мо-
жем, однако, выполнить
интерполяцию между 30
и 40 для получения при-
ближенных значений про-
центильных точек Fs,36- Интерполяция выполняется с величина-
ми, обратными степеням свободы, например, для определения
о.и/Узб решается следующее уравнение;
30 36 o.ss/'a.ao— o.ss/'s.ss
1 1 o.cs/'s.so — o.ss^a.io
30 40
В результате интерполяции получаются следующие процен-
тильные точки:
0.75^3.36~ L43
0,90^346“ 2,25
0,95^3.36 “ 2,86
Р = 3,81 — найденное значение
F = MSb!MSw
0,99^336 ~ 4,38
326
Таблица 15.2
Пример расчетов по методу одяофакторного дисперсионного анализа
(ANOVA) с равными п; данные из таблицы 15.1
2 3 4
4=10 4=10 4 = 10 4 = 10
X. 1 48.40 X. 2 = 48,00 X. а — 57,50 Хи = 53,60
to 10 10 10
£*>-«< £xt2 =480 z X(» = t>7& £Хе< = 536
i=I
10 to 10 to
^Х^ =25 024 £ Х/2-24 392 4 10 £ 2175 £ х?3 ==33 925 4 10 £ £>5,-125 375 2 Хг„- 42 03,
<484)» + (480)’ + (575)’ + (636)’ (2175)’
г>ьь --------------------йз----------------------—
— 119 977,70- 118 265,62= 1712,08
= 125 375 - (434)2 + (W + (575)’ + (636)’ =
= 125 375 - 119 977,70 — 5397,30
..с SSb 1712,08 SS’s, 5397,30
«5» = -^ = —у—570,69 ----.149,93
Одно найденное значение F из данных табл. 15.! лежит ме-
жду 95 и 99 процентилями ^-распределения с 3 и 36 степенями
свободы. Фактически оно лежит около 98 процентиля в распре-
делении 5з,зе- Отсюда, если Но:р, = р2 — рз = |м была верной,
то F-отношение, равное 3,81 или больше, появилось бы с вероят-
ностью, приблизительно равной 0,02. Если бы в этом примере
мы проверяли Нц на уровне а = 0,05, то отбросили бы Но в
пользу Hi, согласно которой не все 4 ц равны. Если мы ориен-
тировались бы на уровень значимости а = 0,01, то не отбро-
сили бы Hv. Мы были бы склонны принять На, даже если бы она
была ложной.
15.12. Однофакторный дисперсионный анализ (ANOVA)
с неравными п
Нередко в J ячейках однофакторного дисперсионного анали-
за ANOVA число результатов не равно. Например, 5 испытуе-
мых могли рассматриваться на 1 уровне фактора, а 10 и 20 дру-
гих соответственно на 2 и 3 уровнях. Методику дисперсионного
327
анализа, которая была разработана выше, можно легко усовер-
шенствовать, чтобы приспособиться к «планам с неравным чис-
лом наблюдений п». В сущности, теория остается прежней; тре-
буются лишь незначительные изменения. Техника вычислений
абсолютно аналогична случаю ANOVA с равными п.
Обозначения
Вы уже привыкли к тому, что Ле значение в /-й группе обо-
значается символом X,j. Когда мы говорили, что t пробегает
значения от 1 до и, а ; —- от 1 до /, то знали, что существовало
/ групп с п измерениями.
Поскольку в данном случае группы могут содержать различ-
ное число значений, необходимо предусмотреть число значений
первой группы Н|, второй группы п2, ... и Лй группы—-п.,. Дан-
ные, собранные в плане, который должен анализироваться одно-
факторным методом ANOVA с неравным числом наблюдений п,
можно представить следующим образом;
1 группа 2 группа 3 группа
^20.
В предыдущем примере 1 группа имела 20 значений, 2 груп-
па— 15, а в 3-й было 18 значений. Следовательно, = 20,
«2 — 15, а пз = 18.
Модель
Относительно исходных совокупностей делаются те же пред-
положения, которые выдвигались для ANOVA с равными п: вы-
борки независимо извлекаются случайным образом из нормаль-
ных совокупностей с равными дисперсиями а2.
Как и прежде, предполагается, что Xtj можно представить в
виде следующей линейной модели:
Хц ~ М + ai + ец>
где X(j — i-e значение /-й группы; ц— среднее J генеральных
средних; а, —разность между средним /-я совокупности, ц, и ц;
ец — разность между Xi} и средним /-й совокупности.
В /-и группе индекс I принимает значения от 1 до Общее
число данных во всех группах обозначим N; конечно, /V =
== П] -|- п2 + • • + nJ- В ANOVA с равными п вводилось огра-
ничение вида а: + • • • = 0. В ANOVA с неравным числом п
принимается допущение, что niai 4- п2а.2 + nJaJ — О- Это — един-
328
ственное существенное отличие в теоретической модели, и оно не
должно вас сильно беспокоить.
Как и прежде, определяются оценки наименьших квадратов
(МНК) для эффектов условий опытов, aj, которые служат для
проверки гипотезы о том, что в совокупности все a.j — 0, то есть
все У генеральных средних равны. МНК — оценка а, представ-
ляет собой разность X j~X~, то есть среднее п} оценок в /-груп-
пе минус среднее всех оценок.
a, =x.j~x.. =—-----------х...
С другой стороны, МНк — оценка ц представляет собой:
Оценка компоненты ошибки, ец, дается выражением
Нуль-гипотеза, которую мы хотим проверить, состоит в том,
что в генеральной совокупности все а, одинаковы и, следова-
тельно, равны нулю. Символически нуль-гипотеза выглядит так:
Но- а( = 0 для всех j.
Эквивалентной формулировкой Я» в терминах J генеральных
средних будет; Ло:/ц = Ц2 = ... = ц/.
Суммы квадратов
Во-первых, определяются сумма квадратов внутри, SSa, и
сумма квадратов между, SSt>. SS10 — просто взвешенная сумма /•
выборочных дисперсий для каждой группы;
зз.=(л-|)*?+(л-1и+ ... +(»,-i)S;-=
= £(Л1~х.1)>+Ё(Л1-х.!р+ ... +Е(х„-х.,)’.
Более простое обозначение предыдущей взвешенной суммы
имеет вид:
^(X/f — X./)2.
329
Взглянув на ожидаемые значения MSb и MSW, то есть на
средние значения обеих величин по повторениям однофактор-
ного эксперимента с неравными п, мы можем заметить, как от-
ношение AfS{, к MSW связано с вопросом «Правильна ли Hof».
Ожидаемые значения MSb и MSa
Мы теперь .убедились в том, что SSw—просто взвешенная
сумма J выборочных дисперсий: = —l)s/. Так как
каждая s2t является несмещенной оценкой одной и той же ге-
иеральной дисперсии о2, то величина E(SSW) — E(nj— 1)о2.
Теперь
В (SS.) = S (п, - о * - «’ S (»/ - 1) = »’(« ~ П-
Поэтому
£(т=т)“'Е<л,5-) = 'Л
Независимо от истинности или ложности Нд, среднее значе-
ние MSW (которое было бы получено в результате усреднения
MSa при большом числе идентичных экспериментов) равно оа,
общей дисперсии каждой из J совокупностей.
Величину E(MSb) вывести несколько труднее, поэтому мы
утверждаем без доказательства истинность следующего выра-
жения:
Е (MSb) = о2 + 1 .
Формула для E(MSb) при неравных п напоминает формулу
E(MSb) для равных п, [См. ур. (15.8).] Они отличаются только
тем, что коэффициент п, с которым все квадратичные отклоне-
«ия pj—р взвешиваются в случае равных п, становится част-
ным весом rij для каждого квадратичного отклонения при не-
равных п.
Основное свойство AfS& сохраняется прежним, как и в случае
равенства п, и это свойство лучше всего проявляется при ана-
лизе E(MSb). Когда Но верна, ожидается появление одинаковых
MSb и MSa и равных о2. Когда Нд ошибочна, ожидаются зна-
чения MSb, превышающие Эти и другие рассуждения, ка-
сающиеся теории распределений, аналогичны случаю равных п
и приводят к методам проверки Нд по Г-критерию.
331
Проверка Но по F-критерию: идея и метод
В случае верности нуль-гипотезы отношение MSb/MSw
будет соответствовать центральному F-распределению с J— ! и
—/ степенями свободы. Когда нуль-гипотеза ошибочна, отно-
шение MSblMSw будет следовать нецентральному /^распреде-
лению, которое имеет большее среднее, чем центральное (см.
рис. 15.2).
Стратегия оценки Но не отличается от той, которая была при-
нята в случае равного числа наблюдений п. Принимается а, оп-
ределяется точка процентиля 100(1—а) по таблице Е-распре-
деления с /—1 и Af—/ степенями свободы, MSb/MSw сравни-
вается с i-aF.r-t, n-j и принимается решение принять или от-
бросить Но-
Таблица 153
Оценке конформизма испытуемых,
которым сообщали, что их мнении в слабой,
средней или сильной степени совпадали
с мнениями студентов в целом
слабое соответствие 2 среднее соответствие 3 сильное соответствие
15 13 11 9 15 12 18 14 12 10
14 13 10 9 15 11 17 14 12 10
14 13 10 9 14 11 16 14 12 10
14 13 10 8 14 10 15 14 12 10
13 13 10 8 14 10 14 13 11 9
13 13 10 8 13 10 14 13 11 8
Был проведен эксперимент, в котором изучалось влияние
сходства восприятия социальной группы на конформизм пове-
дения. Группа из 60 испытуемых случайным образом делилась
на 3 подгруппы: слабое
соответствие — испытуе-
мым этой группы сооб-
щалось, что их мнения
обычно расходятся с мне-
ниями студентов коллед-
жа в целом; среднее со-
ответствие — этим испы-
туемым говорили, что их
мнения согласуются с
мнениями учащихся кол-
леджа довольно часто;
сильное соответствие —
испытуемым сообщалось,
что их мнения, как пра-
вило, совпадают с мне-
ниями учащихся в це-
лом. Затем испытуемых просили высказать суждения по 18 акту-
альным вопросам (смертная казнь, контроль рождаемости и т.д.),
однако прежде испытуемым сообщали, что думают по каждому
вопросу учащиеся в целом. Число раз из 18 возможных сужде-
ний, которое совпадало с мнениями учащихся в целом, рассма-
тривалось в качестве оцениваемого параметра «конформизм».
Фактические «оценки конформизма» 60 испытуемых представ-
лены в табл. 15.3.
12 испытуемых изучались в условиях среднего соответствия;
24 — в условиях слабого, а еще 24 — в условиях сильного. Рас-
сматриваемая нуль-гипотеза состоит в том, что в совокупностях,
из которых, как можно предполагать, эти выборки извлекаются
случайно, средние значения для 3 условий равны. Если мы про-
332
нумеруем группы 1, 2, 3 от слабого к сильному соответствию, то
Нй: pi = цг = цз-
Вычисление сумм квадратов представлено в табл. 15.4.
Таблица 15.4
Пример вычисления сумм квадратов для однофакторного ANOVA
с неравными л; данные из таблицы 15.3
Л; =24
24
У Хп = 273
«2=12
Лз = 24
24
£ Xi3 = 303
t £4,-9085
/-1 |=.|
в + AW + « „ = 8780,833 - 8760.417 20,416
SS№ = 9085 - = 9085 - 8780,833 = 304.167
Число степеней свободы для МЗь и MS& равно соответствен-
но 7—1 = 2 и /V —7 = 60 — 3 = 57. Отсюда MS6 = 20,416/2 =
= 10,208, a A1SW = 304, 167/57 = 5,336. Результаты ANOVA вы-
глядят так: ______________________________
Источник вариации df. MS F
Между груп- пами Внутри групп 2 57 10,208 5,336 1,91
Для проверки нуль-гипотезы Нй о том, что = цг = цз(или,
что равносильно —0^, сравним полученное ^отношение,
равное 1,91, с F-распределеннем с 2 и 57 степенями свободы.
75 и 90 процентили в распределении F2.57 определяются величи-
нами 1,42 и 2,40 соответственно. В повторениях эксперимента
табл. 15.3 F-отношения, превосходящие величину 2,40, будут на-
блюдаться в 10% случаев, когда подтверждается нуль-гипотеза.
15.13. Последствия нарушения допущений, имеющихся
в ANOVA: «устойчивость (рабастность)» ANOVA
Проблема, возникающая (для уровней значимости и мощно-
сти) в случае нарушения предположений при анализе диспер-
сионной модели, представляет большие трудности для специали-
333
ста в области математической статистики. Этого следовало ожи-
дать. Математики выбирают предположения для своих про-
цедур в соответствии с их вероятием и управляемостью. Вероят-
ное предположение — это предположение, которое, по-видимо-
му, относится к реальным данным, например, мы немного при-
обрели бы от процедуры или модели, опирающейся, главным
образом, на предположение о том, что оценки теста IQ имеют
прямоугольное распределение (все оценки одинаково вероятны)
в совокупности испытуемых. Управляемость предположения —
гипотеза, упрощающая множество математических выкладок и
действий. Распространенное допущение о нормальности наблю-
дений по переменным, возможно, является лучшим примером
допущения, которое одновременно вероятно и во многих случаях
управляемо. Множество наблюдений, выполняемых в физиче-
ских и социальных науках, имеют одну моду, большую долю
значений, близких к центру группирования, и очень малое число
значений, существенно отклоняющихся от этого центра. Благо-
даря тому, что среднее и дисперсия выборок из нормального
распределения статистически независимы, значительно упро-
щается статистическая теория, которая строится на предполо-
жении о нормальности.
Не следует удивляться, что положение осложняется, когда
возникает вопрос о влиянии нарушения предположения. Для
ответа на подобные вопросы необходимо выдвинуть другие до-
пущения, которые хотя и более вероятны, но несомненно ме-
нее управляемы (в математическом отношении). «...Мы понима-
ем, что наше исследование следствий нарушения основных пред-
положений будет неполным и мы не сможем его поддерживать
на уровне строгости, принятом в математике» (Шеффе, 1962).
Вспомните, что в простой модели однофакторного диспер-
сионного анализа ANOvA с постоянными эффектами делаются
следующие предположения:
5. Хц = |Л 4~ а? &ti-
2. eij ~ ННР(0, а2), то есть внутри каждой из I групп на-
блюдения нормально и независимо распределены относительно
их среднего с дисперсией о2.
3. Ха, = о.
Первое предположение состоит в том, что наблюдение может
рассматриваться как простая сумма 3 компонент: первая отра-
жает общий уровень результатов измерений (ц); вторая — воз-
растание или убывание независимой переменной, установленное
по результатам всех наблюдений, взятых в группе /, полученной
в условиях /-го уровня; и компонента ец, которая в поведенче-
ских науках относится к «индивидуальным различиям» и «ошиб-
ке измерений». Существуют различные методы, в которых
1 предположение может не выполняться. Один из них характе-
ризуется тем, что эффект условий j, а,, не одинаков для всех
334
испытуемых. Например, некоторые учащиеся могут отличиться
больше, чем другие, в данном опыте.
Предположение 2 утверждает, что е0 для многократных вы-
борок имеют нормальное распределение с нулевым генеральным
средним (ожиданием) и дисперсией о2 и независимы. Мы можем
рассмотреть три различных нарушения этого предположения:
(1) отсутствие нормальности, (2) различные дисперсии в раз-
ных группах, (3) отсутствие независимости. Следствием допу-
щений 1—3 является тот факт, что большое число наблюдений,
рассматриваемых при / условиях, внутри каждой группы
должно подчиняться нормальному распределению, а дисперсия
этого распределения в разных группах должна быть постоянной,
ст2 (очевидно, к среднему такие требования не предъявляются).
Кроме того, если извлекаются повторные выборки и для любой
из [/(/—1)/2] пар испытаний строится диаграмма рассеивания
выборочных средних, то будет наблюдаться нулевая корреляция
средних вследствие предположения о независимости.
Предположение 3 нас не интересует; в нем нет особой необ-
ходимости, поскольку оно просто является следствием выбора
представления в виде трех членов (ц, <zj, е<,).
Отсутствие предположения о независимости заслуживает
внимания. Проверка коррелированных иДа зависимых групп по
/-критерию— подходящая статистическая методика (если срав-
ниваются только 2 варианта условий), когда отсутствует неза-
висимость е<:. В поведенческих науках часто говорят о проблеме
«повторных измерений» (то есть о повторении экспериментов с
теми же самыми людьми при несколько измененных условиях)
при зависимых выборках. (Здесь мы не будем обсуждать про-
блему повторных измерений. Мы вернемся к ней в 18 главе. См.,
например Winer, 1962, гл. 4 и 7):
Мы коснемся только влияния нарушений на уровень значи-
мости предположений о нормальности и однородности диспер-
сий. Пример из последних исследований специалистов по мате-
матической статистике:
1. В предположении истинности нуль-гипотезы находим из
F-таблицы точку' процентиля 1 — а в /^-распределении с J — 1 и
N — J степенями свободы (i-aFj-un-j). (Эта процентильная
точка будет значением, которое превышает (100а) % F-отноше-
иий, полученных в ANOVA в случае, когда верна нуль-гипотеза
и выполняются предположения ANOVA.)
2. Эмпирическими или математическими средствами опреде-
ляется фактический процент F-отношений, превосходящих
когда нуль-гнпотеза правильна, а дисперсии неодно-
родны или совокупности не являются нормальными или когда
имеет место и то и другое.
3. Сравниваются номинальный а и фактический уровень зна-
чимости, то есть процент величин F, превышающих х-т-
Воке (1954, а, Ь) и Бокс и Андерсен (1955) получили неко-
торые предварительные математические результаты по влиянию
835
неоднородности дисперсий в однофакторном ANOVA на а. Боль-
шая часть результатов приводится Шеффе (1962). Эти резуль-
таты воспроизводятся в табл. 15.5-
Табл. 15.5 следует понимать так: если сравниваются 3 ва-
рианта условий и п, = 9, п2 = 5, а п3 — 1 и если генеральные
дисперсии находятся в отношении 1:1:3 (например, </'—10,
о^=10, а] = 30), то вероятность ошибки 1 рода фактически
равна 0,17, тогда как экспериментатор полагает, что она равна
0,05. В этом случае нару-
Табмца 15.5 шенйе предположения об
Влияние неоднородности дисперсий
на вероятность ошибки I рода
в однофакторном ANOVA для номиналь-
ного уровня значимости 0,05
Число групп Отношение С1 —диспср- Размеры выборок, "/ Фактическая вероятность ошибки 1 рода
3 1 -.2:3 5, 5, 5 0,056
3. 9, 3 0,056
7, 5, 3 0,092
3, 5, 7 0,040
3 1:1:3 5, 5, 5 0,059
7 5, 3 0,11
9, 5, 1 0,17
1, 5, 9 0,013
5 1 : I :1 : I :3 5, 5, 5, 5, 5 0,074
9, 5, 5, 5, 1 0,14
1, 5, 5, 5, 9 0,025
7 1:1 ...1:7 3, 3 3 0,12
однородных дисперсиях
было вызвано смещением
вправо (общее увеличе-
ние значений) распре-
деления F-отяошения,
MSblMSw, когда нуль-ги-
потеза верна. Экспери-
ментатор имеет больше
шансов отбросить истин-
ную нуль-гипотезу, чем он
думает.
Одна важная тенден-
ция, наблюдаемая в дан-
ных Бокса, касается свя-
зи между о и распределе-
нием п. Обратите внима-
ние на. то, что когда п
равны, то фактическая
вероятность ошибки 1 ро-
да очень близка к номи-
нальной вероятности а.
Может оказаться, что влияние нарушения предположения об
однородных дисперсиях будет не очень сильным при одинако-
вых п.
Вышеприведенные соображения так или иначе приводят к
следующим выводам:
1. Когда объемы выборок равны, влиянием неоднородности
дисперсий на уровень значимости F-критерия можно пренебречь.
2. Когда объемы выборок и дисперсии неравны, а из сово-
купностей с большими дисперсиями выбирается меньшее число
объектов, вероятность ошибки 1 рода больше а. Иначе говоря,
влияние неоднородных дисперсий в данном случае приводит к
смещению распределения F-отношеиий вправо.
3. Когда объемы выборок и дисперсии не равны, а нз сово-
купностей с большими дисперсиями берется большее число объ-
ектов, вероятность ошибки 1 рода меньше а. Влияние неодно-
родных дисперсий в этом случае должно привести к сдвигу рас-
пределения F-отношений влево.
335
Теперь постараемся выяснить, каково влияние нарушения
предположения о том, что наблюдения в ANOVA берутся из
нормальных совокупностей. Многолетние исследования ясно по-
казали, что влияние нарушения нормальности на номинальный
уровень значимости F-крнтерия крайне незначительно. Резуль-
таты экспериментов, опубликованные Э. Пирсоном в «Biometri-
ка» в 1929 и 1931 гг., показали, что для ANOVA с 2 группами
фактические и номинальные вероятности ошибок 1 рода прибли-
зительно равны в случае, когда выбираются скошенные распре-
деления. Бокс и Андерсен (1955) изложили точное математиче-
ское сопоставление номинального уровня а и фактической веро-
ятности ошибки I рода для различных распределений, не опи-
сывающихся нормальным законом.
Что касается вероятности ошибки 1 рода, то мы можем с
уверенностью заключить, что гипотеза нормальности в ANOVA
Таблица 15.6
Фактические вероятности ошибок I рода при двустороннем
/-критерии для различных ненормальных совокупностей н значений
генеральных дисперсий
1 совокупность 2 совокупность Номинальный уровень значимости
Форма П] Форма П2 0,05 0.01
Нормальное 1 5 Нормальное 1 5 0,053* 0,009*
Нормальное 1 15 Нормальное 1 15 0,040 0,008
Нормальное 1 5 Нормальное 15 0,040 0,006*
Нормальное 1 5 Нормальное 4 5 0,054 0,018
Нормальное 1 15 Нормальное 4 15 0,049 0,011
Нормальное 1 5 Нормальное 4 15 0,010 0,001
Нормальное 4 5 Нормальное 1 15 0,160 0,060
Экспоненциальное ** 1 5 Экспоненциальное 1 5 0,031 0,003
Экспоненциальное I 15 Экспоненциальное 1 15 0.040 0,004
Прямоугольное *** ] 5 Прямоугольное 1 5 0,051 0,010
Прямоугольное 1 15 Прямоугольное 1 15 0,050 0,015
Прямоугольное 1 5 Прямоугольное 4 5 0,071 0,019
Нормальное 1 5 Прямоугольное 1 5 0,056 0,010
Нормальное 1 15 Прямоугольное 1 15 0,056 0,010
Экспоненциальное 1 5 Нормальное j 5 0,071 0,019
Экспоненциальное 1 15 Нормальное 15 0,051 0,014
Экспоненциальное 1 25 Нормальное 1 25 0,046 0.013
Экспоненциальное 1 5 Прямоугольное 1 5 0,064 0,033
Экспоненциальное 1 15 Прямоугольное 1 15 0,056 0,016
Экспоненциальное I 5 Экспоненциальное 4 5 0,083 0,017
* Случаи, когда допущения ANOVA удовлетворялись, рассматривались
как контрольные в процессе эмпирической проверки.
•* Экспоненциальное распределение напоминает верхнюю треть нормаль-
ного распределения.
*** График прямоугольного распределения — прямая горизонтальная ли-
ния, причем асе значения переменной одинаково вероятны.
337
почти не имеет значения. Ее можно нарушить, а вероятность
ошибки 1 рода останется приблизительно равной величине, уста-
новленной экспериментатором, а именно а.
Боно (1960) пересмотрел множество предыдущих исследо-
ваний и представил оригинальную работу, касающуюся наруше-
ния гипотез t-критерия. Оригинальный вклад Боно в исследова-
ние нарушения гипотез A&OVA вызывает интерес, а его статья
хорошо известна и часто упоминается благодаря отличному об-
зору литературы. Учащемуся, начинающему изучать эту область,
стоит внимательно ознакомиться с данной работой.
Боно сравнил фактический уровень с номинальными уров-
нями значимости 0,05 и 0,01 для различных объемов выборки и
нарушений гипотез об однородности дисперсий и нормальности.
Фактические уровни значимости основаны на выборках объема
1000 t-отношений. Полные распределения частот t-отношений,
полученных при выполнении t-проверок для совокупностей, не
характеризующихся нормальным законом распределения, или
совокупностей с неравными дисперсиями, воспроизводятся в
статье Боно 1960 г. Мы приведем только минимум наиболее лег-
ких примеров из работы Боно. Эти результаты описываются в
табл. 15.6. Попытайтесь объединить результаты Боно с выво-
дами Бокса и Пирсона.
Вообще, оказывается, что ANOVA с постоянными эффектами
удивительно нечувствителен к отклонениям от нормальности; а
когда п равны, то и к влиянию неоднородности дисперсий. Бокс-
применил слово «робастность» для характеристики нечувстви-
тельности статистической проверки к нарушению допущений.
15.14. Проверка однородности дисперсий
Необходимо запомнить 2 случая, для которых имеет смысл
проверка однородности генеральных дисперсий: (1) когда хотят
сделать выводы относительно генеральных дисперсий, поскольку
они представляют научный интерес, и (2) когда предполагают
неоднородность дисперсий в дисперсионном анализе, если не все
факторы имеют постоянные эффекты.
Наиболее известный метод проверки однородности группы
дисперсий принадлежит М. Бартлету (1937). Статистики иногда
неохотно обращаются к критерию Бартлета, так как вычисления
трудоемки. Критерий Бартлета требует расчета J выборочных
дисперсий и их логарифмов. Кроме недостатка, связанного с
трудоемкостью вычислений, оказалось, что критерий Бартлета
весьма чувствителен к нарушению очень важной предпосылки,
утверждающей, что 1 выборок образуются из нормальных сово-
купностей (Box, 1953). Если исследуются совокупности, не под-
чиняющиеся нормальному закону, вероятность ошибки 1 рода
(отбрасывание истинной Но) при использовании критерия Барт-
лета может быть намного больше а, выбранного исследовате-
338
лем. Критерий Бартлета настолько чувствителен к предположе-
нию о нормальных совокупностях, что может даже служить хо-
рошим средством оценки нормальности (Box, 1953)1 Метод
оценки однородности дисперсий Шеффе по трудоемкости ариф-
метических операций не уступает критерию Бартлета. Однако
он гораздо менее чувствителен к нарушению предпосылки о нор-
мальности (Шеффе, 1962). Критерий, разработанный Хартли
(см. Biometrika tables for Statisticians, p. 60—61), — полезный и
экономный способ проверки Hs. Он содержит сопоставление от-
ношения максимальной выборочной дисперсии к минимальной с
табличным значением (табл. 31, таблицы биометрики). Критерий
Хартли использует не всю информацию о наблюдениях, касаю-
щуюся неоднородности дисперсии, и следовало ожидать появле-
ния более мощных критериев. Кохрен (1951) предложил крите-
рий, который прост для применения и использует больше ин-
формации, содержащейся в данных, чем метод Хартли. Винер
(1962, р. 96) утверждал, что существует доказательство чув-
ствительности критериев Бартлета, Хартли и Кохрена к допу-
щению, на которое опираются критерии, что I выборок исходят
из нормальных распределений. Для реализации 2 последних
критериев также требуются специальные таблицы.
Ливен (i960) предложил критерий Яо, который и прост в
применении (он использует обычную методику дисперсионного
анализа) и в большинстве случаев нечувствителен к нарушению
гипотезы нормальности. Критерий Ливена — просто однофак-
торный дисперсионный анализ абсолютных значений разностей
между каждым наблюдением и средним группы. Например, дан-
ные эксперимента имеют следующую структуру:
Условия
1 2 ... I
Хп Хц ... Х{1
хп1 Хп1 ... Хп1
Необходимо проверить гипотезу <з\= ... —а]. Никакого
предположения о форме распределений, составляющих основу J
выборок, не делается. Статистика будет опираться на предыдущие
данные при условии, что (I) можно приблизиться к 95 и 99
процентилю, скажем, в распределении статистики, когда Я# вер-
на, и (2) критерий, основанный на этой статистике, обладает
достаточной мощностью для отклонения Яо в случае, когда она
является ложной. Проверяемая по критерию Ливена статисти-
ка— отношение MSb/MSw преобразованных оценок Z,;, которые
связаны с Xi, выражением Z^ — ]Хц— Jtj|. Если F-отношение
превышает точку процентиля 1 — а обычного ^-распределения
с числом степеней свободы I— 1 и У(п— 1), то приходят к вы-
339
воду, что генеральные дисперсии различны примерно с 1 —а до-
верительной вероятностью.
В статье Ливена (I960) содержится описание результатов
исследования свойств этого критерия. Наряду с другими вопро-
сами он изучил соответствие между вероятностью получения
значимого F-отношеняя для Zy и номинальной вероятностью,
принятой исследователем, то есть исследовалось соответствие
выборочного распределения F-отношения для Zy и F-распреде-
ления. Ожидалось, что это соответствие объясняется широко при-
знанной «устойчивостью» дисперсионного анализа с постоян-
ными эффектами. Поскольку дисперсионный анализ с постоян-
ными эффектами устойчив при одинаковом числе наблюдений в
группе, Ливен сосредоточил внимание на этом случае. Устойчи-
вость критерия Ливена изучалась, таким образом, только при
равных п. Математическое обоснование для исследования Ли-
вена оказалось недостаточно четким; эмпирические выборочные
распределения F-отношений, вычисленных для Z>j, сравнивались
с F-распределеиием, имеющим /—I и J(n— 1) степеней сво-
боды. Вообще совпадение номинальной (основанной на F-pac-
пределении) и эмпирической (основанной на совокупности
1000 наблюдений) вероятностей отбрасывания истинной Но было
удивительно близким.
Ливен исследовал также мощность критерия отбрасыва-
ния Но. Было установлено, что мощность весьма удовлетвори-
тельна. При наличии нормальных распределений и J = 2 эффек-
тивность критерия Ливена, связанная с точностью F-критерия,
оказалась приемлемой. Эффективность описывалась диапазоном
0,75—0,96 для различных значений а и различных альтернатив-
ных гипотез Для J выборок эффективность критерия
Ливена по сравнению с приблизительной характеристикой эф-
фективности критерия Бартлета, в предположении нормальных
распределений, находилась в диапазоне 0,83—0,90.
В целом оказывается, что критерий Ливена является «устой-
чивым» критерием (для равного числа наблюдений в J выбор-
ках) проверки гипотезы о равных генеральных дисперсиях,
имеющим удовлетворительную мощность отбрасывания альтер-
нативных гипотез. Простота расчетов и применение стандартных
таблиц F-распределелия делают его особенно привлекатель-
ным по сравнению с более трудоемкими и менад устойчивыми
критериями, которые обычно используются. (См. Glass, 1966а).
15.15. Мощность F-критерия
Мощность конкретного F-критерия зависит от 4 величии: сте-
пеней свободы «между», обозначаемых символом П|, степеней
свободы «внутри», обозначаемых символом пг, величины <р, яв-
ляющейся мерой степени «ложности» нуль-гипотезы, и а, уровня
значимости критерия. Разумеется, в однофакторном ANOvA ве-
340
личина nt == J—1, а величина пг = N — J. Мощность F-крите-
рия определяется для конкретной группы величин gi, pv.
Величина ср имеет следующее определение:
л i
Ф= V ~-------Та5--•
где р. = (gj + ... Ч- что также равно g.
Расчет tp включает а2, генеральную дисперсию, равную для
всех / совокупностей. Обычно а8 не известна; возникает необхо-
димость либо собрать предварительные данные для ее оценки,
делая проницательные предположения относительно ее величи-
ны, либо вести измерения различий между pj в единицах о та-
ким образом, чтобы не было необходимости знать а2 (например,
какова мощность F-критерия, если ри — цг равно величине о/2?).
Когда tp, raj, «2 и а известны, мощность F-критерия можно
определить по таблицам. Например, предположим, что проведен
эксперимент, сравнивающий 3 условия (J = 3). Допустим, су-
ществует п = 11 наблюдений в группе, а проверку нуль-гипо-
тезы по F-критерию следует выполнить на уровне а — 0,05. Мы
хотим оценить мощность F-критерия для следующих альтерна-
тивных гипотез:
Ц|=68, И2 = 66, р3 = 64.
Предположим, что предыдущие эксперименты по изучению
аналогичного явления позволяют считать, что ст2 довольно близ-
ка к 20. Величина ср равна:
Vi i 1(68 - 66И + (66 - ббр + (64 - 66?] /ТГ(8Г
3~20 V 3-20
-Л/Т5--^М7 = 1.21.
Таблицы используются при nt — (/— 1) — 2, п2 — (N— J) =
= 30, а = 0,05 и <р = 1,21. Мощность F-критерия Но по сравне-
нию с альтернативной гипотезой о том, что рм = 68, щг = 66, а
Из = 64, приблизительно оценивается величиной 0,40. Таким об-
разом, в четырех случаях из 10 имеется возможность отбрасыва-
ния Не в пользу Я1, если фактически pi = 68, рг — 66, а рз=64.
Убедитесь в том, что при — J — 1 = 1, пг = М — / = 60,
а = 0,01 и ср = 5,00 мощность F-критерия приблизительно рав-
на 0,94.
Задачи и упражнения
1. В следующих примерах найдите степени свободы для MSb
и MSW:
а. /==2; п = 4; б. 7 = 5; п = 2;
в. / = 3; «1 = 3; «2 — 0; я3 = 4;
г. 7 = 3; «] = 4; п2= 1; п3 = 5;
341
2. Определите критическое значение F = MSn/MS№ для про-
верки Но в следующих примерах:
а. 7 = 2; п = 6; а = 0,01.
б. 7 = 5; п —7; а=0,10
в. 7=3; П|=4; п2 = 6; га3=8; а =0,05
3. Пользуясь лишь следующими данными в таблице ANOVA,
найдите MSt,, MSW и F:
Между груп-
пами
Внутри групп
Общая
dt S3 MS
4 49 81,25 378,60
4. Выполните по F-критерию проверку нуль-гипотезы
(Н/““ й-)2==0 на уровне 0,01 по следующим данным, ко-
торые описывают весовые потери в килограммах испытуемыми,
соблюдавшими 4 различные диеты.
Диета А Диета Б Диета В Диета Г
Хц = 2,7 Х21 =3,6 Х31 = 1,35 Х41 = 2,25 Хм =2,7 М । Х,,==9,45 Х23 = 9 Х33 = 7,65 Х<а = 7,2 Щ1Л тою см О Ч,—— cj со е-У тип >?><><
5. Необходимо проверить нуль-гипотезу Но : pi = ... = щ
при а = 0,05 и для выборок объема п = 5. Пусть (11=10,
g2=10, (13=12, щ= 14 и (15=14; величина а2=8,00. Ка-
кова мощность F-критерия в этих условиях?
16
МЕТОДЫ МНОЖЕСТВЕННЫХ СРАВНЕНИЙ
16.1. Введение
Как правило, вывод ANO VA — это утверждение о том, что нуль-
гипотеза об отсутствии различий в условиях эксперимента истин-
на или ложна для соответствующего уровня значимости (а),
задающего вероятность ошибки I рода. Если нуль-гипотеза от-
брасывается, то утверждение типа «не все генеральные средние
можно считать равными» часто не слишком информативно. По
сравнению с простым утверждением, что выборочные средние
различны, при отсутствии статистического вывода это, разумеет-
ся, большое достижение, но решение отбросить Но ничего не го-
ворит нам относительно того, какие генеральные средние рассма-
триваемых совокупностей различны. Предположим, что для двух
экспериментов, сравнивающих 4 группы и содержащих большие
выборки при малой величине AfSo» = ц2 = Оз = 20, а — 30
в первом эксперименте и hi == 5, цг = 10, цз — 25, щ = 50— во
втором. Вероятно, в обоих случаях экспериментатор должен по-
лучить значимое F-отношение при проверке //0: F (ц/ — jl.)2 —
= 0. При пользовании только простым методом однофакторного
дисперсионного анализа ANOVA, оба варианта приведут к абсо-
лютно одинаковой точке зрения, то есть будет сделан вывод
о том, что Нв ложна на высоком уровне значимости (низкий а),
хотя характер различий между генеральными средними в этих
случаях совершенно иной. Такое положение нас не удовлет-
воряет.
Большинство методов множественного сравнения предназна-
чено для использования после того, как отброшена нуль-гипо-
теза об отсутствии различий. Назначение этих методов состоит
в выделении сравнений между средними, приводящих к отбра-
сыванию Но. Например, в первом эксперименте сравнение fxi и
gs с помощью вычисления р» — ц2 = 20 — 20 = 0 показывает,
что эти 2 средних не обеспечили бы высокую вероятность отбра-
сывания Но, если бы были только эти 2 группы условий. Однаксг
343
p4—gj = 30 — 20= 10 несколько повлияло бы на значимость
различий. Применение методов множественных сравнений к ре-
зультатам первого эксперимента с большими выборками с вы-
сокой вероятностью должно привести экспериментатора к
выводу о том, что Ц|, иг, Из одинаковы, а отличается от них
(превосходит их).
Вероятно, сначала у вас возникнет мысль, что проверка по
/-критерию, выполненная для всех возможных пар средних, вхо-
дящих в f-критерий, позволит выявить, где заключены суще-
ственные различия между средними. Это вполне понятное пер-
вое впечатление; однако такая методология абсолютно неприем-
лема. /-критерий разрабатывался не для подобного применения,
и он лишен смысла в этом случае, /-критерий правильно исполь-
зуется для двух случайных выборок. Совсем другое дело рас-
считывать, что /-критерий окажется валидным для определения
значимости различия между минимальным и максимальным
выборочными средними в совокупности /-средних, /-критерий,
приложенный к максимальным в минимальным /-средним, не
учитывает величины Л Разве не ясно, что если мы принимаем
I = 50 и из одной и той же нормальной совокупности случай-
ным образом извлекается 50 выборок, то /-критерий будет опи-
сывать максимальное и минимальное значения как «существен-
но различные» гораздо чаще, чем предсказывает значение а?
Несмотря на явную непригодность /-критерия, ведущего к полу-
чению значимого f-отношения в дисперсионном анализе, или
множественного /-критерия вместо дисперсионного анализа, этот
метод часто использовался и продолжает использоваться.
Существует несколько доступных методов множественного
сравнения, но мы подробно рассмотрим только два из них. Все
эти методы сравнительно недавно пополнили статистическую
теорию, прячем разработка их относится к 50-м гг. XX в., а на-
чало их применения в поведенческих науках датируется при-
мерно 1957 г. (см. McHugh, Ellis, 1955; Stanley, 1957а; Sparks,
1963; Kenyon. 1965).
Один из наиболее ранних методов был разработан Килзом
(1952) на основе первоначальных исследований Неймана
(1939) и получил название метода Неймана — Кнлза (см. Wi-
ner, 1962, р. 80). Другим исследователем был Дункан (1955).
который предложил новый множественный критерий. Метод
Дункана, вероятно, получил наибольшее распространение в по-
веденческих науках и педагогике; однако до сих пор специали-
сты в области математической статистики преодолевают разно-
гласия или убеждают друг друга в том, что метод обоснован
(см. Шеффе, 1962). Он может представлять определенный
интерес для специалистов в прикладных областях.
Если исследователь хочет сравнить несколько групп условий
опытов с контрольной группой для определения различий ва-
риантов опытов по сравнению с данными одной контрольной
группы, в его распоряжении имеется метод Даннетта (1955)
344
'(см. Winer, 1962, р. 90—91). Одной из сравнительно небольшого
числа опубликованных работ в области педагогики, в которой
использовался метод Даннетта, является статья Скэннела и
Маршалла (1966). С ней стоит ознакомиться. Два наиболее по-
лезных метода множественных сравнений разработаны Тьюки
и Шеффе: Г-метод и S-метод. Хотя оба метода имеют много об-
щего, мы рассмотрим характерные случаи, возникающие при
применении этих методов при решении задач, с которыми вы,
вероятно, встретитесь на практике.
16.2. Т-метод
В однофакторном ANOVA нуль-гипотеза отбрасывалась на
уровне значимости а. Производилось сравнение J условий опы-
тов, а число наблюдений п в каждой группе было равным. В про-
цессе реализации ANOVA все допущения отвечали требованиям,
по крайней мере отсутствовали факты, свидетельствующие о на-
рушении хотя бы одного предположения. Для J условий суще-
ствует /(/—1)/2 пар (го есть сочетаний из J средних по два).
Каждая из них допускает сравнение вида X/ — Х.у, где j j*.
В результате анализа У (У— 1)/2 различий выборочных средних
и применения Т-метода экспериментатор хочет решить, можно
ли ему считать, что ру-ру* не равна нулю, Сначала мы про-
следим, как достигается это решение, а затем обсудим его ве-
роятностные характеристики,
1 этап. Определяются все J (J—_1)/2 сравнений между выбо-
рочными средними вида X.t — Х.р. Например, если_с°*
поставляются три условия, то вычисляются X-i — X .2,
Ха-Х.ъ и Х.2-Х.3.
2 этап. Все разности вида Х.,~ Х.р делятся на yjMSJn,
где MSa, — средний квадрат внутри уровней фактора в
однофакторном дисперсионном анализе (ANOVA), а
п— число наблюдений в любой группе.
3 этап. По таблицам определяется точка процентиля 100(1—а)
для распределения стьюдентизированного размаха со
степенями свободы J и )(п—1). Эта процентильная
точка обозначается \-аЯз, лп-о-
Стьюдентизированный размах — это разность между макси-
мальными и минимальными средними J независимых выборок
по п элементов из нормальной совокупности, деленная на
Существует семейство таких распределений, посколь-
ку для разных пар значений J и п получаются разные распре-
деления. Для выбора конкретного распределения нужны 2 па-
раметра: число выборок J и число степеней свободы для
MSW J(n — 1).
345
-4 этап. Все /(/ — 1)/2 разностей вида X./— Х.у, деленные на
y/MSdn, сравниваются с процентильной точкой. Если
они превосходят i-a<7j,дп-п, то заключают, что Х.,и
Х.р существенно различны, то есть что доказано разли-
чие Ц/ и Jl/%
Рассмотрим следующий пример применения Т-метода. В ре-
зультате эксперимента по сравнению трех методов (1 — 3) с 11
наблюдениями в группе (п = 11), имеем X,t =22,60, = 23,40,
Я,з — 28,50, a A4SM = 4.10. На уровне 0,05 получено значимое
F-отношение.
(этап. Х.1~Х.2 = —0,80-
X.i-X.^— 5,90.
Х.2-Х.3 = -• 5,10. _______
2 этап. Деление предыдущих разностей на -у/4,10/11 =0,610 дает
— 1,311, —9,672 и —8,361.
3 этап. По таблицам мы видим, что о,95<7з,зо = 3,49.
4 этап. Всякое абсолютное значение разности средних, деленное
на y/MSa,ln и превышающее 3,49, является значимым.
Таким образом, можно прийти к выводу на основе Т-ме-
тода, что генеральные средние для 1 и 2 групп не отли-
чаются друг от друга (поскольку 1,311 < 3,49), а сред-
нее 3-й группы отлично и от I и от 2.
16.3 Доверительные интервалы для контрастов
в Т-методе
Построение доверительных интервалов для разностей
X.j — X.f следует рассматривать как важный, возможно, даже
более важный этап, чем принятие решений о значимости разно-
сти. Пользуясь Г-методом, можно построить множество совмест-
ных доверительных интервалов для разностей выборочных сред-
них. Доверительный интервал относительно X., — опреде-
ляется по следующей формуле:
(X./— X-r)± -y/MSv/n. (16.1)
В примере, описывающем роль Г-метода при оценке значи-
мости, мы имели: X. j=22,60, Х.2=23,40, Х.3=28,50, -y/MS^In —
= 0,610, a o,%?j,36=“3,49.
Для построения доверительных интервалов по трем возмож-
ным разностям между средними прибавляют и вычитают
(3,49) (0,610) = 2,13 от каждой разности. Вычисления приво-
дятся в табл. 16.1.
346
Таблица 16.1
Построение доверительных интервалов для разностей
трех выборочных средних с использованием Т-метода
Х.у-Х,. Окончательные расчеты
X.i-X.0=-0^0 (3,49) (0,610) = 2,13 - 0^±2,13 = = (—2,93; 1,33)
Х.1--Х.,=-5,90 2,13 —5,9±2,13 = = (-8,03; -3,77)
Х.2 —• Х-а = —5,10 2,13 -5,1±2,13 = = (-7,23; -2,97)
Обратите внимание, что один доверительный интервал, вклю-
чающий нуль, соответствует незначимой разности выборочных
средних Х.1 и Х.2, тогда как 2 других разности значимы.
Заметьте также, что величина, которую прибавляют и вычи-
тают из разности выборочных средних, одинакова для всех зна-
чений / и /*. Таким образом, определяют i{n-i^MSwln
и прибавляют и вычитают эту величину от каждой из разностей
/(J—1)/2 средних для построения множества совместных дове-
рительных интервалов по Т-методу, Разумеется, цель любого до-
верительного интервала этого типа — покрыть величину ру — ру>.
Совместные доверительные интервалы строятся таким образом,
чтобы доверительная вероятность для каждого интервала не-
была равна величине 1—а. Смысл термина совместный и харак-
тер вывода, который соответствует таким, доверительным интер-
валам, будут раскрыты в следующем параграфе.
В эксперименте, в котором сравниваются 5 групп, осуществ-
ляется 5(4)/2 = 10 сравнений выборочных средних. Доверитель-
ные ннтервалы можно установить для всех 10 результатов срав-
нений по Т-методу с использованием ур. (16.1) и а — 0,05, на-
пример. В множестве из 10 доверительных интервалов некото-
рые интервалы перекроют разность ру— ру, а некоторые—нет.
Аналогичный эксперимент мог бы повторяться неоднократно, до
тех пор пока не будут накоплены тысячи групп с 10 довери-
тельными интервалами. Некоторая часть из указанных тысяч
экспериментов, характеризующаяся тем, что все 10 вычислен-
ных доверительных интервалов для 10 сравнений вида
X.t — Х-г заключают в своих пределах величину ру —-ру, оце-
ниваются значением 0,95, то есть (1 — а). Иначе говоря, в
100(1 — а) процентах опытов, в которых сравнивается / групп
по п элементов в каждой, Т-метод позволит получить /(/— 1)/2
доверительных интервалов, причем все в своих пределах будут
содержать разность ру—цу. В некоторых опытах, возможно».
347
только один из ](] —1)/2 доверительных интервалов не пере-
крывает ц/— Ц/s в других экспериментах более чем один из
группы совместных доверительных интервалов не будет пере-
крывать fij — jif. В большой серии только 100(a) процентов
экспериментов будет иметь одни или более из числа /(У —1)/2
доверительных интервалов, ие перекрывающих р/ — ру.
Понятие множества совместных доверительных интервалов
в корне отличается от более простых понятий доверительных
интервалов, встречавшихся ранее в этой книге. Прежде мы го-
ворили о вероятности того, что доверительный интервал вида
X. ±гол/п содержит ц в своих пределах. Теперь мы говорим
о вероятности того, что в экспериментах с У группами каждая
группа, в которую входит совокупность доверительных интер-
валов, перекрывает рассматриваемые параметры. В вероятност-
ных терминах совокупность интервалов была выборочным про-
странством, по отношению к которому рассматривалась довери-
тельная вероятность 1—а. При наличии множества совместных
доверительных интервалов выборочное пространство — бесконеч-
ная совокупность экспериментов, причем каждый опыт позво-
ляет получить У (У—1)/2 разностей выборочных средних.
Предположим, что для некоторой переменной производится
сравнение 3 групп (У = 3) по 10 представителей (п — 10) и что
Hi = 13. Ц2 = 10, а цз = 5. В ходе экспериментального исследо-
вания можно осуществить 3(2)/2 = 3 сравнения средних, Пред-
ставим себе, что при a = 0,10 по Т-методу выполняется построе-
ние доверительных интервалов для 3 сравнений: X., — Х.2,
X.i — Х.3 и Х-2 — X ,3. Вероятно, процесс извлечения 3 групп с
10 наблюдениями и построения интервалов по Т-методу для
сравнений мог бы повторяться бесконечно. На рис. 16.1 приво-
дятся возможные результаты этого процесса.
Точки представляют разности выборочных средних. Три точ-
ки над единицей по горизонтальной шкале рис. 16.1 представ-
ляют три разности между средними, полученные при первой по-
становке эксперимента. Равные отрезки прямых выше и ниже
каждой точки изображают интервалы, построенные с помощью
Т-метода. Обратите внимание на то. что в первом опыте все 3
доверительных интервала содержат истинные значения цу—цу.
Мы должны ожидать, что это случится в 90% — 100(1—а)
проведенных экспериментов (У — 3, п= 10). Обратите внима-
ние также и на то, что в пятом эксперименте 2 из 3 интервалов
не покрывают разности генеральных средних.
Методу множественных сравнений присущ, по-видимому,
один недостаток при выборе допустимого процента ошибки экс-
перимента. Этот недостаток связан с концепцией эксперимен-
та. Обычно в исследованиях в области педагогики и социальных
наук выбор числа уровней, характеризующих фактор в экспери-
348
менте, произволен. Иногда для осуществления подобного выбора
имеются вынужденные причины. Экспериментатор будет охотно
вводить любое число дополнительных уровней, если они ясны,
для сравнения. Некоторые исследователи в таких случаях выби-
рают «контрольную группу». Определение «фактора» (совокуп-
ность уровней для сравнения) в эксперименте абсолютно произ-
вольно. Однако контраст между методами А и В всегда подразу-
Рис. 1V.I. Множество совместных доверитель-
ных интервалов, построенных по Г-методу для
10 повторений эксперимента, в котором сравни-
ваются 3 условия.
меняет нечто подобное, независимо от того, самостоятелен ли он
или входит в фактор с дюжиной уровней. (См. Wilson, 1962;
Ryan, 1959, 1962.)
Анализ метода Тыоки показывает, что вероятность выявления
значимого контраста между двумя средними (мощность контра-
ста) зависит от 7, числа групп, сравниваемых в опыте. Ширина
доверительных интервалов в окрестности отдельного контраста
в методе Тьюки зависит от 7 (так же, как и от п и MSa). Не
следует допускать, чтобы произвольный выбор числа уровней в
эксперименте оказывал влияние на эти связанные условия
(мощность и ширина интервалов).
349
16.4. S-метод
Метод множественных сравнений Шеффе можно использо-
вать как в тех случаях, когда применим Г-метод, так и в ситуа-
циях, где Г-метод не имеет смысла.
Понятие сравнения (скажем, щ — цг), которое встречалось в
предыдущем параграфе, — это частный случай более общего
понятия контраста-
Определение: Контрастом J генеральных средних |Х[, ..., ц/
называется линейная комбинация
Ф==С|Щ + C2U2 + ••• -f-
такая, что ci -f- с2 -f- ... -f- cj = 0.
Константы Ci, ..., Cj— просто положительные и отрица-
тельные действительные числа, сумма которых равна 0. Таким
образом, ф = ц, -f- рг — 2цз — контраст для 3 средних pi, р2 и
рз, если Ci = 1, Ci = !, с3 = —2, По этому определению раз-
ность между любыми 2 средними образует контраст: например,
ф = цз — ив соответствует Сз=1, с& = —1, а все другие с
равны 0-
Пусть имеется 5 генеральных средних ..., ps. В табл. 16.2
перечислены их контрасты.
Таблица 162
Контраст
С, С, с> с. С,
1- 1-10 0 0
2. - 1(М| + Ц<)/21 -- 1 0 -у 0
3. [(Hi + Н» + |14)/3) - «Иг + Р»)/2] £ 1 1 1 3 2 2 3 ~ ~2
4. Цз —>4 -10 10 0
Любой контраст ф можно оценить при замене ц выборочными
средними, то есть оценка ф параметра Ф определяется выраже-
нием:
ф===сХ1 + С2*-2+ ••• Л-CjX.j. (16.2)
Например, если ф — цз — цз, то оценка ф — разность X .2 — Х.3.
До обсуждения значимости любого оцениваемого контраста
необходимо оценить дисперсию ф. Если выполнен однофактор-
ный дисперсионный анализ ANOVA и найдено значение MSW,
то оценка дисперсии ф задается выражением
<v"s-(v+4+ +4)- <|М>
350
где М5Ш — «средний квадрат внутри»; Cj — константа, на кото-
рую умножается /-е среднее, а л,- — число наблюдений а /-й
группе.
Число степеней свободы df, связанных с оценкой дисперсии,
определяется величиной df для MSW, N — J, где N — общее
число наблюдений в полном однофакторном дисперсионном ана-
лизе, предшествующем S-методу, равно nt -f- п2 -f- ._.. -f-nj.
Например, если 7 = 4, все п равны 10, а ф = Х.| — Х,4, то
оценкой дисперсии будет:
«2 л, с №. °’ 1 о2 , (-1)4 ,,с /24
— МЗД-jO-+ То + То + —П-J — MS, (ду) .
Число степеней свободы для оценки дисперсии равно
N — 1 = 40 — 4 = 36.
Обычно оценка ф нужна для проверки значимости ее отличия
от нуля. Данная проверка позволяет ответить на такие вопросы:
1. Существует ли какая-нибудь разница между реакциями
на обучающую программу с выбором из готовых ответов или
с поисками ответа? pi—
2. Отличается ли среднее для выбора из готовых ответов при
наличии и при отсутствии подтверждения от аналогичного сред-
него для случая поиска ответа? [(pt-f-pa)/2] — [(из + щ)/2].
3. Отличается ли среднее трех уровней положительного под-
крепления в процессе эксперимента от среднего 2 уровней отри-
цательного подкрепления? [(Hi 4-Иг 4-Рз)/3][(ц< 4-Ps)/2].
В процессе проверки значимости контраста средних можно
выделить следующие 5 этапов:
1 этап. Описать и оценить ф. Необходимо определить коэффи-
циенты С|, .... cj, оценивающие рассматриваемый кон-
траст. Если это выполнено, ф получается в результате
подстановки выборочных средних вместо генеральных
средних, например, в ур. (16.2).
2 этап. Найти оценку дисперсии ф. В процессе реализации одно-
факторного дисперсионного анализа ANOVA, предше-
ствующего применению S-метода, оценивается MS». Эта
величина, с, и объемы выборок подставляются в
ур. (16.3) для получения dj.
3 этап. Найти дф. Взять положительный квадратный корень из
dj, которая была найдена на 2 этапе.
4 этап. Составить отношение ф к dj. Величина ф, полученная
на первом этапе, делится на величину 6$, найденную на
3 этапе.
5 этап. Сравнить абсолютную величину отношения с критерием.
Абсолютная величина отношения, найденная на 4 этапе,
сравнивается с величиной квадратного корпя из произ-
ведения (7—1) на процентиль 100(1—а) 5-распреде-
351
ления со степенями свободы /— 1 и N — 3, то есть аб-
солютная величина отношения сравнивается со значе-
нием V(/ — Vi-efj-i.yy-y.
Гипотеза о том, что = 0. отбрасывается, если абсолютная
величина отношения превышает величину корня квадратного из
произведения (/—1) на процентильную точку, то есть отбро-
сить Но: ф — 0. если > л/{3 —- \)x_aF .
Предположим, что производилось сравнение 4 способов изу-
чения уравнивания окислительно-восстановительных химиче-
ских реакции. Данные (оценки теста, содержащего 15 вопро-
сов), полученные в результате эксперимента, приводятся
в табл, 16 3,
Таблица 16.3
Группа Выборочное я
2 7.1 = 10,32 Х.г = 10,54 Л] =20 п2 = 25
3 Х.3 = 12,80 X.4 = 7,17 «з = 20 MSa. = 8,35
При анализе дисперсии этих данных Г-отношение значимо
на уровне 0,05. В данном случае цель S-метода состоит в вы-
явлении групп, приводящих к получению значимого результата.
Вполне вероятно, что будут представлять интерес все воз-
можные лары разностей между выборочными средними. Таким
образом, необходимо определить значимость следующих разно-
стей выборочных средних:
X.i — X.z Х.г—Х.3
Х.У~Х.3 X.2-X.t
X.f — X.1 X.z-X.<
Кроме того, предположим, что исследователю требуется не-
сколько более сложный контраст. Это соответствовало бы слу-
чаю, когда 1 и 2 группы обучали двумя методами, отличающи-
мися друг от друга только тем, что I группа действительно на-
блюдала осаждение хлорида серебра, а вторая — нет. Данные
наводят на мысль, что этот опыт для 1 группы был бесполезен;
фактически 1 и 2 группы могут не различаться. Исследователь
хочет знать, будет ли среднее значение 1 и 2 групп существенно
отличаться от среднего значения 3 группы, обучение которой
производилось по совершенно иному методу. Подобный вопрос
характеризуется контрастом [(jit-f- рг)/2] — цз-
Контрасты, в которых заинтересован исследователь, приво-
дятся в табл. 16.4. Указанные подробности завершают 1-й и 2-й
352
из пяти этапов, которых следует придерживаться. Если мы
подставим данные в формулы табл. 16.4, то будем иметь оценки
и дисперсии контрастов (см. табл. 16.5).
Таблица 16.4
Контраст Оценка контраста Оценка дисперсии контраста
А. —Из. Б. Hj - Из В. Hi —Ит Г. цг — Из Д. Иг — Из Е. Ц8~Н< ж Hi + На ,, /К. Hs х.>-х.г X.!- Y.s X.I-X.4 Х-г — X-з Х.г-Х.4 Х.З-Х.4 Х-i +х.г 7 2 ‘ А!5ш(-±+-1Л «г/ AfSw “-(та+та) «•(та+та) “-(та+'та) Afsd —+-Д+ -J-) \ 1 Яг я8 7
Таблица 165
Контраст Ф ‘5
А, Щ —цг Б. Hi — |4з В. Hi — Г. Иг ~ цз Д- Иг —Из Е. цэ — щ Ж. ((И1 + Цг)/2] - цз —0,22 -2.54 3.15 -2,32 3,37 5.69 -2,43 0,752 0,835 0,969 0,752 0,885 0,969 0,605
В качестве примера вычислений, выполнявшихся втабл. 16.5,
рассмотрим контраст Ж. Контраст равен ф — [(su + Нг)/2]— из!
оценкой ф контраста (1 этап) является
10,32+ 10,54
2
12,86 = -2,43.
Оценка дисперсии контраста (2 этап) следующая:
i + та) =8'35 (та + таг +10 = °.61-
12 Зак. 448
353
Находятся положительные значения квадратных корней
(3 этап) из оценок дисперсии всех 6 контрастов (таблица слева)
—0,22/0,867 == —0,25
—2,54/0,914 «-2,76
3,15/0,985== 3,21
—232/0,867 == —2,67
337/0,94! « 3.59
5,69/0,985=» 5,81
-2,43/0.778 ==-3,12
Для каждого из шести контрастов определяется отношение ф
к (4 этап). Абсолютные величины отношений, найденных
на 4 этапе, сравниваются с V(7 — 1)1-0^j-i. w-J (5 этап).
Л' = 20 + 25 + 20+ 15 = 80, а 7 = 4.0.95Ез,7б = 2,72.
W = V3<72) = 2,86.
Поэтому если какое-либо отношение, найденное на 4 этапе,
больше, чем 2,86, по абсолютной величине, то есть если отноше-
ние выше 2,86 или ниже —2,86, то соответствующий контраст
значим В соответствии с этим критерием контрасты В,Д,Е и Ж
значимо отличаются от нуля по 3-методу при а = 0,05. Таким
образом, исследователь приходит к выводу, что
Hl + 1*2
Ml — R, Ц2 — Р’4» Рэ — *4 И -^-2-------?3
не равны нулю. Нельзя заключить, что отличаются щ и рг или щ
и рэ или ц» и цз- Опубликованные результаты применения 3-ме-
тода в области педагогических и психологических исследований
можно найти в книге Траверса и др. (1964).
16.5. Доверительные интервалы для контрастов
в S-методе
Доверительный интервал в окрестности оценки контраста в
5-методе строится следующим образом:
Ч>±9,У(/-1),_аГ,(16.4)
Естественно, цель доверительного интервала — включить в
свои границы истинное значение контраста генеральных сред-
них, ф.
354
Если ф =s Ci|xt + faga 4--..сщ,, то доверительный интер.-
вал для ф относительно ф образуется так:
(CiX.i 4- СгЛ’.г 4- • • • 4"с-г-^ т)
± -у/MS. + ... + (16.5)
Предположим, например, что ф == щ— рг. Доверительный
интервал для ф был бы следующим;
(X., - X. „) ± MS. +i.) V(;-D,-„F„77i.
Если сначала проверялась значимость разности оцениваемых
контрастов, то применение ур. (16.4) для полученных довери-
тельных интервалов представляется вполне удобным. Построе-
ние доверительных интервалов по S-методу здесь будет показано
на примере, использованном в § 16.4.
Выборочный контраст значимо отличается от 0, если довери-
тельный интервал относительно него не перекрывает 0. Следо-
вательно, контрасты В, Д, Е и Ж в табл. 16.6 соответствуют кон-
трастам, которые существенно отличаются от 0. В случае кон-
траста В можно утверждать с вероятностью, обеспечиваемой
S-методом, что разность между щ и щ несколько больше 0; ве-
роятно. фактически значение разности находится в интервале
0,35—5,95.
Таблица 16.6
Пример построения доверительных интервалов
по S-методу с использованием уравнения (16.4)
Ч (2.861
д —0,22 0,867 (—2,71, 2,27)
Б —2,54 0,9! 4 (—5,17, 0,09)
В 3,15 0,985 (0,35, 5,95)
Г —2,32 0,867 (—4,80, 0,16)
п 3,37 0,941 (0,68, 6,06)
Е 5,69 0,985 (2,89, 8,49)
Ж -2.43 0,778 (—4,66, -0,20)
Аналогично доверительный интервал по контрасту Ж свиде-
тельствует о том, что различие между рз и средним значением
генеральных средних р[ и скорее всего не равна нулю. С дру-
гой стороны, S-метод не позволяет нам с уверенностью заклю-
чить, что pi и цг отличны друг от друга (контраст А).
Доверительные ннтервалы, построенные по S-методу, должны
рассматриваться как совокупность совместных доверительных
12*
355
интервалов. Так же, как и в случае построения интервалов по
Т-методу, относительно каждого индивидуального интервала
нельзя сделать никакого вероятностного утверждения. С другой
стороны, интервалы строятся так, что в целом совокупность ин-
тервалов, которые можно определить в любом опыте, имеет ве-
роятность захвата истинной величины контрастов, оцениваемых
в ее границах, равную 1 — а.
16.6 Сравнение Т- и S-методов
Метод множественных сравнений Шеффе, как правило, пред-
почитается математиками Т-методу вследствие его универсаль-
ности (нет необходимости в равных п) и большей чувствитель-
ности в тех случаях, когда необходимо оценить сложные комби-
нации выборочных средних. Однако вы, вероятно, будете чаще
применять Т-метод.
Очевидно, выбор Т- или S-метода для практического исполь-
зования определяет распределение среди J групп. Одно из
требований Т-метода, которое не обязательно в S-методе,— ра-
венство объемов выборок. Следовательно, Т-метод нельзя при-
менять в случае неравных п. Это утверждение нужно понять
правильно. Скоро мы увидим, что если представляют интерес
только различия среди пар выборочных средних, то Т-метод
значительно лучше с точки зрения возможностей выявления
значимых различий и более узких доверительных интервалов,
чем S-метод. Если значения п не очень сильно различаются, на-
пример nt = 21, П2 = 22 и п$ = 20, то имеет смысл случайным
образом убрать один элемент из l-й группы, два элемента из
2-й группы и применить Т-метод. Случайное исключение из ана-
лиза 3 испытуемых почти не повлияет на результаты и позволит
применить более эффективный Т-метод для сравнения выбороч-
ных средних. С другой стороны, подобная стратегия не устроила
бы нас в том случае, если бы, например, ni = 5, пг ~ 30, а
Пз — 40, поскольку для получения равных п (по 5 элементов)
пришлось бы исключить слишком много данных. В этом случае
целесообразно было бы использовать S-метод, даже если бы
вас интересовали только 3 возможных расхождения между вы-
борочными средними.
Предположим, что после определения значимого Т-отноше-
ния в процессе дисперсионного анализа с равными п экспери-
ментатору надо исследовать различия между J(J — 1)/2 выбо-
рочными средними. Каким методом он может воспользовать-
ся? Или если возможны оба метола, то какой из них следует
предпочесть? Предпочтение отдается Т-методу, поскольку он
обеспечивает выявление большего числа значимых различий в
средних. Кроме того, Т-метод будет давать более узкие довери-
тельные интервалы относительно различий между средними по
сравнению с S-методом.
356
В качестве примера для сопоставления ширины доверитель-
ного интервала относительно X./— Х.р, построенного в Г- и
5-методах, возьмите контраст между Я,? и Я,з в табл. 16.1. Было
установлено, что доверительный интервал при а = 0,05, для
Р и с. 16.2. Схема множественных сравнений 1 средних значе-
ний групп. (Основанная на работе: Hopkins, Chadbourn. 1967.)
Я.г— Я3 есть (—7,23; —2,97). Зеперь установим доверительный
интервал с вероятностью 0,95 для той же самой разности, поль-
зуясь S-методом.
X-2 X.j“—5,1 AfS„, = 4,l п% — П3 = 11
^-4,1(тг + тг) = °.7‘15
V(/- = -?2(ЗЭЗ) = 2,58.
Доверительный интервал относительно Яг— Яз, построен-
ный по S-методу, есть —5,1 ± (2,58) - (0,86) = (-7,32; —2,88).
857
В некоторых случаях в S-методе получится интервал, содер-
жащий нуль, — это означает, что различие между средними
признается несущественным, тогда как Г-метод позволяет полу-
чить доверительный интервал для той же разности, не содержа-
щий нулевого значения, приводя вас, таким образом, к выводу
о существенном различии между двумя средними.
Когда рассматриваются более сложные контрасты по срав-
нению с простой разностью средних значений, например,,
[(gi + Ц2>/2] —рз. то S-метод обладает большими возможно-
стями (и поэтому позволяет получить более узкие доверитель-
ные интервалы относительно оценки контраста), чем постановка
исследования по Г-методу применнтельнок подобным контрастам.
Мы не обсуждали применение Г-метода для контрастов, отли-
чающихся от разности ц/ —и/% поскольку это было бы нецеле-
сообразно, ибо нами разобран S-метод, имеющий предпочтение
в случае более сложных контрастов. Интересную характеристику
обобщенного Г-метода можно найти в работе Гейзера (Guen-
ther, 1964, р. 54—57), а обсуждение метода с математических
позиций — в книге Шеффе (1962).
Применение Г-метода (или S-метода, когда п заметно от-
личаются друг от друга) к различиям между выборочными сред-
ними охватывает почти все случаи применения методов множе-
ственного сравнения в педагогических исследованиях и поведен-
ческих науках. Интерес к более сложным контрастам, для кото-
рых более приемлемым оказался бы S-метод, нс распространен-
ное явление. Бесспорно, однако, что в S-методе просматриваются
благоприятные возможности для исследования интересных и за-
служивающих внимания контрастов.
Сравнительно новый учебник по статистическому выводу
Миллера (1966) является отличным справочником по этим №
другим вопросам.
Задачи и упражнения
Если выражение (X,— X>/.)± 0>95<?Л/йе-
содержит нуля, то различие между Х: и X,• считается значи-
мым на уровне 0,05 по методу Тьюки. Это эквивалентно заклю-
чению о том, что X.I и Х.г существенно различны на уровне
0,05, если _ _
-^=- > ил..
Предположим, что в конкретном эксперименте J = 6, п = 11, а
MSW = 44,00. Какие из перечисленных средних значимо разли-
чаются при а = 0,05 по Г-методу:
=61,25, Х.2 = 64,72, Х.3 = 70,57, Х.4 = 73,42,
X.5 = 81,66, а X.6 = 82,17?
17
ДВУХФАКТОРНЫИ
ДИСПЕРСИОННЫЙ АНАЛИЗ —
ПОСТОЯННЫЕ ЭФФЕКТЫ
17.1. Структура и обозначение данных
Данные, полученные в плане двухфакторного дисперсионного
анализа, классифицируются по двум факторам. Подобные двух-
факторные классификации предметов известны каждому. На-
пример, людей можно разделить в соответствии с полом и про-
исхождением; автомобили можно классифицировать по «годам»
и «маркам».
Рассмотрим пример двухфакторного плана эксперимента, в
котором сравниваются 3 метода обучения чтению. Учеников,
участвующих в этом опыте, можно классифицировать по двум
признакам (наряду с другими): по методу обучения, по кото-
рому они проходят соответствующий курс (фактор А), и по полу
(фактор В). Фактор А, метод обучения, имеет 3, а фактор В,
пол, — 2 уровня. Поскольку и мальчики и девочки в процессе
эксперимента учатся по каждому методу, возможны 6 различ-
ных комбинаций уровней двух факторов. Предположим, что пе-
ременной, которая будет анализироваться при оценке резуль-
тата эксперимента, служит понимание прочитанного, обозначае-
мое символом X. Наблюдения по X получаются в результате
применения стандартизованного теста на понимание прочитан-
ного. Если четырех мальчиков и четырех девочек учили читать
по 1 методу, четырех мальчиков и четырех девочек по 2 методу
и т. д., то полученные данные можно расположить в таблице
и обозначить так, как показано на рис. 17.1.
Всего в этом эксперименте участвуют 24 ученика. — ре-
зультат теста на понимание прочитанного «первого» — про-
извольно выбранного — мальчика, который учился по 1 методу.
Хз24— результат теста «четвертой» девочки, учившейся по 3 ме-
тоду.
Вообще наблюдение в плане двухфакторного дисперсионного
анализа ANOVA обозначается символомХ1;д,где t—индексфак-
тора А, принимающий значения 1, 2..../, / — индекс фактора
В, принимающий значения 1,2, ..., J, a k — индекс, характе-
ризующий наблюдения внутри ячейки (комбинация уровней фак-
359
торов А и В) плана и принимающий значения 1, 2..п. Та-
ким образом, в записи Хщ имеем;
1=1,2,...,! для фактора А,
j=l, 2...../ для фактора В и
k=\, 2.....п для „содержимого ячеек".
Эти обозначения несколько отличаются от обозначений, при-
нятых в главах 15 и 16. В частности, крайний правый индекс
Фактор обучения Фактор В. пол
Мужской (1) Женский (2)
1 2 3
1 х',:: Х113 Х,н Х|2| х122 х 12<
2 х2П Xsii ^213 Х22| Х22з Х224
3 ^313 Х313 Х3;|
Рис. 17,1. Структура данных в
двухфакторном плаке ANOVA
3X2 при 4 наблюдениях в ячейке
(обозначенных Хщ, где <—1.2,3
для метода. /=1, 2 для пола,
a fe = !, 2. 3, 4 —для ученика в
ячейке «метод — пол*).
здесь указывает наблюдения
внутри ячейки, а прежде для
этого служил левый индекс.
Обратите внимание также на
то, что здесь k= 1, 2 ... п,
тогда как для однофакторного
плана было i — 1, 2 ... п.
17.2. Модель для данных
Цель сбора данных состоя-
ла в том, чтобы узнать, как из-
меняются результаты при из-
менении уровней двух факто-
ров, то есть будут ли они для
мальчиков выше, чем для де-
вочек, обеспечивает ли метод 2
более высокие результаты, чем
метод 1 и т. д. В конечном.
итоге, теперь мы создаем весь-
ма абстрактную модель—об-
общение модели, используемой
в однофакторном дисперсион-
ном анализе ANOVA, чтобы,
объяснить в общем виде, ка-
кое отношение к факторам А
и В имеют собранные данные.
Возможно, простейшей моделью данных в двухфакторном
дисперсионном анализе ANOVA оказалась бы та, в которую.
входили бы только 4 вида членов, или «эффектов»: член ц. по-
стоянный для всех результатов; 1 членов сс„ один для каждого,
уровня фактора Д, описывающих смещение данных выше или
ниже р. для результатов на i-м уровне фактора А; J членов
для смещения на каждом уровне фактора В и член е!3й, который,
по существу, компенсировал бы различие между результатом и
суммой остальных членов модели. В соответствии с этой эле-
ментарной моделью оценка Х,зй выглядела бы так:
Xfjk = I* + «< + Р/ +
360
(17.1>
К сожалению, наиболее полезная и широко распространен-
ная модель для данных в двухфакторном дисперсионном ана-
лизе ANOVA несколько сложнее, чем уравнение (17.1). Она от-
личается от уравнения (17.1) членом, который обозначает влия-
ние особого результата сочетания уровня i фактора А с уров-
нем / фактора В. Слово «особый» в этом контексте, означает,
что результат, который получился бы из сочетания уровня I фак-
тора А с уровнем / фактора В, не может характеризоваться
простой суммой at и ₽>. Иначе возможно, что для описания оце-
нок в ячейке i/ потребуется новая величина которая не
является произведением а/ и Ру.'Такой член называется взаимо-
действием. [Понятие взаимодействия двух независимых пере-
менных обязано своим происхождением известному английскому
статистику-генетику Р. Фишеру. Ему принадлежали идеи управ-
ления экспериментом путем рандомизации и исследования эф-
фектов нескольких факторов и их взаимодействий одновременно,
что успешно опровергло распространенное в опытном сельском
хозяйстве в 1900-е гг. утверждение, что «одновременно варьирует
одна переменная». См. Fisher (1925); Stanley (1966b).] Если
в модели для описания данных требуется член взаимодействия,
то знание главного эффекта уровня i фактора А и уровня / фак-
тора В еще не позволяет предсказать результат в ячейке ij.
Взаимодействие несколько напоминает пару поляризованных
линз: свет проходит сквозь каждую линзу в отдельности, но
когда одна линза положена на другую (когда они совмещены),
через пару линз свет не проходит. Отдельные эффекты линз от-
личаются от их совместного эффекта.
Развернутая модель, модель, на которой основан анализ дан-
ной главы, представляет собой:
Хц1г ~ Ц + а1 +Р/ + 6;/^. (17.2)
Без потери общности предполагаем, что члены а, ₽ и а£
в этой модели должны в сумме давать нуль по i н /, то есть
а( = X ₽/ = S аРг/= 0.
В разделе 17.4. мы более детально изучим характер взаимо-
действий в ANOVA и рассмотрим некоторые примеры.
17.3. Оценивание модели по методу
наименьших квадратов (мнк)
Располагая данными и принимая частную абстрактную мо-
дель для интерпретации этих данных, мы пок^ еще стоим- пе-
ред задачей связи данных с моделью. Какие свойства данных
влияют на величину ц в уравнении (17.2)? Каким образом надо
обработать данные, чтобы получить информацию о значениях
<ti, и аДо?
361
С аналогичной общей проблемой мы сталкивались, когда пы-
тались предсказать У по X с помощью прямой или объяснить
различия между уровнями факторов в однофакторном диспер-
сионном анализе ANOVA. Это по сути дела та же самая про-
блема, и наш подход к ее решению не отличается от предыду-
щего. Мы подгоняем модель по уравнению (17.2) к данным та-
ким образом, чтобы удовлетворялся критерий наименьших
квадратов. В этом случае, как, впрочем, и в других, критерий
наименьших квадратов состоит в следующем: (1) условия опы-
тов подставляются в уравнение (17.2) вместо ц. cq ... а/, 0| ...
Фактор А
2
Фактор В
Хш»2 ХП2 = 4 X)2f = 1 Л !22 м> з
Я22| = 5
... fJj; сфл ... (2) последние вместе с данными позво-
ляют путем вычитания определить значения Un ошибок
(3) когда найденная таким способом сумма квадратов ошибок,
становится настолько малой, насколько это возможно, полу-
чаются мнк-оценки ц, а;, 0, и а$ц.
Например, в простейшем плане вида 2X2 получено 8 оце-
нок при п = 2, как показано на рис. 17.2.
Фактор В
Si_________Sa
<Фн а£,2
а$22
Рис. 17.3. и
Мы постулируем следующую модель для данных:
Xi/k — И + а/ + ₽/ + а$н + et/k>
i = l, 2
/=1, 2
k=\, 2
Предполагаемые основные эффекты и эффекты взаимодей-
ствия характеризуют данные рис. 17.2 некоторым способом, изо-
браженным на рис. 17.3.
362
Отсюда, как и предполагалось, следует, например, что
йп = Н + «j + Pi + ори + вц2-
В результате вычитания соответствующих членов мы видим,
что
602 = ^12-(|Л + а, + Pi + арц). (17.3)
Предположим, мы имеем ц = 5, а, = 2, «2=1, ₽i=0.
02 = 1, а все аРо равны нулю. Обеспечит ли это нам минималь-
ную величину суммы восьми квадратов ошибок? Мы можем вы-
числить епг по уравнению (17.3):
б112 = 4 — (5 + 2 + 0 + 0) = — 3.
Аналогичное вычисление оставшихся е^л, возведение их всех
в квадрат и суммирование квадратов дает величину, рав-
ную 132. Возможно ли, что это минимальная сумма квадратов
ошибок? Нет, оказывается, что минимальная сумма квадратов
ошибок получается для следующих мнк-оценок параметров
.модели:
ц = 4 001! = — 0,5
dj = —1,5 ар12 = 0,5
02=1,5 а0л=О,5
Pi = 1 ар22 = “ 0,5
Ь--1
Сумма квадратов оцениваемых ошибок, которые были полу-
чены путем подстановки мнк-оценок в ур. (17.2) вместе с дан-
ными У.д, равна 8,00, минимально возможной величине для лю-
бых наборов [л, &i, Р; и aptj.
Какая же обработка данных позволит получить мнк-оценки?
Как и в случае однофакторного дисперсионного анализа ANOKA,
оценки по методу наименьших квадратов для коэффициентов
модели получаются в результате простого усреднения данных
различными способами- Например, оценка р метода наименьших
квадратов — просто среднее значение 8 значений в таблице 2X2.
Мнк-оценка сц—среднее 4 значений первой строки таблицы
минус среднее всех восьми значений. Мик-оценка Ра— среднее
четырех значений второго столбца минус среднее всех 8 значе-
ний. Мнк-оценка ари—среднее двух значений в ячейке, нахо-
дящейся на пересечении I строки и 1 столбца, минус среднее
1 строки минус среднее 1 столбца плюс спящее всех 8 значений.
Пусть — среднее совокупности данных с определенной
структурой, из которой выбирались значения Лй строки и /-го
столбца. Пусть Д(. будет средним значением 1 в i-й строке;
Д.,—средним / в /-м столбце, а ц — средним всех Напри-
мер, см. рис. 17.4.
363
Мнк-оценки коэффициентов модели в плане ANOVA типа1
2X2 можно охарактеризовать в терминах их определений по-
выборке и величине математического ожидания среднего, кото-
рыми они описываются в генеральной совокупности. Это сдела-
но в табл. ПЛ.
Таблица 17.Г
Оценивание по методу наименьших квадратов в двухфакторном
дисперсионном анализе ANOVA с постоянными эффектами
Фактор В
Фактор А
Рис. 17.4.
Прежде чем перейти к проверке гипотез относительно коэф-
фициентов модели, целесообразно остановиться несколько под-
робнее на толковании смысла взаимодействия факторов А и В.
ПА. Сущность взаимодействий
Кроме самостоятельного интереса, который представляет
анализ влияния одной переменной (независимой) на другую (за-
висимую), исследователи часто спрашивают, будет ли это влия-
ние одинаковым для всех уровней еще одной (второй) независи-
мой переменной. Если оно неодинаково, то говорят, что суще-
ствует взаимодействие между двумя независимыми переменными.
364
Предположим, что экспериментально сравниваются три различ-
ных метода преподавания. Установлено, что один метод сравни-
тельно лучше других для более одаренных учеников, тогда как
другой лучше для менее одаренных. Мы говорим, что между
методом преподавания и способностями ученика существует
взаимодействие.
Пример гипотетических данных, показывающих эффект вза-
имодействия между полом и характером текста для чтения, для
скорости чтения приведен на рис. 17.5. Обратите внимание на
то, что мальчики читают сравнительно быстрее одни тексты;
девочки — другие. Различие в скорости чтения мальчиков и де-
вочек не одинаково для разных текстов. Заметьте, что когда
объединяют мальчиков и девочек, то есть линии усредняются.
------Девочки
------Мальчики
МоЗа История Америки Спорт
Текст Зля чтения
Рис. 17.5. Графическое представление оценок средней скорости
чтения мальчиков и девочек по трем типам текстов для чтения.
то все три группы текстов оказываются одинаково трудными.
Мы говорим, что для «вида текста» не существует основного
эффекта. Кроме того, когда объединяются три читаемых источ-
ника, мальчики и девочки читают одинаково быстро.
Рассмотрим данные рис. 17.6. Здесь снова мальчики читают
сравнительно быстрее по теме «спорт». Хотя девочки явно чи-
тают быстрее мальчиков, их превосходство неодинаково для
разных текстов. Таким образом, существует взаимодействие ме-
жду полом и текстом для чтения (так же, как различие между
полами). Обратите внимание на то, что для взаимодействия тре-
буется просто, чтобы различия между полами по разным тек-
стам были разными — их нельзя устранить, как это наблюда-
лось на рис. 17.5. Вот почему во вступительных абзацах упо-
треблялись выражения «сравнительно лучше» и «сравнительно
быстрее».
Тот факт, что сплошная и пунктирная линии не параллельны,
отражает наличие взаимодействия.
365
А. Демонстрация того, что отсутствие взаимодействия между
двумя факторами влечет за собой параллельность линий на гра-
фике средних по ячейкам..
Предположим, мы имеем план дисперсионного анализа раз-
мером 2X2, как показано на рис. 17.7.
Р и с. 17.6. Графическое представление оценок средней скорости
чтения мальчиков я девочек по треи типам текстов для чтения.
На этой схеме символы р представляют генеральные средние
для строк, столбцов, ячеек и общего итога. Если между двумя
независимыми переменными нет взаимодействия, то среднее
ячейки равно сумме общего среднего с основным эффектом
строки и основным эффектом столбца, например,
Рц — Р + <Pi- — P> + (P-i — р)-
Если взаимодействие есть, то равенство нарушается.
Допустим, мы взяли 4 средних значения ячейки из рис. 17.7,
такие, что (ци — щг) = (nzi — Цгг),— это дает параллельные ли-
нии, показанные на рис. 17.8. Чтобы линии «а рис. 17.8 были па-
раллельны, расстояние между линиями по вертикали должно
3S6
быть одинаковым во всех точках. В частности, расстояние от ци
до Ц12 должно равняться расстоянию от pzi до ра> *.
Предполагая отсутствие взаимодействия по смыслу диспер-
сионного анализа, имеем:
Ип“И + (Й1- — и) + (йч — И).
а
Pi2 = И + (Й1 - — И) + (Й-2 — Ю-
Аналогично,
H2I = Н + (Й2- — и) + (Й-1 — н).
а
Ра = Ц + (Й2 • ~~ I1) + (Й - 2 — Н)-
Два расстояния между парами средних равны. Таким обра-
зом, линии параллельны,
--------Дебочки
.. । Мальчики
Нода История Америки Спорт
Текст Зля чтения
Рис. 17.9. Графическое представление оценок средней
скорости чтения мальчиков и девочек по треи типам
текстов для чтения.
Обратите внимание, что наклоны линий для мальчиков (и, в
свою очередь, для девочек) на рис. 17.5 и 17.6 одинаковы. Сле-
довательно, степень непараллельности и отсюда степень взаимо-
действия на рнс. 17.5 и 17.6 идентичны.
Рис. 17.9 иллюстрирует ситуацию, в которой нет взаимодей-
ствия.
Б. Предостережение
Следует принимать во внимание искусственные причины су-
ществования взаимодействий. Например, рассмотрим рис. 17.10,
иллюстрирующий взаимодействие интеллекта и условий обуче-
ния. В известном смысле определение эффекта взаимодействия
1 Линии, разумеется, не главное, но очень удобное средство, помогающее
визульно определить, будут ли различаться между собой разности. Не прин-
ципиально также, что ось X обозначена символами рц, и jij..
367
в терминах простой суммы генеральных средних и вывод, что
«отсутствие взаимодействия» подразумевает существование па-
раллельных линий при графическом представлении средних,—
неточная интерпретация нашего замечания об «особом» н «не-
предвиденном» исходе, получающемся в результате сочетания
уровней двух факторов. Разумеется, множество графиков средних
для двухфакторных планов имеет непараллельные линии, од-
нако мы испытываем некоторую неловкость, говоря о взаимо-
действиях, когда непараллельные линии образуются просто «с
потолка» при помощи карандаша и бумаги. Это показывает, что
возможности нашей процедуры оценивания по методу наимень-
Рис. 17.10. Пример возможного искусственного взаимодей-
ствия между интеллектом и условиями обучения.
ших квадратов для определения того, какие эффекты взаимо-
действия можно измерить с помощью выражения — й/. —
+ Н, вероятно, не исчерпывают всей полноты наших интуи-
тивных представлений о взаимодействии apv, особом и непред-
сказуемом (по крайней мере, из главных эффектов) результате
сочетания уровней факторов.
В. Два вида взаимодействий
В статистической литературе различают, и это удобно, два
вида взаимодействий: упорядоченные и неупорядоченные. В слу-
чае упорядоченного взаимодействияранговыйпорядоккатегорий
одной переменной по значениям независимой переменной анало-
гичен порядку внутри каждой категории другой независимой
переменной. На рис. 17.6 мы видим пример упорядоченного вза-
имодействия. Рис. 17,10 также представляет упорядоченное вза-
имодействие. Однако не таков рис. 17.5. На нем представлен
пример неупорядоченного взаимодействия. Когда линии не пе-
36Я
ресекаются, говорят, что взаимодействие «упорядочено»; когда
линии пересекаются, взаимодействие «неупорядоченное».
Важность этого отличия с точки зрения интерпретации со-
стоит в следующем. Когда взаимодействие упорядочено, можно
предположить, что если по зависимой переменной оценка дево-
чек выше оценки мальчиков, то превосходство сохраняется для
всех видов текста. Это значит, что даже при наличии взаимодей-
ствий можно сделать простое утверждение общего характера
относительно мальчиков и девочек без определения или ссылки
«а некоторую другую переменную. Однако когда взаимодей-
ствие неупорядоченное, утверждение, что оценка девочек выше
(то есть что они читают быстрее), чем у мальчиков, нельзя ис-
толковать в том смысле, что превосходство сохраняется для всех
видов текстов.
Обычный совет в тех случаях, когда имеется значимое вза-
имодействие, сводится к тому, что полезно изображать средние
значения для различных комбинаций. К сожалению, как пра-
вило, в научных отчетах не приводится достаточное число дан-
ных, позволяющих читателю последовать этому совету.
Следует подчеркнуть, что «упорядоченность» и «неупорядо-
ченность»— свойства графиков. В процессе графической интер-
претации взаимодействия возможен выбор расположения фак-
тора А или В на абсциссе. Те же самые средние ячеек могут
образовать упорядоченное взаимодействие, когда на абсциссе
находится фактор А, и неупорядоченное, когда фактор В.
17.5. Формулировка нуль-гипотез
Если бы на рис. 17.1 на фактор В, «пол», не обращали вни-
мания, то данные были бы идентичны результатам, полученным
в однофакторном эксперименте, сравнивающем 3 метода обуче-
ния. На каждом уровне фактора А было бы получено 8 наблю-
дений, а модель однофакторного дисперсионного анализа
ANOVA предназначалась бы для проверки с помощью методов
статистического вывода гипотезы о том, что 3 генеральных сред-
них, лежащих в основе рассматриваемых методов обучения,
были равны. Эта нуль-гипотеза идентична одной нуль-гипотезе,
представляющей интерес для двухфакторного дисперсионного
анализа. Конкретно, мы хотим знать, позволяют ли данные, на-
копленные в двухфакторном ANOVAt сохранить или отвергнуть
решение об истинности утверждения Яо, что Д1г =й2. — ц3.,
Во всяком двухфакторном дисперсионном анализе ANOVA
нуль-гипотезу для фактора А можно сформулировать следую-
щим образом:
Но ц2. = ...
(нуль-гипотеза для фактора Л).
Обратите внимание, что равенство / генеральных средних,
образующих / уровней фактора А> можно использовать для
«формулировки Но в нескольких эквивалентных вариантах.
369
Поэтому, когда fe = l, 2, п для каждой комбинации
уровней факторов вида ij, ц— среднее значение // генеральных
средних (одно для каждой ячейки), равенство всехцг. означает,
что каждое й(. равно g. Если каждое £,.=!*, то g,. — и = 0
для / уровней фактора А. Так как оц, основной эффект уровня L
фактора А, равен gi.— g, то все а< равны нулю, если нуль-гипо-
теза верна. Следующие формулировки нуль-гипотезы для фак-
тора А эквивалентны:
1. Яо-‘Й1- = ... = g,-,
2- Я0:£(й,. -rf = 0.
3. Я0:£<4 = 0,
4. : все (g,. — g) = 0 и
5. Нй: все at — 0.
В предыдущем обсуждении то, что мы выбрали для рассмо-
трения фактор А вместо фактора Ъ, было несущественным. Раз-
работка нуль-гипотезы для фактора В совершенно аналогична.
В данном случае в отношении фактора В нас интересует откло-
нение или принятие нуль-гипотезы о том, что J генеральных
средних, образующих уровни фактора В, равны. Эквивалентны-
ми описаниями нуль-гипотезы для фактора В являются следую-
щие:
1. Но- й-1 — Д.2= • •• = Д-/,
2. Нй’- =
3. Яо: £$ = 0,
4. Я0:все (g., —g)==0 и
5. HQ: все 0, = 0.
Существует множество вариантов, в которых нуль-гипотеза
относительно основного эффекта, то есть относительно одного
фактора, может оказаться ложной. Для фактора А g(. может
равняться 20,5, а остальные g(. равны 29.1, например. Или
Др — ц2. == 16,65, а g3. = g4. = 17,80- В обоих случаях Но оши-
бочна. Все, что требуется для признания ошибочности Но, сво-
дится к получению, по крайней мере, 2 неравных генеральныг
средних. Альтернативную гипотезу Ht можно сформулировав
следующими эквивалентными способами для фактора А:
1. Hi: g<. =/= gr, где i и /' различны,
2.
370
3. О,
4. Я,: ц;. — ц =£ О по крайней мере для одного I, и
5. Hi: а,- ¥= 0 по крайней мере для одного I.
Каждое из этих эквивалентных утверждений будет справед-
ливым только в том случае, если нуль-гипотеза для фактора А
ложна. Отсюда, если мы отклоняем На, то автоматически прини-
маем Hi.
Вид альтернативной гипотезы для фактора. В совершенно
аналогичен. Читатель может сам написать Ht для фактора В, по
крайней мере, пятью эквивалентными способами.
Остается рассмотреть одну интересную гипотезу, касаю-
щуюся совокупности членов взаимодействия, В § 17.4 наше
внимание было направлено на 2 условия: (1) генеральные сред-
ние на графике параллельны; (2) генеральные средние — не па-
раллельны. Мы видели, что если между Л и В нет взаимодей-
ствия, то ц,-? будет равно ц + (р(. — р) + (£•/ — ц) = ц + а( + ₽/.
Эквивалентное условие состоит в том, что уч/ — + yi- j •“ Р-
Теперь, если это условие выполняется, то
у.ц — цг. — ц./ + р==0 для всех ц,/.
Или, в терминах модели уравнения (17.2),
ар(/ = 0 для всех i и /.
Если линии средних ячеек не параллельны хотя бы в одной
-точке для А, то по крайней мере одно взаимодействие ад,, не
равно нулю. Существует несколько эквивалентных способов фор-
мулировки нуль-гипотезы На и альтернативной гипотезы Ht от-
носительно эффектов взаимодействия. Вот некоторые из них:
1. Но: все - й,/+ Ц) == О,
2. Но: все аД// = 0,
3 Ио- S S (Гц-Г,-
Ц. — О И
л. «„. s £«й;-о.
i=l /=|
1. Н(: — цг. — Й.у + М О
по крайней мере для одного U ,,
2. Hi: аД// =?ь 0 по крайней мере для
одного а₽гу,
3‘ “Р./ +
+ И)г=?ь 0 н
371
Итак, существуют 3 пары гипотез, которые характерны для
двухфакторного дисперсионного анализа ANOVA: (1) Яо и
для фактора А, (2) Но и Hs для фактора В и (3) HQ и для
взаимодействия А и В.
17.6. Суммы квадратов в двухфакторном ANOVA
Как и в однофакторном ANOVA, последовательность про-
верки в соответствии с теорией статистического вывода 3 нуль-
гипотез в двухфакторном дисперсионном анализе требует знания
сумм квадратов, степеней свободы, средних квадратов, ожидае-
мых средних квадратов и F-отношений. Во время путешествия
по этому маршруту вам может показаться, что не существует
явных указателей в направлении к месту назначения. Необхо-
димо запастись терпением, поскольку смысл предварительных
шагов не прояснится до тех пор, пока вы не окажетесь на по-
следнем этапе путешествия.
Существуют 4 источника вариации, как принято говорить в
случае двухфакториого ANOVA: (1) фактор А, (2) фактор В,
(3) взаимодействие А и В и (4) «внутри» ячеек или комбинации
уровней А к В. Мы будем по очереди определять сумму квадра-
тов для каждого источника вариации.
Сумма квадратов для фактора А
Сумма квадратов для фактора А, обозначаемая SS^, пред-
ставляет собой просто произведение nJ на сумму возведенных
в квадрат мнк-оцеиок at
sSj-n/Saj-n/Е(Т,.. - х(17.4>
Вспомните, что at = gi.— р оценивается величиной
средним значением nJ оценок на уровне i фактора А, минус X.,
среднее всех nIJ значений в таблице данных. Сумма по всем F
уровням А этих квадратов оценок, (Xt..—X...)2, называется
суммой квадратов фактора А.
Уравнение (17.4) для SSa не предназначается для легких
вычислений. Мы вернемся к вопросу о расчете SSA в § 17.9.
Сумма квадратов для фактора В
Сумма квадратов фактора В представляет собой произведе-
ние nJ на сумму возведенных в квадрат оценок fj:
ss, - 2 ё;=£ (X,. - х < it .5».
Обратите внимание на то, что п!—число оценок, усреднен-
ных для получения Я,. В SS/ п! было числом оценок, усред-
ненных для получения Я,...
372
Сумма квадратов для взаимодействия А и В
jlfX,,. - Х,..-*.,. + X. ..)’ (17-в)
Заметьте, что, как и прежде, коэффициент, на который умно-
жается сумма, есть число значений, усредненных для получе-
ния Х,3..
Сумма квадратов «внутри» ячеек
Остается еще SSW— сумма квадратов внутри ячеек.
S3. = Г 1, {Х,п - . )>, (17.7)>
Смысл этих 4 сумм квадратов прояснится, когда будут рас-
смотрены ниже соответствующие средние квадраты и их ожи-
дания.
Между прочим, хотя сумма квадратов отклонений каждого
из nil значений относительно X... двухфакторного плана и не
имеет большого значения, она все же точно равна выражению
SSa + SSb + SSab + SSW, то есть
+ + (17.8> •
Член в левой части ур. (17.8) называется полной суммой ;
квадратов и поэтому обозначается символом 55аОли- Полная
дисперсия совокупности nil значений разлагается на 4 аддитив-
ные компоненты: отсюда пошло выражение дисперсионный ана- '
лиз, сокращенно ANOVA или иногда anova.
17.7. Степени свободы
Каждая из 4 сумм квадратов в двухфакторном ANOVA пре-
образуется в средний квадрат путем деления на соответствую-
щее число степеней свободы. Число степеней свободы суммы
квадратов равно числу мнк-оценок эффектов, содержащихся в
сумме квадратов, без числа независимых линейных ограничений,
наложенных на эти оценки. По общему признанию, это трудное
и абстрактное понятие, и здесь мы будем обсуждать некоторые
его детали просто ради полноты картины. SSa рассчитывается
по I мнк-оценкам fit, ...,&/. Естественно и неограничительно'
принять для модели ур. (17.2), что at 4- ... 4- ai — 0. Кроме
того, необходимо предположить, что fit 4- - • • 4- fir — 0. чтобы
можно было найти решение в соответствии с принципом
наименьших квадратов. Действительно, как и требуется.
373
•мик-оценки at удовлетворяют этому ограничению, то есть
•6) + ... + «/= 0. Это легко показать:
Т4,= Т(х,.. -х..,)-о,
поскольку Jf... —среднее I средних значений столбцов Xt...
При вычислении существует I мнк-оценок, которые под-
чиняются одному линейному ограничению; их сумма должна
быть равна нулю. Следовательно, число степеней свободы для
SSa есть I—1. Совершенно аналогичные рассуждения привели
бы к правильному выводу о том, что SSB имеет число степеней
свободы, равное I— 1.
Вычисление SSAB включает II мнк-оценок коэффициентов
аро Ограничения, которые надо наложить на эти оценки для
решения задачи метода наименьших квадратов, заключаются в
равенстве нулю сумм по строкам для любого заданного столбца
и сумм по столбцам для любой заданной строки, то есть
— 0 для каждого i. (17.9)
£$г/ = 0 для каждого /. (17.10)
Из уравнения (17.9) число условий — I, есть еще I ограни-
чений из уравнения (17.10). Не все I1 ограничений, однако,
независимы. То есть, задаваясь ограничениями ур. (17.9) и зная,
что 22равно нулю для / — 1, .... I—1, надо обеспечить
jEajjij— 0. Отсюда независимы только 1-^-1—1 линейных
ограничений на II значений сф1(. Поэтому степени свободы для
SSxb определяются выражением:
//-(/+/ - !) — // —J- J + 1.
Обратите внимание, что его можно представить в виде про-
изведения (I — I) (У — 1).
Сумма квадратов внутри ячеек, SS», фактически является
суммой квадратов nil мнк-оценок членов в модели ур. (17.2).
Любое значение ei)k оценивается выражением = л,# —- Xfj.
Так как ё^ь — отклонение результата от среднего значения
ячейки, то сумма п значений е13& внутри каждой ячейки равна
нулю. Итак, существует II независимых линейных ограничений
на nil значений ёцк- Следовательно, число степеней свободы,
связанное с SS», равно Un — II я» II (п — 1).
Предыдущие результаты можно обобщить следующим обра-
зом:
374
Теперь рассмотрим очень простой пример линейного ограни-
чения. Сколько независимых ограничений существует по данным
таблицы 2X3 на рис. 17.11? (Попытайтесь заполнить 4 про-
пущенных ячейки, сумму по столбцам и общую сумму).
2X3 = 6) минус число независимых линейных ограничений,
наложенных на данные, то сколько степеней свободы имеется
для таблицы данного типа? Иначе говоря, сколько входов ячеек
может варьироваться? Есть ли аналогия степеням свободы для
взаимодействия фактора А с фактором В в факторном плане
вида 2X3?
17.8. Средние квадраты
Для каждой суммы квадратов существует средний квадрат
(сокращенно MS), определяемый делением суммы квадратов на
число степеней свободы:
»<? — SSw
П(п_ .
375
Так же, как и в случае однофакторного ANOVA, средние
квадраты используются на заключительном этапе вычислений,
ведущем к проверке нуль-гипотез.
17.9. Техника вычислений
В этом параграфе мы увидим, как используются расчетные
формулы для определения сумм квадратов и средних квадратов.
Для плана двухфакторного ANOVA. в котором фактор А
имеет / уровней, фактор В — I уровней, а каждая из II ячеек
содержит п наблюдений, 4 суммы квадратов наиболее удобно
получать по формулам табл. 17.2.
Таблица 17.2
Формулы расчета сумм квадратов в двухфакторном дисперсионном
анализе с равным числом наблюдений п
'(gX/"*)’ С?, ,s
ss СшЯ
8 £-1 п[ П.11
/=1
gy(W_ss ss (шЯ
L L n SSB nil
' • - ' ' (i *«*)’
Из совокупности 2500 десятых классов, изучающих геомет-
рию, для участия в эксперименте было выбрано случайным об-
разом 48 классов. Исследователь хотел оценить эффективность
2 различных методов и окружающих условий в процессе изуче-
ния геометрии, а также определить их взаимодействия. Случай-
ным образом классы приписывались в равных количествах че-
тырем комбинациям окружающих условий и метода. По окон-
чании одного семестра исследователь провел одну и ту же
контрольную работу по геометрии в каждом классе. Так как
выборочным элементом является «класс», то в качестве элемента
анализа рассматривается средний класс (округленный до бли-
жайшего целого) по критерию успеваемости. Результаты пред-
ставлены в таблице на рис, 17.12.
376
В предыдущем примере I = !, 2; / = J, 2, a k s= !, ,,., 12.
Некоторые основные расчеты показаны на рис. 17.12. Кроме
того, требуется еще одна величина: сумма всех 48 значений,
возведенных в квадрат.
Эта величина равна:
S Д х'п = 2* + 5! + ... +35’= 14969.
Для определения четырех сумм квадратов по формулам
табл. 17.2 необходимы только те величины, которые показаны
на рис. 17.12.
Фактор В, условия
Лекция в классе (1} Программированное обучение (2) Суммы по строкам
я Тради- g цион- S ныв (1} Е 2, 5, 6, 7, 4, 6 7, 8, 4, 6, 7, 10 12 £ =72 9, 12, 14, 15, 10, 13, 14, 16, 10, 13. 14, 17 12 £ *1г* = 157 S Sx,rt-» /==| I
о. о £ Совре- G мен- ные (2} 10,13,14,16,10, 13 14, 17, 11, 13, 15, 17 12 S *«*“163 21, 25, 31, 33, 22, 26 32, 34, 22, 30, 32, 35 12 £ *Ш = 343 *=| 2 12 £ £ X2/ft = 506
Суммы по столбцам 2 12 J X Х„„-233 j=sl fes=l 2 IS X £ хм-ях> 2 2|? t t E 735
Рис, 17.12. Пример основных расчетов в двухфакторном диспер-
сионном анализе.
Сумма квадратов фактора A, SSa, вычисляется следующим
образом:
SS, = ®+®_JZ3№ _1598.52.
Остальные суммы квадратов определяются так, как показа-
ниже:
SSb=<®£+«_5!Z55L = 146M2.
сс (72)® + (157)2 + (1б3)2 + f343}2 (735)2
‘->ОЛВ-----------------12----------------2• 2 • 12 —
_ 1598>52 _ !463Д)2 _
_Л®1!_ = 188.02.
SS. - 14,969 - ШИМЦв! = 464,75.
377
Суммы квадратов, степени свободы и средние квадраты при-
водятся в табл. 17.3.
Таблица 17.3
Суммы квадратов, степени свободы и средние
квадраты для данных структуры 2X2 на рис. 17.12
Источник вариации dt S3 MS
Фактор А (метод) I- ! = 1 1598,52 1598,52
Фактор В (условия) /— 1 я= ( 1463,02 1463,02
Взаимодействие А и В (/-1)(/-1)=1 188,02 188,02
Внутри ячеек /Цп — 1) — 44 464,75 10,56
17.10. Ожидаемые значения средних квадратов
Теперь настало время снова обратить внимание на цель рас-
четов. Нам требуется критерий, основанный па теории статисти-
ческого вывода, чтобы решить, позволяют ли данные принять
нуль-гипотезу //0 или альтернативу /Лотносительноглавныхэф-
фектов факторов Я и В и эффектов их взаимодействия. Как и а
однофакгорном ANOVA, ожидаемые значения средних квадра-
тов показывают истинность или ложность 3 нуль-гипотез.
Ожидаемое значение (или среднее в длинных рядах) MSw—
среднее всех MS», которое было бы получено, если бы аналогич-
ный двухфакторный план ANOVA выполнялся бесконечно при
независимых наблюдениях. С другой стороны, E(MSW)— дис-
персия совокупности, из которой берутся наблюдения в каждой
ячейке двухфакторного плана ANOVA. Мы будем предполагать,
что дисперсия совокупности, из которой выбираются п наблюде-
ний для каждой ячейки, равна о;. Это позволяет распростра-
нить предположение об однородности дисперсий, как и в одно-
факторном ANOVA.
Если предполагается, что п наблюдений в ячейке ij должны
извлекаться из совокупности с дисперсией а’, то Е (/</) = <7е-
имеет следующий вид:
м С — _____* I *_____________
//(«—!) ~ //(л-1)
Мы заметим, что MSW— среднее /7 выборочных дисперсий
внутри ячеек, то есть
??S‘?
378
Мы видим, далее, что
e(ms.)=4-^4— >££-тД=
i f
Ожидаемое значение MSA— среднее бесконечного множества
MSa, каждое из которых получено в результате независимого
повторения аналогичного двухфакторного плана ANOVA—
I уровней фактора А, I уровней фактора В и п элементов в каж-
дой из II ячеек. В эксперименте 2X2 предыдущего параграфа
величина MSA составляла 1598,52. В гипотетически бесконечной
совокупности MSa существует только одно наблюдение, которое
могло быть получено при повторении аналогичного эксперимен-
та «методы X условия» для новой группы объемом 48 классов,
выбранных случайным образом из совокупности Нам не из-
вестно, будет ли 1598,52 больше или меньше генерального сред-
него значения MSA, то есть ожидаемого значения MSA, E{MSa).
В результате одного повторения эксперимента мы можем
определить одно значение MSA. Однако мы не можем вычислить
E(MSa)' если бы такая возможность существовала, то не было
бы необходимости в теории статистического вывода. Можно вы-
вести алгебраическую формулу для Е(М5д) в терминах пара-
метров модели уравнения (17.2). Сейчас, опуская подробности
вывода, мы просто утверждаем, что Е{М5Л) имеет следующий
вид:
»'S«I
E(MSt) = a; + -ryT~, (17.10
где а; — дисперсия ошибки в уравнении (17,2) и оценивается
величиной MSW, а аг — основной эффект t-го уровня фактора А,
то есть at = jit — р.
Предположим, что неизвестная исследователю истинная ве-
личина (истинная дисперсия «внутри ячейки») равна 15,0 и
что pi. — 12, а Й2. = 22. Тогда ц == ~ (12 4- 22) = 17, cq —
= 12 —17 = —5, a az = 22 — 17 ~ 5. Подстановка этих вели-
чин и J = 2, а п = 12 в ур. (17.11) дает:
г(М5л)= 15,0 + 12 • 2 -1215.
Предыдущие вычисления были выполнены для иллюстрации
смысла членов уравнения (17.il). Необходимо отметить, что в
действительности никто никогда не вычисляет E(MSA). Важно
379
•обратить внимание на связь между выражением для £(М8А) и
истинностью или ложностью нуль-гипотезы относительно фак-
тора А. Заметьте, что третье из нескольких эквивалентных утвер-
ждений Но для фактора Л в § 17.5 состоит в том, что
HQ: X а* —0.Величина, равная, по предположению, 0 вН0 для
фактора А, аналогична величине Sa*, которая появляется в
числителе второго члена выражения для E(MSa). Таким обра-
зом. если На верна, или Sa®==0, то
Е(МЗл) = < + ^- = «;.
С другой стороны, если На ошибочна— в случае, когда Sa,
положительна, — то
£(MsA) = «;- + ^7^i>«:.
Это важное соотношение следует понимать так: если Но вер-
на, то мы полагаем, что MSa nG величине будет равна истинной
• дисперсии внутри ячейки, если Но ошибочна, мы ожидаем,
что MSa будет больше величины а"-.
Ожидаемое значение MSb имеет вид:
Е (MSB) = o's + -Ар- • (17-12)
Нуль-гипотеза Н9 для основного эффекта фактора В пред-
оставляет собой: Нй: Е —0- Но для фактора В верна, то
Ожидаемое значение М8Ав равно
«ЁЕ«й,
Е(М5,,)-<г: + 7ГУ1у^. (17.13)
Нуль-гипотезу для взаимодействия факторов А и В можно пред-
ставить так: Но: У сф^==О- Таким образом, мы видим, что
если для взаимодействия А и В Но верна, то E[MSAb) равно
•<ф если Нп ошибочна, то E(MSA8)> o’-.
Все важнейшие соотношения обобщаются в табл. 17.4.
380
Таблица 17.4
Соотношения между нуль-гнпотезамв и ожидаемыми
значениями средних квадратов
Средний квадрат Ожи тасмый средний квадрат в случае истинности Н, для данного Источника вариации Ожидаемый средний квадрат в случае ЛОЖНОСТИ Но
Фактор A. MSA ’ ,п3 % a'l °‘+ Т-Т
Фактор В, MSg ,, "'Ы °с + у" 'j"
Взаимодействие А и В. MS
и и, <подв
Внутри ячеек, MSW
Если Но верпа, то MSA и MSW имеют одинаковое ожидаемое
значение; если Но ошибочна, то MSa характеризуется ожидае-
мым значением, превышающим а", а ожидаемое значение М5Ш
по-прежнему равно сф Естественно, если оказывается, что М5Л
больше MSa на некотором этапе эксперимента, мы склонны ду-
мать. что Но ошибочна; если MSa и MSw имеют приблизительно
одинаковую величину при тщательном повторении эксперимен-
та, мы склонны считать, что они обе оценивают одну и ту же
величину о-. Сравнения МЗв или MSAB с MSw относятся соот-
ветственно к оценке истинности или ложности нуль-гипотез от-
носительно основных эффектов В и взаимодействия эффектов
А и В в том плане, что сравнение MSA с MSW кое-что говорит
нам о вероятности верности Sa* = 0.
Выяснение, когда MSA (MSB или MSab) настолько больше
MSW, что нам следует считать истинность Нв невероятной, — это
задача об изменчивости значений средних квадратов от одной
реализации двухфакторного эксперимента к другой. Мы рассмо-
трим ее в следующем параграфе.
17.11. Распределения средних квадратов
Прежде чем приступить к вопросу о статистических распре-
делениях 4 средних квадратов в плане двухфакторного AMOVA,
желательно выяснить сущность статистического вывода, рассма-
триваемого в подобной ситуации. В двухфакторном плане § 17.9
в каждой из 2 X 2 == 4 ячеек бралось 12 наблюдений. 48 наблю-
дений можно рассматривать как случайно извлеченные из 4
381
гипотетических совокупностей (одна для каждой ячейки), содер-
жащих бесконечное число объектов классов, которые были бы
получены в идентичных экспериментальных условиях. 48 наблю-
дений на рис. 17.12 будут называться полностью повторенным
экспериментом. Этот полный эксперимент позволил получить-
следующие средние квадраты: MSa — 1598.52, МЗв = 1463,02,
MSab — 188,02 и МЗЮ = 10,56. Вторую полную реплику экспе-
римента можно было бы получить, выполнив аналогичный экспе-
римент для иного множества из 48 классов (12 в каждой ячей-
ке), второе повторение дало бы другие значения для каждого
из 4 средних квадратов. Ясно, что можно было бы реализовать
третье, четвертое, пятое и т. д. повторение эксперимента, причем
каждое из них дало бы свое собственное множество 4 средних
квадратов. Теперь возникает вопрос, каким будет распределение
значений М$А, полученное в результате бесчисленных повторе-
ний эксперимента? Мы задаем аналогичный вопрос отдельно
для MSg, MSab н MSw.
Прежде чем ответить на эти вопросы, необходимо дополнить
нашу модель в уравнении (17.2) некоторым предположением.
Вспомните, что модель уравнения (17.2) сама по себе является
допущением и что в § 17.10 предполагалось, что все дисперсии
гипотетических совокупностей, образующих II ячеек эксперимен-
та, оценивают одну и ту же дисперсию ст’. К этим предположе-
ниям мы прибавим теперь допущение о том, что эти совокупно-
сти являются нормально распределенными.
Распределение MSa
В предположении о нормальности мы знаем, что п наблюде-
ний в каждой ячейке образуют случайную выборку из нормаль-
ного распределения со средним ц,3 и дисперсией ctJ. Каждая
дисперсия ячейки s’( — несмещенная оценка ст’. Кроме того, мы
можем показать, что
а2 п — I
то есть $2/1<т'е имеет распределение, равное распределению хи-
квадрат (df = n — 1), деленному на п—1. Эго утверждение
справедливо для II независимых дисперсий ячеек $г/. Из свой-
ства аддитивности переменных хи-квадрат нам известно, что
Деление на II дает:
£ i. •’< мз
I !__________ Х/лп-»
//aj ~ а’ ~ (л - 1) ’
382
MS^c2' обладает хи-квадрат распределением, df=!J(n — 1),
деленным на II (п — 1). Например, в задаче § 17.9 I = / = 2, а
л =12. Пусть величина <^= 15. Тогда
MSW
15 ~ 44
а одно наблюдаемое значение MSW = 10,56 при 15 df пред-
ставляет собой одно наблюдение из хи-квадрат распределения
(df — 44), которое было преобразовано делением на 44.
Распределение MSa
В этом случае мы должны рассмотреть два варианта: распре-
деление MSA, когда 7f0:SaJ = 0 верна и когда IP ошибочна.
Если Но верна, то
то есть MSAl<3-e имеет распределение ио полным повторениям
двухфакторного плана, которое является распределением хи-
квадрат (af = I — 1), деленным на I — 1.
Рис. 17.13. Распределение MSAlc2e.
Если Но ошибочна, то MSA[ol описывается так называемым
нецентральным хи-квадрат распределением (df = I — 1), делен-
ным на I— 1. Нецентральное хи-квадрат распределение с df =
= I — 1 — математическая кривая, имеющая более высокое
среднее и расположенная, как правило, справа от хи-квадрат
распределения (df = I—1), Связь хи-квадрат распределения с
нецентральным распределением хи-квадрат показана на
Когда Но ошибочна, значения Л15Л имеют тенденцию превы-
шать значения Л15д, получаемые в случае верности Но. Это про-
является в смещении вправо нецентрального распределения хи-
квадрат.
Чем больше величина S<4, тем сильнее выражено смещение
вправо от X/_i/(J—I) значений MSA[<j*. Таким образом.
383
нецентральное распределение хи-квадрат на рис. 17.13 предназна-
чено только для одного конкретного значения Sa2; существует
свое нецентральное распределение х2 для каждого значения
Sa2.
Распределение MSb
Рассуждения о распределениях, касающиеся MSb, совершен-
но аналогичны рассуждениям для MSA.
Если Но'. Sp- = O верна, то
MSb x5-i
Если Но ошибочна, то MSB /о£ имеет нецентральное распреде-
ление хи-квадрат (df = 7 —-1), деленное на 7 — 1.
Распределение MSAB
Если Но: SSap?, — 0, то есть если между факторами А и В
нет взаимодействия, то
°'i ~ -1) </ -1) ’
а именно 7И5лв/а2 имеет распределение хи-квадрат, df—
— (/-—!) (J — i), деленное на (7 — 1) (7 — 1).
Если нуль-гипотеза относительно взаимодействия А и В оши-
бочна, Л15да/а^ описывается нецентральным распределением
хи-квадрат, df = (7—- 1) (7 — 1), деленным на (7—1)(7—1).
Теперь мы можем сделать из предыдущих фактов основные
выводы по данному параграфу. Напоминаем, что отношение 2
независимых переменных хи-квадрат, деленных на соответствую-
щее число степеней свободы, имеет А-распределение.
Предположим, что верна Но: Sa^=0; тогда Л15д^о’~х?_|/(7—• 1).
Независимо от истинности или ложности Но, MS^f^ имеет
распределение хи-квадрат, деленное на П(п— 1).
Теперь
Но обратите внимание на то, что
MS,/»’ MS,
—е ,~j “ ----F‘~'-
(К счастью, мы исключаем а?, не зная ее фактической ве-
личины.)
Мы показали, что отношение MSa к М5ю имеет ^-распреде-
ление с I— 1 и 1!(п— 1) степенями свободы в случае, когда Нц
верна. Таким образом, если величина отношения MSAIMS,a для
повторения двухфакторного эксперимента напоминает «типич-
384
ное» наблюдение из распределения fj-i, (под словом «ти-
пичное» мы подразумеваем, что MSA/MSW не превышает, ска-
жем, 90-й, или 95-й, или 99-й процентиль этого распределения),
мы склонны думать, что Но верна. С другой стороны, если Йо
ошибочна, то мы ожидаем, что величина будет больше
величины МЗц,. Отсюда, если мы получаем очень большую ве-
личину MSA/MSW — величину, которая, оказывается, извлечена
не из F/_), jj(n-i), поскольку она превышает, скажем, 99-й про-
Рис. 17.14. Распределение MSB[MSW для полных повторений
двухфакторного плана в случае истинности и ложности Но
(заштрихованная область содержит 5% отношений, превы-
шающих 95 процентиль ^-распределения)
центиль этого распределения, — то мы думаем, что, вероятно, Но
ошибочна. Когда //o:S§j=;0 верна,
«s.M MS,
Когда Яо:22ар’; = 0 верна, то
msab/^ ... МЗла
-„с...-.-з--—----га-пц-п. и (я-d.
MSa
Влияние ложной нуль-гипотезы иа главные эффекты факто-
ра В или эффекты взаимодействия А и В проявляется в увели-
чении MSb' или MSab без одновременного возрастания AIS»,
приводя, таким образом, для полных повторений плана к рас-
пределению отношений средних квадратов, смещенному вправо
от F-распределения. Подобные соотношения для фактора В при-
ведены на рис. 17.14.
17.12. Проверка нуль-гипотез
Обсуждение этого момента приводит нас к трем отношениям
средних квадратов, называемым ^отношениями:
р F ~MSb р MSab
ГЛ— MS*' MStB> —
13 Зак. 448
385
f Для данных табл. 17.3 эти F-отношения характеризуются
следующими значениями:
„ 1598,52 ... _0 „ 1463,02
^“ТоЗГ”151'38' F‘—щй--138’54-
„ _ 188,02 ,_Qn
f*b—iwra 17,80'
Теперь мы покажем, как можно выполнить статистическую
проверку трех нуль-гипотез, используя F-отношения. Рассма-
триваемые F-отношения подобны F-критерию в однофакторном
ANOVA с постоянными эффектами. F-критернй будет представ-
лен для главных эффектов фактора А.
Во-первых, выбирают уровень значимости а, который, разу-
меется, задает вероятность отклонения Яо:2с^ = О, когда факти-
чески она верна, а, выбранное таким образом, определяет кри-
тическую область, то есть значения отношения MSA/MSW, приво-
дящие к отклонению Я0:2а^ = 0 как истинной нуль-гипотезы.
Данная критическая область охватывает все числа, превышаю-
щие 100(1 — а) процентиль распределения F/-J, гдя-п, то есть
все значения, превышающие i-bFj-i, /j(n-i)- Если расчетная вели-
чина Fa = MSaIMS-u, превышает критическое значение
i_aF/-(, то Но отклоняется. Если Fa меньше критического
значения, то Но не отбрасывается.
Вернемся к примеру на рис. 17.12, чтобы проиллюстрировать
проверку гипотезы. Там мы нашли, что FA = 151,38. Если бы
Яо:2а^ = О была истинной, то распределение FA для повторных
полных повторений планов 2X2 описывалось бы F-распределе-
нием с I—1 = 1 и П(п—1) = 44 степенями свободы. Мы не
хотели бы ошибочно заключить, что Но ошибочна, когда факти-
чески она верна. Действительно, мы хотим разработать такое
правило решения для выбора между Но и чтобы
оно приводило нас к ошибочному решению отбросить Но в поль-
зу Hi только, скажем, в одном случае из 100. Следовательно, мы
собираемся принять риск а = 0,01 совершения ошибки 1 рода.
Поскольку единственным аргументом в пользу Hi служит боль-
шое значение Fa, мы разместим всю критическую область кри-
терия в правом хвосте распределения Fi,u‘, следовательно, кри-
тическим значением критерия становится o.saF]^ По таблицам
мы можем определить, что 99-й процентиль F-распределения с 1
и 44 степенями свободы приблизительно равен 7,25.
Любое F-отношение, превышающее 7,25, будет рассматри-
ваться как доказательство ложности гипотезы 7/o:Sa^ = O. Дан-
ное утверждение служит правилом принятия решений при про-
верке гипотезы. Если в действительности Но верна, то правила
решений будет иметь вероятность а = 0,01 для неправильного
отбрасывания Но-
Для данных рис. 17.12 величина FA равна 151,38. Поскольку
рассматриваемое F-отношение превышает критическое значение
386
7,25, то гипотеза о том, что Sa^==Q, отбрасывается. Приходим
к выводу, что два выборочных средних Xt.. и Х2., значимо
различаются на уровне 0,01.
Аналогично применяется Е-критерий для . гипотезы
/fo:Sp^=0. Таким же образом осуществляется и проверка по
критерию F нуль-гипотезы относительно взаимодействия факто-
ров А и В. Если //o:SSap^=O верна, то FAB имеет распреде-
ление с (/ — 1) (J — I) == I и П (л — 1) = 44 степенями свободы.
Предположим, что мы хотим проверить Нп с риском 0,01 отбра-
сывания Но, когда она верна. Критическое значение, которое
должно превышать FAB и которое рассматривается как доказа-
тельство ложности Но, равно 7,25, 99-му процентилю Е-распре-
деления с 1 и 44 степенями свободы.
Рис. 17.15. Положения F-отношения, равииго, 17,80'относи
тельно F-расиределения с 1 и 44 степенями свободы.
Величина Fab равна отношению 188,02/10,56 = 17,80. Поло-
жение этого эмпирического F-отношения, соответствующего
^-распределению с 1 и 44 степенями свободы — распределение
Fab, которое было бы получено в случае истинности Но,— пока-
зано на рис. 17.15.
Анализируя рис. 17.15, было бы нелепо считать, что 17.80
выбиралось случайным образом из распределения Ei,44, но дока-
зать, что данные подтверждают нуль-гипотезу о том, что
ХЕар^ — О, было бы равноценно этому. Таким образом, вывод
состоит в том, чтобы отбросить Но, а вероятность его ошибоч-
ности намного меньше 0,01.
Так как найдено значимое взаимодействие А и В, то имеет
смысл представить его графически Четыре средних значения
ячеек для данных рис, 17.12 равны 6,00 для традиционного ме-
тода и лекции в классе, 13,08 в случае традиционного метода и
программированного обучения, 13,58 для современного метода и
лекции в классе и 28,58 в случае современного метода и про-
граммированного обучения. Четыре средних значения ячеек
представлены на рис. 17.16.
В отклонении от параллельности двух линий на рис. 17.16
проявляется взаимодействие метода с условиями. С помощью
1Э*
387
f-критерия было установлено, что отклонение двух линий от па-
раллельности явно статистически значимо, то есть существует
очень малая вероятность того, что графическое представление
неизвестных генеральных средних дало бы параллельные линии.
Интерпретация этого взаимодействия состоит в том, что совре-
менный метод обучения подчеркнул превосходство программи-
рованного обучения над обычным уроком. Программированное
Програннироваинае обучение (Bg)
Лекция 8 классе (S,)
5 ?
ТраЗициоигаий
метоЗ(АЛ
(X=9,54j
Современный ЗаЗисимая
нетоЗ М переменная
(X = 21,06)
Рнс. 17.16. График взаимодействия факторов А
и В для данных рис. 17.12.
обучение примерно на 7 единиц лучше школьного урока при
традиционном методе; однако оно на 15 единиц лучше при со-
временном методе. Вероятно, современный метод сам более при-
годен для программирования, чем традиционный метод.
17.13. Обзор двухфакторного
дисперсионного анализа ANOVA
с одинаковым числом наблюдений в ячейке
В общих чертах модель двухфакторного дисперсионного ана-
лиза ANOVA с постоянными эффектами при п наблюдениях в
ячейке строится следующим образом:
1. Для данных постулируется следующая модель:
Xllt = Ц + «/ + ₽/ + + eilk-
2. Предполагается, что п наблюдений в любой одной из //
ячеек происходят из нормального распределения с дисперсией
о^, которая постоянна для каждой ячейки, и что // выборок не-
зависимы.
3. Для каждого из трех f-критериев принимается уровень
значимости а: критерии для проверки нуль-гипотезы о главных
эффектах факторов А и В и эффекте взаимодействия А и В.
388
4. Определяются по таблицам 3 критических значения для
проверки по критерию F. Этими критическими значениями яв-
ляются:
для Fa'- \-aFt~\,H (п-d;
для FB‘ i_eF/-i, ii (п-d',
для Fab- -aF(/-l) {/-!), и pl-1).
5. По формулам расчета сумм квадратов из табл. 17.2 вы-
числяются четыре средних квадрата MSa, MSg, MSab н MSa и
определяются степени свободы.
6. Рассчитываются 3 F-отношения:
msa msb __ msab
ms„ Fb ~ msw Fab ~ MS*,'
7. F-отношения 6-го этапа сравниваются с соответствующими
критическими значениями, найденными на 2-м этапе. Если F-ot-
ношение превышает критическое значение, то соответствующая
нуль-гипотеза отбрасывается па уровне значимости а. Если
F-отношение не превышает критическое значение, то соответ-
ствующая нуль-гипотеза не отбрасывается.
8. Результаты оформляются в табличной форме, как пока-
зано в табл. 17.5.
Таблица 17.5
Табулирование оценок модели
двухфаиторного дисперсионного анализа ANOVA
с постоянными эффектами
Источ ihk вариации df MS F Р
Фактор А (методы) Фактор В (условия) АХВ Внутри ячеек 44 1598,52 1463,02 188,02 10,56 151,38 * 138,54 * 17,80 * Р< 0,001 Р< 0,001 Ж 0,001
• F-отиошеиио значимо на уровне а = 0,01.
Вероятности приводятся в последнем столбце табл. 17.5.
Принято записывать для каждого F-отношения долю р, площади
F-распределения, которая лежит справа от полученного F-отно-
шения. Например, если бы РАв имело величину 3,47. то следо-
вало бы указать, что р находится между значениями 0,10 и 0,0b,
то есть что менее 10%, но более 5% площади распределения
Fj.44 расположено выше 3,47. Сразу стало бы ясно, что нуль-гй-
потезу относительно взаимодействия можно было бы отбросить
при а = 0,10, но не при а — 0,05.
389
17.14. Двухфакторный дисперсионный анализ ANOVA
с постоянными эффектами при неравном числе
наблюдений п
Вы, вероятно, будете удивлены, узнав, что обобщение двух-
факторного ANOVA от случая равных п на случай с неравны-
ми п выполнить не так просто и легко, как в случае однофак-
торного дисперсионного анализа. Все множество двухфакторных
структур данных с неравными п распадается на два подкласса,
один из которых не вызывает никаких практических затрудне-
ний ни в теории, ни в приложении, К сожалению, другой класе
создает проблемы, Остальную часть этого параграфа мы разде-
лим на 2 части, соответствующие двум группам условий для не-
равного числа наблюдений.
Пропорциональные частоты ячеек
Теперь, поскольку мы рассматриваем вероятности различных
ячеек, имеющих разное число наблюдений, нам необходимо-
ввести новую систему обозначения таких чисел. Общее число-
наблюдений в IJ ячейках двухфакторного плана обозначалось-
символом п. Впредь число наблюдений ячейки подобного плана
будет описываться символом пц. Рассмотрим план вида 3X2
(1 — 3, 7 = 2), наблюдения которого показаны на рис. 17.17.
Фактор А (/) Фактор В (!) Суммы строк
1 2
2 3 Суммы столбцов "u'ill’ll -q кг и> ко 1111 « « ~ 7 е в = е а а а = В Щ
Рве. 17.17. Обозначения в факторных планах
с неравным числом наблюдений.
Число наблюдений в ячейке, расположенной на пересечении
первого столбца (i = 1) и первой строки (/ = 1), равно пп=2.
В ячейке на пересечении третьего столбца (1 = 3) и второй
строки (/ = 2) находится «зг = 4 наблюдения.
В конечном итоге возникнет необходимость воспользоваться
числом наблюдений в любой строке или в любом столбце двух-
факторного плана. Обратите внимание, что на рис. 17.17 в пер-
вом столбце 2 4-3-|-2 = 7 наблюдений. Это число определяется
суммированием п{} следующим образом:
3
n.j = П;| 4- п21 4" П3| «= 5L п(।
390
Запись вида n.t для суммарных частот первого столбца со-
ответствует нашему приему использования подстрочной точки
для обозначения суммирования по индексу. Вообще результи-
рующая частота /-го столбца обозначается символом n.j. Общее
число наблюдений 3 строки равно:
2
«3-=n3i+n32=Z«3/=2-+ 4 = 6.
/=1
Всего в i-й строке п(. наблюдений.
3 2
Член п.. обозначает У, £ п{(, что дает общее число наблю-
дений в полной структуре данных. Мы будем пользоваться так-
же известным обозначением Л' для общего числа наблюдений,
то есть определением п, — N. Каков же смысл п2 и «t.?
Для двухфакторного ANOVA с постоянными эффектами при
неравных п можно предложить сравнительно простую схему вы-
числений при условии, что частоты ячеек пропорциональны. Что
подразумевается под пропорциональными частотами ячеек? Ча-
стоты ячеек пропорциональны, если
n,l = ^± (17.14)
«Зля всех II значений пц.
Иначе говоря, условие пропорциональности удовлетворяется
в тех ситуациях, когда для каждой ячейки число наблюдений
равно произведению числа наблюдений во всей строке и во
всем столбце, на пересечении которых лежит ячейка, деленному
на общее число наблюдений *. Обратите внимание, что это усло-
вие обеспечивается для каждого из шести значений на
рис. 17.17:
6-7 „ 9-7 „ 7-6 „
«П— 21 —rt2i— 21 —И31 — 21 —
6-14 . 9-14 с 6-14 .
п12 — “2j“ — 4, «22—~21~ Я 6, «32-2Т~ — 4’
Таким образом, шесть частот ячеек на рис. 17.17 пропорцио-
нальны. Выражение «пропорциональны» здесь означает, что
2 : 3 : 2 = 4 : 6 : 4 и 2:4 = 3:6 = 2:4. Таким образом, группы
частот столбцов пропорциональны друг другу (или столбцу
1 Откуда получилось уравнение (17.14)? Вспомним формулу вероятности
появления двух независимых событий из главы 10, (Рл) (Рв),гяе Рл — вероят-
ность появления события А, а Рв — вероятность появления события В. Ана-
логично, еелн пц/п «определяется» в целом долей л случаев, расположен-
ных в i-й строке, я долей я.. случаев, находящихся в /-м столбце, то оно
будет равно выражению (nijft J(n j/n }. Решите уравнение для n(J сами й
вы получите уравнение (17.14).
391
сумм строк), и три группы частот строк также пропорциональны
друг другу (или строке сумм столбцов) *.
Установив, что частоты ячеек пропорциональны, можно при-
ступить к расчетам, как показано далее. Расчеты будут пред-
ставлены для данных (дальность прыжка с разбега, измеренная
в метрах, для мальчиков и девочек трех групп) рис, 17.18.
Фактор А (группа) Фактор В (пол) Суммы по строкам Средние ст рок
девочки (1) мальчики (2)
(D 3,45 4,50 5,46 3,39 4,26 4,77 2 "1/ X X X „8-23,83 /=1 4=1 4,30
(2) 3,93 3,12 3.57 4,29 4,59 3,54 3,30 3,27 3,15 £ X Х„8-32,76 /=1 4-J 3,64
(3) 3,03 2,07 3,84 2,52 3.18 3,00 2 яч 2, £ X.,8 -17,64 2,94
Суммы по столб- цам з "п = 23,67 < л,2 52 52 (=1 4=1 = 52,56 Ё i £'^/8-76,23
Средние столбцов 3/58 3,75 Общее среднее 3,63
Рис, 17.18, Иллюстративные данные для плана с пропорциональной
частотой ячеек из рнс. 17.17,
Обратите внимание, что в знаках суммирования на рис. 17.18
пц заменяет п в символе суммы всех наблюдений в ячейке ij, то
есть сумма пц наблюдений в ячейке ij обозначается следующим
образом:
2
1 Анализируя иначе, но эквивалентно, случай, когда nij пропорциональ-
ны. можно считать, что каждое Пц состоит из константы пропорциональности
для строки и константы пропорциональности для столбца с,. Тогда п1} =-
пс). Для данных рис. 17.17 3 константами строк будут г; = 2. г2 = 3 и
rs = 2. Две константы столбцов есть с1 = 1 и с2 = 2. Пользуясь этими дан-
ными, находим, например, что л21 = г2с, = (3) (1) = 3.
392
наблюдению в ячейке. Суммы квадратов вычисляются следую-
щим образом:
_ у (£Х‘О _ _ (316,43?+ (232,40? _
— Zu 3 6 “ 3
_ (548,83? = 5I379;235 _ 50202,395 = 1176,840.
ss;-£
= < ’84,33? -4- (179,60? Ц- (184,90? __ (548,83? _
= 50210,860 — 50202,395 = 8,465-
SSxs “ Ё £ Х2ц - SSa - SS'B -
(г
- Л±!-.а---—-== (104,33)2 + (103,60)2 + ...
... +(76,40)2— 1176,840-8,465-в- =
= 51402,919 — 1176,840—8,465 —50202,395 = 15,219.
AfSi получается в результате вычисления MSa по 24 дан-
ным верхней половины рис. 17.22 и умножения на с. SSW опре-
деляется следующим выражением:
/ / "о I i{iх11к)
= 922+ 1 142+ 107г+ ... + 932 —[-2у-+ ... +-^-] —
= 209061 — 205522,933 = 3538,067.
Величина с оценивается так:
= 0,2611.
400
Теперь мы собираемся вычислить средние квадраты и Лот-
ношения: , SS'a 1176,840 MSa — —— — р— = 1176,840. . SS'B 8,465 MSB = -/ = = 4,233. ’5-219 7R]n MS AB — —2— = —2~ = 7,61 °-
MS'. = с = 0,2611 -iy- — 0,2611 (196,559) = 51,322.
/•-отношения для проверки 3 нуль-гипотез представляют со-
бой:
„ MS'. (176.840 ,,
22’93
Fi==^4_^_0.08
В MS'* 55,322
MS'AB 7,610
₽лв ==--т~~--------- 0,15.
АВ MSW 5!,322
Совершенно очевидно, что нет оснований делать вывод о зна-
чимом главном эффекте фактора В — дозы глютаминовой кис-
лоты или эффекте взаимодействия А и В. ^-отношение для фак-
тора А равно величине 22,93, которая превышает o.wFi.ts = 8,28.
Вероятность р получения Fa = 22,93 или больше, если нуль-ги-
потеза для фактора А верна, меньше значения 0,01. Значит,
Но: X я^==0 отбрасывается.
Результаты анализа невзвешеиных средних значений можно
представить в той форме, которая принята для двухфакторного
дисперсионного анализа.
Источник вариации at MS F р
Диагноз (Д) 1 1176,840 22,93 Р < 0,01
Доза глютаминовой кис- 2 4,233 0,08 р > 0,56
лоты (В)
АХ В 2 7,610 0,(5 Р > 0,50
Внутри ячеек 18 51,322
401
17.15. Множественные сравнения в двухфакторном
ANOVA
Отбрасывание нуль-гипотезы относительно главного эффекта
фактора А означает лишь то, что по крайней мере два из / ге-
неральных средних отличаются друг от друга. Отличаться мо-
гут все / генеральных средних, только два из них или любое ко-
личество средних из рассматриваемой группы; К-критерий не диф-
ференцирует этих возможностей. Как и в случае одиофакторного
ANOVA, методы множественных сравнений необходимы для оп-
ределения того, какие пары из / выборочных средних обладают
достаточно большими различиями, чтобы позволить сделать вы-
вод о расхождении основных генеральных средних. Предыдущие
замечания применимы также и к фактору В. Методы множе-
ственных сравнений Тьюки и Шеффе были рассмотрены в
16 главе. В этом параграфе мы покажем, какой метод целесо-
образно использовать в случае двух факторов.
Когда число наблюдений, на которых основаны I выбороч-
ных средних фактора А, одинаково для всех I средних значений,
и нас интересует только /(/ — 1)/2 различий между / генераль-
ными средними, следует применять метод Тьюки. Множество
/(/—1)/2 совместных доверительных интервалов для ц,, —
с доверительной вероятностью 1 —а строится следующим обра-
зом:
где — точка 100(1—а) процентиля в распределении
стьюдентизированного размаха с / и 77— II степенями свободы
(см. табл.); MSa — средний квадрат внутри из двухфакториого
ANOVA, a N/1 — общее число наблюдений, на которых строится
каждое из 1 выборочных средних значений. (Напоминаем, что
это число наблюдений должно быть одинаковым для каждой
группы, когда применяется метод Тьюки.) Когда п в ячейках II
равны, Nil — nJ.
Построение множества совместных доверительных интерва-
лов по методу Тьюки будет показано на данных рис. 17.23, для
которых оказалось, что FB значимо на уровне а = 0,01.
Обратите внимание, что N = 27, I — 2, а I = 3; кроме того,
число наблюдений, по которым оценивается каждое среднее
столбца, равно отношению N[J = 27/3 — 9.
Величина MSB равна 232,78; отсюда FB=232,78/24,62=9,45,
что значимо на уровне 0,01 с 2 и 21 степенями свободы. Необ-
ходимо выяснить, существенно ли отличается I группа от 2 и
3 групп или значимо ли различаются группы 2 и 3?
Относительно трех разностей между парами средних можно-
построить множество совместных доверительных интервалов по
методу, представленному в табл. 17.9. Доверительные интервалы.
402
для ft.i — ц.2 и j!.j — й-з не содержат нулей, следовательно,_мы
делаем вывод о существенном расхождении между X.t. и Х.2.
и между X.,. и Х.3. .Доверительный интервал для й-а и Й-з
включает нуль, не существует доказательства, что й-г и й-з от-
личаются друг от друга. Доверительная вероятность, оцениваю-
щая в равной мере справедливость всех трех заключений, рав.
на 99%.
Фактор В
Ср.‘А»№значе-
иия столбцов Х,1.=2">,44 Х.2.= 16,00 Х.3. = 17,44
Рис. 17.23
Предыдущие методы, разумеется, применимы также к фак-
тору А, причем н-is и N/I — делитель MSW изменяется не-
значительно,
Таблица 17.9
Построение множества совместных доверительных
интервалов относительно разностей между парами
средних по методу Тьюки
Разности сродниц /**57 О.9Л.21 V Nil Доверительный витервал (ур. (17.16)1
X.,. -Х.г. = 9,44 (4.61)^/^—7.62 (1.82. 17,06)
X.t. -Х.а. =8,00 7,62 (0,38, 15,62)
Х-2< — X .з, = — 1,44 7,62 (—9,06, 6.18)
Когда требуется выполнить множественные сравнения сред-
них значений одного фактора в двухфакторном плане, средние
значения строк или столбцов которого основаны на различном
числе наблюдений, следует применять метод Шеффе. Последний
•обсуждался в 16 главе. Единственные изменения в уравнении
(16.5), связанные с тем, что анализируется двухфакторный
ANOVA' состоят в том, что MSv, теперь заменяет «средний квад-
рат внутри ячеек», а вместо пьиспользуются п,,.., ,JVr,
то есть п обозначает общее число наблюдений, на которых осно-
ваны средние значения столбцов (или строк). Формула
403
построения множества совместных доверительных интервалов
для контрастов средних значений строк по методу Шеффе имеет
следующий вид:
<С|Х,.. + ... ... +“-)х
X V(7 ~ 0 i-aF;-i, n-u- (17.17)
Задачи и упражнения
1, Заполнить таблицу дисперсионного анализа и выполнить
проверку по F-критерию 'нуль-гипотез для факторов А и В и
взаимодействия Л и В на уровне значимости а <= 0,01.
Источник варилли df S3 MS
Фактор А 4 64,26
Фактор В 5 46,85
АХВ Внутри 120 1136,53
Итог 149 2411,69
2. Приведенный рисунок характеризует генеральные средние
значения ячеек, строк и столбцов в плане двухфакторного дис-
персионного анализа.
Фактор В
1_______2_________з
Ни == 15 j Цц ~ 10 Bi3 = 5
Нг1 = 5 |ц22 = 10 р23— 15
а. Верна или ошибочна гипотеза HQ: £aJ = O?
б. Верна или ошибочна гипотеза —
в. Верна или ошибочна гипотеза Fo Е = 0?
18
ОДНОФАКТОРНЫЙ и многофакторный
ДИСПЕРСИОННЫЙ АНАЛИЗ:
СЛУЧАЙНЫЕ, СМЕШАННЫЕ
И ПОСТОЯННЫЕ ЭФФЕКТЫ
18.1. Введение
В этой главе преследуются три цели: (!) ввести альтерна-
тиву модели дисперсионного анализа, на которой строились рас-
суждения 15—17 глав; (2) показать сочетание этой новой н
предыдущей модели ANOVA, что очень важно в эксперимен-
тальном исследовании; (3) представить правила получения ос-
новных элементов (суммы квадратов, степени свободы, ожидае-
мые значения средних квадратов и т. д.) дисперсионного ана-
лиза, с которым приходится иметь дело на практике. Эти три
темы будут рассматриваться в указанном порядке.
18. 2. Модель ANOVA со случайными эффектами
В этом параграфе мы опишем модель дисперсионного ана-
лиза и ее применение, которые в корне отличаются от модели
ANOVA с постоянными эффектами, рассмотренной в 15 главе.
К счастью, большое сходство методов 15 главы и тех, которые
предстоит рассмотреть здесь, должно значительно облегчить
изучение материала данной главы. Модель, которую мы будем
теперь разрабатывать, называется моделью дисперсионного ана-
лиза со случайными эффектами.
Мотивы выделения модели ANOVA с «постоянными эффек-
тами» не были выяснены в 15-й главе. Проще понять смысл
«постоянных эффектов», противопоставляя их «случайным эф-
фектам». В модели ANOVA, проанализированной в 15 главе,
нас интересовал прежде всего процесс статистических выводов
относительно множества главных эффектов а,...а/. Мы пред-
ставляли себе бесконечную последовательность повторений экс-
перимента, в каждом из которых было п объектов с / уровнями.
Интерес к / генеральным средним — или, аналогично, к / глав-
ным эффектам — заставил нас рассматривать только те повто-
рения эксперимента, в которых появлялись одинаковые / уровни
405
испытаний. Далее мы э известном смысле фиксировали (в про-
тивоположность возможности варьировать) J совокупностей та-
ким образом, чтобы каждая и только она обеспечивала получе-
ние одной выборки объема и при каждом повторении экспе-
римента.
Теперь мы хотим рассмотреть совокупности, которые при
каждом повторении эксперимента дают выборки, изменяющиеся
благодаря повторениям; сначала мы будем испытывать сово-
купности А. В, и С, а затем О, Е и F. Этот метод следовало бы
принять в том случае, если бы нас интересовали дисперсии сред-
них большого набора совокупностей, лишь незначительное чис-
ло которых можно наблюдать в одном эксперименте. Далее, мы
Модель с постоянными эффектами (/ = 3) X + в/ + « Основные эффекты: О[, а2, а3 Повторение Основные аффекты, вкснсиимени присутствующие эксперимента ври поо1оре11Н11 Модель со случайными эффектами (7 = 3) X + а/ + е Основные эффекты: О;, аг, ..., ам Поатооение Основные эффекты, эксперк4еэто присутствующие «ВС eyHClHl при по8ТОревик
1 at, аг, а3 2 а,, аг, а, 3 af, а2, а3 2 as. O3t. a8 Дю» 2з, а3 а!|, 2ц, О50
Рис. 18.1. Характеристика моделей ANOVA с постоянными
и случайными эффектами.
могли бы случайно выбрать для данного опыта из большого на-
бора совокупностей как выборку в J совокупностей, так и вы-
борки в п наблюдений из каждой совокупности. Если бы мы
снова повторили опыт, то не стали бы «фиксировать» уровни
факторов так, чтобы были снова представлены те же J совокуп-
ностей; скорее, мы выбрали бы другой набор / совокупностей.
Подобно тому, как в модели с постоянными «эффектами» при-
сутствовали «эффекты» вида а, =* щ— ц, в новой модели также
имеются эффекты вида а; == ц, — ц. Однако в то время как
прежде полное множество aj было представлено при каждом
повторении анализа с постоянными эффектами, здесь мы хотим
рассмотреть тот случай, когда при повторении эксперимента
имеется только случайная выборка эффектов д,- Отсюда назва-
ние этой модели — модель ANOVA со случайными эффектами.
Рис. 18.1 — попытка представить графически разницу между мо-
делями с постоянными и случайными эффектами.
Для контроля успеваемости администрация школ проводит
ежегодно в мае в седьмых, восьмых и девятых классах всех
школ проверки по тесту Metropolitan. Часто эти данные ис-
пользуются для сопоставлений. Отмечается ли в школе А более
высокая успеваемость, чем в школе Б? Наблюдается ли в шко-
•406
ле В какой-нибудь прогресс с момента последней майской про-
верки? Администрация понимает, что не все аспекты проверки
стандартизуются. В частности, проверка проводится в разных
школах в разное время дня. Если существует некоторая суще-
ственная изменчивость результатов, связанная со временем про-
ведения проверки, то сравнение школ А и Б говорило бы больше-
о том, когда школы А и Б проводили испытания, чем о том, какая
из школ добилась более высоких показателей. Например, если
школа А проводила контрольную работу в 9 часов утра, когда
учащиеся не были утомлены, а школа Б в 2 часа дня, в конце
уроков, то А могла превзойти Б, даже невзирая на то, что Б
обогнала бы А в случае совпадения времени проверки.
Школьная администрация готовится провести исследование
с целью установить, будет ли «время дня» служить важным ис-
точником дисперсии отметок за контрольную работу.
Мы учтем интересы администрации и постараемся воплотить
их в статистической модели. Во-первых, представим себе сово-
купность 50-минутных периодов с ежеминутным началом в ин-
тервале от 9 до 15-ти час. Существует 360 таких периодов, мно-
го, но вовсе «не бесконечно много». Тем не меиее 360 потенци-
альных моментов начала контрольных рассматриваются как «ги-
гантское» число, и нас совсем не будет интересовать, что все
разрабатываемые методы покоятся на предположении о беско-
нечном числе уровней фактора.
Допустим, что всем учащимся средней школы был пред-
ложен другой вариант контрольной работы по чтению Metropo-
litan (объективное испытание, включающее в себя 44 разнооб-
разные темы), начинающейся в 9 час 35 мин. Период с 9 час
35 мин до 10 час 25 мин утра — 36-й период в совокупности
360 периодов в течение дня. Обозначим среднюю отметку мно-
жества учащихся за этот период символом цзв. Вообще, ц/ —
средняя отметка множества учащихся за /-период, /==1, ...
..., 360.
Руководитель программы испытаний интересуется совокуп-
ностью pj. Различаются ли р;? Вполне вероятно, что различия
имеются; ио велики ли они? Какова изменчивость ц;? Если
бы каждая школа проводила контрольную в 10 час 45 мин
утра, в 13 час 30 мин или в 14 час 15 мин. мы просто поставили
бы эксперимент, сравнивающий эти 3 периода, и проверили бы
гипотезу о том, что — Цз> для модели ANOVA с постоян-
ными эффектами, рассмотренной в главе 15. Однако отдельные
школы могут выбрать для проведения контрольной любой
50-минутный интервал; поэтому нам необходимо получить пред-
ставление обо всех у.}. Дисперсия pj говорит о типах ожидаемых
различий
Теперь формализуем модель со случайными эффектами.
Пусть мы имеем воображаемую бесконечную совокупность зна-
чений ц/. (Нас по-прежнему не смущает, что в нашем примере
только 360 значений ц,.) Обозначим среднее значение всех pj
407
Этот интервал свидетельствует о том, что наше исследование
оказалось крайне бедным информацией. Исследование, обеспе-
чивающее стабильные оценки с2а и о2, то есть узкие доверитель-
ные интервалы для оЦаг, не так легко осуществить; как J, так
и п должны быть довольно большими.
Проверка нуль-гипотезы Яо:ад = О не представляет боль-
шого интереса, в отличие от проверки //0 : X = 0 в модели
с постоянными эффектами. Мы часто весьма скептически вос-
принимаем предположение о том, что небольшие совокупности
средних одинаковы, как, например, в модели ANOVA с постоян-
ными эффектами — случай, для которого мы хотим проверить
гипотезу об отсутствии различий. Разумеется, гораздо реже мы
поражаемся как почти невозможному событию тому, что все
бесконечное число уровней фактора характеризуется одним ге-
неральным средним, как должно быть, если гипотеза Яо; о£ = 0
истинна. Поэтому когда применяется модель ANOVA со случай-
ными эффектами, чаще всего интерес сосредоточивается на оце-
нивании а не на проверке а2 = 0.
Однако если существуют веские причины для проверки
Яо:а£ = О, эту гипотезу можно легко проверить следующим об-
разом: если F = MSb!MSw превышает точку 100(1—а)
процентиля F-распределения с J— I и J(n— I) степенями сво-
боды, гипотезу Н0:о2а = 0 можно отбросить на уровне зна-
чимости а. Например, для данных табл. 18.1 F — MSb!MSw =
= 164,40/33,81 =4,86, что превышает 4,02, 99-й процентиль
в /чзо. Таким образом, гипотезу W0:o| = 0 можно отбросить
при а = 0,01.
Для всех значений о’ выборочное распределение F =
= MSblMSv определяется так:
AfS>, ( па' \
Несколько основных моментов, рассмотренных в этом пара-
графе для модели однофакторного дисперсионного анализа
ANOVA со случайными эффектами, обобщается в табл. 18.3.
В заключение рассмотрим вопрос о последствиях нарушения
предположений модели ANOVA со случайными эффектами.
В 15-й главе мы видели, что нарушение предположения о нор-
мальности не оказывало серьезного влияния на обоснованность
ANOVA с постоянными эффектами; кроме того, неоднородные
дисперсии не страшны в модели с постоянными эффектами, если
все п одинаковы. Однако дело обстоит иначе в случае модели
ANOVA со случайными эффектами. В частности, если эксцесс
случайных эффектов aj = ц} — ц отличается от эксцесса нор-
мального распределения, обоснование доверительных интерва-
415
Таблица 133
Итж вврпвп» И ss S IMS)
Между уроаякнк Внутри уровней Z(»-t) ;>)’ (И'")' , , L n in ££*ь-£Н~- ’* , MS> - MS. *'" n «’ « MS,
(реаудьтаты — средяие классов, округленные до блнжайаего целого часаа, no retry па 73 вопросов) Шкода (,) ЛВВГЛЕЖЗИК Суммы Соеапае
AAAS Програима(/) $ SC/S 31,27 21J6 «1.40 24.29 35,28 36,33 21,2) 31,34 j 35,40 54,56 строк строк 603 30,15 747 37,35 о8Э 34,13
32^0 46,50 34Д2 42,47 33,43 26.30 32.35 j 44,43 30.57
35,58 3I.2S 42,39 36,38 41^7 ЗМ8 27,25 29,31 | 45,4) 31,26
столбпоа 206 165 2SS 193 230 227 >50 192 248 IM 2033
лов для о’/о’2 или проверка Н0:о^ = 0 могут стать серьезными
вопросами. Отсутствие нормальности наблюдений внутри уров-
ней фактора со случайными эффектами не имеет большого зна-
чения.
18.3. Модель ANOVA
со смешанными эффектами
Третья по счету и совершенно иная модель дисперсионного
анализа, о которой будет идти речь, образуется при сочетании
моделей с постоянными и случайными эффектами. Такое объ-
единение двух моделей в модель со смешанными эффектами по-
лезно в экспериментальном исследовании.
Как можно предположить по названию «модель со смешан-
ными эффектами», смешанная модель содержит 2 группы эф-
фектов: постоянную и случайную. Естественно, что модель опи-
сывает данные, накопленные в двухфакторном плане, подобном
двухфакторной модели с постоянными эффектами, рассмотрен-
ной в 17 главе. Один фактор, например, фактор строки, содер-
жит группу I постоянных эффектов; фактор столбца — случай-
ная выборка J случайных эффектов из гипотетической бесконеч-
ной совокупности нормально распределенных эффектов. Рассмот-
рим мысленный эксперимент, в котором эксперты сравнивают
3 элементарные научные программы: (1) программу Американ-
ской ассоциации научного прогресса (AAAS); (2) программу
элементарного научного исследования (ESS); (3) программу
научного курса модернизации исследования (SC7S). Зависимой
переменной в эксперименте является «знание процессов науч-
ного исследования», которая оценивается по результатам спе-
циального теста, состоящего из 75 вопросов. Эксперимент пла-
нируется следующим образом: для участия в опыте отбираются
10 начальных школ; в каждой школе в нашем распоряжении
имеется 6 экспериментальных классов; с помощью случайных
методов по каждой программе в каждой школе обучаются два
класса. Наблюдения зависимой переменной берутся как резуль-
тат проведения испытаний по теме «научные процессы» во всех
60 опытных классах и усреднения оценок учеников в каждом
классе; таким образом, 60 наблюдений в эксперименте образуют
средние значения классов. Результаты эксперимента представ-
лены в табл. 18.4.
Произвольное наблюдение в табл. 18-4 обозначается Хцъ, где
i изменяется по строкам (программа) от 1 до 3, j — по столбцам
(школы) от 1 до 10, a k претерпевает изменения внутри ячеек
(классы) от 1 до 2. В общем, i = 1, ..., I, j = 1, ..., J и
k = 1, .... п. Обозначения те же, что и для двухфакторного
ANOVA с постоянными эффектами.
417
Двухфакторный план табл. 18.4 имеет две группы основных
эффектов плюс одна группа эффектов взаимодействия. Два
главных эффекта — «программа», которая будет называться
фактором Д, и «школы», фактор В. Ясно, что три научные про-
граммы не могут быть взяты из большой совокупности таких
программ и что экспертов не интересовало обобщение вообра-
жаемой совокупности других программ, из которой они, по пред-
положению, могли быть извлечены. Интерес сосредоточен на
том, какую из этих программ следует предпочесть двум другим.
Отсюда 3 главных эффекта фактора А считаются «постоянны-
ми». С другой стороны, 10 школ, представленных в экспери-
менте, можно считать выборкой из совокупности школ; или—•
что более важноэксперты не хотят, чтобы результаты иссле-
дования в процессе эксперимента ограничивались десятью шко-
лами Чтобы быть полезным, вывод о сравнительном превосход-
стве программ должен делаться по данным более чем 10 школ.
Следовательно, 10 школ рассматриваются как случайно выбран-
ные уровни фактора В со случайными эффектами. Так в одном
плане пересекаются постоянные и случайные эффекты фактора.
Структурная модель, постулируемая для наблюдений этого пла-
на, называется моделью со смешанными эффектами;
Хщ — 11 + ai + fy + abtl A~eii^ (18.13)
где XIllt— к-е ..наблюдение в ячейке ij\ ц — обшее среднее
совокупности всех наблюдений; а, — основной эффект (ц, — р)
i-ro уровня фиксированного фактора; Ь<— основной эффект
(jij — ja) j-го уровня случайного фактора; abt} — эффект взаимо-
действия (щ3 — ц,— |Л;-|-ц) ij-ro сочетания постоянного и слу-
чайного фактора, а — ошибка или «остаточная» ком-
понента, которая учитывает вариацию наблюдений внутри
i/'й ячейки.
На члены модели со смешанными эффектами в ур. (18.13)
накладываются следующие ограничения (недопущения):
1. он 4- .. - 4- a.i = 0.
2. Генеральное среднее бесконечного числа bjT из которого в
эксперименте с научными программами представлено только
10 значений, равно нулю.
3. ай), 4- ab21 4- ... 4- ab,, — 0 для всех /.
4. Совокупность бесконечного набора для одного i
(строки) имеет нулевое среднее.
Эти ограничения предполагают, что если мы выполняем сум-
мирование данных структуры табл. 18.4, то постоянные эффек-
ты и эффекты взаимодействия будут «компенсироваться», то
есть складываться до нуля; однако суммирование по столбцам
плана для получения, например, определенного среднего значе-
ния строки не приведет к нулевому значению суммы I величин
bj или 1 величин abl}.
Предположим, мы хотим сравнить X, и А’» , то есть средние
значения классов для программ AAAS и ESS. Эти два средних
418
имеют следующую структуру коэффициентов модели по
ур. (18.13):
Л,.. == J- + а, 4-bt + аЬц + elfj!) j ==
= р 4-а, 4-6. 4-a6t.
Xi.. — р 4- «2 + 6 • +о6?- + «2...
Разность между Х|.и J2. равна:
X].. — Хъ-- — (ctj — ctj) + (a6i. ~ abi-) + (th- —- ё2- ).
Из-за того, что значения ab по J столбцам не дают нуля и
повторение эксперимента при другом наборе/случайных эффек-
тов привело бы к другим значениям abi. и аба, выборочная дис-
персия разности Х{.. — Х2 будет содержать компоненту эффек-
тов взаимодействия, ab. Это обстоятельство будет вполне
оценено при обсуждении ожидаемых значений средних квадра-
тов для смешанной модели. Но прежде чем заняться этим, мы
должны выдвинуть предположения, которые необходимы в слу-
чае смешанной модели, описываемой ур. (18.13).
Относительно коэффициентов модели == ц 4-а, + 6,+
4- aba + e,lf< делаются следующие предположения:
1. Случайные эффекты, Ь} = ц, — р, нормально распределе-
ны с нулевым средним и дисперсией а^.
2. Эффекты взаимодействия вида ab(} распределены нор-
мально по j для каждого i с нулевым средним и дисперсией
3. Компоненты ошибок e,3k распределены нормально и неза-
висимо от b и ab с нулевым средним и дисперсией ог.
Четвертое очень важное предположение необходимо для обес-
печения обоснования проверки гипотезы о постоянных основных
эффектах:
4. Для всех пар уровней постоянного фактора корреляция
(по совокупности случайных эффектов) результатов на одном
и на другом уровне пары должна быть одинаковой. Например,
если в совокупности всех школ корреляция средних результатов
класса для программ AAAS и £SS равна 0,50, то корреляция
в совокупности для AAAS и SC/S и для ESS и SC/S также
должна быть равна 0,50. Позже мы укажем, как следует изме-
нить методы данного параграфа, когда есть подозрение, что 4-е
предположение об однородных корреляциях основательно нару-
шено.
Имея модель и сформулированные предположения, мы мо-
жем приступить к разработке методов проверки нуль-гипотезы
о постоянных и случайных основных эффектах и эффектах вза-
имодействия. Наша цель, далее, состоит в том, чтобы проверить
419
Модель двухфакторного ANOVA со смешанными эффектами
при п = I, то есть при одном наблюдении в ячейке, встречается
часто. Например, 6 объектов (случайный фактор В) можно на-
блюдать в отдельности в 4 условиях испытаний (постоянный
фактор А), как показано на рис. 18.2. Данный план обычно от-
носят к плану с повторными измерениями, поскольку наблюде-
ния объектов выполняются неоднократно. Вообще, в плане с по-
вторными измерениями наблюдение обозначается символом Xtj,
Рис. 18.2
причем i указывает строку, в которой расположено наблюдение,
a j — его столбец. Средние квадраты между строками (постоян-
ный фактор), между столбцами (случайный фактор) и для вза-
имодействия строк и столбцов можно вычислить по расчетным
формулам табл. 18.5, допуская п = 1 и отбрасывая индекс k и
все суммирования по нему. Так как п = 1, то для вариации вну-
три ячеек имеется П (п—1) =0 степеней свободы; таким об-
разом, дисперсию относительно среднего ячейки ij оценить нелозя.
Таблица дисперсионного анализа для существующих источников
вариации представлена в табл. 18.9.
Таблица 18.9
Таблица ANOVA для двухфакторного анализа
со смешанными эффектами при п = I
Источ.,нк вариации 4f £<MS)
Фактор А (постоянный) Z-1 ч. в е й'
Фактор В (случайный) 1 - 1 о2 + aj
В.)аимодействие А н В (/—!)(/—1) °2 + °ab
424
Если мы предполагаем, что I уровней постоянного фактора
будут одинаково коррелировать в совокупности элементов (слу-
чайный фактор), то F = MSa/MSab будет иметь F-распределе-
ние с I—I и (/—I)(J—1) степенями свободы, когда верна
Ло:Ха* = О. Отсюда, для проверки Но на уровне значимости а
F = MSa/MSab можно сравнить с
При п = 1 для модели со смешанными эффектами проверка
нуль-гипотез Но:а1 = О и H0:<Fatl — 0 невозможна.
Важное предположение для проверки /Уо : Ха-— 0, позво-
ляющее обосновать смешанную модель, состоит в том, что кор-
реляции всех пар уровней постоянного фактора в совокупности
1'ис. ш.л. i.xoMii анализа плана с повторными измере-
ниями
уровней случайного фактора должны быть одинаковыми. Нару-
шения этого предположения приводят к увеличению фактиче-
ской вероятности ошибки I рода по сравнению с «номинальным»
значением. Когда ожидаются неоднородные корреляции между
парами уровней постоянного фактора, должны быть приняты
специальные меры для обеспечения обоснованного применения
проверки по F-критерню нуль-гипотезы о постоянных основных
эффектах. Бокс (Box, 1954b) показал, что влияние неоднород-
ных корреляций уровней постоянного фактора должно прояв-
ляться в получении выборочного распределения F — MSa/MSab,
имеющего число степеней свободы меньше I — 1 и (/—I) (J—I).
когда Ио верна. Гринхаус и Гейзер (1959) показали, что в край-
нем случае число степеней свободы может уменьшиться только
до 1 и 1 — 1 для выборочного распределения F = MSa/MSab
при правильной нуль-гипотезе. (См. также Lana, Lubin, 1963).
425
Если ожидаются неоднородные корреляции, то следует пользо-
ваться такими решениями, дающими возможный вариант про-
верки гипотезы:
I. Если F = Л13д/Л13лв превышает точку процентиля 1 —<х
в ^-распределении с I и J — 1 степенями свободы, отбрасываем
Яо : = 0 на уровне значимости а (консервативный крите-
рий}.
2. Если F — MS^IMSab оказывается ниже точки процентиля
1—а в F-распределении с /—I и (I—\)(1—1) степенями
свободы, f/Q:^a2i — 0 не следует отбрасывать на уровне значи-
мости а (очевидный критерий).
3. Если F = MSa/MSab оказывается между j-t в
j-aFr-i,a-i)y-i). необходимо прибегнуть к многомерному методу,
известному как критерий Т2 Хотеллинга (см. Шеффе, 1962 или
Winer, 1962).
Стратегия анализа плана с повторными измерениями пред-
ставлена на рис. 18.3.
18.4. Правила заполнения таблицы ANOVA
В последующих параграфах главы излагается совокупность,
«правил» определения всех входов таблицы дисперсионного ана-
лиза (ANOVA) для широкого класса моделей ANOVA *. Для
планов, у которых каждая пара факторов относится к полностью
сочетающимся или к иерархическим и каждый фактор — случай-
ный или постоянный и внутри минимального подразделения
плана (ячейки) — берется одинаковое число повторений (на-
блюдений), предложены правила, определяющие возможные ис-
точники вариации, их степени свободы, формулы сумм квадратов,
и ожиданий средних квадратов. Если вы овладеете этими про-
стыми правилами, то сложные методы дисперсионного анализа
покажутся вам менее трудными и побудят вас использовать их,
когда это потребуется.
Существует много работ, излагающих правила определения
входов в таблице ANOVA для ряда планов, которые здесь рас-
сматриваются (см. например Bennett, Franklin, 1954; Cornfield,
Tukey, 1956; Guenther, 1964; Henderson, 1959; Шеффе, 1962;
Schultz, 1955; Winer, 1962). Ни один из этих источников, однако,
не повторяется в этом разделе.
Для демонстрации описываемых правил будет применяться
следующий пример с шестью классами. Три из шести классов,
входящих в экспериментальное исследование, образуются госу-
дарственными школами (Pi), а три других —частными школами
(Р2). В каждом классе было 5 условий. Предположим, что каж-
• Эти параграфы основаны на работе Мнлмана и Гласса (Miliman^
Glass, 1967).
426
дый класс разбит случайным образом на 10 подгрупп и что в
каждом из пяти вариантов условий две подгруппы отвечали
а1езависимо. Таким образом, в каждом классе для одной зависи-
Фактор С Фактор Г
Класс Условия
Рис. 18.4. Структура данных примера, использованного
для иллюстрации применения правил ANOVA.
мой переменной X существуют 2 наблюдения, и Xz. Этот план
изображен на рис. 18.4.
18.5. Определение терминов
1 — А. Сочетающиеся и иерархические факторы
Два фактора называются сочетающимися, если каждый уро-
вень (различные категории фактора называются уровнями) од-
ного из факторов встречается с каждым уровнем другого фак-
тора. Иначе говоря, для каждой возможной комбинации
уровней факторов, которые полностью сочетаются, должно су-
ществовать хотя бы одно наблюдение. Таким образом, «тип
школы» и «условия» (имеющие соответственно два и пять уров-
ней) сочетаются, поскольку имеются наблюдения в каждом из
10 сочетаний «школа-условия».
Говорят, что фактор является иерархическим по отношению
ко второму, если каждый уровень первого (иерархического)
встречается только на одном уровне второго. В нашем экспери-
менте «класс» является иерархическим фактором. Ни один из
классов не может быть одновременно в государственной (Pt) и
частной (Pi) школе Если бы, однако, те же самые 3 класса
были включены одновременно в Pt и Рг. то С не был бы иерар-
хическим для Р. Иерархия существует, когда некий уровень од-
ной переменной не встречается со всеми уровнями другой. Так
как Ci при Pt не эквивалентно С4 при Рг, то Ci не встречается
427
на обоих уровнях Р. Обратите внимание, что С\ сочетается со
всеми уровнями Т («условия»); фактор «класс» не является
иерархическим для Т. Для целей нашего обсуждения любой
иерархический фактор должен иметь одинаковое число уровней
на каждом уровне фактора, для которого он является иерархи-
ческим.
1 — Б. Случайные и постоянные факторы
Фактор может считаться случайным, если его уровни, ис-
пользуемые в исследовании, образуют простую случайную вы-
борку из совокупности уровней с нормально распределенными
эффектами. «Ученики» и «классы» — два фактора, которые ча-
сто считаются случайными. Результаты ANOVA можно распро-
странить на совокупность уровней случайного фактора. Когда
в исследовании участвуют все уровни фактора (например, муж-
ской— женский или высокий — средний — низкий), когда ис-
следуются только уровни, интересующие исследователя (напри-
мер, метод А и метод В, а другие методы не представляют
ишереса), или когда используется систематический выбор
уровней, фактор считается постоянным. Результаты ANOVA
можно распространить только на совокупность повторений
эксперимента, в которой представлены конкретные уровни по-
стоянного фактора. Например, исследование, в котором система-
тически использовались третий, шестой, девятый и двенадцатый
классы, позволяет распространить полученные результаты только
на эти 4 класса.
Действительно, положение (постоянное или случайное) фак-
тора зависит во многом от совокупности повторений исследова-
ния, применительно к которой производится обобщение, посколь-
ку оно зависит от способа выбора уровнен. Пять уровней
фактора можно было случайно выбрать из теоретически беско-
нечной совокупности уровней, но фактор оказался бы «постоян-
ным» в том случае, если бы выводы делались для повторений
исследования, в котором появляются только эти 5 уровней.
Это трудный для понимания момент, относительно которого
нам больше нечего сказать.
В нашем примере «классы» рассматриваются как случайный
фактор, а «тип школы» и «условия» — как постоянные. Мы так-
же будем называть «повторы» внутри минимальной ячейки пла-
на иерархическим фактором, который всегда будет случайным и
иерархическим по отношению ко всем другим факторам плана.
18.6. Определение возможных строк
(источников вариации) таблицы ANOVA
II — А. Обозначения
1. Источник вариации фактора, который не является иерар-
хическим по отношению ко всем другим факторам, обозна-
чается заглавной буквой, например А, В, С..
428
2. Источник вариации иерархического фактора обозначается
заглавной буквой, за которой следует двоеточие, а затем буква
или буквы, обозначающие факторы, для которых он является
иерархическим, например, А: В для фактора А, образующего
«иерархию» относительно фактора В.
3. Источник вариации для взаимодействия обозначается ком-
бинацией букв, определяющих взаимодействующие факторы, на-
пример, АВ или АВ : С.
11 — Б. Правила
I. Таблица ANOVA имеет одну строку для каждого фактора
(включая фактор «повторение»).
2, Таблица ANOVA имеет одну строку для всех возможных
(двухфакторных, трехфакторных и т. д.) взаимодействий фак-
торов. Чтобы установить, какие взаимодействия могут суще-
ствовать, все возможные пары, тройки и прочие комбинации
факторов образуются по следующим правилам (если це суще-
ствует «иерархий», отличающихся от «повторов», то будет
2й— k—1 таких взаимодействий, где k — число сочетающихся
факторов):
а) В символе, обозначающем взаимодействие, записать сле-
ва от двоеточия буквы, находящиеся слева от двоеточия у соче-
тающихся факторов. (Если в обозначении фактора никакого
двоеточия нет, то подразумевается, что оно находится справа
от всех букв.)
б) Записать следующие за двоеточием, но без повторения,
те буквы справа от двоеточий в факторах, которые сочетаются.
в) Вычеркнуть любую комбинацию, имеющую букву слева
от двоеточия, которая повторяется справа от двоеточия.
// — В. Пример правил приведенных в 11— Б (по данным
из § 18.3)
I. Р (типы школы), Т (условия), С:Р (классы, образующие
«иерархию» для Р) и R-.PCT (повторения, группирующиеся в
пределах сочетаний Р, С, Т) представляют сочетающиеся и
иерархические факторы н образуют строки в табл, по правилу
II-Б. 1.
2. Возможные взаимодействия этих факторов включают:
РТ, которое сохраняется и при записи в виде ТР,
PC : Р, которое вычеркивается, поскольку Р появляется как
до, так и после двоеточия (правило I! — Б.2в).
ТС;Р, которое остается н может быть записано в виде
СТ-.Р.
РТС: Р, которое также вычеркивается, так как Р появляется
как до, так и после двоеточия.
Все взаимодействия, включающие R-.PCT, вычеркиваются в
соответствии с правилом II — Б.2в.
3. Таким образом, строки таблицы ANOVA в нашем примере
содержат Р, С : Р, Т, PT, СТ : Р и R: РСТ.
429
18.7. Определение степеней свободы для источников
вариации
111—А. Обозначения
1. Число уровней неиерархического фактора обозначается
той же малой буквой, что и фактор. В нашем примере р — 2,
a t = 5.
2. Число уровней иерархического фактора в пределах каж-
дого уровня или сочетания уровней факторов, при котором он
является иерархическим, обозначается строчной буквой слева
от двоеточия, идентифицирующего такой фактор. Например, в
классификации с иерархией типа С; Р число уровней С на каж-
дом уровне Р обозначается символом с (равно 3 в нашем при-
мере). В иерархической классификации R.PCT г обозначает
число повторов в ячейке, равное 2 в нашем примере.
3. Общее число наблюдений N равно произведению всех
строчных букв сочетающихся и иерархических классификаций.
В нашем примере это число равно произведению рХсХ*Х^==
= 2 X 3 X 5 Х2 = 60.
Ill — Б. Правила
L Пусть строчная буква приводится в соответствие с каж-
дой заглавной буквой. Число степеней свободы для любой стро-
ки в таблице ANOVA определяется вычитанием каждой малень-
кой буквы слева от двоеточия и умножением произведения этих
разностей на произведение малых букв справа от двоеточия
2. Для контроля следует прибавить расчетное число степе-
ней свободы кА— 1.
111—В. Пример правил, излаженных в пункте 111 — Б (для
данных из § 18.3}.
1. Число степеней свободы для Р = р— I =(2— 1)= 1.
Число степеней свободы для С: Р — (с— 1)р == (3—1) - 2 = 4.
Число степеней свободы для Т — (t — 1) = (5--- I) = 4.
Число степеней свободы для РТ=(р—l)(i—1) = (2—1)Х
Х(5- 1) = 4.
Число степеней свободы для СТ-.Р=(с—1)(/—1)р =
= (3— 1) (5—1)2 = 16.
Число степеней свободы для R-.PCT = (г—\)pct =
= (2 — 1) (2) (3) (5) = 30.
2 Для контроля, 1-|~4-|-44-44-16-|-30 = А—1=59.
18.8. Вычисление сумм квадратов
IV.—А. Обозначения
1. Заглавная буква X будет использоваться для обозначения
наблюдения над зависимой переменной; индексами будут раз-
личные строчные буквы, которые используются для степеней
430
свободы. Например, Хрс(г используется для обозначения произ-
вольного наблюдения в нашем примере.
2. Строчные буквы также будут использованы для обозначе-
ния верхних пределов индексов. Например, /==1,2.t озна-
чает, что уровни переменной t меняются от 1,2 до уровня /, ко-
торый в нашем примере является пятым.
IV — Б. Правила
1. Для каждой строки в таблице ANOVA выписать степени
свободы {df) в символической форме (то есть пользуясь строч-
ными буквами) и раскрыть их алгебраически. Например, графа
РТ имеет число степеней свободы (р— 1) (/— 1), которое равно
+pt — р—/-f-1. Формула для сумм квадратов источника ва-
риации будет иметь такое же множество членов, что и разверну-
тая запись для степеней свободы (четыре члена в случае взаимо-
действия РТ), и эти члены будут иметь те же алгебраические
знаки, что и соответствующие члены в символической за-
писи df [+, —, —, и + для нашего выражения {р — 1) (/ — 1)].
2. Для каждого члена в развернутом алгебраическом пред-
ставлении df записать многократное суммирование, соответ-
ствующее каждому индексу произвольного наблюдения. Припи-
сать сумме алгебраический знак члена, которому она соответ-
ствует. Например, для члена -f-р/ в алгебраическом выражении
(р—1)(/—I) следует записать:
+ Z Z Z Z XptCf
3. Для каждого выражения многократного суммирования
заключить в круглые скобки X и те знаки суммирования, верх-
ние границы которых не появляются в соответствующем члене
развернутого выражения для df. Например, для члена -f-р/ сле-
дует расположить круглые скобки так:
+ ЕЕ (ЕЕ
4. Возвести в квадрат выражение в круглых скобках и раз-
делить на общее число наблюдений, которые суммируются для
получения величины в круглых скобках. Это число будет опреде-
ляться произведением верхних пределов знаков суммирования
в круглых скобках. Если в круглых скобках не появляется зна-
ков суммирования, то «суммируют» по 1 значению, так что этот
член делится на 1. Тогда часть расчетной формулы для взаимо-
действия РТ, соответствующая члену -f-р/, выглядит так:
+её(еЬ4
431
IV—В. Пример правил, изложенных в пункте IV — Б (для
данных из § 18.3).
В § 18.7 для рассматриваемой задачи было найдено 6 источ-
ников вариации. Таким образом, в процессе анализа плана тре-
бовалось вычислить 6 сумм квадратов. Будут приводиться толь-
ко формулы сумм квадратов РТ и R : РСТ. Попытайтесь запи-
сать оставшиеся формулы в соответствии с правилами IV—Б.1
и IV — Б.4. Для обозначения любогоиаблюдення1ребуется4ин-
декса: Хрс(г.
1. Суммы квадратов для РТ.
Правило I, df для (РТ) = (р — I) {t —-1)= pt — р — t -f- I.
Правило 2. pt — р — f + I:
S S Jj-Xprfr —
-ЁЁЁЁ*„,, + ЁЁЁЁи,л.
Правило 3. pt — p — t 1:
ЁЁ(ЁЬ,л)^Ё(ЁЁр,л)-
- E (Ё i E x^r) + (Ё E Ё Ё .
Правило 4. pt — p — t -j- k
EЁ(ЁЁ^.-<0* _ Ё(ЁЁЁ^)' _
ё(ёее^)' (ЁЁЁЁ-w)’
per + pctr
В результате применения правила 4 получаем расчетную
формулу сумм квадратов для взаимодействия факторов Р и Т.
2. Суммы квадратов для R:PCT.
Правило 1. df для (R: РСТ) — (г—\)pct—pctr — pct.
Правило 2. pctr — pct:
ЁЁЁЁхм^ЁЁЁр«,.
Правило 3. pctr — pct:
EEEE(A«j-EEE(pw„).
432
Правило 4. pctr — pct:
Эта формула дает сумму квадратов для повторений (или
«внутри»).
18.9. Определение ожиданий средних квадратов
V — А. Обозначения
1. Символ о1 2, имеющий слева от двоеточия в индексе только
строчные буквы, соответствующие случайным или конечным
факторам, обозначает дисперсию случайной переменной, лежа-
щей в основе этих случайных и конечных факторов. Например,
Ос:р обозначает дисперсию эффектов, связанных со всеми клас-
сами (С), входящими в совокупность классов, относящихся
к определенному типу школы (Р).
2. Символ о2, содержащий в индексе слева от двоеточия
строчные буквы, соответствующие постоянным факторам, обо-
значает функцию суммы квадратов эффектов переменных, кото-
рые представлены слева от двоеточия !. Так, д2 обозначает функ-
цию квадратов постоянных эффектов, связанных с условиями,
например, о2 = 2а2/(/ — I).
V — Б. Правила
1 Если следующее правило V—Б. 2 не приведет к каким-
либо изменениям, то ожидание среднего квадрата любого фак-
тора содержит о2 в каждой графе таблицы ANOVA, причем в
обозначении этой величины есть все буквы, характеризующие
рассматриваемый средний квадрат.
2. Некоторые компоненты о2 ожидания среднего квадрата,
описанного в пункте V— Б. 1, пропадают в соответствии со сле-
дующим правилом: любая о2, имеющая слева от двоеточия бук-
ву, обозначающую постоянную классификацию, исчезает, за
исключением тех случаев, когда источник вариации среднего
квадрата содержит эту букву. Помните, что если в индексе нет
двоеточия, то двоеточие по определению находится справа от
всех букв.
3. Коэффициент определенного о2 в конкретном среднем
квадрате включает произведение всех строчных букв, не встре-
чающихся в индексе а2.
1 Хотя принято использовать обозначение о2, читателю следует запом-
нить, что для факторов или сочетаний, содержащих постоянные факторы,
о2 не является дисперсией случайной переменной; это просто сумма квадра-
тов констант (постоянных эффектов).
433
V — В. Примеры, правил, изложенных в пункте V — 5 (для
данных из § 18.3).
Один из способов определения ожидаемых значений средних
квадратов заключается в первоначальном перечислении всех
возможных о1 2, последующем исключении выбранных о2 по пра-
вилу V — Б.1, повторном исключении а2 по правилу V — Б. 2 и,
наконец, в присвоении коэффициентов оставшимся компонентам
по правилу V — Б. 3. Эта последовательность будет приведена
здесь.
I. Ожидаемый средний квадрат для любой строки мог бы со-
держать©'’, а], а’ р, ар! и а’( ртак же, кака’ рс('. В E(MS) для
Р вычеркните а], поскольку среди индексов нет р (правило
V—Б.1).
В E(MS) для С: Р уберите ар( а/ и а2р так как ни одна из
них не имеет одновременного сочетания сир среди индексов
(правило V — Б. i),
В E(MS) для Т уничтожьте а2 и а2. р( правило V—Б. 1).
В E(MS) для РТ уничтожьте а’, а2.р и а; (правило V—Б. 1),
В E(MS) для СТ:Р уберите все а2, кроме а2,.р и а2, так
как в их индексах не присутствуют все буквы с, t и р (правило
V—Б. I).
В E(MS) для R.CTP уберите все а2, за исключением о2, по-
скольку ни в одной из них не присутствуют все буквы с, t, р и г
(правило V — Б.1).
2. Вспомните, что С и R считаются случайными, Р и Т —
постоянными. Кроме а2, Е (MS) для Р до настоящего момента
включает о2, с2.р, apf и а2/;р. Теперь а2 содержит постоянный
фактор Р слева от двоеточия, но рассматриваемый средний
квадрат (Р) содержит эту букву, поэтому а2 остается,
имеет только случайный фактор С слева от двоеточия, так что
а2,р также сохраняется. а’р( содержит постоянный фактор t сле-
ва от двоеточия, и t не входит в рассматриваемый средний
квадрат (Р), поэтому ар( исключается. По той же причине
исключается а2,.р. а2, то есть а2.р(с всегда сохраняется, по-
скольку слева от двоеточия должен быть только случайный фак-
тор R.
Кроме о2, E(MS) для С: Р еще содержит только р п
a2f р a2.p сохраняется, потому что С — случайная величина, и,
кроме того, с входит в С: Р. Однако а2,, р содержит t слева от
двоеточия, а Г к тому же постоянна, и t не входит в рассма-
триваемый средний квадрат (С:Р). Итак, <fct. р исключается.
1 Ожидаемый средний квадрат E(MS) для повторов случайного фак-
тора в минимальной ячейке обычно обозначается просто ог или а' Это?
прием реализован и здесь, с2 везде появляется как источник вариации, даже
если г == I, когда для этого источника нет степеней свободы.
434
Кроме a2, £(Л45) для Т пока содержит o’, c'pt и со-
храняется, поскольку t входит в Г. исключается, так как
Р постоянно, и р не входит в Г. o£f.p остается, потому что
С случайно. Обратите внимание, что р находится справа от
двоеточия и, таким образом, не подвержено влиянию правила
V — Б. 2.
Точно так же можно показать, что E(MS) для РТ — это о2,
и ъ'сг.в' а £(MS) для СТ'.Р — о2 и <т2,.р.
3. Коэффициенты уцелевших компонент определяются непо-
средственно по правилу V — Б.З. Например, коэффициент а2.р
представляет собой (/ X г) = (5) (2) = 10. Окончательные ре-
зультаты приводятся в табл. 18.10.
Таблица 18.10
Таблица результатов дисперсионного анализа
(для примера из § 18.3)
И с то чи и я варч It-Ии Е (MS\
р (р —1) = S а2+10а2р + 30а2
С:Р р (с — Н = 4 а2+Юа2.р
Т (/-1)-4 а2 +2а2,.р+ 12а2,
РТ (р —— 1)(/—- 1) = 4 а2 +2а2/;₽ + 6а2<
СТ Р р(с •—1)(/— 1)«» 16 а2 +2о^;р
R-.PCT pct (г — 1) = 30 а2
Итог pctr — I = yV - 1 = 59
18.10. Проверка значимости
Обычно цель исследователя состоит в проверке одной или
более нуль-гипотез о том, что отдельные компоненты дисперсий,
постоянные или смешанные эффекты равны нулю. Для проверки
любой подобной гипотезы сначала определяют источник вариа-
ции, соответствующий компоненте дисперсии, постоянному или
смешанному эффекту, о которых идет речь. Средний квадрат
для этого источника становится числителем F-отношения, стати-
стического критерия, который используется при проверке нуль-
гипотезы. Затем определяют, каково ожидаемое значение сред-
него квадрата, когда компонента дисперсии, рассматриваемый
постоянный или смешанный эффект, равны нулю. Назовем это
новое ожидаемое значение E(MS\H0 правильна). Знаменателем
F-отношения служит средний квадрат, имеющий ожидаемое
значение £(Л15|Д0 правильна). Иначе говоря, нуль-гипотеза
проверяется с учетом отношения 2 средних квадратов таким
435
образом, чтобы оба они обладали одинаковым ожидаемым з>п<
чением в том -'лучае, если рассматриваемая нуль-гипотеза ‘ч-р. а.
Предположим, в нашем примере пас интересовала гипотеза:
tf-~ 0. Так как ожидаемое значение среднего квадрата для Р
содержит Ор, а ожидаемое значение Р равно ожидаемому зна-
чению С :Р при <т*=0, отношение среднего квадрата для Р
к среднему квадрату для С : Р соответствует проверке гипотезы
о том, что а2р = 0.
Если для оценки эффекта не существует соответствующего
F-отношення, иногда допускаются приближенные методы (См.
например. Winer, 1962, р. 199—202.)
Несмотря на то что предыдущие методы проверки значимо-
сти распространены на практике, некоторая доля скептицизма
по поводу свойств распределения /•‘-отношений в смешанных
планах (то есть имеющих как постоянные, так и случайные фак-
торы) была вызвана соображениями, изложенными в § 18 2, ка-
са1ельно предположений для смешанной модели, и, например,
у Шеффе (1962, гл. 8).
Задачи и упражнения
Из совокупности экспертов была извлечена случайная
выборка в 10 человек (J = 10). Каждый эксперт оценивал
независимую случайную выборку, состоящую из 20 детей, по
семибалльной шкале «эмоциональной устойчивости». Диспер-
сионный анализ позволил получить следующие результаты:
Исто ibHK вадизшш dt MS Е t/WS)
Между экспертами 9 10,48 О2 + 20q2
В 1утри 190 9,64 а1
а. Оцените дисперсию экспертов, с£, на материале приведен-
ных данных.
б. Сравните значения д2а и а2- Кто в среднем отличается
больше — дети, которых оценивает один и тот же эксперт, или
эксперты?
в. Постройте 95% доверительный интервал для о^/а2.
19
ОСНОВЫ ПЛАНИРОВАНИЯ
ЭКСПЕРИМЕНТА1
19.1. Введение
Слово «экспериментирование» имеет много значений в поведен-
ческих науках. Чаще всего под ним понимается «эмпиризм», ис-
пытывающий новые подходы и субъективно оценивающий их
эффективность. В этой главе мы рассмотрим более конструктив-
ное исследование, аналогичное исследованиям во многих науках.
Оно предполагает контроль исследователем по крайней мере од-
ной переменной — например метода преподавания арифметики,—
которой он может управлять. Такое экспериментирование отли-
чается от наблюдения над естественно происходящими собы-
тиями тем, что период наблюдения устанавливается исследова-
телем так, чтобы можно было наблюдать потенциально различ-
ные эффекты по крайней мере двух условий (обработок) в ситуа-
ции, когда приписывание объектов (как правило, учеников или
классов) различным условиям выполнено без смещения. «Приро-
да» почти всегда создает смешенные распределения по обработ-
кам, даже перед естественным экспериментом опыты, подвергаю-
щиеся одной обработке, как правило, не сопоставимы с опыта-
ми, предназначенными для другой обработки. Например, в
группе, где курильщики во многих отношениях отличаются от
некурильщиков, любое из этих отличий могло вызвать более
высокую заболеваемость раком легких среди курильщиков
Короче говоря, природа редко распределяет объекты по усло-
виям (обработкам) случайным образом, тогда как осторожный
исследователь почти всегда поступает именно так. Можно опре-
делить контролируемый, с управляемыми переменными, сравни-
тельный эксперимент как исследование, в котором имеющиеся
объекты эксперимента распределены случайно (или просто, или
с ограничениями) по различным обработкам. Вообще говоря,
если мы рассматриваем каждый фактор, которым можно управ-
лять (например, несколько методов преподавания арифметики,
1 Простое, общее изложение этоп темы см в книге. Stanley, 19676.
437
пол; выполнение задания с фиксацией ответов, по сравнению
с выполнением задания про себя при программированном обуче-
нии; или 100% подкрепления в отличие от 50% подкрепления)
и который обладает 2 или более уровнями категорий (напри-
мер, программа SMSG! наряду с двумя другими методами
преподавания математики образовала бы три уровня фактора
«преподавание математики»), можно говорить о комбинациях
уровней факторов, например, шести сочетаниях, образованных
тремя методами преподавания математики, сочетающимися с
двумя уровнями пола (мужской — женский). Это факторный
план 3X2 — один фактор на трех уровнях, сочетающийся со
вторым фактором на двух уровнях.
Основной экспериментальный план включает один или более
факторов, которые либо регулируются исследователем, как по-
казано выше, либо не поддаются регулировке (например, муж-
ской или женский пол, день недели, рост выше или ниже сред-
него). Уровни одного фактора могут сочетаться с уровнями
другого или уровни одного или более факторов могут создавать
иерархию внутри уровней другого фактора. Например, в слу-
чае, когда шесть экспертов (трое мужчин и три женщины) оце-
нивают каждую из 10 категорий по каждой из семи характери-
стик, эксперты группируются внутри пола, поскольку ни один
мужчина — эксперт не является одновременно женщиной — экс-
пертом (то есть уровни экспертов не сочетаются с уровнями
пола, хотя они сочетаются с уровнями категорий и характери-
стик).
Другим примером был бы эксперимент, в котором управляе-
мыми факторами оказались бы непосредственное подкрепление
по сравнению с отсроченным подкреплением и 50%-е подкрепле-
ние ио сравнению со 100%-м подкреплением, причем все уровни
одного фактора сочетаются со всеми уровнями другого, с испытуе-
мыми (то есть людьми), классифицированными по следующим
признакам; мужчина — женщина, блондин — брюнет — рыжий,
ставшие испытуемыми добровольно или недобровольно. Испы-
туемые были бы сгруппированы в 12 «гнезд», образованных
взаимным пересечением пола с цветом волос и с добровольным
участием в эксперименте. Одна четвертая часть испытуемых в
каждом гнезде была бы распределена случайно для определен-
ного сочетания уровней управляемых факторов.
Иерархическая группировка имеет место тогда, когда неко-
торые факторы содержатся в других; например, города могут
группироваться внутри округов, округи внутри штатов, а штаты
внутри регионов. Исследователь мог распределить города по
экспериментальным условиям случайным образом. Он получил
бы план с частичной иерархией и частичным сочетанием, с гео-
1 SMSG означает «Школьная группа по изучению математики», группа,
состоящая из педагогов-математиков, которые первыми ввели курс современ-
ной математики в средних школах США
438
графическими единицами, которые не сочетаются друг с другом,
но сочетаются с уровнями фактора обработки. При этом нет
основания считать, что некоторый город в большей степени удо-
влетворял бы требованиям эксперимента, чем город в другом
штате
Иерархия и сочетание могут иметь место только в тех слу-
чаях, когда существуют по крайней мере 2 фактора. Обратите
внимание, однако, «а то, что иерархия редко встречается, когда
все факторы управляемы.
Понятие «факторного плана» принято некоторыми статисти-
ками для описания полностью сочетающихся групп двух или
более факторов при равном или неравном числе эксперимен-
тальных объектов, распределенных совершенно случайно для
каждого сочетания уровней факторов. (См. Kendall, Buckland,
1957, р. 106). Для одного фактора при случайном распределе-
нии п, экспериментальных объектов по каждому из J уровней
фактора сочетания, разумеется, не было бы. Другие определе-
ния факторного плана включают те случаи, когда возможно
только ограниченное распределение объектов, при условии, что
N имеющихся объектов следует рассматривать как выборку из
двух или более различных совокупностей (например, мужчины
и женщины); каждая такая совокупность определяет уровень
неуправляемого фактора.
Являются ли «рандомизированные блочные планы» фактор-
ными (см. Stanley, 1967, р. 204—205)? В этой главе мы посте-
пенно увидим, что в них входят все сочетания уровней факто-
ров, но с ограничениями на рандомизацию, которая, как пра-
вило, необходима, когда данный экспериментальный объект уже
«связан» с уровнем такого, например, фактора, как пол или по-
сещаемая школа. Ничего страшного не случится, если отнести
любой план, образованный путем сочетания и/нли иерархии
уровней факторов к типу факторных планов, при условии, что
учитываются различия между подобными планами, имеющие
значение для интерпретации результатов эксперимента или со-
стояния исследования.
19.2. Пример
Для примера рассмотрим управляемый эксперимент с че-
тырьмя типами печати, сочетающимися с тремя размерами
шрифта, факторный план 4X3, обеспечивающий 12 сочетаний
уровней факторов: каждый тип испытывается с каждым разме-
ром, а каждый размер — с каждым типом. Это — полный план.
Если мы возьмем 12 учеников и распределим их случайным об-
разом по каждому из 12-ти сочетаний, то получим в результате
одно повторение. Обычно, как минимум, мы будем распределять
24 ученика случайным образом по два для каждого из 12-ти соче-
таний, и тем самым обеспечивать два повторения. Чтобы распола-
гать более эффективными данными, нам может потребоваться
439
распределение более чем двух учеников в каждом сочетании.
Некоторое число повторений, п, позволит получить необ-
ходимую эффективность. Существуют методы определения п.
Как осуществить этот планируемый факторный эксперимент,
включающий 4 типа печати, сочетающиеся с 3 размерами шриф-
та? Разумеется, мы должны решить, какие типы и размеры ис-
пользовать. Вероятно, мы хорошо помним четыре типа печати,
служащие кандидатами для использования в учебнике или книге,
которые мы хотим исследовать Нам также известно, какие три
размера шрифта нужно опробовать в наших целях — это раз-
меры 8, 12 н 16. Четыре типа и три размера образуют 12 соче-
таний уровней факторов, которые исчерпывают все сочетания,
представляющие интерес в этом эксперименте. По терминологии
планирования эксперимента мы имеем два фактора с постоян-
ными эффектами и поэтому применяем модель с постоянными
эффектами, так как мы «извлекли» четыре типа из заданной
совокупности только четырех типов и три размера из рассма-
триваемой совокупности только трех размеров.
Где мы получаем экспериментальные объекты, с которыми
проводим эксперимент? Мы могли бы создать группу, состоя-
щую из случайных 12п индивидов, встретившихся на нашем
пути, или определить совокупность индивидов, такую, напри-
мер, как все учащиеся четвертых классов в большой школьной
системе, и извлечь из этой совокупности случайным образом
12л элементов. Применение первой группы ограничивает воз-
можности строгого статистического обобщения по результатам
эксперимента именно с этими 12п объектами, тогда как извле-
чение экспериментальных объектов случайно из совокупности
позволяет дать статистическое обобщение на эту совокупность,
повышая тем самым внешнюю обоснованность. (У нас, однако,
имеется возможность нестатистического обобщения от членов
локализованной группы к другим представителям, «им подоб-
ным», если мы достаточно знаем о случайно выбранных элемен-
тах. чтобы быть твердо уверенными в том, что ни одна из их ха-
рактеристик, определяющих исход эксперимента, не отличается
сильно от характеристик данной совокупности, что могло бы
повлиять на результаты. В этом трудно убедиться, и в любом
случае мы не располагаем вероятностным основанием для обоб-
щения от локальной группы до какой-либо другой.)
После того как по одному из описанных методов получено
12zi объектов, мы случайно распределяем п из них по каждому
сочетанию уровней факторов, которые обладают общим содер-
жанием, но различными сочетаниями типа и размера. Мы соби-
раемся изменять только тип и размер. Все другие переменные
должны быть постоянными (так, используя в опытах только
мальчиков, сохраняем тем самым фактор пола на одном уровне)
или рандомизироваться во всех 12 сочетаниях уровней факто-
ров. Практически могло, например, оказаться, что все 12 учени-
ков сидят в классе случайно. (Это могло быть при случайном
440
распределении мест учеников в классе.) Если бы ис-
пользовалось неслучайное распределение в классе, то этот
момент пришлось бы рассматривать как часть плана, причем
план стал бы сложнее первоначального 4X3. Контроль допол-
нительных переменных требует большого внимания и искусства,
чтобы эксперимент оказался внутренне обоснованным, то есть
позволил осуществить сравнения, свободные от смещения.
После того как 12л учеников прочитали одинаковый абзац за
одно и то же время при всех идентичных условиях, кроме типа
и размера печатного шрифта, им предлагается общее контроль-
ное задание для определения того, сколько усвоил каждый из
них по конкретному сочетанию типа и размера шрифта, которое
ему досталось. Общая оценка каждого ученика по итогам этого
контрольного испытания даст наблюдения относительно анали-
зируемой зависимой переменной.
19.3. Достоинства и недостатки факторного
планирования
Полные сбалансированные факторные планы (планы, в кото-
рых встречается каждая из возможных комбинаций уровней
факторов с хотя бы одним объектом на комбинацию) допускают
достаточно эффективную проверку более чем одной гипотезы
относительно основных эффектов (например, влияние размера
шрифта или влияние типа) в одном и том же эксперименте. Йх
также используют для исследования взаимодействия двух или
более факторов. Возможно, что наименее эффективный из трех
размеров шрифта в сочетании с наименее эффективным из че-
тырех типов не дает наименьший результат среди 12 сочетаний
уровней факторов. Если эффекты аддитивны, то, зная эффек-
тивность определенного уровня фактора размера шрифта и опре-
деленного уровня фактора типа, можно предсказать эффектив-
ность сочетания этих уровней факторов. Тогда мы говорим, что
два фактора не взаимодействуют. В однофакторных исследова-
ниях нельзя изучить взаимодействие статистически, и тем не ме-
нее существенное взаимодействие может во многом затруднять
обобщение результатов однофакторных экспериментов.
Факторный план сравнительно прост. Он не требует каких-
либо предварительных измерений или «подбора» эксперимен-
тальных объектов, поскольку искажение результатов устра-
няется (в вероятностном смысле) благодаря случайному распре-
делению объектов по комбинациям уровней факторов. С другой
стороны, он допускает вариабельность внутри комбинации
уровней факторов такого же порядка, что и дисперсия истинных
данных между условиями плюс ошибки измерения. Таким обра-
зом, сигналы (истинные эффекты) можно выделить из шума
(внутрикомбинанионная вариабельность), если отношение сиг-
нал— шум является низким. Этот шум (или ошибка, как ее
441
обычно называют) уменьшает мощность применяемых критериев
значимости и увеличивает ширину расчетных доверительных
интервалов. Ошибку истинной опенки можно уменьшить различ-
ными способами, например разбиением на блоки, стратифика-
цией, нивелированием и одновременным варьированием, каждый
из которых зависит от классификации или предварительных из-
мерений экспериментальных объектов, причем эти способы дол-
жны уменьшить внутрикомбинационную вариабельность истин-
ных оценок. Ошибку измерения можно несколько уменьшить,
пользуясь более надежным средством измерения.
Более важно отметить, что выборочную ошибку оценивания
основных эффектов и эффектов взаимодействия можно умень-
шить (и таким образом повысить мощность критериев значимо-
сти), просто увеличивая п, ибо чем больше объем эксперимента,
поставленного на должном уровне эффективности (то есть с не-
значительной ошибкой наблюдения), тем меньше ошибка.
19.4. Разбиение на блоки
Разумеется, часто можно уменьшить изменчивость внутри
уровней факторов по результирующим измерениям путем вы-
бора экспериментальных объектов из однородной подсовокупно-
сти. Например, берутся люди одного возраста, пола, 1Q и соци-
ально-экономического уровня. При этом «ошибка» может зна-
чительно уменьшиться, но за счет ограничения возможности
распространить полученные результаты только на других людей
того же возраста, пола, /Q и социально-экономического уровня,
что и изучаемые в эксперименте. Лучше включить в виде
факторов в эксперимент те характеристики, которые,
по предположению, наиболее тесно связаны с выходным
параметром (параметрами) исследования, то есть с зависимой
переменной (переменными). Факторизация будет уменьшать
ошибку почти в такой же степени, как метод подсовокупностей.
Затем можно проверить взаимодействия переменных состояния
с управляемой переменной (переменными), чтобы определить,
можно или нет обобщить полученные результаты по возрастным
группам, полу и т. д.
Одной из первых классификаций с совмещениями, разрабо-
танных Фишером для сельскохозяйственных исследований, был
рандомизированный блочный план, (См. Fisher, 1925, р. 226—
229.) Когда требовалось посеять в поле V различных сортов
пшеницы, он предложил сначала поделить поле на В блоков
земли, причем так, чтобы плодородие внутри каждого блока
было по возможности одинаковым. Затем каждый блок можно
разделить на V участков, один для каждого сорта пшеницы.
Каждый сорт распределялся случайным образом по каждому
участку в заданном блоке, поэтому в каждом блоке все V сортов
будут посажены за один прием. В результате образовалось
442
В XV сочетаний уровней факторов и BV наблюдений, когда
пшеница созрела. Для изучения структуры наблюдений обрати-
тесь к табл. 1э. 1.
Таблица 19.1
Группировка данных в эксперименте с рандомизированным
блочным планом; обозначения: XBV, где Ь » 1,2 ...В — блоки,
a v — 1,2 ... V — сорта пшеницы; случайные блоки,
постоянные сорта
Блок земли Сорт пшеницы
1 1 2 1 ''
2 В х12 ... х2! ха ... x2V XBt Хвг XBV
Источинк вариации df Е (MSI
Между блоками (а) Между сортами ((5) Блоки X сорта (ар) В —1 (B-D(F-I) аг + а2 + а2 е + ВУ’ „2 _1_ „2
Обратите внимание, что сорта были распределены случайно
по участкам внутри блоков. Фишер показал, что рандомизация
играет решающую роль. Кроме того, В блоков в эксперименте
можно рассматривать как случайную выборку из гипотетической
совокупности блоков, «подобных этим», тогда как V сортов, ве-
роятно, были «заданной совокупностью» сортов пшеницы, то
есть теми сортами, которые интересовали исследователя. Это
смешанная модель: случайные эффекты блоков и постоянные
эффекты сортов. Значения E(MS), представленные в табл 19.1,
таковы, что М£сорто2/М£(й,чоки Хсорта; распределено как
Fу_|, (В_1Ху-|) в соответствии с нуль-гипотезой о том, что V сор-
тов позволяют получить одинаковое количество пшеницы
Выбирая однородные части поля (блоки), а не простое рас-
пределение сортов полностью по воле случая в пределах поля,
Фишер устранил дисперсию между блоками, вызванную сред-
ним квадратом ошибки, и увеличил мощность критерия значи-
мости для сортов. Его не очень сильно интересовала величина
Л45блоиов, за исключением того, что она должна быть по воз-
можности максимальной в условиях данного эксперимента. Об-
щий принцип однородного подбора экспериментального мате-
риала можно распространить за пределы сельского хозяйства
443
на вопросы, представляющие большую важность в поведенче-
ских пауках. В отдельных случаях блоки не целесообразно рас-
сматривать как фактор со случайными эффектами. Кроме того,
в большинстве ситуаций в сочетании уровней факторов будет
присутствовать не одно наблюдение. (Фишер сделал поправку
для некоторых случаев, но чем больше участков в блоке, тем
меньше однородность внутри блока.)
Наше последующее обсуждение основано на трех шкалах:
фактор, оцениваемый во шкале наименований, который мы на-
зовем блоковой переменной; порядковый фактор, называемый
стратифицированной переменной; и фактор в шкале интерва-
лов или отношений, который мы называем нивелирующим. Мы
считаем, что такая терминология более полезна для поведенче-
ских дисциплин, чем одно традиционное выражение «рандомизи-
рованный блочный план». Блоковые, стратифицированные и ни-
велирующие переменные являются скорее классифицирующими,
чем управляемыми величинами Они предшествуют эксперимен-
ту. как, например, в том случае, когда поле было разделено на
блоки, прежде чем различные сорта сеялись на участках вну-
три этих блоков. Рассмотрим теперь каждый из этих 3 видов
факторизации, которые полезны с точки зрения уменьшения
ошибки и расширения возможностей обобщения.
Разбиение на блоки переменной,
оцениваемой по шкале наименований
Известный пример разбивки на блоки — классификация каж-
дого ученика в зависимости от пола и введение этого фактора с
двумя уровнями непосредственно в экспериментальный план.
Физиологический пол не является управляемой переменной, но
в плане эксперимента он рассматривается статистически как
управляемый фактор. Для 2 уровней пола, 3 уровней размера
шрифта и 4 уровней типа печати существуют 2 X 3 X 4 = 24
сочетания уровней факторов, и возникает необходимость в 24а
экспериментальных объектах.
Можно оценить основные эффекты пола, размера шрифта и
типа печати. Кроме того, можно изучить взаимодействие пола
с размером шрифта, пола с типом печати и размера шрифта с
типом печати, а также трехфакторное взаимодействие пола,
размера шрифта и типа печати. Если основной эффект пола зна-
чим, то этот фактор существенно уменьшает дисперсию ошибки.
Если пол взаимодействует с каким-либо из двух управляемых
факторов, то, рассматривая пол как фактор, мы выясняем, как
соответственно ограничить наши обобщения. Например, можно
обнаружить, что девочки считают более легким для чтения тре-
тий, а мальчики первый тип печати. В дальнейшем это могло
бы найти отражение в плане.
Другим примером разбиения на блоки является использова-
лие однояйцевых близнецов в эксперименте, где один фактор
444
изучается на 2 уровнях. Близнец А из каждой пары приписы-
вается случайно уровню управляемого фактора, а близнец В
тогда приобретает другой уровень. При Р парах близнецов имеет-
ся 2Р экспериментальных объектов Существуют три источника
дисперсии — между парами близнецов, между двумя условиями
и взаимодействие пар с условиями Обратите внимание, что мы
располагаем только одним повторением, поэтому непосредствен-
ная оценка значимости невозможна. Если изменчивость среди
пар близнецов значима, то ошибка компоненты существенно
снижается, но, поскольку ради этого жертвуют половиной степе-
ней свободы, возможности статистической проверки условий с
двумя уровнями могут не улучшиться или даже ухудшиться.
В этом плане фактор «пары близнецов» почти наверняка
рассматривался бы как случайный, поскольку нам, вероятно,
хотелось бы обобщить сравнение А и В на совокупность всех
близнецов. Между прочим, таков общественно-научный или
биологический вариант рандомизированного блочного плана
Фишера. Пары близнецов не упорядочены, причем оценка про-
изводится по шкале наименований.
Стратификация переменных, оценивающихся по шкале порядка
Мы называем переменную шкалы порядка, которая исполь-
зуется в экспериментальном плане как фактор, например соци-
ально-экономическое положение каждого испытуемого, страти-
фицирующей переменной. Может быть пять уровнен, скажем,
высокое, выше среднего, среднее, ииже среднего н низкое соци-
ально-экономическое положение, образующих классифицирую-
щий (то есть не управляемый) фактор с пятью уровнями.
Нивелирование переменных шкалы интервалов
или отношений
Для получения так называемой нивелирующей переменной
можно использовать интервальную или приблизительно интер-
вальную шкалу или шкалу отношений. Чтобы уменьшить вариа-
бельность внутри уровней в комбинации факторов, можно сгруп-
пировать экспериментальные элементы до начала эксперимента,
оценивающего, например, понимание прочитанного материала
или рост, которые, по предположению, хорошо коррелируют в
испытаниях с выходным параметром эксперимента. Если су-
ществует Т уровней фактора испытаний и LT эксперименталь-
ных объектов, то следует распределить объекты от максималь-
ного до минимального по предварительно измеренному фактору
на L уровней. На каждом таком уровне один объект распределял-
ся бы случайным образом для каждого из Т испытаний (то есть
Т уровней управляемой переменной), образуя одно повторение
плана L X Т. Если корреляция измерений нивелирующего
445
фактора с выходными параметрами существенно отлична
от нуля, то (как и в предыдущем плане с близнецами) измен-
Таблиц 19.2
Схема данных нивелирующего
плана с повторениями;
обозначения Xla, I = 1,2 ... £
уровней, t — 1,2 ... Т условий,
ai = l, ...,п элементов для каждого
условия внутри каждого уровня*
Уровни Условия
1 2 T
*121 XlTl
1 *112 *122 XlT2
*i!n XlTt
*211 *221 X2Tt
л2!2 *222 K2j2
2 Х21п *22h X2Ta
Х Lit ХЫ
XL12 XL22 XLT2
XLt. XL2n X LTti
к типу 16). Тренд может быть
порядка), например 8-й и 16-й
чивость внутри испытании зна-
чительно уменьшится.
С другой стороны, можно
было взять N = nLT экспери-
ментальных объектов, где п-
больше 1. (В предыдущем па-
раграфе п=1.) Затем следо-
вало распределить по группам
N экспериментальных объек-
тов от максимальногодомини-
мального, причем L = N/nT
групп, и расположить случай-
ным образом п эксперимен-
тальных элементов в каждом
испытании на каждом уровне.
Это позволило бы прове-
рить взаимодействие уровней
с испытаниями, что план при
п — 1 непосредственно не да-
ет. Такой план представлен в
табл. 19.2.
19.5. Упорядочение
уровней факторов
Если имеются три равноот-
стоящих размера шрифта, как,
например, 8, 12 и 16. то су-
ществует три равно распреде-
ленных уровня упорядоченно-
го фактора. Значимый тренд
для размера тина можег быть
линейным, представляющим
равное увеличение (или умень-
шение) при переходе от типа
8 к типу 12 (и ог типа 12
квадратичным (то есть второго
одинаково эффективны, а 12-й
• Можно допустить i = I. 2, .., пи вместо постоянного п. особенно
в тех случаях, если уровни и условия являются одновременно факторами с
постоянными эффектами, как обычно и бывает. Это может быть предпоч-
тительнее тогда, когда число объектов, имеющихся на заданных уровнях
естественной или требующейся классификации, отличается от их числа на
других уровнях Вспомните обсуждение анализа с пропорциональными часто-
тами ячеек. Здесь условием пропорциональности должно быть следующее со-
отношение. Пц= (Л; ) (л
446
намного лучше, или сочетать в себе линейные и квадратичные
компоненты.
Тип печати, как видите, является фактором шкалы наимено-
ваний, а не порядка. В том же исследовании вполне вероятно
наблюдать два или более упорядоченных фактора, например, в
случае, если кто-либо ввел пять одинаково распределенных зна-
чений веса бумаги в процесс исследования печати; тогда при-
шлось бы оценивать различные тренды, которые могли возник-
нуть. (См., например, Winer, 1962, Edwards, 1968 )
19.6. Случайный выбор уровней факторов
Ранее в этой главе отмечалось, что четыре типа печати мож-
но извлечь случайным образом из большой заданной совокупно-
сти типов, для которой надо сделать обобщения. Если бы в этой
совокупности содержалось, скажем, 40 типов, то четыре извле-
ченных типа составили бы 10% от полной совокупности — не-
большой, но едва ли игнорируемый процент. С другой стороны,
если четыре школы выбраны из заданной совокупности в
4000 школ, то 1/10 от 1%, которую составляют в эксперименте
школы от данной совокупности, была бы очень малой долей, так
что можно считать, что четыре школы фактически извлечены
из бесконечной совокупности, причем в этом случае следовало
сказать (пользуясь соответствующей терминологией), что. шко-
лы — фактор со случайнымй эффектами.
Если в эксперименте присутствуют одновременно факторы
с постоянными и случайными эффектами, мы говорим, что для
анализа результатов следует применять смешанную модель. (См.
18 гл. о модели ANOVA со смешанными эффектами.) В педа-
гогических и психологических исследованиях настоящие фак-
торы со случайными эффектами встречаются редко, но мы
предпочитаем действовать так, как если бы уровни фактора, на-
пример учителя, школы, классы, категории или пары близнецов,
извлекались случайно из практически бесконечной совокупности
таких уровней. Мы действуем так, аргументируя это тем, что
используемые конкретные уровни, вероятно, образуют случай-
ную выборку из гипотетической совокупности, применительно к
которой мы хотим делать обобщения: учителя, «похожие на
этих», школы, «как эти», и т. д. Этой логики придерживается
ряд высококвалифицированных специалистов в области матема-
тической статистики, которые горячо спорили друг с другом по
этому вопросу. (См., например. Cornfield, Tukey, 1956.) Если мы
собираемся распространить наши выводы на других учителей,
другие школы и т. п., то нам необходимо применить аналитиче-
скую модель, соответствующую такому обобщению, а не поль-
зоваться моделью, которая применяется в данном эксперименте
только для конкретных уровней.
447
19.7. Естественные и управляемые эксперименты
Выбор уровней факторов из совокупности, превосходящей
количество, которое требуется в эксперименте, обеспечк'чет
управление экспериментом на более высоком уровне по сравне-
нию с методологией выбора, распространенной до начала 50-х гг.
XX в. Различие этих двух подходов заключается в манипулиро-
вании уровнями одного или более факторов параллельно со слу-
чайным распределением объектов по комбинациям уровней фак-
торов. Выбор профессий мог встретиться при обследовании
заработной платы, в котором испытуемые классифицируются
по профессии, полу и семейному положению, например когда
исследуемые профессии извлекаются из большого перечня слу-
чайно. Анализ результатов подобного исследования формально
мог бы осуществляться таким же способом, как и в экспери-
менте, включающем типы печати, пол и семейное положение, но
в данном исследовании мы не производили никаких манипуля-
ций. тогда как в эксперименте с типом печати это имело место.
Разумеется, можно вообразить эксперимент, в котором объ-
екты, представляющие собой сочетание двух полов и трех се-
мейных положений, распределены по профессиям случайно, в
результате чего распределение способностей, интересов, образо-
вания. возраста и т. п. случайно сочетается с профессией, устра-
няя тем самым смешивание профессии с личными характери-
стиками.
Вообще говоря, интерпретация результатов управляемого
эксперимента проще интерпретации аналогичного «естественного
эксперимента». Более известным примером, чем рассмотренный,
является исследование влияния изучения латыни в школе на
лексику английского языка. Если учащиеся выбирают (то есть
добровольно вызываются) или не выбирают изучение латыни,
то исходные данные для двух условий почти всегда будут значи-
тельно отличаться друг от друга, причем учащиеся, изучающие
латынь, сначала будут обнаруживать лучшие знания лексики
английского языка, более высокие IQ и другие показатели по
множеству других познавательных и аффективных переменных.
Если, однако, половину будущих участников группы изучения
латыни можно было бы случайно распределить по девятым и
десятым классам, а другую, скажем, по одиннадцатым и две-
надцатым безвозвратно таким образом, чтобы разочарование и
фрустрация не нарушали эксперимента, проводимого в школе,
то, вероятно, следовало бы беспристрастно сравнить обе группы
в конце учебного года в десятом классе, после того как одна
половина прошла двухгодичный курс латыни, а другая нет.
Вследствие случайного распределения не наблюдалось бы си-
стематического смешивания каких-нибудь априорных перемен-
ных с экспериментальной переменной (то есть изучением латы-
ни). Результаты будут интерпретироваться гораздо проще, чем
в естественном эксперименте.
448
Достаточно только вспомнить те большие трудности, с кото-
рыми встретились статистики при анализе результатов обшир-
ного естественного эксперимента с курением, продолжавшегося
на протяжении многих лет. Является ли курение сигарет одной
из возможных «причин» рака легких? Или других заболеваний?
В результате сравнения большого числа подгрупп людей и экс-
периментов с животными для опровержения правдоподобных
альтернативных гипотез большинство исследователей в этой об-
ласти пришло к выводу о том, что курение действительно увели-
чивает вероятность того, что у человека будет развиваться рак
легких и возникнут некоторые другие болезни, но, поскольку
работа с людьми не была управляемым экспериментом, дока-
зать это подавляющему большинству всех разумных существ все
же не удается. В самом деле, ассоциативный анализ не может
исключить все возможные альтернативные гипотезы, тогда как
управляемые эксперименты, при условии безупречного их выпол-
нения, могут исключить все систематические альтернативы,
оставив лишь случайные флуктуации (обычно с очень малой
вероятностью, в значительной степени контролируемой экспе-
риментатором). Нельзя сказать, что один эксперимент может
быть окончательным или идеальным: так не бывает. Нередко
эксперимент поставит много новых вопросов, а не ответит на
старые, но по крайней мере процесс рандомизированного распре-
деления экспериментальных объектов по комбинациям уровней
факторов устраняет основной источник систематического смеще-
ния, искажающего большинство естественных экспериментов.
Однако контроль иногда достигается ценой уменьшения
внешней обоснованности (то есть обобщенности). Например,
вероятно, невозможно распределить людей случайно по клубам
неопознанных летающих объектов (НЛО) и клубам другого на-
правления (не НЛО) и сохранить смысл такого разделения, как
это имеет место в естественных условиях. Можно попытаться
предложить одним лицам курить, а другим воздержаться от
курения, но, вероятно, это недостаточно хорошо имитировало бы
естественную ситуацию, когда люди определенного темперамен-
та и происхождения не могут воздержаться от курения несколь-
ких пачек сигарет в день, тогда как других это не соблазняет.
Никто не может очень хорошо распределить профессии случай-
ным образом и в то же время со смыслом. Дажеобучение или не
обучение латыни для выбранных учащихся школы за счет
отсрочки этого предмета для половины иа них никогда не осу-
ществляется, насколько мы знаем. Однако этот метод отсрочки
испытания для случайно выбранной группы испытуемых часто
применялся при оценивании эффектов в психотерапии.
Но в целом исследователи в области поведенческих и соци-
альных наук, а также в педагогике не пользуются простыми и
эффективными средствами случайного распределения по сопо-
ставляемым группам даже в том случае, когда это совсем не-
трудно.
449
В этой главе мы только попытались сделать причинные за-
ключения из сравниваемых данных. Вопросы типа «Каково рас-
пределение возраста учительниц первого класса в Калифор-
нии?» и «Кого больше среди директоров начальных школ в
США — мужчин или женщин?» — примеры вполне уместных
вопросов, непосредственно не связанных с причинными заклю-
чениями. При отсутствии большого объема подобной информа-
ции едва ли можно планировать управляемые эксперименты.
Мы можем дать ответы на важнейшие вопросы, пользуясь анке-
тами, опросами и случайными исследованиями. Исследователи
разработали также эффективные аналитические методы для вы-
вода причинных заключений по имеющимся данным. (См., на-
пример, Blaiok, 1964.)
19.8. Другие экспериментальные планы
Поскольку данная книга задумана скорее как систематиче-
ский учебник, а не как справочник, мы не пытались объяснить
или хотя бы упомянуть ряд экспериментальных планов, кото-
рые иногда представляют интерес для ученых в области пове-
денческих наук, в том числе для исследователей в области
педагогики. К ним относятся латинские и греко-латинские квад-
раты. сбалансированные и частично сбалансированные неполно-
блочные планы и дробные факторные планы. (Для ознакомле-
ния с ними см. Cochran, Сох, 1957; Сох, 1958; Winer, 1962; Ed-
wards, 1968; Snedecor, Cochran. 1967; Brownlee, 1965; McLean,
1966, 1967.)
19.9. Ковариационный анализ
Фишер разработал дисперсионный и ковариационный анализ
как процедуру анализа результатов, полученных по факторным
планам разных типов. К сожалению, в данном учебнике мы не
обсуждали ковариационный анализ (ANCOVA), поскольку под-
робное и систематическое изложение его заняло бы много стра-
ниц и изрядно удлинило бы и без того достаточно объемистый
учебник. Основной принцип ANCOVA — использование измере-
ний одной или нескольких априорных переменных, то есть изме-
рений, полученных до случайного распределения объектов по
опытам. Эти измерения проводятся в надежде на то, что будет
учтена регрессия выходных параметров по этим априорным из-
мерениям (то есть что линейная связь априорных измерений X
с апостериорными значениями У будет ощутимой).
Фактически, дисперсионный анализ выполняется для (У—У),
где значения У предсказываются по значениям X обычным спо-
собом по уравнению btX -f- bo. Некоторое осложнение возникает
из-за того, что даже в случае одного только априорного фак-
450
тора будет по крайней мере два его уровня и, следовательно,
не менее двух столбцов значений У. При двух или более априор-
ных факторах должны применяться методы множественной рег-
рессии.
Гипотетический пример применения ковариационного анали-
за поможет прояснить его цели. Предположим, что изучаются
четыре различных метода обучения счету в однофакторном
ANOVA. В качестве априорных переменных для каждого испы-
туемого, предназначенного для участия в эксперименте, исследо-
ватель имеет: словесную оценку способностей (V), количествен-
ную опенку способностей (Q) и предыдущий средний балл (О).
Он случайным образом выбирает rtj (лучше n — N/4) испытуе-
мых для каждого из 4 методов обучения, не обращаясь к оцен-
кам испытания или среднему баллу (СБ). Затем он проводит
эксперимент и в конце его дает всем участникам контрольную
работу по вычислениям однофакторного ANOVA-, это дает воз-
можность получить выходные параметры У. Наконец, он прово-
дит ковариационный анализ данных, чтобы определить по ре-
зультатам использованной в статистическом плане априорной
информации, существенно ли различаются установленные сред-
ине значения четырех методов. Если регрессия конечных оценок
испытания по трем предсказывающим переменным является зна-
чимой, то установленный средний квадрат внутри метода будет
меньше, чем в том случае, когда исследователь не пользовался
этой априорной информацией, обеспечивая тем самым более эф-
фективную проверку значимости и допуская более узкие дове-
рительные границы, построенные для разностей между средними
значениями методов. Структура таких данных представлена в
табл. 19.3.
Таблица /9.3
Структура данных для ковариационного анализа трех предсказывающих
переменных и четырех уровней одного фактора: Vtj, Qtp Gtj и Y(j, где
i= 1,2......................n, a ( = 1,2, 3,4
451
Подробнее об этом анализе (особенно для случая с одной
предсказывающей переменной) см.: Edwards (1968), Brownlee
(1965, р. 376—396), Winer (1962), McNemar (1962), Lindquist
(1953), Шеффе (1962). Для знакомства с иной точкой зрения
на планирование исследовательских проектов большого
масштаба прочтите работу Бейкера (1967). Статистические ас-
пекты теории интеллектуальных тестов изложены в: Lord,
Novick (1968).
В приведенном примере экспериментатор вместо «уравнива-
ния» по одной из трех предсказывающих переменных мог, на-
пример, взять 5 уровней СБ в качестве явного фактора в плане
и затем применить ковариационный анализ, теперь уже с двумя
предсказателями (словесные и количественные оценки сп1)собно-
стей), к оценкам результатов двухфакторного (5 уровней X
X 4 метода) плана. Здесь, однако, он имел бы одни классифика-
ционный (СБ) и один управляемый фактор (метод), первый
из которых, вероятно, коррелирован с каждой из двух предска-
зывающих переменных, тогда как последний благодаря рандо-
мизированному распределению объектов по методам, напротив,
не коррелирован. Исследователь может вычислить соответствую-
щие средние значения для пяти уровней СБ, а также для
уровней четырех методов, аналогично соответствующим
средним значениям для ячеек методов СБ, и проверить значи-
мость как неуправляемых, так и управляемых средних. Он
должен быть особенно внимательным при интерпрета-
ции Л15сб и MScb х методы, так как СБ—неуправляемый
фактор.
Там, где имеется только одна исходная переменная, оцени-
ваемая в процессе эксперимента по шкале интервалов или отно-
шений, желательно сделать ее явным фактором в плане, а не
использовать в методе ANCOVA. Этот вопрос обсуждал Коксом
(1957).
19.10. Квазиэкспериментирование
Хотя рандомизация — метод выбора последовательности пр»
экспериментировании,
«существует множество естественных общественных условий, в которых
исследователь может включить нечто подобное экспериментальному плану
в список методов анализа совокупности данных (например, когда в что
измерять), даже когда полностью потерян контроль над планом опреде-
ляющих условий эксперимента (когда и как испытывать с учетом рандо-
мизации), которые делают возможным Настоящий эксперимент. В общем,
такие ситуации можно относить к квазиэкспериментзльным планам. Од-
на из целей (книги) — способствовать нх распространению и повышению
эрудиции н вопросах анализа типичных ситуаций Но именно потому, что
невозможен полный контроль за экспериментом, в большей степени, чем
для понимания обычных экспериментов, необходимо, чтобы исследователь-
отдавал себе ясный отчет в том, какие именно переменные его частного-
плана не удается контролировать Это необходимо ври оценивании квази-
452
экспериментов, контролирующих списки источников опасности, которые
были разработаны в [этой книге]». (Campbell, Stanley, 1966, р. 34).
Квазиэкспериментировавие, предложенное Кэмпбеллом
(1957) и разработанное впоследствии Кэмпбеллом и Стэнли
(1963 или 1966), по-видимому, представляет собой нечто сред-
нее между управляемым лабораторным экспериментом и не-
управляемым естественным экспериментом.
19.11. Экспериментальный объект
и элемент статистического анализа:
сравнительные эксперименты
с целыми группами
Если статистический анализ эксперимента призван обеспечи-
вать достоверную вероятность вывода о возможностях ложных
заключений на основе данных, то должен существовать компро-
мисс между чисто математическими предположениями относи-
тельно данных, по которым рассчитываются вероятности, и ди-
намикой экспериментальной ситуации. Вероятность ошибки
I рода может оказаться совсем иной, если данные эксперимента
не согласуются со статистической математической моделью, на
•основе которой была получена эта вероятность.
Пример влияния нарушения независимости
параллельных экспериментов
Допустим, что сравниваются методы А и В обучения студен-
тов уравниванию химических реакций. План для сравнения
двух методов предполагает объединение 120 учащихся в 60 пар
с равными способностями и случайное распределение членов
каждой пары по методам А и В. Все 120 испытуемых учатся
у одного преподавателя, но в процессе обучения их необходимо
разделить на четыре группы по 30 человек в каждой. План
можно представить так, как показано на рис. 19.1. Каждый из
четырех квадратов содержит 30 учащихся, которые проходят
обучение в одном классе.
Предположим, что методы А н В сравниваются по наблю-
дениям, какой из партнеров в каждой паре (ученик А или В)
оценивается выше по тесту навыков уравнивания химических
реакций. Это признанный, хотя и не очень эффективный метод
сравнения А и В и выполнения проверки гипотезы; вы можете
воспринимать его как метод, применяемый в непараметрическом
«критерии знаков».
Теперь представим себе, что исследователь провел такой
эксперимент и в каждой из 60 пар учащийся, обучающийся по
.методу В, получил более высокие баллы, чем его партнер. (Разу-
453
меется, это—невероятная совокупность результатов, даже
в том случае, если бы метод В был гораздо лучше метода А.
Мы пользуемся Этим гиперболизированным примером, по-
скольку он более полно отражает точку зрения, которую мы
собираемся принять.) Исследователь рассуждает следующим
образом:
«Предположим, что нуль-гипотеза об одинаковой эффектив-
ности методов А и В действительно верна. Какова в таком слу-
чае .вероятность того, что ученик В получит более высокие оцен-
ки, чем ученик А в каждой из 60 пар? Если метод А действи-
тельно не отличается от метода В, то вероятность того, что уче-
ник В получит более высокие оценки, чем ученик А, для каж-
дой пары равна 1/2. (Случайное распределение учеников в паре
для методов А и В убеждает нас в этом.) Вероятность того, что
у ученика В имеется один шанс опередить ученика А во всех
60 парах, составляет (1/2)®° и является чрезвычайно малой. От-
сюда мы можем уверенно отклонить гипотезу, утверждающую,
что методы А и В одинаково эффективны».
Пара Метод А
2 Ученик 1 Ученик 3
30 Ученик 59
31 Ученик 61
Ш
60 Ученик 119
Метол В
Ученик 2
Ученик 4
И
Ученик 60
Ученик 62
' IV
Ученик 120
Рис. 19.1
В расчетах исследователя подразумевается, что при верности
нуль-гипотезы каждая пара характеризуется независимой воз-
можностью появления события (а именно, что ученик В опере-
жает ученика А), вероятность которого равна 1/2, причем это
предположение заставило его отклонить нуль-гипотезу из-за ее
неправдоподобности при имеющихся данных. Действительно,
каждая соревнующаяся пара — это опыт: одного ученика обу-
чают по методу А; другого — по методу В. Одна пара учеников
образует единичный опыт. Наблюдение относительно превосход-
ства методов А и В на нескольких парах учеников представляет
454
собой параллельные опыты. Существует множество повторений
эксперимента, поскольку существуют конкурирующие пары, ре-
зультаты которых наблюдаются. Наш исследователь сделал
предположение—возможно, необоснованное, — что эти повто-
рения являются независимыми.
Рассмотрим это допущение. Вероятно ли, что если ученик В
оценивался выше ученика А в 1-й паре, то это не повлияет на
шансы ученика В получить более высокие оценки, чем у учени-
ка А во 2-й паре? Когда образуется большое число классов, этот
факт не представляется невероятным. Напомним, что 120 уче-
ников распределялось в четырех отдельных классах. Тот, кто
хоть сколько-нибудь знаком с процессом обучения, знает, что
ученики всего класса взаимодействуют во время обучения таким
образом, что учебный процесс либо ускоряется, либо замед-
ляется.
Вариант 1
А
Вариант 2
Класс I
Нарушитель i
Класс И
Класс I
Нарушитель !
Класс II
Класс Ш
Нарушитель 2
Класс IV
Класс III
Класс IV
Нарушитель 2:
Данные покажут, что метод В лучше
метода А для всех 60 пар учени-
ков.
Данные покажут, что метод А лучше
метода В для 30 пар, а для осталь-
ных 30 пар метод В лучше А.
Вариант 3
Вариант 4
Класс 1
Класс II
Нарушитель 1
Класс I
Класс II
Нарушитель
Класс Ш
Нарушитель 2
Класс IV
Класс III
Класс IV
Нарушитель 2
Данные покажут, что метод А лучше
метода В для 30 пар, а для осталь-
ных 30 метод В лучше А.
Данные покажут, что метод А лучше
метода В для всех 60 нар учеников.
Рнс. 19.2
$55
когда фактически /1 и В одинаково эффективны. Фактически
эксперимент оказался не более чувствительным к выявлению
преимуществ одного метода, чем эксперимент, в котором сравни-
вались бы только две независимые пары учеников.
Исследователь поэтому ошибся в своем первом анализе ве-
роятности ложного заключения, так как он не понял, что прове-
дение эксперимента с целыми классами не позволяет получить
60 независимых повторений эксперимента
ПРИЛОЖЕНИЕ
ОТВЕТЫ НА ЗАДАЧИ И УПРАЖНЕНИЯ
Глава 2
1. а. наименований б. порядка
в. отношений г. наименований
2- a. tf + Xl + Xl+X1, t,.Xt + Xs + Xe
(X, + X, + A)’
а... з£л, 5(Е"-)
» £(Х< + П
s *<(*<+о
Глава 3
2. Ри> = 108,41.
Глава 4
1. Среднее — 2,56; медиана — 2,8; мода = 3,05.
2. Среднее = 3,06; медиана = 3,3.
3. Среднее = 14,34; медиана = 14,45.
4. Среднее = 3(14,34) = 43,02; медиана = 43,35.
5. Среднее = 13,3; общую медиану нельзя определить, зная только отдельные
медианы и п.
6. В точке D.
Глава 5
1. Включающий размах = 21; дисперсия, s2 = 32,34; стандартное отклонение,
s — 5,68; среднее отклонение = 4,22.
459
« - 126,17 - 96,17 -
2. Q-------’— ------!— = 15.
3. «больше, чем»; дисперсия объединенных групп равна величине 66,9.
Глава 6
L а. 0,1587 г. 0,0250 б. 0,9772 д. 0,4987 в. 0,0505 е. 0,6915
ж. 0,8664 2. а. 0.2420 б. 0,2420 в. 0,0317
с. 0,3945 3. а. 50 б. 89 в .6 г. 38 д. 99
Глава 7
I. Браун и Смит получат одинаковую величину коэффициента корреляции, так
как высота в дюймах содержит !2 значений высоты в футах. Линейное пре-
образование X и/или Y не изменит величины коэффициента корреляции.
2 Так как rIlF не может превышать + I, то rxt, = {sxv)/(sxse) s; 1. Нам из-
вестно, что s« = 5, a s„ — 4; отсюда (sxl,)/(5 • 4) 1, то есть slv 20.
3. а г = —0,04.
в. X и У связаны нелинейно. Между ними почти не наблюдается линейной
связи, на что указывает коэффициент корреляции Пирсона, равный —0,04,
Глава 8
2 а. 2.93 б. 1,80 в. 2,06 г. 3,24
4 Пет.
5. В процессе преобразования X в сХ + d bs делится на с, то есть для
преобразованных значений X наклон линии регрессии равен Ь,/с. Так как
и р, — bsX.. то пересечение осн У для преобразованных данных, обозна-
чаемое символом 60, равно Ьд == У,-~(сХ. 4- d) =• У, — biX, — Ьу — =
Глава 9
1. а. точечно-бисернальный б. Ро Спирмена в. рангово-бисериальный
г. г Пирсона д. коэффициент фн е. рансово-бцсериальный
2. г4(, = —0,75.
3 т = 0,60
4. а г, — 0,87. б. т и 0,76.
5. Нет.
Глава 10
1.а. Р(А) "» 13/52 = 1/4 б. Р(А) = 1/52 в. Р(А Л В) =0/52 = О
г P(AUB) = Р(А) + Р(В) — Р(А ЛВ) = (13/52)+ (4/52) — (1/52) .«
= 16/52 = 4/13.
2- ^’^= 1287.
460
3 ]+4 + 6 + 4+1 = 16; 2* =16.
4.
Ожидаемая
’ частота
256
5. а. 0,79 6.0,006 в. (0.6915)3 = 0,331.
6. £(*) = 2у.
Глава И
1. а. 0,10 б. 2,09 в. 1,28 г. 1,29
3. Вероятность определяется величиной 0,02.
4. - £(13 - В (Г,,,) - »/(« - 2).
Глава 12
Ох,
5,00
3,54
2,50
1,77
1,25
0 883
0,224
0,158
2. Следует взять выборку объема 40
3. 95% доверительный интервал простирается от 105,97 до 107,53.
а. (—0,01, 0,65)
б. (-0,89, -0,12)
в. (—0,03, 0,25)
(-0,14, 0,71)
(—0,93, 0,09)
(—0,01, 0,28)
Глава 13
1. а. Нуль-гипотеза Но— гипотеза о параметре или параметрах распределения^,
которую можно или нельзя «аннулировать» (отклонить) на основе до-
казательства, обеспечиваемого выборкой из распределения.
461
б. Альтернативная гипотеза Hi—гипотеза о параметре распределения, ко-
торая определяет значения параметра, отличающиеся от заданных в На.
Если Но отбрасывается, то принимается Hi, и наоборот.
в Ошибка I рода — отбрасывание Но в случае, когда она верна.
г. Ошибка II рода— принятие Но, когда она ложна.
д. Уровень значимости, а, — это вероятность совершения ошибки I рода,
е Мощность критерия, 1 —f), — вероятность отбрасывания Но в случае,
когда она ложна.
ж. Критическая область — все те значения выборочной статистики, в соот-
ветствии с которыми исследователь будет отбрасывать Но, если его вы-
борка дает одно из этих значений.
2. Вероятность ошибки 1 рода приблизительно равна 0,16.
3. а. 0,10 б. 0,95 в 0,95 т. выше 0,99
Глава 14
V( 0,28) (0,72) [(1 /873) + (1/837)]
незначим на уровне 0,01.
2. Полученное значение %2 равно 13,27. 99-й процентиль ^'Распределения
с 4 степенями свободы равен 13,28. Хотя у.2 строго незначим на уровне 0,01,
следует выразить некоторое сожаление относительно объявленной значимо-
сти на уровне 0,02,
Глава 15
I. a. dtb == 1, = б. dff,=4, 4^ = 5.
в, dft, = 2, dfu,~ 10
г. rf/i “2; 7.
2. a о ogFj in — 10,04 6 o.toFt.st = 2.14 в. q.ssEj.is “ 3,68
3. MSb = 20.31 MSa & 6,61 F => 3,07.
4. Таблица ANOVA
Истопник sap. d! MS р
Между группами Внутри групп 13 145,61 4.11 35,43
Отбросить Но на уровне 0,01.
5. Величина <p равна -y/2 = 1,414; n: — J— 1=4; == N —J — 20, a
a = 0,05 По таблицам мощности P-критерия мы видим, что мощность,
I —(5, приблизительно равна 0,60.
Глава 16
Каждая пара средних должна отличаться по крайней мере на величину
o.«9e.«>V'MStB/n =8,32, чтобы считаться существенно различной на уровне
0,05. В соответствии с этим критерием статистически значимыми являются
462
Математическая статистика
и планирование эксперимента
в науках о человеке
Основное назначение предлагаемой советскому читателю книги
Дж. Гласса и Дж. Стэнли «Статистические методы в педагогике
и психологии», по замыслу ее авторов, состоит в том, чтобы
служить учебником для первоначального знакомства с предме-
том, позволяющим в дальнейшем читать и понимать статисти-
ческую литературу. Но это лишь одна из задач, которые авторы
поставили перед собой.
Другое назначение книги — быть справочником по статисти-
ческой технике для людей, которые уже владеют соответствую-
щими идеями и методами, и руководством по планированию
экспериментов и квалифицированной интерпретации их резуль-
татов в конкретных исследовательских задачах. Таким образом,
книга Дж. Гласса и Дж. Стэнли, судя по ее содержанию, может
в течение длительного времени претендовать на роль настольной
книги экспериментатора, чем и определяется достаточно четко
круг ее читателей.
По-видимому, не существует особой необходимости доказы-
вать такому читателю целесообразность и эффективность при-
менения математических методов в таких науках, как психоло-
гия, социология, педагогика и т. п.. — это уже давно подтверж-
дено практикой научно-исследовательской работы в этих обла-
стях и в настоящее время никем не оспаривается.
Математическая статистика ныне является наиболее адек-
ватным инструментом при решении специфических проблем тех
наук, в которых существенную роль играет вариабельность ха-
рактеристик человека как объекта изучения и сложная система
взаимозависимости этих характеристик. При этом на первый
план выдвигаются такие традиционные задачи математической
статистики, как оценка параметров распределений, проверка
гипотез, определение наличия и характера статистических свя-
зей и т. п. Кроме того, как и во всякой экспериментальной
науке, имеющей дело с массовыми явлениями, и в психологии,
и в педагогике исследователь в результате своей работы очень
часто получает такое количество экспериментального мате-
риала, разобраться в котором без помощи всроятностно-стати-
477
стических методов просто невозможно. В этих случаях важное
значение приобретают методы группировки данных, изучение
распределения статистик, выделение скрытых факторов, методы
понижения размерности массивов экспериментальных данных
и т. д. Однако многие экспериментаторы знают, что применение
этих методов — не единственное средство борьбы с «проклятием
размерности». Понизить ее часто можно еще до начала самого
эксперимента путем надлежащего его планирования. Известно
ему также и то, что методы планирования эксперимента и раз-
работаны как раз для тех объектов, выходные характеристики
которых варьируют под влиянием множества случайных фак-
торов.
Во всех этих случаях вопрос ставится о приложении уже
разработанного математического аппарата к конкретной экспе-
риментальной ситуации, и если экспериментатор находит в
книге удовлетворительные ответы па вопросы, связанные с пере-
численными обстоятельствами, то этого уже достаточно для вы-
сокой ее оценки.
Возможен и другой подход, развивающий изложенную точку
зрения и одновременно в определенной степени отрицающий
ее. Речь идет о том, что существующий математический аппа-
рат, развитый в основном для удовлетворения потребностей
физики и наук, отпочковавшихся от нее, аппарат, в абстрактном
виде отражающий явления, изучаемые этими науками, не всегда
соответствует запросам таких областей знания, как, например,
психология, хотя бы потому, что современная математика при
существующей в ней тенденции к обоснованию своих понятий,
исходя из теории множеств, в основном рассматривает объекты
дизъюнктивного характера, в то время как психические про-
цессы, как подчеркнул С. Л. Рубинштейн, этим свойством не
обладают. В подобных случаях конкретные науки (в том числе
и психология) обычно не дожидаются момента, когда матема-
тика преподнесет им готовый инструмент анализа, а порождают
его внутри себя, оттачивают на своих задачах и используют для
решения своих проблем, предоставляя математикам право фор-
мально-логического обоснования корректности метода, эффек-
тивность которого уже проверена практикой. Так, например,
обстояло дело с математическим аппаратом квантовой меха-
ники, аналогичный путь прошел в своем развитии и факторный
анализ.
Возникший в среде психологов и связанный с именами
Н. Спирмена, Л. Терстона, К. Холзингера, Г Хармана и др., а
также такого известного статистика, как К. Пирсон, факторный
анализ использовался для построения математических моделей
способностей и поведения человека. Дискуссии о психологиче-
ском содержании моделей на начальной стадии развития фак-
торного анализа не способствовали привлечению внимания к
нему широкого круга математиков, вследствие чего, оставаясь
долгое время скорее набором рецептов (применение которых
478
требовало большого искусства и интуиции), нежели научным
методом, этот вид анализа теоретическое обоснование с совре-
менных позиций получил лишь 10—15 лет назад, уже после
того, как произошло переосмысление методов самой матема-
тической статистики. Теперь мы можем констатировать, что
факторный анализ—-один из интереснейших и трудных разде-
лов многомерной статистики — давно вышел за рамки психоло-
гии и находит широкое применение в социологии, педагогике,
экономике, биологии, химии, пробивает дорогу в металлургии
и других отраслях прикладной науки, где существенную роль
играют факторы, скрытые от непосредственною наблюдения,
используется при анализе сложных систем...
Можно было бы привести и другие примеры зарождения
нового математического метода в недрах «заинтересованной»
в нем конкретной науки, но здесь для нас более важным яв-
ляется тот факт, что необходимость в разработке математи-
ческого аппарата, который мог бы удовлетворить бурно расту-
щие потребности экспериментальной психологии, отнюдь не ми-
новала. Помимо острых дискуссий по этому вопросу на пред-
ставительных форумах психологов, об этом свидетельствует и
появление конструктивных предложений в виде более или менее
разработанных теоретических построений. Однако процесс раз-
работки «нового» математического аппарата только начинается,
и потребуются еще значительные усилия и со стороны матема-
тиков, и со стороны психологов, прежде чем он будет создан,
при этом от психологов ожидается четкая формулировка тех
проблем, которые нуждаются в «математизации». В то же
время практика убедительно показывает, что разработка мате-
матического инструмента — это еще только половина дела. Со-
вершенно необходимо, чтобы новые идеи попали на благодат-
ную почву. В связи с этим очень актуальной представляется
проблема повышения общей математической культуры психоло-
гов, социологов, педагогов, а решить ее невозможно без созда-
ния прочной (и главное — правильной) методической основы,
без широкого внедрения навыков математического анализа в
повседневную работу экспериментаторов. Поэтому любая книга,
посвященная приложениям математики к проблемам конкретной
науки, подлежит оценке и с этой точки зрения
Говоря о состоянии и перспективах применения математи-
ческих методов в психологии, легко привести множество при-
меров отличного по результатам и квалифицированного их ис-
пользования, хотя для значительной части психологов-экспери-
ментаторов эти методы до сих пор остаются объектом восхище-
ния и .. недопонимания. Наиболее органично математические
методы, в том числе и методы планирования эксперимента и
статистической обработки его результатов, входят в те разделы
психологии, где широко применяются современные технические
средства получения первичной информации (психофизиология,
психофизика, инженерная психология и т. п.). Здесь само обилие
479
информации выдвигает на первый план вопросы ее организации.
Значительно реже эти методы используются в других разделах,
например в педагогической психологии, да и в самой педагогике,
где в большинстве опубликованных работ в качестве результата
математической обработки выступает чаще всего пресловутый
средний балл; в лучшем случае проводится разделение учащихся
на группы по различным признакам при помощи наиболее попу-
лярных статистических критериев, однако при этом нередко
нарушаются элементарные условия их применения
Таким образом, в настоящее время можно констатировать,
что если в педагогике сделаны первые шаги на пути использо-
вания математических методов, если в отдельных разделах пси-
хологии эти шаги постепенно превращаются в уверенную по-
ступь, то до массового привычного владения этим эффективным
инструментом исследования (и в психологии и в педагогике)
все еще далеко. Более того, практика работы по приложению
математики к этим наукам позволяет утверждать, что в среде
психологов и педагогов наблюдается резко диспергированное
распределение по степени владения вероятностно-статистиче-
скими методами — от случаев блестящего их использования до
области растерянности и беспомощности, проявляющихся при
необходимости решения даже такой, например, задачи, как
определение необходимого объема экспериментальной выборки.
При этом особо удручающим обстоятельством является то, что
мода такого распределения лежит именно в этой области. Впро-
чем (поскольку проводить эксперимент все же надо), экспери-
ментатор после недолгих колебаний выходит из подобного со-
стояния, принимая решение ситуативного, чаще всего интуитив-
ного или волюнтаристского характера.
Однако переживание определенного дискомфорта, возникаю-
щего в такой ситуации у добросовестного исследователя, пони-
мающего к тому же, что применение готовых рецептов зачастую
оказывается малоэффективным, а иногда может привести и к
грубым ошибкам, заставляет последнего приняться за изучение
литературы по теории вероятностей и математической стати-
стики— при этом главной целью ставится постижение методо-
логии вероятностно-статистического подхода. С этого момента
у нашего идеального исследователя появляется реальная воз-
можность (если попытка пробиться сквозь чещу чисто матема-
тических трудностей не остановит его раньше) на собственном
опыте убедиться в существовании того пугающего разрыва, о
котором много говорят сами математики, между теоретическими
и прикладными ветвями интересующей его науки, в специфиче-
ской направленности книг по математической статистике, щедро
издаваемых для металлургов, машиностроителей, химиков, ра-
диотехников, экономистов (но только не для педагогов и пси-
хологов), в нарочитой упрощенности одних руководств и не-
оправданном усложнения других и т. д.
480
Прекрасно понимая, что те заманчивые перспективы, кото-
рые открываются на пути использования математических мето-
дов, требуют для своей реализации достаточно надежного фун-
дамента, построить его тем не менее ни психолог, ни педагог
оказываются не в состоянии. И это не их вина. Из книг на рус-
ском языке, призванных ликвидировать пробел в учебной
литературе по основам теории вероятностей и математической
статистике, до недавнего времени они могли выбрать только
одну (Г. В. Суходольский, Основы математической стати-
стики для психологов, Изд. ЛГУ, 1972); и только в самое по-
следнее время вышла в свет удачная книга Е. Ю. Артемьевой и
Е. М. Мартынова, Вероятностные методы в психологии (Изд.
МГУ, 1975). Как и книга Г. В. Суходольского, она предназна-
чена для студентов-психологов младших курсов. Однако такой
ограниченный набор учебной литературы (не считая, конечно,
многочисленных публикаций по применению математических
методов в психологии, социологии, педагогике, читать и пони-
мать которые можно, уже владея определенными навыками в
их использовании), видимо, не может удовлетворить разнообраз-
ные требования широкого круга психологов и педагогов в нашей
стране. Восполнить в определенной мере этот пробел может
предлагаемый вниманию советского читателя перевод книги
Дж. Гласса и Дж. Стэнли «Статистические методы в педагогике
и психологии».
Говоря о ее содержании, следует отметить прежде всего
обилие в книге фактического материала, что само по себе тре-
бует каких-то вех для ориентировки в нем. Но прежде чем их
расставить, необходимо подчеркнуть тот главный эффект, кото-
рый может быть достигнут при изучении книги. Речь идет о вы-
работке нового методического подхода к анализу эксперимен-
тального материала, об умении увидеть в привычных понятиях
их новую сторону, выявить количественные соотношения между
качественными категориями. Заставить себя взглянуть на вещи
глазами статистика — нелегкая задача, но добиться этого —
значит подготовить себя к активному восприятию новых идей
в математике и, быть может, к их генерации Достигнет ли
ли этого уровня читатель — в значительной степени зависит от
него самого. Авторы, во всяком случае, сделали все, чтобы под-
готовить для этого почву, конечно, в тех пределах, которых
позволяет достичь курс прикладной математической стати-
стики.
Книга Дж. Гласса и Дж. Стэнли отличается простотой и
доступностью изложения. Авторы все время помнят, что они
обращаются к читателю с элементарной математической под-
готовкой. Вместе с тем они почти нигде не жертвуют из-за этого
логикой или строгостью изложения. В силу этих причин, а так-
же на основе опыта общения с широким кругом психологов и
педагогов, стремящихся к овладению вероятностно-статистиче-
скими методами, можно утверждать, что чтение этой книги в
481
внутреннего развития самой математической статистики, пла-
нирование эксперимента представляет собой завершающую
конструкцию системы прикладных методов этой науки, или, если
не бояться транспонирования терминов, системы математиче-
ского обеспечения эксперимента. Последнее утверждение отнюдь
не означает, что эта система прекратила свое развитие, — оно
лишь констатирует тот факт, что система обрела свою структуру,
что не препятствует, а скорее способствует дальнейшему совер-
шенствованию ее элементов.
Говоря о содержании книги, можно выразить сожаление по
поводу того, что в ней не нашли отражения многие важные
разделы статистической теории, скажем многомерный метод
статистической классификации, в частности факторный анализ.
Хотелось бы видеть более детальное рассмотрение регрессион-
ного анализа. Если иметь в виду полный объем требований, ко-
торые выдвигает современный уровень развития статистиче-
ского анализа, можно было бы поставить авторам в упрек и
то, что в книге (в основном это касается ее второй части)
не рассмотрены со свойственной им тщательностью вопросы
применения непараметрических критериев, оценок максималь-
ного правдоподобия, детали секвенциального и дискриминантного-
анализа. Однако при этом не следует забывать об основной цели
книги — снабдив экспериментатора определенным запасом доб-
рокачественных знаний в области статистики, раскрыв перед
ним суть статистических методов, обеспечить ему тем самым
возможность дальнейшего самостоятельного успешного продви-
жения в этом направлении. Объем всякой книги ограничен, и
расширение ее тематики неизбежно привело бы к скороговорке,
которая и так уже чувствуется в последней, 19-й главе. В целом
же книга Дж. Гласса и Дж. Стэнли адекватно отражает совре-
менные представления о роли и месте статистических методов
в экспериментальных науках, объектом изучения которых яв-
ляется человек. И если применение статистических методов —
это путь к повышению эффективности научных исследований, то
перевод книги, предлагаемый вниманию советского читателя,—
одно из удачных и надежных средств для их изучения и при-
ложения на практике. Помимо той пользы, которую книга при-
несет при индивидуальном ее штудировании, она благодаря
богатству содержащегося в ней материала, в том числе и оби-
лию специфических примеров, может оказаться полезной и при
разработке программ группового обучения и повышения квали-
фикации соответствующих специалистов (разумеется, при кор-
ректировке с учетом сделанных выше замечаний).
При подготовке к изданию перевода книги на русский язык
были произведены некоторые сокращения. Они касаются наибо-
лее элементарных мест в первых главах книги, повторений, не-
489
•которых упражнений и отдельных примеров. Исключены также
статистические таблицы из приложения. Они весьма громоздки.
Вместе с тем сейчас нет недостатка в хороших статистических
таблицах. Читатель может воспользоваться, например, следую-
щими наиболее полными таблицами: 1) Л, Н, Большее,
Н. В. Смирнов, Таблицы математической статистики, «Нау-
ка», М., 1965. 2) Я. Янко, Математико-статистические табли-
цы, Госстатиздат, М., 1961. 3) Д. Б. Оуэн, Сборник статистиче-
ских таблиц. Изд 2-е, ВЦ АН СССР, М, 1973. 4) А. К. Мит-
ропольский, Техника статистических вычислении, изд. 2-е,
«Наука», М., 1971. 5) R. A. Fisher, F. Y a t е s. Statistical
tables for biological, agricultural and medical research, 4-th ed ,
Oliver and Boyd, Edinburgh, 1953. 6) A. Ha Id, Statistical tables
and formulas, Wiley, N. Y„ 1952, 7) E. S. Pearson, H. O. Har-
tley, Biometrika, tables for statisticians, v. I, 3-th ed., Cam-
bridge Univ. Press, Cambr. 1966.
При переводе встречались некоторые терминологические
трудности. Так, например, английские термины «estimate» и
«score» часто переводятся на русский язык словом «оценка». Од-
нако смысл этих слов совершенно различен. Первое-—это стан-
дартный статистический термин, обозначающий некоторую
функцию от результатов наблюдений, а второе — это, например,
школьная отметка, оценка знаний. В переводе термин «оценка»,
как правило, сохранялся за статистическим значением, а во
втором случае подбирался текстуально подходящий эквивалент.
Вообще при переводе статистических терминов было стремле-
ние придерживаться той практики, которая сложилась в оте-
чественной статистической литературе, особенно в литературе по
планированию эксперимента.
Ю. П. Адлер,
А. Н. Ковалев
СОДЕРЖАНИЕ
От издательства ............................................. 5'
I- ВВЕДЕНИЕ.................................................. 7
2. ИЗМЕРЕНИЕ, ШКАЛЫ И СТАТИСТИКА.............................12
21. Измерение ............................................... 12
2 2. Измерительные шкалы 12
2 3. Переменные и их измерение - ................ 20
2 4. Символы, данные и операции.............................. 22
2 5. Обозначение сигма (S)................................... 23
Задачи и упражнения ... 29
3. ТАБУЛИРОВАНИЕ И ПРЕДСТАВЛЕНИЕ ДАННЫХ.....................30-
3.1. Табулирование данных.................................. 30
3.2. Квантили ............................. ... . 36
3 3 Определение процентилей............................... .37
3 4. Наглядное представление данных ..... . 42
3.5. Графическое представление распределения частот .... 44
36 Запутанные графики....................... - . . . 51
3.7. Общие советы при построении графиков....................54
Зада чи и упражнения...................... .... 55
4. МЕРЫ ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ............................... 58
41. Введение .............................. . . . 58
4 2. Мода .......................................... . 53
4 3 Соглашения об использовании моды............. . .59
4.4. Медиана .................................... . . 69
4.5. Вычисление медианы ... . . ... .60
4 6. Среднее ............................................... 61
4 7 Вычисление среднего..................................... 62
4.8 Свойства среднего........................................64
4 9. Среднее, медиана и мода объединенных групп..............66
4.10. Интерпретация моды, медианы и среднего ................67
4 11 Выбор меры центральной тенденции - ... 68
4.12. Другие меры центральной тенденции - .................71
Задачи и упражнения...........................................72
491
Б. МЕРЫ ИЗМЕНЧИВОСТИ.........................- . 74
5.1. Введение ................................................74
5 2. Размах ..................................................75
5.3 Размах от 90-го до iO-го процентиля.......................76
5 4 Полу-междуквартильный размах ... 76
5 5 Дисперсия ............................................... 76
5 0 Вычисление дисперсии s*.................................. 79
5 7. Стандартное отклонение s ............................. 80
58 Некоторые свойства дисперсии.............................. 80
5.9 Среднее отклонение........................................82
5 10 Стандартизированные данные................................. ч3
5.! I. Асимметрия ...............................................85
5.12. Эксцесс .................................................. 88
Задачи и упражнения..............................................89
8. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ.................................. ... 91
6! Введение...................................................91
62 История нормального распределения..........................91
63. Нормальная кривая........................................ 93
64 Семейство нормальных кривых................................95
6.5. Единичное нормальное распределение как стандарт..........93
6.6. Применение нормальной кривой...........................,98
6.7. Двумерное нормальное распределение.....................160
Задачи и упражнения..........................................102
7. МЕРЫ СВЯЗИ....................................103
7.1 Введение ....................................................103
7 2 Коэффициент корреляции Пирсона, равный произведению момен-
тов ........................................................ ЮЗ
7 3 Формула для вычисления Гх,..................................107
74 Пример вычисления г*у......................................197
7 5 Область изменения гху.......................................ПО
7 6 Влияние преобразования данных на гЖ(1.......................HI
7.7. Интерпретация коэффициентов корреляции......................ИЗ
7 8 Дополнительные замечания об интерпретации г«»..............117
7 9 Дисперсия суммы и разности переменных......................118
Задачи и упражнения..............................................121
8. ПРЕДСКАЗАНИЕ И ОЦЕНИВАНИЕ..................123
8 1 Введение ....................................................123
8 2. Задача оценивания У по X (или X по У)..................... 125
8 3 Постоянство дисперсий и стандартная ошибка оценки............130
84. Связи &о и 51 с другими описательными статистиками........133
8 5 Проверка выполнимости критерия наименьших квадратов для Ь>
и Ья........................................................... 128
8 6. Измерение нелинейных связей между переменными, корреляцион-
ное отношение т|2.............................................. 138
Задачи и упражнения..............................................141
9. ДРУГИЕ МЕРЫ СВЯЗИ...........................142
9 1 Введение ................................................... 142
9 2. Обзоп главы..................................................142
9,3 'Леры связи..................................................145
492
9.4 . Часть корреляции н частная корреляция..................167
9.5 Множественная корреляция и предсказание.................172
Задачи и упражнения...........................................177
10. ВЕРОЯТНОСТЬ ............................................(79
10 1 Введение ................................................179
10 2. Вероятность как математическая система .................180
103. Комбинирование вероятностей..............................182
104 Перестановки и сочетания..................................185
10 5 Биномиальное распределение................ . ... . 189
10 6 Случайность и случайный выбор............................194
10 7 Случайные переменные................................... 196
108 Виды случайных переменных.................................198
109. Вероятность как площадь..................................199
10 10. Ожидания и моменты.....................................200
Задачи и упражнения...........................................201
Л. ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ. ИСПОЛЬЗУЕМЫЕ В СТА-
ТИСТИЧЕСКИХ ВЫВОДАХ.............................206
11 1. Введение ..............................'......................206
11 2. Нормальное распределение...............-......................206
11 3. Распределение хи-квадрат.....................................207
11.4 . Е-распределеняе............................................210
11.5 . (-распределение ...........................................212
116 Соотношения между нормальным, (•_ хи квадрат и Е-распределе-
ниями ..........................................................2'4
Задачи и упражнения.................................................215
12. СТАТИСТИЧЕСКИЙ ВЫВОД: ОЦЕНИВАНИЕ...........217
12.]. Генеральные совокупности и выборки, параметры и статистики 217
122. Случайный выбор............................................218
123 . Идея выборочного распределения.........................219
12 4 Свойства оценок...........................................227
125 Интервальное оценивание..................................233
12. 6 Заключение ..............................................244
Задачи и упражнения.............................................245
13. СТАТИСТИЧЕСКИЙ ВЫВОД: ПРОВЕРКА ГИПОТЕЗ ...... 246
13 1. Введение ................................................. £45
13 2 Научная и статистическая гипотезы..............................246
133 Проверка статистической гипотезы................................249
13 4 Ошибка I рода, уровень значимости и критическая область . . . 254
135 Ошибка И рода, & н мощность ... ................257
односторонние» критерии ...............................
Задачи и упражнения.............................................
262
264
14. ИЗБРАННЫЕ МЕТОДЫ ВЫВОДА..................................265
14 1 Введение ...............................265
14.2. Выводы о среднем значении совокупности, ц...............265
14 3 Использование независимых выборок для выводов относительно
14—1*2 • - . . 268
14.3 Выводы относительно ц, — р2 при использовании зависимых вы-
борок ...... ........................27В
493