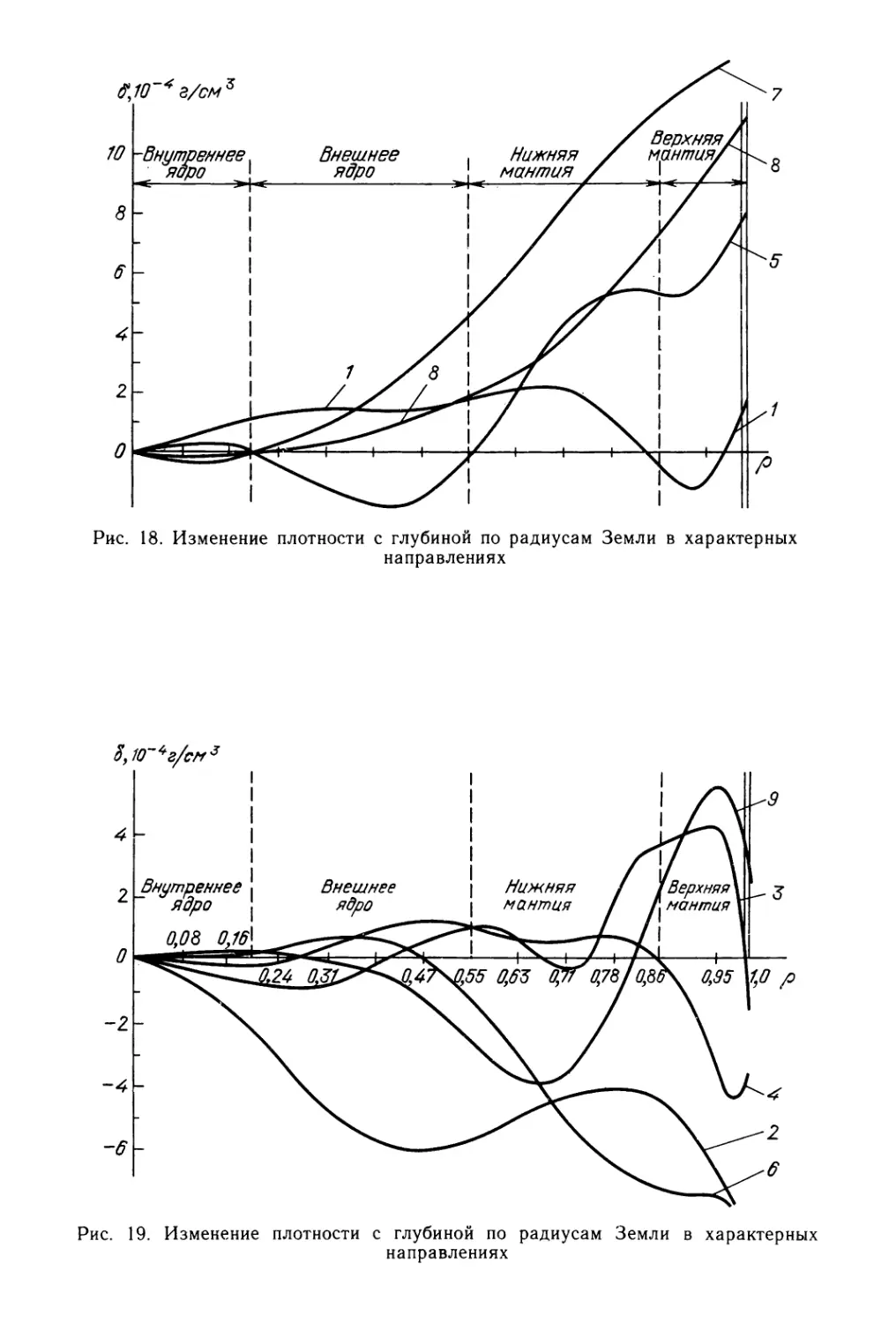
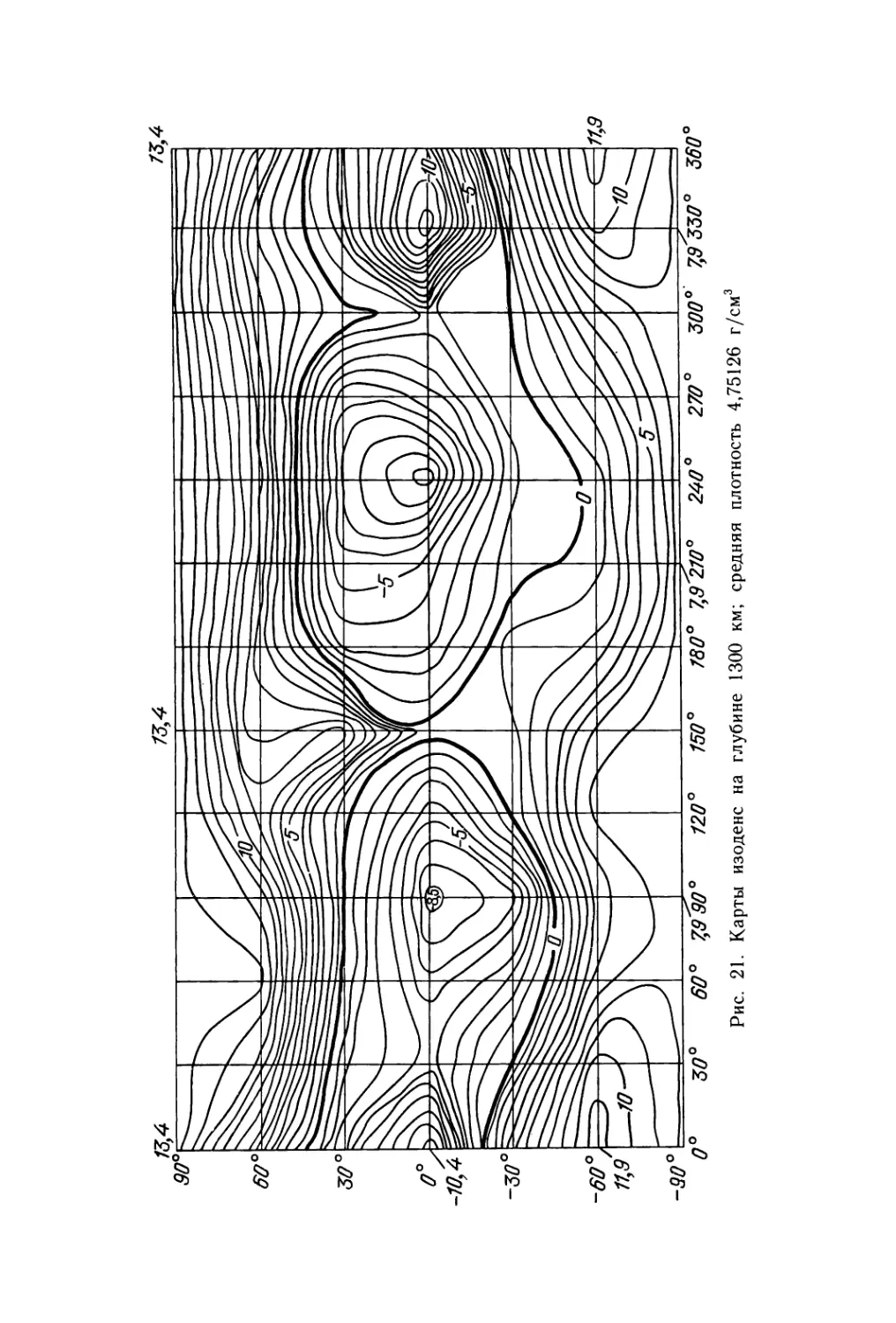
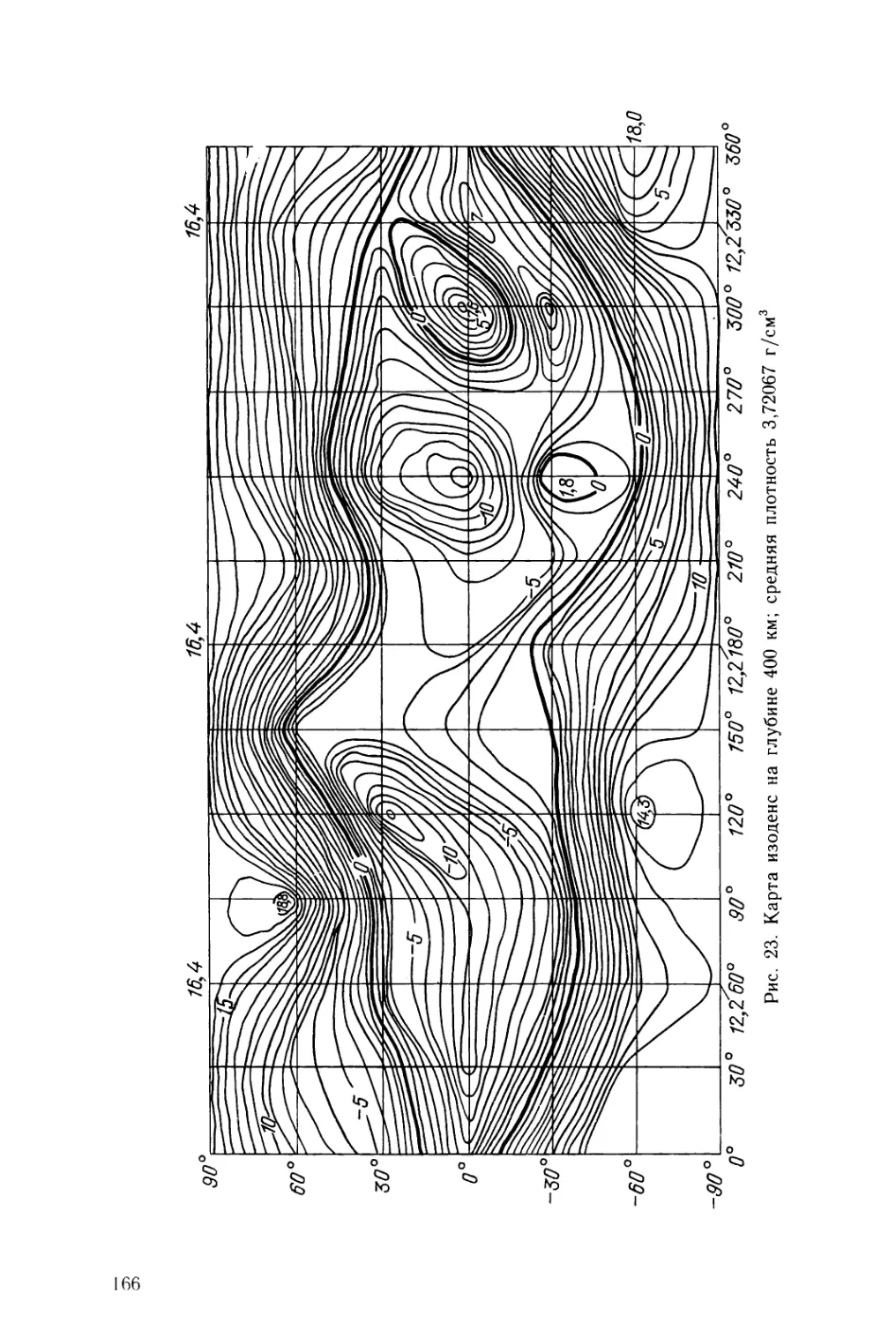
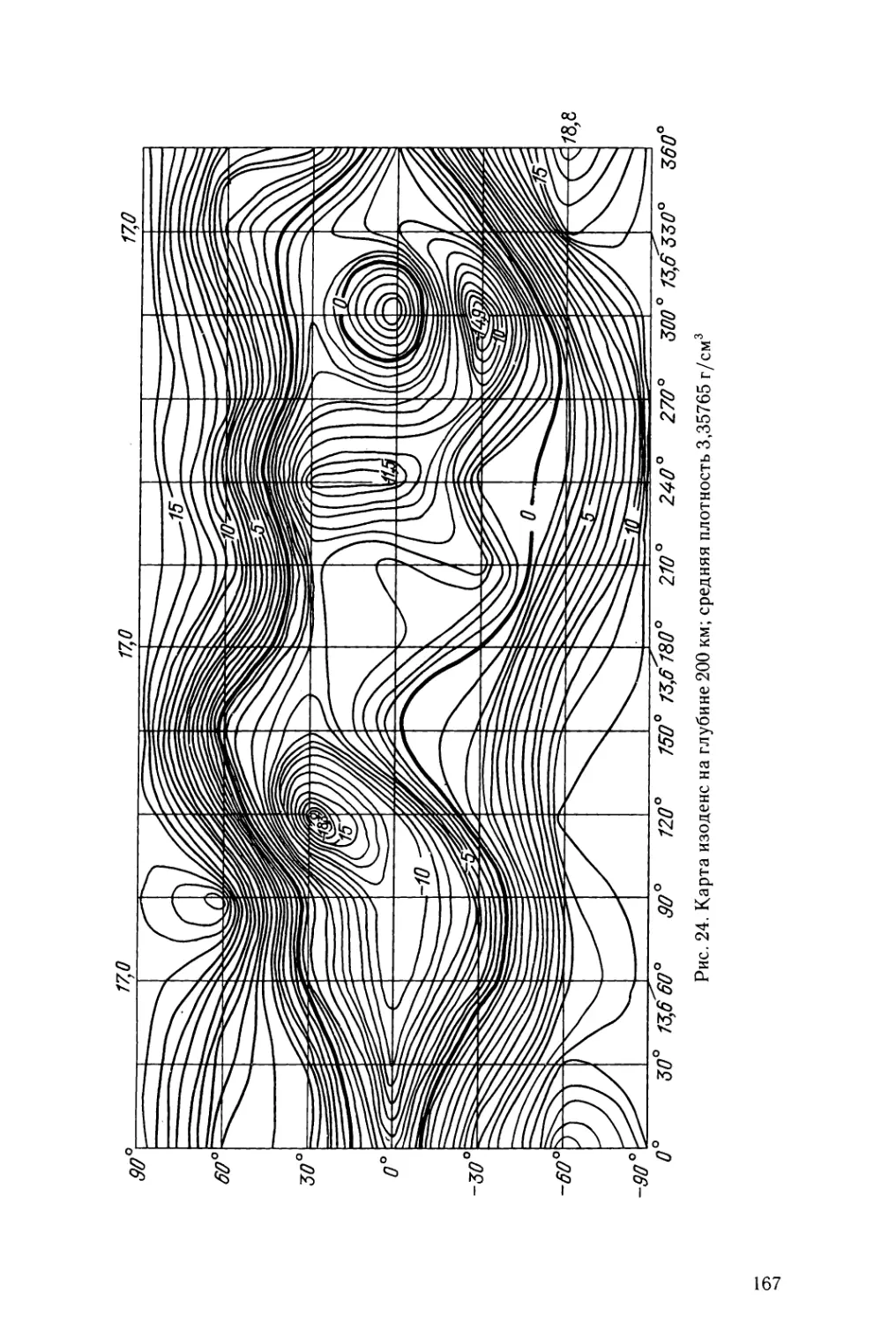
Текст
Г. А. МЕЩЕРЯКОВ
ЗАДАЧИ
ТЕОРИИ
ПОТЕНЦИАЛА
И ОБОБЩЕННАЯ
ЗЕМЛЯ
МОСКВА«НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 9 1
ББК 22.65
М56
УДК 523
Мещеряков Г. Л. Задачи теории потенциала и обобщенная Земля. —
М.: Наука. Гл. ред. физ.-мат. лит., 1991. — 216 с. — ISBN 5-02-014068-6
Подытожены многочисленные оригинальные исследования автора и его коллег,
опубликованные в различных отечественных и зарубежных научных журналах.
Представлены исследования обобщенной Земли: построены и обсуждены глобаль¬
ные модели фигуры и распределения плотности недр планеты. В основу построения
моделей положены решения обратных задач (геодезической и геофизической)
теории потенциала, базирующиеся на использовании современной информации
о Земле, в первую очередь о ее гравитационном поле. Обсуждены свойства ряда
геопотенциала и его мультипольное представление. Рассмотрена потенциалографи¬
ческая задача: многоточечные модели геопотенциала и концепция гравитирующих
дисков. Дан метод определения и учета нецентральности гравитационного поля
Земли, проявляющейся при движении искусственных спутников Земли, и геометри¬
ческая теория их движения.
Для геофизиков, геодезистов, астрономов; может быть использована аспиран¬
тами и студентами указанных специальностей.
Табл. 9. Ил. 27. Библиогр. 237 назв.
Рецензенты:
доктор физико-математических наук В. Я. Скоробогатько,
кандидат технических наук А. Н. Марченко
„ 1605050000-084 ло Л1
М 053(02)-91 98-91
ISBN 5-02-014068-6 © «Наука». Физматлит, 1991
ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1.0 задачах теории потенциала . 7
§ 1. Притяжение точечных объектов 7
§ 2. Основные виды ньютоновских потенциалов притяжения . . 10
§ 3. Разложение внешних потенциалов в ряды шаровых функций . 15
§ 4. Задачи теории потенциала 22
§ 5. Краевые задачи для слабо сжатых эллипсоидов вращения . 27
Глава 2. Мультипольное представление потенциала .... .... 33
§ 6. Максвеллово представление сферических функций и потенциалы
мультиполей 33
§ 7. Нахождение максвелловых параметров сферических функций 39
§ 8. Некоторые общие свойства шаровых, сферических функций и
мультиполей 45
Глава 3. Потенциал притяжения Земли и ее обобщенная фигура . 50
§ 9. Потенциал притяжения Земли и потенциал силы тяжести .... 50
§ 10. Гравитационные мультиполи. Мультипольное представление
геопотенциала 57
§ 11. Мультипольное истолкование основных особенностей фигуры
геоида 64
§ 12. Моменты плотности недр Земли и ее эллипсоид инерции .... 69
§ 13. Основные свойства ряда, представляющего геопотенциал . ... 76
§ 14. О вычислении среднего значения внутреннего потенциала притяже¬
ния Земли 91
Глава 4. Потенциалографическая задача и концепция гравитирующих
дисков 93
§ 15. Многоточечные модели геопотенциала . 93
§ 16. Потенциалографическая задача ... 106
§ 17. Концепция гравитирующих дисков . . 111
Глава 5. Геодезическая обратная задача теории потенциала и фигура
Земли 120
§ 18. Единственность, устойчивость и метод решения . . 120
§ 19. Об определении обобщенных фигур Земли и планет . 129
§ 20. Обобщенная фигура Земли. Нормальная Земля . . 132
Г л а в а 6. Геофизическая обратная задача теории потенциала и распреде¬
ление плотности земных недр 138
§ 21. Единственность, устойчивость и численный метод решения . 138
§ 22. Биортогональная система многочленов в эллипсоиде ... 145
§ 23. Методика построения плотностной модели Земли 149
§ 24. Предварительная глобальная плотностная модель Земли . . 155
§ 25. Замечание об общей обратной задаче теории потенциала . 169
Г л а в а 7. Динамически одноточечные модели геопотенциала и геометриче¬
ская теория движения ИСЗ 170
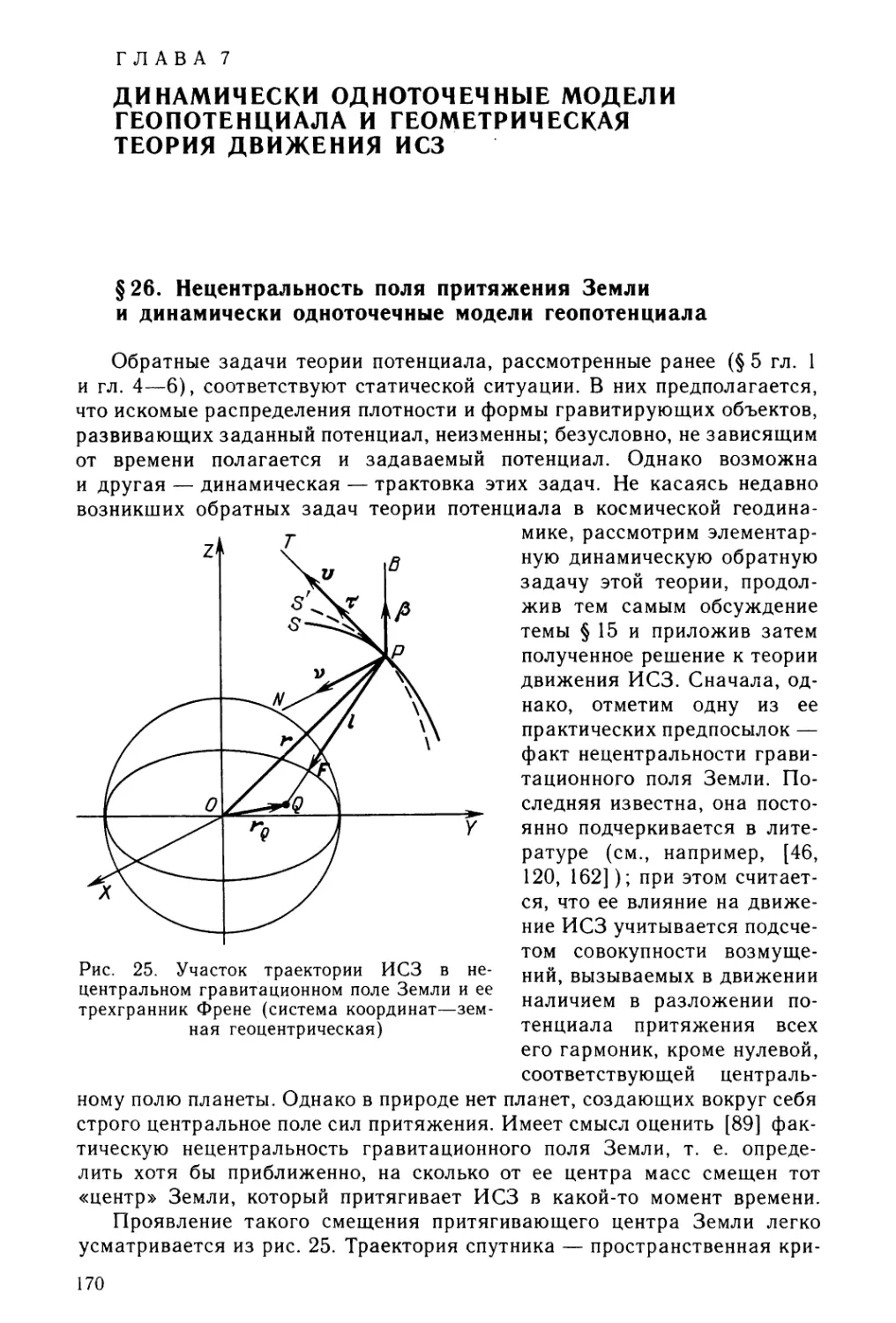
§ 26. Нецентральность поля притяжения Земли и динамически одното¬
чечные модели геопотенциала 170
§ 27. Геометрия орбиты ИСЗ 174
§28. Геометрический метод построения орбит ИСЗ 179
§ 29. О пряхмом методе построения орбит ИСЗ 185
Приложение 191
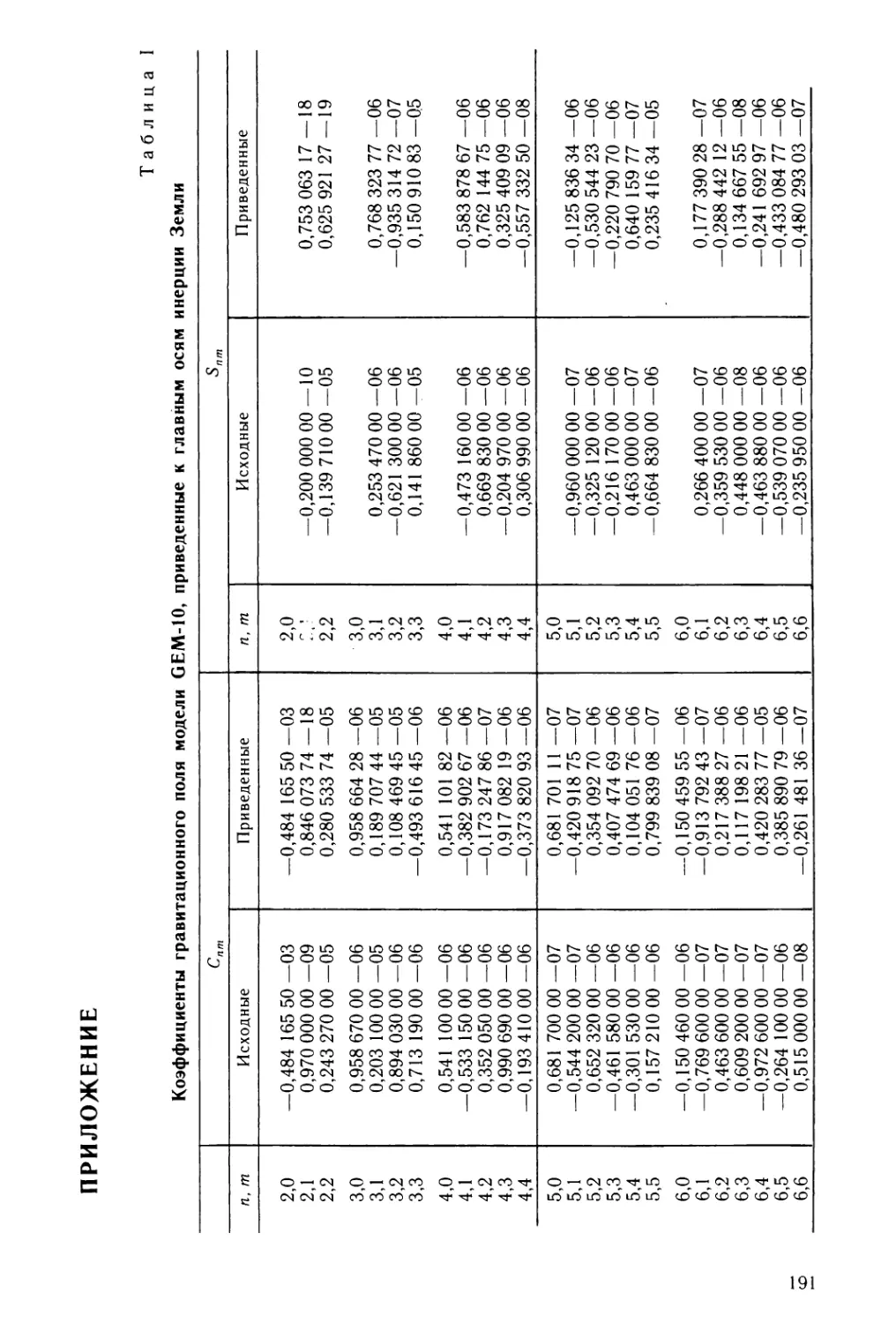
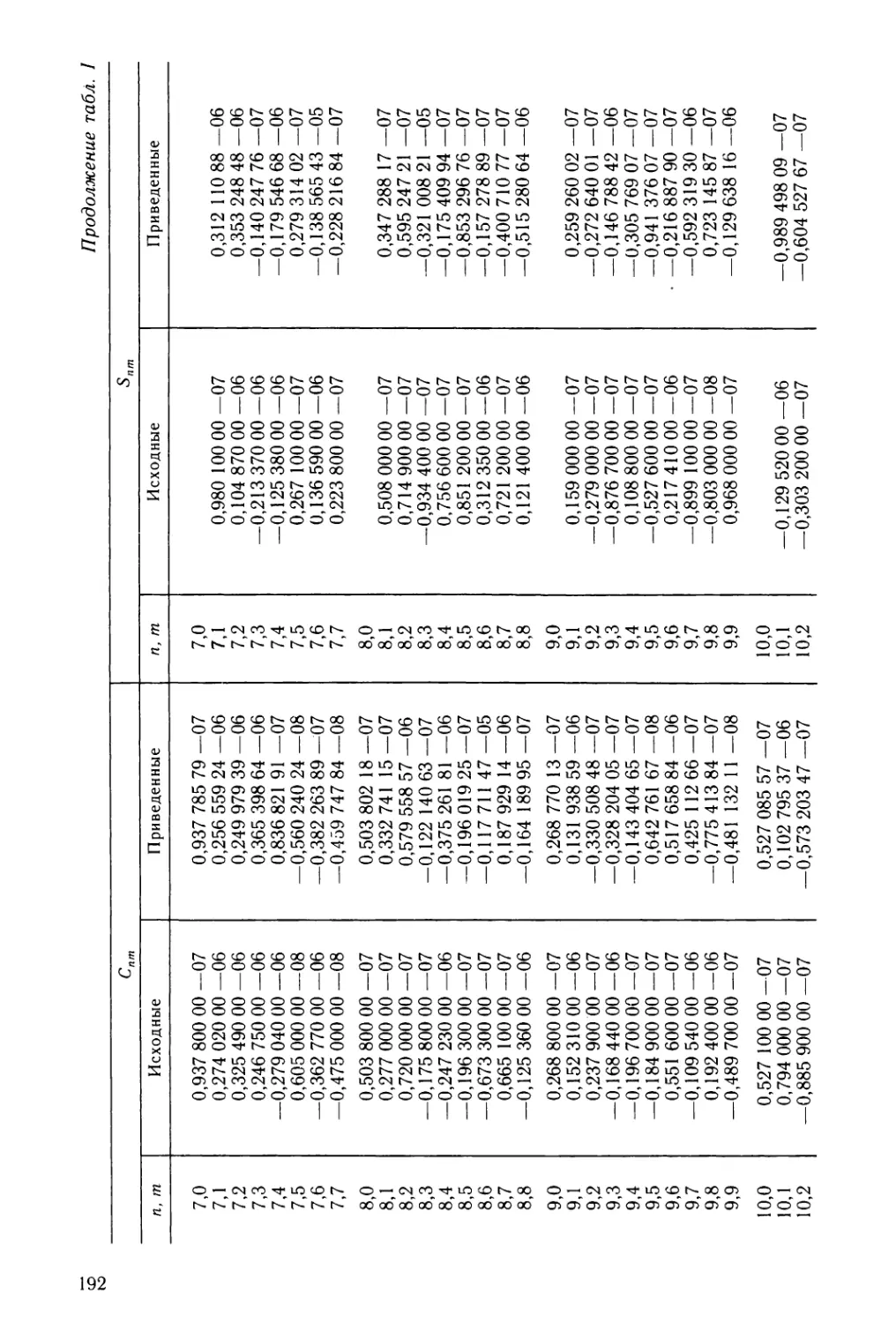
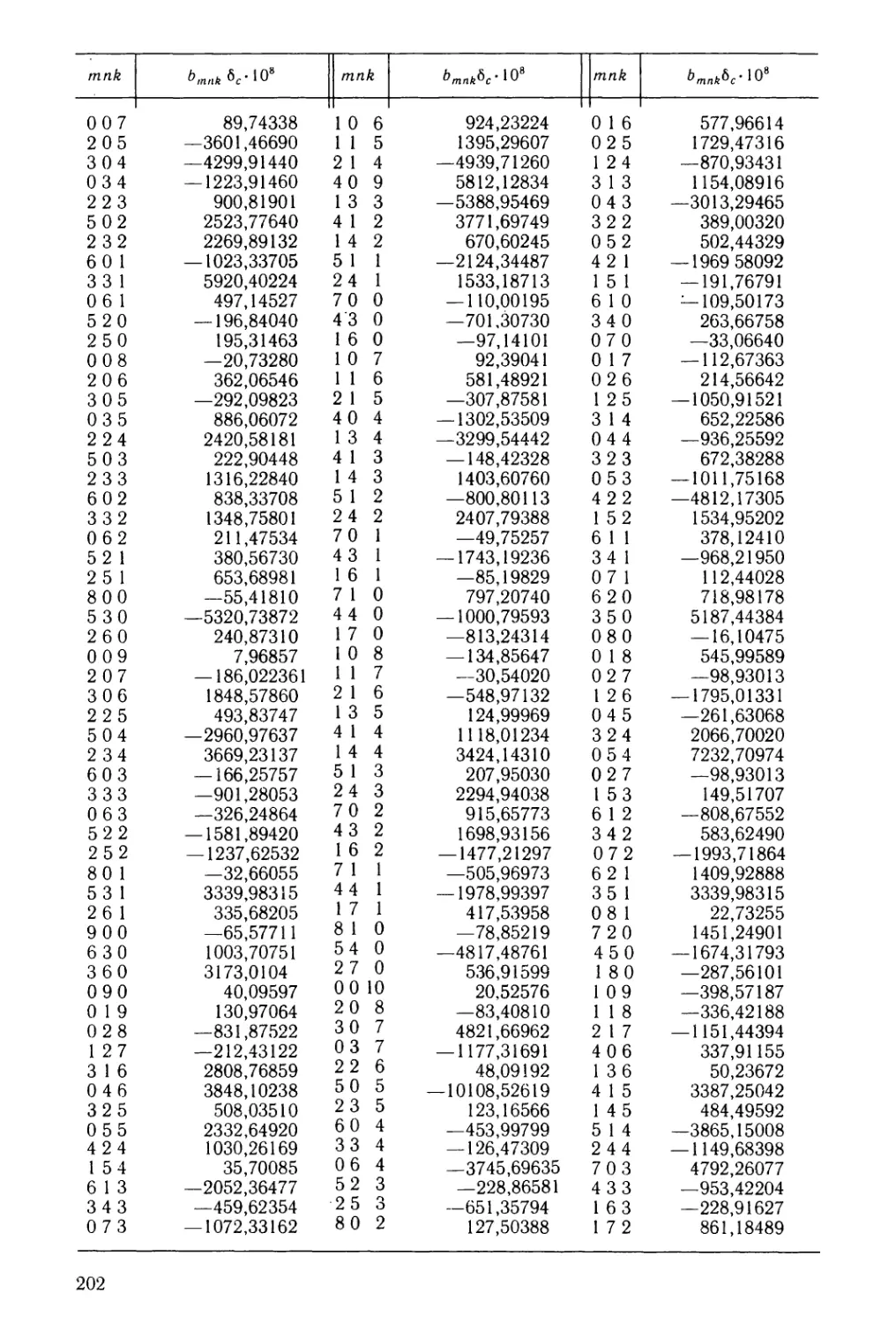
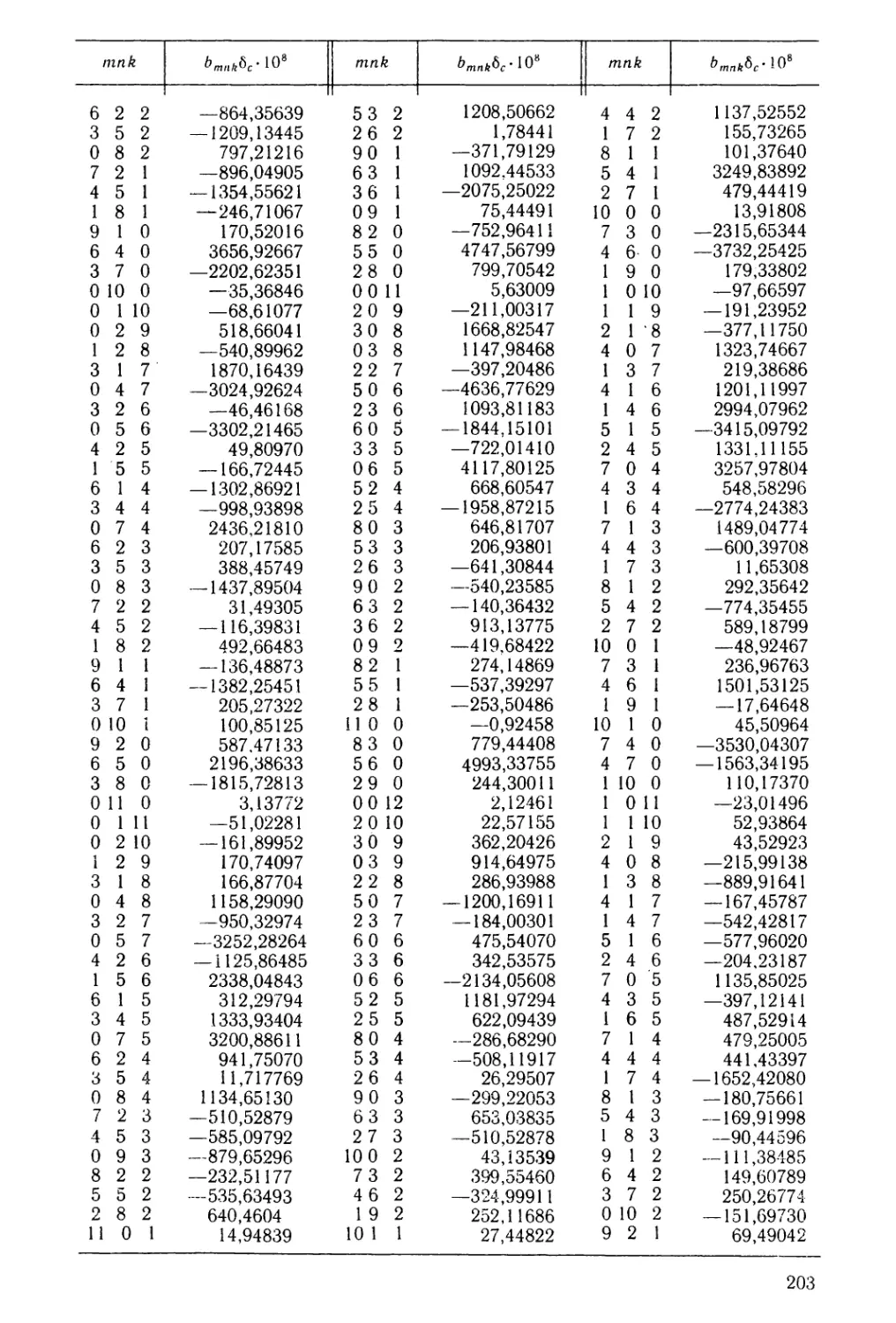
Таблица I. Коэффициенты гравитационного поля модели GEM-10,
приведенные к главным осям инерции Земли 191
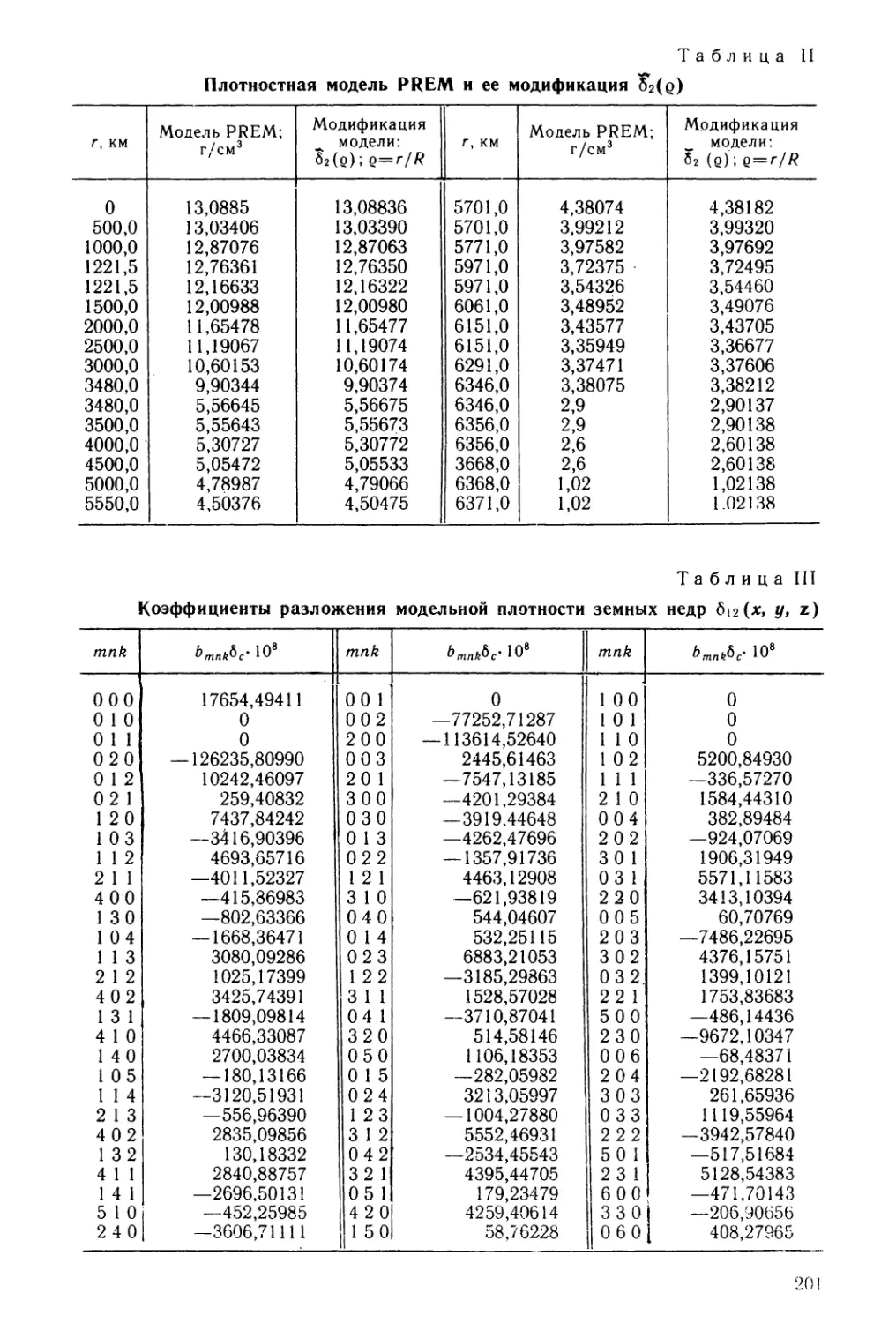
Таблица II. Плотностная модель PREM и ее модификация б2 (р)’ . . . . 201
Таблица III. Коэффициенты разложения модельной плотности земных
недр 612 (х, у у z) 201
Список литературы . 205
ПРЕДИСЛОВИЕ
Основные задачи, рассматриваемые в монографии, суть задачи плане¬
тарной геодезии и геофизики определения обобщенных, а значит, модель¬
ных поверхности Земли и глобального распределения плотности ее недр.
Впервые исследование этих двух проблем было начато и значительно
продвинуто Клеро в его знаменитой книге 1743 г. [47] еще до создания
учения о потенциале, которое появилось лишь через 30 лет (Лагранж,
1773 г.) и сразу же стало прочным фундаментом теории фигуры Земли
(Лаплас) и теории фигур равновесия вращающейся жидкости.
Однако после работ Стокса 1849 г. [147] и особенно Молоденского
1945 г. [ПО] проблема изучения не только обобщенной планетарной
фигуры Земли, но также и детальной, как геоида (квазигеоида), так
и физической фигуры, обособилась от проблемы исследования распреде¬
ления плотности, т. е. в практических целях удалось следствие отделить
от причины. Это оказалось возможным осуществить благодаря замеча¬
тельным свойствам потенциала притяжения, а точнее, на основании
теоремы единственности решения краевых задач теории потенциала.
Геодезическое следствие этой теоремы, данное Стоксом, и его последую¬
щая теория констатировали возможность определения внешнего гравита¬
ционного поля и фигуры Земли без знания распределения плотности ее
недр, хотя при этом еще и привлекались редукции силы тяжести. Моло-
денский [110] освободился и от последнего, вследствие чего основная
проблема геодезии [ill, 115, 127] оказалась независимой от задачи
выявления внутренней структуры планеты. Правда, в последнее время
и в рамках физической геодезии интерпретация и уточнение результатов
ее выводов привели к необходимости исследования взаимосвязей возму¬
щающего потенциала Земли и распределения генерирующих его аномаль¬
ных масс [229].
Задача изучения распределения плотности вещества внутри Земли,
рассмотренная еще Лапласом и Лежандром, вошла в общую проблему
исследования внутреннего строения планеты. С одной стороны, она вышла
из рамок первого приближения Клеро и превратилась в обширную проб¬
лему Клеро — Лапласа — Ляпунова для гидростатически равновесных
планет, и в настоящее время (со счетом на ЭВМ) практическая реализа¬
ция ее возможна до довольно высоких порядков приближения [32]. С дру¬
гой стороны, и, очевидно, это более важно, разработка новых методов
геофизических исследований (особенно при высоких температурах и
давлениях), комплексное их использование, наличие богатейшей инфор¬
мации (сейсмологической, магнитометрической, данных о тепловых пото¬
ках и др.) привели уже к созданию ряда репрезентативных моделей
5
внутреннего строения Земли, как обобщенных — стандартных, так и
региональных [189, 32]. Однако вопросы более детального изучения глу¬
бинных недр планеты (и, в частности, важнейшей их характеристики —
плотности) не только не теряют своей актуальности, но, как известно,
становятся более настоятельными.
При этом представляется, что в плане исследования обобщенных
распределений плотности недр планеты и ее фигуры есть еще не использо¬
ванные возможности. С одной стороны, это — наличие огромнейшей
информации о гравитационном поле в виде моделей геопотенциала,
создаваемых по результатам наблюдений искусственных спутников Земли
(ИСЗ) и наземных гравиметрических измерений, выполняемых не только
на суше, но и в акваториях (а в ближайшей перспективе — ив околозем¬
ном пространстве); с другой — ряд математических теорий (обратных
задач теории потенциала, а более широко, некорректных задач, аппрокси¬
мации функций и т. д.), допускающих на ЭВМ численное решение
исследуемых задач, практически независимо от сложности описывающих
их уравнений и алгоритмов.
Автор предпринял здесь попытку вновь объединенного (как это
было у Клеро) рассмотрения задач изучения формы Земли и распределе¬
ния плотности ее недр, но не на основе гидростатической теории*),
а за счет привлечения нового (теперь уже известного) вида информации,
именно, параметров внешнего гравитационного поля планеты. Он исходит
из известной «теории возмущений», в которой сначала исследуется глав¬
ная часть объекта или явления, а затем находятся поправки, ее уточняю¬
щие. Под главными частями, которые, конечно, могут трактоваться
по-разному (этому далее будет ряд примеров), понимаются обобщенные
(мы воздерживаемся от именования их нормальными) фигура и распре¬
деление плотности, обусловленные внешним гравитационным полем (его
параметрами до некоторого заранее установленного порядка) и такими
факторами, которые наряду с геопотенциалом в основном и определяют
изучаемый объект, характеризуя его фундаментальные свойства: если
фигуру, то это астрономогеодезические, если плотность, то — сейсмологи¬
ческие. Полученные главные части приводят к глобальным планетарным
моделям фигуры и плотности. Региональные и детальные модели можно
строить затем на основе глобальных с дополнительным использованием
иной полезной неучтенной информации на исследуемые районы.
В книге представлены результаты многолетних исследований автора
и его коллег, которым, в особенности А. Н. Марченко и М. М. Фысу,
он выражает глубокую благодарность за активную помощь и самостоя¬
тельную разработку ими ряда вопросов в цитируемых далее совместных
или личных публикациях. Автор благодарит также Винковскую В. Г. за по¬
мощь при подготовке рукописи к изданию.
В связи с обширностью затронутых вопросов возможны разного
рода неточности в выводах и их толковании. Автор заранее благодарит
читателей за критику и с благодарностью воспримет ее.
*) Как это было сделано недавно К. М. Картвелишвили в его работе «Плане¬
тарная плотностная модель и нормальное поле Земли» (М.: Наука, 1982. — С. 93).
ГЛАВА 1
о ЗАДАЧАХ ТЕОРИИ ПОТЕНЦИАЛА
§ 1. Притяжение точечных объектов
Многие явления природы, хотя и имеющие различную физическую
сущность, объясняются — как это установлено экспериментом и прове¬
рено практикой — наличием сил, действующих между точечными объек¬
тами обратно пропорционально квадрату расстояния между ними. Это
отражено фундаментальными законами физики, в соответствии с кото¬
рыми сила F взаимодействия (притяжения или отталкивания) двух
точечных объектов выражается известной формулой
т] т2
F = —С —-у— г • (1.1)
Г
Здесь г — расстояние между точками Q и Р (r=QP=rr°) у в которых
находятся эти объекты с обильностями mi и тг соответственно, причем
для закона Ньютона (тр>0, /=1, 2) — это массы объектов — материаль¬
ных точек, для закона Кулона — это точечные электрические или магнит¬
ные [51, 175, 40, 52] заряды (и тогда m—q^O). Коэффициент пропор¬
циональности С в каждом из трех указанных случаев имеет свой смысл,
а вообще, он зависит от свойств среды, в которой расположены действую¬
щие друг на друга объекты, и от выбранной системы единиц. В случае
закона всемирного тяготения, например, C=G — это гравитационная
постоянная, числовое значение которой по современным определениям
и в соответствии с рекомендациями МГГС [210] составляет
<7=6,672 • 1СГ8 см3 • г“' • с-2. (1.2)
Далее будем следовать, по крайней мере в первых главах, традиции
математической теории потенциала, в которой принято С= 1. Как известно
[40], такое соглашение не претендует на установление «сверхабсолют -
ной» системы единиц механических величин, в которой вместо трех было
бы только две основных единицы (длины и времени), так как принятие
0= 1 привело бы к тому, что размерность силы по (1.1) равнялась
бы размерности квадрата массы, деленной на квадрат размерности длины,
а единица массы в соответствии со вторым законом Ньютона равнялась бы
1 см3/с2, что противоречит действующей системе, по которой эта единица
есть
‘ ^ = 1)5.10* г.
7
Принятие С= 1 делается исключительно для упрощения письма при
теоретических выкладках; при применении их результатов к конкретным
физическим объектам в соответствующие формулы вводится множителем
соответствующий размерный коэффициент С.
Под точечными объектами понимаются объекты природы, имеющие
конкретные конечные размеры, но такие, что диаметр любого из них
во много-много раз меньше расстояния между ними.
Всякий такой точечный объект обильности т, расположенный в фикси¬
рованной точке Q(£, т], 5), создает в окружающем ее пространстве
центральное поле своего действия (так как F ||г), обычно характеризуе¬
мое в любой его точке Р (*, у, z) вектором напряженности f, т. е. силой
действия поля на единичную положительную массу (или единичный
положительный заряд), находящуюся в этой точке:
f = -^ Г0 (г2 = (X.- If +(у- Г!)2 + (2 - С)2), (1.3)
Г
или, несколько строже,
HP)=-^r°QP. (1.3а)
Г QP
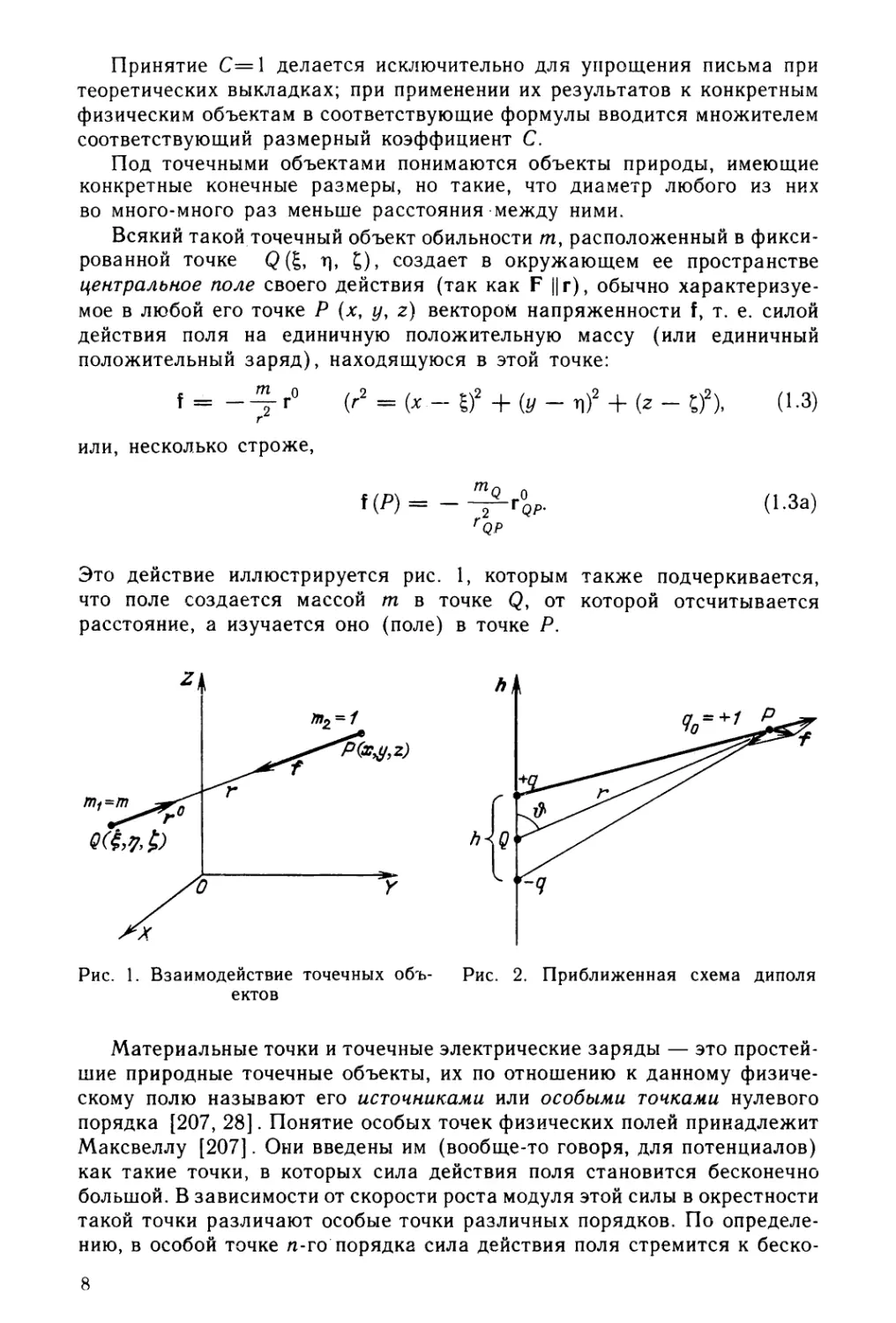
Это действие иллюстрируется рис. 1, которым также подчеркивается,
что поле создается массой m в точке Q, от которой отсчитывается
расстояние, а изучается оно (поле) в точке Р.
Материальные точки и точечные электрические заряды — это простей¬
шие природные точечные объекты, их по отношению к данному физиче¬
скому полю называют его источниками или особыми точками нулевого
порядка [207, 28]. Понятие особых точек физических полей принадлежит
Максвеллу [207]. Они введены им (вообще-то говоря, для потенциалов)
как такие точки, в которых сила действия поля становится бесконечно
большой. В зависимости от скорости роста модуля этой силы в окрестности
такой точки различают особые точки различных порядков. По определе¬
нию, в особой точке n-го порядка сила действия поля стремится к беско¬
8
нечности пропорционально 1 /гп+2 (г — расстояние, отсчитываемое от этой
точки).
Рассмотрим свойственные природе особые точки первого порядка —
диполи (дублеты). Приближенная конструкция диполя (рис. 2) —это
совокупность двух одинаковых по абсолютной величине, но разных по
знаку ( + <7 и —q) электрических (или магнитных) зарядов, отстоящих
друг от друга на малое расстояние /i<Cr. А диполь как точечный объект
(в точке Q) —это такое предельное положение этих зарядов при их
сближении по оси /г, когда Л-М3, a оо, но так, что
Iim /i<7=const=Mi; (1.4)
при этом h может стремиться к нулю произвольным образом: либо оба
заряда навстречу друг другу, либо любой из них к другому, либо еще
каким-либо способом. Скалярная величина М\ называется моментом
диполя, а ось h — осью диполя; ось всегда задается направлением
от отрицательного заряда в приближенной конструкции диполя к ее
положительному заряду.
Вектор Mi = Mih° называется векторным моментом диполя. Очевидно,
что можно полагать Mi = ^h, где под h понимается вектор с модулем,
равным расстоянию между зарядами в приближенной схеме диполя,
и q и h выбраны удовлетворяющими условию (1.4).
Каждый из зарядов приближенной конструкции диполя действует на
пробный заряд <7о= + 1, помещенный в произвольную точку Р, по «закону
обратных квадратов», а их совокупное действие, выражаемое вектором
напряженности f, находится в соответствии с (1.3) и дается формулой
3(МР г)г М,
* = г- о-5)
г6 Г
В сферической системе координат с ее центром в диполе (или в сере¬
дине приближенной конструкции диполя) и с полярной осью, совпадаю¬
щей с осью h диполя, составляющие вектора напряженности суть
2М, cos О Af, sin О
k = —7—- \з • ^ = 0' С-5а)
где Ф — полярное расстояние, Я — долгота, а модуль вектора напряжен¬
ности равен
М
f = -J-У1 + 3 cos2 (1.56)
Из последних формул, приведенных здесь с точностью до размерного
множителя, легко следуют основные свойства диполя как притягивающего
(и отталкивающего) объекта.
Во-первых, диполь (хотя он и составлен из точечных объектов, каждый
из которых действует на пробный заряд обратно пропорционально
квадрату расстояния) воздействует на пробный заряд обратно пропор¬
ционально кубу расстояния; сила его действия везде вне диполя имеет
конечное значение, исчезающее на бесконечности; сам диполь является
особой точкой создаваемого им поля, т. е. особой точкой (или полюсом)
9
первого порядка. Далее (в § 6) будут рассмотрены точечные объекты,
действующие на пробный заряд (или массу) обратно пропорционально
любой целой степени расстояния.
Во-вторых, поле диполя — нецентральное: f || г лишь тогда, когда
пробный заряд находится на оси диполя.
Центральные поля притяжения (отталкивания) создаются точечными
объектами нулевого порядка — материальными точками и точечными
зарядами. Однако имеются и протяженные объекты с центральными
полями притяжения: это тела шарообразной формы, распределение масс
или зарядов в которых зависит только от их удаления от центров этих тел,
являясь непрерывной или даже кусочно-непрерывной функцией. Значит,
притяжение таких тел происходит так же, как и материальных точек —
центров, в которые стянуты массы тел. Последний факт был установлен
еще Ньютоном, что и явилось затем основой создания теории движения
планет Солнечной системы.
Если притяжение рассмотренных простейших точечных объектов
легко поддается расчету, то качественное изучение и числовой подсчет
притяжения протяженных объектов и тел конечных размеров оказываются
технически более трудными и требуют привлечения теории потенциала,
которая возникла именно при решении подобных задач.
Вспомним, что скалярным потенциалом V(х, у, z) заданного в области
Q вектора F=/rJci+/r|/j+/7zk является такая функция, градиент которой
в любой точке Q совпадает с этим вектором: gradl/=F, т. е.
dL- F - F
дх х’ ду у’ dz z'
Вводимая так потенциальная функция позволяет заменить изучение
векторного поля F(x, у, z) изучением скалярного поля V (х, у, z), причем
для приложений важно, что производная потенциала по любому направ¬
лению s выражает составляющую вектора F по этому направлению:
dV/ds=Fs.
§ 2. Основные виды ньютоновских потенциалов притяжения
Классическими типами потенциалов притяжения являются точечный,
объемный и потенциалы слоев — простого и двойного. Напомним их
определения и приведем в описательном порядке их основные свойства,
следуя в основном [40, 143, 59, 50].
Точенным потенциалом V (Р) называют потенциал напряженности
в точке Р(х, у, z) поля притяжения, развиваемого в пространстве по
закону всемирного тяготения материальной точкой массы т, находящейся
в точке Q(xy уу z) (см. рис. 1),
V(P) = V(jc, yt z) = m/r. (1.6)
Здесь, как и раньше, расстояние г отсчитывается от точки Q: г=
= У (х—£)2+ (у—ti)2+ (z—t)'1.
На бесконечности (г->-оо) потенциал равен нулю. Точка Q (источник
поля) является особой точкой поля, и в ней потенциал V неопределен.
10
Во всем пространстве, кроме точки Q, потенциальная функция непрерыв- .
ная, гармоническая (Л1/=0) и имеет таковые же производные всех
порядков.
физический смысл потенциала (1.6) зключается в том, что в любой
точке Р пространства функция V (Р) означает работу, которую надо
совершить против сил поля, чтобы единичную массу перенести из данной
точки поля в бесконечность.
Потенциалом объемных масс (объемным потенциалом) называют
интеграл вида
V(x, у, z) = + л’ 9 d\ А1 di, (1.7)
х QP
или короче
(1-7а)
т т
где т — область, ограниченная поверхностью о и заполненная веществом
с плотностью 6; r=rQP — расстояние между точкой Q(£, т), £) 6 т+а
и точкой Р(х, у, z). Если Р£ т, то потенциал (1.7) является внутренним
потенциалом (К,), точнее, потенциалом на внутреннюю точку, если
Р £ т, то внешним (Ке). Двусторонняя поверхность а предполагается
поверхностью Ляпунова (определение этих поверхностей см. в [59, 143,
50, 157] ; к ним относятся, в частности, поверхности с непрерывной
кривизной). Плотность б предполагается либо принадлежащей классу
С^+а, либо кусочно-непрерывной: б £ Ц\ в точках непрерывности б=
=dm/dT.
Потенциальная функция V=V (х, у, г) задается при помощи тройного
интеграла (1.7), зависящего от координат точки Р (х, у, z) как параметров.
В случае внутреннего потенциала Vx этот интеграл является несобствен¬
ным: в любой точке Р g т подынтегральная функция, точнее 1/г, обра¬
щается в бесконечность. Однако, если плотность б есть функция, ограни¬
ченная в (т+а), то объемный потенциал — функция, непрерывная во всем
пространстве и регулярная на бесконечности, т. е. рИш V=0 и р ^ =(^
где р — радиус-вектор точки Р от произвольного начала; другими сло¬
вами, при удалении притягиваемой точки в бесконечность объемный
потенциал стремится к нулю не менее быстро, нежели 1/р.
Объемный потенциал допускает оценку. Потенциал любого объема
и в любой точке меньше, чем потенциал сферы равного объема на ее центр:
V(P) <2лбнаиб Я2,
где R — радиус сферы, равновеликой по объему телу т.
Если плотность 66СТ+(Р то первые производные объемного потен¬
циала V=V(xy у, z) непрерывны; они вычисляются дифференцированием
подынтегральной функции под знаком интеграла (1.7); поэтому проекции
силы ньютоновского притяжения при переходе через поверхность а
притягивающего тела не испытывают разрыва.
Вторые производные объемного потенциала тела, плотность которого
удовлетворяет условию Гёльдера—Липшица, непрерывны как вне, так
11
и внутри тела, однако испытывают скачок при переходе через его
поверхность. Внешний потенциал удовлетворяет уравнению Лапласа
ДУе=0, т. е. в любой замкнутой области вне тела является гармонической
функцией (значит, имеет там непрерывные частные производные всех
порядков); внутренний — уравнению Пуассона AV'i =—4лб.
Для объемного потенциала интегралы от произведения плотности
тела б на любую гармоническую функцию Н внутри а выражаются
через значения потенциала и его нормальной производной на поверх¬
ности а:
5""---'£-)*■
т а 4 '
Такие интегралы (по объему тела т) называются стоксовыми постоянными
данного тела. В частности, при Н= 1 имеет место формула Гаусса
— 4дМ = \ do,
on
о
выражающая массу М тела через значение нормальной производной его
потенциала на ограничивающей тело поверхности.
Потенциал простого слоя — это поверхностный интеграл вида
= (1.8)
ст
где r=rQpy причем Q(£, т], £) 6 (т, а точка Р (х, у, z) может занимать
в пространстве любое положение. Здесь |ы= |la (Q) —плотность поверх¬
ностного распределения масс на а.
Потенциал У'=У/(х, у, г) простого слоя непрерывной плотности р,
расположенного на поверхности Ляпунова а, — это функция, ограничен¬
ная и непрерывная во всем пространстве вне слоя. Она является гармони¬
ческой функцией (значит, имеет непрерывные производные любых поряд¬
ков) , регулярной на бесконечности. Хотя 1 /г в каждой точке поверхности с
обращается в бесконечность, этот потенциал имеет конечное значение.
Для потенциалов слоев и их производных различают прямые значения,
т. е. те, которые они имеют на слое, и предельные значения, т. е. те,
которые они принимают при приближении к слою с одной или другой
стороны. Прямые значения потенциала простого слоя равны его предель¬
ным значениям.
Производные первого порядка потенциала простого слоя с непрерыв¬
ной плотностью, расположенного на замкнутой поверхности Ляпунова а,
непрерывны как вне а, так и внутри нее; однако при пересечении слоя они
претерпевают разрыв. При переходе из внутренней области во внешнюю
нормальная производная получает приращение, равное 4л,и0 (и-о — плот¬
ность слоя в точке пересечения поверхности). Прямое значение нормаль¬
ной производной потенциала простого слоя равно среднеарифметическому
из ее двух предельных значений (по внешней и по внутренней нормалям).
Двойным слоем обычно называют предельное положение (при h-+-0)
двух простых слоев, расположенных на параллельных поверхностях
(на расстоянии h по нормали п между ними) и несущих в соответствующих
точках электрические заряды, одинаковые по абсолютной величине, но
12
противоположные по знаку. При этом полагают, что при величины
зарядов |^|-^оо, но так, что lirn/i^=const=v. Величину v называют
моментом (или плотностью) двойного слоя. Потенциал двойного слоя
выражается любой из следующих трех формул:
о ' '
V"{P) = \v^do, (1.96)
а г
уЧР) = JL[ VC0S^ У-do + 4-[ VC0-S{y' n)-do + М JVCOS_(z, _tl)_
v 1 dx J r dy J г dt J г
а а о
(1.9в)
в которых п — нормаль к поверхности а, выбираемая так, что стрелка
ее положительного направления находится с той стороны поверхности о,
на которой расположены положительные заряды; r=rQP) Q(£, r\, £) 6а,
a Р(х, у, z) — любая точка пространства; <р — угол между положитель¬
ным направлением нормали п к поверхности о и прямой QP.
В формуле (1.96)da— это элементарный угол «видимости»
элемента do поверхности из точки Р. Формула (1.9в) представляет
потенциал двойного слоя V" в виде суммы проекций на оси координат
сил притяжения трех простых слоев (каждый на а) с плотностями
vcos(*, n), v cos (г/, n), v cos (z, п) соответственно (или первых производ¬
ных по координатам потенциалов этих трех слоев).
Двойной слой можно также называть дипольным слоем, так как иногда
его определяют (см., например, [50]) как такой слой на а, притягиваю¬
щими элементами которого являются диполи с переменным моментом v,
сплошным образом расположенные на поверхности а.
В любой точке Р пространства вне поверхности а, на которой находится
двойной слой и которая предполагается поверхностью Ляпунова, потен¬
циал V" этого слоя имеет определенное и конечное значение, изменяю¬
щееся непрерывно при перемещении этой точки, если только она не попа¬
дает на сам слой. Всюду вне слоя этот потенциал гармоничен
(значит, имеет непрерывные производные всех порядков, также являю¬
щиеся гармоническими функциями) и регулярен на бесконечности, где
он стремится к нулю не менее быстро, чем 1 /р2.
При переходе притягиваемой точки Р через слой потенциал V" слоя
претерпевает разрыв: его прямое значение не совпадает с предельными;
скачок потенциала (в случае слоя на замкнутой поверхности) равен
4jiv, а его прямое значение есть среднеарифметическое из двух предель¬
ных.
Отметим теперь наиболее важные свойства, общие для всех потен¬
циалов V, V\ V".
Все они — гармонические функции вне порождающих их притягиваю¬
щих образований и регулярные на бесконечности.
13
Каждый из них во внешней точке может быть представлен фундамен¬
тальной формулой Грина*)
выражающей, в частности, объемный потенциал тела т суммой потенциа¬
лов простого и двойного слоев, расположенных на поверхности о этого
тела. При применении этой формулы к потенциалам К' и V" слоев
на замкнутых поверхностях под знаком интеграла по о должны фигуриро¬
вать предельное «внешнее» значение нормальной производной (для слу¬
чая потенциала Vfe простого слоя) и предельное «внешнее» значение потен¬
циала V" (для случая двойного слоя, когда должна еще существовать
его нормальная производная [143]),
Любой из потенциалов (точечный, объемный и потенциал слоев)
как функция трех переменных наглядно изображается семейством
уровенных (эквипотенциальных) поверхностей
причем расстояние dn между близкими уровенными поверхностями
обратно пропорционально модулю градиента потенциала, т. е. модулю
силы действия поля,
Приращение каждого из рассмотренных потенциалов {V в— У а) пРи
переходе из точки А, лежащей на уровенной поверхности V=const= VA,
к точке В на уровенной поверхности l/=const= VBy выражает с обратным
знаком работу, совершаемую силами поля при переносе единичной массы
(положительного заряда) из точки А в точку В, и не зависит от пути
этого переноса (поле потенциальное!).
С понятием потенциала сил притяжения тесно связано понятие
потенциала тела самого на себя. Это частный случай потенциала сил
взаимного ньютоновского притяжения двух тел конечных размеров
(каждое из которых может быть трех-, двух-, одномерным с непрерывной
или интегрируемой плотностью) [163, 31], соответствующий тождествен¬
ности притягивающихся тел. Потенциал трехмерного тела т с плотностью б
самого на себя — это шестикратный интеграл
*) Здесь выписан частный случай фундаментальной формулы Грина. В более
общем виде она дает интегральное изображение произвольной правильной (т. е. ко¬
нечной, однозначной и непрерывной вместе со всеми своими производными первых
двух порядков внутри области и на ее границе а) функции суммой потенциалов
слоев (1.10) и объемного потенциала с плотностью, пропорциональной лапласиану
представляемой функции.
V (ху уу z) =const,
dV
I grad V\
14
выражающий гравитационную (потенциальную) энергию Э тела [40, 143]
Э=-П = 6Vdz, (1.11)
т
где V — его объемный потенциал.
Механический смысл гравитационной энергии тела в том, что она равна
работе (с обратным знаком), которую надо совершить, чтобы все рассеян¬
ные в бесконечности частицы данного тела перенести в имеющуюся
конфигурацию этого тела. С точностью до постоянного множителя энергия
выражается также известным интегралом Дирихле [40].
Ляпунов [59] показал, что при заданном объеме тел постоянной
плотности потенциал тела на себя П максимален для шара. Лихтен¬
штейн [57] распространил этот результат на более общий случай: среди
всех конфигураций заданного объема т неоднородной жидкости (с анали¬
тическими и регулярными границами раздела заданных подобъемов с
постоянными значениями плотности) минимум энергии Э достигается при
сферически-симметричном распределении масс жидкости.
§ 3. Разложение внешних потенциалов
в ряды шаровых функций
Приведем сначала лапласово представление [40, 31, 50] объемного
потенциала (1.7), развиваемого телом т переменной плотности 6. Отнеся
пространство к полярной системе координат (р, О, Я), начало которой
находится внутри т, запишем
к,р.«, ц й<>-
т
где dx=p/2sinft'd'0/dA/dp'. Будем считать, что точка Р находится вне
P(/>AV
Рис. 3. К разложению объемного потенциала в ряд
сферы S радиуса R, объемлющей тело т (рис. 3). Тогда р>р' и Л=р'/р<1.
Поэтому обратное расстояние разлагается в абсолютно и равномерно
15
сходящийся ряд по переменной h:
_1_ 1 = 1 =
r Vp2 + р'2 — 2рр' cos t р(1 —2h cosij) + /I2) /2
oo
= £ "+т P»(cos T|i),
n = 0 P
в котором Pn (cos ф) —полином Лежандра (0^ф<1л).
Используя это разложение, имеем
<30
V(p, О, X) = £ Уя(0, X), (1.12)
л = О Р
где
Г„(«, Х) = $6(р', в', X')p'nPn(cosTp)do
т
— так называемые «игреки» Лапласа, сферические функции входящих
в Prt(cos ф) переменных ft, Я, заданных посредством соотношения
cos ф=соэ # cosft'+sinft sin O' cos (A,—V). (1*13)
Ряд (1.12) является сходящимся всюду вне сферы S. С учетом
теоремы сложения многочленов Лежандра функции Лапласа имеют вид
п
Yn(®. *■) = X cos тХ + Snm sin тХ)Р™ (cos &), (1.14)
т = О
а коэффициенты при элементарных шаровых гармониках
—— Pm(cos cos тк
рЛ+1 гп sin тХ
в разложении потенциала (1.12) суть
У - S • *. <||5>
с ПО = 5 6p,nPn(cos O') dx, Sn о = 0.
Т
Эти величины являются стоксовыми постоянными тела т, зависящими от
его формы и строения — конкретно, от плотности б. Стоксовы постоянные
низших порядков имеют простой механический смысл: постоянная
нулевого порядка выражает массу тела, постоянные первого порядка
определяют положение центра масс (центра инерции) тела относительно
используемой системы координат, стоксовы постоянные второго порядка
описывают эллипсоид инерции тела.
Любое п-е слагаемое ряда (1.12), т. е.
Vn(Р- о. Ь) = -^ТГ/„(<►. V’ (1Л6)
16
называется [50] для данного тела т его потенциалом м-го порядка.
Каждый из таких потенциалов — это шаровая функция соответствующего
порядка, а значит, и гармоническая вне а. Потенциалы нулевого и
первого порядков — это потенциал материальной точки в начале коорди¬
нат с массой, равной массе М тела, и потенциал диполя, находящегося
в начале координат. Потенциалы более высоких порядков также имеют
смысл потенциалов точечных объектов, но более сложной структуры
(им посвящен § 6).
Аналогично разложим в ряд шаровых функций потенциал простого
слоя (1.8), полагая поверхность а, несущую слой, ограниченной: она
может быть замкнутой или незамкнутой [88]. Окружив слой объемлющей
сферой S радиуса /?, примем ее центр за начало системы координат
и по использованной уже схеме получим
V'(P) = \ %), (1.17)
о п = 0 Р
где
п
У'Л’Э'. *0 = X {Cam C°S ml + Sfnm Sin mk) Р” (COS '9'),
m = О
причем постоянные слоя выражаются интегралами по поверхности о:
£"} (ив)
' о
С'о — \ w'nPn(cos ft') do, S*„о = 0.
a
При вычислении этих интегралов должен быть принят во внимание
либо способ задания поверхности а, например, ее уравнение вида
p=f (ft, к), либо какие-либо иные
характеристические свойства по¬
верхности слоя, позволяющие
выполнить их подсчет.
Разложим потенциал V"
двойного слоя (1.9) в ряд шаро¬
вых функций для частного слу¬
чая [93], в котором слой пред¬
полагается плоским, занимаю¬
щим ограниченную часть о
плоскости (рис. 4).
Принимая плоскость слоя за
координатную плоскость ху, по¬
местим ее начало О в некото¬
рую точку, принадлежащую
слою, а ось г направим по пер¬
пендикуляру к нему. За положительное направление нормали п к слою
примем отрицательное направление оси г. Тогда потенциал такого слоя
Рис. 4. К разложению в ряд потенциала
плоского двойного слоя
17
примет вид [143]
уЧР) = \ *■>** , з- = j ^dcQ, (1.19)
о (V(JC — I)2 + (у — Tl)2 + г2) a rQP
где zP= ppcos rQP = / p2 + p/S — 2pp'cos ф = p (1 — 2h cos ф + /г2) 1/2.
Описав из начала системы координат в плоскости ху окружность радиуса
/?=Рнаиб+е (е>0 — сколь угодно малая величина), будем искать разло¬
жение V" (Р) в ряд шаровых функций во всем пространстве, внешнем
относительно круга S. В таком случае h=р'/р<3-
Из выражения (1.19) потенциала V" следует, что во всех точках
плоскости Оху вне слоя V" (ху у, 0)=0. Значит, можно считать, что угол ф
принадлежит открытому промежутку (0, 2л), поэтому случаи выполнения
равенств ф=0 и ф=2л могут быть исключены из рассмотрения.
Для получения нужного представления потенциала V" (Р) разложим
1 /rQp в ряд по степеням /?=р'/р- С этой целью вспомним [20, 140, 160]
производящую функцию полиномов Гегенбауэра:
оо
(1 — 2h cos ф + h2)~k = £ Сп(cos ф)/гл;
п = о
степенной ряд в ее разложении является абсолютно сходящимся при
А<1. Значит, в данном случае
V"(P) = -Ц ZpvQ С3/2(cos
и при этом допустимо интегрирование присутствующего здесь ряда.
Но сначала обратимся к теореме сложения многочленов Гегенбауэра,
записав ее при 6=3/2 и 0'=л/2,
СТ (costy) = C3n/2 (cosO cosO'+sinO sinO'cos (X—У)) =
ft n
= У Т + 1 (От + 1) (п - т)! i,(3/ sinmft X
+ m + 1
X ^1+1"(cos О) ■ СТ-1 m(0) C'„(cos (X - V));
т = 0
при ЭТОМ
f
г 0 при i нечетном,
СУ2 + «(0) = { ( _ ! )-/2 (3/2) (* )
1^2)!— ПРИ ' ЧеТН0М-
18
Проинтегрировав почленно ряд, которым выражен теперь потенциал
двойного слоя, получим
, Л 2m + 1(m + 1)(« - m)![(3/2)J2
V" sec ft = I -TPY ^
r (2)n + m + 1
n = 0 m = 0
X
XC7-^m(0)sinmftC^+m(cosft)$v(i, л)р,пС1,(со8(Х-Ь'))<*а. (1.20)
a
Займемся входящими сюда интегралами
/(tm = $vp'"Cil(cos (*-*')) da.
a
Выпишем суммы [20], определяющие Clm (cosy), где у—Х—Х'\
т т
Cj„(cosy)= У cos [(т —2£)у] = ^ cos [(т — 2k)k] cos [(т — 2&)A/] +
6 = 0
т
+ ^ sin [(т — 2fc)X]sin [(т — 2fc)A/].
6=0 6=0
6 = 0
Значит,
Л.т = \ «пт* COS [(п — 2ft) X,] + £ Ьnmk Sin [{т — 2ft)Ц
■ " ' 6 = 0
1 = 0.21)
6 = 0
где
bnmk I
Обозначив еще
2т+‘(т+1)(п-т)![(3/2у2 •/,+„
Мпт = — Ln-m ' ' ’ (1.22)
V /п + т+ 1
запишем
V" sec ft = £ £ М„т sinm ft X
п = 0 ^ т = 0
з ( 'т т Л
X c/i^m (cos ft) J £ a„m* cos [(m - 2ft)X.] + Y sin [(m — 2ft)X,] I.
I 6 = 0 6 = 0 I
Перейдем в последней формуле от полиномов Гегенбауэра к присое¬
диненным функциям Лежандра на основании известной связи между
ними [160]
siny О • С[ i ! (cos О) ——— Р\(cos •0').
' 2У(! /2)у Л
19
И тогда после очевидных преобразований получим
оо п
V" = ctgO £ £ NnmKt\{COSO) X
т = О
где обозначено
т т \
Y, C0S КОТ ~ + У bnmk sin [(т - ЩЦ L
k = О k = о I
= Afram/[2m + 1 (1 /2)т + , ]. (1.23)
Рекуррентная формула [140] для присоединенных функций Лежандра
с одинаковым нижним индексом
Pqp + 2(x) + 2(q + 1 )—jJL=-Pg+i(x) + (р - q)(p + q + 1 )Pq{x) = 0
Д/1 - x2
позволяет написать
ctgft- KXl (cos 0) = -Ss— m + l)>±-". +-2i p:+ ,(cos 0) -
„ . -2(^+l) P"+'2(COsd)-
Используя эту формулу, имеем ’
оо п
'"~v“ ">• »•I 7^ Z (-^тту)
я = О r m = О 4 7
у"=1/" (Р> о, х)= > —^ 2, * х
m = О
X [(и — от + l)(n + m + 2)Р”+,(cos #) + P?+i2(cosfl)] X
X
£ cos К™ - + £ &nm* sin [(m - 2*)Я] I. (1.24)
Получив такое представление потенциала V" двойного слоя, заметим,
что его искомое разложение по шаровым функциям должно иметь вид
= z
— рр+1 ’
Р=1р
где Ур=Ур(д, X) — сферические функции р-го порядка. В таком представ¬
лении V" в отличие от разложений объемного потенциала и потенциала
простого слоя, в которых суммирование начинается с р=0, первым
членом разложения является У\/р2, что связано с поведением V" на
бесконечности, где, как было отмечено в § 2, потенциал двойного слоя
убывает пропорционально 1/р2. Из выражения V" (1.24) видно, что оно
удовлетворяет этому условию. Значит, входящие в (1.24) суммы
X) = Yj (•••)[•• •]{•••} Должны быть сферическими функциями
т = О
(я+1)-го порядка. Однако, не постулируя этого, разложим каждую из
20
этих сумм по элементарным сферическим гармоникам, что, с одной
стороны, подтвердит это положение, а с другой — даст явное выражение
указанных функций, чем и будет завершено получение искомого разложе¬
ния потенциала V" по шаровым функциям.
При разложении fn (Ф, X) по элементарным сферическим функциям
получим
ОО I
где
£ £ (atj cos j'k + р,7 sin jX)P\ (cos 0) = Yn + , (d, %),
i = 0/ = 0
2 i + 1
4л
5 X)P,(cosd)aco, pi0 = 0.
За счет ортогональности сферических функций на единичной сфере о
все ац и рц равны нулю, кроме
(О
Г Dm /„ „„ ОЛ12 f ^nmO^OS tTlX ,
X [Рп + 1 (cos Ф)] |6nm0sin2m)v -^.
i (_ Hr) (n + 2) + l (cos *)]4oo d<»>
_ 2n + 3
a/ = n+i,o 4л
откуда
7i -f 1, m I is I &nm0>
>n+ 1. m J | bnm0
при
(я + m + 2)!
2(m +1) (л — m)!
Таким образом, получим
п + 1
Yn + , (Ф, X) = £ cos sin 1 (cos О),
m = О
где
fc-KH'*'- *** 43?:$* »•*>
И
X = (!L+m + Vl |7А \ Г СТ + т(0)
2(1/2)т+1(2)я + (в + 1 С"-'" (0)-
Заметим, кстати, что выполненный расчет аннулировал отдельное вычис¬
21
ление а,, + 1о, и коэффициенты ап0 определяются первой формулой (1.25)
с учетом Кпт по последней из приведенных формул при т=0.
Перед тем как подставлять полученное выражение сферических функ-
.. ций Гп+1 в разложение (1.24), вспомним формулу (*) на с. 18, вследствие
которой ряд членов этого разложения обратится в нуль, именно в искомом
ряде будут отсутствовать все члены, содержащие КптУ а значит, и
(0) при нечетных разностях индексов п — т. По этой причине
разложение V" не будет содержать секториальных гармоник (ибо
Кп п+1 = 0), поэтому исследуемое представление потенциала двойного
слоя может быть записано в виде
оо п
V"(p)= £ —i-у £ Клт{апт cos тК + bnm sin mk) Рл + , (cos Q), (1.26)
n = 0 ^ m = 0
где
<■*>
Коэффициенты ряда (1.26) Knmanm и Knmbnm, выражаемые форму¬
лами (1.25) и (1.27), зависят от формы двойного слоя и его плотности; они
аналогичны стоксовым постоянным в ряде для объемного потенциала.
§ 4. Задачи теории потенциала
Появление теории потенциала обязано введенному Лагранжем
в небесную механику *) удобному приему исследования сил, действующих
по закону всемирного тяготения. Ньютон считал, что этим законом
может быть объяснено не только движение небесны^ тел, но и фигура
Земли. Поэтому становление теории потенциала (Лагранж, Лаплас,
Лежандр и др.) происходило параллельно с решением практических
задач астрономии, механики и геодезии, связанных с разработкой теории
движения Луны и планет и теории фигуры Земли.
Затем после фундаментальных работ Гаусса по земному магнетизму
и Грина по электростатике и магнетизму теория потенциала превратилась
в мощный аппарат теоретической физики (методы исследования и интег¬
рирования уравнений эллиптического типа) и математического анализа
(способы представления функций при помощи потенциалов).
Разработка классической теории потенциала как одной -из основных
частей математической физики была завершена в начале нашего века
(Ляпунов, Стеклов, Гюнтер и др.) детальным изучением свойств ньюто¬
новских потенциалов и созданием строгих методов решения основных
краевых задач для уравнений Лапласа и Пуассона.
Теория потенциала интенсивно развивается и в настоящее время;
это вызвано необходимостью обобщений известных результатов, введения
новых видов потенциалов и решения разнообразных задач практики,
*) По меткому выражению Идельсона [40] «учение о потенциале возникло в
тот день (Лагранж, 1773 г.), когда было обнаружено» существование функции,
частные производные которой равны составляющим силы ньютоновского при¬
тяжения по соответствующим осям координат.
22
а также необходимостью углубления и обновления основных понятий
и методов классической теории и создания новых обобщенных направле¬
ний в ней (абстрактная теория потенциала).
Остановимся кратко на основных типах задач теории потенциала,
имеющих большое значение при изучении Земли как планеты.
Прямые задачи теории потенциала. После того как введен потенциал
притягивающего объекта (например, планеты), возникает практическая
задача вычисления его значений в фиксированных точках пространства.
Для объемного потенциала эта так называемая прямая (внешняя или
внутренняя) задача теории потенциала ставится следующим образом:
дано тело т, т. е. дана ограничивающая его поверхность а, и указано
распределение плотности 6 его недр. Требуется вычислить объемный
потенциал (1.7) этого тела
V(P) = \^-drQ
JT rPQ
в какой-то заданной точке Р пространства (внешней или внутренней).
Это обычная задача интегрального исчисления. Однако даже в случае тел
постоянной плотности (6=const) интеграл (1.7) в элементарных функ¬
циях выражается только для некоторых областей т простейшего вида,
например для шара и для эллипсоидов вращения (сжатых или вытяну¬
тых), причем для последних окончательные формулы настолько гро¬
моздки, что неудобны для практических приложений. Интегралы по
объему, выражающие потенциалы однородных трехосных эллипсоидов,
были сведены усилиями классиков либо к интегралам по поверхностям
(формула Гаусса, см. [143]), либо при вычислении внутреннего потен¬
циала— к одномерным интегралам (результаты Лагранжа, Гаусса,
Дирихле, см. [143, 31]); внешние же потенциалы эллипсоидов легко
вычисляются затем на основании внутренних из надлежащим образом
составленных пропорций, следуемых из теорем Лапласа, Айвори и
Маклорена о притяжении эллипсоидов [31]. Приведенные примеры пока¬
зывают, что даже в случае потенциалов простейших областей (а тем
более произвольных) невозможно обойтись при их вычислении без квадра¬
турных или кубатурных формул.
Задача вычисления потенциалов тел заданной формы и известной
плотности важна для поисковой геофизики: если на основании геологиче¬
ских, сейсмических или каких-либо других данных удается определить
положение и форму (хотя бы приближенно) тела — залегания полезного
ископаемого, то, вычислив при некоторой предполагаемой постоянной
плотности его потенциал или производные потенциала на дневной
поверхности, можно найти вклад этого тела в реальное гравитационное
поле Земли, что позволит затем методом подбора найти плотность
исследуемого залегания и уточнить его форму. Для этого в руководствах
по гравиразведке [30, 144] приводятся результаты решения прямой
задачи теории потенциала для областей, соответствующих по форме
наиболее типичным геологическим структурам.
Общим решением внешней прямой задачи теории потенциала для
классических видов последнего может считаться разложение потенциала
в ряд шаровых функций (§ 3), коэффициенты которого легко вычисляются
23
по известным форме и плотности притягивающих образований, причем
точка, в которой вычисляется потенциал, предполагается находящейся
за сферой, объемлющей это образование.
Обратные задачи теории потенциала. Эти задачи очевидным образом
связаны с только что рассмотренными прямыми задачами. В обратных
задачах потенциал считается заданным в некоторой области простран¬
ства, требуется найти форму и плотность тела, его развивающего — это
общая (иногда говорят, смешанная) обратная задача теории потенциала.
Если, кроме потенциала, известной считается также форма тела, то
обратная задача именуется геофизической или (особенно в зарубежной
литературе) гравиметрической: в ней искомой является плотность масс
тела. Если же, кроме потенциала, известна плотность тела (например,
она постоянна) или она просто игнорируется постановкой задачи, то
такая задача является геодезической обратной задачей [230, 85]: в ней
ищется форма тела. Любая из этих задач может быть как внешней,
так и внутренней в зависимости от того, в какой области пространства
(относительно поверхности тела) задан потенциал.
Указанные традиционные обратные задачи теории потенциала имеют
единую аналитическую сущность. Действительно, Исследование любой из
них требует рассмотрения объемного потенциала (1.7). В случае геофизи¬
ческой задачи, когда потенциал V(Р) и поверхность о тела т известны,
это выражение относительно искомой плотности б масс тела является
линейным интегральным уравнением / рода. В случае геодезической .
задачи, т. е. при заданных потенциале V(Р) и плотности б (например,
б = const), выражение (1.7) относительно уравнения поверхности
А,) превращается в нелинейное интегральное уравнение также
I рода.
Основополагающий факт, характеризующий обратные задачи теории
потенциала, — это их некорректность; она обусловлена в основном
неустойчивостью (в классическом смысле) решения описывающих эти
задачи интегральных уравнений I рода. Задачи некорректны по Адамару;
при определенных условиях они могут рассматриваться как условно
корректные, или корректные по Тихонову. Общей теории обратных задач
теории потенциала пока нет. При исследовании и решении какой-нибудь
конкретной обратной задачи, существование решения которой не подле¬
жит сомнению, требуется за счет введения дополнительных условий
доказать теорему единственности решения в принятом классе функций
и теорему его устойчивости относительно малых изменений в исходных
данных, а также разработать алгоритм эффективного построения
устойчивого решения.
Отдельные обратные задачи теории ньютоновского потенциала были
впервые исследованы в математике в 30-е годы: сначала были получены
теоремы единственности для внутренней геодезической (конечно, такой
терминологии тогда не было) задачи [184, 183, 213], затем для внешней
[116]. Была обсуждена устойчивость обратных задач [154]. С 40-х годов
они стали интенсивно проникать в поисковую геофизику (обзор исследо¬
ваний в этой области см. в [148], обширная библиография имеется
также в [36]), а в конце 60-х годов и в геофизику планетарную [35, 74];
некоторая задержка использования их в последней связана, очевидно,
24
с отсутствием до середины 60-х годов необходимой надежной информации
о глобальном гравитационном поле Земли.
Обсуждаемые обратные задачи теории потенциала тесно перепле¬
таются с теорией фигур равновесия вращающейся жидкости, с теорией
фигуры Земли и основной геофизической проблемой изучения внутреннего
строения планеты. Однако, несмотря на полученные там значительные
результаты, исследование и решение обратных задач теории потенциала
по определению формы тела и плотности являются актуальными, так как,
во-первых, дают возможность согласовать параметры внешнего гравита¬
ционного поля с «внутренними» характеристиками тела, его развиваю¬
щего, во-вторых, позволяют найти по результатам наблюдений вне Земли
обобщенную фигуру планеты и в глобальных масштабах модельное
распределение плотности ее недр, и, в-третьих, как следствие они могут
быть затем естественной основой построения региональных и локальных
моделей, что особенно важно в связи с постоянным увеличением наблю¬
дательной информации различных видов.
Ниже будут рассмотрены две указанные традиционные обратные
задачи теории потенциала применительно к планетарной геофизике
и геодезии и будут обсуждены постановка и решение в частных случаях
одной новой — потенциалографической — задачи, важной для космиче¬
ской геодезии и планетарной геодинамики и в частных постановках
уже усиленно разрабатываемой в последнее десятилетие, правда с иных
позиций.
Краевые задачи теории потенциала. Как уже отмечалось, ньютонов¬
ские потенциалы в областях, не содержащих притягивающих масс,
являются гармоническими функциями, т. е. в этих областях они удовлет¬
воряют уравнению Лапласа
а объемный потенциал внутри тела, его создающего, удовлетворяет
уравнению Пуассона
Эти два простейших уравнения с частными производными второго
порядка эллиптического типа часто называют дифференциальными
уравнениями теории потенциала.
Перечислим основные внутренние краевые задачи для них. Первая
краевая задача (задача Дирихле): требуется найти функцию К, которая
внутри области т удовлетворяет уравнению Лапласа (или Пуассона),
непрерывна в области (т+ст) и принимает на ее границе заданные
значения
Вторая краевая задача (задача Неймана): надо найти функцию, непре¬
рывную внутри области и удовлетворяющую там уравнению (1.28) или
(1.29), а на границе области — краевому условию
AV=0,
(1.28)
AV= — 4л6.
(1.29)
v I а = Ф-
(1.30)
(1.31)
25
Если ищется гармоническая функция, то заданная «краевая» функция ф
должна удовлетворять равенству
J ф do = 0. (1-32)
о
Если искомая функция должна удовлетворять уравнению Пуассона, то
функция ф должна удовлетворять дополнительному условию
^ ф do = —4л ^ 6 dx. (1.33)
о т
В третьей краевой задаче краевое условие имеет вид
[*v + Иг], - (| 3,)
где а/р = const >0. Условия (1.32) и (1.33) в этой задаче не являются
необходимыми.
В технике и при изучении стационарных тепловых полей часто иссле¬
дуют и решают также смешанные краевые задачи, в которых на разных
частях краевой поверхности задаются условия различных типов, а для
современной физической геодезии существенна задача с «наклонной»
(«косой») производной.
В теории потенциала основополагающее значение имеют также
внешние краевые задачи для уравнения Лапласа. Краевые условия
в них имеют тот же вид, что и для внутренних задач. Но в случае внешних
задач на искомую в бесконечной области вне о гармоническую функцию
накладывается еще требование ее регулярности на бесконечности.
Преобразование Кельвина позволяет внешние краевые задачи сводить
к внутренним.
Коснемся вопроса разрешимости краевых задач. Для первой и
третьей краевых задач имеют место теоремы единственности. Теоремы же
существования решения и его устойчивости при малых изменениях
краевых данных для этих задач справедливы лишь в таких областях т,
которые ограничены поверхностями а Ляпунова.
В случае внутренней задачи Неймана для уравнения Лапласа,
рассматриваемого в области т, ограниченной поверхностью о Ляпунова,
на которой задана непрерывная функция ф, удовлетворяющая условию
(1.32), решение существует; но оно определено с точностью до произволь¬
ного постоянного, т. е. не единственно. Однако решение будет един¬
ственным и будет непрерывно зависеть от краевой функции ф, если,
во-первых, малые изменения этой функции таковы, что не нарушают
равенства (1.32), и, во-вторых, произвольное постоянное слагаемое,
с точностью до которого определено решение задачи Неймана, выбрано
таким образом, что ее искомое решение на а также удовлетворяет этому
равенству, т. е.
\Vda = 0.
26
Для разрешимости внешней задачи Неймана условие (1.32) не
является необходимым: решение существует при любой непрерывной
функции ф, непрерывно от нее зависит и единственно.
Разработано много методов решения краевых задач теории потенциала
для различных видов областей, они подробно описаны в литературе.
Для теории потенциала и вообще для математической физики наиболее
существенны методы, восходящие к Грину; методы, связанные со сведе¬
нием краевых задач к интегральным уравнениям Фредгольма II рода,
используемые, в частности, в теории фигуры Земли, а также исторически
старейший метод Фурье разделения переменных с последующим использо¬
ванием бесконечных рядов. В следующем параграфе, мы приведем
примеры решения краевых задач для уравнения Лапласа в случае
области с границей в виде эллипсоида вращения последним из перечислен¬
ных методов.
§ 5. Краевые задачи для слабо сжатых эллипсоидов вращения
Построением функций, гармонических внутри эллипсоидов вращения,
по их заданным значениям на границе занимался еще Ламе (1839 г.);
решение внешней задачи дал Гейне (1842 г.). В их исследованиях уже
использовались присоединенные функции Р™ Лежандра первого рода,
распространенные на комплексную область; Гейне при этом ввел функции
Лежандра Q™ второго рода [28]. Рассмотрим решение задач Дирихле
[28, 56] и Неймана для указанных областей, причем подробнее остано¬
вимся на второй, так как ее решения в доступной литературе найти
не удалось.
Сжатый вдоль оси вращения Oz эллипсоид £, описываемый уравне-
X* А-Ц* Z*
нием —-[--у = 1? зададим параметрически:
х = a sin # cos X, у = a sin О sin X, z = b cos Ф ^ ^
(0^0^ л, О X <С 2л);
здесь О — полярное расстояние, X — долгота.
Включим эллипсоид Е в триортогональную систему поверхностей.
Для этого достаточно в (1.35) сделать подстановку
а = с ch г], 6 = cshri, (1.36)
где с — линейный эксцентриситет меридионального эллипса эллипсоида
вращения Е: с2=а2—Ь2. Тогда
х = с ch т] sin # cos X, у = с ch т| sin Ф sin X, z = с sh т) cos ft (1.37)
(Ог^г|<Соо, 0<СО^Сл, 0^Х<2л).
Этими равенствами каждая точка (ху у, z) пространства отнесена
к вырожденным эллипсоидальным координатам т), 0, X. Координатные
поверхности r]=const и ,0,= const суть софокусные эллипсоиды вращения
и гиперболоиды вращения (вокруг оси Oz) соответственно; X=const —
плоскости, проходящие через ось Oz. Через каждую точку пространства
проходит только одна поверхность каждого семейства, причем эти поверх¬
ности системы пересекаются попарно ортогонально.
27
Из формул (1.37), вводя r2=x2+y2-\-z2, имеем
sh г| = -у\/г2 — с2 sin2 Ф, ch х\ = -^д/г2 + с2 cos2 Ф, (1.38)
т. е. sh т| и ch т) возрастают вместе с г, т. е. с удалением точки (х, у, г)
от начала координат.
Эллипсоиду £ приписывается ц = const = г]0, причем th г]0 = Ь/а или
sh т|0 = Ь/с.
В криволинейных координатах т], О, к для областей, ограниченных
координатными поверхностями рассматриваемой триортогональной
системы, переменные в операторе Лапласа разделяются, в результате
чего частными решениями уравнения MJ—0 в таких областях являются
выражения вида [28]
и(пт = K(i sh ц)Рп( cos О) [ 5^^ внутри Е, (1.39)
= QmAi Sh л)С(COS Щ вне E. (1.40)
Здесь n и m^in суть целые неотрицательные числа, /=У —I, Р„ и
Q™ — символы присоединенных функций Лежандра соответственно пер¬
вого и второго рода. При т]->-оо функции Q™ (i sh г\) по модулю стремятся
к нулю.
Значит, общие решения уравнения Лапласа для рассматриваемых об¬
ластей могут быть представлены рядами
и- I Z de;Jiu- °-4|>
п = 0 т = 0 )
с произвольными коэффициентами, либо действительными, либо чисто
мнимыми, но такими, чтобы их произведения на соответствующие Uпт
были действительными.
В связи с предыдущим отметим следующее.
Из определения присоединенных функций первого рода по Гобсону
s4m Р (-у\
Р?(г) = (г2 - 1)т/2—-(1.42)
dz
имеем при z—i sh г]
dmP (i sh г])
p:a sh т|) = chm р (1.43)
d (sh т|)
откуда следует, что функции Р™(/ sh т)) действительны при (п=Ьт)
четном и чисто мнимы при (п±т) нечетном.
Из представления функций Лежандра второго рода при помощи
гипергеометрического ряда
Q”(2) = (-I)V - I)m/2 + ” + 1} x
2 + Г (n + 3/2) zn + m + l
^ n + m + 2 n + m + 1 3. 1 \ ,
Xf{~~2 • 2 ■ " + T* -j)(
JO.44)
28
видно, что в случае z=i sh г\ вещественность функций Q"1 (/ sh rj) не зави¬
сит от т, и они действительны при п нечетном и чисто мнимы при п четном.
Таким образом, коэффициенты рядов (1.41) в случае внутренних
задач должны быть действительны при (п±т) четном и мнимы при
(riztm) нечетном, а в случае внешних задач — действительны при п
нечетном и мнимы при п четном.
Далее, в рассматриваемых областях используемые функции Лежандра
однозначны и ограничены, причем Q™ (i sh ц) обращается в нуль при
т|—>-оо. Последнее следует из формулы (1.44), в которой гипергеометри-
ческий ряд является сходящимся по крайней мере при sh г|> 1.
Переходя к краевым задачам, ограничимся случаем областей внутри
и вне слабо сжатых эллипсоидов вращения Е. Под таковыми будем
понимать эллипсоиды, на которых shr]0^l, что обеспечивает естественную
(т. е. без аналитического продолжения их на более широкую область),
сходимость гипергеометрических рядов, фигурирующих в определении
присоединенных функций Лежандра. Для слабо сжатых эллипсоидов
вращения сжатие а их меридиональных эллипсов не может превосходить
а*= (а—6)/а«0,2929.
Такие эллипсоиды, правда, в другом контексте, фигурировали в [31].
Там показано, что потенциал притяжения таких эллипсоидов, имеющих
специальное неоднородное строение (именно, такое, при котором поверх¬
ности равной плотности есть поверхности вращения вокруг оси вращения
эллипсоида, в частности эллипсоидально слоистое), разлагается в ряд
полиномов Лежандра четных порядков, который является сходящимся
всюду во внешнем пространстве вне фокального шара радиуса с, а не
только вне сферы, объемлющей эллипсоид.
Задача Дирихле. Пусть выражающая краевое условие задачи Дирихле
(1.30) функция ф, предполагаемая на Е абсолютно интегрируемой,
задана своим разложением по сферическим функциям
Ряд (1.45) предполагается при этом равномерно и абсолютно сходящимся
на Е.
Тогда решение внутренней задачи Дирихле для эллипсоида вращения
£, обращающееся на его поверхности в заданную функцию /(Ф, к),
оо
п
(1.45)
п = 0 т = 0
где
с (О, X) = (Апт cos ml + Впт sin mX)P”(cos d) (1.46)
и
:}
2n + l (n — m) !
8m 4л (n + m)!
J /(<K, *')PT(cos<K)£?s sin Г d%!
0 0 1
(1.47)
причем
{
2 при m Ф 0
1 при m — 0; все £„0 = 0.
29
которая удовлетворяет перечисленным условиям, имеет вид
оо п
_ _ m P”(i stlT|)
и(Щ. о, х) = X z 17(0, «т,г (L48)
п = 0 m = О 0 sn
а решение соответствующей внешней задачи есть
U(n, *, d_ £ j с(«, t) . <U9>
Q“(* Sh T!0)
причем эти ряды являются абсолютно сходящимися при r)<Crio и т^Ло
соответственно.
Внешняя задача Неймана. Будем искать вне Е регулярное на беско¬
нечности решение уравнения Лапласа
AU=О,
нормальная производная dU/dv которого на Е обращается в заданную
функцию X):
= /(«,*). 0-50)
(Условия, налагаемые на эту функцию, сформулируем ниже. Внешнюю
нормаль к координатным поверхностям ri=const обозначаем через v.)
Решение задачи будем представлять рядом (1.41), в котором Uпт
выражаются формулой (1.40), т. е. будем искать функцию
U= I X /Н Qnm(''sh^)P™(cosd){
п = 0 т = 0 пт) 1
cos тХ, (1.51)
sin тХ, v ’
точнее, значения ее коэффициентов Dnm и £лт, которые обеспечивают
удовлетворение этой функции краевому условию (1.50).
Производная по нормали v к поверхности r]=const от частных решений
(1.40) имеет вид [28]
_д_
dv
[«: (i .ь ч) f? (cos ♦) {5?ns ] -
= cos /V» (rn* Л) 1 dQ^jish Ti)
sin mXj n' ' л/—2 „ , 12 dr\ ■ ^ '
’ с у cos О -f- sh T| 1
А используя представление Гобсона функций Лежандра второго рода
Q:(z) = (z2- (1.53)
dz
получим
dQn& _/J8 ivn/2f ^ <?„(*) , mz dmQn(z)
dz1
to -(«’-'И i: i ^
(функции P™(z) и Qn(z) определены на всей 2-плоскости, кроме разреза
30
по действительной оси от — оо до 1), что при z=i sh rj позволяет вычис¬
лить производную в (1.52); в результате находим
|г[«<.>м)р:(со5<ч(“5™‘]_
[q: + 1 (i sh т|) + т th л Qn (i sh л) ] { ^ (1-55)
cVcos2 О + sh2 T|
Таким образом, нормальная производная искомого решения имеет вид
— = 1 у у М х
dv сУcos2 О + sh2 л п = 0т = о Епт)
X [Qn + ' (i sh л) + т th л-Q? (i sh ц)]Р?(cos в) { jj; (1.56)
В отличие от решения первой краевой задачи, в которой ее краевое
условие представляется рядом по сферическим функциям, здесь прихо¬
дится брать разложение по последним следующей вспомогательной
функции:
F{&, X) = У a2 cos2 О + 62 sin2 О / (Ф, X). (1.57)
Решение имеет вид (1.45) — (1-47). При этом предполагается, что
функция /(Ф, А,) такова, что разложение в ряд сферических функций
соответствующей ей вспомогательной функции А,) является сходя¬
щимся равномерно и абсолютно. Используя это разложение, запишем
,(в' ч'+„‘ Ч К (158)
Va cos ft + b Sin ft П = 0 пг = 0 пт )
Сравнивая теперь-^- | £, следуемое из (1.56) при ti=tio с краевым
условием в виде (1.58), находим коэффициенты искомого решения задачи
°пт \ = — ? / Апт, (1.59)
Епт ) a(?n (/sh Ло) + mbQ™{ish Т]0) I Впт>
которые, как видно из их структуры, действительны при п нечетном
и чисто мнимы при п четном; значит, все слагаемые ряда (1.51) действи¬
тельны. Подчеркнем, что в (1.59) Апт и Впт суть коэффициенты разло¬
жения по сферическим гармоникам вспомогательной функции (1.57).
Заметим, что теперь нормальную производную решения можно пред¬
ставить так:
дУ _ 1
с Ус os2 О + sh2 т|
X у у Апт\ + ‘ sh л) + m th л Q„ (t sh л)] pm , /cos ml, (1.60)
» = [Q” + ,(ishr)0) + mth4oQ7(/shtio)] * IsinmX,
31
откуда, кстати, при т] = г|о легко усматривается выполнение краевого
условия (1.50).
Учитывая ограниченность th r\ (lim th т]=1) и принимая во внимание
Г|->оо
известное неравенство из [28]
ряд (1.58) можно считать при наложенных выше условиях на функцию
/(О, X) при разложении вспомогательной функции F($y X) в ряд сфериче¬
ских гармоник мажорантным рядом для (1.60), что позволяет констати¬
ровать равномерную сходимость ряда (1.60) всюду вне Е.
Ряд (1.51), которым представлено решение внешней задачи Неймана,
является равномерно сходящимся вне Еу коль скоро таковым является
ряд (1.60), составленный из его производных.
Действительно, при преобразовании пространства по Кельвину [143]
относительно сферы радиуса Ъ поверхность Е перейдет в поверхность £*,
бесконечно удаленная точка — в начало системы координат, а каждая
гармоническая функция (частное решение уравнения Д£/=0) ип из
бесконечной совокупности в общем решении (1.51), записанном кратко
перейдет в гармоническую и* внутри £*; последовательность {(У^) частич¬
ных сумм ряда (1.62) перейдет в последовательность {£/*}, причем обе
они суть последовательности гармонических функций. Аналогично будет
и с последовательностями производных. Значит, внутри Е* имеется
последовательность {U*} гармонических функций, которая равномерно
сходится к U*y так как [164] ряд производных (U%)' сходится к (U*)'
равномерно в £* (ибо это присуще преобразуемому ряду (1.60)), а после¬
довательность {U*} сходится в одной точке — в начале координат.
Свойство равномерной сходимости {U%) переносится затем на последова¬
тельность (1.62).
Отметим, что решение внешней задачи Дирихле для эллипсоида
вращения широко привлекается в теории фигуры Земли к исследованию
проблемы Стокса [132, 110 и др.], решение же внутренней задачи будет
использовано при уточнении плотности недр в глобальных и региональных
моделях ее распределения внутри общеземного эллипсоида. Решение
внешней задачи Неймана позволяет восстановить внешнее гравитацион¬
ное поле эллипсоидальной Земли по известным данным о нем на поверхно¬
сти планеты (§20).
(1.62)
ГЛАВА 2
МУЛЬТИПОЛЬНОЕ ПРЕДСТАВЛЕНИЕ ПОТЕНЦИАЛА
§6. Максвеллово представление сферических функций
и потенциалы мультиполей
Применительно к главным задачам теории потенциала Лежандром,
Лапласом и Гауссом была создана и разработана теория шаровых и
сферических функций, которая и поныне остается необходимым аппаратом
не только теории потенциала, но и математической физики вообще,
а также теории фигур планет, в частности, теории фигуры Земли. Важное
дополнение к учению о шаровых и сферических функциях, основанное
на понятии их полюсов (идею о которых высказывал еще Гаусс) и со¬
держащее физическую интерпретацию этих функций, было разработано
Максвеллом [207], алгебраический комментарий к построениям Мак¬
свелла был затем дан Сильвестром [228]. Максвеллово представление
шаровых и сферических функций изложено во многих математических
сочинениях и руководствах [28, 53, 50, 20].
Максвелл применял свою теорию, основанную на фактах явлений
электростатики, к изучению этих явлений; в настоящее время его пред¬
ставление потенциала (гармонических функций) широко используется
в теоретической физике. Еще в начале века Умов [161] впервые вос¬
пользовался этой теорией при изучении земного магнетизма, дав тем са¬
мым «геометрическую» интерпретацию гауссова потенциала магнитного
поля Земли, мультипольный анализ которого получил широкий размах,
однако, только с 60-х годов [201, 232—235, 37, 195—199]. В это же время
он начал использоваться и в геодезии при описании и изучении гравита¬
ционного поля, построении его моделей и расчете орбит ИСЗ [190, 194, 77,
99, 102, 67—70]. Так как максвеллово представление потенциала и
шаровых функций не отражено еще в учебной (геодезической и гео¬
физической) литературе, мы остановимся кратко на его основных поло¬
жениях, предварительно вспомнив лапласово представление сферических
функций.
При рассмотрении разложения объемного потенциала тела т с плот¬
ностью 6 в ряд (1.12) шаровых функций, было отмечено, что каждое
слагаемое (1.16) этого ряда
vn(p, о. ь) = -^гп-ио. Ь). (2.1)
являющееся шаровой функцией п-го порядка (гармоническим однород¬
2 Г. А. Мещеряков
33
ным многочленом п-й степени), называется потенциалом п-го порядка.
Максвелл трактовал его как потенциал специального точечного объ¬
екта — мультиполя дг-го порядка, находящегося в начале системы коорди¬
нат.
Фигурирующая в (2.1) сферическая функция (1.14) может быть запи¬
сана в лапласовой форме
п
Уя(д, к)= £ (с«™ с05 mk + Snn sin m\)P»(cos 0) (2.2)
m = 0
или даже в какой-либо иной.
Не связывая сейчас это выражение с потенциалом какого-либо гене¬
рирующего его образования, вспомним, что оно представляет общий вид
сферической функции дг-го порядка, содержащей 2дг+1 элементарных
(стандартных) сферических функций вида
Р™(cos *0*) | ^ ^ (га ^ дг; дг, га— целые положительные). (2.3)
За счет произвольности Спт и Snm выражение (2.2) описывает
совокупность всех сферических функций дг-ro порядка. Последняя может
трактоваться как (2дг + 1)-мерное евклидово пространство с обычным
образом введенным в нем скалярном произведении при единичном
весе; роль базиса выполняет система элементарных функций (2.3).
Любая функция f (Ф, >,) на сфере со единичного радиуса разла¬
гается в ряд «игреков» (ряд Лапласа)
оо оо п
f (Ф, X) = £ Yn = Yj Z (CnmCOS m% +snm sin mX)P”(cos 0), (2.4)
я = 0 n = 0 m = 0
дающий наилучшее квадратическое приближение f (ОД) по системе (2.3),
если коэффициенты этого ряда определяются формулами
г Ч .... ч . я 2я
^пт
s
\ = е 2п + 1 <п ~ т)1 { { f (o', V)^(cos У) cos т* sin d.V dW\
| &m 4jx (n + m)\ J]M ’ 1 sin mV
(2.5)
= {2 при m Ф 0, s .
m \ 1 при m = 0, n0
Заметим, что на практике для ряда Лапласа (2.4) часто пользуются
полностью нормированными присоединенными функциями Лежандра
Рп (cos #) = Л^гт(2п + 1)|Д|[ Ртп (cos 0), (2.6)
когда квадрат нормы элементарной сферической функции принимается
равным 4л, или частично нормированными (квазинормированными, нор¬
мированными по Шмидту)
Рп (cos О) = Д /гт ;; + g}f?(cos О) (2.7)
34
при квадрате их норм, положенным равным 4л/(2я+1); при этом соот¬
ветственно изменяются и коэффициенты ряда.
Вспомним также, что функции вида
Z<i} (р, О, к)= pnYn(&, X) (2.8)
Z(«> (р, О, Л,)=р-(я+ГЧ^ (#, к) (2.9)
являются шаровыми функциями соответственно внутри и вне единичной
сферы со.
В противоположность представлению (2.2) сферических функций
Максвелл посчитал более естественным и «отчетливым» определять
сферические функции выражением
!-.(♦. (210)
где р — расстояние от центра сферы со единичного радиуса, принятого
за начало системы координат, до произвольной точки пространства;
Mn=const>0 — момент функции Уп (д, А,), считаемый по предложению
Умова всегда положительным, a h,— ее оси (/=1, 2, . . ., п). Заметим,
что после дифференцирования по осям h,, предусмотренным формулой (2.10)
из производной выделяется множитель 1/рл+1, а правая часть этой фор¬
мулы превращается в функцию только от О и А, как раз и являющуюся
сферической функцией. Шаровые функции внутри и вне единичной сферы
определяются затем как обычно, т. е. формулами (2.8) и (2.9); при этом
оси ht считаются также и их осями. Задание всех осей сферической
(шаровой) функции определяет ее однозначно с точностью до постоянного
множителя.
Точки (/=1, 2, . . ., п) пересечения осей функции (2.10) со сфе¬
рой со Максвелл назвал полюсами этой сферической функции. Отметим,
что понятие полюса имеет в основном служебное назначение: полюсы
функции на сфере определяют (фиксируют) в пространстве положение
осей функции, т. е. тех направлений, при дифференцировании по которым
фундаментальной гармонической функции 1/р получается именно кон¬
кретная сферическая функция (2.10).
Так как каждая ось h, функции задается двумя величинами, то ясно,
что выражение в правой части формулы (2.10) содержит 2п + 1 пара¬
метров и поэтому дает общее выражение сферической функции п-то по¬
рядка; частный вид сферических функций порядка п обусловлен значе¬
ниями момента Мп и выбором направлений их осей (или заданием по¬
люсов) .
Если сферическую функцию представить в терминах ее полюсов,
то в ее записи будут присутствовать только косинусы определенных
углов, — это раскрывает некоторый аналитический смысл понятия по¬
люса.
Обозначая косинус угла, образуемого лучом OQ с /-й осью функ¬
ции, через цу, а косинусы углов между осями, имеющими индексы i и /,
через Хц и выполняя дифференцирование по осям, предписываемое
Формулой (2.10), из последней можно получить общую формулу
2*
35
Максвелла
(2.10а)
В этой формуле Xs означает число косинусов Хц, содержащихся в каком-
либо слагаемом сферической функции, в котором число подстрочных
индексов в произведении различных щ и Хц всегда равно п, р/1-25—
число косинусов [х; в том же члене, а 2 (р”-25^5) — сумма всех членов,
содержащих каждый одинаковое число р;- и Хц, S — символ суммирования
по s от s=0 до s=n/2 при четном п и до 5= (п— 1) /2 при п нечетном.
Фигурные скобки, заключающие Уп, означают, что формула (2.10а)
представляет не саму сферическую функцию, а алгоритм образования ее
в виде суммы S, в которой указаны коэффициенты перед суммами 2
произведений определенного числа косинусов \ы; и Хц\ последние суммы
2 должны быть раскрыты в соответствии с заложенным в них смыслом.
Так, например, при п=4 имеем по (2.10а)
(2.11)
(2.11а)
У^=М^ [35/8 [Х1|Х2|Хз[Х4 — 5/8 (|Х1[Х2^34 + (Х1ЦзХ24 + Ц1М'4^23 + М'2М'3^14 +
—(Л2М'4^'13_Т" Р-ЗМ-Л 2-Т 1 /в (?Ч 2^34 | ^13^24“1”^14^2з) ] •
Сферические функции первых порядков имеют вид
Уо=Мо, У 1 = Л11 [11, У2 = М2 (3/2M'lM'2—1 /2^12),
К3 = М3 [5/2М-1М-2М-з —1 /- О11 + Ц.з^-12) ] •
В развернутом виде У2, например, запишется так:
K2=M2(3/2C0S Q*ri2l) cos Q*n^2)-72cos П^П^), (2.116)
где Q* — переменная точка сферы, являющаяся пересечением последней
лучом OQ, Щ1* и П^2) —полюсы У2.
Рассмотрим выражение [21]
( t -а\
r = irPA-T-/• (212)
в котором, как обычно, Рп — символ полинома Лежандра, а Т=
I п 1/2
= ( £ X^t^i J , где t\, t2y • . tn — некоторые параметры. Легко
1 '
показать, что относительно последних выражение W является многочле¬
ном п-й степени. Коэффициентом в слагаемом этого многочлена, содержа¬
щем произведение всех п параметров t\ /2. . . tn, является сферическая
функция Уп при Мп= 1 с аргументами р, и Хц, т. е. выраженная через
свои максвелловы характеристики (Хц) и положение произвольной точки
относительно ее полюсов (р,,).
Перейдем теперь к понятию мультиполя.
Под мультиполем нулевого порядка понимается точечный заряд q
в начале системы координат О, потенциал которого в некоторой точке
36
пространства Q есть
Vo=q/p.
Здесь q — «момент» этого мультиполя: Mo=q, р — расстояние точки Q
от заряда q.
Мультиполь первого порядка — это диполь (см. рис. 2, с. 8). Если он
размещен в начале системы координат, то его потенциал в любой точке Q
1Л = -М,
_д_
dh
Г(7>
где
Mi
момент диполя, hi — направление его оси.
Вычислим теперь в точке Q потенциал И2)
диполями (рис. 5) с одинаковыми моментами Mi
ности начала системы координат О, но t
ориентированными антипараллельно и
расположенными на расстоянии /i2<}>
друг от друга. Осуществим предельный
переход, при котором оба диполя стремят¬
ся совпасть (/гг—^0), перемещаясь вдоль
оси h2 навстречу друг другу и оста¬
ваясь при сближении все время антипа-
раллельными, причем при уменьшении А2
до нуля момент диполя М\ возрастает,
так что
сил, развиваемых двумя
, находящимися в окрест-
Ъо
lim (2! Mih2) = const = М2.
Рис. 5.
Приближенная
квадриполя
В пределе получим новый точечный объ¬
ект — квадриполь (мультиполь 2-го порядка), потенциал которого выра¬
жается формулой
V2 = lim Vi2) =
М,
2! dh{dh2 р
(2.13)
Квадриполь характеризуется моментом М2 и направлениями своих осей
hi и h2.
Аналогично конструируются октаполи (мультиполи 3-го порядка),
тетраполи (мультиполи 4-го порядка) и т. д.
В общем случае мультиполь п-го порядка — это точечный объект,
получаемый в результате предельного перехода, которому подвергаются
Два мультиполя (п—1)-го порядка по описанной выше схеме и потенциал
которого равен
М. 1
Vn = lim V{n) = (- 1 у—f-aj-57 • (2.14)
п 4 ’ n\ dhldh2...dhn р v ’
Обратившись теперь к формуле (2.10) и разделив обе части ее на pn+1,
видим, что слева образуется шаровая функция вида (2.9), совпадающая
с потенциалом (2.1) п-то порядка, а справа — выражение потенциала
(2.14) мультиполя того же порядка, т. е. потенциалы различных порядков
некоторого тела т в его лапласовом разложении (1.12) в ряд шаровых
Функций — это потенциалы мультиполей соответствующих порядков,
Расположенных в начале системы координат. Поэтому введенные Макс¬
37
веллом оси и моменты имеют один и тот же смысл как для сферических
(шаровых) функций, так и для мультиполей соответствующих порядков.
Как уже отмечалось, общая сферическая функция У п (О, X) зависит
от 2п-\-1 параметра. В ее лапласовом представлении — это коэффициенты
Спт, Snm'y в максвелловом — момент Мп функции и 2я величин, опреде¬
ляющих в парах направления ее я осей. И хотя набор этих независимых
параметров в каждом представлении (2я + 1)-мерного пространства сфе¬
рических функций я-го порядка имеет полный ранг, их смысл различен.
В первом случае, т. е. в представлении (2.2), эти параметры суть
коэффициенты Фурье — Лапласа разложения Уп (#, X) по системе ба¬
зисных функций (2.3), т. е. в терминах функционального анализа это
геометрические характеристики функции Уп относительно базиса, при¬
нятого при описании пространства этих функций. Во втором случае,
т. е. в представлении (2.10), максвелловы параметры сферической функ¬
ции суть тоже геометрические (но в обычном реальном трехмерном
пространстве) характеристики данной функции Yn (ft, X), но безотноси¬
тельно какого-либо базиса или системы координат; они выражают
естественные свойства этой функции как таковой, являясь ее инвариант¬
ными характеристиками. Действительно, если пучок заданных векторов
h, в пространстве по «предписаниям» правой части формулы (2.10)
выражает бесконечное множество «подобных» сферических функций, то
фиксация числового множителя Мп выделяет из него одну конкретную
функцию Уп с предписанными ей параметрами.
Указанный пучок векторов hf-, исходящих из особой точки я-го порядка
производной по совокупности направлений этих векторов фундаменталь¬
ной гармонической функции MJр (т. е. исходящих из мультиполя я-го по¬
рядка, расположенного в центре единичной сферы), является простейшим
геометрическим образом, полностью раскрывающим все свойства соответ¬
ствующей ему сферической функции я-го порядка. Очевидно, это и
является «отчетливой» основой определения Максвеллом сферических
функций.
Каждая из формул Максвелла (2.10) или (2.10а) позволяет по¬
строить любую сферическую функцию с заданными осями. Приведем
классические примеры [28].
Пусть все я осей некоторой сферической функции я-го порядка Уп
предполагаются совпадающими. Приняв это общее направление осей
функции за ось г прямоугольной системы координат, можно показать,
что функция с этими осями оказывается зональной сферической, т. е. Уп=
= Рп (cos-O'), где полярное расстояние ft отсчитывается от оси z.
Пусть я—т осей (т — целое, яг<я) сферической функции Уп явля¬
ются совпадающими, а остальные т осей расположены в плоскости,
перпендикулярной к общему направлению указанных ранее я—т ее осей,
и образуют друг с другом последовательно углы, равные п/т. Совпа¬
дающее направление я—т осей примем опять за ось г. Тогда для еди¬
ничной сферы, описанной из начала координат, плоскость, несущая
остальные т осей, будет экваториальной. Если систему координат раз¬
вернуть вокруг оси z так, чтобы ось х совпадала с одной из т осей, то
функция Уп есть тессеральная сферическая: Уп=Р™ (cos ft) cos тХ при
нечетном яг, и Уп—Р™ (cos О) sin тХ при четном. Если же ось х является
38
биссектрисой угла между двумя соседними осями в экваториальной
плоскости, то функция Yп есть Р™ (cos d) sin тХ при нечетном т и
рт (cos Ф) cos тХ при четном т.
Предположим теперь, что все п заданных осей сферической функции Yп
расположены в одной плоскости под одинаковыми, равными л/я, углами
между соседними осями. Тогда, выбрав аналогично предыдущему случаю
систему координат (взяв за ось z перпендикуляр к этой плоскости) и
построив единичную сферу, можно показать, что определяемые этими
осями функции Yn есть секториальные вида Рпп (cos О) cos пХ, либо
Рпп (cos О) sin пХ в зависимости от четности я (так же, как и в случае
тессеральных функций, но при т=п).
Приведем еще лапласову форму записи сферической функции
Yn ($\ заданной ее максвелловыми параметрами (моментом Мп и
направляющими косинусами аь Ьь с,ее осей). Она имеет вид [198, 62, 102]
М п =
У „.(О, X) = —р ^ (А ™ cos тХ + В™ sin тХ) Р„ (cos ft), (2.15)
П' т = 0
где А™, ВУ довольно громоздко выражаются через максвелловы пара¬
метры этой функции при помощи рекуррентных соотношений Джеймса
[198]
2Дт=а; [(1+6J.) аГЛГЛ'-рЖ1] +2ctfAT-i,
(2.16)
2В?=щ [аГбП'-РГ'Л-У] +
+Ь, [(1+б]п)аГЛт_-11 + РГЛГ-+11 ] + 2сяТВТ- ,
(Ло=1, Во=0; бт — символ Кронекера), в которых
а Г = [(1/2) (2 - b'm)(i + m) (i + m - l)]l/2,
РГ=[(1+б°т) (i-m) (i-m-1)] 1/2, (2.17)
y?=[(i+m) (i-m)] 1/2.
§7. Нахождение максвелловых параметров
сферических функций
Введение и использование максвеллова представления сферических
функций предполагает не только знание его характеристик, но и переход
от него к лапласову представлению функций, и обратно.
Если формула (2.10) дает определение сферических функций, то их
явное выражение заключено в общей формуле Максвелла (2.10а). В ней
косинусы углов |а£- и Хц выражаются формулами типа (1.13), т. е. пред¬
полагается, что сфера, на которой задана сферическая функция, пара¬
метризована обычным образом при помощи ft и X. Поэтому переход
от максвеллова представления Yn к лапласову осуществляется простой
подстановкой значений косинусов jbiy и Хц, выраженных в сферических
координатах ft, X, в общую формулу Максвелла (2.10а) и последующими
элементарными преобразованиями получаемого выражения к нужному
виду.
39
Переход от лапласова представления Yn к максвеллову сложнее, и
он требует знания осей и момента этой функции.
Самый простой по идее и естественный метод определения осей и
моментов сферической функции — это метод Умова [161]. Сущность его
заключается в сравнении двух выражений сферической функции Yn:
одного, содержащего 2м+1 максвелловых параметров (момент Мп и
координаты полюсов fy, Хг), и другого, в котором фигурируют — в та¬
ком же числе — ее коэффициенты Лапласа (Cnm, Snm). Однако, если
последние входят в Yп линейным образом, то относительно координат
полюсов выражение сферической функции является трансцендентным
и даже относительно их тригонометрических функций отнюдь не ли¬
нейным. Поэтому таким же сложным оказывается и получаемое указан¬
ным образом уравнение, из которого предполагается определение
максвелловых параметров. Для решения такого уравнения Джеймсом
[195] разработан единообразный алгоритм, часть оригинальных формул
(см. (2.15) — (2.17)) из которого была приведена.
Способ Умова широко используется в геофизике [201, 232—235, 237,
96, 195—197] при изучении магнитных мультиполей низших порядков;
развитие этого способа Джеймсом позволило получить их параметры
до восьмого порядка включительно [196].
Теоретическим обоснованием нахождения полюсов сферических функ¬
ций является теорема Сильвестра [228, 53] о существовании у сфериче¬
ской функции п-го порядка с действительными коэффициентами един¬
ственной системы ее п действительных полюсов. Геометрическая интер¬
претация ее [53] составляет, по сути дела, общую методику определения
максвелловых параметров функции Yn [81], детализированную [98, 100,
62] и апробированную [100, 62] на примере вычисления параметров
гравитационных мультиполей Земли до 15-го порядка.
Обращаясь к этой методике, вспомним сначала формулу Клебша
(см. [28])
Z„(i, n, о| = (-1 pJ+1Z„(*, у, г), (2.18)
в которой Zn (х, у, z) — шаровая функция вне единичной сферы (умно¬
жением ее на р"
этой сферы), а
жением ее на p2n+1 осуществляется переход к шаровой функции внутри
z„(6, п. 0= I (2Л9)
Р + q + r = п
— полиномиальный дифференциальный оператор с переменными
(2-2°)
связанными соотношением, выражающим воздействие оператора Лапласа
на гармоническую функцию:
£2+л2+£2=0. (2.21)
Формула (2.18), с одной стороны, показывает, что каждому однород¬
ному многочлену (2.19) степени п от символических переменных т|, £
40
таких, что выполняется (2.21), соответствует гармонический многочлен
от х, у, 2 степени п [21]. С другой стороны, она конкретизирует вид опе¬
ратора— многочлена (2.19): для каждого гармонического полинома
Z (х> У, г) переменные £, т), £ в полиномиальном операторе связаны
той же функциональной зависимостью друг с другом, что и переменные
х у, z в соответствующем гармоническом многочлене Z„ (х, у, г).
Из формулы (2.18) следует также, что, так как 1/р п+14=0, то
Zn (|, т), £)=0 соответствует Zn (х, у, z)=0. (2.22)
С помощью операторов дифференцирования по осям (2.20) формула
Максвелла, как известно, записывается в равноценном виде (2.106)
Уя(#Д) = (-1Г-е^Л1яП
п- /= 1 р
где линейные формы
Мб. л, Е)=Я/Е+М+*Л (2.23)
отнесены к операторному пространству 0£т]£.
Таким образом, задача представления произвольной шаровой (или
сферической) функции степени п по Максвеллу требует приведения
тернарной формы (2.19) л-го порядка
I
Р + Я + г = п
при условии (2.21), наложенным на ее переменные, к каноническому виду
п
П Ц(1, п, ц
/=1
принимаемому за произведение п линейных форм (2.23).
Нахождение этих форм равносильно нахождению осей (или полюсов)
сферической функции. Определение последних по Сильвестру *) следует
из решения системы уравнений
Г Z„(E, т|, £)= 0, (2.24а)
I 12+П2+С2=0. (2.246)
Рассмотрение поверхностей (2.24) при этом даст общие образующие
конуса (2.24а) и мнимого конуса (2.246), а искомые оси ht функции (2.10)
будут тогда направляющими векторами плоскостей, каждая из которых
содержит по две общих образующих конусов (2.24).
Следуя [53], установим на поверхностях (2.24) общую параметриза¬
цию и и v:
l=[(\-u2)/{\+u2)} v, (2.25а)
г)= [2ы/(1+и2)1 а, (2.256)
t,=iv (t=y— 1), (2.25в)
при которой (2.246) тривиально удовлетворяется, а (2.24а) вследствие
{
*) Теорема Сильвестра (1876 г.) была доказана значительно позднее
(А. Островский [214], 1925 г.).
41
того, что Zn — однородная функция п-й степени, приобретает следую¬
щий вид:
Z„ (|, Z) = vnR2n (и)= О,
где R2n — рациональная функция, легко преобразуемая в алгебраическую
степени 2п с комплексными коэффициентами.
Решая алгебраическое уравнение степени 2п
R2n (<0=0, (2.26)
найдем 2п его комплексных корней uk (£=1, 2, . . ., 2я). Каждый из этих
корней даст на основании (2.25) общую образующую конических по¬
верхностей (2.24)
1 U\ ^Uk у
1= 5Г0» Л = С = «Л
1 -f 1 +
канонические уравнения которой
Б/ (a, H-/Pi )=т|/ (а2+фз) =СА‘ - (2.27)
Следовательно, все эти образующие мнимые. Любая пара таких мни¬
мых образующих определяет плоскость, проходящую через начало си¬
стемы координат 0£л£> поэтому ей соответствует линейная форма вида
(2.23). Таких плоскостей всего С\^= 2п (2п — 1) / 2! = п (2п — 1); причем
уравнение каждой из них имеет вид
Е л i
/ / / /
а1 4~ <Pl а2 + *?2 i
// // // //
а1 + (Pi а2 + (Рг *
Л,5 + В,ц + C,t =
= 0. (2.28)'
Одним штрихом здесь обозначены величины аир, относящиеся в их у-й
(/=1, 2, . . ., п (2п—1)) паре к первой образующей, двумя штрихами —
ко второй; при этом
а\к) + Ф\к) = = TtV- (2-29)
• + «* 1 +4
где индекс (6), соответствующий k-му корню уравнения (2.26), может
принимать «значение» штрих или два штриха в зависимости от того,
к какой образующей в паре относятся аир.
Выбрав путем перебора из п(2п—\) плоскостей (2.28) только действи¬
тельные из них, а таковых, соответствующих комплексно-сопряженным
образующим (2.27), имеется ровно п [53], получим направляющие
косинусы последних
а, *, = -r> ct=^- (Nt = УА? + В? + С?),' (2.30)
i £ iV£-
которые и дают п искомых осей ht сферической функции (2.10).
По направляющим косинусам (2.30) осей сферической функции
(2.10), вычислим положение ее полюсов:
cos ^i=cit tgX—bi/ai (/=1, 2, . . ., n). (2.31)
42
Но так как направления осей сферической функции можно менять
в парах без изменения при этом значения функции [207], то следует
уточнить, какую именно из двух диаметрально противоположных точек
пересечения сферы осью функции надо принять за ее полюс. Проще всего
для этого воспользоваться значениями функции (2.10) во всех 2i точках
(2.31), из которых i точек — полюсы функции, a i— их антиподы. При
этом придется прибегнуть к использованию момента Мп функции (2.10),
который легко находится описываемым далее образом.
При практической реализации описанной методики наиболее трудоем¬
кой процедурой являются составление и решение разрешающего проблему
алгебраического уравнения (2.26) степени 2п, приводимому к виду [98]
У к( Спт У Qk U2k + Snm V Rk u2k +Л = 0, (2.32)
т=0 у k=0 k=0 J
в котором
k
-7Ь
(2.33)
(2.34)
Ф™ = ^ in~m (i = (2-35)
2 Пп\{п-т)\ V
а — биномиальные коэффициенты, даваемые известной формулой
/ Р\ _ Гч — Р(Р ~ 0 • • • (Р ~ <7 + 0
\я) р Р?
Для нахождения корней разрешающего уравнения (2.32) удобнее,
однако, представлять его в общем виде
2 п
У = 0 (2.36)
i = 0
и его коэффициенты при решении конкретной обсуждаемой задачи полу¬
чать из следующей матрицы:
\п
0.0
пп
и0Л
Do, 2
пп
UQ ,2n
)п
1,0
Г)п
и\л
D1,2
Dn
U\>2n
\п
2,0
Г)п
и2,\
D'2,2
Г)п
U2,2n
)п
п, 0
пп
ип, 1
d:,2
Dn
un,2n
элементы которой суть
DI, 2*=ф:CnmQk
Dm, 2k-\-l = ^n^nm^k
(O^k^ n),
(0<£<м —1).
(2.38)
Отметим свойства матрицы D: ее элементы Dnm , принимают построчно
действительные или комплексные значения, в зависимости от того, четно
или нечетно п — т (см. выражения (2.33) и (2.38)); суммы элементов
по столбцам выражают коэффициенты уравнения (2.36).
С учетом последнего просто составляются комплексные коэффициенты
этого уравнения
Ят./
Dn
1
(О < / < 2п).
(2.39)
Найдя таким образом величины dj и вычислив корни уравнения одним
из стандартных методов (например, методом Мюллера), легко определить
величины А, В, С, пропорциональные направляющим косинусам осей
сферической функции из рассмотрения одного из детерминантов вида
(2.28), именно
Al+Вц + С^
1
л £
otf + W
аг-Мрг i
-af+Zp?
—a 2 -HP2 i
=0.
(2.40а)
или
А£>-\-Вт)-{-С£>=
I
л
£
ai-MPi
a'2 + /p2
i
a Г-ФГ
a't-iW
—i
=0,
(2.406)
Разбивка п корней на пары производится после вычисления соответ¬
ствующих каждому корню величин вида a+/Pi и аг+/р2 простым их
перебором, в результате чего и составляются определители (2.40), а зна¬
чит, находятся и величины А, В, С, именно при |3i = pf=Pi и р2=р2 = Р2
по (2.40а):
А = a2=ai = a2, B=—al =—a[ = —a\, C=aiP2—а2рь
и по (2.406):
А = — ct2, В = ocj, C=a2pi — aiP2- (2.41)
По формулам (2.30) и (2.31) вычисляются теперь координаты полю¬
сов О,, сферической функции.
И, наконец, момент Мп функции находится 2лг-(-1 раз по любой из фор¬
мул вида [62]
я!л/2я~ +
(2.42)
следуемым из сравнения правых частей формул Максвелла (2.10) и
Джеймса (2.15).
44
§ 8. Некоторые общие свойства шаровых,
сферических функций и мультиполей
Замечательные свойства шаровых функций и их сужений на сферу —
сферических, обусловлены тем, что, во-первых, шаровые функции —
многочлены, во-вторых, эти многочлены однородные, и, в-третьих, они
гармонические. Основополагающее значение при этом имеют понятия
их осей и полюсов.
С позиций анализа оси гармонических многочленов и полюсы сфе¬
рических функций — это их инвариантные характеристики: они зависят
лишь от данной (каким-либо образом) функции, полностью ее опреде¬
ляют и в принципе независимы от используемой системы координат.
С алгебраической точки зрения максвеллово представление шаровых
и сферических функций является каноническим видом тернарной формы,
подчиненной условию равенства нулю квадратов ее линейно независимых
переменных. И «канонизм» ее заключается не только в наибольшей
простоте, симметрии и общности (по отношению к пространству однород¬
ных многочленов данной степени), но и в отражении им основных свойств
описываемого образа, представляемого результатом последовательного
дифференцирования по особым для данной функции направлениям фунда¬
ментального решения уравнений Лапласа 1/р.
И, наконец, важен физический смысл каждого элемента такого
пространства гармонических многочленов: это потенциал специального
точечного объекта, мультиполя п-то порядка, который строится опреде¬
ленным предельным образом. Приближенная конструкция такого объекта
(не единственная, но простейшая) представляет собой правильную
пространственную решетку зарядов с чередующимися знаками, т. е. си¬
стему 2п точечных зарядов, потенциал которой так же, как и самого
мультиполя п-го порядка, убывает обратно пропорционально удалению
от него в степени (ц+1)-й. За счет последнего мультиполи выгодно
использовать при построении многоточечных моделей потенциалов притя¬
жения планет.
Отметим некоторые свойства шаровых Zn и сферических Yп функций,
используемые далее.
Свойство симметрии следует из определения шаровых функций как
однородных многочленов, за счет которых при любом /г=0, 1, 2, . . . для
шаровых функций в прямоугольных координатах имеем
V2k (—X, —у, -z) = v2k (дг, у, 2),
VWi(-*. —У> ~z) = ~v2k+\{x, у, z)
(2.43)
или в полярных
V2k (р, ft, X) = V2k (р, л—О, я+А,),
^26+1 (р> А,) = ^26+1 (р> п — ft, я + ^)>
(2.44)
а для сферических функций
У2к (О, h) = Y2k(n—Ф, л+А,),
^2fc+l(ft> к) = ^2*+1(л — ft> Л + А,).
(2.45)
45
Свойство симметрии Vп на любой сфере радиуса р и Y п на единичной
сфере заключается в том, что значения их в антиподных точках соответ¬
ствующих сфер одинаковы при п четном и противоположны при п не¬
четном.
При задании внешнего потенциала V какого-либо тела т рядом (1.12)
по шаровым функциям, который является абсолютно и равномерно сходя¬
щимся всюду вне сферы, объемлющей тело т, имеет смысл объединить
в нем все шаровые функции четных порядков (пусть их сумма будет
Учет) и отдельно шаровые функции нечетных порядков (их сумма Кнеч),
т. е. представить потенциал суммой вида
V (х, у, г) = Учет (х, у, z) + V„e4 (х; у, г). (2.46)
Тогда при рассмотрении потенциала V (дс, у, г) на сфере радиуса
p=V?+7+? наряду с формулой (2.46) имеем также
V(—x, —У> —z) = V4eT(x, у, z) — VW4(xt у, z), (2.47)
т. е. за счет симметрии шаровых функций (относительно начала системы
координат) приходим к существенному уменьшению области задания
потенциала. Аналогичный факт имеет место также при учете симметрии
иных составляющих потенциала относительно одной из координатных
плоскостей, именно «естественной» плоскости симметрии, о чем будет речь
далее (§ 17).
Наряду с полюсами сферических функций как инвариантных их харак¬
теристик почти аналогичное значение имеют точки стационарности этих
функций. Переходя к рассмотрению эстремальных свойств [101 ] сфериче¬
ских функций, вспомним, что сферическая функция представляет сово¬
купность значений шаровой функции на сфере радиуса р=1. Поэтому
будем искать условия, при которых однородный гармонический многочлен
Zr = Zn(x, уу z) принимает экстремальные значения на единичной сфере
x2+y2+z2= 1. (2.48)
Это задача на условный экстремум, для решения которой удобно восполь¬
зоваться методом Лагранжа.
Составляя вспомогательную функцию
F„(x, у, z)=Zn(x, у, г) — 72Мх2+(/2+г2— 1), (2.49)
где X — неопределенный множитель Лагранжа, получаем, что координаты
точек экстремума удовлетворяют системе уравнений
dZn dZn dZn
- кх = 0, -г- - Ху = 0, -^-^2 = 0. (2.50)
дх ду ог
Вообще говоря, эта система и уравнение (2.48) дают решение задачи
в общем виде: из них можно найти множитель X и координаты точек
экстремумов. Однако свойство однородности шаровой функции Zn позво¬
ляет дать простую геометрическую интерпретацию такому решению.
Умножая уравнения системы (2.50) последовательно на х, у, z и склады¬
вая их, получаем с учетом формулы (2.48)
dzn dzn dZn
Х^х + У~ду~ + г^Г = х' (251>
46
т. е.
(р, grad Z„)=X, (2.52)
где р = х\ + у\ + zk — радиус-вектор точки экстремума, a grad Zn — гра¬
диент шаровой функции в этой же точке. С другой стороны, поскольку
левая часть формулы (2.51) входит в формулу Эйлера для однородных
функций, запишем также
riZn=%. (2.53)
Кроме того, записав систему (2.50) в виде равенств типа dZJdx=kx,
возводя их в квадраты и сложив с учетом (2.48), получим
I grad Zn | = А,. (2.54)
Теперь ясен смысл множителей Лагранжа при решении обсуждаемой
задачи: каждый из них равен произведению шаровой функции на ее значе¬
ние в соответствующей точке экстремума, а абсолютная величина каждого
из них равна модулю ее градиента в этой точке.
Умножая теперь уравнения (2.50) последовательно на орты координат¬
ных осей i, j, к и складывая результаты, находим
grad Zn=Xр, (2.55)
т. е. в точках экстремумов сферических функций Yn градиент Zn шаро¬
вых функций, связанных со сферическими обычным образом, кол-
линеарен радиусу-вектору р.
Таким образом, нахождение точек экстремумов сферической функции
Yn требует определения собственных направлений векторной функции
g„=grad Zn от векторного аргумента р:
g„=gn(p). (2.56)
которые с учетом (2.50) легко получить из соотношений
1 dZn 1 dZn 1 dZn
дх у ду z dz
(2.57)
Заметим также, что из сравнения формул (2.53) и (2.54) следует, что
в точках экстремума
| grad Z„|= п Zn . (2.58)
Значит, в точках экстремума сферических функций ясный смысл имеет
не только направление grad Zn, раскрываемое формулой (2.55), но и его
модуль, выражаемый формулой (2.58).
Вспоминая теперь, что распределения значений для шаровых функций
Zn подобны на всех сферах, концентрических с единичной сферой,
скажем, что собственные направления векторной функции gn=
=grad Zn(x, у, z) суть те направления p=xi + t/j +zk, в пространстве
по которым шаровая функция на любой сфере p=const^= 1 имеет экстре¬
мальные значения. При этом, учитывая свойство симметрии этих функций,
ясно, что всякая сферическая функция имеет четное число точек экстре¬
мума, среди которых могут быть и совпадающие. При рассмотрении
экстремальных свойств сферических функций пока были обсуждены лишь
47
необходимые условия экстремума, и только привлечение достаточных
условий позволит осуществить полное решение этой проблемы.
Переходя к физической интерпретации вопроса, отметим следующее.
Так как экстремальные значения шаровой функции Zn=Vn, трактуемой
потенциалом л-го порядка, на любой указанной выше сфере суть экстре¬
мальные значения на ней потенциала соответствующего мультиполя п-го
порядка, то в силу (2.58) на этой же сфере в тех же точках также экстре¬
мальное значение имеет и модуль grad Vni т. е. вектора напряженности
поля сил притяжения этим точечным объектом. Значит, рассмотренные
здесь исходящие из мультиполя направления, на которых лежит вектор
притяжения им, — это (так же, как и его оси) инварианты мультиполя
или соответствующей ему шаровой функции.
Как уже подчеркивалось ранее, центральное поле притяжения созда¬
ется только мультиполем нулевого порядка — точечным зарядом (мас¬
сой). Однако оказывается, что в поле, развиваемом мультиполем любого
порядка, могут быть найдены такие направления, в малой окрестности
которых поле обладает свойством центральности: вектор притяжения
точечным объектом направлен к этому объекту (или строго в противо¬
положную сторону). Такие особые направления поля — это только что
рассмотренные инвариантные направления к точкам экстремума сфериче¬
ских функций.
Приведем некоторые результаты исследований на экстремум сфериче¬
ских функций низших порядков.
Сферическая функция Yn нулевого порядка (2.11) как константа
экстремумов не имеет.
Сферическая функция первого порядка Yi (см. (2.11)) приводит
к шаровой функции 1Л= (Mj/p2) Y\. Это потенциал диполя.
Функция Ki имеет два экстремума, в точках на оси диполя на равных
расстояниях от него: max Y\=M\ — в направлении стрелки оси диполя
и min Yi = —М1 в противоположном направлении. Обращаясь к формулам
(1.5а), видим, что и grad V\ имеет там же наибольшие значения по мо¬
дулю, но для этих двух точек — различные направления; и это два единст¬
венных направления «центральности» поля диполя.
Экстремумов квадриполя или соответствующей ему сферической функ¬
ции Y2 или шаровой У2 второго порядка общего вида шесть. Они дости¬
гаются попарно в диаметрально расположенных от квадриполя точках:
две пары их в плоскости квадриполя — одна на биссектрисе угла между
его осями hi и \\2, другая — на биссектрисе дополнительного угла до л;
третья пара — на прямой, перпендикулярной к плоскости квадриполя.
Направления прямых, несущих соответствующие пары этих точек, — это
собственные направления квадратичных форм У2 или Y2.
Остановимся еще на задаче преобразования сферических функций
при вращении системы координат, необходимость чего часто возникает
в математической физике [21], небесной механике [3, 222], геофизике
[227, 198], геодезии [34, 63]. Эта задача решалась неоднократно, однако
представляется, что самый простой численный способ указанных пре¬
образований основан на свойстве инвариантности максвелловых пара¬
метров сферических функций относительно вращения системы коор¬
динат.
48
Задача ставится так. Сферическая функция Y п (ft, А,) дана на единич¬
ной сфере своими коэффициентами Спт, Snm в некоторой (скажем, «ста¬
рой») системе координат Oxyz или, лучше, Ох\Х2Хз. От этой системы совер¬
шен переход к «новой» системе координат Ох{х2хг, оси которой задаются
относительно прежней системы или углами Эйлера или известным образом
выражаемыми через них направляющими косинусами со/Л углов осей
старой системы с осями новой (/ — номер оси старой, к — номер оси новой
системы). Другими словами, считается заданной матрица вращения
системы координат Q=(^jk). Требуется функцию Yn представить в новой
системе сферических координат fl7, Х\ т. е. найти отнесенные к ней лапла-
совы коэффициенты Спт, Snm этой функции. (Все величины в новой системе
координат снабжаем знаком «штрих». Новые сферические координаты
ft', X' предполагаем введенными на сфере по системе Оххх2х3 таким же
образом, как старые ft, X были введены по системе Ох 1*2*3.)
Алгоритм решения этой задачи, основанный на инвариантности
максвелловых параметров Yn:
включает в себя следующие этапы.
1. Нахождение по методике § 7 максвелловых параметров функции
Kn(ft, X): направляющих косинусов ab bb ct (/=1, 2,..., п) ее осей
и момента Мп.
2. Пересчет по заданной матрице вращения направляющих косинусов
осей функции Yn к новой системе координат:
(tr — символ транспонирования).
3. Вычисление по рекуррентным формулам (2.16) величин А'пт,
Впт в новой системе координат, что совместно с моментом М'п=Мп и дает
по формуле (2.15) искомое трансформированное выражение гармоники
Удачный программный вариант этого алгоритма описан в [63] при¬
менительно к пересчету стоксовых постоянных Земли к естественной
системе координат [77], оди которой суть главные оси инерции Земли.
(2.59)
у. «к, V).
ГЛАВА 3
ПОТЕНЦИАЛ ПРИТЯЖЕНИЯ ЗЕМЛИ
И ЕЕ ОБОБЩЕННАЯ ФИГУРА
§9. Потенциал притяжения Земли
и потенциал силы тяжести
Изучение Земли в глобальном и региональном масштабах требует,
в первую очередь, знания ее фигуры а, распределения плотности 6 слагаю¬
щих ее масс и обусловленного ими гравитационного поля. Последнее
описывается фундаментальным соотношением, выражающим потенциал
притяжения Земли
V(P)= Qe( т + а), Рф т. (3.1)
т rPQ
Потенциал W силы тяжести, модуль градиента которой выражает
доступное для измерений ускорение силы тяжести g, это
W(P) = V(P) + Q(P), (3.2)
где
Q(P) = -у-р2 sin2 Ф (3.3)
— потенциал центробежной силы, а (0 = 0,7292115147 • 10-4 рад • с-1
[125] — угловая скорость вращения Земли. Этот потенциал принимается
во внимание только внутри Земли, на поверхности и в ее непосредственной
окрестности.
Подчеркнем, что обычно под т в (3.1) понимается объем всех твердых
и жидких масс Земли. Значит, влияние на ускорение силы тяжести
атмосферы, притяжения небесных тел (Луны, Солнца, планет) и другие
более тонкие эффекты (приливного и неприливного характера) учитыва¬
ются дополнительно в виде поправок. Источники их разнообразны по при¬
роде; они зависят не только от положения, но и от времени, по абсолютной
величине они незначительны и в сумме составляют доли процента. Будем
считать далее гравитационное поле Земли стационарным и обусловленным
лишь двумя факторами: притяжением Земли и ее вращением. Считается
при этом, что Земля обладает свойствами абсолютно твердого тела.
Потенциал притяжения V(P) Земли обладает свойствами объемного
потенциала, перечисленными в § 2, а свойства потенциала Q центробежной
силы очевидны ввиду простого его написания. Поэтому легко констати¬
ровать и свойства потенциала W(P) силы тяжести Земли: он непрерывен,
имеет непрерывные первые производные, а его вторые производные
50
(или некоторые из них) имеют разрыв непрерывности на поверхности
Земли и внутри нее там, где плотность недр меняется скачком. Так как
ДГ=—4я06+2ш2, (3.4)
то заключаем, что вне Земли (6=0) потенциал W есть функция субгармо¬
ническая, а внутри Земли явно не гармоническая: в различных областях
ее может быть супергармонической, гармонической и субгармонической.
Для потенциала силы тяжести имеем также (на основании §2)
dW=g cos(g, ds) ds,
где g — ускорение силы тяжести, а 5 — любое направление, и
dW=-gdh, (3.5)
где dh — элемент расстояния между уровенными поверхностями
(U7=const) гравитационного поля Земли, отсчитываемый вверх по отвес¬
ной линии.
Из уровенных поверхностей потенциала W выделяют такую поверх¬
ность
W=const=W0, (3.6)
которая проходит через нуль футштока (начальный пункт нивелирной
сети), и называют ее геоидом. Эта основная уровенная поверхность при¬
нимается за определяемую в геодезии поверхность Земли: в акваториях
она совпадает (как теперь выяснилось, с точностью до ±1 м) с невоз¬
мущенной (приливами и атмосферными воздействиями) поверхностью
воды, а под сушей является ее мысленным продолжением.
Аппроксимация геоида эллипсоидом вращения, ось которого совпадает
с осью вращения Земли, приводит к обобщенной поверхности планеты
в виде так называемой нормальной Земли. На XVII Генеральной ассамб¬
лее (1979) Международного геодезического и геофизического союза
(МГГС) приняты [210] следующие геометрические параметры эллип¬
соида нормальной Земли GPS-80:
а= 6 378 138,0 м, а= 1 : 298,257. (3.7а)
Расположение геоида относительно эллипсоида GRS-80 дано картой
на рис. 6.
Потенциал W силы тяжести непосредственно не измеряется; из измере¬
ний могут быть получены лишь его приращения (3.5); dh получают
из нивелировок, g доставляет гравиметрия; гравиметрическими прибо¬
рами измеряют ускорение силы тяжести и его производные.
Потенциал W принято выражать рядом вида
^(р. о, /.) =
= ~ ^ 1 + Хо (у) (С""> C0S тХ + Snm sin ГПХ)Р”(COS ft) j +
+ ^Lp2sin2ft, (3.8)
51
или более кратко
f YnV' V OJ2 2 2
W(p, <>,*.) = X ,+T" + Tp sin
я = О р
где
(3.9)
П
Ул(0, X) = GMa" ^ (Спт cos тХ + Snm sin тХ)Р™(cos Ф). (3.10)
т = 0
При этом р — расстояние от начала координат, ft — полярное расстояние,
X — долгота, М — масса Земли, ае — средний радиус ее экваториального
сечения, а СптУ Snm — безразмерные стоксовы постоянные. Каждый
из рядов (3.8) и (3.9) — это, по сути дела, лапласов ряд (1.12), в который
лишь введена гравитационная постоянная G и стоксовы постоянные
СптУ Snm записаны в безразмерном виде: постоянные выписанных здесь
рядов равны постоянным ряда (1.12), деленным на GMa”.
Стоксовы постоянные планеты низших порядков, как уже отмечалось
в §3, имеют простой механический смысл.
Постоянная нулевого порядка Coo=GM — так называемая геоцентри¬
ческая постоянная как размерная величина и Соо= 1 как безразмерная.
Стоксовы постоянные первого порядка выражают в используемой
системе координат координаты центра масс планеты х0, i/o, 2п, именно
х0=аеСц, y0=aeSn, z0=aeC ю, (3.11)
где Сю, Си, Sи безразмерны. Таким образом, если начало системы коорди¬
нат совпадает с центром масс Земли, то ее стоксовы постоянные первого
порядка равны нулю.
Стоксовы постоянные второго порядка определяют эллипсоид инерции
планеты. Вспомним из механики, что
К =\6(y2 + z2)dx, Ву = $ d(z2 + x2)dr, Cz = $ 6(x2 + j/2)dT (3.12а)
TXT
суть моменты инерции тела т относительно координатных осей Ох, Оу, Oz
соответственно и
Оуг = ^ byzdx, Ezx = ^ bzxdx, Fxy = ^ бху dx (3.126)
TXT
— центробежные моменты инерции тела т по отношению к этим осям (про¬
изведения инерции). С учетом выписанных выражений легко устанавли¬
вается, что
С20=1 /2{Ах-\-Ву)—С2, С22=1 /ЛВу — Ах)у
C2l = Ezx, S2l = Dyz, S22=X / 2Е Ху,
где стоксовы постоянные так же безразмерны, как и все фигурирующие
здесь моменты инерции, т. е. моменты (3.12а) и (3.126) предполагаются
в (3.13) поделенными на GMa\.
Если оси используемой системы координат совпадают с главными
осями инерции планеты, то, как известно, произведения инерции обраща¬
ются в нули, а Ах, ВС2 переходят в главные моменты инерции А, В, С
53
(Л<В<:С); в результате в ряде для геопотенциала
С21 = 521 = <S 22 = 0
И
Сго=1/2(А+В)-С, Сп='/<(В-А). (3.14)
Стоксовы постоянные Спт, Snm третьего и более высоких порядков
какого-либо простого механического смысла не имеют. Каждая из них
является линейной комбинацией степенных моментов плотности земных
недр (см. далее § 12).
Определение стоксовых постоянных Земли является одной из главней¬
ших задач геодезии, которая решается как наземными средствами
гравиметрии и физической геодезии, так и в результате обработки специ¬
ально поставленных наблюдений геодезических искусственных спутников
Земли.
Динамическими методами спутниковой геодезии [26, 46, 120, 162]
определяют согласованные наборы гармонических коэффициентов Спт,
Snm геопотенциала (безразмерных, нормированных) и геоцентрических
координат станций наблюдения — совокупность указанных величин назы¬
вают «моделями Земли». Обзоры таких моделей приведены в [71, 126,
18] и наиболее полными моделями являются модели GEM-10C, OSU 81
до 180-го порядка и степени, GPM-2 — до 200-го. Целью вывода моделей
гравитационного поля является не только получение оптимальных
(в смысле приближения к истине) значений гармонических коэффициент
тов, но и создание «инструмента» для надежного дальнейшего прогнози¬
рования орбит тех ИСЗ, которые использованы в выводе данной модели.
Оценка точности моделей выполняется по внутренней сходимости, она
оказывается сильно преувеличенной, так как не отражает систематиче¬
ских погрешностей. Поэтому суждение о реальной точности выводов
следует 1) из сравнения наборов стоксовых постоянных, полученных
в результате наблюдений различного вида (лазерных, доплеровских,
фотографических, гравиметрических), 2) из сравнения аномалий силы
тяжести, вычисленных на основе данной модели, с полученными по грави¬
метрическим данным и 3) из апробирования результатов прогнозиро¬
вания по анализируемой модели орбит ИСЗ, не участвовавших в ее вы¬
воде. Для лучших современных выводов отмечается [125] хорошее согла¬
сие полученных по ним степенных дисперсий (по порядкам в разложении
высоты геоида в ряд сферических функций) с таковыми, найденными
из статистического анализа силы тяжести. Считается [125], что устой¬
чиво определены по чисто спутниковым данным гармонические коэффи¬
циенты геопотенциала до 10—16-го порядков и степеней (зональные —
с погрешностью в несколько единиц девятого знака, тессеральные —
на порядок ниже). Спутниковые выводы стоксовых постоянных Земли
примерно до 10-го порядка точнее, чем гравиметрические, а с 12-го по¬
рядка наибольшую точность определения тессеральных гармоник дают
гравиметрические определения. С 50-го порядка погрешности гравиметри¬
ческих определений оказываются соизмеримыми с величинами находимых
постоянных, и это пока предел для разложения силы тяжести по сфери¬
ческим функциям; вопрос надежности чисто спутниковых выводов
54
Спт и $пт будет затронут в § 13. Далее, в приложении дается табл. I сток¬
совых постоянных модели GEM-10 [202], приведенных по методике §8
к главным осям инерции Земли.
Относимая к фундаментальным геодезическим постоянным геоцентри¬
ческая гравитационная постоянная GM — это размерная стоксова кон¬
станта Соо, которой GRS-80 предписано значение [210]
GM= (398 600,50+0,05) км3 - с-2. (3.76)
Важной числовой характеристикой Земли является также значение
потенциала силы тяжести на поверхности геоида Wo.- Оно может быть
получено [26] осреднением большого ряда значений W, вычисленных
по формуле (3.8) в ряде точек земной поверхности с известными коорди¬
натами (обычно это станции наблюдений ИСЗ) и приведенных к «уровню
моря». В GRS-80 принято
W0= 62 636 860,85 м2 • с~2. (3.7в)
Из потенциала силы тяжести W Земли традиционно выделяют его
главную часть — нормальный потенциал U, полагая, что он развивается
общеземным эллипсоидом, которому при этом приписываются определен¬
ные свойства. Тогда
W=U+T, (3.15)
где Т — остаточная часть потенциала планеты, так называемый воз¬
мущающий потенциал. В нормальный потенциал включают самые крупные
(по числовому значению преобладающие над остальными) гармоники
реального потенциала (Соо и С20), а иногда еще несколько последующих.
Установленный нормальный потенциал U считается затем известным.
Возмущающий потенциал Т также представим рядом шаровых функций,
но с обязательным исключением из него потенциала нулевого порядка
Vo планеты и с соответственно измененными коэффициентами (относи¬
тельно ее реального потенциала) у тех гармоник, которые отнесены
к нормальному; значит, в общем виде
оо
Т= £ Vn. (3.16)
п = 1
Введение нормального потенциала и соответственно нормального
гравитационного поля Земли позволяет каждой точке пространства
отнести аномалию силы тяжести
&g=g—y, (3.17)
в которой под g=—dW/dh понимается значение реальной силы тя¬
жести (оно может быть измерено), а под y=—dU/dh значение
нормальной силы тяжести (оно может быть лишь вычислено). Кропотли¬
вая обработка уже накопленной гравиметрической информации (с необ¬
ходимыми предсказаниями значений Ag на отдельные «белые пятна»)
позволила составить карты осредненных значений Ag на всю поверх¬
ность Земли в пятиградусной ее разграфке и в одноградусной. Схемати¬
ческое распределение Ag на геоиде (при у для уровенного нормального
эллипсоида GRS-80) приведено на рис. 7.
55
§10. Гравитационные мультиполи. Мультипольное
представление геопотенциала
Записывая геопотенциал в виде ряда (3.9) и вспоминая, что его
п-й член как потенциал Vn д-го порядка выражает потенциал мультиполя
того же порядка, естественно последний трактовать с позиций притяже¬
ния гравитирующих масс, а не электростатических зарядов, как это было
в построениях Максвелла.
При обращении геодезии к обсуждаемой теории Максвелла [190,
194, 77] сразу же возникло понятие гравитационного мультиполя
(см. [77]), где и были впервые описаны такие мультиполи низших поряд¬
ков (нулевого, первого, второго). При построении гравитационного
мультиполя надо оперировать с положительными и отрицательными
гравитационными зарядами (или гравитирующими массами). Однако
закон всемирного тяготения предполагает только положительные массы.
При этом сила притяжения F+ пробной массы т2= 1 г, помещенной
в произвольной точке Р, массой т>0, создающей поле и расположенной
в точке Q, коллинеарна вектору г=0? и всегда направлена в противо¬
положную сторону, т. е. к притягивающей точке Q.
Теперь предположим, что в точке Q помещена отрицательная масса
т<0, создающая свое поле притяжения и обладающая по определению
тем свойством, что (при замене знака у этой массы) новое поле, создава¬
емое массой —т, соответствует обычной ситуации поля тяготения,
в котором действует закон Ньютона. В случае поля отрицательной массы
мы полагаем, что вектор F силы «притяжения», т. е. вектор
F_=-F+,
также коллинеарен вектору г =Q/^, но направлен в ту же сторону, что и г.
Наиболее отчетливо характер действия отрицательных масс (или
будем также говорить «отрицательных гравитационных зарядов») прояв¬
ляется в случае притяжения, развиваемого телом произвольного строения,
когда это притяжение представляется в виде суперпозиции притяжения
однородного — осредненного — тела и притяжений, вызываемых вкрап¬
ленными в тело неоднородностями. Так, в теории изостазии в этом случае
говорят об избытке масс (га>0) и о дефекте масс (т<0); последнее
как раз и соответствует обсуждаемым здесь отрицательным массам.
Заменив в схеме построения электростатических мультиполей поло¬
жительные и отрицательные электрические заряды (±^) положитель¬
ными и отрицательными точечными массами (zkm) соответствующих
знаков, получим, ничем не нарушая и не модифицируя схемы, гравита¬
ционные мультиполи.
Гравитационные мультиполи низших порядков уже затрагивались
ранее в § Г. это точечная масса (для поля притяжения особая точка нуле¬
вого порядка) — мультиполь нулевого порядка и диполь — мультиполь
первого порядка (теперь мы его называем гравитационным диполем).
Так как мультиполь п-го порядка есть результат я-кратного дифферен¬
цирования по п осям фундаментального решения 1/р уравнения Лапласа,
то для мулътиполя нулевого порядка дифференцировать 1 /р не приходится
57
ни разу, т. е. осей этот простейший «мультиполь» не имеет; момент же его
равен М0=М, а потенциал есть потенциал точечной массы, массы Земли,
сосредоточенной в начале системы координат:
V0=GM/p. (3.18)
Потенциал гравитационного мультиполя 1-го порядка—диполя
планеты
У, (О, к) Afj cos (nV’, Q*) Л4| (a{x b{y -f- c{z) ^
2 = 2 3 ’
P P P
где Mi — его момент, x, у, z и p, О, X — координаты точки Q, в которой
рассматривается потенциал этого объекта.
Находя по описанной ранее (§8) методике точки экстремумов сфери¬
ческой функции Y1 (О, X), видим, что они (jclt2=±ai, Уii2=±fri,
z 1 2==bCi) совпадают с полюсом П{!) диполя и с антиподной ему точкой,
в которых ext Y\ = zbM\. Находя еще точки экстремума функции Y\ (О, X),
представленной в виде (3.10) через стоксовы постоянные планеты,
и сравнивая результаты, обнаружим, что
а\ = С\\ / N, bi=Sn/N, С[ = Сю / N,
N=^[c2w+C2l{+S2u, M\=GMaJ\l. (3'20)
Учитывая теперь механический смысл стоксовых постоянных первого
порядка (3.11), получим
ai = Xn/L, b\ = yn/L, с{ = z0/L, ^
М{ = GML, L = + У о + 2о-
Значит, момент М\ гравитационного диполя планеты — это произведение
планетоцентрической постоянной GM на его нецентральность L, т. е.
на смещение диполя от центра масс планеты.
Попытаемся теперь дать механическую трактовку гравитационного
диполя. Апеллируя к принятой в физике схеме его построения (§1),
скажем, что планета плоскостью, перпендикулярной к оси диполя и про¬
ходящей через начало системы координат, рассечена на два «полушария»,
массы которых суть М' и М">М'. При этом гравитационные заряды
ztq (2q=M"—М') размещены на оси диполя в точках, симметричных
относительно начала, на расстоянии h друг от друга, выражаемом следую¬
щей формулой:
h = 2Мд/С|0 + С?, + S2U/(M" - М'). (3.21а)
Так как для Земли используемую систему координат пытаются
тщательно совместить с ее центром масс, т. е. практически всегда L=О,
то ясно, что гравитационного диполя Земля не порождает.
Рассмотрим гравитационный мультиполь 2-го порядка — квадриполь.
Параметры гравитационного квадриполя Земли были вычислены впервые
[77] методом Умова. Затем они неоднократно вычислялись и по описанной
здесь методике §7 (например, в [66]). Раскроем геометрическую струк¬
туру гравитационного квадриполя. Возьмем направления его осей hi
58
и h2, найденные в [77], по модели гравитационного поля Земли SAO-1:
0, = 4°37,5', Ф2= 175°22,5', h = X2= 165° 13,3' (3.22)
(значения этих параметров, получаемые и по современным моделям поля,
незначительно отличаются от указанных). Видим, что обе оси гравита¬
ционного квадрироля Земли лежат в плоскости меридиана Хж 165,2°,
отклоняясь от полюсов на угол Ф«4,6°.
Рассмотрим сначала качественную картину гравитационного поля,
создаваемого квадриполем Земли, развивающим потенциал V2=Y2 / р3.
Если считать, что 1Л=0, т. е. начало системы координат совмещено
с центром масс, то поле квадриполя накладывается на сферически-
симметричное поле Vo =GM /р точечной массы М.
Помня, что р — расстояние от центра масс Земли, и полагая р=
=p=const>ae, видим, что на сфере радиуса р сила притяжения квадри¬
полем внешней точки (так же как и его потенциала) пропорциональна
значениям У2. Найдем поэтому последние на каком-либо меридиане
в точках пересечения сферы p=const осью вращения Земли, когда
0=0 и 0=я, и на экваторе этой сферы, т. е. при $=п / 2. Так как
у2= 7г М2 (3|Xip2 — хи 2),
где теперь A,i2=cos (я—2Ф) = —cos 20, то в первом случае
уп°л = _1/2Д|2 (3 COS2^— COS 2^)= — l/2 М2 (1-fcos2^) <0,
и во втором
YlKB='/2M2 (3 siri 2flcos2 (X-X)+cos 2fl)>0.
Отсюда заключаем, что распределение силы притяжения квадриполем
внешней точки таково, что при одинаковых удалениях от центра планеты
она всегда меньше на оси вращения, нежели в точках экваториальной
плоскости. Кроме того, и это важно для_ последующего, в плоскости
экватора она является наибольшей при Х=Х и А,= Х+я и наименьшей при
X==Xztn/2. Значит, если мы хотим представить квадриполь (точечный
объект, расположенный в центре Земли) приближенно в виде системы
четырех точечных зарядов, то необходимо отрицательные заряды (недо¬
статок масс) поместить на оси вращения Земли, а _положительные
(избыток масс) — в плоскости экватора под долготами X и Х+л.
Так как оси квадриполя лежат в плоскости ?t=const, то и заряды, его
образующие, в любой момент стремления их к предельному положению
также расположены в этой плоскости на прямых hi и —hi (рис. 8а),
причем сугубо ориентировочно может быть оценено и расстояние этих
зарядов от центра Земли.
Действительно, если мультиполю нулевого порядка соответствует
точечная масса в центре Земли с массой, равной массе всей планеты,
то присутствие квадриполя объясняется отличием реальной Земли
от ее идеальной сферически-симметричной модели. А основное видимое
различие их в том, что во втором приближении Земля является эллипсои-
.дом вращения с разностью полуосей порядка 20 км. Сопоставляя земной
эллипсоид с равновеликим ему по объему шаром, видим, что экваториаль¬
ному поднятию эллипсоида над сферой соответствует избыток масс,
59
а полярному опусканию эллипсоида — недостаток их. Это дает возмож¬
ность предварительно локализовать (по расстоянию от центра) положение
точечных зарядов приближенно представляемого квадриполя, считая, что
они находятся либо в коре, либо в верхней части мантии.
Однако указанное отличие Земли от идеальной не является единствен¬
ной (и даже главной) причиной, объясняющей квадриполь планеты.
Если бы Земля состояла из эллипсоидальных или даже сфероидальных
слоев и находилась бы в состоянии гидростатического равновесия,
то тогда расположение масс не зависело бы от долготы X, а У2 выроди¬
лась бы в зональную сферическую функцию, С22 и S22 обратились бы
Рис. 8. Схема образования гравитационного квадриполя Земли
в нули и, значит, к было бы неопределимым, а обе оси квадриполя при этом
совпали бы с осью вращения Земли, которая оказалась бы двукратной
осью сферической функции второго порядка. В действительности этого
нет. Значит, уверенное определение и нахождение конкретного
меридиана X, во-первых, говорит об отличии состояния Земли в целом
от гидростатического и, во-вторых, качественно указывает на глобальный
характер расположения масс внутри планеты:_массы Земли более скон¬
центрированы в окрестности меридианов к и Х+л, менее — меридианов
kztn/2. Плоскости этих меридианов совместно с плоскостью экватора
соответствуют плоскостям, которые наилучшим образом, но осредненно,
отвечают плоскостям симметрии масс Земли, точнее, они являются
плоскостями симметрии трехосного эллипсоида инерции Земли. Это
утверждение было высказано нами в [77], а в [101] оно подтверждено
соответствующими вычислениями, результаты которых будут приведены
в §12. _ _
Таким образом, плоскости к и Х+я/2 суть естественные плоскости
главных меридианов планеты, связанных с ее внутренней структурой
и ею обусловленных. Пересечения этих плоскостей друг с другом
и с плоскостью экватора Земли определяют оси натуральной прямо¬
угольной системы координат. Эти оси (ОХ, О У, OZ) суть главные оси
инерции Земли, моменты инерции относительно которых есть Л, Ву С
(.АСВСС).
60
Отмеченные выше концентрация земных масс и их разуплотнение
по направлениям главных меридианов Земли подтверждаются картой
геоида (см. рис. 6).
Меридиан оси В (А,±я/2) проходит в восточном полушарии
(75,2° Ost) через середину Евразии, в западном (104,6° West) примерно
через середину Северной Америки. В восточном полушарии меридиан этой
оси пересекает центральные части территорий, в которых высоты геоида
и аномалии силы тяжести отрицательны, что соответствует как раз мини¬
мальному притяжению за счет V2. В западном полушарии указанная
картина не так отчетлива.
Меридиан оси наименьшего момента инерции А Д+л= 14,8° West),
проходящий через Атлантический океан, также рассекает почти посредине
области положительных высот геоида и, севернее экватора, области поло¬
жительных аномалий силы тяжести. Это и понятно, ибо данный меридиан
проходит вдоль Срединно-Атлантического хребта, рифтовая_долина кото¬
рого предполагается трещиной земной коры. Меридиан 165,2° Ost
рассекает области Восточно-Тихоокеанского поднятия, но хорошего согла¬
сия с картами высот геоида и аномалий силы тяжести здесь не отмеча¬
ется. В принципе его может и не быть, так как при интерпретации располо¬
жения главных осей инерции в теле Земли должно быть принято во внима¬
ние распределение масс по всем глубинам планеты, осредненное каким-то
неизвестным образом. Этот вопрос подробнее будет обсужден далее
в §24, а сейчас перейдем к уточнению приближенной конструкции грави¬
тационного квадриполя Земли, схематически показанной на рис. 8а.
Для этого надо осуществить предельный переход в его схеме, устрем¬
ляя друг к другу заряды в каждой из пар qз, q\ и qi, q2, оставляя их на
главных осях инерции С и А и на осях квадриполя: на оси hi и на анти-
параллельной ей оси —hi соответственно, и беспредельно сближая пос¬
ледние с сохранением их параллельности. Значения обильностей зарядов
q=\qi\ при этом должны увеличиваться, но так, чтобы произведение
qh\h2, выражающее с точностью до константы момент квадриполя, остава¬
лось бы конечной величиной. Исключая окончательную предельную ситуа¬
цию, при которой /ii=0 и /12=0, остановимся на случае таких малых
отрезков h\ и h2 (рис. 86), при которых «бесконечно» близкие, но большие
по абсолютной величине и разноименные по знаку гравитационные
заряды q~ р,, находящиеся в точках (Д, fy, , развивают в пространстве
потенциал
(г,- — расстояния от точечных зарядов р,, выраженных в единицах масс
Земли, до внешней точки Р), оптимально представляющий потенциал
квадриполя Земли, описываемый стоксовыми постоянными 2-го порядка:
4
(3.23)
1/2(Р) = У2(0, X) / р3,
2 (3.24)
Y2 (Ф, l) = GMal Yj ^2т cos т^ sin m^)^?(cos ^)-
61
Оптимальность представления потенциала 2-го порядка У2 потенциа¬
лом К(2) набора четырех точечных масс понимается с позиций критериев
общей методики построения многоточечных моделей геопотенциала
(см. далее § 15) ; здесь, в частности, она означает, что наиболее подходя¬
щей для целей аппроксимации внешнего поля реального квадриполя
Земли является такая его приближенная конструкция, при которой
среднеквадратические а и максимальные Л уклонения уровенных поверх¬
ностей У{2) (P)=const от таковых V2 (P)=const имеют (на уровне моря)
наименьшие значения и по крайней мере первое из них не превосходит
уклонений а* друг от друга эквипотенци^альных поверхностей квадрипо-
лей, полученных по последним моделям геопотенциала (для них о* состав¬
ляет всего несколько сантиметров).
Описанный предельный процесс построения приближенной конструк¬
ции квадриполя реализовывался неоднократно [103, 66, 69] согласова¬
нием по методу наименьших квадратов полей У2 и 1/(2) в узлах карто¬
графической сетки с целью определения параметра jlx (2)=|(ыг| , /= 1, 2, 3, 4,
(рь рз<0, Ц2, Р4>0) варьированием d\=D\ / ае (D2 просто выражается
через D\: D2=D\tg (у/2), у — угол между осями квадриполя).
Точечные массы приближенной конструкции квадриполя, построенной
со специальной целью прогнозирования орбит ИЗС типа LAGEOS, велики:
положительные массы \х2 и р4 на оси наименьшего момента инерции
Л составляют около 539,5 масс Земли (они отстоят от центра масс планеты
на расстоянии примерно 0,52 км) и такие же по абсолютной величине
отрицательные массы pi и р3 на оси наибольшего момента инерции С,
расположенные на оси вращения Земли севернее и южнее экваториальной
плоскости на расстоянии примерно 6,37 км. Такая конструкция квадри¬
поля вряд ли допускает какую-либо геофизическую интерпретацию,
но зато она довольно точно описывает эллипсоид инерции Земли (как
иногда говорят, динамическую фигуру планеты).
Указанные в §7 направления экстремумов сферической функции
У2 (Ф, ^) второго порядка являются для функции, соответствующей
гравитационному квадриполю Земли, направлениями главных осей
инерции планеты [101]. Если геопотенциал отнести к этим осям, то, как
отмечалось, C2i=S2i=S22=0 и между остающимися стоксовыми постоян¬
ными 2-го порядка и параметрами квадриполя Земли устанавливается
[64] простая связь
M2=GMa2 (2С22—С2о), cos у= (§С22-\-С2о) / (2 С22—С2о), (3.25)
и так же просто параметры квадриполя выражаются через главные
моменты инерции Земли:
Мч= GMaf (С-A), cos 7=1-2 (С-В) / (С-Л); (3.26)
причем в этой системе координат S=sin (у/2) просто выражается через
направление одной из осей квадриполя:
S=cos fti.
Остановимся кратко на гравитационном октаполе Земли. Октаполь —
это точечный объект, получаемый в результате предельного сближения
двух квадриполей, антипараллельных по соответствующим осям; его
62
приближенная схема дана на рис. 9. Он характеризуется моментом М3
и направлениями осей hi, h2, h3. Его потенциал
3 3 dh{dh2dh3 р
Параметры гравитационного октаполя Земли впервые были получены
в [60] по стоксовым постоянным 3-го порядка модели SAO-1. Координаты
полюсов (направления осей) оказались равными
^ = 58,6°, >.1 = 288,4°; 02= 143,5°, ^2=295,4°; 03= 108,1°, Х3=20,2°.
Не приводя значения момента и не пытаясь дать какой-либо геофизи¬
ческой интерпретации его (геодезическая интерпретация будет дана
ниже), рассмотрим отдельно его зональную и незональную части. Если
в случае гравитационного квадриполя такое рассмотрение констатирует
отличие состояния недр Земли от гидростатически равновесного, дает
общие суждения о трехмерном характере
распределения плотности вещества плане¬
ты и раскрывает трехосность ее динамичес¬
кой фигуры, то и в случае октаполя это
приводит к определенным выводам о преоб¬
ладающем влиянии некоторых групп гар¬
моник 3-го порядка на внешний потен¬
циал Земли и фигуру геоида.
Действительно, для зонального октаполя
Земли (учитывается только С3о=т^О, осталь¬
ные гармоники 3-го порядка считаем
нулями)
fl, = 02=0, 03= 180°, MfH«l/4Af3,
а для незонального (С3о=0, остальные бе¬
рутся по модели геопотенциала) направления осей отличаются от таковых
для общего октаполя незначительно (в пределах ±10°) и Мзезон лишь на
3 % отличается от М3. Значит, общий октаполь Земли обусловлен преиму¬
щественно тессеральными и секториальными гармониками потенциала,
отражающими асимметрию распределения масс и фигуры Земли в долгот¬
ном отношении. Ранее — по относительно большему значению С3о в на¬
боре всех стоксовых постоянных 3-го порядка — подчеркивалась асиммет¬
рия фигуры Земли лишь относительно экватора («грушевидность» ее).
Обращаясь теперь к гравитационному тетраполю Земли, скажем, что
этот точечный объект как предельное положение двух октаполей, характе¬
ризующийся моментом Ма и четырьмя осями ht, в своей приближенной
конструкции имеет 24= 16 точечных масс. Не приводя здесь его максвел-
ловых параметров, впервые полученных в [61], скажем лишь, что только
одна его ось образует с осью вращения Земли угол примерно 11,5°, осталь¬
ные три тяготеют к плоскости экватора (для них д равны 59°, 72°, 75°).
И здесь имеют определенный смысл построение зонального и незональ¬
ного тетраполей и сравнение их с общим тетраполем Земли.
Это сравнение указанных тетраполей показывает, что оси общего
тетраполя Земли расположены намного ближе к осям незонального
Рис. 9. Приближенная схема
октаполя
63
тетраполя (лишь одна отклоняется от соответствующей оси примерно
на 11°, остальные — на 14-2°), чем к оси зонального, т. е. к оси вращения
планеты; при этом Mje30H»M4, а М\опжх/5М4. Значит, на гравитационный
тетраполь Земли при вычислении его параметров преобладающее влияние
оказывают тессеральные и секториальные гармоники (причем большее —
последние), что при его интерпретации, как и октаполя, подчеркивает
наличие большей асимметрии в распределении масс внутри планеты и в ее
фигуре по долготе, нежели по широте, причем значительнее эта асиммет¬
рия проявляется в приэкваториальной зоне.
Как видно из описания гравитационных мультиполей первых порядков,
каждый из них несет в себе полезную информацию о планете, а учитывая
еще равноценность максвеллова представления шаровых функций лапла-
сову, потенциал силы тяжести Земли, очевидно, в отдельных случаях
может оказаться целесообразным записывать и в мультипольном виде
для которого значения необходимых параметров (Мп и Ьг при /=
= 1, 2, . . . , п) Земли были вычислены А. Н. Марченко до 18—16-го поряд¬
ков для моделей геопотенциала SA0-3 и GEM-6 в его диссертации [64],
а по модели SA0-1 до 16-го порядка они приведены в статье [102].
§ 11. Мультипольное истолкование
основных особенностей фигуры геоида
Использование мультипольного представления геопотенциала при
изучении внешнего гравитационного поля Земли и ее фигуры находится
в стадии становления. Методически начальным этапом этого явилась раз¬
работка способов нахождения параметров мультиполей (§ 7) и обсужде¬
ние результатов их установления по различным наборам стоксовых
постоянных Земли. Первый из этих вопросов рассматривался сначала
автором [77, 81], затем им же совместно с А. Н. Марченко [98, 100],
который, дополнив [62] и апробировав методику определения параметров
мультиполей вычислением их по различным моделям геопотенциала
(SAO-1, 2, 3, 4; GEM-1, 2, 3, 4, 5, 6, 7, 8; GRIM-1, 2), выполнил также
их сравнение и соответствующий анализ [64].
Этими исследованиями показано, что более реалистически находятся
углы между осями мультиполя, нежели направления его осей, так как при
этом исключается систематическая погрешность из-за разворота модели
потенциала Vп данного порядка относительно начала системы координат.
Установлено, что оси гравитационных мультиполей являются чувствитель¬
ными индикаторами изменения поля притяжения планеты: они хорошо
подтверждают рассогласованность исследуемых моделей геопотенциала.
По различным моделям достаточно устойчиво определяются параметры
квадриполя Земли, согласованно находятся параметры мультиполей
третьего—седьмого порядков, а параметры мультиполей более высоких
порядков получаются с большим разбросом. В связи со сказанным
гравитационные мультиполи Земли имеет смысл привлечь к описанию
главной части геоида.
(3.28)
64
Фигура планетарного геоида к настоящему времени уже хорошо
изучена. Еще в доспутниковую эпоху (1952 г.) И. Д. Жонголович [33]
на основании выполненного им по гравиметрическим данным разложения
силы тяжести в ряд сферических функций до 8-го порядка построил
карту высот планетарного геоида над общеземным эллипсоидом. Такие
карты строят теперь почти после каждого нового вывода моделей гео¬
потенциала либо по одним спутниковым данным, либо в комбинации
их с наземными данными. Сравнительно недавно карты морского геоида
были построены по данным спутниковой альтиметрии — по GE0S-3
и Seasat [217, 219].
Фигура геоида является очень сложной, она не коррелирует с топогра¬
фией земной поверхности. Даже обсуждаемая с прошлого века трех-
осность Земли и установленная после запусков первых ИСЗ грушевид-
ность планеты не являются преобладающими особенностями геоида.
Объяснение последним находят в скрытом от нас рапределении земных
недр и считают, что ондуляции геоида в какой-либо точке планеты обус¬
ловлены «либо аномальными массами, расположенными достаточно
глубоко, либо интегральным эффектом большого числа аномальных масс,
расположенных в коре и верхней мантии» [43]. Не углубляясь в геофизи¬
ческую интерпретацию особенностей фигуры геоида, вернемся к его гео¬
метрии. На всех отмеченных картах стабильно выделяются характерные
особенности фигуры геоида как по своему плановому расположению,
так и по высоте (табл. 1). Еще в 1966 г. Каула [46] отмечал устойчивое
Таблица 1
Основные особенности фигуры геоида (ориентировочное расположение экстремумов
его высот) [46]
Местоположение
основных повышений
и понижений геоида
Высота
над
эллипсоидом,
м
Широта,
град
Долгота,
град
В районе Новой Гвинеи
77
—5
150 в. д.
В Северной Атлантике (вблизи Велико¬
70
50
10 з. д.
британии)
К юго-востоку от м. Доброй Надежды
51
—50
40 в. д.
У берегов Перу (Перуанский желоб)
44
— 10
80 з. д.
На юго-восток от Индии
— 110
0
70 в. д.
У берегов Антарктиды (море Росса)
—60
—70
160 з. д.
Западная часть Атлантического океана
—55
20
60 з. д.
Восточная часть Тихого океана (на юго-
—55
20
120 з. д.
запад от Калифорнии)
постоянство в расположении основных экстремумов поверхности геоида:
на всех картах его присутствуют четыре максимума и четыре—пять мини¬
мумов, причем наибольшее понижение геоида находится в Индийском
океане, наибольшее повышение — в районе Новой Гвинеи (некоторые
несовпадения в плане этих ондуляций по данным разных авторов объясня¬
ются, в первую очередь, различием эллипсоидов, над которыми даются
высоты геоида и разными наибольшими порядками гармоник, учитывае¬
мых при построении карт). Мультипольное истолкование обсуждаемых
особенностей геоида и частично его общей фигуры было дано в статье
3 Г. А. Мещеряков
65
[99] и с некоторыми дополнениями в [64]. Так как гравитационные
мультиполи низших порядков уже были описаны в предыдущем пара¬
графе, перейдем сразу к рассмотрению вклада их потенциалов в фигуру
геоида. С этой целью в [64], откуда мы заимствуем приводимую ниже
табл. 2 и рис. 10—12, был рассчитан вклад в ондуляции геоида мульти¬
полей разных порядков, соответствующих моделям геопотенциала
SAO-3 и GEM-6. В табл. 2 приведены среднеквадратические значения
ап ондуляций геоида, обусловленные мультиполем п-го порядка, средне-
л
квадратические значения ондуляций геоида <j* = ^ ok, обусловлен-
k = 2
ных суммой мультиполей от второго до п-го порядков; величины о2 и of
характеризуют ондуляции геоида мультиполя второго порядка относи¬
тельно нормального эллипсоида вращения с а=6378155 м, а= 1/298,255.
Таблица 2
Порядковые характеристики вклада гравитационных мультиполей Земли
в ондуляции геоида
п
ПП'
м
, м
M
<
» м
SAO-3
GEM-6
SAO-3
GEM-6
п
SAO-3
GEM-6
SAO-3
GEM-6
2
16,4
16,6
16,4
16,6
9
2,6
2,3
28,4
28,4
3
18,9
19,0
25,1
25,3
i 10
2,3
2,4
28,5
28,5
4
10,4
10,2
25,6
25,8
И
2,1
1,8
28,4
28,4
5
7,3
6,8
26,7
26,8
12
1,9
1,3
28,4
28,5
6
5,0
5,2
27,3
27,4
13
1,7
1,8
28,6
28,6
7
4,6
4,5
28,0
28,2
14
1,4
1,2
28,7
28,6
8
3,7
2,5
28,1
28,2
15
1,3
1,4
28,7
28,7
16
1,4
1,1
28,7
28,7
Из табл. 2 видно, что наибольший вклад в ондуляции геоида вносят
квадриполь (п=2), октаполь (п=3) и тетраполь (п=4). Действие же
мультиполей более высоких порядков значительно меньше.
Рассмотрение величин а* приводит к выводу о преобладающем влия¬
нии квадриполя и октаполя планеты. Если среднеквадратические значения
ондуляций геоида, построенных по самим моделям SAO-3 и GEM-6 состав¬
ляют около 29 м, то суммарный вклад <т3 квадриполя и октаполя имеет
значение более 25 м. Влияние мультиполей четвертого и более высоких
порядков носит, очевидно, локальный характер. Поэтому остановимся
более детально на обсуждении гравитационных квадриполя и октаполя
Земли.
Рассмотрим качественную картину гравитационного поля, обусловлен¬
ного квадриполем Земли, который развивает потенциал V2—Y2 / р3. Опре¬
деление точек экстремума сферической функции Y2, как обсуждалось
ранее, показывает, что четыре из них находятся в плоскости осей квадри¬
поля, т. е. в меридиане А,«345°, и две — в меридиане ^«75°. Эти точки
являются полюсами соответственно осей С, А и В инерции планеты. При
одинаковых удалениях от центра планеты потенциал притяжения V2
квадриполем внешней точки всегда меньше на оси инерции С:
У2 (С) = —М2 (3—cosy) / 4р3,
66
нежели в плоскости, в которой лежат оси А и В инерции Земли и которая
практически совпадает с экваториальной плоскостью. В последней макси¬
мального значения потенциал притяжения достигает на оси А (под долго¬
тами примерно 345 и 165°)
у2 (А)=м2 (3+cosv) / 4р3
и минимального на оси В(кж75°) инерции Земли
y2 (B) = -(M2cosy) /2р3.
В общем случае для заданного р: УГ2(Л)>К2 (В)>К2 (С). Этот вывод
хорошо подтверждается картой ондуляций геоида, обусловленных квадри¬
полем Земли (по GEM-6) относительно нормального эллипсоида враще¬
ния (рис. 10). Действительно, в области размещения полюсов оси А
Рис. 10. Ондуляции эквипотенциальной поверхности (в метрах), обусловленные
гравитационным квадриполем
квадриполь вызывает поднятия, достигающие 30 м, а в области располо¬
жения полюсов оси В инерции Земли — опускания уровенной поверхности,
достигающие 40 м. Поэтому мы и подчеркнули ранее, что плоскость осей
квадриполя (Х«345°), экваториальная плоскость, а также меридиан
Х«75° тесно связаны с плоскостями симметрии эллипсоида инерции
планеты и ее обобщенной фигурой в виде трехосного эллипсоида [77].
Перейдем теперь к октаполю. В свое время неожиданностью было
получение относительно большого значения параметра С3о, вызывающего
в фигуре геоида асимметрию по отношению к экватору (грушевидность
Земли). Тем не менее раздельное рассмотрение параметров зонального
(соответствующего зональной части Vz) и незонального (соответствую¬
щего незональной части Vz) октаполей планеты приводит к выводу о том,
что гравитационный октаполь Земли обусловлен главным образом
тессеральными и секториальными гармониками третьего порядка. Послед¬
нее, кстати, объясняет и тот факт, что наряду с грушевидностью, вызывае¬
мой коэффициентом Сзо, фигура геоида, соответствующая Vz, имеет
не менее заметную асимметрию в долготном отношении. Это хорошо под¬
67
тверждается картой ондуляций геоида, обусловленных октаполем планеты
(рис. 11), на которой хорошо просматриваются восемь экстремумов
уровенной поверхности Кз=сопз1:: четыре максимума и четыре минимума.
Сравнивая теперь карту рис. 11 с картой геоида по GEM-10В
(см. рис. 6) и более ранними его картами, констатируем, что максимумы
и минимумы эквипотенциальной поверхности, соответствующей октаполю,
хорошо отвечают главным особенностям геоида, получаемого разными
авторами. В целом расхождение в координатах максимумов и минимумов
достигают ±30°, а в среднем составляют ±15°, но сами области эктрему-
мов хорошо перекрываются. Лучшая сходимость наблюдается для восточ¬
ного полушария. Естественно, картой эквипотенциальной поверхности
K3=const не может быть предусмотрено пятого минимума (см. [46],
с. 163) и более «тонких» деталей геоида, имеющих место в его современных
определениях, так как авторы выводов геоида использовали при этом
гармоники гравитационного поля Земли и более высоких порядков, чем
Рис. 11. Ондуляции эквипотенциальной поверхности, обусловленные гравитацион¬
ным октаполем
третий. Примечательным, однако, оказывается тот факт, что основные
особенности сравнительно сложной и асимметричной поверхности геоида
в качественном отношении достаточно хорошо описываются лишь октапо¬
лем планеты, распределение значений потенциала которого обладает
отчетливо проявляющимся на рис. 11 свойством его симметрии (2.44).
Можно отметить также асимметрию расположения максимумов
и минимумов в широтном отношении. Так, в области северного полюса
Земли наблюдается положительная ондуляция, далее следует волнообраз¬
ный «пояс» из трех отрицательных и ниже — «пояс» из трех положитель¬
ных ондуляций, а в области южного полюса — значительное понижение.
При этом «бугорчатое» строение геоида по поясам в долготном отношении
проявляет себя даже заметнее, нежели грушевидность Земли.
Качественно асимметричную форму геоида можно было бы частично
объяснить геофизическими свойствами земной коры, так как топография
68
также асимметрична относительно плоскости экватора. Однако это про¬
тиворечит действительности: на северном полюсе океан, а на южном —
материк. А поскольку влияние земной коры проявляется в гармониках
более высоких порядков чем третий, то можно предположить, что главные
особенности фигуры геоида обусловлены глобальными неоднородностями
масс во всем теле Земли, которыми и объясняется доминирующее влияние
октаполя планеты.
Таким образом, учитывая выводы, сделанные на основании анализа
величин, приведенных в табл. 2, и хорошее согласие рис. 11 с картами
геоидов, полученных в последнее время, можно объяснить теперь основные
особенности фигуры геоида главным образом гравитационными квадри-
полем и октаполем планеты. Если первый характеризует фигуру Земли,
близкую к трехосному эллипсоиду, то второй определяет восемь главных
ондуляций геоида. Рассмотрение же эквипотенциальной поверхности
K4=const, соответствующей тетраполю Земли (рис. 12), усиливает
Рис. 12. Ондуляции эквипотенциальной поверхности, обусловленные гравитацион¬
ным тетраполем
последний вывод, так как наложение поля V4 на поле Кг+Кз почти
не изменяет картину вклада квадриполя и октаполя в фигуру геоида.
Проявление тетраполя заметно главным образом по лучшему выделению
в качественном отношении Южноамериканского поднятия геоида и его
понижения в районе Багамских островов, т. е. тех особенностей фигуры
геоида, которые хуже остальных описываются совместным вкладом
квадриполя и октаполя Земли.
§ 12. Моменты плотности недр Земли
и ее эллипсоид инерции
Продолжая начатое в §9 рассмотрение механического смысла стоксо¬
вых постоянных Земли, обратимся сначала к ее степенным моментам.
Как известно, степенными моментами п-го порядка кусочно-непрерыв¬
ной функции 6=6 (х, у, z), рассматриваемой в области т, называются
69
выражения вида
Ipqr(6) = $ bx?yqzr dx, p + q + г = n, n = 0, 1, 2,... (3.29)
T
Моменты (3.29) допускают различную трактовку.
Если под б подразумевают плотность масс абсолютно твердого тела,
занимающего ограниченную часть пространства т, то выражения (3.29)
называют в механике моментами тела т.
Если б — функция ограниченной вариации в области т, возможно,
даже бесконечной, то интегралы (3.29) в математике называют степен¬
ными моментами функции б.
Если под б понимать плотность распределения вероятности случайных
величин х, у, zy а под т — все пространство, то выражения вида (3.29)
приводят к важнейшим в теории вероятности понятиям моментов много¬
мерных (в данном контексте — трехмерных) случайных величин.
Фундаментальное значение степенных моментов объясняется тем, что
в механике они являются основополагающими понятиями геометрии масс
и динамики тел, в теории приближения функций — основным объектом
изучения так называемой проблемы моментов, в теории вероятностей —
одним из сильнейших,методов исследования случайных величин и случай¬
ных функций, являющимся замечательным созданием русской науки.
Примечательно, что все эти три аспекта теории моментов связаны с именем
Чебышева.
Понимая под т объем планеты, а под б — плотность веществ, ее слага¬
ющих, будем далее интегралы (3.29) называть или степенными момен¬
тами планеты, или степенными моментами плотности ее недр.
В настоящее время все указанные выше трактовки степенных моментов
плотности недр Земли начинают использоваться при глобальном ее изуче¬
нии. Причина этого кроется в содержании классической проблемы момен¬
тов, заключающейся в том, что по известной последовательности (бес¬
конечной или конечной) моментов разыскивается в известной области т
функция б, для которой числа этой последовательности являются
ее моментами.
Механическая интерпретация одномерной задачи моментов для
конечного промежутка [а, Ь] дана Чебышевым в хронологически первой
его работе 1867 г. по проблеме моментов; она заключается в нахождении
верхнего и нижнего пределов для массы, приходящейся на интервал
[а, ?], где а<£<б, по заданным на [а, Ь] первым моментам ее распреде¬
ления.
И при дальнейшем развитии одномерной проблемы моментов как мате¬
матической теории (см. [15]) последней постоянно сопутствовали ее меха¬
нические приложения: так, Стильтьес в 1884 г. и Радо в 1890 г. использо¬
вали первые степенные моменты Земли (ее массу и момент инерции) для
установления пределов изменения плотности земных недр на разных
глубинах в предположении, что плотность есть функция только расстоя¬
ния от центра планеты.
К многомерной, точнее, двумерной проблеме (трехмерная отличается
от нее лишь усложнением формул), математика (Гильдебрандт и Шён¬
берг) обратилась только в 30-е годы текущего столетия, хотя трехмерные
70
степенные моменты Земли (нулевого, первого и второго порядков) в их
механической трактовке, приведенной в §9, использовались в теории
потенциала уже с прошлого века.
Значение трехмерной проблемы моментов для планетарной геофизики
отчетливо оформилось в 1968 г., когда было осуществлено сведёние к ней
обратной задачи теории потенциала [74, 75], в которой по известному
внешнему потенциалу тела заданной формы ищется плотность его масс.
К этому времени, с одной стороны, в геофизике уже накопился ряд фактов,
подтверждающих наличие на значительных глубинах в теле Земли
латеральных вариаций плотности, а с другой — уже имелась достаточная
информация о внешнем гравитационном поле, позволяющая приближенно
решать для планеты усеченную трехмерную проблему моментов.
Из наблюдений, однако, степенные моменты Земли не получают, но они
очень просто связаны с ее стоксовыми постоянными. Каждая стоксова
постоянная планеты, как уже отмечалось ранее, есть линейная комби¬
нация степенных моментов ее плотности. Действительно, записывая
в подынтегральном выражении формулы (1.15) гармонические функции
рпРпп (cos Ф) cosтк и p^cos Ф) sin тХ в прямоугольных координатах,
получаем с учетом (3.29)
где apqr и $pqr — константы, a Ipqr(6) —размерные степенные моменты
вида (3.29), если при этом и стоксовы постоянные Спт и Snm размерны.
Если же в правой части формулы (3.30) подразумеваются безразмерные
стоксовы постоянные, то в левой части этой формулы должны фигуриро¬
вать не Ipqr(6), a Jpqr(б) —тоже безразмерные степенные моменты,
которые связаны с размерными следующим образом:
Соотношения вида (3.30) были рассмотрены И. Д. Жонголовичем
в [34], где впервые был приведен список коэффициентов аир при 4.
Затем этот список был продолжен до az<16 [97], а впоследствии
и до п^9 [106]. В последней статье приведены также общие формулы для
вычисления коэффициентов apqr и $pqr в случае стоксовых постоянных
любой степени п и произвольного порядка т.
Ставя вопрос о нахождении степенных моментов земных недр /pqr
по набору стоксовых постоянных [79], видим, что при всяком порядке п
имеется /л=72 (л+1) (я+2) степенных моментов (3.29) или (3.31),
а известные стоксовы постоянные этого порядка доставляют лишь
s„=2ai+1 линейных соотношений между этими моментами, причем
ln>sn. Значит, для определения моментов нужна дополнительная инфор¬
мация. Она может быть взята из геофизики в виде некоторой известной
модели распределения плотности земных недр. Назовем такую модель
исходной моделью. Для нее при каждом п могут быть вычислены степен¬
ные моменты, скажем, Jpqr\ обозначим их через J°pqr. Подстановка их в соот¬
ношения (3.30) показывает, что С°пгпФСпт и S^m=^=Snm. Для того чтобы
соотношения (3.30), которые будем считать теперь условными уравне¬
(3.30)
V(6)=/wr(6) / {Mai).
(3.31)
71
ниями, удовлетворялись, надо в моменты J°pqr ввести некоторые поп¬
равки vpqr.
Положив
J pqr=J°pqr-\-Vpqn (3.32)
имеем при каждом п всего 1п искомых поправок vpqr=Vj (/= 1, 2, . . .,/„),
удовлетворяющих sn линейным уравнениям связи
X lMrr 1 • ьгчг + Щ = 0 (*'=»• 2, • • Sa), (3.33)
p + <7 + r = n РЯГ '
в которых невязки суть
Wi=C°nm— Спт или Wi — S°nm—Snmr. (3.34)
Если исходная модель выбрана удачно и в среднем она отвечает реаль¬
ному строению планеты, то поправки Vj можно полагать малыми, имею¬
щими разные знаки, и, значит, их можно искать способом наименьших
квадратов:
1п
^ v2} = min. (3.35)
/ = i
Реализация этого условия — в сооветствии с известными вычислитель¬
ными схемами метода наименьших квадратов (МНК) — приводит к таким
поправкам vр введение которых в J°pqr дает моменты Jpqn согласованные
с заданной информацией о гравитационном поле в виде набора стоксовых
постоянных. Конечно, получаемые Jpqr — это лишь квадратические
приближения степенных моментов, но они более реалистичны, нежели
Jpqn соответствующие даже оптимальной (в каком-то смысле) геофизи¬
ческой модели планеты, при построении которой, однако, не учтена
информация о внешнем гравитационном поле. Подтвердим это следующим
фактом. Из вычислительной процедуры МНК следует, что находимые
поправки Vj в моменты являются линейными комбинациями исходных
стоксовых постоянных Cnrn, Snm. Значит, описанная процедура
определения (уравнивания) степенных моментов ничего не дает (приводит
к Vj= 0) для планеты, все стоксовы постоянные которой, кроме Coo = 1,
равны нулю, т. е. для тела со сферически-симметричным распределением
плотности. Во всех остальных случаях она улучшает исходное распределе¬
ние плотности (и}Ф0), видоизменяя его так, чтобы получаемая модель
развивала бы в пространстве наблюдаемое гравитационное поле.
Остановимся на рассмотрении для Земли степенных моментов 2-го
порядка, которых всего шесть, а стоксовых постоянных этого порядка
только пять.
Выполним уравнивание трех моментов J200, /020, /002 (остальные
/110=2522, /101=^21, /011= С21 уравнивания не требуют) в качестве условия
вида (3.30) при сферически-симметричной исходной модели радиуса R и
массы М, для которой
*^200 = Л)20 = Л)02 = до j 5р4 dp = /.
72
В результате получим их квадратические приближения, а значит, по фор¬
мулам (3.12а) и моменты инерции относительно осей принятой системы
координат
Ax=2J+{/3Cw—2С22, Ву=21+'/зС20+2С22, Cz=2J—'г/3С20. (3.36)
Если координатные оси совмещены с осями главных моментов инерции,
то Лх, Ву, Cz выражают, как уже упоминалось, главные моменты инерции
А, В, С. И тогда по известной формуле, определяющей динамическое
сжатие Земли,
Н=[С—1/2(Л + В)]/С,
можно вычислить его значение Н° по параметрам гравитационного поля
С го и С 22 с учетом исходной модели планеты. Оно равно
#°=ЗС2о/ [2 (С20—3/) ]. (3.37)
Приняв за исходную модель планеты однородный шар (/=0,2) и взяв
известное для Земли С2о= —1083* 10~6, получим Н°=0,0027, что, конечно,
сильно отличается от известного его значения Н «0,0033, но в относитель¬
ном виде это составляет более 80 % его действительной величины.
Если вместо однородного шара взять более реалистическую модель
распределения плотности 6=6 (р) недр Земли, то формула (3.37) даст
значение Н с погрешностью в несколько процентов. Конечно, подсчиты¬
вать таким образом динамическое сжатие Земли нет никакой надобности,
ибо его значение более точно выводят из астрономических наблюдений.
Но для некоторых планет и их спутников можно таким способом найти
нижний предел их динамического сжатия
Ят|п=ЗС20/ [2 (С20—0,6) ], (3.38)
если для них известна гармоника второго порядка.
Для Земли динамическое сжатие известно. Значит, рассматривая фор¬
мулу, его определяющую, как соотношение между моментами инерции
А, В, С и Н и присоединяя к нему уравнения вида (3.30) для С2о и С22,
отнесенные к главным осям инерции планеты, имеем относительно /2оо,
7о2о> /002 линейную систему с определителем 2Я/(1—2Н) =^=0, из которой
могут быть найдены эти степенные моменты, а значит, и главные моменты
инерции
А = С20 2С22, В = С20 -jp- + 2С22> С = - (3.39)
Результаты расчета безразмерных главных моментов инерции Земли
по этим формулам с использованием некоторых моделей ее гравитацион¬
ного поля и с разными значениями Н, приводимыми в литературе, даны
в табл. 3 и 4.
Данные этих таблиц, как и не приводимый здесь расчет точности
определения А, В, С по С2о, С22 и Н, показывают, что на точность
вычисленных моментов инерции сильно влияет неуверенное знание дина¬
мического сжатия Земли.
Далее мы будем пользоваться последним из приведенных в табл. 4
значений момента инерции Земли С = 0,3306748. Оно соответствует
73
Таблица 3
Безразмерные главные моменты инерции Земли при Я= 0,0032726
Модели поля
А
В
С
GEM-6
0,3297297
0,3297369
0,3308159
GEM-9
0,3297290
0,3297353
0,3308152
GEM-10
0,3297290
0,3297362
0,3308152
Таблица 4
Безразмерные главные моменты инерции Земли для модели GEM-10
Значения Н
А
В
С
0,0032726
0,3297290
0,3297362
0,3308152
0,0032732
0,3296685
0,3296757
0,3307547
0,0032739935
0,3295886
0,3295958
0,3306748
значению динамического сжатия //=0,0032739935, принятому в теории
вращения Земли [176].
Перейдем к вопросу определения ориентировки эллипсоида инерции,
иногда называемого динамической «фигурой» Земли. При обсуждении
гравитационного квадриполя Земли (§ 10) подчеркивалось, что направле¬
ния главных осей инерции планеты совпадают с направлениями экстре¬
мумов сферической функции У 2 (О, X), соответствующей потенциалу V2
квадриполя. Последние являются собственными направлениями вектор¬
ной функции g2=gradV'2=g2 (р) от векторного аргумента р (§ 8). Решение
задачи Определении точек экстремума (точнее, определения стационарных
точек) сферической функции У2 (ft, X) выполнено в [101], где показано,
что направляющие косинусы собственных векторов квадратичной формы
V2 равны
/, + /2
2с
х2 = =Ь
т1п2 — т2п!
2cs
У2 = ±
т, + т2
2с
п\к ~ п21\
2 cs
z2 = dz
2 с
1\ГП2 — 12ГП\
2 cs
2s
Уъ = ±
2s
2з — =Ь
2s
(3.40)
здесь с=cos (у/2), s=sin (у/2), а у — угол между осями квадриполя
направляющие косинусы осей которого суть (/1, mi, п\) и (/2, m2, п2).
Точки с координатами ±(jcj, у 1, zi) и +(х3, уъ, ^ъ) лежат в плоскости
квадриполя и определяют ось наименьшего момента инерции А и ось
наибольшего момента инерции С соответственно. Точки с координатами
±(*2, У2, z2) задают ось среднего момента инерции В. По указанным
направляющим косинусам осей инерции Земли при необходимости могут
быть вычислены и углы Эйлера, более компактно фиксирующие триедр
естественной системы координат ОАВС.
74
Таким образом, для определения ориентировки, эллипсоида инерции
планеты по известному комплекту ее стоксовых постоянных 2-го порядка
надо еще знать направления осей гравитационного квадриполя и легко
вычисляемый по последним угол между ними. Однако нахождения осей
квадриполя описанными ранее методами (§ 7) при этом можно избежать.
Для этого надо, как это выполнено в статье Абрикосова [1], вычислить
сначала по стоксовым постоянным инварианты квадратичной формы,
описывающей потенциал У2 квадриполя, затем по ним параметры М2 и
р=cos у, которые в совокупности со стоксовыми постоянными дают воз¬
можность найти оси квадриполя из простых алгебраических выражений.
Если ориентировку осей инерции описывать не углами Эйлера или, тем
более, направляющими косинусами (3.40), а углами £, т], £ последователь¬
ных поворотов вокруг всех трех осей принятой системы координат, то
найдем
m« — т, L — L . п,т0 — т,п0
tgE=— L> sin Л . tgC = ■■■■ 7-7С-. (3.41)
п{ — п2 ’ 1 2s 6 ъ s(/j + /2) v ’
Эти формулы дают координаты т|, I полюса оси С и восточную долготу £
оси А.
Преимущество использования именно этих углов («самолетных»,
«кардановых») в том, что, во-первых, они в отличие от углов Эйлера
не приводят к неопределенности даже при совпадении оси инерции С
с осью Oz принятой системы координат, и, во-вторых, именно такая
система углов принимается для описания положения полюса Р оси вра¬
щения Земли, координаты хР, уР которого соответствуют углам ц и £ [1].
Определение ориентировки триедра естественной системы координат
ОАВС по моделям геопотенциала GEM-7, 8, 9, 10, GEM-L2 и Раппа-
1981 привело к следующим результатам.
1. Углы £ит] не превосходят Г'. Средние квадратические ошибки
их определения оказались того же порядка, что и сами углы, а это свиде¬
тельствует о неустойчивости их выводов по существующим моделям потен¬
циала.
2. Западная долгота £ оси наименьшего момента А инерции имеет
значение ^4= 14°56'±4' (среднее из выводов по использованным шести
моделям геопотенциала).
Отсюда следует, что при современной точности моделей потенциала
Земли можно считать, что ось наибольшего момента С инерции Земли
совпадает со средней осью вращения планеты и что параметры ее грави¬
тационного квадриполя можно считать по формулам, полученным по ме¬
тоду Умова в [77] при C2i=S2i=0:
4ct^ $ = - (2 + —-Jk=A tg2X=^-, (3.42)
V V<%2 + SlJ C22
M2 = GMa\ (2У C\2 + s222 - C20), (3.43)
где стоксовы постоянные безразмерны. Однако заметим, что одной из
важных задач современной геодезии является именно определение C2i и S2i.
75
Как известно, при разнообразных теоретических исследованиях
Земли как планеты в целом и особенно для практики заманчиво иметь
в качестве единой системы координат некоторую «абсолютную» систему
координат. Таковой может быть естественная система ОАВСу т. е. система
координат с началом в центре масс Земли и с осями, совпадающими
с направлениями главных осей инерции планеты. При описании гравита¬
ционного поля планеты в такой системе координат OXYZ обращаются
в нули все стоксовы постоянные первого и второго порядков, кроме С20
и С22. В приложении дана табл. I стоксовых постоянных модели геопотен¬
циала GEM-10 [202], приведенных к естественной системе координат по
программе Марченко [63] (см. § 8).
Заметим, что в этой системе координат потенциал второго порядка
У2 (потенциал гравитационного квадриполя Земли) имеет канонический
вид
(3.44)
Такое выражение V2 вместе с тривиальной записью потенциала нуле¬
вого порядка Vo=GM/p и с учетом исчезновения потенциала земного
диполя (1Л = 0) дает образец раскрытия возможностей мультипольного
представления геопотенциала (3.28).
§ 13. Основные свойства ряда, представляющего
геопотенциал
Продолжим рассмотрение классического ряда шаровых функций (1.12)
УЯ(Ы)
X
п~0 РЛ + 1
представляющего потенциал притяжения планеты, записав его для Земли
в развернутом виде
V
= ]Г f-jf) ^ (Спт cos т'к + Snm sin тХ) Р™( cos #). (3.45)
л = 0 ' т = 0
Значение этого ряда уже было раскрыто ранее (§ 9). Коротко оно
сводится к тому, что получаемые по результатам измерений (гравиметрия)
и наблюдений (космическая геодезия) его коэффициенты Спт и Snm —
это те параметры, числовые значения которых в совокупности определяют
и описывают свойства гравитационного поля Земли, а аналитическое
представление каждого из них (см. формулы (1.15) в § 3) отражает его
зависимость (а значит, и зависимость поля притяжения планеты в целом)
от ее формы и внутреннего строения (в смысле распределения плотности
вещества по всему ее объему). Поэтому практически использование как
самого ряда (3.45), так и его параметров в отдельности предполагает
полную взаимосогласованность их как коэффициентов конкретного схо¬
дящегося ряда, рассматриваемого в области его сходимости. И вот
необходимость строгого уяснения выделенных обстоятельств заострила
в последние десятилетия вопрос об исследовании свойств ряда (3.45) и
76
разработок обоснованных методик вычисления на его основе потенциала
и его производных в точках поверхности Земли и в ее ближайшей
окрестности [127, 111, 115, 178, 200, 9, 10, 129, 130, 170—172].
Не входя в эту обширную проблему со многими ее аспектами, оста¬
новимся далее лишь на некоторых возможных интерпретациях этого ряда
и следуемых из них практических выводах.
Но сначала отметим основные свойства ряда (3.45) или (1.12).
Лапласов метод (§ 3) его вывода обусловливает ему равномерную сходи¬
мость всюду вне сферы S, объемлющей планету т, радиуса ^=рнаиб, где
Рнаиб — планетоцентрический радиус-вектор точки поверхности о планеты,
наиболее удаленной от начала координат, обычно совмещенном с центром
масс т. Для Земли полагают R=ae. Скорость сходимости обсуждаемого
ряда в указанной области не превосходит скорости сходимости геометри¬
ческой прогрессии со знаменателем ajр.
Качественно такой же результат следует и из теории гармонических
функций [153], согласно которой ряд (1.12) вне сферы S трактуется
степенным рядом (относительно 1/р), представляющим гармоническую
функцию V в окрестности бесконечно удаленной точки. Этот степенной ряд
равномерно сходится в любой частичной подобласти, целиком со своей
границей принадлежащей области, внешней относительно объемлющей
сферы S.
Сходимость ряда (3.45) в слое pg<^p<.R (ра — радиус-вектор точек
поверхности о планеты), а значит, и на поверхности Земли, ничем не га¬
рантирована, хотя известны случаи, когда обсуждаемый ряд представляет
потенциал не только вне объемлющей сферы S, но и всюду вне поверхности
о тела т, например вне однородного (или даже неоднородного, но эллип¬
соидально-слоистого) эллипсоида.
Лаплас и Гаусс описывали этим рядом потенциал Земли и в точках ее
поверхности (первый — гравитационный потенциал, второй — магнит¬
ный), ограничиваясь в нем несколькими первыми членами.
Отношение к этому ряду геодезистов до самого недавнего времени
кратко, но точно было сформулировано еще в 1888 г. ([141], с. 119):
«Весьма веские соображения заставляют предполагать, что уравнением
(1.12), (3.45) *) определяется потенциал всякого тела во всем (подчерк¬
нуто Ф. А. Слудским) внешнем пространстве. Строгого доказательства
этой в высшей степени важной теоремы, к сожалению, не имеется. Но так
как в справедливости ее не сомневался сам Гаусс, то не будем сомне¬
ваться и мы». Поэтому в геодезии почти до наших дней этот ряд на по¬
верхности Земли принимался без каких-либо оговорок. Безусловно, что
при использовании частичных сумм VN ряда (3.45) при малых А, т. е. при
изучении главной части потенциала, это вполне допустимо. Но в космиче¬
скую эру, когда открылись возможности определять и использовать его
коэффициенты до порядков А, исчисляемых десятками, а теперь и сот¬
нями, задача исследования характера сходимости ряда геопотенциала
и ее скорости приобрела практическое значение и ей стали уделять
большое внимание; были, в частности, безуспешные попытки дать дока¬
зательства сходимости ряда на поверхности Земли, имеется даже обзор
*) По нашей нумерации формул.
77
последних, составленный Моритцом (см. [127]), а состояние проблемы
подробно изложено в его работе [111].
Вопрос убывания коэффициентов ряда геопотенциала исследовался
сначала эмпирически на основании информации о гравитационном поле
Земли, полученной по результатам наблюдений.
Из статистического анализа наборов стоксовых постоянных Земли,
полученных по наблюдениям первых ИСЗ У. М. Каула [46] в 1966 г.
установил формулу зависимости от п степенных дисперсий
^п(Сяа, snm) = X (CL + SU (я ^ 3) (3.46)
т = О
гармоник геопотенциала в виде
а„=10 • 1СГб/г“2, (3.47)
а из независимой обработки данных об аномалиях силы тяжести Л. П. Пел-
линен [124] в 1970 г. также методами математической статистики получил
kg2n= 166ц_1,12мгал2, что дает
<х„=9,3 • 10—6п—2'06. (3.48)
Обе эти формулы в диапазоне дг=100^-200 оправдываются практи¬
чески и на современных моделях геопотенциала.
Скорость сходимости ряда (1.12) в теоретическом плане изучена
в 1977 г. К. В. Холшевниковым [200]. Она зависит как от формы
поверхности о планеты, так и от ее структуры, точнее от гладкости
функции плотности 6 недр планеты (от числа и значения разрывов непре¬
рывности 6). При этом чем мельче структуры планеты и чем ближе они
расположены к ее поверхности, тем более сильно они проявляют свое влия¬
ние на более высокие гармоники Yп потенциала V. Найдена оценка для
потенциала п-го порядка планет земной группы:
\у I = < -CMRn . (3.49)
' p" + 1 ^ n5'V+l ’
где безразмерный множитель 2,4 (на S) зависит от «гладкости»
плотности планеты; отмечено, что сходимость ряда (1.12) определяется
поведением плотности 6 в сколь угодно тонком поверхностном слое.
Сходимость ряда (1.12) на поверхности Земли изучена в [9, 10]. Этот
ряд построен для внешней области относительно сферы S, и для его сходи¬
мости в слое между а и S, как уже отмечалось, в общем случае не может
быть никаких оснований (это имеет место, например, для однородного
эллипсоида, но не для тел произвольной формы). Конечно, можно наде¬
яться, что потенциал будет сходиться и на а или в какой-либо точке
слоя ра^р</?. И если вдруг это окажется так, то надо будет еще удосто¬
вериться, что же тогда представляет его сумма, т. е. совпадет ли она
со значением потенциала притяжения Земли именно в этой точке. Наде¬
яться на это совпадение нельзя, ибо для такой точки рс/?, что не пре¬
дусмотрено методом вывода обсуждаемого ряда, когда почленно интегри¬
ровался ряд производящей функции полиномов Лежандра для случая
р>R. Значит, если и окажется, что в какой-то точке слоя ряд (1.12)
78
сходится, то, очевидно, в этой точке он, скорее всего, представляет какую-
то другую функцию, а не исследуемый внешний потенциал Земли;
примеры исследования поведения ряда на а будут приведены далее.
Для небесной механики Пуанкаре [139] еще в 1886 г. было детально
обсуждено понятие сходимости рядов как с точки зрения математики, так
и с точки зрения астрономии, была разработана теория асимптоти¬
ческих разложений функций и было показано, что подавляющая часть
рядов небесной механики суть ряды асимптотические. С позиций этой
теории и изучаемый ряд (1.12) является в слое между о и S асимптоти¬
ческим степенным рядом (в смысле Пуанкаре).
Поведение ряда (1.12) при увеличении п (при фиксированных Ф и X)
частично таково же, как и простейшего классического асимптотического
ряда ([164], с. 531—532), иллюстрируемого разложением In (1+х),
сходящимся на промежутке (—1,1], а при малых х>\ выражающим
разложение этой же функции, но уже асимптотическое: оно при любом
достаточно малом х>\ сначала (до некоторого п *) имеет убывающую
последовательность частичных сумм, которые затем (при увеличении п)
начинают возрастать и при п-+ оо увеличиваются до бесконечности.
В данном примере, правда, асимптотическое разложение для любого
n^Ln * с определенной точностью представляет и в некоторой области
х>\ вне промежутка сходимости (—1,1] именно функцию In (1+х).
Для потенциала V, т. е. для ряда (1.12), аналогичный факт не доказан.
В [10] показано, что асимптотический ряд (1.12) на поверхности а
Земли начинает расходиться при /1=200-^300; очевидно, эти порядки и
должны определять максимальные степени создаваемых моделей геопо¬
тенциала. Напомним, что при этом имеется в виду лапласов ряд шаровых
функций (3.45) с коэффициентами (1.15).
В связи с расходимостью ряда (3.45) на поверхности Земли в настоя¬
щее время усиленно разрабатываются разнообразные методики вычисле¬
ния таких поправок в стоксовы постоянные Земли, введение которых
должно изменить расходимость ряда на сходимость, способы улучшения
сходимости ряда и предлагают<5я новые ряды геопотенциала, в частности
«сходящиеся во всем пространстве» (но к чему они сходятся внутри
планеты?) [8, 129, 130, 170—172, 215].
Перейдем теперь к аппроксимационной трактовке ряда, представляю¬
щего геопотенциал. Применительно к возмущающему потенциала Т пос¬
ледняя разработана в физической геодезии (см. [111, 115]) и заключа¬
ется в том, что в бесконечной области Q вне сферы, целиком расположен¬
ной внутри а и возможно наибольшего радиуса а (сфера Бьерхаммара),
этот потенциал разлагается в обобщенный ряд Фурье по системе элемен¬
тарных шаровых функций
являющейся полной ортогональной системой в классе гармонических
функций Н (Q)c=L2(Q), регулярных на бесконечности. И тогда имеем
ряд (1.12), в котором суммирование начинается не с п=0, а по крайней
мере с /г=1 и который содержит в себе сферические функции (1.14) с
79
коэффициентами апт> bnm вместо СптУ Snm, даваемыми формулами
^пт 1
Ьпт }
Г(р, О, Х)-^Р>08 0)/С08,п^й.
4ла J pn + 1 '\sinmA,
Заметим, что в теории фигуры Земли множество функций H(Q) су¬
жают: вместо него берут пересечение //(Q) с соболевским пространством
функций Wl (Q), и тогда одной из важнейших задач является установле¬
ние таких числовых значений параметров а и q, которые гарантировали бы
полученному таким образом ряду наилучшее представление возмущаю¬
щего потенциала Т.
Рассмотрим другой вариант построений [82, 84], просто и быстро
доставляющий в области Q (здесь вне объемлющей сферы S радиуса R)
наилучшее квадратическое приближение произвольной гармонической
функции, а значит, и потенциала притяжения планеты.
Пусть Н — множество всех функций, гармонических в неограниченной
области Q (точки поверхности S причисляем к области Q) и регулярных
на бесконечности. В основе построения лежит следующая лемма.
Лемма. Система элементарных шаровых функций
KJ = {-^T^(cosO){Cs°nS^}SW (п. т = 0, 1, 2, т < п)
(3.50)
для множества всех гармонических функций H<^L2(Q) в области Q
является полной и ортогональной системой при любом весе
р=р-(2+х), х>0*). (3.51)
Ортогональность этой системы устанавливается непосредственными
вычислениями; параллельно с этим определяются и нормы функций си¬
стемы (3.50)
2л (п + т)\
- 'j ^ — (2л + 1 + х) Г
!| = 2 п + 1 +1Г 1
2п -f 1 (п — т)\
II «„о II2/ 2п+1+п)_^ (3-52)
2п 4- 1
Полнота системы (3.50) для H<^L2(Q) следует из ее определения и из
возможности представления любой гармонической функции V£H из Q
рядом Лапласа (1.12). На основании этого констатируем, что в Н суще¬
ствует только одна функция (К==0), которая ортогональна (с весом р)
ко всем функциям системы {о)лт}. У всякой же иной функции Уф0, пред¬
ставимой рядом (3.45), имеется хотя бы один коэффициент Спт (или
Snm)t отличный от нуля, вследствие чего
SpV4,
dQ = C || оупт II2ф-0, С=const ^=0,
*) В [82, 84] допущены неточности: считалось х = 0, поэтому все рассмотрение
там относилось практически к Т, а не к любой функции V, и с ошибочных позиций
трактовалась единственность изучаемого ряда.
80
а этого достаточно для полноты определенной в Q системы функций
(3.50), (3.51).
На основании этой леммы любую_ гармоническую функцию £/У,
а значит, и потенциал 1/, в области Q можно единственным образом
аппроксимировать обобщенным полиномом VN по элементарным (стан¬
дартным) шаровым функциям (3.50):
N п
VN = X Y, Илт cos т% Впт sin т%) Р™ (cos ■§) (3.53)
п = 0 Р т = 0
при условии
вдг = S -^(V - VN)2dQ = min. (3.54)
Q P
При этом довольно просто вычисляются коэффициенты Фурье функции
V£H по системе (3.50), которые имеют вид
^пт "| 2п + 1 {п — т)! /Г) ^ D2п + 1 + * \/
Впт}= 2я (rt + т)Т “Г х)а X
X \ У 1 P:(cos#){ cosm* dQ,
J рл + 3 + X * 4 ^ sin
Л„о = + 1 + x) Я2" + 1 + * X
X ) V-~- '3 +— P„ (cos 0) </Q ; • Bn0 = 0. (3.55)
Обобщенный полином (3.53) с коэффициентами (3.55) дает наилучшее
квадратическое приближение любой гармонической функции V в неогра¬
ниченной области Q. Вследствие известных свойств обобщенных рядов
Фурье по полным ортогональным системам квадратическая погрешность
приближения eN при любом фиксированном N имеет наименьшее значение
именно при найденных значениях коэффициентов Апт и Впт. В случае
увеличения N она не возрастает. При N-*oо ряды, найденные для VN,
в среднем сходятся к функции V\ при этом имеет место равенство Парсе-
валя.
Итак, доказана следующая теорема.
Теорема. Внешний гравитационный потенциал V планеты во внешнем
пространстве относительно сферы, охватывающей все массы планеты,
представляется обобщенным рядом Фурье (формула (3.53) при N-^oo)
с коэффициентами (3.55).
Примечание. Хотя при заданном весе (3.51), т. е. при каком-либо
фиксированном значении параметра х, такое представление единственно,
все же в рамках задачи о наилучшей квадратической аппроксимации
потенциала имеет смысл поставить также вопрос об оптимальном значе¬
нии х, реализующем минимум погрешности аппроксимации едг (по пара¬
метру х). Выбор конкретного значения параметра х связан с выделением
сферического слоя вне сферы 5, в котором должна быть обеспечена
наименьшая погрешность приближения.
При описании полного потенциала V всегда должно быть строго
х;>0. А при аппроксимации возмущающего потенциала Г, когда разло¬
жение не содержит нулевой гармоники 1 /р, можно принять и х=0, что
8!
выгодно с точки зрения вычислений: тогда упрощаются выражения коэф¬
фициентов (3.55).
Возможность аппроксимации гармонических функций при различных
весах (3.51) подчеркивает выраженное леммой простое, но важное свой¬
ство системы элементарных шаровых функций (3.50), заключающееся
в том, что эта система вне сферы при любом х>0 является полной
и ортогональной системой функций (базисом) в пространстве гармони¬
ческих функций, регулярных на бесконечности.
Таким образом, классическое представление (1.12) потенциала притя¬
жения вне сферы рядом по шаровым функциям, представляющее локаль¬
ное разложение потенциала в окрестности бесконечно удаленной точки,
трактуется теперь как его глобальное представление, но, конечно, с дру¬
гими коэффициентами (3.55). Коэффициенты Апт и Впт при описании
потенциала рядом по шаровым функциям не менее естественны чем
стоксовы постоянные Спт и Snm, ибо формулами (3.55) наглядно раскры¬
вается их значение как обобщенных коэффициентов Фурье. Они выражены
здесь интегралами по всему внешнему пространству от произведений
шаровых функций, веса и изучаемого потенциала. Последнее отчетливо
объясняет замеченную на основании экспериментальных данных необ¬
ходимость определения гармоник потенциала по равномерно распре¬
деленным наблюдениям за ИСЗ при разнообразных их орбитах, охва¬
тывающих наибольшую часть пространства, внешнего относительно
Земли.
Рассматривая ряд шаровых функций (3.45) как ряд Фурье (3.53) при
N->oo с коэффициентами (3.55), имеет смысл получить компактную
запись последнего. С этой целью, следуя [181], пронумеруем стандартные
шаровые функции (3.50) единым индексом k. Для этого сначала введем
в них третий индекс /:
и перейдем затем от совокупности трех индексов п, ту I к одному — k.
полагая, что он определяется по правилу
Тогда каждой функции с тремя индексами Флт/ будет соответствовать
функция с одним индексом фЛ:
По этому же правилу занумеруем все коэффициенты ряда геопотенциала
при т = 0, / = 1,
при т Ф 0, / = 1, (3.56)
при т Ф 0, / = О,
/2^ —|— 2/72 -f- /— 1.
(3.57)
Ф„т(=Ф*-
(3.56а)
Спт, Snm или Апт, Впт:
при т = 0, / = 1,
при т Ф 0, / = 1,
при т Ф 0, 1 = 0.
(3.58)
82
После этого ряд Фурье для геопотенциала примет вид
оо
V(t) = £ akVk(t), (3.59)
k = О
где t= (р, Ф, Я,) определяет положение внешней точки, а функции <рй (/)
и коэффициенты аА находятся соответственно по (3.56), (3.56а) и (3.58)
с вычислением индекса k по формуле (3.57).
Как при аппроксимации возмущающего потенциала Т в геодезии, так
и здесь при наилучшей квадратической аппроксимации полного внешнего
потенциала V планеты, ряд Фурье содержит два параметра а и q или R и
х. выбор числовых значений которых определяет область и точность
аппроксимации.
Для тел строго сферической формы радиуса R в рядах, представляю¬
щих V или Т, параметр R имеет определенное значение: R=а=ра.
В случае реальной планеты, форма которой отлична от сферической,
важно подобрать наиболее подходящее значение параметра R. И если для
целей геодезии его выгодно отождествлять с радиусом сферы Бьерхам-
мера, то для целей космической геодезии, очевидно, лучше брать средний
радиус планеты R= (рст) ср=/?ср.
Вообще, аппроксимация потенциала планет несферической формы
требует знания ее формы и удачного подбора исходной системы функций
(базиса), по которой следует строить разложение. Так, если для целей
аппроксимации потенциала форму планеты считать сферической, то, же¬
лая сохранить принятое разложение внешнего потенциала по шаровым
функциям, необходимо так выбрать радиус сферы /?, вне которой ищется
разложение потенциала 1/, чтобы в среднем интегралами по Q было
охвачено все внешнее относительно о пространство, в котором этот
потенциал полагаем заданным. При таком выборе R приходится отка¬
зываться от сферы, охватывающей все массы планеты, так как выгоднее
пользоваться сферой с радиусом, равным среднему радиусу планеты Rcp.
Вопрос выбора линейного множителя в разложении геопотенциала V
обсуждался на XXI симпозиуме MAC, где было решено использовать
в формулах для V Земли ее средний экваториальный радиус ае. Однако
исходя из принципа наилучшего квадратического приближения внешнего
потенциала (а не из «эстетических соображений» [45]), в его разложе¬
нии по шаровым функциям имеет смысл брать вместо ае средний радиус
Земли /?ср. Формально область сходимости ряда (1.12) при этом несколько
расширяется за счет добавления к области р>ае еще части пространства,
ограниченной сферами радиусов Rcp и ае, в которой нет масс твердой
Земли.
Однако замена ае на вызовет пересчет безразмерных стоксовых
постоянных планеты. Легко показать, что при этом в стоксовы постоянные
Земли Спт и Snm надо ввести поправки
Д Спт = ~-пСпт, \Snn = ~~nSnm, (3.60)
или, достаточной степенью точности,
ДСпт=1,12. 10—3гсСпш, Д5„т=1,12 • 10“3«Snm. (3.60а)
83
При малых значениях п такие поправки на три порядка меньше самих
гармоник Спт и Snm, т. е. кроме ДС2о, они невелики. А ДС2о = —2,435Х
Х10-6, что, кстати, приводит к поправке в сжатии Земли 6а=31-10~7,
вследствие чего оно оказывается равным 0,0033560=1/297,97 вместо
принятого 0,0033529=1/298,25.
Ясно, что при сопоставлении гармонических коэффициентов потенци¬
ала, определенных при различных масштабных множителях, именно при
ае и при а, надо при переходе от одних к другим учитывать удвоенные
значения поправок (3.60а).
Аппроксимация геопотенциала может быть выполнена с большей точ¬
ностью, если она будет осуществляться вне общеземного эллипсоида по
системе гармоник слабо сжатого эллипсоида (см. § 5), когда «лапласов»
ряд его внешнего потенциала имеет вид
К(ть е, Ь)= X £ °Епт\ятп{1 sh T))P:(cosd)feS^’ (3.61)
п = 0 т = 0 пт)
И еще точнее, если аппроксимация будет реализовываться вне теллуро-
ида. Но если в первом случае решение задачи может быть аналитически
доведено до расчетных формул, то во втором возможно только ее числен¬
ное решение, обремененное почти непреодолимыми трудностями при
построении базисной системы гармонических фукнций вне теллуроида.
Аппроксимация геопотенциала по системе элементарных шаровых
функций приводит к рядам, которые всюду вне сферы Бьерхаммера и, '
в частности, на поверхности Земли, сходятся в среднем. Отсюда, как
известно, еще не следует их равномерная сходимость. В геодезии счи¬
тается [111, 115], что последняя применительно к обсуждаемым
рядам обеспечивается теоремами Рунге — Крарупа и Келдыша — Лав¬
рентьева.
К этому вопросу возможен также иной подход, перед рассмотрением
которого напомним сущность обобщенного суммирования расходящихся
рядов [168, 159], в принципе восходящего к Эйлеру.
Если по некоторому правилу Р ряду £ yk относят число s, называ-
* = о
емое его суммой, то считают, что ряд суммируется к сумме s методом сум¬
мирования Р, что обозначают так:
с»
£ vk = s(P) или lim sn = s(P),
k = о
где sn — частичная сумма, a s(P) — обобщенная сумма исходного ряда.
Классическим методом обобщенного суммирования является метод
средних арифметических, называемый также методом Чезаро [159] или —
применительно к тригонометрическим рядам Фурье — методом Фейера.
В простейшем его виде вводят последовательность (ал) средних арифме¬
тических первых частичных сумм ряда
«о + Sj + • • • +
On = —
п + 1
84
Если при этом оп имеет предел при п-^оо
lim on=s,
Л—► оо
то говорят, что исходный ряд суммируется к сумме 5 методом средних
арифметических (методом Чезаро), и обозначают так:
оо
^ Vk = s(C> 1) или lim sn = s(C, Г).
k = о
При чезаровском определении суммы ряда каждый сходящийся ряд
суммируем к той функции, к которой он сходится, — это так называемое
свойство регулярности метода суммирования. Если же ряд расходящийся,
но предел средних арифметических оп его частичных сумм sA> существует,
то этот предел естественно и принимается за обобщенную сумму ряда.
Известно, что суммы Чезаро — Фейера даже в случае расходящихся
рядов Фурье, но суммируемых в смысле (С, 1), сходятся равномерно при
любом значении аргумента (теорема Харди).
Далее под V будем понимать потенциал притяжения некоторого
тела т, а под Vk — его потенциалы k-х порядков. Так как они гармоничны
вне т вплоть до его поверхности, то и все их чезаровские суммы оп также
функции гармонические, значит, как sk, так и оп суть потенциалы.
Приведем некоторые результаты численного эксперимента суммиро¬
вания (обычного и обобщенного — по Чезаро) ряда геопотенциала в ха¬
рактерных точках поверхности геоида*) (рис. 13—16). На рисунках
приведены значения геопотенциала по его модели 180-го порядка OSU-
81 [218], вычисленные тремя способами на поверхности геоида в регионах
Индийского минимума его ондуляций (рис. 15) и их Гвинейского макси¬
мума (рис. 13), а также в районе Багамских островов (рис. 16) и у берегов
Великобритании (рис. 14).
Сначала геопотенциал вычислялся обычным суммированием по фор¬
муле (3.45); ход изменения его частичных сумм sk показан на рисунках
пунктирными линиями.
Во втором способе выполнено суммирование ряда (3.45) методом
средних арифметических, когда, однако, суммы Чезаро оп образовывались
из частичных сумм 5^=УЛ(д, А,)/р* + 1 ряда (1.12), каждая из которых
включала в себя все 2k -f- 1 гармоник k-й степени, т. е. в суммирующей
формуле всем гармоникам этой степени приписывался один и тот же вес;
соответствующие графики представлены штриховыми линиями.
Наконец, ряд геопотенциала вида (3.59) был просуммирован строго
по Чезаро (С, 1), когда при переходе от частичной суммы sk исходного
ряда к последующей sft+1 добавлялся лишь один член ряда, т. е. функция
(3.56) с соответствующим коэффициентом (3.58); графики таких чезаров-
ских сумм для ряда (3.59) изображены на рисунках сплошными лини¬
ями.
Значения потенциала V вычислялись с сохранением в нем десяти зна¬
чащих цифр, т. е. с погрешностью AV = ±0Д1 м2/с2, что соответствует
*) Вычисления выполнены аспирантами Львовского политехнического инсти¬
тута Н. Ф. Агеевым и А. Д. Баклажко.
85
Рис. 13. Графики значений потенциала притяжения Земли на геоиде в области
Гвинейского максимума его ондуляций (ф=— 3°, Х=145° в. д.), вычисленные тремя
указанными в тексте способами
Рис. 14. Графики значений потенциала притяжения Земли на геоиде у берегов
Великобритании (ср=50°, л,= 10° з. д.)
86
Рис. 15. Графики значений потенциала притяжения Земли в области Индийского
минимума ондуляций геоида (ф=5°, Х=79° в. д.)
Рис. 16. Графики значений потенциала притяжения Земли в районе Багамских
островов (ф = 30°, к = 70° з. д.)
87
определению высот £ геоида над общеземным эллипсоидом с погреш¬
ностью Д£«±1 мм.
Обсуждая на основании приведенных графиков для первого принятого
способа суммирования (пунктирные линии) сходимость ряда (3.45) геопо¬
тенциала с коэффициентами по модели OSU-81, конечно, «обременен¬
ными» погрешностями их определения, видим, что при увеличении п
имеется некоторая тенденция ряда к сходимости, но, во-первых, изменения
его частичных сумм происходят явно не монотонно, во-вторых, ограниче¬
ние счета 180-м порядком не позволяет считать эксперимент суммирования
(таким способом) законченным, в-третьих, и это главное, что уже отме¬
чалось: на поверхности геоида ряд (3.45) является расходящимся.
Поэтому, хотя и нет никаких оснований для сходимости ряда в рассмат¬
риваемых случаях, можно все же, задавшись некоторой точностью ДГ
представления потенциала, установить эмпирически необходимое число N
членов ряда (точнее, порядка шаровых функций), обеспечивающих ее, тем
более, чем здесь взяты самые неблагоприятные случаи, соответствующие
экстремумам высот геоида.
Приняв, например, ДК==ьЮ м2/с2, имеем следующие значения по¬
рядка N усечения ряда (3.45):
в регионе Индийского минимума М = 90
в регионе Гвинейского максимума iV = 104,
в районе Багамских островов Д/ = 51,
у берегов Великобритании jV=100,
т. е., ограничившись такими порядками частичных сумм ряда (3.45) при
его обычном суммировании, можно по нему определить высоту £ геоида
над эллипсоидом с погрешностью Д£«±1 м.
Характерно, что при этом нет какой-то определенной зависимости
порядка усечения ряда от высоты геоида, кроме того, что понижениям
геоида соответствуют меньшие значения N (90 и 51) нежели его повы¬
шениям (104 и 100); последнее скорее всего отражает в соответствии
с выводами [200] меньшую гладкость функции плотности земных недр,
а лучше сказать, более сложную глубинную структуру планеты в регионах
наибольших ондуляций геоида (Гвинейского и в северо-восточной части
Атлантического океана).
Главное здесь, однако, не в этом. Лапласов ряд (3.45) на поверх¬
ности геоида расходится. Но этот же ряд трактуется еще и как ряд Фурье,
и в физической геодезии [115] для нахождения его сумм разработаны
методы устойчивого суммирования. В описываемом же эксперименте
использовано суммирование его по Чезаро в указанных выше двух вари¬
антах. Соответствующие им графики (суммирование по второму и треть¬
ему способам) на рис. 13—16 наглядно подтверждают сходимость чезаров-
с.ких сумм в обоих случаях: начиная со 130—160-го порядков графики
этих сумм «выходят на горизонтальную асимптоту» и выражают значения
потенциала V с погрешностью АК= ± 1 м2/с2, что приводит к возмож¬
ности вычисления высоты геоида £ по получаемым таким способом зна¬
чениям потенциала V с погрешностью Д£«±Ю см.
Анализируя совместно результаты всех трех использованных способов
суммирования ряда геопотенциала, приходим к следующим выводам.
88
1. На поверхности геоида эти способы дают существенно различные
результаты. Даже при N= 180 расхождение между ними может достигать
20 м2/с2, что в переводе на высоты геоида соответствует примерно двум
метрам!
2. Обычным суммированием ряда (3.45) геопотенциала его действи¬
тельного значения получить нельзя ввиду расходимости этого ряда при
р0<R> где R — радиус сферы S, объемлющей Землю.
3. Вычисление потенциала по второму описанному способу рекомендо¬
ваться для практики не может, так как в нем комплектам гармоник
геопотенциала одной степени приписывается один и тот же вес, т. е.
в терминах физической геодезии гравитационное поле при таком методе
суммирования принимается за изотропное.
4. Суммирование по методу Чезаро (С, 1) ряда (3.59) геопотенциала,
члены которого расположены хотя и не строго в порядке убывания их
абсолютных величин и который даже расходится в точках геоида, дает
в реальном анизотропном гравитационном поле Земли такие значения по¬
тенциала V (и, значит, высоты £), которые определяются, во-первых,
равномерно сходящимся процессом вычислений и, во-вторых, на основа¬
нии стоксовых постоянных планеты, полученных по результатам наблюде¬
ний. Поэтому такие значения V могут быть приняты за реальное отраже¬
ние действительности. Вычисление высот геоида с погрешностью, напри¬
мер, ±10 см обеспечивается при этом моделью геопотенциала до 160-го
порядка и степени.
Не останавливаясь на других интересных выводах из приведенного
и аналогичных экспериментов, резюмируем, в заключение, свойства ряда
геопотенциала.
Потенциал притяжения V планеты вне объемлющей ее сферы S ра¬
диуса R представляется лапласовым сходящимся рядом по элементарным
шаровым гармоникам (3.50) с коэффициентами (1.15), выраженными
интегралами по объему планеты. Этот же ряд, если его коэффициенты
представлены интегралами (3.55) по внешности сферы S, есть для этой
бесконечной области уже ряд Фурье, также сходящийся там. Если этим
рядом представить потенциал V на поверхности Земли и всюду вне ее,
то в слое между сферой 5 и поверхностью планеты а, он, во-первых,
уже не будет рядом Фурье, и, во-вторых, окажется рядом расходя¬
щимся.
Если потенциалы V или Т представить рядами Фурье вне сферы
Бьерхаммера и не ставить вопроса о написании для них обобщенных
коэффициентов Фурье типа (3.55) (ибо в интегралы* их выражающие,
войдут значения V или Т в областях между этой сферой и поверхностью
планеты, которых — так же, как и аналитических их продолжений, кстати,
неустойчивых, — мы не знаем), а считать эти коэффициенты подлежа¬
щими определению по результатам наблюдений, то и тогда, во-первых,
для области, внешней относительно поверхности Земли, ряды уже не будут
обладать экстремальным свойством рядов Фурье (не приведут в этой
области к минимуму квадратическую погрешность аппроксимации), и,
во-вторых, на поверхности планеты также будут расходящимися. Много¬
значность при этом трактовки коэффициентов обсуждаемых рядов
объясняется приведенной выше леммой.
89
Исходя из сказанного и желая сохранить форму традиционного
описания потенциала рядом по шаровым функциям, приходится считать
этот ряд на поверхности Земли и в ее ближайшей окрестности расходя¬
щимся и использовать его именно как расходящийся ряд. При этом,
безусловно, возникает вопрос: будет ли потенциал, представимый таким
расходящимся рядом, описывать действительный потенциал Земли?
Непосредственной проверки этого пока сделать нельзя: для этого надо
детально знать то, ради чего, в частности, изучается потенциал притяже¬
ния планеты: ее форму и распределение плотности ее недр. Представля¬
ется, однако, возможным следующий подход к разрешению этого вопроса.
Привлекая простейший метод обобщенного суммирования расходя¬
щихся рядов — метод Чезаро (С, 1) и основываясь на ряде геопотенциала
вида (3.59) с базисными функциями фk(t), определенными формулами
(3.56) с учетом (3.57) и с коэффициентами (3.58), будем постулировать
этот ряд, заведомо расходящийся в слое между сферой, объемлю¬
щей планету, и поверхностью последней (или даже поверхностью
геоида), рядом, описывающим реальный потенциал Земли, при условии,
что все его коэффициенты получены (или получаются) по результатам
наблюдений и измерений. При этом значения .потенциала должны вы¬
числяться не по ряду (3.45) или даже (3.59), а исходя из принимаемого
его определения
v= lim <т„ = lim £ (I - —\ ak<pk{t\ (3.62)
Л-»00 П -У- ОО £ = Q \ П ~Г I /
отражающего равномерную сходимость чезаровских сумм оп расходяще¬
гося ряда (3.59), по следующему алгоритму:
N k \
VttVN = oN= £ (1 - ш)°k(fk{t)' (3-63)
к = О \ /
где N для каждой точки ввиду трехмерности гравитационного поля
и его анизотропности определяется, как и q, эмпирически по заданной
ТОЧНОСТИ (AV) задан
кдг—адг+„К(ДК)задан (<7=1, 2, . . q). (3.64)
Обсуждаемое асимптотическое разложение геопотенциала
ОО
V~ X а*%(<), (3.65)
k = 0
в котором
ф,(0 = ^гтгМ*- *)
Р
(t — совокупность переменных р, О, л, фиксирующих положение точки,
/г=Аг2+2т+/—1, причем в этом ряде содержатся при разных k ансамбли
членов с одной и той же степенью переменной р), совпадает вне объемлю¬
щей сферы с лапласовым рядом потенциала, а на поверхности планеты,
т. е. при выходе за область его сходимости, постулирует значение потен¬
циала в соответствии с правилом суммирования (С, 1), которое приводит
90
к равномерной сходимости чезаровских сумм ряда и на ней. Введенное
определение геопотенциала сходящимся процессом не единственно. Для
физической геодезии выгоднее определить его на основе метода Пуас¬
сона—Абеля, а не на основе метода среднеарифметических. Здесь как
более простой был избран последний; он хотя и слабее первого — дает
сходимость к той же функции, что и метод Пуассона—Абеля.
§14. О вычислении среднего значения
внутреннего потенциала притяжения Земли
Если внешнее гравитационное поле Земли в настоящее время уже
достаточно хорошо изучено, то наши сведения относительно внутреннего
гравитационного поля весьма скудны. В литературе приводятся лишь
модельные представления о внутреннем потенциале и ускорении силы
тяжести внутри Земли, которые соответствуют либо моделям внутреннего
строения сферически-симметричной планеты, либо ее гидростатически
равновесным моделям. Поэтому представляет большой интерес определе¬
ние любой числовой характеристики какого-либо внутреннего поля пла¬
неты по результатам измерений на ее дневной поверхности или даже
в околоземном пространстве. Одной из таких характеристик, поддаю¬
щихся вычислению, является среднеинтегральное значение потенциала
притяжения Земли. Приведем соответствующий вывод [78].
Полагая известным полярный — наибольший — момент С инерции
Земли
С = ^ бг2 dx,
т
где б — плотность земных недр, а г — расстояние точки от оси вращения,
и пользуясь уравнением Пуассона Д1/= —4яСб, можно записать
— 4яGC = ^ r2AV dx. (3.66)
т
Преобразовывая последний интеграл по «большой формуле Грина» и
учитывая, что Д (г2) =4, получим
5 vd{X\ty2) da - IS ^ + y2)^dr - лОС. (3.67а)
та а
Эта формула отнесена к естественной системе координат, т. е. координат¬
ные оси направлены по главным осям инерции планеты; д/дп — диффе¬
ренцирование по внешней нормали к поверхности.
Имеют место также аналогично выводимые формулы, в которых
используются главные моменты инерции А и В:
5 Vd* = т$ v~2} da ~ Т$(г/2 + г2)1^ д0 ~ nGA' (3-676'
та а
^ V dr = V д{Х\+ г2) da - (*2 + г2) -§£- dx - лОВ. (3.67в)
та а
91
Беря среднее из трех» последних выражений и находя по формулам
(3.39) сумму размерных главных моментов инерции
А+В + С= 2- Ц^-М£СМ,
где ае — большая полуось общеземного эллипсоида, С20 — вторая зональ¬
ная гармоника геопотенциала и Н — динамическое сжатие Земли,
получим
5 - I) - IS p’f-*’ - (3.68)
та а
Здесь р=р (О, X) — радиус-вектор точек поверхности планеты: р2=
=x2-\-y2-\-z2. В эту формулу входят потенциал притяжения Земли и его
производная по нормали. Однако последние из наблюдений не получают.
Поэтому введем в правую часть формулы (3.68) потенциал силы тяжести
W == 1/+У2со 2(х2 + у2)= V+1/2(о2г2,
где о — угловая скорость вращения Земли. Тогда после ряда преобразо¬
ваний получим
\Vdx =т$da p^rdG +
т ° °
+ -у-$ (р4 sin 2d) ~ da - 2Я3~ 3 nGMa\C20, (3.69)
СТ
где dW/dn=—g cos a {g — ускорение силы тяжести, а — угол наклона
физической поверхности Земли к поверхности U7=const), а Ф полярное
расстояние.
Эта формула позволяет вычислить среднеинтегральное значение
Vev=±-\vdT (3.70)
т
внутреннего потенциала притяжения Земли: в правую часть (3.69) и
(3.70) здесь входят величины, которые либо известны по результатам
измерений, либо легко могут быть получены по всей поверхности Земли
осреднением по площадкам в пятиградусной или одноградусной раз¬
графке. При этом Землю можно трактовать эллипсоидом, геоидом,
теллуроидом.
Результаты вычисления Vcp для геоида стандартной Земли SAO-1
дали следующий результат:
Vrcp=78 352 300 м2/с2,
а лля теллуроида
1^=78 239 900 м2/с2.
Заметим, что знание Vcp позволяет теперь более обоснованно вы¬
числять гравитационную энергию Земли по определяющей ее формуле
(1.11).
92
ГЛАВА 4
ПОТЕНЦИАЛОГРАФИЧЕСКАЯ ЗАДАЧА
И КОНЦЕПЦИЯ ГРАВИТИРУЮЩИХ ДИСКОВ
§15. Многоточечные модели геопотенциала
Детальное изучение гравитационного поля Земли с помощью ИСЗ
привело к необходимости исследования различных математических форм
описания геопотенциала V и выбора при этом такого его представления,
которое при решении разнообразных практических задач (как спутнико¬
вой геодезии, так и физической) дает в каждом конкретном случае
наилучшие результаты. Наряду с классическим разложением V по шаро¬
вым функциям (1.12) большое распространение получило также его
представление с помощью потенциала системы точечных масс.
Сущность такого представления потенциала притяжения очевидна.
Замена объемного (имеется в виду внешнего) потенциала (1.7а) инте¬
гральной суммой позволяет написать
где rrii — точечные массы внутри планеты, rt — расстояния от них до внеш¬
ней точки Р. Правая часть формулы (4.1) может трактоваться по-разному:
либо как сумма потенциалов набора точечных масс (механическая
трактовка), либо как (обобщенная) кубатурная формула (для интеграла
Стильтьеса, зависящего от параметров), либо как разложение по системе
функций {1 /г£-} неортогонального базиса (математические трактовки)
и т. п. В связи с этим в литературе описаны разнообразные подходы
к построению многоточечных моделей потенциала притяжения планеты.
Считается, что впервые использовать точечные массы как основу
математической модели гравитационного поля для геодезических целей
предложил в 1967 г. Д. Вейтман [231], дав методику нахождения пара¬
метров точечных масс (расположенных на оси вращения Земли), которые
аппроксимируют зональную составляющую гравитационного потенциала
планеты. Однако отметим, что в 1966 г. М. А. Алексидзе [5] дал пред¬
ставление возмущающего потенциала по полной системе фундаменталь¬
ных решений уравнения Лапласа, коэффициенты которого по существу
суть точечные массы, совокупность которых является прообразом строя¬
щихся в настоящее время всевозможных многоточечных моделей потен¬
циалов притяжения планет. Важное значение имело также открытие
в 1968 г. Мюллером и Сьегреном [211] масконов (mass concentration)
на Луне. Указанные исследования Вейтмана и ряда других авторов
N
(4.1)
93
[7, 16, 24, 44] способствовали проникновению в геодезию и плането-
дезию представления внешнего гравитационного потенциала системой
потенциалов точечных масс, так как масконы затем широко аппроксими¬
ровались точечными массами.
Работы, посвященные такому подходу, позволили обнаружить ряд его
преимуществ перед общепринятым разложением гравитационного потен¬
циала V по шаровым функциям. По сравнению с традиционным разло¬
жением в этом случае осложняется вопрос о сходимости ряда, пред¬
ставляющего потенциал на поверхности планеты, но зато достигается
однородность описания V и его производных вне планеты и на ее поверх¬
ности. Последнее облегчает использование комбинаций наблюдений
разнообразного характера (спутниковых, гравиметрических и т. п.). Если
поступление новой информации о гравитационном поле планеты связано
с необходимостью пересчитывать все гармонические коэффициенты ряда
по шаровым функциям, то использование представления ее потенциала
суммой потенциалов точечных масс позволяет локально уточнять описание
поля введением новых точечных масс, незначительно проявляющих свое
действие в отдельных областях. Кроме того, применение традиционного
разложения при построении детальных моделей гравитационного поля
планеты обременено значительными вычислительными погрешностями,
которые связаны с использованием рекуррентных формул при подсчете
присоединенных функций Лежандра больших степеней. Применение моде¬
лей точечных масс лишено этого недостатка и допускает более простое
программирование.
Несмотря на некоторые различия в подходах к рассматриваемому
вопросу, можно указать наметившуюся общую тенденцию использования
при этом критерия способа наименьших квадратов (см., например, [29,
119, 179, 191]). Большинство исследователей считают заданной конфигу¬
рацию точечных масс и определяют лишь величины «точечных источни¬
ков». Нахождение параметров точечных масс описано Сьегреном и др.
[226, 225], Дюфуром [187], Леви [203], Харди и Гопфертом [191, 192]
и др. Авторы перечисленных работ размещали определенное число точеч¬
ных масс на сфере некоторого радиуса р, причем либо в узлах картогра¬
фической сетки [226, 225], либо в вершинах правильных многогранников
[187], или связывали их расположение с местом нулей сферических
гармоник используемой модели потенциала [203]. Харди и Гопферт [191,
192], применив «предсказание по способу наименьших квадратов с ис¬
пользованием мультиквадратических функций», дали формулу для вы¬
числения наиболее оптимального радиуса р указанной сферы для равно¬
отстоящих (или почти равноотстоящих) точечных масс.
Релли и Хербрехтсмейер [220] в 1978 г., использовав формулу Харди
и Гопферта для вычисления р, получили модель 165 точечных масс,
описывающих гравитационное поле Земли. Результаты тестов показали,
что средние аномалии силы тяжести (1°Х1°) представимы с точностью,
характеризуемой стандартным уклонением 20 мгал.
П. Голота [29] в 1979 г. при построении 36-точечной модели гео¬
потенциала распределил массы на сфере определенного радиуса р, а почти
равномерное расположение точечных масс в плановом отношении выбрал
в соответствии с формулами Лунквиста и Джакалии [58], применяемыми
94
при представлении геопотенциала с помощью выборочных функций. В от¬
личие от авторов предшествующих работ Голота аппроксимировал то¬
чечными массами полное гравитационное поле Земли, а не его часть.
В работах Дж. Бальмино [16, 179] использовано уже неравномерное
распределение масс в плановом отношении (и при этом часть точечных
масс на разных глубинах) на основе подмеченного им факта лучшего пред¬
ставления потенциала при размещении масс в точках экстремумов уро-
венной поверхности потенциала силы тяжести. Ананда [177], используя
при построении модели гравитационного поля Луны доплеровские данные
слежения за космическими аппаратами «Аполлон-15», «Аполлон-16» и
«Лунар Орбитер-5», расположил точечные массы на одной глубине
(50 км от поверхности Луны). Но построенная им (с помощью обработки
долгопериодических вариаций средних орбитальных элементов космиче¬
ских аппаратов) модель 117 точечных масс характеризуется также не¬
однородным их размещением в плановом отношении, причем девять масс
соответствуют лунным масконам. В работах Бровара, Юзефовича [24],
Огородовой и др. [119] гравитационное поле Луны аппроксимировано
полем 83 точечных масс, 12 из которых соответствуют масконам, а осталь¬
ные представляют остаточное поле. Эта модель характеризуется тем,
что ее массы уже не сосредоточены на какой-то «оптимальной» сфере,
а имеют разные глубины. Каплан и Кункив [44] предложили комбиниро¬
ванную модель потенциала Луны, состоящую из усеченного ряда сфе¬
рических гармоник и конечного числа членов, выражающих вклад
масконов.
Таким образом, в последних из перечисленных работ, так же как и
в работах Добачевской [185], где предложено строить модель точечных
масс геопотенциала в соответствии с распределением плотности земных
недр по Буллену, сделаны попытки нахождения параметров точечных масс
с учетом структуры планеты. Например, Ананда [177] рассматривал
выбор положений девяти точечных масс, совпадающих с местоположением
известных лунных масконов как «добавление к исходному ряду данных
априорных оценок», остальные же точечные массы (из общего числа
их— 117) он выбирал произвольно «для получения минимальных значе¬
ний коэффициентов корреляции».
В работах Тараканова и др. [151], например, крупнейшие гравита¬
ционные аномалии Земли интерпретируются именно отдельными точеч¬
ными массами, расположенными на глубинах 600-^800 км. Однако этими
авторами решалась чисто геофизическая задача интерпретации главных
ондуляций геоида; вопрос же аппроксимации геопотенциала в смысле
построения модели точечных масс для использования ее в практических
целях геодезии и спутниковой геодезии ими не ставился.
При построении многоточечных моделей потенциала может быть ис¬
пользована обширная информация о планете: это в первую очередь
трехмерные модели распределения плотности ее недр, а не одномерные,
как это указано в работе [185]. Пользуясь такими трехмерными распре¬
делениями, можно, во-первых, выделять регионы в теле Земли с анома¬
лиями плотности и, во-вторых, численным интегрированием по этим ре¬
гионам находить координаты аномалеобразующих точечных масс и их
величины.
95
Большинство исследователей задачу построения многоточечной
модели потенциала не связывают с внутренним строением планеты и
рассматривают как формальную аппроксимацию его суммой потенциалов
определенного числа параметров (точечных масс), используя, по сути
дела, в скрытом виде основную идею построения кубатурных формул.
На практике же наилучшие результаты получают (см., например, [119,
179]) при расположении определенного числа точечных масс в местах
экстремумов уровенной поверхности потенциала силы притяжения пла¬
неты.
В работе Нидхэма [212], которая посвящена использованию точечных
масс для описания детального гравитационного поля, на основании
гравиметрической информации в виде осредненных значений аномалий
силы тяжести по трапециям 1°Х 1°, ЗО'ХЗО' и 5'Х5' получены определен¬
ные соотношения между числом точечных масс, описывающих те или
иные аномалии, их глубиной и размерами площадки, на которой эти
массы расположены. Используя комбинацию спутниковой (в виде набора
стоксовых постоянных до 14-го порядка) и отмечаемой гравиметрической
информации, Нидхэм построил детальную модель гравитационного поля
центральной части США, соответствующую разложению по сферическим
гармоникам примерно до 180-го порядка и степени.
В работах [7, 135], как и в [231], дано решение задачи аппроксимации
потенциала тела вращения потенциалом системы точечных масс, распо¬
ложенных на оси вращения. Критерием качества аппроксимации счи¬
тается совпадение первых членов разложения указанных потенциалов
по зональным гармоникам; задача сводится к классической проблеме
моментов. Такой подход по сравнению с другими подходами дает, оче¬
видно, максимальную близость потенциалов точечных масс (в отмеченном
смысле) к исходному разложению по сферическим гармоникам при мини¬
мально возможном их числе. Однако при численной аппроксимации
зональной части, а тем более и незональной, массы и их расстояния
от центра Земли в общем случае оказываются как комплексными, так
и действительными; массы могут даже «выскакивать» за пределы пла¬
неты. Это несколько осложняет работу с подобными моделями. Поэтому
в своих последних исследованиях авторы [136] оставили за такой мето¬
дикой только роль получения исходной конфигурации масс, которую затем
уточняют для конкретных орбит ИСЗ методом наименьших квадратов.
Таким образом, к настоящему времени имеется ряд моделей гравита¬
ционного потенциала, соответствующих указанным выше особенностям их
построения. Однако точечные массы используются практически для
описания возмущающего потенциала T=V—U. Однако нормальный по¬
тенциал U понимается разными авторами по-разному. Чаще всего в ка¬
честве U выбирается потенциал эллипсоида вращения. Другими словами,
представление гравитационного потенциала планеты суммой потенциалов
точечных масс применяется фактически (за исключением работы Голоты)
обычно в комбинации с разложением по шаровым функциям и служит
в этом случае лишь для описания «тонкой» структуры поля притяжения
планеты.
Однако появление искусственных спутников Земли привело [4] к прак¬
тической необходимости воспользоваться классической задачей двух
96
неподвижных центров (поставленной в небесной механике еще Эйлером)
при аппроксимации некоторой основной части геопотенциала потенциалом
двух комплексных точечных масс (неподвижных центров) с целью по¬
строения некеплеровых (эйлеровых) промежуточных орбит, учитывающих
сжатие Земли.
Основное отличие такого подхода от описанных выше методов по¬
строения многоточечных моделей потенциалов планет заключается не
в числе используемых масс, а в поиске такого аппроксимирующего
выражения гравитационного потенциала, которое, с одной стороны,
достаточно хорошо представляет потенциал реальной Земли, а с другой —
удовлетворяет известной теореме Штеккеля [31], выражающей условия
интегрируемости в квадратурах уравнений движения. Однако при обобще¬
нии результатов Аксенова, Гребенникова и Демина [4] на случай учета
большего числа членов разложения геопотенциала возникают значитель¬
ные трудности. Например, в [48, 49] рассмотрена задача четырех не¬
подвижных центров, а в [12] даже п неподвижных центров. Но при этом
решение уравнений движения в квадратурах получено авторами лишь для
плоского случая.
Таким образом, если решение задачи неподвижных центров широко
используется при получении промежуточных орбит в теории движения
ИСЗ, то для целей детального прогнозирования движения спутника и
при изучении тонкой структуры гравитационного поля одних неподвижных
центров недостаточно. Поэтому именно для указанных целей А. Дрожинер
[186] в 1977 г. предложил использовать потенциал последних лишь
в качестве нормального поля, а детальную структуру геопотенциала
аппроксимировать набором точечных (действительных) масс.
Именно с таким нормальным полем построена в [121] модель М-137
137 точечных масс, в которой в качестве исходной информации использо¬
вались граничные значения аномалий силы тяжести в виде разложения
их по сферическим функциям до 22-й степени с коэффициентами, взятыми
в соответствии с моделью геопотенциала GEM-10. По определенной схеме
итерационным образом по способу наименьших квадратов определялись
все четыре параметра каждой точечной массы. Погрешность аппрокси¬
мации аномалий силы тяжести по всей Земле доведена до ±2,6 мгал.
В работе Плахова [133] рассмотрена роль представления геопотен¬
циала с помощью набора точечных масс при интегрировании диффе¬
ренциальных уравнений движения ИСЗ. Показано, что при использовании
аналитических методов интегрирования многоточечное представление
геопотенциала никаких преимуществ перед разложением потенциала
в ряд по сферическим гармоникам не дает и в этом случае оказывается
даже сложнее. Однако при численном интегрировании появляются до¬
вольно весомые преимущества перед сферическим разложением, обуслов¬
ленные главным образом простотой вычисления правых частей диффе¬
ренциальных уравнений движения ИСЗ. Например, если число сфериче¬
ских гармоник и число точечных масс в разложениях геопотенциала
равны, то вычисление производных от потенциала по координатам при¬
мерно в 4,25 раза эффективнее по сравнению с использованием тради¬
ционного представления. В общем же при численном интегрировании
уравнений движения спутника применение многоточечной формы гео¬
4 Г. А. Мешеряков
97
потенциала ускоряет процесс вычислений на каждом шаге не менее чем
в 1,6 раза.
В последнее время в спутниковой геодезии используются разнообраз¬
ные численные методы, которые по сравнению с аналитическими дают
не худшие, а часто и лучшие результаты. В частности, при численном
интегрировании уравнений движения ИСЗ особенно эффективным оказы¬
вается использование многоточечных моделей геоптенциала. Приведен¬
ный анализ литературы и опыт исследований позволяют утверждать, что
основным критерием выбора того или иного представления геопотен¬
циала для целей прогнозирования орбит ИСЗ должна считаться практиче¬
ская необходимость упрощения процесса программирования и уменьше¬
ния времени счета на ЭВМ. В связи с этим приходится отдавать пред¬
почтение именно точечным моделям потенциала, которые удовлетворяют
следующим требованиям.
1. Число точечных масс не должно быть большим, а это главным
образом связано с выбором их пространственной конфигурации. Поэтому
следует размещать точечные массы под экстремумами уровенной поверх¬
ности и не связывать их конфигурацию с какими-либо геофизическими
гипотезами.
2. Параметры точечных масс, включаемых в модель, должны быть
вещественны.
3. Модель точечных масс должна быть однородна, т. е. из нее не
следует выделять какое-либо нормальное поле, описываемое рядом сфе¬
рических либо каких-нибудь других специальных функций.
При построении многоточечных моделей для целей спутниковой гео¬
дезии целесообразно использовать накопленную информацию о гео¬
потенциале в виде наборов стоксовых постоянных, тем более, что к настоя¬
щему времени наиболее уверенно получены те из них, которые описывают
гравитационное поле Земли в планетарном масштабе, т. е. по наблюде¬
ниям ИСЗ.
Для того чтобы удовлетворить поставленным выше требованиям,
во Львовском политехническом институте была разработана [103, 104,
65] методика построения моделей точечных масс, которая основана
на построении приближенных конструкций гравитационных мультиполей
и свойстве симметрии шаровых и сферических функций. Сущность ее
заключается в следующем. Если обозначить через потенциал при¬
ближенной конструкции мультиполя порядка п, т. е. потенциал системы 2п
точечных гравитационных зарядов (которые имеют одинаковую массу,
но половина их со знаком плюс, а другая — со знаком минус), то потен¬
циал Vп мультиполя примет вид
где ht — расстояния между зарядами, a Rn — погрешность аппроксимации
потенциала мультиполя Vn потенциалом его приближенной кон¬
струкции.
Значит, теперь
Vn = lim V(n> = V(n> + Rn,
(4.2)
(4.3)
n = 0
98
При нахождении параметров точечных масс, рассматриваемых как заряды
приближенных конструкций мультиполей с потенциалами Ил), задача
заключается в таком выборе этих масс, чтобы при суммировании в фор¬
муле (4.3) погрешности Rn компенсировали бы друг друга и выражение
для внешнего гравитационного потенциала с определенной степенью точ¬
ности приняло бы вид
оо
V * Ум = X ^ (4.4)
п = О
Соотношение (4.4) после выполнения в нем сплошной нумерации масс
приближенных конструкций мультиполей приводит к простому выражению
гравитационного потенциала
у„(р. = gmJ^7 + Д 1)1 (4'5)
в котором
гi = д/р2 + Dial — 2рД ае cos yt,
cos y-=cos О cos Ot+sin О sinfy sin (Л,—).
Здесь и дальше полярные координаты i-и точечной массы обозначены
через diy 0£, d—D^ (ае — большая полуось земного эллипсоида);
р, — точечная масса, выраженная в единицах массы планеты (p.=mt/Af);
р, О, X — полярные координаты внешней точки.
Итак, соотношения (4.4), (4.5) предполагают замену потенциала
мультиполя Vп потенциалом V{n) его приближенной конструкции. Это
накладывает определенные условия на конфигурацию каждой совокуп¬
ности 2п точечных масс, ибо расположение последних должно быть вы¬
брано так, чтобы свойства функции Ил) довольно полно отражали свой¬
ства аппроксимируемой ею функции Vn . Тогда наличие общих законо¬
мерностей в распределении значений потенциалов Vn разных порядков
позволит получить общие условия для пространственного положения
точечных масс приближенной конструкции мультиполя произвольного
порядка п. При этом воспользуемся отмеченным в § 8 свойством симметрии
шаровых и сферических функций.
Симметрии распределения значений функции Vп естественно поставить
в соответствие подобное свойство функции Ил). Это достигается проще
всего таким размещением точечных масс, когда они лежат попарно
на одинаковых расстояниях относительно начала координат. Тогда
согласно общепринятой схеме (§6) построения приближенных конструк¬
ций мультиполей на прямых, проходящих через начало координат, сим¬
метрично относительно начала будут расположены точечные массы оди¬
накового знака в случае мультиполя четного порядка и массы разного
знака в случае мультиполя нечетного порядка. При этом потенциал VM
оказывается представленным двумя составляющими: четной Учет,
обусловленной потенциалом приближенных мультиполей четных поряд¬
ков, и нечетной Кнеч, обусловленной массами мультиполей нечетных
порядков. Отсюда следует, что при переходе в (4.5) от параметров
4*
99
точечных «источников» к гармоническим коэффициентам Сп т, Sn m,
входящим в ряд
К, = 1 + (у-) Z C0S тХ +Snm Sin т*0 P”(C0S #) J, (4.6)
получаемый из (4.5) разложением 1 /ri в ряд по полиномам Лежандра,
точечные массы приближенных конструкций мультиполей четных поряд¬
ков связаны ТОЛЬКО СО СТОКСОВЫМИ ПОСТОЯННЫМИ C2k, m> $2k, т (6=1» 2, . . .)
четных порядков
с\
;М_2 I D"( — l )'J j*'"'
2k, т ) j = 1 V ^2/г, m’
(4.7)
а параметры точечных масс мультиполей нечетных порядков — только
со стоксовыми постоянными С2*+1,т» ^2*+i,m (6=0, 1, 2, . . .) нечетных
порядков
2*+1,т) _2 £ Df + yj (4.8)
2fc + l,m J /= 1 t Рг/г-f l,m-
В этих уравнениях
ait0=^(cos^.),
art, т 1 __ 2 (n — m)y pm / ф \ | C0S m V
а/ Г (м + m)! n 1 ''1 sin mb:,
Hn, m ) X /
где P™ (cos Oy) —присоединенные функции Лежандра, а суммирование
по / предполагает учет всего по 2Л/2=2П_1 масс для каждого мультиполя
порядка я, оставшиеся же 2п~1 масс учитываются автоматически.
Выражения (4.7) и (4.8) указывают, что составляющая V4eT равна
сумме всех четных членов разложения (4.6), а Кнеч — сумме шаровых
функций нечетных порядков (такое суммирование законно в силу абсо¬
лютной и равномерной сходимости ряда (4.6)). Поэтому, рассматривая
две произвольные точки, лежащие на одной прямой, проходящей через
начало координат на равных расстояниях от начала, скажем с учетом
свойства симметрии, что если в одной из них внешний потенциал равен
сумме V4eT и Кнеч, то в другой он равен их разности
Ум (х, у, 2) = учет (*, у, z) + Кнеч (х, у, г), (4.9)
V* ( —х, —у, — г) = Учет (*, у, z) — Унеч (х, у, z).
Таким образом, построение описываемым здесь способом приближен¬
ных конструкций мультиполей позволяет сочетать в одной однородной
математической модели гравитационного потенциала важное свойство
(4.9) разложения внешнего гравитационного потенциала в ряд по ша¬
ровым функциям с отмеченными выше преимуществами моделей точечных
масс.
100
Используя в качестве исходной информации набор стоксовых посто¬
янных {Сп т Sn< m) планеты, усеченной до некоторого порядка /г*, мож¬
но находить параметры ру, Dp Оу, kj точечных масс из решения систем
нелинейных уравнений (4.7), (4.8).
При этом необходимы начальные приближения искомых величин,
подстановка которых в (4.7), (4.8) приведет естественно к невязкам
N
vk(k=\, 2, . . ., N). Составляя функцию F = v\ и минимизируя
k = 1
ее каким-либо численным методом, найдем поправки к начальным значе¬
ниям искомых параметров. Начальные приближения лучше всего было бы
выбрать на основании данных геофизики. Угловые координаты (0у. Ху)
положения точечных масс приняты ниже в первом приближении сов¬
падающими с координатами точек экстремумов уровенных поверхностей
Vп = const, что хорошо согласуется как с положением плановых коорди¬
нат экстремумов аномалий плотности разных порядков /г, вычисленных
по распределению плотности трехмерной механической модели Земли,
так и с выводами [179].
Верхними пределами суммирования по j в (4.7) и (4.8) должны
быть некоторые постоянные, зависящие от принимаемого числа точечных
масс приближенных конструкций мультиполей четных и нечетных поряд¬
ков. А при непосредственном решении систем должно приниматься во вни¬
мание еще по одному нелинейному уравнению на каждый мультиполь
Мп = n\q П hh
i = 1
связывающему момент мультиполя Мп с его зарядами q (точечными мас¬
сами) и расстояниями ht между ними, причем последние должны быть
выражены через координаты (Dy, #у-, Kj) точечных масс. Кроме того,
при этом желательно для приближенной конструкции каждого мультиполя
использовать алгебраические соотношения между расстояниями Z)y и ве¬
личинами, характеризующими направления осей h, самого мультиполя.
Не располагая пока ими для произвольного п, такое соотношение прини¬
мается только для мультиполя второго порядка: D\=D2 tg(y/2).
В случае мультиполей высоких порядков п число 2п масс, составля¬
ющих его приближенную конструкцию, является слишком большим,
и в принципе (с практической точки зрения) его можно уменьшить,
предполагая точечные массы мультиполей разных порядков совмещен¬
ными, т. е. аппроксимировать отдельно четную 1/чет и отдельно нечетную
КНеч составляющие. Совмещение отдельно зарядов мультиполей четных и
отдельно зарядов нечетных порядков приводит, в частности, к модели,
точечные массы которой уже только попарно равны по абсолютной вели¬
чине и имеют соответственно одноименные и разноименные знаки.
Формула потенциала A-точечной модели имеет вид
где суммирование по i предполагает учет лишь половины точечных
101
масс модели, вследствие чего такую модель называют моделью двойных
(или сопряженных) масс.
В соответствии с описанной методикой было получено несколько
многоточечных моделей геопотенциала МО [103, 104, 66], Ml [103,
104], М2 [65], М3 [105].
Первая из них МО — пятиточечная — представляет главную часть
потенциала притяжения Земли, описываемую шаровыми функциями нуле¬
вого У0 и второго V2 порядков (см. табл. 5). Так как потенциал У(0)
Таблица 5
Пятиточечная модель МО геопотенциала [66J, построенная по стоксовым
постоянным GEM-10
Номер внецен-
тренных масс
и»-.
единицы
массы
Земли
единицы
экваториального
радиуса
%
град
К
град
1
—539,50280
0,1 • лог2
0,0
0,0
2
539,50280
0,81932823 • 10-4
90,0
165,0656
3
, —539,50280
0,1 • 10“2
180,0
0,0
4
539,50280
0,81932823 • 10“4
90,0
345,0656
GM= 398600,44 км3/с2, ае=6378,138 км, 170,6321149й.
приближенной конструкции мультиполя нулевого порядка совпадает с
потенциалом V0 его предельной конструкции, то одна из точечных
масс модели МО — центральная и У(0)= Vo=GM/p. Потенциал же V2
гравитационного мультиполя 2-го порядка (квадриполя) аппроксими¬
руется потенциалом У(2) его приближенной конструкции — набором че¬
тырех (22=4) точечных масс, размещенных в плоскости наибольшего
С и наименьшего А моментов инерции планеты, причем две отрицатель¬
ные точечные массы расположены на равных расстояниях на оси С
и аналогично две положительные массы — на оси А. Модель МО характе¬
ризуется [66] среднеквадратическим отклонением о уровенной поверх¬
ности, обусловленной потенциалом точечных масс, относительно уровен¬
ной поверхности K0+K2=const, равным всего 0,004 м и максимальным —
0,010 м. Значения точечных масс квадриполя оказались превышающими
массу Земли и не допускают каких-либо геофизических объяснений.
Однако они приводят, как и при аппроксимации первых членов зональной
части геопотенциала потенциалом двух неподвижных центров с комплекс¬
ными массами [4], к хорошей аппроксимации поля V2 полем У(2) четырех
точечных масс.
Модель Ml — тринадцатиточечная — аппроксимирует потенциал при¬
тяжения, описываемый шаровыми функциями нулевого, второго и треть¬
его порядка (У0+У2+У3) и как составную часть включает в себя
модель МО. Потенциал Уз гравитационного мультиполя 3-го порядка
(октаполя) представлен потенциалом У(3) его приближенной кон¬
струкции — набором восьми (23=8) точечных масс, расположенных
под восемью экстремумами уровенной поверхности y3=const. Значение
102
среднеквадратического отклонения о уровенной поверхности, обуслов¬
ленной набором точечных масс модели Ml относительно поверхности
V'0+K2 + Vr3=const, составляет приблизительно 3 м относительно поверх¬
ности геоида, построенного, например, по полному набору стоксовых
постоянных GEM-6, величина а=15,4 м.
Следует отметить, что получение моделей МО и Ml является след¬
ствием дифференцированного подхода к изучению разложения V в ряд по
шаровым функциям, который привел, с одной* стороны, к объяснению
основных особенностей фигуры геоида совместным вкладом гравитацион¬
ных квадриполя и октаполя Земли, а с другой стороны — к соответствию
(по числу) четырех экстремумов (в плоскости осей квадриполя) уровенной
поверхности l/2=const и восьми экстремумов, отвечающих в качественном
отношении главным особенностям фигуры геоида, поверхности Уз=
= const — четырем (22) и восьми (23) зарядам приближенных конструк¬
ций квадриполя и октаполя планеты. Поэтому можно сказать, что основ¬
ная идея построения моделей МО и Ml в первую очередь связана
с физической структурой геоида, в частности, с особенностями его фигуры.
Модель М2 [65] — 97-точечная — включает в себя как составную
часть решение Ml и связана с наиболее уверенно определяемой в настоя¬
щее время из комбинации разнообразных наблюдений частью разложения
по шаровым функциям гравитационного потенциала планеты до 8-го
порядка включительно [128, 216]. Метод построения этой модели основан
уже не на аппроксимации (как при получении решений МО и Ml) каждого
потенциала п-го порядка потенциалом 2п точечных масс приближенной
конструкции мультиполя, а на «совмещении» точечных масс, соответ¬
ствующих мультиполям разных порядков (отдельно четных и отдельно
нечетных), и аппроксимации четной и нечетной ^составляющих разложения
по шаровым функциям [103]. Такого рода обобщение приближенных
конструкций мультиполей отдельно четных и отдельно нечетных порядков,
несомненно, позволило при построении М2 обойтись значительно мень¬
шим числом точечных масс. Решение М2 значительно точнее модели
Ml, о чем свидетельствуют, например, результаты сравнения его с раз¬
личными выводами стоксовых постоянных Земли [651 •
Для модели М3 (127-точечной модели геопотенциала) в качестве
исходной информации были использованы гармонические коэффициенты
Слт, Snm решения GRIM-2 [180] и на основе их определены параметры
точечных масс. Аппроксимируемая функция была выбрана в виде раз¬
ложения потенциала по шаровым функциям, усеченного до 12-го порядка,
с гармоническими коэффициентами, взятыми по GRIM-2.
Согласование потенциалов выполнялось не во всем внешнем прост¬
ранстве, а на полусфере (по сетке 5°Х5°), охватывающей притягива¬
ющие массы планеты. Из ряда получаемых таким образом моделей
в качестве лучшей была выбрана модель 127 точечных масс (вместе с то¬
чечными массами решения Ml), причем 63 точечные массы соответствуют
зарядам приближенных конструкций мультиполей четных порядков и
64 массы — зарядам приближенных конструкций мультиполей нечетных
порядков.
Среднеквадратические отклонения о (на уровне моря) поверхности
VM= const, построенной по модели М3 относительно поверхностей V=
103
= const, построенных по некоторым полным наборам стоксовых постоян¬
ных Земли, составляют для SAO-4,3 (24,24) 6,3 м; GEM-6 (16,16) 5,3 м;
GEM-8 (25,25) 5,5 м. Последние дают возможность заключить, что
многоточечная модель М3 в среднем почти с одинаковой степенью
точности аппроксимирует как поле GEM-6, порядок усечения которого
(16,16), так и поле моделей SAO-4,3 и GEM-8, порядок усечения которых
уже соответственно (24,24) и (25,25). Величина о колеблется в пределах
5-1-6 м. Для сравнения отметим, что для решения Ml параметр о состав¬
ляет примерно 16 м, а для модели М2 принимает значения 6-F7 м.
В приведенном обзоре работ по многоточечным моделям потенциала
было отмечено их использование как при описании глобального поля
притяжения планеты, так и при изучении его региональных и локальных
особенностей. Если описанные модели МО и Ml дают глобальное пред¬
ставление геопотенциала, то их развитие — М2 и М3 — отражают уже
и его региональные особенности; последние две модели также могут
быть основой построения более детальных многоточечных моделей потен¬
циала.
Дальнейшее развитие описываемой методики построения многоточеч¬
ных моделей геопотенциала принадлежит Марченко, Абрикосову и Цюпаку
[69,70], которые для целей космической геодинамики (определение нера¬
вномерности и параметров вращения Земли) дали, скажем кратко,
способ получения моделей точечных масс непосредственно по наблюда¬
тельной информации, за которую принимаются как аномалии силы
тяжести, так и высоты геоида в центрах стандартных (5° X 5к) или
иных трапеций. Построение моделей «двойных», или «сопряженных»,
или даже произвольных точечных масс сведено к решению задачи
нелинейного программирования с регуляризацией по Тихонову. Решение,
например, LPM-1A, представляющее совокупность 135 сопряженных
точечных масс, приводит к среднему квадратическому значению остато¬
чных для сборного набора (Rapp, 1979+GEM-10B) 1654 осредненных
значений высот геоида примерно 1,8. Эта модель описывает геопотенциал
с той же точностью, что и модели GEM-9 и GEM-10, однако при уточнении
орбиты ИСЗ Starlette она дает экономию вычислительного времени
около 30 %.
Подобные по точности представления орбит Lageos и Starlette дает
модель 100 точечных масс Бартелмеса и Кауцлебена *), но, во-первых,
она не является однородной (нормальное поле представлено гармони¬
ками до 4-го порядка и степени по GEM-10), и, во-вторых, в ней —
в качестве исходной информации — использовались производные возму¬
щающего потенциала, которые присутствуют в правых частях уравнений
движения ИСЗ.
Рассмотрим в заключение один общий подход к построению многото¬
чечных моделей потенциала, соответствующий теории наилучших квадра¬
тических приближений функций. Пусть основной системой функций в об¬
ласти Т является подлежащая определению система неортогональных
*) Barthelmes F., Kautzleben Н. Л. New Modelling the Gravity Field of the Earth
by Point Masses; Pap. Present, at the General Assembl. IAG: Symp. C. — Hamburg,
1983. — 18 p.
104
функций {1 /г£}, где
Г1 = \р = (* - У2 + (г/ - л,)2 + (г - У2. Q, (if л,- У е X,
а Г — или все внешнее относительно планеты т пространство, или
какая-либо его подобласть, например, шаровой слой, внутри которого
расположена (или предполагается) орбита космического аппарата, ради
прогнозирования которой производится приближение потенциала, осу¬
ществляемое с весом р=р(х, у, z)>0. Вес будем брать в виде р= 1/р2+х,
где х>0 либо устанавливается априорно, либо подбирается специальным
образом.
Итак, будем аппроксимировать V в области Г обобщенным много¬
членом по системе (1 /г,} с весом /?, т. е. «многочленом» вида (4.1а)
: 1
при условии
т,
(4.1а)
8п = \ р( V — G У —- \ йт -► min. (411)
Определению подлежит выбор подсистемы п функций {1 /rjn, т. е. по¬
ложение точек Qf многоточечной модели, и коэффициентов mt обобщен¬
ного многочлена, т. е. масс вещества, сконцентрированного в этих
точках,— всего 4п параметров.
Необходимые условия minert приводят к следующей системе Ап урав¬
нений:
°,ИИМЧ)'
(4.12)
где в каждой из входящих в нее четырех подсистем /=1,2,. я,
а скалярные произведения имеют обычный вид
(ф, -ф) = ^ р(х, у, г) <р(х, у, 2) ij)(x, у, г) йт.
т
Вычислительные трудности решения нелинейной системы (4.12) очевидны,
но зато преодоление их позволит строить как глобальные модели потен¬
циала, так и региональные (для каждого КА или серии их в любой
105
выделенной подобласти пространства). Ясно, что в согласии с принципом
МНК таким же образом решается наилучшая аппроксимация поля
набором точечных масс относительно заданной какой-либо его транс¬
форманты (вместо самого потенциала).
§ 16. Потенциалографическая задача
Многоточечные модели потенциала притяжения планеты являются
примером его нетрадиционного представления. В настоящее время, как
уже подчеркивалось в предыдущем параграфе, усиленно изыскиваются
и другие способы его описания, именно, такие, которые, повторим,
не теряя в точности, позволяли бы эффективную реализацию их на
ЭВМ. При этом речь идет об описании потенциала с вполне определенными
практическими целями последующего его использования в космической
геодезии и навигации (необходимость экономного — в смысле памяти
и машинного времени—счета орбит искусственных небесных тел), в физи¬
ческой геодезии (при счете возмущающего потенциала и его транс¬
формант) и в других задачах. Такая прикладная задача удобного анали¬
тического представления потенциала иногда рассматривается «автоном¬
но», т. е. вне какой-либо связи ее с формой планеты и с распределением
плотности ее недр. В этой задаче считается заданным потенциал притяже¬
ния планеты т вне объемлющей его сферы: форма планеты и ее строение
либо считаются приближенно известными, либо вовсе игнорируются.
Задачу описания потенциала планеты (как только что обрисованного
«удобного» для практики) естественно называть потенциалографической
задачей — ПЗ [85, 94]; ее постановку уточним несколько позже.
ПЗ примыкает к недавно возникшим в теории ньютоновского потен¬
циала обратным задачам на суммарный потенциал [138] и, в общем,
может рассматриваться либо как специфическая задача последних, либо
как своеобразная их модификация. В задачах суммарного потенциала —
в их физической трактовке — требуется по заданной в некоторой области
пространства гармонической функции найти внутри этой области (внут¬
ренние задачи) или вне ее (внешние задачи) генерирующие притяжение
образования (именно, «объемное» тело, простой слой, двойной слой),
сумма потенциалов которых выражает заданную гармоническую функ¬
цию. Эти задачи в классическом смысле некорректны. Уже имеет¬
ся ряд исследований по выявлению условий разрешимости их [138, 122,
123].
Отличие ПЗ в простейшей ее постановке от задач на суммарный
потенциал заключается в том, что заданная гармоническая функция
(потенциал притяжения планеты) в первой считается представленной
суммой известных потенциалов слоев, а не известной суммой потенци¬
алов искомых слоев, как это свойственно вторым задачам. За счет
указанного такая ПЗ распадается на традиционные обратные задачи
теории потенциала.
ПЗ не нова. Ее впервые решил Лаплас (§ 3), разложив потенциал
притяжения в ряд шаровых функций, который, как было видно, допускает
различные интерпретации и разные формы его записи. Предлагалось
и много других форм описания потенциала планеты, например, по
106
гармоникам сжатого эллипсоида вращения, рядами по функциям Ламе,
потенциалом простого слоя, при помощи мультиквадриковых и других
видов функций, с использованием так называемых неподвижных центров
(мнимых или комплексных), комбинированием различных способов его
аппроксимации в отдельных областях пространства и др.,— и все это
разные методы решения потенциалографической задачи. Обзор и библи¬
ография их имеются в [42, 127,8].
Как видно, некоторые из перечисленных методов отвечают дескрип¬
тивному подходу: как наилучшим образом (в каком-то определенном
смысле, например, с позиций теории квадратических приближений) опи¬
сать потенциал (V или Т) аналитически — при помощи специальных
функций или разложений в ряды. Такому подходу следуют представления
потенциалов рядами по шаровым функциям, по вырожденным эллипсо¬
идальным, по функциям Ламе, методом конечных элементов и некоторые
другие. Если исходить из принципа теории наилучших квадратических
приближений, то для получения удовлетворяющего ему глобального
решения задачи необходимо знать форму планеты, и — в соответствии
с этим — из только что перечисленных представлений V первые дают
строгое решение для планет сферической формы, вторые и третьи —
для планет эллипсоидальной формы (соответственно в виде эллипсоидов
вращения и трехосных эллипсоидов). Использование конечных элементов
предусматривает наиболее точное описание потенциала в отдельных
областях вне реальной планеты. Все эти подходы аналитически осу¬
ществляют аппроксимацию V\ будем считать, что они доставляют реше¬
ние прямой потенциалографической задачи.
Но к описанию потенциала реальной планеты возможен и другой
подход — конструктивный, которому соответствуют обратные потенциало¬
графические задачи: надо отыскать поверхность 5 и на ней располо¬
жить два слоя — простой и двойной (дипольный) или один из них,
сумма потенциалов которых выражала бы потенциал планеты и допускала
бы более простое вычисление его, нежели обычным образом по ряду
шаровых функций.
Возможность постановки таких обратных задач вытекает из фунда¬
ментальной формулы (1.10) Грина, в соответствии с которой объемный
потенциал V тела т представляется суммой потенциалов двух слоев:
V' — простого и V" —двойного, расположенных на поверхности о тела,
V=V'+V",
или даже одного из них. Этот факт имеет основополагающее значение
в математической физике при исследовании и решении краевых задач
теории потенциала. Здесь же обсуждается иной вопрос — вопрос о разно¬
образии форм описания внешнего объемного потенциала V. Значит,
имея образец его выражения в виде (1.10) и учитывая непрерывность по¬
тенциалов слоев (простого и двойного) во внешнем по отношению
к ним пространстве, можно предположить, что изучаемый потенциал
представим суммой
V=k'V'+k"V", (4.13)
в которой коэффициенты k' и k" — постоянные или даже переменные,
107
а потенциалы V' и V", именно потенциал простого слоя
V'(P) =
^ d-Q (Q е S, Р ф S)
Г РП
PQ
(4.14)
и потенциал двойного слоя
V"{P) =
dSQ (QgS, Р ф S)
(4.15)
соответственно с плотностью р и моментом v, отнесены к некоторой
ограниченной гладкой двусторонней поверхности S, расположенной
внутри а и не имеющей с ней общих точек. Предположим также, что
сумма (4ЛЗ) выражает на а и в области между о и 5 аналитическое
продолжение внешнего потенциала {V или Т) во внутрь тела т, если,
конечно, оно существует.
Ясно, что если для заданного тела т мы сможем каким-то образом
разделить его потенциал на две части, которые хотим затем трактовать
потенциалами слоев (соответственно простого и двойного), лежащих
на выбранной априори поверхности S, объемлемой поверхностью о
тела т, то будем иметь две типичные обратные задачи теории потенциала
с присущими им свойствами некорректности. При этом описывающие
их выражения (4.14) и (4.15) —относительно плотностей р и v этих
слоев — являются интегральными уравнениями I рода с непрерывными
ядрами; причем условия разрешимости этих уравнений должны дать
как подтверждение правильности выбора поверхности S, так и правомоч¬
ность принятого разделения V на части V' и V".
Обратные задачи теории потенциала, в которых заданный внешний
потенциал (V или Т) тела т неизвестной формы должен быть пред¬
ставлен суммой (4.13), мы называем обратными потенциалографическими
задачами. Предположим, что коэффициенты k' и k" заданы. Если один
из них равен нулю, а второй единице, то потенциал представляется
только одним слоем — простым или двойным. Поверхность S, несущая
в таких задачах слои (или слой) также может считаться либо известной,
либо даже подлежащей определению. Эти задачи объединяют в себе
ряд задач, известных из практики геодезии. Например, при /г"=0 и k'=\
имеем представление внешнего потенциала планеты потенциалом просто¬
го слоя: за S здесь могут быть приняты размещенные внутри планеты
поверхность сферы или эллипсоида известных размеров, либо поверх¬
ность, параллельная неизвестной поверхности о планеты и находящаяся
внутри последней.
Важно отметить, что ПЗ могут изучаться в дискретной постановке.
Приведем пример. Пусть потенциал V заменяется потенциалом простого
слоя. Если вместо непрерывной плотности р этого слоя искать массы
т, его элементарных площадок, сконцентрированные в некоторых точках
слоя, то придем к рассмотренной ранее задаче построения многоточечных
моделей потенциала. Задавшись при этом поверхностью слоя S, будем
иметь линейную задачу по определению масс т,. Если же поверхность
слоя считать неизвестной, то дискретная постановка обратной потен¬
108
циалографической задачи при /г'=1, £"=0 охватывает общий случай
построения многоточечных моделей потенциала, в которых определе¬
нию подлежат массы mh находящиеся на поверхности S, численно
определяемой искомыми точками концентрации масс (^.= р./ае, fy, Хь
ае= const).
Заметим, наконец, что потенциалографическая задача при k'=k"=\
в дискретной постановке при искомой поверхности обобщает построение
многоточечных моделей потенциала за счет включения в число искомых
параметров этих моделей гравитационных диполей, набор которых соот¬
ветствует потенциалу двойного слоя V". Таким образом, мы приходим
к точечно-дипольным моделям потенциала.
Несколько слов о последних. Так как главная часть потенциала
(или нормальный потенциал) может быть трактована притяжением
центра планеты (или фокального диска), причем в каждом из них
сконцентрирована вся масса планеты, то оставшаяся поправочная часть
потенциала (или возмущающий потенциал) оказывается безмассовой.
Такой возмущающий потенциал пропорционален второй степени обрат¬
ного расстояния; для его представления невыгодно брать точечные массы,
потенциалы которых пропорциональны первой степени этого расстояния.
В качестве нужных точечных объектов отмеченному условию удовлет¬
воряют гравитационные диполи. Их при этом можно описывать присущей
им характеристикой — моментами диполя (дипольными моментами) или
разносить образующие их массы — «заряды» на конечные расстояния,
как это свойственно приближенным конструкциям диполей.
Итак, ПЗ в аналитическом смысле раскрывает многообразные воз¬
можности замены объемного потенциала тела потенциалами других
видов. Для геодезии эта задача позволяет потенциал притяжения пла¬
неты (полный V, либо его главную или возмущающую часть Т) опи¬
сывать различными способами, среди которых можно отыскать наиболее
подходящие для тех или иных практических целей. Заметим, что в случае
представления потенциала V Земли k'ФО и к" Ф 0, а в случае Т /г'=0;
для гидростатически равновесных планет при описании их полного
потенциала /г"=0. Важно также, что потенциалографическая задача
допускает дискретную постановку, что, как отмечено, приводит к много¬
точечным и точечно-дипольным моделям потенциала; кроме того, и само
задание потенциала планеты может быть взято в дискретном виде.
Существенно также, что поверхность S, несущая слои, может считаться
искомой или может считаться заранее заданной. Все эти моменты
должны быть предусмотрены детальной постановкой каждой конкретной
потенциалографической задачи. Но прежде чем переходить к таковой,
сделаем следующие замечания.
От поверхностей S, на которых для описания потенциала V тела
суммой (4.13) — (4.15) предполагается поместить простой и двойной
слои, требуется только возможность размещения на них этих слоев.
Последние должны развивать в окружающем их внешнем пространстве
потенциалы притяжения V' и К", причем возможные разрывы непрерыв¬
ности этих потенциалов и их производных в точках слоев при пересечении
их не влияют на решение рассматриваемой задачи. Поэтому нет необ¬
ходимости брать поверхности S из класса поверхностей Ляпунова; под
109
ними достаточно подразумевать ограниченные гладкие двусторонние
поверхности класса С\ именно такие, которые могут нести на себе
указанные слои, при этом, как уже подчеркивалось, эти поверхности,
будучи расположенными в области т, не должны иметь общих точек
с ее границей — поверхностью а.
Поверхности S могут быть замкнутыми и могут быть незамкнутыми.
Во втором случае они должны быть ограничены одной или несколькими
замкнутыми кривыми. Простейшими такими незамкнутыми поверхностями
S являются области некоторой плоскости, например, области в плоскости
сечения тела т. Очевидно, располагая слои в плоскостях сечений, имеет
определенный смысл выбрать сечения, проходящие через центр масс
тела т и содержащие его диаметр, так как они — как сечения тела —
наиболее полно отвечают ему в целом. Возможность использования
таких плоских слоев подсказывается замечательной трактовкой (см.
[143]) потенциала однородного эллипсоида с полуосями, а>Ь>с по¬
тенциалом неоднородного эллиптического слоя (диска) с полуосями
л/а2— л1Ь2 — с2, расположенного в плоскости, определяемой осями
эллипсоида, перпендикулярного его малой оси.
Обрисовав разнообразные возможности выбора поверхностей S для
описания объемного потенциала V тела т суммой (4.13) — (4.15), мы
представим последним указанным образом потенциал планеты, используя
именно плоские слои в ее экваториальном сечении, учитывая при этом,
что для гидростатически равновесных планет плоскость экватора явля¬
ется естественной плоскостью их симметрии.
Заметим, что потенциалографическая задача (4.13) — (4.15) может
быть сформулирована в обобщенном виде, когда в искомое представление
заданного внешнего потенциала V планеты, кроме потенциалов простого
и дипольного слоев, включаются еще дополнительно слои, несущие
на себе гравитационные квадриполи, октаполи и т. д., вообще, мультиполи
п-го порядка и развивающие в пространстве потенциалы Vn соответст¬
вующих порядков, т. е. когда предполагается
причем все эти слои либо лежат на одной поверхности S, либо на
различных S^n\ но внутри т.
Такая обобщенная ПЗ еще не изучалась. Однако приведем все же
один ее частный — предельный — случай, когда, во-первых, все /г(л'= 1
и, во-вторых, точечные объекты разных типов расположены на одной
замкнутой поверхности S, охватывающей начало системы координат.
Рассмотрим такой частный случай, при котором поверхность S стяги¬
вается в точку, именно в начало системы координат. Тогда из (4.16)
получаем частную сумму классического ряда потенциала V, записанную
в мультипольной форме, что соответствует случаю использования — при
описании поля — только центральных гравитационных мультиполей.
Представление же потенциала V в обобщенной ПЗ предусматривает
использование мультиполей нецентральных и расположенных дискретно
или непрерывно на во внутренней области тела т.
N
(4.16)
п = 1
110
Подобные исследования ведутся и за рубежом. В частности, раз¬
работан *) комбинированный метод представления потенциала мульти-
польными слоями в сочетании с конечными элементами.
Теорию нецентральных мультиполей различных порядков разработал
Марченко [204]. Он дал ее основы, получив общую формулу Максвелла
для потенциала нецентрального мультиполя, позволяющую выразить
последний с помощью комбинаций потенциалов точечных масс и потен¬
циалов диполей, оси которых совпадают с осями рассматриваемого
мультиполя. Так как из потенциалов нецентральных мультиполей, с одной
стороны, легко получить в центральном случае известную систему орто¬
гональных шаровых функций, а с другой стороны, при п=0 — систему
потенциалов точечных масс (неортогональных функций), то сказанное
позволяет считать, что введение обсуждаемого класса функций — потен¬
циалов нецентральных мультиполей — привело к теоретическому обоб¬
щению применяемых для описания геопотенциала некоторых видов обоб¬
щающих базисных функций. Кроме того, в [204] изучен важный под¬
класс осевых (или радиальных) мультиполей, получена рекуррентная
формула для их вычисления, установлены условия, при которых обсужда¬
емые функции могут считаться линейно независимыми и полными, иссле¬
дованы экстремальные свойства потенциалов радиальных мультиполей
на сфере. Последнее позволило выделить существенные параметры изу¬
чаемых функций и создать методику предварительного мультипольного
анализа поля для выбора оптимального (с точки зрения аппроксимации)
местоположения и порядка мультиполя при решении задачи описания
геопотенциала указанными объектами с различной степенью его дета¬
лизации. Показано также, что с помощью преобразования Кельвина
на основе радиальных мультиполей имеется возможность «генерации»
воспроизводящих ядер, которые могут находить применение в вариаци¬
онном методе физической геодезии.
§ 17. Концепция гравитирующих дисков
Рассмотрим теперь один частный случай потенциалографической за¬
дачи.
Будем под 5 понимать площать эллипса или круга, лежащих в эквато¬
риальной плоскости планеты и имеющих центр в центре масс планеты,
возможно наибольших размеров, именно таких, что их контуры, однако,
не касаются контура экваториального сечения планеты (ситуация, ана¬
логичная таковой при введении в физической геодезии сферы Бьерхам-
мара). Другими словами, за S принимаем далее площадь экваториального
сечения планеты, обобщенную эллипсом или окружностью и «сжатую»
незначительно к центру, именно, настолько, что ограничивающие ее
эллипс или окружность становятся «почти» вписанными в это сечение.
И хотя для некоторых планет (Марс, Земля) под S выгодно понимать
площадь эллипса, будем все же далее — в целях описания глобального
*) Hofmann-Wellenhof В. Representation of the Gravitational Potentional by
Multipoles // Mitteilungen der geodatischen Institute der Technischen Universitat
Graz. — Folge 47. — Graz. — 1983. — P. 208.
Ill
гравитационного поля планеты и ради упрощения вычислении — прини¬
мать за 5 круг радиуса
R=ae—е, (4.17)
где ае — экваториальный радиус планеты, а е>0 — некоторая малая
величина.
Потенциал V планеты отнесем к вращающейся вместе с ней прямо¬
угольной декартовой системе координат Oxyz, начало которой совмещено
с центром масс планеты, а ось OZ совпадает с ее осью вращения. Тогда
в соответствии с условиями потенциалографической задачи выразим
V суммой (4.13) при /г'=/г"=1, слагаемые которой суть
V(£ — xf + (Л — У)2 + z2
_zv(g, r))dS
(4.18)
[V(i~— *? + (Л — yf + z2]3 ^4’19^
Здесь x, у, z—координаты произвольной точки Р вне планеты; £, ц —
координаты текущей точки Q плоской области S; р (£, т^) и v (£, ц) —соот¬
ветственно плотность простого и момент двойного слоев, предполагаемыми
принадлежащими к классу функций L%.
При написании этих потенциалов использованы формулы (4.14) и
(4.15), причем в последней за положительное направление нормали п к5
взято отрицательное направление оси Oz. (Заметим, что формулы (4.18)
и (4.19) при R-+oo и при заданных на всей плоскости функциях
р (£, г]) и v(£, л) дают соответственно решения задач Дирихле и Неймана
для уравнения Лапласа в случае полупространства.)
Простой слой, предполагаемый находящимся на площади круга 5 в
экваториальной плоскости планеты и развивающий вне ее и на ее поверх¬
ности потенциал (4.18), будем называть массовым материальным диском
ММД в связи с тем, что круг (или эллипс) S — для создания им в окру¬
жающем его пространстве потенциала V' — приходится считать нагру¬
женным поверхностными массами плотности р (£, л)> общая масса кото¬
рых равна массе планеты.
Двойной слой, образованный сплошным образом расположенными
на S диполями, ориентированными перпендикулярно к его плоскости
и развивающими в своей совокупности всюду вне его (значит, и на
поверхности планеты) потенциал (4.19), будем именовать дипольным
диском ДД на основании того, что свойства этого потенциала — как
потенциала двойного слоя — обусловлены функцией распределения мо¬
ментов диполей v (£, г]), образующих в совокупности этот диск.
В данной потенциалографической задаче требуется определить плот¬
ность р и момент v указанных гравитирующих дисков.
Отметим сначала основные свойства потенциалов (4.18) и (4.19)
введенных дисков.
1. Площадь S гравитирующих дисков выбрана так (см. условие (4.17)),
что потенциальные функции V' (х, у, г) и V" (х, у, z) и их частные произ¬
водные любых порядков суть функции, непрерывные всюду вне S; значит,
112
они и все их производные непрерывны не только во всем внешнем про¬
странстве относительно планеты, но и на ее поверхности о.
2. Из формул (4.18) и (4.19) потенциалов дисков, в сумме выражаю¬
щих внешний потенциал Земли, видно, что потенциал ММД, т. е. У'{Р)>—
четная функция, а потенциал ДД, т. е. V" (Я), — нечетная функция
относительно г. Другими словами, потенциалы V' и V" гравитирующих
дисков — это четная и нечетная части потенциала V планеты относительно
ее экваториальной плоскости. В том случае, когда для какой-либо внешней
точки Р(х, уу z) нет ей симметричной, точнее, последняя попадает во
внутрь планеты или на ее поверхность, то приходится понимать под потен¬
циалом V в такой точке его аналитическое продолжение извне внутрь пла¬
неты, конечно, при условии его существования.
3. Вспоминая (§ 2) разный характер убывания потенциалов слоев по
мере удаления от них, отметим, что в любой внешней точке Р
\V'{P) \ >\V" (Р) I.
Дадим приближенное решение рассматриваемой потенциалографиче¬
ской задачи.
Будем полагать внешний потенциал V планеты заданным набором
стоксовых постоянных
УN={Cпту ^ J
до некоторого порядка N. На основании свойства 2 запишем
V'=V V"=V
V V чет, V V неч,
где Учет и 1/неч — соответственно четная и нечетная части потенциала V
относительно z или относительно cos Ф (Ф — полярное расстояние внешней
точки Р). Значит, исходной информацией о ММД является левая часть
уравнения (4.18), заданная набором параметров
У'и={Спт, Snm)n+m==2k (k=0y 1, 2,. . .), (4.20)
а для ДД — левая часть уравнения (4.19) с набором стоксовых посто¬
янных
У N {^nm> ^ nm\ n-\-m= 2/г+Г (4.21)
Потенциал планеты в усеченном до N-ro порядка ряде VN шаровых
функций содержит (N -f- I)2 стоксовых постоянных. Легко подсчитать, что
усеченный ряд V'N потенциала ММД имеет в своем составе {/2 (N + 1) X
X (N 2) постоянных, в ряде V"N потенциала ДД их общее количество
равно х/2N (N + 1) •
Известно, что всякая функция двух переменных ф(£, г]) е L2S для любо¬
го фиксированного N имеет х/2 (N + l)(/V + 2) степенных моментов
ФМ= 5 SV dS (р + я < АО- (4.22)
Значит, набор (4.20) стоксовых постоянных, определяющий V'N> до¬
ставляет все степенные моменты \xpq плотности ММД, поэтому его плот¬
ность р,= |л(£, г]) может быть восстановлена решением усеченной (до /V-ro
113
порядка) степенной проблемы моментов, конечно, при выполнении
условий ее разрешимости.
Моменты \ipq плотности ММД однозначно вычисляются при этом по
постоянным а'пт и Ь'пт этого диска вида
(г', V — полярные координаты точки Q(£, г\) диска в его плоскости), ко¬
торые, в свою очередь, легко получаются по соответствующим стоксовым
постоянным Спт и Snm из их набора (4.20) путем сравнения коэффициен¬
тов разложения потенциала V' (Р) ММД в ряд шаровых функций с чет¬
ными (в смысле п+т=2k) коэффициентами лапласова ряда потенциала
Почти аналогично находится и момент v>*(£, tj) дипольного диска.
Отличие приближенного решения уравнения (4.19) от описанной проце¬
дуры такового для ММД заключается в том, что таким же образом вводи¬
мые и получаемые постоянные а"т и Ъ"пт, имеющие вид (4.23), но, безуслов¬
но, с функцией v(g, г]) вместо р(£, т|) и иными множителями
А'п'т, выражаются с точностью до коэффициента, зависящего от п и /л, уже
через стоксовы постоянные Сл+1 т и 5л+1 т. Таким образом, разложение
V'N' «впитывает» в себя стоксовы постоянные до (УУ+ 1)-го порядка вклю¬
чительно. Поэтому для решения усеченной степенной проблемы моментов
для функции v(|, г]) до УУ-го порядка требуется учитывать стоксовы по¬
стоянные планеты до (УУ+1)-го порядка.
Подчеркнем одно любопытное обстоятельство. Как известно (см. гл. 6),
обратная задача теории потенциала, в которой по известному внешнему
потенциалу планеты, точнее, по набору ее стоксовых постоянных до неко¬
торого порядка УУ, ищется плотность б распределения ее масс, однознач¬
ного решения не имеет. При сведении этой задачи к трехмерной степенной
проблеме моментов, усеченной до УУ-го порядка, для обеспечения един¬
ственности ее решения не хватает */2п(п—\) моментов на каждый п-й
порядок (п^2). Если же искать плотность р и момент v гравитирующих
дисков ММД и ДД этой планеты, располагая параметрами ее внешнего
поля также до yV-ro порядка, то, как было показано, эти «плотностные»
характеристики дисков могут быть определены однозначно в классе мно¬
гочленов М-го и (УУ— 1)-го порядков. И.хотя эти гравитирующие диски —
абстрактные конструкции, рассмотрение их оказывается небесполезным.
Из обсужденного массового материального диска ММД планеты мо¬
жет быть выделен меньший по размерам фокальный диск ФД, отвечаю¬
щий главной части потенциала, именно, эллипсоиду с эллипсоидально¬
слоистой структурой. Остановимся на этом подробнее.
В классической теории притяжения эллипсоидов [11,31, 143, 149], раз¬
работанной к началу нашего века и ставшей вновь актуальной в связи
с запросами современной физики и астрофизики [113, 169], известна
теорема Маклорена—Лапласа, в соответствии с которой однородные
софокусные эллипсоиды одинаковой массы развивают во внешнем (отно¬
сительно наибольшего из этих эллипсоидов) пространстве одинаковый
потенциал. Предельный случай, при котором эллипсоид сплющивается
(4.23)
114
в плоский диск, был рассмотрен Риманом (см. [143]). Это следствие
римана гласит, что внешний потенциал однородного эллипсоида 3
4 + 4 + 4 = 1 (а > Ь> с) (4.24)
а Ь1 сг
плотности 6=const совпадает с потенциалом простого слоя, распределен¬
ного на площади фокального для 3 эллипса
** + /4=1, 2 = 0 (4.25)
2 2
а — с
с переменной плотностью
2аЬсЬ -у I jc2
У (а2 - с2)(Ь‘
Hi,, „ „ „ \/1 - -о (4-26)
а2 — с2
Из последней формулы следует, что монотонно изменяющаяся плот¬
ность такого простого слоя равна 2abcb/\{a2 — с2)(Ь2 — с2) в центре
эллипса и исчезает на его контуре. Заметим также, что в случае вырожде¬
ния эллипсоида (4.24) в сжатый эллипсоид вращения (а=Ь) эллиптиче¬
ский диск (4.25) превращается в круговой диск радиуса д/а2 _ с2 *)
Обращаясь теперь к неоднородному эллипсоиду 3 со слоистым распре¬
делением масс, рассмотрим [91] интересный для приложения случай тол¬
стых эллипсоидальных слоев, на которые можно разбить эллипсоид.
Будем считать, что внутри эллипсоида Эо=Э построено п софокусных
эллипсоидов Э\, З2,. . Эп, концентрических с Эо и подобно ему располо¬
женных. Пусть в каждом из эллипсоидов 3t (/=0, 1, 2,. . ., /г), полуоси
которого аь bh ch плотность вещества постоянна и равна 6,. Тогда при
переходе из одного эллипсоида в соседний она увеличивается (по направ¬
лению к их общему центру) скачком на величину ht = 6, — 6; _ Значит,
потенциал притяжения такого неоднородного эллипсоида Э на внешнюю
точку представится суммой потенциалов однородных эллипсоидов 3t(i=
=0, 1,2,.. ., ц), каждый из которых может быть заменен потенциалом эл¬
липтического диска
^ bi-°i
с плотностью
2 gM(6,.-6,._,) Г
' v<«? - ■?><*? - 4) V
х2 У2
Г-п — - \ / 1 а2 Л Ь2 с2
Поэтому во внешнем пространстве потенциал неоднородного эллип¬
соида 3 описанной выше слоистой структуры совпадает с потенциа¬
лом эллиптического диска (4.25) с кусочно-непрерывной плотностью р,
*) Из синонимов «диск» и «пластина», используемых в математической и физи¬
ческой литературе применительно к простым, в основном плоским, слоям, мы здесь
пользуемся первым — «диск», который для (4.26) довольно наглядно раскрывает
смысл графика функции р = р(х, у) — в системе координат Oxy\i — поверхности,
ортогонально пересекающей плоскость ху вдоль эллипса (4.25).
115
убывающей от центра диска к его периферии:
.-о л/(а«2 _ сЬ(^ - сЬ V
1 - v^-тИ^ («-.=о).
af — cf bf — с?
(4.27)
Суммированию в этой формуле (л* ^ п) подлежат только те слагаемые,
в которых подкоренное выражение во втором радикале неотрицательно.
Ясно, что в случае сжатого эллипсоида вращения с принятой структурой
эллиптический диск вырождается в круговой, а для шара со сферически
симметричным строением он обращается в материальную точку.
В случае эллипсоида вращения (а = Ь) возможен более общий под¬
ход [95] к геометрии слоистого строения его внутренности, основанный
на законе изменения второго эксцентриситета /2= (а2—с2) /с2 сла¬
гающих его слоев в виде непрерывной функции 1=1(с) их малых полуосей
[о, Со].
Плотность вещества внутри Эо зададим функцией ее распределения
6=6(с) вдоль малой оси эллипсоида. Будем считать эту функцию на
промежутке [0, Со], исключая лишь конечное число точек, невозрастаю¬
щей функцией, имеющей абсолютно интегрируемую производную 6'(с),
а в исключенных т точках — имеющей разрывы первого рАда (скачки
hk<z0\ 6=1, 2,. . ., т) и на правом конце промежутка — односторонний
скачок: 6(с0—0)^=0 и 6(с0)=0.
Можно показать, что при выполнении сформулированных условий
внешний потенциал эллипсоида вращения Эо совпадает с потенциалом
простого слоя, распределенного на площади его фокального круга
х2+У2=ао—с?, 2=0 (4.25а)
с переменной плотностью, выражаемой интегралом Стилтьеса
со
ц(х, у)= -2\f{c)db{c), (4.28)
С*
в котором нижний предел интегрирования с* — положительный корень
уравнения
cl (с) — д/х2 + у2 = 0, (4.29)
а подынтегральная функция
№ = ^+|(c) А1с212(с) - (X2 + у2)> о. (4.30)
Интеграл (4.28) может быть вычислен по формуле (см. [164]),
содержащей в себе интеграл в смысле Римана:
ф, у) = 2
f(c0)6{c0 - 0) - £ f(ck)hk - ^ f(c)d(c)dc
(4.31)
причем суммирование в ее среднем слагаемом для всякой данной точ¬
ки (х, у) диска S предусматривается с такого k* С т, начиная с кото-
116
рого выражение с\ /2 (ck) — (х2 + у2), входящее в f(ck)y уже неотрица¬
тельно.
Таким образом, потенциал на внешнюю точку однородного и даже
неоднородного эллипсоида, но со слоистой структурой, точнее, с эллипсои¬
дально-слоистым строением, может быть заменен потенциалом фокаль¬
ного диска (ФД) этого эллипсоида. Если планеты в начальном, довольно
грубом приближении шарообразны, то в следующем они имеют эллипсои¬
дальную форму, а исходя из первого приближения Клеро его гидро¬
статической теории фигур планет им даже может быть приписано эллип¬
соидально-слоистое строение. Поэтому важность для небесной механики
обсуждаемого здесь факта из теории притяжения эллипсоидов очевидна.
Как указывалось в § 1, при расстояниях между телами, значительно
больших их линейных размеров, взаимное притяжение тел отождеств¬
ляется с притяжением материальных точек с массами этих тел и располо¬
женных в их центрах масс. Более того, притяжение планеты как тела
сферической формы со слоисто-сферической структурой также эквива¬
лентно притяжению заменяющей это тело материальной точкой, или,ска¬
жем фигурально, массивного «шарика» ничтожного радиуса. Теперь же
видим, что притяжение планеты, которая в глобальных масштабах строже
соответствует телу эллипсоидальной формы со слоисто-эллипсоидаль¬
ным строением, более точно можно трактовать притяжением диска —
эллиптического или даже кругового, предположив, скажем, что указан¬
ный «шарик» сдавлен в массивный «эллипсоидик», который и есть как раз
ФД планеты — эллипсоида как предельное положение при его сплющива¬
нии. Возможность такой разной трактовки реальных планет (представле¬
ние их то точками, то дисками, расположенными в экваториальных
плоскостях планет), допустимой при изучении развиваемых ими сил тяго¬
тения, естественно связана с удалением притягиваемых масс от планеты.
При очень больших расстояниях планета притягивает как материальная
точка, при меньших — как ее фокальный диск, а при расстояниях,
сравнимых с размерами самой планеты, — как диск, дополнительно нагру¬
женный иными гравитирующими образованиями, и, наконец, при «беско¬
нечно малых» расстояниях (при расстояниях, во много-много раз меньших
размеров планеты) ее поле притяжения может считаться даже однород¬
ным, конечно, с надлежаще подобранным для рассматриваемой области
пространства вектором его напряженности.
Обращаясь к Земле, скажем, что приведенные здесь формулы (4.27) и
(4.31) дают возможность построить приближенно гравитационное поле
ее ФД, радиус которого легко определяется по полуосям общеземного
эллипсоида (равен примерно 522 км), а плотность его ц — по модельному
эллипсоидально-слоистому распределению плотности 6 вещества внутри
планеты, которое может быть взято из моделей ее внутреннего строения;
при этом плотности эллипсоидальных слоев и скачки плотности на гра¬
ницах оболочек должны быть подобраны так, чтобы масса эллипсоида
(а значит, и диска) была равна общей массе Земли.
Однако больший интерес представляет обратная задача, возвращаясь
к которой, скажем, что в рамках ее решения мы подошли к концепции
гравитирующих дисков (КГД). Сущность последней в том, что потен¬
циал V=V(P) притяжения планеты можно представить следующей
117
суммой:
V=V*+V'+V", (4.32)
где в качестве слагаемых фигурируют потенциалы трех плоских слоев,
находящихся в экваториальной плоскости планеты. Именно,
у* (Р) = G \ >iQ/— (4.33)
s* PQ
— потенциал фокального диска (ФД), или, подробнее, потенциал про¬
стого слоя с плотностью р*=|1*(£, к\), расположенного на площади
фокального круга S* радиуса д/а2 —. b2 общеземного (двухосного) эл¬
липсоида с полуосями а=ае и b(a>b)\
(4.34)
s pQ
— потенциал (безмассового) материального диска (БМД), другими сло¬
вами, потенциал простого слоя с плотностью р,= р,(£, тЦ, находящегося
на площади круга S радиуса R=ae—е(е>0 — сколь угодно малая вели¬
чина) ;
г zpvndSn
V"{P) = G \ Р ° Q- (4.35)
J Г
S PQ
— потенциал дипольного диска (ДД), или, конкретнее, потенциал двой¬
ного слоя с моментом v=v(£, т|), расположенного также на площади
круга S.
Центры кругов S* и S совпадают с центром О масс планеты. Плотности
р*(£, г]), р,(£, г|) и момент v(£, г]) предполагаются в соответствующих об¬
ластях принадлежащими к классу функций, интегрируемых с квадратом.
Напомним, что относительно координаты z каждый из потенциалов
V* и V' простых слоев является четной функцией, а потенциал V' двой¬
ного слоя — нечетной.
Потенциал V* фокального диска выражает потенциал данной неэллип¬
соидальной неоднородной планеты в предположении строго эллипсои¬
дальной ее формы и эллипсоидально-слоистого строения. Он совпадает с
потенциалом общеземного эллипсоида, если последнему приписать ука¬
занную внутреннюю структуру.
Потенциал V* фокального диска выражает нормальный потенциал
U Земли в общепринятом его понятии, значит, V* отражает главную
(т. е. с точностью до малых первого порядка) часть потенциала гидро¬
статически равновесной Земли, представляемой в приближении Клеро
эллипсоидом вращения с эллипсоидально-слоистым строением. Потенциал
V* выражает главную часть потенциала планеты: |К*|^> |К'|+|К"|. Трак¬
товка нормального потенциала Земли потенциалом ФД была обсуждена
в теории фигуры Земли Юркиной [174] исходя из предпосылок проблемы
Стокса.
Потенциалы V' безмассового материального диска и V" дипольного
описывают в сумме V'-\-V"=T возмущающий потенциал Т планеты.
Оба они «безмассовы».
i 18
Так как потенциал БМД — функция, четная по z, то V' обусловлен
такими отклонениями действительной планеты от ее идеальной формы
(уровенного эллипсоида вращения) и идеального (эллипсоидально-слои¬
стого) строения, которые симметричны относительно плоскости экватора.
А вследствие того, что потенциал Vм ДД — нечетная относительно
z функция, то он отражает такие отличия реальной планеты от идеальной,
которые асимметричны по отношению к ее экваториальной плоскости.
В дополнение к объяснению выражения (4.20) заметим теперь, что,
выделяя из МД фокальный диск, последнему приписывают обычно Соо и
С го (иногда и более высокие четные зональные гармоники потенциала),
а все остальные из набора (4.20) относятся к БМД.
Разделение коэффициентов (Cnm, Snm) потенциала планеты на четные
(4.20) и нечетные (4.21) относительно удаления г от экваториальной
плоскости позволяет изучить свойства планеты, связанные с симметрией
или ее нарушением относительно этой плоскости. В подтверждение
сказанного сошлемся на предварительные вычисления *) главной части
плотности v(£, т]) ДД Земли по стоксовым постоянным планеты до 5-го
порядка включительно, показавшие, что ее наибольшее значение, в де¬
сятки раз превосходящее среднее, приходится на область Галапагосских
островов, совпадая с центром Галапагосского спретинга, где имеет место
прорыв земной коры (там находится знаменитый подводный термальный
источник «Черный курильщик»).
*) Вычисления выполнены студентками геодезического факультета Львовского
политехнического института Г. Я. Сцирой и Н. Ф. Гайдаш.
ГЛАВА 5
ГЕОДЕЗИЧЕСКАЯ ОБРАТНАЯ ЗАДАЧА
ТЕОРИИ ПОТЕНЦИАЛА И ФИГУРА ЗЕМЛИ
§ 18. Единственность, устойчивость и метод решения
Как отмечалось в § 4, обратные задачи теории потенциала стали
предметом исследований в математике с начала 30-х годов. Однако
предыстория их более ранняя и связана в теоретическом плане с работами
итальянских ученых начала века [206, 118], а в практическом — с зарож¬
дением и становлением прикладной геофизики в нашей стране, когда
по инициативе В. И. Ленина в 1918 году были начаты исследования
возможностей добычи железа в районе Курской магнитной аномалии,
вызванные жизненно важными нуждами молодой Советской республики
в решении проблемы недостатка рудного сырья. Академик П. П. Лазарев —
заместитель председателя Особой комиссии по изучению Курской магнит¬
ной аномалии (OK КМА) и руководитель геофизических работ исходил
из твердой убежденности в том, что совокупность результатов гравиметри¬
ческих, сейсмических и магнитных наблюдений и измерений даст возмож¬
ность определять залежи рудных тел. Он с сотрудниками разрешили ряд
конкретных задач. Их работы привели к постановке общей обратной
задачи теории потенциала [55], один из частных случаев которой (для
призмы) был в 1923 г. рассмотрен О. Ю. Шмидтом [173], а трудами
Лазарева и его сотрудников представлены обширные теоретические и
экспериментальные исследования, положившие начало отечественной раз¬
ведочной геофизике.
Основные положения обратной задачи теории потенциала были опуб¬
ликованы Лазаревым лишь в 1930 г. В его статье [55] «Об общих условиях
возможности нахождения рудных залежей путем гравиметрического и
магнитного исследования» — в ответ на поставленный вопрос — показа¬
но и подчеркнуто, что даже если задача определения поля по заданным
гравитационным или магнитным массам получает однозначное решение,
то «обратное решение — нахождение по потенциалу или полю магнитных
или гравитационных масс — является задачей неопределенной и задача
не получает однозначного решения» (с. 113 в [55]). А в конце статьи
затронуты возможности исследования Земли как планеты в целом; от¬
мечено, что получается многозначный ответ, если пользоваться только
одними гравитационными данными. «Ответ получается однозначный, если
мы воспользуемся и данными сейсмического исследования» (с. 114).
Практическая реализация такого пути исследования плотности недр
Земли (геофизическая задача) будет описана в гл. 6. Завершающим
звеном теоретической проблематики ОК КМА была известная теорема
П. С. Новикова [116] об единственности определения формы тела
120
по его внешнему потенциалу в классе гладких звездных поверхностей
(геодезическая задача).
Напомним ее содержание (§ 4). Пусть некоторое тело т, состоящее
из вещества плотности 6 и ограниченное поверхностью а, развивает во
внешнем пространстве потенциал
V(P) = TQ> Qex, Рф т. (5.1)
J lPQ
Предположим, что потенциал V(Р) вне тела т известен. Задача
заключается в том, чтобы по нему определить поверхность о тела т.
Эта задача в различных постановках неоднократно изучалась,
кроме Лазарева и Новикова, многими исследователями: Сретенским
[143], Ивановым [38], Лаврентьевым [54], Зидаровым [35, 36], Прилепко
[137, 138], Векком [230] и другими. Ими устанавливались условия
единственности и устойчивости решения, изучались вопросы существова¬
ния и фактического нахождения его — при этом применялись разнообраз¬
ные подходы и методы.
Ниже задача обсуждается в постановке [83, 86, 92], отвечающей
запросам планетарной геофизики и геодезии, наблюдательная информа¬
ция которых содержит в своем составе также данные о потенциале
и его градиенте непосредственно на искомой поверхности. Последнее
позволяет не только рассмотреть теоремы единственности нового типа
(одна из них приводится ниже), но и построить эффективный метод
решения задачи в рамках выполнимости условий этих теорем. Такая
трактовка задачи, когда, кроме задания потенциала вне тела, он или его
градиент считается заданным еще и на искомой поверхности тела, более
близка к реальной ситуации, а фигурирующие в ее постановке условия
менее стеснительны, чем, например, в одной из известных теорем [137],
где для обеспечения единственности решения общей обратной задачи
теории потенциала требуется дополнительное задание потенциала в одной
точке внутри тела. А главное: предлагаемая постановка делает ясным
процесс решения задачи, который в конечном итоге сводится к обратному
интерполированию потенциала (или модуля его градиента) вдоль радиуса-
вектора.
Обсуждаемую задачу будем рассматривать как условно-корректную:
приняв заранее факт существования ее решения в некотором классе
поверхностей, построим сначала формальное решение задачи, докажем
его единственность в принятом классе поверхностей, дадим оценку его
приближенного построения, затем отметим источник некорректности
задачи в изучаемой постановке и обсудим устойчивость ее решения при
приближенно заданной исходной информации.
Будем пользоваться сферической барицентрической системой коорди¬
нат р, Ф, К, т. е. такой сферической системой, начало которой совпадает
с центром масс тела т, чего всегда можно достигнуть при заданном
внешнем потенциале.
Теорема. Обратная задача теории потенциала (5.1), в которой по по¬
тенциалу V=V(p, Ф, А,), развиваемому телом т, ищется его поверхность
о: А,), предполагаемая а) гладкой, б) звездной относительно цент¬
121
ра масс тела т и в) с заранее известной областью изменения барицентриче¬
ского радиуса-вектора
имеет в указанном классе поверхностей единственное решение, если
1) потенциал V тела т всюду вне сферы радиуса а может быть задан
рядом по шаровым функциям (1.12)
описывающим вне поверхности а и на ней внешний потенциал этого тела,
а в слое между а и сферой радиуса а — его аналитическое продолжение;
2) на самой поверхности а потенциал V тела представлен непрерывной
функцией F ее криволинейных координат Ф, к
тела т, a q — постоянная, вводимая следующим условием);
3) радиальная производная потенциала dV/dp такова, что ее разложе¬
ние по сферическим функциям, следуемое из (1.12), в шаровом слое
а<р<сР окрестности поверхности а тела удовлетворяет условию
Комментарии к теореме, а) Как следует из ее формулировки, исход¬
ными данными при исследовании и решении задачи считаются априорные
сведения о размерах тела т в виде неравенства (5.2), непрерывная
функция F в условии (5.3), отражающем задание потенциала «внутрен¬
ним» образом на искомой поверхности, и коэффициенты при элементар¬
ных сферических гармониках в сферических функциях к) ряда
(1.12), удовлетворяющих неравенству (5.5); при этом Y0=M, a Ki=0
в силу выбора системы координат.
б) В отличие от ряда известных постановок задачи, в которых по внеш¬
нему потенциалу ищется тело, близкое к данному, в сформулированной
теореме вместо этого предполагается известной область изменения бари¬
центрического радиуса-вектора. Заметим, что условие 2) позволяет легко
определить его среднее значение:
где со — единичная параметрическая сфера. Числа а^1 и р в неравенстве
(5.2) должны быть установлены на основании известных сведений о теле
а<г<р,
(5.2)
К(р, О, k)\a = F{$, к),
(5.3)
причем
| fcp-f(d. \)\ <С,
(5.4)
2лл
О О
С = (1 - (М - масса
zap
о < q < 1
(5.5)
гср = М/Тср; Fcp = — J F(p, к) da),
(0
122
г, при этом предпочтительно иметь а=гнаим—т], где г|>0 — малая вели¬
чина.
Неравенство (5.4) характеризует степень отклонения заданного потен¬
циала V на искомой поверхности о от его среднего значения на ней,
причем, если вместо (5.2) известно, что [а,р], то правая часть неравен¬
ства (5.4) имеет вид 1 /2 (1—q) еП, где е = (р — а) 6 р — «сжатие» тела т,
а П = М/a — потенциал точечной массы М (находящейся в барицентре
тела т), рассчитанный на расстоянии а от него.
Заметим, что неравенство (5.4) выполняется всегда для тел, ограни¬
ченных уровенной поверхностью потенциала K=const.
в) К условию 1): ряд (1.12) всюду вне сферы радиуса а может счи¬
таться сходящимся в среднем (см. § 13).
г) Условие 3) теоремы, характеризующее гладкость потенциала,
обусловленную внутренней структурой тела т, допускает простую механи¬
ческую интерпретацию: оно означает, что определенная часть (например,
при q=1/2 равная 2/з) гравитационного действия тела т на любую точ¬
ку его поверхности и в ближайшей окрестности ее в виде указанного в ус¬
ловии шарового слоя обусловлена силой притяжения материальной точки
с массой, равной массе М тела т и расположенной в его барицентре.
Приведем конструктивное доказательство теоремы, дав метод построе¬
ния искомой поверхности на основе отмеченной в ней исходной инфор¬
мации.
Составим уравнение, разрешающее задачу. Для этого согласуем на
поверхности о два представления потенциала: «внутреннее», заданное
функцией (5.3), и заданное рядом (1.12), который должен быть взят
при р= г. Из их сравнения имеем
м Т-Гв, X)
т + I = т х)' (5-6)
п = 2
Введя новую переменную
х=\ /г (5.7)
и обозначив
К=К(Ъ, A,) = F(fl, k) / М, (5.8)
получим из (5.6)
* - К - та Z V (5 9)
п = 2
— уравнение относительно х в виде х = ф(х), удобном для итераций.
Временное фиксирование координат О, X любой точки поверхности а (в том
числе и особых точек параметризации — полюсов единичной сферы)
позволяет считать величины К и Yn в уравнении (5.9) постоянными,
и тогда его естественно решать методом последовательных приближений.
При этом произвольная v-я итерация не дает точного значения корня х
уравнения (5.9); будем переменную, от которой зависит его правая часть,
обозначать буквой £, причем
|=1/р, Р6(а.р), (5.10)
123
поэтому правую часть уравнения (5.9) можно записать в виде функции
рассматриваемой на промежутке (^=1/р, g2= 1 /а), на котором она
непрерывна, так как по условию 1) фигурирующий в ней ряд представляет
потенциал, непрерывный во всем пространстве. Таким образом, имеем
формальное решение задачи, предоставленное следующим алгоритмом;
причем последнее равенство выражает полное решение задачи.
Обоснова-ние этого алгоритма требует доказательства сходимости
процесса итераций, получения оценки находимого так корня уравнения
(5.9) и доказательства его сходимости на промежутке (£i, £2). Для этого
достаточно показать (см. например, [22]), что функция <р(£) на замкну-
том промежутке [|*, £**], где \*=\/гкап6>1\ и £**= 1/гнаим<|2, удовлет¬
воряет для любых |'£"6 [£*,!**] условию Липшица с константой L< 1
и — для обоснования единственности корня — что существует такое
1б [£*> 1**\ * при котором ф(£) удовлетворяет неравенству
Вспоминая обозначение (5.8), из предпоследней формулы с учетом
последней имеем
откуда в силу условия 3) заключаем, что на промежутке (£i, £2)
00
(5.11)
00
х = lim tv; tv= К —jrr j Уп £(" t , (5.12)
V+oo m П L 9
n = 2
n = 2
где K=K{$, X) и Уп=Ул(0, X) —функции О, Х\ тогда
х=х(0, Я,), r= 1 /х=/(tl>, X),
(5.13)
|1-Ф(6)|<(1 -L)d,
где d='/2(£**—£*).
Вычислим производные функции (5.11)
(5.14)
оо
и потенциала (1.12)
оо
_/m dV/dp + М/р2
* (У =
-м/р2
-м/р2
124
На основании формулы Лагранжа о конечных приращениях, приме¬
ненной к промежутку [£', £"], теперь легко усмотреть, что функция ф (£) на
этом промежутке удовлетворяет условию Липшица с константой L=
/2, причем значение q соответствует заданному внешнему потен¬
циалу.
Установление равенства L=q показывает, что процесс итераций
(5.12) при произвольном выборе начального приближения £(о)6 [£*> £**]>
например, |(0) = 1/2(£1+Ы, сходится к корню уравнения (5.9) со скоро¬
стью геометрической прогрессии со знаменателем q. При этом, как из¬
вестно, оценка приближения при q<\ может быть охарактеризована
неравенством
где е — предельная погрешность вычисления корня уравнения (5.9),
определяемая по заданной погрешности определения радиуса-вектора г
поверхности о.
Остается доказать единственность корня х уравнения (5.9), находи¬
мого в соответствии с алгоритмом (5.12); для этого надо удостовериться
в существовании такого £, которое удовлетворяет неравенству (5.14).
С этой целью вычислим сначала левую часть неравенства (5.14) в точке
5о= 1 /ро, где р0=гср, причем гср дается формулой, приведенной в коммен¬
тарии б) к теореме.
Находим при фиксированных значениях ft, к
а с учетом условия (5.4) имеем
I lo — <P(io)l < (1 — Я) Р2~р-а- = (1 — ~
т. е. точка £о не удовлетворяет ,(5.14), ибо в последнем неравенстве справа
|Е(„) — *K<7v|£(o) — 4
а в нашем случае, когда q=x/2, более предпочтительным
|i(v) *|<6>
(5.15)
(5.16)
если только
|^(v— 1) £(v)|
м
Теперь
бо-ф(Ео) = (Fcp-F($, к))/М,
фигурирует l/2 — =
125
Однако, ссылаясь на установленную уже сходимость последователь¬
ности итераций (£(v)), всегда можно найти в этой последовательности
такой номер итерации v=p, начиная с которого будет выполняться
*|£(n+i)—О —q)d,
или
1ф№ы)-^)1 <0 -q)d,
т. е. [£*> £**] удовлетворяет неравенству (5.14), что доказывает един¬
ственность корня.
Так как вычисление х= 1/г как корня уравнения (5.9) может быть
выполнено для любой пары значений Ф 6 [0, л], X 6 [0, 2л), то заключаем,
что указанный метод (5.12) дает уравнение искомой гладкой звездной
поверхности а: г=/(Ф, X) = \/x(ft, X). Как следует из предыдущего,
полученная так функция r=f('O', X) единственная и в соответствии с фор¬
мулами (5.12) непрерывно зависящая от исходных данных — даваемых
формулами (3.55) коэффициентов Апт, Впт при элементарных гармониках
в К„(Ф, и функции /(О, >,).
Пример использования метода решения рассматриваемой задачи при¬
ведем для простейшего случая.
Пусть дан внешний потенциал некоторого тела, который зависит
только от р: 1/=К(р), т. е. все К„(0, X) в ряде (1.12) суть тождественные
нули, кроме Yo=My значит, У=М/р. Задан также потенциал на поверх¬
ности тела:
l/|CT=const=c.
В этом случае приведенных данных достаточно для определения а.
Необходимость в итерациях отпадает и сразу из уравнения (5.9) имеем
х =с/М.
Значит, тело т — шар радиуса г=М/с.
Доказав теорему единственности решения (5.12), перейдем к обсуж¬
дению его устойчивости. В теоретическом плане при выполнении условий,
указанных в теореме единственности, и при использовании метода итера¬
ции, вообще говоря, имеет место не только единственность находимого
решения задачи, но, как это следует из формул (5.12), и непрерывная
зависимость его от исходных данных в виде коэффициентов ЛптУ Впт ряда
(1.12) и функции (5.3). Это достигнуто в рассматриваемой постановке
задачи дополнительным заданием потенциала (5.3) на искомой поверх¬
ности о при помощи непрерывной функции F(ft, X) и постулированием
потенциала V на а сходящимся рядом (1.12). При этом первое позволило
перейти от нелинейного интегрального уравнения I рода (5.1) к уравнению
(5.9), неявно определяющему радиус-вектор г, а второе — обеспечить
указанные единственность и устойчивость корня этого уравнения, прини¬
маемого за искомое решение задачи. Таким образом, условия теоремы
внешне позволили снять некорректность с обратной задачи (5.1). Однако
в действительности некорректность, присущая этой задаче, остается и по¬
следнюю приходится рассматривать как условно-корректную, что уже от¬
мечалось выше. Причиной некорректности задачи в обсуждаемой поста¬
126
новке является опять-таки задание потенциала рядом (1.12), который при
фактическом построении решения (5.12) надо неоднократно суммировать,
а как известно, эта операция для рядов Фурье с приближенными коэф¬
фициентами (для ряда потенциала их получают по результатам измере¬
ний) является неустойчивой. В связи с этим для обеспечения устойчи¬
вости решения задачи необходимо иметь не только эмпирические значе¬
ния этих коэффициентов, но и дополнительную информацию о степени их
точности. В зависимости от вида этой информации и от того, какие конк¬
ретные методы суммирования ряда (1.12) будут затем использованы
при решении задачи, могут быть даны различные варианты теоремы
устойчивости решения задачи. Приведем ниже один из них, применив при
этом устойчивое суммирование ряда (1.12) по методике [13, 156] *).
Воспользуемся компактной записью (3.59) ряда для потенциала.
Вместо точных значений коэффициентов ak ряда (3.59) возьмем их
эмпирические, а значит, приближенные, значения ск\
ск=ак+Ук, (5-17)
с малыми (в пространстве /2) погрешностями yh обусловленными погреш¬
ностями измерений, причем пусть
Z укг
k = о
Другими словами, вместо последовательности u=[ak) дана последова¬
тельность и^={ск), для которой р,2= (и, иц) ^т], где р/2 — расстояние в мет-
рике /2: / <*, \
р£,(«.«,) = ( Ео (ck - °к)2 V/2
Значит, вместо ряда Фурье (3.59) с точными коэффициентами ak мы
располагаем рядом
оо
X с*ф*(о
k = о
с приближенными коэффициентами ск.
Требуется найти в классе гармонических функций Я (Q) £ С (Q) функ¬
цию V(t)y аппроксимирующую функцию V (t) по последовательности
чисел {с*}.,близкой (в метрике /2) к последовательности {ak} коэффициен¬
те
тов Фурье функции V (/), т. е. такой., что ^ (ck — akf <1 ц2. При
k = о
этом аппроксимация должна быть такой, чтобы при т]-^0 расстояние
(в метрике С) между функциями V (t) и V (t)
9c(V, V) = maxQ I V - V \ = e-+0.
Воспользуемся одним из оптймальных методов Арсенина устойчивого
суммирования рядов Фурье. Будем считать, что погрешности определения
*) Используемый далее устойчивый метод суммирования рядов Фурье описан
в [13, 156] для функций, заданных в конечной области. Применение преобразова¬
ния пространства по Кельвину позволяет воспользоваться этим методом и в рас¬
сматриваемом случае бесконечной области вне сферы радиуса а.
127
коэффициентов Фурье, т. е. числа yk, являются случайными числами,
удовлетворяющими требованиям:
1) W есть последовательность попарно некоррелированных случай¬
ных чисел;
2) математические ожидания (МО) этих чисел равны нулю, МО (yk) =
= 0, при всех значениях k.
Тогда дополнительное условие, согласно которому интеграл
\ p(t)fAO{V - Vfdil
при фиксированном значении параметра регуляризации ар имел бы наи
меньшее значение по элементам последовательности {£*}, фигурирующей
в стабилизирующем функционале решаемой задачи, приводит [13, 156]
к оптимальной сумме ряда (3.59) с приближенными коэффициентами ck
<5|8!
Однако в стабилизирующие множители
1 МО(т2*)
''<*• - T+VT “ 1 " <5|9)
входят отношения теоретических математических ожиданий случайных
чисел у| и с% которых мы не знаем. Поэтому приходится довольствоваться
их эмпирическими значениями. Тогда, если
МОэмп(у2) _ МО(у|)
МОэмп(с*) _ МО(с2)
где X Р* ^ то
(1 + Р*) >
£ / МОэмп(у?) \
^м_М1“Т55=ч5ТЛ(,)- (5-20>
А так как в нашем случае ср\{t) ^ Q (Q = const>0), то имеем оценку
AV(t) = НС (0 -v(t)\ < (Qt х с1)1/2 •
k = о
т. е. оптимальное суммирование с «эмпирическими» стабилизирующими
множителями вида (5.19) устойчиво к малым изменениям отношений
МО (у1) / МО (с\) в том смысле, что при £-^0 (т. е. в метрике /2) и
ДУ (t)^0 (в метрике С).
Заметим, что в силу условия 2), наложенного на последовательность
{у*}, в предыдущих формулах можно положить МО (y2k)—d(yk)=dky пони¬
мая под dk дисперсию коэффициентов ряда потенциала, совпадающую
с дисперсией погрешностей этих коэффициентов:
d(ck)=d(yk)=dk.
128
Возвращаясь теперь к рассматриваемой обратной задаче теории потен¬
циала, будем считать, что сумма ряда, фигурирующего в уравнении (5.9)
и в формулах (5.12), — а это ряд, представляющий потенциал тела т с вы¬
делением из него первых двух членов при нумерации по п и первых
четырех членов с индексацией по к, получена устойчивым методом (5.20).
Значит, сумма этого ряда в формулах (5.9) и (5.12) устойчива относи¬
тельно исходной информации, включающей данные о коэффициентах
ряда (1.12) и их точности. Полученный результат может быть сформули¬
рован в виде следующей теоремы.
Теорема. Приближенное решение (5.12) обратной задачи теории по¬
тенциала (5.1), для которой выполнены требования теоремы единствен¬
ности, является в указанном классе поверхностей устойчивым относи¬
тельно исходной информации, если, кроме эмпирических значений мате¬
матических ожиданий коэффициентов ряда (1.12), задающего внешний
потенциал тела, известны еще и дисперсии этих коэффициентов.
§ 19. Об определении обобщенных фигур Земли
и планет
Воспользуемся методом решения задачи § 18 при определении физи¬
ческой поверхности Земли и обобщенных фигур планет.
Под обобщенными фигурами планет будем далее понимать такие их
поверхности, при описании которых учтены коэффициенты разложения
потенциала планеты в ряд шаровых функций до некоторого фиксирован¬
ного порядка N. Основную уровенную поверхность планеты будем фикси¬
ровать либо заданием на ней значения потенциала, выводимого по ре¬
зультатам наблюдений, либо заданием координат точки, через которую
она проходит. Физическую поверхность Земли будем полагать прохо¬
дящей через ряд заданных поверхностными координатами точек, в кото¬
рых на основании результатов измерений известен потенциал силы
тяжести.
Рассмотрим метод определения физической поверхности Земли, из
которого как частный случай получим и способ построения ее основной
уровенной поверхности — геоида; при этом будем апеллировать к реше¬
нию обратной геодезической задачи теории потенциала.
Подчеркнем, что здесь не рассматривается основная проблема физи¬
ческой геодезии, т. е. не ставится целью определение с максимально
возможной точностью подробной поверхности Земли и ее внешнего гра¬
витационного поля на основании всей имеющейся к настоящему времени
геодезической и другой информации о планетах. Ниже, во-первых,
ищется обобщенная планетарная фигура Земли как первое и главное
приближение ее реальной поверхности, во-вторых, при решении задачи
внешнее гравитационное поле считается заданным, а не определяемым.
К составу исходной информации мы относим 1) данные спутни¬
ковой геодезии о внешнем гравитационном поле планеты, 2) значения
геопотенциала в нуле футштока, 3) традиционную геодезическую инфор¬
мацию (результаты нивелировок, измерений силы тяжести и астрономиче¬
ских определений координат пунктов), дающую приращения геопотен¬
циала, 4) угловую скорость вращения Земли, 5) априорно известные гра¬
5 Г Д Уичцеряков
129
ницы изменения геоцентрического радиуса-вектора (его наименьшее а и
наибольшее р значения).
Примем для дальнейшего геоцентрическую систему координат р, О, х,
обозначив буквой г искомый радиус-вектор r=/(d, X) физической поверх¬
ности а Земли: г=р|а.
Будем исходить, как и в § 18, из общепринятого разложения потен¬
циала Земли V в ряд шаровых функций (1.12)
отнесены к объемлющей сфере 5, значит, cn=GMa", а Спт, Snm — без¬
размерные стоксовы постоянные, получаемые из результатов наблюдений.
При использовании сферы Бьерхаммера 50 радиуса а и с сохранением
числовых значений Yп (О, X) последние преобразуются к виду
Переходим теперь к определению физической поверхности Земли
по указанной выше исходной информации.
Запишем выражение потенциала силы тяжести W планеты, беря раз¬
ложение потенциала силы притяжения отнесенным к внутренней сфере So
и ограничиваясь в нем некоторым порядком N:
где слагаемое, стоящее вне суммы, есть потенциал центробежной силы
(со — угловая скорость вращения Земли), а с'п, апти Ьпт даны формулами
Пусть в некоторой точке поверхности Земли, астрономические коор¬
динаты которой получены из наблюдений, а значит, обычным образом
с использованием результатов гравиметрической съемки, вычислены и ее
где сферические функции
п
Yn(b, к) = £ {Апт cos тк + Впт sin тк) Р%(cos Ф) =
т = О
п
= сп Y, (Cnmcos mb + Snm sin mk)P™(cos #) (5.21)
П
Km COS тк + bnm sin mk) P%(cos 0) =*= cnZn{&, k), (5.22)
m = 0
где
Cn = GMa”, anm = Cnm + 2,24 • lO^nC,
bnm = Snm + 2,24 • 10~3rtS„m.
(5.23)
(См. замечания об этом на с. 84 после формулы (3.60а).)
Поэтому имеем
(5.24)
(5.23).
130
геоцентрические координаты Ф и к, известно значение геопотенциала
х) = W0 - $ g- dh, (5.26)
L
где Wо — значение геопотенциала на геоиде, т. е. в нуль-пункте нивелиро¬
вок, а приращение потенциала \gdh найдено численно по результатам
L
нивелировок и измерений силы тяжести.
Тогда, сравнивая выражения (5.26) и (5.25), которое должно быть
взято при р = г, имеем
N c'nZJ«, X) оЛ2
+ £ п д"*+’ L + -^-(1 - Р2(cosd)) = W(V, А.). (5.27)
(5.28)
п = 2
Вводя новую переменную
х=а/г,
выполняя элементарные преобразования и обозначив
К = Л* = 1Г(1 -^(cosfl)), <7о = ^. (5-29>
получим из (5.27)
N
Х= К- Л*Х~2 - X £ (5.30)
— основное уравнение, разрешающее задачу. Фигурирующие в нем вели¬
чины /С, Л*, Z„ суть функции д и Х\ значит, для любой данной точки
на земной поверхности они имеют определенные постоянные значения,
и тогда (5.30) является относительно х алгебраическим уравнением сте¬
пени (V +3, уже приведенным к виду х=у(х)% удобному для итераций. Ре¬
шение этого уравнения при любом N (даже достаточно большом)
осуществляется просто. Важнее другое — его исследование: оно также
не вызывает каких-либо осложнений, и на основании известных теорем,
относящихся к методу итераций, легко доказывается, как в предыдущем
параграфе, что процесс итераций для уравнения (5.30) является сходя¬
щимся, а находимый таким образом при любых О, X корень х=у(х)
этого уравнения является единственным и допускает оценку \х—x(v) | <Сг
при любом заданном сколь угодно малом е>0, если только |x(v)—
—x(v_1)|<Ce (здесь v—номер итерации).
Обратимся теперь к построению основной уровенной поверхности
планеты, характеризуемой тем, что на ней U7=const=U70. Оно также
дается решением основного уравнения (5.30), в котором теперь К
(см. формулы (5.29)) имеет постоянное значение:
где R*=GM/Wo — гравитационный масштабный фактор.
Если для планеты неизвестно Wo — значение потенциала силы тяжести
на основной уровенной поверхности, то последнюю можно построить,
5*
131
потребовав, например, прохождения ее через заданную точку про¬
странства г<0), О , А, . Тогда в уравнении (5.30) постоянной К надо при¬
дать следующее значение:
* - 7«\' + 1г*•""> + тг(-тгУ(| - о™»}
(5.32)
Применим полученные результаты к нахождению основной уровенной
поверхности планеты, проходящей через точку экватора- (,0,(0) = л/2) под
такой долготой Х(0), при которой ее радиус-вектор г = гнаиб = ае. Пересчета
стоксовых постоянных при этом делать не будем. Тогда, ограничиваясь
N=2 и приняв х(0)=1, из первой же итерации по основному уравнению
(5.30) при /С, вычисляемом по формуле (5.32), получим известное
уравнение «сфероида» Клеро с долготным членом [83].
Описанный метод итераций широко используется при построении
геоида и при исследовании фигур Луны и планет.
§ 20. Обобщенная фигура Земли. Нормальная Земля
Как уже неоднократно подчеркивалось, потенциал притяжения Земли
определяется, с одной стороны, формой ее поверхности а, т. е. ее фигурой,
а с другой — распределением плотности ее недр б. Поэтому, обращая
формулировку задачи о представлении внешнего потенциала, приходим
к двум традиционным обратным задачам теории потенциала: геодези¬
ческой, в которой искомой по заданному V (или W) является форма
планеты а, и геофизической (гравиметрической), в которой — также
по К — ищется распределение ее недр — функция 6. В отличие от дру¬
гих исследований здесь конкретизирован способ задания потенциала,
именно считается, что он задан классическим рядом по шаровым функ¬
циям, т. е. известными считаются коэффициенты Спт и Snm этого разло¬
жения. Так как последних бесчисленное множество, то на практике,
естественно, используют некоторое конечное их число. Обычно ограни¬
чение как при создании моделей геопотенциала, так и при исполь¬
зовании коэффициентов ряда делают не по числу его членов, принимаемых
в расчет, а по наивысшей степени (иногда говорят — порядка) N удер¬
живаемых гармоник. В § 19 при определении обобщенной фигуры планеты
было подчеркнуто, что она находится по набору стоксовых постоянных
до принятой степени N. За счет ограничения N описанным методом
итераций находится один из действительных корней алгебраического
уравнения (УУ+3)-й степени. Вычисляемая так поверхность планеты
есть обобщенная поверхность (или фигура) N-го порядка. Поэтому
мы говорим о физической поверхности N-го порядка, о геоиде N-rо по¬
рядка, а в гл. 6 будем рассматривать и распределения плотности 6N (х, у, z)
также некоторого фиксированного N-го порядка.
В геодезии принято считать, что в разложениях элементов гравита¬
ционного поля по сферическим функциям имеет смысл при усреднении
гравиметрических данных по трапециям размера z X -г удерживать гармо¬
ники, степень которых не превосходит л/z, т. е. брать N, равное
132
n/z. Такое соответствие N и z переносится и на поверхность обоб¬
щенных фигур планет, т. е. поверхности планет сглажены «обоб¬
щением» до N-ro порядка за счет усреднения их рельефа по площад¬
кам z X z, причем z = n/N.
По алгоритму (5.12) можно вычислить радиусы-векторы любых
точек поверхности планеты. Однако за счет «обобщения» фигуры (за счет
усечения ряда потенциала) мы генерализируем ее в том смысле, что
находимый методом § 19 радиус-вектор r=f(#y X) при конкретных
значениях X относим не только к точке Ф, Ху но и ко всем точкам
ее круговой окрестности радиуса 1,77 Rnjl/N (радиус планеты — в кило¬
метрах). На таких участках фигуры jV-го порядка все неровности рельефа
сглажены и эти участки могут приниматься за площадки сферы
радиусом их средних точек.
Совместное изучение физической поверхности Земли и ее внешнего
гравитационного поля постулировано теорией Молоденского, возникшей
в то время (1945 г.), когда наука еще не располагала такими мощными
средствами исследований, как ИСЗ. Запуск искусственных спутников
Земли (1957 г.) открыл широкие возможности для изучения внешнего
гравитационного поля планеты, а теперь уже накоплена богатейшая
информация о нем: имеются в виду спутниковые модели геопотенциала.
Поэтому параллельно с традиционным подходом физической геодезии
исследования фигуры Земли может оказаться, очевидно, небесполезным и
метод § 19, в котором используется минимум известной информации,
обеспечивающей однозначность и устойчивость решения в произвольной
точке искомой поверхности. Результаты такого решения могут быть
детализированы за счет привлечения в исследуемом регионе данных
других видов измерений, например гравиметрических.
Под обобщенной фигурой Земли часто понимается геоид. И хотя
его построение по любым известным моделям геопотенциала любого
порядка сводится к использованию простой формулы, представляющей
разложение его высоты £ над обобщенным эллипсоидом в ряд сфери¬
ческих функций (см., например, [125]), оно независимо может быть
выполнено и по методике § 19: результаты при этом оказываются
идентичными.
Карты геоида (гл. 3) отражают его сложную форму, обусловленную
скрытым расположением масс. Именно по различиям карт геоида, по¬
строенным по разным моделям геопотенциала, можно наглядно сравни¬
вать свойства этих моделей. Основные качества геоида описываются гар¬
мониками самых низших порядков (рис. 10—12); повышение порядка
моделей, безусловно, детализирует карты геода, однако к полному согла¬
сию их не приводит.
Наиболее известной обобщенной формой Земли является общеземной
эллипсоид, точнее, так называемая нормальная Земля (НЗ) в виде уровен-
ного эллипсоида вращения. Учитывая важность нормальной Земли, под¬
черкнем, что под этим термином понимается обобщенная модель Земли
как планеты в целом, с одной стороны, отражающая ее основные
свойства в осредненном виде, а с другой — наиболее просто пред¬
ставляющая ее для математического описания. Другими словами, НЗ
должна содержать в себе главнейшие сведения о механических качествах
5а г. а. Мещеряков
133
планеты при несложной и удобной для приложений математической
аппроксимации последней.
НЗ при решении научных и практических задач выполняет двоякую
роль: она применяется либо как правдоподобная модель Земли с до¬
статочной точностью заменяющая реальную планету (в астрономии, гео¬
физике, картографии, навигации и т. д.), либо там, где требуется
более высокая точность, как очень хорошее ее первое приближение —
ее главная часть, используемая затем как удобная система отсчета
(в геодезии, гравиметрии, спутниковой геодезии, космической геодина¬
мике и т. д.).
Ввиду основополагающего значения НЗ для науки и техники с конца
прошлого века твердо укоренилась исключительная научная традиция
установления ее параметров как фундаментальных постоянных астро¬
номии и геодезии на крупнейших международных форумах — съездах
Международного Астрономического Союза (MAC) и Генеральных ас¬
самблеях Международного Геодезического и Геофизического Союза
(МГГС). Последние рекомендации современных значений фундаменталь¬
ных постоянных обсуждались в 1971 г. XV Генеральной ассамблеей
МГГС в Москве («Геодезическая референц-система 1967 г.» GRS-67)
и на XVIII Генеральной ассамблее МГГС в Гамбурге, 1983 г. («Геодези¬
ческая референцная система 1980 r.»-GRS-80; см. (3.7а) и (3.76)). Перио¬
дический пересмотр числовых величин основных параметров НЗ и харак¬
теристик нормального гравитационного поля вызван совершенствованием
и увеличением состава и видов наблюдений, по результатам которых
они выводятся, постоянным повышением их точности и увеличивающейся
необходимостью иметь такие значения этих параметров, которые аде¬
кватно отображали бы действительность. Последнее вынуждает об¬
ращаться также к теории НЗ и к ее предпосылкам, в которых, очевидно,
должны быть отображены запросы не только геодезии, но и геофизики,
в которой возникла необходимость создания референционной плотностной
модели планеты, долженствующей не только быть согласованной с гео¬
дезической НЗ, но и составлять с ней взаимосвязанный комплекс — еди¬
ную нормальную Землю. И хотя такой вопрос ставился даже в междуна¬
родном масштабе, ответа на него до сих пор еще нет.
В вычислительном плане эллипсоид НЗ находится просто как такой
эллипсоид вращения (вокруг малой оси), который осуществляет наилуч¬
шую квадратическую аппроксимацию поверхности геоида: для геоида
36-го порядка, построенного по модели GEM-10В, такое наилучшее при¬
ближение дает эллипсоид именно с параметрами GRS-80, причем он ре¬
ализует также наилучшее приближение геоидов моделей SAO-5 и
SAO-6 *).
Наибольшие отступления эллипсоида GRS-80 от геоида (Индийский
минимум минус Гвинейский максимум) составляют в относительной мере
около 1/40 000=0,0025 %.
*) Подтверждающие вычисления приведены в статье Г. А. Мещерякова и
С. Д. Волжанина «Использование метода Lp-оценок при определении параметров
общеземного эллипсоида» (Сб. «Геодезия, картография и аэрофотосъемка». —
Львов, 1983. — Вып. 38).
134
Нормальный эллипсоид принято считать уровенным. А раз он аппрок¬
симирует геоид, т. е. тоже уровенную поверхность, то в связи с тем,
что они необходимо пересекаются, возникает противоречие: нормальный
эллипсоид не может быть уровенным. Действительно, приведение g с гео¬
ида на эллипсоид в точках Индийского минимума и Гвинейского макси¬
мума дает в соответствующих точках эллипсоида 1^0+Ю8-Ю м2/с2 и
Wo—68*10 м2/с2, т. е. искажение реальности для эллипсоида составляет
AU7=176-10 м2/с2, что в относительной мере равно 1 /35 ООО ж 0,003 %.
Таким образом, с одной стороны, нормальный эллипсоид и нормальное
поле по своей точности сопоставимы, а с другой — в тех случаях,
когда нормальным полем хотят заменить реальное внешнее гравита¬
ционное поле Земли, будет ближе к истине установление неуровенного
нормального эллипсоида, что требует переноса на него значений потен¬
циала силы тяжести с геоида, вводя в них поправки на высоту геоида
над эллипсоидом. Поэтому имеет смысл обсудить нормальное поле Земли,
нормальный эллипсоид для которого является неуровенным, но отве¬
чающим всей совокупности имеющихся гравиметрических данных для
планеты.
Переходя к осуществлению этого, но при сохранении нормальной
Земли в форме эллипсоида вращения, например GRS-80, необходимо
решить для него внешнюю задачу Неймана; краевым условием при этом
охватим уже имеющуюся информацию о гравитационном поле Земли, к на¬
стоящему времени полученную по результатам измерений, выполненных
на суше и в акваториях и представленную известными картами ано¬
малий силы тяжести в пятиградусной или одноградусной разграфках.
Приведем решение этой задачи.
Пусть эллипсоид вращения Е (Oz — ось вращения) с полуосями
(а, а, Ь) задан параметрически (см. § 5, формулы (1.35))
х=а cos и sin к, у=а cos и cos к, z=b sin и
(—л/2^а^л/2, 0^к<С 2л), (5.33)
где и — приведенная широта, к — долгота, V а2—Ь2=с — линейный экс¬
центриситет.
И пусть на Е задана нормальная производная dW/dn потенциала
силы тяжести W=U-\-Q, где U — потенциал притяжения масс, располо¬
женных внутри £, a Q — известный потенциал центробежной силы,
действующей на произвольную точку (х, у, z) пространства за счет вра¬
щения Е вокруг оси z с угловой скоростью (О.
Пользуясь подстановкой (1.36)
a=cchr\, b=c sh г|,
отнесем пространство (1.37) к триортогональной системе вырожденных
эллипсоидальных координат (г), О, к): рожденных
х=с ch г] sin ft cos к, у = с ch iq sin *0* sin к, z=c sh iq cos О
(0 ^ г] <C со, О^Ф^л, 0 ^ ^ С 2л),
где «полярное расстояние» Ф=л/2—и.
135
Координатные поверхности r]=const и ,0,= const суть софокусные
соответственно эллипсоиды и гиперболоиды вращения вокруг оси Oz,
к= const — плоскости, проходящие через ось Oz. Эллипсоиду Е приписы¬
вается T|=const=r|o, причем shr\o=b/c\ для земного эллипсоида т]о~
«3,2205.
Вспомним, что (1.38)
sh т\ = -^-д/ г2 — с2 sin О, ch ц = -у д/ г2 + с2 cos2 О,
т. е. и sh г], и ch т] возрастают вместе с г — удалением точки (х, г/, z) от нача¬
ла координат.
Потенциал Q центробежной силы в этих координатах равен
Q = ch2 r\ sin2 Ф. (5.34)
Задача ставится так. Найти вне Е гармоническую функцию U,
регулярную на бесконечности (потенциал масс, находящихся внутри £),
если на Е известна ее нормальная производная
dU г/а лч dW
дп \ Е — f ^ — дп
ab co2sin2d
Г2 ^ ' (5-35)
Дjb с cos
Если решение задачи искать в виде классического ряда вырожденных
эллипсоидальных гармоник (1.51)
Dnm 1 Л#Я/. , ч лт/ ЛЧ f COS т>1,
£У(Л, о, Х) = X X ят )q*(i shti)P?(cosd)f
п = От = 0 ^
sin тк,
то, как показано в § 5 (см. (1.59)), для удовлетворения краево¬
му условию коэффициенты Dnm и Епт должны иметь следующие зна¬
чения:
°пт | = а |
Епт ) [aQ™ + 1 (i sh Т|0) + mbQ™(i sh r|0)] I
где Лпт и Впт— коэффициенты разложения по сферическим гармоникам
вспомогательной функции F (ft, к) =л] b2-\-c* cos^ft f (Ф, X);
при п четном коэффициенты Dnm и Епт чисто мнимые, но тогда и Qn(i sh т])
мнимы, т. е. Dnrm Епт действительны при любых пит.
Ряд (1.51), выполняющий вне эллипсоида Е роль «лапласова ряда»
§ 13 с увеличенной для него областью сходимости, является равно¬
мерно сходящимся всюду вне £, если аналогичными свойствами обладает
разложение Е(Ф, X) в ряд сферических функций; по крайней мере,
при непрерывной | ряд (1.51) вне эллипсоида Е сходится равно¬
мерно. дп
136
Нормальное ускорение силы тяжести в произвольной точке вне Е
дается выражением
преобразуемым на £ в функцию, описывающую краевое условие.
Решения (1.51), (5.36) задачи Неймана для эллипсоида вращения
дают теперь возможность получить нормальное гравитационное поле пла¬
неты, отнесенное к неуровенному эллипсоиду; при этом в предваритель¬
ном (промежуточном) варианте его построения достаточно, очевидно,
dW I
принять в краевом условии -— | Е = у (ft) == g, где осредненные по
широте значения ускорения силы тяжести g могут быть взяты с карты Ag
по пятиградусной разграфке, конечно, как уже говорилось, с пересчетом
в них g с геоида на эллипсоид нормальной Земли GRS-80. Если g брать
по карте Ag с одноградусной разграфкой и, естественно, сохранять
в (1.51) тессеральные эллипсоидальные гармоники, то формулы (1.51)
и (5.36) восстанавливают внешнее гравитационное поле Земли, соот¬
ветствующее всей использованной при его построении наземной и спут¬
никовой информации о нем. Погрешность такого восстановления поля
обусловлена лишь осреднением исходной информации: заменой непре¬
рывной функции (5.35) ее дискретными значениями в точках одногра¬
дусных или пятиградусных трапеций.
Такое нормальное поле Земли может быть использовано вместо
реального, в частности при вычислении правых частей уравнений движе¬
ния ИСЗ при прогнозировании их орбит.
Отметим в заключение следующее. В ряде недавних публикаций *)
была введена и описана сфероидальная нормальная Земля (СНЗ),
отождествленная в них с гидростатически равновесной планетой. Однако
общепринятому определению гидростатически равновесных фигур пла¬
нет она не удовлетворяет. Опуская здесь обсуждение СНЗ, автор остав¬
ляет пока за этой «сфероидальной» Землей роль только такой нормальной
фигуры Земли, которая задается и описывается набором четных зональ¬
ных гармоник геопотенциала.
*) Мещеряков Г. А. О нормальной Земле // Геодезия, картография и аэрофото¬
съемка. — Львов, 1986. — В. 43; Мещеряков Г. А., Агеев Н. Ф. Предварительный
вариант нетрадиционной нормальной Земли. — Там же, 1986. — В. 44; Мещеря¬
ков Г. А., Агеев Н. Ф. Предварительный вариант нетрадиционного нормального
поля Земли. — Там же, 1987. — В. 45; Meshcheryakov G. A., Ageev N. F., Fys М. М.
On the Spheroidal Normal Earth // Proc. Int. Symp. Part I. — Prague, 1987.
W / c[aQ™ + 1 (i sh t|0) + m&Q™(i sh r|0)]
глГП / n\
ГЛАВА 6
ГЕОФИЗИЧЕСКАЯ ОБРАТНАЯ ЗАДАЧА
ТЕОРИИ ПОТЕНЦИАЛА И РАСПРЕДЕЛЕНИЕ
ПЛОТНОСТИ ЗЕМНЫХ НЕДР
§ 21. Единственность, устойчивость
и численный метод решения
В геофизической (гравиметрической) обратной задаче теории ньюто¬
новского потенциала по заданному внешнему потенциалу
V{P) = \~^T' Q{x' у' 2)ет> Р{1, л’ (6Л)
тела т известной формы ищется плотность б слагающего его вещества.
Эта задача уже подробно исследовалась рядом авторов [137, 138, 35,
36], для нее, в частности, доказан ряд теорем единственности с до¬
вольно общими предположениями о заданной поверхности тела и его
искомой плотности. Ниже приведены теоремы, в которых, как и в случае
задачи гл. 5, используется задание внешнего потенциала рядом шаровых
функций.
Учитывая некорректный характер задачи, сузим класс возможных
решений, именно будем искать б в некотором подклассе Ст класса непре¬
рывных функций Ст и для этого случая найдем условия, при которых дан¬
ная задача корректна по Тихонову [154—156]. За Ст принимается
здесь класс непрерывных в замкнутой области т + а функций б, удовле¬
творяющих следующим двум условиям:
1. I б (Q) I < Af, где М — одна и та же постоянная для всех функ¬
ций б (Q) 6 Ст.
2. |б (Qi) — б (Q2) I <LrQiQ2 при любых Qb Q2 6 т 4- а (условие Лип¬
шица с одной и той же константой L для всех функций из Ст).
Соотношение (6.1) относительно искомой плотности является неодно¬
родным интегральным уравнением I рода. Из общей теории интегральных
уравнений известно, что неоднородное уравнение I рода имеет единствен¬
ное решение в некотором классе функций лишь тогда, когда соответст¬
вующее ему однородное уравнение в этом классе функций имеет только
одно тождественно равное нулю решение.
Однородное уравнение, соответствующее уравнению (6.1),
\ dxQ = О, (6.2)
J ‘PQ
*) Здесь (ср. с гл. 1) взаимно изменены обозначения координат
точек Р и Q.
138
имеет простой физический смысл [143]: оно представляет при некоторых
особых распределениях масс р (Q) в теле т такой потенциал этого
тела, который всюду вне т тождественно равен нулю.
При таких распределениях масс тело т называют телом нулевого внеш¬
него потенциала (ТНВП); плотность его
n(Q)=MQ)-MQ) (6.3)
есть разность двух возможных распределений масс внутри т, приво¬
дящих к одному и тому же внешнему потенциалу. Плотность ТНВП
дается [143] формулой
^(Q)== (64)
где W — любая функция из класса С2 дважды непрерывно дифференци¬
руемых функций в замкнутой области т + а, удовлетворяющая условиям
dW I
г|° = 0’ 4!И° = 0-
где п — внешняя нормаль к поверхности а.
Из принадлежности W к классу С2 следует, что функция р (Q)
является равномерно-непрерывной в области т, а значит, она удовлетво¬
ряет условию 1) при постоянной 2М. Кроме того, на основании формулы
(6.3), в которой 6t(Q)£CT (/=1,2), ясна выполнимость для функций
р (Q) условия Липшица с константой 2L. Поэтому можно считать, что
плотность р (Q) ТНВП также принадлежит классу Ст, в котором ниже
ищется решение уравнения (6.1).
В добавление заметим, что если р (Q) ортогональна внутри т ко всем
функциям класса Ст, то тогда W == 0, а значит, p(Q) = 0.
циям; тогда W — любая функция класса С2 при условиях (6.5), а р (Q)
дается формулой (6.4).
В добавление заметим, что если p(Q) ортогональна внутри т ко всем
функциям класса Ст, то тогда W = 0y а значит, p(Q)==0.
Предполагая априори существование решения уравнения (6.1)
в классе Ст, заключаем, что единственное решение этого уравнения воз¬
можно лишь при условии
]<b(Q)»(Q)dTQ = 0, (6.6)
т
где Ф (Q) означает любую функцию класса Ст.
В класс Ст входит непустой подкласс функций Ф*, аналитических
в т (например, Ф*=е*+1/+2). Последние при центральной точке разло¬
жения x=y=z=0, совпадающей с серединой диаметра т, представля¬
ются равномерно сходящимся рядом вида
ф = £ А„№.
Р, <7, Г = 0
Для функций Ф* из формулы (6.6) имеем
\( Ё = f А „Л \х,хр yqzrdt.
т \p>q,r = o J q r = о т
(6.7)
139
Интегралы
Jpqr ~ Jpqrifl) ~ ^ d-TQ (6.8)
т
суть степенные моменты функции p(Q), т. е. моменты плотности ТНВП.
Условие (6.6) теперь принимает вид
оо
Z AMrIMr(v) = о, (6.9)
р, Я, Г = О
и оно наверняка выполняется при равенстве нулю всех моментов / (р).
Таким образом, условие (6.6) распадается на бесконечное множество
условий
$ \i(Q)xpyqzr dxQ = 0 (р, q, г = 0, 1, 2, ...), (6.10)
Т
которые, очевидно, дают возможность охватить условием (6.6) и неана¬
литические функции Ф класса Ст, ибо таковые по теореме Вейерштрасса
можно сколь угодно точно приблизить полиномами
т
X
Р + Я + Г = 0
Теперь ясно, что для построения в области т ТНВП с плотностью р (Q) =
= 0 надо знать все моменты тела искомой плотности 6. Действительно,
если для тела т даны все Jpqn то при этом имеем для двух возможных
в т распределений масс 6i и 62: Jpqr(S\) —Jpqr(&2)=0. Значит, с учетом
определения моментов
^ bxxpyqzrd,T — ^ 62xpyqzr dx = ^ (6j — b2)xpyqzr dx = 0. (6.11)
T T T
Отсюда в силу формулы (6.3), добавления к лемме Пицетти—
Новикова и условий (6.10) следует, что разность р = 6i — 62 =0, а значит,
она выражает плотность ТНВГ1 p(Q) =0.
Всего степенных моментов п-го порядка, как уже отмечалось в § 12,
/п=1/2 (я+1) (л+2), причем sn—2ri-\-\ линейных комбинаций их (по чи¬
слу независимых однородных гармонических многочленов) представляют
стоксовы постоянные тела т, т. е. коэффициенты при шаровых функциях
в разложении внешнего потенциала. Они в данной задаче могут считаться
известными. Значит, располагая еще дополнительно заданными ln—sn=
= 1/2n(n — l) остальными моментами, можно считать, что имеется вся
необходимая информация, обеспечивающая единственность решения
уравнения (6.1). Таким образом, имеет место следующая теорема единст¬
венности.
Первая теорема единственности [74, 75]. Уравнение (6.1) при задан¬
ной поверхности о тела т имеет относительно плотности 6 единственное
решение в классе функций Ст при условии дополнительного задания при
любых п^2 (п=р + ^ + 0
1) либо таких 1 /2ai {п—1) степенных моментов тела искомой плотности,
в которых одночлены xpyqzr негармонические,
140
2) либо таких {/2п(п — 1) линейных зависимостей между моментами
п-го порядка, при которых соответствующие соотношения между одно¬
членами хpyqzr представляют негармонические полиномы,
3) либо (при п>2) а первых и (5 вторых, причем a + p=l/2 п (п— 1).
Эта дополнительная информация должна быть таковой, чтобы, во-первых,
получаемые при любом п системы линейных уравнений относительно мо¬
ментов Jpqr имели отличные от нуля определители, и, во-вторых, находимые
из этих систем величины Jpqr удовлетворяли условиям разрешимости
возникающей при этом проблемы моментов.
Указанные теоремой условия имеют простейший вид; они могут
быть более сложными, например с нелинейными связями между момен¬
тами. Пример такого условия (при п=2) был приведен в § 12.
Данная теорема единственности в работе [14] была распространена
на случай потенциалов в /г-мерных пространствах. Заметим, что, как разъ¬
яснилось обзорными статьями [206, 118], затронутый здесь круг вопросов
был предметом исследований итальянских ученых еще в конце прош¬
лого—начале этого века, когда и было введено понятие о теле нулевого
внешнего потенциала. Использованная здесь лемма о нем и единствен¬
ность определения плотности по степенным моментам обсуждались Пи-
цетти, Боджиа, Лауричелла еще в начале века.
Приведенная теорема сводит геофизическую обратную задачу теории
потенциала к классической проблеме моментов [15]. Использование ее
требует знания бесчисленного множества степенных моментов искомой
плотности. Поэтому важно дать ответ на вопрос: нельзя ли в принципе
вместо задания всех моментов иметь только одну такую (истоко¬
представимую через 6) функцию U (P)=U (£, т], £), которая, будучи
разложенной по некоторым функциям координат точки Р (£, ц> С)*
имела бы в качестве коэффициентов разложения необходимые моменты,
подобно тому, как разложение внешнего потенциала (6.1) в ряд по шаро¬
вым функциям точки Р имеет своими коэффициентами стоксовы постоян¬
ные тела т. Полагая возможным существование множества таких функ¬
ций U (Р), рассмотрим одну из них, свойства которой позволяют
сформулировать еще один вариант теоремы единственности решения
уравнения (6.1) и обрисовать характер возможной необходимой добавоч¬
ной информации, представимой в сжатом виде.
Вторая теорема единственности. В классе функций Ст уравнение (6.1)
имеет единственное решение при условии того, что во внешнем относи¬
тельно а пространстве, точнее, вне описанного вокруг тела параллеле¬
пипеда с гранями, параллельными координатным плоскостям, дополни¬
тельно задана непрерывная функция U (£, г], £), истокообразно предста¬
вимая через 6:
U(l, л. £) = ^ 6Z2 ехр (у + ip + dx. (6.12)
т
При доказательстве теоремы, не умаляя общности, будем считать, что
начало системы координат совмещено с серединой диаметра области т,
а длина полудиаметра этой области принята за единицу; тогда
М<1, M<i>
141
и в силу условий теоремы
|6|>1, Ы>и
Разложим экспоненту, входящую в (6.12), в ряд Маклорена
“Чт+i+iH+x I
N ' п = \р + q + г = п
Умножим обе части этого равенства на bz2d% и затем проинтегрируем их
по объему т. Получаемый ряд справа допустимо интегрировать почленно,
так как ряд
X х ^(fmmy=x,^(t+f+fy
n=\p-\-q + r = n п = I
равномерно сходится в т, ибо имеет мажорантный ряд
К ^ где к = supT |б| < М.
п = 1
В результате имеем
и(1, Л. 0 = $ 6z2 exp (j + + -0 dx =
т
оо
= W«)+£ Yj J7Jp’q'r + 2^'
П = 1 р + q + Г = п
По конструкции этого ряда видно, что в нем нет подобных членов; таким
образом, заданная функция (6.12) дает возможность получить все
моменты вида
Jp,q,r+2(6) (P,q,r=0,1,2,...),
которых при фиксированном п имеется, как легко подсчитать, 1 /2П (п— 1) и
которые вместе с 2/г + 1 линейными соотношениями между моментами
п-го порядка, следуемыми из заданного внешнего потенциала V (Я) после
разложения его в ряд по шаровым функциям, образуют полный комплект
всех 1/2(^+1) (п+2) степенных моментов искомой функции б.
Различный характер разложения функций V (Я) и U (Я), именно
V (Я) — по шаровым функциям, вычисляемым в точке Я, а (У (Я) — по отри¬
цательным степеням ее координат, гарантирует при выбранном виде
(6.12) функции U (Я) получение всех недостающих в разложении V (Я) мо¬
ментов, необходимых для единственности решения задачи в Ст.
Теорема доказана. Она, кстати, выражает совместность системы из двух
интегральных уравнений I-го рода, (6.1) и (6.12).
Эта теорема дает пример необходимой дополнительной информации
в сжатом виде, однако геофизический смысл ее неясен. Поэтому жела¬
тельны поиски других функций, обладающих аналогичными аналитиче¬
скими свойствами, отражающих физические свойства планеты и имеющих
параметры, допустимые для измерений на поверхности Земли или в около¬
земном пространстве.
Установим теперь корректность по Тихонову постановки рассматривае¬
мой геофизической задачи [74].
Во-первых, существование решения уравнения (6.1) относительно
плотности 6 в классе Ст предположено априорно и может описывать
лишь некоторую более или менее правдоподобную модель изучаемого
тела т в смысле его внутреннего строения (расположения масс внутри
него). Было бы лучше искать решение (6.1) в классе кусочно-непрерывных
функций, что полнее отвечало бы истине, однако даже принятое здесь
сужение класса решений позволяет найти первое приближение, которое
аппроксимирует возможное кусочно-непрерывное распределение масс
в теле непрерывным распределением.
Во-вторых, единственность решения данной задачи в классе Ст
обеспечена дополнительными условиями, следуемыми из теоремы.
В-третьих, устойчивость решения является, как это вытекает из тео¬
ремы Тихонова [154], прямым следствием выполнения предыдущих двух
условий (существования и единственности), ибо множество функций
6 (Q) класса Ст образует компакт. Действительно, условие 1) выражает
равномерную ограниченность семейства функций: |6(Q)|^M, кстати,
можно взять М=/ооо; условие 2) приводит к равностепенной непрерыв¬
ности множества этих функций, а замкнутость его также следует из этих
условий.
Как следствие изложенного теперь можно констатировать коррект¬
ность задачи (6.1) при нахождении ее решения 6 в классе С\. с=СТ,
каждая функция которого удовлетворяет условиям
где М, L — некоторые постоянные.
Перейдем теперь к решению задачи, которое в принципе может быть
выполнено разнообразными методами, например, как это сделано в [230],
методом регуляризации. Но поскольку теоремой единственности задача
сведена к степенной проблеме моментов, естественнее получить ее
приближенное решение именно как решение усеченной проблемы момен¬
тов (возможно, высокой степени). В § 12 уже показано, правда на при¬
мере планетарного тела (Земли), как на основании внешнего потенциала
тела, заданного стандартным рядом по шаровым функциям (т. е. коэф¬
фициенты этого ряда — стоксовы постоянные тела Спт и Snm — считаются
известными), можно найти приближенные значения степенных моментов
Jpqr(6) плотности этого тела.
Напомним, что квадратические приближения всех 1п степенных
моментов порядка п находятся при этом на основании известных sn<.ln
стоксовых постоянных этого порядка при условии (3.35)
а — некоторые начальные приближенные значения моментов, под¬
бираемые на основании максимума имеющейся информации о функции 6.
16(Q)|< М, |grad 6(Q)|< L,
П
где
W/=»Wr=/Wr--C (/=>’ 2- • • - *»)•
143
Определение искомых моментов Jpqr выполняется по известной вычисли¬
тельной схеме метода наименьших квадратов, который, как было отмечено
в § 12, не дает решения в случае, когда все стоксовы постоянные тела г,
кроме Соо, равны нулю. А это исключительный случай материальной
точки или шара со сферически-симметричным распределением плотности.
Значит, рассматриваемый способ решения геофизической задачи сведе¬
нием ее к проблеме моментов применим только к таким телам, внешние
потенциалы которых имеют не менее двух ненулевых стоксовых постоян¬
ных. Находимая при этом плотность может быть выражена многочленом
(от х, у, z) N-й степени, где N — наивысший порядок ненулевых стоксовых
постоянных.
Выгода привлечения дополнительного условия (3.35) общеизвестна,
на нем основана теория обработки результатов измерений, квадратиче¬
ская аппроксимация функций, оно используется и при решении некор¬
ректных задач, например в двойственном методе регуляризации Иванова
(при решении операторных уравнений I рода [39]) и т. д. Действенность
этого условия увеличивается при малых Vj и при наличии у них разных
знаков; далее будет показано, как при этом организовать процесс
вычислений.
Физический смысл условия (3.35) заключается в том, что в классе
непрерывных функций ищется такое решение для плотности, степенные
моменты которого в квадратической метрике наименее уклоняются от ее
степенных моментов, соответствующих максимуму уже известной инфор¬
мации о ней (скачки плотности доставляет сейсмология).
Приближенное решение проблемы моментов может быть выполнено
любым из устойчивых, разработанных в последнее время методов
(см., например, [156, 145, 146]). Остановимся на методе ее решения [76],
основанном на теории квадратических приближений. Сначала исследуем
случай сферической планеты радиуса R.
Пусть плотность 6=6 (х, у, z) ^ L2. Такое предположение включает
и соответствующую первой теореме единственности, ситуацию, в которой
принято 6 ^ Ст, а, как известно, CxaL2. Функцию 6, заданную внутри
шара, будем аппроксимировать обобщенным полиномом 6N(x, у, г)
степени N по такой полной системе ортонормированных в т многочленов,
скалярные произведения которых на искомую плотность известны. Поли¬
ном буу найдем в соответствии с принципом теории квадратических
приближений, т. е. при условии
Zn = \ (б — 6N)2dT = min. (6.13)
т
Примем за основную систему функций систему одночленов
\у?УяА (Р, <7, r=0, 1, 2, ...); (6.14)
тогда указанные скалярные произведения обратятся в линейные комбина¬
ции степенных моментов плотности и в соответствии с известным алго¬
ритмом построения наилучших квадратических приближений получим
после преобразований и в записи по исходной системе одночленов
N
6„{х, у, z)= I X (6.15)
m = 0p-\-q-\-f — т
144
где коэффициенты Apqr — функции области и степенных моментов плот¬
ности.
В соответствии с известными свойствами рядов Фурье по полным
ортонормированным системам функций найденный полином 6^ единствен¬
ный; квадратическая погрешность приближения eN не возрастает при уве¬
личении N\ в среднем при N-* оо значение полинома bN сходится к искомой
плотности б.
Представление плотности б конечной суммой ее ряда Фурье (6.15)
может трактоваться как решение рассматриваемой усеченной проблемы
моментов, а если условия разрешимости проблемы моментов выполнены,
то оно единственно.
В качестве примера приведем непрерывное одномерное распределение
плотности недр планеты сферической формы радиуса R, которое дается
простой формулой [80]
б2 (р)=5/Ар [ (5/ооо—7S)+7/Зр2 (5S—ЗУ ооо), (6.16)
где бср — средняя плотность планеты и
S==J200 I $020 I-$002= 1 /2 (A -T2J-]-C), J000= 1 •
Последняя формула (в ней все моменты безразмерные) — результат
осреднения трехмерного распределения бг(х, у, z), полученного в виде ряда
Фурье, усеченного до N= 2; она выражает наилучшее квадратическое
приближение плотности в классе полиномов второй степени.
§ 22. Биортогональная система многочленов в эллипсоиде
При фактическом решении геофизической обратной задачи теории по¬
тенциала применительно к Земле используются, как только что было
обсуждено, ортогональные многочлены трех переменных.
Однако теория ортогональных многочленов многих переменных, в от¬
личие от таковой в случае одной переменной, в научной литературе
освещена недостаточно. И хотя построение указанных многочленов с
помощью процесса Грамма—Шмидта принципиально возможно, однако
оно трудоемко, и позволяет определить лишь первые члены последова¬
тельности. Полученные при этом ортогональные системы, как следует из
опыта их построения для шара и эллипсоида, не обладают свойством
симметрии относительно переменных и для них неизвестны рекуррентные
соотношения, что определенно затрудняет их использование.
Вместе с тем существует ряд систем многочленов многих переменных,
обобщающих некоторые из ортогональных рядов одной переменной. Так,
в [20] рассмотрены две биортогональные системы многочленов в шаре,
каждая из которых «квазиортогональна» (т. е. многочлены общей сте¬
пени N=m-\-n-\-k не ортогональны друг другу, хотя каждый из них
ортогонален всем многочленам иных степеней, отличных от N); при этом
одна из этих двух систем является обобщением многочленов Лежандра
(одной переменной).
Обобщение только что указанных биортогональных систем многочле¬
нов в шаре на случай внутренней области трехосного эллипсоида
т{х2/а2-\-у2/b2-\~z2/c2^\} разработано Фысом [166, 107].
145
В качестве производящих функций вводимых систем многочленов
{№„,„*(*, у, г)} и {(отп*(х, у, г)} приняты функции следующего вида:
ф(х, у, z, а, р, Y) = |^-^г +-р-+-р-- +
+ (7 + $ + Я(‘-7-£-?)]4
(6.17)
(6.18)
ф(х, у, г, а, р, у) =
( I _ 2ах — 2^у _ I а2 _|_ Р2 I V2 \ ~ Т
“V а2 й2 с2 + а2 + Ь2 + с2 )
которые определены и аналитичны по тройкам соответствующих пере¬
менных внутри эллипсоида. Следовательно, внутри т они представимы
соответственно рядами
сю
ф(х, у, 2, а, р, V) = £ Wmnk(x, У. z)ampY. (6.19)
N = m-\-n-\-k = О
оо
ф(х, у, z, а, р, v) = X °w(*> У' z)ampV (6.20)
ЛГ = т + п + /г = 0
по переменным а, р, у, а коэффициентами в них являются многочлены
систем \Wmnk} и {comnfe}, обладающие свойством биортогональности в т:
J У> *)Штпк{х, У, 2)rfT =
Т
'о, если т Ф тх, или п ф пх, или k Ф kx,
lmnky если m = mlt п = п{, k = k{\ \ )
l „ = — sr (V — Объем т).
Lmnk . - 9m. 9/7 9£> ' '
3 VN\
(2N + 3 )m\n\k\a2fnb2nc2k
Перечислим основные свойства многочленов Wmnk (х, у, г). Для них
имеет место формула типа формулы Родрига
( X2 -L у2 4- 22 1 V
<>■z) - i -++v ■-' ) *• M
из которой следует, в частности, что Wmnk(xy у, г) —многочлены
от х, I/, z степени не выше N = т + п + к.
Эта система многочленов обладает также свойством квазиортогональ¬
ности
^ Утпк(х, у, z)Wm^k{{x, у, 2)
т
{
dx =
[о, при т + п + к ф тх + п{ + k{, т — tnx, п — пх
= ^ mjn,*,, или k — kx нечетных;
при m + л + & = + «1 + £, * ' '■
и т — т]у п — пл, к — кх четных;
m,лг,/г, см в [166] .
146
Многочлены Wmnk могут быть представлены в виде линейных комби¬
наций степеней х, у, z
У, z) =
т у (2<, - 1)Н(2/2 - 1)!1(2<3- 1)!!(-1)4 ^
~ 2Nm\n\k\ambnck , , , ,2^, . „ (2'i “ m)\{2t2 - n)!(2<3— ft)! X
*1 + l2 + *3 + *4 = ^
, 2/, - m / fJ \ 2t0 - n t
x(t
где
х(тГ"аг'-(тг ■ (6-24>
2ti—m>0, 2/2—n>0, 2/3—ft>0, /4=W—(/, + /2 + /3). (6.25)
Выпишем легко получаемые выражения многочленов низших степеней:
^000 = 1. (6.26)
Wm = x/a2, Wmo = y/b2, W00i = z/c2,
w - _l2з*2 , / , *2 Л.
Г200 “ 2а2 W "б7 + ^ ’
+ ^ + (627)
'«»-^(т-+ т-+ ■?-')■ г"
ш ^XZ W/ ^У2
w\o\ — 2 2 » ^011 — ~TY-
2дн/
be
Для многочленов Wmnk, степени которых выше второй, имеют место
рекуррентные соотношения вида
(1 + *1)
+ R\) ( 0чЛ z2 y2\
(I + «!> ,
—p—«(»
^>(M
U7
^ m
— 2, n, k
2 \
Z >
\ w
1 my n
\ w
^2>
I m, n,
-(2 + Л, + R3)t(m — l)e(ft — l)-g- Гт, -
-(2 +/?, + /?2)e(m_ i)e(„_ i)_^_H7m_|
— (2 + #2 + Rs)-^yWmn_lk_[s(k — l)e(rt — 1) —
— (2 + 7?,)e(m — l) — Wm_ 1>п>* +(2 + R2)s{n — n- 1,* +
CL b
+ (2 + R3)e(k — ,, (6 28)
где
e(/)={?- если {<0> m Ф 0
w \1, если / > 0,
147
(_L т Ф О Г0- т Ф О
*.(«, п, k) = |« ’ m = о ; Ri{m, п, k) = ji_ т = Q> „ = 0;
{О, т Ф 0 или я ^ О, (6.29")
■1, m = О, я = 0, 6=^0.
Рекуррентные соотношения для многочленов ч>тпк таковы:
®mnk = (2 + /? i)e(m — 1 )-4f 0>m_ ,, n, * + (2 + #2)«(rt — 1) “m, n - 1. * +
+ (2 + /?з)е(/5 — l)-ycom „ , — (1 + R\)s(m — 2)<nm_2 n k —
— (1 "h — 2)(om>n-2,k 0 ~t~ W* 2)com(k — 2> (6.30)
причем многочлены низших степеней суть
о)ооо=1> (Oioo=3x/a2, (i)oio=3y/b , coooi = 3z/c , (6.31)
и
200
a2 ( a2 ')• “020 - ^ ^ l). *002 _ ± - l),
15xy 15xz 15yz
0)110 — 2 l2 ’ 0)101 — 9 2 ’ 0)011 — ,2 2 • (6.32)
Рассмотренные биортогональные системы функций внутри эллипсоида
позволяют строить обобщенный ряд Фурье, представляющий в т произ¬
вольную функцию f^L\\
f~ X (6-331
m + п + k = 0
ИЛИ
/ ~ ^ Cmnk^mnk'
rn п It ^ 0
где
bmnk = ^ Сmnk \ f^mnk dx /lmnk' (6.34)
т ) т
Частичные суммы этих рядов выражают среди многочленов N-n сте¬
пени наилучшее приближение к функции f в среднеквадратическом
смысле. Более того, для разложения (6.33) имеет место обобщенное
148
неравенство Бесселя и равенство Парсеваля
ОО
X bmnkCmnk 5 UmnkWmnk dl < J f rfx, (6.35)
tn + n + k = 0 t T
а значит, и сходимость в среднем [165].
§ 23. Методика построения плотностной модели Земли
Описанные в §21 исследования геофизической обратной задачи
теории потенциала, сведение ее к проблеме моментов и представление
решения последней обобщенным рядом Фурье по некоторой известной
ортогональной или биортогональной системе многочленов (внутри сферы
или эллипсоида) составляют, в своей совокупности, основы общей мето¬
дики построения приближенного распределения плотности 6 внутри
Земли.
Ввиду некорректности задачи такая методика потребует использова¬
ния частичных сумм указанных рядов Фурье очень высоких порядков.
Чтобы уменьшить последние, надо к решению привлечь максимум уже
имеющейся геофизической информации о планете, заключенной, на¬
пример, в репрезентативной стандартной модели ее. Будем таковую
принимать в полном объеме; конкретно, возьмем из нее функцию скачков
и непосредственно совокупность многочленов, параметрически описываю¬
щих распределение плотности между смежными поверхностями ее раз¬
рывов. В связи со сказанным будем считать
б(х, у, z) = 6°(р) + Щх, у, г), (6.36)
где 6и(р) — распределение плотности в эллипсоидально-слоистой модели,
полученной модифицированием исходной стандартной сферически-сим-
метричной модели; ре [0, 1] —безразмерный радиус под широтой ср0~
^35,3°; Д6 (х, у, г) — искомая часть плотности, которая представляет
ее малые отклонения от 6° (р), обусловленные трехмерностью, и описыва¬
ется рядом типа (6.33). При этом малость Д6 (ху уу г) с большим основа¬
нием позволяет использовать при уравнивании степенных моментов
плотности в случае N^>2 принцип наименьших квадратов (3.35), а не¬
прерывность Д6 (ху у, z) обеспечивает более быструю сходимость ее ряда
Фурье (6.33), нежели аналогичного ряда, представляющего саму функ¬
цию 6 (ху уу z)y ибо коэффициенты bmnk для функции Д6 во много раз
меньше таковых для самой плотности 6.
Построение модельного распределения с учетом стоксовых постоянных
до ЛУ-го порядка (N=m-\-n-\-k) будем осуществлять по следующей схеме.
Сначала выполняется преобразование исходной стандартной сфериче¬
ской модели Земли в эллипсоидальную. Для этого в каждом полиноме,
выражающем закон изменения плотности между двумя смежными по¬
верхностями ее разрыва в сферически-симметрической модели в зависи¬
мости от удаления от центра планеты г, последнее заменяется на без¬
размерную величину р, геометрически представляющую безразмерный
радиус-вектор эллипсоида под той широтой сро, которая обеспечивает
равенство объемов и как следствие масс сферического и соответствую¬
щего ему эллипсоидального слоев. Такое простое преобразование позво-
149
ляет считать известной основную часть 6°.(р) плотности земных недр,
описываемую используемой стандартной моделью Земли.
Затем отыскивается поправочная часть плотности Д6 (ху у, z).
При ее определении будем считать, что планета отнесена к вращающейся
вместе с Землей системе координат Oxyz, начало которой совмещено с
центром масс, а оси координат — с главными осями инерции Земли.
Функцию Д6 (х, уу z) будем представлять рядом (6.33). В принятой
системе координат коэффициенты bmnk разложения этой функции при
2 элементарно выражаются через стоксовы постоянные пла¬
неты (при N=2 должно быть использовано еще динамическое сжатие Н,
см. § 12) и установленную основную часть 6° (р) распределения плотности.
Именно
&ооо = 6срЛ -^-$8°(р)р2ф\
\ ср о /
Ь юо= bo\o= booi = b\ io=froi i = bЮ1=0,
^200 = "2^сР Г 2Н~ — ^ + ^ "а—5
|_ \ / ср о ср о
^020 = (6.37)
=Т6CP[5(--|f “ 2С^) - 3 + eW<*P + ^| 6°(p)p2dpj,
^002 = Y«cp^(i 20 - 3 + ^ j 6V p4 dp + -A-j 6°(p)p2 dpj
Здесь 6cp=M/V средняя плотность; M — масса планеты, V — объем зем¬
ного эллипсоида. Значит, по формуле (6.36) с учетом первых членов ряда
(6.33) для /=Д6 имеем
62 {ху у, z)=6° (р)+Д62 (ху у, г). (6.38)
Для уточнения искомого распределения плотности 6 (х, уу z) за счет
стоксовых постоянных 3-го порядка вычисляем приближенные значения
степенных моментов 3-го порядка по определяющим их формулам, при¬
нимая в них 6 (ху уу z)= 62 (х, уу z). Используя их, получаем по методике
§ 12 поправки к этим моментам, а затем и уравненные степенные
моменты 3-го порядка, линейные комбинации которых известного вида
выражают все bmnk при т+«+/г^З. Значит, находим и 6з (х, уУ z).
Описанным образом осуществляется учет всех стоксовых постоянных
до установленного априори порядка Nycjy в результате чего получается
трехмерное модельное распределение 6N (х, у, z), согласованное с пара¬
метрами внешнего гравитационного поля планеты до /VyCT-ro порядка.
Перейдем теперь к расчету главной части распределения плотности
недр в виде указанной модели 62 (х, уу z), в которой будут учтены пара¬
метры внешнего гравитационного поля только до 2-го порядка включи-
150
тельно. Соответствующее распределение выражается приведенными ранее
формулами (6.38), (6.37), (6.33) и исходной стандартной моделью Земли.
За исходную модель примем глобальную механическую модель пла¬
неты PREM — предварительную референцную земную модель [189]. Она
построена на основании современных значений главных астрономо¬
геодезических параметров (масса М, средний радиус R и момент инер¬
ции / планеты) и обширной новейшей сейсмической информации о
планете (данные наблюдений за ее свободными колебаниями, длинно¬
периодными поверхностными, поперечными и продольными объемными
волнами). Эта модель есть «некоторая абстракция» (см. [189]), она
параметрически проста, но благодаря ее геофизическим свойствам, обу¬
словленным использованием при ее построении большого объема резуль¬
татов добротных наблюдений она хорошо представляет Землю в среднем
и даже предназначается на роль референцной модели планеты. Однако
она является сферически-симметричной, т. е. описывает шарообразную
Землю с одномерным (зависящим лишь от одной координаты — удаления
от центра) изменением ее свойств, вследствие чего ею не отражается
хотя бы в общих чертах развиваемое Землею внешнее гравитационное
поле, необходимость согласования стандартных моделей Земли с которым
была подчеркнута еще в 1977 г. [208]. Чтобы добиться этого, имеет смысл
сначала создать на основе PREM модельное эллипсоидальное трех¬
мерное распределение плотности земных недр, согласованное с пара¬
метрами внешнего гравитационного поля до некоторого порядка, а затем
осреднением его получить искомую модификацию модели PREM, уже
отвечающую этому полю.
Для реализации сказанного заменим Землю эллипсоидом вращения
с параметрами ае=6 378 137 м, а= 1/298,257, который равновелик
по объему шару радиуса #=6371 км с массой Л4=5,974 • 1027 г, и возьмем
динамическое сжатие //=0,0032727 (этому значению И соответствует
полярный момент инерции 1С= С=0,3308045). Используем также значе¬
ния стоксовых постоянных Земли до 2-го порядка модели GEM-10В,
отнесенные к главным осям инерции планеты.
На основании этих данных, принимая модель PREM (она дана в при¬
ложении, табл. II) в качестве исходной, по предлагаемой методике
рассчитано модельное эллипсоидальное трехмерное распределение плот¬
ности земных недр 62 (х, у, г). Оно незначительно отличается от исходной
модели: максимальные широтно-долготные вариации плотности относятся
к поверхности и не превосходят 0,001 г/см3 по долготе и 0,0025 г/см3 по
широте. Осредняя 62 (х, у, г) по единичной сфере, получаем искомую
модификацию — модель 62 (р), которая также приведена в табл. II.
Данные таблицы показывают, что эта модификация модели PREM
несет в себе незначительную корректировку в распределении плотности
исходной модели. Однако пересчитанное распределение уже может счи¬
таться отвечающим осредненной структуре внешнего гравитационного
поля (до 2-го порядка включительно). А выполненный при этом «возврат»
к исходной модели является, кроме того, хорошей апробацией обсуждае¬
мой методики. Распределение плотности §2 (х, у, z) не приведено здесь
в связи с тем, что выбор исходных данных о массе и моменте инерции
Земли требует дополнительного обсуждения.
151
Массу Земли М определяют косвенным образом на основании получае¬
мой по результатам наблюдений геоцентрической гравитационной по¬
стоянной GM и измеряемой в лабораторных условиях постоянной
тяготения G. Принимая для них значения GM=39S 600,5 км3- с-2 и
рекомендованное XVII Генеральной ассамблеей Международного Геоде¬
зического и Геофизического Союза G=6,672 • 10~8см3- с-2- г-1, имеем
М=5,97423 • 1027 г, что приводит к средней плотности 6ср=5,51532 г/см3.
Комитетом по стандартной модели Земли рекомендовано для момента
инерции значение /с=0,3308 [117], которому соответствует динамическое
сжатие Земли Я=0,003273 [25]. Учитывая важность референцного
эллипсоидального распределения плотности для теории вращения Земли,
вероятно, целесообразно взять такое значение Я, которое наиболее досто¬
верно с позиций этой теории и согласовано с новейшими данными
о прецессии и нутации Земли, именно Я=0,0032739935 [176]. При этом
значение полярного момента инерции будет: /с=0,3306748 [108].
Возвращаясь к построению глобальной трехмерной плотностной мо¬
дели Земли, будем считать в качестве исходных данных последние при¬
веденные значения массы М, момента инерции 1С и динамического
сжатия Я, а остальную информацию — ту же, что и при модификации
модели PREM. Использование формул (6.38), (6.33), (6.37) позволило
получить эллипсоидальное трехмерное распределение плотности земных
недр 62 (ху у, z), которое из-за громоздкости мы здесь не приводим
(см. табл. 2 в статье [108]).
Использование этого распределения 62 (х, у, z), в качестве репрезента¬
тивного нулевого приближения и необходимого набора стоксовых постоян¬
ных позволяет получать трехмерные распределения dN (х, у, z) более
высоких порядков. Для этой цели составлена программа DENSITY [167],
по которой, в частности, могут быть найдены и числовые значения
коэффициентов разложения bmnk. Для дальнейшего принято Яуст=12.
Выбор такого NyCT обусловлен, во-первых, надежностью числовых значе¬
ний стоксовых постоянных низших порядков, и, во-вторых, практическими
возможностями используемых ЭВМ. Получаемые с помощью программы
DENSITY коэффициенты bmnki соответствующие перечисленной выше ин¬
формации о планете, приведены в табл. III в приложении. Эти коэф¬
фициенты вычислены приближенно, поэтому желательно оценить степень
достоверности их определения.
Так как bmnk — известные линейные комбинации полученных уравни¬
ванием степенных моментов, то осредненной оценкой их надежности при
каждом N могут служить величины отношения весов уравненных значе¬
ний моментов к весам их вычисленных значений по модели (N— 1)-го по¬
рядка. Такие отношения (их числовые значения при различных N при¬
ведены в [79])
(N+ 1)(Я + 2) ^
N N(N - 1)
осредненно характеризуют достоверность модели N-го порядка. Они по¬
казывают большую степень близости этой модели к действительной
Земле по сравнению с моделью предыдущего (N— 1)-го порядка за счет
такого перераспределения масс в последней, после которого модель
152
развивает во внешнем пространстве потенциал притяжения, тождествен¬
ный с потенциалом реальной планеты до N-ro порядка включительно,
например, при N= 12 указанное отношение весов rfi2«l,4. Отмеченное
свойство уравненных степенных моментов переносится на коэффициенты
разложения
12
§12 (х, У, г) = б°(р) + Yj bmnkWmnk(X’ У у Z)y (6.39)
т + п + k = О
с одной стороны, обеспечивая им достаточную степень достоверности
при каждом v=m-\-n+k, а с другой, констатируя факт уточнения модели
в каждой последующей итерации. Отмечаемое улучшение модели пони¬
мается в смысле повышения степени ее близости к реальной Земле
за счет наибольшего согласования ее гравитационного поля с гравита¬
ционным полем планеты.
Хорошим способом проверки надежности коэффициентов bmnk было бы
непосредственное их вычисление по каким-либо неиспользованным нами
данным. К сожалению, таковыми мы не располагаем. Однако имеется
возможность проверки получения набора величин bmnk в одном частном
случае, именно при m-\-n-\-k=3, когда один из таких коэффициентов
непосредственно выражается через стоксову постоянную, конкретно:
b\w= (105/4) 6ср5з2 (6ср — средняя плотность Земли); вычисленный таким
образом коэффициент b\w в пределах точности вычислений совпадает с его
значением, даваемым программой DENSITY, что подчеркивает надеж¬
ность вычисления по ней коэффициентов хотя бы третьего порядка.
Знание коэффициентов разложения (6.39) дает возможность вычис¬
лять модельное распределение плотности в произвольной точке обще¬
земного эллипсоида. Числовые значения многочленов Wmnk при этом
можно получать различными способами, например используя их явное
представление (6.24). В программе DENSITY однако, проведено более
рациональное вычисление Wmnk на основании рекуррентных соотношений
(6.28).
Итак, совокупность приведенных здесь формул при наличии таблицы
в приложении или, что равносильно, программы DENSITY составляет
рабочую основу трехмерной плотностной модели Земли. Предлагаемое
распределение (6.39) кроме основных условий, которым подчинены из¬
вестные плотностные модели Земли, удовлетворяет еще дополнительным
условиям, заключенным в стоксовых постоянных планеты до 12-го по¬
рядка. Благодаря этому такое эллипсоидальное распределение полнее
раскрывает трехмерную структуру земных недр.
Отметим одно важное свойство предлагаемой модели, характеризуемое
сходимостью последовательности используемых 6N\ ведь только при на¬
личии сходимости таких последовательностей обсуждаемая методика
может считаться обоснованной. Характер вывода формулы (6.39),
построенной по биортогональной системе многочленов Wmnk и (amnk внутри
эллипсоида, обеспечивает ряду только сходимость в среднем. Для прак¬
тических приложений желательно было бы установить для {6^} равномер¬
ную сходимость. Однако без дополнительных ограничений на плотность
этого сделать нельзя, тем более неизвестно, как удастся затем проверить
6 Г. А. Мещеряков
153
выполняемость таких условий, если бы они и были установлены. Поэтому
ограничимся ниже численной проверкой сходимости последовательности
{бдг}, полученной при различных (естественно, первых) значениях А'.
При этой проверке, как и вообще при счете bN по программе DENSITY,
широко используется обобщенное суммирование рядов Фурье: конкретно,
при вычислении частичных сумм бдг привлечен известный метод сум¬
мирования по Фейеру—Чезаро (см. § 13).
Возникающее при таком обобщенном суммировании некоторое рас¬
согласование модели б# с использованной информацией о гравитационном
поле в виде набора {Спт, 5лт}дг может быть легко аннулировано введением
соответствующей поправки, вычисляемой только что описанным здесь
/80 -
Рис. 17. Графики распределения аномалий плотности Дбд, по глубине в зависимо¬
сти от N: а — по произвольно взятому радиусу (по оси ординат Д612, 10+ 5 г/см3);
б — в области Индийского минимума £
методом (счета плотности). Кроме того, при построении региональных
моделей необходим учет известной плотности поверхностного слоя. Его
можно выполнить на основе свойств тела нулевого внешнего потенциала
(§21) и решения по [73] тригармонического уравнения для потенциала,
154
дополняющего до НВП потенциал гармонической плотности, восстанав¬
ливающей на о заданную плотность тела т.
Далее будем пользоваться не абсолютными значениями плотности
bN, а ее отклонениями от среднего значения плотности по эллипсоиду Еу
проходящему через точку, в которой вычисляется плотность. Это так
называемые горизонтальные (или латеральные) неоднородности (их
также называют аномалиями плотности)
Дбл,= бл, (х, у, 2) — 6л, (р), (6.40)
где
Мр) = М*> У> z)dS>
Е — эллипсоид х2/а2+у2/Ь2-\-г2/с2=р2, проходящий через точку (*, у, г);
SE — его площадь.
На рис. 17 приведены графики распределения AbN по двум направле¬
ниям: одному, идущему от центра Земли к точке в области Индийского
минимума ондуляций геоида, и другому — к произвольно взятой точке
(ф=55° с. ш., А,= 50° в. д.) в Европейской части СССР (примерно в 90 км
на юго-восток от Казани). Из этих графиков видно, как с увеличением N
изменяется степень детализации распределения плотности. Если при N,
равном 2, 4 и даже 6, наблюдается грубая аппроксимация, дающая лишь
общую качественную картину изменения Дбдг, то при N, равном 8, 10, 12,
распределение плотности по глубине все более детализируется, и графики
становятся более похожими друг на друга, т. е. уже при этих N имеет место
определенная тенденция к их совпадению, которое должно наступить при
дальнейшем увеличении N. Рассмотрение рисунков позволяет надеяться
и на сходимость используемых разложений аномалий плотности no N
по любым направлениям в связи с тем, что, во-первых, вообще последова¬
тельность Дбдг полиномиальная и без каких-либо особенностей,
и во-вторых, в частности, при конкретном N сходимость подтверждена
в двух рассмотренных случаях (один — соответствующий экстремальной
ситуации, другой — произвольной).
§ 24. Предварительная глобальная плотностная модель Земли
Глобальную плотностную модель Земли, представленную в пре¬
дыдущем параграфе своей «рабочей» основой, облечем теперь в цифровую
форму и дадим общую качественную структуру распределения плотности
б 12 (*^> у, z) недр земного эллипсоида.
Кусочно-непрерывная плотность со скачками, заданными моделью
PREM, в осредненном виде совпадает с плотностью этой стадартной
модели, но между каждыми смежными поверхностями ее разрывов
корректируется специально построенным многочленном от х, уу z 12-й
степени Лб12 (х, У, z). Коэффициенты его подобраны так, что выра¬
жаемая им плотность удовлетворяет дополнительно более чем 150 усло¬
виям, предоставляемым надежно полученными параметрами разложения
внешнего гравитационного поля планеты в ряд шаровых функций
до 12-го порядка и степени включительно. Обсуждаемая плотностная
6*
155
модель Земли — это эллипсоидальная модификация модели PREM, согла¬
сованная с реальным внешним гравитационным полем планеты за счет
минимально возможных перемещений масс. Вычисляя значения
612 (х, у, z) в произвольных точках внутри земного эллипсоида,
можно строить глобальную и даже региональные плотностные модели
недр Земли.
Заметим, что глубина везде далее отсчитывается от поверхности
общеземного эллипсоида; таким образом, приводимые ниже карты рас¬
пределения Д612 характеризуют неоднородности на эллипсоидальных
концентрических оболочках Земли, имеющих «приведенную» глубину
d=R4>( 1—р), где р — относительный радиус (0<р<1)’, а /?ф= /?(ф) —
размерный радиус поверхности эллипсоида Е под широтой ср.
Исследуем сначала вопрос изменения плотности с глубиной по харак¬
терным («экстремальным») направлениям, указанным в табл. 6, а также
Таблица 6
Наибольшие ондуляции геоида по спутниковой альтиметрии [219]
Номер
направления
Ондуляции
геоида,м
Примерное расположение
Описание
местоположения
широта,
град
долгота,
град
1
70
—3
145
У острова Новой Гвинеи
2
— 110
5
79
В Индийском океане
3
70
50
— 10
У берегов Великобритании
4
30
30
—70
У Богамских островов
5
56
—55
50
У берегов Антарктиды
6
—56
20
— 120
В восточной части Тихого
океана
на оси вращения Земли (направление № 7 — на Северный полюс,
№8 — на Южный) и в направлении (№ 9) на точку в экваториальной
части Южной Америки (<р=0, А,=60° з. д.). На различных глубинах
по этим направлениям вычислены значения Д612, которые представлены
графиками на рис. 18, 19. Анализ их показывает, что горизонтальные неод¬
нородности простираются практически до центра Земли. С одной стороны,
в ядре они по результатам вычислений незначительны и, в основном,
не превосходят 3 • 10-4 г/см 3; исключение составляет график, соответ¬
ствующий Индийскому минимуму ондуляций геоида, для которого уже
во внешнем ядре неоднородности составляют более чем 8 • 10~4 г/см 3.
С другой стороны, возможно, что наличие неоднородностей в ядре
вообще отражает принятый метод исследования с априори заложенной
аппроксимацией скорее всего дискретного распределения неоднородно¬
стей, о природе которого мало что известно*), непрерывным; рис. 19
тогда представляет сильно сглаженные графики разрывных функций.
Однако, учитывая принятый порядок разложения плотности Ауст=12
(для геофизики это не низкий), можно считать полученные горизонталь¬
ные неоднородности претендующими на отражение реальности.
*) Джекобе Дж. А. Земное ядро. — М.: Мир, 1979.
156
Рис. 18. Изменение плотности с глубиной по радиусам Земли в характерных
направлениях
5,Ю~* г/см3
Рис. 19. Изменение плотности с глубиной по радиусам Земли в характерных
направлениях
Из рис. 18, 19 видно, что по глубине для каждого из исследуемых
направлений положительные и отрицательные аномалии плотности
взаимно нескомпенсированы; более того, для некоторых из них (например,
направление № 2) величины Д612 отрицательны на всем протяжении
глубин, а это подтверждает вывод некоторых исследователей [158], что
недра Земли изостатически нескомпенсированы и можно лишь полагать,
что уравновешен только центр планеты. (В противоположность этому
анЬмалиям Дбдг на эллипсоидальных поверхностных слоях в целом при¬
писана компенсация, т. е. сумма положительных и отрицательных анома¬
лий плотности на них равна нулю; это следует из принятого определения
неоднородностей).
Не останавливаясь на качественном изучении распределения неодно¬
родностей по глубине на каждом из графиков в отдельности, отметим
лишь, что наиболее характерным из них является график 2, соответствую¬
щий Индийскому минимуму ондуляций геоида. Здесь отрицательные
неоднородности простираются до центра Земли, причем они имеют мини¬
мум на глубине 3372 км и локальный максимум на глубине 1372 км.
Указанный минимум приходится на верхнюю часть внешнего ядра, что
близко к выводам сейсмической томографии [188], согласно которым
горизонтальные неоднородности по указанному радиусу захватывают
нижнюю часть мантии, а у нас простираются значительно глубже (на¬
именьшее их значение ниже границы ядро — мантия на глубине
500 км).
Из рис. 18, 19 видно, что изменение плотности по направлениям;
соответствующим минимумам ондуляций геоида (графики 2, 4, 6),
не единообразно — значит, объяснение этих ондуляций не может быть
обусловлено только характером распределения масс под исследуемой
точкой геоида.
На ряде глубин особенности графиков связаны со свойствами земных
недр на этих глубинах. Так, на границе ядра и в прилегающей к нему
области по одному радиусу (график 5) горизонтальные неоднородности
близки к нулю и меняют знак, а по четырем направлениям (графики
2, 3, 4, 9) аномалии плотности имеют локальные экстремумы: один мак¬
симум (по радиусу 3) приходится строго на границу ядро — мантия,
другой (4) ниже ее примерно на 500 км, по радиусам 2, 5, 8, 9 минимумы
расположены: первый ниже на 500 км (2), два других ниже на 700 км,
а четвертый выше ее на 500 км.
Вторая область глубин, имеющая особенности, — это глубины от 1300
до 1800 км. К ней приурочены экстремумы графиков 2, 3, 5, 9 и примерно
постоянное значение аномалий Д612 графиков 4 и 5. В этой области
предполагают залегание аномального тела, порождающего Индийский
минимум ондуляций геоида [151]. Иногда именно на этих глубинах рас¬
полагают точечные массы для наилучшей аппроксимации внешнего потен¬
циала [16, 70].
Третья область, где ярко проявляются особенности графиков анома¬
лий Д612, относится к верхним слоям планеты до глубин порядка 300 км,
захватывающих часть астеносферы. В ней графики 1, 3, 4, 9 имеют пико¬
образные экстремумы; отмечаются значительные градиенты плотности
для графиков 1, 3, 5, 9.
158
Большой интерес представляет распределение плотности (или их ано¬
малий) по оси вращения Земли, вдоль которой направлен ее наибольший
момент инерции С. Только во внутреннем ядре отмечается несимметрич¬
ное распределение плотности вдоль оси вращения: под Южным полюсом
вещество несколько плотнее; а под Северным — разуплотненное (сравни¬
тельно с его состоянием по внутреннему ядру в целом). Затем вдоль оси
вращения планеты отмечается уплотнение (это является следствием
ее вращения), которое увеличивается к поверхности, причем характерно,
что плотность на одинаковых глубинах под Северным полюсом примерно
на 5 • 10-4 г/см3 больше, чем под Южным. Отмеченный факт асиммет¬
ричного распределения вещества вдоль оси вращения отвечает в некото¬
рой степени грушевидности Земли, связываемой обычно с зональной
гармоникой 3-го порядка.
Рассмотрим теперь распределение аномалий плотности 'земных недр
в широтно-долготном простирании, представленное картами А612 на ряде
глубин; рассмотрим характерные из них (рис. 20—24), относя¬
щиеся к мантии на глубинах 200, 400, 700, 1300 и 2891 км. (Мы наме¬
ренно не затрагиваем ниже вопроса о распределении плотности в ядре.
Но уже обсужденные ранее результаты расчета говорят о том, что
во вцутреннем ядре аномалии плотности незначительны — не пре¬
восходят 3 • 10-4 г/см3, а в верхней части ядра имеются неоднородности
разных знаков, значительно большие по абсолютной величине, именно,
до 8 • 10“4 г/см3; при этом довольно любопытно, что аномалии Аб на лу¬
чах, соответствующих экстремумам ондуляций геоида — как положитель¬
ным, так и отрицательным, имеют во внешнем ядре один знак: A6i2<0.
Воздерживаясь по интерпретации этого интересного факта и от утвержде¬
ния о сферически-симметричном строении внутреннего ядра (возможно,
оно таково или очень близко к таковому), отметим, что ответы на эти
вопросы могут быть получены, в частности, и дальнейшим совершенст¬
вованием применяемой здесь методики).
На картах по результатам вычислений значений А612 в узлах карто¬
графической сетки через 30° приведены изоденсы (линии равных значений
аномалий плотности).
Заметим, что всякая карта в изолиниях дает, во-первых, стати¬
ческое (стационарное) значение картируемого объекта, что и отра¬
жается изолиниями изучаемой функции, и, во-вторых, она представ¬
ляет «мгновенное» состояние (на момент составления карты) дина¬
мики явлений, обусловленных этой функцией, так как ортогональные
траектории изолиний — это кривые, касательные к которым в каждой
точке являются градиентами закартированной функции. Значит, карты
изоденс описывают кинематику и динамику вещества внутри Земли.
Эти карты отражают неустойчивость недр планеты. Для устойчивости
должно быть: 1) < 0» то есть должно быть возрастание плотности
с глубиной, и 2) Аб = 0 — отсутствие неоднородностей в направле¬
ниях, ортогональных отвесной линии. Поэтому правильнее было бы
далее соответствующие выводы делать в трехмерном случае с учетом
вертикального градиента плотности, но это не входило в цели описы¬
ваемых исследований.
159
Перейдем к рассмотрению общей картины распределения неоднород
ностей в мантии. В целом по анализу карт на рис. 20—24 она выглядит
следующим образом. За счет вращения Земли, приводящего к сжатию
ее у полюсов, имеет место концентрация вещества около оси вращения
Земли; конкретнее, в полярных областях на всех глубинах вещество
уплотнено, а в приэкваториальных областях — особенно при удалении
от оси вращения — оно является разуплотненным. При этом по глубине
всей мантии максимальное разуплотнение наблюдается в области, через
центральную часть которой проходит ось среднего момента инерции Б
Земли (А,в«75,2° в. д.). Эта область захватывает район Индийского
минимума ондуляций геоида и простирается широтно к Африке (60—
90° в. д.), а «антиподная» область меридиана этого момента инерции
лежит в восточной части Тихого океана под долготой А,ж255° в. д.
Другая естественная меридиональная плоскость планеты, т. е. наимень¬
шего момента инерции Л (>м«14,8° з. д.) проходит по Срединно-Атланти¬
ческому хребту (30—15° з. д.), продолжение этого меридиана через
полюсы располагается восточнее Австралии и Сахалина, т. е. примерно
под 150° в. д. Именно этой области соответствует зона неустойчивости
состояния вещества (а за счет этого и конвективной текучести его),
отчетливо проявляющаяся на глубинах всей мантии.
После такой общей характеристики распределения аномалий в целом
представляет большой интерес описание распределения неоднородностей
хотя бы на указанных выше конкретных эллипсоидальных оболочках.
Рис. 20. Карта изоденс на приведенной глубине 2891 км; средняя плотность на этой
глубине 5,57173 г/см3
Рассмотрим карту аномалий плотности в подошве мантии. Она пред¬
ставлена на рис. 20 («приведенная» глубина 2891 км). Прежде всего
проследим ход нулевой изоденсы (линии равных аномалий плотности),
для которой A6i2=0. Относительно нее на карте представлены области как
уплотнения вещества (Д6>0), так и его разуплотнения (Д6<0). Замкну¬
тых нулевых изоденс на этой карте две. Наиболее протяженная из них
160
окаймляет области разуплотненного вещества под значительной частью
Евразии, Африки, Западной Австралии, Южной и Центральной Америки,
южной части Атлантического и Индийского океанов. Вторая линия
Аб 12== 0 окаймляет значительно меньшую область разуплотнения вещества
под экватором в Тихом океане на юго-восток от Маршалловых островов
под его Центральной впадиной. Максимальное (в глобальном смысле)
разуплотнение вещества (до —9 • 10-4 г/см3) приходится на об¬
ласть, охватывающую Индийский минимум ондуляций геоида и даже
экваториальную часть Индийского океана. Несколько меньшая
(—7 • 10-4 г/см 3) зона разуплотнения вещества имеет место западнее
Южной Африки и в южной части Атлантического океана. Наконец,
третья область разуплотнения попадает под Северо-восточную часть
Южной Америки севернее устья Амазонки. Остальные области подошвы
нижней мантии характеризуются уплотненным веществом. Они занимают
полярные зоны примерно до широты 60° и одну меридиональную полосу
под долготой Х=150° в. д. (восточнее берегов Австралии, Японских остро¬
вов и Сахалина), причем в экваториальной части полосы — в ее верхних
слоях — имеет место тройное сочленение плит (Индийской, Тихоокеан¬
ской и Филиппинской); на данной карте это проявляется седловиной
изолиний (ф=0, Х=150° в. д.), отражающей неустойчивость состояния
вещества нижней мантии. Из этой области вещество мантии, очевидно,
растекается под острова Новой Гвинеи и к Филиппинам и менее интен¬
сивно на восток. Наиболее уплотненное вещество (A6i2=10 • 10-4 г/см3)
на этой глубине находится под Аляской. Следующая область уплотненного
вещества (A6i2=6,5 • Ю-4 г/см 3) приходится на 60° ю. ш. и находится
под акваторией Тихого океана южнее Восточной Австралии. Эти две
области уплотненного вещества, с одной стороны, определяют положение
среднего момента инерции В, ас другой — определяют «очаги» растека¬
ния вещества в экваториальных областях планеты: от южного очага
на северо-запад и от северного на юго-восток.
Вторая карта распределения аномалий плотности отвечает глубине
1300 км, т. е. примерно середине мантии (рис. 21). На этой глубине
опять явно выделяется точка минимакса функции A6i2(jc, у, г) —седло¬
вина изолиний (ф=0°, Х=150° в. д.) под тройным сочленением ранее ука¬
занных плит, от которой на запад и на восток находятся области разуплот¬
нения вещества, а на север и юг — места расположения уплотненных
недр. Можно даже предположить, что на данной глубине именно эта точка
определяет ход нулевой изоденсы, которая в целом является замкнутой
кривой, тянущейся вдоль всей планеты в широтном направлении парал¬
лельно экватору, кроме незначительного участка (в окрестности упомя¬
нутой выше седловины), где имеет место соединение ее северной и южной
ветвей. Таким образом, глобально в приэкваториальной области на этой
глубине имеется зона разуплотнения вещества, кроме указанной «узкой
перегородки» — «меридиональной стены» из уплотненного вещества, рас¬
положенной под долготой Х=150° в. д. Эта «стена» уже на широтах
10° с. ш. и 30° ю. ш. смыкается с приполярными зонами уплотненного
вещества. Отметим, что максимальные'области уплотнения имеют место
в районе Северного полюса и в Атлантическом океане у берегов Антарк¬
тиды (максимум 11,8 • 10-4 г/см3).
161
Теперь об областях наибольших значений разуплотнения вещества.
На экваторе между южной частью подводного Срединно-Атлантического
хребта и Бразильской впадиной имеет место наиболее разуплотненное
вещество (A6i2= — 13,3 • 10-4 г/см3), и эта область совпадает согласно
некоторым литературным источникам [27] с одним из «магических ром¬
бов». Аналогичное тело пониженной плотности пересекается плоскостью
данной карты в восточной части Тихого океана под долготой 120° з. д.
Отрицательная аномалия плотности (A6i2= —10,3 • ТО-4 г/см3) в этом
районе обусловливает «понижение» геоида с его минимальным значением
в точке № 6 табл. 6 (акватория Тихого океана у берегов Калифорнии).
Важно отметить также дополнительное наличие еще двух седловин,
соответствующих неустойчивому состоянию масс. Одна из них попадает
под северную часть Южной Америки (ф=0°, А,=60° з. д.) ; для ее интер¬
претации важны также карты аномалий A6t2 на глубинах 400 и 700 км;
из них видно, что над этой областью залегает «линза» более плотного
вещества, которое, опускаясь, выдавливает вещество мантии на данной
глубине на восток (под устье Амазонки) и менее интенсивно на запад
(под Галапогосские острова). Вторая зона «неустойчивости» распо¬
ложена под большими рифтами Восточной Африки (зона на экваторе
при К от 80° до 50° в. д.), где находится область наибольших упругих
напряжений — большой Восточно-Африканский рифт; этой зоне принад¬
лежит не менее шести «горячих точек».
Рассмотрим теперь рис. 22 — третью карту аномалий Л612; она соответ¬
ствует нижней зоне фазовых переходов — 700 км. Нулевая изоденса
в данном случае окантовывает полосу вдоль экватора с размахом широт
от 15—50° с. ш. до 20—60° ю. ш. Однако и здесь в зоне меридиана момента
инерции В (именно под Х«150° в. д.) выделяется наличие отмеченной
на предыдущей карте «меридиональной стены», которая образует вер¬
тикальное поднятие у полюсов, причем южное из них простирается
от полюса на север до 60—50° ю. ш., а затем в ней образуются два «про¬
вала»: один в районе экватора, второй — в акватории под Охотским
морем. Первый из них — это основная точка гравитационной неустой¬
чивости мантийного вещества. Вид изоденс показывает, что отсюда ман¬
тийное вещество растекается в стороны наибольшего разуплотнения
на запад (под Новую Гвинею и далее вдоль экватора на запад под Индий¬
ский океан) и на восток (под Тихий океан), что может быть следствием
движения вещества из указанных «поднятий» в эту область неустойчи¬
вости с севера и юга. Местом «стока» вещества при этом является упомя¬
нутая на предыдущей карте область вещества с пониженной плотностью
в Тихом океане под долготой 120° з. д., где A6i2= —13 • 10-4 г/см 3. Воз¬
можно, что отмечаемое движение вещества компенсирует противополож¬
ное движение вещества в более высоких слоях, т. е. движение, обуслов¬
ливающее надвиг Индийской плиты на Филиппинскую и Тихоокеанскую.
На данной карте выделяется также несколько меньшая область
разуплотнения на экваторе под Срединно-Атлантическим хребтом, к кото¬
рой приурочен один из «магических ромбов» (согласно карте Сандерсона,
см. [27]). Между областями разуплотнения выделяется под всей север¬
ной частью Южной Америки и на северо-восток от нее до Срединно-
Атлантической области наибольшего уплотнения ее центр, именно
163
Рис. 22. Карта изоденс на глубине 700 км; средняя плотность 4,39769 г/см:
точка с координатами ф = 0°, >. = 60° з. д., для которой Mt2 = 6X
X Ю~4 г/см3 — это своеобразная «линза» толщиной примерно 800 км
и в горизонтальном поперечнике порядка 3000 км, из которой вещество
растекается в две упомянутые выше области разуплотнения (Тихоокеан¬
ское и разуплотнение под Срединно-Атлантическим хребтом).
Зоны наибольшего уплотнения вещества на этой глубине имеют место
в трех областях: Сибирское уплотнение (ф=60° с. ш., Х=90° в. д.), где
A6i2=17 • 10-4 г/см3, под Антарктидой (ф=60° ю. ш., Х=0°), где
A6i2=17 • 10-4 г/см3, и в акватории севернее берегов Антарктиды
(ф=60° ю. ш., А,= 120° в. д.), где Лб2= 12 • 10-4 г/см 3. На общем фоне
разуплотнения выделяется еще локально на этой глубине (как и на глу¬
бине 400 км) в Тихом океане (ф=30° ю. ш., Х= 120° з. д.) уплотненное тело,
расположенное под областью тройного сочленения плит: Антарктической,
Тихоокеанской и Наска.
Четвертая карта (рис. 23) относится к первой зоне фазовых переходов
на глубине 400 км. Здесь более «классически» проявляется разуплотнение
вещества в экваториальной области и его уплотнение в средних и высоких
широтах. Однако, во-первых, здесь отмечаются значительные градиенты
плотности при переходе от средних широт к экватору, во-вторых, большое
разуплотнение вещества вдоль экватора в Индийском океане, в-третьих,
расширение Индийской зоны разуплотнения не только вдоль экватора,
но и в северо-восточном направлении вдоль побережья Азии от Индонезии
к Японским островам, при этом максимум разуплотнения приходится
на восточное побережье Китая в районе устья реки Янцзы (A6i2=
= —12 • 10-4 г/см3). Сохраняются области разуплотнения вдоль эква¬
тора в Тихом и Атлантическом океанах. Однако заметим, что здесь про¬
является дополнительная зона разуплотнения в южной части Южной
Америки (ф=30° ю. ш., >,= 60° з. д.), т. е. под северной частью Арген¬
тины.
На этой глубине отмечаются области уплотненного вещества под
Сибирью (A6i2=18,8 • 10-4 г/см3), под Антарктидой (A6i2=21,8 •
• 10“4 г/см3) и у берегов Антарктиды (A6i2= 14 • 10-4 г/см3). Так же,
как и на предыдущей глубине, под Срединно-Атлантическим хребтом
(ф=0°, А,= 30° з. д.) выделяется точка «стока» вещества, которое течет
сюда из упомянутой выше «линзы» в северной части Южной Америки
и с юго-востока из-под Антарктического уплотнения вещества (ф=
= 60° ю. ш., Х=0°), а также из-под Пиренейского полуострова.
Рассмотрим, наконец, рис. 24 — карту изоденс на глубине 200 км.
Здесь также ход нулевой изолинии опоясывает приэкваториальное
разуплотнение масс, отделяя его от приполярной области с более уплот¬
ненным веществом, захватывающим и средние широты. Наиболее резко
выделяемые области разуплотнения вещества — это области восточного
побережья Китая (Аб12= 18,3 • 10-4 г/см3), Тихоокеанское разуплотне¬
ние, вытянутое вдоль меридиана 120° з. д. от экватора до 30—32° с. ш.
к берегам Калифорнии и захватывающее разлом Сан-Андреас. На этой
глубине более значительно проявляются зоны уплотненного вещества:
Сибирская (A6i2= 19,2 • 10-4 г/см 3) и более растянутая Антарктическая
(A6i2= 18,9 • 10-4 г/см 3), а аномалия плотности под «линзой» в Южной
Америке характеризуется уменьшением уплотнения вещества.
165
166
30° 12,2^60° ~90° ПО1 150° 12£l80° 210°240° 270° 300° 72,2'ш° 360
Рис. 23. Карта изоденс на глубине 400 км; средняя плотность 3,72067 г/см3
167
Рис. 24. Карта изоденс на глубине 200 км; средняя плотность 3,35765 г/см;
Мы не приводим по понятным причинам соответствующей карты
модельного распределения Д612 на поверхности земного эллипсоида.
Описанная модель дает обобщенную картину распределения плотности.
Однако представляется, что использованный на основе обширной инфор¬
мации метод ее представления при помощи многочлена от трех перемен¬
ных 12-й степени в каждой оболочке планеты, границы которых и скачки
плотности на них взяты по результатам сейсмологических исследований,
уже дает возможность исследовать — пусть даже обобщенно и в качест¬
венном отношении — ядро и мантию, исключая из последней литосферу и,
возможно, верхнюю часть астеносферы.
Отметим две основные особенности предварительной' глобальной
плотностной модели Земли.
1. Горизонтальные неоднородности в теле планеты простираются
вплоть до ее центра, отражая тем самым и сферически-несимметричное
строение земного ядра.
2. Распределение плотности земных недр обусловлено в главной своей
части вращением Земли, что приводит на любой глубине к большему
уплотнению вещества в полярных и в средних широтах и разуплотнению
его в экваториальной части планеты; при этом существующее наличие
масс разной плотности (даже на одной глубине) фиксирует расположение
в ней плоскостей главных моментов инерции Земли: экваториальной
плоскости и двух меридиональных (с А,л=14,8° з. д. (±180°), в которой
лежит наименьший момент инерции Л, и с кв=75,8° в. д. (=Ь180°), в кото¬
рой лежит средний момент инерции В).
Охарактеризуем общую предварительно полученную качественную
структуру плотностной модели мантии Земли.
Плоскость наименьшего момента инерции Л обусловлена конкретным
расположением более уплотненного вещества в полярных и средних
широтах, которое на разных глубинах «полуостровами» вклинивается
в приэкваториальный разуплотненный пояс под Срединно-Атлантическим
хребтом (^^15° з. д.) и в окрестности меридиана (Х^150° в. д.), образуя
там зоны неустойчивого расположения земных недр.
Меридиональная плоскость среднего момента инерции В пересекает
области наиболее разуплотненного вещества по глубине всей оболочки
Земли, которые представляют собой своеобразные «воронки» разуплотне¬
ния (конусы дефекта масс), исходящие из середины ядра и поднимаю¬
щиеся вплоть до астеносферы, а «оси» их (кривые линии) в осредненном
смысле соответствуют для одного из них направлению от центра Земли
к точке, близкой к тройному сочленению плит — Тихоокеанской, Кокос
и Наска (ф=0°, Х=240° в. д.), для второго — к Индийскому минимуму
ондуляций геоида. В верхней части мантии ось первого из этих конусов
смещена примерно на 30° на север вдоль разлома между Тихоокеанской
плитой и плитой Кокос к тройному сочленению плит (Тихоокеанской,
Кокос, Северо-Американской); а второго — из района под Цейлоном пере¬
мещена на северо-восток под устье Янцзы; каждый из этих конусов
более похож на изогнутый рог.
Указанные здесь четыре особенности распределения масс внутри
Земли (наличие двух зон неустойчивости вещества и двух «воронок» его
разуплотнения) носят для планеты глобальный характер и определяют
168
в целом внутреннее строение планеты, ее внешнее гравитационное поле,
динамику Земли, намечая тем самым один из подходов к объяснению
конвективных движений в мантии, тектоногенезу и фигуре Земли.
Представляется, что сочетание результатов сейсмического томографи-
рования с данными вычислений плотности 612 (х, у, z) позволит находить
и модельные распределения упругих постоянных.
§25. Замечание об общей обратной задаче
теории потенциала
Коснемся кратко этой задачи, основываясь на результатах § 18 и 21.
Выше были приведены исследования и, в частности, методы прибли¬
женного решения геодезической и геофизической обратных задач теории
потенциала. Их постановкой конкретизировалась форма задания внеш¬
него потенциала: он предполагается заданным стандартным способом,
общепринятым при описании внешних гравитационных полей планет,
именно рядом по элементарным шаровым функциям.
При таком задании внешнего потенциала, как легко видеть, может
быть решена (также приближенно) и общая обратная задача теории
потенциала, в которой по известному внешнему потенциалу ищется
и форма тела, его создающего, и распределение плотности его веществ.
Будем предполагать, что в этом случае выполняются все условия
теорем единственности и устойчивости решения каждой из двух уже
рассмотренных задач: как геодезической, так и геофизической. Тогда
в классе звездных гладких поверхностей искомых тел с непрерывной
плотностью единственным образом могут быть найдены поверхность
и плотность тела, развивающего в окружающем пространстве заданный
потенциал.
Этапы практического построения решения таковы.
Сначала решается геодезическая задача, что дает область расположе¬
ния искомых масс. Затем в найденной области строится ортогональная
или биортогональная система многочленов, которая принимается
за базисную систему функций в этой области. По ней строится обобщен¬
ный многочлен Фурье, которым и представляется приближенно искомая
плотность вещества в уже найденной области.
Возможно, что при реализации этой схемы могут появиться дополни¬
тельные условия, которые придется наложить на поверхность и плотность
искомого тела, а также и на считаемый заданным его внешний потенциал.
Центральным вопросом и в этой задаче является нахождение прибли¬
женных значений всех степенных моментов произвольного порядка, кото¬
рое было описано ранее (в § 12 и 21) и которое из-за возможного наличия
нулевых коэффициентов в разложении заданного внешнего потенциала
в ряд шаровых функций значительно сужает класс возможных решений
искомой плотности.
ГЛАВА 7
ДИНАМИЧЕСКИ ОДНОТОЧЕЧНЫЕ МОДЕЛИ
ГЕОПОТЕНЦИАЛА И ГЕОМЕТРИЧЕСКАЯ
ТЕОРИЯ ДВИЖЕНИЯ ИСЗ
§26. Нецентральность поля притяжения Земли
и динамически одноточечные модели геопотенциала
Обратные задачи теории потенциала, рассмотренные ранее (§ 5 гл. 1
и гл. 4—6), соответствуют статической ситуации. В них предполагается,
что искомые распределения плотности и формы гравитирующих объектов,
развивающих заданный потенциал, неизменны; безусловно, не зависящим
от времени полагается и задаваемый потенциал. Однако возможна
и другая — динамическая — трактовка этих задач. Не касаясь недавно
возникших обратных задач теории потенциала в космической геодина¬
мике, рассмотрим элементар¬
ную динамическую обратную
задачу этой теории, продол¬
жив тем самым обсуждение
темы § 15 и приложив затем
полученное решение к теории
движения ИСЗ. Сначала, од¬
нако, отметим одну из ее
практических предпосылок —
факт нецентральности грави¬
тационного поля Земли. По¬
следняя известна, она посто¬
янно подчеркивается в лите¬
ратуре (см., например, [46,
120, 162]); при этом считает¬
ся, что ее влияние на движе¬
ние ИСЗ учитывается подсче¬
том совокупности возмуще¬
ний, вызываемых в движении
наличием в разложении по¬
тенциала притяжения всех
его гармоник, кроме нулевой,
соответствующей централь¬
ному полю планеты. Однако в природе нет планет, создающих вокруг себя
строго центральное поле сил притяжения. Имеет смысл оценить [89] фак¬
тическую нецентральность гравитационного поля Земли, т. е. опреде¬
лить хотя бы приближенно, на сколько от ее центра масс смещен тот
«центр» Земли, который притягивает ИСЗ в какой-то момент времени.
Проявление такого смещения притягивающего центра Земли легко
усматривается из рис. 25. Траектория спутника — пространственная кри¬
Рис. 25. Участок траектории ИСЗ в не¬
центральном гравитационном поле Земли и ее
трехгранник Френе (система координат—зем¬
ная геоцентрическая)
170
вая. Кеплеров эллипс для некоторой ее точки Р, т. е. невозмущенную
орбиту движущегося в поле Земли спутника, строят в плоскости, содер¬
жащей точку Р орбиты, вектор скорости v спутника в этой точке и центр
масс планеты О, в котором предполагают сконцентрированной всю
ее массу. Но такое предположение не отвечает реальной ситуации.
Сила F притяжения Землей ее искусственного спутника, а вообще говоря,
даже и Луны, исключительно редко расположена на прямой РО и, будучи
приложенной в точке Я, направлена не в точку О, а в некоторую другую
точку Q, находящуюся над или под фокальным диском Земли. Значит,
плоскость мгновенного (действительно, мгновенного!) эллипса спутника
в точке Р должна содержать в себе не точку О, а точку Q, положение
которой по известной силе, кстати, легко найти. Угол между плоскостью
кеплеровой орбиты и плоскостью мгновенного эллипса (на рис. 25 угол
между векторами г и F), просто оценить. Заменяя действительную Землю
общеземным эллипсоидом, видим, что этот угол равен разности между
геоцентрической широтой точки Р и ее геодезической широтой, вычислен¬
ной на высоте спутника. Как известно, этот угол для точки, находящейся
на земном эллипсоиде, имеет максимальное значение при широте 45°
и составляет там около 12', а для точки на высоте, например, орбиты
ИСЗ «Lageos» он около 6', что в линейном виде дает отстояние точки Q
от точки О примерно 22 км. Такова максимальная нецентральность
Земли для спутников на высотах 6—7 тыс. км.
Нецентральность поля Земли проявляется даже и при притяжении
Луны. Соответствующие расчеты «смещения центра масс Земли с пря¬
мой приложения равнодействующей лунного и солнечного притяжения»
были выполнены для различных упрощенных моделей Земли в [23],
см. также [236], где при некоторых значениях «геоцентрической широты»
Луны (18 и 28°) полученные смещения оказались явно непренебрегае-
мыми величинами даже для теории движения Луны («100 м и «140 м).
Представляется, однако, что обсуждаемые оценки наиболее просто можно
получать из сравнения геоцентрической и геодезической широт на высоте
исследуемого движущегося объекта, а не по каким-либо моделям Земли.
Раскрыв значение точки Q как мгновенного центра притяжения ИСЗ,
определим теперь ее местонахождение, предположив, что в ней сосредо¬
точена некоторая масса, которая в данную эпоху притягивает спутник,
заданный своим положением, так же, как все массы Земли или даже как
все гравитирующие массы Солнечной системы. Пусть искомые координаты
точки Q суть а, р, у; вместо массы, сконцентрированной в этой точке,
будем далее определять ее гравитационный параметр \y,=±GrriQ, равный
произведению постоянной тяготения G на искомую массу в точке Q. Эту
точку, кстати, называют в [223, 19] фиктивным притягивающим центром;
мы предпочитаем именовать ее мгновенным центром притяжения; послед¬
ний термин полностью отвечает сущности дела.
Заметим, что сформулированная динамическая задача определения
положения точки Q и сосредоточенной в ней массы по заданному
в некоторой другой точке Р и в ее достаточно малой окрестности значению
гармонической функции U, принимаемой за потенциал точечной массы
mQ> может трактоваться как своеобразная простейшая обратная задача
теории ньютоновского потенциала. Последняя в такой постановке при
171
условии, что точка Р для поверхности уровня U=const является эллипти¬
ческой точкой, имеет легко находимое единственное решение. Однако
если значение потенциала полагать заданным в конечной области прост¬
ранства, содержащей известную точку Ру то такая задача — как обратная
задача теории потенциала — уже неразрешима. Получаемое же ниже
ее решение дает тогда в этой области лишь некоторую аппроксимацию
заданной гармонической функции потенциалом точечной массы.
Итак, в точке Р (х, у, г) и ее малой окрестности имеем заданным потен¬
циал U(P)y который в силу гармоничности является аналитической
функцией координат в этой малой области, а значит, имеет и градиент
F=grad U. Предположим, что потенциал (У (Р) может быть представлен
потенциалом точечной массы, находящейся в некоторой точке Q (а, р, у).
Тогда
U(P) = vl/1, F = ц//2 = U/l, F = Л/и* + u2y+ I]\-
F=\QP\2=(*-a) 2+(</~P) 2+(2-y) 2; (7.1)
_Mx-aO ц .ix (У-PI v Ц(г-Т)
F ’ y F F
Из формулы первой строки имеем
/ = и/л]и2х + и\ + ui ц = Ш = и2/У Ul + и] + и\, (7.2)
а из последней с учетом (7.2) находим
uu„ uui
у
“ = '+ и>' + и1+-Щ' е~9+ +ul
UU.
(7.3)
у = z +
Формулы (7.2) и (7.3) дают полное решение рассматриваемой обрат-
ной задачи в ее локальной постановке: они выражают значение при¬
тягивающей массы (параметра р) и ее положение (а, р, у). Причем это
решение мы считаем зависящим от параметра t — от времени, которым
фиксируется положение точки Р как основы исходной иснформации,
т. е. потенциала U сил тяготения в этой точке, развиваемых либо одним
телом т, либо даже совокупностью таких тел. Этот гравитационный потен¬
циал, отнесенный к заданному моменту t, заменяется потенциалом точеч¬
ной массы rriQ, т. е. для космической геодезии и небесной механики
мы имеем здесь, по сути дела, идеальный случай многоточечных моделей
потенциала — его одноточечную модель. Но эта «идеальность»» достига¬
ется дорогой ценой и на первый взгляд она иллюзорна: находимый так
единственный точечный объект модели является нестационарным, ибо его
параметры суть функции положения точки пространства, для которой
строится модель потенциала. Поэтому модель потенциала, описываемую
выражениями (7.2) и (7.3), можно назвать его одноточечной моделью
с подвижной и переменной массой или, короче, динамически одноточеч¬
ной моделью потенциала.
Приведенные простые рассуждения и тривиально полученный резуль¬
тат позволяют теперь совершенно по-иному — неклассически — подойти
172
к трактовке и изучению орбит небесных объектов (искусственных или
естественных), движущихся в поле сил ньютоновского притяжения.
Обращаясь к движению ИСЗ в заданном гравитационном поле,
скажем, что любой точке Р его траектории соответствует свой мгновенный
центр притяжения Q, определяемый формулами (7.2) и (7.3). Этот
мгновенный центр притяжения Q формирует орбиту спутника в окрест¬
ности ее точки Р. В работе [17] (формула (18)) дано дифференциальное
уравнение, описывающее перемещение фиктивного центра Q в зависи¬
мости от движения точки Р по ее орбите. Упомянутое уравнение получено
там в предположении прямолинейного движения центра Q. Однако вместо
дифференциального уравнения, определяющего радиус-вектор rQ центра
притяжения, из формул (7.3) сразу следует (после умножения их соответ¬
ственно на i, j, к и сложения) значение самого вектора rQ:
г«=г + 1?-+Ъ> + и^та<1и (7-3а)
X 1 у 1 Z
(все входящие в эту формулу величины — функции времени t).
Вектор Гд для всякой точки Р (г=г (t)) единичной массы, движущейся
в отнесенном к геоцентрической инерциальной системе координат прост¬
ранстве под воздействием всех проявляющихся в нем гравитационных
сил, суммарный потенциал которых в данную эпоху t в точке Р равен U,
дает положение мгновенного центра Q притяжения, эквивалентного
по действию всем учитываемым потенциалом U гравитирующих в прост¬
ранстве масс.
Элементарную дугу орбиты в окрестности ее точки Я, формируемую
действием массы \i/G в точке Q, мы относим к мгновенной орбите ИСЗ
в точке Р. Вообще, мгновенной орбитой ИСЗ для ее точки Р в эпоху t будем
называть ту кривую, по которой начиная с этого t двигался бы спутник,
если бы с этого момента времени притяжение всех масс проявлялось бы
на нем так же, как действует неподвижная точечная масса p/G, находя¬
щаяся в точке Q. Мгновенной орбитой является эллипс (при модуле
вектора момента количества движения СФ 0 и постоянной энергии
h<0, см. далее § 28). Реальная орбита ИСЗ в поле гравитационных сил —
это огибающая кривая линия мгновенных эллипсов траектории спутника.
С другой стороны, реальная орбита — это ребро возврата огибающей
поверхности (развертывающейся!) однопараметрического семейства (па¬
раметр — время t) соприкасающихся плоскостей его мгновенных орбит.
Таким образом, если в принятой теории движения ИСЗ выделяют
невозмущенную (кеплерову) и возмущенную орбиты, то в рамках излага¬
емой здесь теории фигурирует мгновенная плоская орбита и реальная
пространственная, причем последняя формируется исключительно
в заданном модельном поле гравитационных сил. Для перехода от такой
пространственной орбиты к действительно наблюдаемой необходимо
учитывать возмущения первой, обусловленные всеми силами негравита¬
ционного характера.
Обратимся теперь к нахождению приращений параметров р, а, р, у,
определяющих мгновенный центр притяжения и соответствующих
перемещению точки Р в соседнюю точку орбиты за промежуток
времени А/. Они выражаются следующими формулами, получаемыми
173
дифференцированием выражений (7.2), (7.3):
Ар=рД/, Да=аД/, Д|3=|ЗД/, Ду=уД/, (7.4)
где
|i = -j^(2 Fo-lfr?)), (7.5)
Г
1 2 UU, .
а = х +-^(Uxu + Ux) - —£Г-(г, '?).
1 2UUU
£ = У + ~^(Uyo + Uy) - —^ (г, г), (7.6)
Г г
1 ... 2 ииг
V = 2 + ~^(Uzo + Uz) - г).
В этих формулах все величины, стоящие в правых частях равенств,
должны быть вычислены в «начальной» точке дуги орбиты (в точке Я);
выражения третьих производных приведены в следующем параграфе.
§27. Геометрия орбиты ИСЗ
Перейдем к изучению движения ИСЗ единичной массы относительно
геоцентрической инерциальной системы координат Oxyz (рис. 26); при
этом будем исходить из только что рассмотренного факта о нецентраль-
ности поля сил, действующих на
спутник: направление силы F,
под действием которой он дви¬
жется, не проходит через начало
О системы координат.
Выпишем дифференциальные
уравнения движения ИСЗ
x=F„ y=Fy, z=Fv (7.7а)
или, короче,
г=F,
(7.7)
где r=r(t)=x(t) \+y(t) j+z(t) k —
радиус-вектор ИСЗ и F=
= F(x, у, z)=Fx\+Fy) + Fzk —
вектор действующей на ИСЗ
силы, причем F=Frp+FHerp: Frp
означает сумму гравитацион¬
ных сил (силы притяжения
Земли, Луны, Солнца и др. тел
Солнечной системы), a FHerp — сумму сил негравитационного характера
(силы сопротивления атмосферы, светового давления и др.).
Остановимся сначала на геометрии движения: построим естественный
трехгранник траектории и выразим ее кривизну и кручение через дейст¬
вующую силу и ее производные.
Рис. 26. Часть дуги орбиты ИСЗ (система
координат — инерциальная геоцентриче¬
ская)
174
Рассмотрим некоторую дугу s орбиты ИСЗ в окрестности ее произ¬
вольной точки Р.
Так как вектор скорости v расположен на касательной Т, орт которой
т, то легко получим последний
Т = (*' + у) + zk),
где v = д/х2 + у2 + i2.
Запишем уравнение касательной Г к орбите
р—г=q\
или
X - * У - у Z — 2
(7.8)
(7.9)
(7.9а)
(7.10)
(X—x)x+(Y—y)y+{Z—z)z=0, (7.10а)
в которых (здесь и далее) р = {Х, У, Z) — радиус-вектор текущей точки
соответствующего геометрического образа, a q — переменный скалярный
множитель.
Уравнение соприкасающейся плоскости траектории ИСЗ имеет вид
и нормальной плоскости
или
(р—г. v)=0
или в координатах
(р—г, v, F) =0
X — х Y — y Z-z
х
Fy
У
F„
z
F„
= 0;
вектор бинормали*)
и ее орт
а уравнение бинормали
В—В л-\-В у]-\-В zk
Р=в/Я,
Р~г=^В
(7.11)
(7.11а)
(7.12)
(7.12а)
(7.13)
*) Обозначение одной буквой В бинормальной прямой и модуля вектора
бинормали В = ! В | не должно привести к недоразумениям; это замечание отно¬
сится и к аналогичному использованию букв Т (касательная прямая и модуль
вектора касательной) и N (главная нормаль и модуль вектора главной нормали).
175
или
у-у
Ви
Z - г
(7.13а)
причем
В =
Ву =
X
F,
В, =
(7.14)
На основании тир (или v и В) имеем теперь вектор главной нормали
N=BXv и ее орт v=pxтили, более подробно,
1
vB
J
ВУ
У
к
В,
и уравнение спрямляющей плоскости
(р—г, v)=0
или
где
(Х-х) Nx+(Y-y) N,+ (Z-z) Nz=О,
в„ в,
в
Вх Ви
—
У z
У г
II
II
х У
х у
(7.15)
(7.16)
(7.16а)
• (7.17)
Из приведенных формул, описывающих все элементы естественного
трехгранника траектории ИСЗ, видно, что только касательная к ней
и нормальная плоскость выражаются через кинематическую характери¬
стику движения — его скорость v, а все остальные, в том числе сопри¬
касающаяся плоскость и нормали (главная и бинормаль), отражают уже
динамику движения и обусловлены силами, действующими на спутник,
т. е. зависят от структуры поля сил. Особо наглядно проявляется это
на кривизне k и кручении х орбиты.
Переходя к их вычислению, введем скалярное произведение а, пред¬
ставляющее связь кинематики движения и его динамики,
<j=(v, F) = (г, T)=xFx+yFy+iFz (7.18)
и, воспользовавшись уравнениями движения (7.7), напишем (по формуле,
определяющей кривизну k пространственной кривой)
k2 = (v2F2 - а2) / (v2
(7.19)
или
k2=
(х2 +у2 +i2)(F2x + F2 + F\)
(xFx + yF + iFz
(i2 + y2 + i2)3
Для вычисления кручения ч орбиты надо иметь третью производную
радиуса-вектора
7 = x'i + у' j + "z k.
176
Найдем ее, дифференцируя по t уравнения движения (7.7а):
dFx
i'Jr~STi = (v> grad F*)>
dF .
I + = (v, grad Fy),
dFz .
У + =(v, grad Fz).
... dF,. .
dFx .
+
4
у
1ч
dy b
dF„ .
dF .
y = ~arx +
~dy~b
dFz .
dFт
2 = +
dy
(7.20)
Вводя матрицу M производных от составляющих силы F
М =
запишем
dFx
dF x
dFx
dx
dy
dz
dFУ
dFy
dFy_
dx
dy
dz
dF_t_
dFz
dFг
dx
dy
dz
r=
Mv *,
■ = (x
. », i)
(tr-
(7.21)
(7.22)
ния). Значит, кручение х траектории ИСЗ может быть вычислено по
известной формуле
(Г, г, 'г')
k2(r2f
(7.23)
в которой r=v, г дается уравнениями движения (7.76), а г и k 2 — форму¬
лами (7.22) и (7.19)
Заметим, что элементы строк матрицы (7.21) равны составляющим
по осям координат векторов grad Fx, grad/7^, grad F7 соответственно.
В дальнейшем мы привлечем еще и четвертую производную текущего
радиуса-вектора орбиты
r<IVWIV)i+i/<,v>j+2<,v>k, (7.24)
проекции которой на координатные оси также легко могут быть вычислены
(в заданном поле сил):
d2Fv
X(IV) = (F, grad Fx) +
dx
■x2 +
d2F
dy
x У2 +
dzF
X -2
dz1
+
+ 2
(
dx dy
ХУ +
d2F
X
dx dz
XZ -f-
d2F
X
dy dz
yt).
d2F
d2F„
d2F„
Ут = (F, grad Fy) + —x2 + -~-y2 + z2 +
+ 2
(
dy*
dz1
dFy •• , dFy •• , ^
——т—XI/ —-—XZ -\ —-
dx dy dx dz dy dz
(7.24a)
,(IV) _
d2F,
= (F, grad F2) + —f i2 +
d2F,
d2F
+ 2
(
dx2
2 У +
dy2 dz
z2 +
d F, . . d2Fz . .
xy -j—-—-— XZ -f-
v dx dz 1
dx dy
dy dz
yi)
177
Приведем также производную скалярного произведения о= (г, г)
по времени
<т=(г, F)+x(grad F„ v) + i/(grad F v) + i(grad F^ v)
6=f*+(t,T)=F*+(t,T). (7.25)
Обсудим теперь кратко характер сил, действующих на спутник.
При написании предыдущих формул имелась в виду произвольная сила F,
действующая на ИСЗ, предполагаемая, с одной стороны, нецентральной,
а с другой — неконсервативной. В этом случае основные теоремы дина¬
мики справедливы только в дифференциальной форме, именно,
теорема о количестве движения:
d\=Vdt\ (7.26)
теорема о моменте количества движения:
(d/dt)(v X v)=r X F; (7.27)
теорема о «живой силе»:
d{v2/2)=(F, dv)\ (7.28)
и ни одна из них при этом не допускает какого-либо первого интеграла.
Хорошо известно, что основную, преобладающую часть действующей
на спутник силы F составляют гравитационные силы Frp, а влияние
негравитационных эффектов на коротких дугах орбиты чрезвычайно мало.
Поэтому примем далее FHerp=0, считая, что их влияние должно учиты¬
ваться после интегрирования уравнений движения, например путем вве¬
дения соответствующих поправок. Значит, дальше всюду считаем, что
F = Frp, т. е. будем рассматривать движение ИСЗ в поле только гравита¬
ционных сил. В таком случае
F=grad£/, (7.29)
где, как уже отмечалось, I] — суммарный потенциал сил притяжения
ИСЗ всеми массами Земли, Луны, Солнца и остальных тел Солнечной
системы. Конечно, при этом имеются в виду такие тела, потенциалы при¬
тяжения которых непренебрегаемы.
Теперь поле сил F — консервативное, поэтому, как известно, из тео¬
ремы «о живой силе» может быть получен один первый интеграл — ин¬
теграл энергии
v2/2 + (— £/)=const. (7.30)
Кроме того, приведенные выше формулы геометрии орбиты для рас¬
сматриваемого случая потенциального поля должны быть переписаны
с тем, чтобы в них фигурировали производные суммарного потенциала U}
который теперь выступает в качестве исходной информации о поле. Это
приводит к следующим заменам:
г _ ди _ п р - ди - п f? d(J
х ~ дх ~ х’ У ~ ду ~ У' г дг г ^ ^
(для краткости, и как это принято, пишем UХУ а не Ux и т. п.).
178
Матрица М (формула (7.21)) превращается в симметричную матрицу
вторых производных потенциала
и»
и.
м =
иух
иуу
и\
и>у
и
Заметим, что если бы на ИСЗ были установлены приборы, предна¬
значенные для определения в текущей точке его орбиты gvadU (т. е. пер¬
вых производных функций U) и элементов матрицы М (т. е. вторых
производных), то геометрию траектории в окрестности какой-либо
ее точки можно было бы описать автономно по данным таких приборов,
конечно, принимая в расчет поправки за негравитационные эффекты.
Как известно, на создание таких приборов сейчас возлагаются большие
надежды [72, 221].
§ 2в. Геометрический метод построения орбит ИСЗ
Определим в нецентральном поле гравитационных сил орбиту ИСЗ
в некоторой окрестности ее произвольной точки Р0. Примем следующий
порядок построения орбиты: сначала для малой дуги траектории ИСЗ (ок¬
рестности точки Ро) построим промежуточную орбиту, за каковую примем
мгновенную (для точки Ро) траекторию ИСЗ, получив ее интегрированием
уравнений движения с правыми частями, отражающими притяжение
мгновенного центра Q. От промежуточной плоской орбиты перейдем
затем к пространственной траектории, т. е. уточним дугу орбиты,
соответствующую некоторому шагу (по времени) ее построения. Вы¬
числение положения конечной точки этой дуги и вектора скорости в ней
позволит считать эти величины начальными для следующего шага. Отли¬
чительной чертой такой методики исследования возмущенного движения
является исключение из нее наиболее трудоемкой операции интегрирова¬
ния уравнений этого движения, обусловленного совокупностью всех
действующих сил.
Под окрестностью любой точки Ро траектории ИСЗ понимается такая
малая, содержащая в себе эту точку дуга орбиты, в пределах которой
движение спутника происходит под действием переменной, но централь¬
ной силы F, развиваемой массой ц/G, находящейся в точке Q (а, |3, у).
Такое механическое понимание окрестности точки Ро траектории естест¬
венно отождествляется с ее геометрическим понятием дифференциальной
окрестности 2-го порядка, ибо при том и другом толковании она опреде¬
ляется производной 2-го порядка f=F, вычисляемой в точке Р0.
Пока ограничиваемся рассмотрением такой дуги орбиты w P0P=sy
которую можно считать плоской, лежащей в ее соприкасающейся плос¬
кости. Значит, в канонических уравнениях изучаемой траектории ИСЗ
предполагаются опущенными малые 3-го и более высоких порядков
(относительно s). С указанной точностью эта дуга пространственной
орбиты (длиною s) отождествляется с плоской дугой ее мгновенной
орбиты. Поэтому определение последней для точки Ро приводит к нахож¬
дению дифференциальной окрестности 2-го порядка пространственной
орбиты.
179
Таким образом, надо проинтегрировать систему уравнений
.?= —ц(х—ос )//3, i?=-|x(y—Р)//3, z=—ц(2—V)//3 (7.33)
при начальных условиях
г|,=,0=(г)р.= Го, г|/=(о=(г)р=г0. (7.34)
Решение этой задачи выполняется элементарно — составлением, как
и в случае центрального поля, интегрируемых комбинаций (см. например,
[31]) или же сведением к этому случаю после параллельного переноса
системы координат Oxyz по вектору rQ. Оба варианта интегрирования
системы (7.33) дают те же первые интегралы, что и для центрального
поля, но с понятной заменой в них x,.i/, z соответственно на х—а, у—(3,
z—у. Это интегралы площадей
(у—P)z—(z—■у)у=си {z—y)x—{x—a)z=c2, (х—а)у— (у—Р)х=с3(7.35)
и интегралы Лапласа
— \i (х—а)/1 + съу—с2к—\\у
— \i(y—P)// + Cii—с3х=Х2, (7.36)
— \i{z—у)/1 + с2х—сху = А*,
где с={ с 1, с2, Сз} — вектор момента количества движения (или вектор
момента скорости) и A,={A,i, Х3) — вектор Лапласа. Последние и здесь
удовлетворяют тем же соотношениям, что и для центрального поля,
именно условию ортогональности
С\А-i -J- с2Х2“I-£3X3=0, или (с, А») =0, (7.37)
и известному равенству
А/ j -{- Л*2 —I— А'3== "I- h {с j -j- С2~\~ ^з)’ или A^=jji^-J-/ic^, (7.38)
в котором h — постоянная энергии, равная удвоенной константе из фор¬
мулы (7.30). Причина этому ясна: здесь также рассматривается централь¬
ное поле, хотя центральное уже относительно мгновенного центра Q.
Таким образом, имеется семь интегралов движения: (7.30), (7.35),
(7.36), связанных двумя соотношениями (7.37), (7.38), т. е. всего пять
независимых интегралов системы (7.33). Они позволяют по данным на¬
чальным условиям (7.34), т. е. по известным для точки Я0 значениям
*0, Уоу Zq; Jtoy уо, z0 в эпоху t0 получить (с контролем) числовые значения
постоянных /г, С\, с2у с3, А,ь Х2, Х3 и построить мгновенную траекторию
ИСЗ в окрестности ее начальной точки Р0. Однако для получения мгно¬
венного движения в окрестности этой точки пока не хватает еще одного
соотношения, содержащего в себе время t.
Уравнения же мгновенной траектории ИСЗ составить легко. Из инте¬
гралов площадей (7.35) после умножения их на (х—а), (у—р), (z—у)
соответственно и сложения результатов имеем
с 1 (х—а) + с2(у—р) + с3(г—у)=0, (7.39)
а из интегралов Лапласа (7.36) после аналогичных действий и простых
преобразований получаем
(х-а) X, -(-(£/—Э) Xj + fz-y) Х3=с2-ц/. (7.40)
180
При произвольных х, у, z соотношение (7.39) описывает плоскость,
а (7.40) с учетом того, что I есть расстояние между двумя точками,
является уравнением поверхности второго порядка. В нашем случае
х, у, z удовлетворяют уравнениям движения (7.33), поэтому совместное
рассмотрение (7.39) и (7.40) дает уравнения мгновенной траектории ИСЗ,
являющейся плоской кривой, лежащей в плоскости (7.39), содержащей
центр притяжения Q и ортогональной вектору с.
Эта плоскость — плоскость мгновенной орбиты — совпадает с сопри¬
касающейся плоскостью реальной траектории спутника в ее начальной
точке Роу поэтому для вектора площадей с устанавливается теперь (на¬
ряду с его известным механическим смыслом) простой геометрический
смысл: вектор площадей с коллинеарен вектору бинормали Э пространст¬
венной траектории ИСЗ: с=^р.
Для дальнейшего исследования мгновенной орбиты и фактического
нахождения ее перейдем к иной системе координат, к такой, в одной из ко¬
ординатных плоскостей которой находилась бы мгновенная орбита. Для
этого исходную — геоцентрическую — систему координат (рис. 26) пере¬
несем сначала параллельно
самой себе так, чтобы старое
начало О совпало с мгновен¬
ным центром Q. Тогда новые
координаты х', у', z' любой
точки пространства будут
*'=*—а, у'=у—$, z'=z—y.
(7.41)
Затем обычным образом
(см. [31]) перейдем от си¬
стемы Qx'y'z' к системе
Q£r|£ (рис. 27), плоскость
Q\г] которой совпадает с плос¬
костью мгновенной орбиты
(7.39) вследствие того, что
положительное направление
оси Q£ мы примем по направ¬
лению вектора площадей с;
ось Q£ направим по вектору
Лапласа Я (он лежит на оси
симметрии мгновенной орби¬
ты и направлен в ее перигей), а ось Qr^ возьмем так, чтобы дополнить
новую систему координат до правой.
Положение новой системы координат Q£r]£ можно задать либо углами
Эйлера Q, со, /, либо направляющими косинусами ее осей Q\, Qtj, Q£,
относительно осей Ох', Оу', Oz' старой системы Qx'y'z'. Углы Эйлера
показаны на рис. 27: это угол прецессии триедра Q£r—долгота
восходящего узла Q, угол собственного вращения триедра — угловое
расстояние перицентра от узла со и угол нутации трехгранника (угол
между положительными направлениями осей Qz' и Q£), или наклонение
орбиты /.
Рис. 27. Участок траектории ИСЗ (система
координат — «орбитальная»)
181
Эйлеровы углы, характеризующие положение плоскости мгновенной
орбиты в пространстве и орбиты в ее плоскости, могут быть получены
в соответствии с общей теорией кеплерова движения [31], т. е. по фор¬
мулам
с, . л/ с? + с\ к
tg £2 = , tgi = , tg о =-т- sin Й. (7.42)
C2 c3 Ъ.
Однако важно заметить, что в рассматриваемом случае нецентрального
движения они, как и параметры орбиты (см. далее) р и е, характери¬
зующие ее размеры и форму, являются зависящими от времени, и всякий
заданный набор их всегда относится к некоторой точке Р орбиты,
считаемой начальной. Если интегралы движения (7.35) и (7.36) по началь¬
ным условиям (7.34) уже получены, то (7.42) теперь дают положение
плоскости (Q и /) мгновенной орбиты и угловое расстояние перицентра
от узла со.
Направляющие косинусы новых осей относительно осей системы
координат Qx'y'z' даются приводимой таблицей.
1
Л
t
г
Aii
С2^3 С3^2
£i_
X
сХ
с
А.2
ГзА-i—CiA-з
С2
у'
А,
сХ
С
А.з
С\Х2—С2 All
Сз
Z
X
сХ
с
Поэтому новые координаты £, т], £ выражаются через исходные х, у, z
следующим образом:
All Ain AlO
6 = -i-(* - а) + — P) + -±(z - т).
- с, (*-«) + ■ -^ (У- P)+ (г-у),
(7.43)
СI Сп Со
z = -±(х - а) + -j-(y - Р) + -j-(z - у).
Формулы обратного перехода имеют вид
. \ е. . С2^з — сз^2 . с\ v
* = « + — I + Т1 + —С,
Ain CqAii с 1 Aiq С(\
у = р + Xs + Д ч + Vs’ (7'44)
. h «. . С1^2 ~~ С2^1 . С3 у
г = V + — I + ^ т, + —С-
182
В новой системе координат уравнения мгновенной (для точки Р0)
орбиты суть
£=0, til=c2-ki, (7.45)
где теперь / = д/g2 + г\2.
Введем полярные орбитальные координаты / и f (f — истинная анома¬
лия) относительно притягивающего центра Q по обычным формулам
£=/ cos /, г|=/ sin /. (7.46)
Тогда из второго уравнения (7.45) имеем
l=p/(\+e cos f) (7.47)
— уравнение мгновенной орбиты в полярных координатах /, f, в котором
р — параметр, е — эксцентриситет, просто выражаемые через уже най¬
денные константы орбиты,
p=c2/\i, е=к/р. (7.48)
Осталось определить шестой — динамический — элемент мгновенной
орбиты или зависящую от него истинную аномалию f в эпоху to, т. е. /0.
Воспользуемся аргументом широты
ц=со + /. (7.49)
Для начальной точки Р0 орбиты этот угол может быть найден по формуле
(см. [142])
tg w0=c3 {zo—y)/ [ci {yo—$)—c2 (xo—a)], (7.50)
после чего с учетом (7.42) легко вычисляются на эпоху to истинная ано¬
малия
fo—u0—со (7.51)
и эксцентрическая аномалия
£o=2arctg(S^±^tg4).
(7.52)
Затем определяется и средняя аномалия М в начальный момент to
Мо=Е0—е sin £0, (7.53)
и с учетом среднего движения п
n = ^f\L/a3/2 (а = р/( 1 — е2)) (7.54)
момент т прохождения спутника через перигей
т = tQ - -i-Mo (7.55)
как последний элемент мгновенной орбиты ИСЗ. Таким образом, полу¬
чены все элементы мгновенного эллипса.
Движение ИСЗ (точнее, проекции спутника на его мгновенную
плоскость) находится также по приведенным формулам, причем поря¬
док определения движения в любой момент времени t таков: по заданному
t определяется средняя аномалия
М=п (*—т), (7.56)
183
по ней из решения уравнения Кеплера
Е—esm Е=М (7.57)
находится эксцентрическая Еу по которой легко определяется и истинная
аномалия f на тот же момент t:
(7.58)
Затем по формуле (7.47) находится /, по которому (совместно с f) вы¬
числяются т|, потом ху у, z и, наконец, составляющие скорости
х, уу z для момента t по следующим формулам [142]:
С Г ^1 • г , С2^3 /, гч|
x = j[~irsmf + л (<? + cos f)\
*=f[-xsin^+ сЛ7/‘"3(е + cos4
i = j[-^S'mf+ С|"2~С2Х' (g + cosfij.
(7.59)
причем имеют место контрольные равенства
~\Jх2 + у2 + z2 = уд/1 + 2е cos / + е2 = +"/* = v.
(7.60)
Заметим, кстати, что теперь на любой момент времени /, для которого
определяется положение ИСЗ на мгновенной орбите, может быть вы¬
числена дуга 5 мгновенного эллипса, пройденная проекцией спутника
на соприкасающуюся плоскость в начальной точке Ро орбиты. Пользуясь
(7.47), имеем
[ V1 + е2 + cos ф
s = p\ — т <*ф. (7.61)
(1 + е cos фу
Так как этот интеграл эллиптический, то он может быть вычислен только
по формулам механических квадратур. Более важна, однако, принципи¬
альная возможность: формула (7.61) позволяет считать известной дугу
мгновенной траектории спутника, т. е. дугу эллипса (7.47).
Итак, только что приведенное интегрирование уравнений движения
ИСЗ в поле точечного источника притяжения Q, смещенного отно¬
сительно центра О масс планеты, доставило как промежуточную орбиту,
так и промежуточное движение. Последнее имеет ясный смысл, оно,
с одной стороны, приближенно отражает реальное движение ИСЗ, заме¬
няя его пространственную траекторию плоской кривой, наиболее к ней
близкой, а с другой (и это более важно) — выражает точное движение
по плоскости промежуточной орбиты ортогональной проекции спутника.
А за счет того, что эта плоскость для пространственной орбиты есть
соприкасающаяся (в начальной точке движения), то значит, теперь име¬
184
ются возможности уточнения и орбиты *) и найденного промежуточного
движения методами дифференциальной геометрии.
Уточнение орбиты (на каждом шаге ее построения) включает в себя
переход к естественной спутникоцентрической системе координат, вы¬
числение инвариантов траектории — кривизны и кручения как минимум
в двух точках дуги, переход от дуги эллипса к дуге пространственной
орбиты и, наконец, вычисление с нужной точностью координат спутника
и его скорости в конечной точке дуги обсуждаемого шага построения
траектории.
§ 29. О прямом методе построения орбит ИСЗ
Геометрические построения траектории спутника (§ 28) осуществля¬
ются согласно традиционному принципу небесной механики, в соответст¬
вии с которым сначала строится промежуточная орбита, а затем вы¬
полняется ее уточнение. И единственное, но основополагающее отличие
в реализации этого принципа лежит в ином выборе промежуточной
орбиты, за каковую вместо кеплерова эллипса ИСЗ в центральном
поле берется его мгновенная орбита в нецентральном поле. Все остальные
отличия наших построений от классических несущественны, и они суть
следствия указанного главного. Значит, общий план изучения орбиты
дифференциально-геометрическими средствами так же, как и обще¬
принятыми методами, заключается в последовательном исследовании
свойств траектории начиная с простейших локальных и кончая объ¬
единением всех их в целое, что и приводит к фактическому нахождению
ее (траектории), а это индуктивный подход к проблеме. Но возможен
и другой подход — дедуктивный: по данным о структуре поля сил и на¬
чальным условиям движения данного спутника найти его траекторию,
а затем исследовать нужные ее свойства. Такая схема изучения орбиты
ИСЗ требует прямого, непосредственного метода ее построения. Рас¬
смотрим его сущность.
Этот метод мы называем прямым методом потому, что в нем исключено
предварительное получение мгновенной (или невозмущенной промежу¬
точной в соответствии с принятыми понятиями небесной механики для
аналитических методов) орбиты, а сразу определяется реальная «воз¬
мущенная» траектория спутника, как это делается в ее численных методах.
Основная идея этого метода (разложение координат точек орбиты в сте¬
пенной ряд), как и сам метод в целом, безусловно, не новы; проблема имеет
давнюю историю, основные вехи которой целесообразно отметить далее.
На характер сил F, действующих на спутник (единичной массы),
ограничений в методе не накладывается: это либо одни гравитационные
силы, либо сумма всех известных сил различного происхождения. Однако
предполагается определенная гладкость их составляющих:
Fx=fi(x, у, z), Fy=f2 (х, у, z), Fz=f3{x, у, г),
именно в некоторой окрестности начальной точки Ро траектории, через
*) Под уточнением орбиты здесь понимается именно переход от плоской к про¬
странственной орбите.
7 Г. А. Мещеряков
185
которую спутник проходит В эпоху t=to, функции fi(x, у, 2,) (/=1, 2, 3)
должны быть непрерывными по всем своим аргументам и удовлетворять
по каждому из них условию Липшица.
В основе метода лежат дифференциальные уравнения динамики точки
(7-7)
x=Fx, y=Fу, z=Fг,
записанные в геоцентрической инерциальной системе координат Oxyz.
Пусть начальные условия (7.34) отнесены к точке /V, выпишем их под¬
робнее:
Xp0 = x(t) \l=tg = x0, yP(j = y(t) | , = ,o = y0, Zpo = z(t)\ ( = ,o = z0, (7.62)
xp0 = x'(t)\t=to = x0, yP(> = y'(t)\ t=,0=y0> zPg=z'(t)\ l=,o=z0. (7.63)
Будем интегрировать уравнения (7.7) при начальных условиях (7.62),
(7.63) классическим методом разложения искомого решения
{*(/), у (0, z(0)= г (t)
в ряд, что при заданных правых частях уравнений системы (7.7) потре¬
буют на деле одних лишь дифференцирований.
В силу требований, наложенных на правые части Д дифференциальных
уравнений (7.7), и при заданных начальных условиях (7.62), (7.63),
скажем, что в соответствии с теоремой Пеано (см. [131]) через начальную
точку (t0y *о, Уо, 20, х0, уо, г'о) проходит по крайней мере одна интегральная
кривая системы (7.7), а в соответствии с теоремой единственности
Осгуда на некотором промежутке (а, b), окружающем точку t=t0,
существует одна и только одна система функций
x=x(t), y=y(t), z=z{t), (7.64)
удовлетворяющих системе (7.7) и принимающих при t=to вместе с их
соответствующими производными значения (7.62), (7.63); полученное
на промежутке (а, Ь) решение может быть продолжено в обе стороны.
Если дополнительно предположить, что правые части ft уравнений
(7.7) аналитичны в окрестности t=to по х, у, z и /, то по теореме Коши
и функции (7.64) как решения системы (7.7) также будут аналити¬
ческими функциями t. Значит, искомое решение, определяемое в этой
области, где выполняются все условия, наложенные на правые части
уравнений системы (7.7), представляется сходящимся рядом (для крат¬
кости три скалярные функции (7.64) объединены в одну — векторную)
Г(0 = г(/„ + АО = £ ± г<"> (*0) (ДО", (7.65)
или при сокращенных обозначениях г(п) (/0)=Гоп) и (Дt)n=&tn
rM = го “h г0Д/ + г — |- г —— + + • • • (7.65а)
Этот ряд описывает реальную траекторию ИСЗ в поле гравитационных
сил. Действительно, в этом случае правые части уравнений движения
186
аналитичны по всем своим аргументам: во вращающейся с Землей
системе координат они гармоничны и, значит, аналитичны по пространст¬
венным координатам, а функциональная структура матрицы перехода
от этой системы координат к инерциальной показывает, что они, во-пер¬
вых, аналитичны также по времени, и, во-вторых, сохраняют свою анали¬
тичность по координатам инерциальной системы. При учете же в рамках
данного метода сил негравитационного характера необходимо предвари¬
тельное выяснение их свойств, в частности аналитичности их состав¬
ляющих.
Практическая реализация аналитического по своей сути прямого
метода интегрирования уравнений движения ИСЗ должна осуществляться
численно. При некотором заранее установленном шаге Д/ строится дуга
орбиты ^Р0Р[ по формуле вида (7.65а), при этом г0 и f0 задаются
начальными условиями (7.62), (7.63), Го=Ря = Ро в силу интегрируемого
уравнения (7.7), а последующие производные, например г0 и rb(IV), в началь¬
ной точке Ро орбиты вычисляются на основании ранее приведенных
формул (7.20), (7.24а), в которых частные производные составляющих
Fx, Fy, Fz действующей на спутник силы по координатам и проекции
вектора скорости v=r должны быть взяты в начальной точке Ро орбиты.
Таким образом, формула (7.65а) сразу дает дугу траектории ИСЗ
в окрестности ее известной точки Р0 с достаточно высокой степенью
точности, если, конечно, в этой точке надежно известна структура
поля сил, определяющих движение спутника в ее окрестности. Последнее
в настоящее время можно считать гарантированным для поля гравита¬
ционных сил при расчете орбит внеатмосферных спутников. Вопрос учета
негравитационных сил требует дополнительных исследований для каж¬
дого конкретного ИСЗ.
Получив по формуле типа (7.65а) положение ИСЗ на эпоху t\ = /о + АС
т. е. точку г (С), и удостоверившись в достаточной точности ее определения
(в противном случае уменьшаем шаг), находим затем значение его
скорости v в найденной точке:
V, = *(/,) = г0 + r'0At +'г0^ + r(0lv>^f + ■■■ (7.66)
Имея теперь точку Рi, т. е. ri = r(C), и значение скорости ИСЗ
в ней, т. е. ft = r(/i), и вычислив в ней все нужные величины, характе¬
ризующие поле сил, принимаем эту точку за начальную и переходим
к следующему шагу построения дуги ^PiP2, и так по шагам
строим искомую траекторию ИСЗ в заданном поле действующих на него
сил.
Для практической реализации метода надо иметь формулу для выбора
шага At интегрирования уравнений движения (7.7). Проще всего его полу¬
чить по первому из опускаемых членов ряда (7.65).
Если при вычислении траектории учитываются члены ряда (7.65) до
некоторого порядка п^З *), то вводя априорно абсолютную погрешность
*) Большее сокращение ряда, например до п=2, приводит к замене дуги
орбиты на каждом шаге интегрирования дугой плоской кривой, что для счета явно
невыгодно.
7*
187
'п
.= 16г | ее построения, имеем
(7.67)
Входящая сюда производная г(л + 1), вычисляемая в начальной точке Р0
орбиты, может быть оценена с использованием легко получаемых прибли¬
женных формул вида
в которых р — гравитационный параметр мгновенного центра притяжения
Q, отражающий в окрестности точки Р0 траектории ИСЗ действие
всех учитываемых гравитационных сил.
Не сравнивая прямого способа интегрирования уравнений движения
с применяемыми другими численными методами, сошлемся на уже имею¬
щиеся [114] результаты их сопоставления в пользу первого. Подчеркнем
лишь его главное отличие от них: довольно кропотливые и требующие
большой тщательности операции интегрирования правых частей уравне¬
ний движения на каждом шаге в указанных методах заменены в об¬
суждаемом более простой операцией дифференцирования составляющих
сил притяжения (по сути, потенциала и его производных) и последующим
вычислением их в начальных точках шагов построения орбиты.
Итак, выше было рассмотрено интегрирование уравнений (7.7)
движения ИСЗ при начальных условиях (7.62), (7.63) методом раз¬
ложения искомого решения в ряд: обсуждены существование решения
(7.65) в окрестности начальной точки траектории, единственность и схо¬
димость, приведена методика построения орбиты. Однако ряд (7.65)
допускает и иное толкование.
Ставя вопрос изучения в заданном поле сил траектории ИСЗ в окрест¬
ности ее произвольной точки Р0 (при t=to) с известными координатами
(7.62) и при известной скорости движения v=r(fo)=ro в ней, можно
сразу «разложить движение в ряд», т. е. представить исследуемую
орбиту рядом вида (7.65), сохраняя в нем определенное число первых
слагаемых и вычисляя коэффициенты такого ряда на основании уравнений
его движения (7.7). Это, с одной стороны, доставляет каноническое
представление (7.65а) орбиты ИСЗ, аналогичное в некотором смысле
каноническому представлению пространственной кривой, а с другой —
дает метод непосредственного построения (по шагам) его траектории.
Как бы, однако, мы ни смотрели на ряд (7.65), он и его первые
частные суммы описывают главную часть движения ИСЗ. Чтобы повысить
точность представления траектории спутника на каждом шаге ее по¬
строения и по возможности увеличить последний, надо, однако, иметь
удобные формулы для вычисления последовательных производных г('г)
(при 3) в начальной точке каждого шага. Для этого надо знать струк¬
туру поля сил в окрестности такой точки, ибо нужные производные суть
dt’
(7.68)
188
Производные действующей на ИСЗ силы F вычисляются по правилам
дифференцирования сложной функции (см., например, приведенные выше
формулы (7.20), (7.24а)), и в них входят, в свою очередь, две группы
производных: во-первых, частные производные (различных порядков)
силы по координатам, и, во-вторых, производные последние (также разных
порядков) по времени. Указанные производные второй группы в начальной
точке шага построения орбиты просто выражаются через начальные
условия (7.62), (7.63) и ранее найденные частные производные силы
по координатам. Вычисление же этих производных, т. е. производных пер¬
вой группы, связано со свойствами поля сил F и требует их конкретного
задания.
Под силой F в прямом методе понимается сумма всех учитываемых
сил, действующих на спутник, т. е.
F = £ grad V, + £ ТГР. (7.69)
i k
где Vt — потенциалы притяжения Земли, Луны, Солнца, планет и т. д.,
a Ffrp — силы негравитационного характера; все они должны быть
записаны в инерциальной системе координат, зафиксированной своим
началом в центре масс Земли.
Исходя из такого общего задания поля сил нельзя, очевидно, со¬
ставить каких-либо универсальных алгоритмов для последовательного
определения производных г(п), входящих в основную формулу (7.65)
метода. Это возможно только в отдельных частных случаях. Так, напри¬
мер, для поля сил центральной точечной массы удобная процедура
вычисления этих производных, как и само основное разложение (7.65)
были даны Лагранжем еще в 1778 г., а исследования области сходимости
выполнены в начале нашего века У. Гамильтоном и Ф. Мультоном
(см. [150]). Непосредственное использование разложения Тейлора (7.65)
при совместном интегрировании уравнений небесной механики, т. е. при
решении задачи N тел, было всесторонне исследовано в 1970 г. В. Ф. Мя-
чиным и О. А. Сизовой [114], которые, применив способ Д. Ф. Стеф-
фенсена (1956, 1957 гг.) последовательного вычисления производных,
требующий введения вспомогательных функций*), условно назвали ме¬
тод, разработанный ими, методом Тейлора—Стеффенсена. И если в [114]
детально разработан случай задачи пяти точечных тел, то в работе [134]
обсуждены возожности применения метода Тейлора — Стеффенсена при
определении возмущенного движения ИСЗ в поле тяготения Земли,
представляемом ее многоточечной моделью, хотя число масс при этом
довольно велико (обычно 100). В последние годы при прогнозировании
*) Применительно к задаче двух тел Лагранж пользовался, по сути дела, тремя
вспомогательными переменными (одна алгебраически связана с г, это и=г~3, и
две — р и q — дифференциальным образом выражены через г2, именно через
первую и вторую ее производные по времени (см. [112]). В методе Стеффенсена
фигурируют две вспомогательные функции, за которые принимаются непосредст¬
венно г2 и г-3 (см. [114]). За счет последнего осуществляется линеаризация
системы интегрируемых уравнений движения, которая естественно дополняется при
этом зависимыми линейными дифференциальными уравнениями, определяющими
введенные функции [134].
189
орбит ИСЗ отрабатывались и другие варианты использования метода
Тейлора — Стеффенсена [41].
Однако прямой метод имеет более широкое значение, он вообще
занимает исключительное положение среди всех известных методов не¬
бесной механики, что обусловлено, в первую очередь, возможностью
его трактовки не только как способа интегрирования уравнений движения,
но и как непосредственного способа описания и построения орбиты:
его использование в общем случае требует лишь исследования отбрасыва¬
емых членов разложения ряда (7.65), и в принципе в разложении
можно сохранить сколь угодно много членов и определять движение
на значительные интервалы времени; в частных же случаях вычисления
траекторий ИСЗ последовательное применение его по шагам достаточно
обосновано и может использоваться на практике.
В таком трактовании метода он может использоваться при про¬
гнозировании орбит ИСЗ не только для поля сил точечных масс [134], а в
общем случае поля всех учитываемых сил (7.69). И тогда можно ограни¬
читься сначала счетом приведенных выше ((7.20) и (7.24а)) производных
третьего и четвертого порядков, что соответствует учету вторых и третьих
частных производных потенциала притяжения. В настоящее время при
интегрировании уравнений движения ИСЗ даже самыми эффективными
методами (см., например, [134]), привлекают только первые (без которых
счет вообще невозможен), а при уточнении орбит иногда и вторые
производные потенциала. Однако преобразование и развитие известных
формул Каннингхэма [182], выполненное недавно Абрикосовым [2],
позволяет экономично считать производные потенциала и более высоких
порядков.
В заключение скажем, что сущность прямого метода построения
орбит ИСЗ в заданном поле сил (7.69) при начальных условиях (7.62),
(7.63) и устанавливаемом шаге построения (7.67) выражается форму¬
лами (7.65), (7.66) со счетом в последних производных (7.20), (7.24а)
с привлечением либо формул Абрикосова, если потенциалы Земли, Луны
и т. д. заданы комплектами стоксовых постоянных, либо по элементарно
получаемым выражениям частных производных потенциалов наборов
точечных масс, если используются многоточечные модели гео- и селено-
потенциала.
Возвращаясь, наконец, к названию описанного метода, подчеркнем,
что это «трижды прямой» метод: во-первых, он доставляет непосредствен¬
ное построение траектории ИСЗ, хотя и может интерпретироваться
как метод интегрирования уравнений его движения; во-вторых, он позво¬
ляет получать сразу «возмущенную» всеми учитываемыми источниками
сил орбиту, минуя построение какой-либо промежуточной орбиты; и,
в-третьих, в нем все нужные производные находятся прямым диффе¬
ренцированием сил (или потенциалов) без введения — для их вычисле¬
ния — каких-либо вспомогательных функций, как это требуется в мето¬
дах Лагранжа и Тейлора — Стеффенсена.
Коэффициенты гравитационного поля модели GEM-10, приведенные к главным осям инерции Земли
ч
VO
о
4
5
CL
с
I I
со —■
CD СМ
О О
СО LO
ю см
CD
о" o'
Ю CD CD CD 00
O' О О О О
I I I II
СО Ю О О
00 CD N О Ю
СО ^ О
СМ -—1 '—1
СО СО о
00 ю о
СО СО Ю
h- 05 —I
о" о о"
00 Tf О СМ
t-- О СО
00 — ^ СО
СО СМ Ю N
00 СО СМ Ю
iCD Г'- О ID
o' о" о" о'
I I
о о
о о
о о
о —
о г-
о о
О СО
СМ —
о о"
ООО
ООО
ООО
14. О CD
Tt СО 00
СО — —
Ю СМ ^
СЧ <Я ~
о" о' о"
CD CD CD CD
О О О О
INI
О О О О
CD СО h- О
-00 0)0)
со О Tf CD
N CD О О
tJ- CD CM СО
o" o' о' o'
I I
o^-- см^ o, — CM^CO o, — CM^CO ^
CM С i см" со' со" со" со" Tt*"
III IIII II I II
ID CO CO
CD N CO
— О ID
^ СО О
00 Tt* 00
^ 00 CM
o" o" o"
t*- t^- О CD
CD О CD —
CD N CD
00 О 00 CO
ID 00 О О
О — —
o" o" o" o"
— CM
о о
— о
— CM
^ 00
ID CO
o" o"
N CM О
rf 00 CM
CM О 00
CO h— CO
h- —
— 05 CO
o" o" o"
I II I
CO CT> ID
ООО
I I I
ООО
ID О О
ID О О
CD О N
— о CM
^ О СО
00 ^
^ О СМ
о" о" о"
CD ID CD CD
О О О О
1111
О О О О
о о о о
о о о о
NODD
CD — О —
00 СО СО
Ю О О —
О) СМ 00 N
о" о" о' о"
CD CD
О О
I I
— СО
тг со
1D Ю
CD CD CD
ООО
I I I
ООО
ООО
ООО
ID О —
О CD ^
СМ О СО
ID О О
СО О —
о" о" о"
О — СМ О^ — СМ^ О О — СМ^ о ^
см" см" см' со" со" со" со" -Я Tf" Tt*'
CD CD с
О О <
I I I
CD ^
CO ^
00 ID
ID О
CM CO
-Ю
o" o'
I I I
ON^t
h- h- CO
О О CD
DID-
h- — ^
О О ID
CM ^ CO
CM CO CM
o" o" o"
t"- CD 00
ООО
I I I
О CM N
О rt- CD
CO CO
00 Tf
00 CO
— CM —
o' o' o"
CD CD N
ООО
I I I
CM Tf CO
О 00 О
CD О CM
— СО О
Tt* CO 00
Я 4. Я
o' o' o"
I I I
CO CO I
ООО'
I I I
ООО
О CM N
О — —
О Ю CD
CD CM —
О CO CM
o" o" o"
I I
I I
О о
о о
о о
о со
О 00
со ^
CD CD
^ CD
о" о"
II I II
ООО
ООО
ООО
О СО о
TMDO
CD О 00
CDDTf
СМ СО
ООО
ООО
ООО
00 ID
00 О О
СО О ID
CD СО СО
Tf ID СМ
О О О О О О
I III
О — CM, СО ^ О^ — СМ СО^ ^ 1D^ СО^
ID" ld" id" ld" id" ld" CD" CD" CD" CD" CD" Сd" CD"
■ CO CO CO t—
5 0 0 0 0
I I I I
CD N CD С
О О О С
I I I
— 00
О —
ь- о
— о
00 см
О ^
о" о"
CM — о
DMDD
O'tOOO
t"- Tt* О
ID О О О
CO’t-N
О CM 00
LD О 00
^ h- СО
О СО N
Ю — —
— О CM
00 СО О —
О 00 О 00
— СМ 00
N О ID -
— СМ 00 CD
— Tt- СО СМ
ОООО ООООООО
I I
h- h- I
О О '
I I
II II II I II II
о о
о о
см
—I Tf
00 ^
CD ID
ОООО
СМ 00 СО —
СО ID ID СМ
СМ —■ —
LD СО О LD
<Я 'Я ‘Я я
о" о" о" о"
I I
о, — CM СО, Ю
ю" ю" ld" Ю ld" ld"
О О
О о
о о
CD О
^ CD
О О
ID CD
— h-
О о
о о
CD СМ
СО о
CD О
Tf CD
5 0 0 0
5 0 0 0
ООО
ООО
CD — О
CM tJ* lD
СО —
О CM ID
ООООООО
I I
I I
O, — CM CO Tt lD^ CO
CD CO CD CD CD CO CD
191
Продолжение табл.
I I
00 00 CD
00 Tf N
О 00 N
— Tf Tf
-IN(N
CMCOO
Ю
CO CO —
o' o' o'
CD N Ю N
О О О О
I I I I
OO CN CO Tt
DOrf 00
CD ^ Ю CD
tJ* —< CD —
lOCOiOCN
О О 00 00
N N CO W
— CS — CS
o' o' o' o'
I I I
I I
I I
—с —
—I CM CM
00 N- 00
00 Tt- О
(M(MO
N LD —■
ПЮ CO
o' o' o'
Tf CD
О N
О CD
О О
^ CM
LO CO
N Ю
o' o'
I I
00 О О
Г- — 00
(NN(N
NOLO
Ю О —
— rf lD^
o' o' o'
'-NON-N-N-CDNCD
000000000
1 II II I И I
^^WNNOONCD
DOtJ-OOOICOOO-
OODCDNDlOOO
00 CD I"- oo — tF CO
Is- N CO 00 CO —■ CD
О О
CD ^
CM CD
О CM
Ю N
(NN
o' o'
— CD CM <
-rf — 05 (
05 CM Ю I
о о” о' о' о' о о
CD Ю -
4f О "
— СО с
III I
Г"- N
о о
I I
00 N
о см
тГ ю
о ^
00 о
О CD
о'о'
I I
1111
CD N-
о О О
I I I
о о
о о
2 °
о n
—. 00
О Tf
00 О
О —
О О
о о
о о
N 00
СО СО
СО Ю
—I см
см —
о' о'
I I
ООО
ООО
- Ю ОО
N СО СО
CD СО СМ
см — см
о' о' о'
N N
О О о
I I I
ООО
ООО
ООО
ООО
О 05 ^
00 ^ ^
О — со
1DSC
N N- со
ООО
N CD
о о
Mill
о о о <
о о о <
ООО
О о LO
CD см СО
CD —1 см .
LO lO 1 С
N 00 СО I
о о
о о
см ^
о о о' о' о о о о
I I
о о
о о
о о
о о
о о
о о
Ю N
— см
о' о'
I
N N N '
ООО'
I I I
ООО
ООО
ООО
ООО
N- 00 СО
CD 00 N
N О CM
00 — Ю
о' о' о'
1111
о о о о
о о о о
о о о о
— ООО
Tt — О О
N- 05 СО 00
— О О CD
СМ 00 00 о
о' о' о' о'
I I
о о
о о
о о
см о
LO см
О со
см о
— СО
о' о'
I I
о. °i Я Я Я Я Я Я Я Я Я Я Я Я Я
N N-' N N tC iC N-' tC oo' CO CO CO CO CO CO CO CO
Я °i Я Я Я Я Я Я Я
о о о о о о о о о о
о — см_
о' о' о'
N
CD
CD
CD
N
00
N
00
N
N
CD
CD
N
LD
CD
N
N
CD
N
N
N
oo
CD
N~
N~
00
о
1
О
1
О
I
О
I
о
О
I
о
1
о
1
О
I
о
1
О
I
О
I
О
I
О
1
О
I
О
I
О
I
O
I
о
1
O
I
О
1
O
I
о
1
О
I
О
I
О
I
О
I
1
о
1
1
О
1
Tt*
, ,
1
tJ"
1
о
1
1
00
1
Ю
1
N-
1
CO
1
1
LD
1
N
1
Tj<
1
LD
1
CO
1
05
1
00
1
ID
1
ID
1
N-
1
Tt*
1
CD
1
1
N
см
СО
CD
о
СМ
00
00
—
—
Ю
CD
00
CM
Я
—
05
—
LD
О
CD
CD
00
CD
00
—
LD
о
О
00
о
СО
N
CM
00
o
—*
05
—*
05
05
о
00
00
Tf
Я
00
CM
CO
CM
00
ID
N
О
см
Tf
CD
Tt*
о
Th
ID
CD
i—i
CM
00
N-
CO
О
О
О
CD
LD
CO
n
Ю
о
СО
00
СМ
СМ
N
00
N
LD
CM
О
N
05
N
05
ID
CM
tJ*
N-
CD
—
—
N
CD
о
Ю
CD
о
СМ
05
CO
см
О
CM
LD
CD
n
IN-
00
_
О
00
CO
CM
N-
LD
ID
1—<
СО
ID
CD
СО
CD
00
iD
о
со
N
CM
N
05
00
CD
CD
CO
CO
CM
rt-
CM
00
о
CM
см
СО
00
Ю
со
ID
СО
ID
CO
Я
—1
—1
CM
я
CO
CO
CD_
Я
N-
оооооооо
ООООООООО
oooooooooo
I I I
I I I
NCDN
ООО
I I I
Ю Ю СО
00 о о
о г- см
N СМ СО
(NON
LD — LD
IN
CD
CD
CD
CD
00
CD
00
N
N
N
N
CD
N
N
N
CD
N
CD
N
CD
N
N
N
CD
CD
N
О
I
О
I
О
I
О
I
О
I
о
1
О
I
О
I
О
I
О
1
О
I
О
I
О
1
О
1
О
I
О
I
О
I
О
I
О
I
О
О
О
I
О
I
О
1
О
I
О
I
С5
1
О
1
О
1
О
1
О
1
О
1
о
1
О
1
О
1
О
1
о
1
О
1
О
1
О
1
о
1
О
1
О
1
О
1
О
1
О
О
О
1
О
1
О
о
1
О
1
О
О
о
о
О
о
О
о
о
о
о
о
о
о
О
о
о
о
О
о
о
О
О
о
о
о
О
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О
о
о
о
О
о
о
о
о
о
о
о
см
05
LD
Tf
о
N
о
о
о
о
о
со
о
о
о
CD
о
о
тГ
о
о
о
TJ*
о
о
00
о
Tf
N-
О
о
N
о
00
о
о
00
см
со
СО
СО
00
СО
05
N
05
CD
ID
N
1^.
Ю
CD
05
ю
СМ
LD
СО
N
о
LD
N
CD
СО
ID
Ю
00
см
N
00
CD
05
см
05
со
N-
СМ
rf
N
о
CD
N
о
N-
см
N
05
N
CD
СМ
CD
ID
СО
CD
05
00
ID
О
05
00
05
СМ
со
CM
СМ
CD
СО
Tt*
ю
СМ
N
—
СМ
—
CD
CD
—
СМ
—
СМ
—
—
—
LD
—
—
rt*
оооооооо
ооооооооо
INI I
> о о о
I I I
о о о о
I I
N
N N
О
i
О О
1 1
1
о
1 1
о о
о
о о
о
о о
о
о о
—
О 05
N
Tj* ID
СМ
05 00
ID
N 00
ООО
О- я. Я Я Я Я Я Я
г^Г г^Г (С tC fC tC [С Я
Я я Я Я Я Я Я. Я Я
оо' оо' СО СО СО СО об СО СО
СО — CM СО Я ID CD N 00 О
ооооооооо о
о — см
о' о' о'
192
(DON-
ООО
I I I
СП —' СО
Tf О N-
СО — сг»
ЮСОЬ
— ^ о
СМ — 1П
о" о" о" о" о"
II II
N- О О СО N-
о о о о о
I I I II
00 СО Ю Ф1 *Ф
О СМ —I 00 N-
О) СО О
о см о
О СО СО
о о
N N Ф
со —
о о" о"
I I
CM N-
CM П-
О СО
CM Ф
ю —
Ф N-
Г- N- СО I
О О О С
I I I
СО Ь- 00
О Ф CD
о — ю
см N- ю
см см о
О со о
О О со
см со —
о" о" о"
I I I
I I I
I I I I I I I I I
N 00
о ю
СО N-
—< N-
о ю
00 Ф
о о
o' o'*
со со
см Ф
00 о-
СО СО
о см
СО 00_
о' о"
I I
— — см см
СП СМ О СО
СО О) СО СО
ф СО 00 00
N- Ю СП N
СМ — см Ф^
o' o' о” o'
IN 00
см о
юсм.
о" о"
I I
) со О со С
) О СМ СО С
« —I — ю
) 05 ф сп
- 00 см см
00 со СО
— ^ СО
г- — —
o' о" о
СО со
—.
Ф 00
N- 00
о ю
N- N
о —
о см
Ю СО
— 00
ю ю
CM N
оо оо N
ООО
I I I
ф —■ ю
ооом*
о о n-
СО СМ СО
СО СО Ф
-—1 М" N
см ф о
см Ф —
о о о о о о о
I I I
N
N-
о
1
о
1
1
см
1
N.
СО
ю
ю
ф
СО
см
ф
СО
СО
о
ф
ч.
О
о"
о"
I I I I I II I
о о
о о
о о
— о
Tf
о
ю о
—, N
о" о"
I I
о о
о о
о о
о о
N N.
Ф СП
CM N
Ф IN
о* о"
I
о о о о
о о о о
оо о о
о о о о
О 00 со со
’tOCOO)
О СМ со СП
Ю 00 Ф СМ
o' о" o'" o'
N
со
N-
N n
N
N-
N-
N
IN
о
1
о
1
о
1
о о
1 1
о
1
о
1
о
1
о
1
о
1
1
о
1
о
1
о
1 1
0:0
1
о
1
о
1
о
1
о
1
о
о
о
о
OI о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
СО
о
о о
о
о
о
о
о
СП
00
см
00. ю
ю
ф
00
СП
о
со
Ф
ю
СО.00
00
ф
ф
ф
00
СП
со
см
N ф
со
со
ю
со
00
ОО-
СО
LO СО
о
см
со
—4
ю
I
ооооооооооо
I I I II I II
N
N
N
СП N
N-
N-
n-
N
n-
00
N-
N
N
о
1
о
1
о
1
о о
1 • 1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
1
о
1
о
1
о
о
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
N
о
00
ф
ф
05
N-
00
о
со
—1
ф
ф
о
о
о
см
in
ф
см
N
ю
со
05
ф
СП
00
N
СО
00
CD
Ф
05
о
ф
ю
ф
см
—
00
со
СО
см
—
см
со
*—1
со
ю
о о о о
о о о о о о о
о"
о о
о О —
О ф^ LO <0 N 00^ О —^ 0_ — CQ СО Ф. Ю СО^ N СЮ СП ——
о" о o’ o' о о о" о ——" —" ——Г —Г —Г ——Г — —Г
о_ —см.
см" см" см" см" см" см" см" см" см" см" см" см" см" со" со" со"
СП N
N
N
N
N
00
п-
N-
п-
CD
ь-
t—
оо
N-
п-
о о
1 1
о
1
©
о
1
о.
1
о
j
о
1
o
1
о
1
о
1
о
о
о
о
1
о
1
о
1
о
1
о
1
о
1
1 1
СО Ф
1
00
1
ф
1
ф
,
1
СО
1
1
о
1
CD
CD
ю
СП
1
IN
1
со
1
05
1
1
п-
1
о
о n
N
м
05
СО
05
LO
о
см
см
CD
о
CD
CD
со
со
IN-
СП CD
CD
CD
ф
N-
LO
CD
о
00
CD
N-
IN
CD
со
СО
CD
CD
— СП
о
со
о
со
ю
о
о
-3*
см
—1
ю
00
п-
00
со
ю
— 00
00
ю
СО
CM
со
ю
05
о
см
05
—
СО
ю
00
о
СП ю
—«
см
_
CD
00
Tj*
П-
00
о
СП
см
о
со
00
CD
см
ю
СО CD
о
СП
см
СО
CD
Ю
СО
IN-
00
СО
СП
со
05
о
ф —<
ю
CD
CD
CM
CD
05
Tt*
05
со
—<
—1
СО
CD
о о о о
о о
о о
oooooooooooo
N-
00
N-
N-
00
00
N-
IN-
00
IN
оо
N-
п-
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
О
I
О
I
о
1
о
1
о
1
о
1
о
1
о
1
1
05
1
1
см
00
1
00
1
CD
1
о
1
со
1
О
1
tJ*
1
CD
1
N-
1
CD
1
п-
1
со
1
CD
00
05
со
СО
IN
05
CD
00
—1
СМ
о
05
ю
IN-
Tt-
N-
о
со
IN
00
00
см
00
О
00
05
см
СО
о
со
СО
00
00
05
о
СО
05
см
ю
СП
О
о
■«*
^1-
00
со
о
00
CM
ю
CD
со
—
Tt*
00
N-
LO
Is-
СП
см
N-
00
о
05
CD
00
г-
со
05
СМ
05
о
05
05
п-
см
CD
05
CM
г*-
CD
N-
см
05
о
00
см
СО
со
—1
ю
см
со
CM
см
—1
—
СЯ
СО
00
oooooooooooo
о"
ООО
IIIII
ОО N-
N
N-
00
N
CD
CD
N-
00
N
N-
N
N.
N-
00
00
N-
N
N-
О о
1 1
О
1
О
1
о
1
о
1
о
1
О
1
О
1
О
1
О
1
О
1
О
1
О
I
о
1
о
1
о
1
о
1
о
1
о
1
1 1
о о
1
о
1
о
1
о
1
о
1
о
1
о
I
О
1
о
1
о
1
о
1
о
1
О
1
о
1
о
1
о
1
о
1
о
1
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
05
со
о
о
о
о
о
о
о
о
о
о
о
о
о ю
00
СО
о
CD
со
N
о
05
ю
CD
см
■*#*
о
о
со
00
о
In ^
CD
00
00
00
CD
N
N-
со
см
00
00
о
о
00
CD
00 см
ю
05
СО
о
СМ
О
N
00
CD
LO
см
о
05
ю
00
Tt*
00
05 05
Ю
СО
00
ю
СМ
—<
00
со
см
ю
о" о"
о"
о о
ООО
ООО
о о
о о о о о о о
I I
N-
N
00
N
N
N-
00
N
N-
IN
00
N-
СО
N
N- N
о
1
о
j
о
1
О
1
О
I
О
I
о
1
О
1
О
I
О
1
о
1
О
1
О
О
I
О о
1 1
1
о
1
о
1
о
1
о
1
О
1
О
1
о
1
о
1
О
1
о
1
о
1
о
о
1
О
1 !
О О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О О
о
о
о
о
о
о
о
о
о
о
о
о
о
О О
о
о
см
тГ
см
о
05
"ф
о
CD
о
ю
ю о
ю
о
см
ю
’ф
00
СП
ю
00
о
N
CD
05
— 05
СП
CD
N
N
см
см
CD
N-
N
00
N
СО
00
СМ
CD СО
СО
LO
Tt*
-Ф
N
00
—-
СМ
со
—<
CD
■ф
•ф -Ф
о о о о о о
1 1
о о о о о о о
I 1 1 1
ООО
1
оооооооо ————————————
О. ~~1 °~}
см см см см см см см см см см см см см со" со" со"
193
Г'-Г-.ООГ'-ООЬ-Г'-ООСООО^Г^Г'-ОО
(MNtDOOCOlOTtO
0 050(M05CD(N(N
TfOl-iOOOlMX)
NCO^CDOOlOCO'tOCO
—'^^CDCO—■ — 00 00O5CO
g *§
a oo —
(D Ю CO Tf Ю Oi ’t ЮЮ - Ю
NNCDTf--0O5OOOCOO
CN СП G\ — CN ^ t"- CD CS СП —„
o' О o' o' О о' О о' О О О
OCOOinN0(DOO(M(NlOCO(N-
ON'tO0in0CDW0OlONCO
(N00N-C
SS88S
.^-NOTf-^CONO)
00 t^- h- 00 00
ooooooooooo oooooooooooooo ooooo
lO0O(NOOCOOOO-OOO)(MON
OOOJ’-in-iOCOtNlO-CCOlW^
00 CM П- CO_ —^ ^ ^ CN CM CD СЧ CM^ CD^ CM_
o' o o' o’" o' o' о' О* о' О o' o' o' o'
CD CO CM О
—' N Ю Ю 00
О CD 00 —« CO
СО О О О О
СО — ^ CM 00
ооооо
нннтнп
ooooooooooo
sssllissilfe
CXD -- CD^ Ю —I ID ^ CO CO О CD
o' o' o' o' o' o' o' o' o' o' o'
I III I
h-h-OOt^t^OOt^-OOt^OOt^-t^.t^-00
oooooooooooooo
00008000000000
58888?
JNON-C
58?
58?
iCCDNNCM’tNLOCDOOCOO^O
CM^CO-COO)CM(DNNNOllOlO
СО-нЮ-CMCD --^-нЮСОСМтГ Tf
o' o' o' О О
OOOOOOOOO
II II I
00 r-- h- 00
Mill
88888
ff
О — CM CO O-CMCOTt
CO D_ CD_ П- 00 <0 —; — — 0_ — CM^ CO Tt D^ CD^ СЮ СП —^ ~ ^ O^ — CM_ CO ^ D^
CO CO CO CO CO CO CO CO CO CO CO Tf' t}-' Tt Tt Tt rt d'd'd" d d'd'
?!!??Г1Т1Г1 Iff!!!
CHCMOOCDOCO — ЮСОО
CMOOOCMCDOt^-CDCD^1 —
ЮЮООООСОСОООСМООО
i'COCDQ-^-^lOOO
СМСОЮООЮСО — DOOD
lOCMCDOJWOONTfN^iO-CO'tO CM —> CO CM CM —
CO CO —> СО О — 00 CO — CD Ю О Tt* D — CD CM CM 00 D
CDCO-O-OTfOoO'tOOO-N^ -CDCDNIOCO
OINCOOOOCONIOCO-COCDCD-N О О CD Tf- O) ’t
-(DO-NO-ONNC^NCMO)^ О^ООЮтГО
oooooooo<
CO-ONIMO'tNcOCMOiOfNiOCM SSJiOOON
<N —i CM СО CO CM ~ CM^ 00 <N » CN — CO —
o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o'
I I I I I I I I I I
NOONNONNNNNN NNNN0ONNNNNNN0ONN 00 00 OO 1^- t^- 00
00007 = 00000 0000000 = 00000 = 0 = = = 0 = 0
|8|88|||8|8IIIIIJIIIIIIIII111111
ЮОО-О0-ООСМО CMCOt— —'DCMCD^COCMCDOOO—'O CD ^ 00 CM D
OCDTfOO - rf D - CM О cOt-'-OOOOCOCDDDOO—'Ю—■ — ЮФМ^ЮОО
CM О CD CO 00 — СМ^^СОЮ (N -4 СО СО Ю СО CM СО СО Ю СМ^ 00^ СО (N СО^ОО^ Ю Ю
о о о' о' о' о о' о' о' о' о о' о' о' о' о' о' о' о' о' о' о' о' о' о' о о' о' о' о' о о
О —' СМ СО О - СМ со Tf
СО ^ D CD <ХЭ СП — — —I <D — СМ^ СО Tt Ю CD_ СЮ СП — —О — СМ^ СО ^
СО СО СО СО СО СО СО СО СО СО СО ^ Tf rf ^ тр ^ ^ ^ lo' Ю d' Ю d'd'
194
LD CO Tf
CO СО 00
'tOlN
00 со 00
CM CO
о CO CO
Tf 00 CO
00 LO Tf
o' o' o'"
- h- oo t
> О О С
I I
Tf Tf
о CM
П- Ю
00 Ю
о CM
ID CO
СО О
Tf сю
o' o'
CO b- CM
о — Tf
id CO —
00 CO CM
ID 00 't
NCMCJ)
h- 00 CM
— —I CO
I I
CO 00
CO 00
LD —
CM 00
CM 00
CO CM
I I
о о о о о
о о
I
I ! I I I I II
. h- 00
з О О
I I
ID b>-
— О
Ь- 00
Tf О
СО О
— СМ
Tf 00
оо ь-
— 00
—I Tf
О СО
CM id
О О О О
О) Г-
00 СП
СМ Ю
h- О
ID СО
f^Tf
о' о'
СО СТ. Г-
'—- тГ 05
^ — о
Tf СО
О) со см
СО —; со
о' о о'
СО Tf
СО Tf
О) 00
СО СО
00 —<
СМС|
о' о'
I I
П- 00
о о
I I
со со
Ю СМ
СО t—
CONN
ООО
I I I
Tf 00 00
— СО О
СО О О
О со о
00 05 Tf
- см п- оо
5 СМ 00 00
- — — 00
О О С
I I
^ п-
о о
I I
о о
I I
— о
см см
ю см
СО СО
ю —
см eg
о' о' о' о'
Tf СО
СО 00
ID СМ
п- со
СП о
О СП N
ООО
I I I
О со СО
— СП —
СМ 00 о
см ^ см
со — со
СП —I
о' о' о'
t"- 00
о о
I I
n-t^00n-t^00b-00
оооооооо
I n I I I I I
о о
о о
о о
о о
Tf Tf
LD О
00 п-
со СО
о' о' о' о'
о о
о о
СО О
со со
f- Tf
СО LD
о о
о о
о о
о о
О со
Tf Tf
ID СП
00 —
о' о'
Г-- О- Г— I
ООО'
I I I
I I
П- 00
о о
I I
о о о о
о о о о
—I о см о
О LD О О
п- со Tf со
— СО СМ со
о' о' о' о'
I I I
ООО
ООО
СП Tf* СО
озюсо
СО LD О
— со см
о' о' о'
о о
о о
см о
о о,
о о
00 О
Tf Tf
со см
СО Tf
о' о' о о
I I I
Ю 00
ID 00
со СП
00 п-
о о
I I
о о
о о
о о
о о
О со
о о
— 00
00^ СО
о' о'
п- оо
о о
I I
о о
о о
о о
о о
00 О
— см —
о' о'
п- п- ОС
ООО
■I I I
ООО
ООО
ООО
ООО
— СП о
ID П- О
г-, ь- см
О С4 00_
о' о' о' о' о'
П- 00
о о
I I
о о
о о
о о
о о
ю о
I I
о о
о о
о о
о о
СП П-
СМ Tf
п- ю
см —
о' о'
I
I I
о о
о о
о о
о о
О LD
СО Tf
Ю —1
СП —
о' о'
ООО
ООО
ООО
ООО
О СО о
Tf О СП
Tf ю Ю
—I Tf Tf
о' о' о'
lOlDiOlDlDiOlOlOlOiO СОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСОСО
I I
00
r-.
п-
00
п-
00
со
п-
СО
п-
п-
п-
00
00
00
Г"-
t"-
п-
СО
С"-
п-
h-
оо
05
п-
со
оо
о
1
О
I
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
О
1
О
1
о
1
о
1
о
1
о
1
о
1
о
1
о
О
I
о
1
о
1
о
1
о
1
о
1
о
1
о
1
1
со
1
О
1
00
1
о
1
СО
1
00
1
05
1
1
LD
1
со
1
СП
1
ID
1
r^-
1
1
г*-
1
Tf
1
CM
1
1
СП
1
00
1
ID
1
о
1
Tf
1
О
1
СО
1
ID
1
1
о
1
г-
1
Tf
1
05
CO
00
п-
см
СП
СО
со
h-
LD
—X
см
ID
ь.
CM
05
05
05
00
СО
ID
о
00
h-
см
Tf
5
LD
о
1^-
00
00
00
ю
п-
ID
ю
п-
О
Tf
со
о
СО
СП
СО
Tf
Tf
о
СО
СО
г—,
00
СО
05
п-
О
ID
СП
см
00
СМ
CO
h-
п-
о
см
05
Tf
СП
СМ
СО
СО
Г--
СО
LD
oo
СП
со
см
г-
см
00
05
05
00
05
О
СО
05
00
о
05
CO
00
СО
Tf
см
со
СП
СО
Tf
Tf
см
Tf
СП
со
П-
00
05
ю
LD
Tf
00
Tf
О
LD
СО
СМ
Tf
СП
CO
Tf
СП
о
h-
СО
00
см
05
00
_<
п-
00
Tf
_
CO
см
о
со
00
СМ
_
СО
Tf
CM
оо
СО
05
СО
05
LD
О
СП
со
со
00
см
СО
Tf
см
СО
LD
LD
П-
СП
00
см
СО
п-
LD
ID
о
со
см
h-
00
Tf
Tf
—1
со
Tf
СО
—
СО
СО
СМ
со
Tf
Tf
—
05
CO
LD
—
со
—
—"
—
—
Tf
CM
CM
со
—
—■
СО
Tf CM -
00 см с
— 00 l
ID 00 t
CM 00 с
— О •
о' о' о' о' о' о' о' о' о' о' о' о' о' о' о' о' о' о' о' о'
I М I III
о о
I
о о о о о
о о
I
о о о о о о
I I I
п- п-
п-
п-
f"
00
п-
п-
00
00
г-.
п-
00
г-
п- п-
00
п-
f-
ь-
п-
п-
00
00
п-
00
о о
1 1
о
1
о
1
o
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
оо
1 1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
1 1
о о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1 1
о о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
П- 05
00
ID
п-
о
Tf
ю
о
со
о
СО
fr.
о
ю
о
00
00
о —
о
о
СО
СО
СО
п-
h-
СП
см
о
о
ID
о
—1
f- Ю
СП
Tf
п-
см
см
LD
СО
см
о
со
Tf
ID
00
f-
Tf О
оо
см
о
СО
00
СО
о
СО
СО
Tf
05
05
см
о
00 п-
со
CM
СП
о
Tf
со
05
05
см
о
СО
05
05
00
Tf
LD
Tf СО
г-
Г"-
Tf
п-
Tf
Tf
ю
см
см
05
о
со
Tf
со
СМ LD
см
—1
—
00
со
см
со
—
СО
со
см
—1
со
со
>—1
—
см см
см
см
—
—
со
—
СО
’—■
Tf
05
—
СО
со
оооооооооо
ооооооооооооооооо
оооооооо
I I I
О — CM СО Tf id
СО h- 00 СП ——I —^ — — —
lD ld' id ld' ю' ld' Ю LD lo' ld'
О — CM CO Tf Ю CO
о, '1 ^ ^ ^ °°, ’“I
CO CD со CO CO CO CO 0 CO CO CO CO CD CO CO CO CD
О — CM CO Tf ld со П-
П-' (С П-' п-T
195
Продолжение табл.
05 h-
о о
I I
Ю
Tt- CD
— О
см ю
со о
СО CD
CM CD
00 Ю
o' o'
(^.ООГ'-^ООООГ'-ОО
оооооооо
I I II I I I I
CD CM
00 О
О CM
CM —
CD CO
oT o'-
I
(0 — 0
— CM CM
— СП ^
МПОО
LO CO CO
— CM ^
o' o' o'
I I I
CD 00 CD
CM CD rt-
^ — О
00 —
СО Ю CM
ID — Cg
o' o' o'
I I
Г'-
Г"-
00
00
Г"-
Г'-
оо
г^-
Г--
Г"-
Г--
оо оо
о
1
о
1
о
1
о
1
о
1
о
1
О
I
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
О О
I I
1
см
1
см
1
ь-
1
Г--
1
со
1
о
1
О
1
00
1
о
1
1
1
о
1
ю
1
CM
1
СП
1
СО
1 1
СО CD
о
Ю
со
см
00
со
см
00
00
о
г^-
о
со
СО
Ю СО
о
CD
—м
CD
CD
см
CD
со
CD
О
ю
00
00
см
ю
CD СП
о
h-
t"-
о
00
CD
СО
00
ь-
CD
СО
о
00
со
СО Ь-
СО
о
ю
о
Г'-
СП
о
Ь-
CD
—
00
о
СО СМ
СП
см
ь-
h-
О
СО
СМ
CD
см
ю
СО 00
00
00
t'-
СО
CD
см
CD
ю
Г--
о>
00
CD
Tf
Г- CD
—
СО
СМ
см
—
—
СМ
■'f
—
—
CM
—
со
Ю —
о о
I
oooooooooooooooo
II I II
I I I I I I I I I I
о о
о о
о о
о о
о о
о см
00 о
см см
о' о'
I
о о
о о
о о
о о
00 ю
о о
о о
о о
о о
LD 00
00 00
ю о
о о о о
о о о о
о о о о
о о о о
CD О — О
^ CD СМ Ю
-N-N
h-
h-
00
00
1"-
00
00
t"-
Г--
!>■
Г"-
Г--
00
00 h-
О
I
о
1
С5
о
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о о
1 1
1
О
1
о
о
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1 1
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
05
см
о
о
г-
о
о
г-.
со
CD
05
см
см
о
О 00
см
СП
00
_
о
1—,
05
05
СО
СО
г-.
00
00
CD
ID
h- —
05
ю
о
см
00
05
о
h-
см
о
05
см
о
00
СО 05
см
со
05
00
—
см
СО
00
—
—
СО
—
—
ID СМ
оооооооо
оооооооооооооооооо
I I
III I
I I I
t— t"— t— t"— t"— t— t—
00 00 00 00 00 00 00 CXD 00 00 00 00 00 00 00 00 00 00 00
Г--
00
00
г^-
t'-
00
Г-- 00
00
Г-.
Г"-
00
г-.
h-
h-
о
г-
ь-
оо
00
00 00
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о о
1 • 1
o
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
7
о
1
о
1
о
1
о
О
1
о
1
О О
I I
3
1
05
1
см
1
00
1
1
ь-
1
1
СП
1
CO
1 1
о —
1
CM
1
СП
1
ю
1
СП
1
Ю
1
1
LD
1
1
1
ю
1
со
1
00
1
1
см
о
1
CD
1
1 1
Г"-
ас
о
00
СО
1^-
СП
CD
h-
CD
CM
—
05
со
05
см
г-
00
CD
t"-
ID
CD
—
ID
f-.
т*« CD
<v
см
СО
о
CD
СП
h-
ID
— 00
00
г-
t"-
Ю
05
Г--
CD
со
00
о
05
о
05
Ю
00
CD
f-.
см
05
о
ID
о —
05
ь-
о
00
со
CD
см
CD
CD
CD
—*
СО
CD
CM CM
со
ю
CD
00
CD
00
CM 05
05
CM
СО
CM
CD
00
о
—
—
05
о
—
—
"Ф
CD
ID 00
к
00
CD
о
ID
t^.
CD
LO
r- CD
CO
00
05
о
Tf
см
о
ID
СО
CM
ID
05
О
00
tJ- ID
О-
со
со
о
1—1
1—1
О CD
о
о
t"-
о
■'f
05
Ю
05
со
со
—
СО
h-
ID
CM CM
Е
Г--
см
СО
—
CM
—
— —
—
—
г-.
СО
со
см
—
СО
—
см
—
CD CO
oooooooooo
1 1 1 1 II
ооооооооооооооооооо
1 1 1 1 1 1 III
N00 00NNNN00NN t"-OOOOl"-f^OO^OOl>-C'-OOl^-^-OOOOl^OOOOOO
oooooooooo ооооооооооооооооооо
I I I I I I I I I I I I I I I I I I I I I I I I I I I I I
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
CM
о
о
ь-
см
05
о
см
о
о
о
—
CD
о
05
о
со
г^
о
см
о
о
о
о о
ID
со
СО
ю
СП
05
CD
Ю
СО
00
''f
CD
Г--
05
05
CD
см
00
05
05
оо
со
00
о о
00
см
05
CD
ID
ю
05
см
о
СО
Ю
см
СО
|>-
см
CD
со
00
t"-
ID СМ
CM
ю
05
см
см
—
—
см
см
см
—
см
СП
—
ю
—
CD
см
см
—
—
СО
CD ID
oooooooooo
II III
^0^0 — CMCO^LOCDt--
Г'-Т (С [С tC гС оГ t^T (С (С
ооооооооооооооооооо
II I I I I I I
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
196
00 00 00
ООО
I I !
о — —
СП ID CD
rt* 00 тр
СО — Ю
СМ Ю О
— 00
СМ СО О
ю —см
о" о' о"
CD 00
о о
I I
t"- CD
О 00
— о
О О
CD СО
LO О
CD ~
— CD
о" о"
1111
h- 00 Г"-
о о о
I I I
СО О О
CM -**
00 —* 00
00 CD
СО СО CM
— I" '
О Ю 00
— СО ~
о" о' о"
h- 00
ООО
I I I
— см —■
CD Г-
СМ Ю ^
— СО О)
00.ON
Ь- СП ~
СО О О
СП 00^ СО^
о' o' о"
OCON
05 ID —
00 СО О
h- СО 00
05 1^- со
00 t'- CD
О 00 Ю
СО СМ^ тр
о" o' o'
) h- CD 00 I
> О О О <
I I I
Ю 00 N
h- CM CD
CD Tf
CO 05 LO
О О 05
N ООО
CM — 00
—^ CO
о о" о
I I
CO CM
CM CO
00 b-
П- ID
05 00
ID tJ-
— О
CO —
o'" o'
CD 05
CD 00
CO CD
05 o
CM h-
— <0
о o'
I I II I II I I
CO ^
Tf CO 05
CM CD 05
00 00 о
00 05 О
CO^ CM^ CD
o' o' o'
CM
CD Ю
CM h-i
CD 05
CM Tt4
Ю rf
o' o'
LD 05 О CO
05 ^ О 00
CD О Tf
CM 00 О CD
1DCOO-
C0^ CN CD СП
o' o' o~ o'
I I I
05 LD 00
Tf — Tf 00
00 CO CM
CO ^ rf О
iD't--
CM^ 00 ~
o' 0“ o' o'
I I
00
00
00
b-
l>-
00
00
b-
h-
f"-
00
h-
00
t"-
t"-
00
00
05
05
f"-
00
r- 00
0
1
О
I
0
1
0
1
0
1
0
1
0
1
0
1
0
1
О
1
0
1
0
1
0
1
0
1
0
1
О
I
О
I
0
1
0
1
O
I
0
1
0
1
0
1
О
I
0
1
О
I
О
I
О
I
0
1
0
1
0
1
О
I
0 0
1 1
1
0
1
О
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
О
1
0
1
0
1
0
1
0
1
0
1
О
1
О
1
0
1
0
1
О
1.
0
1
0
1
0
1
О
1
0
1
О
1
О
1
О
1
0
1
0
1
0
1
О
1 1
0 0
0
О
0
0
0
0
0
0
0
О
0
0
0
0
0
О
О
0
0
О
0
0
0
О
0
О
О
О
0
0
0
О
0 0
0
О
0
0
0
0
0
0
0
О
0
0
0
0
0
О
О
0
0
О
0
0
0
О
0
О
О
О
0
0
0
О
0 0
0
О
0
0
0
0
0
0
0
О
0
0
0
0
0
О
О
0
0
О
0
0
0
О
0
О
О
О
0
0
0
О
00
0
О
0
0
05
00
0
0
t"-
h-
0
CO
0
О
00
0
О
0
ID
CD
О
—H
О
О
О
CO
0
b-
О
Tf 0
0
05
_H
CO
0
00
0
ID
CD
CD
CM
ID
Tf
CO
Tf
О
05
CD
00
CO
CO
CD
_
ID
О
О
05
rt4
CM
ID
—' ID
00
ID
05
0
CM
0
05
05
00
CM
00
CM
ID
t"-
00
LD
CM
4—
h-
’'f
00
1—1
b-
CO
CM
0
CD
CO
—. 00
CO
CM
CM
00
CM
CO
CM
—■*
CM
00
00
CM
CM
—
CO
’—1
05
—•
—1
CM
00
—i ^
00000000000000
III II I III
о о о <
I I I
000000000000000
I I I II I I
I I II I I II I II II
ОС 00 N t
О О О С
I I I
• h- О
5 О —>
I I
h- r- 00 h- h- b-
0000000
I II II I I
^ CM
05
CM
СП
0
ID
05
О
CD
CM
CM
rt4
—4
О
00
00
00
Tt*
00
CO
05
r-
lD
CO
05
00
00
Г4-
0
О
CM СП
f-
CM
—1
ID
0
СО
CM
CO
t"-
LD
0
t--
00
CD
CD
CO
LD
CM
CM
Tf
00
CM
Tj4
CD
r^-
CO
^ CD
CM
Ю
CM
00
00
О
см
CO
CD
CD
00
co
О
00
ID
CM
П-
05
00
,—,
CO
05
CD
00
0
co
00
05 ID
CD
Tt4
CO
1—1
CO
CD
LD
0
b.
CM
CM
CO
00
CM
ID
О
h-
05
ID
h-
ID
«—
05
b-
ID
05
N-
05
ID
ID
05 CD
00
00
ID
О
Tt4
СП
О
00
CO
05
CO
CO
CD
CD
t-~
b-
CM
05
rt4
CM
CM
—*
О
0
CM
Ю
ID
r^
00
CO CM
CM
LD
05
0
СП
ь-
CD
05
CM
00
r-
Tj*
CM
05
00
"34
CD
Tt*
CM
LD
ID
CM
1—
00
00
rt4
05
П- —<
CD
Tt4
CO
LD
0
О
см
Ю
CM
CM
CM
CM
0
CD
CD
CD
ID
rt4
00
О
b-
05
Ю
05
CO
CM
05
О
— CM
05
ID
CM
—4
t".
СО
ID
ID
—_
ID
CD
r-
—*
CO
CM
CD
CO
h-
05
r^-
CM
CM
CD
CM
00000000000000000000
II I I ! I I
OOOOOOOOOOOOOOOO
I II I II I
00
O О
I I
-07
-07
00
О
I
r>.
О
I
00
0
1
00
О
I
t".
O
I
-08
-07
00
0
t"-
O
I
00
0
1
00
0
1
0
1
h-
O
I
t"-
O
I
r-
0
1
00
О
I
Is-
O
I
00
0
1
00
0
1
h-
О
I
00
0
1
00 00
0 0
1 1
t-
О
I
05
0
1
О
I
О
I
0
1
00
О
I
r-
О
I
f'-
0
1
h-
O
I
1 1
88
88
1
О
О
1
О
О
1
0
0
1
О
О
1
О
О
0 0
0 0
0
0
1
О
О
1
0
0
0
0
1
0
0
1
О
О
1
О
О
1
0
0
1
О
О
1
О
О
1
0
0
1
0
0
1
О
О
1
0
0
1 1
0 0
0 0
1
О
О
1
0
0
1
О
О
1
О
О
1
0
0
1
О
О
1
О
О
1
0
0
1
О
О
88
О —
О О
О О
^ CM
О
О
О
О
О
LD
0
0
0
8
О
8
h-
0 0
0 0
O CM
0
0
0
О
О
05
0
0
0
0
0
0
8
О
О
CO
8
CO
0
0
ID
О
О
О
О
О
05
0
0
0
0
0
0
8
О
0
0
0
88
О О
О
О
b-
8
О
О
О
О
О
О
LD
0
0
0
О
О
О
О
О
t"-
0
0
CD
О
О
LD
Tt Tt
h- 00
—■ CM
'^J4 05
CD О
CO —
CD
LD
CD
05
00
CD
^t4
05
05
LD
00
CM
h- CM
^ 05
h- CM
ID
00
CD
Tt4
CM
CM
CO
СП
LD
CD
О
CM
CO
05
CM
t>.
СП
CM
05
CO
ID
00
CD
Tt4
CM
0
CO
ID
OO
Tt4
CM
CD
00
~ Tf
00 —
CD 05
f-
t"-
CM
О
О
LD
ID
О
CM
00
CD
CM
ID
05
LD
Tt4
CD
CO
П-
CM
Tt4
CO
00
CO
CM
o' о o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o'
О — CMCO^iDCDl^-OOCn
О — CM со Ю CD^ h- 00 05 — — —' —1 —1 ^1. 1 ^ ^1.
0505050505050505050505050505050505050505
О — CM CO ^ LD
O-<MC0M*iDCDN00C5--'-'^--
o' o' o' o' o' o' o' o' o' o' o' o' o' o' o' o'
CMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCM
197
Продолжение табл.
I ! N I
П ■ —
tJ-ON
COON
Ф —' ©
00)Ю
© СО —
о" о" о"
00 CD
N О
СП СП
— 00
N 00
©^ —I
о" о"
I I
N
00
N
00
N
05
N
00
CD
00
N
N
N
со
N
N
со
N
N
00
со
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
О
I
О
I
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
f
о
1
о
1
о
1
1
СО
1
ф
1
1
©
1
1
см
1
о
N
1
1
СМ
1
1
N
1
оо
1
©
1
N
1
1
ф
1
ф
1
©
N
1
ф
ф
сО
см
N
©
см
ф
©
СО
см
©
о
ф
©
о
со
N
ю
о
©
СО
00
00
N
N
CD
со
00
00
N
©
©
©
о
СО
со
со
00
ф
I
со
Ф
СО
N
05
ф
СО
©
N
СО
СО
см
©
©
со
см
©
©
СО
©
ф
со
о
ф
о
CD
05
05
N
ф
©
ф
о
N
СО
см
см
©
СО
N
со
05
ф
ф
N
СМ
со
ф
ф
со
©
см
©
о
©
со
см
©
©
©
N
ф
о
CD
ф
N
со
СО
00
см
©
со
.-м
ф
см
см
N
см
©
©
©
см
CD
N
00
ф.
—*
—Ч
—
©
см
—•
—1
©
©
ООО
о"
о о о о о
о”
о о о о
о о
о о о о о
II II I I I II II
§§£
I I I
82 =
о оо со
Ф CO
°0 Ю rf
^ О CD
— СО О
°° CD CM
О o'©"
I I I I I I I I I I I I I I I I I I
О о
о о
ООО
ООО
> о о о
> о о о
"ООО
о с
о с_
О Ф с
CD —■ О Ф —■
(MO)NCO"t
СП —^ N СМ О
о*" о" o' о" o'
I I I
00 00N-N.N-00©N-
оооооооо
I I I I I II I
о о
о о
о о
о о
CD О
о о
о о
о о
о о
— о
" СМ СО
5 © о
< —I ©
Г о о"
I
ООО
ООО
ООО
ООО
О О CD
N N см
ю о —
—« см —<
о" о" О С
I I
ООО
ООО
СП о о
no©
о см о
— 00 ©
ООО
ООО
ООО
ООО
СМ 00 О
СМ 00 Ф
CD см со
см — —■
o' о" o'
I
I
ООО
ООО
ООО
ООО
ООО
N ф —I
— © о
05 СП —<
o' сТ о'
о о
о о
о о
о о
—* СО
СО СО
СО СО
о" о"
I I
ООО
ООО
ООО
ООО
О О 00
Ф N Ф
05 Ф О
CD^CH —
о" о" o'
I I
ООО
ООО
ООО
ООО
о о ©
CM Ф со
СО 05 CD
05 05 —1
© N 00 © О о—'CMCO^LCCDt^-00 05 0—'
-н — — — СМ О—'CMCO'^iDCDf-.OOCn — — —' —> — —' — — —< —« СМСМ О — СМ СО
©
©
N
со
о
©
N
оо
©
СО
ОО
о
СО
N
N
о.
СО
©
N
оо
со
п-
со
©
©
со
п-
N- со
о
1
о
!
о
1
о
1
7
о
1
о
1
о
i
о
1
о
1
о
1
7
о
i
о
1
о
1
о
1
о
1
о
!
о
1
о
1
о
1
о
1
о
1
о
j
о
1
о
1
о
1
о
1
о
i
О О
I i
1
1
со
1
СО
1
со
1
со
1
СО
1
см
1
©
1
©
1
о
1
со
1
ф
1
см
1
о
1
см
1
N
1
©
1
©
1
см
1
©
1
©
ф
1
о
1
см
1
©
1
N-
1
см
1
ф
1 1
© ф
ф
о
©
ф
о
о
о
О0
см
—1
ф
ф
©
СО
о
см
©
©
ф
оо
ф
о
©
N.
оо
© ©
со
©
N
о
со
N
оо
©
©
CO
©
—4
о
N
©
N
о
©
©
©
©
©
©
N-
©
©
©
— N-
со
©
о
ф
ф
со
ф
ф
1—1
©
N
©
ф
ОО
©
ф
©
ф
СО
о
ф
см
см
©
N-
©
о
ф
© ©
СО
©
©
см
©
о
см
N
о
*—1
N
о
—-
со
ф
N
ю
—ч
п»
N.
ф
ф
см
о
о
© ©
со
©
©
СО
см
о
©
N
см
©
N
N
со
со
©
©
ф
со
ю
см
см
,—,
см
—
©
см
_*
N.
© со
©
со
со
©
©
см
©
со
CO
см
©
©
©
N
ф
N
ю
©
©
ю
о
оо
©
©
СО СО
ф
ф
ф
©
со
©
ф
©
CM
©
©
—•
—<
N
см
©
см
©
©
см
см
см
ф
ф
©
см —
о о о о о
оооооооооооооооооооооо
о о
о" о"
III II
II I I I I
о
1
со
о
1
со
о
1
СО
о
1
со
о
1
©
о
1
N>
о
1
оо
о
1
-07
-08
со
о
1
о
1
оо
о
1
оо
о
1
о
j
со
о
1
со
ср
1
-09
N.
о
1
N-
о
1
о
оо
о
1
©
о
1
N-
о
1
N-
о
N-
о
1
©
о
1
00
о
1
оо
©
1
-07
-08
1
о
о
1
о
о
1
о
о
1
о
о
1
о
о
1
о
о
1
о
о
1
о
о
о о
о о
1
о
о
1
о
о
1
о
о
1
о
о
1
о
о
1
о
о
1
о
о
о
о
1
о
о
1
о
о
о
о
1
о
о
1
о
о
1
о
о
о
о
1
о
о
1
о
о
1
о
о
1
о
о
1 1
о о
О о
о
о
©
о
о
о
о
о
о
8
о
8
о
о
о
о
8
8
о
88
—■ о
о
о
о
8
о
о
о
о
о
о
с
о
о
СО
О
о
о
о
о
о
о
о
о
о
о
©
8
©
о
о
г-
о
о
о
8
с
о
о
оо
о
о
ф
о
о
о
о
О
о
о
о
о
о
о
о
о о
о о
— о
©
со
СО
N-
см
ф
со
ф
©
ф
см
см
о
©
со
©
©
©
см
©
ф ©
о ©
см со
ф
ф
см
о
о
см
о
©
©
©
©
N-
©
см
см
©
©
©
©
см
о
оо
©
©
©
©
©
©
со
©
о
со
©
©
СО
см
со
00
СО
о
со
СО
©
©
ф
N-
©
см ©
CM N-
—. ©
о о о о о
оооооооооооооооооооооо
II I II I I I I I
i I
CD N 00 05 О
О — CMCOT*"lDCDt"-a0050 —
—1 —^ СМ О^ —CN ©^ Ф^ © CD N 00^ СП — —^ — —н — ^ «
SSSSS ^^^CMCM^^^CM^^CMCMCMCMCMCMCMC^CMCNCM см см см см
О^ —(N СО
см" см см" см
198
N- 00
о о
I I
N- CO
о о
СО О
N Ю
Ю 00
гр СО
СО —■
ion
o' 0“
00 00 с
О о с
I I
СО 00 ’
СМ СМ I
CM N-
00 n-
гр 00
N о
— гр
СО (О
о" o'
I
I I
00ЮЮ
гр СО О
О IN СО
N- 00 СМ
СО гр СО
~
o' о" о"
I I
I I I
со со о
Т* -Ч —Н
00 N со
СМ СМ гр
СО 00 ю
in гр см
СО СО Ю
СМ —I —^
o' 0“ о"
I I I i I I I I
—. о —'
о- со см
-ON
тр CO гр
I"- ю СО
lO — CM
ю со CM
СО СО гр
СО гр СО
— — СО
О О гр
N СМ
00 СО гр
(О О N
тр N- N-
—. тр CD
CO CM О
ю CM CM
000000000
I I
N-NNOOOOCOOONNC
OOOOOOOOOO
I I I II I II I I I I I II II
- 00 00 00 С
5 О О О С
COO-
СО СО СО
О гр СО
СО — О
со ю
СМ —-^СО
o' 0“ о”
О 00 ю
Ю О 00
05 00 00
СО Ю О
— СО СО
Тр —1
N000
— О —
гр N- О
СМ СО О
гр О СО
тГ О-
СМ СО гр
СМ — СМ
гр 05 СО
00 О со
ю см ю
СМ СО 00
СО О О
СМ 00 со
со о ю
СО гр О С
О СО СО L
СО СО О)
N — СМ
COiON
О СО СМ
- СМ Ю
CM LO СМ
00 СО
О) гр
СО О
СО со
05 СО
СМ см
o' o' o' o' o' o' o' о о о о о о о
1111
I I I
N- N-
00
00
N.
00
N
N-
N
N
00
00
00
N-
N
N- N-
00
00
О О
I I
О
I
О
1
О
I
О
1
О
I
О
I
О
О
I
о
1
о
1
о
1
о
1
о
1
О о
1 1
о
1
0
1
1 1
О о
1
О
1
о
1
О
1
о
1
О
1
О
О
1
О
о
1
о
о
1
о
1
о
1 1
о о
1
о
1
0
о о
о
о
о
О
о
о
о
о
о
о
о
о
о
о о
о
0
о о
о
о
о
О
о
о
о
о
о
о
о
о
о
о о
о
0
о о
о
о
о
О
о
о
о
о
о
о
о
о
о
о о
о
0
СО о
о
о
N*
О
ю
о
N
СО
о
о
о
см
см
05 гр
о
0
N- СО
о
00
СМ
ю
о>
ю
гр
О)
о
N-
ю
00
СО
СО ю
N-
со
О СО
СО
N-
N-
00
N-
N-
СО
05
U0
см
о
00
ю
со о
гр
N-
СО —
00
гр
—*
05
СМ
СМ
—ч
—
N-
—
05
—«
—__
— см
05
СО
o' о о" о" о o' о" o' о” о" о" o' о" о" о" о" о" о" o'
N-
N-
N-
N-
00
N-
00
00
00
о
00
N-
00
00
00
00
N-
О
о
1
О
1
о
о
•|
о
1
о
1
о
1
о
1
7
о
1
о
1
0
1
о
1
о
1
0
1
0
1
О
1
о
1
о
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
0
1
о
1
о
1
0
0
О
о
о
о
о
о
о
о
о
о
о
о
0
о
о
0
0
о
о
о
о
о
о
о
о
о
о
о
о
0
о
о
0
0
о
о
о
о
о
о
о
о
о
о
о
о
О
о
о
0
О
о
см
ю
о
СО
о
о
о
о
о
со
о
о
о
0
05
ю
СО
ю
00
см
00
ю
ю
гр
о
гр
00
см
СО
05
гр
СО
со
о
ю
00
ю
00
СО
05
о
N-
Гр
см
о
05
ю
см
—
—*
см
—
00
ю
СО
СО
05
—<
см
ю
гр
—
—
ОООО
ооооооооооооо
О — СМСО^ЮСОЬОООО - СМ о — CMCO^LOCON-
тр_ lO со N 00_ О —^ ^ ^ ^ — — —I см. СМ_ СМ^ О —^ СМ^ О гр LO СО N 00_ 05 — —^ — — — —^ — —
см" см" см" см" см" см" см" см" см" см" см" см" см" см" см" см" см" см" см" со" со" со" со" со" со" со" со" со" со" со" со" со" со" со" со" со" со"
смсмсмсмсмсмсмсмсмсмсмсмсмсмсмсмсмсмсм смсмсмсмсмсмсмсмсмсмсмсмсмсмсмсмсмсм
О IN
IN
00
N
00
о
о
00
IN
N
00
05
N-
IN
00
05
N.
оо
N-
00
00
00
00
05
00
00
05
00
00
00
N-
00
00
N-
00
05
— 0
1 1
0
1
0
1
о
1
о
1
7
7
о
1
0
1
0
1
о
1
о
1
о
1
0
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
0
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
1 1
СМ N.
1
00
1
1
СО
1
N.
1
N-
1
05
1
05
1
ю
1
0
1
гр
1
см
1
см
1
0
1
05
1
со
1
1
00
1
N.
1
о
1
со
1
СО
1
СО
1
о
1
N-
1
1
N.
1
05
1
N-
1
05
1
СО
1
ю
1
N-
1
05
1
05
1
N-
см —
05
СО
о
см
см
N-
N
—
05
со
05
N-
со
гр
N
N-
см
00
СО
LO
см
со
см
00
ю
см
ю
Гр
00
05
см
СО
СМ 05
CM
05
СО
ю
см
о
со
гр
см
СО
со
о
ю
ю
1—1
гр
05
,
05
СО
ю
00
00
СО
см
тр
ю
ю
ю
СО
ю
см
со
О 05
00
ю
05
см
00
ю
СО
со
N
ю
—с
см
СО
00
СО
05
см
о
о
ю
о
05
со
00
05
СО
ю
см
ю
СО
05
05
о см
0
N-
ю
00
со
05
гр
о
гр
—
—
гр
со
см
—
05
см
гр
гр
ю
N-
СО
о
05
N
со
N
о
о
ю
05
СО
СО
05
00 00
0
гр
00
со
СО
05
00
05
ю
05
со
со
СО
см
00
см
со
Гр
СО
N-
о
ю
ю
со
со
—н
Гр
со
со
00
ю
со
со
о
—
U0 —
СО
гр
СО
05
см
СО
гр
00
СО
СО
05
00
СО
о
см
0
о
00
см
00
05
о
N-
05
см
СО
о
о
со
Гр
Гр
Гр
оо
05 см
гр
см
—
гр*
N-
СО
05
см
см
Ю
СО
—
со
.—1
—
-г
см
см
N.
см
ю
см
см
см
СО
N-
со
00
см
N-
ооооооооооооооооооо
III II 1 II 1 1 1
оооооооооооооооооо
1 INI 1 1 1 1 1 1 1 1
05 00
N
00
N.
00
00
о
N-
N-
00
N-
00
N
N-
00
о
N.
00
N.
00
оо
00
00
00
00
00
00 00
00
00
N
00
00
N-
00
00
о о
1 1
о
1
о
1
о
1
о
1
о
1
7
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
7
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о о
1 1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
1 1
о о
1
о
1
о
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1 1
оо
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о о
со
о
N.
о
о
о
о
со
о
00
о
о
05
о
о
о
Гр
о
о
о
о
о
о
о
о о
о
о
N-
о
о
N-
о
о
О СО
со
г—1
05
05
о
СО
05
—
о
00
Гр
05
N-
о
см
о
Гр
см
ю
05
ю
05
05
о
05 СО
о
LO
00
—<
N-
СО
05
со
со 05
N-
СО
оо
05
о
о
см
N.
Гр
о
05
о
о
N-
о
со
о
00
со
см
см
СО
N« N
о
ю
о
Гр
Гр
ю
Гр
05 СО
00
см
со
—
см
—
см
N-
см
Гр
ю
Гр
см
со
см
Гр
ю
со
00
— см
Гр
СО
Гр
СО
см
о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о" о"
О-СЧСО-^ЮСОКОООО-СМ О — CMCOrpLOCON
’t lO (О N СО О —1 —1 —1 —I — —— — СМСМСМО — CMCO^IO<ON-000> — — —— —
199
Продолжение табл.
I м I I
о о о о о о
I I II
II I I I I I I I I
N 00 00 с
О О О С
I I I
> Г"- 05
> о о
I I
00 N-
о о
I I
00 Г"- 00 Г
о о о с
I I I
о
Ю
CD
LD
СП
CM
CD
00
О
ID
N-
N
LD
CM
CO
ID
CD
N
CD
СП
О
О
00
_
N
N
N
сч
CM
00
О
00
LD
N-
IN
CO
СЧ
Ю
05
—«
—'
00
Tt-
00
CD
CD
00
LD
СП
00
N
CM
CD
СО
CM
ID
СП
CO
N
СП
CM
''f
CD
CM
CO
LD
N
О
co
CD
N
СП
CD
CO
CO
ID
О
CD
CD
00
о
CD
05
00
LD
05
О
00
CO
>D
05
ID
N-
ID
N
О
О
CD
00
CD
CM
00
N-
О
00
''f
00
О
N
—
СП
ID
о
CM
О
Ю
CD
CD
CD
О
СП
N
05
N
00
ID
LD
ID
ID
N
—
ID
О
О
CD
CD
CM
N-
_
CO
CD
СП
CD
CD
N-
00
ID
''f
00
CD
_
IN
CM
CO
СП
CO
rf
—
N-
N
СП
CD
CD
00
N-
О
О
о
О
N
00
N
О
О
CM
О
о
00
О
СП
CD
CD
CM
СП
О
00
00
CO
In
—1
00
05
CM
CO
CM
—
N
CM
CM
—
CD
—•
CM
CM
СП
CM
CD
оосооооооооооооо
INI II II I
о о
I I
о о о о о о
I I I
Is- 00 N-
о о о
00 00 00
о о о
I I I I I I
ООО
ООО
ООО
ООО
ООО
—< СО ^ CM IN. СП
О Ю CD CD Tt- о
—I
o' о" о" о* о-' о"
III II
ООО
ООО
ООО
ООО
О О IN-
00
N-
о
IN
00
00
00
N
N-
N-
N
00
00
00
00
00
00
00
00
00
N
00 (
О
I
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
о
1
о
о
1
о
1
о
1
о
1
о
1
О
1
о <
1
1
О
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
о
1
о
1
о
1
о
1
о
1
о
1
о
о
1
о
1
О 1
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о«
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о«
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О 1
о
со
о
о
о
о
о
00
СО
со
о
о
о
о
о
о
о
о
о
о
о
О 1
СО
о
N
о
N
о
см
о
ID
LD
00
00
00
ID
CD
ID
_|
см <
CD
о
см
см
см
Tt*
со
о
СП
о
о
N
IN
00
О) ■
—
со
IN
N-
СП
*—
CD
со
ID
см
см
СП
00
CD
1
ОООООООООООООООООООООС)
I I
I I I
00 О О — СЧ со O-^CSfC'tlOCDNCOO^O-CNCO't
СЧ^ СЧ^ см СЧ О^ — CM СО Tt ID CD^ N С» СП — — — — СМ CM CS СМ_ СЧ
СО СО СО*" со" со" со" ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ч*<"
CM CM CM CM СМ СМ см СЧ СЧ СЧ СЧ СЧ СМ СЧ СЧ СЧ СЧ СМ СЧ СЧ СЧ СЧ СЧ СЧ СЧ СЧ СЧ сч сч сч сч
n о
о о
I I
00 N 00 00
О О о о
I I II
I I
. 00 00 00 IN 1
5 О О О О <
1111
I I I I I I I I
N N !
о о <
I I
I I I I I I I
00
00
о
см
00
N
СМ
СП
СО
CD
LD
00
05
CO
IN
CM
05
СП
05
CM
00
05
05
CD
OO
CO
05
IN
IN
см
LD
CD
ID
LD
см
00
Ю
CM
CO
О
ID
—1
00
—«
00
IN
—1
CD
CO
о
ID
05
C-l
CM
—<
00
uO
CO
см
см
N
О
LD
<У)
ID
О
00
00
СП
LD
00
CD
CD
СП
CO
ID
05
00
о
CO
CO
CO
05
CO
О
N
N
00
о
CD
О
СП
СП
N
O)
со
N
о
05
ID
CO
Tf
О
CO
CM
О
о
CM
CD
N
00
СМ
00
—
СП
00
О)
ID
00
CM
CM
CM
СП
О
IN
СП
CM
05
00
00
о
N
CD
О
LD
CD
05
см
см
СМ
LD
N
rh
00
О)
ID
N-
ID
—
05
N
05
IN
CD
о
00
ID
О
CD
LD
О
о
ID
LD
00
О)
О)
СМ
СП
СО
СО
00
ID
ID
О
CM
О
T—1
CM
CO
CD
о
О
LD
О
LD
CO
CD
со
СМ
СО
—1
CM
ID
CO
T—^
CO
CO
N
—„
—,
<N
CO
—
LD
N
CM
О О О О о" о"
: I I
ОООООООООООООООООООООС
I I I
III II
I I
I I
00
05
N
N
N
00
00
00
00
N-
00
N
00
N
N
N
00
N
N
00
N
00
00
N
оо
N
00
00
СП
05 00
о
1
о
1
о
1
О
1
О
1
о ■
|
о
1
о
1
о
1
о
1
о
1
о
1
о
1
О
I
О
I
О
1
о
1
О
1
О
1
о
1
О
1
о
1
о
1
о
1
о
1
О
1
о
1
О
I
О
I
О О
I i
1
о
1
о
1
о
1
о
1
о
1
О
1
о
1
о
о
1
о
1
о
1
о
1
о
1
О
1
О
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
о
1
О
1
о
1
О
1
1 !
О О
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
О
О о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о о
о
о
о
ID
о
о
о
о
см
о
о
05
о
N
о
CD
о
о
см
о
00
о
о
о
о о
СО
о
ч*
CD
ID
N
ю
00
ID
N
CD
СО
см
см
CD
_
05
СП
N
Tt-
со
ID
00
05
N
о
О id
00
00
см
О
СО
со
N
СО
о
о
CD
CD
СО
см
00
со
со
05
о
о
CD
N
о
ю
О LD
N
—<
СМ
—ч
05
см
—
—
’—'
<—*
>-*
см
N
CD
—Ч
со
00
—<
1
*—'
N
CD
CD
СМ см
О О О О
о" о"
ооооооооооооо
о"
ооооооооооо
II I III I
I I I
- ^ O — C4 00 rflD'DlNC0050 — СМСО'Ф
O^ ’—^ CM_ CO ID CO N 00 О T—1 —■* <—■ -—- —< -—i — —£\i c\) r\j
СЧСЧСЧСЧСЧСЧСЧСЧСМСЧСЧСМСЧСЧСЧСМСМСЧСМСМСЧСЧСЧСЧСМ
200
Таблица II
Плотностная модель PREM и ее модификация F2(q)
г, км
Модель PREM;
г/см3
Модификация
модели:
Mq); g=r/R
г, км
Модель PREM;
г/см3
Модификация
модели:
52 (q); g=r/R
0
13,0885
13,08836
5701,0
4,38074
4,38182
500,0
13,03406
13,03390
5701,0
3,99212
3,99320
1000,0
12,87076
12,87063
5771,0
3,97582
3,97692
1221,5
12,76361
12,76350
5971,0
3,72375
3,72495
1221,5
12,16633
12,16322
5971,0
3,54326
3,54460
1500,0
12,00988
12,00980
6061,0
3,48952
3,49076
2000,0
11,65478
11,65477
6151,0
3,43577
3,43705
2500,0
11,19067
11,19074
6151,0
3,35949
3,36677
3000,0
10,60153
10,60174
6291,0
3,37471
3,37606
3480,0
9,90344
9,90374
6346,0
3,38075
3,38212
3480,0
5,56645
5,56675
6346,0
2,9
2,90137
3500,0
5,55643
5,55673
6356,0
2,9
2,90138
4000,0
5,30727
5,30772
6356,0
2,6
2,60138
4500,0
5,05472
5,05533
3668,0
2,6
2,60138
5000,0
4,78987
4,79066
6368,0
1,02
1,02138
5550,0
4,50376
4,50475
6371,0
1,02
1.02138
Таблица III
Коэффициенты разложения модельной плотности земных недр 6t2 (х, yf z)
mnk
ЬтпФс• Ю8
mnk
bmrnfic- Ю8
mnk
bmnk&c- Ю8
000
17654,49411
00 1
0
1 00
0
0 1 0
0
002
—77252,71287
1 0 1
0
0 1 1
0
200
— .113614,52640
1 1 0
0
020
— 126235,80990
003
2445,61463
1 02
5200,84930
0 1 2
10242,46097
20 1
—7547,13185
1 1 1
—336,57270
02 1
259,40832
300
—4201,29384
2 1 0
1584,44310
1 20
7437,84242
030
—3919.44648
004
382,89484
1 03
—3416,90396
0 1 3
—4262,47696
202
—924,07069
1 1 2
4693,65716
022
— 1357,91736
30 1
1906,31949
2 1 1
—4011,52327
1 2 1
4463,12908
03 1
5571,11583
4 00
—415,86983
3 1 0
—621,93819
220
3413,10394
1 30
—802,63366
040
544,04607
005
60,70769
1 04
— 1668,36471
0 1 4
532,25115
203
—7486,22695
1 1 3
3080,09286
023
6883,21053
302
4376,15751
2 1 2
1025,17399
1 22
—3185,29863
032.
1399,10121
402
3425,74391
3 1 1
1528,57028
22 1
1753,83683
1 3 1
— 1809,09814
04 1
—3710,87041
500
—486,14436
4 1 0
4466,33087
320
514,58146
230
—9672,10347
1 40
2700,03834
050
1106,18353
006
—68,48371
1 05
— 180,13166
0 1 5
—282,05982
204
—2192,68281
1 1 4
—3120,51931
024
3213,05997
303
261,65936
2 1 3
—556,96390
1 23
— 1004,27880
033
1119,55964
402
2835,09856
3 1 2
5552,46931
222
—3942,57840
1 32
130,18332
042
—2534,45543
50 1 !
—517,51684
4 1 1
2840,88757
32 1
4395,44705
23 1
5128,54383
1 4 1
—2696,50131
05 1
179,23479
600
—471,70143
5 1 0
—452,25985
420
4259,40614
33 0
—206,90656
240
—3606,71111
1 50
58.76228
060
1 408,27965
201
mnk
b,„nk 6C-I0“
mnk
ЬтпФс- Ю8
mnk
ЬтпФс' Ю8
007
89,74338
205
—3601,46690
304
—4299,91440
034
— 1223,91460
223
900,81901
502
2523,77640
2 32
2269,89132
60 1
— 1023,33705
33 1
5920,40224
06 1
497,14527
520
— 196,84040
250
195,31463
008
—20,73280
206
362,06546
305
—292,09823
035
886,06072
2 24
2420,58181
503
222,90448
233
1316,22840
602
838,33708
332
1348,75801
062
211,47534
52 1
380,56730
2 5 1
653,68981
800
—55,41810
5 30
—5320,73872
260
240,87310
009
7,96857
2 07
— 186,022361
306
1848,57860
225
493,83747
504
—2960,97637
234
3669,23137
603
— 166,25757
333
—901,28053
063
—326,24864
522
— 1581,89420
252
— 1237,62532
80 1
—32,66055
53 1
3339,98315
2 6 1
335,68205
900
—65,57711
630
1003,70751
3 60
3173,0104
090
40,09597
0 1 9
130,97064
028
—831,87522
1 27
—212,43122
3 1 6
2808,76859
046
3848,10238
325
508,03510
0 55
2332,64920
424
1030,26169
1 54
35,70085
6 1 3
—2052,36477
343
—459,62354
0 7 3
— 1072,33162
1 О 6 924,23224
1 1 5 1395,29607
2 1 4 —4939,71260
40 9 5812,12834
1 3 3 —5388,95469
4 1 2 3771,69749
1 4 2 670,60245
5 1 1 —2124,34487
2 4 1 1533,18713
70 0 —110,00195
4 3 0 —701,30730
16 0 —97,14101
1 0 7 92,39041
1 1 6 581,48921
2 1 5 —307,87581
4 0 4 —1302,53509
1 3 4 —3299,54442
4 1 3 —148,42328
1 4 3 1403,60760
5 1 2 —800,80113
2 4 2 2407,79388
7 0 1 —49,75257
4 3 1 —1743,19236
1 6 1 —85,19829
7 1 0 797,20740
44 0 —1000,79593
1 7 0 —813,24314
10 8 —134,85647
1 1 7 —30,54020
2 1 6 —548,97132
1 3 5 124,99969
4 1 4 1118,01234
1 4 4 3424,14310
5 1 3 207,95030
2 4 3 2294,94038
7 0 2 915,65773
4 3 2 1698,93156
1 6 2 —1477,21297
7 1 1 —505,96973
4 4 1 —1978,99397
1 7 1 417,53958
8 1 0 —78,85219
54 0 —4817,48761
2 7 0 536,91599
0 0 10 20,52576
20 8 —83,40810
30 7 4821,66962
03 7 —1177,31691
22 6 48,09192
5 0 5 —10108,52619
23 5 123,16566
6 0 4 —453,99799
3 3 4 —126,47309
0 6 4 —3745,69635
52 3 —228,86581
2 5 3 —651,35794
80 2 127,50388
0 1 6
577,96614
025
1729,47316
1 24
—870,93431
3 1 3
1154,08916
043
—3013,29465
322
389,00320
052
502,44329
4 2 1
— 1969 58092
1 5 1
— 191,76791
6 1 0
— 109,50173
340
263,66758
070
—33,06640
0 1 7
— 112,67363
026
214,56642
1 25
— 1050,91521
3 1 4
652,22586
044
—936,25592
323
672,38288
053
— 1011,75168
422
—4812,17305
1 52
1534,95202
6 1 1
378,12410
34 1
—968,21950
07 1
112,44028
620
718,98178
350
5187,44384
080
— 16,10475
0 1 8
545,99589
027
—98,93013
1 26
— 1795,01331
045
—261,63068
324
2066,70020
054
7232,70974
027
—98,93013
1 53
149,51707
6 1 2
—808,67552
342
583,62490
072
— 1993,71864
62 1
1409,92888
35 1
3339,98315
08 1
22,73255
720
1451,24901
450
— 1674,31793
1 80
—287,56101
1 09
—398,57187
1 1 8
—336,42188
2 1 7
— 1151,44394
406
337,91155
1 36
50,23672
4 1 5
3387,25042
1 4 5
484,49592
5 1 4
—3865,15008
244
— 1149,68398
70 3
4792,26077
433
—953,42204
1 63
—228,91627
1 72
861,18489
202
mnk
ЬтпФс- Ю8
mnk
*wVio8
mnk
bmnkbc' Ю8
6
2
2
—864,35639
53
2
1208,50662
4
4
2
1137,52552
3
5
2
— 1209,13445
26
2
1,78441
1
7
2
155,73265
0
8
2
797,21216
90
1
—371,79129
8
1
1
101,37640
7
2
1
—896,04905
63
1
1092.44533
5
4
1
3249,83892
4
5
1
— 1354,55621
36
1
—2075,25022
2
7
1
479,44419
1
8
1
—246,71067
09
1
75,44491
10
0
0
13,91808
9
1
0
170,52016
82
0
—752,96411
7
3
0
—2315,65344
6
4
0
3656,92667
55
0
4747,56799
4
6
0
—3732,25425
3
7
0
—2202,62351
28
0
799,70542
1
9
0
179,33802
0 10
0
—35,36846
00 11
5,63009
1
0 10
—97,66597
0
1
10
—68,61077
20
9
—211,00317
1
1
9
— 191,23952
0
2
9
518,66041
30
8
1668,82547
2
1
8
—377,11750
1
2
8
—540,89962
03
8
1147,98468
4
0
7
1323,74667
3
1
7
1870,16439
22
7
—397,20486
1
3
7
219,38686
0
4
7
—3024,92624
50
6
—4636,77629
4
1
6
1201,11997
3
2
6
—46,46168
23
6
1093,81183
1
4
6
2994,07962
0
5
б
—3302,21465
60
5
— 1844.15101
5
1
5
—3415,09792
4
2
5
49,80970
33
5
—722,01410
2
4
5
1331.11155
1
5
5
— 166,72445
06
5
4117,80125
7
0
4
3257,97804
6
1
4
— 1302,86921
52
4
668,60547
4
3
4
548,58296
3
4
4
—998,93898
25
4
— 1958,87215
1
6
4
—2774,24383
0
7
4
2436,21810
80
3
646,81707
7
1
3
1489,04774
6
2
3
207,17585
53
3
206,93801
4
4
3
—600,39708
3
5
3
388,45749
26
3
—641,30844
1
7
3
11,65308
0
8
3
— 1437,89504
90
2
—540,23585
8
1
2
292,35642
7
2
2
31,49305
63
2
— 140,36432
5
4
2
—774,35455
4
5
2
— 116,39831
36
2
913,13775
2
7
2
589,18799
1
8
2
492,66483
09
2
—419,68422
10
0
1
—48,92467
9
1
1
— 136,48873
82
1
274,14869
7
3
1
236,96763
6
4
1
— 1382,25451
5 5
1
—537,39297
4
6
1
1501,53125
3
7
1
205,27322
28
1
—253,50486
1
9
1
— 17,64648
0 10
1
100,85125
11 0
0
—0,92458
10
1
0
45,50964
9
2
0
587,47133
83
0
779,44408
7
4
0
—3530,04307
6
5
0
2196,38633
56
0
4993,33755
4
7
0
— 1563,34195
3
8
0
— 1815,72813
29
0
244,30011
1
10
0
110,17370
0 11
0
3,13772
00 12
2,12461
1
0 11
—23,01496
0
1
11
—51,02281
20 10
22,57155
1
1
10
52,93864
0
2 10
— 161,89952
30
9
362,20426
2
1
9
43,52923
1
2
9
170,74097
03
9
914,64975
4
0
8
—215,99138
3
1
8
166,87704
22
8
286,93988
1
3
8
—889,91641
0
4
8
1158,29090
50
7
— 1200,16911
4
1
7
— 167,45787
3
2
7
—950,32974
23
7
— 184,00301
1
4
7
—542,42817
0
5
7
—3252,28264
60
6
475,54070
5
1
6
—577,96020
4
2
6
— 1125,86485
33
6
342,53575
2
4
6
—204,23187
1
5
6
2338,04843
06
6
—2134,05608
7
0
5
1135,85025
6
1
5
312,29794
52
5
1181,97294
4
3
5
—397,12141
3
4
5
1333,93404
25
5
622,09439
1
6
5
487,52914
0
7
5
3200,88611
80
4
—286,68290
7
1
4
479,25005
6
2
4
941,75070
53
4
—508,11917
4
4
4
441,43397
3
5
4
11,717769
26
4
26,29507
1
7
4
— 1652,42080
0
8
4
1134,65130
90
3
—299,22053
8
1
3
— 180,75661
7
2
3
—510,52879
63
3
653,03835
5
4
3
— 169,91998
4
5
3
—585,09792
27
3
—510,52878
1
8
3
—90,44596
0
9
3
—879,65296
100
2
43,13539
9
1
2
— 111,38485
8
2
2
—232,51177
73
2
399,55460
6
4
2
149,60789
5
5
2
—535,63493
46
2
—324,99911
3
7
2
250,26774
2
8
2
640,4604
1 9
2
252,11686
0
10
2
— 151,69730
11
0
1
14,94839
10 1
1
27,44822
9
2
1
69,49042
203
mnk
bmncfic' Ю8
mnk
bmnkbc- Ю8
mnk
Ьmnk^c' Ю8
8
3
1
—232,17613
7
4
1
— 163,38704
6
5
1
455,49428
5
6
1
262,49826
4
7
1
—242,32698
3
8
1
— 11,79565
2
9
1
50,90729
1
10
1
6,77575
12
0
0
— 1,15895
11
1
0
—9,11866
10
2
0
33,64420
9
3
0
203,35733
8
4
0
—213,83908
7
5
0
—771,89256
6
6
0
389,25934
5
7
0
797,23453
4
8
0
— 197,00231
3
9
0
—228,34119
21
0
0
24,85325
1
11
0
7,90717
0 12
0
1,90649
СПИСОК ЛИТЕРАТУРЫ
1. Абрикосов О. А. Об определении направлений главных осей инерции Земли //
Кинематика и физика небесных тел. — 1985. — Т. 1, № 6.'— С. 69—71.
2. Абрикосов О. А. О вычислении производных потенциала- притяжения Земли
для целей спутниковой геодезии и геодинамики // Кинематика и физика небес¬
ных тел. — 1986. — Т. 2, № 3. — С. 51—58.
3. Аксенов Е. П. Специальные функции небесной механики. — М.: Наука,
1986.— 318 с.
4. Аксенов Е. П., Гребенников Е. А., Демин В. Г. Обобщенная задача двух непо¬
движных центров и ее применение в теории движения искусственных спутни¬
ков Земли // Астрон. журн. — 1963. — Т. 40, № 2. — С. 363—372.
5. Алексидзе М. А. Об одном представлении аномального гравитационного
поля // ДАН СССР. — 1966. — Т. 170, № 4. — С. 828—830.
6. Андерсон Д. А., Дзевонский А. М. Сейсмическая томография // В мире
науки. — М.: Мир, 1984. — № 12. — С. 16—25.
7. Антонов В. А. Представление гравитационного поля планеты потенциалом
системы точечных масс // Тр. Астрон. обсерватории ЛГУ. — 1978. — Т. 34. —
С. 145—155.
8. Антонов В. А., Тимошкова Е. И., Холшевников К. В. Сравнительные свойства
различных представлений гравитационного поля Земли//Тр. I Орловской
конф. — Киев: Наук, думка, 1982. — С. 93—105.
9. Антонов В. А., Холшевников К. В. О сходимости ряда геопотенциала на зем¬
ной поверхности. I // Астрон. журн. — 1980. — Т. 57, вып. 6. — С. 1323—1330.
10. Антонов В. А., Холшевников К. В. О сходимости ряда геопотенциала на земной
поверхности. II // Астрон. журн. — 1982. — Т. 59, вып. 4. — С. 763—768.
11. Аппель П. Фигуры равновесия вращающейся однородной жидкости.—
Л. — М.: ГТТИ, 1936. — 374 с.
12. Аразов Г. Т. Решение плоской задачи п неподвижных центров // Celest.
Mech. — 1977. — V. 16, № 1. — P. 42.
13. Арсенин В. Н. Об оптимальном суммировании рядов Фурье с приближенными
коэффициентами // ДАН СССР.— 1968. — Т. 183, № 2. — С. 257—260.
14. Атаходжаев М. А., Салихов Ш. И. К вопросу единственности в обратной
задаче теории потенциала // Краевые задачи для диф. уравнений. 4. — Таш¬
кент: Изд-во ФАН УзССР, 1974. — С. 94—98.
15. Ахиезер Н. И. Классическая проблема моментов.— М.: Физматгиз, 1961.—
310 с.
16. Бальмино Дж. Представление потенциала Земли с помощью совокупности
точечных масс, находящихся внутри Земли // Использование искусственных
спутников для геодезии. — М.: Мир, 1975. — С. 178—183.
17. Батраков Ю. В. Промежуточные орбиты, аппроксимирующие начальный уча¬
сток возмущенного движения // Бюл. ИТА. — 1981. — Т. XV. — № 1 (164). —
С. 1—5.
18. Батраков Ю. В. Использование ИСЗ для решения задач планетарной геодезии
и геодинамики // Изучение Земли как планеты методами астрон., геофиз. и
геодезии. — Киев: Наук, думка, 1982. — С. 195—200.
19. Батраков Ю. В., Макарова Е. Н. Обобщенный метод Энке для изучения
возмущенного движения//Бюл. ИТА.— 1979. — Т. XIV.—№ 7 (160).—
С. 397—401.
205
20. Бейтмен Г., Эрдейн А. Высшие трансцендентные функции. Т. I. — М.: Наука,
.1965. — 294 с.
21. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции Т. II. — М.: Наука,
1974. — 295 с.
22. Березин И. С., Жидков И. Я. Методы вычислений. Т. II. — М.: Физматгиз,
1960. — 620 с.
23. Бондарева М. Д., Юркина М. И. Оценка смещения центра масс Земли с прямой
приложения равнодействующей лунного и солнечного притяжения. — М., 1980
(Деп. /ОНТИ ЦНИИГАиК (Деп. от 18.03.1980. — № 24—80) — С. 6—19.
24. Бровар В. В., Юзефович А. П. Параметры лунных масконов. // Современные
проблемы позиционной астронометрии. — М.: Изд-во МГУ, 1975. — С. 303—
312.
25. Буллен К. А. Плотность Земли. — М.: Мир,. 1978. — 437 с.
26. Бурша М. Основы космической геодезии. II. Динамическая космическая гео¬
дезия. — М.: Недра, 1975. — С. 280.
27. Гаврилов В. П. Феноменальные структуры Земли. — М.: Наука, 1978. — 152 с.
28. Гобсон Е. В. Теория сферических и эллипсоидальных функций. — М.: ИЛ,
1952. _ 476 с.
29. Голота П. Представление гравитационного поля Земли с помощью потенциала
точечных масс. // Наблюдения искусств, спутников Земли. — Варшава—
Лодзь, 1979. — No. 18. — С. 159—169.
30. Гравиразведка: Справочник геофизика. — М.: Недра, 1981. — 397 с.
31. Дубошин Г. Н. Небесная механика: основные задачи и методы. — М.: Наука,
1968. — 799 с.
32. Жарков В. Я., Трубицын В. Я. Физика планетных недр. — М.: Наука, 1980. —
448 с.
33. Жонголович И. Д. Внешнее гравитационное поле Земли и фундаментальные
постоянные, связанные с ним // Тр. ин-та теоретич. астрономии. — М. — Л.:
Изд-во АН СССР, 1952. — Вып. III. — 126 с.
34. Жонголович И. Д. Потенциал земного притяжения // Бюл. ИТА. — 1957. —
Т. 6, № 8. — С. 505—523.
35. Зидаров Д. Я. О решении некоторых обратных задач потенциальных полей и
его применения к вопросам геофизики. — София: Изд-во Болгарской Акаде¬
мии Наук, 1968. — 154 с.
36. Зидаров Д. Я. Обратна гравиметрична задача в геопроучването и геоде-
зията. — София: Изд-во на Българската Академии на науките. 1984. —
278 с.
37. Золотов И. Г. О представлении геомагнитного поля при помощи мультипо¬
лей // Геомагнетизм и аэрономия. — 1966. — Т. 6, № 3. — С. 556—567.
38. Иванов В. К- Обратная задач потенциала для тела, близкого к данному //
Изв. АН СССР. Сер. мат. — 1956. — Т. 20. — С. 793—818.
39. Иванов В. К. О приближенном решении операторных уравнений I рода//
Журн. вычисл. математики и мат. физики. — 1966. — Т. 6, № 6. — С. 17—21.
40. Идельсон Н. И. Теория потенциала и ее применения к вопросам геофизики. —
Л. — М.: ГТТИ, 1932. — 348 с.
41. Иодис В. Я. Повышение точности и перспективы численного метода Тейлора—
Стеффенсена. // Всесоюзная конф. «Исследование гравитационного поля и
природных ресурсов Земли космическими средствами» (тезисы докладов). —
Львов, 1984.— С. 15—17.
42. Использование искусственных спутников Земли для геодезии. — М.: Мир,
1975. _ 432 с.
43. Кан М. А. Определение фигуры Земли и аномалий масс по возмущениям орбит
искусственных спутников//Земная кора и верхняя мантия. — М.: Мир,
1972. — С. 25.0—263.
44. Каплан М. Г., Кункиев Б. Г. Модель потенциала Луны с учетом влияния
масконов // Использование искусств, спутников для геодезии. — М.: Мир,
1975. — С. 370—382.
45. Каула У. М. Обзор геодезических параметров // Фундаментальные постоян¬
ные астрономии. — М.: Мир, 1967. — 382 с.
46. Каула У. М. Спутниковая геодезия. — М : Мир, 1970. — 170 с.
206
47. Клеро А. Теория фигуры Земли, основанная на началах гидростатики. —
М. — Л.: Изд-во АН СССР, 1947. — 358 с.
48. Козлов И. С. Задача четырех неподвижных центров и ее приложения к теории
движения небесных тел // Астрон. журн. — 1974. — Т. 51, № 1. — С. 191 —198.
49. Козлов И. С. Интерпретация и приложения задачи четырех неподвижных
центров // Астрон. журн. — 1975. — Т. 52, № 3. — С. 649—655.
50. Котляков Н. С., Глинер Э. Б., Смирнов М. М. Основные дифференциальные
уравнения математической физики. — М.: Физматгиз, 1962. — 767 с.
51. Кринчик Г. С. Физика магнитных явлений. — М.: Изд-во МГУ, 1985. — 335 с.
52. Крылов А. Н. О земном магнетизме. — Петроград: Ред.-изд. отдел морского
комиссариата, 1922. — 184 с.
53. Курант Р., Гильберт Д. Методы математической физики. Т. I. — М. — Л.:
Гостехиздат, 1951. — 476 с.
54. Лаврентьев М. М. О некоторых некорректных задачах математической фи¬
зики. — Новосибирск: Наука. Сиб. отд-ние, 1962. — 92 с.
55. Лазарев П. П. Сочинения. Т. III. Геофизика. — М. — Л.: Изд-во АН СССР,
1950.— 278 с.
56. Лебедев Н. Н. Специальные функции и их приложения. — М.: Гостехиздат,
1953. — 379 с.
57. Лихтенштейн Л. Фигуры равновесия вращающейся жидкости. — М.: Наука,
1965. — 252 с.
58. Лундквист С., Джакалья Дж. Е. О. Представление геопотенциала с помощью
выборочных функций. // Использование искусств, спутников Земли для геоде¬
зии. — М.: Мир, 1975.— С. 184—192.
59. Ляпунов А. М. О некоторых вопросах, относящихся к проблеме Дирихле. //
Работы по теории потенциала. — М. — Л.: Гостехиздат, 1949. — 178 с.
60. Марченко А. Н. О вычислении элементов октаполя Земли // Геодезия, карто¬
графия и аэрофотосъемка. — 1976. — Вып. 23. — С. 54—61.
61. Марченко А. Н. О гравитационном тетраполе Земли .// Геодезия, картография
и аэрофотосъемка. — 1976. — Вып. 24. — С. 63—68.
62. Марченко А. Н. О вычислении моментов гравитационных мультиполей
Земли // Геодезия, картография и аэрофотосъемка. — 1977. — Вып. 25. —
С. 35—41.
63. Марченко А. Н. Преобразования стоксовых постоянных при вращении коорди¬
натной системы // Геодезия, картография и аэрофотосъемка. — 1977. — Вып.
26. — С. 46—55.
64. Марченко А. Н. Использование мультипольного представления потенциала
при изучении гравитационного поля Земли: Канд. дис. — Львов, 1979. —
180 с.
65. Марченко А. Н. Модель точечных масс глобального гравитационного поля
Земли // Геодезия, картография и аэрофотосъемка. — 1980. — Вып. 32. —
С. 81—90.
66. Марченко А. Н. Вариант простейшей модели гравитационного поля Земли. //
Наблюдения ИСЗ. — М., 1984. — № 21 (1982). —С. 138—140.
67. Марченко А. Н. Описание гравитационного поля Земли системой потенциалов
нецентральных мультиполей. I. Теоретические основы метода // Кинематика и
физика небесных тел. — 1987. — Т. 3, № 2. — С. 54—62.
68. Марченко А. Н. Описание гравитационного поля Земли системой потенциалов
нецентральных мультиполей. II. Предварительный мультипольный анализ //
Кинематика и физика небесных тел. — 1987. — Т. 3, № 3. — С. 38—44.
69. Марченко А. Н. и др. Модели точечных масс и их использование в орбитальном
методе спутниковой геодезии. I. // Кинематика и физика небесных тел. —
1985. — Т. 1, № 4. — С. 53—61.
70. Марченко А. Н. и др. Модели точечных масс и их использование в орбитальном
методе спутниковой геодезии. II. // Кинематика и физика небесных тел. —
1985. — Т. 2, № 5. — С. 72—80.
71. Медведев П. П. Методы и результаты спутниковой геодезии // Итоги науки и
техники. Геодезия и аэрофотосъемка — М.: ВИНИТИ, 1980. — Т. 16. — 111с.
72. Медведев П. П. Исследование гравитационного поля и фигуры Земли новыми
методами космической геодезии. // Итоги науки и техники. Геодезия и аэрофо¬
тосъемка. — М.: ВИНИТИ, 1980.— Т. 17.
207
73. Мейман Н. Об одной краевой задаче для полигармонических уравнений //
ДАН СССР. — 1941. - Т. XXXIII. № 4. — С. 275—278.
74. Мещеряков Г. А. О корректности одной обратной задачи теории потеницала //
Изв. АН СССР. Физика Земли. — 1969. — «№8. — С. 54—59.
75. Мещеряков Г. А. О единственности решения одной обратной задачи теории
потенциала // Сиб. мат. журн. — 1970. — Т. XI. — № 5.
76. Мещеряков Г. А. Динамическая фигура Луны и распределение плотности
лунных недр // Астрон. журн. — 1973. — Т. 50, № 1. — С. 186—199.
77. Мещеряков Г. А. О мультипольном представлении гравитационного потен¬
циала//Геодезия, картография и аэрофотосъемка.— 1974. — Вып. 19.—
С. 63—72.
78. Мещеряков Г. А. О среднем значении внутреннего гравитационного потенци¬
ала Земли//Геодезия, картография и аэрофотосъемка. — Львов, 1974.—
Вып. 19. — С. 61—62.
79. Мещеряков Г. А. Использование стоксовых постоянных Земли для уточнения
ее механических моделей // Геодезия, картография и аэрофотосъемка. —
1975. — Вып. 21. — С. 23—30.
80. Мещеряков Г. А. О фигуре Марса // Астрон. журн. — 1975. — Т. 52, № 2. —
С. 374—379.
81. Мещеряков Г. А. О нахождении полюсов сферических функций // Геодезия,
картография и аэрофотосъемка. — 1976. — Вып. 23. — С. 61—66.
82. Мещеряков Г. А. Новая интерпретация представления внешнего гравитацион¬
ного потенциала рядом шаровых функций // Геодезия, картография и аэрофо
тосъемка. — Львов, 1978. — Вып. 28. — С. 68—74.
83. Мещеряков Г. А. О сфероиде Клеро, обобщающем поверхность Марса //
Картографирование Луны и Марса. — М.: Недра, 1978. — С. 28—35.
84. Мещеряков Г. А. О наилучшей квадратической аппроксимации геопотенци-
ала // Наблюдения ИСЗ, № 20. — София:- Изд-во БАН, 1982. — С. 264—269.
85. Мещеряков Г. А. Обратные задачи теории геопотенциала (лекция на Межд.
зимней школе «Теор. и эксп. вопросы планетарной геодинамики», 29.IX—
9.Х. 1983). — Киев. 1983. — 32 с.
86. Мещеряков Г. А. Об одной обратной задаче теории потенциала. // Диффе¬
рент уравнения и их применения. — Львов: Вестн. ЛПИ, 1983. — № 172. —
С. 92—93.
87. Мещеряков Г. А. Использование метода итерации при определении обобщен¬
ных фигур планет. / Ргос. Int. Sym. «Figure of the Earth, the Moon and other
planets» Monograph Series of VUGTK- — Praha, 1983. — P. 143—154.
88. Мещеряков Г. А. О представлении потенциала планеты суммой потенциалов
двух простых слоев // Геодезия, картография и аэрофотосъемка. — 1984. —
Вып. 39. — С. 51—60.
89. Мещеряков Г. А. Основы геометрической теории движения ИСЗ. — Львов,
1984. — 37 с. (Деп. Укр. НИИНТИ; № 509 Ук. — 85ДЕП.)
90. Мещеряков Г. А. Представление потенциала притяжения Земли суммой по¬
тенциалов плоских слоев (концепция гравитирующих дисков) // Тезисы докл.
Всесоюз. конф. «Исследование гравитационного поля и природных ресурсов
Земли космическими средствами». — Львов, 1984. — С. 8—9.
91. Мещеряков Г. А. О представлении потенциала планеты суммой потенциалов
плоских слоев // Геодезия, картография и аэрофотосъемка. — 1984. — Вып.
40. — С. 79—86.
92. Мещеряков Г. А. Об определении физической поверхности Земли с использо¬
ванием параметров геопотенциала, определяемых методами космической
геодезии // Наблюдения ИСЗ. — М., 1984. — № 1 (1982). — С. 131 —137.
93. Мещеряков Г. А. О разложении по шаровым функциям потенциала двойного
слоя, расположенного в плоскости экватора // Геодезия, картография и аэро¬
фотосъемка. — 1985. — Вып. 41. — С. 75—81.
94. Мещеряков Г. А. Потенциалографическая задача и концепция гравитирую¬
щих дисков // Ргос. 5th Int. Symp. «Geodesy and Phvsics of the Earth». —
Potsdam: Veroff. d. Erde, 1985. — N 81. —Teil 11. —S. 78—87.
95. Мещеряков Г. А. Представление потенциала притяжения Земли суммой по¬
тенциалов двух простых слоев. //Observation of ASE, N 23 (1984).—
P. 199—209.
208
96. Мещеряков Г. А. и др. Мультипольный анализ глобального геомагнитного
поля для интервалов различной длительности и вековые вариации этого
поля // Геомагнетизм и аэрономия. — 1979. — Т. XIX, № 4. — С. 722—731.
97. Мещеряков Г. А., Голикова А. В. О степенных моментах плотности земных
недр // Геодезия, картография и аэрофотосъемка.— 1976. — Вып. 24.—
С. 68—77.
98. Мещеряков Г. А., Марченко А. Н. Об уравнении, определяющем оси сфери¬
ческих функций // Геодезия, картография и аэрофотосъемка. — 1976. —
Вып. 24. — С. 77—81.
99. Мещеряков Г. А., Марченко А. Н. Мультипольное истолкование основных
особенностей фигуры геоида // Геодезия и картография. — М.: Недра,
1976. — № 6.— С. 14—24.
100. Мещеряков Г. А., Марченко А. Н. Нахождение осей гравитационных мульти¬
полей // Геодезия, картография и аэрофотосъемка. — 1977. — Вып. 25. —
С. 42—47.
101. Мещеряков Г. А., Марченко А. Н. Об экстремальных свойствах сферических
функций, описывающих внешний гравитационный потенциал Земли // Геоде¬
зия, картография и аэрофотосъемка. — 1978. — Вып. 27. — С. 88—96.
102. Мещеряков Г. А., Марченко А. Н. О максвелловых параметрах гравитацион¬
ного поля Земли. // Наблюдения искусств, спутников Земли. — Варшава—
Лодзь,1978. — № 18.— С. 171 — 187.
103. Мещеряков Г. А., Марченко А. Н. О новом подходе к представлению гравита¬
ционного потенциала планеты потенциалом системы точечных масс //
Астрон. вестн. — 1979. — Т. XIII, № 4. — С. 193—202.
104. Мещеряков Г. А., Марченко А. Н. Модель точечных масс геопотенциала, полу¬
ченная на основе его мультипольного представления // Геодезия, картография
и аэрофотосъемка. — 1979. — Вып. 29. — С. 52—61.
105. Мещеряков Г. А., Марченко А. Н. О многоточечных моделях геопотенциала. //
Изучение Земли как планеты методами астрономии, геофизики и геодезии. —
Киев: Наук, думка, 1982. — С. 121 —131.
106. Мещеряков Г. А., Фыс М. М. О связи степенных моментов плотности земных
недр со стоксовыми постоянными // Геодезия, картография и аэрофо¬
тосъемка. — 1979. — Вып. 30. — С. 100—113.
107. Мещеряков Г. А., Фыс М. М. О биортогональных системах многочленов внутри
эллипсоида // Теорет. и прикл. пробл. вычислит, мат. — М.: Ин-т прикл.
пробл. мат. АН СССР, 1981. — 120 с.
108. Мещеряков Г. А., Фыс М. М. Трехмерная и рефернцная плотностные модели
Земли // Геофиз. журн. — 1986. — Т. 8, № 4. — С. 68—75.
109. Мещеряков Г. А., Фыс М. М. Трехмерная плотностная модель Земли /
Львовск. политехнич. ин-т. — Львов, 1987. . 42 с. (Деп. в Укр. НИИНТИ
04.05.88. № 1054—Ук. 88).
110. Молоденский М. С., Еремеев В. Ф., Юркина М. И. Методы изучения внешнего
гравитационного поля и фигуры Земли // Тр. ЦНИИГАиК. — М., 1960. —
Вып. 131. — С. 1—251.
111. Моритц Г. Современная физическая геодезия. — М.: Недра, 1983. — 390 с.
112. Мультон Ф. Р. Введение в небесную механику. — М. — Л.: ОНТИ, 1936.—
479 с.
113. Муратов Р. С. Потенциалы эллипсоидов. — М.: Атомиздат, 1976.— 143 с.
114. Мячин В. Ф., Сизова О. А. Совместное интегрирование уравнений небесной
механики численным методом Тейлора—Стеффенсена // Бюл. ИТА. — Л.:
Наука, 1970. — Т. XII, № 5 (138). — С. 389—400.
115. Нейман Ю. М. Вариационный метод физической геодезии. — М.. Наука,
1979. — 198 с.
116. Новиков П. С. Об единственности решения обратной задачи теории потен¬
циала // ДАН СССР. — 1938. — Т. 18, № 3. — С. 165—168.
117. Обращение Комитета по стандартной Земле МСГГ//Физика Земли.—
1976. — № 11. — С. 80—81.
118. Оганесян С. М., Старостенко В. И. Тела нулевого внешнего потенциала:
о забытых работах и современном состоянии теории // Физика Земли. —
1985. — № 3. — С. 49—62.
209
119. Огородова Л. В., Юзефович А. П., Бобко Г. В. Представление аномального
гравитационного поля Луны полем точечных масс. // Современные проблемы
позиционной астрономии. — М.: Изд-во МГУ, 1975. — С. 312—317.
120. Основы сгГутниковой геодезии / Под ред. Изотова А. А. — М.: Недра,
1974. — 315 с.
121. Остач О. М., Агаева И. Н. Аппроксимация внешнего гравитддионного поля
Земли моделью гравитирующих точечных масс. // Изучение Земли как пла¬
неты методами астрономии, геофизики и геодезии. — Киев: Наук, думка,
1982.— С. 106—114.
122. Павлов Г. А. К обратной задаче суммарного потенциала ма£с // Дифференц.
уравнения. — 1976. — Т. 12, № 1. — С. 109—117.
123. Павлов Г. А. Разрешимость обратных задач теории потенциала//Диффе¬
ренц. уравнения. — 1982. — Т. XVIII, № 10. —С. 1772—1779.
124. Пеллинен Л. П. Статистический анализ силы тяжести // Изв. вузов. Геодезия
и аэрофотосъемка. — 1970. — Вып. 5. — С. 43—50.
125. Пеллинен Л. П. Высшая геодезия. — М.: Недра, 1978. — 264 с.
126. Пеллинен Л. П. Современное состояние и перспективы планетарных исследо¬
ваний гравитац. поля Земли. // Изучение Земли как планеты методами
астрономии, геофизики и геодезии. — Киев: Наук, думка, 1982. — С. 55—63.
127. Пеллинен Л. П., Нейман Ю. М. Физическая геодезия // Итоги науки и тех¬
ники. Геодезия и аэрофотосъемка. Т. 18. — М.: ВИНИТИ, 1980.— 132 с.
128. Пеллинен Л. П., Остач О. М. Вопросы совместного использования спутниковых
гравиметрических и астрономо-геодезических данных для определения фигуры
и гравитационного поля Земли. // Наблюдения искусств, небесных тел. —
1976. — № 15. — С. 26—62.
129. Петровская М. С. Построение всюду сходящегося разложения геопотенци¬
ала // Наблюдения искусств, небесных тел. — 1975. — № 15, ч. 2. — С. 537—
563.
130. Петровская М. С. Обощение ряда Лапласа в теории потенциала // Динамика
движения искусств, спутников Земли. — М, 1978. — С. 47—48.
131. Петровский И. Г. Лекции по теории обыкновенных дифференц. уравнений. —
М.: Наука, 1970. — 279 с.
132. Пицетти П. Оасновы механической теории фигуры планет. — М. — Л.: ГТТИ,
1933. — 170 с.
133. Плахов Ю. В. О роли точечного представления внешнего геопотенциала
в астродинамике // Исслед. по геодезии, аэрофотосъемке и картографии. —
1978. — Вып. 3 (1) — С. 51—56.
134. Плахов Ю. В. Применение теории возмущения в космической геодезии. —
М.: Недра, 1983. — 199 с.
135. Полещиков С. М. О построении вещественной системы точечных масс, пред¬
ставляющих гравитационное поле планеты // Вестн. ЛГУ. — 1984. — № 1. —
С. 95—99.
136. Полещиков С. М., Холшевников К. В. Построение системы точечных масс,
представляющих гравитационное поле планеты, по спутниковым наблюде¬
ниям // Вестн. ЛГУ. — 1984. — № 7. — С. 76—86.
137. Прилепко А. И. Об единственности определения формы и плотности тела в об¬
ратных задачах теории потенциала // ДАН СССР. — 1970. — Т. Ф193, № 2. —
С. 288—291.
138. Прилепко А. И. О разрешимости обратной задачи объемного потенциала пе¬
ременной плотности // Сиб. мат. журн. — 1970. — Т. 193, № 2. — С. 288—
291.
139. Пуанкаре А. Избранные труды. Т. 1. Новые методы небесной механики. —
М.: Наука, 1971. — 771 с.
140. Рыжик И. М., Градштейн И. С. Таблицы интегралов сумм, рядов и произведе¬
ний. — М. — Л.: Гостехиздат, 1951. — 464 с.
141. Слудский Ф. А. Общая теория фигуры Земли. // Избр. геодез. тр. — М.:
Недра, 1967. — 237 с.
142. Справочное руководство по небесной механике и астродинамике / Под ред.
Дубошина Г. Н. — М.: Наука, 1976. — Изд. 2-е. — 862 ч.
143. Сретенский Л. Н. Теория ньютоновского потенциала. — М. — Л.: Гостехиздат,
1946. — 318 с.
210
144. Старостенко В. И. и др. Методика решения прямых задач гравиметрии и
магнитометрии на шарообразных планетах. — Киев: Наук, думка, 1986. —
112 с.
145. Старостенко В. И. Вопросы теории и методики интерпретации гравиметри¬
ческих наблюдений устойчивыми численными методами: Автореф. докт. дис. —
М. — 1976. — 35 с.
146. Старостенко В. И., Оганесян С. М. Устойчивые операторные процессы и
их применение в задачах геофизики // Изв. АН СССР. Физика Земли. —
1977. _ № 5. — С. 61—75.
147. Стокс Д. О силе тяжести на земной поверхности: Статьи и силе тяжести. —
М.: Изд-во геод. лит-ры, 1961. — 152 с.
148. Страхов В. Н. и др. Состояние и перспективы развития в СССР теории интер¬
претации гравитационных и магнитных аномалий // Физика Земли. —
1982. — № 5. — С. 11—23.
149. Субботин М. Ф. Курс небесной механики. — Л. — М.: Гостехиздат, 1949.—
Т. 3. — 280 с.
150. Субботин М. Ф. Введение в теоретическую астрономию. — М.: Наука, 1968. —
800 с.
151. Тараканов Ю. А., Черевко Т. Н. Интерпретация крупнейших гравитационных
аномалий Земли // Изв. АН СССР. Физика Земли. — 1979. — № 4. —
С. 25—41.
152. Тектоносфера Земли. — М.: Наука, 1979. — 531 с.
153. Тиман А. Ф., Трофимов В. Н. Введение в теорию гармонических функций. —
М.: Наука, 1968. — 206 с.
154. Тихонов А. Н. Об устойчивости обратных задач//ДАН СССР. — 1943.—
Т. 39, № 5. — С. 195—198.
155. Тихонов А. Н., Арсенин В. Я■ Методы решения некорректных задач. — М.:
... Наука, 1979. — Изд. 2-е. — 284 с.
156. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. — М.:
Наука, 1974. — 224 с.
157. Тихонов А. Н., Самарский А. А. Уравнения математической физики. —
М.: Наука, 1972. — 735 с.
158. Тяпкин К. Ф. Новая ротационная гипотеза структурообразования и геоизоста-
зии // Геофиз. журн. — 1980. — Т. 11, № 5. — С. 40—46.
159. Уиттекер Э. Т., Ватсон Дж. И. Курс современного анализа. Ч. I. — М.: Физ-
матгиз. 1963. — 342 с.
160. См. [159]. — Ч. II. — 515 с.
161. Умов Н. А. Построение геометрического образа потенциала Гаусса как прием
изыскания законов земного магнетизма: Избр. соч. — М. — Л.: Гостехиздат,
1950. — 555 с.
162. Урмаев М. С. Орбитальные методы космической геодезии. — М.: Недра,
1981. — 256 с.
163. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления.
Т. III. — М. — Л.: Гостехиздат, 1949. — 783 с.
164. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления.
Т. II. — М.: Наука, 1966. — 800 с.
165. Фыс М. М. О сходимости в среднем биортогональных рядов внутри эллип¬
соида // Дифференц. уравнения и их приложения. — Львов: Вища шк„
1983. — С. 131 — 132.
166. Фыс М. М. Методика построения модельных распределений плотности, потен¬
циала силы тяжести внутри земного эллипсоида: Канд. дис. — Львов,
1985. — 129 с.
167. Фыс М. М. Методика построения распределений плотности, потенциала и
ускорения силы тяжести внутри земного эллипосида. — Львов, 1985. —
29 с. (Рукопись деп. в УкрНИИНТИ, № 471. — УК—85 Деп.)
168. Харди Г. Расходящиеся ряды. — М.: ИЛ, 1951. — 504 с.
169. Чандрасекхар С. Эллипсоидальные фигуры равновесия. — М.: Мир, 1973. —
288 с.
170. Чуйкова Н. А. Построение сходящегося во внешнем пространстве разложения
потенциала притяжения эллипсоида произвольного эксцентриситета // Тр.
I Орловской конф. — Киев: Наук, думка, 1982. — С. 120—121.
211
171. Чуйкаова Н. А. Новое доказательство сходимости ряда Лапласа на физиче¬
ских поверхностях планет // Вестн. МГУ. Сер. 3. Физика. Астрономия.
1984. — Т. 25, № 1. — С. 22—28.
172. Чуйкова Н. А. О некоторых возможностях представления потенциала притя¬
жения произвольного тела рядом, сходящимся всюду вне его поверхности //
Вестн. МГУ. Сер. 3. Физика. Астрономия. — 1985. — Т. 26. № 5. — С. 77—81.
173. Шмидт О. Ю. Математическое определение тяжелых подземных масс по на¬
блюдениям вариометром Этвеша // Т. Особой комиссии по иссл. Курской маг¬
нитной аномалии. — М., 1925. — Вып. 6. — С. 51—64.
174. Юркина М. И. О проблеме Стокса // Изв. вузов. Сер. Геодезия и аэро¬
фотосъемка. — 1977. — № 1. — С. 63—70.
175. Яновский Б. М. Земной магнетизм. Т. 1. — Л.: Изд-во ЛГУ, 1963. — 445 с.
176. Яцкив Я. С. Нутация в системе астрономических постоянных. — Киев, 1980.
(Препринт/АН УССР. Ин-т теор. физики, ИТФ—80—95Р). — 59 с.
177. Ananda М. P. Lunar gravity: a mass point model // J. Geophys. Res. — 1977. —
V. 82, N 20. — P. 3049—3064.
178. Arnold K. Beweis der gleichmassigen Konvergenz der Kugelfunktionsentwick-
lung fur das Gravitationpotential der Erde im Aussenraum // Vermessung-
technik. — Bd 26, N 7. — S. 222—226.
179. Balmino G. La pepresentation du potentiel terrestre par masses ponctuelles//
Bull. geod. — 1974. — N 111. — P. 85—108.
180. Balmino G., Reigber C.f Moynot B. The GRIM—2 Earth gravity field model //
Veroff. Dtsch. geod. Kommis. Bayer. Akad. Wiss. — 1976. — N 86. — P. 34.
181. Brosche P. Representation of the Systematic Differences in Position and Proper
Motions of Stars by Spherical Harmonics // Veroff. Astron. Rechen. Inst.—
Heidelberg, 1966. — N 17. — P. 5—27.
182. Cunningham L. E. On the computation of the spherical harmonic terms needed
during the numerical integration of the orbital motion of an artificial satellite
Celes // Mech. — 1970. — V. 2. — P. 207—216.
183. Dive P. Attraction des ellipsoides homogenes et reciproques d’un theoreme
de Newton//Bulletin de la Societe Mathematique de France.— 1931.—
V. LIX.
184. Dive P. Sur l’identite de deux corp possedant le potential newtonien, dans une
region interieuer commune // Comptes rendus. — 1932. — V. 195. — P. 597—
599.
185. Dobaezewska W. Okreslenie potencjalu sily ciezkosci Ziemli metoda mas punk-
towvch // Geod. i kartogr. — 1974. — V. 23, N 3. — P. 239—245.
186. Drozyner A. Potential and mascons//Artif. Satell. — 1977. — V. 12, N 1. .
P. 19—26.
187. Dufour H. M. La representation du potential terrestre par der functions regio-
nalyses // Bull. Inform. Just, geogr. nat. — 1971. — prepr., s. 1., s. a. — 13 p.
188. Dzevonski A. M. Mapping the Lower Mantle: Determination of Lateral Hetero¬
geneity in P velocity up to degree and order 6 // J. of Geophys. Res. — 1984. —
V. 89, N 137. — P. 5929—5952.
189. Dzevonski A. М., Anderson D. L. Preliminary reference Earth Model // Phys.
Earth and Planet. Inter. — 1981. — V. 25. — P. 297—356.
190. Groten E. On the spherical harmonics series of geopotential at the Earth’s
surface // Bull, geodes. — 1968. — N 88. — P. 227—239.
191. Hardy R. L. Pcasearch results results in application of multiquadric equations to
surveying and mapping problems // Surv. and Mapp. — 1975. — V. 35, N 4. —
P. 321—332.
192. Hardy R. L., Gdpfert W. M. Least squares prediction of gravity anomalies,
geoidal undulations and defflections of vertical with multiquadric harmonic
functions // Geophys. Res. Lett. — 1975. — V. 2, N 10. — P. 423—426.
193. Heikkinen M. Solving the shape of the Earth by using digital density models //
Rep. of Finnish Geodetic Inst. — Helsinki, 1981. — 70 p.
194. Hotin M. Matematical Geodesy // Washington D. C. — 1969. — 416 p.
195. James R. W. On recurrence relation for multipole coeficients // Pure and Appl.
Geophys. — 1967. — V. 68, N 3. — P. 83—89.
196. James R. W. Mutlipole analysis. 1. Theory and geomagnetic multipoles 1965.0 //
Austral. J. Phys. — 1968. — V. 21, N 4. — P. 456—464.
212
197. Jamse R. W. Mutlipole analysis. 2. Geomagnetic secular variation //Austral.
J. Phys. — 1969. — V. 22, № 4. — P. 481—495.
198. James R. W. Transformation of spherical harmonics under change of reference
frame // Geophys. J. R. Astr. Soc. — 1969. — V. 17. — P. 305—316
199. James R. W. A review of basic computations with spherical harmonics in
geomagnetism // Pure Appl. Geophys. — 1973. — V. Ill, № 10. — P. 2273 —
2285.
200. Kholshevnikov C. On convergence of an asymmetrical body Potential expansion
in spherical harmonics // Celestial Mechanics. — V. 16. — 1977. — P. 45—60.
201. Kilczer G. Die geometrische Structur des erdmagnetischen Quadrupolmoment—
Tensors // Gerlands Beitrage zur Geophysik. — 1964. — Bd 73. — 290 S.
202. Lerch F., Putney D. Godard Earth model for oceanographic applications
(GEM—10B and GEM—10C) //Mar. Geodes. — 1981. — V. 5, № 2.—
P. 145—185.
203. Levie S. L. Jr. Simple mass distribution for the Lunar Potential//Moon.—
1971. — V. 3, № 3. — P. 315—325.
204. Marchenko A. N. On the Representation of the Earth Gravitational Potential
by Means of the System of Potential of Non-Centric Multipoles // Proc.
Int. Symp. «Figure and Dynamics of the Earth, Moon and Planets». —
Prague, 1986. — P. 443—475.
205. Martinec Z., Pec K. Three-dimantional density distribution generating the ob¬
served gravity-field of planets. P. I. The Earth // Proc. Int. Symp. «Figure and
Dynamics of the Earth, Moon and Planets». — Prague, 1986. — P. 129—152.
206. Marussi A. On the densiti distribution in bodies of assigned outer Newtonian
attraction //Bolletino di Geofisica Teorica ed Applicata.— 1980.—V. XXII,
№ 86. — P. 83—94.
207.Maxwell J. C. A treatise on Electricity and Magnetism. — Oxford, 1881.—
V. 1. — 2d ed. — 464 p.
208. Mescheryakov J. A., Deineka I. P. A variant of the earth’s mechanical model //
Geofys. sb. — 1980. — V. 25. — P. 9—19.
209. Mescheryakov G. A., Marchenko A. N., Tatevian S. K., Sorokin N. A. On the use
of Point Mass Models of the Geopotential for Orbit Prediction // Adv. Space
Res.—Great Britain. COSPAR, 1981.—V. 1. — P. 1—6.
210. Moritz H. Fundamental Geodetic Constant // Proceedings of the IAG XVII Ge-
ner. Assemb. IUGG/IAG. — Canberra, 1979. — 34 p.
211. Muller P. М., Sjogren W. L. Mascons: Lunar mass concentrations // Science. —
1968. — V. 161. — P. 680—684.
212. Needham P. E. The formation and evaluation of detailed geopotential models
based on point masses. — The Ohio State University. Report of the Departament
of Geodetic Science. — 1970. — Report № 149. — 69 p.
213. Nikliborc W. Eine Bemerkung uber die Voiumpotentiale//Math. Zeit. —
1932. — Bd 35. — S. 625—631.
214. Ostrowski A. Die Maxwellsche Erzengung der Kugelfunktion//Jahrsber.
Dentsch. Math. — 1925. — Bd 33. — S. 245—251.
215. Petrovskaya M. S. Formulas Simplifications and Accuracy Improvement in the
Approximation of the Geoid Heights // Proc. Int. Symp. «Figure and Dynamics
of the Earth, Moon and Planets». — Prague, 1986. — P. 305—322.
216. Rapp R. H. Special Studv Group 5.36 Earth models // Trav. Assoc. Int. Geod. —
1976. — V. 25. — P. 404—410.
217. Rapp R. H. Global anomaly and undulation recovery using GEOS-3 altimeter
data. — Columbus, 1979. — 49 p. — (Report Dep. Geod. Sci/Ohio State Univ.;
No 285).
218. Rapp R. H. The Earth gravity field to degree and order 180 using SEASAT
altimer data, terrestial data and other data. — Dep. of Geod. Sci. Rep. № 322. —
OSU, Columbus, Ohia, 1981.
219. Rapp R. H. Global Atlas of sea surface heights based on the adjusted SEASAT
altimeter data. — Columbus, 1982. — 63 p. (Report Dep. Geod. Sci/Ohio
State Univ.; № 333).
220. Reilly S. R.t Herbruhtsmeier E. H. A systematic approach to modeling the
geopotential with point mass anomalies//J. Geophys. Res.— 1978. — V. 83,
№ B2. — P. 349—361.
213
221. Schwarz К. P. Capabilities of airborne gradiometry for gravity estimation; Bull,
geod e sci. affini. — 1977. — V. 36, № 2. — P. 195-214.
222. Sidlichovsky M. Problem of three bodies. . . // Bull. Astron. Inst. Czechosl. —
1983. — V. 34, № 2. — P. 65—74.
223. Shaikh N. A. A new perturbation method for computing Earth—Moon trajecto¬
ries; Astron. Acta. — 1966. — V. 12, № 3. — P. 207—211.
224. Skorvanek M. The inverse gravimetric problem for the Earth // Veroff. Zentral.
fur Phys. der Erde. — 1981. — Bd 3. — S. 464—475.
225. Sjogren W. L., Muller P. M. e. a. Lunar surface mass distribution from dynami¬
cal point mass solution // Moon. — 1971. — V. 2, № 3. — P. 338—353.
226. Sjogren W. L. e. a. Mars gravitv field based on short-are technique // J. Geo-
phys. Res. — 1975. — V. 80, № 20. — P. 2899—2908.
227. Stern D. Classification of magnetic shells //J. Geofys. Res. — 1965. —V. 70,
№ 15. — P. 3629—3634.
228. Sylvester J. J. Note of spherical harmonics, 1876 in Collected Mathematical
Papers. V. 3. — Cambridge, 1909. — P. 37—51.
229. Tscherning С. C., Sanso F. Choise of Norm for the Density Distribution of the
Earth (Prep. Intern. Workshop «Density Distribution of the Litosphere». —
ETH, Lurich, May 28—31, 1985).
230. Week N. Inverse Problem der Potential theorie // Appl. Anal. — 1972. —
V. 2, No. 2. — P. 195—204.
231. Weightman J. A. Gravity, geodesy and artificial satellites a unifield analytical
approach. // The Use Artif. Satellites for Geodesy. Publ. Nat. Techn. Univ.
Athens. — 1967. — V. 2. — P. 467—486.
232. Winch D. E. The fourth order geomagnetic multipole: the sedecimupole // Pure
and Appl. Geophys. — 1967. —V. 67, № 2. — P. 112—122.
233. Winch D. E. The fifth order geomagnetic multipole: the duotrigintupole // Pure
and Appl. Geophys. — 1967. — V. 68, № 3. — P. 90—102.
234. Winch D. E., Malin S. R. C. Changes in geomagnetic multipole coefficients //
Pure and Appl. Geophys. — 1969. — V. 74, № 3. — P. 16—22.
235. Winch D. E., Slaucitajs L. Geomagnetic multipoles 1965 // Pure and Appl.
Geophys. — 1966. — V. 65, № 3. — P. 95—101.
236. Yurkina М. I. On Substantionen of the Dynamical Theory of the Earth’s Rotation;
Proc. Int. Symp. «Figure of the Earth, the Moon and other Planets». Monograph.
Series of VUGTK- — Prague, 1983. — P. 31—35.
237. Zilahi-Sebess L. On the geomagnetic quadrupolefield // Acta Techn. Hung. —
1961. — V. 37. — P. 403—426.
Научное издание
Мещеряков Герман Алексеевич
ЗАДАЧИ ТЕОРИИ ПОТЕНЦИАЛА И ОБОБЩЕННАЯ ЗЕМЛЯ
Заведующий редакцией Г. С. Куликов
Редактор J1. П. Русакова
Художественный редактор Т. Н. Кольченко
Технический редактор И. Ш. Аксельрод
Корректор Л. С. Сомова
ИБ № 32485
Сдано в набор 20.04.89. Подписано к печати 13.03.91.
Формат 60X90l/i6-
Бумага тип N° 2. Гарнитура литературная.
Печать офсетная.
Уел. печ. л. 13,5. Уел. кр.-отт. 13,5. Уч.-изд. л. 15,91.
Тираж 870 экз. Заказ № 1110. Цена 3 р. 50 к.
Издательско-производственное и книготорговое объединение «Наука»
Главная редакция физико-математической литературы
117071 Москва, Ленинский проспект, 15
Отпечатано в Четвертой типографии издательства «Наука»
630077; Новосибирск-77, ул. Станиславского, 25
NAUKA PUBLISHERS
Main Editorial Board for Physical
and Mathematical Literature
15, Leninsky prospect, Moscow, W-71, 117071, USSR
POTENTIAL THEORY PROBLEMS
AND THE GENERALIZED EARTH
German A. MESHERJAKOV, D. Sc.
Abstract:
Investigations of the generalised Earth have been presented, global models
of the figure and distribution of the density of the planet“s entrails have been
calculated and concerned. The author prefers to name them „generalised1* instead
of „normal**. Inverse problems (geodetic and geophysical) of the potential theory,
developped using latest data about the Earth and its gravity field, have been
assumed as a basis of models calculation.
External gravity field (with its parameters determined up to certain order
and some other information are determinating generalised figure and distribution
of density. So it would be astronomogeodetic information for figure and seismologi-
cal — for density.
General parts, obtained in such a way, lead to planet global models of figure
and density. Regional and detailed models must be constructed on the basis
of such giobal ones in accordance with some other unregistered information about
region researched.
The author didn’t try to cover the main ideas of work by abstract mathematical
language. He thought the problems concerned in the book, and partually solved,
are very important for the practice and put forward naturally, in a simple way.
So they could be solved by comparatively simple mathematical means.
Contents:
Introduction. Ch. 1. On potential theory problems. Ch. 2. Multipole repre¬
sentation of the potential. Ch. 3. The attraction potential of the Earth and its gene¬
ralized form. Ch. 4. Potentialographical problem and conception of gravitating discs.
Ch. 5. Inverse geodetical problem of the potential theory and the Earth*1 figure.
Ch. 6. Inverse geophysical problem and distribution of the density of the Earth inte¬
rior. Ch. 7. Dinamically one-point models of geopotential and geometrical theory
of artificial satellite movement. Supplement.
Author:
Mesherjakov German Alexejevich, the chief of the chair of theory of mathematical
processing of geodetical measurement of Lvov polytechnical institute, professor,
Doctor of Science. He heads a group of research workers, who are studying gravity
fields of the Earth, the Moon and other planets. They are using gravity fields
parameters for exploration of the planet’s figures, distribution of the den¬
sity and other its characteristics.
The author wrote more than 150 articles, which were published in various
science publications, including international ones; he is the author of two mono¬
graphs.