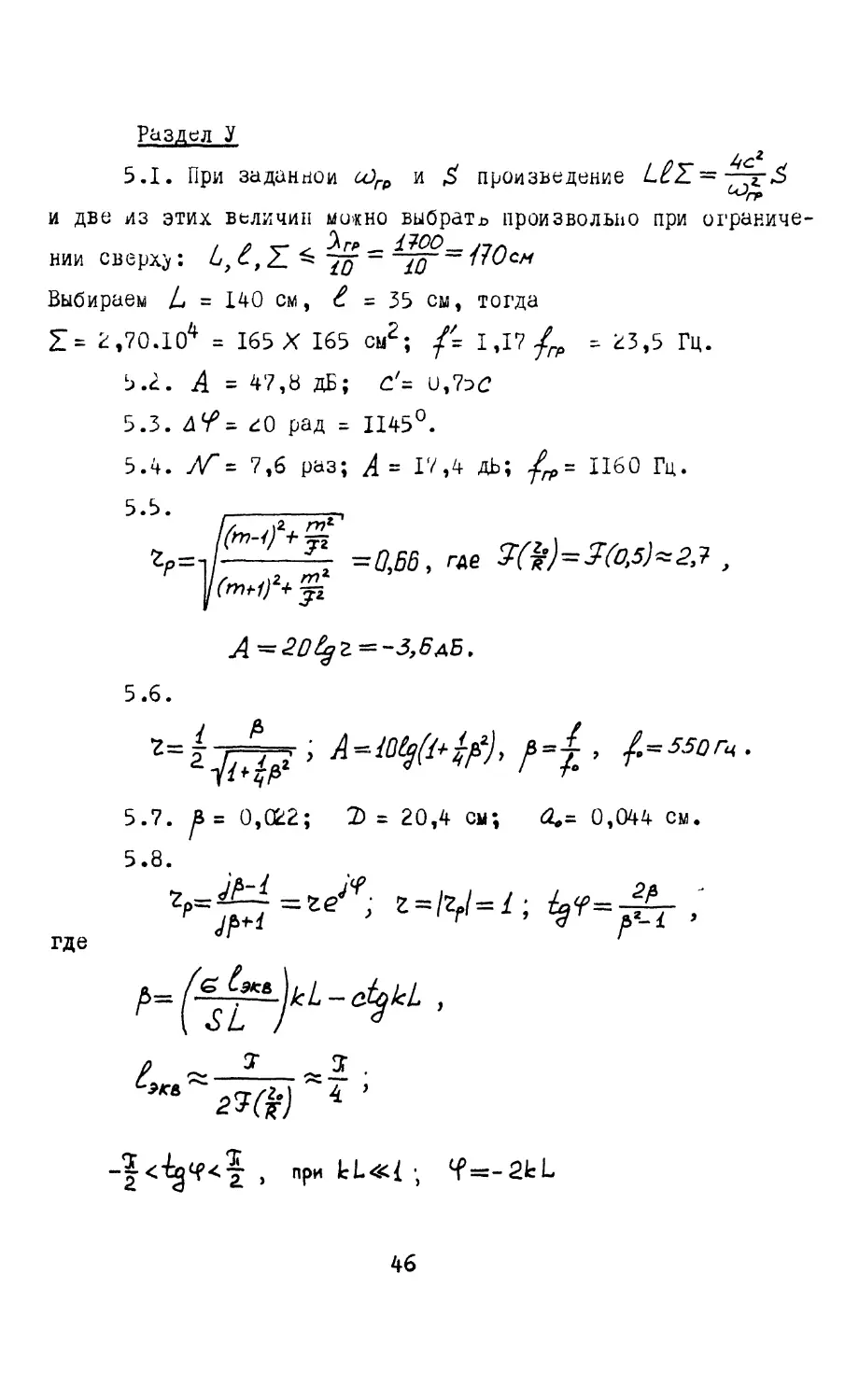МОСКОВСКИЙ ОРДЕНА ЛЕНИНА
И ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. М. В. ЛОМОНОСОВА
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА АКУСТИКИ
С. И. I
ЗАДАЧИ ПО ТЕОРИИ 31УКА
ИЗДАТЕЛЬСТВО МОСКОВСКОГО УНИВЕРСИТЕТА
1976

Рецензенты: профессор В.М# Лопухин,
профессор М.Д. Карасев
Издательство Московского университета, 1976 г.

ПРЕДИСЛОВИЕ
Настоящий сборник задач по теории звука составлен по
материалам занятии» проводившихся в течение ряда лет со
студентами кафедры акустики физического факультета МГУ.
Состав задач соответствует в основном программе курсов лекций,
читаемых на кафвдре акустики МГУ, однако настоящий сборник
задач может быть полезен и студентам других учебных заведении
как пособие при упражнениях.
Для помощи при решении задач в книге приведены таблицы
специальных функции и график (импеданс-диаграмма)» при помо-
помощи которого возможно быстрое решение задач по распространению
звука в слоистых системах по направлению нормали к слоям.
В конце книги приведен список вспомогательной литературы
и ответы в виде алгебраических выражении и численных результатов.
Все задачи решаются в системе единиц СГС, наиболее
принятой в акустике.
Автор будет весьма благодарен всем использующим сбор-
сборник задач в своей работе за замечания и указание желательных
добавлении или замеченных в тексте погрешностей.

I. Скорость звука. Интенсивность звука. Эффект Допплера
Литература [If 2, 3].
I.I. Рассчитать звуково'й барьер скорости самолета, ког-
когда скорость его равна скорости звука на высоте 9 км, где
температура -70^С, и сравнить его со звуковым барьером при
0°С на уровне моря. Зависит ли барьер от атмосферного дав-
давления?
1.2. При какой температуре в градусах Цельсия скорость
звука в газе удвоится по сравнению со скоростью при 0°С и
при какой станет в два раза меньше?
1.3. Звуковая волна с уровнем интенсивности 147 дБ пол-
полностью поглощается при нормальном падении на плоский слой
пористого вещества толщиной 5 см. Рассчитать, через сколько
времени нагреется этот слой на 1°, если его удельная тепло-
теплоемкость 0,2 кал на градус.
1.4. Плоская звуковая волна в воздухе с частотой
1000 Гц при температуре 0°С имеет уровень интенсивности
134 дБ над дорогом Ро = 2Л0~** дан/см . Вычислить амплиту-
амплитуды звукового давления, скорости и смещения частиц, а также
амплитуду колебаний температуры в этой волне»
1.5. Уровень интенсивности звуковой волны при прохож-
прохождении через перегородку ослаодяется с 97 до 51 дБ. Рассчи-
Рассчитать приближение, без использования таблиц логарифмов
(зная лишь ??2sO,3), во сколько раз уменьшилось звуковое
давление.
1.6. Определить показатель преломления звука (л) при
переходе из водорода в углекислоту. Скорость звука подсчи-
подсчитать, зная молекулярный вес газов (/г?) и отношение теплоем-
костей (jf-f* э которое равно 1,4 для двухатомных газов
и 1,3 для многоатомных.
1.7. Подсчитать фокусное расстояние (L) ультразвуко-
ультразвуковой двояковогнутой латунной линзы, находящейся в водной
среде. Радиус кривизны вогнутых поверхностей линзы 50 см;
линза при расчете считается тонкой. Скорость продольных
звуковых волн в латуни 3,4.1Сг см/с и в воде 1,5.1Сгсм/с.

1.8, Интенсивность звука в морской воде убывает
вследствие поглощения на величину f> дБ/кы. Коэффициент
поглощения уб s 0,036i t где / - частота, выражаемая
в килогерцах. Определить, на каком расстояния от источни-
источника сферическая волна уменьшается по амплитуде в 100 раз
при частотах 10 и 100 кГц,
1.9. Из воздуха на поверхность воды падает вертикаль-
вертикально звуковая волна с частотой 100 Гц и интенсивностью 97 дБ.
Определить, какой уровень звукового давления будет регист-
регистрировать приемник, находящийся на глубине I см под поверх-
поверхностью воды.
1.10. Скорость звука в воде в зависимости от темпера-
температуры Т в градусах Цельсия определяется формулой
С = 1450 + 4,6 Т (м/с).
Считая, что Т с глубиной (Н) падает по линейному закону
с градиентом 0,5 град/м начиная с 20°С, определить радиус
кривизны (?) звукового луча, выходящего горизонтально из
точки, лежащей на глубине 5 м. Радиус кривизны определяет-
определяется формулой %~Т « гДе Q ' градиент скорости звука.
Определить, на каком расстоянии (I) звуковой луч отклонит-
отклонится книзу на 50 м.
1.11. Плоская звуковая волна падает по нормали из воз-
воздуха на границу со слоем углекислоты и частично отражает-
отражается, частично проходит через нее. Определить коэффициент от-
отражения ( Zp) на границе, а также во сколько раз (t) от-
отличается амплитуда прошедшей волны от амплитуда падающей*
Определить отношение амплитуды звукового давления в макси-
максимумах и минимумах отраженной волны. Для воздуха
С s 3,4.10^ см/с;рс= 41; для углекислоты С =2,6.Ю^см/с;
рС= 51.
1Л2. Найти скорость (С) звука во взвеси воздушных
пузырьков в воде при процентном содержании воздуха /?=0,01
считая, что во взвеси суммируются сжимаемости, а плотность
при малом ft близка к плотности воды.
ДЛЯ ВОДЫ МОДУЛЬ |ПРУГОСТИ а?^ г2,2Л0^0ДВ/С]Г, ДЛЯ
воздуха 9^ = 1*43.Ю5 дн/см2.

I.13. Найти выражение для вектора интенсивности звука
при суперпозиции двух плоских волн одинаковой частоты, имею-
имеющих интенсивности Ьн и C/t и разность фаз <Р , в случае
одинакового направления обоих волн; противоположного направ-
направления волн.
1.14. Длинный товарный поезд идет со скоростью U м/с.
Когда он подходит к тоннелю в отвесной вертикальной стене,
машинист дает гудок с частотой / П*. Звук гудка и его эхо
слышат машинист и сторож, находящийся вблизи последнего ва-
вагона (на земле). Какой частоты звук гудка и его эха слышит
каждый из них? Какой частоты ( Ajf ) биения они услышат?
1.15. Самолет летит к вертикальной скале со скоростью,
равной половине скорости звука и- ~ , и излучает корот-
короткие тональные отрывки (цуга) с частотой /= 1000 Гц. Ка-
Какую частоту A') имеет эхо-сигнал, отраженный от скалы?
1.16. Плоская волна, распространяющаяся в воздухе с
частотой 1000 Гц, имеет амплитуду звукового давления ро=~
2.10*"^ бар (порог слышимости). Определить амплитуду смещения
( Ще ) и амплитуду скорости ( Ц ) частиц среды. Тот же рас-
расчет сделать для уровня интенсивности в 160 дБ над порогом
слышимости.
1.17. Определить вектор интенсивности звука J на ли-
линии, соединяющей два противофазных источника звука с круго-
круговой частотой и) , находящихся на расстоянии 2.Н друг от
друга, в среде со скоростью звука С и плотностью f в
функции расстояния 2 от средней точки прямой, соединяющей
источники•
1.18. Два точечных источника, находящиеся в воздухе
на расстоянии й см, синфазно излучают звук с частотой
/ Гц. Под каким углом ( d ) к линии, соединяющей источ-
источники, звук в дальнем поле будет на 6 дБ слабей, чем вдоль
этой же, осевой,линии на том же расстоянии от средней точ-
точки между источниками?
1.19. Определить ослабление (л) звука частоты 1000Гц
при прохождении по нормали через стальную пластину толщи-
толщиной 2,54 см (I дюйм), разделяющую два резервуаре с водой.
(Плотность стали 7fI i/cm3; скорость продольных волн в
сталм 6,1.10^ см/с).
6

П. Звуковые водны в трубе постоянного сечения
(длинноволновое приближение)
Литература [I, 2].
2.1. Возбуждающий звук поршень помещен у одного конца
трубы (сс= 0), наполненной воздухом ( ?= 3,44.10^ см/с,
рс= 42), у которой площадь поперечного сечения равна 10 см2,
а второй поршень, механический импеданс которого надо опре-
определить, помещен у другого конца трубы (:г= 30). Измерение
давления звуковой волны показало, что максимальная амплиту-
амплитуда давления в точках х = 3; х* 15; х = 27 равна Ю&рМи-
нимальная амплитуда давления, равная 6,57 бар, получилась в
точках X = 9, X = 21. Найти из этих данных механический
импеданс второго поршня (Z^)f частоту звука (/) и амплиту-
амплитуду колебаний возбуждающего поршня ( ^о).
2.2. Возбуждающий звук поршень помещен в одном конце
трубы, длина которой 86 см, а площадь поперечного сечения
10 см2. Второй конец трубы закрыт диафрагмой, механический
импеданс которой ( Rt ^JJ^ ) требуется определить. Импеданс
в точке возбуждения (исключая импеданс поршня) имеет следую-
следующие значения:
R
3
100
0
-71
200
42
1260
300
147
-365
400
420
0
500
189
126
600
840
-840
700
67
76
800
1260
1680
Какова действительная (ф) и мнимая (С?) части механи-
механического импеданса диафрагмы при тех же частотах? Нанести на
кривую значения Rt и J€ в функции частоты (/)• Принять
рс = 42.
2.3. Безразмерный, удельный импеданс в некоторой точке
(X) трубы при частоте ? = 344 Гц равен /=+/7.
При каком условии на границе возможен данный случай?
Какая величина импеданса будет на расстояниях 25, 50, 75,
100 и 125 см 01 исходной точки? Скорость звука 3,44Л0^см/с.
2.4. Два одинаковых порвня каждый с массой 10 г без
трения колеблются в противоположных концах цилиндрической
7

трубы длиной 34,4 см с площадью поперечного сечения 10 см*.
Один поршень приводится в движение силой lOQexpQlot) дин.
Скорость звука С = 3f44.I0^ см/с.
а) Нанести на график амплитуду смещения и амплитуду
скорости другого поршня в функции частоты @< f < 250 Гц);
б) нанести на график амплитуду смещения и амплитуду
скорости другого поршня в функции частоты B50 Гц^/<500Гц).
2.5. Поршень с ничтожным механическим импедансом
вставлен в один конец цилиндрической трубы с поперечным се-
сечением 10 cir, заполненной воздухом (С = 3,44.10 см/с). Дру-
Другой конец трубы отстоит на ? см от поршня и закрыт жесткой
пластинкой. Поршень приводится в движение периодической си-
силой
а) Длина трубы ?= 34,4 см. Вывести выражения для ско-
скорости (%г) и смещения (п) поршня в функции t от t = о
до Ь 1/2;
б) длина трубы 1= 34,4 см, другой конец трубы открыт.
Вывести выражения для скорости и смещение поршня и нанести
их на график.
2.6. Найти коэффициент иiрадения звука { 2р) от кругло-
круглого отверстия радиуса 2,= 5 см в боковой стенке бесконеч-
бесконечной трубы диаметра <?- 2ъо = 25 см. Построить частотную ха-
характеристику коэффициента отражения в пределах от 100 до
5000 Гц. Импеданс отверстия вычислить по формуле
где р в 1,2.Ю~3 г/см; С = 3,44.10^ см/с.
Построить частотную характеристику коэффициента отраже-
отражения в пределах 100 < \ < 5000 Гц.
2.7. Рассчитать основную резонансную частоту трубы
длиной ? = 2 м и диаметром 2г* = 3,0 см, закрытой с одной
стороны,.заполненной воздухом и закрытой с другой стороны
резиновой пленкой толщины 0,2 мм с массой на единицу площа-
площади р1 ш 2,2.10"^, имеющей собственную частоту в отсутствие
трубы 250 Гц.
2.8. На конце трубы сечения ^= 100 см2, заполненной
воздухом ( С = 3,44.10^ см/с), стоит возбуждающий звук пор-
8

шень с импедансом Z=*R+JJ t где R= 4200 мех.ом,
О = -4200 мех.ом при частоте 344 Гц. Рассчитать импеданс
при той же частоте в точках на расстоянии Х= 25, 50, 75
и 100 см от конца трубы исхода из теоретических формул.
2.9. Показать, что при наличии небольшого, чисто ре-
реактивного, удельного, безразмерного импеданса jJ в
конце трубы и твердой стенки в ее начале резонансная часто-
частота (?' ) по сравнению с резонансной частотой закрытой с
обоих концов трубы ( /o-^f ) увеличивается при
$ > 0 и уменьшается при Oi < 0.
2.10. Амплитуда звукового давления в различных точках
(х) отрезка трубы (длины t ), возбуждаемой в начале си-
силой H!~%C0*o)t и замкнутой на начальный и конечный
поршни с импедансом Zo и Ze * выражается формулой
где Z и 2S - модуль и фаза коэффициента отражения в кон-
конце трубы, Ar=^r и А - постоянная величина, не зависящая
от ос и ? .
Показать, по каким формулам величины Z , 5 и /4 ,
а также /С^ и /}*<>,«в стоячей волне могут быть определены,
если измерены звуковые давления в трех точках трубы ( а ; р2
ft ръ ) с координатами з:,; осг %и ocs.
2.II. В бесконечной трубе поставлено на расстоянии L
друг от друга большое число слоев с удельным сопротивлени-
сопротивлением Ri . Найти коэффициенты отражения Zi и lz на входе
первого слоя при таких частотах ? и <Д , когда
Ic^-rtX и kz?-(n+?)j и показать, что в первом
случае при RH^{ будет ?<^ , а во втором —

Ш. Нормальные волны в волноводах с жесткими стенками
Литература [I, 3].
В данном разделе рассматриваются волноводы^заполнен-
ные воздухом.
5.1. Найти грапичные частоты возникновения волновых
мод (/л, п ) при т,п<3 в бесконечной трубе прямоуголь-
прямоугольного сечения со сторонами CL = 10 см, ё> = 15 см.
3.2. Найти граничные частоты возникновения волновых
мод ( /??, п ) при т,п<3 в бесконечной круглой трубе ради-
радиуса Ъв = Ю см.
3.3. Исследовать дальнее звуковое поле в бесконечной
прямоугольной трубе сечения п*& ( a>i ), в начальном
сечении которой на площади a<xi>i , расположенной в цент-
центре, колеблется поршень со скоростью U— Uceocp(jcot)9
где со=2$1 • Задается: <2 = 17 см; ?= 8,5 см;
j±^^L--j-j <2, а< лежат вдоль оси ее ; ?, 6i - вдоль
оси у . Поле исследовать на частотах /у = 500 Гц и
/2 = 2100 Гц.
ЗЛ. Найти звуковое поле в бесконечной прямоугольной
трубе сечения йхё ( &>& ), в начальном сечении кото-
которой на площади щели длиной й и шириной cL , расположен-
расположенной у края площади <2х8 , задана скорость U^U.expCJLot).
Вычислить вектор плотности потока мощности по оси тру-
трубы на частоте /<^'
3.5. В круглой бесконечной трубе радиуса Si, = 6 см
задана скорость U^iuexpCJcot) в начальном сечении B=0)
на площади коаксиального круга радиуса ?, = 2 см.
Определить частоты первых трех критических частот ?;
/2; /3 • Исследовать звуковое поле на оси трубы (ось И )
при частотах /'=^A - 5 ТО) и /'=*/, A+5.Ю).
На какой из двух частот 1-я мода будет бегущей волной и во
сколько раз {Я) ее амплитуда превысит амплитуду 0-й моды;
какова будет ее скорость d ? На каком расстоянии 2У от
начала затухающая 1-я мода ослабеет в в раз?
3.6. Вычислить в функции частоты среднюю плотность по-
потока звуковой энергии для отдельной волновой моды в беско-
бесконечной по длине прямоугольной тр^бе сечения CL*$> при
10

в начальное сечении B=0) скорости
U^U.CoijfX'Codoot , где А-Щ ; m = I, 2, 3;...; сторо-
сторона а расположена по оси ос ; сторона ? - по оси у .
3.7. Найти выражение для звукового поля в квадратной
бесконечной по длине трубе (сторона квадрата а ), в цент-
центре начального сечения которой B=0) колеблется квадратный
поршень (со стороной <2, ^колеблющийся с амплитудой скорос-
скорости ио и угловой частотой и) .
3.8. Ьывести выражение коэффициентов разложения потен-
потенциала скорости звука по характеристическим функциям для бес-
бесконечной прямоугольной трубы сечением &х? для произ-
произвольно заданного распределении скоростей ^o
в начальном сечении трубы ( 2=0).
3.9. Исследовать звуковое поле в бесконечной круглой
цилиндрической трубе радиуса Zo = 10 см, если в начальном
сечении ( z » 0) задано распределение скоростей по закону
где ( VnZ ) п -й корень уравнения JoCvnz) = 0.
Определить амплитуду звукового давления на оси трубы {г-о)
при частоте в два раза выше со^ЦС # Будет ли возбуждаться
в трубе плоская волна?
3.10. Определить присоединенную массу прямоугольного
отверстия, расположенного в центре квадратной трубы путем
— jM^
вычисления суммарной кинетической эьергии T —
всех неволновых мод, возникающих при постоянной амплитуде
осевой колебательной скорости U^UoeczpOcvt) , задаваемой
в зоне отверстия.
3.II• Вывести формулу для кинетической энергии звуко-
звуковых волн в объеме бесконечной по длине круглой цилиндричес-
цилиндрической трубы (радиуса 2О ), в начальном сечении которой ко-
колеблется (вдоль оси трубы по закону U=u0eocp(joot) ) круг-
круглый, коаксиальный с трубой, поршень радиуса ?, . Предпола-
Предполагается, что волновое число к намного меньше первого соб-
собственного волнового числа Vo4 .
Написать выражение присоединенной массы поршня. Необ-
Необходимые формулы для расчета:
II

г.) /при m=
г.
' ~* ' имеет те же значения.
3.12. Вывести выражения для коэффициентов Арп и Вр„
разложения звукового поля в бесконечной круглой трубе радиуса
Zo в ряд по бесххелевым функциям:
при заданном в начальном сечении B=0) распределени коле-
колебательной скорости (по оси 2 ) по закону #
(формулы для справок: литература [6] и в задаче 3.II).
3.13. Определить звуковое поле в бесконечной круглой
цилиндрической трубе радиуса 2о и длины ? , если в началь-
начальном сечении B=0) задано поршневое движение с амплитудой
скорости U. и частотой и) на площади коаксиального с осью
трубы B ) круга радиуса ?у . Найти присоединенную массу
поршня в длинноволновом приближении.
3.14. Вычислить присоединенную массу круглого централь-
центрального отверстия радиуса ?у в перегородке, стоящей перпендику-
перпендикулярно к оси (z ) круглой бесконечной (в обе стороны) трубы
радиуса 1* (для случая частот, меньших первой критической
частоты ( co<?V9ic % в функции отношения ^ = ^=0,25;
0,4 и 0,6.
3.15. В бесконечной круглой трубе (радиус Zo ) колеблет-
колеблется коаксиальный круглый поршень (радиус Z1 ) со скоростью
U^U^ecjcpCJcot). Определить звуковое поле в трубе и найти
выражение для суммарной кинетической энергия неволнового поля
в приближении длинных волн (Ic2o<&i ). Найти выражение для при-
присоединенной массы поршня.
12

3.16. Определить звуковое поде в бесконечной прямоуголь-
ной трубе сечения dx& , в начальном сечении которой
(Z = 0) на площади Я,*^ » расположенной в углу прямо-
прямоугольника йх? , задана скорость колебаний u=u.eccp(jtcjt)
вдоль оси трубы ( е ). Определить интенсивность звука ( J )
на частотах ниже первой критической частоты при следующих
данных: <2= 5 см; ё= Ю см; 3,= Z см; 4= ^ см.
3.17. Определить присоединенную массу (J/) круглого от-
отверстия радиуса 7+ в перегородке бесконечной квадратной
трубы (со стороной & ) в функции от отношения ? = ^ *
13

1У» Звукопоглощающие систеуы (в воздушной среде)
Литература [l].
Присоединенная масса отверстия площади $ в перегород-
перегородке, стоящей поперек трубы, и имеющей площадь А , равна:
4.1. Определить при помощи импеданс-диаграммы коэффици-
коэффициент поглощения звука системой, состоящей из пяти слоев порис-
пористого материала с активным удельным иыпедансом R1—2pc , стоя-
стоящих на расстоянии L = 25 см друг от друга перед твердой стен-
стенкой (последний слой отстоит от твердой стеики также на 25 см).
Расчет произвести на частотах j~ = 680 и 340 Гц.
4.2. Пользуясь импедаьс-диаграммой, рассчитать коэффици-
коэффициент поглощения звука трехслойной системой, стоящей перед твер-
твердой стенкой, при нормальном падении з^ука.
Расстояние первого слоя от стсиы ?н = 20 см, удельное
сопротивление RH-5pc ; расстояние второго слоя от первого
<^= 10 см, удельное сопротивление R12~2.pc ; расстояние
третьего слоя от втирого 1Ъ~ 5 с&, удельное сопротивление
/?,3 = °i5Pc • Расч<-т сделать для частот 100, 500 и 2000 Гц.
4.3. Определить коэффициент поглощения звука, распростра-
распространяющегося в круглой трубе на частотах 500, 1000 и 2000 Гц,
если на расстоянии ^ = 1,7 см от конца трубы, закрытого жест-
жесткой стенкой, помещена первая жесткая перегородка с отверстием
посередине диаметра d = 0,4 см, закрытым поглощающим матери-
материалом с удельным сопротивлением Ri = 12 мех.оь на см . На рас-
расстоянии iz = ,3,4 см от первой перегородки помещена вторая
жесткая перегородка с теми же величинами d и R ; на расстоя-
расстоянии 1Ъ- 17 см от второй перегородки помещена^ третья такая же
перьгородка. Площадь сечения трубы Х= I см^.
4.4. Коэффициент отражения вольы давления на конце трубы
выражается следующим образом:
14

где #,¦??- безразмерные активнее и реактивное сопротивле-
сопротивления на конце трубы; г-=е^2г ; 2& - фаза коэффициента отра-
отражения. Показать, что на плоскости комплексного переменного
( R1, J/, ) кривые равного поглощения ( ol= 1- ъ2 )^
( ?-3oyust ) и равной фазы (?~?W?) при отражении на конце
представляют семейство окружностей. Найти уравнения этих ок-
окружностей*
4»5. I) Расчитать толщину слоя (I), диаметр отверстий
(oi)9 расстояние ( d ) между ними для однослойного резонансного
звукопоглотителя с жесткой рередней стенкой и с отверстиями
по квадратной решетке при задании получить*>О/Гъ интервале частот
55-240 Гц» Материал в отверстиях имеет удельное сопротивление
^f= I мех.ом/см2.
2) Задача аналогичная (I), но материал, закрывающий отвер-
отверстия, имеет сопротивление ?,= 4 мех.ом/см2.
3) Задача аналогичная (I). Поглотитель расчитывается на ин-
интервал частот 45-55 Гц при о^>0,9; сопротивление материала
в отверстиях Ri = I мех.ом/см^ (см^;стр. 18§|).
4*6• Определить зависимость от частоты коэффициента погло-
поглощения звука ( о(. ) при нормальном падании на резонансный погло-
поглотитель с жесткой тонкой передней стенкой с квадратными ячейка-
ячейками со стороной 4 см, глубиной 10 см и диаметром отверстия 2 см,
которое закрыто пористым материалом с удельным сопротивлением
5 мех.ом/см2.
4*7..Рассчитать по приближенным формулам р, стр» I89J
геометрические размеры резонансного звукопоглотителя, глубину
резонансного слоя ( i ) и диаметр ( d ) круглых отверстий,
расположенных по квадратной решетке на расстоянии ( а. ) друг
ох друга, чтобы обеспечить коэффициент поглощения звука
о?>0,8 в диапазоне 200-800 Гц» Сопротивление в отверстиях
принять равным I мех.ом, а толщину листа, в котором сделаны
отверстия резонаторов, принять равной 0,3 см.
15

4.8. Найти модуль и фазу коэффициента отражения звука
(при нормальном падении звука)частоты <{ от твердой поверх-
поверхности, на которой по квадратной решетке с шагом "а11 располо-
расположены круглые каналы глубины t и площади & . Определить
модуль и фазу коэффициента отражения в диапазоне частот до
10 000 Гц в функции kl^^l 9 приняв З.= аг= 16 см2;
/^ = 4 см2; ^s 5 см.
4.9. Найти модуль и фазу коэффициента отражения з^ука
частоты / при нормальном падении на твердую поверхность, на
которой по -квадратной решетке с швгом и и площадью ячеек ?
расположены каналы глубиныси площади ?=7~ , причем на вхо-
входе в каналы сосредоточен пористый материал с удельным сопро-
сопротивлением Лу = I мех.ом/см . Принять й= 4 см, ? = 4 см%
I a 5 см, построить график модуля и фазы коэффициента отра-
отражения звука в функции ki^^E в диапазоне частот до
10 000 Гц.
4.10. Рассчитать по приближенным формулам [I, стр.189]
резонансный звукопфглотитсль с глубиной резонансного слоя
t , диаметром круглых отверстий d , расположенных по
квадратной решетке с взаимным расстоянием а , который обес-
обеспечивает коэффициент поглощения <^ > 0,98 в диапазоне частот
от 100 до 120 Гц. Толщина листа с отверстиями ё = 0,5 см.
11II. Найти модуль Z и фазу 2S коэффициента отраже-
отражения от слоя жидкости толщины t , налитого на жесткую поверх-
поверхность, при падении звука под углом &L к нормали. Построить
график модуля и фазы коэффициента отражения для случая, ког-
когда жидкостью является вода, слой имеет глубину t - 30 см,
угол падения равен 0,1 рад и частота меняется от 0 до Ю кГц.
4Л2. й некоторой точке труоы удельный импьдьнс
Z^Rj-hj^ 9 где ?, = 42 мех.ом/см2 и Д, = -42 мех.ом/см2
на частоте ^ = 344 Гц. Считая, что при 18°С скорость звука
равна 344 и/с и рс = 42 мех.ом/см2, определить удельный им-
импеданс в точках на расстояниях 25; 50; 75 и 100 см от началь-
начальной. <хЪ*
4.13. Труба площадью 4СТ скачкообразно перехо-
переходит в точке с координатой *«? в бесконечную трубу сече-
сечения Л5*—^8*^ • На сколько децибел &L слабей звук,
отраженный от переходного сечения,по сравнению с падающим?
16

У. Сложные звукопроводы. Фильтрьи Рупоры. Резонаторы
Литература [I, 2, 5]. Вспомогательные формулы см. в
разделе 1У.
5.1. Рассчитать многоячейчатый фильтр низких частот с
граничной частотой у^= 20 Гц для канала сечением ^=30см
при условии нкакочастотного приближения теории. Определить
возможные значения сечения (Z ) и длины (^) камер расшире-
расширения, вставляемых между отрезками канала ? , ииею щи ш длину
(?). Определить, на какой частоте /' выше /^ затухание
составит 10 дБ на I ячейку.
5.2. Фильтр низкой частоты представляет канал с периоди-
периодически меняющимся сечением. Камеры расширения имеют сечение ?
и длину L , соединительные патрубки в перегородках имеют
сечение S и длину t . Задаются размеры Z.= 100 см;
t- 25 см; $= 30 х 30 см2; Z = 100 х 100 см2. Определить,
на сколько децибел А ослабнут волны частоты /'= 1,01^г/>
после прохождения 20 ячеек фильтра. Определить фазовую ско-
скорость волн {С') при частоте 20 Гц.
5.3. Фильтр высокой частоты представляет сооои трубу ди-
диаметром Ъ = 50 см. В боковой поверхности трубы имеются отвер-
отверстия диаметра d = Ю см, центры которых расположены вдоль
длины трубы ьа расстоянии L = 20 см друг от друга; в отвер-
отверстия заделаны трубки длиной t = 10 см.
Вычислить сдвиг фазы &Ч> для звука с частотой /-^/гр;
получающийся в результате прохождения фильтра длиной 4 м.
5.4. Глушитель мотора представляет собой цилиндрическую
трубу диаметра 2> = 2 см. В боковой поверхности трубы вдоль
ее длины расположены отверстия диаметра cL = I см, центры ко-
которых находятся на расстоянии L = Ь сь друг от друга; в от-
отверстия заделаны трубки длины t s 2 см. Определить граничную
частоту /п> .
Во сколько раз {N) и на сколько децибел (А ) уменьшится
амплитуда дль частоты /= 0,9^/^, , если длина глушителя
40 см.
5.5. Груба площадью сечения ?-3"^2 скачкообразно
переходит в бесконечную трубу сечения ^ = ^ = хг^ , где
17

/Г7>1. Определить, учитывая присоединенную массу, на сколько
децибел (AL ) отраженный от переходного сечения звук будет
слабей падающего, если принять /^ = 4; i*.= ^4r . Присоеди-
Присоединенная йасса на переходном сечении Л- f
5.6. Рассчитать в функции частоты коэффициент отражения
A) и коэффициент ослабления звука (А ) (в децибелах) при
прохождении через бесконечную квадратную трубу сечением 25см ,
если в стенке трубы имеется сбоку отверстие диаметром 2 см,
за которым присоединен объем 200 см3,
5.7. Рупорный громкоговоритель возбуждается поршнем пло-
площадью S = 100 ^Г см*1. Объем перед поршнем через плоскую пред-
рупорную камеру малой длины соединяется с рупором экспоненци-
экспоненциальной формы (бесконечным), устье которого имеет площадь
ё = k ОТ см2.
Определить коэффициент расширения р и выходной диа-
диаметр Ъ рупора длиной 150 см при условии, что на частоте
100 Гц его сопротивление излучения составляет 0,8 от предель-
предельного (высокочастотного). Рассчитать, какую амплитуду ао дол-
должен иметь поршень для получения мощности 10 вт на частоте
100 Гц,
5.8. Определить частотную зависимость коэффициента отраже-
отражения звука ( Zp ) по амплитуде и фазе на конце круглой трубы
сечения So-XR*- 20 см , если в твердой тонкой перегородке
на конце трубы имеется отверстие площадью ^-CTZo ; 2,= I см,
за которым лежит закрытый отрезок такой же трубы длиной
/, s ю см (резонатор). Трение в отверстии не учитывается.
Функцию фока рассчитать по формуле раздела 1У.
5«9. Рассчитать фильтр низких частот, включаемый в волно-
волновод (трубку) диаметром с/= I см так, чтобы его граничная час-
частота ^р была равна 500 Гц, Определить затухание А в деци-
децибелах на одну ячейку фильтра при / = 2/^>.
Рассчитать, какая задержка по времени (г) получится на
одну ячейку фильтра и какая будет фазовая скорость (С) звука
в фильтре,
5,10, Бесконечная фильтровая цепочка состоит из круглой
трубы диаметром Ъ = 10 см с жесткими тонкими перегородками,
18

стоящими на расстоянии L = 10 см друг от друга и имеющими
в центре круглые отверстия диаметром d-rt сы. Определить
частотную характеристику фильтра и нанести ее на график.
11II. Рассчитать собственную частоту воздушного резонато-
резонатора в форме колбы с горлом длиной ?=10 см, диаметром
с г. = ц. см и сферической полостью объемаУдиаметроы ZlR = 20 см.
Расчет провести в длинноволновом приближении.
5.12. Рассчитать собственную частоту и добротность (fl)
воздушного резонатора в ^орме прямоугольного параллелепипеда
с ребрами а=<5= 100 см и h = 80 см (высота) с круглым от-
отверстием в центре верхней грани (п>6) с площадью ?- 200 см,
проводимость отверстия принять равной (приближенно) его диа-
диаметру. Потери на излучение рассчитать по формуле дли пульси-
пульсирующего в свободном пространстве сферического излучателя с
площадью ? ; трение в горле не учитывается.
5.13. Рассчитать собственную частоту и добротность (Q)
воздушного резонатора в форме прямоугольного параллелепипеда
с ребрами п-&= 80 cm и /? = 60 см (высота) с круглым отверс-
отверстием в центре верхней грани (а>6) с площадью *?=Тг/=150 см*1,
к которому примыкает открытая трубка того же диаметра длиний
15 см с открытым концом. Проводимость трубки (/О рассчитать
с поправкой на концы; трение в горле не учитывается. Сопротив-
Сопротивление излучения рассчитывается по формуле /^=^Те- ; про-
проводимость для отверстия на конце труоки с фланцем равна
Н!=4ъ , для отв;|сгия без фланца \(**Вго .
5.14. Определить собственную частоту резонансной системы,
состоящей из закрытого снизу цилиндрического объема высотой
& = {0 си и диаметром t><* 40 см, закрытого с верхней стороны
стальной пластинкой толщиной cl = 0,05 см (заделанной по
краю) и имеющей экран (фланец) большого размера. Эквивалент-
Эквивалентные параметры пластинки вычислить приближенно, исходя из ре-
резонансной частоты круглой пластинки в отсутствие упругого
объема.
Определить амплитуду колебаний в центре пластинки при
воздействии звуковой волны с частотой /= 600 Гц и уровнем ин-
интенсивности 100 дБ, падающей по оси цилиндра сверху вниз.
6-2232
19

5.15. Рассчитать собственную частоту^резонатора, состо-
состоящего из двух равных объемов по 1000 см3, соединенных труб-
трубкой длиной 5 см и диаметром 2 см. Трубку рассматривать как
сосредоточенную систему, учтя присоединенную массу с обоих
концов по формуле для отверстия в бесконечной стенке (см.ра^д.Т).
Рассчитать добротность резонатораB,если в трубку заложен
пористый материал с удельным сопротивлением I мех.ом.
5.16. Определить резонансную частотуДбарабана диаметром
80 см и глубиной 50 см, закрытого мембраной толщиной 0,1 см,
сделанной из материала с плотностью 1,8 и натянутой о" силой
2 х 10 дин на ом. Определить амплитуду колебаний^ центре
мембраны при воздействии звуковой волны с частотой 100 Гц и
уровнем интенсивности 97 дБ, падающей на мембрану по нормали
к ее поверхности.
5.17. Определить резонансную частоту^стальной "мембраны"
телефона, имеющей диаметр 2 г* = 5 см, толщину ol= 0,04 см и
зажатой по краю, считая объем полости под мембраной равным
Vs 30 см3.
5.18. Найти радиусы B,) сферических резонаторов типа
Гельмгольца и радиусы (?•) круглых отверстий в их сферической
оболочке при собственных частотах 100; 200; 400 и 800 Гц, ес-
если добротность всех резонаторов одинакова Q= 100. Проводи-
Проводимость отверстий резонаторов считать равной их диаметру. Сопро-
Сопротивление излучения отверстия рассчитать по формуле для пульси-
пульсирующего излучателя в свободном пространстве при кг,« I.
5.19. Как изменится резонансная частота воздушных полос-
полостей голосового аппарата, если вместо воздуха эти полости будут
наполнены гелием. Возможно ли определить в атмосфере гелия
произношение гласных "у" и "и", формантные частоты которых в
воздухе равны для "у" 500 и 900 Гц и соответственно для "и"
500 и 2000 Гц? Скорость звука в гелии вычислить, зная его мо-
молекулярный вес и отношение удельных теплоемкостей.
5.20. Резонатор Гельмгольца имеет собственную частоту
500 Гц при температуре 20°. Какова будет собственная частота
этого резонатора, если он наполнен воздухом при температуре
200° или -170°?
20

5.21. Определить резонайсную частоту fl воздушного
пузырька в воде, иуеющего радиус I см и заполненного опреде-
определенной массой воздуха при атмосферном давлении, если он бу-
будет погружаться на глубину 10 км? Будет ли влиять на резонанс-
резонансную частоту данного пузырька сила поверхностного натяжения?
5.22. Определить основную резонансную частоту закрытой
трубы длиной L » 20 см с сечением 8 см , в боковой стенке
которой, на расстоянии t- 10 см от конца присоединен резо-
резонатор объема Vs 10 см3 с входным отверстием площадью
? = 0,5 см2.
21

У1. Излучение и рассеяние звука сферой и цилиндром
Литература [I, 2], таблицы 1-5.
6.1 • Определить интенсивность (^/) рассеянного жесткой
сферой звука в функции полярного угла -9 при значениях вол-
волнового параметра k?<>- 3,2. Расчет диаграммы проводится че-
через угловой интервал д-д - 10°. Начертить диаграмму направ-
направленности.
6.2. Точечный источник с производительностью Д,= ?4дЗ,
расположенный на полюсе жесткой сферы, излучает в воду звук
с частотой 10 кГц; радиус сферы соответствует условию
kZo = 2,4. Суммарная излучаемая мощность равна 5 х 10""^ Вт.
Определить интенсивность звука^в направлении полярной оси
на расстоянии 100 м от центра сферы и выразить ее в децибелах
относительно нулевого уровня давления ро* 2 х 10""*^ бар(эфф.)
6.3. Вывести выражения для коэффициентов {ито> итуу и^у )
разложения в ряд по сферическим функциям потенциала скорос-
скоростей для излучения звука сферой (радиус 1О ), на поверхности
которой задано распределение скоростей uC-d^JeospCjcvt), в
зависимости от полярного и азимутального углов. Изложить
весь ход вывода коэффициентов с объяснениями (см. [1,стр.2141).
6.4. Поверхность сферы радиуса Тс = 2 см колеблется с
радиальной составляющее
^ j
Определить интеьсивность излучения CJ в функции угла г?
при kzo- 0,5 и полную излучаемую мощностьД,предполагая
У»2О и 1.
6.5. Поршень радиуса 10 см вставлен в поверхность сферы
радиуса 20 см. Радиальная скорость на поршье iQeocpCJcot)
см/с. Найти полную излучаемую мощность звука Л в функции
частоты в диапазоне 6^ if. < I000 Гц. Начертить полярную диаг-
диаграмму интенсивности звука при волновых параметрах 0,6
( ^= 164 Гц) и1,8(/= 488 Гц).
6.6. Найти выражение для характеристики направленности
3) излучения звука в вертикальной плоскости (по интенсив-
гг

ности) полоской малой угловой ширины л-9 = 1°, опоясываю-
опоясывающей сферу по экватору ( •& = 90°) и колеблющейся со скоростью
uoeocp(Ja>t) (производительностью i4,-2X*.d-9 ) по нор-
нормали к поверхности сферы при ( ?г„= 0,5). Начертить характе-
характеристику направленное m^tffl).
6.7. Определить, во сколько раз (,/V") уощность излучения
точечного источника, расположенного на полюсе Сферы при зна-
значении kZe = 3, отличается от мощности такого же источника
при kio = 4.
6.8. Определить, во сколько раз (Jf) отличается мощ-
мощность, излучаемая двумя противофазными точечными источниками
с одинаковой производительностью, расположенными на полюсах
сферы при ??*= 3, от мощности, излучаемой такими же источни-
источниками при /:&= 2.
6.9. Определить интенсивность и начертить диаграмму на-
направленности тонкого (шириной Д-д ) излучающего звук пояса,
расположенного по экватору сферы, радиуса 1О , колеблющего-
колеблющегося по закону A*sAiCo62.lf-exp(Ju>t) (где </> - азимут). Вол-
Волновой параметр kzo считать весьма малым.
6.10. Какую силу?надо приложить, чтобы жесткий (невесо-
(невесомый) баллон диаметром ?Z*=c/= 20 см совершал колебания в во-
воде с амплитудой п^ 5 см и частотой /= 10 Гц.
11II. Вывести выражение для диаграммы направленности ли-
линейного источника, расположенного по образующей бесконечного
цилиндра радиуса to при азимуте ф = 0, колеблющегося по
нормали к поверхности цилиндра со скоростью U-U0eocp(joot)
и, приняв jcZo—^rZo-i » определить отношение интенсивнос-
интенсивности 3(о) в дальнем поле го направлению $ = 0 к интен-
интенсивности <#A80°) при азимуте % = 180°.
6.12. Вывести выражение для диаграммы направленности
(в дальней зоне) бесконечно длинной плоской полоски ширины
иаи, колеблющейся в воде с колебательной скоростью
U^U^eccpQ'oot) по нормали к плоскости бесконечного плос-
плоского экрана, плоскость которого совпадает с плоскостью полос-
полоски. Вычислить, при каких частотах будут иметь место значения
ka = 6, 10, 20, если #= 20 см и при каких углах с нор-
нормалью к плоскости пластинки S? интенсивность звука Судет
23

равна нулю и максимуму Ч? для этих трех случаев.
6.13. Определить круговую частоту^обственных радиальных
колебаний воздушного пузырька радиуса *• в воде при атмос-
атмосферном давлении исходя из величины упругости его объема и ко-
колеблющейся массы (которая практически равна присоединенной
массе воды).
Зная сопротивление излучения пульсирующей сферы, опреде-
определить добротность колебательной системы пузырька (?})•

УП. Поршневой излучатель. Обнаружение эхо-сигнала
Литература [I, 2, 7].
При решении задач этого параграфа необходимы следующие
сведения:
а) интенсивность звука на оси гидроакустического порш-
поршневого излучателя мощности Л (с радиусом *о ) с экраном,
имеющего коэффициент концентрации У* , равна на расстоя-
расстоянии 1 от центра поршня
7 Я <
где Jb - коэффициент затухания звука.
Звуковое давление в воде равно &х
б) коэффициент затухания в морской воде (в дБ на км)
в функции частоты ? (кГц) определяется эмпирической форму-
формулой
в) интенсивность эхо-сигнала от сферы радиуса R э на-
находящейся на расстоянии X , при локации в море поршневым
излучателем (с экраном) мощности /7 с коэффициентом кон-
концентрации J" , равна
г) интенсивность эхо-сигнала бесконечного цилиндра ра-
радиуса R при тех же условиях, как и для сферы
д) обнаружение эхо-сигнала приемником, реагирующим на
звуковое давление не меньше ро 9 возможно при условии
Р2
25

7.1. Круглая поршневая диафрагма диаметром 30 см-2г*
(с большим фланцем) излучает в воду на частоте 30 кГц звуко-
звуковую мощность 10 Вт.
а) Определить (пренебрегая затуханием звука), на каком
предельном расстоянии можно обнаружить звук при помощи при-
приемника с чувствительностью I бар.эфф (сопротивление излуче-
излучения диафрагмы считать равным R*Sf>c , где ?=эгг*);
б) определить, по каким направлениям 9п излучение
звука будет отсутствовать;
в) определить предельную дальность по направлению пер-
первого бокового лепестка 9' диафрагмы направленности.
7.2. Круглая поршневая диафрагма диаметром 30 см
(с большим фланцем) излучает в воду на частоте 30 кГц звуко-
звуковую мощность П s 10 Вт. Определить, на каком предельном рас-
расстоянии можно обнаружить звук приемником с чувствительностью
I бар.эфф., учтя затухание звука в море (сопротивление излу-
излучения диафрагмы считать равным R**$J)C , где $**yzi).
7.3. Точечный излучатель с производительностью (силой)
Q3^v излучает звук с частотой ? в морской воде.
Определить эффективную амплитуду звукового давления р€
на расстоянии 7 (кы), учтя коэффициент затухания в морской
воде.
Задачу решить для трех различных заданий:
кГц
10
20
30
км
6
2
I
см3/с
24
1.33
7Л. При излучении точечного источника с производитель-
производительностью Qc при частоте / = 30 кГц на расстоянии 2= I км
амплитуда звукового давления равна ОД бара.
Определить производительность (силу) источника Ф> ,
учитывая коэффициент затухания звука в морской воде.
7.5. Рассчитать звуковое давление на горизонтальной оси
поршневой диафрагмы радиуса R = 15 см, колеблющейся (в
бесконечном экране) в морской воде с амплитудой ?,= 10 см
26

при частоте 30 кГц на расстоянии Z - I км и 2 кмэ учитывая
коэффициент зьт^ханиа /2> в зависимости от частоты.
7.6. Гидролокатор с поршневым излучателем (диаметр
2г*= 10 см) излучает при частоте 50 кГц мощность 10 Вт в
горизонтальном направлении.
а) Определить, на каком расстоянии может быть принят
эхо-сигнал от сферы диаметра 5 м с учетом затухания в морс-
морской воде, если минимальное давление, регистрируемое системой,
равно I бар#эфф.
б) Определить то же расстояние для частоты ^?= 25 кГц.
7.7. Поршневой излучатель радиуса &,= 4,5 см с экра-
экраном (с горизонталх-ной осью) излучает под водой (на глубине
h = 10 м ) звуковую мощность Л на частоте /=100 кГц и
должен лоцировать сферу радиуса R = 40 см, находящуюся на
той же глубине на расстоянии Zi = 140 м при условии, что
прямой луч закрыт круглым экраном (радиуса S = 0,5 м), по-
поставленным перпендикулярно к оси на расстоянии ^2= Пот
центра поршня.
а) Выяснить, возможно ли осуществить гидролокацию в та-
таких условиях и, если возможно, на каком предельном расстоя-
расстоянии?
б) Какова минимальная мощность излучателя для осущест-
осуществления локации на боковом луче диафрагмы с учетом затухания
в морской воде, если риемник регистрирует минимальное давле-
давление рь бар.эфф.?
7.8. Определить минимальную мощность поршневого гидро-
гидроакустического излучателя с радиусом 15 см (с экраном) для
осуществления на частоте 30 кГц и на первом боковом лепестке
диаграммы направленности локации сферы радиуса 20 м, находя-
находящейся в море на расстоянии I км, если приемник, находящийся
рядом с излучателем, может принять сигнал со звуковым давле-
давлением р> I бар (эфф).
7.9. Поршневой гидроакустический излучатель с горизон-
горизонтально направленной осью имеет отношение диаметра B г* )
к длине волны ( 1 ) ?~ = 1,70. Излучаемый в воде на глу-
глубине h = 15 и звуковой импульс с тональной набивкой отража-
отражается от вертикальной плоскости, стоящей на расстоянии х от
27

излучателя и от свободной поверхности воды, и приходит об-
обратно к излучателю в разные моменты времени с интервалом
At .
Исследовать, при каких условиях амплитуды импульса, от-
отраженного от плоскости и от свободной поверхности, равны на
поверхности излучателя и с каким интервалом времени At
яридут отраженные импульсы, если А = 15 м. Расчет провести
без учета затухания в среде для значений волнового параметра
kz*= 1,703" и kx0- 2,720Г .
Для расчетов следует использовать таблицы бесселевых
функций.
7.10. Поршневой излучатель (радиус ъ,= 15 см) с экра-
экраном излучает в морской воде мощность Л = 10 Вт в горизон-
горизонтальном направлении и создает на расстоянии 1 * 3,44 км
амплитуду давления ро (эфф.)
Не учитывая затухание в среде, определить, чему равна
частота излучателя и какая эффективная амплитуда давления
имеет место в центре поршневой диафрагмы, если ро соответст-
соответствует четырем различным уровням 94; 100; 106; 112 дБ над ну-
нулевым уровнем 2 х 10~^ бар. При расчетах принять
рс = 1,5 х 1Сг и сопротивление излучения /?*Spc,nae ?-3iz?,
11II. Летучая мышь может обнаружить эхо-локацией сферу
диаметром Ъ = 2 см на расстоянии ^= I и. Определить, на
каком расстоянии *1г она сможет обнаружить при помощи сиг-
сигнала той же интенсивности длинный стержень того же диаметра.
7.12. Ультразвуковой излучатель дельфина имеет мощ-
мощность П = 0,1 Вт и коэффициент концентрации у= 50 при час-
частоте ^ = 80 кГц.
а) Определить, на каком расстоянии дельфин может локи-
локировать цилиндр радиуса Ro = 20 см, стоящий вертикально, ес-
если слуховой аппарат дельфина регистрирует давление, соответ-
соответствующее не менее 40 дБ над нулевым уровнем
Ро = 2 х 10"^ бар.эфф.
б) Ту же самую задачу решить для ?„ = 2 см.
28

7.13. Определить, на каком расстоянии ос от излучателя
будет воспринят эхо-сигнал в море от вертикального цилиндра
радиуса Ri = 10 см, если эхо-сигнал такого же излучателя от
сферы радиуса Rz = 10 см, отстоящей на расстоянии ?- 100 м,
воспринимается с такой же амплитудой как от цилиндра, так и
от сферы. Длина волны звука значительно меньше ^ и ^ •
Задачу решить при задании а) 1 = 100 кГц; б) / = 30 кГц.
Литература
1. Ржевкин С.Н. Курс лекций по теории звука. Изд-во МГУ,
I960.
2. Морз §. Колебания и звук. М., ГШ, 1949.
3. Исакович М.А. Общая акустика. М., "Наука", 1973.
4. Стрелков СП. Введение в теорию колебаний. М.-Л.,
1951.
5. Фурдуев В.В. Электроакустика. М., ГТТИ, 1948.
6. Янке ?•, ЭвдвК| Леш Ф.Специальнйе функции. М., "Наука','
1964.
7. Сташкевич А.П. Акустика моря. Л., "Судостроение", 1966.
29

IX. Таблицы и графики
Таблица I
Функции Лежандра для сферических координат
0°
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
tr
0°
5
10
15
20
25
I.0000
I.0000
I.0000
I.OuOO
i.oooo
I.OuOO
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
I.0000
Is fa*)
I.0000
0.9437
0.7840
0.5471
0.2715
0.0009
P, Ccos &)
I.0000
0.9962
0.9848
0.9659
0.9397
0.9063
0.8660
0.8192
0.7660
0.7071
0.6428
0.5736
0.5000
0.4226
0.3420
0.2588
0.1736
0.0872
0.0000
ftcotd)
I.0000
0.9216
0.7045
0.3983
0.0719
-0.2040
рг(соз&)
I.0000
0.9886
0.9548
0.8995
0.8245
0.7321
0.6250
0.5065
0.38Ck
0.2500
0.II98
-0.0065
-0.1250
-0.2321
-0.3245
-0.3995
-0.4548
-0.4886
-0.5000
P7(cosfr)
I.0000
0.^962
0.6164
0.2455
-0.1072
-0.3441
1.0000
0.9773
0.9106
0.S042
0.6640
0.5010
0.3248
0.1454
-O.lk5?
-0.1768
-0.3002
-0.3886
-0.4376
-0.4452
-0.4130
-0.3449
-0.2474
-0.I29I
0.0000
I.0000
0.9623
0.8352
0.6847
0.4750
0.2465
0.0234
-0.I7I4
-0.3190
-0.4063
-0.4275
-0.3852
-0.2891
-0.1552
-0.0038
+0.1434
0.2659
0.3468
0.3750
1.0000
0.8675
0.5218
0.0962
-0.2518
-0.4062
1.0000
0.8358
0.4228
-0.0428
-0.3617
-0.3896
30

Продолжение таблицы I
30
35
40
45
50
55
60
65
70
75
80
85
90
Pstcosd-)
-0,2233
-0.3691
-0.4197
-0,3757
-0.2545
-0.0868
+ 0,0898
0,2381
0,3281
0,3427
0,2810
0,1577
0,0000
pjcotf)
-0.3740
-0.4П4
-0.3236
-0.1484
+ 0,0564
0.2297
0.3232
0.3138
0.2089
0.0431
-0.I32I
-0,2638
-0,3125
R(c*s9)
-0,4102
-0.3096
-0.1006
+ 0.I27I
0.2854
0.3I9I
0,2231
0,0422
-0.1485
-0.2731
-0.2835
-0.1778
0.0000
8 («**)
-0.3388
-0.II54
+ 0.1386
0.2983
0.2947
0.1422
-0.0763
-0.2411
-0.2780
-0.1702
+ 0.0233
0.2017
0.2734
§6»s9)
-0.1896
+ 0.0965
0.2900
0.2855
0.I04I
-0.1236
-0.2679
-0.2300
-0.0476
+ 0.1595
0.2596
0,1913
0.0000
31

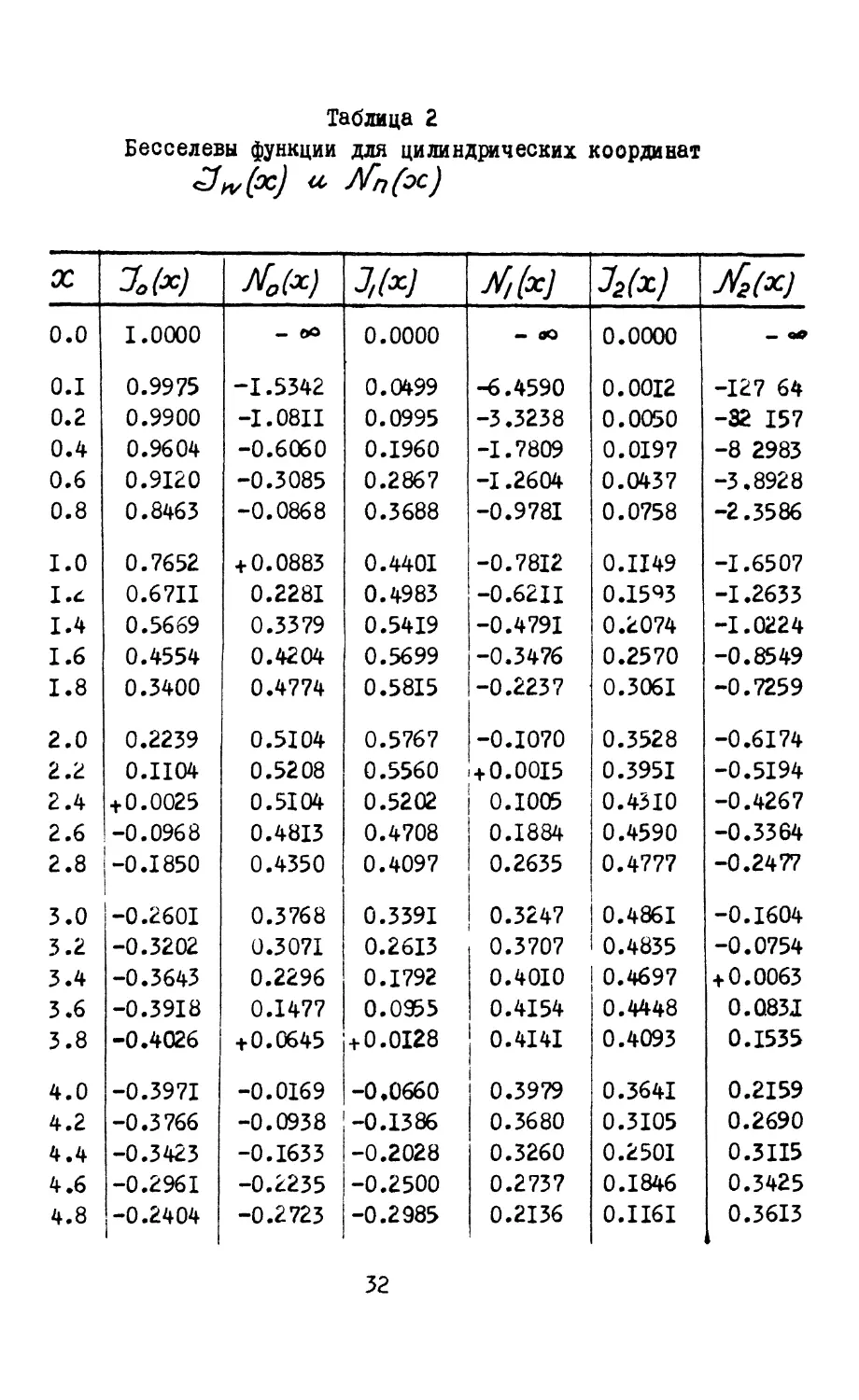
Таблица 2
Бесселевы функции для цилиндрических координат
X
0.0
0.1
0.2
0.4
0.6
0.8
1.0
1.С
1.4
1.6
1.8
2.0
г .г
г л
2.6
2.8
3.0
3.2
3.4
3.6
3.8
4.0
4.2
4.4
4.6
4.8
1.0000
0.9975
0.9900
0.9604
0.9120
0.8463
0.7652
0.67П
0.5669
0.4554
0.3400
0.2239
0.II04
+0.0025
-0.0968
-0.1850
-0.2601
-0.3202
-0.3643
-0.3918
-0.4026
-0.3971
-0.3766
-0.3423
-0.2961
-0.2404
-1.5342
-I.08II
-0.6060
-0.3085
-0.0868
+ 0.0883
0.2281
0.3379
0.4204
0.4774
0.5104
0.5208
0.5104
0.4813
0.4350
0.3768
0.3071
0.2296
0.1477
+0.0645
-0.0169
-0.0938
-0.1633
-0.2235
-0.2723
0.0000
0.0499
0.0995
0.1960
0.2867
0.3688
0.4401
0.4983
0.5419
0.5699
0.5815
0.5767
0.5560
0.5202
0.4708
0.4097
0.3391
0.2613
0.1792
0.0955
+ 0.0128
-0.0660
-0.1386
-0.2028
-0.2500
-0.2985
-6.4590
-3.3238
-1.7809
-I.2604
-0.9781
-0.7812
-0.62II
-0.4791
-0.3476
-0.2237
-0.1070
+ 0.0015
0.1005
0.1884
0.2635
0.3247
0.3707
0.4010
0.4154
0.4I4I
0.3979
0.3680
0.3260
0.2737
0.2136
0.0000
0.0012
0.0050
0.0197
0.0437
0.0758
0.II49
0.15^3
0.2074
0.2570
0.3061
0.3528
0.3951
0.4310
0.4590
0.4777
0.4861
0.4835
0.4697
0.4448
0.4093
0.3641
0.3105
0.2501
0.1846
0.II6I
-127 64
-32 157
-8 2983
-3.8928
-2.3586
-1.6507
-1.2633
-1.0224
-0.8549
-0.7259
-0.6174
-0.5194
-0.4267
-0.3364
-0.2477
-0.1604
-0.0754
+ 0.0063
0.Q83I
0.1535
0.2159
0.2690
0.3II5
0.3425
0.3613
32

Продолжение таблицы Z
X
5,0
5.2
5.4
5.6
5.8
6.0
6.2
6.4
6.6
6.8
7.0
7.2
7,4
7.6
7.8
8.0
-0.1776
-0.П03
-0.0412
+ 0.0270
0.0917
0.1507
0.2017
0.2433
0.2740
0.2931
0.3001
0.2951
0.2786
0.2516
0.2154
0.I7I6
Ж(Х)
-0.3085
-0.3212
-0.3402
-0.3354
-0.3177
-0.28b2
-0.2483
-0.2000
-0.1452
-0.0864
-0.0250
+ 0.0339
0.0907
0.1424
0.1872
0.2235
К*)
-0.3276
-0.3432
-0.3453
-0.3343
-0.3II0
-0.2767
-0.2329
-0.I8I6
-0.1250
-0.0652
-0.0047
+ 0.0543
0.1096
0.1592
0.2014
0.2346
0.1479
0.0792
+ 0.0101
-0.0568
-0.II92
-0.1750
-0.2223
-0.2596
-0.2858
-0.3002
-0.3027
-0.2934
-0.2731
-0.2428
-0.2039
-0.I58I
+ 0.0466
-0.0217
-0.0867
-0.1464
-0.1989
-0.2429
-0.2769
-0.3001
-0.3119
-0.3123
-0.3014
-0.2800
-0.2487
-0.2097
-0.1638
-0.II30
ЛГмМ
0.3677
0.3617
0.3429
0.3152
0.2766
0.2299
0.1766
0.II88
+ 0.0586
-0.0019
-0.0605
-0.II54
-0.1652
-0.2063
-0.2395
-0.2630
33

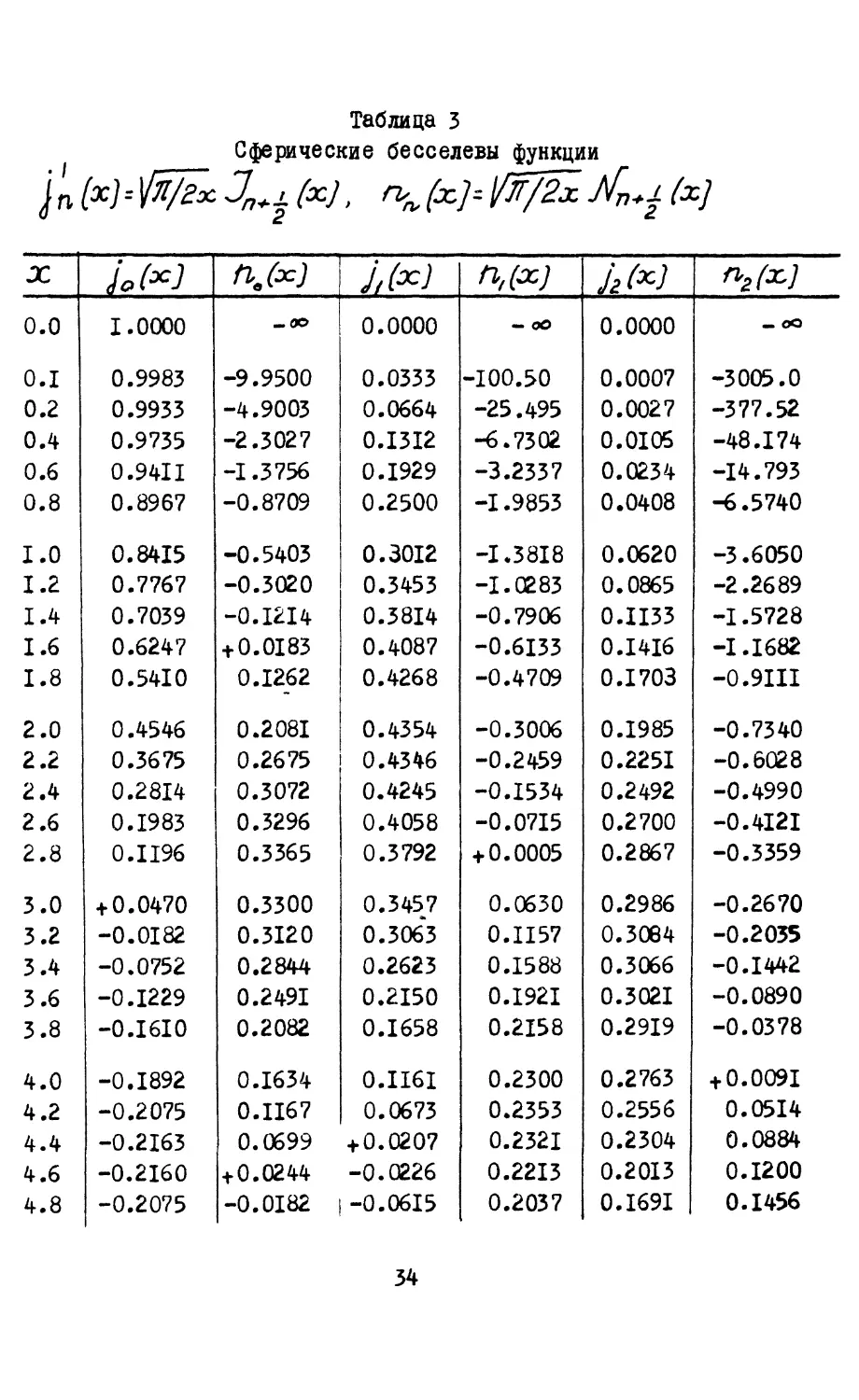
Таблица 3
Сферические бесселевы функции
X
0.0
O.I
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
2.2
2.4
2.6
2.8
3.0
3.2
3.4
3.6
3.8
4.0
4.2
4.4
4.6
4.8
Jot*]
I.0000
0.9983
0.9933
0.9735
0.941I
0.8967
0.8415
0.7767
0.7039
0.6247
0.5410
0.4546
0.3675
0.2814
0.1983
0.II96
+ 0.0470
-0.0182
-0.0752
-0.1229
-0.I6I0
-0.1892
-0.2075
-0.2163
-0.2160
-0.2075
-oo
-9.9500
-4.9003
-2.3027
-1.3756
-0.8709
-0.5403
-0.3020
-0.I2I4
+ 0.0183
0.1262
0.2081
0.2675
0.3072
0.3296
0.3365
0.3300
0.3120
0.2844
0.2491
0.2082
0.1634
0.II67
0.0699
+ 0.0244
-0.0182
Ш
0.0000
0.0333
0.0664
0.I3I2
0.1929
0.2500
0.3012
0.3453
0.3814
0.4087
0.4268
0.4354
0.4346
0.4245
0.4058
0.3792
0.3457
0.3063
0.2623
0.2150
0.1658
0.II6I
0.0673
+ 0.0207
-0.0226
-0.0615
- oo
-100.50
-25.495
-6.7302
-3.2337
-I.9853
-1.3818
-1.0283
-0.7906
-0.6133
-0.4709
-0.3006
-0.2459
-0.1534
-0.0715
+ 0.0005
0.0630
0.II57
0.1588
0.I92I
0.2158
0.2300
0.2353
0.2321
0.2213
0.2037
JiM
0.0000
0.0007
0.0027
0.0105
0.0234
0.0408
0.0620
0.0865
0.II33
0.I4I6
0.1703
0.1985
0.2251
0.2492
0.2700
0.2867
0.2986
0.3064
0.3066
0.3021
0.2919
0.2763
0.2556
0.2304
0.2013
0.I69I
n2fjt)
— oo
-3005.0
-377.52
-48.174
-14.793
-6.5740
-3.6050
-2.2689
-1.5728
-1.1682
-0.9III
-0.7340
-0.6028
-0.4990
-0.4I2I
-0.3359
-0.2670
-0.2035
-0.1442
-0.0890
-0.0378
+ 0.0091
0.0514
0.0884
0.1200
0.1456
34

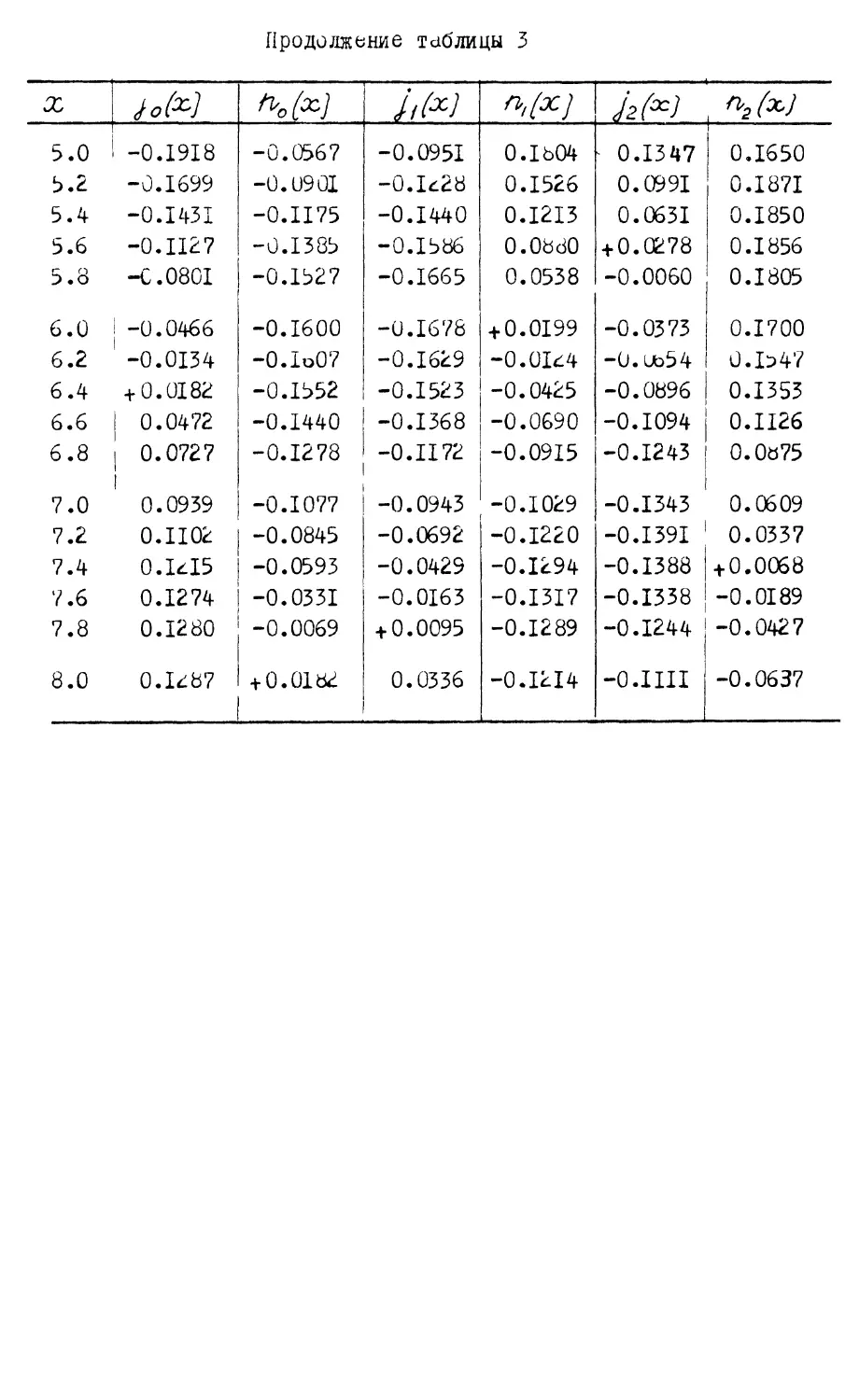
Продолжение таблицы 3
X
5.0
Ь.2
5.4
5.6
5.8
6.0
6.2
6.4
6.6
6.8
7.0
7.2
7.4
V.6
7.8
8.0
-0.I9I8
-0.1699
-0.I43I
-0.112:7
-С.0801
-0.0466
-0.0134
+ 0.0182
0.0472
0.0727
0.0939
0.П02
0.UI5
0.1274
0.1280
0.U87
-0.0567
-0.U90I
-0.II75
-0.1385
-0.1527
-0.1600
-0.1о07
-0.1552
-0.1440
-0.1278
-0.1077
-0.0845
-0.0593
-0.0331
-0.0069
+ 0.01с^
-0.0951
-0.1^28
-0.1440
-0.1586
-0.1665
-0.1678
-0.1629
-0.1523
-0.1368
-0.II72
-0.0943
-0.0692
-0.0429
-0.0163
+ 0.0095
0.0336
пй(х]
0.1604
0.1526
0.I2I3
O.ObdO
0.0538
+ 0.0199
-0.0U4
-0.0425
-0.0690
-0.0915
-0.1029
-0.1220
-0.1294
-0.I3I7
-0.1289
-0Л214
<¦ 0.1347
0.0991
0.0631
+ 0.0278
-0.0060
-0.0373
-О.иь54
-0.0896
-0.1094
-0.1243
-0.1343
-0.I39I
-0.1388
-0.1338
-0.1244
-0.IIII
П2(эс]
0.1650
0.I87I
0.1850
0.1856
0.1805
0.1700
О.Ъ47
0.1353
0.II26
0.0675
0.0609
0.0337
+ 0.0068
-0.0189
-0.0427
-0.0637

Таблица 4
Фазовые углы и коэффициенты амплитуд для излучения и рассеяния
звука сферой J4, *ка = B1их,/ц) =(соа/с)
На
0.0
0.1
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
2.2
2.4
2.6
2.8,
3.0
3.2
3.4
3.6
3.8
4.0
4.2
4.4
4.6
4.8
5.0
на
2.0
2.2
2.4
2.6
2.8
3.0
3.2
3.4
3.6'
3.8
4.0
4.2
4.4
4.6
4.8
5.0
За
во
100.5
25.50
6.731
3.239
2.001
I.4I4
1.085
0.8778
0.7370
0.6355
0.5590
0.4993
0.4514
0.4I2I
0.3792
0.3514
0.3274
0.3066
0.2883
0.2721
0.2577
0.2448
0.2331
0.2225
0.2128
0.2040
*5
51.31
27.14
15.25
9.021
5.573
3.576
2.371
1.620
I.I37
0.8183
0.6043
0.4583
0.3577
0.2881
0.2399
0.2065
0.00°
0.02
0.15
I.I2
3.41
7.18
12.30
18.56
25.75
33.68
42.19
51.16
60.49
70.13
80.01
90.08
100.32
110.70
121.20
131.79
142.47
153.22
164.03
174.91
185.83
196.79
207.79
-0.01°
-0.02
-0.04
-0.10
-0.20
-0.37
-0.68
-I.I6
-I.9I
-2.99
-4.48
-6.43
-8.79
-11.45
-14.15
-16:56
со
2000
250.1
31.35
9f408
4.101
2.236
1.426
I-02I
0.7931
0.6529
0.5590
0.4918
0.44II
0.40II
0.3686
0.3415
0.3184
0.2985
0.28II
0.2657
0.2519
0.2396
0.2285
0.2184
0-2091
0.2006
323.7
155.2
79.69
43.38
24.83
14.83
9.206
5.907
3.904
2.649
1.Ш
1.308
0.948
0.701
0.529
0#407г
0.00°
-0.01
-0.08
-0.58
-Ь82
-3.80
-S.I4
-8.II
-8.97 .
-8.25
-5.87
-1.97
+3.21
9.44
16.50
24.23
32.49
41.18
50.23
59.37
69.15
78,92
88.88
98.97
109.20
119.55
129.98
4
0.00°
0.00
0.00
-0.01
-0.01
-0.03
-0.06
-0.11
-0.21
-0.38
-0.66
-1.09
-1.73
-2.65
-3.92
-5.58
-
5637
354.6
70.73
22.67
9.434
4.646
2.583
1.584
1.057
0.7629
0.5901
0.4837
0.4148
0.3676
0.3333
0.3071
0.2862
0.2688
0.2540
0.24II
0*.2296
0.2194
0.2I0I
0.2016
0.1939
2370
1030
483.5
242.2
128.2
71.28
41.34
24.88
15.49
9.933
6.545
4.418
3.050
2.148
1.542
I.I26
<Рг
0.00°
0.00
0.00
-0.01
-0.06
-0.25
-0.70
-1.59
-3.07
-5.19
-7.7?
-10.40
-12.49
-13.51
-13.14
-II.31
-8. II
-3.73
+ 1.65
7.86
14.75
22.20
30.12
38.44
47.08
56.00
65.16
0.00°
0.00
0.00
0.00
0.00
0.00
0.00
-0.01
-0.02
-0.03
-0.06
-0.12
-0.22
-0.37
-0.61
-0.98
*1
-
- -
5906
785.5
188.9
62.97
25.82
12.22
6.426
3.667
2.236
1.444
0.9823
0.7036
0.5308
0.4214
0.3508
0.3042
0.2723
0.2496
0.2326
0.2193
0.2084
0.1992
0.I9I2
0.1840
-
7790
3343
1541
755.6
390.7
211.7
119.5
70.01
42.3.9
26.44
16.94
11.13
7.479
5.130
3.587
0.00°
0.00
0.00
0.00
0.00
-0.01
-0.02
-0.08
-0.22
-0.51
-1.05
-1.97
-3.38
-5.34
-7.80
-10.54
-13.16
-15.17
-16.17
-15.9-4
-14.41
-11.67
-7.84
-3.08
'+2.47
8.7С
15.4€
А,
<?*;
0.00°
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
-0.01
-0.02
-0.04
-0.07
-0.12
-
-
-
2058
547.8
186.9
75.74
34.84
17.66
9.669
5.635
3.459
2.220
I.48I
1.024
0.7334
0.5443
0.4195
0.3364
0.2807
0.2432
0.2174
0.1994
0.1863
0.1764
0.00°
0.00
0.00
0.00
0.00
О.00
0.00
0.00
-0.01
-0.02
-0.06
-0.15
-0.32
-0.64
-I.I8
-2.02
-3.27
-5.00
-7.23
-9.83
-12.58
-15.10
-17.00
-17.95
-17.79
-16.47
-14.04
-
-
-
-
5002
4
0.00°
0.00
0.00
0.00
0.00
2407 0.00
1219 | 0.00
645.8 ; 0.00
356.1 , 0.00
203.6 0.00
120.2 0.00
73.09
45.06
/29.24
19.16
12.»
>
0.00
0.00
0.00
0.00
-0.01
Вклейка Зак .2332. Стр.36-37

Таблица 5
Фазовые углы и коэффициенты амплитуд для излучения и рассеяния
звука цилиндром
Да
0.0
ол1
0.2
ОЛ
0.6
0,8
1.0
1.2
1.4
1.6
1.8
2.0
г.г
2.4
?•6
2,8
3.0
3-2
3.4
3.6
3.8
4-0 .
4.2
4.4
4.6
4.8
5 Л
/са
2.0
2.2
2.4
2.6
2.8
3.0
3.2
3.4
3.6
3.8
4.0
4.2
4.4
4.6
4.8
5.0
Со
&>
12.92
6.651
3.583
2.585
2.091
1.793
1.593
1.447
1.335
1.246
I.I73
I.II2
1.060
I.0I4
0.9743
0.938$
.0.9071
0.8785
0.8524
0.8286,
0.8067
0.7865
0.7678
0.7503
0.7341
GL7I88
22.07
12.82
7.834
4.999
3.309
2.261
Iw590
1.149
0.8534
0.6539
0.5190
0.4287
0.3693
0.3312
, 0.3071
. 0.2921
п
0.00°
.44
1.71
6.28
I2;82
20.66
29.39
38.74
48.52
58.62
68.%
79.49
90.15
100.93
III.81
122.75
133.76
144.82
155.92
107.06
178.23
189.42
200.04
211.88
223.14
234.42
JL45,7I
fs
-0.04°
-0.10 .
-0.22
-0.45
-0.86
-1.53
-2.59
-4.18
-6.41
-9.35
-12.92
-16.83
-20.62
-23.74
-25.76
, -26.44
OP
63.06
15.55
3.875
1.844
1.199
0.9283
0.7884
0.7035
0.6453
0.6019
0.5676
0.5392
0.5152
0.4944
0.4700
0.4597
0.4450
0.4317
0.4195
0.4084
0.3980
0.3885
0.3796
0.3713
0.5535
0.3662
Ce
130.8
68.99
38.65
Z2.18
14.03
8.967
5.922
4.025 i
2.805
2.000
1.456
1.082
0.82II
0.6374
0.5081
0.4177
0.00°
-45
-1.82
-6.97
-13.62
-18.73
-20*50
-18.94
-14.80
-8.84
-1.61
+6.52
15.31
24.57
34.20
44.11
54.24
64.55
75.01
85.58
96.25
107.01
117.83
128.72
139.65
150.64
161.66
n
0.00°
0.00
-0.01
-0.08
-0*06
-0.13
-0.25
-0.47
-0.83
-1.41
-2.30
-3.60
-5.42
-7.85.
-10.88.
-1Л.40
Qt
OO
2546
318.2
39.71
Ц.72
4.922
2.529
1.503 •
1.012
0.7627
0.*6309
0.5573 ,
0.5130 1
0.4836
0.4624
0.4457
0.4319
0.4198
0.4090
0.3992
0.3901
0.3816
0.3737
0.3662
0.3592
0.3525
0.3462
Cy
903.5
432.1
221.4
120.2
68.58
40.86
25.27
16.16
10.65
7.200
4.985
3.526
2.542
1.865
1.391
1.054
n
0.00°
0.00
-0.Ш
-0.14
-0.69
-2.09
-4.77
-8.91
-14.06
-19.03
-22.49
-23.69
-22.56'
-19.45
-14.75
- 8.84
- 1.99
+ 5.59
13.73
2.33
31.29
40.55
50.06
59.77
69.66
79.70
89.87
0.00°
0.00
0.00
0.00
0.00
-0.01
-0.02
-0.04
-0.07
-0.14
-0.26
-0.46
-0.77
-1.26
-2.00
-3.06
—
9565
600.7
II9.6
38.20
15.'81
7.712
4.212
2.504
1.596 ,
1.086
0.7898
0.6158
0.5136
0.4535
0.4175
0.3952
0.3804
0.3698
0.3617
0.3549
0.3480
0.3434 |
0.3383 !
0.3334
0.3287
Cm
7144
3090
1452
725.6
383.4
212.6
122.9
73.80
45.80
29.29
19.24
Й.95
8.907
6.252
4.471
3.251
n
0.00°
0.00
0.00
0.00
-0.01
-0.06
-0.20
-0.57
-1.35
-2.77
-5.08
-8.44
-12.71
-17.32
-21.41
-24.15
-25.09
-24.19
-21.64
-17.71
-12.66
-6.72
-0.04
+ 7.22
14.97
23.13
31.62
/i
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
-0.01
-0.02
-0.04f
' -0.08
-0.14
-0.25
-0.42
—
-
-
1595
382.9
127.3
52.03
24-54
12.85
7.290
4.405
2.801
1.861
1.287
0.9265
0.6965
0.5496
0.4566
0.3987
0.3631
0.3412
0.3275
0.3187
0.3126
0.3081
0.3044
-
-
4941
2418
1248
674.6
380.0
222Д
I34.I
83.43
53.32
34.92
23,40
16.00
11.15
rf
0.00°
0.00
0.00
0.00
0.00
0.00
0.00
-0.02
-0.06
-0.16
-0.37
-0.79
-1.55
-2.80
-4.73
-7.46
-II. CH
-15.13
-19.29
-22.81
-25.11
-25.90
-25.14
-22.95
-19.54
-15.10
-9.81
ft
0.00
>0.00
0.00
0.00
0.00
0.00
0.00
o*.oo
0.00
0.00
0.00
0.00
-0.01
-0.01
-0.02
r0.04

Таблице
Наименование
единицы
Длина
Скорость
Ускорение
Таблица
S
i единиц измерения и обозначений
Обозначение
Единица
измерения
сантиметр
сантиметр
в секунду
сантиметр
на сек.квая
Сокращен-
Сокращенное обоз-
обозначение в
сист. СГС
см
см/с
р.см/с2
Связь меж-
хсгс
I м = К^су
1м/с=10^см/с
1м/с2=10см/с
Эффективные амплитуды колебательных смещений, скоростей и
ускорений обозначаются теми же буквами с
Масса
Плотность
Площадь
Объем
Время
Частота
Частота угловая,
или циклическая
Температура
Плоский угол <
Телесный угол
Сила
Давление
Нулевой уровень
звукового давле-
давления (эффект)
Ji, m
р
?, s, H, ?
У
}
1
и)
Т
?2
гт ф
о
р>
р*
грамм
грамм на
куб. санти-
сантиметр
квадратный
сантиметр
кубический
сантиметр
секунда
(секунда),
герц
радиан в
сек.
градус по
шкале Цель-
Цельсия или
Кельвина
градус,
радиан
стерадиан
дина
дина на
квадр#сан-
квадр#сантиметр (в
акустике -
бар)
о ТП™* тшн/pi
С «1U ДНЯ/ vl
(бар)
индексом |!е!Ч
г
г/см3
см2
С
_
Гц
рад/с
°С, °К
рад,0
стер
да
?5/сГ
(бар)
2
1
I Ki^IC^r
1кг/м3=Ю
г/см3
1м^=104см^
_ q fi 4
lM3=IObCMd
I с = I с
I Гц = 1 Гц
I рад/с =
= 1 рад/с
Т°К=2?3+Т°С
1рад=A80/^)
1стер=1стер
I н=105дн
I н/м2 =
=10 дн/см^
—
36

Продолжение таблицы б
Наименование
единицы
Эффективная амп-
амплитуда давления
Добротность
Модуль Юнга
Модуль сдвига
Модуль объемной
упругости
Динамическая
вязкость
Скорость звука
Интенсивность
(сила) звука
Обозначение
Л
Q
Ё
а
с
у
Уровень интенсив- /
ности звука (лога- ь
рифмический)
Удельное акусти-
акустическое сопротив-
сопротивление (импеданс)
Z
Механическое со-
сопротивление акус- гг
тической системы ^т
Волновое число
Длина волны
к
х
Единица
измерения ;
дина на кв.
см
безразмерно
дина на
АДЭ. V/H
дина на
кв.см
дина на
кв.см
дина-секун-
дина-секунда на квадр.
сантиметр
сантиметр
в секунду
дина-секунде
иокращен-
UVV \J\J\J*J
начение в
сист. СГС
дн/см2
дн/см2
дн/см2
ДН/СМС
дн.с/см2
см/с
t 3pr.c/ciic
на квадр.сан- \
тиметр
ДБ
дина-секунда
на кубич.см
дина-секунд*
на сантимет!
единица на
сантиметр
сантиметр
безраз-
безразмерный
дн.с/см3
1 , з
) ДН.С/СМ^
сы-1
см
'Связь между
единицами С
и СГС
lH/Людн/с-г
Ih/m^sICUh/cm2
1н/м2=Юдн/см2
1н/м =10дн/с^
2
1н.с/м =Юдн.с/с1г
Im/ossIO^cm/c
—
1н.с//аь=1 дн/см3
Iн.с/м=1дн.с/см '
1м"*1=1 (Г2 см
1м=1(гсы
37

X. Ответы и, решения
Раздел I
1.1. гГ= 1000 км/ч и 1200 км/ч независимо от давлении.
1.2. 819° и -205°С.
1.3. 484 дня.
1.4. у^яа 1000 бар(эфф); ч4^ 25 см/с; амплитуда смещения^
ё=в^0,004 см; амплитуда ускорения ^^ 1,37-10^см/с^;
лТ = 0Д°.
1.5. В 200 раз.
1.6. гг- 3&5-4О**Т ; в водороде С = 12,50.104см/с;
/77
в углекислоте С = 2,60.10 см/с; показатель преломления
П = 0,48.
1.7. L = 45 см.
1.8. 3,5 и 0,157 км,.
1.9. Около 28 дн/см^ (бар).
1.10. Ы 470 м.
1.11. гР = -0Д07; t = i-lzpl=09Q93\ ?^=1,36.
1.12. Суммарный модуль упругости J; = ~ + ~^ ? С7 =12Ом/с.
1.13. Для одинакового направления * '
по частоте
для противоположного направле-
направления: ^/=^-q.
I.I4. Машинист слышит гудок с частотой /
эхо - с частотой /—^с / • разница
/-/¦-^/. ^ ¦
Сторо» слышит гудок с частотой /"=7fzr » a эхо-с час-
частотой /'^Л-/; рьзность частот /"-/"^-^^Z •
Машинист и сторож услышат биения с частотой 4^=^ef.
1.15.
38

.16. 5е=7,75.1(Г10 см; ^е= &Ц%,= ^.ЭО.Ю^сы/с; при
160 дБ получатся величины в 10 раз большие*
положительное направление оси ? — от средней точки к источ-
источнику.
I.I9. /2=0,86.
Раздел П
/= 1^0 Гц; ^в= 2,28.КГ5см.
2.2. /?*=#, ^"^^5^ ПРИ /= 200,^00,600 и 800 Гц;
ПРИ /=100,300,500 и 700 Гц.
2.3. Импеданс на конце трубы должен Оыть равеь нулю. Импеданс
в точках 3: = 2!>, 50, 75, 100 и 1^5 см будет равен:
2.4. Ответ в форме г{
2.5. а) Закрытая труба
б) открытая труба
2 -6 •
2.7. из резонансной частоты мембраны и>„=Ц^^ находат-
ся натяжение пленки V = 2,11.10^ дн/см. Безразмерный им-

педанс на конце трубы ?А- jooaspc » где ^-^г*,>
смещение в центре ?=^~ , тогда %<=—?$J^=~J ~JTf
Условие резонанса ^^-'^^^rt откуда 1с?
?« 77,7 ГЦ.
г.8. Импеданс при ас - 25, 50, 75 и 100 см равен соот-
соответственно 4200 A+J ); 4200 {1-J ), 4200 ( l+j ) и
4200 ( {-J ) мех.ом.
2.9. Резонансная частота / определяется из выражений
в которых ' 1с=Ш, При %<О, ?'>/ труба как бы укора-
укорачивается; при Ц>0; ?*d труба как бы удлинняется.
2.10.
Должно быть 2)/<^, <bz>i9 где
2.II.

Раздел Ш
3.1. rf10 = 1700Гц; /2о= 3400 Гц; /„ = ИЗО Гц;
?г = 2260 Гц; 4м = 'сC° Гц» А = 2880 Гц; /а,= 3580 ГЦ.
3.2. /и= 2070 Гц; /,г = 5800 Гц; Д = 1000 Гц;
4 = 2400 Гц; 4 = 4630 Гц; /2о = 1650 ГЦ; ? = 3630 Гц;
/2г= 540J Гц.
при f = 2Д.103 Гц; йго= 0,532; ^= 0,3*
при / = ЗЛО3 Гц; 0&* 0,213; *р= 0,75ic.
с
при ^^ga в дальнем поле остается только 1-й член
3.5. Уу = 3450 Гц; ^(= 6320 Гц; /3= 9170 Гц;
С; Zi- 50 см.
3.6. « , *tJ*
3.7.
41

5.Ъ. Требуется дагь детальный вывод коэффициентов «*т„
разложения потенциала скоростей в бесконечный ряд;
но}п - О, I, Zy 3 ....
3.9. Амплитуда звукового давления на оси
Плоская волна возбуждается только при п = 0.
3.10.
?• у
з.и.
) - корни уравнения ^
3.12. Изложить ход вывода коэффициентов.
3.13. Звуковое давление в зависимости от Z , н и
Присоединенная масса:

3.14.
) л 0p
3.15. Звуковое давление в функции t ,ги t :
где
где
Iтах^ 2 9 *
3.16.
3.17.
где
=>" =1

Раздел 1У
4.1. При /t= 680 Гц; <^= 0, при /г= 340 Гц; ol= 0,76.
4.2. о4,в= 0,52; о^,0= 0,ь2;^гом= 0,92.
4.3. о^* 0,71; Чл>о^ 0,4; ^* 0,18.
4 Л. Окружности равного поглощения
окружности равной фазы / { )*_ / i
4.5. I) I* 27 см;^= 0,86 см; Л= 8,5 см. 2) <f= 27 см;
d= 1,74 см; ^г= 6 см. 3) ? = 31 см; ^= 9,7 сь; ^2= 61 см.
4.6. Максимумы коэффициента поглощения о^= 0,555 полу-
получаются при частотах, соответствующих корням уравнения
Ъ,ЪЬК\с1-ск$кЫО ; ^= 1200 Гц; /? = 3220 Гц; /s = 5000 Гц.
При частотах /=/?1 ^7-Ю5 Гц, <^ = 0.
4.7. t - b,I3 см; ^ = 1,75 см; CL = 6 см.
4.8. Приняв функцию Фока ^i^.&S^l^ получим
фаза ^ близка к 0, за исключением узкой области частот близ
корней уравнения @,106-сф^ )=0, соответствующих частотам
1= 1500 Гц; /=4600 Гц; ^=* 7900 Гц, где фаза перескакива-
перескакивает с +90° на -90°, оставаясь далее близкой к нулю до следующе-
следующего корня.
4.9.
44

Корни уравнения @,07k?-ctgke)=0 соответствуют
частотам /f ««I570 Гц;/2«4740 Гц;/3 « 8000 Гц;
при /=^» ;**# ; при кЫпгу ?-п^9 г={.
4.10. Выбрав г,= I мех#ом/сыг, получим ^= 31,2 см;
с^= 1,77 см; <2= 10,3 см.
11II. Модуль коэффициента отражения г-ltpl-i;
"
Г
J
=1 Д3.10"; в формуле Ч^ - углы падения;
и преломления; >(r2=i|i 9 Угол 2i = 0 при к2
и достигает значений 1^ , когда IДЗЛО
г 2780^ t 0,22 Гц.
4.12.
i \); Z/0,50) =f>c (i-J);
?рЦ); Z<(lfi0) =
4.13.
где A =
при

Раздел У
5.1. При заданию и и)гр и ? произведение LiZ.^ —r
и две из этих величин ми«но выбрать произвольно при огракиче-
/ ?> ^Г s ^Гй _ 1100— S7S)
нии сверху: L, с, Z ^ -Jq - 5~ ~ //с/с*
Выбираем А = 140 cw, <f = 33 см, тогда
?х г$70.Ю4 = 165 X 165 см2; /4 1,17/гр - ^3,5 Гц.
Ь.?. 4 = 47,8 дБ; с'= U,7dC
5.3. ЛУ^ ^0 рад = 1145°.
5.4. И/"= 7,6 раз; Л= 17,4 дЬ; ^= 1160 Гц.
5.5.
где
Нщ =т^ гйе
5.6.
5.7. S= 0,012; 2)= 20,4 см; (^= 0,044 см.
5'
ЧЗ-"*''-*-<; ^-^в
при

5.9. Зная %ГР , определим 4*в = 377, где 4*в- Длина
трубок диаметра do между камерами расширения; L и $ -
- длина и сечение кауер ( SL-V ). Величины /- и 4*в должны
быть меньше -|р = 6Ь см. Выбираем L = 8 см; 4^= 2,95 см,
?=16 см с некоторым приближением так, чтооы 4«в^=377;
?-?**?- 2.0,647*, = 2,95 - 0,64 = 2,31 см; Г = 0,637мс ;
скорость звука с''= 1570 см/с.
5.10.
Первая полоса непропускашш лежит между ?Й/}= -I и
G^/J = +i; I^L* 0f93f ^ = 510 Гц; ^А=Т; ^= 1700 Гц.
Для-второй полосы непропускания i^^f^', -f3- 1915 Гц;
^ = 3440 Гц.
5.II-
«* = €*$[ = 590г*; ?=
концевая поправка дает ? = 82 Гц.
5.12. /о= 25 Гц; Q = 177.
5.13. /„= 21,5 Гц;<3 = 540.
5.14. /в = 77 Гц.
5.15. /, = 170 Гц; Q = 6,4.
5.16. ^ =62 Гц; действующая сила 35,6.105 дн; импе-
импеданс IJ9.I05 дн.с/см3, амплитуда колебаний при 100 Гц
47

5.17. Упругость объема У на два порядка меньше упругос-
упругости мембраны и ей можно пренебречь
/%«
5.18.
^Ри ^pfs35 iOO; 200, 400, 500 Гц получим соответстъенно
t, =3,4 см; г«= 1,7 см; г»= 0f85 cm; te= 0f425 см.
5.19. Резонансные частоты в гелия для гласных "у" и
"и" будут соответственно 1450; 2660 и 1450/Гласные "у11 и
"и" будут совершенно неузнаваемы.
5.20. Q^= 442 м/с; С^ 221 м/с.
5.21. // = 316/, ;гд* ?= 340 Гц;
/= 107.1СГ Гц « 107 кГц; силы поверхностного натяжения
почти не влияют.
5.22.

Раздел П
6.1. Привести таблицу 36$) и начать диаграмму на-
направленности.
6.2. С/= 0,788^-; ? = 124,7 ДБ; Д = 3*7 бар.
в .4. n^/ci
6.5. Ш = 300 эрг/с; '0= 1Д ,
6.6.
характеристика направленности
при -?=0, &Й/«/ ; при т? =55°, <?E5о)=0,93;
при 90°, tf (90°) = 0,89.
6.7. jiT = 2,43
6.8. X = 2f65.
6.9.
Ч i
6.10. 3>= 13,2.10е дн = 13,5 кГ.
11II. 3@)_
ш

ю-
0,
6
10
20
7
II
25
,15
,9
.8
<^=90
* <= 20.5°
6.13. «t-
о* размера пузырька.
Q «завшсио
50

Раздел УП
7.1. а) Предельная дальность 205 км; б) 9^ 12°; #2=22°;
Р^ = 33,5°; в) ??й15,6°; предельная дальность 26 км.
7.2. 5,35 км.
7.3. Во всех трех случаях Ре = ОД бар(эфф.).
7.47<L,33 см3/с
7.5. 19,8 бар(эфф.) и 4,95 бар(эфф-).
7.6. а) 260 м; б) 239 м.
7.7. а) Локация возможна на боковых лучах, углы которых с
осью излучателя io$>bj\H — ^ ; для луча, осуществ-
осуществляющего локацию, {q§~?k. > б) Локация возможна
при /7 ^ 184 Вт.
7.8. 36 Вт.
7.9. Условие выполняется при ос = 7,7 ; &t = 134 мс
при X = 15,6 ; &t = 292 мс.
7.10. Давление в центре диафрагмы 10; 20; 40; 80 бар; час-
частота 5, 10, 15 и 20 кГц.
7.11. ^(^ = 5,8 м.
7.12. а) 440 м; б) 320 м.
7.13. а) 330 м; б) 720 м.
51

С. о ц е р х а н и е
1. Скорость зв\ка. Интенсивность звука. Эффект стр#
Дрпплера, 4
П. Звуковые волны в трубе постоянного сечения.
(длинноволновое приближение) 7
Ш» Нормальные волны в волноводах с жесткими стен-
стенками Ю
1У. Звукопоглощающие системы (в воздушной среде) 14
У. Сложные звукопроводы. Фильтры. Рупоры, Резона-
Резонаторы 17
У1. Излучение и рассеяние звука сферой и цилиндром 22
УП. Поршневой излучатель. Обнаружение эхо-сигнала 25
УШ. Литература 29
IX. Таблицы v графики 30
X. Ответы и решения 38
Сергей Николаевич Ржевкин
Задачи по терии звука
Редактор Р.Д. Солод¦
Художественный редактор Н.D.Калмыкова.
Заказная.
Подписано к печати!йг?-1976 г.
Л.-53684. Формат 60x90/16
Бумага тип.* 3
Уел.печ.л.3,25+2 вкл.@,375 п.л.)
Уч.-изд.л.З,03
Зак.2232 Тираж 350 экз.
Цена 18 коп.
Издательство
Московсого университета
Москва,К-9,ул.ГЕРЦЕНА, 5/1
Типография Изд-ва МГУ
Москва,Ленинские горы.

V
Импеданс-диаграмма
Коэффициент поглощения^- ——т~* ЦИФРЫ на окружности равной фазы (S)
означают ф- при У±>0) jf^ ^?.' пои 7jf <c?. Цифры на окружности равного
поглощения означают Wl9iaN= §fc
Вкладка зак.2232