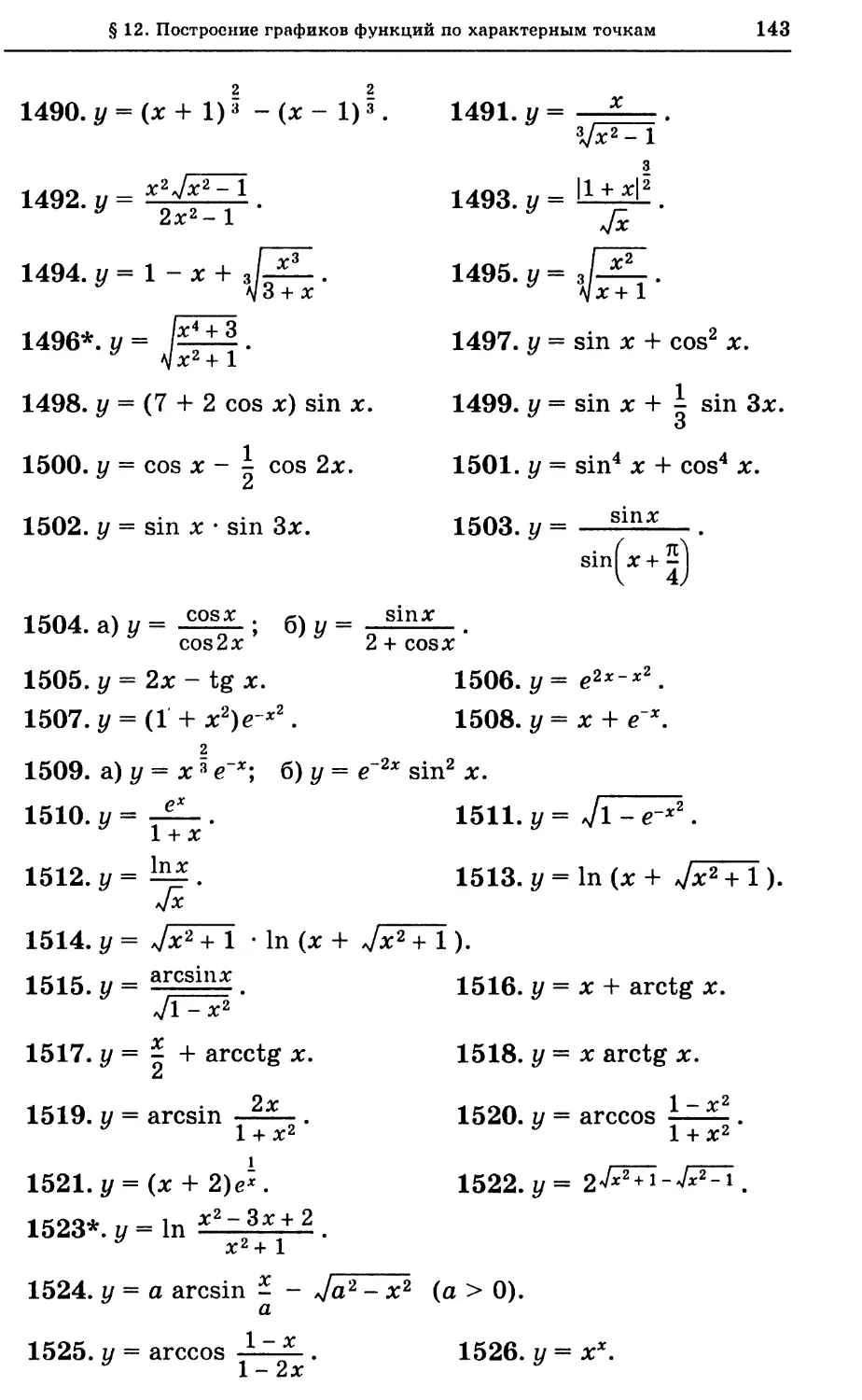r n n	X^4AjpCOS t tcos2t), 1
Б.П. Демидович .i
Сборник
задач и упражнений
по математическому г
анализу
Vi
I \ | I
X!—Д| СШл 1
у I-a sin t;
х-а cos!'t,
y~nsiryt;
x=aCo^t,
y\=asin2i:

Б.П. Демидович
СБОРНИК
задач и упражнений
по
математическому анализу
Учебное пособие
для вузов
ACT (Ш5Ь
ACT • Астрель
Москва *2005

УДК 517(076.1)
ББК 22.161я73
ДЗО
Оформление обложки
дизайн-группы «Дикобраз»
Демидович Б. П.
ДЗО Сборник задач и упражнений по математическому ана¬
лизу: Учеб, пособие для вузов / Б. П. Демидович. — М.: ООО
« Издательство Астрель»: ООО « Издательство ACT », 2005. —
558, [2] с.: ил.
ISBN 5-17-010062-0 (ООО «Издательство ACT*)
ISBN 5-271-03601-4 (ООО «Издательство Астрель»)
В сборник включено свыше 4000 задач и упражнений по важнейшим
разделам математического анализа: введение в анализ; дифференциаль¬
ное исчисление функций одной переменной; неопределенный и опреде¬
ленный интегралы; ряды; дифференциальное исчисление функций не¬
скольких переменных;' интегралы, зависящие от параметра; кратные
и криволинейные интегралы. Ко всем задачам даны ответы.
Для студентов физических и механико-математических специально¬
стей высших учебных заведений.
УДК 517(076.1)
ББК 22.161я73
Подписано в печать с готовых диапозитивов 25.10.04.
Формат 60 х 9071в. Гарнитура «Школьная». Уел. печ. л. 35,0.
Доп. тираж 10 000 экз. Заказ № 296.
ISBN 5-17-010062-0 (ООО «Издательство ACT»)
ISBN 5-271-03601-4 (ООО «Издательство Астрель»)
© ООО «Издательство Астрель», 2002

ПРЕДИСЛОВИЕ
Как и многие математики, я дважды пользовался этой очень
популярной книгой: первый раз, когда меня учили анализу, а
затем, когда сам учил ему других. Рад подготовке очередного
издания задачника Б. П. Демидовича и с особым чувством бла¬
годарности откликаюсь на предложение его сына, В. Б. Демидо¬
вича, написать по этому поводу предисловие.
Итак, несколько слов об этом замечательном университет¬
ском задачнике по математическому анализу и о его авторе, про¬
фессоре Московского государственного университета Борисе
Павловиче Демидовиче.
Б. П. Демидович (1906—1977) был родом из Белоруссии, где
его отец Павел Петрович Демидович служил учителем и одно¬
временно с успехом занимался этнографией и местным фольк¬
лором, за что был даже избран членом-сотрудником Император¬
ского Общества Любителей Естествознания, Антропологии и Эт¬
нографии при Московском университете. Сам Борис Павлович,
закончив Белорусский государственный университет, тоже не¬
сколько лет учительствовал, а затем поступил в аспирантуру
Научно-исследовательского института математики и механики
Московского государственного университета. В аспирантуре он
занимался под общим руководством Вячеслава Васильевича Сте¬
панова, имея своим непосредственным руководителем Виктора
Владимировича Немыцкого. Именно они в значительной степени
и определили основную область научной деятельности Б. П. Де¬
мидовича: классический математический анализ и теория обык¬
новенных дифференциальных уравнений.
П-о окончании аспирантуры Б. П. Демидович был зачислен
ассистентом механико-математического факультета Московско¬
го государственного университета на кафедру математического
анализа. С того времени, на протяжении более сорока лет он яв¬
лялся сотрудником этой кафедры, став после защиты кандидат¬
ской диссертации ее доцентом, а после защиты докторской дис¬
сертации — ее профессором. Кроме того, он преподавал и в дру¬
гих вузах Москвы. Многие из его непосредственных учеников
стали кандидатами и докторами наук.
Профессионализм и богатейший педагогический опыт Б. П. Де¬
мидовича нашли отражение в его научных работах (их около
шестидесяти), в том числе в монографиях и учебных пособиях,
получивших признание как у нас, так и за рубежом.

4
Особое место в этом ряду занимает предлагаемый читателю
сборник задач. Первое его издание, материал которого Б. П. Де¬
мидович собирал более пятнадцати лет, вышло в свет в 1952 году.
Книга сразу приобрела известность и стала основным универси¬
тетским задачником по математическому анализу. В дальней¬
шем в задачник вносились некоторые авторские коррективы, но
лишь в незначительной мере, поскольку первоначальная струк¬
тура книги оказалась очень удачной. К настоящему времени за¬
дачник выдержал множество переизданий на русском языке, пе¬
реведен на многие иностранные языки и используется во многих
странах мира.
Развитие математики со временем приводит к новым, обычно
объединяющим отдельные факты понятиям, методам, концеп¬
циям, языку. Это часто затрагивает и, казалось бы, законченные
фундаментальные разделы. В полной ^мере это относится также
к дифференциальному и интегральному исчислению с его ны¬
нешней инвариантной трактовкой дифференциала и законов
дифференцирования, с языком дифференциальных форм и ин¬
тегрированием форм, позволившем написать современную фор¬
мулу Ньютона—Лейбница. Этот язык и общая формула Стокса
и сейчас не всегда присутствуют не только в задачниках, но и в обя¬
зательных курсах анализа. На стыке нескольких областей мате¬
матики находятся также асимптотические методы — важный
и, благодаря своей эффективности, весьма полезный математи¬
ческий аппарат, элементы которого, подобно теории пределов
и формуле Тейлора, желательно видеть в задачниках по анализу.
Но высшие разделы анализа предполагают у обращающегося к ним
наличия определенных навыков и техники. Ведь исполнение
сколь-нибудь серьезного музыкального произведения немысли¬
мо, если исполнитель не владеет инструментом.
Опыт показал, что задачник Б. П. Демидовича позволяет сту¬
денту приобрести необходимые навыки в использовании аппара¬
та классического анализа. Предлагаемый задачник — одно из
основных университетских учебных пособий для упражнений по
математическому анализу.
В. А. Зорич,
профессор кафедры
математического анализа
механико-математического
факультета МГУ

Часть 1
Функции
одной
переменной

РАЗДЕЛ I
ВВЕДЕНИЕ В АНАЛИЗ
§ 1. Вещественные числа
1.	Метод математической индукции. Чтобы доказать, что некоторая
теорема верна для всякого натурального числа л, достаточно доказать:
1) что эта теорема справедлива для п = 1 и 2) что если эта теорема спра¬
ведлива для какого-нибудь натурального числа л, то она справедлива
также и для следующего натурального числа п + 1.
2.	Сечение. Разбиение рациональных чисел на два класса А и В назы¬
вается сечением, если выполнены следующие условия: 1) оба класса не
пусты; 2) каждое рациональное число попадает в один и только в один
класс и 3) любое число, принадлежащее классу А (нижний класс), мень¬
ше произвольного числа, принадлежащего классу В {верхний класс). Се¬
чение А/В определяет: а) рациональное число, если или нижний класс А
имеет наибольшее число или же верхний класс В имеет наименьшее чис¬
ло, и б) иррациональное число, если класс А не имеет наибольшего числа,
а класс В — наименьшего числа. Числа рациональные и иррациональные
носят название вещественных или действительныхХ).
3.	Абсолютная величина (или модуль). Если х — вещественное чис¬
ло, то абсолютной величиной {модулем) |jc| называется неотрицательное
число, определяемое следующими условиями:
Для любых вещественных чисел х и у имеют место неравенства
4.	Верхняя и нижняя грани. Пусть X = {х} — ограниченное множе¬
ство вещественных чисел. Число
В дальнейшем под словом число мы будем понимать веществен¬
ное число, если не оговорено противное.
2) Запись х € X означает, что число х принадлежит множеству X,
-х, если х < 0;
х, если х > 0.
|*| - ы < |* + у\ < |*| + ы.
т = inf {*}
называется нижней гранью множества X, если:
1)	каждое х € Х* 2) удовлетворяет неравенству
х > т;
2)	каково бы ни было е > 0, существует х' € X такое, что
х' < т + е.

§ 1. Вещественные числа
7
Аналогично число
М = sup {*}
называется верхней гранью множества X, если:
1)	каждое х € X удовлетворяет неравенству
х < М,
2)	для любого е > О существует х” € X такое, что
х">М- е.
Если множество X не ограничено снизу, то принято говорить, что
inf {*} = -оо;
если же множество X не ограничено сверху, то полагают
sup {*} = 4-00.
5.	Абсолютная и относительная погрешности. Если а (а * 0) есть
точное значение измеряемой величины, а х — приближенное значение
этой величины, то
Д = |jc - а\
называется абсолютной погрешностьюу а
— относительной погрешностью измеряемой величины.
Говорят, что число х имеет п верных знаков, если абсолютная по¬
грешность этого числа не превышает половины единицы разряда, вы¬
ражаемого /1-й значащей цифрой.
Применяя метод математической индукции, доказать, что для
любого натурального числа п справедливы следующие равенства:
1.	1 + 2 + ... + /» = "iZLtJJ.
2
2	12 + 22 +	+ п2 = п(ге + 1)(2д+1)
6
3.	I3 + 23 + ... + п3 = (1 + 2 + ... + п)2.
4.	1 + 2 + 22 + ... + 2я-1 = 2Л- 1.
5.	Пусть
а1п] = а(а - К) ... [а - (п - 1)й] и а[0) = 1.
Доказать, что
(а + й)1"1 = £ Сп а1п-т№тК
т - О
где С™ — число сочетаний из п элементов по т. Вывести отсюда
формулу бинома Ньютона.

8
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
6.	Доказать неравенство Бернулли:
(1 + хг)(1 + х2) ... (1 + хп) > 1 + хх + х2 + ... + хп9
где xlf х2, ...» хп — числа одного и того же знака, большие -1.
7.	Доказать, что если х > -1, то справедливо неравенство
(1 + х)п >1 + пх (п> 1),
причем знак равенства имеет место лишь при х = 0.
8.	Доказать неравенство
п\ <	при п > 1.
Указание. Использовать неравенство
(1 + ;г7тГ *2 <-*• *• •••>•
9.	Доказать неравенство:
а)	2! • 4! ... (2п)! > [(п + 1)!]я при n > 1.
б)	1 .3 ... 2п^1 <	1
2	4	2 n J2n+1
10.	Доказать неравенства:
а)	1 +	+ -р + .. + -р > Jn (п > 2);
л/2	л/3	Jn
б)	п'" 1 > (п + 1)" (п > 3);
в)
г) (2л)! < 22"(п!)2.
sin хк (0 < xk < я; k = 1, 2, ..., /г);
11.	Пусть с — положительное число, не являющееся точным
квадратом целого числа, и А/В — сечение, определяющее веще¬
ственное число Jc , где в класс В входят все положительные ра¬
циональные числа Ъ такие, что Ь2 > су а в класс А — все остальные
рациональные числа. Доказать, что в классе А нет наибольшего
числа, а в классе В нет наименьшего числа.
12.	Сечение А/В, определяющее число \f2 , строится следую¬
щим образом: класс А содержит все рациональные числа а такие,
что а3 < 2; класс В содержит все остальные рациональные числа.
Доказать, что в классе А нет наибольшего числа, а в классе В —
наименьшего.
13.	Построив соответствующие сечения, доказать равенства:
а)	л + л = .Д8; б) л/2Тз = 7ё .

§ 1. Вещественные числа
9
14.	Построить сечение, определяющее число .
15.	Доказать, что всякое непустое числовое множество, огра¬
ниченное снизу, имеет нижнюю грань, а всякое непустое число¬
вое множество, ограниченное сверху, имеет верхнюю грань.
16.	Показать, что множество всех правильных рациональ¬
ных дробей — , где тип — натуральные числа и 0 < т < п> не
п
имеет наименьшего и наибольшего элементов. Найти нижнюю
и верхнюю грани этого множества.
17.	Определить нижнюю и верхнюю грани множества рацио¬
нальных чисел г, удовлетворяющих неравенству
г2 < 2.
18.	Пусть {-х} — множество чисел, противоположных чис¬
лам х € {х}. Доказать, что:
a)	inf {-х} = -sup {х}; б) sup {-х} = -inf {х}.
19.	Пусть {х + у) есть множество всех сумм х + у> где
х € {*} и у € {у}.
Доказать равенства:
а)	inf {х + у} = inf {х} + inf {у};
б)	sup {х + у) = sup {х} 4- sup {у}.
20.	Пусть {ху} есть множество всех произведений ху, где
х € {х} и у € {у}, причем х > 0 и у > 0.
Доказать равенства:
a)	inf {ху} = inf {х} inf {у}; б) sup {ху} = sup {х} sup {у}.
21.	Доказать неравенства:
а)	\х-у\> ||х| - |у||;
б)	\х + хх + ... + хп\ > \х\ - (|Xj| + ... + |х„|).
Решить неравенства:
22. |* + 1| < 0,01.
24. |х| > \х + 1|.
26. |* + 2| + |ж - 2| < 12.
28. ||х+ 1|-|ж- 1|| < 1.
30.	Доказать тождество
23. \х-2\> 10.
25. \2х - 1| < \х - 1|.
27. |х + 2| - |х| > 1.
29. |х(1 - *)| < 0,05.
31.	При измерении длины в 10 см абсолютная погрешность
составляла 0,5 мм; при измерении расстояния в 500 км абсолют¬
ная погрешность была равна 200 м. Какое измерение точнее?
32.	Определить, сколько верных знаков содержит число
х = 2,3752,
если относительная погрешность этого числа составляет 1%.

10
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
33.	Число
х= 12,125
содержит 3 верных знака. Определить, какова относительная по¬
грешность этого числа.
34.	Стороны прямоугольника равны:
х = 2,50 см ± 0,01 см,
у = 4,00 см ± 0,02 см.
В каких границах заключается площадь S этого прямоугольни¬
ка? Каковы абсолютная погрешность А и относительная погреш¬
ность 8 площади прямоугольника, если за стороны его принять
средние значения?
35.	Масса тела т = 12,59 г ± 0,01 г, а его объем V = 3,2 см3 ±
±0,2 см3. Определить плотность тела и оценить абсолютную и от¬
носительную погрешности плотности, если за массу тела и его
объем принять средние значения.
36.	Радиус круга
г = 7,2 м ± 0,1 м.
С какой минимальной относительной погрешностью может быть
определена площадь круга, если принять п = 3,14?
37.	Известны измерения прямоугольного параллелепипеда:
х = 24,7 м ± 0,2 м,
у = 6,5 м ± 0,1 м,
z = 1,2 м ± 0,1 м.
В каких границах заключается объем V этого параллелепипе¬
да? С какими абсолютной и относительной погрешностями мо¬
жет быть определен объем этого параллелепипеда, если за его
измерения принять средние значения?
38.	С какой абсолютной погрешностью следует измерить
сторону квадрата х, где 2 м < х < 3 м, чтобы иметь возмож¬
ность определить площадь этого квадрата с точностью до
0,001 м2?
39.	С какими абсолютными погрешностями А достаточно
измерить стороны х и у прямоугольника, чтобы площадь его
можно было вычислить с точностью до 0,01 м2, если ориенти¬
ровочно стороны прямоугольника не превышают 10 м каж¬
дая?
40.	Пусть 8 (jc) и 8 (у) — относительные погрешности чисел х
и у, 5 (ху) — относительная погрешность числа ху.
Доказать, что 8 (ху) < 8 (х) + 8 (у) + 8 (х)5 (у).

§ 2. Теория последовательностей
11
§ 2. Теория последовательностей
1.	Понятие предела последовательности. Говорят, что последова¬
тельность хи х2, ...» хп, ... имеет своим пределом число а (короче, схо¬
дится к а), т. е.
Нш хп = а,
л — СЮ
если для любого е > 0 существует число N = N (е) такое, что
\хп - а\ < е при п> N.
В частности, хп называется бесконечно малойу если
Нш хп = 0.
л — оо
Последовательность, не имеющая предела, называется расходя¬
щейся.
2.	Признаки существования предела.
1)	Если
Уп<хп< гп
И
lim уп = lim гп => с,
л * оо	Л —• оо
то
lim д:л = с.
П — оо
2)	Монотонная и ограниченная последовательность имеет предел.
3)	Критерий Коши. Для существования предела последовательнос¬
ти хп необходимо и достаточно, чтобы для любого е > 0 существовало
N = N (е) такое, что
\хп — хп + р| < е,
если только п > N и р > 0.
3.	Основные теоремы о пределах последовательностей. Предпола¬
гая, что существуют
lim хп и lim упУ
П — оо	п — ОО
имеем:
1)	если х„ < г/„, то lim *„ < Нш г/„;
л ’ оо	п — ОО
2)	lim (д:л + у„) = lim + lim г/„;
а — оо	п — оо	л — оо
3)	lim (х„ (/„) = lim хп lim j/„;
п — ОО	п — ОО	л — ОО
v	lim *„
4)	lim — =	—— , если lim yrt ^ 0.
{/„	lim уп	П-ОО

12
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
4.	Число е. Последовательность
(1 + ;Г ->
имеет конечный предел
lim {1 + iV = е = 2, 718 281 8284... .
л - °о V п)
5.	Бесконечный предел. Символическая запись
lim хп = °о
п ОО
обозначает, что, каково бы ни было Е > 0, существует число N = N (Е)
такое, что
|л:л| > Е при п> N.
6.	Предельная точка. Число £ (или символ оо) называется частич¬
ным пределом (предельной точкой) данной последовательности хп (п =
= 1, 2, ...), если существует ее подпоследовательность
xPi, хРг, .... хРп, ... (1 < Pi < р2 < ...)
такая, что
lim х =
п — ОО
Всякая ограниченная последовательность имеет по меньшей мере
один конечный частичный предел (принцип Больцано—Вейерштрас-
са). Если этот частичный предел единственный, то он же является ко¬
нечным пределом данной последовательности.
Наименьший частичный предел (конечный или бесконечный) по¬
следовательности хп
lim хп
п — оо
называется нижним пределом, а наибольший частичный предел ее
lim хп
п — ОО
называется верхним пределом этой последовательности.
Равенство
lim хп = lim хп
п — ОО	п — ОО
является необходимым и достаточным условием существования преде¬
ла (конечного или бесконечного) последовательности хп.
41. Пусть
п
п+ 1
(л= 1, 2, ...).

§ 2. Теория последовательностей
13
Доказать, что
lim хп = 1,
п —► оо
определив для каждого е > 0 число N = N (е) такое, что
\хп - 1| < £, если п> N.
Заполнить следующую таблицу:
£
0,1
0,01
0,001
0,0001
...
N
42.	Доказать, что хп (п = 1, 2, ...) есть бесконечно малая (т. е.
имеет предел, равный 0), указав для всякого е > 0 число N = N (е)
такое, что \хп\ < £ при п> N, если:
а)
LD1
п
б) =
2 п ,
п*+ 1 ’
в) хп =
г)	= (-1)" • 0,999".
Для каждого из этих случаев заполнить следующую таблицу:
8
0,1
0,001
0,0001
...
N
43.	Доказать, что последовательности:
а)	хп = (-1)"п, б) хп= 2-f" , в) хп = lg (lg п)	(п > 2)
имеют бесконечный предел при п —► со (т. е. являются бесконечно
большими)у определив для всякого Е > 0 число N = N (Е) такое,
что \хп\ > Е при п> N.
Для каждого из этих случаев заполнить следующую таблицу:
Е
10
100
1000
10 000
...
N
44.	Показать, что
х„= п^п (п = 1, 2, ...)
не ограничена, однако не является бесконечно большой при
л — оо.
45.	Сформулировать с помощью неравенств следующие ут¬
верждения:
a) lim хп = оо; б) lim хп = -оо; в) lim хп = +оо.

14
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
Предполагая, что п пробегает натуральный ряд чисел, опре¬
делить значения следующих выражений:
46. Иш
л —* оо fl2 4- 1
J. am V^siiin!
п+ 1
1 + а + а2 + ... + ал
48. Ш
п -* оо
47. lim ^ Jn+ 1 - 7л j.
49. lim —(-2)" + 3”—
n —• оо (-2)"*1 + Зл*1
50.	lim 1' It (И < !. N < !)•
51.	lim [\ + А + ... + 'ЦГ).
л —* оо \П2 П2	П1 )
. 2 + 3 _
+ (-1)п-1я|
п п
/г 1
92
+ ~ + ..
+ (»-i)2i
/г3
п3 J '
+ 2!+ ...
+ (2л- 1 )2~|
Л3
п3 J
ьА+А
+ .| 2л- 1>
22 23
2" )
+ — +
...+ 1 1
2 3
п(п+1)J
57. lim ( 72 1/2 «72... 2"72).
Л — оо V	У
Доказать следующие равенства:
58. lim
О
II
*1<
59. lim
2л = 0.
л — оо
Л — ОО
л!
60. lim
^ = 0 (а > 1).
61. lim
.1*-
II
О
л — оо
а"
л — ОС
Л!
62. lim
Я — оо
/г<7Л = 0, если Ы < 1.
63. lim
Л -* оо
"Та = 1
64. lim
1ое"Л - 0 (а > 1).
65. lim
л7л = 1,
л — ОО
п
/I — оо
66. lim
— = 0.
л -* оо
"7л!
а)	100/1 + 200 или 0,01/г2?; б) 2П или /I1000?;
в)	1000л или п\?
68.	Доказать, что
lim fi-f. ..^ziUo.
л — оо V 2	4	2 п )
Указание. См. пример 9 б).

§ 2. Теория последовательностей
15
69.	Доказать, что последовательность
+ (п — 1, 2, ...)
монотонно возрастает и ограничена сверху, а последовательность
2/n = (l + ^) (n = 1, 2, ...)
монотонно убывает и ограничена снизу. Отсюда вывести, что эти
последовательности имеют общий предел
lim fl + lV-lim Г1 + 1Г‘-в.
л — ОО V	flj	П-+ ОО V	tlj
Указание. Составить отношения Хп* -1
неравенством примера 7.
70.	Доказать, что
и воспользоваться
Уп- 1
О	< е - (l + ГГ < 3 („ = 1,2, ...).
V п) п
При каких значениях показателя п выражение ^1 + будет
отличаться от числа е меньше чем на 0,001?
71.	Пусть рп (д = 1, 2, ...)— произвольная последователь¬
ность чисел, стремящаяся к +оо, и qn (п = 1, 2,...) — произвольная
последовательность чисел, стремящаяся к -оо (prt, qn £ [-1, 0]).
Доказать, что
72.	Зная, что
lim Г1 + i) = е,
п-°° \ п)
доказать, что
lim
п —' оо
(1 + 1 + !
= е.
Вывести отсюда формулу
е = 2 +
2!
+
OjL
п\п *
где 0 < 0Л < 1, и вычислить число е с точностью до 10 5.
73.	Доказать, что число е иррационально.
(*)

16
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
74.	Доказать неравенства
75.	Доказать неравенства:
а)	—Ц- < Inf 1 + -] < i , где п — любое натуральное число;
п+1 V п) п
б)	1 + а < еа, где а — вещественное число, отличное от нуля.
76.	Доказать, что
lim п ( а" - l) = In а (а > 0),
п — оо V	)
где 1п а есть логарифм числа а при основании е= 2, 718... .
Пользуясь теоремой о существовании предела монотонной и
ограниченной последовательности, доказать сходимость следую¬
щих последовательностей:
Р1 _L_ л_ Рп
10'
целые неотрицательные числа, не превышающие 9, начиная с рх
U
3
77. хл=Ро+Y5 + — +^ (и=1.2,...), гдеpt (i = 0,1,2,...) —
78.*.- 12 • И ... " + 9
1
2п-1
81.	хх = J2 , х2 = J2 + J2 , ...,	= V2 + л/2~+ ... + л/2 , ... .
п корней
Пользуясь критерием Коши, доказать сходимость следую¬
щих последовательностей:
82.	= а0 + axq + ... + anqn, где
|aj < М (k = 0, 1, 2, ...) и |</| < 1.
83	х = s*n ^ + s*n2 4. sin п
п 2 22 *“ 2л
84	д: = cos^- + cos2!	cosn!
12
2-3
л(/г + 1)
Указание. Воспользоваться неравенством
1^1 1

§ 2. Теория последовательностей
17
86.	Говорят, что последовательность хп (п = 1, 2, ...) имеет
ограниченное изменение, если существует число С такое, что
1*2 “ *il + 1*3 “ *г! + ••• + |*„ - *„ - il < С (п = 2, 3, ...)•
Доказать, что последовательность с ограниченным изменени¬
ем сходится.
Построить пример сходящейся последовательности, не имею¬
щей ограниченного изменения.
87.	Сформулировать, что значит, что для данной последова¬
тельности не выполнен критерий Коши.
88.	Пользуясь критерием Коши, доказать расходимость по¬
следовательности
Х„ = 1 + \ + i + ... + - .
89.	Доказать, что если последовательность хп (п= 1, 2, ...)
сходится, то любая ее подпоследовательность хп также сходится
Гп
и имеет тот же самый предел:
lim хр = lim хп.
/1 — 00 п /1 — 00
90.	Доказать, что монотонная последовательность будет схо¬
дящейся, если сходится некоторая ее подпоследовательность.
91.	Доказать, что если
lim хп = а,
п — «х>
ТО
lim \хп\ = \а\.
/1 — 00
X
92.	Если хп —► а, то что можно сказать о пределе lim ?
п-оо
93.	Доказать, что сходящаяся числовая последовательность
ограничена.
94.	Доказать, что сходящаяся числовая последовательность
достигает либо своей верхней грани, либо своей нижней грани,
либо той и другой.
Построить примеры последовательностей всех трех типов.
95.	Доказать, что числовая последовательность хп (п = 1, 2, ...),
стремящаяся к +°о, обязательно достигает своей нижней грани.
Найти наибольший член последовательности хп (п = 1, 2, ...),
если:
96. хп =
2п
Jn
100 + п
1000*
97. xt
98. х.
п\

18
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
Найти наименьший член последовательности хп (п = 1, 2, ...),
если:
99. хп = п2-9п- 100.	100. хп = п +	.
п	П
Для последовательности хп (п = 1, 2, ...) найти inf хпУ sup хп9
Иш хп и lim хп, если:
п —* ОО	я — оо
101. а) = 1 - -;	6)xn = (-l)n-1 (2 +
/i	V	nj
Ю2 .*.-1=1£+1±£1Е.
д	2
103. дс„ « 1 + -5- cos 25 .
/1+1 2
«(«-о
104. *„ = 1 + 2 (-1)" + 1 + 3 • (-1)
2
105. хп = cos
/1+1 О
106. хп = (-1)"п.
107. *„ = -п[2 + (-1)"].
108. хп = и*-1»”.
109. х„ = 1 + п sin ^ .
110. хн- * .
п п- 10, 2
Найти lim хп и lim д:л, если:
П — ОО л * оо
lll.*„- n* , cos2"71.
я 1 + п2 3
112. х„=(1 + у-(-1)Л+8т^
113. - ”, sin2 n7t .
л+1 4
114. л:„ = а/ 1 + .
115. *„= cos" ^25.
О
Найти частичные пределы следующих последовательностей:
116 -
1
1 3
1
7 1
2Л -
1
* 2
’ 2 ’
4 9 4
’ 8 ’
8’ 2"
2"
> •
117. 1,
1
1 + 1
1
1 + 1.i
+ 1.
1
2 ’
2
’ 3 ’
3 2
3
4 ’
1
• • • э
1 +
1 1
+ 1
1
э • • • • ^
+ 1,
1
п
п ’ 2
п
/1-1
п
/г +
118 !
1
2 1
2
3 1 2
3 4
lie. 2
’ 3 ’
3 ’ 4
’ 4’
4’ 5 ’ 5 ’
5 ’ 5
» •••
1 1
4’ 2
1	1
4 ’ 3
119. лг„ = 3^1 —	+ 2 (-1)».
120. хп = ![(« +ft)+ (-!)» (в-ft)].

§ 2. Теория последовательностей
19
121.	Построить пример числовой последовательности, име-
щей в качестве своих частичных пределов данные числа
•••»
122.	Построить пример числовой последовательности, для
которой все члены данной числовой последовательности
d\ >	• • • > dnt • • •
являются ее частичными пределами. Какие еще частичные пре-
делы обязательно имеет построенная последовательность?
123.	Построить пример последовательности:
а)	не имеющей конечных частичных пределов;
б)	имеющей единственный конечный частичный предел,
но не являющейся сходящейся;
в)	имеющей бесконечное множество частичных пределов;
г)	имеющей в качестве своего частичного предела каждое
вещественное число.
124.	Доказать, что последовательности хп и уп = хп nJri
(п= 1, 2, ...) имеют одни и те же частичные пределы.
125.	Доказать, что из ограниченной последовательности хп
(п = 1, 2, ...) всегда можно выделить сходящуюся подпоследова¬
тельность хп (п = 1, 2, ...).
г П
126.	Доказать, что если последовательность хп (п = 1, 2, ...)
не ограничена, то существует подпоследовательность хр такая,
что
lim хв = оо.
П-оо Ип
127.	Пусть последовательность хп (п= 1, 2, ...) сходится, а
последовательность уп (п = 1, 2, ...) расходится. Что можно ут¬
верждать о сходимости последовательностей:
а) хп + упУ	б) хпуп7
Привести соответствующие примеры.
128.	Пусть последовательности хп и уп (п = 1, 2, ...) расходят¬
ся. Можно ли утверждать, что последовательности:
а) хп + уп;	б)
также расходятся?
129.	Пусть lim хп = 0, и уп (т = 1, 2, ...) — произвольная
П — оо
последовательность. Можно ли утверждать, что lim хпуп = О?
я — оо
Привести соответствующие примеры.

20
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
130.	Пусть
Иш хпуп = 0.
#1 — оо
Следует ли отсюда, что либо lim хп = 0, либо lim уп = 0?
Л — оо	л —* Оо
Рассмотреть пример: хп = 1 *	, уп = 1	(п = 1, 2, ...)•
Сл	Сл
131.	Доказать, что:
а)	lim хп + lim уп < lim (*„ + у„) < lim + lim уп;
/1 — 00	л — оо	Л - * ОО	л — оо	л — ОО
б)	Иш л:л + lim i/n < lim (хл + yn) < lim хл + lim уп.
Л — ОО	л — оо	л — оо	л — ОО	л — оо
Построить примеры, когда в этих соотношениях имеют место
строгие неравенства.
132.	Пусть л:Л > 0 и уп > 0 (п = 1, 2, ...). Доказать, что:
а)	Иш ж/ lim уп < lim (хл1/л) < lim • Шп уп;
л — оо	Л — ОО	Л —* ОО	л — оо	Л — оо
б)	Иш X.. Шй Уп < Пш (*„!/„) < Шп • Шп 1/л.
л — оо	л — ОО	л — ОО	л — ОО	л — ОО
Построить примеры, когда в этих соотношениях имеют место
строгие неравенства.
133.	Доказать, что если lim д:п существует, то какова бы ни
л — оо
была последовательность уп(п= 1, 2, ...), имеем:
а)	Шп (хл + t/„) = Иш + Шп ул;
Л — ОО	л — оо	Л — ОО
б)	Шп (*„«/„) = Иш *„ • Шп уп (хп > 0).
Л — оо	л — ОС)	Л — ОО
134.	Доказать, что если для некоторой последовательности jcrt
(л = 1, 2, ...), какова бы ни была последовательность уп (п = 1,
2, ...), имеет место по меньшей мере одно из равенств:
а)	Шп (хп + (/„)= Шп хп + Шп уп
Л — оо	Л — оо	л — оо
или
б)	Шп (х„уп) = Шп хп • Шп уп (хп> 0),
Л — оо	л—оо	л — оо
то последовательность — сходящаяся.
135.	Доказать, что если > О (n = 1, 2, ...) и
Иш хп • Иш — = 1,
л — оо	п-*оо хп
то последовательность — сходящаяся.

§ 2. Теория последовательностей
21
136.	Доказать, что если последовательность хп (п = 1, 2, ...)
ограничена и
lim (*й 4 , - хп) = О,
А1 - ♦ ОО
то частичные пределы этой последовательности расположены
всюду плотно между ее нижним и верхним пределами:
Z = lim хп и L = lim лгп,
—* ОО	П —* ОО
•т. е. любое число из отрезка [Z, L] является частичным пределом
данной последовательности.
137.	Пусть числовая последовательность х2, ..., хЛ, ...
удовлетворяет условию
О < хт + п< хт + хп (т, п= 1,2, ...).
х
Доказать, что lim — существует.
П —* оо л
138.	Доказать, что если последовательность хп (п = 1, 2, ...)
сходится, то последовательность средних арифметических
= - (*i + *2 + ••• + *п) (и = 1» 2, ...)
п
также сходится и
lim
,1 — 00
Xj + Х2 + ... + Хп
П
lim хп.
П — оо
Обратное утверждение неверно: построить пример.
139.	Доказать, что если
lim хп = +оо,
П —► ОО
ТО
X, + х2 + ... + хп . ^
lim —			2 = +оо.
п -* оо	П
140.	Доказать, что если последовательность хп (я = 1, 2, ...)
сходится и хп > 0, то
lim nJxlx2...хп = lim
П — оо	/I —* оо
141.	Доказать, что если > О (n = 1, 2, ...), ТО
lim	= lim	,
п — ОО	П — ОО д;л
предполагая, что предел, стоящий в правой части последнего ра¬
венства, существует.

22
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
ТО
142.	Доказать, что lim -2- = е.
п~*°° nJn\
143.	Доказать теорему Штольца, если
а) Уп + i > Уп (п= 1, 2, ...);	б) lim уп = + оо,
п — оо
« — х
в)	существует lim 		 ,
Уп + \- Уп
lim ^ = lim
«-00	У/.	« -* 00 Уп+\-Уп
144.	Найти:
a) lim — (а > 1); б) lim
/I — +О0 ап	П-+ 4 00 л
145.	Доказать, что если р — натуральное число, то:
a) lim
П — оо
1р+2р+... + лр _ 1 .
лр+1 Р+1’
б) lim
П -* оо
Пр + 2Р + ... + пр п '
\ = Ь
V пр Р+
) 2’
в) lim
П —» оо
1Р + 3Р + ... + (2я- 1/ _
2Р
Р+ 1
пИ
Р+ 1 '
146. Доказать, что последовательность
Хп = 1 + i + i + ... + - - In п (n = 1,2, ...)
Z о	И
СХОДИТСЯ.
Таким образом, имеет место формула
1+i + — + ... + i = С + In /I + en,
2	3	п
где С — 0,577216... — так называемая постоянная Эйлера и
£л —* 0 при п —> оо.
147. Найти
lim [—Ц-
п —* сю \fl + 1
п + 2
+
148. Последовательность чисел хп (п
следующими формулами:
±).
2 п)
= 1,2,...) определяется
= а, *2 = 6.	= ^"-i g*"'2 (« = 3, 4, ...)•
Найти lim xn.
n -* CO
149. Пусть хл (n = 1, 2, ...) — последовательность чисел, оп¬
ределяемая следующей формулой:
*„>0,	! = |(жп + (п = О, 1, 2, ...).
Доказать, что lim jcn = 1.

§ 3. Понятие функции
23
150. Доказать, что последовательности хп и уп (п = 1, 2, ...),
определяемые следующими формулами:
= а, уу = b, хп+ j = Jxnyn , уп + j =	,
имеют общий предел
Ц (a, b) = lim хп = lim уп
/I — сю	П — оо
(iарифметико-геометрическое среднее чисел а и Ъ).
§ 3. Понятие функции
1.	Понятие функции. Переменная у называется однозначной функ¬
цией /от переменной х в данной области изменения X = {*}, если каждому
значению хеХ ставится в соответствие одно определенное действительное
значение у — f(x), принадлежащее некоторому множеству Y = {у}.
Множество X носит название области определения или области су¬
ществования функции f(x); Y называется множеством значений этой
функции. В простейших случаях множество X представляет собой или от¬
крытый промежуток (интервал) ]а, Ь[ = (а, Ь): а < х < Ь> или полуоткры¬
тые промежутки ]а, Ь] = (а, b]: а < х < b и [а, Ь[ = [а, Ь): а < х < Ь, или
замкнутый промежуток (сегмент) [а, Ь]: а < х < Ь, где аиЬ — некоторые
вещественные числа или символы -оо и +оо (в этом сл^ае равенства иск¬
лючаются).
Если каждому значению х из X соответствует одно или несколько
значений у = f(x), то у называется многозначной функцией от х.
2.	Обратная функция. Если под х понимать любое значение, удов¬
летворяющее уравнению
f(x) = у,
где у — фиксированное число, принадлежащее множеству значений Y
функции {(х)у то это соответствие определяет на множестве У некото¬
рую, вообще говоря, многозначную функцию
* = ГЧу),
называемую обратной по отношению к функции f(x). Если функция
у = f(x) монотонна в строгом смысле, т. е. f(x2) > f(xx) (или, соответствен¬
но, f(x2) < f(xi)) при х2> xl9 то обратная функция х = f~](y) является
однозначной и монотонной в том же смысле.
Определить области существования следующих функций:
151. у =	.	152. у = J3x-x3 .
153. у = (х - 2) JZ±£ .

24
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
154. а) у = log (jc2 - 4);
б) у = log (х + 2) + log (х - 2).
155. у = Jsin(Jx).
156. у = л/cos х2.
157. у = lg (sin .
158. у - & .
Б1ПЛХ
159. у = arcsin .
1 + x
160. г/ = arccos (2 sin х).
161. у = lg [cos (lg x)].
162. i/ = (х + |дф Jxsin2nx .
163.	у = ctg ях + arccos (2*).
164.	i/ == arcsin (1 - x) + lg (lg x).
165. а) у = (2*)!; б) у
= log2 log3 log4 x; в) у = Vlgtgx .
г) у = Vsin2x + л/sinЗх (0 < х < 2я).
Определить области существования и множество значений
следующих функций:
166. у — J2 + х - х2.
167. i/ = lg (1 - 2 cos x).
168. у = arccos - .
1 + X2
169. у = arcsin (lg ^ j .
170. у = (-1)*.
171.	В треугольник АВС (рис. 1), основание которого АС = b
и высота BD = А, вписан прямоугольник KLMN, высота которого
NM = х. Выразить периметр Р прямоугольника KLMN и его пло¬
щадь S как функции от х.
Построить графики функций Р = Р (х) и S = S (х).
172.	В треугольнике АВС сторона АВ = 6 см, сторона АС = 8 см
и угол ВАС = х. Выразить ВС = а и площадь S треугольника АВС
как функции переменной х. Построить графики функций а = а (х)
и S = S (х).
В
Рис. 1
Рис. 2

§ 3. Понятие функции
25
173.	В равнобедренной трапеции ABCD (рис. 2), основания
которой AD = а и ВС = b (а > Ь)9 а высота НВ = h9 проведена
прямая MN || НВ и отстоящая от вершины А на расстоянии
AM = я. Выразить площадь S фигуры ABNMA как функцию пе¬
ременной х. Построить график функции: S = S (jc).
174.	На сегменте 0 < х < 1 оси Ох равномерно распределена
масса, равная 2 г, а в точках этой оси х = 2 и х = 3 находятся
сосредоточенные массы по 1 г в каждой. Составить аналитиче¬
ское выражение функции т = т (х) (—оо < х + оо), численно рав¬
ной массе, находящейся в интервале (-оо, х)9 и построить график
этой функции.
175.	Функция у = sgn х определяется следующим образом:
[-1, если х < 0;
sgn д: = J 0> если х = 0;
I 1,еслих>0.
Построить график этой функции. Показать, что
\х\ = X sgn X.
176.	Функция у = [х] (целая часть числа х) определяется
следующим образом: если х = п + г, где п — целое число и 0 < г < 1,
то [х] = /г. Построить график этой функции.
177.	Пусть
у = п(х) (х> 0)
обозначает число простых чисел, не превышающих числа х. По¬
строить график этой функции для значений аргумента 0 < х < 20.
На какое множество Еу отображает множество Ех функция
У = f(x)> если:
178. у = *2,	Ех = {-1 < х < 2}.
179. у = lg х,	Ех = {10 < jc < 1000}.
180.	у — — arcctg х9 Ех = {-оо < х < оо}.
Ех={ 0<М< 1}.
Ех= {1 < |х| < 2}.
Переменная л: пробегает интервал 0 < х < 1. Определить,
какое множество пробегает переменная у9 если:
183. у = а 4- (Ь - а)х.	184. у =	•
185‘ У = 2^Т ’	186> У = ^Х~Х* •
187. у = ctg ях.	188.1/ = х + [2х].
к
181.	у = ctg Н ,
4
182.	у = М,

26
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
189.	Найти /(О), /(1), Я2), Я3), Я4), если
Я*) = х4 - 6х3 4- Их2 - 6х.
190.	Найти Я~1)> Я“0,001), ЯЮО), если
f(x) = \gx2.
191.	Найти f (0,9), f (0,99), f (0,999), f (1), если
f (x) = 1 + [х].
192.	Найти Д-2), /(-1), /(0), /(1), /(2), если
193.	Найти /(0), f(-x), f(x + 1), f(x) + 1, /Qj , щ , если
194.	Найти значения х, для которых: 1) f(x) = 0; 2) f(x) > 0;
3) f(x) < 0, если:
a) f(x) = х - х2; б) f(x) = sin 2 ; в) f(x) = (х 4- |x|)(l - x).
195.	Найти <p(x) = f{x + h)~f{x), если:
а) Я*) = ax + 6; 6) f(x) — x2; в) Я*) = a*.
196.	Пусть
Показать, что
f(x 4- 3) - ЗЯ* + 2) 4- ЗЯ* + 1) - Я*) = 0.
197.	Найти целую линейную функцию
если ЯО) = -2 и ЯЗ) = 5.
Чему равны f(l) и f(2) (линейная интерполяция)?
198.	Найти целую рациональную функцию второй степени:
если Я“2) = 0, ЯО) =1, Я1) = 5.
Чему равны f(-l) и Я0,5) (квадратичная интерполяция)?
199.	Найти целую рациональную функцию третьей степени:
если Я-1) = 0, Я0) = 2, Я1) = "3, Я2)=5.
1 + X при -ОО < лс < о,
2х при 0 < х < 4-оо.
f(x) = ax2 4- bx 4- с.
Я#) = ax 4- by
f(x) = ax2 4- 6x + c,
Я#) = ax3 4- bx2 4- cx 4- <i,

§ 3. Понятие функции
27
200.	Найти функцию вида
f(x) = а + bcx9
если /(0)=15, f(2) = 30, /(4) = 90.
201.	Доказать, что если для линейной функции
f(x) = ах + b
значения аргумента х = хп (п = 1, 2, ...) образуют арифметиче¬
скую прогрессию, то соответствующие значения функции уп = f(xn)
(п = 1, 2, ...) образуют также арифметическую прогрессию.
202.	Доказать, что если для показательной функции
значения аргумента х = хп (п = 1, 2, ...) образуют арифметиче¬
скую прогрессию, то соответствующие значения функции уп = /(хп)
(п = 1, 2, ...) образуют геометрическую прогрессию.
203.	Пусть функция f(u) определена при 0 < и < 1. Найти
области определения функций:
f(x) = ах (а> 0)
а)	Я sin х); б) Д1п х); в)	•
204.	Пусть
Я*)= |(в* + а-*) (а > 0).
Показать, что
Я* + у) + Ял: - у) = 2f(x)f(y).
205.	Пусть
Я*) + Я*/) = /(2).
Определить 2, если:
a)	f(x) = ах;
б) Я*) = i ;
г) Яж) = log .
В) Яж) = arctg х (|х|) < 1;
Найти <р[<р(х)], \|/[\|/(х)], ф[\|/(х)] и ц/[ф(х)], если:
206.	ф(х)«=х2и\|/(х) = 2х.
207.	ф(х) = sgn х и \|/(х) = i .
208. ф(х) =

28
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
209.	Найти f[f(x)], f{f[f(x)]}, если /(*) = -±- .
210.	Пусть
fn(x) = f(f(...f(x))).
'	V	'
п раз
Найти fn(x)y если f(x) = 		.
J1 + х2
211.	Найти f(x)9 если f(x 4- 1) = х2 - Зх 4- 2.
212.	Найти f(x)y если / 4-ij = *2 + (Н ^ 2 j .
213.	1. Найти f(x)y если = х 4- Jl + х2 (х > 0).
2.	Найти f(x)9 если f f—1 = х2.
\х + 1)
Доказать, что следующие функции являются монотонно воз¬
растающими в указанных промежутках:
214.	f(x) = х2 (0 < х < 4-00).
215.	f(x) = sin jc	.
216.	fix) - tg * (-jj < * < |).
217.	f(x) = 2x 4- sin x (-00 < x < 4-oo).
Доказать, что следующие функции являются монотонно убы¬
вающими в указанных промежутках:
218.	f(x) = х2 ( оо < х < 0).	219. f(x) = cos х (0 < х < п).
220.	f(x) = ctg х (0 < х < л).
221.	Исследовать на монотонность следующие функции:
a)	f(x) = ах 4- Ь;	б) f(x) = ах2 + Ьх + с;
В) f(x) = х3;	г) fix) =	;
сх + d
д)	f(x) = ах (а> 0).
222.	Можно ли почленно логарифмировать неравенство?
223.	Пусть ср(х), \j/(x) и f(x) — монотонно возрастающие функ¬
ции. Доказать, что если
ср(х) < f(x) < \|f(x)y
то
ф[ф(*)] < ЛЯ*)] < ф[ф(*)].

§ 3. Понятие функции
29
Определить обратную функцию х = сp(t/) и ее область сущест¬
вования, если:
224.	у = 2х + 3 (—оо < х < +оо).
225.	у = х2; а) -оо < х < 0; б) 0 < х < +оо.
226.	у =	(х * -1).
227.	у = л/1 - х2 ; а) -1 < х < 0; б) 0 < х < 1.
228.	у = sh х, где sh х = | (ех - е~х) (-оо < х < +оо).
229.	у — th х, где th х =	~ е * (-оо < х < +оо).
ех + е х
)х, если -оо < х < 1;
х2, если 1 < лс < 4;
2х, если 4 < х < +оо.
231.	Функция /(х), определенная в симметричном интервале
(-Z, 0» называется четной, если
/(-•ж) = /(л:);
и нечетной, если
/(-*) = ~f(x).
Определить, какие из данных функций f(x) являются четны¬
ми, а какие нечетными:
a) Дх) = Зх - х3;	б) /(х) = V(1 - #)2 + а/( 1 + л:)2;
в)	Да:) = а* + а“х (а > 0); г) f(x) = In ;
Д) fix) = In (х + J1 + х2 ).
232.	Доказать, что всякую функцию Дх), определенную в
симметричном интервале (-Z, Z), можно представить в виде сум¬
мы четной и нечетной функций.
233.	Функция Дх), определенная на множестве Е, называет¬
ся периодической у если существует число Т > 0 (период
функции — в широком смысле слова!) такое, что
Дх ± Т) = Дх) при х € Е,
Выяснить, какие из данных функций являются периодиче¬
скими, и определить наименьший период их, если:
a)	Дх) = A cos Хх + В sin А.х;
б)	/(я) = sin х + ^ sin 2х + ^ sin 3x;
Cj	О
b) f(x) = 2 tg | - 3 tg |; r) f(x) = sin2 x;
д)	f(x) = sin x2;	e) f(x) = Vtgx;
ж)	f(x) = tg Jx ;	з) /(x) = sin x 4- sin (x J2).

30
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
234.	Доказать, что для функции Дирихле
, ч ]1,если храционально,
* * *	[0,если х иррационально,
периодом является любое рациональное число.
235.1.	Доказать, что сумма и произведение двух периодиче¬
ских функций, которые определены на общем множестве и пе¬
риоды которых соизмеримы, есть функции также периодиче¬
ские.
2.	Функция fix) называется антипериодической, если
f(x + Г) = -/(*) (Т > 0).
Доказать, что fix) — периодическая функция с периодом 2Т.
236.	Доказать, что если для функции fix) (-00 < х < +оо) вы¬
полнено равенство fix + Т) = &/(*), где k и Т — положительные
постоянные, то fix) = агф(л:), где а — постоянная, а ср(х) — перио¬
дическая функция с периодом Т.
§ 4. Графическое изображение функции
1.	Для построения графика функции у = f(x) поступают следующим
образом:
1)	определяют область существования функции X = {*};
2)	выбирают достаточно густую сеть значений аргумента xit х2* ..., хп
из X и составляют таблицу соответствующих значений функции
«// = f(xi) (i= 1, 2, ..., п);
3)	наносят систему точек Mt(xn t/,) (/ = 1, 2, ..., л) на координатную
плоскость Оху и соединяют их линией, характер которой учитывает по¬
ложение промежуточных точек.
2.	Чтобы построить грамотно график функции, следует изучить об¬
щие свойства этой функции.
В первую очередь нужно: 1) решив уравнение f(x) = 0, определить
точки пересечения графика функции с осью Ох (нули функции);
2) установить области изменения аргумента, где функция положитель¬
на или отрицательна; 3) если возможно, выяснить промежутки моно¬
тонности (возрастания или убывания) функции; 4) изучить поведение
функции при неограниченном приближении аргумента к граничным
точкам области существования функции.
В этом параграфе предполагается, что свойства простейших элемен¬
тарных функций — степенной, показательной, тригонометрических и
т. п., известны читателю.
Пользуясь этими свойствами, можно, не проделывая большой вы¬
числительной работы, сразу рисовать эскизы графиков многих функ¬
ций. Другие графики иногда удается свести к комбинации (сумме или
произведению и т. п.) этих простейших графиков.

§ 4. Графическое изображение функции
31
237.	Построить график линейной однородной функции
У = ах
при а = 0,	1, 2, -1.
238.	Построить график линейной функции
у = х + b
при 5=0, 1, 2, -1.
239.	Построить графики линейных функций:
я) у = 2х + 3; б)у= 2 - 0,1*; в)у = -|-1.
240.	Температурный коэффициент линейного расширения
железа а = 1,2 • 10~6 К'1. Построить в подходящем масштабе гра¬
фик функции
I	= f(T) (-40 К < Т < 100 К),
где Т — температура и I — длина железного стержня при темпе¬
ратуре Т, если I = 100 см при Т = 0 К.
241.	По числовой оси движутся две материальные точки.
Первая в начальный момент времени t = 0 находилась на 20 м
влево от начала координат и имела скорость vY = 10 м/с; вторая
при t = 0 находилась на 30 м вправо и от точки О и имела
скорость и2 = -20 м/с. Построить графики уравнений движений
этих точек и найти время и место их встречи.
242.	Построить графики целых рациональный функций 2-й
степени (параболы):
я) у = ах2 при а = 1,	2, -1;
б)	у = (х- *0)2 ПРИ *о =	1» 2> “1;
в)	у = х2 + с при с = 0, 1, 2, -1.
243.	Построить график квадратного трехчлена
у = ах2 + Ъс + с,
приведя его к виду
у = у0 + а(х - х0)2.
Рассмотреть примеры:
а)	у = 8* - 2х2;	в) у =	-х2 +	2х -	1;
б)	у = х2 - 3* + 2;	г) I/ =	| я2 +	х +	1.
244.	Материальная точка брошена под углом а = 45° к плос¬
кости горизонта с начальной скоростью о0 = 600 м/с. Построить
график траектории движения и найти наибольшую высоту
подъема и дальность полета (считать g - 10 м/с2, сопротивлени¬
ем воздуха пренебречь).

32
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
Построить графики целых рациональных функций степени
выше второй:
245. у = *3 + 1.	246. у = (1 - х2)(2 + х).
247. у = х2 - х4,	248. у = х(а - х)2 (а + х)3 (а > 0).
Построить графики дробно-линейных функций (гиперболы):
1 - JC
1 + ЛГ '
249. z/ = ± .	250. z/ =
х
251. Построить график дробно-линейной функции
ах+ b
У =
сх + d
(ad - be * 0, с * 0),
приведя ее к виду г/ = г/0 ■+"
т
х-х0
Зх+ 2
Рассмотреть пример у =
2 х — о
252.	Газ при давлении р0 = 1 Па занимает объем V0 = 12м3.
Построить график изменения объема V газа в зависимости от дав¬
ления р, если температура газа остается постоянной (закон
Бойля—Мариотта).
Построить графики дробных рациональных функций:
253.	у = х + i.
X
254. у = х2 + i (трезубец Ньютона).
255. у = * + \ .
256. у =
1 + *2
(кривая Аньези).
257. у -
258.1/ =
260. г/ =
2*
1 + *2
1
1-л:2
(серпантин Ньютона).
1 + л:
-? +
1
1-л:
259. у =
261. у =
1 — лс2
1 .
1 + х
А + —i— .
X2 1-х
262.	у = (*+1)(*~2).
J (х- 1)(х+ 2)
263.	Построить эскиз графика функции
„_ ах2 + Ьх + с ,	.
— —;v— («1^0),
сцл: + bj
приведя ее к виду
у = kx + т +

§ 4. Графическое изображение функции
33
Рассмотреть пример
_ jc2 — 4с.х -ь 3
У х +1
264.	Построить график изменения силы притяжения F мате¬
риальной точки, находящейся на расстоянии х от притягиваю¬
щего центра, если F = 10 Н при х = 1 м (закон Ньютона),
265.	Согласно закону Ван-дер-Ваалъса объем V реального га¬
за и его давление р при постоянной температуре связаны соот¬
ношением
(p+i) (V-b)-c.
Построить график функции р = p(V), если а = 2,6=0,1ис = 10.
Построить графики иррациональных функций:
266.	у = ±7- х - 2 (парабола).
267.	у = ±xjx (парабола Нейля).
268.	у = ±^7Ю0 - х2 (эллипс).
269.	у = ±Jx2 - 1 (гипербола).
270.	у = ± /7^^ •	271. у = ±лг«/Ю0 - х2.
272. у = ±дс JlQ*_ х (циссоида).
273.1/ = ±,/(*2-1)(9-*2) .
274.	Построить график степенной функции у = хп при:
а) п = 1, 3, 5;	б) п = 2, 4, 6.
275.	Построить график степенной функции у = лс'1 при:
а) п = -1, -3;	б) /г = -2, -4.
276.	Построить график радикала у = "i/x: при:
а) /п = 2, 4;	б) т = 3, 5.
277.	Построить график радикала у = "7^ » если:
а) т = 2, /г = 1;	б) /п = 2, k = 3;	в) /?г = 3, k = 1;
г)	/гг = 3, /г = 2;	д) ап = 3, k = 4;	е) /?г = 4, k = 2;
ж) m = 4, /г = 3.
278.	Построить график сложной показательной функции у = ах
1

34
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
279. Построить график сложной показательной функции
у = еу1, если:
а) ух = х2;
б) ух = -л:2;
*)Уг=-х‘>
Ds.-i;
д) J/i = -^:
280.	Построить график логарифмической функции у = loga х
при а = i , 2, е, 10.
281.	Построить графики функций:
а) у = In (-х),	б) у = -In (х).
282.	Построить график сложной логарифмической функции
у = In уи если:
а) г/j = 1 + х2;	б) ух = (х- 1)(х - 2)2 (х - 3):>;
В) lJi = ГТх;	г> У1 = Д :	д) ух = 1 + <?х.
283.	Построить график функции у = log* 2.
284.	Построить график функции у = A sin х при А = 1, 10, -2.
285.	Построить график функции у = sin (х - дс0), если х0 = 0,
я л Зя _
4 ’ 2 ’ 4 ’
286.	Построить график функции у = sin пх> если п = 1, 2, 3,
1 1
2	’ 3 ’
287.	Построить график функции у = a cos я + b sin дс, приведя
ее к виду г/ = A sin (дс - дс0).
Рассмотреть пример: у = 6 cos дс + 8 sin х.
Построить графики тригонометрических функций:
288.	у = cos я.	289. у = tg х.
290. г/ = ctg дс.	291. у = sec дс.
292. I/ = CSC ДС.
294.1/ = sin3 дс.
296.1/ = sin х • sin Здс.
293. у = sin2 дс.
295. I/ = ctg2 х.
297. i/ = ±Vcosx .
Построить графики функций:
298. у = sin дс2.
300.	а) у = cos- ;
х
299. п = sini .
* л:
б)у = sin дс • sini .

§ 4. Графическое изображение функции
35
301.	а) у = tgS ;
302.	у = х ^2 + sin i j .
304. у = SIM.
X
306. у = ±2~* л/sin 71 л:.
308. у = In (cos лс).
1
o-i/ч	sinx
310.	у = в
б)	z/ — seci .
303.	у = ±лД - лс2 sin-.
л:
305. у = е* cos лс.
COSJC
307. у =	2.
1 + ЛС2
309. у = cos (In лс).
Построить графики обратных круговых функций:
311.	г/ = arcsin лс.
313. у = arctg лс.
315.1/ = arcsin - .
317.1/ = arcctg i .
319. i/ = arcsin (cos лс:).
321. у = arctg (tg лс).
312.	у = arccos лс.
314. у = arcctg лс.
316. у = arccos i .
*
318. z/ = arcsin (sin лс).
320. z/ = arccos (cos лс).
322. у = arcsin (2 sin лс).
323. Построить график функции у = arcsin yl9 если:
1-х
а) у 1
б) i/i =
1 -
2 ’
2*
i+*
г) ух = е*.
1 + х2 ’
324.1. Построить график функции у = arctg ylt если:
а) г/, = х2; б) у, =
1
в) ух = In х; г) У! =
1
sin д:
2. Построить графики функций:
а) у = лс3 - Зле + 2;
г2
б) г/ =
B)^kFT’
д)	у = 3 sin (J + |);
ж) у = —^ ;
1-21"'
(1-х)(1 + х)2’
г) у = Jx(l-x2);
е) у = ctg
яле
1 + *2’
3)	у = lg (х2 - Зх + 2);

36
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
и) у = arcsin |
I! -sln*)
; к) у = arctg(^-y
*а) У lo§>cos дс
sin лс;
м)у = (sin х)с1ех.
325.	Зная график функции у = /(лс), построить графики функ¬
ций:
а) у = -/(*);	б) у = /(-лс);	в) у = -/(-лс);
г) у = /(лс - *о);	Д) У = */о + Я* “ *о); е) у = /*(2*);
ж) у = /(&лс + &) (Л * 0).
326.	Пусть
.. ч ]1 - W при Н < 1;
Кх)=\ 0	приМ>1.
Построить графики функций:
у = \[Кх - 0 + f(x + О]
при f = О, f = 1 и £ = 2.
327.	Построить графики функций:
а)	у = 2 + VI - *;	б) г/ = 1 — е"х;
в) у = In (1 + лс);	г) у = -arcsin (1 + я);
д) z/ = 3 + 2 cos Зле.
328.	Зная график функции у = /(лс), построить графики
функций:
а) г/ = |/(*)|; б) г/ = | (1/(*)1 + /(*));в) у = \ (|Л*)1 - /(*));
г) у = fz(x); д) у = Тя*);
ж) У = /(/(*)); з) у = sgn f(x);
329.1.	Пусть
f(x) = (х — а)(Ь - х)
е) у = In f(x);
и) у = [/(*)].
(а < Ь).
Построить графики функций:
а) у = Кх);	б) у = /2(*);
г)	у = 7/(*);	д) У = е/(х);
ж) у ~ arcctg /(лс).
е) у = lg /(лс:);
2. Построить графики функций:
a) z/ = arcsin [sin /(лс)];	б) z/ = arcsin [cos /(лс)];
в)	z/ = arccos [sin /(лс)];	г) г/ = arccos [cos /(лс)];
д)	z/ = arctg [tg /(лс)],
если: 1) /(лс) = лс2; 2) /(лс) = лс3.

§ 4. Графическое изображение функции
37
330.	Зная графики функций у = f(x) и у = g(x), построить гра¬
фики функций:
а)	у = fix) + g(x); б)у = f(x)g(x); в) у = f(g(x)).
Применяя правило сложения графиков, построить графики
следующих функций:
331. z/ = 1 + х + е*.	332. у = (х + I)"2 + (х - I)"2.
333.1/ = х 4- sin х.	334. г/ = х + arctg х.
335.1/ = cos х 4- | cos 2х 4- | cos Зх.
336.	у = sin х - i sin Зх + i sin 5x.
3	5
337.	у = sin4 x 4- cos4 x.	338. г/ = |l - x| 4- |l 4- x|.
339.	у = |1 - x| - |1 + x|.
340.	Построить графики гиперболических функций:
а)	у = ch х,	где	ch х =	i	(е* 4-	е	*);
б)	a-sh *,	где	sh дг -	|	(г- -
в)	у = th х,	где	th х =	.
спх
Применяя правило умножения графиков, построить графики
функций:
341.	у = х sin х.	342. г/ = х cos х.
343. z/ — х2 sin2 х.
345. г/ = с-*2 cos 2х.
347. у = [х] |sin лх|.
349.	Пусть
346. у — х sgn (sin х).
348. у = cos х • sgn (sin х).
Построить график функции у = f(x)f(a - х), если:
а)	а = 0;	б) а = 1;	в) а = 2.
350.	Построить график функции у = х + Jx sgn (sin лх).
Построить график функции у = —, если:
fix)
352. /(х) = х(1 - х)2.
354. f{x) = In х.
351.	Дх) = х2(1 - х2).
353. Л*) = sin2 х.
355. Я*) = е* sin

38
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
356. Построить график сложной функции
где и = 2 sin *, если
У = f(u),
357. Пусть
fin) =
-1 при -оо < и < -1;
и при -1 < и < 1;
1при 1 < и < +оо.
ф(*)= |(* + |*|) И \|/(*)
J*, если jc < 0;
[я2, если х > 0/
Построить графики функций:
а) у = Ф[Ф(*)];
в) у = ф[ф(*)];
358. Пусть
1, если \х\ < 1;
0, если |*| > 1
и \|/(*)
Построить графики функций:
а) У = ф[ф(*)];
в) у = ф[ф(*)];
б)!/ = ф[ф(*)];
г) У = ф[ф(*)]-
J2 - *2, если |*| < 2;
12, если |*| >2.
б)*/ = ф[ф(*)];
г) У = ф[ф(л:)].
359. Функцию /(*), определенную в положительной области
* > 0, продолжить в отрицательную область * < 0 таким образом,
чтобы полученная функция была: 1) четной; 2) нечетной, если:
a) fix) = 1 - *; б) /(*) = 2* - *2; в) /(*) = V* ;
г) Я*) = sin *; д) fix) = е*;	е) /(*) = In *.
Построить соответствующие графики функций.
360. Определить, относительно каких
симметричны графики функций:
а) у = а*2 Ч- 6* + е;
вертикальных осей
+
1 .
(I-*)2’
в) у = Ja + х + Jb - х (0 < а < b);
г) у = а + b cos *.
361. Определить, относительно каких центров симметричны
графики функций:
а) у = а* + 6;
б) */ =
а* + fr .
с* + d 9
в) у = а*3 + Ь*2 + сх + d;
г) у =
1
* - 1
д) у = 1 + V*- 2 .

§ 4. Графическое изображение функции
39
362.	Построить графики периодических функций:
а)	у = |sin х\;	б) у = sgn cos х;
в)	У = f{x), где /(л:) = А ^2 -	,
если 0 < х < 2Z и f{x + 2/) = /(я);
г)	у = М-2Ц];
д)	I/ = (дс), где (х) — расстояние от числа х до ближайшего
к нему целого числа.
363.	Доказать, что если график функции у = f(x) (-00 < х < 4-оо)
симметричен относительно двух вертикальных осей х = а и х = b
(b > а), то функция f(x) — периодическая.
364.	Доказать, что если график функции у = f(x) (-00 < х < +оо)
симметричен относительно двух точек А(а, у0) и Б(6, ух) (Ъ > а),
то функция f(x) есть сумма линейной функции и периодической
функции. В частности, если у0 = у lf то функция f(x) — периоди¬
ческая.
365.	Доказать, что если график функции у = f(x) (-00 < х < Ч-оо)
симметричен относительно точки А(а, у0) и прямой х = b (6 ^ а),
то функция f(x) — периодическая.
366.	Построить график функции у = f(x) (-00 < х < +оо), если
f(x + 1) = 2f(x) и f(x) = jc(1 - *) при 0 < л: < 1.
367.	Построить график функции
У = /(*) (-°° < * < +°°),
если:
f(x + л) = f(x) + sin л: и /(дс) = 0, при 0 < х < п.
368.	Построить график функции у = у(х), если:
а)х = у - уя;	6)х=	;
1 + «г
в)	х — у — Хп у\	г) х2 = sin у.
369.	Построить график функции у = у(х), заданных парамет¬
рически, если:
а)	х = 1 — t9 у = 1 - t2;
б ) х = t + ^ , г/=^ + ~;
в)	л: = 10 cos £; у = sin £ (эллипс);
г)	л: = ch ty у = sh t (гипербола);
д)	х = 5 cos2 £;	1/ = 3 sin2 £;
е)	л: = 2(£ - sin t)\ у = 2(1 - cos f) (циклоида);
ж)	х = t + \ft у у = lJt + 1 (£ > 0).

40
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
370.	1. Построить графики неявных функций:
а)	х2 - ху + у2 = 1 (эллипс);
б)	х3 + z/3 - Зху = 0 (декартов лист);
в)	Jx + 4у = 1 (парабола);
2 2
г)	х3 + у3 = 4 (астроида);
д)	sin х = sin i/;
е)	cos (ял:2) = cos (пу);
ж)	ху = ух (х > 0, у > 0);
з)	х-\х\ = у- \у\.
2. Построить графики неявных функций:
a)	min (л:, у) = 1;	б) max (л:, у) = 1;
в)	max (|*|, |j/|) = 1;	г) min (х2, у) = 1.
371.	1. Построить графики функций г = г(ф) в полярной сис¬
теме координат (г, ср), если:
а)	г = ф (спираль Архимеда);
б)	г — - (гиперболическая спираль);
Ф
в)	г = -ЯЦ- (0 < ф < +оо);
Ф+ 1
JL
г)	г = 22л (логарифмическая спираль);
д)	г = 2(1 + cos ф) (кардиоида);
е)	г = 10 sin Зф (трехлепестковая роза);
ж)	г2 = 36 cos 2ф (лемниската Бернулли);
з) ф=	(Г> 1);
и)	ф = 2я sin г.
2.	Построить в полярных координатах гиф графики следую¬
щих функций:
а)	ф = 4г - г2; б) ф =	; в) г2 + ф2 = 100.
1 + rz
3.	Построить в полярных координатах гиф графики функ¬
ций, заданных параметрически (t > 0 — параметр):
Ф = 1 - 2"‘ sin Ц ,
г = 1 - 2 * cos § .
372.	Приближенно решить уравнение
л:3 - Зл: + 1 = 0,
построив график функции у = л:3 - Зл: + 1.
а)
ф = t COS2 ty
r = t sin2 ty
6)

§ 5. Предел функции
41
Графически решить следующие уравнения:
373.	х3 - 4х - 1	= 0.	374.	х4	-	4х + 1 = 0.
375.x = 2 '.	376.	lg	х	= 0,lx.
377. 10' = х2.	378.	tg	х	= х (0 < х <	2я).
Графически решить системы уравнений:
379.	х + у2 = 1,	16л:2 + у = 4.
380.	л:2 + у2 = 100, у = 10(л:2 - л: - 2).
§ 5. Предел функции
1.	Ограниченность функции. Функция f(x) называется ограничен¬
ной на данном промежутке (а, Ь), если существуют некоторые числа т
и М такие, что
т < f{x) < М
при х € (а, Ь).
Число т0 = х {/(*)} = max т называется нижней гранью функ¬
ции f(x)y а число М0 = sup {f(x)} = min М называется верхней гранью
х 6 (о, Ь)
функции f(x) на данном промежутке (а, Ь). Разность М0 - т0 называется
колебанием функции на промежутке (а, b).
2.	Предел функции в точке. Пусть функция f(x) определена на мно¬
жестве X = {л:}, имеющем точку сгущения а. Запись
lim f(x) = А	(1)
х — а
обозначает, что для каждого числа £ > 0 существует число 8 = 8(e) > 0
такое, что для всех х, для которых f(x) имеет смысл и которые удовлет¬
воряют условию 0 < \х - а\ < 8, справедливо неравенство
|/(х) - А\ < е.
Для существования предела функции (1) необходимо и достаточно,
чтобы для каждой последовательности хп -* а, хп & а (хп € X; п = 1,2,
...), было выполнено равенство
lim Дх„) = А.
л — со
Имеют место два замечательных предела:
1) lim	= 1, 2) lim (1 + х)х = с.
х —* 0 X	х —» 0
Критерий Коши. Предел функции f(x) в точке а существует тогда
и только тогда, если для каждого е > 0 найдется 8 = 8(e) > 0 такое, что
I fix') - Ях")| < Е,

42
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
как только 0 < \х' - а\ < 8 и 0 < \х" - а\ < 8, где х' и х" — любые точки
из области определения функции f(x).
3.	Односторонние пределы. Число А' называется пределом слева
функции f(x) в точке а:
А' = lim f(x) = f(a - 0),
х -• и -0
если
|А! - f(x)| < £ при 0 < а - х < 5 (е).
Аналогично, число А" называется пределом справа функции f(x) в
точке а:
А” = lim f(x) = f(a + 0),
х — а +0
если
[А" - f(x)\ < е при 0 < х - а < 8(e).
Для существования предела функции f(x) в точке а необходимо и
достаточно, чтобы
f(a - 0) = f(a + 0).
4.	Бесконечный предел. Условная запись
lim /(*) = оо
х — а
обозначает, что для любого Е > 0 справедливо неравенство:
|/(л:)| > Е, если только 0 < \х - а\ < 8(£).
5.	Частичный предел. Если для некоторой последовательности
хп -* а (хп *= а) имеет место равенство
lim f(xn) = В,
п — оо
то число (или символ оо) в называется частичным пределом (соответ¬
ственно конечным или бесконечным) функции f(x) в точке а.
Наименьший и наибольший из этих частичных пределов обознача¬
ются через
lim f(x) и lim /(*)
х — О	X (I
и называются соответственно нижним и верхним пределами функции
f(x) в точке а.
Равенство
lim f(x) = lim f(x)
x “a	x-a
необходимо и достаточно для существования предела (соответственно
конечного или бесконечного) функции /(х) в точке а.

§ 5. Продел функции
43
381.	Показать, что функция, определяемая условиями:
f(x) = /г, если х = — ,
п
где тип — взаимно простые числа и п > О, и
/(я:) = 0, если х иррационально,
конечна, но не ограничена в каждой точке х (т. е. не ограничена
в любой окрестности этой точки).
382.	Если функции f(x) определена и локально ограничена в
каждой точке: а) интервала, б) сегмента, то является ли эта
функция ограниченной на данном интервале или соответственно
сегменте?
Привести соответствующие примеры.
383.	Показать, что функция
л*) =
1 + X2
1 + х4
ограничена в интервале -оо < х < +оо.
384.	Показать, что функция
f(x) = - cos -
X	X
не ограничена в любой окрестности точки х = 0, однако не явля¬
ется бесконечно большой при х —► 0.
385.	Исследовать на ограниченность функцию
f(x) = In х • sin2 5
в интервале 0 < х < £.
386.	Показать, что функция
/(*) =
х
1 + JC
в области 0 < х < +оо имеет нижнюю грань т = 0 и верхнюю
грань М = 1.
387.	Функция f(x) определена и монотонно возрастает на сег¬
менте [а, Ь]. Чему равны ее нижняя и верхняя грани на этом
сегменте?
Определить верхнюю и нижнюю грани функций:
388.	/(*) = *2 на [-2, 5].
389.	f(x) = —— на (-оо, +оо).
1 + X2

44
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
390.	f(x) =	на (0, +оо).
391.	fix) = х + i на (0, +оо).
392.	f(x) = sin x на (0, +oo).
393.	f(x) = sin л: + cos * на [0, 2я].
394.	f(x) = 2х на (-1,2).
395.	/(jc) = [jc]: а) на (0, 2) и б) на [0, 2].
396.	f(x) = х - [х] на [0, 1].
397.	Определить колебание функции f(x) = я2 на интервалах:
а) (1; 3); б) (1,9; 2,1); в) (1,99; 2,01); г) (1,999; 2,001).
398.	Определить колебание функции f(x) = arctg i на интер¬
валах:
а) (-1; 1); б) (-0,1; 0,1); в) (-0,01; 0,01); г) (-0,001; 0,001).
399.	Пусть m[f] и M[f] — соответственно нижняя и верхняя
грани функции f{x) на промежутке (а, Ь).
Доказать, что если fi(x) и f2(x) — функции, определенные на
(а, Ь), то
m[fi + /2] > mUi] + лМУ2]»
М[Л + /2] < М[А] + М[/2].
Построить примеры функций /^лс) и f2(x), для которых в пос¬
ледних соотношениях имеет место:
а) случай равенства и б) случай неравенства.
400.	Пусть функция f(x) определена в области [а, +°о) и ог¬
раничена на каждом сегменте [а, Ь]. Положим: т(х) = inf /(£),
дг
М(х) = sup /(£).
а < £ < х
Построить графики функций у = /п(л:) и у = М(я:), если:
а) /(*) = sin я; б) /(л:) = cos х.
401.	С помощью «е — 8»-рассуждений доказать, что
lim х2 = 4.
л* — 2
Заполнить следующую таблицу:
Е
од
0,01
0,001
0,0001
8

§ 5. Предел функции
45
402.	На языке «Е — 8» доказать, что
lim гг
х- 1 (1
= 4-00.
Заполнить следующую таблицу
Е
10
100
1000
10 000
...
8
403.	Сформулировать с помощью неравенств следующие ут¬
верждения:
a) lim fix) = b; б) lim fix) = b;	в) lim fix) = 6.
x-*a	xa -0	x —* a +0
Привести соответствующие примеры.
Сформулировать с помощью неравенств следующие утверж¬
дения и привести соответствующие примеры:
404.	a) lim fix) = b; б) lim fix) = b; в) lim f(x) = b.
X —oo	X — -oo	x — +00
405.	a) lim fix) = oo;
x — a
в)	lim f(x) = +oo;
x — a
д)	lim	f(x)	=	-oo;
x - a-0
ж)	lim	/*( jc)	=	oo;
x — a + 0
и)	lim	f(x)	=	+oo.
x — a + 0
406.	a) lim fix) = oo;
X — OO
в) lim f(x) = +oo;
X — oo
д) lim f(x) = -oo;
X — -OO
ж)	lim	f(x)	=	oo;
X — +00
6) lim f(x) = -oo;
x — a
r) lim f(x) = oo;
x — a - 0
e) lim f(x) = 4-oo;
x — a-0
з) lim f(x) = -oo;
x — a + 0
6) lim /(jc) = -OO;
X — oo
r) lim f(x) = oo;
X — -oo
e) lim f(x) = 4-oo;
X — -oo
з) lim f(x) = -oo;
X — +oo
и) lim f(x) = +oo.
x — +00
407.	Пусть у = fix). Сформулировать с помощью неравенств,
что значит:
а)	у -* b -	0 при х —► а;	б) у	b - 0	при х	—► а - 0;
в)	у —>- b -	0 при л:	a 4- 0;	г) 1/	6 4- 0	при х	—► а;
д)у b + 0 при х -* а - 0; е) у -+ b 4-0 при х —► a 4-0;
ж) г/ —► 6 - 0 при х * оо;	з) г/ —3>6-0 при х -оо;
и)	У Ь -	0 при х	—* +оо;	к) у	—* b 4- 0	при х	—► оо;
л) у —>> b 4-	0 при х	-оо;	м) у	—1- b 4- 0	при х	—* 4-00.
Привести соответствующие примеры.

46
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
408.	Пусть
Р(х) = а0хп + а1хп~1 + ... + ап>
где ai (i = 0, 1, ..., п; п > 1, а0 ^ 0) — вещественные числа.
Доказать, что
lim \Р(х)\ = +оо.
X — ОО
409.	Пусть
R(x) =
где а0 ^ 0 и 60 ^ 0.
Доказать, что
а0хп + аххп~1 + ... + ап
b0xm + blxm l + ... + bm *
lim
х * оо
|Ж*)| = <
оо, если /г > т;
~ , если п = /и;
0, если п < т.
410. Пусть
ад =
Q(*)’
где Р(х) и Q(x) — многочлены от х и
Р(а) = Q(a) = 0.
Какие возможные значения имеет выражение
lim
х -* а
Р±х)?
Q(X)
Найти значения*следующих выражений:
411. а) lim
*2-1
б) lim
2х2 - х- 1	х — 1 2л:2-
412. lim d + *)(1 + 2*)(1 + Зу)- 1 в
* х-0	х
х- 1
в) lim
2л:2 -л: - 1
413.	lim Ц + ^М1*6*?.
* — о л:2 + л:5
414.	lim .t.1?*) t nx) 1 (тип — натуральные числа).
х-+ о	х2
415. Ит ^-1)^-2)^-3)^Т4)(у-5)<
х-*оо	(5л:- I)5
416. Ит
X — оо
(2л:-3)20(Зл: + 2)30
(2л: + I)50

§ 5. Предел функции
47
417. lim {*+1H*2+l) - (*"+1),
х — оо	!±I
[(ЛЛГ)” н- 11 2
418. lim
X2 - Ъх + (
з jc2 - 8* + 15
420. lim
х4 - Зх + 2
>1 х5-4х + 3
422. lim
424. a) lim
х3 - 2х- 1
1 х5- 2х- 1 *
X + X2 + ...хп - п ,
419. lim **~2*+2 .
х — 1 *4-4* + 3
421.1im *3:2*02~4* + 8.
х-2 я4 - 8*2 + 16
423. Ит ..^2-х-2)3° ,
х —* 2 (JC3 - 12л: + 16)10
► 1
х - 1
б) Ит
2х + 1
1 л:50 - 2х + 1
хт — 1
425. Ит 	 (тип — натуральные числа).
х - 1 Хп - 1
426.	lim ~ а") ~ па" \{хга) (п — натуральное число).
х-а	(х - а)2
427. Ит
(п+ 1 )х+п (	_
(х-1)2
(п — натуральное число).
428
. lim --- - ^ п ^ (тип — натуральные числа).
х+ £1 + (* + 2а
+ ... +
430. Ит -
« —► оо /I
429. lim iff
/I * оо л[Л
(*+Э, + (‘+?),+
Указание. См.'пример 2.
431.	Ит 12+32+ - +(2»~1)2-
«-.оо	22 + 42 + ... -f (2/г)2
432.	Ит Г13 + 23+„- + п3 -”1.
п - оо V	я3	4у
Указание. См. пример 3.
433.	Ит 13 + 43 +.72 + ::: МЗ^- 2)2 .
« —* оо [1 + 4+ 7+ ... + (Зя-2)]2
434.	Определить площадь криволи¬
нейного треугольника ОАМ (рис. 3),
ограниченного параболой у =	> осью
Ох и прямой х = а, рассматривая ее как
предел суммы площадей вписанных
прямоугольников с основаниями -,
п
где п
Рис. 3

48
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
Найти пределы:
*]х + Jx + Jx
Jx+ 1
435. lim
X — +00
437. lim «А + 2x - 3
Jx-2
439. lim	+	.
x~*a	Jx2 - a2
441. lim 5£EI±2.
*		2 X3 + 8
443.	lim ^-±2£--5 .
*	-8	*Vi-2
Л /l . у _ 1
444.	lim —	 (/г — целое число).
* — o	*
436. lim Jk±Mk±Uk.
*-+°° V2x+1
438. lim dlZLll.
x - -e 2 + V*
440. lim ^±.13-2^I
*-з x2 - 9
442. lim
*-i6 T^_4
lim Vl-2x-x2-(l + x)
445. lim
x —* о	л:
446. lim V8 + 3x - x2 -_2
x -* о	tf + tf2
447. lim
x —* 0
У27нПс- V27- *
*+ 2*V^
448. lim Л±Ъ_ЛЕ5,
*-° S/l + X- Vl - X
449. lim
x-*7 i/x + 9-2
451. lim
450. lim -
x —» 0
1 + 5-4
3	V
1 + T
-Я
vi + 5x-(l + x)
452.	lim + ax~ V1 (тип — целые числа).
x — О	х
453.	lim тЛПШШ^± (m и „ _ целые числа).
х -* О	X
454.	Пусть Р(лс) = ахх + a2.r2 + ... + апхп и т — целое число.
Доказать, что lim ^ * Р(-ХУ—1 = — .
х —»о	х	т
Найти пределы:
т Гх — л
455. 1. lim 	 (тип — целые числа).
* -1 0/х - 1
2. lim
х-1
1 - Jx 1 -3Jx

§ 5. Предел функции
49
456 lim (1-V*)(l-V*)-- (l-nV*)
' х->1	( 1 - Х)п~ 1
457,	lim [J(x + а)(х + b) - х].
X —' +оо
458.	lim ( Jx + Jx + Jx - Jx 1 .
459.	lim x
x — +00
^Jx2 + 2x- 2 Jx2 + x
460.
lim
x -* a +0
\
/
461.	lim (3Jx3 + x2 + 1 - Ух3 - x2 + 1
X —* oo V
462.	lim (3Jx3 + Sx2 - Jx2 - 2x 1.
463.	lim x* [(* + l)5 - (jc - 1)*] .
X - ' oo
464.	lim x312 {Jx +2 - 2 Jx + 1 + Jx 1.
465.	lim [nJ(x + a^.^Jx + an) - jcJ .
466.	lim	1) (n — натуральное число).
* - 4oo	Xn
467.	lim +.x2.t.xl.7,*).. (n — натуральное число).
x~* 0	. X
468.	Изучить поведение корней хх и х2 квадратного уравне¬
ния ах2 + Ьх 4- с = 0, у которого коэффициент а стремится к нулю,
а коэффициенты b и с постоянны, причем b ^ 0.
469.	Найти постоянные а и b из условия:
lim (£i±JL	=0.
*-.oo V я+ 1	У
470.	Найти постоянные a, nb/(i= 1, 2) из условий:

50
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
Найти пределы:
471. lim
473. lim
sin 5 а:
х -* 0 X
sinmx
472. lim 21££.
х — °о X
х —> п SinПХ
. (тип — целые числа).
474. а) lim -—; б) lim ; в) lim х ctg Зле.
х —> О X2	X-О X
475. lim tg£^shH
х-о sin3 а:
477. lim
х-0
cosa: - cos3a:
y2
x - О
476. lim sin5*-sin3* _
x — o sina:
1 + sina: - cos a:
478. lim
x -* о 1 + sinpa: - cospa:
479. lim tg 2x tg^5 - arj ,
nx
480. lim (1 - x) tg
x — l	2
481. Доказать равенства:
a) lim sin x = sin a; 6) lim cos x = cos a;
x — a
2/i-l
в) lim tg x = tg a (a * ----1 n; n = 0, ±1, ±2, ...1.
x — a	V	2	У
Найти пределы:
482. lim si^-sina.
x — a	X — CL
484. lim *К-**Д.
x —* a X — CL
486. lim sec*~seca.
x —* a	X — CL
483. lim cosx-cosa.
x — a X — CL
485. lim £fr?.-c-jg.g.
x —* о	X — CL
487 lim cosec* ~ coseca
* x -a	a: - a
488	lim s^n(fl +	- 2sin(a + a:) + sina
‘ x-o	x2
489	lim cos(fl + 2дс) ~ 2cos(a + x)+ cos a
‘ x-o	a:2
490.	Um tg(a+2x)-2tg(a + ^) + tga _
x * О	X2
491.	lim ctg(fl + 2x) ~ 2ctg(a + x) + ctga ^
* x-*0	x2
492 lim s^n(fl + *)sin(a + 2a:) - sin2a
‘ x —» О	x
2 sin2 x + sina: - 1
493. lim
я 2sin2a:- 3sina: + 1
494 lim 1 ~ cosxcos2xcos3a:
* x-o	1 - cosa:

§ 5. Предел функции
51
495. lim
■(*-!)
it 1- 2 cos*
3
496. lim	.
x~3 COS^X +
497. lim tg(a + x)tg(a-x)-tg»a
x-+0
498. lim -	1-?-****
r_ я 2 - ctgx - ctg3X
4
500. lim
* — 0 Vl + *sinx- Jeosx
502. lim ^ -.ЯРР*2.
x - 0	1 - COS*
499. lim V1 +tgx-7l+ sinx
* x-’O	X3
501. lim	.
sin^x
503. lim
x"*° 1- COS(V^)
504 lim * ~ cos Хл/cos 2 дс у cos 3jc
’ Д о	x2
505.	lim f sin Jx + 1 - sin л/r 1,
ДС —* foo V	/
506.	a) lim f 1 + *"\ i-* ; 6) lim	l~x ; в) lim	l~* .
х_>0\2 + л:у	л- — l V 2-f лу	x — +°o v 2 + я:/
i - ,7x
l-Vi
507. lim
X — OO
(x + 2 V"2
Ux-lJ ■
509. lim
Я — '■»
(sin" 2nn 1.
1 3rt+lJ
510 lim [Щ + *)]“".
4
511. lim
x * oo
(**-Г\;Т7
U2 + i; *
' x2 + 2x - 1
512. lim f*!+jy*.
X — oo \x2 — 2J
513. lim (
x * 0 V
514. lim xJl - 2x .
x * 0
,2x2-2x-2) *
515. lim
x — oo
f x + aYY
\x- a)
516. lim (aJ*+bl) (a1>0,a2>0).
х-'+со\а2х+Ь2) 1
517. lim (1 + x2)cle2x.
x —* 0
518. lim (1 4- sin nx)ctenx.
x - 1
519. a) lim (} + ;
x-*0 vl + sinX)
6) lim ( 1 + tg* Vin3jc.
x — о VI + sinxv
520. lim (
x — a *
'sin^rb e
< sin a)
521. lim f cos* P .
x-o Vcos2jcj

РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
522. lim (tg x)ig s
523. lim (sin x)tgJ
“hWr'ir'
526. lim XJcos л/г .
x — 0
528. lim cos'1 -£= •
Jn
530. lim x[ln (x + 1) - In x].
x — +oo
525. lim f sin - + cos -1 .
x-oo V x	x)
527. lim fa±£V.
x-oo \П- 1J
529. lim ISil + fEl.
x — 0	X
531. lim hLx~ln.a (a > 0).
x-a x-a
532. lim [sin In (л: + 1) - sin In x]. 533. lim	x + ^
X —* +oo	J	x-*+oo ln(X*°+X+l)
535. lim 42 + fx).
x~*+oo (3 + e2x)
534. lim fig
x — oo V 1 + 100x2)
536.	lim
ln(l + l/x + i/x)
537.	lim log(*+*) + log(*-*)-21ogx (jc > 0)
л -0
h2
538. lim
lntg(^ + axj
x — о	sinbx
In
539. lim jncosa* .
x — 0 In COSOX
540. a) lim
x * 0
f nx +	1 - n2x2>>
X+JT-X2
541. lim ——- (a > 0).
x — 0 X
543. lim **'ae
(a > 0).
x — a x-a
"i + x-2*
545. a) lim
Vl + x-3*
B) lim	;
^ x — l sin(rcxP)
6) Um ?n_(nx+Vl-n^ #
ln(x + Jl - X2)
542. lim ^(a > 0).
x-a x-a
544. lim ^x +	.
6) lim fUSin^cosaxy^
x - 0 V 1 + sinxcospxy
Г) lim .. “"Ч”'2*)	.
x-1 ln[cos(jt 2*)]
546.
lim tg" f 2 + Г).	547. lim
a —oo V4 П)	x — 0
gax _ gPx
548.	lim	(a > 0).
x-a xP-aP
550.	lim P-,:*+..°*~*-2gjt
A - О	Л2
x - о sin ax - sin(3x
549.	lim	(a > 0).
x-A X-Ь
(a > 0).

§ 5. Предел функции
53
551.	lim (* + ДГ’(* + ЬГ\
п -* оо (х + а +b)2x *t, + h
552.	lim /гГ'Д/зс - ll (jc > 0).
л — оо V	/
553.	lim /г2	- n + \fx^ (х > 0).
554.	lim	(a > 0, b > 0).
555.	lim (пЯ + Ф)а (a > 0, b > 0).
n — oo V 2 у
556
. lim f ^
x- о V
+ b* + c*
(a > 0, b > 0, c > 0).
557.	lim f+	(a > 0) 6 > 0, c > 0).
дг — о V a + fr + c ;
558.	lim	V (a>0,b>0).
x —* 0 V. CLX + bx )
559. lim
ax - bx
560. lim
x-a (ax-bx)2
a°x - ax"
♦ a ax - x°
(a > 0, b > 0).
(a > 0).
561.	a) lim	;	6) lim M1+1D.
X — —oo ln( 1 + 2X)	X-*+oo ln(l + 2*)
562.	lim In (1 + 2X) In (1 + Ц .
x -	V xj
563.	lim (1 - x)\ogx 2.
x —* 1
564.	Доказать, что lim — = 0 (a > 1, n > 0).
x — +oo ax
565.	Доказать, что lim	=0 (a > 1, e > 0).
x-+oo Xе
Найти пределы:
566.	a) lim	;	6) lim ln(*2 + g*) .
x — о ln(x4 + e2x)	x-+oo ln(x4 + e2x)
567.	lim ln(1 + *gJ> .
X~^° ln(x + Jl + JC2)
568.	lim [(* + 2) In (jc + 2) - 2(x + 1) In (x + 1) + x In x\.
X — +oo

54
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
569. lim
х — +0
(
In (х In а) • In
lna*
In
x
(a > 1).
570. lim fIn * + l • ln-2 £±Tl.
x — +oo \	x + Jx2 _ l	X-1J
571.	lim VI+*sin*-l .
x —* o ex2-l
572.	lim со»(***)-сов(хе-«) .
x -0	X3
X	x2+ 1
573.	lim (2е^ - l)“.
574. lim (2 - x) 2 .
X — 1
575. lim
1 - sina+Pjc
7(1- sinex)( 1 - sinPjc)
576. a) lim — ;	6) lim — —~ 1 ;
(a > 0, P > 0).
x — 0 X
thx
дг —• 0 X*
b) lim 	 (см. пример 340).
x —* 0 X
577. a) lim r ч (см. пример 340);
x —* о ln(ch3x)
6) lim SW*2 + x - sh Jx2 - x
chx
578. a) lim
X -* +oo
shjc - shfl ,
x — a X — CL
6) lim
eh* - cha ,
x * a X- a
Inch*
x - о lncosx
в) lim
579.	a) lim (x - ln ch x); 6) lim e*'"2x eSinx
x — о thjc
( ch^2
580.	lim
/1 — 00
n
cos-
V	П)
581.	lim arcsin \—- .
x —► oo	1 + X
582.	lim arccos ( Jx2 + x - x),
x — +oo	V	J
***• arcte ФЬ ■
584.	lim arcctg —- * -.
Ji + x2
585.	lim arctg(x + /t)-arctgx
л —* о	h

§ 5. Предел функции
55
In
l + x
l-x
586.	lim 	.
x - о arctg( l + x) - arctg( l-x)
587. lim Гn arctg		 • tgn (? + #-11
n-oo L	n(x2+ 1) + X V4 2n)i
588.	lim x (% - arctg —?--).
x-oo	V4	x+1J
589.	lim x f- - arcsin x .
*-,0° V2	Jx2 + 1,
590.	lim [l +	.
rt-oo L	Tl J
591.	a) lim -i- e *2;	6) lim x In x.
x - О X100	x — + 0
592.	a) lim f Jx2 + x - x); 6) lim (Jx2 + x
593.	a) lim (Jl + x+x2 - Jl - x + x2);
X — -OO
6)	lim (Vl + x+ x2 - Jl - x + x2).
x — +00
594.	Найти
/i = lim f(x) - lim /(x),
X — +oo	x — -oo
если
/(ж) = In x + ^2 + fl2
X+ >s/x2 + b2
595.	a) lim arctg —-i— ; 6) lim arctg .
x -* +0	1 - x x -* 1 +0	1 - X
596. a) lim —1— ;	6) lim —.
x — -0	-	x —*■ +0	-
1 + ex	1 + ex
597.	a) lim	; 6) lim	.
x —* -oo	X	x —* +oo	X
598.	Доказать, что:
а)	—2 + 0 при x — -oo;
l + x
б)	— 2 - 0 при x ->• +oo.
l + x
599.	Доказать, что:
а)	2х — 1 - 0 при х — -0;
б)	2х — 1 + 0 при х — +0.
-х).

56
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
600.	Найти /(1), /(1 - 0), Я1 + 0), если f(x) = х + [х]2.
601.	Найти /(/г), f(n - 0), f(a + 0) (n = 0, ±1, ...), если f(x) =
= sgn (sin nx).
Найти пределы:
602. lim x 1 cos-.
603. lim жГЛ.
x * 0 А/ X
x - 0 IXJ
604. lim sin [njn2 + 1 ] .
П — ОО V /
606. lim sin sin ... sin x.
/1 — 00 "v" '
л раз
605. lim sin2 (njn2 + n).
n * oo
607. Если lim cp(jc) = А и lim cp(jc) = Б, то следует ли отсюда, что
х — а	х -* А
lim \|/(ф(л:)) = В?
х -* а
Рассмотреть пример: ср(лт) = - при х = £ , где р и q — взаим-
Ч	Ч
нопростые целые числа и ф(я:) = 0 при х — иррациональном;
\|/(jc) = 1 при х ^ 0 и \|/(лг) = 0 при х = 0; причем х —► 0.
608.	Доказать теоремы Коши: если функция f(x) определена
в интервале (а, +со) и ограничена в каждом конечном интервале
(а, 6), то:
а)	lim	= lim [f(x + 1) - f(x)];
X -* +оо X	X — +оо
б) lim [ft*)] 1 = lim	(f(x) >0 0),
X-.+00	x — 1-00	/(x)
предполагая, что пределы в правых частях равенств существуют.
609.	Доказать, что если: а) функция f(x) определена в области
х > а; б) ограничена в каждой конечной области а < х < Ь;
в)	lim [f(x + 1) - f(x)] = оо, то
X -> +оо
lim	= оо.
X— +оо X
610.	Доказать, что если: 1) функция f(x) определена в облас¬
ти х > а; 2) ограничена в каждой конечной области а < х < Ь;
3)	для некоторого натурального п существует конечный или бес¬
конечный предел
Urn К*+!)-/(*) = l,
X —-ЮС)	ХП
lim Й£1 -_i_.
x- +oo JC"+ 1	/1+1
TO

§ 5. Предел функции
57
611.	Доказать, что
a)	lim fl + iV-e*; б) lim (l + х +	+ ... +	= в*.
п-оо in)	,,-оо I	2!	»!;
612.	Доказать, что
lim п sin (2пеп\) = 2я.
л — сю
Указание. Использовать формулу (*) примера 72.
Построить графики функций:
613.	а) у = 1 - jc100;	б) у = lim (1 - х2я) (-1 < х < 1).
п » оо
614.	а) г/ =	(х > 0); б) у = lim	(х > 0).
1 + X100	п-оо 1 + Хп
615.	у = lim *" ~ (X * 0).
п - ОО хп + X п
616.	у = lim /х2 +
617.	г/ = lim Vl + х'1 (х > 0).
618. у = lirn „J1 + х" + (^J	(х > 0).
619.	у = lim ■■ xnt2 - (х > 0).
n-оо а/22', + х2л
620.	а) у = sin1000 x;	б) у = lim sin2" x.
/I — OO
621.	у = lim	+	(*>0).
n —* оо	П
622.	у = lim (x - 1) arctg x".
/1 — 00
623.	*/ = lim «Д + e"(* + 1).
/г — оо
624.	a) */ = lim ^	;
t — +oo 1 + etx
б) у = lim -J— In - (jc > 0).
xt&2n 4. fx
625.	a) у = lim 	i-	 (x > 0);
" "00 tg2" — + 1
б)	у = lim д: sgn |sin2 (п!ти:)|;
П — OO
в)	построить кривую
lim 'i/Wn + \y\n = 1.
/I - OO

58
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
626.	Асимптотой (наклонной) для кривой у = f(x) называет¬
ся прямая у = kx + b, для которой
lim [/(*) - (kx + b)] = 0.
х — сю
Используя это уравнение, вывести необходимые и достаточ¬
ные условия существования асимптоты.
627.	Найти асимптоты и построить следующие кривые:
а)У= г	5 5
х2 + х - 2
в)	у — 3Jx2 - х3 ;
д) у= In (1 + ех);
б)	у = Jx2 + х ;
г) У =
<?* - 1 ’
е)	у = л: + arccos - .
s2" 1
(2л)! J
Найти следующие пределы:
628.	lim Г -SILL. +	+ .
п —»оо L (л + 1)! (л + 2)!
629.	lim [(1 4- jc)(1 + л:2)(1 4- хА) ... (1 + х2п)], если |х| <1.
п оо
630.	lim fcos S cos S ... Cos .
»-oo (	2	4	2";
631.	Пусть
lim SLSl =1,
x —» 0	\J/(*)
где vi/(jc) > 0 и am„ => 0 (m = 1, 2, ...) при n > °o, t. e. |amn| < e при
m = 1, 2, ... и n > N(e).
Доказать, что
lim [cp(aln) + ср(а2л) + ... + ср(алл)] =
л — оо
= lim [\у(а1п) + V|/(ot2n) + ... + 1|/(а,ш)],	(1)
Л — оо
предполагая, что предел в правой части равенства (1) существует.
Пользуясь предыдущей теоремой, найти пределы:
вз2- л	«зз- 1 (™ *?) •
k
634. lim ^ ^ап2 - lj
П(-, + й-
636. lim П cos .
«-00
(а > 0).

§ 5. Предел функции
59
637.1.	Последовательность хп задана равенствами:
хх = Ja , х2 = Ja + л/а , х3 = Ja + 7а + Ja , ... (а > 0).
Найти lim хп.
П — °о
2.	Последовательность задается следующим образом:
= 0, х2 = 1,
+ *»-г) (»=2, 3, ...).
Найти lim хп.
П-* оа
3.	Последовательность уп определяется с помощью последо¬
вательности хп соотношениями:
Уо = х0, уп = хп-ахп_1 (п=1,2,...),
где |а| < 1. Найти lim хп, если lim уп = Ь.
Л — Оо	п~* ОО
4.	Последовательность хп определяется следующим образом:
*о=1> *«=7ТТ— (тг = 1, 2, ...).
Найти lim хп.
п * оо
Указание. Рассмотреть разности между хл и корнями уравне-
1
НИЯ X = 		 .
1 + X
638. Последовательность функций
Уп = Уп(х) (0 < ж < 1)
определяется следующим образом:
а>1/,-§, уп=	("=2,3, ...);
6)1/1“	УЯ=|	(тг = 2, 3, ...).
Найти lim уп.
639. 1. Пусть х > 0 и t/n = Уп-№~ хУп-\) (п =	2» •••)• Дока¬
зать, что если yt > 0 (i = 0, 1), то последовательность уп сходится и
lim
Уп х
1
Указание. Изучить разность -
У ГГ

60
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
2.	Для нахождения у = Jx , где х > О, применяется следую¬
щий процесс: у0 > 0 — произвольно,
Доказать, что lim уп = л/д;.
/I — ОО
Указание. Использовать формулу
/	/-л2
г/„- V* _ \ Уп-\- V*
(п > 1).
y„ + Jx \y„_l + Jx/
640.	Для приближенного решения уравнения Кеплера
х - £ sin х = m (0 < £ < 1)	(1)
полагают
х0 = m, хх = т 4- £ sin д;0, ..., дг„ = /п -Ь £ sin дг„_ х, ...
(метод последовательных приближений).
Доказать, что существует £ = lim д:„ и число £ является един-
/1 — 00
ственным корнем уравнения (1).
641.	Если соЛ[/] есть колебание функции f(x) на сегменте
I* - 41 < h (Л > 0), то число
Щ[П = lim О),,[/]
Л - о
называется колебанием функции f(x) в точке £.
Определить колебание функции /(jc) в точке д; = О, если:
a) f(x) = sin- ;
х
в) f(x) =	4- sin ;
6)	f(x) = — cos2 i ;
X2	X
г)	f(x) = - arctg - ;
Я	X
Д) fix) =
sin*
e) fix)
i *
1 + ex
ж)	f(x) = (l + |*|) ~x.
642.	Пусть f(x) = sin i. Доказать, что, каково бы ни было
число а, удовлетворяющее условию -1 < а < 1, можно выбрать
последовательность хп^> 0 (/г = 1,2,...) такую, что
lim f(xn) = а.
П — ОО

§ 6. О-символика
61
643.	Определить
I = lim f(x) и L = lim f(x),
* —> 0	x^°
если:
a) f(x) = sin2 - + - arctg - ; 6) f(x) = (2 - x2) cos - ;
x n	x	x
в) f(x) = ^1 + COS2	* .
644.	Определить
l	= lim /(я) и L = lim f(x)9
X —* oo	x * °°
если:
a) /(*) = sin x\
в) f(x) = 2	;
6) f(x) = x2 cos2 x;
r) f(x) =
1 + jc2sin2^:
(x > 0).
§ 6. О-символика
1.	Запись
(p(jc) = 0(v|/(jc)) при x € X
обозначает, что существует постоянная А такая, что
|ф(*)1 < -АМ*)1
для х € X.
а)
Аналогично пишут
<р(*) = 0(»|»(х))
при х -* а,
(2)
если неравенство (1) выполнено в
некоторой окрестности
Uа точки
а (х 5й а). В частности, если \|/(jc) & 0 при х € UA (х & а), то соотношение
(2) заведомо имеет место, если существует конечный lim	^ о.
х —* a V|/( JC)
В этом случае будем писать ф(д:) = 0*(\|/(л:)).
Если
lim	= k ^ 0 (р > 0),
х - о хр
то ф(лг) называется бесконечно малой порядка р относительно бесконеч¬
но малой х. Аналогично, если
lim	= k * 0 (р > 0),
X —‘ оо ХР
то \\f(x) называется бесконечно большой порядка р относительно беско¬
нечно большой х.

62
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
2.	Запись
ф(лг) = о(ц/(л;)) при х -* а
обозначает, что
Ф(л;) = a(*)i|/(x) (х € Ua, х * а),	(3)
где «(*) -* 0 при х-* а. Если \у(х) ^ 0 при х € Ua> х & а, то равенство (3)
эквивалентно утверждению
lim 3>l£l = 0.
х-« \p(jc)
3.	Функции ф(лг) и \р(лг) называются эквивалентными (ф(лг) - \|/(х))
при х —* а, если
Ф(л:) - \j/(jc) = o(\|/(jc)) при х -* а.	(4)
Если \|/(л:) 5й 0 при х € Ua, х & а, то из (4) имеем
lim 2i£l - 1.
х-а \|/(л:)
При х -* 0 справедливы следующие соотношения эквивалентности:
sin х ~ х; tg х ~ х; ах - 1 ~ х In а (а > 0);
In (1 + х) - х;	1/(1 + х) - 1 - - .
Вообще
<р(лг) + о(ср(х)) - <р(х).
При нахождении предела отношения двух бесконечно малых (или
бесконечно больших) функций, если х -* а, данные функции можно
заменять эквивалентными.
645.	Считая центральный угол АОВ = х
(рис. 4) бесконечно малой 1-го порядка, опре¬
делить порядки малости следующих величин:
а) хорды АВ; б) стрелки CD; в) площади секто¬
ра АОВ; г) площади треугольника АВС; д) пло¬
щади трапеции АВВХАХ; е) площади сегмента
АВС.
646.	Пусть o(f(x)) — произвольная функ¬
ция, имеющая при х -* а более низкий поря¬
док роста, чем функция f(x), и 0(f(x)) — любая
функция, имеющая при х~* а тот же порядок роста, что и функ¬
ция f(x)9 где f(x) > 0.
Показать, что:
a) o(o(f(x))) = o(f(x));	б) 0(о(/(*))) = o(f(x));
в) о(0(/(*)» = o(f(x));	г) 0(0(f(x))) = 0(f(x));
д)	0{f(x)) + o(f(x)) = Q(f(x)).

§ 6. О-символика
63
647.	Пусть х —* 0 и /г > 0. Показать, что:
а)	СО(хп) = 0(хп) (С ^ 0 — постоянная);
б)	0(хп) + 0(хт) = 0(jc") (/г < т);
в)	0(jc")0(jcm) = 0(лг" + т).
648.	Пусть х -+ +оо и /г > 0. Показать, что:
а)	СО(хп) =
б)	О^'1) + 0(jcm) = 0(хп) (п > т)\
в)	0(хп)0(хт) = 0(хп + '").
649.	Показать, что символ ~ обладает свойствами:
1)	рефлективности: ф(л;) - cp(jc);
2)	симметрии: если ф(д;) - v|/(jc), то vj/(jc) ~ ф(*);
3)	транзитивности: если ф(л;) - vj/(jc) и vj/(x) - %(х)9 то ф(д:) - %(х).
650.	Пусть jc —^ 0. Доказать следующие равенства:
ж) (1 + х)п = 1 + пх + о(х).
651.	Пусть х +оо. Доказать следующие равенства:
652.	1. Доказать, что при достаточно большом х > 0 имеют
место неравенства:
е) arctg i = 0(1);
в)	х + х2 sin x = 0(х2);	г)	= о
а) х2 + 10х + 100 < 0,001х3; б) In1000 х < V* ;
в) х10ех < е2х.
2. Доказать асимптотическую формулу
при х —> -foo.

64
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
653.	Пусть х —5► 0. Выделить главный член вида Схп (С — по¬
стоянная) и определить порядки малости относительно перемен¬
ной х следующих функций:
а) 2х - Зх3 + д;5;	б) J\ + х - Jl-x ;
в)	Jl - 2х - Vl - 3jc ;	г) tg х - sin х.
654.	Пусть х —5► 0. Показать, что бесконечно малые
__i_
a) f(x) = -р- ;	б) /(*) = е *2
тле
не сравнимы с бесконечно малой хп (п > 0), каково бы ни было
/г, т. е. ни при каком п не может иметь место равенство
lim	= k, где k — конечная величина, отличная от нуля.
х-0 Хп
655.	Пусть х -* 1. Выделить главный член вида С (х - 1)п и
определить порядки малости относительно бесконечно малой
х - 1 следующих функций:
а) х3 - Зх + 2;	б) 3Jl - Jx ;	в) In х;
г)	ех - е;	д) Xх - 1.
656.	Пусть х —*> +оо. Выделить главный член вида Схп и оп¬
ределить порядки роста относительно бесконечно большой х сле¬
дующих функций:
а) *2 + 100* + 10 000;	б)	■■■	— ;
х3 - Зх + 1
в) 3Jx2 - х 4- Jx ;
г)
а/ 1 + л/1 + *fx .
657. Пусть д;
+оо. Выделить главный член вида С( -
и
определить порядки малости относительно бесконечно малой -
х
следующих функций:
a) 5	б) ^Х+ 1 “ ^ ’
в)	7* + 2 — 2л/* + 1 + л/* ; г) i sini .
л:	д:
658.	Пусть д: —5► 1. Выделить главный член вида С^—и
определить порядки роста относительно бесконечно большой
следующих функций:
г) -4—;
втяд:
61
д)а^
В)
VT

§ 7. Непрерывность функции
65
659.	Пусть х —5► +оо и fn(x) = хп (п = 1, 2, ...). Доказать, что:
1)	каждая из функций fn(x) растет быстрее, чем предшест¬
вующая функция fn _ ^х);
2)	функция ех растет быстрее, чем каждая из функций fn(x)
(тг= 1, 2, ...).
660.	Пусть х —* +°° и fn(x) = nJx (п = 1, 2, ...). Доказать, что:
1)	каждая из функций fn(x) растет медленнее, чем предшест¬
вующая функция fn-i(x);
2)	функция f(x) = In л; растет медленнее, чем каждая из функ¬
ций /„(*) (тг= 1, 2, ...).
661.	Доказать, что, какова бы ни была последовательность
функций
fiM> /2(*)> •••> fn(*)> •••	(*о < х < +оо),
можно построить функцию f(x), которая при х —► +оо растет бы¬
стрее, чем каждая из функций fn(x) (п = 1, 2, ...).
§ 7. Непрерывность функции
1.	Непрерывность функции. Функция f(x) называется непрерывной
при х = х0 (или в точке л:0), если
lim f(x) = f(x0)y
x^xQ
т. е. если функция f(x) определена при х = х0 и для каждого £ > 0 су¬
ществует 5 = 5(е, л:0) > 0 такое, что при \х - х0\ < 8 для всех значений
f(x)> имеющих смысл, выполнено неравенство
\f(x) - f(x0)\ < е.
Функция f(x) называется непрерывной на данном множестве
X = {jc} (интервале, сегменте и т. п.), если эта функция непрерывна в
каждой точке множества X.
Если при некотором значении х = л:0, принадлежащем области оп¬
ределения X = {я} функции f(x) или являющемся предельной точкой
этого множества, равенство (1) не выполнено (т. е. или (а) не существует
число f(x0), иными словами, функция не определена в точке х = х0> или
(б) не существует lim f(x)> или (в) обе части формулы (1) имеют смысл,
но равенство между ними не имеет места), то х0 называется точкой раз¬
рыва функции f(x).

66
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
Различают: 1) точки х0 разрыва первого родау для которых сущест¬
вуют конечные односторонние пределы:
/(*о - 0) = lim /(*) и f(xо + 0) = lim f(x)
х —’ xQ - О	x—x0 + 0
и 2) точки разрыва второго рода — все остальные. Разность
f(x0 + 0) - f(x0 - 0)
называется скачком функции в точке х0.
Если выполнено равенство
/(*0 - 0) = f(x0 + 0),
то точка разрыва х0 называется устранимой. Если по меньшей мере
один из пределов f(x0 - 0) или f(x0 + 0) равен символу оо, то х0 назы¬
вается точкой бесконечного разрыва.
Если выполнено равенство
fix о - 0) = fix о)	(или fix о + 0) = fix0))9
то говорят, что функция fix о) непрерывна слева icnpaea) в точке х0.
Для непрерывности функции /(*) в точке х0 необходимо и доста¬
точно равенство трех чисел:
fix0 - 0) = fix0 + 0) = fix0).
2.	Непрерывность элементарных функций. Если функции fix) и
gix) непрерывны при значении х = х0, то функции
a) fix) ± gix); б) fix)gix); в) igix0) * 0)
Six)
также непрерывны при х = х0.
В частности: а) целая рациональная функция
Pix) = а0 + ахх + ... 4- апхп
непрерывна при любом значении х; б) дробная рациональная функция
а0 + а1х+ ... + апхп
Ь0 + Ьгх+ ... + Ьтхт
непрерывна при всех значениях ху не обращающих знаменателя в нуль.
Вообще основные элементарные функции: хпу sin х, cos	tg х, ах,
log0 xf arcsin x, arccos xy arctg xy ... непрерывны во всех точках, где они
определены.
Более общий результат следующий: если функция /(*) непрерывна
при х = х0 и функция giy) непрерывна при у — fix0)y то функция gifix))
непрерывна при х = х0.
3.	Основные теоремы о непрерывных функциях. Если функция fix)
непрерывна на конечном сегменте [а, Ь]у то: 1) fix) ограничена на этом сег¬
менте; 2) достигает на нем своей нижней грани т и верхней грани М imeo-
рема Вейерштрасса); 3) принимает на каждом интервале (а, Р) С [а, Ь] все
промежуточные значения между /(а) и /(Р) imeopeMa Коши). В частности,
если /(а)/(Р) < 0, то найдется значение у (сх < Y < Р) такое, что /(у) = 0.

§ 7. Непрерывность функции
67
662.	Дан график непрерывной функции у = f(x). Для данной
точки а и числа е > О указать геометрически число 5 > 0 такое,
что If(x) - f(a)I < е при \х - а\ < 5.
663.	Требуется изготовить металлическую квадратную плас¬
тинку, сторона которой х0 = 10 см. В каких пределах допустимо
изменять сторону х этой пластинки, если площадь ее у = х2
может отличаться от проектной у0 = 100 см2 не больше чем:
а)	на ±1 см2; б) на ±0,1 см2; в) на ±0,01 см2; г)на±Е(см2)?
664.	Ребро куба заключается между 2 м и 3 м. С какой абсо¬
лютной погрешностью А допустимо измерить ребро х этого куба,
чтобы объем его у можно было вычислить с абсолютной погреш¬
ностью, не превышающей е м3, если:
а)	е = 0,1 м3;	б) е = 0,01 м3; в) £ = 0,001 м3?
665.	В какой максимальной окрестности точки х0 = 100 ор¬
дината графика функции у = Jx отличается от ординаты у0 = 10
меньше чем на е = 10 п (п > 0)? Определить размеры этой окрест¬
ности при п = 0, 1, 2, 3.
666.	С помощью «е - 5» -рассуждений доказать, что функция
f(x) = х2 непрерывна при х = 5.
Заполнить следующую таблицу:
£
1
0,1
0,01
0,001
...
6
667.	Пусть f(x) = i и е = 0,001. Для значений х0 = 0,1; 0,01;
0,001; ... найти максимально большие положительные числа
8 = 5(е, х0) такие, чтобы из неравенства \х - дс0| < 5 вытекало бы
неравенство \f(x) - f(xQ)\ < е.
Можно ли для данного £ = 0,001 выбрать такое 8 > 0, которое
годилось бы для всех значений х0 из интервала (0, 1), т. е. такое,
что если |д: - д:0| < 8, то |/(jc) - f(x0)\ < е, каково бы ни было значение
*о € (0, 1)?
668.	Сформулировать на языке «£ - 8» в положительном
смысле следующее утверждение: функция /(х)9 определенная в
точке х0, не является непрерывной в этой точке.
669.	Пусть для некоторых чисел £ > 0 можно найти соответ¬
ствующие числа 8 = 8(е, лг0) > 0 такие, что \f(x) - f(x0)\ < £, если
только \х - л:0| < 8.

68
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
Можно ли утверждать, что функция fix) непрерывна в точке
xQ, если:
а)	числа £ образуют конечное множество;
б)	числа е образуют бесконечное множество двоичных
дробей е = ^ (га = 1,2, ...)•
670.	Пусть дана функция
fix) = х + 0,001[д;].
Показать, что для каждого е > 0,001 можно подобрать
5 = 5(е, jc) > 0 такое, что |fix') - f(x)\ < в, если только \х' - х\ < 5,
а при 0 < £ < 0,001 для всех значений х этого сделать нельзя.
В каких точках нарушается непрерывность этой функции?
671.	Пусть для каждого достаточно малого числа 5 > 0 су¬
ществует £ = £(8, х0) > 0 такое, что если \х - jc0| < 5, то выполнено
неравенство \f(x) - /(jc0)| < £. Следует ли отсюда, что функция fix)
непрерывна при х = х0? Какое свойство функции f(x) описыва¬
ется данными неравенствами?
672.	Пусть для каждого числа £ > 0 существует число
8 = 8(е, х0) > 0 такое, что если\f(x) - f(x0)| < £, то \х - х0\ < 8. Следует
ли отсюда, что функция f(x) непрерывна при значении х = х0?
Какое свойство функции описывается этими неравенствами?
673.	Пусть для каждого числа 8 > 0 существует число
£ = £(8, х0) > 0 такое, что если \f(x) - f(x0)\ < £, то \х - х0\ < 8.
Следует ли отсюда, что функция f(x) непрерывна при х = х0?
Какое свойство функции f(x) описывается данными неравенствами?
Рассмотреть пример:
arctg ху если х рационально,
л - arctg Ху если х иррационально.
674.	С помощью «£ - 8»-рассуждений доказать непрерыв¬
ность следующих функций:
а)	ах + b;	б) х2;	в) х3;
г)	Jx ;	д) ifx ;	е) sin х;
ж) cos х;	з) arctg х.
Исследовать на непрерывность и изобразить графически сле¬
дующие функции:
675.	f(x) = \х\.
676. fix) =
у2	А
	, если х^ 2;
х- 2
А, если х = 2.

§ 7. Непрерывность функции
69
677.	f(x) = —-—-, если х ^ -1 и /(—1) — произвольно.
(1 + х)2
678.	a) Д(х) = НМ , если х ^ 0 и /х(0) = 1;
б)	/2(*) =	, если х * 0 и /2(0) = 1.
679.	f(x) = sin i , если д: ^ 0 и /(0) — произвольно.
680.	/(х) = х sin i , если х ^ 0 и /(0) = 0.
681.	/(х) = е *2, если д: ^ 0 и /(0) = 0.
682.	f(x) = —р , если д:^ 1 и /(1) — произвольно.
1 + е~1
683.	f(x) = х In х2, если д: ^ 0 и /(0) = а.
684.	/(х) = sgn х.
685.	/(х) = [х].
686.	/(х) = Jx -[Jx].
Определить точки разрыва функций и исследовать характер
этих точек, если:
687. у =
689. у =
(1 + х)2‘
х2- 1
х3 - Зх + 2
688. у =
1 + х
1 + х3'
1 1
690.j/=^4
X - 1 х
691. у=-±-
smx
693. у = cos2 -
х
- cosпх
2
695. у =
cos-
	X
cos -
х
697. у = Jx arctg - .
699. у = -i-
lnx
692. i/= /Ц-^
V 4-х
694. I/ = sgn ^sin
696. у = arctg i .
x
ДС + 1
698. 1/ = e x .
700. у = —i— .
1 - el~J

70
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
Исследовать на непрерывность и нарисовать эскизы графи¬
ков следующих функций:
701. у = sgn (sin х).
703. у = х[х].
705. у = х2- [х2].
т7-»- 4;]-
709'» - И «"
711. у = sec2 - .
702. у = х - [дс].
704. у = [дс] sin пх.
70в-*'-[;]•
708. у = sgn ^ cos	.
710. у = ctg ^ .
712. у = (-1)1*4
713.у“ arctg (i + ^ 1-^).
714. у -
x*sm*x
715. у =
716. у = In
(х+1)(х-3)
sin(x2)
_i
717. у = е *.
718. у = 1 - е .
719. у = th
2л:
1 - JC2
Исследовать на непрерывность и построить графики следую¬
щих функций:
720.у= lim
л- оо 1 + Х'1
722. у = lim Vl + х2'1.
П — оо
724.i/= lim
(л: > 0).
я* - Л'
л — оо l + (2sinx)2n
* + xzen
721.i/= lim
/I — ОО пх + п х
723. у = lim cos2'1 х.
л — ОО
725. у = lim [х arctg (л ctg х)].
Л — ОО
727. у = lim М1±£!У .
*	«-+00 1п(1 + е1)
726. у - lim
я - оо 1 + епх
728.	у = lim (1 + дс) th tx.
t — +оо
729.	Определить, является ли непрерывной функция:
730.	Пусть
Дд.) _ |2х, если 0 < х < 1,
’2-х, если 1 < х < 2.
_ jex, еслих<0,
f\x) ~ 1 а + х, если х > 0.
При каком выборе числа а функция /(х) будет непрерывной?

§ 7. Непрерывность функции
71
731.	Исследовать следующие функции на непрерывность и
выяснить характер точек разрыва, если:
\х2 при 0 < х < 1,
а) fix) = 12 - ж при 1 < х < 2;
б) т = |
х при |jc| < 1,
1 при \х\ > 1;
\ _£/ \ I COS^ при|х| < 1,
В) f(x) = <	2
\\х - 1| при |jc| > 1;
г) fix) =
Д) fix) = |q
ctg2 nx для нецелого x,
для целого х;
sin пх для рационального х9
для иррационального х.
732.	Функция d = d(x) представляет собой кратчайшее рас¬
стояние точки х числовой оси Ох от множества точек ее, состоя¬
щего из отрезков 0<jc<1h2<jc<3. Найти аналитическое
выражение функции d, построить ее график и исследовать на
непрерывность.
733.	Фигура Е состоит из равнобедрен¬
ного треугольника с основанием 1 и высо¬
той 1 и двух прямоугольников с основа¬
ниями 1 каждый и высотами, равными 2
и 3 (рис. 5). Функция S = S(y) (0 < у < +оо)
представляет собой площадь части фи¬
гуры Еу заключенной между паралле¬
лями У = 0 и У = у, а функция b = Ь(у)
(О < у < +оо) есть длина сечения фигуры Е
параллелью У = у.
Найти аналитические выражения функций S и Ь9 постро
ить их графики и исследовать на непрерывность.
734.	Доказать, что функция Дирихле
%(х) = lim | lim cos'1 (nmlx)
m —oo n —oo
разрывна при каждом значении х.
735. Исследовать на непрерывность функцию
fix) = хх(х)9
где хМ — функция Дирихле (см. предыдущую задачу). Постро¬
ить эскиз графика этой функции.

72
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
736. Доказать, что функция Римана
„ ч - , если х = — где /пип взаимно простые числа;
f(x) = < п	п
[ 0, если х иррационально,
разрывна при каждом рациональном значении х и непрерывна
при каждом иррациональном значении х. Построить эскиз гра¬
фика этой функции.
737.	Исследовать на непрерывность функцию f(x), заданную
следующим образом:
/(*>=
пх
П + 1 *
если х есть несократимая рациональная дробь — (п > 1), и
п
fix) = \х\,
если х — иррациональное число. Построить эскиз графика этой
функции.
738.	Функция f(x) =	определена для всех значений
х2
аргумента х, кроме х = 0. Какое значение следует приписать
функции fix) в точке х = 0, чтобы эта функция была непрерыв¬
ной при х = 0?
739.	Показать, что при любом выборе числа /(1) функция
fix) = будет разрывна при х = 1.
740.	Функция fix) теряет смысл при х = 0. Определить число
/(0) так, чтобы fix) была непрерывна при х = 0, если:
a) f(x) =	;	б) fix) =	;
\f\Tx-\	х
1	I
в)	fix) = sin x sin - ;	г) fix) = (l + x)x;
__i_
Д) fix) = — e *2;	e) fix) = xx (x> 0);
X*
ж) f(x) = X In2 X.
741.	Обязательно ли будет разрывна в данной точке х0 сумма
двух функций fix) + gix), если:
а)	функция fix) непрерывна, а функция gix) разрывна
при х = #0;
б)	обе функции fix) и g(ar) разрывны при х = х0? Постро¬
ить соответствующие примеры.

§ 7. Непрерывность функции
73
742.	Обязательно ли произведение двух функций
f(.x)g(x)
терпит разрыв непрерывности в данной точке х0, если:
а)	функция f(x) непрерывна, а функция g(x) разрывна в
этой точке;
б)	обе функции f(x) и g(x) разрывны при х = х01
Построить соответствующие примеры.
743.	Можно ли утверждать, что квадрат разрывной функции
есть также разрывная функция?
Построить пример всюду разрывной функции, квадрат кото¬
рой есть функция непрерывная.
744.	Исследовать на непрерывность функции f[g(x)] и £[/(#)],
а)	f(x) = sgn х и g(x) =14- jc2;
б)	f(x) = sgn x и g(x) = х(1 - x2);
в)	f(x) = sgn x и g(x) = 1 4- x - [х].
745.	Исследовать на непрерывность сложную функцию
У “ /(и)> где и = ф(*), если:
(О < * < 1).
746.	Доказать, что если f(x) — непрерывная функция, то
есть также непрерывная функция.
747.	Доказать, что если функция f(x) непрерывна, то функция
где с — любое положительное число, также непрерывна.
748.	Доказать, что если функция f(x) непрерывна на сегменте
[а, 6], то функции
если:
х при х рациональном;
2	- х при х иррациональном
F(x) = |/(*)|
также непрерывны на [а, Ь].

74
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
749.	Доказать, что если функция f(x) и g(х) непрерывны, то
функции
ф(*) = min [/(х), g(x)] и ф(х) = max [f(x), g(x)]
также непрерывны.
750.	Пусть функция f(x) определена и ограничена на сегменте
[а, Ь]. Доказать, что функции
т(х) = inf {/(^)} и М(х) = sup {/(£)}
непрерывны слева на сегменте [а, Ь].
751.	Доказать, что если функция f(x) непрерывна в проме¬
жутке а < х < +оо и существует конечный lim f(x), то эта функ-
х — +оо
ция ограничена в данном промежутке.
752.	Пусть функция f(x) непрерывна и ограничена в интер¬
вале (а:0, +оо). Доказать, что, каково бы ни было число Т, най¬
дется последовательность хп —► +°о такая, что
lim [f(xn + Т)- /(*„)] = 0.
п-* оо
753.	Пусть ср(лг) и Щх) — непрерывные периодические функ¬
ции, определенные при -оо < х < +оо и
lim [<p(jt) - v|/(jc)] = 0.
х —* 4-00
Доказать, что
ср(*) = \|!(Х).
754.	Доказать, что все точки разрыва ограниченной монотон¬
ной функции являются точками разрыва 1-го рода.
755.	Доказать, что если функция f(x) обладает следующими
свойствами:
1)	определена и монотонна на сегменте [а; Ь];
2)	в качестве своих значений принимает все числа между
f(a) и /(b),
то эта функция непрерывна на [а, Ь].
756. Показать, что функция f(x) = sin	, если х * а и /(а) = О,
принимает на любом сегменте [а, Ь] все промежуточные значения
между /(а) и /(b), однако не является непрерывной на [а, Ь].
757.	Доказать, что если функция f(x) непрерывна на интер¬
вале (а, Ь) и хи х2у хп — любые значения из этого интервала,
то между ними найдется число £ такое, что
№ = i [/(*,) + fix2) + ... + /(*„)].
п

§ 8. Обратная функция. Функции, заданные параметрически
75
758.	Пусть f(x) непрерывна в интервале (а, Ь) и
I = lim f(x) и L = lim f(x).
х —'• а	х а
Доказать, что, каково бы ни было число А, где I < Л < L, су¬
ществует последовательность л:/,->а(/г=1,2, ...) такая, что
lim f(xn) = Л.
П — СО
§ 8. Обратная функция.
Функции, заданные параметрически
1.	Существование и непрерывность обратной функции. Если функ¬
ция у = f(x) обладает следующими свойствами: 1) определена и непре¬
рывна на интервале (а, Ъ); 2) монотонна в строгом смысле на этом ин¬
тервале, то существует однозначная обратная функция х = f"1(y)9 опре¬
деленная, непрерывная и соответственно монотонная в строгом смысле
на интервале (А, Б), где А = lim f(x) и В = lim f(x).
х — а+0	дг — 6-0
Под однозначной непрерывной ветвью многозначной обратной
функции данной непрерывной функции у = f(x) понимается любая од¬
нозначная непрерывная функция х = g(y), определенная в максималь¬
ной области ее существования и удовлетворяющая в этой области урав¬
нению f[g(y)] = у.
2.	Непрерывность функции, заданной параметрически. Если функ¬
ции ф(0 и \|/(0 определены и непрерывны в интервале (а, (3) и функция
ф(0 строго монотонна на этом интервале, то система уравнений
* = ф(0> У = V(0
определяет у как однозначную непрерывную функцию от х:
у = чЧф'Ч*)),
на интервале (а, Ь), где а = lim <p(t) и b= lim ф(0-
t — а +0	< — р - 0
759.	Найти обратную функцию дробно-линейной функции
= ax_+_b _bc7t о).
сх + d
В каком случае обратная функция совпадает с данной?
760.	Найти обратную функцию х = х(у), если
У = * + [*].
761.	Показать, что существует единственная непрерывная
функция у = у(х) (-оо < х < +оо), удовлетворяющая уравнению
Кеплера
у - е sin у — х (0 < е < 1).

76
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
762.	Показать, что уравнение
ctg х = kx
для каждого вещественного k (-00 < k < +00) имеет в интервале
О < х < я единственный непрерывный корень х = x(k).
763.	Может ли немонотонная функция у = f(x) (-00 < х < +оо)
иметь однозначную обратную функцию? Рассмотреть пример:
\ху если х рационально;
у 1-х, если х иррационально.
764.	В каком случае функция у = f(x) и обратная функция
х = f~l(y) представляют одну и ту же функцию?
765.	Показать, что обратная функция разрывной функции
у = (1 4* х2) sgn х
есть функция непрерывная.
766.	Доказать, что если функция f(x) определена и строго мо¬
нотонна на сегменте [а, Ь] и
lim /(*„) = /(а) (а < хп < Ь),
П-* оо
ТО
lim хп = а.
п — оо
Определить однозначные непрерывные ветви обратных
функций для следующих функций:
767.	у = х2.	768. у=	2х- х2.
769‘ У = ТТх* •	770- у =	sin
771. у = cos *.	772. у =	tg х.
773.	Показать, что множество значений непрерывной функции
у = 1 + sin #, соответствующих интервалу (0 <х < 2 я), есть сегмент.
774.	Доказать равенство
arcsin л: + arccos л: =
п
775.	Доказать равенство
1	71
arctg х + arctg - = - sgn х (х * 0).
ОС Z
776.	Доказать теорему сложения арктангенсов:
X -{- I/
arctg х + arctg у = arctg	+ ея,
где е = г(х, у) — функция, принимающая одно из трех значений:
0, 1,-1.

§ 8. Обратная функция. Функции* заданные параметрически
77
Для каких значений у при данном значении х возможен раз¬
рыв функции е? Построить на плоскости Оху соответствующие
области непрерывности функции е и определить значение этой
функции в полученных областях.
777.	Доказать теорему сложения арксинусов:
arcsin х + arcsin у = (-1)е arcsin [xj\ - у2 + yjl - х2 j + еп
(W < 1, Ы < l), где
и
Е = 0, если ху К 0 или х2 + у2 < 1,
Е = sgn ху если ху> 0 и х2 + у2 > 1.
778.	Доказать теорему сложения арккосинусов:
arccos х + arccos у = (-1)е arccos [ху - J1 - x2Jl - у2 j + 2пе
(W < 1* \у\< 1)» где
£ = О,
И
£ “ 1>
если х + у > О,
если х + у < 0.
779.	Построить графики функций:
а)	у = arcsin х + arcsin J1 - х2 ;
б)	у = arcsin(2jcVl - х2) - 2 arcsin х.
780.	Найти функцию у = у(х), заданную уравнениями:
х = arctg ty у = arctg t (-°° < t < +оо).
В какой области определена эта функция?
781.	Пусть
х = ch ty у = sh t (-оо < t < +oo).
В каких областях изменения параметра t переменную у мож¬
но рассматривать как однозначную функцию от переменной х!
Найти выражения у для различных областей.
782.	Каковы необходимые и достаточные условия того, чтобы
система уравнений
* = <р(0, у = v(0 (а < t < Р)
определяла бы у как однозначную функцию от х?
Рассмотреть пример: х = sin2 £, у = cos2 t.
783.	При каких условиях две системы уравнений
х = ср(0» «/ = W) (a <t < Ь)
и
Ж = ф(Х(т))> У = ф(х(*)) (а < т < Р)
определяют одну и ту же функцию у = у(х)1

78
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
784.	Пусть функции ф(лг) и \|/(x) определены и непрерывны на
интервале (а, Ъ) и
А = inf ф(л:), В = sup ф(л:).
а<х<Ь	а<х <Ь
В каком случае существует однозначная функция f(x), опреде¬
ленная в интервале (А, В) и такая, что
\|/(jc) = f(<p(x)) при а < х < Ы
§ 9. Равномерная непрерывность функции
1.	Определение равномерной непрерывности. Функция /(х) называ¬
ется равномерно непрерывной на данном множестве (интервале, сегменте
ит. п.)Х = М, если f(x) определена на X и для каждого е > 0 существует
8 = 8(e) > 0 такое, что для любых значений х\ х" 6 X из неравенства
\х' - х"\ < 8
следует неравенство
I fix9) - f(x")\ < е.
2.	Теорема Кантора. Функция f(x), определенная и непрерывная на
ограниченном сегменте [а, Ь\, равномерно непрерывна на этом сегменте.
785.	Цех завода вырабатывает квадратные пластинки, стороны
которых х могут принимать значения в пределах от 1 до 10 см.
С каким допуском 8 можно обрабатывать стороны этих пласти¬
нок, чтобы независимо от их длины (в указанных границах) пло¬
щадь их у отличалась от проектной меньше, чем на е? Выполнить
численный расчет, если:
а)	е = 1 см2; б) е = 0,01 см2; в) е = 0,0001 см2.
786.	Цилиндрическая муфта, ширина которой е и длина 8,
надета на кривую у = V* и скользит по ней так, что ось муфты
остается параллельной оси Ох. Чему должна быть равна длина 8,
чтобы эта муфта свободно прошла участок кривой, определяе¬
мый неравенством -10< х < 10, если:
а)е = 1; б)е = 0,1; в) е = 0,001; г) е произвольно мало?
787.	В положительном смысле сформулировать на языке
«£-8» утверждение: функция f(x) непрерывна на некотором
множестве (интервале, сегменте и т. п.), но не является равно¬
мерно непрерывной на этом множестве.
788.	Показать, что функция
№ = -
X
непрерывна в интервале (0, 1), но не является равномерно непре¬
рывной в этом интервале.

§ 9. Равномерная непрерывность функции
79
789.	Показать, что функция
/(х) = sin -
х
непрерывна и ограничена в интервале (0, 1), но не является рав¬
номерно непрерывной в этом интервале.
790.	Показать, что функция
f(x) = sin х2
непрерывна и ограничена в бесконечном интервале -оо < х < +оо,
но не является равномерно непрерывной в этом интервале.
791.	Доказать, что если функция f(x) определена и
непрерывна в области а < х < +оо и существует конечный
lim f(x),
х —» +оо
то f(x) равномерно непрерывна в этой области.
792.	Показать, что неограниченная функция
f(x) = х + sin х
равномерно непрерывна на всей оси -оо < х < +оо.
793.	Является ли равномерно непрерывной функция f(x) = х2
на интервале
а)	(-Z; Z), где I — любое, сколько угодно большое поло¬
жительное число;
б)	на интервале (-оо, +оо)?
Исследовать на равномерную непрерывность в заданных об¬
ластях следующие функции:
х
794.	f(x) =
*± — Л'
795.	f(x) = In х
796.	f(x) =
sin*
797.	fix) = ex cos -
X
798.	fix) — arctg x
799.	fix) = Jx
800.	/(*) = * sin *
(-1 < x < 1).
(0 < x < 1).
(0 < x < я).
(0 < x < 1).
(-OO < X < +oo).
(1 < X < +°o).
(0 < x < 4-oo).
801.1.	Показать, что функция fix) = l2HHl равномерно непре-
X
рывна на каждом интервале
Jx = (-1 < х < 0) и J2 = (0 < х < 1)

80
РАЗДЕЛ I. ВВЕДЕНИЕ В АНАЛИЗ
по отдельности, но не является равномерно непрерывной на их
сумме
J1+J2 = {0< \х\ < 1}.
2.	Доказать, что если функция f(x) равномерно непрерывна
на каждом из сегментов [а, с] и [с, &], то эта функция является
равномерно непрерывной на суммарном сегменте [а, 6].
802.	Для е > 0 найти 8 = 8(e) (какое-нибудь!), удовлетворяю¬
щее условиям равномерной непрерывности для функции f(x) на
данном промежутке, если:
а)	f(x) = Ъх - 3	(-оо	< х < +°о);
б)	f(x) = х2 - 2х -	1	(-2 < х < 5);
B)/(*)=i	(0,1<х<1);
г) f(x) = Jx	(0 < X +00);
д)	f(x) = 2 sin X -	COS X (-OO	< x < +00);
е)	f(x) = jc sin i	(x &	0) и /(0) = 0 (0 < jc < тс).
803.	На сколько равных между собой отрезков достаточно
разбить сегмент [1, 10], чтобы колебание функции f(x) = х2 на
каждом из этих отрезков было меньше 0,0001?
804.	Доказать, что сумма и произведение ограниченного чис¬
ла равномерно непрерывных на интервале (а, Ь) функций равно¬
мерно непрерывны на этом интервале.
805.	Доказать, что если ограниченная монотонная функция
f(x) непрерывна на конечном или бесконечном интервале (а, 6),
то эта функция равномерно непрерывна на интервале (а, 6).
806.1.	Доказать, что если функция f(x) равномерно непре¬
рывна на конечном интервале (а, 6), то существуют пределы
А = lim f(x) и В = lim f(x).
х — а + 0	х — 6-0
Верна ли эта теорема для бесконечного интервала (а, Ъ)?
2.	Доказать, что для того, чтобы функцию f(x)9 определенную
и непрерывную на конечном интервале (а, Ь), можно было про¬
должить непрерывным образом на сегмент [а, 5], необходимо и
достаточно, чтобы функция f(x) была равномерно непрерывна на
интервале (а, 6).
807.	Модулем непрерывности функции f(x) на промежутке
(а, Ь) называется функция
(0Д5) = sup \f(x,) - f(x2)I,
где xx и x2 — любые точки из (а, 6), связанные условием \хх - х2\ < 8.

§10. Функциональные уравнения
81
Доказать, что для равномерной непрерывности функции fix)
на промежутке (а, Ъ) необходимо и достаточно, чтобы
lim о)/(5) = 0.
5-0	'
808.	Получить оценку модуля непрерывности соД8) (см. пре¬
дыдущую задачу) вида
0,(8) < С8а,
где С и а — константы, если:
а)	f{x) = х3	(0<*< 1);
б)	fix) = Jx	(О <л;<а)и(а<л:< 4*оо);
в)	f(x) = sin х + cos х (0 < х < 2л).
§ 10. Функциональные уравнения
809.	Доказать, что единственная непрерывная функция fix)
(-00 < х < +оо), удовлетворяющая для всех вещественных значе¬
ний х и у уравнению
f(x + y)=f(x) + m,	а)
есть линейная однородная функция
fix) = ах,
где а = /(1) — произвольная константа.
810.	Доказать, что монотонная функция fix), удовлетворяю¬
щая уравнению (1), есть линейная однородная.
811.	Доказать, что функция fix), удовлетворяющая уравне¬
нию (1) и ограниченная в сколь угодно малом интервале (-£, е),
есть линейная однородная.
812.	Доказать, что единственная не равная нулю тождествен¬
но непрерывная функция fix) (-00 < х < 4*оо), удовлетворяющая
для всех значений х и у уравнению
fix + у) = fix)fiy),	(2)
есть показательная функция
fix) = ах,
где а = /(1) — положительная постоянная.
813.	Доказать, что не равная нулю тождественно функция
fix), ограниченная в интервале (0, е) и удовлетворяющая урав¬
нению (2), есть показательная.
814.	Доказать, что единственная не равная нулю тождествен¬
но непрерывная функция fix) (0 < х < 4*оо), удовлетворяющая
для всех положительных значений х и у уравнению
f(xy) = fix) + fiy),

82
РАЗДЕЛ 1. ВВЕДЕНИЕ В АНАЛИЗ
есть логарифмическая функция
f(x) = loga X,
где а — положительная константа.
815.	Доказать, что единственная не равная нулю тождествен¬
но непрерывная функция /(*) (0 < х < +°°), удовлетворяющая
для всех положительных значений х и у уравнению
fixy) = f(x)f(y),	(3)
есть степенная функция
fix) = *a,
где а — постоянная.
816.	Найти все непрерывные функции f(x) (-00 < х < +°°),
удовлетворяющие для всех вещественных значений х и у
уравнению (3).
817.	Показать, что разрывная функция
f(x) = sgn х
удовлетворяет уравнению (3).
818.	Найти все непрерывные функции fix) (-оо < х < +оо), удов¬
летворяющие для всех вещественных значений х и у уравнению
f(x + у) + fix - у) = 2f(x)fiy).
819.	Найти все непрерывные ограниченные функции fix) и
giх) (-оо < х < +°°), удовлетворяющие для всех вещественных
значений х vl у системе уравнений:
fix + у) = fix)fiy) - gix)giy),
six + у) = f(x)giy) + fiy)gix),
и, сверх того, условиям нормировки:
/(0) = 1 и gi 0) = 0.
и
Указание. Рассмотреть функцию
820. Пусть
Fix) = fix) + g*i х).
A fix) = fix + Ax) - fix)
A2 fix) = Д{Д/(*)}
суть конечные разности функции fix) соответственно первого и
второго порядков.
Доказать, что если функция fix) (-оо < х < +оо) непрерывная
и Л2fix) = 0, то эта функция линейная, т. е. fix) = ах + Ь, где а и
b — постоянные.

РАЗДЕЛ II
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
§ 1. Производная явной функции
1. Определение производной. Если х и xt = х + Ах — значения не¬
зависимой переменной, то разность
А у = f(x + Д*) - f(x)
называется приращением функции у = f(x) на сегменте [х, л-J.
Выражение
у'-Пх)- lim %L,	(1)
Ах — о Ал:
если оно имеет смысл, носит название производной, а сама функция
f(x) в этом случае называется дифференцируемой.
Геометрически число f'(x) представляет собой угловой коэффициент ка¬
сательной к графику функции у = f(x) в точке его х (tg а = f'(x)) (рис. 6).
2. Основные правила нахождения производной. Если с — постоянная
величина и функции и = и(х), v = v(x), w = w(x) имеют производные, то
1)	с' = 0;
2)	(си)' = си';
3)	(и + v - ш)' = и' + v' - w';
4)	(uv)' = u'v + uv';
5)	f-T = u'v~ uv: (v*0);
\vj	v2
6)	(un)' = nun~ lu' (n — постоянное число);
7)	если функции у = f(u) и и = (р(лг) имеют производные, то
Ух = УиН'х-

84
РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
3. Основные формулы. Если х — независимая переменная, то
1
I. (хп)' = пхп '1 (п — постоянное число). IX. (arcctg х)'=
П. (sin х)' = cos х.
III. (cos х)' = -sin х.
1 + x2'
X.	(ax)' = ax\na(a>0); (ехУ = 6х.
XI.	(logaxy
(a>0);(lnx)'=i.
jclna	x
IV. (tg*)' =
COS2X
1
V. (ctg *)' = --
VI. (arcsin x)' =
sin2x
1
VII.	(arccos x)' = -
VIII.	(arctg x)' =
J1- x
1
XII. (sh x)' = ch x.
XIII. (ch x)f = sh x.
1
c\i2X *
1
л/Г^Х2
1
XIV. (th x)' =
XV. (cth x)' = -
sh2x '
1 + x2
4.	Односторонние производные. Выражениями
f, Um flx + Afl-Ji*1,
Ajc - -о	Ддс
r+w= hm fL*-±-4£lrJL*i
Дх —* +o	Ajc
определяются соответственно левая и правая производные функции /(дс)
в точке х.
Для существования производной f'(x) необходимо и достаточно, чтобы
Г-(х)=П(х).
5.	Бесконечная производная. Е!сли функция f(x) непрерывна в точке х и
lim f{x + &x)-f{x) =00t
дх - о	Ах
то говорят, что в точке х функция f(x) имеет бесконечную производную.
В этом случае касательная к графику функции у = f(x) в точке х пер¬
пендикулярна к оси Ох.
821.	Определить приращение Ах аргумента х и соответствующее
приращение Ау функции y = lgx> если х изменяется от 1 до 1000.
822.	Определить приращение Ах аргумента х и соответствующее
приращение А у функции у = \ , если х изменяется от 0,01 до 0,001.
х2
823.	Переменная х получает приращение Дх. Определить
приращение А у, если:
а) у = ах + Ь; б) у = ах2 + Ьх + с; в) у = ах.

§ 1. Производная явной функции
85
824.	Доказать, что
а)	A[f(x) + g(x)] = Дf(x) + Дg(x);
б)	Д[f(x)g(x)] = g(x + Ax)Af(x) + f(x)Ag(x).
825. Через точки А( 2, 4) и А'(2 + Ах, 4 + А у) кривой у = х2
проведена секущая АА'. Найти угловой коэффициент этой секу¬
щей, если:
а)Дх=1;	б)Дх = 0,1;	в)Дх=0,01;
г)	Ах произвольно мало.
Чему равен угловой коэффициент касательной к данной кри¬
вой в точке А?
826.	Отрезок 1 < х < 1 + h оси Ох с помощью функции у = х3
отображается на ось Оу. Определить средний коэффициент рас¬
тяжения и произвести численный расчет, если:
a)	h = 0,1;	б) h =0,01;	в) h = 0,001.
Чему равен коэффициент растяжения при этом отображении
в точке х — 1?
827.	Закон движения точки по оси Ох дается формулой
101 + 5t2,
где t — время в секундах их — расстояние в метрах. Найти сред¬
нюю скорость движения за промежуток времени 20<£<20 + Д£
и выполнить численный расчет, если:
a)	At;	б) Д£ = 0,1;	в)Д* = 0,01.
Чему равна скорость движения в момент времени t = 20?
828.	Исходя из определения производной, непосредственно
найти производные следующих функций:
а)	х2;	б) х3;	в) - ;	г) Jx ;
х
д) \[х ;	е) tg х;	ж) ctg х; з) arcsin х;
и)	arccos х; к) arctg х.
829.	Найти /'(1), f'(2) и /'(3), если
f(x) =(х-1)(х- 2)2(х - З)3.
830.	Найти f'(2), если
f(x) = х2 sin(^: - 2).
831.	Найти /'(1), если
f(x) = х + (х - 1) arcsin
р-
4х +1

86
РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
832.	Найти Иш	, если функция f(x) дифференциру-
jc —* а	х - а
ема в точке а.
833.	Доказать, что если функция f(x) дифференцируема и
п — натуральное число, то
Шп п|у(* + ^ - /(ж)] = Г(х).	(1)
Обратно, если для функции f(x) существует предел (1), то
можно ли утверждать, что эта функция имеет производную? Рас¬
смотреть пример функции Дирихле (см. задачу 734).
Пользуясь таблицей производных, найти производные сле¬
дующих функций:
834.	у = 2 + х- х2. Чему равно у'( 0); y'^|j ; у'( 1); у'(-Ю)?
835. у =
3
- 2х. При каких значениях х:
а )у'(х)= 0;	б)у'(х) = - 2;
836. у = а5 4- 5а3х2 - хъ.
в) у\х) = 10?
837. у =
&	Л I U
838. у = (* - а)(х - Ь). у'(|) .
839. у = (х + 1)(х + 2)2(х + З)3.
840.	у = (х sin а + cos а)(х cos а - sin а).
841.	у = (1 + пхт)( 1 + тхп).
842.	а) у = (1 - х)(1 - х2)2(1 - х3)3; б) у = (5 + 2х)10(3 - 4х)20.
843.	у = ± + А + А .
хх2- X3
844.	Доказать формулу
(
ах + ЬУ
сх + d)
а b
с d
(сх + d)2 ’
Найти производные функций:
2х
845. у =
847. у
1-х2
(1-х)2(1 + х)3
849. у = (1~х)р .
*	(1 + х)ч
851.	у = х 4- Jx 4- 2/* •
846. у
\ + X - X2
1 — X + X2
848. у = (?-«2)(3-**).
(1-х)2
850. у = A’Li-.a:)17.
у 1 + х
852.	у = I + А. + J- .
* Л *Ji

§ 1. Производная явной функции
87
853. у = З/*2 - -р •	854. у
V*
855.	у = (1 + *)л/2 + *2 УЗ + х3 .	856. (/:
856.	у = n+ni/(l-*)m(l + *)" .	857. у ■
■iHl-	859.,
л/х + Jx~+ Jx .	861. г/
cos 2х - 2 sin х.	863. г/=
sin(cos2 х) • cos(sin2 х).	865.1/
sin[sin(sin х)].	867. у
= Хл/Т + Х2 .
= m + V(l-JC)m(l+^)n.
X
Ja2 - х2
858. у = з
860. у -
862.1/
864. у
866. у
COS*
2sin2* '
sin* - *cos*
cos*+ *sin*"
tg * - | tg3 * + | tg5 *.
6 0
437ctg2* + Vctg8*.
sin[cos2(tg3 *)].
2-;.
868. у
870.1/
872.	y
873.	у
875. у
877. у
879.	у
880.	у = ex[l + ctg
882. у
884.	у -
885.	i/:
887.1/
869. i/1
871. у
874.1/
876. у
878. у
-[■
=
1-х2
sin X
_ (1 + х)2
COS X б
asinfrx- bcosbx
Ja2 + b2
]
881. у
883.1/
ьм1Ка
4- a*" + a0* (a > 0). 886. у
ln(ln(ln *)).	888. у
41 + *2(* + л/ГТ*2)
= lll+ljl+l/x.
: (2 - x2) cos x+2x sin x.
= sin" x cos nx.
sin2x
sinx2 *
= 1
cosnx ’
= tg|-Ctg|.
= sec2 - + cosec2 - .
a	a
— л-Х2
= e* (*2 - 2* + 2).
__ ln3 • sinx + cosx
3*
= ex + eeX + eeeX.
= lg3 X2.
= ln(ln2(ln3 *)).

88
РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
889.	у
890.	у
891.	у
892.	у
893.	у
894.	у
895.	у
896.	у
897.	у
898.	у
899.	у
900.	у
901.	у
903. у
905.	у
906.	у
907.	у
908.	у
909.	у
910.1/
I	ln(l + *)-i lnd + xV^L-.
1	1г| *2~ 1
4 1 хг + 1 '
1	_|_ 1 in *4
4(1 + х4) 4	1 + х4 ’
1 ln *73-
2л/б *7з + Т2*
i jn i + * _j_ Tfe jn i + *7fe
1-fe	l-x l-k	l-xjk
Jx+1 - ln(l 4- Jx + 1 ).
(0 < k < 1).
ln(* + Jx2 + 1).
x ln(* 4- 7l + x2 ) - 7l + X2 .
* ln2^* 4- TTT^2 j - 2jl+x2 ln(* 4* JTTx2 4- 2x.
Z Jx2 + a2 4- у ln I* 4- Jx^Ta2 j .
■ -4= In + (a > 0, b > 0).
2jab Ja-xJb
Jl-x2 + 3 ln l.t-'H-*2.
X4	X
In tgf.	902.j/ = lntg(j + |).
- ctg2 x + ln sin x.	904. у = ln /■ ~ sin*
2	6	* VI + sin*
cos*
2 sin2*
+ In
f-
+ cos*
sin*
In b + acosx+ jb2-a2smx ^ ^ у <
a + bcos*
-	(In3* + 3 In2 x + 6 ln x + 6).
*
—	In i -	1
4*4	*	16*4 *
! (1 - Vl + *2 )2 + 3 ln(l + Ifl + X2 ) .
1п[1чЧп(1+1"1)].

§ 1. Производная явной функции
89
911.	у = *[sin(ln х) - cos(ln х)].
912.	у = In tg | - cos x • In tg x. 913. у = arcisn |.
z	z
914. г/ = arccos
72
915. у = arctg — .
916. у
918.	у
919.	у
920.	у =
922. у ■
924. у ■
926.	у
927.	у ■
928.	у
930. у
4 arcctg —.
72	*
917. у = Jx - arctg Jx .
Л
л: + Jl - х2 • arccos х.
in /—+ arctg Jx - Jx.
\1 + я
921. z/ = arcsin(sin jc).
= л: arcsin
arccos -.
x
arccos(cos2 x).
-- arccos J1 - x2 .
= arcctg fsin£±cos^ ^
vsinx - cos л:/
923. у = arcsin(sin x - cos x).
\ + X
925. у = arctg
1-д:
Va2 - b2
= arcsin
arctg
1 — JC2
1 + X2 ’
1
Г О
V Va + b
tg -
2
929.1/
(a>b> 0).
1
arccos2(jc)2
arctg д; 4* i arctg (д;3).
931.	у = ln(l 4- sin2 д:) - 2 sin x • arctg (sin д;).
932.	у
ln( arccos
'	Jx
ji)
= In
x + a
Jx2 + b2
+ arctg \
933.	у ■
934.	у =
935.	у ■
936.	у
937. у = jc(arcsin х)2 + 2 Jl - дс2 arcsin л: — 2*.
£ 7«2 - х2 + 2f arcsin 2 (а > 0).
2	2	cl
i In i£±nL + 4 arctg 2x~ 1
д:2- дс + 1
7з
хЛ+l _ 1
472 x2-xj2+l 2j2
In
73
arctg
xj2
938. у =
arccosjc + l|n 1 - л/l - jc2
*	2	\ + JT~x2'

90
РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
939. у = arctg Jx2-1 - ~^=.
Jx^l
940 apgM +1 1пЦг.
ЛПГ2 2	1 + х
r\A~t к 		1	Х^	+1	1	1	а/З
941'!'- 15 1п l^TTF " Jyl “** S?n-
942. у = —^— - arcctg *6.
1 + л:12
-1—+ V3 arctg	.
+ 3Jx + 3Jx3
943. у = In 1-</*
7l + 37* + \Jx*
944.	у = arctg	_	.
1	+ TT3*2
945.	у = arcctg -- ~-2—-■ (a > 0).
2	Jax-x2
946. у =	7Г - 2x - jc2 +2 arcsin .
2	J2
947.	у = ± InSfiULt* - I arctg
4 VTTP-ж 2
948.	у = arctg(tg2 jc).
949.	j/ = JT^lc2 • In ЙН* +i in+ arcsin*.
Vl + *	2 i + VT^2
950.	г/ = л: arctg Jt - i ln(l + дс)2 - i (arctg jc)2.
951. у = ln(ex + 7l + e2x).
qkq _ о( sinasin* ^
95o. у — arcsin 		 .
vl - cosacosav
952. у = arctg(* + Jl + x2).
954.	у = -Ц In A2 + 2 *7j + J arctg T*2+ 2
473	7*2 + 2 + xS 2	л:
955.	у = arctg -0= - -i- In У1 + *4~*У2 .
2a/2	УГ+л*4 4л/2 7i + jc4 + jCa/2
956.	у = ^"f2 - A arcctg	.
1 + *2	72	TT1^2
957.	i/ = arccos(sin *2 - cos *2).
958.	i/ = arcsin(sin *2 ) + arccos(cos *2).
959.	у = em arcsln *[cos(/n arcsin *) + sin(/n arcsin x)].

§ 1. Производная явной функции
91
960.	а) у = arctg ех - In / f 2x— ; б) у = J1 + л/Г+1/1 + х4 ;
V е2лг +1
в) у = arcctg
яг
г) у = ln2(sec 2
961.	у = х + Xх + х*г (х> 0).
962.	у = Xх“ + ха* + ах* (а > 0, х > 0).
963.	у = Xjx (лс > 0).
964.	у = (sin *)cos * + (cos *)sin *.
965.	1. у = (In jc)x : jc1u *.	2.i/= rarcsm(sin**)-p2* .
Larccos(cos2*)J
966.	у = logx e.
967.	у = ln(ch x) +	.
969.	у = arctg (th x).
970.	у = arccos .
971.	!,-£*+5^1 arctg (£3 th |)	(0 < |6| < a).
972.	Найти производную функции
у = ln^cos2 х + J1 + cos4* j ,
вводя промежуточное переменное и = cos2 *.
Приемом, указанным в примере 972, найти производные
функций:
973.	у = (arccos х)2 j^ln2(arccos х) - ln(arccos х) +	.
974.	у = i arctg(l/l + *4) + 71п^1 + х4 + 1 .
2	4 i/T7x*-l
975.	= e l2arcsin(e *2) + 1 ln(1 _ *-2*»).
Vl - е-2х2	2
976. у =
ат
1 - а2дг
1 + а2х 1 + а2х
arcctg а х.

92
РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
977.	Найти производные и построить графики функций и их
производных, если:
а)	у = |*|;	б) у = *|*|;	в) у = 1п|*|.
978.	Найти производные следующих функций:
а)	у = |(* - 1)2(* + 1)3|;	б) у = |sin3 *|;
в )у = arccos — ;
г)	у = [х] sin2 пх.
Найти производные и построить графики функций и их про¬
изводных:
1-х	при -оо < х < 1;
979.	у = < (1 - *)(2 - х)	при 1 < х < 2;
-(2 - х)	при 2 < * < +°о.
f (х - а)2(х -	Ь)2	при а < * < Ь;
вне отрезка [а, Ь].
980. у
Их
10
QM 1, = \х	при * < 0;
УвА- у 11п(1 + *) при * > 0.
arctg х
при |*| < 1;
982. у =
5	sgn * +	при |*| > 1.
х‘е-
983.	у=\г
при 1*1 < 1;
при |*| > 1.
984.	Производная от логарифма данной функции у = /(*) на¬
зывается логарифмической производной этой функции:
Найти логарифмическую производную от функции у, если:
а)у = *Д^;	б) у = -^-з/ 3~* ;
у VI+ *	1-*V(3 + *)2
в)	у = (*-<*,)“>(*-а2)"2 ...(*-ал)°»; г) у = (* + Jl + x2 )\
985.	Пусть ф(*) и \|/(*) — дифференцируемые функции от *.
Найти производную от функции у9 если:
а)	у =	;	б) у = arctg ;
в)	у = vixl/y(x) (ф(*) * 0; ф(*) > 0);
г)	у = log*,) \|/(*) (ф(*) > 0; ф(*) > 0).

§ 1. Производная явной функции
93
986.	1. Найти у\ если:
а) у = f(x2);	б) у = /(sin2 х) + /(cos2 *);
в)	у = /(<?*) • еПх);	г) у =/{Я/(*)]Ь
где /(и) — дифференцируемая функция.
2.	Найти /'(О), если
Я*) =	- 1)(х - 2) ... (* - 1000).
987. Доказать следующее правило дифференцирования опре¬
делителя /1-го порядка:
fll(X) fl2(X)
• Л„(*)
t
n
/п(*) fu(x) ••
• fm(x)
fik(x) fki(X) ..
f kn(X)
W2
II
/'»(*) /’*2(*) •
• /'**(*)
fnM fni(x) •
•• fnnW
fni(x) fm(x) •
•• /„,.(*)
988. Найти F'(x), если
989.	Найти F'(x), если
л: — 1 1	2
—3 х	3
-2 -3*+1
ад =
X X2 X3
1	2х Зх2 •
О 2	6*
990.	Дан график функции. Приближенно построить график
ее производной.
991.	Показать, что функция
f(x) =
2 • 1
лг sm -
х
О
при х & 0;
при х = 0
имеет разрывную производную.
992.	При каком условии функция
/(*) =
« • 1
хп sm -
х
О
при х ^ 0;
при х = О
а)	непрерывна при х = 0;
б)	дифференцируема при х = 0;
в)	имеет непрерывную производную при х = 0?
993.	При каком условии функция
\х\п sin г-7- при х & 0,
/(*) = { 1*1"
при х = 0
О

94
РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
(т > 0) имеет:
а)	ограниченную производную в окрестности начала ко¬
ординат;
б)	неограниченную производную в этой окрестности?
994.	Найти f\a), если
f(x) = (* - а)ф(*),
где функция ф(*) непрерывна при х = а.
995.	Показать, что функция
f(x) = \х- а|ф(*),
где ф(*) — непрерывная функция и ф(а) ^ 0, не имеет производ¬
ной в точке а.
Чему равны односторонние производные /1(а) и /+(а)?
996.	Построить пример непрерывной функции, не имеющей
производной в данных точках: аи а2, ..., ап.
997.	Показать, что функция
fix) = X1
(х*0) и /(0) = 0
имеет точки недифференцируемости в любой окрестности точки
х = 0, но дифференцируема в этой точке.
Построить эскиз графика этой функции.
998.	Показать, что функция
fix) =
Xя,
0,
если х рационально;
если х иррационально,
имеет производную лишь при х = 0.
999.	Исследовать на дифференцируемость следующие функ¬
ции:
а)	у = |(* - 1)(х - 2)2(* - З)3|; б) у = |cos х\;
в)	у = \п2 - х2\ sin2 х;	г) у = arcsin(cos *);
-—- (jc -Ч-1)2	при |*| <1;
4
|*| - 1	при |*| > 1.
Для функции f(x) определить левую производную /'_(*) и пра¬
вую производную /*+ (*), если:
1000.	Я*) = |*|.	1001. fix) = [*] sin л*.
я
COS-
*
1002.	f(x) = *
1003.	f(x) = л/sin*2
(* * 0),
/(0) = 0.

§ 1. Производная явной функции
95
1004.	f(x)	(* * 0), /(0) = 0.
1 + е*
1005.	f{x) = Jl - е-*2.	1006. f(x) = |1п \х\\ (л: * 0).
1007.	fix) = arcsin .
1 + x2
1008.	fix) = ix -2) arctg -J—	(* * 2), /(2) = 0.
X — Ct
1009.	1. Показать, что функция f(x) = * sin i при * 5* 0 и /(0) =
О	непрерывна при x = 0, но не имеет в этой точке ни левой, ни правой
производной.
2.	Пусть х0 — точка разрыва 1-го рода функции /(*). Выра¬
жения
/'_(*о)= Шп /(*o + *W(*o-0)
и
// /_ ч _ lim Н*о + ^) - /(*<> + 0)
1 + \х0)	Л_+0	I
называются обобщенными односторонними (соответственно ле¬
вой и правой) производными функции f(x) в точке х0.
Найти (*0) и /+(^0) в точках разрыва х0 функции f(x)9 если:
a)	fix) =	;	б) fix) = arctg ;
в) Л*) = -Ц .
1 + е*
1010.	Пусть
№~
хг, если л: < х0;
ах + Ъ, если х > *0.
Как следует подобрать коэффициенты а и Ъ, чтобы функция
fix) была непрерывной и дифференцируемой в точке х = х0?
1011.	Пусть
fix),
ах + Ь9
если х < х0;
если х > х0у
где функция f(x) дифференцируема слева при х = х0.
При каком выборе коэффициентов а и Ъ функция F(x) будет
непрерывной и дифференцируемой в точке х0?

РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1012.	На сегменте а < х < Ъ построить сопряжение двух по¬
лупрямых
у = kx(x - а) (—°° < х < а) и у = k2(x - Ъ) (Ь < х < +оо)
с помощью кубической параболы
(где а и b — неизвестные параметры) так, чтобы получилась
гладкая кривая.
1014.	Можно ли утверждать, что сумма
не имеет производной в точке х = х0, если:
а)	функция f(x) имеет производную в точке х0, а функ¬
ция g(x) не имеет производной в этой точке;
б)	обе функции /(*) и g(x) не имеют производной в точке х0?
1015.	Можно ли утверждать, что произведение
F(x) = f(x)g(x)
не имеет производной в точке х = х0, если:
а)	функция /(*) имеет производную в точке х0, а функ¬
ция g(x) не имеет производной в этой точке;
б)	обе функции /(*) и g(x) не имеют производной в точке х0?
Рассмотреть примеры:
a)	f(x) = х, g(x) = |*|;	б) f(x) = |*|, g(x) = |*|, где *0 = 0-
1016.	Что можно сказать о дифференцируемости функции
F(x) = f(g(x))
в данной точке х = х0, если:
а)	функция f(x) имеет производную в точке х = g(x0), а
функция g(x) не имеет производной в точке х — х0;
б)	функция f(x) не имеет производной в точке х = g(x0),
а функция g(x) имеет производную в точке х = х0;
в)	функция f(x) не имеет производной в точке х = g(x0)
и функция g(x) не имеет производной в точке х = х0?
Рассмотреть примеры:
у = А(х - а)(х - Ь)(х - с),
где параметры А и с подлежат определению.
F(*) = f(x) + g(x)
a) f(x) = *2, g(x) = |*|;
б) /(*) = |*|, g(x) = х2;

§ 1. Производная явной функции
97
1017.	В каких точках график функции
у = х + V sin*
имеет вертикальные касательные?
Построить этот график.
1018.	Может ли функция f(x) в точке ее разрыва иметь:
а)	конечную производную; б) бесконечную производную?
Рассмотреть пример: /*(х) = sgn х.
1019.	Если функция f(x) дифференцируема в ограниченном
интервале (а, Ь) и
lim f(x) = оо,
X —• о
то обязательно ли
1) lim /*'(*) = оо; 2) lim |/'(*)| = +оо?
х -* а	х~* а
Рассмотреть пример: f(x) = - + cos i при jc
л:	х
0.
1020.	Если функция f(x) дифференцируема в ограниченном
интервале (а, Ъ) и
lim А*) = оо,
то обязательно ли
lim f(x) = оо?
л: — а
Рассмотреть пример: /(*) = 1/х при х —3► 0.
1021.	Пусть функция f(x) дифференцируема в интервале
(jc0, +оо) и существует lim f'(x). Следует ли отсюда, что сущест-
X — +оо
вует lim f'(x) ?
X — +00
Рассмотреть пример: f(x) =	.
1022.	Пусть ограниченная функция f(x) дифференцируема в
интервале (*0, +оо) и существует lim f'(x). Следует ли отсюда,
X — ОО
что существует lim f(x) конечный или бесконечный?
X —• ОО
Рассмотреть пример: /(*) == cos (In х).
1023.	Можно ли почленно дифференцировать неравенство
между функциями?
1024.	Вывести формулы для сумм:
а)	Рл = 1 + 2х + Зх2 + ... + пхп~\
Qn = I2 + 22х + 32х2 + ... + п2хп-х;
Указание. Рассмотреть (х + х2 4- ... + хп).
б)	= sin х + sin 2jc + ... + sin nxy

98
РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1025.	Вывести формулу для суммы:
Sn = ch х + 2 ch 2х + ... + п ch пх.
Указание. Sn = (sh х + sh 2х 4- ... + sh пх)'.
1026.	Пользуясь тождеством
cos^ cos^ ... cos ——
2	4	2п
вывести формулу для суммы:
sin*
sn = I tg - + - tg - + ... + — tg —.
2 e 2	4 s 4	2“	2"
1027.	Доказать, что производная четной дифференцируемой
функции есть функция нечетная, а производная нечетной диф¬
ференцируемой функции есть функция четная.
Дать геометрическую интерпретацию этого факта.
1028.	Доказать, что производная дифференцируемой перио¬
дической функции есть функция снова периодическая с тем же
периодом.
1029.	С какой скоростью возрастает площадь круга в тот мо¬
мент, когда радиус этого круга R = 10 см, если радиус круга рас¬
тет равномерно со скоростью 2 см/с?
1030.	С какой скоростью изменяются площадь и диагональ пря¬
моугольника в тот момент, когда одна сторона его * = 20 м, а другая
сторона у = 15 м, если одна сторона прямоугольника уменьшается
со скоростью 1 м/с, а другая возрастает со скоростью 2 м/с?
1031.	Из одного и того же порта одновременно вышли паро¬
ход А в направлении на север и пароход В в направлении на вос¬
ток. С какой скоростью возрастает расстояние между ними, если
скорость парохода А равна 30 км/ч, а парохода В равна 40 км/ч?
1032.	Пусть
jx,	если0<*<2;
№ = \2х -2,	если 2 < х < +оо,
и S(x) — площадь, ограниченная кривой у = /(*), осью Ох и пер¬
пендикуляром к оси Оху проведенным в точке х (х > 0).
Составить аналитическое выражение функции S(*), найти
производную S'(*) и построить график функции у = S'(*).
1033.	Функция S(*) есть площадь, ограниченная дугой ок¬
ружности у = Ja2 - х2 , осью Ох и двумя перпендикулярами к
оси Ох у проведенными в точках 0 и *	< a j.
Составить аналитическое выражение функции S(*), найти
производную S'(x) и построить график этой производной.

§ 2. Производные обратной функции, функции, заданной параметрически
99
§ 2. Производные обратной функции,
функции, заданной параметрически,
и функции, заданной в неявном виде
1. Производная обратной функции. Дифференцируемая функция
у = f(x) (а < х < Ъ) с производной f'(x) ^ 0 имеет однозначную непре¬
рывную обратную функцию х = Г1(у)> причем обратная функция также
дифференцируема и справедлива формула
2. Производная функции, заданной параметрически. Система
уравнений
где cp(f) и \|/(0 — дифференцируемые функции и (р'(0 ^ 0, определяет у
в некоторой области, как однозначную дифференцируемую функцию от х:
У = ¥(Ф~'(*)).
причем производная этой функции может быть найдена по формуле
3.	Производная функции, заданной в неявном виде. Если диффе¬
ренцируемая функция у = у(х) удовлетворяет уравнению
то производная у' = у'(х) этой неявной функции может быть найдена из
уравнения
где F(xy у) рассматривается как сложная функция переменной х.
(Более подробно о дифференцировании неявных функций см. разд. VI, § 3.)
1034.	Показать, что существует однозначная функция у = у(х),
определяемая уравнением
и найти ее производную у'х.
1035.	Показать, что существует однозначная функция
у = y(x)f определяемая уравнением
F(x, у) = 0,
т;№. »)]“ 0.
у3 + 3у = х,
у - esin у = X (0 < £ < 1),
и найти производную у'х.

100	РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1036.	Определить области существования обратных функций
х = х(у) и найти их производные, если:
а) у = х + In х (х > 0);	б) у = х + ех;
в)	у = sh х;	г) у = th я.
1037.	Выделить однозначные непрерывные ветви обратных
функций х = *:([/), найти их производные и построить графики,
если:
Л) у- 2х2 - х4; б )у=	; в) у = 2в'* - е~2*.
1038.	Построить эскиз графика функции у = у(х) и найти про¬
изводную у'х(х), если: jc = -1 + 2£ - £2, у = 2 - 3£ 4- £3. Чему равна
*/'*(*) при х = 0 и при л; = -1? В какой точке М (л:, i/) производная
V’JLx) = 0?
Найти производные у'х (параметры положительны), если:
1039.	л: = ill - Jt,
1040.	х = sin2 t,
1041.	x = a cos f,
1042.	лг = a ch t,
1043.	x = a cos3 t,
1044.	jc = a (t - sin 0»
1045.	x = e2* cos2 t,
у = Jl-lft.
у = cos2 £.
z/ = b sin £.
i/ = b sh t.
у = a sin3 £.
z/ = a (1 - cos £)•
i/ = e2t sin2 t.
1046.	л; = arcsin ■■■■ 	, у = arccos ■	1	.
л/ГТТ2	л/ГТТ2
1047.	Показать, что функция у = z/(a;)> определяемая систе¬
мой уравнений
л; = 2£ 4- |4 I/ = Ы2 + 4ф|,
дифференцируема при t = 0, но ее производная в этой точке не
может быть найдена по обычной формуле.
Найти производные у'х от следующих функций, заданных в
неявном виде:
1048.	х2 4- 2 ху - у2 = 2л;. Чему равно у' при х=2иу=4и
при дс = 2 и I/ = О?
1049.	у2 = 2рл; (парабола).	1050. ~	^ = 1 (эллипс).
а2 о2
2 2 2
1051. Jx + Jy = Ja (парабола). 1052. х3 + у3 = а3 (астроида).
1053.	arctg ^ = In Jx2 + у2 (логарифмическая спираль).

§ 3. Геометрический смысл производной
101
1054.	Найти у'х, если:
а)	г = аср (спираль Архимеда);
б)	г = а (1 4- cos ер) (кардиоида);
в)	г = аепщ (логарифмическая спираль),
где г = Jx2 + у2 и ф = arctg ^ — полярные координаты.
§ 3. Геометрический смысл производной
1. Уравнения касательной и нормали. Уравнения касательной МТ
и нормали MN к графику дифференцируемой функции у = f(x) в точке
его М (х, у) (рис. 7) соответственно имеют вид:
где X, У — текущие координаты касательной или нормали, а у' — f'(x) —
значение производной в точке касания.
2. Отрезки касательной и нормали. Для отрезков касательной и
нормали: РТ — подкасательная, PN — поднормаль, МТ — касатель¬
ная, MN — нормаль (рис. 7); учитывая, что tg а = у\ получаем следую¬
щие значения:
3.	Угол между касательной и радиусом-вектором точки касания.
Если г = /(ф) — уравнение кривой в полярной системе координат и (3 —
угол, образованный касательной МТ и радиусом-вектором ОМ точки
касания М (рис. 8), то
У - у = у' (X - х),
Y - у =* —1 (X - х),
У
РТ = U. , PN = \уу%
У
мт= R. Vi + у’2, млг = |^|71 + г/'2.
у’
У
О У
х
О
Рис. 7
Рис. 8

102 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1055.	Написать уравнения касательной и нормали к кривой
у = (х + 1)V3 - х
в точках: а) А (-1; 0); б) В (2, 3); в) С (3, 0).
1056.	В каких точках кривой
у = 2 + х - х2
касательная к ней:
а)	параллельна оси Ох;
б)	параллельна биссектрисе первого координатного угла?
1057.	Доказать, что парабола
у = а(х - хх)(х - х2)	(а & 0, хг < х2)
пересекает ось Ох под углами а и Р ^0<a<|,0<P<|j,
равными между собой.
1058.	На кривой
у = 2 sin х (-71 < х < 71)
определить те участки ее, где «крутизна кривой» (т. е. \у'\) пре¬
вышает 1.
1059.	Функции
у = х и уг = х + 0,01 sin 1000ти;@
отличаются друг от друга не больше чем на 0,01. Что можно ска¬
зать о максимальном значении разности производных этих
функций?
Построить соответствующие графики.
1060.	Под каким углом кривая
у = In х
пересекает ось Ох?
1061.	Под какими углами пересекаются кривые
у = х2 и х = у2?
1062.	Под какими углами пересекаются кривые
у = sin х и у = cos х?
1063.	1. При каком выборе параметра п кривая
у = arqtg пх (п > 0)
пересекает ось Ох под углом, большим 89°?

§ 3. Геометрический смысл производной
103
2.	Показать, что кривая у = |л:|а касается,
а)	оси Оу при 0 < а < 1;
б)	оси Ох при 1 < а < +оо.
3.	Показать, что для графика функции
\\х\ау если а * 0, х * 0;
^	[1, если х = 0,
предельное положение секущей, проходящей через точку А (0, 1),
есть ось Оу.
1064.	Определить угол между левой и правой касательными
к кривой: а) у = J1 - е~а2х2 в точке х = 0; б) у = arcsin -
1	+ х2
в точке л: = 1.
1065.	Показать, что касательная к логарифмической спирали
г=аетф
(аит — постоянные) образует постоянный угол с радиусом-век¬
тором точки касания.
1066.	Определив длину подкасательной к кривой
У = ахпу
дать способ построения касательной к этой кривой.
1067.	Доказать, что у параболы
у2 = 2рх:
а)	подкасательная равна удвоенной абсциссе точки
касания;
б)	поднормаль постоянна.
Дать способ построения касательной к параболе.
1068.	Доказать, что показательная кривая
у = ах (а > 0)
имеет постоянную подкасательную. Дать способ построения ка¬
сательной к показательной кривой.
1069.	Определить длину нормали к цепной линии
у = a ch-
а
в любой ее точке М (х0, у0).
1070.	Доказать, что у астроиды
2 2 2
хз + уз = дз (а > 0)
длина отрезка касательной, заключенного между осями коорди¬
нат, есть величина постоянная.

104 РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1071.	При каком соотношении между коэффициентами а, Ъ
и с парабола
у = ах2 4- Ьх + с
касается оси 0x1
1072.	При каком условии кубическая парабола
у = хг 4- рх 4- q
касается оси 0x1
1073.	При каком значении параметра а парабола
у = ах2
касается кривой у = \п х!
1074.	Доказать, что кривые, у = f(x) (f(x) > 0), у = f(x) sin аху
где f(x) — дифференцируемая функция, касаются друг друга в
общих точках.
1075.	Показать, что семейства гипербол
х2 - у2 = а, ху = b
образуют ортогональную сетку, т. е. кривые этих семейств пе¬
ресекаются под прямыми углами.
1076.	Доказать, что семейства парабол
у2 = 4а (а - х) (а > 0)
и
у2 = 4Ь{Ь + х) (b > 0)
образуют ортогональную сетку.
$ 1077. Написать уравнения касательной и нормали к кривой
х=2 t-t2, y=3t-t3
в точках: a) t = 0; б) t = 1.
1078.	Написать уравнения касательной и нормали к кривой
г = 2t+f2 I/ = 2t~t2
1	+ t* 9 У 1 + f3
в точках: a) t = 0; б) t = 1; в) t = °о.
1079.	Написать уравнение касательной к циклоиде
х = a (t - sin t)t у = а (1 - cos t)
в произвольной точке t = t0. Дать способ построения касательной
к циклоиде.
1080.	Доказать, что трактриса
х = a ^ln tg | 4- cos *j , у — a sin £ (а > 0, 0 < t < ri)
имеет отрезок касательной постоянной длины.

§ 4. Дифференциал функции
105
Написать уравнения касательной и нормали в заданных точ¬
ках к следующим кривым:
1081.	-2L-
100
+ *1 = 1,
64
1082. ху + In у = 1,
М(6; 6,4).
М( 1; 1).
§ 4. Дифференциал функции
1.	Дифференциал функции. Если приращение функции у = f(x) от
независимой переменной х может быть представлено в виде
А у = A (x)dx + o(dx)y
где dx = Ал:, то линейная часть этого приращения называется дифферен¬
циалом функции у:
dy = А (x)dx.
Для существования дифференциала функции у = f(x) необходимо и доста¬
точно, чтобы существовала конечная производная у' = /'(*)> причем имеем:
dy = y'dx.	(1)
Формула (1) сохраняет свою силу и в том случае, если переменная
х является функцией от новой независимой переменной (свойство
инвариантности первого дифференциала).
2.	Оценка малых приращений функции. Для подсчета малых прира¬
щений дифференцируемой функции f(x) можно пользоваться формулой
f(x 4- Ал:) - f(x) ~ f'(x)Ал:,
относительная погрешность которой сколь угодно мала при достаточно
малом |Ajc|, если f'{x) & 0.
В частности, если независимая переменная х определяется с пре¬
дельной абсолютной погрешностью, равной А*, то Ду и — предельные
абсолютная и относительная погрешности функции у = f(x) — прибли¬
женно выражаются следующими формулами:
Л,/ = ИЛ, и
8,=
1083.	Для функции
/(*) = л:3 - 2л: + 1
определить: 1) А/(1); 2) df( 1) и сравнить их, если:
а)Ал:=1; б) Ал: =0,1; в) Ал: = 0,01.
1084.	Уравнение движения дается формулой
х = 5£2,
где t выражается в секундах и х — в метрах.
Для момента времени t = 2 с определить Ал: — приращение
пути и dx — дифференциал пути и сравнить их, если:
а) А£ = 1 с; б) At = 0,1 с; в) At = 0,001 с.

106 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Найти дифференциал функции у> если:
1085. у = -.
X
1087.#-£ In
X — CL
х + а
х
1086. у = - arctg - (а * 0).
а	а
1088. у = In \х 4- Jx2 + а |.
1089.	у = arcsin - (а * 0).
а
1090.	Найти:
a) d (хех);
д) d (Ja2 + хг);
ж) d 1п(1 - х2);
+ 1 in tgf£+5l
L2cos2Jt:	2	ч2 4)
6) d (sin x - x cos x);
«о
з) d (arccos jij j ;
Пусть и, v, w — дифференцируемые функции от х. Найти
дифференциал функции у9 если:
1091. I/ = uvw.
1092. у = i .
V2
1093. у =	1	.	1094. г/ = arctg -.
Ju^Tv2	v
1095.	i/ = In Ju2 + v2.
1096.	Найти
a)
d
d( x3)
(x3 - 2jc6 - x9);
B) d(sin£);
d(cosjc)
6)
d f эшаЛ .
d(*2)l x ) *
r)
«*<<«*) •
d(ctgx) ’
^ d(arcsine)
7 d(arccosjc) *
1097.	В круговом секторе радиус Я = 100 см и центральный
угол а = 60°. Насколько изменится площадь этого сектора, если:
а)	радиус его R увеличить на 1 см;
б)	угол а уменьшить на 30'?
Дать точное и приближенное решения.
1098.	Период колебания маятника определяется по формуле
Т =

§ 4. Дифференциал функции
107
где I — длина маятника и g = 9,8 м/с2 — ускорение свободного
падения.
Насколько нужно изменить длину маятника I = 0,2 м, чтобы
период Т увеличился на 0,05 с?
Заменяя приращение функции дифференциалом, найти при¬
ближенно следующие значения:
1099.	VT02 .	1100. sin 29°.
1101. cos 151°.	1102. arctg 1,05.
1103.	lg 11.
1104.	1. Доказать приближенную формулу
Ja2 + х ~ а 4- — (а > 0),
2	а
где |х| <£. а (соотношение А « В между положительными А и В
означает, что А весьма мало по сравнению с Б).
С помощью этой формулы приближенно вычислить:
а)	Л ;	б) л/34 ;	в) JT20
и сравнить с табличными данными.
2.	Доказать формулу
Ja2 + х = а +	- г (а > 0, х > 0),
2
где 0 < г < —-.
8 а
1105.	Доказать приближенную формулу
nJan + х ~ а + —(а > 0),
пап
где |л;| а.
С помощью этой формулы приближенно вычислить:
а)	з/9 ; б) i/80 ;	в) l/lOO ;	г) 10Л000 .
1106.	Сторона квадрата х = 2,4 м ± 0,05 м. С какими предель¬
ной абсолютной и относительной погрешностями можно вычис¬
лить площадь этого квадрата?
1107.	С какой относительной погрешностью допустимо изме¬
рить радиус R шара, чтобы объем его можно было определить с
точностью до 1%?
1108.	Для определения ускорения свободного падения с по¬
мощью колебания маятника пользуются формулой

108 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
где I — длина маятника, Т — период его колебаний. Как отра¬
зится на значении g относительная погрешность 8 при измере¬
нии: а) длины Z; б) периода Т?
1109.	Определить абсолютную погрешность десятичного ло¬
гарифма числа х (х > 0), если относительная погрешность этого
числа равна 8.
1110.	Доказать, что углы по логарифмической таблице тан¬
генсов определяются точнее, чем по логарифмической таблице
синусов с тем же самым числом десятичных знаков.
§ 5. Производные и дифференциалы высших порядков
1. Основные определения. Производные высших порядков от функ¬
ции у = f(x) определяются последовательно соотношениями (предпола¬
гая, что соответствующие операции имеют смысл!):
Если функция f(x) имеет непрерывную производную Рп)(х) на ин¬
тервале (а, Ь), то кратко пишут: f(x) Е С(п) (а, Ь). В частности, если f(x)
имеет непрерывные производные всех порядков на (а, Ь), то употребля¬
ется запись: f(x) Е С(00) (а, Ь).
Дифференциалы высших порядков от функции у = f(x) последова¬
тельно определяются формулами
/<»>(*)-{/^Ч*)}'	(п= 2,3,...).
dny=d(dn~'y) (л- 2,3,...),
где принято dly = dy = y'dx.
Если х — независимая переменная, то полагают:
d2x = d3x= ... = 0.
В этом случае справедливы формулы
dny — y{n)dxn и у^ У .
2. Основные формулы:
I. (ахУп) = ах 1пп а (а > 0); (ех){п) = ех.
III.
IV. (хт)(п) = т(т - 1) ... (т - п + l)jcm“я.
V. (in*)<">, W:1!,?_-!)!.

§ 5. Производные и дифференциалы высших порядков
109
3.	Формула Лейбница. Если функции и = ф(х) и v = ф(х) имеют про¬
изводные п-го порядка (/i-кратно дифференцируемы), то
(ш>)(л)=£ С1пи^Чп~1\
I = о
где и{0) = и, и{0) = v и С'„ — число сочетаний из /г элементов по /.
Аналогично для дифференциала dn(uv) получаем
dn(uv) = ^ Clndn~1 udlVy
i = 0
где положено d°u = и и d°i> = п.
Найти I/
1111. у = X
VI + X2
1113. у = <г*2.
1115. I/ = (1 + х2) arctg х.
1117. у = х In х.	1
1119.	у = х [sin (In х) + cos (In х)].
1120.	Найти у(0), у\0) и г/"(0), если
У = gsin* cos	ху
LLL*.y= —=.
Vl - x2
1114. z/ = tg x.
1116 arcsinx
Vl - ЛГ2
лУ -L -
1118. у * In /(x).
Пусть и = ф(х) и v = \|/(х) — дважды дифференцируемые
функции. Найти у", если:
1121.i/= а2.	1122.	г/ = In й.
1123. у = a/u2 + и2 .	1124.	у = uw (и > 0).
Пусть /(х) — трижды дифференцируемая функция. Найти у"
и г/'", если:
1125. у = f(x2).	1126.	у = /(1) .
1127. у - /(ех).	1128.	у = Д1п х).
1129. у = Аф(х)), где ф(х) — достаточное число раз дифферен¬
цируемая функция.
ИЗО. Найти d2y для функции
У = ех
в двух случаях:
а)	х — независимая переменная;
б)	х — промежуточный аргумент.

110 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Считая х независимой переменной, найти d2y, если:
1131. у = JT+х2 .	1132.1/=^.	1133. t/ = x*.
Пусть и и v — дважды дифференцируемые функции от пере¬
менной х. Найти <22г/, если:
1134. у = uv.	1135. у = ± .
1136.	у = umvn (тип — постоянные).
1137.	у = а“ (а > 0).	1138. £/ = In Ju2 + v2.
1139.	у = arctg - .
V
Найти производные у'х, г/'2,	от функции у = */(*), заданной
параметрически, если:
1140. х=2t-t2y	y=3t- t3.
1141.	х = a cos t, у = a sin £.
1142.	jc = a (f - sin t),y = a (1 - cos *)•
1143.	* = e* cos £,	1/	= sin £.
1144. д:-Г(0,	V=tnt)-f(t).
1145.	Пусть функция г/ = f(x) дифференцируема достаточное
число раз. Найти производные х\ х'\ х"\ х1У обратной функции
х = f~l(y), предполагая, что эти производные существуют.
Найти у'х9 у"г, от функции у = у(х)9 заданной неявно:
1146.	х2 + у2 = 25. Чему равны у', г/" и г/'" в точке М(3, 4)?
1147.	у2 = 2р*.	1148. х2 - ху + у2 = 1.
Найти г/i и у”2 у если:
1149. у2 + 2 In у = jc4. 1150. -У*2 + у2 = aearctg * (а > 0).
1151.	Пусть функция f(x) определена и дважды дифференци¬
руема при х < х0. Как следует подобрать коэффициенты a, b и с,
чтобы функция
Г /(*),	если д: < x0i
~ [ а(х - х0)2 + Ь(х - х0) + с, если х > х0,
была дважды дифференцируема.
1152.	Точка движется прямолинейно по закону
s=10 + 20*-5*2.
Найти скорость и ускорение движения. Чему равны скорость и
ускорение в момент времени t = 2?

§ 5. Производные и дифференциалы высших порядков
111
1153.	Точка М (х, у) равномерно движется по окружности
х2 + у2 = а2, делая один оборот за время Т. Найти скорость v и
ускорение w проекции точки М на ось Ох, если при t = 0 точка
занимала положение М0 (а, 0).
1154.	Тяжелая материальная точка М (х9 у) брошена с на¬
чальной скоростью v0 в вертикальной плоскости Оху под углом
а к плоскости горизонта. Составить (пренебрегая сопротивлени¬
ем воздуха) уравнение движения и определить скорость и и ус¬
корение w, а также траекторию движения. Чему равны наиболь¬
шая высота поднятия точки и дальность полета?
1155.	Уравнения движения точки
х = 4 sin wt - 3 cos wty у = 3 sin wt + 4 cos wt
(w — постоянно).
Определить траекторию движения, скорость и ускорение.
В следующих примерах найти производные указанного по¬
рядка:
1156.	у = х(2х - 1)2(* + З)3; найти г/(6) и i/<7).
1157.	у = ^ ; найти у'".
1158.	у = Jx ; найти г/(10).
1159.	у =	; найти г/(8).
1160.	у ~ ~	; найти i/(100).
Jl-x
1161.	«/ = д:2е2х; найти у(20).
1162.	у = ^ ; найти у<10).
1163.	г/ = л: In х; найти i/<5).
1164.	у =	; найти i/(5).
1165.	у — х2 sin 2х; найти у(50).
1166.	у = —s--x- ; найти у'”.
1167.	у = sin л: sin 2jc sin Зле; найти z/(10).
1168.	у = jc sh х; найти z/(100).
1169.	у — ех cos х; найти ylv.
1170.	у = sin2 jc In jc; найти z/(6).

112 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
В следующих примерах, считая х независимой переменной,
найти дифференциалы указанного порядка.
1171.	z/ = *5; найти d5y.
1172.	у = -р ; найти d3y.
Jx
1173.	у = х cos 2х; найти d10y.
1174.	у = ех In х; найти d4y.
1175.	у = cos х • ch х; найти d6y.
В следующих примерах найти дифференциалы указанного
порядка, если и — функция от х9 дифференцируемая достаточ¬
ное число раз.
1176.	у = и2; найти d10y.
1177.	у = еи\ найти dAy.
1178.	г/ = In гг; найти d3y.
1179.	Найти d2yy d3y и d4y от функции у = /(х)9 считая х функ¬
цией от некоторой независимой переменной.
1180.	Выразить производные у" и у'" от функции у = f(x)
через последовательные дифференциалы переменных х9 у9 не
предполагая х независимой переменной.
1181.	Показать, что функция
у = Сх cos х + С2 sin х9
где Cj и С2 — произвольные постоянные, удовлетворяет уравнению
</" + !/= 0.
1182.	Показать, что функция
I/ = Сх ch х + С2 sh х9
где Сг и С2 — произвольные постоянные, удовлетворяет уравнению
У"-У = 0.
1183.	Показать, что функция
У = С1ех'х +С2ех*х,
где Cj и С2 — произвольные постоянные иХХ9 Х2 — постоянные,
удовлетворяет уравнению
у" - (A,j + Х2)у' + АлХ2у = 0.
1184.	Показать, что функция
у = хп[С1 cos (In я) + С2 sin (In jc)],
где Ci и С2 — произвольные постоянные ил — постоянная, удов¬
летворяет уравнению
х2у" + (1 - 2п)ху' + (1 + п2)у = 0.

§ 5. Производные и дифференциалы высших порядков
113
1185.	Показать, что функция
JL,	/
у = еЩ Ci cos + Со sin -^1 + е Щ С3 cos — + С4 sin —1,
V J2	JV V V2	J2>)
где С1? С2, С3 и С4 — произвольные постоянные, удовлетворяет
уравнению
У™ + У = 0.
1186.	Доказать, что если функция /(я) имеет производную /г-го
порядка, то
[/(а* 4- 6)](л) = anfn\ax 4- b).
1187.	Найти Р{п\х), если
Р(х) = а0д:л 4- ахл:л “ 1 + ... + ап.
Найти у{п)
1188. у =
, если:
ах+Ь
сх + d
1189. у =
1
х(1 -х)'
1190^=^72-
Указание. Разложить функцию на простейшие дроби.
1191. у = —.
VI-2л:
1193. I/ = sin2 лс.
1195. у = sin3 х.
1197.	у = sin ах sin bx.
1198.	у = cos ах cos Ъх.
1200. у = sin2 ах cos bx.
1202. у = х cos ах.
1204.	у = (х2 + 2* + 2)е~х.
1206. у = ех cos х.
1208.	у = In	.
9 а-Ьх
1209.	у = еах Р(х), где Р(х)
1210.	у = х sh х.
1192. у = —
VI + х
1194. у = cos2 я.
1196. г/ = cos3 х.
1198.	у = cos ах cos Ьдс.
1199.	у = sin ах cos bx.
1201. у = sin4 х + cos4 х.
1203. у = х2 sin ах.
1205.	г/ = - .
*
1207. у = ех sin х.
многочлен.
Найти dny, если:
1211.	у = *ле*.
1212. у «
* *

114	РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1213.	Доказать равенства:
№
1)	[еах sin (bx 4- с)](л) = еах(а2 4 Ь2)2 sin (Ъх 4 с 4 жр),
пл
2)	[еах cos (bx 4 с)](л) = еах (а2 4 Ь2)2 cos (Ьл: 4 с + жр),
где
sin ф =	— 	- , cos ф = а .
л/а^Ть2	л/а2 + Ь2
1214.	Найти р(л), если:
а) у = ch ал: cos Ьл:;	б) г/ = ch ах sin Ьл:.
1215.	Преобразовав функцию f(x) = sin2p л:, где р — натураль¬
ное число, в тригонометрический многочлен f(x) = ^ Ak cos 2kx,
k = 0
найти f{n\x).
Указание. Положить sin х— —: (t - t)f где t = cos x 4 i sin x и
La l
t = cos x - i sin x, и воспользоваться формулой Муавра.
1216.	Найти f{n\x), если:
a)	f(x) = sin2p +1 х; б) f(x) = cos2p х; в) f(x) = cos2p + 1 х,
где р — целое положительное число (см. предыдущую задачу).
Если
f(x) = f^x) + if2(x),
где i — мнимая единица и fx(x)9 f2(x) — действительные функции
от действительной переменной х, то по определению принимаем:
/'(*) = Пх) + if'2(x).
1217.	Используя тождество
_L_ = If J_ - J-)
л:2 + 1 2i\x-i x + i) ’
доказать, что
=	sinK" + П arcctg *]•
* +	(1 + *2)~
Указание. Применить формулу Муавра.
1218.	Найти п-ю производную от функции
/(х) = arctg х.
Найти /*л)(0), если:
ш,'‘|м~1|-ьт..„: б)/м-
1220. a) f(x) = х2еах; б) f(x) = arctg х;
х
Jl - X
в) fix) =
arcsin х.

§ 5. Производные и дифференциалы высших порядков
115
1221.	a) f(x) = cos (/7i arcsin х); б) f(x) = sin (m arcsin x).
1222.	a) f(x) = (arctg x)2;	6) Дх) = (arcsin x)2.
1223.	Найти Д'1)(а), если
Д*) = (х - а)Лф(х),
где функция ф(х) имеет непрерывную производную (п - 1)-го по¬
рядка в окрестности точки а.
1224.	Доказать, что функция
Д*) =
х2п sin -, если х ^ О,
х
О,	если х = О
(п — натуральное число) в точке х = 0 имеет производные до п-го
порядка включительно и не имеет производной (п + 1)-го порядка.
1225.	Доказать, что функция
Д*) =
если х у* О,
если х = О
бесконечно дифференцируема при х = 0.
Построить график этой функции.
1226.	Доказать, что многочлены Чебышева
Тт(х) = cos (т arccos х) (т = 1, 2, ...)
удовлетворяют уравнению
(1 - х2)Г"(х) - хТпг{х) + rn2Tm(x) « 0.
1227.	Доказать, что многочлены Лежандра
рЛх) = 2^ К** - 1)ml(m)	= °» !> 2> -)
удовлетворяют уравнению
(1 - х2)Р”{х) - 2хР'т(х) + т(т + 1)Рт(лг) = 0.
Указание. Продифференцировать т 4-1 раз равенство (х2 -1 )ц'=2тхи>
где н = (х2 - l)w.
1228.	Многочлены Чебышева—Лагерра определяются фор¬
мулой
Lm(x) = cx(xmO(m) (m = 0, 1, 2, ...).
Найти явное выражение для многочлена Lm(x).
Доказать, что Lm(x) удовлетворяет уравнению
xL”(x) + (1 - x)L'm(x) + mL(x) = 0.
Указание. Использовать равенство хи' + (х - т)и = 0, где и = хте~х.

116 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1229.	Пусть у = f(u) и и = <р(х), где f{u) и (p(*) — /г-кратно
дифференцируемые функции.
Доказать, что
В - ± лмПи),
k= 1
где коэффициенты Ал(х) (k = 0, 1,	п) не зависят от функции f(u).
1230.	Доказать, что для п-й производной сложной функции
У = /(*2) справедлива формула
^ = (2x)nfM(x2) + “LH—11 (2х)п - 2fin " ^(х2) +
dxn	1!
+ п(п~ 2)(/l~3)(2,r)п~4/(п~2)(х2) + ...
1231.	Многочлены Чебышева—Эрмита определяются фор¬
мулой
#„,(*) = (-l)me*2 (<r*2)<w> (m = 0, 1, 2, ...).
Найти явное выражение для многочленов Нт(х).
Доказать, что Нт(х) удовлетворяет уравнению
Н^(х) - 2хН'т(х) + 2тНт(х) = 0.
Указание. Использовать равенство u' + 2хи = 0, где и = ех2.
1232.	Доказать равенство
(*“ “ 1 е* )(п) =	.
хп + 1
Указание. Применить метод математической индукции.
1232. Доказать формулу:
а)	(хЧп х) = п\ ^1п х + j (х > 0);
k = i
б)	£ё(“г) = [Сп (д:) sin *"Sn(x) cos
где
Сп(х) = 1 -
2!
х2"
(2л)!’
S„(x) = х -
3!
дг2п~1
(2л- 1)! *

§ 6. Теоремы Ролля, Лагранжа и Коши
117
1233.	Пусть — = D обозначает операцию дифференцирования и
f(D) = £ pk(x)Dk
— символический дифференциальный многочлен, где pk(x) (k =
= 0, 1, ...» /г) — некоторые непрерывные функции от х.
Доказать, что
f(D){eXxu(x)} = eXxf(D + Х)и(х),
где X — постоянно.
1234.	Доказать, что если в уравнении
akxhy^] = О
к = О
ПОЛОЖИТЬ
х = е\
где t — независимая переменная, то это уравнение примет вид:
]Г akD(D-l)...(D-k+l)y=0,
к = О
где D = А .
at
§ 6. Теоремы Ролля, Лагранжа и Коши
1.	Теорема Ролля. Если: 1) функция f(x) определена и непрерывна
на сегменте [а, Ь]; 2) /(*) имеет конечную производную f'(x) внутри этого
сегмента; 3) f(a) = f(b), то существует по меньшей мере одно число с из
интервала (а, Ь) такое, что
Пс) = 0.
2.	Теорема Лагранжа. Если: 1) функция f{x) определена и непре¬
рывна на сегменте [а, Ь]; 2) f(x) имеет конечную производную /'(х) на
интервале (а, Ь), то
f(b) - f(d) = (b - a)f'(c), где a < с < b
(формула конечных приращений).
3.	Теорема Коши. Если: 1) функции f(x) и g(x) определены и непре¬
рывны на сегменте [а, Ь]; 2) f(x) и g(;t) имеют конечные производные
/'(х) и g'(x) на интервале (а, Ь); 3) /'2(jc) -I- g'2(x) & 0 при а < х < Ь;
4)	g(a) * g(b), то
f(b)-f(a) = Ш
g(b)-g(a) g'(c)'
где а < с < Ь.

118 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1235.	Проверить справедливость теоремы Ролля для функции
f{x) = (х - 1)(х - 2)(х - 3).
1236.	Функция
f(x) = 1 - 3Jx*
обращается в нуль при хх = -1 и х2 = 1, но тем не менее f'(x) ^ О
при -1 < х < 1. Объяснить кажущееся противоречие с теоремой
Ролля.
1237.	Пусть функция f(x) имеет конечную производную f'(x)
в каждой точке конечного или бесконечного интервала (а,'Ь) и
lim f(x) = lim f(x).
х a +0	x-~ b-0
Доказать, что
Пс) = О,
где с — некоторая точка интервала (а, Ь).
1238.	Пусть: 1) функция f(x) определена и имеет непрерыв¬
ную производную (п - 1)-го порядка f{n ~ 1](х) на сегменте [х0, хп];
2) f(x) имеет производную /i-го порядка fin)(x) в интервале (х0, хп)
и 3) выполнены равенства
f(x0) = fixt) = ... = f(xn) (х0 < *i < ... < хп).
Доказать, что в интервале (*0, хп) существует по меньшей ме¬
ре одна точка £ такая, что
/(Я)Й> = 0.
1239.	Пусть: 1) функция f(x) определена и имеет непрерыв¬
ную производную (р + q)-ro порядка + г/)(х) на сегменте [а, b];
2) f(x) имеет производную (р 4- q + 1)-го порядка + q + x)(jc) в
интервале (а, Ь); 3) выполнены равенства
Да)=Г(а)=... = /(р>(а) = 0,
= m = ... = №) = 0.
Доказать, что в таком случае
+ (С) = 0,
где с — некоторая точка интервала (а, Ь).
1240.	Доказать, что если все корни многочлена
Рп(х) = а0хп + агхп ~1 + ... + ап (а0 * 0)
с действительными коэффициентами ак (k = 0, 1, ..., п) вещест¬
венны, то его последовательные производные Р,[(х), Р„(х), ...,
Р{п ~1)(х) также имеют лишь вещественные корни.

§ 6. Теоремы Ролля, Лагранжа и Коши
119
1241.	Доказать, что у многочлена Лежандра
1 dn г/ 2
РП(Х) =
2nn\dxn
{(X2 - 1)"}
все корни вещественные и заключены в интервале (-1, 1).
1242.	Доказать, что у многочлена Чебышева—Лагерра
LAx)-s£-.(fe-‘)
все корни положительные.
1243.	Доказать, что у многочлена Чебышева—Эрмита
Нп(х) = (-1Ге*г£-п(е**)
все корни вещественные.
1244.	Найти на кривой у = xz точку, касательная в которой
параллельна хорде, соединяющей точки А (-1, -1) и В (2, 8).
1245.	Верна ли формула конечных приращений для функции
/(*)=!
на сегменте [а, Ь]> если ab < О?
1246.	Найти функцию 0 = 0(лг, Ах) такую, что
f(x + Ах) - fix) = Axf\x + 0Ajc) (0 < 0 < 1),
если:
a) f(x) = ах2 + Ъх + с (а* 0); б) f(x) = х3;
В) /(*) = i ;	г) f(x) = ех.
1246. 1. Пусть f(x) € С(1) (-оо, +оо) и для любых х и h спра¬
ведливо тождество:
f(x + h) - f(x) = hf'(x).
Доказать, что
f(x) = ах + b,
где а и Ъ — постоянные.
2.	Пусть fix) € С(2) (-оо, -h оо) и для любых х и h справедливо
тождество:
f(x + h) - fix) = hf'[x + I] .
Доказать, что
fix) = ах2 + Ъх + с,
где а, 6 и с — постоянные.

120 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1247.	Доказать, что если х > 0, то
I
k = 1
Jx + 1 - Jx = 	 			 ,
2jx + Q(x)
где i < 0(jc) < |, причем
lim 0(*) = I,
4
lim 0(*)=I
x — +oo	Z
1248. Пусть
fix) = <
S-x2
2
1
л:
при 0 < x < 1,
при 1 < X < +оо.
Определить промежуточное значение с формулы конечных при¬
ращений для функции f(x) на сегменте [0, 2].
1249.	Пусть /(х) - /(0) = */'(£(*)), где 0 < £(*) < х. Доказать,
что если
f(x) = х sin (In х) при х > 0 и /(0) = 0,
то функция £ = £(#) разрывна в любом сколь угодно малом ин¬
тервале (0, е), где е > 0.
1250.	Пусть функция f(x) имеет непрерывную производную
f\x) в интервале (а, Ь). Можно ли для всякой точки £ из (а, Ь)
указать две другие точки хг и х2 из этого интервала такие, что
= т (х1<$<х2)?
Х2 - Х\
Рассмотреть пример: fix) = х3	(-1 < х < 1), где £ = 0.
1251.	Доказать неравенства:
а)	|sin х - sin у\ < \х - у\;
б)	РУр~1 ix - у) < хр - у9 < рхР~1 (х - у), если 0<у<хир>1;
в)	|arctg а - arctg Ъ\ < \а - Ь\;
г)	IzA < in 2 <	если 0 < b < а.
а	b Ъ
1252.	Объяснить, почему не верна формула Коши для функций
f(x) = х2 и giх) = JC3
на сегменте [-1, 1].
1253.	Пусть функция f(x) дифференцируема на сегменте
[х19 х2], причем хх х2 > 0. Доказать, что
1
*1-*2
*1 х2
fixi) f(x2)
= т - ът,
где < £ < х2.

§ 6. Теоремы Ролля, Лагранжа и Коши
121
1254.	Доказать, что если функция f(x) дифференцируема, но
не ограничена на конечном интервале (а, b), то ее производная
f'(x) также не ограничена на интервале (а, Ь). Обратная теорема
не верна (построить пример).
1255.	Доказать, что если функция f(x) имеет в конечном или
бесконечном интервале (а, Ь) ограниченную производную /'(*),
то f(x) равномерно непрерывна на (а, Ь).
1256.	Доказать, что если функция f(x) дифференцируема в
бесконечном интервале (х0, +оо) и
lim f\x) = О,
X -*• +оо
ТО
lim	= О,
х -* +оо X
т. е. f(x) = о(х) при х
1257.	Доказать, что если функция f(x) дифференцируема в
бесконечном интервале (х0, +оо) и
f(x) = о(х) при х -+ +оо,
то
lim \f'(x)\ = 0.
X — +оо
В частности, если существует lim f\x) = k, то k = 0.
* — +оо
1258.	1. Доказать, что если: 1) функция f(x) определена и не¬
прерывна на сегменте [х0, X]; 2) f(x) имеет конечную производ¬
ную f'(x) в интервале (*0, X); 3) существует конечный или бес¬
конечный предел
lim f\x) = f\x о + 0),
X — JC0+OO
то существует соответственно конечная или бесконечная одно¬
сторонняя производная fl(x0) и
П(Х о) = Пх о + 0).
2.	Показать, что для функции
f(x) = arctg	(х 1) и /(1) = 0
существует конечный предел lim f'{x), однако функция f(x) не
X —* 1
имеет односторонних производных /1(1) и /|( 1). Дать геометри¬
ческую иллюстрацию этого факта. Однако в этой точке сущест¬
вуют обобщенные односторонние производные (см. 1009.2).

122 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1259.	Доказать, что если f'(x) = 0 при а < х < Ь, то
f(x) = const при а < х <Ь.
1260.	Доказать, что единственная функция f(x) (-00 < х < +°°),
имеющая постоянную производную
f'(x) = k,
есть линейная функция
f(x) = kx + b.
1261.1.	Что можно сказать о функции f(x)> если fn\x) = 0?
2.	Пусть f(x) € С(00) (-°о, + °°) и для каждого х сущест¬
вует натуральное число пх (пх < п) такое, что
= о.
Доказать, что функция f(x) есть полином.
1262.	Доказать, что единственная функция
У = У(х) (-оо < х < +оо),
удовлетворяющая уравнению
у' = Ху (к = const),
есть показательная функция
у = СеХх,
где С — произвольная постоянная.
Указание. Рассмотреть (уе~Хх)'.
1263.	Проверить, что функции
f(x) = arctg ,
g(x) == arctg x
имеют одинаковые производные в областях: 1) х < 1; 2) х > 1.
Вывести зависимость между этими функциями.
1264.	Доказать тождества:
а)	2 arctg х + arcsin 			 = я sgn х при \х\ > 1;
1 + х2
б)	3 arccos х - arccos (Sx - 4х3) = п при \х\< i .
1265.	Доказать, что если: 1) функция f(x) непрерывна на сег¬
менте [а, 6]; 2) имеет конечную производную f'(x) внутри него;
3)	не является линейной, то в интервале (а, Ь) найдется по мень¬
шей мере одна точка с такая, что
\Пс)\ >
т-т
Ъ-а
Дать геометрическую иллюстрацию этого факта.

§ 7. Возрастание и убывание функции. Неравенства
123
1266.	Доказать, что если: 1) функция /(х) имеет вторую про¬
изводную f"(x) на сегменте [а, Ь] и 2) f'(a) = /'(b) = 0, то в интер¬
вале (а, Ь) существует по меньшей мере одна точка с такая, что
|Г(С)| * iw> - л«)1-
1267.	Автомобиль, начав двигаться из некоторого пункта А,
закончил свой путь через время t9 пройдя при этом расстояние
s. Доказать, что в некоторый момент времени ускорение движе¬
ния автомобиля было не меньше .
§ 7. Возрастание и убывание функции. Неравенства
1.	Возрастание и убывание функции. Функция f(x) называется воз¬
растающей (убывающей) на сегменте [а, 6], если
f(x2) > f(xi) при а <	< jc2 < Ь
!
(или соответственно f(x2) < f(xx) при а < хх < х2 < Ь).
Если дифференцируемая функция /(х) возрастает (убывает) на сег¬
менте [а, Ь], то
/'(*) > 0 при а < х < b (или f\x) < 0 при а < х< Ь).
2.	Достаточный признак возрастания (убывания) функции. Если
функция f(x) непрерывна на сегменте [а, Ь] и внутри него имеет поло¬
жительную (отрицательную) производную /'(*)> то функция /(дс) возрас¬
тает (убывает) на [а, &].
Определить промежутки монотонности в строгом смысле
(возрастания или убывания) следующих функций:
1268.	у = 2 + х - х2.	1269. у = Зх - Xs.
2
1270*^1+*.-
1272. у = х + sin х.
1274. у = cos 5 .
1273. у = х + |sin 2х\.
1275. у = 2f .
W 9.x
1276.1/ = хпе~х (п> 0, х > 0).
1278. f(x) = х( J + sin In л: j ,
1277. у = х2 - In дс2.
если jc > 0 и /(0) = 0.
1279.	Доказать, что при увеличении числа сторон п периметр
рп правильного n-угольника, вписанного в окружность, возрас¬
тает, а периметр Рп правильного n-угольника, описанного около
этой окружности, убывает. Пользуясь этим, доказать, что рп и
Рп имеют общий предел при /г —► оо.

124 РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1280.	Доказать, что функция
возрастает на интервалах (-°°, -1) и (0, +оо).
1281.	Доказать, что целая рациональная функция
Р(х) = а0 + агх + ... + апхп (п > 1, ап ^ 0)
является монотонной (в строгом смысле!) в интервалах -л:0)
и (х0> +°°), где х0 — достаточно большое положительное число.
1282.	Доказать, что рациональная функция
^ = а0 + а\Х+ ... + апхп
Ь0 + Ъхх + ... + Ьтхт
(апЪт * 0),
отличная от тождественной постоянной, монотонна (в строгом
смысле!) в интервалах (-°°, -х0) и (*0, +°°), где х0 — достаточно
большое положительное число.
1283.	Обязательно ли производная монотонной функции
является монотонной? Рассмотреть пример: f(x) = х + sin х.
1284.	Доказать, что если cp(jc) — монотонно возрастающая
дифференцируемая функция и
|/'(*)| < ф'(^)| при х> х0,
то
|/(^) - /(*о)| < ф(л:) - Ф(^о) при х> х0.
Дать геометрическую интерпретацию этого факта.
1285.	Пусть функция f(x) непрерывна в промежутке а < х < +оо
и сверх того /'(х) > к > 0 при х > а, где k — постоянная.
Доказать, что если f(a) < 0, то уравнение f(x) = 0 имеет один
и только один действительный корень в интервале
а, а -
1286.	Функция f(x) называется возрастающей в точке х0,
если в некоторой окрестности \х - х0\ < 8 знак приращения функ¬
ции Af(x0) = f(x) - f(x0) совпадает со знаком приращения аргу¬
мента Ах0 = х - х0.
Доказать, что если функция f(x) (а < х <Ъ) возрастает в каж¬
дой точке некоторого конечного или бесконечного интервала
(а, 6), то она является возрастающей на этом интервале.
1287.	Показать, что функция
f(x) = х + х2 sin |, если х * 0 и /(0) = 0,

§ 7. Возрастание и убывание функции. Неравенства
125
возрастает в точке х = 0, но не является возрастающей ни в каком
интервале (-£, в), окружающем эту точку, где е > 0 произвольно мало.
Построить эскиз графика функции.
1288.	Доказать теорему, если: 1) функции ср(лг) и \|/(лг) /г-крат-
но дифференцируемы; 2) cp{k\x0) = \\f{k)(x0) (k = 0, 1, ..., п - 1);
3) cp(n)(x) >	при х > х0, то имеет место неравенство
(р(х) > \f/(x) при X > х0.
1289.	Доказать следующие неравенства:
а)	ех > 1 + х	при х ^ х0;
б)	х - ^ < 1п(1 + х) < х при х > 0;
X
в)	х - -- < sin х < х при х > 0;
б
г)	tg х > х + ^	при 0 < х < ^ ;
о	2
1 1
Д) (*а + уа)а > (*р + г/р)р при *>0, у>0и0<а<(3.
Дать геометрическую интерпретацию неравенств а) — г).
1290.	Доказать неравенство
2	тс
- х < sin х < х при 0 < х < - .
л	2
1291.	Доказать, что при х > 0 имеет место неравенство
(
•1 +
1Г
х)
< е <
X + 1
1292.	У арифметической и геометрической прогрессий число
членов и крайние члены соответственно одинаковы и все члены
прогрессий положительны. Доказать, что у арифметической
прогрессии сумма членов больше, чем у геометрической.
1293.	Исходя из неравенства
£ (а** + Ьк)2 > 0,
Л= 1
где х, ak, bk (k = 1, ..., п) вещественны, доказать неравенство Коши
k = 1
Z аА < Z а* ■ Z
и2
bk ^
k= i
k = i
1294.	Доказать, что среднее арифметическое положительных
чисел не больше среднего квадратичного этих же чисел, т. е.
1
п
п
Z Xk<

126 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1295.	Доказать, что среднее геометрическое положительных
чисел не больше среднего арифметического этих же чисел, т. е.
'\JxlX2...Xn < i(Xj + Х2 + ... + Хп).
Указание. Применить метод математической индукции.
1296.	Средней порядка s для двух положительных чисел а и
b называется функция, определяемая равенством
А „(а, Ь) =	> если « * О,
и
Д0(а, b) = lim As(a, Ь).
s — О
В частности, получаем: при s = -1 среднее гармоническое;
при s = 0 среднее геометрическое (доказать!); при s = 1 среднее
арифметическое; при s = 2 среднее квадратичное.
Доказать, что:
1)	min (а, Ь) < Дя (а, 6) < max (а, Ь);
2)	функция Дя (а, 6) при а ^ b есть возрастающая функция
переменной s;
3)	lim As (а, 6) = min (а, ft);	lim As (а, b) = max (a, ft).
S — -oo	5 — 4-00
Указание. Рассмотреть [In Д, (a, b)].
as
1297.	Доказать неравенства:
а)	ха - 1 > а(л: - 1) при а> 2, х> I;
б)	'i/je - nJa < nJx - а , если п> I, х > а > 0;
в)	1 + 2 In х < х2 при х > 0.
§ 8. Направление вогнутости. Точки перегиба
1. Достаточные условия вогнутости. График дифференцируемой
функции у = f(x) называется вогнутым вверх или выпуклым вниз (вог¬
нутым вниз или выпуклым вверх) на сегменте [а, Ь], если отрезок кривой
У = № (а<х<Ь)
расположен выше (соответственно ниже) касательной, проведенной в
любой точке этого отрезка. Достаточным условием вогнутости графика
вверх (вниз), в предположении существования второй производной
f"(x)> является выполнение неравенства
/"(*) > 0 (f"(x) < 0) при а < х <Ь.

§ 8. Направление вогнутости. Точки перегиба
127
2. Достаточное условие точки перегиба. Точки, в которых меняется
направление вогнутости графика функции, называются точками пере¬
гиба. Точка х0, для которой либо f"(x0) = 0, либо f'\x0) не существует,
причем f\xо) имеет смысл, есть точка перегиба, если f"{x) меняет свой
знак при переходе через значение х0.
1298.	Исследовать направление вогнутости кривой
y=l + 3Jx
в точках А(-1, 0), Б(1, 2) и С(0, 0).
Найти промежутки вогнутости определенного знака и точки
перегиба графиков следующих функций:
1299. у = 3х2- х3.
1300. у- “2 . (о > 0).
у а2+х2 v 7
5
1301. у = х + X*.
1302. у = л/ГГ*2.
1303. у = х + sin х.
1304. у = е-*2.
1305.	у = In (1 + х2).
1306.	у = х sin (In х) (х > 0).
1308. Показать, что кривая
1307. у = хх (х>0).
имеет три точки перегиба, лежащие на одной прямой.
Построить график этой функции.
1309.	При каком выборе параметра h «кривая вероятности»
у = jLe-hV (Л > 0)
Jn
имеет точки перегиба х = ±а?
1310.	Исследовать направление вогнутости циклоиды
х = a(t - sin t), у = а( 1 - cos t) (а > 0).
1311.	Пусть функция f(x) дважды дифференцируема в про¬
межутке а < х < +оо, причем: 1) f(a) = А > 0; 2) f(a) < 0;
3)	f"(x) < 0 при х > а.
Доказать, что уравнение f(x) = 0 имеет один и только один
действительный корень в интервале (а, +оо).
1312.	Функция f(x) называется выпуклой снизу (сверху) на
интервале (а, 6), если для любых точек хг и х2 из этого интервала
и произвольных чисел и Х2 (A,j > 0, Х2 > 0,	+ Х2 = 1) имеет
место неравенство
/(Xi*! + Х2х2) < Xifixj) + X2f(x2)

128 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
(или соответственно противоположное неравенство)
/(А.!*! + Х2х2) >	+ X2f(x2).
Доказать, что: 1) функция /(*) выпукла снизу на (а, Ь)9 если
f"(x) > 0, при а < х < Ь\ 2) f(x) выпукла сверху на (а, Ь)9 если
f"(x) < 0, при а < х <Ъ.
1313.	Показать, что функции
хп (п > 1), ех, х In х
выпуклы снизу на интервале (0, +°°), а функции
хп (0 < п < 1), In х
выпуклы сверху на интервале (0, +оо).
1314.1.	Доказать неравенства и выяснить их геометрический
смысл:
а)	| (хп + уп) >	(х > 0, у > 0, х * у, n > 1);
б)	~Т~ > е 2 {х * уУ’
в)	х In х + у In у > (х + у) In , если х > 0 и у > 0.
2.	Пусть f"(x) > 0 при а < х < Ь. Доказать, что
firr1) < lU{Xl) + f(X2)]
при любых х19 х2€ [а, Ь].
1315.	Доказать, что ограниченная выпуклая функция всюду
непрерывна и имеет односторонние левую и правую производ¬
ные.
1316.	Пусть функция f(x) дважды дифференцируема в интер¬
вале (а, Ь) и /"(4) * 0, где а <^<Ь.
Доказать, что в интервале (а, Ь) можно найти два значения
хх и х2 такие, что
f(X2) ~ f(Xl) _
jc2-*i
1317.	Доказать, что если функция f(x) дважды дифференци¬
руема в бесконечном интервале (дг0, +оо) и
Иш /(дг) = 0, lim /(х) = 0,
х-*х0+0	х — +оо
то в интервале (дг0, +оо) имеется по меньшей мере одна точка £
такая, что /"(£) = 0*

§ 9. Раскрытие неопределенностей
129
§ 9. Раскрытие неопределенностей
Правило Лопиталя. Случай 1-й: раскрытие неопределенности ви¬
да jj . Если: 1) функции /(х) и g{х) определены и непрерывны в некото¬
рой окрестности С/е,) точки а, где а — число или символ оо, и при х —>
а обе стремятся к нулю:
lim f(x) = lim g(x) = 0;
x —• a	x — a
2) производные f'(x) и g'(x) существуют в окрестности UE точки а, за
исключением, быть может, самой точки а, причем одновременно не об¬
ращаются в нуль при х а; 3) существует конечный или бесконечный
предел
lim
х -* а
£1*1
то имеем
Пш 11*1 = Пт £1*1.
ж-* a g(x) х -+ a g' (X)
Случай 2-й: раскрытие неопределенности вида —. Если:
оо
1) функции f(x) и g(x) при да стремятся к бесконечности:
lim f{x) = lim g(x) = оо,
x~* a	x a
где a — число или символ °o; 2) производные f'(x) и g'(x) существуют
для всех xt принадлежащих некоторой окрестности Ut точки а и отлич¬
ных от а у причем
f'2(x) + g'2(x) * 0 при х 6 Ue и х * а;
3) существует конечный или бесконечный предел
то
lim £1*1,
X — a g (л:)
lim Я£] = lim
х * и g( х)	х * и
£1*1
Аналогичные правила справедливы для односторонних пределов.
Раскрытие неопределенностей видов 0 • оо, оо - оо, 1°°, 0° и т. п.
путем алгебраических преобразований и логарифмирования приводит¬
ся к раскрытию неопределенностей двух основных типов:
0 оо
- и — .
Под окрестностью Ut точки а понимается совокупность чисел х9 удов¬
летворяющих неравенству: 1) 0 < \х - а\ < е, если а — число; 2) |jc| > i , если
е
а — символ оо.

130 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Определить значения следующих выражений:
1318. lim
sina*
х —* о siпЪх
1319. lim g^*-cos*,
х-0
1320. lim ЛГУ.-.Д .
х - • о х — sin л:
1322. Иш .
П tgX
Х 2
1324. lim Vtg*-1
х - - 2 sin2 л: - 1
4
1326. lim
1 - cos л;2
1321. lim ЛВ*Х- 12tg* ,
x-+o 3sin4jt - 12sin:e
1323. lim ^g*-1.
1325. lim ^.+ 1)~2(gJ-l) _
x-+0	X3
1327 lim arcsin2* - 2arcsine
* x-o	x3
x^o x2sinx2
1328.	lini ^ Ja arctg - Jb arctg j .
1329.	lim *-—pnx (a > 0).
x -> 0
1331. lim MfinH)
x —»о ln(sin&:e)
1333.	lim coB(Bin«)-cos«
x-0	X4
1330. lim {„ х'~х ) .
x —* 1 Vlnx- x+ 1J
1332. lim -'-n-(cosa*).
x — o ln(cosbjc)
1334.	lim ifj- - -L) .
x —* o Athx	tgxj
1335.	lim Arsh (sh x) - Arsh (sin л:)	Arsh x = ln(jc+
shx-sin^
x — 0
1336. lim ^ (e > 0).
X-+00 Xе '	’
1337.	lim — (a > 0, n > 0).
X — f oo etf-r
1338.	lim -SJ-.
x — о л:1000
1340. lim In л: • In (1 - x).
x- 1-0
1342. lim xx.
x —• +0
1344. lim (x*x - 1).
x * 0
1346. lim x} ~x .
X- 1
1348. lim (tg x)tg2*.
n
X~* 4
1350. lim fin .
x +0 \ xj
1339.	lim xV0’01*.
X — +00
1341. lim xe In л: (e > 0).
x — +0
1343. lim xxX ~ *.
x — 0
1345. lim x1 + lnjr.
x —* +0
1347. lim (2 - x) ^ .
X —♦ 1
1349. lim (ctg x)sin *.
x - о
1351. lim ftg -Si-Y'*.
x — oo v	2x + 17

§ 9. Раскрытие неопределенностей
131
1352. lim te'l
х-а vtgа)
ctg(x-o)
1353. lim |
ж-O
fa*- jelna'
jelnb,
1355. lim
X — 1
f— --
Unx x
1356. lim f ctg x - ^ .
i-«\	xj
1357. lim
Jm Г	1	1 1.
*-0 Lln(AT+Vm2) ln(l + ЛС) J
1358. lim
ax - xa
x - a x-a
(a > 0).	1359. lim <1 + *^~e
1360. lim (а + хУ~аХ (a > 0).	1361. lim f- arctgjcY.
x~* 0	X2	x-* +oo V7t	J
1362. lim (th x)x.
1363. a) lim Гагсвжплгу.
x -* 0 V x )
В) lim
x-0 V X J
6) lim f^V;
* —» 0 \ x J
Д) lim
( Arshjc"\j
x-+0 V x J
1_ 1 /JC
1364. lim
x —* o	e
1366. lim {22HV2.
x-+ о V ch# )
Г) lim f arctg^y1,.
где Arsh x = In (x + J1 + x2).
(o	\i/x
1365. lim - arccos x
x-o\n	)
1367. lim 	lnch* .
x~*° mJoh.x - Vchx
1368.	a) lim f	;	6) lim	.
*-ol 2 J	*-+oo (In*)*
1369.	lim \l/x* + x2 + x + 1 - Jx2 + x + 1 • ln(e* + *)l.
X-+oo L	x J
1370.	lim ^(x + a)1* - x1 + x7°~^.
1371.	Найти lim ^ , если кривая у = f(x) входит при д: —► О
х — о х
начало координат (0, 0) (lim f(x) = 0) под углом а.
х * О

132 РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1372.	Доказать, что Пт л/(х) = 1, если непрерывная кривая
х — +о
у = f(x) входит при х —* +0 в начало координат ( lim f(x) = 0) и
х — +о
при 0 < х < г целиком остается внутри острого угла, образован¬
ного прямыми: у = -kx и у = kx (k^ °°).
1373.	1. Доказать, что если для функции f(x) существует вто¬
рая производная /"(*), то
/"(*) = Иш f(x+h) + f(x-h)-2f(x) _
/г —* 0	ll2
2.	Исследовать на дифференцируемость в точке х = 0 функ¬
цию:
1
/(*> = s
х
1
2
1
ех- 1
если х ^ 0;
если х = 0.
3.	Найти асимптоту кривой
У =
(х > 0).
(1 + *)*
1374.	Исследовать возможность применения правила Лопи-
таля к следующим примерам:
a) lim
*zsin-
х ,
sin*
б) lim
sin* ,
*oo *+Sin*
в)	цт g~2x(cos* + 2 sin*) + e~x2sin2* .
x-++°o	<rx(cos*+sin*)
r\ um l + * + sin*cos*
1	jc-oo (* + sin*cos*)esinx ’
1375.	Найти предел отношения площади кругового сегмента,
имеющего хорду Ь и стрелку А, к площади равнобедренного треуголь¬
ника, вписанного в этот сегмент, если дуга сегмента при неизменном
радиусе R стремится к нулю. Пользуясь полученным результатом,
вывести приближенную формулу для площади сегмента: S
§ 10. Формула Тейлора
1. Локальная формула Тейлора. Если: 1) функция /(*) определена
в некоторой окрестности |* - *0| < е точки *0; 2) /*(*) имеет в этой окрест¬
ности производные /*'(*), •••, fn~l)(x) до (п - 1)-го порядка включительно;
3) в точке *0 существует производная п-го порядка Рп)(х0)9 то
п
f(x) = ^ ак(х - х0)к + о(х - х0)п,
k = 0
(1)

§10. Формула Тейлора
133
где
„ _ /<*>(*<,)
°к ft!
В частности, при х0 = 0 имеем
(6 = 0, 1,	п).
№ = Z +	(2)
к = О
При указанных условиях представление (1) единственно.
Если в точке х0 существует производная /(л +	т0 остаточный
член в формуле (1) может быть взят в виде 0*((* - л:0)л + !).
Из локальной формулы Тейлора (2) получаем следующие пять важ¬
ных разложений:
I.	ех = 1 + * +	+ ... + ^ + о(лг").
II.	sin *-«-§: + ...+(-!r-'jg^+obP).
III.	сое ж - 1 - |j + ... + (-1)" ^ + 0(х2я + ■).
IV.	(1 + х)т = 1 + тх + т^т~ ^ Ж2 + ...
+ т(т-1)...(т-п+1) х„ + о(хП)
п\
V. In (1 + х) = х - ^ + ... + (-1)" -1 — + о(хп).
2	п
2.	Формула Тейлора. Если: 1) функция f(x) определена на сегменте
[а, Ь]; 2) f(x) имеет на этом сегменте непрерывные производные /'(*), ...»
f{n " 1)(jc); 3) при а < х < b существует конечная производная /(л)(л;), то
п - 1
т = Y <* - а>*+ д»(*>
k = о
где
Rn(x) _ fM{a + Q{x-a}) (JC _ау (0 < 0 <
п\
(остаточный член в форме Лагранжа), или
Д„(*) - /<n)(-7+-0|.(";,T---- (1 - 0,)л‘ \х - а)” (0 < 9, < 1)
(п- 1)!
(остаточный член в форме Коши).
1376.	Многочлен
Р(х) =1 + Зх + 5хг- 2х3
расположить по целым неотрицательным степеням двучлена х + 1.

134 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Написать разложения по целым неотрицательным степеням
переменной х до членов указанного порядка включительно сле¬
дующих функций:
до члена с х4. Чему равно /(4)(0)?
1 - х + х2
100
1377. f(x) =
1378.	^		гг до члена с х“
(l-2*)40(l + 2*)60
1379.	mJam + х (а > 0) до члена с х2.
1380.	V1 - 2х + xs - 3Jl - Зх + х2 до члена с х2.
1381.	е2х~х2 до члена с хь.
1382.	—— до члена с х4.	1383. Vsin л:3 до члена с х13.
ех- 1
1384. In cos х до члена с х6	1385. sin (sin х) до члена с х3.
1386. tg х до члена с х5.	1387. In до члена с хб.
х
1388.	Найти три члена разложения функции f(x) = Jx по це¬
лым неотрицательным степеням разности х - 1.
1389.	Функцию f(x) = Xх - 1 разложить по целым неотрица¬
тельным степеням бинома х - 1 до члена с (х - I)3.
1390.	Функцию у = a ch - (а > 0) в окрестности точки х = 0
а
приближенно заменить параболой 2-го порядка.
1391.	Функцию f(x) = л/1 + х2 - х (х > 0) разложить по целым
неотрицательным степеням дроби ~ до члена с ^ .
1392.	Найти разложение функции f(h) = In (х + h) (х > 0) по
целым неотрицательным степеням приращения h до члена с hn
(п — натуральное число).
1393.1.	Пусть
f(x + h) = f(x) + hf\x) + ... + —fn\x + 0Л)
n\
(0 < 0 < 1), причем fin + 1}(x) * 0.
Доказать, что
lim 0 = -i- .
/1-0 n+1
2. Пусть при x —>> 0 имеем
f(x) = 1 + kx 4- o(x).
Доказать, что

§ 10. Формула Тейлора
135
3.	Пусть f(x) € С(2)[0, 1], /(0) = /(1) = 0, причем \f"(x)\ < А при
х £ (0, 1). Доказать, что
\f'(x)\ < ^ при 0 < * < 1.
4.	Пусть f(x) (-оо < х < +оо) — дважды дифференцируемая
функция и
Mk = sup |/(Л)(л:)| < +оо (k = 0, 1, 2).
-оо < ДГ < | IX)
Доказать неравенство
Ml < 2М0М2.
1394. Оценить абсолютную погрепшость приближенных формул:
а) е* ~ 1 + л: +	+ ... + ^ при 0 < х < 1;
б) sin х ~ х
при |jc| <
2 ’
в)	tg д: ~ х +	при |дс| < 0, 1;
О
г) Jl + X ~ 1 + £ - ~ при 0 < X < 1.
2	8
1395.1.	Для каких х справедлива с точностью до 0,0001 при¬
ближенная формула:
cos х = 1 - — ?
2
2. Доказать формулу
nJan + х = а +
пап~1
(п > 2, а > 0, X > 0), где 0 < г < ^-1	.
2п2 а2п~1
1396.	С помощью формулы Тейлора приближенно вычислить:
a) V30 ;	б)	V250 ;	в) 12 * *Т4000 ;
г)	Je ;	д)	sin 18°;	е) In 1, 2;
ж)	arctg 0,8;	з) arcsin 0,45;	и) (1, I)1,2
и оценить погрешность.
1397.	Вычислить:
а)	е с точностью до 10“9;
б)	sin 1° с точностью до 10~8;
в)	cos 9° с точностью до 10-5;
г)	л/5 с точностью до 10 4;
д)	lg 11 с точностью до 10 5.

136 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Используя разложения I—V, найти следующие пределы:
г2
1398.	lim
jc —* О
1399.	lim
х —* О
cos* - е
gxsin х — х(1 + х)
1400.	lim х2 (Jx + 1 + Jx - 1 -2 Jx).
X — 4-00
1401.	lim (%/xCl -f xb - Vx(i - xh).
X — 4*00
1402.	lim ^ ж3 - л:2 + |j e' - Jxfi + 1 j.
1403.	lim a\+aJ~2 (a > 0).
jr-0	X2
1404.	lim [* - x2 ln^l + !jj .
1405.	lim f i - -±-) .
x-o U sin*;
1406.	a) lim if! - ctg x);
*-o x\x	J
в) lim 1-(С05/)8|',х;
6) iim sin (sinx) - xi/1 - x2.
д 0
* - 0
г) lim sh(tgx)-x
x —* 0	v*
Для бесконечно малой при л: —> 0 величины у определить глав¬
ный член вида Схп (С — постоянная), если
1407.	у = tg(sin х) - sin(tg х).
1
1408.1/ = (1 + х)х - 1.	1409. // = 1 - (1 *	.
1410.1.	При каком подборе коэффициентов а и b величина
х - (а + b cos х) sin х
будет бесконечно малой 5-го порядка относительно *?
2. Подобрать коэффициенты Ап В так, чтобы при лг-^0 имело
место асимптотическое равенство
ctg* = rrlS+0(*5)-
3.	При каких коэффициентах А, Б, С и D справедлива при
д: —> 0 асимптотическая формула
ех __ 1 + Ах + В х2
1 + Cx + Dx2
+ 0(*5).

§11. Экстремум функции. Наибольшее и наименьшее значения функции 137
1411. Считая |л:| малой величиной, вывести простые прибли¬
женные формулы для следующих выражений:
1412.	Считая * малым по модулю, вывести приближенную
формулу вида
х = a sin * + (3 tg х
с точностью до члена с х5.
Применить эту формулу для приближенного спрямления дуг
малой угловой величины.
1413.	Оценить относительную погрешность следующего пра¬
вила Чебышева: круговая дуга приближенно равна сумме боко¬
вых сторон равнобедренного треугольника, построенного на хор-
~ /4
де этой дуги и имеющего высотой /- ее стрелки.
§ 11. Экстремум функции.
Наибольшее и наименьшее значения функции
1.	Необходимое условие экстремума. Говорят, что функция f(x) имеет
в точке *0 экстремум (максимум или минимум), если функция определена
в двухсторонней окрестности точки х0 и для всех точек х некоторой об¬
ласти: 0 < |* - х0| < 5, выполнено соответственно неравенство
f(x) < f(x о) или f(x) > fix о).
В точке экстремума производная f'(x0) = 0, если она существует.
2.	Достаточные условия экстремума. Первое правило. Если: 1) функ¬
ция f(x) определена и непрерывна в некоторой окрестности \х -х0| < б
точки *0 такой, что производная f'(x0) равна нулю или не существует
(критическая точка); 2) f(x) имеет конечную производную f'(x) в области
О < |х - х0| < 6; 3) производная /'(*) сохраняет определенный знак слева
от х0 и справа от х0, то поведение функции f(x) характеризуется сле¬
дующей таблицей:
Знак производной
Вывод
* < *0
* > *0
I
+
+
Экстремума нет
II
+
-
Максимум
III
-
+
Минимум
IV
-
-
Экстремума нет

138 РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Второе правило. Если функция f(x) имеет вторую производную
/"(*)> причем в некоторой точке х0 выполнены условия
f\xо) = 0 и f"(xо) * О,
то в этой точке функция f(x) имеет экстремум, а именно:
максимум, когда f"(x о) <0, и минимум, когда f"(x 0) > 0.
Третье правило. Пусть функция f(x) имеет в некотором интервале
\х - х0\ < 8 производные /'(*), •••» fn~l(x) И в точке х0 производную f(n)(x0),
причем
f(k)(xo) = 0 (k = 1, ..., п - 1), fin\xQ) * 0.
В таком случае: 1) если п — число четное, то в точке х0 функция f(x)
имеет экстремум, а именно: максимум при f (л)(я:0) < 0 и
минимум при f{n\x0) > 0; 2) если п — число нечетное, то в точке х0
функция f(x) экстремума не имеет.
3.	Абсолютный экстремум. Наибольшее (наименьшее) значение на
сегменте [а, Ь] непрерывной функции f(x) достигается или в критиче¬
ской точке этой функции (т. е. там, где производная f'(x) или равна ну¬
лю, или не существует), или в граничных точках а и b данного сегмента.
Исследовать на экстремум следующие функции:
1414.	у = 2 + х - х2.
1415.	у = (х - I)3.
1416.	у = (х- I)4.
1417.	у = хт (1 - х)п (тип — целые положительные числа).
1418.	у = cos х + ch х.
1419.	у = (* + 1 )J V*.
1420.	i/=[l + x+ — ... + —)ех (п — натуральное число).
1421.	у = |х|.
1422.	у = х* (1 - х)~3.
1423.	Исследовать на экстремум в точке х = х0 функцию
f(x) = (х - х0)пф(*)
(п — натуральное число), где функция ср(л:) непрерывна при х = х0
и ф(л:) * 0.
1424.	Пусть f(x) =	, f'(x) =	и х0 — стационарная
Q(x)	Qz\x)
точка функции f(x), т. е. Pi(x0) = 0, Q(x0) * 0.
Доказать, что
sgn /"(лг0) = sgn Р; (х0).
1425.	Можно ли утверждать, что если функция f(x) в точке
х0 имеет максимум, то в некоторой достаточно малой окрестнос¬
ти этой точки слева от точки х0 функция f(x) возрастает, а справа
от нее убывает?

§11. Экстремум функции. Наибольшее и наименьшее значения функции 139
Рассмотреть пример:
Дх) = 2 - х2 ^ 2 4- sin , если х * 0 и /(0) = 2.
1426.	Доказать, что функция
f(x) = е х2, если х^Ои /(0) = О,
имеет в точке х = 0 минимум, а функция
£(х) = хе *2, если х^Ои £(0) = О,
не имеет в точке х = 0 экстремума, хотя
/(,,)(0)=0, в<я>(0) = 0 (и = 1, 2, ...).
Построить графики этих функций.
1427.	Исследовать на экстремум функции:
а) Дх) = е w ^ V2 + sin	при х ^ 0 и ДО) = 0;
б) Дх) = е W ^ л/2 + cos	при х^Ои ДО) = 0.
Построить графики этих функций.
1428.	Исследовать на экстремум в точке х = 0 функцию
f(x) = |д:| ^ 2 + cos i j , если х^Ои ДО) = 0.
Построить график этой функции.
1429. у =
Xs - бде2 + 9х - 4.
1430. у = 2х2- х4.
1431.у =
х(х - 1)2(* - 2)3.
1432. и = х + 1.
*
1433. у =
2х
1 + X2 ’
1434. у — х1~1х + 2 .
* х*+2х+\
1435. у =
л/2х - д:2 .
1436. у = х\[х - 1 .
1437. у =
хе“*.
1438.1/ = 7* In х.
1439. у =
In2*
X
1440. I/ = cos х -f i
* 2
1441.у=
10
1442. i/ = arctg x - |
Сл
1 + sin2* *
1443. у =
ех sin х.
1444. i/ = |x|e"lx "

140 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Найти наименьшие и наибольшие значения следующих
функций:
1445.	f(x) = 2х	на	сегменте	[-1; 5].
1446.	f(x) — х2 — 4х + 6 на сегменте [-3; 10].
1447.	f(x) = \х2 - Зх + 2| на сегменте [-10; 10].
1448.	f(x) = х + i	на	сегменте	[0,01; 100].
1449.	f(x) = л/5 - 4х на сегменте [-1; 1].
Найти нижнюю грань (inf) и верхнюю грань (sup) следующих
функций:
1450.	f(x) = хе~0,01х на интервале (0, +оо).
1451.	f(x) = ^1 + * +	+ ... + е~х на интервале (0, +оо).
1452.	f(x) =	на интервале (0, +оо).
1453.	f(x) = е~%2 cos х2 на интервале (-°°, +°о).
1454.	1. Определить нижнюю и верхнюю грани функции
/(£) = з + ф на интеРвале х < £ < +°°* Построить графики функций
М(х) = sup /(£) и 7n(x)= inf /(£).
X « ' £ < + <»	X < £ < + «>
2. Пусть
М* = sup|/<*>(x)l, к = 0, 1,2
х
Найти М0, Mj и М2, если /(лс) =	.
1455.	Определить наибольший член последовательности:
а)	2^ (п = 1, 2, ...);
2"
в)	nJn (л = 1, 2, ...).
1456.	1. Доказать неравенства:
а)	\3х - х3\ < 2 при |лс| < 2; б)б)	27ГГ <	+ (1 - *Y < 1,
б)
Jn
п+ 10000
(п = 1, 2, ...);
если 0<х< 1 ир> 1;
в)	лст (а-х)п<
тпПп а т+п
(т + л)т + п
при т>0,л>0и0<л:<а;
г) < nJxn + ап < х + а (х > 0, а > 0, п > 1);
2~
д)	|а sin х + Ъ cos х\ < л/а2 + Ь2.

§11. Экстремум функции. Наибольшее и наименьшее значения функции 141
2. Доказать неравенства
2	< . х2+Л . < 2
3	х2 + х + 1
при -ОО < X < +оо.
1457.	Определить «отклонение от нуля» многочлена
Р(х) = *(* - 1)2(х + 2)
на сегменте [-2, 1], т. е. найти
ЕР = sup |Р(х)|.
-2 < х < 1
1458.	При каком выборе коэффициента q многочлен
Р(х) = х2 + q
наименее отклоняется от нуля на сегменте [-1, 1], т. е.
ЕР = sup |jP(jc)| = min.
-1 < X £ 1
1459.	Абсолютным отклонением двух функций f(x) и g(x)
на сегменте [а, b] называется число
А = sup |/(х) - g(*)|.
« < .г < b
Определить абсолютное отклонение функций:
f(x) = х2 и g(x) = х3
на сегменте [0, 1].
1460.	Функцию
f(x) = X2
на сегменте [х1У х2] приближенно заменить линейной функцией
g(x) = (Xj + х2)х + b
так, чтобы абсолютное отклонение функций f(x) и g(x) (см. пре¬
дыдущую задачу) было наименьшим, и определить это наимень¬
шее абсолютное отклонение.
1461.	Определить минимум функции
f(x) = max {2|х|, |1 + х|}.
Определить число вещественных корней уравнения и отде¬
лить эти корни, если:
1462.	х3 - 6х2 + 9х - 10 = 0.
1463.	х3 - Зх2 - 9х + h = 0.
1464.	Зх4 - 4х3 - 6х2 + 12х - 20 = 0.
1465.	х5 - 5х = а.
1466.	In х = kx.
1467.	= ах2.
1468.	sin3 х • cos x = а при 0 < x < n.
1469.	ch x = kx.

142 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1470.	При каком условии уравнение
х* -f рх -f q = 0
имеет:
а)	один вещественный корень;
б)	три вещественных корня?
Изобразить соответствующие области на плоскости (р, q).
§ 12. Построение графиков функций
по характерным точкам
Для построения графика функции у = f{x) нужно: 1) определить об¬
ласть существования этой функции и исследовать поведение функции
в граничных точках последней; 2) выяснить симметрию графика и пе¬
риодичность; 3) найти точки разрыва функции и промежутки непре¬
рывности; 4) определить нули функции и области постоянства знака;
5)	найти точки экстремума и выяснить промежутки возрастания и убы¬
вания функции; 6) определить точки перегиба и установить промежут¬
ки вогнутости определенного знака графика функций; 7) найти асимп¬
тоты в случае существования их; 8) указать те или иные особенности
графика. В частных случаях общая схема упрощается.
В задачах, отмеченных звездочкой, точки перегиба определяются
приближенно.
J2
Построить :
1471. у=3х- х2.
1473. у = (х + 1)(х - 2)2
1475**'-гЙ1Тб-
1477-»=<w
1479
1	10 +
1472. у = 1 + х2 -	.
у 2
1474*. у =	.
у 1 + ЛГ4
1476*. у = (1 + ж)(1_ж)2
1478-Игт!)‘-
1480. у = —-— .
У (1-л;2)2
1482*. у =	•
х3+ 1
1483. у = —- ^ + — .
1 + х Зх2 1-х
1485. а) г/ == ±JSx2 - х4 ; б) у = —=
Jx2 + 1
1484. у = (х - 3) Jx .
х - 2
I486, у = ±J(x - 1)(х-2)(х-3). 1487*. у = Ух3 - х2 -
1488. у=Ух~2 -Ух2 + 1 .	1489. // = (х + 2)2 - (л

§12. Построение графиков функций по характерным точкам
143
2 2
1490. у = (х + 1) * - (х - 1)5 .
1491. у =
1]х2 - 1
1492.у
_ x2Jx2- 1
2х2- 1
\1 + х\2
Jx
1494. у = 1 - * +	•
V3 + х
• </= g±l.
У *1х2+ 1
-•JS-
1496*
1498.у = (7 + 2 cos л:) sin х.
1500. у = cos х - i cos 2х.
w 2
1502. у = sin x • sin Зх.
1493. у
1495. у
1497. I/ = sin х + cos2 х.
1499. у
1501. у
1503. у
sin х + i sin 3jc.
sin4 * + cos4 x.
sin л:
1504.	a )y- -22S3L; б) у =	.
cos2:c	2 + cosjc
1505.	i/ = 2л: - tg л:.	1506. i/
1507. y = (1 + jc2)c-^2.
1509.	a) у = x* e~x; б) у = e~2x sin2 x.
1510.	у =	.	1511. у =
y l + x	y
1512. у =lM.	1513. у =
Jx
sin^x + ^
e2*-*2.
1508. у = x + e‘*.
7l - e-*2.
In (x + 7x^+1 ).
л/ л.
1514. i/ = л/л:2 + 1 • In (x + Jx2 + 1).
* ~ ^ ~	arr.sin r
1515. i/ = argsin^
J1 - л:2
1517. i/ = | + arcctg jc.
1519. i/ = arcsin - —	.
1 + л:2
1521. i/ = (x + 2)e* .
1523*. у = In
y	x2+1
1516. y = x + arctg л:.
1518. у
1520. i/
1522. i/
x arctg x.
1- x2
= arccos 	.
1 + x2
2 Jx2~+1 - Jx2 -1 (
1524.	у = a arcsin - - Va2 - л:2 (a > 0).
a
1525.	i/ = arccos - ~ * .	1526. у
*	1 - 2л:	*
= Jt

144 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1527*. у = X* .	1528. у = (1 + х) *.
1529*. у = х (1 + I)' (х > 0).
1530*. у =
с» -*г
1 + х2
(без исследования вогнутости).
Построить кривые, заданные в параметрической форме:
1531.x=(l±lif,	y=itLpi.
4	4
1532. х= 2t - t2,
1533*. х= —j,
у = St - fs.
y=W~L'
1534.	x = -£i- ,
1-t2
1535.	jc = t +
1536.	x = a cos 2f,
1537.	Jt = cos4 tf
1538.	x=tlnt,
y 1 + t2 ‘
г/ = H- e~2*.
i/ = a cos 31 (a > 0).
у = sin4 £.
1539.	x	, y = atg4 (a > 0).
COS’11
1540.	jc = a (sh t - t)y у = a (ch t - 1) (a > 0).
Представив уравнения кривых в параметрической форме, по¬
строить эти кривые, если:
1541.	х3 + уя - 3аху = 0 (а > 0).
Указание. Положить у = tx.
1542.	х2 + у2 = х4 + уА.	1543. х2у2 = х3 - у3.
1544.	ху = ух (х > 0у у > 0).
1545.	Построить график кривой:
ch2 х - ch2 у = 1.
Построить графики функций, заданных в полярной системе
координат (ср, г) (г > 0):
1546.	r = а + b cos ф (0 < а < Ь).
1547.	r= a sin Зф (а > 0).	1548. г =	(а > 0).
1549*. г = a-У^- , Где ф > 1 (а > 0).
Ф- 1
1550*. ф = arccos^-^-i .

§ 13. Задачи па максимум и минимум функций
145
Построить графики семейств кривых (а — переменный
параметр):
1551. у = х2 - 2х + а.	1552. у = х + — .
х
1553. у - х ± Ja( 1 - х2) •
1554. у = £ + е“х.
у 2
1555. у = хе п .
§ 13. Задачи на максимум и минимум функций
1556.	Доказать, что если функция f(x) неотрицательна, то
функция
F(x) = Cf2(x) (С>0)
имеет в точности те же точки экстремума, что и функция f(x).
1557.	Доказать, что если функция cp(jc) — монотонно возрас¬
тающая в строгом смысле при -оо < х < +оо, то функции
f(x) И ф(/(*))
имеют одни и те же точки экстремума.
1558.	Определить наибольшее значение произведения m-й и
/1-й степеней (т > 0, п > 0) двух положительных чисел, сумма
которых постоянна и равна а.
1559.	Найти наименьшее значение суммы m-й и п-й степеней
(//г > 0, п > 0) двух положительных чисел, произведение которых
постоянно и равно а.
1560.	В каких системах логарифмов существуют числа, рав¬
ные своему логарифму?
1561.	Из всех прямоугольников данной площади S опреде¬
лить тот, периметр которого наименьший.
1562.	Найти прямоугольный треугольник наибольшей пло¬
щади, если сумма катета и гипотенузы его постоянна.
1563.	При каких линейных размерах закрытая цилиндриче¬
ская банка данной вместимости V будет иметь наименьшую пол¬
ную поверхность?
1564.	В данный круговой сегмент, не превышающий полу¬
круга, вписать прямоугольник с наибольшей площадью.
1565.	В эллипс
вписать прямоугольник со сторонами, параллельными осям эл¬
липса, площадь которого наибольшая.

146 РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
1566.	В треугольник с основанием Ъ и высотой h вписать пря¬
моугольник с наибольшим периметром.
Исследовать возможность решения этой задачи.
1567.	Из круглого бревна диаметра d вытесывается балка
с прямоугольным поперечным сечением, основание которого рав¬
но b и высота h. При каких размерах балка будет иметь наиболь¬
шую прочность, если прочность ее пропорциональна bh2l
1568.	В полушар радиуса R вписать прямоугольный паралле¬
лепипед с квадратным основанием наибольшего объема.
1569.	В шар радиуса R вписать цилиндр наибольшего объема.
1570.	В шар радиуса R вписать цилиндр с наибольшей полной
поверхностью.
1571.	Около данного шара описать конус наименьшего объ¬
ема.
1572.	Найти наибольший объем конуса с данной образующей L
1573.	В прямой круговой конус с углом 2а в осевом сечении
и радиусом основания R вписать цилиндр с наибольшей полной
поверхностью.
1574.	Найти кратчайшее расстояние точки М(р, р) от пара¬
болы у2 = 2рх.
1575.	Найти кратчайшее и наибольшее расстояния точки
А(2, 0) от окружности х2 + у2 = 1.
1576.	Найти наибольшую хорду эллипса ^ 4*^ = 1 (0 < 6 < а),
а2 о2
проходящую через вершину В (0, -Ь).
X ^	м2
1577.	Через точку М(х, у) эллипса + f- = 1 провести ка¬
ст2 о2
сательную, образующую с осями координат треугольник, пло¬
щадь которого наименьшая.
1578.	Тело представляет собой прямой круговой цилиндр, за¬
вершенный сверху полушаром. При каких линейных размерах
это тело будет иметь наименьшую полную поверхность, если
объем его равен V.
1579.	Поперечное сечение открытого канала имеет форму
равнобедренной трапеции. При каком наклоне <р боков «мокрый
периметр» сечения будет наименьшим, если площадь «живого
сечения» воды в канале равна S, а уровень воды равен h?
1580.	Извилистостью замкнутого контура, ограничивающе¬
го площадь S, называется отношение периметра этого контура
к длине окружности, ограничивающей круг той же площади S.
Какова форма равнобедренной трапеции ABCD (AD || ВС), об¬
ладающей наименьшей извилистостью, если основание AD = 2а
и острый угол BAD = а?

§ 13. Задачи на максимум и минимум функций
147
1581.	Какой сектор следует вырезать из круга радиуса R, что¬
бы из оставшейся части можно было свернуть воронку наиболь¬
шей вместимости.
1582.	Завод А отстоит от железной дороги, идущей с юга на
север и проходящий через город Б, считая по кратчайшему рас¬
стоянию, на расстояние а. Под каким углом ф к железной дороге
следует построить подъездной путь от завода, чтобы транспор¬
тировка грузов из А в Б была наиболее экономичной, если стои¬
мость провоза тонны груза на расстоянии 1 км составляет по
подъездному пути р р. по железной дороге q р. (р > q) и город Б
расположен на расстоянии Ъ севернее завода А?
1583.	Два корабля плывут с постоянными скоростями и ии
по прямым линиям, составляющим угол 0 между собой. Опреде¬
лить наименьшее расстояние между кораблями, если расстояния
их от точки пересечения путей в некоторый момент были соот¬
ветственно равны а и Ь.
1584.	В точках А и Б находятся источники света соответ¬
ственно силой Бх и S2 кандел. На отрезке АБ = а найти наименее
освещенную точку М.
1585.	Светящаяся точка находится на линии центров двух
непересекающихся шаров радиусов R и г (Б > г) и расположена
вне этих шаров. При каком положении точки сумма освещенных
частей поверхности шаров будет наибольшая?
1586.	На какой высоте над центром круглого стола радиуса
а следует поместить электрическую лампочку, чтобы освещен¬
ность края стола была наибольшей?
Указание. Освещенность выражается формулой
где ф — угол наклона лучей к плоскости стола, г — расстояние источ¬
ника света от освещаемой площадки, /0 — сила источника света.
1587.	К реке шириной а построен под прямым углом канал
шириной Ь. Какой максимальной длины суда могут входить в
этот канал?
1588.	Суточные расходы при плавании судна состоят из двух
частей: постоянной, равной ар., и переменной, возрастающей
пропорционально кубу скорости. При какой скорости и плавание
судна будет наиболее экономичным?
1589.	Груз, лежащий на горизонтальной шероховатой плос¬
кости, требуется сдвинуть с места приложенной силой. При ка¬
ком наклоне этой силы к горизонту ее значение будет наимень¬
шим, если коэффициент трения груза равен k?
1590.	В чашку, имеющую форму полушара радиуса а, опущен
стержень длины I > 2а. Найти положение равновесия стержня.

148 РАЗДЕЛ И. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
§ 14. Касание кривых. Круг кривизны. Эволюта
1.	Касание л-го порядка. Говорят, что кривые
1/ = ф(х) и 1/ = 1|/(*)
имеют в точке х0 касание п-го порядка (в строгом смысле!), если
(р{к\х0) = \|/(Л)(*о) №=0,1,..., л)иф(я + 1)(jc0) * i|/(rt + 1)(лг0)- В этом случае
при х * Xq имеем:
ф(*) - ц(х) = 0*[х - х0]п + К
2.	Круг кривизны. Окружность
(* - S)2 + (у - п)2 = -R2.
имеющая с данной кривой у = f(x) касание не ниже 2-го порядка, назы¬
вается кругом кривизны в соответствующей точке. Радиус этого круга
R={i±Ml1
\у"\
1
называется радиусом кривизны, а величина k = — — кривизной.
R
3.	Эволюта. Геометрическое место центров (£, г|) кругов кривизны
(центры кривизны)
*	y'(l + i/'2)	_	, 1 + z/'2
^ =	—-й—г, ri = y + —*-
у"	у"
называется эволютой данной кривой у = f(x).
1591.	Подобрать параметры k к b прямой
у = kx + b
так, чтобы она имела с кривой
у = хЛ - Зх2 + 2
касание порядка выше первого.
1592.	При каком выборе коэффициентов а, b и с парабола
у = ах2 + Ьх + с
имеет в точке х = х0 касание 2-го порядка с кривой у = ех1
1593.	Какой порядок касания с осью Ох имеют в точке х = О
кривые:
а) у = 1 - cos х;	б) у = tg х - sin х;
В) у = ех - (l + X + y) ?
1594.	Доказать, что кривая у=ех2 при л: ^ 0 и г/ = 0 при х = О
имеет в точке х = 0 с осью Ох касание бесконечно большого порядка.
1595.	Найти радиус и центр кривизны гиперболы
ху= 1
в точках: а) М (1, 1); б) N (100; 0,01).

§14. Касание кривых. Круг кривизны. Эволюта
149
Определить радиусы кривизны следующих кривых:
1596.	у2 = 2рх (парабола).
1597.	^ + ^ =1 (а > b > 0) (эллипс).
а2	о2
1598.	= 1 (гипербола).
а2 о2
2 2 2
1599.	х3 + у 3 = а 3 (астроида).
1600.	л: = a cos £, у = Ъ sin £ (эллипс).
1601.	х = a (£ - sin 0» I/ = а (1 - cos £) (циклоида).
1602.	х = a (cos £ + £ sin £), у = а (sin £ - £ cos £) (эвольвента круга).
1603.	Доказать, что радиус кривизны линии 2-го порядка
у2 = 2рх - qx2
пропорционален кубу отрезка нормали.
1604.	Написать формулу радиуса кривизны линии, заданной
в полярных координатах.
Определить радиусы кривизны кривых, заданных в поляр¬
ных координатах (параметры положительны):
1605.	г = аср (спираль Архимеда).
1606.	г = аетр (логарифмическая спираль).
1607.	г = а (1 + cos ср) (кардиоида).
1608.	г2 = a2 cos 2ф (лемниската).
1609.	На кривой у = In х найти точку, кривизна в которой
наибольшая.
1610.	Максимальная кривизна кубической параболы у =
(О ^ х +оо, k > 0) равна . Найти точку х, в которой достига¬
ется эта максимальная кривизна.
Составить уравнения эволюты кривых:
1611.	у2 = 2рх (парабола).
1612.	= 1 (эллипс).
2 2 2
1613.	х3 + уя = а3 (астроида).
1614.	х = a In	У- - Ja2 - у2 (трактриса).
1615.	г = аеотф (логарифмическая спираль).
1616.	Доказать, что эволюта циклоиды
х = а (£ - sin £), I/ = а (1 - cos £)
есть также циклоида, отличающаяся от данной только положением.

150 РАЗДЕЛ II. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
§ 15. Приближенное решение уравнений
1. Правило пропорциональных частей (метод хорд). Если функция
f(x) непрерывна на сегменте [а, Ь] и
тт < о,
причем /' (х) 5* 0 при а < х < Ьу то уравнение
/(*) = 0 (1)
имеет один и только один действительный корень £ в промежутке (а, Ь).
За первое приближение этого корня можно принять значение
хг = а +
где
8, = -
	(м
т-Па)
(ь ~ а).
Применяя далее этот способ к тому из промежутков (а, д^) или (д^, Ь),
на концах которого функция f(х) разнозначна, получим второе прибли¬
жение х2 корня £ и т. д. Для оценки л-го приближения хп справедлива
формула
I*» - 41 <
fix „)
т
(2)
где т = inf \f'(x)\, причем
а<х<Ь
Иш х„ =
п — ОО
2. Правило Ньютона (метод касательных). Если f"(x) ^ 0 на сег¬
менте [а, Ь] и f(a)f"(a) > 0, то за первое приближение корня £ урав¬
нения (1) можно принять значение
Повторяя этот прием, получаем быстро сходящиеся к корню £ по¬
следовательные приближения £л (п = 1, 2, ...), точность которых оцени¬
вается, например, по формуле (2).
Для грубой ориентировки полезно нарисовать набросок графика
функции у = /(д:).
Пользуясь методом пропорциональных частей, определить
с точностью до 0,001 корни следующих уравнений:
1617.	х3 - 6х + 2 = 0.	1618. х4 - х - 1 = 0.
1619. х ~ 0,1 sin х = 2.	1620. cos х = х2.
Пользуясь методом Ньютона, определить с указанной точно¬
стью корни следующих уравнений:
1621.	х2 +	= 10дг (с точностью до 10_3).
1622.	х lg х = 1 (с точностью до 10~4).

§15. Приближенное решение уравнений
151
1623.	cos х • ch х = 1 (с точностью до 10 3) (два положительных
корня).
1624.	х + ех = 0 (с точностью до 10“5).
1625.	х th х = 1 (с точностью до 10"6).
1626.	С точностью до 0, 001 найти три первых положитель¬
ных корня уравнения
tg х = х.
1627.	С точностью до 10"3 найти два положительных корня
уравнения
1 _ х

РАЗДЕЛ III
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Простейшие неопределенные интегралы
1.	Понятие неопределенного интеграла. Если функция f(x) опреде
лона и непрерывна на промежутке (а, Ь) и F(x) — ее первообразная, т. е
F'(*) = f(x) при а < х < Ъу то
J f(x) dx = F(*) + С, а < х < by
где С — произвольная постоянная.
2.	Основные свойства неопределенного интеграла:
a) d £ J f(x) dx j = f(x) dx; 6) J d<b(x) = Ф(х) + C;
в) jAf(x) dx = A J f(x) dx (A = const; A * 0).
r) J U(x) + £(*)] dx = J fix) dx + j*g(x) dx.
3.	Таблица простейших интегралов:
I.
И.
III.
IV.
V.
VI.
VII.
VIII.
jV
dx =
4 C (n* -1).
/14-1
= In 1*1 + C (x * 0).
dx
arctg x + С,
2 ^-arcctg x + C.
l + x
1 — x
+ C.
arcsin x + С,
-arccos x + C.
ji
iiS-i -
|* dx
J Vl - x2
f dx = 111 \x + Jx~±l \ + C.
J Jx4A
J a* dx = у— + C (a > 0, a * 1); J ex dx = ex + C.
Jsin x dx = -cos x + С.	IX. J" cos дг </s- = sin л: + C.

§ 1. Простейшие неопределенные интегралы
153
X. f -Ц- = -ctg х + С.
J Sin^JC
XII. j*sh х dx — eh x + C.
XIV. f 4^7- = “Cth x + C.
J shzx
4.	Основные методы интегрирования.
а) Метод введения нового аргумента. Если
Г f(x) dx = F(x) + С,
XIII. Jch x dx - sh x + C.
XV. f -4r- = th * + C.
J ch2*
J f(u) dii = F(u) + C,
где и = (p(jt) — непрерывно дифференцируемая функция,
б)	Метод разложения. Если
/(*) = Л(*) + /2(*)»
то
f(x) dx = I /*,(х) dx + I f2(x) dx.
| f(x) dx = J f,(x) dx + J
в)	Метод подстановки. Если f(x) непрерывна, то, полагая
х = <р(0.
где ср(0 непрерывная вместе со своей производной (р'(£), получим
Jf(x) dx = |/(ф(О)ф'(О dt.
г) Метод интегрирования по частям. Если и и и — некоторые дип-
ференцируемые функции от х, то
I и dp ~ ии —
v du.
Применяя таблицу простейших интегралов, найти следую-
хцие интегралы:
1628.
|(3 - X2)3 dx.
1629.
j*x2(5 - x)4 dx.
1630.
j*(l - х)(1 - 2х)(1 - Зх) dx.
1631.
1632.
Г (z + 2! + «Л dx.
J \Х X2 Xs)
1633.
1634.
tfx-2 -VP+l d
) ifx
1635.
dx.
J x -lTx
1636.
f ( 1 ” jc2) dx•
1637.
Г(У27г-;!Д1-Г dXt

154
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1638. f V*4 + *:4 + 2 dx.
J X3
1640. f p*..
J 1 - x2
’ Jl + x2 + Jl - x2 dx
1639. f .
J 1 + x2
1642
Jl-x*
1643
1645.
\
, jV^Ti-TF^l dx_
Jx*- 1
f2^1-51"1 dx.
J 10*
1644. J(2* + 3*)2 dx.
1646. f	dx.
J ex+ 1
TO
1647.	j (1 + sin x + cos x) dx.
1648.	J JT - sin2x dx (0 < x < n).
1649.	Jctg2 x dx.	1650. j*tg2 x dx.
1651. J(a sh л: + b ch x) dx.	1652. Jth2 x dx.
1653.	Jcth2 x dx.
1654.	Доказать, что если
J f(x) dx = F(x) + C,
J f(ax + b) dx = i F(ax + b) + C (a * 0).
Найти интегралы:
1655. f .
J x + a
1657. JVb7
Zx dx.
1659.
1
dx
i66i. J
1663.J
(5*-2)2
dx
2 + 3x2 ’
dx
1656. J(2x-3)10 dx.
1658. f dx
J
1660.
J2 - 5x
J 1-*
J2-Zx2
1665. J («"* + e2x) dx.
1662.
1664.
f dx
J 2-Зд
Sx2
dx
f	dx
J JZx2
1666. J(sin5x - sin5a) dx.

§ 1. Простейшие неопределенные интегралы
155
1667.
r dx
1668. j
Г dx
' sin2^23: + 5j
| 1 + cos*
1669.
C dx
1670. j
Г dx
1 1 - cos* *
| 1 + sin*
1671.
f [sh(2* + 1) + ch(2* -
1)] dx.
1672.
f dx
J ch2-
2
1673.
I—,-
'■hi
Путем надлежащего преобразования подынтегрального вы¬
ражения найти следующие интегралы:
xdx
1674. J
1676. f
1678.
1680.
\
Указание, рр =2d(Jx).
Jx
1683.
1685.
1687.
1689.
1691.
J
In2*
dx.
1693.
1695. J sin5 * cos * dx.
1697. | tg x dx.
1699.
Г _sir
J 37si
sin* + cos*
dx.
1675. J x2 *V 1 + x3 dx.
3-2*2*
1677. j
( 1 + *2 )
xdx
1679. j
* *3rf*
4 + *2 *
*8 - 2 ’
dx
1681. I
* . 1 <
sin - • -
(1 + x)Jx
J
* .
1682.
*1 *
rf*
7*2+1
dx
1684. j
dx
xjx2 - 1
3 *
(*2 + l)2
xdx
1686. (
* *2 dx
3 *
(*2-1)2
J
(8*3 + 27)'
dx
1688. j
dx
7*(i + *)
*Jx(l - x)
xe~x2 dx.
1690. J
* exdx
2 + e* ’
dx
1692. 1
Г dx
J
J\ + e*x
dx
*ln*ln(ln*)
sin* dx.
1694.
1696. f
J Jcos3x
1698. J ctg x dx.
Sinjc - COSJC

156
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1700. a) f ■■■ sin-*-^  - dx; б) Г -^= dx;
J Ja2sin2x+ b2cos2л:	J Vcos2*
B) f _£OSX_ dx.
J V cos 2 x
1701. f 	^	.
J sin2xifctgx
1703. f
J sin л:
1705. f 4^.
J sh*
1.707. f ■, shxchx dx.
J Vsh4* + ch4*
1709. f	dx.
J 1 + x2
r) f	dx.
J Jch2x
1702. f ——^	—.
J sin2л: + 2cos2*
1704. f
J cos л:
1706. f 4r- •
J chx
1708. J
dx
1710.
J
ch 2xl/th2x
		dx
(arcsin^)2>s/l - x2
1711
1713. j
1715. |
1717.J
. f / In(* + Jl + X2) dx
J V 1 + x2
1719.
J
*;+; dx.
Указание. ( 1 + 4 ] dx = d f х - -|.
V X2) l х)
"I"! dx.
1714. f x*dx .
х4+ 1
J (*5 + l)4
п
x2dx
1716 f 1 in ^ + xdx
Л + хп + 2
l-x2lni-xaX-
cosxdx
1718 f sinxcosx dx
J2 + cos2*
JL 0 AU» I A 1АЛ*
J sin4* + cos4*
2;-®’х dx.
1720. f xdx
9х-4х
J Jl + X2 + J(1 + X2)
Применяя метод разложения, вычислить следующие интег¬
ралы:
1721.
a) j x2(2 - 3x2)2 dx;
6) j *(1
H
43
о
/*-ч
*
1
1722.
f \ + x dx.
J 1-*
1723. |
X2 »
-=— dx.
1 + x
1724.
f - dx.
J 3 + *:
1725.)
ИЩах.
1 + x2
1726.
f <2-*)2 dx
1727. J
x2 dx
\ 2-x2
(l-*)100
1728.
f ~^T dx-
J *+ 1
1729. J
dx
Jx + 1 + Jx - 1

§ 1. Простейшие неопределенные интегралы
157
1730.
\xJT
Ьх dx.
_ 1	2
Указание, * = --(2 - 5 л:) + - .
о	5
1731.
/
xdx
Vi - з*
1733. f -
J (ЛГ-1)(* +
1734.
1736.
1738.
1732.
J x3 Vl +x2
2 dx.
3)'
I
н и e. 1 = i [(* + 3) - (* -
4
!>]•
dx
1735.
x2 + x- 2 ’
dx
1737.
{x2 - 2)(x2 + 3) ’
xdx
1739.
x* + 3x2 + 2'
2)
f
J (x + 2)(* + 3)‘
f 	—	(a ^ 6).
J (x + a)2(x+ by
1740. f 	—	 (a2 * £>2).
J (x2 + a2)(x2 + b2) v	'
1741.
1743.
1745.
1746.
1747.
1749.
1751.
1753.
1754.
sin2 x dx.
sin x sin(x + a) dx.
f cos x ‘ cos § dx.
J 2	3
J sin ^ 2x - cos ^ Зл; + dx
1742. J cos2 x dx.
.744. J sin 3x • sin 5jc dx.
sin3 x dx.
sin4 x dx.
ctg2 x dx.
sin2 3x sin3 2x dx.
dx
sin2 x cos2 x *
1748.
1750.
1752.
cos3 x dx.
cos4 x dx.
tg3 x dx.
Указание. 1= sin2 x + cos2 x.
dx
1755.
s
sin2 x cos x
1757. f	dx.
J sinx
1756.
1758.
J-
dx
sin* cos3*
f dx
J COS4 Л

158
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1759.j
% dx
l + ex'
1760. j
l + e2x
1761.j
sh2 x dx.
1762. j
ch2 * dx.
1763.J
sh x sh 2x dx.
1764. |
J
ch * • ch Sx dx.
1765. j
Г dx
sh2*ch2* *
Применяя подходящие подстановки, найти следующие
тегралы:
1766.
x2 3«/l -* dx.
1767. J
[ jc3(1 - 5л:2)10 dx.
1768.
*2 dx.
1769. J
f ** dx.
J2- x
' Jl - X2
1770. j
j* *5(2 - 5л:3) * dx.
1771.
J* cos5 x • Jsinx dx.
1772. j
f sin*cos3* Алл
1 1 + cos2*
1773.
f sin2* dx.
1774. j
Г In xdx
1 COS6*
1 xjl + \nx
1775.
f dx
1776. j
Г dx
1 г ‘
e2 + cx
1 Vl + ex
1777.
f arctgV* dx
I Jx 1 + x'
Применяя тригонометрические подстановки х = a sin t,
х = a tg t, х = a sin2 J и т. п., найти следующие интегралы (па¬
раметры положительны):
1778.
f dx
1779. J
A
x2dx
J - ‘
J (l-*2)2
Jx2 -2
dx
1780.
Jl - x2 dx.
1781. f
3 ■
J
(*2 + a2)2
1782.
1783. J
' X 1 x dx.
Л/ 2 a - *
1784.
f dx у r
J J(x-a)(b-x)
,
а з а н и e. Применить подстановку
x — a = (b — a)sin2 t.
1785.
J(x - a)(b - a) dx.

§ 1. Простейшие неопределенные интегралы
159
Применяя гиперболические подстановки х = a sh t, х = a ch t,
ит. п., найти следующие интегралы (параметры положи¬
тельны):
1786. f Ja2 + х2 dx.	1787. f x*dx dx.
J	J Ja2 + x2
1788.	f	dx.
J Vx + a
1789.	f ■■ ■ d	1790. f J(x + a)(x + b) dx.
J J(x + a)(x + b)	J
Указание. Положить
x + a = (fi - a) sh2 t.
Применяя метод интегрирования по частям, найти следую¬
щие интегралы:
1793.
1795.
1797.
1799.
1801.
J
И¥)
1791. | In х dx.
dx.
xe~x dx.
x3<r*2 dx.
x2 sin 2x dx.
x3 ch 3x dx.
1803. | arcsin x dx.
1805. I x2 arccos x dx.
!
I
1807. J In (x + Jl + x2) dx.
1809. J arctg Jx dx.
Найти следующие интегралы:
1811.
1813.
х5ех3 dx.
*(arctg x)2 dx.
1815. f
J V1 + X2
1792. J xn In x dx (n * 1).
1794. J Jx hi2 x dx.
1796.
1798.
1800.
1802.
1804.
x2e~2x dx.
x cos x dx.
x sh x dx.
arctg x dx.
x arctg x dx.
1806. | arcs*n? dx.
Г2
1808.
1810.
1812.
1814.
1816.
1
Г x In 1ЛЛ dx.
J 1-*
J sin x • In (tg x) dx.
(arcsin x)2 dx.
X2 In i—£ dx.
1 + x
Ы
X2)2
dx.

160
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1817. j
P dx
(a2 + x2)2'
1818. j
|* Ja2 - x2 dx.
(•
1819.
Jx2 + a dx.
1820.
x2 Ja2 + x2 dx.
1821.
x sin2 x dx.
1822.
•
e-Г* dx.
J
1823.
x sin Jx dx.
1824. I
[ *earctex3 dx.
J
J
(1 + X2)2
1825.
• ^arctgx
» dx-
1826.
[ sin (In x) dx.
J
(1 + X2)2
J
1
1827. J
J* cos (In x) dx.
1828.
•
eax cos bx dx.
1829.
J* eax sin bx dx.
1830.
e2x sin2 x dx.
1831.
j* (ex - cos x)2 dx.
1832. j
Г arcctge* dx.
| ex
1833.
Г dx.
1 sm2*
1834. J
f xdx dx
1 cos2* ■
1835.
f xeX dx.
I (*+i)2
Нахождение следующих интегралов основано на приведении квад¬
ратного трехчлена к каноническому виду и применении формул:
х
IV.
V.
= - arctg - + С (а ^ 0).
а
1 Г ^х _ 1
J а2 + х2 а
п. f dx = —
J а2 - х2 2с
ш- J^-±iln|“!±*!!|+c'
Г
J Ja2 - *
J
4- С (а * 0).
arcsin - + С (а > 0).
2	а
= In I* + Jx2±a21 + С (а > 0).
Jx2±a2
VI. f xdx = ±4a2±x2 + С (a > 0).
J Ja2±x2
VII.	f Ja2 - x2 dx = -л/я2 ~ *2 + — arcsin - -f С (a > 0).
J	2	2	a K '
VIII.	J V*2±a2 d* = ZJx2±a2 ± j 1п|л; + Jx2±a21 + C (a > 0).

§ 1. Простейшие неопределенные интегралы
161
Найти следующие интегралы:
Г 	dx
J а
1836.
1838. Г —
J з*
+ b х2
dx
(аЪ * 0).
I
2-2х- 1
dx.
L
x3dx
х4 - х2 + 2
1840/f
J x2+ x+ 1
1842. J
1844.	J
1845.	J
1837
1839. J x
1841.
dx
x2-x+2
xdx
4 - 2x2 - 1
xdx
J-
1843. f x%dx-
J *6-*3-
2*cosa + 1
2 ‘
dx
3 sin2 x - 8 sin x cos x + 5 cos2 x
dx
sin* + 2cos* + 3
TO
и
1846. J
dx (b * O’».
1847. Г
dx
	 v/*
Ja + bx2
J
Jl - 2x-x2
1848. J
dx
1849. J
dx
Jx + X2
J2x2- x + 2
1850. Доказать, что если
У = ax2
+ bx + c 0),
Г dx _ J_ in
uL
+ Jay
+ С при
a > 0
J Jy Ja
2
Г
— = -J— arcsin
-y’
— + С при a < 0.
J
4y 4~a
Jb2 - 4ac
iSSl.J
xdx
1852. J
x+l... л
Jb + x - x2
Jx2 + * + 1
1853. а)
Г xdx
6,J
cos xdx
J VI - 3jc2 - 2л/
Jl + sin* + cos2*
1854. J
x3dx
1855. J
* + X3 (
Jx4-2x2-l
л/1 + X2- X4
1856. J
dx
1857. f
dx
xjx2 + x + 1
J
x2Jx2 + * + 1
1858. J
dx
1859. J
dx
(x + l)Jx2 + 1
(x - l)Jx2 - i
1860. f
dx
1861. f
л/2 + x - x2
J
(x + 2)2Jx2 + 2x -
5
J
dx.
dx.

162
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1862. j
./2 + x + x2 dx.
1863. J
Jx4 + 2x
1864. j
\~x + x.2 dx.
1865. j
• л:2 + 1
xjl + X - X2
xjx4 + 1
2-1
dx.
х dx.
§ 2. Интегрирование рациональных функций
Применяя метод неопределенных коэффициентов, найти сле¬
дующие интегралы:
1866. Г —	 dx.	1867. f 	—
J (х-2)(х+5)	J (я; + 1)(дг+ 2)(х +
1868. Г х'Чх
J Х2+Х~2
3)'
Г 	£
J х4+5:
5х2 + 4
cbr.
4-2х3-2х2 + х+1
2 + 5х + 4
4 + 5л:2 + 4
<2л\
1870.
1872- J (»!№-.)
1874‘ J (лс + 1)(я; + 2)2(х + З)3
1875.	f —	 dx
J Xs + X
1876.	Г •£
J х4
1878.» f —
1880» J
1882. J
1884. f -4^-r
1886. f -4^-:
J jc6+ 1
dx
2 - 4x + 4)(л:2 - 4л: + 5)
dx
J л:(1 + л:)(1 + x + л:2) *
xdx
x3 - 1
1887. f 	—
J (1 + ж)(1 + Хг)(\ + X
■h
■)'
1888
1889.
5 - X4 + X3 - X2 + X - 1
x2dx
f
J v4 i Ow,
i869- J
1871. J
+ 6л:
dx.
xdx
x3 - Зл: + 2
1873.
1Ы:
Зл: + 2
dx.
1877. f
J (x+ 1)(л;2+ 1)
1879. f 	—x
J (x-l)Hx
1881. f -P--
J л:3 + 1
1883. f —~~7 •
J *4-l
1885. f -~~—r •
J л:4 + л:2+ 1 •
2+ 2л:+ 2)
9

§ 2. Интегрирование рациональных функций
163
1890. При каком условии интеграл
ах2 + Ьх + с
I
dx
х3{х- I)2
представляет собой рациональную функцию?
Применяя метод Остроградского, найти интегралы:
dx
1891. f 	—
1893. f —
J (x2 + l)3
1895. J
1897.
dx
(*4 + l)2
■J (*4-l)3
1892. f —
J (x
1894-1
1896.
3+ 1)2
x2dx
+ 2x+ 2)2
2 + 3x-2
1)(ДГ2 + x + 1)2
dx.
Выделить алгебраическую часть следующих интегралов:
1898.
1900.
Г *2+ 1
J (Х4 + Х2+1
Г 4хГ) - 1
J (х5 + я + 1)
dx.
dx.
1899.
Г dx
J (х3 + л: + 1)
1901. Найти интеграл
j
dx
х4 + 2л:3 + Зле2 + 2л: + 1
1902. При каком условии интеграл
Г q«« + 2px + Y. dx
J (ах2 + 2bx + с)2
представляет собой рациональную функцию?
Применяя различные приемы, найти следующие интегралы:
1903.
1905.
1907.
1909.
1911.
X3 dx.
(*-l)100
1904.
x3dx
xs + 3 ’
1906.
		 dx.
1908.
x(xs + Sx4 + 2)
xndx
1910.
jc8 + Зя;4 + 2 '
у2л - 1
* dx.
1912.
xn+\
Г xdx
J х2- 1
j* X2 + X
J *e+l
f x*c
J (*10-
J lx
dx.
x4dx
lO)2
x9dx
10 + 2x5 + 2)2
Г jc3n~1
’ J (x2n + 1
l)2
dx.

164
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1913.
Г dx
J jc(jc10+2)’
1915. f —dx.
) дс(1 + дс7)
1917. f ■ Л- V ;
J JC4 + JC2 + 1
1919. f *1Z*. dx.
J **+ 1
1914.
1916.|
1918. J
/Г
dx
(jc10 + l)2
1920
jc(jc4- 5)(jc5- 5jc + 1)
		jc2- 1
JC4 + JC3 + JC2 + JC + 1
dx.
dx.
dx.
f £l±i
‘J jc6+1
1921. Вывести рекуррентную формулу для вычисления ин¬
теграла
dx
'■ -Ji
(ajc2 + bx + c)n
Пользуясь этой формулой, вычислить
(a ^ 0).
/з =
I (*2
dx
г2 + JC + I)3
Указание. Использовать тождество
4a (ajc2 + fcjc + с) = (2ах + Ь)2 + (4ас - Ь2).
1922. Применить подстановку t =
х + b
для вычисления ин¬
теграла
/ =
j
	dx
(jc + а)т(х + Ь)п
(тип — натуральные числа). Пользуясь этой подстановкой,
найти
j
	dx
(jc - 2)2(jc + З)3 ’
1923.	Вычислить
ji
Рп(х) dx,
(х-а)пч 1
если Рп(х) есть многочлен степени п относительно х.
Указание. Применить формулу Тейлора.
1924.	Пусть jR(jc) = #*(jc2), где R* — рациональная функция.
Какими особенностями обладает разложение функции R(x) на
рациональные дроби?
1925.	Вычислить
Г dx
J (1 + х)2"’
где п — целое положительное число.

§ 3. Интегрирование иррациональных функций
165
§ 3. Интегрирование иррациональных функций
С помощью приведения подынтегральных функций к рацио¬
нальным функциям найти следующие интегралы:
dx
1926.
1928
1930
Г dx
J 1 + Jx
Jx
x3j2~-
1927.
j
Г xl/2 + x
J x + 1/2 + x
f 	 dx
J (1
dx.
(1 + \JxfJx
1932. Г	dx ■-
J 3J(x + l)2(x - 1
V(3
1934.	J
1935.	f 	-!
J 1 A- Jx
1929
1931
1933
a:(l + 2 Jx + l/x)
f 1 7.JX.± \ dx.
J 1 + 3Jx + 1
f ^TT-^ri dx.
J Jx+ 1 + Jx - 1
x dx
J
dx
a)n + J(x - 6)n" 1
dx
• л/х + J1 + X
Указание. Положить x =
4Jx3(a - x)
(n — натуральное число)
к2 - 1
2u
(a > 0).
1936. Доказать, что интеграл
i
R [x, (x - a)n (x - &)"] dx,
где R — рациональная функция и p, q, дг — целые числа, явля¬
ется элементарной функцией, если
р + q = /г/г,
где /г — целое число.
Найти интегралы от простейших квадратичных иррацио-
нальностей:
1937. f х2 dx.
1938.»j
dx
J л/1 + X + X2
(x + 1 )Jx2 + X + 1
1939 f
1940. J
Jx2 + 2x + 2 дх
J (1 — JC2)^/l — JC2
X
1941. f xdx
19121
' .l-* + *2. rf*.
J (1 + x)J 1 - X - X2
Jl + X - X2
Применяя формулу
f Ы*1 dx = Qn _
i(*) у + X J
dx
>
J У
У

166
РАЗДЕЛ 111. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
где у = Jax2 + bx + с , Рп(х) — многочлен степени п, Qn _ t(x) —
многочлен степени п - 1 и X — число, найти следующие интег¬
ралы:
1943.
dx.
I. (
*3 dx.
1944. j
/
• x™dx
J
Jl + 2х - х2
•
Jl + X2
x3 - бдс2 + 11 JC — 6
Jx2 + 4jc + 3
•J
xAJa2-x2 dx.
1946.
. 1
* dx
1948. J
dx
J
x3Jx2 + 1
x4Jx2- 1
1 1
• dx
1950. J
• dx
J
(x-l)3Jx2+3x+l
(jc+ 1 )5Jx2 + 2x
.. При каком условии интеграл
С alx2 + blx + cl
J Jax2 + bx +
dx
Jaxz + bx + c
представляет собой алгебраическую функцию?
Найти J	^Ху где ^ = ^ах2 + Ьх + с , разлагая рациональ¬
ную функцию на простейшие дроби.
1952. j
xdx
1953.
(x- l)2Jl + 2x- x2
1954.j
Jx2 + x+ 1 d
(x + l)2
1955.
1956. J
xdx
1957.
(x2- 3jc+ 2)Jx2- 4jc+ 3
1958. j
* dx
1959.
(x2+l)Jx2-1
1960. I
f ^+2 dx
I дс2+1
Г 	xdx
J (х2 - 1 )Jx2 - х - 1
Г	х2
J (1 + x)Jl + 2х - х2
Г 	dx
J (1 + x2)Jl - X2
Г	dx
J (i-x4)jr+T2'
dx.
Приводя квадратичные трехчлены к каноническому виду,
вычислить следующие интегралы:
dx
1961.
f
J (х2 + дс + 1)
(JC2+ X + 1) л/ X2 + х- 1
1962.	f
J (4- 2х + x2)j2 + 2х- хг
1963.	f 	(,x+l)dx _
J (x2 + x+ 1 )Jx2 + X + 1

§ 3. Интегрирование иррациональных функций
167
1964. С помощью дробно-линейной подстановки х = - + Р*
1 +1
вычислить интеграл
1965. Найти
j
I
dx
(х2 - х + \)Jx2 + X + 1
dx
(х2 + 2)j2x2 - 2х + 5
Применяя подстановки Эйлера:
1) Jax2 + bx + с = ±Jax 4- г, если а > 0;
2)	Jax2 + bx + с = Х2 ± Jc , если с > 0;
3)	*/а(х - хх)(х - х2) = 2(х - jc2),
найти следующие интегралы:
1966;J
dx
1967.
х + Jx2 + х + 1
1968. J
xjx2 - 2x + 2 dx.
1969.
1970. j
dx
[1 + Jx(l + х)]г
Jr
и
dx
+ Jl-2x- х2
х - Jx2 + Зх + 2
+ Jx2 + Зх + 2
dx.
Применяя различные методы, найти следующие интегралы:
1971.
1973.
Г 	!
J Jx2 + 1
J
-Jx^l
dx
1972
' f 	2
J (l-JC
xdx
J2 + J1 - x + лДТх
c3)Vl - *2
1974. f -*±Л±* + *г. . dx.
J 1+X+Jl + X+X2
1976. f ...(^-1?d3C	.
J (x2+ 1)V*4+ 1
1978. Г — --x-	- .
J xV*4 + 2x2 - 1
1975. f ■	da:.
J a/x + Jx+ 1
1977. f (*2 + 1)rf* .
J (x2-l)Jx4+l
1979.	f (*2 + l)dx ^
J xjx4 + x2 + 1
1980.	Доказать, что нахождение интеграла
J R(x, Jax~+~b , JcxT~d) dXy
где Я — рациональная функция, сводится к интегрированию ра¬
циональной функции.

168
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Интеграл от дифференциального бинома
J хт(а + Ъхп)р dxу
где т, п и р — рациональные числа, может быть приведен к интегри¬
рованию рациональных функций лишь в следующих трех случаях (тео¬
рема Чебышева):
Случай 1. Пусть р — целое. Тогда полагаем х = zN, где N — об¬
щий знаменатель дробей тип.
Случай 2. Пусть т + - — целое. Тогда полагаем а + Ьхп = гл,
п
где N — общий знаменатель дроби р.
Случай 3. Пусть HULL + р — целое. Тогда применяем подста-
новку ax~n + b = zN\ где N — знаменатель дроби р.
Если п = 1, то эти случаи эквивалентны следующим:
1) р — целое; 2) т — целое; 3) т + р — целое.
Найти следующие интегралы:
Jx
1981.J
Jx3 + х4 dx.
1982. J
d + 'V^)2
1983.J
xdx
1984. j
x''dx
л/1 + \[х?
Jl - X2
1985.J
dx
1986. J
* dx
Vl + X3
i/l + X4
1987. J
Л
dx
1988. j
dx
x4Jl + x6
1989. Г
УЗх-х3 dx.
1990.В
каких случаях интеграл
Jl + xm
dx.
где т — рациональное число, представляет собой элементарную
функцию?
§ 4. Интегрирование тригонометрических функций
Интегралы вида
J sinm х cos" х dXy
где тип — целые числа, вычисляются с помощью искусственных пре¬
образований или применением формул понижения.

§ 4. Интегрирование тригонометрических функций
169
Найти интегралы:
1991. j
cos5 * dx.
1992. J
|* sin6 * dx.
1993.
cos6 * dx.
1994.
%
sin2 * cos4 *
dx.
1995.
sin4 * cos5 * dx.
1996.
%
sin5 x cos5 x
dx.
1997.
sin3jc dx.
COS4 *
1998. J
f cos4x dx
| sin3 *
1999.
Г dx
2000.
Г dx
1 sin3* ’
| cos3 * ’
2001.
Г dx
2002.
Г dx
| sin4*cos4* ’
| sin3 x cos5 x ’
2003.
j* dx
) sin*cos4* ’
2004.
j* tg5 x dx.
2005.
j* ctg6 * dx.
2006.
f s5n4fx dx.
J COS6 *
2007.
Г dx
2008.
Г dx
J Vsin3*cos5*
J cos* Vsin2*
2009.
Г dx
2010.
C dx
J Vtgic
) l/tgx
2011. Вывести формулы понижения для интегралов:
a) In = J sin" х dx;	б) Кп = J cos'1 х dx (п> 2)
и с их помощью вычислить
j sin6 х dx и J cos8 x dx.
2012. Вывести формулы понижения для интегралов:
a) /„ = f 4s- ;	б) Кп = f	(га > 2)
J sin"*	J cos'1*
и с их помощью вычислить
\4±- и f_d
J sin’* J cos7*
Следующие интегралы вычисляются с помощью применения формул:
I. sin a sin Р = | [cos(a - Р) - cos (а + р)].
И. cos a cos р = | [cos (а - Р) + cos (а + Р)].
III.	sin a cos Р = - [sin (а - Р) + sin (а + Р)].
dk

170
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Найти интегралы:
2013. I sin Ьх cos х dx.
2014.
2015.
cos х cos 2x cos Sx dx.
x . X
- sin -
2	3
sin x sin ? sin ? dx.
2016.
2017.
2018.
sin jc sin(jc 4- a) sin (jc 4- fr) dx.
cos2 ax cos2 bx dx.
sin3 2x • cos2 Sx dx.
Следующие интегралы вычисляются путем применения тождеств:
sin (а - (3) = sin [(х 4- а) - (х 4-Р)],
cos (а - Р) = cos [(х + а) - (х 4- Р)].
sin(jt + b)
dx
Найти интегралы:
2019. f —	^
J sin(jc + a)si
2020.	Г
J sin(jc + a)cos(JC + b)
2021. f 	—	.
J cos(* + a)cos(jc + b)
2022.	J dx
2023.	J
sinjc - sina
dx
cosjc + cos a
2024. J tg x tg (x + a) dx.
Вычисление интегралов вида
J R (sin x, cos x) dx,
где R — рациональная функция, в общем случае приводится к интегри-
X
рованию рациональных функции с помощью подстановки tg - = t.
Сл
а) Если выполнено равенство
Я (-sin х, cos х) = -R (sin х, cos х)
или
R (sin х, -cos х) = -R (sin х, cos х),
то выгодно применять подстановку cos х = t или соответственно sin х = t.

§ 4. Интегрирование тригонометрических функций
171
б)	Если выполнено равенство
R (-sin *, -cos *) = R (sin х, cos х),
то полезно применять подстановку tg х = t.
Найти интегралы:
2025. 1	dx
/п
sinx- cosjc + 5
2026.
J (2 +
dx
cos*) sin*
2027.	f 	sini*	 dx
J sin*+ 2 cos*
2028.	f —^— при: a) 0 < e < 1; 6) e > 1.
J 1 + ECOS*
2029.	f sin2* dx.	2030. f ——
J a2sm2* +
xdx
. + ECOS*
f ■ 5in2*	 dx.
J 1 + sin2*
2°3i. f 2 . fs2
J (a2sin2* +
2033. J
2035. Г -
J si
b2cos2x
+ b2 cos2*)2
dx
1
(asin* + bcos*)2
dx
sin4 x + cos4 x
2032.
2034. f —
J sin3* +
2036.
Sin* COS*
sin* + cos*
xdx
dx.
COS3*
2037. f sin.2~y ~	dx.
J sin4* + cos4*
2039. f 		4?-— .
J Sin6* + COS6*
2041. Найти интеграл
Г sin2 jeeps2*
J sin8 *+cos8;
2038. f s}»xcos? dx.
J 1 + sm4*
2040. Г —-
J (Sin2*
dx.
dx
: + 2 cos2*)2
l
dx
asin* + bevsx
приведя знаменатель к логарифмическому виду.
2042. Доказать, что
Г ax sin* + bicosjc ,	.	, „ , i .	, .	i ,
—4			 dx = Ax + В In a sin x + b cos * + C,
J asin* + bcos*
где А, В, C — постоянные.
Указание. Положить
a, sin x + bx cos x = A (a sin x + b cos x) + В (a cos x - b sin *),
где А и В — постоянные.
Найти интегралы:
2043.	а) f -sin*-c°s*
J si
2044.	f ——— .
J 3 + 5tg*
sin* + 2 cos*
dx
dx;
б) Г -г—s
J sin*-
sin*
3cos*
dx.
f a\Sin* + 6,COS* ,
2045.	—			 dx.
J (asin* +bcos*)2

172
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2046. Доказать, что
I
a,sinx+ bxcosx + с, ,	.	, „, i .	, ,	.1.
—				 dx = Ах + В In a sin д: + о cos х + с +
asinx + bcosx + с
+ С
J
clx
asinx-t- bcosx + с 9
где А, В, С — некоторые постоянные коэффициенты.
Найти интегралы:
2 cos л: - 3
2047. f rinjt+2cos«-3 ^
J sin* - 2cos* + 3
2048.
2049.
Г 	sin д:
J J2 + sin* -
J
J2 + sinx + cos*
2 sin л: + cosx
3sinx + 4cosjc - 2
2050. Доказать, что
л2
dx.
dx.
i
a1sin2jc+261sinxcosJC+Cjcos2:»:	_
asinx + bcosx
= A sin д: + В cos x + C
где А, Б, C — постоянные коэффициенты.
f dx
J a sin x + b
+ bcosx 9
Найти интегралы:
■ 4 sin Jt cos* + 3cos2Jt
2051.	J Sinf£
2052.	J
sin л: + cosx
sin2x - sin xcos x + 2 cos2 x
dx.
dx.
!
sinx + 2cosjc
2053. Доказать, что если (a - cf + b2 ^ 0, to
ajsinx + bx cosjc	,	_ . Г dux
asin2JC+ 2bsinjccosjc
£
+ C COS2 X	J A>lU2 + Ai	J ^2^2 +
2 + ^2
где А, Б — неопределенные коэффициенты, Xl9X2 — корни урав¬
нения
a - X b
b с - X
— 0 (Xi ^ A2),
щ= (a - XJ sin x + b cos x и kt =
a - X,
(i= 1, 2).

§ 4. Интегрирование тригонометрических функций
173
Найти интегралы:
2054. f 2sin*-cos*,. dx.
J 3sin2.x + 4cos2x
2055.
(sinx + cosjc)dx
sin2* - 4sin*cos* + 5cos2*
it
2056. I .йп£^1£ов« dx.
+ 4sin*cos*
2057. Доказать, что
dx
f	^
J (asin* +
Asin* + В cos*
bcosx)n (asin* + bcosx)n~ 1
+
+ c f
J (asin* + 6c<
bcosx)n ~2 ’
где A, B9 C — неопределенные коэффициенты.
dx
2058. Найти J
,оказг
(sin* + 2cos*)3
2059. Доказать, что
dx
Asm*
+ b cos*)" (a + bcos*)"-
+ В
Jsr
dx
+ C
+ bcosx)n~1
dx
bcosx)n
+
(H * W),
и определить коэффициенты А, Б и С, если п — натуральное чис¬
ло, большее единицы.
Найти интегралы:
2060. f 	sinxdx	2061.
J cosjcVl + sin2*
2062.	f .
J J2 + sin 2*
2063.	f ——dx
J (l + i
1
Sinz*
COS2*Vtg*
dx.
ecos*)2
cos”~1* ^ e
2064. f 	—
J gin-«2^5
(0 < e < 1).
dx.
x + a
Указание. Положить t
2

174
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2065. Вывести формулу понижения для интеграла
j
f . х - а>
sin
. х + а
sin—-—
dx
(п — натуральное число).
и
§ 5. Интегрирование
различных трансцендентных функций
2066.	Доказать, что если Р(х) — многочлен степени п, то
J P(x)eaxdx = еах	+ ... + (-1)л	+ С.
2067.	Доказать, что если Р(х) — многочлен степени п, то
| Р(х) cos ах dx =	Р(х) - ^	- ...] +
+ cosa*r Р'(х) -	+ pV(x) - ... 1 + с
a2 L	a2	a4	J
f Р(х) sin ах dx — - £2ёНГ р(х) -	+ p,v{x) _ ...1 +
I	CL [_	CL	CL	_J
ЁМ£Г P'ix) -	+ P%*1 - ... 1 + с.
a2 L	a2 a4	J
+
Найти интегралы:
2068. J х3е3х dx.
2069. J
1* (x2 - 2x + 2)e-x dx.
2070.J
j* х5 sin 5x dx.
2071. j
|* (1 + x2)2 cos x dx.
2072.J
j* x7e~x2 dx.
2073. J
j* х2е^* dx.
2074. J
J* eax cos2 bx dx.
2075. J
|* eax sin3 bx dx.
2076. j
j* xex sin x dx.
2077. j
|* x2ex cos x dx.
2078.J
|* xex sin2 x dx.
2079. J
j* (x - sin x)3 dx.
2080. I
[ cos2 л/x dx.

§ 5. Интегрирование различных трансцендентных функций
175
2081. Доказать, что если R — рациональная функция и числа
а19 а29 •••, ап соизмеримы, то интеграл
J R (еа'\ еа*х, ..., ea-x)dx
выражается в виде элементарной функции.
Найти интегралы:
2082.
Г dx
J (1 + е*)2‘
2084.
(* dx
J е2х + ех-2‘
2086.
м
2088.
{dx-
2090.
Г dx
J л/1 + е* + а/1 - ех
2091. Доказать, что интеграл
2083. J
V2' dx.
1 + ех
2085. (
dx
X X X
J
1 + е* + е* + е*
2087. j
• dx
Jex- 1
2089. I
*je2x + 4ex - 1 dx.
где R — рациональная функция, знаменатель которой имеет
лишь действительные корни, выражается через элементарные
функции и трансцендентную функцию
f dx = И (еах) + С,
где
2092. В каком случае интеграл
I РШе’
где Р Г — 1 = а0 + — +...+ — и а0, а,, а„ постоянны, пред-
\xj	X	хп
ставляет собой элементарную функцию?

176
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Найти интегралы:
2093.J
'(l-if r-dx.
2094.
,r'dx-
2095.j
2097. j
e2x dx
2096.
f dx
x2 - 3x + 2 '
* x4e2\dx.
(x-2)2
J (*+l)2
Найти интегралы, содержащие функции In f(x)9 arctg f(x),
arcsin f(x), arccos f(x), где f(x) — алгебраическая функция:
2098.	j* In'1 x dx (n — натуральное число).
2099.	J x3 In3 x dx.	2100. J
2101. f In [(x + a)x + “ (x + £>)* + fc] -	^—-.
J	(x+a)(x+b)
2102.	J In2 (x + Jl + x2 ) dx.
2103.	| In (Vl -x + Л + x) dx.
dx.
2104.
[ 1пх , dx.
2105. I
x arctg (jc -f- 1) dx.
J
(1 + x2Y
J
2106.
Jx arctg Jx dx.
2107. J
x arcsin (1 - x) dx.
2108.
arcsin Jx dx.
2109. J
Г x arccos - dx.
1 x
2110.
f arcsin dx.
1 1 + X
2111. j
[ arccos* dx.
(1-x2)2
2112.
f x arccos x dx
{\-X2)2
2113.
j* x arctg x In (1 + x2) dx.
2114.
Г г 1л 1 + x dr
2115.j
Г \n(x + *Jl + x2)dx
I 111 •
1 1-*
1 *
(l + x2)2
Найти интегралы, содержащие гиперболические функции:
2116.
J sh2 x ch2 x dx.
2117.
ch4 x dx.
2118.
j* sh3 x dx.
2119.
•
sh x sh 2x sh Sx dx.

§ 6. Примеры ua интегрирование функций
177
2120.
2122.
th х dx.
Jthx dx.
dx
2121. J cth2 x dx.
2123'a)J sh* + 2ch«’
S)J wTJhJ'-
2124. J sh ax sin bx dx.
dx
6) f 	,
J sh2jc - 4shjcchjc + 9ch2:t
chxdx
r)
J
3sluc - 4ch*
2125. I sh ax cos bx dx.
i
§ 6. Примеры на интегрирование функций
x2dx
Найти интегралы:
2126. J
dx
2127.
X6(l + X2) ’
2128. j
dx
2129.
1 + X4 + X8 ’
2130. j
dx-
2131.
2132. f / * _ dx.
J V 1 - xjx
2133.
2134. J
' dx
2135.
\jx2( l - x)
2136.j
dx
xjx4 - 2x2- 1
2137.
2138. J
(1 + x)dx
x + Jx + x2
2139.
2U0- J
(2x + 3) arccos (2x -
3) dx.
2141.]
|" x In (4 + x4) dx.
2142.
2143. j
Г xln(l + Vl + *2) dx
1 Jl + x2
г
2144.
x Jx2 + 1 Injx2 - 1
dx.
2145.
* In * dx.
Jl - x2 Jl-X
2146.
2147.
Г ”п4ж я dx.
sin8 X + COS8 X
2148.
J (1-х2)3
f dx
J Jx + \[x
f	x + 2
J x2JT^x'
I
In
I
X2
dx
xjl + X3+ X
l + yr^x2
Jl-X2
dx.
(1 + x)2
1
arcsinjt . 1 + x2
Jl-X2
dx.
I
J:
dx
(2 + sin*)2
dx
sinxjl + cosjc

178
РАЗДЕЛ III. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2149. f ах* +.b arctg х dx.
J х2 + 1
2151.
2153.
2155.
1
Г 	sii
J УГ7
x \nx
(1 + X2)2
sin 2*
dx.
dx.
COS4*
'arctgx djc>
Г x4arctg
J 1 + x2
2157. f + dx
J (1-л:2)2
2159.	J* jc(1 + лс2) arcctg xdx.
2160.	| a:*(1 + In x) dx.
i. Г arctge2_
J e2(l + ex)
f 	dx
J (e*+1 + l)2-(ex~1 + l)2
2162
2163
2165
2167
f i±sin£e, djc.
J 1 + COS*
'. J x \x\ dx.
2169. J j|l + jc| - |1 - *|
2171. J max (1, x2) dx.
dx.
2150
, j* ax2 + b
'J x2-l
In
*- 1
X + 1
dx.
2152. f 2LSE£&£ dx.
J JTTlx2
2154. f »ia£S£252 dx.
J л
4T
f x arcctgx ,
J (1 - л:2)2
2156.
2158. J JUT* arcsin x dx.
2161.
I
arcsine*
dx.
2164. J Vth2x+ 1 dx.
2166. J |jc| dx.
2168. | (* + I*
2170. J e-W dx
: dx.
. j* cp(jc) dx, где cp(jc) — расстояние числа x до ближайшего
2172
целого числа
2173. J [х] |sin 7i*| dx (* > 0).
2174.	f f(x) dx, где f(x) = \1 f при J*J J 1;
J	[ 1 - |*| при 1*1 > 1.
*	[ 1, если -°o < * < 0;
2175. I f(x) dx, где /(*) = < x + 1, если 0 < * < 1;
l 2x, если1<*<+°о.
2176. Найти
J Xf"(x)
dx.

§ 6. Примеры на интегрирование функций
179
2177. Найти
J П2х)
dx.
2178. Найти f(x), если f'(x2)
(х > 0).
2179.	Найти f(x), если: a) /'(sin2 х) = cos2 х;
б)Г(1пх) = -11при°<Х<1; И /(0) = 0.
[х при 1 < X < +00
2180.	Пусть f(x) — монотонная непрерывная функция и
f~l(x) — ее обратная функция. Доказать, что если
1
f(x) dx = F(x) + С,
то
I
f~\x) dx = xf~\x) - F(f~\x)) + C.
Рассмотреть примеры: a) f(x) = xn (n> 0);	6) f(x) = ex\
B) f(x) = arcsin x; r) f(x) = Arth x.

РАЗДЕЛ IV
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Определенный интеграл как предел суммы
1. Интеграл (в смысле Римана). Если функция /*(х) определена на
[а, Ь] и а = х0 < хх < х2 < ... < хп = Ь, то интегралом функции /(х) на
сегменте [а, b] называется число
ь	^
f f(x) dx = lim У /&)Д*„	(1)
J	max|A*,|-0 ^
а
где xt < ^ < X/ + j и Ах, = х* + j - х*.
Для существования предела (1) необходимо и достаточно, чтобы
нижняя интегральная сумма
п- 1
£_ = у /п,Дх,
»- о
и верхняя интегральная сумма
_ п - 1
■S = £ М,Дх„
/ = 0
где
т} = inf /(х) и Mj= sup /(х),
ДГ,<Х<Х(|,
имели общий предел при шах |AxJ -* 0.
Функции /(х), для которых предел в правой части равенства (1) су¬
ществует, называются интегрируемыми (собственно) на соответствую¬
щем промежутке. В частности, а) непрерывная функция; б) ограничен¬
ная функция, имеющая конечное число точек разрыва; в) ограниченная
монотонная функция, — интегрируема на любом конечном сегменте.
Если функция /(х) не ограничена на сегменте [а, Ь], то она собственно
неинтегрируема на [а, Ь].
2. Условие интегрируемости. Необходимым и достаточным услови¬
ем интегрируемости на данном сегменте [а, b] функции f(x) является
выполнение равенства
lim
тах|Дх(.| -♦ 0
п - 1
I
i = 0
WjAXj = 0,
где Wj — колебания функции f(x) на сегменте [xlt xi+ J.

§ 1. Определенный интеграл как предел суммы
181
2181.	Найти интегральную сумму Sn для функции
f(x) =1+х
на сегменте [-1, 4], разбивая его на п равных промежутков и
выбирая значения аргумента ^(i=0, 1, п - 1)в серединах
этих промежутков.
2182.	Для данных функций f(x) найти нижнюю Sn и верхнюю
Sn интегральные суммы на соответствующих сегментах, деля
их на /г равных частей, если:
а)	f(x) = г3 [~2<х< 3];
б)	/(*) = Jx [0 < х < 1];
в)	f(x) = 2х [0<х< 10].
2183.	Найти нижнюю интегральную сумму для функции
f(x) = х4 на сегменте [1, 2], разбивая этот сегмент на п частей,
длины которых образуют геометрическую прогрессию. Чему ра¬
вен предел этой суммы при п -* оо?
2184.	Исходя из определения интеграла, найти
т
J (у0 + gt) dt,
о
где Т, v0y g постоянны.
Вычислить определенные интегралы, рассматривая их как
пределы соответствующих интегральных сумм и производя раз¬
биение промежутка интеграции надлежащим образом:
2 1
2185.
I
-1
х2 dx.
2186
J
ах dx (о > 0).
2188. cos t dt.
2187. J sin xdx.	2188. J
0 0
b
2189.	J (0 < a < b).
a
Указание. Положить ^ = Jx~x~[ (i = 0, 1, ..., n).
ь
2190.	j* xm dx (0 < a < b; m * -1).
a
Указание. Выбрать точки деления так, чтобы их абциссы х{ об¬
разовывали геометрическую прогрессию.

182
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ь
2191
■J
dx
х
(О < а < b).
2192.	Вычислить интеграл Пуассона
j In (1 - 2а cos х + а2) dx
о
при: a) |а| < 1; б) |а| > 1.
Указание. Воспользоваться разложением многочлена а2л - 1 на
квадратные множители.
2193.	1. Пусть функции f(x) и ср(х) непрерывны на [а, 6]. До¬
казать, что
Нш
max|AXj| —1* О
Ь
А£<)Ф(0/)Д*/ = f
; = п	"
f(x)ty(x) dx,
где xt < ^ < xt + j, xt < 0, < Xj + , (i = 0, 1, .... п - 1) и Axt = х, + , -
- х, (х0 = о, хп = Ь).
2. Пусть функция f(x) ограничена и монотонна на [0, 1]. До¬
казать, что
J/M
о
dx -
я ±'(я) -°(я>
3.	Пусть функция f(x) ограничена и выпукла сверху (см. за¬
дачу 1312) на сегменте [а, Ь]. Доказать, что
ф - a) tWtfW < J f(x) dx<(b-a)f .
а
4.	Пусть f(x) € С<2> [1, +оо] и fix) > 0, f\x) > 0, fix) < 0 при
я € [1, +оо). Доказать, что
£ Ш = | fin) +
П
J f(x) dx + 0(1)
i
при п —* ОО.
5.	Пусть f(x) € С(1) [а, Ь] и
ь
Дп = j* f(x) dx -	^ f^a + k
а	*= 1
Найти Нш тгДп.

§ 1. Определенный интеграл как предел суммы
183
2194.	Показать, что разрывная функция
/(*) = sgn (sin s'!
интегрируема на промежутке [0, 1].
2195.	Показать, что функция Римана
ф(х) =
О,	если х иррационально;
- , если х = — ,
п	п
где тип (п > 1) — взаимно простые целые числа, интегрируема
на любом конечном промежутке.
2196.	Показать, что функция
f(x) = - - Г-1, если х ^ О
X LXJ
и /*(0) = 0, интегрируема на сегменте [0, 1].
2197.	Доказать, что функция Дирихле
Х(х)
0,	если хиррационально;
1,	если храционально,
не интегрируема на любом промежутке.
2198.	Пусть функция f(x) интегрируема на [а, ft] и
fn{x) = sup f(x) при xL < х < xt + j,
где
xi, = a + ^ (b - a) (i = 0, 1, ..., n; n = 1, 2, ...).
Доказать, что
ь	b
2199.	Доказать, что если функция f(x) интегрируема на [a, ft],
то существует последовательность непрерывных функций (рДя)
(п = 1, 2, ...) такая, что

184
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2200.	Доказать, что если ограниченная функция f(x) интег¬
рируема на сегменте [a, ft], то абсолютная величина ее |/(л;)| также
интегрируема на [а, ft], причем
dx.
2201.	Пусть функция /(х) абсолютно интегрируема на сегмен-
ь
те [а, ft], т. е. интеграл J \f(x)\ dx существует. Является ли эта
а
функция интегрируемой на [а, ft]?
Рассмотреть пример:
1,	если х рационально;
-1, если х иррационально.
2202.	Пусть функция f(x) интегрируема на [а, ft] и А < f(x) < В
при а < х < ft, а функция ср(лг) определена и непрерывна на сегмен¬
те [А, 5]. Доказать, что функция cp(/(jc)) интегрируема на [а, 6].
2203.	Если функции f(x) и ср(лг) интегрируемы, то обязательно
ли функция /(cp(jc)) также интегрируема?
Рассмотреть пример:
J 0, если jc = 0;
1\х) ” 1 1, если х 5* 0,
и ф(д;) — функция Римана (см. задачу 2195).
2204.	Пусть функция f(x) интегрируема на сегменте [А, В].
Доказать, что функция f(x) обладает свойством интегральной
непрерывности, т. е.
ь
lim Г \f(x + h) - f(x)| dx = 0,
h -* о J
a
где [a, fc] с [А, В].
2205.	Пусть функция /(я) интегрируема на сегменте [а, 6].
Доказать, что равенство
ь
J f 2(x) dx = 0
п
имеет место тогда и только тогда, если f(x) = 0 во всех точках
непрерывности функции /(*:), принадлежащих сегменту [а, &].

§ 2. Вычисление определенных интегралов с помощью неопределенных
185
§ 2. Вычисление определенных интегралов
с помощью неопределенных
1.	Формула Ньютона—Лейбница. Если функция f(x) определена и
непрерывна на сегменте [а, Ь] и F(x) — се первообразная, т. е. F'(x) = f(x), то
г
f(x)dx = F{b)-F{a) = F(x) .
I
ь
Определенный интеграл J* f(x) dx при f(x) > 0 геометрически пред-
а
ставляет собой площадь S, ограниченную кривой у = f(x), осью Ох и
двумя перпендикулярами к оси Ох: х = а и х = b (рис. 9).
2.	Формула интегрирования ио частям. Если f(x), g(x) 6 С(1)[а, Ъ], то
Ь	н h
Г f(x)g\x) dx = f(x)g(x) - Г g(x)f\x) dx.
3.	Замена переменной. Если: 1) функция /(х) непрерывна на сегмен¬
те [а, Ь]; 2) функция ф(0 непрерывна вместе со своей производной ф'(/)
на сегменте [а, Р], где а = ф(а), b = ф(Р); 3) сложная функция Дф(0) оп¬
ределена и непрерывна на [а, Р], то
ь	Р
J кх) dx = J mt)W(t) dt.
a	(jt
Применяя формулу Ньютона—Лейбница, найти следующие
определенные интегралы и нарисовать соответствующие криво¬
линейные площади:
2206.
I
\fxdx.
-1
л
2207.
J sin х dx.
П

186
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Л
2208.
Г dx
J 1 + х2
2209.
2210.
Л
sh 2
I
1
2
J
1
2
dx
Jl - X2
dx
J Jl +X2
sh 1
1
2212. J — dx
2211
I11-
x\ dx.
2*cosa + 1
(0 < а < 71).
-l
2л
2213.
Ь
dx
ecosx
(О < e < 1).
2214.
I Таг
dx
-l
n
2
2215.
J(1 - 2ax + a2)(l - 2bx + b2)
(ab * 0).
(|a| < 1, |&| < 1, ab > 0).
Г 	dx
J a2sin2Jt + b
b2 cos2 л:
2216. Объяснить, почему формальное применение формулы
Ньютона—Лейбница приводит к неверным результатам, если:
а)
Jt
-1
2217. Найти
2я
■ >
б)|
0
1
Г А
Г 1
J dx
-1
1
1^1 + 2*
sec2xdx ,
2 + t g2x
dx.
в) j £0rote
-1
100 л
2218. Найти
i ^
cos2jc dx.
С помощью определенных интегралов найти пределы следую¬
щих сумм:
2219. lim
f-L + 2
\П2 П
2	п - 1
2	м2
2220.
Пт (—5— + —5— + ... + —1—1.
п~*оо \П+ 1
л + 2
п + п

§ 2. Вычисление определенных интегралов с помощью неопределенных
187
lim ( п + п +	+ —Л—)
'/1 — 00 1л2+12 я2 + 22	"	п2+п2)
2221
2222. lim -{sin -
/х — оо П\	П
+ sin 22 + ... + sin	.
п	п )
2223.	lim V+ 2f+ - + пР (р > 0).
л — оо	ПР+г
2224.	lim if /ГД + /ГД + ... + /ГД")
/1-00 nV V л V Л	V ЛУ
Найти:
nJn\
2225. lim
/1 — 00 Л
2226. lim Г1 у f( а + k^\\.
/i-оо Lai	V	n /J
i
Отбрасывая равномерно бесконечно малые высших поряд¬
ков, найти пределы следующих сумм:
sin — + 1
' 1 +
2
) sin?f
n2 \
V
n.
) n2
+
{
1 + n~1
\
n
sin fcLLi}*].
2228. lim sin 2 • V 	3—-.
„-°° n pTj 2 + cos—
n
n
J(nx + k)(nx + k + 1)
2229. lim ^			 (x > 0).
( i
2230. lim
/1—00
On	On
Z	4- ... +
Al+ 1 n , 1
2
л >\
2"
n + i
nJ
2231. Найти:
b	b	b
— f sin x2 dx, 4- f sin *2 dx, -гг f sin *2 dx.
dxj	da J	db J
2232. Найти:
•v*2
a)	-p f JYTt2 dt; 6) -p f _^L_ ; в) -p f cos (mf2) dt.
dx J	/ГГТ4 dx J
П	„2 ^	sin *

188
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2233.	Найти:
л
J
cosx2dx
a) lim SL-
х —> О	X
I
ех dx
в) lim —
х — 4*оо
f‘
2x2dx
j*(arctgx)2dx
б) lim Q		— 	;
*-+0° Jx2+1
г) lim	f(nx)dx,
n ► oo J
если f(x) € C [0, +oo] и f(x) —► А при x —► +oo.
2234.	Доказать, что
f ex dx dx ~ — ex
J	2x
о
при X OO.
2235.	Найти
lim
x — +o
sin*
J Jtg xdx
_Q
tgx
о
2236.	Пусть f(x) — непрерывная положительная функция.
Доказать, что функция
jtf(t)dx
ср(х) = ±
jf(t)dx
о
возрастает при х > 0.
2237. Найти:
2
<2х, если /(х) =
х
2
при 0 < х < 1,
при 1 < х < 2;
1
о
dxy если f(x) =
х	при 0 < х < t,
t *	при t < х < 1.

§ 2. Вычисление определенных интегралов с помощью неопределенных
189
2238. Вычислить и построить графики интегралов I = /(а),
рассматривая их как функции параметра а, если:
a) I = J* х\х - а| dx;
°>Ч
б) J = f ■-	.>п2*	-dx;
J l + 2acos* + a2
si nxdx
Jl - 2acos* + a2
Применяя формулу интегрирования по частям, найти сле-
дующие определенные интегралы:
In 2
11
2239. f хех dx.
2240.
I x sin * dx.
J
0
J
0
2л
<*
2241. J* х2 cos * dx.
о
2242.
J" |ln x\ dx.
e
Л
2243. f arccos * dx.
J
2244.
Г * arctg * dx.
J
0
0
Применяя подходящую замену переменной, найти следую¬
щие определенные интегралы:
1 п
2245. f xdx .
2246
f x2 4аг - x2 dx.
X
1
J
0
0,75
ln2
2247. f dx
2248.
f *Jex - 1 dx.
J (* + l)Jx2+ 1
0	v 7
1
J
0
2249. f arcsin Jidx
J Jx(l-x)
2250.	Вычислить интеграл f 		dx, полагая х - - = t.
J 1 + х4	х
-1
2251.	Объяснить, почему формальная замена х = ср(0 приво¬
дит к неверным результатам, если:
1 1
а) dx, где t = х3;
I
-1
Ггт
б)|ттЬ- гда*-7!
dx
sin2* 5
где tg х = t

190
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2252.	Можно ли в интеграле
J x3Jl - х2
dx
положить х = sin t?
2253.	Можно ли в интеграле / л/Г - х2 dx при замене пере-
о
менной х = sin t в качестве новых пределов взять числа к и - ?
2254.	Доказать, что если Дх) непрерывна на [а, Ь], то
ь	1
J Дх) dx = (Ь - а) j* Да + (b - а)х) dx.
а	0
2255.	Доказать равенство
а	а2
J x3f(x2) dx = | J хДд;) rfx (a > 0).
о	0
2256.	Пусть f(x) — непрерывная функция на сегменте
ь
[А, В] D [а, Ь]. Найти Г Дх + у) dy при [а - х, b - х] С [А, В],
dx J
a
2257.	Доказать, что если f(x) непрерывна на [0, 1], то
п	л
2	2
а) J Дsin х) dx = j* /(cos x) dx;
6)	J x/(sin x) dx = ~ J /(sin x)
о	0
dx.
2258.	Доказать, что для непрерывной на [-Z, Z] функции Дх)
имеем:
i	i
1) J Д*) dx = 2 J Дх) dx,
-/	о
если функция Дх) четная, и
2) J /(х)
-I
dx = 0,
если функция Дх) нечетная. Дать геометрическую интерпрета¬
цию этих фактов.

§ 2. Вычисление определенных интегралов с помощью неопределенных
191
2259.	Доказать, что одна из первообразных четной функции
есть функция нечетная, а всякая первообразная нечетной функ¬
ции есть функция четная.
2260.	Вычислить интеграл
Jt1 +Х_ хУ"’ dx
введя новую переменную t = х 4-
х
2261.	В интеграле
J /(х) COS X
dx
выполнить замену переменного sin х = t.
2262.	Вычислить интеграл
1
dx,
J | cos<4)
где п — натуральное число.
2263.	Найти интеграл
/т
xsinx
+ COS2X
dx.
2264.	Найти интеграл
1
l + f4x)
dxy
если
x3(x - 2)
2265.	Доказать, что если f(x) — непрерывная периодиче¬
ская функция, определенная при -оо < х < +оо и имеющая пе¬
риод Т, то
Iм
а
dxy
где а — любое число.

192
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2266.	Доказать, что при п нечетном функции
X	X
F(x) = J sin" х dx и G(x) = J cos" x dx
о	0
периодические с периодом 2n; а при n четном каждая из этих
функций есть сумма линейной и периодической функций.
2267.	Доказать, что функция
F(x) =
- \ т
dx,
где f(x) — непрерывная периодическая функция с периодом 7\
в общем случае есть сумма линейной функции и периодической
функции периода Т.
Вычислить интегралы:
1
2268. J х(2 - х2)12 dx.
0
е
2270. J (х In х)2 dx.
1
-1
2272. Г dx .
J xjx2 - 1
-2
3
2274. j* arcsin Jrf^dx-
0
2n
2276. f . , dx——.
J Sin4 X + COS4 X
0
я
2278. J {x sin x)2 dx.
0
In 2
J sh4 x
2269.
2271.
2273.
j* xdx
J x2 + x+ 1
9
J x У l - X
1
J Xlf>ji
dx.
-i- Sxs dx.
0
2я
2275. f 	——
J (2 + cosa;)(3 +
cosx)
Jsi
2277. sin x sin 2x sin 3x dx.
2279. j* ex cos2 x dx.
о
2280.
dx.

§ 2. Вычисление определенных интегралов с помощью неопределенных
193
С помощью формул понижения вычислить интегралы, зави¬
сящие от параметра л, принимающего целые положительные
значения:
2281.1п
я
2
о
2283.1п =
2282.1п
2284. /„
2285. /„ = f ■ х"-х ■
J
2286.1п
2287.1п
Я
4
К
sin£_2_cosjf\
sinx + cos xj
2n+ 1
я
2
Jcos" *dx-
0
1
J (1 - x2)ndx.
0
1
J xm (In x)n dx.
о
Если f(x) = fi(x) + if2(x) есть комплексная функция от действитель¬
ной переменной х> где fi(x) = Re f(x), f2(x) — Im f(x) и i2 = -1, то по
определению полагают:
Очевидно, что
| f(x) dx = | fx(x) dx + i J f2(x) <
Re j* /(*) dx = jRe /(x) d*,
ImJ* f(x) dx = Jim f(x) dx.
2288. Пользуясь формулой Эйлера
показать, что
j
е1* = cos х 4- i sin x9
О, если m & n,
2ti, если m = n
(пит — целые).
2289. Показать, что
Г с<« +*d* = е*(а + *Р)-еа(а+/Р)
J	а+*Р
(аи(3 — постоянные).

194
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пользуясь формулами Эйлера:
cos х = -(е1Х 4- е '*), sin х = — (е1ДГ - е tx),
вычислить интегралы (тип — целые положительные числа):
2290.
f sin2m д: cos2" д: dx. 2291. Г
J	J	sinx
о	о
я	я
2292. Г cps(2n +_1)х dx	2293. j* cos„ х
J COSX	J
о	о
я
2294.	/ sin" х sin пх dx.
о
Найти интегралы (л — натуральное число):
я
2295.	J sinft" 1 х cos (п 4- 1)х dx.
о
я
2296.	j* cos'1" 1 х sin (n 4- l)x dx.
о
2я
2297.	J e-ax cos2n x dx.
dx.
cos nx dx.
j
2298. In cos x • cos 2nx dx.
2299. Применяя многократное интегрирование по частям,
вычислить
интеграл Эйлера: В(т, п) = J хт *(1 - х)л 1 dx, где
тип — целые положительные числа.
2300. Многочлен Лежандра Рп(х) определяется следующей
формулой: Рп(х) =
Доказать, что
1	d";[(je*- in (п = 0, 1, 2, ...).
2 nnidxn
j* Рт(х)Рп(х) dx = <
О,	если т ^ п9
2п+ I
, если т = п.

§ 2. Вычисление определенных интегралов с помощью неопределенных
195
2301.	Пусть функция f(x) собственно интегрируема на [а, b]
и F(x) — функция такая, что F'(x) = f(x) всюду в [a, &], за иск¬
лючением, быть может, конечного числа внутренних точек
с, (/ = 1, ... , р) и точек а и Ь, где функция F(x) терпит разрыв
1-го рода («обобщенная первообразная»). Доказать, что
ь
f f(x) dx = F(b - 0) - F(a + 0) - £ [F(Ci + 0) - F(ct - 0)].
2302.	Пусть функция f(x) собственно интегрируема на сег¬
менте [а, Ь] и
X
F(x) = С + J № d\
а
— ее неопределенный интеграл.
Доказать, что функция F(x) непрерывна и во всех точках не¬
прерывности функции f(x) имеет место равенство
F\x) = f(x).
Что можно сказать о производной функции F(x) в точках раз¬
рыва функции f(x)7
Рассмотреть примеры:
а)	=1 (п = ± 1, ±2, ...) и f(x) = 0 при х * i ;
б)	f(x) = sgn x.
Найти неопределенные интегралы от ограниченных разрыв¬
ных функций:
2303.
J sgn х dx.
2304.
sgn (sin x) dx.
2305.
J*[jc] dx (x > 0).
2306.
x[x] dx (x > 0)
2307.
|(-l)w dx.
2308.
f f(x) dx, где f(x) = -
j 1, если \x\ < Z,
1 Л II»
J
0
[ 0, если \x\> l .
Вычислить определенные интегралы от ограниченных раз¬
рывных функций:
3	2
2309. f sgn (х - х3) dx.
2310. J [ех] dx.

196
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
п + 1
2313.	J In [х] dxy где п — натуральное число.
1
1
2314.	j* sgn [sin (In x)] dx.
0
2315.	Найти J |cos x\ Jsinx dx, где E — множество тех значе-
E
ний сегмента [0, 4л], для которых подынтегральное выражение
имеет смысл.
§ 3. Теоремы о среднем
1.	Среднее значение функции. Число
ь
M[f] = ^ J № dx
а
называется средним значением функции f(x) на промежутке [а, Ь].
Если функция f(x) непрерывна на [а, 6], то найдется точка с € (а, Ь)
такая, что
ми] = т.
2.	Первая теорема о среднем. Если: 1) функции f(x) и ф(д;) ограни¬
чены и соответственно интегрируемы на сегменте [а, Ь]; 2) функция ф(х)
не меняет знака при а < х < Ь, то
ь	ь
J f(x)cp(x) dx = ц J Ф(л:) dx,
а	а
где т<р<Мит= inf f(x), М = sup f(x);
а < x<b	а < x<b
3)	если, сверх того, функция f(x) непрерывна на сегменте [а, Ъ], то
р = /(с), где а< с < Ь.
3.	Вторая теорема о среднем. Если: 1) функция f(x) и ф(х) ограни¬
чены и собственно интегрируемы на сегменте [а, Ь]; 2) функция ф(х) мо¬
нотонна при а < х < Ь, то
ь	Е,	ь
J f(x)<p(x) dx = ф (а + 0) J f(x) dx + ф(Ь - 0) J f(x) dx,
a	at,
где а < £ < b;

§ 3. Теоремы о среднем
197
3) если, сверх того, функция <р(*) монотонно убывающая (в широком
смысле!) и неотрицательная, то
ь	К
J /(лг)ср(д:)	dx = (р(а	+ 0) J	f(x)	dx (а	< £ <	Ь),
а	а
а если функция ф(лг) монотонно возрастающая (в широком смысле!) и
неотрицательная, то
ь	ь
j* Л*)Ф(*)	dx = ср(Ь	- 0) J	f(x)	dx(a<^<	b).
2316. Определить знаки следующих определенных интегра¬
лов:
2я
2я
а) Г х sin х dx;
J
б) f
J х
0
0
2
1
в) f х32* dx;
г) f JC2 In .
J
J
-2
1
2
, Определить, какой интеграл больше:
я
я
2
2
а) Г sin10 х dx или
J
Г sin2 x dje;
J
0
0
х dx.
б,|
1	1
е~х dx или J e~*2dx;
о	о
2я
в) J е~х2 cos2 х dx или j* е~х2 cos2 х dx.
О	я
2318.	Определить средние значения данных функций в ука¬
занных промежутках:
а)	fix) = х2 на [0, 1];
б)	f(x) = Jx на [0, 100];
в)	f(x) =10 + 2 sin х + 3 cos х на [0, 2л];
г)	f(x) = sin х sin (х + ф) на [0, 2л].
2319.	1. Найти среднее значение длины фокального ради¬
уса-вектора эллипса
г = -—2	 (0 < в < 1).
1 - есовф

198
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2.	Найти среднее значение скорости свободно падающего те¬
ла, начальная скорость которого равна i>0.
2320.	Сила переменного тока изменяется по закону
i = i0 sin^ + ф) ,
где i0 — амплитуда, t — время, Т — период и ср — начальная фа¬
за. Найти среднее значение квадрата силы тока.
2321.	Пусть fix) € С [0, 4-00) и lim fix) = А. Найти
X -* +оо
X
lim - Г fix) dx.
х — +оо х J
О
Рассмотреть пример f(x) = arctg х.
х
2322.	Пусть j* f(t) dt = х/(0л:). Найти 0, если:
о
a) f(t) = tn (п > -1);	б) f(t) = In t\
в) f(t) = е*.
Чему равны lim 0 и lim 0?
х — +0	х,— +оо
Пользуясь первой теоремой о среднем, оценить интегралы:
2323. f -	-4?
J 1 + 0,5совл:
о
юо
2325
+ 100
■ dx.
2326.1.	Доказать равенства:
1
2.	Найти:
a)	lim f _£L-;
е — о J ел:3 + 1
где а > О, b > 0 и fix) € С [0, 1].
2324.
j
Jl + х
dx.
a) lim Г dx = 0; б) lim Г sinn х dx = 0.
л — oojl + л;	П-ОО J
о	о
fee
б) lim Г f(x)4z ,
е-*+0 J X

§ 4. Несобственные интегралы
199
2327. Пусть f(x) непрерывна на [a, 6], а ф(лг) непрерывна на
[а, Ь] и дифференцируема на (а, 6), причем
ф'(*) > 0 при а < х < Ь.
Доказать вторую теорему о среднем, применяя интегрирова¬
ние по частям и используя первую теорему о среднем.
Пользуясь второй теоремой о среднем, оценить интегралы:
2331. Пусть функции ср(х) и \j/(jc) интегрируемы на промежут¬
ке [а, Ъ] вместе со своими квадратами. Доказать неравенство
Коши—Буняковского
2332. Пусть функция f(x) непрерывно дифференцируема на
сегменте [а,Ь] и f(a) = 0.
Доказать неравенство
1. Несобственная интегрируемость функций. Если функция f(x)
собственно интегрируема на каждом конечном сегменте [а, Ь]> то, по
определению, полагают
200 л
2328. Г 51Rldx.
100л
ь
а
b
2330. sin х2 dx (0 < а < b).
а
а
а
а
Ь
где М = sup |/(х)|.
а < х < Ь
2333. Доказать неравенство
lim Г dx = 0 (р > 0).
п — ОО I	X
п
§ 4. Несобственные интегралы
ь
f(x) dx =
а
а
(1)

200
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Если функция f(x) не ограничена в окрестности точки b и собст¬
венно интегрируема на каждом сегменте [а, Ъ - е] (е > 0), то прини¬
мают
Ь	Ь-Е
J f(x) dx = lim^ J f(x) dx.
a	a
(2)
Если пределы (1) или (2) существуют, то соответствующий интеграл
называется сходящимся, в противном случае — расходящимся (в эле¬
ментарном смысле).
2. Критерий Коши. Для сходимости интеграла (1) необходимо и до¬
статочно, чтобы для любого е > 0 существовало число Ъ = Ь(е) такое, что
при любых Ъ' > Ъ и Ь" > Ъ было бы выполнено неравенство
№ dx
< е.
Аналогично формулируется критерий Коши для интеграла типа (2).
3.	Признаки абсолютной сходимости. Если \f(x)\ несобственно ин¬
тегрируема, то соответствующий элементарный интеграл (1) или (2) от
функции f(x) называется абсолютно сходящимся и является интегра¬
лом заведомо сходящимся.
Признак сравнения I. Пусть \f(x)\ < F(x) при х > а.
Если
+оо
J F(x) dx сходится, то интеграл
а
+оо
J f(x) dx сходится абсо-
а
ЛЮТНО.
Признак сравнения II. Если \|/(лг) > 0 и ср(лг) = 0*(\|/(дс)) при х —1» +оо,
+оо	+оо
то интегралы J ф(дс) dx и J \|/(лг) dx сходятся или расходятся одновре¬
менно. В частности, это имеет место, если <р(лг) ~ \|/(лг) при х —► +оо.
Признак сравнения III. а) Пусть
л*)"°*ё) при *
+оо.
В таком случае интеграл (1) сходится, если р > 1, и расходится, если
1.
б) Пусть
л*) = 0*((б^я) при
В таком случае интеграл (2) сходится, если р < 1, и расходится, если
р> 1.

§ 4. Несобственные интегралы
201
4.	Специальный признак сходимости. Если: 1) функция ф(х) моно¬
тонно стремится к нулю при х —1» +оо и 2) функция f(x) имеет ограни¬
ченную первообразную
х
Fix) - J № d%,
а
то интеграл
+оо
J f(xyp(x)dx
а
сходится, вообще говоря, не абсолютно.
В частности, интегралы
+ оо	+ оо
J dx и J f^dx («> 0)
а	а
сходятся, если р > 0.
5.	Главное значение (в смысле Коши). Если функция f(x) такова,
что при любом е > 0 существуют собственные интегралы
с - е	b
J f(x) dx и j f(x) dx (a < с < b),
то под главным значением в смысле Коши (v. р.) понимается число
b	-с-е	Ь
J f(x) dx + J f{x) dx
a	c + e
J
v. p. I f(x) dx = lim
Аналогично
/. p. I f(x) dx = lim I f(x) dx.
J	a- +oo J
Вычислить интегралы:
+oo
2334. f Ц- (a > 0).
J x2
a
+oo
f dx
J 1 + X2 *
-oo
1-00
f dx
J X2 + X - 2 ‘
2336.
2335. J In x
	c
VT
dx.
2337. Г ■ ,
J ITT*
-1
+od
2338.
2339.
f dx
J (jc2 + jc +
l)2 '

202
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2340.
2342.
2344.
о
+ оо
)
dx
2341. f
1+ X2
J
0
-t oo
dx
2343. f
(2-x)Jl-x
J
l
О
-f oo
хЫх dx.
2345. f
(1 + X2)2
J
0
dx.
dx
ЛГл/1 + Х5+ X10
2346.	J е ах cos Ъх dx (а > 0).
о
+ оо
2347.	| еах sin Ъх dx (а > 0).
С помощью формул понижения вычислить следующие несоб¬
ственные интегралы (п — натуральное число):
+оо
2348.1п
пе~х dx.
Г„= J хпе
о
+оо
, / = f	^	 (ас - Ь2 > 0).
" J (ax*+2bx+c)" 1	’
—оо
+ оо
2350. In = f 			-.
J х(х+ 1)...(х + п)
2349.1п =
1
1
2351./„= f x"dx ■
J J(1 - x)(l + X
J(l-x)(l + x)
2352. In = f —r——,— •
J chn+1x
о
+ oo
2353. a) J In sin x dx; 6) J In cos x dx.
0
f ei |sin*-CQS*| dX'
J	J sin л:
2354. Найти
где E — множество тех значений х интервала (0, +°°), для кото¬
рых подынтегральное выражение имеет смысл.

§ 4. Несобственные интегралы
203
2355.	Доказать равенство
+ оо	+оо
J ах + ~ j dx = i J f( Jx2 + Aab) dx,
о	о
где a > 0 и b > 0, предполагая, что интеграл в левой части равен¬
ства имеет смысл.
2356.	Средним значением функции f(x) на интервале (0, +оо)
называется число
X
M\f\ - lim I f № d\.
x — -boo x J
0
Найти средние значения следующих функций:
a) f(x) = sin2 х + cos2 (xj2); 6) f(x) = arctg x;
в) f(x) = V^sin x.
2357. Найти:
a) lim x f dt;
X-+0 J t2
X
+ oo
xe~ldt
в) lim
jc —» 0
In
1
pl + t4dt
6) lim a			:
X —* 00	Xs
r) lim xa[f-^-dt,
x-0 J ta+ 1
где a > 0 и f(t) — непрерывная функция на сегменте [0, 1].
Исследовать сходимость интегралов:
4-00	4оо
2358.
Г x2dx
J *4 - х2 + 1 ’
о
2
2360. Г .
J 1пл:
0
1
2362. J хр1пч ±dx.
О
4оо
2364. Г arct%a* dx (а * 0).
J хп
2359.
I
1
4оо
dx
\lx2 + 1
2361. J xp ~ 1e~x dx.
0
4-oo
2363. f -^—dx (n> 0).
J 1 + xn
0
-400
2365. J ln(1+-^ dx.
Xn

204
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2366. f xmarct?*dx (п > 0).
J 2 + хп
2368.
f sin2*
J *
dx.
2367. f	(n>0).
J 1 + *"
0
n
2
I
2369
sin'’* cos’*
2370. a) f xndx-;	6) f
J ЛТх* J
dx
Jx*
2371.
f dx
J xp+ x<i'
2373. J ln-(sLn-^ dx.
2375.
0
+ oo
J
J~X
2372.
2374.
f b*
J 1-*
0
+ oo
J
dx.
xP\n<ix
dx
xP(\nx)<i(\n\nx)r
2376.
a> f ;	7Г.—Ц;—;	j- <ai < аг < ••• < ««);
+ oo
6) J X°\x - lp I
dx.
Pm(x) ,
2377. f	d*, где Pm(x) и Рп(л;) — взаимно простые мно-
J *п\Х)
0
гочлены соответственно степеней тип.
Исследовать на абсолютную и условную сходимости следую¬
щие интегралы:
+ 00
2378. J	dx.
о
Указание. |sin х\ > sin2 х.
+ 00
2379.	Г	dx.
J * + 100

§ 4. Несобственные интегралы
205
2380. a) J хр sin (xq) dx (q ^ 0);	6) J sin (sec x) dx;
о
+ oo
в) J x2 cos (ex) dx.
о
2381. f	(q > 0).
J 1 + хч
о
+ oo
+°° sinfar +
2382. f — 	—• dx.
J *"
Г P (x)
2383.	sin x dx, где Pm(a;) и Pn(x) — целые многочлены
J * n\X)
a
и Pn(x) > 0, если x > a > 0.
+ oo
2384.	1. Если J f(x) dx сходится, то обязательно ли f(x) —► 0
а
при х -* +оо? Рассмотреть примеры:
+ оо	+оо
a) J sin (х)2 dx; б) J (-1)1*21 dx.
о	о
2. Пусть f(x) € С(1) [х0, +оо), \f'(x)\ < С при х0 < х < +°о и
+ оо
J |Дд:)| dx сходится. Доказать, что f(x) —► 0 при х —► +оо.
хо
+ оо
Указание. Рассмотреть интеграл J f(x)f'(x) dx.
хо
2385.	Можно ли сходящийся несобственный интеграл
ь
dx
J fix)
от неограниченной функции f(x), определенной на [а, Ь], рас¬
сматривать как предел соответствующей интегральной суммы
t = 0
где xt < ^ < х{ + 1 и	+ 1 - Xj?

206
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2386. Пусть
4 ОО
J f(x) dx
(1)
сходится и функция ф(л;) ограничена. Обязательно ли сходится
интеграл
J* /(лг)ф(л;) dx?
(2)
Привести соответствующий пример.
Что можно сказать о сходимости интеграла (2), если интеграл
(1) сходится абсолютно?
+ оо
2387.	Доказать, что если J f(x) dx сходится и f(x) — моно-
а
тонная функция, то f(x) = О ^ .
2388.	Пусть функция f(x) монотонна в промежутке 0 < х < 1
и не ограничена в окрестности точки х = 0.
Доказать, что если существует
1
то
J f{x) dx,
о
1
; 14!) - j л*>
k= 1	n
2389.	Доказать, что если функция f(x) монотонна и ограни¬
чена в интервале 0 < х < а и существует несобственный интеграл
J №
dx,
то
lim хр 41 f(x) = 0.
.Г — 4 0
2390. Показать, что:
1
a) v. Р- J ~ = 0;
-1
+ оо
в) V. р. J sin х
j
dx
l - х2
= 0;
dx = 0.
6) V. p.

§ 5. Вычисление площадей
207
2391. Доказать, что при х > 0 существует
И х = v. р.
Г <£.
J
0
Найти следующие интегралы:
+ оо
2
2392. v. р. Г , а* .
2393. v. р. f ?* .
* J х2 - Зх + 2
^ J х\пх
0
1
+ оо
2
ч-оо
2394. v. р. f } + * dx.
J 1 + X2
2395. V. р. f arctg
J
~оо
-ОО
dx.
§ 5. Вычисление площадей
1.	Площадь в прямоугольных координатах. Площадь S плоской фи¬
гуры А1А2В2В1 (рис. 10), ограниченной двумя непрерывными кривыми
у = У\(х) и у = у2(х) (у2(х) > Ух(х)) и двумя прямыми х = а и х = Ъ (а < Ь),
равна
S = J* [j/2(*) - </i(*)l dx.
2.	Площадь фигуры, ограниченной кривой, заданной в парамет¬
рическом виде. Если х = *(£)> У = у(0 [0 < t < Т] — параметрические
уравнения кусочно-гладкой простой замкнутой кривой С, пробегаемой
против хода часовой стрелки и ограничивающей слева от себя фигуру
с площадью S (рис. 11), то
т	т
S	= - J y(t)x\t) dt= J x(t)y\t) dt,
0
0
У
О
Рис. 10
Рис. 11

208
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ИЛИ
Т
S- \ J [x{t)y’{t)-x'{t)y(t)\dt.
о
3.	Площадь в полярных координатах. Площадь S сектора ОАВ
(рис. 12), ограниченного непрерывной кривой г= г(ф) и двумя
полупрямыми ф = а и ср = Р (а < Р), равна
Р
■S = | J Л<Р) dф.
а
2396. Доказать, что площадь прямого параболического сег¬
мента равна
s= ! bh,
где b — основание и h — высота сегмента (рис. 13).
Рис. 12
Найти площади фигур, ограниченных кривыми, заданными
в прямоугольных координатах.1*
2397.	ах = у2у ау = х2.
2398.	у = х2, х + у = 2.
2399.	у = 2х - х2, х + у = 0.
2400.	а) у = |lg jc|, i/ = 0, х = 0,1, х = 10;
б)	I/ = 2х, у = 2, * = 0;
в)	у = (* + I)2, х = sin Щу у = 0 (0 < у < 1).
2401.	у — дс; I/ = дс + sin2 х (0 < л: < я). **** Все параметры в этом и следующих параграфах раздела IV счита¬
ются положительными.

§ 5. Вычисление площадей
209
2403.	£| + g = 1.
а2 Ъ2
2404.	у2 = х\а2 - х2).
2405.	у2 = 2ул;, 27ру2 = 8(х -р)3.
2406.	А*2 + 2£л;у + Су2 = 1 (А > О, АС - В2 > 0).
2407.	у2 = ---*■■■ ■■ (циссоида), х = 2а.
zo — х
2408.	дс = а In —t..V?2.~ ^ - ^/а2 - у2, у = 0 (трактриса).
2409.	у2 =	*"	2 (х > 0; п > -2).
(1 + хп + 2)2
2410.	у = e"*|sin х\, у = 0 (х > 0).
2411.	В каком отношении парабола у2 = 2л; делит площадь
круга л:2 + у2 = 8?
2412.	Выразить координаты точки М(х, у) гиперболы л;2 - у2 = 1
как функции площади гиперболического сектора S = ОМ'М, огра¬
ниченного дугой гиперболы М'М и двумя лучами ОМ и ОМ', где
М'(х, -у) — точка, симметричная М относительно оси Ох.
Найти площади фигур, ограниченных кривыми, заданными
параметрически:
2413.	х— a(t - sin £), у = а(1 - cos £) (0 < £ < 2л) (циклоида)
и у = 0.
2414.	л; = 2£ - £2, у = 2£2 - £3.
2415.	х = a (cos £ + £ sin £), у = a (sin £ - £ cos £) (0 < £ < 2л)
(развертка круга) и л; = а, у < 0.
2416.	л; = а (2 cos £ - cos 2£), у = а (2sin £ - sin 2£).
2417.	a) х = — cos3 £, у = ^ sin3 £ (с2 = а2 - 62) (эволюта эллипса);
а	о
б)	х = a cos £, у = asin2* .
2	+ sin£
Найти площади фигур, ограниченных кривыми, заданными
в полярных координатах:
2418.	г2 = a2 cos 2ф (лемниската).
2419.	г = a (1 + cos ср) (кардиоида).
2420.	г = a sin Зср (трилистник).
2421. г = —^  (парабола), ф = - , ф = - .
1 - совф	4	2

210
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2422. а) г =
1 + ecoscp
б) г = 3 + 2 cos ср;
а) г = -—£
(0 < в < 1) (эллипс);
2423.	г = a cos ср, г = a (cos ср + si
2424.	Найти площадь сектора, ограниченного кривой
ср = г arctg г
2425.	Найти площадь фигуры, ограниченной:
а)	кривой г2 + ср2 = 1;
б)	лепестком кривой ср = sin (яг) (0 < г < 1);
в)	линиями ср = 4г - г3, ср = 0;
г)	линиями ср = г - sin г, ср = я;
д)	замкнутой кривой г = —L ? ф — _ZLL .
1 + t2	1 + t
Перейдя к полярным координатам, найти площади фигур,
ограниченных кривыми:
2426.	х3 + у3 = 3аху (лист Декарта).
2427.	х4 + у4 = а2(х2 + у2).
2428.	(х2 + у2)2 = 2а2ху (лемниската).
Приведя уравнения к параметрическому виду, найти площа¬
ди фигур, ограниченных кривыми:
1.	Длина дуги в прямоугольных координатах. Длина дуги отрезка
гладкой (непрерывно дифференцируемой) кривой
у = у(х) (а< х<Ь)
2 2 2
2429.	х3 + у 3 = а 3 (астроида).
2430.	х4 + у4 = ах2у.
Указание. Положить у = tx.
§ 6. Вычисление длин дуг
ь
s = Jl + у'2(х) dx.
а
равна

§ 6. Вычисление длин дуг
211
2.	Длина дуги кривой, заданной параметрически. Если кривая С
задана уравнениями
* = x(t), у = y(t)	Т)у
где x(t), y(t) € С(1) [£0> Т], то длина дуги кривой С равна
= jjx'Ht) + y'4t)dt.
3.	Длина дуги в полярных координатах. Если
Г-Г(ф) (а < ф < Р),
где г(ф) 6 С'11 [а, Р], то длина дуги соответствующего отрезка кривой
равна
s =
г'2(ф) dcp.
Длины дуг пространственных кривых см. в разд. VIII.
Найти длины дуг следующих кривых:
2431.1/=	(0<х<4).
2432.	у2 = 2рх(0<х< х0).
2433.	и = a ch^ от точки А (0, а) до точки В (Ь, к).
а
2434.	у = ех (0 < х< х0).
2435.	х— | у2 - | In у (1 < у < е).
2436.	у = a In—(0 < х < Ь < а).
а2 - х1
2437.	у = In cos л; (0 < х < а < 5).
2438.	х = а 1па + л/а2"У- - Ja2 - у2 (0 < Ь < у < а).
У
2439.	у3 =	{0 < х < | а).
у 2а- х V	3	)
2 2 2
2440.	х3 + г/3 = а 3 (астроида).
2441.	х = — cos31, у = ~ sin3с2 = а2 - Ь2 (эволюта эллипса),
а	Ь
2442.	х = cos4 t, у = sin4 t.
2443.	х = а (£ - sin 0» £/= а(1 “ cos 0 (0 < * < 2я).
2444.	х = a(cos £ + t sin *)> у = a (sin t - t cos t) при 0 < t < 2я
(развертка окружности).

212
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2445.	а) х = a (sh t - t), у = a (ch t - 1) (0 < t < Т);
б)	х = ch3 t, у = sh3 t (О < t < T).
2446.	г = сир (спираль Архимеда) при О < ср < 2я.
2447.	г = аетф (т > 0) при О < г < а.
2448.	г = а (1 + cos (р).
2449. г= —-£	 f|q>| < ?! •
1	+ coscp V 2 )
2450.	г = a sin3 ® .
2451.	r=atg| (0<(р< 2я).
2452.	а) Ф = |( г + 1) (1 < г < 3);
б)	(р = Jr (0 < г < 5);
Г
в)	<р = J (0 < г < R);
О
г)	г = 1 4- cos t, ср = t - tg~ (0 < t < Т < я).
2453.	Доказать, что длина дуги эллипса
х — a cos t9 у = b sin t
равна длине одной волны синусоиды у = с sin ~ , где с = Ja2 - fr2.
b
2454.	Парабола 4ау = я2 катится по оси Ох. Доказать, что фо¬
кус параболы описывает цепную линию.
2455.	Найти отношение площади, ограниченной петлей кривой
»-±(i ~x)Ji-
к площади круга, длина окружности которого равна длине кон¬
тура этой кривой.
§ 7. Вычисление объемов
1. Объем тела по известным поперечным сечениям. Если объем V
тела существует и S = S(x) [а < х < Ь] есть площадь сечения тела плос¬
костью, перпендикулярной к оси Ох в точке х, то

§ 7. Вычисление объемов
213
2. Объем тела вращения. Объем тела, образованного вращением во¬
круг оси Ох криволинейной трапеции
а < л: < &, 0 < у < у(х)>
где у(х) — непрерывная однозначная функция, равен
ь
Vx = п J у2(х) dx.
а
В более общем случае объем кольца, образованного вращением во¬
круг оси Ох фигуры а< х < Ь, ух(х) < у < у2(х), где ух(х) и у2(х) — не¬
прерывные неотрицательные функции, равен
ь
V=n J [yl(x)- у\(*)] dx.
а
2456.	Найти объем чердака, основание которого есть прямо¬
угольник со сторонами а и Ь, верхнее ребро равно с, а высота
равна h.
2457.	Найти объем обелиска, параллельные основания кото¬
рого суть прямоугольники со сторонами А, В и a, b, а высота
равна h.
2458.	Найти объем усеченного конуса, основания которого
суть эллипсы с полуосями А, В и a, b, а высота равна h.
2459.	Найти объем параболоида вращения, основание кото¬
рого S, а высота равна Н.
2460.	Пусть для кубируемого тела площадь S = S(ar) его по¬
перечного сечения, перпендикулярного к оси Ох, изменяется по
квадратичному закону:
S(*) = Ах2 + Вх + С [а < х < 6],
где А, Б и С — постоянные.
Доказать, что объем этого тела равен
v= |[s(a) +	+ S(«] ,
где H = b - a (формула Симпсона).
2461.	Тело представляет собой множество точек М(х, у, г),
где 0 < г < 1, причем 0<лг<1,0<у<1, если 2 рационально, и
-1 < х < 0, -1 < у <0, если г иррационально. Доказать, что объем
этого тела не существует, хотя соответствующий интеграл

214
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Найти объемы тел, ограниченных следующими поверхностями:
2462.	£?+*£=l,z=£*f2 = 0.
а2 Ь2	а
2463.	^	— 1 (эллипсоид).
а2	о2	с2
2464.	^ + g-5!=1,* = ±c.
а2	Ъ2	с2
2465.	х2 + z2 = а2, г/2 4- z2 = а2.
2466.	:с2 + у2 + z2 = а2у х2 + у2 = ал:.
2467.	z2 =	b (а	-	л:),	л:2	+	у2 = ал:.
2468.	~	^	=	1 (0	<	z	< а).
a2 z2	9
2469.	x + y + z2=lyX=09y = 0yZ = 0.
2470.	л:2 + у2 + z2 + ху + yz + zx = а2.
2471.	Доказать, что объем тела, образованного вращением во¬
круг оси Оу плоской фигуры
а < х < by 0 < у < у(х)у
где у(х) — однозначная непрерывная функция, равен
ь
V = 2я f ху(х) dx.
Найти объемы тел, ограниченных поверхностями, получен¬
ными при вращении отрезками следующих линий:
2472.	у =	(0 < х < а) вокруг оси Ох (нейлоид).
2473.	у = 2х - х2у у = 0: а) вокруг оси Ох; б) вокруг оси Оу.
2474.	у = sin Ху у = 0 (0 < х < я): а) вокруг оси Ох; б) вокруг
оси Оу.
2475. у = б(|)2, у = Ь
X
а
а) вокруг оси Ох; б) вокруг оси Оу.
2476.	у = е~ху у = 0 (0 < х +оо): а) вокруг оси Ох; б) вокруг оси Оу.
2477.	л:2 4- (у - Ь)2 = а2 (0 < а < Ь) вокруг оси Ох.
2478.	л:2 - ху + у2 = а2 вокруг оси Ох.
2479.	у = e~xJsinx (0 < х < +оо) вокруг оси Ох.
2480.	х = a (t - sin 0» У = а (1 " cos t) (0 < t < 2я), у = 0:
а)	вокруг оси Ох; б) вокруг оси Оу; в) вокруг прямой у = 2а.
2481.	х = а sin3 ty у = Ъ cos3 t (0 < t < 2я): а) вокруг оси Ох;
б)	вокруг оси Оу.

§ 8. Вычисление площадей поверхностей вращения
215
2482.	1. Найти объем тела, образованного вращением площа¬
ди петли кривой
х = 2t - I2, у = At - t2
вокруг: а) оси Ох; б) оси Оу.
2. Доказать, что объем тела, образованного вращением во¬
круг полярной оси плоской фигуры
0<а<ф<(3<л, 0 < г < г(ф)
(Ф
иг— полярные координаты), равен
Р
sin ф сйр.
Найти объемы тел, образованных вращением плоских фигур,
заданных в полярных координатах:
2483.	1. г = а (1 + cos ф) (0 < ф < 2л): а) вокруг полярной оси;
б)	вокруг прямой г cos ф =
а
4 ’
2. (х2 + у2)2 = а2{х2 - у2): а) вокруг оси Ох; б) вокруг оси Оу;
в)	вокруг прямой у = х.
Указание. Перейти к полярным координатам.
2484.	1. Найти объем тела, образованного вращением фигу¬
ры, ограниченной полувитком спирали Архимеда
г = аф (а > 0; 0 < ф < л),
вокруг полярной оси.
2. Найти объем тела, образованного вращением фигуры, ог¬
раниченной линиями:
ф = лг3, ф = л,
вокруг полярной оси.
2485.	Найти объем тела, образованного вращением фигуры:
а < г < а л/2 зт2ф
вокруг полярной оси.
§ 8. Вычисление площадей поверхностей вращения
Площадь поверхности, образованной вращением гладкой кривой
АВ вокруг оси Ох, равна
в
Р = 2л j* \у\ ds,
л
где ds — дифференциал дуги.

216
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Найти площади поверхностей, образованных вращением сле¬
дующих кривых:
2486■y = xj* (О < х < а) вокруг оси Ох.
2487.	у = a cos|| (|jc| < Ъ) вокруг оси Ох.
й О
2488.	у = tg х ^0 < х < вокруг оси Ох.
2489.	у2 = 2рх (0 < х < х0): а) вокруг оси Ох; б) вокруг оси Оу.
y2	«у2
2490.	±- +	=1 (0 < b < а): а) вокруг оси Ох; б) вокруг оси Оу.
а2 о*
2491.	х2 + (у- Ь)2 = а2 (6 > а) вокруг оси Ojc.
2 2 2
2492.	х ® + z/3 = аз вокруг оси О*.
2493.	«/ = а ch^ (\х\ < b j : а) вокруг оси Ох; б) вокруг оси Оу.
2494.	±х = а In — VglzJtf -	- у2 вокруг оси О*.
2495.	jc = а (£ - sin £), у = а (1 - cos £) (0 < £ < 2я): а) вокруг
оси Оде; б) вокруг оси Оу; в) вокруг прямой у = 2а.
2496.	л: = а cos3 £, I/ = а sin3 £ вокруг прямой у = х.
2497.	г = а (1 + cos ср) вокруг полярной оси.
2498.	г2 = а2 cos 2(р: а) вокруг полярной оси; б) вокруг оси Ф = ~ ;
в) вокруг ОСИ ф = 7 .
4
2499.	Тело образовано вращением вокруг оси Ох фигуры,
ограниченной параболой ау = а2 - х2 и осью Ох. Найти отноше¬
ние поверхности тела вращения к поверхности равновеликого
шара.
2500.	Фигура, ограниченная параболой у2 = 2рх и прямой
х = £, вращается вокруг прямой г/ = р. Найти объем и поверх¬
ность тела вращения.
§ 9. Вычисление моментов. Координаты центра масс
1. Моменты. Если на плоскости Оху масса М плотности р = р(у) за¬
полняет некоторый ограниченный континуум £1 (линию, плоскую об¬
ласть) и (о = (o(i/) — соответствующая мера (длина дуги, площадь) той

§ 9. Вычисление моментов. Координаты центра масс
217
части континуума £2, ординаты которой не превышают уу то k-м момен¬
том массы М относительно оси Ох называется число
Мк = lim у р (у,)у* Да)(.у,) = Г ру* dco(y) (ft = 0, 1, 2, ...),
тахД^-О f-d	J
где ДУ/ = У/ - У/ -1 и Дш(у,) = о>(у,) - <i)(y,. ,)•
Как частные случаи, получаем при k = О массу М, при /г = 1 — ста¬
тический момент, при /г = 2 — момент инерции.
Аналогично определяются моменты массы относительно координат*
ных плоскостей.
Если р — 1, то соответствующий момент называется геометрическим
(момент линии, плоской фигуры, тела и т. д.).
2. Центр масс. Координаты центра масс (*0, у о) однородной плоской
фигуры площади S определяются по формулам
_ m\v) _ м[х)
х0 —, У о	s ,
где М, М[х) — геометрические статические моменты фигуры отно-
сительно осей Оу и Ох.
2501.	1. Найти статический момент и момент инерции дуги
полуокружности радиуса а относительно диаметра, проходяще¬
го через концы этой дуги.
2. Найти статический момент дуги параболы
у2=2р*(0<*<
относительно прямой х = £ .
2502.	1. Найти статический момент и момент инерции одно¬
родной треугольной пластинки с основанием b и высотой h отно¬
сительно основания (р = 1).
2. Найти моменты инерции 1Х = М2Х) и /у = М2У) относитель¬
но осей Ох и Оу параболического сегмента, ограниченного кри¬
выми
ау = 2а* - х2 (а > 0) и у = 0.
Чему равны радиусы инерции гх и гу> т. е. величины, определяе¬
мые соотношениями
J,= Sr2x,Iy= Sr2y,
где S — площадь сегмента?

218
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2503.	Найти моменты инерции однородной эллиптической
пластинки с полуосями а и Ь относительно ее главных осей (р = 1).
2504.	1. Найти статический момент и момент инерции одно¬
родного кругового конуса с радиусом основания г и высотой h
относительно плоскости основания этого конуса (р = 1).
2. Найти момент инерции однородного шара радиуса R и мас¬
сы М относительно его диаметра.
2505.	Доказать первую теорему Гульдена: площадь поверх¬
ности, образованной вращением плоской дуги С вокруг не пере¬
секающей ее оси, лежащей в плоскости дуги, равна длине этой
дуги, умноженной на длину окружности, описываемой центром
масс дуги С.
2506.	Доказать вторую теорему Гульдена: объем тела, обра¬
зованного вращением плоской фигуры S вокруг не пересекаю¬
щей ее оси, расположенной в плоскости фигуры, равен произве¬
дению площади S на длину окружности, описываемой центром
масс этой фигуры.
2507.	Определить координаты центра масс круговой дуги:
х = a cos (р, у = a sin ср (|(р| < а < п).
2508.	Определить координаты центра масс области, ограни¬
ченной параболами ах = /у2, ау = х2 (а > 0).
2509.	Определить координаты центра масс области
+ Й < 1	(0 < * < а, 0 < у < Ь).
а* Ьг
2510.	Определить центр масс однородного полушара радиуса а.
2511.	Определить координаты центра масс С (ср0, г0) дуги ОР
логарифмической спирали г = aem{fi (т > 0) от точки 0 (-°°, 0) до
точки Р (ф, г). Какую кривую описывает точка С при движении
точки Р?
2512.	Определить координаты центра масс области, ограни¬
ченной кривой r= а (1 + cos ф).
2513.	Определить координаты центра масс области, ограни¬
ченной первой аркой циклоиды х = a (t - sin t), у = а (1 - cos t)
(0 < t < 2тг) и осью Ox,
2514.	Определить координаты центра масс тела, образован¬
ного вращением площади 0 < х < а; у2 < 2рх вокруг оси Ох,
2515.	Определить координаты центра масс полусферы
д:2 + у2 z2 — a2 (z > 0).

§10. Задачи из механики и физики
219
§ 10. Задачи из механики и физики
Составляя соответствующие интегральные суммы и находя
их пределы, решить следующие задачи:
2516.	Определить массу стержня длины I = 10 м, если линей¬
ная плотность стержня меняется по закону 5=6 + 0,3* (кг/м),
где * — расстояние от одного из концов стержня.
2517.	Какую работу надо затратить, чтобы тело массы т под¬
нять с поверхности Земли, радиус которой R, на высоту hi Чему
равна эта работа, если тело удаляется в бесконечность?
2518.	Какую работу надо затратить, чтобы растянуть упру¬
гую пружину на 10 см, если сила в 1 Н растягивает эту пружину
на 1 см?
Указание. Использовать закон Гука.
2519.	Цилиндр диаметра 20 см и длины 80 см заполнен паром
под давлением 10 Па. Чему равна работа пара при уменьшении
его объема в два раза, если температура пара остается постоян¬
ной?
2520.	Определить силу давления воды на вертикальную стен¬
ку, имеющую форму полукруга радиуса а, диаметр которого на¬
ходится на поверхности воды.
2521.	Определить силу давления воды на вертикальную стен¬
ку, имеющую форму трапеции, нижнее основание которой
а = 10 м, верхнее 5 = 6м и высота Л = 5 м, если уровень погру¬
жения нижнего основания с = 20 м.
Составляя дифференциальные уравнения, решить следую¬
щие задачи.
2522.	Скорость точки меняется по закону
v = v0 + at.
Какой путь пройдет эта точка за промежуток времени [0, Т]1
2523.	Однородный шар радиуса R и плотности 5 вращается
вокруг своего диаметра с угловой скоростью со. Определить ки¬
нетическую энергию шара.
2524.	С какой силой материальная бесконечная прямая по¬
стоянной линейной плотности Ро притягивает материальную
точку массы т, находящуюся на расстоянии а от этой прямой?
2525.	Определить, с какой силой круглая пластинка ра¬
диуса а и постоянной поверхностной плотности 80 притягивает
материальную точку Р массы т, находящуюся на перпендику¬
ляре к плоскости пластинки, проходящем через ее центр Q, на
кратчайшем расстоянии PQ, равном Ь.

220
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2526.	Согласно закону Торричелли скорость истечения жид¬
кости из сосуда равна
v = cj2gh,
где g — ускорение свободного падения, h — высота уровня жид¬
кости над отверстием и с = 0,6 — опытный коэффициент.
За какое время опорожнится наполненная доверху верти¬
кальная цилиндрическая бочка диаметра D= 1м и высотой
Я = 2м через круглое отверстие в дне бочки, если диаметр от¬
верстия d = 1 см?
2527.	Какую форму должен иметь сосуд, представляющий со¬
бой тело вращения, чтобы понижение уровня жидкости при ис¬
течении было равномерным?
2528.	Скорость распада радия в каждый момент времени про¬
порциональна его наличному количеству. Найти закон распада
радия, если в начальный момент t = 0 имелось количество радия
Q0, а через время Т = 1600 лет его количество уменьшится в два
раза.
2529.	Для процесса второго порядка скорость химической
реакции, переводящей вещество А в вещество Б, пропорциональ¬
на произведению концентрации этих веществ. Какой процент веще¬
ства В будет содержаться в сосуде через t = 1ч, если при t = 0
имелось 20% вещества Б, а при t = 15 мин его стало 80% ?
2530.	Согласно закону Гука относительное удлинение е
стержня пропорционально напряжению силы а в соответствую¬
щем поперечном сечении, т. е. е = — , где Е — модуль Юнга.
Е
Определить удлинение тяжелого стержня конической фор¬
мы, укрепленного основанием и обращенного вершиной вниз, ес¬
ли радиус основания равен Б, высота конуса Н и плотность р.
§ 11. Приближенное вычисление определенных интегралов
1. Формула прямоугольников. Если функция у = у(х) непрерывна
и дифференцируема достаточное число раз на конечном сегменте [а, Ъ]
иЛ =	, X/ = а + ih (i * 0, 1, ..., n), yt = y(xt), то
n
b
J y(x) dx = h(y0 + У1 + ... + yn -1) + Rn,
a
где

§11. Приближенное вычисление определенных интегралов
221
2.	Формула трапеций. При тех же обозначениях имеем
ь
J у(х) dx — h (Уо + Ух + У2 + — + Уп-1 ] + Я*.
а
где
Rn=-{b\a2)h2f”&')
3.	Параболическая формула (формула Симпсона). Полагая л = 2fe,
получим
ь
J у(х) dx = §[(у„ + 1/2*) + 4(у, + Уз + ... + 2/2*-1) +
+ 2(у2 + У А + — + У2*-г] + Я„,
где
дд = -l.fi ^ f 1У(5") (а<Г<Ь)-
2531.	Применяя формулу прямоугольников (п = 12), прибли¬
женно вычислить
2л
J jc sin х dx
о
и результат сравнить с точным ответом.
С помощью формулы трапеций вычислить интегралы и оце-
нить их погрешности, если:
1
1
2532. f лЛх (п
J 1 + X
0
Л
2
= 8).
2533. f ,d* (п — 12).
J 1 + х3
0
2534. J Jl-isirv
0
lxdx (п = 6).
С помощью формулы Симпсона вычислить интегралы:
9
л
л
2535. Jx dx
1
(П = 4).
2536. 73 + cosxd (п = 6).
0
Л
2
2537. J dx
0
(п = 10).
1
2538. f xdx (n = 6).
J ln(l + x)
0

222
РАЗДЕЛ IV. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
2539.	Принимая п — 10, вычислить константу Каталана
1
G= J V^dx.
о
2540.	Пользуясь формулой
1
я _ f dx
4 J 1 + х2 ’
о
ВЫЧИСЛИТЬ число п с точностью до 10-5.
1
2541.	Вычислить J е*2 dx с точностью до 0,001.
0
1
2542.	Вычислить J (ех - 1) ln^ dx с точностью до 10-4.
о
2543.	Вычислить с точностью до 0,001 интеграл вероятностей
+ оо
J е~х2 dx,
о
2544.	Приближенно найти длину эллипса, полуоси которого
а = 10 и b = 6.
2545.	Построить по точкам график функции
х
у = J* dt (0<х< 2п),
0
приняв Ах = 71/3.

РАЗДЕЛ V
РЯДЫ
§ 1. Числовые ряды. Признаки сходимости
знакопостоянных рядов
1. Общие понятия. Числовой ряд
оо
а, + а2 + ... + ап + ... = ^ ап
(1)
П = 1
называется сходящимся, если существует конечный предел
lim Sn = S (сумма ряда),
где Sn = ах + а2 + ... + а„. В противном случае ряд (1) называется расхо¬
дящимся.
2. Критерий Коши. Для сходимости ряда (1) необходимо и достаточ¬
но, чтобы для любого е > 0 существовало число N = N(z) такое, что при
п > N и р > 0 (пир — натуральные числа) было выполнено неравенство
то: 1) из сходимости ряда (2) следует сходимость ряда (1); 2) из расхо¬
димости ряда (1) следует расходимость ряда (2).
В частности, если ап ~ Ъп при п -* со, то ряды с знакоположитель¬
ными членами (1) и (2) сходятся или расходятся одновременно.
Признак сравнения II. Если
|Sn + p-S„|= £ а> <е-
В частности, если ряд сходится, то
lim ап = 0.
3. Признаки сходимости
Признак сравнения I. Пусть кроме ряда (1), имеем ряд
Ъх + Ъ2 + ... + Ъп + ... .
(2)
Если при п> п0 выполнено неравенство
то а) при р > 1 ряд (1) сходится и б) при р < 1 расходится.
!) Значение символа О* см: раздел I, § 6, п.1.

224
РАЗДЕЛ V. РЯДЫ
Признак Даламбера. Если ап > 0 (п = 1, 2, ...) и
Иш ^ =q,
то а) при q < 1 ряд (1) сходится и б) при q > 1 расходится.
Признак Коши. Если ал > 0(п= 1, 2, ...)и
Иш фп = д,
то а) при q < 1 ряд (1) сходится и б) при q > 1 расходится.
Признак Раабе. Если ап> 0 (п = 1, 2, ...) и
Иш п{ ——- 1
= р.
то а) при р > 1 ряд (1) сходится и б) при р < 1 расходится.
Признак Гаусса. Если ап > 0 (п = 1, 2, ...) и
JLl_ =Х+ н +
an+1	Л Я1 + Е
где |0„| < С и е > 0, то: а) при X > 1 ряд (1) сходится; б) при X < 1 ряд расхо¬
дится; в) при X = 1 ряд (1) сходится, если р > 1, и расходится, если р < 1.
Интегральный признак Коши. Если /(х) (я > 0) — неотрицательная
невозрастающая функция, то ряд
оо
I л»)
п = 1
сходится или расходится одновременно с интегралом
-foo
J f(x)dx.
1
Доказать непосредственно сходимость следующих рядов и
найти их суммы:
2546. 1 - i + i
2	4
(-1)-1
2 "-1
+ ... .
2547
+ ... .
2548. i +
3_ + _5
2
2г 23
2549. -i-
4- J-
1-2
2-3
2550. -±-
+ -!-
1 -4
4-7
+
1
3 4
+ ... +
+ ... .
1
п(п + 1)
+ ... +
1
(3л-2)(3л+ 1)
+ ... .
+ ... .

§ 1. Числовые ряды. Признаки сходимости знакопостоянных рядов
225
2551. a) q sin а + q2 sin 2а + ... + q" sin па + ...;
6) q cos а + q2 cos 2а + ... + qn cos na + ... (|g| < 1).
oo
2552.	£ (Jn + 2- 2ТЙТТ + Jn).
П — 1
OO
2553.	Исследовать сходимость ряда ^ sin nx.
n = 1
Указание. Показать, что при х * kn (k — целое) невозможно,
чтобы sin пх -+ 0 при п —* оо\
оо
2554.	Доказать, что если ряд ап сходится, то ряд
п = 1
оо	Рп + 1 - 1
£ Ап, где Ап =	£ а, (рг = 1, рх < р2 < ...),
» =1	' = рл
полученный в результате группировки членов данного ряда без
нарушения порядка их следования, также сходится и имеет ту
же сумму. Обратное неверно; привести пример.
оо
2555.	Доказать, что если члены ряда ^ ап положительны и
п = 1
оо
ряд АЛ, полученный в результате группировки членов этого
п = 1
ряда, сходится, то данный ряд также сходится.
Исследовать сходимость рядов:
2556.	1 - 1 + 1 - 1 + 1 - 1 4-....
2557.	0,001 + л/оГШ + VoToOl +
1
2560.
1 + 1
+ 1
+
1! 2!
3!
1 + 1 +
1 +
1
3
5
7
1 +
1
+
1001
2001
1 +1 +
1 +
3
5
+ — +
п\
+ ...
2 п- 1
-J- + ...+ 	I
3001	ЮООл+1
+
2л- 1
+ ..
2562.1 + 1 + 1 + ... +		-1-
З2 52	(2п-1)2
+ ... .
2563. -1 + 1
+ ^ + ... + *
V2 2а/3 Зл/4	njn +1
+ ... .
2564. —Lr + -Д= +
УП 73^5
1
+ ... .
7(2п - 1)(2я + 1)

226
РАЗДЕЛ V. РЯДЫ
2565.	Доказать, что ряд чисел, обратных членам арифмети¬
ческой прогрессии, расходится.
оо	оо
2566.	Доказать, что если ряды ^ ап (А) и ^ Ьп (В) сходятся
п = 1	л = 1
оо
и ап< сп< bn(n= 1, 2, ...), то ряд ^ сп (С) также сходится. Что
п = 1
можно сказать о сходимости ряда (С), если ряды (А) и (Б) расхо¬
дятся?
2567.	Пусть даны два расходящихся ряда
оо	оо
£ а»и £
л = 1	л = 1
с неотрицательными членами.
Что можно сказать о сходимости рядов:
оо	оо
а) £ min(a„, Ьп) и б) тах(а„, 6„)?
Л = 1	Л = 1
2568.	Доказать, что если ряд ^ ад (а > 0) сходится, то ряд
п = 1
оо
также сходится. Обратное утверждение неверно; привес-
п = 1
ти примеры.
2569.	Доказать, что если ряды ^ aj и ^ 6^ сходятся, то
л = 1	л = 1
сходятся, также ряды
ы.
£ MJ> £ (ая + Ьп)2,	£ ь
л = 1	л = 1
2570.	Доказать, что если
л = 1
lim пап = а ^ 0,
л — оо
то ряд ^ ад расходится.
л = 1
2571.	Доказать, что если ряд ^ ад с положительными и мо-
л = 1
нотонно убывающими членами сходится, то
lim пад = 0.
л — ОО

§ 1. Числовые ряды. Признаки сходимости знакопостоянных рядов
227
2572. Является ли сходящимся ряд ап> если
п = 1
Иш (аЛ + х + ап + 2 + ... + ап +р) = О
П оо
при р = 1, 2, 3, ...?
Пользуясь критерием Коши, доказать сходимость следую¬
щих рядов:
2573.	а0 + g + ... +	+ ... (|а„| < 10).
2574.	2*2* + 2*£|* + ... + “М* + ....
2	22 2Л
2gyg ^ cos*- cos 2* + cos 2*- cos3* +
+ COS/IJC- COS(ft + 1)* +
П
2.
cos* + cos*2 +	+ cos*re +
I2
22
п*
Указание. Использовать неравенство
1	<_!
п
	гг = —i-r - - (П= 2, 3,...).
п(п-1) п-1 п
Пользуясь критерием Коши, доказать расходимость следую¬
щих рядов:
2576.1	+ i + i + ... + - + ... .
2	3	п
2577. а)1 + ±—i+i + i- ±+ ... ;
2	3	4	5	6
б)
+
1
Л~2	л/2~3
+ ... +
Jn(n+ 1)
4- ... .
Пользуясь признаками сравнения, Даламбера или Коши, ис¬
следовать сходимость рядов:
2578 1000 + 10002 + 10003 +	+ 10°°л +
1!
2!
3!
п\
2579.	If +if +
2580.	I! + L +	+ ... + 21 + ... .
З3
2581. a) Li! + 2!_2! +
22
6) Li! +3^2!
' 1 22
пп
23 • 3!
З3
+ ...+ L"! +
+ »LJ« + ... + L2! +
З3	n"

228
РАЗДЕЛ V. РЯДЫ
2582.	+... + ^¥ +...•
2	24	2®	г»2
2583 1000 + ЮОО 1001 + Ю00 Ю01 Ю02 +
13
2584. - + i-l + t 1™ + ... .
13 5
2 2 6 2 6 10
2585. а) £ (71 - 3Т2)(Т2 - 5л/2) ... (72 - 2n + i/2).
Л = 1
б) £ ап, где а„ = <
П= 1
1 2
-, если л = ш ,
п
, если п^пг
»I «П тт^т
(тп — натуральное число);
sin2fca
п= 1	*
7.2
cos2fea
2586. У	.	2587. V Л " .	2588. У — .
, ^2 + ij"	«=» (д + I)"	»-« "ТЬ^г
2589. а) £
Л"
п= 1 (2л2 + л+ 1) 2
V /1(Л - 1)
п±1; б) Z 2-+3"’
■> S Цт-З'
п = 2
г) 72 + 72 - 72 + J2-J2 + A + J2-J2 + J2 + J2 +....
Указание. */2=2 cos 7 .
4
2590. Доказать, что если
л-00 а„
то ап = о(д?), где > g.
lim = ^-1 =q(an> 0),
П = 1
2591.1.	Пусть для членов знакоположительного ряда ^ ап
(ап > 0) выполнено неравенство
< р < 1 при п > п0.

§ 1. Числовые ряды. Признаки сходимости знакопостоянных рядов
229
Доказать, что для остатка ряда
•R„ = a„ + i + ап + 2 + •••
имеет место оценка
Л-Л0+ J
Rn < а„о •	—— , если п > л0.
2. Найти, сколько членов ряда
v [(2л)!!]2
La (4л)!! ’
п = 1 v 1
где (2л)!! = 2 * 4...2л, достаточно взять, чтобы соответствующая час¬
тичная сумма Sn отличалась от суммы ряда S меньше, чем на е = 1(Г6.
2592.	Доказать, что если
Hm	= q < 1 (ап> 0),
п —• оо ап
оо
то ряд ^ ап сходится.
п = 1
Обратное утверждение неверно. Рассмотреть пример
1
2
+ -L + -L
22	.З2
4- ... .
с»
2593.	Доказать, что если для ряда ^ ап (ап > 0) существует
л = 1
lim Ь.±> =д,	(А)
п — оо ап
то существует также
Иш = Я•	(Б)
п — ОО
Обратное утверждение неверно: если существует предел (Б),
то предел (А) может и не существовать. Рассмотреть пример
у ИЫГ.
La 2n+1
л = 1
2594.	Доказать, что если
lim 1Jan =q (ап> 0),
П — оо
оо
то: а) при q < 1 ряд ^ а„ сходится; б) при q > 1 этот ряд расхо-
л = 1
дится (обобщенный признак Коши).

230
РАЗДЕЛ V. РЯДЫ
Исследовать сходимость рядов:
2595. £
П~ I
со acos2-^-
2596. У ——
Zj 2"
2597. а)
оо
пЧЛ + (-1)"]".
3"
б) у (\ + cosл^2”-111,1
2-* V 2 + cos п)
Пользуясь признаками Раабе и Гаусса, исследовать сходи¬
мость следующих рядов:
2598-©' + (1т)' + (Ш)' + --
**4(a>0'6>0'd>0)-
2601. У 			Щ	—.
& (2+Л)(2 + 72)...(2 + Л)
(7>0).
2600, У —.
La Пп*Р
П = 1
п\п~Р
2602.	У -
2603.	У Р(/>+1)-(/> + га-1) • -L.
Z-r	п!
Я = 1
2604.	У Г(1-3 5...(2п-1))Г . J,
La. L 2 • 4 • 6...(2n) J ПЧ
П = 1
2605.	V	^ +	ip > 0, q > 0).
n4"i L<7(<7+l)...(<7 + n-l)J
2606.	Доказать, что если для знакоположительного ряда
^ ал (ап > 0) при /I —► оо выполнено условие
1 + ^ + о(-1,
п = 1
Ап
+ 1
ТО
где е > 0 произвольно мало; причем, если р > 0, то ап | 0 при
п -* оо, т. е. ап при п > л0, монотонно убывая, стремится к ну¬
лю, когда п * оо.

§ 1. Числовые ряды. Признаки сходимости знакопостоянных рядов
231
Определив порядок убывания общего члена ап9 исследовать
оо
сходимость заданного ряда ап9 если:
п = 1
2607.	ап = n' + ain,-l +■■■ + *, Где пч +	1 + ... + Ъ. > 0.
пч + Ъхп<*-1+ ... + ЪЦ	1
2608.	ап= — sin - .
ПР п
2609.	ап = (7(яТТ) - У In3^1 (п > 1).
/1+1
2610.	ап = lnp (sec 5 j .
2611.	ап -log^l + ^) (а > 0, Ъ > 0).
2612...-[е-(1 +1)7.
2613.	а) о„ = —Ц- ; б) о„ =	.
1 + -5-	1 + 1
п 1пл	п п
2614.	Доказать признак Жамэ: знакоположительный ряд
оо
ап (ап > 0) сходится, если
п = 1
(1 - ч[ап) JL. > р>\ при п > п0,
in п
и расходится, если
(1 - ф~п) ^ < 1 при п > п0.
оо
2615.	Доказать, что ряд ^ о„ (ап > 0) сходится, если сущест-
1п—
П = 1
вует а > 0 такое, что -—- > 1 + а при п> п09 и расходится, если
ln/t
ini
-—- < 1 при п> п0 (логарифмический признак).
In/г
Исследовать сходимость рядов с общим членом:
2616. а„ = п'пх(х> 0).
2617.а.=
" (lnlnn)1""
2618.	а„ =	.
(1пп)|п1пп
(п > 1).
(л > 1).

232
РАЗДЕЛ V. РЯДЫ
Пользуясь интегральным признаком Коши, исследовать схо¬
димость рядов с общим членом:
2619.	а) ап = —^— (п > 1); б) ап = ——---т--,—г
n\np/i	n(ln/i)^(lnln/i)
2620.	Исследовать сходимость ряда:
ОО
а) V 	In2 ' ln3...In(ra+ 1)	 .	0);
1	L, ln(2+p)-ln(3+p)...ln(n+l+p) ^
П = 1
о° . .
б)	V , где v(n) — число цифр числа п;
п2
п = 1
(п > 2).
°° 1
В) S 1л(п!)'
п= 2
2621.	Пусть \п(п= 1, 2, ...)— последовательные положи¬
тельные корни уравнения
tg х = х.
Исследовать сходимость ряда
S
л = 1
2622.	Доказать, что ряд ап с положительными монотонно
« = 1
убывающими членами сходится или расходится одновременно
ОО
с рядом ^ 2па2П.
п = О
2623.	Пусть /(#) — положительная монотонно невозрастаю-
оо
щая функция. Доказать, что если ряд f(n) сходится, то для
остатка его
Rn= £ Я*)
п = 1
справедлива оценка
+оо
J /(jc) dx < Rn< f(n + 1) + J f(x) dx.
П+ 1	/1+1
oo
Пользуясь этим, найти сумму ряда V — с точностью до 0,01.
Z-f пг
п= 1

§ 1. Числовые ряды. Признаки сходимости знакопостоянных рядов
233
2624.	Доказать признак Ермакова: если f(x) — положитель¬
ная монотонно убывающая функция и
Вт	- Л,
f(x)
оо
то ряд f(n) сходится при X < 1 и расходится при X > 1.
л = 1
оо
2625.	Доказать признак Лобачевского: ряд ^ ал с положи-
Л = 1
тельными монотонно стремящимися к нулю членами сходится
или расходится одновременно с рядом
оо
S Р. ■ 2-.
т Я О
где рт — наибольший номер членов ап> удовлетворяющих нера¬
венству
аЛ>2" (/1=1,2, ..., рт).
Исследовать сходимость следующих рядов:
ОО /	— I ■ ' '	оо
2626. ]Г	2627. ^ (Jn+a -\JrF+n+b).
П = 2	Л = 1
2628 £ Кйг - i5h) • I, (я -f5?) •
ОО _	.	ОО
2630. У iniiii}.
^ Ла
л = 1
2632.
л = 1
°°	а In я + Ь
2634. £ ecinn.d,
Л = 1
2631. £ е-3^.
Л = 1
ОО	1
2633. £ (n»2+i - 1).
Л = 1
°°	1
Z —-—•
л = 1 ln2^sinij
2635.
2636
1 (-;)'
Л = 1
( сЬ^Л
п
cos—
I
2638. у -2L.
2637. In
л = 3
V
оо	,
2639. У тг^-.
„ = 2 (1ПЛ)Л
2640.
Е 1 а
л * 1
п _ Ь" + с"
2
(а > О, Ь > 0, с > 0).

234
РАЗДЕЛ V. РЯДЫ
2641. £ (пп" - 1).
п = 1
2642- £	[1п	~ ln ( sin Л“)] ‘
п-1
оо
2643.	£ д-(Япл + с1п2л) (о > 0).
П = 1
°°	9 п
2644.	У -	—		— (о > 0, Ь > 0).
(п + а)п + ь(п + Ь)п + а
п * 1
2645.	V ■ll'Ltiilll- .
А 2! • 4!...(2п)!
П = 1
оо
Исследовать сходимость рядов ^ ыл со следующими общи¬
ми членами:
л — 1
°646 и — f
2647.
I/ =
1
2646. u„ j i + xt.
0
un
n
Ji/mpdx
(п + 1)л
0
Л+ 1
2648. u„- J sin2xdx.
nn
n
n
2649.
«« =
J e~J* dx.
n
2650. u„- f s}n3xdx.
J 1 + Ж
2651.
ы„ =
1! + 2! + ... + n\
(2л)!
ln2fe
2652. и =
па
Заменив последовательности яЛ (л = 1, 2, ...) соответствую¬
щими рядами, исследовать сходимость их в ряде:
2653. *„ = 1 + -^ + — + 4г - 2 Vn.
л/2	л/л
lnfe _ (Inл)2
2 ’
2655. Сколько примерно надо взять членов ряда, чтобы найти
его сумму с точностью до 1(Г5, если:
*>Ё>
2654. х, - Т Н!
k = 1
п = 1
п = 1
п = 1

§ 2. Признаки сходимости знакопеременных рядов
235
§ 2. Признаки сходимости знакопеременных рядов
1.	Абсолютная сходимость ряда. Ряд
£	(D
П = 1
называется абсолютно сходящимися, если сходится ряд
£ к|.	(2)
п = 1
В этом случае ряд (1) также сходится. Сумма абсолютно сходящегося
ряда не зависит от порядка слагаемых.
Для определения абсолютной сходимости ряда (1) достаточно при¬
менить к ряду (2) известные признаки сходимости для знакопостоянных
рядов.
Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется
условно (не абсолютно) сходящимся. Сумму условно сходящегося ряда
путем перестановки слагаемых можно сделать равной любому числу
(теорема Римана).
2.	Признак Лейбница. Знакочередующийся ряд
Ь1-Ь2 + Ь3-Ь4 + ... + (-1)л-1Ьп + ...
(Ъп > 0) сходится (вообще говоря, не абсолютно), если: а)Ьп> Ьп + х
(п= 1,2, ...)и б) lim bn *= 0. В этом случае для остатка ряда
п — оо
Лп = (-1ГЬя + 1+(-1)» + 1Ьл + 2 + -
имеем оценку
Rn = (-l)nQnbn + l(0<Q< 1).
3.	Признак Абеля. Ряд
оо
X «А	<*>
п = 1
оо
сходится, если: 1) ряд ^ ап сходится; 2) числаЬп(п = 1,2,...)образуют
п = 1
монотонную и ограниченную последовательность.
оо
4.	Признак Дирихле. Ряз (3) сходится, если: 1) суммы Ап ** ^ at
i = 1
ограничены в совокупности; 2) Ьп монотонно стремится к нулю при п~* оо.
2656.	Доказать, что члены не абсолютно сходящегося ряда
можно без перестановки сгруппировать так, что полученный но¬
вый ряд будет абсолютно сходящимся.

236
РАЗДЕЛ V. РЯДЫ
2657.	Доказать, что ряд ^ ап является сходящимся, если вы-
п = 1
полнены условия: а) общий член этого ряда ап стремится к нулю
оо
при /г —► об) ряд ^ Ап9 полученный в результате группировки
п = 1
членов данного ряда без нарушения их порядка, сходится; в) число
pn+i~l
слагаемых а19 входящих в член Ап =	^ at (1 = pi с р2 < ...),
i=Pn
ограничено.
2658.	Доказать, что сумма сходящегося ряда не изменится,
если члены этого ряда переставить так, что ни один из них не
удаляется от своего прежнего положения больше чем на т мест,
где т — некоторое заранее заданное число.
Доказать сходимость следующих рядов и найти их суммы:
2659.	1-I+T-S+ — -
2	4	8
2660.	l +	+	.
2	4	8	16	32
2661.	1-1+I-1+I-I+... .
2	3	4	5	6
Указание. Применить формулу 1 + - +
+ — = С + In /I + £л,
п
где С — постоянная Эйлера и lim еп = 0.
п — ОО
00 1
2662.	Зная, что V	= In 2, найти суммы рядов, полу-
1	п
п = 1
ченных из данного в результате перестановки его членов:
а)	1 + 3	2	5	7	4	+-’
1	1.1	1	1	.
б)	1 ' 2 '	J + I	"	6	' 8	+ -	•
2663.	Члены сходящегося ряда
оо
I
п = 1
Jn
переставить так, чтобы он стал расходящимся.

§ 2. Признаки сходимости знакопеременных рядов
237
Исследовать сходимость знакопеременных рядов:
л
(-1)"
2664. £
л = 1
/1=1
2
>л
1)п(
2л+100у.
Зл+1 J ’
♦i
_ 1 _ 1
4 5
2666. Пусть
£ (-D4.
(1)
п = 1
где Ьп > 0 и Ьп 0 при п оо. Следует ли отсюда, что ряд (1)
сходится? Рассмотреть пример
у (-1)я. 2 + (-1)л.
Л
/1=1
Исследовать сходимость рядов:
00	1 1ЛЛ
2667. У
п 4
п = 1
2668.
п sin2/t
у (-1)" SS:
л=1
оо	/-
2669. У (-1)"—^
п +
/1=1
100
2670
. у ■.
„ = 2 л/я + (-1)"
ОО
2671. sin (п л/n2 + ft2).
/1=1
”	/ 1V
2672. V til
П
\Л\
n=i
2673.	a) V И; б) У -l-cos™i.
к, ^ ПУ2 ln2« rt+1
2674.	Доказать, что знакочередующийся ряд
&i “ &2 + &з “ Ь4 + ••• + (~1)Л гЬп + ...	(Ьп > 0)
сходится, если
Ьп
Ъ
п + 1
1 + £
П
где р > 0 (см. 2606).

238
РАЗДЕЛ V. РЯДЫ
Исследовать на абсолютную (кроме 2690) и условную сходи¬
мости следующие ряды:
2676. У
^ ПР
П 3 1
2677. ln[l + Ь1£].
я 3 2
2679. V ЫН.
х+ п
п = 1
2681. У -J-1)"'1	.
2683. У (-1)" й—1 -±-.	2684. У
^'	n+1 too[Z	А	2"
Я3 1	V»	П = 1
2685. У ЫП.
к *2л
J0L / 1 \(7п |
2687. £ ^—
Я 3 1
ПР
2676. У tDlZl
п=1	„ п
2п8т2,,д:
П = 1
2678. £ (-1)л
л
2680. У —i
[л +
(-1Г
Н [л + (-1)Т’
п 3 2
2682. 2
• ля
sin—
4
к 31 np+sin^
оо sin 22
2686. У —
a-* In л
я = 2
2688. У
^ л
Ппп|
Л 3 1
2689.	У (-1)""1 Г1 • 3 ' Ь...(2п- 1)У
A v ' I 2-4 -6...(2п) J
Я 3 1
ОО .	.9
2690.	]Г
81ПЛ • 81ПЛ*
п 3 1
2691.	£ sin л2.
л = 1
Указание. Доказать, что lim sin п2 * 0.
п -» ОО
2692.	Пусть
р/„ч = а0ж<, + а|ДУ-1 + ...+а,
1	'	60x« + b1x«-i+... + 6f
— рациональная функция, где Оо ^ О, Ь0 ^ 0 и \$>0хч + Ъххч~1 + ...
... + t>J > О при х > По.
Исследовать на абсолютную и условную сходимости ряд
£ (-1 )пЩп).
п 3 Я0

§ 2. Признаки сходимости знакопеременных рядов
239
Исследовать сходимость рядов:
2693.	+	+
1 р	2 ч	3 р	49	5 р 69
2694.1 +

±
+
±
4-
_
4* ...
Зр
2 р
5 р
Ip
4 р
2695. а) 1
4-
1

±
+
1
+
1_

— 4-
1
+ -L-JL +
3 р
1 р
5 р
7 р
3 р
9 р
Но 5о
6)1

2_
4-
1
+
±

2
-f
1 +
1
-1+1+.
2 9
3 р
4 р
59
6 р
7 р
8ч 9 р
2696. Доказать, что ряды
ч _ , sin2л: ,	. Зх ,
а)	sin х + —-— 4- sin—- 4- ... ,
2	3
б)	cos х + SSLte + соеЗх +
не абсолютно сходятся в интервале (0, л).
2697.	Для рядов
I
п = 1
COS/IX
ПР
’ I
л = 1
sin/IX
ПР
(О < х < п)
определить для совокупности параметров (р, х): а) область абсо¬
лютной сходимости; б) область неабсолютной сходимости.
2698.	Исследовать сходимость рядов:
оо
/1 = 2
(-1 )ач/п.
In П
оо
в> I
п= 10
sin л
п + 10 sin/г
2699.	Для ряда
6>i
*1п("4).
ln(ln/i)
оо
I (-1Г
п = 1
-1 (1 + р)(2 + р)...(п + р)
n\n<i
определить: а) область абсолютной сходимости; б) область услов¬
ной сходимости.
2700.	Исследовать сходимость ряда
где ("Л = m(w-l).-(w-»+l)
V п)	п\

240
РАЗДЕЛ V. РЯДЫ
2701.	Если ряд ^ ап сходится и
п = 1
lim ^ = 1,
п — оо ап
то можно ли утверждать, что ряд ^ Ьп также сходится?
п = 1
Рассмотреть примеры:	и Г(.г1). -f II
п = 1 'v'1	л = 1 L Vя	71 j
оо
2702.	1. Пусть ^ art — не абсолютно сходящийся ряд и
/1=1
оо
N+ai N
2 ’ '
l = 1
Доказать, что
lim ^ =
n-oo P„
i = 1
2. Доказать, что сумма ряда
(-Пя + 1
п = 1
ПР
для каждого р > 0 лежит между ± и 1.
2703.	Сколько членов ряда следует взять, чтобы получить его
сумму с точностью до е = 10 г’ в ряде:
(-1У + 1.
а) У
« -1 7^+1
б) у sinn ?
«-1 Л
2704.	Доказать, что если члены ряда
1-1 + 1-1+1-...
2	3	4	5
переставить так, чтобы группу р последовательных положитель¬
ных членов сменяла группа q последовательных отрицательных
членов, то сумма нового ряда будет
In 2+ ±1п*.
2	q

§ 3. Действия над рядами
241
2705.	Доказать, что гармонический ряд
1
останется расходящимся, если, не переставляя его членов, изме¬
нить их знаки так, чтобы за р положительными членами следо¬
вало бы q отрицательных (р ^ q). Сходимость будет иметь место
лишь при р = q.
§ 3. Действия над рядами
Сумма и произведение рядов. По определению полагают:
оо	оо	со	оо	оо	оо
а) £ а"1£ к = Z {а»± ь"); б) Е а« £ь"= Xс-’
/1=1	/1=1	/1=1	/1=1	/1=1	/1=1
где
сп = а1Ьп + а2Ьп- 1 + ••• + апЬ 1-
оо
Равенство а) имеет неформальный смысл, если оба ряда У ая и
п = 1
оо
У* сходятся, а равенство б) — если, сверх того, по меньшей мере
п = 1
один из этих рядов сходится абсолютно.
2706.	Что можно сказать о сумме двух рядов, из которых:
а) один ряд сходится, а другой расходится; б) оба ряда расхо¬
дятся?
2707.	Найти сумму двух рядов:
X [h +	+ х [з^
/1=1
п= 1
+
(-1Г* Л,
Л3 J
Найти суммы следующих рядов:
п = 1
2709. £
cos-
2 пп
п = 1
2п
2710.	£ ж®уР*2']	(N<1).
/1 = 0
2711.	Показать, что у — • £	= 1-
л = 0	‘	/1 = 0

242
РАЗДЕЛ V. РЯДЫ
2712.	Показать, что	= ]Г (п + 1)<7Л (Ы < l] •
п = О '	п = О
2713.	Показать, что квадрат сходящегося ряда
есть ряд расходящийся.
I
п = 1
(-1)-1
Jn
2714.	Доказать, что произведение двух сходящихся рядов
Z
п = 1
И)*'1
па
(а > 0) и ^
п = 1
(-1Г-1
лР
(Р>0)
есть ряд сходящийся, если а + Р > 1, и расходящийся, если
а + Р < 1.
2715.	Проверить, что произведение двух расходящихся
рядов
1 -
I
п = 1
3
и 1 +
есть абсолютно сходящийся ряд.
§ 4. Функциональные ряды
1. Область сходимости. Совокупность Х0 тех значений х, для кото¬
рых сходится функциональный ряд
“i(*) + “2(*) + — + “»(*) + —.	(1)
называется областью сходимости этого ряда, а функция
п
S(x)= lim V щ(х) (х в Х0)
п — ОО jL-J
/= 1
— его суммой.
2. Равномерная сходимость. Последовательность функций
fl(x), f2(x)	/■„(*),...	(*)
называется равномерно сходящейся на множестве X, если:
1)	существует предельная функция
f(x) = lim fn(x) (х е X);
л — ОО
2)	для любого числа е > 0 можно указать число N - N(e) такое, что
|Л*) - /»(*)! < е
при п> N и х € X.

§ 4. Функциональные ряды
243
В случае равномерной сходимости последовательности (*) к f(x)
используют обозначение:
fn(x)^f(x).
Функциональный ряд (1) называется равномерно сходящимся на
множестве X, если равномерно сходится на этом множестве последова¬
тельность его частичных сумм:
«„(*) = £«,(*) (п-1,2,...).
1= 1
3.	Критерий Коши. Для равномерной сходимости ряда (1) на мно¬
жестве X необходимо и достаточно, чтобы для каждого е > 0 существо¬
вало число N = ЛГ(е) такое, что при п > N и р > 0 было выполнено нера¬
венство
|Sn+,(*)-S„(*)| =
п+р
I = п + 1
< е для всех х € X.
4.	Признак Вейерштрасса. Ряд (1) сходится абсолютно и равномер¬
но на множестве X, если существует сходящийся числовой ряд
с\ + с2 + ... + сп + ...
(2)
такой, что
|иЛ(*)| < сп при х € X (п = 1,2, ...).
5.	Признак Абеля. Ряд
£ ап(х)Ьп(х)
(3)
/1=1
оо
сходится равномерно на множестве X, если: 1) ряд ^ ап(х) сходится
п= 1
равномерно на множестве X; 2) функции bn(x) (п = 1, 2, ...) ограничены
в совокупности и при каждом х образуют монотонную последователь¬
ность.
6.	Признак Дирихле. Ряд (3) сходится равномерно на множестве X,
N
если: 1) частичные суммы аЛ(лг) в совокупности ограничены;
п = 1
2) последовательность bn(x) (п — 1, 2, ...) монотонна для каждого х и
равномерно на X стремится к нулю при п со.
7.	Свойства функциональных рядов, а) Сумма равномерно сходя¬
щегося ряда непрерывных функций есть функция непрерывная.
б) Если функциональный ряд (1) сходится равномерно на каждом
[а, Р] С (а, Ь) и существуют конечные пределы
lim ип(х) - Ап (п - 1, 2, ...),
х — а

244
РАЗДЕЛ V. РЯДЫ
то: 1) ряд ^ Ап сходится; 2) имеет место равенство
п = 1
Еи»(ж) = X
lim ип(х)
в) Если члены сходящегося ряда (1) непрерывно дифференцируемы
оо
при а < х < b и ряд производных ц!(*) сходится равномерно на
п = 1
интервале (а, Ь), то
^ [ ic “"(*) ]= х ц-(лс) при х ^ («. &>•
п = 1
г) Если члены ряда (1) непрерывны и этот ряд сходится равномерно
на конечном сегменте [а, Ь], то
Ь	оо Ь
f I S “«(*)	= £ f «*„(*>
•J L«-i -1 я = 1 '
(4)
Вообще формула (4) верна, если Rn{x) dx -+ 00 при я -* 0, где
/*„<
Rп(х) =	^	Это последнее условие годится также и для случая
i = п + 1
бесконечных пределов интеграции.
Определить области сходимости (абсолютной и условной) сле¬
дующих функциональных рядов:
2716. У —
ХЛ
2717
п = 1
. у
^ 2п-\\\ + х)
п=1
2718. У -Л-(—V. 2719. У
L, n+ll2*+lj	Za 2-4...(2л) ll + *2J
#1=1	#1=1
2720. £ !Lj£lxa(l-x)n. 2721. £ ^
2"sin2£
2
#1=1
2722. У	.	2723. У 2^,(?>0;0<кп).
^ (х + п)р	jLi l + п"	'
П = 1
оо
2724.	(РЯД Ламберта)

§ 4. Функциональные ряды
245
оо	и	оо
2725. £ Р**П)] •	2726. £ y-j£j
П = 1
2727. У 	—
A (1 + *)(1 + *2)...(1 +
П = 1
А, (1 + *)(1+*2) ...(1 + ЛГ»)
00 00 1 1
2728. V пе~пх.	2729. У -±- * 	±— .
" "/Г?	1 + а2"*2
п = 1
n = 1 «/Й!
ОО	111
2730.	]Г (2 - х)(2 - х2 )(2 - *2 )(2 - ж ") (х > 0)
П = 1
00
2731.	У (Е±£12.
Z-i лл +*
п = 1
оо
2733. У	(I/ > 0)
^ п + уп у
п = 1
2732. У	(ж > 0; у > 0).
jL<xn + yn	*
п = 1
2734. ^ n7Wn2 + |j/|»2.
П = 1
ОО	00	/	\
2735.	(* > °)-	2736. £ tg" Г ж + jO .
п = 1	Л = 1
+оо
2737.	Доказать, что если ряд Лорана artxrt сходится при
П - -оо
* = и при х = х2 (tal < |jc2Q > то этот ряд сходится также при
|*il < \х\ < \х2\.
2738.	Определить область сходимости ряда Лорана
+ оо
I йхп
п = -оо
и найти его сумму.
2739.	Определить области сходимости (абсолютной и услов¬
ной) рядов Ньютона:
ч	^ л:1"1	1 хм	ч ^ {ех)пу\п\
а) У —Г; б) У ——- ;	в) у i—<-f— ,
п\	пР п\	Пп
п = 1
п = 1
где xw = х(х - 1)—[л: - (п - 1)].
оо
2740.	Доказать, что если ряд Дирихле У — сходится при
* пх
п = 1
х = х09 то этот ряд сходится также при х > х0.

246
РАЗДЕЛ V. РЯДЫ
2741.	Доказать, что для равномерной сходимости на множе¬
стве X последовательности fn(x) (п = 1, 2, ...) к предельной функ¬
ции /(х) необходимо и достаточно, чтобы
lim {supгл(*)} = О,
П — ОО х 6 X
где rn(x) = |/(х) - fn(x)\.
2742.	Что значит, что последовательность fn(x) (п = 1, 2, ...):
а) сходится на интервале (х0, +о°); б) сходится равномерно на
каждом конечном интервале (а, 6) с (х0, +оо); в) сходится
равномерно на интервале (х0, +оо)?
2743.	Для последовательности
fn(x) = xn (п = 1,2,...) (О < х < 1)
определить наименьший номер члена N = N(e, х), начиная с ко¬
торого отклонение членов последовательности в данной точке х
от предельной функции не превышает 0,001, если х = ^,...
1
• • • >   > ....
"l/lO
Сходится ли эта последовательность равномерно на интерва¬
ле (0, 1)?
2744.	Сколько членов ряда
I
sin пх
п(п + 1)
следует взять, чтобы частичная сумма Sn(x) отличалась при
— оо < х < 4-00 от суммы ряда меньше чем на е? Произвести
численный расчет при:
а) е = 0,1;	б)е = 0,01;	в) 6 = 0,001.
2745.	При каких п будет обеспечено выполнение неравенства
Исследовать последовательности на равномерную сходи¬
мость в указанных промежутках:
2746.	fn(x) - хп; а) 0 < jc < i ; б) 0 < х < 1.
Z
2747.	fa(x) = xn-xn + 1; 0 < * < 1.
2748.	fn(x) = х" - х2а; 0 < * < 1.

§ 4. Функциональные ряды
247
2749.	fn(x) = -i- ; 0 < х < +оо.
х+ п
2750.	/„(*) = , пх ; 0<х<1.
1	+ п + X
2751.	fn(x) =	; а) 0 < x < 1 - е; б) 1 - е < * < 1 + е;
в)	1 4- е < х < +оо, где е > 0.
2752.	fn(x) =	; а) 0 < х < 1; б) 1 < х < +оо.
1 + п2х2
2753.	/л(х) = 1х2 + — -, -оо < х < +оо.
V Л2
2754.	/л(х) = п (Jx + l - Jx j ; 1 < х < +оо.
2755.	а) /л(х) -	; -оо < * < +оо;
п
б) /„(*) = sin - ; -ОО < х < +оо.
п
2756.	a) fn(x) = arctg пх; 0 < х < +оо;
б)	fn(x) = х arctg пх; 0 < х < +оо.
2757.	fn(x) = еп(х " *>; 0 < х < 1.
2758.	fn(x) = е ~(х~п)2; а) -I < х < Z, где I — любое положитель¬
ное число; б) -оо < х < +оо.
2759.	/л(х) = -1п—;0<х<1.
п п
2760.	fn(x) = ^ 1 + ^ j ; а) на конечном интервале (а, Ъ);
б)	на интервале (-оо; +оо).
2761.	fn(x)
2762.	/л(х)
2763.	/л(х)
п(х”
—
1); 1 < х < а.
о/ТТ
хп
; 0< х < 2.
п2х,
если 0 < х < i ;
п
\ "2(
2
- х 1, если i < х <
2 .
у
) п
п
о,
если х > - ,
п
на сегменте 0 < х < 1.

248
РАЗДЕЛ V. РЯДЫ
2764.	Пусть f(x) — произвольная функция, определенная на
сегменте [а, 6], и
fn(x) = [ИМИ (п= 1,2,...).
п
Доказать, что
/„(*)=*/(*) (а<х<Ъ)
при п *
2765.	Пусть функция f(x) имеет непрерывную производную
f'(x) в интервале (а, 6) и
fnM = «[ /( Ж +	- f{x) j .
Доказать, что fn(x) /'(дс) на сегменте а < х < (3, где а < а < (3 < Ь.
п - 1	1	✓	.X
2766.	Пусть fn(x)= -л л: + -J, где f(x)— непрерывная
i = О
на (~°°, +°°) функция. Доказать, что последовательность fn(x)
сходится равномерно на любом конечном сегменте [а, 6].
Исследовать характер сходимости следующих рядов:
оо
2767.	хп на интервале: а) |*| < q, где q < 1;б) |jc| < 1.
п = О
оо
2768.	а) V ^ на сегменте -1 < х < 1;
< п2
п — 1
оо
б)	У ^ на интервале (0, +°о).
^ п\
п = 0
2769.	jjr (1 - х)хп на сегменте 0 < х < 1.
п = О
2770.	У Г— -	; -1< * < 1.
U n + lj
/1=1
2771.
£ f(n-i)*+:
; 0 < х < +оо.
fax [(n- 1)* + \](nx+ 1)
°° 1
2772. У 		гг	тт; 0 < х < +оо.
(Jt+ п)(х+п+ 1)
/1=1
2773- 1. аПкТТ
пх
.	(1 + *)(1 + 2лс)...(1 + пж)
б)	е < х < +оо.
; а) 0 < х < е, где е > 0;

§ 4. Функциональные ряды
249
2774. Пользуясь признаком Вейерштрасса, доказать равно¬
мерную сходимость в указанных промежутках следующих
функциональных рядов:
а)1	-°° < ^ < +°°; б) ]Г “72"» -2 <*<+00;
я = 1	/1=1
ОО	оо
в) У i-	хл 2 •0 < х < +00; г) У , п*5 2» W < +°°;
Z-» 1 + п4х2	Л*I 1 + пьх2
п = 1	л = 1
°° 2	1
Д) У -£=(*"+ *-«), 1 < Н< 2;
п=1 ^Г!	2
е)	У , |*| < а, где а — произвольное положитель-
"' [1]'
ное число;
Ж) У Sinn* , И < +0О;	3) У S255* , |*| < +00;
к	к п
л = 1	п = 2
00	00	о
л) У *2е~ях, 0 < * < +оо; м) У arctg „	, Ы < +оо.
Ли	Ли	X2 + п3
п = 1
п = 1
Исследовать на равномерную сходимость в указанных про¬
межутках следующие функциональные ряды:
оо
2775.	V -1-—- на сегменте: а) е < х < 2п - е, где е > 0;
Ли п
п = 1
б) 0 < х < 2п.
2776.	У 2я sin-i-; 0 < * <+оо. 2777. У til! ; 0 < * <+оо.
Z-i	3я*	х+п
П = 1
п = 1
Указание. Оценить остаток ряда.
”1”—U
2778. У И)" ;0<*<2л.	2779. У ^	;|х|< 10.
кг n + smx	к\ V«2 + ех
	2 пк
оо COS——
2780. У 3 ; -оо < * < +оо.
к\ Jn2+x2

250
РАЗДЕЛ V. РЯДЫ
2781.	у	; 0 < ж < +оо.
„„1	Jn + X
2782.	у И?'*1. ; 0 < х < +оо.
n=l Jn(n+X)
2783.	Может ли последовательность разрывных функций
сходиться равномерно к непрерывной функции?
Рассмотреть пример
fn(x) = -ц(х) (/г = 1, 2, ...),
п
где
\|/(д;) =
0,	если хиррационально;
1,	если х рационально.
оо
2784.	Доказать, что если ряд |/n(*)| сходится равномерно
п = 1
оо
на [а, Ь], то ряд ^ /„(я) также сходится равномерно на [а, &].
п = 1
оо
2785.	Если ряд ^ /„(я) сходится абсолютно и равномерно на
л = 1
оо
[а, &], то обязательно ли ряд |/„(л:)| сходится равномерно на
п = 1
[а, &]?
оо
Рассмотреть пример ^ (—1)л(1 - ar)*1, где 0 < х < 1.
п = 0
2786.	Доказать, что абсолютно и равномерно сходящийся ряд
оо
у fn(x) (0< * < 1),
л = 1
где
fn(x) = <
0,
i sin2(2n + Чис),
п
если 0 < х < 2 (п +1};
если 2~(п + 1} < х < 2~п;
0,	если 2 п < х < 1,
нельзя мажорировать сходящимся числовым рядом с неотрица¬
тельными членами.

§ 4. Функциональные ряды
251
2787. Доказать, что если ряд
оо
п= 1
члены которого суть монотонные функции на сегменте [а,Ь], схо¬
дится абсолютно в концевых точках этого сегмента, то данный
ряд сходится абсолютно и равномерно на сегменте [а, Ь].
2788. Доказать, что степенной ряд
Ё ап*п
п = 0
сходится абсолютно и равномерно на любом сегменте, целиком
лежащем внутри его интервала сходимости.
оо
2789. Пусть ап-* оо так, что ряд V LL
\п
/1 = 1
сходится. Доказать,
00 1
что ряд V 	 сходится абсолютно и равномерно на любом
" х-ап
n=i
ограниченном замкнутом множестве, не содержащем точек ап
(n= 1, 2, ...)•
2790. Доказать, что если ряд ^ ап сходится, то ряд Дирихле
/1=1
Z— сходится равномерно при х > 0.
пх
п = 1
2791. Пусть ряд ап сходится. Доказать, что ряд апе
n = i
п=1
сходится равномерно в области х > 0.
2792.	Показать, что функция
/(*)= У ^
П
sin пх
3
/1=1
непрерывна и имеет непрерывную производную в области
—ОО < X < +оо.
2793.	Показать, что функция
«*>- z
1
{п-хУ
а) определена и непрерывна во всех точках, за исключением це¬
лочисленных: х = 0, ±1, ±2,...; б) периодическая с периодом, рав¬
ным 1.

252
РАЗДЕЛ V. РЯДЫ
2794.	Показать, что ряд
[пхе'пх - (п - 1)хе~(п ~ Vх]
п = 1
сходится неравномерно на сегменте 0 < х < 1, однако его сумма
есть функция, непрерывная на этом сегменте.
2795.	Определить области существования функций f(x) и ис¬
следовать ее на непрерывность, если
a)/(*)= £ (x+ij;
П = 1
б) f(x) =
S
п = 1
х+л(-1)" .
х2+п2
оо
■>«*>- Е. <1тЬ>
п = 1
2796.	Пусть гл (Л = 1, 2, ...) — рациональные числа сегмента
[О, 1]. Показать, что функция
ОО I	I
№ = X зг*1 (0 < * < 1)
k = 1
обладает следующими свойствами: 1) непрерывна; 2) дифферен¬
цируема в иррациональных точках и недифференцируема в ра¬
циональных.
2797.	Доказать, что дзета-функция Римана
«*>-1 г
П = 1
непрерывна в области д: > 1 и имеет в этой области непрерывные
производные всех порядков.
2798.	Доказать, что тэта-функция
е(*) =
+ оо
I
s —С
g-nn2X
определена и бесконечно дифференцируема при х > 0.
2799.	Определить области существования функции f(x) и ис¬
следовать ее на дифференцируемость, если:
a) fix) = V tlp£;	б) Я*)- У -&-г
П + Х	L-t п2+х2
п = 1
2800.	Показать, что последовательность
fn(x) = - arctg Xя (п = 1, 2, ...)
п
сходится равномерно на интервале (-оо, +оо), Но
[ lim /п(дс)]' _ j * lim f'n{ 1).

§ 4. Функциональные ряды
253
2801.	Показать, что последовательность
fn(x) = х2 + i sin х 4- 5j
сходится равномерно на интервале (-оо, +оо), но
[ lim fn(x)Y * lim f'n(x).
2802.	Определить, при каких значениях параметра а:
а) последовательность
Ш = п«хе-пх	(1)
(п = 1, 2, ...) сходится на сегменте [0, 1]; б) последовательность
(1) сходится равномерно на [0, 1]; в) возможен предельный пе¬
реход под знаком интеграла
1
lim Г fn(x) dx.
П -» ОО J
о
2803.	Показать, что последовательность
fn(x) = пхе~пх (п = 1, 2, ...)
сходится на сегменте [0, 1], но
1	1
I* [ lim /„(*)] dx * lim f fn(x) dx.
J П-ЮО	n-> OO J
0	0
2804.	Показать, что последовательность
/„(*) = nx(l - x)n (n = 1,2,...)
сходится неравномерно на сегменте [0, 1], однако
lim Г fn(x) dx= Г lim fn(x) dx.
Л — OO J	J n —* 00
2805.	Законен ли переход к пределу под знаком интеграла
в выражении
1
lim f т —--- dxl
л-оо J 1 + П2Х4

254
РАЗДЕЛ V. РЯДЫ
Найти пределы:
2806.	lira У	.
Х-+1-0	п Хп+1
п = 1
2807. lim
im V (xn-xn + 1).
-1-0
n = 1
2808. a) lim V —p—; 6) lim V ■ ■** ■.
*-+0 La 2ntl	x-oo La 1 + пгхг
n = 1	n = 1
2809.	Законно ли почленное дифференцирование ряда
Ё arct^?
п = 1
2810.	Законно ли почленное интегрирование ряда
п =
на сегменте [0, 1]?
2811.	1. Пусть f(x) (-сю < х < +°о) — бесконечно дифферен¬
цируемая функция и последовательность ее производных fn\x)
(п = 1, 2, ...) сходится равномерно на каждом конечном интер¬
вале (а, Ь) к функции cp(jc). Доказать, что ср(д:) = Сех, где С — по¬
стоянная величина. Рассмотреть пример /„(*:) = е-(*-л>2, n= 1,
2, ... .
2.	Пусть функции fn(x) (п = 1, 2, ...) определены и ограниче¬
ны на (-°°, +оо) и fn(x)=Zcp(jc) на любом сегменте [а, Ь]. Следует
ли отсюда, что
lim sup/(x) = supcp(x)?
п — ОО X	X
§ 5. Степенные ряды
1.	Интервал сходимости. Для каждого степенного ряда
а0 + аг(х - а) + ... + ап(х - а)п + ...
существует замкнутый интервал сходимости: \х - а\ < R, внутри кото¬
рого данный ряд сходится, а вне расходится. Радиус сходимости R оп¬
ределяется по формуле Коши—Адамара
i - Пт "7Й •

§ 5. Степенные ряды
255
Радиус сходимости R может быть вычислен также по формуле
R = lim
п — оо
если этот предел существует.
ОО
2.	Теорема Абеля. Если степенной ряд S(х) = ^ апхп ^|л:| < R j схо-
п = о
дится в концевой точке х = R интервала сходимости, то
5(Д)= lim S(x).
х — Д-0
3.	Ряд Тейлора. Аналитическая в точке а функция f(x) в некоторой
окрестности этой точки разлагается в степенной ряд
Л*) = £ f^(x-a)k.
Остаточный член этого ряда
Д„(*) = fix) — ^	(х ~
к = 0
может быть представлен в виде
R„ix) =	«(*-«))	+1 (0 < е < 1)
(л+ 1)!
(форма Лагранжа) или в виде
Rnix) =	“U (1 - 01)"(* - а)" +1 (0 < в, < 1)
п\
(форма Коши).
Необходимо помнить следующие пять основных разложений:
I. е" = 1 + х +	+ ... + ^ + ... (-оо < х < +оо).
уЗ	, у2п— 1
И. sin х - х - |у + ... + (-1)П	(2п1Т)! + •"	(~°° < Х < +00)'
III.	cosx=l-g +...+(-l)"^j +... (-оо < х < +оо).
IV.	(1 + х)п = 1 + тх +	х2 + ...
+ т(т-	п+ 1) х„ + ы<х< 1}.
п\
1п(1 + *) = X- Щ ^ - ... + (-1)я-1 — + ... (-1 < х< 1).
Z о	Н
V.

256
РАЗДЕЛ V. РЯДЫ
4. Действия со степенными радами. Внутри общего интервала схо¬
димости \х - а\< R имеем:
оо	сю	сю
а) £ ап(х - о)" ± £ Ъп{х-а)п= £ (а„ + Ьл)(а: - а)л;
л = О
л = О
б)	£ а„(* - а)" ^ Ь"(х ~аУ= X С^Х ~ а)"’
л = О	л = 0	л = О
где cn = a0bn + а,Ь„ -, + ...+ а„Ь0;
- 00 -| 00
в)	^[£ ап(х - a)"J = ^ (л + 1 )а„ + ,(л: - а)л;
"л = 0
л = 0
_ _ °о	_	оо
Г)|[£ а„(*-а)л]</* = С + £ ^^(*-а)л+'.
л = 0	л = О
5. Степенные ряды в комплексной области. Рассмотрим ряд
оо
сп(х-а)\
л = 0
где
cn = a„ + ib„, a = a + «Р, z = x + iy, i2=-1.
Для каждого такого ряда имеется замкнутый круг сходимости |лс - а\ < R,
внутри которого данный ряд сходится (и притом абсолютно), а вне расхо¬
дится. Радиус сходимости R равен радиусу сходимости степенного ряда
I Ы-*
л = 0
в действительной области.
Определить радиус и интервал сходимости и исследовать по¬
ведение в граничных точках интервала сходимости следующих
степенных рядов:
2812.	V
Zj пр
Л = 1
2814. У ^Щхя.
А <2п>!
00 / 1 \ 2
2816. £ f i + ij" xn.
Л = 1
2819-£«-1>"[етл
Л = 1	4
2813. У ?Л+(-2)"(ж + 1)».
^	Л
л = 1
оо
2815. a "2 лс” (0 < a < 1).
2817. У 4^"(а> 1).
.4-1 «"2

§ 5. Степенные ряды
257
оо
2820.	V т(т-1)...(т-п+1) х„
П\
л = 1
ОС
2821.	*я (а > О, Ь> 0).
Л = 1
ОО	оо
2822.	У —Ц- (а > 0, b > 0). 2823. У (а > 0).
/-< a" + bn	jL, „Гп у
- _ 1 - _ 1 u
П = 1
п = 1
2824.
,f?i V«2+ 1
2826. £
/I = 1
2829. £
л = 2
2828. У [3 + Н)'1|У'.
^	Л
л = 1
ОО	2
2830.	У
2"
Л = 1
2831.	а) V W*1 ^/l (ряд Принсгейма);
П
2825. У	х\
(2п+1)!!
/i = i
2827.|; (1+|+... + !)*-.
1п п
л = 1
л = 1
Z10v(«)
	(1 - х)’\ где v(/i) — число цифр числа п\
п
л = 1
в) Z М-Т-
£—1	\ Sill П)
л = 1
2832. Определить область сходимости гипергеометрического
ряда
1 + jc + a(g+i)P(P+i) *2 +
1	• Y 1 • 2 • y(Y + 1)
+ g(g+ 1)...(а + n - 1)P(P + l)...(P + n - 1) yn + _ _
1-2 ... п • y(Y+ 1)...(Y+	1)
Найти область сходимости обобщенных степенных рядов:
2833. У -J—fi—Щ" .	^ 1-г-я
jLu 2л+1ч1 + л:/
л = о
2835.
Zxn
2п2'
2834. V — sin£.
Lu хп 2п
л = 1
™	( IV»2
283в-1(1 + я
Л = 1
2837-z 3i£?tsnx
л = 1

258
РАЗДЕЛ V. РЯДЫ
2838.	Функцию
f(x) = X3
разложить по целым неотрицательным степеням бинома х + 1.
2839.	Функцию
/(*) = (а 5й 0)
разложить в степенной ряд: а) по степеням я; б) по степеням би¬
нома х - Ь, где b & а; в) по степеням - . Указать соответствующие
х
области сходимости.
2840.	Функцию f(x) = In х разложить по целым неотрица¬
тельным степеням разности х - 1 и выяснить интервал сходи¬
мости разложения. Найти сумму ряда
л = 1
Написать разложения следующих функций по целым неот¬
рицательным степеням переменной х и найти соответствующие
интервалы сходимости:
2841.	/(*) = sh х.
2842.	f(x) = ch х.
2843.	f(x) = sin2 x.
2844.	/(*) = ax (x > 0).
2845.	f(x) = sin(jn arcsin x).
2846.	f(x) = cos(|lI arcsin x).
2847.	Написать три члена разложения функции f(x) = Xх по
целым неотрицательным степеням разности х - 1.
2848.	Написать три члена разложения функции
/(*) = (1 + *)*
(х & 0) и /(0) = е по целым неотрицательным степеням перемен¬
ной х.
2849.	Функции sin (х + h) и cos (х + h) разложить по целым
неотрицательным степеням переменной h.
2850.	1. Определить интервал сходимости разложения в сте¬
пенной ряд функции
/(*)=
X
х2- 5х + 6
а) по степеням х; б) по степеням бинома х - 5, не производя са¬
мого разложения.

§ 5. Степенные ряды
259
2. Можно ли утверждать, что
о°
Z	si
п = 1
sin *
на (-оо, +оо) при N —► оо?
Пользуясь основными разложениями I—V, написать разло¬
жения в степенной ряд относительно х следующих функций:
2
2851.	.
2853. sin3*.
1
2852. cos2*.
„ю
2854.
1-*
2855.
2856.
(1-*Г
2857.	In /pi.
Vi-*
2858.
Jl - 2x
1 + * - 2*2
Указание. Разложить данную дробь на простейшие.
2859.
2861.
2862. а)
2863
12-5*
6 - 5* - х2
1
1-х-х2'
1
2860.
1 + * + х2
*cosa- х2
; б) f(x) =
1 - 2*cosa + х2
1 + * + х2 + *3
2864.
(1-х)(1-**)
Чему равно/(1000>(0)?
jc sin a
1 - 2*cosa + х2'
2865.
arsha
2866.
1 - 2a:cha + x2
2867.	In (1 + a: + a;2 + x3).
2868.	ex cos ° cos (a; sin a).
Указание. Применить формулы Эйлера.
(1-**)л/ГГ£5
Разложив предварительно производные, путем почленного
интегрирования получить разложения в степенной ряд следую¬
щих функций:
ОО .	1	+ 1
2869.	f(x) = arctg *. Найти сумму ряда V	.
^	2 п — 1
л = 1
2870.	/(*) = arcsin *.
2871.	/(*) = In (* 4- Vl + х2).
2872.	/(*) = In (1 - 2* cos a + *2).

260
РАЗДЕЛ V. РЯДЫ
2873.	Применяя различные методы, найти разложения в сте¬
пенной ряд следующих функций:
а)	fix) = (1 + jc)ln(l + *);
б)	f(x) = i In + | arctg jc;
в)	f(x) = arctg	;
r) fix) = arctg 2^5 ;
Д) fix) — x arctg x - In Jl + x2 ;
е)	f(x) = arccos (1 - 2x2);
ж)	f(x) = x arcsin x + Vl - x2;
з)	f(x) = x In (x + Vl + x2) - Vl + x2.
2874.	Используя единственность разложения
h2
fix + Л) - /(X) = л/'(*> +	/"(*) + ....
найти производные л-го порядка от следующих функций:
a) f(x) = ех
2875.	Функцию
б) fix) = е*; в) fix) = arctg х.
fix) = In
2+ 2х + х2
разложить по целым положительным степеням бинома х + 1.
2876.	Функцию
1
/(*) =
1-х
разложить в степенной ряд по целым отрицательным степеням
переменной х.
2877.	Функцию
fix) = In х
разложить в степенной ряд по целым положительным степеням
дроби .
дг + 1
2878.	Функцию
разложить в степенной ряд по целым положительным степеням
дроби —.
1 + X

§ 5. Степенные ряды
261
2879. Пусть
т- £
п = О
£2
п\ '
Доказать непосредственно, что
fWf(y) = fix + у).
2880. Пусть по определению
sin х =
Z ^
п = О
Х2п+ 1
(2 л + 1)! ’
COS X =
оо
I <-1>*
п = О
*2я
(2л)Г
Доказать, что:
a) sin х cos х = | sin 2jc; б) sin2 jc + cos2 jc = 1.
2881. Написать несколько членов разложения в степенной
ряд функции:
№ =
-1
Производя соответствующие действия со степенными ряда
ми, получить разложения в степенные ряды следующих функ
ций:
2882. fix) = (1 + х)е х.
2884. fix) = In2 (1 - *).
2886. fix) = ех cos х.
2888. f(x) =	.
1 + X
2890.	fix) = (m*)2.
2883. fix) = (1 - xf ch Jx .
2885. fix) = (1 + x2) arctg x.
2887. fix) = ex sin x.
2889. fix) = (arctg xf.
Написать три члена разложения (отличные от нуля) в степен¬
ной ряд по положительным степеням переменной х следующих
функций:
2891.	fix) = tg х.
2893.	fix) = ctg x - i .
2892. fix) = th x.

262
РАЗДЕЛ V. РЯДЫ
2894.	Пусть разложение sec х записано в виде
00	v
sec х = V —2- х2п.
(2л)!
п = 0
Вывести рекуррентное соотношение для коэффициентов Еп
(числа Эйлера).
2895.	Разложить в степенной ряд функцию
f(x)=—±==	(н<1).
Jl-2tx + x2 v	'
ОО
2896.	Пусть f(x) =	Написать разложение функции
л = 0
F(x) =	.
ОО
2897.	Если ряд апхп имеет радиус сходимости Rl9 а ряд
п = 0
ОО
Ьпхп — радиус сходимости R2, то какой радиус сходимости
л = 0
R имеют ряды
ОО	ОО
а) £ (а„ ± К)хп; б) £ апЬпхп?
/1 = 0	/1 = 0
2898.	Пусть
Z = lim
п — оо
Яд
и L = Иш
+1
л —* оо
a„ + i
п = 0
Доказать, что радиус сходимости Я степенного ряда ап#л
удовлетворяет неравенству
I	< Я < L.
2899.	1. Доказать, что если Длс) = an#n, причем
л = 0
|n!a„| < М (n = 1, 2, ...),
где М — постоянная, то: 1) f(x) бесконечно дифференцируема в
любой точке а; 2) справедливо разложение
м- У 2%£И(х-аГ (W<+°°).
П\
п = 0

§ 5. Степенные ряды
263
2.	Пусть /(х) € С(ао)(а, Ь) и |/(л)(х)| < сп (п = О, 1, 2, ...) при
х € (а, Ь). Доказать, что функция f(x) разлагается в степенной ряд
оо
f(x) = £ ап(х - х0)л (*0 € (а, Ь)),
п = 0
сходящийся в интервале (а, Ь).
3.	Пусть /(*) € С(00) [-1, 1] и /<л)(х) > 0 (п = 0, 1, 2...) при
лс € [-1, 1]. Доказать, что в интервале (-1, 1) функция f(x) раз¬
лагается в степенной ряд
оо
fix) = £ а„хл.
п = 0
Указание. Используя монотонность производных f{n\x) для ос¬
таточного члена Rn(x) ряда Тейлора функции f(x)t получить оценку
|Я„(*)|< |*|л + 1/(1).
2900.	Доказать, что если: 1) ап > 0; 2) существует
ОО
Нш V апхп = S,
x^R-о
« = о
ОО
то ^ anRn = S.
л = 0
Разложить в степенной ряд функции:
2901. f e~f2 dt.
2902. f
dt
л -t*
J
J
0
0
X
2903. f — dt.
X
2904. f
arct® xdx.
J *
0
J
0
X
/•	1 J 1
2905.	I ^ (i + t) (написать четыРе члена).
о
Применяя почленное дифференцирование, вычислить суммы
следующих рядов:
2906.	x + ^ + ^ + ... .
3	5
А* 3	у 5
2907.	х - ~	- ... .
3	5

264
РАЗДЕЛ V. РЯДЫ
2908. 1 + |f + g + ... .
2909.
1-2	2*3
+
3-4
2910. 1 + \х +	+ i-r-l*3 +	•
2	2-4	2-4-6
Указание. Производную ряда умножить на 1 - х.
Применяя почленное интегрирование, вычислить суммы
рядов:
2911.	х + 2х2 + Зх3 + ... .
2912.	х-4х2 + 9х3 - 16х4 + ... .
2913.1	• 2х + 2 • Зх2 + 3 • 4х3 + ... .
2914.	Показать, что ряд
ОО
«-1.
п = 0
х*п
(4 п)!
удовлетворяет уравнению
ylv = y.
2915.	Показать, что ряд
п = 0
хп
(л!)2
удовлетворяет уравнению
ху" + у' - у = 0.
Определить радиус и круг сходимости степенных рядов в
комплексной области (z = х + iy):
2916.	£
п = 1
(*-*-*>"
л • 2"
2917.	У
(1 + 0"г"
(л+ 1)(л + 2) ’
2918 V 	п'гП
* Z- (1 + 0(1 + 2/)...(1 + л/)
2919.
/1=1
г”
па+Ф •
2920. У <*-*7" .
n(l-eia)n
n=i
2921.	Пользуясь формулой бинома Ньютона, приближенно
вычислить V9 и оценить ошибку, которая получится, если взять
три члена разложения.

§ 5. Степенные ряды
265
2922.	Приближенно вычислить:
a)arctgl,2;	б) 1°Jl000 ; в) ;
Je
г)	In 1,25 и оценить соответствующие погрешности.
Пользуясь соответствующими разложениями, вычислить
с указанной степенью точности следующие значения функций:
2923.	sin 18° с точностью до 10"5.
2924.	cos 1° с точностью до 10~6.
2925.	tg 9° с точностью до 10'3.
2926.	е с точностью до 10"6.
2927.	In 1,2 с точностью до 1(Г4.
2928.	Исходя из равенства
п _	1
- = arcsin-,
6	2
найти число л с точностью до КГ4.
2929.	Пользуясь тождеством
S	= arctg| + arctg|,
ВЫЧИСЛЙТЬ ЧИСЛО 71 с точностью до 0,001.
2930.	Пользуясь тождеством
! “ 4 arctg| -arctg^,
определить число 7С с точностью до 10-9.
2931.	Пользуясь формулой
In (п + 1) = In п 4- 2 Г -—-—Г + ■ - -—— + ... 1,
v 7	\_2п +1	3(2л +1)3 J
найти In 2 и In 3 с точностью до 10-5.
2932.	С помощью разложений подынтегральных функций
в ряды вычислить с точностью до 0,001 следующие интегралы:
1
4
a) f e~x2dx;
J
6)!
Г e xdx\
0
2
2
1
в) f 2iMdjc;
г> I
Г cos x2 dx;
J X
0
0

266
РАЗДЕЛ V. РЯДЫ
д) J *£dx;
О
100
dx
+ оо
2
з) Г т==;
j vrric<
0
1
2
и) J 1п(^^)^;	к) J
10
1
2
w4 f arcsinx
ЛЧ —
dx;
0
1
м) I Xх dx.
\
о
2933.	Найти с точностью до 0,01 длину дуги одной полуволны
синусоиды
у = sin х (0 < х < л).
2934.	Найти с точностью до 0,01 длину дуги эллипса с полу¬
осями а = 1 и b = \ .
2
2935.	Провод, подвешенный на двух столбах, расстояние меж¬
ду которыми равно 21 = 20 м, имеет форму параболы. Вычислить
с точностью до 1 см длину провода, если стрелка прогиба h = 40 см.
§ 6. Ряды Фурье
1. Теорема разложения. Если функция f(x) кусочно-непрерывна и
имеет кусочно-непрерывную производную f'(x) в интервале (-/, /), при¬
чем все точки разрыва £ регулярны (т. е. /(£) = ^ [/"(£, ” 0) + /(£, + 0)]), то
функция f(x) на этом интервале может быть представлена рядом Фурье
ОО
v а0 ,	(	ппх . ,	. пкх\	/1ч
fix) = у + 2, [«nCOS— +&„sin—J,	(1)
n = 1
где
ft*) cos^ da: (n = 0, 1, 2, ...)
-1
1
b„ = yj fix)sm^dx(n=l,2, ...)
(2)
(2')

§ 6. Ряды Фурье
267
В частности:
а) если функция /(х) четная, то имеем
оо
Л*)- у + £
ап cos
пкх
I ’
(3)
где
1
о
б) если функция f(x) нечетная, то получаем
со
(4)
где
1
ъп = | J f(x) sin^y^ dx (л = 1, 2, ...)•
. ЛЯХ
о
Функцию f(x)y определенную в интервале (О, Z) и обладающую в нем
приведенными выше свойствами непрерывности, можно в этом интер¬
вале представить как формулой (3), так и формулой (4).
2. Условие полноты. Для всякой интегрируемой на интервале (-Z, I)
вместе со своим квадратом функции f(x) формально построенный ряд
(1) с коэффициентами (2), (2') удовлетворяет равенству Ляпунова
3.	Интегрирование рядов Фурье. Ряд Фурье (1), даже расходящий¬
ся, интегрируемой по Риману в интервале (-Z, I) функции f(x) можно
интегрировать почленно в этом интервале.
2936.	Функцию
разложить в ряд Фурье.
2937.	Каков будет ряд Фурье для тригонометрического мно¬
гочлена
f(x) = sin4 х
п
Рп(х) = ^ (a* cos ix + Р; sin ix)l
2938.	Разложить в ряд Фурье функцию
f(x) = sgn х (-я < х < я).

268
РАЗДЕЛ V. РЯДЫ
Нарисовать график функции и графики нескольких частных
сумм ряда Фурье этой функции.
Пользуясь разложением, найти сумму ряда Лейбница
у (-1)"-1
La 2п-1 '
П = 1
Разложить в ряд Фурье следующие функции:
2939
А, если 0 < х < I;
О, если I < х < 2Z,
где А — постоянная, в интервале (0, 21).
2940. f(x) = х в интервале (-л, л).
2941. f(x) =
к- х
в интервале (0, 2л).
2942. f(x) = \х\ в интервале (-л, л).
\ах> если л < х < 0;
2943. f(x) =
Ъх, если 0 < х < л,
где а и Ъ — постоянные, в интервале (-л, л).
2944.	f(x) = л2 - х2	в интервале (-л,	л).
2945.	f(x) = cos а#	в интервале (-л,	л) (а —	не	целое).
2946.	f(x) = sin ах	в интервале (-л,	л) (а —	не	целое).
2947.	f(x) = sh ах	в интервале (-л,	л).
2948.	f(x) = еах	в интервале (-/i,	h).
2949.	f(x) = х	в интервале (a, a + 2Z).
2950.	f(x) = лс sin лс	в интервале (-л,	л).
2951.	f(x) = дс cos х в интервале
Разложить в ряд Фурье следующие периодические функции:
2952.	f(x) = sgn (cos х).
2953.	f(x) = arcsin (sin x).
2954.	f(x) = arcsin (cos x).
2955.	/(*) = x - [x].
2956.	f(x) = (jc) — расстояние x до ближайшего целого числа.
2957.	f(x) = |sin x\.
2958.	/(лс) = |cos x\.
2959. /(л:) =
a'
nsmnx
n = 1
(N< l).
sin*

§ 6. Ряды Фурье
269
2960.	Разложить в ряд Фурье функцию
f(x) = sec * ^ с * с .
Указание. Вывести соотношение между коэффициентами ап и
2961.	Функцию f(x) = х2 разложить в ряд Фурье: а) в интер¬
вале (-я, тс) по косинусам кратных дуг; б) в интервале (0, я) по
синусам кратных дуг; в) в интервале (0, 2тс).
Нарисовать графики функций и сумм рядов Фурье для слу¬
чаев а), б) и в).
Пользуясь этими разложениями, найти суммы рядов:
почленным интегрированием получить разложение в ряд Фурье
на интервале (-я, я) функций х2, х3 и х4.
2963.	Написать равенство Ляпунова для функции
2962.	Исходя из разложения
*=2]Г (-1)я + 1 21
оо
,л + 1 81ППХ
(-я < X < я),
П
п = 1
J1 при \х\ < а;
[О при а < \х\ < я.
Исходя из равенства Ляпунова, найти суммы рядов:
оо
оо
п = 1
и
2964.	Разложить в ряд Фурье функцию
3 ху
Ху
1,
Пользуясь формулами
cos х =	+ t)9
z
sin X =
где t =eixvit =e ,x, получить разложение в ряд Фурье следующих
функций:

270
РАЗДЕЛ V. РЯДЫ
2965. cos2mx (т
2966.
2967.
<7 sin*
1 - 2</cosJt+ q2
целое положительное число).
(Ы < 1).
J_=_2l
1 - 2</cos* + q2
(Ы < !)•
2968.	1-gcos* (|?| < 1).
1	- 2</cos* + q2
2969.	ln(l - 2q cos x + q2) (|g| < 1).
Разложить в ряд Фурье неограниченные периодические
функции:
2970.	f(x) = In
2971.	f(x) = In
sin-
2
cos^
2
tg2
2972.	/(*) = In
2973.	Разложить в ряд Фурье функцию
fix)
JlnJR
dt (-71 < x < n).
2974.	Разложить в ряд Фурье функции
* = x(s), у = y(s) (0 < s < 4а),
дающие параметрическое представление контура квадрата:
О < * < а, 0 < у < а, где s — длина дуги, отсчитанная против хода
часовой стрелки от точки 0(0, 0).
2975.	Как следует продолжить заданную в интервале ^ 0,
интегрируемую функцию f(x) в интервал (-71,я), чтобы ее разло¬
жение в ряд Фурье имело вид
оо
/(х) =	ап cos (2л - I)* (-71 < х < я)?
п = 1
2976.	Как следует продолжить заданную в интервале ^ 0,
интегрируемую функцию /(х) в интервал (-я, я), чтобы ее разло¬
жение в ряд Фурье имело вид
оо
fix) = ^ ba sin (2п - 1)дс (-я < х < я)?
/1=1

§ 6. Ряды Фурье
271
2977.	Функцию
разложить в интервале ^ О, |j :
а)	по косинусам нечетных дуг;
б)	по синусам нечетных дуг.
Нарисовать графики суммы рядов Фурье для случаев а) и б).
2978.	Функция f(x) антипериодична с периодом л, т. е.
Какой особенностью обладает ряд Фурье этой функции в ин¬
тервале (-я, л)?
2979.	Какой особенностью обладает ряд Фурье функции f(x)
в интервале (-л, л), если f(x + л) = f(x)?
2980.	Какими особенностями обладают коэффициенты Фурье
аЛ, Ьп (п = 1, 2,...) функции у = f(x) периода 2л, если график функ¬
ции: а) имеет центры симметрии в точках (0, 0),	, 0^ ; б) имеет
центр симметрии в начале координат и оси симметрии х = ±- ?
С*
2981.	Как связаны между собой коэффициенты Фурье аЛ, Ьп
и а„, Рп (л = 0, 1, 2, ...) функций cp(jc) и \|/(jc), если
2982.	Как связаны между собой коэффициенты Фурье аЛ, Ъп
и ал, (Зл (п = 0, 1, 2, ...) функций cp(jc) и \|/(jc), если
2983.	Зная коэффициенты Фурье ап,Ьп(п = 0, 1,2, ...) интег¬
рируемой функции f(x), имеющей период 2л, вычислить коэф¬
фициенты Фурье ап, Ьп (п = 0, 1, 2, ...) «смещенной» функции
/(х + К) (h = const).
2984.	Зная коэффициенты Фурье ап> Ъп (п = 0, 1, 2, ...) интег¬
рируемой функции /(х) периода 2л, вычислить коэффициенты
Фурье Ап> Вп(п = 0, 1, 2, ...) функции Стеклова
fix + я) = -fix).
Ф(-*) = ф(х)?
ф(-х) = -ф(*)?
J т<%.
х-h

272
РАЗДЕЛ V. РЯДЫ
2985. Пусть f(x) — непрерывная функция с периодом 2п
и ап, Ъп (п = 0, 1, 2, ...) — ее коэффициенты Фурье. Определить
коэффициенты Фурье Ап, Вп(п = 0, 1, 2, ...) свернутой функции
я
F(x) = IJ*mf(x + г) dt■
-л
Пользуясь полученным результатом, вывести равенство
Ляпунова.
§ 7. Суммирование рядов
1. Непосредственное суммирование. Если
ип = Vn + 1 - vn (п = 1, 2, ...) и Игл = Уоо,
то
В частности, если
ип =
+1 • • •+ m
где числа a, (i = 1, 2, ...) образуют арифметическую прогрессию со зна¬
менателем d9 то
= -
1
md апап+1.. .ап + г
В некоторых случаях искомый ряд удается представить в виде ли¬
нейной комбинации известных рядов:
V- (-1)Л + 1 , о V- 1 Я2 ^ (-1)я+1 Я*
S S	1п2: 15"? I Чг- - 12 "’• "•
/1=1 /1=1 /1=1
оо
2. Метод Абеля. Если ряд ап сходится, то
/1 = 0
оо	оо
Za„= lim V апх\
л:— 1-0
п = 0
/1 = 0
Сумма степенного ряда ^ апхп в простейших примерах находится
/1 = 0
с помощью почленного дифференцирования йли интегрирования.

§ 7. Суммирование рядов
273
3.	Суммирование тригонометрических рядов. Для нахождения
сумм рядов
со	оо
У ап cos пх и у bn sin ля
п = о	л = 1
их обычно рассматривают как действительную часть и соответственно
как коэффициент мнимой части суммы степенного ряда в комплексной
оо
области у CLnzny где z = е'х.
п = о
Здесь во многих случаях полезен ряд
оо
У — =in—!—	(И < 1).
п 1-х
п = 1
Найти суммы рядов:
2986. —
1-3	3-5	5 7
2987.
1	+ А-+А_+....
1-2-3	2-3-4	3-4-5
1
1 + 1
2988. —- -i- + —+ ...
1-2	2-3	3-4	4-5
ОО
2989 V 	—
Zj (п+ 1)(л + 2)(л + 3) ’
п = 1
2990.
оо
	 (т — натуральное число).
п(п + т)
п = 1
2991.
1 +_!_ + 1
1-2-3	3-4-5	5-6-7
+ ...
2992 L
п = 2
оо
2994. V *	■.
Z-f п(2п + 1)
«=1
2996. V 2ln+JJ
п\
л = 0
оо
2998. У 	-4
Z-f n2(n + 1)2(л + 2)2
л=1
00	/	1 чл
3000. у —^—- .
^ л2 + п - 2
/1 = 2
3001.	Пусть Р(х) = а0 +	+ ... + am*m. Найти сумму ряда
2993. У	2п~ 1—
А л2(2л + I)2
/1=1
°° 2
2995. У
л!
л=1
оо
2997. у 2/ 1 --а ■
Zj п2(л+ I)2
п = 1
2999. У ИГ».
А (2л + 1)!
/1 = 0

274
РАЗДЕЛ V. РЯДЫ
Найти суммы следующих рядов:
3002. V 2.+JL*».
^ 2лл!
п = 0
3004. V (~1)"(2га2+ !)jc2n.
4-i	(2я)!
3003
у хп
' ^ (л+1)!	‘
л = О
л = О
3005. £
л = о
(л+1)!
П2Хп
(2л + 1)!
С помощью почленного дифференцирования найти суммы
рядов:
3006. У £
4-1 п
п = 1
3007.
/1=1
(~1)п-1хгп
О	'
V (~1Г
4—t	п(2п-1
3008. £
л = о
4л +1
3009. V aia + d) --[g+l?.-	х* ы> 0).
^	d-2d...nd
n = 1
Указание. Производную ряда умножить на 1 - х.
ЗОЮ. i £ + i-if+ LJ-1(2V + ... .
3	2	3-бЫ 3 • 6•9V2/
С помощью почленного интегрирования найти суммы рядов:
ЗОН. jr п^хп ~ 1.
п = 1
3012.	£ га(п + 2)лгл.
п = 1
3013.	У t1)*2".
л!
п = О
Используя метод Абеля, найти суммы следующих рядов:
*°ЫЛ-\ + 17-Г0+ -•
з°15-1" I + I " I + ••• •
3016. 1 - i +	- i-4-| + ••• •
2	2-4	24-6
З017л + И + Н1 +

§ 7. Суммирование рядов
275
Найти суммы следующих тригонометрических рядов:
3018. У
t	п
п = 1
оо
3020. £
cos л*
3019 у cos/
" п
п = 1
sin л ос sin л*
п = 1
3021. £
sin2 лает л*
п = 1
3022. ]Г "-*>«.
3023. £
П= 1
п = 2
3024 V cos(2n~1)х
Z-,	(2/1-1)2
П = 1
3025. V (-i)o- i_sinvt£_ ,
^	Л(Л +1)
п = 1
3026.
ZCOSTl*
л!
/1 = 0
3027. Построить кривую У	= о.
л2
л=1
Найти суммы следующих рядов:
ОО
3028. У Кдт1)!]2(2ж)а".
“	(2л)!
n = i
зо29- £
3030.
/1 = 0
1!
+
2!
3!
*+1	(*+!)(*+ 2)	(* + 1)(* + 2)(х + 3)
+ ... .
3031.
а2 + х а2 + х а3 + *
°°
(л = 1, 2, ...) и ряд У — расходящийся.
°2	+ ... при условии, что * > 0, ап > 0
3032. ■ х--~ +	- +	* - + ..., если: а) |*| < 1; б) |*| > 1.
1-х2	1-х4	1-х8
3033. V 		^
Z-f (1 - *")(! - хп+1
если: а) |*| < 1; б) |*| > 1.

276
РАЗДЕЛ V. РЯДЫ
§ 8. Нахождение определенных интегралов
с помощью рядов
С помощью разложения подынтегральной функции в ряд вы¬
числить следующие интегралы:
1 1
3034. f In —— dx.	3035. f	t
3036.
J In	3035. J
0	0
j K.i_f dx
0
1
3037.	jVUnU -xi)dx (p> 0, q> 0)
0
1	+oc
3038.	J In x • In (1 - x) dx.	3039. J
xdx
e2nx_ 1
0
+ oo
3040.
Г xdx
J ex+ 1
3041. Разложить по целым положительным степеням модуля k
(0< k< 1) полный эллиптический интеграл 1-го рода
Л,
E(k) = J
d(p
Jl - fc2sin2(p
3042. Разложить по целым положительным степеням модуля k
(0< k < 1) полный' эллиптический интеграл 2-го рода
&
E(k) = j* Jl - fc2sin2(pd(p.
3043. Выразить длину дуги эллипса
х — a cos ty х = Ь sin t (0 < t < 2п)
с помощью ряда, расположенного по целым положительным сте¬
пеням эксцентриситета.
Доказать равенства:
1
3044. Г ^ = У -1,
] Xх	Пп
п	п = 1

§ 9. Бесконечные произведения
277
tw
3045.	f <r*2sin ax dx= i V SzDlnL a2n +1.
J	2Zw2n+l)!
0	n = О
2	я
3046.	J ecosx cos (sin x) cos nx dx= ^ (n = 0, 1, 2, ...).
Найти:
3047. J eacosx cos (a sin x - nx) dx (n — натуральное число).
о
я
J-
3048.
а: sin a (
2acosa: + a2
Указание. См. пример 2864.
я
3049.	J In (1 - 2a cos x + a2) dx.
0
3050.	Доказать формулу
+ O0
f _^djc=I-Ii + 2!	..
J a + * a a2 a3
о
... +(-l)n-1	+ (-1)»§а21,	(1)
an	an+l
где а>0и0<9Л<1.
С какой точностью выразится интеграл
j
е~х
100 +а:
dx,
о
если в формуле (1) взять два члена?
§ 9. Бесконечные произведения
1. Сходимость произведения. Бесконечное произведение
оо
PlPz-Pn- = ]~J рп	(1)
п = 1
называется сходящимся, если существует конечный и отличный от нуля
предел
Нш ГТ р, = lim Рп = Р.
п-~оо А. ±	п - оо
i = 1

278
РАЗДЕЛ V. РЯДЫ
Если Р = 0 и ни один из сомножителей рп не равен нулю, то произ¬
ведение (1) называется расходящимся к нулю; в противном случае про¬
изведение называется сходящимся к нулю.
Сходимость произведения (1) равносильна сходимости ряда
^ 1пр„.	(2)
п= п0
Необходимым условием сходимости является
lim р„ = 1.
П — ОО
Еслирп = 1 4- а„ (л = 1, 2,...) и а„ не меняет знака, то для сходимости
произведения (1) необходимо и достаточно, чтобы был сходящимся ряд
£ «„ = £(р„-1).	(3)
п = 1	п = 1
В общем случае, когда ал не сохраняет постоянного знака и ряд (3)
сходится, произведение (1) будет сходиться или расходиться к нулю
вместе с рядом
£“•“ Ё(р"-1)2
2.	Абсолютная сходимость. Произведение (1) называется абсолют¬
но или условно (не абсолютно) сходящимся в зависимости от того, аб¬
солютно или условно сходится ряд (2). Необходимым и достаточным
условием абсолютной сходимости произведения (1) является абсолют¬
ная сходимость ряда (3).
3.	Разложение функций в бесконечные произведения. При
-оо < х < +оо имеют место разложения
cos х = J~J £ 1 -
п = 1
_4£f_1
(2п-1)2я2_Г
В частности, из первого при х = ^ получаем формулу Валлиса
5 = П 2п > 2п
2	11 2л- 1 * 2л+Г
п = 1
Доказать следующие равенства:
808‘-П(1-й-г
л = 2
3052. П п!-1 -
11 л3+1 3
п = 2
оо
3053. П Г1 - , 2 , 1 - 1.
11 L л(л+ 1)J 3
л = 2
3»54.П[1 + (1П
л = 0

§ 9. Бесконечные произведения
279
3055. Д cos ф, = \ .	3056. Д cosfn
sinjc
3057. Ц chfn =
л = 1
3059. 5 = 2
£. = sh*
2" x
2
3058. Д (1 + *2Л) = (M < !)•
л = 0
2
V2 ^2 + J2 J2 + J2 + J2
3060.
3 n
3 n
2 к
П Зл-l Sn+l 3/3
л = 1	v
Доказать сходимость и определить значения следующих бес¬
конечных произведений:
3061. п ^
3062
■ П [ 1 + п(п + 2)]
(-1)"
3063. П ('оЯ + о^оП + II •	3064. ГГ а п (а > 0).
11 (2л + 3)(2я + 5)	11
л = 1	л - 1
оо	сх>
3065. Следует ли из сходимости произведений Пр*и П 9»
п = 1	л = 1
сходимость произведений:
оо	оо	оо	оо
а) Д (р„ + <7„); б) Д р\; в) Д pnqn\ г) Д
Л = 1	Л = 1	Л = 1	Л=1
Исследовать сходимость следующих бесконечных произ¬
ведений:
оо
30ввП я-
л = 1
оо
30в8-П(1 + г.)'
Л = 1
“П(Й)'-
3067. П	■
11 п(п + 2)
л = 1
оо
3069. П ( 1 - п)'
3071. ГГ n2 + ain + bi t где п2 + ап + b> 0 при п > п0.
11 п2 + ап + Ь
3072. Д (” °')(П	'(Я	где n0 > bt (t = 1, 2, .... р).
11 (n-bi)(,n-b2)...(n-bp)

280
РАЗДЕЛ V. РЯДЫ
3073
3075
■гШ-
л = О
п-Н-
л = 1
ОО	х
3077. П ( 1 +	•
л = 1
оо
3079. Ц(1- хп).
п = 0
3074. ГТ —.
, Jn2+ 1
П = 1 v
ОО
3076. П "V» •
л - 1
ОО	£
3078. f|( 1 “	«где о 0.
л = 1
3080. П(1+ £).
3081. Л
1 +
хп
3082.
( т\р
sin-
х
\ п J
оо	оо
3083. n(l + g)cosg. 3084.
л = 1	л = 1
оо
3085.	Vln(n + J:)- Inn .
п = 1
оо
3086.	Доказать, что произведение cos хп сходится, если
л = 1
оо
СХОДИТСЯ ряд Y\ Хп •
л = 1
оо
3087.	Доказать, что произведение П tg(i + а-) (1а«1< i)
л = 1
оо
сходится, если абсолютно сходится ряд ^ ап.
п = 1
Исследовать на абсолютную и условную сходимости следую¬
щие бесконечные произведения:
3088
+	3089. П[1 + ^]
3090-n[1 + t^r:]'	8091-П [1 + 1к?]-
л = 2

§ 9. Бесконечные произведения
281
Jn
3092. ГГ -=-*
!л «£+(-1)«
оо
3094. J]	.
3096
1 + fcV--
3093.	га*-1)”
п = 1
ОО г
3095.
3098.	Показать, что произведение
fi + i + IVi- J,
V J2	2 A	J2
сходится, хотя ряд
fJL + Г) +Г--Ц н
v,/2	2)	{ j-2)
расходится.
оо
3099.	Показать, что произведение (1 + ал), где
1 + -L + Г
7з з,
К
'JL + JU (
7з 3J 1
< Ja)
-1
если п = 26 - 1,
л'
ап=<
-L +
I + _L,
если п = 2k,
Jk
* ft,/*
оо
оо
хотя оба ряда
Е«ли
^ а„ расходятся.
п = 1
Л = 1
3100.	Пусть
а*)- £ Л
п = 1
{дзета-функция Римана) ирп (п = 1, 2, ...) — последовательные
простые числа.
Доказать, что
пО-?)"-«*>•
п = 1	гп

282
РАЗДЕЛ V. РЯДЫ
3101.	Доказать, что произведение
П(“г)"
л = 1
И ряд
°о
п = 1
где рп (п = 1, 2, ...) — последовательные простые числа, расхо¬
дятся (Эйлер).
3102.	Пусть ап > 0 (п = 1, 2, ...) и
_£«_=l + £+	(е > 0).
<*„♦ 1	n U1+V
Доказать, что
Указание. Рассмотреть
оо
Нш а„П? = а, ГГ — { 1 + -Т.
л -* о©	1. JL ап \ п)
л = 1
3103.	С помощью формулы Валлиса доказать, что
1 • 3 • 5...(2л - 1) _ _1_
2 • 4 • 6...(2л)
3104.	Доказать, что выражение
л _ п\еп
O'п
имеет отличный от нуля предел А при п —► оо.
Вывести отсюда формулу Стирлинга
nl=An+*en(l + е„),
где lim ел=0иА = J2п .
П — оо
Указание. Искомый предел представить в виде бесконечного
произведения
оо
А = lim ап = а{ ]~Т	.
л — оо	х х а„
л = 1
Для определения константы А воспользоваться формулой
Валлиса.

§ 9. Бесконечные произведения
283
3105.	Согласно Эйлеру гамма-функция Г(х) определяется
следующей формулой:
Г(х) = lim
П —* °0
	п\пх
х(х+ !)...(* + п)’
Исходя из этой формулы:
а)	представить функцию Г(х) в виде бесконечного про¬
изведения;
б)	показать, что Г(л:) имеет смысл для всех действитель¬
ных х, не равных целому отрицательному числу;
в)	вывести свойство
Г(* + 1) = хГ(х);
г)	получить значение Г(п) для п целого и положительного.
3106.	Пусть функция f(x) собственно интегрируема на сег¬
менте [а, Ь] и
8„ = — , fia = f(a + i&„) (i = 1, 2, .... n).
Доказать, что
lim П (1 + bJin) = e
П —* 00	1 A
J f{x)dx
3107.	Доказать, что
lim
n * oo
PJ(a + ib)
У' (a + Lb)
где a > 0 и b > 0.
3108.	Пусть fn(x) (n = 1, 2, ...) — непрерывные функции на
oo
интервале (a, V) и |/n(jc)| < cn (n — 1, 2,...), где ряд у cn сходится.
n = 1
Доказать, что функция
оо
F(x) = J] I1 + Ш\ (l/.(*)l < 1)
п= 1
непрерывна на интервале (а, Ь).
3109.	Найти выражение для производной функции
F(x) = Y\ [1 + /„(*)].
л = 1
Каковы достаточные условия существования F'(x)l
3110.	Доказать, что если 0 < х < у, то
Ига +	= 0.
у(у+!)...({/ +п)

284
РАЗДЕЛ V. РЯДЫ
§ 10. Формула Стирлинга
Для вычисления л! при больших значениях п полезна формула
Стирлинга
n + ^L
л! = J2nh ппе ,2я	(0 < 0„ < 1).
Пользуясь формулой Стирлинга, приближенно вычислить:
3111. lg 100!
3113.
1-3-5.„99
2 -4 -6...100
3112. 1 • 3 • 5 ... 1999.
3114. сТоо •
3115. -	.	3116. f (1 - х2)ь0 dx.
20!30!50!	J v 7
о
2 п
3117.	J sin200 х dx.
0
3118.	Вывести асимптотическую формулу для произведения
(2л-1)!!= 1-3-5...(2л-1).
3119.	Приближенно вычислить С%п , если л велико.
3120.	Пользуясь формулой Стирлинга, найти следующие
пределы:
a) lim nlfn\;
п —* 00
В) Иш -	 п	;
л-°° nJ(2n - 1)!!
б) Иш -5-;
п^°° nJn\
Г) lim iMl.
л —• 00 Inn"
§ 11. Приближение непрерывных функций
многочленами
1.	Интерполяционная формула Лагранжа. Многочлен Лагранжа
( = о	о) - (х,- x,.i)(x,-хи1)...(х,- хп)У‘
обладает свойством Рп(хt) = yt (i = 0, 1, ...» л).
2.	Многочлены Бернштейна. Если f(x) — непрерывная на сегменте
[0, 1] функция, то многочлены Бернштейна
вп(х) = У /ГЛс'ях'( 1
Н KnJ
при п-* оо сходятся равномерно на сегменте [0, 1] к функции f(x).

§11. Приближение непрерывных функций многочленами
285
3121.	Построить многочлен Рп(х) наименьшей степени л,
принимающий заданную систему значений:
X
-2
0
4
5
У
5
1
-3
1
Чему приближенно равны Рп(-1), Рп( 1), Рп(6)?
3122.	Написать уравнение параболы у = ах2 + Ьх + с, прохо¬
дящей через три точки: А (х0 - hy у_г)у В (*0, у0), С (х0 + h, уг).
3123.	Вывести формулу для приближенного извлечения кор¬
ней i/= Jx (1 < х < 100), используя значения х0 = 1, у0= 1;
хг = 25, ух = 5; х2 = 100, у2 = 10.
3124.	Вывести приближенную формулу вида
sin х° « ах + Ьх3 (0 < х < 90; х — arc л:°),
используя значения
sin 0° = 0, sin 30° = |, sin 90° = 1.
Пользуясь этой формулой, приближенно найти:
sin 20°, sin 40°, sin 80°.
3125.	Построить для функции f(x) = \х\ на сегменте [-1, 1] ин¬
терполяционный многочлен Лагранжа, приняв за узлы точки:
3126.	Заменив функцию у(х) многочленом Лагранжа, при¬
ближенно вычислить
2
J у(х) dx,
0
где
х
0
0,5
1
1,5
2
У(х)
5
4,5
3
2,5
5
3127.	Составить многочлены Бернштейна Вп(х) для функций
х9 х2, х3 на сегменте [0, 1].
3128.	Написать формулу многочленов Бернштейна Вп(х) для
функции f(x)9 заданной на сегменте [а, Ь].

286
РАЗДЕЛ V. РЯДЫ
3129.	Приблизить функцию fix) = М * х- на сегменте [-1, 1]
А
многочленом Бернштейна В4(х).
Построить графики функций у =	и у = B4(*).
А
3130.	Приблизить функцию /(*) = |*| при -1 < х < 1 много¬
членами Бернштейна четного порядка.
3131.	Написать многочлен Бернштейна Вп(х) для функции
f(x) = екх (а<х< Ь).
3132.	Вычислить многочлен Вп(х) для функции f(x) = cos х
на сегменте -Ц < л: < 5 .
2	2
3133.	1. Доказать, что |*| = lim Рп(х) на сегменте [-1, 1], где
а-**)'
2. Пусть /(jc) G С[а, Ь] и
ь
Мк= j xkf(x)dx = О (fe = 0, 1, 2, ...)•
а
Доказать, что /(*) = 0 при л: € [а, Ь].
Указание. Использовать теорему Вейерштрасса об аппроксима¬
ции непрерывной функции многочленами.
3134.	Пусть f(x) — непрерывная 2я-периодическая функция
на отрезке [-я, я] и ап, Ъп (л = 0, 1, 2, ...) — ее коэффициенты
Фурье. Доказать, что тригонометрические многочлены Фейера
Л	«-I f	| ч
а„(х) = у +	1-“) (ai cos ix + б; sin где)
i = 1
равномерно сходятся к функции fix) на отрезке [-я, я].
3135.	Построить многочлен Фейера а2л _ i(jc) для функции
fix) = \х\ при -я < х < я.

Часть 2
Функции
нескольких
переменных

РАЗДЕЛ VI
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1. Предел функции. Непрерывность
1.	Предел функции. Пусть функция f(P) = f(xu х2,...»хп) определена
на множестве Е, имеющем точку сгущения Р0. Говорят, что
lim f(P)=A,
р-р0
если для любого е > 0 существует 5 = 5 (е, Р0) > 0, такое что
\т~А\<г
при Р € Е и 0 < р (Р9 Р0) < 5, где р (Р, Р0) — расстояние между точками
РиР0.
2.	Непрерывность. Функция /(Р) называется непрерывной в точке
Р0, если
lim f(P) = f(P0).
р~р0
Функция f(P) непрерывна в данной области, если она непрерывна в
каждой точке этой области.
3.	Равномерная непрерывность. Функция f(P) называется равномер¬
но непрерывной в области G, если для каждого £ > 0 существует 5 > О,
зависящее только от е, такое, что для любых точек Р' и Р" из G имеет
место неравенство
If(P') - f{P")I < Е
при р (Р\ Р") < 5.
Функция, непрерывная в ограниченной и замкнутой области, рав¬
номерно непрерывна в этой области.
Определить и изобразить области существования следующих
функций:
3137. и - VI-*2 + Jy2- 1 •
3139. и =	1	.
Jx2 + у2 - 1
3136. и = * + Jy .
3138. и = J1 - х2 - у2 .

§ 1. Предел функции. Непрерывность
289
3140. и = J(x2 + у2 - 1)(4 - х2 - у2).
3141. и = /0х1 + У2-*г •	3142. и = VI ~(х2 + у2).
Л/ 2л: — л:2 — у2
3143. и = In (-х - у).	3144. и = arcsin
3145.	и = arccos	.
х + у
3146.	и = arcsin —п + arcsin (1 - у).
У2
3147.	и = Jsin(x2 + у2).	3148. и = arccos г •••.
*Jx2 + y2
3149.	и = In (xyz).
3150.	и = In (-1 - х2-у2 + z2).
Построить линии уровня следующих функций:
3151. г = х + у.	3152. г = х2 + у2.
3153. z = х2 ~
3155. 2=2.
X
У
3154. 2 = (х + у)2
3156.2 =
1
х2 + 2 у2
3157. 2 = Jyx .
3159. а) г = |*| + |у| - |* + у|;
в)	2 = max (|*|, |j/|);
3158. 2 = \х\ + у.
б) 2 = min (*, j/);
г) 2 = min (х2, у).
2х
3160.2=	+
3161.	2 = *» (* > 0).
3162.	2 = хуе~х (*>0).
3163. 2
(а > 0).
3164.	2 = arctg „ -У ■■■ (а > 0).
Xz + У2 - Л2
3165.	2 = sgn (sin х sin у).
Найти поверхности уровня следующих функций:
3166.	и — х + у 4- 2.
3167.	и = х2 + у2 + 22.
3168.	и = х2 + у2- 22.
3169.	и = (х + у)2 + 22.
3170.	а = sgn sin (я2 4- i/2 + 22).
н рс:

290 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Исследовать характер поверхностей по данным их уравне
ний:
3171. z = f(y- ах).	3172. 2 = f(Jx2 + y2).
3173. 2 = xf[^ .	3174. 2 =	.
3175. Построить график функции
F(t) = /(cos t, sin t),
где
3176.	Найти f{ 1, U-) , если f(x, у) =	,
V я/	x2 + y<
3177.	Найти /(я), если
(*>0).
3178.	Пусть
2= 4у + /(V*- 1).
Определить функции /иг, если 2 = х при у = 1.
3179.	Пусть
2 = X + у + f(X - у).
Найти функции /иг, если z= х2 при у = 0.
3180.	Найти /(я, у), если /^ х + у, & j = х2 - у2.
3181.	Показать, что для функции
имеем
lim {lim f(x, у)} = 1; lim {lim f(x, у)) = -1,
jc -» 0 у-* О	t/ — 0 JC — 0
в то время как lim /(я, у) не существует.
х — 0
У~* о
3182.	Показать, что для функции

§ 1. Предел функции. Непрерывность
291
имеем
lim {lim fix, у)} = lim {lim /(x, у)} = 0,
jc “*■ 0 i/ —► 0	t/ — 0 x —* 0
тем не менее lim f(x, у) не существует.
х * О
У~* О
3183.	1. Показать, что для функции
fix, у) = (х + у) sin i sin 1
* У
оба повторных предела lim {lim f(x, у)} и lim {lim f(x, у)} не су¬
де — О у — 0	(/ —* 0 х — О
ществуют, тем не менее существует lim f(x9 у) = 0.
х — О
У-О
2. Существует ли предел
lim
_2.f У. ?
х — о л;2 + г/2
3. Чему равен предел функции
fix, у) = х2е<х2-у~>
вдоль любого луча х = t cos а, у = t sin а (0 < t < +оо) при t-+ +оо?
Можно ли эту функцию назвать бесконечно малой при х —> +оо
и у -* +оо?
3184.	Найти
lim {lim /(х, г/)} и lim {lim /(дс, у)},
х-* а у-* Ь	у —* b х —* а
если:
а)	fix, у) = 4^ , а = оо, Ь = оо;
л:2 + I/4
б)	/(X, у) =	, а = 00, ь = +0;
1 +
в)	/(л:, у) = sin	, а = оо, ft = оо;
+ у
Г) /(х, у) = -±- tg	,а = 0,Ь = оо;
ху 1 + ху
Д) /(х, у) = log* (х + у), а = 1, & = 0.
Найти следующие двойные пределы:
3185. lim „ Х + У
х-*оо X
у-*00
2 _
ху + у2
3186. lim
х2 + у2
х4 + у4'
3187.
lim
х — о	л:
у-а
3188. lim (л:2 + у2)е-<1+»>.
X — +оо
у -* + °°

292 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3190. Иш (х2 + у2)	.
х —* 0
у-0
3192. lim	.
Jx2 + у2
3193. По каким направлениям ср существует конечный предел:
X
a) lim е*2*»2;	б) lim е*2-»2 • sin 2ху,
р — +0	р -* +оо
если х = р cos фИ1/=р sin ф?
3189. lim
(~гЯхг
X —■ +оо
у — +оо
V*2 + у2)
/
X2
1 \-£—
3191. lim
1 + ± )х + у
■-С н
1 1
а 8
/**
X)
Найти точки разрыва следующих функций:
3194. и =
3196. и =
3198. и =
1
Jx2 + y2
х +у в
х3 + у3 ’
1
sin jc sin у
3200.	и == —— .
хуг
3195. и = -&L .
х + у
3197. и = sin — .
ху
3199. и = In (1 - х2 - у2).
3201.	и — In 		-	 				.
J(x - а)2 + (у- b)2 + (г- с)2
3202.	Показать, что функция:
a) f(x, у) =
2ху
х2+ у2 9
О,
если х2 + у2 * О,
если х2 + у2 = О,
непрерывна по каждой переменной хиув отдельности (при фик¬
сированном значении другой переменной), но не является непре¬
рывной по совокупности этих переменных;
б) /(*, у) =
	, если х2 + у2 * О,
х4 + у4
О,	если х2 + у2 = О,
в точке О (0, 0) непрерывна вдоль каждого луча
х = t cos а, у = t sin а (0 < t < +°°),
проходящего через эту точку, т. е. существует
lim f(t cos а, t sin а) = /(0, 0);
I — о
однако эта функция не является непрерывной в точке (0, 0).

§ 1. Предел функции. Непрерывность
293
3203.	1. Исследовать на равномерную непрерывность линей¬
ную функцию
и = 2х - Зу + 5
в бесконечной плоскости Е2 =
|*| < +00, \у\ < +00
2. Исследовать на равномерную непрерывность в плоскости
Е2 = ||*| < +оо, \у\ < +оо
функцию
и = Jx2 + у2.
3. Будет ли равномерно непрерывной функция
f(x, у) = sin
к
1-х2 -у2
в области х2 + у2 < 1?
4.	Дана функция
и = arcsin - .
У
Является ли эта функция непрерывной в своей области опреде¬
ления Е?
Будет ли функция и равномерно непрерывной в области Е1
3204.	Показать, что множество точек разрыва функции
/(*> У) = х sin - , если у & 0 и f(x, 0) = 0, не является замкнутым.
У
3205.	Доказать, что если функция f(x, у) в некоторой области
G непрерывна по переменной х и равномерно относительно х не¬
прерывна по переменной у, то эта функция непрерывна в рас¬
сматриваемой области.
3206.	Доказать, что если в некоторой области G функция
f(xf у) непрерывна по переменной х и удовлетворяет условию
Липшица по переменной у, т. е.
I/(*, У') ~ /(*, У")I < LW ~ У"1
где (#, у') € G, (я, у") € G и L — постоянная, то эта функция не¬
прерывна в данной области.
3207.	Доказать, что если функция f(x, у) непрерывна по каж¬
дой переменной х и у в отдельности и монотонна по одной из
них, то эта функция непрерывна по совокупности переменных
(теорема Юнга).

294 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3208.	Пусть функция f(x> у) непрерывна в области а < х < А,
b < у < В, а последовательность функций ф„(а:) (п = 1, 2, ...) схо¬
дится равномерно на [а, А] и удовлетворяет условию b < фп(л:) < В.
Доказать, что последовательность функций
Fn(x) = f(x, (р„(х)) (п =1,2,...)
также сходится равномерно на [а, А].
3209.	Пусть: 1) функция f(x, у) непрерывна в области
R(a < х <А;Ь < у < В); 2) функция ф(д:) непрерывна в интервале
(а, А) и имеет значения, принадлежащие интервалу (6, В). До¬
казать, что функция
В(*) = /(*, ф(*))
непрерывна в интервале (а, А).
3210.	Пусть: 1) функция /(я, г/) непрерывна в области
R(a< х < А; b < у < В); 2) функция л: = ф(и, и) и у = \j/(u, у) не¬
прерывны в области R' (а' < u < A'; b' < и < В') и имеют значения,
принадлежащие соответственно интервалам (а, А) и (Ь, В). До¬
казать, что функция
В(и, и) = /(ф(ы, и), ф(и, у))
непрерывна в области R'.
§ 2. Частные производные. Дифференциал функции
1.	Частные производные. Результат частного дифференцирования
функции нескольких переменных не зависит от порядка дифференци¬
рования, если все производные, входящие в вычисление, непрерывны.
2.	Дифференциал функции. Если полное приращение функции
f(x, у, z) от независимых переменных х, у, г может быть представлено
в виде
Д/(а:, У, г) = ААх + ВДу + CAz + о(р),
где А, В, С не зависят от Да:, Д у, Аг и р = л/(Д*)2 + (Ду)2 + (Аг)2 , то функ¬
ция /(я, у, г) называется дифференцируемой в точке (а:, у, г), а линейная
часть приращения ААх + ВДу + СДг, равная
<*/(*, У у г) =	(*, у, z) dx + /' (*, у, г) dy +	(*, у, г) dz, (1)
где dx = Да:, dy = Ду, dz = Дг, называется дифференциалом этой функ¬
ции.
Формула (1) сохраняет свое значение и в том случае, когда перемен¬
ные xf у, z являются некоторыми дифференцируемыми функциями от
независимых переменных.

§ 2. Частные производные. Дифференциал функции
295
Если х, у у z — независимые переменные, и функция f(xt у, г) имеет
непрерывные частные производные до /I-го порядка включительно, то
для дифференциалов высших порядков имеет место символическая
формула
d"f(x, у, z)=	+ dylj- + dz^j f(x, у, г).
3.	Производная сложной функции. Если w = f(x, yt z) — дифферен¬
цируема и X = ф(и, i>), у = \|/(и, и), z = X (и, и), где функции ф, \|/, % диф¬
ференцируемы, то
dw __	dwdx	+	dwdy	+	dwdz
ди	дхди	дуди	дгди9
dw =	dwdx	+	dwdy	+	dwdz
dv	dxdv	dydv	dzdv*
Для вычисления производных второго порядка функции w полезно
пользоваться символическими формулами:
dhv_ «ГрЛ+оЛ+р JLV ,,, +	+ ЭД1Э12 ,
ди2	V 1 Эл:	*Э1/	Эи Эл:	Эи ду ди дг
d4 2w
диди
-('■■s+4+J,|s)(4+4+J!,s)" +
ду
+ дР+дш + dQidw + ДД1 Эш
Эп Эл:	Эп Э£/ dv дг 9
где
= f2* о, =
4.	Производная в данном направлении. Если направление 1 в про¬
странстве Oxyz характеризуется направляющими косинусами:
{cos a cos Р cos у} и функция и = /(л:, у, г) дифференцируема, то произ¬
водная по направлению 1 вычисляется по формуле
ди	ди	t ди	о	.	ди
-гг =	— cos а	+ — cos	Р	+	~ cos у.
Э/	дх	ду	дг
Скорость наибольшего роста функций в данной точке по модулю и на¬
правлению определяется вектором — градиентом функции:
gradual+ ^j +
дх ду
модуль которого равен
|grad и\ =

296 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3211.	1. Показать, что
П(х, b)=±[f(x, Ь)1
2. Найти /' (я, 1), если
/(*, у) = х + (у - 1) arcsin
3212.	1. Найти f'x (0, 0) и /' (0, 0), если
f(x, у) = Vху .
Является ли эта функция дифференцируемой в точке 0(0, 0)?
2.	Является ли дифференцируемой в точке 0(0, 0) функция
/(*, у) = Ух3 + у3 ?
3.	Исследовать на дифференцируемость в точке 0(0, 0) функ¬
цию
/(*, у) = е х2 + у2 при х2 + у2 > О
и /(0, 0) = 0.
Найти частные производные первого и второго порядков от
следующих функций:
3213.	и = *4 4- у4 - 4*У.
3215. и = 4 •
У2
3217. и = х sin (х + у).
3219. и = tg— .
У
3221. и = In (* + у2).
3223. и = arctg-^tK-.
1 -ху
3225. и =	1	.
л/*2 + у2 + Z2
2
3227.	и= хг.
3214.	и — ху +
3216. и =
Jx2 +
3218. u =
2.
*
У2
У
3220. и =
3222. и = arctg^ .
х
3224. u = arcsin —*	.
Jx2 + у2
3226. u =	.
3228.	и= х«г.

§ 2. Частные производные. Дифференциал функции
297
3229.	Проверить равенство
Э2и _ д2и
дхду дудх9
если:
а) и = х2 - 2ху - Зу2; б) и = ху2 ;
в)
и = arccos
3230.	1. Пусть f(x, у) = ху—^—^ , если х2 + у2 * 0 и /(0, 0) = 0.
X2 + у2
Показать, что
Гху (0, 0) * fyX (0, 0).
2. Пусть
1	0	при х = у = 0.
Существует ли f"y(0, 0)?
3231.	Пусть и = f(x, у у z) — однородная функция измерения п.
Проверить теорему Эйлера об однородных функциях на следую¬
щих примерах:
а) и = (х - 2у + 3z)2; б) и = х ■ ■— ; в) u = (-V .
л/л:2 + у2 + г2
3232.	Доказать, что если дифференцируемая функция
u = f(xf у у z) удовлетворяет уравнению
I „Эи , „Эи _
+ у— + z— = /ш,
Эу Эг
то она является однородной функцией измерения п.
Указание. Рассмотреть вспомогательную функцию
т) _	tz)
3233.	Доказать, что если f(x9 уу z) — дифференцируемая од¬
нородная функция измерения /г, то ее частные производные
f'x (Ху у у z)y f'y (х9 у у z), f'z (Ху у у z) — однородные функции изме¬
рения п - 1.

298 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3234.	Пусть и = f{x, у у г) — дважды дифференцируемая од¬
нородная функция измерения п. Доказать, что
( X+ 2^-1 и = п(п - 1 )и.
К ох	с)у	дг)
Найти дифференциалы первого и второго порядков от сле¬
дующих функций (х9 у9 г — независимые переменные):
3235.	и = хтуп.	3236. и = £ .
У
3237. и — Jx2 + у2 .
3239. и = в**.
3241.и=
3238. u = Injx2 + у2 .
3240. и = ху + yz + zx.
х2 + у2
3242. Найти d/(l, 1, 1) и d2/(l, 1, 1), если
f(Xy У у
3243.	Показать, что если
и = Jx2 + у2 + 22 ,
то d2u > 0.
3244.	Предполагая, что я, г/ малы по модулю, вывести при¬
ближенные формулы для следующих выражений:
а) (1 + х)т(1 + у)п; б) In (1 4- х) • In (1 + у); в) arctg * + У .
1 + art/
3245.	Заменяя приращение функции дифференциалом, при¬
ближенно вычислить
а) 1,002 • 2.0032 • З,0043; б) 1>031	- ;
37(0, 98)1/1765*
в)	VI, 02*+ 1,97»; r) sin 29° • tg 46°; д) 0.971'05.
3246.	На сколько изменятся диагональ и площадь прямо¬
угольника со сторонами дг=6ми1/=8м, если первая сторона
увеличится на 2 мм, а вторая сторона уменьшится на 5 мм?
3247.	Центральный угол сектора а = 60° увеличился на Да = 1°.
На сколько следует уменьшить радиус сектора R = 20 см, чтобы
площадь сектора осталась без изменения?
3248.	Доказать, что относительная погрешность произведе¬
ния приближенно равна сумме относительных погрешностей
сомножителей.

§ 2. Частные производные. Дифференциал функции
299
3249.	При измерении радиуса основания R и высоты Н ци¬
линдра были получены следующие результаты:
R = (2,5 ± 0,1) м; Н = (4,0 ± 0,2) м.
С какой абсолютной погрешностью А и относительной погреш¬
ностью 8 может быть вычислен объем цилиндра?
3250.	Стороны треугольника а = (200 ± 2) м, Ъ = (300 ± 5) м
и угол между ними С = (60 ± 1)°. С какой абсолютной погреш¬
ностью может быть вычислена третья сторона с треугольника?
3251.	Показать, что функция
/(*, у) = J\xy\
непрерывна в точке (0, 0) имеет в этой точке обе частные произ¬
водные fx (0, 0) и fy (0,0), однако не является дифференцируемой
в точке (0, 0).
Выяснить поведение производных fx (х, у) и fy (х, у) в ок¬
рестности точки (0, 0).
3252.	Показать, что функция
/(*. У) =
ху
Jx2 + у2
если х2 + у2 ^ 0 и /(0, 0) = 0, в окрестности точки (0, 0) непре¬
рывна и имеет ограниченные частные производные fx (х, у) и
fy У)> однако эта функция недифференцируема в точке (0, 0).
3253.	Показать, что функция
f(x, у) = (X2 + у2) sin 1	,
X2 + у2
если х2 4* у2 & 0 и /(0, 0) = 0, имеет в окрестности точки (0, 0)
частные производные fx(x9 у) и fy(x, у), которые разрывны в
точке (0, 0) и неограничены в любой окрестности ее; тем не менее
эта функция дифференцируема в точке (0, 0).
3254.	Доказать, что функция f(x, у) имеющая ограниченные
частные производные fx (х, у) ти fy (х, у) в некоторой выпуклой
области Е, равномерно непрерывна в этой области.
3255.	Доказать, что если функция f(x> у) непрерывна по пе¬
ременной х при каждом фиксированном значении у и имеет ог¬
раниченную производную fy (х, у) по переменной у, то эта функ¬
ция непрерывна по совокупности переменных х и у.

300 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Найти указанные частные производные в следующих задачах:
3256.	^	, если и = х-у + х2 + 2 ху + у2 + х3 -
- 3х2у -у3 4- jc4 - Ах2у2 4- у4.
дх4 ’ дх3ду ’ Элг2Эу2
3257.
3258.
3259.
3260.
3261.
д3и
дх2ду
д6и
дх3ду3
д3и
дхдудг
д3и
дхдудг
Э 4и
дхдуд^дг]
, если и = х In (ху).
, если и = х3 sin у + у3 sin х.
, если и = arctg ■ —,
1 — JCl/ — JCZ — 1/Z
, если ы =
, если ы = In
V(Jf-^)2+(y-n)2
3262.	. если и = (х- х0У (у - у0)4.
3263.	, если « -	.
дхтдуп
х-у
3264.	:^т Пц , если ы = (jc2 4- i/2)e* +
Эл:тЭул
3265.	, если ы = jq/ze* + у + г.
dxPdy<idzr
3266.	Найти /^\.и)(0, 0), если /(jc, i/) = е* sin у.
3267.	Показать, что если
и = f(xyz)y
то
д3и
F(t)y
дхдудг
где t = xyZy и найти функцию F.
3268. Найти dAUy если и = jc4 - 2х3у - 2ху3 4- уА 4- jc3 - 3jc2i/ -
- 3jci/2 4- у3 4- 2jc2 - ху 4- 2у2 4- jc 4- у 4- 1.
Э4и Э4и Э4и Э4и „ д4и 9
и	'
Чему равны производные
Эл:4 ’ дх3ду ’ дх2ду2 ’ дхду3 ду4
Найти полные дифференциалы указанного порядка в сле¬
дующих примерах:
3269.	d3Uy если и = jc3 4- у3 - Зху (х - у).
3270.	d3Uy если и = sin (jc2 4- у2).
3271.	d10u9eели и = In (jc 4- у).

§ 2. Частные производные. Дифференциал функции
301
3272.	d6w, если и = cos х ch у.
3273.	d3w, если и = хуг.
3274.	d4w, если и = In (xxyyzz).
3275.	dnw, если и = еах + by.
3276.	dnw, если w = Х(л:)У(у).
3277.	dnw, если w = /(х 4- у 4- г).
3278.	dnw, если w =	+ ь* + сг.
3279.	Пусть Рп(л:, у, г) — однородный многочлен степени л.
Доказать, что
dnPn(x, у, 2) = n! Pn(dx, dy, d2).
3280.	Пусть
Эл:	Эу
Найти Aw и A2w = A(Aw), если:
а) и =
х .
JC2 + у2 *
3281.	Пусть
Найти Aw, если:
б) w = Injx2 + у2 .
Aw =
Э2ц Э2ц
d22 Эу2
a) w = sin л: ch у;	б) w = Injx2 + у2 .
3282.	Пусть
AjW =
A2w =
Э2цЭ2ц
Эл:2 Эу2
4-
Э2ц
022 ’
Найти AjW и A2w, если:
-a) w = л:3 4- у3 4- 23 - 3xyz; б) и =	■	— .
Jx2 + у2 + 22
Найти производные первого и второго порядков от следую¬
щих сложных функций:
3283. и = f(x2 4- у2 4- 22).

302 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3286.	Найти 2.^ , если
ахоу
u = f(x + у, ху).
3287.	Найти А и = ^	^	^ , если
ох2	ду2 дг2
и = f(x 4- у + г, х2 + у2 + г2).
Найти полные дифференциалы первого и второго порядков
от следующих сложных функций (я, у и г — независимые пере¬
менные):
3288.	и = /(f), где t = х + у.
3289.	и = /(f), где f = |.
3290.	и = f(*Jxz + у2).
3291.	и = /(f), где t = xyz.
3292.	и = /(*2 + i/2 + z2).
3293.	u = /(£, t|), где £ = ax, t] = by.
3294.	и = /(£, r|), где £ = x + у, ц = х - у.
3295.	и = /(£, т|), где £ = ху, Л = ~ •
3296.	и = /(х + у, г).
3297.	u = /(х + у + г, х2 + у2 + г2).
3298.	и = f (-,&) .
\у х)
3299.	и = /(х, у, г), где х = t, у = t2, z = t3.
3300.	и = /(£, т|, О, где £ = ах, ц = by, С = cz.
3301.	и = /(£, л, О, где £ = х2 + у2, ц = х2 - у2, £ = 2ху.
Найти dnu, если:
3302.	и = f(ax + by + cz).
3303.	u = f(ax, by, cz).
3304.	и = /(£, ri, О, где £ = ajX + bti/ + схг, ц = a2x + b2y + c2z,
C = a3x + b3y + c3z.
3305.	Пусть и = /(г), где г = Jx2 + у2 + z2 и / — дважды диф¬
ференцируемая функция. Показать, что
А и = F(r),
где А и =	— оператор Лапласа, и найти функцию F.

§ 2. Частные производные. Дифференциал функции
303
3306.	Пусть и и v — дважды дифференцируемые функции и
Д — оператор Лапласа (см. задачу 3305). Доказать, что
где
A(uv) = uAv + i>Aи + 2Д(и, и),
*/ v __ диди , диди , ЭиЭи
1 ’ * дхдх дуду дгдг'
3307.	Показать, что функция
и = 1па/(л: - а)2 + (у - Ь)2
(а и b — постоянные) удовлетворяет уравнению Лапласа
д2и ^ д2и _ q
дх2 ду2
3308.	Доказать, что если функция и = w(jc, у) удовлетворяет
уравнению Лапласа (см. задачу 3307), то функция
\х2 + у2 х2 + у2)
также удовлетворяет этому уравнению.
3309.	Показать, что функция
1	(■*-Ь)2
и =—±—е Аа2*
2	ajnt
(аиЬ — постоянные) удовлетворяет уравнению теплопроводности
ди _ 2д±и
dt дх2 *
3310.	Доказать, что если функция и = и(х, t) удовлетворяет
уравнению теплопроводности (см. задачу 3309), то функция
и = -^—е 4fl2/ и( — , - —
аЯ	УаЧ аЧ
) (t > 0)
также удовлетворяет этому уравнению.
3311.	Доказать, что функция
где г = J(x - а)2 + (у - b)2 + (z - с)2, удовлетворяет при г ^ 0 урав¬
нению Лапласа

304 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3312.	Доказать, что если функция и = и(х, у, г) удовлетворяет
уравнению Лапласа (см. задачу 3311), то функция
1 ,.(k2x k2y k2z\
v ~r U{~ ’ r* ’ r4'
где k — постоянная и г = Jx2 + у2 + г2 , также удовлетворяет это-
му уравнению.
3313.	Доказать, что функция
Схе~аг + С2еаг
и = -!	—,
Г
где г = Jx2 + у2 + z2 и Си С2 — постоянные, удовлетворяет урав¬
нению Гельмгольца
д2и д2и
дх2 ду2
д2и
дг2
= аи.
3314.	Пусть функциии их = иг(х, у, г) и и2 = и2(х, у, г) удов¬
летворяют уравнению Лапласа Аи = 0.
Доказать, что функция
о	= Uj(x, у, г) + (х2 + уг + г2)и2(х, у, z)
удовлетворяет бигармоническому уравнению
А(Аи) = 0.
3315.	Пусть /(*, у, г) есть т раз дифференцируемая однород¬
ная функция измерения п.
Доказать, что
[Х§х +У§у + Z§zY ^Х'у'2) = 71 ~ 1)—“ т + 1)Л*. г/»*)•
3316.	Упростить выражение
sec * ~ 4- sec i/ ^ ,
дх	ду
если
2	= sin у + /(sin х - sin у),
где / — дифференцируемая функция.
3317.	Показать, что функция

§ 2. Частные производные. Дифференциал функции
305
где / — произвольная дифференцируемая функция, удовлетво¬
ряет уравнению
ХЪ± + 2у^ = пг.
дх а ду
3318.	Показать, что
2 = yf(x2 - у2),
где / — произвольная дифференцируемая функция, удовлетво¬
ряет уравнению
у2'дх + ХУду = Х2'
3319.	Упростить выражение
ди	ди	ди
дх	ду	дг 9
если
Ы = X* - i Х3(у + г) + | x2yz + f(y- X, г- х),
где / — дифференцируемая функция.
3320.	Пусть
х2 = VW, у2 = ЮГ, Z2 = UV
и
/(*» I/, 2) = F(u, г, w).
Доказать, что
xf’x + yfy + zf'z =	•
Предполагая, что произвольные функции ф, \|/ и т. п. диффе¬
ренцируемы достаточное число раз, проверить следующие равен¬
ства:
3321.	i/~ -	= 0, если z = ф(х2 + у2).
идхду	w г/ /
3322. х2^ -ху(£ + у2 = 0, если z= £- + q){ху).
.дг
дг
ду
3*
3323.	(х2 - у2) Р- + хур- = XI/2, если 2 = еуф
dx <я/
3324.	+ ау^ + [32 — = пи, если u = хЛф(-^ ,	.
дх *ду ^ дг	Чха х$)
(	Х2\
уе2У2

306 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3325.	х^+у^+г^ = и + ^ , если и= ^ In * + х<р( - . -1.
дХ ду 02	2	2	\Х X)
3326.	~~ =	, если и = ср(л: - at) 4- \|/(jc 4* at).
at2 ox2
3327.	- 2|Д^- +|^-0, если и = xy(x + у) 4- y\\f(x 4- у).
3328.	- 0.	« - Ф© + *»(“) •
3329-	,0+24<g.+!)*|f=„,„-,,u.
если u = xa + x1" "	•
3330-	|S=|IS’eCJIHU = ^ + ^
Путем последовательного дифференцирования исключить
произвольные функции (р и \|/:
3331. 2 = X + ф(ДС1/).
3333. z = <p( Jx2 + y2).
3335. и = <p(J , К) .
3337.2	= ф(*)Ф(У)-
3339. г = *ф(^) + yw(^j •
3332.2	= ^).
3334. и = ф(х - у, у - 2).
3336. 2 = <р(х) + v|/(i/).
3338.2	= ф(дс + у) + ф(л; - у).
3340.	2 = ф(дл/) +	•
3341.	Найти производную функции
z = х2 -у2
в точке М( 1, 1) в направлении Z, составляющем угол а= 60°
с положительным направлением оси Ох.
3342.	Найти производную функции
2	= X2 - Ху + у2
в точке М (1, 1) в направлении Z, составляющем угол а с поло¬
жительным направлением оси Ох. В каком направлении эта про¬
изводная имеет:
а) наибольшее значение; б) наименьшее значение;
в)	равна нулю?
3343.	Найти производную функции
2 — In (х2 4- у2)

§ 2. Частные производные. Дифференциал функции
307
в точке М (jc0, у0) в направлении, перпендикулярном к линии
уровня, проходящей через эту точку.
3344.	Найти производную функции
2=1-
в точке м( — , —1 по направлению внутренней нормали в этой
точке к кривой:
+ Ml
а2 Ъ2
= 1.
3345.	Найти производную функции
и = хуг
в точке М (1, 1, 1) в направлении Z{cos a, cos р, cos у}-
Чему равен модуль градиента функции в этой точке?
3346.	Найти модуль и направление градиента функции
и =
г
где г = Jx2 + y2 + z2 , в точке М0 (х0, у0, z0).
3347.	Определить угол между градиентами функции
и = х2 + у2 - г2
в точках А (е, 0, 0) и Б (0, е, 0).
3348.	На сколько отличается в точке М (1, 2, 2) модуль гра¬
диента функции
и = х 4- у + z
от модуля градиента функции
v = x + y + z + 0,001 sin (10CinJx2 + у2 + z2)?
3349.	Показать, что в точке М0 (jc0, у0, z0) угол между гради¬
ентами функций
и = ах2 + by2 + cz2
и
и = ах2 4- by2 4- cz2 4- 2/пл: 4- 2ш/ 4- 2рг
(а, 6, с, /п, /г, р постоянны и а2 4 62 4 с2 ^ 0) стремится к нулю,
если точка М0 удаляется в бесконечность.

308 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3350.	Пусть и = /(jc, г/, г) — дважды дифференцируемая
функция. Найти —^	, если cos a, cos Р, cos у — направ-
ol2 ul\olJ
ляющие косинусы направления I.
3351.	Пусть и = /(х, у, г) — дважды дифференцируемая
функция и
lx {cos а1э cos Р1? cos yj, l2 {cos а2, cos P2, cos y2},
h {cos a3, cos p3, cos y3}
— три взаимно перпендикулярных направления.
Доказать, что:
б)
д2и
+
_ Э2и
. Э2ы
, д2и
di\
ы\
Bll
Э*2
Эу2
02 2
3352. Пусть и = и(х9 у) — дифференцируемая функция и при
у = х имеем
и(х, у) = 1 и ~
Найти ^ при у = х2.
°У
3353.	Пусть функция и = ы(л:, i/) удовлетворяет уравнению
Э2ц _ Э2ц __ q
дх2 ду2
и, кроме того, следующим условиям:
и(х, 2х) = х, их (х9 2х) = jc2.
Найти ихх(Ху 2х)у и'ху(х9 2x)f иуу(Ху 2х).
Полагая z = z(х9 у), решить следующие уравнения:
3354.	Й-0.	3355. 2Ц- = 0.	3356. ^ = 0.
ох2	дхау	дуп
3357.	Полагая и = и(х, у, г), решить уравнение
ЭЗц =0.
дхдудг
3358.	Найти решение 2 = г(л:, i/) уравнения
т =х2 + 2У>
ду
удовлетворяющее условию z(x, х2) = 1'.

§ 3. Дифференцирование неявных функций
309
3359.	Найти решение z = z(x, у) уравнения
d2Z _ о
ду2
удовлетворяющее условиям: z(x, 0) = 1, z'y(х, 0) = х.
3360.	Найти решение z = z(x, у) уравнения
d2z
дх ду
= X + У,
удовлетворяющее условиям: г(х, 0) = х, 2(0, у) = у .
§ 3. Дифференцирование неявных функций
1.	Теорема существования. Если: 1) функция F(x, у> г) обращается
в нуль в некоторой точке А0(х0, у0, z0); 2) F(x, у, z) и F'x(xt у, z) опреде¬
лены и непрерывны в окрестности точки Д,; 3) F2'(x0, у0> z0) ^ 0, то
в некоторой достаточно малой окрестности точки Д)(х0, у0) существует
единственная однозначная непрерывная функция
г = f(x, у),	(1)
удовлетворяющая уравнению
F(x, у, z) = 0
и такая, что z0 = f(xQi yQ).
2.	Дифференцируемость неявной функции. Если, сверх того,
4)	функция F(x, у у z) дифференцируема в окрестности точки
Ао (*о> Уо> 2о)> т0 функция (1) дифференцируема в окрестности точки
А0(х0, у0) и ее производные ^ и —^ могут быть найдены из уравнений
Эх ду
dF	dFdz	= 0	Э£	dFdz	= 0
Эх	ЭгЭх 9	ду	дгду
(2)
Если функция F(x, у, z) дифференцируема достаточное число раз, то
последовательным дифференцированием равенств (2) вычисляются так¬
же производные высших порядков от функции z.
3.	Неявные функции, определяемые системой уравнений. Пусть
функции F,(Xi, ..., хт; уи ..., уп) (i = 1, 2, ..., л) удовлетворяют следую¬
щим условиям:
1)	обращаются в нуль в точке Ао(х10, ..., хт0; у10> ..., уп0),
2)	дифференцируемы в окрестности точки А0;
d(F F )
3) функциональный определитель —11 ’—— * 0 в точке А,.
д(«/„ • -,Уп)

310 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
В таком случае система уравнений
Fi(xu хт; уи	= 0 (/= 1, 2, л)	(3)
однозначно определяет в некоторой окрестности точки А0(я;10,	хт0)
систему дифференцируемых функций
У1 = fix 1, .... хт) (i = 1, 2,	л),
удовлетворяющих уравнениям (3) и начальным условиям
fi(xw, хт0) - у,а (i - 1, 2,	л).
Дифференциалы этих неявных функций могут быть найдены из сис¬
темы
т
I
1
эр,. .
/г
I
k = 1
(i= 1, 2,	n)1).
3361.	Показать, что разрывная в каждой точке функция Дирихле
f 1,если * рационально,
I	0,если * иррационально,
удовлетворяет уравнению
У2-У = 0.
3362.	Пусть функция f(x) определена в интервале (а, Ь). В ка¬
ком случае уравнение
тУ - 0
имеет при а < х < b единственное непрерывное решение у = 0?
3363.	Пусть функции f(x) и g(x) определены и непрерывны
в интервале (а, Ь). В каком случае уравнение
f(x)y = g(x)
имеет в интервале (а, Ь) единственное непрерывное решение?
3364.	Пусть дано уравнение
*2 + у2 = 1	(1)
и пусть
У = У(х) (-1 < х< 1)	(2)
— однозначная функция, удовлетворяющая уравнению (1).
1)	Сколько однозначных функций (2) удовлетворяет уравне¬
нию (1)?
1} При формулировке большинства задач этого раздела без оговорок
предполагается, что выполнены условия существования неявных функ¬
ций и их соответствующих производных.

§ 3. Дифференцирование неявных функций
311
2)	Сколько однозначных непрерывных функций (2) удовлет¬
воряет уравнению (1)?
3)	Сколько однозначных непрерывных функций (2) удовлет¬
воряет уравнению (1), если: a) i/(0) = 1; б) z/(l) = О?
3365.	Пусть дано уравнение
*2 = У2	(1)
и пусть
У = УМ (“°° < * < +°°)	(2)
— однозначная функция, удовлетворяющая уравнению (1).
1)	Сколько однозначных функций (2) удовлетворяет уравне¬
нию (1)?
2)	Сколько однозначных непрерывных функций (2) удовлет¬
воряет уравнению (1)?
3)	Сколько однозначных дифференцируемых функций (2)
удовлетворяет уравнению (1)?
4)	Сколько однозначных непрерывных функций (2) удовлет¬
воряет уравнению (1), если: а) у( 1) = 1; б) у(0) = 0?
5)	Сколько однозначных непрерывных функций у = у(х)
(1-8<д;<1+8) удовлетворяет уравнению (1), если у(1)^ 1 и 8
достаточно мало?
3366.	Уравнение
*2 + у2 = х4 + у4
определяет у как многозначную функцию от х. В каких областях
эта функция: 1) однозначна, 2) двузначна, 3) трехзначна, 4) че¬
тырехзначна?
Определить точки ветвления этой функции и ее однозначные
непрерывные ветви.
3367.	Определить точки ветвления и непрерывные однознач¬
ные ветви у = у(х) (-1 < х < 1) многозначной функции у, опре¬
деляемой уравнением
(хг + у2)2 = х2- у2.
3368.	Пусть f(x) непрерывна при а < х < b и ср(у) монотонно
возрастает и непрерывна при с < у < d. В каком случае уравнение
Ф(У) = /(*)
определяет однозначную функцию
У = Ф'ЧЯ*))?
Рассмотреть примеры: a) sin у + sh у = х; б) е v = -sin2 х.

312 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3369.	Пусть
Х = у + Ф (у),	(1)
где ф(0) = 0 и |ф'(«/)| < k < 1 при —а<у<а. Доказать, что при
-г < х <г существует единственная дифференцируемая функция
у = У(х)> удовлетворяющая уравнению (1), и такая, что у(0) = 0.
3370.	Пусть у = у(х) — неявная функция, определяемая урав¬
нением
* = ky + ср (у),
где постоянная k & 0, и ф{у) — дифференцируемая периодиче¬
ская функция периода со такая, что |ф'(г/)| < \k\- Доказать, что
У = - + Щх)9
где \|/(jc) — периодическая функция с периодом |А|со.
Найти у' и у" для функций у, определяемых следующими
уравнениями:
3371.	х2 + 2ху -у2 = а2.
3372.	Injx2 + у2 = arctg^ •
3373.	у - г sin у = л: (0 < е < 1).
3374.	** = у* (л: * у).
3375.	у = 2х arctg^ .
3376.	Доказать, что если
1	+ ху = /г(* - у),
где /г — постоянная величина, то имеет место равенство
dx _ dy
1 4- JC2 1 + у2 ’
3377.	Доказать, что если
д:2!/2 + я2 + у2 - 1 = 0,
то при ху > 0 имеет место равенство
dx + dy = 0
«/I-*4
3378.	Доказать, что уравнение
(х2 + у2)2 = a2(*2 - у2) (а ^ 0)
в окрестности точки х = 0, у = 0 определяет две дифференцируе¬
мые функции: I/ = i/iOr) И1/ = t/2(^)- Найти у\ (0) и i/'2 (0).

§ 3. Дифференцирование неявных функций
313
3379.	Найти у' при х = 0 и у = 0, если
(х2 + у2)2 = 3х2у - у3.
3380.	Найти у', у" и у"', если х2 + ху + у2 = 3.
3381.	Найти у\ I/" и у”' при х — 0, у = 1, если
х2 - ху + 2у2 + х - у - 1 = 0.
3382.	Доказать, что для кривой 2-го порядка
ах2 + 2 Ьху + су2 + 2dx + 2ei/ + / = 0
справедливо равенство
Для функции 2 = 2(х, у) найти частные производные первого
и второго порядков, если:
3383.	х2 + у2 + z2 = а2.
3384.	г3 - Здгг/2 = а3.
3385.	х + у + г = ег.
3386.	г = 4х2 - у2 • tg *	.
Jx2-y*
3387.	jc + у + z = еНх + у + 2).
3388.	Пусть
д;2 + у2 + z2 - Ъхуг = 0	(1)
и
/(*, у, z) = xy2z3.
Найти: a) fx (1, 1, 1), если г = 2(х, г/) есть неявная функция,
определяемая уравнением (1); б) fx (1,1, 1), если у = г/(х, 2) есть
неявная функция, определяемая уравнением (1). Объяснить, по¬
чему эти производные различны.
3389.	Найти	при х = 1, у = -2, г = 1, если
Эх2 ЭхЭг/ Эг/2
х2 + 2у2 + Зг2 + ху - 2 - 9 = 0.
Найти d2 и d229 если:
3390.	+ g + 2| = 1.
а2 Ь2 с2
3391.	Х1/2 = х + у + 2.
3392.	£ - In 2 + 1.
z	У

314 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3393.	z — х ■+■ arctg—^— .
Z — X
3394.	Найти du, если гг3 - 3(дс + у)и2 + г3 = 0.
3395. Найти
д2г
дхду
, если ^(л: + у + г, х2 + у2 + г2) = 0.
3396.	Найти ^ и ^, если F(x - у, у - z, z - х) = 0.
с)лг Эг/
3397.	Найти ^ ~ и , если F(x, х + у, х + у + z) = 0.
ох оу ох2
3398.	Найти:
1)	. если F(xz, yz) = 0;
2) d2z, если: a) ,F(* + z, у + z) = 0; б)	| j = 0.
3399.	Пусть z = 2(х, i/) — та дифференцируемая функция, оп¬
ределяемая уравнением
г3 - xz + у = О,
которая при х= 3, г/= -2 принимает значение 2=2. Найти
<22(3, -2) и d22(3, -2).
3400.	Пусть * = д:(г/, 2), г/ = г/ (д:, 2), 2 = 2 (я, г/) — функции,
определяемые уравнением F(x, г/, 2) = 0.
Доказать, что
Эх Эг/ Эг = _i
Эг/ dz Эх
3401.	Найти ^ и ^ , если х + I/ + 2 = О, дс2 + у2 + 22 = 1.
dz dz
3402.	Найти:
а)	7Г'	* "Г! и ’ при * = 1. У = -1. 2 = 2, если
d2 rf2 dx2 dz2
x2 + у2 = 122, д: + г/ + 2 = 2;
б)	~ ~ ~ и ^ , если д;и - yv = 0, i/u + дп> = 1.
Эх Эу ox оу
3403.	Система уравнений
хе"
+ 2 ии = 1,
1 + и
= 2х
определяет дифференцируемые функции и = и(х, у) и и = и(х, у)
такие, что и(1, 2) = 0 и и(1, 2) = 0. Найти <2гг(1, 2) и <2l>(1, 2).

§ 3. Дифференцирование неявных функций
315
3404.	Найти du, dv, d2u и d2v, если
и + v = х + у,
sin и _ х
sin и у
3405.	Найти du, dv, d2u и d2v при де=1,г/=1,и=0, у = 5
4
если
и
ех cos -
У
Л
х
Z • У
е* sin - =
v = У_
У Л ’
3406.	Пусть
jc = t + Г1, у = t2 + Г2, 2 = f3 + Г-3.
Найтии 4Ц.
аде аде 4де2 4де2
3407.	В какой области плоскости Оху система уравнений
де = и + и, у = а2 4- v2, z = а3 + и3,
где параметры а и v принимают всевозможные вещественные
значения, определяет z как функцию от переменных де и у! Най¬
ти производные ~ и ~.
ах ау
3408.	Найти:
а) и ^ в точке и = 1, v = 1, если
ох оу
х = и 4- In v,
у = v - In и,
г = 2а + v;
f)2X
б)	в точке и = 2, у = 1, если
дхду
х = cos cp cos ф, у = cos ф sin ф, z = sin ф.
3409.
де = a cos и, у = и sin v, z = l>.

316 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3410.	Пусть функция z = z(x, у) определяется системой урав¬
нений:
г дс =	+ и,
<У = еи~09
[ Z — UV
(и и v — параметры). Найти dz и d2z при и = 0 и v = 0.
3411.	Найти ^ и ^ , если
ох дх2
Z = х2 + у2,
где у = у(дс) определяется из уравнения
л:2 - ху + у2 = 1.
3412.	Найти ~ и ^, если
Эя dy
и =
ДС + Z
y + z ’
где z определяется из уравнения
zez = яе* + уеу.
3413.	Пусть уравнения
х = ср(гг, о), у = \|/(u, u), z = х(и,
определяют z как функцию от х и у. Найти ^ и ~ ,
Эдг dy
3414.	Пусть
* = ф(и, о), у = \|/(гг, и).
Найти частные производные первого и второго порядков от об¬
ратных функций: и = и(х, у) и и =	у).
3415.	Найти	^	> если:
оде dy Эдс dy
а)	* = и cos - , у = и sin - ;
и	и
б)	х =	+ и sin и, у=еи-и cos у.
3416.	Функция и = и(х) определяется системой уравнений
[ и = f(x, у, z),
Ш*, !/, 2) = 0,
[h(x, у, *) = 0.
Найти ^ и^.
dx dx2

§ 3. Дифференцирование неявных функций
317
3417.	Функция и = и(х, у) определяется системой уравнений
[ и = f(x, у, г, t),
\ g(y, z, t) = О,
[h(z, t) = 0.
Найти и ^ .
ах ау
3418.	Пусть
х = /(гг, v9 w)y у = g(u9 г;, гг;), z = h(u9 г;, гг;).
тт “ Эгг Эгг Эгг
Наити — , г- н — .
ах ау аг
3419.	Функция z = г(х9 у) удовлетворяет системе уравнений
| /(*, у у г, t) = О,
I ^Г(^> У» 2, ^) О,
где t — переменный параметр. Найти dz.
3420.	Пусть и = f(z)y где г — неявная функция от переменных
хну у определяемая уравнением z = х + г/ср(г).
Доказать формулу Лагранжа
дпи
дуп
0я"1
Эл:я-1
Указание. Доказать формулу для п = 1 и применить метод ма¬
тематической индукции.
3421.	Показать, что функция z = z(x9 г/), определяемая урав¬
нением
Ф (х - azy у - bz) = 0,	(1)
где Ф (гг, и) — произвольная дифференцируемая функция от пе¬
ременных гг и и (а и b — постоянные), является решением урав¬
нения
a^z + &Эг = j
ах ау
Выяснить геометрические свойства поверхности (1).
3422.	Показать, что функция z = z(х9 у)9 определяемая урав¬
нением
Ф(х-х, у-уоЛ=0>
vz-z„ z-zj
где Ф (гг, и) — произвольная дифференцируемая функция от пе¬
ременных гг ир, удовлетворяет уравнению
(* “ х°^ + (у~ Уо)% = 2 " 20*
Выяснить геометрические свойства поверхности (2).

318 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3423.	Показать, что функция z = z (х, у), определяемая урав¬
нением
ах + by + cz = Ф (х2 + у2 + z2),	(3)
где Ф(гг) — произвольная дифференцируемая функция от пере¬
менной и и а, b и с — постоянные, удовлетворяет уравнению
(су -bz)~ + (az - сх== Ъх - ау.
дх	ду
Выяснить геометрические свойства поверхности (3).
3424.	Функция z = z(x> у) задана уравнением
х2 + у2 + г2 = r//(j) .
Показать, что
(х2 -у2- z2)^ + 2 хур- = 2xz.
дх	ду
3425.	Функция z = г(х, у) задана уравнением
Показать, что
F(x + zy~\ у + zx'1) = 0.
= г-ху.
3426.	Показать, что функция z = z(x, у), определяемая сис¬
темой уравнений:
[ х cos а + у sin а + In z = /(а),
1 —х sin а + у cos а = /'(а),
где а = а(х, у) — переменный параметр и /(а) — произвольная
дифференцируемая функция, удовлетворяет уравнению
= 22.
3427.	Показать, что функция z = z(x, у), заданная системой
уравнений:
z — (хх + У- + /(а),
а
о = X - У- + /'(а),
а
удовлетворяет уравнению
dzdz _ 1
дхду

§ 4. Замена переменных
319
3428.	Показать, что функция z = z(x, у), заданная уравнениями
[г - f(a)f = х\уг - а2),
[z - /(а)]Г(а) = ах2,
удовлетворяет уравнению
Э£0£
ЭдсЭу
= *г/.
3429.	Показать, что функция z = z(x, i/), заданная уравнениями
г = ад: 4- уср(а) + \|/(а),
О = х + у(р'(а) + \|/'(а),
удовлетворяет уравнению
d^zd^z _ ( d2z\2 = 0
дх2 ду2 \дхду)
3430.	Показать, что неявная функция z = z(x, у), определяе¬
мая уравнением
у = *ср (г) + \|/(2),
удовлетворяет уравнению
Э^2 _ 9 Э2Э2_Э^2_
V3i/J Эдс2 дхдудхду чЭдсу ду2
§ 4. Замена переменных
1. Замена переменных в выражении, содержащем обыкновенные
производные. Пусть в дифференциальном выражении
А = Ф(дс, у, у’х , у"х , ...)
требуется перейти к новым переменным: t — независимой переменной
и и — функции, связанным с прежними переменными х и у уравнениями
х = /((, и), у = g(t, и).	(1)
Дифференцируя уравнения (1), будем иметь:
, Э< Эи '
V + Ku't
Э	t ди '
Аналогично выражаются высшие производные ухх , ... В результате мы
получаем
А Ф|(^, 1/, ut , 11ц , ...).

320 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. Замена независимых переменных в выражении, содержащем
частные производные. Если в дифференциальном выражении
о = Ff г ^ дг_	д^г д2г д2г
V *	’ дх 9 ду 9 дх2 9 дхду 9 ду2 9
положить
X = f(u, и), у = #(а, и),
(2)
где а и l> — новые независимые переменные, то последовательные част-
дг дг
ные производные — , — , ... определяются из следующих уравнении:
дх ду
дг	__	dzdf_ _j_ дг dg
ди	дгди	дуди	9
дг	_	дг df	дг dg
ди	дхди	дуди9
и т. п.
3.	Замена независимых переменных и функции в выражении, со¬
держащем частные производные. В более общем случае, если имеем
уравнения
х = Да, v, w), у = g(uy vy w)y г = h(u> v, w)>	(3)
где uyv — новые независимые переменные и w = w(u, v) — новая функ-
дг дг
ция, то для частных производных — ,	, ... получаем такие уравне-
dx ду
ния:
дг(df + д£ЭиЛ +	dz^fdg	+	д£диЛ	_ dh	{	dhdw
дх\ди	dwdu)	ду\ди	dwdu)	ди	dwdu 9
дг(df_	df dw\	.	дг(д£	,	Э|[ЭиЛ	= dh	,	dhdw
ЭдгчЭи	dwdv)	dy\dv	dwdv)	dv	dwdv
и т. п.
В некоторых случаях замены переменных удобно пользоваться пол¬
ными дифференциалами.
3431.	Преобразовать уравнение
у'у'" - з у"2 = х,
приняв у за новую переменную.
3432.	Таким же образом преобразовать уравнение
у'УУ - ЮуУУ" + 15у"3 = 0.
3433.	Преобразовать уравнение
у" + ” У' + У = О»
приняв х за функцию и t = ху — за независимое переменное.

§ 4. Замена переменных
321
Вводя новые переменные, преобразовать следующие обыкно¬
венные дифференциальные уравнения:
3434.	х2у" 4- ху' 4- у = 0, если х = е1.
3435.	у’" = ^ , если t = In |х|.
3436.	(1 - х2)у" - ху' 4- тг2у = 0, если х = cos £.
3437.	у" + у' th х + -2^- у = 0, если х = In tg|.
Ж
3438.	у" 4- p(x)y' 4- g(x)y = 0, если у = ue Хщ , где р(х) € С(1).
3439.	х4у" 4- хуу' - 2у2 = 0, если х = ^ и у = ие2<, где u = u(t).
3440.	(1 4- х2)2у" = у, если х = tg t и у = —— , где и = и(£).
cost
3441.	(1 - х2)2у" = -у, если х = th £ и у =	, где и = и(£).
сп£
3442.	у"4-(х4-у)(1 4-у')3 = 0,еслих = и4-£иу = и-£,гдеu = u(t).
3443.	у'" - х3у" 4- ху' - у = 0, если х = у и у = у , где u = и(£)-
3444.	Преобразовать уравнение Стокса
„ = 	А*/	^
(х - а)2(х - Ь)2
полагая
и = —У—г , £ = In
x-b
и принимая и за функцию переменной t.
3445.	Показать, что если уравнение
g+pWg+,(*)„- о
преобразовать подстановкой х = ф(£) в уравнение
§ + р(^ +^=0’
то
[2Р&Ш) + <У(ШО(ОР = I2p(x)q(x) + «/(*)][<7(*)]4 •
3446.	В уравнении
Ф(г/, у', у") = О,

322 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
где Ф — однородная функция переменных у, у\ у"> положить
X
judx
У =е*	.
3447.	В уравнении
F(x2y", xiу) = О,
где F — однородная функция своих аргументов, положить
у'
и = х—.
У
3448.	Доказать, что уравнение
у"'(\ + у'2) ~ Зу'у"2 = О
не меняет своего вида при томографическом преобразовании
а£ + Ь1ц + с1 _ а2\ + Ь2ц + с2
а£> + Ьг| + с 9 ^	а£>+Ьг\ + с
Указание. Данное преобразование представить в виде компози¬
ции простейших преобразований:
х = аХ + рУ + у, y = Y;
Хх = а£ + Ьг| + с, Yj = а2% + Ь2г\ + с2.
3449.	Доказать, что ьиварциан
S[x(t)] =
*ПП - ЗГ^]2
x'(t)	2 L дс' (£) J
не меняет своего значения при дробно-линейном преобразовании:
у-аЦЩ М_6с^0).
* cx(t) + d v	'
Преобразовать к полярным координатам г и ф, полагая
х = г cos ф, у = г sin ф, следующие уравнения:
3450.	*И.='*±Ё.
dx х- у
3451.	(xjf - у)2 = 2ху(1 + у'2).
3452.	(х2 + у2)2у" = (х + yy’f.
3453.	Преобразовать к полярным координатам выражение
Х + УУ'
ХУ' -У

§ 4. Замена переменных
323
3454.	Кривизну плоской кривой
К - I у "хх 1
выразить в полярных координатах гиф.
3455.	В системе уравнений
^ = У + kx(x2 + у2), g - -JC + fty(x2 + у2)
перейти к полярным координатам.
3456.	Преобразовать выражение
W=x^ -у*!*,
df2 у dt2
введя новые функции г = Jx2 + у2, ф = arctg £ .
3457.	В преобразовании Лежандра каждой точке (х, у) кри¬
вой у = z/(x) ставится в соответствие точка (X, У), где
X=y',Y=xy'-y.
Найти Г, У" и Г".
Вводя новые независимые переменные Е, и г|, решить следую
щие уравнения:
3458.	^	~ , если Е = х + г/иг| = х-[/.
dx dt/
3459.	ур- -	= 0, если £ = х и п = х2 + у2.
ах	оу
3460.	ар- + Ър = 1 (а ^ 0), если £ = хип = 1/-Ь2.
dx	dy
3461.	хр + t/^ = г, если £ = х и ц = ^ .
Эх	ду	х
Принимая иииза новые независимые переменные, преобра¬
зовать следующие уравнения:
3462.	хр + Jl + у2 р = XI/, если
Эх	dt/
и = In х и у = In (у + */1 + У2 )•
3463.	(х + у)^ - (х - у)^ = 0, если
Эх	Эу
и = In Jx2 + у2 и v = arctg - .
х

324 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3464.	х^ + I/~ = 2+ Jx2 + i/2 + 22 , если
дх	ду
U=-KV=Z + 4х2 + у2 + Z2 .
X
3465.	4- у— = - , если
ах	ду	г
u=2x-z2kv=-.
z
3466.	(х + 2)~ 4- (у +	= jc 4- у 4- 2, если
дх	ду
u = x + znv = y + z.
3467.	Преобразовать выражение
(г + ех+(г + е*)¥■ - (г2 - ех + «),
дх	ду
приняв за новые независимые переменные
£ = у 4* ze~x, г| = х 4- ze~y.
3468.	Преобразовать выражение
полагая
*= UD, 1/= |(И2“ У2)-
3469.	В уравнении
ди.ди.ди_п.
дх ду дг
ПОЛОЖИТЬ
£ = *, У\ = у- X, £ = Z ~ X.
3470.	Преобразовать уравнение
приняв х за функцию, ay и z — за независимые переменные.
3471.	Преобразовать уравнение
а, - г)| + а, + 2)| - °,
приняв х за функцию, а и = у — z, и = у + z — за независимые
переменные.

§ 4. Замена переменных
325
3472.	Преобразовать выражение
ду)
приняв х за функцию и и = xz, и = yz — за независимые пере¬
менные.
3473.	Решить уравнение
(у 4- z 4- и+ (х 4- z 4- и+ (л: + I/ 4-	= л: + у + z,
dt/	02
положив = х - и, ец = у - и, = z - и.
Перейти к новым переменным и, v, w, где ю = и>(и, у), в сле¬
дующих уравнениях:
3474.	- х^ = (у - х)г, если
Эл:	ду
и = х2 + у2, v = - 4- i , w = In 2 - (л: 4- у),
х у
3475.	х2^- + у2^ = г2, если
Эх ду
и = Ху V = - - i , Ю = i - - .
I/ л:	2 л:
3476. (XI/ 4- г)~ 4- (1 - у2)^ = л: 4- yz, если
Эл:	dt/
и = yz - X, V = XZ - у, w = ху - 2.
3477-Нйч (*!)' -
х = иеш, у = vew, z = ше".
3478.	Преобразовать выражение
полагая
I/ = In Jx2 4 у2 , V = arctg 2,Ш=Х + 1/ + 2,
где w = и>(и, у).
3479.	Преобразовать выражение
д _ dz . dz
дх ' ду'
полагая и = л:ег, у = г/ег, w = ze*, где w — и;(ы, у).

326 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3480.	Решить уравнение
х^ +ydJi +2^£ = ц+*2,
ОХ ду 02	2
ПОЛОЖИВ 4=-»Г) = У-, С, = z, w = - , где W = U>(%, Г), Q.
2 2 2
Преобразовать к полярным координатам гиф, полагая
х = г cos ф, I/ = г sin ф, следующие выражения:
3481.	w = xdr? -ydJL.
ду дх
3482.	w = хр + I№.
дх ду
3483
-©■♦(Г
3484. w = ^ +
Э*2
2	'Э|Л2
ду)
д2и
ду2
3485. w = х2^У + 2ху^~ + у2.
Эл:2	дхду ду2
348в.„ = ^-2^+^||-(,|+!,|)
/ =
ЭлгЭу	ду2
3487.	Преобразовать выражение
ЭиЭи _ диди
дхду дудх9
положив х — г cos ф, у = г sin ф.
3488.	Решить уравнение
Э2ц _ ?д2и
dt2	дх2 9
введя новые независимые переменные:
^ = х - at, У) = х + at.
Приняв и и у за новые независимые переменные, преобразо¬
вать следующие уравнения:
3489.2^| + д2г
дх2
дхду ду2
и = х + 2у + 2
Э2г + Эг + Эг = 0> если
дх
И
ду
и — х — у — 1.
3490.	(1 +	+ (1 + J/2)0 + »| + »| - 0. если
и = ln(JC 4- Jl + лс2) и и = 1п(1/ 4- VI 4 у2).
3491.	4- 2Ьху^^- 4- су2~| = 0 (а, 6, с— постоянные),
дх2	дхду	ду2
если
и = In х и v = In I/.

§ 4. Замена переменных
327
3492. р + р = 0, если
Эх2 ду2
х
и =
X2 + у2
И У =	^—-
X2 + I/2
3493. p+p+tn2z = 0, если
Эх2 Эг/2
х = еи cos у и у = еи sin у.
3494-ё-!'р-1|-0(!'>0,'всл”
и = х — 2 Jy и у = х + 2 л/г/.
3495. х2^| ~ У2 Т1 = °> если
Эх2 Эг/2
и = ху
и у = - .
У
3496.	x2g-(x2 + y2)||+y2p = О, если
и = X + Ц И и = 1 + 1 .
* У
3497.	xyg - (*» + </2)Ц + хур +	+	= О, если
И = I (JC2 + У2) И V = ху.
3498.	х2|^§ - 2х sin у^Ц^- + sin2 у|^| = О, если
Эх2	Эхду	Эу2
и — X tg У- и V — X.
6	2
3499.	х|^§ - у^| = 0 (х > 0, у > 0), если
Эх2 с)у2
X = (и + у)2 и у = (и - у)2.
3500.
Э2г
•(1 + |)’’если
ЭхЭу V ду)
и = х и у = г/ + z.
3501. С помощью линейной замены
£ = X + Xjy, Т1 = х + Х2у
преобразовать уравнение
Ар + 2Врр + Ср = О,
Эх2 Эхдг/ Эу2
(1)
дхду
где А, В и С — постоянные и АС - В2 < 0, к виду
if“- = о.
Найти общий вид функции, удовлетворяющей уравнению (1).

328 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3502. Доказать, что вид уравнения Лапласа
не меняется при любой невырожденной замене переменных
х = ср(и, v)9 у = ц(и, v),
удовлетворяющей условиям:
Эср _ Э\ц Э(£ _ _Эф
ди Эи ’Эи ди *
3503.	Преобразовать уравнения:
а) Дц =	+ |р = 0;	б) Д(Ди) = 0,
полагая и = /(г), где г = Jx2 + у2.
3504.	Какой вид примет уравнение
д21У
дхду
4- cw = 0,
если положить w = /(и), где и = (х - х0)(у - у0)?
3505.	Преобразовать выражение
А =
гд2и
ЭЛГ2
+ */
Э2ц
ЭлгЭг/
, Эи
Эх*
полагая
х +у = Х, у = ХУ.
3506.	Показать, что уравнение
2!* + 2хи2 — + 2(и - ы3)- + х2и2г = О
Элг2 У дх КУ У ’ду У
не меняет своего вида при преобразовании переменных
х = uv и
3507.	Показать, что уравнение
д2г + о д2г + д^г _ q
дх2 дхду ду2
не меняет своего вида при замене переменных
и = X + 2 И У=1/4-2.

§ 4. Замена переменных
329
3508.	Преобразовать уравнение
XV—- + uz-2-^
Удхду У дудг
+ XZ
дхдг
= 0,
полагая х = г|£, у = z = £г|.
3509.	Преобразовать уравнение
d2z	д2г	d2z д2г	d2z	d2z	_ q
дх2!	дх\	0*3	д*,0*2	0*10*3	0*20*з
полагая у1 = х2 + х3 - хи у2 = хг + х3- х2, у3 =	+ х2 - *3.
3510.	Преобразовать уравнение
гд2и
д2и
дх2
ду
дг2
д2и
' дх ду
+ 2X2
дхдг
+ 2yz
дудг
= 0,
полагая £ = - , ri = - , С = у - z.
х	х
Указание. Записать уравнение в виде А2и - Аи = 0, где
А =
±
дг ’
3511.	Выражения
преобразовать к сферическим координатам, полагая
х — г sin 0 cos ф, у = г sin 0 sin ф, z = г cos 0.
Указание. Замену переменных представить в виде композиции
двух частичных замен
х = R cos ф, у = R sin ф, г = г
и
R = г sin 0, ф = ф, z = г cos 0.
3512.	Преобразовать уравнение
введя новую функцию w и полагая w = z2.

330 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Приняв мииза новые независимые переменные и w= w(u> и)
за новую функцию, преобразовать следующие уравнения:
3513.	+2^ = - , если u=-,v = x,w = xz-y.
ду2 ду	х	у
3514.	Щ - 2^Ц- +	= 0, если и = х + у, и = Я, ш = - .
ах2 дхду ду2	х	х
3515.	+ 2-^- +	= 0,еслиu = x + y,v = x-y,w = xy-z.
Ох2	дхду	ду2
3516.	+
дх2
д2г
дхду
z, если и = 2L±Jf f D = Х—И 9 w = 2еу.
£t	Lt
3617- в
о д 2z
дхду
= 0, если
и= X, V = X + у, W = X + у + Z.
3518. ,1 -	1,1 - Лр -	, если
х = sin и, у = sin v, z = ew.
351Э. (1 - ^2)g - |f - 2лс| - i 2 = О (W < 1), если
и = i (у + arccos jc), 0 = i (у - arccos *), w = z\j 1 - jc2 .
z	z
3520. Щ - 2
dJC2 dy2
если
u = je + y, v = x - y, w = - 	- - .
V*2- у2
3521.	Доказать, что всякое уравнение
Э2е , Эг , lDz
Э*ду дх ду
+ cz = О
(а, Ьу с — постоянные) путем замены
2 = иеах + *уу
где а и (3 — постоянные величины ии = и(х9 у), можно привести
к виду
+ CiU = 0 (Ci — const).
дхду

§ 4. Замена переменных
331
3522.	Показать, что уравнение
д2и _ ди
дх2 ду
не изменяет своего вида при замене переменных
*' = *
У
U
Гу
е 4у ,
где и' — функция переменных х' и у'.
3523.	Преобразовать уравнение
<7(1 + q)
д22
дх2
- (1 + р + q + 2pq)
д2г
дхду
+Р(1+Р)р=°>
где Р = — И а = — , ПОЛОЖИВ и=Х + 2,и=и + 2,и)=Х + и + 2,
дх	ду
считая, что w = w(u9 v).
3524.	Преобразовать уравнение
положив х = у = ел, 2 = и = б"", где w = w(^9 ц, О-
3525.	Показать, что вид уравнения
д^гд^г _ ( д2г\2 = Q
Эл:2 Эу2 чЭлгЭуу
не меняется при любом распределении ролей между переменны¬
ми х9 у и 2.
3526.	Решить уравнение
fdz\2 d2z _ 9Э2Э2 д2г , ГЭг^2 Э22 _ q
Iду) дх2	дхду дхду 1Эл7 ду2
приняв х за функцию от переменных у и г.
3527.	Преобразовать уравнение
А(т’	+ 2в(т’ г)ГГ- +с(г’	=0
VЭл: ду) дх2	\дх ду) дхду \дх ду) ду2
применяя преобразование Лежандра
X=^,Y=^,Z = *^+i/^-z,
Эл:	ду	дх ду
где Z = Z(X, Y).

332 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 5. Геометрические приложения
1.	Касательная прямая и нормальная плоскость. Уравнение каса¬
тельной прямой к кривой
УяФ(0. 2 = x(f)
в точке ее М(х> у, г) имеет вид
X — х = Y-y = Z-2
dx	dy	dz
dt	dt	dt
Уравнение нормальной плоскости в этой точке:
2.	Касательная плоскость и нормаль. Уравнение касательной плос¬
кости к поверхности z = f(x, у) в точке ее М(х, у, z) имеет вид
Z-»-^-(X-x)+^(Y-y).
dx	dy
Уравнение нормали в точке М есть
X — х = Y-y = Z-z
dz	dz	-I
dx	dy
Если уравнение поверхности задано в неявном виде F(x, уу z) = О,
то соответственно имеем
|^(Х-*)+ ^(Y-y)+ g(Z-2) = 0
— уравнение касательной плоскости и
X — х
. Y-y .
_ Z-,
dF
dF
dF
дх
э«/
dz
— уравнение* нормали.
3.	Огибающая кривая семейства плоских кривых. Огибающая кри¬
вая однопараметрического семейства кривых /(*, у, а) = 0 (а — пара¬
метр) удовлетворяет системе уравнений:
/(*, у у а) = 0, f'a (Ху у у а) = 0.
4.	Огибающая поверхность семейства поверхностей. Огибающая по¬
верхность однопараметрического семейства поверхностей F(xy у, z, а) = 0
удовлетворяет системе уравнений:
F(Xy у у Zy а) = 0,	% (*, z/, 2, ос) = 0.
В случае двупараметрического семейства поверхностей Ф(х, у, 2, а, (3) = 0
огибающая поверхность удовлетворяет следующим уравнениям:
Ф(*, у у Zy а, Р) = 0, Ф;(*, у у Zy а, Р) = 0, Фр(*, у9 2, а, Р) = 0.

§ 5. Геометрические приложения
333
Написать уравнения касательных прямых и нормальных
плоскостей в данных точках к следующим кривым:
3528.	х = a cos a cos t,y = а sin а cos £, 2 = а sin £; в точке £ = £0.
3529.	jc = a sin2 t> у = b sin £ cos £, 2 = c cos2 £; в точке £ = ^.
3530.	у = x, z = x2; в точке M(l, 1, 1).
3531.	я2 + 22 = 10, у2 + z2 = 10; в точке М(1, 1, 3).
3532.	х2 + у2 + г2 = 6, д: + у + 2 = 0; в точке М(1, -2, 1).
3533.	На кривой
х — t9 у — £2, 2 == £3
найти точку, касательная в которой параллельна плоскости
х + 2у + z = 4.
3534.	Доказать, что касательная к винтовой линии
jc = a cos £, у = a sin £, 2 = Ь£
образует постоянный угол с осью 02.
3535.	Доказать, что кривая
jc = ае* cos £, у = ае* sin t, z = аег
пересекает все образующие конуса я2 + у2 = 22 под одним и тем
же углом.
3536.	Доказать, что локсодрома
tg(l +1) = еН ^ = const^
где ф — долгота, ц/ — широта точки сферы, пересекает все мери¬
дианы сферы под постоянным углом.
3537.	Найти тангенс угла, образованного касательной в точке
М0(х0, У о) к кривой
Z = f(x, у),
х- х0 = у-у о
cos a	sin а
где f — дифференцируемая функция, с плоскостью Оху.
3538.	Найти производную функции
Jx2 + у2 + Z2
в точке М(1, 2, -2) в направлении касательной в этой точке к
кривой
х — £, у ~ 2£2, z = -2£4.

334 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕхМЕННЫХ
Написать уравнения касательной плоскости и нормали в точ¬
ке М0 к следующим поверхностям:
3539.	2 = я2 + у2; М0( 1, 2, 5).
3540.	х2 + у2 + г2 = 169; М0(3, 4, 12).
3541.	2 = arctg^; М0( 1, 1, 5) .
3542.	ах2 + by2 + сг2 = 1; М0(х0, у0, 20).
3543.	z — у 1п~ ; М0( 1, 1, 1).
3544.	2 1 + 2 5 =8; М0(2, 2, 1).
3545.	х = a cos vp cos ф, i/ = 6 cos vp sin ф, 2 = c sin vp; М0(ф0, vj/0).
3546.	x = г cos ф, у = г sin ф, 2 = г ctg а; М0(ф0, г0).
3547.	х — и cos v9 у = и sin и, 2 = аи; М0(ио, v0).
3548.	Найти предельное положение касательной плоскости к
поверхности:
X — U + V, у = и2 + У2,	2 = U3 + У3,
когда точка касания М(и9 v) (и & v) неограниченно приближается
к точке М0(и0, vo) линии края и = v поверхности.
3549.	На поверхности
х2 + 2у2 + З22 + 2ху + 2xz + 4г/2 = 8
найти точки, в которых касательные плоскости параллельны ко¬
ординатным плоскостям.
3550.	В какой точке эллипсоида
у2	f(2
2L + \L + 2L
а2 Ь2 с2
= 1
нормаль к нему образует равные углы с осями координат?
3551.	К поверхности
х2 + 2у2 + З22 = 21
провести касательные плоскости, параллельные плоскости
х + 4г/ + 62 = 0.
3552.	Доказать, что касательные плоскости к поверхности
xyz = а3 (а > 0) образуют с плоскостями координат тетраэдр по¬
стоянного объема.
3553.	Доказать, что касательные плоскости к поверхности
Jx + Jy + Jz = Ja (a>0)
отсекают на осях координат отрезки, сумма которых постоянна.

§ 5. Геометрические приложения
335
3554.	Доказать, что касательные плоскости к конусу
проходят через его вершину.
3555.	Доказать, что нормали к поверхности вращения
(f* 0)
пересекают ось вращения.
3556.	Найти проекции эллипсоида
х2 + у2 + z2 - ху= 1
на координатные плоскости.
3557.	Квадрат {0 < jc < 1, 0 < z/ < 1} разбит на конечное число
частей а диаметра < 5. Оценить сверху число 5, если направления
нормалей к поверхности
z = 1 - х2 - у2
в любых точках Р(х, у) и Р\{хХ9 уг)9 принадлежащих одной и той
же части а, отличаются меньше чем на 1°.
3558.	Пусть
^ = f(x, у), где (*, у) € D,	(1)
— уравнение поверхности и ф(Р1э Р) — угол между нормалями
к поверхности (1) в точках Р(х9 у) € D и Рх(х19 уг) £ D.
Доказать, что если область D ограничена и замкнута, а функ¬
ция f{x9 у) имеет ограниченные производные 2-го порядка в об¬
ласти D, то справедливо неравенство Ляпунова
Ф(Л, Р) < Ср(Л, Р)9	(2)
где С — постоянная и p(Pi, Р) — расстояние между точками Р и Р1в
3559.	Под каким углом пересекается цилиндр х2 + у2 = а2
с поверхностью Ъг = ху в общей точке M0ix09 у09 20)?
3560.	Показать, что координатные поверхности сферических
координат х2 + у2 + г2 = г2, у = х tg ф, х2 + у2 = г2 tg2 0 попарно
ортогональны.
3561.	Показать, что сферы
х2 + у2 + z2 = 2ах, *2 + «/2 + г2 = 2Ьу, х2 + у2 + 22 = 2сг
образуют триортогональную систему.

336 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3562.	Через каждую точку М(х9 у9 г) проходят при А.= Х19
X = Х2, X = А,3 три поверхности второго порядка:
*2	. У2 + Z2
а2-Х2	Ь2-Х2	с2-Х2
= -1
(а > Ь > с > 0).
Доказать ортогональность этих поверхностей.
3563.	Найти производную функции и=х+у+гв направ¬
лении внешней нормали сферы х2 + у2 + г2 — 1 в ее точке
М0(х0, у0, г0). В каких точках сферы нормальная производная
функции и имеет:
а) наибольшее значение, б) наименьшее значение,
в)	равна нулю?
3564.	Найти производную функции и = х2 + у2 + г2 в направ¬
лении внешней нормали эллипсоида	=1в его точке
а2 о2 с2
М0(*0, I/о» 20).
3565.	Пусть ^ и ^ — нормальные производные функций и
on дп
и v в точке поверхности F(x, у, г) = 0. Доказать, что
&uv)-u&+v&
Найти огибающие однопараметрических семейств плоских
кривых:
3566.	х cos а + у sin а = р (р = const).
3567. (х - а)2 + у2 = ^ .
3568.	у = kx + j (a = const).
k
3569.	у2 = 2px + p2.
3570.	Найти кривую, огибаемую отрезком длины Z, концы ко¬
торого скользят по осям координат.
у2	п2
3571.	Найти огибающую эллипсов — +	= 1, имеющих по-
а2 о2
стоянную площадь S.
3572.	Найти огибающую траекторий снаряда, выпущенного
в безвоздушном пространстве с начальной скоростью v09 при
варьировании в вертикальной плоскости угла бросания а.
3573.	Доказать, что огибающая нормалей плоской кривой
есть эволюта этой кривой.
3574.	Исследовать характер дискриминантных кривых се¬
мейств следующих линий (с — переменный параметр):
а)	кубических парабол у = (х - с)3;
б)	полукубических парабол у2 = (х - с)3;

§ 6. Формула Тейлора
337
в)	парабол Ней ля у3 = (х - с)2;
г)	строфоид (у - с)2 = х2?Lz_£ .
а + х
3575.	Определить огибающую семейства шаров радиуса г,
центры которых расположены на окружности х = R cos t,
I/ = JF? sin £, 2 = 0 (£ — параметр, R > г).
3576.	Найти огибающую семейства шаров
(х - t cos а)2 + (у - t cos Р)2 + (z - t cos у)2 = 1,
где cos2 а + cos2 Р + cos2 у = 1 и t — переменный параметр.
3577.	Определить огибающую семейства эллипсоидов
+ и! + г! « 1,
Ъ2 с2
объем которых V постоянен.
3578.	Найти огибающую семейства сфер радиуса р, центры
которых расположены на поверхности конуса х2 + у2 = г2.
3579.	Светящаяся точка находится в начале координат. Оп¬
ределить конус тени, отбрасываемой шаром
(X - Х0)2 + (у- Уо)2 + (2 - 20)2 < R2,
2	, 2 , 2 . у-,2
если Х0 + Z/o + 20 > R •
3580.	Найти огибающую семейства плоскостей
z- z0=p(x- х0) + q(y - уо),
если параметры р и q связаны уравнением
p2 + g2= 1.
§ 6. Формула Тейлора
1.	Формула Тейлора. Если функции f(x, у) имеет в некоторой ок¬
рестности точки (а, Ъ) непрерывные все частные производные до п + 1
порядка включительно, то в этой окрестности справедлива формула
/(*, у) - Па, Ь) + £ 1[(Ж - а)|- + (у - b)|J Да, 6) + R„(x, у), (1)
где
я„(*> у) = ^Y)i[(« ~а)|- +	f(a + Qn(x ~a)’b + ®п(у - Ъ))
(о < е„ < 1).

338 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2.	Ряд Тейлора. Если функция f(x> у) бесконечно дифференцируема
и Иш = Rn(x, у) = 0, то эта функция допускает представление в виде
п — оо
степенного ряда
1
f(x, у) = f(a, b) + £	Ь)(х - а)‘(у - Ь)’.	(2)
i*i> 11
Частные случаи формул (1) и (2) при а = Ъ = 0 соответственно носят
названия формулы Маклорена и ряда Маклорена.
Аналогичные формулы имеют место для функции более чем двух
переменных.
3.	Особые точки плоских кривых. Точка М0(х0, у0) дифференцируе¬
мой кривой F(x, у) = 0 называется особой, если
о,	1/о) = 0,	F;(x0, i/o) = О, FI (*0> Уо) = 0.
Пусть М0(х0, у0) — изолированная особая точка кривой класса С<2) и числа
А = F”x (х0, у0), В = F'x'y (*„. у0), С = F''y (*„, у0)
не все равны нулю. Тогда, если:
1)	АС - В2 > 0, то М0 — изолированная точка;
2)	АС - В2 < 0, то М0 — двойная точка (узел);
3)	АС - Б2 = 0, то М0 — точка возврата или изолированная точка.
В случае А = В = С = 0 возможны более сложные типы особых точек.
У кривых, не принадлежащих классу гладкости CS2), могут быть особен¬
ности более сложной природы: точка прекращения, угловые точки и др.
3581.	Функцию /(я, р) = 2jc2 - ху - у2 - 6л: - Зу + 5 разложить
по формуле Тейлора в окрестности точки А(1, -2).
3582.	Функцию f(x, г/, г) = я3 + у3 + 23 - Злгг/г разложить по
формуле Тейлора в окрестности точки А(1, 1,1).
3583.	Найти приращение, получаемое функцией
f(x, у) = х2у + ху2 - 2ху,
при переходе от значений х =* 1, у = -1 к значениям хх = 1 + h,
Уг = -1 + k.
3584.	Разложить /(х + h, у + k, z + /) по целым положитель¬
ным степеням величин A, k и Z, если
/(я, у, г) = Ал:2 + By2 + Сг2 + 2£>л:1/ + 2Exz 4- 2Fi/2.
3585.	В разложении функции
/(X, 1/) = X?
в окрестности точки А(1, 1) выписать члены до второго порядка
включительно.

§ 6. Формула Тейлора
339
3586.	Разложить по формуле Маклорена до членов четверто¬
го порядка включительно функцию
f(x, у) = Jl-x2-y2.
3587.	Вывести приближенные формулы с точностью до чле¬
нов второго порядка для выражений:
a) cos£;
cos у
б) arctg | + * + У ,
1 -Х + у
если |х| и \у\ малы по сравнению с 1.
3588.	Упростить выражение
cos(x + у 4- z) - cos х cos у cos 2,
считая ху у у z малыми по модулю.
3589.	Функцию
Fix, у) = ^ Wx + л> У) + fix, У + h) +
+ fix - h,y) + fix, у - h)]- fix, у)
разложить по степеням h с точностью до h4.
3590.	Пусть /(Р) = /(*, у) и Pi(Xiy у<) (i = 1, 2, 3) — вершины
правильного треугольника, вписанного в окружность с центром
в точке Р(Ху у) радиуса р, причем хх = х + р, уг = у. Разложить
по целым положительным степеням р с точностью до р2 функцию
Др) = I ШРг) + fiPZ) + ЯРз)]-
3591.	Разложить по степеням h и k функцию
bxyf(x, у) = fix + h, у + k) - fix + h, у) - fix, у + k) + fix, у).
3592.	Разложить по степеням р функцию
271
•F(p) = -^J" fix + р cos ср, у + р sin ф) cfcp.
о
Разложить в ряд Маклорена следующие функции:
3593.	fix, у) = (1 + x)mil + у)п.	3594.	fix, у)	= 1п(1 + х	+ у).
3595. fix, у) = ех sin у.	3596.	fix, у)	— ех cos у.
3597. fix, у) = sin х sh у.	3598.	fix, у)	= cos х ch	у.
3599.	fix, у) = sin(jt2 + у2).
3600.	fix, у) = 1п(1 + лг)1п( 1	+	у).

340 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3601.	Написать три члена разложения в ряд Маклорена
функции
1
fix, у) = J (1 + x)‘*»dt.
О
3602.	Функцию ех + у разложить в степенной ряд по целым
положительным степеням биномов х - 1 и у + 1.
3603.	Написать разложение в ряд Тейлора функции f(x, у) = -
У
в окрестности точки М( 1, 1).
3604.	Пусть z — та неявная функция от х и у, определяемая
уравнением гъ - 2xz + у = 0, которая при х = 1 и у = 1 принимает
значение 2=1.
Написать несколько членов разложения функции z по воз¬
растающим степеням биномов х - 1 и у - 1.
Изучить типы особых точек следующих кривых и примерно
изобразить эти кривые:
3605.	у2 = ах2 + х3.	3606. х3 + у3 - 3ху = 0.
3607. jc2 + у2 = х4 + у4.	3608. х2 + у4 = х6.
3609. (х2 + у2)2 = а\х2 - у2).	3610. (у - х2)2 = х5.
3611.	(а + х)у2 = (а - х)х2.
3612.	Изучить форму кривой у2 = (х - а)(х - Ь)(х - с) в зави¬
симости от значений параметров а, Ь, с (а < Ъ < с).
Исследовать особые точки трансцендентных кривых:
3613.	у2 = 1 - е~х2.
3615. у = х In х.
3617. у = arctgf-Д—).
vsinxy
3619.	i/2 = sin х2.
3614.	у2 = 1 - е-*3.
3616. у = -2— .
1 + е*
3618. у2 = sin^ .
3620.	i/2 = sin3 х.
§ 7. Экстремум функции нескольких переменных
1.	Определение экстремума. Пусть функция f(P) = f(xl9 хп) оп¬
ределена в окрестности точки Р0. Если или f(P0) > f(P), или f(P0) < f(P)
при 0 < р(Р0> Р) < 8, то говорят, что функция /(Р) имеет экстремум (со¬
ответственно максимум или минимум) в точке Р0.
2.	Необходимое условие экстремума. Дифференцируемая функция
f(P) может достигать экстремума лишь в стационарной точке Р0, т. е.

§ 7. Экстремум функции нескольких переменных
341
такой, что df(P0) = 0. Следовательно, точки экстремума функции f(P)
удовлетворяют системе уравнений
/;; (*!, .... х„)= 0 (t= 1,.... п).
3.	Достаточное условие экстремума. Функция f(P) в точке Р0 имеет:
п
а)	максимум, если df(P0) = 0, d2f(P0) < 0 при \dxt\ ^ 0,
i = 1
п
б)	минимум, если df(P0) = 0, d2f(P0) > 0 при \dxt\ ^ 0.
/ = 1
Исследование знака второго дифференциала d2f(P0) может быть про¬
ведено путем приведения соответствующей квадратичной формы к ка¬
ноническому виду.
В частности, для случая функции f(x, у) двух независимых пере¬
менных х и у в стационарной точке (дг0, у0) (df(x0, у0) = 0) при условии,
что D — АС - В2 * 0, где А — f”x (дс0, У о), В = f'x'y (х0, у0), С = f”y (х0, у0),
имеем:
а)	минимум, если D > 0, А > 0 (С > 0);
б)	максимум, если D > 0, А < 0 (С < 0);
в)	отсутствие экстремума, если D < 0.
4.	Условный экстремум. Задача определения экстремума функции
f(P0) = f(xx, ..., хп) при наличии ряда соотношений (р^Р) = 0 (t = 1, ...,
т; /п < п) сводится к нахождению обычного экстремума для функции
Лагранжа
цр) = т + £ хдаср),
/ = 1
где Xi(i— 1, ..., /п) — постоянные множители. Вопрос о существовании
и характере условного экстремума в простейшем случае решается на
основании исследования знака второго дифференциала d2L(P0) в стацио¬
нарной точке Р0 функции L(P) при условии, что переменные dxx,...» dxn
связаны соотношениями
У dx} = 0 (i = 1, ..., т).
j= 1 °Xj
5.	Абсолютный экстремум. Функция f(P), дифференцируемая в ог¬
раниченной и замкнутой области, достигает своих наибольшего и на¬
именьшего значений в этой области или в стационарной точке, или в
граничной точке области.
Исследовать на экстремум следующие функции нескольких
переменных:
3621.	z = x2 + (y- I)2.
3622.	z = x2-(y- l)2.

342 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3623.	г = (х-у + I)2.
3624.	2 = х2 - ху + у2 — 2х + у.
3625.	2 = *У(6 -х-у).
3626.	2 = х3 + у3 - 3ху.
3627.	а) 2 = х* + у* - х2 - 2ху - у2;
б) 2 = 2л:4 + у4 - х2 - 2у2.
3628. 2 = ху 4* —— 4* —— (л: > 0, у > 0).
х у
3629.2	= xyjl-g-g (а > О, b > 0).
3630. 2 = ах + ьУ + с.	(д2 + Ь2 + с2 * 0).
4хг + уг + 1
3631.	2= 1 - л/*2 + У2 •
3632.	2 = е2х + 3!,(8л:2 - 6ху + 3у2).
3633.	2 = ех2~« (5 - 2л: + у).
3634.	2 = (5л: + 7у - 2Ь)е-<х*+ х«+^.
3635.	2 = л:2 + ху + у2 - 4 In х - 10 In у.
)•
3637.	z = sin х sin у sin (х + у) (0 < х < п; 0 < у < я).
3638.	z = х - 2у + Injx2 + у2 + 3 arctg^ .
3639.	z — ху 1п(х2 + у2).
3640.	2 = х 4- у + 4 sin х sin у.
3641.	2 = (х2 4- i/2)e -О'2**'2).
3642.	и = х2 4- у2 + z2 + 2х + Ау - 6г.
3643.	и = х2 + у2 + z2+ 12ху + 22.
3644.	и = * +	— +2 (х > О, I/ > 0, 2 > 0).
Ах у х
3645.	и = xi/223(a - х - 2у - 32) (а > 0).
3646.	(л: > 0, у > 0, г > 0, а > 0, 6 > 0).
X у 2 Ь
3647.	и = sin л: + sin у + sin z - sin (x + у + z) (0 < x < n; 0 < у < л;
О < 2 <7t).
3648.	и = хгх2 ...хпп (1-х1-2х2- ,..-пхп)(х1 >0,х2 >0, ...хп >0).
3649.	м = л:. + — + — + ... + -£&- + — (л;, > 0, i = 1, 2, ... п).
*1	*2	Хп-1 *»
3636. 2 = sin х 4- cos у + cos (х - у) ( 0 < X < 5 ; 0 < I/ < 5
V	Z	2

§ 7. Экстремум функции нескольких переменных
343
3650.	Задача Гюйгенса. Между двумя положительными чис¬
лами а и Ъ вставить п чисел хг, х2, ..., хп так, чтобы значение
дроби
	Х\Х2 • • •Хп
(а + хг)(х1 + х2)...(хп + Ь)
было наибольшим.
Найти экстремальные значения заданной неявно функции z
от переменных х и у:
3651. х2 + у2 + z2 - 2х + 2у — £z - 10 = 0.
3652. х2 4- у2 4- z2 - xz - yz + 2х 4- 2у 4- 2z - 2 = 0.
3653.	(х2 + у2 + z2)2 = а\х2 Л-у2- z2).
Найти точки условного экстремума следующих функций:
3654.	z = ху, если х 4- у = 1.
3655.	z = - 4- ^ , если х2 4- у2 = 1.
а о
3656.	z = х2 + у2 у если - +2 =1.
а о
3657.	a) z = Ajc2 4- 2Bxi/ + Ci/2, если x2 4- у2 = 1;
б)	z = л;2 4- 12лгг/ + 2у2, если 4х2 4- у2 = 25.
3658.	2 = cos2 л: 4- cos2 у, если х - у = Ц .
4
3659.	и = * - 2г/ 4- 2г, если х2 4- i/2 4- z2 = 1.
3660.	u = xmynzp, если
л: 4- z/ 4- 2 = а (тгс > 0, л > 0, р > 0, а > 0).
3661.	и — х2 Л- у2 Л- z2, если
$ +$ + § =1 (а > b > с > 0).
3662.	и = xy2z3, если х 4- 2у 4- З2 = а (х > 0, у > 0, z > 0, a > 0).
3663.	а) и = xz/2, если х2 4- у2 + z2 = 1, * + у 4- z = 0;
G) и — ху 4- £/2, если х2 + I/2 = 2, у + z = 2 (* > 0, 1/ > 0,
2> 0).
3664.	и = sin х sin у sin 2, если х + у + z = 5 (х > 0, у > 0, 2 > 0).
2

344 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
если
х2 + у2 + z2 = 1, х cos а 4- у cos (3 + z cos у = О
(а > b > с > 0, cos2 а 4- cos2 Р + cos2 у = 1).
3666.	и = (х - £)2 + (у - г\)2 4- (г - О2, если
Ах 4- By + Cz = 0, х2 + у2 + z2 = R2,
—= —3— = —, где cos2 а 4- cos2 Р 4- cos2
cos а cosp cosy
3667.	и = х\ 4“ х\ 4- ... 4- х2п, если
^ + ... 4- ^ = 1	(а, > 0; i = 1, 2, ... л).
«1	«2	«п
3668.	и = х\ 4- х?2 4- ... + х^ (р > 0), если
хх 4- х2 4* ... 4* хп = а (а > 0).
3669.	и = ~ 4- ^ 4- ... 4- — , если
*1 *2 *»
Pl*l + Рг*2 + ••• + $пХп = 1
£=1,2, ... л).
3671. Найти экстремум квадратичной формы
п
“ - X а« К = а;<)
при условии	= 1.
i = 1
3672.	Доказать неравенство
если л > 1 и * > 0, у > 0.
Указание. Искать минимум функции г = - (хп 4 ул) при условии
а
х + у - s.

§ 7. Экстремум функции нескольких переменных
345
3673.	Доказать неравенство Гёлъдера
Указание. Искать минимум функции
п
при условии	alxi = А.
/ = 1
3674.	Доказать неравенство Адамара для определителя
А = |aJ порядка л:
Указание. Рассмотреть экстремум определителя А = |aj при на¬
личии соотношений
Определить наибольшие (sup) и наименьшие (inf) значения
следующих функций в указанных областях:
3675.	z = х - 2у - 3, если 0<*< 1, 0 < у < 1,0<jс + у < 1.
3676.	z = х2 + у2 - 12х 4- 16у, если х2 + у2 < 25.
3677.	2 = х2 - ху 4- у2, если |x| 4- |у| < 1.
3678.	и = х2 4- 2у2 4- 3z2, если х2 4- у2 4- г2 < 100.
3679.	и = л: 4 I/ 4- 2, если х2 4- у2 < z < 1.
3680.	Найти нижнюю грань (inf) и верхнюю грань (sup) функ-
в областях х > 0, у > 0, z > 0.
3681.	Показать, что функция z = (1 4- еу) cos д: - уеу имеет
бесконечное множество максимумов и ни одного минимума.
3682.	Является ли достаточным для минимума функции f(x, у)
в точке М0(х0, г/0), чтобы эта функция имела минимум вдоль каждой
прямой, проходящей через точку М0?
Рассмотреть пример f(x, у) = (х - у2)(2л: - у2).
л
2 4 = s, (t = 1, 2, ... п).
дии
u = (x + t/ + 2)e-(* + 2!, + 3z)

346 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3683.	Данное положительное число а разложить на п поло¬
жительных сомножителей так, чтобы сумма обратных величин
их была наименьшей.
3684.	Данное положительное число а разложить на п слагае¬
мых так, чтобы сумма их квадратов была наименьшей.
3685.	Данное положительное число а разложить на п поло¬
жительных множителей так, чтобы сумма заданных положи¬
тельных степеней их была наименьшей.
3686.	На плоскости даны п материальных точек Рг(х19 уг)>
Р2(х2, у2)9	Рп(хп> Уп) с массами, равными соответственно т19
т2, ...» тп.
При каком положении точки Р(х9 у) момент инерции системы
относительно этой точки будет наименьшим?
3687.	При каких размерах открытая прямоугольная ванна
вместимости V имеет наименьшую поверхность?
3688.	При каких размерах открытая цилиндрическая ванна
с полукруглым поперечным сечением, поверхность которой рав¬
на S, имеет наибольшую вместимость?
3689.	На сфере х2 + у2 4- z2 = 1 найти точку, сумма квадратов
расстояний которой от п данных точек Mf,xl9 yif z) (i = 1, 2, ... n)
была бы минимальной.
3690.	Тело состоит из прямого кругового цилиндра, завер¬
шенного прямым круговым конусом. При данной полной по¬
верхности тела, равной Q, определить его измерения так, чтобы
объем тела был наибольшим.
3691.	Тело, объем которого равен V, представляет собой пря¬
мой прямоугольный параллелепипед, нижнее и верхнее основа¬
ния которого завершаются одинаковыми правильными четырех¬
угольными пирамидами. При каком угле наклона боковых гра¬
ней пирамид к их основаниям полная поверхность тела будет
минимальной?
3692.	Найти прямоугольник данного периметра 2р9 который
вращением вокруг одной из своих сторон образует тело наиболь¬
шего объема.
3693.	Найти треугольник данного периметра 2р9 который
вращением вокруг одной из своих сторон образует тело наиболь¬
шего объема.
3694.	В полушар радиуса R вписать прямоугольный паралле¬
лепипед наибольшего объема.
3695.	В данный прямой круговой конус вписать прямоуголь¬
ный параллелепипед наибольшего объема.

§ 7. Экстремум функции нескольких переменных
347
3696.	В эллипсоид
+у1
а2 Ъ2 с2
= 1
вписать прямоугольный параллелепипед наибольшего объема.
3697.	В прямой круговой конус, образующая которого I на¬
клонена к плоскости основания под углом а, вписать прямо¬
угольный параллелепипед с наибольшей полной поверхностью.
3698.	В сегмент эллиптического параболоида - = ~	^,
с а2 о2
z = с вписать прямоугольный параллелепипед наибольшего объ¬
ема.
3699.	Найти кратчайшее расстояние точки М0(х0, у0> z0) от
плоскости Ах 4- By + Cz + D = 0.
3700.	Определить кратчайшее расстояние d между двумя
прямыми
*-*i = У~У\ = z-zi
"Ч	пх	рх
х-х2 = у-у2 в г-22
/П-2	^2	Pi
3701.	Найти кратчайшее расстояние между параболой у = х2
и прямой х — у — 2 = 0.
3702.	Найти полуоси центральной кривой второго порядка
Ах2 4- 2Вху 4- Су2 = 1.
3703.	Найти полуоси центральной поверхности второго по¬
рядка
Ах2 + By2 + Cz2 + 2Dxy + 2Eyz 4- 2Fxz = 1.
3704.	Определить площадь эллипса, образованного пересече¬
нием цилиндра
плоскостью
Ах 4- By + Cz = 0.
3705.	Определить площадь сечения эллипсоида
у2	1/2
— + + — = 1
а2 Ь2 с2
плоскостью
х cos а 4- у cos Р 4- z cos у = 0,
где cos2 а 4- cos2 Р 4- cos2 у = 1.

348 РАЗДЕЛ VI. ДИФФ. ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3706.	Согласно принципу Ферма свет из одной точки в другую
попадает за кратчайшее время.
Предполагая, что обе точки расположены в различных опти¬
ческих средах, разделенных плоскостью, причем скорость распро¬
странения света в первой среде равна а во второй v2, вывести
закон преломления света.
3707.	При каком угле падения светового луча на боковую
грань призмы с преломляющим углом а и показателем прелом¬
ления п угол отклонения луча (т. е. угол между падающим и
выходящим лучами) будет наименьшим? Определить этот угол
наименьшего отклонения.
3708.	Переменные величины хи у удовлетворяют линейному
уравнению
у = ах + Ь,
коэффициенты которого требуется определить. В результате ря¬
да равноточных измерений для величин хи у получены значения
х19 уi (£= 1, 2, ..., /г).
Пользуясь способом наименьших квадратов, определить
наивероятнейшие значения коэффициентов а и Ь.
Указание. Согласно способу наименьших квадратов наивероят¬
нейшими значениями коэффициентов а и b являются те, для которых
сумма квадратов погрешностей
£ Д? = £ (<**/ + Ь- уд2
1=1 1=1
будет наименьшей.
3709.	На плоскости дана система п точек Mt(xi9 у) (i = 1, 2, ...
..., л). При каком положении прямой х cos а 4-у sin а - р = 0
сумма квадратов отклонений данных точек от этой прямой будет
наименьшей?
3710.	Функцию х2 на интервале (1,3) приближенно заменить
линейной функцией ах 4- b так, чтобы абсолютное отклонение
А = sup \х2 - (ах 4- b)\ (1 < х < 3)
было минимальным.

РАЗДЕЛ VII
ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
§ 1. Собственные интегралы, зависящие от параметра
1.	Непрерывность интеграла. Если функции /(х> у) определена и не¬
прерывна в ограниченной области R[a < х < А; Ъ < у < В], то
А
F(y) = J fix, у) dx
а
представляет собой функцию, непрерывную на сегменте Ь < у < В.
2.	Дифференцирование под знаком интеграла. Если сверх указан¬
ного в 1°, частная производная f’y (х9 у) непрерывна в области Я, то при
Ь< у < В справедлива формула Лейбница
А	А
^ J fix, y)dx = J fy (*, у) dx.
a	a
В более общем случае, когда пределы интеграции являются диффе¬
ренцируемыми функциями ф(у) и i|j(y) параметра у и а < <р(у) < А,
а < ¥(у) < А при Ь < у < В, то имеем
ч(у)
Ту J Кх'У^ах =
ф(у)
v(y)
= fiwiy), y)¥iy) - fi<t>iy)> yWiy) + J f'y ix, y) dx b< у < B.
<P(y)
3. Интегрирование под знаком интеграла. При условиях 1° имеем
В А	А В
fix, у) dx =
Ь а
3711.	Показать, что интеграл
1
f(x, у) dy.
F(y) = J fix, у) dx
О
от разрывной функции f(x, у) = sgn (х - у) является функцией
непрерывной. Построить график функции и = F(y).

350
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
3712.	Исследовать на непрерывность функцию
Пу) - Г	dx,
J х2 + у2
где функция f(x) непрерывна и положительна на сегменте [0, 1].
3713.	Найти:
1	+ос
a) lim f -
а — 0 J 1
dx
+ х2 +а2
в)	lim Г х2 cos ах dx;
а —0 J
о
б) lim Г Jx2 + а2 dx;
а-* О J
-1
1
г) lim f 	—	;
i+(i+-T
z
д)	lim f e~R
R-^oo J
sin 0
dQ.
3714.	1. Пусть функция f(x) непрерывна на сегменте [А, Б].
Доказать, что
lim i f [/(* + h) - /(f)] dt = f(x) -f(a) (A < a < x < B).
h — o h J
a
2. Пусть: 1) фп(х) > 0 (n = 1, 2, ...) на [-1, 1]; 2) <pn(x)=tO при
i
n oo на 0 < £ < \x\ < 1; 3) J* фл(х) dx -* 1 при n —> oo.
-i
Доказать, что если /(x) € С [-1, 1], то
i
lim Г /(лг)ф„(лг) dx = ДО).
П -» oo J
3715.	Можно ли совершить предельный переход под знаком
интеграла в выражении
1	X2
lim f £ еdx?
y-oj у2
0
3716.	Можно ли вычислить по правилу Лейбница производ¬
ную функции
1
F(y) = J In Jx2 + у2 dx
о
при г/ = 0?

§ 1. Собственные интегралы, зависящие от параметра
351
3717.	Вычислить F'(x), если
*2
F(x) = J е~хУ2 dy.
X
3718.	Найти F'(a), если:
cos а
a) F(a) = J еа^' ~ *2 dx;
б) F(a)
sin a
b + a
I
a + a
a
sinax
dx;
в)ад=| lnil±a£]^;
0
a
r) F(a) = J /(jc + a, x - a) dx;
or x + a
д) F(a) = J* dx J* s^n + */2 ~ a2) dy.
0 x-a
3719. Найти F”(x)y если
F(x) = J (x + y)/(y) dy,
где f(x) — дифференцируемая функция.
3720. Найти F"(x), если
ь
F(x) = J /(y)|x - y| dy,
где a < b и /(у) — непрерывная на [a, &] функция.
3721.1. Найти F"(x), если
Л Л
*■(*) = ^5 | Л* + S + л) (Л > 0),
о о
где f(x) — непрерывная функция.
2. Найти F(n)(x), если

352
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
3722.	Доказать формулу
= + ‘-1-*•••■>• «
О
Пользуясь формулой (1), получить оценку:
dn ( sinx\
dxn\ х J
n+ 1
при x €	+oo).
3723.	Функцию f(x) = x2 на промежутке 1 < x < 3 приближен¬
но заменить линейной функцией а + Ъх так, чтобы
з
J (а + Ъх - х2)2 dx = min.
i
3724.	Получить приближенную формулу вида
J1 + х2 ~ а + Ьх (0 < а < 1)
из условия, что среднее квадратичное отклонение функций а + Ьх
и J1 + х2 на данном промежутке [0,1] является минимальным.
3725.	Найти производные от полных эллиптических интег¬
ралов
2
E(k) = j* Vl-&2sin2(p cfcp,
о
71
2
F(k) = f -—is.	(0 < k < 1)
J
и выразить их через функции E(k) и F(k).
Показать, что E(k) удовлетворяет дифференциальному урав¬
нению
E"(k) + i E'(k) +	= 0.
k	1 — k2
3726.	Доказать, что функция Бесселя целого индекса п
я
Jn(k) = - f cos(mp - х sin ср) с?ф
Jtj
О
удовлетворяет уравнению Бесселя
x2J” (х) + xJ’n (х) + (х2 - n2)Jn(x) = 0.

§ 1. Собственные интегралы, зависящие от параметра
353
3727.	Пусть
а
где функция ф(х) непрерывна вместе со своей производной (p'(jc)
на сегменте 0 < х < а.
Доказать, что при 0 < а < а имеем
Г(а) = ^ + f	dx.
Tot J Ja- х
Указание. Положить х = at.
3728.	Показать, что функция
1
и(х) = J К(х, y)v(y) dy,
О
где
К(х, у) =
х (1 - у), если х < у;
у (1 - х)9 если х> у,
и и(у) непрерывна, удовлетворяет уравнению
и"(х) = -и(х) (0 < х < 1).
3729.	Найти F^y (х, у), если
ху
F(x, у) = J (х - yz)f(z) dz,
X
У
где f(z) — дифференцируемая функция.
3730.	Пусть f(x) — дважды дифференцируемая функция и
и(х) — дифференцируемая функция.
Доказать, что функция
x + at
и(х, О = | lf(x - at) + f(x + af)] + ^ J F(z) dz
x-at
удовлетворяет уравнению колебания струны
d2U _	9д2и
dt2	дх2
и начальным условиям: и(х9 0) = f(x)9 и\ (х9 0) = F(x).

354
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
3731.	Показать, что если функция f(x) непрерывна на сегмен
те [О, I] и (х - £)2 + у2 + г2 * 0 при 0 < £ < Z, то функция
1
и(х, у
__aig.	—
*J(x - £)2 + у2 + z2
удовлетворяет уравнению Лапласа
д2и ,	, dhi _ q
дх2 ду2 дг2
Применяя дифференцирование по параметру, вычислить
следующие интегралы:
п
2
3732.	J In (a2 sin2 х + b2 cos2 х) dx.
о
п
3733.	J In (1 - 2а cos * + а2) d*.
о
п
2
3734.	f arctg(«tg^)dx,
J tgx
О
я
2
3735.	f lni±^2^ **- (|a| < l) .
J 1- a cos* cos* v	J
0
3736.	Пользуясь формулой
l
arctg* _ f dy
* J 1 + x2y2 9
0
вычислить интеграл
l
f arctg* dx
J * ЛТТ*'
0
3737.	Применяя интегрирование под знаком интеграла, вы¬
числить интеграл
1
J dx (а > О, Ь > 0).
О

§ 2. Несобственные интегралы, зависящие от параметра
355
3738.	Вычислить интегралы:
1
а)	f sin fIn il—	dx;
J V X) inx
0
1
б)	J* cos^ln	dx (a > 0, b > 0).
о
3739.	Пусть F(k) и E(k) — полные эллиптические интегралы
(см. задачу 3725). Доказать формулы
k
а)	J F(k)k dk = E(k) - k\ F{k);
0
k
б)	J E(k)k dk = |[(1 + k2)E(k) - klF(k)],
0
где k\ = 1 - k2.
3740.	Доказать формулу
J xJ0(x) dx = xJi(x),
где J0(x) и Ji(x) — функции Бесселя индексов 0 и 1 (см. задачу
3726).
§ 2. Несобственные интегралы, зависящие от параметра.
Равномерная сходимость интегралов
1. Определение равномерной сходимости. Несобственный интеграл
1
f(xy у) dx,
(1)
где функция f(xy у) непрерывна в области а<х< +°о, ух < у < у2У называется
равномерно сходящимся в интервале (уи у2)У если для любого е > 0 сущест¬
вует число В = В(е) такое, что при всяком b > В имеем
1
f(x,y)dx
< е (У\<У< Уз)-

356
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
Равномерная сходимость интеграла (1) эквивалентна равномерной
сходимости всех рядов вида
оо
I
п = О
I
/(X, у) dx,
(2)
где а = а0 < а, < а2 < ... < а„ < а„ +
< ... и lim ап - +оо.
П — оо
Если интеграл (1) сходится равномерно в интервале (уи у2), то он
представляет собой непрерывную функцию параметра у в
этом интервале.
2. Критерий Коши. Для равномерной сходимости интеграла (1) в
интервале (уи у2) необходимо и достаточно, чтобы для любого 6 > 0 су¬
ществовало число В = Б(е) такое, что
ft"
J' f(x, у)dx
ft'
< е
(У1<У< Уг)>
если только Ь' > В и Ь" > В.
3.	Критерий Вейерштрасса. Для равномерной сходимости интегра¬
ла (1) достаточно, чтобы существовала не зависящая от параметра у ма¬
жорирующая функция .F(*) такая, что
1)	I/(*, у)I ^ jF(*) при а < х < +°о,
+оо
2)	J F(x) dx < +°о.
а
4.	Аналогичные теоремы имеют место для несобственных интегра¬
лов от разрывных функций.
Определить области сходимости интегралов:
3741.
f е~ах
J 1 + х
о
4-00
I-
dx.
3743. |
х»
3742.
3744.
xcosxdX'
Х<!
f ХСО\
J ХР +
о
2
f dx
J |lndp
3745.
j, cos—
f —l-^dx.
J nJ 1 - xz
0
4-00
3746. f sin* dx(p> 0).

§ 2. Несобственные интегралы, зависящие от параметра
357
При помощи сравнения с рядами исследовать сходимость
следующих интегралов:
+оо	4-00
3747.
f ZZZdx.
J х + а
3749.
о
+оо
J
3748. Г ■ - xdx , (га > 0).
J 1 + xnsm2x
о
4~оо
dx
3750.
Г sin(* +
J хп
&dx.
3751.	Сформулировать в положительном смысле, что значит,
что интеграл
4-оо
• dx
J f(.X, у) I
сходится неравномерно в заданном интервале (у19 у2).
3752.	Доказать, что если: 1) интеграл
4-оо
| dx
J fix, у) I
сходится и 2) функция cp(x, у) ограничена и монотонна по х, то
интеграл
J* /(х)<р(х, у) dx
сходится равномерно (в соответствующей области).
3753.	Доказать, что равномерно сходящийся интеграл
4-оо
Т’Н)
1= j е ул о1 dx (0 < у < 1)
1
нельзя мажорировать сходящимся интегралом, не зависящим от
параметра.
3754.	Показать, что интеграл
4-оо
/= J aeaxdx
О
сходится: 1) равномерно в любом промежутке 0 < а < а < Ь;
2) неравномерно в промежутке 0 < а < Ь.

358
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
3755.	1. Доказать, что интеграл Дирихле
+оо
/ = |
о
сходится: а) равномерно на каждом сегменте [а, 6], не содержа¬
щем значения а = 0; б) неравномерно на каждом сегменте [а, Ъ],
содержащем значение а = 0.
2.	Исследовать на равномерную сходимость интеграл
+ 00
J ха
1
в следующих промежутках: а) 1 < а0 < а < +°о; б) 1 < а < +°о.
3.	Показать, что интеграл
I
о
dx
*а+ 1
сходится неравномерно в интервале 1 < а < +оо.
Исследовать на равномерную сходимость в указанных про¬
межутках следующие интегралы:
1
3756.	a) J ^ (0 < а < 1);
о
б) J е “* sin х dx (0 <а0< а < +°о).
о
4-00
3757.	J хае~х dx (а < а < Ь).
О
4-00
3758.	f 22^ dx (-оо < а < +оо).
J 1 + х2
-оо
4-оо
3759. f -—(0 < а < +°°).
J (*-а)2+1
о
4-оо
3760.	a) J ^M-e-^dx (0 < а <+оо);
О
+ оо
б) f I¥£dx (О < 10).
J xjx

§ 2. Несобственные интегралы, зависящие от параметра
359
+ 00
3761. Г
е-ах cosxdx
J
ХР
1
4 со
3762. f
Vae-"*2 dx
J
0
+ оо
3763. f
е-(х-а)г dx;
J
-со
4-сю
3764. а)
Г е-х2(.1 + У2)
о
+ оо
б) Г sis*! dx
J 1 + XP
0
(0 < a < +oo), где p > 0 фиксировано.
(0 < a < +oo).
a) a < a < b; 6) -oo < a < +oo.
sin x dy (-00 < x < +°o);
ip> 0).
3765. Подобрать число b > 0 так, чтобы
f 	< в при 1,1 < р < 10, где в = 10 6.
J 1 + хр
ъ
1
j* хр ~ 1 In'7 i djc; а) р > р0 > 0; б) р > 0 (q > -1).
0
1
3767. f	■ dx (0 < п < +оо).
J л/Г^2
3766.
3768. f sin± 4*	(0 < п < 2).
J х хп
3769.
Г x*dx	(|a, < Г|
J \J(x- 1)(лг- 2)2 ^	2J
3770. Г sina* dx (0 < a < 1).
J VI* - ocl
J\x - a|
и
3771. Интеграл называется равномерно сходящимся при дан¬
ном значении параметра, если он равномерно сходится в неко¬
торой окрестности этого значения. Доказать, что интеграл
a dx
а2х2
сходится равномерно при каждом значении а ^ 0 и не сходится
равномерно при a = 0.

360
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
3772.	Законен ли переход к пределу под знаком интеграла в
выражении
+оо
lim Г ае~ах dx?
а -» +оо J
0
3773.	Функция f(x) интегрируема в промежутке (0, +оо). До¬
казать формулу
+ оо
lim
а — +оо
+ оо
J f(x) dx.
о
3774.	1. Доказать, что если f\x) абсолютно интегрируема на
[а, +оо], то существует lim f(x).
X — ОО
2. Доказать, что
+оо
lim Г f(x) sin пх dx = О,
n-*oo J
О
если f(x) абсолютно интегрируема в промежутке (0, 4-оо).
3775.	Доказать, что если: 1) f(xy у) =► f(xy у0) в каждом ко-
+оо
нечном интервале (а, Ъ); 2) \f(xy у)| < F(x)y где Г F(x) dx < 4-оо, то
+ оо	+оо
lim f(xy у) dx = lim f(xy у) dx.
У^Уо J	J	У^Уо
a	a
3776.	1. Вычислить интеграл
+oo	+oo
J lim +
0	0
используя предельный переход под знаком интеграла.
2. Пусть f(x) непрерывна и ограничена на [0, +оо). Доказать,
lim -
г/ —* о п
+оо
I
ЩЩчх-Ц 0).
X2 + у2
что

§ 2. Несобственные интегралы, зависящие от параметра
361
3777.1.	Найти
+ оо
dx
хп + 1
2. Доказать, что интеграл
*“)-1
е-(х-а)2 dx
есть непрерывная функция параметра а.
3778. 1. Показать, что
F( а) =
1 sin-
= —
J ха
dx
есть непрерывная функция в интервале 0 < а < 1.
2. Определить точки разрыва функции
F(a) = J
Построить график функции у = F(a).
Исследовать на непрерывность в указанных промежутках
следующие функции:
3779.	F(а) = J	при а > 2.
0
+оо
3780.	F(a) = J dx при а > 0.
1
П
3781.	F(а) = f sinx s dx при 0 < а < 2.
J дс“(я-дс)“
3782. F(a) =
0
+ оо
1
О
-Ьоо
|sinjc|a
dx при 0 < а < 1.
3783,
Да) = J ае~ха2 dx при -оо < а < +оо.

362
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
§ 3. Дифференцирование и интегрирование
несобственных интегралов под знаком интеграла
1.	Дифференцирование по параметру. Если: 1) функция /(*, у) не¬
прерывна вместе со своей производной fy (*, у) в области а < х < +°°,
+ оо	4-00
Уi < У < Уг> 2) I f{xy у) dx сходится; 3) J fy (*, у) dx сходится равно-
а	а
мерно в интервале (уи у2), то
4-00	400
щ J /(*. у) dx = J fy (х, у) dx
а	а
при ух < у < у2 (правило Лейбница).
2.	Формула интегрирования по параметру. Если: 1) функция
f(xy у) непрерывна при х > а и ух < у < у2
;2)J
f(xt у) dx сходится рав-
(1)
номерно в конечном сегменте [уи у2], то
У 2 +оо	+оо	У 2
J dy J f(x, у) dx = J dx J f(x, y)dy
У i«	«	У\
Если f(x, у) > 0, то формула (1) верна также и для бесконечного
промежутка (уи у2) в предположении, что внутренние интегралы равен¬
ства (1) непрерывны и одна из частей равенства (1) имеет смысл.
3784.	Пользуясь формулой
1
- 1 Wv = I
J
х” * dx = - (п > 0),
п
вычислить интеграл
1
I = j хп 1 lnm х dx, где т — натуральное число.
3785.	Пользуясь формулой
f -£	*= <«>
J х2 + а 2 Ja
0),
вычислить интеграл
+оо
/ = Г ——-, где п — натуральное число.
J (x2 + a)n + 1

§ 3. Дифференцирование и интегрирование несобственных интегралов
363
3786.	Доказать, что интеграл Дирихле
/(a)- J
О
———— dx
X
имеет при а * 0 производную, однако ее нельзя найти с помощью
правила Лейбница.
Указание. Положить ах ** у.
3787.	Показать, что функция
:dx
F(а)« Г -—2S**.
J 1 + (* + а)2
о
непрерывна и дифференцируема в области -оо < а < +оо.
3788.	Исходя из равенства
ь
- f dy,
-j
вычислить интеграл
+ 00
J е °*“-е *** ^ (а > О, b > 0).
о
3789. Доказать формулу Фруллани
+ оо
f	dx = д0) 1п6 (а > 0, 6 > 0),
J	X	CL
О
+оо
где f(x) — непрерывная функция и интеграл j* dx имеет
А
смысл при любом А > 0.
Применяя формулу Фруллани, вычислить интегралы:
4-00
3790.	J cosax- cosbx dx (a > 0, b > 0).
0
4-oo
3791.	J sinax-sinft* (a > 0> b > 0).
0
4-oo
3792.	J arctgax-7arctg»x dx (a>0)b> 0).
0

364
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
С помощью дифференцирования по параметру вычислить
следующие интегралы:
4-00
3793. J e ax2~e ^2 dx (а > О, Р > 0).
О
4-оо
4-оо
3794.	(а > О, Р > 0).
О
4-оо
3795. J	- sin тх dx (а > 0, |3 > 0).
о
4-оо
3796. J 01z£±
cos тх dx (а > 0, (3 > 0).
0
Вычислить интегралы:
1
3797.	J М1 ~ а2*22) dx (|а| < 1).
0	^
1
3798.	J	dx (|а| < 1).
о	х
4-оо
3799.	f arctga* dx.
J x2Jx2- 1
1
4-oo
3800.	f lnif + xpdx.
J	P2 + JC2
n
0
4-oo
4-oo
ggQj f arctga* arctgP*
* J *2
о
4-oo
dx.
4-oo
3802.	f .l»(lt-a.2x.2).ln(1 + P2^2)djc.
J	x4
0
3803.	Вычислить интеграл Эйлера—Пуассона
4-оо
/= J e-*2dx,
О
одя из формулы
/2 =
= J е~*2 dx J xe~x2y2dy.

§ 3. Дифференцирование и интегрирование несобственных интегралов
365
Пользуясь интегралом Эйлера—Пуассона, найти следующие
интегралы:
+ оо
3804.	J е-(а*2+2<>*+с) dx (а > 0, ас - Ь2 > 0).
—оо
+ оо
3805.	J (ахх2 4- 2bYx + c1)e-(ax2 + 26x + c>djc (a > 0, ас - b2 > 0).
-оо
+оо
3806.	J е~а%2 ch bx dx (a > 0).
-oo
4-00
3807.	*2)dx (a > 0).
о
+ oo
3808.	f e ax2-e^x2dx (a > 0, P > 0).
J	X2
0
4-00
3809.	J e~a%2 cos bx dx (a > 0).
о
4-00
3810.	a) J xe~ax2 sin bx dx (a > 0);
о
4-oo
6) J x2ne~x2 cos 2bx dx (n — натуральное число),
о
3811.	Доказать, что
5
lim Jx Г e~axt2 dt — (a > 0, 5 > 0).
x — 4-oo J	tya
-8
3812.	1. Исходя из интеграла
-foo
1(a) = J e-ax^^-dx (a > 0),
0
вычислить интеграл Дирихле
4-oo
£>(p)= J sislid*.
0

366
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
2. Какой примерно вид имеет график интегрального синуса
y = Six,
где
Si*-J
sinf
dtl
Используя интегралы Дирихле и Фруллани, найти следую¬
щие интегралы:
+ оо
3813 f е~а*г - cospx dx (а>0)
J х2
о
+ оо
3814.	J sina*sinp«dx (|a|^|p|j.
О
+оо
3815.	J sina*cosp*da.
3816.
О
+оо
I
О
+ 0О
sin3 &х
X
dx.
3817.
I (-
sin а х у
dx.
о
+оо
3819.
; dx.
х
Г sin4*
J *2
о
+оо
3820.	J sin<q*-sin?p*djt. (ар^0).
О
+оо
3821.	J siy2) dx.
^sina*j3
3818. J [ j
0
+oo
3822.	J e~kx sina*sinP* dx (fe > o, a > 0, p > 0).
0
3823.	Найти разрывный множитель Дирихле
-boo
D(x) = - f sin X cos Xx^
к j	X
для различных значений x. Построить график функции у = D(x).

§ 3. Дифференцирование и интегрирование несобственных интегралов
367
3824.	Вычислить интегралы:
a) v. р. f	dx. 6)v.p. f SBS3£ dx.
J x + b	J x+b
3825.	Пользуясь формулой
тЬ - J ‘-•""’'“у-
вычислить интеграл Лапласа
Г cost
J 1 +
L = |
r2
3826.	Вычислить интеграл
г _ f xsinax
1 J 1 + *
dx.
Вычислить интегралы:
3827.
Г sin2*
J 1 + x2
dx.
3828,
о
+ oo
Г cos ад:
'■ J а**2)2
о
+oo
dx.
3829. f	„соапа,х— dx (a > 0, ac - b2 > 0).
J ах2 + 2Ь* + с
о
3830.	Пользуясь формулой
+oo
1 = 2 f e_xy2 dy (JC > Q)
*Jx *]n J
0
вычислить интегралы Френеля
+ oo
+oo
Г sin(*2) dx =
| f
dx;
J
2 J
fx
0
0
+oo
+oo
Г cos (x2) dx =
l f
^dx.
J
0
2 J
0
Jx

368
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
Найти интегралы:
3831.	J sin (ах2 + 2Ъх + с) dx (а * 0).
-оо
+ оо
3832.	J sin х2 cos 2ах dx.
—оо
+оо
3833.	J cos х2 cos 2ах dx.
-ОО
3834.	Доказать формулы:
+ оо	+оо
1Ч Г совал: , _ я	0\ Г л; sin ал; * _ я
1} J ^2 dx~Ta 8Ш аа; 2) J ^TJi- dx ~ ~ 2 C°S а“’
О	о
где а & 0 и интегралы понимаются в смысле главного значения
Коши.
3835.	Найти преобразование Лапласа
F(p) « J е*№ dt (р> 0)
для функции f(t)9 если:
а)	f(t) = tn (п — натуральное число);
б)	т = 7i ;
в)	№ = е“';
г)	f(t) = te~at;
д)	f(t) = cos t;
е)	№ =	;
ж)	/(0 = sir* aV* •
3836.	Доказать формулу (интеграл Липшица)
+оо
Г e~atJ0(bt) dt =	1 (a > 0),
J	Ja2 + fe2
я
где J0(x) = I f cos(x sin (p) d(p — функция Бесселя 0-го индекса
nj
о
(см. задачу 3726).

§ 4. Эйлеровы интегралы
369
3837.	Найти преобразование Вейерштрасса
+оо
e'(x'y)2f(y)dy’
-ОО
если:
a) f(y) = 1; б) f(y) = у2\ в) f(y) = е2ау; г) f{y) = cos ay.
3838.	Многочлены Чебышева—Эрмита определяются фор¬
мулами
Нп(х) = (-1 Уе*2 £-п (е-2) (п = 0, 1, 2, ...).
Доказать, что
4-0°	г
*	0,	если т& п;
}	-	2.„!Л, вслЯт-„.
-ОО	*■
3839.	Вычислить интеграл
<р(х)=—^— Г е 2	(Oj > 0, о2>0),
2а ПО 102 J
-оо
имеющий важное значение в теории вероятностей.
3840.	Пусть функция f(x) непрерывна и абсолютно интегри¬
руема на промежутке (-оо, +оо).
Доказать, что интеграл
и(х, t) = 	i—
2	njnt
удовлетворяет уравнению теплопроводности
ди _ 1 д2и
dt a2dx2
и начальному условию
lim и(ху t) = f(x).
о
§ 4. Эйлеровы интегралы
1.	Гамма-функции. При х > 0 имеем:
О
Основное свойство гамма-функции выражается формулой понижения
Т(х + 1) - хТ(х).

370
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
Если п — целое положительное число, то
Г(п) = (п - 1)!; г( « + |) =	Л ■
2.	Формула дополнения. При х, не равном целому числу, имеем
Г(х)Г(1 - х) =
smTtJt
Эта формула позволяет определить гамма-функцию для отрицатель¬
ных значений аргумента.
3.	Бета-функция. При х > 0 и у > 0 имеем
1
В(*. у)= J t'-'a-ty-'dt.
о
Справедлива формула
3841.	Доказать, что гамма-функция Г(х) непрерывна и обла¬
дает непрерывными производными всех порядков в области х > 0.
3842.	Доказать, что бета-функция В(я, у) непрерывна и обла¬
дает непрерывными производными всех порядков в области х > 0,
У> 0.
С помощью эйлеровых интегралов вычислить следующие ин-
тегралы:
1
a
3843.
Г Jx - х2 dx.
3844. [x24a?~-
J
0
J
0
4-оо
4-oo
3845.
f
3846. f dx.
J U + *)2
J l + x*
0
0
71
4-00
2
3847.
Г x 2dx
3848. f sin6 x
J 1 + x4 *
J
0
0
1
3849.
f dx (n > 1).
j Vl-X»
3850. J х2пе~х2 dx (п — целое положительное).

§ 4. Эйлеровы интегралы
371
Определить область существования и выразить через эйлеро¬
вы интегралы следующие интегралы:
+ оо
3851.
J
0
+ оо
3853.
J
0
Ь
3854.
а
1
3855.
f
3857
f 2Z±dx (п > 0).	3852. f
J l + xn	J (1 + *)"
о
f *mdx (a> 0, b> 0, n> 0).
J (a + bxnf
f	XY dx (0 <a<b;c> 0).
J (x+c)mtn + 2
71
2
(m > 0).	3856. f si
o	J
n
2
jtg-«
dx.
3856. J sinm x cos'1 x dx.
о
: dx.
3858. f ■-dx fo < \k\ < l). 3859. f «-** dx (n > 0).
J (1 + fccos*)" V 1 1 J	J
о
+ oo	1
3860. J xme-*"dx.	3861. J (in i)
0	0
+ oo	i-oo
3862. J xpe-axlnxdx (a > 0).	3863. J
dx.
dx.
3864. a) f	dx-, 6) f Z^dx; в) f	dx.
J 1 + x	J 1 + %3	J 1 +%4
3865.
f xP~1
J (1 +
- X*l-
0
+ oo
x)\nx
■ dx.
3866.
J z^Ldx (0 < p < 1).
Указание. Этот интеграл можно рассматривать как
lim [В(р, е) - В(1 - р, е)].
е — со
+ оо	1
3867. J dx (0 < а < р).	3868. J In Г(*) dx.

372
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
3869
J In Г(х) dx (а > 0).	3870. J* In Г(л;) sin пх dx.
а	0
1
3871. J In Г(х) cos 2ппх dx (п — натуральное число).
Доказать равенства:
1 1
3872.
J VT^T4 J
x2dx _ к
Л - х4 J Jl-x4 4
и	0
Ч-оо	Ч-оо
3873.	J е~х* dx • J x2e~x*dx = -2- .
0	0	*
п +°°	j
3874.	Ц f *— dx = Qj"(2я)^.
т = 1 о
4-оо
3876. lim f e-*ndx = 1.
n-*oo J
О
4-оо
Используя равенство ^	J tm~le~xt dt (х > 0), найти
интегралы:
4-оо
3876. J
0
совал:
хт
4-сю
3877. f
sin ал:
хт
3878.	Доказать формулы Эйлера:
а)	J tx leu cos a(kt sin a) dt = cos ал:;
о
4-оо
б)	J tx ~ 1е~и 008 “ sin(A.t sin а) dt = sin ах
о
(Х> 0, *> 0, -|< а< |).

§ 5. Интегральная формула Фурье
373
3879.	Найти длину дуги кривой
rn = ап cos щ (а > 0, п — натуральное).
3880.	Найти площадь, ограниченную кривой
\х\п + \у\п = ап (п > 0, а > 0).
§ 5. Интегральная формула Фурье
1. Представление функции интегралов Фурье. Если: 1) функция
f(x) задана на оси -оо < х < +оо, 2) кусочно-непрерывна вместе со своей
производной f\x) в каждом конечном промежутке и 3) абсолютно ин¬
тегрируема на интервале (-оо, +оо), то во всех своих точках непрерыв¬
ности она допускает представление в форме интеграла Фурье:
где
f(x) = J [а(Х) cos Хх + b(X) sin Хх] dX,	(1)
о
-f ОО	-f оо
а(Х)=± f № cos d\ и b(k) = i f f(£) sin Ц, d\.
n J	я J
В точках разрыва функции f(x) левая часть формулы (1) должна быть
заменена на | [f(x + 0) + f(x - 0)].
Для четной функции f(x)9 с тем же замечанием относительно точек
разрыва, формула (1) дает:
где
/(*) =
+оо
cos Хх dXy
+оо
a(X) = | J т cos Ц, d^.
о
(2)
Аналогично для нечетной функции f(x) получаем
+ оо
f(x) = J b(X) sin Хх dX,
о
(3)
+оо
Ь(Х) - | | №) sin ц, d\.
0
где

374
РАЗДЕЛ VII. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
2. Представление функции интегралом Фурье в интервале (0, +°°).
Функция f(x), заданная в интервале (0, +°°), и кусочно-непрерывная
вместе со своей производной f(x) на каждом конечном интервале (a, b) С
С (0, +°°), абсолютно интегрируемая на (0, +°°), по желанию может быть
представлена в данном интервале или формулой (2) (четное продолже¬
ние), или формулой (3) (нечетное продолжение).
Представить интегралом Фурье следующие функции:
3881. f(x) =
1, если \х\< 1;
О, если |jc| > 1.
3882.	fix) — i*®11 Х> если J*| <
10, если |л:| > 1.
3883.	f(x) — sgn (х - a) - sgn (дс - Ь) (Ь > а).
h { 1 - если Ы < а;
3884.	fix) = ^ I а) 11
0,	если |х| > а.
3885.	f(x) =
3886.	fix) =
3887.	fix) =
а‘ + хс
(а > 0).
(а > 0).
а* + х*
Jsin*, если |х| < п;
10, если |х| > п.
3888. fix) =
cosx, если |дс| < ^ ;
0, если \х\ > |.
Сл
3889. f(x) = <
Asinwi, если |f| <	;
О)
0,	если \t\ > —
0)
(п — натуральное число).
3890.	f(x) = е-М (а > 0).
3891.	fix) = е~°№ cos рх (а > 0).
3892.	fix) = е~°М sin р* (а > 0).
3893.	fix) = е~*2.
3894.	fix) = хе~*г.

§ 5. Интегральная формула Фурье
375
3895.	Функцию
f(x) = е~х (0 < х < +оо)
представить интегралом Фурье, продолжая ее: а) четным обра¬
зом; б) нечетным образом.
Найти преобразование Фурье
+ оо	I
F(x) = -L f f(t)e4tx dt= -L Иш f f(t)e-“x dt
J2n J	J2n 1 +0° J
-OO	-/
для функции f(t)9 если:
3896.	f(x) = <Г“М (a > 0).
3897.	f(x) = xe~aM (a > 0).
if
3898.	f(x) = e 2 .
-if
3899.	/(*) = e 2 cos ax.
3900.	Найти функции ф(л:) и \|/(jc), если:
+ оо
а)	J Ф(у) cos ху dy = -^—г;
о
+•00 б)б)	J ф(у) sin ху dy = ех (х > 0).
0

РАЗДЕЛ VIII
КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 1. Двойные интегралы
1.	Непосредственное вычисление двойного интеграла. Двойным ин¬
тегралом от непрерывной функции f(x, у), распространенным на огра¬
ниченную замкнутую квадрируемую область £1, называется число
f(x, у) dx dy = lim Y Y f(x,, у,)Ах,Ьу,,
max ДхЛ -*■ 0
max|At/j —> 0	1	1
где Ajc* = xl + j - xly Ayj = у} + х - у} и суммирование распространяется на
те значения i и у, для которых (xit yj) € £1.
Если область £1 задана неравенствами
я
а< х< Ь, ух(х) < у < у2(х),
где уг(х) и у2(х) — непрерывные функции на сегменте [а, Ь], то соответ¬
ствующий двойной интеграл может быть вычислен по формуле
ь у2(х)
у) dx dy = j* dx J f(x, y) dy.
Q	a yx{x)
2.	Замена переменных в двойном интеграле. Если непрерывно диф¬
ференцируемые функции
X = х(и, и), у - у(и, и)
осуществляют взаимно-однозначное отображение ограниченной и зам¬
кнутой области £1 в плоскости Оху на область £2' в плоскости Ouv, и
якобиан
/_ °(х’ У)
D(u, v)
сохраняет постоянный знак в £1 за исключением, быть может, множе¬
ства меры нуль, то справедлива формула

§ 1. Двойные интегралы
377
В частности, для случая перехода к полярным координатам г и ср по
формулам х — г cos <р, у — г sin (р имеем
JJ f(x> у) dx dy = JJ f(r cos cp, r sin cp)r dr dcp.
a	a
3901.	Вычислить интеграл
JJ xу dx dy,
1
О ч у < 1
рассматривая его как предел интегральной суммы, разбивая об
ласть интеграции на квадраты прямыми
x=-,y=J-	(i, j= 1, 2, .... п- 1)
п	п
и выбирая значение подынтегральной функции в правых верх¬
них вершинах этих квадратов.
3902.	Составить нижнюю £ и верхнюю S интегральные сум¬
мы для функции f(x, у) = х2 + у2 в области 1<х<2, 1<у<3,
разбивая последнюю на прямоугольники прямыми
x=l + -,y=l + ^i (i, j = 0, 1	п).
п	п
Чему равны пределы этих сумм при п °о?
3903.	Вычислить приближенно интеграл
я
dxdy
хг + уг<,2Ь
л/24
+ X
2+у2
аппроксимируя область интеграции системой вписанных квад¬
ратов, вершины которых Ду находятся в целочисленных точках,
и выбирая значения подынтегральной функции в вершинах этих
квадратов, наиболее удаленных от начала координат. Сравнить
полученный результат с точным значением интеграла.
3904.	Приближенно вычислить интеграл
JJ Jx + y dS,
s
где S — треугольник, ограниченный прямыми х — 0, у = 0 и
х + у = 1, разбив область S прямыми х = const, у = const, х + у = const
на четыре равных треугольника и выбрав значение подынтеграль¬
ной функции в центрах масс этих треугольников.

378
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
3905. Область S{jc2 + у2 < 1} разбита на конечное число квад¬
рируемых частей ASt (i = 1, 2, ..., п) диаметра меньше чем 5. При
каком значении 8 будет обеспечено выполнение неравенства
и/1
sin (jc + у) dS - ^ sin (х, + t/f)AS,
где (*„ у,) 6 AS,?
< 0,001,
/ = i
Вычислить интегралы:
i i
1 X
3906. f dx f (* + у) dy.
3907. f dx f
J J
0 0
J J
0 *2
2n a
3908.	J dip J r2 sin2 cp dr.
0 0
3909.	Доказать равенство
JJ X(x)Y(y) dx dy =
R
J
Y(y) dyt
если R — прямоугольник: a< x< A, b < у < В и функции Х(х)
и Y(y) непрерывны на соответствующих сегментах.
3910. Вычислить
А В
I = J dx J /(*, у) dy,
а Ь
если
3911. Пусть /(*)
а< х< Ь.
Доказать неравенство
г-Ь	-,2
\^f{x)dx
f(x, у) = F'x'y(x, у).
непрерывная функция в промежутке
< (b - a)j f(x) dx,
где знак равенства имеет место лишь, если f(x) = const.
Указание. Рассмотреть интеграл
ь ь
J dx J [f(x) - f(y)f dy.

§ 1. Двойные интегралы
379
3912.	Какой знак имеют интегралы:
a) JJ* 1п(х2 + у2) dx dy;
М + Ы<1
б) IT	VI - (X2 - у2) dx dy;
х2 + у2< 4
в)	JJ arcsin(* + у) dx dyl
О < JE < 1
-1 < у < 1 -X
3913.	Найти среднее значение функции
f(x, у) = sin2 х sin2 у
в квадрате 0 < дс < я, 0 < у < п.
3914.	Пользуясь теоремой о среднем, оценить интеграл
j = f f 	dxdy
JJ 100+cos2jc-»-
W + M<io
cos2 у
3915.	Найти среднее значение квадрата расстояния точки
круга (х - а)2 + (у - Ь)2 < Й2 от начала координат.
В задачах 3916—3922 в двойном интеграле J J f(x, у) dx dy
о
расставить пределы интегрирования в том и другом порядке для
указанных областей Q:
3916.	Q — треугольник с вершинами О (О, 0),А (1, 0), В (1,1).
3917.	Q — треугольник с вершинами О (0, 0), А (2, 1), В (-2, 1).
3918.	Q — трапеция с вершинами О (0, 0), А (1, 0), В (1, 2),
С( 0, 1).
3919.	Q — круг х2 + у2 < 1.
3920.	Q — круг х2 + у2 < у.
3921.	Q — параболический сегмент, ограниченный кривыми
у — х2 и у — 1.
3922.	Q. — круговое кольцо 1 < х2 + у2 < 4.
3923.	Доказать формулу Дирихле
а х
J dxj f(x, у) dx =
о о
J dy J f{x, у) dx
о у
(а > 0).

380
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Изменить порядок интегрирования в следующих интегралах:
2х
2-х
3924. j* dx j* f(x, у) dy. 3925. j* dx j* f(x, y) dy.
X2
T-1
l-x2
3926. j* dx J /(x, y) dy.	3927. J dx J	/(x, y) dy.
-Jl - X2
J2x - j
-1
2n
J2ax
3928. J dx J f(x, y) dy. 3929. J dx J f(x, y) dy (a > 0).
1	2~x	0	hax-x*
e lnx	271 sin*
3930. j* dx j* f(x, y) dy. 3931. j* dx J f(x, y) dy.
10	oo
Вычислить следующие интегралы:
3932.	j*j*jcp2 dx dy, если область Q ограничена параболой
у2 = 2px и прямой х = 2 (р > 0).
3933. Г Г dxdy ^а >	если область Q ограничена кратчай-
J J V2 а - х
Q
шей дугой окружности с центром в точке (а, а) радиуса а, касаю¬
щейся осей координат, и осями координат.
3934.	j*j* \ху\ dx dy, если £2 — круг радиуса а с центром в на-
Q
чале координат.
3935.	j*J (х2 + у2) dx dy, если Q — параллелограмм со сторо-
Q
нами у = х, у = х + а, г/ = а и г/ = За (а > 0).
3936.	j*j* г/2 da; dp, если Q ограничена осью абсцисс и первой
Q
аркой циклоиды jc = a(t - sin 0» У = я(1 ~ cos t) (0< t< 2п).
В задачах в двойном интеграле Jj* f(x, у) dx dy перейти к по-
Q
лярным координатам г и ср, полагая х = г cos ср и у = г sin ср, рас¬
ставить пределы интегрирования, если:
3937.	Q — круг jc2 + у2 < а2.
3938.	Q — круг х2 + р2 < ajc (a > 0).

§ 1. Двойные интегралы
381
3939.	Q — кольцо а2 < х2 + у2 < Ь2.
3940.	Q — треугольник 0<лс<1;0<г/<1-лс.
х2
3941.	Q — параболический сегмент -а < х < а; — < у < а.
а
3942.	В каком случае после перехода к полярным координа¬
там пределы интегрирования будут постоянные?
Перейти к полярным координатам г и ср, полагая х = г cos ср
и у = г sin ср, и расставить пределы интегрирования в том и дру¬
гом порядке в следующих интегралах:
1
1
1 J1-X2
3943.
J
dx f f(x, у) dy.
3944. f dx f f(x, y) dy.
0
J
0
J J
0 l-x
2
xJZ
1 *2
3945.
J
dx f f(Jx2 + y2) dy.
3946. f dx f /(*, y) dy.
0
J
X
J J
0 0
3947.
J.
Г f(x> y) dx dy, где область Q ограничена кривой
Q
(x2 + у2)2 = a2(x2
- y2) (x > 0).
Полагая, что г и ср — полярные координаты, изменить поря¬
док интегрирования в следующих интегралах:
п
2 acoscp
3948. J dtp J /(ф, г) dr (а > 0).
a Vsin 2 <р
3949.	J dcp j* (/ср, г) dr (a > 0).
о	о
а ф
3950.	J dcp J /(ср, г) dr (0 < а < 2п).
Перейдя к полярным координатам, заменить двойные интег¬
ралы однократными:
3951.	f f /(Jx2 + у2) dx dy.
х2 + у2<1
3952.	j*J f(Jx2 + у2) dx dy, где Q = |i/| < \x\; \x\ < 1
Я fl*)dxdy-
x2 + y2<x
3953.

382
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Переходя к полярным координатам, вычислить следующие
двойные интегралы:
3954.	JJ Jx2 + y2dx dy.
х2 + у2<а2
3955.	JJ sin//*2 + У2 dx dy.
n2 < x2 + y2 < 4it2
3956. Квадрат S{a < x < a + h9 b < у < b + h}9 (a > 0, b > 0) c
помощью системы функций
U=	V = Jxy
преобразуется в область S'. Найти отношение площади области
S' к площади S. Чему равен предел этого отношения при h -* 0?
Вместо х и у ввести новые переменные и и v и определить
пределы интегрирования в следующих двойных интегралах:
Ь рх
3957. J dx J /(х9 у) dy (0 < а < Ь; 0 < а < (3), если
и — Ху V
= а.
2	2-х
3958.	J dx J /(Ху у) dyf если и = х + у9 v = х - у.
0	1-х
3959.	JJ f(Xy у) dx dy9 где область Q ограничена кривыми
о
Jx + Jy = Ja у х = 9, у = 0 (а > 0), если
х — и cos4 Vy у = и sin4 v.
3960.	Показать, что замена переменных
* + У = 5. У =
переводит треугольник 0<jc< 19 0 < у < 1 - х в единичный
квадрат 0<£< 1,0<Г|< 1.
3961.	При какой замене переменных криволинейный четырех¬
угольник, ограниченный кривыми ху = 19 ху = 29 х - у + 1=0,
х - у - 1 = 0 (х > 0, у > 0), перейдет в прямоугольник, стороны
которого параллельны осям координат?

§ 1. Двойные интегралы
383
Произведя соответствующие замены переменных, свести
двойные интегралы к однократным:
3962.	JJ f(x + у) dx dy.
1*1 + М < 1
3963. Г Г f(ax + by + с) dx dy	(а2 + b2 * 0).
*2 + t/2< l
3964.	JJ f(xy) dx dy, где область Q ограничена кривыми
Q
xy = 1, xy = 2, у = *, у = 4* (* > 0, у > 0).
Вычислить следующие двойные интегралы:
3965.	JJ (х + у) dx dy, где область Q ограничена кривой
о
х2 + у2 = х + у.
3966
|| (W + M) dxdy.
М + Ы<1
3967.	JJ Jl -	~ cte dy, где область Q ограничена эллип¬
сом 2* + g - 1.
a2 b2
3968.	||	(x2 + y2) dx dy.
x4 + y4^l
3969.	JJ (x + y)dx dy, где область Q. ограничена кривыми
у2 = 2х, х + у = 4, х + у = 12.
3970.	JJ jci/ rfjc dy, где область Q. ограничена кривыми xy = 1,
х + у= |,
* 2
3971.	JJ |cos (jc + у)| d* dy.
О < X < 71
О < у < я
3972.
Я
2 + у2<1
|| VIУ - Х2\ dx dy.
dx dy.
N<i
0<j/<2
3973.

384
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Вычислить интегралы от разрывных функций:
3974. JJ sgn (х2 -у2 4-2) dx dy.
х2 + у2 < 4
3975.	JJ [х + у] dx dy.
2
0<j/<2
3976.	JJ J\y - х2\ dx dy.
JJ хтуп dx dy = О,
х2<у< 4
3977. Доказать, что
х* + уг^аг
если тип — целые положительные числа и по меньшей мере
одно из них нечетно.
3978.	Найти
lim -Ц ГГ f(x, у) dx dy,
p-о яр2 JJ
Х2 + У2 P2
где f(x, y) — непрерывная функция.
3979.	Найти F'(t), если
F(t) = f f ey2 dx dy.
0<x<t
0 <y<t
3980.	Найти F'(t), если
F(t)= JJ Jxz + yz dx dy.
(X-t)2 + (y~t)2<: 1
3981.	Найти F'(t), если
F(t) = JJ f(x, y) dx dy (t > 0).
ДC2 + l/2 < *2
3982.	Доказать, что если f(x, i/) непрерывна, то функция
*	Je + t/-£
u(x, i/) = | J J /(£, л)
o	*>-x + y
удовлетворяет уравнению

§ 2. Вычисление площадей
385
3983.	Пусть линии уровня функции f(x> у) — простые замк¬
нутые кривые и область S(ul9 v2) ограничена кривыми f(x, у) =
и f(x9 у) = v2.
Доказать, что
JJ f(x, у) dx dy = |
S(VVV2)	VX
vF'(v) dv9
где F(u) — площадь, ограниченная кривыми /(jc, у) — щ и /(jc, у) = и2.
Указание. Область интегрирования разбить на части, ограни¬
ченные бесконечно близкими линиями уровня функции f(x> у).
§ 2. Вычисление площадей
Площадь области S, расположенной в плоскости Оху> дается фор¬
мулой
5 =
Я-
s
Найти площади, ограниченные следующими кривыми:
3984.	ху = a2, jc + у = | а (а > 0).
3985.	у2 = 2pjc + р2, р2 = -2gjc + q2 (р > 0, р > 0).
3986.	(jc - у)2 + jc2 = а2 (а > 0).
Переходя к полярным координатам, вычислить площади, ог¬
раниченные следующими кривыми:
3987.	(jc2 + у2)2 = 2а\х2 - у2); х2 + у2 > а2.
3988.	(jc3 + у3)2 = jc2 + р2, jc > 0, р > 0.
3989.	(х2 + у2)2 = а(х3 - Зху2) (а > 0).
3990.	(х2 + у2)2 = 8а2ху; (jc - а)2 + (р - а)2 < а2 (а > 0).
Вводя обобщенные полярные координаты г и ср по формулам
jc = ar cosa ср, р = 6r sina ф (г > 0),
где a, b и а — надлежащим образом подобранные постоянные, и
учитывая, что -	= aa&r cosa~1 ф sina_ 1 ф, найти площади,

386
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
ограниченные следующими кривыми (параметры считаются по¬
ложительными):
3991. ^ + Ul = * + К.
Ъг
3
h k
r2	j,2
3992-^ + ^-|i+fe;A:-0-!'-0'
s993-(s + Й* " P + ё <»>°.!'>0)-
3994.a)^+g),=g-g(«>0,i,>0,;
6)f£ + u)* =
; U bj c4
з995--Л
Производя надлежащую замену переменных, найти площади
фигур, ограниченные следующими кривыми:
3996.	х + у = а, х + у = Ь,у = ах, у = (Зд: (0 < а < Ь; 0 < а < (3).
3997.	лсг/ = а2, дгг/ = 2а2, г/ = х, у = 2х (х > 0; у > 0).
3998.	а) г/i 2 = 2рх, у2 = 2qx, д;2 = 2п/, д;2 = 2sy (0 <р < q; 0 < г < s);
б)	д:2 = ау, х2 = 6г/, д:3 * 5 = су2, Xs = dy2 (0 < а < 6; 0 < с < d);
в)	у = ад;р, */ = Ъхр, г/ = сд;7, г/ = dx*7 (0 < р < q; 0 < а < Ь;
О	< с < d).
-=£,в-=£ (*> о, г/> 0).
а о а о
4000.	£ +	= 1, где X принимает следующие значения:
А А- с3
i с2, ^ с2, ^ с2, 5 с2 (JC > 0, у > 0).
3	3	3	3	у
4001.	Найти площадь, ограниченную эллипсом
(aj* + Ь±у + сх)2 + (а2д; 4- 62i/ + с2)2 = 1,
где
5 = агЬ2 - а2Ьг ^ 0.

§ 3. Вычисление объемов
387
4002.	Найти площадь, ограниченную эллипсами	= с2
сп*и Stl^U
2 2
(и = и 1, и о) и гиперболами ■»- — - ■	■	= с2 (и = i>i, и2) (0 <ил< и2;
cos2 v	sin2 v
0 < vx < v2y х > 0, у > 0).
Указание. Положить х = с ch и cos l>, у — с sh и sin и.
4003.	Найти площадь сечения поверхности
х2 + у2 + z2 - ху - хг - уг = а2
плоскостью х + у + г = 0.
4004.	Найти площадь сечения поверхности
i + 1+1=о
X у Z
плоскостью 2=1- 2(х + г/).
§ 3. Вычисление объемов
Объем цилиндроида у ограниченного сверху
непрерывной поверхностью г = f(x, у)у снизу
плоскостью 2 = 0 и с боков прямой цилиндри¬
ческой поверхностью, вырезающей из плоскос¬
ти Оху квадрируемую область Q (рис. 14), равен
V =
У) dx dy.
4005.	Нарисовать тело, объем которого равен интегралу
1	1-х
= Jd* J (х2 + у2) dy.
О о
4006.	Изобразить объемы, выражаемые следующими двой¬
ными интегралами:
a)	JJ	(x + y)dxdy;	б)	||	Ji-^-l^dx dy;
0<х+у<1	**</?<-,
х»0,у>0	7 ,
в)	JJ	(x2 + y2)dxdy;	г)	JJ	Jx2 + у2 dx dy;
М + Ы<1
хг + уг < X
д) JJ Jxydx dy\ е) j*J sin njx2 + у2 dx dy.
1 < JC < 2
x < у < 2x
xz + y*<l

388
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Найти объемы тел, ограниченных следующими поверхностями:
4007.	2 = 1 + jc + у, 2 = 0, х + у = 1, х = 0, у = 0.
4008.	х + у + z = а, х2 + у2 = R2, jc = 0, г/ = 0, 2 = 0 (а > Лл/2 ).
4009.	z = х2 + у2, у = х29 у = 19 z = 0.
4010.	2 = COS X COS у, 2 = 0, \х + 1/| < 5 , |jc - i/| < 5
4011.	z = sin^ , z = 0, у = х, у = 0, х = п.
4012.	z = лгу, лг + г/ + 2 = 1,2 = 0.
Переходя к полярным координатам, найти объемы тел, огра¬
ниченных следующими поверхностями:
4013.	г2 = ху9 х2 + у2 = а2.
4014.	z = х + у, (х2 + у2)2 = 2;п/, 2 = 0 (л: > 0, у > 0).
4015.	z = x2 + у29 х2 + у2 = х9 х2 + у2 = 2х9 2 = 0.
4016.	х2 + у2 + z2 = a2, я2 + у2 > а|х| (а > 0).
4017.	х2 + у2 - аг = 0, (х2 + у2)2 = а2(х2 - у2)9 z = 0 (а > 0).
4018.	2 = е-<*2 + *2>, 2 = 0, х2 + у2 = Л2.
4019.	2 = с cos я*/*2 + У2, z = 0, у = jc tg а, у = jc tg (3, (а > О,
Z d
с> 0, 0 < а < (3 < 2я).
4020.	2 = jc2 + у29 2 = jc + у.
Найти объемы тел, ограниченных следующими поверхностя¬
ми (параметры предполагаются положительными):
4021.^+£+^=1,^+£=£?(2>0).
Ъ2
Ъ2
4022.*? +Й = -1, *f =1.
ь2
&2
4023. ~ +	*!+£=* +И*,
Ь2 с
/2\2
+
&2
* 1,2
0.
0.
«“■ё+й
4025. (2 + «V + 2! = 1, * = о, у = 0, г = 0.
\а Ъ) с2
4026. г! + и! + г! = 1, f£f + кГ)2 = г!
а2 Ь2 с2	U2 b2J й2
4027.	z2 = ху, х + у = а, х + у = b (0 < а < Ь).
у1
г>2
4028.	z = jc2 + у2, л:у = а2, ху = 2а2, у = |, у = 2л;, z = 0.
4029.	z = л;у, л;2 = у, х2 = 2у, у2 — х, у2 = 2х, г = О.

§ 4. Вычисление площадей поверхностей
389
4030.	z — с sin^^ , z = 0, ху = а2, у = ах, */ = Рх (0 < а < Р; х > 0).
а2
4031.	2 — х 2 + [/2,2 = 0, х + t/ = 1, х = 0, г/ = 0.
4033.	a) 2 = с arctg^ ,2 = 0, V*2 + У2 = а arctg^ (г/ > 0);
-Ш
6) z=ye а , ху = а2, ху = 2а2,у = т,у = п, z = 0 (0 <т< п).
4034.	— + ^ + — = 1, х = 0, у = 0, 2 = 0 (п > 0).
ап Ъп сп	*
4035.	+ £)" +	= 1, х = 0, у = 0, 2 = 0 (п > 0, т > 0).
§ 4. Вычисление площадей поверхностей
1.	Случай явного задания поверхности. Площадь гладкой криволи¬
нейной поверхности г = 2(х, у) выражается интегралом
Q
где Q — проекция данной поверхности на плоскость Оху.
2.	Случай параметрического задания поверхности. Если уравнение
поверхности задано параметрически:
X = x(uf V), у = у(и, и), 2 = 2(и, V),
где (и, v) € Q, Q — ограниченная замкнутая квадрируемая область и
функции х, у и 2 непрерывно дифференцируемы в области Q, то для
площади поверхности имеем формулу
р= дхдх + di/di/ _|_ Э2Э2
dudv dudv dudv *
где

390
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4036.	Найти площадь части поверхности аг = ху, заключен¬
ной внутри цилиндра х2 + у2 = а2.
4037.	Найти площадь поверхности тела, ограниченного по¬
верхностями х2 + г2 = а2, у2 + г2 = а2.
4038.	Найти площадь части сферы х2 + у2 + z2 = а2, заклю-
X ^ It 2
ченной внутри цилиндра -- + £- = 1 (Ь < а).
а2 о2
4039.	Найти площадь части поверхности г2 = 2д:г/, отсекаемой
плоскостями х + у = 1, х = 0, у = 0.
4040.	Найти площадь части поверхности х2 4- у2 4- г2 = а2,
расположенной вне цилиндров х2 + у2 = ±ах (задача Вивиани).
4041.	Найти площадь части поверхности z = Jx2 4- у2, заклю¬
ченной внутри цилиндра х2 + у2 = 2х.
4042.	Найти площадь части поверхности z = Jx2 - у2, заклю¬
ченной внутри цилиндра (х2 + у2)2 = а2(х2 - у2).
4043.	Найти площадь части поверхности z = |(д:2 - i/2), вы¬
резанной плоскостями х - у = ±1, х + у = ±1.
4044.	Найти площадь части поверхности х2 + у2 = 2az, заклю¬
ченной внутри цилиндра (х2 + у2)2 = 2а2ху.
4045.	Найти площадь:
а)	части поверхности х2 4- у2 = а2, вырезанной плоскос¬
тями х + z = 0, х - z = 0 (х > 0, у > 0);
3
б)	части поверхности (я2 + у2)2 + z = 1, отсекаемой
плоскостью 2 = 0;
в)	части поверхности ^	+ ^ = 1, вырезанной
г)
плоскостями х=0, 1/ = 0иг = 0;
JC2	I] 2	/ч	и
части поверхности — -	= 22, вырезанной поверх-
а Ь
ностью ^	^ = 1 (г > 0);
а2 о2
д)	части поверхности sin 2 = sh л: • sh у, отсекаемой плос¬
костями х = 1 и х = 2 (у > 0).
4046.	Найти поверхность и объем тела, ограниченного по¬
верхностями х2 + у2 = 122, х 4- у + 2 = 2а (а > 0).
4047.	Найти площадь части сферы, ограниченной двумя па¬
раллелями и двумя меридианами.

§ 5. Приложение двойных интегралов к механике
391
4048.	Найти площадь части геликоида
х = г cos ср, у = г sin ф, z = /цр, где 0<г<а, 0<ф< 2л.
4049.	Найти площадь части поверхности тора
х = (Ь + a cos \|/) cos ф, I/ = (6 + a cos \j/) sin ф, 2 = а sin \|/
(0 < а < 6), ограниченной двумя меридианами Ф = ф1э ф = ф2 и
двумя параллелями \|/ == \j/i, \j/ = \j/2.
Чему равна поверхность всего тора?
4050.	Найти телесный угол со, под которым виден из начала
координат прямоугольник x = a>090<y<b90<z<:C.
Вывести приближенную формулу для со, если а велико.
§ 5. Приложение двойных интегралов к механике
1.	Центр масс. Если х0 и у0 — координаты центра масс пластинки О,,
лежащей в плоскости Оху> и р = р(*, у) — плотность пластинки, то
х°= м JJP*dx dy'Уо=1 h JJ*pydx dy> w
a	q
где M = JJ p dx dy — масса пластинки.
Q
Если пластинка однородна, то в формулах (1) следует положить р = 1.
2.	Моменты инерции. 1хм1у — моменты инерции пластинки Q,, ле¬
жащей в плоскости Оху, относительно координатных осей Ох и Оу —
выражаются соответственно формулами
Ix = J J РУг dx dy, Iу = JJ рхг dx dy,	(2)
a	a
где p = p(jc, y) — плотность пластинки.
Рассматривается также центробежный момент инерции
IXIJ ~~ я рху dx dy.	(3)
Q
Полагая р = 1 в формулах (2) и (3), получим геометрические момен¬
ты инерции плоской фигуры.
4051.	Найти массу квадратной пластинки со стороной а, если
поверхностная плотность пластинки в каждой точке пропорцио¬
нальна расстоянию этой точки от одной из вершин квадрата и
равна р0 в центре квадрата.

392
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Найти координаты центра масс однородных пластинок, ог¬
раниченных следующими кривыми:
4052.	ау = х2, х + у = 2а (а > 0).
4053.	Jx + jjy — Ja , х = 0, у = 0.
2 2	2
4054.	хз 4-у* = а} (х > 0, у > 0).
4055.	{- + jfV = Ц (петля).
\а	Ъ)	с2
4056.	(х2 + у2)2 = 2а2ху (х > 0, у > 0).
4057.	г = а (1 + cos ср), ср = 0.
4058.	х = a (t - sin t)9 у = а (1 - cos £) (0 < £ < 2л), у = 0.
4059.	Найти координаты центра масс круглой пластинки
х2 + г/2 < а2, если плотность ее в точке М (х9 у) пропорциональна
расстоянию точки М от точки А (а, 0).
4060.	Определить кривую, описываемую центром масс пере¬
менной площади, ограниченной кривыми:
У = J2px> у = 09 х — X.
Найти моменты инерции 1Х и 1у относительно осей координат
Ох и Оу площадей (р = 1), ограниченных следующими кривыми:
4061.	г + I = 1> Г + \ = 1> У = 0 (*i > °> Ъ2 > 0, h > 0).
Oj ft	U 2 it
4062.	(х - а)2 + (у - а)2 = а2, х = 0, у = 0 (0 < х < а).
4063.	г = а (1 + cos ср).
4064.	х4 + у4 = а2(х2 + у2).
4065.	ху = а2, ху = 2а2, х = 2у, 2х = у (х> 0, у > 0).
4066.1.	Найти полярный момент
Io = JJ (*2 + у2) dx dy
s
площади S, ограниченной кривой
(х2 + у2)2 = а2(х2 - у2).
2. Найти центробежный момент инерции 1ху однородной фи¬
гуры, ограниченной кривыми
ay = x2f ах = у2 (а > 0).
4067.	Доказать формулу
I, = ч + Sd\

§ 5. Приложение двойных интегралов к механике
393
где It, /,о — моменты инерции фигуры S относительно двух параллель¬
ных осей I и 10, из которых 10 проходит через центр масс фигуры, a d —
расстояние между этими осями.
4068.	Доказать, что момент инерции плоской области S от¬
носительно прямой, проходящей через центр масс О (0, 0) и со¬
ставляющей угол а с осью Ох, равен
I	= Ix cos2 а - 2Ixy sin а cos а + Iy sin2 а,
где 1Х и 1у — моменты инерции области S относительно осей Ох
и Оу, а I — центробежный момент:
рху dx dy-
s
4069.	Найти момент инерции правильного треугольника со
стороной а относительно прямой, проходящей через центр масс
треугольника и составляющей угол а с его высотой.
4070.	Определить силу давления воды на боковую стенку х > 0
цилиндрического сосуда х2 + у2 = а2, 2 = 0, если уровень воды в нем
z = h.
4071.	Шар радиуса а погружен в жидкость постоянной плот¬
ности 8 на глубину h (считая от центра шара), где h> а. Найти
силу давления жидкости на верхнюю и нижнюю части шаровой
поверхности.
4072.	Прямой круговой цилиндр, радиус основания которого
равен а, а высота Ь, целиком погружен в жидкость плотности 8
так, что центр его находится на глубине Л под поверхностью воды,
а ось цилиндра составляет угол а с вертикалью. Определить силу
давления жидкости на нижнее и верхнее основания цилиндра.
4073.	Определить силу притяжения однородным цилиндром
х2 + у2 < а2, 0 < г < h, материальной точки Р (0, 0, b), если масса
цилиндра равна М, а масса точки равна т.
4074.	Распределение давления тела на площадку смятия
1
дается формулой р = Ро( 1 ~ ^ ~	1 • Определить среднее дав-
V а2 о1)
ление тела на эту площадку.
4075.	Луг, имеющий форму прямоугольника со сторонами
a mb, равномерно покрыт скошенной травой с погонной плотно¬
стью, равной р. Какую минимальную работу надо затратить, что¬
бы собрать все сено в центре луга, если работа по транспортиров¬
ке груза массой М на расстояние г равна НМг (0 < k < 1).

394
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
§ 6. Тройные интегралы
1. Непосредственное вычисление тройного интеграла. Если функ¬
ция f(x, у у г) непрерывна, а область V ограничена и определяется сле¬
дующими неравенствами:
хг < X < Х2, уг(х) < у < у2(х), 2г(Ху у)< 2< 22(ху у),
где Ух(х)у у2(х)у 2х(ху у)у г2(х, у) — непрерывные функции, то тройной
интеграл от функции f(x, у, z), распространенный на область V, может
быть вычислен по формуле
*2 У2^	Х2(х, у)
/Л ^Х’ У’ 2*dx dy dZ = J dX J dy J ^*’ y’ 2^dz'
V	Xx yx(x) Xt(x,y)
Иногда удобно также применять формулу
Х2
JJJ f(x, у, z) dx dy dz = J dx JJ f(x, y, z) dy dz,
V	x. S(x)
где S(x) — сечение области V плоскостью x = const.
2. Замена переменных в тройном интеграле. Если ограниченная
кубируемая замкнутая область V пространства Охуг взаимно однознач¬
но отображается на область V пространства O'uvw с помощью непрерыв¬
но дифференцируемых функций
л: = х(и, о, w), у = у(и, и, w), 2 = z(w, о, ш),
причем
j =	У’,2) ^ о при (иу Vy w) 6 V\
D(UyVyW)
то справедлива формула
JJJ У> ^ dX ^ dZ =
v
= JJJ f(x(u, Vy w)t y(Uy Vy w)y 2(Uy Vy w))\l\ du dv dw.
v•
Как частные случаи, имеем:
1) цилиндрическую систему координат ф, г, Л, где
х = г cos ф, у = г sin ф, 2 = hy
D{x, У, z) - г
П(ГуЦ>у1г) ’

§ 6. Тройные интегралы
395
2) сферическую систему координат ср, ц/, г, где
х = г cos ср cos ц/, у = г sin ф cos ц/, z = г sin ц/,
^ cos v.
D(r, Ф, Ф)
Вычислить следующие тройные интегралы:
4076.	j*j*J xy2zs dx dy dz, где область F ограничена поверхно-
V
СТЯМИ Z = ху> у = Ху X = 1, 2 = 0.
4077.	Г Г Г —— , где область V ограничена поверхно-
J J J (I + X + у + z)3
V
стями x + y + z=l9x=09 г/ = 0, 2 = 0.
4078.	^ dy dzy где область V ограничена поверхно-
стями х2 + у2 + z2 =Д, х = 0, у = 0, z = 0.
+ ^ + ~^dx dy dz> где область F ограничена
поверхностью
*1 + ч! + £?
а2 Ь2 с2
1.
4080.	Jj*J л/#2 + у2 dx dt/ d-г, где область F ограничена по¬
верхностями
х* + Г * 2% 2 = 1
Различными способами расставить пределы в следующих
тройных интегралах:
1	1 - X X + у
4081.	J dx j* dy j fix, у у z) dz.
000
1	Jl-x2	1
4082.	f dx f dy f f(x9 у, z) dz.
-1 _vrr^2 7^77
1	1	x2 + y2
4083.	J dxj dy J
f{x, y, z) dz.

396
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Заменить тройные интегралы однократными:
X ^ X)	11	х + у
4084.	J d^j drij ДО dC-	4085. J dxj dy J f(z) dz.
0 0 0
4086. Найти
о 0
J d*J dyj f(x, y, z) dz,
a b c
если f(x, y, z) = F'X'JZ (x, у, z) и a, b, с, А, В, C — постоянные.
Переходя к сферическим координатам, вычислить интегралы:
4087. Г (Г Jx2 + у2 + z2 dx dy dZy где область Vограничена по¬
верхностью х2 + у2 + z2 = z.
1	Jl - х2	J2 - х2 - у2
4088.	'
0	0	4^4^
4089.	Перейти к сферическим координатам в интеграле
J cfo: J dy J z2 dz.
Jx2 + у2 + z2 j dx dy dz.
где область V ограничена поверхностями z = х2 +у2,х = у,х = 1,
у = О, z = 0.
4090.	Произведя соответствующую замену переменных, вы¬
числить тройной интеграл
ш;
где V — внутренность эллипсоида ~	^	^ = 1.
а2 о2 с2
4091.	Перейдя к цилиндрическим координатам, вычислить
интеграл
JJJ (*2 + у2) dx dy dz,
V
где область V ограничена поверхностями х2 + у2 = 2z, z = 2.
4092.	Вычислить интеграл
dz.
где область V ограничена поверхностями z = ay2, z = by2, у > О
(О < а < Ь), z = ах, z = $х (0 < а < Р), z = h (h > 0).

§ 6. Тройные интегралы
397
4093.	Найти интеграл JJJ xyz dx dy dz, где область V распо-
к
ложена в октанте л:>0,1/>0,2>0и ограничена поверхностями:
_ 	 X2 + у2	X2
Z = 	2- . 2 —
т
, ху = а2, ху = Ъ2, у = ах у у = (Зх
(О < а < Ь; 0 < а < |3; 0 < т < п).
4094.	Найти среднее значение функции
f(x, у, z) = х2 + у2 + z2
в области х2 Л- у2 + z2 < х + у + z.
4095.	Найти среднее значение функции
ld + id + d
fix, у, z) = е**а2 ь2 с2
в области + У- + — < 1.
а2 Ъ2 с
2 &2 С2
4096.	Пользуясь теоремой о среднем, оценить интеграл
dxdydz
- ш
х2+ 2 + z2<R2
J(x - а)2 + (у - b)2 + (z - с)2
где а2 + Ь2 + с2 > Л2.
4097.	Доказать, что если функция fix, у, z) непрерывна в об¬
ласти V и
JJJ ^х’Уг z^dx dy dz=0
v
для любой области со С V, то fix, у, z) = 0 при ix, у, z) 6 V.
4098.	Найти F\t), если:
а )Л(0 =	/я f(х2 + у2 + z2) dx dy dz,
x2 + y2 + z2it2
где f — дифференцируемая функция;
б) F(t) = ш fixyz) dx dy dz ,
0<x<t
0
0 < z< f
где f — дифференцируемая функция.

398
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4099. Найти
ш
хтупгр dx dy dz,
где т, п и р — целые неотрицательные числа.
4100. Вычислить интеграл Дирихле
JJJ* xpy4zr (1 - х- у- z)sdx dy dz,
V
(р > 0, q > 0, г > 0, s > 0),
где область V ограничена плоскостями x + y + z = 19х = 09 г/ = О,
2=0, полагая
Х + у + z = {,9 Z/ + 2 = ^T1,2 = £ti£-
§ 7. Вычисление объемов
с помощью тройных интегралов
Объем области V выражается формулой
V =
dx dy dz.
Найти объемы тел, ограниченных следующими поверхностями:
4101.	2 = х2 + у2, z = 2х2 + 2у2, у = х, у = х2.
4102.	2 = х + у, z = ху, х + у = 1,х = 0, у = 0.
4103.	х2 + г2 = а2, х + у = ±а, х - у = ±а.
4104.	02 = х2 + у2, 2 = Jx2 + у2 (а > 0).
4105.	аг = о2 - х2 - у2, z = а - х - у, х = 0, у = 0, z = 0 (а > О).
4106.	2 = 6 - х2 - у2, 2 = V*2 + у2 .
Переходя к сферическим или цилиндрическим координатам,
вычислить объемы, ограниченные поверхностями:
4107.	х2 + у2 + z2 = 202, х2 + у2 < 22.
4108.	(*2 + у2 + 22)2 = о2(*2 + у2 - 22).
4109.	(лс2 + у2 + 22)3 = Зхуг.
4110.	х2 + у2 + г2 = а2, х2 + у2 + г2 = б2, лс2 + у2 = г2 (г > 0)
(О < а < Ь).

§ 7. Вычисление объемов с помощью тройных интегралов
399
В следующих примерах удобно пользоваться обобщенными сфери¬
ческими координатами:
г, ф и \|/ ^ г > 0; 0 < ф < 2л; -5 < ф < 5 j,
вводя их по формулам
)х = ar cosa ф cosp ф,
у = b г sina ф cosp ф,
z = cr sinp ф
(а, с, а, Р — постоянные),
У> z) = aPaber2 cosa "1 ф sina " 1 ф cos2p " 1 ш sinp "1 ш.
1)(Г,ф, ф)
Вычислить объемы тел, ограниченных следующими поверх¬
ностями:
4111. f£! + к! + *2Л2
(*1 + м1 + *Г\ = *
■ U2 Ь2 с2; /г ■
б) Гг! + г£? + £Г|2 = £?+2£?-£?
' U2 62 cV a2 b2 с2
4113.	— + и! + 2!-1, *!+«£!-*.
а2	Ь2	с2	а2 Ъ2 с
4114.	*! + И! + 2! = 1.
a2	b2	с4
Пользуясь подходящей заменой переменных, вычислить
объемы тел, ограниченных поверхностями (параметры предпо¬
лагаются положительными):
4116.	а) Гг + И +	- ! + ? (* > о, 0 >0, г > 0);
\а	Ь	с)	h	k
6) Cl + g + f)’ - s - J > о. * > °>-
4117. а) Г- + ? + -V = (х > 0, у > 0, z > 0);
\а	b	с)	аЬс	*	’

400
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4118. а)
= 1 (х > 0, у > 0, 2 > 0);
4119.	z = х2 + у2, г = 2(х2 + у2), ху = а2, ху = 2а2, х - 2у,
2х = у (х > 0, у > 0).
4120.	x2 + z2 = а2, х2 + г2 = Ъ2, х2 - у2 - г2 = 0 (х > 0).
4121. (хг + у2 + z2)3 =
а6*2
хг + уг'
4122.
f£? + 2? + 5fV = 5 .
' U2 Ъг с2) h
О2 ft2 с2
£ + 2
4123.	-2-5- = 2 arcsin (*+2+51,£+2=1,* = 0,* = а.
£ + 2 + 5	л	® w a о
а b с
£ + 2 + 5
4124.	£ + 2 + 5 = in а_Ь_с ^ х = 0>	2 = 0,	2+5=0,
а Ь с	х + К	Ь с
а &
г + г + 5 = 1.
а Ь с
4125.	В каком отношении объем шара х2 + у2 + z2 < 4az делит
поверхность jc2 + i/2 + az = 4а2?
4126.	Найти объем и поверхность тела, ограниченного по¬
верхностями х2 + у2 = az, z = 2a - Jx2 + у2 (a > 0).
4127.	Найти объем параллелепипеда, ограниченного плос¬
костями
atx + Ьм + c,z = ± Л4 (£ = 1, 2, 3),
если
А =
а\ &i ct
^2 *-2
а3 Ь3 с3
* 0.

§ 8. Приложения тройных интегралов к механике
401
4128.	Найти объем тела, ограниченного поверхностью
(агх + Ьгу + сгг)2 + (а2х + b2y + c2z)2 + (а3х + Ъ3у + c3z)2 = Л2,
если
А =
ах Ьх сх
а2 ^2 С2
а3 ^3 С3
* 0.
4129.	Найти объем тела, ограниченного поверхностью
zfx^
h{a2
п- 2
(п> 1).
4130.	Найти объем тела, расположенного в положительном
октанте пространства Oxyz (х > 0, у > 0, z > 0) и ограниченного
поверхностями:
— + ^ + — = 1 (т > 0, п > 0, р > 0), х = 0, у = 0, z — 0.
ат Ъп ср
§ 8. Приложения тройных интегралов к механике
1.	Масса тела. Если тело занимает объем 7и р = р (х> у, г) — плот¬
ность его в точке (х, у9 z), то масса тела равна
М = JJJ р dx dy dz.	(1)
v
2.	Центр масс тела. Координаты центра масс (л:0, у0, z0) тела вы¬
числяются по формулам
*°=b JJIрх dx dy dz'
v
Уо = iJJJ Ру dx аУ dz>
V
= j^JJJ Р2 dx ХУ dz-
(2)
2„ =
Если тело однородно, то в формулах (1) и (2) можно положить р = 1.
3. Моменты инерции. Моментами инерции тела относительно
координатных плоскостей называются соответственно интегралы
I ху
V	V
/« - JJJ РУ2 dx dy dz.
рх2 dx dy dz9

402
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Моментом инерции тела относительно некоторой оси I называ¬
ется интеграл
It =
рг2 dx dy dz9
где г — расстояние переменной точки тела (х, у, г) от оси L В частности
для координатных осей Ох, Оу и Ог соответственно имеем:
Py	PyU	Iи	f UY	^П?У ^ 9. Дг	191
Моментом инерции тела относительно начала координат назы¬
вается интеграл
h
JJJ Р(*2 + У2 +	**х dy dz.
v
Очевидно, имеем
Io ~ I х у I у г	1гхя
4.	Потенциал поля тяготения. Ньютоновым потенциалом тела в
точке Р (х у у у г) называется интеграл
и(х, у у г) - ш pK,U)«.
где V — объем тела, р = р(£, r|, Q — плотность тела, и
Г= «/($- X)2 + (Г) - у)2 + (С - Z)2 .
Материальная точка массы т притягивается телом с силой, проек¬
ции которой Ху У, Z на оси координат Ох, Оу, Ог соответственно равны:
*=GTx= gJ7J dr]
V
Y=Gl=GIIIpv
z=Gl=Ginp^^dTidC’
где G — гравитационная постоянная.
4131.	Найти массу тела, занимающего единичный объем
0< х< 1, 0< г/ < 1, 0< z < 1, если плотность тела в точке М (х, у, z)
дается формулой р = х + у + z.
4132.	Найти массу тела, заполняющего бесконечную об¬
ласть х2 + у2 + z2 > 1, если плотность тела меняется по закону
р = p0e~k^x2 + y2 + z2, где р0 > 0 и k > 0 постоянны.

§ 8. Приложения тройных интегралов к механике
403
Найти координаты центра масс однородных тел, ограничен¬
ных поверхностями:
•у 2	*/2	ji2
«ЗЗ.^-^-с.
4134.	z = х2 + у2, х + у = а, х = 0, у — 0, z = 0.
4135.	х2 = 2рг, у2 = 2рх, х = £ 2 = 0.
4136.	2l+s	+	£i=1’;c = 0>y	=	0’z==0-
а2 Ь2	с2
4137.	х2 + z2 = а2, I/2 + -г2 = а2 (г	>	0).
4138.	х2 + у2 = 2г, jc + у = 2.
4139.	+ |! +	(х>0, i/>0, 2>0,а>0, &>0,
Va2 Ь2 с2; а&с
с> 0).
4140.	z = х2 + у2, z = \ (х2 + I/2), х + у = ±1, х ~ у — ±1.
Z
4141.	— + ^ + ~ =1, jc = 0, п = 0, z = 0 (/г > 0, х > 0, у > 0, z > 0).
ап Ьпсп
4142.	Определить координаты центра масс тела, имеющего
форму куба:
0<х<1, 0<у<1, 0<2<1,
если плотность тела в точке (jc, у, г) равна
2a-l 2р - 1 2у - 1
р = X 1~а у 1_Р Z 1_Y ,
где 0<a<l,0<p< 1, 0 < у < 1.
Определить моменты инерции относительно координатных
плоскостей однородных тел, ограниченных следующими поверх¬
ностями (параметры положительные):
4143.	^ + И + - = 1, х = 0, у = 0, г = 0.
а Ь с
4144.	г|	+	g	+	г| =	1.
а2	Ь2	с2
4145.	—	+У-	=г-,г	= с.
а2	Ь2	с2 ’
414в.а)£! + g +2|-1, *?+£=*;
Ъг
i/2
б)£ +И1 =25, £ +2
а2	Ъ2	с а Ь
Ъ2
z
с

404
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4147 а) (— + ^	1 « £? + й! -	•
' U2 Ь2	c2j а2 &2 С2 ’
б) (а)" + (£Г + {сУ = !- * = °. У = 0, 2 = 0 (п > 0;
jc > 0, у > 0, z > 0).
Определить моменты инерции относительно оси Ог однород¬
ных тел, ограниченных поверхностями:
4148.	z = х2 + у2, х + у = ±1, jc-i/ = ±1, 2 = 0.
4149.	а) *2 + у2 + 22 = 2, *2 + i/2 = 22 (г > 0);
6) (х2 + у2 + 22)3 = а52.
4150.	Найти момент инерции неоднородного шара
X2 + У2 + 22 < #2
массы М относительно его диаметра, если плотность шара в те¬
кущей точке Р(ху у у г) пропорциональна расстоянию этой точки
от центра шара.
4151.	Доказать равенство
= /, + Md2 у
1 *0
где It — момент инерции тела относительно некоторой оси Z,
/,о — момент инерции относительно оси /0, параллельной Z и про¬
ходящей через центр масс тела, d — расстояние между осями и
М — масса тела.
4152.	Доказать, что момент инерции тела, занимающего
объем Vу относительно оси Z, проходящей через его центр масс
О (0, 0, 0) и образующей углы а, р, у с осями координат, равен:
/, = Ix cos2 а + Iy cos2 Р + 1г cos2 у -
- 2Кху cos а cos Р - 2КХ2 cos а cos у - 2Куг cos Р cos у,
где 1Х, 1у, 1г — моменты инерции тела относительно осей коор¬
динат и
ш рху dx dy dZy Kxz = JJJ pxz dx dy dzy
V	V
Куг= Ш pyz dx dy dz
— центробежные моменты.
4153.	Найти момент инерции однородного цилиндра х? + у2 < а2,
z = ±hy плотности р0 относительно прямой х = у = z.

§ 9. Несобственные двойные и тройные интегралы
405
4154.	Найти момент инерции относительно начала коорди¬
нат однородного тела плотности р0, ограниченного поверхностью
(х2 4- у2 -f z2)2 = а2(х2 4- у2).
4155.	Найти ньютонов потенциал в точке Р(х, у, г) однород¬
ного шара Е,2 4- г|2 4-	< R2 плотности р0.
Указание. Положить, что ось 0£ проходит через точку Р(х, у, z).
4156.	Найти ньютонов потенциал в точке Р(х, у, г) сфериче¬
ского слоя r\ < £2 4- г|2 4- ^2 < R\, если плотность р = f(R), где
/ — известная функция ий= *Д2 4 ц2 + С,2.
4157.	Найти ньютонов потенциал в точке Р(0, 0, 2) цилиндра
4- Г|2 < а2, 0 < £ < Л, постоянной плотности р0.
4158.	С какой силой притягивает однородный шар
£2 4- ц2 + г;2 < д2
массы М материальную точку Р(0, 0, а) массы т?
4159.	Найти силу притяжения однородным цилиндром
£2 4- ц2 < а2, 0< А
плотности р0 точки Р(0, 0, г) единичной массы.
4160.	Найти силу притяжения однородным шаровым секто¬
ром плотности р0 материальной точки единичной массы, поме¬
щенной в его вершине, если радиус шаровой поверхности равен
Д, а угол осевого сечения сектора равен 2а.
§ 9. Несобственные двойные и тройные интегралы
1. Случай бесконечной области. Если двумерная область О, не огра¬
ничена и функция f(xy у) непрерывна на £2, то по определению полагают:
JJ fix, у) dx dy - Jim Я f(x, у) dx dy,	(1)
a	" Q.
где Q,n — любая последовательность ограниченных замкнутых квадри¬
руемых областей, исчерпывающая область Q. Если предел в правой час¬
ти существует и не зависит от выбора последовательности Qn, то соот¬
ветствующий интеграл называется сходящимся; в противном случае —
расходящимся.
Аналогично определяется несобственный тройной интеграл от не¬
прерывной функции, распространенный на неограниченную трехмер¬
ную область.

406
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
2. Случай разрывной функции. Если функция f(x, у) непрерывна в
ограниченной и замкнутой области £2 всюду, за исключением точки Р(а, 6),
то полагают:
JJ /(*> У) dx dy = ^lim^ JJ f(x, у) dx dy,	(2)
я	q -ut
где UE есть область диаметра E, содержащая точку Р, и в случае сущест¬
вования предела рассматриваемый интеграл называют сходящимся; в
противном случае — расходящимся.
Предполагая, что вблизи точки Р(а, Ь) имеет место равенство
«,.!,)-Sfeii,
где абсолютная величина функции ф(х, у) заключена между двумя по¬
ложительными числами т и М и г = J(x - а)2 + (у- b)2, получим, что
1) при а < 2 интеграл (2) сходится; 2) при а > 2 — расходится.
Аналогично определяется несобственный интеграл (2), если функ¬
ция /(х, у) имеет линию разрыва.
Понятие несобственного интеграла от разрывной функции легко пе¬
реносится на случай тройных интегралов.
Исследовать на сходимость несобственные интегралы с бес¬
конечной областью интегрирования (0 < т < |ф(х, у)| < М):
Я ^kixiv-
х2 + у2> 1
4162.
«63. JJ
0^у<1
dxdy
(i + |*h(i + M«)'
-JE&iti-ds dy.
(l + x2 + y2)p
4164.	ff гр4.УТ (p>0,q>0).
JJ W'+M*
M + M>i
4165.	f f	dy.
JJ (х + уУ
х + у> 1
4166.	Доказать, что если непрерывная функция /(х, у) неот¬
рицательна и5л (/i= 1, 2, ...)— какая-нибудь последователь¬
ность ограниченных и замкнутых областей, исчерпывающая об¬
ласть S, то
dx dy = lim
п -* °о
dx di/,
где левая часть имеет смысл одновременно с правой или не имеет его.

§ 9. Несобственные двойные и тройные интегралы
407
4167.	Показать, что
lim j*j* sin (jc2 + у2) dx dy = я,
\x\ < n
M < n
тогда как
lim J*J sin (x2 + y2) dx dy = 0
x2 + y2 < 2nn
(n — натуральное число).
4168.	Показать, что интеграл
Я i^dxdy
х>1,у>1
расходится, хотя повторные интегралы
+ оо +оо	4-оо 4-оо
f dx f x2-V*dy и f dy Г xl~y*dx
J	J (*2+</2)2 y J *) (x2 + y2)2
1 1
1 1
сходятся.
Вычислить интегралы (параметры положительны):
4169. JJ Щл.
4170.
4171.
Ху > 1
X > 1
Я
х2 + у2 ^ 1
Я
dxdy
х + у>1
0<х< 1
+ У)Р
dxdy
л/1 -х2-у2
4172.
Я
4173.
Я ;
*> х2 + 1
dxdy
х2 + у2> 1
dxdy
(х2 + у2)р
+ Уг
4174. JJ e-(x + y)dx dy.
О < х < у
Переходя к полярным координатам, вычислить интегралы:
4-оо 4-оо
4175.
4176.
4177.
J J е-^г*УгЫх dy.
-оо _оо
f-oo 4-00
J J e~(x2+y2)cos (*2 + У2) dx dy.
-ОО —оо
foo + оо
J J e~{x2 + y2)s*n	+ У2)	dy.

408
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Вычислить интегралы:
4-00 4-оо
4178.
И eax2 + 2bxy + cy2 + 2dx + 2ey + ( fa dy, ГДв О. < 0, CLC ~ Ь2 > 0.
-оо — оо
4179. ff eK^^dx dy.
г* и*
а2 Ь2
4180
4-оо 4-оо
г г _Г£! + 2е^й + й:	,	ч
L I хуе °2 аЬ ь* dx dy fO < |е| < lj ,
Исследовать на сходимость несобственные двойные интегра¬
лы от разрывных функций (0 < т < |ср(лг, у)| < М):
4181. Г Г dfd^-, где область Q. определяется условиями:
JJ Х2 + у2
\у\ < х2; х2 + у2 < 1.
4182. f f ,	, ■ dx dy.
JJ (x2 + xy + y2)i>
x2 + y2<l
4183.
1*1 + M < 1
4184.	f Г dx dy.
J J I*-#
0 0
4185.	ff /1 ^{Xiy)2^dX Л»•
JJ (1 -x2-y2y
X2 4- у2 < 1
4186. Доказать, что если: 1) функция ср(:с, у) непрерывна в
ограниченной области а < х< А, Ь< у < В; 2) функция f(x) не¬
прерывна на сегменте а<*<АиЗ)р< 1,то интеграл
сходится.

§ 9. Несобственные двойные и тройные интегралы
409
Вычислить следующие интегралы:
4187. ff In *	- dx dy.
J J Jx2 + у2
x2 + y2< 1
a jc
4188.
Мжг
0 0
J(a-x)(x-y)
(a > 0).
4189. J| In sin(x - у) dx dy,
где область Q ограничена прямыми г/ = 0, у = х, Jt = я.
4190. f f dxdV .
JJ	Jx2 + у2
x2 + y2<x
Исследовать на сходимость следующие тройные интегралы:
4191.
х2 + у2 + г2 > 1
4192.	Г Г Г ——dxdydz, где 0 < m < |ф(х, у, г|<М.
JJJ <x2 + u2 + z2)p
Я/	(дЖу2Л)Р dX dy d2' ГДб0<т<	У’ 21 < М~
л:'2 +	+ г'2 < 1
4193.	Г Г Г	. (р > 0, q > 0, г > 0).
JJJ \х\р+\у\ч + \г\г ^
|дс| + Ы + |г|>1
а а а
4194.	f f f 	f{x1y,z)dxdydz	, Где 0 < /га < |/(дс, у, z\ < М,
| J J (1У~ ф(*)]2 + [г-\у(х)]2}р
(х) — непре{
Шdxdyd
\Х+У-i
0 0 0
а ср(л;) и \|/(jc) — непрерывные функции на сегменте [0, а].
dxdydz
■ z\p
М <’i
М < 1
W<1
4195
Вычислить интегралы:
4196. Г f f	.
JJJ XPylZ'
0 0 0
4197 f f f	dxdydz
' JJJ (x2 + y2 + z2)3
х2 + уг + гг>1
4198.
Ш <r
x2 + y2 + г2 < 1
-foo 4-00	4-00
dxdydz
x2 - y2 - z2)p
4199.	JJj* е^х2 + У2 + г2Ых dy dz.
-OO _oo -oo

410
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4200.	Вычислить интеграл
+ оо 4-00 +оо
I
—ос
3	3
где Р(хх, х2, *з)= £ S a4xixj(ay = ayi) — положительно опре-
i=l / = 1
деленная квадратичная форма.
§ 10. Многократные интегралы
1. Непосредственное вычисление кратного интеграла. Если функ¬
ция f(x 1, х2,..., яп) непрерывна в ограниченной области £2, определяемой
неравенствами
х[ <	< х'{ ,
Х2 (^l) ^	^ Х2
Г	^ dXst
Хтг (*^1> *^2» • • • » Xn - 1 ) ^ Хп ^ Хп (Х1 > *^2> * * * >	- 1 )»
где х[у х'{ — постоянные числа, x^xj, х2 (*i)> •••» xh(xi> х2* •••» *n-i)>
я" (л^, лг2,л:л-1) — непрерывные функции, то соответствующий мно¬
гократный интеграл может быть вычислен по формуле
JJ... J f(x,, *2, ... , хп) dXi dx2 ... dxn =
a
Xl	X2(Xt)
= J dxt J dx2 ... J f(xu x2, ..., xn)dxn.
x‘2(xt)
xn<xi	*»-!>
2. Замена переменных в кратном интеграле. Если: 1) функция
f(x 1, л:2, ...» хп) равномерно непрерывна в ограниченной измеримой об¬
ласти £2; 2) непрерывно дифференцируемые функции
*< = Ф/Й1.^2. •••> D (i“ 1.2	п)
осуществляют взаимно однозначное отображение области £2 простран¬
ства Оххх2 ... хп на ограниченную область £2' пространства	и
3) якобиан
_ Р(хи х2, ...,хп)
Da и^-Лп)
в области £2', то справедлива формула
/(*„ х2, .... хп) dxt dx2... dxn =
= JJ • J ЛФ1* Ф2. Фл) W dl\ di>2 ■■■ dln-

§10. Многократные интегралы
411
В частности, при переходе к полярным координатам (г, (pi, (р2, ..., (рЛ_ О
по формулам
Хх = Г COS (р!,
х2 = г sin (р! cos ср2,
Xn-l = Г Sin Ср! sin (р2 ... sin (рл _ 2 COS Cpn _ j,
хп = г sin cpj sin ср2 ... sin срл _ 2 sin срл _ 1#
r D(x„ JC2, JC„)	. п — 2	• п-Ч
1= п,		ZL = г” 'sin" 2 ф! sin" ф2 ... sin ф„ _ 2-
2)(г,ср„
4201.	Пусть К(х, у)—непрерывная функция в области R(a <*<£>;
а<у < Ь) и
бь 6
Кп (х, у) = J J* ... J К (*, tx)K (tlt t2)... К (tn, у) dti dt2 ... dtn.
a a a
Доказать, что
b
кп + т + i(x, y)= J Ka (x, t)Km (t, y) dt.
a
4202.	Пусть f = f(xl9 x2f ...» xn) — непрерывная функция в об¬
ласти 0 < х{ < х (i = 1, 2, ..., п). Доказать равенство
X	Х\	ХП-1	X	X	X
J dx, J dx2	... J fdxn=j dxnj djcn_i	... 1	/ dxx	(n	> 2).
0	0	0	Q	xn	x2
4203.	Доказать, что
J du J dt2... J f(t0f(t2)... /(*„) dtn = i J № d%
0 0 0 0
где f — непрерывная функция.
Вычислить следующие многократные интегралы:
1	1	1
4204.	a) J J ... J {х\ + х\ + ... + х\) dxx dx2 ... dxn\
00	о
1 i	i б)б)1Н (хх + х2 + ... +лгл)2 dxx dx2 ... <2лгл.
оо о

412
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4205.1п
dxx dx2 ... dxn.
Xj >0,x2> 0	xn >0,
*1 + x2 + ... + xn < a
1
х\ хп- 1
4206.
J
<2*! Г <2лг2 ... ххх2 ... xndxn.
J J
0
0 0
4207.
ГГ... Г JXl + x2+ ... + xndxr dx2
*1
J J J
l>0.*2>0	*„>0.
+ дг2 + ... + *„«!
4208. Найти объем /i-мерного параллелепипеда, ограничен¬
ного плоскостями
anxl + а12х2 + ... + ainxn = ±А, (i = 1, 2,	п),
если Л = |aiy| ^ 0.
4209.	Найти объем п-мерной пирамиды
h + h + ... + is < 1, * > о (i=l,2	га)
а\ а2	°п
(а, > 0, i = 1, 2,	я).
4210.	Найти объем n-мерного конуса, ограниченного поверх¬
ностями
2 2
*1 . *2
2 „2 „2
2
2	2
*я_1
= —9> хп=ап.
а1 «2	ал-1 ал
4211.	Найти объем п-мерного шара
2 , 2 . . 2^2
+ д;2 + ... + *л < аг.
4212.	Найти /и x2ndxx dx2 ... <2лгл, где область Q. опреде-
ляется неравенствами
2,2,	,2	^-2 h ^	/ h
Xi + х2 + ... +	< a2, -- <	< - .
4213.	Вычислить
JH
dxxdx2...dxn
Гл 2	2	2
4\-Хх-Х2-	хп

§10. Многократные интегралы
413
4214. Доказать равенство
X	*1	*Л-1
J dxx J dx2... J f(xn) dxn = J	du■
0 0 0
4215. Доказать равенство
о	о
J*i dxjjx2dx2... ff(xn + 1)dxn + 1 =
0
x
= f (x2 - u2)n f(u)du.
2nn\ J
4216. Доказать формулу Дирихле
pj-i p2-1 p, -l
*i x2 ... xn dxj d*2... dxn =
+ *2 + ••• + xn ^ 1
=	Г(р,)Г(ра)...Г(р„)
ЦР1 +P2+ •• + Pn+ i)
(Pl,p2. —,Pn> 0).
4217. Доказать формулу Лаувилля
f(xx + x2 +... + xn)xj1	1... xP„n 1 dx j d*2... d*„ =
X1 + X2+... + X)1< 1
= Г(р,)Г(ра)...Г(р.)
T(Pl+P2+ • - +Pn)
1
| f(u)uPl+P2 + +p"~ldu (pltp2, ...,p„> 0),
0
где f(u) — непрерывная функция.
Указание. Применить метод математической индукции.
4218. Привести к однократному интегралу n-кратный интег¬
рал (п > 2)
JJ ... | /(л/*1+*2+ — + *п
j dx1 dx2 ... dxn
распространенный по области х\ + х\ + ... + х2п < R2, где /(и) —
непрерывная функция.

414
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4219.	Вычислить потенциал на себя однородного шара ра¬
диуса R и плотности р0, т. е. найти интеграл
,/=Ро Г ГГ f f f dxldyldzldx2dy2dz2
2	П,2
2 2 2 . d2
Х1 +У1 + 21
2 2 2 . о2
х2 + у2 + г2 ^ Я
где гг> 2 = 7(^1 “ хг)2 + (У 1 - У2)2 + (*i - z2)2 .
4220.	Вычислить n-кратный интеграл
2^jjT fcj*. + с
/ = 1
dxx dx2
n>
n
если ^ a^XjXj {atj = ay7) — положительно определенная квадра-
тичная форма.
§11. Криволинейные интегралы
1. Криволинейный интеграл 1-го рода. Если f(x, у, 2) — функция,
определенная и непрерывная в точках гладкой кривой С
* = x(t), у = y(f), 2 = z(t)9 (t0< t< Т)	(1)
и ds — дифференциал дуги, то
т
J f(x, у, 2) ds = J f(x(t)9 y(t), z(t))«Jx,2(t) + y'2(t) + z'2(t) dt.
Особенность этого интеграла состоит в том, что он не зависит от направ¬
ления кривой С.
2. Механические приложения криволинейного интеграла 1-го ро¬
да. Если р = р(лг, у, г) — линейная плотность в текущей точке (х, у> z)
кривой С, то масса кривой С равна
М = J* р(х, у у z) ds.
с
Координаты центра масс (х0, у09 г0) этой кривой выражаются фор¬
мулами
*0
хр(х9 у у z) dSy
zp(xf у у z) ds.

§11. Криволинейные интегралы
415
3.	Криволинейный интеграл 2-го рода. Если функции Р = Р(х, у, z)f
Q = Q( х, у, г), Я = R(x, у у г) непрерывны в точках кривой (1), пробегае¬
мой в направлении возрастания параметра t, то
J Р(Ху у, г) dx + Q(x, у у z) dy + R(xt уу г) dz =
с
т
= J {P(x(t), y(t), z(t))x\t) + Q(x{t), y(t), z(t))y'(t) +	(2)
*0
+ R(x(t), y(t), z(t))z'(t)} dt.
При изменении направления обхода кривой С этот интеграл изменяет
свой знак на обратный. Механический интеграл (2) представляет собой
работу переменной силы {Р, Q, Я}, точка приложения которой описы¬
вает кривую С.
4.	Случай полного дифференциала. Если
Р(Ху у у z) dx + Q(Xy у у г) dy + R(x, i/, z) dz = duf
где и = u(Xy yf z) — однозначная функция в области F, то независимо от
вида кривой С, целиком расположенной в области V, имеем
J Р dx + Q dy + Rdz = и(х2, у2, z2) - u(ac,, ylt г,),
c
где (xlf ylt zx) — начальная и (x2, y2, z2) — конечная точки пути. В про¬
стейшем случае, если область V односвязна и функции Р, Q и R обладают
непрерывными частными производными первого порядка, для этого не¬
обходимо и достаточно, чтобы в области V были тождественно выпол¬
нены следующие условия:
dP	= dQ	c)Q = ЭЯ	ЭЯ = ЭР
dy	дх	dz	ду 9	дх	dz *
Тогда, в простейшем случае стандартной параллелопидальной об¬
ласти Vy функцию и можно найти по формуле
X	у	г
Р(Ху у у z)dx+	Q(x о, у у z)dy +	R(x0, у0У г) dz + с,
*о	Уо	2о
где (лг0, Уо, zQ) — некоторая фиксированная точка области V и с — про¬
извольная постоянная.
Вычислить следующие криволинейные интегралы 1-го рода:
4221.	J (х + у) ds, где С — контур треугольника с вершинами
с
0(0, 0), А (1, 0) и В (0, 1).
и(Ху у у Z)
-

416
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4222.
ds9 где С — арка циклоиды
х = a (t - sin t)9 у = а (1 - cos t) (0 < t < 2л).
4223.	J (х2 + у2) ds, где С — кривая
с
д; = a (cos t + t sin £), у = a (sin t - t cos £) (0 < t < 2л).
4224.	J jm/ (is, где C — дуга гиперболы
с
x = a ch t9 у = a sh *	(0 < £ < f0).
i i\	22g
4225.	д;3 + i/3 (is, где C — дуга астроиды д;3 4- уг = a3.
с
4226.	j* e*lx2 + v2 ds9 где С — выпуклый контур, ограниченный
с
кривыми г = а, ф=0,ф=- (гиф — полярные координаты).
4
4227.	J \у\ ds9 где С — дуга лемнискаты
(*2 + у2)2 = а2(*2 - у2).
4228.	j х ds9 где С — часть логарифмической спирали г = аек(р
с
(k > 0), находящаяся внутри круга г < а.
4229.	J Jx2 + y2ds9 где С — окружность я2 + у2 = ах.
с
/* /7 о	у
4230.	— , где С — цепная линия у = a ch - .
J г/2	а
с
Найти длины дуг пространственных кривых (параметры по¬
ложительны):
4231.	х = 3*, у = З*2, 2 = 2*3, от О (0, 0, 0) до А (3, 3, 2).
4232.	д; = е-* cos t9 у = sin £, 2 = е"*, при 0 < £ < +оо.
4233.	у = a arcsin -,2=7 ln^—^ от О (0, 0, 0) до А (д;0, у09 20).
а 4 а + х
4234.	(д; - у)2 = а (д: 4- у), х2 - у2 = ^х2 от О (0, 0, 0) до
о
А (х0, у0, z0).

§11. Криволинейные интегралы
417
4235.	х2 + у2 = сг, У = tg- от О (0, 0, 0) до А (*0, у0, г0).
X с
4236.	х2 + у2 + z2 = a2, Jx2 + у2 ch ^arctg = а от точки
А (а, 0, 0) до точки В (х, у, 2).
Вычислить криволинейные интегралы 1-го рода, взятые
вдоль пространственных кривых:
4237.	j* (х2 + г/2 + г2) <2s, где С — часть винтовой линии
с
л; = a cos t9 у = a sin £, 2 = bt (0 < t < 2п).
4238.	J х2 ds9 где С — окружность
с
л:2 + I/2 + z2 = а2, л: + у + z = 0.
4239.	J* 2 ds, где С — коническая винтовая линия
с
х = t cos t9 у = t sin £, 2 = t (0 < t < ^0).
4240.	J* 2 ds, где C — дуга кривой x2 + у2 = z2, у2 = ax от точки
с
О	(0, 0, 0) до точки А (а, а, J2 ).
4241.	1. Найти массу кривой х = a cos t, у = b sin £ (а > b > 0;
О < t < 2л), если линейная плотность ее в точке (х, г/) равна \у\.
2.	Найти массу дуги параболы
у2 = 2рх
если линейная плотность параболы в текущей точке М(х, у) рав-
на |у|.
3.	Найти массу дуги кривой х = at, у = У-t2, z= 113 (0 < t < 1),
2	о
плотность которой меняется по закону р =
4242.	Вычислить координаты центра масс дуги однородной
кривой у = a ch- от точки А (0, а) до точки В (b, h).

418
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4243.	Определить центр масс дуги циклоиды
х = a (t - sin t), у = а (1 - cos t) (0 < t < я).
4244.	1. Найти статические моменты
Sy=jxds,Sx=ly
ds
дуги С астроиды
2 2 2
х* + у3 = а3 (х > 0, у > 0)
относительно осей координат.
2. Найти момент инерции окружности
х2 + г/2 = а2
относительно ее диаметра.
3.	Найти полярные моменты инерции
10 = | (*2 + У2) ds
С
относительно точки О (0, 0) следующих линий: а) контура С
квадрата шах {|л;|, \у\} = а; б) контура С правильного треугольника
с вершинами в полярных координатах
P(a,0),Q(a,	Д(а,
4.	Найти средний полярный радиус астроиды
2 2 2
х* + i/3 = а® ,
т. е. число г0 (г0 > 0), определяемое формулой
г	2
I0 = sr0,
где /0 — полярный момент инерции астроиды, относительно на¬
чала координат (см. 4244.3) и s — длина дуги астроиды.
4245.	Вычислить координаты центра масс контура сфериче¬
ского треугольника х2 + у2 + г2 = а2; х > 0, у > 0, г > 0.
4246.	Найти координаты центра масс однородной дуги
х = el cos t, у = ег sin t9 z = ef (-00 < t < 0).
4247.	Найти моменты инерции относительно координатных
осей одного витка винтовой линии,
L
х = a cos £, у = a sin t9 z =	£ (0 < * < 2я).

§11. Криволинейные интегралы
419
4248.	Вычислить криволинейный интеграл 2-го рода
J * dy - у dx,
ОА
где О — начало координат и точка А имеет координаты (1, 2),
если: а) ОА — отрезок прямой линии; б) ОА — парабола, ось ко¬
торой есть Оу; в) О А — ломаная линия, состоящая из отрезка ОВ
оси Ох и отрезка ВА, параллельного оси Оу.
4249.	Вычислить
J х dy + у dx
ОА
для путей а), б) и в), указанных в предыдущей задаче.
Вычислить следующие криволинейные интегралы 2-го рода,
взятые вдоль указанных кривых в направлении возрастания па¬
раметра:
4250. J (х2 - 2ху) dx + (у2 - 2ху) dy, где С — парабола
с
у — х2 (-1 < * < 1).
4251.	j* (х2 + у2) dx + (х2 - у2) dy, где С — кривая
с
у = 1 - |1 - *|	(0 < * < 2).
4252.	Г (х + у) dx + (х - у) dy, где С — эллипс ~	^ = 1,
J	а2 о2
с
пробегаемый против хода часовой стрелки.
4253.	j* (2а - у) dx + х dy, где С — арка циклоиды
с
х = a (t - sin t), у = а (1 - cos t) (0 < £ < 2л).
4254.	J) (х + У№х—Щ—У^У-, где С — окружность х2 + у2 = а2,
I	х +У
пробегаемая против хода часовой стрелки.
4255.	j>	’ где	— контур квадрата с верши-
ABCDA
нами А (1, 0), В (0, 1), С (-1, 0), D (0, -1).

420
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4256.	J dx sin у + dy sin х, где АВ — отрезок прямой между
АВ
точками А (0, п) и В (я, 0).
4257.	£ dy arctg^ - dx, где ОтА — часть параболы у = х2
ОтАпО
и ОпА — отрезок прямой у = х.
Убедившись, что подынтегральное выражение является пол¬
ным дифференциалом, вычислить следующие криволинейные
интегралы:
(2,3)
4258
4260
». х dy Л- у dx.
(-Ь2)
(3,-4)
4259. f х dx + у dy.
(0,1)
(2,3)
Г (* + у) dx + (X - у) dy.
(0.1)
(1.1)
4261.	J (х - y)(dx - dy).
(i,-D
(a, b)
4262.	Г f(x + y)(dx + dy), где f(u) непрерывна.
(0,0)
(1.2)
4263.	J У»Х~Х^У вдоль путей, не пересекающих оси Оу.
(2,1)
(6,8)
4264.
(1.0)
ло координат.
(*2- 02>
f xdx+\
У . Jx2 + у2
ИМ
вдоль путей, не проходящих через нача-
4265. J ср(лс) dx + \|f(y) dy, где ср и \|/ — непрерывные функ¬
ции.
(*1 .у,)
(3,0)
J (х4 + 4xi/3) dx + (6х2у2 - by4) dy.
(-2,-1)
4266.

§11. Криволинейные интегралы
421
(1.0)
4267.	Г	ydjc вдоль ПуТей, не пересекающих пря-
J (х-уУ
(0.-1)
мой у = X.
(2, п)
4268. J (l-g cos ^ j dx + ^ sin 2 + К cos 2 j dy вдоль путей,
(1.л)
не пересекающих оси Ог/.
(а,Ь)
4269.	ех (cos у dx - sin у dy).
(0,0)
4270.	Доказать, что если f(u) — непрерывная функция
и С — кусочно-гладкий замкнутый контур, то
j) f(x2 + у2)(х dx + у dy) = 0.
С
Найти первообразную функцию z, если:
4271. dz = (х2 + 2ху - у2) dx + (х2 - 2ху - у2) dy.
4272. dz =
ydx - xdy
Зх2 - 2ху + 3у2 '
4273 dz = (*2 +	+ $y2)dx + (х* - 2ху + y2)dy _
(х + уУ
4274. dz = e*[etf(jic - у + 2) + у] dx + ex[ev(x - у) + 1] dy.
4275. dz =
д " + Я| +1 ц
дхп*гдут
0 n + m + 1 ц
d* + г		 dy.
дхпдут*1
4276.dz
Э ”+Я| *1
дхл+2дут~'
+ т+1
0xn-l^m+2
> где
г = Jx2 + у2.
4277. Доказать, что для криволинейного интеграла справед¬
лива следующая оценка:
J Р dx + Q dy
с
< LM,
где L — длина пути интеграции и М = max Jp2 + Q2 на дуге С.
4278. Оценить интеграл
^я ~
f
х2 + y2=R2
ydx - xdy
(x2 + xy + y2)2 ’
Доказать, что lim IR = 0.
Я — оо

422
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Вычислить криволинейные интегралы, взятые вдоль простран¬
ственных кривых (координатная система предполагается правой):
4279.	J {у2 - z2) dx + 2 yz dy - х2 dz9 где С — кривая x = t9y = t29
с
z = t3 (0 < t < 1), пробегаемая в направлении возрастания параметра.
4280.	J у dx + z dy Л- х dz9 где С — виток винтовой линии
с
х = a cos t9 у = a sin t9 z = bt (0 < t < 2я), пробегаемой в направ¬
лении возрастания параметра.
4281.	J (у - z) dx + (z - jc) dy + (x - y) dz9 где C — окружность
c
jc2 + у2 + z2 = a2, i/ = jc tg a (0 < a < n)9 пробегаемая против хода
часовой стрелки, если смотреть со стороны положительных х.
4282.	J х2 dx + z2 dy + х2 dz9 где С — часть кривой Вивиани
с
х2 + у2 + z2 = а2, х2 + у2 — ах (z ^ 09 а > 0), пробегаемая против
часовой стрелки, если смотреть с положительной части (х > а)
оси Ох.
4283. J (у2 - z2) dx + (z2 - х2) dy + (х2 - у2) dz9 где С — контур,
с
ограничивающий часть сферы х2 + у2 + z2 = 1, х > 0, у > 0, z > 0,
пробегаемый так, что внешняя сторона этой поверхности остается
слева.
Найти следующие криволинейные интегралы от полных
дифференциалов:
(2, 3,-4)
4284.	f х dx + у2 dy - z3 dz.
d.1.1)
(6,i,i)
4285.	J yz dx Л- xz dy + xy dz.
(1,2,3)
(■*2’
4286. f —f + ydy.t ?d.z , Где точка (xl9 yl9 zx) расположена
J Jx2 + y2 + г2
(*!•*!■*!>
на сфере дг + у* + zl = a2, а точка (x29 y2> z2) — на сфере лг + г/2 +
+ z2 = Ъ2 (а > 0, Ъ > 0).

§12. Формула Грина
423
(*2’ ^2’ Z2)
4287.	J ф(дг) dx + \|/(г/) dy + %(х) dz, где cp, у, X — непре-
рывные функции.
(х2,у2,г2)
4288.	J* f(x + у + z)(dx Л- dy Л- dz)9 где f — непрерывная
(xl,yvzl)
функция.
(*2’^2’г2)
4289.	j* f(Jx2 + у2 + z2 )(х dx + у dy + z dz), где f — не-
(Xvyv 2j)
прерывная функция.
Найти первообразную функцию и9 если:
4290.	du = (х2 - 2yz) dx + (у2 - 2xz) dy + (z2 - 2xy) dz.
4291.	du = ( 1 - 1 + 4) dx + (2 + dy - Ц-dz.
\ у z) \z y2) 17 z2
4292.	du = (x + y-z)dx + (x + y-z)dy + (x + y + z)dz ^
x2 + y2 + z2 + 2xy
4293.	Найти работу, производимую силой тяжести, когда
точка массы т перемещается из положения (xl9 yl9 zx) в положе¬
ние (х2, у2* z2) (ось Oz направлена вертикально вверх).
4294.	Найти работу упругой силы, направленной к началу
координат, значение которой пропорционально расстоянию от
материальной точки до начала координат, если эта точка описы¬
вает в направлении против хода часовой стрелки положительную
четверть эллипса ^	^ = 1.
а2	о2 *
С	I
4295.	Найти работу силы тяготения F = — , где г = Jx2 + у2 + z2 9
г2
G — гравитационная постоянная, действующей на единичную
массу, когда последняя перемещается из точки Мг (х19 у19 гг) в
точку М2 (x29y29z2).
§ 12. Формула Грина
1. Связь криволинейного интеграла с двойным. Если С — замкну¬
тый простой кусочно-гладкий контур, ограничивающий конечную од¬
носвязную область S, пробегаемый так, что область S остается слева, и

424
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
функции Р (х, y)nQ (х, у) непрерывны вместе со своими частными про¬
изводными первого порядка P’f (х, у) и Q'x (х, у) в области S и на ее
границе, то имеет место формула Грина
£р(*, у) dx + Q (х,	dx dy.	(1)
С	s
Формула (1) справедлива также и для конечной области S, ограни¬
ченной несколькими простыми контурами, если под границей С послед¬
ней понимать сумму всех граничных контуров, направление обхода ко¬
торых выбирается так, что область S остается слева.
2. Площадь плоской области. Площадь фигуры S, ограниченной
простым кусочно-гладким конутром S, равна
S = j) х dy = - j) у dx = i j) (x dy - у dx).
c	c	c
В этом параграфе, если не оговорено противное, предполагается, что
замкнутый контур интегрирования простой (без точек самопересече¬
ния) и пробегается так, что ограниченная им область, не содержащая
бесконечно удаленной точки, остается слева (положительное направле¬
ние).
4296.	С помощью формулы Грина преобразовать криволиней¬
ный интеграл
I = j) Jx2 + у2 dx + у[ху + In (х + Jx2 + у2)] dy,
с
где контур С ограничивает конечную область S.
4297.	Применяя формулу Грина, вычислить криволинейный
интеграл
I = (х + у)2 dx - (х2 + у2) dy,
К
где К — пробегаемый в положительном направлении контур тре¬
угольника АВС с вершинами А (1, 1), В (3, 2), С (2, 5).
Проверить найденный результат, вычисляя интеграл непо¬
средственно.
Применяя формулу Грина, вычислить следующие криволи¬
нейные интегралы:
4298.	j) ху2 dy - х2у dx, где С — окружность х2 4- у2 = а2.
с

§12. Формула Грина
425
4299.
dx - {х- у) dy, где С — эллипс
+ £ = 1.
b2
4300.	j> е*[(1 - cos у) dx-(у- sin у) dy], где С — пробегаемый
с
в положительном направлении контур, ограничивающий об¬
ласть 0<x<n, 0<у< sin х.
4301.	j) е~(х2~У2) (cos 2ху dx + sin 2ху dy).
х2 + y2=R2
4302.	На сколько отличаются друг от друга криволинейные
интегралы
h= J (х + yf dx - (х- у)2 dy,
АтВ
h= [ (х + у)2 dx-(x- у)2 dy,
АпВ
где АтВ— прямая, соединяющая точки А( 1, 1) и Б (2, 6), и
АпВ — парабола с вертикальной осью, проходящая через те же
точки А и Б и начало координат?
4303.	Вычислить криволинейный интеграл
J (ех sin у - ту) dx + (ех cos у - т) dy,
АтО
где АтО — верхняя полуокружность х2 + у2 = ах, пробегаемая
от точки А (а, 0) до точки О (0, 0).
Указание. Дополнить путь АтО до замкнутого прямолинейным
отрезком ОА оси Ох.
4304.	Вычислить криволинейный интеграл
J* [ф(У)ех - ту] dx + [<р\у)ех - т] dy,
АтВ
где ср(г/) и ф'(у) — непрерывные функции, а АтВ — произволь¬
ный путь, соединяющий точки A(xlf yY) и Б (х2, у2)> но ограничи¬
вающий вместе с отрезком АБ площадь АтВА данной величины S.
4305.	Определить две дважды непрерывно дифференцируемые
функции Р (х, у) и Q (х, у) так, чтобы криволинейный интеграл
I	= j) Р (х + а, у + Р) dx + Q (х + а, у + Р) dy
с
для любого замкнутого контура С не зависел от постоянных а и |3.

426
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4306.	Какому условию должна удовлетворять дифференци¬
руемая функция F (х, у)9 чтобы криволинейный интеграл
где С — простой замкнутый контур, не проходящий через начало
координат, пробегаемый в положительном направлении.
Указание. Рассмотреть два случая: 1) начало координат нахо¬
дится вне контура; 2) контур С окружает начало координат.
С помощью криволинейных интегралов вычислить площади,
ограниченные следующими кривыми:
4308.	х = a cos t, у = Ъ sin t (0 < t < 2п) (эллипс).
4309.	х = a cos3 t, у = b sin3 t (0 < t < 2п) (астроида).
4310.	(х + у)2 = ах (а > 0) и осью Ох (парабола).
4311.	х3 + у3 = 3аху (а > 0) (петля декартова листа).
Указание. Положить у = tx.
4312.	(х2 + у2)2 = а2(х2 - у2) (лемниската).
Указание. Положить у = х tg ф.
4313.	Кривой х3 + у3 = х2 + у2 и осями координат.
4314.	Вычислить площадь, ограниченную кривой
(х + у)п + m + 1 = ахпут (а > 0, п > 0, т > 0).
4315.	Вычислить площадь, ограниченную кривой
J F (х, у)(у dx + х dy)
АтВ
не зависел от вида пути интегрирования?
4307.	Вычислить
с
п
= 1 (а > 0, b > 0, п > 0)
и осями координат.
Указание. Положить - = cos п (р, ^ = sin п ср.
4316.	Вычислить площадь, ограниченную кривой
(а > 0, Ъ > 0, п > 1)
и осями координат.
4317.	Вычислить площадь петли кривой
(а > 0, Ъ > 0, с > 0, п > 0).

§12. Формула Грина
427
4318.	Эпициклоидой называется кривая, описываемая точ¬
кой подвижной окружности радиуса г, катящейся без скольже¬
ния по неподвижной окружности радиуса R и остающейся вне
нее.
Найти площадь, ограниченную эпициклоидой, предполагая,
R
что отношение - = п есть целое число (п > 1).
г
Разобрать частный случай г = R (кардиоида).
4319.	Гипоциклоидой называется кривая, описываемая точ¬
кой подвижной окружности радиуса г, катящейся без скольже¬
ния по неподвижной окружности радиуса R и остающейся вну¬
три нее.
Найти площадь, ограниченную гипоциклоидой, предпола-
р
гая, что отношение - = п есть целое число (п > 2).
р
Разобрать частный случай г = - (астроида).
4
4320.	1. Вычислить площадь части цилиндрической поверх¬
ности х2 + у2 = ах у вырезанной поверхностью х2 + у2 + г2 = а2.
2. Доказать, что объем тела, образованного вращением во¬
круг оси Ох простого замкнутого контура С, расположенного
в верхней полуплоскости у > 0, равен
4321.	Вычислить
У2 dx.
Г_ 1 iXdY-YdX
2л f X2 + Y2 '
С
если X = ах -f by, Y = сх + dy и простой замкнутый контур С
окружает начало координат (ad - be) ^ 0).
4322.	Вычислить интеграл I (см. предыдущую задачу), если
X = ф(д:, у), Y = V|/(jc, у) и простой контур С окружает начало ко¬
ординат, причем кривые ф(х, у) = 0 и \}/(jc, у) = 0 имеют несколько
простых точек пересечения внутри контура С.
4323.	Показать, что если С — замкнутый контур и I — про¬
извольное направление, то
j> cos (1, n) ds = 0,
с
где п — внешняя нормаль к контуру С.

428
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4324.	Найти значение интеграла
/ = j) [х cos(n, х) + у cos (п, у)] ds9
с
где С — простая замкнутая кривая, ограничивающая конечную
область S, ип — внешняя нормаль к ней.
4325.	Найти
lim \ <£ (F • n) dst
d(S) - о S J
с
где S — площадь, ограниченная контуром С, окружающим точ¬
ку (х0, t/0), d(S) — диаметр области S, п — единичный вектор
внешней нормали контура С и F{X, У} — вектор, непрерывно
дифференцируемый в S + С.
§ 13. Физические приложения
криволинейных интегралов
4326.	С какой силой притягивает масса М, равномерно рас¬
пределенная по верхней полуокружности х2 + у2 = а2, у > 0, ма¬
териальную точку массы /п, занимающую положение (0, 0)?
4327.	Вычислить логарифмический потенциал простого
слоя
и(ху У) = ф
с
где к = const — плотность, г = V(E> - х)2 + (Л ~ У)2 и контур С есть
окружность £2 + Г|2 = R2.
4328.	Вычислить в полярных координатах риф логарифми¬
ческие потенциалы простого слоя
2л	2л
Ix = J cos /п\|/ lnid\|/ и /2 = J sin m\\f In~ с?\|/,
о	о
где г— расстояние между точкой (р, ф) и переменной точкой
(1, \j/), а т — натуральное число.
4329.	Вычислить интеграл Гаусса
U(x, у)-$ SSS&Jllds,
С
где г =	- х)2 + (Л - у)2 — длина вектора г, соединяющего точ¬
ку А(х9 у) с переменной точкой М(£, г|) простого замкнутого глад¬

§13. Физические приложения криволинейных интегралов
429
кого контура С, (г, п) — угол между вектором г и внешней нор¬
малью п к кривой С в точке ее М.
4330.	Вычислить в полярных координатах р и ср логарифми¬
ческие потенциалы двойного слоя
2п	2п
Кj = J cos m\\f CQS(^r? n) d\\f и К2 = J sin m\\f —dy,
о	0
где r — расстояние между точкой A (p, ср) и переменной точкой
M (1, v|/), (г, n) — угол между направлением AM = г и радиусом
ОМ = п, проведенным из точки О (0, 0), и тп — натуральное
число.
4331.	Дважды дифференцируемая функция и = и(х, г/) назы¬
вается гармонической, если Дц ^	= 0. Доказать, что и
ох2 ду2
есть гармоническая функция тогда и только тогда, если
с
где С — произвольный замкнутый контур и — производная
дп
по внешней нормали к этому контуру.
4332.	Доказать, что
Я1Ш) +(tS) ]dx dy = -\\ut^udx dy+ j>u|-nds>
s	s	c
где гладкий контур С ограничивает конечную область S.
4333.	Доказать, что функция, гармоническая внутри конеч¬
ной области S и на ее границе С, однозначно определяется своими
значениями на контуре С (см. задачу 4332).
4334.	Доказать вторую формулу Грина на плоскости
я
S
А и Ли
dx dy = ф
ди до
дп дп
и V
с
и V
3
где гладкий контур С ограничивает конечную область S и ^
дп
производная по направлению внешней нормали к С.

430
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4335.	Пользуясь второй формулой Грина, доказать, что если
и = и(х, у) — гармоническая функция в замкнутой конечной об¬
ласти S, то
й ■ й |>	"1п''д£Уе'
с
где С — граница области S, п — внешняя нормаль к контуру С,
(х, у) — внутренняя точка области S и г = V(4 ~ х)2 + (Л ~ У)2 —
расстояние между точкой (х, у) и переменной точкой (£, Л) кон¬
тура С.
Указание. Вырезать точку (х, у) из области S вместе с бесконеч¬
но малой круговой окрестностью ее и применить вторую формулу Грина
к оставшейся части области S.
4336.	Доказать теорему о среднем для гармонической функ¬
ции u (М) = и(х, у):
U (м) = ^ j) u(£, ri) cfs,
С
где С — окружность радиуса R с центром в точке М.
4337.	Доказать, что функция и(х, у), гармоническая в огра¬
ниченной и замкнутой области и не являющаяся постоянной в
этой области, не может достигать своих наибольшего и наимень¬
шего значений во внутренней точке этой области (принцип мак¬
симума).
4338.	Доказать формулу Римана
где
я
S
Ци] M[v]
и V
dx + Q dy,
L[u] =
д2и
дхду
+ а
ОХ
+ си,
M[v] =
d2v
дхду
+ CV
(а, Ъ, с — постоянные), Р и Q — некоторые определенные функ¬
ции и контур С ограничивает конечную область S.
4339.	Пусть и = и(х, у) и v = и(х, у) — компоненты скорости
установившегося потока жидкости. Определить скорость изме¬
нения количества жидкости в ограниченной контуром С области
S.	Какому уравнению удовлетворяют функции и и и, если жид¬
кость несжимаема и в области S отсутствуют источники и стоки?

§14. Поверхностные интегралы
431
4340.	Согласно закону Био—Савара электрический ток iy
протекающий по элементу проводника dsy создает в точке про¬
странства М(ху у, г) магнитное поле напряженностью
сМ = fe^rxfs).
Г3
где г — вектор, соединяющий элемент ds с точкой М, и. k — ко¬
эффициент пропорциональности.
Найти проекции НХУ Нуу Н2 напряженности магнитного поля
Н в точке М для случая замкнутого проводника С.
§ 14. Поверхностные интегралы
1. Поверхностный интеграл 1-го рода. Если S — кусочно-гладкая
двусторонняя поверхность
х = х(и, v)y у = у(иу и), z = z(uy и), ((а, и) € £2)	(1)
и /(я, у у г) — функция, определенная и непрерывная в точках поверх¬
ности Sy то
JJ fix, уу г) dS = JJ f(x(uy v)y y(uy v)y z(uy v))*jEG-F2 du dvy (2)
s	£2
где
= dxdx + Э1/Э1/ + Э2Э2
ЭаЭи ЭаЭи ЭаЭи'
В частном случае, если уравнение поверхности S имеет вид
2 = z(xy у) ((ху у) е а),
где z(xy у) — однозначная непрерывно дифференцируемая функция, то
JJ f(x, у, z) dS = JJ f(x, у, г(х, у))	+(|f) dx dy'
S	о
Этот интеграл не зависит от выбора стороны поверхности S.
Если функцию f(xy уу г) рассматривать как плотность поверхности
S в точке (ху уу г), то интеграл (2) представляет собой массу этой поверх¬
ности.

432
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
2. Поверхностный интеграл 2-го рода. Если S — гладкая двусторон¬
няя поверхность, — ее сторона, характеризуемая направлением нор¬
мали n {cos a, cos Р, cos у}, Р = Р(х> У у 2), Q = Q(x, у, z), R = R(x, у, г) —-
три функции, определенные и непрерывные на поверхности S, то
JJ Р ей/ dz + Q dz dx + R dx dy =
s+
= JJ (P cos a + Q cos P + R cos y) <&S.	(3)
s
Если поверхность S задана в параметрическом виде (1), то направ¬
ляющие косинусы нормали п определяются по формулам:
A	D
cos a = —	■ — , cos Р = —., -    	,
±7а2 + В2 + С2	±JA2 + B2 + C2
с
cos у = —===== ,
±JA2 + B2 + C2
где
А
д(У>*)
д(и, v)
>В
д(г> *)
д(и, v)
С
Э(а, v) 9
и знак перед радикалом выбирается надлежащим образом.
При переходе к другой стороне S" поверхности S интеграл (3) меняет
свой знак на обратный.
4341.	На сколько отличаются друг от друга поверхностные
интегралы
I\ = JJ (X2 + у2 + Z2) dS,
S
/2 = JJ (х2 + у2 + z2) dP,
р
где S — поверхность сферы х2 + у2 + z2 = а2 п Р — поверхность
октаэдра \х\ + \у\ + \г\ = а, вписанного в эту сферу?
4342.	Вычислить
ЯгА5'
S
где S — часть поверхности х2 + z2 = 2az (a > 0), вырезанная по¬
верхностью z = Jx2 + у2 .
Вычислить следующие поверхностные интегралы 1-го рода:
4343.	JJ (х + у + z) dS, где S — поверхность
s
х2 + у2 + z2 = a2, z > 0.

§14. Поверхностные интегралы
433
4344.	f| (х2 + у2) dS, где S — граница тела
s
Jx2 + у2 < Z < 1.
4345. Г Г	——г, где S — граница тетраэдра
JJ (1 + Х + у)2
S
х + у + z < 1, х> 0, у> 0, z> 0.
4346.	JJ \xyz\ dS, где S — часть поверхности z = х2 + у2, от-
s
секаемая плоскостью z = 1.
4347.	j*J , где S — поверхность эллипсоида и h — расстоя-
s
ние центра эллипсоида до плоскости, касательной к элементу dS
поверхности эллипсоида.
4348.	JJ z dS, где S — часть поверхности геликоида
s
х = u cos vy у — u sin Vy z = v (0 < u < a; 0 < v < 2n).
4349.	|| z2 dS, где S — часть поверхности конуса
s
x = r cos (p sin a, у = r sin (p sin a, z = r cos a
(0<r<a;0<(p< 2л) и a — постоянная ^0 < a < | j .
4350.	JJ (лгу + i/2 + 2л:) dS, где S — часть конической поверх-
s
ности z = Jx2 + у2 , вырезанная поверхностью
х2 + у2 = 2ал:.
4351.	Доказать формулу Пуассона
I
JJ /(a# + 6i/ + cz) dS = 2^J f(uja2 + b2 + c2) duf
s	-i
где S есть поверхность сферы x2 + у2 + z2 = 1.
4352.	1. Найти массу параболической оболочки
2=| (Х2 + У2)	(0 < 2 < 1),
плотность которой меняется по закону р = г.

434
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
2.	Найти массу полусферы
х2 + у2 + z2 = а2 (г > 0),
плотность которой в каждой ее точке М (х, у> г) равна - .
а
3.	Найти статические моменты однородной треугольной
пластины
х + у + z = а (х> 0, у>0У z > 0)
относительно координатных плоскостей.
4353.	Вычислить момент инерции однородной сферической
оболочки
*2 + у2 + z2 = a2 (z > 0)
плотности р0 относительно оси Oz.
4354.	Вычислить момент инерции однородной конической
оболочки
-2+и1-Г2=° (0 <*<Ь)
а2 а2 Ъ2
плотности р0 относительно прямой
х __ ц _ z — Ъ
10 0 ‘
4355.	Найти координаты центра масс:
а)	части однородной поверхности z = Jx2 + у2, выре¬
занной поверхностью х2 4- у2 = ах;
б)	однородной поверхности z = Ja2 - х2 - у2 (х > 0; у > 0;
х + у < а).
4356.1.	Найти полярные моменты инерции
/° = JJ(*2 + J/2 + г2) dS
S
следующих поверхностей S:
а)	поверхности куба max {|jt|, \у\9 \z\} = а;
б)	полной поверхности цилиндра х2 4- у2 < R2; 0 < z < Н.
2. Найти моменты инерции треугольной пластинки
х + у + z = 1 (х > 0; у > 0\ z > 0)
относительно координатных плоскостей.

§14. Поверхностные интегралы
435
4357.	С какой силой однородная усеченная коническая по¬
верхность
х = г cos ср, у = г sin ф, z = г (0 < ф < 2тс, 0 < b < г < а)
плотности р0 притягивает материальную точку массы т, поме¬
щенную в вершине этой поверхности?
4358.	Найти потенциал однородной сферической поверхно¬
сти х2 + у2 + z2 = a2 (S) плотности р0 на точку М0(л;0, у0, z0), т. е.
вычислить интеграл
S
где г = J(x - х0)2 + (у- у0)2 + (2- г0)2 .
4359.	Вычислить
JC + l/ + Z = f
где
I - х2 ~ у2 - z2, если
если х2 + у2 + z2 < 1;
если х2 + у2 + z2 > 1.
Построить график функции и = F(t).
4360.	Вычислить интеграл
х2 + 1/2 + г2=<2
где
f(x, у, Z) =
х2 + у2,	если х > Jx2 + у2 .
О,	если х < Jx2 + у2 .
4361.	Вычислить интеграл
s
где S — переменная сфера
(£ - х)2 + (л - у)2 + (С - г)2 = t2,
И
если £,2 + г|2 + £2 < а2.
если £2 + Г|2 4- £2 > а2,
предполагая, что
г = V*2 + у2 + z2 > а > 0.

436
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Вычислить следующие поверхностные интегралы 2-го рода:
4362.	JJ(xdydz 4- ydzdx 4- zdxdy), где S — внешняя сторона
s
сферы х2 + у2 4- z2 = а2.
4363.	JI f(x) dydz + g(y) dzdx + h{z) dxdyt где f(x)>	g(y)9
s
h(z) — непрерывные функции и S — внешняя сторона поверхно¬
сти параллелепипеда 0 < х < а; 0 < у < Ь; 0 < z < с.
4364.	“ z) dydz 4- (z - х) dzdx 4- (х - у) dxdy9 где S —
s
внешняя сторона конической поверхности х2 4- у2 = z2 (0 < z < h).
4365.	JJ	' где s _ внешняя сторона
у2	ц2	2%
эллипсоида —	-f	f-	+	—	= 1.
а2	Ъ2	с2
4366. ^x2dydz + у2 dz dx 4- z2 dx dy9 где S — внешняя сто¬
рона сферы (х - а)2 4- {у - b)2 + (z - с)2 = Я2.
§15. Формула Стокса
Если Р = Р(х9 у, 2), Q — Q(x, у, 2), i? = R(x, у, 2) — непрерывно диф¬
ференцируемые функции и С — простой замкнутый кусочно-гладкий
контур, ограничивающий конечную кусочно-гладкую двустороннюю
поверхность S, то имеет место формула Стокса:
Р dx 4- Q dy 4- R dz =
Я
cos а
cos(3 cosy
_Э_
э_
дх
ду
dz
Р
Q
R
где cos a, cos (3, cos у — направляющие косинусы нормали к поверхности S,
направленной в ту сторону, относительно которой обход контура С соверша¬
ется против хода часовой стрелки (для правой координатной системы).
4367. Применяя формулу Стокса, вычислить криволиней¬
ный интеграл
фydx 4- zdy 4- xdz,
с
где С — окружность х2 4- у2 4- z2 = а2, х 4- у 4- z = 0, пробегаемая
против хода часовой стрелки, если смотреть с положительной
стороны оси Ох.
Проверить результат непосредственным вычислением.

§15. Формула Стокса
437
4368.	Вычислить интеграл
j) (х2 - yz) dx + (у2 - xz) dy + (z2 - xy) dz,
Ат В
взятый по куску винтовой линии
х = a cos ф, у = a sm ф, z = — ф
2 л
от точки А (а, 0, 0) до точки В (а, 0, Л).
Указание. Дополнить кривую АтВ прямолинейным отрезком
и применить формулу Стокса.
4369.	Пусть С — замкнутый контур, расположенный в плос¬
кости х cos а 4- у cos Р + z cos у - р = 0 (cos а, cos Р, cos у — на¬
правляющие косинусы нормали плоскости) и ограничивающий
площадку S. Найти
*
dx dy dz
cos a cosP cosy
x у z
где контур С пробегается в положительном направлении.
Применяя формулу Стокса, вычислить интегралы:
4370.	£ (у + z) dx + (z 4- х) dy + (х + у) dz, где С есть эллипс
с
х = a sin21, у = 2а sin t cos t, z = a cos21 (0 < t < л), пробегаемый
в направлении возрастания параметра £.
4371.	j)(i/ - z) dx + (z - x) dy + (x - y) dz, где C — эллипс
c
x2 + y2 = a2, - + ^ = 1, (a > 0, h > 0), пробегаемый против хода
a Л
часовой стрелки, если смотреть с положительной стороны оси Ох.
4372.	j) (г/2 + z2) dx + (х2 + z2) dy + (х2 + у2) dz, где С есть кривая
с
л:2 + у2 + z2 = 2ifar, х2 + у2 = 2гл: (0 < г < Я, z > 0), пробегаемая так,
что ограниченная ею на внешней стороне сферы х2 + у2 + z2 = 2Rx
наименьшая область остается слева.

438
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4373.	<р (у2 - z2) dx + (22 - х2) dy + (х2 - i/2) d2, где С — сечение
с
поверхности куба 0 < л: < а, 0 < I/ < а, 0 < г < а плоскостью
о
л; + I/ + 2 = ^а, пробегаемое против хода часовой стрелки, если
смотреть с положительной стороны оси Ох.
4374.	ф i/2z2 dx + z2x2 dy + *2i/2 d2, где С — замкнутая кривая
с
л; = a cos t, у = a cos 2£, 2 = a cos 3£, пробегаемая в направлении
возрастания параметра t.
4375.	Доказать, что функция
W (х, у, z) = kifj cos^ n) dS (k = const),
где S — площадка, ограниченная контуром С, n — нормаль к
поверхности S и г — радиус-вектор, соединяющий точку про¬
странства М (х, I/, г) с текущей точкой А (£, г|, Q контура С, яв¬
ляется потенциалом магнитного поля Н, создаваемого током i,
протекающим по контуру С (см. задачу 4340).
§ 16. Формула Остроградского
Если S — кусочно-гладкая поверхность, ограничивающая объем V,
и Р = Р (х, у, z), Q = Q (х, у, z)> R = R (х, у, г) — функции, непрерывные
вместе со своими частными производными 1-го порядка в области V + S,
то справедлива формула Остроградского:
If
{р
cos а + Q cos Р + R cos у) dS =
+ +mdxdydz,
ду dzj У '
где cos а, cos Р, cos у — направляющие косинусы внешней нормали к
поверхности S.
Применяя формулу Остроградского, преобразовать следую¬
щие поверхностные интегралы, полагая, что гладкая поверх¬
ность S ограничивает конечный объем V и cos a, cos Р, cos у —
направляющие косинусы внешней нормали к поверхности S:
4376.
4377.
V
V
x3dyd2 + y3d2dx + 23dxdy.
yzdydz + 2xd2dx + xydxdy.

§16. Формула Остроградского
439
4378. я JCCOSg-b у COSft + 2COSy rfg
Jx*
+ уг + 2г
4379. f Г (i^ cos a 4- ^ cos P 4- ~ cos yl dS.
J J \dx	dy	dz J
4381.	Доказать, что если S — замкнутая простая поверхность
и 1 — любое постоянное направление, то
я
cos(n, 1) dS = О,
где п — внешняя нормаль к поверхности S.
4382.	Доказать, что объем тела, ограниченного поверхностью
S, равен
V= | JJ(jc cos a 4- у cos (3 + 2 cos у) dS,
где cos a, cos P, cos у — направляющие косинусы внешней нор¬
мали к поверхности S.
4383.	Доказать, что объем конуса, ограниченного гладкой
конической поверхностью F (лс, у, г) = 0 и плоскостью
Ах 4- By +- Cz 4- D = 0, равен
F-lSH,
где S — площадь основания конуса, расположенного в данной
плоскости, и Н — его высота.
4384.	Найти объем тела, ограниченного поверхностями: z = ±с и
)х = a cos и cos v + b sin и sin v,
у = a cos и cos v - b sin a cos у,
z = с sin и.
4385.	1. Найти объем тела, ограниченного поверхностью
х = и cos v, у = и sin у, <г = -и 4- a cos у (и > 0, а > 0)
и плоскостями: лс = 0 и 2 = 0.
2. Найти объем тела, ограниченного тором
)х = (6 4- a cos ij/) cos cp,
у = (b + a cos \|/) sin ф, (0 < а < 6).
2 = a sin ij/.

440
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4386.	Доказать формулу
^ | IJJ ^Хг у’z' ^dx dy dz
X2 + у2 + z2 < t2
Я
f(x, у, z, t) dS +
xt + yt + z'-t*
Ш Sf
x2 + y2 + z2<t2
dx dy dz (t > 0).
С помощью формулы Остроградского вычислить следующие
поверхностные интегралы:
4387.	j*j*:x:2 dy dz 4- у2 dz dx 4- z2 dx dy, где S — внешняя сто¬
рона границы куба 0 < д: < а, 0 < i/ < а, 0<2<а.
4388.	JJ х3 dy dz 4- у2 dz dx 4- z3 dx dy> где S — внешняя сто¬
рона сферы
x2 + y2 + z2 = a2.
4389.	JJ(jc - у + z) dy dz 4- (y - z + x) dz dx 4- (z - x 4- y) dx dy,
где S — внешняя сторона поверхности
\x - У 4- г\ 4- \у - z 4- х\ 4- \z - х 4- у\ = 1.
4390.	Вычислить
JJ (х2 cos а 4-у2 cos (3 + z2 cos у) dS,
где S — часть конической поверхности х2 4- у2 = z2 (0 < z < h) и
cos a, cos (3, cos у — направляющие косинусы внешней нормали
к этой поверхности.
Указание. Присоединить часть плоскости
2 = Л, *2 + у2 < h2.
4391.	Доказать формулу
V	S
где S — замкнутая поверхность, ограничивающая объем V, п —
внешняя нормаль к поверхности S в текущей точке ее (£, r|, О,
г = V(£ - х)2 + (г| - у)2 + (С - г)2 иг — радиус-вектор, идущий от
точки (х, у, г) к точке (£, r|, Q.

§16. Формула Остро градского
441
4392. Вычислить интеграл Гаусса
Их, у, 2) = |j£2^dS,
где S — простая замкнутая гладкая поверхность, ограничиваю-
хцая объем V, п — внешняя нормаль к поверхности S в точке ее
(£, r|, Q, г — радиус-вектор, соединяющий точку (х, у, г) с точкой
(4, л. О и Г = л/(^-х)2 + (л-у)2 + (С-2)2 .
Рассмотреть два случая:
а)	поверхность S не окружает точку (х, у, г),
б)	поверхность S окружает точку (х9 у, г).
4393. Доказать, что если
Л — д2и , с)2и , ()2и
~ с)х2 ду2 dz2
и S — гладкая поверхность, ограничивающая конечное тело V,
то справедливы следующие формулы:
a) JJ dS = JJJ А и dx dy dz;
S	V
+ JJJ uAu dx dy dz,
v
где и — функция, непрерывная вместе со своими частными про¬
изводными до второго порядка включительно в области V + S, и
^ — производная по внешней нормали к поверхности S.
on
4394. Доказать вторую формулу Грина в пространстве
ш
Аи Av
dx dy dz =
ди ди
дп дп
и V
•У
и V
dS,
где объем V ограничен поверхностью S, п — направление внешней
нормали к поверхности S и функции и = и(х9 у, z)f v = v (х9 у9 z)
дважды дифференцируемы в области V + S.
4395.	Функция и = и (х9 у9 z)9 обладающая непрерывными
производными до второго порядка включительно в некоторой об¬
ласти, называется гармонической в этой области, если
— д2и , г)2и , д2и

442
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Доказать, что если и — гармоническая функция в конечной
замкнутой области V, ограниченной гладкой поверхностью S, то
справедливы формулы:
где п — внешняя нормаль к поверхности S.
Пользуясь формулой б), доказать, что функция, гармониче¬
ская в области V, однозначно определяется своими значениями
на ее границе S.
4396.	Доказать, что если функция и = и(х, у, z) — гармони¬
ческая в конечной замкнутой области V, ограниченной гладкой
поверхностью S, то
где г — радиус-вектор, идущий из внутренней точки (х, у, г)
области V в переменную точку г|, Q поверхности S,
поверхности S в точке (£, Г|, Q.
4397.	Доказать, что если и = и(х, у, г) — функция, гармони¬
ческая внутри сферы S радиуса R с центром в точке (х0, у0> z0), то
(теорема о среднем).
4398.	Доказать, что функция и = и(х9 у, z), непрерывная в
ограниченной замкнутой области V и гармоническая внутри нее,
не может достигать своих наибольшего и наименьшего значений
во внутренней точке области, если эта функция не является тож¬
дественной постоянной (принцип максимума).
4399.	Тело V целиком погружено в жидкость. Исходя из за¬
кона Паскаля, доказать, что выталкивающая сила жидкости
равна весу жидкости в объеме тела и направлена вертикально
вверх (закон Архимеда).
4400.	Пусть St — переменная сфера (£ - х)2 4- (г| - у)2 -t- (£ - z)2 =
= t2 и функция /(£, ц, 0 непрерывна. Доказать, что функция
г = */(£ - х)2 + (г| - у)2 + (С - г)2 > п — вектор внешней нормали к
S,

§17. Элементы теории поля
443
удовлетворяет волновому уравнению
д2и
ду2
д2и , д2и , д2и __ д2и
дх2 ду2 дг2 dt2
и начальным условиям: u\t = Q = 0, ^ I = f(x9 у, z).
dt |« = о
У казание. Производную ^ выразить тройным интегралом.
at
§ 17. Элементы теории поля
1.	Градиент. Если и(г) = и(х, у, z), где г = х\ + у\ + zk, есть непре¬
рывно дифференцируемое скалярное поле, то градиентом его называ¬
ется вектор
gradu=^i+^j+^k
дх ду дг
или, короче, grad и = Vu, где V = i Д- + j Д + к Д . Градиент поля и в
дх ду дг
данной точке (х, г/, г) направлен по нормали к поверхности уровня
и(х, у, г) = С, проходящей через эту точку. Этот вектор для каждой точ¬
ки поля по модулю
г
ч-ЛеИЭЧе)
и направлению дает наибольшую скорость изменения функции и.
Производная поля и в некотором направлении l{cos a, cos Р, cos у}
равна
ди	,	,	ди	,	ди	п ,	ди
— = grad и • 1 = — cos а	+	— cos	Р +	— cos у.
Э/	дх	ду	дг
2.	Дивергенция поля и ротация (вихрь) поля. Если
a(r) = ах (xt z/, г) i + ау (х, у, г) j + аг (х> у, г) к
есть непрерывно дифференцируемое векторное поле, то скаляр
дах	даи	даг
дх	ду	дг
называется дивергенцией или расходимостью этого поля.
Вектор
rot а = V х а =
i
j
к
Э_
Э_
±
дх
ду
дг
ах
ау
носит название ротации или вихря поля.

444
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
3. Поток вектора через поверхность. Если вектор а(г) порождает
векторное поле в области Q, то потоком вектора через данную поверх¬
ность S, расположенную в Q, в указанную сторону, характеризуемую
единичным вектором нормали n{cos a, cos (3, cos у), называется интеграл
dS = J*J(ax cos a + ay cos P + az cos Y) dS,
s	s
где an = an — нормальная проекция вектора. Формула Остроградского
в векторной трактовке принимает вид
9
ап
Jj*J* div a dx dy dz,
v
где S есть поверхность, ограничивающая объем F, и п — единичный
вектор внешней нормали к поверхности S.
4.	Циркуляция вектора. Линейным интегралом от вектора а(г),
взятым по некоторой кривой С {работа поля), называется число
J
a dr =
j* axdx + ау dy + а2 dz.
с
Если контур С замкнут, то линейный интеграл называется цирку¬
ляцией вектора а вдоль контура С.
В векторной форме формула Стокса имеет вид
j) a dr = J*J (rot а)л dS,
С	S
где С — замкнутый контур, ограничивающий поверхность S, причем
направление нормали п к поверхности S должно быть выбрано так, что¬
бы для наблюдателя, стоящего на поверхности S, головой по направле¬
нию нормали, обход контура С совершался против хода часовой стрелки
(для правой системы координат).
5.	Потенциальное поле. Векторное поле а(г), являющееся градиен¬
том некоторого скаляра и:
grad и = а,
называется потенциальным, а величина и называется потенциалом поля.
Если потенциал и — однозначная функция, то
J a dr = и (В) - и (А).
АВ
В частности, в этом случае циркуляция вектора а равна нулю.
Необходимым и достаточным условием потенциальности поля а, за¬
данного в поверхностно односвязной области, является выполнение ус¬
ловия
rot а = О,
т. е. такое поле должно быть безвихревым.

§17. Элементы теории поля
445
4401.	1. Найти модуль и направление градиента поля
и = х2 4- 2у2 4- 3z2 4- ху 4- Зд: - 2у - 6z в точках: а) О (0, 0, 0);
б)А(1, 1, 1) и в) Б (2, 0, 1). В какой точке градиент поля равен
нулю?
2. Пусть
а = ху - г2.
Найти модуль и направление grad и в точке М (-9, 12, 10). Чему
равна производная ~ в направлении биссектрисы координатно-
о1
го угла хОу!
4402.	В каких точках пространства Охуг градиент поля
и = хг + у3 4- z3 - 3хуг
а) перпендикулярен оси Oz\ б) параллелен оси Oz; в) равен нулю?
4403.	Дано скалярное поле
и = Ini
г
где г = J(x - а)2 + (у - Ь)2 + (х - с)2 . В каких точках пространства
Oxyz имеет место равенство
|grad и\ = 1?
4404.	Построить поверхности уровня скалярного поля
и = Jx2 + у2 + (z + 8)2 4- Jx2 + у2 + (z - 8)2.
Найти поверхность уровня, проходящую через точку М (9, 12, 28).
Чему равен шах и в области х2 4- у2 4- z2 < 36?
4405.	Найти угол ср между градиентами поля
и = ——2L
л:2 + у2 + г2
в точках А (1, 2, 2) и Б (-3, 1, 0).
4406.	Пусть дано скалярное поле
и = -р=== •
V*2 + у2 + Z2
Построить поверхности уровня и поверхности равного моду¬
ля градиента поля.
Найти inf и9 sup u, inf |grad и\9 sup |grad и\ в области 1 < z < 2.

446
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4407.	С точностью до бесконечно малых высших порядков
найти расстояние в точке М0 (д:0, у0, г0) между двумя бесконечно
близкими поверхностями уровня
и (ху у у г) = с и и (х, у, г) = с + Ас,
где и (*0, у0, 20) = с (grad и (х0, «/о» 2о) * о )•
4408.	Доказать формулы:
а)	grad (и + с) = grad и (с — постоянно);
б)	grad си = с grad и (с — постоянно);
в)	grad (и + v) = grad и + grad v;
г)	grad uv= и grad v + v grad u\
д)	grad (и2) = 2и grad и;
е)	grad f'(u) = f'(u) grad и.
4409.	Вычислить:
a) grad r; 6) grad г2; в) grad - , где r = V*2 + y2 + z2.
r
4410.	Найти grad Дг), где r = Jx2 + y2 + z2.
4411.	Найти grad(cr), где c — постоянный вектор иг — ради¬
ус-вектор из начала координат.
4412.	Найти grad{|c х г|2} (с — постоянный вектор).
4413.	Доказать формулу
grad f(u9 v) = grad и + grad v.
аи	dv
4414.	1. Доказать формулу
V2 (uv) = и V2v 4- v V2u + 2 Vu Vy,
где
V = i
э_
Эл:
V2
vv-fe
11
Эу2
+
11
дг2‘
2. Доказать, что если функция и = h(jc, I/, 2) дифференциру¬
ема в выпуклой области Q и |grad ы| < М, где М — постоянная,
то для любых точек А, В из Q имеем:
|и (А) - и (В)| < Мр (А, В),
где р(А, В) — расстояние между точками А и В.
4415.	Для функции и = и(х, уу г) выразить grad и: а) в ци¬
линдрических координатах; б) в сферических координатах.

§17. Элементы теории поля
447
4416.	Найти производную поля н = ^ 4- ^ 4- ^ в данной
а2 о2 с2
точке М(х9 у у г) в направлении радиуса-вектора г этой точки.
В каком случае эта производная будет равна величине гради¬
ента?
4417.	Найти производную поля и = - , где г = Jx2 + у2 + z2,
г
в направлении 1 {cos a, cos (3, cos у}.
В каком случае эта производная равна нулю?
4418.	Найти производную поля и = и (х9 у9 г) в направлении
градиента поля v = v (х9 у9 z).
В каком случае эта производная будет равна нулю?
4419.	Написать в ортах векторное поле
если
а = с х grad и9
и = arctg——	 и c = i + j + k.
Jx2 + у*
4420.	Определить силовые линии векторного поля
а = х\ + у] + 2zk.
4421.	Доказать непосредственным вычислением, что дивер¬
генция вектора а не зависит от выбора прямоугольной коорди¬
натной системы.
4422.	Доказать, что
div а (М) = lim ~ Г [ ап dS9
d(S)-+ 0 V J J
S
где S — замкнутая поверхность, окружающая точку М и огра¬
ничивающая объем V9 п — внешняя нормаль к поверхности S,
d(S) — диаметр поверхности S.
4423.	1. Найти дивергенцию поля
= -ix + jy + kz
Jx^+V2
в точке М (3, 4, 5). Чему приближенно решен поток П вектора а
через бесконечно малую сферу (х - З)2 + (у - 4)2 + (z - 5)2 = е2?
2. Найти
i
j
к
Э
э_
э
дх
Эу
дг
<*>*
Юу
0)г

448
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4424.	Доказать, что:
а)	div (а + b) = div а 4- div b;
б)	div (нс) = с grad и (с — постоянный вектор, и — скаляр);
в)	div (на) = и div а + a grad н.
4425.	Найти div (grad н).
4426.	Найти div [grad /(г)], где г = Jx2 + у2 + г2. В каком слу¬
чае div [grad f(r)] = О?
4427.	Вычислить: a) div г; б) div - .
г
4428.	Вычислить div [/*(г)с], где с — постоянный вектор.
4429.	Найти div [/(г)г]. В каком случае дивергенция этого
вектора равна нулю?
4430.	Найти:
a) div (н grad н); б) div (н grad н).
4431.	Жидкость, заполняющая пространство, вращается во¬
круг оси Ог против часовой стрелки с постоянной угловой ско¬
ростью О). Найти дивергенцию вектора скорости v и вектора ус¬
корения w в точке М (ху у у г) пространства в данный момент вре¬
мени.
4432.	Найти дивергенцию гравитационного силового поля,
создаваемого конечной системой притягивающих центров.
4433.	Найти выражение дивергенции плоского вектора
а = а(г, ср) в полярных координатах гиф.
4434.	Выразить div а(х9 уу z) в ортогональных криволиней¬
ных координатах и, v, w9 если
х = f(Uy Vy w)9 у = g(Uy Vy w), z = h(Uy Vy w).
Как частный случай получить выражение div а в цилиндриче¬
ских и сферических координатах.
Указание. Рассмотреть поток вектора а через бесконечно малый
параллелепипед, ограниченный поверхностями и = const, v — const,
w = const.
4435.	Доказать, что:
а)	rot (a + b) = rot a + rot b;
б)	rot (ua) = и rot a + grad (и x a).
4436.1.	Найти: a) rot r; 6) rot[/(r)r].
2. Найти модуль и направление rot а в точке М (1, 2, -2),
если
a«Ki+2j + £k.
г х у
4437.	Найти: a) rot сf(r); б) rot [с х /(г)г] (с — постоянный век¬
тор).
4438.	Доказать, что div (а х b) = b rot а - a rot b.

§17. Элементы теории ПОЛЯ
449
4439.	Найти: a) rot (grad и); б) div (rot а).
4440.	Жидкость, заполняющая пространство, вращается во¬
круг оси l{cos a, cos (3, cos у} с постоянной угловой скоростью со.
Найти ротацию вектора линейной скорости v в точке простран¬
ства М (х, I/, г) в данный момент времени.
4441.1.	Найти выражение ротации плоского вектора а = а (г, ср)
в полярных координатах г и ф.
2. Выразить rot а (х, у, г): а) в цилиндрических координатах;
б) в сферических координатах.
4442.1.	Найти поток вектора г: а) через боковую поверхность
конуса х2 + у2 < z2 (0 < г < /г); б) через основание этого конуса.
2. Найти поток вектора а = iyz + jxz + kxy: а) через боковую
поверхность цилиндра х2 + у2 < а2 (0 < z < h); б) через полную
поверхность этого цилиндра.
4443.	Найти поток радиуса-вектора г через поверхность
2 = 1 - л/*2 + у2 (0<2<1).
4444.	Найти поток вектора а = хЧ + у2j + z2k через положи¬
тельный октант сферы х2 + у2 + z2 = 1, х > 0, у > 0, z > 0.
4445.1.	Найти поток вектора а = у\ + zj 4- хк через полную
поверхность пирамиды, ограниченной плоскостями х = 0, у = 0,
z = 0, х + у + z = а (а > 0).
Проверить результат, применяя формулу Остроградского.
2. Найти поток вектора
а = jc3i + i/3 j + z3k
через сферу х2 + у2 + г2 = х.
4446.	Доказать, что поток вектора а через поверхность S, за¬
данную уравнением г = г (и, и) ((и, v) € Q) равен
.s	а
где ап = ап и п — единичный вектор нормали к поверхности S.
4447.	Найти поток вектора а = т^- (т — постоянная) через
г3
замкнутую поверхность S, окружающую начало координат.
4448.	Найти поток вектора
/ = 1
где ех — постоянные и гх — расстояния точек М, (источники) от
цеременной точки М(г), через замкнутую поверхность S, окру¬
жающую точки М{ (i = 1, 2, ..., п).

450
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4449.	Доказать, что
JJ ^dS = JJJV2u dx dy dz,
где поверхность S ограничивает тело V.
4450.	Количество теплоты, протекающее в поле температуры
и за единицу времени через элемент поверхности dS, равно
dQ = -kn grad и dS,
где k — коэффициент внутренней теплопроводности и п — еди¬
ничный вектор нормали к поверхности S. Определить количе¬
ство теплоты, накопленное телом V за единицу времени. Ис¬
пользуя скорость повышения температуры, вывести уравнение,
которому удовлетворяет температура тела (уравнение тепло¬
проводности).
4451.	Находящаяся в движении несжимаемая жидкость за¬
полняет объем V. Предполагая, что в области V отсутствуют ис¬
точники и стоки, вывести уравнение неразрывности
+ div(pv) = 0,
где р = р(х, у у z) — плотность жидкости, v — вектор скорости,
t — время.
Указание. Рассмотреть поток жидкости через произвольный
объем (о, содержащийся в V.
4452.	1. Найти работу вектора а = г вдоль куска винтовой ли¬
нии г = ia cos t + ja sin t + kbt (0 < t < 2n).
2.	Найти работу поля
a-Ii+Ij + Ik
у г x
вдоль прямолинейного отрезка, соединяющего точки М (1, 1, 1)
и АГ(2, 4, 8).
3.	Найти работу поля
а = iey ~ 2 + \ег “ * + кех ~ у
вдоль прямолинейного отрезка между точками О (0, 0, 0) и
М( 1, 3, 5).
4453.1.	Найти работу поля
а = (у + z)i + (z + х)] + (х + у)к
вдоль кратчайшей дуги большого круга сферы х2 + у2 + z2 = 25,
соединяющей точки М (3, 4, 0) и N (0, 0, 5).

§17. Элементы теории поля
451
2. Найти работу вектора а = /(г)г, где f — непрерывная функ¬
ция, вдоль дуги АВ.
4454.	1. Найти циркуляцию вектора
а = -yi + х] + ck
(с — постоянная): а) вдоль окружности х2 + у2 = 1, z = 0; б) вдоль
окружности (х - 2)2 + у2 = 1,2 = 0.
2. Найти циркуляцию Г вектора а = grad ^arctg ^ вдоль кон¬
тура С в двух случаях:
а) С не окружает ось Oz\ б) С окружает ось Oz.
4455.	Дано векторное поле
а = -*рi -	j + Jxyzk.
Jx Jz
Вычислив rota в точке М( 1, 1, 1), приближенно найти цирку¬
ляцию Г поля вдоль бесконечно малой окружности
\(х - I)2 + (г/ - I)2 + (г - I)2 = в2,
|(л: - 1) cos а + (у - 1) cos (3 + (z - 1) cos у = 0,
где cos2 а + cos2 (3 + cos2 у = 1.
4456.	Плоский установившийся поток жидкости характери¬
зуется вектором скорости
w = и(х, у)i + v(x, y)j.
Определить: 1) количество жидкости Q, протекающее через замкну¬
тый контур С, ограничивающий область S (расход жидкости);
2) циркуляцию Г вектора скорости вдоль контура С. Каким уравне¬
ниям удовлетворяют функции и и и, если жидкость несжимаема и
поток безвихревой?
4457.	1. Показать, что поле
а = yz (2х + у + z)i + xz (х + 2у + z)j + ху (х 4- у + 2z) к
потенциальное, и найти потенциал этого поля.
2. Убедившись в потенциальности поля
“	1‘	3*»	3“’
(I/ + Z)2	(У+2)2	(1/ + 2)2
найти работу поля вдоль пути, соединяющего в положительном
октанте точки М (1, 1, 3) и N (2> 4, 5).

452
РАЗДЕЛ VIII. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
4458.	Найти потенциал гравитационного поля
создаваемого массой тп, помещенной в начале координат.
4459.	Найти потенциал гравитационного поля, создавае¬
мого системой масс /?г£ (г = 1, 2, ...» /г), помещенных в точках
= 1, 2, ..., п).
4460.	Доказать, что поле а = f(r)г, где f(r) — однозначная не¬
прерывная функция, является потенциальным. Найти потенциал
этого поля.
4461.	Доказать формулу
grad Jjjjp(Q)^ | = -JJp(Q) nf + JJJ gradQ p(Q)^,
где S — поверхность, ограничивающая объем V, n — внешняя
нормаль к поверхности R, г— расстояние между точками
Р(х, у, г) и Q(£, r\, Q.
4462.	Доказать, что если а = grad и, где
+ оо
и(х, у, г) =	& dt, dr\ dC
-oo
г = V(£ - x)2 + (Л - У)2 + (C - 2)2 >
TO
div a = p(x, у, 2)
(предполагая, что соответствующие интегралы имеют смысл).

ОТВЕТЫ
Раздел I
16.0; 1. 17.-72; 72. 22. -1,01 < * < -0,99. 23. х < -8; х > 12.
24. х< -i. 25. 0 < х <	26. Ы< 6. 27. х > -i . 28.	< х< 1.
2	3	' '	2	2	2
29. ь-М < X < Ъ.-Ш ; Р.+.Ш < х <	. 31. Второе. 32. Два знака.
33. Не превышает 0,41%. 34. 9,9102 см2 < S < 10,0902 см2; Д < 0,0902 см2;
8 <0,91%.	35. 3,93 г/см3 ±0,27 г/см3; 5 <7,3%.	36. 8 <3,05%.
37.	172,480 м3 < V < 213,642 м3; V = 192,660 м3 ± 20,982 м3; 8 ~ 12%.
38.	Д < 0,17 мм. 39. Д < 0,0005 м. 42. а) ЛГ > 1; б) N > /I; в) N > 1 +	;
б	Ve	lg2
г)	N > ;	~ 2330 lgi . 43. a)N>E;6)N>	V ; в )N> Ю10. 46. 0.
l^U, УУУ	£	V, Ck J
47. 0. 48. 0. 49. i . 50.	. 51. i . 52. i . 53. i . 54. ^ . 55. 3. 56.1. 57. 2.
3	1 -a 2	2	3	3
67. а) второе; б) первое; в) второе. 72. е = 2,71828... . 92. Равен 1, если
а^Ои принадлежит [-1; 1], или не существует, если а = 0. 96. х3 = 1 i .
8
®7. Хюо =	98. х1000 =	Ю00!	~	' Ю452, 99. х4 = х5 = —120.
100. х10 = 20.101. а) 0; 1; 1; 1; б) -з|; 5; -2; 2.102.-1; li ; 0; 1.103.0; 2; 0.
Ск	£л
104. -4; 6; -4; 6. 105. -|; 1;	; 1. 106. -ОО; 4-00; -ОО; 4-00. Ю7. —ОО; —1;
-ОО; -ОО. 108. 0; +°°; 0; +°°. 109. —ОО; 4-00; -ОО; 4-00. 110. -5; 1,25; 0; 0.
111.	; 1. 112. -{е+±^\е+ 1. 113. 0; 1. 114. 1; 2. 115. 0; 1. 116. 0; 1.
117. 1; i; 1; ...;0. 118. Все вещественные числа, заключенные между
2	3
О	и 1, включая последние. 119. 1; 5.	120. а; Ъ. 127. а) расходится,
б) может как сходиться так и расходиться. 128. а) нельзя; б) нельзя.
129. Нет. 130. Нет. 144. а) 0; б) 0.147. In 2.148. i (а + 26). 151. -°° < х < +°°,
3
х 5й -1. 152. -оо < х < - V3 и 0 < х < л/3 . 153. -1 < х < 1. 154. a) |jc| > 2;
б) х > 2. 155. 4fe2jt2 < х < (2k + 1)2к2 (ft = 0, 1, 2, ...). 156. |х| < и
< М <!<«*■> (*-1.2....). 1ет-5Т1<*<д
И

454
ОТВЕТЫ
_2ftTl <х< ~2Г+2 *k ~	2’	158- * > °> х* п (л = !* 2> •••)•
1	Ггл-Ля
159.-i < л:< 1.160.1л:- Щ< 5 (Л - 0, ±1, ±2, ...). 161. 101	2> < х <
3	6
Гг а + -Пи
< НГ 2> (k = 0, +1, +2, ...). 162. х = -1, -2, -3, ... и л: > 0. 163. л: < О,
л: * -л (л = 1, 2, ...). 164. 1 < х < 2. 165. а) х = i 1, |, 2, ... ; б) х > 4;
в)Ы + 5 < *< kn + 5 (ft= 0, +1, ±2 ...); г)0«*<|и^<*<^.
4	2	о о	Z
166. -1 < * < 2; 0 < у < li . 167. 2tot + 5 < * < 2йя + ^ (ft = 0, ±1, ±2,...);
2	3	о
-оо < I/ < lg 3. 168. -оо < * < +оо; 0<у< п. 169.1 < л: < 100; -2 <i/<2.
La	La
170. х =	, где я и д — целые числа; у = ±1. 171. jP = 26 -I- 2 Г 1 — ^) л:
2д+1	V hj
(О < х < Л); S = Ьх ^ 1 -	(0 < х < Л). 172. а = Vl00^96cosjc (0 < х < я);
S	= 24 sin х (0 < х < я). 173. S = —я2, если 0 < х <	; S = л( х - ^--^1,
а-Ь	2	V 4 у
а - b ^	^ а + b . о _ ь Г а + b (а-х)2!		, а + b
2	2	L 2 а - 6 J	2
174. т(х) = 0, если -°° < х < 0; т(х) = 2х, если 0 < х < 1; т(х) = 2, если
1<х<2; т(х) = 3, если 2 < х < 3; т(х) = 4, если 3 < х < +°о.
178. Еу = {0 < у < 4}. 179.	= {1 < у < 3}. 180. Еу = {0 < у < 1}.
181.	Еу = {1 < |i/| < +оо}. 182. Еу = {1 < у < 2}. 183. а < у < Ъ при а <Ъ
и b < у < а при а> Ь. 184. 1 < у < +оо. 185. О > у > -оо и +°° > у > 1.
186. О < у < i . 187. +оо > у > -00. 188. О < у < i и § < г/ < 2. 189.0; 0;
La	La	La
0; 0; 24. 190. 0; -6; 4. 191.1; 1; 1; 2. 192. -1; 0; 1; 2; 4. 193.1, ^ ,
1-х
х - 1	1 + X
. 194. а) /(х) = 0, если х = -1, х = 0 и х = 1;
2	+ х* 1 + х * х +1 * 1-х
/(х) > 0, если -оо < х < —1 и 0 < х < 1; /(х) < 0, если -1 < х < 0 и
1	< х < +оо; б) /(х) = 0, если х = ±i ; f(x) > 0, если 1
k	2k + 1
< х < ~ и
2k
2k+\
< X <
2k + 2
1
(k = 0, 1, 2, ...); /(x) < 0, если
1
< х <
и -— < х < -
2k	2/г + 1
2k+ 2	2/г+1
(& = О, 1, 2, ...); в) /(х) = 0, если х < 0 и х = 1; f(x) > О,
если х < 0 и х = 1; /(х) > 0, если 0 < х < 1; f(x) < 0, если 1 < х < +оо.
195. а) а; б) 2х + h; в) а* •	. 197. f(x) = | л: - 2; /(1) = i ; /(2) = 2? .
п	3	3	3
198.Я*)=2*2+И* + 1; Я-1) 1; Я0,5) = 2±1. 199. f(x) = jX3-
17
10

ОТВЕТЫ
455
- lx2 - ^х + 2. 200. f(x) = 10 + 5 • 2х. 203. a) 2Am < * < л + 2Агл
(k = 0, ±1, ±2); б) 1 < х < е; в) х > 0, х * k (k = О, 1, 2,...). 205. а) г = х + у;
б) г =.*£.; В)г=	; г) z =	. 206. ф(ф(*)) = *4; ф(ф(*)) = 22*;
ф(\|/(де)) = 22х; ф(ф(*)) = 2 *2. 207. ф(ф(де)) = sgn х; ф(ф(л:)) = х (лс *■ 0);
ф(ф(дс)) = ч/(ф(ас)) = sgn х ix * 0). 208. ф(ф(ас)) = ф(х); ф(ф(х)) = \|/(х);
ф(ф(дс)) = ф(ф*)) = 0. 209.	—; д: (х * 0, х * 1). 210. fn(x) =	*	.
*	Л + пхг
211. дс2-5дс + 6. 212. л:2 - 2	> 2|J . 213. 1. 1-tiLt*? . 2. fix) = (j^f •
221. а) Возрастает при a > 0 и убывает при а < 0; б) при а > 0 убывает
в интервале ^ -оо, - Aj и возрастает в интервале ^ -А, +°° j ; в) возрас¬
тает; г) при ad-Ьс> 0 возрастает в интервалах ^ -оо, и ^	, +оо j ;
д)	возрастает при а > 1 и убывает при 0 < а < 1. 222. Можно, если
основание логарифмов больше 1. 224. ^-2 (-оо < у < +оо). 225. a) -Jy
(О < у < +оо); б) JTy (0 < у < +оо). 226. (у * -1). 227. а) -л/Г^
(О < у < 1); б) -л/Г^2 (0 < у < 1). 228. Arsh у = In (у + л/Гму1)
(-оо < у < +оо). 229. Arth у = i In (-1 < у < 1). 230. х = г/, если
2	1 ~ у
-оо < у < 1; х — а/у , если 1 < у < 16; х = log2 у9 если 16 < у < +оо.
231. а) Нечетная; б) четная; в) четная; г) нечетная; д) нечетная.
О «г
233. а) Периодическая, Т = =^- ; б) периодическая, Т = 2к; в) периодиче-
л
ская, Т = 6я; г) периодическая, Т = я; д) непериодическая; е) периоди-
2
ческая, Т = к; ж) непериодическая; з) непериодическая. 241. t = 1 г с,
з
* = -з|м. 243.х0 = -±,
.. _ 4ас - Ь2
244. у = х -
х2
36000
9 км; 36 км.
251. х0 =	: Уо = - • 252. р = if (F > 0). 263. fe = -, /п = 0,6 ,abh
с	с	V	а\	а\
п = ±- iaxb-ab,), д:0 = --- 264. (/=12.287. А = «/а*~Гь* ; sin^ = -2,
«1 а?	ai	*	А
cos х0 = т •	356. у — 2 sin я, если |д: -	< - , и I/ = (-1)*, если
А	6
5	< |* - лй| < ik = 0, ±1, ±2, ...). 357. а) у = | (* + |*|); б) и в) у = х2,
если х > 0; у = 0, если л: < 0; г) у = х, если л: < 0; у = я4, если л: > 0.

456
ОТВЕТЫ
358. а) у = 1; б) у — 1, если 1 < |д:| < л/3 ; у — 0, если |х| < 1 или \х\ > J3 ;
в)	г/ = 1, если |я| <1; у = 2, если |я| >1; г) г/ = -2, если |х| > 2; у = 2 - (2 - х2)2,
если \х\< 2. 359. При л: < 0 имеем: а) 1) f(x) = 1 + х> 2) /(дс) = -(1 + х);
б) 1) f(x) = -2х - х2, 2) f(x) = 2х + х2; в) 1) f(x) = J-x , 2) f(x) = -J^x ;
г)	1) f(x) = -sin 2) f(x) = sin x; д) 1) f(x) = <T*,	2) f(x) = -<TX;
e)	1) f(x) = In (-x), 2) /(x) = -In (-x). 360. a) x = - A ; б) x = ± ; в) x = ^ ;
r) x = kn(k = 0, ±1, ±2, ...). 361. a) (jc0, ax0 + b), где x0 — произвольно;
6)	; в) (x0, Уо), где x0 = -■£- и y0 = ах? + ЪхI + сх0 + d; г) (2, 0);
v с с)	6а
д)	(2, 1).	372. Корни: -1,88; 0,35; 1,53.	373. 2,11; -0,25; -1,86.
374.	0,25; 1,49. 375. 0,64. 376. 1,37; 10. 377. -0,54. 378. 0; 4,49.
379. х,	0,57, I/, = -1,26; х2	0,42, у2 = 1,19; х3 = 0,45, у3 = 0,74;
х4 « 0,54, ул = -0,68. 380. х, = -1,30, г/, = 9,91; х2 = 2,30, у2 = 9,73;
х3 = -0,62, у3 = -9,98; х4 = 1,62, у4 = -9,87. 382. а) Вообще говоря, нет;
б) да. 385. Ограничена сверху и неограничена снизу. 387. /(а) и (b).
388. 0; 25. 389. 0; 1. 390. 0; 1. 391. 2; +°о. 392. -1; 1. 393. -Jl; JI.
394. |;	4.	395. a)	0,1; б) 0, 2. 396. 0; 1. 397. а) 8; б) 0,8; в) 0,08; г) 0,008.
398. а)	я;	б) л;	в) л; г) л.	411. а) 1; б)-; в) i.	412.6. 413.10.
О	2
1	*	/ол30	_2in±i!
414. \ пт{п - т). 415. 5‘5. 416. ^	. 417. п 2	. 418. -± . 419. ± .
420. 1. 421. i . 422. i . 423. f|V°. 424. a)	; б) 2-1. 425. 2 .
4	3	\2J	’	2	’	24	л
426. PterJ) а"-2. 427. "<n + х) . 428.	. 429. х + 2 . 430. х2 + ах + ^ .
2	2	2	2	3
431. 1. 432. i. 433. 3. 434.	435. 1. 436. -1. 437.	438. -2.
2	3	^3
439. -1= . 440. --1 . 441. -1-. 442. i . 443. ±2 . 444. ± . 445. -2. 446. ± .
J2a	16	144	4	5	л	4
447.	.	448. |. 449. 4-1.	450.	-1.	451. -i . 452. ^ - Ё . 453.	1 + £ .
27	2	27	36	2	m л	т п
455. 1.	£	.	2. i	.	456. 1.	457. i (а + Ь). 458. i .	459. -± . 460. 1.
т	2	п\	2	2	4
461.	|. 462. 2. 463. |.	464.	-1.465.	± (а, + а2 + ... + а„). 466. 2".	467. 2/г.
468. lim	Xj = °о, lim	х2 =	-£ .	469.	а = 1, 6 = -1. 470. а, = +1;	bt = + i
(i = 1, 2). 471. 5. 472. 0. 473. (-if'“2* . 474. a) ±; б) 1; в) 1. 475. i .
п	2	3	2
476. 2. 477.4. 478.1. 479. i . 480.1. 482. cos a. 483. -sin a. 484. sec2 a
p	2	n

ОТВЕТЫ
457
(а ^ (2k + 1)$, k = 0, ±1, ...)•	485. - , * (а ^ to, где k — целое).
2	sin2a
486. sina- (а ^ (2& + 1)- , где k — целое). 487. - c°soa (а * &л, где k —
cos2 а	2	sin2 а
целое). 488. -sin а. 489. -cos а. 490. £sina да + 1)5, где k — целое).
cos3 а	2
491. 2 со- - (а * fcrc, где Л — целое). 492. 5 sin 2а. 493. -3. 494. 14.
sin3 а	2
495. -L . 496. -24. 497. -™2а (а * (26 + 1)5 , где k — целое). 498. 5 •
^	cos4 а	2	4
499. i . 500. |. 501. -i . 502. J2 . 503. 0. 504. 3. 505. 0. 506. а) |;
б) Ji; в) 1. 507.1. 508.0. 509.0. 510.0. 511.1. 512. е3. 513.1. 514. в”2.
515. е2а. 516. О, если ах < а2; +°°, если ах > а2; е °1 , если ах = а2. 517. е.
з
518. с"1. 519. а) 1; б) Je . 520. <?ct*a (a* to — целое). 521. е* . 522. в"1.
JT2
523.1.	524. е~2. 525. е. 526. i . 527.ex + l. 528. е т . 529.1. 530.1.
Те
531. 1. 532. 0. 533. 1. 534. -2. 535. 2 . 536. |. 537.	. 538. 2“ .
а	5	2	2	хг	. Ь
539. (J)2. 540. а) 0; б) п.	541. In a. 542. a“	In	2 .	543.	a“ In	ea. 544. e2.
545. a) § ; 6)eP2-“2; в) 2;	г)-2. 546. e2. 547.1. 548. |a°-P.	549. a6 In a.
550.	ax In2 a. 551. e^a + b\ 552. In x. 553.	In	x.	554.	ф .	555. Jab.
556.	Va&c . 557. (aa6V) . 558. -J- . 559. f lnSV' • 560. a““ In a.
JTb	v b)
561. a) 0; 6) |il|. 562. In 8. 563. -in 2. 566. a) |; б) 1. 567. 1. 568. 0.
2
569. In a2. 570. ± . 571. i . 572. -2. 573. e2. 574. e* . 575.	. 576. a) 1;
8	2	M
6) i ; в) 1. 577. a) I; 6) 2 sh |. 578. a) ch a; 6) sh а; в) -1. 579. a) In 2;
6) 1. 580. e”2. 581.	. 582. 5 . 583. -5 . 584. ^ . 585. -i-;. 586. 2.
2	3	2	4	1 + x2
2
587.	. 588. i . 589. 1. 590. e* . 591. a) 0; 6) 0. 592. a) +00; 6) 1.
593. a) -1; 6) 1. 594. 1. In Ц. 595. a) f ; 6) -f . 596. a) 1; 6) 0. 597. a) 0;
6)1. 600. 2; 1; 2. 601.0; (-l)"'1; (-1)". 602.0. 603.1. 604.0. 605.1.606.0.

458
ОТВЕТЫ
613.	б) у = 1, если |дс| < 1; у = 0, если |х| = 1. 614. б) у = 0, если 0 < х < 1;
у = |, если х = 1; у = 1, если 1 < х < +°°. 615. z/ = -1, если О < И < 1;
г/ = О, если |х| = 1; г/ = 1, если \х\ > 1. 616. у = |х|. 617. г/ = 1, если О < х < 1;
X2
у — Ху если х > 1. 618. z/ — 1, если О < х < 1; у = Ху если 1 < х < 2; г/ = — ,
если х > 2. 619. у = О, если О < х < 2; г/ = 2 V2 , если х = 2; у = х2, если
х > 2.	620. б) у = 0, если х * (2& + 1)|; у = 1, если х = (2& + 1)^
(k = 0, ±1, ±2, ...). 621. у = In 2, если 0 < х < 2; г/ = In xf если х > 2.
622. у = 0, если -1 < х < 1; г/ = | (л: - 1), если х > 1. 623. у = 1, если х < -1;
у = ех + 1у если х > -1. 624. а) у = х, при х < 0; г/ = |, при х = 0; у = 1,
при х > 0; б) i . 625. а) у = Jx при 0<х<1и4й-1<х<4& + 1; z/ = х
х
при 4&-3<х<4&-2и4&-2<х<4&-1; z/=|(Vx + х) при x = 2k- 1
(k = 1, 2, 3, ...); б) z/ = О, если х — рационально; z/ = х, если х — ирра¬
ционально; в) контур квадрата шах{|х|, \у\) = 1. 627. а) х = 1, х = -2у у
' 111
= х — 1; б) г/ = х + - при х оо уУ = -х- - при х -оо; в) у = - - х; г)
у — х при х —* +°о, у = 0 при х —►	д) у = 0 при х -°о, z/ = х при
* -» +оо; е) у = х + 5 . 628. 0. 629.	. 630.	. 632. 1. 633. £ .
’ у	2	1-Х	X	6	2
634. i In а. 635. Je. 636. е т. 637. 1.1(1 + УГ+4а). 2. |. 3.	.
Z	Z	О	1 — CL
4.	2^Ь-1. 638. a) Jl + x - 1; б) 1 - Л-х . 641. а) 2; б) +°°; в) 0; г) 1;
д) 2; е) 1; ж) 2 sh 1. 643. а) ( = -1, L = 2; б) Z = -2, L = 2; в) I = 2, L = е.
644. а) I = -1, L = Г; 6)1 = 0, L = +оо; в) I = 1, L - 2; г) Z = О, L = +°о.
645.	а) Первого порядка; б) второго; в) первого; г) третьего; д) третьего;
1
е)	третьего. 653. а) 2х; б) х; в) — ; г) ^ . 655. а) 3(х - I)2; б) (- ~	;
2 2 3л/2
2 1 3
в)х-1; г)е(х-1); д)х-1. 656. а) х2; б) 2х2; в) х3; г) х® . 657. a) fij ;
61 KS!; ■- Iffl1: г> (S'-■658- *> 1(A)16>л (А11 »>
г)	1 • -j- ; д) —. 663. а) 9,95 < х < 10,05; б) 9,995 < х < 10,005;
я 1-х х- 1
в)9,9995<х< 10,0005; г) «/ЮО - £ <х< «ДООТё. 664Д< А; а)Д<3,7мм;

ОТВЕТЫ
459
б) Л <0,37 мм; в) А <0,037 мм. 665.100[1 - ПГ(л + 1)]2 < * < 100[1 + НГ<п+1)]2;
а) 81 < х < 121; б) 98,01 < * < 102,01; в) 99,8001 < х < 100,2001;
2
г)	99,980001 < * < 100,020001. 666.5 = min (£ , 1667.8 = ГН«_ а о,001 х\ ;
а) 8 ~ 10"5; б) 8 ~ 10~7; в) 8 ~ 10~9. Нельзя. 669. а) Нельзя; б) можно.
671. Нет; ограниченность в точке х0. 672. Нет; если функция f(x) опреде¬
лена в конечном промежутке (а, Ь), то эти неравенства выполняются всег¬
да; если по меньшей мере а или b равно символу оо, то lim \f(x)\ = +оо.
X — ОО
673. Нет; однозначность и непрерывность обратной функции. 675. Непре¬
рывна. 676. Непрерывна, если А = 4, и разрывна при х = 2, если А * 4.
677. Разрывна при х = -1. 678. а) Непрерывна; б) разрывна при х = 0.
679. Разрывна при я = 0. 680. Непрерывна. 681. Непрерывна. 682. Разрывна
при х = 1. 683. Непрерывна при а = 0 и разрывна при а & 0. 684. Разрывна
при х = 0.	685. Разрывна при х = k (k — целое). 686. Разрывна при
х = k2 (k = 1, 2, ...).	687. х = -1 — точка бесконечного разрыва.
688. х = -1 — устранимая точка разрыва. 689. л; = -2 и jc = 1 — точки
бесконечного разрыва. 690. х = 0 и х = 1 — устранимые точки разрыва;
х = -1 — точка бесконечного разрыва. 691. х = 0 — устранимая
точка разрыва; х = kn (k = ±1, ±2, ...) — точки бесконечного разрыва.
692. х = ±2 — устранимые точки разрыва. 693. х = 0 — точка разрыва
2-го рода. 694. х = i (k = ±1, ±2, ...) — точки разрыва 1-го рода; х = 0 —
k
о
точка разрыва 2-го рода. 695. х = 0их = - ■■■■ (k — 0, ±1,...) — устранимые
2k + 1
точки разрыва. 696. х = 0 — точка разрыва 1-го рода. 697. х = 0 — уст¬
ранимая точка разрыва. 698. х = 0 — точка разрыва 2-го рода.
699.	х = 0 — устранимая точка разрыва; х = 1 — точка бесконечного разрыва.
700.	х = 0 — точка бесконечного разрыва; х = 1 — точка разрыва 2-го рода.
701.	х = kn (k = 0, ±1, ±2, ...) — точки разрыва 1-го рода. 702. х = k
(k = 0, ±1, ±2, ...) — точки разрыва 1-го рода. 703. х = k(k = ±1, ±2, ...) —
точки разрыва 1-го рода. 704. Функция непрерывна. 705. х = ±Jn
(п = 1, 2, ...) — точки разрыва 1-го рода. 706. Ж = i (ft = +l, ±2, ...) —
k
точки разрыва 1-го рода; х = 0 — точка бесконечного разрыва. 707. х=\
k
(k = ±1, ±2, ...) — точки разрыва 1-го рода; х = 0 — устранимая точка
о
разрыва. 708. х = ■	(k = 0, ±1, ±2,...) — точки разрыва 1-го рода;
(2k + 1)я
х = 0 — точка разрыва 2-го рода. 709. х — ±- и х = ±— (k = 1, 2, ...) —
«	Jk
точки разрыва 1-го рода;, х = 0 — точка разрыва 2-го рода. 710. х = \
k
(k = ±1, ±2, ...) — точки бесконечного разрыва; х = 0 — точка разрыва
2
2-го рода. 711. х = 	=-— (k = 0, ±1, ±2, ...) — точки бесконечного
(2k+ 1)л

460
ОТВЕТЫ
разрыва; х = 0 — точка разрыва 2-го рода. 712. х = ±Jn (п = 1, 2, ...) —
точки разрыва 1-города. 713. * = 0, х = 1 и л; = 2 — точки разрыва 1-города.
714. х *= kn (k = 0, ±1, ±2,...) — точки бесконечного разрыва. 715. х = ± Jkn
(k = О, 1, 2, ...) — точки бесконечного разрыва. 716. х = -1 и х = 3 —
точки бесконечного разрыва. 717. х = 0 — точка разрыва 2-го рода.
718. х = 0 — устранимая точка разрыва. 719. х = ±1 — точки разрыва
1-го рода. 720. у = 1, если 0 < х < 1; I/ = |, если х = 1; у = 0, если х > 1;
х = 1 — точка разрыва 1-го рода. 721. у = sgn х; х = О — точка разрыва
1-го рода. 722. у = 1, если |х| < 1; z/ = я2, если |х| > 1. Функция непре¬
рывна. 723. у = 0, если х ^ Лл; у = 1, если х = Лл (Л = 0, ±1, ±2, ...);
х = kn — точки разрыва 1-го рода. 724. у = х, если \х - kn\ < ^ ; у = |,
если х = Лл±|;1/ = 0, если ^ < |лг - Лл| < 5^ (Л = 0, ±1, ±2, ...); х = kn ± ^ —
точки разрыва 1-го рода. 725. I/ = ^ х, если Ля < х < Ля + ^ ; z/ = - | х,
если kn + 5 < х < Ля + я; I/ = 0, если х = kn + ^ (Л = 0, ±1, ...); х = -^ —
точки разрыва 1-го рода. 726. у = х при х < 0; у = х2 при х>0. Функция
непрерывна. 727. у = 0 при х < 0 и г/ = х при х > 0. Функция непрерывна.
728. у = -(1 + х) при х < 0; у = 0 при х = 0иу = 1+ х при х > 0; х = 0 —
точка разрыва 1-го рода. 729. Нет. 730. а = 1. 731. а) Функция непре¬
рывна; б) х = -1 — точка разрыва 1-го рода; в) х = -1 — точка разрыва
1-го рода; г) х = k (k = 0, ±1, ±2, ...) — точки бесконечного разрыва;
д)	х ^ k (k = 0, ±1, ±2, ...) — точки разрыва 2-го рода. 732. d = -х при
-со < х < 0; d — 0 при 0 < х < 1; d = х - 1 при 1 < х < |; d = 2-х при
| < х < 2; d = 0 при 2 < х < 3; d = х - 3 при 3 < х < +°о. функция
непрерывна. 733. S = Зу - ^ при 0 < у < 1; S = | +2у при 1 < у < 2;
5	11
S	= - + у при 2 < у < 3; S = ~ при 3 < у < °°; функция — непрерывна;
Ъ = 3 - у при 0<1/<1; Ь = 2 при 1 < z/ < 2; fr = 1 при 2 < z/ < 3; fr = О
при 3 < у < +°°; х = 2 и х = 3 — точки разрыва первого рода. 735. Разрывна
при х и непрерывна при х = 0. 737. Разрывна при всех отрицатель¬
ных значениях и положительных рациональных значениях аргумента.
738./(0) = 0,5. 740. а) 1,5; 6)2; в) 0; г) е; д) 0; е) 1; ж) 0. 741. а) Да;
б) нет. 742. а) Нет; б) нет. 743. Нет. Пример: f(x) = 1, если х — раци¬
онально, и /(х) = -1, если х — иррационально. 744. a) f(g(x)) непрерывна,
g(f(x)) разрывна при х = 0; б) f(g(x)) разрывна при х = -1, х = Оид: = 1,
g(f(x)) = 0 непрерывна; в) f(g(x)) и g(f(x)) непрерывны. 745. Д<р(х)) = х.
759. * = zlJLLk; а + d = 0.	760. х = у - Л, если 2k < у < 2k + 1
су-а

ОТВЕТЫ
461
(к = 0, ±1, ±2, ...)•	764. /(/(х)) = х. 767. х = -Jij (О < у < +°о);
х = Jy (О < у < +°°). 768. х = 1 - Л-у (-°° < у < 1); х=1 + Jl-y
(-00 < у < 1). 769. л; =	(-1 « у < 1), * = 1 + J1~y2 (0 < ||/| < 1).
У
770.	л: = (-1)* arcsin у + kn (k = 0, ±1, ±2, ...)	(-1 < у < 1).
771.	jc = 2kn ± arccos у (k = 0, ±1, ±2, ...) (-1 < у < 1). 772. л: = arctg у + кк
(k = 0, ±1, ±2, ...) (-оо < у < +оо). 776. е = О, если ху < 1; е = sgn х,
если ху > 1. 779. а) у =	, если -1 < л: < 0, у = 2 arcsin л: ~	» если
О < jc < 1; б) у = -(я + 4 arcsin х), если
-1 < л: < -—г , г/ = 0, если
Л
<*< — ;i/ = ft-4 arcsin л:, если -5L	1.780.*/= £ -*(-£ <*<£).
Л Л	Л	2	\ 2	2)
781. у = Jx2- 1 (1 < х < +°°); у = Jx2- 1 (1 < х < +°о). 782. Для всех f,
для которых ф(<) = х, где х — произвольное значение функции ф(*),
функция \}/(0 должна иметь одно и то же значение. 783. Множество
значений х(т) при а < т < |3 должно быть интервалом (а, Ь). 784. Для
всех значений х, для которых ф(я) = ц, где и — произвольное число из
интервала (А, В), функция \j/(jc) должна принимать одно и то же зна¬
чение. 785. |5| < ~ см. а) 0,5 мм; б) 0,005 мм; в) 0,00005 мм.
786. а) 5 < i; б) 8 < 2,5 • 1(Г4; в) 5 < 5 • Ю"7; г) 8 < ^ (е < 1).
4	2	4
793. а) Да; б) нет. 794. Равномерно непрерывна. 795. Не является
равномерно непрерывной. 796. Равномерно непрерывна. 797. Не явля¬
ется равномерно непрерывной. 798. Равномерно непрерывна. 799. Рав¬
номерно непрерывна. 800. Не является равномерно непрерывной.
802. а) 8=|; б) 8 = |; в) 8 = 0,01е; г) 8 = е2 (е < 1); д) 8 = |;
5	8	о
е) 8 = min (§, ^-]. 803. п > 1 800 000. 808. а) о>,(8) < 38; б) оь(8) < JE ;
<0/(8) <	: в) (0/(8) < 8л/§ •	818. f{x) = cos ах или f(x) = ch ах.
J2a
819. f(x) = cos ax; g(x) — ± cos ax (a = const).
Раздел II
821. Дг = 999; Д(/ = 3. 822. Ax = -0,009; Д|/ = 990 000. 823. a) Ay = аД*;
6) Ay = (2ax + b)Ax + a(Ax)2; в) Ay = ax(a&x - 1). 825. a) 5; 6)4,1; в) 4,01;
г)	4 + Ax; 4. 826. З + ЗЛ + Л2; a)3,31;73; 6) 3,0301; в) 3,003001; 3.
827. a) i>Cp = 215 м/с; б) оср = 210,5 м/с; в) иср = 210,05 м/с; 210 м/с.
828. а) 2х; б)3х2; в)(х *0); г)-Ц (х > 0); д) -L. (*#0); е)
*2	2 Jx	3 V**
COS2JC

462
ОТВЕТЫ
(х * (2k - 1)5, k = 0, ±1,...); ж) —±- <* *kn,k = 0, ±1,...); з) —L=
г	sin *	VI-*2
(И < 1); и)——L= (|лг| < 1); к) . 829. -8; 0; 0. 830. 4. 831. 1 + \ .
Vl - X2	1 + х	4
832. /'(а). 834. у' = 1 - 2х; 1, О, -1, 21. 835. у' = х2 + х - 2; а) -2; 1;
б) -1; 0; в) -4; 3. 836. ЮЛ - 5л:4. 837. -2-. 838. 2х - (а + Ь).
a + о
839. 2(х + 2)(х + 3)2(3x2 + 11 +9). 840. х sin 2а + cos 2а. 841. гпп[хт ~1 +
+ хп~1 + (т + п)хт + п- ‘]. 842. a) -(1 - х)2(1 - х2)(1 - л3)2(1 + 6х +.
+ 15л:2 + 14л:3); б) -20(17 + 12л:)(5 + 2л:)°(3 - 4л:)19. 843.	±
<* 54 °)- 845- (W 56 !)• 848- (fiV+2V)*'
847.
1 - * + 4*2
(1-*)3(1 + *)4
(Ы * 1). 848. 12-6*-6*3+2*3+5х*-Зд+ (х * ^	_(1 - *)*-Ч(р +<?)+(Р~ g)*l
(1 - *)3	(1 + х)Ч + 1
(х * -1).	850.	~ (Я + 1)* - (Р + Я " I)*2] (* * -1).
(1 + *)
851. 1 +
2 Jx з3Л*
(х > 0).
852. -Л -
2хЛ Зх3Л
(х > 0).
853.	— + — (л: > 0). 854. 1 + 2x2. 855. 6+ 3* + 8х2+ 4х3 + 2х* + Зл+
33Л хЛ	Л + хг	ЛТх2 V(3 + x3)2
(X * if*).	856. 	(n-m)-{n + m)x _	857. 	a?_	< |а|)_
(re + m)»W( l-*)"(l + x)"	(nt-yrzv
858.	(|*| * 1). 859. 		. 860.
X X	(1 + ж3)2	8 Л^х^Л^х^^х^Л
(x > 0).	861. Л	1	•	1	(x * 0, л: * -1, л * -8).
УхЧ1 + Л)г lj(i + i/l + Л)г
862. -2 cos jc(1 + 2 sin x).	863. x2 sin x. 864. -sin 2x • cos(cos 2x).
865. n sin" ~ 1 x • cos(n + l)x. 866. cos x • cos(sin x) • cos[sin(sin jc)].
867.2elnx(eos*8ln«»-jsln«COB*») {y?* M.k=h2,...). 868.-1 + cof * (x * tot,
sin2*2	2 sin3*
fe = 0, +1, +2,...). 869. nsin^ ( x* 2^-1 n,k — целое! .870.	^	-.
cosn+1* v	2	)	(cos* + *sin*)2
871. (x * tot; k = 0, ±1, ±2, ...). 872. 1 + tge x (x * (2k + 1)|;
-16cos—
k = 0, ±1, ±2, ...). 873.
8
3sin4*Vctg*
(x * knt k — целое). 874.
a sin
з 2*
^ x 5*	, k — целое j . 875. -3 tg2 * * sec2 x • sin(2 tg3 x) • cos[cos2(tg3 *)]-

ОТВЕТЫ
463
х * 5 + kn, k — целое). 876. -2хе-*г. 877. --t- • 2 ts* sec2i • In 2.
3	)	x2	x
878. *V. 879. x2e'x sin *. 880. e*(sin*~ cosx) * 2Ая> k _ целое)
2 sin32
2
881. -1+31jn23 sin x. 882. Ja2 + b2 eax sin bx. 883. e*[l + e*x(l + e8'*)].
884. i/ (In |	(x > 0). 885. a° xa“-1 + ax° '1 a'" In a + axa“x In2 a.
886.5 lg e • lg2 x2 (x * 0). 887.	1	. (x > e). 888.  	,-6—r- (x > e).
x	*ln*ln(ln*)	x\nx ln(ln3*)
(1.,)=(..,■) <* =■ -»• 89°- ZTZ <W =■ >»• 891- «rby “ *°>-
J)-893- „--..и,-.-,	(»>-■)•
895.	1	. 896. In (л; + Jx~2TT ). 897. In2 (x + Jx2+ 1). 898. V*2 + a2 •
Jx^Tl
899. —1—- fW< Is). 900.-	-5	 (0 < x < 1). 901.-i- (0<x-2fat<Jt,
a-bx2 v	4bJ	хь _ x2	sin*
k — целое). 902. —i— Г|jc — 2Arrr| < £ , & — целое!. 903. -ctg3 jc (0 < x - 2&Я < я,
cos* V	2	У
k — целое). 904. i— f * ^	~ 1 n,k — целое!. 905. cos^* (0 < x - 2kn < я,
cos* V	2	J	sin3*
k — целое). 906. ^-2-. 907. -I”!* (x > 0). 908. i- In * (* > 0).
1	a + bcosx	x2	'	x5
1	+ x + i + Ini
909.	—	. 910. 		£	£	. 911. 2 sin (In *) (x > 0).
1 + Vl + X2	^1 + *lnij|4 + *ln^i + lnijj
912. sin x-lntgjefoc*- 2kn < 2 , k — целое! . 913. ——— (|*| < 2).
V	2	/	л/4 - x2
914.	, 1			(I* - 1| < Л ). 915. -f£i- (a * 0). 916. -J— (x *0).
Vl + 2*- x2	x +a	x + z
917.	— (л: > 0). 918. -		 arccos x (|*| < 1). 919. arcsin /—£- (x > 0).
2(l + x)	JT^x2	41 + x
920. 			 (Ы > 1). 921. sgn (cos x) { x	2—0г-~- я, k — целое! .
|*|л/*^Л	^	2	>
922^щ^^совх (х*2кк,к-целое). 923. sinf+-Я9.?£ (o<x-kii< 5,
Vl + cos2 x	Vsin 2 *	v	2
ft — целое). 924. sgn*- (0 < Ы < 1). 925. —i— (* * 1). 926.1 fx * ? + Am,
У	7l _ X2	1 + X2	V 4

464
ОТВЕТЫ
k — целее 1. 927.	i	. 928.	(х * 0). 929.
)	a + bcosx	1 + х2
(|х| < 1). 930. j-—^ . 931. -2 cos х • arctg (sin х). 932.
l + xe
J1 - x4 arccos3 (x2)
	1
2xjx- larccos-~r
Jx
(x > 1). 933. 		a';f-	(* > -a). 934.	. 935.	1	(* * -i).
(x + a)(x2 + b2)	x3+l
936. -J-j (|*| * -1). 937. (arcsin xf (|*| < 1). 938.	(0 < |jc| < 1).
941.^
939. ,	(x > 1). 940. xarccosx
942.
(X2- l)3'2
12х*
(1 + x12)2
. 943. 		i	 (x < 1). 944.	1	(|jc|< 1). 945. —±
(1 -x)lfx
2 JT-
Jax- x2
(0 < * < a). 946. x* (\x +1\<J2). 947.	1	. 948.
sin2x
Jl-2x-x2
vr
sirrx + cos4x
£_ • in ll—Z (|*| < 1).
		2	1 + X
(x * ^я, k - целое). 949.	- —x
950. -£i_ arctg*. 951. —. 952.	1	. 953. sinqSgn(coss- cosa)
1 + x2	л/ГТТ2*	2(1 + x2)	1-cosacosx
(cos x cos a). 954. 	1	■ ■ ■ (0 < |x| < 1). 955.	(|x| ^1).
(х4-!)*/*2*^	l-?4
956.
(1 + x2)2
—= (1*1 < 1).	957. 2f(cos*2+sin*^ Г0 < |*| < ЬЛ>,
Vl - x2	Vsin(2x2) '	V' 2/
fe = 0,1, 2,... j . 958. 2x[sgn(cos x2) + sgn(sin x2)]	^ , & = 0, 1, 2, ...'j.
959.
2m
Jl^T2
. ^m(arcsin x) CQS m (arcsin *)	(|*| < 1).	960. a)	J
6)
; в)
r)
6jl+^IT+iJl+x4lj(l+iJT+x*)2 V(l+x4)3	x3cos-^-(sin“+ cos-У /ctg —-
x2V x2 x2>W x2
!1*ЭД1п2 • 8|п<2Ух) • ЬЧ**2*). 961.1 +*^(1 + In*) + ****' Г1 + ln*+ln2*)
3	V*2 • cos223*^	'
(x > 0). 962. Xa~lxx° (1 + a In x) 4- axx°x + In a In xj + x?axX In a( 1 + In x)
- - 2
(x > 0). 963. x* (1 - In x) (x > 0). 964. (sin x)1 + cos x • (ctg2 x - In sin x) -
- (cos x)1 + sin x (tg2 x - In cos x) ^ 0 < x - 2&7t < 11 k — целое j .
965. 1. ^n^);1)1 [x - 2 In2 x + x In x ln(ln x)] (x > 1). 2. y' = 2y\	x

ОТВЕТЫ
465
^]n arcsinsin2* +nrf»tg2JcT sin* • sgn(cos*) _ cos* • sgn(sin*)
arccos(cos2*)	Larcsin(sin2 x)Jl + sin2* arccos(cos2^)VTT~cos2lc
kn
2
k = 0, +1 , ...)• 966.	e)2 (x > 0, * * 1). 967. th3 *.
968. --2— (x > 0). 969. —5— . 970. sgn(sh*) (x * 0). 971.	.
sh3*	ch2*	ch*	b + achx
972. - —-?fn.2—— . 973.arccos x In (arccos x) (|jc| < 1). 974.-----*--—■
Jl + COS4*	Jl - X2	1/(1 + *4)3
975. _2nc-»2arcsin(e-»2) (д. * Q) 97g ia**\na arctg a-x (a > 0)> 977 a) sgn x
,2	(1 + a2x)2
(l-e-2*2)2
(* * 0); 6) 2\x\; в) i (* * 0). 978. a) (x - 1)(* + 1)2(5* - 1) sgn (* + 1);
6) | sin 2x • |sin x\; в) —--— (|*| > 1); r) л[*] sin 2nx. 979. у' = -1 при
2	xjx 2 - 1
-oo < * < 1; у' = 2x - 3 при 1 < x < 2; if = 1 при 2 < x < +oo.
980. i/' = 2(x - a)(x - b)(2x - a - b) при x € [a, ft]; у' = 0 при x € [a, ft].
981.	у' = 1 при * < 0; t/' = —при 0 < x < +oo, 982. f = ——- при
1 + x	1 + x2
-1 < x < 1; у' = i при |д:| > 1.	983. у' = 2*e~*2 (1 - *2) при |*| < 1;
у' = 0 при |*| > 1. 984. а)
б)
54 - 36* + 4*2 + 2*3
*(1-*2)’	'	3*(1 - *)(9 - х2)
(х * 0, * *= 1,
л; * +3); в) V ; г)
^ х - at
/= 1
71	.985. а) Ф(*),Р'(*)+ Ч'(*)¥'(*) ((^(х) + \f(x)*0);
Jl + х2	J<p2(x) + ф2(;с)
б)(ф,(х)у(х)-ф(х)<(х)) (^)+^(х)^0);в)Ф(х)у^у)	1	Ч>'(*) _<£l£l talKx)
Ф2(я) + Ф2(х)	(фМчЧ*) ф2(х)
г) Я!li*l _J_ -	1ш1*1 .986.1. а) 2xf'fx2); 6) sin 2x[/'(sin2 л:) - /'(cos2 л:)];
’ ф(*) 1пф(х) ф(*) 1п2ф(х)	>	!\ h > и V 2	'
в)	ел*> [е* /'(е*) + /'(*)/(е*)]; г) /'(*)/' [/(*)]/'{/ [/(*)»; Д) Ю00! 988. З*2 + 15.
989. 6*2. 992. а) п > 0; б) п > 1; в) п > 2. 993. а) л > т + 1; б) 1 < п < т + 1.
994. (р(а). 995. fL (а) = -ф(а), fL(a) = ф(а). 999. а) Недифференцируема
при * = 1; б) недифференцируема при * = —^-^я, ^ — целое; в) диф¬
ференцируема всюду; г) недифференцируема при * = kn, к — целое;
д)	недифференцируема при * = -1. 1000.	= /+ = sgn * при * * 0 и
(0) = -1, /+ (0) = 1. 1001. fL (*) = fL (л:) = п[х] cos я* при * ^ целому числу;
(k) = л(& - 1)( fl (k) = 7tfe(-l)fc при k целом. 1002. fL (*) = f+ (*) =
(cos 2 + 5 sin s) sgn (cosg при * ^ ^ (ft - целое); fL (j^j) -

466
ОТВЕТЫ
= -(2ft + 1)5 , r+(- (2k + 1)5 . 1003. fl(x) = fl(x) =	при
J2kn < \x\ < J(2k+ 1)л (ft = 0, 1, 2, ...); /1(0)	1, fl(0) = 1;
/' (7(2ft+l)n)=+oo, f±(j2kK)-±oo (ft-1, 2,...). 1004. Л(Jc) = /X(Jc) =
1 + fl + ±>'
- ----- при * * 0; fl (0) = 1, fl (0) = o. 1005. /1 (x) = fl (ж) = -££=
(1 + Д)
при x * 0; /1(0) = -1; fl (0) = 1. 1006. fl(x) = fl (x) = 5 , Где e = -1
при 0 < |ж| < 1 и е=1 при 1 < |ж| < +0°; fl (+1) =-1, fl (+1) = 1.
1007. Г.(ж) = /* (ж) = 2s?1n^~2JC^ при х * +1; fl(+1) = +1, fl (+1) = ±1.
1008. fl(x) = fl (x) = arctg ^2 “ (x-2¥+ 1 ПРИ x * 2;	^	= +f •
1009.1. a) fl (0) = -1, fl (0) = |; 6) fl (1) = fl (1) = |; в) fl (0) - fl (0) - 0.
1010. a - 2x0; b = -Xq. 1011. a = fl(x0)\ b = f(x0) - x0f_(x0).
1012. A
	 0^2 ^1
(6 - a)2 * C ki + k2
1013. а = -5^,Ь = -^Ц. 1014. а) Можно;
б) нельзя. 1015. a) Нельзя; б) нельзя. 1016. a), б), в) Функция F(jc) может
как иметь производную F'(x), так и не иметь ее. 1017. х = kn (k = О,
±1, ±2, ...). 1018. а) Не может; б) может. 1019. 1) Не обязательно; 2) обя¬
зательно. 1020. 1) Не обязательно. 1021. Не следует. 1022. Не
следует. 1023. Вообще говоря, нельзя. 1024. а) Рп =	(п+1)хП + пхп + 1.
Qn
__ 1 + х- (п+ 1)2хп+ (2п2 + 2п- 1)хп+1-п2хп +
(I-*)3
б) S„ =
sinMsin'lii*
2 2 .
sin-
2
П =
„sin£sin2^*-sin2M
2 2	2_
2 sin2 2
2
1025. S„ =
nsh^sh^n + ijx - sh2
nx
2
2sh2%
2
1026. Sn = ± ctg f-n - ctg *. 1029. 40л см2/с. 1030. 25 м2/с; 0,4 м/с.
1031. 50 км/ч. 1032. S(x) = у , если 0 < х < 2; *S(jc) = х2 - 2х + 2,
если х > 2; S'(x) = х, если 0 < л: < 2; 5'(л:) = 2л: - 2, если х > 2.
1033. £(*) = 1^1 Ja2- х2 + ^ arcsin ^ ; S'(*) = Ja2 - х2 sgn х (0 < |лг| < а).
2
1034. у' =	1	.1035. у; = -—i	. 1036. a) -оо < у < +оо; х‘ = -2- ;
* 3(z/2 + 1)	* 1-ecosy	°	у х+1

ОТВЕТЫ
467
■ ;в)-оо<у< +OOJ	—Ц
41 +у2
б) -ОО <у< +00; X' = —i
у 1 - X + у	’ у
= -Jl + ~JT^y (-оо < у < 1); х2 = -Jl - JPy
1); х4 = Jl + Jl -у (-ОО < у < 1);
'	= pL
~ \х(Х- X2) V ~ 1’ 2’ 3’ 4^’	*« "	У”** У'' 4i *2 = А
(О < у < 1); x’l = ^ (i = 1, 2); в) *! = —1п(1 + -/1-1/) (-°° < у
Х2 - In LLtO (0 < у < 1); *; = -2(^тт^) (i = х’ 2)-1038- ^ = ~|
I; -3; -| и -|; (-4 4). 1039. J-LL- /*)\ (t > 0, t * 1). 1040. у’х = -
2	2	Vt(l-Vt)
ix = -- ctg t (0 < |f| < к). 1042. у’х = - cth t (|<| > О
а	а
Х'„ = т-Ц. 1037. а) х
У 1-у2
(О « у < 1); *3 - Jl-JTTy (0 < у <
1	= _ ПГ (о < у < 1); *2 = pl
41-у У ’	‘	41 -у
< 1);
<(1 + t)\
(О < х < 1). 1041. у’х = -Ц
1043. у'х = -tg t ^ 2k£ 1	— целое j . 1044. у'х = ctg | (t * 2kn, k
’>■ у'х = tg t ■ tg (t + 5^ ( t * 5 + kJi, t * | + fere). 1046. y'x = sgi
^ 1 ГМ&	= 1- X - У - 5 . _1 1A4Q P 1ЛССП —b2X inei _ /1
целое). 1045. y'x
(0 < |t| < +oo). 1048. у' -	5 ; -i . 1049. £ . 1050.	. 1051. - I
x-y 2	2	у	a2y	4
1052. -з^ . 1053.	. 1054. a) tg (<p + arctg <p); 6) ctg ^ (q> *
Ф*±у); в) tg (ф + arctg 1) .	1055. a) у = ifl (x + 1); у = -Щ(х +
б) у 3, * = 2; в) * = 3, у = 0. 1056. а) (± , 2 Г); б) (0, 2). 1058. |х| < 2 и
V 2	4/	3
Щ < Ы < я. 1059. max \у\ - у1 = 10я = 31,4. 1060. 5.1064. а) 2 arctg Л :
3	4	|а|
б)	5. 1066.	1*1. 1069. =4. 1071. Ь2 - 4ас	= 0. 1072. f+ faV	=	0.
2	|„|	|а|	\3J	\2)
1073. а -	.	1077. а) Зх - 2у = 0, 2х +	Зу = 0; б) 3* - м - 1	°	О,
х + Зг/ - 7 =	0.	1078. а) у = х> у = -х\ б) Зл:	- у - 4 = 0, х + Зу - 3	~	0;
в)	у = -х; у = х. 1079. у - 2a = (х - at0) ctg ^ . Касательная к
циклоиде перпендикулярна к отрезку, соединяющему точку касания с
точкой соприкосновения катящегося круга. 1081. Зх + by - 50 = О,
5л: - 3у - 10,8 = 0. 1082. л: + 2у - 3 = 0, 2л: - у - 1 = 0. 1083. Д/( 1) = Ал: +
+ 3(Дл:)2 + (Ал:)3; df( 1) = Дл:. а) 5, 1; 6)0,131,0,1; в) 0,010301, 0,01.
1084. Дл: = 20Д^ + 5(Д02, dx = 20Д*; а) 25 м, 20 м; б) 2,05 м, 2 м;

468
ОТВЕТЫ
в)	0,020005 м, 0,02 м. 1085. -Ц (х * 0). 1086.	. 1087.
х2	а2 + х2	х2-а2
(|*| * |а|). 1088. dx . 1089. sgna dx (|*| < |а|). 1090. а) (1 + x)exdx;
Jx2 + a	Ja2 - х2
б) * sin * dx; в)(* * 0); r) 2~ dx (* > 0); д) -xdx - ; e) ———
x4	2xji	(1_ж2)|
(|*| < 1); ж)	(|*| < 1); з) —p= (M > 1); и)	(* * | + kn,
1 — X	% Jx 2 _ 1	COS X \	Ct
k — целое!!. 1091. vw du + uw dv + uv dw. 1092. vdu~^udv (u 0).
)	u3
1093. _udu±vdv {u2 + v2 > 0)	1094 Vdu-Udv {u2 + y2 > Q)
3	u2+u2
(u2 + v2)2
1095. udu + vdv. (и2 + v2 > 0). 1096. a) 1 - 4*3 - 3*6; 6) -i- ( cos * -	;
u2 + v2	2x2 v	x )
в)	-ctg x (x * knt k — целое); г) -tg2 x ^x * ^ + &я, k — целое! j ; д) -1
(|jc| < 1). 1097. а) Увеличится на 104,7 см2; б) уменьшится на 43,6 см2.
1098. Увеличить на 0,0223 м. 1099. 1,007 (по таблицам: 1,0066).
1100.0,4849 (по таблицам: 0,4848). 1101. -0,8747 (по таблицам: -0,8746).
1102. 0,8104 = arc 46°26' (по таблицам: arc 46°24'). 1103. 1,043 (по таб¬
лицам: 1,041). 1104.1. а) 2,25 (по таблицам: 2,24); б) 5,833 (по таблицам:
5,831); в) 10,9546 (по таблицам: 10,9545); 1105. а) 2,083 (по таблицам:
2,080); б) 2,9907 (по таблицам: 2,9907); в) 1,938 (по таблицам: 1,931);
г)	1,9954 (по таблицам: 1,9953). 1106.0,24 м2; 4,2%. 1107. 5Я<0,33%.
1108. а) 5, = 8,; б) 5, = 28г. 1109. 0,438. 1111. ffi-tl*?). 1Н2.
* * (1 + *2)3'2 £
(I-*2)2
(|*| < 1). 1113. 2е *2 (2*2 - 1). 1114.	(* *	k = 0, ±1, ...).
115. _2*_ + 2 arctg *. 1116. -ii— +	(|*| < 1). Ц17. I
1 + *2	6	(I-*2)2	(1-*2)5/2	4 1	'	х
х > 0). 1118.	(Я*) > 0).	1119. -2 sin (In *) (* > 0).
/ \Х)	х
120.1/(0) - 1,1/40) = 1,у"(0) = 0.1121.2(ии" + и'2). 1122. У '- “'2 -
и2	V2
w > 0). 1123.	+ VU2^U'V~ “°')г (U2 + и2> 0). 1124. у" = и° х
(и2 + V2)312
[( V^ + v' In и J + vuu"~2u'* +	+ и" In и J. 1125.1r = 4*2 Г(*2) +
+ 2 f'(x2); iГ = 8*3 f'"(x2) + 12* f"(x2). 1126. y" = J- H -) + — f( i);
X4 \xj X3 \xj
		■ MS ■ MS' 1127-	«V>,

ОТВЕТЫ
469
у= е3*Г\ех) + зe2xf"(ez) + exf'(ex). 1128. у" = \ [Г(1п х) - f\\n х)];
I/"' = ^ [Г(1п х) - ЗГ(1п х) + 2/"(In ж)]. 1129. </" = ф'2(х)Г(ф(х)) + ф"(х)Дф(х));
у" = ф'3(х)Г"(ф(х)) + Зф'(х)ф"(х)/"(ф(х)) + ф"'(*)/'(ф(*)). ИЗО. а) е* dx2;
б) ex(dx2 + d2x).	1131. —.	1132.	21n*~3dx2 (x > 0).
(l + *2)3/2	xz
1133. xx ^(1 + In x)2 + ij dx2. 1134. и d2v + 2 du dv + v d2u.
1135. (Цс/2“-. “**21- 2du(0du^udv) (l) > 0) 1136> um - 2 vn- 2{[m(m _ l)v2 x
V*
x da2 + 2mnvu du dv + л(л - 1 )u2 do2] + uv(mv d2u + nu d2v)}.
1137. au In a(du2 In a + d2u). 1138. [(v2 - u2) du2 - 4uv du dv + (u2 - v2) dv2 x
x (u2 + v2)(u d2u + v d2v)(u2 + y2)-2 (u2 + v2 > 0).	1139. [-2uv du2 +
+ 2(a2 - v2) du dv + 2uv dv2 + (и2 + v2)(v d2u - и d2v)](u2 + v2)~2
(u2 + v2> 0). 1140. y" =
4(1 - 0 *
8(1 - O3
(f*l). 1141.i/" =
1 ,
a sin3*
y"' =	(t *kn,k — целое).
y a2sin-Ч v	'
(t * 2knt k — целое). 1143. у" =
1142. у" = -
4 a sin4 -
2
t
cos-
2
4 a2 sin7 * ^
2
V2cos3(t + |)
_ e~2*(2sin* + cos*)
V2cos5^* +
(**3
+ kn,k = 0. +1, ±2. ...) . 1144. y” = ^ ; i,'" = ™ (fV) * 0).
1145.	x'" = -У’У'"-ЗУ"2;	ЮУу-у” + W3
y' y'z	y'b	yn
(y'*0). 1146.	-Ц,	-§, -§§, -2§-	1147. в., -El, 3£f.
I/ yz y* 4	64	1024	I/ yz yb
1148. y' = ZILlJL, y" =
x~2y J
(x-2y)3 ’
4	64	1024
1149.1,'-^;
(дс - 2z/)5	1 + z/2
</" = тгЧг, • t3*1 + ^2>2 + 2*4 ^ " ^>1- 115°- у' = ***: у" = У*+У,,? •
1151. a = | /"(*o); b = f'(x0); c = /(x0).	1152. 20 - Ш, -10; 0, -10.
1153. u =	sin — w =	cos — t. 1154. x = o0l cos a,
(/ = o0l sin a - ^ ; о = Jvl~ 2v0gtsina +g2 t2 ; w= g-, y= x tga-——;
l;°g2p ; ^ sin 2a. 1155. x2 + y2 = 25; 5|d)|, 5d)2. 1156. j/(e) = 4-61; ym = 0.
1157. j/'" = -ат{т+Щт + 2)	^ Q) 115g> y,io) = _
17!!
210x9Vx
(JC > 0), где nil

470
ОТВЕТЫ
обозначает произведение натуральных чисел, не превышающих числа л, и
одинаковой четности с ним, т. е. 17!! = 1 • 3 • 5 ... 17. 1159. i/(8)= ^
(х * 1). 1160. (/100) = —1971(399 - х)— (х к 1161 ^20) = 220е^(х2 + 20х + 95).
10	А1
1162.	«/<10> = е* £ (-1)'^77. где Л',0 = 10 • 9 • ... (11 - £) и А?0 = 1.
i = 0
1163. I/<®> = - А (х > 0).	1164. i/<5> = ^ - Ш in* (JC > 0).
1165. j/<50) = 250 ^-х2 sin 2х + 50х cos 2х + sin 2х j. 1166. у'" =
= 27(1-Зх)3-36 sin3a;- 27(1-Зя)»-28 cos Зх * Ij. 1167. 0(,о> =
(1-Зх)3	(1-Зх)т
= -28 sin 2х - 218 sin 4х + 28 • З10 sin 6л:. 1168. у{100) = jc sh jc -h 100 ch x.
1169. 01V = -4ex cos x.	1170. i/<*> =	+ flM -	+ «fl sin 2x +
x6 \ x5 x3	:c J
+ (§2 - Ш + 122 + 32 In x) cos 2x. 1171. 120 dx5. 1172. -—^-= dx3
vxe	X<	x3	)	8 x3Jx
(x > 0). 1173. -1024(x cos 2x + 5 sin 2x) dx10. 1174. e* (in x + 4 - ^ +
+ — - dx4. 1175. 8 sin x sh x dx®. 1176. 2ud10u + 20 du d9u +
X3	X*)
+ 90 d2u d8u + 240 d3u d7u + 420 d4u d6u + 252(d5u)2.	1177. e“(du4 +
+ 6du2 d2u + 4 du d2u + 3 d2u2 + d4u).	1178.	- ?-d-u-<*±“ + Ё!“ .
u3	и2	и
1179. d2y - i/" dx2 + j/' d2x; d3«/ = i/'" dx3 + 3y" dx d2x + y' d3x;
d4y = J/IV dx4 + 6j/'" dx2d2x + 4^" dx d3x + 3^" d2x2 + j/' d4x.
dx dy
dx
dx dy
-Sd2x
dx dy
d2x d2y
d3x d3y
d2x d2y
l; у ~ —
dx3 ’ y	dx5
1187. i*n)(x) = a0«!
1188.	C-1)*'‘?l?r	. И89.	+	1—]. 1190. (-l)"n! x
(cx + d)"*1	Lx"*1	(1 — x)n *1J
x Г	1	 - 	1	1.	1191. Ц»	1) (x < i).
Цх-2)»*1	(x- 1)"*Ч	(1 - 2X)" 3	2
1192. H)"*1:1 ' 4 - .	5)(3я + 2x) (п>2;х*-1). 1193.-2"'1 cosf 2x+22l.
3"(1 + x)"*1/3	v	'	\	2)
1194. 2" - 1 cos ( 2 x + 2£) . 1195. | sin (^ + y) ~j sin (3x + 25) .
1196. | cos^x+yj + y cos^3x+yj . 1197. iS-gX. cos [ (a-b)x + у] -

ОТВЕТЫ
471
сов[(а + Ь)*+^].119Ь&^ coe[(a-ft)*+22] +	x
x cos ((a + b)x + 25 J . 1199.	sin ((a - b)x + 25 J + (a+^>)n x
xsin((a + b)x+^j.l200. ^cos(bx+22) - i2a^b)n cos [(2a-6)x + 25) -
- (2a + b)n cos [ (2a +
b) x +
nnl
2 J
1201.
4" _ 1 cos (4x + 25).
1202. a" x cos ( ax + 25)
+ nan "1
1 sin
(“+?)•
1203. an [x2 - п(^п;1)] x
x sin (ax + y) - 2nan " 1 x cos (ax + ^) . 1204. (-I)ne-X[x2 - 2(n - l)x +
+ (n - l)(n - 2)].	1205. ex |±	+ V(-l)* »("-!)•••(«-*+1)1.
\X	JCA+1	)
1206.	ex • 2"/2cos(x + 25).	1207. ex • 2n/2 sin (x + 25).
1208.	Ka + bxV + (-l)”'1 (a - bx)n] (|x| < |2|).
1209.	eax{anP(x) + C'nan-'P'(x) + ... + P(n)(x)]. 1210. | {[(x + n) -
(-l)"(x - n)] ch x + [(x + n) + (-l)"(x - a)] sh x}.	1211. dny = ex ( x" +
dxn
+ n2xn ~1 + n*(n ~ 1‘>2 x" -2 + ... + all dxn. 1212. tii^lJlnx-Vi
2!	J	xn +1	f^i
(x > 0). 1214. a) (a2 + b2) * • j^cos ^/icp - ch ax cos [bx +	-
-	sin ^ mp - sh ax sin ^bx +	; 6) (a2 + b2) 2 j^cos (шр - ch ад: x
x sin ^bx + — 'j + sin ^ /мр — sh ад: cos	J , где cos (p = «	° - ,
sin ф = A . 1215. fn\x) = V (“1У + *2" ’2* + 1 (p - fc)n CL cos Г (2p -
*4l>	L
-	2k)x + 25] . 1216. a) £ (-1У + k('2p~22P+1^	> sin [(2p “ 2k +
A = 0
+ l)x + 25];	6) ^ 2n-2p + 1(p - k)nCh2p cos [(2p - 2k)x + 25];

472
ОТВЕТЫ
В) £ {(2p---*i-^Cl., cos [(2p - 2k + l)x + f] ). 1218.	x
*•-0 '	‘	(1 + jr2)2
X sill (rt arcctg x) (x * 0). 1219. a) ^[2" + 1 + (-1)"]; б)	(n > 1).
1220.	a) n (я - l)a" ~ 2;	6) f2k\0) = 0, f2k b '>(0) = (-1)*(2/г!) (k = 0, 1,
2, ...); в) f2k\0) = 0, f2k + '> = (0) = [1 • 3 ... (2k - l)]2 (k = 0, 1, 2, ...).
1221.	a) f2k)(0) = (-l)*/n2(m2 - 22) ... [m2 - (2k -2)2], f2"' " (0) - 0;
6) f2k\0) = 0, f’(0) - m, /<2* + "(0) = (-l)*m(m2 - l2)...[m2 - (2k -l)2]
(ft- 1,2,...). 1222. a) f2k)(0) = (-1)* " 1 • 2(2fc -1)! ^1 + | + ... + j^Tt) «
f2k- "(0) = 0 (k = 1, 2, ...); 6) f2k) (0) = 22* - ' [(ft - l)!]2, /<2ft" »> (0) = 0
(k = 1, 2, ...).	1223. n! <p(a).	1228. LJx) = (-l)m [xm - m2xn-1 +
+	xm~2 + ... + (-l)m mil. 1231. Hm(x) = (2x)m -	(2x)m~2 +
1*2	J	1.
+ m(m ~ l>(m ~ 2)(m - 3) (2a-)m - 4 _ _	1236. При x = 0 не существует
конечной производной f(x). 1244.А (-1, -1), С (1, 1). 1245. Не верна.
1246. а) 0=|
б) 0 =
х2 + хАх + i(Ax)2 - х
V	3
Ах
(х > 0, Ад: > 0);
B)0 = £ft+f "О (^ + Д*)>0); Г>0=^ 1п^- 1248.с=| или
J2 . 1250. Вообще говоря, нет. 1261. f(x) = с0 + схх + ... + + сп _ {хп ~ \
где= 0,1,..., п-1) постоянны. 1268. При	< х < | функция возрастает,
при | < х < +°° убывает. 1269. При < х < -1 функция убывает, при
-1 < л: < 1 возрастает; при 1 < х < 4-оо убывает. 1270. При -оо < х < -1
функция убывает, при -1 < х < 1 функция возрастает; при 1 < х < +оо
убывает. 1271. При 0 < х < 100 функция возрастает; при 100 < х < +оо
убывает. 1272. Функция возрастает. 1273. В промежутках (— , — + ? I
V 2	2	3 /
j убывает (k = 0, ±1,
±2,...). 1274. В промежутках^,^) и ( '2*71 * ’2*Тг) ФуНКЦИЯ
возрастает; в промежутках	, ^) и [~± , -_L_) убывает
(k = 0, 1, 2, ...). 1275. При -оо < х < 0 функция убывает; при 0 < х <
функция возрастает; в промежутках (^	+5
V 2	3	2	2

ОТВЕТЫ
473
возрастает; при	< х < +°° убывает. 1276. При 0 < х < п функция возрастает;
при п< х< -К» убывает. 1277. Убывает при -со <дг<-1и0<х<1; возрастает
7п 0. 1Яя , 0(._ ч
при -1<л:<0и1<л:< +оо. 1278. В промежутках
, е
функция возрастает; в промежутках е
-2кл V? + 2кп
, е 12
'J убывает
(к = 0, ±1, ±2,...). 1283. Не обязательно. 1298. В точке А кривая вогнута
вверх; в точке В вогнута вниз; С — точка перегиба. 1299. График при
-°о < х < 1 вогнут вверх; при 1 < х < +°° вогнут вниз; х = 1 — точка
перегиба. 1300. При |л:| < — — вогнутость вниз; при \х\ > ~ — вогнутость
л	л
вверх; х = ±-2- —точки перегиба. 1301. При х < 0 — вогнутость вниз;
л
при х > 0 — вогнутость вверх; х — 0 — точка перегиба. 1302. Вогнутость
вверх. 1303. При 2kn < х < (2к + 1)л — вогнутость вниз; при
(2k + 1)я < х < (2к + 2)л — вогнутость вверх; х = kn — точки перегиба
> /1
(к = 0, +1, ±2, ...)• 1304. При |х| <	— вогнутость вниз; при |л:|
вогнутость вверх; х = ±	— точки перегиба. 1305. При |дг| < 1 —
вогнутость вверх; при |jc| > 1 — вогнутость вниз; х = ±1 — точки
2Ал - —	2 Ая+2
перегиба. 1306. При е 4 < х < е 4
2кп + -	2кт—
>	4 < х < е 4
— вогнутость вверх; при
кл + -
вогнутость вниз; х = е
точки
перегиба (к = 0, ±1, ±2, ...). 1307. Вогнутость вверх при 0 < х < +ос.
1309. h =
аЛ
1310. Вогнута вниз (при а > 0).	1318. £ .	1319. 1.
1320. 2. 1321. -2. 1322.
1323. -i. 1324.1. 1325.1. 1326.1.
3	3	6	2
1327. 1. 1328. 2^ . 1329. 1 In а. 1330. -2. 1331. 1. 1332. (. 1333. 1.
3	ab	6	V Ь)	6
1334. ? . 1335. 1. 1336. 0. 1337. 0. 1338. 0. 1339. 0. 1340. 0. 1341. 0.
3
1342.1.	1343.1. 1344.-1. 1345. е*. 1346. в1. 1347. г”. 1348. е'1.
1349. 1.	1350. 1.	1351. 1.	1352. е“»2
= (а * ^£, к -
целое
1353. е5(,п2"- 'лЧ). 1354. 1 . 1355. 1.1356. 0. 1357.	. 1358. ая(1п а - 1).
1359.	. 1360. —. 1361. е’* . 1362.1. 1363. а) е«; б) ; в) е1; г) е 2;
2	а

474
ОТВЕТЫ
д)	е 6 . 1364. е 2 . 1365. е * . 1366. е 1 . 1367.
. 1368. a) Je ; б) 0.
1369.-i. 1370. а. 1371. tg а. 1373. 2. ДО) =	• 3. у = ± (х + ±1.
1374. а) Правило Лопиталя неприменимо, предел равен нулю; б) пра¬
вило Лопиталя неприменимо, предел равен 1; в) формально применен¬
ное правило Лопиталя дает неверный результат, равный 0, предел не
существует; г) применение правила Лопиталя незаконно и приводит
к неверному результату, равному нулю, предел не существует. 1375. |.
О
1376. 5 - 13(* + 1) + 11(* + I)2 - 2(х + I)3.1377.1 + 2х + 2х2 - 2х4 + о(х4);
-48. 1378. 1 + 60* + 1950*2 + о(хг). 1379. а + —- - (от~ V** + о(х2).
1380. 1 х2 + х3 + о(*3). 1381. 1 + 2х + + х2 - \ х3 - \ х4 - -L + о(*5).
6	3	6	15
1382.	+ 0(х4).	1383. х - £ -	+ о(*13).
2	12	720	18	3240
1384.	+ о(хв). 1385. х-^ + о(х3). 1386. х+^ + ^ + о(х5).
12	45
15
1387.	- J£- - _|1_ + о(*в). 1388.1 + i (х - 1) - i (х - I)2 + о((* - I)2).
6	180	2835	2	8
1389. (х - 1) + (* - I)2 + \ (х - I)3 + о((х - I)3). 1390. у = а + £ + о(х2).
2	2 а
1391-т--;гз + <>Ш. 1392Лп*+ “ - Т~г +••• +(-1)"-1-^- + 0(ЛЛ).
2х 8*3	\х3)	х 2хг	пхп
1394. а) Меньше
(71+1)!’
б) не превышает
3840 ’
в)	меньше 2 • 10"
г)	меньше . 1395.1.1*| < 0,222 = arc 12°30'. 1396. а) 3,1072; б) 3,0171;
16
в)	1,9961; г) 1,64872; д)0,309017;е)0,182321;ж)0,67474 = агс38°39'35";
з)	0,46676 = arc 26°44'37"; и) 1,12117.1397. а) 2,718281828; 6)0,01745241;
в)	0,98769; г) 2,2361; д) 1,04139. 1398.	. 1399. 1.1400. -А. 1401. |.
1402. i . 1403. In2 а. 1404.1.1405.0.1406.а) А ; б) If ; в) А ; г) 1.1407. ^ .
6	2	3	90	2	3	30
1408. х2. 1409. £ . 1410.1. а
2
|;Ь = -1.2.А = -|;В = --^.З.Л= 1,
3	3	5	15	2
в = й*с = -|^=^-1411-а)й:б)1";в)ш;г)т-1412-а = 1;
Р = i . 1413.	, гдеа— половина центрального угла дуги. 1414. Максимум
3	180
у = 2^ при х — |. 1415. Экстремума нет. 1416. Минимум у = 0 при х = 1.
4	а
1417. Минимум у = 0 при х = 0, если т — четное, и экстремума нет при
х = 0, если т — нечетное; максимум у —
ттпп	т
—-—- при х =	; минимум
(т+П)т+п	/71+71

ОТВЕТЫ
475
у = 0 при х — 1, если п — четное, и экстремума нет при х = 1, если /г —
нечетное. 1418. Минимум у = 2 при х = 0. 1419. Минимум у = 0 при
х = -1; максимум I/ = Ю10е"9 ~ 1 234 000 при х = 9. 1420. Максимум
г/ = 1 при х = 0, если п — нечетное, и экстремума нет при х = 0, если п —
четное. 1421. Минимум у = 0 при х = 0.1422. Максимум у = 1 ЗД ~ 0,529
о
при х = i ; минимум г/ = 0 при х = 1; экстремума нет при х = 0.
3
1423. Минимум Дх0) = 0, если ср(х0) > 0 и п — четное; максимум Дх0) = О,
если (р(х0) < 0 и п — четное; Дх0) — не экстремум, если п — нечетное.
1425. Нет. 1427. а) Минимум ДО) = 0; б) минимум ДО) = 0.1428. Минимум
ДО) = 0. 1429. При х = 1 максимум у = 0; при х = 3 минимум у = -4.
1430. Минимум у = 0 при х = 0; максимум у = 1 при х = ±1. 1431. При
х =	~ 0,23 минимум у ~ -0,76; при х = 1 максимум у = 0;
при х = —	~ 1,43 минимум у ~ -0,05; при х = 2 экстремума нет.
6
1432. При х = -1 максимум у = -2; при х = 1 минимум у = 2. 1433. При
х = -1 минимум у = -1; при х = 1 максимум у = 1. 1434. При х = \
5
минимум у =	. 1435. При х = 0 и х = 2 — краевой минимум г/ = 0; при
Z4
х = 1 максимум у = 1. 1436. При х = ? минимум у =	1/2 ~ -0,46;
4	8
при х = 1 экстремума нет. 1437. При х = 1 максимум у = е~1 ~ 0,368.
1438. При х = +0 краевой максимум у = 0; при х = е"2 ~ 0,135 минимум
у = -- ~ -0,736. 1439. При х = 1 минимум у = 0; при х = е2 ~ 7,389
е
максимум у =	~ 0,541. 1440. При х = kn (k = 0, ±1, ±2, ...) максимум
е2
у = (-1)* + - ; при х =	+ 2kn (k = 0, ±1, ±2, ...) минимум у =
2	3	4
1441. При х — kn (k = 0, ±1, ±2, ...) максимум г/ = 10; при х = n^k +
(ft = 0, ±1, ±2, ...) минимум у = 5. 1442. При х = 1 максимум у = -~
4
- i In 2 ~ 0,439. 1443. При х = -5 + 2rcft (ft = 0, ±1, ±2, ...) минимум
2	4
I/ = -^Р е 4 + 2*я. при * =	+ 2ftix (ft = 0, ±1, ±2, ...) максимум
2	4
у = $ е * + 2кп л 1444. При х = -1 максимум у = ё~2 ~ 0,135; при х = О
минимум у = 0 (угловая точка); при х = 1 максимум у = 1. 1445. i ; 32.

476
ОТВЕТЫ
1446. 2; 66. 1447. 0; 132. 1448. 2; 100, 01. 1449. 1; 3. 1450. 0;	~ 36,8.
е
гг ЗЯ
1451. 0; 1. 1452. 0; ± (1 + Л) = 1,2.	1453. -Ц е 4 =-0,067; 1.
1454. 1. т(х) = -i , если -°о < х < -3; т(х) = } + * , если -3 < х < -1;
6	3 + х2
т(х) = 0, если -1 < х < +°о; М(х) = | , если -оо < х < 1; М(д:) = ^ *2,
если 1 < д: < +оо. 1455. а) ~ 1,77 • 107; б) ^ ; в) Л ~ 1,44.
1457.	~ 4,85. 1458. q = -|. 1459. ^ . 1460. £(дг) = (хх + х2)д: -
- i (jCj + лг2 + бд^д^); A = - (д^ - дг2)2. 1461. |. 1462. Один корень: (3, -foo).
о	о	о
1463. Один корень: -оо < х1 < -1, если h > 27; три корня: -оо < хх < -1,
-1 < д;2 < 3 и 3 < дг3 < +°о, если -5 < h < 27; один корень: 3 < х3 < +оо,
если h < -5. 1464. Два корня: -оо < д^ < -1 и 1 < х2 < +оо. 1465. Один
корень: -°° < хх < -1, если -оо < а < -4; три корня: -оо < хх < -1,
-1 < д:2 < 1 и 1 < дг3 < +оо, если -4 < а < 4; один корень: I < хг < +оо,
если 4 < а < +оо. 1466. Один корень: 0 < хх < 1, если -оо < k < 0; два
корня: 0<дг,<7 и i < х2< +°°, если 0 < k < - ; корней нет, если k > i .
k k	e	e
1467.	Корней нет, если a < 0; один корень: -оо < хх < 0, если 0 < а < ^ ;
4
три корня: -оо < хх < 0, 0 < д:2 < 2 и 2 < дг3 < +оо, если ^ < а < +оо.
4
1468.	Два корня при |а| < Зл/З /16; нет корней при |а| >	. 1469. Два
корня: 0 < IjcJ < ^ и £ < |л:2| < +оо, где £ ~ 1,2 — положительный корень
уравнения: cth х = х, если \k\ > sh £ ~ 1,50; корней нет, если \k\ < sh
1470. а) ^	^ >	+ ^ < 0. 14711}. Симметрия относительно
начала координат. Нули функции: д: = 0ид; = ±~ л/3 ±1,73. Минимум
у = -2 при х = -1; максимум у = 2 при л: = 1. Точка перегиба л: = 0, у = 0.
1472. Симметрия относительно оси Оу. Нули х = ±Vl + л/3 ~ ±1,65.
Минимум у = 1 при х = 0; максимум у = 11 при л: = ±1. Точки перегиба:
х = ±4г ~ ±0,58; у = 1 ^ . 1473. Симметрия относительно точки А (1, 2).
V3	18
Нули: д: = -1 и х = 2. Минимум у = 0 при л: = 2; максимум у = 4 при
х = 0. Точка перегиба: х = 1, у = 2. 1474. Симметрия относительно оси Оу.
!) К задачам на построение графиков не везде даются полные ответы.

ОТВЕТЫ
477
Нули функции: х = ±J2 ~ ±1,41. Максимум у = 2 при х = 0; минимум
у = 1 - ^ ~ _0,12 при х = ± л/2 + л/5 ~ ±2,06. Точки перегиба: х1>2 = ±0,77,
1/12 = 1,04; лг3>4 ~ ±2,67, 1/3 4 ~ -0,010. Асимптота у — 0. 1475. Точки
разрыва: * = 2 и х = 3. Нули: д; = ±1. Минимум у = -(10 - 796 ) ~ -0,20
при х = 7	~ 0,42; максимум у = -(10 + л/96 ) ~ -19,80 при
5
х = 7 + /24 ~ 2,38. Точка перегиба: х ~ -0,58, у ~ -0,07. Асимптоты:
5
л: = 2,д; = Зиг/=1. 1476. Точки разрыва: д^ = -1 и лг2 = 1. Нуль функции
х = 0. Точек экстремума нет. Точка перегиба *~-0,22,z/~-0,19. Асимп¬
тоты: д: = -1,л:=1иг/ = 0. 1477. Нуль функции х = 0. Точка разрыва
1 о
jc = —1. Минимум у = 0 при д: = 0; максимум z/ = -9 — при д: = -4. Точек
перегиба нет. Асимптоты: д; = -1 и у = х - 3. 1478. Минимум z/ = 0 при
дг = _1; точка перегиба х = -4, z/ = ~~ . Асимптоты: л: = 1 и у = 1.
1479.	Максимумы г/ = -34^j + 142 = -8,82 при * = -3 + /^ « -3,56 и
I/ = 0 при д: = 0; минимум у = 34~ -0,06 при д; =	3 ~ 0,56.
32	2
Точка перегиба х = i , У = ~tz • Асимптоты: л: = —1 и у = х - 3.
5	45
1480.	Симметрия относительно начала координат. Точек экстремума нет;
точка перегиба х = 0, у = 0. Асимптоты: д: = -1, х = 1 и г/ == 0.
1481.	Минимум у = 131 при д; = 5; точки перегиба: д: = -1, у = 0. Асимптоты:
х = 1иу = х + Ь. 1482. Минимум у = 2~ при д; — 2; максимум z/ ~ -3,2
3
при х ~ -2,4; точка перегиба д: = 0, у = 8. Асимптоты: д: == -1 и z/ = х.
1483. Симметрия относительно оси Оу. Нули функции: д: = ±^Р ~±0,79.
4
Точек экстремума нет. Точки перегиба: x = ±J^ ~ ±0,71, z/ = -21. Асимптоты
д: = -1, д: = 0, х = 1 и у = 0. 1484. Область существования: 0 < х < +°°.
Нули: х = 0 и х = 3. Минимум у = -2 при д: = 1; краевой максимум z/ = 0
при д: = 0. Вогнутость вверх. 1485. а) Область существования: \х\<2*/2 ~ 2,83.
Симметрия относительно начала координат и осей координат. Нули:
д; = 0ид; = ±2л/2. Максимум \у\ — 4 при д: = ±2; минимум \у\ = 0 при
х = 0; краевой минимум \у\ = 0 при х = ±2j2 . Точек перегиба нет;
б) нуль функции х = 2. Минимум у = - Тб ~ -2,24 при л; = -0,5. Точка перегиба
=-^ь/П =-i,18; у, =~ -2,06 и *2 =	~ 0,42; у2*=-1,46.

478
ОТВЕТЫ
Асимптоты: у = -1 при х —> -°° и у = 1 при х —*■ +°°. 1486. Область
существования: 1<л:<2иЗ<^< +°о. Нули: х = 1,х = 2их = 3.
Максимум у = \ Vl2 ~ 0,62 при х = - ~ ^ ~ 1,42; краевые минимумы
3	3
\у\ = 0 при х = 1, 2 и 3. 1487. Минимум у = 0 при х = 1; максимум
у = | V3 ~ 1,06 при х =	; точка перегиба х = -1, у = 0. Асимптота:
у — х — — . 1488. Симметрия относительно оси Оу. Минимум у = -1 при
3
х = 0. Вогнутость вниз. Асимптота: у = 0.1489. Симметрия относительно
начала координат. Нуль функции: х = 0. Минимум у = -l/l6 ~ -2,52
при х = -2; максимум у = Vl6 при х = 2. Точка перегиба: х = 0, у = 0.
Асимптота: у = 0. 1490. Симметрия относительно оси Оу. Минимум
у = 1/3 ~ 1,59 при х = ±1; максимум у = 2 при х = 0. Вогнутость вниз.
1491. Симметрия относительно начала координат. Точка разрыва:
х = ±1. Нуль функции: х = 0. Минимум у = — ~ 1,38 при х = */3 ;
V2
максимум у = при х = -*/3 . Точки перегиба хх = 0, ^ = 0 и х2 3 = ±3,
V2
у2|з = ±1- . 1492. Область существования функции: \х\> 1. Симметрия
относительно оси Оу. Краевой минимум у = 0 при х = ±1. Вогнутость
вниз. Асимптоты: у = | при х —► +°° и у =	при х —► -°°. 1493. Область
3	г~	1
существования функции: х > 0. Минимум у = -	~ 2,60 при х = - .
о
Вогнутость вверх. Асимптоты у = jc -h — и х = 0. 1494. Область сущест¬
вования: х > 0 и х < -3. Нуль функции х = ^	~ 4,30. Минимум
у = 13 при х = -4; краевой максимум у = 1 при х = 0. Вогнутость вверх.
К	1
Асимптоты: у = - - 2х при х —► -°°; у = -- при х —>- +°°; х = -3 при
х —*■ -3 - 0. 1495. Минимум у = 0 при х = 0; максимум у = \fi ~ -1,59
при х = -2. Точки перегиба: хх = -(2 - JS ) ~ -0,27, ух =	~ 0,46;
х2 = -(2 + л/3) ~ -3,73, у2 = -sj5 +	~ -1,72. Асимптота х = -1.
1496.	Симметрия относительно оси Оу. Функция положительная. Максимум
у = V3 ~ 1,73 при х = 0; минимум у = J2 ~ 1,41 при х = ±1. Точки перегиба:
х1>2 ~ ±0,47; у12 ~ 1,14 и х3 4 ~ ±4,58, */3>4 ~ 4,55. Асимптоты у = ±х.
1497.	Период функции: Г = 2л; основная область 0 < х < 2я. Нули функции:

ОТВЕТЫ
479
jCj = я + arcsin
«/5-1
2
1,21я и л:2 = 2я - arcsin
л/5- 1
2
~ 1,79я. Минимумы
у = 1 при л: = £ и у = -1 при х = ^ ; максимум i/ = 1 i при х — ^ и
2	2	4	6
л; = ^ . Точки перегиба: д^ = arcsin	~ 0,32я, ^ = 19 * ^	~ 1ДЗ;
6	8	32
х2 — я — arcsin - tVP ~ 0,68я, i/2 =	; дг3 = я + arcsin * ~ 1,20я,
8	32	8
„ = 19-ЗТзЗ
У 3	on
~ 0,055; х4 = 2я - arcsin
Узз-i
8
1,80я, 1/4 =
19-ЗУзз
32
1498.	Период функции: 2я; основная область -я < х < я. Симметрия
относительно начала координат. Нули: хг = 0 и д:2 3 = ±я. Минимум
у =	л/15 ~ -7,3 при х = -arccos 1 ~ -0,42я; максимум у=Щ «Д5 ~ 7,3
8	4	8
при л;
arccos
1
4
0,42я. Точки перегиба: хх = 0, У\ = 0;
*2,з = iarccos «±0,8471, у2,3 = ±|| -Дб =±2,54; *4>5 = ±я, {/4,5 = 0.
1499.	Период функции: Т = 2я; основная область: -я < л: < л. Симметрия
относительно начала координат. Нули: хх = 0 и д:23 = ±я. Минимумы:
у = -| л/2 ~ -0,94 при д; = и д; = -5 , у = | при д: = |; максимум
У = ~\ при х = - % у у = | V2 при д: = ^ и д: = ^. Точки перегиба:
*i = 0. J/1 “ 0; *2>3 = ±arcsin ~ ±0,37я, у2,3 = ±^ «/30 = ±0,81;
*4-5 = ±(я - arcsin ) = ±0,63я, ^4>5 = ±^ 730 ; *6,7 = ±я, i/в>7 = 0.
1500.	Период функции: Г = 2я; основная область [-я; я]. Симметрия
1 - /з
относительно оси Оу. Нули функции: д:12 = ±arccos -- ^	~ ±0,62я.
11	з
Минимумы: у = - при х = 0; у = -1- при д; = ±я; максимумы: у = -л
2	2	4
при л: = ±2 . Точки перегиба: д:12 = ±arccos 1 f ~ ±0,18я, i/1>2 ~ 0,63;
3	8
дг34 =‘±arccos ~ № ~ ±0,70я, уЗА ~ -0,44. 1501. Период функции:
Т= |; основная область £ - ^	. Симметрия относительно оси Оу. Функ¬
ция положительная. Максимум у = 1 при х = 0; минимум г/ = | при
д: = ±7 . Точки перегиба: д;, 2 =	, i/t 2 = ? ■	1502. Период функции:
4	’	8	’	4

480
ОТВЕТЫ
Т = л; основная область	J . Симметрия относительно оси Оу. Нули
функции: Xj = 0h х23 = ±^ . Минимумы г/ = 0 при х = 0 и у = -1 при я: = ±^ ;
максимум у = Tz при я: = ±arccos \ ~ ±0,21л. Точки перегиба:
16	4
*i 2 = ±5 arccos 1	~ ±0Д1 л, (/12 == 0,29; х3 4 = + i arccos 1 ~	«
2	1о	2	1о
- ±0,36л, г/3>4 =~ -0,24. 1503. Период функции: Т = к; основная область
q —
0	< х < л. Точка разрыва: х =	. Нули: хх = 0, х2 = л. Экстремумов
4
/2
нет, функция возрастает. Точка перегиба: я: = - , г/ =	. Асимптота
о —
я: = — . 1504. а) Период функции: Т = 2л; основная область [-л; л].
4
Симметрия относительно оси Оу. Нули функции: *1,2 = ±5 .Минимум
у = 1 при я; = 0; максимум г/ = -1 при я: = ±л. Точки перегиба: х12 = |;
у12 = 0. Асимптоты: я: = ±^ и я: = ±— ; б) период функции: Т = 2л, основная
/о
область -л < я: < л. Функция нечетная. Минимум г/ =	~ -0,58 при
3
я: =	; максимум у =	~ 0,58 при я: = ~ . Точка перегиба: хх = 0,
У\ = 0; яг2,3 = +л, i/2 з = 0.1505. Центры симметрии (kn, 2kn). Нули функции:
я^ = 0 и я:2 з ~ ±0,37л, .... Максимумы у = ^ - 1 + 2kn при х = ^ + kn,
минимумы г/ = -^5 - 1 + 2&л^ при я: =	+ kn j . Точки перегиба:
Oh-4-1
х = kn, у = 2&л. Асимптоты: я: = ——1 л (Л — целое). 1506. Симметрия
относительно прямой х — 1. Функция положительна. Максимум у = е
при х = 1. Точки перегиба я:1>2 = I ± ф , уи2= */е ~ 1,65. Асимптота у = 0.
1507. Симметрия относительно оси Оу. Функция положительна. Максимум
у = 1 при х = 0. Точки перегиба: я:12 = —	~ ±1*22, */12 =| е ^ ~ 0,56.
Асимптота у = 0. 1508. Функция положительна. Минимум i/ = 1 при
я: = 0. Вогнутость вверх. Асимптота у = х при х —* +оо. 1509. а) Функция
неотрицательная; нуль х = 0. Минимум у = 0 при я: = 0; максимум
У=31пе* ~ 0*39 при х = |. Точки перегиба: я^ =	~ -0,15, г/л ~ 0,34
V9	о	о

ОТВЕТЫ
481
и х2 = ^ + ^ ~ 1,48, у2 ~ 0,30. Асимптота у = 0 при х -+ +оо; б) функция
о
неотрицательная. Минимум у = 0 при х = kn (k = 0, ±1, ±2, ...); макси-
1	-( 2ft + Ijrt
мумы у = ~ е 2 при * = ^ + kn. Точки перегиба = (-1) ^ + Ля,
1	-[2Л + 1(-1)*1я
ук = | е L	J . 1510. Функция положительна при * > -1 и отрицательна
при * < -1. Минимум у = 1 при * = 0. Вогнутость вверх при х > -1 и
вогнутость вниз при *<-1.1511. Симметрия относительно оси Оу. Функ¬
ция неотрицательная; нуль * = 0. Минимум у = 0 (угловая точка) при
*	= 0. Вогнутость вниз. 1512. Область существования функции: * > 0.
Нуль функции * = 1. Максимум у = - ~ 0,74 при * = е2 ~ 7,39. Точка
с
перегиба: * = е8/3 ~ 14,33, у = - с~4/3 ~ 0,70. Асимптоты: * = 0 при * —*• +0
о
и I/ = 0 при * —* +оо. 1513. Симметрия относительно начала координат.
Нуль * = 0. Точек экстремума нет; функция возрастающая. Точки пе¬
региба: * = 0, у = 0. 1514. Симметрия относительно начала координат.
Нуль функции * = 0. Функция возрастает. Вогнутость вверх при * > 0
и вогнутость вниз при * < 0; О (0, 0) — точка перегиба. 1515. Область
существования функции: |*| < 1. Симметрия относительно начала коор¬
динат. Функция монотонно возрастает. Вогнутость вверх при * > 0 и
вогнутость вниз при * < 0; точка перегиба: * = 0, у = 0. Асимптоты:
*	= ±1. 1516. Симметрия относительно начала координат. Нуль функ¬
ции: * = 0. Точек экстремума нет; функция возрастающая. Точка пере¬
гиба: * = 0, у = 0. Асимптоты: у = * - | при * —* -оо и у = * + | при
х —* +оо. 1517. Нуль функции * ~ -5,95. Минимум у = \ + ? ~ 1,285
2	4
при * = 1; максимум у = -| + ~ ~ 1,856 при * = -1. Вогнутость вверх
при * > 0 и вогнутость вниз при * < 0; точка перегиба * = 0, у = |.
Асимптоты: у = | + я при * —>- -оо и у = | при * —► +оо. 1518. Симметрия
относительно оси Оу. Функция неотрицательна; нуль * = 0. Минимум
у = 0 при * = 0. Вогнутость вверх. Асимптоты: у = -%х- 1 при * —> -оо
и у = ^ * - 1 при * —*• -boo. 1519. Симметрия относительно начала
координат. Нуль функции * = 0. Минимум у = (угловая точка) при
*	= 1; максимум у = | (угловая точка) при * = 1. Точка перегиба * = 0,
у = 0. Асимптота у = 0.1520. Симметрия относительно оси Оу. Функция

482
ОТВЕТЫ
неотрицательна; нуль х = 0. Минимум у = 0 при х = 0 (угловая точка).
Вогнутость вниз. Асимптота у = я. 1521. Точка разрыва функции х = 0.
Нуль функции jc = —2. Минимум у =	-6,59 при * = 2; максимум
I/ = i - 0,37 при х = -1. Точка перегиба * = -|, */=§£* - 0,13.
е	5	5
Асимптоты: jc = 0hi/ = x + 3. 1522. Область существования функции
|*| > 1. Симметрия относительно оси Оу. Краевой максимум у = 2 & ~ 2,67
при * — ±1. Вогнутость вверх. Асимптота у = 1. 1523. Область сущест¬
вования функции * < 1 и * > 2. Точки пересечения с осями координат
, 0 j. Максимум у ~ 1,12 при * =	~ -0,72. Асимптоты
* = 1,* = 2иг/ = 0. 1524. Область существования функции |*| < а. Точки
пересечения с осями координат: (0, -а) и (0,67а, 0) (приблизительно!).
Функция монотонно возрастает. Краевой минимум у = а при * = -а
(0,1п2)и(|
и краевой максимум у = | а при х = а. Вогнутость вверх. 1525. Область
о
существования функции: * < 0 и х> - . Краевой минимум у = 0 при
3
2
* = 0; краевой максимум у = к при * = - . Вогнутость вниз при * < 0 и
3
о
вогнутость вверх при х> - . Асимптота у = - . 1526. Область существо-
3	3
вания: * > 0. Функция положительна. Минимум у =	- 0,692 при
х = - ~ 0,368; краевой максимум у = 1 при * = +0. Вогнутость вверх.
е
1527.	Область существования функции * > 0. Краевой минимум у = 0
1
при * = +0; максимум у = ее ~ 1,44 при х = е. Асимптота у = 1.
1528.	Область существования: * > -1, * ^ 0. Функция положительна.
Устранимая точка разрыва: * = 0. Точек экстремума нет, функция убы¬
вающая. Вогнутость вверх. Асимптоты: * = -1 и у = 1. 1529. Функция
монотонна при * > 0. Краевой минимум у — 0 при * = +0. Асимптота
у = е^х -	. 1530. Функция положительна. Симметрия относительно
оси Оу. Точки разрыва: * = +1. Минимум у = е при * = 0; максимум
у = -i- - 0,15 при * = ±л/3 . Четыре точки перегиба. Асимптоты: х = -1
Aje
при * —>- -1 + 0; * = 1 при х 1 - 0 и у = 0 при * —>- °о. 1531. Функции
* и у — неотрицательны; *min = 0 при t = -1; ytnUl = 0 при t = 1. Вогнутость
вверх при t > -1 и вогнутость вниз при t < -1. 1532. Точки пересечения
с осями координат: (0, 0) при t = 0; (+2л/3 - 3, 0) при t = ±J3 и (0, -2)
при t = 2; *max = 1 и утлх = 2 при t = 1 (точка возврата); ymin = -2 при

ОТВЕТЫ
483
t = -1. Вогнутость вверх при t < 1 и вогнутость вниз при t > 1.1533. Точка
пересечения с осями координат: (0, 0) при t = 0; хтАХ = 0 при t = 0,
*luin = 4 при t = 2;y убывает при возрастании £. Точка перегиба (-0,08; 0,3)
при £ ~ -0,32 (приближенно). Асимптоты: у = 0, х = -£ и у = ± - 2 .
2	2	4
1534.	Точка пересечения с осью Оу: (0, 1) при £ = 0; точка пересечения
с осью Ох: (-1, 0) при £ = оо. Краевые экстремумы: Jtmin = 0 и утАХ = 1
при £ = 0; д:шах = -1 и ymin = 0 при £ = оо. Точек перегиба нет. Асимптота
у = |. Вогнутость вверх при |f| > 1 и вогнутость вниз при | < 1.
1535.	Функции х и у — положительные; *min = 1 и ymin = 1 при £ = 0
(точка возврата). При £ < 0 — вогнутость вверх; при £ > 0 — вогнутость
вниз. Асимптота у = 2х при £ —>- +оо. 1536. Основная область: [0, я].
Точки пересечения с осями координат:	, 0 j
« = 5;(-a,0)nPHf=2;Jo>^) При*-2р;(|,о)
при< = 5;(0;--|) при
при i . Экстремумы:
6
*„,а* = а и |/тах = а при t = 0; ymi„ - -а при t = |; *min = -а при t = |;
о,.
«/max = « при £ = у ; хтах = аи i/min = -а при £ = я. Вогнутость вверх при
0	< £ < ^ ; вогнутость вниз при | < t < п. 1537. Функции х и у — неот¬
рицательные и периодические; основная область 0 < £ < ^ . Экстремумы:
*min = 0 и утм = 1 при t = |; дсшах = 1 и утЫ = 0 при t = 0. Вогнутость
вверх. 1538. Область существования: £ > 0. Симметрия относительно
прямой х + у = 0. Экстремумы: *min = “- ~ -0,37, у = -е ~ -2,72 при
е
£ = i ; утАХ = - , л: = е при t = е. Точки перегиба: х1 = - J2e~& ~ 0,34,
е	е
I/! = -j2e-& ~ 5,82 при £ =	~ о,24 и х2 = J2e^ , у2 = J2e~*^ при
£ —	~ 4,10. При £ = 1 — изменение знака вогнутости. Асимптоты:
х = 0 и i/ = 0. 1539. Функции л: и I/ — периодические с периодом Т = 2я;
основная область -я < £ < я. Симметрия кривой относительно осей коор¬
динат. Кривая имеет две ветви. Экстремумы: xmin = а, у = 0 при £ = 0;
*max = “а> У = 0 при £ = +Я. ВОГНУТОСТЬ ВВврХ при -Я<£<-| И 0 < £ < ^ ;
вогнутость вниз при -5 < £ < 0 и ^ <у<п. 1540. Симметрия относительно
6	а
оси Оу; ytnm = 0, л: = 0 при £ = 0. Вогнутость вниз. 1541. Параметрические
уравнения: х = ?g*3, у = j*g^3 (-оо < £ < +оо). Симметрия относительно

484
ОТВЕТЫ
прямой у = х. Точка пересечения с осями координат О (0, 0) (двойная
точка). *шах = l/i ~ 1,59а при у = а\[2 ~ 1,2а; утлх = al/i при х = al/2 .
Асимптота х + у + а = 0. 1542. Симметрия относительно начала коор¬
динат, осей координат и биссектрис координатных углов; О (0, 0) —
изолированная точка. Точки пересечения с осями координат: (±1, 0) и
(0, +1). Mniin = 1 при у = 0; |*LX =	- 1,10 при ы = Л * 0,71;
М.н1,. = 1 при х = 0; |(/|П1М = Л±Ж при W = Л • 1543. Параметрические
уравнения: х =	, у = —— , где t = ^ (-°° < £ < +°о). Кривая имеет
две ветви. Симметрия относительно прямой х + у = 0. Экстремумы:
=* | V2 » 1,89,1/ = -| V4 « -2,38 при t—\/2* -1,26;	= -| Ш ,
х = 2 зД ПрИ i = -JI к -0,79. Точки перегиба: х, = 2,18, ух ~ -4,14 при
2	у 2
t = ~3Jl(7 + 3j5) ~ -1,90; х2 ~ 4,14, ух ~ -2,18 при t = -3J|( 7-Zjl) ~ -0,53
при t = -SJ2 — изменение знака вогнутости. 1544. Кривая состоит из
1	1 + !
прямой у — х и гиперболической ветви л: = (1 + 0 * , х = (1 4- 0	1
(-1 < t < +оо). е) — двойная точка. Вогнутость вверх при х * у. Асимп¬
тоты: х = 1 и у = 1. 1545. Область существования: |*| > In (1 4- л/2) ~ 0,88.
Симметрия относительно осей координат. Краевой минимум \у\ = 0 при
х = ±ln (1 4- J2 ). Вогнутость вниз при у > 0 и вогнутость вверх при у < 0.
Асимптоты: у = х и у = -х. 1546. Область существования функции: г > 0,
|ф| < а, где а = arccos • Кривая замкнута. Симметрия относительно
полярной оси. Максимум г = а 4- b при ф = 0; краевой минимум г = 0 при
ф = ±а. 1547. Область существования: 0 < ф < 5 ;	< ф < я; ^ < ф < ~ .
Л-
Функция г — периодическая с периодом . Кривая замкнута и имеет
о
три одинаковых лепестка. Оси симметрии: ф =	, Ф = и ф =
6	6 2
Начало координат О (0, 0) — тройная точка. При 0 < ф < ^ имеем:
и
максимум г = а при ф = ^ и минимум г = 0 при ф = 0 и ф = £ .
6	3
1548.	Область существования функции: |ф| < 5 и S < Ы < I п> период ^ .
6	2	6	3
Минимум г = а при ф = 0 и ф =	. Асимптоты: ф = ±|,ф = ±| и ф =	.

ОТВЕТЫ
485
1549.	Спираль, имеющая начало координат своей асимптотической точ¬
кой; г монотонно убывает при возрастании ср. Асимптота ср = 1.
1550. Область существования г
75-1 _
при г =
л
i ; минимум (р = arccos 1
-0,62. Краевой максимум ср = п
arc 75°30/ при г = 2. Асимптота
г cos ср = 1 при г —► +оо. 1551. Семейство парабол с вершинами (1, а - 1)
(минимумы). Точки пересечения с осями координат: (0, а) и (1 + Jl-a , 0)
(при а < 1). Вогнутость вверх. 1552. Семейство гипербол при а ^0 и
прямая у = х при а = 0. Минимумы у = 2|а| при х = |а| и максимумы
у = -2\а\ при х — -|а| (а ** 0). Асимптоты у = х и х = 0. 1553. Семейство
эллипсов при 0 < а < +°о; семейство гипербол при -°о < а < 0; прямая
у = х при а = 0. Все кривые семейств проходят через точки (-1, -1) и
(1, 1). При у > х имеем: 1) максимум у = Jl + a при х = - -	, если
л/Г+а
а > 0; максимум у = -Jl + a при х =	, если -1 < а < 0; краевые
Jl + a
минимумы у = +1 при х = +1 (а ^ 0); 2) вогнутость вниз. При у < л:
имеем: 1) минимум у = -Jl + a при х = -- 1 — , если а > 0; минимум
Jl + a
у = Jl + a при х —	1 — , если -1 < а < 0; краевые максимумы у = +1 при
Jl + a
х — +1; 2) вогнутость вверх. Асимптоты: у — (1 + J^a )х и у = (1 -
при а < 0. 1554. Семейство показательных кривых, если а *= 0; прямая
у = 1 + |, если а = 0. Общая точка семейства (0, 1). Минимумы
-i- (1 + In 2а) при л: = i In 2а, если а > 0; у монотонно возрастает,
2а	а
если а < 0. Асимптота у = |. 1555. Семейство кривых, проходящих
через точку (0, 0) и имеющих в ней общее касание с прямой у = х. Мак¬
симум у = ае~1 ~ 0,37а при х = а, если а > 0; минимум у = ае“1 при х = а,
если а < 0. Точка перегиба х = 2а, у = 2а<Г2 ~ 0,27а. Асимптота у = 0.
f тп * 1
1558. аП1А,"ттпП % 1559. (/п + л) [	. 1560. Основание системы лога-
(т + п)т + п	\ттпп)
1
рифмов не должно превышать - 1,445. 1561. Квадрат со стороной 7s .
1562. Острые углы треугольника 30° и 60°. 1563. Высота банки Н = з/~
равна диаметру ее основания; полная поверхность Р = 3Jb4nV2.
1564. cos ср = cosa +	, где 2а — дуга сегмента и 2ср — дуга,
4
стягиваемая стороной прямоугольника. 1565. Стороны прямоугольника

486
ОТВЕТЫ
а Л и b Л.1566. Если h > 6, то периметр Р вписанного прямоугольника
с основанием х и высотой у имеет краевой максимум при у = h; если
h < b, то Р имеет краевой минимум при у = 0; если h = b, то периметр
Р постоянен. 1567. b =	, h = d . 1568. Измерения параллелепипеда
— , — и . 1569. -^т Л3.1570. tlR2 (1 + л/5)~81% поверхности шара.
Л Л Л зТз
1571. Объем конуса равен удвоенному объему шара. 1572.	/3.
9<Уз
1573. Если tg а < |, то максимум полной поверхности цилиндра дости¬
гается при г =
R
2(1 -tga)
, где г — радиус основания цилиндра. Если
tg a > i , то при r = R имеем краевой максимум. 1574. р( V2 - 1)	•
2	^ 2
1575. 1; 3. 1576. Если 6 < -2=, то максимум длины хорды МВ = — , где
Л	с
с2 = Ja2 - Ъ2 и точка М имеет координаты л: и р, достигается при
л: = л/a2 - 262 ; z/ = ~ ; если 6 >	, то краевой максимум длины
с2	с2	72
хорды МБ =26 достигается	при	л: =	0,	I/ =	6.	1577.	*	=	, у	= -4= ; аб.
72	72
Joy
1578. Максимум поверхности достигается при r = h= з — , где г — радиус
V 5 71
основания цилиндра и Л — его высота. 1579. ср = 60°. 1580. Трапеция,
описанная около окружности. Боковые стороны АВ = CD = a sec2 |.
1581. a = 2я ~ arc 294°, где а — центральный угол оставшегося
сектора. 1582. ср	= arccos	2	,	если arccos 2	>	arctg	7 ; ср	=	arctg 7 , если
р	р	о	о
arccos 2 < arctg 2 . 1583. -. 1584. AM = [ 1 + ,/fiY .
P	b	Ju2 + v2 - 2uucos0	'
1585. Расстояние светящейся точки от центра большего шара равно
х = —-—-, если а > г + R - и х = а - г, если г + Б<а<г + Б где
■ (й1
1+
(- £\ -
а3 + 63J2.
1588. v = з/— , где k — коэффициент пропорциональности. 1589. arctg k.
*J2k

ОТВЕТЫ
487
1590. При I < 4а угол наклона стержня определяется из формулы
cos а =	; при I > 4а положения равновесия нет. 1591. k = -3;
16а
2
Ь = 3; у = 3(1 - л). 1592. а = I ех°; b = е*»(1 - *0); с = е*» ( 1 - л0 +	.
1593. а) Первый; б) второй; в) второй. 1595. a) У2 , (2, 2); б) 500 000,
а	з
(150, 500 000) (приблизительно!). 1596. pf 1 + —V. 1597.	,
V р )	ао
з
где е = ^2~— эксцентриситет эллипса. 1598. (£2*2~9\У f где
а	ао
е = У*2 + Ь2 — эксцентриситет гиперболы. 1599. 3|ахр|3.1600. ^ (1 - е2 cos21) 2,
а	о
з
где е — эксцентриситет эллипса. 1601.2 J2au . 1602. at. 1604., (г * [ 2^2—:.
|r2+ 2r'2- rr"|
3
1605. (fl2 + f2}2.1606. гУГ+^Г2.1607. ? л/2^. 1608. ^ . 1609.	.
2	a2 + r2	3	3r	\J2	2 '
1610. x0 ~ 680 m. 1611. Полукубическая парабола 27pri2 = 8(£ - p)3.
2	2	4
1612. Астроида (a£)3 + (6ц)3 = c3, где c2 = a2 - 62. 1613. Астроида
(£ + ц)3 + (^ - Л)3 = 2a 3. 1614. Цепная линия ц = a ch^ . 1615. Лога-
а
m(y - и \
рифмическая спираль р = тае у 21 .	1616. £ = ла + а(т - sin т);
Л = ~2а + а(1 - cosт), гдеx-t-n. 1617. х, = -2,602; х2 = 0,340; х3 = 2,262.
1618.	хх = -0,724; х2 = 1,221.1619. л: = 2,087 = arc 119°35'. 1620. ±0,824.
1621. хх = 0,472; х2 = 9,999. 1622. Xj = 2,5062.1623. Xj = 4,730; х2 = 7,853.
1624. я: = -0,56715. 1625. х = ±1,199678. 1626. Xj = 4,493; х2 = 7,725;
х3 = 10,904. 1627. xj = 2,081; х2 = 5,940.
Раздел III
В ответах этого раздела ради краткости произвольная аддитивная
постоянная С опущена.
1628.21х - 9л3 + § л5 - I л7. 1629. ^ х3 - 125л:4 + 30л5 - 12 л® + I л7.
5	7	3	3	7
1630. х - Зх2 +	i± х3 - ? х4. 1631.	х —	— —	2	In |х|.	1632. a In |х|	-	^	.
3	2	х	11	1	1	х	2х2
1633.	-хУх	+	2 Ух.	1634.	\ xifx	-	£хЧ/2Р	+	\	\[х*.
3	5	17	3
1635.	(l + ltf-fji^ + I . 1636. li£i±Z}. 1637.2л- ^ bJl2x^ +%\/Ъхг.
Ifx^ 2	5	8 '	li/x	5	2

488
ОТВЕТЫ
1638. In |дг| - —A . 1639. * - arctg л:. 1640. -л: + i In |I±*| . 1641. x + 2 ln|*zi|.
4*4	2 И _ x\	\x + 1
1642. arcsin x + In (x 4- J1 + x2 ). 1643. In
X + Jx 2 - 1
X + Jx2 + 1
. 1644.	+2 -51 +-Ц-.
In4 ln6 In 9
1645.	+ —3— fil . 1646. i e2x -ex + л:. 1647. x - cos x + sin x.
ln5V5;	5In2 V2)	2
1648. (cos x + sin x) • sgn(cos x - sin x). 1649. -x - ctg x. 1650. -x + tg x.
1651. a ch x + b sh x. 1652. x - th x. 1653. x - cth x. 1655. In \x + a\.
4
1656. JL (2л:-3)11.1657.-i(1 -Зл:)5.1658.-? J2^bx . 1659.		?	.
22
15(5* - 2)2
1660.	*J(l-x)2.	1661. ^ arctg^ л: J) .	1662.
276
In
72 + * *fs
Ji-хЛ
1663. arcsin J|J. 1664. -1 In|*л/3 + 73x2-2 1.1665. -(e-x + | e“2x).
1666. -x sin 5a - | cos 5x. 1667. -1 ctg ^ 2x + 2 j. 1668. tg |. 1669. -ctg |.
1670. tg(2-|j.	1671. | [ch (2x + 1) + sh (2x - 1)].	1672. 2 th |.
1673. -2 cth |. 1674. -л/Г^Г2. 1675. ± (1 + x3)2. 1676. -I In |3 - 2x2\.
1677.i— . 1678. i arctg ^ . 1679. -i- In
2(1 + **)	4	6 2	872
^ - 72
72
. 1680.2 arctg 7* .
1681. cos i . 1682. -In
i + 7*^+1
1683. -arcsin Л • 1684. ---*	.
W
1685. —1— .	1686. i V8*3 + 27 .	1687. 2 sgn x ln(7M + 7i*+Tj)
7*23!	8
(x(l + x) > 0). 1688. 2 arcsin 7* • 1689. -| e-*2. 1690. In (2 + ex).
1691. arctg ex. 1692. -In (e~x + Jl + <r2*). 1693. i In3 *. 1694. In |ln (In x)|.
О
1695. i sin0 x. 1696. -Д=.	1697. -ln|cosx|. 1698. In |sin x|.
6	Vcos*
1699. | Vl-sin2x. 1700. a)	+	(a2 *b2); 6) In |72cos x +
2	az-b2	72
+ 7cos2x |; в) -i; arcsin ( 72 sin x); r) In (72 ch x + Jc\\2x).
72	72
1701. -| Vctg3x . 1702. arctg (^j. 1703. In |tg ||. 1704. In | tg[| + 5)
1705. In I th ^1. 1706. 2 arctg ex. 1707. -i- Inf 'Щ* + 7sh“x + ch4x ) .
I 2|	272 V 72	'

ОТВЕТЫ
489
1708. 31/th* . 1709. - (arctg л:)2.1710. -—-— . 1711. - ln2(x + Jl + x2).
2	arcsin*	3
1712. -1 arctg . 1713. -i- In *2-*-/g+ 1
J2	xj2	2 J2 x2 + xj2+l
. 1714. -
15(jc5 + l)3
/ n f 2
1715.	—In I x 2	+ 7l + x"4 2) при n * -2; -ir In |x| при n = -2.
и + 2 V	72
1716.	1	In2 — .	1717.	—	arcsin f /1	sin x	1. 1718.	i	arctg	(tg2 x).
4	1-x	72	43	)	2
1719.	-1-	 In I3*-2*!. 1720.2jl + Jl + x~*. 1721. a) \ x3 - x5 + ? x7;
2(ln3-ln2)	|3*+2'|	3	5	7
6)	~ *)'2. 1722.	-x - 2 In |1	- x|.	1723. |	(1 - x)2 + In	|1	+ x|.
1724.	9x	- fa:2	+	lx3	-	27 In |3 +	x|.	1725.	x	+	In (1	+	x2).
2	3
1726. 4: In
72
Л-
72 - X
+ 21n|2-xzl-x.l727.
1
1728. £ - £
5	4
99(1 - л)"	49(1 -jc)98	97(1 -x)91
3	3.
+	^ + x - In |x + 1|. 1729. i Г (x + 1) 2 - (x - 1) 21.
3	2	3 L	J
3	3	7	4
1730. -8+,30x(2 _ 5xyz 1731. -I±|* (1 - Злг)5.1732. 4-(l + x2)3 - fo+x2)3.
о (о	111	14	о
1733. - In |*._M.	1734. i In linil.	1735. arctg x - 4= arctg •
4 |x + 3|	3	\x+2\	72	J2
1736.
1739.
1072
In
• - 72
x +
72
2x + a + b
- _i_	arctg JL	. 1737. In klili	. 1738. A	In Ц	.
573	73	(x + 2)2	2 x2 + 2
	 + —In |*±“|. 1740. —A— f i arctg £ -
(a - b)2(x + a)(x + b) (a-6)3	|x+6|	a2 - b2 \ b	b
- 1 arctg £) (|a|	* |ft|). 1741. £ -	I sin 2x.	1742. £ + A	sin 2x.
a	a)	2	4	2	4
1743. - cos a - -	sin (2л: + a). 1744. ~	sin 2 л: - ^	sin 8*. 1745. 3	sin f +
24	4	16	6
+ 3 sin ~ . 1746. cos { bx + £•) + cos ( x +	. 1747. -cos x +
56	10 v	12/	12 V 12/
+ 1 cos3 x. 1748. sin x - i sin3 x. 1749. | x - \ sin 2x + sin 4x.
3	3	8	4	о 2
1750. 3 x + i sin 2л: + i sin 4л:. 1751. -л: - ctg jc. 1752. i tg2 x + In |cos jc|.
8	4	32	2
1753. cos 2л: - ^ cos 4л: + cos 6л: 4- cos 8x + -i- cos 12л:.
"л	J	48	128	192
16
64
1754. tg л: - ctg л:. 1755. —J- + In |tg ( f
sin*	V 2	4/
1756.
2 cos2*
+ In |tg x|.

490
ОТВЕТЫ
1757. In |sin x| - \ sin2 л:.	1758. tg * 4- \ tg3 л:.	1759. x - In (1 4- ex).
и	О
1760. x + 2 arctg e*. 1761. -2 + I sh 2x. 1762. 2 + I sh 2x. 1763. \ sh3 л:.
2	2	2	4	3
1764. i sh 2x + | sh 4x. 1765. -(th x + cth x). 1766. -y|g(9 + 12* +
+ 14jc2)(1 - x) * . 1767. -1 e65050*2 (1 - 5л:2)11.1768. - A (32 + 8л: + 2x?)j2^~x .
1769. -JL(8 + 4л:2 + 3xi)4lrx2.	1770. -!Lt|A*-3(2 - 5л:3)3.
1771. f§ - | sin2 x + sin4 л:] «/sin3 л: . 1772. -1 cos2 x + i ln(l + cos2 л:).
\o 7	11	/	2	2
x
1773. i tg3 л: + i tg5 л:. 1774. \ (-2 + In л:)-Л+ 1пл;. 1775. -л: - 2e 2 +
3	5	4
+ 2 In (1 + e2). 1776. л: - 2 In (1 + Jl+7*). 1777. (arctg Jx f. 1778. —2— .
1779. 2 J^2 + In |л: + 4x^21.	1780.	2 4^Zx2 + \ arcsin 2.
Lt	Li	Li	CL
1781. —-g	. 1782. -Ja2 - x2 4- a arcsin * . 1783.	Jx(2a-x) 4-
a2Ja2 + x2	a	2
4- 3a2 arcsin . 1784. 2 arcsin	• 1785. 2x~ (q + b) J{x- a){b- a) 4-
4-	arcsin i .	1786. | Ja2 + x2 + £ In (x 4- Ja2 + x2).
1787. | Ja2 + x2 - ~ In (x 4- Ja2 + x2). 1788. Jx2 - a2 - 2 a In {Jx-a 4-
4- Jx + a ), если x > a; - Jx2 - a2 4- 2a In (J- x + a 4- J- x- a ), если x < -a.
1789. 21n (Jx + a 4- Jx + b), если х4-а>0их4-Ь>0;-2 1п( J- x - a 4-
4- J- x-b ), если х4-а<0их4-Ь<0. 1790. ------ J{x 4 a){x 4 b) -
4
In (4^~a +4^~a), если х4а>0ил:4б>0. 1791. x(ln x - 1).
4
1792. 2HI fin л: - -ЦЛ (n * -1).	1793. -i (1п2л: + 21m: + 2).
п + IV	л + 1/	x
з
1794. | x2 (1п2л: - 11пл: + |j. 1795. -(л; + 1)е'х. 1796. (V + х + |] .
1797. -2!±1 е-*2. 1798. л: sin л: + cos л:. 1799.	—1 cos 2х 4- - sin 2х.
2	4	2
1800. х ch х - sh x. 1801. ^ 4- sh Зх -	4- ch 3x.
1802. x arctg x - 1 In (1 4- x2). 1803. x arcsin x 4- J1 - x2 . 1804.	4-
£ 2

ОТВЕТЫ
491
+ i±£f arctg x. 1805. -Li*!	+ *! arccos л:. 1806.
2	9	3	*
In
i +7Г
. 1807. X In (x + Jl+IT2)- ЛТх*. 1808. д:-Ц^ In !±^ .
2	1 - л:
1809. -л/J 4- (1 4-*) arctg V* .	1810. In tg | - cos л: * In tg *.
1811. i (jc3 - l)ex*.	1812. x(arcsin jc)2 4- 2jl - x2 arcsin x - 2x.
о
1813. (arctg x)2 - л; arctg x + i In (1 + л:2). 1814. x2 - | In |1 - x2} +
Z	Z	о	о
+ ^ In |ki*|.	1815. Jl + x2 111 (x + Jl+x2) - x. 1816. -—*— +
+ 1 arctg x. 1817. ——£		 + arctg * (a * 0). 1818. f	+
2	2a2(a2 + x2)	2 a3	a	2
4- ^ arcsin p: (a 5* 0).	1819. ~ Jx^Ta 4-2 In |jc 4- Jx2 + a |.
1820. ^2jc' + a2) 7a2 + *2 - ^ In (x + Ja2 + x2). 1821. ^ - £ sin 2* -
8	8	4	4
-	. 1822. 2(Jx- \)е-Г* . 1823. 2 (6 - x)Jx cos Jx - 6 (2 - x) sin J~x .
8
1824. -(1-*)<’!,rctl!'. 1825. (1 + x)e’"'Atx . 1826. £ [sin (In x) - cos (In x)].
2jl
2 Jl
acosbx + frsinfrx eax
a2 + b2
1827. | [sin (In x) 4- cos (In *)].
1829. asinbx-bcosbx ^ lg30 eff (2 - sin 2x - cos 2x). 1831. £ + 1 sin 2x -
a2+b2	8	2	4
- ex(cos x 4- sin x) 4- | e2x. 1832. -x 4- | In (1 4- e2x) - e~x arcctg (ex).
1833. ~[x 4- ctg x * In (e sin x)]. 1834. x tg x 4- In |cos x\. 1835.	.
J\a\ + xj\b\ ^ если ab < 0.
1836. —1= arctg { x - 1, если ab > 0; sgna-. In
ЛЬ У 4a J	2 J^b
1837. — arctg
Л	Jl
J\a\-xJ\b\
2x~ 1 . 1838. i In \ x~1\. 1839. In
\Zx + 1
4л/2
x2 - (л/2 + 1)
x2 + (j2-l)
1840. £ In (x2 4- x 4- 1) 4- arctg ^
2	л Л
. 1841. i In (x2 - 2x cos a 4 1) 4
2
4- ctg a * arctg -—(a * Ля, & — целое). 1842. 1 In (x4 - x2 4- 2) 4-
sina	4
+ -^= arctg 1*1^1.1843. i ln{|x3 + l|(x3 - 2)2}. 1844. i In |3si»*-5c.os*l.
2v«	V7	9	2 I sinx-cosx I
(-!*■)
1845. arctg
1846. i к	4 Ja 4 Ьх2 ), если b > 0;
Jb

492
ОТВЕТЫ
-i- arcsin ( x /--1, если a > 0 и b > 0. 1847. arcsin . 1848. In \x 4-
\	4 a)	72	I
+ 1 + VF+x | . 1849. J| In ( * - i + Jx2- ijc + lj . 1851.-J5 + X-X2 +
4- i arcsin ^j=- •	1852. Jx2 + x + 1 4-| In ^ jc + | 4- Jx2 + x+ 1 j .
1853. a) —i— arcsin 4*2 * 3; 6) arcsin 2si"x~1-	1854. 1 7*4 — 2x2 — 1 +
2л/2	Vl7	3	2
+ i In |лг2 - 1 + «/*4 + 2x2 - 11. 1855.	«/1 + л;2 - x4 + | arcsin 2*^Г 1.
1856. -In
х + 2 + 2jx2 + x + 1
x
.1857,
dEHHl +1 arcsin
x ^	|jr|75
(Nl>#
1858. --L In
72
1-*+ 72(1 + *2)
1 +д:
1860.
5^
2 + 2* - 5	+	1
x + 2
1859. arcsin .	(|*| >72).
I*- 1172
(I* + i| > 76).
x + 7
—- arcsin 	—
575	|лг + 2|Тб
1861.	2--~ J2 + x - x2 + | arcsin 2£_Jt.	1862.	72 + x + x2 +
4	8	3	4
+ I In (i + x + J2 + X + X2 ) .	1863.	7x4 + 2x2- 1 - \ In ]jc2 +
o	)	4	Сл
+1+7*4 + 2x2 - 1|. 1864-71 + *- x2 +1 arcsin 1—?^-In
2	75
2 + X+ 2J1 + X-X2
х-Ц < £
2 2
) . 1865. In
(x + 2)4	1
jf2 — 1 + 7*4 + 1
1867. ~ In ,
2	|(*+1)(jc+3)3
1868. ±- - £L +	-
.	1866. In I* - 2| + In \x 4- 5|.
З*7	5д:6 , Идс* 21д;4
9
8
6
4.	43*!	- §5*!	4- 171* 4- I	In I—-—l—I	. 1869. x 4- i	In |*| - ~	In |дс	- 2|	4-
3	2	3 |(jc + 2)102,|	6	1 1	2	1	1
4- In |jr - 3|. 1870. x + \ arctg л: - | arctg £. 1871. -	1
3	3	3	2
	 + i In |3E_=_1|
3(.r - 1)	9	L+2
1872. -i- + i In \x2 - ll.
x+1	2	1	1
1873.
-	5*:-6- ■ + 4 In \*zl\.
д:2 - 3jt + 2	\x - 2
1874. 9^2+50^ + 68 + 1 ln |(x + l)(x + 2)ll4	1875. -	3*2 t3:r_:2	+
4(x+2)(x+3)2	8 I (* + 3)>7 I	8(jc - 1)(дг+ 1)=*
+ i- In |*±2|. 1876. arctg * + f ln 4^4 • 1877.1 arcctg л; + i ln	.
16	|x-l|	6 x2 + 4	2 Б 4 x2 +1
Ш8.	- «Й, (« - 2). urn. -5^+i |„	e«+1).
1 arctg	. 1881. | ln	+ -±= arctg	.
1880. In
IДГ + 1
7з
7з
X2 - X + 1
7з
7з

ОТВЕТЫ
493
1884.
In Х~±Х^Л + -J- arctg -*JL
4j2 x2-xj2 + l 2j2
1 - X2
1885. i In *--+ x + 1 +
4 x2 - x + 1
+ -J— arctg y2 1. 1886. -i- In - + *4j? *■*- + 1 arctg x + i arctg x3.
2л/3	хТЗ	473	1 - хТЗ + хг 2	6
1888. i In If ~ 1)2 - 4= arctg
6 x2 + *+l	73
1889.
2x- 1
1887.	J—4 + i In <1 + *>2 + I arctg x -	arctg
6(1 + *)	6	1-x + x2 2	з7§	7з
In ^+2y + 2 +
+ | arctg (x + 1) - 2 arctg (2x + 1).
5	5
1891. —
x2 + x + 2
S(x-l)(x+ l)2
+ J_ in |*±I|. 1892.
16
\x- 1
1890. a + 2b + 3c = 0.
—£— + 1 In i£±ill +
3(x3 +1)	9 x2 - x + 1
+ arctg .	1893. x(3f2 + 5I + § arctg x. 1894. 	i
3J3	3	8(х2+1)2	8	x2 + 2x + 2
+ arctg (x + 1). 1895.
In
rV2 + 1
4(*4+l)	16V2 x2-xj2+l Sj2
— arctg ,
x2 - 1
1896. - 5?- + g- - + 1 In Iх-41 + -A_ arctg 2£±1.1897. — — — n* +
3(*2 + *+l)	9	*2 + *+l зТз * 7з	32(x4 -1)2
+ In	-M arctg X. 1898. —*3 + -2*—
128 U+l| 64 ё	6(x4 + *2+l)
. 1899.
1900. --
x5 + x + 1
1902. ay + cot = 2b(3.1903.
(весь интеграл!). 1901
1	3
_8*4 + 8дг2 + 4x - 1
28(*3 + x+l)2
	 + —— arctg 2x
3(*2 + * + 1) зТЗ	73
2*+ 1
96(*-1)9с	97(jc- l)97	98(x- l)98	99(*-1)"
1904. i In\^4\ - i arctgдс2.1905. -i- arctg . 1906. i In -(*2+1>2 +
8	|**+1|	4	473	73	12	x4-x2+l
+ i arctg jc3 +	1
3
— arctg -x2~—
273	73
1907.
— In
x4 + 2
In
x4 + 1
1908.	f—^— + ——
кин*1»-™	2715
In
Tio
716
)•
1910.
xb + 2
1_
10
10(xlo + 2xh+2)
1912. -i- f arctg - -£!_) (/i * 0). 1913. -±- in	. 1914.
2/i l & дг2л + ly v 7	20	x10 + 2
1916.
+ i- In
10 *10+1
1915. i In —Jill— .
7	(1 + x7)2
1917.
-p arctg
V3	xV3
ii=i. 1918. 4= In 2*2 + (1 ~ 7S)x + 2 1919
75	2x2 + (i + 75)*+2
2a* + b
1920. arctg *+ i arctg jc3. 1921. In =
(д - 1)Д(а*2 + bx + c)n_1
£l + i
In xU1 .
4 4
(х4 + 2)1
- In |x"
+ l|)(n^0).
. 1914.
1 +
10( лг10 + 1)
i In
I x(xA - 5) I
5
U5 - 5x + l|
1 In
x4 - х2Л + 1
472
x4 + x2j2 + l"
. 2д - 3 . 2а г
!«-• л-1 Д '’-1’

494
ОТВЕТЫ
где А = 4ас - Ъ2\ /3
2х+1	+	2х+1
6(х2 + х+1)2	3(х2 + л:+1) з^/з
+ arctg 2jc+1
7з
/	1	 dt; -L(-i +
(ft-a)m + n-1J	fm	625 V *
t2
3* - ^ -3 ln|t|),
1922. / =
(ft- a)m + n"1 J tm
где	1923.	-J] fc|/_ ffij0	In \x - a|.
x+3’	^ k\(n - k)(x - a)n~k
k = о
1924. i?(x) = P(x2) + Vy Г—^^—1, где P — многочлен,
fTijTi 4a< ~ x) tj (a/ + jc),,/-l
±ai (i = 1, ...» k) — корни знаменателя, — постоянные коэффи-
n
циенты. 1925.	^ cos 71	^ • In ^ 1 - 2x cos	+ x2 j 4-
± Y
n t—i
sin	arctg	2,1
2 л
i7C(2fe - 1)
2n
. 1926.2 7* - 2 In (1 + 7*)-
4*7* - 1
1928. 2f4-
1927. 3 ln 	r 2 x3j*r	FI - -n= arctg r
4 (l + l/x) (l-l/x + 21/*)*	2,/7	77	4
- | <2 _ 2 in I* - 1| + i$ ln (t2 + t + 2) - -Ц= arctg , t - V2 + x.
2	4	8	877	77
1929. 6f - 3t2 - 2i3 + f t4 + f ts - | f + 3 ln (1 + f2) - 6 arctg t, где
Z	5	7
t=6*fcTl. 1930.	2—- - —i— . 1931. ^	+ i ln|jc+ л/^231 |.
(1 + Vi)2 l + \fx	2	2	2	1	1
1932.
_з cm
2 ух - 1 *
1933. -
at3
+ a in l + tj2 + t‘ + a arctg f
где
l + «4	472	1 -tj2 + t2 272	tj2
t = 41^ . 1934. —2-пЩ±. 1935. £ +Jx - i 7*(l + x)-iln(Jx + TTFi).
V x	a-b>ix-a	2	2	2
1937.	Jl + x + x2 - | ln + x + Jl + x+x2^.
1938.	-ln
2 - * + 2 Jx2 + x + 1
+ R) - 72 ln
x+ 1
X+2 + J2R
1939.	2~* , 71 -л:2 • 1940. R + ln (x + 1 +
3(1 -x)2
где R = Jx2+2x+2 . 1941. arcsin l±2* +
Л
1942.	1 ~^x 7l + x - x2 - ii arcsin	•
1943.-M+SX + 2X*	- x2 - 4 arcsin i—^ . 1944.	£-x3 +
6	J2	V256	128
+ In
3 + x + 2j\ - x - x2
1 + x
~5 _ 9 д.7 _|_ rmr
‘	\ uiak (aAx _a2x3 ,
21
2
63
2

ОТВЕТЫ
495
+ —1 Ja2 - х2 + ~ arcsin 1946.	- И* + 37^ 7х2 + 4х+3 -
6 J	16	|a|	V 3	3	)
- 66 In |x + 2 + 7*2 + 4x+31.	1947. - JL ЛсШ. + i In ^ <fxl — •
2л:2	2	|x|
1948. Zjltkjx2-!. 1949.7^rLz4-Jx*+3x+1 --j^ln (* + V/5 + 2.J?it3.*±l
20(x-l)2
1950. Jx + 3 Jx* + 2x - | arcsin p-1-,,
8(x+l)2	8	|x+lj
40^5	x-1
где x < -2 или x > 0.
1951. 4а(са, + bb,) = 8а2с, + 3Ъ2ах (а * 0).
-Л In
1952.
/1 + 2х
А/ 2(1-
х)
V2
1954.
1955.	Jl + 2x- х2 - 2 arcsin
72 + л/l + 2x - x2
1Q*Q * nrp^in 1 In
3x + 1 - 2jx2- x-1
1 — X
‘2 |x-i|7§ 2
x + 1
7x2+x+ 1 +ln f
X + i + 7*2 + X+1 1 + i In
2 ; 2
1 - x + 2 Jx2 + x + 1
X + 1 l
X + 1
Ll* - ± arcsin jia/L.
72	72	l1 + *l
c72
1956. -MHEH - 2 arcsin p-i- (x < 1 или x > 3). 1957. 4= arctg ■,	.
x-1	\x-2\	72	7ГГх2
1958.
1
272
In
x72 + 7^1
хТг-Тх2^!
1959.
2ТГ
In
7Г
+ X* + X
72
I960. In (x+T^T2 ) - arctg. 196I. J_ in
*	76
472 ТГТхг-хТг
(2x+1)72+ 73(x2 +x- 1)
(2x+1)72-73(x2+x-1)
1962.	arcsin ^	#	arctg ^+2x-x^	_	1	in 7б+72 +	2х-х2
73	3	(1-х)л/2	л/б л/б - 72 +	2х - х2
1963.	2(X~J-L. 1964. arctg^2 + 3:— +-LIn <- + \Щ~ 4Чхг +х+ 1)
37*2+х +1	л/2	(х-1)л/2 Тб	Jx2- х + 1
если х + 1 >0.1965. In 72(2х2 - 2х+5)-Jx+lj _ i arctg 72х2-2х+5
672	72(2х2-2х + 5) + (х+ 1) 3
1966.
X + 1
+ 4 in
2(2г+1)
- 2 arctg z, где z =
|2z + 1|3 ’
где
г = х + 7х2+х+ 1 . 1967. In lizil
1 + 7l - 2х- х2
1968. i
О
1 [(г - l)3 + (г - I)'3] +
+ [(г -l)2 +(z-1)’2] + [(г -1) + (г -1)1]
+ | 1п|г-1|,где2 = х+ 7*2- 2x+ 2 ,
1969. -
			 		4	 +5 In |z - l| - In |z - 2| - In |z + 1|,
18(z + 1)	6(2+ 1)2	4	1	1	27	1	1	108	1	1
где г = J*2+3*+2 . 1970. 2(3~4z> ■ + -2- In ^+1 + 2z
*+l	6(1 — 2 — 22)	5^5	7Е-1-2Х
+ 7x(l + x).	1971. £ (7*2 + 1 + Jx^l) + i In
4	4
, где z = -x +
X+ Vx2+ 1
Tx2

496
ОТВЕТЫ
1972. i Vz -	f In 1Л±ШШ1±1 - 2 arctg	, где z = fi£ .
3	31/12 ^ zV3-Vl2l2+l	zJl-V	1-x
1974. Jl + x + x2 +
1973. -Д + * ~ Jl - x - Л arcsin x.
Л
+ i In l + 2x+27l + x + x2 _ 1975 2 Г	+ 2 + JC2 1 _ 2 Г(Х + 2 _ *2 1 .
2	(2 + x+27l + x + x2)	3L	J 5|_
1976.—±: arcsin
Л
^-.1977.-4 In
x2+ 1
У2
хЛ + л/х4+ l| _ 197S, i
X2 - 1
arcsin
! л
(|x| > Jj2-1). 1979. i In хг(2хг + 1 + 2Vx'1 + x2 + 1) _ 1981 1 J(x + x2)s _
2	x2 + 2 + 2jx* + x2 + 1	3
- i±l* Vx + x2 + i In (Vx + л/1 + лг) при x > 0.	1982. f x« - 4x2 +
8	8	5
i	-	i	^
+ 18x6 + _3£L - 21 arctg x5 .	1983. | z5 - 2г3 + 3z, где z = Jl + l/x*.
I	5
1 + x3
1984. —z + ? z3 - г4 - где z = Vl - x2.1985. A In 2l+£±l - J_ arctg =ALiJ.,
3	5	6	(z-1)2 Д	73
где z =
VT
1986.	7 In |i±i| - i arctg 2, где 2 = A^1 + x*.
a.	4	|2 — l| 2	л:
1987.	I In ^4 + i In 4—+ t + -Л= arctg , где z = 6УГ7^’.
6	2 + 1	12	*2-z+l	2V3	2Л
1988.	I z4 - I z9, где z
-<R-
1989.
-	3*	- I in -fc-tA)2..
2(z3 +1)	4 z2 - z + 1
- j
.-«Hir
, где z ==
1990. m = ^ , где k = ±1, ±2, ... .
k
1991. sin x - \ sin3 x + i sin5
3	5
X. 1992. 4 * ~ 7 sin 2л: + 4 sin 4л: +
16	4	64
+ 4 sin3	2*. 1993. A *	+ 7	sin 2л: + 4	sin 4л: - -L	sin3 2л:. 1994. 4	-
48	16	4	64	48	16
_ sin4л: _|_ sin32x jggg sin5л: _ 2sin7* sin0x j^ggg _cos2* _j_ cos3 2* _
64
_ cos5 2 x
320
1999. -
48
64
96
:. 1997. 1,
_ 1
1998.
cos л: -
cos3 л:
-lln
Itg *|
3cos3x
cos л: ’
2
2 sin2*
2
1 2|
oC0Sf + i In
itg г|.
2000.
sin*
+ i In
Itg f-
+ *)
2sin"* 2
1 2
2 cos2 л:
2
1 6 V 2
4)
2001. -8 ctg 2x - I ctg3 2x.	2002. ASj2 + 2A|f* -	+ 3 In |tg x|.
2003.	Л— + —i— + In Itg i|.
соэл:	Зсоз3л:	2
2004.	Ц1* -	- In |cos x|.
4	2	11
2005.	-x -	- ctg x. 2006.	. 2007. -2 Vctgx + | Vtg3* .
5	3	5	3

ОТВЕТЫ
497
2008. 4 In № + |W + *;>| - 4 arctg
где
t = Vsinx.
2009,
(1-03(1-^3)I	2	tJi 9
I. _L- in 2г + гЛ+\ _ 1 arctg iAi 2 = Ttgl. 2010. i In {z2+P\ +
2j2	z2- zj2 + 1 Л 2 1	4	z<-z2+l
+ 4 arctS . где z = № • 2011. /„ = -C0S£sit£_L* + 'Ll! J„_2;
2	V3	n	n
К„ = -sinxcos^Jx + ft—1 ^я_2.	/6 = -A cos X sin5 x - £ cos x sin3 x
n
b_
24
- Д- cos xsin x + x; jRl8 = i sin x cos7 x 4- sin xcos5 x 4- sinxcos3 x 4-
16	16	8	8	48	192
4- sin x cos x 4- x. 2012. In = -
128 128 n
cosx
4. ;l ~ 2 r .
+ 		 1 n-2>
K =
(n - l)cosn_1x
x n-2 jr . г __ cut) Л
+ ^Tif'-2’ In - w
(n - l)sinn" lx n - 1
cosx _ 3cosx ц_ 3
x 8sin2x 8
+ § In tg I ;
Zr _ SinX
л7
4- 5sinx 4. 5sinx
6cos6x	24 cos4 x	16 cos2 x
+ -5- In tg (~ + 2V 2013. — — cos 4x -
16	V2 4J	8
\ cos 6x 2014. 2 +
12	4
sin2x , sin4x , sin6x
8
16
24
.2015. 2 cos£ - cos— -
2 6 10 6
--5- COS	— cos . 2016. -i cos (a - 6) cos x - i cos (x 4- a 4- b) 4-
14	6	22	6	2 v	4
4- -L cos (3x + a + b). 2017. 2 +	4-	+
12	4	8a	86	16(a-6)
4- sin2(fl t . 2018. cos 2x + -p- cos 4x 4- cos 6x - cos 8x 4-
16(a + b)	16	64	48	128
+ -i- cos 12x.	2019. —-i—— In I sin(ff , если sin (a - b) * 0.
192	sin(a-6) |sin(x+a)|
2020.	i	in|sin(x + o)|, если cos (a-b)^ 0.2021.—Д—- ln|cos(* + b)|,
cos(a-fc) |cos(x + 6)|	sin(a-fc) |cos(x + a)|
если sin (a - b) * 0. 2022.	 In
cos a
sin^“
2
(cos a ^ 0). 2023. —— In
sin a
	0x - a
cos—-—
2
x + a
x + a
cos——
2
c°s—
1	1	1	3tg| +1
(sin a * 0). 2024. -x 4- ctg a • In —22M— (sin a * 0). 2025.	arctg	-— .
|cos(x + a)|	Jb	Л
2026. - In ~ cosx)(2cosx)2	2027. -- (2 sin x 4- cos x) 4- -4- x
6	(lcosx)3	5	bjb
x In
N
X + arctg 2 ^
2 J
2028. a) ~ arctg (	f) ’ еСЛИ 0 4:1 e < 1;
6)	2 In £ + cosx+jJ£2. 1 S.1]H , если e > 1. 2029. x - 4= arctg (*/2 tg x).
Ve2^!	l + ecosx	J2
2030.-i- arctg (• 2031.. Щ^-L.■ 4--1- arctg ^ (ab * 0), где z = tg x.
ab	V b J	(a2z2 + b2)	2 ab3	b

498
ОТВЕТЫ
2033. 		22Н	.
a(asinx + bcosx)
2032. i (sin x - cos x) - -i- In |tg fi + 5)
2	2л/2 I v2 87
2034.-i In <sinx + cosx)2 _ 1 arct Г2cosx_-±inXA _ 2035 1 arct Гt£2*t
6	1 - smxcosx /3	V 73sin x '	Л	у Л }
2036.1
J2 + J2 arctg ■ -ц ■	- л/2 - V2 arctg u
74 + 272	74-272
72 V 72
, где u = tg 2л:.
2037. -7- In ^~sin2* . 2038. i arctg (sin2 л:). 2039. arctg f 1 tg 2* )
2J2 J2 + sin2x	2	V2	j
lnh(i+I)
272 T2+sin2x
2040. -	2
.. , 0. +-^F ar°tg -7= , где z = tg x. 2041.—-
4(z2+2)	472	72
л/а2 + b2
где cos cp = - ■ — — и sin (p = a . 2043. a) -- - 2 In Isin x + 2 cos xl;
7a2+ft2	5	5
б) 0,1л: + 0,3 In |sin x - 3 cos x\.	2044. || + ^ In |5 sin x + 3 cos x\.
2045.
_afti - axb л
a2 + b2 asinx + bcosx
+ 2£ii££iin|tg(|+|)
(a2+ft2)2
, где cos (p =
Ja2 + b2
5tg^+l
и sin cp = — —— . 2047.	+ 7 In Isin x - 2 cos x + 3| - - arctg	?— .
7S^Tb2	5	5	1	1 5 e 2
2048. ^ - i tg (% - •;) - 7 In (72 + sin x + cos x). 2049. f л: - | In |3 sin x +
2	2	V.2	8/	2	5	5
+ 4 cos x - 2| + —4= In
5721
T7+T3^2tg|- lj
T7-73(2tg|-l)
+ 272 ln Itg f£ + 2) . 2052. i (sin x + 3 cos x) + ln
I v2 8;	5	575
2051. -sin x 4- 3 cos x +
T5-l + 2tg|
T5+l-2tg|
2054. -4	arctg f- i ln	Л •	2055. f arctg	(sin л: - 2 cos x) +
7з	v 7з )	4	2- smx	5
+	1	. jn	75+ 2 sinx + cos*	2056	3	In	T2(sinx+	cosx)+ 1
107б	Тб -2sinx-cosx	4л/2	| У2(sinx +	cosx) - 1
Уз + T2(sinx - cosx) 2058	2 sinx- cosx +	1 i L f x , arctg 2^
‘ 10(sinx+2cosx)2 юУ5 I ё V2 2 J
4л/б
x ln
л/3-У§(8тх- cosx)
2059	^	^	 d _	(2n — 3)a q = —	n - 2
(/i-l)(a2-ft2) ’	(/i — 1)(д2 — 62)*	(ti- l)(a2- ft2)*
2060. 4 In	fin2* .	2061. 2jigx - -7- ln *S*tT^tgx +j +
7§	|cosx|	2л/2 tgx - J2tgx +1
+ 4= arctg iHil (tg x > 0). 2062. if arcsin f rinx-coexY| _ 1 ln (sin x +
72	tgx-1	21	V 7з )) 2

ОТВЕТЫ
499
4- cos х 4- J2 + sin 2*). 2063. -
esinx
(1 - e2)(l + ecosx)
(1 - e2)2
2064. --	cos j * ^ sin —2“j (cos a * 0). 2065. In = 2/n_j cos a -
- /л_2 +	tn~\ где n > 2 и t — sin £1“ ( sin	' . 2068. e3x ^ -
-	^	- JU . 2069. -e~x(x2 4- 2). 2070.	- ^ + §1^ cos 5* 4-
3	9	277	7	V 5	25	625У
4- № - ^ 4- -fi-1 sin 5*. 2071. (21 - lOx2 4- x4) sin л: - (20* - 4*3) cos *.
V 5	125	3125/
2072.	(x6 + 3x4 +6x2 + 6).	2073. 2e'(t5 - 51* + 20t3 - 60t2 +
+ 120/ - 120), где < = Vi. 2074. eax\± + acos^V 2bsin2bxl
’	L2 a	2(a2 + 4b2) J
2075 — pHosinb*~ 6cos6*) _ asin35x- 35cos35x1	2076 — r*fsin * —
4	L (a2 + b2)	(a2+ 952)	J*	2
-	cos *) 4- cos *]. 2077. ^ [*2(sin * 4- cos *) - 2x sin * 4- (sin * - cos *)].
A
2078.	~ yjj(2 sin 2x 4- cos 2x) 4- i (4 sin 2x - 3 cos 2x) J .
2079.	| x4 4- | x2 4- 3*2 cos * - *^6 sin * 4- | sin 2*^ - ^5 cos * 4- | cos 2x j -
-	1 cos3 *. 2080.	£	+ i	Jx sin (2 Jx) 4- A	cos (2 Jx). 2082. * 4- -i—	-
3	2	2	4	1 + ex
-	In (1 + ex). 2083. ex - In (1 + ex). 2084. -i + I In \ex - 1| + i In (ex + 2).
2	3	6
2085. x - 31Ы (1 + e* )Jl + e
3 arctg e6 .
2086. * 4-
1 + e4
2087. -2 arcsin
и-
2088. In (ex 4- Je2x - 1) 4- arcsin (e x).
2089. *]e2x + 4ex-l 4 2 In (ex 4 2 4 Je2x + 4ex-l) -
arcsin
2ex - 1
•Л
2090.- ±e-x(JT+7x- JiT7x) + i In (/1 + e1 ~ 1?( 1 ~	- g*). 2092. a, +
2	4 (JTTP+ 1)(1 + J\ - ex)
+ <h + £2 + ... + . Л" _ = о. 2093. ex f 1 -	. 2094. -<TX - li (e‘x).
1!	2!	(л - 1)!	V */
2095. e4 li (e2x “4) - e2 li (e2x ' 2). 2096. ^ . 2097. ^ ( x2 + 3x + ^ -
—22-1 + (64e4 + li (e2x*4).	2098. x[ln"x-n In"'1 x + n(n- 1) In'*-2 x + ...
x-2)

500
ОТВЕТЫ
... + (-1Г -1 • п (п - 1) ... 2 In * + (-1)лл1)]. 2099. f In3 х - 2 1п2 * +
4 V	4
+ 5	In	X -	JL) . 2100. --i- f	In3 * + 5 In2*	4- 5 In * + 21.2101.	In (* + a) x
8	32;	2x2 V	2	2 4J	v '
x In	(*	+	b). 2102. л: In2 (x + Jl + x2)	- 2jl + x2 In (*	+ Jl + *2 ) + 2*.
+ *ln( Vl - x	+ Jl + x)	+	i arcsin x.	2104.	-*ln* -
2103.
JTTx2
-ln(* + УТТ*2). 2105.-£ + \ In (*2 + 2*+ 2) + ^ arctg (x + 1). 2106. -2 +
2	2	2	3
+i In (1 + x) + arctg Jx . 2107.J2x - x2 +	arcsin (1 - x).
3	3	4	4
2108. i Jx- x2 + (* - 1) arcsin Jx . 2109. -5SM Jx2- 1 + ~ arccos i .
2	2	2	X
2110. -2 sgn (1 - x)Jx + (1 + x) arcsin Ф . 2111.	- In л/П^х2.
1 + x
Jl-
2112.
arccos*
Jl ~ :
+ I In .	2113. л: - arctg * + (±±£f arctg * - £1 x
2	1 — X	V 2	2)
x [In (1 + x2) - 1]. 2114. * - ——— In
1 v ’	1	2	l-x
x In (x + JT+T2).	2116. -f +	.
8	32
. 2115. -In Jl + x2 + —x
Jl + x2
2117	— + sh2x + sh4x
8	4	32
2118. ф - ch x. 2119.	. 2120. In ch x. 2121. * - cth x.
3	24	16	8
2122.
!. 0,5[ln (e2* + Je4x - 1) + arcsin (e-2*)]. 2123. a) \ arctg 3'1/2 (2 th £ + l); 6)
Л	\	2 J
_L arctg — --r 3 ; в)	arctg
75	75 зТП
3th^
		2
7П
; r) -| * - | In |3 sh * - 4 ch *|.
2124.
acha*sinfr* - 6sha*cos6*
a2 + b2
2125.
acha*cosfr* 6sha*sin6*
a2 + b2
2126. ———	+ -i- - i	- arctg	x. 2127. |	* + **	- i	In |i±*|.
5xs 3x3 x	&	8 (l-x2)2	16	11_jc|
2128. -i- In l+?J} + x2 - -i- arctg . 2129. 2jx - 33Jic + 6«7x -
473 1-хЛ + х2 273	хТз
- 6 In (®7x + 1) (x > 0). 2130.	(15 + lOx + 8x2)Jx(l - x) + | arcsin Jx
(0 < x < 1). 2131. -2 VlTx2 - In 1 +	2 (|x| < 1). 2132. -§ Jl-xJx
x	1*1	3
(x > 0). 2133.	(8 - 4X2 + Зх4) JYTJc2.2134 i In У+ 2)2, - 73 arctg
15	2	1 - z + z2
где z = з/-—- . 2135. -i In
V *	3
2 + x3 +2 Jl + x3 + x6
. 2136. i arccos £i±l
2	x2T2

ОТВЕТЫ
501
2137.	- \	- 2 arcsin л: (И < 1). 2138.	(1 + х)2 +	х
х Jx + x2 + | In | л: + | + Jx + x2 | (х > 0; л: < -1). 2139.	-
- 1 In <1 + x'>\ + л/З arctg . 2140.-3*+21 7-*2 + 3*-2 + (x2 +
2	1 + x + x2	S	4	V
+ 3* - arccos (2* - 3) (1 < x < 2). 2141. -x? + ^ In (4 + *4) + 2 arctg ^ •
3
2142. --1 —x* arcsin * 4- \ (arcsin x)2. 2144.	Jx^+1 4- (y2f-l)2 x
xIn 7*2- 1 - - In Jx2+1-1 (|^ >	2145.	- In	-
з 4x2 +1 +1	U-*	J\^x>
-i arcsinx-In 1 + x- (0<*< 1).2146.
2	xK
4- —arctg ■
2tg£+l
3(2 + sin*) ' зТз	7з ’
2147 — In ^ + 4 */2 + cos4*	2148	1	_ 1 in л/2 + 7l + cos*
J2 7-4V2-cos4*	Vl + cos л: 2j2 J2 - Jl + cos*
2149. аГ* arctg x - i In (*2 4-1)1 - (arctg *)2. 2150. a f * In |£zJJ -
L	2	J 2	V |*+l|
- In \x2 - 1|) + i±± In2 1*^11.	2151. -_iM—. + i In	(* > 0).
1	1 )	4	I jc +1|	2(1 + x2)	4	1 + x2	’
2152. Jl + x2 arctg x - In (x + Jl + x2). 2153. -In (cos2 x + Jl + cos4*).
2154.	- 2+/2 JlTT2 arccos * (|*| < 1). 2155.	- ( x - x
9	3	6 V 3 /
x arctg x+ \ (arctg x)2 + § In (1 + x2). 2156.	x*2- arctg *.
2157. ln(x + 7l + x2j + J_ in Л + х2-хЛ ^ <	2158 _2f + £ Jl-x2 X
2(1 - x2)	472	JlTT2 + xj2	4	2 v
x arcsin * + A (arcsin ж)2 (1*1 < 1). 2159. £ + i(l + л:2)2 arcctg x.
4	4	12	4
2160. ** (* > 0).	2161. * - e~x arcsin (ex) - In (1 4- Jl - e2x) (* < 0).
2162. * - In (1 4- e*) - 2e 5 arctg e* - ^ arctg e^ . 2163.	[x - In (1 4-
+ e* ch 1)1 -	. 2164. -2 In (th x + Vl + th2* ) + 4= In ^ + th2* + ^th3?.
4shl	72 TTTtPi-^thjc
2165. ex tg ^.	2166.	.	2167.	.	2168. 2£? (* + И).
2	2	3	3
2169. ^ + £l 4-(* ~	. 2170. e* - 1, если * < 0; 1 - е~х> если x>0.
2171. *, если |*| < I? y + I s^n x’ если ^ >	2172. | 4- i ^(*) -

502
ОТВЕТЫ
х I 1 - 2 I (x) -
2174. x - ^ при |л:| < 1; x - £ \x\ + i sgn x при |*| > 1.	2175. x, если
3	2	6
-oo < x < 0; ^ + x, если 0 < x < 1; x2 + ^ , если x > 1. 2176. xf'(x) - f(x).
2177. i f(2x). 2178. /(x) = 27*. 2179. a) x - ^ ; 6) f(x) = x при -oo < * < 0;
f(x) = e* - l при 0 < x < Ч-oo.
, где (x) = x - [х].	2173.	{|л:| - (-l)1*1 cos ял:}.
n
Раздел IV
2181.12|.2182. a) S_„=16i	+g,S„=16l +П5 +g;
10230	= 10230 2"
»(2?-l)’	"	«(2?-l)
2183. S = 31.
"72-1 . 31
;	. 2184. u0T + ± gT2. 2185. 3. 2186. ^ .
"732-1	5
lna
2191. In £.
a
2187.1. 2188. sin x. 2189.1	- I. 2190.
a	b	m +1
2192. а) 0, если |a| < 1; б) я In a2, если |a| > 1. 2193. 5.	[/(a) - f(b)].
2201. Вообще говоря, нет. 2203. He обязательно. 2206. 11 i. 2207.2.
4
2208. 5 .	2209. ? .	2210.1.	2211.1.	2212. —5— .
6	3	2 sin a
2213.
2л
Jl^72'
2214. —Lr In 1 +	. 2215.	. 2216. а) Подынтегральная функция -
Jab 1-Jab	2M	x
и ее первообразная In |л:| разрывны в промежутке интеграции [-1, 1];
б) функция -i= arctg [ Щ=г)» играющая роль первообразной, разрывна
Л v Л'
1	2
при 0 < х < 2я; в) функция arctg - разрывна при х = 0. 2217. - .
X	о
2218. 20072 . 2219. 1. 2220. In 2. 2221. 2 . 2222. 2 . 2223. -J- .
2	4	я	р+1
ь
2224. | (2 72 - 1). 2225. I. 2226.1.	/(x)dx. 2227. |я. 2228.	.
2229.х + 1.	2230. -J- .	2231.0; -sina2; sinЬ2.	2232.a) 2xJT+x* ;
2	1п2

ОТВЕТЫ
503
2242
б)	--- -	■ ; в) (sin х - cos х) cos (я sin2 х). 2233. а) 1; б) ; в) 0.
Jl + X12 Jl + X*	4
г)Л. 2235.1. 2237. а) §; б) |. 2238. a) i - £, если а < 0; i - £ + ^ ,
6	2	3	2	3	2	3
если 0<а<1;^-|, если а > 1; б) ^ , если |а| < 1;	, если |а| > 1;
2	3	2	2 Or
в)	2, если |а| < 1; если |а| > 1. 2239. | In 2240. я. 2241. 4я.
.2(1-	2243.1. 2244.??	-	2245.1. 2246.?^.
V	е)	3	2	6	16
2247. 4= In	. 2248. 2 - 5.2249.	. 2250. 4= • 2251. а) Обратная
Л	7	2	4	72
3	1
функция jc — ±£2 двузначна; б) функция л:= - разрывна при t = 0; в) не
существует однозначной непрерывной ветви функции х = Arctg t, опре¬
деленной на конечном сегменте и пробегающей значения от 0 до я.
о	5
2252. Нет. 2253. Можно. 2256. f(x + Ъ) - f(x + a).	2260. | е2.
1	о
2261.	J [/(arcsin t) - /(я - arcsin 0] dt + J [/(2я + arcsin t) - /(я - arcsin t)] dt.
0	-1
2262.	An.	2263.	^ .	2264.	arctg	P - 2jc.	2268. 315-i.
4	27	26
2269. 1 In 3 - — . 2270. A e3 - J-. 2271. -66 5 . 2272. -5.2273. #2-.
2	273	27	27	7	3	270
2274. £ n - 73 .	2275. 2я (± - -±~).	2276. 2nj2 .	2277. ± .
3	V73	272^	6
2278. § -5.2279. | (e* - 1). 2280. | 1п2-^.ШЛ,= М! J,
если
n = 2k;	/„ =	, если n = 2fe + 1.	2282. Cm. № 2281.
(2&+1)!!
2283. (-1ГГ7 - (l - 1 + 1 - ...	2284. 22" СйУ
L4 v 3	5	2n-lJJ	(2л+1)!
2285. См. № 2281. 2286. /„ =	. 2287. In = (-1)" -In 72 +|[l-
- i + ... + (-1)"-1 i] 1.2290. ■■■ ?№рУ-№пУ:		. 2291. О, если n четное;
я, если n нечетное. 2292. (-1)Ля.	2293.	•	2294. 4 sin ?? .
7	2n 2" 2
2295. 0.	2296. 0 . 2297.	(1 -е-2“я)[ Cj. + 2g‘cL--2;-(/n-2*)»] ‘

504
ОТВЕТЫ
2298. -5- (-1)*-1. 2299.	.2302. В точках разрыва функции
4 п	(т + п- 1)!
f(x) производная F'(x) может как существовать, так и не существовать.
2303. |*| + С. 2304. arccos (cos *) + С. 2305. *[*] - l*W-|l+ l) + С.
2306. i!liJ - l*l(l*l+l)(2|*l+l) + c 2307. C + i arccos (cos nx).
2	12	n
2308. i (|l + *| - 11- *|) + C. 2309. -1.	2310. 14 - In 7!	2311. 5° .
2	71
2312.	■ 2313. In n! 2314. -th 2 . 2315. 5 . 2316. a) б) +; в) +; г) -.
4	2	3
12 1
2317. а) Второй; б) второй; в) первый. 2318. а) ± ; б) ; в) 10; г) - cos (р.
3	3	2
2319.1.	. Р-	 = Ъ — малая полуось эллипса. 2. uCD = i (о0 + их), где vx —
л/1-е2	2
конечная скорость тела. 2320. i ig . 2321. А. 2322. а) 0 = i— ; б) 0 — - ;
2	л + 1	б
в)	0 = i In	lim 0= 1, lim 0= 1. 2323.55 + 12 0 (|e| < 1).
X	X	x —0	2 jt--oo	3	3
2324. Заключается между —и ^. 2325. 0,01 - 0,0050 (0 < 0 < 1).
10V2	10
2326.2.	a) 1; 6) /(0) In £ . 2328. -jj- (0 < 0 < 1). 2329. ? 0 (|0| < 1). 2330. §
a	50n	a	a
(|0|< 1). 2334. i. 2335.-1. 2336. n. 2337.7t. 2338. 5 ln 2. 2339. -*5..
"	«	3	ЗТЗ
2340.
2я
зУз
2341. 4:. 2342. 2.2343. i ln f 1+41- 2344.0. 2345. 2-1.
Л	2	5 l Js)	2
w
2346. —2— . 2347.	. 2348. In = nl 2349. /„ =	^ • -22—.
a2 + b2	a2 + b2	n	n (2n- 2)!!	„.1
(ac-62)	2
П
2350. In = n! (-1)* + ln (k 4- 1), где Ckn — число сочетаний из n
k = l
элементов no fe. 2351. In =	, если n — четное, и In=	,
если n — нечетное. 2352. In = (n~ тс, если n — четное, и In= С—-p.;.: ,
л!!	n\\
если л —нечетное. 2353. а)-1 In 2; б)In 2.2354.	.2356.а)1;
б) £ ; в) 0. 2357. а) 1; б) ~ ; в) 1; г) i /(0). 2358. Сходится. 2359. Сходится.
2	3	(X
2360. Расходится. 2361. Сходится при р > 0. 2362. Сходится, если р > -1
и q > -1. 2363. Сходится, если т> п - т> 1. 2364. Сходится при

ОТВЕТЫ
505
1	< п < 2. 2365. Сходится при 1 < п < 2. 2366. Сходится, если т > -2,
п - т > 1.	2367. Сходится при п > 0 (а ^ 0).	2368. Расходится.
2369. Сходится, если р < 1, q < 1.	2370. а) Сходится при п > -1;
б)	Сходится. 2371. Сходится, если min (р, g) < 1, max (р, g) > 1.
2372. Сходится. 2373. Сходится. 2374. Сходится, если р > 1, q < 1.
2375.	Сходится при р > 1, q произвольном, г < 1 и при р=1,д>1,г<1.
я
2376.	а) Сходится, если,< 1 (/ = 1, 2, ..., п)> Р/ > 1; б) сходится при
i= 1
а> -1, Р> -1, а + Р< -1. 2377. Сходится, если Рп(х) не имеет корней
в промежутке [0, +оо] и п > т + 1. 2378. Сходится не абсолютно.
2379. Сходится не абсолютно. 2380. а) Сходится абсолютно, если
-1 < BJlL < 0; сходится условно, если 0<	< 1; б) сходится;
Я	Я
в)	сходится. 2381. Сходится абсолютно, если р > -2, q > р + 1; сходится
условно, если р>-2,р<д<р+ 1. 2382. Сходится условно при 0 < п < 2.
2383. Сходится абсолютно при п> т + 1; сходится условно при
т < п < т + 1. 2385. Нет. 2392. In |. 2393.0. 2394. л. 2395.0. 2397. —.
2	3
2398. 4i . 2399. 4l. 2400. а) 9,9 - 8,1 lg е = 6,38; б) 2 - -L ~ 0,56;
2	2	In 2
в)	i + 5 ~ 0,97. 2401. 5.2402. па2. 2403. nab. 2404. £ а3. 2405. §5 Др2.
3	к	2	3	15
2406.	71	. 2407. Зла2. 2408. ^ . 2409. — . 2410. i cth 5 = 0,546.
JAC-B2	2	л + 2	2	2
2411. (Зя + 2) : (9л - 2). 2412. х= chS, у = shS. 2413. Зла2. 2414. -5-.
15
2415. ^ (4л5 + Зл). 2416. бла2. 2417. а) 25 • £1; б) я а2	- 9 ) .
3	8 ab	ч^З /
2418. а2. 2419.5м!. 2420.^. 2421.^(3 + 472)- 2422. а) ■ М2 •
2	4	6	§
(1-Е2)*
б) 11л;в) 1.2423.(л-1)^ .2424. | ( 1-1п2 + -Ь) .2425.а) | ;б) 1 ;в)4± ;
г)	я( 1 +	; д) я(1 - 5] а2. 2426. | а2. 2427. па2 Л . 2428. а2. 2429. | ла2.
2430.	. 2431.	(10 TlO - 1). 2432. 2
Нх°+%)
+ pin
х0 + ‘
[I
2433. 7л2-а2 . 2434. х0 - 72 + 7l + е2г" - In 1 + ^ + g2*°. 2435.	.
1 + 72	4
2436. а In £+! - b. 2437. In tg f 5 + ^ . 2438. a In ? . 2439. 4а( 1 +
a-b	V4 2)	b	\

506
ОТВЕТЫ
+ л In	. 2440. 6а. 2441. 4-^3~6*). 2442. 1 +	. 2443. 8а.
72 >	*Ь	72
72ch^+7chT
2444. 2л2а.	2445. а) 2 ch £ TchТ -1\- Л In 	-——	;
^	2	)	1 + 72
б) i (ch2 2Т — 1). 2446. ла71 + 4я2 +2 In (2л +71 + 4л2). 2447. А+Е? а.
2	2	т
2448.8а. 2449. р[ 72 + In (1 + Л )]. 2450.	. 2451. а(2я - th я).
2452. а) 2 + i In 3; б) 6i ; в) sh Я; г) Т. 2455.	= 0,73. 2456. ^ (2а + с).
2	3	5л/3	6
2457. £ [(2А + а)В + (А + 2а)Ь]. 2458. ^ [(2А + а)В + (А + 2а)6].
6 6
2459. 1SH. 2462. 2 аЬс. 2463. i nabc. 2464.	.	2465.	а3.
2	3	3	3	3
2466. | а3 (я - Я . 2467. Ща2*1аЬ. 2468. ^ . 2469.	. 2470.	а3.
3	V о)	15	2	15	3
2472. I каЬ2. 2473. а) ^; б) ^. 2474. а) %; б) 2я2. 2475. а) яаЬ2;
7	15	3	2	15
б) . 2476. а) 5 ; б) 2л. 2477. 2я2а2Ь. 2478.	. 2479. -—5— .
’	6	'2	'	3	5(1-е-2*)
2480.	а) 5л2а3;	б)6л3а3; в) 7л2а3.	2481. а) ^ лаб2; б) ^|ла2Ь.
2482.1.	У, - || л; F, = ^ л. 2483.1. а) | ла3; б) ^ л2а3. 2. а) 2£! [ Л х
х In (1 + 72) - |1; б) Щ ; в) .	2484. 1. | (л4 - 6я2)а3. 2. |л.
3J 4л/2	4	3	3
2485. ^ . 2486. ^ Г2lTl3 + 2 In ^±Ш) . 2487. 2а7я2а2 + 4Ь2 +
272	243 V	2 J
+ ^ In	.	2488. я[ (ТВ - Л ) + In ($-LlK-$.r	.
2489. а) у [(2д:0 + p)j2Pxo + P2 ~ P2]; 6) f [ (P + 4*0) Лхо(Р+2хо) “P2 x
.2490.а)2лй2 + 2ла&£1Н111£ ;б)2ла2+	in ^ (1 + ejj ,
xln J2xq+Jp + 2xo
■Гр
где e =	~1,2 — эксцентриситет эллипса. 2491. 4я2а6. 2492. ~ па2,
a	5
2493. a) ла ^ 2b + a sh ^) J б) 2ла ^ а + b sh jj - a ch £ j .
2494. 4яа2.

ОТВЕТЫ
507
2495. а) ^яа2; б) 16я2а2; в) ^яа2. 2496. ^ а2 (472 - 1). 2497. ^яа2.
3	3	5	5
2498. а) 2яа2 (2 - Л ); б) 2яа2 Л; в) 4яо2.	2499.	[14 VB +
1283Vl0
+ 17 In (2 + Jb )]« 1,013. 2500. V = ^p2; P = 2яр2[(2 + 72 ) + In (1 + Л)].
3
2501.1.	M, = 2a2; M2 =	. 2. ^ [72 + 5 In (1 + «/2 )]. 2502.1. Af, = ^ ;
2 8 6
f ■2-- Я - I ^ “ I •Л ■ “O3-^ ^ •
M<f-> = na^b 2504.1. M, =	, M2 = £ r2/»3. 2. / = | MJR2. 2507. *„ =
4	12	30	5
-«fip;	- 0. 2508. (|a, la). 2509. (|f, Щ). 2510. (o. 0, §«).
2511. ф0 = ф - a, где a = arctg ; r0 — - mr ■■ . Логарифмическую спи-
Vl + 4m2
раль r0 = •-am - em(<Po + a). 2512. ф0 = 0, г0 = l а. 2513. х„ = па, у0=%а.
Jl + Am2	6	6
2514. x0 = | а, у0 = 0. 2515. ( О, 0,	. 2516. 75 кг. 2517. Ah = rng^j ,
где Л — радиус Земли; Д» = rtigR. 2518. 5 Дж. 2519. 1740 Дж. 2520. § а3.
2521. 708 i Т. 2522. v0T + § Г2. 2523.	лбо)2!?5. 2524. Проекции силы
3	2	15
притяжения на координатные оси: X = О, У =	, где fe — гравита-
а
ционная постоянная. 2525. 2nkmb0 [1 - ь ], где k — гравитационная
V	Ja2 + b2'
постоянная. 2526. Примерно 3 часа. 2527. Сосуд должен быть ограни*
чен поверхностью, образованной вращением кривой у = СхА вокруг
вертикальной оси Оу. 2528. Q = Q0 • 2"^° . 2529. 99,92%. 2530. ^ .
о Е
В ответах на приближенное вычисление определенных интегралов
даны табличные значения. 2531. -6,2832. 2532. 0,69315. 2533. 0,83566.
2534. 1,4675. 2535. 17,333. 2536. 5,4024. 2537. 1,37039. 2538.0,2288.
2539. 0,915966. 2540. 3,14159. 2541. 1,463. 2542. 0,3179. 2543. 0,8862.
2544.51,04.
2545.
X
0
л
3
2л
3
п
4л
3
5л
3
2п
У
0
0,99
1,65
1,85
1,72
1,52
1,42

508
ОТВЕТЫ
Раздел V
2546.	2.2547. 2.2548. 3. 2549.1. 1550. i . 2551. а) , Jslna		;
3	2	3	1- 2</cosa + q2
б) —7 cos a - q2_m_ e 2552. 1 - J2 . 2553. Сходятся лишь при x = kn (k —
1 - 2gcosa+ q2
целое). 2556. Расходится. 2557. Расходится. 2558. Сходится.
2559. Расходится. 2560. Расходится. 2561. Расходится. 2562. Сходится.
2563. Сходится. 2564. Расходится. 2566. Может как сходиться, так и
расходиться. 2567. а) Может как сходиться, так и расходиться;
б) расходится. 2578. Сходится. 2579. Сходится. 2580. Сходится.
2581. а) Сходится; б) расходится. 2582. Сходится. 2583. Сходится.
2584. Сходится. 2585. а) Сходится; б) сходится; в) сходится при лю¬
бых а и х. 2586. Сходится. 2587. Расходится. 2588. Расходится.
2589. а) Сходится; б) сходится; в) сходится; г) сходится. 2591. 2. п > 13.
2595. Сходится. 2596. Сходится. 2597. а) Сходится; б) сходится.
2598. Сходится при р > 2. 2599. Сходится при > 1. 2600. Сходится
а
прир > |. 2601. Сходится. 2602. Сходится при р + q > 1. 2603. Сходится
при q > р. 2604. Сходится при | + q > 1.	2605(h). Сходится при
a(q - р) > 1. 2607. Сходится при q > р 4- 1. 2608. Сходится при р > 0.
2609. Сходится прир > 0.2610. Сходится при р > |. 2611. Сходится при
1. 2612. Сходится при р> 1. 2613. а) Расходится; б) расходится.
2616. Сходится при х < i .	2617. Сходится. 2618. Расходится.
е
2619. а) Сходится при р > 1; б) сходится при р > 1, q произвольном и
при р = 1, q > 1.	2620. а) Расходится; б) сходится; в) расходится.
2621. Сходится. 2623.1,20. 2626. Сходится при a > |. 2627. Сходится, ес¬
ли а = |. 2628. Расходится. 2629. Сходится. 2630. Сходится при а > 2.
2631. Сходится. 2632. Сходится. 2633. Сходится. 2634. Сходится, если
с = 0, - < -1.	2635. Расходится. 2636. Сходится, если а ^ 0.
а
2637. Сходится. 2638. Расходится. 2639. Сходится. 2640. Сходится, ес¬
ли а = Jbc . 2641. Сходится, если а < -1. 2642. Сходится, если a > |.
2643. Сходится при аь > е> с = 0 и при ас> 1. 2644. Сходится при а + Ъ > 1.
2645. Сходится. 2646. Сходится. 2647. Сходится. 2648. Расходится.
2649. Сходится. 2650. Сходится. 2651. Сходится. 2652. Сходится при
a < 2. 2653. Сходится. 2654. Сходится. 2655. а) N > 100 000; 6) N > 12;

ОТВЕТЫ
509
в)	N > 4. 2659. |. 2660. l|. 2661. In 2. 2662. а) | In 2; б) I In 2.
2664.	Сходится. 2665. а) Сходится; б) сходится. 2666. Не следует.
2667. Сходится. 2668. Сходится. 2669. Сходится. 2670. Расходится.
2671. Сходится. 2672. Сходится. 2673. а) Расходится; б) сходится.
2675.	Абсолютно сходится при р > 1; условно сходится при 0 < р < 1.
2676.	Абсолютно сходится при р > 1; условно сходится при 0 < р < 1.
2677.	Абсолютно сходится при р > 1; условно сходится при | < р < 1.
2678.	Абсолютно сходится при \х - nk\ < 7 (k — целое); условно сходится
4
при х = nk ± 7.2679. Сходится условно при любом х, не равном целому
4
отрицательному числу. 2680. Абсолютно сходится при р > 1; условно
сходится при 0 < р < 1. 2681. Абсолютно сходится при р > 2; условно
сходится при 1 < р < 2. 2682. Абсолютно сходится при р > 1; условно
сходится при i < р < 1. 2683. Условно сходится. 2684. Абсолютно схо-
дится. 2685. Расходится. 2686. Условно сходится. 2687. Абсолютно схо¬
дится при р > 1; условно сходится при 1 < р< 1. 2688. Расходится.
£4
2689.	Абсолютно сходится при р > 2; условно сходится при 0 < р < 2.
2690.	Сходится. 2691. Расходится. 2692. Абсолютно сходится при
q > р + 1; условно сходится при р < g < р + 1. 2693. Абсолютно сходится
при р > 1, q > 1; условно сходится при 0 < р = q < 1. 2694. Абсолютно
сходится при р > 1; условно сходится при р = 1. 2695. а) Абсолютно схо¬
дится при р > 1; условно сходится при р = 1; б) абсолютно сходится при
р > 1, q > 1; условно сходится при 0 < р = q < 1. 2697. а)р > 1; б) 0 < р < 1.
2698. а) Сходится; б) сходится; в) сходится. 2699. а)д>р+1;
б)р<д<р+1.	2700. Сходится абсолютно при т > 0; сходится
условно при -1 < т < 0.	2703. а) п > 1 000 000; б) п > 1,32 • 1016.
2706.	а) Расходится; б) может как сходиться, так и расходиться.
2707.	- . 2708. - . 2709. -- . 2710.	. 2716. Сходится абсолютно при
3	4	7	1-ху
\х\> 1. 2717. Сходится абсолютно при х > 0; сходится условно при х = 0.
2718. Сходится абсолютно при х >-- и при х < -1. 2719. Сходится абсо-
и
лютно при |л:| ^ 1 и сходится условно при * = -1. 2720. Сходится аб¬
солютно при	3 < * < | и при | < * <	-	2721. Сходится
абсолютно при \х - nk\ < ^ (k = 0, ±1, ±2, ...).	2722. Сходится абсо-
6
лютно при р > 1 и х * k (k = -1, -2, ...) и сходится условно при 0 < р < 1,
* ^ fe. 2723. Сходится абсолютно при q > р + 1 и сходится условно при

510
ОТВЕТЫ
р < g < р + 1. 2724. Сходится абсолютно при \х\ < 1. 2725. Сходится абсо¬
лютно при |jc| < 1. 2726. Сходится абсолютно при \х\ * 1. 2727. Сходится
абсолютно при х ^ -1. 2728. Сходится абсолютно при х > 0. 2729. Схо¬
дится абсолютно при 0 < \х\ < +°о, если \а\ > 1; расходится, если \а\ < 1 или
если х = 0. 2730. Сходится абсолютно при х = 2 и при х > е. 2731. Схо¬
дится абсолютно при х > 1. 2732. Сходится, если 0< min(x, у) < 1.
2733. Сходится абсолютно при \х\ < 1, 0 < у < +°° и при \х\ > 1, у > \х\;
сходится условно при х=-1,0<1/< 1. 2734. Сходится абсолютно при
max (|х|, |у|) < 1. 2735. Сходится абсолютно при: 1) 0 < х < 1, -оо < у < +оо;
2)jc=1,i/>1h3)jc>1,i/>2. 2736. Сходится абсолютно при \х - kn\ < - ,
4
где k — целое число. 2738. i < \х\ < 2; ——- . 2739. а) Сходится
абсолютно при х> 0, сходится условно при -1 < х < 0; б) сходится
абсолютно при р 4- х > 1 и при х = 0, 1, 2, ..., сходится условно при
0 < р + х < 1; в) сходится абсолютно при: 1) \х\ < 1, у — произвольно;
2) х = ±1, у > |; 3) х — произвольно, у = 0, 1, 2, ...; сходится условно
при х = 1, -^ < у < ^ . 2743. При е = 0,001 и х = nj0, 1 , N > 3т. Нет.
2744. п > — . 2745. п > 26. 2746. а) Сходится равномерно; б) сходится не-
£
равномерно. 2747. Сходится равномерно. 2748. Сходится неравномерно.
2749. Сходится равномерно. 2750. Сходится равномерно. 2751. а) Схо¬
дится равномерно; б) сходится неравномерно; в) сходится равномерно.
2752. а) Сходится неравномерно; б) сходится равномерно. 2753. Сходит¬
ся равномерно. 2754. Сходится неравномерно. 2755. а) Сходится равно¬
мерно; б) сходится неравномерно. 2756. а) Сходится неравномерно;
б) сходится равномерно. 2757. Сходится неравномерно. 2758. а) Сходит¬
ся равномерно; б) сходится неравномерно. 2759. Сходится равномерно.
2760. а) Сходится равномерно; б) сходится неравномерно. 2761. Сходит¬
ся равномерно. 2762. Сходится равномерно. 2763. Сходится нерав¬
номерно. 2767. а) Сходится равномерно; б) сходится неравномерно.
2768. 1. Сходится равномерно. 2. Сходится неравномерно. 2769. Схо¬
дится неравномерно. 2770. Сходится равномерно. 2771. Сходится нерав¬
номерно. 2772. Сходится равномерно. 2773. а) Сходится неравномерно;
б) сходится равномерно. 2775. а) Сходится равномерно; б) сходится не¬
равномерно. 2776. Сходится неравномерно. 2777. Сходится равномерно.
2778. Сходится равномерно. 2779. Сходится равномерно. 2780. Сходит¬
ся равномерно. 2781. Сходится равномерно. 2782. Сходится равномер¬
но. 2783. Может. 2785. Не обязательно. 2795. а) Существует и непре¬
рывна при \х\< 1; б) существует и непрерывна при |jc| < +оо; в) сущест¬
вует при \х\ < +оо, разрывна при х = 0. 2799. а) Существует и дифферен¬
цируема при х -k (k = 1, 2, 3, ...); б) существует при \х\ < +оо, диф-

ОТВЕТЫ
511
ференцируема всюду, за исключением х = 0.	2802. а) а произвольно;
б) а < 1; в) а < 2. 2805. Нет. 2806. i In 2. 2807. 1. 2808. a) 1; б) ^ .
2 6
2809. Законно. 2810. Да. 2812. Я = 1; (-1; 1). При х = -1 сходится абсо¬
лютно, если р > 1, и условно, если 0 < р < 1; при х = 1 сходится абсо¬
лютно, если р > 1, и расходится, если р < 1. 2813. R = |; ( ~| ;~|) • При
3 V 3	3 J
х = сходится условно; при jc = расходится. 2814. Я = 4; (-4; 4).
о	3
При х = ±4 расходится. 2815. R = +оо; (-оо, +оо). 2816. R = i ; f — i ; i).
e \ e eJ
При x = ±i расходится. 2817. R = +oo; (-oo, +oo). 2818. R = 2; (-1, 3).
e
При x = -1 сходится абсолютно, если р > 2, и условно, если 0 < р < 2;
при х = 3 сходится абсолютно, если р> 2, и расходится, если 2.
2819. Я = 2Р; (-2Р, 2Р). При х = -2Р сходится абсолютно, если р> 2, и
расходится, если р< 2; при х = 2Р сходится абсолютно, если р > 2, и
сходится условно, если 0 < р < 2. 2820. Я = 1; (-1, 1). При х = -1 схо¬
дится абсолютно, если ап > 0, и расходится, если т < 0; при х = 1 схо¬
дится абсолютно, если ап > 0, и сходится условно, если -1 < т< 0.
2821. R = min [ i ; - | ; (-Я; Я). При х = -Я сходится условно, если а> Ь,
\а Ь)
и абсолютно, если а < Ь; при х = Я расходится, если а > 6, и сходится
абсолютно, если а < Ъ. 2822. Я = max (а, 6); (-Я; Я). При х = ±Я расхо¬
дится. 2823. Я = 1; (-1; 1). При х = +1 сходится абсолютно, если а > 1,
и расходится, если а < 1. 2824. Я = 1; (-1, 1). При х = ±1 сходится аб¬
солютно. 2825. Я = 1; (-1; 1). При х = -1 сходится условно; при jc = 1
расходится. 2826. Я = 1; (-1, 1). При х = -1 расходится; при х = 1
сходится условно. 2827. Я = 1; (-1; 1). При х = ±1 расходится.
2828. R = i ; ( -i ; 1) . При л: = ±1 расходится. 2829. R = |; (	, |) .
При х = ±| расходится. 2830. Я = 1; (-1; 1). При дс = ±1 сходится
3
абсолютно. 2831. а) Я = 1; (-1; 1). При х = ±1 сходится условно;
б)	при 0 < х < 2 сходится абсолютно; при х = 2 сходится условно;
в)	сходится лишь при х = 0. 2832. Я = 1; (-1, 1). При х = -1 сходится абсо¬
лютно, если у-а-р>0, и сходится условно, если -1 <у-а-р<0; при
х = 1 сходится абсолютно, если у-а~Р>0, и расходится, если у - а - Р < 0.
2833.*>0.2834.|х|> i.2835.0<|*|<+00.2836. *>-1.2837.|х-И< 7 >
А	4
где k — целое число. 2838. -1 + 3 (х + 1) - 3 (х + I)2 + (х + I)3.

512
ОТВЕТЫ
»» а) £ ^ (Н < W); б| £	(la - t| < |„ - % .) - £ ^
(Ы>И). 2840. У (-1Г1 (£^122 (0 < * < 2); In2.2841. V	(Ы< +оо).
п	*—* (2п + 1)!
л = 1	я = О v	'
2842. Е (f5i (W < +оо)-	2843- „?(_1)Л+1 SS*2n (W < +оо)-
2844. £ igg *"(|*| < +«>). 2845. и* + >-(1 ■ ~ ^ х3 + ^1~ И2К32 - И2) х5 +...
л = О
(|*| < 1). 2846.1 - ^ *2 -	х4 - ... (|*| < 1). 2847.1 + (* - 1) +
+ (* - I)2 +	+ ... (О < * < 2). 2848. е( 1 - | + 11 х2 - ^ *3 + ... )
(|х| < 1). 2849. sin (х 4- h) = sin х 4- h cos х - — sin х cos х + ... (|Л| < 4-оо);
2!	о!
cos (х 4- Л) = cos х - h sin х - ^ cos х 4- ^ sin х 4- ...	(|Л| < +оо).
2!
3!
2850. 1. а) (-2; 2); б) (3, 7). 2. Нет. 2851. V	(|*| < +оо).
' п\
я = О
2852. 1.1 + £ (-1)" gg *2" (Ы < +оо). 2853. | £ (-1)'	(2|> + 1},
кп + 1	32я~ 1 x2n + 1
(1*1 < +оо).	2854. £ *" (|*| < 1).	2855. £ (п + 1)*л (|*| < 1).
л = 10	л = О
2856. * + £ t2"-,1)»*» + ‘	•	2857. £	(|*| < 1).
л = 1	л = О
2858. | £[1 - (-2)”]*" (|*| < I).	2859. £ [l +	*„ (|*| < 1).
л = 1	л = О
2880-5 £[л+1^^]*',(|*|<1). 2861. £ап*п,гдеап=^[(^1)"М +
л = 1	л = О	**
+ (-1)"	*'] (числаФибоначчи). 2862.а) £ хп sin 2я<"+1) (|*| < 1);
оо
б) ^ с„х", где cn = 1, если n = 4&; cn = -1, если n = 2k 4- 1; сп = 0, если
л = О
n = 2k + 2 или n = 2ft + 3 (Л = 0, ±1, ±2, ...). /<1000> (0) - 1000!.
2863. ^*" cos not (|*| < 1). 2864. у *” sin па (|*| < 1). 2865. х" sh па
п = 1	л = О	л = О
(1*1 < e-W). 2866. У	х2" (1*1 < 1). 2867. Y Н)-‘+11+(-1)"К-1)2 х"
(2л)!!	п

ОТВЕТЫ
513
оо	сю	2n + 1
(-1 < х < 1). 2868. V х" (|х| +оо). 2869. Y (-1)" £—- (|х| < 1); 5
*—*п\	2п + 1	4
л = 0	п - О
2870. х + Y	(|х| < 1). 2871. х + Y I (-1)"
4* (2п)!! 2п+1	„ -, 1	(2л)!! 2/1+1,
00	СО	1
(|х| < 1). 2872.-2 У	х” (|л:| < 1). 2873. а) х + У(-1)п+1	—-
^	п\	^	п(п+1)
л-1	п= 1
(-1 < X < 1); б) у	(-1 < х < 1); в) arctg 2 + V	*2n “ 1
' 4 л + 1	'	2 п - 1
2"(2n + 1)
(W < л/2 ); д) ]Г(-1)‘
,П + 1	X*
2п(2п-1)
(W < 1); е) 2\х\	1 + X (2"	*Г ■ gfTY при 0 < * < 1 и -1 < х < 0;
I	п - 1	'
ж)	1 + — + У ](2п- 1)" х2”*2 I (|*|< 1);з)_1 + £! + у (-1)" (2п~1)!! X
'	2	^ (2л + 2!!)2/г+1 4 1	} '	2	^ } (2л + 2)!!
П = 1 1	'	Л = 1
X (|д) < 1). 2874. а) е*г Г (2лг)Л + ZllZLjJJ (2 xf ~ 2 + ^{п~}Кп7ЛМгЛ} х
2 п + 1	L	1!	2!
х (2+...] ; б) £££ «' [ а" +	в" -'* +	а"-V +...] ;
,ч (-1)“'1 л! Гу”-1 ■ (п-1)(п-2) л-з + (п-1)(п-2)(п-3)(п-4)тП-5_	1
' (1 + х2)» L	3!	5!	”’J‘
2875. £ ^14(х + 1)2л (-2 < х < 0).	2876. -]Г ^ (|х| > 1)-
и = 1	п = 1
2877. У —-— ((х > 0).	2878.	+ f <2”~ 1>» Г^_Г‘
^ 2n+l\x+lJ у '	1 + х	(2л)!! U + xJ
л = 0	л = 1 v '
(х>.2881.1 - i х- ± X?-± х3-...(И < 1).2882.1 + £	*■
п = 2
(Н < «°>. 2883. £	^ +	«■ (W < «Ч, г» 0! - 1.
(-1)! = оо, (-2)! = оо и т. д. 2884. 2 £ ( ! + | + ... + I) (-1 < х < 1).
22cos—
2885. х + 2 У	х2л +1 (|х| < 1).	2886. Y 	±- хл (|х| < +°о).
4п2 -1	п\
2887. ]Г —_1 хл (|х| <+оо). 2888. £	(-l)"'1^ 1 + | +... + 1^хл
Л = 1	Л = 1 I	‘

514
ОТВЕТЫ
(-1 < *< I)-	2889. £ (-l)n- 1 ( 1 + | + ... +	£ (W< 1).
n = 1
289°. £	"j>V- (H<= D- 2891.*+ 1**+^ *• + ... (W<!).
2892.	x -	+ A,» + ... (W< !). 2893.-1,- -L,> - Jj,’ - ...
<W< *)• 2894.£„= 1, £
к = О
(-1)*
E„.k
(2h)\(2n-2h)\
= 0. 2895. P0 (*) = 1;
pfn_(2»-l)!! Г yn_ n(n-l) rn-2 + n(n-l)(n-2)(n-3) „-4 _	1
nK ) n\ L 2(2n -1)	2 • 4 • (2n- l)(2n- 3)	J
oo	л
(n > 1) (многочлены Лежандра). 2896. ^ s„xn, где sn = ^ aft.
n = 0	A = 0
2897. a) Д > min (Д„ Д2); б) Д > fi^2. 2901. V (-1)"	■ (|х| < +оо).
п\(2п + 1)
/1 = 0 4 7
Ё (_1>“ i£vTT: <и4 ■>• 2905- *+ т - д + ё - - (W < »•
2906.
. i In (|х| < 1).	2907. arctg x (\x\ < 1).	2908. ch x (\x\ < +oo).
a	L — X
2909. 1 + In (1 - x) (H < 1). 2910. —L= (-1 < x < 1). 2911.	*
x	Jl - X	(1_*)
(H < !)•	2912.	(\x\ < 1).	2913.	(\x\ < 1).	2916. Д = 2;
(x - l)2 + (у - l)2 < 4. 2917. R= -L;x2 + y2<±. 2918. Д = 1; *2 + y2 < 1.
J2	2
2919. Д = 1; x2 + y2 < 1. 2920. Д = I 2 sin |l; (x - cos a)2 + (y - sin a)2 <
< 4 sin2 |. 2921. 2,080. 2922. a) 0,87606 = arc 50°11'40"; 6) 1,99527;
в)	0,60653; r) 0,22314. 2923.0,30902. 2924.0,999848. 2925.0,158.
2926. 2,718282.	2927. 0,1823.	2928. 3,1416.	2929. 3,142.
2930. 3,141592654. 2931. In 2 = 0,69315; In 3 = 1,09861. 2932. a) 0,747;
6)2,835; в) 1,605; r) 0,905; д) 1,057; e) 0,119; ж) 0,337; з) 0,927;
и)	8,041; к) 0,488; л) 0,507; м) 0,783. 2933. 3,82. 2934.4,84. 2935. 20,02 м.
О	1	1
2936. 2 - ± cos 2х + i cos 4х. 2937. Ряд Фурье совпадает с многочленом Рп (х).
8	2	8
2938. 5 V *™(Ч7Л)х ; 5 .	2939. % ~ — f	sin (2fe + 1) S*
4	^ 2k -14	2 п 2ft +1 v	' l

ОТВЕТЫ
515
2940. 2 V (-1)" + 1 sinnx 2941. V sinnx . 2942. 2 - ± V cos(2fe+l)x
2-i	n	2-,	n	2 n 2-,	(2k+l)2
2943 (a-b)n _ 2(g - 5) у cos(2fe+ l)x + / + м у ,_ly. + l sinnx
4	n 2-,	(2k + 1)	v ' 2-, y '	n ’
2944. 2 n2 + V	cos nx. 2945.	Г » + V (-1)" +« “cosnxH
3	2-, пг	it L2t Ь '	'	,!-a!j
Л = 1	Л = 1
oo	oo
2946 2 sinTta	(-!)" + ln sinnx	2947 ^s^17lfl V* (~l)n + 1 л sinnx
я	n2 - a2	n	n2 + a2
2948. 2 sh a/i
1
2a/i
+ ]
Л
nna
cos
(a/i)2 + (ял)2
2949. a + Z +
2950. 1 - i cos x + 2 V £	■ cos nx. 2951. — V 	n sin 2nx.
2	Lj n2- i	я Zj (4л2-l)2
2952. if )( i)*cos(2fe-t l)xl 2953. 4 у (-1)* . sin (2fe + 1) x.
я t". 1	2fe+1 I	п±(2к+1)*
2954. 4 V cos(2fe + l)x 2955 1 _ 1 у sin2nnx (x * целом числу).
я	(2/г+1)2	2 я	л
2956. i - if cos2n(2n + 1)х	2957 2 _ 4 у cos2fex 2958 2 +
4 я2 '	(2л+1)2	я я ^ 4/е2 — 1	я
+ 4 у (-1)*:1 cos 2kx. 2959. —g— + 2 У cos лх. 2960. 4 In (1 + Л ) +
п 2-. 4ft2-1	1 - a2 ^ 1-о	я '	'
А = 1	п = 1
+ Ё |(“1У'[2 + | £ ti^sin^Jcos(8fe + 4)x .+£	1п(1 + «/2) +
+ — У	sin (2 т - 1)5] cos 8Ах 1. 2961. а) — +4 V lzl)2 cos nx
л 2-, 2т- 1	4j	f	' 3	2-i n2
(-it < x < л); б) 2л У	sin nx - - V	.?inC2fe I-1)*	(0 < x < л); в)	4lE? +
’	’	2-. n	n 2-.	(2k +1)3	3
+ 4 У	- 4л У 21М£ (0 < x < 2л); 5i, 5i , 5? . 2962. x2 = 2? +
2-‘- n2	2-i n	6	12	8	3
OO	00	.	00	.
+ 4 У (-1)"	x3 = 2л2 У (-l)n + 1 s--n-- + 12 У (-1)" &пЛ* ;
2-i	n2	2-i	n	2-i	n3

516
ОТВЕТЫ
*4 = ±я4 + 8я2 У (—1)л	+ 48 У tD^lcosnx. 2963.	;
я	"	л2	л4	2
П = 1	Л = 1
^2- 3?.?.±3af 2964 2 _ _9_ у i.	ММ + J_ V cosMM (0 < *< 3).
6	3	2я2 А л2	3	2я2 <11 л2 v	’
п = 1	П = 1
2965.	A.CL + 2^гт £ С?ж-‘ cos2ftx. 2966. J ff*einnx (Ы < 1).
А = 1	п=1
СЮ	00	оо
2967.1 + 2 ^ cos пх (|g| < 1). 2968. ^ qn cos ял:. 2969. -2 ^ ^ cos пх.
/1=1	п = О	/1=1
2970. -In 2 - V SSSM.	2971. -In 2 + Y tl)"",??™*.
п	п
/1=1 /1 = 1
2972. -2 У <=os(2fe+l)s 2973. у sin(2fc + 1)*	2974. ws) » а _
*,о	2л+1	(2ft + l.)2	2
_4af —L._ cos	+ 1° У -LIL- einiM±H2E2;i,(e)-2 -
я2 I>0 (2ft +1)2	2a	n2Z-(2ft+l)2	2a ,J,W 2
4a ^
я2 2-*
l
(2fe + l)2
cos (2fe+ 1)7IS + 1“ у .LUli sin (2ft + 1)я$
2a	я2	(2fc+l)2	2a
A - 0 '	'	A = 0
2975. Д-х) = Л*); Дя - л:)	f(x). 2976. Д-х) = -Дх); f(n - х) = Дх).
2977.
•*>\Ё Ifeb? -	‘»<"+ '>*1 (0<	1);
б)
2(-1)*<'1
(2ft + I)2
+ §
feftTTjSj -(2ft+l)x[l(
2 J
(п = 0, 1, 2, ...). 2979. a2„_, = ft2n-1 = 0 (л = 1, 2, 3, ...). 2980. а) ап = О,
Ъ2к - 1 = 0; б) а„ - 0, Ь2к = 0.	2981. а„ = а„, Р„ = -ft„.	2982. ап = -а„,
Р„ = Ьп. 2983. а„ = а„ cos nh + ft„ sin nh, ft,, = ft„ cos nh - a„ sin nft.
2984. A, = a0, A„ = a„	= ft„ (n - 0, 1, 2, ...). 2985. A = aj ,
+ ft2; S„=0(«= 1, 2, ...)
2986. i . 2987. ± . 2988. 2 In 2 - 1.
2	4
2989. 1.2990. i f 1 +	i	+ ... + II.	2991. In 2 - ±.	2992. 5.2993.1.
4	ml	2	m)	2	4
2994. 2 (1 - In 2). 2995. 2e. 2996. 3e2. 2997. ^ - 3. 2998. *1 - Щ .
3	4	16
2999. i (cos 1 - sin 1). 3000. ± (4 In 2 - 1). 3001. e* (ccmxm + am_ ,xm ‘1 + ...
2 6
... + a0), где коэффициенты ak (k = 0,1,..., m) определяются из равенства
P(n) = amn(n- 1)... (n - m + 1) + am_ xn (n- 1)...(л - m 4- 2) + ... + axn + Oq.

ОТВЕТЫ
517
3002. е'2 (j + 1 ).3003.(х2 + х + i) ± . 3004. (l - |T) cosx-
-	£ sin x. 3005. i f sh л/i - ch Jx 1, если x > 0; i fsin J\x\ -
2	4 V Jx	'	4
-	cos vw ] , если x<0. 3006. In jl— . 3007.2* arctg * - In (1 + *2) (|x| < 1).
3008. i arctg x +
3010.(4- !)'> -
3013.(1 + 2*2)e*2.
3017. 2.	3018.
2
3020. i In
2
• x + a
sin—-—
2
x- a
a
i	In i±^ (|*|< 1). 3009.(1- *)'3 - 1 (|*| < 1).
1. 3011.	(|*| < 1). 3012.	(|*| < 1).
3014. -2- + i In 2.	3015. 2 .	3016. i •
зТз 3	4	72
2z* (0 < * < 2rt).	3019. -In | 2 sin || (0 < * < Zn).
. 3021. 2, если 0 < * < 2a; 0, если a < * < Zn - 2a;
4
-2 , если 2я - 2a < * < 2я. 3022. 2 sgn * (|*| < я). 3023. | (^ 1 -	-
-	2 sin* (|*| < я).	3024. 2? - 5|*| (|*| < я).	3025. f (1 + cos*) -
2	8	4	2
-	sin x In ^ 2 cos |j (\x\ < я). 3026. eC08 x cos (sin x) (|x| < +oo). 3027. x = in,
y= jn (i, y= 0, ±1, ±2, ...). 3028. 2 (arcsin x)2 (|x| < 1). 3029. ^ +
+ -JL^L- arcsin ^ , если x > 0; j-i- -	ln ^ +^4--— , если x < 0.
? (4~*)5
(4-x)2
1
3030.
x- 1
3031.	.	3032.
x
t*-; 6)	*
i - * i - *
3033. a)
(l-*)2’
6)
(*-1)2
3034.1.	3035.1 + £3033.g.
2
3037. - У		i	.	3038. 2 — —	. 3039. J- .	3040. 2!	. 3041. F(fe) =
Z-f	n(p+nq)	6	24	12
-I 1 +
2л- 1
i [Ц-I **•) • 3M2- «*> -1 j1 - i PtU2]’ x
. 3043. 2яа £l - e2 -	j “•••]» где e — эксцентри-

518
ОТВЕТЫ
ситет эллипса. 3047. 2м: . 3048. In (1 + а) при |а| < 1 и In (1 + ±)
п\	а2 V а)
при |а| > 1. 3049. О при |а| < 1 и к In а2 при |а| > 1. 3050. 2 • 10 6. 3061. |.
3062.2.	3063. |.	3064. <Г,п2.	3065. а) Нет; б) да; в) да; г) да.
3066. Расходится к нулю. 3067. Сходится. 3068. Сходится при р> 1.
3069. Расходится к нулю. 3070. Сходится при любом р. 3071. Сходится,
если ах = а. 3072. Сходится, если ^ at = ^ Ъг 3073. Расходится к ну-
I = 1	< = 1
лю. 3074. Сходится. 3075. Сходится. 3076. Сходится. 3077. Сходится
при любом х. 3078. Сходится при любом х. 3079. Сходится при |jc| < 1.
3080. Сходится при |jc| < 2. 3081. Сходится при \х\ > е. 3082. Сходится
при любом х. 3083. Сходится при \х\ < 1, р, произвольных и при х = ±1,
р> 1, q> |. 3084. Сходится при любом х и р. 3085. Расходится.
3088. Сходится условно. 3089. Расходится. 3090. Сходится абсолютно,
если р> 1; сходится условно, если | < р< 1.	3091. Расходится.
3092. Расходится. 3093. Расходится. 3094. Сходится условно. 3095. Схо¬
дится условно. 3096. Расходится. 3097. Сходится абсолютно при а > 1;
сходится условно при ^ < а < 1.
3109. F'(x) = F(x) V -AifL;
f?, ! + /„(*)
X ]fn(x)\ < +°°i l/H(*)l < (n = 1, 2,...), где ^ cn< +00.3111. 157,970 +
n - 1	П = 1
+ 0 • 0,0004 (0 < 0 < 1).	3112. 102866 • 7,7 • f 1 + —2—) (|0| < 1).
3113. 0,0798 • (l + 3У (|0| < 1). 3114. 1028 • 1,378 • (l + JL) (|0| < 1).
3115. 1042- 4,792 • (l + ifo) (|0|< 1). 3116.0,124 ■ (l + JL) (|0| < 1).
e„
3117.0,355 * (l + e|o) (I0! < 1)* 3118‘(2w “ 1)!! = & i2n)"e n*Wn <f°«i < !)•
3119. 2L e6n (|en| < 1). 3120. a) 1; б) e; в) |; г) 1. 3121. P3(x) = 1 -	* -
Jnn	*	21
~Ux2+hx3; РзЫ) s 3,43: Ps(1) “ ~1>57: Рз(6> * 8-43- 3122‘ V-Vo +
+ y' ~y~ 1 (X - x0) + У' ~ 2yl+, У ~ 1 (x - x0)2. 3123. у = 0,808 + 0,193* -
6tl	Ah*

ОТВЕТЫ
519
- 0,00101л:2.3124. sin *° ~	Г 1 - f-f-f 1; sin 20° = 0,341; sin 40° = 0,645;
288 L V150/ J
sin 80° « 0,994. 3125.P(x)= I (7л:2- 4л:4). 3126.71. 3127. B„(x) = x;
О	О
3128. Bn(x) = £ f(a +	где l = b - a.
3129. Bn{x) = 1 (1 - *)(1 + x? + i (1+ x)*. 3130. B2n (x) = \	x
3136.	Полуплоскость у > 0. 3137. |jc| < 1; \y\ > 1. 3138. Круг x2 + y2 < 1.
3139. Внешность круга x2 + у2 > 1.	3140. Кольцо 1 < x2' 4- у2 < 4.
3141. Луночка х < х2 + у2 < 2х. 3142. -1 < х2 + у < 1. 3143. Полуплос¬
кость х + у < 0. 3144. Пара вертикальных углов \у\ < М (* * 0).
3145. Пара тупых вертикальных углов, ограниченных прямыми у = 0
и у = -2х, включая границу без общей вершины О (0, 0). 3146. Криво¬
линейный треугольник, ограниченный параболами у2 = х9 у2 = и пря¬
мой г/ = 2, исключая вершину О (0, 0). 3147. Семейство концентриче¬
ских колец 2nk < х2 + у2 < к (2k + 1) (fc = 0, 1, 2, ...). 3148. Внешность
конуса х2 + у2 - z2 = 0, включая границу за вычетом вершины.
3149. Совокупность четырех октантов пространства. 3150. Внутрен¬
ность двуполостного гиперболоида х2 + у2 - z2 = -1.3151. Параллельные
прямые. 3152. Концентрические окружности. 3153. Семейство равно¬
сторонних гипербол с общими асимптотами у = ±х. 3154. Параллельные
прямые. 3155. Пучок прямых с вершиной в начале координат, за выче¬
том вершины. 3156. Семейство подобных эллипсов. 3157. Совокупность
равносторонних гипербол, асимптотически приближающих к осям ко¬
ординат и расположенных в I и II квадрантах. 3158. Семейство двузвен¬
ных ломаных линий, вершины которых расположены на оси Оу.
3159. а) I и III квадранты при 2 = 0; семейство двузвенных ломаных ли¬
Раздел VI

520
ОТВЕТЫ
ний, звенья которых параллельны осям координат, а вершины распо¬
ложены на прямой х + у = 0 при г > 0; б) линии уровня — стороны углов,
параллельные положительным направлениям координатных осей Ох и
Оу с вершинами на прямой у = х; в) семейство контуров квадратов с
общим центром О (0, 0), стороны которых параллельны осям координат
Ох и Оу при г > 0; точка 0(0, 0) при г = 0; г) прямые, параллельные оси
Ojc, если г < 0; стороны углов, параллельные координатной оси Ох и
положительной полуоси Оу, с вершинами на параболе у = jc2, если г > 0;
положительная полуось Оу, если 2 = 0. 3160. Пучок окружностей, про¬
ходящих через начало координат (не включая этого начала!) и ортого-
С	С + х
нальных к оси Ох. 3161. Кривые у =	. 3162. Кривые у = ^—- .
In jc	lnx
3163.	Семейство окружностей с центрами на оси Ojc, ортогональных к
окружности х2 + у2 = а2. 3164. Семейство окружностей, ортогональных
к оси Оу и проходящих через точки (-а, 0), (а, 0), за вычетом последних.
3165. Прямые х = тк и у = пк (т, п = 0, ±1, ±2, ...), при г = 0;
система квадратов тк < х < (т 4- 1)я, пк < у < (п + 1)я, где (-1)т + п = 2,
при 2 =-1 или 2 = 1. 3166. Семейство параллельных плоскостей.
3167.	Семейство концентрических сфер с центром в начале координат.
3168.	Семейство двуполостных гиперболоидов при и < 0; семейство
однополостных гиперболоидов при и > 0; конус при и = 0. 3169. Семей¬
ство эллиптических цилиндров, общей осью которых является прямая
jc + у = 0, 2 = 0. 3170. Семейство концентрических сфер х2 + у2 + г2 =
= кп (п = 0, 1, 2, ...), при и = 0; семейство сферических слоев кп<х2 +
+ у2 + 22 < к(п + 1), где (-1)" = и, при и = -1 или и = 1. 3171. Цилинд¬
рическая поверхность с направляющей г = /(у), х = 0, образующие ко¬
торой параллельны прямой у = ах, 2=0. 3172. Поверхность вращения
кривой 2 = /(*), У = 0 вокруг оси 02. 3173. Коническая поверхность с
вершиной в начале координат и направляющей: х = 1, 2= /(у).
3174. Коноид с направляющей: х = 1, 2 = /(у), образующие которого
параллельны плоскости Оху. 3176. /^1,	= /(jc, у).	3177. Jl + jc2 .
3178. /(0 = 2 + f2; 2 = jc - 1 + Ту (jc > 0).	3179. /(*) = jc2 - jc;
2	=	+ (x -yf. 3180. f(x, y)=x2. 3183.2. Нет. 3. 0; нет. 3184. a) 0,1;
6) i , 1; в) 0, 1; г) 0, 1; д) 1, °°. 3185.0. 3186. 0. 3187. a. 3188. 0. 3189. 0.
A
3190.1.	3191. e. 3192. In 2.	3193. a) 5 < <p < ^; 6) 5 < cp < ^ и
— < ф < 7Г . 3194. Точка разрыва: x — 0, у - 0. 3195. Все точки прямой
4	4

ОТВЕТЫ
521
х + у = 0. 3196. О (0, 0) — точка бесконечного разрыва; точки прямой
х + у = 0 (х* 0) — устранимые точки разрыва. 3197. Точки, располо¬
женные на осях координат. 3198. Совокупность точек прямых х = тк и
у'= пк (т, п = 0, ±1, ±2, ...). 3199. Точки окружности х2 + у2 = 1.
3200. Точки координатных плоскостей: х*=0, у = 0 и z = 0. 3201. (а, Ь, с).
3203.1.	Равномерно непрерывна. 2. Равномерно непрерывна. 3. Нерав¬
номерно непрерывна. 4. Функция непрерывна на Е, но неравномерно.
3211. 2. f'x(x, 1)= 1.	3212. 1. /;(0, 0) = 0, f’y(0, 0) = 0; функция
недифференцируема в точке О (0, 0). 2. Функция недифференцируема
в точке О (0, 0).	3. Функция дифференцируема в точке О (0, 0).
3213. ^ = 4х3
дх
8ху\ ^ = V - 8х2у,	= 12х2 - 8у\	= -16*«,,
f2!H = 12(/2 - 8х2. 3214.
ду2
ду
Эи
дх
дх2
дхду
= j,+ I,!>“=*-*,|!H=0, Э2“
У ду
дх2
ЭхЭу
Э2и _ 2х 3215 — = -i- df£ = — Э2и _ Q Э2и _ _2_ д2и _ 6х
ду
3216. ^ =
Эх
Эх
ду
ди _ _
у* дх2
ху
дхду
д2и = _ Зху2
ду2
д2и
(х2 + у2)312 ’ Эу (х2 + у2)312’ Эх2 (х2 + у2)5/2’ ЭхЭу
-	3217- к -	«>+ *-<*+»>•
I** = х cos (х + i/),	=2 cos (х + у) - х sin (х + у),	= cos (х + у) -
ду	дх2	дхду
-xsin (х+у),	= -х sin (х + у). 3218. |н =	=-*£1£!,
Э 2u __
дх2
ду2
_2sinx2 + 4x2cosx2 д2и
У	9 дхду
2xsinx2
д2и
ду2
У ду
2cosx2
3219.	=
дх
= 2х г*2 ди ^.х2 „гх2
3j/
У*
Эх2
- sec2— + Ц-2 sin *-2 sec3 —,
У У У2	У У
д2и _
= -£г sec2*!
4х3 • х2
	 ОТ Г» _
sec3
х2 д2и
_ 2х2
sec2—
. 2х4
sin
— sec3—.
дхду
г/2 ^
У
3 У
У ’ Эу2
У3
У
г/ s'"
3220.
Эи =иа.»-1
Эх У ’
II
ху In X,
Э2и
Эх2
=у(у-
1)ху‘
2 Э2и
’ЭхЭг/
= ху~
*(i
+ у In х),
Э2и _
Xй In2 X (х :
>0).
3221.
Эи _
. 1
Эи = 2 у
д2и
_ _
1
ду2
Эх
Х + у2
ду
х + у2
9 Эх2
(х + у2)2 ’
д2и
2 у
д2и
в 2(х-
•У2)
99.9.9. ди
=
Эи .
_ X
дхду
(х + у2)2
' ду2
(x+i
!/2)2 ‘
* Эх
ду
х2 + у2
д2и _
. _ 2ху
д2и
_ X2
"S'2
д2и .
2ху
3223
Эи
_ 1
Эх2
(х2 + у2)2 ’
дхду
(X2
+ У2)
2’ ду2
2 + у2)2"
* Эх
1 + X2
Эи _
1 Э£|
и __ _
2х
Э2и =
0,
Э2и _
-_1а_
(XJ/ * 1).
1 + у2 Эх2
(l + x2)J
! ’
дхду
ду2
а + </2)2
3224 — = JssL. ди _ _ xsgnу д2и _ _	2х|у| д2и _ (х2 - j/2)sgn.y
дх х2 + у2 * ду х2 + у2’ дх2 (х2 + у2)2* дхду (х2 + у2)2	1

522
ОТВЕТЫ
д2и _
2х|у| QOOK —
	 X
Э2и _
2х2 - у2 - 22
№
(*2 + У2)2 ''
Эх
(х2 + у2 + z2)3/2
’ Эх2
(х2 + у2 + z2)s/2
Э2ц ,
Зху
3226.
= if*r,3u=.
-гГгУ
, ^ -Ггу In 2
дхду
(х2 + у2 + 22)5/2
Эх
xvyJ Эу
М
Эг VyJ у
д2и __
Эх2
z(z - IV xY Э2и =
х2 VyJ Эу2
. £i£±JJf:
г/2 1
xV Э^и = (хУ
у) ’ dz2 VyJ
In2*,
У
Э2ц = -Zi(xY
дхду ху\у)
д2и
дхдг
- (1 + 2'"
г).
у)
Э2ц = UxY
dydz У VyJ
(! + ;
-1";) (?>0)
3227. jji£ = 1£й |i£ = HIM , |if -_K« in *, |ll2 -	, |!й - “Isf* ,
Эл:	xz ду z dz z2	dx2 x2z2	dy2	z2
=MiM(22+ „In*),	- j£±ids*li£, 1^.	=
022	9-4 v 17	г)гЭ?7	гг2	ЭлгЭг	лгг3	ihtdz
дхду
_ulnx(z + ylnx) (жг * 0)	3228. |S£ — К! u, — zy-'u In х, ^ =
z3	Эх х ду	dz
= уги In * In у,	1') u, |^| = zy*~2u (2 - 1 + гуг In л:) In *,
Эх2	х2	Эу2
(1 +уЧпх),	=
х	ЭхЭг
1^1 - уги (1 + уг In х) In X In2 у,
OZ2
д2и
дхду
= У*и\№ (1 + у* In х),	= у* *а In х [1 4- z In у(1 + у* In х)] (х > О, у > О),
х	дудг
3230. 2,fXy (0, 0) не существует. 3235. da = xm~lyn~1(my dx + + дх dy),
d2u = xm " 2у" " 2[m(m - l)y2 dx2 + 2mn xy dx dy + n(n - 1) x2 dy2].
3236. du = У^-^У , d2u = -1 dy (ydx- x dy). 3237. du = *** + V*» ,
У2	У3	Jx2 + y2
(ydx-xdy)2 3238 da = xdx + ydy # д
(x2 + y2)3/2 ‘	‘	x2 + y2 *	(x2 + y2)2
3239. da = (у dx + x dy); d2a = е*у[у2 dx2 +2(1+ xy) dx dy +
+ x2 dy2].	3240. da = (y + z) dx + (z + x) dy + (x + y)dz,
d2u = 2(dxdy + dydz + dzdx). 3241. du =	+ УЛУ),
(x2 +у2)2
= 2z[(3x2 - y2)dx2 + Sxydxdy + (3y2 - x2)dy2 \ - 4(x2 + y2)(xdx + ydy)dz
(x2 + y2)3
3242. dx - dy, -2(dx - dy)(dy + dz). 3244. а) 1 + mx + лу; б) xy; в) x + y.
3245. a) 108,972: 6) 1,055; в) 2,95; r) 0,502; д)0,97. 3246. Диагональ
уменьшится приблизительно на 3 мм; площадь уменьшится приблизи¬
тельно на 140 см2. 3247. Уменьшить на 1,7 мм. 3249. А — 10,2 м3; 8 ~ 13%.
3250. А ~ 7,6 м. 3251. fx (х, у) и fy (х, у) не ограничены в окрестности
точки (0, 0). 3256.
Эх4
24,
Э*ц
Эх3Эу
О,
д4и
Эх2Эу2
-16.
3258. _	= -6(cos х + cos у).
Эх3Эу3
3259.
д3и
дхдудг
= 0.
3257.
д3и
Эх2Эу
= 0.
3260.
Э3ц
дхдудг

ОТВЕТЫ
523
= е*»* (1 + 3хуг + х2у2г2).	3261. . д4ц =	+ 48(х-ОТу-Л)2, где
дхоуд^дц г4	г8
r = J(x-W + (y-п)2 • 3262. |J^S. = р!у!. 3263. 3irl)TigLtS-M»*+"»y>.
3264.	+ у[х2 + у2 4- 2(mx 4- пу) 4- m (m - 1) + л (л - 1)]. 3265. (х 4- р) х
х (г/ 4- д)(г 4- г) е* + у + г. 3266. sin 25 . 3267. F(f) = /'(0 + 3ff'(0 + t2f'"(t).
3268.	d4u = 24 (с^л:4 - 2d*3 dy - 2d* dy3 + dy4); ^ = 24, ^	12,
ax4	dx3dy
эЙЬ = °’ £ip “ “12>	“ 24- 3269-‘ d3“ - 6 (d*3 - 3d*2 dy +
4- 3dx dy2 4- dy3). 3270. d3u = -8 (x dx 4- у dy)3 cos (x2 4- y2) - 12 (x dx 4-
+ у dy)(dx2 + dy2) sin (*2 + y2). 3271. d10M = -9!^+^У)1> .	3272. d*u -
= -(dx6 - I5dx4 dy2 4- I5dx2 dy4 - dy6) cos x ch у - 2dx dy (3dx4 -
-	10dx2 dy2 4- 3dy4) sin x sh у.	3273. d3u = 6dx di/ dz. 3274. d4u =
= 2 (^	^ .	3275.	dnu = eax + by (a dx + b dy)n. 3276. dnu -
v x3 у3 23;
- £ cj	(y) dxn~k dy*. 3277. dnu = fin) (x +у + г) (dx + dy + dz)\
* = 0
3278. dna = ea* + by + сг (a dx 4 b dy 4- c dz)n. 3280. a) Au = -a, A2u = u;
6) Au = 1, A2u = 0. 3281. а) A и = 0; б) A и - 0. 3282. a) AjU = 9[(*2 - yz)2 4-
4- (y2 - xz)2 4- (z2~ xy)% A2u = 6 (x 4- у 4- 2); 6) Axiz = i , где г = Jx2 + у2 + z2 ,
г4
A2u = 0. 3283.	= 2*/'(*2 + y2 + z2);	= 2f'(x2 + y2 + z2) + 4*2 П*2 +
*»■**§+ +	-r; (x.i)	(*.*):
S: --?fi (*•;MS- 5) + ;«(*•;) +	(*•;);
& -S «('•;)- ? «(* 9' j*«(* 91> $ - $ * (* 9 +
+ jf/S (*• »)-3285’S ■	+ »,'! + !“fi -xr, + x»r.ig -
-*y«':	= «'1 + y2/22 + У2*2/зз	+ 2y/i'2 + 2yz/j3 + 2y2z/^ ;
|^f =	+ 2*2z/23 + xV/3'3 ; 0 = ^/з'з 5	= xyf'k + *уг2^'3 +
+ */i'2 +*z/'i'3 + 2*yz/23 + /2 + z^3;	=xyf"3 +*y2/23 +*y2zf3'3 +y/J ;
- ^y/2'3 +	+ xf’3.3286.	= T.'i + (* + У)/Гз + *tf ft* + П ■

524
ОТВЕТЫ
3287. Ди = 3/;', + Цх + у + а) ГГ, + 4(х2 + у2 + z2)f'22 +6f, .
3288.	du = f(0(d* + dy); d2u = /"(О (d* dy)2. 3289. du = f (О хаУ~УЛх ;
d2u = /"(О	- 2f\t) dx{xdy~ydx). 3290. du = f • ?-ах + УаУ ;
*3	V*2 + y2
d*u = r ■	+	+ r • (ydx~xdy)2.3291. du = AO do d2u = ПО dt2 +
X2+U2	2
(x2 + y2)2
4- /'(f) d2f, где d£ = yz dx 4- zx dy 4- xy dz и d2f = 2(z dx dy + у dx dz 4-
+ x dy dz). 3292. du = 2f' - (x dx + у dy + z dz); d2u - 4/" • (x dx 4-
+ у dy + z dz)2 4- 2/' • (dx2 4- dy2 4- dz2).	3293. du= a f[ dx + bf2 dy;
d2u = a2/(i dx2 4- 2abf[2 dx dy 4- b2 /22 dy2. 3294. da = /; • (dx 4- dy) 4-
4- f2 • (dx - dy); d2a - /;; • (dx 4- dy)2 4- 2/i'z * (dx2 ~ dy2) 4- /Ц • (dx - dy)2.
3295.	du= f[ ■ (y dx + x dy) + f'2 •	; d2u =	•(yd* + x dy)2 +
У2
+ 2A, • y2dx2Z.xldUl + /» • {ydx-xdyy +2f, ,dxdy_2f’2 .(ydx-xdy)dy
3296.	da = /{ • (dx 4- dy) 4- f2 • dz; d2a = f[\ • (dx 4- dy)2 4- 2/J'2 • (dx 4-
4- dy)dz 4- /22 * dz2. 3297. da = /{ • (dx 4- dy 4- dz) 4- 2/£ * (x dx 4- у dy 4-
4- z dz); d2a = /JJ • (dx 4- dy 4- dz)2 4- 4/i'2 * (dx 4- dy 4- dz)(x dx 4- у dy 4-
4- z dz) 4- 4/22 (x dx 4- у dy 4- z dz)2 4- 2/2 • (dx2 4- dy2 4- dz2).
xiydx-xJyXzJU-ydz) +	. (zdy-ydz)2 _ 2f . (ydx-xdy)dy _ 2f, x
y2z2	z4	y3
x (zrfy -ydz)dz _ 3299 du =	+ 2<f- + 3t2y» ) d2u =	+ 4(^-2 +
+ 4t2/^2 + 6(2/'Гз +12f3A, + 9<4/зз + 2/2 + 6tf3)df2.	3300.	du	=
= a/J dx 4- bf'2 dy 4- c/J dz; d2a = a2/Vi dx2 + b2f22 dy2	4- c2	/£'3	dz2	4-
4- 2abf[,2 dx dy 4- 2ac/y3 dx dz 4- 2fec f2'3 dy dz. 3301. da = 2/J	• (x	dx	4-
4- у dy) 4-2/g ' (x dx - у dy) 4-2/з * (y dx 4- x dy); d2a =	4f[\	• (x	dx	4-
+ i/ tfy)2 + 4/22 '(x dx - у dy)2 4- 4/33 • (y dx 4- x dy)2 4- 8/J'2 • (x2 dx2 -
- y2 dy)2 4- 8/!з • (x dx 4- у dy)(y dx 4- x dy) 4- 8/23 • (x dx - у dy) x
x(y dx 4- x dy) 4- 2/i • (dx2 4- dy2) 4- 2 /2 * (dx2 - dy2) 4- 4/J • dx dy.
3302. dna = /*л) (ax 4- by 4- cz)(a dx + b dy + c dz)n. 3303. dnu = (a dx ^ +
V
4- b dy ^ 4 c dz /(£, T), О* где £ = ax, ri = fey, £ = cz. 3304. dnu =

ОТВЕТЫ
525
= [ dx[a,| + a2± + a3 |) + dy (b,| + b2± + b3 1) + dz (c,| +
+ c2± + c3|)]" m, Г), 0. 3305. F(r) = f\r) + l f(r). 3316. 1. 3319. xyz.
3331. xp- - yp- = x. 3332. 2*|* + y^ - 2z. 3333.	- *1!2 =0.
Эл:	dy	Эх Эу	Эх Эу
3334. ^	+ р:	+ 2“	= 0. 3335. jc|“	+ i/|“	+ z^
Эх Эу Эг	Эх Эу Эг
0. 3336. ^ = 0.
ЭуЭх
3337. z^- =	3338.	- 0. 3339. х^ + у^ = z.
ЭуЭх ЭхЭу	Эх2 Эу2	Эх Эу
3340.*2^Ц-/^ + ;*ф -j/^ =0.3341.1-73.3342.^ =cosa + sina;
Эх2 Эу2 Эх Эу	Э/
а) a = 7; б) a = ^; в) а = ^ и а = —.	3343.
4	4	4	4
_	3 п
7п
Г~2	2
л/*0 + Уо
3344. ^ J2(a2 + b2). 3345.	= cos a + cos P + cos y; |grad u\ = Js .
ab	ol
3346. |grad a| = i ; cos (grad иГ*) = - — , cos (grad uTy) =	,
rl	'о	r0
cos (grad u^z) =	, где r0 = Jxl + yl + z\ . 3347.5. 3348.- 3142.
r0	2
3350.	cos2 a + ^ cos2 p + cosy + 2^- cos a cos p +
dl2 dx2	dy2	K dz2 ' дхд у	K
+ 2^ cos a cos у + 2^ cos P cos y. 3352. ^ = -0,5. 3353. u” (x, 2x) =
ЭхЭг	ЭуЭг	Эу
=	(х, 2х) = -4х/3, и”у (х, 2х) = 5х/3.	3354. z = хф(у) + ф(у).
3355.	2 = ф(х) + \|/(у).	3356.	z - ф0(х) + уф^х) + ... + уп “ 1 фп _ ^х).
3357. и = ф(х, у) + ф (х, 2) + % (у, 2).	3358. u = 1 + х2у + у2 - 2х4.
3359. 2 = 1 + ху + у2. 3360. г = х + у2 + 0,5ху (х + у). 3362. Множество
нулей функции /(х) должно быть нигде не плотным на интервале (а, 5),
т. е. нули функции f(x) не могут целиком заполнять никакой интервал
(a, р) <= (а, Ъ). 3363. Множество нулей функции /(х) должно быть нигде
не плотным на интервале (а, Ь), причем каждый нуль £ функции /(х)
одновременно есть нуль функции g(x) и сверх того существует конечный
предел lim [g(x)//(x)]. 3364. 1) Бесчисленное множество; 2) две; 3) а) одна;
б) две; 3365. 1) Бесчисленное множество; 2) четыре: у = х; у = -х;
у = |х| и у = -|х|; 3) две; 4) а) две; б) четыре; 5) одна. 3366. 1) Нигде;
2) 0 < |*| < 1, |*| = JLlM ; 3) * - 0,1*1 = 1; 4) 1 < |*| < J1+2^ ; однознач¬
ные ветви: у = eJl + Jl + X2-x4 (|д|<	y = eJl-Jf^T*

526
ОТВЕТЫ
1 < |jc| <	9 Где в = -1, 1. 3367. Точки ветвления: (-1, 0), (0, 0),
(1, 0); у = г(х)^8х2+1~^х^^ (\х\ < 1), где е(х) = -1, 1,
sgn X и -sgn X.
3368.Множество значений функции ср(у) должно иметь общие точки с
множеством значений функции fix), 3371. у' =	• у” = — «~2..
х-у	(х-у)3
3372. у' = * *±JL ; у" =	.	3373. у' = —±— ; у" = .-£51пУ ..
X-у	(x-yr	1-ECOS у	(1 — £ COSI/)3
3374 и' = У2(г~1плс) • и" = Уг1у(1-1пх)г-2(х-у)(1-1пх)(1-1п1/)-х(1-1п1/)2|
у х2(1-1п{/),{/	x3(l-lnj/)3
3375. у’= И; у" = 0. 3378. у\ (0) = -1; у'г (0) - 1. 3379. у\ (0) = 0;
у'2ф) --733 ; у'3(0) = 73.3380. у' --Щ* ; у" =
18
21/	(х+2у)°;У	(x+2y)f
162х
Э2г _ _х_ц .	Э22 _ _у2 + z2
дхду
9 ду2
3384.
_ —X .
dz
=
. Э 22 _
_x2 + 22 .
5
2
' э у
2
’ dx2
23
dz
dz _
X 2
dx
Z
2- ХГ/ ’
dy
22 — Xy ’
z(z* -
-2xyz2 -x
2У2) dz _
(z2-
■ xi/)3
Эх
X + y
+ 2
X2
+ У +
2- l)3 ’
dx
x2-i/2 ’
дх2 (z2-xy)3*dy2	(z2 - ху)3 1 дхду
_ dz _	1	. Э22 _ д2г _ д2г _ _ х + у
dz __ _ уz . Э2 2 _ _	У22	.	Э22 _ хуг . Э22 = __ x2z
Эу х2-у2’ дх2 С*2-*/2)2’ ЭлтЭг/ (х2 - у2)2 1 ду2 (x2-i/2)2*
3387 Эг _ dz =_1; |!| =pf	=	3388. а)-2; б)-1.3389.
дх ду	дх2	ЭхЭу Э{/2	'	’	дх2 5
= -i ; ^2 =	. 3390. dz - -Si	+ к£ё) ; d2z -	Г(*! +
дхду 5 ду2 125	2 l a2 b2 J	z3 Lla2
!‘>di*11 ~ “)dS ■
d2z= -2{y(l-Uz)dx2+ l* + У- г(1 + xy)\dxdy + x(\- xz)dy2} 3392 dz =
(1 ~xy)2
- гЛМ*х_ + гйу) агг _ _z2{ydx-xdy)2 _	3393. dz = dx - 	(*- *№	;
y(x+z)	y2(x + z)3	(x-z)2 + y(y +1)
d2z = Ш.х.-.1){У+Шх-г)2 + у2\ d 2	3394 d = _u2{dx+dy)-z2dx
\(x- г)2 + y(y + 1)|3 y	u\2(x + y)-u)
3395.	= ~4i*~ z} [F32 F[[	- 2F[ F'2 F['2	+ F[2 F22 ] -
ЭхЭг/	(i^ +22F2)3	1	2	12	1	22 j
3396	— = ^ ~	= ^2 ~
* Эх	-F’3 ’ dy F’2 - F3
2(F\ +2xFj )(F[ + 2yF’2 )F\
(F[ + 2zF2 )3

ОТВЕТЫ
527
33»7.| - -(l + &£*■)■. | - -(l + S-); g - -*-■[**«! +
+ 2rxi + F& ) - 2(F[	+ Fi )Fi (F['3	+ Щ ) + (JPJ +	)2^ ].
3398. 1)
d2z
dx2
= -(xF;	+ yFi r3 • [y2z2(Fi2 F[\ - 2Fi Fi F['2 + F'2	) -
„2
-2z(xF( + yFi )FJ2 ]; 2) a) d2z = -
72, _ W', -2FI f- f;- + f;2f^
(fi + f{ )3
(dac-dy)2;
d2z = --4- (2da:2 - bdx dy 4- 2dy2).
243
6)d2z-f'rVl	d^)2-33"-dz=|
3401. ^ = 2^1; *1 = .
dz x-y dz x-y
3402. a) ^ = 0, ^ = -1,	= -I; б) ^	+	; !*£ =
' dz	dz	dz2 dz2 4’	; dx x* + y* dx
r = 22^£й; jj2--££±H£ (a:2 + y2 > 0). 3403. du = -± dy,
*2+z/2 Эу x2 + y2 dy x2 + y2	3
do = -d* + - dz/.
3 y
3404 da = (s*nt? + xcosv)dx - (siruz - xcosv)dy .
jt cos lm- у cos и	8 9
dv —-(sint?- ycosu)dx+ (sinu + ycosu)dy . ^2u __	= (2dscosy-xdy siny)du _
X COS V + у COS Ы	*	X COS У + I/ cos и
_ (2dycosu-ydusinu)du 3405- du _ l(dx + di,); dy = *dy- l(dx_dy).
x cos v + у cos и	2v	y'	4 w 2	w
d2u = da:2; d2u = i (da: - dy)2. 3406. ^ = 2(t+±)‘,p = 3 f f2 i + 1
2	dx \ t) dx \ t2 )
8 -2; ё -16(1'+ 7) - ^ * » t■ f, - -3“к I -!1<»+»>1:* ■”>•
3408 a) — = 3 . Э2 = _ 1 . Э 2z = 26 . ч Э^£ = _ sin2<p + cos2ф cos2 ц/
‘	' dx 2 9 dy 2 *	' dxdy 121 ’	' dx2	sin3<p
3409	= sin2i> d2z = _cos2y 32z = _sin2y
dx2
9 dxdy
dy2
3410. dz = 0;
d2Z = I (dx2 - dy2). 3411. 42 = 2(*Ца!) ; p. =	+ 6a
2 v	y	dx	x-2у dx2 x-2y (x-2y)3
3412. 2“ - -i- + (■»-*•	ДС) ex - г du = _ x+z + (y + l)(y - x) ey - г>
da y + z (z+l)(y + z)	dy (y + z)2	(z+l)(y+z)2
3413	=-I Г^5!!^ _Эл»Э2£>| Эг =_1	Г„е г =	_ Эу/Э^
dx I \dudv dvduj 9 dy I [dudu duduj *	dudv dudv
3414 du	_ ldj|j .	du	_ _ 1 Эф .	d2u	_ _J_	lfdvj/d£(g _ ЭфЭ2ф
dx 1 dv *	dy	I du *	dx2 73	|1ЭшЭи2 dvdu2
-	^2(f) -	- ЭфЭ2У|/"| (<ht\2 \. d2u = J_
V dvdudv	dv dudv) dudv \dv dv2 dv dv2 J IduJ j dxdy I3
к') ,
4 \dv
/"ЭфЭ2ф _
ЧЭу du2

528
ОТВЕТЫ
Эф Э2 \|/
ди
Э2\|/ЛЭфЭу|/ ГЭф Э2ф _Эф Э2\|/^/"ЭфЭц/ЭфОц/А _|_ру|/Э2ср _ЭфЭ2цЛ дер Эху
ди2)диди чЭиЭиЭи dvdudv)\dudv диди) \dvdudv диди2) диди
д2и _ __1_ |/"9vj/3£cg _ ЭфЭ2фЛ fdtjA2 _ о fdy д2ср _ OcgdM Ocgdtj) _|_ fchj/Э^ф _
ди2 13\\диди2 диди2) чЭуу	\dvdudv	диди2) диди \ди ди2
, где / =	-2S2S.	3415. а) ^	= cos - ; ^	= sin 2.;
и и ди dvdu	ох	и ду	и
_ ЭфЭ2ф>|
ди dv2) v3ij
ди _
«л. ^
uj * di/
v , V V
= cos - 4- - sin - ;
и и и
гг\ ди
б)Гх
_ sinu
eu(sinv - cosv) + 1
• =
~(eu - cos и)
. dv _
eu + sin v
dx
u|<?"(sinu- cosu)+ lj
’ dy
u\ e"(sinu- cosu)+ 11
I . d2u
_ 1 1
d(g, h)
Ij * dx2
l\ \
d(y. z)
l 'Эх
Z-)2g +
d(f.g)
f/.i-
+ 12$-
dz) S
d(y, г)
1 'Эх
dy
г = d(g, h)	т _ d(g, h)	т _ D(f, g, h)	0417 ди	_ df . ди	_ df	, J-jjdjf
2 d(ztx)'	3 d(x,y)	D(x,y,z)'	дх дх* ду ду 1\ду*
где/,- Црй и /2 = |Mi.3418.^ =	^ = Ц-, |2 = £, где /, =
д(г, t)	д(х, t)	дх I ду I dz I
-»№	мы. л--L1ЦМ»,
d(v,w)	d(v, w)	d(v, w)	D(u,v,w)	J3
гдеЛ = |^,/2= |^,/з= 1^.3431.*'" +xx'5 = 0.3432. xlv = 0.
Э(х, f) * Э(у,t)	d(z, t)
3433.	- t(42)* = 0. 3434. ^ + I/ = 0. 3435. ^ - 3^-if + 2& -6y = 0.
dt2	1<Ш	di2 w	di3 di2 dt *
3436. ^ + n2u = 0. 3437.	+ m2y = 0. 3438. и" + Г q(x) - ip2(x) -
dt2	dt2 *	L*v ’ 4y ' '
-^P'(x)lu = 0.3439. ^+(u + 3)^ + 2u = 0.3440. ^ =0.3441.^ =0.
2 J	afz	ai	a£2	at2
3442.	+ 8uf= 0.	3443. t5 ^ + (314 + 1)^ +	= 0.
dt2	\dt)	dt3	a£2 dt
3444 u" -u' =	Ф (1» u* u'+ u2)= 0. 3447. Для/ + и2 - ц, a, 1) = 0.
3450. 4^ = r. 3451. r'2 = -~S^2-(P r2. 3452. rfr2 + 2r'2 - rr") = r'3.
d<p	sin2(p
3453. £ .	3454. К = lr.2+lr? .T rf”\.
(r2 + r'2)2
ЁГ = fcr3-	ЁФ = -1
df	’	df
3455.

ОТВЕТЫ
529
3456. w=4- { -г2^2) • 3457. Г *= л:; Y" = 4т: У” =	• 3458. z = cp(x + у),
af V afy	у	у"3
где ср — произвольная дифференцируемая функция. 3459. г = ф(лг2 + у2).
3460. z = — + ср(у - 6z).	3461. z = х(р(й').	3462. ^	^ = е“ sh и.
а	\Л7	Эи dv
3463.	= Эг _ 3464 Э£ = 1 3405 Эг = £ . £i±i£ 3466. @11+v- z)|^ +
Эи dv
dv
dv
du
+ (и + 2i> - z)~ = a + у - z. 3467.
dv
ex + y - z2
-x* -ifc
1 - e e ,hl
. 3468.
3469. ^ - 0.	3470. ^	^ .
^	У
3471. ¥ + 2* = 2.
du dv v
ШШ
u2 + v2
3472. A =
ax. dxV
. 3473. ^	^	^ + 3u + (e* + e" + e<) = 0.
Э£ Эп Э£
3474.
^ = 0. 3475. ^ - 0. 3476. ^ = 0. 3477. u2 f|^V + v2	=
dv	du	dv	\du)	\dvj
e2“( 1 - ^cos2u|
=	. 3478. —-—^		 . 3479.A = ^ ^ . 3480. ^ = & .
du dv	dw	du dv	Э£ £
du
3481. w =	. 3482. w =	. 348З. w =	+ iffiiV . 3484. w = ^ +
Эф	dr	ydrj r2\d(pj	dr2
+ 1 Эи + 1 dju 3485 w =r2^u 3486 w = 3Jb 3487 7 _ 1(ЭиЭ£ _ ЭисЫ
г dr г2 Эф2	Эг2	Эф2	/лЭгЭф ЭфЭгУ
3488. и = ф(д: - at) + vp(jc + at), где ф и \|/ — произвольные функции.
3489.3^-	=0.3490. ^ + Ilf* =0.3491.af	+ 2Ь^4~ +
dvdu du	du2 dv2	V du2 du)	dudv
+ b( T1 - !r) - °- 3492. T1 + Щ = °- 3493. |^|
V dv2 dv)	du2 dv2	du2
+ ^4 + m2e2uz = 0.
3494.
Э2г _
dudv
0.	3495.
Э2г _ 1 dz
3496.
dv2
d2z _
dz
dudv 2udv	dvdu u(4-uv)dv
3497. (u2-v2)f2- = v*/. 3498. |!f --£Ц|2.3499.^- +^Ц(^ -
ЭиЭи Эи	Эи2 и2+и2Эи	ЭиЭи и2 - v2 \ du
где А.» и \п — корни уравнения А + 2 ВХ + СХ2 = 0. 3503. а) А и =	+ i— ;
dr2 rdr

530
ОТВЕТЫ
б) Д(ДU)	=	+ Щ	_ 1£и	+ 1 rfu в	3504. upL + Ё!2	+ Сш - 0.
dr4 г dr3 г2 dr2 г3 dr	du2 du
-уш?+й-з508-«|(«|)+'>1;(’'1;)+|;э1(?§ -
-	+«й+*Й) •ш jjf+ Й+ Й= °-3510 $ ■ °-
3511. Л,» - (&)’ + i(|)’ ♦	i M - I[i ( H&) +	x
(»»ea)
1 d2u
sin203(p2
]■ ^ hb + m - (S'+(i)
3513. PZ - 0. 3514. PZ -0. 3515. PZ -L 3513. PZ + P?- - 2ш.
du2	dv2	du2 2	du2 ouov
3519.
3524.
d2w
dud v
d2w
dt,2
+ (-
-11
Э2а; _
0. 3518.
02W
u
dv2
3u2
dv2

w
3520.
|!i£ +
d2w _
> 4sin2(u-
du2
dv2
, 32Ш
, d2w
' дш
+ ^2 +
+ (e‘
" -1) ГГ:
Эл2
э;2
Эл
a; v
41
©'♦(S'--
3523. 1^- = 0.
dudv
<dx]J
,dO
3526. * = уф) + ф). 3527. A(X, Y)g - 2B(X. Y)^ + C(X. Y)g - 0.
3528.
*-*0	= У-Уо
-cos a sin *0	- sin a cos t0
cos *0
2 - 20 = (л: - л:0) cos a tg t0 +
+ (y - y0) sin a tg t0, где x0 = a cos a cos £0, i/0 = a sin a cos *o> 2o = a sin *<>•
3529. * +2 = 1, j, = £ ; a* - cz = ± (a2 - c2). 3530.	= Ц-1;
ас	2	2	112
* + у + 2z = 4. 3531. 2-=-^ = ^	^ ; Зх + Зу - z = 3. 3532. * + z = 2,
*	3	3-1
j/ + 2 = 0;*-z = 0. 3533. Af, (-1,1, -1); M2 (	• | •	• 3537- tg Ф -
= f'x (X0, y0) cos a + f'y (x0, y0) sin a. 3538. jf =	. 3539. 2x + 4y - z -
-5 = 0;	= ILlI = IzA . 3540. 3* + Ay + 12z = 169; | = й = ^.
3541. 2 = f - | (* - v);
*-*o = У-Уо = *-*o
ax о	bi/o cz0
3544. л: + у - 4z = 0;
“p =	. 3542. ал:0л: + by0y + cz0z = 1;
3543. * + у - 2z = 0;	2Ц± =	.
= *Ц_2 = £z_i .	3545. - cos \|/0 cos cp0 +
11-4	a

ОТВЕТЫ
531
, и	•	.2 •	1 xsec\i/0sec<p0- a р see \i/0 cosec ф0 - b zcosec\i/0-c
+ cos \|/0 sin epo + - sin \j/0= 1;		——	= -	—	—— =	—— ,
be	be	ac	ab
3546. x cos ер, + у sin фо - г tg a = 0; r°cos(p° = У-'*™** = 2 ~ ^tga
coscp0
sm<Po
-tga
3547. ax sin v0 - ay cos v0 + v0z = au0v0;
x - u0 coso0 _ у - u0smv0 _ z - av0
asmun
-acosu0
“0
3548. M - Ц + ± = 2.	3549. A(0, ±2j2,T2j2); В(±2, T4, ±2);
u« *4
Ua
C (+4, +2, 0). 3550. л: = +2f , t, = ±¥, z= , где d= Ja2 + b2 + c2.
a	a	a
3551. x + 4p + 6z = ±21.	3556. x2 + y2 - xy = 1, 2 = 0; 3p2 + 4x2 = 4,
x = 0; 3x2 + 4z2 = 4, у = 0.	3557. 6 < 0,003.	3559. cos cp =
2bz0
a*/a2 + b2
3563. ^ = x0 + z/o + z0; a) x0 = 1/0 = 20 = -4= ;	6) x0 = p0 = *o = “4= »
V3	V3
в) на окружности x + 1/ + 2 = 0, x2 + y2 + z2 = 1. 3564. ~ —	2	— .
on [~2	~2	~2
xo + Уо + £0
*Ja4 b4 c4
3566. x2 + y2 = p2. 3567. у — ±x. 3568. p2 = 4ax. 3569. Огибающей нет.
2 2 2 2
3570. x2 + у2 = l2 .3571. \xy\ =	. 3572. у = £«-£*? . 3574. а) у = 0 —
2я	~ 2
2*	2 v20
огибающая (геометрическое место точек перегиба); б) у = 0 — огибаю¬
щая; в) у = 0 — геометрическое место особых точек (точек возврата);
г)	х = 0 — геометрическое место двойных точек, х = а — огибающая.
3575. Тор (4х2 + у2 - Rf + z2 = А 3576. лг2 sin2 a + у2 sin2 3 + г2 sin2 у -
- 2 xy cos a cos 3 _ 2хг cos a cos у-2 у z cos 3 cos у = 1. 3577. \хуг\ = V
3578. |г± Jx2 + у2 | = pV2. 3579
* У
2
+
У *
2
+
Z X
xо Уо
Уо z0
*0 Уо
АпД
2
< R2(x2 + у2 + г2). 3580. (х - х0)2 + (у - у0)г = (г - г0)2. 3581. /(лг, у) =
= 5 + 2(лг - I)2 -(л: - 1 )(у + 2) - (р + 2)2.	3582. /(лг, у, г) = 3[(лг - I)2 +
+ (г/ - I)2 + (г ~ I)2 - (х - Щу -1) - (х- 1)(г - 1) - (у - lMz - 1)] +
+ (л; - I)3 + (у - I)3 + (z - I)3 - 3(л: - 1)(г/ - l)(z - 1). 3583. Д/(1, -1) =
- Л - 3k + (-Л2 - 2hk + к2) + (h2k + hk2). 3584. f(x + h, у + к, г + l) =
= f(x, у у г) + 2 [h(Ax + Dy + Е) + k(Dx + By + F) + l(Ex + Fy + Cz)] +
+ f(hy k, Z).	3585. xy = 1 + (x - 1) + (x - l)(p - 1) + R2( 1 + 0(x - 1),
1 + 0(p - 1)) (0 < 0 < 1), где Д2(х, y) = | *[ ^ & dx - In x • dy j + 3 ^ dx +

532
ОТВЕТЫ
+ 1пж • dy j ^-jLdx2 + - dx dy j + dx3 - ^ dx2 dy и dx = x - 1,
dy=y- 1.	3586. 1 - | (x2 + у2) - | (л;2 + у2)2.	3587. a) 1 - ± (л:2 - г/2);
б) 5 + * - лгу. 3588. -(ху + хг + у г). 3589. F(x, у) = ^ (f'x'x +	) +
+ U'L, + С. )+•••• 3590. Др) - «ж, у) + ^ [(/" (ж, у) + & (ж, у)].
3591. Д = /(л:, у) = hk Г+ V У	ЭV<*. у) 1.3592. F(p) -
7	LOjcЭг/.	т\(п-т)\ дхтдуп~т]
= Я*. У) + £ (Д-2(|)2” Д"Я*, У), где Д - g + |i .	3593. 1 + m* +
+ «У +	+ й1^У2 + ... <И< 1. Ы< 1).
3594. £ (-1):--(^n-1j!^(H + |y|<i).3595. f; f;(-ir-giiL
т,п = 0	т = 0 « = 0	'	'
<М< +°°, |у| ~ +00).	3596. У У (-1)"-^Ц; (И< +°°, |у| < +оо).
т = 0 п = О
3597.	£ £ (-1Г (2riXIl). (W " +°°’ Ы = +0O>-
m = 0 n = 0	v	,v	'
3598.	£ 2 (-‘''(iSfe <H <+0°.H< «°>. 3599. f
m = 0 n = 0	n = 0
(x2 + y2< +00). 3600. У У (-l)m +	(|ж| < 1, |y| < 1). 3601. f(x, y) =
m = 1 n = 1
= 1 + i(* - t) 3602-1 t (x'Vr1}" (W < +°°’	+0°>-
00
3603. £ (-1)"[1 +(X- l)Ky - 1)" (-0° < x< +00, о < у < 2). 3604. г = 1 +
n = 0
+ [2(* - 1) “ (У ~ 1)] - [8(* - l)2 - Ю(л: - 1 )(y - 1) + 3(у - l)2] + ... .
3605. (0, 0) — изолированная точка, если a < 0; точка возврата,
если а = 0; двойная, если а > 0.	3606. (О, 0) — двойная точка.
3607. (0,0) — изолированная точка. 3608. (0,0) — изолированная точка.
3609. (О, 0) — двойная точка. 3610. (0,0) — точка возврата (второго
рода). 3611. (О, 0) — двойная точка. 3612. Если а < Ъ < с, то кривая
состоит из овала и бесконечной ветви; если а = Ь < с, то А (а, 0) —
изолированная точка; если а < Ъ = с, то В (Ь, 0) — двойная точка; если
а = Ь = с, то А (а, 0) — точка возврата. 3613. (О, 0) — двойная точка.
3614. (О, 0) — точка возврата. 3615. (О, 0) — точка прекращения.
3616. (О, 0) — угловая точка. 3617. х= кп (к — 0, ±1, ±2, ...) — точки
разрыва 1-го рода. 3618. х = 0 — точка разрыва 2-го рода. 3619. х = 0 —

ОТВЕТЫ
533
двойная точка. 3620. х = kn (k = 0, ±1, ±2, ...)— точки возврата.
3621.	2min = 0 при х = 0 и у = 1. 3622. Точек экстремума нет. 3623. Не¬
строгий минимум 2=0в точках прямой х - у + 1 = 0. 3624. 2niin = -1
при х = 1 и у = 0. 3625. 2шах = 108 при х = 2, у = 3; нестрогий минимум
2 = 0 при х = 0, 0 < у < 6; нестрогий максимум 2 = 0 при х = 0,
-ОО < у < 0 и 6 < у < +°°.	3626. 2min = -1 при X = 1 и у = 1.
3627. a) 2lnin = -2 при л:1 = -1,1/1=-1ил:2 = 1,1/2 = 1; экстремума нет при
х = 0 у = 0; б) максимум 2 = 0 при х = 0, у = 0; минимум 2 = -1 i при
о
х= ±\у у = ±1; седло г = -1 при х = 0, у = ±1, и седло 2 = -i при
2 8
у = 0. 3628. Минимум 2 = 30 при х = 5 и у = 2. 3629.2min = -
аЬ
зТз
при - = - £ = +-— ; Zmax = ^ при £ = 2 =	. 3630. 2шах = л/а2 + Ъ2 + с2
а Ъ JI	73	а	Ь Jз
при х = - у у = - у если с > 0; 2lllin = -*/а2 + Ь2 + с2 при х = - у у = - у если
с	с	с	с
с < 0; экстремума нет, если с = 0, а2 + Ь2 ^ 0. 3631. 2max = 1 при х = 0 и
у — 0. 3632. Минимум 2 = 0 при х = 0У у = 0; седло 2 = | е-2 при х =	,
у = -|. 3633. Седло г = е3 при л: = 1, I/ = -2. 3634. Максимум 2 = е 13 ~
~ 2,26 • 10 6 при х= 1, у = 3; минимум г = -26 е 52 ~ -25,51 при х = -— ,
I/ = -^ . 3635. Минимум 2 = 7 - 10 In 2 ~ 0, 0685 при л: = 1, z/ = 2.
3636. 2„шх = |л/3 при ле = 5 и у = |. 3637. zmin =	при л; = у = у ;
гтпх = ПРИ * = У = | • 3638. Седло г=-1 + |1п2+2л = 1,70 при
8	3	2	4
х = 1, у = 1. 3639. Минимум 2 = -J- ~ -0,184 при х = у = ±—±0,43;
2е	J2e
максимум 2 = — при х = -у = ±—^— ; экстремума нет в стационарных
2*	J2~e
точках л: = 0, г/ = ±1 и л: = ±1, у = 0.	3640. Стационарные точки
* =	(_1Г +1 + (т +	^ = 15(_1)т + 1 +	(т’ п = °’	±2’ ->•
Экстремум 2 = тл +	+ ^3 j (-l)m 1 1 + 2 • (-1)", если тип различной
четности (максимум при т нечетном и п четном, минимум при т чет¬
ном и л нечетном); экстремума нет, если ти п одинаковой четности.

534
ОТВЕТЫ
3641. 2min = 0 при х = 0 и у — 0; нестрогий максимум z = е 1 при
х2 + у2 = 1. 3642. umin = -14 при х — -1, у = -2, z = 3. 3643. Минимум
и = -6913 при * = 24, у = -144, г = -1. 3644. Минимум и = 4 при л: = |,
I/ = 1, г = 1. 3645. ишах = ~ при х — у — 2 — |; нестрогий экстремум и = 0
при I/ = 0, х 9й 0, z *0, дг + 2i/ + Зг 5й а. 3646. Минимум и =	ПРИ
4	v 16&
* = | xVl 6а14Ь , г/= i %/16a4b , z = |	• 3647. Максимум и = 4 при
х — у — z — |; краевой минимум и = 0 при лг = у= 2 = 0и2 = у = 2 = я.
6
3648
Г 2	2
• Ищах = -Т			2 при JCt = л:2	=	•••	= Хп =	—		.
тах и2 + л+2;	*	1	2	п л2 + д + 2
— — 2 „
3649.	Минимум и = (п + l)2n+1 при хх = 2Л+1, л:2 =	хп = jcx .
3650.	Числа a, jclf л:2, ...» xni b составляют геометрическую прогрессию
со знаменателем q = a+i - . 3651. Минимум zx — -2 и максимум z2 — 6
при дс = 1, у = -1. 3652. zmin = -(4 + 2л/б ) при х = у = -(3 + Тб );
2тах = 2л/б - 4 при Х = у = -(3 ~ Тб ). 3653. Нестрогий минимум 2 =
272
при х2 + у2 =	, 2 < 0; нестрогий максимум 2 = при х2 + у2 =	,
8	272	8
г > 0.	3654.	= 1 при * = |, у = |.	3655. 2„lin =	при
~ _ ьt	.. _ _ ае . ,	_ л/о2 + Ь2   „ _ be _ at
J*7b*,y	тш И1 р
где е - sgnab * 0. З656.гт.х=	при * =	у-
3657. a) 2min = Х1э 2тах = Х2, где Xj и Х2 — корни уравнения (А- Х)(С -X)-
- Б2 = 0 и Xj < Х2; б) максимум z = 106i при * = ±1 i , у = ±4; минимум
4	&
2 =-50при* =±2,2 =+3.3658. Экстремум 2 = 14- при* = £ + ^ ,
72 8 2
у — -2 + (Л * 0, ±1, ±2, ...) (максимум, если k — четное, и мини-
8 2
1	9
мум, если k —* нечетное). 3659. umin = -3 при дг = - ±, у = ^, 2 = -
2 .
3 ’
3	при *= 1, р = -|, 2-|.	3660. Цщах = -ат П*Р.т”'пПРР при
3*3	3	тах (/д + л + р)т + п+р

ОТВЕТЫ
535
— = ^ = - =			. 3661. umin = с2 при х = 0, у = 0, z = ±с; итах = а2
ш п р	fit + п + р
при х = ±а, у = О, г = 0. 3662. ышах = (|) при л: - у = г - |. 3663. a) umln =
= -Г^ пРи*=У=-^ иг=-1.д: = 2 = 1 и!/ = -1,1, = г=1и
3 76	76	76 76 76	76
лс = ^’и'-=^прилс=г/ = ^и2=^’" = г = -^ иу = ^’
1	2
у = г = - — и х = — ; б) Условный максимум и = 2 при х = 1,
Тб	Тб
у = 1, г = 1. 3664. итм = | при х = у = г = 5.3665. umln = X, и umax = Х2,
где X, и Х2 - корни уравнения X2 -	+ в +	X + fesiS +
+ S2& +	= О (X. < Х2).	3666. umln = mAcosa + Bcos^+Ccos^
а2с2 a2b2) V 1	21	A2 + B2 + C2
и,„ax = R2- 3667. Umin =
при xi= —
a<
(i- 1, 2,
3668. umm
_ aP
nP-
4 /=1
при
а
= 1, 2, ...,
л). 3670. итвх
а2
°п X,
.аге при —
«1
Хо х„
•2 •«
1«
II
II
1а
II
- при xt = s (i = 1, 2, .... rt). 3669. umin = [ X a/ajp) )
( Z ) ' (f “ 1
= (	-	V<!* «2 *-*«» а“1а“2	а"»
Vaj + a2 + ... + aj
=	-	. 3671. Экстремумы и = X определяются из уравнения
dj + a2+ ... + a„
\ai} - X8/y| = О, где 8/y = 0 при i j и 8^ = 1. 3675. Inf z = -5, sup г — —2.
3676. Inf z = -75; sup z = 125. 3677. Inf z = 0; sup 2= 1. 3678. Inf и = 0;
sup a = 300. 3679. Inf и =	; sup и = 1 + */2 . 3680. Inf и = 0; sup и =
= e-1 ~ 0,37. 3682. Нет. 3683. Минимум равен — . 3684. Слагаемые равны.
nJa
i
i i
3685. Множители равны хь:
«я	«1	«■
аах а2 ...а„
(i= 1, 2, ..., л),
(а,)"
где ос, (t = 1, 2, ..., п) — соответствующие показатели степеней;

536
ОТВЕТЫ
acLi ol22...CLn
i-'i-+JL +
1 (<2
наименьшее значение суммы (— + — +
\ax a2	aJ
1 n	l"	n
3686. x = —- У m,xh у = — У где M = V m*. 3687. Измерения
M ,4i	м Н	,4i
ванны V2F, V2F, £ V2F. 3688. Я = 2Я = 2 /Ж , где R — радиус
2	V Зя
цилиндрической поверхности и Н — ее образующая. 3689.	xh
N £-1
-.n	irt	{ п л2 s' п л2 s' п \2
У=* Jj £ У1,г = — £ 2„гдеЯ -	+ (Yy,l + (Уг/) -Минимальная
сумма квадратов расстояний равна п -2N +	(*f + i/f + z? ).3690. Угол
о
наклона образующих конуса к его основанию равен arcsin - . 3691. Угол
о
наклона боковых граней пирамид к их основаниям равен arcsin |.
о
3692. Стороны прямоугольника ^ и ^ . 3693. Стороны треугольника
О	о
«» ^ и ^ • 3694. Измерения параллелепипеда ^и -5-.
2	4	4	7з	7з 7з
3695. Высота параллелепипеда равна i высоты конуса. 3696. Измере-
о
ния параллелепипеда % , и ~ .	3697. Высота параллелепипеда
Тз л/2	л/2
Л = I sin а • -te°S., если а > arctg л/2 , и Л = 0, если 0 < а < arctg л/2 .
2tga- V2
3698. Измерения параллелепипеда a, b и £ . 3699. i^-*? t + Сг°+	.
2	л/А2 + В2 + С2
3700. с/ =
±д
У1-|/2 *1-*2
т1	пх	рг
т2	п2	р2
. гдеД = J
Ш\ пх
т2 п2
2
+
п1 рг
П‘2 Р2
2
+
Pi "Л
р2 т2
3701.	. 3702. Квадраты полуосей а2 = и Ь2 = Х2 являются корнями
4л/2
уравнения (1 - ХА) (1 - ХС) -Х2В2 = 0. 3703. Квадраты полуосей а2 = Х19
Ь2 = Х2 и с2 = Х3 являются корнями уравнения
АЛ - 1 DX FX
ZU ВЛ-1 ЯЛ
FX EX СХ-1
= 0.

ОТВЕТЫ
537
3704. 2^ -М2 + В2 + С2.3705.	яа&с ■	. 3707. Угол паде-
|С|	Ja2 cos2a + 62cos2(3 + с2 cos2y
ния равен arcsin ^ п sin ~j ; отклонение луча равно 2 arcsin ^ п sin - а.
3708. Искомые коэффициенты а и Ъ определяются из системы уравнений
я	я
a[*x] + Ь[*1] = [дсу], a[xl] + Ъп = [i/l], где [*{/] = £	[*1] = £ х„
<= 1	i= 1
я
[г/1 ] = ^ У(. Задача имеет определенное решение, если ^ (л:/ - xjf ^ 0.
3709. tg 2а =
~ГГ. _ 1 V"
2 (ху-хц)
Ч/) __п = х cos а + w sin а, где а: = i V л:;,
и2 — (1Л2 I	Л “i
—	1 т-ч	7	1
ху — — ЛГ/I/, и т. п. суть средние значения. 3710. 4* - 1; Amin = ± .
Раздел VII
3711. F(y) = 1, если —оо < у < 0; F(y) — 1 — 2 г/, если 0 ^ у ^ 1;
F(i/) = “1» если 1 < у < +оо.	3712. F(i/) разрывна при у = 0.
3713. а) 2 ; б) 1; в) |; г) In ; д) 0. 3715. Нельзя. 3716. Нельзя.
4	3	1 + е
X2
3717.	F(x) = 2хе~** - е'*3 - f у2е~^г dy. 3718. a)-(ea|5in 0,1 sin а +
+ е0'008 “I cos а) + J Jl - х2 еа^1 ~х2 dx; 6)^1 +	sin а(6 + а) -
sinu
u
- (А 4- sin a(a + а); в) - ln(l + a2); r) /(a, -a) + 2 f f'u (и, v) dx, где
v a a + aj	a	J
о
u2 + u	a2
и = * + аио = *-а;д)2а J sin (y2 + a4 - a2) dj/ + 2 J sin 2x* cos 2ax dx -
- 2a J dx J cos (x2 + y2 - a2) dy. 3719. F"(x) = 3f(x) + 2x f(x).
0	x — it
3720. F"(x) = 2f(x), если x € (a, b), и F"(a:) = 0, если x € (a, b).
3721. 1. F"(x) =	, где A2 f(x) = f(x + 2A) - 2f(x + Л) + fix').
h2
2. F^x) = (n - 1)!Дх).	3723. 4* - П.
3
3724. 0,934 + 0,428a:

538
ОТВЕТЫ
(приблизительно!). 3725. g -	g - jjjfpj - £.
3729. F'x'y (x,y) = x(2 - 3y2)f(xy) + ^/(j) + x2y( 1 - у2)Г(ху).
3732. я In	3733. О, если |a| < 1; я In a2, если \a\ > 1.
3734. | sgn a In (1 + |a|).
3737. In ^±4 • 3738‘ a> arctg
3735. я arcsin a.
b - a
3736. | In (1 + 72 ).
	. 6* 11 62+ 25+ 2
1 + (a + 1)(5 + 1) *	2 Шд2 + 2a + 2
3741. a > 0.
3742. Max (p, 7) > 1. 3743. lEzil < 1. 3744. p < 1. 3745. /г < 0 и n > ± .
17 1	2
3746. p > 1.3747. Сходится при a > 0 и при a = --/l-~ 1 я (тг = 1, 2, ...).
3748. Сходится при л > 4. 3749. Сходится при р > 1. 3750. Сходится
при -1 < п < 2. 3755. 2. а) Сходится равномерно; б) сходится неравномерно.
3756. а) Сходится неравномерно; б) сходится равномерно. 3757. Схо¬
дится равномерно. 3758. Сходится равномерно. 3759. Сходится
неравномерно. 3760. а) Сходится равномерно; б) сходится равномерно.
3761. Сходится равномерно. 3762. Сходится неравномерно. 3763. а) Схо¬
дится равномерно; б) сходится неравномерно. 3764. а) Сходится нерав¬
номерно; б) сходится равномерно. 3765. b > Ю70. 3766. а) Сходится
равномерно; б) сходится неравномерно. 3767. Сходится равномерно.
3768. Сходится неравномерно. 3769. Сходится равномерно. 3770. Схо¬
дится равномерно. 3772. Нет. 3776.1.	3777.1. 1. 3778.2. а = ±1.
3779. Непрерывна. 3780. Непрерывна. 3781. Непрерывна. 3782. Непре-
рывна. 3783. Разрывна при a = 0. 3784. LzlUml. 3785. 5 • (2" ~	* 2)
пт*1	2	(2п)!!
3788. In ^ . 3790. In $ . 3791. 0. 3792. 5 in 2 . 3793. i In £ .
a	a	2	5	2a
ym v). 04 vo.
a2 + m2
3794. In L2-g)2;(2P)2; 3795 arctg 1 _ arctg a
(a+p)2,t+2«*	m	m
3797. —rc(l - л/1-a2). 3798. itln 1 + ^ ~	.3799. \ sgn a • (1 + |a| - VT+oT2
L*	&4
3800. i In (|otJ + P|) (P * 0).	3801. I In fo+Py*11 (a > 0, P > 0).
3802. ^ [aP(a + P) + a3 In a + P3 In P - (a3 + P3) ln(a + P)] (a > 0, P > 0).
о
3803.
2
3804.
c- h2
3805.
(a + 2 52)a1
- 4abbl + 2a2c1 fit ~
2a2	Vfl ^
-b2

ОТВЕТЫ
539
3806. /"Л.	3807. Qe'la. 3808.	~ Л).	3809. \ £ е~*‘ .
Ча	2	2ча
ь2
381°*а) С ^; б) (_1)В2^ £~п <е'62) • 38121- 5 sgn Р- 2. Функция
нечетная. При х > 0 минимумы в точках 2kn и максимумы в точках
(2k - 1)я, где k = 1, 2, 3, ... Асимптоты у = ^ при * —* +оо и I/ = -|
при л: -*• -оо. 3813. я!й - Jna. 3814. i In . 3815. О, если |а| < |(5|;
2	2	|ос — р|
7 sgn а, если |а| = |р|;	£ sgn а, если |а| > |р|.	3816. ? sgn а.
4	2	4
3817. 2 Ы 3818. ^а|а|.	3819. 2.	3820. £ In |“|.	3821. 2.
2' 1	8	1 '	4	8	|р|	4
3822. ^ arctg ^	^ arctg + * In	11'. 3823. Щх) = 1
2	2	2	2	4 л2 + (а+р)2
при |*| < 1; D(x) = i при х = ±1; D(x) = 0 при |*| > 1. 3824. а) я sgn a cos ab\
а
б) п sgn a sin аЬ. 3825. 2 е-М. 3826. 2 Sgn ae‘w. 3827. 2(1 - е-2).
2	4	4
3828. 5Й±М)е-Н 3829. к cos—	_ 3830
4
1 /я.	1 /я
Jac -Ь2~ а	2^2*	2 v2 *
3831.	sin(^2£^f + 2ggn	. 3832. Jn cos (a2 + 2). 3833. Jn sin (a2 + |j.
3835-а)^:б)^;В)?^ПРИР>а:Г)(^;Д)^;е)1П(1 + р);
ж)	«у.я в 4Р 3837. а) 1; б) х2 + i ; в) е2ах + а2; г) i е 4 cos a*.
2 рл/р	2	2
лг2
3839. (р(л:) = -1= е"2°2, где а = Jo\ +	. 3843. 5.3844. ^ . 3845. -2- .
Ол/2я	»	16	2^/2
3846.
2я
зТз
. 3847. -2- . 3848.	. 3849. —2— . 3850.	*)!! Jit.
272	512	_„:_n	2»*'
nsin-
л
3851. —2— (0 < т < п). 3852. В (л - т, т) (0 < т < л). 3853. ^(Y) " х
_ тп	п \bj
X В (, р - Ш±1) Го <	< р ). 3854. - -С» ~ а>"	, В (т И-1, л +1)
V д	д А п )	(а + c)n + 1(b + с)т+1
(т > -1, л > -1).	3855. ± В р- , 1 - ±1 (л < 0 или л > 1).
т \т	п)

540
ОТВЕТЫ
3856. i В(, 5L±i) (т>-1, п>-1). 3857. —5— (|л| < 1). 3858.
и \ и	и )	О П/ЧР.^^
2„„„ U JL
COS
2
2"-1
(1 - k2)2
хВ (1' |) 1» > »>• 3859 ; г © I» > О)- **»• й г (=^)	5 0) •
3861. Г(р+1)(р>-1).	3862. 4- rri£±r1Jl (P>-1).	3863. -n2cosPn
dp I аР+1 J	8т2ря
з
(0 < р < 1).	3864. а) к3 1 + cofPn (0 < р < 1); б) J- л2; в) -2^1.
sm3prc	27	32^2
(0 <р < 1, О < q < 1). 3866. л ctg кр. 3867. ^tg|5.
tgf
3865. In
2
tgf
3868. In
л/2я
3868. In 72it. 3869. In J2n + a (In a - 1).	3870. 1 ( 1 + In |).
3871. -i-.	3876.
4 n
2Г(т)сов^
(a > 0).	3877.
2r(m)sin^5
(a > 0).
3879. aB fi .	3880.
l2 2 n)
2ofr7l'|
n \n)
■0
3881. Дх) = - f cos Xx dX.
я J A
3882. Дх)-? f	sin Xx dX. 3883. Дх) = 2 f gfrte-.gfcS^f—») dX
Я J Л.	Я J	A
о	0
+ oo	+ co
3884. Дх) = — f 1_ °°saX cos Xx dX. 3885. —A— =i Г e-“A cos Xx dX.
,v ’ na J X2	a2 + x2 a J
3886. ——- = f e^sin Xx dX. 3887. Дх) = 2 f ^5 sin Xx dX. 3888. Дх) -
a2 + x2 J	я J 1 - A2
+0° COS ^7-
2ялА
= 2 f 	2 cosXjc dX. 3889. ДО = — f “V sin Xt dX. 3890. Дх) =
я J 1 - А2	я J A2 - w2
о	о
+ oo	+oo
- 2s f S22±£ dX. 3891. Дх) = “ f Г—-Ц	, + -—7-	-1 cos Xx dX.
я J A2 + a2	я J L(A-P)2 + a2 (A+P)2 + a2J
о	0
f OO
3892. fix) =	f 	AsinA*	 dX 3893 X2 = J_ x
Д } я J [(A. - P)2 + a2||(A + P)2 + a21	J~n
x2
x2
x f e 4 cos Xx dX, 3894. xe~x2 = -i- f Xe 4 sin far dX.	3895. a) e * =
J	2ТЙ J

ОТВЕТЫ
541
+ оо	+оо
= | J 92SLI dX (0 < x < +oo); 6) e"x = 2 |	dX (0 < x < +oo).
О	О
3896. F(x) = /1 • —2— . 3897. F{x) = -i fe—2*— . 3898. F(x) = e‘^ .
*ln x2 +a2	' '	»Jn(x2+a2)2	' '
xi+of
3899.F(x) = c 2 chax.3900.a)<p(y) = e«(y>0);6)V|i(y) = - • -У— (y>0).
71	1 + y2
Раздел VIII
3901. 1.3902. S-i2-H+_^;S=^+lI+-^;13l. 3903.9,88.
4	3 n Zn2	3 n 3n2	3
Точное значение 2я(7 - ,/24) = 13,20. 3904.0,402. Точное значение 0,4.
3905.	8 < 0,00022. 3906. 1. 3907. i . 3908. ^ . 3910. / = F (А, В) -
- F (А, 6) - F(а, В) + F (а, Ь). 3912. а) Отрицательный; б) отрицательный;
в)	положительный. 3913. - . 3914. 1,96 < I < 2. 3915. а2 + Ь2 + ~ .

542
ОТВЕТЫ
2-U
+ J dy J (f(x, у) dx. 3925. J dy J f(x, y)dx + J dy J f{x, y) dx.
2	VL	-1	-27Г77/	0	-2 JTTy
2
l Vy	о Ji -1/2	i
3926. | dy | f(xt y) dx. 3927. J dy J f(x, y) dx + j dy J fix, y) dx.
3928. J dy J fix, y) dx. 3929. J dy
2-У
VI -V*
a - Ja2 - y2
-VT7,
J f(x, y)dx+ J f(x, y) dx
4b U	4b (4	1	Г	A	II niVOIIIj/
+ J	dy J	fix, y)	dx.	3930.	J	dy	J	fix,	y) dx.	3931.	J	dy	J	fix, y)	dx	-
a	^2	0	ry	0	nrcsinj/
2 a
0	2n + arcelnny
- J dy | f(x, y) dx. 3932.	. 3933. ( 2 V2 - |'jaja. 3934. ^ .
-1	л - arcsinr/
2л	a
3935. 14a4.	3936.	.	3937. J d(p J rf (r cos ф, r sin ф) dr.
0	0
it
2	a cos<p	2n |ft|
3938.	J* c£q>	j*	rfir cos cp, r	sin	(p) dr.	3939.	J	dcp	J	rf (r cos cp, r sin (p) dr.
л	0	0	|<||
2
-Lc«ec(.*!)
osiny
4 сов2ф
3940.
I* I rf (r cos (p, r sin cp) dr. 3941. J dcp J rf (r cos cp, r sin cp) dr +
3n	a
4	ein<p
asincp
СОВ2ф
+ J* dcp j* rf (r cos cp, r sin cp) dr + J dcp J rf (r cos cp, r sin cp) dr.
Зл
4
3942. В том случае, если область интеграции ограничена двумя концент¬
рическими окружностями с центром в начале координат и двумя лучами,
4	С08ф
исходящими из начала координат. 3943. j* dcp J* rf (r cos cp, r sin cp) dr +
о	0
Л	1	л
2	81ПФ	1	2
+ J dcp J rf (r cos cp, r sin cp) dr = J r dr j f (r cos cp, r sin cp) dcp +
4

ОТВЕТЫ
543
Г- nrcsin- j;
75 г 2 1
Г r dr Г /(r cos cp, r sin cp) dcp. 3944. f dcp f
rf(r cos cp, r sin cp) dr =
J J J J
arccos- J_co8ec^4>+^
7 + arccos-^—
1 4 rj2
я 2
3 С08ф
Г r dr f /(r cos cp, r sin cp) dcp. 3945.
f d<p f rf (r)dr =
J J
j j
-p arccos—ip
75 * rj2
я 0
4
272	4	;
~ J rf (r№r + J (f ” arccos -) r/(r) dr.	3946. Jdcpx
0	272	°
1
aiesin'
Л + 4r2-
СОвф
1 arcsn
2r
x 1 r/(r cos cp, r sin cp) dr = Г r dr
J
/(r cos cp, r sin cp) dcp +
sing»
0
0
cos2«p
r- arcsln^-^p-—-
J2 2 r
я
4 a,
fcos2<p
-f Jrdr
j f(r cos cp, r sin cp) dcp. 3947.
]<*.
J r/(r cos cp, r sin cp) dr =
1
arccos-
r
я
4
0
a
1	r2
-arccos—
2	o2
arccos-
a a
= f rdr
f /(r cos cp, r sin cp) dcp.
3948.
f dr f /(<p, r) dq>.
J
0
J
1	r2
--arccos—
2	o2
J J
0 nrj1jr
—arccos—
о
a
5- -arcsin^-
2 2 a2 a a
1
3949. f dr
f /(cp, r) dcp. 3950. f dr f
/(cp, r) dcp. 3951. 2я Г r/(r) dr.
J
0
J J J
1	r2 Or
-arccos—
2	o2
0
3952. к J rf(r)dr + J ^ к - 4 arccos i j r/(r) dr. 3953. | J f(tg (p) cos2 cp dcp.
0	1	я
2
3954.2.	3955. -6я2. 3956. - • 62 +	+ A) + (ft + A)2 + (2& + h)Jb{b +h} .
3	5 Ja(a + h)(Ja+ Ja+ h)(Jb+ Jb+ h)
3	ft	p	24-u
|(£)5.3957.	J	u du	J	f(u, uv) dv. 3958.	| J da J	; “zJ'j	rfu.
a	a	1 -u
я
2	a
3959.4J* sin3 v cos3 vdv j uf (u cos4 у, и sin4 y) du. 3961. и = лгу, у = x - у.

544
ОТВЕТЫ
3962. | f(u) du. 3963. 2 J Jl - u2 f(uja2 + b2 + c) du. 3964. In 2 J /(a) du.
-i	-i	i
3965. 2.3966. |. 3967. % nab. 3968. -b . 3969. 543. 3970. 13L - ln 2.
2	3	3	15	128
3971. 2n. 3972. £ n. 3973. § + 2 . 3974. £ л + 8 ln i±7| . 3975. 6.
16	3	4	3	Д
3976. | (4-372 +473).	3978. f(0,0).	3979. -F(t), если t > 0.
3980. 2 f f	* + У djc dt/. 3981. F'(t) = f (f cos cp, t sin cp) dcp.
JJ	J
(x-o2 + (y-02< 1	0
3984.	- 2 ln 2^ a2. 3985. | (p + g) Jpq . 3986. Jia2. 3987. ?-7|~.2 a2.
3988
.. 2 + ^ ln(l + 72).	3989. 2£f.	3990. a2^ + arcsin ^ .
3991. 2“*(“! + *f). 3992.	“1 + *1) + “!*!] . 3993. 2^2! +	,
4	U2 *2J	3 ЬзТз^Л^	A2*2J	6U2	k2)
3994. a)	; 6) -7. -(a6).s. 3995. — . 3996. (P~ «)(62- a2)
; 6hHak + bh)2 ’ 1260 c8	70	2(a + 1)(B + 1)
3997. 2- ln 2.
2
2(a+ 1)(P+ 1)
3998. a) | (q - p)(s - r); 6) ± (ft5 - as)(<r3 - d~3);
B) (p/l)"(?+!)(»” " a^)(c3999. a) ^ ab; 6) ^ ( arctg | +
+ Ш ab. 4000. c4 (7l0 - 2) arcsin i . 4001. £ . 4002. ^ [(u, - n,)(sh 2u, -
257	о	3	|o|	4
- sh 2u,) - (u2 _ «i)(sin2u2 - sin 2w,)]. 4003. \ na2. 4004. -^L. 4007. - .
3	7 77	6
4008. 25!“ - 2 R3. 4009. ^ . 4010. n. 4011. n. 4012. И - 2 ln 2.
4	3	105	12
4013. -i-r2(if)a3.	4014. 5.	4015. £jjt. 4016. ±£a3. 4017. 2Bl.
37S	8	32	9	8
4018. л(1 - e «2). 4019. 2a2c • (p-«)(^~2). 4020. 2.4021. | nabc(2 - Л).
4022. I nabc(2 J2 - 1).	4023. ^22&£.	4024. §Jta5c. 4025. ^ .
4026. I abc (Зл + 20 - 16 72 ). 4027.	^ . 4028. | a4. 4029. |.

ОТВЕТЫ
545
r3(i)	rfiym
4034.	. 4035. аЬс Ui Ы
Зп2 рГЗ^|	2т + п гП+2'|
V п)	\т п)
. 4036. \ па2 (2 72 - 1). 4037.16а2.
О
4038. 8а2 arcsin - .	4039. — .	4040. 8а2.	4041. nj2 .	4042. — .
о	72	2
4043.	(1 + | 1п3) + | arctS j= ■	4044. ^ (20 - Зл).
4045. а) 2а2; б) | [3 ТТо + In (3 + 7Т0)]; в) | аЪс (1 + ±)'' [(i + ± +
+ ^)2 -£]sr)| ab (272 - 1) arctg ; д) | In (c + e'1). 4046. S = 4л(3 +
+ 273 )а2; V = ^ а3. 4047. (ф2 - <Pi)(sin ф2 - sin V|/,) В2, где ф„ <р, —
73
долготы меридианов, \|/i, \|/2 — широты параллелей, R — радиус сферы.
4048. к I aja2 + /г2 + h2 In	|. 4049. S = а(ср2 - cpi)[& (\|/2 “ Vi) +
+ a (sin \|/2 - sin \|/j)]; 4тс2а&. 4050. со = arcsin
. fec ; w ~ ^ ■
V(a2 + b2)(a2 + c2)	“2
4051. ^ [2 + 72 In (1 + 72 )]. 4052. *0 - -5 ; </o - f a- 4053. *0 = «/0 = f •
6	Zoo
4054. *„ = </o “ ^a. 4055. % = ^ 5 Уо -	• 4056. *0 = Vo = f •
4057. *0 = § а; у,, = ^	4058. x0 = ла; y0 = | a. 4059. *0 = ~f ; Уо ” 0-
О	S#7l	D	5
4060. Парабола y0 = | 730pxo . 4061. Zx = ^	(ft = |ft, - ftj).
4062.	(16 - 5л). 4063. Ix = z„ - 49ла<
32
32
.4064./ =/„
Зла4
472"
4065.	Zx = 7у = | a4. 4066.1. Z0 = ^ . 2.	. 4069. Za =	. 4070. X = ah2;
Y = 0, где Xy Y — проекции силы давления на оси координат Ох и Оу.
4071. Рх = тш25 [h ~ |aj;P2 = тш25 + | a j . 4072. Проекция силы
давления на оси Ох и Oz, расположенные в вертикальной плоскости, про¬
ходящей через ось цилиндра, из которых ось Ох — горизонтальная, а ось
Ог — вертикальная, соответственно равны: Хх = -тш2Ъ ^ Л - | cos a j sin a,

546
ОТВЕТЫ
Zx = -па2Ъ {^h - | cos a j cos a; X2 = na2b + | cosaj sin a,
Z2 = па2Ь + | cos aj cos a. 4073. Проекции силы притяжения на
оси
Ох, Оу, Огу соответственно, равны: X = 0, У = 0, Z = -ZkrrjM
a2h
{\b\-\b-h\+ Ja2 + (b-h)2 -Ja2 + b2}y где£ — гравитационная постоянная.
4074. рф = \ р0.4075. А = Ы 2abja* + b2 + a3 In ^ .-/°21&г + рз ln a + Ja* + bt
4076. -±-.	4077. i ln 2 -	.	4078. i. 4079. |jtabc. 4080. 2,
364	2	16	48	5	6
4081. j dx |j dz J f(x, y, z) dy + j dz J f(x, y, z) dy
0^00	x	2-x
1	, г	1-tf	11-//
- I	dz П	dy	J	f(x, y, z)	dx	+	j	dy	j	f(x, y, z)	dx	.
0	0	z-y	x	0
1	1	Jz2-x2	1	x	Jz2-y2
j	dx	j	dz	J	flx, y,	z)	dp =	J dz	J	dp	J	/(x, p, z)
1x1 0 -x
4082.
dx.
4083. J dx J dz J f(x, y, z) dp + J dz J /(x, p, z) dp
0 0 0 ,2 /	2
*	л/г-х*
\	Jx	\	11	2	1
= | dz	|	dp |	/(x, p, z) dx + J dp |	/(x, p, z) dx • + J	dz J	dp x
0 I 0	Л ®	1 /ГЛ
1 * 1
X J f(x, y, z) dx. 4084. | J (x - Z,)2 f(Z)dl,. 4085. | J (2 - z2) /(x)dz +
2
+ | J (2 - z2) f(x)dz. 4086. F (А, В, C) - F (A, B, c) - F (A, b, C) -
1
- F (a, В, C) + F (Ay b, c) + F (a, Б, c) + F (a, b, C) - F (a, b, c).
i
2	nrctg-
4	СОвф
C08(f> C08 Ц/
4087.^.4088.^(272 -1).4089. J dtp J cosvpdy J ^f(r)dr
sinip
СОВ^ф

ОТВЕТЫ
547
4090.	4091. И!.	4092.	- Щ - ±) *<Л.
4093' Я (£ - Й №' “ “*> [ Л ( 1 + 7jT>) + 4	5 '
4п
В3
;, где 1е| < 1.4098. a) F(t) = 4nt2 f(t2);
4095.3(е- 2). 4096. и = п ,
3 Ja2 + b2 + с2 + OR
б) F'(t) = “ [ F(t) + JJJ xyz f(xyz) dx dy dz J , где £>0иУ={0
О < у <	0 < z < 0*	4099. О, если одно из чисел m, п и р нечетное;
4я . (ш- 1)!!(л- 1)!!(р- 1)!!
т+п + р+ 3	(/тг + л-f-p-h
если числа т, п к р четные.
4100. r(P+ 1)r(?+ 1)!Xr+ !).r.(s..t.l) . 4101. 1.. 4102. -1.4103. 2 а3(Зя - 4).
Г(р + q + r+ $ + 4)	35	24	3
4104.	.	4Ю5. 3- (3я - 4). 4106. ^ я. 4107. яа3. 4108. ^ . 4Ю9. ± .
6	24v	3	472	2
4110. | (2 - 72)(63 - а3). 4111. 5 • ^. 4112. а) ^ abc; б)	.
4113.	(3 - 75 ). 4114. ^ abc. 4115. ^	/5 Г2(У). 4116. a) ^
12	5	3 ty2 V 4 /	60
(“V
abc \hJ лллн (i be gr\ abc >1110 „ \ abc .
— 77ft • 4U7-a) 5Ш00; б) T • 4118‘a) 90 ’
h k
xfs +51	+5!V6)
u a; U2	'
61 I5S; ■> sf**-im- ?л 412°- ^ “ “"’MD-4m- f°‘-4122
x (1 - e’1). 4123. § abc. 4124. 5 abc Q - ±j . 4125. 37 : 27. 4126. V =
nabc2
3 h
5 na3
6
S	= ^ (672 + 575 - 1). 4127. Sh^2fl3.4128. ^ . 4129.	^ .
3 ti sin —	^
4130.
abc
mn + mp + np
-Yi-W)
UtLYnLlpJ.. 4131. |. 4132. 4яр0(i +	+ 4) e-k.
,{! + ! +Г|	2	Vk	k2
U n p)
4133.	( 0, 0, | с у 4134. x0 = i/o = | a; z0 = ^ a2. 4135. x0 ” J/o = 0;
Z° = T76^‘	^o=|a;«/0=|b; г„=§с. 4137. *o = i/o = 0; 2o ~ ^ •
4138. *0-00-1; *o=§-	4139. *„ - |^a; y0 =	2o = Цс.

548
ОТВЕТЫ
4uo.	о; ,0-i. aa.ii.ti.u.t
Г(»)'(Э
4142. х0 = а;
и =а. z — v 4143 / = аЬс3 • / = а*Ьс • 7 = fl^3g 4144 7 = JL nabc3-
У о Р* *о у. *i*o. ixy	> 1уг лп »1гх АП . «am. ixy тише,
.г __ па3Ьс. г _
1 * Л/г лл > *хг
2abc3 ,лк„ 1л\. г _2а63С/1Лс„ о^оч. г _2а3Ьс
nab3c
V = ВПаЗЬс: 7« -	4145- ^ - nF • -	20 • -	20
4146. а) Ixy = £Sg. (15я - 16); /„ = ^ (Ю5я - 272); 1уг = £±2± (105я - 92);
б) /,у = | яаЬс3; /„ = | nab3c; 1уг = | яа3Ьс. 4147. a) 1уг =	а36с;
/гх=^5я1а&3	7	5^-аЬс3; б)	;
"	25672	"	12872	"	5"2
г = JL • Л?Ш • аз6с;
(!)
аЪс3. 4148.1г =	.
15
r<iym	r<iw*)
_	i	\п) \п)	,3 r	1	v/iy vn;
"=57Ii '“<1Гe
4149.a) I2 =	(472 - 5); 6) 5 a\ 4150. £ МД2. 4153.1=Ц-{ a2 + \ h2 ) , где
15	5	9	3 V 3 у
Af = 2яр0а2/г — масса цилиндра. 4154. /0 = п а Ро. 4155. а = 27ip0	^ ,
если г < R; и = Ро, если г > Rt где г = */x;2 + у2 + г2 . 4156. и =
3 г
2
= 4я J /(р) min ^ , р j dp, где г = 7*2 + y2 + z2.4157. и = яр0
(А - г) х
: 7«2 + (А - z2) + г7а2 + z2 - [(Л - 2) |А - z| + ф|] + а21п
h - z+ Ja2 + (А - г)2
Ja2 + z2 - z
4158.	X = 0; У = 0; 2 =	, если |а| > Д, £ = ~^^а, если |а| < Д.
4159.	X = 0; У = 0; Z = -2np0G{Ja2 + г2 - 7а2+(Л-г)2 - (|г| - |Л - г|}.
4160.	X = 0; У = 0; Z = -Gp0itein2 а. 4161. Сходится при р > 1.
4162. Сходится при р > 1 и q > 1.4163. Сходится при р > |. 4164. Сходится
при — + i <1.	4165. Расходится. 4169. 	-	 (р > а > 1).
р (7	(р-9)(д-1)
GMm ,

ОТВЕТЫ
549
4170. _L_ (р > 1). 4171. 2л. 4172. -5- (р > 1). 4173. nj2(j2-l).
Р- 1	Р- 1
4174. ± . 4175. л. 4176. 5 . 4177. £ . 4178. 4= е5 , если 8 =
2	2	2	7§
а 6
b с
А =
a b d
bee
d е f
. 4179. - ab. 4180. --71-. 4181. Сходится. 4182. Сходится
е	2
2(1 - е2)2
при р < 1. 4183. Сходится при - + i >1. 4184. Сходится при р < 1.
Р Я
4185. Сходится при р < 1. 4187. 5 . 4188. тш. 4189. In 2. 4190. 2.
о	о
4191. Сходится при р > |. 4192. Сходится при р с |. 4193. Сходится
при i + i + i <1.	4194. Сходится при р < 1. 4195. Сходится при
Р Я г
р < 1.	4196. (1 - рГЧ1 - дГ'(1 - г)1 (р < 1, q < 1, г < 1). 4197. ^ .
О
3	I—
4198. 2лв(| , 1 - р ] (р < 1). 4199. л1.4200. № , где Д = |a,J. 4204. а) 5 ;
б) п(3п+ х). 4205. — . 4206. — . 4207.			. 4208. 2Л-2Г'--?.
12	п\	2 Пп\	(п - 1)!(2л + 1)	|Д|
4209.
:. 4210. —^
п - 1
2
„ „	_ /ion я2а" >4010 я 2 an~lh3
а1а2...ап. 4211.	. 4212.	.
<1*0	-Кт1)
nt 1	п 1	^
4213. -5-i—.	4218.	f f(Ju)ur' du. 4219. и = ^|л:
От1) 01)J-
2Ро Л5-
4220
где 5 = \а J и А =
a,j bt
bj с
— окаймленный определитель.
4221. 1 + 72.4222. ^а3. 4223. 2л2а3(1 + 2л2). 4224. ^(ch* 210 - 1).
15
4225. 4 J . 4226. 2(еа - 1) + 5 аё‘. 4227. 2аг(2 - 72 )• 4228. ^Ч*/,** ■
4	1 + 4л35
4229. 2а2. 4230. 5 . 4231. 5. 4232. 73 . 4233. |*0| + kl, где |*„| < а.
4234.
472
^+2{~Г
4235. f 1 + ^] 7^ •4236.« V2 arctg —М-
Ч ос )	Ja2_

550
ОТВЕТЫ
4237. ^ (За2 + 4n2b2)Ja2 + b2 . 4238. § па2. 4239. ± [ (2 + tl)2 -2^].
3	3	3
4240. -^-= Г 100 738 - 72 - 17 In	. 4241.1. 2Ь ( Ь + aarcsinE),
25672 L	17	J	V	е )
где е - ^а*~Ь‘ — эксцентриситет эллипса. 2. | p*(2j2 -1). 3.1£ (373 -1) +
+ | ta«±Ml.4242.*b-b-aJEIi;»b-! + —£*== • 4243.х* = у0 = |а.
4244. 1. Sx = Sy= ! а2. 2. ла3. 3. а) ^ а3; б) ^ а3. 4. ro= -j=-
4245. *„ = «,„ = 20 = |2.4246. *о = § ! J/o = ~|!	| • 4247. /х -	-
=	74л2а2 + Л2 ; /г = а274л2а2+Л2 .	4248. а) 0; б) |; в) 2.
4249. а) 2; б) 2; в) 2. 4250. -±|. 4251. |. 4252. 0. 4253. -2ла2. 4254. -2л.
15	о
4255. 0. 4256. 0. 4257. 2 - 1. 4258. 8. 4259. 12. 4260. 4. 4261. -2.
4
а + Ь	х2	У 2
4262. J /(u) du. 4263. -|. 4264.9. 4265. J ср(лг) dx + J у(у) dy. 4266. 62.
0	х\	У\
4267.1. 4268. л + 1. 4269. е“ cos Ъ - 1. 4271. z - ^ + х2у - ху2 - £ + С.
3	3
4272. -J- arctg	+ с. 4273. z = -	, + In \х + у\ + С.
272	2у72	(* + !/)2
4274. z = е + »(х - у + 1) + ые* + С. 4275. z -	+ С.
дхпдут
4276. z =	f arctg 2] + С. 4278. |/д| < |5.4279. i. 4280. -ла2.
Эх-Эу™ V	yJ	1-га Д2	35
4281. 2л 72 а2 sin - а ] . 4282. -S|! . 4283. -4. 4284. -53^ . 4285. 0.
хй	У2	г2
4286. Ъ - а. 4287. J ср(х) dx + J \у(у) dy + J x(z) d-z. 4288.
xi	У\	*i
j
/(a) da.
Jxl + yl + zl
4289. J а/(а) da. 4290. a = | (x3 + $/3 + z3) - 2xi/z + C.
I 2	2	2
J*i + y +zi
4291. a = x - - + ££ + C. 4292. a «= In *J(x + y)2 + z2 + arctg —— + C.
у z	x + у

ОТВЕТЫ
551
4293. А = -mg (z2 - zx). 4294. A =	(a2 - Ь2),	— коэффициент
упругости. 4295. A = Gfi - —1, где rt = Jx* + y\ + zf (i = 1, 2).
'Г1 r2y
4296. / = f f y2 dx dy. 4297. -46? . 4298. ^ . 4299. -2тшЬ. 4300.	(e? - 1).
J J	3	2	5
4301. 0. 4302. /, - I2 - 2. 4303.	. 4304. mS + ex* (p(y2) - ex> <p(yj) -
О
- m(y2- y,) - j (x2 - x,)(y2 + y,). 4305. P = ||, Q = ft* +	, Где и —
дважды дифференцируемая функция и k — постоянная величина.
4306. ^ [jcF(jc, у)] = A [yF(*, у)]. 4307. 1) / = 0; 2) / = 2я. 4308. nab.
ох	ду
4309. | яab.	4310. 2f .	4311. | a2.	4312. a2.	4313.1+-^.
8	62	3 9я/з
4314. jB(2m + 1, 2n + 1).
4315.
4316. ^
n
n
4317.	. 4318. я (n + 1)(« + 2)^; 6яr2. 4319. я (n - l)(n - 2)r>\
бяг2. 4320.1. 4a2. 4321. sgn (ad - be). 4322. / = £ sgn V), где сумма
распространена на все точки пересечения кривых ф (л:, «/) = 0 и \|/ (я, у) = О,
лежащие внутри контура С. 4324. / = 2S, где S — площадь, ограни¬
ченная контуром С. 4325. Х^(х09 у0) + Yy(x0, у0). 4326. Проекции силы
на оси координат равны: X = 0; У =	, где G — гравитационная
па2
постоянная. 4327. и = 2nxR In ~ , если р = Jx2 + у2 <R;u = 2kkR In - , если
р > R. 4328. /j = — pm cos тф, /2 = p“m sin тф, если p > 1. 4329. и = 2я, если
m
точка A(x9 у) лежит внутри контура С; и = я, если точка А(д:, у) лежит на
контуре С; a = 0, если точка А(х, у) лежит вне контура С. 4330. Кг =
= 7tpm cos тф, 1*Г2 = ярш sin тф, если 0 < р < 1; Кх = О, К2 = 0, если р = 1;
2^ = cos тф, 1^2
Оц	ди =
дх	ду
-~j sin тф, если р > 1. 4339. Q = JJd* dy;
^	s
* “ “i [(Л -	^ - (С “ -г) dy];
0.
4340. Я

552
ОТВЕТЫ
я„ = ki	г) dx-a- х) dz}; Нг = ki ^1[Й- х) dy-( n - у) dx].
С	с
4341. /, - I2 = (4я - 2j3)a4.	4342. 7-nj2a3.	4343. яа3.
4344. 2(1 + 72).	4345.	+ (7§- 1) In 2.	4346. И5Ф^.1.
4347. 15 обе fЛ + Л + Л) •	4348. я2[а./Г+а2 + In (а + УГГ^)].
3	\а2	о2	с2)
4349. ^ sin а cos2 а (о < а < ^]. 4350. Ц J2 а4. 4352.1. ?.д(1 + 6-/3)
2	V	2;	15	15
2. яа2. 3. -51.4353. | яр0а4. 4354.	. 4355.a) *0 = % ;
2л/3	3	12	2
Уо = 0; 20 = а; б) *„ = у0 = -5- ; г0 = 5 (V2 + 1).	4356.1. а) 40а4;
9л	2V2	л
б) яЯ£д(Д + Н)2 + | Н3 J . 2. у| . 4357. Проекции силы притяжения на
оси координат X = 0; Y = 0; Z — nkmp0 In |. 4358. и = 4яр0 min ^а, 1 j ,
где r0 = Jxl + yl + zl. 4359. F(t) = 5L (3 - если И < Л ; F(t) = 0,
если И > 73 .	4360. F(0 = я(8~5^) *<.	4361. F = 0, если t < г - а;
6
F ” -I [а2 - (г - I)2], если r-a<t<r + a;F = 0, если t > г + а (< > 0).
4362. 4яа3. 4363.	+ eW~g<,0) +	аЪс. 4364. 0.
4365.	-12 (а262 + а2с2 + Ъ2с2).	4366. ^ (а + Ь + c)R3. 4367. -па2 Л ■
аос	3
4368. ^.	4369. 2 пл S. 4370. 0.	4371. -2яа (а + К).	4372. 2яДг2.
4373. -|а3. 4374. 0. 4376. 3 [[[ (х2 + у2 + г2) dx dy dz. 4377. 0.
V
4378.2JJJ
V
dxdydz
aJx2 + y2 + 22
. 4379. jjj
V
A и dx dy dz, где A и =
ox2
, d2u , d2u
dy2 dz2
4380. 0.	4384. 15 ( a2 +	|c|.	4385.1. | a3. 2. 2я2а26.	4387. За4.
4388. Ш яа8.
4389. 1.	4390. -541
2
4392.	а) / - 0; б) I - 4я.

ОТВЕТЫ
553
4401.1.	a) grad и (0) = 3/ - 2у - 6k; |grad и(0)\ = 7, cos а = |, cos Р —	,
cos у = -5 ; б) grad и (А) = 6/ 4- 3у, |grad и (А)| = 3 Jb , cos а =	,
7	л/5
cos Р = -р , cos у = 0; в) grad и (В) = 7/, |grad а (Б)| = 7, cos а = 1, cos (3 = 0,
V5
cos y = 0; grad ц = 0в точке M (-2, 1,1). 4401.2. grad и (М) = 12/ - 9; - 20k,
Igrad и (М)| = 25, cos а = ||, cos Р =, cos у =	; |^ = А .
4402. a) jcz/= 22; б) jc = t/ = 0 и х = у = z; в) х = у = z. 4403. г =1.
4404.	+1^-1 (и > 16);	= 1; шах и = 20.
и2 - 256 и2	960	1024
о
4405. cos ф = —- . 4406. Поверхности уровня — полости конусов; поверхности
равного модуля градиента — торы, inf и = 0, sup и = 1; inf |grad и\ = 0,
sup Igrad и\ - i . 4407.:	j-j^l	. 4409. a) I; б) 2r; в) . 4410. /'(r)J .
2	|gradu(x0, y0,20)|	’ r'	’ r3	Wr
4411. c. 4412. 2r(c • c) - 2c(c • r). 4415. a) grad u = ^ er + e„ + ^ e2, где
dr rd(p v dz
er = icos ф 4- jsin ф, еф = -isin ф + jcos ф, ez = k — орты, касательные к соот¬
ветствующим координатным линиям; б) grad и = |^ег+	^ + —I—^ ем,
Эг гЭ0	г sin 0 Эср v
где er = i cos ф sin 0 + j sin ф sin 0 + k cos 0, ee = i cos ф cos 0 + j sin ф cos 0 -
- k sin 0, еф = -i sin ф 4- j cos ф — орты, касательные к соответствующим
координатным линиям. 4416. ^ = — , где г = Jx2 + у2 + z2 ; ^ = Igrad и\,
Эг г	Эг
если а = Ь = с. 4417.
ди __ _ cos(/, г) . ди
Ы	г2 ’ Ы
0, если 1JL г. 4418.
ди __ grad и grad у .
Э/ Igrad и|
^ - 0. ег-ли grad и I grad ». 4419. а - t(J^,+y»H(.£557t+«»)+h(«-y)»
Э'	(x2+y2 + z2)Jx2 + y2
4420. g = с,л:, г = с2хг. 4423.1. div а (М) —	; П = де3. 2. 0.
125	125
4425. div (grad и) = А и, где Да =	. 4426. f"(r) + - /'(г);
дх2 ду2 дг2	г
f(r) = с 4- — , где chcj — постоянные. 4427. а) 3; б) - . 4428. (с • г),
г	гг
4429. 3/(г) + rf(r); (/г) = 4 > гДе с постоянна. 4430. а) и Ди + (grad а)2;
г3
б) а Ди 4- grad а • grad и, где Да — оператор Лапласа. 4431. div v = 0;
div w = -2co2.	4432. О, вне притягивающих центров. 4433. div а =

554
ОТВЕТЫ
= “ Гт" (гаг) + ^г*1, где а., а0 — проекции вектора а на координатные
г Lor	оф J	у
линии ф = const и г = const. 4434. div а = г	(MNau) + ^ (NLav) +
LMN 1ди	ди
+ (ЬМаш)^ , где ам, а„, аш — проекции вектора а на соответствующие
координатные линии и L = |17ЧЕНЕГ ’М = «ЩЧЕЧЁГ ’
N =*	+(^) +Ш ‘ ®сли г» Ф» 2 — цилиндрические координаты,
то div а = “ Ц“ (гаг) + ^ + г^“] I если г, 0 и ф — сферические
координаты, то div а = r2^nQ [j- (r2^ sin 0) + (ав sin 0) +	.
4436.1.	а) 0; б) 0. 2. rot а (М) = i - j + § k, |rot а (М)| = ± ЛИ ,
cos а = —, cos (3 = ■	, cos у = -Ш- .	4437. а)^И[гх с];
ли	ЛИ	ЛИ	г
б) 2f(r)c + [c(r • г) - r(c • г)].	4439. а) 0; б) 0.	4440. rot v = 2ш.
4441.
.1. rot а = - (гаф) - к, где аф и аг — проекции вектора а
соответственно на координатные линии г = const и ф = const.
2 »> — - йг - Й+ (S - Й * + ; [*<■* - Й
где аг = ах cos ф + ау sin ф, аф = -ах sin ф + ау cos ф, а2 = аг\
б)rota = = 7ibй (а*sin0)-$] e'+lr[sb'^-i{га^]е° +
+ 1	^Га®^ ~~	] вф* ГДе °г = fljc C0S ^ S^n ® + аУ s*n ^ s*n ® + а* C0S
ае = ах cos ф cos 0 + ау sin ф cos 0 - аг sin 0, аф = -а, sin ф + ау cos ф.
4442.1.	а) 0; б) лЛ3. 2. а) 0; б) 0. 4443. л. 4444. ^ . 4445.1. 0. 2. 5 .
8	5
П	-л
4447. 4лт. 4448. ^ е,. 4450.	= div (Л grad и), где с — удельная
теплоемкость и р — плотность тела. 4452. 1. 2л2Ь2. 2. 81~ * In 2.
гв
3. | (3 + е4 - 12е2). 4. -12. 4453. J f(r) г dr. 4454.1. а) 2л; б) 2л. 2. а) Г = 0;

ОТВЕТЫ
555
б) Г = 2кп, где п — число оборотов контура С вокруг оси Oz.
4455. rot а(М)—j - 2k, Г = ^n(cos Р + 2 cosyje2.4456. Q= JJ
s
г - Я (к +1) * ^ s - • I -1: •4457-1- “ -	+»+2>+c-
S
2. i. 4458. и = ~. 4459. и (x, у, z) = V — , где rt — расстояние
3	r	i = i r<
переменной точки M (x, у, z) от точки Mt (i = 1,2,..., л).
4460. u (я, у, z) = f f/(f) dt, где r = Jx2 + y2 + z2.

СОДЕРЖАНИЕ
Предисловие 	 3
Часть 1
Функции одной переменной
Раздел I 4
Введение в анализ
§	1.	Вещественные числа	 6
§	2.	Теория последовательностей	 11
§	3.	Понятие функции	 23
§	4.	Графическое изображение функции	 30
§	5.	Предел функции	 41
§	6.	О-символика	 61
§	7.	Непрерывность функции	 65
§	8.	Обратная функция. Функции, заданные параметрически	 75
§	9.	Равномерная непрерывность функции	 78
§ 10.	Функциональные уравнения	 81
Раздел II
Дифференциальное исчисление функций одной переменной
§	1. Производная явной функции	 83
§	2. Производные обратной функции, функции, заданной
параметрически, и функции, заданной в неявном виде	100
§	3.	Геометрический смысл производной	101
§ 4.	Дифференциал функции	105
§	5.	Производные и дифференциалы высших порядков	108
§ 6.	Теоремы Ролля, Лагранжа и Коши	117
§	7.	Возрастание и убывание функции. Неравенства	123
§ 8.	Направление вогнутости. Точки перегиба	126
§	9.	Раскрытие неопределенностей	129
§ 10.	Формула Тейлора	132
§ 11.	Экстремум функции. Наибольшее и наименьшее значения функции . . 137
§ 12.	Построение графиков функций по характерным точкам	143
§ 13.	Задачи на максимум и минимум функций	145
§ 14.	Касание кривых. Круг кривизны. Эволюта	148
§ 15.	Приближенное решение уравнений	150
Раздел III
Неопределенный интеграл
§	1. Простейшие неопределенные интегралы	152
§	2. Интегрирование рациональных функций	162

СОДЕРЖАНИЕ
557
§	3. Интегрирование иррациональных функций	165
§	4. Интегрирование тригонометрических функций	168
§	5. Интегрирование различных трансцендентных функций	174
§	6.	Примеры на интегрирование функций	177
Раздел IV
Определенный интеграл
§	1. Определенный интеграл как предел суммы	180
§	2.	Вычисление определенных интегралов с помощью неопределенных . . 185
§	3. Теоремы о среднем	196
§	4.	Несобственные интегралы	199
§	5.	Вычисление площадей	207
§	6.	Вычисление длин дуг	211
§	7. Вычисление объемов	212
§	8. Вычисление площадей поверхностей вращения	215
§	9. Вычисление моментов. Координаты центра масс	216
§	10. Задачи из механики и физики	219
§	11.	Приближенное вычисление определенных интегралов	220
Раздел V
Ряды
§	1.	Числовые ряды. Признаки сходимости знакопостоянных рядов	223
§	2.	Признаки сходимости знакопеременных рядов	235
§	3. Действия над рядами	241
§	4.	Функциональные ряды	242
§	5.	Степенные ряды	254
§	6.	Ряды Фурье	266
§	7.	Суммирование рядов	272
§	8.	Нахождение определенных интегралов с помощью рядов	276
§	9.	Бесконечные произведения	277
§	10.	Формула Стирлинга	284
§	11.	Приближение непрерывных функций многочленами	284
Часть 2
Функции нескольких переменных
Раздел VI
Дифференциальное исчисление функций нескольких переменных
§	1.	Предел функции. Непрерывность	288
§	2.	Частные производные. Дифференциал функции	294
§	3.	Дифференцирование неявных функций	309
§	4.	Замена переменных	319
§	5.	Геометрические приложения	332
§	6.	Формула Тейлора	337
§	7.	Экстремум функции нескольких переменных	340
Раздел VII
Интегралы, зависящие от параметра
§	1. Собственные интегралы, зависящие от параметра	349
§	2. Несобственные интегралы, зависящие от параметра.
Равномерная сходимость интегралов	355

558
СОДЕРЖАНИЕ
§	3. Дифференцирование и интегрирование несобственных интегралов
под знаком интеграла	3G2
§	4.	Эйлеровы интегралы	3G9
§	5.	Интегральная формула Фурье	373
Раздел VIII
Кратные и криволинейные интегралы
§	1.	Двойные интегралы 	376
§	2.	Вычисление площадей	385
§	3.	Вычисление объемов	387
§	4.	Вычисление площадей поверхностей	389
§	5.	Приложения двойных интегралов к механике 	391
§	6.	Тройные интегралы	394
§	7.	Вычисление объемов с помощью тройных интегралов	398
§	8.	Приложения, тройных интегралов к механике 	401
$	9.	Несобственные двойные и тройные интегралы	405
§ 10.	Многократные интегралы	410
§11.	Криволинейные интегралы	  414
§ 12.	Формула Грина	423
§ 13.	Физические приложения криволинейных интегралов	428
§ 14.	Поверхностные интегралы	431
§ 15.	Формула Стокса 	436
§ 16.	Формула Остроградского	439
§ 17.	Элементы теории поля	  443
ОТВЕТЫ	453

Учебное издание
Демидович Борис Павлович
СБОРНИК ЗАДАЧ И УПРАЖНЕНИЙ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Редакция «Образовательные проекты»
Ответственный редактор Е. С. Гридасова
Технический редактор Л. Б. Чуева
Общероссийский классификатор продукции ОК-005-93, том 2;
953005 — литература учебная
Санитарно-эпидемиологическое заключение
№ 77.99.02.953.Д.000577.02.04 от 03.02.2004 г.
ООО «Издательство Астрель*
129085, Москва, пр-д Ольминского, д. За
ООО «Издательство ACT*
667000, Республика Тыва, г. Кызыл, ул. Кочетова, д. 28
Наши электронные адреса: www.ast.ru
E-mail: astpub@aha.ru
ОАО «Санкт-Петербургская типография № 6*.
191144, Санкт-Петербург, ул. Моисеенко, 10.
Телефон отдела маркетинга 271-35-42.
По вопросам приобретения книг обращаться по адресу:
129085, Москва, Звездный бульвар, дом 21, 7 этаж
Отдел реализации учебной литературы
«Издательской группы ACT»
Справки по телефону: (095)215-53-10, факс 232-17-04

V=4 (2 sin t - sin2t).
«{
5){
»){
Х = 4СЩ£ 1
y~asint;
x-a
x\=a
y\=a
Профессор Борис Павлович
Демидович свыше 40 лет работал
на кафедре математического
анализа Московского государст¬
венного университета. Им написаны
более 60 научных работ, в том числе
монографии и учебные пособия,
получившие признание как в нашей
стране, так и за рубежом.
Задачник Б. П. Демидовича —
одно из самых известных
и значительных вузовских учебных
пособий последних десятилетий.
Он переведен на многие
иностранные языки и используется
в разных странах мира.
♦Сборник задач и упражнений
по математическому анализу»
адресован студентам и препода¬
вателям физических и механико¬
математических факультетов
университетов и педвузов,
а также высших технических
учебных заведений.