И.И.Ляшко, А.К.Боярчук, Я.Г.Гай, ГП.Головач
МАТЕМАТИЧЕСКИЙ АНАЛИЗ:
ВВЕДЕНИЕ В АНАЛИЗ, ПРОИЗВОДНАЯ, ИНТЕГРАЛ
Справочное пособие по высшей математике. Т. 1
М.: Едиториал УРСС, 2001. — 360 с.
«Справочное пособие по высшей математике» выходит в пяти томах и
представляет собой новое, исправленное и существенно дополненное издание
«Справочного пособия по математическому анализу» тех же авторов. В новом
издании пособие охватывает три крупных раздела курса высшей математики —
математический анализ, теорию дифференциальных уравнений, теорию функций
комплексной переменной.
В том 1 включен материал по следующим разделам курса математического
анализа: введение в анализ, дифференциальное исчисление функций одной
переменной, неопределенный и определенный интегралы.
Пособие предназначено для студентов, преподавателей и работников физико-
математических, экономических и инженерно-технических специальностей,
специалистов по прикладной математике, а также лиц, самостоятельно
изучающих высшую математику.
Оглавление
Глава 1. Введение в анализ 5
§1 . Элементы теории множеств 5
§2. Функция. Отображение 13
§3. Действительные числа 20
§4. Комплексные числа 31
§5. Векторные и метрические пространства 35
§6. Предел последовательности 42
§7. Предел функции 66
§8. Непрерывность функций 97
§9. Равномерная непрерывность функций 106
Глава 2. Дифференциальное исчисление функций одной переменной 111
§ 1. Производная явной функции 111
§2. Дифференциал функции 127
§3. Производная обратной функции. Производная функции, заданной
параметрически. Производная функции, заданной в неявном виде 133
§4. Производные и дифференциалы высших порядков 137
§5. Теоремы Ролля, Лагранжа, Коши 147
§6. Возрастание и убывание функции. Неравенства 156
§7. Направление выпуклости графика функции. Точки перегиба 161
§8. Раскрытие неопределенностей 166
§9. Формула Тейлора 173
§10. Экстремум функции. Наибольшее и наименьшее значения функции 182
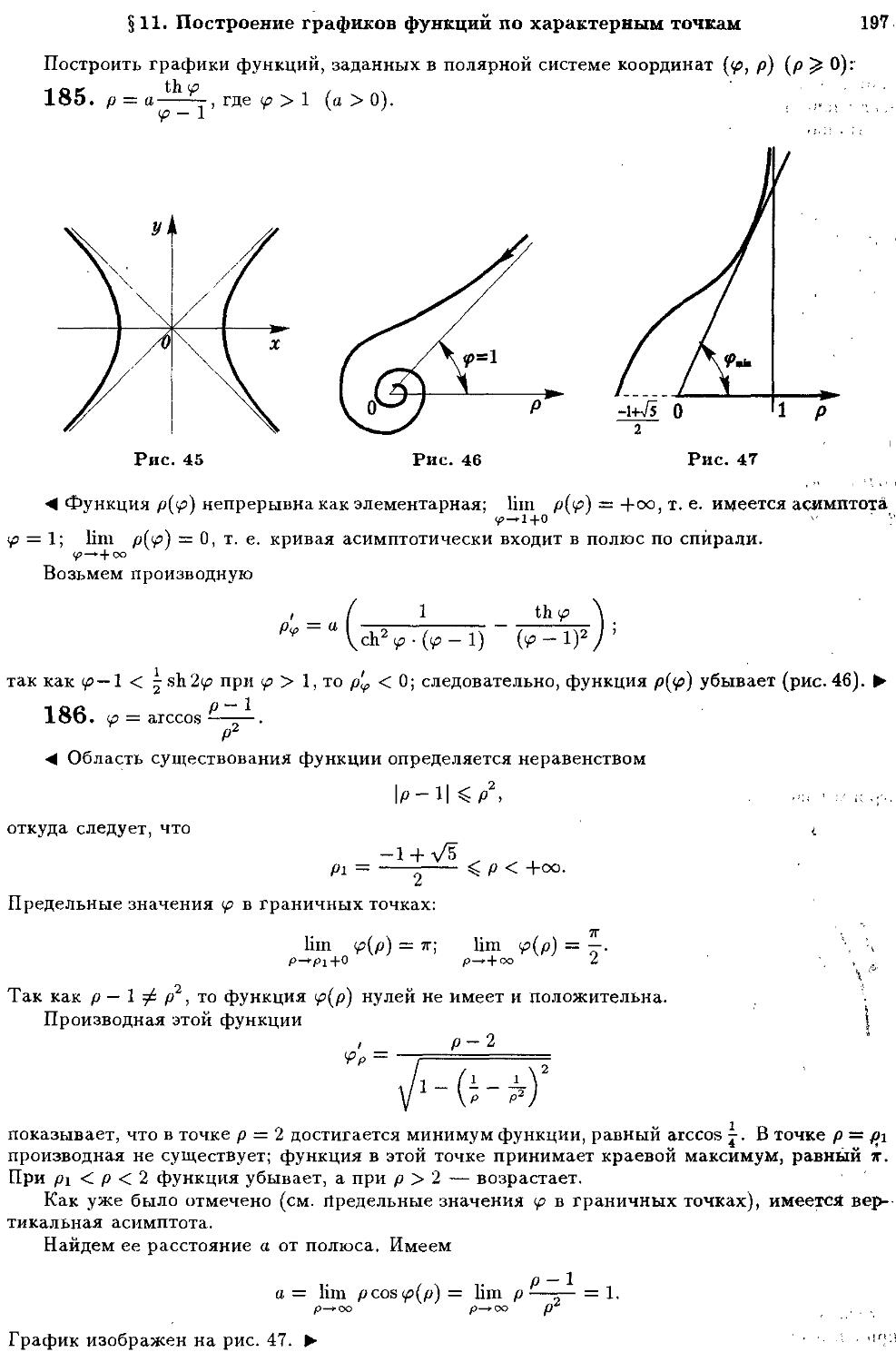
§11. Построение графиков функций по характерным точкам 187
§12. Задачи на максимум и минимум функции 200
Глава 3. Неопределенный интеграл 206

§1. Простейшие неопределенные интегралы 205
§2. Интегрирование рациональных функций 221
§3. Интегрирование иррациональных функций 233
§4. Интегрирование тригонометрических функций 241
§5. Интегрирование различных трансцендентных функций 246
§6. Разные примеры на интегрирование функций 248
§7. Интегрирование вектор-функций и функциональных матриц 251
Глава 4. Определенный интеграл 253
§1. Интеграл Римана 253
§2. Основные теоремы и формулы интегрального исчисления 263
§3. Интегрирование вектор-функций, комплекснозначных функций и
функциональных матриц 291
§4. Несобственные интегралы 297
§5. Функции ограниченной вариации 311
§6. Приложение определенного интеграла к решению задач геометрии 314
§7. Общая схема применения определенного интеграла. Задачи из
механики и физики 332
§8. Интеграл Стилтьеса 336
§9. Приближенное вычисление определенных интегралов 345
Ответы 353

От издатепьства
"Справочное пособие по высшей математике", первый том которого Вы дер-
держите в руках, не является книгой, совершенно незнакомой российскому читателю.
Первые три тома представляют собой исправленное и дополненное переиздание двух-
двухтомного "Справочного пособия по математическому анализу" тех же авторов, хорошо
известного среди студентов под обиходным названием "Анти-Демидович" и ставшего
редкостью в вузовских библиотеках. Четвертый и пятый тома издаются впервые и по-
посвящены соответственно теории функций комплексной переменной и теории диффе-
дифференциальных уравнений.
Пособие построено на материале широко известных задачников — "Сборника
задач по математическому анализу" под редакцией Б.П.Демидовича, "Сборника задач
по теории функций комплексной переменной" Л.И.Волковысского с соавторами,
"Сборника задач по дифференциальным уравнениям" А.Ф.Филиппова и ряда других.
Все пять томов объединены общей идеологией "решебника": в каждой главе содер-
содержится необходимый теоретический материал, изложены и проиллюстрированы много-
многочисленными примерами методы решения основных типов задач, приведены упражне-
упражнения для самостоятельной работы, ответы на которые помещены в конце книги.
В первом томе рассматриваются следующие разделы курса математического
анализа: введение в анализ (с элементами теории множеств, теорией действительных и
комплексных чисел, теорией векторных и метрических пространств, теорией преде-
пределов) — первая глава; дифференциальное исчисление функций одной переменной —
вторая глава (по сравнению с предыдущим изданием сюда добавлены два параграфа,
касающиеся построения графиков функций и задач на минимум и максимум функции);
неопределенный интеграл — третья глава; определенный интеграл (включая интеграл
Стилтьеса, приложения определенного интеграла к решению задач геометрии, механи-
механики и физики, методы приближенного вычисления определенных интегралов) — четвер-
четвертая глава. В процессе подготовки нового издания были исправлены замеченные опе-
опечатки и приложены значительные усилия к тому, чтобы не внести новых.
В заключение мы благодарим Вас, дорогой читатель, за оказанное нам доверие и
надеемся, что эта книга станет для Вас хорошим помощником.

Глава 1
Введение в анализ
1. Элементы теории множеств
1.1. Логические символы.
В математике часто некоторые словесные выражения заменяют посредством символов.
Так, например, символом V заменяют выражение "для произвольного", или "для любого", или
"какого бы ни было", а символом 3 — выражение "существует", или "йайдется". Символы V
и 3 называются кванторами.
Запись А => В {импликация) означает, что из справедливости высказывания А вытекает
справедливость высказывания В. Если, кроме того, из справедливости высказывания В вы-
вытекает справедливость А, то записываем А -Ф» В. Если А -Ф» В, то высказывание В является
необходимым и достаточным условием для того, чтобы выполнялось высказывание А.
Если предложения А и В справедливы одновременно, то записываем А А В. Если же
справедливо хотя бы одно из предложений А или В, то записываем А\1 В.
1.2. Операции над множествами.
Математическое понятие множества элементов принимается в качестве интуитивного.
Множество задается правилом или признаком, согласно которому определяем, принадлежит
ли данный элемент множеству или не принадлежит.
Множество обозначают символом А = {х}, где х — общее наименование элементов мно-
множества А. Часто множество записывают в виде А = {а, Ь, с,...}, где в фигурных скобках
указаны элементы множества А.
Будем пользоваться обозначениями:
N — множество всех натуральных чисел;
Ъ — множество всех целых чисел;
(Q) — множество всех рациональных чисел;
R — множество всех действительных чисел;
С — множество всех комплексных чисел;
Ъа — множество всех неотрицательных целых чисел.
Запись а € А (или А Э а) означает, что элемент а принадлежит мно-
множеству А.
Запись а ? А (или А ^ а) означает, что элемент а не принадлежат
множеству А.
Множество В, все элементы которого принадлежат множеству Л, назы-
называется подмножеством множества А, и при этом записывают В С. А (или
А Э В) (рис. 1). Всегда А С А, так как каждый элемент множества,
естественно, принадлежит А. Пустое множество, т. е. множество, не со-
содержащее ни одного элемента, обозначим символом 0. Любое множество
содержит пустое множество в качестве своего подмножества.
Определение 1. Если А С В А В С А, то А и В называются
равными множествами, прг1 этом записывают А = В.
Определение 2. Если А С J, то множество элементов множества
J, не принадлежащих А, называется дополнением множества А к мно-
множеству J (рис. 2).
Дополнение множества А к множеству J обозначают символом CjA
или просто СМ, если известно, к какому множеству берется дополнение.
Таким образом,
С:тА = {х : х € J A x g А}. Рис. 2
Рис. 1

6 Гл. 1. Введение в анализ
Если А С J, В С J, то иногда дополнение множества В к множеству А называют разностью
множеств А и В и обозначают А\В (рис. 3), т. е.
А\В = {х:х €АЛх <? В}.
Пусть А и В подмножества множества J.
Определение 3. Объединением множеств А и В называется множество (рис. 4)
AU В = {х :х еАУ х€ В}.
Аналогично, если Aj, j = 1, п, подмножества множества J, то их объединением будет
множество
п
Aj¦ = {х : х € Ах V х € А2 V ... Vie An).
Определение 4. Пересечением подмножеств А и В называется множество (рис. 5)
А Л В{х : х € А А х € В}.
п
Аналогично, символом |~) Д, обозначают пересечение подмножеств Aj, j = 1, п, множе-
множества J, т. е. множество
п
Если каждому ^ € Л/ сопоставлено некоторое множество .А^, то говорят, что задано
семейство множеств {^}, ft € М. В этом случае множество (J Л^ = {ж : все х такие, что
х € Л^ хотя бы для одного fi € Л/} называют объединением семейства множеств {^}, ц €
М, а множество |~) Л^ = {i : i € Лм V/г € Л/} — пересечением этого семейства.
Определение 5. Симметрической разностью двух множеств А и В называется мно-
множество, определяемое объединением разностей А\В и В\А (рис. 6).
Симметрическую разность обозначают символом А Л В.
Определение 6. Два элемента а и Ъ называются упорядоченной парой, если указано,
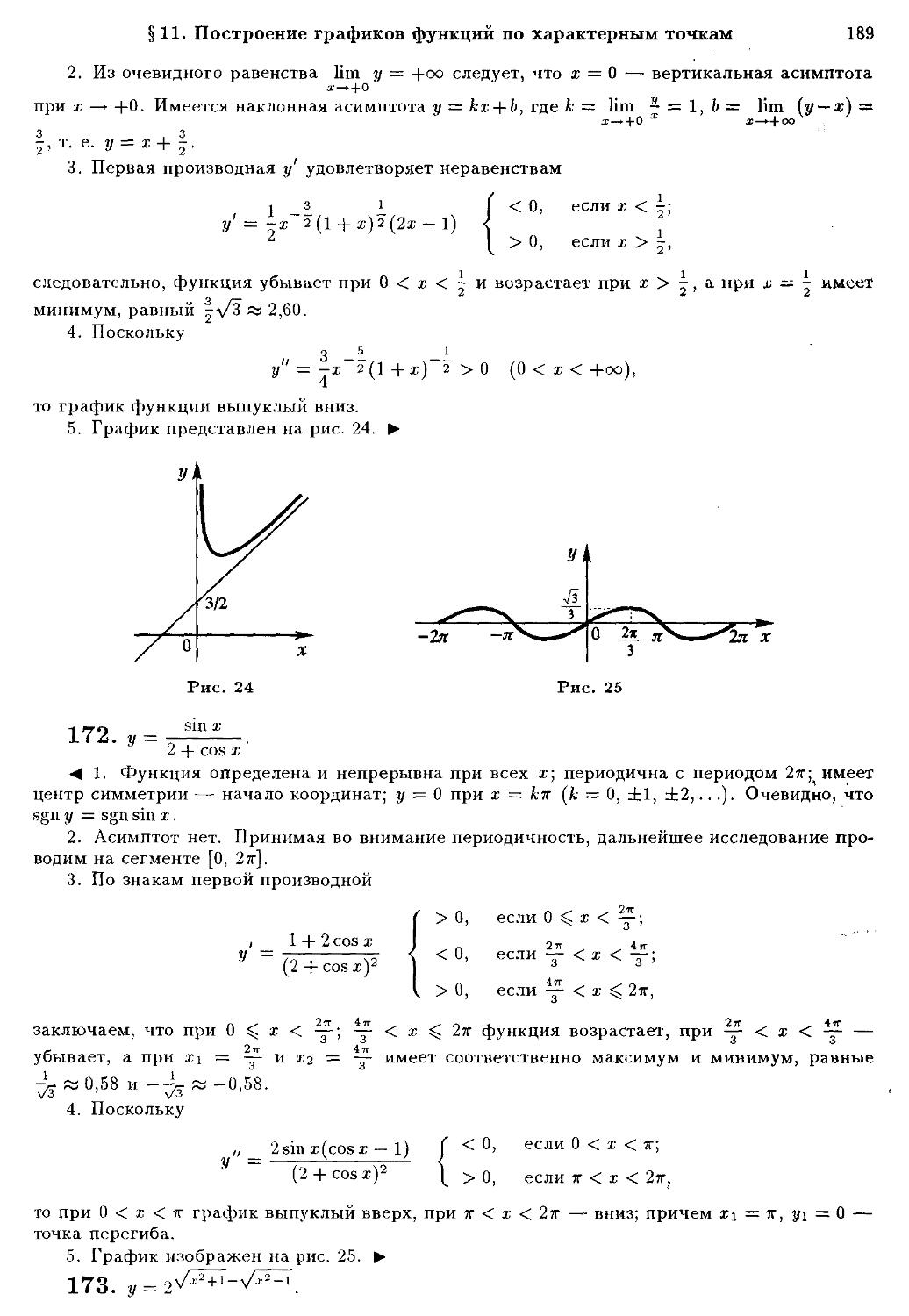
какой из этих элементов первый, какой второй, при этом ((а, 6) = (с, d)) <=>¦ (а = с Л 6 = d).
Упорядоченную пару элементов а и 6 обозначают символом (а, Ъ).
Аналогично определяется упорядоченная система из п элементов ai, аг, ..., ап, которую
обозначают символом (ai, а2, ..., an)- Элементы ai, аг, • ¦ •, ап называются координатами
упорядоченной системы (ai, «2, •••, а„).
Определение 7. Совокупность всевозможных упорядоченных пар (а, Ъ), где а ? А,
Ь € В, называется произведением множеств А и В и обозначается символом Ах В.
Аналогично, символом Ai х А2 х ... х А„ обозначают произведение множеств Aj С J,
j = 1, it, т. е. совокупность всевозможных упорядоченных систем (ai, а2, ¦¦¦, ап), где aj €

§ 1. Элементы теории множеств 7
1.3. Булева алгебра.
Пусть А, В и D — произвольные подмножества множества J. Тогда непосредственно из
определений объединения, пересечения и дополнения вытекают следующие предложения:
1) Аи В С 3, АГ\ В С. J (замкнутость операций объединения и пересечения);
2) A\J В = В \J А, А Л В = В Л А (коммутативность операций объединения и пересече-
пересечения);
3) A U (В U D) = (A U В) U D, А Л (В Л D) = (А П В) Л D (ассоциативность операций
объединения и пересечения);
4) A U (В П D) = (A U В) Л (A U D) (дистрибутивность операции объединения относи-
относительно операции пересечения);
А Л (В U D) — {А Л В) U (А Л ?)) (дистрибутивность операции пересечения относительно
операции объединения);
5) АиА = АпА = А;
6) (Л U В = В) & {А Л В = А);
7) Аи 0 = A, An J = A, An 0 = 0, Аи J = J;
8) A U СМ = J, А П СА = 0,
Если для элементов множества а = {А, В, С, ... } определены объединение U и пересече-
пересечение П, для которых выполняются отношения 1)—8), то тройка (<r, U, П) называется булевой
алгеброй. Таким образом, если а — семейство всех частей множества J, то (ay U, П) —
булева алгебра.
1.4. Принцип двойственности.
Для произвольных подмножеств А и В множества J справедливы равенства
С (Л и Я)=О4ПСЯ, С (Л Л Я) = СМ и СВ. A)
Свойства, записанные равенствами A), называются принципом двойственности. Их
можно прочитать следующим образом: дополнение к объединению множеств равно пересече-
пересечению их дополнений, а дополнение к пересечению множеств равно объединению их дополнений.
Без труда принцип двойственности переносится на произвольное число подмножеств Лм; при
этом записывают
[J f] f]\JA,. B)
В этом случае символ дополнения С можно менять местами со знаком U или П, при этом
знаки эти переходят один в другой.
1.5. Алгебра множеств.
Пусть J — некоторое множество, a P{J) — система всех подмножеств множества 3.
Определение 1. Непустое семейство R С P{J), замкнутое относительно операций
объединения, пересечения и разности множеств, называется кольцом множеств.
Определение 2. Множество Е называется единицей семейства множеств Е, если
Е 6 Е и \М € ? справедливо равенство А Г\ Е = А.
Определение 3. Кольцо множеств, содержащее в качестве своего элемента единицу,
называется алгеброй множеств.
Определение 4. Семейство множеств S С P{J) называется полукольцом, если оно
содержит пустое множество и если ЧА € S и ЧА\ С А существуют такие множества
Аг, Аз, ..., Ап € S, что
А = Ai U A2 U ... U Ап,
где символ U означает объединение непересекающихся множеств.
1. Доказать справедливость отношений 1)—8) пункта 1.3.
^1) По определению 3, п. 1.2,
AU B = {x €J :x GAV х еВ},
следовательно, из включения х ? Аи В следует х € J, т. е. Аи В С J¦
Аналогично, по определению 4, п. 1.2,
А П В = {х € J : х € А Л х € В},
поэтому из включения х € А П В следует включение А П В С J ¦

8 Гл. 1. Введение в анализ
2) Поскольку высказывание х ? А V х € В равносильно высказыванию х ? В V х ? А, то
AuB={x&J:xeA\/x€B} = {xeJ:x€B\/x€A} = BuA.
Второе равенство доказывается аналогично.
3) В силу свойств логического символа V, имеем
AV (В V D) = {х € J : х € AV х е (В U ?))} = {i€ J:i €iv(i efl Vi€ ?>)} =
= {х е J : (х ? А V х ? В) V х € D} = {х е J : х е (А 1) В) V х ? D] = (A U В) U D.
Второе равенство из 3) доказывается аналогично.
4) Имеем
A U (В П D) - {х € J : i € А V х € (В Л ?>)} =
= {a;€j:i€ylV(ieBAiefl)} = {i€j:(i€J4Vj;gfl)A(i€vlVt€i))} =
= {х € J : (х € A U 5) Л (х € A U ?))} = (A U В) П (Л U ?>).
Второе равенство доказывается аналогично.
5) Пусть х g A U А, тогда ж€АЛхбА,т. е. х € А и, тем самым, справедливо включение
A U А С А. Обратное включение А С A U А непосредственно следует из определения
объединения. Из двух последних включений вытекает равенство A U А — А.
Равенство А П А = А доказывается аналогично.
6) Предположим, что справедливо равенство А П В = А. Тогда
(А Л В = А) =>• (А С А Л В) =>• (Л С В).
Пользуясь полученным включением, находим
Аи В = {х € J : х е AV х € В} С {х е J : х ? В V х ? В} = В.
А поскольку Аи В Э В, то Аи В = В. Таким образом,
{АпВ = А)=>{АиВ = В). A)
Пусть теперь Аи В — В. Тогда справедливы импликации
(AUB = B)=>{AU В С В)=> (АС В).
Пользуясь включением А С В, находим
Ar\B = {x€j:x€AAxeB}D{x€J:x€AAxeA}=A.
А поскольку справедливо и обратное включение А П В С А, то ЛпЯ = А, следовательно,
(лия = я)^(/1пв = 4 B)
Из A) и B) следует (An В = А) & {А 1) В = В).
7) Если x&AU0,tox?AVx?0. Поскольку множество 0 не содержит ни одного
элемента, то из х € A U 0 следует ж € Л, т. е. i U 0 С А, что совместно с включением
A U 0 Э Л равносильно равенству Аи 0 = А.
Далее, wi0QAf\0Q0 непосредственно следует равенство А П 0 = 0.
Поскольку А С J, то А П J = {х € J : х € А Л х € J}.D {х € J : х € А Л х € А} = А,
что совместно с включением А Г\ J С. А влечет равенство А Г\ J = А.
Наконец, непосредственно из включений J С A U J С j следует равенство A U J = 3.
i 8) Согласно свойству 1),
AUCAC3. C)
Пусть х € .7, тогда если i € >t, то х € Л U СМ; если же х 0 А, то i € СА и снова
а; € A U СЛ. Таким образом, из х € ,7 следует ж € A U СА, т. е.
J С A U СА. D)
Из C) и D) следует равенство
A U СА = J. E)
Для доказательства равенства А П СА = 0 покажем, что множество А П СА не содержит
ни одного элемента. Действительно, согласно равенству E), любой элемент множества J
принадлежит А или СА. Если х € А, то х g СА и, следовательно, х 0 А П СА. Если же х €
СД, то х ? Л (так как если бы х g А, то х ? СА), и снова ij?An СА. Поскольку множество
А П СЛ не содержит ни одного элемента, то это множество пустое, т. е. А П СА = 0. >

§ 1. Элементы теории множеств 9
2. Доказать принцип двойственности:
С (A U В) = САГ\СВ, A)
С (А Л В) = CM U СВ ;. -(-2)
(см. равенства A), п. 1.4). ¦
¦4 Докажем равенство A) (равенство B) доказывается аналогично). -: ,
Пусть i € С (Л U В), тогда, согласно равенству E) предыдущей задачи, х ? A U В, т. е.
х g А Л х g В. Отсюда х € СМ Л х € СВ, а следовательно, х € СА П СВ. Таким образом,
С (A U В) С СМ ЛСД. C)
Предположим теперь, что х € СМ П СВ. Тогда х € СА Л ж € СВ, т. е. ж ? А Л х & В, л
значит, х $ Аи В и х g С (A U В). Отсюда
С{AU В) С САП СВ. D)
Из включений C) и D) следует равенство A). > ,
3. Доказать равенства
Аи(АпВ) = Ал(АиВ) = А. .;.'¦¦»¦ Ш
< Пользуясь свойствами 4) и 5) задачи 1, получаем первое из равенств A): /,
A U (А Л В) - (A U А) Л (A U В) = А П {A U В).
Остается доказать, что А Л (A U В) = А. Если i€v4n(AUfl), loigiAigAUfiHi
следовательно,
А Л (A U В) С А. B)
Если же i ? А, то i? AU5, а значит, х € А Л (A U В), т. е. ' • ' v •¦•¦ ¦'
А С А Л (A U В). C)
Из включений B) и C) следует второе из равенств A). > '
4. Доказать равенства:
а) ССА = А; б) CJ = 0; в) С0 = J. ; ,
¦4 а) Если i € ССА, то i ^ СА, а поэтому х g А и справедливо включение ССА С Л.
Наоборот, если х € А, то х & СА, а поэтому х € ССА и справедливо включение А С CGA.
Из доказанных включений следует равенство а). >
б) Множество CJ пустое, так как отрицание х ? CJ справедливо для любого х € 3¦
в) Если 1€.7,тох^0,а поэтому х g С0 и, следовательно, J С С0. Поскольку всегда
С0 С J, то из последних двух включений следует равенство в). > ¦ '
5. Доказать справедливость включения
(А\В) С (A\D) Л (D\B). ."¦'"';¦.
¦^ Пусть i € (А\В), тогда х € А Л х ? В. Если при этом x^D, то i € (Л\Р) и,
следовательно, i 6 (А\?>) U (D\B). Если же i 6 D, то поскольку i ^ 5, находим,. чтри
х € (D\B), а поэтому х € (А\?>) U (D\B). Таким образом, как при х ? ?>, так ипри
i € D из условия i € (А\В) следует х € (A\D) U (D\B), что равносильно доказываемому
включению. >
6. Определить множества Аи В, А П В, А\В, В\А, А Л В, если:
а) А = {i : 0 < х < 2}, В = {х : 1 ^ х ^ 3};
б) А = {х : I2 - 3i < 0}, В = {х : х2 - 4х + 3 ^ 0};
в) А = {х : \х - 1| < 2}, В = {х : \х - 1| + |х - 2| < 3}.
< Пользуясь определениями объединения, пересечения, разности и симметрической (раз-
(разности множеств, находим:
a) A U В = {х : @ < х < 2) V A ^ х ^ 3)} = {х : 0 < х ^ 3}; . , r i
А Л В = {х : @ < х< 2) Л A ^ х ^ 3)} = {х : 1 ^ х < 2}; , г /.'; .,.,',' „,,
А\В = {х:@<х<2)Лх?[1, 3]} = {х : 0 < х < 1}; "¦;-Лг г''.,',..(,'
В\А= {i : A ^ х ^ 3) Лх ?]0, 2[} = {х :2 ^х ^ 3}; . , , . ,
АДВ= {х :(A\B)U(B\A)} = {x:@<x < 1) V B ^ х ^3)}. ,.,.¦.-,»

10
Гл. 1. Введение в анализ
б) Поскольку х2 — Зх < 0 для 0 < х < 3, то А = {х : 0 < х < 3}. Неравенство х2—4х + 3 ^ 0
справедливо для — оо < х ^ 1 и3^г< +оо. Обозначим D = {я : —оо < х ^ 1}, i? = {х : 3 ^
х < +оо}, тогда В = D U Е. Используя свойства операций над множествами, находим:
AU В = AU (D U Е) = Аи D I) Е = {х : @ < х < 3) V
V (-оо < х < 1) V C < х < +оо)} = {х : -оо < х < +оо);
А Л 5 = А Л (Д и Е) = (А П ?>) и (А Л ?) = {х : @ < х sg 1) V х € 0} = {х : 0 < х ^ 1};
= {i : (я б Л Л х € ?>) V (I € А Л i б Е)} = (A\D) U (Л\?) = {х : 1 < х < 3};
= (?) и Е)\А = {х :(х € Dv х е Е) Лх ?А] =
= {x:(x€DAxgA)V(x6E/\x?A)} = (D\A) U (E\A) =
= {х : (-оо <i<0)vC^i< +oo)};
АДВ = АД(Ви?)- И\(?> U Е)) и ((?) U Е)\А) =
= {х : A < а; < 3) V (-оо <i^0)VC^i< +oo)} =
= {х : (-со <i^0)vA<i< +oo)}.
в) Запишем явное выражение для множества А = {х : —2 < х — 1 < 2} = {х : — 1 < х < 3}.
Затем, решая неравенство |х — 1| + |а; — 2| < 3, находим явное выражение для множества
В = {х :0 < х < 3}. Тогда
Л U В = {х : (-1 < х < 3) V @ < х < 3)} = {х : -К х < 3};
Л Л Д = {х : (-1 < х < 3) Л @ < х < 3)} = {х : 0 < i < 3};
А\В = {х : (-К х < 3) Л х ?]0, 3[} = {х : -К х ^ 0};
В\Л = {х : @ < х < 3) Л х ?] - 1, 3[} = 0;
Л Л В = (Л\5) U (В\А) = А\В = {х : -К х ^ 0}. >
в
D
Рис. 7 Рис. 8
7. Имеем Л = {(х,у) : \х\ + \у\ < 5} (рис. 7), 5 = у,
{(,у)>/+ »} (р),
(рис. 9). Показать, что A <Z В С. D.
ч ¦« Пусть (ж, у) € Л, тогда |х| + |у| < В. Отсюда
х2 + У2 ^ \/х2 + 2|z||jf| + у1 = \х\ + \у\ < S,
Рис. 9
т. е. (ж, у) € В, что, в свою очередь, влечет выполнение нера-
неравенства
тах{|х|, \у\} < \/х2 +у2 < S,
а следовательно, и включение (х,у) ? D. Таким образом,
Л С В С D. > Рис. 10
8. Пусть Л = {х : 2 ^ х ^ 4}, В = {у : 1 ^ у ^ 3}. Изобразить на плоскости хОу
множество точек Ах В.
¦4 Поскольку Л х В = {(х,у) : B ^ х ^ 4) Л A ^ у ^ 3)}, то Л х Д есть совокупность
точек прямоугольника, ограниченного прямыми х = 2, х = 4, j/ = 1,j/ = 3 (рис. 10). >

§ 1. Элементы теории множеств 11
9. Показать, что семейство R, замкнутое относительно объединения и разности, является
кольцом.
< Пусть А и В — произвольные множества семейства R. Поскольку А Л В = А\(А\В) ,
а А С R, А\В С R, то А Л В С R. Следовательно, семейство R замкнуто относительно
объединения, пересечения и разности, т. е. является кольцом. >
10. Показать, что семейство R = {«, 0}, состоящее из непустого множества а и пустого
множества 0, образует кольцо. Является ли это кольцо алгеброй?
< Семейство R содержит своими элементами объединение a U 0 = а и разности а\0 —
а, 0\а = 0. Поэтому R замкнуто относительно объединения и разности, т. е., согласно
предыдущему примеру, является кольцом. А так как элемент а € R содержит все остальные
множества семейства R, то « — единица семейства, аи — алгебра. >
11. Пусть множество J = {«, ft, 7} состоит из трех элементов, a P(J) — семейство всех
подмножеств множества J.
а) Записать все алгебры, которые можно построить из элементов множества P{J), и
указать их единицы.
б) Описать все кольца, которые можно построить из элементов множества P{J).
в) Описать все полукольца, которые можно построить из элементов множества P(J) и
которые не являются кольцами.
< а) Простейшими алгебрами являются: семейство {0}, состоящее из одного пустого
множества; три алгебры
{{«}, 0,}, {{/?},0}, {{7}, 0},
состоящие из двух элементов с единицами, соответственно равными {«}, {ft}, {7} (см- пре-
предыдущий пример); шесть алгебр
{{«, ft}, {«}, {ft}, 0}, {{«, 7}, {«}. {7}, 0},
Ш. 7}. М. М, Я}, {{«,ft},0},{{»,y},0}, {{ft, У},0},
единицами которых соответственно являются множества {«, ft}, {а, у}, {ft, у}, {a, ft},
{«, 7}, {ft, f}- Легко видеть, что любое из этих семейств замкнуто относительно объединения
и разности; четыре алгебры
{J, {«, ft}, {7}, 0}, {J, {«, 7}, {ft}, 0}, {J, {ft, 7}, {«}, 0}, U, e>),
единицей которых является множество J. Наконец, объединение всех перечисленных алгебр
{J, {«,/>}, {«,7}, {/?, 7}, {«}- {ft}, {7}, 0}
также является алгеброй с единицей J.
б) Все приведенные в пункте а) алгебры, естественно, являются кольцами. Других колец
нет.
в) Всякое кольцо является полукольцом. Действительно, из условия, что А и А\ С А
принадлежат кольцу R, следует, что
A = AiUA2, где А2 = A\Ai С R-
Кроме того, в нашем случае можно построить примеры полуколец, которые не являются
кольцами. Например, семейства
{{«}, Ш, 0}, {{«}, {7},0}, {{/»}, М, Я},
{{«, ft}, {7}, 0}, {{«, у},{ft}, 0}, {{ft,i}, {«}-W-
В самом деле, в каждом из шести семейств пересечение любых двух элементов семей-
семейства принадлежит этому семейству. Далее, каждый непустой элемент семейства имеет в
качестве своего подмножества только само множество, поэтому, например, для семейства
{{ft, 7}> {«}, 0}, имеем
{ft, 7} = {ft, 7} U 0 = {ft, 7}, {«} = {«} U 0= {«},
т. е. второе условие определения полукольца выполняется. Полукольцом является любое
семейство, содержащее {«}, {ft}, {7}, 0, но не совпадающее с P(J)'-
{{«, ft}, {«}, {/»}, {7}, 0}, {{«, 7}. {«}> М- {7}, «I И Т. Д.

12 Гл. 1. Введение в анализ
Покажем, например, что семейство S = {{а, /3}, {а}, {/?}, {у}, 0} — полукольцо. Действи-
Действительно, пересечение любых двух элементов семейства S снова является элементом S. Далее,
для всякого элемента .*> справедливо разложение: {а, /?} = {a} U {/?}, {а} = {a}, {/?} = {/?},
{у} = {7} на непересекающиеся множества. Таким образом, семейство S — полукольцо. >
12• Пусть три числа а, Ь и с удовлетворяют неравенствам а < с < Ь. Показать, что
семейство
S = {[а, Ь], [а, с], [с, Ь], [а, с[, [с, с], ]с, Ь], 0},
состоящее из сегментов и полусегментов, образованных точками a, b и с, является полуколь-
полукольцом, но не кольцом.
Ч Пересечение любых двух элементов семейства S есть элемент этого же семейства, т. е. S
замкнуто относительно операции пересечения. Далее, любой элемент семейства S допускает
разложение на непересекающиеся части, принадлежащие 5. Например,
[а, Ь] = [a, c]U]c, Ъ] = [a, c[U[c, c]U]c, b] = [a, c[U[c, b], [а, с] = [a, c[U[c, с] и т. д.
Семейство 5 не является кольцом, так как оно не замкнуто относительно объединения. На-
Например, [a, c[U]c, b] не принадлежит S. >
13. Доказать, что
(AnB)x(DnE)=(AxD)n(B хЕ). A)
^ Пусть (х, у) € (А П В) х (D П Е), тогда х ? А П В к у ? D С\ Е, что равносильно
тому, что х ? А Л х ? В и у ? D Л у € Е. А поскольку х € А Л у € D, то (х, у) € А х D.
Аналогично, из х?ВЛу?Е следует (х, у) € В х Е. Таким образом, (х, у) € (А х D) П
(Вх?) и
(;1ПВ)х(Вп?)С(ЛхВ)П(Вх4 B)
Предположим теперь, что (х, у) € ((Л х D) П (В х Е)). Тогда (х, у) ? (А х D) Л (х, у) €
(В х Е) и, следовательно, х ? А Л у € D и х € В Л у ? Е. Отсюда г€/1пВ и у ? D П Е,
т. е. (х, у) € ((А П В) х (D П Е)) и справедливо включение
(А х D) П (В х Е) С (Л П В) х (D П ?). C)
Иэ включений B) и C) следует A). >
Упражнения для самостоятельной работы
1. Доказать равенства:
ММ II li
(см. равенства B) п. 1.4), где ц принадлежит произвольному множеству.
2. Пусть А С В к D произвольные множества. Доказать справедливость включений:
л) AC\D CBC\D; 6)AUDcBuD.
3. Доказать, что если АС В /\ A G D, то А С В П D.
4. Доказать, что если А С D Л В С D, то АН В С D.
5. Доказать справедливость равенств:
а) A AB = (AL)B)\(A П В); б) A U В = (А А В) А (А П В); в) А\В = А А (АП В).
6. Доказать, что для симметрической разности справедливо включение
_ AABC((AAD)L)(BAD)).
7. Доказать справедливость включений:
а) (Ai U Аа)\(В» U В2) С (Ai\Bi) U (Л2\В2);
б) (CM, U O42) A (C5i и СЯ2) С C((CMi А СВХ) П (СМ2 А СЯ2)),
где .А,, А2, Bi, B2 — подмножества множества J.
' 8.'Доказать что:
а) {Ах U Аг) А {Вх U 52) С {Ах А Вх) U (Л2 А В2);
¦ б) (Л'хПАг) Д(В, ПВ2)С(Л1 ДВ,)П(Л2 Д52);
" '-..вХ (АД'Д2) Д Ei\B2) с (А, А В,)\(Л3 А В2),
где Ai., A2, В\, В2 — подмножества множества J.
9. Определить множества A U В, АП В, А\В, В\А, А А В, если:

§ 2. Функция. Отображение 13
а) А = {х:-4<х< 1}, В= {х :0<z<4}; "!
б) А= {х :х2 -х-2>0}, В = {х : 6х - х2 ^ 0}; 1>: '
в) А = {х : sin жх = 0}, В = {х : cos ^ = о}. ' ';
10. Определить множества A U В, АГ\ В, А\В, В\А, А А В, если:
а) А = {(х, у) : х2 + у2 ^ 1}, В = {(х, у) : \х\ + \у\ ^ 1};
б) А = {(х, у) : тах(\х\, \у\) ^ 1}, В = {(х, у) : |*| + |у| < 1};
в) А = {(я, у) : Н + |у| < 2}, В = {(», у) : ^(я - 2)» + (у - 2)' < 2};
г) Л = {(г, у) : sjx* + у* ^ 2], В = {(х, у) : maxflz + 1|, |у + 1|) ^ 2}.
11. Определить множество А х В, если: ,.
а) А = {х : -2 < х ^ 1}, В = {у : -3 ^ у < 1};
б) Л = {г : 0 ^ х ^ 1}, В = D х Е, где D = {у : 0 ^ у ^ 2}, ? = {г : 0 ^ z <. 3};
в) А = {х : — оо < г < +оо}, 5 = {у : sin^y = 0};
г) А = {х : sin жх = 0}, В = {у : —оо < у < +оо].
12. Пусть множество J состоит из четырех элементов a, ft, у и S, a P(J) — семейство
всех подмножеств множества J, включая и пустое множество. . '"'¦'•'
а) Построить примеры алгебр, единицами которых являются соответственно множества:
{а}, {а,/}}, {«,/9,7}. {«,/?, 7, «}•
б) Построить пример кольца, которое содержит в качестве своих элементов множества
{а, /3, у, 8}, {а}, {/}}, {у}, {8}. Будет лн это кольцо алгеброй? *
в) Построить пример полукольца (но не кольца), содержащего множество {а,/},у,6}'.
13. Показать, что множество всех сегментов, полусегментов и интервалов на числовой
прямой является полукольцом, но не кольцом.
14. Показать, что семейство всех прямоугольников вида
П = {(х, у):а<х^Ь, c<y^d],
где а, Ь, с и d — действительные числа, причем а < Ь, с < d, является полукольцом, но не
кольцом.
15. Какими множествами следует дополнить семейство, рассмотренное в задаче14; чтобы
оно превратилось в кольцо?
16. Доказать, что:
а) (Аи В) xD = (A xD)U(BxD); б) А х (В U D) = (А х В) U (A x D).
17. Доказать, что:
а) (А\В) xD = (A xD)\{BxD); б) А х (B\D) = (А х В)\(А х D).
18. Доказать, что
(AU B)x(DU E) = (Ax D)U(B xD)U(Ax E)U(Bx E).
§2. Функция. Отображение '
2.1. Функция. J
Определение. Отображением множества Е в множество F, или функцией, опре-
определенной на Е со значениями в F, называется правило, или закон /, который каждому
элементу х € Е ставит в соответствие определенный элемент f(x) € F.
Элемент х € Е называют независимым переменным, или аргументом функции /, элемент
f(x) € F называют значением функции /, или образом; при этом элемент х € Е называется
прообразом элемента f(x) € F.
Отображение (функцию) обычно обозначают буквой / или символом / : Е —*• F, указывая
тем самым, что / отображает множество Е в F. Употребляется также обозначение, х *-*
f(x), указывающее, что элементу х соответствует элемент f(x). Иногда функцию удобно
задавать посредством равенства, в котором содержится закон соответствия. Например, можно
говорить, что "функция / определена равенством f(x) = у/х2 + 1, х € jo., b]n. Если "у" —
общее наименование элементов множества F, т. е. F = {у}, то отображение / : Е '—* F
записывают в виде равенства у = f(x) и говорят, что это отображение задано явно!.5 *:

14 Гл. 1. Введение в анализ
2.2. Образ и прообраз множества прн заданном отображении.
Пусть задано отображение / : Е —> F и множество D С Е.
Определение 1. Множество элементов из F, каждый из которых является образом
хотя бы одного элемента из D при отображении f, называется образом множества D и
обозначается f(D).
Очевидно,
f(D) = {f(x)eF:xeD}.
Пусть теперь задано множество Y С F.
Определение 2. Множество элементов х 6 Е таких, что f(x) € Y, называется
прообразом множества Y при отображении f и обозначается f~l{Y)-
Ясно, что
r\Y) = {xZE:f(x)?Y}.
Если у € F, то f~l(y) = {х 6 Е : f(x) = у}. Если при каждом у € F множество /~х(у) состоит
не более чем из одного элемента х € Е, то / называется взаимно однозначным отображением
Е в F. Впрочем, можно определить взаимно однозначное отображение / множества Е на F.
Определение 3. Отображение f : Е —> F называется:
инъективным (или инъекцией, или взаимно однозначным отображением множества
Е в F), если (х ф х') =*• (f(x) ф f(x')) или если Vy 6 F уравнение f(x) = у имеет не более
одного решения;
сюръективным (или сюръекцией, или отображением множества Е на F), если
f(E) = F или если Vy 6 F уравнение f(x) — у имеет, по крайней мере, одно решение;
биективным (или биекцией, или взаимно однозначным отображением множества Е
на F), если оно инъективно и сюръективно или если Vy 6 F уравнение f(x) = у имеет одно
и только одно решение.
2.3. Суперпозиция отображений. Обратное, параметрическое и неявное
отображения.
Определение 1. Пусть f : Е —* F, a g : F —> G. Поскольку f(E) С F, то отображение
g каждому элементу f(x) € f(E) С F относит определенный элемент g(f(x)) ? G.
Таким образом, каждому х G Е посредством правила g о f поставлен в соответствие эле-
элемент (д о f)(x) = g(f(x)), g(f(x)) € G. Тем самым определено новое отображение (или новая
функция), которое назовем композицией отображений, или суперпозицией отображений, или
сложным отображением.
Определение 2. Пусть f : Е —> F — биективное отображение и F = {у}. В силу
биективности f каждому у g F соответствует единственный образ х, который обозначим
через f~i(y), и такой, что f(x) = у. Таким образом, определено отображение /-1 : F —* Е,
которое называется обратным отображению f, или обратной функцией функции /.
Очевидно, отображение / обратное отображению /~'. Поэтому отображения / и /~'
называют взаимно обратными. Для них справедливы соотношения
Определение 3. Пусть <р : П —> X, ф : U —* Y, причем хотя бы одно из этих отобра-
отображений, например <р, биективно. Тогда существует обратное отображение (р" : X —> П, а
значит, ф о <р~' : X —* Y.
Определенное таким образом отображение называется заданным параметрически с помо-
щькготображений tp : Q —<¦ X, ф : U —>У, причем переменное из П называется параметром.
Определение 4. Пусть на множестве G — X xY определено отображение Т: G —> Д,
г()е множество Д содержит нулевой элемент. Предположим, что существуют множества
Е С X, В С Y такие, что при каждом фиксированном х € Е уравнение Т(х, у) = 0 име-
имеет единственное решение у & В. Тогда на множестве Е можно определить отображение
f : Е —> В, ставящее каждому х € Е в соответствие то значение у € В, которое при
указанном х является решением уравнения Т(х, у) = 0.
Относительно так определенного отображения у = f(x), х Е Е, у € В, говорят, что оно
задано неявно посредством уравнения f(x, у) = 0.
Определение 5. Отображение f : Е —* F называется продолжением отображения
g : D —> F, ад — сужением отображения f, если Е D D и f(x) = д(х) Vx € D.
Сужение отображения / : Е —> F на множество D С Е иногда обозначают символом /|о-

§ 2. Функция. Отображение 15
Определение 6. Графиком отображения / : Е —> F называется множество
G = {(*, /(*)) : х € Е, /(*) е F).
Ясно, что G С Е х F.
14. Пусть отображение f : R —> [—1, 1] задано равенством /(г) = sin x.
Найтиа)/{0); в)/('); .),('); г) / A) ; д) / ([-', f ]) ; e)/(]-f,f[);
Ж)/([°'Я); з) /([О, 27Г]); и)/^); к) /"' (|) 5 л) /"' (^Щ ; м)Г'(^);
н) Г»([-1, 1]); о) /-'(]-!, 1[); п) /-'([°.|])-
•^ Пользуясь таблицей тригонометрических функций, находим:
а) /@) = sin 0 = 0; б) / (f) = sin f = \;
д) Имеем /(—f) = —1, /(§) = 1, причем, если аргумент синуса пробегает значения
от —j до ^, то значения синуса изменяются от —1 до +1. Следовательно, /([— §, §]) =
{sini :—^^х^^} = [—1,1]. Аналогично находим:
з) /([0, 2*]) = {sinz : х € [0, 2^]} = [-1, 1].
и) Поскольку sin х = 0, если х = кк, к € Z, то
/~'@) = {г: sin i=0}.
к) Если sini = i, то i = (-l)narcsin j + nv = (-l)"f + »jt, « € Z. Поэтому Z (?)-
1)"^+К7Г, « 6 2.
Аналогично предыдущему находим:
м) /-1 (^) = |«-: sin x = ^} = (-l)nf + ят, n E Z.
н) Согласно определению 2, п. 2.2,
/"'«-1. i]) = К* ¦¦ /(*) = «in * е [-1, i]}.
Покажем, что/~'([—l, 1]) = К. В самом деле, пусть х G /~'([—1, 1]) и а = sin г, тогда f(x) =
а, а € [—1, 1], а поэтому х = (( — 1)" arcsin а + пп), а: € К, и, следовательно, /~'([—1, 1]) С М.
Если х € R, то sini € [-1, 1] и as e f~\[-\, 1]), т. е. R С /"^([-l, 1])- Таким образом,
/-'([-1,1]) =R.
о) Из равенств sini = ±1 находим множество А = {х : х = ¦% + пж, п € Ъ\ значений х.,
которые не принадлежат /~'(] — 1, 1[). Поэтому, в силу предыдущего пункта, /~х(] — 1, 1[) =
п) Имеем /"' ([о, ?]) = {х : sin i 6 [о, |] }. Пусть х € /"' ([о, |]) и а = sin г, тогда
а € [О, |] и х = (-l)narcsin i + «тг, п 6 Z.
Пусть п = 2А: — фиксировано, тогда х = arcsin a + 2fc;r, причем при изменении a of 0 до
j переменное i изменяется от 2кя до Bfc + j) х, т. е. г € [2ктг, Bк + g-) я-] .
Пусть п = 2А. + 1 — фиксировано, тогда х = —arcsin a + Bfc + l):r, и если а изменяется от О
до j, то переменное х изменяется от Bк + \)т до Bк + |) п, т. е. г € [Bк + g) ж, Bк + 1)я-|.,
Таким образом,
»+
!) -

16 Гл. 1. Введение в анализ
Справедливо и обратное включение, поскольку при х ? [2kv, Bfc + i) ж\ или х ? [Bfc + |-)тг,
BJt + 1)тг] значение sin х € [О, -]. Поэтому
1 ([»¦ Ш = (и
Ь (+9 ]) (и [(+!) *¦
15. Доказать, что если / : Е —> F и А С Е, В С Е, то справедливо равенство
/(Л U 5) = /(Л) U f(B). A)
^ Согласно определению 1, п. 2.2, имеем
/(Лив) = {/(*):г е лив}.
Пусть /(я) € /(Л U В), тогда г € (Л U В), т. е. х € Л V г € 5. Но если г € Л V г € В, то
/(я) € /(Л) V /(г) € /(В) и /(г) € (/(Л) U /E)). Этим доказано включение
/(Л U В) С (/(Л) U/(Я)). B)
Пусть f(x) € (/(Л) U /E)), тогда f(x) € /(Л) V /(г) € f(B), откуда г € Л V г € 5, т. е.
i € (Л U В), а поэтому /(г) ? /(Л U В) и
(/(Л) U/(В)) С/(Л U В). C)
Из B) и C) непосредственно следует A). >
16. Доказать, что если / : Е —> F и А С F, В С F, то справедливы равенства:
а) ГХ(Л П В) = /"'(Л) П /"'(В); б) /-'(Л\В) = /-'(^/"'(В);
в) Г1 (A U В) = Г1 (A) U Г \В).
4 а) Пусть х € /~'(^ П В), тогда /(х) € (А П В), т. е. f(x) е Л Л /(х) € В. Но тогда
х € /~Х(Л) Л х g /~'(В), а следовательно, х € (/~'(Л) П /~'(В)). Таким образом, доказано
включение
Г1 (А П В) С (Г1 (А) П Г1 (В)).
Для доказательства обратного включения предположим, что х € (/~'(Л) П f~1(B)). То-
Тогда i G /"'О4) Л х е /~'(.В); отсюда /(х) € Л Л /(i) € В, а поэтому /(я) € (Л П В) и
я € /-1(Л П В). (Следовательно,
Из доказанных включений следует равенство а).
б) Пусть х € /-'(Л\В), тогда /(*) е (Л\В), т. е. f(x) € Л Л /(*) 0 В. Но тогда
I € f~1(A) Л х 0 f~1(B), а следовательно, х € (/~'(^)\/~1E))- Таким образом,
Г1(Л\В)С{Г1(А)\Г1(В)).
Если г е (/-'(AJV/'^B)), то_х е Г1 (А) Ах <? Г1 {В). Отсюда /(*) € Л л/(*) € В,
т. е. /(аг) € (Л\В). Но тогда х € / Х(Л\В), что доказывает справедливость включения
(Г*(а)\гЧв))сгЧа\В),
обратного доказанному выше. Из этих включений следует равенство б).
в) Если х € f~\A U В), то f(x) € (Л U В). Отсюда /(г) € Л V /(я) € В, а тогда
I € /~Х(Л) V х € f~l{B), т. е. i € (/-1(Л) U /"^В)). Таким образом,
Г1(АиВ)с(Г1(А)иГ1(В)).
Если же предположить, что х € (/~'(л) и /~'E))> то х € /"Ч-4) V х € f~\B) и
/(i) € Л V /(х) € В или /(х) € (Л U В), откуда х € /д-4 U В). Следовательно,
(Г1 (A) U Г1 (В)) С Г1 (A U В),
что вместе с обратным включением равносильно в). >
17. Пусть / : Е —> F, Р — семейство подмножеств множества Е, Q — семейство
подмножеств множества F. Обозначим
Q:AeP}, /"•(<?) = {Г1(Д)€Р: В €Q}.

§ 2. Функция. Отображение
17
Доказать, что: а) если Q — кольцо, то / 1(Q) — также кольцо; б) если Я — кольцо, то
f(P) не обязательно является кольцом.
¦4 а) Поскольку Q кольцо, то из 5Х € Q, В2 € Q следует (Вх U B2) € Q, Ei\B2)t Я-
Тогда, согласно предыдущему примеру,
/-xEi) U Г\В2) = Г1(ВХ U В2) € Г\Я)\ Г\Вх)\Г1(В2) = Г\Вг\В2) € Г1 (Я),
т. е. f~1(Q) — кольцо.
б) Пусть Е = {а, Ъ, с, d), F = {а', 6', d'}, /(а) = а', /F) = /(с) = 6', /(<*) = d'. Семейство
Я = {{а, Ь, с, d}, {а,Ь}, {c,d), 0}
является кольцом, однако /({a, b})\f({c, d}) = {а', 6'}\{Ь', d'} = {а'} ? /(Я) = {{а', Ь.', d'},
{а', Ь'}, {Ь1, с'}, 0}, т. е. /(Я) не является кольцом. >
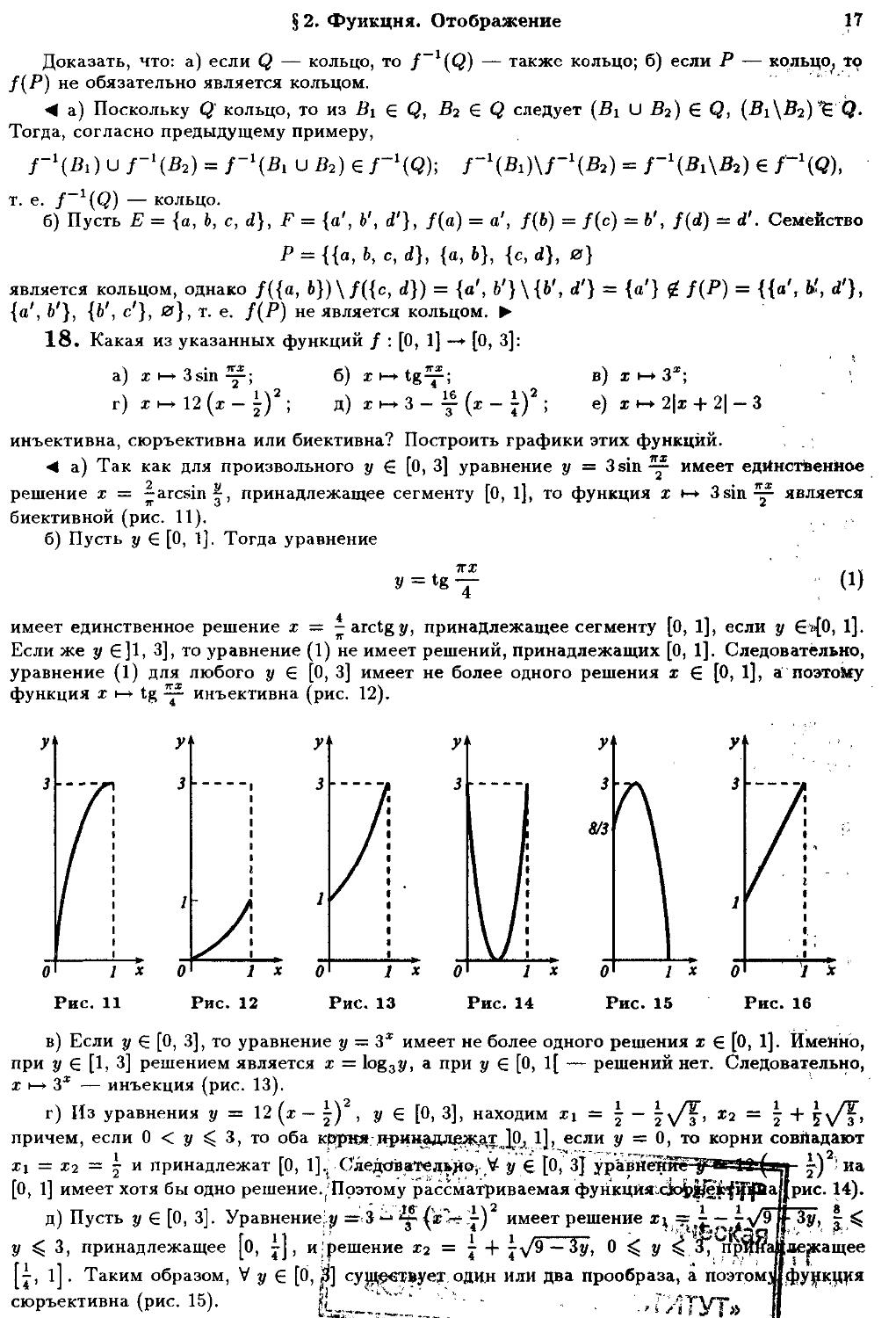
18. Какая из указанных функций / : [0, 1] —> [0, 3]:
а) х ь-^ 3 sin ~r~; б) х i—> ^ё~т~5 ^) ^ *~* ^ > ¦
г) г ^ 12 (х - |J ; д) х н- 3 - f (г - jJ ; е) х ь* 2|х + 2| - 3
инъективна, сюръективна или биективна? Построить графики этих функций.
¦4 а) Так как для произвольного у € [0, 3] уравнение у = 3sin-^ имеет единственное
решение х = -arcsin j, принадлежащее сегменту [0, 1], то функция х *-* 3sin^ является
биективной (рис. 11).
б) Пусть у € [0, 1]. Тогда уравнение
У = tg — A)
имеет единственное решение х — ^arctgy, принадлежащее сегменту [0, 1], если у &<{0, 1].
Если же у €]1, 3], то уравнение A) не имеет решений, принадлежащих [0, 1]. Следовательно,
уравнение A) для любого у € [0, 3] имеет не более одного решения х ? [0, 1], а поэто»у
функция х I—> tg 2j? инъективна (рис. 12).
О 1х
Рис. 12
О 1х
Рис. 13
У
3
№
О 1х
Рис. 15
О 1х
Рис. 16
в) Если у € [0, 3], то уравнение у = 3* имеет не более одного решения х € [0, 1]. Именно,
при у € [1, 3] решением является х = log3y, а при у € [0, 1[ — решений нет. Следовательно,
х 1—> 3* — инъекция (рис. 13).
г) Из уравнения у = 12 (х - ?) , у € [0, 3], находим xt = | - j^/f, х2 = | + ?\/f,
причем, если 0 < у ^ 3, то оба корня • принадлежат JO, 1], если у = 0, то корни совйадают
xi = х2 — 2 и принадлежат [0, 1], Следовательно, V у € [О, 3J уравнение-^
[О, 1] имеет хотя бы одно решение.'Поэтому рассматриваемая функция cjo^gieK^iJ^Bajlрис. 14).
д) Пусть у € [0, 3]. Уравнение:.у =¦ 3 -^ ^ ^«ле-lj) имеет решение х^ = i — JV9fr Зу, | ^
у ^ 3, принадлежащее [0, -], и;решение х2 = j + уу'Э — Зу, 0 ^ у ^ 3^ принаддежащее
fj, l]. Таким образом, V у € [0, ^] суре«твует один или два прообраза, а поэтомч|функ,1Ц?Я
[j ]
сюръективна (рис. 15).
T'/iTYJ»

18 Гл. 1. Введение в анализ
е) Пусть у € [0, 3]. Тогда уравнение у = 2\х + 2\ — 3 при у € [1, 3] имеет единственное ре-
решение х = ^у~> если у € [0, 1[, то это уравнение не имеет решений, принадлежащих сегменту
[О, 1]. Следовательно, х *-* 2\х + 2\ — 3 — инъекция (рис. 16). >
19. Дана функция f(x) = tgx, — < х < —, найти обратную ей.
< Покажем, что данная функция является биекцией / :]у-, Щ- [—> К- С этой целью
обозначим х = 2?г + г, ~§ < г < J- Тогда V у € R уравнение у = tgx принимает вид
у — tg г, г € ]— ^, § [. Отсюда г = arctgy и, пользуясь тем, что х = 2ж + г, находим
х — 27r + arctg у; причем если у € М, то х € ] гр -у- [, т. е. биективность функции установлена.
А поскольку каждому у € 1R соответствует единственное значение х € ] -у, -j- [, то обратную
функцию /~ : R —+ ] -у-, ¦— [ определяет соответствие у н-> 2я- + arctg х, х 6 ] -у, -у [. >
20. Написать явные выражения функций, заданных параметрически:
а) х = a cost, у = а sin t, 0 ^ t ^ я-; б) г = а cos t, у = а sin t, я- ^ t $С 2я- (а > 0).
¦< а) Поскольку функция t к->• a cost, < € [0, я-], является биекцией [0, я-] —> [—а, а], то V г 6
[—а, а] из равенства х = a cos t находим единственное значение < = arccos -, принадлежащее
сегменту [0, ff]. Подставив это значение во второе равенство, получим
у = a sin I arccos —
Т. е. у = у/а2 — х2, х € [—а, а].
б) Обозначим я- + г = t. Тогда, если г € [0, я-], то t € [т, 2я-], при этом первое равенство
Приводится к виду х = —a cos г.
Функция т t-* —a cos г является биекцией [0, я-] —> [—а, а], поэтому V г € [—а, а] находим
г — arccos (—¦¦) = я- — arccos- и t = 2я- — arccos |. Подставив найденное значение t во второе
равенство, получим
у = -\Л2 - х2, х е [-а, а]. >
21. Написать явное выражение для функции / : —, — —> [4я-, Ьп], заданной неявно,
Посредством равенства
sin х — cos у = 0, г € -г-, — I > у € [4тт, 5jt]. A)
¦< Для любого фиксированного х G [^р ^] имеем sin х = ?, ? S [—1, 1]- Поэтому A)
равносильно уравнению cos у = </, которое на сегменте [4тг, 5я-] имеет единственное решение.
Этим доказано существование функции
/:[?.?]-[4., Ч.
Для записи аналогичного выражения функции / преобразуем равенство A) к виду
¦ /"¦ ^\
sin х — sin I у I = 0.
Отсюда
1--+У г + --г/
2 sin = cos j- = 0.
Приравняв к нулю каждый множитель, находим два значения у:
У = х - | + 2пп, п е Z, B)
| я?1 .- • C)
В случае B) из условия х € [—¦, у-] следует у € [{2п + 1)п, Bм + 2)я-] и не принадлежит
[4ff, 5тг] V« € Z, т. е. у = i — | + 2п7г не является значением функции / ни при каком п € Z.

§ 2. Функция. Отображение 19
В случае C) из условия i g [^, у] следует у € [Bп - 2)тг, B« - 1)тг] С [4тг, 5ir] при п = 3.
При этом значении п из C) находим явное выражение функции /
13я- ГЗя- 5тг1
* = -* + —, «е[т,т].^
Упражнения для самостоятельной работы
19. Пусть отображение / : К —> [—1, 1] задано равенством f(x) = cos г.
Найти: а) /@); 6)/(f); B)/(f); r)/(f); „)/([-?§]); e)/fl-f, f Q ;
ж)/([0, ?]); з)/([0,2»]); и) Г»; к)/^); л) /"» (f) ; м) /"» (f) ;
н)/-1([-1,0]); o)/-([o,f]); n) /- ( [-f, f ]) .
20. Для отображения / : [о, ^J —> R, заданного равенствами
a) /(i) = tgi; 6) f(x) = ctgx,
найти: /([0,f]), /([o,=]), /([f,f]), /"'QO, 1]), /
21. Доказать, что если / : Е —<• F, А С ?, 5 С Е, то:
а) /(Л п В) С (ДЛ) П /(Я)); б) (f(A)\f(B)) С /(Л\В).
22. Пусть f : Е^ F, AC F, В CF. Доказать, что если А С В, то /"'(Л) С /~
23. Доказать, что если f : Е -^ F и А С Е, В С F, то:
*) АСГЧНА)); б) /(Г'E)) = В; в) f(A)nB = f(Anf-1(B));
г) (/(Л) ПЙ = 0)#(ЛП /-'E) = 0); Д) (/(А) С В) # (А С
24. Какая из функций / : [— 1, 1] —»¦ [0, 1]:
а) х •—> cos Щ-; б) ху-*—х2 + \\ в) a; i—>" |а;|;
г >-> -J-; д) i^ -*-; е) г к 2* J
инъективна, сюръектияна или биективна? Построить графики.
25. Найти биективное сужение функций:
a) f(x) = х2, х €R; б) f(x) = sin г, х € К;
г) f(x) = sin j, x > 0; д) /(z) = 10*, z € R;
26. Найти функции, обратные данным:
в) fix)
е) fix)
= sin x,
— COS X,
= ctgz,
= cos г, x
= x3
xe
xe
GR;
+ 1 + 1, i €
La ' :
[-77Г
x €]- tr,
f];
. -ex];
0[.
b) f(x) = cosx, хе[2я-,3тг]; г)
д) /(x) = tgx, x€]+f, t[; e)
27. Найти явное выражение для функций, заданных параметрически:
а) * = ¦??, У = т^> 0^t<+oo; б) х = ??, v = f^, -oo < t ^ 0 (а>0).
28. Найти явное выражение для функции / : [я-, 2ж\ —» [-^, -^], заданной неявно
cosi+smy=0, x € l?r, 2я-], у € [—, -j-J .
29. Найти явное выражение для функции / : [я-, 2я-] —>¦[§, Щ-\, заданной неявно
cos х + sin у — 0, г € [я", 2я-], у € [§, ^р] . . .

20 Гл. 1. Введение в анализ
§ 3. Действительные числа
3.1. Бинарные отношения и бинарные операции.
Определение 1. Бинарным отношением в множестве Е называется всякое подмно-
подмножество В из произведения Е х Е.
Определение 2. Бинарное отношение 12. называется отношением эквивалентности
в множестве Е, если подмножество "Я:
а) рефлексивно: (а, а) ? "Я Va ? Е;
б) симметрично: ((а, Ь) ? Я) =>• (F, а) ? ~Я);
в) транзитивно: ((а, Ь) ? Я Л F, с) ? '#) =>• ((а, с) е 'Л).
Вместо (а, 6) ? 7? часто пишут а ~ Ъ или а = Ь.
Определение 3. Бинарное отношение П называется отношением порядка в множе-
множестве Е, если оно:
а) рефлексивно: (а, а) ? П Va ? ?;
б) транзитивно: ((а, 6) € П Л F, с) € П) =>• ((а, с) € П);
в) антисимметрично: ((а, 6) 6 П Л F, а) € П) =>¦ (а = 6).
При этом говорят, что отношение П упорядочивает Е. Вместо (a, b) € П часто пишут
а ^ Ь, или а С Ь.
Если Va, b ? Е всегда (а, Ь) € П или F, а) € П, то говорят, что множество Е вполне
упорядочено.
Определение 4. Внутренней бинарной операцией на множестве Е называется ото-
отображение f : Е х Е —<• Е.
Пусть заданы два множества Е и F.
Определение 5. Внешней бинарной операцией на множестве Е называется отобра-
отображение f : Ex F — Е.
Определение 6. Множество Е, обладающее внутренней бинарной операцией Т, назы-
называется группой, если:
1) операция ассоциативна: (а Т Ь) Т с = а Т (Ь Т с) Va, b, с ? Е;
2) имеется нейтральный элемент: Эе ? Е такое, что Va ? Е справедливо равенство
аТе = еТа = о;
3) всякий элемент, имеет симметричный: Va ? Е За ? Е такое, что аТа = аТа=е.
Если, кроме того,
4) операция Т коммутативна, то группа называется коммутативной или абелевой.
Если операция Т есть сложение, то группа называется аддитивной, если Т есть умноже-
умножение, то группа называется мультипликативной.
3.2. Аксиомы поля действительных чисел.
Определение 1. Множество R = {а, Ъ, с, ...} называется полем действительных
(или вещественных) чисел, если для его элементов установлены бинарные отношения и
бинарные операции, подчиненные перечисленным ниже аксиомам.
Аксиомы сложения
СО. В множестве R определена внутренняя бинарная операция — сложение
К х К -> R : (а, Ъ) (-¦ а + 6,
которая каждой паре элементов a, b ? R однозначно ставит в соответствие некоторый элемент
множества R, называемый их суммой и обозначаемый символом а + Ь. При этом выполняются
следующие аксиомы:
C.I. (a -+¦ Ь) + с = а + (Ь + с) (ассоциативный закон).
С.2. В И? существует элемент, называемый нулем и обозначаемый символом 0, такой, что
Va€R
a + 0 = a.
С.З. Va € К существует такое число (—a) ? R, что выполняется равенство
а + (-а) =0.
С.4. Va, Ь ? U
a + b = b + а.
Таким образом, множество R является аддитивной абелевой группой.

§ 3. Действительные числа 21
Аксиомы умножения
У.О. В множестве R определена внутренняя бинарная операция — умножение
R х К -> U : (а, Ъ) >-* а • Ь,
которая каждой паре элементов а, Ь € R однозначно ставит в соответствие некоторый эле*
мент множества R, называемый их проозбеЭеноез» и обозначаемый символом а ¦ Ь. При'этом
выполняются следующие аксиомы:
УЛ. (а -Ъ) • с = а ¦ (Ь ¦ с) Va, b, с € R (ассоциативный закон).
У.2. В R существует элемент, называемый еЭоноцей и обозначаемый символом 1, такой,
что Va € К справедливо равенство
a • 1 = a.
У.З. Va € К\{0} существует элемент a € R, называемый обратным чдслу а, такой, что
a-a =1.
У.4. а-Ъ = Ъ-а Va,b€№.
Следовательно, множество ненулевых элементов множества К является мультиплика-
мультипликативной абелевой группой.
Д.1. Операция умножения дистрибутивна относительно сложения, т. е.
= a-b + a-c Va, Ь, с € R.
Множество {а, Ь, с, ...}, удовлетворяющее аксиомам С, У и Д, называется числовым по-
полем. Это же множество без аксиомы У.4 называется телом.
Аксиомы порядка
П.О. В множестве К задано отношение ^, которое вполне упорядочивает К:
П.1. а ^ a Va € К (рефлексивность).
П.2. (a $C b Л b $С а) =$¦ (а = 6) (антисимметричность).
П.З. (а ^ 6 Л b ^ с) =*¦ (а ^ с) (транзитивность).
П.4. Va, b € К или а ^ 6, или 6 ^ а, или то и другое.
Следующие две аксиомы связывают отношение порядка и бинарные операции:
ПП.1. Если а, Ь, с € К и а $С Ь, то а + с ^ Ь + с.
ПП.2. ИзО^а и 0^6 следует 0 ^ ab Ча, Ь ? К. !l
Аксиома о верхней грани - ;
Определение 2. Множество А С М называется ограниченные сверху, если существу-
существует элемент М С К такой, что а ^ Л/ Va ? А, про этоз« число М называется верхней
гранью множества А. ,. :»
Определение 3. Верхняя грань М* множества А называется точной верхней гранью
множества А, если всякая другая верхняя грань М множества А не меньше числа М*.,
Точная верхняя грань множества А обозначается символом sup .А.
В.О. Всякое ограниченное сверху множество 4сМ имеет точную верхнюю грань.
3.3. Расширенное множество действительных чисел. ..
Определение. Множество Ш = R U {—оо, +оо}, состоящее из элементов множества R
и двух символов —оо и +оо, называется расширенной системой действительных чисел;
причем выполняются следующие условия:
а) —оо < а < +оо,
а — оо = —оо, а + оо = +оо, = =0 Va ? R;
—оо +оо
б) если a > 0, mo a • (—оо) = —оо, a ¦ (+оо) = +оо;
в) если а < 0, то a • (—оо) = +оо, a • (+оо) = —оо.
Символ —оо +оо называется минус (плюс бесконечностью.

22 Гл. 1. Введение в анализ
3.4. Основные характеристики действительного числа.
Будем для простоты обозначать через К одновременно множество всех действительных
чисел, упорядоченное пространство действительных чисел и упорядоченное поле действи-
действительных чисел, различая смысл обозначения по тексту изложения. Например, если записано
х € R, то здесь К — множество действительных чисел. Если сказано, что х ^ у в К, то под
R понимаем упорядоченное пространство. Наконец, если записано х + у < z в К, то К озна-
означает упорядоченное поле действительных чисел. В случае, если по тексту изложения не ясен
смысл обозначения, то будем пользоваться более сложными обозначениями.
Для действительного числа х введем следующие характеристики: |i| — модуль х, sgn x —
знак х, х+ — положительная часть х, х~ — отрицательная часть х. Они вводятся по пра-
правилам:
i*4 i;,
с,
о,
если х
если i
если i
если х
<
>
0,
0;
о,
0;
если х > 0,
sgn х = \ О, если 1 = 0,
если х < 0;
+ _ J xi если х .> и, _ _ j и, если х ^ О,
если i < 0.
Очевидны следующие соотношения между этими характеристиками Vz 6 К:
x = |x|sgnx, |x| = xsgnx, х = х — х~,
\~\ _ _+ I _~ г+ _ \Х\ "Г" Ж -_ РГ? Г Т Ч
|Л| ЛТЛ, Л о' О' \ '
При решении задач часто применяются неравенства
Вместе с указанными характеристиками полезно также рассмотреть функции К —» R :
х \г+ |х|, х (-+ sgnr, i I—> i+, x —* х~, графики которых изображены на рис. 17—20. Первая и
вторая функции являются мультипликативными отображениями, поскольку из определения
этих функций следуют равенства
\ху\ — |х||у|, sgn(iy) = (sgn i)(sgn у) V(x € К, у 6 К).
Каждая из указанных функций, за исключением "sgn", обладает свойством: множество
точек, расположенных выше ее графика, является выпуклым, т. е. если две точки на плоско-
плоскости расположены выше графика функции, то и все точки отрезка, соединяющего их, также
расположены выше. Такие функции называются выпуклыми. Если функция / определена на
числовой прямой R и является выпуклой, то V(ii 6 К, хг € Щ выполняется неравенство
C)
Это неравенство очевидно: его левая часть есть ордината точки графика с абсциссой *' 2*3 ,
а правая часть — ордината точки отрезка с той же абсциссой, расположенного выше графика
(рис. 21). Выпуклые функции будут подробно изучены в § 5, гл. 7.
Применив неравенство C) к выпуклым функциям х *-* \х\, х н-> i+, x i—> х~, получим
важные оценки
|x + »|<|x| + |»|, (х + у)+ <1++з,+ , (х + у)~ <я- + зГ, D)
справедливые V(r 6 К, у € Щ.
Из всех перечисленных характеристик действительного числа наиболее важной является
его модуль. Под основными свойствами модуля числа понимают следующие:
1) Vr€K (|x| = 0)=*(x = 0);
2) V(A€R, r€ К) |Ах| = |А||х|;
3) V(x€R, у eR) \х + у\^\х\+\у\.
¦, , Последнее неравенство называется неравенством треугольника, поскольку оно имеет гео-
геометрический смысл в слунае, когда х € С, у € С (см. § 4).

§ 3. Действительные числа
3.5. Метод математической индукции.
Пусть запись А(к) означает, что высказывание А истинно при указанном к €
метода математической индукции в следующем:
I Л {А(к) =*¦ А(к + 1) Vifc € N)) => (А(п) V» 6 N).
23
i. Суть
О
-1
Рис. 18
У
О
Рис. 19
О
Рис. 20
х, d2
Рис. 21
22. Доказать, что в множестве R имеются единственные нуль и единица.
Л Предположим, что в множестве К имеется два нуля Oi и <h. Тогда, согласно аксиомам
С.2 и С.4, имеем
Oi =0i +02 =02+0i =02.
Аналогично, если li и Ь единицы в R, то, согласно У.2 и У.4,
li=b'b = b-li = Ь. >
23. Доказать, что: а) уравнение а + х = Ь имеет единственное решение х = —а + Ь; 6)
уравнение ах — Ь имеет единственное решение х — а~хЬ.
< а) Число —а + Ь удовлетворяет уравнению а + х = Ь. В самом деле: а + (—а + Ь) =
(а + (—а))+Ь = 0 + Ь = Ь. Других решений нет. Действительно, если х € К —другое решение,
то
-а + Ь- -а + Ь,
—а + (а + х) = — а + Ь,
(-а+а) +х = -а + Ъ,
0+i=i =-а+ 6.
б) Аналогично число а~хЬ удовлетворяет уравнению ах = Ь:
Если х g R — какое-либо другое решение уравнения ах = Ь, то
а~16 = а-1Ь, а~\ах) = а-1Ь, (а а)х = а Ъ,
1 ¦ х — а~1Ь. х = а~1Ь. >
24. Элемент а ? Е называется регулярным относительно внутренней бинарной операции
Т, если Vi, у ? Е
{а Т х = а Т у) Л (х Т а = у Т а) => г = у. ;
Доказать, что всякий элемент с 6 К регулярен относительно сложения, а1 всякий ненуле-
ненулевой элемент с 6 R регулярен отиосительно умиожения. ; '

24 Гл. 1. Введение в анализ
4 Докажем, что произвольный элемент с 6 К регулярен относительно сложения. В силу
коммутативности сложения (с + а = с + 6) & (а + с = b + с). Поэтому достаточно показать,
что (с + а = с + 6) =*- (а = 6).
На основании предыдущего примера и ассоциативности сложения имеем
а = -с. + {с + Ь) = (-с + с) + 6 = 0 + 6 = Ь.
Аналогично доказывается, что Vc ? R\{0} регулярен относительно умножения. >
25. Обозначим Е = {/} — множество функций / : А —> А, А С К- Пусть на этом
множестве определена внутренняя бинарная операция
Е х Е-* E:(f,g) н- / о д.
а) Показать, что эта операция ассоциативна.
б) Определить регулярные элементы этой операции.
4 а) Для доказательства равенства
(f og)oh = f o(g oh)
достаточно показать, что образы любого элемента х € А совпадают. Пусть х € А, п; = h(x),
v = g(u). Имеем
((/ о д) о h)(x) = (/ о g)(h(x)) = (/ о д){и) = f(g(u)) = f(v),
(д о h)(x) = g(h(x)) = д(и) = v,
следовательно, (/ о (д о h))(x) = f((g о h)(x)) = f(v), т. е. образы элементов х совпадают и
ассоциативность доказана.
б) Отображение / назовем регулярным слева, если (/од = /оК) => (д = h), и регулярным
справа, если (д о / = h о /) =>> (д = h). Ясно, что отображение регулярно, если оно регулярно
слева и справа.
Покажем сначала,- что отображение / регулярно слева тогда и только тогда, когда оно
инъективно.
В самом деле, если / инъективно и fog = foh,To для любого х 6 А
(Ш*)) = ПЦх))) => (д(х) = h(x)) ^{g = h).
Если же / не инъективно, то на множестве А существуют различные числа х и у, образы
которых совпадают: f(x) = /(»/). Выберем отображения д и h такими, чтобы д{а) = х,
h(a) = у для некоторого а ? А. Поскольку х ф у, то из f о д = f о h не следует равенство
д = h, т. е. / не будет регулярным слева.
Покажем теперь, что / регулярно справа тогда и только тогда, когда функция / сюръек-
тивна.
Если / сюръективно, то Vi 6 А существует такое и ? А, что /(«) = х. Тогда
(д о / = h о /)=>(,(*) = Цх)) ЧхЕА.
Если же / не сюръективно, то до f = ho f для тех отображений д и h, сужения которых
совпадают на множестве f(A). Однако отображения д и h могут быть различны, поскольку
могут принимать различные значения на множестве A\f{A).
Таким образом, для того чтобы отображение / было регулярно, необходимо и достаточно,
чтобы оно было биективным. >
26. Множество А С К называется ограниченным снизу, если Эт 6 К такое, что Va 6 А
выполняется неравенство m ^ а; при этом число m называется нижней гранью. Нижняя
грань я»* множества А называется точной нижней гранью множества А, если всякая другая
нижняя грань т множества А не больше т*. Точная нижняя грань множества А обознача-
обозначается символом МЛ.
Доказать, что всякое ограниченное снизу множество А имеет точную нижнюю грань,
причем, inf А = — sup{—А), где —А = {—х}, х € А.
•^ Согласно условию, Зт 6 К такое, что х ^ т Vi 6 А, откуда —х ^ — т, т. е. множество
—А ограничено сверху. Согласно аксиоме В.0, 3sup{—А) = М*. Тогда —х ^ М* Vi 6 А,
поэтому — М* ^ i Vi ? Л, следовательно, — М* — нижняя грань множества А. Если N
— любая другая нижняя грань множества +Л, то — N— верхняя грань множества —А, а
поэтому — N ^ М* = sup{— А}, откуда N ^ — М, так что — М* = — sup{—А} является точной
нижней гранью множества А. >

§ 3. Действительные числа . 25
27. Доказать теорему Архимеда: если а > 0, a b — произвольное действительное 4UCJHQ,.
то существует такое п 6 Ъ, что (и — \)а ^.Ь, па > Ь. .,;-..
•^ Докажем сначала, что Эп 6 Z такое, что па > 6. Для доказательства предположим
обратное, т. е. ка ^.Ь VA; € Ъ. Тогда множество {ка} ограничено сверху и, согласно аксиоме
В.О, имеет точную верхнюю грань sup{fca} = М* ^ 6. Поскольку число М* — а не является
верхней гранью множества {ка}, то Зра 6 {ка} такое, что М* — а < ра ^ М*\ Отсюда
(р + \)а > М*, (р + 1) € Z, что противоречит определению числа М*. Источник противоречия,
в предположении, что ка ^ 6 VA: 6 Z. Следовательно, существует число к ? Z такое, что
fca > 6.
Аналогично доказывается, что Зт 6 Z такое, что та < 6. Сегмент [та, ка], содержащий
точку Ъ, делится точками (т + l)a, (m + 2)а,... , (ifc — l)a на fc — m сегментов; одному из них
принадлежит точка 6. Следовательно, существует п € Z такое, что (п — \)а ^ 6 < па. >
28. Доказать, что для произвольно заданного положительного числа е существует такое
натуральное число п, что
- < с.
Л Полагая в теореме Архимеда Ь = -, а = 1, приходим к неравенству по • 1 > -, »о € Z.
А так как - > 0, то пб € N. Тогда Vn > «о, п € N, справедливо неравенство п > по > - или
29. Пусть а п f) произвольно заданные действительные числа, причем Of < /?. Доказать,
что существует рациональное число г, заключенное между числами а и 0.
4 Обозначим h = fi — а. Согласно предыдущему примеру, 3n g N такое, что
Согласно теореме Архимеда, существует т ? S такое, что
m m+ 1
— <a < .
п п
Отсюда и из неравенства A) получаем
п п
n и n
Таким образом, а = ^— < /3. >
30. Показать, что множество всех правильных рациональных дробей —, где тип —
натуральные числа и 0 < т < я, не имеет наименьшего и наибольшего элементов. Найти
точную нижнюю и точную верхнюю грани этого множества.
•^ Пусть т и п @ '< т < п) — любые натуральные числа. Тогда из очевидных неравенств
т _ 2т 2т - 1 т _ 2т 2т +1 -
« 2и 2п ' п 2га 2п
следует, что множество правильных рациональных дробей не имеет наименьшего и наиболь-
наибольшего элементов.
Покажем, что inf { ^ } = 0, a sup { ~} = 1 •
Согласно теореме Архимеда, для произвольно заданных е > 0 и т € N найдется таКОе"
п € N, n > т, что п > —. Тогда — < с. Отсюда и из неравенства — > 0 следует;
что inf {-^-} = 0. Аналогично для произвольно заданных с > 0 и р € N найдется такое
натуральное число т, что т > р'1~''. Отсюда -т— > 1 — с, т. е. при n = p + m имеем
— > 1 — с, а это вместе с неравенством — < 1 означает, что sup | — | = 1. > >
31. Пусть {х + у} есть множество всех сумм х + у, где г € {х} и у € {j/}. Доказать
равенства:
a) inf {ж + J/} = inf{i} +inf{j/}; б) sup{i + у} = sup{i} + sup{«/}.
¦4 а) Так как из х ^ m, i 6 {х}, и j J mi, } 6 {у}, следует, что г + у *? тр.-\-тх,,.
(х + у) 6 {x + j/}, то существование inf{i} = т* и inf {у} = то* влечет за собой существование

26 Гл. 1. Введение в анализ
inf {г + у}. Ясно, что х + у ^ т* + т*. Далее, для произвольного с > 0 существует такой
элемент (х' + у') € {х + у}, что
т* + т\ ^ х + у' < т* + ml + с,
поскольку существуют1 такие х' € {х} и у' g {у}, что тп* ^ х' < т* + | и т* ^ у' < т* + ^.
Следовательно,
inf {я + у} — х' +у' = inf {z} +inf{j/}.
Равенство б) предлагаем доказать самостоятельно. >
32. Пусть {ху} есть множество всех произведений ху, где х 6 {х} и у ? {у}, причем
х ^ 0) у ^ 0. Доказать равенства:
a) inf{ry} = inf{r}inf{y}; б) sup{i»/} = sup{i} sup{y}.
4 Докажем равенство б) (равенство а) предлагаем доказать самостоятельно). Так как
из х < М, х 6 {х}, х ^ 0, и у < Mi, j 6 {у}, у ^ 0, следует, что гу < Л/Mi, то из
существования sup{i} = М* и sup{y} = М* вытекает существование sup{iy}. Из неравенств
М* -?i < г < М*, М* - ?2 < У 4: М* следует, что М*М* - (ciM* + е2М' - ?i?2) <
ху ^ M'Mi*. Поскольку величина eiMi* +егМ* — С1С2 может быть сколь угодно малой, то
sup{iy} = М*М* = sup{i}sup{y}. >
33. Пусть X = (-± —-—|, п 6 N. Доказать, что inf X - 0, supX = 1.
•^ Пусть с > 0 — произвольно заданное число. Тогда из неравенств
0<Ь^ТТ<?' 1-?<5 + 2^ГТ<1'
справедливых при всех п > ~ge, вытекает, что inf X = 0, sup X = 1. >
34. Доказать неравенства:
а) \х-у\> ||х|-Ы|; б) \х + Х1 + Х2 + ¦ ¦ ¦ + хп\ > \х\ - (\xi\ + |х2| + ... + |х„|).
< а) Применяя к сумме (х — у) + у неравенство треугольника, приходим к неравенству
из которого получаем
Меняя местами х и у, находим
Отсюда
-|*-»|<И-Ы. B)
Из неравенств A) и B) следует а).
б) Пользуясь неравенством треугольника, получаем
|х| = |(х + Xi + Х2 + ... + Х„) - (Xl + XJ + . . . + Хп)\ <
< \х + Х\ + Х2 + ... + Хп\ + |ll + 12 + • • ¦ + Хп\ <
< \х + XI +Х2 + ... + Х„| + \xi\ + \Х2\+ ... + |хп|,
откуда непосредственно следует неравенство б). >
35. Решить уравнение
|х| + |х-1| + |х-2| -2,5 = 0.
¦* Имеем
{-Зх + 0,5 = 0, если х € ] - со, 0[,
-1 + 0,5 = 0, еслих€[0, 1[,
+х — 1,5 = 0, если х 6 [1, 2[,
+3х - 5,5 = 0, если х € [2, +оо[.
Отсюда заключаем, что на промежутках ] — со, 0[, [2, +со[ решений нет, а на промежутке
[0, 1[ имеем корень х = 0,5 и на [1, 2[ — корень х = 1,5. >

§ 3. Действительные числа 2t
36. Найти сумму '¦
Sn = arctg - + arctg - + arctg — + • • • + arctg ^j.
4 Применим метод математической индукции. Поскольку ;
,9i = arctg -, S2 = arctg - + arctg - = arctg 2 8 = arctg -,
2 2 8 l-J-8 3 ....,-. j\
2 1 ~ + - 3 ' ¦'
S3 = arctg - + arctg — = arctg 3 2 18t = arctg -, ''.''..
О 1 О 1 — — . ТС .
3 18
то можно предполагать, что
Sn = arctg ^y, n€N. . ' A)
А так как
Sn+1 = arctg _ + arctg ^__ = arctg
и равенство A) справедливо при п = 1, то, согласно индукции, оно справедливо при всех в. >
37. Применяя метод математической индукции, доказать, что для любЬго натурая!!«ого
числа п справедливы следующие равенства: '-¦''<
а) г* +22 + ... +п2 ="(» + 1)B" + 1). б) 13+23+...+г,3 = A + 2+...+«)«. ^
6
Л а) При п = 1 равенство справедливо. Предполагая справедливость равенства при п,
покажем справедливость его и при п + i. Действительно, > '..
что и требовалось доказать.
б) При п — 1 справедливость равенства очевидна. Из предположения справедливости его
при п следует , ,f , г-
I3 + 23 + ... + п3 + (» + IK = A + 2 + ... + nf + (п + IK =
= A + 2+ ...
Учитывая равенство 1 + 2 + ... + п = "^" ', получаем
I3 + 23 + ... + «3 + (п + IK = A + 2 + ... + п + (п + I)J,
т. е. утверждение справедливо и при п + 1. >
38. Доказать формулу бинома Ньютона
где С™ — ———: г-г (число сочетаний из п элементов по т), к\ = 1-2 ... к, причем полагают'
т\(п — ту. , "
0! = 1. ' .
4 При п = 1 имеем
?п=0
Остается показать, что из предположения справедливости утверждения для н следует, что
п+1
ГГ! .¦:¦'.¦¦¦ ' ¦¦!.'.( \г -.Ш

28 Гл. 1. Введение в анализ
В самом деле,
п п
(a + 6)n+1 = (а + Ь)(а + Ъ)п = (а + 6) JT С?ап-тЬт = ? С^а
m=0 m=0 m=0
n n+l rc
On а о + > On a 6 ^ a + > (On + ^n )a 0+6
m—О m=l m=l
Используя соотношения
Cn +<^n = m! (n - m)! + (m - 1)! (n + 1 - m)! = m! (n + 1 - m)! = Cn+1' Cn+1 = Cn+1 = *'
окончательно имеем
n n+l
/ j^ Zl'i*1"^'^ П+1 , ^ ^|T71 71+1—TTOlTTO , 1П+1 ^T ^""*T71 П+1 —'TTllTn ^
m—\ m=0
39. Доказать неравенство Бернулли
A + Xi)(l + Xi) . . . A + 1„) ^ 1 + Xi + X2 + • • ¦ + Xn,
где x\, xi, ... , xn — числа одного и того же знака, большие — 1.
¦4 При п = 1, 2 неравенство очевидно. Пусть неравенство справедливо при п. Покажем
справедливость его при п + 1. Имеем (при Xi > —1)
= 1 + Х\ + Х2 + ... + Х„ + Xn+i + (Xi + 12 + • ¦ ¦ + Xn)xn+i ^ 1 + Ц + 12 + . . . + In + Х„+1 .
Здесь использовано неравенство
(Х1 + Х2 + ••• + Х„)хп+1 ^ 0,
справедливое при любых Xi одного знака. >
40. Доказать, что если х > — 1, то справедливо неравенство
A + х)п^1 + пх, »>1,
причем знак равенства имеет место лишь при х = 0.
¦4 Требуемое неравенство непосредственно следует из предыдущего примера, если поло-
положить там Хх = хг = ¦ ¦ ¦ = хп = х. Если х = 0, то Vn > 1 имеем знак равенства. Покажем,
что при п > 1 и х > —1 получим строгое неравенство A + х)п > 1 + пх. При п = 2 это
очевидно: A + хJ ~ 1 + 2х + х2 > 1 + 2х. Далее, если A + х)" > 1 + их, то
A + z)n+l = A + i)n(l + х) > A + nx)(l + х) = 1 + пх + х + пх2 > 1 + (п + 1)х. >
41. Доказать, что если ц > 0 Vi; = 1, п и iii2 • • • хп — 1, то
XI + Х2 + . . . + Хп ^ П, A)
при этом
(*1 + 12 + • • • + Хп = «) -Ф^ (li = 1 Vi = 1, n).
•^ Для доказательства применим метод математической индукции. При п = 1 неравенство
A) справедливо и при этом имеет место только знак равенства. Если п = 2 и iii2 = 1, то
обязательно один сомножитель, например xi^l,ax2^1- Тогда из очевидного тождества
XI + Х2 = Х1Х2 + 1 + (Х1 - 1)A - 12) B)
и условия х\хг = 1 следуют неравенство х\ + хг ^ 2 и условие (х\ + хг = 2) -О (ц = i2 = 1).
Предположим теперь, что для произвольных к положительных чисел xi, хг, ¦ ¦ ¦ , Хк, про-
к
изведение которых равно единице, справедливо неравенство У2 Xi ^ к, причем
\
, = jfc & (xi = 1 Vt = ТД).

§ 3. Действительные числа 29
Рассмотрим произведение к + 1 положительных чисел xi, хг, ¦ ¦ ¦, Xk+i, для которых
Х\Х2 ¦ ¦ ¦ Хк+1 = 1.
Если не все хг равны единице, то найдутся числа как большие, так и меньшие единицы. Не
ограничивая общности, будем считать, что х\ > 1, Хг < 1. Тогда, по предположению, для к
положительных чисел (xyX'z), хз, ¦ ¦. , Хк+1, произведение которых равно единице, справедли-
справедливо неравенство
(xix2) + xz + ... + Хк+1 ^ к, C)
причем
[xiX-2 + Хз + ¦ ¦ ¦ + Хк+\ = к) & {х\Х2 = Х3 = ¦ ¦ ¦ = Хк+1 — 1)- D)
Складывая тождество B) с неравенством C), получаем неравенство
xi + Х2 + ¦ ¦ ¦ + xk+i > к + 1 + (xi - 1)A - х2) ^ к + 1
и условие
{Х1+Х2+ ... + Хк+1 = к + 1 + (И - 1)A - Х2}) «• {(Х!Х2) = Х3= ... = Хк+1 = 1),
из которого следует, что
k + l)&(xi = l Vi = l,k + 1). >
42. Пусть х, > 0, х, ? К, Vi = ТГ», а
—j j j— (среднее гармоническое),-
Xi X'2 ' ' ' Xn
)/п — л/ххх2 . ¦. х„ (среднее геометрическое),
. х\ +х2 + ... + хп
fn = (среднее арифметическое).
Доказать, что ~/п ^ г/„ ^ $„ и при этом Gп = г/п = 60 ^ («1 = 12 = . •. = in).
Л Произведение п положительных чисел
XJ_ Х2_ Хп _ ' :
>/п 1/п " »?п ' • .,. ; ' ;
поэтому, согласно предыдущему примеру, их сумма
1 I-.--H >п.
Цп Цп П„
к
Отсюда )/„ ^ ^„. При этом знак равенства достигается тогда и только тогда, когда — = -3- =
... = —^ = 1, т. е. когда х\ = Х2 = ... = яп- По только что доказанному
„/1
Цп V Xl X2 X" n Tn
11 1 ¦ i :|-
откуда 7„ < )/„ и уп = цп, если — = — = ... = — = 1, т. е. если ц = х2 = ... = хп. >
43. Доказать неравенство Коши—Буняковского
где xi, yi (jI = 1, ?») — произвольные действительные числа. В каких случаях в указанио»-
неравенстве имеет место знак равенства?
п
4 Из очевидного неравенства ^(i>< + J/;J ^ 0 получаем неотрицательный при всех
п п п
значениях t квадратный трехчлен t ^ x] + 2t ^ ^iJ/t + ^2 у\ ^ 0> поэтому
Ч - Е*» Е^ ¦<•¦

30
Гл. 1. Введение в анализ
Знак равенства имеет место тогда и только тогда, когда x{t + yi = 0, г = 1, re, т. е. когда
существует такое число Л ^ 0, что yt = Xxi, i = 1, я, или когда все Xi, г = 1, п, или все yi,
t = l, re, равны нулю. >
Доказать неравенства:
•< Неравенства а) и б) являются следствием неравенства г/п ^ ?п из задачи 42 при Хк = к
и Хк = к2 (к = 1, п) соответственно.
Доказательство неравенства в) проведем с помощью метода математической индукции.
При п = 1 неравенство очевидно. Предполагая его справедливым при п, покажем, что оно
справедливо и при п + 1. В самом деле,
1 3
2 I
2n-
2н 2n
<
2n + l
2n + 2
<
1
'2я + 3 V 4 + 8я + 4 л/2« + 3 "
45. 1 + 4= + 4= + ¦ • • + 4= > V». » 2 2.
V2 л/3 лД
При п ^ 2 имеем
46. nn+
11 11
л/2 -/3 л/п V™
•< При « = 3 неравенство очевидно. Предполагая, что неравенство справедливо при ге,
докажем справедливость его и при п + 1, т. е. докажем, что (п + 1)п+2 > (м + 2)n+1, если
Умножив обе части последнего неравенства на ^n J^.1—, имеем
Но так как ^^^ = Г+2п+Л " > (я + 2)n+1, то требуемое доказано. >
47.
2
?sinz, 0
, А; = 1, м.
•< При я = 1 неравенство справедливо. Докажем, что
жив справедливость исходного неравенства.
В самом деле, если 0 ^ Хк ^ ж, то
sin
k=l
n+l
sinifc, предполо-
п+1
sm I > xk I cos i
n+i + cos I 2_^Xk I smi»+i
\k=l I
k=l
|COSIn+1| +
COS > Ifc
sinin+i
k=\
n+1
+ sin in+j ^ > sin it + sm in+j =
48. Bre)!<22n(n!J, я> 1.

§ 4. Комплексные числа 31
•4 При н = 2 неравенство очевидно. Исходя из справедливости его для п, покажем
справедливость его для »»+1. В самом деле, . vi' :;;: '
B» + 2)! = Bu)!B» + l)Bn+2) < 22n(re!JBn + l)Bn + 2) < \. .",'"\w ,У '
< 22n(n!JBr. + 2J = 22"+2((n + 1)!}*. *
Упражнения для самостоятельной работы
30. Пусть {~х} — множество чисел, противоположных числам х 6 {х}. Доказать^ что:
а) inf{ — х} = — sup{z}; б) sup{ — х) — — inf{i}. '
31. Применяя метод математической индукции, доказать неравенства:
а)п!>п?,п>2; б) Bп - 1)! < я2", п > 1; в) f>p < ^Г* , п, р ? N. , ,
fc=i
32. а) Доказать, что для любого выпуклого n-угольника справедливо равенство ?>»>!*
п'~ ' , где Z)n — число диагоналей. . !
б) Доказать, что для любого выпуклого многогранника справедливо соотиошеиие п
Рп = 2, где Вп — число вершин, Рп — число ребер, п — число граней.
33. Доказать неравенства:
а)
б) (xi + 12 + ... + хп) (^ + ^ + ... + j^j Z п2, х, > 0, i = Т77Г;
в)
34. Вычислить суммы:
а) 1- 11+2-2! +... +п-п\; б) I4 + 24 + ... + п*; в) Is + t + ... + re5.
35. Доказать, что:
J2 к (к + 1) ... (А; + го - 1) = -~^п (я + 1) ... (re + m),
где т — натуральное число.
Пользуясь этой формулой, вычислить суммы:
а) 1-2 + 2-3+ ... +п(п + 1); б) 1-2-3 + 2-3-4+ ... + ге(ге + 1)(ге + 2);
в) 1-2-3-4 + 2-3-4-5+ ... +я(п + 1)(п + 2)(п + 3).
36. Доказать, что
1 / 1 1 \
~ m ^m! (n+l)(n+2) ... (n+m-1) ^ '
где m — натуральное число.
Пользуясь этой формулой, вычислить следующие суммы:
1 , 1, , 1 ¦ fi4 _J_ , _J_ ,
1-2 "•" 2-3 "Г • ' • "f n(n+l) ' U^ 1-2-3 "•" 2-3-4 "Г • • .
1-2 "•" 2-3 "Г • ' • "f n(n+l) ' U^ 1-2-3 "•" 2-3-4 "Г • • . T n(n+1)(n+2) > ". , .
B) ! . __!_ . . !
"-' 1-2-3-4 ^ 2-3-4 5 T • • • "Г n(n+1)(n+2)(n+3) ' ' ;, ,
37. Решить уравнения:
a) |x + l| + |x| + |x-l| = 6; 6) x|x + 2|-|x + l|-(x + l)|x| + l = 0.
§ 4. Комплексные числа ' '
4.1. Комплексные числа и действия над ними.
Определение. Комплексным числом z называется упорядоченная пара (х, у) дей-
действительных чисел х и у. При этом равенство, сумма и произведение упорядоченных пар,
а также отождествление некоторых из ниа: с действительными числами определяются
следующим образом:
1) два комплексных числа z\ = (xi, у\) и Z2 = (жг, 2/г) называются равными, если Х\ я?
Х2 U У\ = J/2/ ! ¦'¦' - ¦ *Л

32 Гл. 1. Введение в анализ
2) суммой комплексных чисел z\ и zi называется комплексное число z вида
Z = (Xl+ X2, У\ + У2)\
3) произведением комплексных чисел z\ и гг называется комплексное число
Z = (Z1X2 - У\У2, Х\У2 + Х2У1);
4) множество комплексных чисел (х, 0), х 6 К, отождествляется с множеством дей-
действительных чисел R.
Разностью комплексных чисел z\ и z%, называется комплексное число z такое, что гг+г =
z\ откуда находим z = z\ - z2 = (xi - хг, у\ - Jte).
Частным комплексных чисел z\ и Z2 называется комплексное число z такое, что zi ¦ z —
z\. Отсюда находим
/ Л-УХУ2 \
х\+у\ ' х\ + у\ )¦
Комплексное число @, 1) обозначается символом i = @, 1). Тогда @, 1) • @, 1) = (—1, 0),
т. е. i2 = — 1. Произвольное комплексное число z можно записать в виде
z = (х, у) = (х, 0) + @, у) = (х, 0) + @, 1)(у, 0) = х + iy.
Эта запись называется алгебраической формой комплексного числа. Комплексное число z =
(х, —у) = х — iy называется сопряженным по отношению к комплексному числу z = (х, у) =
х + iy.
4.2. Геометрическая интерпретация комплексного числа.
Всякое комплексное число z = (x, у) можно изобразить как точку на плоскости с ко-
координатами хну. Плоскость, на которой изображаются комплексные числа, называется
комплексной плоскостью, при этом ось Ох называется действительной, а Оу — мнимой.
Расстояние г точки z от нулевой точки, т. е. число г = ух2 + у2 = yzl,, называем
модулем комплексного числа z и обозначаем символом |г|.
Число
arctg -, если х > 0,
arctg - + ir, если х < 0, у ^ 0,
arctg |- — Я", если х < 0, у > 0,
^sgn у, если х = 0
называем аргументом комплексного числа z и обозначаем символом в = arg z. При заданном
г углы, отличающиеся на 2мг. п 6 Ъ, соответствуют одному и тому же числу. В этом случае
записываем Arg z = arg z + 2птг, п 6 Z , и arg z называем главным значением аргумента.
Числа г и в называют полярными координатами комплексного числа z. В этом случае
z = (х, у) = (г cos в, г sin в) = r(cos в + г sin в)
называется тригонометрической формой комплексного числа.
Если z\ — (ri cosflj, ri sin <?i), z-i = (гг cos02, ri sin Q-i), то
z\Zi = (nr2cos@i+02), nr2sin@i+02)),
— = [- COS@! - в2), — Sin@! - в2)) .
Zi \Г2 Г2 /
Для возведения в степень комплексного числа z = (rcosfl, rsin0) применяем так называ-
называемую формулу Муавра
zn = (rn cos пв, rn sin пв).
Корень «-й степени комплексного числа z находим по формуле
= y/r cos , Vrsm I , к = 0, n — 1. A)
V n n /
49. Доказать, что:
a) Z! + Z2 = zx +z2; б) гТг? = zi ¦ z2;
•^ ПуСТЬ Zl = (Xl, yi), Zi = (X2, У2)-

§ 4. Комплексные числа , 33
а) По определению сопряженного числа
г\ + Z2 - (Xi +X2, 2/1 +2/2) = (Xl +X2, -У1 -У2) = (Xi, -3/l) + (X2. -З/2) = 2J +22.
б) Имеем гГгг" = (xiX2 - 2/j2/2, X1J/2 + X2J/1) = (xix2 - J/iJte, -Xi3/2 - Х2З/1) =
(xi, -3/i)(x2, -J/2) = zi • z2.
в) Запишем комплексное число z в тригонометрической форме z = (г cos в, rsinfl), тогда
z = (rcos( —в), rsin(—в)). Пользуясь формулой Муавра, имеем
(г)" = (rncos(-n0), rnsin(-n0)) = (rn cos п9, -rn sin пв) = (rncosn6, r" sin ti0) = (гп). >
50. Выполнить указанные операции: • .. , i
а) B - 0B + О2 - C - 20 + 7; б) A + О4; в) ^ + ?j . '
М С комплексными числами, записанными в алгебраической форме, операции сложения,
вычитания и умножения можно производить так же, как и с действительными биномами. При
этом пользуемся тем, что г2 = —1, г3 = г2 • г = —г, г4 = i3i — —i2 = 1 и т. д.
а) Имеем
B - 0B + гJ - C - 20 + 7 = B - 0B + О2 + 4 + 2» =
= B + 0(B - 0B + 0 + 2) = B + 0D + 1 + 2) = 14 + 7».
б) Согласно формуле бинома Ньютона, .
A + О4 = 1 + 4г + 6i2 + 4г3 + i4 = 1 + 4t - 6 - 4t + 1 = -4.
_ 27 , ;Ы-Л 135 -60-Л , 45 , .-6у/5 1
-64+* 64 ~ "бТ ~ г 64 + бТ +t 64 ~ бТ
51. Найти частное комплексных чисел:
! в)
2
2 l 2 • '
М Формулу для нахождения частного комплексных чисел z\ и хг запишем в виде
Z\ _ Z\ ¦ Zi _ Z\ ¦ Zi
Zi Zi -Z1 \Z2\2
Пользуясь этой формулой, находим
1 _ -i _ . 1 _ 1 -t _ 1 -i _ 1_ _ i_
aj 1 ~ |i|a " Ц ' l + i~ \l + i\2 ~ 2 ~2 2; • -: '
52. Представить следующие комплексные числа в тригонометрической форме:
а) -3; б) -»; в) 1 + i; г) -1 + гЧ/З.
•^ Имеем: , .¦ / -и,
а) | - 3| = 3, 9 = я-, -3 = 3 (cos я- + г sin ж);
б) | - .-| = 1, 9 = -f, -i = cos (-f) + isin (-f) ; ;
в) |1 + t| = л/2, в = -7, 1 + » = л/2 (cos f + isin f);
r) I - 1 + iV3| = 2, 9 = ^, -1 + »л/3 = 2 (cos ^ + ism ?f) .>
53. Вычислить:
a)(l+V3K°; 6) (^-tV2J0; „) AZ^
"-' Д) B + 2iL1; е)(->/з
а) Представим комплексное число в тригонометрической форме
1 + »УЗ = 2 (cos | + isin 0 ,

34 Гл. 1. Введение в анализ
затем, применив формулу Муавра, получим
A + гУзK0 = 230 (cos ^ + isin *?) = 230.
б) Аналогично предыдущему находим
= 2- (cos (-*?)
и в триг
) яЛ . . / яЛ
в) Представляя числитель и знаменатель дроби в тригонометрической форме, вычисляем
частное
затем, использовав формулу Муавра, находим
" ( (§) (D) ((?) (?)) - ••
№)" - (- (-§)+<* (-D)" - (-(-?
l + i _ v^(sf +isinf) 1 / 7ir . . 7ir
Г) 7Г^ " 2>/3 (cos (-f) + isin (-f)) ~ ^VCOSli +tSm 12 J;
/ l + i V1 1 / 77л- ,.. 77л-\
I —= I = y= I cos h «sm I =
VV3-i3/ 6sVe V 12 12 У
5тг , . . 5тг
й+tsm 12
д) B + 2i)il = (V8L1 fcos - + isin -У' = (V8L1 (cos — + isin —) = 820B + 2i).
\4 4/ \4 4/
54. Найти все значения корней: а) у\; б) V —1 — г'л/з".
•^ а) Запишем комплексное число 1 в тригонометрической форме
1 = cosO° +isinO°,
затем по формуле A), п. 4.2, находим
^=cosltl+isin2^l! jt = 0, 1,2, 3.
4 4
Следовательно,
¦УТ = cosO0 + isinO° = 1 при it = 0, y/l = cos | + isin f = i при fc= 1,
v'T = cos 7Г + г sin 7Г = — 1 при fc = 2, v'T = cos ¦— + i sin -^- = — i при fc = 3.
б) Записав комплексное число —1 — i\/3 в тригонометрической форме
находим
V-l -»V3 = л/2 I cos-2 Hsin— I, k = 0,1,2.
V 3 3 /
Отсюда
у — 1 — 1л/3 = л/2 (cos (—jp) + isin (—^)) , A: = 0,
(cos (Ч-) + tsin (t1)) . k = l,
-1 - »V3 = ^2 (cos (i|l) + isin (if)) , Jb = 2. >

§ 5. Векторные и метрические пространства 35
55. Решить уравнение г6 + 1 = 0. ,
М Имеем z — \f-\. Для вычисления всех значений \/~—\ применим формулу A), п. 4.2,
6/—т -я- + 2ктг . . -я- + 2кт , -—=
zk = V-l = cos |-isin , к = 0, 5.
О О
Отсюда zo = <**(-j)+ism (--)= — --, z, = cos - + tsin -=_ + -,
тг . . Я' 5ir . . 5ir \/3 t
*2 = cos - + ism - = », г3 = cos — + tsin — = —— + -,
II D D i I
lie . . 7я- Уз i 9ir . . 9я-
6 О 2 2i 6 6
Упражнения для самостоятельной работы
38. Доказать, что a) z\ — z-i = z\ — zr, 6) If1) = f1 в) P(z) = P{z), где z t-* P(«)'—'
алгебраический многочлен с действительными коэффициентами.
39. Выполнить указанные операции:
a) A + j\/3N; б) ^т?; в) f^ (х2 + у2 # 0).
40. Найти действительную и мнимую части следующих комплексных чисел:
41. Показать, что множество комплексных чисел, в котором введены операции сложения
и умножения, образует поле.
42. Найти модули и аргументы следующих комплексных чисел:
a) (_4 + 3iK;6) A + 08A-и/3)~6;в) 1 + cos f +isinf.
Найти все значения следующих корней:
43. уТ. 44. v'-l +*• 45. ff^A. 46. ^64.
Найти корни уравнений:
47. z2 + E - i2)z + 5A - г') = 0. 48. г2 + A - »2)г - »2 = 0.
49. (г + г')п + (г-г)п = О.
50. Доказать, что модуль комплексного числа является абсолютным значением, т. е. \г\
удовлетворяет условиям: . '
1) |z| > 0 Л (|z| = 0 ¦«• z = 0); 2) |ziz2| = |zi||z2| Vzi,z2€C; ' .
3) jzi + z2| <|zi| + |z2| Vzb z2 €С.
51. Доказать, что модуль комплексного числа удовлетворяет неравенству
§ 5. Векторные и метрические пространства
5.1. Векторное пространство.
Определение 1. Векторным пространством над полем К = {Л, /*,&", ... } называется
множество Е = {х, у, z, ...}, в котором определены:
I. Внутренняя бинарная операция Е х Е —^ Е : (х, у) *->¦ х + У, относительно которой
множество Е является абелевой группой:
1) х + (у + z) = (х + у) + z; 2) х + в = х;
3)х + (-х) = 0; 4)х + у = у + х
• *'?'!* '
(здесь в — нулевой элемент группы). , . .
II. Внешняя бинарная операция К х Е —> Е : (Л, х) i-> Ax, удовлетворяющая следующим
аксиомам:
5) Л(х + у) = Лх + Ху; 6) (Л + /i)x = Лх + цх;
7) (А^)х = А(^х); 8) 1 -х = х.

36 Гл. 1. Введение в анализ
, Элементы векторного пространства Е называют векторами (или точками), а элементы
поля К — скалярами.
Если K,= R, то Е называется действительным векторным пространством, а если
К. = С, то Е называется комплексным векторным пространством.
Определение 2. Всякое подмножество V векторного пространства Е, обладающее
двумя бинарными операциями пространства Е и являющееся векторным пространством
над полем К, называется векторным подпространством пространства Е.
В произвольном векторном пространстве выполняются следующие свойства:
1)Хв = в; 2)О-я = 0; 3) (-1)х = -х.
5.2. Нормированные векторные пространства.
Понятие абсолютного значения распространяется на векторные пространства над норми-
нормированным полем К.
Определение. Нормой в векторном пространстве Е называется отображение
Е ->¦ R+ : х i-> ||х||, R+ = {а €К:0<а <+оо},
удовлетворяющее следующим аксиомам:
... .1)
2)
. ) ЦН || ||||
3) \\х + у\\ ^ ||х|| + \\y\\ V х, у е Е (неравенство треугольника).
5.3. Евклидово пространство.
Определение 1. Пусть Е — векторное пространство над полем R. Отображение
Ё х Е —<• R : <р(х, у) = {х, у), которое каждым двум элементам х и у из Е ставит в со-
ответствие действительное число, обозначаемое символом (х, у), называется скалярным
произведением, если V х, р, z 6 Е a VAgR выполняются следующие аксиомы:
1)¦<*, У) = <», х);
2) <я+ »,*> = (в, *) + <»,«);
3) {Аа:, у) = Л(х, у);
4) (г, г) > О Л ({х, х) = 0) ^ (х = 0).
Определение 2. Векторное пространство, в котором определено скалярное произведе-
произведение, называется евклидовым пространством.
5.4. Метрическое пространство.
Определение. Множество Е = {х, у, z, ...} называется метрическим простран-
пространством, если определено отображение Е х Е —<• К^ : (х, у) i-> p(x, у), которое Эля любых х
и у; ставит в соответствие неотрицательное действительное число р, удовлетворяющее
следующим аксиомам:'
1) И*, ») = 0) =»(* = »);
2) р (х, у) = р (у, х) Ч х, у & Е (аксиома симметрии);
. 3) р(г, у) ^ р(х, г) -(- p(z, у) V х, у, z 6 ? («еравемсгово треугольника^.
Элементы метрического пространства называются точками, а число р(х, у) называется
расстоянием между точками х и у или .метрикой пространства 2?.
Всякая часть F метрического пространства Е, в которой определено отображение FxF —<•
R.*,,,делающееся сужением отображения Е х Е —> К+ : (х, у) i-> р(х, у), называется ле-
трическил< подпространством, а определенная в нем метрика — индуцированной метрикой.
Метрическое подпространство само является метрическим пространством.
5.5. Окрестности.
Определение 1. Открытым (замкнутым) шаром с центром в точке хо и радиусом г
в метрическом пространстве Е называется множество
{х 6 Е : р(х, х0) < г} ({х 6 Е :р(х, х0) ^ г».
Открытый (замкнутый) шар обозначается S(xo, r) E(хо, г)).
Аналогично определяется открытый (замкнутый) шар в векторном нормированном про-
пространстве.
Определение 2. Открытым (замкнутым) шаром с центром в точке xq и радиусом г
в векторном нормированном пространстве Е называется множество
.{х € Е : ||х - хо|| < г} ({х 6 Е : ||х - хо|| < г}).

§ 5. Векторные и метрические пространства Щ
Определение 3. Открытый шар с центром в точке Хо и радиусом 6 называется 6-
окрестмостью точки хо- , !I fI
На действительной прямой К открытый (соответственно замкнутый) шар радиуса Ь, ёст%,
интервал ]хо — 6, хо + б[ (соответственно сегмент [хо — 6, хо + 6]). '»'"'"
56. Пусть Кт — множество всевозможных упорядоченных систем т действительны*
чисел (xi, Х2, ¦¦¦, хт). Пусть в множестве Rm определены: внутренняя бинарная опердцвд
Кт х Йт —> Кт, которая для любых двух элементов х = (xi, ..., хт) и у = (yi, ¦¦ ¦ t Ут)
множества Кт ставит в соответствие элемент :
х + у = (xi +»i, ..., хт + ут), .., -,<¦,
называемый суммой х' и у; внешняя бинарная операция R X Кт -* Кт, которая для любого
X € Кт и любого А 6 R ставит в соответствие элемент ¦-.;¦! <; <;
Лх = (Лх1; ..., Ахт),
называемый произведением Л на х.
Показать, что К — векторное пространство над полем К. '" ' - ' ^
4 Сначала покажем, что множество Rm является аддитивной абелевой группой. Дей-
Действительно, для произвольных х = (xi, ..., xm), у = (s/i, ..., Ут) и z = {z\, ..., im) в'силу
ассоциативности действительных чисел, имеем ' " ' '
X + (У + Z) = (Xl + (yi + Z\), . . . , Xm + (Ут + Zm)) =
= ((Xl +Vl) + Zl,...,(xm+ ym) + Zm) ^ C*'+f|4 Щ
Обозначим 9 = 0 = @, ..., 0), тогда Vx € Km выполняется равенство x-f O {
. .., Xm + 0) = (Xl, ..., Xm) = X. Для ЛЮбоГО X 6 К"* ПОЛОЖИМ -X = (-Xl, * v.<, ..
тогда х + (—х) = (xi — xi, ..., xm — xm) = @, ..., 0) = 0. Наконец, в силу коммутативности
сложения действительных чисел i'
.., Ут+Xm) = (»1, •••, 3/m) + (ll, . . ., Хт)
Следовательно, все четыре аксиомы абелевой группы выполнены. ¦ '• ¦
Далее, из определений внешней и внутренней бинарных операций и свойств действителен
ных чисел непосредственно следуют равенства: , .
= A(xi +yi, ..., Xm+ym) = Dxi+yi), ..., A(xm + Ут)) = p
= (Axi +Xyi, ..., \Хт +At(m) = (Axi, ..., \хт)+ (Ajfi, ..., Хут) — ->
= Х(хи ..., Xm)+X(yU ..., 3/m)i=
(Л + /*)х = (Л + /*)(*!, ..., хт) = ((Л + /*)хь ..., (Л + /*)хт)=
= (All +/1X1, ..., Aim + fiXm) = {Xxi, ..., Axm)+ (/*Xl, ..., ЦХт) 4= >,
= А(хь ..., xm) + /i(ib ..., im>=
, ..., цхт) = A'(/i
1 • X = A • Xi, . . . , 1 • Xm) — (Si, . . . , Xm) = X, , г „ip.
для произвольных х и у из Km и любых А и /1 из К. Таким образом, аксиомы, оп^ейёЛЙЬщие1
векторное пространство, выполнены, а поэтому Rm является векторным простраиствсййг Щ$.
полем К. > - . : дг) ¦ !i-
57. Пусть 9Л — множество всевозможных прямоугольных матриц вида ' *' -¦'<•¦¦? с,
(аи Oi2 ••¦ «in .
021 022 ¦•• 02„ | _ (о^.^
Cml «m2 • • • Зтп
где a,j € К, » = 1, m, j = 1, п.
Суммой матриц А'= (а,у) и В = D,-у) назовем матрицу
011+6п 2 + Ь\2 ... aj
В = | a21 + 621 022 + 622 ••• di
ml + iml Om2 + 6m2 . . . Clmn + Ътп

38 Гл. 1. Введение в анализ
а произведением матрицы А на число Л € К — матрицу
(Лап А<ц2 ••• А<п„ \
Ла21 Ла22 ¦ ¦ • Ло2п 1
\ат\ \ат2 ... \ат„ J
Показать, что ?ЭД — векторное пространство над полем К.
А Множество 9Л матриц А = (atJ) размера т х п можно отождествить с пространством
Rm" векторов х = (an, ..., ain, • • •, ami, • • •, <*тп) при помощи взаимно однозначного соот-
соответствия (uij) «-> (an, ..., п\п, ..., ami, • ••, amn)- При этом для любых (o,j) 6 9Л, (bij) 6 9Л
и А€К
(oij) + (bij) «-> (аи + Ьп, • ••, ain +bin, ..., ami +6mi, ..., amn +bmn),
A(o,j) <-»¦ (Aan, ..., Aain, ¦ ¦ •, Aami, ..., Aamn)
(т. е. пространство 9Л изоморфно пространству Rm" относительно сложения элементов из
ЯЛ и умножения на скаляры поля R). Таким образом, 9Л — векторное пространство над
полем К. >
58. Доказать, что пространство К превращается в нормированное векторное простран-
пространство, если для произвольного х = (xi, хг, ..., xm), x 6 Кт, положим
||х|| = s/x\ + x\+ ... +х2т.
•^ Для доказательства достаточно проверить выполнение аксиом 1)—3) пункта 5.2.
1) Очевидно, ||х|| > 0 и (||х|| = 0) & (х = 0).
2) Для любого х 6 Кт и VA 6 К имеем
A)
+ ... +(AzmJ = л/F^xf+xl-t- ...+х2т =
3) Покажем, что для любых х = (xi, х2, ..., хт) и у = (ja, y2 ут)
B)
Записывая неравенство B) в координатной форме
и возводя обе части в квадрат, после упрощения получаем неравенство
C)
эквивалентное неравенству B). Неравенство C) называется неравенством Коши—Буня-
ковского; его справедливость уже доказана (см. пример 43). Следовательно, равенство A)
задает норму в Rm. >
59. Доказать, что векторное пространство СОТ, элементами которого являются матрицы
размера т X и, является векторным нормированным пространством, если для произвольной
матрицы А = (aij), г', = 1, т., j' = 1, н, положить
Выполнение первой аксиомы нормы очевидно. Далее УА€КиУ.Аё9Л имеем
т п т п т п
II I mVVi i i\i
т. е. вторая аксиома также выполняется.

§ 5. Векторные и метрические пространства 39
Остается проверить выполнение неравенства треугольника. Пусть А, В 6 9W — произ-
произвольно заданные матрицы размера т хп, тогда "
jn n т п т п т п
\\А+в\\ = ЕЕ 1°*+w < EE(ia"i + !*•>!) = ЕЁ i°yi+ЕЕ i*o-i = in»+рн-
i = l j=l i = l J=l i=l j=\ i=l j=\
Таким образом, все аксиомы нормы выполняются, а поэтому равенство A) задает норму
в ЯЛ, превращая его в векторное нормированное пространство над полем R. > ; -X
60. Пусть С множество всевозможных ограниченных функций / : [а, Ъ] —>¦ К. :/
Показать, что множество С становится векторным нормированным пространствам иад
полем К, если для произвольной функции / положить
||/||= sup |/(*)|. A)
хб[а,Ь]
•^ Легко убедиться, что С является векторным пространством над полем К, если равенство
(/+</)(*) =/(х) + <7(х), хе[а,Ъ]
определяет сложение в С, а
(А/)(х) = А/(х)
— умножение на скаляр поля R.
Остается проверить, что для числа ||/||, определенного формулой A), выполняются все
аксиомы метрики. •'
1) Поскольку \f(x)\ ^ 0, то H/II = sup |/(х)| ^ 0; кроме того, ||/|| = 0 тогда и только тогда,
когда |/(ж)| = 0, т. е. когда / : [о, 6] —<• 0, а такое отображение является нулевым элементом
векторного пространства С.
2) Для произвольной функции / € С и любого Л 6 К имеем
||А/||= sup |A/(*)|= sup |A||/(x)| = |A| sup |/(х)| = |А|||/||. ' ¦' г.
х6[а,6] х?[а,Ь] *?[а,Ь] ..
3) Из неравенства треугольника для абсолютного значения и свойств точной верхней г
ни следует неравенство
|/(О+ g(x)K |/(О|+ |ф)и sup |/@l+ sup |g(OI = Ш + 1Ы1 V/,eeC, V«€
з||, то точная верх-
также ограничена
Поскольку множество {\f(x) + g(x)\}, x 6 [а, Ъ], ограничено числом ||/|| +
няя грань этого множества, которая, согласно равенству A), равна ||/ + ff|
этим же числом. Следовательно,
sup |/(х) + «,(х)| = ||/ + «,|К 11/11 +1Ы1,
х€[а,Ь)
что и завершает проверку аксиом метрики. > ;
61. Показать, что для произвольного векторного нормированного пространства1 f? — .
{х, у, z, ... } справедливо неравенство ¦ ••!•-
11М|-1ЫМ<11*-»11- ' О)
•^ Согласно неравенству треугольника,
откуда
Меняя местами х и у, имеем
- У|| = ||х - у\\
или
-||х-2,||^||х||-|Ы1- C)
Из B) и C) непосредственно следует A). > •¦..-,

40 Гл. 1. Введение в анализ
62. Доказать, что векторное пространство ?ЭД (см. пример 59) становится евклидовым
пространством, если для произвольных двух элементов А = (<*;_,) и В = (&,-_,) положить
• •¦ ¦<,Для доказательства достаточно проверить, что (А, В), определяемое равенством A),
удовлетворяет четырем аксиомам скалярного произведения (см. п. 5.3). Выполнение трех
первых аксиом непосредственно следует из определения числа {А, В):
т п т п
1) (а, в) = Е Ё ayjt,- = Е Е »уву = (в- л);
2) для произвольных матриц Л = (aij), В = Fij) и С = (cij) имеем
3) пусть УЛеЯН и УЛбК, тогда
(\А, В) =^2^2\а,3Ь„ = Л]Г5>Л, = \(А, В);
1=1 j=i i=i j=i
. .4) для любой матрицы А 6 ЯП находим
откуда следует, что {А, А) ^ 0 и (Л, Л) = 0 тогда и только тогда, когда все элементы ма-
матрицы А равны нулю, т. е. когда А = в, где в — нулевой элемент векторного пространства
SW. Следовательно, выполняются все аксиомы скалярного произведения, т. е. равенство A)
задает скалярное произведение в векторном пространстве 9Л, поэтому 931— евклидово про-
пространство. >
63. Показать, что нормированное векторное пространство Е = {х, у, z, ... } становится
метрическим, если для любых элементов х и у из Е положить
р(х, у) = \\х-у\\.
А Покажем, что выполняются аксиомы метрики (см. п. 5.4). Действительно, из свойств
нормы вытекает, что: •
1) р(х, у) = ||х — у\\ ^ 0, причем р(х, у) = 0 тогда и только тогда, когда х — у = в, т. е.
2) р(х, у) = ||х - 2,|| = ||(-1)(» - х)|| = | - 1| . Иг, - х|| = ||у - х|| =р(у, х);
3) р(х, у) = ||х - у|| - ||х - z + z - у\\ <С ||х - z\\ + ||* - у|| = р (х, z) + р (г, ») V г, », г 6 ?.
Следовательно, все аксиомы метрики выполняются, поэтому Е — метрическое простран-
пространство. >
Упражнения для самостоятельной работы
52. Доказать, что множество C{f, g, h, ...} всевозможных отображений множества Е в
векторное пространство F над полем К само является векторным пространством над тем же
полем К.
53. Показать, что множество комплексных чисел С образует векторное пространство над
полем действительных чисел К.
54. Показать, что векторное пространство Кт становится нормированным, если для лю-
любого элемента х = (xi, Х2, ..., хт) норму ||х|| введем одним из следующих равенств:
а) ||х|| = |xi| + |х2| + ... + |хт| (октаэдрическая норма);
б) llxll = max |xi| (кубическая норма).
l<i<m

§ 5. Векторные и метрические пространства
55. Какие из равенств ;» о Л1&
т
a) ||x||=?fc-M; б) ||х|| /
к=1 V •=!
в) ||х|| = |*i| + |x2| + ... +|xm_i|; г) ||х|| = max сн\х{\, at > 0; д) ||х|| = max \ц\
l^i<m l^t^m—1' >.
задают норму в векторном пространстве К?
56. Показать, что в векторном пространстве 9Я, элементами которого являются матрицы
А = (o,j) размера m X п, норму ||Л|| можно ввести одним из следующих равенств: -!"'''
•0 1ИН = ,/Ё ? Ф б) 1И11 = ,?ах ? 1°'>1; в) ИИ = ™« Е 1««1; О
\/i = lj = l ^'^mj=l 1^<ni=l
57. Пусть 9Л то же, что и в предыдущем примере. Указать, какие из равенств
a) 1И11 = JEE«u4, «y>o; б) |И||=\/Е Е«у;
у i=i>=i V '=1 >=I
в) 1ИП = E E «oiaoi «о > °; г) 1И11 = 1m*xnai>la'>l> ai> > 0;
д) \\A\\ = max (Vjj|atJ|, «<> < 0; e) \\A\\ = max ау|ау|, «ij > 0, m > 2
задают норму в пространстве 0Л.
58. Исходя из определения метрики, доказать, что в пространстве Rm расстояние между
произвольными точками х = (xi, X2, ..., Хт) и у = (yi, 3/2 j/m) можно определить одним
из равенств:
a) p(x> ») = WE(Xl ~»"J; б) р(х,У) =
в) p(x, t/) = max |x,- - j/;|; г) р(х, у) =
i=l 1<«<т
59. Непосредственной проверкой аксиом метрики показать, что в пространстве,!
ментами которого являются матрицы размера т Хп, расстояние между
ками (матрицами)
можно ввести одним из равенств:
а) р(а, в) = .ЕЕК-У!; б) рИ. в) = ,
у.-=1>=1 i<'<m
в) р(Л, В)= max Ela'V~"*O'h г) PC' В) = тах
60. Пусть Е — метрическое пространство с метрикой р : Е х Е —+ Ш . ¦ *"*'¦ ¦1)ч''"'
Показать, что если, кроме того, Е и векторное пространство, то оно является нормирован-
нормированным пространством с нормой ||х|| = р(х, в), где х — произвольный, а в — нулевой элементы
пространства Е. ' ;'
61. Изобразить множество точек, которое является замкнутым (открытым) Шаром В¦''ifi?H
трическом пространстве К2, если метрика р определена одним из следующих равенств: '•' "'лI
а) р(х, У) = \/(Xl -yiJ + (Х2 - Ы2; б) р(х, у) = |xi - »i| + \х2 - уф ; ,/,,,,,„„;
в) р(х, у)= max |xi-t/i|; г) р(х, у) = ¦
Д) Р (х, у) = bf^ + Ь^; е) р (х, у) = max {b

42 Гл. 1. Введение в анализ
§ 6. Предел последовательности
6.1. Понятие последовательности.
Определение. Последовательностью элементов множества Е называется отобра-
отображение
N —> Е : п t—> хп,
щ. f. функция, которая каждому натуральному числу п € N ставит в соответствие эле-
элемент х„ g E.
Для записи последовательности употребляем обозначения (хп), или х\, X2, ...,хп, ...,или
хп = /("), п ? N.
Элементы х\, Х2, ¦ ¦¦, хп, • ¦• называются членами последовательности, а хп — общим
членом последовательности.
Множество Е может быть различным, например: М, Шт, С[а, ft], ЯЛ и т. д. Если Е = М,
то последовательность называется числовой, если ? = Мт, — векторной, если ? = С[а, ft],
— функциональной, если Е = ЯЛ, — матричной и т. д. В каждом из этих случаев множество
всевозможных последовательностей образует векторное нормированное, а следовательно, и
метрическое пространство.
6.2. Сходящиеся последовательности и их свойства.
Сначала рассмотрим числовые последовательности.
Определение. Последовательность (хп) действительных чисел называется сходя-
сходящейся, если существует действительное число а и Эля произвольного е > 0 существует
натуральное число т такое, что Эля всех п > т справедливо неравенство
\хп - а\< е.
При этом число а называют пределом последовательности (хп), что символически запи-
записывают
lim хп = а или хп —> а при п —> оо.
С помощью логических символов определение запишется следующим образом: числовая
последовательность (х„) называется сходящейся, если
Бели последовательность не является сходящейся, то ее называют расходящейся.
Теорема. Если последовательности {хп) и (j/n) действительных чисел сходятся и
lim in = a, lim у„ = b, то
n-»oo n-*oo
lim (xn + Уп) = a + b, lim xnyn — аЬ,
n—*oo n—*oo
lim — = ? (yn ф 0 V n 6 N, b ф 0).
n— oo J/n 0
6.3. Признаки существования предела.
1. Если уп ^ хп ^ 2П V»i > «о и lim yn = lim zn — а, то 3 lim in = a.
2. Монотонная и ограниченная последовательность имеет предел.
3. Числовая последовательность (хп) имеет конечный предел тогда и только тогда, когда
Ve > 0 3 т € N : V п > т А V р € N =>¦ |г„+р - хп\ < е
(критерий Коши).
6.4. Число е.
Последовательность и н> A + -J , п € N, имеет конечный предел, называемый числом е:
lim A + -А =е = 2,718 281 828 459 045 ...

§ 6. Предел последовательности 43
6.5. Предел в несобственном смысле.
Определение 1. А-окрестностью "точка +оои ("точки —со") называется множе-
множество точек Ш, удовлетворяющих неравенству
Д < х < +оо (-оо < х < -Д);
А-окрестностью "точки оо" называется множество точек R, не принадлежащих сег-
сегменту [—Д, Д].
Определение 2. Числовая последовательность (in) имеет предел +оо (—оо), или стр0-
мится к +оо (—оо), если
V Д > 0 Эт € N : Vn > га => хп > Д
(V Д > 0 Эт е N : Vb > т => хп < -Д).
Числовая последовательность (хп) имеет предел оо, если УД >0 3 mgN: Ум > п» aj>
М>Д.
6.6. Частичные пределы. Верхний и нижний пределы.
Определение 1. Если частичная последовательность (inj) сходится, то ее предел
называется частичным пределом последовательности (хп).
Определение 2. Число о?Й называется предельной точкой числовой последователь-
последовательности {хп), если любая ее окрестность содержит бесконечное число членов последовЛгпеяь-
ности.
Частичный предел последовательности является одновременно и ее предельной точкой.
Определение 3. Наибольший [наименьший) частичный предел числовой последователь-
последовательности (х-п) называется ее верхним (нижним) пределом и обозначается символом
lim xn ( lim xn)-
n—*oo n—*oo
Теорема. Любая числовая последовательность имеет верхний и нижний пределы.
6.7. Сходящиеся последовательности в метрическом пространстве.
Определение. Последовательность (хп) элементов метрического пространства flttet-
зывается сходящейся, если существуют элемент а € Е и Эля любого е > 0 натуральное
число т такое, что V п > т справедливо неравенство р(хп, а) < е.
В этом определении натуральное число m можно заменить положительным действитель-
действительным числом а, поскольку из неравенства п > а следует п > [а] = т.
Если в Шт задана последовательность с членами xn = (sin, i2n, •••, Хтп), Л 6Nt та-
такая, что существует lim xin, i — 1, т, то эта последовательность сходится и справедливо
равенство ~*
lim хп = ( Hm x\n, Um i2n, ••-, lim xmn)-
n—*oo n—*oo n—*oo n—*oo
Аналогично, если в QJl задана последовательность
М „(*)
iu а12 ...
Л*= | | , *€N,
"ml am2
такая, что 3 lim a\,q', p = 1, w, 9 = 1, m, то эта последовательность сходится и справедливо
к—*оо
равенство
lim Л* =
lim a^ lim a^} ... Urn
koo koo fc*oo
lim a^ lim a(^ ... lim a
k — 00 k—*oo fc—*oo
64. Доказать, что последовательность (in) = ( ) сходится к числу 2.
4 Имеем \хп — 2| = |^-^- — 2| = ^. Для любого е > 0 3 m ? N такое, что ^ < в
пример 28). Тогда V п > m справедливо неравенство — < е и, следовательно, |хп — 1{ < с,
т. е. lim in = 2. >

•44 Гл. 1. Введение в анализ
65. Доказать, что:
a) lim qn = 0 при \д\ < 1; б) lim дп = оо при \д\ > 1.
т»—»оо п—»оо
¦4 а) Если q = 0, то равенство а) очевидно. Пусть е > 0 — произвольно и 0 < |</| < 1.
Тогда, пользуясь неравенством Бернулли, получим
Отсюда
б) Пусть |g| > 1 н Д > 0 — произвольно. Тогда из неравенства
1*1" = 0 + (Ы -1))" > 1 + »(\я\ -1) > "(Ы -1) > а
находим, что
Найти следующие пределы:
л 3 ', 5
Положим 5„ = |
Тогда
2"
2»
2n-\
2"+!
+CI + J-+ |
2V222
2n+1
Таким образом,
lim 5„ = lim 1 Н Ц = bm 1 + 2 =
„_«, " „_«, у 1 _ I 2П ) П-ОО V 2"~2 2" /
= lim 3 - lim —^ - 2 Um ^ + Um — = 3.
п—><х> п—>оо i" ^ п—со Г п—>оо Z"
Здесь воспользовались тем, что
и п
A + 1)" 1 + w + ^il+...+1 sL
для произвольного е > 0, если п > 1 + -, т. е. lim ^ = 0. >
п-1
•< Заметим, что
П + 2^3 + • • • + п(в + 1) = Г ~ 2) + 12 " з) + • • • + (n " V+1) = г ~ 7Г+
Тогда
= 1. >
68. lim^-v^-v^... 2V2).

§ 6. Предел последовательности 45
¦4 Так как уД¦ \Д¦ \/2 ... 2^2 = 2г+4 + " +2^ = 21~^ = —р- и при п > 2
2^
= М2гМ = fl+h^-lj J > (
т. е.
V У V / V /
1
то 22" —> 1 при п-юо и предел последовательности равен 2. >
Доказать следующие равенства:
69. lim —- = 0.
п—оо »»!
< Равенство следует из неравенства
2П _ 2 2 2 2 /2\п_9/2\п
<'ni~l'"n^ \l) ~2\з)
и из того, что (|)П —<¦ 0 при п —> оо (см. пример 65). >
70. lim — =0, а> 1.
п—*оо Оп
¦4 Пусть т — целое и т ^ к. Тогда
где Ъ = ^/а > 1. Но
«"_'*_ " 2п
при ?г —> оо; тогда, применяя теорему о предельном переходе в произведении, получаем, ЧТО
((^г) ->0 при п —> оо, откуда следует требуемое. >
71. lim 21 = 0.
n—оо П!
Равенство нулю предела следует из очевидного неравенства
0<
Н
1 2 ¦" m m + 1 ¦" n m!
п—т
<е,
справедливого при любом е>0 и т+1>|а|, если п достаточно велико. >
72. lim nqn — 0, если \q\ < 1.
¦< Доказательство следует из того, что
|ngn| = К = —, b > 1 (см. пример 70). >
я
73. lim \/a = 1.
п—*оо
^ При а ¦=¦ 1 равенство очевидно. Пусть а > 1, тогда у/а > 1 и (см. пример 40)
а = A+(у?-1))" > l + n(yj-l) >n{tya-l),
откуда получаем, что 0 < %/а — 1 < ^ < е при n > j (е > 0), т. е. у/а —>¦ 1 при п —> оо.
Если 0 < а < 1, то ~ > 1 и по доказанному w - —> 1 при я-юо Но тогда
hm va = «m —= = -^ = 1. >
п—»оо п—»оо п I\ ,.
hm
n-oo

46 Гл. 1. Введение в анализ
74. lim ^ = 0, а>1.
П—гОО 11
•4 Так как lim —¦ = 0, Ь > 1 (см. решение примера 70), то ¦— < -^ < 1 при достаточно
большом п. Положим Ь = а?, где а > 1, а е > 0 — произвольное. Тогда < < 1
2
или 1 < п < а2п
Логарифмируя последнее неравенство, имеем 0 < logan < en, откуда 0 < ——— < е при
достаточно большом п. Из последнего неравенства и следует утверждение. >
75. lim у/и = 1.
п-юо
¦4 Из очевидного неравенства
следует, что | \/п — ]| < \/~г < е ПРИ произвольном е > 0 и при всех »» > 1 + 2е 2. >
76. lim -^= = 0.
п—юо -ун!
Щ Покажем сначала, что
Применим метод математической индукции. При я = 1 неравенство справедливо. Далее,
если оно справедливо при «, то для я + 1 имеем
Последнее неравенство справедливо, так как
(л , ^"-1 | " ¦ "("-1) J_. , п(п
\ п) ~ п 2! '«2+-+
п!
Существование и равенство нулю предела вытекает из неравенства
. 1 1 I
Т „/7^ п 6'
справедливого для любого е > 0 при всех »г > -. >
77. Доказать, что последовательность (хп), где
—
монотонно возрастает и ограничена сверху, а последовательность (уп), где
moh^vohho убывает и ограничена снизу. Следовательно, они имеют общий предел:
A \ П /¦ | \ П+ 1
1 + - = lim A + - I = e.
Я/ п—оо \ П/

§ 6. Предел последовательности 47
Согласно неравенству примера 40, имеем
A _ Г-^У+1—> 0 - -4т)—-1.
У (п + 1Jу га V п + 1/ я
Л
О + ;гГ+
п3 + п2 — п
т. е. х„ /", а «/„ \. Далее, хп < уп и 0 < уп - хп — (l + ?)" ^ < ^ —» 0 при я -> ooj откуй»
(»/п - хп) —> 0 при га -> оо. ¦ • -
Следовательно, lim хп = lim j/n = е- >
78. Доказать, что
A \ п о » . , , '
1 + -) < -, я е N. .......
»/ га
A \"
1 Н— I будет отличаться от числа е меньше
чем на 0,001?
•< Согласно примеру 77, имеем (l + ~) > е. Тогда
y<<<
я/ я » я 1000
при
79. Пусть (рп) — произвольная последовательность чисел, стремящаяся к +оо, и (qn) —•
произвольная последовательность чисел, стремящаяся к —оо. Доказать, что < Ч
lim I + — = lim 1 + — = е.
.. —оо у рп J n~oo \y qnj
¦4 Пусть (я*) — произвольная последовательность целых чисел, стремящаяся к
гда из неравенства ¦. » <';¦,•
К1 + ~) ~е<е при п > N(e), e > 0,
К, \пк / , \"fc * ¦ '
1Н I — е < е при л* > N(e), т. е. lim II Н ) = е.
"* / nt-.oo \ ™* / . ,
Если произвольная числовая последовательность (я*). Р* > 1> стремится к -?оо, то суще-
существует такая последовательность целых чисел (я*), что пк «J рк < я* + 1 и я* —> +оо. Так
как левая и правая части очевидного неравенства
1 + ~
1 Н 1 = е.
Если произвольная последовательность чисел (</*), — Як > 1, стремится к —оо, то, полагая
?* = -Пк, получаем
80. Поскольку lim (l Н—) = е, доказать, что
п —• оо \ ?1 /
Вывести отсюда формулу

48 Гл. 1. Введение в анализ'
где 0 < вп < 1) и вычислить число е с точностью до 10~5.
Щ Переходя к пределу в неравенстве
п 2! я2 3! я3 . . . .
4- , «(» - 1) . . . (W - fc + 1) J_ в(п - 1) ... 2 • 1 1 ¦ ¦ - •
+ "•"'" *! . " п* п! я»
2! \ n/ 3! V nj \ nj k\ \ n) \ n) \ n
n —» со, получим неравенство
02 + 1 + 1+... + ! = ^
справедливое при любом к. Так как в множестве {ук} нет наибольшего элемента, то при
к = п
«/« = 2+1+1+... + 1<е>
т. е. знак равенства невозможен. Кроме того,
Таким образом, х„ < уп < е и lim xn = е. Отсюда следует, что lim yn = е.
п—»оо п—*оо
Переходя к пределу в неравенстве
1,1, , 1 ,
-Уп-
)| + (п + 2)! + • • • + („
1 Л 1 1 \ 1 я + 2
(и + 1)'Д n+2 (n+2J '") (я + 1)! я + 1 я-я!
при фиксированном и и т-»оо, получаем
0< е-уп < -—-.
я • п!
Обозначим вп = е~\л , 0 < вп < 1. Отсюда получаем требуемое.
Неравенство Q < е — у„ < ^~ < 10~5 справедливо при я ^ 8. Отсюда
81. Доказать неравенство
¦4 Левая часть неравенства справедлива при п = 1; далее, ПО индукции
-LW
так как неравенство (я + 1) (^-) (~7~) -* 1 эквивалентно неравенству (l + —) < е
(справедливость последнего следует из примера 77).
¦ Правая часть неравенства следует из того, что (см. пример 42)
82. Доказать неравенства:
/ а) ——°- < In 11 Н— ) < —, где я — любое натуральное число;
. < я +1 V я / и ! ,
б) 1 + а < еа, где п — действительное число, отличное от нуля.

§ 6. Предел последовательности
а) Логарифмируя неравенство (см. пример 77)
,.,
получаем п In (l + ^) < In e = 1 < (n + 1) In (l + ?•), откуда следует неравенство а). - -l
б) Покажем сначала, что
^ < 1пA + г) < г, • ' ¦ A)
где г — любое рациональное число, отличное от нуля и большее —1. Пусть г s? тр > CL Тогда,
в силу неравенства а), получаем
—^—т)
n + m — U
n +
11 1 m- '
<-+ + ... + < — = r,
n n +1 n + m — 1 n
+> ^ -
r) >___ + __+... +___>__ = __^. = __i
откуда следует неравенство A) для г > 0.
Если же —1 < ri < 0, то, полагая —п = г, 0 < г < 1, имеем
откуда -^ <ln(l + n)<-г, т. e. y^-<ln(l + r1) <n. , '
Пусть а — произвольное действительное число, большее —1, отличное от нуля.
существует такое рациональное число г, что
(например, любое рациональное число г, содержащееся между действительными числами в
и Va2 +4 +a- 2). Тогда • >
Следовательно, ln(l + а) < а (а > -1, a # 0) и 1 + a < ea (rt > -1, а ф ff)i ЕайгГс**к —1,
то неравенство 1 + а < еа очевидно, поэтому неравенство 1 + a < ea справедливо при всех
афО. >
83. Доказать, что
/ I \ • • ¦ ¦¦ -¦'¦ ¦-<< i%> ¦"
lim nan—1= In a, a>0,
где In а есть логарифм числа а при основании е = 2,718 ....
< Из
1, откуда
Из неравенства (l + ?•)" < е < (l + ^гг)" находим, что 1<п|еп—lj< 1+j^
\ ¦./''..< i
/ I \
lim n I en — 1 1 = 1.
n-oo у / • ¦ .
A \ / 1п_а \ / _i_ \ n " » '
an — 1J = n(e n — 1J = zn [ег» — 1J In а, где zn s= j^-j —> +оо
при п —> оо. Обозначим ап = [г„] (целая часть), так что а„ ^ г„ < ап + 1 и ,1 < — ^ —.
Отсюда получаем неравенства
In а • а„1 eon+i — 1] < уп < 1па(а„ + 1I еа» — 1 J, | _,,..t с«й
— In а(е""+1 — 1J +1па(ап + 1)(е"»+1 — 1} <з/„<1па-а„(еа» —lj +lnof e-an' — 1 j.

Так
Гл. 1. Введение в анализ
как последовательность (ап(еа>« — 1J j является подпоследовательностью сходящейся
последовательности (п (е « — 11 1, то
lim cvn(ea» — 1 I = lim n «» — 1) = 1.
Применяя утверждение 1, п. 6.3, получаем
/ / J_ \ / JL \\
lim yn = lim In a • cvn(ea» — 1) +lna( ea» — 1 I I = In a, a > 1.
n-*oo n—oo Y V / \ / J
Если же 0 < a < 1, то
yn = n (a n _ 1 j = n j 1 I =
Где b — - > 1. А так как bn —> 1 и н (i>« — 1J —> Ini при n -> oo, то
lim J/n = — Inb = — In - = In a, 0 < a < 1. >
n—*oo a,
84. Пользуясь теоремой о существовании предела монотонной и ограниченной последо-
последовательности, доказать сходимость последовательности (хп), где
<t Имеем ¦ 2*1 = 1 + 57Г+Г > 1> следовательно, последовательность возрастает.
Ограниченность следует из неравенств
Таким образом, последовательность, согласно утверждению 2, п. 6.3, сходится. >
Пользуясь критерием Коши, доказать сходимость следующих последовательностей
где:
, Q к sm I sin 2 sin н ..
2 22
Пусть Vc > 0. Тогда
2" '
sin(n + 1) sin(n + 2) sin(n + р)
| sin(?i + 1)| | sin(n +
2n+i ' 2n+2
^ 1
|sin(n+p)|
1
" 2п+р
При n > — log2c и всех натуральных р. >
86, i«
cosl! cos 2!
cos n!
¦, n 6 N.
1-2 2-3 '•••' „(„
¦4 Для произвольного е > 0 и при всех натуральных р имеем
cos(n 4-1)! cos(n + 2)! cos(n+p)!
(n+2)(n
(n + p)(n+p

§ 6. Предел последовательности 5J>,
+ + + 1
•• + (n+p)(n+p
n +1 n + 2 n + 2 n + 3 n + p п+Я + l n + 1 n + p + 1 я +
V«> 1-1=ЛГ(е). >
87. Последовательность (xn) имеет ограниченное изменение, если существует
сло с, что
\Х2 -Xi\+\x3-X2\+ ... +\xn — Xn-l\ <С, П € N. '
Доказать, что последовательность с ограниченным изменением сходится1.
Построить пример сходящейся последовательности, не имеющей ограниченного
ния.
¦4 Из условия вытекает, что последовательность (j/n), где
уп = \х2-Х1\ + \хз-хг\+ ¦¦¦ +\*п-х„-1\, ¦'¦ -•'1;i
сходится (как ограниченная и монотонно возрастающая). Далее, так как (уп) — сходящаяся
последовательность, то
|хп+р — Хп\ = \Хп+1 — Хп + Sn-2 — Sn-1 + . . . + Хп+р ~ Xn+p-l\ ^
^ \%п+1 — Хп\ + \х„-2 ~ ^п-11 + • • ¦ + |*п+р - Хп+р-1 | = |j/n+p - $ni < e
при п > Л^(е) Vp > 0, т. е. последовательность (хп) сходится. - *
Очевидно, последовательность ; '; 1-К- к
сходится; однако она не имеет ограниченного изменения, так как при любом А > 0 неравен-
неравенство , ¦,"; j,.
\х2-х1\ + \х3-х2\+ ... +\x2n-xin-l\ = 1 + 1 + 1+ ••• +^ZT >1 + ^ + J+ '••• +« >
справедливо при п > ел — 1. >
88. Пользуясь критерием Коши, доказать расходимость последовательностей {хп), где:
а)*„ = 1 + ?+...+?, пеЩ 6)Kn=;^ + ^J+...+i^I n€N.
•< Пусть е — произвольное число из интервала ]0, j[.
а) Поскольку f
i i 1.1. , 1 . Р , . ,. Г а.
'—^ —' и + 1 п + 2 п+р п+р'
а при р = п
\х , -х \>1->е
для всех »г, то последовательность расходится.
б) Расходимость последовательности следует из того, что
= 1 при п=р-
89. Доказать, что сходящаяся последовательность достигает либо своей точной верхней
грани, либо своей точной нижней грани, либо той и другой. Привести примеры посл(зя&ва4
тельностей всех трех типов.
•* Пусть lim х„ — а. Предположим, что хп < а (хп > в) Vn € N. Тогда существует наи-
поо
меньший (наибольший) элемент последовательности, который будет точной нижней (-
гранью. Если последовательность содержит элементы как меньшие а, так и большие а или

52 Гл. 1. Введение в анализ
некоторые элементы, равные а, то во всех этих случаях последовательность имеет как наи-
наименьший, так и наибольший элементы, т. е. достигает своих точной нижней и точной верхней
граней.
Приведем примеры последовательностей всех трех типов:
l)(*n)=(^), zi=0 = inf{*n}; 2) (*„) = (i) , xi = 1 = sup{xn};
' 3) («„) = (bill) , Xl = _i = inf {Xn}, X2 = \ = sup{xn}.V
Найти наибольший член последовательности (хп), если:
< 90. xn = g.
Щ Условимся наибольший член последовательности (хп) обозначать символом max xn ¦ Из
неравенства
т О
Хп 4
справедливого дри п > 2, вытекает, что последовательность (хп) монотонно убывает. Поэто-
Поэтому Наибольший член содержится среди элементов х\, хг, хз. Находим, что
9
тахх„ = хз = -•
_ 1000"
•Ьп — ;
¦Щ Так как -~^- = ~rf, т° при п > 999 последовательность монотонно убывает, а при
п < 999 — возрастает. Следовательно,
1ППЛ1000
maxin = цооо = ™ и 2,49 • 10*и. >
Для последовательности (хп) найти inf{xn}, sup{xn}, lim xn и lim х„, если:
92. xn = (-ir
^ Так как все элементы последовательности (х„) содержатся в последовательностях
Xjn-i в 2 + 2п^д, i2n = —2 — ^ и X2n < X2n-i, причем последовательность (хгп-i) мо-
монотонно убывает, а последовательность (хгп) возрастает, то
xi = sup{xn} = 5, lim хп = Urn x2n-i = 2,
n—<-oo n—*oo
12 =inf{in} = --, lim xn = lim x2n =-2.
Z n—*oo n—*oo
11V
'¦4 Имеем i4n-2 < i2n-l < X4n, причем (х4„_2) убывает, а (х4П) возрастает. Поэтому
inf{in} = lim xn = lim x4n-2 = lim (l - ) = 0,
П—КХ) П—*ОО П—*OO \ 471 — 1 /
(An \
1 + —" = 2. >
4u -|- 1 /
Найти lim xn и lim xn, если:
• оо
2тгп
n-*oo n-*oo
,2
^ Так как 1зп-2 < хзп-i < хзп и в последовательности (хзп-г), (хзп-i) и (хзп) сходятся,
г v v -(Зп-2J 1
Ьш хп = hm хзп-2 = hm —jr = --,
,,,..,. n—oo n — oo n-.,oo 2A + Cn — 2)^) 2
t "X \^
lim х„ = lim хзп = lim ' ,j = 1. >
1 + 1y
n-.oo n-»oo

§ 6. Предел последовательиости
95. Xn=(l + -У (-1)" + sin —. , .!.' ' 'V v, ,5;«i
¦4 Выделяя из всех членов данной последовательности восемь подпоследовательности^
(ХЯп-з), . ¦*¦',-' >.. ¦¦¦
. . ¦¦- I - ¦- ¦ ,'t) ;i
легко убедиться, что наименьший и наибольший частичные пределы имеют соответственно
подпоследовательности , > stV' ^!:'
B \ 8п— 3 j / 1 \вп-гв ¦:'.,! -.:' iMHtirt
1+в Г) 7=' 18п-6=A + ^ т) +.1. ,,'*
Поэтому ... .,.,:-¦¦¦>'•' щ> ¦
( ( 1 \8"-3 1 \ 1 •¦г?> '¦ 'ВЙ'Г'Н
lim хп = Um х8п-з = lim —11 + 7= = —е =,
-^оо п—оо п—оо \, Ч 8П — 3/ ¦s/2J у/2
// 1 \8n-6 \
lim х„ = lim i8n-6 = lim 1 + + 1 = е + 1. >
n—*oo n—*oo n—*оо \ Ч оТ1 — и / / ¦ I ¦ (.
2
2 W^T ¦ ;
n + 1 4
4 Имеем Х4п < х*п-з < Z4n-i < х*п-2, откуда '".. .1 Гр
lim in = lim x4n = 0, lim xn = lim itn-2 = Urn :-- al |» , ,,,,1 ^
n—*oo n—*oo n—*oo n—.oo n—^oo 4U — 1
. " ,-,¦ ¦¦¦¦;-r,.<>', -- >>•"¦* > Л
Найти частичные пределы:
g7 1 1 1 3 1 7 J_ 2"-l
' 2' 2' 4' 4' 8' 8' ""¦' 2n> 2n ' ¦'" ' . ,: ,
4 Из членов данной последовательиости составим две сходящиеся подпоследовательности:
х„ = ф? и х„ = 'д. Их пределы lim in = lim —• = 0, lim f = lim 2~'' = 1 будут
частичными пределами. . .л . ?в-
Так как все другие сходящиеся подпоследовательности входят в состав этих двух^то
гих частичных пределов нет. > л'" '
ЛП 1 11 11 1
|. i+i- i.
п'
п'"'' я- 1 п' п+ 1' ""
¦4 Члены данной последовательности составляют сходящиеся Подпоследовательности х>> «в
^ и Хкп = ^ + j^ (&, n € N), которые имеют соответственно пределы 0, i (fc € N). > х
QQ I I 1 I 1 1 I i i i
2' 3' 3' 4' 4' 4! 5' 5' 5' 5' '•" : ,' ; - ' =\"I; 8в
¦4 Очевидно, все рациональные числа г @ < г < 1) являются членами данной, после-
последовательности. Пусть а — любое действительное число такое, что 0 ^ а '< 1;' тогдМ щж
достаточно большом натуральном т неравенство ' i
а+ < 1
справедливо при всех п ? N.
Для каждого натурального числа п среди членов данной последовательн©с*и найдется
такое рациональное число гп, что
а < гп < а-\
Отсюда следует, что lim rn = а, т. е. а — частичный предел. Аналогично рассматривает**
случай, если 0 < а < 1. > ., ,(.
100. Построить числовую последовательность, имеющую в качестве своих частичных
пределов данные числа:
ai, а2, ..., ар.

54 Гл. 1. Введение в анализ
¦<,Обозначим Xfcn = с*к + —, к = 1, р, п € N. Так как последовательности х*п сходятся
к числам а*, А; € N, то искомой последовательностью может быть, например, последователь-
последовательность
+ 1 а 1а -а - а - а - а +- а +-
, ' , ¦ ¦ ¦, р , 2' 2' '''' р 2' ' " ' п' п' ' р п.', ''''
составленная из членов последовательностей (х/с„), Л € N. >
101. Построить числовую последовательность, для которой все члены данной последо-
последовательности
а\, а2, ..., а„, ...
являются ее частичными пределами. Какие еще частичные пределы обязательно имеет данная
последовательность?
¦< Из членов последовательностей х„ = а„, Хкп = а* + ^т^ (п, к € N) составим последо-
последовательность с членами
1 11 111
0,1, 0,1 + -, а2, ai + -, а2 + -, аз, ai + -, а2 + -, аз + -, а4, ...,
I оо 4 4 4
которая имеет своими частичными пределами: 1) пределы последовательностей (хкп), т. е.
члены последовательности (an) и 2) частичные пределы последовательности (а„). >
102. Построить последовательность:
а) не имеющую конечных частичных пределов;
б) имеющую единственный конечный частичный предел, но не являющуюся сходящейся;
в) имеющую бесконечное множество частичных пределов;
г) имеющую в качестве своего частичного предела каждое действительное число.
4 а) Например, хп = п.
б) Пусть (in) — последовательность, стремящаяся к конечному пределу а, (уп) — беско-
бесконечно большая последовательность; тогда последовательность xi, j/i, x2, j/2) ...,х„, уп, ...
является расходящейся и имеет единственный конечный частичный предел а.
в) Примеры 99 и 100.
г) Построим последовательность, содержащую все рациональные числа ±-, где р и q —
натуральные числа:
1 I 1 -1 1 Л i -- - -- I I _1 - _1
' ~ ' 2' ' 3' ~3' 3' ~3' 2' ~2' Т' Т' 4' "¦•' п' ~п' п1 п1""
п — 1 я — 1 я п п пп п
¦ • • ' п ' п ' г* - 1' п - 1' • • •' 2 ' 2 ' 1 ' 1 ' '''"
Тот факт, что любое действительное число является частичным пределом, доказывается ана-
аналогично решению примера 99. >
103. Доказать, что последовательности (хп) и (уп) = (xn -s/n) имеют одни и те же
частичные пределы.
¦< Так как lim у/п — 1 (см. пример 75), то lim рч/р^ = 1, где (рп) — произвольная
п—юо п—*оо
подпоследовательность ряда натуральных чисел.
Пусть а — частичный предел последовательности (хп) и lim хр„ = а. Тогда, применяя
п—*оо
теорему о предельном переходе в произведении, находим
lim yPn = lim xPn ptfpZ = lim xPn lim ptfpZ=a,
n—*oo n—*oo n—*oo n—*oo
x..,ei, a — частичный предел последовательности (j/n)-
Пусть теперь j) — частичный предел последовательности (уп) и lim уЧп = /?. Поскольку
п—*оо
д/п > 0, то определена подпоследовательность (хп) = (Уп п " I, а следовательно, и подпосле-
подпоследовательность (хЯп) = I Удп(Яп) Чп I, которая имеет своим пределом число f). >
104. Пусть последовательность (х„) сходится, а последовательность (уп) расходится.
Что можно утверждать о сходимости последовательностей:
а) (*„ + »„); б) {хпУпI
Привести соответствующие примеры (для случая б)).

§6. Предел последовательности ,BS
¦4 а) Последовательность (хп + Уп) расходится. Если бы она сходилась, то сходилась
бы и разность последовательностей (хп) и (хп + Уп)- Но это невозможно в силу того^ЦЯс/
(х„ - (х„ + уп)) = -(j/n) а («/„) — расходится. " ';;!ГВД
б) Последовательность может как сходиться, так и расходиться. Например:
1) последовательность (хп) = (—) сходится, а последовательность (уп) = ((—1)") расхо-
расходится, однако их произведение (хпуп) = ( ^~J 1 образует сходящуюся посяедбвателйго'сй»;
2) последовательность (хп) = („XI") сходится, а (уп) = I п1\п ) расходится; их произве-
произведение (х„з/„) = (^^Тр~) тоже расходится. > ,.(
105. Доказать, что:
a) lim хп + lim yn ^ lim (х„ + ;/„) ^ lim xn + lim yn;
n—*oo
б) lim хп + lim yn ^ Urn (xn + Уп) ^ lim in + lim yn.
n—*oo n—*oo п—*оо n—*oo n—*oo
Привести пример, когда в этих соотношениях имеют место строгие неравенства.
Замечание. Если из последовательности (хп) выделить некоторую подпоследовательность (yi
то
lim хп S; lim Д<;„ •
А а) Поскольку нижний предел последовательности является ее предельной точкой, То
lim (хп + Уп) = lim (хг„ + 2/г„), _Um_xrn = lim imrn .
п—*оо n—»oo n—юо n—*oo
В силу замечания, имеем
lim in + lim yn ^ lim xr^ + lim ут„ = lim xmrn + Jmi_j/rn ^ lim xmrn + fan Ут^^
n—*oo
Далее, поскольку {xmrn +ymrn) является подпоследовательностью сходящейся последователь-
последовательности (хГп +Уг„),ТО
lim (хг„ +уГп) = lim (xmrn +2/тгл). > ч,:^,
п—*оо п—*оо
А так как, кроме того, последовательность (xmrn) сходится, то и последовательность
также сходится, так что - '•.?
lint утгт1 = lim УтГп,
п—*оо п—*оо
и полученное неравенство можно переписать в виде
lim хп + lim j/n ^ lim xmrn + lim УтТп = lim (xmrn + УтГп) = lim (жп + Уп).
и—*оо п—юо п—*оо п—*оо п—*оо п—*оо
Левая часть неравенства а) доказана. Учитывая это и тот факт, что
lim (-уп) = - lim yn,
п—*оо п—.оо
получаем
Um (in + г/,,) - Um j/n = lim (xn + yn) + lim (-yn) ^ lim ((xn + yn) + (-yn))= Um
n—*oo n—*oo n—*oo n—*oo n—*oo " 71-+0O
Отсюда вытекает правая часть неравенства а).
Неравенство б) доказывается аналогично.
Построим пример, когда в данных соотношениях имеют место строгие неравенства.
^, n6N.
Тогда х„ + «/n = (-1) 2
lim х„ = -1, lim xn = 1, lim yn = -1, lim yn = 1, lim (xn+yn) = —1, lim (хп+Уп),^-1. >
n—*oo n—>co n—*oo n—»oo n—*oo n—»-oO
106. Пусть xn ^ 0 и j/n ^ 0, n € N. Доказать:
a) lim xn ¦ lim yn ^ lim (xnyn) ^ lim xn • Um ;/n; ¦ ¦¦ , ¦. ¦ ••¦!.•

56 Гл. 1. Введение в анализ
6) Цп> Sn • Um Vn < lim (xnyn) < lim xn ¦ Um yn.
n*5o n*oo n*oo n*oo n*oo
f n-*5o n*oo n*oo n-*oo n—*oo
" Привести пример, когда в этих соотношениях имеют место строгие неравенства.
Щ Докажем случай а) (случай б) доказывается аналогично).
Если х„ = О, п 6 N, или lim хп = 0, то соотношение а) очевидно.. Остается рассмотреть
случай, когда Um xn > 0. Тогда хп > 0, начиная с некоторого номера.
.... ,,';, ..¦, „ j П-.ОО
Пользуясь замечанием в примере 105 и обозначениями
Um (хпуп) = Um (хг„уГп), Um хт„ = lim xmrn,
п—»оо п—*оо п—*оо п-*м
имеем
Цт х„ ¦ Цт уп ^ Цт жг. ¦ Цт уг. = Цт хтг_ ¦ lim уг. ^ Um im • lim ;/m .
П—>ОО П—»ОО П —OO П—>ОО П-.ОО П-»ОО П-.ОО П — OO
Поскольку (!!mrjmrj — подпоследовательность сходящейся последовательности {хГпуГп),
то
^ : n—»oo n-*oo n-»oo n n
А так как подпоследовательность (tmrj сходится к отличному от нуля пределу, то подпосле-
подпоследовательность (УтГп) также сходится, т. е. Цт утг_ = Цт УтТ„ ¦ Следовательно,
n—*t» п—«оо
lim хп ¦ Um yn? Um imf, • Um ymr.= Um ftm.il.Vm.ll)= lim (хпУп)-
П-~*ОО fl—-ИЗО Tl—*OO Tl—*OO 71-^OO П-^ OO
1 Таккм образом, левая часть неравенства а) доказана. Если Um yn = 0, то правая часть
71-^ОО
неравенства а) очевидна, ибо в таком случае Um уп = 0, а поэтому Um (хпуп)=0. Пусть
Т1-^ОО • 71-^ОО
to »n > 0. Тогда, согласно доказанному и тому, что lim — = ., 1—, получаем неравеи-
ti**eb' ¦ ''• ' п-->со ^п "т Уп
€СТО, .. . •¦ • П~°°
ыл _^_ Цт (хпуп) = Цт —• Цт (хпуп) ^ Um (—(хпуп)) = lim xn,
Цт уп п—оо п-»оо 3/п п-»оо п—оо \уп ' п—оо
иэ которого следует правая часть неравенства а).
Приведем пример, когда в данных соотношениях имеют место строгие неравенства. Пусть
' . .'. '¦ '-¦'¦ j п(п+1)
¦ \у-<\>
- jy^fn « 1, lim г„ = 3, _Цт_з/„ = -, Um yn = -, Um (inj/n) = -, Um A„з/„) = -. >
n-*^o n-roo n~»oo Z n—»oo L n—.oo Z n—»oo J
"хОТ. Доказать, что если Шп %п существует, то какова бы ни была последовательность
(>п)ж получим^
''-'" -! : Um (хп + Уп) = Um xn + Um з/„.
п-*оо п-^оо п—»оо
-, Ч Имеем (см. пример 105)
lin» (хп + уп) ^ Um хп + Um з/„, Um (in + з/n) ^ Um in + Um yn.
n—*oo n—*oo
Поскольку lim xn = lim xn = lim хП1 то в предыдущих соотношениях возможен только
о
п-^оо п—*оо
^j Доказать, что если для некоторой последовательности (zn), какова бы не была
последовательность (уп), имеет место по меньшей мере одно из равенств:
, ,,al Цт (х„ + Vn) s» lim xn + lim уп или б) lim (хпуп) = Um хп ¦ Um уп, хп ^ О,
то последовательность (жп) — сходящаяся.

6. Предел последовательности 57
•^ Пусть условие а) выполнено, (j/n) — любая последовательность и уп =,—*§¦ TofS*
условия а) следует ' ' ' • ¦' ¦ »•;,
t _ _
lim х„ + lim (—х„) = lim хп — lim in == lim;(an •*-»»>)i
поо noo noo noo n^oo"
.) '<»¦-
откуда lim xn = lini xn, т. е lim xn существует. При выполнении условия б) полагаем
уп = —1- Тогда из б) вытекает, что lim (—хп) = — lim хп, или lim хп = lim xn и сдова
убеждаемся в существовании предела последовательности (хп)- > " ¦'
109. Доказать, что если хп > 0 и '* "м '
I
lim хп ¦ lim — = 1,
Х
п—>«
то последовательность (хп) — сходящаяся. ' vsif
¦4 Из условия примера и того, что lim — = -р , вытекает, что lim %n яг Цщ хп,
п—> оо
т. е. (х„) ^сходящаяся последовательность. > •<-,,, , ,ч /
110. Доказать, что если последовательность (хп) ограничена и '" ; .. ' ' -'11-ь>
lim (xn+i - хп) = 0, , .у\ , Г|1[
п—*оо - -„ ¦;¦„: ,,
то частичные пределы этой последовательности расположены всюду плотно между tjQ}
и верхним пределами: s
/ = lim xn и i = lim xn, .: ,. ¦ * *¦•
n—*oo n—*oo
т. е. любое число из отрезка [f, i] является частичным пределом данной последователь
А Покажем, что любая точка а, принадлежащая интервалу ]?, L[ является частичнММ
пределом последовательности (хп), т. е. покажем, что любая е-окрестнрсть точки а содержит
бесконечное число элементов последовательности (хп).
Пусть е > 0 -— такое произвольное фиксированное число, что е-окрестности тоЧек /, о и L
не имеют общих точек. Согласно условию, существует такое число N{e), что |ln+l ""'sinl "*? W
при п > N(s). , .>.-'¦ '''
Поскольку I — частичный предел, то в е-окрестности точки I найдется элемент жм, с ,
индексом pi большим, чем N(e). По той же причине в е-окрестности точки L сущест^уЛ
элемент хЧ1 с индексом q\ большим, чем pi. А так как расстояние между соседними элемен-
элементами при п > АГ(е) меньше 2е, то среди натуральных чисел п, для которых р\ < » < fi,.
существует хотя бы одно такое число ri, что элемент хГ1 принадлежит е-окрестн&Й|# ^вИЙЁК
а.
Далее, существует элемент х?2 с индексом |>2 большим, чем ?i, И такой, что kpj; KpWMJkfr
лежит е-окрестности точки /. Следовательно, среди номеров п; для которых qi < п <i*fjj,
найдется такой номер гг, что элемент хГ2 принадлежит е-окрестности точки а., Про^^кад
этот процесс до бесконечности, убеждаемся в существований бесконечного числа эл'еме
последовательности (хг„), принадлежащих е-окрестности точки а. Следователь'нв|'Э1;^311 *ч
дельная точка, а так как а — произвольная точка интервала ]/, L[ то требуемое утверждение
доказано. >
111. Пусть числовая последовательность (хп) удовлетворяет условию 0?^< ;Ц|'$ $"т'-f
хп, т, п € N. Доказать, что lim — существует. :Г ,
п—»оо П _ ' ¦" . * '.
< Имеем 0 < хп ^ xi + ii + ... + xi = rcxi, 0 ^ — Sj xi, n = 2, 3, ... , n
следовательно, последовательность (^f-j ограничена и существует
грань а — inf { — }. Пусть е > 0 — произвольное, тогда существует1"таКЬЙ
™ <г Z™. s п л- I " ••¦¦:; ¦¦';.. ¦¦•¦-'¦
Всякое целое число п может быть представлено в виде п = дт + г
чисел: 0, 1,2, ..., т — 1. Полагая для большего единообразия хо = 0,
Хп = Xqm+r ^ 1т + 1щ + ¦ • • + Хт + 1Г = qXm + Хг,

Гл. 1. Введение в анализ
Хп _ Хдт+г дхт + Хг __ Хт q
Л qm + г ^ qm + г т qm + г п
1г
п
Поскольку
m + г n 2 n
xr ограничено и существует такое число N(e), что при п >
А тогда «^ — <« + f + f = a + e при м > iV(e), так что lim — = а. >
п
112. Доказать теорему Теплица: пусть 1) Рпк > 0; 2) у^ Рпк = 1; 3) lim Pnk = 0
*—' п-»оо
при каждом фиксированном к; 4) lim х„ = а. Тогда последовательность с членами tn =
п—юо
п
EJ°nfcs;/e сходится u liin <„ = о.
(sal
¦^ Из условия 4) вытекает существование такого числа N = А^е), что неравенство
|х„-а|< |
выполняется для всех п > N(e)\ далее, из этого же условия вытекает существование такого
числа М > 0, что
для всех п. Наконец, из условия 3) следует существование такого числа по = По(е) > N, что
для всех п > по.
-Пользуясь этими неравенствами и условиями 1)—2) теоремы, получаем
Рпк(хк — о)
JV - о| + PnN.
- а\+ ...
-а\
п
для всех п > по, т. е. lim tn — lim J2 РпкХк = a.
nюо n»oo
2
n—юо n—»oo k=1
113. а) Доказать что если последовательность (хп) сходится, то последовательность
средних арифметических (?„), где
?п = -(*1 +Х2 + ... +Х„),
также сходится и lim ?n = lim х„.
п—*оо п—*оо
б) Доказать, что если последовательность (у„) сходится и у„ > 0 V« g N, то последова-
последовательность средних гармонических
также сходится и lim 7n = lim j/n-
-4 в) Доказать, что если lim yn = +оо, то
lim 7n = +оо и lim $n = +оо,
где fn — среднее гармоническое, а ?„ — среднее арифметическое из чисел j/i, j/2, • • ¦, S^n-

§ 6. Предел последовательности 59
¦4 а) Если положить Рпк = ^ (к = 1, п; п € N), то для Р„к и in будут выполнены *се
п
условия примера 112, причем tn = У^ PnkXk — ?п- Следовательно, lim ?ге = lim xn-
д.=1 п-*оо т»—юо
б) Пусть
- (А,- = 17п), ** = 3/п- • '
»i г/2 ' ' ' Уп
Тогда все условия примера 112 будут выполнены, причем tn = fn. Следовательно, lim уп "»
lim 2/„.
п—*оо
в) Покажем, что если lim — = 0, то lim — = 0. А это эквивалентно тому, что liin; ^n e
п—*оо Уп п—*оо ^п п—*оо . :_
+оо. Используя пример 112 и полагая
" >¦¦ \ 1 , -
-Pnfc = - (* = 1, П), Хп = , -
П Уп . . -л//*
п -.»-•-
получаем, что tn = У] РпкХк = — и lim — = lim — = 0.
ц — l "*п п—*оо 7п п—*оо Уп , ,¦ - ,: ; ^
Утверждение, что lim ?n = +°о, следует из неравенства (см. пример 42) уп ^ {п И К»
71—tOO
того, что lim уп = +оо. >
п—»оо
114. Доказать, что если последовательность (хп) сходится и хп >'О, То
lim д/х1Хг •.. xn = lim xn. _>
n—*oo n—oo
Имеем (см. пример 42)
П _ . „ Xi + X2 + . . . + Xn
7п = J_ _1_ —Г ^ Vl2 п ^
*1 """ *2 *п
А поскольку lim yn = lim ?n = lim xn (см. пример 113), то
н—*оо п—*о
lim Уигг • • • хп ~ lim х„. >
115, Доказать, что если Vn € N хп > 0, то
V »; г Хп
lim Vх" = "m >
п-»м п—*оо Xn—1
предполагая, что предел, стоящий в правой части последнего равенства, существует.
^ Доказательство следует из того, что
,• „/ ,. / Х2 Хз Хп ,. Хт,
иш s/xn = lim \ x\ ¦ — • — ... = urn
(см. пример 114). >
116. Доказать, что lim n = e.
Х\ XI Хп-1 П-.ОО Хп-1
А Заметим, что
где xn = ^V- Поскольку liin -^2— = lim fl Л—Ц-)" = e, то на основании примера 115
"¦ n-.oo xn-l n — oo v n-1/
получаем требуемое утверждение. > , > .ь;й-
11 Т. Доказать теорему Штольца: если >
a) V« 6 N «/n+i > J/n; б) Иш j/n = +оо; в) существует Um , mo
n—.oa n—oo уп ~ Уп—1 п:
,. Хп ,. Хп
lim — = lim
n—oo J/n n-»oo J/n ~ J/n—1

60 Гл. 1. Введение в анализ
¦4 Пусть lim *"~*n-', — а (а — конечное). Тогда если считать, что у0 = 0, х0 = 0 и
п—са " »п-1
р _ Ук - Ук-1 , _ у— у _ ХХ
J пк — j л — -I, /I, Л.ух —
У
j , , ,
Уп Уп — Уп-1
то получим выполнение условий теоремы Теплица (пример 112) для Р„к и Хп, причем tn =
'л
Следовательно, lim — = lim tn = lim Х„ = lim д"~а;"~1 = a.
n—*<x> Уп n-.oo n—юо n—*oo ^n Уп—I
Если lim *"~**~1 = +oo, то повторяем приведенные выше рассуждения для последова-
п—юэ Уп Уп — 1
тельности ( — ), предварительно убедившись, что xn+i > хп, начиная с некоторого по € N ,
и lim xn = +оо. >
п—*оо
118. Доказать, что если р — натуральное число, то:
1 + 2+ ... +п 1 Л + 2+ ...пр п
а) Ьт — ' = ; б) hm
в) hm
-;
^ Р+/ 2'
3" + . .. + Bп + 1)р 2"
= .
ПР+1 р+1
¦4 Для доказательства применим теорему Штольца (пример 117). Докажем пункт б) (пунк-
(пункты а) и в) доказываются аналогично).
б) Если положить хп — (р + 1)AР + 2Р + ... + ир) - пр+1, уп = (р + 1)гар, то
Г.+ 1 - Уп n-оо (р + l)((n + 1)р - IIP)
(р + 1) (np + pit"'1 + ?i?=±lnP-2 + ... + l)
= lim
j ^
(p + 1) (nP + pnP-1 + V&^-nP-2 + ... +1 - nPJ
Соберем коэффициенты при одинаковых степенях п. Затем разделим числитель и знамена-
знаменатель на пр-1 и обозначим через о (-) сумму всех членов со степенями не выше —1; получим
n —oo J/n+l — J/n n^°° p(p + 1) + О (^-j ^
119. Доказать, что последовательность (in), где
Xn = 1+ -+-+... H In 7i,
2 3 n
сходится. Таким образом, имеет место формула
1 + \ + \ +•••+- = О + Ь п + с„,
где С = 0,577216 ... — так называемая постоянная Эйлера и еп —> 0 при п-» оо.
¦4 Так как xn+i — х„ = ^у — 1п(п + 1) + In п = -^-^ — In (l + i) < 0 (см. пример 82, а)),
то Последовательность (хп) монотонно убывающая. Кроме того, она ограничена снизу:
ln(l + 1) + In (l + i) + In (l + i) + ... + In (l + I) - In n =
= In I 2 —^ ) = In > > 0.
\23 n nJ n n+1
Поэтому существует конечный предел С, а тогда справедливо представление
1 +- + -+...+ 1П П = С + ?„,

§ 6. Предел последовательности ' fil
где е„ —¦ 0 при п —¦ оо. > . ,; ,., д. *- , ¦'.
120. Найти lim (—j— + -^— + ... + -LY
п—оо \П + 1 П + 2 2п) .. . . .... ¦
•« Пусть г„ = 1 + \ +...+ \. Тогда
1 1 j • ' ¦.'¦¦' ••'¦'¦' ¦ ¦¦'¦¦ '¦' "''
—— + -—х + ¦ • ¦ + — = г2„ - г„ = In 2n + e2n - In n - е„ = In 2 + (еа„ - е„) . • i
(см. пример 119) и , ....,..>
lim ( - + -+...+—¦]= In 2. > ' ' '¦¦ " .
п^оо \П + 1 П+2 2П)
121. Последовательность (х„) определяется формулами
, Хп-1 + Хп—2 г о л \
—а, х2 = о, х„ = (и = 3, 4, ...).
Найти lim in.
П—*ОО
•Ц Имеем
Подставляя эти выражения в очевидное равенство , . -.....>. ч».1:
Х„ = XI + (Х2 -Xl) + (x3 -Х2) + . ч + (in -Zn-l)/' , _ .,- ,, ^.rf
получим, начиная со второго слагаемого, геометрическую прогрессию, сумма которой
откуда
,. ,. / 2(Ъ-а) Ь-а {-\)п\ а + 2Ь ^
\хш хп = hm (а + \ + —— ^^- = —г—. >
п—»оо п—*оо V о о J / **
122. Пусть (хп) —последовательность чисел, определяемая следующей формулой: *
хо > 0, х„+1 = - (хп Н ), п€^о.
2 V х„/
Доказать, что щп хп = 1.
п —оо .'i ' - ' ¦ "V
А Поскольку хо > 0 и х„ + — ^ 2, то последовательность (in) ограничена снизу Чи-
Числом 1. А из неравенства xn+i = \ (хп + —) ^ in, справедливого для rn ^ 1, вытекает,
что данная последовательность монотонно убывает. Следовательно, существует конечный
предел а, причем а ^ 1. Переходя к пределу в равенстве , . I ЛЯ 4
находим, что а = ? (о + ^) . Отсюда о2 = 1 или а = ±1. Но так как Vn € N х„ % 1", то о 'зав I.11?
123. Доказать, что последовательности (х„) и (j/n), определяющиеся формулами
, , Хп +Уп :' . > ,; I
XI = a, J/1 = о, Xn+i = у/ХпУп, Уп+i = ,
имеют общий предел /г(а, 6) = lim xn — lim yn (арифметико-геометрпческое среднее чнеея
п—*оо п—*оо \ '
а и Ь). ' : (_..,.
¦4 Из условия примера следует, что Vn € N хп ^ 0, j/n ^ 0. Используя известное неравен-
получаем
Хп + Уп

62 Гл. 1. Введение в анализ
А Так-Как Sn+l = \/ХпУп > V^T = In, Уп+1 = Хп+Уп ^ уп, ТО, ВВИДУ ТОГО ЧТО Хп < Уп <
J/1, Уп ^ in ^ ii, последовательности (in) и (j/n), в силу утверждения 2, п. 6.3, имеют
конечные пределы А и В соответственно. Переходя к пределу в равенстве
_ In + Уп
2 ¦ > :
получаем, что А = В. Общее значение этих пределов называется средним арифметико-
геометрическим и обозначается символом ц(а, Ъ). >
Найти пределы:
Ц Поскольку
1 _
1 - р- —
то, записывая произведения в виде
, Л - ^, Я,
/ _ _1_Л / 1_> / _ М ^3 2_4 ^5
V 22А 3V "¦¦ V п2) 22 ' 32 ' 42
2' в '
находим, что
Имеем
Тогда
'
l-4 2-5 3-6 (н-1)(п
n-oo\2-3 3-4 4-5 "¦ n(n + l
.. 1 п + 2 1
^ооЗ п 3
Найти пределы векторных последовательностей (хп), где:
" \\ п ) • L + iJ J"
Поскольку каждая из последовательностей координат сходится, то, согласно п. 6.7,
lim хп = lim 1 , lim = (е, е ). >
г v - f!L±! !i±i H + 1N\
п ~ V п ' 2н ' " *"' mn ) '
^ Аналогично предыдущему примеру находим
у (л. п+1 п + 1 »+1\ Л 1 1\
hm х„ = I hm , hm ——, ..., hm ) = I 1, -, ..., — . >
128. xn = fTy2+^, V
•^ Покажем, что существуют пределы последовательностей каждой из координат. Из
неравенств 2 < л/2 + 2" < 2 л/2 и того, что lim т/2 = 1, следует lim л/2 + 2п = 2. Далее, из
неравенств
находим, что
1 < У2 + 2-™ < \/3, 1 < \/2 + 2- < \/3 -
lim \/2 + 2~" = 1, Бт У2 + 2- = 1.

§ 6. Предел последовательности <Ш
Поскольку пределы последовательностей координат существуют, то существует И предел век-
векторной последовательности, а поэтому , , ,,
lim х„ = ( lim л/2 + 2n, lim \Л + 2-", lim \/2
п—*оо \n—*oo n—*oo n—юо
129. Xn = (Xln, X2n, . . . , Imn), ГДе
\ n + 1 Ji +
4^т+ ¦•• +г7
+ 2 it + m
•* Обозначим у„ =z\ + ~ + ... + -i. Из примера 119 следует, что
уп = C' + lnn + 7n,
где С — постоянная Эйлера, а 7п —* 0 при п —*¦ оо. Тогда
Xin — »(l + i)n - Уп = С' + 1п(A +t)n) +7(l+i)n - С-Ып-Уп =ln(l
Поскольку уп —<¦ 0, 7A+0" ~+ ° ПРИ w —»¦ со, то
lim г^„ = ln(l + »'), г = 1, т.
п—*оо
Следовательно,
Шп хп = ( lim ц„, lim i2n, ..., lim imn] =Aп2,1пЗ, ..., lti(m + 1)). >
П—*QQ \П—»0О П—*0О П—*ОО /
130. Пусть задана векторная последовательность (хп), где ' ' .-.--«.i
евклидова норма которой стремится к бесконечности.
Обязательно ли существование хотя бы одной последовательности координаты (xin), стре-
стремящейся к бесконечности? Рассмотреть пример
Нет, не обязательно. В предложенном примере евклидова норма
_ /A-(-!)")»»* ЛГ+(-1
стремится к бесконечности при п ^ оо. Однако ни одна из последовательностей координат
не стремится к бесконечности. Действительно, для последовательностей координат
lim х\п =в +со, lim nn = 0; lim tin = +co, lim g2ti — 0
n—*oo n—>oo n—*oo n—>(»
и, следовательно, оо не является пределом ни для одной из этих :
131. Найти предел последовательности (А„) = (а\™'), г = 1, р, j — 1,: д, где
1 . 1 . . 1
,-,-,' , ¦ о i • • • ¦ , ¦ i если 3 >
Ji + ut+1 п + гп + 2 п + рг
1
—, если i = ,
" 1 1 .1
¦ п + jn+1 n + jn + 2 '" п + in'
Сначала докажем, что каждая из последовательностей п н-> а\"', i = 1, р, j — 1,'
сходится. Пусть, например, j > г. Тогда (см. пример 129)
а(п) = 1 1 1
°ij n+in + 1 n+in + 2
''"' '» "
+ + ) ( +

64 Гл. 1. Введение в анализ
где xin —* ln(l + /) при « —+ со. Отсюда
а\? = *j» - К» -+ ЬA + j) - ln(l + 0 = In ji
Аналогично при i > j находим, что
при п —+ со.
in
1 +)
при n —> oo.
Наконец, если г = j, то сц" = — —> 0 при п —«¦ со.
Таким образом, все последовательности fa,"'1 сходятся, поэтому
lim Л„ = f Km a\f) =
132. Найти
lim
n—*oo
/О In | In | ... In f \
In | 0 In | ... In f
ln± ln| 0 ... laf
\ In f In f In f ... 0 /
l
(
lg» n+sin n
Все элементы матрицы являются сходящимися последовательностями, поэтому
И 1 1
lim
п—*оо
+
lg « n+sin n
.. п 1
lim lim тг7
П—*ОО 11 -(- 1 П—>(
Um ^ Um ^P
n—oo Jl n—oo in
lim
n-*oo
10 0
= V 0 I 4
Упражнения для самостоятельной работы
Доказать следующие равенства:
63. lim t=1
n
где т — натуральное число.
„-.oo (
64. lim f ,-i
П-.00 \Vn2
65. lim
+
+ • • • + , x ^ = 1.
1
—, где p — натуральное число.
+1
n
- n-'i, S fc(fc+i)-1(*+m+i) = ^гЬ> где m — натуральное число.
67. Um *zi __
E'
_ j gg
69. Пусть жо > 0 — произвольно,
l / \
Доказать, что lim a;n = %/**•

§ 6. Предел последовательности 65
70. Последовательность (х„) определяется соотношениями rn+i = рхп + q, р ф 0, xi —
произвольно. При каком условии последовательность (хп) сходится? Найти, в случае ее
сходимости, предел.
71. Доказать неравенство (l -\—J 2 > е.
72. Доказать неравенства
73. Найти ton ^, 0 < Л < 1.
п—юо п
Пользуясь теоремой о существовании предела монотонной и ограниченной последователь-
последовательности, доказать сходимость следующих последовательностей (хп), где:
74.xn = Tfc + ^+...+JzI. 75. rn=(iL)( L)(L)
С помощью критерия Коши исследовать на сходимость следующие последовательности
(хп), где:
76- *» = пЬъ + ?rk + • • • + m n = 2, з,....
77. xn = i-^ + n?lf+...+j-J-) n = 2,3,....
78. Пусть ai ^ (i2 ^ a? ^ ... ^ 0. Доказать, что последовательности F'„) и (<тп), где
Sn = tii + «2 + • • • + tin, Cn = tii + 2ti2 + • •. + 2na2n,
или обе сходятся, или обе расходятся.
79. Доказать, что последовательность EП), где
Sn ~ 2~пГ^2 + зп^Т + • • • + TThTFTT' и = 2, 3, ... ,
сходится при р>1 и расходится при р ^ 1.
80. Доказать, что для любой последовательности (оп) с положительными членами спра-
справедливы неравенства: '
а) lim a"'1 ^ lini ^/а^; б) lim Vfa^ ^ lim ""+1 .
Найти пределы векторных последовательностей (хп), где
84. хп = ( ^/3" + 2п, ^/Зп +4", ^Зп +6").
n+1 ' v v ~"^n ¦ ¦ ¦ "n I ' ГД<3 « ~ m\(n-m)<
Найти пределы матричных последовательностей {An), где
86. а„ = ((l -(- i)J"), «= ТГр, i = 177
((п+1K-п2 (;.+2K-п3 (п+3L-п4
п
(п-1)а-пг (n-2K-n3 (n-3L-n4
89. Доказать, что
ton /lni?n = lim An ¦ lim .Sn,
если пределы матричных последовательностей существуют и все члены последовательностей
являются матрицами одного размера.

66 Гл. 1. Введение в анализ
90. Пусть матричные последовательности (Ап) и (Вп), где Ап = (а\"), В„ = (bff), и
векторная последовательность (хп), где xn = (xin, %2п, ¦ ¦ ¦, хч„), сходятся, причем
lim А„ = A, lira В„ = В, lim xn = х,
П—*ОО П—*0О П~*ОО
а матрицы С = (а3), G = (д]к) и вектор у = (уи у2, ..., уч), г = Т~р, j = TTq, к - Т~г —
постоянные.
Доказать, что:
a) lim АпВп = АВ; б) lim СВ„ = С В; в) lim AnG = AG;
п—»со п—«-оо п—>оо
г) lim ЛпХп — Ах; д) lim Лпу = Лу.
п—»о
7. Предел функции
7.1. Предельная точка множества. Предел функции в точке.
Определение 1. Пусть X С К- Число хо 6 К называется предельной точкой множе-
множества X, если
Ve > 0 Зу 6 X, у # яо : |у- ко| < г.
Из определения следует, что любая окрестность точки хо содержит точку из множества
X, отличную от хо. Сама точка хо может принадлежать, а может и не принадлежать мно-
множеству X.
Определение 2. Значение +оо есть предельная точка множества X, если VM 6
R3j/ &X :у> М.
Значение —оо есть предельная точка множества X, если
vm е к з у е х •. у < м.
Определение 3. Точка х ? X, не являющаяся предельной точкой множества X, назы-
называется изолированной точкой множества X, т. е.
36 >0: 5(i, 6) fll = {i}.
Определение 4. Число жо G К называется предельной точкой множества X С R,
если из этого .множества .можно выделить последовательность (гп) различных точек, схо-
сходящуюся к хо.
Определения 1 и 4 эквивалентны.
Пусть / : X —»• R и хо — предельная точка множества X.
Определение 5 (Гейне). Функция f имеет предельное значение при х —+ Го (или в
точке Хо), если существует такое число Л g R, что Эля произвольной последовательности
(хп) значений х € (]а, Ь[\{*о}), сходящейся к точке хо, соответствующая последователь-
последовательность значений функции (f(xn)) сходится к точке А.
Определение 6 (Коши). Функция / имеет предел при х —+ хо, если
3/l€lRAVg>03«>0:0<|r-ro|<^=^ \f(x) - A\<s.
При этом число А называем пределом (или предельным значением) функции / в точке хо
и записываем
lim f(x) = А или f{x) —+ А при х —> хо-
Определения Гейне и Коши эквивалентны.
Введем понятие одностороннего предела.
Определение 7 (Гейне). Функция f имеет в точке, хо предел слева (справа), если
существует такое число А 6 R, что для произвольной последовательности (х„) значе-
значений х, а < хп < хо {хо < хп < Ь), сходящейся к точке Хо при п —? оо, соответствующая
последовательность (f(xn)) значений функции f сходится к точке А.
Определение 8 (Коши). Функция / имеет в точке хо предел слева (справа), если
3A6RAVe>03^>0:0<io-i<«@<i-io<«)=> \f(x) - А\ < е.

§ 7. Предел функции 67
Число А называем пределом слева (справа) функции / в точке хо и обозначаем
Дю-0) (/(ю+0)) или lim f(x) ( lim f(x)).
Функция / имеет предел в точке хо тогда и только тогда, когда в этой точке существуют
и равные между собой пределы слева и справа.
Теорема (критерий Коши). Функция f имеет конечный предел в точке^хо тогда и
только тогда, когда
Ve > 0 3 5 > 0 : @ < \х - хо\ < 6 Л 0 < \у - хо\ < 6) =*• \f{x) - f(y)\ < e.
Особую роль играют два замечательных предела:
l)li
=1; 2) Um(l+r)x =е.
Х+0
Если lim f(x) = A, lim g(x) — В, то
Um (/(*) + g{x)) = А + В; lim f(x)g(x) = АВ; lim 44 = 4 (*(*) »* °- B »*
7.2. Ограниченность функции.
Функция / : X —* К, X С К, называется ограниченной на множестве X, если существуют
числа т и М такие, что т ^ f(x) ^ М, х ? X.
Число то = inf \f(x)} называется точной нижней гранью функции /, а число Jlfo ==
х?Х
sup {/(ж)} — точной верхней гранью функции / на множестве М. Разность Afo — n»o найи-
вается колебанием функции f на множестве X.
Если функция / : X —> К имеет конечный предел в точке хо € X, то она ограничена в
некоторой окрестности этой точки.
7.3. Символы Ландау. Эквивалентные функции.
Пусть хо € R, а 5 = {X, Y, Z, ...} — семейство всех интервалов пространства R, которые
либо все содержат точку хо как внутреннюю, либо все они имеют точку хо своим концом
только левым или только правым для всех интервалов множества В. Тогда VX € В А УУ €
в=> xnY &в, х ев az cx=> z ев.
Пусть Т = {/, g, h, ...} — семейство числовых функций, обладающих одним из следую-
следующих свойств: '
1) для произвольной функции / ? Т в множестве В существует содержащий точку хо
интервал X, на котором функция / определена, кроме, быть может, самой точки хо;
2) для произвольной функции / е Т в множестве В сущчсъъуех интервал, имеющий своим
концом точку хо, на котором / определена.
Определение 1. Если lim f(x) = 0, mo функция f называется бесконечно малой при
х—ха
х —+ хо/ если lim f(x) = со, то функция f называется бесконечно большой при ас -р* Jto-
х~х0
Определение 2. Если для функций f, g € Т, f : X —* К, у : Y —* R, существует
интервал Z С X П Y ? В, X ? В, Y ? В, и такое конечное число А > 0, что V» € Z,
креме, быгоь сможет, сал<ой точки го, выполняется неравенство
\д(х)\ < Л|/(г)|,
то записываем
9 = O(f)
при х —> хо. При этом функции fug называем функциями одного порядка при х —»¦ во-
Если Ve>0 3ZcXnYsB такое, что Vr G Z кроме, быть может, самой точки х<у,
выполняется неравенство
I*(*)| < е|/(г)|,
то записываем
9 = o(f)

68 Гл. 1. Введение в анализ
при х —* хо. При этом в случае д(х) —»• 0, f(x) —> 0 при х —+ io считаем, что функция д есть
бесконечно малая более высокого порядка, чем /; если же д(х) —> се, f(x) —> схэ при х —>¦ х0,
то считаем, что бесконечно большая функция д имеет порядок роста ниже, чем /.
Если существует интервал Z € В такой, что Vi G Z\{xo] f(x) ф 0, то запись д = О(/)
означает, что отношение ОЧ- ограничено при х G Z\{xo], а запись </ = о(/), что ^*^е —+ О
при I —¦ 1о-
Символы Оно называются символами Ландау,
Определение 3. Функции g и f называются эквивалентными, если f — g = o(g), т. е.
если Ve > 0 3Z G В такое, что Vr € Z\{xo] выполняется неравенство
\f(x)-g(x)\<e\g(x)\.
При этом записываем / ~ д, а равенство / = д + о (</) называем асимптотическим
равенством.
Пусть f, д?Т и д{х) > 0 Vz 6 Y G -В, тогда
lim
Справедливы асимптотические равенства
sinx = х + о(х), tgx = x + o(x) при х —> 0.
7.4. Частичные пределы.
Если для некоторой последовательности (х„) значений аргумента функции /, сходящейся
к хо, справедливо равенство lim f(xn) — А, то число А называется частичным пределом
п—*оо
функции / в точке Хо- Наибольший и наименьший частичные пределы обозначаем через
lim f(x) и lim f(x) и называем соответственно верхним и нижним пределами функции f в
хх х
х—ха
точке
Очевидно,
3 lim f(x) -& Urn f(x) = lim f(x).
x*x яя хХ
7.5. Предел функции комплексной переменной.
Определение 1. Последовательность N —»• С : п р—<¦ zn называется сходящейся, если
Эг 6 С Л Ve > 0 Зт ? N : V» > m =Н«„ - г| < е.
Аналогично последовательность комплексных чисел (zn) сходится к оо, если
VJV Эгп € N : Vn > т =*• \zn\ > N.
Последовательность (zn), где zn = rn + ij»n, сходится к точке 2 = а + ib тогда и только
тогда, когда
lim xn = a, lim yn — Ь.
Пусть zo — предельная точка множества D С С.
Определение 2 (Гейне). Функция г н-> /(г), z Q D, D С С, ил<еет предел при z —> zo,
если
ЗА € С Л V(zn) С !>\{zo} : lim гп = -z0 =>¦ Um /(г„) - А.
п—ьоо п—>оо
Определение 3 (Коши). Функция z t-> f(z) имеет предел при z —* го, если
ЗА eCAVe > 0 35 > 0:0 < \z - zo\ < 6 => \f(z)-A\ < е.
133.. Показать, что функция
т
п, если х = —, где тип — взаимно простые целые числа,
•''¦¦' ^0, если х — иррационально,
конечна, но не ограничена в каждой точке (т. е. не ограничена в любой окрестности этой
точки).
¦Щ Пусть х = - — произвольное рациональное число. Тогда г и = -^ * - при к —> оо,
т. е. попадает в любую окрестность точки х = -. А так как /(rfc) = kq —»• схэ при к —> оо, то
функция / не ограничена в любой окрестности точки х.

§ 7. Предел функции 69
Пусть, далее, х = а, где а — иррациональное. Тогда существует последовательность
рациональных чисел г,¦ = —, г € N, такая, что lim — = а. При этом lim (ft = +00. По-
Чг I—.ОО '• 1-.00
скольку / ( — I =</!—>¦ +оо при t —> 00, а точки последовательности ( ^ ) попадают в любую
окрестность точки а, то функция не ограничена. >
134. Если функция / определена и локально ограничена в каждой точке: а) интервала, б)
сегмента, то является ли эта функция ограниченной на данном интервале или соответственно
сегменте? Привести соответствующие примеры.
¦4 а) Вообще говоря, нет. Например, функция f(x) = - ограничена в окрестности любой
точки интервала ]0, 1[, но не является ограниченной на этом интервале, так как f{xn) —*¦ +00
при хп = ^ —> 0 , а 0 < х„ < 1 при п = 2, 3,
б) Функция ограничена. Для доказательства предположим противное: пусть функция
неограниченная. Тогда для любого натурального числа п существует хп € [а, Ь], где [а, 6] —
сегмент, указанный в условии задачи, такое, что
f(Xn) > П.
А так как а ^ х„ ^ Ь (т. е. (хп) — ограничена), то существует подпоследовательность
(хкп), (хкп) С {хп), такая, что
lim хкп = с € [о, Ь].
П—ЮО
По условию, / локально ограничена в окрестности любой точки, т. е. существуют такие Ь > О
и Е > 0, что
|/(z)|<?, xe]c-6, с+6[.
Кроме того, существует такое число N, что кп > Е при п > N и Хкп 6 ]с — 6, с + 6[, а тогда
f(xkn) > кп > Е. Полученное противоречие доказывает утверждение. >
135. Показать, что функция
ограничена в интервале ] — оо, +оо[.
¦4 Ясно, что f(x) > 0, т. е. функция ограничена снизу. Далее, из неравенства A — х2J >
Х2 , 1+х2 1 х2 13
О следует, что -ц^ ^ -, а поскольку 1 + х ^ 1, то -^7 = J+^т + jq~T ^ 1 + J = г-
Следовательно, 0 < f(x) ^ j, —00 < х < оо. >
136. Показать, что функция
fix) = — cos —
XX
не ограничена в любой окрестности точки х = 0, однако не является бесконечно большой при
х —* 0.
¦4 Пусть хп — —. Очевидно, при п —> оо значения хп попадают в любую окрестность
точки х = 0. Требуемое утверждение вытекает из того факта, что lim |/(i2n)| = 00 , а
п—.оо
f(x2n-l) = 0, « 6 N. >
137. Исследовать на ограниченность функцию
f(x) = In x ¦ sin2 —
в интервале ]0, е[. '
4 Так как 0 ^ sin2 - ^ 1, а функция х н-» In г; монотонно возрастающая, то f(x) ^
max{0, Ing}, т. е. / ограничена сверху.
Далее, положим хп = 2n+i • Тогда, начиная с некоторого номера «о> все хп попадают"
в интервал ]0, е[. При этом f(xn) = In -—^ = — In (l + A1 + j)) > — (n + |) -+ —00 при
n —*¦ 00, т. е. /не ограничена снизу. >
138. Показать, что функция /, где
'<•) = т

70
Гл. 1. Введение в анализ
в области 0 ^ х < оо имеет нижнюю грань т = 0 и верхнюю грань М = 1.
¦4 Очевидно, 0 ^ тт^1 0 ^ i < оо. Пусть е — произвольное и 0 < е < 1. Тогда
f{x) = т^ < ? при 0 < х < 727- Следовательно, inf {/(я)} = 0.
Далее, очевидно, j~^ < 1, 0^i<oo. С другой стороны, для указанного ранее е
1-е
/(*) =
> 1 — е при ж >
т. е. sup {/(г)} = 1. >
139. Функция / определена и монотонно возрастает на сегменте [а, 6]. Чему равны ее
точная нижняя и точная верхняя грани на этом сегменте?
А Так как / монотонно возрастает на [а, Ъ], то /(а) ^ f(x) ^ /(Ь) Vi G [а, Ь].
Пусть е > 0 — произвольное и такое, что /(а) + е < /(&). Тогда существует х' ? [а, Ь]
такое, что
f(a)^f(x')<f(a)+e
(например, х' = а), т. е. inf {/(ж)} = /(я)-
Аналогично, если f{b)~e < /F), то существует х" ? [а, Ь] такое, что f(b)—e < f{x") ^ /(Ь)
(например, г" = Ъ).
Следовательно, sup {/(i)} = f(J>). >
140. Определить колебание функции f(x) = х2, i 6 К, на интервалах: а) ]1; 3[;
б) ]1,9; 2,1[; в) ]1,99; 2,01[; г) ]1,999; 2,001[.
¦4 На каждом из указанных интервалов сужения заданной функции монотонно возрастают
и имеют на концах этих интервалов конечные предельные значения, в силу чего являются
ограниченными. Следовательно,
а) Мо - то = /C - 0) - /A + 0) = 9 - 1 = 8;
б) Мо - то = /B,1 - 0) - /A,9 + 0) = 4,41 - 3,61 = 0,8;
в) Мо - то = /B,01 - 0) - /A,99 + 0) = 4,0401 - 3,9601 = 0,08;
г) Мо - та = /B,001 - 0) - /A,999 + 0) = 4,004001 - 3,996001 = 0,008. >
141. Пусть m[f] и M[f] — соответственно нижняя и верхняя грани функции / на
промежутке ]а, Ъ[.
Доказать, что если /i и /2 — функции, определенные на ]а, Ъ[, то
a) m[fi + h] > m[h) + m[f2); 6) M[h + f2] ^ [f,] + M[f2].
А Докажем неравенство а) (неравенство б) доказывается аналогично). Обозначим mi =
inf {fi{x)}; 1П2 = iuf {fi{x)}. Тогда fi{x) ^ mi и /2A) > m.2, x 6 }a, b[. Складывая
a<x<6 a<3;<6
последние неравенства, получаем fi(x) + /2A) ^ "»i + «12, x ? ]a, b[, откуда m[fi ¦+ /2] ^
[/] []
ц+п2 m[/i] + m[/2]. >
142. Показать, что функция f(x) = sin -, x ? K\{0}, не имеет предела при х
Требуемое утверждение следует из того, что последовательность х„ = я.
.A+2я.)
0.
¦ п
при и —+ оо стремится к нулю, а f(xn) = ( — 1)" вовсе не имеет предела. >
143. С помощью "е — ^''-рассуждений доказать, что lini x2 = 4. Заполнить следующую
аг-.2
таблицу:
е
0,1
0,01
0,001
0,0001
¦4 Пусть г > 0 — произвольно. Тогда
|*2-4| = |(х--2J
как только 0 < \х — 2| < т/4 + е — 2 =
выполняться, если
>
> —
- 2|2 + 4|х - 2| ^ в,
. Последнее неравенство тем более будет
ТТ^ + 2 2^4 +? 2л/4 + 4е + е2 2B + е)

§ 7. Предел функции
Пусть е = jjjr. Тогда 6 (j^r) == 4,10„ ,2 и
.A0-) = JL; «A0-») = jL; *A0-») = jij; «A0-*) = -J-. >
144. На языке "?—5" доказать, что
& (х -
= +00.
Заполнить следующую таблицу;
Е
b
10
100
1000
10 000
Пусть Е > 0 — произвольно. Тогда
71
как только (х — IJ < -g или 0 < \х — 1| < --^ = 5 (?). Отсюда находим, что
^;
; «A0000) - ^.
145. Пусть Р(х) = аохп + air"" + ... + ап, где а; (г = 0, п)— действительные числа.
Доказать, что lim |.P(x)| = +оо.
X—*0О
Ч Не ограничивая общности, будем считать, что ао ф 0. При достаточно больших |ж|
ао + f- ... + —
г хп
|ао|
2
Так как Urn \х\п ¦ ^ = +оо, то Um \P(x)\ = +оо. >
146. Пусть
п-1+ ... +а„
где ао ф 0 и bo ф 0. Доказать, что
{со, если ге > т,
—, если п = т,
0, если » < т.
¦4 Пусть п > т. Тогда
+ ^+-.-+^
> х
Оо
при достаточно больших |i|. В силу того что lim |r|n
х—*оо
Если п = т, го
= со, имеем lim R(x) = оо..
a0
—- при x —* со.
bo
Наконец, если п < m, то при достаточно больших |г| имеем
<
2ao
~Ъо~
откуда следует, что lim R(x) = 0. >

72 Гл. 1. Введение в анализ
147. Пусть х —¦ 0. Доказать следующие равенства:
а) х sin \fx = i2-fo(i2J; б) \цх = о(х е), е > 0;
i
в) {1 + х)п = 1 + пх + о{х); г) arctgi =
М Записанные равенства следуют из того, что
. .. ЯБШл/х ,. ,. _?1 ,. — lnt 1
a) lim г*— = 1; б) um x In х — lim —-—= 0, t——;
X2
в) A + i)n = 1 + nx + C*z2 + ... + xn = 1 + hi + (<?2* + • • • + i")! =1 + nx.+ a(x)x,
где a(x) = Clx + ... + i" -¦ 0 при х -*-0;
r)|aictgi|<f. >
148. Пусть x —>¦ 0. Выделить главный член вида Схп (С — постоянная) и определить
порядки малости относительно переменной х следующих функций:
а) х\-* Bi-3i2+x5);
б) х i
н* (V1 + х - л/1 - z);
в) ih (\/l — 2x — ^1 — 3z); г) x h-> (tgx — sinx).
•* а) Из того что 2x - Зх2 + x5 = 2x + (-3x + x4)x = 2i + n(x)x, где a(x) -* 0 при х -* 0,
следует, что 2х - Зх2 + i5 = 2x + о (х), т. e. Cxn = 2x, « = 1.
б) Из равенства lim +x~~v ~x — \ следует, что Gx = x, « = 1, т. e. y/1 + x — \/l ~ ж ~ x•
i—O *
в) Поскольку
l~2x-(l-x) 1 - x - -У1 - Зх ^ _ 11
I—0
то Cx11 = jx2, n = 2.
г) Имеем Um ts*~3si"x = i поэтому C'x3 = V, « = 3. >
x—»0 x / ^
149. Пусть x —> +сю. Выделить главный член вида Схп и определить порядок роста
относительно бесконечно большой х следующих функций:
, з / .
а) х и* ух2 — х 4- л/^5 б) ж 1-+ у 1 + V 1 + л/ж-
¦< а) Поскольку
bill
= П
то
= хз, п= |.
б) Имеем v/l + \J\ + у/х = х» \/х~* + д/х + 1 ~ хв , поэтому С'х" = х» (п = |) . >
Решить примеры (при решении некоторых из них заменить бесконечно малые функции
эквивалентными им):
15U. a) lim i '—-^ '—; б) lim -; в) lim
' i—O X2 Х-.1 Хп - 1 'x-lVl-Xm 1-Х"/
(т, и — натуральные числа).
М а) Разлагая по формуле бинома Ньютона, получаем
х—О
= lim
i—о
2
б) Полагая x = l-ft(<—>0 при х —¦ 1) и пользуясь принципом отбрасывания бесконечно
малых,, находим
,. xm-l ,.
hm = lim
n 1
.. mt + o(t) ,. mt ro
= km ———f-+ = lim —- = —.
t +{t) t
m = lim ) —- = km ———f-+ = lim —
—1 Xn - 1 t-0 A + <)"-! t—0 «t +0{t) t—0 «t

§ 7. Предел функции 7$
в) Пусть х = 1 + t. Тогда t —> О при х —¦ 1. Имеем «
.. / га п \ _ / ?t
,—.1 V 1 — Тт 1 — Т« / t_n
= lim
t-o V,"* + Clt2 +o(t2) mt + C^t2 +o(t2)
= Hm (nCl-mC2n)t2+o(i2) = =
t—o mut2 -f q (<2} mn 2
151. hm -( x + - + x+— +...+ ж + i -^- •
n—oo « \\ П/ \ П / \ П J I
< Используя результаты примера 37, а), получаем
= lim - nx + —- ¦ ~^-—— + ^ ; v -^ I = x + ax + —. >
n—'oo 71 \ H 2 71 6 / 3
¦.со v
•* Имеем
I2 + 32 + ¦¦¦ 4- Bn - IJ
(см. пример 37, а)). Вычитая из второго равенства первое, получаем
I2 I З2 | ... | Bа IJ -
Тогда
I2 + З2 + ... + Bп - IJ _ пDп2 - 1) -
п^ 22 + 42 + ... + B«J "" п-^о 2п(п + 1)Bп + 1)
,. I3 + 43 + 73 + ... + (Зп - 2K
п^ A4-4 + 7+ ...+(Ы-2)У
¦^ Имеем (см. пример 37, б))
I3 + 43 + 73 + .., + (Зп - 2K = C • 1 - 2K + C • 2 - 2K + C • 3 - 2K + ... + (Зп - 2K =
= 27A3 +23+33+ ... +«3)-54A2 + 22+ ... +п2) + ЗбA+2+ ... + п) - 8п =
_ 54 Ч» + 1)Bп + 1) + 36 ¦&+? _ 8п;
Поскольку в числителе и знаменателе высшая степень п равна 4, то предел дроби равен
отношению коэффициентов при м4, т. е. 3. >
154. lim yfx.
¦4 Предполагая, что х0 > 0, положим х = хо + *. Ясно, что t —¦ 0 при х —> хо. Считая
|t| < Хо, имеем
жо 1 - — .
' " Хо
откуда lim ^/ж = lim \/xo + t = >Ухо^. >
1-10 '—0

74
Гл. 1. Введение в анализ
155. lim
1
¦< Разделив числитель и знаменатель на -y/*i получим
156. Um
4 Имеем
\J x + \/x
Um —
x—*-f oo
fx — y/a + y/x — a
= Um
X—*-f OO
= 1. >
lim
у/х — у/а у/х — а
+
2 2
= lim
1
i—о V^z2 — a2 (-y/i + л/а) y/x + a
= lim
Ix-a 1
¦ H—;=
157. lim
9 + 2х - 5
- 2
¦< Очевидно,
lim
- 5
= lim
= 2 lim
12
= —-. >
5
*-s уУх-2 x-.b (I_8)(V^4T2
Замечание. При решении примеров 155—157 использованы результаты примера 154.
1 ко ,. л/1 + х — 1 , .
lOo. Um (п — целое число).
х-~0 X
•< Положим iyi + х — 1 = t. Тогда х = A + i)n — 1. Считая, что |i| < 1, имеем 1
у/Г+"х < 1 + |х|, откуда lim у/\ + х = 1, т. е. t —>• 0 при х —¦ 0. А тогда
_J _ ?
" — 1 t—o n< -f o(t) n
= lim
Следовательно, у"/\ + х = 1 + ^ + о (i), x —¦ 0. >
/x +2 - лУх + 20
159. Um
Ух + 9 - 2
Имеем при х —> 7
+
= 3
^p = 3 (l + ^y^) + о (х - 7),
о (х - 7),
= 3
Таким образом,
Ш
27'
160. Um =

§ 7. Предел функции 75
•« Положим \/1 +5х = t. Ясно, что < -+ 0, если х -* 0. Тогда i = j((l + tM - 1) и
km
5х -
. lim =
= lim
= lim
= lim
+
(m и « —целые числа).
lim =
х—*Q
Пользуясь результатом примера 158, имеем
ТЩ У1 + ах - 1) + 71 + Рх - 1
= lim
x-0
v »/ГГ7 v
= lim \/\ + fix ¦ a lim
x—o x—o
1
~-2->
h p urn —!: -J- = —I .
ax x—o px n m .
162. Пусть jP(x) = aix + a,2X2 + ... + anxn и m — целое число. Доказать, что
Так как Р(х) —* 0 при х —¦ 0, то
Urn (ai
1*°
(см. пример 158). >
Найти пределы:
163. lim -^-——_ (т цп — целые числа).
х — 1 ух — 1
¦4 Положим х = A + t)mn. Тогда t -> 0 при 1-»1и
,. Vx"-1 ,. A
(см. пример 150, б)). >
164. Ц ^
.•С-.1 A-Х)"
Полагая 1 — х = t (t —¦ 0 при х —> 1), получаем
lim
= lim
t-»o
II I- J-
2 3 ¦"" n ~ »!
(воспользовались решением примера 158). >
Решить примеры (в примерах 165—168 избавляемся от радикалов в числителе и переходим
к выражениям с очевидными предельными значениями): '
165. lim х(\/х2 +2х - 2\Л2 + х + х).
2х(ч/х2 + 2х - х - 1)
=
hm х(\/хг+2х — 2\/х-* + х + х) = lim

76
= lim
x—*-|-
166. lim (
¦^ Прибавляя и вычитая г, получим
Гл. 1. Введение в анализ
-2
167. шп ( \/(х + ai)(x + а2) . . . {х + а„) - х).
X —»-f ОО
•* Положим ^ = <, тогда < —> +0 при х —у +оо и
(х -f ai)(x + а2) ... (х + а„) - х =
где P(t) = (ai +a2 + • • • 4-a,.)< + (aia2 +aia.3 + ¦ •• + an_ian)t2 + ... + a\a2 ¦¦¦ antn.
Используя результат примера 162, находим, что искомый предел равен
(х -
168. hm
i—+00 X"
-4 Имеем
.m Q - л/х^Т)" + (x + Vx^^T)" =
xn
lim
x->+00
= lim
1
4- lim
x—*-f 00
1--V =0 + 2" = 2". >
. 4-х2 4-х)" - (Vl 4-х2 -x)"
169. hm — (« — натуральное число).
¦^ Возводя в п-ю степень и приводя подобные члены, получаем
lim
i—о
х)" - {у/Т+1?- х)" ,.
' J — = li
= lim — nx
—0 x у
(\Л + я2)" 4-o(x)j =
Найти пределы:
i и-п .. sin mx
17U. lim — .
i—jr Sin ПХ
¦4 Положим x — n + t,t —>0. Тогда
.. sinmx .. sinfrnn + mt) ,. (—l)msinmt
hm = lim —Ц ' r^ = lim *-.—'- =
I-.» smni t—o sin(«7r 4- nt) t—o (—l)nsin«t
n t—o m< sin nt
171. lim
1 — COS X
i—o x-'
Пользуясь первым замечательным пределом, находим
1 -cosx ,. 2 sm у ,. 1
hm = hm ^-A- = hm -
x-*o 2
-о г^
x—0 X*
sinf\2
Таким образом, 1 — cos x = ^- 4- о (х2) при х —¦ 0. >

§ 7. Предел функции 77
172. lim ——.
.x—0 I
4 Из неравенства |1 — cosi| = 2sin2 |- < |x| вытекает, что
,. , tgi sin i 1
km cosi = 1, lim = km • = 1.
x—0 x—0 X x—0 X COSX
Таким образом, tg i = i 4- о (i) при i —¦ 0. >
i wo ,¦ sin5i— sin 3x
173. lim : .
x—0 Sin I
4 Пользуясь асимптотическим разложением, находим
,. sin5i— sin 3i ,. 5i — 3i + o(x)
km = lim . = 2. >
x—o sm i x—o x -f о (x)
1 ТЛ i- 1 + sin i — cos i
174. Urn : .
x—0 1 4- Sin pi — COS pi
¦^ Поскольку при i —> 0 имеем 1 — cosi = o(i), 1 — cospx = o(x), sinx = x + о (as),
sin pi = pi -f о (i), то
,. 14-sin i—cosi .. i 4- о (i) 1
lim = km -y^r = -. >
x—o 1 4- smpi — cos pi x—o pi 4- 0 (x) p
175. Доказать равенства:
a) lim sin 1 = sin a; 6) lim cos 1 = cos а; в) lim tg 1 = tg а, а ф —-—тг; n € Z.
X—.a
0
6)
а) Имеем
^ sin 1 — sin a\
Аналогично
0 ^ cos 1 -
— 2 sin
- cos a\ =
1 — a
2
: 2 sin
COS
I -
2
1 4" a
2
a .
^ 2 sin -
1 4- a __,
2 ~*
с
i
— a
2
\x — a|, lim sinx = sin a.
la; — a| и lim cos x = cos a.
L ?
lim sin x
в) lim^ tg x - '~°cosx = ~ = tg а, если cos а ф 0, т. е. если a ^ ^^т, n € Z. >
x—-a
Найти пределы:
i wo .. sin 1 — sin a
17b. km .
x—a X — a
¦^ Очевидно,
sin i-sin a ,. 2 sin ?^? cos ?|i sin ^p- x + a
lim = Inn =— = lim —^~ ¦ lim cos —-— = 1 • cos Л = cos a
^ lim cos
x—a I
i->o i - x—a
1
(здесь воспользовались тем, что cosi —* cosb при i —¦ Ь). >
177. km CteX~ctea.
x—a X—a
¦^ Пользуясь формулой разности котангенсов, находим
,. ctgi— ctga sin(a — 1) 1 ,- ( sin(a —1)\ 1 ,. 1 1
km —2 2_ = llm __v _L . — llln i L . _ . lim _ = - л
x—a x — a x—.a sin i • sin a x — a x—a V a — 1 у sm a x—a sin x sm a
a ф kw, k€ Ъ: >
-trro у cos (a -f 2i) — 2 cos (a -f 1) -f cos a
x—0 I2
< Выражение в числителе преобразуем в произведение, имеем
,. cos (а + 2х) - 2 cos (а + х) + cos а ,. 1 / „ . х . ( Зх\ . х . / х\\
km ^ ^ r-i—I—' = km -5- -2sin - sm a + — + 2sin -sin a + - )) =
x—0 X x—0 X^\ L \ & / I \ ill
A I X \
-• 2 sin - ¦ 2 sin - cos (a + x) I = - cos a. >
хг I I )

78
Гл. 1. Введение в анализ
j.m ctg (a + 2ж) - 2 ctg (а -f х) + ctg a
х—0 X2
Аналогично предыдущему
2s)-2ctg(a
^ J_ {a + 2l)_ctg(a+x))_(ctg(a + l)
х—0 X'
+ —
i—о х2 \sin(a + 2z)sin(a-f x) sin(a-f z)sina
_ У f 1 /втаЛ2
х—о ysin(a -f х) К х ) si
2cos(a
sin asin(a -f 2i)
а ф kir,
2 cos a
к € Z. >
180. lim
2 sin2 i + sin i — 1
I—1 2 sin2 i — 3 sin i + 1
6
¦< Разлагая числитель и знаменатель на множители, получаем
.. 2 sin2 х +sini — 1 ,. (sin i -f l)Bsini — 1) .. sin x + 1
liin —-r-2 —-: = hm f-. (; . -f = hm = -3.
x—? 2sm'i i - 3smi + 1 X^Z (smi - l)Bsini - 1) ^...isini-l
бб б
181. U
Um .
-' cos(x+f)
¦4 Разлагая числитель на множители, имеем
= lim
182. Um
cos (x + f)
sin (x - f)
cosicos
-sm (j - ij
= lim
= -24. >
После очевидных преобразований находим
x)tg(a-x)-tg2a = Um J_
x—о
x—ox2
i% a tg-'i
= hm
_ 2\ =
x—o x2
4 4 cos 2a
г a — 1) = tg a — 1 = :—. >
183. lim . .=—
x—o Vl + x sin x —
¦< Уничтожая иррациональность в знаменателе, получаем
„2
lim
= hm
соах) ,. л/1 + ^ sin x 4- л/cos ж
'- = lim -—= Л .
= Л
lim , , = hm Ц:
х—0 -у/1 + X sin X — д/cOS I *—0 1+ISlnl — COSI
Если х —»¦ 0, то 1 + isin х —> 1, а тогда (см. пример 144) VI + х sin * —¦ л/l = !• Аналогично
¦ 1 при х —>¦ 0. Далее, 1~^sx — | ('"^Г^ ) ~* J
при
0- Следовательно,
т/1 + i sin х + v/cos i 4
—i-а». ^— = з •
„2 ^^ т
¦юл ,¦
184. lim
sin х

§ 7. Предел функции
¦^ Вычтем и прибавим в числителе единицу, тогда
,. i/cos х — v^cos х (л/cos х — 1 1 — лУсов х \
hm г-5 = hm -—г-5 1 г^ =
*—о sin i i—o у sin x sm x J
= lim
( cos x — 1 1 — cos x 1 ^ _
\sin2 x(v/cos~x + 1) sin2 x 1 -f -J/cos x + v'cos2 x /
r—0 V Sin X(VCOS X
_ .. 1 — cosx ( x \2 ( 1 1
•¦2 Vsinx/ \ д/сБТх + l I -f ^/coFx + tycos2xj 2
hm
x-0 X^
12"
Здесь воспользовались тем, что д/cosx —¦ 1 при х —> 0, а это следует из примеров 175 и 154. >
185. Доказать, что
lim (sin y/x + 1 — sin \fx) = 0.
Действительно,
| sin \/х + 1 — sin
2 sin
sin
4-
< e при x > -L =
Докажем следующие утверждения:
A) lim ах = а1о,а>0; Б) lim In i = In юI
&—*Xo x—*xo
B) lim (m(i))v(i) = аь при условии, что V« > 0 3 6 > 0 : 0 < \х -хо\ < 6 =» @ < |u(r)-o| <
е) Л @ < |«°(ж) - Ь| <е).
Ч А) Достаточно рассмотреть случай а > 1. Имеем
I _i
Поскольку lim an = Hm a n = 1, то для произвольного е > 0 существует такое по, что
n—юо п—*о
ax°
<a "o
Тогда при 11 — io| < — имеем
Б) Имеем
1 < a "o < a* x° < a "" < 1 -\ ,
ax0 ax°
e при |x-xo|< ±.
при n > 1. Таким образом, при п > 1
n / \ n/ n
Пусть e > 0 — произвольное число, не превосходящее j- Тогда существует такое По, что
Если взять
-е < In (l - —) < In (l + —) < e.
\ no/ \ no/
L < XXQ 1_
По Xo «0

80 Гл. 1. Введение в анализ
то для разности In х — In хо = In I I -f x~^° J получим следующую оценку:
(j _ ±Л < ь Л + ?
\ по / V
_? < 1п (j _ ±Л < ь Л + ?и?!>) < Ь Л + J_
Ю / V «о
или |In x — In io| < e, если только \х — xo\ < xo?-
В) Согласно условию и пункту Б),
u(i)lnM(i) —> Ып а при х —у хо-
Тогда, на основании А), имеем
lim (и(х)) v ' = lim е у ' *- ' = е = а = lim и(х) 1
Х—Х0 1—10 \*^*0 J
Найти пределы:
186. Urn fiL±
¦^ Согласно утверждениям А)—В), имеем
.. / 1 + 2 у2 f 2 i + 2|
lim = lim exp < x In > .
Поскольку In *J\ i < О ПРИ достаточно больших x, a lim x2 = +oo, то искомый предел ра-
равен 0. >
Замечание. Решение примеров 187—192, 200, 201, 208, 209, 210 основано на простом примере
раскрытия неопределенности 1°°.
Пусть lim и(х) = 1, lim v(x) = оо. Тогда, на основании утверждения В), получаем
lini и" = lim A + (и - 1)) «-1 = exp
х х
>< lim (и — l)v > .
^х-*х0 J
187.
I2 — 2
¦^ В нашем случае м = ^2^; и = ж2; (и — 1)и = J5~~j- Следовательно,
.. Z^ + iV2 /,. зх2 \ з
Inn — = exp < Inn ——- } = е . >
х-оо ^I2 - 2у (_х^оо I2 - 2 J
1 ОО !• /1 2\ctg2x
loo. lim(l + х ) 6 .
¦^ Аналогично предыдущему
lim(l + х2H4'* - exp (lim г2ctg2г) - exp \ lim ( — ) > = е. >
.т-о U^o J ^х-,0 \tgxj J
189. Uin(l+sinxx)ctglri.
.т-»1
¦^ Очевидно,
lim A + sin nx)ctg "^ = exp ¦< lim sin тгх ctg жх > = exp < lim cos tti > = e".
190. lin , 1 .
x—0 \ 1 -f Sin I

§ 7. Предел функции 81
Имеем
.. /1 + tgiNiuT^ f,. tgx-sinx 1 1 (..
km , . = ехр < hm -^ : - } = ехр < hm
*—o\l + sinx/ U^o 1 + sinx sinxj [i^o
2sin2f \ 0
г > = еи = 1. >
191. Hm
Hm ().
я—О \ 1 + Sin X )
•Ц На основании примечания о раскрытии неопределенности вида 1°°, при вычислении
предела показательно-степенного выражения и" имеем
1 + sin x sm x
Поскольку при z —> 0 tg х — sin х = tg i A — cos я) ~ у-, 1 + sin x ~ 1, sin x ~ x , то
?!. j
lim (m — l)v = lim -\ = -.
Таким образом,
Цщ( ре^, >
x—o \ 1 + sm i /
192. lim (sm-4-cosiI.
-Ц Поскольку sin i + cos ^ = ~ + 1 + ° (~) пРи i-»oo, lim (sin ~ + cos 1) = 1, то
193. U
.t—0 X
На основании утверждения В), имеем
lim 'ПA+Х) = limlnf(l+x)-) =lne = l.
Таким образом, ln(l + x) = x + о (х) при х —> 0. >
194. lim
*" + <x>ln(x10+X + l)'
< Вынося за скобки в числителе и знаменателе старшие степени х и пользуясь утвержде-
утверждением Б), находим
1п(х2-х + 1)
hm . . .„ ~ — lim
х-- + оо 1п(х1у + X + 1) I-.+OC
195. lim — г^ —, х > 0.
< На основании свойств логарифмов и утверждения Б), получим
= lim —- lg II 5" ) =
л—о К2 \ х2 I
,пй ,. In cos ах
196. hm —.
х—О In COS OX

82 Гл. 1. Введение в анализ
¦4 Пользуясь асимптотическими равенствами (см. примеры 178 и 193), получаем
,. lncosa* ,. l(^)) Ц+ „(,)
lim :— = Inn —-. г- = шп —~^-z = lim -тт—- = -pr.
x-olncosbx —оьЛ ь^. + о^2Л ^о_ь^, + 0(х2) ^ol!t2 b2
(Iх — 1 A 4- ж)** — 1
197. a) lim , a > 0; 6) lim (ц — действительное).
ж—О X х-> О Ж V
¦* а) Пусть а* — 1 = t. Тогда t —> 0 при s —»¦ 0, поэтому
,. а1 — 1 ,. tin a ,. In a .
lim = lim —; = lim —; г-гт" = In a-
*-о х t~oln(l+t) t^oln(l+tI/t
Таким образом, ах = 1 + ж In a -f о (г) при г —»¦ 0 {ех = 1 + х + о (г)).
б) Очевидно, lim A+'r)" = lim е"'°(.1^)-1 иМ1±й = „ так как мьA + в) - 0 при
I —> 0, lim .—г = 1, lim ' = 1 (на основании утверждения Б); примеров 197, а) и
193). Таким образом, A + хI* = 1 + цх + о (х) при as —>¦ 0. >
ino 1- 1 — cos''s , „
1Уо. шп (и — действительное).
ас-.О X2 '
Л Используя результат предыдущего примера, получаем
.. 1 — cosM т. _ . A + (cos х — I))** — 1 1 — cos x _ ц
x—.0 X2 x—.0 COS X — 1 X2 2
inn л ,. e*' -(cosi)^ e4 ,. a1-!" „ . ,. eax* cos2a s - 1
199. a) hm Ц ^—; 6) hm , a > 0; в) hm ъ , a^0,
< а) Имеем
e1" -(cosx)^ __ exl_-J_ l-(cosa)^
x'- "" "¦"¦ xs" + i2
На основании примеров 197, а) и 198 находим, что искомый предел равен 1 + ~.
б) После очевидных преобразований получим
a*-.* ea—-I „-.(l + ^r-l
х — а
Предел первого слагаемого (см. пример 197, а)) равен аа1па. Предел второго слагаемого
(см. пример 197, б)) равен аа. Следовательно,
,. а — х а, а а, а
lim = а шо-о = a In -.
х—а х — а е
в) Имеем
, еа*2 cos2" ж - 1 _ (еа*2 - 1) cos2a ж+cos2a г - 1 еах* - 1 2а 1 - cos2a x
ах*
¦ a cos х —
Поскольку lim 5—rvcos2ax = a, lim ' с°^—- = а, то предел всего выражения равен
х—0 аг х—>0 х
нулю. >
200. lim Ж*~а", а > 0.
X — а X — а
< Представим функцию: х_а = <р(г) в виде суммы двух слагаемых: (р(х) — х_а—Ь
х_а = (pi(x) + <p2{x). Очевидно,
Vi(s) - ^~ Ti "lns-
(х — a) In х

§ 7. Предел функции 83
Так как при х -+ а еа1пж —» а°, е /х_а\1п~1 —> 1, In х —> In а, то lim <pi(x) = a°lna. Далее,
. n *-»« -——
a
Окончательно получаем lim *д_° = аа In а + аа = аа 1п(ае). >
лщ ,. (I +sin ж cos as \
ZU1. lim ; —
i—о у I + sin s cos px )
4 Ищем предел показательно-степенного выражения «"; имеем (при х —> 0)
. _ cos as — cos fix cos3 s _
I + sin s cos fix sin2 s
Следовательно,
nnn ,. ' Si
1 l
i—i sinir((x'3 — 1) + 1) »-*i sinir(x'3 — 1) ~ *-»i яр(х'3 — 1)
_ A + t)a -1
(здесь воспользовались результатом решения примера 197, б)). >
ог»«» .• 2B1)
203. lim
*-i In(cos(?r2x))'
4 Полагая sin2(ir2*) = t, получаем
,. sin2Gr2x) .. t ,. t
lim r—;—Ц —¦ = lim -, = lim —; = —2
x-*i ln(cos (¦k2x)) t-*o-ln(l — t) t—o—-+ o(t)
(здесь воспользовались формулой ln(l —<) = —< + о (<)). >
204. lim Ж° ~ °° , a > 0.
•< Полагая s — a = t и пользуясь результатом примера 197, б), получаем
1)'3_1 t-0 /? • 1 + о (t)
205. lim —— , a >0.
h—0 Л2
¦< Используя результат примера 197, а), находим
— X-\-h I x~-h о»»-
ЛГУ/* -i. I1*' ~T ">) I* ~T "/
ZUD. lim ^-; ' ,\„ , ',.
x_h/a-l\ , 3
= lim a —; = a In a. >

84 Гл. 1. Введение в анализ
4 Используя второй замечательный предел, после очевидных преобразований находим
(х + а)х+а{х+Ъ)х+ь (( Ъ
207. lim n2(y/x- n+y/x), x > 0.
n—оо
M Имеем (см. 197, а))
= е-а~ь. >
п—юо п—оо —к П + И
208. lim f^+^V, a>0, i>0.
¦^ Аналогично предыдущему примеру имеем
= exp <^ lim -*— 1 In S =
г 1 j I r = e = vab.
- - /J
bm
n-oc V 2
(l ,.
= exp { - lim
l2
¦ С.
\
'а+Ь+
1
, а > О, Ь > 0, с > 0.
Обозначим /(ж) = +'' +с . Очевидно, /(ж) -* 1 при х —> 0. Тогда
,. (а+ +Ь+ +с+ \* Г,. /(х) - 1
lim ( = exp < lim —^
i-o V а + Ь + с / I х-о х
Поскольку
ж—о х а + 6 + с 1—о V ж х х I
_ а In а + ЫпЬ + с In с
= а+Ь+с
1
то искомый предел равен (а°Ь сс)а+ь+с. >
1
210. lim (аХ +Ь* ) Х , а > О, Ь > 0.
*-о \ а1 + Ьх J '
/а^+Ь\ Г /(х) - 1
lmi ;— = exp < lim —^
¦4 Имеем
где /(ж) — " ."У.. -+ 1, так как lim а1 = 1, limb* = 1, lim ax — 1, lim Iх = 1 (см.
а +6 1—0 1-0 1-0 х-О
утверждение А)). Поскольку
/(я) - 1 а*" + Ь*2 - а- - Ь*
bm t^—L = llln : : =
1—0 x
= hm — 5—x H 3—s = - - (ln a + In b),
я-о a^ + bx \ x2 x2 x x J 2
-i(lna+ln Ь)
то искомый предел равен е 2

§ 7. Предел функции 85
211. lim i—~^, а > 0, * > О.
х—о (ах — Ьху
<4 Поскольку (см. пример 197, а)) а*2-**2 = х2 In f + o(i2), (аж-ЬхJ = (iln f + o(x)J =
s2ln2f+ о(х2),то
x2lnf + 0(x2) x2lnf / «x-i
= Ь *2 ln2 | + 0 (s2) = bm ^^ = (In -J .
Ьо (a- - | ^
212. lim ln(l +2*)lii Cl + -V
.T— + OO V Xj
¦4 Воспользовавшись асимптотическим равенством примера 193, находим
lim ln(l+2*)ln (l + -) = lim (sln2 +ln(l + 2~*))m ( +
= lim (x\n2 + 2~x + oB'x))(- + o(-)) =3b2=ln8.
213. Доказать, что
к
¦4 Поскольку lim -^ = 0, а > 1 (см. пример 70), то одновременно будет и
xk
lim — =0, a > 1. A > 0.
Следовательно, по заданному е > 0 найдется такое натуральное число N, что при n > N
выполняется неравенство
Пусть s > JV + 1; положим п = [х] (целая часть х). Тогда п> N и n^i<n + l, так что
ах ап
Это и доказывает наше утверждение. >
214. Доказать, что
lim ° =0, а > 1, ? > 0.
¦4 Положим хе = t. Тогда
? t—н
В силу равенства (см. пример 74) lim °ga" = 0, имеем
п
Вш = 0
n-*oo ?J /V
Пусть ?] > 0 — произвольное. Тогда существует такое натуральное число N, что при п > N,
i
п
Для t > iV + 1 положим п = [<]. Тогда п > N ип^Кв + 1, так что
г п
т. е. lim ~~- — 0, а тем самым и lim °^° * = 0. >

86 Гл. 1. Введение в анализ
Решить примеры (при решении примеров 215, 216 используются формулы
ех-е~х , ех + е~х shs
sh s = : ch x = ; tn x = ——,
2 2 chs
а также формулы гиперболической тригонометрии):
о, к sll а: chz-1 ths
Zxo. a) km ——; б) hm ; в) hm .
х^О X i—O Хг х-+0 X
¦4 а) На основании примера 197, а), имеем
km = km = km e • = 1.
x^O X x-+0 2x x-~0 2s
Отсюда sh s = s + о (s) при s —> 0.
б) На основании а), находим
, chs-1 ,. 2sh2f 1
km т.— = km — = km —
x-*0 Xz x-~0 Xz i—0 2
Таким образом, chs = l + ^ + o (s2) при s —•¦ 0.
в) Используя результат решения а) и утверждение А), получаем
..ths ,. sh s 1
km = km • —— = 1. >
x->o x x-*o x ch s
216. km f.2*
i—о In(ch3s)
¦4 Используя результаты решения примера 215, имеем
,. sh2s .. {x + o{x)f .. (i + o(s)J s2 2
km ¦-. = km —j-*—§—^—u r- = km -f x " = km ¦§ = -. >
\2 *¦'/ 2 ^ ^ 2
Доказать следующие равенства:
21 Т. lim arctg s = arctg So.
< Пусть so > 0 и s > 0. Положим arctgs — arctgs0 = t. Тогда для произвольного е > 0
имеем
|arctgs-arctgso| = |<| ^ |tgt|= ^ *° <|s-so|<?,
как только |s —so| < 5 (s) = e. Таким образом, соотношение доказано для So > 0. Если so < 0,
то доказательство сводится к уже рассмотренному случаю, поскольку arctg ( —s) = —arctgs.
Справедливость требуемого соотношения при So = 0 вытекает из очевидного неравенства
0 ^ |arctg х — arctg 0| = |arctg s| < |s|. >
218. km arcctg s = arcctg so.
¦4 Пользуясь тождеством arctgs + arcctgs = j, справедливым при всех значениях s,
получаем
km arcctg s= lim ( arctgs I = —— arctg so = arcctg so- >
x-+xo x^x0 \2 /2
219. lim arcsin x = arcsin so, —1 ^ so ^ 1.
< Заметим, что если 0 ^ s < 1, то arcsin s = arctg . x , а если 0 < s ^ 1, то arcsin s =
arcctg ' д x . Поэтому для so ? ]0, l[ имеем
..... s s0
km arcsm s = km arctg : = arctg —. = arcsin so.
В точке io = 1 имеем (см. пример 218)
lim arcsin x — lim arcctg = arcctg 0 = — = arcsin 1.
.-c—>! —0 x—> 1— 0 X 2

§ 7. Предел функции 87
Случай —1 ^ so < 0 сводится к уже рассмотренному, так как arcsin(—х) = —arcsina;. А по-
поскольку для точки so = 0 левое и правое предельные значения равны нулю, то доказательство
завершено. >
220. lim arccosx = arccosso, — 1 Sj So ^ 1.
¦4 Поступая аналогично предыдущему примеру и используя тождество
arcsm s + arccos s = —,
получаем требуемое соотношение. >
221. a) lim arctga; = —; б) lim arctg s = — —;
X —<-+OO 2 X—.— OO 2
в) lim arcctg ж = 0; r) lim arcctg i = тт.
X —t-+0O X~* — OO
¦4 а) Пусть e > 0 — произвольное. Тогда из неравенства х > tg (| — е) = Е(е) вытекает,
что arctg s > j — е, т. е.
О < - - arctg х < е Уж > Е{е).
б) Имеем lim arctg x = — lim arctg i = — ?.
X—* — OO X—»-(-OO
в) Используя то, что arcctgs = — — arctgi, получаем
lim arcctg i = lim I arctg x) = =0.
X—+OO X—+OO \2 /22
г) Аналогично
,. ,. (ж \ v ( ir\
lim arcctg x = bm — - arctg z) = — --— ]=ff. >
ж—-oo x->-oo \2 / 2 V 2/
Найти пределы:
ooo arcsinai
ZZZ. lim , aiO.
x—0 S
•4 Поскольку Urn arcsin s = 0 и Urn ^HL? _ цт . F«ini = 1, To
,. arcsinai ,. arcsinai
lim = bm ¦ a = a. > ^
x->0 s x->o ai l,i _
223. lim^te a^O.
x-*0 I
¦4 Из того, что lim arctg i = 0, следует, что
я—0
,. arctg as ,. arctg as
lim 2— = lim —-— • a = a. >
x-+o x x->o tg (arctg as)
224. lim t( + ft)t
¦4 Поскольку lim (arctg (s + h) — arctg s) = 0, то
h—*0
lim arCtg (x + h)- arctSx _ i;m tg (arctg (г+ /t)-arctg s) _ x + h-x
П, I H, I ~Йо ^(l + i^ + fe
225. a) lim ri 6) lim
' a;0 I ' I—+0
ri ) r-.
a; 0 I ' I—+0 I
1 + ex 1 + ex
l
¦< а) Если s —+ —0* то > —oo , a e* —+ 0, поэтому lim т- = !•
x—-о1+eS
б) Если же s —* +0, то > +oo и т- —> 0, т. е. искомый предел равен 0. >
1+е*
226. lim sinGTY n2 + 1).

88 Гя. 1. Введение в анализ
М Записав последовательность уп — sin^Vn2 + 1) в виде уп = sm{z(y/n2 + 1 — и + п)),
получим
Urn sin(ir\/n2 + 1) = lim sin ((к\/п2 + 1 — тгн) + тгп ) =
п—юо п—юс V /
= lim (-1)" sin (t(\Jn2 +1- n)) = lim (-1)" sin * . = 0. >
n—t-oo \ / n-*oo V?l^ —(— 1 —|— Tl.
227. lim sin2Gr\/7t2 + n).
4 Аналогично примеру 226 имеем
lim sin2Gr\/n2 + n) = lim sin2 ((тг\/п2 + n — nz) + nz) —
n-*oo n—t-oo \ /
= lim sin2 I ?r(\Jn2 + n — n) I = lim sin2 —, = 1. >
n-*oo \ / n—юо
228. Если lim tp(x) = А и lim V'C*) = 5, то следует ли отсюда, что lim ф((р(х)) = В?
я—*а X—*А X-+CL
Рассмотреть пример: <р(х) = - при х = -, где р к q — взаимно простые числа и i^(i) = 0
Я Я
при х иррациональном; ф(х) = 1 при х ф 0 и ^>(х) = 0 при s = 0, причем х —>• 0.
¦< Из условия примера следует, что для произвольного е > 0 существует такое <г = <г(е) >
0, что
№(«)-л|<в) A)
как только
Q<\u-A\<a, B)
т. е. неравенство A) выполняется для всех значений м из и-окрестности точки А, исключая
саму точку А.
Далее, согласно условию задачи, для произвольного <т > 0, в том числе и для а из нера-
неравенства B), существует такое 6\{(т(е)) = S (е) > 0, что для всех х, удовлетворяющих условию
0< \х-а\<6(с), C)
функция и = <р(ж) удовлетворяет неравенству
\V{x) -А\<<т, D)
причем, не исключается случай, когда <р{х) — А.
Но при и = <р(ж) = А функция ф(и) = ф{<р(х)) может быть вовсе не определена или же
определена, но ее значение ф(А) ф lim ф(и). В обоих случаях неравенство C) не обеспечи-
и-*А
вает выполнение неравенства A). Для того чтобы из условий lim <р{х) = A, lim ф(х) = В
х-*а х—*Л
вытекало равенство lim ф((р(х)) = В, достаточно, чтобы <р(х) ф А при х ф а. В предложен-
ном примере это условие не выполняется. >
229. Пусть для всех х € ]хо, жо + 1], где Хо — фиксировано, выполнены условия:
1) Рпк{х) > 0, к =17^; 2) ^Pnfc(s) = 1;
k = l
3) lim Pnk(x) = 0 при каждом фиксированном к; 4) lim ип(х) = /.
п—*оо п—*оо
п
Доказать, что lim tn = 1, где tn = )^Pnk(x) иь(х).
п—юо
к=1
4 Пусть е > 0 — произвольное. Из условия 4) следует существование такого числа N =
N(e, х) > 0, что \и„{х) — /| < | для всех п > N. Из этого же условия следует существование
такого числа М > 0, что
\ип(х)\^М, \un(x)-l\^2M Vn€N.
Из условия 3) вытекает существование такого числа но = но (г, х) > N, что
< тггтр, к = T7TV, Vn > по.

jj 7. Предел функции 89
Из этих неравенств и условий 1), 2) следует неравенство
*=1
-J|+ ... + PnN(x)\uN(x) - l\
PnN+l\uN+l(x) -l\+ ... + Pnn(x)\un{x) ~ l\ «
+ UPnN+l(x) + ... + Pnn(l)) <|+|=« Vf» > ПО.
Следовательно, lim tn — I. >
п—<-оо
230. Доказать теоремы Коши: если функция f :]а, +оо[—+ R ограничена в каждом ко-
конечном интервале ]а, Ь[, то
a) lim ^= lim (/(* + 1) - /(z)); б) lim (/(z))= = lim ^'Д^, /(z) > с > О,
предполагая, что пределы в правых частях равенств существуют.
в) Доказать, что если lim (/(ж + 1) — /(я)) = +°° и / огракичека снизу на каждом
кокечкси интервале ]а, Ь[, то
¦< а) Для доказательства воспользуемся примером 229, полагая при этом, что
Рт(х) = ^—, Рпк(х)=—¦—, к = 2^п, 0<хо<1^ю + 1, хо
Ml(s)=ZiL±i)> Un{x)=-f(z + n)-f(x + n-l), n = 2, 3, ....
Тогда in = Y2 Р"к(х)ик(х) = V~ . Все условия теоремы выполнены, поэтому
fc=i
а,
lim tn = lim ^^ + "^ = lim (/(s + n) -f(x + n- 1)) = /.
Поскольку / не зависит от х, то из последнего равенства следует, что
lim 1^1= lim
б) Поскольку f(x) ^ с > 0, то определена функция F(x) — In f(x). Пусть lim v . ' = /.
Тогда, пользуясь теоремой пункта а) и возможностью предельного перехода в показателе
степени, получаем требуемое
Um (/(s))i = hm exp < —-^-^ } = exp < lim
+ ^^ " + 1 S J \H
= exp( lim (b/(z + l)-In/(*))}= lim
(_! —4OO J X—+ OO
в) Для произвольного Е > 0 существует такое число го > 0, что при х > хо
f(x + 1) - /(г) > IE.
Отсюда следует, что f(x + п) — /(г) > 2пЕ и
/(а + п) ^ /(а) + 2пД?
X + II X + П
Поскольку /(ж) ^ о > 0 при so < х ^ So + 1, то существует такое число но, что
X + И

90 Гл. 1. Введение в анализ
при Vn > По, т. е. если t = х + п, х0 < х ^ so + 1, п > «о, то
что эквивалентно требуемому утверждению. >
231. Найти пределы:
а) lim (Ins)*; б) lim I-)* .
' Ж-. + 00 ' я—+00 \X)
¦4 а) Воспользуемся результатом примера 230, б), находим
1 ln(s + l) lns + ln(l + M / ln(l + i)\
lim (Ins)* = lim \ + ' = lim r-i si. = Mm 1 + —i si - i.
б) Аналогично а) получаем
Um f-V = lim *±! = i. >
X
232. Доказать, что если: 1) функция / определена в области х > а; 2) ограничена в
каждой области а < х < Ь; 3) существует предел
конечный или бесконечный, то
lim
т+1
х+оох
¦4 Пусть / — конечное. Тогда из условия следует, что
lim /(s + ")-/(s + "-l)
n-оо (х + п)т+1 - (х + п - 1)т+1
Воспользуемся примером 229, полагая
к = 2, n, 0<so<x^so + l, so > a,
получим tn = У "L . Все условия примера 229 выполняются, поэтому
lim *„ = lim
lim /
«-*«, (s + ra)
не зав
а поскольку предел —— не зависит от ж, то последнее равенство эквивалентно тому, что
^11^^- = ^-^.
Пусть / = +оо. Тогда из условия 3) следует, что
(s + п)"^ -(* + »-1Г+1 _ 0
n->oo f(x + П) - f(X + 11-1)
а поскольку последовательность
((s + nr+1-(s + n-ir+1)~=i,
монотонно возрастая, стремится к +оо, то таким свойством обладает и последовательность

§ 7. Предел функции 9Ц
Положив
/(s + n) /(ж + п)
к = 2, п, 0<so<s^so + l, so > a,
, (s + l)m+1 (s + n)m+1 - (s + n - l)m+1
gl(l) = W' "^ /(, + „)-/(« + »,-!) ' П = 2'3
и воспользовавшись примером 229, получим
" (s + n)m+1
<n = У j Pnk(x) uk(x) — K >• 0 при n -* oo,
откуда и следует требуемое утверждение. >
233. Доказать, что lim nsinBiren!) = 2ir.
¦4 Имеем (см. пример 80)е = 1 + 1 + ^+...+^ + -^, 0 < вп < 1, причем
. f , п+i \ , n+i ,
= п • п! ( — + -7- — = Н -, 2:ттг —> 1 при п —* оо,
\(n + l)! (n + l)(n + l)\J n + 1 (n + 1J v '
Пользуясь этим, получаем
lim n sinB7ren!) = lim «sin ( 2тгп! уп -\ -1 = lim nsin -= lim —^———¦'1'к%п = 2я\ >
п
Построить графики функций:
234. у = lim у/1 +х", х > 0.
п—*оо
< Если 0 < х ^ 1, то 0 < у/\ + яп ^ л/2, и так как lim л/2 = 1, то lim ^l -f xn = 1.
П—ЮО П—*ОО
Если же 1 < х < +оо, то ^/1 + х" = s ^*/^г +1 и Г/-^-
при п -с оо, поэтому '
lim л/1 + xn = x.
П-+ОО
,, Г 1, если 0 < s < 1,
Следовательно у = < i ^ ^ ,
и 1 х, если 1 < s < +оо.
Построить график предлагаем читателю. >
235. у = Хт^ r/l + s" + Г у J , s ^ 0.
Имеем
если
/s2\" // 1 \ " / Х\" п/-
— =s{/(- +х +1<х\/3, если1<8<2;
\ Lt j у \ Ж / V Z /
А так как lim л/3 = 1, то окончательно имеем
1, если 0 ^ s sj 1,
s, если 1 < х < 2,
я2
—, если 2 ^ s < +оо.

92 Гл. 1. Введение в анализ
Построить график предлагаем читателю. >
236. Построить кривую
Um vlxl" + \у\п ~ *•
< Поскольку 0 < mJ*(Liti | \п\ ^ 2, если |х| ^ 1, \у\ ^ 1, \х\ + \у\ ф 0, то
max(|x|n, \y\n)
(см. пример 73), и, следовательно,
lim ^FT№=nlinwnaX(|x|, Ы)
т. е. тах(|х|, |у|) = 1 и графиком служит контур квадрата с вершинами в точках (±1, ±1).
Это следует из того, что точки А(±1, \у\), \у\ ^ 1, В(\х\, ±1), |х| < 1, принадлежат графи-
графику. >
Найти следующие пределы:
237. lim (A+х)A+х2)A+х4) ... A + х2п)),если |х|<1.
п-*оо
4 Умножив и разделив выражение, находящееся под знаком предела, на 1 — х, получим
Шп (A + х)A + х2)A + х4) ... A + х2")) =
П> ОО
= Um
= um Um .
п—оо 1-Х п->« 1-Х 1—1
238. lim I cos — cos — ... cos — I , i ф 0.
n-»oo \ 2 4 2" /
4 Умножив и разделив на 2П sin ф? выражение, предел которого ищем, найдем
.. / X X X \
lim cos — cos — ... cos — 1 = hm
n-oo V 2 4 2n/ n-oo
;f ¦¦¦CoSi^r-2"-1sin^r_
2" sin ^
smi .. smi ^ smi
= hm -—:—— = lim . a = . >
n^oo 2" Sin — n—oo X SU1- X
239. Пусть lim ) ' = 1, где ф(х) > 0 и атп =$0, m G N, при п-*оо,т. e. |amn| < с
x— 0 ф(Х)
при тп € N и п > N(e).
Доказать, что
lim (v?(«in) + v(«2n) + ¦ • • + v(ann)) - lim (V"(«in) + ^(«2п) + • • • + Ф(апп)), A)
noo
(
n—*oo
предполагая, что предел в правой части равенства A) существует.
4 Поскольку lim ^Ц = 1 и с*т„ =4 0, то Ve > 0 3N = iVfe) такое, что V?i > iV
х0 ^'vx/
откуда, в силу условия ф(х) > 0, имеем
< a + ?
ln) + Ф{<*2п) + • • • + Ф(ППП)
Исходя из этого неравенства, а также из условия существования предела в правой части
равенства A), заключаем, что предел числителя существует и равен пределу знаменателя. >
Используя равенство A) предыдущего примера, найти следующие пределы:
240. Um fV

§ 7. Предел функции 93
¦4 Поскольку lim — г = 1 (см. пример 158), а -у =t 0 при п —*¦ оо, то
п—*оо _2_ п
Зп2
* Л г V^ * ! r »(» + !) 1
-г- - 1 = hm У —? = - hm -*—z—*• = -. >
/ п—си ^—' ЗП2 6 п—оо П2 6
п—си
—? = - hm z= -.
ЗП2 6 п—оо П2 6
241. Urn
„_оо
к=1
. ка
¦^ Здесь lim —j^p— = 1 и -f =t 0 при п —*¦ оо, поэтому имеем
п п
lim у sin -г = hm У -г- = lim —ij—j—^ = -. >
„_оо I—* II2 п—оо ^--' П2 п-оо 2П2 2
fc=l k=l
к
/ \
242. EmV а?-1 , а>1.
¦4 Имеем lim. —т = 1 (см. пример 197, а)) и -^ =$ 0 при п —> оо. Таким образом,
"—оо -о In a n
п2
т
.. \^ ( -т ,\ ,. v^^'lna 1 г n(n + l) I
km > a n= _ i = hm > ——- = In a hm \ , > = - In a. >
^^ \ / n—оо ^^ П2 n—oo 2П2 2
k=l
243. hm ТТ A + АЛ .
¦4 Имеем
" I n
Um П f1 + -t) = exp < i™ Vin (i + -V
„_ooll\ П2/ r|^^ V П2
V П2
in (i + 4) к
Поскольку lim г = 1 и -у =t 0 при п —*¦ оо, то
п —оо — "
п2
"°° 2
П
244. lim
¦4 Легко убедиться, что
hm —-—-=-=—— = 1 и —5- =$ 0 при п —> оо.
п—оо *¦ ° 2?»3
2пЗ
Поэтому
A;a I .. г—v ка
—= = exp < lim > I
,. т-т A;a I .. г—v ка I
lim I I cos —= = exp < lim > In cos —= > —
n-.oo ¦*•¦»• Ilijil I n-«oo *—' 11^11 I
,. Afc2a0 f ,. n(n + l)Bn + l)a2l -^
- hm > —- > = exp < - hm -^ —^ r—^— > = e 6 .
n-oo ^ 2П3 Г I n-co 2 • 6 ¦ П3 Г
= exp

94 Гл. 1. Введение в анализ
В примерах 245 и 246 перейти к пределу в показателе степени на основании утвержде-
утверждения А).
245. Последовательность (хп) задана равенствами ii = у/а, хг = \/а + у/а, хз =
Vе "t" va + V^i • • •> гДе а > 0- Найти lim xn.
* п-*оо
М Заметим, что хп = у/а + xn-i> п = 2, 3, .... Применяя метод математической индук-
индукции, убеждаемся, что последовательность хп = у/а + xn-i монотонно возрастает и ограничена
сверху, например, числом А > j + л/j + о. Следовательно, по известной теореме, имеем
lim хп = I ^ О,
п—>оо
причем I ss у/а+1, откуда находим, что
t_ V4T+T+1
2
246. Если ctift[/] есть колебание функции / на сегменте \х — ?| ^ А, А > 0, то число
wof/] = lim Wft[/1
ft-0
называется колебанием функции f в точке (.
Определить колебание функции / в точке х = 0, если:
а) f(x) = sin -; б) /(х) = — cos2-; в) /(г) = х B + sin-); r) /(x) =-arctg-.
X XX \ X / 7ГХ
•4 Согласно определению колебания фунхции в точке, имеем:
а) wh[f] = sup^ {sin i } - mi^ {sin i } = 1 - (-1) = 2,
/ wo[/l = lim C4ift[/1 ss lim 2 = 2;
LJJ ft_0 L J ft—0
б) Wh[f\ = sup {^cos2 1} - mf^^cos2 i} > sup {^cos2 ^} = *V, где ib —
целые числа такие, что |fc|ff^ ^. Поэтому
wh[/] = +оо, u>a[f] = +оо;
в) 0 ^ Wft[/] = sup {x B + sin i) } - inf {x B + sin i) } ^ ЗЛ - (-ЗЛ) = 6ft,
wh[/] = 0, wo[/] = 0;
r) Wft[/]= Bup^i arctg 1} - mf^iarctgl} = \ - (-1) = 1;
^o[/] = lim Uh{f] — lim 1 = 1. >
ft-*o ft-*o
247. Определить / = lim f(x) и L = lim/(x), если
лг-»О ^—0
19 1
f(x) = sin2 - + - arctg-.
X TV X
4 Поскольку inf {sin2 -} = 0 при x = xn = — —, n g N, a
2 1 f 2 11
lim — arctg — = inf < — arctg — > = —1,
n-*oo 7Г Xn 1.7Г X J
A О 1 \ / 0 \
sin2 —I arctg — ) = lim (sin2 птг -| arctg (—птг)) = —1.
X 7Г X/ n—oo V 7Г /
TO

§ 7. Предел функции 95
Аналогично, поскольку sup {sin2 - J = 1 при х = хп = ,t 2 , , п € N , a lim -arctg — =
'sup {| arctg ^} = 1, то
. _ / . 2 1 2 1 \ ,. ( . 2 тгA + 2w) 2 тгA + 2п) \
Z = hm sin - + - arctg - I = lim sin —— + - arctg —i— '- )
s—0 \ X It X/ n — oo ^ 2 7Г 2 J
= 1. >
248. Пусть функция гие1, где z = х + iy, определена посредством равенства
ег = lim (l + -Y. A)
Показать, что
ех = ex(cosy+ isin.y). B)
Вывести отсюда формулу Эйлера:
2 ' w 2i -
Представим последовательность пи (l + ?±i2i)n B тригонометрической форме
где <р я arctg ^^, а затем применим формулу Муавра. В результате приходим к последова-
последовательности
п
п >-* I 1 Н 1 ~- ) (cos nifi +1; sin nip).
Поскольку (l + ^ + o(^)Jx/n+oA/n) -+e, f (^ + о (?)) -<¦ x при п -+ со, то
\ ?8 П2 ) \\ П 1l2 J
при n —¦ oo.
Далее, согласно примеру 223,
n<p = n arctg —7— = n ( —7 H о ( - ) ) = 2/ + о A)
n + x \n + x \nj) v
при n —* 00. Поэтому (см. пример 175, a), 6)) cos?np —+ cosy, siting —+ sin у при п —* 00.
Таким образом,
J -+ ex(cosy + isiny)
при Ji —> 00, что доказывает равенство B).
Полагая в равенстве B) х = 0, получаем
е'у = cosj/ + г sin У- C)
Заменив в последнем равенстве у на —у, имеем
e~ty = cosy — ismy. D)
Из равенств C) и D) находим
е'и + e~iy . eiy - e~tv
cosy= , smj/ = j. . >

96
Гл. 1. Введение в анализ
Упражнения для самостоятельной работы
Найти точную верхнюю и точную нижнюю грани функции / : Е —*¦ F. Указать точки
х, у € Е (если они существуют) такие, что /(х) = sup{/(i)}, f(y) = inf {/(x)}.
91. /(х) = ?., |х| 4 1. 92. /(х) = I, х G ]-1, 1[\{0}.
93. /(х) = х2, 1 < х < 2. 94. /(х) = х2, -1 sS x sj 2.
95. /(х) =
96. /(х) = arcsin(sin х), x € К.
_(x _ iJ) i ^ i < :
97. f(x) - arccos(cosi), x € R. 98. /(x) = arctg ?, x ^ 0, /@) = 0.
99. Определить колебание функции /(х) = -, x g K\{0}, на интервалах:
a) ]10-7, 10-6[; 6) ]10-n-\ 10-"[; в) ]10"n, 10"l; г) ]106, 107[; д) ]10", 10n+1 [.
100. Определить колебание функции f(x) = sin ? на интервалах:
1 1 1 l Г. рл 1 —5— -i- f- ^ 1 2 i г. \ i х* J_ г
' J 407Г> 20?T I' ' J 407Г' 397Г I' / J 2ПП+Ж' ПЖ [' Г' J 4П7Г+7Г' П7Г L'
Показать, что:
101. A + х)" = 1 + пх + "("~^х2 + о (х2) при х -> 0.
102. х + cosx = ОA) при х ->¦ 0.
103. e-^l + х-1I = 1 - jx-1 + О(х-2), х > 2.
104. A + х + О(х")I = ехх + О(х1) при х -юо.
105. (хе2х-")п = ©(е12-*), х > 0.
106. а) е°<»> = 1 + о(х), х^О; б) о (/(х) • д(х)) = о (/(х)) • О(д(х)), х - х0.
107. ^/х" = у/х~о Н— у хо~"(х — Хо) + о (х — хо), х —»¦ хо.
Найти пределы:
N.
117.
118. Доказать неравенства
где ifc > 0, 0 ^ Afc < 1 (Jt = 1, п), ^ А, = 1.
п
119. Пусть: 1) 0 ^ Хкп ^ 1; 2) Y2 ^<=" = 1; 3) Um Anfc = 0 при каждом фиксированном
k=l
Ь; 4) х„ > 0, п е N; 5) lim х„ = I. Тогда lim П Х1"п = '•
п~*оо п—юо . j
Найти пределы:
(l-sin x)(cos2 x+l)~- sin 2x
120. Um , ^ .
121. Um -
х—О
124. Um
Х-+ОО
-. 122. lim
x—О
. 125. lim
ex cos a:— 1
-. 126. Um

§ 8. Непрерывность функций 97
Найти I = lim f(x) и L = lim /(x), если:
127. /(x) = sin x + cos(x\/2). 128. /(x) = sin2(x\/2) + 62 cos2'
129. /(x) = sin2(x\/2) - A +sm2zJ. 130. /(г) = (l+i)*si
141 -Ft r\ ( Л 1 M1 ± ci>i^ ¦>¦ 1QO 4"( r\ V X /
JL О X • J yJL) — I ^ -f- ~ I -p M U Jj . ±O?. J yJL j — _ , . 5 •
§ 8. Непрерывность функций
8.1. Определение непрерывности функции.
Определение 1. Функция / : X —г R, X С К, называется непрерывкой в точке
хо 6 X, если выполняется одно из эквивалентных условий:
1) Ve > 0 3E > 0 : (Vi € X) (|i - io| < Й) =Ф-
|у(ж) _ f(xD)\ < е; A)
2) Эля произвольном послеЭовательности (хп) значений хп € X, сжоЭящейся при п —> с»
к точке хо , соответствующая последовательность (/(хп)) значений функции сходится при
п —> оо к /(х0);
3) lim /(х) = /(хо) или /(х) — /(хо) —> 0 при х — io —> 0;
4) Ve > 0 Э 8 > 0 такое, что
/(]х0 - «, хо + 6[) С }/(х0) - е, f(x0) + e[
или, что то же самое,
f : ]хо — 8, xq + 5[ —> ]/(хо) ~ ?, /(хо) + е[.
Из определения непрерывности функции / в точке хо следует, что
lim /(х) = / I lim х ) .
\ /
Определение 2. Если функция f непрерывна в каждой точке интервала ]а, Ь[, то
функция / называется непрерывной на этом интервале.
Определение 3. Функция / :]а, хо] —> R (/ : [хо, Ь[^> Щ называется непрерывной в
точке хо слева (справа), если выполняется одно из эквивалентных условий:
1) Ve > 0 35 > 0 такое, что неравенство A) выполняется, как только хо — 5 < х ^ аго
(хо ^ х < хо + 8);
2) Эля произвольной последовательности (хп) значений х„ 6 ]а, Хо] (хп € [хо, Ъ[), схо-
сходящейся к точке хо, соответствующая последовательность (/(х„)) значений функции /
сходится к f(xo);
3) lim f(x) = f(x0) I lim /(x) =/(x0) или, короче, если /(х0 —0) = /(хо) (/(хо +
ixO утх+О J
4) Ve > 0 3 6 > 0 такое, что
f(]x0 - в, хо]) С ]/(ю) - е, /(хо) + ?[ (/([хо, хо + 8[) С ]/(хо) - е, /(х0) + е[).
Функция f : X —> Ш непрерывна во внутренней точке хо 6 X тогда и только тогда,
когда она в этой точке непрерывна слева и справа. •
Теорема 1. Если функция g : Т -* X, Т С R, X С К, непрерывна в точке to € Т, а
функция / : X —> R непрерывна в точке хо € X, где хо = з(^о), то композиция /о g : Т —> R
непрерывна в точке to ¦
Теорема 2. Пусть функции f : X —> К и # : X" —* К, I ct, непрерывны в точке
хо ? X . Тогда функции
1 + 9, Sa и L (g(xo)^O)
непрерывны в точке хо ¦
Все элементарные функции непрерывны в области существования.

98 Гл. 1. Введение в анализ
8.2. Непрерывность вектор-функций и функциональных матриц.
Определение. Вектор-функция х t-> f(x), f(x) = (/i(x), ... , fn(x)), x ? X, называется
непрерывной в точке хо 6 X, если
lim f(x)=f(x0).
X X
Функциональная матрица х >-+ А(х), где А(х) = (a,j(x)), г = 1, т, j = 1, п, называется
непрерывной в точке хо 6 X, если
lim А(х) = А(х0).
х-+х0
Вектор-функция f непрерывна в точке х0 6 X только и только тогда, когда в этой
точке непрерывна каждая из функций х ь-+ fi(x).
Функциональная матрица х i-+ А(х) = (а.Дх)) непрерывна в точке хо ? X тогда и
только тогда, когда в этой точке непрерывны все элементы матрицы х \—> atJ(x), г —
1, то, j = 1, п.
8.3. Точки разрыва функции и их классификация. Особые точки функции.
Определение. Если функция f : X —> R не является непрерывной в точке хо ? X, то
говорят, что она терпит разрыв в этой точке. При этом точка хо, называется точкой
разрыва функции f.
Точки разрыва функции / классифицируем следующим образом:
1. Пусть хо € X — точка разрыва функции / и существует lim f(x), конечный или
Х~*Х0
бесконечный. При этом:
а) если lim f(x) конечный, то Хо называем точкой устранимого разрыва функции /;
х-*ха
б) если lim fix) = оо, то io называем точкой разрыва типа полюса.
х—хо
2. Если lim f(x) не существует, то точку ю ? X называем точкой существенного
х--х0
разрыва функции /. При этом:
а) если существуют конечные пределы /(хо — 0), /(хо + 0) (/(хо — 0) ф f(xo + Q)), то точку
хо называем точкой разрыва первого рода функции /;
б) все остальные точки существенного разрыва называем точками разрыва второго рода
функции /.
Поскольку в изолированной точке хо 6 X функция / : X —> М непрерывна, то ее точками
разрыва могут быть лишь предельные точки х ? X.
8.4. Основные свойства непрерывных функций.
Определение 1. Функция / : [а, Ъ] —* К называется непрерывной на сегменте [а, Ь]
если они непрерывна на интервале ]а, Ь[ и в точке а непрерывна справа, а в точке b —
слева.
Пусть функция / : [а, Ь] —*¦ R непрерывна на сегменте [а, Ъ], тогда: 1) она ограничена на
этом сегменте; 2) если т = inf {/(х)}, М = sup {/(x)}, то на сегменте [a, b] существуют
х€[а,Ь] хе[а,Ь]
точки xi и Х2 такие, что /(xi) = т, /(хг) = М [теорема Вейерштрасса); 3) принимает
на каждом сегменте [а, /3], [а, /3] С [а, 6], все промежуточные значения между /(а) и /(/?)
(теорема Коши). В частности, если f(a)f(ji) < 0, то найдется такое значение у (а < у < /?),
что /G) = 0.
Определение 2. Функция f :]a, b[ —> К называется кусочно-непрерывной на интер-
интервале ]а, Ъ[, если она непрерывна во всех точках этого интервала, кроме конечного числа
точек разрыва первого рода и конечного числа точек устранимого разрыва.
249. С помощью "е—6"-рассуждений доказать непрерывность следующих функций:
а) ih+ai + t, aySO, igR; б) 1 ни2, 1 g I; в) х 1-+ x3, x 6 R; г)ги л/х, х > 0;
д) x !-+ yfx, x € R; e) x i-»- sin x, x € M; i)ih cos x, x б R; 3) x t-> arctg x, x б К.
¦4 а) Выберем е > 0 произвольно. Для любого фиксированного хо 6 R имеем
\ах + b — ахо — Ц — \a\\x — хо\ < е, если |х — хо\ < -,— = 6.

§ 8. Непрерывность функций
б) Пусть е > 0 — произвольное и хо € К. Тогда .
|х2 - xl\ = |(х - хоJ + 2хй(х - хо)\ «С |х - хо\2
¦¦> 'тчонаид-">!{п:)Н Л.9.
как только |х — Хо| < \/|хо|2 + ? — |хо| = 8.
в) Пусть е > 0 — произвольное, но такое, что 0 < е < 1. Имеем |х3 — ж|| = |х2 + xxq +
Xq||x — xoj. Пусть |х — хо| < 1. Тогда \х\ < |хо| + 1, поэтому
|х3 - х30\ < C|хо|2 + 3|хо| + 1)|х - хо| < е, ¦-, ¦¦¦• •
как только
1 ~и'^ЗЫ2+3|х0| + 1
г) Для произвольного ? > 0 и Хо > 0 имеем
|х-хо| \х-
= 8.
+
если \х — хо\ < е^/хо — 8.
д) Для любого ? > 0 и хо € К\{0} имеем
|х-хо|
е,
I I 3 / 2 с
если |х — хо| < - \/Хд е = Ь.
Непрерывность функции в точке хо = 0 следует из неравенства |у^| = \J\X\ < ?, справедли-
справедливого при |х| < е = о.
е) Для любого е > 0 имеем
I sin х — sinzol =
„ . х — хо х + Хо
2 sm cos
при \х — хо\ < 8 — г.
ж) Аналогично предыдущему
'MtMt,J~>f> •, I.
I cos х — cos хо | =
-2 sin
. х — хо . х +
< е
При |х — Х0| < 6 = ?.
з) Пусть [хо| > 0 и |Л| = |х-хо| < |хо|. Если arctg(xo + ft)-arctgio = t, то tgt г=
а так как |i| ^ |tg<| при [i| < ^, то
|arctg(a;0 + h) -arctgxo| = |t| < |tgt| =
если |ft| - |x - xo|
\h\
1+xZ+hxo
(l + sg)g _
+
Непрерывность функции х \-^ arctg х в точке х = 0 следует из неравенства
|aictg х — arctg 0] = |arctg x| < |х|. >
Исследовать на непрерывность следующие функции:
• IV '' '
250. /(х-) = (-1)
(cosx+smx)
, х € К.
•4 Пусть = п, тогда х принадлежит полуинтервалу \(п — 1)тг + j, пж + J •
Сужение функции / на каждый из полуинтервалов [(» — 1)т+ j, "Т + j [, tl ?Z,
х »-> (-l)n(cosx + sinx) + 2\/2n A)

100 Гл. 1. Введение в анализ
непрерывно. Остается проверить непрерывность функции / в точках nir + j, rt 6 Z. Из A)
находим
(cosx
f(mr+--o)= Мтж (-l)"(c
4
(п-1)т+J) =(-1)" (сов((п-1)т +j)+sm((n-l)T+|))+2V^(n-l). B)
Далее, полагая в B) вместо н число п + 1, получаем
+J) = (-l)n+1 (cos(nT +J) +sin
Итак, значения функции / в точках пж+j, п € Z, равны ее соответствующим предельным
значениям слева в этих точках. Поэтому функция / непрерывна в каждой из точек пж +
-, п 6 Ъ. А так как ранее установлена непрерывность во всех промежуточных точках, то она
непрерывна на всей числовой прямой. >
251. /(х) = arctg •!—= + ж , х ф пж + ^, f [пж + —) — «7г, п G Ъ, х G К.
у/2 L 27г J \ 2/
< Если [^|~] = » и х ф п-к + ^, п ? Z, то х ? ] ?17Г — f, "тг + § [• Сужение функции /
на каждый из интервалов ] пж — ~, птг + ^ [, п 6 Z, есть непрерывная функция
х I-+ arctg —=г + П7г.
¦ л/2
Остается проверить непрерывность функции / в точках я7г + f, и € Z. Имеем
/ 7Г \ / t? X
f I пж -\ 0 ) = lim arctg —^=- + и;
V 2 / «-„„+?-о V >/2
7Г \ , / tg I . . \ 7Г
П7Г Н 1-0 = hm arctg -3— + Ы + 1)ж ] = пж + -.
2 У x_n7r+i+0 V ' V2 / 2
Таким образом, / (пж + ^ — 0) = / (н7г + ^ + о) Vn 6 Z, и, следовательно, функция / непре-
непрерывна наК. >
252. /(х) = [х]([х] - (-1)W cos жх), х 6 R.
А Пусть [i] = п, тогда п ^ х < п + 1, is 6 Z. Сужение функции / на полуинтервалы
X I—* п(« — ( — 1)" COS 7ГХ)
непрерывно. А так как значение /(») = «(« — 1) равно предельному значению слева /(п —0) =
lim (?»— 1)(« — 1 — ( —I)" cos7rx) = js(js — 1), то функция / непрерывна на множестве R. >
253. /(х) = Ы, хек.
¦< Если к ^ х < к + 1, к 6 2, то [х] — к, и, следовательно, / — непрерывна. Если
же хо = к, то /(А;) = к, f(k — 0) = Нш [х] = к — 1, т. е. функция / терпит разрыв при
хо = к, к € 7L >
Определить точки разрыва и исследовать характер этих точек, если:
254. f{x) = 2__i х ^ _i, /(_!) = о.
А Имеем
lim f{x) = —оо; lim f(x) — — оо,
следовательно, х = —1 есть точка разрыва типа полюса. >
255. /(*) = ^РЩ-, х е R\{-i, о, 1}, /(-1) = /@) = /A) = о.
Х-1 X
А Функция / непрерывна при х € R\{ —1, 0, 1} как элементарная. Поскольку
1- -г/ ч 1- X — 1 . . I — 1 -г, ч г Ж — 1 г,
lim /(х) — им = Т00; um /(х) = am = — 1; lim /(x) = lim = 0,

§ 8. Непрерывность функций 10*1
то х = — 1 есть точка разрыва типа полюса, х = 0 — точка разрыва первого рода, а в точке
х = 1 функция / непрерывна. >
256. /(x) = cos2-, х^О, /@) = 1.
X
¦4 Пусть хп = ~^, уп = Bп^1Oг, п 6 N. Тогда х„ —>• 0, уп ->¦ 0 при п ->¦ оо, однако
/(х„) —>¦ 1 , a f(yn) —* 0 при п —> оо. Следовательно, lim f(x) не существует и х — 0 — точка
разрыва второго рода. >
257. /(х) = arctg -, хфО, /@) = 0.
-Ч Пусть е > 0 — произвольное. Тогда существует х0 > 0 такое, что — > tg (^ ~ е),
откуда tg — > f —?• В силу возрастания арктангенса для 0 < х < io и подавно arctg - > ——е.
т. е. lim arctg ~ = § •
Аналогично показывается, что lim arctg — = . Следовательно, i = 0 — точка разрыва
.г- ——0 ' х 2
первого рода. >
258. /(х) = {-ж=, Хфц,хф\, /(о) = /A) = о.
1-е1-'
-Ч Имеем
,. 1 ,. Т^ 1-х
lim 5— = lim j— • = Ч-°°,
J, —±0 -г— х-~±\1 X
\ — е1-х 1 _ е1-х
т. е. х = 0 — точка разрыва типа полюса. Далее,
lim j— = 0, lim j— = 1,
x-»l—0 _ т- I —1 + 0 . -j
1 — e1-^ 1-е 1~x
поэтому х = 1 — точка разрыва первого рода. >
259. f(x) = x[x], х ей.
¦4 Если [х] = и, то х 6 [и, п + 1[ и сужения функции / на полуинтервалы [п, п + 1[
х I—> их, х ? [n, ii + 1[,
непрерывны при любом и ? Z. А так как /(п) = «2, /(» — 0) = lim (?i — 1)ж = (?i ^- l)n, то
х—*п — О
точки х = и являются точками разрыва первого рода. >
260. /(х) = [x]siri7rx, х?М.
-Ч Пусть [ж] = и, тогда п ^ х < п + 1 и сужения функции / на [и, п + 1[
х 1—» «siii7rx, ж g [л, л + 1[, ?8 € Z,
непрерывны. Остается исследовать непрерывность в точках х =?s, n € Z. Имеем
/(») ='«siiurn = 0, /(п — 0) = lim (n — 1) sin 7ri = (is — l)sin7T?s = 0,
т. е. /(«) = f(n — 0) и функция / непрерывна на R. >
261. /(х) = х [i] , х / 0, /@) = 1.
•Ч Функция / непрерывна на каждом из полуинтервалов —j < х ^ —, rt € Z\{0},
поскольку ее сужения х t—>• »»х на эти полуинтервалы непрерывны. Далее, / (—J = 1,
/ (—+ о) = lim х [-] = ^-, поэтому в точках х = —, п € Z\{0}, функция / терпит
.1-1+0
разрыв первого рода.
Рассмотрим неравенство
1 п + 1
П+1 L X J
справедливое для х ? ] ^tj, ~[> « € N. Если п -+ оо, то х —г +0, и из A) следует, что
lim /Ы= Um х [i] = 1.
j: — + 0 х — + 0 L:l'J

102 Гл. 1. Введение в анализ
Если [i] = -п, то -» < i < -п + 1, -^ < х < ^, и
Если п -» оо, то i -» —0, и из B) находим, что lim /(х) — lim iH =1. Таким образом,
/@) в= /(+0) = /(—0) = 1, т. е. при 1 = 0 функция непрерывна. >
262 f( 1 — / sin* для рационального, х
• J(x) — \ о для иррационального х.
^ Пусть xq ф 71, 71 6 Z, —произвольно, (хп) —последовательность рациональных чисел,
сходящаяся к io, a (tn) — последовательность иррациональных чисел, сходящаяся к хо- Из
равенств lim f(xn) = lim sin7rxn = sin7rxo Ф 0 и lim /(tn) = 0 вытекает, что lim /(x) не
71—*OO П—KX 71—*CO X-*Xq
существует, т. е. хо — точка разрыва второго рода.
ЕСЛИ Же Хо = 71, 71 6 Z, ТО
\f(x0) - /(х)| < | sin тгх| = | sin(im + тг(х - ?г))| =
= | cos Tresin тг(х — га)] = | sin тг(х — хо)| < тг|х — хо| < ?,
если \х — Хо| < — = 6. Следовательно, хо = и — точки непрерывности функции /. >
263. Доказать, что функция Римана
Г —, если х = —, где тип — взаимно простые числа,
\ 0, если х — иррационально,
разрывна при каждом рациональном значении ж и непрерывна при каждом иррациональном
значении х.
^ Пусть Хо = — рациональное, так что /(хо) = -. Очевидно, последовательность
(ПР+1 \ Р д v г ( 71U+1 \
) рациональных чисел сходится к - = хо при п —» оо. А так как lim / ( -i:— I =
lim — = 0, то каждая рациональная точка - является точкой разрыва.
п—>оо "* q
Пусть cv — произвольное иррациональное число, а (х„) = ( — | — произвольная
довательность рациональных чисел, сходящаяся к а. Тогда lim gn = оо и
lim f{xn) = lim f(^-)= lim — = 0 = /(«).
А так как /(х) = 0 при х иррациональном, то равенство lim /(х„) = /(«) = 0 справед-
справедливо для любой последовательности (хп) с произвольными членами, сходящейся к ирраци-
иррациональному числу с*. Таким образом, функция / непрерывна при каждом иррациональном
значении х. >
264. Исследовать на непрерывность функцию
/ п+7' если х — несократимая дробь —, п ^ 1,
^ |х|, если х — иррациональное число.
^ Пусть хо — рационально, т. е. хо = ^, п Js 1. Согласно условию, /(хо) = ~^г{-
Поскольку Хк = -^ > ^ = хо при к —* оо , a lim f(xk) = lim ^rr = ~ Ф -?rj = f(xo),
то функция / терпит разрыв при всех рациональных значениях аргумента.
Пусть теперь хо — иррационально, а (х/,-) = ( — ) — произвольная последовательность
рациональных чисел, сходящаяся к хо. Тогда lim |m*| = оо, lim |7i*| — ос и
.. ., . ,. ть v "пГ f |х| = /(хо), еслихо>0, ,,х
lun f(xk) = .hm —— = hm ^-Ц- = хо = \ '_' , если хо - 0> A)

§ 8. Непрерывность функций 108Г
Отсюда вытекает, что функция разрывна при отрицательных иррациональных зн&ч^гаыпо'ар-
гумента.
Если Хк —* хо при к —> оо, причем хи ^ 0 — иррациональные числа, то
lim f(xk) = lim \хк\ = \хо\ = /(хо)-
к—*оо fc—*оо
Таким образом, функция / непрерывна только при положительных иррациональных зна-
значениях аргумента. > '. ; ¦
265. Пусть функция / непрерывна и ограничена в интервале }хо, +оо[. Доказаяъ,,что
какое, бы ни было число Т, найдется последовательность хп —> +оо такая, что
lim (/(*„ +Т)-/(*„)) = 0. . , • !
п-»оо ,
М Пусть Т > 0 — произвольное. Рассмотрим разность /(х + Т) —/(х). Возможны ДЙй <
случая: . • ¦
1) существует конечное число х' JS го такое, что разность /(х + Т) — /(ж) сохраняет
постоянный знак для всех ж ^ х ;
2) для произвольного Е ^ хо существует х* > Е такое, что /(х* + Т) — /(х*) — 0.
В первом случае последовательность (f(x' + nT)) монотонна, а поскольку она и ограни-
ограничена, то существует конечный предел lim /(ж' + пТ) = I, так что
lim (/(x'+(n
?г—'Со
причем х,п = х' + пТ —> +оо при п —* оо.
Во втором случае существует такая бесконечная последовательность (хп) значений х,
х > хо, что х„ —» +оо при 7г-^оо и /(еп + Т) — f(xn) = 0, т. е.
lim (/(е„ + Т)-/(е„)) = 0.
п—>со ..
Случай, когда 2Л < 0, заменой х + Т — t приводится к уже рассмотренному. >
266. Пусть ip и ф — непрерывные периодические функции, определенные при i ?М и
lim (ч>(х) — ф(х)) = 0. Доказать, что <р(х) = Ф{х), х ? К.
¦4 Пусть Ti — период функции р, а Тг — период функции^. Пр;едпд^о^;им, чтс|.(^
), т. е. существует такая точка х = t, что
Возьмем е > 0 произвольное, но меньшее, чем —. В силу непрерывности функции <р в
точке х = t для указанного е > 0 существует 6 > 0 такое, что
A)
<р в
B).
как только |/;.| < 6. Согласно условию, существует такое натуральное число к, что
кТ2) - ф{1 + кТ2)\ < е, а тогда Vr?i € N имеем
\<p(t + mkT2) - ф>(г + mkT2)\ <е. ' C)
Из неравенств B), C) и периодичности функций (риф следует неравенство
|<p(t) - (/;(t)| = |<p(t) - <p(t + miT2) + у.(< + mA,-T2) - ФЦ + mhT2)\ <
< \tp(t) - <p(t + mkT2)\ + \<p(t + ткТг) - ф{Х + mkT2)\ =
= \<p(t) - tp(t + mkT2 ~ nTi )| + \<p(t + mkT2) - ф(г + raffi)| < e + e = 2e, , ^,D)
если только •¦..,-.; !• ¦
|mfcT2-nTi| < 6. E)
Но мы выбрали такое число е, что 2е < М¦ Таким образом, неравенство D) противоречит
равенству A). Источник противоречия — в предположении существования точки х — t, в
которой \ip(t) — Ф(г)\ — М > 0. Следовательно, такой точки не существует, т., е. ip(x) =.ф(х)., ,
— оо < х < +оо.
Остается показать, что при произвольных заданных числах Т\, кТ2 и 6 существуют целые
числа ш > 0 и п, удовлетворяющие неравенству E). .
Если Т2 и Ti — рациональные, то это очевидно.

104 Гл. 1. Введение в анализ
Пусть Тг и Т\ — иррациональные. Если обозначим -jr- = I, jr = а> т0 неравенство E)
запишем в виде
\ml- п\ < а. F)
Для доказательства последнего неравенства разобьем интервал [0, 1] на [—] + 1 равных
частей ([а] — целая часть числа а) длиной уут—, причем, к каждому из частичных интер-
интервалов условимся приписывать его левый конец и не приписывать правый.
Рассмотрим множество чисел
.и-рп.м-м,..., ([I
каждое из которых принадлежит одному из построенных нами частичных интервалов. По-
Поскольку частичных интервалов [^-] + 1, а чисел G) имеется [—] + 2, то существует хотя бы
один интервал, содержащий два числа
pi - \pl] я ql- [ql], p<q, (8)
множества G). Но так как длина интервала равна -r-pj—, то разность между числами (8)
меньше этой длины, т. е.
\qi - [,,i] -Р1 + Ml = К? -p)i - Ы - №\ < тт
Обозначая q — р = m (га > 0), [ql] — [pi] = n и подставляя вместо 1иаих значения, получаем
6
кТ2
-, или \mkT2 — nTi | < 6. >
267. Доказать равенство arcsin х + arccos х = —.
Имеем
¦к . Зтг
^ arcsin х 4- arccos х ^ —.
Поскольку sin (arcsin x-\- arccos x) = 1, то arcsin x + arccos x = ^
неравенства заключаем, что к = 0. >
268. Доказать формулу сложения арктангенсов:
х + у
arctg х + arctg у = arctg h етг,
1 - ху
где г принимает одно из трех значений 0, 1, —1.
¦4 Имеем
tg (arctg x + arctg у) = —, tg ( arctg
1 - ху
1- ху
поэтому
х -\- у
arctg х + arctg у = arctg ; h еж,
где е 6 Ъ. Поскольку |arctgx + arctg y\ =
1 — ху
arctg **? + еж
Отсюда и из предыдущего
х + у
< ж, а
arctg -±Zi.
A)
?, ТО
е может принимать только три значения: 0, 1, —1. Вычисляя косинусы от левой и правой
частей равенства A), получаем
, cos еж =
1 - ху
1, если I?/ < 1,
— 1, если ху > 1.

§ 8. Непрерывность функций 105
Следовательно, функция (х, у) >—> е(х, у) терпит разрыв, если у = -, где х — любое
фиксированное число. Заметим, что если ху < 1, то е = 0, а при ху > 1 е = ±1 (так как е
может принимать только три значения 0, 1, —1).
Пусть ху > 1 и х > 0. Тогда у > 0 и
arctg х > 0, arctg у > 0, a arctg — — < 0.
1-ху
В равенстве A) слева стоит непрерывная положительная функция, следовательно, и справа
должна стоять положительная функция, а поэтому еж > 0, т. е. е — +1.
Аналогично, если ху > 0 и я < 0 (у < 0), то е = — 1. >
269. Исследовать на непрерывность вектор-функцию
V x x x I
f(O) = (l, 1, 0).
< Функция f при х ф 0 непрерывна, поскольку ее координаты непрерывны при этих
значениях аргумента. Далее,
lim fix) = (lim ^-^, lim -, bin -—^-^ ] = A, 1, 0),
X-.0 Vc-.O X a—0 X Л.-.0 X I
поэтому функция x i—> f (г) непрерывна и при х = 0. >
2/0. Исследовать на непрерывность функциональную матрицу
х GK.
< Функциональная матрица непрерывна на К, так как все ее элементы непрерывные на
функции. >
Упражнения для самостоятельной работы
Исследовать на непрерывность следующие функции:
133. /(x) = arcsinx, \х\ ^ 1. 134. /(х) = arccos х, |х| ^ 1.
135. /(х) = arctg я, х G К. 136. /(х) = arcctg x, x G R.
137. /(х) = е—~-, х ф 0, /@) = 1. 138. /(х) = lj^~^-, х > -1, х ф 0, /@) =0.
139. /(.г) = arctg ^, х ф | + А,'тг, / (f + кж) =0, t g Z.
140. /(х) = sin x arcsin ^?, х ф | + fcir, / (f + fcir) = 0, fc G Z.
141. /(x)= I |X2'' !E!^ !; 142. /(*) =
143. f(x) = (-1) ["^T"] (sin x + cosx) + 2^2 [^^J , i G K.
144. /(x) = ^ arctg ^ + f sgn x, x # 0, /@) = 0.
145. /(я) = -М + 1 + ?.+ ... +^, x^ l. 146. /(i) = [
147. f(x) = -x [^] + 1 + ^ + ... + i^, x g ]0, 1].
iJ
148. f{x) = | *~ И' * | ^Q 149. f(x) = [x]sin тгх, х G R.
150. f(x) = { * ' " ' 151. /(x)=< x ' *^">
x + 1, x ^ 0. I y/2 + x, x ^ 0.
Определить точки разрыва и исследовать их характер:
152. /(х) = sin р-, 1^0, /@) = 0.
153. /(х) = arctg ^f + т [^~] . г / | + пх, / (| + ш) = 0, п € Z.
154. /(х) = arctg 3t?W2H' + тг [ih?j ; х ^ BИ + 1)*-, f(Bn + 1)тг) = 0, п 6 Z.

Гл. 1. Введение в анализ
155. f{x) = arctg ^*/±l, /(±1) = f.
156- /(*) = ,g»,J,g,+a. * / I + **> / (f + **) = °-
157. /(х) = tgx, х- / f + fcTr, / (f + Ьг) = 0, fc € Ъ.
158. /(i) = arcsin (sin e) arctg -Л-, x ф нтт, /(нтг) = 1, м ? Z.
159. /(i) = In arcctg i, z / 0, /@) = 0. 160. /(я) = tg \, x ф 0, /@) = 0.
Исследовать на непрерывность вектор-функции:
161. f(x) = (cosx, sinx, 1), i?R.
164. f(i) = 1 v л >x , LJI—j , ..., LJt—^ I , если x € J — 1, +oo[\{0} и i@j =
(л/2, 2л/2, ..., mv/2).
165. f(z) = (l + i)j,(l + 2i)x,...(l+mi)H, есяи.1 € ]-l, +oo[\{0} и f@) =
(e,e2,...,em).
Исследовать на непрерывность функциональные матрицы:
1вв.А(х)=( 1 siY * ),хе
у ' V cos х 1 1 — х )
167. Л(*)=(№),
168. А(х) = (a,j(i)), где аи(г) = A + га;)^, г = 1, т, j = 1, н, х € ]-1, оо[\{0} и
169.
170.
, где ah(x) = (l + ~) х* , х ф 0 и Л@) = Е.
'"!' ' ; ' А(х) =
^ о ... о \
о Л- ... о
0 0
, х ф О, Л@) = Е.
1
§ 9. Равномерная непрерывность функций
9.1. Определение равномерной непрерывности.
Определение. Функция f : X —* К называется равномерно-непрерывной на множе-
множестве X, если
Ve > 0 Э S > 0 : Vx, у G X А \х - у\ < S =Ф |/(х) - /(у)| < е.
Если функция / не является равномерно-непрерывной, то это означает следующее:
Эе> (т > 0 :Чх, у?Х Л \х-у\ <6^- \f{x)-f(y)\ > e.
9.2. Теорема Кантора.
Теорема. Если функция f : [а, Ь] —> К непрерывна на сегменте [а, Ъ], то она равномерно-
непрерывна на этом сегменте.
271. Показать, что функция /(х) = -, х ? ]0, 1[, непрерывна на интервале ]0, 1[, но не
является равномерно-непрерывной на этом интервале.
¦4 Функция / непрерывна, как всякая элементарная функция. Покажем, что она не явля-
является, равномерно-непрерывной на интервале ]0, 1[.

Пусть хп = ^, уп =
§ 9. Равномерная непрерывность функций
у^, п € N. Тогда
е
!-1в7
, ;\
- Уп\ -
О при п —> оо,
т. с. разность \хп — уп может быть меньше любого наперед заданного положительного числа.
Однако \f(xn) — f(yn)\ = |гс + 1 — n — 1 — е| = е Ve > 0. Следовательно, функция / не является
равномерно непрерывной на интервале ]0, 1[. >
272. Показать, что функция /(ж) = sin — непрерывна и ограничена на интервале ]0, 1[,
X
но не является равномерно-непрерывной на этом интервале.
М Ограниченность функции / очевидна, а непрерывность следует из того, что функции
у i-t sin у, у ? R, х н-т ^, х € ]0, 1[, непрерывны, а поэтому их композиция также непрерывна.
Пусть хп = ^гг, уп = ~^, и € N. Тогда \х„ - г/„| = (п+1)A2га^1) -+ 0 при п -+ оо,
в то время как |/(х„) — f(yn)\ = 1 ;? е Ve G ]0, 1]. Следовательно, функция / не является
равномерно-непрерывной на ]0, ] [. >
273. Показать, что функция f(x) = sin x непрерывна и ограничена на числовой прямой
К, но не является равномерно-непрерывной на этой прямой.
М Ограниченность и непрерывность очевидны, а равномерная непрерывность отсутствует,
так как
O, I],
1, п €
несмотря на то, что
Сп - Уп\ =
= -> О
при п —» оо. >
274. Доказать, что если функция / определена и непрерывна в области а ^ х < +оо и
существует конечный предел Jim /(ж), то / равномерно-непрерывна в этой области.
•^ Из существования предела следует, что
Ve >0Э?> а : Ve, у Е]Е, +оо[ => \f(x)-f(y)\ < е. A)
Фиксируем такое Е > 0 и рассмотрим сегмент [a, 2jS]. Согласно теореме Кантора, функция /
равномерно-непрерывна на [а, 2Е], т. е. Ve > 0, в частности, для е, указанного ранее, ЭЙ > О
такое, что Vx', у € [«, 2?] Л \х — у\ < А =>• |/(л) — /(?/)| < е. Не ограничивая общности, считаем,
что Ь < Е. Тогда из условия \х — у\ < 6 следует, что оба числа хну большие Е или оба
меньшие 2Е. В том и другом случае для любых х и у, больших а, из условия jx—j/| < S следует
неравенство \f(x) — f(y)\ < е, что устанавливает равномерную непрерывность функции / на
[а, +оо[. >
275. Показать, что неограниченная функция f(x) — х + sin x равномерно-непрерывна
нд всей числовой прямой К.
¦4 Для произвольного е > 0 имеем
| sin ж — sin j/| =
. х— у х + у
sm cos
-2\х-у\ <е
I/O) ~ f(y)\ = U' - .V - (sin x - sin y)\ < |x -
X yj , _ .^-- —~
для всех х и (у, удовлетворяющих неравенству |х — у\ < | = й. >
276. Являются ли равномерно-непрерывными функции:
а) /(я) = х2, .г е ]-/, 1[; б) /(х) = х2, х G R?
< а) Пусть е > 0 произвольно задано. Тогда
I/O) - f(y)\ = \х2 - у2\ = \х + у\ \х - у\ ^ (|х| + \у\)\х - у\ < 21\х - у\ < ?
при Vx, у g ] — l, 1[л \е — у\ < Yi~ *> т- е- / — равномерно-непрерывна на ] — /, /[.
б) Функция / не является равномерно-непрерывной, так как при хп = п -\—, уа = п,
п ? N. имеем |.г„ - у„\ = ^ -* 0 при п -+ оо, a \f{xn) - f(yn)\ = 2 + \ > 2 ^ ? Ve ?]0, 2]. >

108
Гл. 1. Введение в анализ
м- Исследовать на равномерную непрерывность следующие функции:
277. f(x)=I^-I, xe[-i, 1].
< Функция непрерывна на [—1, 1], а поэтому по теореме Кантора и равномерно-непре-
равномерно-непрерывна. >
278. f(x) = \nx, i€]0, 1[.
¦4 Равномерная непрерывность отсутствует, так как если хп = е~", уп = е"", п € N, то
\х„ - уп\ = j=± -> 0 при и ^ оо, а |/(х„) - f(yn)\ = 1 > е Ve G ]0, 1]. >
279. f(x)= ^А х€]0, тг[.
•^ Рассмотрим функцию F(x) = /(х) при х € ]0, ir[, F@) = 1, F(ir) = 0. Поскольку функ-
функция F непрерывна на сегменте [0, 1], то, по теореме Кантора, она и равномерно-непрерывна
на этом сегменте, а следовательно, и на интервале ]0, тг[. >
280. fix) = ex cos-, *е]0, 1[.
¦4 Положим хп = j^r> Уп = Bn-H)ir' П
однако
Iх" ~ Уп
2пBп
0 при п —* оо,
1/(*п) " /(У»I = ?2п" +е<2»+1)- > 2 Vn e N.
Следовательно, функция не является равномерно-непрерывной. >
281. /(г) = arctgz, х <= R.
•^ Равномерная непрерывность следует из того, что (см. пример 268)
|arctg? - arctg ?/| =
arctg
х-у
- У
+ху
< \х - у < е
при \х — у\ < 5 = е. >
282. /(е) = ism г, 0 ^ х < +оо.
•^ Пусть хп — пп, уп = пж + —, н. € N, тогда |х„ — уп\ = — —» 0 при п —» оо ,
а |/Ы - /(»п)| = (и* + i) | sin (n* + i) | = (J№ + I)sini = (тг + ^)^ - тг при
n
n -* оо. Следовательно, |/(in) — /(j/n)| > f VV > m, и функция не является равномерно-
непрерывной. >
283. Для е > 0 найти S > 0 (какое-нибудь!), удовлетворяющее условиям равномерной
непрерывности для функции /, если:
а) /(х) = х2 - 2х - 1, -2 s$ х <? 5; б) /(х) = ^/Ё, 0 < х < +оо.
¦4 а) Имеем
1/(*) - /Ы1 = I1" " 2х -1-У2 + '2у + Ц = \х2 - у2 - 2 (х - у)\ ^
^\х + у\\х-у\ + 2 \х -у\Ц (|х[ + |v| + 2)|* -у[ЦГ2\х-у\< е,
если |х -у\ < ^ = *.
б) Пусть е > 0 — произвольное. Если числа х и у такие, что
О ^ х < е\ 0 ^ у < еп, A)
то 0 ^ -у/х < ?, 0 ^ ?/у < е и |х — у\ < е" = S. Отсюда следует, что |/(х) — f(y)\ =
I у/%— ^/у\ < ? при \х — у\ < еп ~ 8. Если же A) не выполняется, т. е. хотя бы одно из чисел
х или у не меньше еп, то
Тогда
< ?
при |ж - i/| < е" = 5. >

§ 9. Равномерная непрерывность функций 109
284. Доказать, что сумма и произведение конечного числа равномерво^меирерывнййс на
интервале ]а, Ь[ функций равномерно-непрерывны на этом интервале.
¦4 Достаточно рассмотреть случай двух равномерно-непрерывных на ]а, Ъ[ функций / и
д. Согласно условию,
Ve > 0 3«! > 0 : Vs, у G ]а, Ь[Л |х - у\ < «i => |/(х) - /(у)| < |, A)
Ve>0 352 >0:Vx, уЕ]а, Ь[Л \х - у\ < 62 => \f{x) - f(y)\ < ^. B)
Если |е — у\ < 6, 6 = min{6i, б2}, то будут выполняться оба неравенства A) и B). Тогда
непрерывность суммы следует из неравенства
|/(*) + д(х) - f(y) - д(г/)К \f(x) - f(y)\ + \g(x) - д(у)\ < | + | = е,
справедливого Ve, ?/ €]а, Ь[, если |i — у\ < б. '>
Равномерная непрерывность произведения вытекает из того, что
|/(х) д(х) - f(y) д(у)\ = |/(х) д(х) - f(x) g(y) + f(x) g(y) - f(y) g(y)\ <
< |/(х)| \д(х) - д(У)\ + \д(у)\ \f(x) - f(y)\ < L\ + М|,
если \х -у\ < 6, х в ]а, Ъ[, у G ]а, Ь[, где L = sup \f(x)\, М = sup \g(x)\. >
285. Доказать, что если ограниченная монотонная функция / : }а, Ь[—*¦ R непрер|1вна"
на конечном или бесконечном интервале ]а, Ь[, то эта функция равномерно-непрерывца йа
интервале ]а, Ь[.
¦4 Из условия следует, что существуют конечные пределы
/(а + 0)= lim /(х), /F-0)= lim Hx).
X—.а+0 I—>Ь—О
Если а и 6 — конечны, то, полагая /(а) = /(а + 0), /(Ь) = f(b — 0), получаем непрерывную
функцию / на сегменте [а, Ь], которая, в силу теоремы Кантора, равномерно-непрерывна иа
[а, Ь]. ¦ -
Если одно из чисел а, Ъ или оба эти числа равны — оо, соответственно +оо, то рассуждая,
как и при решении примера 274, снова убеждаемся, что функция / равномерно-непрерыв-
равномерно-непрерывна. >
286. Модулем непрерывности функции / :}а, Ь[—> R называется функция
где Wf(S) = sup \f(x) — f{y)\, x и у — любые точки из ]а, Ь[, связанные условием \х — у\ ^ 8.
Доказать, что для равномерной непрерывности функции / на ]а, Ь[ необходимо и доста-
достаточно, чтобы lim tu/(<5) = 0.
6—*~{-0
-4 Необходимость. Пусть lim u>f(S) = 0. Тогда
6—>-f О
Ve > 0 Э«1 > 0 : Vx, у 6 ]о, Ь[Л V<5 < «i => w/E) < е.
Так как a>/F) = sup \f(x) - /(j/)|, то
е Vx, у G ]а, Ь[Л \х - У| < в,
т. е. функция / равномерно-непрерывна на ]а, Ъ[.
Достаточность. Пусть / — равномерно-непрерывна на ]а, Ъ[, тогда
\/е > 0 36 > 0 : Vx, у G ]a, Ь[Л |х - у| < « = |
Но тогда при тех же условиях относительно х и у имеем
w/(«)= sup
|
т. е. lim UfE) = 0. >

110 Гл. 1. Введение в анализ
Упражнения для самостоятельной работы
Исследовать.на равномерную непрерывность следующие функции:
171. Дх) = у/х2 + 1, х G R. 172. Дх) = /Ё2" In x, 1 < х < +оо.
173. Дх) = л/г1 In х, 0 < г < 1. 174. /(е) = у/х, 0 < ж < +оо.
175. /(х) = ^, 0 < х < +оо. 176. /(ж) = ^г, -1 < г < 0.
177. Дх) = Чф-, i e R. 178. f(x) = х + In x, 1 ^ х < +оо.
179. /О) = х-lux, х 6 ]0, 1[. 180. f(x) = е-*2, х &R.
181. Дх) = ^—, х G R. 182. /(г) = x2lnx, х > 1.
183. Дх) = xcosx, х е R. 184. /(х) = x2cosx, х € [0, п].
185. /(х) = х3 + х2 + 1, х ?R.

Глава 2
Дифференциальное исчисление
функций одной переменной
§ 1. Производная явной функции
1.1. Основные определения.
Определение 1. Пусть дана функция f :]a, b[—> R. Разность Дж = х — хо (х, Хо ?]а, Ь[)
называется приращением аргумента в точке хо.
Ощэеделение 2. Разность Д/(ю) = /(хо + Дх) — f(xo) называется приращением
значений функции f в точке хо ¦
Определение 3. Если существует предел (конечный или бесконечный)
Лх-—О
то он называется производной (конечной или бесконечной) функции f в точке хо-
Определение 4. Пределы (конечные или бесконечные)
/i(xo)= lira MM, /;ы= Нт М?°1
' Да;—-0 Де V Да;—+0 Дж
называются соответственно левой и правой производными функции f (конечной или бес-
бесконечной) е точке хо ¦
Во всех этих определениях бесконечный предел понимается как один из символов +оо
иди — оо.
Определение 5. Если функция f терпит разрыв первого рода в точке хо, то выраже-
выражения
/1(*о-0)= Inn /(«o
4
/|(IO + 0)= Hm
Ax ч ai-+o Дж
называются соответственно левой и правой в расширенном смысле производными функ-
функции f в точке Хо ¦
Необходимо помнить, что во всех этих определениях приращение Дж стремится к нулю
произвольно.
Приращения Дх и ДДяо) могут быть как сколько угодно большими, так и сколько угодно
малыми.
1.2. Правила вычисления производных.
Если функции / и g имеют конечные производные при х G ]а, Ъ[, то
1) (<*i/ + »2g)' = aif + а2у', «i, №2 —постоянные;
2) (/</)' = fg' + f'y; 3) (f) ' = ^2, ^(x) ф 0.
1.3. Производная сложной функции.
Если функции f : и i—>- /(u), <р : х у-* и = ф{х) имеют конечные производные f'u и <р'х,
то (f(<f(x)))':1! = fL(<p(x))<p'x. Значком внизу обозначена переменная, по которой вычисляется
производная.

112 Гл. 2. Дифференциальное исчисление функций одной переменной
1.4. Таблица производных.
Если х — независимая переменная, то справедливы формулы:
Зг; 2) (а*)' = а*Ьа, а > 0,
3) (sin х)' = cos х; 4) (cos х)' — — sin x;
5) (tgz)'=^_; 6) i
/ V ° / cos2 x ' '
/ cos x smar
7) (arctga;)'= y^; 8) (arcctg x)' = -^;
9) (arcsina:)' = A-^; Ю) (arccosa:)' = - J__
11) (logax)'=I!L-., a>0, a^l, (lnx)'=±; 12) (shx)' = chx;
13) (chx)' = sbx; 14) (thx)'=^;
15) (cthx)' = -^; 16) ^
17) (aithx)^^, |х|<1; 18) (|x|)' = sgu x, x ф 0;
19) ([ж])' = 0, x ф к, к е X.
1.5. Производная степенно-показательиой функции.
Если функции и : х •-> и(х) и л : ? >—> «(а;) имеют конечные производные, то
1.6. Производная от вектор-функции и матричной функции.
Если компоненты вектор-функции f : х >—> (fi(x), /2B:), • • • , fn{x)) имеют конечные про-
производные, то
Аналогично, если элементы матричной функции А : х i-+ (atJ (х)), где (а,_, (а;)) — функциональ-
функциональная матрица порядка in х и, имеют конечные производные a,j[x), то производная матричной
функции вычисляется по формуле
(аи{х) ai2(*) ¦¦• ain(x)
а'21(х) а'22(х) ... а'2п(х)
«miW a'm2(x) ... a'mn(x)
1.7. Производная от комплексной функции скалярного аргумента.
Если го : х ы- и(х) + iv(x) и функции и : х i—> и(х), г> : а; н-> л(а;) имеют конечные
производные, то производная функции го вычисляется по формуле
W = и -\- IV .
1. Определить максимальное приращение Да; аргумента х и соответствующее прираще-
приращение Д/(хо) функции / : х ь-+ lg х в точке хо = 1, если х изменяется от 1 до 1000.
¦^ Используя определения 1 и 2, п. 1.1, имеем
Да; = 1000 - 1 = 999, Д/(а;0) = lg 1000 - lg 1 = 3. >
2i. Определить максимальное по абсолютной величине приращение Да; аргумента х и со-
соответствующее приращение Д/(а;о) функции f : х >—* —j в точке хо = @,1, если х изменяется
от 0,01 до 0,001.
¦^ Аналогично предыдущему находим
Д* = 0,001 - 0,01 = -0,009, Д/(х0) = у—]-^ - j-^ = 99 • 104. >
Примеры 1 и 2 показывают, что приращения Ах и Af{xg) могут принимать какие угодно значе-
значения.

1. Производная явной функции
113
3. Переменная х получает приращение Ах в точке ж0, т. е. Ах — щ,— #л». йвредечить
приращение Д/(жо), если:
a) f (*) = (*, sinx, О; 6)f(*)=2TZ+i4=i;'' в) /(х)
¦^ Согласно определению 2, п. 1.1, имеем:
a) Af (xo) = f (ж) — f (хо) = (х — хо, sin a; — sin жо, ех — ех°) =
ж, 2 sin cos ( xq + ^-
'-О'
б)
/(.о) = ^ -
4Дг
ж" \i\x
sh°X0
¦Да;) D-жо)D-а;о-Да;)'
In ?о^ _ /^ а;" - хо In ^"
sh а; — sh жо О
In
>sh^ch(:ro + ^)
4. Найти /'A), если:
a) f(x) = (х — 1) arcsin
б) f (x) = (arctga;, 2х, In ж);
г) /(а;) =
tgx arcsm (ж — 1)
Используя определение 3, п. 1.1, получаем:
а) /'(!)= Иш
б) f'(l) = д1™0
в) /'A) = д1иао
Дж
Ах
= - sin 1 + г;
4
г) /'A)= lim ^
(l + Да;) - tgl arcsin
Следующий пример показывает, насколько важно произвольное стремление Дет к нулю в опреде-
определении производной.
5. Доказать, что вектор-функция
г ( ¦ и \ -
i : х Н-+ I a: sin a;, V'la;). e
ж sin -, х ф О,
, i \ I х sin , 1 f (J, ,. „
где ф(х) = <. 1 не имеет производной в точке х = 0.
I U, X — U,
¦^ Для того чтобы вектор-функция имела конечную производную, необходимо и доста-
достаточно, чтобы каждая компонента ее имела конечную производную. Покажем, что функция ф
не имеет производной в точке х = 0.
По определению 3, п. 1.1, имеем
™'{0) = lim sin -—.
Если взять Да; = тт >¦ 0, к —*• ос, к ? N, то sin -г— = sin 2fcx = 0. Если же Ах — , „. , то
при А; —> ос sin -г~ —> 1. Таким образом, производная ф'(й) не существует. >

114 Гл. 2. Дифференциальное исчисление функций одной переменной
¦ Найти производные следующих функций:
6. f(i) = |'\/h"j-2 \/3 + х\ sin(cos2(sin34x5)), e~4;c3j.
¦^ Каждая компонента лектор -функции имеет конечную производную, поэтому, согласно
пункту 1.6, находим
fix) =
'(х) = ((\Л+ ** \Д+ *Л")' . («« (cos2(sin3 4х5)))', (е)') =
-^=L.= \Д + х;! + л/2 + г? —— Х - cos (cos2 (sin3 4х6)) x
\/2 <- .г2 (л/3 + х3J
х sinBsin3 4х' ) • 60 sin2 4x -cos4x -х , — 12х
7. /(г) = sm(cos r J -|- ;ros(siu r).
¦^ Согласно пункту 1.7, имеем
/ (г) == I sin(cos .(;)) + j(cos(sin x)) = — sin x cos(cos х) — г cos x sm(sm x). >
sin 2x cos2i
sh:(x <-|ь!х
¦^ Пользуясь пунктом i.0, находим
,, ^ (sm 2^)' (cos2x)' \ _ ( 2cos2x -2 sin 2a;
¦' •' ^ (нЬ .Ь-)' (th3x)' J ~ \ 3ch3x 3sh3x
9. Найти проилг.однуи> от лектор—функции
f : х i~- ! arcsin -j—j, [x]sin2 -кх ) .
•4 При \r\ > ! п r ./. 4. /t g 1,,
f'(x) = I I arcspi --¦ j {[:t-lsiii* -,r,tV j =
' -==== | ¦-¦: j , ([x])'sin27rx + THsm25rx = ( — 5r[x]sin
При |x| > i их = /„¦, /,¦ g Ж, рассматриваем левую и правую производные функции
у : х у-* [х] sin 1гз . Имеем, но определению 4, п. 1.1,
/ -,, .. [/[sin2™ ,. [k + h]K2h2
У±{к) = luu —¦ ; = hill r = 0.
х— к±0 Т — Д.' h—*±0 Л
Поскольку у'{к} — тг[А'] sui 2тгА- — (I, то ?/(х) = 7r[x]sin25rx при всех х. Следовательно,
/'{.<;) --г ( Д=, тг[х] sin 2жх) , |х| > 1. >
10. Найти производную or матричной функции
«п(х) а12(х)
¦^ ' Х h у '»2l(Xj A22(X
где
arctg х при |х| ^ 1,
~ sgn х -Ь ^— при |х| > 1,
/ , / ч J x'c~x при |х| ^ 1
«12(xj = «21 (Х) = < j 1
L ; при|х| > 1,
а22(з;) = \х\.

§ 1. Производная явной функции 115
Сначала вычисляем производные от элементов данной матрицы. При \х\ ф 1'и-х ф О
1
1
а[1(х)={ [
при \х\ < 1,
при \х\ > 1,
= sgnz.
Далее ищем односторонние производные функций aij(x) в точках х = 1, х = — 1 их = 0:
+0
оп_(-1) = Inn
/i—* —О
о'п_A) = lim
Л — -0
arct8 A
Oi2-(—1) = lim
— = - lim r((l-2ft + ft2)(l+2/»-,
e Л-.+0 ft
- 1) = 0..
+ v * />-+o h
Аналогично находим a[2±{^) = 0, a'22±@) = ±1. Таким образом, окончательно получаем
^ 2xe-*\l-x*) ^
2\
'2*е-* (I-*2
0 Sgll ?
sgnx
при 0 < |х| < 1,
при|х| > 1;
i 0
О
/
Поскольку an_( —1) = +оо, то конечной производной матричная функция в точке х = —1 не
имеет. В точке х = 1 выполняется равенство /+A) = /1A), поэтому /'A) = /+A) = /1A)-
В точке х = 0 односторонние производные, хотя и существуют, но не равны между собой,
поэтому /'@) не существует. >
11. Доказать, что если функции a.ij = aij(x), г, j = 1, п, имеют конечные производные,
то производную от определителя D (ж) = det (a,-j(a;)) можно найти по одной из формул:
ац(х) oi2 (а;) ... ащ(х)
D'(x) =
... (l2n(x)
<*nl(*) <«»2(x)
-E
х) «12(ж)
a2i(z) «2г(ж) ...
... апп(х)
Поскольку по определению определителя
ап{х) ... ащ(х)
О22(х) ... Я2п(х)
am (ж) оп2(а;) ... а„„(х)
on (ж) ... "u.(x) ... а1„(х)
021C;) ...
... а'пк(х) '... апп(?)
A)
'B)
ani{x) an2(x) ... ann(x)

116 Гл. 2. Дифференциальное исчисление функций одной переменной
где s — Число инверсий в перестановке [ii, »2, ..., гп], то
-D'(x) =
~^Уа'ч1ач2 ¦ ¦ ¦ "'•" +
•' a'»n + ¦ • • +
an
«21
f
Cti2 ... din
&12 . • • tl2n
пп2 пп?
+
Ли
021
0
0l2 ¦
022 •
/
. . Oln
. . dnn
+ ...+
On
• • • <*(nn =
а1п
021 Я22 • • • «2ti
т. е. получаем формулу B).
Аналогично, исходя из представления
D (х) =
получаем формулу A). >
Приведем примеры вычисления производной функции в точке и ее окрестности.
12. Показать, что функция
/ : х
имеет разрывную производную.
¦^ При х ф 0 элементы данной матрицы имеют конечные производные, которые вычисля-
вычисляются по правилам пунктов 1.2 и 1.3. Поэтому по правилам пункта 1.6 при х ф О
2х sin cos - 1
х х
О 2хех'
x2
0
0
sin -
X
0
о А
1 •
x \
e"' )
x =
o,
o,
/':*
В точке х = 0 по определению 3, п. 1.1, имеем
1 2 • 1
Л sin r
«и @) = lim
/i—о Л
где
Таким образом,
= 0, о'12@) = 1, а21@) = 0, а22@) = 0,
( 2 • 1 _? л
у ч I X S1I1 —, X f U,
аи W ~ | о х х — {)
ai2{x)-x, o2i(a;) = 0, a22(x) = e* .
2х sin i — cos - 1
О 1
О О
= 0.
Исследуем теперь на непрерывность матричную функцию tp. При х ф 0 элементы ее —
элементарные функции, поэтому по известной теореме функция <р непрерывна при х ф 0.
Далее, рассматриваем
2х sin — — cos — 1
*0 2хех'
lim ф(х) = lim
Поскольку
lim ( 2 х sin cos —
а.-»0 \ Ж X

; 1. Производная явной функции
117
не существует, то lim <p(x) также не существует. Следовательно, функция (д разрывна в точке
х = 0. >
13. При каком условии функция
f:x^\x\nsm-^, хфО, и /@) = 0, то > 0,
\х\
имеет: а) ограниченную производную в окрестности начала координат; б) неограниченную
производную в этой окрестности?
а) При х ф 0 производная находится по правилу 2), п. 1.2:
1
f':x~ n\
п\х\п sgn x • sin
i in—m — 1
m\x\ Sgn X ¦ COS ¦
(а)
\х\™ \х\
При х = 0 функция х н-> sin щ^- производной не имеет, поэтому указанное выше правило
применить нельзя. Использовав определение 3, п. 1.1, находим, что
|A|"sin '
/'@) = lim
h—+0
h
= lim
w
sgn Л
существует только при и > 1 и равна нулю. Следовательно, производная существует в окрест-
окрестности начала координат при и > 1. Очевидно, она ограничена при п — т — 1 ^ 0, т. е. при
н Js 1 + т.
б) Как видим по (а), производная будет неограниченной, если и — 1 < 0 или п — т — 1 < 0,
откуда н < 1 или и < 1 + ш, т. е. достаточно, чтобы выполнялось неравенство п < 1 + т.
С другой стороны, для существования /'@) необходимо иметь п > 1. Таким образом, если
1 < п < т, то / является неограниченной в рассматриваемой окрестности. >
14. Показать, что функция
0,
*# 0,
х = 0,
в любой окрестности начала координат имеет точки, в которых конечная производная не
существует, но имеет конечную производную в точке % = 0.
¦^ Функция х ь^ х2 имеет производную всюду. Функция х ь-> cos ^ I имеет производную
всюду, за исключением точек х = 0 и х = Хк = гт—г, к ? Z. Поэтому производную функции
/ при х ф 0 и х ф Xk можно найти как производную от произведения х cos — . В точках же
х = 0 и х = х.к производную / вычисляем, используя определения 3 и 4, п. 1.1. Поскольку
^ = h cos - |, то
/'@) = lim h
т. е. / имеет производную в точке х = 0. Далее,
= 0,
—?—) = lim -
2k+ 1/ i,^±o h
2
2 А: 4
im
-1
1
h
+ »)
cos
2
/
{
7TBJfc + 1)
2 + 0
k + l)
lim —
Bi + IJ /.-±o
т. е. производная f'(xk) не существует. Поскольку Ve > 0 3 к ? Z : |а;^| < е, то в любой
е-окрестностн начала координат имеются точки, в которых производная не существует. >
15. Показать, что функция
f:x
0,
ж ?
а; ?
имеет производную лишь в точках х^ = ктг, к ?

118
Гл. 'I. Дифференциальное исчисление функций одной переменной
¦^ В точках х ф г): функция / разрывна, поэтому не может иметь производной при х ф
Далее, в точках г, — :гк по определению 3, п. 1.1, имеем
Если хк + h е с,)), то /(.г* + /г) = кт2(.гч- 4- /г) = sin2 k и ]im
/1 — 0
= lim ^i^ = 0. Если же
Л
+ ft ? КУО1, то /(it + /t) = !) )i Hin ii?t±Zll = о. Таким образом, f'(xk) = 0. >
Для функции / nainn левую /1 п правую f'+ производные, если:
16. f :j ^ ([..¦] sin ir.t, -'--Tb/-(i,nf@) = @,0).
¦^ По определешпо ), к. 1.1, f'± : x к- (//±(ж), /^(ж)). Поскольку при х ф к, к g Z,
существует /[{г) — тгГг] cos 7Г.с. то /i'|.(x) = /i_(^j = ir[x] cos 7ГЖ при ? ^ А;. Аналогично при
x ф 0
—, поэтому /2+(г) = /2_(i) = /2B;) при ж ^ 0.
Далее вычш .чяом j[r\k) ;i /^(O). Имеем
,. J J.i л, -j- if. i
н—±0
откуда
откуда
Таким образом.
fl<»)= Urn M^MO)=lim _!
1 >
1 + eft
- \ w[x]c.oswx,
1
ex
+ e*
если x ф к, к
Г[{к)= \{-1)кктг,
l +
1 + e
если к ф 0. Если /.- —
r;.u)-=@, о),
r, 1). >
17. /:.^- ч/l -f-'--'.
¦^ Функция ," : и >-- \/ч. имеет конечную производную при и > 0. Функция ф : х н->
а = 1 — е~' имн'1 И(юнзводнук> при всех ж. Поэтому, если ж ф 0, то функция / имеет
производную и ее можно найти как производную от сложной функции. Итак, при х ф 0
имеем

§ 1. Производная явной функции
В точке х - 0 находим Д@) и /1@):
119
/±@) = lim i\/l -е- = lim ^
i.J-14 _ V/ -I <_ —— 11111 _
/.—±o h /«—±o Л
18. Показать, что функция
arcsin x~ 1 / ~
SUl — , I/O,
o, x 1 = 0,
непрерывна в точке х = 0, но не имеет в этой точке ни левой, ни правой производной.
•^ Поскольку lim ( arcsl" sin i ) = 0, /@) = 0, то по определению непрерывности в точке
h—'0 \ /
функция / непрерывна в нуле. Далее,
f(h) - /@) ,. arcsin Л2 . 1
- ' —)l-j- = lim — sm —.
ft л—±о h2 ft
Если h = hk = тт.— и к —> ±oo, то lim —rj—-sin j— = 0; если же h = hk = „, _. пи и
arcsin lit j
fc —> ±OO, TO illll 2 SUl -.— = 1.
A: —±oo hk hk
(Следовательно, односторонние производные не существуют. >
19. Найти в расширенном смысле производные fL(xo) и f\.(xo) в точках разрыва хо
функции /, если:
а) / : ж
,3ч
; б) / : х н-> sgn (а; - а; ).
а) г-о — 0 — точка разрыва первого рода. Сначала найдем /(±0). Имеем
/(±0)= li
л
lim
л—±о я
Далее, согласно определению 4, п. 1.1,
/±@) = hm
= hm
/i—±o
Л2
= lim
lim
л-.±о h
+ ft-i ,. vT+ft-i ,. ft ,i
-г— = inn ¦ lim —r = ±-.
|ft| h-r±0 ft h-»±0 |ft| 2
6) xi = 0, ,г-2,з = ±1 — точки разрыва. Находим:
/(±0) = lim sgn ft(l - ft2) = ±1,
/A ± 0) = hHin sgn (A + ft)(l - A + ftJ)) =
('огласно определению 4, п. 1.1, получаем
/i@) = Inn 5
= Um f
h —±0
ft h-±o ft
= Km sgn_(-2ft-3ft2-ft3)±1 = Hm Ti±
h —±0 ft ft —±0 ft
Л —±0
нш
h->±0 ft
20. Может ли функция / в точке ее разрыва иметь конечную производную, бесконечную
производную:

120
Гл. 2. Дифференциальное исчисление функций одной переменной
¦^ Известно, что функция, имеющая конечную производную в некоторой точке, обязатель-
обязательно непрерывна в ней. Следовательно, в точке разрыва конечной производной функция иметь
не может.
Что же касается бесконечной производной, то, как показывают примеры, ответ положи-
положителен.
Действительно, взяв f(x) = sgn х при х = 0, имеем
/1@) = lim
lim ^
__o ft
цш I = +оо>
и—о h
= Urn
Urn
л-+о h
ljm I = +оо. >
ft-+o h
21. Можно ли утверждать, что сумма F(x) = f(x) + д(х) не имеет производной в точке
х = хо, если: а) функция / имеет производную в точке хо, а функция д не имеет производной
в точке хо', б) обе функции / и д не имеют производной в точке xq!
¦^ а) Исходя из определения 3, п. 1.1, имеем
Пхо) = 1Ш1
(D
p = кш (^ + Р)
h—o \ h h J
Пусть производная функции / в точке хо существует, а производная функции д не су-
существует. Тогда lim —li??l = f'(xo), lim —у°' не существует. Следовательно, предел в A),
как легко установить от противного, не существует, т. е. производная F'(xo) не существует.
б) В некоторых случаях производная F'(xo) может существовать несмотря на то, что обе
функции / и д ее не имеют. Например, если F(x) = ф(х) + {<р(х) — ф(х)), где if имеет
Производную в точке Хо, а V' не имеет. >
22. Можно ли утверждать, что произведение F(ж) = f{x)g(x) не имеет производной в
точке х = хо, если: а) функция / имеет производную в точке хо, а функция д не имеет;
б) обе функции / и д не имеют производной в точке хо?
¦^ а) Вообще говоря, нет. По определению 3, п. 1.1, имеем
F'(xo) = lim
A)
Анализируя A), приходим, в частности, к такому выводу. Если функция д определена при
|х-ю| < S F > 0), /(so) = 0,
М (М = const), то F'(xo) существует. Например,
если f(x) = х, д(х) = [х\, х0 = 0, то F'@) = 0.
б) Если пределы lim
ло
; °'
и lim
л—о
не существуют, но выполняются, например, усло-
д(хо) = О,
Ag(xo)
h
М,
функции fug непрерывны в точке х = Хо,
то предел A) существует. Это видно на примере функций / : х >—> |х|, д : х н-> |а;|. Обе функции
не имеют производных в точке х = 0, однако их произведение f(x)g(x) = х2, очевидно, имеет
производную, равную нулю. >
23. Пусть / : Е С К —*¦ К, где множество ? имеет предельную точку а:о ? ?. Конечный
предел
lim ШМ = f'E(xo) A)
^^*D Ж — Хо
назовем производной функции f в точке хо по множеству Е.
Найти производную по множеству Е в точке хо для функции /, если:
|
а)
б) /(х) =
на ? =
¦^ а) Множество Е имеет единственную предельную точку хо = 0. Используя формулу
A), получаем
/в(so) = lim = 0.

§ 1. Производная явной функции 121
б) Любая точка из множества R является предельной для множества Q. Согласно A),
рассматриваем только те предельные точки, которые принадлежат Q. Пусть хо ? Q. Тогда
Je(xo) = lim —^^ -—- = lim = 2хо. >
х-**хо X — Хо *—**о X — Хо
(хбФ) (*6Ф)
24. Пусть a, b : R — ?п, а = (а^х), а2(х), ... , ап(х)), b = Fi(x), 62(х), ... , 6„(х)),
ж ? ]с, d[. Компоненты а,, Ь; имеют конечные производные на ]с, d[. Показать, что скалярное
произведение (а, Ь) также имеет производную и ее можно найти по формуле
(а, Ь)' = (а', Ь) + (а, Ь').
•^ По определению 3, п, 1.1, имеем
(а, Ь)' = lim i((a(*o + h), Цх0 + h)) - (а(аг0), b(x0))) =
= lim - ((а(ю + h) - a(x0), b(x0 + h)) + (a(x0), b(x0 + h) - b(i0))) =
= lim ((^Y2^-, b(*o + A)) + L(x0), Щ^-Y) = (a'(«o), b(x0)) + (a(x0), b'(x0)) .
При установлении этого результата мы воспользовались следующими утверждениями:
а) Производные а' и Ь' существуют, поскольку, по условию, существуют производные от
их компонент.
б) Скалярное произведение обладает свойством непрерывности, поэтому можно совершить
предельный переход под знаком скалярного произведения.
в) Скалярное произведение обладает однородностью, поэтому множитель ft можно вне-
внести под знак скалярного произведения.
г) Вектор-функция у непрерывна в точке хо. >
25. Пусть f :]а, Ь[—* Е, где Е — евклидово пространство. Примем, по определению, в
качестве производной функции f в точке хо ? ]а, Ь[ предел
f(xo)= lim -±-(t(xo+Ax)-t(xo)). A)
Дл-*О 1ЛХ
Показать, что если А(х), у(х) — соответственно функциональная матрица и вектор-функция,
имеющие конечные производные на ]а, Ь[, то производная А(х)у{х) вычисляется по формуле
(А(х) у(х))' = А'(х) у (*) + А(х) у'(х).
¦^ Используя определение A), имеем
(А(х)у(х))'\ _ =lim]-{A{xo+h)y{xo + h)-A(xo)y(xo)), x0 ? ]а, Ь[. B)
Поскольку существуют производные А'(хо), y'(so), то существуют пределы lim
А'(хо), lim ft" = y'l^o), и из B) предельным переходом находим
(А(х)у(х))'\ = lim ^i^ly^o + h) + lim А(хо)Щ^- = А'(хо)у{хо) + A(xo)y'(xo). >
lx-Хц ;,^Q fi h_0 fl
26. Пусть A(x) — квадратная матрица, имеющая конечную производную и обратную
матрицу А~1(х). Показать, что
(А-^х))' = -А-\х)А'(х)А-\х).
¦^ Пользуясь определением A) из примера 25, сначала устанавливаем, что для произведе-
произведения матриц А, В, имеющих конечные производные, справедлива формула
на основании которой
(А(Х)А-\х))' = А'{х)А-\х) + А{х) {АГ

122 Гл. 2. Дифференциальное исчисление функций одной переменной
Отсюда, в силу тождества А(х)А~1(х) = / (единичная матрица), следует
А'(х)А~1(х) + А(х) (А~1(х))' = 0 (нуль-матрица).
Наконец, умножив слева обе части этого равенства на А~1(х), приходим к требуемой форму-
формуле. >
27. Пусть А(т) — матрица, имеющая конечную производную. Всегда ли справедлива
формула
(Ап(х)У = пАп-1(х)А'(х), пеШ A)
¦^ Уже при ге = 2 замечаем, что приведенная формула, вообще говоря, не выполняется.
В самом деле,
(А2(х))' = (А(х)А(х))' = Л'(х)А(х) + А(х)А'(х).
Отсюда также видим, что формула A) будет справедливой, если матрицы А(х) и А\х) пе-
перестановочны. Оказывается, что и в общем случае перестановочность матриц А(х), А'(х)
является достаточным условием правильности формулы A). В самом деле, поскольку в си-
лу A)
(Ап+1(х))' = (Ап(х)А(х))' = (А"(х))' А(х) + Ап(х)А'(х) = пАп-\х)А1{х)А{х) + Ап(х)А'(х) =
= пАп~\х)А(х)А'{х) + Ап(х)А'(х) = {п + \)Ап{х)А'(х),
то, в соответствии с методом математической индукции, заключаем, что формула A) спра-
справедлива Уп € N. >
28. Найти сумму I3 -f- 23 + 3я + ... + пл.
¦4 Поскольку Г3 + 23.к + 33х2 + ... + п3!71 = (xQn(x))', где
(см.: Ляшко И. И. и др. Справочное пособие по математическому анализу. К., 1978. Ч. 1, с.
220), то
I3 + 23 + З3 + ... пя = liiu (xQn(x))' = lim Qn(x) + lim Q'n{x) =
.и —1 х — 1 j;~l
„2
l)Bn-H) n(n2 -1)(Зи + 2)
6 ' 12
29. Пусть
. , . / sill их cos их \ .
A(x) = \ ¦ , и = const.
' \ — COSUX Sill ШХ I
Показать, что матрица А(х) удовлетворяет дифференциальному уравнению
А"{х) + ш2А(х) = 0, А"(х) - (А'(х))'.
¦^ Имеем
.// - ( cos от — sinL/ir \ .//. . 2 ( sin uix coscjx
А (х) = ш . ] , А (х) = —из
' \ S1I1 и)Х COS UX I У ' \ — COS WX S111 СОХ
откуда и следует указанное уравнение. >
30. Пусть Sn(x) = [ + хА+:—j (- . . . -| j—, где А — постоянная матрица. Установить
дифференциальное уравнение, которому удовлетворяет Sn(x).
¦^ Вычисляя производную, находим
Далее, умножая выражение для ,Чп(х) на А и вычитая полученное из S'n(x), имеем
S'n - ASn + ^-An+1 = 0.
и!

§ 1. Производная явной функции
Это и есть требуемое уравнение. >
Упражнения для самостоятельной работы
Найти производные следующих функций:
-, /• 5.1 1 — 1 I Ь s
123 i
2. /: х>->4\/л/х~+2-1 -2л/2 arctg
3. /:a:_>l
4.
1
*i г- г!
е 2 +л/2е 4 +1 , 1
8>/2 ?i ,- *i
е 2 — -у/2 е 4+1
5. /ни arctg -v/cos 2г — -v/cos 2z.
15.
л/2е 2
<2х. 6. / : х I—> sin2 (w cos ax) + cos2(o;sm ax).
-; 7 . 9. / : x i—> arcsm (cos иг- + sin nz).
ch a^+cos ax J \ ' /
sm(arcsin ax + arccosax). 11. / : t н isina(/?x + 7).
14. / : x 1— ctg(otg(fearctg(cx))).
16. f : x^ e-'2si«(-^). 17. f : x ^1п"Aп(>Ппса;)
18. f:xi->xsinx + (sinx)x. 19. f : x ^ x*** . 20. / :
Найти производные следующих вектор-функций:
21. f : х 1—> (arccos i, arcsin (sin г), sin и(г), cos «(г)) .
22. f : x >
23. f : жн+ Btac, 3t-i3, sin wt, cosujz:). 24. i:
25. f : уз и-> (p(ip) sin 9s, /o(y) cos уз, уз2 — яуз, уз3 — ?2уз) .
26. f : р к- (/>smy3(p), pcosip(p), <p2(p) - xip(p), уз3(р2) - х2уз(р2)).
27. f:ib Csin(e2a), esi x, ip{sm2 x), p(cos2
eatcosi, eQtsint, и G) , u(sint)).
28. f:x^
29. f:In
30. a) f :х
), arctg ;
)), /з (sin и (»(!
6) f : x ^ (i|/(
V
31. На кривой найти точки, в которых касательная к лей коллинеарна указанному век-
вектору, а кривая описывается следующим радиусом-вектором (к евклидовом конечномерном
пространстве Е):
а) f : X ь^ Ccos«, 4sin«, Щ, 0 ^ < < 2тт, а = @, 4, 5);
б) f : < >-+ (t, t2, t3), 0 ^ * < 4, a = B, 4, 6);
в) f : t \-> (e/, t~\ sht), -00 < < < +00, a = A, -1, 0).
32. Найти величину скорости движения материальной точки по кривой, если радиус-
вектор ее имеет вид:
a) f (t) = (sin t, 3cost) в момент t = ж; 6) f (<) = (sint^, 3cost2) в момент t = ¦>/?;
в) f (t) = (sin -, cos i, -) в момент t — -.
33. На данных траекториях найти точки покоя, если траектории описываются следующи-
следующими вектор-функциями:
a) f :*ь-+ (sm^z), cos(ta), cht); 6) f : 11-* t\i2 +A - x)t, It1 -xt+\, — + x2t - \7x);
в) f : 11-* (xt + 2t2 + U, 2xt + \t2 - 4t+ З) .
34. Показать, что траектории, которые описываются следующими вектор-функциями,
ортогональны:
a) fi : t t—*¦ (t sin t, t cos t, 1) и f2 : i *-* (i cos <, — t sin t, 2);

124 Гл. 2. Дифференциальное исчисление функций одной переменной
6)f1:f^(i|/1(f)|)M2(f), u\t)) и f2:t-> (^, -f,
35. Найти кинетическую энергию системы материальных точек с массами тк, движу-
движущихся по следующим траекториям:
а) ffc : t у-* I ^-, sin a;t, coswt 1 (A; = 1, n; rrik — 1);
б) ffc : < i—>• (arcsin (sin kt), arccos (cos&f)) (k = 1, n; rrik = &p).
36. Найти производные следующих комплекснозначных функций:
a) / : 2 н-> 2 In 2 + ге х ; б) / : t и е'
в) / : x н-+ cos2 (ж + г23); г) / : 2 ь-> In
Найти производные следующих матричных функций:
'Sl,22 Cl,22 >| qe f,_( ^
th22 Ctll22
с(соз«2-(-«sin «ж);
2
37. / : x '
39. / : x i
41. / : x i
42. / : a; i
2 I
COSuM
Sill LOX
X
Sinx(sinr 2) lll^ln* 2)
arccos (arctg (arsli xx)) 1 \x — \x\\
tilu . . . ti(x)) , ,".,;. > ln(u(x)\nu(x)
О
ln |cos f
Вычислить производные функций / по множеству, если:
43. f(x) = е*2 при х = ^, н 6 N.
44. /(г) = sin 2ж при а: е ?',?'={ 1, |, \, \, \, \,...}.
45. /B;) = г1пA+23) при хеЕ, Е= {l, л/2, |, ^3, f, ^4, ... } .
46. /(*) = ^ при а: е ?, Е = Q.
47. Пусть а = л(х), Ъ = Ь(х), с = с(х) — вектор-функции (а(х), Ь(х),
имеющие конечные производные. Доказать, что:
а) [&(х), Ъ(х)]' = [а'(г), b(*)] + [а(х), Ь'(*)];
б) (л(х)Ъ(х)ф))' = (&'(х)Ъ(х)с(х)) + (&(х)Ъ'(х)с(х)) + (&(х)Ъ(х)с'(х)).
48. Найти производные от следующих определителей:
а)
6 Е3),
г)
; 6)
X
X
X
2
3
22
23
x"
x3
x4
xb
; в)
e
2a;
e
e31
e
3 a;
4x
e
e
e
sin г sin 2г sin За- sin 4г
sin 2x sin Зг sin Ax sin 5г
sin Зг sin 4x sin 5x sin 62
sin 4x sin 5г sin 62 sin 7x
49. Пусть A(x), B(x) — функциональные матрицы, имеющие конечные производные.
Показать, что
(det (ЛB)ВB)))' = (det А(х))' det В(х) + det A(x) (det ВB))' .
Найти производные функций /, если:
l2 7T2 X ? (Q),
х е R\(Q).
sill2 7T2,
U,
50. /B) =
51. a) f(x) = inf {cos^}; 6) f(x) = sup
53. a) /B) = ^(^B)); 6) /B) = <р(ф(х)); в)
с, если |г| ^ 1,
$}. 52. /(a:) = cos~ lim a;2"
= V(y(^)); г) /(г) = Ф(Ф(х)), где
если |2| > 1,
ф(х) =
1,
если 0 ^ х < +оо,
если — оо < 2 < 0.

§ 1. Производная явной функции 125
54. f(x) = Нш Y[ chp"- 55. a) f(x)— lim Ё m arctg J^Z^jfji
П , ,4. П-1
o) f(xj = lim || I 1 + sm —3- I; в) }\x) = lim 2_, sln (—г % ) ¦
Вычислить правую и левую производные следующих функций:
56. а) /:ги^(-), где ip(t) — расстояние до ближайшего целого числа;
6)/:ih min(tg x, 2 - sin 2ж), -| < г < \\ в) / : х н+ тахD|1|-1, а;2).
57. /:ги [г2]| smira;2|. 58. а) / : х ь+ ^-j—, 2; ^ 1, /A) = 1;
= (>.
59. а) / : х н-, lim exsln ' ; б) / : х ^ lim e
t — 00 t-»oo
Г 3
60. /:ги Ы[х], г ^ 1. 61. / : х ^ < lsm7ra;l2. ^ € Q,
(о, хе
62. Найти f'-(xo) и /4(хо) в точках разрыва х0 функции /, если:
63. При каком условии функция
f : х ^ \хBа [\х\2?} , хфй, и /@) = 0
имеет конечную производную при х = О?
64. Пусть
/*(*) = ЕШ*С>'A-*)"-, ^ен.
1 = 0
Вывести рекуррентное соотношение для функций fk ¦
65. Найти числа Дини
V±f(x) = 1h^-ul±hkzm.t V±f(x)= lim
Л—±0 " л^±о
для функций:
66. Найти -ОгоС11); если
Указание. Функцию Dk искать в виде
где A, a, b — функции, подлежащие определению.
Вычислить производные функций /, если:
60. /:»«| + H»-W- 5)A-2|»-И-;|).
70. Доказать, что множество точек, где функция / имеет неравные правую и левую
производные, не более чем счетно.
71. Показать на примерах, что в общем случае
f'+(x0) Ф f'(x0 + 0) и f!_(x0) ф /'(so - 0).

126 Гл. 2. Дифференциальное исчисление функций одной переменной
72. Можно ли утверждать, что если }'\хо + 0) — f'(xo — 0), то функция / непрерывна в
точке х0?
73. Производная для последовательности (хп) определяется по формуле
i,, = in+i — хп, п € N.
Найти:
а) (*„»„)'; б) Aп*„)'; в) (г-)'; г) (*„ + »„)'; д) (?(*„))'; e) (^)';ж) B")';
з) (sin»2)'; и) (arctgn)'.
74. Написать уравнекие касательной к кривой, радиус-вектор которой
а) f (t) = (sint, cost, 4t), в точке М (~, ~, тг) ;
б) f (t) - (arctgt2, arcsint, sht, cht), в точке М@, 0, 0, 1).
75. Написать уравнение нормальной плоскости к кривой, радиус-вектор которой
a) f (t) = (t, t2, <3), в точке МA, 1, 1);
6) f (t)= ^—T, ln|/(t)|, at2, tcht, sht при t- 1, где a = W%- - e~2 -1.
76. Найти угол между кривыми в точке их пересечения, если радиусы-векторы кривых
fi(t) и f2(t) описываются формулами:
а) f:(t) = (e~2t, -щ-, tht), f2(t) = (t + 1, sin3t, tesht);
б) fi(t) = (t, t2, t3, t4, ts), f2(t) = (sint, sin 2t, sin 3t, sin4t, sin5t).
77. Показать, что вектор-функция X : 11—> (sin t, — cos t, e~t)T удовлетворяет уравнению
где
78. Подобрать вектор-функцию f так, чтобы вектор-функция X : t >—> (t, t2, t3) удовле-
удовлетворяла уравнению
/ -2t 2 t~3 \
X'(t) = A(t)X{t)+f(t), где А(г)=[ 0 -t 1 .
V t-1 о о /
79. Показать, что вектор-функция X : t н-> diag A(t) удовлетворяет уравнению
где
sin t cos t \ fd\ — f cos ^ + cos ^^
sin t — cos t J ' \ sin t — 1
80. Убедиться, что комплекснозначные функции
х2 + 3i
/ни cos \x + г sin Аг и / : а; н^ —5 т
ж'1 — лг
соответственно удовлетворяют уравнениям:
a) f'(x)-i\f(x) = O; б) (x2 + 3i)f'(x) + 12xif2(x) = 0.
81. Найти производные от собственных чисел матрицы A(t), если:
ч .,.. / t t2 ^ .. ., , /sht cht
a) A(t) = , ,4 ; б) АИ) =
' w у <3 t4 у ' I \ ) у _ch( sht
/ 1 t t2 \ /sint cost 0
в) A(t) = ( t t2 t3 I ; r) A(t) = I -cost sint -1
/ V 0 1 t

§ 2. Дифференциал функции 12?!
82. Найти угол между предельными положениями касательных в точке перелома непре-
непрерывной кривой, описываемой вектор-функцией:
> „ , / . irt к b ,,\ ,\ j. ^ ( (t, i2 + 1. ^ + 1. <4 + 1) Ч\ пРи — оо < t ^ О,
а) I :4н> (sin -т-, cos —, t — 1 ); б) I : t *-> [ v . 2t 3t <un ,-, ^ , , ,
y V 2 > 2 ' i/> / у Bt, e , с , f ) у при 0 <t< +oo.
§ 2. Дифференциал функции
2.1. Основные определения.
Определение 1. Функция f : Е —> К называется дифференцируемой в точке хо g ?,
предельной для множества Е, если ее приращение Д/(жо), соответствующее приращению
аргумента х, может быть представлено в виде
Af(x0) = А(хо)(х - хо) + и(х - хо), A)
где и)(х — х0) = о (х — хо) npti х —+ хо ¦
Определение 2. Отображение d : h ь-> Л(з;о)Л, Л € К, называется дифференциалом
функции f в точке, хо, а величина ^(lo)'* — значением дифференциала в этой точке.
Для значения дифференциала функции / принято обозначение df или df(xo), если тре--
буется знать, в какой именно точке он вычислен. Таким образом,
df(xo) = A(xo)h.
Разделив в A) на х — х$ и устремив х к xq, получим А(хо) = / (i'o). Поэтому \/Л € К
имеем
d/(x0) = f'(xo)h. B)
Сопоставив A) и B), видим, что значение дифференциала df(xo) (при f'(xo) ф 0) есть главная
часть приращения функции / в точке Хо, линейная и однородная в то же время относительно
приращения h = х — хо-
2.2. Критерий дифференцируемости функции.
Для того чтобы функция / являлась дифференцируемой в данной точке хо, необходимо
и достаточно, чтобы она имела в этой точке конечную производную.
2.3. Инвариантность формы первого дифференциала.
Если х — независимая переменная, то dx = х — хо (фиксированное приращение). В этом
случае имеем
Если х = tp(t) — дифференцируемая функция, то dx = <p'(to)dt. Следовательно,
df{<p{to)) = (/(p(to)))'t dt = f'x(<p{to))<p't{to) dt = f'(xo)dx,
т. е. первый дифференциал обладает свойством инвариантности относительно замены аргу-
аргумента.
2.4. Формула малых приращений.
Подставив B) в A) и отбросив ш(х — хо), получаем формулу малых приращений:,
; df(xo)
f'(xo)(x - хо), D)
позволяющую при малых значениях х — хо приближенно вычислять значения функции / в
точках х, близких к точке x.q, где значения функции / и ее производной известны.

128 Гл. 2. Дифференциальное исчисление функций одной переменной
2.5. Правила дифференцирования функций.
Если скалярные функции и и v дифференцируемы, то:
a) d(u ± v¦) = du ± rfu; б) d(uv) = и dv + v du;
B)rfЫ = —^—- v^°> r) rf(/(«)) = /(«)<*«•
Если вектор-функции и и v дифференцируемы, то:
a) cf(u± v) = rfuirfv; 6) rf(u, v) = (^u. v) + (u, rfv);
в) rf(Au) = urfA + Arfu (A — скалярная функция).
Если и и v — скалярные дифференцируемые функции, то
d{u ± iv) = du ± г dv, г = —1.
Если А, В — дифференцируемые матричные функции, и — дифференцируемая вектор-
функция, то:
a) d(A±B) = dA±dB\ 6) d(Au) = (<L4)u + Adu; в) d(AB) = (dA)B + AdB.
Дифференцируемы ли функции /, если:
3.1. Af(x0) = Ч sin(x -xo) + (Z/l + (x- x0J - 1) ф(х -жо),где
Так как существует конечный предел
x-*xa X — Xo j;-*x,, I X — Xo X — Xo I
ln\h\
то функция / дифференцируема в точке Хо и df(x0) = 2dx. >
32.
¦^ Поскольку
Д/Yl) / - — i'
lim v ; = lim j (г - 1K + (г - 1) з ) = oo,
x — l X — 1 ;c-»l у
то функция / не дифференцируема в точке х = 1. >
33. Aflxo) = (sin —-—
>) (
\ X — Хо
¦А Рассмотрим предел
Af(xo) Л. 1пA + (^а;о)) . 1 ..
lim ^—'-= lim —^ i ^-^-sm , Inn
X X' X Х X X
i—j.u Ж — Хо \х-*х0 X — Хо X — Хо х-^х0 X — Хо
Поскольку
1пA + (г - хоJ) А ,. е1^0 - 1
lim — '— = 0, lim = 1,
то существует конечная производная вектор-функция f:
f'(z0) = @, 1).
Следовательно, вектор-функция f дифференцируема и
<Zf (го) = @, \)dx = @, dx).>
1
34.
arcsm I е (х~хо)~ I |г — хо|3 + х — Хо
х — Хо 2 s

§ 2. Дифференциал функции 129
¦^ Вычислив пределы
л х_ i_ /|Л,Р \ / 1\
lim — arcsin е л.2 = lim е л2 ft," = 0, lim ( ^—|-1 I = 1, lim ftsgn (tg у- } =0.
h—*0 II h—*0 h—t-0 V R / h—t-0 \ ft/ '
lim — I . j = lim ( —p— J lim ( Ift-I^2 sgnft 1 = 0,
получим
, Д/(жо) _ ( О 1
т. е. матричная функция / дифференцируема в точке хо, и
О 1 \ , _ ( 0 dx
\ / \
Найти:
2 / 1 \
35. a) d(xex ); б) d I arcsin т—г I .
¦^ 1-й способ. Согласно определению 2, п. 2.1, находим
a) d(xe/2) = (if *2)' dx = ех2 Bж2 + 1) dx;
= f arcsin щ ) dx = , ' .
2-й способ, а) Согласно формул б), п. 2.5, имеем
По формуле г), п. 2.5, d(ex ) = ех d(x2) = e* 2xdx. Таким образом,
d(xe^) = в** dx + 2х2ех* dx = ех*Bх2 + 1) d*.
б) Пользуясь формулой г), п. 2.5, имеем
d ^arcsin pj = (arcsin и)'rb, и = Щ. ^и = ^ (^J
поэтому окончательно
d I arcsin т—г I =
V \х\
36. d(uv~2).
•^ По правилу дифференцирования дроби (см. в), п. 2.5), находим
. { и \ v2du — ud(v2) du 2udv
d — = т—i—'- = — r—, v ф 0. >
\v21 vi v2 v3
37. d I arctg — j .
¦^ Используя формулы в) и г), п. 2.5, имеем
v du — и dv
л I и\ 1
d I arctg — I = —•
Л Поскольку
Л.)-^«.)-^. О)
где и — дифференцируемая функция некоторой переменной, то данные примеры можно ре-
решить двумя способами.

130
Гл. 2. Дифференциальное исчислеиие функций одной переменной
а) Обозначая и = х' и пользуясь первым равенством A), имеем
-r/r-(z3 - 2х6 - хэ) = 4-(и - 2и2 - и3) = (и - 2и2 - и3)' = 1 - 4м - Зи2 = 1 - Ах3 - Зхв, х ф 0.
а(хл) аи
Такой же результат можно получить, пользуясь вторым равенством A):
б) Вводя обозначение и = х2 и используя первое равенство A), имеем
d fsu\x\__ d /sm-v/мЛ /sin-v/a\ _ -v/mcos -v/m — sin -v/м _ xcos i — sin x
~/ ~ dZ V~W = V~W = W^ ~ ^3 '
Если же воспользуемся вторым равенством A), то получим
а
d(x2)
cos Л-— sin х
х cos x — sin a;
2xdx
39. Заменяя приращение функции дифференциалом, найти приближенно sin 29°.
¦^ Значение sin 29° относительно мало отличается от sin 30°, так как и а = 29° отно-
относительно мало отличается от «о = 30°. Поэтому для приближенного вычисления sin 29°
воспользуемся формулой D), п. 2.4, взяв f(x) =sma:. Тогда получим
sin 29° и sin — — (sin x)'
Х=И 180
360
= 0,484 ... . >
40. Доказать формулу у а? + х = а -\ г, а > 0, х > 0, где 0 < г < ——.
2и он
¦^ Если считать х: малым (х <С а2), то по формуле малых приращений получим
¦ х = а + —.
2а
Погрешность этой приближенной формулы
A)
2a (\/a2 + x + a) 2a (л/а2 + x + aJ
тем меньше, чем меньше а: > 0. Однако для любых х > 0 она меньше -—^ и, как следует из
A), л/а2 + х = а ¦+- ^ — г, что и требовалось доказать. >
41. Доказать приближенную формулу л/ап + х а а -| ^zfi a > 0, где \х\ <С а".
¦^ Поскольку |ас| «С а", то к функции f : у *-* л/1 + г/, где t/ = -^, эффективно применима
формула малых приращений:
откуда
на основании чего
— И a fl + -i-
42. Найти df(x), если:
a) f (г) = I е -1 , sin(«z: ), cos(az: ), sli ( = j J ; 6) f(x) = e ;
r) f(x) =
arcsin (te4) arctg x2
1
'У>- x*+3ix + 4i + 5' '; ¦"">- \ 0
Используя формулу df(x) — /'(ac)rfac, имеем:
2
5l/'@)|2* sin ал:

а) df(x) = [~3kx2e-
б) df(x) = (cos(a>z2) ¦
§ 2. Дифференциал функции
, 2ах cos(ax2), -4ах3 я'ш(ах*), ± ch (j;
131
(— sm(a:r2) + icos(ax2)) dx;
Г) (*/(*) =
/l-t8x<>
0
i|/'@)|2*ln2
dx.
Под \А\, A — (aij), понимаем величину
\A\ =
Поскольку
/'(и) =
О ^|/'(
, то |/'@)| =
In2 2,
откуда |/'@)| =
= . Таким образом,
df(x) =
43. Пусть при вычислении функциональной матрицы A{i) была допущена погрешность
dA(t). Предполагая, что существует A~l(t), найти приближенно погрешность вычисления
А~ (t), которая будет соответствовать dA[i),
¦4 Поскольку A(t)A~l(t) - I, то
~l + A(d(A~1)) = 0) =
((dA)A
44. Пусть A(t) — квадратная функциональная матрица с модулем |Л| =
\
Е 4w.
где a,j — ее элементы, дифференцируемые на некотором интервале. Оценить модуль диффе-
дифференциала ее собственных чисел как функций t.
¦^ Собственные вектор-функции X и соответствующие им собственные числа А, как ска-
скалярные функции переменной t, удовлетворяют спектральному уравнению:
A)
Считая для определенности, что |X.(f)| =
на Х(<), получаем
Дифференцируя B), находим
d\ = (d(AX), X) + (АХ, dX) = ((dA)X, X) + (AdX, X) + (AX, dX),
I^'WI2 = 1> и умножая равенство A) скалярно
i
(A(t)X(t),X(t)) = \(t). B)
откуда
\(dA) X||X| + \A dX\\X\ + \AX\\dX\
\dA\\X\2
= \dA\ + 2\A\\dX\. >
45. Пусть дифференцируемая функция tp такова, что f((p(t)) = ( на [to, t{\, где / —
дифференцируемая функция и /^ не равна нулю. Найти d(p.

132
Гл. 2. Дифференциальное исчисление функций одной переменной
¦4 Поскольку функции / и ip дифференцируемы, то сложная функция / о ip также диф-
дифференцируема и
= dt)
Упражнения для самостоятельной работы
Найти дифференциалы следующих функций:
83. а) / : х н
arctg
-**
_
3;
3
б) /:i^ -arctg (Jj)a +1;
в) / : i ь* 1п(м2(г) + (г)); r)/:iH и2(\лх) + D
85. a) / : <p >-* p(<p) cosy, 6) f : tp >-* p{ip)sin(w
во. a.) j . i ь* fXt+x4 > °) J '• 1 *~* 2—t к '
в) у t x н^ cos x -\* x sin 3a? 5 rjf'.x *~*+ e
(ei e2 e3 \
и(х) v(x) w{x) ;
sin x cos x 1 /
в) f :ih (sinwii, sinw2X, ... , sin ш„х); г) f : x >-» u(x){eu^x', tgu(x), «(x));
fl)f:x^(i|/(x)|, «2(x)).
89. / : г i
91. /:i
93. f : < к
1л ¦> i. 1
90. /: ih I sgn'c e |x|
V [x] sin[x]
*+» ^2-' ). 92. /:.
sin(tx) cos(tj() /
an(t) ai2(<) • • • ain(<)
d2l(^) ^22 (^) ¦ ¦ ¦ Я2п(^)
Oml(t) Sm2(l) • • • a>mn(t)
V Xn(t)
94. Пусть f (ж) = (fi{x), h{x), ... , fn(x)), где /i, i = 1, n, — дифференцируемые функ-
функции. Найти d(\f(x)\),
95. Пусть f(x) = (aij(x)), i, j — 1, n, — дифференцируемая функциональная матрица.
Найти d(\f(x)\).
96. Приближенно вычислить:
а) sin 16°; б) arctg 100; в) arcsinO,99.
97. Показать, что при х ~^> Хо > 0
ж 1
arctgx«---.
98. Пользуясь приближенными формулами
cos х и 1 ——, sin х и х + «х3, |х| < 1,
найти коэффициент а.
Указание. Ввести в рассмотрение тождество sin х — 2 sin j cos j.

i 3. Производная обратной функции
133
Найти df(O), если:
100. /(x) = {u(x))v{x)
101. /(x) = arcsin^
ln(l+g)
= -\dx, «@) = е, v@) = l.
, «@) = l, d@) = л/2.
102.
0' 103. /(ж) =
/l+3i4-2
X = 0.
104. f(x)=[ SISSL51, Г1Л2± ) , х ^ 0, и f @) = @, 1).
1=0.
105. f (x) = (rS^ii, !=g±fi, |ф), * * 0, и f @) = (О, О, О).
106. /(*) = (
ln(i+x2eI)
,. . х#0,и/@)=( ° ° .
ч 0 x2lnx/ \Ои/
107. Пусть а*, = (o*i, оа-2, ¦¦• , акп), а* € Еп, к = 1, п, — векторы, имеющие общее
начало. Абсолютное значение определителя
аи «12 •. • a>in
О21 О22 •¦• «2п
назовем объемом фигуры Р = {х\х g Е", х — flioi + б2<»2 + ••• +б„а„, 0 ^ б; < 1, » = 1, п},
которую принято называть параллелотопом.
Найти объемы бесконечно малых параллелотопов, построенных на касательных векторах,
проведенных в точках пересечения следующих кривых:
a) fi(t) = (t, t2), fa(t) = (<3, t); 6) ft(t) = (t, t\ t3), fa(«) = (t3, <2, *), ««(*) = (sinT<, *, **);
в) fi(t) = (t, <2, t3, t4), f2(<) = (t2, t3, t\ t), fa(t) = (<3, <4, t, t2), f*(«) = (t4, t3, t\ t).
§ 3. Производная обратной функции. Производная
функции, заданной параметрически.
Производная функции, заданной в неявном
виде
3.1. Производная обратной функции.
Дифференцируемая монотонная функция / :]о, Ъ[~* К с необращающейся в нуль произ-
производной имеет обратную дифференцируемую функцию f~l, производная которой вычисляется
по формуле
3.2. Производная параметрически заданной функции.
Если функция / задана параметрически
х = <p{t), У = il>{t), a<t<0,
где у = /(х) и функции <^ и ф дифференцируемы, причем tp (t) ф 0, то

134 Гл. 2. Дифференциальное исчисление функций одной переменной
3.3. Производная неявно заданной функции.
Если у = f(x) — дифференцируемая функция, заданная уравнением F(x, у) = О, т. е.
F(x, f(x)) = 0 на некотором интервале ]а, Ь[, то во многих случаях ее производную можно
найти из уравнения
±{F(x,f(x))) = 0.
46. Показать, что существует функция у = f(x), определяемая уравнением
у — е sin у = ж, 0 ^ е < 1,
и найти производную / (х).
Ц Функция (р : у н-> х = у — е sin у — дифференцируемая на ] — оо, +оо[, и ее производная
ip : у \—> 1 — е cos у
положительна. Следовательно, функция (р, будучи строго монотонно возрастающей, имеет
обратную, также монотонно возрастающую и дифференцируемую функцию /. Ее производ-
производная
?>'(у) 1 - '
47. Определить область существования обратной функции х — 'р(у) и найти ее произ-
производную, если
у = х +\п х, х > 0.
Ц Поскольку (х +1п^)' = 1 + - > 0, то функция / : х t—> х + In x строго монотонно
возрастает при х > 0. Следовательно, она имеет обратную и
,, 1 х
При 0 < х < +оо имеем —оо < у < +оо, т. е. обратная функция существует на всей
числовой прямой. >
48. Выделить непрерывные ветви обратных функций х = р(у) и найти их производные,
если у = 2х — ?4.
¦4 Функция / : х н-> 2х2 — хА — дифференцируемая, и ее производная f':xt-+ 4x(l — х2) со-
сохраняет знак на интервалах ] —оо, —1[, ] — 1, 0[, ]0, 1[,]1, +оо[. Следовательно, на каждом из
соответствующих интервалов ] — оо, 1[, ] 0, 1[, ]0, 1[, ] — с», 1[ существует дифференцируемая
обратная функция. Обозначив через <?>;, г = 1, 4, эти функции (х = (^э; (»/)), имеем
yi :] - оо, 1[- ]-оо, -1[, ?>2 :]0, 1[-* ]-1, 0[,
V3 :]0, 1{-+]0, 1[, ^ :] - оо, 1 [ —*] 1, +оо[,
причем, судя по знаку производной
1
4х A — х2)
функции fi и </Эз монотонно возрастают, а функции у>2 и tp\ монотонно убывают. Решив
уравнение х — 2х + у ¦= 0 относительно ж, можно получить функции tpi в явном виде:
- V1 - У, х =
Найти производные f'(x), если:
49. х = Vi^Vt, у = s/i-Vt (у = /(ж)).
Ц Найдем сначала

§ 3. Производная обратной функции 135
Далее, пользуясь формулой пункта 3.2, имеем
50. y = (e'sint, e'cost, e'), х = t + t5 (y = f(z)).
Ц Поскольку dy = (ci(e'sint), d(e'cost), d{et)) = (sin t + cos t, cos t — sin t, \)eldt, б?ж =
+ 5t4)«ft, то
dy_ _ /e'(sint + cos<) e'(cos< - sin<) e' \
, . _ dy_ _ /e(
51. »/ = c:os3 t + «sin3 t, x = 2t- cost (j2 = -1; у = f(x)).
Ц Поскольку
dy — (-3cos2 tsmt+3ism2tcost)dt, dx = B + sin t) dt,
то
, . rf«/ 3sin2t ' _,t .
t — sin t 1 — cos t
sh t ch t
Имеем
1 — cost sm ( I , ,- 2\ и
, . i j at, ax = ,i A -)-1 ) at,
ch t sh t / ' v y
A—cos t sin t \
I + ?"* 1 + ? I
Найти производные /' функций f : x *-* у, заданных уравнениями:
53. х2 + 2ху — у2 = 4х.
Ц Пусть г/ = f(x) — дифференцируемое решение данного уравнения. Тогда
x2+2xf(x)-(f(x)J = 4x A)
на некотором интервале. Поскольку все члены в тождестве A) дифференцируемы, то из A)
после дифференцирования получаем
2х + 2/(х) + 2х/'(х) - 2/(х)/'(х) = 4,
откуда
2 2_
54. 13 + уз = 1.
Ц Подставив в данное уравнение дифференцируемое решение у = /(ж), получим тожде-
тождество
xf +(/(x))f = 1,
дифференцируя которое, имеем
Отсюда находим
55. Найти /'(а:), если »/ = /B:) и р = ауз (р, уз — полярные координаты).

136
Гл. 2. Дифференциальное исчисление функций одной переменной
¦4 Поскольку у = pcostp, х = psin<p, то у = apsinip, ж = aipcosip. Далее, dy = a(si
ipcostp) d<p, dx — a(cosy> — yjsin ip) dip. Отсюда, если a(cosip — tpsin ip) ф 0, находим
sin
у cos ip
J \x) — -r— — :
dx cos ip — ip sin уз
56. Найти f'i(x) и f^x), если функции /j и /г заданы неявно системой уравнений
у\ - yl + За; = 2,
¦4 Подставляя значения yi = fi{x) и yi = /2A) в данную систему уравнений, приходим
к тождествам
дифференцируя которые, получаем
/?(*№)-/а
Отсюда, если определитель
находим
(x) h(x)
1=0,
Упражнения для самостоятельной работы
108. Показать, что следующие уравнения имеют единственные действительные решения
? = /(*):
а) х = Зу + sin у2 + cos у - 1 + ^у3; б) ж = 12у5 - iOy4 + 40у3 - ЗОу2 + 15t/ + 1.
Найти одностороннюю производную функции у = fix), заданной параметрически, если:
109. х = 2t-t2, у = it - t3 , в точке t - 1.
110. х =t + З-^Т+1, у = 2t- ЮуТ+Т, в точке t = 0.
111. ж = sin2 t, у = cos2 t, в точках t = 0 и < = §-
Найти /'(ж), если у = /(а:) и:
112. arctg (ж2 + у2) - \п{ху) -1=0. 113. sin — + — + ,/ж2 + у2 = 0.
114. „^T+f, , + Ф(х + у + у2) = 1 (У> — дифференцируемая функция).
+ V' (frO = 2- 116- ^(V'(sin J/) + 2j/ - 3) - 8ж + 4 = 0.
117. arcsin VBy + ж2 + 1) = arctg (у3). 118. e~*2(y)+*2 - 4 - у2 .
Вычислить /'@), если у = f(x) и:
119. z2sini+ | sin ж = 0, х ф 0, и /@) = 0.
120. ж2arctg!+tg(x + г0- I =0, х ф0, и /@) = J.
Найти /{(ж) и /г(ж), если ?/i = /](ж), г/г = /2(г) удовлетворяют уравнениям:
ТОТ ЛУ1Х+У2 s'n х 1 ^- o|2 _i «ч|2 ™,2 1-о-о
^а±. с — 1 — X, </} "I •''1/2 ^~ "^ ¦ 1аа<
123. yi + V'(yi + 3/2) + 3/2 + sin а; = 0, У>(г/2 + з/| 4
Вычислить Д/@) и rf/@), если у — fix) и:
124. ж = t2 + |t|, у = t3 + t, At = dt = 1. 125.
126. ж = j/5 +53/.
Найти ,/'(ж), если j/ = f(x) и:
115. ф
= t* -4t2, у = ts - 5t, At = rft =
127. у = (sin*, cost, t), x = ;it + t3. 128. у = (sh2t, ch2t, tht), x = sht.
129 У = 0ШТГ- x = t + rt2. 130. г/ = е21? + в"'2, х = ^L.

§4. Производные и дифференциалы высших порядков 137
sin2t cos2t
131. у=^2 <3|.= —. 132. V=^
133. у = (sinB/2 + i2), cosB/2 + <2), t), z = 5t + t5
134. у = (V(M), *, t3), ^ = 2^(<2). 135. у = (^(t), </>(t2), ^(t3)), x =
§ 4. Производные и дифференциалы высших
порядков
4.1. Основные определения.
Определение 1. Пусть производная некоторой функции f дифференцируема. Тогда
производная от производной этой функции называется второй производной функции f и
обозначается /". Таким образом,
/"(*) = (/'(*))'¦
Определение 2. Если дифференцируема (п — 1)-я производная функции f, то ее п—й
производной называется производная от (п — 1)-й производной функции f и обозначается
/<">. Итак,
Число « называется порядком производной.
Определение 3. Дифференциалом п-го порядка функции f называется дифференциал
от дифференциала (?( — 1)-го порядка этой же функции. Таким образом,
dnf(x) = d(dn-1f(x)), d°f(x) = f(x), пеК
Если х — независимая переменная, то dx = const и d2x = d3x = ... = dnx = 0. В этом
случае справедлива формула
dnf(x) = fn(x)(dx)n.
4.2. Производные я-ro порядка от основных элементарных функций.
Справедливы формулы
(ax)w = ax]nna, a > 0;
(sin z)<n) = sin (x + ~"j ;
(cos *)<"> = cos (x + ™) ;
(a;m)(n) = m(m - 1) ... (m - n + 1)жт-";
4.3. Формула Лейбница.
Если и и v — ?(-кратно дифференцируемые функции, то
:'=0
4.4. Производные n-го порядка вектор-функции, комплекснозначнои и матричной
функций.
Если компоненты вектор-функции f :ih (/i(z), /2(ж), ••• , fk{x)) n-кратно дифферен-
дифференцируемы, то
f(«)(x) = (/<")(х), йп\х), ... , /^(х)) , • «Tf (х) = (rf"/i(x), dTMx), ... , <«"/*(«)).
Аналогично для комплекснозначнои функции / и матричной функции А имеем формулы:
/<">(*) = «(П)(^) + *"(П)(^); «*"/(*) = dnu(x)+idnv(x);

138 Гл. 2. Дифференциальное исчисление функций одной переменной
?\х) ... а[пк\х) \ /dnau(x) ... d"alk(x) \
; d"A{x)=[ .
V dnan(x) ... dnaik(x) )
Найти /"(ж), если:
57. /(x) = sin(a;2).
Ц По определению 1, п. 4.1, имеем
f'(x)= (sin(x2)J = 2x сов(ж2);
f"{ T\ — I f'(T\\' — f1r тя(т2\\' — 9 СС1ч(т2\ — i-r2 ciiifT2^ Ь-
Oo, f[x) = (x + i) e ' .
Ц Поскольку (u(x) + iv{x))' = xi'(x) + iv'(x), то при дифференцировании комплекснознач-
ной функции число i играет роль обыкновенной постоянной, поэтому
59. f(x) = (sin a:2, cosz2, x2).
Ц Для нахождения производной от вектор-функции следует продифференцировать ка-
каждую ее компоненту, поэтому имеем
f'(ж) = Bа; cose2, -2:rsini2, 2x);
f"(x) = B cos ж2 - 4ж2 sins2, -2 sin ж2 - 4ж2 cos ж2, 2). >
Ы). fix) = ,2 ,2
v ' I sh ж ch ж
Ц Для нахождения производной от матричной функции следует продифференцировать ее
матрицу поэлементно:
A 1 \ / sin х sh x \
со>я% ^2 ¦ />)=2 2^2 2 ,_ 2"с: 2 .>
2ж ch ж 2х sh х / \ сах + 2ж sh ж sh ж + 2ж ch ж /
61. f (х) = (\шр(х), и(х),
v(x)
Поскольку
'м(ж)У _ u'(x)v(x)-u(x)v'(x)
(р(х) ' \
то f'(a;) =(—,«, " "~"" ).
62. Найти 2/"', если ?/ = /(ег)-
Ц По правилу дифференцирования сложной функции имеем
y' = f'(ex)ex
(в этом примере штрих у / означает производную по аргументу ех).
Для вычисления второй производной пользуемся определением 1, п. 4.1, указанным выше
правилом, а также правилом дифференцирования произведения.
В результате получим
у = (/ (е ) е ) = / (е ) е + f (е ) е .

§4. Производные и дифференциалы высших порядков 139
Аналогично находим третью производную
у'" = /'"(е-) в31 + 3/"(О е2х + f'(ex) e'. >
63. Найти d у для функции у = ех, если:
х — независимая переменная; х — промежуточный аргумент (зависимая переменная).
Ц Первый дифференциал обладает свойством инвариантности, поэтому в обоих случаях
dy = d(ex) = exdx.
Далее, по определению 3, п. 4.1,
d2y = d(dy) = d(exdx).
Дифференцируя последнее произведение, получаем
d(exdx) = d(ex)dx + ex d(dx). A)
Если х — независимая, то dx = const = h. Следовательно, d(dx) = d2x = 0 и из A)
находим
d2y = d(ex)dx = exdxdx = ex(dxJ.
Если же х — промежуточный аргумент, то dx, вообще говоря, не является постоянной и
поэтому d(dx) = d2x ф 0. Тогда из A) получим
d2y = ex(dxJ + e* d2x = ex ({dxJ + d2x) . >
64. Найти d2y, если у = arctg —, где и, v — дважды дифференцируемые функции
v
некоторой переменной.
Ц Используя инвариантность формы первого дифференциала, имеем
vdu — udv vdu — udv
dy = d arctg - I = I arctg - dl-)= —-j ¦
\ v I \ v I \vJ i + t^y
где штрихом обозначена производная по (^-) .
Далее, по определению 3, п. 4.1,
и2 +v2
,2 , [ v du — udv
d y = dI
du — udv\
) ,
U2 + V2 /
I
\ U2 +
откуда, по правилу дифференцирования частного, имеем
-2 _ d(vdu — adv)(u2 +v2) — (v du — udv)(d(u2 + v2)) -.
d у _ ______ . (i)
Поскольку d(v du — udv) = dv du+v d2u — dudv — ud2v = v d2u — и d2 v, d(u2 + v2) = d(u2)+d(v2) =
2и du + 2v dv, из A) окончательно находим
2 _ vd2u - ud2v 2(uv((duJ - (dvJ) + (v2 - u2)dudv)
' У ~~ u2 + v2 («2 + ^2J ¦ ^
65. Найти производные у'х, y"xi, y% от функции у = f{x), заданной параметрически,
если х = 2t - t2, y = :it-t3.
Поскольку y'x = ?(/(x)) = Mf = %, то
_d{M-t3)_C-3t2)dt_3
Ух~ dBt-t2)- B-2t)dt -2
Ди Л i i \ d(v'x)
алее, yx2 - ^(?b) = ~^—, поэтому
\dt
dBt-t2) 2(\-t)dt 4A-t)
Аналогично у"ъ = ^{у'х'з) = (<* , поэтому
d ( 3 I 3dt
2/13 ~ dBt-t2) ~ 2A -t)rft ~ 8A -tK'
>

140 Гл. 2. Дифференциальное исчисление функций одной переменной
66. Найти у'х, у'х-2 от функции у = f(x), заданной уравнением
х2+у2
Ц Пусть у = f(x) — дважды дифференцируемое решение данного уравнения. Тогда
дифференцируя тождество x2 + (f(x)J = 5х(/(х)K по х, получаем 2x+2f(x)f'(x) = 5(/(i)K +
\bxf(x)f'(x), откуда
Далее, по определению второй производной и правилу дифференцирования частного, име-
имеем
= Bх - 5/3(х))'A5х/2(х) - 2/(х)) - {2х - 5/3(х))A5х/2(х) - 2f{x))' =
A5xp(x)-2f(x)y
_ B0/3(х) - 75х/4(х) - 60х2/(х) + 4х)/'(х) - 4/(х) + 75/5(х)
A5х/2(х)-2/(х))*
Подставляя значение /'(х), окончательно получаем
„ _ 1500xf(x) - 120х3 + 150х2/3(х) - 250 f(x)
' (Х) ~ A5х/(х)-2)з/2(х) • *
Найти производные и дифференциал указанного порядка:
II _.
к * | Л тт " A00)
D { . у = —===. Найти уу '.
VI — х
¦4 Преобразуем данную функцию к виду, удобному для дифференцирования, и применим
одну из формул пункта 4.2:
j/10°) = 2
A00)
68. y = xshx. Найти г/100'.
< Применяем формулу Лейбница, положив и = х, v = shx, и получаем
100
уA00) = (х sh х)A00) = Y^ °koo {x){k\sh х){10°-к) = С?™ х sh х + Clw ch x = х sh x + 100 ch x. >
69. у = и2. Найти d10y.
¦4 Применяя формулу Лейбница к произведению у — ии, получаем
10 4
2Q ^ "Л ,' ' 1Q ' V А ¦ ¦ in ¦ С 5 2
Д у ГГ! Л (^/ in ц tt Ц "И, Т^ ^ / C'iq U U U tt ~\~ ОIП ( " ^ ) ~
i=0 i=0
70. Выразить производные у" и у'" от функции у = f(x) через последовательные
дифференциалы переменных х и у, не предполагая х независимой переменной.
¦^ Используя определение 3, п. 4.1, а также правило дифференцирования произведения,
получаем
dy = f\x)dx, A)
d2y = f"(x)(dxJ+f'(x)d2x, B)

§ 4. Производные и дифференциалы высших порядков 141
2 f'{x)d3X. /;,> C)
Из формул A) — C) имеем последовательно
"_fn( ,d2y-y'd2x_dxd2y-dyd2x
У — J Vх) -
(dxy (dx)
^=(dw{{dxJd3y
Найти y^n\ если:
у'" = /'"(x) = -J—((dxJ d3y -3d2xdxd2y + 3 {d2xf dy ~ dx dydzx). >
" x2-3x + 2'
Представляя данную дробь в виде
1 1
и применяя одну из формул пункта 4.2, получаем
</") = (-1)пп!
A-1)»+»
72. ?/ = sin3
sin3 х.
Представляя у в виде
3 . 1 .
у — — sin х. sin Зж
4 4
и пользуясь одной из формул пункта 4.2, находим
(п) 3 . / ПЯЛ 3" .
-т- • >
73. у = shi4 х
¦< Преобразовав у к виду
У = - + -CQsiX,
4 4
получаем
ТА , а + Ьх
74. , = In —.
а — ох
Ц Первую производную этой функции запишем в виде
Далее, по одной из формул пункта 4.2, после (н — 1)-кратного дифференцирования получаем
у(п) = (_!)»-!(„ _ 1}, (» + хуП + („ _ 1}! A _х
75. Доказать равенства:
п
1) (е sm(oa;4-c))v ' = е (а + о J sinlox + с + п<р);
/V V1// V'/ V11'/'
п
где
Ь а
z, COS if -

142 Гл. 2. Дифференциальное исчисление функций одной переменной
¦Ц Умножив левую часть первого равенства на г и сложив с левой частью второго равен-
равенства, получим
(еах cos(bx + с))(п> + (ieax sm(bx + с))(п) = eic(e(a+i")x){n) = е'с(а + Ьг)п e(a+bt)x =
= (а2 + Ъ2)^ e^+bi)x+ic+inv = (а2 + b2^f ea*(cos(bx + c+nip) + ism{bx + с + nip)).
Отсюда по аксиоме равенства комплексных чисел и следуют доказываемые формулы. >
76. Преобразовав функцию / : х \—* sin2p х, где р — натуральное число, в тригонометри-
тригонометрический многочлен
р
f(x) = у ^Ак cos'2kx,
найти jK (х).
< Сначала с помощью формул Эйлера и бинома Ньютона преобразуем функцию / в
тригонометрический многочлен. Имеем
Во второй сумме, стоящей в скобках, введем новый индекс суммирования к1, полагая к =
2р — -к'. При атом, использовав известную формулу С^р = C?t~k, получим
sin2"* =
-1)
Ч ^2р -"я "V, У)" т 92р '
А: = 0 к = 0
Далее, по одной из формул пункта 4.2,
(sin2p i)(n) = ^0^- ]Р(-1)*с?, 2п(к - р)п cos B (к - ¦
к=0
— р) cos I 2 (к — р)х Н—— ) . >
( ( . Используя тождество — = — : : . доказать, '
х2 + 1 2г \х — г ж + г/
) (-l)"w!
= ~^ ~~t+T sin(()l + Х) arcctg ж)-
Сначала и раз продифференцируем указанное тождество:
~ 2i
Далее, применяя к комплексным числам (ж — г) п 1 и (х + г) п 1 формулу Myавра, имеем
2
' (-1)" »l!
(cos(w + \)tp - isin(?i + l)v>) = — ; n+1 sin(w

§ 4. Производные и дифференциалы высших порядков 143
где <р = arg (х + г) = | — arctg х — arcctg x. >
78. Найти /(п)@), если f(x) = arctg*.
¦4 Дифференцируя / два раза, получаем
~2х f
J ^x>-
откуда A + x2)f"{x) + 2xf'(x) = 0.
Применяя к полученному тождеству формулу Лейбница, находим
A + x2)fn)(x) + 2 (» - 2)xf<-n~1\x) + (» - 2)(п - 3)/<"-2)(х) +
+ 2xfin-1)(x) + 2 (п - 2)/(n-2)(i) = 0.
Подставив х = 0, имеем рекуррентное соотношение
из которого при п четном находим /^^(О) = 0, а при п = 2k + 1, последовательно полагая
к = 0, 1, 2 ... , — формулу
) = (-l)*Bfc)!, к е Zo. >
79. Вычислить / "'@), если /(а:) = cos(m arcsin x).
< Дифференцируем / и возводим найденное выражение в квадрат, а затем дифференци-
дифференцируем полученное еще раз и приходим к тождеству
A - x2)f"(x) - xf'{x) + m2f(x) = 0.
Дифференцируя это тождество и — 2 раза с помощью формулы Лейбница, получаем
A - x2)f^>(x) - 2х(п - 2)f^-V>(x) - (п - 2)(п - 5)f(n-2)(x) -
- xfn-l\x) - (n - 2)/(n)(x) + m2/(n)(x) = 0.
Отсюда при х = 0 следует рекуррентная формула
из которой при п = 2к, к ? N, с учетом начального значения /@) = 1 находим
/Bfc)@) = (-I)*m2(m2 - 22) ... (m2 - B* - 2J).
Аналогично, полагая в A) п — 2к + 1, к ? N, и учитывая значение /'@) = 0, приходим к
равенству
80. Доказать, что функция
, Г i2nsmi, хфО,
\ 0, 1 = 0,
и € N, в точке х = 0 имеет производные до и-го порядка включительно и не имеет производ-
производной (и + 1)-го порядка.
< Поскольку lim i^- — 0, то /'@) = 0. Предположим, что для некоторого натурального
к ^ п — 1 (п = '2, 3, ...) /^@) = 0. Покажем, что тогда и f^k+1\0) = 0. Действительно,
поскольку
( I) '
]Г С1 2»Bп - 1) ... Bп - * + i + 1) х2"-^1' (sin I) ' ,
х^0, A)
то по определению производной
) = lim /W(*)-/W@) = Hm у- с, 2иBи_1) ... B»-*+i + l) x2»-*+-i Csin I)(°= о.

144 Гл. 2. Дифференциальное исчисление функций одной переменной
Здесь учитываем то, что функция (sin-) содержит член вида ^г sin ^ или j^F cos - (в
зависимости от того, четное или нечетное к).
Итак, с помощью метода математической индукции мы показали, что /^@) = 0 Vfc =
Наконец, полагая в A) к = п, замечаем, что lim f(n\x) не существует, т. е. функция /'"'
разрывна в нуле. Следовательно, она не может иметь производной в этой точке. >
Упражнения для самостоятельной работы
Найти n-ю производную функции /:
136. Дх) = е*2. 137. /(х)=,,_6в,7^„_6. 138. /(*) = xV'OO- 139. /(х) = г»^
140. Найти /'(х), если
/(ж)=
Л(х) /2(х)
Л'ОО Ш
fn(x) ф)
Найти n-ю производную:
141. Дх) = (sin2x, sin2 х, х*), * 6 N. 142. /(х) =
143. /(х)=^-. 144. /(x) = xV*.
1
145. /(х) = xsinCx + 2i). 146. f(x) =
X
„n+1
2n
147. Пусть u = u(x), v = v(x) есть п-кратно дифференцируемые вектор-функции. Тогда
(u(x), v(x))(") = ± С* (u(fc)(x), v(»-*)(x)) .
fc=o
Доказать это.
148. Доказать, что формула Лейбница (н-кратного дифференцирования произведения)
справедлива также для матричных функций А = Л(х) и В = В(х), т. е.
если А к В есть n-кратно дифференцируемые функции.
Найти n-ю производную, используя примеры 147, 148:
149. f (х) = (u(x), v(x)), если:
а) и(х) = (sinx, sin2x, ... , sin nx), v(x) = (e.x, e2x, ... , e"*);
б) u(x) = (cos x, cos 2x, ... , cos nx), v(x) = (x, x2, ... , xn).
150. f(x) = A{x)B(x), если:
, ., ¦. ( sin nx
a) A(x) =
cos nx \ _, . / sh Jtx chnx
. , B(x) —
— cos nx sin nx J y ' у —en nx sh nx
(
i+« (
4 1
lnx ln2x
1 xn x^
151. Показать, что функция
у = /(х) = de""* + С-2.е~хшх (oj, С\, С'г — постоянные)
удовлетворяет уравнению у" + ш2у = 0.
152. Показать, что функция
s = s(t) = p-

§ 4. Производные и дифференциалы высших порядков 145
где к, д — постоянные, является решением уравнения '
m-r-j = тпд — к (~г\ , т = const.
153. Показать, что вектор-функция
/0\ / 2cos< \ / 2sint \
х : t у-* С А 1 I е + С2( 2cos< I + С3( 2sin< ),<?,= const,
V 1 / V 3 cos t - sin t / V 3 sin t + cos t /
удовлетворяет уравнению -^ = Ax, где
/ -1 -2 2 \
A = -2 -1 2 1 .
V -3 -2 3 /
154. Показать, что вектор-функция
+ C5 I 0 I e + Ce I 1 1-е
1 \ /0
0 ]e-" + Ce 1
\ -i / V -i /
удовлетворяет уравнению -^ = Ax, где
( 3 -1 ~M
A= -1 3 -1 .
V -l -l з /
155. Показать, что если некоторая вектср- функция х = х(<) удовлетворяет уравнению
-^ = Ах, где А — постоянная матрица, то она является решением уравнения
%?=Апх VngN. ¦' - i!
156. Найти 2^(А~1(х)), где А~*(х) — обратная к А(х) матрица.
157. Показать, что решения системы уравнений -^ = х3 — у, -^ = х -\-у3 являются также
решениями системы
158. Найти /"@), если /(х) = x3(sin(lnm |х|) + cos(lnm |х|)), х / 0, и /@) = 0, где
Является ли непрерывной вторая производная в нуле? Можно ли подобрать значение
параметра т таким образом, чтобы существовала /'"@)?
159. При каких значениях а функция / : х i-> |i|asin -, х ф 0, и /@) = 0 имеет
непрерывную вторую производную?
160. Найти f"(x), если f(x) = ч>{ф(х)) и
И<2, .„.л_/ е', |х|<2,
|х| > 2.
161. Вычислить вторую в обобщенном смысле производную функции / в точке ее разры-
разрыва, если /(х) = ^^т^-
162. Вычислить вторую производную функции /~ : х t-+ у, обратной для функции
/ : у I—> х, если:

146 Гл. 2. Дифференциальное исчисление функций одной переменной
а) х = у + у3; б) х = у + sin у.
163. Вычислить d2f(O) функции / : х н+ |i|<* arctg тщ, х ф О, и /@) = 0.
164. Найти /"@), если у = f(x) и х = 2< - t2, г/ = (< - IL.
165. Найти f"(x) функции у = f{x), заданной параметрически:
л , It, t < 1, , . Г -arcsin*,
x(t) = ' •¦'*• — * "•
166. Вычислить вторую производную функции у = f(x), заданной неявно уравнением
sin(xy) = х + ?/-|,г/>0,в точке х = |.
167. Найти /500C')) если:
168. Вычислить /'@), если функция f : х *-* у задана уравнением г/5 + х3 + х2 — у2 — 0 и
дважды непрерывно дифференцируема в окрестности точки х = 0.
Вычислить /*г'0)@), если:
169. /(х) = Bin(x2). 170. /(*) = Yr^fpr.
171. /A)= pi^-. 172. j/ = /(*), i=2<-<2, г/ = 3<-<3.
тт u d2 f f ar^i
Найти J^ ', если:
173. f(x) = sm(u(x)v(x)). 174. /(x) = arcsin ^~j. 175. /(x) = u{x) e.~v''{x\
176. /(x) = ln(«(V(x))). 177. f(x)= (u(x) + «(x), 2g). 178. f(x)
179. у = f(x); a) j/(<) = < sin t, i(<) = <cos<; 6) y(<p) = p(<p) sin ^, i(v) = ^(v) cos^j.
180. y = f(x); y(t) = (sint, cost tg<): x@ - 3t + i3.
181. » = /(x) ;y{t) =
182. » = /(x); y@= ..__
Вычислить d^V в указанной точке:
183. у = /(а:), х3 + j/3 = Зж2у2 + 1 в точке М@, 1).
184. у = /О), 3xrj - 2уь - а;2 + у2 + 1 в точке М@, 1).
185. г/ = /(а:), у = х\п(х2 + у2) в точке МA, 0).
186. Пусть компоненты f,(x) вектор-функции f : i и (/i(x), /2A),... , /п(х)) удовле-
удовлетворяют системе уравнений
Найти f"{x).
187. Пусть функциональная матрица А(х) удовлетворяет уравнению
А2(х)В(х) + А(х)С(х) = Е,
где В(х), С(х) — дважды дифференцируемые матрицы, Е — единичная матрица.
Найти А"(л:), если А(х) коммутирует со своей производной.
188. Найти d4f(x), если f(x) = и2(х)у3(х).
189. Найти d2f{x), если f(x) = A(u(x))B(v(x)), где А, В — матричные функции.
190. Найти (I2f(x), если /(ж) = |</з(м(ж))|, где ip — вектор-функция.

§ 5. Теоремы Ролля, Лагранжа, Коши 147
§ 5. Теоремы Ролля, Лагранжа, Коши
5.1. Теорема Ролля.
Пусть функция / : [а, Ь] —* К непрерывна на сегменте [а, Ь] и имеет конечную или беско-
бесконечную производную внутри этого сегмента. Пусть, кроме того, /(а) = f(b). Тогда внутри
сегмента [а, Ь] найдется точка ? такая, что
5.2. Теорема Лагранжа.
Если функция / : [а, Ь] —> К непрерывна на сегменте [а, Ь] и имеет конечную или беско-
бесконечную производную во внутренних точках этого сегмента, то 3? б]а, Ь[ такое, что
/F)-/(в) = /'(?)(*-«)¦
5.3. Теорема Кошн.
Если каждая из функций fug непрерывна на [о, Ь] и имеет конечную или бесконечную
производную на ]а, Ь[ и если, кроме того, производная д'(х) ф О на ]а, Ь[, то Э? €]а, Ь[ такое,
что справедлива формула
/(Ь) - /(а) = /'(О
д(Ь)-д{а) д'(О'
Если дополнительно потребовать, чтобы д(а) ф <?С>)> то условие д'(х) ф О можно заменить
менее жестким:
(Г(х)J+(,У(х)JфО Vre]a,i[.
81. Пусть функция / имеет конечную производную /' в каждой точке конечного или
бесконечного интервала ]а, Ь[ и
Нш f(x) = lim f(x).
.г-_а+0 х — Ь — 0
Доказать, что / (с) = 0, где с — некоторая точка интервала ]а, Ь[.
¦4 Пусть интервал ]а, Ь[ конечен и lini f{x) = lim f(x) = С, С = const. Рассмотрим
фЗ ПК ЦИК)
/ f(x)> если х ?]a' 6t'
6 при x = а и x — о.
Она непрерывна на сегменте [а, Ь] и имеет конечную производную на интервале ]о, Ь[, причем
F(a) = F(b). По теореме Ролля па интервале ]a, b[ найдется такая точка с, что F'(c) =
f'(c) = Q.
Если интервал ]«, Ь[ бесконечный, то, в силу существования конечной производной функ-
функции /, непрерывности функции / и существования конечных, равных между собой, ее пре-
предельных значений при х —» а + 0 и х —* Ь — 0, при достаточно малом е > 0 прямая у = С + с
или прямая у = С — е пересечет кривую j/ = /(x), по меньшей мере, в двух точках, которые
обозначим с\ и с2. Для функции / на сегменте [а, сг] выполнены все условия теоремы Рол-
Ролля, поэтому на интервале ]ci, сг[ (а значит, и на интервале ]а, Ь[) найдется такая точка с, что
Г{с) = 0. '
Рассмотрим теперь случай, когда lim f(x) ¦=¦ lim /(x) = со. Тогда как в случае
конечного, так и бесконечного интервала ]а, Ь[ уравнение f(x) = А (где А > 0 — любое
число, фиксированное, когда lim /(ж) = lim f(x) = +сю) или уравнение f(x) = —А (в
j;—.u + O j: —Ь —0
случае, когда lim /(х) = Цш /(ж) = — со) всегда имеет два различных корня, которые
л—11+о .t—ь—о
обозначим ai п Q2. Применяя теорему Ролля к функции / на сегменте [п\, а2], приходим к
выводу, что на интервале ]fti, «г[ (а значит, и на ]«, Ь[) существует, по меньшей мере, одна
такая точка с, что /'(с) = 0. >
82. Пусть: 1) функция / определена и имеет непрерывную производную (п — 1)-го
порядка на сегменте [хо, х„]; 2) / имеет производную я-го порядка в интервале ]хо, хп[; 3)
выполнены равенства /(хо) = f(xi) = . .. = f(xn), ю < xi < ... < хп. Доказать, что в
интервале ]хо, хп[ существует, по меньшей мере, одна точка ? такая, что /^ (?) = 0.

148 Гл. 2. Дифференциальное исчисление функций одной переменной
¦4 На каждом из сегментов [a;,_i, я,-], г = 1, п, выполнены все условия теоремы Ролля для
функции /, следовательно, существует не меньше п точек ?, €]яо, хп[ таких, что /'(?>) = 0.
Для функции /' на каждом из сегментов [?>, ?j + i], j = 1, п — 1, выполнены все условия
теоремы Ролля, поэтому существует, по меньшей мере, п — 1 точка 1)к €]яо, яп[ такая, что
f"(jik) = 0, к = I, п — 1. Продолжая рассуждать таким же образом, приходим к выводу, что
в п — (п — 2) = 2 точках интервала ]хо, хп[ f^n~l\(,i) = 0, i = 1, 2. Применяя теорему Ролля к
функции /^п~1' на сегменте [d, B], получаем, что существует хотя бы одна точка ? €]хо, хп[
такая, что /(п)(?) = 0. >
83. Доказать, что если все нули многочлена
Рп(х) = аохп + а\Хп~ +...+ап, а0 ф 0,
с действительными коэффициентами а^, к = 0, п, действительны, то его последовательные
производные Р'п, Р,", ... , Р„~~1' также имеют лишь действительные нули.
¦4 Предполагая, что все нули различные, по теореме Ролля получаем, что Рп{х) имеет п — 1
действительный нуль; РЦ{х) будет иметь уже п — 2 действительных нуля и т. д. Но так как при
дифференцировании многочлена степень многочлена уменьшается на единицу, то получается,
что все нули производных будут действительны. Если какой-то нуль многочлена кратный, то
он же будет нулем и для производной от многочлена, т. е. также действительным. >
84. Доказать, что у многочлена Лежандра
все нули действительны и заключены в интервале ] — 1, 1[.
¦4 Многочлен Un(x) = (х2 — 1)" имеет на сегменте [—1, 1] 2п действительных нулей: ii =
Х2 — ... = хп = — 1; Xn+i = хп+2 — ... — Х2п — 1. Согласно предыдущей теореме, многочлен
Рп(х) имеет п действительных нулей, расположенных, по теореме Ролля, в интервале ] — 1, 1[,
что и требовалось доказать. >
85. Доказать, что у многочлена Чебышева—Лагерра
все нули положительны.
¦Ц Рассмотрим функцию <р : х t-+ хпе~х. Поскольку <р@) = lim <p(x) = 0, то существует
х~*-\- со
такая точка ?i ?]0, +оо[, что ^'@) = 0 (см- пример 81). Очевидно, <р'@) = lim <р'(х) = 0,
Х — + ОЭ
поэтому, в силу теоремы Ролля н на основании решения примера 81, найдутся точки ^2 €]0, ^i[
и ^з б]6, +оо[ такие, что <р"(^0 = 0, i = 2, 3. Кроме того, <р"@) = 0. Таким образом, tp"
обращается ъ нуль в трех точках полуоси х Jj 0. Поскольку ^ @) = lim tp-3\x) = 0
при j = 0, п — 1, то, применяя теорему Ролля и пользуясь п — 3 раза результатом решения
примера 81, получаем, что функция ip(n~1^ обращается в нуль в п + 1 точках, лежащих на
полуоси 1^0, причем одна из этих точек х = 0. Эти точки являются концами п отрезков,
на каждом из которых к функции ^"~1) применима теорема Ролля, поэтому существует, по
меньшей мере, и таких точек ijh > 0, что ?^п'('д) = 0. Очевидно, ^"'@) ф 0. Поскольку
Ln(x) = ехцу-'1)(х) есть многочлен п-тл степени, имеющий п нулей, то его нули — точки ijk,
причем 7/^ > 0, к = 1, п. >
86. Доказать, что у многочлена Чебышева-Эрмита
все нули действительны.
¦4 Рассмотрим функцию и : х и-> е~х . Очевидно, lim и^3\х) = 0, поэтому функции v>3',
х-*оо
j = 0, п, удовлетворяют условиям примера 81 на интервале ] — оо, +оо[. Повторяя рассужде-
рассуждения, проводившиеся при решении предыдущего примера, приходим к выводу, что и' обраща-
обращается в нуль, по крайней мере, в одной точке этого интервала; и" — в двух точках; ... ; чг™' —

§ 5. Теоремы Ролля, Лагранжа, Коши 149
в п точках. Поскольку Нп(х) = (—1)пех и'п'(х) есть многочлен n-й степени, имеющий ровно
п нулей, то его нули совпадают с нулями функции irn' и все эти нули действительны. >
87. Найти функцию в = в(хо, Дх) такую, что /(хо + Дх) —/(хо) = Дх/'(хо +0 Дх), если:
а) /(х) = ах2+6х + с, афО; б)/(х) = х3; в) /(х) = -; г)/(х) = е*.
X
¦Ц Применяя формулу конечных приращений Лагранжа к каждой из функций а) - г),
имеем:
а) а(х0 + ДхJ + 6(х0 + Дх) + с- (ах2 + Ьх + с) = ДхBа(х0 + в Дх) + Ь), откуда в = |;
-*„ + «/*„ Д*+|(Д*J+*;|
б) (хо + ДхK -xjj =ЗДх(х0 + <9ДхJ, откуда <9(х0, Дх) = * -^ , х0 > О,
Дх > 0;
г) ех° + х -ех° ¦¦
88. Пусть
~— при 0 ^ х ^ 1,
- при 1 < х < +оо.
Определить промежуточное значение с формулы конечных приращений для функции / на
сегменте [0, 2].
¦Ц Исследуем функцию / на дифференцируемость в точке х = 1. По определению одно-
односторонних производных, имеем
= Um _l.
Д
2 ) ' ^ ' д*-.+о Дх Vl + Дх
Функция / дифференцируема на сегменте [0, 2]. Применяя формулу конечных приращеинй
к функции / на сегменте [0, 2], находим
/B) - /@) = 2/'(с), 0 < с < 2.
Поскольку /B)= I, /@)=|,
— х при 0 < х ^ 1,
— ^2 при 1 < х < 2,
—2с при 0 < с ^ 1,
— \ при 1 < с < 2,
откуда с.\ = -, С2 = л/2 — два промежуточных значения. >
89. Пусть функция / имеет непрерывную производную /' в интервале ]а, Ь[. Можно пи
для всякой точки ? из ]а, Ь[ указать две другие точки xi и хг из этого интервала, если
т 1€
XI — Х\
< Если на интервале ]а, Ь[ /'(х) ) 0 и / отлична от постоянной на любом отрезке,
являющимся частью ]а, Ь[, то / возрастает на ]а, Ь[. Тогда дпя любых xi, %i €]a, 6[, i2 > xi>
имеем
)
Х2 - Xi '
и для тех точек интервала, в которых /'(х) = 0, равенство
Г(о = 0
Х2 — Xi
невозможно. Например, для функции /цн х3, —1 ^ х ^ 1, при любых xi, хг б] — 1, 1[
выполняется неравенство
х\ — X? 2 2
?^=Х+ХХ2+Х2 >0
Х2 -

150
Гл. 2. Дифференциальное исчисление функций одной переменной
следовательно, для точки ? = 0 значений аргумента х\ и Х2, о которых говорилось в условии
задачи, не существует. Приведенные рассуждения не исключают, однако, положительно-
положительного ответа на поставленный вопрос для некоторых классов функций, удовлетворяющих всем
условиям теоремы Лагранжа. >
90. Доказать неравенства;
Д р
a) |smz — sin j/| ^ \х — у\; б) рур~1 (х — у)
хр — ур
pxv~l(х — у), если 0<}<гиу>1;
\i . . . а — Ь , а а — Ь
в) |arctga — arctg Ъ\ ^ \а — 6|; г) < In j < —-—, если 0 < о < о.
Ч По формуле Лагранжа, имеем:
а) sinx — sin у = (х — у) cos f, откуда |sin x — sin j/| = | cosf ||x — j/| ^ \x — y\;
б) x" - yv = р?р~Х{х -У), У < S < x, откуда (х - y)py1 < xp - yp ^ (x -
в) arctg о — arctg Ь =
2
(a — 6), откуда |arctg a — aictgb|
r) In a — In i = j(a — 6), a < ? < 6, откуда ^- < In ^ < ^j— >.
91. Доказать, что если функция / дифференцируема, но не ограничена на конечном
интервале ]о, Ъ[, то ее производная /' также не ограничена на интервале ]о, Ь[.
¦4 Пусть функция / дифференцируема на ]а, Ь[ и не ограничена при х —*¦ 6 — 0. Возь-
Возьмем произвольную последовательность (хп), сходящуюся к Ь слева. Тогда существует такой
номер N, что при Vn > N выполняется неравенство |/(in)| > А, каким бы А > 0 ни было.
Фиксируем любое число т > N и рассмотрим при п > т разность f(xn) — f(xm)- Применяя
теорему Лагранжа к функции / на сегменте [хт, хп], находим
f(Xn)-f(xr
= \f'((mn)\,
где xm < fmn < хи. При достаточно больших п левая часть, в силу условия задачи, больше
любого наперед заданного положительного числа, откуда следует неограниченность произ-
производной /' при х —" Ь — 0.
Обратное утверждение неправильно: из неограниченности производной в интервале не
следует неограниченность функции на этом интервале, например: /:ги л/х, 0 < х < а. >
92. Доказать, что если функция / дифференцируема в бесконечном интервале ]хо, +оо[
и
ton /'(*) = 0,
Mm
/oo
= 0,
т. e. f(x) = o(x) при x —> +oo.
¦Ц Пусть (а;,,) — произвольная последовательность значений аргумента такая, что хп —+
+оо. Тогда Ve > О ЭТУ : Vn > N справедливо неравенство
1/'(«»I < f • (!)
Фиксируем но > N и, взяв и > п0, применим теорему Лагранжа к функции / на отрезке
[х„0, Хп]:
/(х„) -/(х„0)
где х„0 < fntl0 < х„.
В силу неравенства A), из B) имеем
f(xn) - /(хп„)
Из C) получаем неравенства
f(xno) _ Л _ ?п^\ ? < /(х„) < /(хПо) + Л _ ?^о.\ ?
х„ V х„ / 2 хп хп V х„ / 2'
B)
C)
D)

§ 5. Теоремы Ролля, Лагранжа, Коши
При больших ?(, очевидно, справедливо неравенство
151
a A ~~ ~f~~) i" < 2 всегДа ПРИ " > "о, тогда, используя неравенство D), при По > №Й*при
достаточно больших п > по получим неравенство
E)
< ?.
Поскольку (^'п) — произвольная бесконечно большая последовательность, все члены ко-
которой положительны, то имеем
lim
= 0 ) =*¦ (Дх) = о(х)) при х -* + оо. >
93. Доказать, что если функция / дифференцируема в бесконечном интервале ]хо, +оо[
1С f(x) = о(х) при х —> +оо, то
lim \f'(x)\ = 0.
х—> + оо
В частности, если существует lim f'{x) = к, то к = 0.
¦Ц Допустим, что
lim \f(x)\=A, Афй,
X—*-f СС
тогда Ve @ < е < А) ЭВ такое, что при х > В выполняется неравенство
\f'(r\\ ~> л - f A)
Фиксируем xi > В и возьмем х > xi. Применяя теорему Лагранжа к функции / на сегменте
[xi, x], получим, принимая во внимание неравенство A),
fix) -
B)
Переходя в неравенстве B) к пределу при х —> +оо, получим
lim
г1—.-f оо
а;
а это противоречит условию f(x) — о(х). Таким образом, Л = 0, т. е. lim ]/'(x)l = 0.
Допустим теперь, что существует lim f\x) = &• Тогда для произвольной последова-
тельности (хт), хт > 0, хт —> +оо, имеем
lim /'(xm) = i,
т—+оо
т. е. Ve > 0 ЭМ такое, что при т > М выполняется неравенство
k-e<f'(xm)<k+e. C)
Взяв та > М и т > то, получим, применив теорему Лагранжа к функции / на сегменте
хт) — J\Xma) _ м
Из неравенства C) следует неравенство
}, imo ^ ч"г
<
D)

152 Гл. 2. Дифференциальное исчисление функций одной переменной
Переходя к пределу в неравенстве D) при т —> +оо, получим
к - е
lim
Jk + e.
, откуда, в силу произвольности
Поскольку lim f\Xrn> = о, то получаем к — е^О,
т — оо Лm
s, следует, что к = 0. >
94. Доказать, что если функция / непрерывна на сегменте [а, Ь], имеет конечную произ-
производную внутри него и не является линейной, то в интервале ]а, Ь[ найдется, по меньшей мере,
одна такая точка с, что
/(*) - /(«)
>
Ь-а
А Разбивая произвольным образом сегмент [а, Ь] на к частей точками ао = хо <
< ... < х„ = Ь, получаем
1/F)-/(«)! =
По формуле Лагранжа имеем
i = 0, »-l,
где Ах, = ж,_(-1 — х,.
Таким образом, приходим к неравенству
A)
Функция / отлична от линейной, поэтому существует такое разбиение сегмента [а, Ь], что
среди чисел |/'(?;)| найдется наибольшее, отличное от нуля, которое обозначим |/'(?)|. Тогда
из A) получим строгое неравенство
1/F) - /(в)
> = (ь -«I/'@1.
откуда
>
95. Доказать, что если функция / имеет вторую производную на сегменте [а, Ь] и /'(а) =
f'(b) = 0, то в интервале ]а, Ь[ существует, по меньшей мере, одиа точка с такая, что
А Если f(x) = const, то утверждение очевидно. Предположим, что функция / отлична
от постоянной. Из условия f'(a) = f'(b) = 0 следует, что / отлична от линейной функции.
Применяя формулу Коши конечных приращений к функциям / и tp : х i-+ ^x "' на сегменте
Га, ^—1 и к функциям / и ф : х н-> ' ~д' на сегменте \—^-, b], получаем
»(/(*?*)-/(«))_ /46) _,,
—;
/(^J) = /46) «±
F - аJ * - 6 ' 2
Складывая полученные равенства, находим
8(/(>) - /(«)) = /46) , /46)
(Ь -аJ А-а + 6_?,-
A)

§ 5. Теоремы Ролля, Лагранжа, Коши 153
Поскольку /'(а) = f'(b) = 0, то правую часть последнего равенства можно записать в виде
/'F) /46) _ /46)-/4«) /'(Ь) - /46) _ f«,n >
где а < г/1 < ?i, ?i < ?/2 < Ь- Оценивая по абсолютной величине A), с учетом B), имеем
Предположим, что /F) ^ /(а) (в противном случае доказательство тривиально: точкой с
может служить любая точка интервала ]а, Ь[). В силу нашего предположения, хотя бы одно
из чисел |/"(»/i)| или |/"(»/г)| отлично от нуля. Обозначим
|/"(с)|
Тогда имеем
откуда
(знак равенства не исключаем, так как возможен случай, когда \f"{Vi)\ = l
96. Доказать^ что если вектор-функция f : К —> ?п имеет непрерывную производную на
сегменте [а, Ь], то справедливо неравенство
|f(i)-f(a)| <(*-<») шах |f'(x)|.
•4 Функция F : х н-*¦ (f (Ь) — f (а)){х — а) — f (x)(b — а) дифференцируема на сегменте [а, 6],
на концах сегмента принимает одно и то же значение, поэтому по теореме Ролля 3? ?]а, Ь[
такое, что
F'tf) = 0, или (f D) - f(a)J = (f(?), (f (ft) - f (a)))(i - a).
Оценивая обе части полученного равенства по модулю, приходим к неравенству
|f(i)-f(a)|<|f'(OI(*-«)- A)
Поскольку функция |f'| непрерывна на [а, 6], то по теореме Вейерштрасса оиа принимает
максимальное значение max|f'(a:)| в некоторой точке х € [а, Ь]. Следовательно, |f'(OI =
max|f (х)|, и на основании A) получаем доказываемое неравенство. >
97. Доказать, что если вектор-функция F : К —> Е2 а) непрерывна на [а, 6]; б) диффе-
дифференцируема в интервале ]а, Ь[; в) производная F'(a;) ф 0 в ]а, Ь[, то 3? б]а, Ь[ такое, что
РD) - Р(а) = AF'(^),
где А — некоторая постоянная.
•4 Пусть F : х 14- (/(s), ff(z)), (/(ж), ff(a;)) 6 Е2. Тогда функции / и д, в силу условий
а) и б), непрерывны на сегменте [а, Ь] и дифференцируемы в интервале ]а, Ь[. Кроме того,
(f'(x)J + (д'(х)J ф 0 по условию в). Следовательно, по теореме Коши, 3? б]а, Ь[ такое, что
Если, например, /'(?) ^ 0, то
РF) - Р(а) = (/(*) - /(а),
где
л k
Упражнения для самостоятельной работы
191. Убедиться на примере функций /, д, <р, что ни одно из трех условий теоремы Ролля
не является излишним, если:
— (- г^—, если а < х < 4,
0, если ж = а, х = Ь;

154 Гл. 2. Дифференциальное исчисление функций одной переменной
д : х >—* \х\, — 1 5$ ж $С 1; j!;iH-t sin x, 0 $J x <J —.
192. Для вектор-функции f : х н-> (ж sin ж, ж cos ж), ж € [0, ^] , найти такое ? € ] О, ^ [, что
193. Доказать, что если / 6 Сч'" + 1)([а, 6]), то Э? €]а, Ь[ такое, что
/(х-) - lm{x) = /^^rIwm+i(a;),
где
Wm+l(z) = (х — Хо)(х — Xi) . . . (х — Хт), а = Хй < Xi < ... < Хт = Ь,
Укйзание. Ввести в рассмотрение функцию z : х и-> /(ж) — Lm(x) — A:(x)wm+i (x), где fc(S)
выбирается из условия -(х) = 0.
194. Пусть вектор-функция f : R —> Еп, п ^ 3, непрерывно дифференцируема на сег-
сегменте [а, Ь], а < Ъ. Всегда ли можно найти такое ? б]я, Ь[, чтобы вектор fF) — f(a) был
коллииеарен f'(?)?
Рассмотреть пример
f(x) = (cos г, sin ж, х), х 6 [0, 7г].
195. Справедлива ли теорема Лагранжа для дифференцируемой на сегменте [а, Ь] функ-
функции / : х I—- fi(x) + г/2(г), где г — л/-Т?
Рассмотреть пример
fix*-' cos x + г sin х, ж € 0, —
196. Пусть f — дифференцируемая на интервале ]а, Ь[ вектор-функция такая, что f'(x) =
О на ]а, Ь[. Что можно сказать о функции f ?
197. Пусть А — дифференцируемая на интервале ]а, Ь[ матричная функция такая, что
А'(х) = 0, х g]a, b[. Что можно сказать о функции Л?
198. Пусть 1,? : ж н-> х — ',ул , где / — дважды дифференцируемая на [а, Ь] функция,
причем f'(x) ф 0. Для данного в и функции / найти то множество X С [а, Ь], для которого
выполняется неравенство
\<р(х) - р(у)\ ^ е\х - У\, х,Уех,
если:
а) f:xi-+x-cosx, в= \, х € [0, f ] ; б) / : х н- х tgx - 1, в = \, х е [О, |] .
199. Пусть 9 : < ь- /(г) - /(*) - f'(t)(x _*)-..._ /(»)(*)Ifzi? - Д(х - <)Р, * € [а, х], Р > О,
А = const; функция / имеет (п + 1)-ю производную на [о, х]. Доказать, что Vp > 0 Э? б]«, х[
и такое А, что
/(,) = ± Ш^1{х - af
f
(формула Тейлора с остаточным членом в общей форме).
200. Пусть матричная функция А : х i—> A{x) непрерывно дифференцируема на сегменте
[а, Ь] и |Л(ж)| = . / ^2 |а,,(х)|2, где (iij(x) — элементы матрицы А{х). Тогда справедлива
оценка
\А(Ь)-А{а)\^ max \A'(x)\(b - а).
Доказать это.

j 5. Теоремы Ролля, Лагранжа, Коши
155
201. Доказать, что если вектор-функции f и g непрерывны на сегменте [а, Ь] и диффе-
дифференцируемы в интервале ]а, Ь[, то Э? €]а, Ъ[ такое, что
- {(a),
- g(«), f @)-
202. Пусть функции / и </ вместе со своими производными до п— го порядка включитель-
включительно непрерывны на сегменте [а, Ь] и имеют производную (в + 1)-го порядка в интервале ]а, Ь[.
Тогда Э? €]я, Ь[ такое, что
\ / П /j>
к=1
Доказать это.
Указание. Рассмотреть функцию <р : х \
, где
x) = Л„F)г„(х) - г„F)Л„(ж),
— сю, +оо[); 2) Уж, ft ? К выполняется тождество
203. Пусть: 1) / €
3) /"(х) ф 0. Доказать, что: а) если в = в(х), то в(х) = \; б) если \0'(х)\ < +оо и в = $(h),
то lim 6(h) = i
204. Пусть
^0, д'(к)
Найти предельные значения в(х) при ж —¦ +0 и с —> +оо.
205. Пусть функции / и </ дифференцируемы на сегменте [а, Ь], причем
0. Тогда 3^ €]а, 5[ такое, что
Показать это.
206. Показать, что производная функции
Г
/:ih ^ x2 sm(|lnx) , х ^ О,
О,
х = О,
непрерывна при ж ^ 0, однако функция ?, удовлетворяющая соотношению f{x) = /'(?(?)):?,
О < ?(ж) < х, является разрывной.
207. Доказать, что если /' непрерывна и монотонна на сегменте [0, ft], причем /@) =,0,
то функция ? непрерывна на этом сегменте (см. пример 206).
208. Доказать неравенства:
а) |ж-г/К \х'2\лх-у2\пу\ < Зе|х - у\ Уж, у € [1, е];
б) |x2arctgx-2/2arctgt/| < l-^-\x - у\ Уж, у € [0, 1].
209. Доказать неравенства:
Цх-у] Ух, г/€]-оо, +оо[;
)/| Ух, »/€ [1, +оо[.
б)
S1I1 -Т—S]
Х — У
X
In —
а. _
1 И
1
В
— cos г/

156 Гл. 2. Дифференциальное исчисление функций одной переменной
210. Доказать, что последовательные приближения, определяемые формулой
Fpxn r -I
сходятся к корню уравнения х = еех, если 0 < ее < 1.
211. Доказать, что последовательные приближения, определяемые формулой
Хп+1=ЛХ„+1, Хо = A, 1)т, 1 = A, 0)т,
где А = I 2 * I , сходятся в Е2 к решению уравнения X = АХ +1, если е2 < -.
§ 6. Возрастание и убывание функции.
Неравенства
6.1. Возрастание и убывание функции.
Определение. Функция f называется возрастающей (убывающей) на сегменте [а, Ь],
если f(x2) > f{xi) (или соответственно /(жг) < f{xi)) Vki, X2 € [а, Ь] и xi < Х2-
6.2. Критерий возрастания (убывания) функции.
Для того чтобы имеющая конечную или бесконечную на промежутке X производную
функция / возрастала (убывала) на нем, необходимо и достаточно, чтобы выполнялись усло-
условия: а) /'(г) > 0 (f'(x) ^ 0); б) /'(ж) не обращается в нуль ни на каком сегменте [а, ft],
составляющем часть промежутка Х([а, ft] С X).
Определить промежутки возрастания и убывания следующих функций:
98. f:x^^.
¦4 Поскольку f'(x) = хТ~хB — х In 2) при х € ]о, ^[, то на интервале ] 0, — [ функция
/ возрастает. В интервалах ] — оо, 0[ и ] jj^, +°o[ производная функции / отрицательна,
следовательно, / убывает на каждом из этих интервалов. >
99. /:i^i л/- + sin(hi х) 1 , если х > 0 и /@) = 0.
¦4 Дифференцируя /, получаем
х>0,
откуда f'(x) > 0, если sin (in ж + jj > ——. Решая последнее неравенство, находим интерва-
интервалы возрастания функции /:
BI 77-I-ZW71 ——
интервалах е 12 , е. 12
-—тт+2ктт —
e 12 , ei2
функция / убывает, поскольку на них f'(x) < 0, к € Ъ. >
100. Доказать, что функция /:гн A-)—J возрастает на интервалах ] — оо, —1[ и
]0, +оо[.
¦4 Покажем, что в указанных интервалах производная функции положительна. При х > 0
/'(*) - /(*) (ln(x + 1) - In х - -i-^.) .
Применив формулу конечных приращений к функции х !-> In х на сегменте [х, х +1], получим
1
Ы(х + 1) — In ж = -, где х < $ < х + 1,

§ 6. Возрастание и убывание функции. Неравенства, 157
в силу чего /'(х) = f(x) (j- ^у j > 0 при х > 0. . t.
Далее, пусть —оо < х < — 1. Тогда
где f = — х, 1 < f < +оо. По формуле Лагранжа
где t - 1 < ?t < t, поэтому f'(x) = f(-t) (jz^ - j-j > О при 1 < t < +00, или /'(г) > 0 при
-оо < х < —1. >
101. Обязательно ли производная монотонной функции является монотонной?
¦Щ Не обязательно. Функция / : i и 2i + sin x монотонно возрастает на всей числовой
прямой, поскольку ее производная /' : ж н* 2+cos x положительна Уг ? К. В то же время сама
производная, рассматриваемая на интервале ]—оо, +оо[, очевидно, не является монотонной. >
102. Доказать, что если <р — монотонно возрастающая дифференцируемая функция и
|/'(ж)| ^ р'(х) при х ^ so, то
\f(x) - f(xo)\ ^ <р(х) - <р{х0) при х ^ г0.
Дать геометрическую интерпретацию этого факта.
¦4 Поскольку функции / и <р удовлетворяют всем условиям теоремы Коши о среднем
значении, то справедливо равенство
/0О-/Ы
iplx) — <~ .-и -\
откуда |/О) - /Оо)| «S \v>(x) - <р{хо)\ = <р(х) - ч>(х0).
Геометрически это неравенство означает, что приращение монотонно возрастающей диф-
дифференцируемой функции будет не меньше приращения всякой другой дифференцируемой
функции с меньшим или равным абсолютным значением производной. >
103. Пусть функция / непрерывна в промежутке а ^ х < +оо и, сверх того, f'(x) > к >
О при х > а, где к — постоянная. Доказать, что если /(а) < 0, то уравнение f(x) = 0 имеет
один и только один действительный корень в интервале а, а —
J
¦4 Применяя теорему Лагранжа к функции / на сегменте а, а + ^ , имеем
Из условия /'О) > к > 0 находим
откуда
к
Функция / на концах сегмента а, а + У1' принимает значения разных знаков, поэтому,
L J
по теореме Коши о промежуточных значениях, существует такая точка ? € а, а + у'' ,
что /(?) = 0. Докажем, что она единственная на этом интервале. Если допустить, что на
нем найдется такая точка ?i, что /(?i) = 0, то по теореме Ролля на интервале ]?, ?i[ (если
$i > ?) или на интервале ]?i, ?[ (если ?i < ?) найдется такая точка ?г, что / (?г) = 0, а это
противоречит условию f'(x) > к > 0 при х > а. >

158 Гл. 2. Дифференциальное исчисление функций одной переменной
104. Доказать, что если: 1) функции ip и ф в-кратно дифференцируемы; 2) ^ (хо) =
ф^^хо), к = 0, и — 1; 3) р(п\х) > ф \х) при х > хо, то справедливо неравенство ip(x) >
ф(х) при х > хо.
^ Применим к функции <г"~ ' = ip^n~1' -у"' теорему Лагранжа о среднем на сегменте
[хо, х]. Имеем
u("-1}(x-) - «("-^(жо) = м(п)(?)(ж - хо),
откуда, в силу условий 2) - 3), находим и^п~1\х) > 0, х > хо- Аналогично доказываем, что
и("~2)(х) > 0 и т. д., и(х) > 0, т. е. <р(х) > ф(х) при х > х0. >
105. Доказать следующие неравенства:
а) ех > 1 + х при х ф 0; б) х < 1пA + х) < х при х > 0;
х3 . х3 тг
в) х — < sin х < х при х > 0; г) tg х > х + —- при 0 < х < —;
о J 2,
д) [ха + у") а > (х" +уе')Р при х>0,2/>0 и 0<а<,а.
¦< а) Обозначив <р(х) = е/, t/)(x) = 1 + х и замечая, что <р@) ~ ф@), ^Ч3-) > Ф'(х) ПРИ
ж > 0, на основании предыдущего примера заключаем, что у(х) > vH3-) при х > 0.
Полагая х = —< при х ^ 0, получаем
Поскольку уз@) = ф@), tp'(t) > V''(*) ПРИ * > 0, то ip(t) > ф(г) при t > 0, т. е. е* > 1 + х при
ж < 0.
б) Обозначим
<р(х) = х-~, V>(s) = 1пA + х), ?/(х) = х, х ^ 0.
Очевидно, у'(О) = Ф{®) — »/@), у'(-х) < Ф'{х) < ч'(а;) ПРИ ^ > 0, поэтому, на основании
предыдущего примера, имеем
<р(х) < vH^) < v(x) при ж > 0.
в) Пользуясь обозначениями
х3
>р(х) — х —, ф(х) = sin х, ?;(х) = х,
имеем <р@) = V'@) = »;@), (р1 (х) < ф'(х) < ч'(х) при х > 0 и х ^ 2ктг. На основании
предыдущего примера справедливы неравенства
ip(x) < ф(х) < ц(х), х > 0, хф 2ктг, к € N.
При х = 2ктг имеем неравенства
0 < 2Л-7Г,
т. е. <рBА)тг) < фBкж) < 1)Bк-к), к 6 N. Таким образом, при х > 0 выполняются неравенства
р(ж) < ф(х) < ?;(ж).
г) Обозначим
X3 7Г
<p(x) = tgx, ^(г) = ж + у. ° < х < 2'
Очевидно, ip@) = 0@), уэ'(х) > ф'(х) при 0 < х < -j (так как р'(х) = 1 + ig2x, ф'(х) =
1 +х2, tg2x > х2 при 0 < х < ^) . Пользуясь предыдущим примером, можем утверждать, что
¦ ip(x) > ф(х) при 0 < х < ~.
I I
д) Неравенство [ха + уа)« > (х'3 + у0I3 при любых фиксированных х > 0, г/ > 0 и всех
«, 0 < а < /?, эквивалентно неравенству

§ 6. Возрастание и убывание функции. Неравенства 159
Для доказательства последнего обозначим - = t и рассмотрим функцию
ip : z t-> (tz + 1I, 0 < z < +оо. ¦.,. . ,
Ее производная
отрицательна при 0 < z < + oo, поэтому функция tp убывает; следовательно, <р(л) > у(/3) при
О < с* < /? < +оо, т. е. справедливо неравенство
(ха + уа)^ >(х13 + /У
при х > 0, г/>0, 0<а<,3, что и требовалось доказать. >
106. Доказать, что при х > 0 справедливо неравенство
Если неравенство выполняется, то, логарифмируя его, придем к неравенству
которое требуется доказать. Обозначая - = t, t > 0, получаем неравенство
Правая его часть доказана при решении примера 105; докажем теперь левую часть неравен-
неравенства. Обозначим ip(t) = •jry, V'(^) = ln(l + t) и рассмотрим функции <р и ф при t ^ 0.
Очевидно, у@) = V»@)> v'(*) = nit)* < ^'(*) = Г+7 ПРИ * > 0- Следовательно, на основании
неравенства, доказанного в примере 104, можно утверждать, что >p(t) < ф(?) при t > 0, т. е.
-—? <Ьх{\ + -) при х > 0, что и требовалось доказать. >
107. Доказать неравенства:
а) ха - 1 > а(ж - 1) при а ^ 2, ж > 1;
б) л/г — -\/а < yjx — а при п > 1, ж>а>0;
в) 1 + 2 In ж ^ х2 при ж > 0.
¦^ а) Обозначив ip(x) = ха — 1, ^>(ж) = а(ж — 1), имеем: <р(\) = У'A) = 0, уз'С^) > Ф'{х) при
cv Js 2, х > 1. На основании неравенства, доказанного в примере 104,
ip(x) > •0(ж) ПРИ « ^ 2> ж > 1.
б) Аналогично доказательству а) имеем при в > 1, х > а > 0:
ip(x) = л/г— л/а. ^(ж) = \/х~^~п> У(а) = V'(a) — 0>
(js'C^) < Ф'(х)> поэтому v(x) < ^(ж)-
в) Обозначив ip(x) = 1 + 21пж, ф(х) = х2, замечаем, что при х — 1 значения функций
if> и v совпадают, а при ж > 1 выполнено неравенство ф'(х) < ф'(х), поэтому на основании
примера 104 справедливо неравенство ip(x) < ф(х) при х > 1. Пусть 0 < х < 1. Тогда,
полагая t = —, 1 < t < +oo, имеем
откуда v'i(^) < VJi(^) ПРИ 1 < * < +oo, т. e. tp(x) < ф(х) при 0 < х < 1. Приняв еще во
внимание очевидное равенство узA) = V'(l)> приходим к выводу о том, что <f>(x) < ^/>(г) Vz > О,
что и требовалось доказать. >

160 Гл. 2. Дифференциальное исчислеиие функций одной переменной
Упражнения для самостоятельной работы
Найти интервалы возрастания следующих функций:
212. /: in arccos—-. 213. / : ж н+ \х\ае-**, а > 0. 214. / : ж н+ ж (l + i)*.
215. /:gt->arth Г * . 216. / : X -> У, x = tIn f, г/ = Ц^.
sin(,+ 7)
217. / : X -> У, ж = t3 + 1, j/ = exp(v/2lr<-sint2 + cost2), 0 ^ t ^ §.
218. f : X ->Y, x = a(t-sint), у = o(l -cost), 0 ^ f ^ 2tt.
219. / : X -> У, ж = asin3t, г/ = icos3f, 0 ^ t ^ 2тг.
220. /:y>N -^-. 221. /: ip >-* tpe'^ . 222. / : 93 >-+ sin 93.
223. f : X ->Y, x = pcosy>, j/ = psinp, p = ^, <p ^ 0.
224. / : X -> У, г = pcosDp - p3), j/ = psinDp - p3).
225. / : X —¦ У, x3 + г/3 — Зжг/ = 0 (j/ > 0, / — дифференцируемая функция).
226. / : X - У, х2г/2 - г3 + г/3 = 0. 227. /:X-^y,2; + j/ = ze*".
228. / : X — У, ж + у - cos(x + 2у) = 0.
Исследовать на монотонность следующие функции:
229. f :х^B + х)ЫA + х)-2х. 230. /:ги ^у, г^ 1.
231. f :Х -> У, z = sinf-t+?, j/ = 4f5-5f4 + l.
232. р = iptgip, if > 0 (р, <р — полярные координаты).
233. Являются ли возрастающими на отрезке [1, 2] функции: а) / : ( н [г]; б) / : х н-»
(ж -г- 1)[х]; b)/:ii-»i, если ж € Q?
234. Доказать, что сумма и произведение положительных функций, одна из которых
монотонно возрастает, а другая не убывает, есть функция монотонно возрастающая.
Доказать следующие неравенства:
235. 2М1±1|±^
236. ^ту Ь A + i) + In2 (I + I) - ^fp > 0 при х > 0.
237- г " §7 + if ~ • • • ~ (?7 <sin^<^-^+|f-...+ jf^T, ж > 0, п б N.
238. !_? + ?- _-^^COs*^l-?+...+^I»eN.
239. еж > 1 + ж + ^ + • • • + ^-, ж > 0, п € N.
240. sins ^ i|Gr-z), 0 ^ х ^ ж. 241. созж < 1 - ^г, |я| ^ §.
242. а) tg х ^ т^ при О^ж^^; б)tgж^ -тг-^ пр^и f < г < f •
243. ^i ^ a + ^~^(х - 1)жа~2, ж > 1, а ^ 2. 244. sin ж + tg ж > 2ж, 0 < ж < f.
245. ix < 1 + ^~ при К х < е. 246. f^ s-^~ > 0, |г| < тг.
247. Пусть а = (ai, аг, ... , a,,), b = (Ь1( Ьг, . • • , Ьп), с — векторы из Еп. Доказать, что
тогда
/ A F Е\
det f В G > О,
V Е G С )
где А = а2, В = Ь2, С = с2, ? = (а, с), F = (а, Ь), G = (Ь, с).
248. Пусть / дифференцируема на [а, Ь], /(а) = 0 и ЗА € К такое, что \f'(x)\ ^ A\f(x)\
на [а, 6]. Доказать, что /(ж) = 0 Vi6 [a, i].
249. Пусть х, у € Кп. Будем считать х > у (х < у), если Хк > Ук (жь < Ук) V& = 1, в (та-
(такое отношение между некоторыми векторами называется их частичным упорядочиванием). В
связи с данным отношением будем называть вектор-функцию х : t к-<• (x\(t), жг(<), ... , xn(t)),
t € [a, 6], монотонно возрастающей (убывающей) на интервале Г С [а, Ь], если У<1( <2 € Г из
(*! ><2) =*¦ (х(<0 > х(<2)) (x(fi) < x(f2)).
Показать, что вектор-функция х : t н-> (sinf, cost, te~' ) возрастает на JO, J [.
Для вектор-функции f найти интервалы монотонного возрастания (убывания), если:

§ 7. Направление выпуклости графика функции 161
250. f : (м B|cosf| + |cos2i| + 4f, \t + ^ sin it + l) .
253. Матричную функцию А : (и (a,_,(f)) (г, j = 1, в) будем называть монотонно
возрастающей (убывающей) на интервале ]а, Ь[, если Vfi, <2 €]а, i[ из (<i > <г) =*¦ (()
A(h)) (Л(*!)<Л(<2)). __
Для матриц Л и В считаем Л > Д (Л < В), если а;у > 6;j (a,j < bij), i, j = 1, п.
Найти интервалы монотонности для следующих матричных функций:
sin** *2 ( 2
\ л . t / sill f + I sin t| cos t + | cos t\ \
I 1 + arcsin t2 t sin t J
§ 7. Направление выпуклости графика функции.
Точки перегиба
7.1. Выпуклость графика функции.
Определение. Говорят, что график дифференцируемой в интервале ]а, Ь[ функции f :
]а, Ь[—f К имеет на нем выпуклость, направленную вниз (вверх), есл« о» лежит в пределах
указанного интервала не ниже (не выше) любой своей касательной.
Теорема. Достаточным условием выпуклости графика функции вниз (вверх), если функ-
функция всюду на интервале ]а, Ь[ имеет конечную вторую производную, является выполнение
неравенства f"(x) ^ 0 (f"(x) ^ 0) при а < х < Ъ.
7.2. Точки перегиба.
Определение. Точка Мо(хо, г/о) графика функции f, имеющего касательную, называ-
называется точкой перегиба этого графика, если существует такая окрестность точки го оси
абсцисс, в пределах которой график функции f слева и справа от хо имеет разные напра-
направления выпуклости.
Теорема. Точка Mo{xQ, f(x0)), для которой либо f"(x0) = 0, либо f"(xo) не существу-
существует, есть точка перегиба, если f"(x) меняет знак при переходе через точку хо-
Найти промежутки выпуклости определенного знака и точки перегиба графиков следую-
следующих функций:
108. f:xi-^-ix2 -х\ х €К.
М Вторая производная f"(x) = 6A — х) положительна при х < 1 и отрицательна при
х > 1. Следовательно, согласно теореме пункта 7.1, на интервале ] — оо, 1[ график функции /
имеет выпуклость, направленную вниз, а на интервале ]1, +оо[ — выпуклость, направленную
вверх. Согласно определению пункта 7.2, точка МоA, 2) есть точка перегиба графика. >
109. / :х^хх (х>0).
¦4 Поскольку вторая производная f"(x) = xx ((In х + IJ + -) > 0 при х > 0, то, сог'Ласио
теореме п. 7.1, график данной функции имеет выпуклость, направленную вниз. >
110. При каком выборе параметра h "кривая вероятности"
h>o,
имеет точки перегиба I ±<т, —-=e
¦4 Судя по знаку второй производной f"(x) — ~y^Bh2x2 — 1) e~h x , заключаем, что при
х = ±-у57" имеются перегибы (при переходе через эти точки вторая производная меняет знак).
Поэтому требуемое значение h получим из равенства I it, = т) =>¦ I h = ^ I, <Т > 0. >

162 Гл. 2. Дифференциальное исчисление функций одной переменной
111. Пусть функция / дважды дифференцируема в промежутке а ^ х < +оо, причем:
1) f(a) = А > 0; 2) /'(а) < 0; 3) f"{x) ^ 0 при х > а. Доказать, что уравнение /(ж) = 0 имеет
один и только один действительный корень в интервале ]а, +оо[.
^ По формуле конечных приращений Лагранжа при х > а получаем
f(x) = A + (x-a)f'{^(xj), a<fc<x, A)
/'(х) = /'(а) + (х-а)/"F(х)), а<&<х. B)
Из условия /"(?2) ^ 0 следует, что /'(i) < 0 при х > а, поэтому функция / убывает на
интервале ]а, +оо[. Из формул A) и B) находим
/(х) = Л + (х - a)f'(a) + (х - a)(fc - a)/"FF))- C)
В силу условий /'(а) < 0, /"(&(?i)) ^ 0, из формулы C) следует, что при достаточно большом
хо > а значение функции отрицательно. Поскольку функция / непрерывна на сегменте
[а, хо], то по теореме Коши о промежуточных значениях существует такое xi €]a, xq\, что
f(x\) = 0. Функция / не может обратиться в нуль ни в какой иной точке, отличной от xi,
так как убывает на интервале ]а, +оо[. >
112. Функция / называется выпуклой снизу (сверху) на интервале ]а, Ь[, если для любых
точек ii и 12 из этого интервала и произвольных чисел Ai и А2, Ai > 0, А2 > 0, Ai + А2 = 1,
имеет место неравенство
/(Am +X2X2) < \if(xi) + \2f(x2)
(или соответственно противоположное неравенство
/(А,ц + \2х2) > Ai/(ii) + A2/(z2)).
Доказать, что функция / выпукла снизу на ]а, Ь[, если f"(x) > 0 при а < х < Ь, и / выпукла
сверху на ]а, Ь[, если f"(x) < 0 при а < х < Ь.
•^ Пусть f"(x) > 0, х g]a, b[, и пусть Ai > 0 и Аг > 0 — произвольные числа, удовлетво-
удовлетворяющие условию Ai + А2 = 1. Если ii и Х2 — любые точки интервала ]а, Ъ[ и х\ < х2, то
точка Aiii + A2I2, очевидно, лежит между ними. По формуле Лагранжа имеем
/(Aixi + А2х2) - /(xi) = А2(х2 - х,)/'F), A)
где xi < 6 < Am +A212, и
/(х2) - /(Am + A2X2) = Xi(x2 - xi)/'F), B)
где Ain + A2I2 < ^2 < %2- Умножая левую и правую части равенств B) и A) на Аг и Ai
соответственно и вычитая из первого полученного равенства второе, находим
А2/(х2) + Ai/(xO = /(A,i, + А2х2) + AiA2(x2 - и)/"F), C)
где ^i < ?з < ?2 ¦ В силу условий Ai > 0, А2 > 0 и /"(?з) > 0, имеем
А2/(ж2) +Ai/(n) >/(Au;1 +A2I2),
т. е. / выпукла снизу на ]а, Ь[.
Если же f"(x) < 0 на ]а, Ь[, то функция ip : х к->¦ —f(x) по доказанному выше выпукла
снизу на ]а, Ь[, в силу чего имеем
Aiv(ii) + А2^(е2) > ^(AiXi + A2I2),
откуда Ai/(ii) + \-2f{x2) < f(\iXi + A2I2). Полученное неравенство показывает, что / вы-
выпукла сверху на ]а, Ь[. >
113. Показать, что функции (pi : x t^ хп (п > 1), ip2 : x ь-> е1, 933 : I •-»¦ ilni, I > 0,
выпуклы снизу на интервале ]0, +оо[, а функции -ф\ : х у-у хп @ < п < 1), ф2 : х i-»- In i
выпуклы сверху на интервале ]0, +оо[.
^ Дифференцируя дважды данные функции, находим
tf() {l)n-2 '() " ^'() V;'() A)^ ^'() 4
При х g]0, +оо[ имеем ^"(ж) > 0 (j = 1, 3), V;!'(?) < 0 (fc = 1, 2), поэтому, на основании ре-
результата, полученного при решении предыдущего примера, можем утверждать, что функции
ipj выпуклы снизу, а функции фк выпуклы сверху на интервале ]0, 4-оо[. >

§ 7. Направление выпуклости графика функции 163
114. Доказать, что ограниченная выпуклая функция всюду непрерывна и имеет одно-
односторонние левую и правую производные.
•^ Предположим для определенности, что функция / выпукла снизу на интервале ]о, Ь[. В
силу ограниченности / на ]а, Ь[, Зс > 0 такое, что |/(х)| ^ с. Пусть хо €]о, Ъ[ и приращение
аргумента h > 0 в этой точке взято такое, что точки xq — h и хо + h также принадлежат
]а, Ь[. Поскольку / выпукла снизу, то справедливо неравенство f(xo + h) + f(xo — h) >2/(id)>
которое перепишем в виде
f(x)-f{xo-h)<f(xo + h)-f(xo). A)
Из неравенства A) получим систему неравенств
/(х0 - Щ - /(хо - {к + l)h) < /(хо + h) - /(хо) <
<f(xo+{k+l)h)-f(xo + kh), k = 0,n-\, B)
при условии, что точки хо — (к + l)h, хо + (к + l)h [к = 1, п — 1) принадлежат интервалу
]о, Ь[. Суммируя неравенства B) по к от 0 до а — 1, приходим к неравенству
f(xo)-f{xa-nh) < f{xo + h)_ f{xo) < f{x0+nh)-f(xo)t C)
из которого, принимая во внимание ограниченность функции /, получаем
^. . D)
Каким бы ни было е > 0. при всех п > | —1 имеем
|/(*о + Л)-/Ы|<е, E)
если h удовлетворяет условию
0 < h < min
Г Ъ — хо хо — а ~\
т\ , \.
{. п п )
Непрерывность функции / в любой точке интервала ]а, Ь[ доказана. Докажем существование
односторонних производных функции. Пусть h > hi > 0. Тогда справедливы неравенства
/(яо + М/Ы . f(xo + h)-f(xo) f{xo-hi)-f{xo) /(хо - h) - f(xp)
а) hi < h ; б) =л! > =л •
В самом деле, записав hi = Oh, 0 < в < 1, видим, что неравенство а) эквивалентно неравен-
неравенству
0/(хо + h) + A - 0)/(хо) > /(хо - hi),
а неравенство б) эквивалентно неравенству
0/(хо - h) + A - 0)/(хо) > /(хо - hi),
каждое из которых справедливо в силу выпуклости снизу функции /.
Таким образом, функция ip : h i-+ Hxo+hj-f{xo) убывает при ^ ^ _|_о и ограничена снизу
числом — -j^-, а функция ф : h —> -h~ ^х°' возрастает при h —> +0 и ограничена сверху
числом y~. Поэтому существуют пределы
h
lim ip(h) = f+{x0), lim ф(К) = fL(x0). >
+0 /+0
115. Доказать, что если функция / дважды дифференцируема в бесконечном интервале
]хо, +оо[ и lim /(x) = 0, lim /(x) = 0, то в интервале ]хо, +оо[ имеется, по меньшей
ir^i'o + 0 j-> + oo
мере, одна такая точка ?, что /"(?) = 0.
•^ В силу выполнения условий задачи 81, в интервале ]хо, +оо[ 3^i такая, что /'(?i) = 0.
Поскольку /(х) = о(х) при х —> +оо, то на основании решения примера 93 заключаем, что
lim |/Чя)| = 0-
X—*-f ОО
Тогда, в силу примера 81, в интервале ]^i, +oo[ 3? такая, что /"(?) = 0. >

164 Гл. 2. Дифференциальное исчисление функций одной переменной
Упражнения для самостоятельной работы
Найти интервалы выпуклости следующих функций:
254. / : ж и* A + ж2) е~х'2 + ж. 255. / : ж и* arccos ~~ + Зж - 8.
256. / : х ь+ -Т7^= - 5ж. 257. /:ik-^-1 + 3i.
\Л2-1 J l+л:
258. /:Х->У, ж = (* + 1J, у = (i-1J. 259. / : X -* У, ж = shi - i, у = chi - 1.
260. f : X ->Y, x = tlnt, y = -6et-3f.
261. /:Х-»У, ж = A + <) ( , у = A +<) ( . 262. /:^и+-,0<^<|.
263. f : <p t-^ p = ip — tp2, tp ^ 0 (p, tp — полярные координаты).
264. Исследовать направление выпуклости графика функции / : X —> У, заданной неявно
уравнением ж3 — у3 — Зх2у — Зу -(- 1 = 0 в окрестности точки М{ — 1, 0).
265. Исследовать на перегиб в нуле графики следующих функций:
.. , Г ж3 sin-, ж ^ 0, . , Г ж5 cos-, ж/: 0,
а)/:жи*^ б)/:ж(><
' J \ 0, ж = 0; ; •* \ 0, ж = 0.
266. Пусть / — выпуклая снизу на интервале ]а, Ъ[ функция. Доказать, что
где о < Ж1 < ж2 < ... < хп = Ь, п ^ 2.
Используя неравенство предыдущего примера, доказать неравенства:
267. ^•¦(»;.-M<B_i + ;_|=r)n|WeN-
268. ^/Ж]Ж2 ... ж„ ^ -(ж: + ж2 + • • • +жп), ж!' > 0, г = 1, п.
269. а) 1а + 2а+ ... +па ^ п(^)", а ^ 1, п € N;
1-- -
270. х"+г/3"+*" > (а'+^+*)", i > 0, у > 0, z > 0, ж ^ у, ж ^ z, у ^ z, n > 1.
Доказать неравенства:
271. 2J *¦ Л. > | при п > по > 1.
Указание. Использовать вьшуклость вниз графика функции
272. f^ 5!!1?? ^ о при 0 ^ ж < т.
п
Указание. Рассмотреть функцию / : х t-* V^ $ш 'х при 0 < х < тт.
273. Доказать, что сумма конечного числа функций, выпуклых вниз, есть функция, вы-
выпуклая вниз.
274. Доказать, что функция / : ж н-+ lim /п(ж), ж g]a, Ъ[, где /i, /2, ...,/„,... —
п—*оо
выпуклые вниз на ]а, Ь[ функции, является выпуклой вниз функцией.
275. Доказать, что если: 1) р, ^ 0 и pi +рг + • • • + Рп > 0; 2) функция / непрерывна и
выпукла снизу, то
•* \ Р1+Р2+ ¦+Рп ) ^ Р1+Р2+-+РЛ
(неравенство Иенсена).
276. Доказать, что если функция / :] — оо, +оо[—> R непрерывна и выпукла снизу, то
3<р : х >-> ах + Ъ (а, Ъ g R) такая, что Уж g] — оо, +оо[ справедливо неравенство
/(ж)> ах + Ъ.

§ 7. Направлеиие выпуклости графика функции ' 165
277. Число А 6 R называется вторым производным числом Шварца фуикции / в точке
х, если Э(еп) такая, что lim е„ = 0, е„ > О, и . , , •¦•¦<¦¦.
11 — ОО
А= lim jr(f(x+en)-2f(x) + f(x - en)). .'.'„,',
Доказать, что если все вторые производные числа Шварца непрерывной функции / неотри-
неотрицательны, то эта функция выпукла вниз. .:¦
278. Доказать, что если / — выпуклая вниз функция такая, что о ^ f(x) ^ Ъ Vi € [а, 0],
и h — возрастающая выпуклая вниз функция, определенная на [а, 0], то сложная функция
у : х I-»- h(f(x)) также является выпуклой вниз. ¦'¦¦"•
279. Доказать, что если /i, /2, ... , fn — выпуклые вниз функции на ]о, Ъ[, то функция
/;ги max fi(x) также выпукла вниз на ]а, Ь[. ¦'¦'.<
1 <J i <J 71 ...
280. Если: 1) функция / :] - оо, +оо[-> R выпукла вниз; 2) f(x) > 0 Vi ф 0; 3) Эр > 1
такое, что f(8x) = 9pf(x), x G] — оо, +оо[, и V61 ^ 0, то функция h : x i-> (/(i))p является
выпуклой вниз на ] — оо, +оо[. ,;,i ¦
281. Пусть в, > 0, а, > 0 (i = 1, к), ^ б1,- = 1. Доказать, что
1=1 1=1
Отсюда, в частности, вывести, что
а%1~е ^ва + {1-в)Ь Va, 6>0 @ < в ^ 1).
282. Положив в предыдущем примере
a = —-, Ъ ¦¦
J=l J=l
получить неравенство Гёльдера для сумм
где ij > 0, ?/j ^ 0. .,.„
283. Числовой областью постоянной матрицы А = (ач), где а;> € С, г, j = 1, п, называ-
называется множество всех комплексных чисел вида
E
где жу = «j + ipj, «j, /?j G К (г2 = -1). , . Л ¦
Показать, что для любой матрицы А граница числовой области G на комплексной, плос-
плоскости z является выпуклой замкнутой кривой, т. е. отрезок, соединяющей любые две точки
кривой, погружен в С!.
284. Матрица А = (atJ), i, j = 1, п, называется эрмитовой, если А* = А (т. е. 5ji ='a\j).
Показать, что матрица А явл"яется эрмитовой тогда и только тогда, когда ее числовая область
представляет собой отрезок действительной оси.
285. Пусть 1 ^ р ^ 2 и а,, 6; > 0 (г = 1, п). Тогда
< '=' + '=1

166 Гл. 2. Дифференциальное исчисление функций одной переменной
Доказать это.
286. Множество М С Е" векторов f называется выпуклым в Еп, если Vfi, f2 ? М Л V6 €
[О, 1] 3f € М : 0fL + A - 6>)f2 - f. При этом множество векторов {0fi + A - 6>)f2, 0 < в < 1}
называется отрезком, соединяющим векторы fi и f2.
Показать, что множество векторов
М = {f |f = (х, у), f G ?2, OOAjJO, |f| <; 1}
является выпуклым в Е .
287. Показать, что множество М = {f |f = (sinx, cos ж), f g E2, 0 ^ ж ^ ^ } не является
выпуклым в Е2.
288. Показать, что множество
Af = {f|f =(х1]х2, ... ,4 f eEn, |f|<l}
(единичный шар в Е") является выпуклым множеством в Еп.
289. Пусть задана функция / : f/ С Еп ь-> R, где U — выпуклое подмножество. Функцию
/ будем называть выпуклой на U, если Vx, у G U Л V# ? [0, 1] справедливо неравенство
f{6x + A - в) у) < 0/(х) + A - в)/(у). х>
Показать, что функция / : х н^ |х|, х G Еп, выпукла на Еп.
290. Доказать, что если / —выпуклая на U С Еп функция, то Vx; € U (х; = (хц, i2i, • • • ,
Xni), x; € ?" Vt = 1, п) выполняется неравенство
где at > 0, i' = 1, ?(, и ^ а, = 1.
291. Доказать, что если / — выпуклая на U функция и г ? R, то подмножество S Q U
всех векторов х, для которых /(х) ^ г, является выпуклым.
292. Показать, что если компоненты fi(x) вектор-функции f являются значениями вы-
выпуклых функций /,, 1'. = 1, п, на некотором отрезке [а, 6], то функция F : х н-+ {f(x), А), где А
— любой постоянный вектор, А = (Ai, А-г, ... , Ап), Ai ^ 0, из Еп, также выпукла на [а, 6].
293. Показать, что если элементы aij(x) матричной функции Л:к-» (аг](х)), х G [а, 6],
являются значениями выпуклых на [а, Ь] функций a,j : x i-+ а.Дж), то для любой постоян-
постоянной матрицы В с неотрицательными элементами функция F : i и (^(ж)> ^)> х € [ai Ч>
также выпукла. Под скалярным произведением матриц А и В понимаем величину [А, В) —
= Y2aij(x)btJ, где 6,j — элементы матрицы В (проверить выполнимость аксиом скалярного
•'¦J
произведения в ?"*).
294. Пусть функции а,• : х >-» а,-(ж), Ь, : х i—> h,(x) неотрицательны, выпуклы и возрастают
на [a, b] Vi = 1, к. Показать, что в этом случае функция F : ж i-+ (а, Ь)— скалярное
произведение векторов а — (ai(i), ... , а„[х)), Ъ — (bi(x), ... , Ьп{х)) — выпукла на [а, 6].
§ 8. Раскрытие неопределенностей
8.1. Раскрытие неопределенностей вида -. Первое правило Лопиталя.
Если функции fug определены в некоторой окрестности точки а [х ф а), где а —
число или символ оо, и при х ^ а обе стремятся к нулю, а производные /' и </' существуют
' В случае, когда U — отрезок действительной оси, это определение выпуклости совпадает с опре-
определением выпуклости вниз.

§ 8. Раскрытие неопределеииостеи 167
в упомянутой окрестности, за исключением, быть может, самой точки х = а, причем одно-
одновременно не обращаются в нуль при ж ф а, и существует конечный или бесконечный предел
Шп
х~а д'(х)
8.2. Раскрытие неопределеииостеи вида —. Второе правило Лопиталя.
Если функции fug при х —> а обе стремятся к бесконечности, а производные /' и д'
существуют для всех х, принадлежащих некоторой окрестности точки о и отличных от о,
причем (/'(ж)J + (д'(ж)J ф 0 в упомянутой окрестности и х ф а, существует конечный или
бесконечный предел
lim Ш,
х~а д'(х)
д(х) *-.<, д'(х)
Найти пределы:
116. lim **+1(Ь * + !)-*
1—1 1-Х
•^ Функции / : х 1—> ж1+1Aпж + 1) — ж и j : i и l-i, i > 0, i ^ 1, удовлетворяют
следующим условиям:
1) lim /(ж) = lim д(х) = 0;
я:—.1 ж—*1
2) их производные /':1и ж1+1Aпж + l).(l + i + ln ж) + ж* — 1, д' : х н-+ — 1 существуют
при ж > 0;
3) существует lim ^ = -2; 4) (/'{ж)J + (з'(ж)J ^ 0 при х > 0.
Следовательно, применимо первое правило Лопиталя, согласно которому имеем
t\ ж*+1A1-+ж1)~Ж = J*\ т§ = -2 • >
117. lim
x^l 111 Ж — Ж + 1
•^ Функции /iihi'-i и д : х \—> In ? — ж + 1,ж>0,ж/:1, удовлетворяют следующим
условиям:
1) lim /(ж) = lim д(ж) = 0;
X —1 Х^1
2) производные f : i и ^(lni + 1) — 1 и j':ih 1 существуют в достаточно малой
окрестности точки ж = 1;
3) (/'(i)J + (g'(i)J /: 0, х ф 1, в указанной окрестности;
4) согласно предыдущему примеру, существует конечный предел
Ь, ЙО = iS •+1(^1+1)— = -2.
Следовательно, применимо первое правило Лопиталя, и мы имеем
fix) ж1*1 (In ж + 1) — х
lim -)— = Km Ц ' = -2. >
x-i д(ж) х-,1 1 - ж
118. ю = lim — ( — 1 . '
х-.о х у til ж tgжy
. п -- , 111 1 \ ,— TTT)\fnl chxsin x—sh x cos a:
•^ Преобразуя функцию и : ж и-> - I ^-^ — ^—- I, ж € К\{0|, к виду и : ж >—> xshxsinx '
замечаем, что функции /:ги сЬжэтж — вИжсовж, j:i и ж sh ж sin ж удовлетворяют усло-
условиям первого правила Лопиталя. Поскольку существует
-f / . , л sh х sin x
,. / (ж) 2sh ж sin ж л— г— 2
lim ,; , = Urn : ; : ; = lim -г : . г = -,
^q п {X] х—-+ 0 sh X SIH X ~l~ XI Cil X SIH X ~\~ Sll X COS X ) x *-0 ^ x sin x |^ i sin x |^ sn i "
xx x x
то, согласно указанному правилу, w = -. >

168 Гл. 2. Диффереициальиое исчисление функций одной переменной
Замечание. Для нахождения lim ]/l можно было бы применить правило Лопиталя (дважды),
х->0 9 \х)
однако здесь, как и в других подобных примерах, удобнее (с вычислительной точки зрения) поль-
пользоваться замечательными пределами.
119. w= limo (e~^x-10Q, xx -'
•^ Поскольку для вектор-функции
w= lim ( e"я"00, хх -1 \ = ( lim e ^x"", lim
x~+0
то находим пределы каждой из компонент в отдельности. Имеем
1 50
lim е *2 ж-100 = lim iL_ - 50! lim e~y = О
х->0 х->+оо еу у—> + оо
(здесь второе правило Лопиталя применено 50 раз).
Для второй компоненты предварительно применяем представление и" = e"'nu, и > 0, и
проводим некоторое преобразование с тем, чтобы можно было воспользоваться правилом
Лопиталя:
lim i*1 ' = lim e V aMna: / = e"
X-.+0 x —+0
(Здесь мы воспользовались непрерывностью функции х ь-> ех и теоремой о пределе произве-
i 2
дения). Для нахождения а = lim ж In х = lim —=т применяем второе, а для нахождения
Х-.+0 Х-.+0 ^
Ъ — lim t| первое правило Лопиталя. Имеем
1п2х 21п:Е-^ ,. -21пх -|
Inn — = lim —¦ = lim :— = Inn —— = 0,
х—>+0 Х~г х->+0 —Х~2 х->+0 Х~1 х—+0 —
х2
х\п х -I t -¦
Ш11 : = llin = 1.
х—+о xlnx t—-о г
Поэтому окончательно w = @, 1). >
•^ Для нахождения предела вектор-функции вычисляем пределы каждой из ее компонент.
Поскольку компоненты представляют собой степенно-показательные выражения, то приме-
применяем представление и" = е"'п ", и > 0, и, приведя соответствующие неопределенности к виду
j, пользуемся правилом Лопиталя. Имеем
= о,
B \ х lim x\n{— arctgxl
— arctgx) = е1—+°° т = ег,
7Г /
где г = Шп
1-1-х2 arctgx 2
i—fi— =
lim (th x)x = lim e

§ 8. Раскрытие неопределенностей ьг V&9
где ¦ , .•:.-.'.
1 1 2
z= lim iln(ths) = Um th* ' f*x = -2 lim -^—=-2 lim -?— = 0.
/ -- \
Следовательно, w = I 1, e », 1 . >
121. Найти предел матричной функции
i
/sinx\—^ /arctffx\
у J x2 ^ 6—j
при х —? 0.
•^ Поскольку lim А(х) = ( lim aij(x) ), где aij{x) — элементы функциональной матрицы
х—*а \х—*а /
А(х), то вычисляем предел данной матрицы поэлементно. Имеем
J_ , sini ¦'..-...,
.. /SIlll\x2 z Ш —— , r.
lim = e , где z = lim ^—.
x—о \ x ) x—o i^ i '• " ¦' :'¦'
Применяем правило Лопиталя ¦'"'¦•'''
x x cos s—sin x ,. x cos ж —sin i ,. —isinx 1
г
.. х х cos х— sin x x cos ж —sin i
= lim -—: • ~ = lim — = lim
2 2 23
lim : = lim — = lim = .
x—о 2ismi x2 x~о 2i3 1-.0 6i2 6
Аналогично получаем для всех других элементов:
lim ( lrc %x ) * = e", г = lim ¦—¦— = lim —-—
x->0 \ X / x — 0 X* x—0 arctgx
x — A + i2)arctgx ,. —2i arete i 1
= hUo 2x^ = Umo 6^~ = ;
Arsh j: _ X — Arsh X
у i ni = ii л ^ xt. - 1. x !< _ X \/1 + Х2
)^ ] МГ5П X
^ г 1- 1П х г х
= е , z = lim = lim •
х~0 X2 x^O Arshx
1 .. x — u(x) 1 —i Arsh x _ 1
(здесь введено обозначение и(ж) = л/1 + ж2 Arsh ж);
Итак, окончательно имеем
122. lim A-
1
1 \
1 ..
Г !+* 1
х—*0 ZX ?
1
.__. . (Ifl
¦"¦" ty
J, ^ , ,,1
2
•^ Неопределенность оо — оо приводим к виду ^, получим
!_ 1 _ ех -1-х
х ех - 1 ~ ^(е111 - 1)
и, дважды применив правило Лопиталя, имеем
lim е* ~ 1 ~ж - li ех-1 _ е1 _ 1
х™ х(ех - 1) ~ хЛо ег - 1 + жех ~ xl-^o ехB + i) ~ 2 '

170 Гл. 2. Дифференциальное исчислеиие функций одной переменной
123. w= lim fl±-flV' X.
х—о \ 2 /
•^ Неопределенность 1°° приводим к виду ео t получаем
/i + e-\cth* (И
\ 2 )
и, применяя правило Лопиталя, имеем:
Um \ ' = lira 1+е* 2 = -.
i-.o th х Ж-.0 ch х 2
i
Таким-образом, w = е? . >
124. Исследовать на дифференцируемость в точке х = 0 функцию
~ ~ ^1Г> если х / 0;
-, если х = 0.
•^ Исследовать на дифференцируемость функции в точке х = 0 означает установить су-
существование конечного предела
Предел A) будем искать по правилу Лопиталя, для чего мы должны убедиться, что чи-
числитель в A) стремится к нулю при х —> 0. Проверка с применением правила Лопиталя
показывает, что
,. /1 1 1\ ,. 2ех - 2 - х - хе* ,. ех - 1 - хех 1 ,. -хех
Ьо U " ^Т ~ 2 J = Ьо 2х(е^ - 1) = 1™о 2 (е-A + х) - 1) = 2 1™о 2е^ + хе^ = °"
Итак, в формуле A) имеем неопределенность вида -. Применяя к A) правило Лопиталя
трижды, получаем
2ех - 2 - х - де" ге" - 1 - е* -
l hm
lim — = lim — ^ = lim
" " 4ж(е1 - 1) +2х^ех
-ех(т.Л-Л\ Л . Л
¦*-.о 2ж2(е1-1) х~о 4х(ех - 1)-(-2х2еж
-хех ,. -е*(ж + 1)
~ ""о 4(е« - 1) + e'(Sx + 2х2) " ГГо A2 + 12х + 2х2) е« ~ 12' J у ' ~ 12'
125. Найти асимптоту кривой
Л+*
•^ Уравнение наклонной асимптоты имеет вид у = fcx + б. Использовав уравнение кривой,
находим fc и Ь:
, х" 1 1
А; = hm т^-—гг = Ьт —^ = -,
Ъ = lim
( xi+x х\ /1 1\1 //'1\л:\
^+оо \A +х)х e.J Х-+00 I 1 -|- Ij el е2 х^+оо \ V х) )
2е"
Таким образом, получаем уравнение асимптоты у — |- + —. Обоснование законности
многократного использования правила Лопиталя мы предоставляем читателю. >

§ 8. Раскрытие неопределенностей
126. Возможно ли применение правила Лопиталя к пределу
171
lim
*->о sm х
•^ Функции / : x (—> i2 sin - и j : i и sin ж,, ж € R\{0}, определены и непрерывны в
окрестности точки ж = 0 (исключая точку х =0); их производные /':ih 2xsin - — cos - и
д : х ь-> cos ж одновременно существуют при х ф 0; выражение (f'(x)J + (g'(x)J = cos2x +
cos2 - - 2ж sin - + 4ж2 sin2 - ф 0 при i/Ои
hm
/(я)
i-f-f = km
g(x) X—-0
A)
Поскольку lim [2x sin -) (cos ж) г = 0, a lim (cos -) (cos x) l не существует, то предел A)
также не существует. Следовательно, применение правила Лопиталя в данном примере не-
невозможно. >
Отметим, что
ж sm - х ( \\
lim —; — = lim — • lim I ж sin — 1=0.
1-.0 sin x 1-.0 sm ж I-.0 \ xl
127. Найти
det
z — lim
x--0
sm x
ex - 1 1 + x2
det
ж cos ж tg х
¦4 Данные определители как функции переменной ж удовлетворяют всем условиям пра-
правила Лопиталя в некоторой окрестности точки х = 0. Поэтому, применяя правило, получаем
det
z — lim
J-.0
-1 \+хг
det
ж sm ж
е* 2ж
det
cos x — ж sm i cos x
shi e*
+ det
X COS I tg Ж
сЬж е*
det
1 1
0 1
det
0 0
1 1
Упражнения для самостоятельной работы
Найти следующие пределы:
295. lim _j!'° !Г'?-^! _^ ¦ 296. lim \'~\^" . 297. Urn .
298. lim
302.1^^^A
304. lim (v'i4 +x3 + 2i + 1 - V4i2 + i + 1 + vV + аж4 + 1).
305. lim
306. lim
307. lim

172
308-
Гл. 2. Дифференциальное исчисление функций одной переменной
309. lii
310. lim
Х-+0
7 I V
j/(l+xK-lj
312. lim
. 311. lim
. 313. lim
314.
/ arcsin х \ х2 / ars
-. 315. lim sinxh-xx). 316. Um tgx(l - xx).
x—+ 0 x— + 0
317. lim
I—+0
320. Hm
te2. 318. lim "" ^*)
arc
319. u
x—.4-0 arcsin (ex —1)
321. lim ( *'9П9'°;° д) 3:r2 ¦ 322. lim '-* ' ? > °-
arcsin (ex —l)
Sill 7ГЛ' —COS ¦
324. Um
326. Um
325. Um
sm x cos i
2
tgz
I
1
shx
Iu2(l
i
i
+ i)
arcsin i
. 327. lim ~
Ж X
,2n-l
x sm i i
i tgi
328. Пусть функции fugs некоторой окрестности U точки а, за исключением самой
точки а, имеют производные до (п + 1)-го порядка включительно. Пусть, далее, выполняются
условия:
1) Um f(x) - lim f'(x) = ... = lim /(n)(i) = 0;
x—-a, x—*a x~-*<z
2) Um g{x) = lim g'(x) = ... = lim g(n)(i) = 0; 3) 3 lim '[iTl^l =l,leR;
4) производная ^п+1^(ж) /0в окрестности U. Тогда
km ; ч7 = lim i
()
Доказать это.
329. Пусть функции / и д в некоторой окрестности f/ точки а, за исключением самой
точки а, имеют производные до (п + 1)-го порядка включительно. Пусть, далее, выполняются
условия:
1) Um f(x) - lim f'{x) = ... = Um /(n)(i) = +oo;
x—* a л; —* a ' a- —* a
2) Um g(i) = Um g'(x) = ... = lim g{n)(x) = +oo; 3) 3 lim ^"l'!^ =!,lel;
x—a x—a x—a x—a 9V x '(x)
4) производная g^n+1^(x) /0в окрестности t/. Тогда
lim =h 4^
x — a g(l) x-a g<"+1)(l)
Доказать это.

§ 9. Формула Тейлора • i 173
§ 9. Формула Тейлора
9.1. Формула Тейлора на промежутке.
Пусть / :]а, 6[ — R и 3/<n+1) на ]о, Ь[. Тогда Vi, ю €]о, 6[Л Vp > О 30 такое, чэс^.спра-
чэс^.справедлива следующая формула:
f(x) = /(х0) + 1'Ы(х - хо) + • • • + /П^1О)(Д - Ю)" + Лп+1(я),
где ¦ :
Дп+1(х) = ^х°)П+%-^-Р+1/^\хо + в(х - хо)), 0<*<1, A)
(остаточный член в форме Шлемильха—Роша). Из A) при р = п + 1 получаем остаточный
член в форме Лагранжа
Rn+i{x) = (*(~'"j^' /("+i)(^o + tfi(x
а при р = 1 — остаточный член в форме Коши ,
Д„+1 (X) = (Ж ~ ^}"+i A - ^2)П/(П+1)(^ + 02(T - Хо)), 0 < 02 < 1.
9.2. Локальная формула Тейлора (или формула Тейлора с остаточным членом В
форме Пеано).
Если функция /, определенная в некоторой окрестности точки хо, имеет конечную про-
производную /("'(хо), то справедливо представление
Дх) = /(х0) + /'(хо)(х - хо) + ... + f{n\x0){x - Хо}П + о((х - хо)я),
л!
X —> Х0.
9.3. Пять основных разложений.
Положив во всех формулах Тейлора пунктов 9.1 и 9.2 хо = 0, получим соответствующие
формулы Маклорена. Из локальной формулы Маклорена вытекает пять основных разложе-
разложений:
I. ех = 1+х+^+ ... +^- + 0{хп), х-*0; . ..
II. sinx = x-ff+...+(-l)n-1g^T + 0(x2"), х-0;
III. cosx = l-f + ... +(-l)ngT + 0(x2"+1), x-0;
IV. A + Х)'" = 1 + mi + ^~^-Х2 + ... + т(т-1)(т-2)...(т-п+1)д„ + о^„^ х -> Q;
V. ln(l + i) = i-y+...+ (-1Г v + o{xn), 1 — 0.
9.4. Формула Тейлора для вектор-функцин.
Пусть вектор-функция f :]а, Ь[—> ?*" имеет производную (п + 1)-го порядка на ]а, Ь[.
Тогда Vx, хо б]а, 6[Л Vpj > 0 3#j , j = 1, fc, такие, что справедлива формула : , , '
i=0 ' ' '
rHef(x) = (/1(x), /2(x), .... Д(х)),
(X - X0)"+i
j
ri+i (x) — (лп+1, Лп+1, ... , Лп+
Для вектор-функции справедлива локальная формула Тейлора.
Написать разложения следующих функций по целым положительным степеням перемен-
переменной х до членов указанного порядка включительно: :;4t'¦'¦''¦-'¦•

174 Гл. 2. Дифференциальное исчисление функций одной переменной
1 4- 4- 2
128. / : х I—> до члена с х . Чему равно /^ @)?
1 — х + хг
Ц Представляя значение функции / в виде
и пользуясь разложением IV
(l+x3) = 1 -х3 + о(х5), х —О,
получаем
/(х) = 1 + Bх + 2х2)A - х3 + о(х6)) = 1 + 2х + 2х2 - 2х4 + о(х4), х — 0.
Сравнивая полученное выражение с разложением в общем виде (см. пункт 9.2), находим
?~У^ = -2, откуда /D)@) = -48. >
1Z9. е до члена с х .
< Полагая t = 2х — х2 и используя разложение I, имеем
, f f t* tb 5
= 1 + Bx - x2) + ^Bx - x2J + ... + iBi - x2N + o(x5), x — 0,
(мы учли, что o(tb) = oBx — x2M = o(x5) при x —¦ 0). Выполняя далее соответствующие
действия и записывая в разложении члены до х5 (х6, х7, ... вносим в о(х5)), окончательно
получаем
е2*-*2 = 1 + 2х + х2 - -х3 - -х4 - —х6 + о(х6), i -» 0. >
3 о 15
130. Vsinx3 до члена с х13 .
Ц Положим х'' = t и воспользуемся разложением функции sin < по формуле Маклорена:
<< + U
о I2U
а также разложением IV. Тогда получим
I / <2 <4 \ з I I
I _ _ + _ + o{tb) \ =<3(l + ft(<)K
V 3 9 K
3 \ 6 120 J 9
Ш + "(I») — f, Ш
131. In cos x до члена с х .
Ц Применяя разложения V и II, получаем
1 , / ^~9— 1, , -2% 1 / 2 sin4 х sin6 x , 7\ I
In cos x = In V 1 — sm^ x = - ln(l — sm x) = - I — sin x 1- o(x ) I =
2 V у
1 (( x3 x;
2 \\ 6 12
2 X6 X4 X6 X4 X6 ~G Л -2 -4 -6
132. sin(sin x) до члена с х .

§ 9. Формула Тейлора 175
Пользуясь разложением II, имеем
sin х
... . . SX1L X 4 .
sin(sm x) = sm x — Ь o(sm xj =
/ x3 \ 1 i3
= ( x + o(x4) I (x3 + o(x4)) 4- o(sin4 x) = x 1- o(i4). >
133. tg x до члена с х .
Ц Поскольку функция tg x нечетная, то ее разложение в окрестности точки 1 = 0 имеет
вид
^х = Ах + Вх3 + Сх&+о(х6), х —0, A)
где А, В, С — коэффициенты. Записывая A) в виде
sin х = (Ах + Вх3 + Сх5 + о(х6)) cos x
и используя разложения II и III, получим
° + о(х°), х -<• 0.
Отсюда, приравнивая коэффициенты при одинаковых степенях х, находим
~~ ' ~ 3' ~ 15'
Таким образом,
х3 2 ь
tgz = x + — + — х + о(х ), х — 0. >
134. Найти три члена разложения функции / : х i—*¦ \[х по целым положительным
степеням разности х — 1.
Ц Воспользовавшись формулой Тейлора с остаточным членом в форме Пеано, получим
f{x) = /A) + /'A)(х - 1) + ?Sp-(x - IJ + о((х - IJ), х - 1.
Затем находим
и, подставив эти значения в полученную формулу, окончательно имеем
f{x) = 1 + 1(х _ 1) _ 1(х - IJ + оЦх - IJ), х - 1. >
/ о
135. Функцию / : х I—*¦ ach —, а>0,в окрестности точки х = 0 приближенно заменить
параболой второго порядка.
Ц Поскольку
, х 1 / Е _?\ х2 2
ch— = -(ea+e " =1 + —^г + о(х ), х —<¦ 0,
a / \ / La*
то /(х) = a + |^ + о(х2), х — 0. >
136. Функцию f : х i—> \/1 + х2 — х, х > 0, разложить по целым положительным
, 1 1
степеням дроби — до члена с —г ¦
X Хл
< Преобразовывая выражение ^1 + х2 — х и пользуясь разложением IV, получаем
1

176 Гл. 2. Дифференциальное исчисление функций одной переменной
137. Функцию/ : х I-»- : -, х g] — оо, +оо[, разложить по формуле Тейлора с
остаточным членом в форме Лагранжа. Разложение вести в окрестности точки хо = 1 и
найти первые три члена разложения.
^ Искомое разложение имеет вид
Найдем значение функции и ее производных в точке х = 1. Имеем
3 1
Таким образом,
J \ 1 — лс V / йЛ ' Ч' /^
138. Пусть
/(х + ft) = /(х) + ft/'(x) + . . . + ^/(П)(* + «А), A)
где 0 < в < 1, причем /(п+1)(х) ^ 0. Доказать, что lim в = -.
h_»o Jt + 1
Ц Поскольку /(п+1)(х) существует, то по формуле Маклорена с остаточным членом в
форме Пеано запишем
f(x + h) = f(x) + hf(x)+...+^f\x)+f(x)
п\ (тс -f- I)!
Вычитая из равенства A) равенство B) и сокращая на -^-, имеем
fn\x + вк) - fn\x) _ /("+1)(x) o(h)
ft n+1 ft '
откуда
O. B)
п + 1 h
Переходя к пределу при ft —> 0 в этом выражении и принимая во внимание, что /(п+1'(х) ф 0,
находим lim в = —i—. >
139. Пусть / € С'B)([0, 1]) и /@) = /A) = 0, причем ЗЛ > 0 : |/"(х)| < A Vx e]0, 1[.
Доказать, что |/'(х)| < — Vx e [0, 1].
Ц По формуле Тейлора имеем
/@) = /(х) - х/'(х) + /"F)у, 0 < 6 < х < 1;
/A) = /(х) + /'(х)A - х) + /"(ft)Il^-, 0 < х < 6 < 1,
откуда
f'/T\ — _ I f"(f,\r2 — f"(t- Л { Xi— I fl ^ т ^ 1
J I.'*'; ~ о I •> v^l^* J 1,42,1 ,. I i и ^ x ^ i.
V /
Оценивая это равенство по абсолютной величине, получаем
А 2
Но так как 0 ^ 2х2 — 2х + 1 ^ 1 при 0 ^ i ^ 1, то |/'(i)| ^ у, что и требовалось доказать. >
140. Пусть / — дважды дифференцируемая на ] — оо, +оо[ функция и
Мк= sup \f(k){x)\<+ao, А; = 0Г2.

§ 9. Формула Тейлора 177
Доказать неравенство М\ ^ 2МоМ?.
Ц По формуле Тейлора имеем
f(xo)=f(x) + f'(x)(xO-:
откуда
\f'(x)\\xo -x\ + |/"(О1|Я°2Я|2 < M° + М'У + M*Y'
Поскольку Mo + Miy + ^M2y2 J? О при всех у, то М? ^ 2Л/оЛ/г. >
141. С помощью формулы Тейлора приближенно вычислить:
' a) sin 18°; б) arctgO,8.
Ц а) Согласно формуле Маклорена с остаточным членом в форме Лагранжа,
. ,„о ¦ т тг 1 тг3
811118 =smw=To-6-W
где |Д7|< i.^. Итак,
0,314159 f! _ ^869604 (9.869604J
' \ 600
10 V 600 ' 12-105; 'V 600 т 12-105
х 0,314159 A - 0,016449 + 0,000079) и 0,зб9017.
б) Применяя формулу Тейлора, имеем при хо = 1
arctg 0,8 = arctg (ю - 0,2) я arctg хо - (arctg x)'\x=XQ • 0,2 + - • 0,04 (arctg i)"|x=xo -
- i ¦ 0,008 (arctg i)'"|x=Xo »j-0,l- 0,01 - 0,00066 « 0,67474.
Поскольку (arctg i)D)|x=Xo = 0, (arctg x)(-s>l\x=( = 24 1~,1°(.?Л( < 12 при 0,8 < ? < 1, то по
формуле остаточного члена в форме Лагранжа получаем оценку погрешности
|Д| < — @,2M < 3,2 • 10~5. >
142. Вычислить:
a) cos 9° с точностью до 10~5; б) л/б с точностью до 10~4.
^ а) Определим число членов разложения функции косинуса по формуле Маклореиа для
достижения заданной точности. Его можно получить из оценки остаточного члена в форме
Лагранжа. Так как 0<^ = ^^-<^-,i = j^,to "'.""
/ \Bra+21l , _ ч 2п4-2 _2п+2
< 10~5,
' 202п+2Bп
откуда п ^ 2. Таким образом,
cos9° ~ 1 - I (—У + - AЛ* ~ о
~ 2 V20/ 4! V20/ ~ '
•"»•
б) Функцию / : х I—*¦ д/i, z ;> 0, разложим по формуле Тейлора в окрестности точки
= 4: '
где
/? Г^ - B»-1)!! (-!)"(*-4)"+

178 Гл. 2. Дифференциальное исчисление функций одной переменной
Полагая в разложении х = 5, получаем
Из условия
находим, что п ^ 4. Тогда из A) следует
Используя разложения I—V, найти следующие пределы:
I х'\
cos х — ехр I I
143. lim V > .
х-*0 I4
Ц Применяя разложения I и III, получаем
/ х2\
cos х- ехр (—- ) 1 f х2 xi
~ Т+ 24 + °^ ' "
144. Шп ({/х6 + Is - v/
X—*+ОО
^ Преобразовав выражение, находящееся под знаком предела, и применив разложение
IV, имеем
Lm (ух + х ~ Vх - х ) = hm х A + - -II =
X—+0О X—+оо \\ X/ \ Х) ]
з-*
145. lim
X3
" = evl"u
Пользуясь представлением и" = evl"u, и > 0, и разложениями I, V, находим
lim х 3A - esmlIncosa:) = lim
i\
In cos i .. lnfl — sin x) 1 ,. sin x + o(x) 1
= — lim = — lim —^ = - lim ^—'- = -. >
x-.o i2 x-o 2x2 2 x-.o x2 2
146. w= lim x~3(sh(tgi) -x).
< Здесь применяем разложение I, а также используем разложение tg x = х + ^- + o(i4).
Имеем
,. tgx+ j tg3 х + о(х3) - х х+ ^ + о(х3) + ^ + о(х3)-х 1
w = km 2 = lim =* —2 = -. >
х—*о з:13 х—*о ? 2
Для бесконечно малой при х —* 0 величины у определить главный член вида Схп (С —
постоянная):
147. у = tg(sini) -sin(tgi).
•* Прежде всего установим разложение

§ 9. Формула Тейлора 179
Действительно, представляя tgx в виде sini(cosi) и используя разложения II—IV, полу-
получаем
X -| о с
tg х — sin хA — sin2 x) 2 = sin i-|— sin3 x + — sin5 x -\—- sin7 x + o(x8) =
2 8 16
s x7 if x3 xb
5 7
+16"
что и требовалось доказать. Используя эту формулу, а также упомянутые разложения, полу-
получаем
, . , . , N . sin3 x 2.5 17.7 te3i
у = tg (sm x) - sm(tg x) = sin x -\ h — sm x+ —~ sin x -Щх + -^
о 15 olo b
tg6x tg7x . 8, x3 x5 x7 if x3 is\ 2 f X3V
17 _7 x2 2 6 17 7 1 / Xs ,2
„з ~ \ з
откуда Cxn = |j-. Следовательно, С = —, n = 7. >
148. y=(l + x)*-l.
^ Применяя разложения I и V, получаем
/2 \
у = ехЫA+х) - 1 = xln(l + х) + о(х2) = х х - ^- + о(х2) ) + o(i2) = х2 + о(х2), х — 0.
Итак, Сх11 = х2. Следовательно, С = 1, п = 2. >
149. у = 1- A + д)х.
е
Ц Используя формулу и" = е"'п ", и > 0, а также разложения V и I, находим
—1 ^
= 1 - ехр |-| + 0(х)| = 1 - ^1 - | + о(х)) + о(х) = | + 0(х), х - 0;
~ о ' ~~ 9 ' *
4-1 Ь
150. Подобрать коэффициенты А к В так, чтобы при х —>¦ 0 было справедливо равен-
равенство
Имеем
cos х 1 + j4x2
sm x x + BxJ
откуда (х + Bx3) cos я = A -f- Лх2) sin x + O(x7). Используя разложения II и III, получаем
/24 \ /35
(x + Bx3) 1 - — + — + O(x6) I = A + Ax2) [x - — + — + O(x
откуда
х ~ У

180 Гл. 2. Дифференциальное исчисление функций одной переменной
Следовательно, -~ + В =А-1-, i - f = ^ - |, откуда А = -§, В = -±. >
151. При каких коэффициентах А, В, С и D справедлива при х —+ 0 асимптотическая
формула
1 + Ах + Дх2 5
Ц Имеем
е"A + Сх + Dx2) = 1 + Ах + Вх2 + О{хь). A)
Поскольку ех = 1 + х + |у + |^- + ^ + О (У5), то из A) получаем
+ Сх + Dx2) = 1 + Ах + Вх2 + О{хь),
откуда, записывая в разложении члены до х4 включительно, находим
1 + Сх + Dx2 + x + Сх2 + Dx3 + ^ + jx3 + у х4 + ^ + ^х4 + |1 = 1 + Ах + Вх2 + О(х5).
Отсюда, приравнивая коэффициенты при одинаковых степенях х, приходим к системе урав-
уравнений:
СГ+1 = Л, D+^+Uo, D + C+l = B, j + j+f^O,
решив которую, получаем
152. Считая \х\ малой величиной, вывести простые приближенные формулы для следу-
следующих выражений:
V 100/
Ц а) Пользуясь разложением IV, получаем
1+х Jl-x ,л .1. 1 , ,1. .-I
\ = A+х)зA-х) з - A - х)з A + х) 3 =
Vl + x V ' К ' У ) \ -г )
ix - \х2 + о(х2)) (l + \х + \г + о(Х2)) -
l - \х - \х2 + о{х2)) (l - |х + ^х2 + 0(х2)) = ix + о(х2) « ix.
б) Применяя разложение V, приходим к приближенной формуле
In 2 In 2 ^ 100 In 2 70
153. Вектор-функцию fun ( — arctgx ) , х g R\{0, —2}, разложить по целым
\х х + 2 /
положительным степеням бинома х — 1 до члена с (х — 1) включительно.
Ц Искомое разложение может быть получено в результате применения формулы Тейлора
для вектор-функции (см. пункт 9.4):
Цх) = fA) + f'A)(х - 1) + 1 f"(l)(x - IJ + R3.
Поскольку f(l) = A, i, f); f A) = (-1, |, I); f"(l) = B, -±, -1-), то
где R3 — остаточный член в какой-либо форме. >

§ 9. Формула Тейлора ' 181
Упражнения для самостоятельной работы
Разложить по формуле Тейлора следующие функции:
330. / : х н-+ (sinz)smit, х > 0, в точке хо = 1 до члена с (х — IJ включительно.
Остаточный член взять в форме Пеано.
331. / : х I—> tg (х + х2) в точке хо — 1 до члена с (х — IJ включительно. Остаточный
член взять в форме Пеано.
332. / : х ы- !^=, i > 0, в точке i0 = 1 до члена с (х — IK включительно. Остаточный
член взять в форме Пеано.
333. /:гн хе~х~, х 6 R, в точке i0 = 2 до члена с (i — 2J включительно. Остаточный
член взять в форме Лагранжа.
334. /:iki arctgx, igR, в точке io = 1 до члена с (х — IJ включительно. Остаточный
член взять в форме Коши.
335. / : х I—*¦ Vl — i2 arcsin х, \х\ < 1, в точке хо = 0 до члена с i5 включительно.
Остаточный член взять в форме Пеано.
336. f : х I—* (cos(sinz), sm(cosz), es'ax), x ? R, в точке io = 0 до члена с z4.
337. f : ж i—* (/i(x), /2B), /3A)) в точке io = 0 до члена с i5, где
/2(*)=;^Pzl. ^#0, /2@) = -i; /3(x)
Пользуясь локальной формулой Маклорена, получить разложения по целым положитель^
ным степеням х до членов наибольшего или указанного порядка включительно следующих
функций:
О, х = 0.
339. / : х i—* ех . Справедливо ли разложение
Г -—
340. f:x^l е г2. х^°> (до члена с I10).
^ 0, х = О
Оправедливо ли разложение
341. / : X -v У, i = 2< - <2, j/ = 3< - <3 (до члена с i3).
342. / : X -+ Y, x = 2t + sint, у = <е' (до члена с х3).
343. / : X -+ Y, x = t-t2, y^At-t* (до члена с i3).
344. / : X —v У, у7 + у - i = 0 (до члена с х6).
Пользуясь формулой Маклорена с остаточным членом в форме Лагранжа, получить раз-
разложения по целым положительным степеням х до членов указанного порядка включительно
следующих функций:
345. / : х у- \ х* ' х^0' (до члена с х2).
[1,1 = 0
346. / : X —' Y, i4 + У4 +smxy = 1 (до члена с х3 на отрезке [—1, 1]).
347. /ли ех^, х > 0. Справедливо ли разложение
348. Пусть / : х >-+ cos(D(x)), где D — функция Дирихле. Справедливо ли разложение
cos(D(x)) = 1-

182 Гл. 2. Дифференциальное исчисление функций одной переменной
Найти выражение для R2n+2(x).
Подобрать коэффициенты А, В, С таким образом, чтобы при i -t 0 справедливы были
следующие асимптотические равенства с наиболее возможным их порядком точности (уста-
(установить этот порядок относительно х):
349. arctgx=f±|f^ + O*(x"). 350. arcsin x = f±|? + О'(х").
351. ln(l+x) = ^ + O-(x"). 352. VT^=^ + O*(x").
353. A+х)* = 1+^+,f2+O*(x"). 354.
Оценить абсолютную погрешность приближенных формул:
355. cosx и 1 - у- + §^ при |х| ^ 1. 356. л/§^« 1 + ^ при |х| > 103.
357. arctgx « f - j при |х| > 102.
з зз
358. sin(asin(u>x)) т ашх — -—-— при |au>x| < 0,1.
359. /'(х) к Нх+ь>-Н*) при \h\ ^ 0,1. 360. /'(х) к f{*+h)-nx-h) при |Л| ^ Од
361. / (x) » -1 l—i^r-1 s—- при |ft| ^ 0,1.
362. Пусть / удовлетворяет уравнению /'(х) = _F(/(x)), где F — известная, достаточное
число раз дифференцируемая функция. Пусть
flx) ~ f(x + h)~ Я*)
1 (-х' ~ h
Тогда /(х + h) — /(х) и /i_F(/(x)). Оценить |/(х) — /*(х)|, где /* — удовлетворяет уравнению
363. Пусть / удовлетворяет уравнению /'(х) = F(f(x)), где F — известная, достаточ-
достаточное число раз дифференцируемая функция. Оценить |/(х) — /*(х)|, где /* удовлетворяет
уравнению
Г (х + h) + 4/*(х) - 5/*(х - h) = 2h{2F(Г (*)) + f (Г (х - Л))).
Используя разложения I - V, найти следующие пределы:
1 хх2
е- 3 „3 х9 , (cos x-f-sin x) 8 — 1 1——
364. Urn "°о5 дГсЬ д)"; ¦ 365. lim ^ 1S ¦
е2
/ _j_ \
366. lim х2е х - Ух2 + СУХ + 1).
367. lim ( X> XV * s" . 368. lim ¦hO~ch«)-in(ch.h,)_
§ 10. Экстремум функции. Наибольшее и
наименьшее значения функции
10.1. Экстремум функции.
Определение. Пусть функция f определена всюду в некоторой окрестности точки
с. Будем говорить, что функция f имеет в точке с локальный максимум (минимум),
если найдется такая окрестность точки с, в пределах которой значение /(с) является
наибольшим (наименьшим) среди всех других значений этой функции.
Локальный максимум и локальный минимум объединяются общим названием экстремум.
10.2. Необходимое условие экстремума.
Если функция дифференцируема в точке с и имеет в этой точке экстремум, то /'(с) = 0.
Определение 1. Корни уравнения /'(х) = 0 называются стационарными точками
функции /.
К точкам, подозрительным на экстремум, следует отнести и такие, в которых производная
функции / не существует.
Определение 2. Стационарные точки и точки, в которых производная функции не
существует, называются критическими точками этой функции.

§ 10. Экстремум функции 183
10.3. Достаточные условия экстремума.
Первое правило. Пусть функция / дифференцируема всюду в некоторой окрестности
точки с, за исключением, быть может, самой точки с, и непрерывна в точке с. Тогда, если в
пределах указанной окрестности производная /' положительна (отрицательна) слева от точки
с и отрицательна (положительна) справа от точки с, то функция / имеет в точке с локальный
максимум (минимум). Если же производная /' имеет один и тот же знак слева и справа от
точки с, то экстремума в точке нет.
Второе правило. Пусть функция / имеет в данной точке возможного экстремума конеч-
конечную вторую производную. Тогда функция / имеет в точке с максимум, если /"(с) < 0, и
минимум, если /"(с) > 0.
Третье правило. Пусть п — некоторое целое положительное число и пусть функция у =
/(х) имеет в некоторой окрестности точки х = с производную порядка п — 1, а в самой точке
с — производную м-го порядка. Пусть в точке х = с выполняются следующие соотношения:
f'(c) = /"(с) = ... = /"-^(с) = 0, /<">(С) ф 0.
Тогда, если п — четное число, то функция у — /(х) имеет локальный экстремум в точке
с, а именно: максимум, если f(n\c) < 0, и минимум, если рп'(с) > 0.
10.4. Абсолютный экстремум.
Наибольшее (наименьшее) значение непрерывной на сегменте [а, 6] функции / достигает-
достигается либо в критической точке этой функции, либо в граничных точках а и 6 этого сегмента.
Исследовать на экстремум следующие функции:
154. / : х н+ хтA - х)п, х eU, m, n € N.
•4 Находим производную функции / и приравниваем ее к иулю
= (т + n)*"-1^ - X)-1 (-?- - х) = 0.
\ 711/ ~\~ 11 /
Корни этого уравнения xi = 0 (т > 1), Х2 = 1 (» > 1), хз = т"? будут стационарными
точками. Проверим достаточные условия.
Пусть 0 < е < ¦^^- При т четном f'(—e) < 0, f(e) > 0, следовательно, в точке х\ = 0
функция / имеет минимум, равный нулю.
Аналогично для точки Х2 = 1: при п четном /'A — е) < 0, /'A +е) > 0, поэтому функция
/ в этой точке имеет минимум, равный нулю; при п нечетном /'A — е) > 0, /'A + е) > 0, т. е.
экстремума нет.
Наконец, для точки хз = *" имеем
+ п +
Таким образом, в точке х3 функция / имеет максимум
f( ™ \ =
\т + п)
Случай, когда т = 1 (п = 1), предлагаем читателю рассмотреть самостоятельно. >
I 2
155. /:хн-цзA-х)з)Х?К.
•4 Приравнивая к нулю производную данной функции, находим стационарную точку х\ —
|. В точках xi = 0 и хз = 1 конечная производная не существует. Пусть 0 < е < -, тогда ,
Следовательно, при х\ = j функция имеет максимум, равный - \/4- При хг = 0 экстре-
экстремума нет, а при хз = 1 функция имеет минимум, равный нулю. >
156. /пие 1*1 (л/2 + sin-J, хфО, и /@) = 0.

184 Гл. 2. Дифференциальное исчисление функций одной переменной
•4 Исследуем знак приращения функции / в точке х = 0. Имеем
Д/@) = е N (л/2 + sin-J > 0
при всех х ф Q. Следовательно, функция имеет при х = 0 минимум, равный /@) = 0. При
1^0 рассмотрим уравнение f'{x) = 0. Очевидно,
/ль х~2е 1*1 ( (т/2 + sin - ) sgnz - cos - ) , х ф 0.
\ \ X I X )
Поскольку sin - + cos ^ $С л/2, то производная при переходе через точки, в которых она
обращается в нуль, знака не меняет, поэтому других экстремальных значений, кроме /min =
/@) = 0, функция не имеет. >
Найти экстремумы следующих функций:
157. / : х v-+ arctgx hi (I + х2), i?R.
•4 Производная /' : х ^ -±±^ = 0 при х = 1. Поскольку /'A - е) > 0, а /'A + е) < 0,
0 < е < 1, то в точке х = 1 функция имеет максимум, равный j — -\п 2. >
158. f -.х^ 1Ф4*-11, хек.
•4 Из выражения для производной /': х i-+ e"'1" 'sgnx — Izle"'*' sgn (x — 1), х ф 0, х^ 1,
видим, что точки ?i = —1, Х2 = 0 и х3 = 1 подозрительны на экстремум.
О наличии экстремума и его характере судим по знаку производной при переходе через
точки х; (i = 1, 2, 3). Имеем
/'(—1 + е) < 0, /'( —1 — е) > 0 (максимум, равный е~2);
/'(—е) < 0, /'(е) > 0 (минимум, равный 0);
/'A — е) > 0, /'A + е) < 0 (максимум, равный 1)
(е. — достаточно малое положительное число). >
159. Найти наименьшее и наибольшее значения функции/: х i—> x —Зх + 2| на сегменте
[-10, 10].
•4 Находим производную
/' : 1-й Bz-3)sgn(x2 -Зх + 2), х ф 1, х ф 2;
отсюда получаем точки, подозрительные на экстремум:
ii = | (/' (|) = О); Х2 = 1; хз — 2 (производная не существует). Сравнивая между собой
|
числа
/(хх) = 1, Дх2) = 0, Дх3) = 0, /(-10) = 132, /A0) = 72,
приходим к выводу, что наибольшее значение функции равно 132, а наименьшее равно 0. >
160. Найти точную нижнюю (inf) и точную верхнюю (sup) грани функции / : х ь->
е~х cos г на интервале ] — со, +со[.
•4 Принимая во внимание четность функции /, рассматриваем ее на полуинтервале х ^ 0.
Иэ выражения /' : х ь-> —2у/2хе~х cos(j — х2) видим, что точки х\ = 0 и ха, = y-j- + 2&7Г,
fc € Zo, подозрительны на экстремум. Сравнивая числа
1, f{xk) = -Le-?-2k", fceZo, lim /(x) = 0,
Т/2 Х^+ОО
заключаем, что
1 _2lL
inf f(x)=—e 4, sup /(ж) = 1. >
-сс<л;<+сс ^/2 -со<;с<+со
161. Определить iiif/($) и sup /(?) функции / : ? н-> -j на интервале ]х, +оо[.
3 + ?
•4 По производной /' : ? н-> ' ~ ^~%. находим точки, подозрительные на экстремум: ?i =
-3,6 = 1- Затем из чисел/(-3) =-i,/A) = |, Hm ^/(?) = ^, Hm^/($) = 0 выбираем
наибольшее и наименьшее.

§ 10. Экстремум функции 185
Пусть х ^ 1. Тогда g^p- ^ i- и sup /(?) = /A) = j. Если х > 1, то sup /(?) =
3". Следовательно,
Пусть х ^ -3. Тогда ^ > -± и я<^ /(О = -?•
Пусть -3 < х < -1. Тогда -I < i? < о и inf /(?) -
Наконец, если х ^ — 1, то *'г2 ^ /(+оо) = 0 и inf /(?) = 0.
Следовательно,
(
inf /(O<
{ 0, х>-1.
162. Определить наибольший член последовательности (ап), если ап = V">
•^ Полагая п = х, элементы последовательности (ап) можно считать значениями диф-
i_
ференцируемой функции /:ihu, i>0, т. е. а,, = /(»)¦ Пусть стационарная точка io
функции / удовлетворяет неравенствам fc $С хо < к+1, к € N. Тогда, если последовательное;!!,
(и,,) имеет наибольший член (шаха,,), то он равен большему из чисел: oi, аи,
--2
По производной /'ли хх A — lnx) находим стационарную точку хо = е, в которой,
очевидно, достигается максимум /. Следовательно, к = 2. Сравнивая числа а\ = 1, аз = v2
и а,з = \/3, получаем: шаха,, = V^ и 1,44. >
163. Доказать неравенство
-^ ^жр + A -х)р ^ 1, если O^x^l ир>1.
•4 Рассмотрим функцию /: ii-> ip + (l- х)*1. Ее производная /':ги р(хр~1 — A — хI")
обращается в нуль в точке х — \- Сравнивая числа /@) = 1, / (-J = 2р-1 , /A) = 1, находим,
что max /(x) = l, min fix) = '_. . Отсюда следует доказываемое неравенство. >
2 х2 + 1
164. Доказать неравенство — ^ —т. ^ 2 при —оо < х < +оо.
3 х1 + х + 1
•4 Доказательство основано на сравнении четырех чисел:
/max (я), /min(x), Hill /(х), Шп /(х),
X—•¦ — ОО X—>-J-OO
где /(х) = (х2 + 1)(х2+х + 1)~1.
(Следовательно, при х = 1 достигается минимальное значение функции /, равное -, а при
х = — 1 — максимальное, равное 2. >
165. Определить "отклонение от нуля" многочлена
Р(х) = х(х-1J(х + 2)
на сегменте [—2, 1], т. е. найти Ер = sup |P(x)|.
^ Находим
Р'(х) = (х - 1J(х + 2) + 2(х - 1)х(х + 2) + х(х - IJ.
Из уравнения Р'{х) = 0 находим
XI = 1, Х2,3 =
Сравнивая значения /(xi), /(хг), /(хз) и /( — 2), получаем, что

186 Гл. 2. Дифференциальное исчисление функций одной переменной
166. При каком выборе коэффициента g многочлен Р(х) = х2 + д наименее "отклоняется
от нуля" на сегменте [—1, 1], т. е. Ер = sup |-Р(х)| принимает минимальное значение?
•4 Сравнивая числа Р@) = д, Р(±1) = д + 1, находим, что
W<1
т. е. sup |Р(х)| = \д + || + |. Далее, имеем
min ?p = min max{|g|, \g + 1|) = min < \q + -
+ -1 = -
при g = -?. >
167. Абсолютным отклонением двух функций / и д на сегменте [0, 1] называется число
Д = sup |/(x)-ff(x)|.
Определить абсолютное отклонение функций / : х н-+ х2 и д : х i-+ i3 на сегменте [0, 1].
-4 Дифференцируемая на [0, 1] функция tfl : х н-> /(х) — р(х) на концах этого отрезка
принимает равные значения (р@) = </эA) = 0 и на интервале ]0, 1[ имеет единственную ста-
стационарную точку х = -.
Следовательно,
Л=тах{И0)|,|,(^|}=|,(|)| = ±^
168. Определить минимум функции
/ : х н+ max{2|i|, |1 + х|}.
¦4 Если 2|х| ^ |1+х|, то max{2|i|, |1+х|} = 2\х\. Значит, / : х ь->- 2|i|, если -оо < х ^ -|
или х ^ 1. Далее, если 2|х| < |1 + х|, то тах{2|х|, |1 + х|} = |1 + х\. Следовательно,
/ : х ь-? \х + 1| при — - < х < 1. Таким образом,
2|х|, если х 0 ] — -, 1 [.
По производной
fi Г 1, если — | < х < 1,
|_ 2sgn х, если х ^ [ — —, l] ,
видим, что точки xi = — - и Х2 = 1 подозрительны на экстремум. Сравнивая числа / у— -) =
з и /A) = 2, находим /m;n = |. >
Упражнения для самостоятельной работы
Исследовать на экстремум следующие функции:
где х ф 4> l+? + V + V=0,
369.
I2 х3
-1,
370. /:х~( ехр(^т). ^±L
(_0, x = lVx = -1.
371. f:x*^+J2 s-^, OSC х^тг. 372. / : x ь^ |x|s A - хOB - х)э , х
373. /:ih 4^, 0 < x< тт. 374. /: ги |а;|чД|1 - х| чД.
375. /:xh+cos100x + cli100x. 376. / : х н+ j(cosx + | cos x|).
377. /:Х — У, х = 3t — t3, jr = 4* — *4, 0 ^ t ^ 1.

§ 11. Построение графиков функций по характерным точкам 18Т
378. f :v^ 1 + cos^, 0 < <р < f. 379. / : X -> Y, х3 + у3 + х2у + 1 Ь 0.
Найти минимумы следующих функций:
380. / :х i-+max{chz + ±, 4-chx}. 381. /:х ^ max{l -|i + 3|, 1- |i|, 1 -(s-2J}.
Найти максимумы следующих функций:
382. /: xh^min{x + 5, lnx, 1-х). 383. /: x н+ min j-x, (x + 2J - ^, _In*-1°(*+1>\
Найти наибольшие значения следующих функций:
384. /:ih(i- 1J(х - 2J, -3 ^ х ^ 4. 385. / : х ь^ , з^-зг' -1 < z $ 1.
(х п *¦ 1x1 <Г it ii
sin a; J ^ I I ^ ' cos ^ cos — ... cos ~
2+~Т~ 387. ^
,
(
. n 2-cosa;cos i ... cos i
4, X = 0. 2 n
Найти наименьшие значения следующих функций:
388. /: IH ^ + \х3 - ^-х2 - |х + 1, -3 ^х ^2. 389. /:ih f2sinfc7ra:> 1 < ж ^ 4.
390. / : X -> Y, х3 + у3 - 4,5xi/ = 0 @,5 ^ х < 1,5; 0 < у < х), f — непрерывная
функция.
391. /:ih -sin(a.smx), 0 ^ х ^ |, a > 0.
В следующих задачах для данных функций / определить их приближения /* так, чтобы
sup |/(x) —/*(ж)| был минимальным (функция /* называется чебышевским приближением):
392. / : х н-+ х2; /* : х н- а0 + ахх2 + а2х\ 0 ^ х ^ 1.
393. f : х i-^ е"; f* : х i-^ а0 + aix + а2х2, 0 ^ х < 1.
394. /^ке1;/':^ 2±?, 0 ^ х ^ 1.
395. / : х н-> х3 - 6х2 + 6х + 1; /* : х >-* аох, 1 ^ х ^ 5.
Найти наименьшие и наибольшие значения следующих функций:
. / : х н+ е~^ (л/2 + sin ^-V х ^ 0, х € [-тг, тг].
396
397. /ни! - hi | sin z |, x ф кт, к(_^ на отрезке [_47Г) ^
Найти inf/(x), sup/(x) следующих функций:
398. / : x ь^ e" f^+sinxj, x^ j, /(f) =—1 на интервале ]0, +oo[.
399. / : я н-> | sin x - |x - a|| иа ] - 1, l[.
В следующих задачах для данных функций / найти приближения /* ? {/*} так, чтобы
sup |/(х) - Г (х)| - inf sup |/(х) - Г(х)|,
0<х<+со {/*}д;>0
где
+ aix + ct2X2, 0 ^ х ^ хо,
i + 6ix + бгх2), хо < х < +оо.
400. /:хь^ -~. 401. /:х и A+х2)е~х.
402. /:iH(l-i!)e-. 403. /:ih л/1 + я + х2'е~х.
§ 11. Построение графиков функций по
характерным точкам
Исследование и построение графика функции у = /(х) целесообразно проводить по сле-
следующей схеме:
1. Определить область существования функции, периодичность, точки пересечения с
осью Ох и интервалы знакопостоянства, симметрию графика функции, найти точки раз-
разрыва и интервалы непрерывности.
2. Выяснить вопрос о существовании асимптот.
3. Найти интервалы монотонности функции и точки экстремума.

188
Гл. 2. Дифференциальное исчисление функций одной переменной
4. Указать интервалы сохранения направления выпуклости и точки перегиба графика
функции.
5. Построить график функции.
Построить графики следующих функций:
169. „ = 4Й
/x2 + 1
•4 1. Функция определена и непрерывна при всех
х, положительна при х > 2 и отрицательна при х < 2;
2/B) = 0.
2. Из lim у = ±1 следует, что i/ = 1 — асимптота
X —*±0О
графика функции при х —> +оо, а у = — 1 — при х —*¦
— оо.
3. Поскольку производная
У =
2х+ 1
< 0 при х < -j;
> 0 при х > -i,
/(х* + IK
то функция убывает при х < — | и возрастает при х >
—-, а при х = —- имеет минимум, равный — у/Ех —2,24.
4. Судя по знакам второй производной:
У =
< 0 при х < —
> 0
з+\ДТ.
заключаем, что при х < —
з+уТГ
вверх, при —
< х < -
< 0 при 2=^1 < х,
я —1,18 и х > ~~3 g 41 rj 0,42 график функции выпуклый
график выпуклый вниз; точки перегиба ц ~ —1,18; ?/i я
8 g
-2,06 и х2 и 0,42; j/2 « -1,46.
5. График функции изображен на рис. 22. >
170. y=Vx*- v/^+T.
< 1. Функция определена, непрерывна и отрицательна при всех х; ее график симметричен
относительно оси Оу, поскольку у(х) = у(—х).
2. Поскольку предел lim i/ равен нулю, то i/ = 0 — асимптота; других асимптот нет.
3. По знакам производной
У1,
У =
2((х2
Зхз(х2
< 0 при i < 0;
> 0 при х > 0
заключаем, что функция убывает при х < 0 и возрастает при
х > 0, а при х = 0 имеет минимум, равный —1.
4. Поскольку
2 *
2
у" = --х~г (
з ( (х2
t 4 го
з+3х3 -x~j <0
+оо),
то график функции выпуклый вверх и точек перегиба нет.
5. По полученным данным строим график функции (рис. 23). >
т. ,= И±Д.
1. Функция определена, непрерывна и положительна при всех х > 0.

§11. Построение графиков функций по характерным точкам 189
2. Из очевидного равенства lirn у = +оо следует, что х = 0 — вертикальная асимптота
при х —> +0. Имеется наклонная асимптота у = кх + Ъ, где к — lim - = 1, Ъ = lim [у — х) =
х—*+0 х х—*+оо
j, т. е. у = х + -.
3. Первая производная у' удовлетворяет неравенствам
1 з 1
-х 2A + хJBх-1)
< 0, если I < ^;
> 0, если х > -,
следовательно, функция убывает при 0 < х < j и возрастает при х > -, а при х; — - имеет
минимум, равный ^у/Ъ ~ 2,60.
4. Поскольку
3 _i _1
У" = -X 2A+2;) 2>0 @ < X < +0О),
то график функции выпуклый вниз.
5. График представлен на рис. 24. >
172.» = -
з
-2л
Рис. 25
2 + cos х
^ 1. Функция определена и непрерывна при всех х; периодична с периодом 27г; имеет
центр симметрии — начало координат; у = 0 при х = &7Г (А; = 0, ±1, ±2,...). Очевидно, что
sgn у = sgn sin x.
2. Асимптот нет. Принимая во внимание периодичность, дальнейшее исследование про-
проводим на сегменте [0, 2ж].
3. По знакам первой производной
1 + 2 cos х
> 0, если 0 ^ х < ^-;
У =
B + cosxJ
заключаем, что при 0 $С х •
убывает, а при xi = -^- и
^«0,58 и -^«-0,58.
4. Поскольку
-|^; -j- < х
„ _ 2 sin x(cosx — 1)
У = B + cos xJ
> 0, если ^ < х ^ 2тг,
^ 27Г функция возрастает, при -^- < х < —¦ —
< 0, если 0 < х < ir;
> 0, если 7Г < х < 27Г,
то при 0 < х- < 7г график выпуклый вверх, при ж < х < 2к — вниз; причем ii = тг, у\ = 0 —
точка перегиба,
5. График изображен на рис. 25. >
173. у = ¦2^+1-^-'1.

190
Гл. 2. Дифференциальное исчисление функций одной переменной
•^ 1. Функция существует, непрерывна и положительна при всех х > 1 и при х < — 1;
причем у > 1 при этих значениях х; график симметричен относительно оси Оу; у(—1 — 0) =
2,A + 0) = 2^.
2. Поскольку lim у = 1, то у = 1 — асимптота при х —*¦ оо.
X—>± СО
3. Имеем
( \ 1 \. . Г >0, еслих<-1;
у = ху
|1п2
/x2 +1 л/х2 - 1 у I < 0, еслих>1,
следовательно, функция при х < —1 возрастает, при х > 1 — убывает, а в точках х = ±1
имеет краевой максимум, равный 2 (функция /(х), а$Сх<а(/?<х$С6) имеет в точке
а (Ь) краевой максимум, если существует полуокрестность ]а, 6[С [а, «[ (]?, /?[С]/3, Ь]) такая,
что f(a) > f(x) (f{b) > /(х)) для всех х из этой полуокрестности. Аналогично определяется
краевой минимум).
4. Из очевидного неравенства
У = 2/ш2
> у In 2
In 2 >0
следует, что график выпуклый вниз.
5. График изображен на рис. 26. >
У,
-1 0
+1 х
1/1
1
—¦——
0 е *
Рнс
27
1
XI =
Рис. 26
174. j/ = хх,
•^ 1. Функция определена, непрерывна (как суперпозиция элементарных функций у =
и положительна при х > 0.
Ill X
2. lim у = lim ex = 1, поэтому у = 1 — асимптота при х —» +оо.
3. Из неравенств
> 0, если 0 < х < е;
< 0, если е < х < +оо,
вытекает, что при 0 < х < е функция возрастает, при е < х < +оо — убывает, а при х = е
1
имеет максимум, равный ее ; кроме того, г/(+0) = 0.
4. Исследование точек перегиба и направления выпуклости опускаем.
5. График изображен на рис. 27. >
175. » = fi + x)i.

§ 11. Построение графиков фуикций по характерным точкам 191
•^ 1. Функция определена при х > — 1; х ф 0; положительна и непрерывна в этой области.
Поскольку lim A + х)^ = е, то х = 0 — точка устранимого разрыва.
х—*0
2. Из соотношений liai у = + оо: lim у — 1 вытекает, что х = — 1 асимптота
.т__1+0 * —+оо
графика функции при х —> —1 + 0, а у = 1 — при х —^ + оо.
3. Производная
У = У
1
lu(l+x)\
—^—'- I;
х)
+оо
отрицательна. Действительно, полагая в неравенстве примера 90, г) ~- = %., имеем неравен-
неравенство
0),
которое справедливо и при — 1 < х < 0. Пользуясь этим неравенством, получаем
1 1пA+хЛ ( 1 х
У =У
х)
= 0.
Таким образом, функция убывает при всех х из области определения.
4. Покажем, что вторая производная
//
У = У
X2
— B1пA + х)
^ чхA+х) х<
положительна. С, этой целью рассмотрим функцию
Поскольку
(ДхгK
> 0; -1 < х < +оо и р@) = 0, то <р(х) < 0, ZJ
если -1 < х < 0 и <,з(х) > 0, если 0 < х < +оо. Тогда ^(р(х) > 0
при —1<х<0, 0<х< +оо; при этих же значениях х производная
у" > 0. Поэтому график функции выпуклый вниз.
5. Исходя из этих данных, строим график (рис. 28). >
176. y = x( iy
¦4 1. Функция определена, непрерывна и положительна при всех х > 0; у(+0) =
lim х exp Ixln (l + -) \ = 0.
2. Имеется наклонная асимптота у = кх + 6, где
fc = lim - = lim A + - ) = е;
х^+оо X х^+оо \ X/
Ь = lim (у — ex) = lim х (ехр <х1пAн— ) > — е ) =
а;^ + сс я —+со V L \ X/J /
= lim х fexp/x (--tfracUx2+o(\)))-e] = Urn e f-i + оA)) = --.
х_+оо Ч I \Х \Х2 I ) ) I X-+OO V. 2 V V 2
3. Имеем
Отсюда следует, что функция возрастает при х > 0.
4. Вторая производная
^ =, (-2 ь Л + П +ь2 Л 14 _ х + 3
^A + х) \ х) \ х) хA + х
положительна. Чтобы в этом убедиться, введем новую переменную t — - и применим теорему
примера 104, полагая там
к = 4.

192
Гл. 2. Дифференциальное исчисление функций одной переменной
Тогда все условия теоремы 104 будут выполнены. Следовательно, у" > 0 при х > 0 и график
функции при этих значениях выпуклый вниз.
5. График функции изображен на рис. 29. >
177. « =
х2'
Л
Рис. 29
< 1. Функция определена, непрерывна и положительна при всех значе-
значениях х, за исключением точек х = ±1, в которых функция терпит разрыв,
причем
j/(—1 — 0) = 0; у(-1 + 0) = +оо;
График функции симметричен относительно оси Оу.
2. Имеются асимптоты х = —1 при х—+—1+0их = 1 при х
у = 0 при х —* оо.
3. Находим производную
1 „ .2
1 -0;
у' = 2хйе1-*2
Поскольку у' > 0 при —оо < а; < — л/3; 0<х<1; 1<х< л/3, то функция при этих значениях
х возрастает; далее, }/' < 0 при —л/3 < х < — 1; —1 < х < 0; л/3 < х < +оо, следовательно,
в этих интервалах функция убывает; в точке х = 0 имеется минимум, равный е, а в точках
х = л/3, х = —л/3 достигается максимум, равный -~д я 0,15.
4. Вычисляя вторую производную
2:се (з _ х2J + х2 A - х2) (9 + х2 + 7х4 - х6)
A-х2LA+х2J
убеждаемся, что у" > 0 при |х] < 1. Далее, у"(у/1,1) > 0; у"(у/И) < 0 и у"(г) —г +0 при
х —> +оо. Следовательно, в каждом из интервалов ]1, л/3[, ]\/3, +оо[, а в силу четности
функции и в каждом из интервалов ] — оо, —л/3[, ] — у/3, —1[ имеется по меньшей мере по
одной точке перегиба.
5. График изображен на рис. 30. >
Построить кривые, заданные в параметрической форме:
178. х =2t-t2, у = 3t-t3.
•^ 1. Функции x(i) и y(t) определены и непрерывны при
— оо < t < +оо; причем при этих значениях t : —оо < х ^ 1;
—оо < у < +оо.
Следовательно, функция у = у(х) (как функция пере-
переменного х) определена при — оо < х $ 1.
2. Поскольку x(t) —>¦ —оо, y(t) —» Т00, ~/Ч —* i°° ПРИ
t —с ±оо, то график функции асимптот не имеет.
3. Производная
Рис. 30
3 1 -Г
dx
2 1 -*
при ti = — 1 (xi = —3) обращается в нуль, а при <2 = 1
= 1) имеет устранимый разрыв, причем
lim
t->i ax
4. Вторая производная
dx2 4 A-tK
имеет разрыв в точке 4 = 1. Заполним таблицу:

§ 11. Построеяяе графиков функция по характериым точкам
t
X
У
dy
dx
d?y
dx2
-OO < t < -1
-oo < x < -3
-2 < у < +oo
&<°
-1<* < 1
-3 < x < 1
-2 < у < 2
§ >°
1 < t < +oo
-OO < X < 1
-oo < j/ < 2
?>°
Из таблицы следует, что при —оо < х < —3 функция у(х) убывает; при —3 < х < 1 —
возрастает; при х = —3 имеет минимум, равный —2, а при х = 1 — максимум, равный 2.
Если х возрастает от —оо до 1, то график функции у = у{х) сохраняет выпуклость,
направленную вниз; если х убывает от 1 до —оо, то выпуклость направлена вверх; A, 2) —
точка перегиба.
5. Пользуясь полученными данными, строим график (рис. 31). >
¦4 Функция x(t) определена и непрерывна при —оо < t < 1; 1 <t < +оо, причем х = 1 —
вертикальная асимптота при t —* 1. Из равенства x(t) = t + 1 + j—^ следует, что я = t + 1 —г
наклонная асимптота. Находим производную x'(t) = (tl~]2 • Очевидно, что на интервалах
] — оо, 0[, ]2, +оо[ функция x(t) возрастает, а на интервалах ]0, 1[, ]1, 2[ — убывает; хтах = О
при t = 0; zmjn = 4 при t = 2.
График функции x(t) изображен на рис. 32.
Рис. 31
Рис. 32
Рис. 33
Функция y(t) определена и непрерывна при всех значениях t, кроме t = ±1; причем
t = — 1 и t = 1 — асимптоты. Поскольку y'(t) = — ' +1,2 < 0, то функция «/(*) убывает при
всех t из области определения (рис. 33). .
Из этих исследований вытекает, что функция у — у(х) определена при —оо < х ^ 0;
4 < х < +оо. Поскольку x(t) —<¦ ±00, y(t) —*¦ +0 при t —* ±00; x(t) —>¦ —|, y(t) —> ±00 при
i —>¦ — 1 ± 0, то у = 0 и х = — | — асимптоты графика функции у = у(х). Кроме того, | —> |,
— - при t —* 1, следовательно, у = | — j — наклонная асимптота.
1аходим производные
dy_ = _
dx
d2y
- IK (t3
откуда получаем, что у"хъ = 0 при to ~ —0,32; <i = 1; причем х(<о) ~ —0,07; y(to) ~ 0,37.
Сначала построим графики функции на отдельных интервалах.
Если -оо < t < -1, то -оо < х < -|; -оо < у < 0; у'х < 0; у < 0 (рис. 34). Если
— 1 < t ^ 0, то —j
+оо. Вторая производная у'^ > 0 при —1 < t < to

194
Гл. 2. Дифференциальное исчисление функций одной переменной
и у < 0 при t0 < t < 0; следовательно, при t = to получаем точку перегиба (хо, Уо), где
хо х -0,07; уо « 0,37 (рис. 35).
Рис. 34
0 X
Рис. 35
Рис. 36
У,
Рис. 37
Рис. 38
Пусть 0 ^ t < 1. Тогда -оо < х < 0, -оо < у ^ 0, у'х > 0, у > 0 (рис. 36). Если
1<<^2,то4^х< +оо, | sj у < +оо, у^ > 0, у"хъ < 0 (рис. 37). Наконец, если 2 < t < +оо,
то х ^ 4; 0 < у < |; уя < 0; у^ > 0 (рис. 38).
Окончательный график изображен на рис. 39. >
180. x = t + e-', y = 2t + e-2'.
•^ Функции x(t) и y(t) определены и непрерывны при всех t. Из определения асимптоты
следует, что х — t, у = 2t — асимптоты при t —+ +оо соответственно графиков функций x(t)
и y(t). Имеем x'(t) = 1 - е""'; х'@) = 0; x"(t) = е~' > 0 при всех t; у'(*) = 2 (l - e~2t),
у'@) = 0; y"(t) = 4e' > 0 при всех t. Таким образом, zm;n = 1 при t — 0; ym;n = 1 при
t = 0. Графики функций x(t) и y(t) выпуклы вниз (рис. 40, а, б).
ЛГ J ,
Рис. 39
Рис. 40
Если -оо < t < 0, то 1 < х < +оо, 1 < у < +оо, у'х = 2 (l + e-t) > 0; у^'2 = -2 (е( - l) >
0. Если же 0 < ( < +оо, то 1 < х < +оо; 1 < у < +оо; уя > 0; у^'2 < 0.
Следовательно, функция у = у(х) возрастает, ее график выпуклый вниз при t < 0 и
вверх — при t > 0.
В точке х = 1 функция у(х) имеет минимум, равный 1.

§ 11. Построение графиков функций по характерным точкам
Далее, - —* 2; у — 2х —> О при t —+ +00, поэтому прямая у = 2х
является асимптотой графика функции при t —+ +00 (рис. 41). >
195
181. х =
Рис. 41
cos^t' * 6 " v'»>-
Л Так как функции x(i) и y(t) известны, то относительно функции
у(х) выясним следующие вопросы: симметрию, экстремум, участки и ха-
характер выпуклости графика функции и существование асимптот.
Поскольку x(i) = х(—i); y(t) = —y(—t), то график функции у = у(х)
симметричен относительно оси Ох, а так как x(t) = — х(ж + t); y(i) —
у(ъ + t) и х (| + i) = — х (^ +1) ; У (f + <) = у (^f +i) (о < i < §) , то О
график функции у(х) симметричен относительно оси Оу.
Следовательно, для построения всего графика достаточно знать гра-
график функции у(х) при х>0иу>0,т. е. при 0 ^ t < ~.
Производная у'х = sin t > 0 при 0 < t < ^, следовательно, функция
у = у(х) возрастает на этом промежутке, причем х —+ +оо; у —^ +оо при t —+ ^ — 0.
Вторая производная у'^2 = j^ cos5 tsin1 > 0 (о < t < |), откуда следует, что при 0 <
t < § график функции у(х) выпуклый вниз.
Так как х —> +оо только при t —> ^ — 0 и у —* +оо только при
t —> j — 0, то вертикальных асимптот нет.
Для выяснения вопроса о существовании наклонной асимптоты
у = кх + b рассмотрим пределы
А; =
lim
~~ ~
= lim
tg3t
= 1,
Ь= lim [}/(<)- x(t)] = a liin (tg3t L-Л =-оо.
t_*. Ц о t—*¦ ~ —О ^ COS Т /
2 2 РИС. 42
Следовательно, асимптот нет.
График кривой при всех t (cost ф 0) изображен на рис. 42. >
Представив уравнения кривых в параметрической форме, постро-
построить эти кривые, если:
 СО 2,24,4
1OZ. х -f у =х + у .
¦^ Очевидно, что график функции симметричен относительно осей коордииат. Предста-
Представим кривую при х>0иу^0в параметрическом виде, положив у = tx (t ^ 0):
Вычисляя производные х' и у', выясняем вопрос об экстремумах
функций x(i) и y(t):
Отсюда следует, что при t = 0 достигается минимум функции x(t), Рис. 43
равный 1 (у — 0); при t = \А/2 — 1 достигается максимум функции x(t), равный у—jt-
( у = 77? ); ПРИ t = V л/2 + 1 достигается максимум функции y(t), равный у у (^ = ТТ? ) •
Нетрудно проверить, что в точках пересечения кривой с координатными осями существует
касательная к кривой (рис. 43). >
1QQ2233
loo. х у = х — у .
•^ Полагая у = txr получим

196
Гл. 2. Дифференциальное исчисление функций одной перемеиири
Если параметр t изменяется в интервалах ] — оо, 0[ и ]0; +оо[, то переменная х может
принимать все значения от —оо до +оо; следовательно, функция у — у(х) определена при
всех значениях х.
Из параметрического представления кривой получаем равенства
У = -х2 - - + —, у2 = x-t+t2,
из которых непосредственно вытекают асимптотические соотношения: у2 ~ х при t —+ ±0
(при этом х —> +00, у —> ±оо); у ~ х при t —> ±00 (при этом х -+ ±00, у —<• —оо).
Полагая в исходном равенстве х — у = и, z + у = г>, получим равенство {у2 — и2) =
12и2и + 4и3, которое указывает на симметрию графика кривой относительно оси v = 0, т. е.
относительно прямой х + у = 0.
Вычисляя производные
dx 2 + t3 ' dx2 B + t3K
находим, что при to = — л/2 я —1,26 \хо = -^л/2 я 1,89; уо =
водные у'х и у не существуют, а у'х = 0 при <2 = ~\ 2 ~
—^л/4~ —2,38j обе произ-
произ-0,79 (х2 = |v^ я 2,38;
Далее, ^'2 = 0 при Ь = - \
0,53 (хз и 4,14; уз и-2,18).
-1,90
2,18;
-4,14) и при t3 = -
)
Пользуясь этими данными и таблицей
1
а;
У
&i
— СО
*1 <
— оо
S/
<
я;
<
т
С2
1
<
<
<
< '1
: +оо
< VI
0
0
<i <
*о <
VI <
У'г
Л
X*
t <t0
X < Ху
У < УО
< 0
> 0
to <
*0 <
УО <
У'х
У"г
t < t2
х < Х2
У <У2
> 0
< 0
'2 <
х2 <
УЗ <
У'х
у
' < 13
х <х3
У <У2
<о
<о
'3
х3 <
— оо
У
У
<
X
<
1
X
I2
t <0
< +оо
У < У3
<0
>о
0 < t
-00 <
-00 <
»i
У"х1
< +оо
X < +ОО
У < +оо
>0
< 0
строим
график функции у = у(х) (рис. 44). >
184. Построить график кривой ch х — ch у = 1.
-^ График кривой симметричен относительно координатных
осей, так как при замене х на —х и у на —у уравнение кривой
вида не меняет.
Если х > 0; у > 0, то уравнение ветви кривой примет вид
sh х = ch у, откуда х = In I ch у + у 1 + ch2 у \.
Имеется асимптота х = ку + Ъ, где
Рис. 44
k = lim ^^ = 1; b = Шп (х(у) - у) = 0. •
Найдем производную
откуда следует, что функция х = х(у) возрастает при у > 0, а в точке у = 0 достигается
минимум, равный In (l + \/2~) .
Далее,
„ 2 ch у
*у' = —Т>°,
(г + ch2 у) 2
откуда вытекает, что кривая выпукла вниз при у > 0. Принимая во внимание симметрию
кривой относительно осей координат, строим график функции (рис. 45). >

§ 11. Построение графиков функций по характерным точкам
Построить графики функций, заданных в полярной системе координат (уз, р) [р ^ 0):
185. о — а
197
th
"^ , где уз > 1 (а > 0).
1 Р
Рис. 45
Рис. 46
Рис. 47
¦4 Функция р(уз) непрерывна как элементарная; lim р(уз) =+оо, т. е. имеется асимптота
уз = 1; lim р(уэ) = 0, т. е. кривая асимптотически входит в полюс по спирали.
Возьмем производную
1 thy?
так как уз —1 < - sh2y3 при уз > 1, то p'v < 0; следовательно, функция /э(уз) убывает (рис. 46). >
186. уз = arccos .
Р2
¦4 Область существования функции определяется неравенством
откуда следует, что
+ Д
Pi = 2 ^ р
Предельные значения уз в граничных точках:
lim уэ(р) = тг; lim уэ(р) = -.
Так как р — 1 ф р2, то функция уз(р) нулей не имеет и положительна.
Производная этой функции
/ р-2
\ '
показывает, что в точке р = 2 достигается минимум функции, равный arccos -. В точке р = pi
производная не существует; функция в этой точке принимает краевой максимум, равный я\
При pi < р < 2 функция убывает, а при р > 2 — возрастает.
Как уже было отмечено (см. Предельные значения уз в граничных точках), имеется вер-
вертикальная асимптота.
Найдем ее расстояние о от полюса. Имеем
а= lim рсоэуз(р)= lim p
р-\
= 1.
График изображен на рис. 47. >

198 Гл. 2. Дифференциальное исчисление функций одной переменной
Построить графики семейства кривых (а — переменный параметр):
187. у = х ± у/а(\-х2).
^ Рассмотрим два случая: a) s > 0 и б) о < 0.
а) а > 0. Область существования функции: 1 — х2 ^ 0, т. е. |х| ^ 1. Нули функции:
xi,2 = ±л/у^-; при — yjY^Z < х < * ФУНКЦИЯ У = х + \/а A — х2) положительна, а при —1 <
x < л/ут^ отрицательна; при — 1 < х < \/jt^ функция у = х — \Ja A — х2) отрицательна, а
при \/тт~ < х < 1 — положительна.
Находим производную
и' = 1 ±
Отсюда следует, что функция у = х + ^/а A — х2) достигает при х = л/^ту максимума,
равного л/а + 1, а функция у — х — \Jа A — х2) достигает при х = —\1~~г{ минимума, равного
Точки х = ±1 являются точками "стыка" этих ветвей.
Из выражения для второй производной
а
У" = ±-
вытекает, что график первой ветви функции выпуклый вверх, а второй — вниз (рис. 48).
При изменении о от 0 до -f оо получим семейство эллипсов, проходящих через точки
(-1, 1) и A, 1) (рис. 49);
Рис. 48
Рис. 49
б) а < 0. Область определения функции — |х| > 1. Асимптоты у = kix + 6; у = fc2x + 6,
График изображен на рис. 50. >
а-
188. у = хе. и .
•^ Рассмотрим два случая: а > 0 и а < 0.
1. о > 0. Функция положительна при х > 0 и отрицательна при х < 0. Находим
производную
у=е .A--

§ 11. Построение графиков функций по характерным точкам 199
Отсюда следует, что при х — а достигается максимум, равный ~. Далее,
-- ( х 2\
У = е ° ( т >
откуда следует, что в точке х = 2а имеется перегиб функции у, причем при х < 2а график
функции выпуклый вверх, а при х > 2о — вниз. Так как хе а —*¦ 0 при х —> +оо, то прямая
у = 0 является асимптотой графика функции при х —> +оо.
2. Если а < 0, то, как легко видеть, этот случай сводится к предыдущему, если в нем
заменить у на —у, а х на —х.
Рис. 50
а>0
Рис. 51 Рис. 52
График семейства изображен на рис. 51, 52. >
Упражнения для самостоятельной работы
Построить графики следующих функций:
404. а) /(х) = sup {sinx, cosx, tgz}; б) /(х) = inf {sin x, cosx, tgx}.
405. x = icost, y = tsint, z = t. 406. x = ocost, y = acos2i, z = cos3t.

200 Гл. 2. Дифференциальное исчисление функций одной переменной
Найти геометрическое место точек, координаты которых удовлетворяют следующим урав-
уравнениям:
407. A-х2 - 11-х2!J + у2 = 0.
408. B - х2 - |1 - х2| - |1 - у\ - \у\) B - у2 - |1 - у2\ - |1 - х| - |х|) = 0.
409. х2 + у2 + 9 - |х2 + у2 - 1| - |2 - у\ - \у + 3| - |х| - |5 - х| = 0.
410. 2 - у - \1 - х - у\ - \1 + х - у\ - \у\ = 0.
§ 12. Задачи на максимум и минимум функции
189. Доказать, что если функция /(х) неотрицательна, то функция F(x) = с/ (х) (с > 0)
имеет в точности те же точки экстремума, что и функция /(х).
•^ Для определенности предположим, что в точке хо функция f(x) достигает максимума.
Тогда существует такое к' > 0, что для всех х из окрестности 0 < \х — хо| < 6 справедливо
неравенство /(ж) < /(хо).
Так как /(х) ^ 0 и с > 0, то из последнего неравенства следует:
c/2(z) < с/2(хо), т. е. F{x) < F(x0).
Последнее означает, что в точке ко функция -F(x) достигает максимума. В случае минимума
поступаем аналогично. >
190. Доказать, что если функция tfi(x) монотонно возрастает в строгом смысле при
—оо < х < +оо, то функции f(x) и ip(f(x)) имеют одни и те же точки экстремума.
М Пусть в точке хо достигается максимум функции f(x). Тогда при всех х из окрестности
0 < |х — Хо| < 6 справедливо неравенство
f{x) < /Ы = /о.
Так как функция <р(х) монотонно возрастает в строгом смысле, то из неравенства / < /о
следует неравенство
?>(/) < ?>(/о).
что и требовалось доказать. Аналогично, предположив, что в точке хо функция tp (/(x))
достигает (максимума, придем к выводу, что функция /(х) также достигает максимума. >
191. В каких системах логарифмов существуют чи-
числа, равные своему логарифму?
¦4 Пусть у — основание искомой системы логарифмов.
Тогда согласно условию имеем
log^x = х (х >0, у > 0, уф 1).
1
откуда у = х х .
Функция у уже исследована нами в примере 174. Из
1
ко —
. jo него следует, в частности, что у не превышает ута.х = ее ,
т. е. во всех системах с основанием у @<у<ее, у ф 1)
такие числа существуют. >
192. В данный круговой сегмент, не превышающий полукруга, вписать прямоугольник
с наибольшей площадью.
Л Пусть высота прямоугольника х, ширина 2у.
Если обозначить через 2а дугу сегмента, а через 2<р — дугу, стягиваемую стороной пря-
прямоугольника, то получаем, что у = Rsinip; х = ОЕ — OB = R(cosip — cos а) (рис. 53). Следо-
Следовательно, площадь прямоугольника равна
S = 2ху — 2R2 sin ^(cos tp — cos a).
Приравнивая нулю производную
S'(<p) = 2R2 B cos <p — cos ip cos tv — l) = 0,
4 /
С
R ?'
1 E "---
1
i / \

§ 12. Задачи на максимум и минимум функции 201
находим, что
cos а + л/cos2 а + 8 cos а — л/cos2 а + 8
COS VI = SV
Дуга V2 не подходит по смыслу задачи.
Так как $'((pi — е) > 0; S'(<p\ -f е) < 0 (е > 0 — достаточно малое), то при
cos a + \/cos2 a +
cos vi =
4
функция S(v) имеет максимум. >
193. В эллипс — + — = 1 вписать прямоугольник со сторонами, параллельными осям
эллипса, площадь которого наибольшая.
•^ Пусть х и у — длины полусторон прямоугольника. Тогда 5 = 4ху, причем х и у —
кординаты точки, лежащей на эллипсе. Для упрощения следует записать параметрические
уравнения эллипса:
х = a cos t, у = b sin t.
Тогда ,9 = 2absin 'It, откуда 5max = 2ab, при t = j> л x — ^Я' У — ^T^- ^
2 2
194. Через точку M(x, у) эллипса — + ^- = 1 провести касательную, образующую с
осями координат треугольник, площадь которого наименьшая.
•^ Уравнение касательной к эллипсу в точке с координатами (хо, уо) имеет вид:
ххр ууо_ _ 1
« а2 Ь2
откуда следует, что касательная отсекает от координатных осей отрезки длиной — и —.
2.2
Следовательно, площадь треугольника S = — .
Если уравнение эллипса параметризовать, то S = si^ 2t, откуда 5min = об при t = -;
ь
195. Поперечное сечение открытого канала имеет форму равно-
равнобедренной трапеции. При каком наклоне <р боков "мокрый периметр"
сечения будет наименьшим, если площадь "живого сечеиия"-воды в ка-
канале равна S, а уровень воды равен ft? '
¦4 "Мокрый периметр" Р определяется по формуле (рис. 54):
A)
sm v
Рис. 54 Площадь "живого сечения" воды:
S = h(a + hctgv). B)
Из формул A) и B) находим
п S , 2ft
Р= -r-hctg<p+-—
и, S1I1 (?
Производная функции Р, равная
1
2 cos v ]
показывает, что при V = f достигается минимум функции Р. >
196. "Извилистостью" замкнутого контура, ограничивающего площадь S, называется
отношение периметра этого контура к длине окружности, ограничивающей круг той же пло-
площади .S'. . •
Какова форма равнобедренной трапеции ABCD (AD\\BC), обладающей наименьшей "из-
"извилистостью", если основание AD = 2о и острый угол BAD = a?

Гл. 2. Дифференциальное исчисление функций одной переменной
С < Пусть П — "извилистость" трапеции. Тогда, согласно опре-
определению, имеем (рис. 55):
П= L
D где S = BC+2aABsma; L = 2AB + ВС + 2a.
Так как
с- 55 2а - ВС = 2АВ cos a, A)
то, обозначая АВ = х, получим
. . _ 2а + x(l — cos а)
у/ж\/Bа — х cos а)х sin a
Исследуя функцию Q(x) на экстремум, находим, что она имеет минимум при .
2 а
х = a sec —.
Из A) получаем ВС = 2а tg2 у; так как половина высоты трапеции г = | sin а равна рассто-
расстоянию от точки О(а, г) до стороны АВ, то в найденную трапецию можно вписать окружность
радиуса г. >
197. Какой сектор следует вырезать из круга радиуса R, чтобы из оставшейся части
можно было свернуть воронку наибольшей вместимости?
< Если под а понимать центральный угол оставшегося сектора, то объем конуса V равен
R3
24тг2
Исследование этой функции от а на экстремум показывает, что максимум ее достигается
при
198. Два корабля плывут с постоянными скоростями и и v по прямым линиям, соста-
составляющим угол в между собой.
Определить наименьшее расстояние между кораблями, если в некоторый момент рассто-
расстояния их от точки пересечения путей были соответственно равны а и Ъ.
v'^ -^ По теореме косинусов имеем
г2 = (а + utf + (Ь + vtf - 2(а + ut)(b + vt)
¦^ rff (рис. 56), где г — расстояние между кораблями в произвольный момент
¦в времени t.
__^ Исследуя функцию r2{i) на экстремум, находим, что
" а U ' 11. , Ч а и
i. , you -г avj cos и — аи — bv
Рис. 56 г (. oj - , о - ^
Подставляя to в r2(t), получим
\ub — va\ sin в
rmin —
у/и2 — 2uv cos в + v2
Если и поменять на —и, то в силу тождеств
sinGr — в) = sin в и cos(tt — в) = — cos в
lub-t-fal sin в
получим rmin = / ' =¦ >
л/и2—2иу cos 9+v2
199. Светящаяся точка находится на линии центров двух непересекающихся шаров
радиусов R и г (R > г) и расположена вне этих шаров.
При каком положении точки сумма площадей освещенных частей поверхностей шаров
будет наибольшей?

§ 12. Задачи на максимум и минимум функции
203
< Найдем сумму площадей освещенных частей поверхностей как функцию расстояния х.
Имеем (рис. 57)
S = 2wR(R - x0) = 2wR2 (l - —) ;
Si = 2жг
где а — расстояние между центрами шаров.
Исследовав функцию S + .S'i = / на экстремум, находим значение х, при котором дости-
достигается максимум этой функции; при этом
откуда а^ r+ R\l—.
Если же производная /'(х) < 0, то максимальное значение функции / (х) достигается при
х\ = а — г; при этом выполняется неравенство
a < r + R\—. >
V г
Рис. 57
а
Рис. 58
Рис. 59
200. На какой высоте над центром круглого стола радиуса а следует поместить элек-
электрическую лампочку, чтобы освещенность края стола была наибольшей?
А Под освещенностью / понимается величина
где г — расстояние от источника света до точки наблюдения, к = const, <p — угол, изобра-
изображенный на рис. 58. Имеем
откуда находим высоту хо, при которой достигается максимум функции 1(х): хо = -т=. >
201. К реке шириной а м построен под прямым углом канал шириной Ь м. Какой
максимальной длины суда могут входить в этот канал?
< Длина корабля I, как следует из рис. 59, равна
Ь а
sin ip cos ip'
Исследовав на экстремум функцию /, получаем, что минимальное значение она принимает
при
t а/Г
у = arctg л/-.
Таким образом, максимально возможная длина корабля равна
з
I
из -f
м. >

204 Гл. 2. Дифференциальное исчисление функций одной переменной
202. Суточные расходы при плавании судна состоят из двух частей: постоянной, равной
а руб., и переменной, возрастающей пропорционально кубу скорости. При какой скорости v
плавание судна будет наиболее экономичным?
¦^ Предположим, что судно прошло S км за Т суток. Тогда расходы R будут равны
Ta + kTv3,
где к — коэффициент пропорциональности. Но так как Т = —, то
откуда находим скорость, при которой расходы минимальны:
а
v =
203. Груз весом Р, лежащий на горизонтальной шероховатой плоскости, требуется
сдвинуть с места приложенной силой. При каком наклоне этой силы к горизонту величина ее
будет наименьшей, если коэффициент трения груза равен к'?
¦^ Проектируя приложенные к грузу силы на горизонтальное напра-
направление, из условия равновесия их получаем (рис. 60):
Г = Fpk = (Р - F sin ip)k = FT = F cos <p,
откуда F = , . kF. .
J к sin v'+cos tf>
Исследовав функцию F(ip) на экстремум, находим, что при ip =
arctg к величина силы F будет наименьшей. >
204. В чашку, имеющую форму полушара радиуса а, опущен
стержень длины I > 2а.
Нантн положение равновесия стержня.
¦^ Найдем потенциальную энергию П стержня относительно дна чашки. Имеем П = mgh,
где h = - sin ip + у — высота центра тяжести стержня относительно дна чашки (рис. 61).
Далее, так как tgip = ^5f = yfzfi то получаем х =
—a cos 2ip.
Использовав уравнение полуокружности, находим, что
у = а(\ — sin 2<p).
Итак, П = тд ( j sin ip + аA — sin 2ip)j . Поскольку стержень стре-
стремится занять положение с минимумом потенциальной энергии,
то необходимо найти ipo, при котором достигается Пт[п. Имеем
Рис. 61
COS ipo =
I + V/2 + 128а2
16а
Так как cos<,3 ^ 1, то равновесие возможно только для I ^ 4а; при / > 4а равновесие невоз-
невозможно. >

Глава 3
Неопределенный интеграл
§ 1. Простейшие неопределенные интегралы
1.1. Определение неопределенного интеграла.
Определение. Функция F : X —* К, X С К, называется первообразной или прими-
примитивной функции f : X —* К, если функция F непрерывна на X и имеет производную, равную
/(х) во всея: точках интервала X, зп исключением счетной его части.
Если функция F имеет производную, равную /(х) в каждой точке интервала X, то функ-
функция F называется точкой первообразной или точкой примитивной функции /.
Совокупность всех первообразных функции / на интервале X называется неопределен-
неопределенным интегралом от функции / и обозначается символом J f(x)dx. Если F — любая перво-
первообразная функции / на интервале X, то ¦ ... .«..,»—,
1
f(x)dx =
где С — произвольная постоянная.
1.2. Основные свойства неопределенного интеграла:
a) d(Kff(x)dx) = f(x)dx; б) / dF{x) = F(x) + С;
B)fXf(x)dx = Xff(x)dx, А€К\{0}; г) J(f(x) + g(x)) dx = J f(x) dx + J g(x) dx.
1.3. Таблица простейших интегралов:
I. Jdx=x + C. II. fx"dx = *^г±С, n? -1^
r 'r:\  '" ""I
III. /f =lnM + C. IV. /щ---1 arctSx + C>
V- J^=|ln|^| + C. VI.
i+x2 I -arcctg x + C, ,
arcsinx -j; C,-
— arccosx + C.
VII. / d* ^ =Iu|x + Vx2±l| + C. VIII. Jaxdx = JT^ + C, a > 0, о.ф\\
f exdx — ex + C.
IX. Г sin x dx = — cos x + C. X. Г cos x rfx = sin x + C.
J sin2 я: ' J cos2 я: *
XIII. J sli x dx = cli x -f C. XIV. J chx dx = shx + С
XV. Г -^ = -ch x + С XVI Г -?f- = th x + С
1.4. Основные методы интегрирования. '
а) Метод введения нового аргумента. Если Jf(x)dx = F(x)+C, то f f(u)du = F(u)+C.
б) Метод подстановки. Если J f(x)dx = F(x) + С, х ?Х, то, полагая
х = v(t), <p:Y-+X,
где <р — непрерывная функция вместе со своей производной <р', получим
/ о ip(t) ¦ ip'(t) dt = F о ip(t) + С.

206
Гл. 3. Неопределенный интеграл
в) Метод интегрирования по частям. Если и и v — дифференцируемые функции и для
функции uv' существует первообразная, то
/ udv = uv — I v du.
1. Доказать, что если / /(х) dx = F(x) + С, то
f(ax + b)dx = -F(ax + b) +
, а / 0.
Имеем
f(ax + b)dx = -f(ax + b) d(ax + b),
поэтому, применяя метод введения нового аргумента, получаем
/ f(ax + b)dx = - / /(ax + 6) d(ax + b) = - / /(и) du = -F(u) + С,
J « J a J а
где и = ах + b.
Например, пользуясь таблицей интегралов, находим:
J <*2+x2 aj 1 + (?) а а J V«2 - х2 J ЛД _ f?J
arcsin - + C;
= ln
- ±1
+Co =1п|х+\/х2±а2|+С, C=Co-ln|o|;
dx _1 / <f(f) 1
x2-fl2 а У (|J_! 2a П
Применяя таблицу простейших интегралов, найти следующие интегралы:
2.
/¦__dx__
J 1 + sin x
деем
У 1
Имеем
+sinx
l+cos(f-х)
If 2 "*
(f - f)
J x«-2
^ Поскольку
У X2 - a2 - 2a
П
x + a
то, согласно примеру 1,
У^х_=1 / d{x*) = 1 ь
У x8-2 4 У (х*J-(л/2J 8л/2
x4-2
x4+2
+ C. >
4.
хл/х2 +1

§ 1. Простейшие неопределенные интегралы
Имеем при х ф О
dx
dx
sgn x dx
1 +
(*)¦
поэтому
+
/
1 7
d A
1 +
(А)'
ч
dx
Поскольку
dx sgn x dx
207
то
J
xVx2 - 1
:(r)
= -arcsin 7—r + С. >
6.
dx
Пользуясь тем, что |х| = xsgnx, имеем
sgnx
¦2 1 + -^
П.+ Х3
¦¦ + c.
При решении на х было наложено ограничение х ф 0. Однако непосредственной провер-
проверкой устанавливаем, что , х есть первообразная функции j-z—.„i2 для всех х Q К. >
7. / /« ,
У у/хA+х)
¦4 Из неравенства хA + х) > 0 находим область определения X — {x:x>0Vx< —1}
подынтегральной функции. Имеем при х > 0
У ^(i + x) У vWi
Аналогично при 1 + х < 0
/dx f dx f
\/x(l + i) У V-x - 1^/-^ У ^/l
Или, объединив оба решения, получим
=2sgnxlnfv/R+y/|x
/
У
/x(l+x)
, х?[-1, 0].

208
Гл. 3. Неопределенный интеграл
8.
¦4 Подынтегральная функция определена при 0 < х < 1, поэтому
/ dx f dx f d(y/x~) . /-,„.
I — = / - =2 / ч v ' = arcsrn л/х + С. >
Имеем
9
dx
+ e2
f dx I dx I
J Vl + e2x ~ J exy/e~2x + 1 ~ J
- »> I sin x с
J v/a2 sin2 x
x cos xdx
\/a2 sin2 x + b2 cos2 x
M Поскольку sin x cos x dx = "n/ ,2^2^°" " 1 T0
/sin x cos x dx _ 1 f d(a2 sin2 x + b2 cos2 x) _
ч/о2 sin2 x + b2 cos2 x a ~ " J \l a2 sin2 x ¦
V o2 sin2 x + b2 cos2 x
I dx
J sin x
\Ja2 sin2 x + 62 cos2 a;
11.
¦4 Имеем
dx
dx
dx _
sin x 2 sin f cos f 2 tg f- cos2 f-
поэтому
12. ( JL-
J cosx
= ln
+ C, x ф lew, к € Z. >
Аналогично предыдущему примеру находим
4 2
cosx У sin (I +x)
•^ Преобразовав подынтегральное выражение, при х ^ 0 получим
/dx _ f dx f dx _ f
sh^~ J 2sh|chf =У 2 th fch2f =У
thf
= ln
th-
+ a. >
ч > I sll X ,
14. / </r
/ch 2 ж
¦4 Очевидно,
f shx 1 / c((V2clix) . 1 /- rrr-,,,, ^
/ —==== («ж = —= / — v y — —-=hi(V2chx + Vch2x) + C. >
J Vch 2* V2 У ^(лДсИхJ-! лД
-j г / sh x ch x <Z
/ . /„1.4„ , „1,
dx
„1,4.,
С

§ 1. Простейшие неопределенные интегралы
209
¦4 Имеем
sh х ch x dx
sh x ch x dx
sh 2x dx
d(ch2x)
\/sh4x + ch4x /(sh3»+ch3»)a+(c
у 2
Тогда
shxchxdx
/ shxchxdx 1 / </(cli2x) 1 , / , n ГГТ: Г\ _
/ = —-= / ,,v ; = = —-= In (ch 2x + Vch22x + 1 I + С -
J y/stfx+dSx 2л/2У v/ch22x + l 2л/2 V /
ln
_Lln f EL??
2л/2 V л/2
16.
dx
ch2 x Vth2x
Очевидно,
— 3 / th
ch2xVth2x J
Вычислить следующие интегралы:
17. / Vl -sin2a:(ix.
¦^ Поскольку
\/l — sin 2i = \/(cos x — sin xJ = | cos x — sin x\ = (cos x — sin x) sgn (cos x — sin x),
то, обозначив 7(x) = J л/l — sin 2x dx, находим
—(sinx -f cosx) + G'_i, — — 2тг^х<^ — тг,
sin x + cos x + C'o, j — я- $C x < ^,
-(sin x + cos x) + C':, j ^ x < j + ж,
(-l)"(sin x + cos x) + Cn, f + (m - l)ir ^ x < \ + гиг,
Поскольку первообразная непрерывна, то должно выполняться равенство
+ **-<)), *ez,
т. е. (-l)fc+1(sin хк + cos ifc) + Ck+i = Km (-l)fc(sin x + cos x) + C\, где хк = j + fcir, A; € Z.
Отсюда приходим к равенству —\/2 + Cfc+i = л/2 + Си- При А: = 0 находим G'i = 2^2 + Со;
далее, при А: = 1 получаем 6'г = 2л/2 + C'i = 2 • 2л/2 + Со. С помощью метода математической
индукции устанавливаем, что Сп = 2л/2п + С, где С = Со — произвольная постоянная.
Наконец, преобразуя неравенство ^ + (п — 1)тг ^ х < | + пж к виду ,Т,»
X — - + Я"
я < i <п
находим, что
Таким образом,
\ ж I г-
- sm2x dx = {-\)\- -I (sin х + cos x) + 2V2
/
f dx_
j sin2 x + 1
+ С. >

210 Гл. 3. Неопределенный интеграл
¦^ Преобразуя подынтегральное выражение, находим
dx
т, .. _ f dx _ f
{X)~ J sin2x + 2cos2x~y (tg2x
2)
_ 1
~ V2 S
где пж ~ § < x < § + '•"¦> '* ? Z. Из непрерывности первообразной следует
HGZ,
т. е.
~Т
Отсюда находим C'n+i = -j= + С'„ или С, = ^ + С, где С = Со. Поскольку п <
в € й, то n = L~2w J' ^'леД0вательн01
< п +1,
является точной первообразной на R. >
А. *У •
I - (IX.
J х* + 1
Из равенства
следует, что
20.
Имеем при х ф 0
- dx =
Поэтому
+ О =
In
= In^
2л/2 х2+хл/2+1
С >
arctg^
л/2 л/2
x<0,
если х > 0.
Согласно определению, первообразная должна быть непрерывной, следовательно, /(—0) =
/(+0), т. е. ^д + С'_1 = -^д + С\. Если найдем С-х = —?д + С, С': = ^ + С, где С
— произвольная постоянная, и положим 7@) = С, то условие /(—0) = /(+0) = 7@) будет
выполненным, а определяемый интеграл запишется в виде
21.
/ J§t
Ae
(l)
•^ Рассмотрим случай, когда Л ^ 0. Пусть [х] = ?i, тогда п^я<
первообразной х >-* 1(х) на полуинтервалы [п, п + 1[, п € N, получаем
ndx n
для сужения

§ 1. Простейшие неопределенные интегралы 211
В силу непрерывности первообразной 1(п) = 1(п — 0), т. е. — д^г + С" = ""Х^Т + Cn-\
или Сп = д^л- + С'п-1, »i € N. Отсюда последовательно находим
Ci = i + Со = j + С, где Со = С,
Поскольку 7i = [х], то из B) и C) окончательно находим
М ^ _ . И , 1 Л , 1 , А. ^ ¦ J_
1А
J
Предположим теперь, что А = 0. Тогда для х € [п, я + 1[, п € N, получим
х)= / -dx = nlnx + С„.
п
Поскольку первообразная непрерывна, то справедливо равенство 1(п) = 1(п — 0). Отсюда,
аналогично рассмотренному выше случаю, находим
6'„ = - In 2 - In 3 - ... - In 7i + С.
А так как 71 = [х], то
Г"|
U dx = [х] In х - In 2 - In 3 - ... - ln[x] + С = [x] In x - ln([x]!) + C.
Таким образом,
J xX+1
)C> если Хф 0,
C, еслиА = 0.
Найденная первообразная не является точной первообразной. Действительно, точная
первообразная имеет в каждой точке области существования производную, равную подын-
подынтегральной функции. Однако подынтегральная функция имеет счетное множество точек раз-
разрыва первого рода, поэтому не может быть значением производной. > ,
•Ц Положим -4= = t, тогда х = j? и dx = —^. При этом, если х g ]0, 1], то t € [1, +оо[.
В результате замены приходим к интегралу
'/
Согласно предыдущему примеру, получаем (полагая А = 2)
Возвращаясь к старой переменной, окончательно имеем
где х €]0, 1]. >
Применяя различные методы, вычислить интегралы:
23. fx(l-xI0dx.

212 Гл. 3. Неопределенный интеграл
¦4 Пользуясь очевидным тождеством х = 1 — A — х), получаем
/ хA - жI0 dx = /A - хI0 dx - / A - x)u dx =
= -JA - х)
- хI1 d(l - х) = -^A - хI1 + ^A - хI2 + С. >
24
7 A-х
dx.
¦4 Разлагая функцию ihi по формуле Тейлора в окрестности точки х = 1, получаем
Поэтому
f x2dx Г A-хJ-2A-х) + 1 , f dx
f dx 1 1 1
+ У A - xI00 ~ 97 A - x)97 ~ 49 A - x)98 + 99 A - x)9
С, Х
¦4 Уничтожая иррациональность в знаменателе, получим
у/Х +
= 1 I 7xTTd(x + l)-i I ^fx~=\d{x-\)= \ (^(x + lK- ^(x-lK) +C, x>l. >
26. I x3s/l+x2dx.
¦4 Поскольку х'3(/х = j((l + х2) - 1) d(l 4-х2), то
f х3 v/l 4- х2 dx- = i / ГA 4- x2)f - A 4- x2
27. Л
2)!
+ x2) = ^(i + x2K-^(i + x2M+a >
x2 4- x - 2'
Имеем
1
x^ ¦
следовательно,
dx
dx
J (x+2)-(x-l) 1_
Л(х+2) 3(х-1)(х + 2) ~ 3
dx \ 1
V^\~T+2)'
x-1
x + 2
C. >
28-
xdx
¦ 3x2 + 2 '
Поскольку x dx = j d(x2) и
/ xdx
J x* + 3x
. / sin4 x dx.
[ [
3x2 + 2 2 У x2 + 1 2 У х2 + 2 2 x2 + 2
x2 + l x2 + 2'
1 х^У1_
2 2 + 2 "*"

§ 1. Простейшие неопределенные ннтегралы : ,213
¦^ Интегрируя тождество
. 4 /l-cos2x\2 1 1
sin x = =
4 2/42
l-cos2x\2 1 1 „ 1 2
cos 2х + - cos 2x =
4
11 1 + cos 4x 3 1 n 1
= - - - cos 2x + = - - - cos 2x + - cos 4x,
4 Z о о Z о
получаем
х dx = — — sin 2x + — sin 4х + С. >
8 4 il
/sin4
30. ftffxdx.
¦^ Имеем
/tg3xdx = /tgx(-i--l)dx= /tgxd(tgx)-
/ / \ COS jb / §
31.
хф-+кте.+
dx
Sill X COS2 X
Пользуясь тем, что J -r^ = In tg f I + С (см. пример 11), находим
/dx f cos2 x + sin2 x f dx f sin x
5— = / : : dx = / ^ h / — dx = ln
Sill X COS2 X J Sin X COS2 X J Sill X J COS2 X
tRTT
kv
32.
sin x
Пользуясь равенством ., \ = —d(ctgx), находим
. /
м
/ ch x ch Ъх dx = - / (ch 2x + ch 4x) dx = - sh 2x + - sh 4x + C. >
33. / ch x ch 3i dx.
¦^ Имеем
Применяя метод подстановки, найти следующие интегралы:
34. /x3(l-5x2I0dx.
¦4 Полагая 1 — 5х2 = t, находим х dx = —-^dt; x3(l — 5х2I0 dx = ^{tn — tio).dt, следова-
следовательно,
-A2 -fH\ 1 , гг 2 >
1 + ООЖ . 2U1 . ^ ^
/3/, ,. 2чЮ , 1 /,,11 ,1
хA-5х) dx=-J(t -t
[-r?=dx.
J л/Г^г"
35.
Пусть л/l — ж2 = t, тогда ' 'г = —dt и
/ si
— (R 4- 4-т2 4- Чт4^ \ /i — т2 4- Г'
л*-
+ COS2 X
n „ I Sill X COS ? ,
OD. / — г— dx.

214 Гл. 3. Неопределенный интеграл
¦4 Полагая 1 + cos2 x = t, получим sin x cos x dx = — у. Тогда
1 fl-t 1 1 1 2 1 2
dx=2y-rdt=2ln|t|-2t + C=2lnA+COS ^)C0S
/¦sin
J T
37. I -jt=.
J VI + e*
X
M Положив t = e 2 } находим
/ dx ^ = -2 / ~— = -2ln(t
38. f —
0 = x - 2ln(l + Vex + 1) + C. >
dx
ж2\3/2 '
Если положить х = sint, то dx = cos tdt и при |х| < 1
dx f dt
' = tg (arcsin x) + С = + С. >
1-х2
39
/ x
¦^ Положим x = jjtI^. Если x G ]-oo, -V2[, то t e ]-J, o[, если же x G]V2, +oo[, to
< € ]0, j [. Заметив, что для этих значений х и t sgnctg 2t = sgn t = sgn x, будем иметь
/
- sgn ctg 2t
&Ml />b2t + cos
Из равенства sin 2t = -jr = Д'8^, учитывая, что |tgt| < 1 при |t| < j, находим
x i Vx2 2
tgt =
vi
если x > т/2,
если x < — т/2.
Таким образом,
= sgnx —Wl - -j+sgnzln
x + \Д2 - 2 + С = i-чД2 - 2 +ln
x+ V*2 -2
+ С >
40./vF
^ Полагая х = asint, получаем
/ \[a? - x2 dx = a2 cos2 tdt = — / A +cos2t)dt =
a2 / 1 \ a2 xx2 i
= — (t + - sin 2t) + С = — arcsin - + —Va2 - x2 + C,
41. f dx
^ Положив x = a tg t, имеем при a ф О
/_^ = 4/,
J \/(х2 + a2K «27
/ V~^x~dX'
x ^a. >
• a >

§ 1. Простейшие неопределенные интегралы
Пусть х = a cos 2t. Тогда . / ~^ = ctg t, dx = — la sin 2t dt и
215
/la x ^ _ _4(j /
]/ a — x J
( —j— sjn 2*) + С = aarcsin - - \l a2 - x2 + C,
\2 4 / a
—a ^ i < a. >
2a -x
dx.
¦4 Полагая x — 2a sin2 t, получаем (см. пример 29)
/ xj—-—dx = 8a2 / sin4 tdt = a2 (u - 2 sin 2t + - sin 4t) +C =
J \j 2a — x J \ 4/
= 3a2 arcsin J — -\/xBa - x) + C, 0 ^ x < 2a. >
V 2fl Л
44.
I
dx
= 2t + C = 2arcsinA/| + С, а < ж < Ъ. >
¦^ Положив х — a = F — a) sin2 f, после простых преобразований получим
J y/(x - a)(b - х) ~
45. / v/a2+x2dx.
¦< Пусть x = asht, тогда dx = achtdt. Следовательно, \/a2 + ж2 = ya2(l +sh2<) = achi
\/я2 + x2 dx = a /
J
a
Т
Из равенства shf = -—j— = ^ находим, что е' = ° ¦ Поскольку е' > 0, то t = In |ж +
Va2 + х2[ - lna. Очевидно, sh2t = 2shtcht = 2sh.t\/\ +sh2t = 2 |a/i + |j.= f|v^
поэтому окончательно получаем
/• . x . „2
/ v/a2 + x2 dx = - \Ja2 + x2 + — In \x + \Ja2 + x2\ + C. >
46.
//х - а
\ / dx.
V х + а
Ч Подынтегральная функция определена при х < — а и при ж ^ а. Пусть ж ^ а. Тогда,
полагая х — а = 2ash2f, получаем
\h—^-dx = 4as
J \J x + a J
Учитывая, что ash2t = лД2 - a2, sht = J^ = -'"/"' , t = 1п(д/ж + а + т/ж - а)-1п\^а,
окончательно получаем
/ 1 / dx = v/x2 — a2 — 2aln(\/x + a + y/x~—~~a) + C.
J У x+a v KW у J
Если x < —a, то, полагая x + a = —2ash2t, имеем
/jx — a f
\ / dx = -4a / sh2t dt = -a sh 2t + 2a< + С =
V x + a У
= —\/x2 + a2 +2aln(V—x — a + \/—x + a) + C. >

216 Гл. 3. Неопределенный интеграл
47. f y/(x + a)(x+b)dx.
4 Предполагая, что b>ayix + a>0,x + b>0, положим х + а, = (Ь — a)sh2tf. Тогда
Поскольку t = ln(^/x + а + л/аГ+Т) — In л/b — a, sh At = ?^^t \/(x + a)(x + Ь) ¦ то оконча-
окончательно имеем
Х+"+
а)(х+Ь)-
*—-^
Если же ж + и < О, х + 6 < О, b > а, то, полагая х + b = — (b — a)sh2t, получим
/(ж + а)(х +b)dx = - ^ ~ а> I (ch 4t - 1) dt = - -
16
sh«
Применяя метод интегрирования по частям, найти следующие интегралы:
48. / х2 arccos х dx.
4 Интегрируя по частям, находим
з
/ i arccos x rfx = I arccos x d I — I = — arccos x + - / —r=
У J V 3 J 3 3 J V1
= — arccos x
-\ I x2d(\/l-x2) = — arccosx - ^- \/l - ж2 + i f \/l - x2 d{x2) =
^- arccosx - 1-0 - x2 - ^,/A - x2K + C,
3 3 9
49
arcsin x
/arcsir
x
¦< Имеем
/arcsin x, / . ,/l\ 1 . / dx
r— dx = I arcsin x a = arcsin x + I —.
x2 J \ xj x J x.y/\ - x2
Последний интеграл вычисляется следующим образом:
f dx _ f dx _ f sgnxd(|x|) _
d I A
Л -1
+ С = In
1 +л/1 -
Окончательно имеем
arcsin x , arcsin x
A
A/p __
D Jb —
111
1 + VI - x2
+ C. >
50. / arctg \fx dx.

§ 1. Простейшие неопределенные интегралы
¦4 Методом интегрирования по частям, находим
217
/ г.1 г xdx I ( \ 1
/ arctg л/ж dx = ж arctg Vx - —- = х arctg лД ~ / I 7-7= ~ о /-,, ,—Г
= х arctg л/ж — V? + / ——— = ж arctg у/х — л/х + arctg д/Ё + С, х ^ 0. >
J 1 + ж
51. / arcsin2» rfx.
¦4 Имеем
/arcsin х dx = х arcsin2x — / . arcsin xdx = x arcsin x + 2 / arcsin x d(\/l — ж2) =
= x arcsin2x + 2 yl — x2 arcsin ж — 2x + С, \х\ ^ 1. >?
52. / ж arcsin2ж </ж.
¦^ Интегрируя по частям и используя предыдущий пример, находим
/ х arcsin2 ж dx = х I arcsin2 ж dx — / arcsin2 ж dx = (ж — 1) / arcsin xdx =
= (ж - 1) (ж arcsin^ + 2\/l - ж2 arcsin ж - 2ж J + С, \х\ < 1. >
CQ / dx
' J («2+Ж2J-
¦^ После очевидных преобразований, интегрируя по частям, получаем
2
[ dx _ \_ [ (а2 + ж2) -ж2 _ J_ ж 1 Г ж ^ 1
У (а2 + ж2J - „2 у (а2+х2J </ж- a3arCtga + а2 У 2 Va2 +
= J_ ж ж 1_ I _
~ a3 g а 2а? (а2 + ж2) 2а2 J a
. / \/а2 — х2 dx,
ж 1 ж _
2а2(а2+х2) + 2^ МС S a +
54. / \/а2 — х2 dx, \x\ ^ а.
¦^ Интегрируя по частям, находим
dx = x\Ja? — х
/ \Jаг —
J
У ^ j ГЗ -, /(x2-a2)+a
J v«2 — х2 J ya2 — x2
= ж \1 а2 — ж2 — / л/а2 — х2 dx + a arcsin —(- С.
J ' " '
(
а \
Решая это равенство относительно f у/а2 — х2 dx, получаем
''а2 — ж2 dx = — \/а2 — ж2 Н arcsin —(- С, а ф 0. >
2 2 а
55. / x2vV
¦4 Имеем
[ x2y/a2+x2dx= f xd(l(a2 +х2M ) =5.(а2+ж2I -| [ (а2 + х2)\/а2 + х2 dx + С =
J J \3 / 3 3У
--Г / \/a2+x2dx+C.

218 Гл. 3. Неопределенный интеграл
Вычисляем последний интеграл:
/
V
/ \Ja
J Va2 + х2 V J л/a2 + ж2
- / \/a
2 + x2dx = -\/a2 + ж2 + — In |x + \/a2
2 + i2 dx + a2 In |ж + \/a2
С
Окончательно получаем
I x2s/a
J
2+x2dx=
a2 + x2 - — ln\x + ^/a2 + x2\ + C. >
8
56 jx sin л/ж dx.
Ч Замечая, что х dx = 2(л/жK d(A/ic)> и интегрируя по частям, получаем
/ ж sin л/ж dx = 2 / (л/жK sin л/ж <г(л/ж) = -2 / (л/жK d(cos л/ж) =
• б / xcos л/ж^(л/ж) = — 2л/ж^ совл/ж 4- 6 / х d(sin л/ж) =
J J
= — 2vx? cos л/ж 4- 6xsin л/ж — 12 / v/*siiiv'ii!(v'') =
'S л/ж 4- 6x sin л/ж 4-12 / л/ж d(cosл/ж) =
/ж 4- 6x sin л/ж 4- 12л/жсозл/ж — 12 sin л/ж 4- С =
= 2л/жF -x)cos,/x 4-6(x - 2) sin л/7 4-С, х Js 0. >
¦^ Интегрируя по частям, имеем
/arctgx /• arctgi t arctgx
лс- i / ^ ,/ arctgx\ xc I Л
arctg x I' i/ arctgx\ arctgx arctg^; Г arctg x
^ / __V /_ __ I Jj.
откуда 7 =
2V1
arct«* + C. >
58. h = / eax cos bx dx, h = / eox sin 6x dx.
Очевидно,
59
/i = - cosbxd(eax) = -eaxcosbx + - f eax sinbx dx =-eax cosbx + ~I2;
a J a a J a a
I2 = — / sin bx d(eal) = — eax sin 6x / eax cos 6x dx = — eax sin bx 1\;
a J a a J a a
. eaa(acos bx + bsin bx) eaI(asin 61 — 6cos bx)
Ji = 2 ,2 1- G; h = , ,, h G. >
a2 + 62 a2 4- b2
. / e2x sin2 x dx.

§ 1. Простейшие неопределенные интегралы 219
¦^ Используя предыдущий пример, получаем
/ е2х sin2 х dx = - j e2x dx-~ I e2x cos2x dx = -e2x - ie2x(sin 2x + cos 2x) + C. If .
Нахождение следующих интегралов основано на приведении квадратного трехчлена к канониче-
каноническому виду и применении формул:
; ? + С, афО.
IV.
а —х*
xdx
V. J-;=== hi |a.-+ УЭТГа2] + С, а > 0. VI. J ^_ _
VII. J vV2 — x2 dx = | \/a2 — x2 + ^-arcsin^ + С, а > 0.
VIII. f Vx2 ±a2dx= fx/cc2 ±а2 ± ^-lii|x + N/i2 ±a2| + C.
Найти интегралы:
= ±^а2 ± ж2 + С.
Имеем
J Зх2 — 2х 1
/х fix
х4 - 2х2 - 1 '
i-l
+ C, x#-|, хф1. >
Очевидно,
х dx
x* - 2x2
_ 1 I d(x2 - 1) 1
- 1 ~ 2 J (x2 - IJ - 2 ~ 4%/2
x2 - 1 + у/г
+ с, хф±\/г + \/2. р-
62.
x2 + ж + 1
Пользуясь свойством г), п. 1.2, получаем
J sin x
63
¦4 Имеем
+ 2 cos x + 3 '
dx
w
= arctg
§2 +
' — Ж < X < Ж ¦
Из непрерывности первообразной следует
1(ж + 2н7г — 0) = 1(ж + 2пж + 0), п € Z, —(- С'п = — — + Cn+i, Cn+i = х + Cn.
2 ^
Отсюда находим C'n = пт + С, где С = Со — произвольная постоянная. Поскольку 2пж — ж <
х < ж + 2«7Г, т. е.
2тг
Таким образом,
I(x) = arctg —2-
2ТГ
= Um /(ж), n'€Z. >
X—>7Г+2П7Г

220
Гл. 3. Неопределенный интеграл
64.
х dx
/5+I-I2
Очевидно,
xdx
(х - \) dx 1
- х — х2 \/5 4- х — х2 2
dx
откуда
/xdx г—
V5 + x-x2=V5-
,5. / , ^ .
У Vz4 - 2х2 - 1
x-x2 + -arcsm-7=r + C, - 2
¦л/27
Имеем при |х| > \/1 4- V2~
х3 dx _ ^2d(x2) (x2-l)d(x2 -1)
2 - IJ - 4
1_
4 2
откуда
— 1
С. >
вв./
Имеем при — 1 «С х ^ 2
g 2x
- — arcsin —-—
67.
- х 4- х2) dx
- X2
¦4 При |х — i <^, i/0, имеем
х - 1
4- х - х2 J хл/1 + i-x2 J л/1 + z-x2
В первом интеграле положим т^г = t. Получим
= dx.
I dx f
7 xVl 4-ж - х2 У y^t2
= -In
2 + ж + 2л/Г+ ж - ж2
Второй интеграл вычисляется непосредственно:
[ (x-Vydx f {~2x + l)dx 1 / rf(x~;) /ГТ 7 1
/ ; = = - / . — - / —, =—v/l + x — x2
J Vl+x-x2 J 2Vl 4- * - x2 2J /Г77 ГТ7 V 2
¦ 2s-
arcsm =
/5
Г77 ГТ
4 Iх 2/
Окончательно имеем
У = - In
2 4- x + 2%/Г4- а; - ж2
— yl + х — х2 arcsin -j= Н С. >
2 л/5
68. f -^±L=

§ 2. Интегрирование рациональных функций
При х ф 0 имеем
I х2 + 1 , / 1 + ^ , У <* (а - i
/ —. ах = sgn х / —. dx = sgn x I —,
J xv^TT J .ОГТТ J . // _n2
221
X2 +
= sgn ж • In
+ G = sgn ж • In
ж2 - 1 + л/х*
+ C. >
Упражнения для самостоятельной работы
Найти интегралы:
1. jyr^T
. з.
^j. 4./a2cx2;bfsin2j. д./-,%.
10. Г ^__. ц. f-^|-. 12. fcos3X<b. 13. fe-^-^di. 14. [e*2*dx.
J cos a- sin2 x J cos4 x J J J
15. /cosi-f. 16. /^Jx. 17. /^t=. 18. /tg4zrfx. 19. /cos2xdx.
20. fxV^Tldx. 21. /(x + !)V*2+x + lrfx. 22. / (-3i+*+1)'i* ¦ 23. f <x+^d
2
24./^,х>1. 25. f$ /
lrfx. 22.
26. /ln[x]dx, x > 2. 27. / p^y, x > 1.
35. f л/1 - 2x2 + x4 dx. 36. /arcsin (sinx)dx, x 6
38. /х3л/ГТ^"йх. 39. /x2(l + xJ0dx. 40. /
Методом подстановки найти следующие интегралы:
37. arccos (cosx) dx,
44>
пг. 46.
. 50. f-^-dx. 51. f
. 52. f .1*'|Г^х i •
49. \х2ф
Применяя метод интегрирования по частям, найти следующие интегралы: : > ;
54. fx3lnxdx. 55. fx3sinxdx. 56. Г xdf . 57. fx2cosxdx. 58. Гхsin2 xdx.
J J J sin3x J J
^®" / sin5 д. ¦ 60. / cos5x ¦ 61. /tg7xdx. 62. / arcsin f dx. 63. / -^ arcsin x dx. >
64. /x2arctgxdx. 65. /^arctg^dx. 66. /xarcctgxdx. 67. / ar^fx dx. 68. Jx3eaxdx.
69. feaxcos2xdx. 70. fl-^fdx. 71. fln2xdx. 72. fx2ln2xdx. 73. f^-dx.
74. /ln(x + \/a2 + x2)dx. 75. /x2ln(x + л/х2 — a2)dx. 76. /xshxdx. 77. Jxsb.2xdx.
78. fx3chxdx. 79. Г iarcsinI rfx. 80. Г arcsin x arccos x dx. 81. Г /'"" dx.
§ 2. Интегрирование рациональных функций
Известно, что правильная дробь
Q(x)
к
1 = 1
>=1

222 Гл. 3. Неопределенный интеграл
где нули квадратных трехчленов ajx2 + bjx + qj комплексные, допускает разложение
Q(s)
' ' ' + UjX2 + bjX + Cj
Постоянные А\,, J3j/^ и С'// находятся методом неопределенных коэффициентов.
В некоторых случаях постоянные А„, An-i, ¦ ¦ ¦, Ai в разложении
'( X~) '
A)
B)
соответствующие множителю (х — xi)n, удобно находить следующим образом.
Умножив равенство B) на (х — х\)п, получим
(х - л)" Ах + (х -
)п~Г
r(x) " V -iy^n-1 i . . . i v~ ~i, -щ -r v~ ~i; , ч •
Заметив, что все слагаемые правой части равенства C) при х = х\ равны нулю, находим
C)
А -
г(х)
D)
Далее, продифференцировав равенство C), получим
г(х)
откуда находим
А -
E)
Продолжая описанный процесс, получим формулу
Ап-к = тт
к\ \г(х)
(*)
, к — 0, п - 1,
F)
используемую для определения постоянных Ап, An-i, . .., А\, соответствующих множителю
(х -Х1)п.
Аналогично вычисляются постоянные разложения A), соответствующие другим действи-
действительным нулям многочлена х (-> Q(x).
Применяя метод разложения рациональной дроби на простейшие множители, вычислить
следующие интегралы:
69. / x3 + 1
J х3 - 5х2 +
6х
¦ dx.
Выделив целую часть
= 1 +
5х2 -
-5г2+6г'
а затем разложив знаменатель правильной дроби на множители, получим
i3 - 5г2 + 6х ~ г(г-2)(г - 3) ~ ~х + х-2 + х-3'
Согласно формуле D), имеем
(г - 2)(х - 3)
г(г - 3)
__9
-~2' ~
х2 - 6х +
х(х-2)
аг=3 '
28
3 '

§ 2. Интегрирование рациональных функций
Интегрируя тождество
13 + 1 ..11 9 1 28 1
223
х3 - Ьх2 + 6х
окончательно получаем
6 х 2 ат-2 3 х-3'
/^Т^^Г^ = - + ^Ь|х|-|1п|г-2| + ^1п|х-3| + С, х-
•6а:
J х3-Ъх-
Аналогично предыдущему имеем
X X
В
_С_
i3-3i+2 ~ (х-1J(х+2) ~ (х-\J + (х-1) + х + :
Пользуясь формулой F), находим
А =
х +2
Таким образом,
У* г^г _ 1 У* rfx 2 f dx 2
J ж3 - Зх + 2 ~ 3 J (х - IJ + 9 У х- 1 9
dx
х+2
1 1
JT-1
+ 2
71
¦/
Имеем
(г + 1)(х + 2J(г + 3K х+1 + (г + 2J (х + 2) ¦*" (г + 3K "*" (г + ЗJ
Пользуясь формулой F), последовательно находим
А =
1
1
= -1,
_ -Qc + 3K-3(x
D =
= 2,
5 ,
'V
(x + lK(r + 2J + (x + 1)Цх + 2K + (x
2)
i=-3
17
' 8 '
Подставив найденные коэффициенты в разложение A) и проинтегрировав, получим
17,
9х2 + ЬОх + 68
4 (г + 3) 8
+C'

224
Гл. 3. Неопределенный интеграл
dx
Имеем
x(x + l)(x2 + x -
По формуле D) находим первые два коэффициента:
А В Сх + Р
~ х х + 1х2+х + 1
A)
А =
(х + 1)(х2 + х + 1)
= 1, В =
= -1.
Далее приводим разложение A) к общему знаменателю
1){х2 + х
Вх(х2 + х + 1) + (Сх + D){x2 + х);
затем сравниваем коэффициенты при х' их, получим систему
О = А + В + С,
+ D + C,
из которой находим С = 0, D = — 1. Проинтегрировав A), получим
dx , i i , i . i / dx
J
X2 + X + 1
= ln
x+1
Г + 1
2 2х -4- 1
—= arctg ¦=- + С, х ф -1; 0.
73.
¦4 Поскольку х3 + 1 = (х + 1)(я2 — х + l)i то
J
Обычным методом получаем систему
0 = А + В,
0 = -А + В
С,
Отсюда А = |, В = —|, С = |. Таким образом, при х ^ —1
(»- \) dx
2 j + 4
1 2х - 1 ^
arcts + C
1 2х - 1
74. /-^т-
Имеем
dx f
Bx + C
откуда получаем х = А(х2 + х + 1) + (Вг + С)(х — 1);
0 = А + В,
1=А-В + С,

§ 2. Интегрирование рациональных функций 225
Решая полученную систему, находим
А-1 Я- г С-1
Следов ательно,
<¦">¦>
¦4 Поскольку
14 + 1 = (х2 + IJ - 2х2 =(г2+1а
то разложение подынтегральной функции на простые дроби ищем в виде
1
Из тождества
1 = (Ах +
получаем систему уравнений
+ 1
х2 +гл/2 +
В)(х2 - гл/2 + 1)
х3
х2
X
х°
0 = А + С,
0 = -у/2А +
0 = А — у/2 В
1 = B + D.
1 ' г2-гл/2 + 1
+ (Cz + ?>)(z2+a
B + y/2C + D,
+ С + y/2D,
Отсюда Л = —С = —т=, В = D = -. Следовательно,
Г х + ^ dx 1 / ^-^ dr_ i / г + #
J x2 + xy/2 + 1 2^2 J x2 - хл/2 + I 2^/2 J x2 +xy/2~+l
1 / dx 1_ / я-^ 1 f dx =
4J (r+^\2+' 2V2J x^-xy/2 + 1 X+4J (T v^V^1
= -1= In ^ + ГЛ^+^ + -^(arctg (xV2 + 1) + arctg (*>/2 - 1)) + С
4л/2 i2 — хл/2 + 1 2т/2
Учитывая формулы сложения арктангенсов (см. пример 268, гл. I), окончательно получа-
получаdx
. х + х\/2 + 1 1 гл/2 тг
In = = arctg 7г Н r= six) + С,
*V2 + l 2Д hl-x2 2у/2 К >
где
{+1, если х > 1,
О, если |г| = 1,
— 1, если х < —1,
76.
7A) = Hm I(x); /(-1) = lim I(x). >
r4 + i2 + Г
•* Поскольку г4 + д;2 + 1 = (х2 + IJ - х2 '= (х2 - х + 1)(х2 +1 + 1), то разложение ищем в
виде
1 _ Ах + В Сх + D
14+12+1 Х2+Х + 1 X2 — Х + 1'

226 Гл. 3. Неопределенный интеграл
Из тождества 1 = (Ах + В)(х2 — х + 1) + (Сх + D)(x2 + х + 1) получаем систему
0 = А + С,
D,
Отсюда А = В = —С = I) — -. Таким образом,
J х* + z2 + 1 ~ 2 J i2 + х + 1 2,/ г2 - х + 1
1 , х + х + 1
arctg
+ 1 2г - 1 . _
-=- + arctg 7F- ] + С.
Заметим, что (см. пример 268, гл. I)
2i + l 2х- 1
arctg -= 1- arctg ^^ = arctg
1-г2
л/3 ь л/3
где функция е(х) определена в предыдущем примере, а значения арктангенса в правой части
в точках х = ±1 равны предельным значениям в этих точках.
Окончательно имеем
da;
1. г2 + г + 1
Ш
arctg
f' Л/ ^
+ х2 + 1 4 " х2 - х + 1 т 2Vf —-«• 1 - х
С. >
77.
/ Ах
J ?пп"-
Сначала преобразуем подынтегральную функцию
= (х4 + 1) + A - ж4) = 14
2(x6
1-г4
х2 -1
2 (г2 + l)(z* -t4l) 2A'-гЧ 1)A + х2) ~ 2 (г2 + 1) 2 (г6 + 1) 2 (г4 - г2 + 1)'
Первые два слагаемых легко интегрируются, поэтому найдем разложение на простые дро-
дроби только последнего слагаемого. Имеем
-х2 + 1
Ах + В Сх + D
-у + \ = (Ах + В)(х2 - V3 г + 1) + (б'г + .
О = А + С,
V3 г + 1);
В
й~А- л/35 + С +
D,
Отсюда А = —С = —jz, В — D = j, поэтому
1 _ 1 х2 1
х6 + 1 ~ 2(х2 + 1) + 2 (х6 + 1) +
Интегрируя это равенство, получаем
х2 - лДх + Г
78
f Ах _1
J ze+ 1 ~2
1 з
arctg г + - arctg х Н
6 ^6 6
1 , х2+уДх
ш
+ I3 — X2 + X — 1 '

§ 2. Интегрирование рациональных функций
227
А Поскольку хь - х4 + х3 - х2 + х - 1 = х*(х - 1) + x2(z -1) + (я - 1) = .(ж - 1)(х4 + х2 +1) =
(i — 1)(х2 + х + l)(i2 — ? + 1), то разложение подынтегральной функции на простые дроби
имеет вид
1 _ А Вх + С Рх + Е
ХЪ — I4 + Ж3 — Х2+Х — 1 Х — 1 Х2+Х + 1 X2 — X + 1'
Из тождества 1 = A(xi + i2 + 1) + (Вх + С)(х - 1)(х2 - х + 1) + {Dx + Е)(х3 - 1) получаем
систему
решая которую, находим
Таким образом,
О = -2В + С+Е,
0 = А + 2В- 26',
О = -В + 1С - D,
/ах2 + 6а
2 + х + 1 V3
+ с
-г^— аг представляет собой рациональную
79. При каком условии интеграл
функцию?
< Интеграл представляет собой рациональную функцию, если в разложении
ах2 + Ьх + с А В D
х3(х — IJ I
_ А_ В_ D_
I3 2
Е
х (х-1J ^ х-1
коэффициенты D и F равны нулю. Предполагая последнее, имеем
ах2 + Ьх + с = А{х2 - 2х + 1) + В(х3 - 2х2 + х) + Ех3.
Приравнивая коэффициенты при одинаковых степенях х, получаем систему
О = В + Е,
а- А-2В,
6= -2А + В,
Исключая из этой системы неизвестные А, В и Е, находим требуемое условие:
Применяя метод Остроградского (см.: Л я ш к о И. И. и др. Математический анализ. К.,
1983. Ч. 1, с. 381), найти интегралы:
80.
. / —
J (х-1J(х+1K'
¦4 Имеем
/х dx
(*-1J(х
Ах2 +Вх + С
х -
х + 1
Дифференцируя обе части равенства, находим
х _ (х2 - 1)BАх + В)- (Зх - ЩАх2 +Вх + С) ¦ D
+
Приводя к общему знаменателю и приравнивая числители, получаем
• = -Ах3 + (А - 2В) х2 + (-2А + В - 36') х + С - В +
+ D(x - 1)(х3 + Зг2 + Зг + 1) + Е(х* г- 2х2 + 1).

228
Гл. 3. Неопределенный интеграл
Приравнивая коэффициенты при одинаковых степенях х в обеих частях этого тождества,
получаем систему
О = D + E,
решая которую, находим
О = -A + 2D,
0 = Л- 2В -2Е,
1 = -2 А + В - 36' - 2D,
Следовательно,
х dx
1+2
81.
(х -1JA +1K
dx
Тб]
1 + 1
1-1
С,
< Имеем
dx
Ах2 +Вх
Х3+1
Ex + F
х2 - х + 1
Дифференцируя и приводя к общему знаменателю, получаем тождество 1 = — Axi — 2Bx3 —
ЗСх2 + 2Ах + В + D(xb - xi + х3 + х2 - х + 1) + (Ex + F)(i4 + i3 + i + 1), откуда
О = D + E,
0 = -2B
E+F,
+ F.
0 = -36' + D + ?,
0 = 2Л-? + ? +
1 = B+D + F;
= C=0, B=\,
= -E=2-,
Таким образом,
J
82.
x2dx
+ 2x +2J'
Имеем
x2dx
Ax + В
2 2x - 1 _ .
arctg ^-+C, !#-!.>
Зл/3
¦ +
I —
J *2-
Cx + D
¦ dx.
откуда, дифференцируя и приводя к общему знаменателю, получаем тождество
х2 = А(х2 + 2х + 2) - (As + В)Bх + 2) + (С'ж + Z»)(r2 + 2х + 2).
Для определения неизвестных получаем систему
0 = С,
1 = -А + 2С + D,
О = -2B + 2C + 2Z»,
решая которую, находим
0 = 2Л-25 + 2Д,
Л = 0, 5 = 1, С = 0, .
= 1.

Тогда
83
§ 2. Интегрирование рациональных функций
xdx
229
" J (*4
J \
1
arctg(r + l) + C.
da:
1J
¦< Имеем
Г dx_
J (*4 + l
Ах3 + Да
х
Х2 +сх + р Г
4 + 1 +J
Ex3 + F г2 + Gx + Н
dx,
откуда
= (ЗАх2+2Вх + C)(i
О = -Л + F,
0 = -2B + G,
О = -ЗС + Н,
. Вх2+ С'х + D) + (х4 + I)(?z3 + Fx2+ Gx + Я);
-3 0 = -4Z» + ?,
0 = 2В + G,
1 = С + Я.
Решая систему, получаем
= B = D = E = F = G = 0, С'=-, Н=-.
4 4
Следовательно,
/ с
J (^4
¦ +
3 f dx
1J xi +1'
Пользуясь результатами примера 75, окончательно находим
dx х 3 . х2 +
где е(х) — то же, что и в примере 75. >
'
/
Применяя метод Остроградского, интеграл представим в виде
dx Ах7 + Вх6 + Схъ + Dx* + Ex3 + Fx2 + Gx + Н f Kx3 + Lx2
(x4 - lJ (ж4 - IJ J xi - 1
Дифференцируя и приводя к общему знаменателю, получаем тождество
5C'i4
ЪЕх2 + 2Fx + G)-
- 8x3(Ax7 + Bxe + Gxb + Dx* + Ex3 + Fx2 + Gx + Я) +
+ (i8 - 2x + l)(Kx3 + Lx2 +Л + N).
Сравнивая коэффициенты при одинаковых степенях х в обеих частях равенства, имеем
0 = К,
0 = -A + L,
0 = -2В + М,
0 = -ЗС + N,
0 = -4D - 2if,
0 = -7А - ЪЕ - 21,
0 = -6В -6F -2М,
0 = -5С -7G - 2N,
0 = -4Z» -%Н + К,
0 = -
0 = -2F + M,
1 = _G + 7V.
Решая систему, получаем
~,
.
Таким образом,
J
dx
7хь - Их 21
+
i4 - IK ~ 32 (i4 -IJ + 32 J z4-l
dx

230
Гл. 3. Неопределенный интеграл
Вычисляя последний интеграл, окончательно получаем
dx
¦ +
21
х - 1
(x4 -IK 32 (ж4 -IJ 128
Выделить рациональную часть следующих интегралов:
¦dx.
21
- ^arctgr + C. >
х2 + \
Имеем
[ х2 + 1
J (х4 + ж2 +
¦dx =
Ах3 + Вх2 + С
Ехъ
¦ dx,
Г4 + X2 + 1 ./ Xi + X2 + 1
откуда получаем тождество
х2 + 1 = (г4 + х2 + 1)(ЗАх2 + 2Вх + С) - Dг3 + :
+ Вх2 + Сх + D) + (xi + х2 + 1)(Ех3 + Fx2 + Gx + Я).
Из системы уравнений
0 = Е,
Q = -A + F,
0 = -2B+G+E,
Н,
0 = -4D + G + E,
1=ZA-C + H +
0 = 2B-2D + G,
1=С + Н
находим А = ^, С =\, В = D = G = 0, F = \, Н = |.
Таким образом, рациональная масть равна выражению
х +2х
6 (х* + х2 + 1) '
86. / . .4J'^~1 „dx.
< Разложение ищем в виде
Ах* + Вх3 + Сх2 + Dx + E
¦dx =
I
Fxi + Gx3 + Ex2 + Kx
xb + x + 1
dx,
отсюда получаем тождество
г5 1 = (хь + х + 1)DАг3
4г5 - 1 = (хь + х + 1)DАг3 + ЗВж2 + 2Сх + D) -
- Ei4 + 1)(,4г4 + 5х3 + Сх2 + Dx + Е) +
+ (х& + х + 1)(-Fr4 + Gr3 + Нх2 + Л"г + X);
решая систему уравнений
0 = -А + G,
X
0 = -25 +Я,
0 = -ЗС + Л',
4 = -4Z» + L + F,
-1 = D-E + L,
находим А = В = С! = Е — F — G = Н = К = L = О, D = —1. Таким образом, интеграл
сводится к своей рациональной части:
— х
хь + х + 1'
Применяя различные методы, найти следующие интегралы:
от I х + х j
О 1 . / —-. ах.
J х^ + \
4 Имеем

§ 2. Интегрирование рациональных функций 231
Используя пример 73, окончательно имеем < :
х2 + х , 1 t з , 1 2i-2 - 1 1 , (г2 + IJ
j__ .._*__ + -—arctg 7^ + 7T7lnd 1ГТ"
Полагая х = <, находим
(* - 3) df
/ *4-3 = 1_ /¦
У x(z8 + 3x4+2) X 4 У
Разложение функции на простые дроби ищем в виде
<-3 Л 5 С
+ +
= —+ •:—7 +
t t + 1 t + 2'
откуда < - 3 = A(t + \)(t + 2) + 5<(< + 2) + Ct(t + 1).
Полагая последовательно t = 0, —1, —2, находим
= 4,
Таким образом,
„4 ,
/т2п-1
dx.
¦^ Имеем
У х»+1 нУ х» + 1 ~ пУ гг» + 1 ( }~
где —оо < г < +оо при четном п к х ^ —1 при нечетном п ф 0. >
Умножая числитель и знаменатель на xi, получаем
if ( J ¦ ^ Ж ^l f Г(^+) A rf/ 5ч =
5 / W~ х™ + 1 ~ (*« + 1
1 / г
То 1
91. f-l^L-dx.
¦4 Полагая i7 = t, получаем
1 /"/1 2
j
l(ln )<| - 2In ]1 + <1) + С = jln A ^J7J + C, r/0;-l. >

232 Гл. 3. Неопределенный интеграл
92. / /V dx.
J Xi + X2 + 1
¦^ Имеем при х ф О
У х2 + 1
J I4 + X2 + 1
Имеем при х ф I
х2 + 1 л У l + js . У ^(^-1) 1 . х2 - 1 . fd
¦j j dx = I -—— dx = I j = —-p arctg -=- + < ,,
i _- 1 L J C'i, если x > 0,
CT2, если a; < 0.
Вследствие непрерывности первообразной имеем
где Ф(х) — первообразная подынтегральной функции.
Таким образом,
С, х = 0.
93.
4 + x3 + s2 + x + 1
После очевидных преобразований имеем
х2 -1
1 - 4т у
-?+1+- + ^" J
f rl ( Л- — Л. -\
¦± + а>
¦4 Аналогично предыдущему примеру имеем
У *"-* dx-1- i g4~1 d(x2) -
J * J '
2^ (-а+^Г-2
95. / E+idx.
•^ Производя надлежащие преобразования, получаем
/ ^Г-ГТ dx= }X f 4+ 2 Х,ч dx = / -y-^— + / 4-Л =
J x6 + 1 _/ (z2 + l)(x4 — s2 + 1) J x2 + 1 J s6 + 1
J ' J
96. Вывести рекуррентную формулу для вычисления интеграла 1п = I -,—j
J (ax
= Jl
. Пользуясь этой формулой, вычислить /3
^ Используя тождество
rfx
теграла 1п = / т—^ ч—>
J (as2 + is + с)"
ах2 +Ъх + с= — {Bах + bf + Dас - б2))
и производя замену 2ах + 6 = t, получаем
/п = ^г/
, . ч„ , где Д = 4ас-й2.

§ 3. Интегрирование иррациональных функций 233
Интегрируя по частям /n-i, получаем
а)-Ч Dа)-1A-») /
+ Д)"-1 а _/
, A
, A п) /
t2 + Д)" ^ ; а J (*2
т Da)n-1t o/i \т .2A— п)Д г
. е. /„_! = 2aj,4A),-i - 2A - »)Л,-1 + \а In.
Решая это равенство относительно 1п, находим
n~ ДA — w)(t2 + Д)" A - п)Д n~1'
Подставляя вместо t его значение, окончательно имеем
_ 2ах + Ъ 2п -3 2а
" ~ (м - 1)Д(аа;2 + Ьх + с)" + га-1 ' Д" "~1-
В предложенном примере a = Ь = с = 1, ?г = 3, Д = 4. Таким образом,
2х + 1 . / dx 2s+ 1 2s+ 1 2
+ 1 /
' х + !)' J
6(s2+x + lJ ' J (s2+s + lJ 6(s2 + s + lJ 3(s2 + s + l) зу х2+х + 1
2x + 1 2z + 1 4 , 2x +
V3
Упражнения для самостоятельной работы
Методом неопределенных коэффициентов найти интегралы:
х^^+6 dx- 88-/(^Тб^) dx- 89' / (*-1)»(*» + 1) ^'
90. f_ -^ 91. Г *^ 92. Г . f~f~l dx.
J *D+л;2JA + я-2) J x7-4xs+6x3-4x J x^+x4+x3+x2+x+l
Найти рациональную часть в следующих интегралах:
93. /ffi^dx. 94. / {?-1'+3'Ц?K ¦ 95. /(f^ds. 96. / '""^а**"
§ 3. Интегрирование иррациональных функций
С помощью приведения подынт
дующие интегралы:
/х ч3/2 4- т
V3/ dx, хф-\.
х+ ^/2Т^
С помощью приведения подынтегральных выражений к рациональным функциям найти
следующие интегралы:
3
Полагая х -\- 2 = t , имеем
_34 3j2
* *
К последнему интегралу применим метод неопределенных коэффициентов:
3t2 - 6f Л Bt + C
{t-l){t2+t + 2) t-\
Отсюда находим
А---, В--, С---
и вычисляем интеграл
Г
J (t-
з (_to_ \± [ tl d
4J«l+4Jl4( + 2

234
Окончательно имеем
Гл. 3. Неопределенный интеграл
/
3 3 3 15
: dx — —t4 1 In I* — ll +
4 2 4 ' '8
27
98
/x dx
. a > 0.
i/хЦа - x)
'(а-х)
Заметим, что
I= [xdx=== Г prd 0<x<a.
J i/x3{a-x) J V a~x
Цх3{а-х)
Подстановка -?^, = t4 приводит к интегралу рациональной функции
Интегрируя по частям, находим
[ dt at f
a I 7 = Г ' ° / ~
dt
Последний интеграл вычислим путем преобразования подынтегрального выражения:
— t2) 1 /" 1 i j2 i f ^2
Г dt _ 1 /" A-и2) + (l -12) i [i+t2 lft2
I _ — — I „ ^ — — I _ ?(? — — I —
I \ -\-1 2 I 1+tf 2 / 1 +1 2/1
-1 fllAdt.1 [±z±dt-1 [J^LzjL+1 f d(' + i)
arctg
Таким образом, окончательно получим
а , t2
+
+ 7-^= arctg
4л/2
+ C.P-
In
99.
(и — натуральное число).
Заметим, что
/
dx
Г dx_
)"-i J */rx-±\n-i
Положим Z=± = tn. Тогда -r-^ = -р^-Г dt и
x—a ^ (x—aJ b—a
n ft,. 11 f , и ^. n n x — b _
= I / 7^-T rft = I / dt ~ I X + C= I \ + C-
b — a J f1-1 ft — a J b — a b — a \ x — a
Применяя формулу
Г Pn\
J Ь
x)
dx = Qn-x(x)y + X / —,
где у — V'ax2 +bx + c, Pn(x) — многочлен степени n, Qn-i(x) — многочлен степени и — 1 и
А — число, найти следующие интегралы:
100.
¦^ Имеем
- х2
= dx.
J VI + 2х - х2
'/¦
dx

§ 3. Интегрирование иррациоиальных функций
235
Дифференцируя это тождество и приводя к общему знаменателю, получаем х3 = BАх
2х - х2) + (Ах2 + Вх + С')A - х) + Л, откуда
з
1 = -ЗА,
0 = 5А-2В,
О = 2Л + 35 -С,
О = 5 + С + А,
5 ,. 19
Таким образом, окончательно имеем при \х — 1| < у/2
х3 dx 2х2 + 5х + 19 I ~ л . х-1 „
- \Л + 2х - х2 + 4 arcsin —-=- + С. >
/4 /~1 Г [ A2Х4 -
х у/ а2 — х2 dx = I ,
J V^
. х-1
dx =
= (Ax* + Bx4 + Cx3 + Dx2 + Ex + F) \/a2 - x2 + Л / f* ,
J Va2 — x?
откуда
a2!4 - xe = EЛг4 + 45i3 + 36'z2 + 21>a; + E)(a2 - x2) - x(Axb + Bx* + Cx3 + Dx2 + Ex + F) + A.
Для определения коэффициентов разложения сравниваем коэффициенты при одинаковых
степенях х:
-1 = -6А,
О = -55,
а2 = 5а2 А - 46',
О =45а2 -3D,
Из этой системы находим
А=\, 5 = 0, С—?,
Следовательно,
/¦
102
О = 36а2 - 2Е,
О = 21>а2 - F,
О = Еа2 + Л.
—?, F = 0, A=fl.
а х
— arcsin ]-r + 6,
16 а
•/¦
•4 Применяя подстановку х + 1 = i, получаем
¦¦/¦
ds
-/тй
Имеем
Дифференцируя по |t| и приводя к общему знаменателю, получаем тождество —1<| =
(ЗА|<|2 + 2B\t\ + 6')A - \i\2) - \t\(A\t\3 + 5|<|2 + C\t\ + D) + А, откуда
-1 = -4А, Щ
О = -35, |t|°
О = ЗА - 26',
0 = 25-1»,
Л=\, 5 = 0,
А = -|.

236
Гл. 3. Неопределенный интеграл
Таким образом,
1
? +
3
4|z + l|3 8|x + l|
1 П7 arcsin • г + С =
(z + 1J 8 |x + l|
3a;2 + Gx + 5
/x2 + 2 x - | arcsin , * t. + C, x < -2, x > 0.
|x + l|
103
•^ Имеем
' / r2 ,1
dx.
/ж2 +2 (а;2 + 1)л/х2 + 2
'/
/?+2
Для вычисления интеграла J
f dx
применим подстановку
= Ы(х + ^х2 + 2).
= t. Тогда
dt
Следовательно,
/x^~+~2 ГТТГл i x
- dx = ln(x + \/хг + 2) + arctg ¦
: + С. >
xz + 1 ч ' ' ' ~ лД2 + 2
Приводя квадратные трехчлены к каноническому виду, вычислить следующие интегралы:
104.
¦^ Имеем
[ x2(l*
J D - 2х + х2)у/2 + 2х - х2
I x2dx I dx Г Bx
~ J D - 2х + x2)yj2 + 2х - х2 ~ J л/2 + 2s - х2 J D - 2х + х2
-4)dx
2)у/2 + 2х ~ х2
Первый из этих интегралов вычисляется непосредственно:
[ f ^ -
J V2 + 2х - х2
dx
. х- 1
= arcsin —-==-.
Ко второму интегралу применим подстановку х — 1 = г. Тогда он преобразуется к инте-
интегралу
2г-2
C + г2)л/Г
который раскладывается на два интеграла
= 1^ф_^1
dz
(з
Первый из них вычисляется с помощью подстановки \/3 — z2 = t:
т = ?= In
VE-t
Возвращаясь к переменной х, получаем
1 , V6 + V2 + 2x-x
\/6 лД - л/2 + 2x - x2
Для вычисления интеграла lt = —2f-
"
полагаем
= t: тогда
2 f
dt

§ 3. Интегрирование иррациональных функций
Таким образом, окончательно имеем
л/2(х -
237
= arcsm
In
л/3 л/б л/б - л/2 + 2s - ;
2 л/2
= — arctg
+ C. >
. С помощью дробно-линеинои подстановки х =
1+1
V2 + 2x - x2
t
- вычислить интеграл
= /-з—
dx
¦ ' " ¦ x + l)\/x^ + x-
Применяя предложенную подстановку, получаем
2
2
но,
Числа cv и /У определяем так, чтобы коэффициенты при t были равны нулю. Следователь-
2а/3 - а -Р + 2 = 0, 2cv/? + а + /? + 2 = 0.
Решая систему, находим cv = 1, ji = — 1. Тогда
-2 dt 2 , 3t2 + l
+ l
:, dx =
Л2+з
2 + x + 1 = t ?t (для случая, когда 1 + t > 0, т. е. если х > —1).
Таким образом,
I = -2
/' (t + l)<tt = -2 /
tdt
-2
dt
Для вычисления первого из этих интегралов применим подстановку лЛ2 + 3 = и. Тогда
tdt
2л/2 -л/З
Возвращаясь к переменной х, получаем
= 4= in
ж +1)
Ct2 + l)\/<2 + 3 л/б
Второй интеграл вычисляется с помощью подстановки
rfz 1
ж2 - х + 1
/-
J Ci2
: arctg -
1
= т= arete
л/2 A-
Окончательно имеем
= 4= In
л/6
A + х)л/2 + ^(s2 + х + 1)
лД2 - х + 1
Применяя подстановки Эйлера:
1) \/ах2 + ix + с = ±л/«х + г, если а > 0;
2) у ах2 + Ьх + с = xz ± i/^> если с > 0;
3) у ах2 + ix + с = уа(х — Xi)(x — Хг) = г(х — Xi), найти следующие интегралы:
106. /= / d*

238 Гл. 3. Неопределенный интеграл
¦^ Здесь а = 1 > 0, поэтому применим первую подстановку
Отсюда х =
l+2z>
(l+2zJ
\/х2 + X + 1 = -X + 2.
- dz. Подставив эти значения в интеграл, получим
2z2+2z + 2 ,
Разложение подынтегральной функции ищем в виде
С
z(l + 2zJ (l+2zJ 1 + 2г г'
Для определения неизвестных А, В к С получаем систему 2 = 25+4С; 2 = А+В+4С; 2 =
С, откуда А = -3; В = -3; С = 2.
Таким образом,
dz f dz ^ f dz 3 1
z гтг — 3
где г = х +л/х2 + х + 1, х ^ -1. >
107.
. + Vl - 2x - x2 '
Поскольку С = 1 > 0, то, применяя вторую подстановку Эйлера
Е — 1 = Vl ~~ 2х — х2, получаем
-t2 +2t + l
=/¦
J l
-dt.
Разлагаем подынтегральную функцию на простейшие дроби:
-t'2+2t + l _A В Ct + D
Приводим последнее равенство к общему знаменателю
-t2 + 2t + 1 ее A(t3 - t2 + t - 1) + B(t3 + t) + (Ct + D){t2 - t)
и приравниваем коэффициенты при одинаковых степенях t:
0 = А + В + С,
-1 = -A-C + D,
2 = A + B-D,
1 = -А.
Отсюда находим А = — 1, 5 = 1, С = 0 и D = 2.
Следовательно,
dt f dt Г dt
t-1
- 2 arctg t + С,
где xt - 1 + VI - 2s - z2. >
108.
5 / x ~ v^
' J x + V?
+ Зх + 2
„ .. , v_'2+3x + 2
Здесь х2 + Зх + 2 = (х + 1)(х + 2), поэтому можно положить: Vl'2 + Зх + 2 =¦ t[x + 1)
(третья подстановка Эйлера). Имеем
-2<2-4<
dx = —
2< dt
x2 + Зж + 2
dx =
Разложение подынтегральной функции ищем в виде
-2t2-4t
Л
откуда
-2<2 -4t = A(t-2){t
¦ B(t-2){t2-
+ D(t-2)(t
C(t2 -
С
+ 2)(t2
:+3<-f
2t
E(t -
¦3t2 + 3t+ 1).

§ 3. Интегрирование иррациональных функций 239
Полагая последовательно % = —1, 1, 2, находим А — -, D — - к Е = ~2?¦ Далее,
приравнивая в тождестве коэффициенты при <4 и t3, получаем систему 0 = С + D + Е; 0 =
В — С + D + 2Е, откуда находим остальные неизвестные:
Г - 1? Я - 5
~ ~Т08' ~ TIT
Таким образом,
Интеграл от дифференциального бннома
¦bxn)pdx,
где in, п и р — рациональные числа, может быть приведен к интегрированию рациональных
функций лишь в следующих трех случаях:
1. Пусть р — целое. Полагаем х = t , где JV — общий знаменатель дробей т и п.
2. Пусть — целое. Полагаем а + bxn = tN, где N — знаменатель дроби р.
п • .
3. Пусть \-р — целое. Применим подстановку ах~п + 6 = t , где N — знаменатель дроби
V-
Если п = 1, то эти случая эквивалентны следующим: 1) р — целое; 2) т — целое; 3) m + р —
целое.
Найти следующие интегралы:
109. / \Д3 + z4 dx.
•4 Имеем при х > 0, а также при х < — 1
= / \/х3 + X4 dx = / Х2(Х~1 +1J dx.
Здесь п = —1, т — 2 и ' — целое. Поэтому, полагая х~ + 1 = t , получим / =
"/ (^§Т = -2^ -2/4, где /„ = / ф±р, п = 3, 4.
Для вычисления последнего интеграла найдем рекуррентную формулу. Пусть
Интегрируя по частям In~i, имеем
/ _ = / dt = * _ 2( -U f t2<lt =
П i I С/2 _ o2\ti-1 С/2 _ „2\п \l I I С/2 _ „2\п
откуда
_ t 2n - 3
Последовательно применяя эту формулу (при a = 1), получаем
3(^ - 1K - lh =
± 1 _
3(<2-1K 3^4(<2-1J А ) 3(<2 - IK "*" 12(<2 - IJ 4 \2(р - 1) 2
_ ± Г, —
2 '
t < 1
3(<2 - IK 12(t2 - IJ 8(t2 - 1) 16

240 Гл. 3. Неопределенный интеграл
Возвращаясь к переменной х, окончательно имеем
/= J7-
8z2+2a;-3 I
24
х-1+± + а»
110
7A+^5
•dx.
Здесь р = — 2. Применяя первую подстановку е = ? , получаем
Поскольку
то окончательно имеем
г fdt _ 1 ftd/ г \ t | i arct t
- 4t3 + 18* -| j - 21 arctg t + C, t = x6. >
111
d x
+ <Jx
В нашем случае т = 1, ?г = -, p = — j и ^jp- = 3. Положим 1 + хз = t2. Тогда
f xdx __ [ 2 ,,2 , 3 s з
J \/l + Ух? J
где <= \/l + Vx2. >
112. / t/3x-x3dx.
4
•^ Здесь m = j, ?г = 2, p = | и ^^- +р = 1. Положим За; 2 — 1 = t3. Тогда
f _ / 3/ 3J _ 9 / *3rft _ ? /" ,/ 1 ^ _ 3t 3 Г dt
- I \j x- x x - -- - - \ts + i) ~ 2(t3 +1) 2 / <3 + Г
Поскольку (см. пример 73)
f dt 1, (< + lJ 1 . 2t — 1
/ -; = - In -^ — arctg -=—,
J t3 + 1 6 t2 -1 + 1 уД V3
то окончательно имеем
лД .2* - 1 ,,
*УЗТ хз .— .—
где t — -*—'-—:—, 0 < х < V3, x ^ — V3. >
Упражнения для самостоятельной работы
Найти интегралы от иррациональных функций:
с. 99. / -
97. / J?tu2 dx- 98- 12У+9т*+'б*1*Лх-
юо. / /**~3\ 1 dx- i°i- / *fizh- 102- / 8ж'+!/^+
-^ . 104. / —
103.
= di.
106. J.-ySL=(ix. ЮТ. / it у 4 . 108.

§ 4. Интегрирование тригонометрических функций 241
§ 4. Интегрирование тригонометрических функций
Интегралы вида
Г
Kmxcosnxdx,
где т и п — целые числа, вычисляются с помощью искусственных преобразований или при-
применением формул понижения степени.
Найти следующие интегралы:
\. I —'-z—dx.
J Sill X
астям, получаем
/ cos4 х 1 [ з , ( 1 \ 1 /cos3 х [ cos2 х \
I . з dx = ~тг / cos xd . , = -- ^-^ h3 / — dx -
J sin3 x 2J Ism2 a;/ 2\sm2i J sm x у
113.
•^ Интегрируя по частям, получаем
3 cos x 3
= cos ж = In
2 2 sin2 x 2
ь 2
h в Z. >
114.
dx
Аналогично предыдущему
/dx _ fd (ctgx) ctgz f cos2 x _ cos е t
sin3 ж J sin x sin а; у sin3 x sin2 ? у si
/ dx _ 1
У sin x 2
Г dx
J sin3 r cos5 x
dx
sin3 a;
ln
tg:
115
Имеем
tg3x
tg
116. jtg'xdx.
¦4 Очевидно,
/. 5 , 1 /\ 2 i42^(sec2x) sec4s 2 , 1, , 2 ч . ^,
tg I (ii = - / fsec x - 1) —^—т—i = sec i + - ln(sec x) + С =
I J sec2x 4 2
tg x tg2x
s
ln|cosz|
[tg&xdx= f i^x(-L--\)dx=i^-- [
J J \ cos2 x J 4 J
cos2 x
**f
— In I cosxl + C. >
117
. / ctgex dx.
После очевидных преобразований имеем
Vsm x

242 Гл. 3. Неопределенный интеграл
dx
118.
3
с
..з
¦4 Полагая <3 = sini, х ф —-, имеем
2
У dx [
rf(sini) _ Г dt _ 3 Г dt 3
1, (l-<) , УЗ 2< + l , 1, (l + <) , УЗ 2<-l
= - 4In «?тттт +—arctg ^тг + iIn ibrri+ —arctg -jr =
i, (i + <J(<2+< + i) Уз Уз<
119. Вывести формулы понижения для интегралов:
а) 7„ = / sin" х dx; б) Кп - / —, п > 2.
' J J cos"z
^ Интегрируя по частям, получаем:
а) 1„ = — / sin" i d (cos x) = — cos i sin" i + (n — 1) / sin"~2 x cos2 xdx =
= — cos i sin" x + (n — 1)/„_2 — (« — l)jfn,
откуда
In = —((« — 1)Лг-2 — cos x sin" x), ii = 3, 4, ... .
. r. /d(sini) sin i . /" sin21 sin x . .
б) Kn= I K ' = — (w + 1) / -Г5— dx = — (n + l)Kn+2 + (n + l)Kn,
' J COSn+1 X COSn+1 X J COS"+2 X COSn+1 X ' У '
откуда
x ф ^ + А.-7Г, fc e Z. >
2
С помощью формул:
I. sin « sin /J = — (cos(a — /?) — cos(a + /?));
II. cos «cos /J = — (cos(a — /?) + cos(a + /3));
III. sin «cos ji = -(sin(a — /?) + sin(a + ji))
найти интегралы:
120. / sin isin — sin — dx.
< Имеем
/.x.i 1 f ( x 3i\ . x
sin x sin — sin — dx = - I cos cos — sin — dx =
2 3 2 J V 2 2 / 3
. x . 5i . 7i . Пг\
- sm - + sm — + sm — - sin -— I
6 6 6 6/
3 x 3' 5i 3 7i 3 Hi
2COS6-10COST-T4COST+32COS —
121. / sin32icos23idi.
^ Используя формулу III, имеем
/sin 2xcos 3x dx — - / Csin 2i — sin6i)(l+cos 61) di =
if/ 3 3 1 \
= — / I 3 sin 2i sin 4x -\— sin 81 — sin 61 — — sin 12i I dx =
8 J \ 2 2 2 /

§ 4. Интегрирование тригонометрических функций
241
3 3 3 1 1
= — — cos 2х -\ cos 4х cos 8х Н cos 6х -\—— cos 12,х + С. >
Применяя формулы:
IV. sin(« - /?) = sin((x + or) - (х + /J));
V. cos(« - ji) = cos((x + of) - (x + /9)),
найти интегралы:
122. / —
/ sinfi + a)sin(x + b)
¦^ Имеем
[ dx 1 Г sin((x + a)- (x+b)) _
J sin(x + a)sin(x + b) sin(u — b) J sin(? + a)sin(i + b)
- г ( f cos(x + b) _ /" cos(x + a) rf \ _ 1
sin (a — b) \J sin(x + 6) J sin(x + a) y sin(a —
6)
sm(x + 6)
-t-t ;—r
sin(x + a)
sin(a - b)
123.
sin i — sin a
Из тождества cos a = cos
следует
/—d\ =_j_ /с08((^)-(у)
у sin x — sin a 2 cos a J sin ^y2- cos ^j5-
124. I tgxtg(x + a)dx.
sin
C,
cos g/0, sin x /^ sin a. >
Имеем
/, \ , rfcosxcos(x + a) + smxsm(x + a) \ ,
tg i tg(x + a) dx = / i '——-—r—^ '- - 1 dx =
v ' J \ cosxcos(x + a) J
-I
cos a
cosx cos(x + a)
dx — x — —x + ctg a In
cos(x + a)
sin a / 0, cos i^O, cos(x + a) /: 0. >
Интегралы вида
R(sh\x, cosx)dx,
где R — рациональная функция, в общем случае приводятся к интегрированию рациональных
функций с помощью подстановки tg ^ = t. ,,¦ -¦ ^
а) Если выполнено равенство *.
R(— sinx, cosx) = — K(sil\x, cosx)
или
R(smx, —cosa;) = —K(sinx, cosx),
то выгодно применять подстановку cos ж = t или соответственно sin а; = t.
б) Если выполнено равенство I ., !
R(— siux, — cosx) = R(smx, cosx),
то применяем подстановку tg x = t.
i ... I
Найти интегралы:
125
J 2 sin x — cos x + 5

244
Гл. 3. Неопределенный интеграл
¦4 Полагая t = tg |-, Bн — 1)тг < x < B?г + 1)тг, п ? Z, получаем
3t
3tgf
<?„.
Из непрерывности первообразной следует
Ц2п1г + 7Г - 0) = /Bп7г + 7Г + 0), -^= + С„ = -^: + С„+1,
v 2л/5 2^
откуда находим С„ = ^ + С, где С = Со — произвольная постоянная. Из неравенств
2птг < х + 7Г < B?i + 2)тг; ?t < ^-^- < п + Л следует, что и = [^^"] ¦ Таким образом,
2.
/= lim /(.т) = " "t, тг,
.г._Bп+1),г *¦ ; 2^5
г, и ? I >
126. / =
¦dx.
Г-
sin х + cos8 x
Положим t = tg2tf, ^-— j<x< f- + ^ n 6 Z. Тогда
dt л/2 - 1 / dt
t2 + 8
'2 + V2
arctg -
Из условия непрерывности первообразной следует
7Г 11%
I + T
7Г 71.7Г
- + c?l--- 4
4 2 4
откуда (по аналогии с примером 125) находим
2 +
2 -
- + C'n+i,
Следовательно,
/(x) =
С'„ = \ { V2 + V2 - \J2 - л/2 ) п + С, С = Со,
2 tg2.c
arctg ft
127. Доказать, что
dx
I
A sin x + В cos x
(u sin x + i cos z)" (a sin x + bсо;
где j4, В, С — неопределенные коэффициенты.
cos x Г
.si)» ' J (asi
dx
a sin x + bcos x)n 2 '

§ 4. Интегрирование тригонометрических функций
Интегрируя по частям, получаем
245
т _ /" d{—acosa; + isin х) _ — a cos x + b sin x . . f
J (a sin i + icos i)™+1 (a sin i + bcos г)"+1 J
(a cos x — bsin xJ dx
— a cos x + bsin ?
(a sin i + bcos x)
(a sin i + 6 cos i)"+2
Г (acosxbsinxJ
+ bsin ? , . Г (acosx— bsinxJ + (bcosx + asinxJ ,
bcos x)"+1 'у (a sin x + bcos x)"+2 '
откуда
1
128. Найти
J (^
(n-l)(a2+b2)
dx
(a sin x + bcos x)"+2
b sin i — a cos x
(asm.,: + ?, cos.,:)'
(sin x + 2 cos xK '
Используя доказанную выше формулу, находим
dx
2 sin x — cos x
(sin i + 2cosi):
10
129. Доказать, что
dx
(f+ ^
2 sin x — cos x
(sin x + 2 cos xJ
+ C> г # fcjr - arctg 2. >
/dx _ A sm г у dx i. с I — I I =? Ш
(a + bcosx)" ~ (a + bcosx)"-1 J (a + bcos z)™-' J (a + bcos x)"~2 ' '"' ^ U'
и определить коэффициенты Л, 5 и С, если и — натуральное число, больше единицы.
М Интегрируя по частям, получаем
J (a +
dx
') cos х
bcos x)n~2 J (a + bcosx)n~
"~1
d sin x
+bcosx)n~l
bsinx
f
J (a
)-i " (П " 1} j (a
b2 sin2 x
= a/-1 + (a+6cosx)
откуда, используя тождество b2 sin2 x = —(a2 — b2) + 2a(a + icos x) — (a + bcos xJ, находим
*'
-—
(tt + OCOSl)"
6 sill x
Bn — 3)a
-1 ~
Таким образом,
( )
(n - l)(a2 - i2) -1 ~ (n - l)(a2
(n-l)(a2 -i2)'
n ^
^ Bn - 3)a
2)'
(n-l)(a2-b2)
/
1
если: а) 0 < e < 1; 6) e > 1.
+ e cos I
¦4 Положим t = tg |, B?i - 1)тг < z < B)j + 1)тг, n G Z. Тогда
а) / =
arctg
g ^ + n
л/1 — e V 1 + ? V1 — e2
Аналогично решению примера 125 находим
/ rf:r _ 2 f dt
~ J l+scosx~l-ej t2 + ii^ '
-e ^, 2 л/1 - e tg |
+ Cn = arctg ^_ 2 + С„.
1 2 /1 +
I — е2
VI + ? yl — е2
/(Bн + 1)тг) = Urn Их),
х—Bп+1)тт
Х

246
Гл. 3. Неопределенный интеграл
б) 1 =
/е2 -1
131. Найти [
имении
+ С, I /: 2П7Г + Т. >
-, если 0 < е < 1.
+ecosiJ
Применим формулу, полученную в примере 129. Полагая а = 1, Ъ = е, м = 2, получаем
dx \ ( —esini , f dx \
A + ecosxJ 1-е2 I 1+ecosx J 1+ecosx/
1 / -esinx 2 , V1 -e tg |
1-е2 \ 1 + ecosi
x ф Ъгж + я-,
IBпж + тг) = lim /(x). >
Упражнения для самостоятельной работы
Найти интегралы от тригонометрических функций:
Ю9. Г- а»,. 110. Г . , Iх з ¦ HI- Г . dx. . ¦ 112. fr-—^ гу.
J ^cos ar+sin л;L J sin x-j-cos° л; J cos° л;—sin ° x J (sin x-\-2 sec x)*
113. f^-j^ . 114. f f 115. /•«"+""» rfj, не. Г t-|2—.
J sin4a:c:osa- J sin jcos j л/sin4 ar+cos4 x л/sin 2a; J 4+3 tg a;
§ 5. Интегрирование различных трансцендентных
функций
132. Доказать, что если Р(х) — многочлен степени п, то
P(x)eaxdx =e°
М Доказательство проводится с помощью метода интегрирования по частям. Имеем
/ Р(х) еах dx = \<?аХР{х) - \ I eaxP\x) dx =
= Ie«P(x) - - (-еахР'{х) - - [ еахР"(х) dx] =
a w а \^а a J J
{x) P'{x)
Применяя метод математической индукции, находим
kTT JeaxP(k+1)(x)dx,
Положив к = и и приняв во внимание, что Р^п+1^(х) s 0, получим требуемую формулу. >
133. Доказать, что если -Р(х) — многочлен степени п, то
Р"(х)
т \ j sm ax I г./ \
Р(х) cos ox dx = ( -Р(х) —
+с и

P(x)smaxdx =
5. Интегрирование трансцендентных функций 247
cosax (и1 . Р"(х)
a \ ' a' <r
. sin ax
у ' a2
¦4 При доказательстве используем пример 132. Заменяя там а на га, где г = л/—1, полу-
получаем
a a' aJ
Пользуясь формулой Эйлера и разделяя действительные и мнимые части, находим требу-
емое. >
Г
134. Доказать, что интеграл / R(x)eaxdx, где R — рациональная функция, знамена-
знаменатель которой имеет лишь действительные корни, выражается через элементарные функции и
трансцендентную функцию
h х = / .
J hxx
X
ч/
f At
где li x
Рациональная функция представляется в виде
R(x)^1
К(Х)~ N(x)'
где М(х) и N(x) — многочлены. Выделяя целую часть (если она имеется) рациональной
функции, получаем
где т,к — кратность корня х,, Aij — неопределенные коэффициенты. Наконец, интегрируя
R (х), получаем
Первый интеграл вычисляется /-кратным интегрированием по частям (/ — степень
гочлена Р(х)). Вычисляя второй интеграл, находим
[ eaxdx [ а { 1
%к J (У J6 \ (il)(
[ eaxdx
J (х-хиУ
, a f eax dx _ ^ах ( 1 а
i-lj {х-ХкУ-1 ' \ (i-Щх-хку-1 (i-l)(i-2)(x-xky-2
\ а' Г еах dx _ '¦••
(i-l)(i-2)...l J x-xk
¦+ •••
- l)(x - xky-i T (• - l)(i - 2)(x - xky-* T • • • T (• - l)!(x - xk)
ai-2eaxk r ea(x~xk) / j
Итак,
тк
R(x)eaxdx~ Ri(x) + Y^^2AkiIik. >
А: 1 = 1

248 Гл. 3. Неопределенный интеграл
135. В каком случае интеграл / Р\ — )exdx, где Р\ — ) =
J \х/ \х/
ao + — +...+ — и
х х"
j, aj, . . . , а„ — постоянны, представляет собой элементарную функцию?
•^ Используя обозначения примера 134 и интегрируя по частям, получаем
= аоех + аи К (е') -ех + а2 И (ех) - —^ - -2- + -?- li (е1) - ... - "
v z ч 2х2 2х 2 ' (п — I)!"
Отсюда следует, что если
то данный интеграл есть илементарная функция. >
Найти интегралы:
136. [(l--Yexdx.
Используя обозначения примера 134 и интегрируя но частям, получаем
+ А?) ех dx = ех - 411 (ех) - -ех +411 (ех) = ех (\--\+ С,
х2 J х \ х!
1 - -У ех dx= ( (l - - + А
х) J \ х х
Упражнения для самостоятельной работы
Найти интегралы от следующих трансцендентных функций:
117- f пГ"^2 dx. 118. f — dx. 119. frr^ZTW- 12°- f-ГГ-- 121- fcl^xdx.
122. /cb.2xsh.2xdx. 123. / Ti-3X+2 dx¦
§ 6. Разные примеры на интегрирование функций
Найти интегралы:
137.
7 Г dx
• J l+x*
•4 Представляя знаменатель в виде, 1 + z4 + xs = (xi + IJ — xi = (г4 + x2 + l)(r4 — x2 + 1),
разложим подынтегральную функцию на простые дроби:
= х + 1 1х
1 + xi + Xs 2 у х4- + х2 + 1 хА - х2 + 1
Интегрируя последнее выражение почленно, получаем
У (г. _iJ + 3 \
0, если ж = О,
/
Итак, искомый интеграл равен
1 (_ _.--, , ,,.. хЧ^з+1 , |sgn^+C)
5vf I arct«:
a;2—i\/3+l
если
если х = 0. >
B + siai)

§ 6. Разные примеры на интегрирование функций 249
М Пользуясь результатом примера 131, находим
/dx __ f ^(f") _ г __ ! cosx 2 f dx
B + sinxJ ~ ~ J 72 + cos fz. _ .ЛJ ~ ~~ ~ 3 ' 2 + sin x 3 J 2 + sin x '
последний интеграл вычислим с помощью универсальной подстановки t = tg |-, 2птг —тг < х <
7Г + 2гатг, в ? Zo,
/(I
J 2+smi уД
Из условия /(тг + 2итг — 0) = /(тг + 2п7г + 0), аналогично тому как мы поступали при решении
примера 125, находим
С„ = —=п + С, С = Со, 2п7г — тг < г < тг + 2гетг.
V3
Таким образом,
г, ч f dx I cos а: 4 2tg| + l 4 Гх + тг]
/w = i BT-^ = 3 2T^ + 3^arctg^7T~ + 37fl^rl+c' a^2re'r + 'r'
7г)= lini
139,. Лх^а:.
.геем
/
При ж > 0 имеем
аналогично при х < 0
х dx = -— + Ci
х2
х dx —
В точке а: = 0, согласно определению первообразной, должно С\ = Сг = С, где С —
произвольная постоянная. Поэтому при всех х имеем
J\x\dx=*jsgnx +C=^- + С. >
140. / (p(x)dx, где (р(х) — расстояние числа х до ближайшего целого числа.
М Из условия задачи <р(х) — \х — п\, п— -^.х<п + -, п¦ ? Zo, поэтому
1(х) = / ipfr) dx = -(х — та)|х — п\ + Сп, и — тг < х < п + -.
J ' 2 ' 2 2
Из непрерывности первообразной получаем
т. е. i + С„ = -i + C,1+i, C'n+i = С„ + j, откуда С'„ = J + С, где С = Со — произвольная
постоянная.
Поскольку ?г ^ ж + ^ < ?г + 1, то м = [ж¦+ i] . Окончательно находим
1 Г 1
141. [x]\siiiKx\dx.

250 Гл. 3. Неопределенный интеграл
¦4 По определению целой части имеем
[х]| sin жх\ = ( — l)"nsin жх, n^x<?i + l,
Поэтому
/Wl-ir
?icosttx + С„,' п ^ х < п
Из непрерывности первообразной в точках х = п + 1 получаем равенства
(-1)
71+1
м cos жх + Оп
Jtll
х=п+1
п+2
(п + l)cOS7TI + С„+1
х=п+1
откуда
C'n+i = С'„ + 2"+1 . Решая это уравнение, получаем С„ = С + —, С — Со ¦¦ Поэтому
/
[x]\smnx\dx=
¦ cos жх + n\ \- С, n ^ x < n + 1.
7Г
Поскольку х изменяется в указанных пределах, то всегда п = [х]. Таким образом, окон-
окончательно имеем
[[х]\бм
с1х = И(
С,
где С — произвольная постоянная. >
142. Пусть f(x) — монотонная непрерывная функция и /-1(х) — ее обратная функция.
Доказать, что если / f(x)dx — F{x) + С, то
У ГЧх)^ = хГх(х) - F(r\x)) + С
В силу условия теоремы, справедливо равенство
Интегрируя его по /^(х), получаем
/¦
откуда
Упражнения для самостоятельной работы
Пользуясь различными методами, найти следующие интегралы:
124. Г / еГТ-dx. 125. Г /!%д dx. 126. Г /"" rfx. 127. Г ^
J (f31 +1) J vcosJ 2i J %/созл 2х •> sin x Vcos2x
X. 129. f Г*"'" Д' rfx ¦ 130. f ; . X^fX Г5-. 131. Г I-. ^^ ГЗ".
J 1 + cos x J \x sin x+cos x)^ J (sin x—x cos .tj*
• Г 7TT ^"- 134. Г xx(\ 4- In x) da;. 135. Г arcS]" e rfx.
128. [
J
J
136. j
139. f
J
133-
+ Sln.f J CO3l(lTCOSl)
- 137. /(|i + l|-|l-i|)di. 138.
140.
l. 141.
, x>0.

§ 7. Интегрирование вектор-функцнн 251
§ 7. Интегрирование вектор—функций и
функциональных матриц
Теорема 1. Вектор-функция F = (Fi, F2, ..., Fm) является первообразной вектор-
функции f = (/1, /2, ..., fm) на интервале X ? М тогда и только тогда, когда на этом
интервале функции Ft являются первообразными функций /,, i = I, m.
Теорема 2. Аналогично, функциональная матрица В = (bij) является первообразной
на интервале X функциональной матрицы А = (ai3) тогда и только тогда, когда на атом
интервале функции bij являются первообразными функций aij, % = 1, го, j = 1, п.
Найти интегралы от вектор-функций:
М Если неопределенный интеграл указанной вектор-функции обозначим символом I, то,
согласно теореме 1,
dx
, [ dx _ /" <Zi ,, /" dx
= (arcsini, arcsin-, arctgi, - arctg - I + С, |i| < 1,
где C^M4 — постоянный вектор. >
¦4 Аналогично предыдущему примеру
I(x) = (In |1 + х|, In x/l + i2, ..., In У1+хт) + C. >
145. / (cos x, cos 2x, ..., cosmx) dx.
Имеем
, / . sin 2i sin mi \
(cos x, cos2x, ... , cosmx) rfi = Ism x, —~?)i • • • > J +
Найти интегралы от функциональных матриц:
/• / sin г sin 2i sin3i sin4x \
146. / I cosi cos2i cos3i cos4i I dx.
J \ tgi tg2i tg3i tg4i J
¦^ Пусть А — первообразная матрица, тогда
cos2x cos За: cos4x
— COS I
A{x) = I sin x
2
sin 2x
2
— In I cos i| —In \/|cos2i| — In
и интеграл равен функциональной матрице х (-» j4(x) + С, где С — постоянная матрица.
147.
r. / (a,ij)dx, где aiy = i>, i = 1, m; j = 1, n, x > 0.
При фиксированных г и j
i ,¦ tti
x 3 dx = . . 1 J + Ci,.
J+7
i±i -
Следовательно, f(aij) dx = (Ьц)-±С, где Ьц = ^- x 1 , а С = (c;j) — постоянная матрица. >

252 Гл. 3. Неопределенный интеграл
148. Доказать, что
(E + Ax)ndx= —!— A-\E + Ax)n+1 +C, A)
где Е — единичная, А, С — постоянные матрицы одного порядка и матрица А — невыро-
невырожденная, п — натуральное число.
•4 Для доказательства достаточно показать, что производная левой части равенства A)
равна подынтегральной матрице. По правилу дифференцирования произведения матриц име-
имеем
-±—А-1(Е + Ax)n+l)= Al ((? + АхуА + (? + Ax^-'AIE + Ах)+ ... +А(Е + Ах)п) .
?i ~J~ J. / 'fl -|— 1
А так как матрицы А и Е + Ax коммутативны, то
\E + Ax)n+l)' = -^~A(n + \)(E + Ax)n = (E + Ax)n. >
/11 \ J
11 ~\~ 1
Упражнения для самостоятельной работы
Найти интегралы от вектор—функций:
142. /(sin r, cosx)dx. 143. /(tgx, tg2x, tg3x)dx, x g ] 0, f [.
144. /(xsinx, xsin2x, ..., z sin mz) dr. 145. j(xex , x3ex , xbex ) dx.
146. J(x, x2, ..., xm)dx. 147. /(x, x2, ..., x'n)lnxdx, x>0.
Найти интегралы от (функциональных матриц:
148.
/2х + cos 2r х cos х + sin х -| 1- cos x In x
Х in х
— х sin х + cos х + ^^ — sin x In r cos 2x + 2 ~^—
X X ,
/ / -\/i \ Г I х ° ° \'
149. / Х ¦'"'¦" Г dx. 150. \0х 0
/(¦
/10 0 \\
151. / |? + Л 0 sinx 0 j dx.
V 0 0 cosx //
152. Пусть все элементы квадратной функциональной матрицы х ь^ /4(г) имеют произ-
производные на интервале ]ц, Ь[. Доказать, что на этом интервале справедливы равенства:
а) /(Л(х)Л'(х) + Л'(х)Л(х)) dx = А2{х) + С;
б) J(A2(x)A'(x) + Л(х)Л'(х)Л(х) + Л'(х)Л2(х)) dx = А3(х) + С.
153. Доказать, что
/ (А(х)±В(х) + {~-хА{х)) В(х)) dx = А(х)В(х) + С,
где А и В — квадратные функциональные матрицы.
154. Пусть А — постоянная квадратная матрица. Матрицу eAl определим посредством
равенства
еАх - lim (E+-AxY .
п—*оо п
Доказать, что
/ еАх dx = АеАх + С,
где С — произвольная постоянная квадратная матрица.

Глава 4
Определенный интеграл
§ 1. Интеграл Римана
1.1. Верхний и нижний интегралы Римана. Критерий интегрируемости функции.
Определение 1. Разбиением П сегмента [а, Ь] называется конечное множество точек
{х0, xi, . . . , хп}, где а — х0 < Х\ < ... < хп — Ь.
Пусть / : [а, Ь] — К и / — ограниченная на сегменте [а, Ъ] функция, а П — произвольное
разбиение этого сегмента.
Верхней и нижней интегральными суммами, соответствующими разбиению П, называют-
называются числа
п— 1 п—1
1 = 0 ! = 0
где М, = sup {f(x)},m,= inf {f(x)}, Ax, = x,+1 - хг.
Определение 2. Числа
[ fdx=mi{Sn(f)}, [ fdx = sup{Sn(f)},
J fn> J {n} -
гЭе точные грани берутся по всем возможным разбиениям сегмента [а, Ь], называются со-
соответственно верхним и нижним интегралами Римана функции f на сегменте [а, Ь].
Определение 3. Функция f называется интегрируемой по Риману на сегменте [а, Ь],
если J f dx = J f dx, а общее значение, верхнего и нижнего интегралов называется интегра-
ь
лом Римана функции f на этом сегменте и обозначается J f(x)dx.
а
Класс всех интегрируемых по Риману функций / обозначают / € R [а, Ъ].
Критерий интегрируемости. Для того чтобы ограниченная функция / : [а, Ъ] —* К
была интегрируемой на сегменте [а, Ъ\, необходимо и достаточно, чтобы Ve > 0 существо-
существовало такое разбиение П этого сегмента, что 0 ^ '5п(/) — 5п(/) < е.
Сокращенно критерий интегрируемости записывают следующим образом:
/eJi[o,li]#Ve>0 ЗП : 0 ^ 5п(/) - Sn(f) =
1 = 0
(здесь 10, = Мг — т, — колебание функции / на сегменте [a;;, Xi+i]).
1.2. Интеграл Римана как предел интегральных сумм.
Пусть П — произвольное разбиение сегмента [а, Ь] и ^(П) = max Axi. На каждом
О^г^п—1
сегменте [х,, х1 + 1] возьмем произвольную точку ?, и образуем так называемую интегральную
сумму

254 Гл. 4. Определенный интеграл
. . Полагаем liin Sn(f) =¦!, если Ve > О 35 > 0 :
<*(п)-о ч '
Теорема. Если:
ь
1) при d(U) -* 0 aiiin 5п(/) = /, то f ? R[a, Ъ] и J f(x) dx = /;
а
Ь
2) / 6 R[a, b], то 3 lim ^ ,Sn(/) = Jf(x)dx.
Эта теорема устанавливает два эквивалентных определения интеграла Римана.
1.3. Некоторые классы функций, интегрируемых по Риману.
Теорема 1. Если f ? С[а, Ь], то / g R[a, b].
Теорема 2. Если f монотонная на сегменте [а, Ь] функция, то / € R[a, Ь].
1.4. Мера 0 Лебега и мера 0 Жордана.
Определение 1. Мерой цЗ сегмента 3 = [а, Ь] [мерой \ij интервала J =]а, Ъ[) назы-
называют его длину, т. е. число Ъ — а.
• • Определение 2. Множество X С К имеет лебегову меру 0, если Ve > 0 существует
такое счетное покрытие W = {3 у, j g N} этого множества сегментами J j {счетное
оо оо
покрытие W = {Jj; j € М} интервалами i7j), меры которых fij, что ^ V4 < е, г&е ^ t4 =
lim
n-*oo
Примером множества лебеговой меры 0 может служить произвольное счетное множество
точек X С К.
Определение 3. Множество XcR имеет жорданову меру 0, если Ve > 0 существует
такое конечное покрытие W = {3}\ j = 1, п} (W = {3}\ j = 1, п}) этого множества
п
сегментами 3} {интервалами 3j), меры которых \ij, что JJ t4 < е.
3 = 1
Примером множества жордановой меры 0 может служить любое конечное множество
точек X С М, а также любое счетное множество точек Y С R, имеющее конечное число
предельных точек.
Из определения 3 следует, что всякое множество жордановой меры 0 имеет лебегову
меру 0.
Теорема (Лебега). Пусть f : [а, Ъ] —* R — ограниченная функция и Е С [а, Ь] — мно-
множество ее точек разрыва. Функция f интегрируема по Риману на сегменте [а, Ь] тогда и
только тогда, когда Е — множество лебеговой меры 0.
Согласно теореме Лебега, классу интегрируемых по Риману функций принадлежат огра-
ограниченные функции, множество точек разрыва которых не более чем счетное или имеет жор-
жорданову меру 0.
1.5. Интегралы функций, заданных на произвольных ограниченных множествах.
Множества, измеримые по Жордану.
Определение 1. Пусть Е С X С R. Функция \Е : X —> R, где
I \ _ Г 0, если х ? Х\Е,
Х{-Х) ~ \ 1, если х ? Е,
называется характеристической функцией множества Е.
Определение 2. Пусть Е С [а, Ъ] С К, / : [а, Ь] —> R — ограниченная функция. Если
fxE €Я[а,Ь], то
ь
/л/ , , def /
f(x)dx= I
a^ / f{x)XE{x)dx.

§ 1. Интеграл Римана 255
Определение 3. Пусть Е с[а, Ь] С R, / : 2? —»¦ R — ограниченная функция. Продолжим
функцию f на весь сегмент [а, 6], образовав функцию
О, если х 6 [а, Ь]\Е.
Если функция F интегрируема на сегменте [а, 6], то
ft
I f{x)dxd= I F{x)dx.
E a
Определение 4. Ограниченное множество Е С R, граница которого имеет лебегову
меру О, называется измеримым по Жордану, а интеграл ¦
ft
j dx- j xB(x)dx,
E a
где [а, b] — произвольный сегмент, содержащий множество Е, называется жордановой ме-
мерой множества Е, или его длиной.
1.6. Свойства интеграла, выраженные равенствами.
1) Если / € R[а, Ъ], то и с/ 6 R[a, b], с — const, причем
б б
/ cf(x)dx = с I f(x)dx.
а а
2) Если /, з € R [а, Ь], то и (/ ± д) € R [а, Ь] и при этом
ft ft ft
J(f(x)±g(x))dx= f f(x)dx±J g(x)dx.
a a a • •.-•¦.'
3) Если / 6 R[a, Ъ] и с е]а, Ь[, то
Ь с Ь
I f(x) dx = I f(x) dx + / f(x) dx (свойство аддитивности); \
а а с ' -
4) Если сужения функции / : [а, 6] -» R на сегменты [а, с] и [с, Ъ] интегрируемы, то
/ 6 R[a, b] и при этом
6 с 6
/ f(x)dx = J f(x)dx + j f(x)dx.
а а с
1.7. Свойства интеграла, выраженные неравенствами.
1) Если функция / интегрируема на [а, Ь] и /(я) > 0 Vx € [а, Ъ], то J f(x)dx > 0; ertin
а
ft
f(x) ^ 0, / 6 C[a, b] и /(х) •? 0 на [а, Ь], то / /(x) dx ^ c> 0, где с — некоторая постоянная.
2) Если /(х) ^ g(x) Vx 6 [a, b] и /, д 6 Л [о, *], то ^ -

256 Гл. 4. Определенный интеграл
1.8. Формулы замены переменной и интегрирования по частям.
а) Пусть выполнены условия: 1) / € С[а, Ь]; 2) сегмент [а, Ъ] является множеством значе-
значений некоторой функции а; : / 1—i- g(t), a ^ t ^ /3, имеющей на ]а, /?[ непрерывную производную;
3) д(а) = а, д(/3) = Ъ.
Тогда справедлива формула замены переменной
ь /з
f(x)dx= f f(g(t))g'{t)dt.
б)Формула интегрирования по частям.
Если и, v ? C^l\a, b], то
ь
/ь г
u(x)i/(x) dx = u(x) v(x) — I v(x)u
'{x)dx.
В примерах 1—5 интегралы Римана вычисляются с помощью интегральных сумм 5п(/)-
Для любой интегрируемой по Риману функции /: [a, i] -> R имеем
независимо от выбора разбиения П и точек ?, ? [xi,x;+i], поэтому при решении указанных
примеров разбиения П и точки ?, выбираются определенным образом.
Вычислить следующие интегралы:
4
1. (\+x)dx.
-1
•^ Функция / : i и 1 + I, — 1 ^ х ^ 4, принадлежит классу С[— 1, 4], следовательно,
/ ? R[a, b]. В силу линейности функции /, удобно при произвольном разбиении П сегмента
[—1, 4] взять ?, = х' *'+l . Тогда интегральная сумма Sn(f) равна самому интегралу. Имеем
= xn - xo + ^ = (xn - xo) A + ) = 12,5,
так как хо = —1, in = 4. Следовательно,
4
Г
(l+x)(Zx = 12,5. >
-l
ь
2.
!. / хт dx, 0 < и < Ъ, тф -1.
•^ Выберем такое разбиение П, чтобы длины сегментов [х;, x;+i] образовывали геометри-
геометрическую прогрессию, и возьмем ?, = х,. Тогда
•• ¦ -л— j. ^^" f /'М" л r'г'^» I(ь\™ Л
х, = ход , i = 1, и, х0 = и, 1„ = 6, G=1- , fj = о - , Axi = a[-\ - - 1 ,
\aj \aj \aj \ \aj I
(^) » - 1

§ 1. Интеграл Римана 257
Поскольку d(H) —+ 0 при к-юои
ь bm+1 _ а1""*
то I xm dx = lim Su(f) — • >
Ja d(n)—о то + 1
ь
3. / ^, 0<а<6.
¦4 Пусть П = {xo = a, xi, ..., х„ = b] — произвольное разбиение сегмента [a, b]. Подын-
Подынтегральная функция интегрируема на [а, 6], в силу чего, как говорилось выше, lim 5д(/)
существует и не зависит от выбора точек &. Полагая & = ^/хТхЦТ, получим
а Ь'
ь 2 2
Следовательно, Г -J = lim Sn(/) = г- >
{ *2 <п)-о а Ь
тг
4. / sin x dx.
~i, имеем
n-l
4 Взяв П = {xi = «^; i = 0, ?г}, ^ = ж;,
П —1 ,— / 7Г 7Г ^
Принимая во внимание, что d(J[) —> 0 при ?г —+ оо, находим
5. j 1пA — 2acos х + a2) eta при \а\ < 1 и |а| > 1.
¦* Возьмем П = {хк — -^к; к = 0, ?г}, ?к = Хк- Тогда d(W) —* 0 при п -* оо. Обозначив
е'1 = cos а; + г sin x, z = t~tx = cosx — г sin x, получим
п1
xi ttV ilk\ ( -iZk\ Ti («-1)(«2"
= -In I I « - e n a-e n = — In -^ ^-—
?г!Х\ /V /и a + 1
Если |«| < 1, то lim Sn(f) = 0, так как а2п —* 0 при п —* оо.
d(II)-*0
Если |«| > 1, то, представляя <?п(/) в виде
a + 1

258 Гл. 4. Определенный интеграл
получим, что lim .Ь'п(/) = Иш 5'п(/) = 7г1пл . Следовательно,
), если |а| < 1,
rln а2, если jorj > 1.
о
6. Пусть функция / : [а, Ь] —> R монотонна на сегменте [a, ft]. Доказать, что
ь
•^ Если / ? R[a, b], то при любом разбиении П сегмента [а, Ь] и произвольном выборе
точек ?; 6 [х,, x.+i] выполняются неравенства
ь
x)dx ^ .Ьп(/), Sn(f) ^ ЬП(Л ^ >Ьп(/),
в силу которых
ff{x)dx-Sa{f)
Для монотонной функции / при разбиении сегмента [a, ft] на ?г равных частей имеем
- Su(f) = Ь~=^- |/(i) - f(a)\ = О (I) .
Обозначив "?n(/)-s-n(/) = *' ПОЛУЧИМ- ЧГ0 j f{x)dx- Sn(f) = & (sn(f) - Sn(f)J =
__ a
O(i), так как |^| < ]. >
7. Пусть f,<p? (-'[a, b]. Доказать, что
ь
lim <rn(fip) = / f(x)tp{x)dx,
d(n)-o J
где <) ^()()
t = 0
n-1
¦^ Из оценки |.S'n(/^)-<Tn(/^)| ^ J2 1/(^011^(^0 ~v{(i)\ Дхч ограниченности функции /,
t = 0
условия ip G R[a, b] и оценки |<p(^i) — <р(?01 ^ ш>. гДе ш> — колебание функции ip на сегменте
[хг, Xi+i], получаем, что lim ($n(f<p) - сп(/^)) = 0.
d(n)O
Следовательно, lim сп(/"р) = lim Sn(f<p)= I f(x)ip(x)dx.&-
<1(П)-*0 d(n)—0 J
a
8. Доказать, что функция Дирихле % '¦ [°i Ч ~* ^> гДе
0, если х иррационально,
1, если х рационально,
не интегрируема на сегменте [а, 6].
•^ Функция х ограничена и разрывна в каждой точке сегмента [а, 6]. Согласно теореме
Лебега, \ не интегрируема на этом сегменте. >

§ 1. Интеграл Римана 259
9. Доказать, что функция Римана / : [а, Ь] —> R, где
г 1 m
... —, если х = —,
|^ 0, если х иррационально,
ь
а т и н (н ^1) — взаимно простые целые числа, интегрируема на [а, Ь] vs. I f(x)dx = 0.
а
•^ В примере 263, гл. 1. доказано, что функция Римана непрерывна в каждой иррацио-
иррациональной точке сегмента [а, 6] и разрывна в каждой его рациональной точке. Поскольку она
ограничена и множество ее точек разрыва счетное, то, согласно теореме Лебега, /€Д[а, Ь].
При любом разбиении П сегмента [а, Ь] каждый сегмент [х,, ?,+1] содержит иррациональ-
иррациональные точки, поэтому Sn(f) = 0, в силу чего
ь
= [ fdx= f f(x)dx = 0.
J J
sup{Sn(/)}
{п} -
10. Доказать, что разрывная функция /лн sgn f sin — J , 0 < x ^ 1, интегрируема на
полуинтервале ]0, ]].
¦4 Функция / разрывна на счетном множестве точек X = {хк = \; к 6 N} и ограничена.
Множество X имеет одну предельную точку х = 0, поэтому имеет жорданову меру нуль.
Функция F : [0, 1] —> R, где
, Г 0, еслигеХи{0},
1 j ~ \ f(x), если х е [О, 1[\{Х U {0}},
ограничена на сегменте [0,1], а множество ее точек разрыва X U {0} имеет жорданову меру О,
следовательно, F ? Д[0, 1]. Согласно определению 3, п. 1.5, / ? R]0, l]. >
11. Доказать, что сужение ограниченной на сегменте [a, b] функции / на множество
Е = {а} интегрируемо на множестве Е и
f(x)dx = O.
Образуем функцию F : [a, b] —> R, где
О, если а < х ^ Ь.
ь
Функция F интегрируема на сегменте [а, Ь] и J F(x)dx = 0, так как при /(а) ф 0 она
а
разрывна лишь в одной точке, а при любом разбиении П сегмента [а, Ь) имеем Sn{F) — О,
Ь а
J F dx = J F(x)dx = 0. Обозначим J f(x)dx = J f(x)dx. Согласно определению З, п. 1.5,
- a E a
a
получаем / f(x) dx = 0. >
a
12. Пусть / : [a, b] —> R — ограниченная на сегменте [a, b] функция. Разбиением П'
сегмента [а, Ь] в направлении от точки Ъ к точке а назовем множество точек П = {хо =
b, xi, ..., хп — а}, где ц > r,-+i, г = 0, п — 1. На каждом сегменте [xj-ц, я;] выберем
произвольную точку ?; и образуем сумму
1 = 0

260
Гл. 4. Определенный интеграл
Если 3 lim <?п'(/) = I't To говорим, что функция / интегрируема на сегменте [а, Ь) в
направлении от точки 6 к точке а и записываем
а
I'= ff(x)dx.
а а о
Доказать, что если / 6 R[a, b], то существует / f(x)dx, и при этом / f(x)dx — — I f(x)dx.
Ь Ь а
¦4 Если точки разбиения П = {го = a, xi, ..., х„ = Ь) совпадают с точками разбиения П',
а точки fj 6 [xj, xj+i] совпадают с точками ?i 6 [xi, x;+i], то Srt'(/) = — ?п(/), где Sn(f) =
Е /A>)Дг>- Поскольку 3 Um 5П(/) =//(х) dx, то 3 lim Sn-(Я = -//(*)<**•>
i=o <п)—о а 4П')—о a
i=o
13. Пусть / : [а, 6] -* К, / g R[a, Ь], А ^ /(х) ^ В и ф : [А, В] — К, ф 6 С[А, В],
д = ф о f : [а, Ъ) —+ R. Доказать, что д (z R[a, b].
М Из условия / ? Л [а, 6] следует, что функция / удовлетворяет критерию Лебега инте-
интегрируемости по Риману.
Композиция д = ф о f непрерывна в каждой точке непрерывности функции /, поэтому
также удовлетворяет критерию Лебега. Следовательно, д 6 R[a, b). >
Заметим, что утверждение, содержащееся в доказанной теореме, в общем случае теряет силу, если
условие непрерывности функции ф заменить условием ее интегрируемости. Пусть, например,
ф:[0, 1]->R, /: [а, 6]-> К,
, . | 0, если у = 0, , . Го, если х иррациональное,
^»> = \ 1, если уф 0, ^)=( I еслиж=^
где т и n (?i ^ 1) — взаимно простые целые числа.
Функция / интегрируема на сегменте [а, 6] (см. пример 9), а функция ф интегрируема на сегменте
[О, 1]. Вместе с тем функция ф о / : [о, 6] —> К, где
ф о f(x) =
О, если х иррациональное,
1, если х-рациональное,
не интегрируема на сегменте [а, 6] (см. пример 8).
14. Пусть / g R[a, b]. Доказать, что |/| 6 R[a, Ь] и
[ f{x)dx ^ f\f{x)\dx.
•^ Поскольку функция / удовлетворяет всем условиям теоремы Лебега, то этим же свой-
свойством обладает и функция |/|. Из неравенств — |/(х)| ^ f(x) ^ |/(хI> х 6 [а> Щ> и свойства
2), п. 1.7, следует, что
6 6 6 Ь Ь
-J\f(x)\dx^ff(x)dx^J\f(x)\dx, т.е. jf{x)dx ^ J \f{x)\dx. >
а о. а а а
Заметим, что из интегрируемости |/| не следует, вообще говоря, интегрируемость /; например,
функция / : [а, 6] —* К, где
1, если ее рациональное,
—1, если х иррациональное,
не интегрируема на [о, 6], хотя функция |/| интегрируема на этом сегменте.

§ 1. Интеграл Римана 261
15. Пусть / 6 R[a, b], ip e R[a, b]. Доказать, что ftp 6 R[a, b].
¦4 Если функции / и <р имеют точки разрыва, то множества этих точек являются мно-
множествами лебеговой меры 0 каждое, а объединение этих множеств будет в общем случае
множеством точек разрыва функции ftp. Поскольку это объединение является множеством
лебеговой меры 0, то функция ftp удовлетворяет критерию Лебега интегрируемости по Ри-
ману. >
16. Доказать, что если ограниченные на сегменте [а, Ь] функции / и tp совпадают всюду
на нем, за исключением лишь множества X С [а, Ь] жордановои меры 0, то либо эти функции
интегрируемы на [а, Ъ) и
ь ь
J f(x)dx = fip(x)dx,
либо они не интегрируемы на [а, Ь].
¦4 Если / ? R[a, b), то, согласно теореме Лебега, множество точек разрыва функции /
имеет лебегову меру 0. В силу условий примера, множество точек разрыва функции tp также
имеет лебегову меру 0, поэтому ip ? R[а, Ь]. Согласно свойству 2), п. 1.6, функция а = /—<р
интегрируема на [a, b], a из примера 14 следует, что \а\ 6 R[a, b]. При произвольном раз-
разбиении П сегмента [а, Ь] каждый сегмент [xi, ?;+i] содержит хотя бы одну точку, в которой
ь
\а\ — 0, следовательно, Sn(\a\) = 0, sup{5n(/)} = / И dx = 0, / \а(х)\ dx = / |а| dx = 0. По-
скольку
J a(x) da
/ |«(х)| dx, то / а(х) dx = J{f{x) - tp(x)) dx = f f(x) dx - f ip{x) dx = 0.
Таким образом, J f{x)dx = J <p(x)dx.
a a
Если предположить, что / ^ R[a, b], a ip 6 R[a, b), то, согласно доказанному, должно
быть / 6 R[a, b] и получаем противоречие.
Следовательно, <р $. R[a, b]. >
Из примера 16 следует, что если / ? R [а, 6], то не изменяя свойства интегрируемости и величины
интеграла, значение функции / на множестве жордановои меры 0 можно заменить произвольны
ми конечными значениями.
Ь
17. Пусть / ? R[a, b]. Доказать, что равенство / / (x)dx = 0 выполняется тогда
a i
и только тогда, когда f(x) = 0 во всех точках непрерывности функции /, принадлежащих
сегменту [а, Ь].
ь
¦4 Необходимость. Доказательство будем проводить от противного. Пусть Jf2[x)dx= 0, /
а
непрерывна в точке хо б]а, Ь[ и f(xo) ф 0. Из непрерывности функции / в точке хо следует,
что /2(х) > 0 в некоторой окрестности S(xo, S)- Используя свойство аддитивности интеграла,
имеем
b xq—6 xq-{-6 Ь Xfj-\-S
f(x)dx= f f(x)dx+ f f(x)dx+ I f(x)dx> J f{x)dx = c,
a a xq—6 xo + 6 xtj—6
где с > 0 — постоянное число. Получили противоречие, так как
ь
J
f(x)dx = 0.
Достаточность. Пусть f{x) = 0 в каждой точке непрерывности. Из того что / 6 R[o, b]
следует, что /2 € R [а, Ь]. При любом разбиении П сегмента [а, Ь] каждый сегмент [xi, Xi+i]
содержит точки непрерывности функции / (в противном случае при некотором разбиении Й

262 Гл. 4. Определенный интеграл
сужение функции / на какой-то сегмент [xi, x,+i] было бы всюду разрывным на нем и, со-
согласно теореме Лебега, следовало бы, что / ^ R[a, Ъ]).
Таким образом, при любом разбиении П имеем
ь
.S'n(/2) = 0, f f2dx = [ f2(x)dx = suV{Sn(f2)} = 0. >
J J {п} -
— a
18. Пусть функция / : [a, b] —+ К ограничена и вогнута1' на сегменте [а, 6]. Доказать,
•^ Вогнутость функции / означает, что функция —/ выпукла, следовательно, / ? С [a, b]
(согласно примеру 112, гл. 2).
Таким образом, / g R[a, Ь]. Используя свойство вогнутости, находим
Интегрируя по ? в пределах [О, Ъ — а] и производя замены а + ? = t и Ъ — ? = z получаем
(Ь-а. Ь-а \ Ь
j f{a + t)dt+ J f{b-t)dA =Jf(x)dx. A)
0 0 /a
Выполнив разбиение П = {ж, = о + i^r; t = 0, п} и взяв & = ж;, получим, что Ах; =
Ь-а
и
11-1 11-1
i — a v—ч „ / .b — a\ b — a
п 1 п 1
•Ьп(/) = > / [а + г = -} /1 о+-6
i i
i=0 i=0
В силу вогнутости функции /, имеем
i
i = 0
Принимая во внимание, что й(П) —* 0 при » —* со, получим, перейдя к пределу при п —> со
в левой и правой частях последнего неравенства,
ь
J
B)
Сопоставляя неравенства A) и B), получим доказываемые неравенства. >
19. Вычислить / x2smxdx.
о
•^ Сначала дважды применим формулу интегрирования по частям, п. 1.8., а затем вос-
воспользуемся решением примера 4. Получим
2 2 2
2 2 2
/i2 sin i (fa = —х2 cos ж +2 / х cos ж tfa = 2 I ж sin x 2 — I sin xdx )=2l 1)=тг-2
о J \ о J J V2 /
0 0 0
1' Вогнутые функции иногда называют выпуклыми вверх.

§ 2. Основные теоремы и формулы 263
Упражнения для самостоятельной работы
Вычислить определенные интегралы следующих функций, составляя интегральные суммы
¦?п(/) и переходя к пределу прн d(H) —* 0:
1. iK хя, -3 ^ х ^ 5. 2. iw у/х, 0 $ х $ 1. 3. х ь+ З1, 0 ^ ж ^ 7.
4. х I—<¦ cos х, О^ас^^. 5. xi—>• 2 + 5х, —З^ас^б.
Найти следующие пределы:
(
8. lim f_=J + -=J +... +_» V 9. lim У("+1)("+2)-2".
Доказать интегрируемость следующих функций:
10. ? и- [|] - 2 [±], 0 < х $ 1. 11. х ^ Их", 1 < х <С 10,5, а > 0.
12. х i-> 4^-, 1 ^ х $ 40, Л > 0. 13. х ь-+ [х2], 2 $ ж $ 17.
14. х- [^], 0,5$ $х$10.
15. Пусть / € Д [а, Ь] и /(ж) > 0. Обозначим /&„ = /(а + к8п), 8„ = ^^. Доказать, что
п ь ( ь \
lim ^ 51 /*» = ^ / /(:с) dx, lim V/i./2n .../„„ = exp ^ ^ / In /(x) dx ^ ,
?г —• oo ¦ . n —* оэ I I
k=l a \ a J
,. П b — a
lim — = .
16. Пусть / g 61B) [1, +oo[ и /(x) ^ 0, /'(ж) ^ 0, f"(x) ^OVig [1, +oo[. Доказать, что
17. Пусть /S C'B)[a, 6] и
Найти lim и At>.
7t^CO
§ 2. Основные теоремы и формулы интегрального
исчисления
К важнейшим теоремам и формулам интегрального исчисления относят: основную тео-
теорему интегрального исчисления, формулу Ньютона—Лейбница, теоремы о среднем, а также
формулы замены переменной и интегрирования по частям (последние две приведены в пунк-
пункте 1.8).
2.1. Определенный интеграл как функция верхнего предела.
Теорема 1. Еоли f g R[a, Ъ], то функция
х ' .
Ф : х к / f(t) dt, a ^ x $6,
непрерывна на сегменте \а, Ъ\.
Теорема 2. (основная теорема интегрального исчисления). Функция
Ф : х к / f(t) dt, a ^x s^b,

264 Гл. 4. Определенный интеграл
где / : [а, 6] —* R, / € R [а, 6], дифференцируема в каждой точке х € [а, Ъ], в которой функция
f непрерывна, и при этом Ф'(х) = f(x).
Теорема 3. (основная формула интегрального исчисления). Если f ? R[a, b] и мно-
множество точек разрыва функции f не более чем счетное, a F — произвольная первообразная
функции f на сегменте [а, Ъ], то справедлива формула
b
[ f{x)dx = F(x
= F(b)-F(a),
называемая формулой Ньютона—Лейбница.
2.2. Теоремы о среднем.
Первая теорема о среднем. Если f ? R[а, Ь], g € R[а, Ъ] и д{х)-^ О (</(х) ^ 0)
Vi ? [а, 6], то справедлива формула
ь ь
I f{x)g{x)dx = ц I g(x)dx, т^ц^М, A)
а а
гдет= inf {f(x)},M= sup {/(i)}.
Если / € С[а, Ь], то формула A) принимает вид
ь ь
j f(x)g(x) dx = f(t) j g{x) dx, t € [a, b]. B)
a a
Если / € C[a, b], g(x) = 1, то
(x)dx = f(t)(b-a), t?[a,b]. C)
Вторая теорема о среднем. Если
1) функция / : [а, Ь] —» К не возрастает на сегменте [a, b], f[x) J 0 Vi ? [а, Ь] и
g € R[a, b], то Э? € [а, Ь] такое, что
ь Z
J f(x)g(x)dx = f(a) J g(x)dx; D)
a a *
2) / we убывает на [a, b], f(x) ^ 0 Ух € [a, b] и g € R[a, b], mo 3ij G [a, b] такое, что
ь ь
f f{x)g(x)dx = f(b) f g(x)dx; E)
J J
a 7]
3) / монотонна на [a, b] и g € R[a, b], mo 3? € [a, b] такое, что
ь ( ь
J f[x)g[x) dx = f(a) J g(x) dx + f(b) J g[x) dx. F)
а а ?
Формулы D)—F) называют формулами Бонне.
Применяя формулу Ньютона—Лейбница, вычислить следующие интегралы Римана:
4я-
dx
20./= /1
J 1
+ ? COS X '
О

§ 2. Основные теоремы и формулы 265
Согласно примеру 130, гл. 3, функция , > ¦
7^=Bк + 1), х = 7г + 2Ьг, к
v у' °
разной фун
Лейбница имеем
является первообразной функции х t-* t, tcO3 я > i ЕЙ, 0 ^ е < 1. По формуле Ньютона—
a2 sin2 х + б2 cos2 х
о
Преобразуя подынтегральную функцию к виду
1 2
a2 sin2 х + V2 cos2 i (a2 + 62)A+ е cos 2i)'
где е = ц2 2 , и произведя в интеграле замену 2х = t, получим аналогично решению преды-
предыдущего примера
ТГ
= _!_ -
2 . lo / I
? COS <
1 < 2 ¦ / Л-и* м , 2?г г*+*Л * ^
¦¦лтсЪ\\1ч-гггхЪт; ) + л т1-7пг-|I =2Й
10
Используя формулу Ньютона—Лейбница, вычислить интегралы от разрывных функций
путем построения их первообразных на всем промежутке интегрирования:
(х —
Щг) dx> /(I) = Л- 2) 'E = I
В
•4 Функция / не определена в точках х = 0 и ж = 2 сегмента [—1, 3], а подынтегральную
функцию можно записать в виде
Г0Ь = (arctg/(х))', хеЕ,
и функция х I—> arctg/(ж), х ? Е, является первообразной ограниченной на множестве
функции Y+72 ¦ Согласно определению 3, п. 1.5, имеем
ч 0, если х = 0 или х = 2.
Первообразную Ф функции F на сегменте [—1, 3] строим следующим образом:
arctg fix), если — 1 ^ х < 0, и lim arctg/(е), если х = О,
л:—*—0
arctg/(г), если 0 < х < 2, и lim arctg/(х) + Ci, если а; = О,
I —+ 0
lim arctg /fx) + С\, если х = 2,
1-»2—О
arctg/(х), если 2 < х ^ 3, и lim arctg/(x) +Сг, еслиа; = 2.

266
Гл. 4. Определенный интеграл
Следовательно, получаем
{ arctg/(х), если — 1 ^ х < О,
arctg f(x) - it, если 0 $ х < 2,
arctg f(x) - 2тг, если 2 $ х $ 3,
гдеФ@) = -|, ФB) = -|тг.
Применив формулу Ньютона—Лейбница, находим
/ = фC) - Ф(-1) = arctg /C) -2т- arctg /(-1) = arctg Щ - 2тг. >
23./=
sin4 x + cos4
•^ Принимая во внимание равенство sin4 ж + cos4 х = |A +ecos4x), где е = -, к произведя
в интеграле замену 4х — t, получим, используя решения примеров 20 и 21,
87Г
dt
+ ? COS <
: arctg
8тге
= 2л/2тг.
24
31,5
. /= j [x]dx.
•4 Построим первообразную функции / : х »-+ [х], 0 ^ х < +оо, имеющей разрывы первого
рода в точках х = п, п ? N.
Если i ?]п — 1, м[, то f{x) = п — 1; если ж ё]и, п + 1[, то /(ж) = п. Таким образом,
функция Fn-i : х (—>¦()»— 1)х + С„_1, Сп-\ ? К, является первообразной сужения функции /
на интервал ]п — 1, »[, а функция Fn : х \—> пх-\- Сп, С„ ? К, является первообразной сужения
функции / на интервал ]п, п + 1[. Из условия непрерывности первообразной в точках х = п
получаем -Fn-i(" - 0) = Fn(n + 0), т. е. (п - 1)п + Сп-\ = «2 + С„, откуда С„ = С„_1 - п,
п 6 N. Полагая п = 1, 2, . . . , получаем С\ = Со — 1, Ст. = С\ —2 = Со —3, Сз = Сг — 3 = Со —6,
С4 = Сз - 4 = Со - 10, ..., С„ = Со - п(п+1); с0 = const.
Поскольку » = [х], х е [п, » + 1[, то Г' --г--п М(М+^
функции /.
По формуле Ньютона—Лейбница кмеем
= х[х] —
является первообразной
25.
/ = -FC1,5) - F(Q,5) = 31,5 • 31 - 31 • 16 = 480,5. >
sgn (sin x) dx.
А Функцию / : x »-+ sgn (sin x), x € К, представим в виде
f^~, x e Ш\{кж; к S Щ,
\ШХ x G {ктг; к GZ].
Поскольку f(x) = slax _ ПрИ x ф fcv^ то непрерывная функция F : x i—> arccos (cosx),
yl —COS2 Л.'
cc ? R, является первообразной ограниченной разрывной функции /. Следовательно,
/ = F{20ir) - F(-IItt) = arccos 1 - arccos (-1) = —к. >
26.
= J(-l)[x] dx.

§ 2. Основные теоремы и формулы 267
•4 Поскольку ( — lyx' = sgn(sm7r:r), igK, то, принимая во внимание решение предыдущего
примера, имеем
г L I \
1 = — arccos (cos tzx)
= —(arccos 1 — arccos ( — 1)) = —1. >
27
. / = j[e*]dx.
о
•4 Функция x t-+ [e1], 0 ^ x < +oo, разрывна в точках х„ = Inn, n. = 2, 3, .... Пусть
х е]х„, х„+1[. Тогда •
/ [е*]rfx = их + Сп, С„ € К, Сп - const.
Если х €]х„+1, i»+2[, то
/ \сх\ dx = (п + 1)х + С„+1, Сп+1 = const.
Из условия непрерывности первообразной функции х i-+ [е1], 0 ^ х < +оо, в точках а;п
получаем зависимость между С'п и Crn+i:
С'п+1 = С„ - 1п(п + 1), n S N.
Полагая последовательно в полученном равенстве п = 1, 2, ... , находим
С'п = С — In n!, С = const.
Таким образом, функция F : х i-> [e^Jac — ln([e1]!), 0 ^ ж < +оо, является первообразной
функции х I—> [е1], 0 ^ х < +оо.
Поскольку [е2] = 7, то / = FB) - F@) = ([е*]х - 1п([е*]!))|* = 14 - In 7!. >
28. /= /sgn(sin(lnx))dx, ?=]0,1].
-4 Функция F : [0, 1] -+ R, где
pi \ _ j sgn (siii(hi ж)), если x €]0, 1],
I Oi если x = 0,
ограничена на сегменте [0, 1], а множество X = {хк — е~к1Т; к g N} ее точек разрыва счетное,
следовательно, F € R [0, 1], и, согласно определению 3, п. 1.5, имеем
/ sgn(sin(lni)) dx = / F(x)dx.
Е 0
Обозначим F{x) = fsgn(sm(lnx))dx, x > 0. Если e~(fe+1)'r < х < е~кк, то ^(ж) =
(-l^^x + Ck, где к = [-^р], t'fc = const. Если же e~(*+2)ir < х < е~(А:+1)'г, то jF(i) =
(-1)кх + С'к + i, Ck+i = const.
Из условия F(e~{k + 1>" - 0) = _F(e~(fc+1)lT + 0) находим
откуда C'fc = Co - 2(е-7Г - е~2ж + ... + (-l)k"ie~kiT), Co = const. Следовательно, F{x) =
(-l)L .Г i-2(e"r-e"+...+(-l)l * J еГ ж J ж) + С'о, причем ^@) = lim Ck =
Таким образом,
6 =——i = th-.
+ e-17 e.-* + 1 2

268 Гл. 4. Определенный интеграл
б
29.
/г ч • жх j
[ж] sin -^-a1-
Ч Рассмотрим F(x) = J[x]sin ^ dx, x ~^ 0. Если i ?]« —1, п[, то .F(x) = — (тг — 1)— cos ^р +
Cn_i, С'п-1 = const. Если же х €]п, п.+1[, то F(x) — ~п~ cos ^ + Cn> Cn = const. Из условия
F(n — 0) = F(n + 0) получаем
,, 6 П7Г _
О„ = — cos ——h O,,-i,
7Г 6
откуда
С„ = Со + - ( COS ^ + COS — + ... + COS — ) .
7Г 4 6 6 6 У
Следовательно,
f(i) = [i]cos \- - (cos- + cos 2- + ¦•¦ +cos[k]-) +Co, / = /^F-0) - F@) = —. >
30. /= / i sgn (cos x) dx.
7Г
Ч Рассмотрим /"(г) = Jxsgn (cosж) dx, x € К. Подынтегральная функция разрывна в
точках хк = ^ + А;л-, fc € Z, поэтому
2 , г
/"(г) = (-l)fc— + Cfc, если i € — + {к - 1Oг, — -\-ктт ,
Из условия -F(xfc — 0) = ^(xfc + 0) находим
Ck+i = (—1) ( — + ктг\ +Ck,
¦ +ж\ + ... + (~^)к~1 ( —Ь (к ~ 1OГ) + Со, Со = const.
Поскольку к = I —'—— , то
Следовательно,
/3 \2 , /5 \2 /7 \2 /9 \2 1 / тг\2 93
42 У 42 / 42 У 42 У 2 4 4У 32
2
Иногда пределы различных сумм вычисляются путем приведения их к интегральным сум-
суммам для интегрируемых функций. При переходе к пределу при п —+ оо получаем интегралы,
которые вычисляются с помощью формулы Ньютона—Лейбница.
Вычислить:
31. lim Sn, Sn = -±— + —J— + ...+^-.
Ч Записав 5» в виде

§ 2. Основные теоремы и формулы
приходим к выводу, что это нижняя интегральная сумма для функции х i-t- -~, О
,
269
1,
при разбиении П = {х, = ^; «¦ = 0, п} сегмента [0, 1] и выборе ?, = я,. Поэтому
1
lim Sn = [ -^- =
П-.00 J 1 + X
0
32. Um Sn, Sn = -IJl + -
n— oo n \ V П
¦х)
= ln2. >
Ч Поскольку 5„ = i
i = 1, «, Дг-, = —, то
I = Ё /№) Ax^ - гДе
^, 0 ^ x ^ 1, fc = x< = ?,
Г - 2(
п —* оо / 3
О
п
33. lim S», ,S'n = sin — Yj ^—.
n
Ч Поскольку sin г- = z + ° (^з) и Um ° ( "Г I У^. 1 !ПГ = °> т0
lim .S'n = lim —
Но -
п-оо „_oon^2 + COS
,k)L\Xk, где /1X1 — гт-г—, и 5j ж
kn ¦
тогда
1 / dx
= 2] 1+0,5
5 cos.
L 2тг
(см. пример 20). >
34. lim Sn, Sn =
•^ Представим ,S'n в виде
2»
9 - I
L
2"
Y
" ^-^ 1 + —
1 = 1 m
где S^ = - f^ 2 n , ,bl2) = i J3 TTT"- Из оценки 0 < ,bl2) < ^| = - следует, что lim Sn2) = 0,
1
21 rfx = -i-
In 2
поэтому
In 2'
Используя правила Лопиталя и теорему 2, п. 1.3, раскрыть неопределенности вида у, и^Ц:
а-
J cos <2 d<
35. lim .
i —+0 X

270 Гя. 4. Определенный интеграл
Ч Применяя первое правило Лопиталя и теорему 2, п. 1.3, получаем
¦X
Jcos t2 dt
г
urn
= lim -^ /
cos <2 (Zt = lim cos <2 = 1. >
36. lim
X —*+oo
'fe'dt
Применяя второе правило Лопиталя два раза, находим
2 / х ч 2 ,.
Л] -МГ^Л! 2е^Ге'2Л
lim
X—>- + О
= lim
я; —*-f со
= lim
„2х2
2 Г ен Л ¦?- f e'2 d<
J ax J
= lim 5 = 2 lim ; —
x—*-foo f'-
dx
= 2 lim
1
=2 lim — = 0. >
l
37. Пусть / ? G'[0, +oo[ и f(x) —>¦ А при ж —»¦ +oo. Найти lim / f(iix)dx.
о
А Произведя в интеграле замену пх = t, получаем
1 п
lim / f(nx)dx= lim — / f(t)dt= lim tpn,
о о
:r
где ipn — значения функции <р : ж ь-> ^ J f(t)dt, 0 < х < +оо, в точках ж„ = и, п € N.
о
Следовательно,
lim
5„ = lim - /
f(t)dt.
Если Л = 0, то Ve > 0 ЭД > 0 : Уж > Д => |/(*)| < |. Поскольку в рассматриваемом
случае функция / является ограниченной, то ЗМ > 0 : \f(x)\ ^ М Уж 6 [0, +оо[.
Пусть ж > Д. Тогда
1 У /(<)
= ^ У /(*) Л + ~ J
f(t) dt.
Из оценок
получаем оценку
д
/
f(t)dt
МД 1
х х
J
f(t)dt
X
i
f(t)dt
< e,
если x >

§ 2. Основные теоремы и формулы
Следовательно, lim <pn = А = 0.
п—юо
Если А ф 0, то Ve > 0 3Ai >0:У:с>Д1=>>1-е< /(ж) < А + е. При х > Дх имеем
f(t)dt= I f(t)dt+ ff(t)dt> [ f(t)dt+(A-e)(x-&i).
271
Поэтому
lim /
Г-+ + СО J
f(t)dt = oo.
Применяя второе правило Лопиталя, получаем
X X
lim i / /(t) it = lim — / f{t) dt = lim /(i) = A.
-r—»+co X J Л.—»-foo dx J л:—*+oo
0 0
Следовательно, lim <р„ = А. >
n-~oo
/x'2
ef dt ~ при x —> +oo.
2x
Докажем, что lim
~
lim
= lim
= 1, применив второе правило Лопиталя:
X
2/е' dt + 2xex
= lim
= lim
h I = lim
\
+ 1
\
= lim
e1 +2i2eI
1=1- >
С помощью замены переменной с последующим применением формулы Ньютона—Лейб-
а вы
39.
ница вычислить следующие ннтегралы:
0,75
). 1= / **
J (x + l)Vx2 + 1
¦4 Полагая -—у = t, получаем: х = - — 1, dx = — -^, х2 + 1 = -^ — - + 2; тогда
-/
(-1)
+ 4V2
40.
А В неопределенном интеграле f ут§7 dx, x € К, произведем замену переменной по фор-
формуле х =(,i^0. Тогда
dt l ¦ 4= + с = 4= arcts ^-^ + с, х е
у2 у 2 XV 2

272
Гл. 4. Определенный интеграл
В примере 20, гл. 3, показано, что функция
F :х<-
V? arctg TW
0,
где е(х) = —-^sgnx, является первообразной функции х
Следовательно, / = еA) — е( — 1) = А=. >
2
41. 7= / (l+i--)e*T«<fa.
если х =? 0,
если х = 0,
_ i+*2 ~ ,
0,5
^ Произведем в интеграле замену х + - = t. Здесь каждому 2 < t ^ 2,5 соответствует два
значения а:, поэтому представим интеграл на сегменте [0,5; 2] в виде суммы двух интегралов
на сегментах [0,5; 1] и [1, 2] : / = h + h, где
lx =
0,5
2
= / (l
Так как в интегралах 1\ и h соответственно имеем х = *2
2
h =0,5/et(l- J + t- \/t2 - 4
7 V v <2 - 4
2,5
, х =
t
-2 ' Т0
+
- 4
2,5
/ =
— 4
t2 -4
2,5 2,5
= / e(d\/t2 -4+ / е'\/t2 - 4d< =
2 2
2,5 2,5
2,5 Г . Г
- / e'V<2 -*dt+ / e'
2тг
42. В интеграле I — I f{x) cos x dx произвести замену переменной по формуле sin x = t.
о
М Представим интеграл / в виде суммы интегралов на четырех сегментах [к^, (к + 1) j] >
к = 0, 3, на каждом из которых функция х v-> sinx, 0 ^ х ^ 2тг, монотонна. Тогда на
сегментах [—1, 0] и [0, 1] определены функции, обратные сужениям синуса на указанные
четыре сегмента. Если х € [о, ^], то х = arcsini, 0 ^ t ^ 1. Если х € [^, тг] , то х =
тг — arcsini и t убывает от 1 до 0. Если х € [тг, — тг] , то х = тг — arcsini и t убывает от 0
до —1. Если х 6 [j-тг, 2тг], то х = 2тг + arcsini, —I ^ t ^ 0. Таким образом, после указанной
замены получаем
10 -1 О
/ = / /(arcsin t)dt + f{^~ arcsin t)dt+ / /(тг - arcsin <) dt + / /Bir + arcsin <) rft =
0 1 0 -1
0 1
= / (fBir + arcsin t) — /(тг — arcsin <)) Л + / (/(arcsin <) — /(тг — arcsin <)) dt. >
С помощью формулы интегрирования по частям и получаемых рекуррентных соотноше-
соотношений вычислить следующие интегралы:

§ 2. Основные теоремы и формулы
273
2
43. 1= /sin11
х dx.
Интегрируем по частям, полагая sinxdx =dv(x), sin" 1 x — u(x). При этом имеем
In = cos x sin" x
}
+ (п - 1) / sin""
1L J
/ } } \
i lsm"~2xdx- /sin" xdx):
¦ x cos^ xdx = {n-\)[ I ski xdx- I sin" x dx | =
о о
Получили рекуррентное соотношение In — -—In-2, с помощью которого находим
In =
Bfc-l)M тг
——>-¦-, если» =2*.
2fc)!!
если и = 2к + 1.
2
44. /n= /<
О помощью замены ^ — x = t убеждаемся в том, что J cos" xdx = Г sin" xdx. >
о
2
о
45. /n =
¦< Интегрируя в пределах от 0 до j тождество
tg2nxdx = tg2n~2xd(tgx) -tg2n~2xdx,
получаем рекуррентную формулу
г 1
1п =
2n - 1
с помощью которой находим
1п =
<-')•'•-<-)•
\к—п
где /о = / rfx = ^.
о
Вводя новый индекс суммирования п — к = т, окончательно получаем
-cos.;^2"+! ,
) dx-
sm x + cos x

274 Гл. 4. Определенный интеграл
¦4 Произведя в интеграле замену J — х = t, получим
7Г
т
1п = -
4 +/„-1 = -—+ /„-1.
Последовательно используя полученную рекуррентную формулу л — 1 раз, имеем
где 1о = J tgt dt = J Co°V = ^cos*
2
47. /Bm, 2n) = sm2m x cos2n x dx.
^ Полагая cos x rfx = dv(x), sin2 x cos2" 1 x = и(х) и применяя формулу интегрирования
по частям, находим рекуррентное соотношение
In — 1
1Bт, 2п) = -1Bт + 2, 2п - 2),
2?п + 1
пользуясь которым п — 1 раз и принимая во внимание решение примера 43, получим
Bга - 1)Bп - 3) ... 3 ¦ 1
/Bт, 2п) =
+ 1)Bт + 3) ... Bт + 2п - 1)
Bп-1)!!Bт + 2п - 1)!!
1Bт + 2п, 0) =
•1)Bт + 3) ... Bт + 2и - 1))Bт + 2п)!! 2 2Bт + 2ге)!!
_ ;гBп)!Bт)! _ тгBп)!Bт)!
2m+n+i (m + n)!2m+nm!n! 22"!+2"+1 m!jt!(m + n)!'
48. /„ = xm(lnx)ndx, E=]0,l].
Е
¦4 Согласно определению 3, п, 1.5, имеем
1
/„= f F(x)dx,
о
Г хт(Ы х)п х € Е
(х) = < *¦ ' ' _ ' Функция F непрерывна справа в точке х = 0, так как
lim F(ж) = 0, следовательно, F € R[0, 1]. Интегрируя по частям, получим
-F(x)
->h
Рассуждая аналогично относительно интегралов /n-i, /n-2, • • • , /i, находим
п!
/п = (-1) 7—TTw"^0'
где /о = Г хт dx — —— . Окончательно
J 7П4-1
In = (-1)"
(m

§ 2. Основные теоремы и формулы 275
Примеры 49—54 являются теоремами, которые могут быть использованы при вычислении
некоторых интегралов и рассмотрении отдельных вопросов теории.
49. Доказать, что для непрерывной функции / : [—I, I] —+ К имеем:
1) / f(x)dx = 2 / f{x)dx, если функция /
четная;
-I О
i
i J f{x)dx = 0,
-i
2) / f(x)dx = О, если функция / нечетная.
В силу свойства аддитивности интеграла справедливо равенство
о
-I -I
Полагая в первом интеграле х = —t, имеем
i i
I f(x)dx= j f(x)dx+ I f(x)dx.
Если / четная функция, то f(x) +/(—х) = 2f(x), 0 ^ х ^ I, и получаем 1). Если / нечетная
функция, то f(x) + f(—x) = 0, 0 ^ х ^ /, и получаем 2). >
50. Доказать, что одна из первообразных четной функции есть нечетная функция^ а
всякая первообразная нечетной функции является четной функцией.
¦4 Пусть / € R [—1, I] и является четной функцией. Тогда любая функция
х
F : х н-> / /(<) dt + С, С = const,
является первообразной функции / на сегменте [— I, I] (множество точек разрыва функции /
не более чем счетное).
—х
Рассмотрим интеграл J f(t)dt, произведем в нем замену — t = z и воспользуемся четно-
о
стью функции /. При этом получим
X
{-x) = -Jf{z)dz + <
Следовательно, {F(-x) = -F(*)) *> (С = 0), т. е. лишь функция х н-> f f(t)dt, -I < х $ /¦,
о
является нечетной.
Пусть / — нечетная на сегменте [—I, I] функция и f € R [—1, I]. Тогда
X
f(x)dx= f(t)dt + C, С = const.
о
Рассмотрим произвольную первообразную функции /

276 Гл. 4. Определенный интеграл
принадлежащую множеству < J f(t)dt + C>. Имеем
/
FA-') = J /(<) dt + Cj = -[ /(-,) dz + Cj = j f(z) dz + C, =
0 0 0
Следовательно, F3 является четной функцией. >
51. Доказать, что если / : К —¦ К является непрерывной периодической функцией,
имеющей период Т, то
а+Т
f(x)dx = Jf(x)dx,
о
где а — произвольное действительное число.
4 В силу свойства аддитивности интеграла, имеем
а+Т Т а+Т
j f(x)dx= I f(x)dx+ j f{x)dx.
a a T
Из условия периодичности функции / следует, что
а+Т а+Т
j f(x)dx= J f(x-T)dx.
т т
Произведя замену х — Т = t, получаем
а+Т
f(x-T)dx = J f(t)dt.
Следовательно,
о+Т а Т Т
j f(x) dx = J f(x) dx+ [ f(x) dx = J f(x) dx. >
a 0 a 0
52. Доказать, Что при нечетном п функции
х х
F : i i-t / sin" tdt, G : x i-f / cos" 1
'tdt
о о
— периодические с периодом 2ж, а при п четном каждая из этих функций есть сумма линейной
функции и периодической функции.
Щ Доказательство проведем для функции F. Пусть « = 2то +1, то € N. Тогда
1+21Г 1+21Г
F(x + 2*)= / sin2m+1<rf<=F(ir)+ f sin2m+1 tdt.
0 x
Аналогично решеиию примеров 51 и 49 нмеем
x+2ir 2ir it
/ sin2m+1trft= fsm2m+ltdt= f sia2m+1 tdt = 0.
x 0 -1Г
Следовательно, F(x + 2jt) = F(x), т. e. F — периодическая функция с периодом 2я\

§2. Основные теоремы и формулы 27Д-,
Если п — 2т, т € N, то • -,
1-п
F{x + 2тг) = F(x) + I sin2m x dx.
Поскольку функция х I—> sin2ma;, x 6 R, имеет период тг, а ее сужение на сегмент [—§¦, §]
является четной функцией, то
7Г »
2тг тг J ,2
/ sin2m х dx = 2 I sin2m x dx = 2 / sin2m x dx = 4 I
• 2т Л :¦; ч !( iHU-i ¦¦'.-'¦Л
sm xax.
0
Следовательно,
27Г 2
Cm= fSin2mxdx = 4 fsm
7 7
Bт)!!
о о
(см. решение примера 43). Таким образом, F{x + 2#) — F(t) — Ст.
Рассмотрим функцию ф : х н-> F(x) — ^-х, х 6 Ш. Поскольку ф(х + 27г) = F(x + 2к) —
функцией, в силу чего
т. е. функция F представима в виде суммы 2тг-периодической функции ф и линейной (одно-
(однородной) функции х н-> атх. > , , ,. г, t ,.-,;„„||
53. Доказать, что функция
X
f:XK jf(t)dt, *gR,..
где / — непрерывная периодическая функция с периодом Т, в общем случае есть сумма
линейной функции и периодической функции периода Т. \
¦4 Согласно теореме 2, п. 2.1, функция F дифференцируема Vx€lR, и при этом F'(x) = f(x).
В силу периодичности /, имеем F'(t + Т) = /(<). Интегрируя на сегменте [хо, х], находим
F(x + T)- F(xo+T) = F{x). Поскольку , ,.j
= / f{t)dt=ff(t)dt = C, С = const,
то F(x + T) - F(x) = С. Если С = 0, то F(x + Т) = F(x) и F является периоди^ско:^
функцией с периодом Т. Если С ^ 0, то введем в рассмотрение функцщо ( . ,,,,'.*,,,.
$:x^F{x)-j;x,- i€R. tl! ;iit ¦•'^I *
Поскольку Ф является периодической функцией с периодом Т, то
F{x) = ${x)+ax, x€U, a-f'
есть сумма периодической и линейной (однородной) функций. > i•¦<: , i . - ¦; ",i't,. ел i-я
54. Доказать, что если / € С[0, 1], то: •>¦'
2" 7 тг -,,,. \ ¦ -IT. ' '' ' ',;</ |
1) / /(sinx)rfx=: / /(cosx)rfx; 2.) / x/(sin x) dx = — I f(sinx)dx..

278 Гл. 4. Определенный интеграл
•4 1) Полагая ~ — х = t, получим
тг тг
~2 0 "г"
/ /(sinx)dx = - / /(cosi)dt = / /(cost) dt.
о Но
2
2) Запишем
тг тг
/x/(sin x) dx = / x/(sin(;r — х)) dx
J
о о
и положим ж — х = t, получим
тт тг тг тг
/ x/(sin x) dx = {ж - t) /(sin t)dt = ir / /(sin t)dt- / </(sin t) di,
0 0 0 0
откуда
7Г 7Г
/x/(sinx) dx = — I f(sinx)dx. >
2 J
о о
В примерах 55—62 рассматриваются различные интегралы. Некоторые из них вычисля-
вычисляются путем использования формул Эйлера
е'х = cosx + г sin х, е~'х = cosx — г sin x.
Вычислить интегралы:
200 тг
55. / = / л/l — cos2x dx.
J
о
200тг
М Поскольку / = л/2 J | sin x\ dx и функция х i—> | sin х|, х € R, периодическая с периодом
о
Т = тг, то, согласно примеру 51, имеем
I = 200\/2 / sin х dx = 400л/2. >
/ si
о
56. /
тг
= /
J 1
+ cos2 x
о
¦< Так как / = J xf(sinx)dx, где /(<) = 2_;2 , то, согласно примеру 54, получаем
о
тг О
ж f sin x , 7г f d(cos х) ж , . ° ж2
I = — I т.— dx = — I ¦—* -г— = —arctgfcos х) = —• >
2 J 2- sin2 x 2 J 1 + cos2 x 2 ьу ' п 4
О тг
57. /= / ^-^ 5-rfx, аек.
у 1 + 2«cosx + аг
о
М Если « = 1, то I = f 1+^'cnos^ dac = /sin2 | rfx, где Е = [0, тг[. В этом случае J = §•

§ 2. Основные теоремы и формулы
При а ф 1 представим / в виде / = ^ A\ — h), где
COS X 1 1
279
= /
J \
+ е cos z '
. + ? COS X
? ?2 ^ ?2(l+COSxW ?2 ?2'
'+а2' |в|^-
Следовательно, / = t2,x 2. (тг — A — е2)^).
(/ / \ \ Iп—^
, 2 arctg ( л/|~| tg - J H—,27Г ¦ [^~] ) = Г (см. пример20),
то
Принимая во внимание, что I —\ при « = 1, получаем
2'
если |«| ^ 1,
—2-, если|а|>1.
2тг
68././
B + cos х)C + cos x)
Из тождества 1 = C + cos x) — B + cos x) следует, что
2тг
J I
+ ?l COS X
где ?i = -, 62 = г. Так как
2тг /
/ dx - ( 2 arct (
J I + ?j cos г 1 yi _e? Г ^
1-е, , х
tg
+ ?2 COS X '
2;r [x + TT
2;r
^ • >
59- / =
Л Поскольку lim ""„^ = », lim ^~ = (—1)п+1»г, то
7Г
/sin nx , ( r, \ ,
—. dx = / f(x)dx,
smx J
при x ? E,
при г = 0,
при х = тт.
Л i an. j.
х) = < n
( (-1)П+
Из формул Эйлера следует, что sinfcx = j^(e'kx — е~'ка:)! к = 1, и, следовательно,
Е-
к=1
2(cos(ji — 1)х + cos(n — 3)х + ... + cos x), если и четное,
2(cos(n — 1)х + cos(n — 3)х + ... + cos х) + 1, если п нечетное.

280 Гл. 4. Определенный интеграл
Поскольку /cos(n - k)xdx,= ""^"jffi » 0, * = 1, 3, .,. , n r- 1, то
я
/sin «х , [ .. ч , Го,
smx J I *•
E
если п четное,
если п нечетное.
60. / =
E
E
cosBn
4 Функция х !-<• С2О" д i * € Е, имеет предельное значение при х -+ |, равное
(-1)пBп + 1), поэтому
/cosBn + 1)х ,
(с<"<2
(-1)
Согласно формулам Эйлера, имеем
COSB» + 1)х = I(e«2-+i)- + e^2"*»)-), cos x = i(e-* + e~ix)
2i ¦ L
n
/(*) = 2 ^(-l)*'1 c»2|« - (* - l))x + (-1)", 0 ^ x ^ тт.
kml
Следовательно,
1 =
J ' t~* ' J "
fc_! sin 2(n - (k - l))x
2(« - (k - 1))
о
i
61. / as / cos nx cos" x dx.
4 С помощью формул Эйлера находим
cosnzcosnx = ' +1 (е'"х + е~"**)(е'* +е~11)" =
too
1 1 /i=i ^U \ 1 1 ^
— — 4- [ NT^ Пкei2("—k)x i \^ Ск -&кх I _ _ I _ Х^ пк
\к=0 fc=l / fc=l
Интегрируя полученное выражение на сегменте [0, я-] и принимая во внимание равенства
я
/ cos 2Jbx dx = 0, к = 1, п,
о
получаем/••=^-. I^i ¦••¦> t ¦¦ ¦-' ¦•¦¦ *.-.ми „¦.¦•.. у.
я
1,62. 1 =, I sinuxsin" xiix. ¦ .
J
о

§ 2. Основные теоремы и формулы 28Г
¦4 Произведем в интеграле замену х = | +1. При этом получим •¦ " " ' s '?*•«« ^я-ч.П
Я я
* ? ' > • * / ¦:¦¦ ¦ '
/ = sinn- / cos"i cos nt dt -f со*»»— f cos?? spiitf &
__7Г Я
2 "I
Так как функция t ь-+ cos" t sin n<, — j ^ < ^ j, нечетная, то, согласно примеру U9* =HMeSj*S
Следовательно,
cos" t sin nt dt =0.
2
= sin n— / cos" t cos «t <|^
2 у , ¦•.¦»•; ••
В предыдущем примере показано, что
1 . 1
i
cos" t cos nt = — + — J2 On cos 2b.
Принимая во внимание равенства
2 я
/ cos 2kx dx = — sin 2Jbx | ^ = 0, к s= 1, rt,
2
находим
2
sinn- /¦
-f
63. Многочлен Лежандра определяется формулой
Доказать, что
О, если тфп,
5^у, если то = п.
у
-1
•^ Рассмотрим при m < п интеграл s • : >, г.н, • ,!>i/
1
/d" 2 m
JxnU
-1
и вычислим его, применив формулу интегрирования по частям m раз. При этом получим ..
1 .
(х2 - 1)п dx = (-l)mm\4 Йх*-1У" =»0, ' -*^A)

282 Гл. 4. Определенный интеграл
так как зрг(х ~ 1)
= 0 при к = 0, н — 1.
-1
Многочлен Рп(х) отличается от многочлена -j-^{x2 — 1)п лишь постоянным множителем,
а многочлен Рт{х) является линейной комбинацией степеней хк, к = О, т, поэтому из A)
следует, что
/ Рп(х)Р,п(х) dx = О, если т < п.
— 1
1 1
Если т > п, то, очевидно, J Pm(x)x" dx = О, в силу чего j Pm{x)Pn(x) dx — 0.
-1 -1
1
Таким образом, J Рт(х) Pn{x) dx — 0, если т ф п.
Рассмотрим интеграл
1
—1 —1
и для его вычисления применим п раз формулу интегрирования по частям, получим
1
Многочлен (х2 — 1)" имеет коэффициент 1 при старшем члене, поэтому dx2n (х2 — 1)" = Bп)!
Следовательно,
- - ^ /<•' - "¦ <• - <-
-1 0 0
(в силу четности функции х \—> (х2 — 1)", —1 ^ х ^ 1). Произведя в интеграле замену
arcsin х = t и принимая во внимание решение примера 43, находим
_ 2B»)!
n ~ 22"(!J
/costit
22"(»!J J ~ 22"(п!JB» + 1)!! ~ 2n + V *
о
64. Пусть f ? R[a, Ь] и функция х н-> F(x), а ^ х ^ 6, такая, что F'(x) = /(ж) всюду
на [о, 6], за исключением конечного числа внутренних точек а, г = 1, р, и точек а и 6, в
которых .F терпит разрывы первого рода.
Доказать, что
/
Дх) dx = F(b - 0) - F{a + 0) - ^(F(c, + 0) - F(c, - 0)).
Образуем функцию x i-> ^1A), о ^ г ^ 6, где
{F(r), если ж €]ci, c,-+i[,
F(c,- + 0), если x = Ci, j = 07"p, c0 = a, cp+i = b.
Пусть П — произвольное разбиение сегмента [a, b], в число точек которого входят с,, г =
1, р. Применяя на каждом сегменте [ху, Xj+i], j = 0, н — 1, формулу конечных приращений,
получим
п—1 п—1 п — 1
j'=0

§ 2. Основные теоремы и формулы 283
Вместе с тем сумма S'n(f) имеет вид .,. i ,
5°(Л = ?(*i(c.4i)--Fi(ci)) = Л(с1)-^(Со) + Л(С1Н.1)-^1(Ср)+^(^(с,-+1-0)-^(с;+0)) =
1 = 0 1=1
р-1
= FF - 0) - F(a + 0) + F(ci - 0) - F(cp + 0) + ^(F(c,+1 - 0) - F(c, + 0)) =
i=i
p
= F(b - 0) - F(o + 0) - J2(F(Ci + °) ~ F(Ci ~ °))-
t=i
ь p
Поскольку / e R[a, b], то lim Sa{f) = //(x)dx = FF - 0) - F(a + 0) - X2(-F(c' + °) ~
4П)—0 a i=1
F(c--O)). >
65. Используя теоремы о среднем, определить знаки следующих интегралов:
2
3 dx.
Е -2
а)/= fS~dx, ?=]0, 2тг]; б) I = f x32*
Е
а) Функция F .- [0, 2тг] -> К, где
F{x)={ *?> ec™x?E>
{ 1, если г = О,
непрерывна на сегменте [О, 2w], поэтому F ? R[0, 2х], причем
2тг
/ sin а; / .
/ dx = I F(xj dx.
Е О
Из свойства аддитивности интеграла следует, что
2тг тг
¦ dx
/ F(x) rfi- = / F(x) dx+ F(x) dx = тг / —
7Г
2тг
(в интеграле f F(x) dx произведена замена х — 7г = t). Применив первую теорему о средней,
тг
получим
о
откуда следует, что / > 0.
б) Запишем I = h + h, где
0 2
/i = I x*2xdx, h= I x32xdx,
-2 a
и произведем в 1\ замену х = —t, получим
2
1 = 2 / x3sh(xln2)dx.

284 Гл. 4. Определенный интеграл
Согласно первой теореме о среднем, имеем
2
n2) / x3
= 2sh(?ln2) / x3dx
0
Следовательно, / > 0. >
66. Пусть / € С[0, +оо[ и 3 lim fix) = А, А <= К. Найти
lim If
х— +оо X J
Рассмотреть /(t) = arctgt, 0 ^ t < +oo.
¦4 Поскольку 3 lim f(x) = А, то Ve > 0 ЭВ > 0:
X—t-+OO
Рассмотрим при х > В интеграл
I j f(t) M=
Так как / 6 R[Q, В], то' f f(i)dt — С, С = const. Согласно первой теореме о среднем, имеем
о
Оценим а(х) =
при
х > В. Имеем
а(х) =
С
В
\с-№в\
1/@-^1
\С-
е
2'
так как В ^ ( ^ х. Поскольку |С — /@-8| = const, то при достаточно больших х > 0 будет
выполняться неравенство "~ ^ — < §> следовательно, и неравенство а(х) < е, из которого
следует, что
;.•. ¦¦ i '; „• , .,, lim —
Если /(*) = arctgi, 0 ^ t < +oo, то
lim — / arctg tdt = —. >
Оценить интегралы:
dx
вт.,./т
+ 0,5 cos х
Представим / в виде I ~ h + h, где
l+0,5cosx'
dx
1 + 0,5 cos х

§ 2. Основные теоремы н формулы 285
Заменяя в интеграле /г переменную по формуле 2х—х = t, убеждаемся в том, что /з — /l ¦
Следовательно, ' " '
7 = 27, = '' <*
о
dt _
2
Функция / : х !-¦ Г -—j-, 0 ^ х ^ х, удовлетворяет на сегменте [0, х] всем условиям
jj l+2cos2- *
теоремы Лагранжа о конечных приращениях, в силу чего имеем
Так как \ < —г < 1, то справедлива оценка — < 1 < 4х, или -™ < / — |х < ?¦.
3 1+2 сор i 3 3 3 3
Обозначив * = (/—j^j : -^, получим
/ = !*. +1*0 к»<i >
3 3 '
100
68. Г
= J *
+ 100 —
о
^ Поскольку функция х i-> д+^00 , 0 ^ х ^ 100, монотонная, а функция х »-* е~*, 0 < i <
100, непрерывная, то к 7 можно применить вторую теорему о среднем (формулу F) п. 2.2).
Тогда получим .
? юо
7 = 0,01 I e.-*dx + 0,005 / е~* dx = 0,01 A - е"*) + 0,005 (е~* - е00), 0 < ? < 100.
о (
Так как ? = 100 0, 0 < в < 1, то 7 принимает вид .
7 = 0,01 - 0,005 (е00 в - е00) = 0,01 - 0,005#i,
где*, =е-1ООв-е-100, 0<вг < 1. >
200ir
69. I
1001Г
" / ^
-< Функция х I— i, ЮОя- ^ х ^ 200тг, монотонная, а функция х »-»• sinz, ЮОх < х ^ 200л-,
непрерывная, поэтому применим формулу F), п. 2.2. При этом получим
2001Г
1
Следовательно, 0 < 7 < ^оЫ • Обозначим в = I : ^оЫг' тогДа -^ = joo 0 < в < 1. ^
2оо ¦;¦'
70. 7= /sm7rx2dx.
100
После замены переменной по формуле irx2 = i, получим
200г1г
- 2V5F J St Л>
1002 IT

286 Гл. 4. Определенный интеграл
Воспользовавшись формулой F), п. 2.2, имеем
=J—\ 1—- [ smtdt + —Ц= / s'mtdt I = 1 "**, 10027г<?<2002тг.
2v^F I 1OO0F J 2OO0F У / 4007Г
\
Очевидно, 0 < / < ~, поэтому / = ^, 0 < в < 1. >
ь
71. /=
•^ Функция ih-^, a^t^i, убывает на сегменте [а, 6], а функция х н-> cosx, a ^ х ^ 6,
непрерывна на нем, поэтому, согласно формуле D), п. 2.2, имеем
s
= ——. I cos x dx = ""* s /-""'" , a < ? < b.
sin ? — sin a
у/а
Из оценки | sin ? — sin a| < 2 следует, что
2 т 2
7= </< -7=.
Va va
Обозначив в = I : -д, получим
2
72. Доказать, что liiu / sin" x dx =0.
п~оо J
о
•^ При доказательстве можно было бы воспользоваться результатом решения примера 43.
Мы воспользуемся первой теоремой о среднем.
Представим /n = J sin" x dx в виде In = In + In , где
о
7Г ? 7Г
/1:) = / sin"zdx, In2) = I smnxdx,
7Г ?
2'~2
0 < е < тг — произвольное, наперед заданное число.
При любом п € N справедлива оценка
7Г ?
2"~2
Так как sin" x < sinn 1г,0<г<^ — |,то
Поскольку /„ > 0, то убывающая последовательность (Д ) ограничена снизу и
3 lim /i1) = С, С > 0.

§ 2. Основные теоремы и формулы 287
Следовательно,
№ = С+ап, #2, =<? + &,,
где «п, Рп —бесконечно малые последовательности.
Согласно первой теореме о среднем, имеем
/^зш^л, о<*„<!-!,
откуда получаем С = ""^"„" ; т- е- С' — бесконечно малая последовательность. Так как'
С = const, то С = 0. >
п+р
73. Доказать равенство lim / dx = 0, р > 0.
п — со J X
^ Функция t ь -, n ^ i ^ u~\~p, убывает, а функция x i—> sinx, n <J x sj ra+p, непрерывна
на каждом сегменте [п, п + р], поэтому, применив вторую теорему о среднем (формула D),
п. 2.2), получим
7 f sin x 1 f . cos n — cos ?n
/„ = / dx = — I sin x dx = , ?i < ?n < « + P-
J x n J n
n n
Из ОЦеПКИ |/„| = |cosn-eo.«fn| ^ 2_ следует> что Jjm /n _ Q ^.
n n n—>oo
74. Пусть / : [a, b] —> R, 9 : [0, i] —> R — непрерывные функции, причем функция
f дифференцируема на интервале ]о, Ь[ и ip'(x) ^ 0. Доказать вторую теорему о среднем
(формула F), п. 2.2), применяя интегрирование по частям и используя первую теорему о
среднем.
6
•^ Рассмотрим интеграл / = f f{x)tp(x)dx и применим к нему формулу интегрирования
по частям, полагая dv(x) = f{x)dx, u(x) — <р(х). При этом получим , ,
f [ \ f f С \ f f
I = f <p(x) / f(t) dt \ -I ip'(x) / f(t) dt\dx = ip(b) / f(x) dx - (ip(b) - (p(a)) / /(x) dx
\ J / J \ J / J J
a a a a a a
(применив к интегралу f I <p'{x) j" fit) dt j dx первую теорему о среднем). Применение этой
a \ a /
х
теоремы законно, поскольку функция х t-> f f(t)dt, a sC x ^ 6, непрерывна, а <р'{х) ^ 0
согласно условию.
После несложных преобразований получаем
I = <р(Ь) f f{x) dx + ip(a) f f{x) dx.
ь 4
Если f G R[a, b], то средним значением функции f на сегменте [а, Ь] называется число
ь
Найти средние значения функций на указанных сегментах:
75. р= 3- , 0<<р<2тг, 0<е<1.
1-е cos ц>

288 Гл. 4. Определенный интеграл
Ч Согласно определению, имеем
х,, ч V f dip pi 2 ( 1 + е <р\
М(р) = — / = — arrt.g . /_Л__ tg — +
vr; 2ж7 1-е cos<p 2ж l^/l- е2 IV1-6 2/
27Г [ip + 7Г
2ж
2тг
(см. пример 20).
Из аналитической геометрии известно, что е = ^-— , р = —, где а — большая полуось
эллипса, b — его малая полуось. Подставив вместо е и р их значения, получим М(р) = Ъ. >
76. / : х 1—> sin х sin(x + ip), 0 ^ х ^ 2ж.
¦^ Исходя из определения среднего значения функции, имеем
2тг 2л
M(f) = — / sin х sin(x + <р) dx = — / (cos <p — cosBx -f <fi)) dx =
2w J 4k J
о о
77. Найти среднее значение скорости свободно падающего тела, начальная скорость
которого равна vo.
^ Скорость свободно падающего тела в момент времени t выражается формулой
v(t) = vo + gt,
где д — ускорение свободного падения.
Согласно определению, получим
так как f = ^Ьа
78. Сила переменного тока изменяется по закону
г = г0 sin
/2?rt
где го — амплитуда, t — время, Т — период, <р — начальная фаза.
Найти среднее значение квадрата силы тока.
•4 Поскольку г2 — »о sin2 (Щт + <р) = *-f (l — cos (~- + 2ip)) , то
т
!< = —.>
о
79. Пусть f ? R[a, Ъ] и д ? R[a, b]. Доказать неравенство Коши—Буняковского
F \ 2 Ь Ь
jf(x)g(x)dx\ <Jf2(x)dxJg2(x)dx.
а /а а
4 Так как / € R[a, b] и д € R[a, b], то
ь ь ь
Обозначим а = J f2(x)dx, ft = J f(x)g(x)dx, 7 = J g2(x)dx и рассмотрим два возможных
а а а
случая:

§ 2. Основные теоремы н формулы
289
1) (у = 7 = 0;2) хотя бы одно из чисел а или у отлично от нуля.
1) Пусть а = 7 = 0. Интегрируя неравенство
\f(x)g(x)\ ^ i(/2(x) + д2(х)), а < х < 6,
получаем
откуда ^ = 0 и доказываемое неравенство выполняется.
2) Пусть, например, 7 > 0- Тогда при всех t € К выполняется неравенство (/(х) +
tg(x)J ^ 0, интегрируя которое получаем
It2 + 2/И + а ^ 0, t e R.
Следовательно, дискриминант квадратного трехчлена
неположителен, т. е. р2 — ау ^. 0. Таким образом, /?2 ^ «7- >
80. Пусть / 6 С^[а, Ь] и /(о) = 0. Доказать неравенство
ь
М2 ^(Ь-а) J fn{x)dx,
где М = sup {|/(x)|}.
•^ Запишем неравенство Коши—Буняковского в виде
\
J f(t)g{t)dt < J P(t)dt Jg*{t)dt,
где g(t) = /'(t),
b. Оно принимает вид
X XX
J f»(t)dt Jdtz Jf'
'(t)dt
откуда получим неравенство
\
X
f fa
(принимая во внимание, что /(о) = 0).
Левая часть последнего неравенства лишь усилится, если в ней положить х = Ь, а в правой
части можно взять и то значение х € [о, 6], при котором непрерывная функция х \-* |/(х)|,
а ^ х ^ 6, достигает своей точной верхней грани М. Следовательно, справедливо неравенство
fl2{x)dx.
Упражнения для самостоятельной работы
Вычислить интегралы, построив первообразные подынтегральных функций на всем про-
промежутке интегрирования и применив формулу Ньютона—Лейбница:

290 Гл. 4. Определенный интеграл
150,2 35,5 125,3
18. / [х)хЫх. 19. / $dx. 20. / &dx. 21. / [x2]dx. 22. / Щ
1,3 2,4 1,2 </Г$ 0,04 L J
100,2 20
23. / [x]|sin7rx|dx. 24. / max(l, x2) dx.
0,25 -10
Вычислить определенные интегралы:
29 3/ г 2уД In 5 1
25. Г V(;-2) dx. 26. f ."* . 27. Г '"^T^dx. 28. f(arcSin xL dx.
{ 3+ V(x-1Y J xJ(x*-2)b I «*+3 J V >
3
2тг
29. /"e-'siiiTrxdx. 30. Г _,_ a+cosx dx. 31. f Icos (in i) I rfx, n € N.
J J l+2acosl+a2 J I V xl I '
0 0 e-2'™
тг
32. fek"ciinxdx. 33. /rj^T^x. 34. /^fyj-dx. 35. / e~mx cos2n+1 x dx.
-10 0 _5
2
1 27Г ~2 n
36. fijifi~T*-dx. 37. / а+ь^О5 д ¦ 38. / (а2 51п2х+б^совД1J • 39- /sin2lixt/x, ?t € N.
Решить уравнения:
X X
41 Г ^* -- Л. А2 Г ^г _. ^
v/2 * In2 * * ~
43. Найти абсолютные экстремумы функции / : % н-> J (а^"Д.а ^*, —1 ^ х ^ 1.
о
44. Исследовать на экстремум и найти точки перегиба графика функции
х
/:1^/D-1)((-2JЛ, хеК-
о
sin2 х cos2 x
45. Доказать тождество J arcsin \/idt-\- J arccos \fidi — ~.
46. Доказать, что
l.~*-l _ (n-l)xn-nx"-1+l
47. Вычислить среднее значение функции / : х i-t- eX , 0 ^ х ^ 2.
48. При каком а среднее значение функции х н-> In х, 1 ^х^о, равно средней скорости
изменения функции?
Показать, что:
49. f </ /4_*;_i3 < 4^2- 50. 0,5 < / ,d_^2n < f, ti^l.
l
51. 0,78 < / .dx a < 0,93.
Доказать равенства:
52. а/'=?^г=1п2-з^->О<в<1. 53.
100 100
Показать, что:
200 _5x
< —. 55. О < / -—: dx < 0,01. 56.
0 "V'T- 2° 0 20+X
20 2 1
10 0
200
** l- о « п^а^Л к* Г *™ ™ J 0,005 26
19

§ 3. Интегрирование вектор-функций 291
59. Определить знак интеграла / = J x2lnxdx.
0,5
7Г 2тг ¦
60. Какой интеграл больше: I\ = J" е~х cos2 х dx или /г = / е~х cos2xdx?
61. Найти lim Г-
#
62. Найти lim / /(х)^, где а > О, Ь > О, / <= С[О, 1].
ас
§ 3. Интегрирование вектор-функций,
комплекснозначных функций и
функциональных матриц
3.1. Интеграл Римана вектор-функцин.
Пусть f : [а, Ь] —<¦ Кт — вектор-функция с компонентами /,, j = I, m, являющимися огра-
ограниченными на сегменте [а, Ь] функциями. Рассмотрим произвольное разбиение П сегмента
[а, Ь] и образуем при любом выборе точек ?; € [xi, x,+i] сумму
которую назовем интегральной суммой вектор-функции f на сегменте [а, 6]. Согласно опре-
определению операции сложения в пространстве Rm, интегральная сумма Sn(f) имеет вид
Sn(f) = En(/l), Sn(/3), • • • , Sn{fm)), A)
где Sn(fj) = X/ /j(?')^x' — интегральные суммы функций /,, j = 1, го. Пусть ^(П) =
i=0
max Дх;. Полагаем lim Sn^fJ^I, если Ve > 0 36 > 0 : УП V d(U) < 8 => |Sn(f) - I| < е.
0^ign 1 <(ПH
)
Определение. Определенным интегралом вектор-функции f но сегменте [о, ft] назо-
вем предел
lim Sn(f) = I,
d(n)-.o v
если он существует.
Если вектор-функция f имеет определенный интеграл на сегменте [о, 6], то будем ее на-
называть интегрируемой по Риману на этом сегменте, а ее интеграл обозначать символом
ь
J f (x) dx. Множество всех интегрируемых на сегменте [о, Ь] вектор-функций f будем обозна-
обозначать f ? Я [о, 6].
Теорема. Вектор-функция f : [о, Ь) —> Rm интегрируема на сегменте [а, Ь] тогда и
только тогда, когда каждая ее компонента f}, j — 1, m, интегрируема на этом сегменте.
Принимая во внимание эту теорему, получаем, что если f€K[a, ft], то
Ь I Ь Ь Ь \
ff(X)dx= I f fl{x)dx, j f2{x)dx, ..., I fm{x)dx\ .
B)
Отметим, что замена переменной в интеграле Jf(x)dx сводится к замене переменной
a
Ь
в каждом из интегралов J/j(x)dx, j = 1, m, поскольку интегрирование вектор-функции f
a
приводит к интегрированию т числовых функций.

292 Гл. 4. Определенный интеграл
Если вектор-функции f и g интегрируемы на [а, Ь] вместе со своими производными f' и
g', то справедливы формулы интегрирования по частям для скалярного и векторного произ-
произведений этих функций:
Ь ft
y<f(x), g'(x)><*x = (f(x), g(x))|* - /V(x), g(x)><Zx,
a a
J[f(x), e'(x)]dx = [f(x), g(x)][ - J[f (x), g(x)]dx.
C)
D)
3.2. Интеграл Римана комплекснозначной функции.
Определение. Для функции f : [а, Ь] —¦ С, где /(х) = м(х) + iv(x), образуем при про-
произвольном разбиении П сегмента [а, Ъ] и любом выборе точек ?, ? [xj, Xj+i] интегральную
сумму
J=0 j=0
ь
ГогЭа J f(x)dx = lim 5п(/), если этот предел существует.
d(n)-o
Множество всех интегрируемых по Риману комплекснозначных функций / будем обозна-
обозначать / € R[a, Ъ].
Теорема. 3 lim Sn(f) & 3 lim Sn(u) Л 3 lim Sn(v), причем
d(n)o wy d(n)o v ' d(n)o v '
Urn Sn(f)=( Km 5п(м), Km Sn(
n)o ' yd(n)o d(n)o
(v) ) .
Таким образом, комплекснозначная функция / интегрируема по Риману на сегменте [а, Ъ]
тогда и только тогда, когда и € R[a, Ъ], v ? R[a, b] n при этом
ь ь ь
I f{x) dx= I u(x) dx + i I v(x) dx. A)
a a a
Если комплекснозначная функция / интегрируема на сегменте [а, Ь], то комплексно-
сопряженная ей функция / интегрируема на этом сегменте. Тогда и произведение / • / = |/|2
является интегрируемой числовой функцией, причем
j f(x)f(x) dx = J(u2(x) + v\x)) dx.
B)
3.3. Интеграл Римана функциональной матрицы.
Если х *-* А(х) = (aij(x)), а ^ х ^Ъ, — функциональная матрица размера пхт, элемен-
элементами которой являются ограниченные на сегменте [а, Ъ] функции, то она является элементом
векторного пространства 53Л над полем R, причем в этом пространстве определена интеграль-
интегральная сумма 5п(.А) = (.S'n(aij)) при произвольном разбиении П сегмента [а, Ъ] и любом выборе
точек ?; € [xi, xi+i]. Полагаем
b
I
A(x)dxd=f Km Sa(A),
если этот предел существует.
Теорема. 3 lim Sn(A) -ФФ- 3 lim 5д(а,у), i = 1, n, j = 1, m,
d(n)O d(n)-»O
lim Sa(A)=( Urn Sn(aij)).

§ 3. Интегрирование вектор-функций 293
Таким образом, функциональная матрица А(х) интегрируема на сегменте [а, Ь] тогда и
только тогда, когда на этом сегменте интегрируемы все ее элементы aij и при этом'
ь / ь \
[ f \ -.
A(x)dx=\ ai3(x)dx\, i = 1, п, j = 1, то. A)
V /
" \а /
Класс всех интегрируемых на сегменте [а, Ъ] функциональных матриц А будем обозначать
AeR[a,b].
ю
81. Вычислить I = / {\/х, 2х)dx, рассматривая его как предел интегральной суммы.
о
¦4 Поскольку у/х е R[0, 10] и 2х 6 Л [0, 10], то (л/х, 2х) е R[0, 10] и при любом разбие-
разбиении П сегмента [0, 10] и произвольном выборе точек ?; 6 [a;,-, x;+i] получим
, lim 5ПBХ)), где 5П(
' i=0 t=0
Разбивая сегмент [0, 10] на п равных частей и полагая ?, = х, = г'^-, получим
>=0
(приняв во внимание, что Дя, = —).
/ ч П—1 ?
Рассмотрим числовую последовательность (гп) = ( —), где хп = ^ л/«, Уп = »>2. Так
1„+1 - хп ,. у/п ,.
lim = Inn 5 — = lim
как существует
li
то, согласно теореме Штольца, существует
з 20
lim ,S'n(V^) = 10 2 lim zn = —
((П)^0 n —оо 3
10
io 2"-2^ ,. 10 210-2V 210-l
и bn то
n е,„, io 2"-2^ ,. 10 2-2V 2-l
Поскольку ,ЬПB- J = — • —io и bin — • —^ = —; ,
2ТГ-1 n-»oo П Л— In 2
2» -1
210 - 1
d(n)-o "v > In 2 •
Следовательно, 1= (^-Vw, 2]°~' j. >
l
82. Вычислить I = / f(x)dx, где
1 1
^ l' ^/A _ 2ax + a2)(l - 2bx + b2)
0 < a < 7Г, |a| < 1, |6| < 1, ab > 0.
Согласно формуле B), п. 3.1, имеем
\ I хг — 2х cos а + 1 /
dx
- 2ax + a2)(l - 2bx + b2)

294
Гл. 4. Определенный интеграл
поэтому интегрирование вектор-функции f на сегменте [—1, 1] сводится к вычислению двух
определенных интегралов числовых функций.
Очевидно,
1 1
_ I dx _ f d(x-cosa) _ 1 / х — costvNI1 _
J x2 — 2icostv + l J (x — cos aJ + sin2 a sin a \ sin a /|-i
-l -l
1 / 1 — cos a 1 + cos a\ 1/ / a\ f aX\ ж
= -. arctg : h arctg : = arctg tg -I + arctg ctg - II = —: .
sin a \ sm a sma / smnV \ 2) \ 2)) 2 sm a
В интеграле
h =
dx
-i
a 1
- 2ax + a2)(l - 2bx + b2)
b 1
1
2-fab J
dx
-l
где A= — + —, В = - + —, произведем замену, полагая у/{А — х)(В — х) = t(A — x). Тогда
получим2 1а 2 2Ь
= _L /
dt
t2 - 1
In
t - 1
|b+l | P?
I a + l I V Ь
Окончательно имеем
Ь-1
a — I
b+l
a+l I V Ь
In
1 . l + Val
In
83. Вычислить 1=1 {f{x)> &{x)) d? i
где
f
^ Поскольку g(i) = v'(z), где v(i) =
то, согласно формуле (З), п. 3.1, получим
2, earctgI), f (x) =
x
I = (t(x), v(x)>|; - J{f(x), v(x)> dx = Л/l + x' In (x + x/l + x2) + ^^
0
7 v+ci+*»>f/x
7Г 1
^7=-l- / — Tdx.
V2 ^ (l + x2M
Полагая в последнем интеграле arctg x = t и интегрируя по частям, находим
7Г
1 I
/ea.rctgi у gt
з- йг = / е cos tdt = — (cos t + sin t)
0 v / 0
Окончательно получаем I = л/21п (l + л/2~) — -. >
l
84. Вычислить 1= /[f(a;), g(*)]rfa;, где f(x) = (x, x2, x3), g(x) = (ex, e2x, e3x).

§ 3. Интегрирование вектор-функций 295
/ 2а; За; \
Так как g(x) = v'(x), где v(x) = lex, ^-, ^—), то согласно формуле D), п. 3.1, имеем
1
I = [f (x), v(x)]|1_1 - J[f(x), v(x)] dx = [f A), v(l)] - [f (-1), v(-l)] -
+ к I - / е2х dx - 2 I xex dx
\ J J
Вычисляя интегралы и принимая во внимание, что
(l)]-[f(-l), v(-l)]=i(|sh3-ch2) +j ^2chl-|ch3) + k(ch2 - 2sh 1),
окончательно получим
sh3 сЬЗ + 2
где i, j, k — орты осей координат. >
ЬЗ + 2ЫбЫ + 12~Л + k (ch 2 - - sh 2 + 4ch 1 - 6sh
7Г
85. Вычислить /= / z(x) dx, где z(x) = eI(cos2 x + г sin2 x).
о
¦4 Применив формулу A), п. 3.2, получим
/ ex(l + cos2x)dx +i / eI(l -cos2x)dx I .
J J J
/
о
Интегрируя по частям, находим
I = -(e^fl + cos 2x + гA - cos 2x))
2
о о
Поскольку
7Г Л1
+ 2A - i) / ex sin 2ж das) = e" - 1 + A - i) / e1 sin 2x <ix.
TV TV
fexSm2xdx = \m f eA+2l)l dx =
l+2i
о о
9 7Г -i
то / = e" — 1 + (i — l)(e7r — 1)— = C — 2г). >
5 5
2тт
OC тт r I mx —imx i I 0, есЛИ 1П ф П,
8о. Доказать, что 1=1 ее dx = { ' г '
I I 2тг, если т = п.
о
¦4 Применяя формулу Эйлера, получим
е1"^"1 = е1{п-т> = cos(n - т)х + isin(n - т)х.
Если т = п, то em:l:e-im:r = \^ следовательно,

296
Гл. 4. Определенный интеграл
Если т ф п, то
I — I cos(n — in)x dx + г / sin(n — т)х dx = sin(n — т)г| + icos(n — m)x\ = 0.
о о
l
87. Вычислить 1=1 A(x)dx, где
an (x) ai2(x
a,2i(x) a,22(x
a,2i(x) = x3 {/l +x2, a22{x) = ^ °i ' n , 0 < z < 1.
/2 + cos 2ж
Согласно формуле A), п. 3.3, имеем
<i\\\x)dx J ai2{x)d,x
A(x)dx= | o,
J a2i(ijaa; J агг!,*)"*
о о
и решение примера сводится к вычислению четырех интегралов.
Интегрируя тождество . г+ ' 2 = ^^у — ^—, находим
1
/ an (г) dx = I arctg x -= arctg —-= J
о
Поскольку д4.3д2+2 ~ ^5Т7 ~ 7^+2 и xdx = \d{x2), тс
7Г 1
d(x2) \ _ 1 х2 + 1
х2 + 2 I ~ 2 г2 + 2
1,4
Так как х3 dx = \х2 d(\ + х2) = ?(A + г2) - 1) d(l + ж2), то
Ja2l(x)dx=1-J((l + x2)-i-[\+x*)
Принимая во внимание тождество 2 + cos 2а: = 3 — 2 sin2 x, находим
siax) _
о о
Окончательно получаем
I =
-. arcsin I 1 / — sm x
= —— arcsin
— sin I
3 j

§ 4. Несобственные интегралы 297
Упражнения для самостоятельной работы
Вычислить следующие интегралы:
63. /f(x)dx)f(x)=(^T, ^А 64. fA(x)dx,
1 ¦ , .
cos5 ж-y/sin х
sin scos" х
2
и \ у/2=х 1+cos2*
2 / ^7 \
65. fA(x)f(x)dz,A(x)=[ VX \ , f(x) = (In2 x, arctgx).
1 \ * х J
1
66. /(f(x), g(x))dx, f(x) = (i3, 1п(х + vTTI5)), g(x) = (e-^2, 1).
§ 4. Несобственные интегралы
4.1. Несобственные интегралы первого и второго рода.
Определение 1. Пусть J — [о, Ь[ — полуинтервал числовой прямой К, причем b может
быть символом +оо, а функция f : J —> R интегрируема на любом сегменте [а, Ь1] С 3 ¦
ь1 ь-о
Если существует конечный предел lim Jf(x)dx, то его обозначают символом Jf(x)dx,
а а
если SgM, a символом J f(x)dx, если Ъ = +оо. В этом случае говорят, что функция f ин-
ь1
тегрируема в несобственном смысле на J, a lim f f(x)dx называют несобственным
(или обобщенным) интегралом функции f на J (первого рода, если b = -\-oo, и второго
рода, если b € R).
ь
Определение 2. Если J =]о, Ь], f : J-^Ш и если lim f f(x)dx существует и конечен,
а'-.а + Оа,
Ь Ь
то будем обозначать его символом J f(x)dx, если а ? R, или символом J f(x)dx, если
а+0 —оо
а = —оо.
У ь-о
Определение 3. Если lim J f(x) dx = J f(x)dx существует, то говорят, что не-
Ъ1 —>Ь—О
а а
6 — 0 +(Х>
собственный интеграл J f(x)dx или J f(x)dx сходится (существует). Если этот предел
а а
Ь —0 +оо
не существует ('или бесконечен), то говорят, что интеграл I f(x)dx или I f(x)dx pac-
а а
ходится (соответственно расходится к оо).
ь-о
Теорема (критерий Коши). Интеграл J f(x]dx сходится тогда и только тогда, когда
а
х2
I f(x) dx —> 0 при Х\ —> Ъ — 0 и Х2 —> b — 0.
4.2. Абсолютная сходимость.
Ь-0
Определение 1. Если интеграл J \f(x)\dx сходится, то говорят, что интеграл
Ь0
J f(x)dx абсолютно сходится.

298 Гл. 4. Определенный интеграл
Ь-0
Если / : [а, Ь[—<¦ Ш — неотрицательная функция, то сходимость интеграла J f{x)dx
а
означает его абсолютную сходимость.
х
Пусть f(x) ^0 Vi 6 [а, Ь[, f(x) jt о. Тогда функция F:ih f f(t)dt, а ^ х < Ъ, воз-
а
Ь-0
растает вместе с х, а интеграл J f(x)dx существует тогда и только тогда, когда множество
а
J f(t)dt > ограничено сверху на полуинтервале [а, Ь[.
а J
Ь-0
Если же f(x) ^ 0 Vi ? [а, Ъ[ и интеграл J f(x) dx не является сходящимся, то интеграл
а
Ь-0
f f(x)dx = +оо.
а
Ь-0
Если интеграл J f(x) dx сходится, то будем писать
ь-о
/
f(x)dx < оо.
Определение 2. Всякий сходящийся несобственный интеграл, абсолютно расходящий-
расходящийся, будем называть условно сходящимся.
Заметим, что если / € R[a, Ъ], то
ь-о ь ь
J f(x)dx= I f(x)dx= f f(x)dx.
a a a + 0
4.3. Алгебраические свойства несобственных интегралов.
1) Пусть / : [а, 4[-»Ми сужение функции / на любой сегмент [а, Ь'] С [а, Ь[ интегрируемо
по Риману на нем. Тогда функция af, a = const, интегрируема на [a, b'] Vtv e R.
Ь-0 х
Следовательно, если 3 J f(x)dx= lim f f(t) dt, то
a a
b-0 b-0
3
/ af(x)dx = a I f[x)dx.
2) Пусть / : [a, b[—*¦ R, g : [a, 6[—> R — функции, сужения которых на любой сегмент
[а, Ъ'] С [а, Ъ[ интегрируемы по Риману на нем. Тогда атим же свойством обладает и сумма
¦ь—о ь—о
/ + </> следовательно, если существуют интегралы J f(x)dx и J g(x) dx, то
a a
lim (f(t) + g(t))dt= lim f(t)dt+ lim g(t)dt,
x^b-0 J x^b-oj x-b-oj
a a a
в силу чего
t—О Ь—О Ь—О
f (f(x) + g(x))dx= f f(x)dx+ f g(x)dx.
a a a
Таким образом, множество Е функций / : [a, &[—<¦ R, интегрируемых по Риману на всяком
ь-о
содержащемся в [а, Ь[ сегменте [а, Ь'] и имеющих сходящиеся интегралы J f(x) dx, образуют

§ 4. Несобственные интегралы 299
Ь-0
векторное пространство над полем К, а отображение / i-»- J f(x)dx пространства Е в К
а
есть линейная форма.
4.4. Замена переменной в несобственном интеграле и формула интегрирования по
частям.
ь-о
1) Пусть / : [о, Ь[-* К, / 6 С[й, Ь[, и / f(x)dx < со. Пусть [а, /?[ — другой полуинтервал
а
из К, причем а, а ? R, но /? и 6 могут быть как конечными, так и бесконечными. Пусть
функция д : [а, /?[—*¦ R возрастает на полуинтервале [а, /?[ и имеет на нем непрерывную
производную д' всюду, за исключением счетного множества точек, и, кроме того,
</([«, /*[) С [а, Ь[, д(с) =а, д(р - 0) = Ъ - 0.
Тогда справедлива формула замены переменной в несобственном интеграле
Ь-0 /3-0
I f{x)dx= J f(g(u))g'(u)du. A)
2) Пусть / ; [а, Ь[-+ R, (/ : [а, Ь[^ R, /, (/ 6 С^На, ^[» и а — конечное число. Тогда,
применив формулу интегрирования по частям на сегменте [а, х] С [а, Ь[, получим
X X
j f(t) g'(t) dt = f(x) g(x) - /(a) g(a) - J f'(t)g(t) dt.
B)
Если при ж —> Ь — 0 любые два из трех членов равенства B) имеют конечный предел, то
и третий член этого равенства имеет предел, поскольку произведение /(а) д(а) определено.
ь—о ь—о
Если, например, существуют интегралы J f(x)g'(x)dx и J f'(x)g(x) dx, то существует
a a
произведение /F — 0) д(Ъ — 0).
ь-о
Если же существуют интеграл J f{x)g'(x)dx и произведение /F — 0) д(Ь — 0), то суще-
t-o
ствует и интеграл J f\x)g{x)dx.
а
В каждом из рассмотренных случаев имеем
6—0 о —U
I f(x) д\х) dx = f(b - 0) д(Ъ - 0) - /(a) c/(a) - / /'(*) с/(х) dx.
C)
Формула C) называется формулой интегрирования по частям несобственных интегра-
интегралов.
4.5. Случай внутренней особой точки.
Пусть функция / : [а, 6]\{с} —> R, где с g]a, Ь[, имеет интегрируемые по Риману сужения
на любые сегменты [а, а'] С [а, с[ и [с', Ь] с]с, 6]. Тогда полагаем
ь с-о ь
f /(*) dx =' / /(*) dx + / /(х) dx, A)
a a c+0
если каждый из интегралов, входящих в правую часть A), существует, и будем называть
несобственный интеграл сходящимся.
Если хотя бы один из этих интегралов не существует, то говорят, что несобственный
интеграл расходится.

300 Гл. 4. Определенный интеграл
4.6. Признаки сравнения и признаки Абеля и Дирихле.
1) Если / и у — неотрицательные функции, определенные на полуинтервале [а, +оо[ и
интегрируемые на любом сегменте [а, х] С [а, +оо[, примем f(x) ^ </(*)> то
X X
[ /(*) dt sC f
(j(t)dt, а ^ х < +оо,
+ ОО + ОО
и из сходимости интеграла J g(x)dx следует сходимость интеграла J f[x)dx, а из расхо-
а а
+ оо +оо
димости интеграла J f(x) dx следует расходимость интеграла J д(х) dx.
а а
2) Пусть / : [а, +оо[—*• К — интегрируемая по Риману на любом сегменте [а, Ъ'] функция,
бесконечно малая при х —>¦ +оо, того же порядка, что и функция х н-»¦ —, а > 0. Тогда
+ ОО
J f(x)dx сходится при »>1 и расходится при а $С 1.
а
3) Пусть [а, Ъ[—> R — интегрируемая по Риману на любом сегменте [а, Ь1] С [а, Ъ[ функция,
имеющая при х —> Ь — 0 тот же порядок роста, что и функция х ь-*• Л , А > 0. Тогда
ь-о
J f(x)dx сходится при А < 1 и расходится при А ^ 1.
+
Теорема (признак Абеля). Пусть f : [а, +оо[^ R, д : [а, +оо[—*¦ М, / f(x)dx cxodum-
а
+ ОО
ся, а функция g монотонна и ограничена. Тогда интеграл J f(x)g(x)dx сходится.
а
Теорема (признак Дирихле). Пусть f : [а, +оо[—> R, g : [а, +оо[—» К и функция f
X
имеет ограниченную первообразную х \—»¦ f f(t)dt, а ^ х < +оо, а функция g монотонно
а
стремится к нулю при ж —*¦ +оо. Тогда интеграл J f(x)g(x)dx сходится.
а
4.7. Главное значение расходящегося несобственного интеграла.
+ 00
Пусть /:1^Ви интеграл J f(x) dx расходится.
— со
Если функция / интегрируема по Риману на всяком сегменте числовой прямой и если
А
существует lim / f(x) ^х, то его называют главным значением в смысле Коши расходяще-
гося интеграла и обозначают
+ 00
V.
— oo —A
Ь
+ 00 A
'• P- / f(x)dx= lim / f(x)dx.
J A^ + oo J
Пусть / : [a, b]\{c.} —>¦ R, с €]a, b[, и интеграл J f{x) dx расходится.
a
c-c Ь
Если при любом достаточно малом е > 0 существуют интегралы J f(x)dx и J f(x)dx и
a c+e
существует
Ь \ Ь
(
f /(*) dx + f f(x) dx = v. p. / f(x) dx,
c+e

§ 4. Несобственные иитегралы 301
то его называют главным значением в смысле Коши расходящегося интеграла.
Вычислить следующие несобственные интегралы:
I. In = f COS
88. In = / cos Inx In cos x dx.
о
•^ Согласно определению 1, п. 4.1, имеем
X
In = lim / cos 2nt In cost tit.
Применим формулу интегрирования по частям к интегралу
х
[
= I cos2ntln cost dt,
о
полагая cos 2ntdt = dv, In cost = и. Тогда получим
X
/„ > (x) = -— sin 2nt In cos t H / sin 2nt tg t dt =
о
x
1 In cos x 1 f cosBn — l)t — cosBn + l)t ,,
^ — . 4- — / ^ ^~- — at.
2»t (sin 2nx)~x An J cost
0
Аналогично тому, как было показано в примере 60, запишем
'" Ч* ^ * 1
— =2> (-1) cos2(n-fe)t + (-l) ,
fc=i
= 2 ^(-l)* cos 2(n - (it - l))t + (-1)".
k=l
Следовательно,
t_i sin 2(n — к)х 1
1) -^
Переходя к пределу при х —> — — 0, получим
г _. / ^п-1 Т , 1 ,:... Ь COS X
»-» JL
+ lim
4 2n x_5_o -2j»(sin2na;)-2cos2nx
х(х + 1)...(х + п)ш
1
•^ Поскольку ,х .—. . < р-, 1 ^ ж < +оо, то, согласно признаку 2), п. 4.6, интеграл
In сходится, так как
/
4

302 Гл. 4. Определенный интеграл
Согласно определению несобственного интеграла, имеем
In = lim / -, -^— = lim ii^tx).
Разлагая правильную дробь ;. . l ,t,n>. на сумму простых дробей, находим
1 Ah (-1)* _ kC*
t + k' Д * ~ fc!(n - Jfc)! l ; n! '
Следовательно,
Так как сумма биномиальных коэффициентов С*, стоящих на четных местах, равна сумме
биномиальных коэффициентов, стоящих на нечетных местах, то
lim
'"* °° k=o
в силу чего lim In J~[ (x + k)^1^ G" =0.
11
Таким образом, 7„ = ^ J] (-l)fc+1C* ln(l + it). >
-f oo
nn T f -axcosBm — l)x
oU. Вычислить Ym = / e. ^ — ax a > 0.
j cos ж
0
< Функция /: in e-«*cosBm-i)^ ^ ^4^^ i fc = f + fc?T, Л ? Zo, имеет особые то-
iKH
x/c. Поскольку существует lim /(г) = ( —1) Bm — l)e V2 / , то функция t
0 ^ t < +oo, где
)m+1BtB-l)e-e(f + l"r)
f(i), если t
()
интегрируема на любом сегменте [0, х], х > 0.
Так как множество {хк} имеет лебегову меру 0, то
; = / F(t) dt,
0
поэтому Im = lim jF(t)dt. На основании решения примера 60, имеем
Следовательно,
I F(t)dt = {~\)'n-1 \l " j +2^(-l)"~J f e~at cos 2(m-n)t dt.

Поскольку е at cos 2(m — n).
~at cos2(?n- ?t)idt = Re
4. Несобственные интегралы
= Ree(-a+i2(m-n»', го
(-a + t2(m-n))t
303
= Re
a2 + 4(m — nJ
„—at
— a + i 2(m — ?t)
(cos 2(m — ?t)t + ism 2(m — «)<)( — я — i2(m — n))
— n) sin 2(m — ra)t — a cos 2(m — n)
axB(m — ?t)sin 2(m — n)x — a cos 2(m — n)x) + a).
— ?^)
a2 + 4(m - ?t)
Таким образом,
Im = lim ( (-l)m"
a2 + 4(m - nJ
x (e axB(m — n) sin 2(m — n)x — a cos(m — n)x) + a) J =
_ (-1)-1 ^ (-1)" _ (-1)
~" a Z^ a2 + 4(m — nJ a
n=l v j—i
+ 00 +00
91. Доказать равенство / f lax-\—I dx = — I f (y x2 + 4ab) dx, где a > 0 и 6 > 0,
J \ x) a J
2 i 4,2 ¦
о о
предполагая, что интеграл в левой части сходящийся.
+ 00
J
+
Обозначим / = J f(ax -j- -) dx и произведем замену ах + - = t, предварительно
представив / в виде / = /i + /г, где
V a +oo
/i = / / (ax + -I ds, /2 = / /(aj; + -)dx.
J \ x) J \ x)
После замены переменной получим
2V/ab
h~ 2a J f{t)V~W^ab
+ OO
dt,
- 4ab
dt,
+ OO
-|-OO
=- f -ДШ
/
¦4a6 a
2V/ab 2V/ab
Полагая в интеграле \Jt2 — 4ab = z, имеем
+ 00
+
1 f
= - /
f(\/z2 + 4ab)dz. >
+ oo
92. Если интеграл / /(г) dx сходится, то обязательно ли /(х) —>• 0 при х —> +оо?

304 Гл. 4. Определенный интеграл
+ 00
•^Необязательно. Рассмотрим, например, интеграл Френеля 1= J sinx2dx. Произведя
в нем замену х2 = t, получим
+ 00
1 / sin t ,
=-J -?dt = Il
+00
sin t
+о
sin t
+0
Поскольку lim —¦=¦ = 0, то I\ существует. Интеграл /г сходится по признаку Дирихле,
X
поскольку —7= 1 0 при t —*• +оо, а функция х \~* fs'mtdt = cos 1 — cos ж, 1 ^ х < +оо,
1
ограничена числом 2 Vs €]l, +оо[. Следовательно, / сходится, а функция х t-t sin x2, 0 ^
х < +оо, не имеет предельного значения при х —+ +оо.
+ оо
Рассмотрим также I = J x sin ж4 da; и произведем в этом интеграле замену х2 = t. При
о
+ °°
этом получим сходящийся интеграл / = - J sint2 dt. Вместе с тем функция х i—> г sin ж4,
+ оо
О ^ х < +оо, не ограничена при ж —+ +оо. (Следовательно, несобственный интеграл f f(x)dx
а
может сходиться и в случае, когда функция / не ограничена при х —* +оо. >
+ 00
93. Доказать, что если интеграл / f(x) dx сходится и / — монотонная функция, то
fix) = о I — ) при x —* +oo.
\x )
M Из сходимости интеграла следует, что |/(ж)| —+ 0 при х —> +оо (в противном случае
интеграл расходился бы, так как функция / в силу монотонности должна быть знакопосто-
янной при всех достаточно больших х, поэтому функция х
}f(t)dt
, а ^ х < +оо, была
а
бы неограниченной при х —> +оо). Таким образом |/| — монотонно убывающая функция.
Поскольку интеграл сходится, то для него выполняется критерий Коши:
Ve > О ЗЛ > а : Van > А Л \/х2 > А
f(x)dx
< е.
Фиксируем произвольное хо > А и рассмотрим при х > х0 интеграл
х
Jf(t)dt.
Так как |/| — монотонно убывающая функция, то \f(x)\ ^ |/(яо)| при х > Хо, поэтому
\f(x)\(x-xQ)<
а:
1
f(t)dt
< е.
Поскольку lim жо|/(ж)| = 0, то из последнего неравенства следует, что lim xflx) — 0, т. е.
X—* + оо :г^+оо
f(x) = о ( — ) при х —> +оо. >
94. Найти представление ^-функции Римана с помощью несобственного интеграла.
М В примере 21, гл. 3, показано, что

§ 4. Несобственные интегралы 306
Если А > 0, то . *
+ ОО
1
Исследовать на сходимость несобственные интегралы:
95
2
Из неравенства Ых < х — 1, 1 < х < 2, следует неравенство (In х) > (х — I), поэтому
2 2
dt f dt
Так как lim In -—^ — +оо, то интеграл J -^ расходится, следовательно, согласно пункту
4.5, интеграл / — расходящийся. >
96. / =
¦4 Сравним в правосторонней окрестности точки х = 0 подынтегральную функцию с
функцией f : х 1-^ ~, О < х < ~, i < А < 1, рассмотрев предел
,. In (sin a;) I In (sin ж) ctgz
lim —v _ ¦ : — = lim —^ = lim 2 т- —
i —+0 Jx X* .г-^ + 0 i-Л x —+ 0 n x _A-i
г 2 (i-'V1 2
= lim y, r = lim jt 1— = ^
(так как А + j > 1).
При x —* +0 подынтегральная функция имеет порядок роста ниже, чем функция /. Так
как интеграл
+о +о
сходится, то, согласно признаку сравнения 3), п. 4.6, интеграл / сходящийся. >
97. / =
х''\пчх'
1 + 0
< Произведем в интеграле замену переменной, полагая In ж = t. Тогда получим
+ <5О
-1
+ 0
Представим / в виде I = h + I2, где
1 +оо
h = I ^^ dt, h =
+0

306 Гл. 4. Определенный интеграл
еA—p)i
При t —> +0 функция t i-> ———, 0 < t ^ I, g > 0, pgR, имеет тот же порядок роста,
что и функция ti-+ —, 0<t^l, а при q ^ 0 интеграл 7i не является несобственным.
Следовательно, согласно признаку сравнения 3), п. 4.6, интеграл h сходится, если q < 1,
и расходится, если q ^ 1.
При t —>• +оо функция t i—>- ^—^—, 1 ^ t < +оо, р > 1, убывает быстрее любой функции
вида t >-+ —, 1 ^ t < +оо, « > 1, так как в этом случае при любом q 6 R имеем
lim : — = 0,
t-»+oo V> ta
следовательно, интеграл 7г сходится при р > 1. Если р ^ 1, то 7г расходится.
Таким образом, интеграл 7 сходится лишь при q < 1 и р>1. >
98. 7 =
+о
•^ Представляя 7 в виде I = h + h, где
1 +ОО
/ sin2 x f sin2 ж
7i = / (fa, h= I dx,
J x J x
+ 0 1
видим, что интеграл h существует, поскольку 3 lim ^r~ =0.
Записав 7г в виде
+ 00 / / X X _
h — - / dx = - lim / / —¦— dt
1 / 1 - cos 2x 1 I / / й< / cos
— - I и = - lim / /
2 J x 2 U-+00 \J t J t
+ 00
cos 2л:
и приняв во внимание, что lim f — = lim In ж = +оо, а интеграл Г cos da; сходится по
I — +OO J ' Ж-. + ОО j ^
признаку Дирихле, делаем вывод о том, что интеграл 7г расходится.
Следовательно, интеграл 7 расходящийся. >
+ ОО
99. 7= / dx .
J хР + хч
М При р = q, очевидно, интеграл 7 расходится, поэтому исследуем его при р ф q.
Пусть р < q. Представляя 7 в виде 7 = 7i + 72, где
1 +00
7i
+ 0 1
исследуем интегралы 1\ и 7г в отдельности.
Поскольку хР+хЧ = хрцл.хЯ-Р) и я9~р —+ 0 при х —+ +0, то подынтегральная функция в
7i имеет при р > 0 тот же порядок роста, что и функция ik -, 0 < х ^ 1, р > 0. Если
р ^ 0, то интеграл 7i существует.
Следовательно, согласно признаку сравнения 3), п. 4.6, 7i в рассматриваемом случае
сходится, если р < 1, и расходится, если р~^\-
Исследуем 7г, представляя подынтегральную функцию в виде
1 +00
/A f I
~TJ—4' /2= /
При х —+ +оо f(x) = О (^j), следовательно 7г сходится при }>1и расходится, если q ^ 1.
Таким образом, если р < q, то 7 сходится при всех р < 1 и g > 1.
Если р> q, го, очевидно, исследуемый интеграл сходится при всех р > 1 н g < 1.

§ 4. Несобственные интегралы 307
Оба рассмотренных случая легко объединяются в один: 7 сходится, если mm{p, q} < 1,
max{p, q) > 1. >
100
+ oo
. I = / "* . dx, где Рт(х) и Pn(x) — взаимно простые многочлены степеней
J "п\х)
+ 0
соответственно m и п.
М Если многочлен Рп(х) имеет действительные нули х = Xi на интервале ]0, +оо[, то
интеграл расходится, согласно признаку 3), п. 4.6, так как при х —>• xi подынтегральная
функция будет иметь одинаковый порядок роста с функцией
(здесь S\xt, S) — ^-окрестность точки ж;).
Если же многочлен Рп(х) не имеет действительных нулей на интервале ]0, +оо[, то при
х —> +оо ртл\ = О ( n_m ) и интеграл 7 будет сходиться согласно признаку сравнения 2), п.
4.6, если п — т > 1, и будет расходиться при и — m ^ 1. >
Исследовать на абсолютную и условную сходимости следующие интегралы:
+ ОО
101.
1.7=/" sin ж
+ 0
Представим 7 в виде 7 = 7i + 12, где
1 +00
+ 0
Рассмотрим при 0 < «1 < »2 < 1 интеграл
х2
/sin i
/= / —dx.
Так как 0 < ^^- < 1 при xt ^ х ^ Х2, то 0 < I < х2 — Xi, поэтому I —> 0 при xi —* О,
—<¦ 0, в силу чего интеграл /i сходится согласно критерию Коши.
Поскольку
/ sin t dt
2 Vs б]1, +оо[, а функция ih j, 1 ^ х < +оо, убывая,
стремится к нулю, то интеграл li сходится по признаку Дирихле.
Из сходимости интегралов 1\ и 12 следует, что интеграл 7 сходится.
Из неравенства |sins| ^ sin2 ж, справедливого Vj; ? R, решения примера 98 и признака
сравнения 1), п. 4.6, приходим к выводу, что интеграл
sm ж
! dx
х
1
расходится, следовательно, I — абсолютно расходящийся интеграл. >
+ °° . /
= [s^±±
J xa
+ 0
-4 Пусть 7 = h + h + h + h 1], где
+oo
f
1 +oo 1 x +co
/sin x cos - f sin ж cos - fcosx sm - /" cos x sin -
^—i dx,- h = / ^ <*ж, 7з = / ^ rfx, 74 = / j—a- rfx,
+0 1 +0
') Такое представление возможно для тех значении параметра а, при которых интеграл
существует.

308 Гл. 4. Определенный интеграл
а затем произведем в интегралах 1\ и /з замену - — t. Тогда получим
+ ?°
С ros t sin —
h
—. 1 т^ ^
/cos t sin - f sin t cos —
из чего следует, что интегралы /i, /4 и /2, /3 однотипны. Поэтому достаточно исследовать
интегралы /г и h и результат исследований автоматически перенести на интегралы h и /з.
Поскольку lim cos — = 1, то Эхо > 1 •'
Х-.+ ОО X
Vz > Z0 =>• - < COS - < 1, < 2- < ,
1
cos —
поэтому —^- | 0 при х -* +оо и « > 0.
Функция х и-* sin ж, 1 ^ х < +оо, имеет ограниченную первообразную Vz € [1, +оо[.
Таким образом, при а > 0 интеграл /г сходится по признаку Дирихле.
Покажем, что /г расходится при а ^ 0. Пусть задано произвольное 0 < е < 1. Положим
/? = —а и возьмем такое п 6 N, чтобы выполнялось неравенство cos- > - при х ^ 2пк.
Bп+1)тт
Применяя первую теорему о среднем к интегралу J xfi sin x cos i йж, получим неравенство
2П7Г
Bп+1)тг
jk- i
/xp sin x cos — dx
X
2wr
= 2?,Z cos
из которого, согласно критерию Коши, следует расходимость интеграла /г при а ^ 0, по-
поскольку Veo > 1 Зи 6 N такое, что 2пъ > xq. Следовательно, /г сходится лишь при а > 0.
Из проведенных выше рассуждений следует, что h сходится лишь при 2 — а > 0, т. е. при
а<2.
Таким образом, интегралы 1ч и /з одновременно сходятся, если 0 < (V < 2.
sin - 1
Исследуем интеграл 1± с помощью признака Дирихле. Так как 0 < — < —-гг при всех
- ха xa+L
х
х>1, « + 1>0,а функция х t-+ Jcostdt, 1 ^ ж < +оо, ограничена, то /4 сходится при
1
(V + 1 > 0, т. е. при а > —1. Следовательно, h сходится при а < 3, а оба интеграла сходятся
одновременно при — 1 < а < 3. Так как ] — 1, 3[П]0, 2[=]0, 2[, то интеграл / сходится при
О < а < 2.
Исследуем интеграл Ii на абсолютную сходимость. Из неравенств
1 - со.ч 2х _ sin2 x |sinzcosi| j
4xa ~ 2xa xa ^ xa'
выполняющихся при всех достаточно больших х > 1, следует, что 12 сходится абсолютно при
(V > 1, а при (v ^ 1 абсолютно расходится.
Следовательно, h абсолютно сходится, если 2 — а > 1, т. е. при а < 1. Поскольку
множества {а ? R : а > 1} и {« 6 R : « < 1} не пересекаются, то интегралы /г и /з не могут
одновременно абсолютно сходиться ни при каких общих значениях а ? R. Поэтому интеграл
/ абсолютно расходится. >
+ ОО
103. /= / x2cos(ex)dx.
о
Полагая в интеграле ех = t, получаем
+ O0

§ 4. Несобственные интегралы 309
Применив второе правило Лопиталя, находим
ln2t In* 1
km = 2 Inn — = 2 lim - - 0.
t—*+oo t t—*+oo t t—*+oo t
Следовательно, -^— [ 0 при t —> +oo.
Поскольку функция ж i-> J cost dt = sin ж — sin 1, 1 ^ x < +oo, ограничена, то, согласно
l
признаку Дирихле, интеграл / сходится.
Из неравенства -^-^lcos<| ^ ~[^ cos2 t, справедливого для всех t > 1, следует, что инте-
интеграл
-f ОО -J-OO +ОО
l
J t 2 J t ^ 2 J t
расходится, так как Г -^—^-dt= lim f\n2td(lnt)= liin -In3 x =+oo, а интеграл
cos 2t dt
сходится по признаку Дирихле. >
Найти следующие пределы:
104. lim [S2ii(ft.
l
Применив первую теорему о среднем к интегралу I(x) = J ^p- dt, получим
Пусть :сб]О, YIl[> где ? > 0 —произвольное, наперед заданное. Тогда cos?(- — l) > ^
следовательно, 1(х) —+ +оо при х —> +0. ,
Применив второе правило Лопиталя, имеем ,. .
г/ \ г// ч COS X
Иш М = Нш Ш. = lim Z^f = !. ^
1 A)'
105. lim ^
lim =. ¦ ¦ -
¦•—+0 In ^ • ,
При любом а > 0 интеграл J ^j- it сходится согласно признаку Дирихле. Поэтому
+ ОО _( J t
Г ^-— tZt = С, С = const, и lim -^ ; = 0. Следовательно,
lim -1-——: = lim j—.
S- + 0 111 -1 *~ + ° In -

310
Гл. 4. Определенный интеграл
Из неравенства 1(х) = I dt Jj е a(hxa — In z) следует, что lim I(x) = +00, поэтому,
J t x-.+o
согласно второму правилу Лопиталя, получаем
liln щ
*-+° In ^
л:
106. Доказать, что при х > О 31i ж = v. р. / -—.
+ о
1-е 2
¦4 При любых 0</<<1 и 0<е<1 существуют интегралы Ii — J ^, /г = / ^7, а.
При 0 < х < 2 справедливо разложение j-^ = —j- + - + О(х — 1), поэтому
lix = lim (In \t —
e~+0
+ 2
Если x > 2, то получим
dt
dt f dt
dt
107. Найти v. p.
•^ Квадратный трехчлен ]/ = x2 — 3i + 2 имеет действительные нули х\ — 1 и ж2 = 2,
следовательно,
+ оо 3 +оо
/dx _ /" dx f dx
x*-3x + 2 ~V' PJ x2 -3z + 2 + J г2 - Зг
= lim I In
?-.+0
-2
X -1
ln
з
2-м
ln
x-2\\3 \ t-.2
-j- lim In
X — 1
— 1
= - In 2 + lim
H-. + 0
] + lim b- = In-. >
1— H) 1- + 00 Ж — 1 2
Упражнения для самостоятельной работы
Вычислить следующие интегралы:
67. Г -^з". 68. Г ^=. 69. f
70.

§ 5. Функции ограниченной вариации 311
+ ОО +ОО +ОО
71. / e~"xcosbxdx, а > 0. 72. / е~ах sin Ьх dx, а > 0. 73. / ^з+fjjT, п 6 N.
п П П
О О
+ оо + оо
74. Г ,„гг,1^„, «с-fc2 >0. 75. Г e-axsin2n xrfx, a > 0.
()
" ~2
76. a) /i = /insin x dx; 6) I2 = /in cosx <2x.
' о о
Исследовать на сходимость следующие интегралы:
+ О0 + ОО 1 +ОО 7Г
77. Г ^Ц-. 78. Г —|^-з-. 79. f dx . 80. f д <*t2> rfx. 81. f
J l+i4 sin2 1 J l + x2sin2:r J eI-cosi J i+l J
0 ,0 0 0 0
7Г +00 +00 +00 / ] 1\
82. [!»»?? d*. 83. f ,fx .. . 84. Г Л"^. 85. f xne~V +^) dx.
J x J l-f(ln x)n J J
0 0 0 —00
+ 00
86. / sin(z+ i) ^§.
0
Доказать неравенства:
+ CO -f OO
87. — j < / C°2S °д dx < j ¦ 88. 0 < f e—;r da; < —y.
0 2
+ 00 _„ +00
20 ' 2П
89' w < / TTf55" dx < П + 5? • 90- fi < / I+f^ dx<^ + io-
1 0
+ 00 +00
91. 0 < Г e" dx < -, n > 1. 92. 1 - - f е~х" dx < 1 + -, n > 1.
J 71 71 J 71
1 0
1 1
93. Доказать, что lim fn2xn~1(l — x) dx ф / lim n xn (l-x)dx.
0 0
* +00
94. Доказать, что если интеграл J f(%) dx абсолютно сходится, то
о
lim / /(a;)|sina:|d2; = ^ / f(x)dx.
п^°° о "о
95. Доказать равенство
+0 о
96. Доказать, что несобственный интеграл / sin2 (ir (x + ^)) dx расходится.
о
Найти:
7Г
1 +оо 2тг
97. v. р. Г —р—, 0 < а < Ъ. 98. v. p. Г -^т. 99. v. p. f при а > 1.
*^ J а — bcosx' г J 1-х3 ^ J 1— а cos a: r
b
0 0
§ 5. Функции ограниченной вариации
Определение 1. Пусть f : [а, Ь] —> К, П — произвольное разбиение сегмента [й, Ь],
п — 1
Afi = /(x;+i) — f(xi), Vn(f;a,b)= ^|Д/,-|. ?исло Vn(/; a, 6) называется eapuayueu функ-
i=0
/ no разбиению П, а число V(/; a, 6) = sup{Vn(/; a, 6)}, гЭе точная верхняя грань бе-
{п}
рется по всем возможным разбиениям П сегмента [а, Ь], называется полной вариацией
функции / на сегменте [а, Ь].
Если V(f; а, Ь) < со, то говорят, что / — функция ограниченной вариации.

312 Гл. 4. Определенный интеграл
Определение 2. Пусть f : [а, Ь] —<¦ Rm, П — произвольное разбиение сегмента [а, Ь],
п — 1
Af; = f(xi+i) — f(xi), Vn(f; a, b) = Y^ l^1"»!* г^е | • | — евклидова норма в пространстве Rm .
i=o
Число V(f; а, Ь) = sup{Vn(f; а, Ь)}, где точная верхняя грань берется по всем возможным
{п}
разбиениям сегмента [а, Ь], называется полной вариацией вектор-функции f на сегменте
[а, Ъ].
Если V(f; а, Ь) < оо, то говорят, что вектор-функция f — функция ограниченной вариа-
вариации.
Теорема 1. Пусть f : [а, Ь] —<¦ Rm. Для того чтобы вектор-функция f была функцией
ограниченной вариации на [а, Ь], необходимо и достаточно, чтобы каждая ее компонента
fj, j — 1, т, имела ограниченную вариацию на этом сегменте.
Теорема 2. Если f : [а, Ь] —* R, g : [а, Ь] —> R — функции ограниченной вариации на
[а, Ь], то f -\-у и fg также функции огрщшченной вариации на [а, Ь].
Следствие. Если функции f и g монотонно возрастают на [а, 6], то f — у есть
функция ограниченной вариации на [а] Ь]: '¦
Теорема S. Пусть f : [а, Ь] —+ R'" — вектор-функция ограниченной вариации. Тогда:
1) V(f; а, у) = V(f- a, x) + V(f; x, у), если а^х ^у ^Ъ;
2) функция Vf : х к-» V(f; а, ж) непрерывна на [а, Ь], если f ? С[а, Ъ].
Теорема 4- Пусть f : [а, Ь] —+ R — функция ограниченной вариации на [а, Ь]. Тогда
существуют такие неубывающие функции р : [а, 6] —> R, q : [а, Ь] —>¦ К, что р(а) = q(a) = 0
и Vi 6 [а, Ь] выполняются равенства
f(x) - f(a) = р(х) - q(x), (I)
V(f;a,x)=p(x)+q(x). B)
Функции р я ij соответственно называют функциями положительной и отрицательной
вариаций функции /.
108. На примере функции / : [0, 2] —> R, где
. _ Г ж sin j, если 0 < ж <С 2,
•^^ = \ 0, * если ж = О,
убедиться в том, что непрерывная на сегменте функция не обязательно имеет ограниченную
вариацию.
¦4 Функция / непрерывна в области определения.
Пусть П = {О, 0^_ , 2>2 ... , -, -,2} — разбиение сегмента [0, 2]. Тогда полная вари-
еп —* 0 при п —+ оо, С — постоянная Эйлера. Следовательно, Vn(/; 0, 2) —> +оо при >г —* оо
и множество {Vn(/; 0, 2)} не ограничено сверху. >
109. Найти функции положительной, отрицательной и полной вариаций функции / :
i и 3i2 - 2хя, -2 ^ х ^ 2.
Найдем сначала функцию ж к-+ V(/; —2, ж), —2 ^ ж ^ 2, приняв во внимание, что
^-2,2].
Пусть П — произвольное разбиение сегмента [—2, ж], —2 ^ ж <С 2. Тогда
п—1 п—1
1 = 0 i = 0
(по формуле конечных приращений Лагранжа).
Следовательно, Vn(/; —2, ж) = Л'п(|/'|), где 5п(|/'|) — некоторая интегральная сумма
функции t н-> |/'(t)|, —2 ^ t ^ ж, в силу чего получаем
X
V(f; -2, х) = J\f
(t)\dt =
= <
-2
х
•- / /'(<) Л = -/(ж) + 28, если - 2 < а; < 0,
2
0
- / /'(<) Л + / /'(t) Л = /(ж) + 28, если 0 < ж < 1,
-2 0
0 1
- / /'(t) dt + J f'(t) dt- J f'(i) dt = 30 - /(ж), если 1 < ж

§ 5. Функции ограниченной вариации 313
Согласно формулам A) и B), имеем
{О, если - 2 < х < О,
/(х), если 0^1,
1, если 1 ^ х < 2,
{-/(г) + 28, если - 2 < х ^ 0,
28, если0<*<1, >
-/(г) + 29, если 1 < х < 2.
110. Пусть / : [и, li] -» К — функция ограниченной вариации на [a, b], р и q — функции
положительной и отрицательной вариаций функции /, a pi и qi — возрастающие на сегменте
[а, Ь] функции и f — pi — </i. Доказать, что
V(p; а, Ь) <; V[pi; а, Ъ), V{4; а, Ъ) < V(gi; а, Ь).
< Согласно теореме 4, функции р к дне убывают на сегменте [а, Ь] и р(х) ^ 0, q(x) ^ 0
Ух €]а, Ь], так как р(а) = (/(а) = 0.
Из формулы B) следует, что Ух G [а, Ъ]
р(х) = V(f; а, х) - q{x) 2 0, д(х) = V(f; а, х) - р{х) > 0,
следовательно, справедливы неравенства
g(x)^V(f;a,x), p(x) ^ V(f; а, х), а < х < Ь. A)
Поскольку / = pi — </1, то
V(/; а, х) = V(pi -gi;a,x), а ^ х < 6.
Рассмотрим при произвольном разбиении П сегмента [а, Ь] вариацию
Vn(/; a, b) = Vn(pi - </i; a, b) =
n-l
\—^ i
|pi(xi+i)-pi(x.)| < Vri(pi; а, Ь).
1=0
Тогда V(f; a, b) ^ V^(pi; a, b). Аналогично, V(f; a, b) ^ V[g\; a, b). Из монотонности функ-
функций p и </, а также из того, что p(a) = </(a) = 0, получаем, что
V(p; а, Ъ) = рF), V(95 а, Ъ) = </F).
Тогда из неравенств A) следуют неравенства
V(p; а, Ъ) = р(Ъ) < V(f; а, Ь) ^ V(Pl; а, Ь), V(g; а, Ь) = д(Ъ) < V(f; а, Ъ) < V(qv, a, Ь). >
111
X
. Пусть д е R[a, Ь], /(х) = / 'g(t)dt, g+(t) = max{</(t), О}, (/"(t) = min{</(t), 0}.
а
Доказать, что / — функция ограниченной вариации на [а, Ь] и что ее функции вариации
задаются равенствами
XXX
;a,x) = j\g{t)\dt, P(x) = jg+(t)dt, д(х) = J g~(i)dt.
а а а
¦4 Пусть П — произвольное разбиение сегмента [а, ж], а < х ^ Ь. Тогда, согласно опре-
определению вариации, получим
n-l
Vh(/; a, x) =
1 = 0
/
g(t)dt

314 Гл. 4. Определенный интеграл
где inf {g(t)} ^ (*, ^ sup
Следовательно, f \g\ dt ^ V(f; a, ж) ^ J\g\dt, а так как j 6 й[а, i], то и |<7| € R[a, b], в
- , N
силу чего V(f; a, x) = J |f/(t)| dt. По теореме 4 имеем
а
д; х
р{х) - q(x) = J g(t) dt, p(x) + q(x) = J \g(t)\ dt.
a a
Следовательно,
P(x)= \Jg(t)(\ + sgng(t))dt=Jg+{t)dt, q(x)= ^ jg(t)(sgn g(t) - 1) dt = jg~{t) dt. >
112. Пусть /:[«,/?] —> R — функция ограниченной вариации на сегменте [а, /3], a
функция f : [о, J] -> 1 удовлетворяет условию Липшица на сегменте [а, Ь], причем [а, Ь] Э
/([а, /?]). Доказать, что композиция F о f есть функция ограниченной вариации на сегменте
[<*, /»]¦
¦4 Функция F удовлетворяет условию Липшица на сегменте [а, Ъ], если существует такое
число L = const, что Vsi, X2 € [а, 6] =>• |-F(a;i) — F(x2)\ ^ X[a;i — жг|-
Пусть П — произвольное разбиение сегмента [а, /3]. Тогда получим
i=0 i=0
Из полученного неравенства следует, что композиция Fof имеет ограниченную вариацию
на сегменте [а, /?]. >
Упражнения для самостоятельной работы
100. Пусть / : [а, Ъ] —> К — функция ограниченной вариации на сегменте [a, b], а <р :
[а, Д-> I - монотонная функция и [а, Ь] Э ?>([«, /?])• Доказать, что композиция / о <р
является функцией ограниченной вариации на сегменте [а, /?].
101. Доказать, что полная вариация функции F : х н-> f f(t)dt, а ^ ж ^ Ь, / € Л [а, Ь],
а
равна
102. Доказать, что если функция х i—»¦ /(ж), а ^. х ^. Ь, имеет ограниченную вариацию на
сегменте [а, 6] и |/(ж)| > е > 0 Vs G [а, Ь], то функция х ь-+ тг^т, а ^ ж ^ Ь, также является
функцией ограниченной вариации на этом сегменте.
103. Вычислить: а) V (sin х; 0, 2п); б) У (cos ж; 0, 2тг).
104. Вычислить функции положительной, отрицательной и полной вариаций функции
х (-> [ж]- I, 0 ^ ж ^ 2.
§ 6. Приложение определенного интеграла к
решению задач геометрии
6.1. Длина дуги спрямляемой кривой.
Определение 1. Путем в Rm будем называть непрерывное отображение f : [a, b] ~*
Шт, [а, Ъ] С R.

§ 6. Приложение определенного интеграла 315
Определение 2. Если непрерывное отображение f : [о, Ъ] —> Rm биективно, то путь
будем называть дугой.
Определение 3. Следом дуги f : [а, Ь] —* Rm или кривой у называется образ сегмента
[а, Ь] при отображении f:
7 = {У € Rm : 2/, =/Дх), а^х^Ъ, j = l,m}.
Определение 4. Пусть f — дуга в пространстве Rm. Если f(a) = fF) u f(xi) ()
Эля любой пары различных точек xi и хг из интервала ]а, Ъ[, то кривая у называется
простой замкнутой кривой.
Определение 5. Кривая у спрямляема, если вектор-функция f имеет ограниченную
вариацию на сегменте [а, Ь], а длиной кривой у будем называть полную вариацию V(f; а, Ь).
Теорема. Если eeKviop-функция f : [а, Ь] —> Rm непрерывна на сегменте [а, Ь], то
кривая у спрямляема, а ее длина I может быть вычислена по формуле
= J\i\x)\dx, A)
где |f'(*)| У (
Рассмотрим частный случай теоремы, когда т = 2, а кривая у задана параметрическими
уравнениями х = <p(t), у = i>(t), a ^ t ^ /3. Тогда |f'(t)| = \/?>'2(<) + ^/2(<) и формула A)
принимает вид
ip'4t) + xl><2{i)dt. B)
Для случая m = 3, когда кривая 7 задана параметрическими уравнениями х — <p(t),
у = ф(г), z — х(<)> а ^ t ^ ^i ПРИ выполнении всех условий теоремы имеем
= f
В частном случае, когда кривая у в R2 представлена в виде /i(x) = х, /г(х) = f(x),
а ^. х ^.Ь, где / : [a, ii] -> R, / ? C'^'fa, 6], формула B) принимает вид ¦ : :>
Если же кривая 7 в!2 задана в полярной системе координат, т. е. параметрическими
уравнениями ¦ .
х = p(<p)cos<p, у = p{<p)sm<p, <po^<p^<pi, p : [<р0, tpj] -+ R+, p € CA)[v50, Vi]>
то формула B) принимает вид .. •
Ч>2
= J
E)
В частном случае, когда кривая в полярной системе координат задана в виде <р = ?>(р),
Pi ^ P ^ P2 , то в интеграле E) следует произвести замену переменной. После замены получим
следующую формулу:
р?
I = [ у/1 + (р<р>(р)I dp. F)

316
Гл. 4. Определенный интеграл
6.2. Вычисление площадей плоских фигур.
Определение 1. Криволинейной трапецией называется плоская фигура Ф, ограни-
ограниченная снизу сегментом [а, Ь] оси Ох, сверху — графиком непрерывной неотрицательной
функции / : [а, Ь] —> R, с боков — отрезками прямых х = а и х = Ъ (рис. 62).
Теорема 1. Криволинейная трапеция — квадрируемая фигура, а ее площадь Р вычисля-
вычисляется по формуле
I
Р= / f(x)dx.
A)
Если непрерывная функция / : [а, Ь] —> Ш меняет знак на [а, Ь], то J f(x)dx равен алге-
алгебраической сумме площадей криволинейных трапеций, расположенных над осью Ох и под
ней.
Если плоская фигура Ф ограничена снизу графиком непрерывной функции /i : [a, b] —* R,
сверху — графиком непрерывной функции /г : [а, Ь] —>¦ К, с боков — отрезками прямых х = а
и х = Ъ (рис. 63), то ее площадь можно вычислить по формуле
б
Р
¦/<
B)
Рис. 62
Рис. 63
Определение 2. Криволинейным сектором называют плоскую фигуру, ограниченную
двумя лучами, составляющими с полярной осью углы ip = a, ip = fi, и непрерывной кривой
у, заданной уравнением р = р{ф), р ^ 0, а ^ tp ^ f).
Теорема 2. Криволинейный сектор — квадрируемая плоская фигура, площадь Р кото-
которой можно вычислить по формуле
p
-У-
C)
Пусть Ф — односвязная область в К2, ограниченная гладкой замкнутой кривой у, задан-
заданной параметрическими уравнениями х = ?(t), у = уA)> to ^ t ^ t\ (кривая у называется
гладкой, если в каждой точке t сегмента [to, ii] функции х и у непрерывно дифференциру-
'2( '2
() @)
Предположим, что Ф — выпуклая ориентированная плоская фигура, обход границы кото-
которой совершается против хода часовой стрелки при изменении параметра t от to до fi. Тогда
площадь Р фигуры Ф может быть вычислена по любой из следующих формул:
P=-Jy{t)x\t)dt,
D)
Р= [ x(t)y'(t)dt,
E)

С. Приложение определенного интеграла
P=l-j{x(t)y\t)-y{t)x'{t))dt.
317
F)
Если фигура Ф не выпукла, но ее можно с помощью прямых, параллельных оси Оу, раз-
разбить на выпуклые части, то к каждой такой части применимы формулы D)—F). Складывая
полученные результаты, опять придем к формулам D)—F), справедливым для вычисления
площади всей фигуры Ф.
6.3. Вычисление объемов тел.
Определение. Пусть f : [а, Ь] —+ К, / <Е С[а, Ь]. Тело Т, образованное вращением вокруг
оси Ох. криволинейной трапеции Ф, ограниченной графиком функции f, отрезками прямых
х — а, х — Ь и сегментом [а, Ь] оси Ох, будем называть телом вращения.
Теорема 1. Тело вращения Т кубируемо и его объем можно вычислить по формуле
V
"I
f{x)dx.
A)
Рассмотрим тело Т, содержащееся между плоскостями х = а и х — Ь. Предположим, что
всякое сечение Ф(а:) тела Т плоскостью, перпендикулярной к оси Ох в точке х ? [а, Ь], есть
квадрируемая плоская фигура, площадь которой Р(х) нам известна.
Теорема 2. Если тело Т кубируемо, а функция Р : х >—<• Р(х), а «С х ^.Ь, интегрируема
на [а, 6], то объем V тела Т можно вычислить по формуле
V =
(x)dx.
B)
Найти длины дуг кривых у, заданных в пространстве R2:
113. 7 = {(х, у) е К2 : у2 = 2рх, 0 < i ^ ж0) j) > 0}.
¦4 Применим формулу D), п. 6.1, приняв во внимание симметрию множества точек
{М(х, j) 6 tJ : 0 ^ 1 ^ хо, у2 = 2рх} относительно оси Ох:
= (ty/p + P + p hl(t + sjp +
114. 7 =
В качестве неременной интегрирования возьмем у. Формула D), п. 6.1, принимает вид
i i
Л dy.
Следовательно,
l/U^H^H^ + T
115. 7 = {{х, у) €К2 : х = o(sht-<), y-a(clit- 1), 0 < t

318 Гл. 4. Определенный интеграл
¦4 Воспользуемся формулой B), п. 6.1, получим
х (t) = a(ch t — 1), у (t) = a sh t,
¦ 1) = 2a2(ch2t-cht) =
Следовательно,
T
Длину кривой вычислим с помощью формулы E), п. 6.1. Имеем
,, ,_ р sin <р
COS ifJ A -+- COS <?>L A + COS (рK 4 COS6 |- '
-Е / ^ -
~ 2 J cos3 f -
os' f ~ 2P7 cos^t
0 0 0
cos<(l -sin2*)
dz
—
dz f z2
-г2J
о
1
V5
= 2р
/ dz
7 l-
л/2;
Для вычисления длины кривой -у воспользуемся формулой F), п. 6.1, получим
3 3
118. Доказать, что длина эллипса 71 = {х = a cos<, у = b sint, 0 ^ t ^ 2тг} равна длине
одной волны синусоиды 72 = (у = с sin —, 0 < х < 2тгЬ} , где с = у а2 — Ь2.
1 Ь '

§ 6. Приложение определенного интеграла 319
¦4 Обозначив длины эллипса и одной волны синусоиды соответственно через 1\ и fe >
получим
2л- 2тт
'i = / \/x'2{t) + y'2(t)dt = /" V^2 sin2 t + b2 cos2 tdt,
о
2жЬ
h = [ \/l+y'2(x)dx = I J1 + ~ cos2 I rfx = '
о о
2Л-6 2тг
+ (a2-b2)cos2^<i (j\ = / a/«2 cos2 t + Ъ2 sin2 tdt
0 - , 0
(в интеграле произведена замена | = t).
Поскольку функции t н^ sin2 t, t t-+ cos2t, t G R, периодические, с периодом Г = тг, то,
согласно примеру 51, имеем
7Г 7Г
тг 2" 1
h -2 \/а2 sin2 < + Ь2 cos2 < rf< = 2 / V a2 sin2 t + b2 cos2 t dt = 4 / \/a2 sin2 t + b2 cos2 t Л.
о
Аналогично имеем
л/a2 cos2 t + b2 sin2 t dt.
Заменяя в последнем интеграле переменную по формуле |- — t = г, получаем
= / v a2 si
h = I v«2 sin2 z + b2 cos2 zdz = \\. >
о
Вычислить площади плоских фигур, ограниченных графиками следующих функций:
119. ?! + ? = !, М<«-
а2
¦4 Плоская фигура является эллипсом с полуосями х = а и х = Ь. Используя симметрию
точек эллипса относительно осей координат, вычислим площадь Pj его четвертой части. Со-
Согласно формуле A), п. 6.2, получим
a . 2
/I 9 ' Г
\ /1 - —dx = ab /cos2 tdt =-ab
\ a2 J 4
(здесь произведена замена - = sint). Окончательно имеем, что Р = 4Р\ = каЬ. >
120. Ах2 + 2Вху + Су2 = 1, Л > О, АС - В2 > 0.
•* Решая относительно а: уравнение Ах2 + 2Вху + Су2 — 1=0, получаем
X = -B*±JA-<AC-Bw_t A_{AC_B2)y^0.
Следовательно, \у\ ^ \ А ^_д2 = Ь. Искомую площадь вычислим по формуле B)-, п. 6.2,
которая в рассматриваемом случае принимает вид
б
Р= f(x1(y)-X2(y))dy,

320
Гл. 4. Определенный интеграл
где
=
=
-Ву-у/А-(АС-В*)у*
Таким образом, имеем
б
2
= — JAC - В2 / cos2 tdt=— JAC - В2 = Ж
A v J A v у/АСГ^
(в интеграле произведена замена arcsin | = t). >
121. у = е~х\ sin х\, у = 0, х > 0.
¦4 График функции у : х у-> e~x\smx\, 0 ^ х < +оо, не имеет точек пересечения с осью
Ох, являющейся его асимптотой при х —* +ОО. Поэтому множество точек плоскости хОу,
ограниченное графиком функции у и положительной полуосью R+ , не является квадрируемой
фигурой в обычном понимании.
Рассмотрим множество площадей
х
Р(х)= / e~(\smt\dt, х еШ
и положим
Pd= lim
я; —<¦ + oo
+ ОО
I sin ж| rfx.
Представляя Р в виде суммы
Р
и заменяя в каждом интеграле переменную по формуле х — къ = t, получаем
_».,,. _t sin < +cost
= И / е *|sinz|ete = Jim^ /
= lim
п—*оо
= lim
п—*оо
Jim
Вопрос вычисления площади фигуры свелся к вычислению суммы
убывающей геометрической прогрессии.
Таким образом, имеем
1 е2+е~2
1
Рис. 64
122. ж = a(cos t +1 sin t), )/ = a(siii < — < cos<), 0 ^ t ^ 27r, и отрезком
луча х = a, i/ ^ 0.
•* Рассмотрим плоскую фигуру М К N RP, ограниченную разверткой
круга и отрезком луча х — а, у «С 0 (рис. 64). Искомая площадь Р равна
сумме площадей треугольника МОР и фигуры MKNRPOM. Очевидно,
Рамор = яа2, так как ОМ = а, \МР\ = 2ка.
Переходя к полярным координатам р и ip, получим
2 2,2 2,, . ,2ч . Smt -t COSt
р =х +у =a(l + t), tg*5= .,,¦
cos t + t

§6. Приложение определенного интеграла 321
Для вычисления площади фигуры MKNRPOM воспользуемся формулой C), п. 6.2, а затем
перейдем в интеграле от переменной tp к переменной t.
Дифференцируя левую и правую части равенства
sin t — t cos t , ¦
tg <j3 = : , ' ' '¦' '
cos t + t sm t
находим
_ 1 d fsint - t cost} _ t2 jf
^~ 1 + fiin'-'""J '
~ VcOS (+( Sill t)
Следовательно,
l/2 a2 f A + t
Pmknrpom = - / p2{ip)d(p = — /
Окончательно имеем
123. x = a cost, у = —
2 + sin ¦„
¦4 При возрастании ( от 0 до т переменная х убывает от а до —а и при этом переменная
у = ii(<) принимает неотрицательные значения, возрастая от 0 до | при изменении t от О
до ^ и убывая от ^ до 0 при изменении t от ^ до -к. Если же t возрастает от т до 27Г, то
переменная х возрастает от —а до а, и значения переменной у = ?г(<) в интервале ]7Г, 27г[
больше значений у = ii(t) в интервале ]0, 7г[, так как sin t < 0 при < ?}тт, 2ъ[. Следовательно,
уравнения ж = a cosi, у — t описывают замкнутую кривую с точками возврата (а, 0) и
7Г
(—а, 0). При этом интеграл Pi = J ydx равен площади фигуры, ограниченной кривой L\(t)
о
2тг
и сегментом [—а, а] оси Ох, взятой со знаком " —", а интеграл Рг = J уdx равен площади
7Г
фигуры, ограниченной кривой ?г@ и сегментом [—а, а] оси Ох. Поэтому искомая площадь
Р равна алгебраической сумме Р\ и Рг:
о
2-it
dt
8 \ /"
sin2 t - 2 sin t + 4 ) rft = -Этта2 + 8а2 /
2 + sm < / J
2 + sin t
о
Поскольку функция t >-* 2+lin t, t € R, периодическая с периодом 2к, то, согласно Примеру
51, имеем
2тг
/• At Г At
J 2 + sin t ~ J 2 + sin t ~
V3
— 7Г
Окончательно получаем, что Р = 7га I —1= — 9 ] . >
V^ J
124. x = 2t-t2, y = 2t2 -f.
¦4 Кривая, ограничивающая плоскую фигуру, имеет точку самопересечения в начале ко-
координат, поэтому в примере речь идет о вычислении площади, ограниченной петлей кривой.
Так как х = у = 0 при f = 0 и t = 2, To0^t^2.

322 Гл. 4. Определенный интеграл
Применив формулу F), п. 6.2, получим
2
Р= -
2 V 5
15'
Найти площади плоских фигур Ф, ограниченных кривыми, заданными в полярных коор-
координатах:
125. Р= р ..-*..-*
1 - cos tp 4 r 2
Применив формулу C), п. 6.2, получим
126. Р=
Р
-, 0 < б < 1 (эллипс).
+ е cos tp
Согласно формуле C), п. 6.2, и решению примера 131, гл. 3, имеем
1 = т/-
dip
2A -е2) \ 1 + е cosz
2 / /l-? г\ 2тг
' л/Т^? arctg V V Г+7 g 2 У 7Г^
127. p = L,p=J-,
ip sin у)
sin у)
Множество точек •< (^, р) € R2 : — sj р ^ ^—, 0 < tp ^ ~ > не является плоской квадри-
= li
руемой фигурой в обычном понимании, поэтому Р = lim P(e), где
Поскольку lim (ctge-i)= lim ^-iti = lim -+ = 0,тоР= lim P(e)=-. >
128. p = a cos^j, /9 = a(cos^) -(- sin y>), M @, — 1 €Ф.
Ч Точки окружности {р = a cos tp, \tp\ ^ ^} симметричны относительно полярной оси, а
радиус этой окружности равен |. Из неравенства а cos ^ sin tp < a(costp + sin tp) sin y>, спра-
справедливого при 0 < tp < j, следует, что полуокружность {р = acos^, 0 ^ tp ^ ¦-} целиком при-
принадлежит той части круга, ограниченного окружностью {р = a(cos <р + sin tp), — ~ ^ <р ^ -^ |,
которая лежит над полярной осью, поэтому точка М, лежащая на полярной оси и принадле-
принадлежащая по условию фигуре Ф, не может принадлежать множеству точек
< a sin tp cos tp ^ p sin ^ ^ a(cos ip + sin tp) sin tp, 0 < tp ^ —¦ ^ С К2.

§ 6. Приложение определенного интеграла 323
Следовательно, фигура Ф является объединением полукруга |р ^ acos(p, 0 ^ <р ^ |- j, пло-
площадь которого ^|~, и части Фх, круга {р ^ a(cos <? + sin у), — J ^ <p ^ "f"}> лежащей под
полярной осью, площадь которой Р^1 вычисляется по формуле
о о
а2 Г
= у /
а2 /*
= у
а2
cos2w
1
Таким образом, /> = ^^ + ^" (f — j) = X^71" ~ -1)' *"
129. Найти площадь плоской фигуры, ограниченной лепестком
кривой {tp = sin жр, 0 ^ р ^ 1}.
^ При возрастании р от 0 до - угол ^ возрастает от 0 до 1, а при
возрастании р от j до 1 угол ^ убывает от 1 до '0' (рй'с. 65), поэтому
выражение
1 0 1
+ 1
= ^ J Р\'{Р) dp
0 10
определяет искомую площадь, взятую со знаком " —", так как первое
слагаемое в левой части написанного равенства равно площади сег-
сегмента ОтВ, а второе слагаемое равно площади сектора ОАВ, взятой
со знаком " —". Следовательно,
1 . / 1 \ 1
1 2 / ,1 f
I p sin жр dp I = / р si
° "" J / J
о /
1/2
Рис. 65
„ . 2 , 7Г I 2 S1I1 7Г/9
"=-- IP cosжpdp = -- р
i \ ж
psin тгр с(/э =
= р-
COS7T/3
— / cos жр dp = \-
—7Г
7Г2
sm TTfl
X30. Найти площадь плоской фигуры, ограниченной кривой
¦^ Из условия р ^ 0 следует, что t ^ 0. Поскольку р = 0 при t = 0 и р —» 0 при < —¦¦+оо,
то 0 ^ t < +oo. (.следовательно,
о о
Интегрируя с помощью метода Остроградского, получим
¦*2 I I j о 1
Р = 2жа2 -
f
131. Найти площадь фигуры, ограниченной петлей листа Декарта х3 + у3 = Заху.
¦< Параметризуем лист Декарта, полагая у = tx. Тогда параметрические уравнения петли
листа Декарта примут вид
За*
У =
ЗаГ
0 ^ t < +оо.
Для вычисления площади воспользуемся формулой F), п. 6.2, приняв во внимание, что
(*(*)„'(*) - y{t)x\t)) dt = X2{t) d №?) = 0^ dt.

324 Гл. 4. Определенный интеграл
Следовательно,
¦+OO +00
0 3
=9?_ f t2 di _ За2
2 7 A + <3J - 2
d(l+f) _ 3 2 1
1 — — CL ———
t3J 2 1+t3
r- +
132. Вычислить площадь фигуры, ограниченной замкнутой кривой, заданной уравнени-
уравнением х* + у* = а2 (х2 + у2).
М Перейдем к полярным координатам по формулам
х = р cos ip, у = р sin ip.
Поскольку кривая симметрична относительно осей координат, то 0 ^ ip ^ 2тг. Уравнение
2 о2
кривой, ограничивающей плоскую фигуру, принимает вид р — sin4 ^cos4—'
Применяя формулы C), п. 6.2, и принимая во внимание решение примера 23, получаем
2тг
Ра1
=а1 /
2 J sin i
=
H- cos4 ^ 2
133. Вычислить площадь фигуры, ограниченной кривой, заданной уравнением х +у =
ах2 у,
^ Параметризуем кривую, полагая у = tx. Тогда
i t2
х = а -, у = а -г, у ^ 0.
Переменные ж и у обращаются в нуль при t — 0 и стремятся к нулю при t —* оо, а множество
точек кривой
симметрично относительно оси Оу. Следовательно, плоская фигура ограничена двумя симме-
симметричными относительно оси Оу петлями, лежащими в верхней полуплоскости плоскости хОу,
и поэтому искомая площадь равна удвоенной площади фигуры, ограниченной одной петлей:
-foo
P= j (X(t)y'(t) - y(t)x'(t)) dt= J X2(t) d (Ш\ =г J Щ^.
О 0 0
С помощью подстановки у — - легко убедиться в справедливости равенства
+ ОО +ОО
,,4п—т—2
О
в силу которого имеем
+ 00 _ +оо +оо +оо +оо
= f t2dt [ tUt - l [ l( l \ - * 1 f dt 1 f
-J A+P)*-J (l+t*)*- 4j Vl + **J" 4A+**) 0 +4У 1 + <* У l
+ 00 +0O ^
Поскольку - f jT^T — j / 1114 (согласно равенству A)), то
1+t*
О О
+ 0О
о

§ 6. Приложение определенного интеграла 325
где F(t) — A- arctg —^ + -?д sgn 1 при t ф 0 и F@) = 0 (см. пример 20, гл. 3). Окончательно
получаем
8V2 8V2
Прежде чем решать примеры на вычисление объемов тел с помощью формул A) и B), п.
6.3, рассмотрим два примера на доказательство. При этом получим полезные формулы для
вычисления объемов тел.
134. Доказать, что объем V тела Т, образованного вращением вокруг оси Оу криволи-
криволинейной трапеции
Ф={(*,3/)€К2: а^я^б, 0 ^ у ^ /(*)},
где / : [а, Ь] —» R — непрерывная на сегменте функция, равен
ь
V = 2* I xf(x)dx.
а
Ч Пусть П = {хо = о, Ei, ... , хп = Ь} — произвольное разбиение сегмента [о, Ь]. На ка-
каждом сегменте [ж,-, ж.+i], i = 0, п — 1, рассмотрим два прямоугольника, в основании каждого
из которых лежит сегмент [ц, хц-i], а боковые стороны равны пи и Mi, где
m, = min {f(x)}, Mi = max {/(i)}.
Объединения всех однотипных прямоугольников образуют две ступенчатые фигуры, одна
из которых вписана в фигуру Ф, а другая описана вокруг нее. При вращении этих ступеича-
тых фигур вокруг оси Оу получим два кубируемых тела Ti и Ti, составленные из кольцевых
цилиндров.
Объемы тел Ti и Тг соответственно равны
п—1 п—1 п—1
Рассмотрим функцию <р : х *-+ 2icxf(x), а ^ х ^ 6. Так как <р € Я [о, Ь], то Ve > 0
п—1 п—1
ЗП : Sn(v) — Sn{v) < |, где Sn{<fi) = ХЗ 2TMjiCi+i Axt, Sn{v) = J
~ i=o ~ i=o
Из очевидных равенств
1=0 t=0 1=0
n—1 n—1 n—1
t=0 1=0 1=0
следует, что УТз - V't, = Sn(v) - Sn(<p) - 7n, где 7n = ^ я-(Л/,- +гп,)Дг?. Оценивая у„,
- i=o
получаем |7n| ^ 2кМ(Ъ — о)й(П), где М = max {/(ж)}, d(U) = max Дх;.
Принимая во внимание неравенство Sn(<p) — Sn(<p) < § и выбирая разбиение П таким,
чтобы выполнялось неравенство 2жМ(Ь — а)й(П) < |, получим неравенство Vr3 — Vri < е, из
которого следует, что тело Т кубируемо (в силу включений Т\ С Т С Ti).
ь ь ь
Поскольку lim Vr, = 2vfxf(x)dx, lim Vr2 = 2vfxf(x)dx, то У = 2я-fxf(x)dx. >
135. Доказать, что объем У тела Т, образованного вращением вокруг полярной оси
Фигуры Ф = {(р, р) е U2 : 0 ^ а ^ ip ^ /? ^ я-, р = /o(v>), /» ^ 0}, /э 6 С[а, 0], равен
/8
У=^ /p»sin^. A)

326
Гл. 4. Определенный интеграл
Ч Пусть П = {<fio = a, <pi, ... , <рп = ft} — произвольное раз-
разбиение сегмента [a, ft], а Ф< — плоская фигура, ограниченная от-
отрезками лучей tp = <pi, tp = <?>i+i и куском кривой <р >—>• p(<fi),
<fii ^ If < V'i + l (РИС 66).
Обозначим М, = max {p(v)}> m> = min {р{<р)} и
рассмотрим два тела Т\ и Тг, образованных вращением вокруг
*р полярной оси двух плоских фигур, составленных из круговых сек-
секторов, имеющих соответственно радиусы Mi и то; и центральный
Рис. 66 угол A<pi = ?>i+i —<pi, t = 0, п — 1. Из определения тел Т, Ti и Тг
следуют включения Тг С Т С Ti.
Вычислим объемы тел Т\ и Тг, используя для этого известную из геометрии формулу для
вычисления объема шарового сектора, имеющую вид V = -irR2h, где h — высота шарового
сегмента, R — радиус шара. Имеем
п-1 п-1
VTi =
3/ ч 4
i (cosp.- - cos?>,+i) = -тг
sin
sin
i=0
TZ 4
7-2 = з "
з .
' sm
1=0
Обозначим y' ^'
разность объемов
= i^,, sin^; = max {sinip}, sinip = min {sin ip) и рассмотрим
/f - то?) sin <pi sin -y1.
yTl - Vt2 = -я-
i=0
Из неравенств (Mf — mf) sin (pi ^ Mf sin ipi — mf sin ^i, sin ^p- < ^*- следует неравенство
п-1
y Y,Mf sin Vi ~ m* sin ti) Apt = 5n(/) - Sn(f),
t=0
где / : <p >-* -2-p3(<p) sin ip, a ^ (p ^ /3, — непрерывная на сегменте [а, /3] функция. Так как
/ € R[a, ft], то Ve > О ЗП : 0 < 5П(/) - Sn(f) < е, следовательно, VTl - Vr2 < e. Таким
образом, тело Т кубируемо, а его объем V можно вычислить по формуле A), так как
VTi -Vt2<y
р
2 г
lim Vt, — lim Vjv = — f / P (<p)sin<pd<p.
г(п)-.о d(n)—o ¦* 3 у ч '
Вычислить объемы тел, ограниченных поверхностями:
136. Параболоида вращения, площадь основания которого равна S, а высота равна Н.
Воспользуемся формулой B), п. 6.3. Поверхность параболоида вращения задана урав-
урав«/2
у (
нением z = х2 + у2, а в любом ортогональном сечении тела плоскостью z = с, 0 < с < Н,
2 2
V = тг / г rfz =
получим круг х' + у' < с. Таким образом, множество сечений тела, ограниченного поверхно-
поверхностью z = х2 + у2, является множеством кругов радиуса г, площади P(z) которых равны wz.
Согласно формуле B), п. 6.3, получим
я
жН2 SH_
~2~'
так как, согласно условию, жН — S. >
а2 о2 с2
^ Тело ограничено однополостным гиперболоидом и кусками плоскостей z = ±с. В силу
симметрии точек тела относительно плоскости хОу, достаточно вычислить объем части тела,
лежащей в полупространстве z ^ 0, и удвоить результат.

§ 6. Приложение определенного интеграла
327
В ортогональном сечении тела плоскостью z — с\, 0 < с\ < с, получаем зляипс
2 2
$ -\—-z—у . ^ = 1, поэтому площадь P(z) поперечного сечения тела плоско-
стью, согласно решению примера 119, равна жаЬ I 1 + |з")- Применив формулу B), п. 6.3,
получим
с с
V = 2 I P(z) dz = 2жаЬ [ A + Z— J dz = -тгабс. >
о о
1 ЯЛ 2 4- 2 4- 2 2 24- 2 —
-^ Тело ограничено частью поверхности кругового цилиндра и двумя кусками сферы, а
плоскость хОу делит его на две равные части. Поэтому рассмотрим ту часть тела, которая
лежит в полупространстве z ^ 0. В сечении этой части тела плоскостью, перпендикулярной к
оси Ох, получим криволинейную трапецию, площадь Р(х) которой вычисляется по формуле
~ *2) ~ У2
Р(х) = 2 I
о
Тогда искомый объем V получим, применив формулу B), п. 6.3:
a
V = 2 [ P{x)dx.
о
Вычислим сначала Р{х), произведя в интеграле подстановку t = arcsm
Р{х) =
v
/
О, т
Подставляя полученное Р(х) в формулу для вычисления объема У, находим
а
V = 2 f(a2 - х2) Tarcsin J-~ + ^Л dx = 2(h + h),
где
h = / (a2 — ж2) arcsin 4 / dx, h — I (a — x)y/ax dx =—a3.
J у a + x J 15
о о
В интеграле h произведем замену х = atg2<f, 0 SC <p SC —, получим
IT
T
= a3 J V(l - t
(

328 Гл. 4. Определенный интеграл
Окончательно имеем
139. Найти объем тела, ограниченного поверхностью, полученной в результате враще-
вращения графика функции х2 + (у — 4J = о2, |х| ^ а, 0 < о < 6, вокруг оси Ох.
¦4 Вращающаяся окружность радиуса а с центром в точке (О, Ь) имеет две оси симметрии:
ось Оу и прямую у = 6. Уравнения верхней и нижней частей окружности относительно
прямой у = 6 имеют соответственно вид
ув = Ы- у/еР — х2, ун = 6 — iy/а2 — ж2, |ж| ^ а.
Применив формулу A), п. 6.3, получим
а а
= * /(«/в -ун) <*я = 8*6 / \/а2 -
х2 dx = 8тга2Ь / cos2 tdt = 2;r2 a2 6. >
140. Найти объем тела, ограниченного поверхностью, полученной в результате враще-
вращения графиков функций х = a(t — sint), у = а(\ — cost), 0 ^ t ^ 2я-, и у = 0:
1) вокруг оси Ох; 2) вокруг оси Оу; 3) вокруг прямой у = 2а.
¦4 1) Применив формулу A), п. 6.3, получим
2ira 2lr 2тг
/ 2 3 // 3 3 / . 6 t
V — 7Г /у (/ж = тга / A — cos t) dt = 87rot / sin — dt =^
J J J 2
oo о
)r
ir 2f
sin6 г dz = Z2ira3 ¦— ¦ — = I
6!! 2
(здесь воспользовались решением примера 43).
2) Объем тела вычислим по формуле, доказанной в примере 134:
= 2k xydx = 2ira3 (t - sint){1 - costJ dt =
о о
/ 2lr 21Г
= 2*o3 I t(\ - costJ dt - I sin t(l-costfdt I = 2*a3 I t(l - costJ dt =
\J J I J
\0 0 /0
2ir 2ir
= 2*a3 ft(~-2cost+^~)dt = ^a3 ftdt = бтг3a3
о
2lr 21Г \ 2lr
о
2ir
(здесь мы приняли во внимание равенства /sin 1A — costJrft = f sint(l — coslJ rf< = 0,
о
2ir
/( |)
о
3) Перейдем к новой системе координат по формулам у\ = у — 2а, х\ = ж. При этом
получим У = Vi — V2, где Vi — объем кругового цилиндра, высота которого равна 2па и
радиус основания равен 2а, а объем Рг вычисляется по формуле
2ira 2ir
Vi = v y2dx = was (A-costJ-4A-cos t)+4)(l+cost) dt = ж2 а3.

§ 6. Приложение определенного интеграла
329
Поскольку Vi = 8тг2а3, то V = 7тг2а3. >
141. Найти объем тела, образованного вращением плоской фигуры, ограниченной пе-
петлей кривой у ~ {х — 2t — t2, у = Ы — t3, t € К}, вокруг: 1) оси Ох: 2) оси Оу.
-* 1) Поскольку х — у = 0 при t = О и при t = 2, то 0 ^ < ^ 2. При возрастании
параметра t от 0 до 1 переменная ж также возрастает от 0 до 1, а при возрастании 1 от 1 до
2 переменная х убывает от 1 до 0, поэтому
2 1 2 2
У f 2 f 2
= -,г f y2dx-w f y2dx = -w fy2dx = 2x /(t -
2) Для вычисления объема воспользуемся формулой примера 134 и примем во внимание
соображения, высказанные при рассмотрении случая 1). Тогда получим
2 12 2
V = -2тг / ху dx - 2тг / ху dx = -2тг / ху dx = II = -2тг /B* - t2)D< - t3J(l - t) dt =
64
105
ж. >
142. Найти объем тела, образованного вращением плоской фигуры, ограниченной гра-
графиком неявно заданной функции (х2 +у2J = а2(х2 — у2), вокруг: 1) оси Ох; 2) оси Оу; 3)
прямой у = х.
< 1) Перейдем к полярным координатам х = р cos <р, у = р sirup. Уравнение кривой ицерт
вид р = ал/cos 2<р, \<р — kir\ ^ j, к = 0, 1. Принимая во внимание "симметрию точек кривой
относительно полярной оси и прямой р cos<fi = 0, воспользуемся решением примера 135. При
этом получим
Т о
V — -тг / a3 cos2 2<fi sin <pdip = —-— / B cos2 <p — 1) 2 d(cos (p) =
4тга3
3\/2
; - 1J dt =
ЗУ2
Зл/2
2) Возьмем луч ip = ^ в качестве полярной оси системы (р1, в)
(рис. 67). Тогда р'(в) = р(у'), # = -(§-?>) =у-^-
Применим теперь формулу, доказанную в примере 135, при-
приняв при этом во внимание, что плоская фигура симметрична и
что sin# < 0. Имеем
Y J(p'
F)f\ sin 6\d0 =
3 4
(cos 2V)
sin (V - |
Рис. 67
Ажа'
з /• з
/ cos 2 2<р cos tpd<p =
^=r
4
/ A — 2 sin
sin <p) =
з
-<2J dt =
/ cos z dz =
4тга3 ЗП ж_
Зл/2 ' 4!! ' 2

330 Гя. 4. Определенный интеграл
3) Возьмем луч <р = j в качестве полярной оси системы (р1, в) (рис. 68). При этом имеем
Принимая во внимание симметрию фигуры и неравенство sin в ^ 0, согласно формуле
примера 135, получим
V= —
[ - ¦ Г *\
I cos 2 2(р sm I (р — — I
dip.
2 4
Произведем в интеграле подстановку <р — j = — i. При этом имеем
V =
-^- / sin 2 2t si
sin t dt -
cos? ( sin? <d(sin<) = -^-тга3 /
о о
После замены -^ — 1 = и* находим, что V =
•f оо -f оо
-Z2L
3 т
Л гДе
(согласно решению примера 133).
Интегрируя по частям, получаем
Рис. 68
.
-+ОО
3
8
О
u2 du
При решении примера 133 показано, что J . " ц4".д = jtj^. Сле-
довательно, I = ^, V = =_^_. >
Упражнения для самостоятельной работы
Вычислить длину кривой 7) если:
105. 7= {(«, У)
106. 7 = {
107. 7 =
108. 7=-! (ж,
100. 7 = {(ж, у) € R2 : ж = a cos5 t, у = a sin5 (, 0 ^ < < 2я-}.
110. 7 = {(ж, J,z)el3:i = « cost, у = а sint, г = it, 0 ^ t ^ to}.
111. 7 = {(ж, у, z) g R3 : х2 = iy, 2xy = 9z, 0 ^ x ^ xo}.
112. 7 = I (x, y, z) € K' : «/ = a arcsin —, z = j In "_ , 0 ^ ж ^ жо } •
113. 7 = {(ж, j/, z)?R3:i = at, у = VSabt2, z = 2bt3, 0 ^ t < to].
114. Найти длину кривой, заданной уравнением л/х + ^/у = л/а, от точки @, а) до точ-
точки (а, 0).
115. Парабола у = {(х, у) g R2 : 4aj/ = х2, г 6 R} катится по оси Ох. Доказать, что ее
фокус описывает цепную линию
Найти площадь плоской фигуры Ф, ограниченной:
2 2 2
116. Графиком астроиды хз + уз = аз .

§ 6. Приложение определенного интеграла 331
117. Графиком функции, заданной уравнением xi + у4 — х2 + у2.
118. Графиком подэры эллипса (х2 -+¦ у2J — а2х2 -+¦ Ъ2у2 .
119. Графиками функций у2 — Аах, х2 -+¦ у2 = 2ах, 2х — у = 4а и лежащей над осью Ох.
120. Петлей строфоиды (а — х)у2 = (а + х)х2.
121. Графиком функции, заданной уравнением (у — хJ = х3 и отрезком оси Ох.
122. Графиком функции, заданной уравнением \/^+ уь = 1> и отрезками осей коорди-
координат.
123. Эллипсом jj + L = 1 и лежащей вне круга х2 + у2 = ai.
124. Графиком кривой, заданной уравнением р = a cos4y.
125. Графиком равнобочной гиперболы р2 cos2<fi = а2, — <fio ^ <р ^ Уо-
126. Графиками функций, заданных уравнениями р2 cos 2ip = 4а2 cos4 <р v. p2 cos 2<р = а2.
127. Петлей кривой, определяемой уравнением х1 -{¦ у7 = ах3у3,
128. Графиком функции, заданной уравнением я2?/2 = 4(х — 1) и прямой, проходящей
через точку перегиба графика.
129. Вычислить площадь криволинейного квадрата, принадлежащего обоим эллипсам
х2 у2 х2 у2
а2 Ь2 Ь2 а2
Найти объемы тел, ограниченных поверхностями, полученными в результате вращения
следующих кривых:
130. 7 = {(х, у) € М2 : у = sinх, 0 ^ ж ^ я-} вокруг оси Ох.
131. 7 = {(я, 2/) € R2 : Bа - ж)у2 = х3, 0 ^ ж < а ^ 2} вокруг оси Ох.
132. 7 = {(я> 2/) € К2 : ж = a(t — sin<), j/ = аA — cost), 0 ^ t ^ 2тга} вокруг пересекающей
ее прямой у — ка, 0 < fc < 2 (вычислить объемы получающихся двух тел вращения).
133.7 = 1 (xi У) € R2 : у = д34" з, х S R > вокруг своей асимптоты.
134. Кривая, заданная уравнением р3 = а3 совЗу, вращается вокруг полярной оси. Опре-
Определить объем тела, полученного в результате вращения фигуры, ограниченной петлей, лежа-
лежащей в третьем квадранте.
136. Сегмент круга радиуса R, соответствующий центральному углу 2а, вращается во-
вокруг своей хорды, Определить объем тела вращения.
136. Куб с ребром о вращается вокруг своей диагонали. Определить объем тела, полу-
полученного в результате вращения одной из граней куба.
137. Ребро куба а. Определить объем тела, полученного в результате вращения одной из
граней куба вокруг диагонали противоположной грани.
138. Кривая, заданная уравнением xi+yi = 2аху2, вращается вокруг оси Оу. Определить
объем тела, ограниченный полученной поверхностью вращения.
Найти объемы тел, ограниченных поверхностями:
139. S = {(х, у, z) eR3 : х2 + 4у2 = 8z, х2 +4у2 = 1, z = 0}.
140. S = {(х, у, z)eU3 : у2 = 2р(а-х), х - z = 0, х - 2z = 0}.
141. 5 = {(х, у, г)?К3 :z2 = (a-x- у)а, х = 0, у = 0, z = 0}.
142. S = {(х, у, z) е К3 : z2 - Ь(а - х), х2 + у2 = ах].
143. 5 = {(*, у, г)еК3 : j/2 + z2 = a2ch2f, -Ъ < х < Ъ).
144. В прямой круговой цилиндр (стакан) радиуса г налита вода. Ось наклонена под
углом а к горизонту. Часть дна, покрытая водой, является сегментом с центральным углом
2ip. Найти объем воды.
145. Три взаимно перпендикулярные прямые являются осями трех круговых цилиндров
одинакового радиуса г. Определить объем общей части всех трех цилиндров.

332 Гл. 4. Определенный интеграл
§ 7. Общая схема применения определенного
интеграла. Задачи из механики и физики
7.1. Аддитивная функция промежутка.
Если всякому сегменту [cv,/9], содержащемуся в фиксированном сегменте [а, Ъ], отвечает
значение определенной физической или геометрической величины Р([а, /9]), то Р называют
функцией промежутка.
Определение. Функция Р : [cv, /9] i—> -P([cv, /9]), [cv, /9] С [а, Ь], называется аддитивной,
если
V7 € ]«, fi[ => P([a, /9]) = P([cv, 7]) + P([7, /9]).
Теорема. Пусть Р : [cv, /9] i-> P([cv, /9]), [a, /9] С [a, 6], — аддитивная функция, а р :
[a, b] —> K, p € C[a, Ь], такая функция, что Р([хо, х]) = p(x — xo) + o((x — xq)), x —<• xq,
Vio € [a, Ь]. Тогда справедлива формула
ь
o(x)dx. A)
7.2. Вычисление статических моментов, моментов инерции, координат центра
тяжести плоских кривых и фигур.
Пусть {Mj(xj, yj)} —система материальных точек плоскости хОу с массами rrij, j = 1, п.
Величины
п п
3 = 1 3 = 1
называются соответственно статическим моментом и моментом инерции этой системы то-
точек относительно оси Ох.
Если на гладкой кривой f — {(х, г/) € К2 : у = f(x), а ^ х ^ Ь} равномерно распределе-
распределена масса с линейной плотностью /* = 1, то статическими моментами и моментами инерции
кривой 7 относительно осей координат называются соответственно величины
ь ь
Мх= I f{x)sj\+f'(xfdx, Mv= I xs/l + f'(zJdx, A)
b b
_ I , I — _ f 2 , —
I,-Jf(xWl+f4x) dx, ly-J x VI+ /'(*) dx, B)
a a
а координаты ее центра тяжести С(?, »/) вычисляются по формулам
I I
где I — длина кривой -у.
Предположим, что криволинейная трапеция Ф лежит по одну сторону оси Ох и что она
однородна. Статическими моментами и моментами инерции этой трапеции относительно осей
Ох и Оу называются соответственно величины
ь ь
Mx = Sm^x) J f'2(x)dx, My = sgn f(x) f xf(x)dx, D)
a a
6 0
Ix=ljf(x)\f(x)\dx, Iy = Jx2\f(x)\dx, E)
a a
а координаты ее центра тяжести С(?, »/) вычисляются по формулам
? - ~р"' '' - ~р~> ( )

i 7. Применение определенного интеграла
333
где Р — площадь трапеции. * ' " ' ' "¦"
Если плоская однородная фигура имеет ось симметрии, то ее центр тяжести лежит на
этой оси.
143. Определить координаты центра тяжести плоской фигуры ... ;.
Г Х2 2 Ч
Ф = { (х, у) € R : -=¦ + тт < 1, 0 ^ х ^ а, 0 ^ у < 6 } .
\ п О I
4 Применяя последовательно формулы D) и F), получим
м =ь~1 ( -xl\d =-Г - —\Г = —
~ 3 '
irafc 4a . irab 46
и ' 4 Зж' 4 Зж
(поскольку площадь фигуры Ф равна жаб). >
144. Найти моменты инерции 1Х и 1У параболического сегмента Ф, ограниченногр
, 0 ^ х ^ 2а, и отрезком оси Oi.
графиком фз'нкщш х н-^
U
¦^ Согласно формулам E), имеем
2а
2.-^
145. Найти координаты центра тяжести однородного полушара радиуса а.
¦^ Ось Oz является осью симметрии полушара
Т = {(х, у, z) € М3 : х2 + у2 + z2 < а2, г ^ 0},
поэтому центр тяжести находится на этой оси. Приняв шаровой пояс, нижнее основание ко-
которого находится на расстоянии z от плоскости хОу и высота которого равна dz, за цилиндр,
высота которого равна высоте шарового пояса, а основание равно нижнему основанию ша-
шарового пояса (кругу радиуса г = л/а2 — z2), вычислим приближенно статический момент dM
шарового пояса относительно плоскости хОу, равный -к(а2 — z2)zdz. Тогда
М
а
Поскольку объем полушара равен ^жо2, то
С =
гм
3
= —а.
Следовательно, С(^, ?/, С) = (о, 0, j-a) . >
146. Определить силу давления воды на вертикальную перегород-
перегородку в канале, имеющую форму полукруга радиуса а, диаметр которого
находится на поверхности воды.
¦4 Обозначим через 1(х) длину горизонтальной прямой, проведенной
на расстоянии х от АВ (рис. 69). Приняв полоску, содержащуюся меж-
между горизонтальными прямыми, отстоящими от АВ на расстояниях х и
x + dx, за прямоугольник с основанием /(х) и высотой dx, можем прибли-
приближенно вычислить давление Р([х, х + dx]), испытываемое этой полоской, применив правило

334
Гл. 4. Определенный интеграл
гидростатики, согласно которому давление воды на полоску, погруженную в нее, равно пло-
площади полоски, умноженной на глубину погружения:
Р{[х, х + dx}};
Согласно формуле A), п. 7.1, имеем
'¦ xl(x) dx = 2х\
= -«
147. Диск толщиной h и радиусом г состоит из вещества с плотностью 6 и совершает п
оборотов в секунду. Какую работу нужно затратить, чтобы его затормозить?
^ Согласно теореме об изменении кинетической энергии, ее приращение за некоторый
промежуток времени равно работе, совершенной приложенными к телу силами за тот же
промежуток времени:
Г - То = А.
Здесь Т — кинетическая энергия в конечный момент, То — начальная кинетическая энергия
тела, А — работа внешних сил. Поскольку тело абсолютно твердое, то работа внутренних
сил равна нулю.
В конце промежутка времени тело остановилось, значит, Т = 0. Следовательно, То = —А.
Знак минус соответствует затрачиваемой работе.
При вычислении кинетической энергии выделим кольцевой цилиндр радиуса р, 0 < р ^ г,
толщина которого dp и высота h. Его объем с точностью до бесконечно малых более высокого
порядка, чем dp, равен 2vhpdp, а масса dm равна 2wShpdp (рис. 70).
Линейная скорость v точек диска, находящихся на расстоянии р от оси
вращения, равна шр, где ш — угловая скорость диска. Так как диск совер-
совершает п оборотов в секунду, то ш = 2жп с~1. Следовательно, v = 2-кпр.
Кинетическая энергия кольцевого цилиндра приближенно равна
dTo = — dm = - ш р dm ~ wSui hp dp.
Согласно общей схеме применения интеграла, получаем
Рис. 70
Следовательно, А = —To = —T38n2hr4. >
2 р3 dp = 4ir3 Sn2 h
/¦
= TZ36nhri
F,
dt
148. Электрические заряды отталкивают друг друга с си-
i ——, где e.j и е-2 — величины зарядов, а г — расстояние
между ними. Определить работу, необходимую для того, что-
рИ(. 71 бы приблизить заряд ег = 1 к заряду t\ из бесконечности на
расстояние, равное R.
4 Элементарная работа dA равна произведению силы на
элементарное перемещение и на косинус угла между направлением силы и направлением
перемещения: dA = F cos a dr (рис. 71). В рассматриваемом случае имеем dA = F2drcosw =
— F2 dr = —^ dr, так как -F2 = fi ¦ Согласно общей схеме применения интеграла, находим
А
R
[ dr fl
J т г
= !¦>
Упражнения для самостоятельной работы
146. Однородная прямоугольная пластина со сторонами а и Ъ разбивается на две части
параболой, вершина которой совпадает с одной из вершин прямоугольника и проходит через
его противоположную вершину. Найти центры тяжести верхней Si и нижней 5*2, частей
прямоугольника.

§ 7. Применение определенного интеграла 335
147. Найти координаты центра тяжести однородной фигуры, ограниченной осями коор-
координат и параболой л/х + ^/у = \/а.
148. Найти статический момент однородной фигуры, ограниченной графиками функций
м *"* Т+х? и х 1~^ х'2' х ^ "^' относительно оси Ох.
149. Найти координаты центра тяжести однородной фигуры, ограниченной графиком
функции, заданной уравнением у2 = ах3 — х4.
150. Найти декартовы координаты центра тяжести однородной фигуры, ограниченной
графиком правой петли лемнискаты Вернулли р2 = a cos2y>.
151. Найти декартовы координаты центра тяжести части логарифмической спирали р =
aev , f 4 V 4 ""¦
152. Найти момент инерции боковой поверхности конуса, радиус основания которого R
и высота //, относительно его оси симметрии.
153. Найти положение центра тяжести однородного конуса.
154. Радиусы оснований усеченного прямого кругового конуса равны R и г, высота h,
плотность ц. О какой силой действует он на материальную точку массы т, помещенную в
его вершине?
155. Капля с начальной массой М падает под действием силы тяжести и равномерно
испаряется, теряя ежесекундно массу, равную т. Какая работа силы тяжести за время от
начала движения до полного испарения капли? Сопротивлением воздуха пренебречь.
156. Треугольная пластинка, основание которой о = 0,4м, а высота h = 0,3м, вращается
вокруг своего основания с постоянной угловой скоростью ш = 5тгс-1. Найти кинетическую
энергию пластинки, если толщина ее d = 0,002 м, а плотность материала, из которого она
изготовлена, ц = 2200кг/м .
157. Пластинка в форме треугольника погружена вертикально в воду так, что ее основа-
основание лежит на поверхности воды. Основание пластинки а, высота h.
а) Вычислить силу давления воды на каждую из сторон пластинки.
б) Во сколько раз увеличится давление, если перевернуть пластинку так, что на поверх-
поверхности окажется вершина, а основание будет параллельно поверхности воды?
158. (Стержень длиной I вращается вокруг своего конца, совершая п оборотов в секунду.
Определить величину натяжения в точке прикрепления, если вес единицы длины стержня
равен <т, а центробежная сила для массы т, движущейся по окружности радиуса г с угловой
скоростью w, равна mrui .
159. Под действием нагрузки / проволока длиной I с поперечным сечением 5 и модулем
Юнга Е получает удлинение А1 равное -g-;. Определить удлинение этой проволоки под дей-
действием своей тяжести, если она висит вертикально. Удельный вес вещества проволоки равен
ц.
160. От нагрузки в 9,8 Н проволока растягивается на 0,01м. Какую работу надо совер-
совершить, чтобы растянуть ее на 0,04м?
161. Какую работу надо затратить, чтобы насыпать кучу песка конической формы ради-
радиусом 1,2м и высотой 1м, если плотность песка 2000кг/м ?
162. По закону Джоуля количество тепла, выделяемого постоянным током, равно Rci2t,'
где с = 0,24 — постоянная, R — сопротивление, t — число секунд, г — сила тока. Найти
выделяемое тепло для неременного тока г = acosbt.
163. По закону Торричелли скорость вытекающей жидкости равна \/2gh, где h — глубина
отверстия под уровнем жидкости. Определить время вытекания воды из конической воронки
с вершиной внизу, имеющей площадь основания Р, высоту h и отверстие в вершине площадью
(Т.
164. Цилиндр радиуса 0,15 м и высотой 0,6 м наполнен воздухом под давлением 9,8 •
104 Н/м . Какую работу надо совершить при изотермическом сжатии газа до объема в два
раза меньшего?
165. Точка движется по оси Ох, начиная от точки A, 0), так что скорость ее численно
равна абсциссе. Где будет находиться точка через 10 с после начала движения?

336 Гл. 4. Определенный интеграл
§ 8. Интеграл Стилтьеса
8.1. Верхний и нижний интегралы Стилтьеса. Критерий интегрируемости.
Пусть / : J —<¦ R, J — [а, Ь], — ограниченная на сегменте J функция, а : J —* К
— неубывающая на этом сегменте функция, П = {а = хо, xi, ... , хп = 6} — произвольное
разбиение сегмента J. Образуем верхнюю и нижнюю интегральные суммы
Ti — 1 тг — 1
Sn(/, а) = ]ГМ, Дог;, ,S'n(/, a) = Y^rnt Да;,
где
М{= sup {/(x)}, m, = inf {/(х)}, Дог; = a(x,-+i) - ог(х;),
и введем в рассмотрение числа
/ fda = inf (Sn(f, a)}, I fda = sup{,Sn(/, a)},
J <n> J {П} -
которые называются соответственно верхним и нижним интегралами Стилтьеса.
Определение. .Если J fda = J fda, то общее значение верхнего и нижнего интегралов
назовем интегралом Стилтьеса функции f no функции а (или относительно функции а)
и обозначим его
ь
J
f(x)da(x).
Множество всех функций /, интегрируемых по С'тилтьесу относительно функции а на
сегменте [а, Ь], обозначим / е ,$'(cv)[a, b].
Из этого определения следует, что при о'(х) = х интеграл Стилтьеса совпадает с интегра-
интегралом Римана функции / на сегменте J.
В общем случае функция а может быть разрывной на J. Функцию о; называют инте-
интегрирующей функцией.
Теорема (критерий интегрируемости).
/ € S(a)[a, b] О Ve > О ЭП : 0 ^ Sn(/, a) - Sn(f, a) < е.
8.2. Интеграл Стилтьеса как предел интегральной суммы.
Пусть П — произвольное разбиение сегмента J, d(U) = шах Дх,-. На каждом сегменте
O^i^n —1
[xi, ?,41] возьмем произвольную точку ?; и образуем сумму
п-1
;=о
которую назовем интегральной суммой Стилтьеса.
Полагаем lim .S'n(/, o*) = I, если
Ve > 0 35 > 0 : УП Л d(U) < 5 <S> \SB(f, a) - I\ < е.
Теорема. Если:
1) при d(U) — 0 3 lim.S'n(/, а), то f € S(a)[a, b] и
^
ь
Зп(/,«) = J f(x)da(x);

§ 8. Интеграл Стилтьеса
ЗД7
2) f?S(a)[a, b], cv ? С[а, b], то 3 lim Sn(f, a) = J/(x)dcv(r). • H ?4 .* ;'
d(H)~ 0 a
Эта теорема устанавливает два эквивалентных определения Интеграла Стилтьёса.Ч
8.3. Основные свойства интеграла Стилтьеса. '
Теорема 1. Если:
1) / € S(a)[a, Ь], д ? S(a)[a, Ь], то (/ + д) ? S(a)[a, 6], с/ € S(a)[a, Ь], с = const, u при
этом
ь ь ь ь ь
f(f + д)(х) da(x) = f Дх) da(x) + f g(x) da(x), J cf{x) da(x) = с I f(x) da(x);
2) /, 9 € .S»[a, 6], /(i) ^ g(x) Vx € 7, mo
ь ь '
J
g(x)da(x);
3) / ? S(a)[a, b] и если с ? ]u, b[, mo f ? S(a)[a, с] Л / ? S(a)[c, b] и при этом
ebb
J f{x) da(x) + J fix) da(x) = J fix) da(x);
4) / ? S(a)[a, b] и если |Дх)| ^.M4x?~J, то
/(x)cia(x) < M(a(fc) — a(a));
5) / ? ,S'(ai)[a, b] и f ? S((v2)[a, b], mo f ? .S'(ai + «г)[а, b] и при этом
ь ь ь
f f{x)d{al+a2){x)=: f f(x)dai(x)+ //(x)da2(x);
a a a ¦.';.",•.<.'¦',
6) / ? S(a)[a, b] и с — положительное число, то f ? S(ca)[a, b] и '' ' l> ' .
ь ь
/"/(x)d(c«(x)) = c //(x)d«(x).
a a
Следует отметить, что в случае интеграла Римана справедливо и обратное свойству 3)
утверждение: если / ? R[а, с] и f ? R[c, b], то f ? R[a, b]. . ¦ ¦, ¦
с ь '
Для интеграла Стилтьеса из существования J'/(x)(ia'(x) и J fix) da(i) не следует, вооб-
a с
Ь
ще говоря, существование Г Дх) do'(x).
Теорема 2. Пусть f ? Ь\п)[а, Ъ], А ^ Дх) ^ S Vx ? [а, Ъ], <р ? С[А, В] и д = f о f :
[а, Ь] -> К. Гогйа </ € S(a)[a, b].
Теорема 3. Если f ? S(a)[a, b] и д ? S(a)[a, b], то:
1) f9 € S(«)[o, Ц;
2) I/! € 5(«)[a, Ь] ti
') Если а разрывна, то возможен случай, что / 6 S(a)[a, Ь], а lim Sn(f> a) не существует (см.
d(n)-»0
пример 154).

338 Гл. 4. Определенный интеграл
Теорема 4 (формула интегрирования по частям). Пусть f : [а, Ь] —> R, д : [о, Ь] —+ R
и существует какой-либо из интегралов Стилтъеса J f(x)dg(x), J g(x) df(x). Тогда суще-
а. а
ствует и другой интеграл, причем справедлива формула
ь ь
J f(x) dg{x) = f(x)g(x)\»a - J g(x) df(x).
A)
8.4. Классы функций, интегрируемых по Стилтьесу.
Теорема 1. Если функция f непрерывна ко сегменте [а, Ь], то f € S(a)[a, b].
Теорема 2. Если функция f монотонна на сегменте [а, !»],««? С[а, Ь], то f ? S(a)[a, b].
Теорема 3. Если f 6 Я [а, Ь], а а удовлетворяет условию Липшица на [а, 6], то f &
S(a)[u,b].
Пусть h : J —-г К — функция ограниченной вариации на сегменте J = [a, b], f : J -^Ш, —
произвольная функция. Согласно теореме 4, § 5, функция h представима на J в виде
ft = «-/?,
где (* и /? — неубывающие на этом сегменте функции.
Определение. Полагаем
ь ь ь
J f(x)dh(x)^ [ f{x)da(x)- j f(x)dp{x), A)
a a a
если f ? S(a)[a} b], f € S(C)[a, b], и при этом будем писать f € S(u)[a, b].
.г
Теорема 4- Если f € R[a} Ь], tp G R[a, b], g(x) = t/o + / y(t) ^? a ^ x <i b, yo = const, mo
a
f € S{g)[a, b] и при этом
ff{x)dg(x)= I f(x)V{x
)dx. B)
8.5. Вычисление интеграла Стилтьеса.
Теорема. Пусть f ? С[а, b], а функция g кусочно-непрерывна на [а, Ь] и имеет инте-
интегрируемую на этом сегменте производную </', которая существует в каждой точке непре-
непрерывности функции д. Пусть хо — «, ^Г, ••• , im — b — точки разрыва функции д и ее
производной д'. Тогда справедлива формула
ь о
Jf(x)dg(x)=ff(x)g'(x
) dx + f{a)(g(a + 0) - 9@)) +
m-l
- д(ь - 0)) + Y, 1«Кя« + о) - g(xl - o)). A)
8.6. Теорема о среднем и оценка интеграла Стилтьеса.
Теорема 1. Пусть f : [а, Ь] —> R, m ^ f(x) ^ M Vx 6 [о, Ь], </:[«, 6] —>¦ К не убывает на
[а, Ь] и f g S(g)[a, h]. Тогда справедливы формула
ь
[ f(x)dy(x)=ti(g(b)-g(a)), A)
а
где т ^ // ^ М.

§ 8. Интеграл Стилтьеса 339
Следствие. Если f ? С[а, Ь], то 3? € [а, 6]:
ь
J
B)
Теорема 2. Если f ? О[а, Ь] и д : [о, Ь] —> R — функция ограниченной вариации на [а, Ь],
то справедлива оценка •
ь
J
f(x)dg(x)
MV(g; а, Ъ), C)
где М — max |/(i')|, V(g; а, Ь) — полная вариация функции д.
149. Пусть функция а возрастает на [a, b], a ^ xq ^ Ь, а непрерывна в точке хо,
ь
f(xo) = 1 и f(x) = 0, если х ф хо. Доказать, что / € S(a)[a, b] и / f(x)dn(x) = 0.
а
М Из непрерывности функции а в точке xq следует, что
Ve>035>0:Vx€ S{x0, 8} =^ \а{х) - а{хо)\ < ^.
Пусть П — такое разбиение сегмента [а, 6], что </(П) < S. Если точка xq принадлежит
сегменту [,r,, j:;+i] при некотором 0 ^ г ^ м — 1, то 5п(/, «) = o<(xi+i) — cv(ij) = а(ж;+г) —
fv(xo) + «(^o) — о?(х;) < г, Sn(/, f*) = 0, следовательно,
0 s? 5П(/, or)-Sn(/,a)<e и / € .S(or)[a, 6].
Поскольку ,S'n(/, or) = 0 при любом разбиении П сегмента [а, Ь], то
= sup{5n(/, a)} = [
{п} - J
1 = 0. >
150. Функции Д, : [—1, 1] —> R, j = 1, 2, 3, определены следующим образом: Д,(х) = 0,
если х < 0, Д,(*) = 1, если х > 0, Да@) = 0, Д2@) = 1, Дз(О) = 1.
Пусть / — ограниченная функция на [—1,1].
а) Доказать, что / g S(pi)[—1, 1] <S> /(+0) = /@) и что в этом случае
1
б) Сформулировать и доказать аналогичный результат для Дг •
в) Доказать, что / ? .Ь'(/Зз)[— 1, 1] -О / непрерывна в точке # = 0.
г) Пусть / непрерывна в точке х = 0. Доказать, что
ill
[ f(x)dlh{x)= f f(x)dl]2(x)= f f(x)dp3(x)-.
J <J <J
А а) Необходимость. Если / ? S(/Ji)[—1, 1], то, согласно свойству 3), теорема 1, п. 8.3,
10 11
f eS{/h)[-l, 0]A/€S(/Ji)[0, l]A[f(x)dp1(x)=lf(x)dp1(x)+[f(x)dp1(x)=[f(x)dp1(x),

340 Гл. 4. Определенный интеграл
о
так как J f(x)dfh(x) = 0.
Из существования J f(x)d[li(x) следует, что Ve > 0 существует такое разбиение П сег-
о
мента [0, 1], что
Поскольку j3i(xi+1) - /?i(z;) = 0, если г'. ф 0, и /?i(xi) - /?i(x0) = 1, то
i) = wo<?, A)
где wq — колебание функции / на сегменте [хо, xi] = [0, xi]. Тогда для любого разбиения П*
такого, что 4(П*) < <i(n), получим неравенство
Sn« (/, ДО - Sw (/, ДО = wj < e, B)
из которого, согласно критерию Бэра, следует, что функция / непрерывна справа в точ-
точке х = 0:
Достаточность. Пусть /(+0) = /@), т. е. функция / непрерывна справа в точке х = 0.
Тогда Ve > 0 3 5 > 0: на интервале ]хо, хо + 6[ колебание uif функции / удовлетворяет
неравенство uif < e.
Возьмем произвольное разбиение П сегмента [—1, 1], в которое входит точка х = 0, такое,
чтобы d(U) < S. Тогда 0 ^ ?п(/, /8i) - 5п(/, /8i) < е, следовательно, / € 5(/?i)[-l, 1].
Поскольку при любом разбиении П сегмента [—1, 1], содержащем точку х = 0, выполня-
выполняются неравенства
1
mi ^ I f{x)dfI{x)^M1, C)
где mi = inf {/(x)}, Mi = sup {/(х)}, и lim iih = lim Mi = /@), то
б) Рассуждая аналогично, получаем
/ е s(/J2)[-i, i] «• Л-о) = /(о).
1
и при этом f /(х) f//?2(x) = /@).
в) Пусть П — произвольное разбиение сегмента [—1, 1] и точка х = 0 не входит в П.
Если 0 € ]xJt xJ + i[, то Sn(/, Дэ) —,S'n(/, /?з) = ш,, где Wj — колебание функции / на сегменте
[xh xJ+i]. Следовательно, (ш3 — 0 при Й(П) -> 0) О (/(-0) = /@) V /(+0) = /@) V /(-0) =
/()/() /())
Если точка х = 0 входит в разбиение П и принадлежит сегменту [х^, ij + i], то .S'n(/, /Зз) —
¦9п(/, /?з) = j(^j + wj )> гДе uj — колебание функции / на сегменте [х3, 0], шу' —
колебание функции / на сегменте [0, ary+i]. Следовательно,
5п(/, Дз) - Sn(/, Дз) -+ 0 при <г(П) - 0 <» lim /(x) = /@),
— х—'О
т. е. / непрерывна в точке х = 0. Таким образом, (/ ? 5(Дз)[—1, 1]) О (/ непрерывна в
точке х = 0, и при этом
i

§ 8. Интеграл Стилтьеса 341
г) Если / непрерывна в точке х = 0, то одновременно выполняются все предыдущие
случаи и при этом
1 1 1
/ /(*) d^{x) = I f(x) df}2{x) = I f{x) dp3(x) = /@). >
-l -i -l
151. Используя обозначения задачи 150, доказать, что /?2 € 5(/?i)[— 1, 1] несмотря на то,
что lim 6'n(/?2, Pi) не существует.
•* Интегрируемость функции /?2 по функции /?i следует из случая а) примера 150, причем
1 i
При любом разбиении П сегмента [—1, 1] и произвольном выборе точек & € [ж;, Zi+i],
j¦ = 0, п — 1, имеем, если 0 ? [iJ: Xj+i]:
Sn@2 Pi) = Y^p2(?,)(Pi(xi i)-Pi(x))= I ^' если^>^°>
' ' / j \ )\ \ ) у v i/j \ q^ если ?j < 0.
Следовательно, lim 5n(/?2, /?i) не существует. >
Этот пример показывает, что условием а ? С[а, Ь], о котором говорится в теореме пункта 8.2,
нельзя пренебрегать. ' ¦ ''
152. Показать, что
о
М Интегрирующая функция ih[i]-i,0^i^ J, представлена в виде разности неубыва-
неубывающей функции i н [i], 0 ^ i ^ 3, и возрастающей функции яь->я,0^ж^З, следовательно,
согласно определению интеграла Стилтьеса по интегрирующей функции ограниченной вари-
вариации, имеем
/ х d([x] - х) = х d[x] - xdx.
0 0 0
Функция х t—r [x], 0 ^ х ^ 3, терпит разрывы первого рода в точках z = 1, ? = 2 и х = 3, а
функция f : х у-г х, О^х^З, непрерывна в каждой точке сегмента [0, 3], поэтому, согласно
решению примера 151, получаем
з
з
Поскольку J х dx = -, то окончательно имеем
о
.5
J
9 _ 3
9 ~" О '
153. Пусть pi — точки сегмента [а, Ь] такие, что а = ро < Pi < ••• < Рп =Ь. Пред-
Предположим, что функция д : [а, Ь] —<• К не убывает на сегменте [а, Ъ] и постоянна на каждом
интервале ]pi, p,+i[, i = 0, п — 1. Пусть / : [а, Ь] —>"R, / € С[а, Ь]. Вычислить
f(x)dg(x).
/¦

342 Гл. 4. Определенный интеграл
¦4 Функция д терпит разрывы первого рода в точках pi, а функция / непрерывна на
сегменте [а, Ь]. На основании решения примера 151 можно утверждать, что / ? S(g)[a, b],
причем
ь
J /(*) dg(x) = f(po)(g(po + 0) - д(ро)) +
о) - 3(р,)) + (д(р<) - 9(р, - о))) + f(pn)(g(Pn) - д(Рп - о)) =
= f(a)(g(a + 0) - 9(а)) + ^ /(р,)(з(Р. + 0) - з(р. - 0)) + /(Ь)(9(Ь) - д(Ь - 0)). >
154. Пусть G(x) = h(x) + д(х), а < х < Ъ, где /г € C'A)[a, i], Л'(г) > 0 Vx g [а, Ь], а д и
/ — функции, заданные в предыдущем примере. Вычислить
ь
JfdG(x).
¦4 Поскольку G — неубывающая на сегменте [а, Ь] функция, равная сумме двух неубыва-
неубывающих на этом сегменте функций, то, согласно формуле A), п. 8.5, имеем
ь ь ь
f f(x) ,Ю(х) = f f(x) dh(x) + J /(*) dg(x).
a a a
h b
Поскольку h G CYO[a, b], то J f(x)dh(x) = J f(x)h'(x) dx, следовательно, получаем
a a
Ь b b
J f{x) dG(x) = j f(x)h'(x) dx + j f(x) dg(x),
b
где J f(x) dg(x) вычисляется по формуле, полученной в предыдущем примере. >
a
155. Пусть / G С[а, Ь], р ? R[a, b], p(x) > 0 Ух ? [а, Ь]. Доказать, что
(. ь
f f(x)dP(x)= I f(x)p(x)dx,
X
= J
где Р(х) = I p(t)dt, a < x sC b.
a
¦4 Рассмотрим произвольное разбиение П сегмента [a, b] и составим интегральную сумму
Стилтьеса функции / по функции Р:
i=0
^i-i-i
Составим также риманову интегральную сумму интегрируемой на сегменте [a, b] функции fp:
п — 1

§ 8. Интеграл Стилтьеса 343
и рассмотрим разность
ХТ
.Vn(/, P) - Su(fp) = ^ /(?,) I f p(x) dx - р(Ь) Дх; 1 .
i=0 ' ^
Согласно первой теореме о среднем, имеем
p(x)dx = /л, Ait, mi ^ Hi ^ Mi,
где го, = inf {7>(я)}, ^ = SUP {р(х)}- Принимая во внимание оценку |/(х)| ^ М,
а ^ х ^Ь, М = const, неравенство \/ц— p(?i)\ ^ t»>i, где ш, —колебание функциир на сегменте
[х,, x,+ i], а также интегрируемость функции р, получаем, что Ve > О 38 > 0:
п—1
|.Ь'п(/, Р) - .?п(/р)| < М ^ш, Дх, < е,
1=0
для каждого разбиения П, для которого с((П) < 8.
ь
Таким образом, 3 lim 5П(/, Р) = lim Sn(fp) =j /(x)p(x) dx. Следовательно,
b Ь
f e S(P)[a, Ц и / Дх) dP(x) = f /(x)p(x) dx.
a a
2
2
156. Вычислить
— 2
(x + 2, если -2^1-^-1,
2, если - 1 < x < 0,
x2 + 3, если 0 < х ^ 2.
•^ Функция у пмеет скачки, равные 1, в точках х = — 1 и I = 0, а ее производная #'
имеет вид
{1, если - 2 ^ х < -1,
0, если - 1 < х < 0,
2х, если 0 < х ^ 2.
Применяя формулу A), п. 8.5, получаем
2-12
//' Г т2 9 2 17
xdg(x) = xdx + 2 / x2dx + (-l) -1+0-1 = ^- ' 3
-2 -2 О
157. Пусть на сегменте [а, Ь] оси Ох расположены массы, непрерывно распределенные
и сосредоточенные в точках х3, j = 1, п. Найти статический момент этих масс относительно
начала координат.
< Пусть j; н^ Ф(х), а ^ х ^ Ъ, — количество массы на сегменте [а, х] С [а, Ъ], причем
Ф(а) = 0. Тогда Ф — неубывающая функция. Пусть П — произвольное разбиение сегмента
[а, Ь] на п частей. Тогда на сегменте [х,, x,+ i] содержится масса Ф(х;+х) — Ф(х;) = ДФ(х;).
В частности, на сегменте [хо, х{\ содержится масса Ф(Х]) — Ф(а) ^ 0 (в силу предположе-
предположения Ф(«) = 0). Считая в каждом случае массу сосредоточенной на правом конце сегмента
[xi, Ki + i], получим приближенное значение статического момента dM всей массы относи-
относительно начала координат в виде
п — 1
dM и ^х,+1 ДФ(х.) = Sn(x, Ф),
1 = 0
2 -2
о-1=Т^

344 Гл. 4. Определенный интеграл
где 5'п (х, Ф) — интегральная сумма Стилтьеса функции х по функции Ф. Переходя к пределу
при <2(П) —> 0, получим для вычисления искомого статического момента М формулу
ь
М = I х<1Ф(х).
а
Если х н-» /л(х) — линейная плотность непрерывно распределенной массы, то Ф'(х) = ii{x).
В точках х}, j = 1, т, функция Ф разрывна и в каждой из этих точек ее скачок равен
массе rrij.
Применяя формулу A), п. 8.5, для вычисления интеграла Стилтьеса, находим
*
М — j xft,(x) dx -f
y ^
Полученная формула показывает, что интеграл Стилтьеса позволяет объединить с помо-
помощью одной интегральной формулы разнородные случаи непрерывно распределенных и сосре-
сосредоточенных масс.
Упражнения для самостоятельной работы
7Г
166. Пусть /:ih sin х, (р : х t—> x2 — Зх + 5, О^х^ ^. Вычислить J f(x) d<p{x).
о
167. Пусть /:1И13, 0^i^l,jj:iHi, если ~- < х < |, <р@) = 0, к = Т~п.
1
Вычислить J f(x) d<p(x).
168. Пусть /:ih»i, (зии [х2], 0 ^ х ^ 5. Вычислить Jf(x)d<p(x).
о
169. Пусть / : х ь-> х2, 0 ^ г ^ 1, <р(х) = 0, если х G [О, \ [ и г G ] ?, l], <p (j) = 1.
1
Вычислить J f(x) d<p(x).
о
170. Пусть /:ii-h2, O^i^l, <p(z) = 1, если ж 6 ]0, 1[, <р@) = <рA) = 0. Вычислить
з Г 0, если х = —1,
171. Вычислить J xd<p(x), где <р(х) = < 1, если — 1 < х < 2,
-1 I -1, если 2 ^ х ^ 3.
2 2 2
172. Вычислить / xdip(x), f x2 d¦?(*), /(х3 + l) d<p(x), где
—2 —2 —2
{х + 2, если - 2 ^ х ^ -1,
2, если - 1 < х < О,
3, если 0 < х ^ 2.
173. Пусть / — функция ограниченной вариации на сегменте [0, 2тт\ и /Bт) = /@).
Доказать, что каждый из интегралов
2тг 2тг
J /(х) cos их dx, J
о о
/(x) cos их dx, f f(x)sinnx dx
V( f- 0 2-х)
не превосходит ' —L по абсолютной величине.

§ 9. Приближеииое вычисление определениых иитегралов 345
§ 9. Приблиэкенное вычисление определенных
интегралов
1°. Формула прямоугольников. Если функция у(х) 6 С^[а, b]; h — -jp; Xi = а + ih
[i = 0, 1,... , n); г/0,) = yi, то
ь
/ y(x) dx = h (j/o + yi + ¦ ¦ • + J/n-i) + Rn,
Й(b — a
n = L-7
2°. Формула трапеций. Если у — у(х) 6 С^2'[а, 6], то при тех же обозначениях имеем
ь
J \ 2 "''
а :
3°. Формула парабол (формула Симпсона). Пусть у = у(х) € С^'[а, Ь]. Полагая
п — 2к, можно получить формулу Симпсона
У(х) dx = - ((j/o + У2к) + 4(j/l + J/3 + • • • + У2Д.-1 ) + 2 (j/2 + 2/4 + • • • + 2/2fc-2)) + Дп,
27Г
/
Примечание. Если имеет место формула
где Z{ — приближенное апачетхие вслпчппт1 г, гичисленное по некоторой формуле, то говорят,
что эта формула в некотором классе функций имеет п—й порядок точности (М > О — постоянная,
не зависящем от /i). ,
Таким образом, формула прямоугольников имеет в классе у G СA>[а, Ь] первый порядок точности,
формула трапеций в классе у ? СB)[а, Ь] имеет второй порядок точности, формула парабол в
классе у ? СТ*)[«, 6] имеет четвертый порядок точности.
Часто вместо нормы || • ||о берут другие специальные нормы, выбор которых зависит от характера
решаемых задач. В дальнейшем отрезок [а, 6] с выделенными на нем точками ж,- = a + ih (i =
0, 1,..., ?i) будем называть равномерной сеткой с шагом h; точки деления х{ называются узлами
сетки.
158. Применяя формулу прямоугольников (п = 12), приближенно вычислить / =
х sin х dx и результат сравнить с точным ответом.
о
¦4 Рассмотрим равномерную сетку на отрезке [0, 2т] с шагом h = ^, тогда it = г^ (г =
О, 1, 2,..., 12). По формуле прямоугольников, имеем
7 11 ч / и
7
/
/
ii 2 11 . 2 /11
, 7Г \—v . 7Г . .Ж Ж v^ . . *7Г Ж I \~л
х sin х dx и — > г — sin г — = — > г sin — = >
6 z_/ е 6 36 ?-j 6 36 \ ?—i
0 .=о ;=о \<=1
cos 6x ¦ sin -ух
sin |
т2 / (б sin 6х • sin —х - y cos yx ¦ cos6l) sin |
36 sin2^

346
Гл. 4. Опредоленныи интеграл
- COS - COS 6 Я Sill -?- ?
sin ~
ж
36
• 2 it
sin -
6 12 6 v '
12
(взяли ж Я 3,14; v3 и 1,73). Точное значение интеграла / = —2т = —6,28 .. . . >
159. С! помощью формулы трапеций вычислить интеграл
I =
1 .sin" х dx (n = 6)
и оценить погрешность формулы.
¦^ Построим на отрезке И), ^| равномерную сетку с шагом h = -rj: {х; = г-^;
г = 0, 1, 2, 3, 4, 5, б} . По формуле трапеций
я- B + Vz , l
7 ~ 12 I 4
)
тг
= —
24
тг /2 + лД 1 \-v / 1F\
о + -р > л/7 + cosi- =
2 л/2 ^ V 6 /
i=i /
\/i4-(- v3 + v7^ + л/п + л/13 + \/l4 - л
4о
1,4677
Оценим погрешность формулы трапеии": для jt;jto оценим Rn. Очевидно,
' ,2; inax |/ '(»/)[•
В нашем случае max
Таким образом, |Д„
1 - \ sin2
I
14 VU '
< 0,002. >
160. О помощью формулы ('импсона вычислить интеграл
¦^ Деля отрезок [0, 1] на четыре равных части (Л = j), по формуле Симпсона имеем
^ ((?/о + 2Д) + 4(yi + уя) + 2у2) и ^A + 0,5 + 3,76471 + 2,56 + 1,6) = 0,78539. >
161. Принимая и — 10 , вычислить константу Каталана
arctg x
¦^ Построим равномерную сетку с шагом h = 0,1 {х; = г/г; г = 0, 1,...,10} и вычислим
приближенно G по формуле (!импсоиа
G = — ((?/о + 2/ю) + 4(i/i + 2/з + 2/5 + 2/7 + 2/э) + 2(j/2 + 2/4 + 2/6 + 3/8)) •
Вычисляя соответствующие значения функции с точностью до пяти знаков после запятой,
получаем у0 = 1; 2/ю = 0,78540; 2/о + 2/ю = 1,78540; ?/i = 0,99668; 2/3 = 0,97152; уъ = 0,92730;

§ 9. Приближенное вычисление определенных интегралов 347
уг = 0,87246; у9 = 0,81424; 4(«/i + у3 + ys + ут + уя) = 4 • 4,58220 = 18,32880; у2 = 0,98698;
t/4 = 0,95127; j/6 = 0,90070; у а = 0,84343; 2(«/2 + ?/4 + у6 + «/8) = 2-3,68238 = 7,36476. Подставляя
вычисленные значения, находим
1,78540 + 18,32880+ 7,36476 _ с
, и — 0,Л. ,.>
1
162. Пользуясь формулой — = I , вычислить число ж с точностью до 10~4.
4 J 1 + х2
о
1
¦4 Мы уже вычислили в задаче 160 интеграл J *3 с помощью формулы Симпсона, взяв
о
к = 2 . Оценим погрешность формулы. Поскольку (см. пример 77, гл. II)
(х . 2) ^ 4! при х 6 [0, 1], следовательно,
\Rn\ < — ¦---
Используя результат задачи 160, находим it й 4- 0,78539 = 3,14156. Сравнивая получен-
полученный результат с табличным тг = 3,141592... , видим, что все четыре цифры после запятой
правильны. >
1
163. Вычислить / е.х dx с точностью до 0,001.
о
¦4 Вычислять интеграл будем по формуле Симпсоиа; поскольку (в1 ) ^ 228 при
х ? [0. 1], то шаг сетки выбираем из условия (оценивая погрешность формулы парабол) Ы1 <
Деля отрезок [0, 1] на 10 равных частей, получаем
1
/ ех" dx. ss — ((«/о + 2/ю) + 4(«/i + j/3 + Уъ + уч + У я) + 2(«/2 + Vi + Уъ + у»)) ¦
о
Вычислим значения функции ех в узлах сетки с точностью до 10~5 (можно вычислить,
используя, например, формулу Тейлора). Имеем уа = 1, г/ю ~ 2,71828, у\ и 1,01004,
j/з « 1,09417, «/5 и 1,28733, «/7 и 1,63230, j/9 ss 2,24789, j/2 и 1,04081, j/4 и 1,17351,
ye и 1,43332, j;8 и 1,89648, j/0 + j/ю a 3,71828; 4(j/i + J/з + Уъ + 2/7 + Уя) и 4 • 7,27173 = 29,08692;
2(г/2 + 2/4 + 2/G + Ы и 2 • 5,54412 = 11,08824;
/¦
-^-C,71828 + 29,08692 + 11,08824) = 43'^344 ~ 1,46311.
о
Получили три верных цифры после запятой. >
1
164. Вычислить / (ех — 1Iп — dx с точностью до 10~4.
J x
о
¦4 При х —г 0 (ег —1Iп^ -+ 0, поэтому интеграл Римана существует. Производная
четвертого порядка подынтегральной функции имеет весьма сложный вид и оценить ее труд-
трудно; более того, уже первая производная подынтегральной функции неограничена на [0, 1]. В

348
Гл. 4. Определенный интеграл
принципе мы можем воспользоваться формулой Симпсона, однако оценку погрешности про-
произвести не сможем. Поэтому поступим следующим образом. Разложим по формуле Тейлора
функцию 1 — ех по степеням х:
где R(x) = ^ф~, 0 < с < 1. Запишем подынтегральную функцию в виде
f{x) = (\-ex)lax
и обозначим через <f(x) функцию
х2 х3 х* х5 хе
Очевидно, /(х) = <р(х) + Ri(x), где Ri(x) = \nxR(x). Оценим |i?i(x)|
при х ?
[О, 1]. Поскольку lim хт1пж = 0; In 1 = 0, то функция Ы = 1жт1пх| достигает абсолютного
х—О
максимума в некоторой внутренней точке отрезка [0, 1]. Дифференцируя z(x), получаем
1
z'(x) — х6 + 7x6lnx. Приравнивая нулю z'(x), находим, что в точке х = е 7 функция |г(х)|
достигает абсолютного экстремума, равного
1
max |z(x)| =
Те'
Так как |й(х)| < ~ при х € [0, 1], получаем оценку \f(x) — <р(х)\ = \Ri(x)\ < у^\' Таким
образом,
{f(x)-<p(x))dx
поэтому вместо интеграла функции /(х) будем вычислять интеграл от функции <f(x). Задан-
Заданная точность будет обеспечена, если в процессе вычисления интеграла функции <р(х) погреш-
погрешность вычислений не превзойдет 10~4.
Интегрируя функцию <р(х) по частям, имеем
1 1
I f(x)dx*i I <p(x)dx =
= ф(х)\п х
х5 х6 ,
720+7Г'
4 18 96 т 600 6-6! ^ 7-7!'
где
t2 . х3 х4 х5 хв . х7
• In 1 — lim ф(х)\п х = 0.
x—»0
С точностью до 10 в имеем
- = 0,250000; — = 0,055556; —=0,010417; ^- = 0,001667; -i-= 0,000231;
4 18 96 600 6 • 6!
/A -e'jlni
xdx a 0,250000 + 0,055556 + 0,010417 + 0,001667 + 0,000231 = 0,317871 и 0,3179. >
165. Вычислить с точностью до 0,001 интеграл вероятностей / = I е х dx.

§ 9. Приближенное вычисление определеиных интегралов
Интеграл сходится, поэтому Ve > 0 3Ai > 0 такое, что при А ^ Ai
e-x2dx<e.
А
Если мы нашли А\, то можем записать при А ^ А\
А +оо
/ = / е~х dx + Д, где R = / е da:.
=1 е~*2 dx + R, где R = /
о л
л-З
Возьмем е = 10 и постараемся определить оптимальное А, т.е. такое, чтобы промежуток
[0, Л] имел по возможности небольшую длину. Проще всего поступить следующим образом:
-ТОО 2 -t-oo ^
допустим, мы нашли такое А, что J e~x dx < е; тогда и интеграл J e" dx < с;
А
-}- со -}-оо Л-}- J
/е-а&- / e~x2dx= J
A+l
+ оо
О < / е~х dx — I e~x dx = I e~x dx — e~f < e,
A A+l A
где А < $ < А + 1 (по теореме о среднем).
Полученное неравенство эквивалентно неравенству
Подставляя e = 10 3 , получим
^ > Vln 1000 « \/б,907755 и 2,628
и в качестве А можем взять А = 2,6.
Можно получить более тонкую оценку для А. Допустим, найдено такое А, что
Л = / e~x* dx <e.
А . ' , i ¦
Произведя замену х2 — t [dx — —7= ), получим
-f-OO
2Л
.-л2
Из условия е2л < е. находим АеА > —, In А + А2 > In jj, откуда Л > Win ^7 — In А. Так
как должно быть А > 2 при е = 10~3 , под радикалом можем взять In 2 вместо In A:
А > ^1пЮ00-21п2 и у/6,90775 - 1,38628 = у/5,52147 = 2,35.
Таким образом, взяв, например, А = 2,4, можем записать
2,4
е"*2 dx < 10~3.
о о
Наша задача сводится теперь к вычислению с точностью до 10~3 интеграла
2,4
7= fe-^dx.
'}
о

350 Гл. 4. Определенный интеграл
Мы могли бы поступить здесь, как и в предыдущей задаче 164: аппроксимировать функ-
функцию е~х полиномом. Но в связи с тем, что промежуток интегрирования имеет длину 2,4, а
степени B,4)п растут довольно быстро, нам пришлось бы для обеспечения нужной точности
взять больше 15 членов разложения в формуле Тейлора.
Интеграл I будем вычислять по формуле Симпсона. Найдем г/4' функции у = е~х .
Поскольку г/D) = 4г/ (з - 12х2 + 4х4) , то |г/D)(х)| ^ 4C - 12 • 5,76 + 4 • 33,1776), х 6 [0; 2,4],
: 1, а функция z = 3 — 12х2 + 4х4 монотонно возрастает при х > л/-. Таким
образом, г/4)(з:)| ^ 4- 66,5904 = 266,3616, 0 ^ х ^ 2,4. Оценивая погрешность R формулы
Симпсона
находим для нашего случая
Из условия \R\ < 10~л получ
h <
Для получения заданной точности можем взять h = 0,1.
Рассмотрим сетку на отрезке [0; 2,4]: uji, = {х, = 0,1»; г = 0, 1, ..., 24}. Для обеспече-
обеспечения заданной точности значения подынтегральной функции в узлах сетки будем вычислять
с пятью значащими цифрами после запятой. Имеем г/о = 1; 2/24 я 0,00315; гд я 0,99005;
2/2- Я 0,96079; г/,3 я 0,91393; yt я 0,85214; г/5 я 0,77880; г/6 я 0,69768; г/7 я 0,61263;
3/8 Я 0,52729; у9 я 0,44486; у\0 « 0,36788; уп я 0,29820; 2/12 я 0,23693; зпз и 0,18452;
2/14 я 0,14086; 3/1.5 « 0,10540; ущ я 0,07731; уп я 0,05558; у18 я 0,03916; уу9 я 0,02705;
2/20 я 0,01832; г/21 я 0,01216; у2г я 0,00791; </2з я 0,00504; г/о + 2/24 и 1,00315;
12 11
j/2j-i я 4-4,42822 = 17,71288; 2^Гy2j я 2 • 3,92627 = 7,85254;
Г 1_ /
^30V т J=1 У-! /
Рассмотрим точное значение / = ~ = 0,8862... , а также ошибку R = I — I = 0,0006 =
6 • 10~ . Полученная точность превысила заданную. >
166. Приближенно найти длину эллипса, полуоси которого а = 10 и b = 6.
¦^ Параметрическими уравнениями эллипса являются х = lOcost, у = 6suit, 0 <С t sC 27r,
а длина его дуги
= 4
о о
Вычислим интеграл с помощью формулы Оимпсоиа, разделив отрезок [0, ^] на 6 равных
частей (Л = Tj) ¦ Будем вычислять значения подынтегральной функции в узлах сетки шн =
{ih; i = 0, 1, 2, 3, 4, 5. 6}:
: / \/ш cos2 t + 36 sin2 < Л = 8 / tJIT + 8cos2xdx.
2,0 = 5, з/б = 3, j/, = \/17 + 4\/3 я ^/23,928 я 4,892; г/2 = -у/П + 4 = \/гТ я 4,583,
2/з = л/и я 4,123; г/4 = vT7^-~4" = %/Гз я 3,606; г/5 = \П7 - 4\/3 я 00,072 я 3,174;
уо+уе = 8; 4 ((/1+3/3 + 2/5) «48,756; 2 (г/2 + г/4) я 16,378.
Подставляя полученны" значения в формулу парабол, находим:
I ~ ^(.s + 48,756 + 26,378) = W?_LlM*i « 5]>056. >

§ 9. Приближенное вычисление определенных интегралов
351
167. Построить по точкам график функции у = / dt @ ^ х ^ 2т), приняв Ах = —.
J t 3
О .. г
¦4 Рассмотрим сетку шл = {х; = ^S * = 0, 1, 2, 3, 4, 5, б} . Значения функции у(х) в узлах
ки:
7Г 27Г
ЗГ ~ Т
/sin a- / sin х , / sin x ,
dz; «/2= / dx; уз = / ах;
о о ., , ,
Т 2л
/sin х / sin x
dx; «/6 = /
х 7 х
2/о = 0; г/1 =
2/4 =
¦ dx.
X J X
0 0 0
Задача сводится к приближенному вычислению шести интегралов.
Рассмотрим на отрезке [0, 2ж] сетку шь = |х; = t-^; г' = 0, 1,..., 24} ; очевидно, узлы сет-
сетки Ш)г являются узлами сетки ш;,. Вычислять интегралы будем по формуле Симпсона.
Находя значения функции дискретного аргумента yi =
sln*< в узлах сетки п>н, получим j/o = lim sla.x> = i- и
0,2618; j7i x 0,2590; у2 = 0,25; у3 « 0,235*9; г/4 и 0,2165;
j/5 ss 0,1932; уб я 0,1666; у7 » 0,1380; j/8 я 0,1083; уд я
0,0785; j/io = 0,05; j/n я 0,0235; у12 = 0; J7i3 я -0,0199;
*- j/и я -0,0357; yi5 я -0,0471; j/16 я -0,0541; j/17 И
л -0,0568; yig и -0,0555; j/i9 И -0,0508; у2о ~ -0,0433;
j/21 я -0,0336; «722 » -0,0227; г/2з ~ -0,0112; y2i - 0.
Очевидно,
27г л
Рис. 72
1
г/1 ~ г (г/о + г/4 + 4(«/i + j/3) + 2«/2) =
2,9579
0,9860;
г/2 я - I «7о + з/8 + 4
:*-1+2
г/з я - I г/о + г/12 + 4 ^ г/2^-1 + 2
*;=!
- г/о + г/16 + 4
к-1 + 2
*;=1
10
к=1
9
т I г/о + «/го + 4
/;-1 + 2
«.•=1
12
11
Ус
1 /
- I г/о + г/24 + 4 ^^ 3/2*1-1 + 2 ^^ ;
\ fc=l fc=l
4,
5
5
4
4
,9407
3
,5570
3
,1635
3
,5247
3
,2568
1,6469;
i 1,8523;
i 1,7212;
i 1,5082;
i 1,4189.
При х е]0, тг[ г/'(г) > 0, а при х б]тг, 2тг[ «/'(х) < 0; «/"(х) < 0 при х 6 JO, ^"[. Таким
образом, у(х) в интервале ]0, 7г[ возрастает, а в интервале ]т, ^г[ убывает; на интервале
]0, -j-[ функция y(j;) выпукла сверху. График функции изображен на рис. 72. >
Упражнения для самостоятельной работы
ю
174. Вычислить In 10 = J -^-, используя правило Симпсона при п = 10. Найти модуль
о
перехода от натуральных логарифмов к десятичным. Сравнить с табличным значением.

Ответы
Глава 1
9. a) A U В = {ж : -4 < ж < 4}, А П В = {х : 0 < ж < 1}, А\В = {х : -4 < х < О}, В\Л =
{ж : 1 < ж < 4}, Л Д В = {х : (-4 < х < О) V A < х < 4)}; б) Л U В = {х : -1 < х <
6}, А П В = {ж : О < ж < 2}, А\В = {ж : -1 < ж < О}, В\А = {х : 2 ^ х < 6}, А Д В -
{х : (-К х < О) V B < х < 6)}; в) A U В = А, А П В = В, А\В = {г : г = 2n, n € Z},
В\А = 0, А А В = {х:х-2п,п€Щ. 10. a) A U В = В, А П В = А, А\В =
0, В\А = А Д В = {(ж, у) : -1 < ж < 1, VI-ж2 < |у| <: 1 - |х|}; б) A U В = А, А П
В = В, В\А = 0, А\В =т1Дй = {(ж, у) : -1 < х < 1, 1 - |х| < \у\ ^1}; в) A U В =
{(х,у):(\х\ + \у\ < 2) V ((ж - 2J + (у - 2J < 4) }, А п В = {(х, у) : 0 < х < 2, 2 -
л/4х - ж2 < у < 2- ж}, А\В= {(ж, у) : (-2 < х < 0, 2 - х < у < 2 + х) V (О < х < 2,
-2 +ж < у ^2-У4х-ж2)}, В\А = {(ж, у) : (о <х < 2, 2-г ^у < 2 + V4i - х2) V
B < ж < 4, |у - 2| < л/4ж - ж2) }, А Д В = (А\В) U (В\А). 11. а) Множество точек пря-
прямоугольника, ограниченного прямыми ж = —2, ж = 1, у = —3, у = 1, причем стороны,
лежащие на прямых х = —2, у = —3, не принадлежат множеству А х В. б) Параллеле-
Параллелепипед, ограниченный плоскостями х = 0, х = 1, у = 0, у = 2, z = 0, z = 3. в) Прямые,
параллельные оси Ож и проходящие через точки @, я), где п ? Ъ. г) Прямые, параллельные
оси Оу и проходящие через точки (и, 0), п g Z. 24. а), б), в) — сюръектнвные функции;
г) — биективна; д), е) — инъективные. 25. a) f\\_(X> oj> /Im + <х>[> ^) /|г21цг-
п € Z, /|f2mr+jr/2 2ПЯ-+37Г/21' п ^ ^- 27. а) х = \J2ay — у2, 0 ^ у < 2о; б)х = —д
0<у<2а. 28. у = -х + ^. 29.y = x-f. 34. а) (п + 1)! - 1; б) ±п(п + 1)Fп3 +9п2 - 1);
в) ^и2(н + 1JBп2 + 2п + 1). 37. о) ± 2; б) 0 ^ х < +оо. 39. а) 26; б) ^^;
в) x2~xf^y?*y ¦ 40. а) Кег = -1, lmz = 0; б) Rez = 2, Imz = |; в) Rez = 2, Imz = 0.
42. a) \z\ - 125, arg z = - § + 3 arctg |; 6) |z| = 0,25, arg z = 0; в) |z| = \/2cosyj-,
argz= f. 43. -1, i^. 44. ^2(cos45° + isin 45°), ^2(cos 165° + isin 165°), ^2(cos285°+
isin285°). 45. 2(cos^ + jsm^), ip = 30°, 90°, 150°, 210°, 270°, 300°. 46. 2(cosv + isin<p),
<p = 0°, 60°, 120°, 180°, 240°, 300°. 47. zi = -2 + i, z2 = -3 + i. 48. z\ = 2i, z2 = -1.
49. гл = ctg^ii, к = 0,n-l. 55. а), б), г). 57. а), в), г). 73. 0. 81. (e, e2, ... , em).
82. (e, л/ё, ..." Ve)- 83. (In 2, In 3, ... , ln(m + 1)). 84.C,4,6). 85. B, Ve). 86. (e°).
87.
2 6 12
-2 -6 -12
88.
0
91. sup{/} = /(-1) = -i inf{/} = /A) = 1.
92. sup{/} =
111.
112.
, inf{/} = -oo. 93. sup{/} = 4, ii
113.
= 0.
114. JL.
108. 2. 109. ||.
115.
110. |,
116. -
2m ' " v "'"¦'••••-"•• * 4m'
l
117. е^й. 120. j. 121. -f. 122. ^. 123. e. 124. e. 125. i. 126. \/2. 127. / = r2,
i = 2. 128. / = 0, I = 1 + b2. 129. /=-2,1 = 1. 130. / = 0, L = e. 131. J = e,
? = e + 1. 132. / = |, L = f. 133. Непрерывна. 134. Непрерывна. 135. Непрерывна.
136. Непрерывна. 137. Непрерывна. 138. Функция терпит устранимый разрыв в точке
х = 0. 139. Функция терпит разрыв в точках ж = ^-ffcir, к g Ъ. 140. Функция терпит разрыв
в точках ж = ? + Агтг, fc ? Z. 141. Непрерывна. 142. Фуикция непрерывна только в точках
ж = кж, к е Z." 143. Непрерывна. 144. Непрерывна. 145. Непрерывна. 146. Непрерывна.
147. Непрерывна. 148. Непрерывна справа в точках ж = п, п g Z. 149. Непрерывна.
150. Непрерывна. 151. Непрерывна. 152. х = 0 — точка разрыва второго рода. 154. х —
Bк + 1)тг, п ? Z, — точки устранимого разрыва. 155. х = ±1 — точки разрыва второ-
второго рода. 156. ж = |- -f А.-7Г, fc € Z — точки устранимого разрыва. 157. х = j + &тг,
А; € Z, — точки разрыва типа полюса. 158. х = nir, п € Z, — точки устранимого разрыва.
159. х — 0 — точка разрыва второго рода. 160. ж =
-, п g Z, — точки разрыва второго
1гBп+1) >
рода. 161. Непрерывна. 162. Непрерывна. 163. Непрерывна. 164. Непрерывна. 165. Не-

354 Ответы
прерывна. 166. Непрерывна. 167. х = ^f^-, j = 1, п, г = 1, т, к ? Z, — точки разрыва.
168. г = 0 — точка разрыва. 169. х = 0 — точка устранимого разрыва. 170. х = 0 — точка
разрыва. 171. Равномерно-непрерывна. 172. Равномерно-непрерывна. 173. Равномерно-
непрерывна. 174. Равномерно—непрерывна. 175. Равномерно—непрерывна. 176. Не являет-
является равномерно-непрерывной. 177. Равномерно-непрерывна. 178. Равномерно-непрерывна.
179. Равномерно-непрерывна. 180. Равномерно-непрерывна. 181. Не является равномерно-
непрерывной. 182. Не является равномерно-непрерывной. 183. Равномерно-непрерывна.
184. Не является равномерно—непрерывной. 185. Не является равномерно—непрерывной.
Глава 2
1пх)))И(х) = (ЬхГ. 22. (-2«
4«3(z)sh«4(x), 5м4(х)спм5(х))м'(а;). 24. ((acos* - sin t)eat, (asin t + cost)eat, -±u' (\) ,
«'(sin t) cost) . 25. (p'(<p) sin <^> + ^(v) cos yi, ^'(^) cos<?> — ^(^) sin <^, 2<p — x, 3(p2 — x2).
27- Bcos(e2:c)e2*, esin * sin 2а;, ф'(ят2 x)sin2x, -<p'(cos2 x) sin 2x). 30. а)
б) i-щ, 2sinx + xcosx, 2cosx - х sin x J х. 31. а) C, 0, 0). 32. а) 1. 33. a) t = 0,
;; б) t = 1, х = ±4. 35. а) ~ (ш2п + ^-У t ф 1; б) \{и2 + 1), t = 1.
произвольное;
36. в) -sin2(z + ix3)(l +3ii2). 39. (^2-</J V V ' '«(»»)/ v y; .
ш cos wx
. ш cos wx \
v^\/i+^-2 . 43.0. 44. 2cos2;2. 48. a) 0; 6H. 50. f'(k) = 0, если к ? Z;
—wsinwx 1 /
,, __, \r//\ I — sin x', 0 $C a: ^ тг, _ . ^,, ч Ch x sh r
не существует, если хфк. 51. а) /'(х) = | 0> ,г ^ ж < +оо. ' 54- / (ж) = ^ ~ ^ >
х#0: 72. Нет. 73. а) х'пУп+1 +хпу'п, /'@) = 0. 74. а) х = ^A + <), ?/= ^A-<), г = тг + 4*.
Ж +4
75. а) х + 2у + Зг = 6. 81. а) 0; 4*3 + 1. 82. a) arccos 4тг- 83. а) 2*3-**+*+i dx
88. а) @,1, 2х,. ..,„,-')*,. 92. (^ *^Н ^ ) ((,, „) + (^, ,))•
94. '^i^ly^- 96. а) 0,275 .... 100. 3tZx. 107. a) dt2; 5dt2. 109.3. 115. |. 119.0.
126. #@) = f. 127. /'(х) = (cos(, -sin*, 1K^. 132.
134 ( t'ttynU+st*) 1 „.2\ l 137 , iy, i
VI»|-V'(I»I)V''(I»I)' ' J 2(v(t2) + 2t-V(t2))- 1<J(- V ^ "-
156. 2(Л(х).4'A-)JЛ-1(ж) - ^-'(«^"(x^-^x).
"( "
/e C4i + ) e ( + 8<1 e (\П + )\
1в1' 5A+44K ^ 4з 284 ^125 / ^ S^ ~ 197. Л -
const. 254. При |x| > \lt; выпукла вниз. 255. При х < 0 выпукла вверх; при х > | выпукла
вниз. 256. На ]0, 1[и]3, +оо[ выпукла вверх; при 1 < а; < 3 выпукла вниз. 257. При х > — ]
выпукла вниз. 258. Выпукла вниз при ( > — 1. 259. Выпукла вверх. 260. При 0 < ( < е"

Ответы 355
и ( > е выпукла вверх. 261. Выпукла вниз. 262. Выпукла вверх. 264. Слева от точки
х = -1 выпукла вниз. 265. Перегиба нет. 295. 0. 296. \. 297. 0. 298. |. 299. ?.
301. 0 при а = Ь, с = 0. 302. b(| - ^), если о = 9ЫпЗ. 304. |. 305.0. 306.1. 307.0.
309. 1. 310. е~о. 312. -^е.ё, п = 2. 313. —2sh |, и = 0. 314. О, га < 2. 315. 1.
316.1. 318.0. 320. е". 321. е1. 322.0. 323. (-1, 0, l). 324. ("I" ?)• 325.^.
359. Указание. Функцию / разложить по степеням А. 364. 0.
404.
{ $С ж $С arcsin ~;
sin ж, f
cos г, — ^ $С ж $С arcsin
, ¦ \/^—1 -^ 7Г ^ 37Г
tg ж, arcsin —5— ^i<j, т $: ж < —.
Функция /(ж) — 2тг-периодическая.
6)
405. Спиралевидная кривая, лежащая на конусе ж2 + г/2 — г2 = 0. 406. Двойная 2х-
периодическая (по t) кривая, лежащая на параболическом цилиндре у — -ж2 —а. В проекции
на плоскость OYZ — петлевидная кривая, симметричная относительно оси OY. 407. От-
Отрезок \х\ $С 1. 408. Внутренняя часть - квадрата. 409. Внутренняя часть прямоугольника
0^ж^5, -3 ^ j ^ 2 с выброшенным полукругом (л/*0 +2/2 ^ 1- 410. Плоскость треуголь-
треугольника с вершинами М\(-\, 0); Мг@, 1); Л/зA, 0).
Глава 3
1. -i(l - 4х)^/1 -4г. 2. arctg(z + 2). 3. i arctg (ж + j) . 4. p^r ln(a2 cos2 ж + b2 sin2 ж).
6. tgf, х/т + гЛя-. 7. ^arctg(x2>1). 8. ^ In f?=i, |x| # 1. 9. -|-
10. ln|tg(f + f)|-ctgx-x, x^^. 11.
15. -sini, ж
16. Mn3^, x > 0.
О
20. i(x3.+ 1I.
- tgx + ж, ж = f + к*.
23. In |x + 1 + \/2 + 2x + x2|.
29. iln3(l - ж2), |*| < 1. 30. -(x2 +
x — j, если —oo < ж < 1; ж — ^-, если —1 $Ci < 1; :V~I+J> если 1 ^ ж < +oo.
^T. 39. _L(X
. + .

356 Ответы
\х\ > а. 44. ^ (V*EZ _ (^EpV) , |ж| > а. 45. i
46. i(Va2-*2K + aVa2 - x2 - a3 In
, |х| < а. 47.
. 51. ln(zVx2 + 1 +
48. е V'+*2 . 49. 2arcsin § + f (x - 2)л/4-х2, |x| ^ 2. 50. In
V^4 + x2 + 1). 52. -In ^44^2^1 ¦ 53. j^j- — g^- — - — arctg j. 54. ^j-ln x — yg-, x > 0.
55. Cx2-6)sinx~(x3-6x)cosx. 56.-x ctgx-ln | sinx|. 57. 2zcosx + (x2-2)sin x. 58.^--
i»inB3:) cosBx) _ cosi 3cosi ,3, I, .-el _n sin х , 3 sin x , 3. I, /* , jt\|
—4 • ¦ 59> -4Й^Т-Пп^+в1п|18г|- 60- 4^1Т7 + ?7г^+?1п|1ёB +l)|-
61. i-tg6r- jtg4x+ jtg2x+ln|cosx|. 62. ж arcsin | + л/4 - x2, |x| < 2. 63. - ^ arcsin x -
^. M < 1. 64. ?arctgx-^ + iln(l + x2). 65. -iarctgf-iln^, x # 0.
66. ^tiarctgx + f. 67. -^arctgx+iarctgx + i. 68. e" (? - 3-g- + % - ^
69. ^j («cos2 x + 2sin xcosx + |). 70. -^ - i, x > 0. 71. xln2 x - 2xln x + 2x, x > 0.
72. ^-ln2 ж—2|-lnx+2^-, x > 0. 73. —l^j^ —2-!j-i —2-, x > 0. 74.
75. ^-ln(x +
2K aVi1-»2 —„ , , __ a;sh2i ch 2x x2
— *—5 • 76. xchx — shx. 77. —- g —.
78. (x3 + <>x)slix - Cx2 + 6)chx. 79. x - y/l - x2 arcsin x. 80. (^ - 2\/l - x2) arcsin x -
x arcsin2 ж + 2x + y/l - x2, \x\ ^ 1. 81. f^fe*, ж # -2. 82. ((^ - 7) sing - ^'~^2 cos ж) tx.
c' в*. л ~ii.4.n; • BO, — T7-3—ГТЗ'~^7Тя—ЙТТШ I — 11,
Д-у/3"
i+\/3
L. 90. ib|x|-^ln
1; 2. 92. x — In Ix
•x, x ф ±1. 87. ^
-. 89. - arctg x + - In ^7—-
• 4 4 |a.'— 1
Ф0. 91. -
. 93.-^. 94. -
x ?4 -1. 95. ^W. 96. ^^- (весь интеграл). 97. 21n |\/x~+T- 1| -
l—IJ
-1. 98. |arctg(f±iJ, x#-2. 99.
. 101. I arcsin x -
21n(x+ ^ + V^2 + x + l). 103. -^= In
А2 + 2з:+2-У2(з:+1)
! arctg -
|x|^l. 102. 2(x3 + l)Vz2 + x + l +
^+1 "~~
2A/f2J^f+2_ 8<x+2)
j arctg Vx2 + 1. 105. -Wctg X%Z?± --ЪЫ ^3A+1^!^+1)^ + ^
. in M +'+V' +i\ 107- _i_ + i. _ ^ где f _ y'ii+i, x # 0. 108. |(
3) \Vl + y/x, x ^ 0.1O9. -jctg(x+ f)-7Vctg3 (x+ f),110. ^ln |tg (f + f) | + | arctg(sin x~
cos x), sin x ^ — cos x. 111.— ^— In I tg ? I
/ /- „ arctg . . In
^ч/5+2 + y^cost
Sill X*. XXa* 1 *¦/л 1 „:„ ^
^ 0.
д/cos4 .тЦ-sin4 ,-c—cos 2д
nrf-- 113- ln l^ls+l) I ~
115. arcsin(sinx — cosx). 116. ~| +
,,-i. , -sinrl. 117. '" .. 118. -—+ ali(eaI), x # 0. 119. i th f - 7 th3 f.
Zb ' 1 a^( 1 + ax) x \ / > ' 2262
120. j^ + iwctg(shx). 121. ^ + ^+f. 122. 5||? - |. 123. e4 Ii(e2A-2)) -
cos2x>0. 126. -^~, cos2x > 0. 127. -i arctg ^== -jIn
/cos 2x+cos
/cos 2x—cos

Ответы
357
128. arctg Vcos 2x - v^cos 2x. 129. xtgf. 130. ^П+со!*' 13Ь *см»-"пя- 132- ж+
tg(f-fj,x/-f+ тмг,пе2. 133. -tgf+ln|tg(f+ §)|. 134. **, «>0..
л: x / X \
in e1 — ln(l + л/1 — f2*) + я, — oo < x < 0. 136. —2e~^ arctg e^ -*¦ arctg2 (eajrfj
- ln(l + ex). 137. i(|l + x|(l + x) + A - x)|l - x|). 138. -|\/l - r^/r, 0 ^ x < 1.
140. In
n=l
Глава 4
1.136. 2. |. 3. 2i^. 4.1. 5.85,5. 6.16. 7. f. 8. f. 9. 4e-J.
18. 37,5 • 150,2* - i(l,3* + 24 + 3* + ... + 150*). 19. ^ + f (?
20-lniiiTrT- 21. 74V/74^-(^+^+...+v/74)-2v/57- 22. 0,92
17.
-/'(o))t
51
1-5-0,22. 23. 22??. 24.^. 25.8+^5*. 26. #+=#. 27. 4-тт. 28. ^ - 3*2 + 24:
30. О, если |o| < 1; -, если |a| = 1;
9\Д
]b\ < a. 38. ^?
если |a| > 1. 31. 4w. 32.
iiM. n\a\- 36. r . 37. -
40. *. 41. x = 2. 42. 2ln2. 43.
/A), min f(x) = /(-i). 44. /min = /A) = -%; точки перегиба: B, -f), (f, -^f).
47. 2 + ln^-. 48. При a = e. 59. / < 0. 60. h > h- 61.1. 62.
63. (iln i - I arctg ±, I in 4^) -64. V^
65.
x, «2), где Л1 = ^ (ln22- i
l
|arctg2-fL
66. l
+ |arctg 2-|-f, ;cv2 = Aп4Iп|+|Уп|
69. f(^-
70. f(i-o)(o + 3b). 71.-3^. 72. -Л,. 73. -^br • ff1^. 74. M! .
8V ;v -1 аНЬ2 а2 + Ь2 2a-»> Bn-2)\! Bn-2)!!(oc-b2)nT7! i
75- „(„На'Ха'Я-с.^п»)- 76- Л = /3 = -f In 2. 77. Сходится. 78. Расходится. 79. Рас-
ходится. 80. Расходится. 81. Сходится. 82. Расходится. 83. Расходится. 84. Сходится
абсолютно при и > 1; при п $С 1 расходится. 85. Сходится. 86. Сходится.
98.
/fc2_a2 a
ж + [x], p(x) = [x], q(x) = x, 0 ^ x
108.6a. 109. | B+ '"^У^) a. 110.
114.
116. Ittb2.
99. 0. 103. a) 4; 6) 4. 104. V([f] - f; 0, x) =
2. 105. 1 + Мп|. 106. ash12-. 107. aln*?!
2 2 (i ' О
111. хо + ^&. 112. xo + zo. 113. xo +
г0. ill. ^11Ц1 + V^J + a. 116. J-7T0-. 117. тг^2. 118. f (a2 + Ь2). 119. |D0 -,
Зтг)а2. 120. ^4~^. 121. 0,1. 122. |^. 123. oftarcsin ^|. 124. Площадь фигуры,
ограниченной одной петлей, равна ^-. 125. ^-ln tg (j + ^о) . 126. (тг + 1)а2. 127. ~.
128. 8 (J\ + -щ - arctg J\ + -^Л . 129. 4о6 arctg ^. 130. ?у. 131. 8тго3 In (l - ^-) -
тг (y + abDa + Ь)\. 132. VY = 1га3 (Bfc2 - 6it + 5)f0 - |Bit2 - 13it + 15)V2fc - *2)• V2 =
- 6k + 5)(ir -fo) + jBA:2 -13it + 15)\/2it - fc2), где t0 = arccos(l - k). 133. rV.
3(sina-acoSa-^). 136. f^. 137.^. 138. tfV^. 138. i.
134. |iro3. 135. 2ira

358
140. Ц^-JTa
142. Ц
Ответы
143.
гъ
б а — I
144. \rz ctgar(B
). 14Б.8B-^)г3. 146. (^, f) и (ff, 2Ё). 147. (f, f). 148. f + i.
149.(^,0). 150.(^,0). 161. ("f-2^, f'Sf)- 152. ^,r«eM-
масса боковой поверхности конуса. 153. На одной четверти высоты, считая от основа-
основания. 154. 2ттутцк I 1 ' == j , где у — гравитационная постоянная. 155. я6т2 ¦
156.
°-h2d«2»
0L905 Дж. 157. а) ^1; б) в два раза. 158. 2ж2п212а. 159. ^.. 160. 0,785 Дж.
161. 2264,4* Дж. 162. ^(<+~1). 163. ~\Щ- 164. 1324,35л-In 2 Дж. 165. х = е10.
166. -1. 167. Щ^-- 168. Ел/fc. 169. i. 170. -1. 171. -5. 172. Ц-; Ц-; ^-.
174. In 10» 2,31; М= г^г «0,433.

Оглавление
Глава 1. Введение в анализ 5
§ 1. Элементы теории множеств 5
§2. Функция. Отображение 13
§3. Действительные числа 20
§4. Комплексные числа 31
§5. Векторные и метрические пространства 35
§6. Предел последовательности 42
§7. Предел функции 66
§8. Непрерывность функций 97
§9. Равномерная непрерывность функций 106
Глава 2. Дифференциальное исчисление функций одной
переменной Ш
§1. Производная явной функции 111
§2. Дифференциал функции 127
§3. Производная обратной функции. Производная функции, заданной
параметрически. Производная функции, заданной в неявном виде 133
§4. Производные и дифференциалы высших порядков 137
§5. Теоремы Ролля, Лагранжа, Коши 147
§6. Возрастание и убывание функции. Неравенства 156
§7. Направление выпуклости графика функции. Точки перегиба 161
§8. Раскрытие неопределенностей 166
§9. Формула Тейлора 173
§10. Экстремум функции. Наибольшее и наименьшее значения функции 182
§11. Построение графиков функций по характерным точкам 187
§12. Задачи на максимум и минимум функции 200
Глава 3. Неопределенный интеграл 206
§1. Простейшие неопределенные интегралы 205
§2. Интегрирование рациональных функций 221
§3. Интегрирование иррациональных функций 233
§4. Интегрирование тригонометрических функций 241
§5. Интегрирование различных трансцендентных функций 246
§6. Разные примеры на интегрирование функций 248
§7. Интегрирование вектор-функций и функциональных матриц 251
Глава 4. Определенный интеграл 263
§1. Интеграл Римана 253
§2. Основные теоремы и формулы интегрального исчисления 263
§3. Интегрирование вектор-функций, комплекснозначных функций и
функциональных матриц 291
§4. Несобственные интегралы 297
§5. Функции ограниченной вариации 311
§6. Приложение определенного интеграла к решению задач геометрии 314
§7. Общая схема применения определенного интеграла. Задачи из механики и
физики 332
§8. Интеграл Стилтьеса 336
§9. Приближенное вычисление определенных интегралов 345
Ответы 353

Ляшко Иван Иванович, Боярчук Алексей Климентьевич,
Гай Яков Гаврилович, Головач Григорий Петрович
Справочное пособие по высшей математике. Т. 1: Математический анализ: введение
в анализ, производная, интеграл. — М: Едиториал УРСС, 2001. — 360 с.
ISBN 5-354-000I8-1
«Справочное пособие по высшей математике» выходит в пяти томах и представляет собой новое,
исправленное и существенно дополненное издание «Справочного пособия по математическому анализу»
тех же авторов. В новом издании пособие охватывает три крупных раздела курса высшей математи-
математики — математический анализ, теорию дифференциальных уравнений, теорию функций комплексной
переменной.
В том I включен материат по следущим разделам курса математического анализа: введение
в анализ, дифференциальное исчисление функций одной переменной, неопределенный и определенный
и н те фалы.
Пособие предназначено для студентов, преподавателей и работников физико-математических,
экономических и инженерно-технических специальностей, специалистов по прикладной математике,
а также лиц, самостоятельно изучающих высшую математику.