Автор: Яглом И.М. Шклярский Д.О. Ченцов Н.Н.
Теги: математика задачи по математике школьная математика
Год: 1976
Текст
Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом
ИЗБРАННЫЕ ЗАДАЧИ И ТЕОРЕМЫ ЭЛЕМЕНТАРНОЙ МАТЕМАТИКИ
Арифметика и алгебра
Книга содержит 350 задач, относящихся к алгебре, арифметике и теории
чисел, По своему характеру эти задачи значительно отличаются от стандартных
школьных задач. Большинство из них предлагалось в школьных математических
кружках при МГУ и на математических олимпиадах. Книга рассчитана на
учащихся старших классов средней школы. Задачи, доступные учащимся 7-го —
8-го классов, отмечены особо. Даны подробные решения всех задач; более
трудные задачи снабжены указаниями. Настоящее, пятое, издание существенно
переработано:—оно упрощено и охватывает материал последних олимпиад.
СОДЕРЖАНИЕ
Предисловие 4
Указания к пользованию книгой 7
Задачи- 9
1. Вводные задачи (1 — 29) 9
2. Перестановки цифр в числе (30—45) 17
3. Задачи на делимость чисел (46 — 96)' 18
4. Разные задачи из арифметики (97 — 149) 24
5. Решение уравнений в целых числах (150—171) 33
6. Матрицы, последовательности, функции (172 — 210) 36
7. Оценки сумм и произведений (211 — 234) 47
8. Разные задачи из алгебры (235 — 291) 53
9. Алгебра многочленов (292—320) 62
10. Комплексные числа (321—339) 67
11. Несколько задач из теории чисел (340—350) 71
Решения 75
Ответы и указания 363
Литература 381
ПРЕДИСЛОВИЕ
Первое издание настоящей книги вышло в свет
в 1950 г.; эта книга открывала серию «Библиотека ма-
тематического кружка». Около 15 задач в первоначаль-
ном варианте книги было заимствовано из рукописи
одного из основателей кружка при МГУ Давида Оска-
ровича Шклярского (1918—1942), в возрасте 23 лет
погибшего в партизанском отряде в Белоруссии. При
этом влияние Додика Шклярского на всю работу, про-
водимую в Москве с интересующимися математикой
школьниками, и, в частности, на книги серии «Библио-
тека математического кружка» было настолько значи-
тельным, что постановка его фамилии на первое место
в списке авторов этих сборников является вполне уме-
стной1). В 1954 г. эта книга была переиздана в значи-
тельно переработанном и дополненном виде; в 1959
и в 1965 гг. книга снова переиздавалась, но уже без
существенных изменений.
Сборники «Избранных задач и теорем элементарной
математики» построены на материалах школьных ма-
тематических кружков и математических олимпиад. Они
содержат задачи «олимпиадского» типа, т. е. такие, для
понимания условий и для решения которых вполне
достаточно знания курса математики средней школы,
однако методы решения этих задач, зачастую, являются
непривычными для школьной практики, приближаясь
к приемам, с которыми сталкиваются математики в сво-
ей исследовательской работе. В отличие от большин-
) Относительно истории школьного математического кружка при
МГУ и московских математических олимпиад и роли, которую сыг-
рал здесь Д. О. Шклярский, см. вводную статью В. Г. Болтянского и
И. М. Яглома к книге [I] (числа в квадратных скобках отсылают чи-
тателя к списку литературы — см. ниже стр. 381—384).
ства задачников, предназначенных для учащихся сред-
ней школы, эти сборники ставят своей целью не столько
закрепить и углубить знания читателя, полученные им
в школе, сколько ознакомить его с рядом новых для
него методов и идей и привить вкус к самостоятельным
изысканиям. В связи с этим здесь почти полностью
отсутствуют задачи, для решения которых достаточно
только формального усвоения школьного курса матема-
тики. Очень слабо представлены в сборниках наиболее
привычные для школьников типы задач «на сообрази-
тельность», скажем, задачи на искусственные методы ре-
шения уравнений и систем уравнений высших
степеней; зато сборники содержат много задач с нестан-
дартными формулировками, требующих для своего ре-
шения новых подходов.
При подборе задач больше внимания уделялось тем
разделам элементарной математики, которые находят
продолжение в современных исследованиях (для приме-
ра назовем темы: «Матрицы/последовательности, функ-
ции» или «Алгебра многочленов»). Некоторые циклы
задач излагают в переработанном и приспособленном
для школьников виде отдельные вопросы, которые обыч-
но относят к «высшей» математике (скажем, элементы
теории чисел). Отдельные задачи заимствованы из со-
чинений классиков математики и из статей, напечатан-
ных в научных математических журналах.
Книга предназначена для интересующихся матема-
тикой учащихся старших (7—10) классов средней шко-
лы. Она может быть также положена в основу работы
школьного математического кружка; при этом руково-
дителю (и участникам) кружка может оказаться полез-
ной и дополнительная литература, указанная в списке
на стр. 381—384. Перед решением задач полезно про-
честь «Указания к пользованию книгой» (стр. 7—8).
В связи с некоторой необычностью содержания сбор-
ники «Избранных задач и теорем» могут показаться
трудными читателю, привыкшему к «стандартным» за-
дачникам, предназначенным для учащихся средней
школы. Тем не менее опыт математических кружков и
олимпиад показывает, что собранные здесь задачи для
достаточно настойчивого школьника вполне доступны.
При переработке книги для нового издания мы ста-
рались ее, по возможности, упростить—для этого из
нее были исключены все без исключения задачи, номера
5
которых помечались во 2-м —4-м изданиях двумя звез-
дочками (в «Указаниях к пользованию книгой» эти за-
дачи рекомендовалось рассматривать как «теорию», чи-
тая их решения сразу после условий), а также наиболее
трудные из задач, номера которых были помечены одной
звездочкой: хотя таким образом из книги выпало не-
сколько интересных задач, но зато она стала доступнее
в качестве пособия для самостоятельной работы учащих-
ся. Некоторые задачи были опущены потому, что они
показались нам менее интересными, чем другие; два
последних цикла задач исключены как «слишком тео-
ретические» (так, например, задачи этих циклов было
невозможно решать «в разбивку»). Взамен исключенных
книга дополнена рядом новых задач, в основном заим-
ствованных из материалов последних московских, все-
союзных и международных олимпиад. Из-за резкого
увеличения числа предлагавшихся на олимпиадах задач
мы исключили из книги список номеров таких задач
(который ныне должен был бы содержать больше поло-
вины всех номеров).
Использование при работе над книгой материалов
математических олимпиад превращает когорту нынеш-
них «олимпиадчиков»: И. Бернштейна, И. Васильева,
Г. Гальперина, Ю. Ионина, А. Лемана, А. Савина,
А. Толпыго, А. Тоома и многих других, в соавторов этого
сборника; особо хочется отметить помогавших автору
своими советами В. Гутенмахера и Л. Макара-Лиманова.
Значительное содействие оказала мне в моей работе
также и Л. И. Головина. При всем том я не знаю, уме-
стно ли специально выражать здесь всем перечисленным
'лицам свою признательность: заботу об интересующих-
ся математикой школьниках я воспринимаю как наше
общее дело, в котором все мы участвуем, отдавая тем
самым свой долг людям, которые некогда учили нас (и
в этой связи мне снова хочется помянуть моего учите-
ля Д. Шклярского).
II. М, Яглом
УКАЗАНИЯ К ПОЛЬЗОВАНИЮ КНИГОЙ
Настоящая книга состоит из условий задач, ответов и указаний
К ним и решений. Ради удобства читателей «Ответы и указания»
помещены в конце книги; так же как и «Решения», они напечатаны
мелким шрифтом.
Номера задач, решение которых не требует знаний, выходящих
за пределы программы 8-го класса средней школы, набраны курси-
вом; решение большинства из этих задач доступно даже семиклас-
сникам. Звездочкой отмечены задачи, которые кажутся автору более
трудными. При этом не исключено, разумеется, что читателю пока-
жется относительно легкой какая-нибудь из отмеченных нами задач,
или, наоборот, его серьезно затруднит задача, не отмеченная звез-
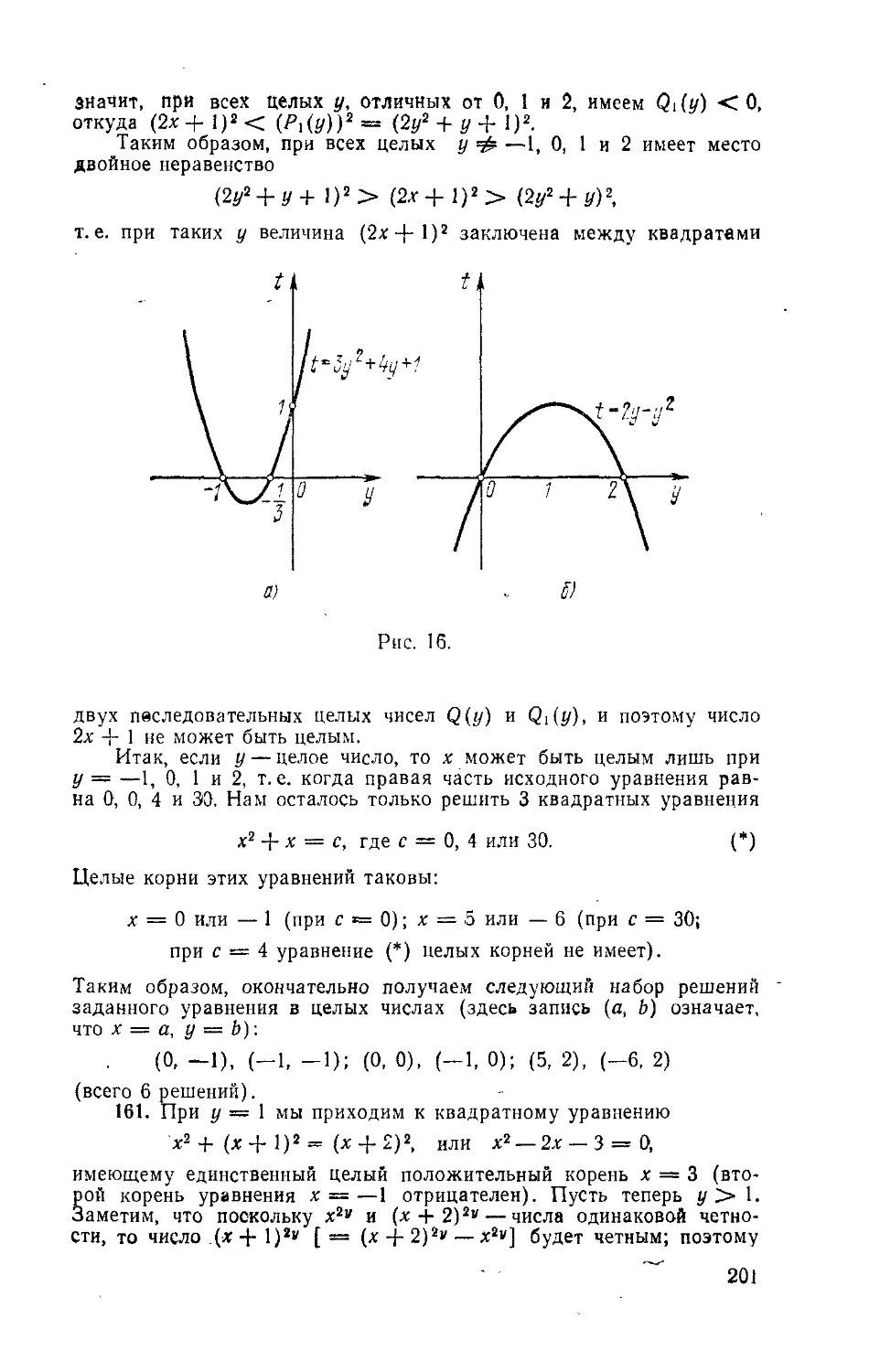
дочкой,— ведь точных критериев, определяющих трудность задачи,
не существует.
Читателю рекомендуется попытаться самостоятельно решить
заинтересовавшую его задачу, не заглядывая в указание или в реше-
ние. Если эта попытка не увенчается успехом, то следует посмотреть
указание или ответ, знание которого тоже может облегчить решение
задачи. Если же и после этого задача не будет решена, то следует
прочитать решение задачи. Если задачу удалось решить, не загляды-
вая в указание, то рекомендуется сравнить ответ с приведенным
в «Ответах и указаниях» (если таковой там имеется) и при расхо-
ждении попытаться обнаружить свою ошибку. Если же ответы
совпадут, то полезно сравнить свое решение с приведенными в книге.
Если в книге дано несколько решений задачи, интересно сравнить
их между собой. Этот порядок может быть нарушен по отношению
к задачам, отмеченным звездочкой,— здесь можно рекомендовать
иногда с самого начала ознакомиться с указанием и только после
этого приступить к решению задачи.
Как правило, задачи сборника независимы одна от другой; лишь
изредка решение задачи использует предложение одной из соседних
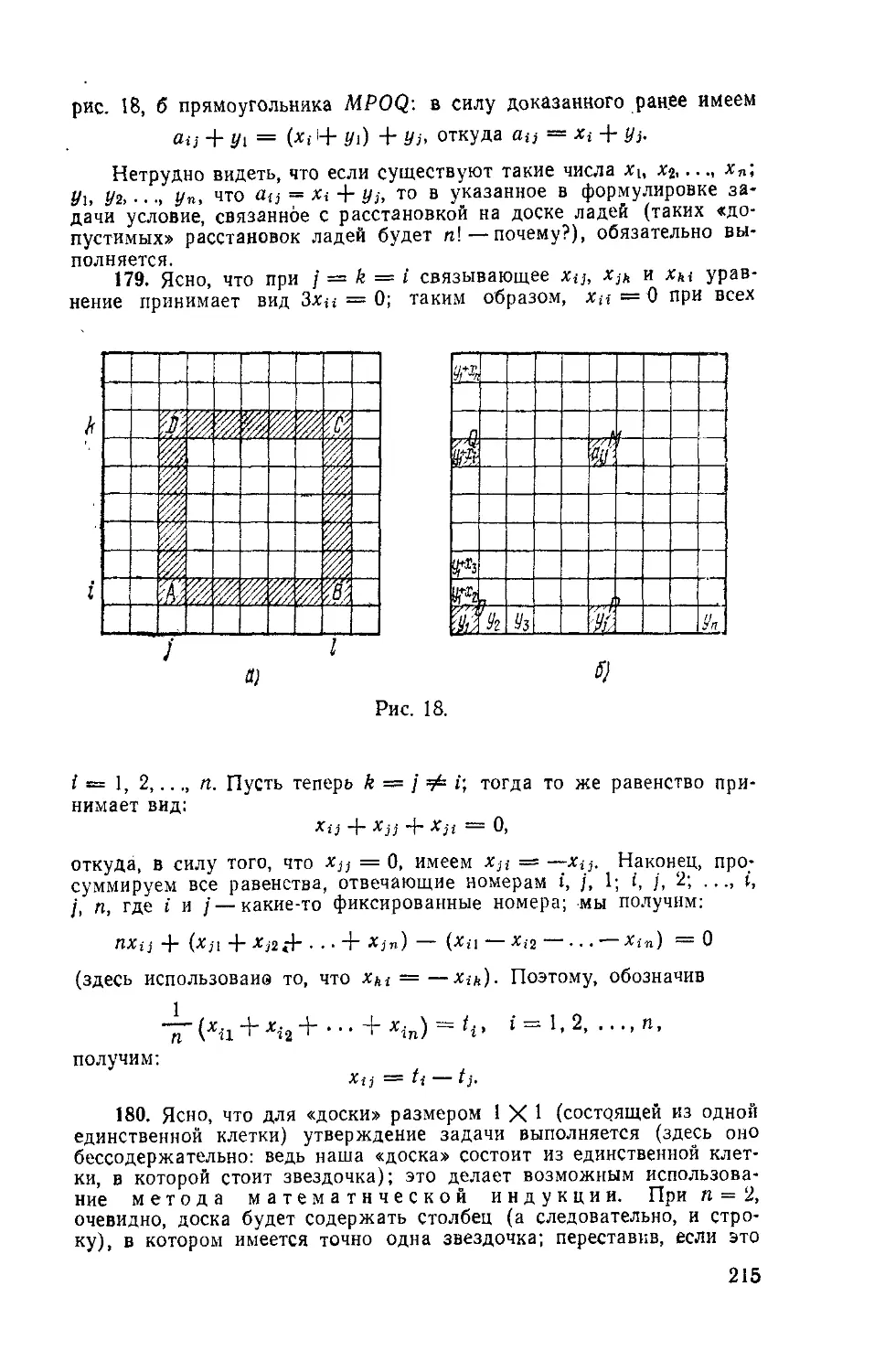
с ней задачи. Исключением в этом отношении являются лишь два по-
следние цикла задач: «Комплексные числа» и «Несколько задач из
7
теории чисел» — в этих циклах задачи более тесно связаны друг
с другом.
Причины, по которым те или иные задачи объединены в один
цикл, могут быть различными: иногда это общность методов и поста-
новок вопросов (таков, например, цикл «Алгебра многочленов»),
иногда — внешнее сходство условий задач; иногда специальный цикл
составляют задачи смешанного содержания, почти не связанные
между собой. Некоторые циклы состоят из задач, связанных между
собой настолько тесно, что их естественно решать подряд (такова,
например, значительная часть цикла «Задачи на делимость чисел»
и весь цикл «Перестановки цифр в числе»); эти циклы задач могут
служить темой специальных занятий математических кружков (при-
чем здесь может оказаться полезной и указанная в конце книги до-
полнительная литература). Иногда циклы задач можно естественно
разбить на части, различающиеся по методам решения и условиям; эти
части циклов отделяются одна от другой черточками. Следует от-
метить, что названия циклов часто являются условными и передают
только их общее содержание: для многих задач невозможно точно
определить, к какому циклу их следует отнести.
Задачи сборника рекомендуется решать не «в разбивку», а выбрать
сначала определенный цикл и потратить некоторое время на решение
задач этого цикла; лишь после ознакомления с одним циклом (кото-
рое, конечно, вовсе не должно состоять в решении всех илн большин-
ства его задач) следует перейти к другому циклу, и т. д. При этом,
разумеется, переходить от одного цикла к другому вовсе не необхо-
димо именно в том порядке, в котором циклы расположены в книге.
В конце некоторых из решений задач указаны возможные обоб-
щения условий задачи; в других случаях читатель сам увидит воз-
можность расширительного толкования стоящего перед ним вопроса
или придумает другие задачи, родственные собранным в этой кни-
ге — и этими возможностями никак не следует пренебрегать. В од-
ном случае в книге сохранена (идущая от И. М. Гельфанда) наро-
чито неопределенная формулировка условия задачи, оставляющая
широкий простор инициативе читателя (см. задачу 194 на Стр. 43);
в иных случаях родственную постановку вопроса учащийся сможет
предложить сам.
В известном смысле продолжением этой книги являются после-
дующие сборники задач, входящие в «Библиотеку математического
кружка» и объединенные с этой книгой общим списком авторов,
а также другие книги серии «Библиотека математического кружка»
(см. список литературы ь конце книги).
ЗАДАЧИ
1. ВВОДНЫЕ ЗАДАЧИ
Собранные здесь задачи, как правило, являются просто упражне-
ниями для развития логического мышления и не связаны ни с каким
определенным разделом математики; впрочем, в этот цикл входят и
несколько задач, которые можно отнести к арифметике (см., напри-
мер, задачи 25—29). Часть задач этого цикла можно связать с тео-
рией графов (о ней см., например, названную на стр. 383 книгу
[43]), изучающей системы точек (вершин графа; рис. 1, а), некото-
рые из которых связаны между собой линиями (ребрами графа);
иногда на этих линиях стрелками указано направление движения по
ребру — и тогда граф называется ориентированным (рис. 1, б'). На
языке теории графов можно, скажем, сформулировать те из ниже-
приведенных задач, которые касаются транспортных сетей (причем сеть
дорог с односторонним движением по ним естественно изображать
ориентированным графом) или отношений знакомства между людьми:
группу лиц можно изобразить системой точек, соединяя между собой
те пары точек, которые соответствуют знакомым ')•
) В задачах этого цикла отношение знакомства всегда считается
симметричным, т. е. полагается, что если А знаком с В, то В знаком
с А; если отказаться от этого условия, то систему знакомств придется
изображать ориентированным графом.
9
Большинство задач этого цикла не требуют почти никаких знаний
по математике; с этой точки зрения они доступны учащимся 5-х—6-х
классов средней школы. Впрочем, при решении некоторых задач ис-
пользуется метод математической индукции (см. о нем
[42]), который изучается лишь в старших классах школы. В реше-
нии других задач может оказаться полезным так называемый
«принцип клеток» Дирихле1), в образной форме часто фор-
мулируемый следующим образом: пусть мы имеем 7 кроликов и
5 клеток (или, вообще, m кроликов и п<т клеток); тогда, если рас-
садить этих кроликов по клеткам, то хотя бы в одной клетке обяза-
тельно окажутся два (или более) кролика.
1. 200 учеников выстроены прямоугольником по
10 человек в каждом поперечном ряду и по 20 человек
в каждом продольном ряду. В каждом поперечном ряду
выбран самый низкий ученик, а затем среди отобранных
20 выбран самый высокий; с другой стороны, из тех же
200 учеников в каждом продольном ряду выбран самый
высокий ученик, а затем среди отобранных 10 выбран
самый низкий. Кто из двоих окажется выше (если это
разные лица) —самый низкий из самых высоких учени-
ков, или самый высокий из самых низких?
2. Каждый из людей, когда-либо живших на земле,
обменялся с другими определенным числом рукопожа-
тий. Доказать, что число людей, обменявшихся нечет-
ным числом рукопожатий, четно.
3. Доказать, что среди любых шести человек най-
дутся либо трое попарно знакомых, либо трое попарно
незнакомых.
4. На заседании присутствуют несколько человек
(разумеется, больше одного человека — иначе какое
же это было бы «заседание»?).
а) Может ли быть, что никакие двое из присутствую-
щих не имеют одинакового числа знакомых?
б) Доказать, что при любом числе участников засе-
дания может случиться так, что никакие трое из при-
сутствующих не имеют одинакового числа знакомых.
5. На некотором собрании присутствовало 2п чело-
век, каждый из которых был знаком не менее чем с п
присутствующими. Доказать, что за круглый стол на
4 лица можно посадить четырех из присутствующих так,
чтобы каждый сидел между своими знакомыми.
6. На конгресс приехало большое число ученых; од-
ни из них были раньше знакомы друг с другом, другие —
*) Поль Лежен Дирихле (1805—1859) — выдающийся не-
мецкий математик.
10
нет. При этом оказалось, что никакие два ученых, имею*
щих одно и то же число знакомых, не имеют общих зна-
комых. Доказать, что среди присутствующих на кон-
грессе ученых найдется ученый, знакомый ровно с одним
участником конгресса.
7. На конгресс приехало 1000 делегатов из разных
стран. Известно, что каждые трое из них могут говорить
друг с другом без помощи остальных (однако при этом
возможно, что одному из трех лиц придется служить
переводчиком для двух других). Доказать, что всех
делегатов конгресса можно так разместить в гостинице
с двуместными номерами, что в каждом номере будут
помещены делегаты, которые могут говорить друг
с другом.
8. На международной конференции присутствуют
17 ученых. Каждые два из них беседуют друг с другом
на определенном языке; при этом всего все 17 человек
знают три языка. Доказать, что среди участников кон-
ференции найдутся трое, которые говорят друг с другом
на одном и том же языке.
9. На некотором собрании присутствовало п человек.
Известно, что каждые два знакомых из них не имеют
никаких общих знакомых, а каждые два незнакомых
между собой лица имеют ровно двух общих знакомых.
а) Доказать, что все присутствующие имеют одно и
то же число знакомых.
б) При каких п возможно условие задачи?
10. В городе «Многообразие» живут 10 000 жителей,
каждые два из которых либо враждуют, либо дружат
между собой. Каждый день не более чем один житель
города может «начать новую жизнь», т. е. перессорить-
ся со всеми своими друзьями и подружиться со всеми
врагами; при этом любые три жителя могут подру-
житься между собой. Доказать, что все без исключения
жители могут подружиться между собой. Какого на-
именьшего числа дней наверное достаточно для этого?
11*. В стране Оз имеется несколько замков, из каж-
дого из которых ведут три пути. Странствующий ры-
царь вые\ал из своего родового замка и пустился в
путешествие по стране. Рыцарь любит разнообразие;
поэтому, доезжая до очередного замка, он каждый раз
поворачивает налево, если в предшествующий раз
повернул направо, и поворачивает направо, если до
этого он повернул налево. (Проезжая первый на своем
11
пути замок, рыцарь может повернуть в любую сторону.)
Докажите, что когда-нибудь рыцарь вернется в свой
замок.
12*. При дворе короля Артура собрались 2п рыцарей,
причем каждый из них имеет среди присутствующих
не более п— 1 врагов. Доказать, что Мерлин — совет-
ник Артура — .может так рассадить рыцарей за круг-
лым столом, что ни один из них не будет сидеть рядом
со своим врагом.
13. а) Известно, что среди 80 монет имеется одна
фальшивая, более легкая, чем остальные, имеющие
все одинаковый вес. При помощи четырех взвешиваний
на чашечных весах без гирь найти фальшивую монету.
б) Известно, что среди п монет есть одна фальши-
вая, более легкая, чем остальные, имеющие все оди-
наковый вес. Каково наименьшее число k такое, что k
взвешиваниями на чашечных весах без гирь всегда
можно выделить фальшивую монету?
14. Некоторые из 20 металлических кубиков, оди-
наковых по размеру и внешнему виду, алюминиевые,
остальные — дюралевые (более тяжелые). Как при по-
мощи не более 11 взвешиваний на чашечных весах без
гирь определить число дюралевых кубиков?
Примечание. В задаче предполагается, что все кубики мо-
гут быть алюминиевые, но дюралевыми все они быть не могут (ведь,
если бы все кубики оказались одного веса, то без этого условия мы
никак не смогли бы определить, алюминиевые они или дюралевые).
15*. Среди 12 монет имеется одна фальшивая. Из-
вестно, что фальшивая монета отличается по весу от
настоящих, но не известно, легче она настоящих или
тяжелее. Настоящие монеты все одного веса. С помощью
трех взвешиваний на чашечных весах без гирь выделить
фальшивую монету и одновременно установить, легче
она или тяжелее остальных.
Примечание. В условиях задачи 15 тремя взвешиваниями
можно выделить фальшивую монету не только из 12, но и из 13 мо-
нет; в последнем случае нельзя, однако, определить, легче или тяже-
лее фальшивая монета, чем настоящая. Для случая 14 монет необхо-
димы уже четыре взвешивания.
Можно также доказать (однако это доказательство является до-
вольно сложным!), что если у нас имеется произвольное число N мо-
нет, одна из которых является фальшивой и имеет иной вес, чем ос-
тальные, то наименьшее число k взвешиваний на чашечных весах без
гирь, обеспечивающее возможность найти эту монету и одновременно
указать, легче ли она или тяжелее остальных, равно logs (2^4-3), если
12
2Л'4-3 является целой степенью тройки, и равно [1og3(2ЛГ-1-3)] 4-1,
если 2W+3 степенью тройки не является (т. е. если число log3(2n4-3)
— не целое; квадратные скобки здесь обозначают целую часть
числа — см. стр. 37); при N = 12 это и дает нам k — 3. Было бы инте-
ресно также указать, чему равно наименьшее число kt взвешиваний,
позволяющих в этих общих условиях лишь найти фальшивую мо-
нету, не определяя, легче ли она или тяжелее остальных (при ==
= 12 или 13 число k\ = 3, а при N = 14 уже kt = 4; общее значе-
ние величины = kt(N) пока, кажется, никем не определено).
По поводу решения общей «задачи об W монетах» (опирающе-
гося, впрочем, на далекие от содержания настоящей книги идеи) см.
книгу [44], где также подробно обсуждаются причины; с которыми
связан возникший в последние десятилетия большой интерес матема-
тиков и связистов к задачам типа задач 13—15.
16. а) К хозяину гостиницы однажды пришел по-
стоялец, не имевший денег, но обладавший серебряной
цепочкой, состоящей из семи звеньев. Хозяин согласился
держать этого постояльца неделю, при условии, что тот
будет ему ежедневно отдавать в виде платы одно из
звеньев цепочки. Какое наименьшее число звеньев надо
распилить для того, чтобы владелец цепочки смог ежед-
невно в течение семи дней расплачиваться с хозяином
(быть может, забирая у него при этом отданные ранее
звенья и выдавая взамен их другие)?
б) Цепь состоит из 2000 звеньев. Какое наименьшее
число звеньев надо распилить для того, чтобы любое
число звеньев от 1 до 2000 можно было набрать, взяв
некоторое число из образовавшихся частей?
17. В городе Лиссе все станции метро связаны
между собой, т. е. с любой станции можно проехать
(возможно с пересадками) на любую другую. Доказать,
что при этом можно закрыть одну станцию метро (без
права проезда через нее) так, чтобы с любой из остав-
шихся станций можно было проехать на любую другую
станцию.
18*. На всех улицах города Зурбагана существова-
ло двустороннее движение. Когда, однако, городским
властям потребовалось произвести ремонт всех доррг,
они вынуждены были временно ввести на части улиц
одностороннее движение, оставив движение на осталь-
ных улицах двусторонним; после этого, напротив, одно-
сторонним было сделано движение по тем улицам, кото-
рые ранее не ремонтировались, а по улицам, где движе-
ние ранее было односторонним, снова было разрешено
ехать в обоих направлениях. При этом в период ремон-
та дорог в обоих случаях можно было проехать
13
из любого пункта Зурбагана в любой другой. Дока-
зать, что в Зурбагане можно ввести одностороннее дви-
жение по всем улицамч так, чтобы проезд из любого
пункта города в любой другой оставался возможным.
19*. В стране Дельфинин имеется п городов, каждые
два из которых соединены шоссе, причем движение по
всем шоссе является односторонним. Доказать, - что
если п=И=2 или 4, го направления движения по шоссе
можно выбрать так, чтобы из каждого города в любой
другой можно было попасть с заездом не более чем еще
в один город; если же п=2 или 4, то так движение
организовать нельзя.
20*. В Швамбрании имеется 100 городов; при этом
если два города А и В не соединены прямой телефон-
ной связью, то имеются регулярные авиарейсы из А
в 5 и наоборот, а если между А и В прямая телефон-
ная связь есть, то таких рейсов нет. Известно, что
в Швамбрании каждые два города могут быть (может
быть — через- посредство нескольких промежуточных
пунктов) соединены между собой телефоном и что из
каждого города в каждый другой можно долететь
самолетом,— возможно, с несколькими посадками
в пути. Докажите, что в Швамбрании имеются такие
4 города, что из каждого из них можно и дозвониться
и долететь в любой другой, используя, в случае необ-
ходимости, в качестве промежуточных пунктов лишь
два других города этой четверки.
21. Можно ли ходом шахматного коня попасть из
левого нижнего угла доски в правый верхний, побывав
на каждом поле ровно один раз?
22. Задача о короле-самоубийце. На шах-
матной доске размером 1000X1000 клеток стоит белый
король и 499 черных ладей. Доказать, что при произ-
вольном положении фигур (и при произвольной игре
черных) король может «сыграть в поддавки», т. е. за
ряд ходов стать на находящееся под боем одной из
ладей поле, вынудив тем самым себя побить. (Фигуры
на нашей доске ходят по обычным правилам.)
23. 12 полей расположены по кругу и на четырех
соседних полях стоят четыре разноцветные фишки:
красная, желтая, зеленая и синяя.
Одним ходом можно передвинуть любую фишку
с поля, на котором ина стоит, через четыре любых поля
на пятое (если оно свободно) в любом из двух воз-
14
можных направлений. После нескольких ходов фишки
могут стать снова на те же четыре поля. Как они мо-
гут при этом переставиться?
24. Среди принятых в университет студентов имеет-
ся ровно 50 знающих английский язык, ровно 50 знаю-
щих французский язык и ровно 50 знающих немецкий
язык (при этом, раз*умеется, среди студентов могут
быть такие, которые знают сразу два или даже все
три языка, так что общее число знающих хоть один
язык студентов, вообще говоря, меньше 3-50=150).
Докажите, что всех студентов можно разбить на 5 та-
ких (вообще говоря — не совпадающих по численности)
групп, что в каждой группе ровно 10 человек будут
знать английский язык, ровно 10 человек — француз-
ский и ровно 10 человек — немецкий
25. а) На спортивных соревнованиях выступают
20 спортсменов; судят соревнования 9 судей. Каждый
судья расставляет в своем списке соревнующихся в по-
рядке от 1-го до 20-го в соответствии с тем, как он рас-
ценил их выступления, причем впоследствии оказалось,
что оценки всех судей разнятся не слишком значитель-
но: ни один спортсмен не получил у двух судей места,
отличающиеся более чем на три. В основу окончатель-
ного распределения мест положено «среднее место»
спортсмена по оценкам 9 судей, т. е. сумма всех при-
писанных ему мест, деленная на число судей (на 9).
Каково наибольшее возможное значение «среднего
места» лучшего из 20 спортсменов?
б) Теннисная федерация присвоила квалификацион-
ные номера всем теннисистам страны: 1-й номер — силь-
нейшему из них, 2-й — следующему по силе, и т. д.; при
этом известно, что в состязании теннисистов, номера
которых в квалификационном списке разнятся более
чем на две единицы, всегда побеждает теннисист с мень-
шим номером. 1024 теннисиста страны устраивают
соревнования по олимпийской системе, т. е. так, что
после каждого этапа соревнований все проигравшие
выбывают из игры, а оставшиеся разбиваются на пары
соперников в следующем туре случайным образом.
Спрашивается, какой наибольший номер может иметь
победитель таких соревнований?
26*. Спартакиада продолжалась п дней; на ней бы-
ли разыграны Af комплектов медалей; при этом в 1-й
День был вручен 1 комплект медалей и 1/7 часть от
16
оставшегося их количества; во 2-й день — 2 комплекта
медалей и 1/7 часть от оставшегося их количества;
в предпоследний, (п—1)-й день— (п—1) комплект меда-
лей и 1/7 часть всех оставшихся медалей; наконец, в по-
следний день были вручены п последних комплектов
медалей. Сколько дней продолжалась спартакиада и
сколько комплектов медалей на ней разыгрывалось?
27. Пять приятелей, один из которых имел обезья-
ну, купили однажды мешок орехов, которые они пред-
полагали утром следующего дня поделить между собой.
Однако ночью один из приятелей проснулся и захотел
орехов; он разделил все орехи в мешке на пять равных
частей, причем у него остался один лишний орех, кото-
рый он отдал обезьяне, и взял себе пятую часть. Вслед
за ним проснулся другой из хозяев орехов; не зная, что
орехи уже кто-то брал, он разделил все оставшееся со-
держимое мешка снова на пять частей, причем остав-
шийся лишний орех отдал обезьяне, и взял себе пятую
часть. Затем последовательно проделали ту же опера-
цию оставшиеся трое приятелей; при этом каждый из
них, не зная о поступке остальных, делил все орехи
на пять частей, брал себе пятую часть и каждый раз
оставался один лишний орех, который отдавали обезья-
не. Наконец, утром все пятеро вместе достали мешок,
разделили оставшиеся орехи на пять частей, а один
орех, оказавшийся лишним, снова отдали обезьяне.
Требуется определить наименьшее число орехов в меш-
ке, при котором возможен подобный раздел их.
28. Два брата продали принадлежащее им дбоим
стадо овец, взяв за каждую овцу столько рублей, сколь-
ко было овец в стаде. Полученные деньги братья по-
делили следующим образом: сначала старший браг
взял себе десять рублей из вырученной суммы, затем
взял десять рублей второй брат, после этого первый
брат взял еще десять рублей, и т. д. При этом младше-
му брату не хватило десяти рублей; поэтому он взял
все оставшиеся после дележа мелкие деньги, а кроме
того, чтобы дележ был справедливым, старший брат
отдал младшему свой перочинный нож. Во что был
оценен перочинный нож?
29. а) С какого дня чаще начинается новый год:
с субботы или с воскресенья?
б) На какой день недели чаще всего приходится
30-е число месяца?
16
2. ПЕРЕСТАНОВКИ ЦИФР В ЧИСЛЕ
30. Какие целые числа от зачеркивания последней
цифры уменьшаются в целое число раз?.
31. а) Найти все целые числа, начинающиеся с циф-
ры 6 и от зачеркивания этой цифры уменьшающиеся
в 25 раз.
б) Доказать, что не существует целых чисел, кото-
рые при зачеркивании первой цифры уменьшаются
в 35 раз.
32*. Целое число уменьшается в 9 раз при зачер-
кивании некоторой его цифры; при этом полученное
число тоже делится на 9.
а) Доказать, что для того, чтобы разделить получен-
ное число на 9, тоже достаточно вычеркнуть в нем
одну цифру.
б) Найти все целые числа, удовлетворяющие усло-
вию задачи.
33. а) Найти все числа, которые при зачеркивании
третьей цифры уменьшаются в целое число раз.
б)* Найти все числа, которые при зачеркивании
второй цифры уменьшаются в целое число раз.
34. а) Найти наименьшее целое число, начинающее-
ся с цифры 1 и такое, что если переставить эту цифру
в конец, то число увеличится втрое. Найти все такие
числа.
б) Какими цифрами могут начинаться отличные от
нуля целые числа, увеличивающиеся втрое от переста-
новки первой цифры в конец? Найти все такие числа.
35. Найти наименьшее натуральное число, оканчи-
вающееся цифрой 6, которое увеличивается в 4 раза
при перенесении его последней цифры в начало числа.
36. Доказать, что нет целых чисел (отличных от
нуля), которые от перестановки начальной цифры в ко-
нец увеличиваются в 5 раз, в 6 раз или в 8 раз.
37. Доказать, что нет целых чисел (отличных от
нуля), которые увеличиваются вдвое от перестановки
начальной цифры в конец.
38. а) Доказать, что нет отличных от нуля целых
чисел, которые от перестановки начальной цифры в ко-
нец увеличиваются в 7 или в 9 раз.
б) Доказать, что нет отличных от нуля целых чисел,
которые увеличиваются в 4 раза от перестановки на-
чальной цифры в конец.
2 Д. О., Шклярский и др. 17
39. Найти наименьшее целое число, начинающееся
цифрой 7 и уменьшающееся втрое от перестановки
этой цифры в конец Найти все такие числа.
40. а) Доказать, что отличное от нуля целое число
не может быть меньше в 2, 3, 5, 6, 7 или 8 раз своего
обращенного (т. е. числа, состоящего из тех же цифр,
записанных в обратном порядке).
б)* Найти все целые числа, которые в 4 раза или
в 9 раз меньше своего обращенного.
41 а) Найти шестизначное число, которое увеличи-
вается в 6 раз, если три последние цифры числа, не
меняя их порядка, переставить в начало числа.
б) Доказать, что не существует восьмизначного чис-
ла, увеличивающегося в 6 раз при перестановке четырех
последних цифр на первые четыре места с сохранением
их порядка.
42. Найти шестизначное число, произведения кото-
рого на 2, на 3, на 4, на 5 и на 6 записываются теми
же цифрами, что и оно само, но в другом порядке.
43. Найти все трехзначные числа, равные среднему
арифметическому всех чисел,- получающихся из задан-
ного числа всевозможными перестановками его цифр
(включая, разумеется, и «тождественную перестановку»,
оставляющую все цифры числа на месте).
44. Пусть А — некоторое целое положительное чис-
ло, А'— число, составленное из тех же цифр, но пере-
ставленных в каком-то другом порядке. Доказать, что
если Д-(-А'=1010, то А делится на 10.
45. Пусть М — некоторое 17-значное число, N— чис-
ло, полученное «переворачиванием» М, т. е. записывае-
мое теми же цифрами, следующими, однако, в обратном
порядке. Доказать, что хотя бы одна цифра десятичной
записи числа ЛТ-рУ — четная.
3. ЗАДАЧ И НА ДЕЛ ИМОСТЬ Ч ИСЕЛ
Начатые задачами этого цикла темы, в основной своей части от-
носящиеся к «высшей арифметике» — к теории чисел,— находят не-
которое продолжение в дальнейших разделах книги, в первую оче-
редь— в циклах 4, 5 и 11. По поводу общих идей, лежащих в основе
решения многих из приведенных ниже задач, читателя можно отослать
к статье (45], брошюре [46] или к изложениям начал теории чисел
(см., например, связанные с так называемой «теорией сравнений»
разделы учебников [64] — [67] или статьи [68]). Особо хочется по-
рекомендовать читателю в связи с материалом настоящего цикла за-
дач раздел 2 книги [5], по характеру изложения наиболее подходя-
щий для учащихся старших и средних классов школы.
18
46. Доказать, что при всяком целом п
а) п3— п делится на 3;
б) п5 — п делится на 5;
в) п7— п делится на 7;
г) п11— п делится на 11;
д) п13— п делится на 13.
Примечание. Отметим, что п9— луже не обязатель-
но делится на 9 (например, 29 — 2 — 510 не делится на 9).
Задачи а) — д) составляют частные случаи одной более общей
теоремы: см. ниже задачу 340 (стр. 71).
47. Доказать, что при всяком целом п
а) З6"— 2б" делится на 35 (здесь п 0);
б) и5 — 5п3 + 4п делится на 120;
в) п2 + Зп + 5 не делится на 121.
48. Доказать, что при всех целых тип
а)* тп(т60—п60) делится на 56 786 730;
б) т5 + 3т4п— 5т3п2—15т2п3 + 4тп4 + 12п5 нерав-
но 33.
49. При каких целых положительных п число 20” +'
+ 16" — 3"—1 делится на 323?
50. Существует ли такое натуральное число п, что
п2 + п + 1 делится на 1955?
51. Какие остатки может давать сотая степень це-
лого числа при делении на 125?
52. Доказать, что если целое число W взаимно просто
с 10, то 101-я степень числа W оканчивается теми, же
тремя цифрами, что и (V (так, например, 1233101 окан-
чивается цифрами 233, а 37101 — цифрами 037).
53. Найти трехзначное число, всякая целая степень
которого оканчивается тремя цифрами, составляющими
первоначальное число.
54*. Пусть N— четное число, не делящееся на 10.
Какова будет цифра десятков числа №°? Какова будет
цифра сотен числа Л200?
55. Доказать, что сумма
Р + 2* + 3* + ... + п\
где п есть произвольное целое положительное число, а
k нечетно, делится на 1+2+3+...+п.
56. Вывести признак делимости чисел на 11.
57. Число 123456789(10)(11)(12)(13)(14) написано
по 15-ричной системе счисления, т. е. это число равно
2*
19
(14) + (13) • 15+ (12) • 154- (11) • 153 + ... + 2-I5l2+1513.
Какой остаток дает оно при делении на 7?
58. Доказать, что единственными числами К такими,
что если N делится на К, то и любое число, полученное
из JV перестановкой цифр, делится на К, являются 1,
3 и 9. (Для К — 1 это свойство очевидно, для К = 3 и
Л = 9 следует из известных признаков делимости на
3 и на 9.)
59. Найти наименьшее целое число, записываемое
одними единицами, которое делится без остатка на
число 333...33.
100 троек
60. Пусть а — последняя цифра целого числа N = 2\
А — число, в которое обращается N, если зачеркнуть
в нем эту последнюю цифру. Доказать, что при всех
й>»3 число аА делится на 6.
61. Доказать, что 27 195s—10887s+I0 1528 делится
без остатка на 26 460.
62. Доказать, что И10—1 делится на 100.
63. Доказать, что 22225555+55552222 делится на 7.
64. Доказать, что число, составленное из Зп одина-
ковых цифр, делится на 3" (так, число 222 делится на
3, число 777 777 777 делится на 9, и т. д.).
65. Найти остаток от деления на 7 чисда
1010+ 10(’°3)+ ... 4- 10(,о,О).
66. а) Найти последнюю цифру чисел 9(Э’’, 2П*'.
б) Найти две последние цифры чисел 2999, З999.
в) * Найти две последние цифры числа 14<14М).
67. Доказать, что
а) две последние цифры десятичных записей чисел
9®9 и 9s*9 (где, например, 9э9 означает Э^) одинаковы;
б)* шесть последних цифр десятичных записей чи-
-+7 77^77
сел 7 и 7 одинаковы.
68. а) Какова последняя цифра числа
(... (((77)7)7) )
(возведение в степень 7 повторяется 1000 раз)? Каковы
две последние цифры этого числа?
20 •
б) Какова последняя цифра числа
( Ь(77)) 1
7\т- ...)
записанного с помощью 1001 семерки, аналогично числу
задачи а), однако с иным порядком возведения в сте-
пень? Каковы две последние цифры этого числа?
69*. Определить пять последних цифр числа
( (9<"0 1
/у = 9\9-- .J
записанного с помощью 1001 девятки аналогично числу
задачи 686).
70. При каких натуральных п сумма 5пД-п5 делит-
ся на 13? Каково наименьшее п, удовлетворяющее это-
му условию?
71. Каковы две последние цифры числа
п“+(п+ 1)“+(п + 2)“+ ... +(п + 99)а,
где п — произвольное целое неотрицательное число и
а) а = 4; б) а = 8?
72*. Найти последние 1000 цифр числа
W = 1 + 50 + 502+ 503+.. .+50999.
73. Натуральное число М делится на 7; доказать,
что если число цифр числа делится на 6, то при пере-
носе последней цифры в начало мы получим число (V,
также делящееся на 7.
74. Сколькими нулями оканчивается произведение
всех целых чисел от 1 до 100 включительно?
В дальшейшем мы будем пользоваться следующим обозначением:
1-2-3-4... (л — 1) • п — п\
(читается: п факториал). Так предыдущую задачу можно короче
сформулировать так: сколькими нулями оканчивается число 100! ?
75. а) Доказать, что произведение п последователь-
ных целых чисел делится на п!.
б) Доказать, что дробь есть число целое,
если только а + +
в) Доказать, что (п!)1 делится на
21
г)* Доказать, что произведение п последовательных
целых чисел, образующих арифметическую прогрессию,
разность которой взаимно проста с п!> делится на п!.
Примечание. Задача 75г) является обобщением задачи 75а).
76. Делится ли на 7 число сочетаний из 1000 эле-
ментов по 500?
77. а) Найти все числа п между 1 и 100, такие, что
(п—1)! не делится на п.
б) Найти все числа п между 1 и 100, такие, что
(п—1)! не делится на п2.
78*. Найти все целые числа п, делящиеся на все
целые числа, не превосходящие ^п.
79. а) Доказать, что сумма квадратов пяти последо-
вательных целых чисел не может быть полным квадра-
том целого числа.
б) Доказать, что сумма одинаковых четных степеней
трех последовательных целых чисел не может равняться
четной степени целого числа.
в) Доказать, что сумма одинаковых четных степеней
девяти последовательных целых чисел не может рав-
няться никакой степени целого числа (разумеется,
с показателем, большим 1).
80. а) Пусть А и В — два различных семизначных
числа, каждое из которых составлено из всех цифр от
1 до 7. Доказать, что А не делится на В.
б) Из всех цифр от 1 до 9 составить три трехзнач-
ных числа, относящихся друг к другу как 1:2:3.
81. Квадрат целого числа оканчивается четырьмя
одинаковыми цифрами. Какими?
82. Доказать, что если обе стороны прямоугольника
и его диагональ выражаются целыми числами, то пло-
щадь прямоугольника делится на 12.
83. Доказать, что если все коэффициенты квадратно-
го уравнения
ах2 + Ьх + с — 0
— целые нечетные числа, то корни уравнения не могут
быть рациональными.
84. Доказать, что если сумму простых дробей
_L+_L_+_J_
(п — целое число) обратить в десятичную, то получен-
ная дробь будет смешанной периодической.
22
85. Доказать, что числа
а) Л/==4 + ±+...+ ±;
б> л? = -г-ь„-тг + 4-2+--- + п-Ьг:
и) =т + 4 + • • • + 2^п
(п, т — целые положительные) не могут быть целыми.
86. а) Доказать, что дробь -4 з^2^. i несократима
ни при каком целом значении а.
б) Указать все (натуральные) числа, на которые
может оказаться сократимой дробь g+ф-? при целом п.
87. 1953 цифры выписаны по кругу. Доказать, что
если при чтении этих цифр в направлении вращения
часовой стрелки, начиная с какой-то цифры, получится
1953-значное число, делящееся на 27, то и при чтении
этих цифр в том же направлении, начиная с любого
другого места, тоже получится 1953-значное число, де-
лящееся на 27.
88. Доказать, что существует делящееся на 51000 чис-
ло, десятичная запись которого не содержит нулей.
89. Доказать, что все числа вида 10 001, 100 010 001,
1 000 100 010 001,...— составные.
90. Доказать, что каждые два числа последователь-
ности
24-1, 22+1, 24-4- 1, 28 4- 1, 2164- 1, ..., 22"-4-1, ...
являются взаимно -простыми.
Примечание. Из результата настоящей задачи, в частности,
следует, что существует бесконечно много простых чисел (см. также
по этому поводу задачи 234 и 349) В самом деле, если бы число про-
стых чисел было конечным, то не могло бы существовать бесконечно
много чисел, каждые два из которых взаимно просты.
91. Доказать, что если одно из чисел 2"—1 и 2n4- 1,
где п > 2, простое, то второе является составным (при
п = 2 оба числа 2n—1 = 3 и 2" 4* 1 = 5 — простые).
92. а) Доказать, что если р и 8р— 1 —простые числа,
то 8р 4-1 — составное число.
б) Доказать, что. если р и 8р2 -ф 1 — простые числа,
то 8р2 — 1 — простое число,
23
93. Доказать, что квадрат любого простого числа,
кроме чисел 2 и 3, при делении на 12 дает в остатке 1.
94. Доказать, что если три простых числа, больших
числа 3, образуют арифметическую прогрессию, то раз-
ность прогрессии делится на 6.
95*. а) Десять простых чисел, меньших 3000, состав-
ляют арифметическую прогрессию. Найти эти числа.
б) Доказать, что не существует 11 простых чисел,
меньших 20 000, которые составляли бы арифметическую
прогрессию.
96. а) Доказать, что из пяти последовательных целых
чисел всегда можно выбрать одно, взаимно простое со
всеми остальными.
б) Доказать, что из 16 последовательных целых чи-
сел всегда можно выбрать одно число, взаимно простое
со всеми остальными.
4. РАЗНЫЕ ЗАДАЧИ ИЗ АРИФМЕТИКИ
97. Число А записывается в десятичной системе счис-
ления при помощи 666 троек, а число В—.при помощи
666 шестерок. Из каких цифр состоит произведение А-В?
98. Найти частное и остаток от деления числа А, за-
писываемого с помощью 1001 семерки, на число 1001.
99. Найти наименьший квадрат, начинающийся с
шести двоек.
100. Существуют ли такие целые числа тип, что
т2=п2+1954?
101. Дописать к 523 ... три цифры так, чтобы полу-
ченное шестизначное число делилось на 7, на 8 и на 9.
102. Найти четырехзначное число, которое при деле-
нии на 131 дает в остатке 112, а при делении на 132
дает в остатке 98.
103. а) Доказать, что сумма всех n-значных чисел
(п>2) равна 494 99 ... 9 55 00 ... 0 (так, сумма всех
(п—3)раз (п—2)раз
трехзначных чисел равна 494 550, а сумма всех шести-
значных чисел 494 999 550 000).
б) Найти сумму всех четырехзначных четных чисел,
которые можно записать цифрами 0, 1, 2, 3, 4, 5 (одна и
та же цифра в числе может повторяться).
104. Сколько и каких цифр понадобится для того,
чтобы записать все целые числа от 1 до 100 000 000 вклю-
чительно?
24
105. Все целые числа выписаны подряд, начиная от
единицы. Определить, какая цифра стоит на 206 788-м
месте.
106. Будет ли дробь 0,1234567891011121314..., ко-
торая получится, если выписать после нуля подряд все
целые числа, периодической?
107. Каждое из целых чисел от единицы до мил-
лиарда включительно заменяется суммой цифр числа;
однозначные числа при этом, разумеется, не меняются,
а остальные уменьшаются. Затем каждое из вновь по-
лученных чисел снова заменяется суммой его цифр —
и так до тех пор, пока не получится миллиард одно-
значных чисел. Каких чисел будет больше среди полу-
ченных чисел — единиц или двоек?
108. Может ли являться полным квадратом целое
число, запись которого в десятичной системе счисления
содержит
а) некоторое количество шестерок и некоторое ко-
личество нулей;
б) цифры 1, 2, 3, 4, 5, 6, 7, 8, и 9 (каждую — по од-
ному разу), причем цифра 5 стоит на последнем месте?
109. На карточках написаны все пятизначные числа
от 11111 до 99 999 включительно (число таких чисел,
очевидно, равно 88889). Затем эти карточки произволь-
ным образом выложили в одну цепочку. Доказать, что
полученное таким путем 444 445-значное число (444 445 =
= 88 889-5) не является степенью двойки.
ПО. Найти все десятизначные числа такие, что 1-я
цифра числа равна числу нулей в его десятичной запи-
си, 2-я цифра —числу единиц, и т. д. вплоть До десятой
цифры, равной числу девяток в записи числа.
111. На какое целое число надо умножить 999 999 999,
чтобы получить число, состоящее из одних единиц?
112. Пусть А — некоторое натуральное число. До-
казать, что существует бесконечно много таких (нату-
ральных) чисел У, записываемых цифрами 1, 2, ..., 9
(без нулей!), что числа N и AN имеют одинаковые сум-
мы цифр ’).
*) Оговорка об отсутствии нулей в десятичной записи чисел N
связана с тем, что если приписать к записи N любое число нулей в
конце, то суммы цифр чисел N и AN, разумеется, не изменятся; по-
этому без этой оговорки из существования одного удовлетворяю-
щего условию задачи числа N сразу же следовало бы существование
бесконечного множества таких чисел.
25
113. Пусть п^2 и at, a2, .все не более, чем
n-значные неотрицательные целые числа, сумма цифр ко-
торых четна, а bi, b%, ...— те не более чем п-значные
числа, сумма цифр которых нечетна. Доказать, что
<21 ~Т 0-2. + • < • ~ 01 + 02 'Г • • •
при всех (натуральных) т<п. Будет ли верно утверж-
дение задачи также и при
114. В числовом треугольнике
1
1 1 1
1 232 1
1367631
каждое число равно сумме трех чисел, расположенных
в предыдущей строке над этим числом и его соседя-
ми справа и слева; в случае отсутствия в предыдущей
строке одного из двух таких чисел они заменяются
нулями.
Доказать, что в каждой строке, начиная с третьей,
найдется четное число.
115. Дана треугольная таблица чисел:
0123............. 1956 1957 1958
1 3 5 ............. 3913 3915
4 8 ............... 7828
в которой каждое число (кроме чисел верхней строки)
равна сумме двух стоящих над ним чисел предшествую-
щей строки. Доказать, что последнее число, стоящее в
самой нижней строке этой таблицы, делится на 1958.
116. Расстояние от пункта А до пункта В равно
999 км. Вдоль соединяющей А и В дороги стоят кило-
метровые столбы, на которых указаны расстояния до А
и до В — надписи на них выглядят так:
О | 999, 1 | 998, 2 | 997. 999 | 0.
Сколько из этих столбов таких, на которых имеются
лишь две различные цифры?
*117. Мальчик, проезжая в автобусе мимо кинотеатра,
успел заметить только часы (но не минуты!) начала
26
четырех сеансов:
1-й сеанс — 12 час. ... мин.;
2-й сеанс—13 час. ... мин.;
7-й сеанс — 23 час. ... мин.;
8-й сеанс — 24 час. ... мин.
Как по этим данным восстановить начала всех сеан-
сов (предполагается, что продолжительность всех вось-
ми сеансов одинакова)?
118. Шоссе, по которому круглосуточно ходит авто-
бус, пересекает железную дорогу. По дороге каждый
час проходят два поезда, которые достигают шоссе
ровно в п час. и в п час. 38 мин., где п принимает все
значения от 0 до 23; каждый раз, когда проходит поезд,
опускается на 5 мин. шлагбаум, преграждающий путь
по шоссе. Требуется так составить расписание автобу-
сов, чтобы они ходили с одним и тем же интервалом
Т мин. между машинами и чтобы ни одна машина не
задерживалась на переезде. При каких интервалах
между автобусами, меньших получаса, так спланировать
движение возможно?
119. Чему равно наибольшее возможное значение
отношения трехзначного числа к сумме его цифр?
120. Вычеркнуть 100 цифр из числа
12345678910111213...979899100
так, чтобы полученное после этого число было
а) возможно большим; б) возможно меньшим.
121. Из всех цифр от 1 до 9 составить три трехзнач-
ных числа, произведение которых было бы
а) наименьшим; б) наибольшим.
122. Сумма нескольких последовательных целых по-
ложительных чисел равна 1000. Найти эти числа.
123. а) Доказать, что всякое число, не являющееся
степенью двойки, может быть представлено в виде сум-
мы по меньшей мере двух последовательных Целых по-
ложительных чисел, а для степеней двойки такое пред-
ставление невозможно.
б) Доказать, что всякое составное нечетное число
может быть представлено в виде суммы по меньшей
мере двух последовательных нечетных чисел, а ни одно
простое число нельзя представить в таком виде. Какие
27
четные числа можно представить в виде суммы несколь-
ких последовательных нечетных чисел?
в) Доказать, что каждую степень целого полржи-
тельного числа п (разумеется, с показателем, большим 1)
можно представить в виде суммы п последователь-
ных нечетных чисел.
124. Доказать, что произведение четырех последо-
вательных чисел в сумме с единицей дает полный
квадрат.
125. Имеется 4п положительных чисел, таких, что
из любых четырех попарно различных можно составить
геометрическую пропорцию. Доказать, что среди этих
чисел найдется п одинаковых.
126. Даны 27 гирь, веса которых равны соответствен-
но I2, 22, З2, ..., 272. Разложить эти гири на три группы
равного веса.
127. Имеется 13 гирь, каждая из которых весит це-
лое число граммов. Известно, что любые 12 из них
можно разложить на чашках весов, по шесть на каж-
дой чашке, так, что наступит равновесие. Доказать, что
все гири имеют один и тот же вес.
128*. Четыре (произвольные) числа a, b, с, d выпи-
саны рядом друг с другом. Под этими числами выписы-
вается новая четверка чисел ai—ab, bt — bc, cl = cd,
di — dcr, под ними выписываются числа a2=aj6i, b2=b}a,
c2—Cidi, d2=diOi, и т. д. Доказать, что либо все полу-
ченные таким образом четверки чисел различны, либо
все они, начиная с некоторой, совпадают между собой.
129. Дан произвольный набор из N (где W—полная
степень двух: N=2k) чисел а;, а2, ..., а^, каждое из ко-
торых равно 4-1 или —1. Исходя из этих чисел, следую-
щим образом составляется новый набор чисел, каждое
из которых также равно +1 или —1: a't — агаг, а'2==
= a2a3, ..., dN_t — aN_iaN, = затем по числам
aj, а’2, .... a‘N точно так же находятся числа а", а2, ...
..., dN, и т. д. Доказать, что в конце концов мы полу-
чим набор, состоящий из одних лишь чисел +1.
130*. Пусть а\, а2, .... ап, где п>2,— целые числа;
по этим числам составляется новая система чисел
aj_±a «*4-43. ' = fzL-<+.fln а’ =
“1 2 u2 2 ’ ’ п—1 2 ’ п
ап 4- а, , ,
— -2-g—;по числам ар а2, .. .,апточно так же находят-
28
„ ( ai + \ - n
ся числа аД = —2— )’ fl2> • • •’ an> и т- п- Доказать, что
если все получаемые таким путем числа — целые, то
al==a2=. .. — ап.
131. Пусть х—1, у, z — произвольные три числа; х\,
у\, 2[ — абсолютные величины |х—у|, |#—z|, |г—х|
попарных разностей этих чисел; х2, У2, — абсолютные
величины попарных разностей чисел хь у\, Z\ (т. е.
числа |Xi—yi |, \yt—Z]|, \zi—Xi |); х3, уз, z3— абсолют-
ные величины разностей чисел х2, у2, z2, и т. д. Извест-
но, что для какого-то п тройка чисел х„, уп, zn не отли-
чается от тройки чисел х, у, г. Чему равны числа у и г?
132*. а) Даны четыре произвольных целых положи-
тельных числа А, В, С, D. Доказать, что если образо-
вать из них четыре числа Ai, Вь Сь Dit равных соот-
ветственно разностям между А и В, между В и С, между
С и D и между D и А (мы каждый раз вычитаем мень-
шее число из большего), затем из чисел Ai, Bit С\, /Д
образовать точно так же новую четверку чисел Д2, В2,
С2, D2, и т. д„ то через несколько шагов мы обязательно
придем к четверке нулей.
Так, например, начиная с четверки чисел 32, 1, ПО, 7,
мы последовательно получим
32, 1, но, 7;
31, 109, 103, 25;
78, 6, 78, 6;
72, 72, 72, 72;
О, 0, 0, 0.
б) Сохраняет ли силу утверждение задачи а),' если
(положительные) числа А, В, С, D являются рациональ-
ными, но не обязательно целыми? А если эти числа
иррациональны?
133*. а) Расположить числа от 1 до 100 таким об-
разом, чтобы никакие 11 (не обязательно последователь-
ных!) из этих чисел не следовали одно за другим в
порядке возрастания или убывания.
б) Доказать, что в каком бы порядке ни располо-
жить числа от Г до 101, всегда из этих чисел можно
выбрать 11 (не обязательно последовательных!) чисел,
29
которые следуют одно за другим в порядке возрастания
или убывания.
134. а) Из первых 200 целых чисел от 1 до 200 вы-
брано 101 число. Доказать, что среди выбранных чисел
найдется пара таких, что одно из них делится на
другое.
б) Выбрать из первых 200 целых чисел 100 чисел так,
чтобы ни одно из них не делилось на другое.
в) Доказать, что если хотя бы одно из 100 целых
чисел, не превосходящих 200, меньше 16, то одно из
втих чисел обязательно делится на другое.
135. Доказать, что
а) из любых 52 целых чисел всегда можно выбрать
два, сумма или разность которых делится на 100;
б) из любых 100 целых чисел всегда можно выбрать
несколько чисел (быть может — одно), сумма которых
делится на 100;
в) если числа задачи б) положительны и не превы-
шают 100, а их сумма равна 200, то можно отобрать
несколько чисел так, чтобы их сумма равнялась 100;
г)* из любых 200 целых чисел можно выбрать 100
чисел, сумма которых делится на 100.
136. Дана невозрастающая последовательность a)f
аг, ..., ап положительных чисел, сумма которых равна 1,
а самое большее из них равно где k—целое:
gT- — О-t о-, д3 ап 0, Oj -f- a, -f- ... яп — 1.
Доказать, что из этих чисел можно выбрать k таких
чисел, что самое маленькое из них больше половины
самого большого.
137. По кругу выписаны р крестиков и q нуликов;
число пар стоящих рядом крестиков обозначим через а,
а число пар стоящих рядом нуликов — через Ь. Дока-
зать, что а—Ь—р—q.
138. Пусть /1, /г, • /п — это числа 1, 2, ..., п, но
только расставленные в каком-то, воообще говоря, новом
порядке. Доказать, что при п четном произведение
(1—11) (2—ii) (3—/3)...(п—i„) может быть как четным,
так и нечетным; однако при п нечетном оно обязательно
четно.
80
z 139. Дано n чисел хь х2, -*з, ..хп, каждое и» кото-
рых равно +1 или —1. Доказать, что если Х1Х2+Х2Х3+...
.. .+xn-.lxn+xnXi=0, то п делится на 4.
140. Доказать, что совокупность всех десятизначных
чисел, записываемых исключительно цифрами 1 и 2, мож-
но разбить на такие две группы, что запись суммы лю-
бых двух чисел из одной группы будет содержать не
менее двух цифр 3.
141. Из цифр 1 и 2 составлено пять 100-значных чи-
сел; при этом известно, что у каждых двух чисел ровно
в г разрядах совпадают цифры, однако ни в одном раз-
ряде не совпадают все пять цифр. Доказать, что это
возможно лишь в том случае, если г заключено в пре-
делах: 40г£>^60.
143. Имеютвя ма набора знаков «+» и «—» по
1958 знаков в каждом наборе. Доказать, что за некоторое
число «шагов», на каждом из которых позволяется
менять произвольно выбранные 11 знаков 1-го набора,
можно 1-й набор превратить во 2-й. (Наборы считаются
одинаковыми, если у них на одинаковых местах стоят
одинаковые знаки.)
143*. Шахматист для тренировки играет не менее од-
ной партии в день; при этом, чтобы не переутомить-
ся, он играет не более чем 12 партий в неделю. Дока-
зать, что можно найти несколько таких последователь-
ных дней, в течение которых он сыграет ровно 20
партий.
144. Пусть N—произвольное целое положительное
число. Доказать, что существует целое число, кратное
N, которое в десятичной системе счисления записывает-
ся одними лишь цифрами 0 и 1. При этом, если W
взаимно просто с 10 (т. е. не делится ни на 2, ни на 5),
то существует делящееся на W число, составленное из
одних только единиц (если N не взаимно просто с 10,
то, разумеется, никакое число вида 11 ... 1 не может
п раз
делиться на Лг)-
145. Расположить на числовой оси систему непере-
.крывающихся (не имеющих общих внутренних точек или
общих концов) отрезков длины 1 так, чтобы для любой
(бесконечной) арифметической прогрессии (с произволь-
ным первым членом прогрессии и какой-угодно раз-
ностью!) хоть один ее член попал внутрь одного из от-
резков нашей системы.
81
146. Пусть т и и—-два взаимно простых целых по-
ложительных числа. Доказать, что если дроби:
/я 4- я 2 (« -|- я)
т ’ т ’
m 4- я 2 (яг + я)
я ’ я
3 (яг 4~ я) (яг — 1) (яг -4 я),
яг ’ ' • ’ ’ яг ’
3 (яг 4- я) (я—1)(яг4-я)
я ’ ' ’ ’ ’ я
изобразить точками на числовой оси, то в каждый из
интервалов (1, 2), (2, 3), (3, 4), ..., (m4-n—2, т-\-п— 1)
оси попадает ровно одна из дробей (см. рис. 2, где по-
ложено т = 3, п — 4).
Рис. 2.
147*. Пусть ai, а2, а3..а„ — какие-то целые поло-
жительные числа, такие, что каждое из этих чисел мень-
ше 1000, а общее наименьшее кратное любых двух чи-
сел больше 1000. Доказать, что сумма обратных величин
чисел яь я2, «з. .. я„ меньше двух.
148*. Дробь — с нечетным простым знаменателем
р=/=5 разложена в бесконечную периодическую десятич-
ную дробь. Доказать, что если число цифр в периоде
дроби четно, то среднее арифметическое всех цифр пе-
риода равно 4,5 (т. е. совпадает со средним арифмети-
ческим всех цифр 0, 1,2,..., 9; это означает, что «боль-
шие» и «маленькие» цифры встречаются в периоде дро-
би одинаково часто). Если же число цифр в периоде
дроби нечетно, то среднее арифметическое всех цифр
обязательно отлично от 4,5.
149*. Доказать, что если разложить дроби
Я1 «2 Яз °П
р ' р2’ р3> ’ рп' " ’
(р — простое, отличное от 2 и 5, Яь я2, .... я„ ...— ка-
кие угодно целые числа, взаимно простые с р) в беско-
нечные периодические десятичные дроби, то несколько
первых дробей (может быть, одна) будут иметь одина-
32
ковое число цифр в периоде, а каждая из последую-
щих — в р раз больше цифр в периоде, чем предыдущая.
Так, например, 4-= 0,(3), 4-= 0,(4), 44= 0,(370),
14=0,(987654320), ™ имеет 27 цифр в периоде, ^4 име-
ет 81 цифру в периоде, и т. д.
5. РЕШЕНИЕ УРАВНЕНИЙ В ЦЕЛЫХ ЧИСЛАХ
150. а) Найти четырехзначное число, являющееся
точным квадратом и такое, что его первые две цифры
равны между собой и последние две цифры также равны
между собой.
б) Двузначное число в сумме с числом, записанным
теми же цифрами, но в обратном порядке, дает полный
квадрат. Найти все такие числа.
151. Найти четырехзначное число, равное квадрату
суммы двух двузначных чисел, образованных двумя
первыми и двумя последними цифрами числа.
152. Найти все четырехзначные числа, являющиеся
полными квадратами и записываемые
а) четырьмя четными цифрами;
б) четырьмя нечетными цифрами.
153. а) Найти все трехзначные числа, равные сум-
ме факториалов своих цифр.
б) Найти все целые числа, равные сумме квадратов
своих цифр.
154. Найти все целые числа, равные -
а) квадрату суммы цифр числа;
б) сумме цифр куба числа.
155. Решить в целых числах уравнения:
а) 1! 4-2! 4-3! + ... 4-х! = y*-t
б) 114-2!+314-...+*! = у’.
156. Сколькими способами можно разложить 2" на
сумму четырех квадратов целых положительных чисел?
157. а) Доказать, что равенство
x2+y2+z2=2xyz
Для целых х, у, г верно только при x=y=«z=0.
8 Д. О, Шклярсквй в др, 33
б) Найти целые числа х, у, z, v, такие, что
x2^-y2-j-z2+v2—2xyzv.
158*. а) При каких целых значениях k возможно
равенство
x’-f-r/’-f-z2—kxyz,
где х, у, z — целые положительные числа?
б) Найти в пределах первой тысячи всевозможные
тройки целых чисел, сумма квадратов которых делится
на их произведение.
/59. Решить в целых числах уравнение
х3—2у3—4z3 = 0.
160. Решить в целых числах уравнение
x24-x=«/4+y3+i/2+i/.
161. Решить в целых положительных числах урав-
нение
х2!'+(х4-1)2“= (х-ф2)2".
162. Решить в целых числах х, у, г уравнение
Рх + х + ... + х = z.
у корней
163*. Доказать, что уравнение х24~х-Н = рр имеет
решения в целых числах х, у для бесконечно многих
простых значений коэффициента р.
164*. Найти четыре целых (положительных) числа
таких, что квадрат каждого из них, сложенный с сум-
мой трех остальных, тоже является полным квадратом.
165. Найти все пары целых чисел, сумма которых рав-
на их произведению.
166. Сумма обратных величин трех целых положи-
тельных чисел равна единице. Каковы эти числа?
167. а) Доказать, что уравнение + -у » -у, где
п>1 — натуральное число, имеет при п простом ровно
три решения в натуральных числах х, у (где решения
х~а, у°=Ь и х=5, у=*а при а^Ь считаются различны-
ми), а при составном п — более трех решений.
б) Найти все решения в целых числах уравнения
задачи а) при п—14.
34
в)* Решить в целых числах х, у, z уравнение
-L —у” =“7’ (Указать формулы, дающие все решения).
168. а) Найти все целые положительные, не равные
между собой числа х, у, удовлетворяющие уравнению
xv=yx.
б) Найти все рациональные положительные, не рав-
ные между собой числа х, у, удовлетворяющие уравнению
ху=ух
'(указать формулу, дающую все решения).
169. В шахматном турнире участвовали два учени-
ка 7-го класса и некоторое число учеников 8-го класса.
Каждый участник играл с каждым другим один раз. Два
семиклассника набрали вместе 8 очков, а все восьми-
классники набрали одинаковое число очков (в турнире
каждому участнику за выигранную партию засчитывает-
ся 1 очко, а за партию, окончившуюся вничью, 1/2 очка).
Сколько восьмиклассников участвовало в турнире?
170. В шахматном турнире участвовали ученики 9-го
и 10-го классов. Каждый участник, играл с каждым дру-
гим один раз. Десятиклассников было в 10 раз больше,
чем девятиклассников, а они набрали вместе в 4,5 раза
больше очков, чем все девятиклассники. Сколько уче-
ников 9-го класса участвовало в турнире и сколько они
набрали очков?
171*. Ц елочис л ен ним треугольником на-
зывается треугольник, длины сторон которого выража-
ются целыми числами. Найти все целочисленные треу-
гольники, периметр каждого из которых равен его пло-
щади.
Задача 171 открывает большую тему в учении о решении уравне-
ний в целых числах; мы здесь не затрагиваем ее глубже именно в
связи с ее необъятностью (эта проблематика частично освещена в
указанной в списке литературы книге [53]). Так, например, пред-
ставляет интерес вопрос о целочисленных треугольниках с углами,
соизмеримыми с «полным» углом в 360°,— можно доказать, что ника-
ких углов, соизмеримых с полным углом и отличных от 60“, 90° и
120°, целочисленный треугольник иметь не может, причем нетрудно
получить формулы, дающие длины сторон всех целочисленных тре-
угольников с данным углом а. где а=60°, или 90°, или 120° (цело-
численные прямоугольные треугольники часто называют пифаго-
ровыми треугольниками). Можно также искать целочисленные
3* 35
треугольники, величины двух углов которых имеют Заданное отноше-
ние, скажем, один угол вдвое, втрое, впятеро или вшестеро больше
другого,— например, несложно доказать, что наименьший целочис-
ленный треугольник, один угол которого вдвое больше другого, име-
ет стороны 4, 5, 6, в то время как наименьшие возможные длины
сторон целочисленного треугольника, один угол которого вшестеро
больше другого, таковы: 30 421, 46 656, 72 930. Дальнейшие задачи
возникают, если, скажем, накладывать определенные условия н на
углы и на стороны целочисленного треугольника: так, нетрудно
указать сколь угодно много пифагоровых треугольников,
у которых гипотенуза или один катет являются полными квадратами,
но не существует ни одного пифагорова треугольника, сразу
две стороны которого являлись бы полными квадратами. При этом
среди целочисленных прямоугольных треугольников (пифагоровых
треугольников), гипотенуза каждого из которых является полным
квадратом, существует бесконечно много таких, сумма катетов ко-
торых тоже дает полный квадрат, однако стороны всех таких тре-
угольников весьма велики: как показал еще в 1643 г. П. Ферма !)>
наименьший из пифагоровых треугольников, стороны которых удов-
летворяют этим условия^, имеет стороны:
а=1 061 652 293 520
6 = 4 565 486 027 76Ь,
с=4 687 298 610 289.
6. МАТРИЦЫ, ПОСЛЕДОВАТЕЛЬНОСТИ,
ФУНКЦИИ
Матрицей размера тХп (или (тХп) -матрицей) называется
просто таблица чисел, имеющая т строк и п столбцов; так, например,
ниже выписаны (2X4)-матрица, (3X3)-матрица (квадратная матри-
ца 3-го порядка), (ЗХ1)-матрица и (1Х5)-матрица [(1Х«)-матрицы
и (пгХ1)-матрицы называются также векторами—соответствен-
но векторами-строками и векторами-столбцами}:
1/2 — 1/2 1/3 1/7
2/7 — 4/3 3/4 0
3 —2
— 11
12
0 7
1 —1
УГ
Уз
2
1
[10 —9 8 —7 6].
Матрица, все элементы которой представляют собой целые числа,
называется целочисленной — так, из выписанных выше матриц
целочисленными являются вторая и четвертая (но не первая и не
третья). Термин «матрица» пока не вошел в школьную программу по
математике и не используется в нижеследующих задачах; однако
большая важность этого понятия (см., например, [55] или [56]) за-
ставляет нас упомянуть этот термин в названии настоящего цикла.
*) Пьер Ферма (1602—1665) — великий французский матема-
тик, один из основоположников теории чисел.
36
Числовой последовательностью называется упорядочен-
ный набор чисел
fli> а2, Оз, • •. > вп, ...
(чаще всего — бесконечный). Для задания последовательности надо
указать правило образования ее членов at, а2, ,.»то правило может
иметь вид формулы, позволяющей по произвольно заданному номе-
ру п вычислить число Ап, или алгоритма, указывающего, как тем
или иным путем найти вп для любого конкретного значения п. Так,
например, для фигурирующей в нескольких из задач этого цикла так
называемой последовательности Фибоначчи1)
1, 1, 2, 3, 8, 8, 13, 21, 34, 55, 89, 144, 233, ... (*)
(числа Фибоначчи; о них см. [57] или [58]) этот алгоритм
задается правилами2):
й! а2 = 1; ап » + a„_t при п > 2. (**)
Впрочем, в математике приходится иногда иметь дело и с так назы-
ваемыми «случайными госледовательностями», образование членов
которых не регулируется жесткими правилами (ср. с задачей 192).
Под функцией y = f(x) понимается закон /: х у отобра-
жения множества X «допустимых» значений аргумента х в множество
У значений функции у, при этом каждому значению хеХ должно
соответствовать единственное значение р—/(х). В «высшей арифме-
тике» (в теории чисел) главный интерес представляют функции, свя-
занные с целыми числами — такие, для которых область определения
X или область У значений функции состоит из целых чисел. Если
область определения X = {1, 2, 3, ...} есть множество всех натураль-
ных чисел, то аргумент х функции чаще обозначается буквой п; при
этом сама функция «*-*• у(п) или п-^ап есть просто числовая после-
довательность {й1, а2, аз, Типичным (и часто встречающимся)
примером функции, у которой область значений У состоит из целых
чисел, является так называемая целая часть [х] числа х, т. е.
наибольшее не превосходящее х целое число (так что, например,
[2,5] =2, [4] =4, [—3,2] =—4); близкой к [х] является и функция
(х) — ближайшее к х целое число (если таких чисел два, то (х)
принимается равным большему из них, так что (2,5) =3, (4) =4,
(—3,2) =«—3; ср. графики функций [х] и (х) на рис. 3, а, б). В не-
которых вопросах математики встречается также функция {х} =
«=х—[X]—дробная часть числа х (рис. 3, в; для сравнения на
рис. 3,г изображен график функции |х— (х) |, указывающей отклоне-
ние х от ближайшего целого числа). Но наибольшую роль в теории
чисел играют «чисто арифметические» функции, для которых и об-
ласть определения X и область значений У состоят из целых чисел;
*) Леонардо Пизанский по прозвищу Фибоначчи
(1180—1240)—крупнейший математик европейского средневековья.
2) Существуют и другие описания чисел Фибоначчи (*)—так,
например, из правил (**) можно вывести явную формулу
1 |71 + 1/б'|п [l -г 1/б\п1
“•“УбН 2 ) 2 /J
•ависимости n-го числа Фибоначчи ип от его номера л.
37
в качестве примеров таких функций можно назвать фигурирующие
в некоторых из собранных ниже задач число делителей т(я)=»тп
(натурального) числа п, сумму его делителей о(п)=о„ или (неявно
участвующую в задаче 197) так называемую функцию Мёбиуса )
ц(н), равную 1 при п=1, равную 0 при п, кратном хоть одному
квадрату натурального числа, -и равную (—I)4 при п = р.р?... р!:,
где Pi, рг.... рк — попарно различные простые числа. [Заметим,
кстати, что все три функции т(п), о(н) и р,(н) обладают так назы-
ваемым «мультипликативным свойством»: если <р(п) любая из этих
функций,, то <р (щп2) — <р(щ) -<р (п2) для любых двух взаимно про-
стых натуральных чисел гц и п2.]
Собранные в этом цикле задачи являются довольно разнообраз-
ными по содержанию и по методам их решения; в частности, в не-
которых задачах используется так называемая «целочисленная ре-
шетка» — множество всех точек плоскости с целочисленными коорди-
’) Август Фердинанд Мёбиус (1790—1868) —выдающийся не-
мецкий математик, специализировавшийся, в первую очередь, в об-
ласти геометрии.
за
натами, плодотворность применения которой в теоретико-числовых
исследованиях была установлена еще Г. Минковским *) и Г. Ф. Во-
роным * 2).
172. Числа 1, 2, 3......п'
ратной таблицы:
1 2
п + 1 п + 2
2/1 4* 1 2л 4~ 2
расположены в виде квад-
3 ... п “
п 4- 3 ... 2/г
2/i 4~ 3 ... Зн
(/г — 1) п 4-1 (л — 1) п 4-
(/? — 1) п 4- 3 . . . п®_
Из этой таблицы выбирается произвольное число, а
строка и столбец, содержащие это число, вычеркивают-
ся. Затем из оставшихся чисел снова выбирается одно
число, и снова вычеркиваются.строка и столбец, содержа-
щие это число,— и так до тех пор, пока в таблице не
останется единственное число,которое автоматически по-
падает в число отобранных. Чему равна сумма всех вы-
бранных таким путем чисел?
173. Квадратная таблица из п2 клеток заполнена
целыми числами от 1 до п так, что в каждой строке и в
каждом столбце таблицы встречаются все числа от 1
до п. Доказать, что если таблица симметрична относи-
тельно диагонали, ведущей из ее левого верхнего уг-
ла в правый нижний угол, и п нечетно, то на этой диа-
гонали встретятся все числа от 1 до п. Будет ли вер-
но это утверждение также и в том случае, когда «четно?
174. п2 целых чисел от 1 до п2 выписаны в квадрат-
ную таблицу размером п\п: при этом число 1 стоит на
любом месте в таблице; 2 принадлежит строке, порядко-
вый номер которой равен номеру столбца, которому при-
надлежит 1; число 3 принадлежит строке, номер которой
совпадает с номером столбца, содержащего число 2,
и т. д. На сколько отличается сумма чисел строки, со-
держащей число 1, от суммы чисел столбца, содержа-
щего число п2?
’) Герман Минковский (1864—190*6)—выдающийся немец-
кий ученый, внесший большой вклад в геометрию, в физику (теория
относительности) и в теорию чисел; один из основоположников «гео-
метрической» теории чисел.
2) Георгий Федосьевич Вороной (1868—19*08)—выдающийся
русский математик, один из основоположников «геометрической» тео
рии чисел.
89
175. Дана прямоугольная таблица размером
во все клетки которой вписаны некоторые числа. Разре-
шается одновременно менять знаки у всех чисел одной
строки или у всех чисел одного столбца. Доказать, что,
применяя эту операцию несколько раз, мы всегда можем
прийти к таблице, у которой суммы чисел каждой стро-
ки и каждого столбца неотрицательны.
176. 800 чисел выписаны в виде прямоугольной таб-
лицы, имеющей 100 строк и 80 столбцов; при этом про-
изведение суммы всех чисел любого столбца на сумму
всех чисел любой строки равно числу, стоящему в пере-
сечении этого столбца и этой строки. Известно, что чис-
ло, стоящее в правом верхнем углу таблицы, положи-
тельно. Чему равна сумма всех составляющих таблицу
чисел?
177. 64 неотрицательных числа с общей суммой 1956
записаны на 64 клетках шахматной доски; при этом из-
вестно, что сумма чисел, выписанных на каждой из двух
диагоналей доски, равна 112, и что числа, занимающие
клетки, симметричные относительно одной или симмет-
ричные относительно другой диагонали, равны между со-
бой. Доказать, что сумма чисел, выписанных в любом
ряду (т. е. в любой строке или в любом столбце) доски,
меньше 518.
178. В клетках шахматной доски размером п\п рас-
ставлены некоторые числа так, что при любой расста-
новке на доске п ладей, никакие две из которых не бьют
-друг друга, сумма закрытых этими ладьями чисел будет
одной и той же. Обозначим число, стоящее на пересече-
нии i-й строки доски и /-го ее столбца, через at}. Дока-
зать, что существуют два таких набора чисел xh х2, ...
...,>х„ и z/i, t/2, .... уп, что ач=х4+^.
179. В клетках шахматной доски размером п\п рас-
ставлены числа; число, стоящее на пересечении р-й
строки и q-ro столбца, обозначено через хР5. Доказать,
что если для любых ц / и k (где l^t, /, k^n) имеет
место тождество хч+хй+хм=0, то существуют п таких
чисел /1, /2, , tn, что Xij—ti—tj.
180. В некоторых клетках шахматной доски размером
п\п стоят звездочки; известно, что если вычеркнуть лю-
бой набор строк доски (только, разумеется, не все!), то
найдется столбец, в котором имеется ровно одна неза-
черкнутая звездочка. (В частности, если вовсе никакие
строки не вычеркивать, то тоже найдется столбец,, в ко-
40
тором имеется ровно одна звездочка.) Доказать, что если
вычеркнуть любой набор столбцов (но не все), то най-
дется строка, в которой имеется ровно одна незачеркну-
тая звездочка.
181*. Во всех, кроме одной, клетках шахматной до-
ски размером п\п стоят знаки «+», а в одной клетке
стоит знак «—»; при этом
а) п = 4 и знак «—» стоит с краю доски, но не в
ее углу;
б) п = 8 и знак «—» стоит не в углу доски.
Разрешается одновременно менять все знаки в одном
(произвольно взятом) столбце, или в одной (произволь-
ной) строке, или в одном (произвольно выбранном)
«наклонном» ряду, параллельном диагонали доски.
(В частности, можно изменить знак в любом угловом
поле, которое образует самостоятельный «наклонный
ряд».) Доказать, что любым числом «допустимых» изме-
нений знаков нельзя избавиться от знака «—», т.е. прий-
ти к доске, во всех клетках которой стоит знак «+».
182. а) Во всех клетках шахматной доски размером
8X8 стоят знаки «+» или «—». Разрешается, выделив
на доске любой квадрат размером 3X3 или 4X4, поме-
нять знаки во всех клетках этого квадрата. Мы хотим
при помощи подобных операций добиться того, чтобы все
стоящие на доске знаки стали знаками «+»; всегда ли
это возможно?
б) Во всех клетках (обыкновенной) шахматной до-
ски стоят натуральные числа; разрешается увеличивать
на единицу все числа, стоящие в клетках любого «мало-
го» квадрата из четырех соседних клеток доски, или все
числа, стоящие в (любых) двух соседних строках доски,
или, наконец, все числа, стоящие в двух (любых) сосед-
них столбцах доски. Всегда ли подобными операциями
можно добиться того, чтобы все числа доски делились
на 10?
183. а) Имеются три кучки камней; играющему с
ними мальчику разрешается брать по одному камню од-
новременно из всех трех кучек или удваивать число кам-
ней в одной (произвольной) кучке. Сможет ли мальчик
за несколько подобных «ходов» выбрать из кучек все
камни?
б) Во всех клетках прямоугольной таблицы, имею-
щей 8 строк и 5 столбцов, расставлены натуральные чис-
ла. Разрешается удвоить число одного столбца (любогс)
41
или вычесть единицу из всех чисел одной строки. Дока-
зать, что несколькими «допустимыми» преобразования-
ми таблицы чисел можно добиться того, что во всех ее
клетках окажутся одни нули.
184. Таблица из двух столбцов целых положительных
чисел и какого-то числа строк выписывается по следую-
щему правилу. В верхней строке мы пишем произволь-
ные числа а и Ь; далее под а выписываем (целое поло-
жительное) число П1, равное -у-, если а четно, и равное
-т;.....если а нечетно, а под b выписываем число bi = 2b.
Далее мы поступаем с числами а\ и bi точно так же, как
раньше поступили с числами а и Ь: под at мы пишем
а, а. — 1
число а2, равное если сц четно, и равное , если
а\ -нечетно; под Ь\ же мы пишем число b2 = 2bi. Под а2
и Ь2 мы располагаем числа а3 и Ь3, образованные из а2
и Ь2 точно так же, как числа а2 и Ь2 образуются из чисел
«1 и bi, и т. д.; этот процесс мы кончаем в тот момент,
когда доходим до некоторого числа п„=1 (которому от-
вечает число b„=2bn-i). Доказать, что сумма всех стоя-
щих в правом столбце чисел bt, которым отвечают не-
четные числа а, (здесь t = 0, 1, ..., п; под«0 и Ьо мы
понимаем числа а и Ь), равна произведению ab.
185. Доказать, что каждое натуральное число либо
является числом Фибоначчи (членом последовательно-
гти Фибоначчи (*), см. стр. 37), либо может быть пред-
ставлено в виде суммы нескольких (различных). чисел
Фибоначчи.
186. Доказать, что сумма никаких восьми последова-
тельных чисел Фибоначчи (см. задачу 185) не является
числом Фибоначчи.
187. Доказать, что если натуральное число п делится
на 5, то и n-е число Фибоначчи ип (см. задачу 185) так-
же делится на 5.
188. Найдется ли среди 100 000 001 первых чисел Фи-
боначчи (см. вадачу 185) число, оканчивающееся че-
тырьмя нулями?
189. Последовательность чисел аь а2, а3,... образо- _
вана по следующему правилу: ai = 1; ап = nn-i ——
ап—1
при «>1. Доказать, что 14<Lflj«)<; 18.
12
190. Последовательность чисел а.\, а2, а3,..., ап тако-
ва, что
«1 = 0, |«2, = ]«14-11, |«з| = |а24-1 ]>•••, |«п| = |а„_14-11.
Доказать, что среднее арифметическое °2л + <>„
п
1
всех чисел не меньше —g-.
191*. Последовательность натуральных чисел а0, а1;
«2, аз, составляется по следующему правилу:
«о, «1, а2=|«о—«i|, «з= |«i—«2|»...
(и вообще ап=|«„_2—an-i| при всех п^2); продолжа-
ется последовательность до первого нуля. Известно, что
каждое входящее в последовательность число не превос-
ходит 1967. Какое наибольшее количество чисел может
содержать такая последовательность?
192. Подряд выписывается бесконечная последова-
тельность цифр aia2a3a4,..., где под ai, a2, аз, ai,... по-
нимается любая из цифр, кроме девятки. Доказать, что
среди чисел ai, aia2, aia2a3, aia2a3a4,... (где под aia2
понимается число ai-10-(-a2, и т. д.) имеется бесконечно
много составных.
193. В последовательности 1975... каждая цифра,
начиная с пятой, равна последней цифре суммы пред-
шествующих четырех цифр; Встретятся ли в этой после-
довательности
а) подряд цифры 1234; б) вторично четверка цифр
1975?
194. Выписываются подряд все числа, кратные
девяти:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117,... (*)
и для каждого из этих чисел находится сумма его цифр:
9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 18, 9, 9,... (**)
На каком месте последовательности (**) впервые
появится число 81 и каково будет следующее за ним
число? Что раньше встретится в этой последовательно-
сти: 4 раза подряд число 27 или 3 раза подряд число
36? Что еще можно сказать о чередовании чисел в по-
следовательности (**)?
195. Рассмотрим следующую последовательность на-
боров (натуральных) чисел. Первый набор 1а образуют
43
две единицы 1,1. Затем между этими числами вставим
их сумму 1 + 1 = 2; мы получим набор Л: 1, 2, 1. Потом
между каждыми двумя из чисел набора Ц вставим сум-
му этих чисел; мы получим набор /2:1-, 3, 2, 3, 1; затем,
поступая таким же образом и с набором /2, мы придем
к набору /3:1, 4, 3, 5, 2, 5, 3, 4, 1, и т. д. Сколько раз в
миллионном наборе /юооооо встретится число 1973?
196. Имеется (конечная) последовательность нулей
и единиц такая, что различны все пятерки последова-
тельных цифр, которые можно из нее выделить (причем
эти пятерки могут, разумеется, и перекрываться по-
добно пятеркам 01011 и 01101, расположенным так:
...0101101...). Доказать, что если последовательность
I 1
нельзя продолжить е сохранением сформулированного
ее свойства, то первые четыре цифры последовательно-
сти совпадают с ее последними четырьмя цифрами.
197. В одну строку выписаны. все делители числа
N=2-3-5-7-ll-13-17-19-23-29-31-37. Под числом 1 и те-
ми числами, которые представляют собой произведение
четного числа простых множителей, подписано число
+ 1, а под числами, представляющими собой произведе-
ние нечетного числа простых множителей, подписано чис-
ло — 1. Доказать, что сумма всех выписанных в нижней
строке чисел равна нулю.
198. Пусть р и q — два взаимно простых натураль-
ных числа. Натуральное число п условимся называть
«хорошим», если его можно представить в виде px-]-qy,
где х и у — целые неотрицательные числа, и «плохим»
в противном случае.
а) Доказать, что существует такое число А, что если
сумма двух целых чисел равна А, то обязательно одно
из них «хорошее», а второе — «плохое».
б) Если числа р и q заданы, то как найти число все-
возможных «плохих» натуральных чисел?
199. Доказать, что если число п неотрицательно, то
его можно (и притом единственным образом!) предста-
(х 4- у)2 -J- Зх + у
вить в виде п =------, где х и у — целые не-
отрицательные числа.
200. Пусть t — произвольное положительное число;
число несократимых дробей -у-, числитель р и знамена-
тель q которых не превосходят t, обозначим через d(t\,
44
Чему равна сумма
е л/100\ । ^/юо\ । j/100\ . । л/ЮО\ । j /lOOV
^ = d(Tj + d(l-J + d(Tj+---+d^j + d (йб)?
201. Доказать следующие свойства целой части чис-
ла (см. стр. 37):
1) +
n\ гт Г х 1
2) , л —целое число}
з) [*+4-] = 12*1-и;
4) [X] +р +4] + [х +4] +•••+[*+ —-1] = [пх].
202. Упростить сумму
« + 2М
2fe+i ]
где п — целое положительное число.
203*. Доказать, что если р и q— взаимно простые
целые числа, то
Г <7 1 , Г^71 > ГJ2.1 I I Пр — В ?1 _ (р — 1) (<7— 1)
204. Доказать, что
а) Т1+т24-т3+ ... 4-т„=
где т„ — число делителей натурального числа nj
б) <h4"оз~FОз4* • •
1 । п Г 1 । о Г 1 1 I
-] + 2[-] + 3[Т]+.
где ая — сумма делителей натурального числа п.
46
205. Существует ли такое целое положительное чис-
ло п, что «дробная часть» числа (2-|-)/2)п,т. е. разность
((2 + /2 )"} = (2 + V2 )п - [(2 + /2 )п],
(см. стр. 37) больше 0,999999?
206*. а) Доказать, что при любом целом положитель-
ном п число [(2 + ]/3 )”] нечетно.
б) Найти наивысшую степень 2, на которую делится
число [(1 +УЗ)"].
207. Доказать, что если р — простое число, большее 2,
то разность
[ (2 +У5)₽] — 2p+I
делится на р.
208*. Доказать, что если р — простое число, то раз-
ность
гр п
. р
делится на р (С„— число сочетаний из п элементов
по р; п — произвольное целое положительное число, не
меньшее р).
„ „5 11-10-9-8-7 .со „ъ Г И1
Так, например, Си == = 462; Си — -т- =•
1 ч* • о • 4 ’ и I и I
= 462 — 2 делится на 5.
209. Указать все такие числа а, что числа [а], [2а],
.], ..., [Уа], где N—фиксированное натуральное
г . г п Г А п г
а
число, все различны и числа —
_2
а
_3
а
тоже все различны.
В задаче 209 требуется найти такое число а, чтобы были различны
числа [а], [2а], [За]...... [Wa] и [0], [20], [30]....... [W0], где
0=-^~. Более содержательной является задача об определении та-
ких а и 0 (где уже не обязательноР чтобы бесконечные
последовательности [а], [2а], [За],...; [0], [20], [30],... состояли
из попарно различных чисел; так, например, можно доказать, что
выписанные последовательности содержат все без исключения нату-
ральные числа, причем каждое число — ровно по одному разу, в том
и только в том случае, когда а иррационально и + Т “ 1.
V* О
46
210*.Доказать, что в равенстве
(N — произвольное целое положительное число) можно
заменить все дроби ближайшими к ним целыми чис-
лами:
'(относительно обозначений см. стр. 37).
7. ОЦЕНКИ СУММ И ПРОИЗВЕДЕНИЙ
211. Сколько цифр имеет число 2100?
212. а) Доказать, что
11 1 3 5 99_ 1
15 <10|/Г< 2'4’6 100 10 •
б) * Доказать, что
J_____________3_ 5 99 1
' 2 ' 4 ' 6 ' " • ' 100 < 12 '
Примечание Результат задачи б), очевидно, представляет
собой усиление результата задачи а).
213. Какое из чисел больше: 31” или 1714?
214. Какое из чисел больше:
.2 ,.з
а) Л= 222 или В = З3 , где в записи числа А фи-
гурируют 1001 двойка, а в записи числа В— 1000 троек;
,4’’
б) В или С = 4 , где в записи числа С фигуриру-
ют 999 четверок? (В этой задаче под а^г 1
всюду
понимается .)
215. Доказать, что в десятичной системе счисления
записи чисел 1974” и 1974” +2" при любом натураль-
ном п содержат одинаковое количество цифр.
216. Среди всех чисел вида 36т—5”, где т и п — на-
туральные числа, найти наименьшее по абсолютной ве-
личине.
47
217. Доказать, что
2100 /-,50 2>«®
---7= с 1 оо "17Г
10/2 10
(Cioo — число сочетаний из 100 элементов по 50).
218. Что больше 99" 4-100" или 101" (п— целое по-
ложительное число)?
219. Что больше 1ОО300 или 300!?
220. Доказать, что для любого целого положитель-
ного п
! 1 \п
2< 1 +— <3.
\ п 1
221. Что больше (1,000001)1000 000 или 2?
222. Что больше 10001000 или 100I999?
223. Доказать, что для любого целого п>6
( п\п ~ , [ п\п
V2J М •
224*. Доказать, что при т>п (т, п — целые поло-
жительные числа)
! 1
а) 1 + —
' \ т 1
Lf
п ) 4
Так, например, 11 +-тЙ == 2-|-, a fl + у)
64 „ 10 о 1
/ j \т+1
б) 1 + —
к т /
1 \п+1
(п>2).
। 1 27 3
Так, например, U + f) а
256 о 13 3
81 ~ d81 8 ‘
Из задачи а) следует, что в последовательности чисел 11 + у I ’
/ 1 V ! 1 \з / 1 \П
11 <4? ~2~) , каждое последующее чис-
ло больше предыдущего. А так как, с другой стороны, ни одно из
чисел не превосходит 3 (см. задачу 220), то при величина
/ 1 \п
11 + "J" 1 стремится к некоторому определенному пределу (заклю-
48
ченному, очевидно, между 2 и 3). йтот предел обозначается бук-
вой е; приближенно он равен 2,71-8281828459045...
Аналогично, задача' б) утверждает, что в последовательности
/ 1 \» / 1 Г / 1 \6 I 1 \«+1
чисел II + I > Н •}- у I , + «••• каж'
дое последующее меньше предыдущего. А так как все эти числа
/ 1 уЖ
больше 1, то величина 1 + — 1 при п, неограниченно возрастаю-
щем, стремится к какому-то пределу. При этом числа второй пос-
ледовательности все более приближаются к числам первой последо-
I 1 уж / 1 V1 1
вательности (отношение /1 + — I : 1 + — I = 1 — все меньше
отличается от 1); следовательно, этот предел должен равняться тому
же самому числу е. Число е играет в математике очень большую
роль и встречается в самых разнообразных вопросах (см., например,
задачу 225 или примечания к задачам 231 и 234).
225. Доказать, что при любом целом п, большем шес-
ти, справедливы неравенства
п \п / п\п
< п! < ,
/ 1 г
где е = 2,71828 ... есть предел выражения U+yl
при ОО.
Этот результат является усилением результата задачи 223. Из
него, в частности, следует, что для любых двух чисел а, и а2.
таких, что ai<e<a2 (т. е., например, для Oi = 2,7, а2 = 2,8 или
01 = 2,71, о2=2,72, или «1 = 2,718, а2 = 2,719. и т. д.) при всех п,
больших некоторого определенного числа (различ-
ного для различных а,) имеют м е с тон еравенства
п \п , . I п \п
— > л! _> — .
«1 / /
Таким
числа
/ II \П
1а/
образом, число е является той «границей», которая отделяет
I п \п
а такие, что I у | растет «быстрее» л!, от чисел а таких, что
растет «медленнее» л! (существование такой границы следу-
ет из задачи 223).
/ п \п
Действительно, — < л! при любом л, большем шести (ибо
\a> 1
I п\п\ „
аг > е, а при я>6, в силу задачи 226, nl> ly I I. Далее, из резуль-
татов задач 220 и 224 вытекает, что при л>3 выполняются
4 Д. О. Шклярский и др.
49
неравенства
Л>е>(1+4') ”П+1Хп+ 1)". у'’й>”+у’п+ 1
71-—
следовательно, при величина у п убывает, если п растет.
_ пг-
Легко видеть, что при п достаточно большом, у п ^становится сколь
угодно близким к единице: это следует, например, из того, что
, 10V~ъ k
lg V 10 =^при достаточно большом k будет сколь угодно малым.
jv— е
Выберем теперь N так, чтобы выполнялось неравенство у N < —;
п>— , С
тогда при тем более будет у' откуда, в силу результа-
/ п \п I п\п
та задачи 225, следует, что п! <
но
Неравенство задачи 225 допускает значительное уточнение.
А именно, можно показать, что при больших п число п! приближен-
ие С есть постоянное число, равное К2л:
(точнее, можно доказать, что при п, стремящемся к бесконечности,
отношение
стремится к единице — см. задачу 161 книги [6]).
226. Доказать, что
m < Р + 2й + з* + ... + nk < О + JLV+1 1 nk+i
/С "Г 1 \ <1 / к~г *
(п и k — произвольные целые числа).
Примечание, Из результата задачи 226 следует, в частно-
сти, что
l* + 2fe + 3ft+... + 1
nt» X1 “ИГ
227. Доказать, ^то при всяком целом п>1:
. 1 1 , 1, ,1^3.
а' 2<'п+1‘'п + 2+ ,,,+2я<4’
1 < Д+~1 + п+1 + • • • + зТДЛ <2-
50
228*. а) Определить целую часть числа
1 j—L j—! [_ _1_ j_ _L 1
/2 /3 Т /4 /1 000 000'
б) Определить сумму
_J_____ , 1 ' । 1। , ____L_._
1/10000 "И 1/10001 "Г 1/10002 ~ У1 000 000
_!_
с ТОЧНОСТЬЮ ДО 50‘
229*. Найти целую часть числа
_L + _1_ + _L. +_J__________.
у 4 у 5 /б f/ 1 000 000
230. а) Определить сумму
+ ! 1
10s ' ll2 “ 12s “ ' • • “ 1000s
с точностью до 0,006.
б) Определить сумму
_L + _L-± I 1
10! ~ 11! “ 12! т ~ 1000!
с точностью до 0,000000015.
231. Доказать, что сумма
1 + т + т + т + • • • + т
превзойдет любое наперед заданное число N, если толь-
ко п достаточно велико.
Примечание. Результат настоящей задачи может быть зна-
чительно уточнен. А именно, можно показать, что рассматриваемая
сумма 1+"2" + "з" + -4' + •••"!“ ПРИ больших п мало отличает-
ся от log п (логарифм берется при основании е — 2,718 ...). Точнее
говоря, можно доказать, что при любом п разность
1 + т + т+“, + ’п"_ [ogn
не превосходит единицы (см., например, [6]).
232. Доказать, что если в сумме
1 + —+ —+ —4- + —
1 2 3^ 4 ^ л
4* 61
вычеркнуть все члены, у которых в знаменателе встре-
чается цифра 9, то сумма оставшихся членов при лю-
бом п будет меньше 80.
233. а) Доказать, что при любом п
1 + Т + Т + Гб + 2д + ••• + 72<2'
б) Доказать, что при любом п
1 -L _L । _L _L J. I
* -Г 4 -Г 9 -Т 16 г -Г „2 4
Очевидно, что неравенство задачи б) является усилением нера-
венства задачи а). Еще более сильный результат содержится в за-
даче 332. Именно из этой.задачи вытекает, что при любом п сумма
1 + Т + Т + • • ‘ + Г2
меньше чем -g- =1,6449340668... (но для любого числа Л\ меньшего
ла
чем -g-, например для А= 1,64 или .4=1,644934, можно найти такое
п, что сумма 1 + -j- + . 4 будет больше N).
234*. Рассмотрим сумму
1+ — + — + — 4- — + — + — + — + — + .. 4 —
‘ 2 3 5 7 1113 17 19 ' р'
где в знаменателях дробей стоят все простыв числа от 2
до некоторого простого числа р. Доказать, что эта сум-
ма может быть сделана больше любого наперед задан-
ного числа N (для этого следует только выбрать чис-
ло р достаточно большим).
Примечание. Результат настоящей задачи может быть зна-
чительно уточнен. А именно, можно показать, что при больших р
,11111 1
сумма 1+"2" "Ь'з'4'5"4_7' + у| + -- -4 —сравнительно мало от-
личается от log log р (логарифм берется при основании е = 2,718...).
Точнее говоря, можно доказать (см., например, [6] или [69]), что
при любом р разность
1 4 2 + 8 + б + 7 + П + ' ‘ ‘ + р —1°8 l°g Р
не превосходит числа 15.
Отметим еще, что сравнение результата настоящей задачи с ре-
зультатами задач 232 и 233 позволяет утверждать, что простых чи-
сел имеется в ряду всех целых чисел «довольно много» (в частности,
52
из этой задачи следует, что их бесконечно много). Можно,
например, сказать, что простые числа встречаются в ряду натураль-
ных чисел «чаще», чем квадраты или чем числа, в записи которых
нет цифры 9, поскольку сумма обратных величин всех квадратов или
сумма обратных величин всех целых чисел, в записи которых не фи-
гурирует девятка, ограничены, а сумма обратных величин всех про-
стых чисел может быть сделана сколь угодно большой.
8. РАЗНЫЕ ЗАДАЧИ ИЗ АЛГЕБРЫ
В то время как большая часть содержания настоящей книги от-
носится к арифметике (и к «высшей арифметике» — к теории чисел),
циклы задач 8—10 посвящены алгебре. При этом при решении от-
дельных задач этих циклов могут оказаться полезными, например,
представление о так называемой основной теореме ал-
гебры, утверждающей, что каждое алгебраическое уравнение сте-
пени п (с вещественными или с произвольными комплексными
коэффициентами) имеет-ровно п (вещественных пли комплексных)
корней (которые, однако, не обязаны быть все различны); форму-
лы Виета'), указывающие связь корней уравнения с его коэффи-
циентами; знание правил деления «углом» произвольных многочле-
нов; тригонометрическая форма или геометрическое представление
комплексных чисел (см. в конце книги литературу к циклам 8—10).
235. Доказать, что
(а -|- b Д- с) 333 — а333 — &333 — с333
делится на
(а b -j- с)3 — а3 — Ь3 — с3.
236. Разложить на множители выражение •.
а10 4- а5 4- 1.
237. Доказать, что многочлен
д.9999 | д.8888 | £1Ш | д-6666 J д-5555 | д-4444 j д-3333 | д.2222 |
4-х11114-1
делится на х9 4- х3 4“ + x<i + + я4 + х3 + х2 + 1.
238. а) Разложить на множители выражение
а3 4~ Ь3 4- с3 — ЗаЬс.
б) Воспользовавшись результатом задачи а), найти
общую формулу для решения кубического уравнения
х3 4- рх 4- <7 == 0.
*) Франсуа Виета (1540—160'3)—видный французский ма-
тематик, один из создателей современной алгебраической символики
4а тем самым » и алгебры).
53
Примечание, Отметим, что результат настоящей задачи поз-
воляет решить всякое уравнение третьей степени. Действительно,
пусть
х3+Ах2-\-Вх-\-С = О
есть какое-то кубическое уравнение (коэффициент при х3 всегда
можно считать равным 1, так как в противном случае мы можем
разделить все уравнение на этот коэффициент). Сделаем в этом
уравнении подстановку: х=у+с. Тогда получим:
у3 + Зсу2 + Зс2у + с3 + А (у2 + 2су + с2) + В (у + с) + С => О,
или
у3 + (Зс + А) у2 + (Зс2 + 2Ас + В)у + (с3 + Ас2 + Вс + С) =0.
Л Л
Отсюда видно, что положив с =—"у(т. е. х =у — -д-), мы ПРН"
дем к уравнению
(ЗА2 2Л2 , D
^9 3 +В
У +
У3 +
I № Л3 АВ '
\ 27 + 9 ~ 3 +С
= 0,
которое имеет такой же вид, как и уравнение данной задачи:
У3 + РУ + Я = 0, где р =
Л2 2Л3 АВ ,
з+о>7-"27~3 ~гС'
239. Решить уравнение
У а— У а + х — х.
240*. Найти действительные корни уравнения
х- + 2ах + — а+ У а2 + х — ± (0 < а < 4-У
' 1 16 F 1 16 \ 4 /
241. Найти действительные корни уравнения
х + 2V х + 2Ух + 2l'x + 2VЗх = х
, п радикалов
(все квадратные корни считаются положительными).
242. Решить уравнение
1~] г »= х
' (в выражении слева знак дроби повторяется п раз).
243. Найти действительные корни уравнения
+ з _ 4 - 1 + Ух + 8-бУх^1 = 1
(все квадратные корни считаются положительными),
54
244. Решить уравнение
|х4-11 — | х | +31 х— 11 —2|х—2| = х4-2.
245. Решить уравнение
, х , х (х—1) х (х—1)(х — 2) ,
1 — 1 1-2 ПГз н
])п х(х—1)(х —2) ... (х — п) q
246. Решить уравнение х3—[х] =3, где, как обычно,
[х] — целая часть числа х (см. стр. 37).
247. Система двух уравнений второй степени
f х2 — уг — О,
Цх —а)24-у2= 1
имеет, вообще говоря, четыре решения. При каких зна-
чениях а число решений этой суммы уменьшается до
трех или до двух?
248. а) Решить систему уравнений
( ах + у — а2,
I х + ay = 1.
При каких значениях а эта система вовсе не имеет ре-
шений и при каких имеет бесконечно много решений?
б) Тот же вопрос относительно системы
( ax-j-y = а3,
( х 4- ay = 1.
в) Тот же вопрос относительно системы
ах + У + 2 = 1 >
х 4-ш/ 4- z = а,
Л +.У + az — а2-
249. Найти условия, которым должны удовлетворять
данные числа ои, аг, аз, а« для того, чтобы система 6
уравнений с 4 неизвестными
Х{ 4- aia2‘,
xi 4- хз — оиаз,
Xi 4- хь = ак^,
Xj 4~ -^з — а2аз,
х2 4- Х4 = а2а4,
. х3 4- Х4 = аза4
55
имела решения. Найти значения неизвестных х{, х2,
Уз, х^
250. Сколько действительных решений имеет система
| х + у = 2,
( ху — Z2 = 1 ?
251. Найти все вещественные решения системы
f x34-z/3 = 1,
I х4 + у4= 1.
252. Найти всевозможные решения х, хь х2, х3, х4, х3
системы уравнений:
Xj + х3 = ХХ2, Х2 4- Х4 = ХХ3, Х3 -|- Х3 = хх4,
х4 4- Х1 «В ХХб, Хб 4- Х2 = ххь
253. Найти всевозможные системы таких четырех ве-
щественных чисел, что сумма каждого из них с произ-
ведением остальных равна 2.
254. Решить систему четырех уравнений с четырьмя
неизвестными
| а—b | у 4-1 а—с | z4-1 а—d 1t'= 1,
|й—а\х 4-|6—c|z4-|b—d|/=l,
| с—а | х4- ] с—b | у 4-|с—<ф=1.
|d—a|x4-|d—b|z/4-|d—c\z =1;
здесь a, b, с, d— какие-то четыре попарно различных
вещественных числа.
255. Дана система п уравнений с п неизвестными
хь x2v..х»:
ах! + Ьхг 4- с = xt, axl 4- Ьхй 4- с = х,( ...
..., axn-i + bxn-t 4- с = хп, ахп 4- Ьхп 4- с = х4
(здесь а#=0). Доказать, что эта система не имеет ни
одного решения, если (Ь—I)2 — 4ас<0, имеет единст-
венное решение при (Ь— I)2 — 4ас == 0 и более одного
решения при (Ь — I)2 — 4ас>0.
256. Пусть все числа alt а2, ..., а„ (где п^2) поло-
жительны; сколько вещественных решений имеет систе-
ма уравнений:
XiXi=alt х2хг=а2, .х»Х1=аж?
53
257. а) Сколько корней имеет уравнение
sinx-J^?
б) Сколько корней имеет уравнение
sin х 1g х?
258. Известно, что
ai — 4а2 -К Злз^О,
п2 — 4п3 О,
«98 — 4 (2дэ Заюо^ о,
^99 —’ 4^100 *h 3(2] 5^0,
(2100 — 4(21 -}- 3(Z2Jg:0.
Пусть (21 — 1; чему равны тогда числа а2, аъ, ..Яюо?
259. Пусть a, b, с, d — какие угодно четыре положи-
тельных числа. Доказать, что три неравенства
аb<.cd,
(a-[-b) (c+d) <ab-\-cd,
(а 4- b) cd<_ (с + d)ab
не могут иметь место одновременно.
260. Доказать, что дробь
2 — ]^ 2+^2 + ^2 + ... + '^2
2 — V 2 + К2+ ... +/2
где в числителе стоят п радикалов, а в знаменателе —
(п — 1) радикалов, при любом п^1 будет больше-^-.
261. Произведение трех положительных чисел равно
1; их сумма больше суммы обратных величин этих чи-
сел. Доказать, что из трех рассматриваемых чисел одно
больше единицы, а два остальных — меньше единицы.
262. Сумма 1959 положительных чисел аь «2, а3, ...
..., (21959 равна 1; доказать, что сумма всевозможных
произведений по 1000 разных сомножителей из числа
наших чисел меньше 1. [В число рассматриваемых про-
изведений включаются все, отличающиеся друг от друга
хоть одним сомножителем, ио не произведения,
57
отличающиеся только порядком сомножителей — такие
произведения считаются одинаковыми и засчитывается
из них лишь одно.]
263. Пусть /V^2 — некоторое натуральное число. Че-
му равна сумма всех дробей вида —> где т и п —
взаимно простые натуральные числа такие, что 1^т<
<Zn^.N и
264. 1973 положительных числа сц, а2, аз, . . ., «1973
таковы, что
а? = а? = а? = ... = (ai972)a‘”3 = (а1973)а‘.
Доказать, что — а^2.
265*. Доказать, что если xt и х2 — корни уравнения
х2— 6х + 1 = 0, то х" 4~ Х2 при любом целом п являет-
ся целым числом, не делящимся на 5.
266. Может ли выражение
(а1 4“fl2'4“ • • • +а999 4-Оюоо) 2 =
=«14-^2+ • • • +<2999“|-niooo"r2a1tz.,-r2a:1a34- ... 4-2й99эают,
где некоторые из чисел ait а2, ..., a999, a100o положитель-
ны, а другие отрицательны, содержать одинаковое чис-
ло положительных и отрицательных попарных произве-
дений?
Рассмотрите аналогичную задачу для выражения
(П14-Й24“ • • • 4~^9999~Ь^1ОООо) 2-
_267. Доказать, что любую целую степень числа
]Д2 — 1 можно представить в виде — VN— 1 , где N —
целое число_ (так, например, (]Д2 — 1)- = 3— 2]/2=-
= ]/9’-^/8, а (/Г-1)3=5/Г-7=К50-К49’).
268. Доказать, что выражение 999994-111111 КЗ нель-
зя представить в виде (Л 4- ВУ3 )2, где А и В — це-
лые числа. _
269. Доказать, чтой 2 нельзя представить в виде
Р+яУг\ где р, q, г—рациональные числа. ____________
(п 4- Vп2 — 4^ т
—L_L2----/
где т, п^2 — натуральные числа. Доказать, что А
. k 4-
можно также представить в виде А = —!—, где
k — натуральное число.
53
271. Существуют ли такие рациональные числа х, у,
z и t, что при некотором натуральном п
(х + уУ2)-п + (г + t У1)2п = 5 + 4/2?
272. Даны две бочки бесконечно большой емкости.
Можно ли, пользуясь двумя ковшами емкости/2лит-
ров и 2—/2 литров, перелить из одной из них в другую
ровно 1 литр воды?
273. При каких рациональных х выражение Зх2 —
— 5х + 9 будет представлять собой квадрат рациональ-
ного числа?
274. Дискриминант Д = р2—квадратного уравне-
ния х2+рх-|-<7 = 0 имеет величину порядка 10; доказать,
что если при округлении свободного члена q уравнения
мы изменили его на величину порядка 0,01, то значения
корней уравнения изменятся на величину порядка
0,001.
275. Округлением числа мы назовем целое число,
отличающееся от исходного менее чем на 1. Доказать,
что любые п положительных чисел можно округлить так,
что сумма любого количества этих чисел будет отличать-
ся от суммы их округлений не более чем на
276. В десятичной записи положительного числа а
отброшены все десятичные знаки, начиная с четвертого
знака после запятой, т. е. взято округление с недостатком
а0 числа а с точностью до 0,001. Полученное число а0 це-
лится на само число а и частное снова округляется с не-
достатком с той же точностью. Указать все числа, кото-
рые при этом могут получиться.
277*. Пусть а — произвольное иррациональное число.
Очевидно, что каково бы ни было целое число п, та из
0 12 3
дробей ряда — = 0,—, —, —,..., которая ближе всего
к се, отличается от а не больше чем на половину—. Дока-
зать, что существуют такие п, для которых дробь со зна-
менателем п, наиболее близкая к а, отличается от а
меньше чем на 0,001 • —•
278. а) Доказать, что если а записывается десятичной
дробью 0,999..., начинающейся со 100 девяток, то и
59
Va = 0,999... записывается десятичной дробью, начинаю-
щейся со 100 девяток. ______________
б)* Вычислить значение корня j/0,1111... 111 с точ-
ностью до 1) 100; 2) 101; 3) 200; 4) 300 знаков после
запятой.
279. а) Что больше
2,00000000004
1.0JJJЭЭ0ЭДЭ4)2 4- 2,00000000004 ИЛИ
2,00000000002 ,
(1,00000000002)2 + .2,00000000002 ’
б) Пусть й>6>0. Что больше
1 4-а + а2+ 1 + Ь+ &2+ ... + Ьп~\
---!----1-!'--------- ИЛИ —1-----!!------------— ?
1 4-а + а2 -I- . .. +ап 1 4- b 4- Ь2 4- ... 4- Ьп
280. Даны п чисел ai, а2, а3, ..ап. Найти число х,
такое, чтобы сумма
(х—ai)2+ (х—а2)2+ ... 4~(х—ап)2
имела наименьшее возможное значение.
281. а) Даны четыре действительных попарно нерав-
ных числа ai<G2<«3<«4. Расположить эти числа в та-
ком порядке fli,, й;2, й,„ ait (iu i2, i3, ii—те же номера 1,
2, 3, 4, только как-то переставленные), чтобы сумма
- ф = (fli, — а,-,)2 4- (й1а — а,,)2 4- (а;, — ait )2 4- (й1( — й^)2
имела наименьшее возможное значение.
б)* Даны п действительных попарно неравных чисел
йь й2, й3..... ап. Расположить эти числа в таком поряд-
ке й{2, й;3).... ain, чтобы сумма
ф = (Oil - й<2)2 + (щ, - й{,)2 4- ... 4- (й1п_, - а1пу 4-
+ («in — «<.)а
имела наименьшее возможное значение.
282. а) Доказать, что каковы бы ни были действи-
тельные числа йь й2, ..., й„; blt b2.Ь„, всегда
ai 4" bl 4- fli 4" 4- ... 4- ]/"йп 4" Ьп
> /(«14- а, 4- ...4-ап)2+(&14-^4-... 4- W2.
При каких условиях имеет место равенство?
60
б) Пирамида называется прямой, если в основание
пирамиды можно вписать окружность и центр этой
окружности совпадает с основанием высоты пирамиды.
Доказать, что прямая пирамида имеет меньшую боковую
поверхность, чем всякая другая пирамида той же высо-
ты, основание которой имеет ту же площадь и тот же
периметр.
Примечание. Неравенство задачи а) составляет частный
случай так называемого неравенства Минковского, сог-
ласно которому
Vа1 + ь1 + ••• + if+Kaf 4- 62~Ь ••• + 11 + •••
... + Vап + ь2п + ... + /2 >
> /(01 +... + апу+^ + ... + Ьпу + ... + (Z1 + ... + гп)2.
283*. Доказать, что при любых - значениях действи-
тельных чисел Oi, а2,..., ап имеет место неравенство
У^01 + (1 — of + (1 — о3)2 4- ...
... + /а2п_1 + (1 - а2) + /а2 + (1~«1)2 > П-Р-
При каких значениях этих чисел левая часть нера-
венства точно равна правой части?
284. Доказать, что если числа Х[ и х2 по абсолютной
величине не превосходят единицу, то
/1 - Xi2 4- /1 -xf< 2^
При каких значениях xi и х2 левая часть этого неравен-
ства точно равна правой части?
285. Что больше cos sin х или sin cos х ? - ---
286. Доказать, не пользуясь логарифмическими таб-
лицами, что
•а) + iogTn > 2; б) л ~ logn 2 > 2‘
287. Доказать, что если а и (} — острые углы и а<{5,
то
a) a—sin а<£—sin 0, б) tga—a<tg£—
288*. Доказать, что если а и В — острые углы и а< В,
Т0^<Ц1.
а . ф
61
289. Найти соотношение между arcsincos arcsinx и
arccos sin arccos x.
290. Доказать, что каковы бы ни были коэффициенты
азь «зо, • • •, «2, «ь сумма
cos32x+a3i cos 31х4-«зо cos 30х-|- ... +а2cos 2хщ cosx
не может принимать при всех х только положительные
значения.
• 291. Пусть некоторые из чисел ait а2, ..ап равны
4-1, а остальные равны —1. Доказать, что
2 sin (а, + + + ... + 45" _
= й, 2 + й, Vi -|- й, 1'2 4" - • "Ь апГ"2.
Так, например, при al — a2—...=an=i получаем:
2 sin (1 + 4- + 4 + ... + 45“ - 2 cosjgj =
= Vi+Vi+
п корней
9. АЛГЕБРА МНОГОЧЛЕНОВ
292. Найти сумму коэффициентов многочлена, полу-
чающегося после раскрытия скобок и приведения подоб-
ных членов в выражении
(1 — 3x4-Зх2)743 ( 1 4-Зх—Зх2)744.
293. В каком из выражений
(14-х2—X3) 1000 И (1—Х24-Х3)1000
будет стоять после раскрытия скобок и приведения по-
добных членов больший коэффициент при х20?
294. Доказать, что в произведении
(I—X-f-X2—Х34-... —х"4-х’°°) X
X (14-*4-*24-... 4-х"4-х100)
после раскрытия скобок и приведения подобных чле-
нов не останется членов, содержащих х в нечетной
степени.
62
295. Найти коэффициент при х50 после раскрытия ско-
бок и приведения подобных членов в выражениях:
а) (1 + х) 1000 -j-х(1 -J-х) 999 + х2(1 + х) 998 + ... + х1000;
б) (1+х)+2(1+х)2+3(1+х)8+... + 1ООО(1+х) 1000.
296 *. Определить коэффициент при х2 после раскры-
тия скобок и приведения подобных членов в выражении
(.. ,(((х—2)2—2)Q—2)2—,., —2)\
k раз
297. Н айти остаток от деления многочлена
х+х3+х9+х27+*81+*243
а) на х—1; б) на х2—1.
298. Неизвестный многочлен дает при делении на
х—1 остаток 2, а при делении на х—2 — остаток 1. Ка-
кой остаток дает этот многочлен при делении на
(х—1) (х—2)?
299. При делении многочлена х1951 — 1 на х4+х3+
Ч-2х2+*+1 получаются частное и остаток. Найти в
частном коэффициент при х14.
300. Найти все многочлены Р(х), для которых спра-
ведливо тождество
хР(х—1) = (х—26)Р(х).
301. Дан многочлен Р(х) =aQxn+aixn~i-1t-.. .4-an_ix+,
z-|-a„ с .
а) натуральными; б) целыми
коэффициентами а^, at, , ап; сумму цифр числа Р(п)
обозначим через s(n) (ясно, что величина s(n) имеет
смысл лишь в том случае, если число Р(п) —натураль-
ное; в противном случае s(n) просто не существует).
Доказать, что если последовательность s(l), s(2),
s(3),... содержит бесконечно много чисел, то она содер-
жит бесконечно много одинаковых чисел.
302. Доказать, что многочлен х200у200-М нельзя пред-
ставить как произведение f(x)-g(y) двух многочленов:
от одного переменного х и от одного переменного у.
303. Квадратный трехчлен р(х) —ах2-[-Ьх-[-с таков,
что уравнение р(х)==х не имеет (вещественных) корней.
Доказать, что тогда и уравнение р(р(х))=х также не
Имеет вещественных корней.
СЗ
304. Квадратный трехчлен р(х)=ax2-^bx-i-c таков,
что если | х | 1, то и |р(х) | 1. Доказать, что в таком
случае из |х| ^1 следует также |р\(х) | 2, где pi(х) =
= сх24-&х4-а.
305. Доказать, что если Xj — корень уравнения
ах2+&х+с=0, (1)’
а х2— корень уравнения
—ах2+Ьх+с=0, (2)
то найдется промежуточный между ними корень х3 урав-
нения
~ х2 + Ьх + с = 0, (3)
т. е. такой, что либо xi^x3^x2, либо xi^x3^x2.
306. Пусть а и £ — корни уравнения
х2+рх4-<7=0,
а у и б — корни уравнения
x2+Px+Q = 0.
Выразить произведение
(а-Г)(Р-"Г) х—б)(р—б)
через коэффициенты данных уравнений.
307. Даны два уравнения:
х2+«х+1 = 0, х24-х4-а = 0.
Определить все значения коэффициента а, при которых
эти уравнения имеют хотя бы один общий корень.
308. а) Найти целое число а такое, что
(х—а) (х—10) +1
разлагается в произведение (x-{-b) (x-j-c) двух множи-
телей с целыми b и с.
б) Найти такие отличные от нуля не равные между
собой целые числа а, Ь, с, чтобы многочлен четвертой сте-
пени с целыми коэффициентами
х(х—а) (х—Ь) (х—с) + 1
можно было представить в виде произведения двух
других многочленов < целыми коэффициентами.
64
309. При каких отличных друг от друга целых числах
ai, а2, .ап многочлены с целыми коэффициентами
а) (х—ai) (х—а2) (х—а3)...(х—ап) — 1,
б) (х—aj (х—а2) (х—а3)...(х—а„) + 1
разлагаются в произведения других многочленов?
310*. Доказать, что при любых отличных друг от
друга целых числах ai, а2, ..ап многочлен
(х—ai)2(x—а2)2... (х—an)2+l
не разлагается в произведение двух других многочленов
с целыми коэффициентами.
311. Доказать, что если многочлен
Р(х) =aoxn+aixn~1+.. .+a„_ix4-an
с целыми коэффициентами принимает при четырех целых
значениях х значение 7, то он не может принимать зна-
чение 14 ни при каком целом значении х.
312. Доказать, что если многочлен 7-й степени с це-
лыми коэффициентами
а0х7+a1x6+a2x54-a3x4+a4X3+a5*2+fl6X-|-a7
при 7 целых значениях х принимает значения +1 и —1.
то его нельзя представить в виде произведения двух мно-
гочленов с целыми коэффициентами.
313. Доказать, что если многочлен с целыми коэффи-
циентами
Р(х) =аохп+а1хп~1-]г.. .у-ап-1х+ап
принимает при х—0 и х=1 нечетные значения, то урав-
нение Р(х)=0 не имеет целых корней.
314*. Доказать, что если многочлен
.Р(х) =a0x"4-aixn_1+a2x’,_2+.. .-{-an_ix+a„
с целыми коэффициентами при двух целых значениях
х—р и x—q (p>q) равен по абсолютной величине 1 и
уравнение Р(х)=0 имеет рациональный корень а, то
. Р + <7
р—q равно 1 или 2 и а = —
315*. Доказать, что многочлены
а) x2222 + 2x2220 + 4x22‘8 + 6x2216 + 8x22I4+. ..
.. .4-2218х44-2220х2+2222;
б) х250+х249+х248+х24'’+х243+.. .4-х2+х+1
б Д. О, Шклярский и др.
65
не могут быть разложены в произведения многочле-
нов с целыми коэффициентами.
316. Доказать, что если два многочлена с целыми, ко-
эффициентами в произведении дают многочлен с четны-
ми коэффициентами, не все из которых делятся на 4, то
в одном из перемножаемых многочленов все коэффици-
енты—четные, а в другом—не все четные.
317. Доказать, что все рациональные корни много-
члена
Р(х) —х”+а1х’,-1+а,2х’г~2-Ь.. .+ап-{х+ап
с целыми коэффициентами и с коэффициентом при стар-
шей степени х равным 1, являются целыми.
318*. Доказать, что не существует такого многочлена
Р(х) =aoxn+ajx’'-1+.. .+an-ix-j-an,
что все числа Р(0), Р(1), Р(2), являются простыми.
Примечание. Предложение, сформулированное в задаче,
было впервые доказано Л. Эйлером1). Ему же принадлежат при-
меры многочленов, значения которых'при многих последовательных
целых значениях х являются простыми (так, например, в случае
многочлена Р(х)~$2— 79x4-1601 80 чисел Р(0)=1601, Р(1)=1523,
Р(2), Р(3), ..., Р(79) являются простыми).
, 319. Доказать, что если многочлен
Р(х) ==%"^-Л1Хп-1+Л2хп-2+. . .-h4n-i*+Xn
при всех целых значениях х принимает целые значения,
то его можно представить в виде суммы многочленов
ад= 1,л(х) = х,р2(х) = Ц4^,...
п /х(х—1)(х—2).,.(х —n + 1)
•••, rn(X)- i ,2 -З...П ’
обладающих тем же свойством (в силу задачи 75 а)),
взятых с целыми коэффициентами.
320. а) Доказать, что если многочлен п-й степени
Р(х) принимает целые значения при х==0, 1, 2, ..., п, то
он принимает целые значения и при всех целых значе-
ниях х.
*) Работавший, главным образом, в России и в Германии швей-
царец Леонард Эйлер (1707—1783) был, бесспорно, крупнейшим
математиком XVIII в., внесшим значительный вклад во все разделы
математической науки.
66
б) Доказать, что всякий многочлен степени п, прини-
мающий при каких-то п-ф1 последовательных целых зна-
чениях х целые значения, принимает целое значение при
всяком целом х.
в) Доказать, что если многочлен Р(х) степени «при-
нимает целые значения при х=0, 1, 4, 9, 16,..., п2, то он
принимает целое значение и при любом целом значении
х, являющемся полным квадратом (но не обязательно
принимает целые значения при всех целых х).
Привести пример многочлена, принимающего целые
значения при каждом целом значении х, являющемся
полным квадратом, но при некоторых других целых х
принимающего дробные значения.
10. КОМПЛЕКСНЫЕ ЧИСЛА
321. а) Доказать, что
cos 5a=cos5 a—10 cos3 a sin2 a-j-5 cos a sin4 a,
sin 5a=sin5 a—10 sin3 a cos2 a 4*5 sin a cos4 a.
б) Доказать, что при каждом целом п
,сог па = cosn a — С2 cos"-2 a sin2 a-j- Cn cos"-4 a sin4 a —
— Cn cos"-8 a sin8 a + .. .,
sin na = C1, cos"”’1 a sin a — Cn cos"-3 a sin3 a 4*
+ Cn cos"-5 a sin8 os — ...,
где обозначенные точками члены, закон образования ко-
торых легко подметить, выписываются до тех пор, пока
сохраняют смысл биномиальные коэффициенты.
Примечание. Задача б), очевидно, является обобщением
задачи а).
322. Выразить tg6a через tga.
323. Доказать, что если х -ф — = 2 cos а, то хп -ф =
Х X
=2 cos па.
324. Доказать, что
sin ф ф sin (ф 4- а) ф sin (ф 4- 2a) 4- ... 4" sin (ф ф па) —
(п ф 1) a . / па \
sin--g--sin ср 4- -g-
а
б*
67
и
cos <p + cos (<р -f- a) -f- cos (<р 4- 2а) 4- • • • + cos (<р 4- ««) =
, (п 4- 1) а / , па \
sin------------------------------------g---cos I <р + — I
а
sin —
325. Упростить
cos2 a4~cos2 2а4-- • ^cos2 «а
и
sin2 a4~sin2 2а4-. • .4-sin2 па.
326. Упростить
cos а 4- Cn cos 2а 4" C2 cos За 4~ • • • 4~ Cn cos na4~
4- cos(n 4- l)a
и
sin a 4- Cn sin 2a 4- C2 sin 3a 4- ... 4- Cn—1 sin na 4-
4- sin(n 4- l)a.
327. Доказать, что если tn, n, p — произвольные це-
лые числа, то
. тл . пл . 2тл 2пл , . Зтл . Зпл ,
sin — sin---4 sin----sin----к sin — sin----4 ...
P p p P ' p p '
... + sin (?~ Sin ~
p p
--если tn 4- n делится на 2p, a tn — п не делится
на 2/7;
= -у, если tn — п делится на 2р, а т 4~ п не делится
на 2р;
О, если т 4- п и т — п одновременно делятся или
одновременно не делятся на 2р.
328. Доказать, что
2л 4л , 6л . , 2мл
C0S 2TTI + C°S 2ГП +.C0S 2Т + Т + • • • + C0S 2пД-Т =
______1_
“ 2 •
68
829. Составить уравнение, корнями которого явля-
лись бы числа:
\ • о Л . 9 2л • п Зл • 9 /2 л
a) sin2 н—П. sin2 О—r~i> sin2 о—г-,,. sin2
' 2/г + Р 2/г + Р 2/г + Р ’ 2/г + Р
б) ctg2_— cto2—?£L_ ctg2 Зл ctg2 -
’ 2n+ p big 2„+ p “S 2«+ !’•••’ 2n + Г
330. Упростить суммы:
я) ctg2 ——— 4- ctg2 ——— 4- ctg2 ——-—I- 4- ctg2 ————:
aj LLS 2n + 1 ё 2м п- I й 2zi + 1 + ' ё 2/г 4- Г
о зт i q 2л . л Ззт ।
6) cosec2 2— + cosec- 2— + cosec2 2— + ...
о /2Л
...4-COSec22—.
331. Упростить произведения:
. . я . 2л . Зл . пл
a) sin6—--г sin =—r-r sin^r——; ... sin^——r
' 2n 4- 1 2n -J-1 2/i 4- 1 2я 4“ 1
и
л . 2л . Зя . (n — 1) л
sin-к- sin — sin s— ... sin '—;
2/7 2/7 2/7 2/7
n 2л Зл /гл
6) COS --—Г COS S-j—r COS 5-—т ... COS s-~7
' 2/7 4- 1 2/7 4- 1 2/7 4- 1 2/7 4- 1
и
л 2л Зл (/7 — 1) л
COS — COS S— COS 5— . . . COS -S——.
2/7 2n 2n 2/7
332. Вывести из результатов задач 330 а) и б), что
при любом целом положительном п сумма
1 + + •••-+ 72
/. 1 V. 2 \ лг
заключается между 11 ~ 2п у; Д1 ~~ 27'~4-~l / ~б~ и
(1-------—) (1 4----—) —.
V 2п 4- ijV ~ 2я 4- 1/ 6
Примечание. Из результата задачи 332, в частности, сле-
дует, что
. , _1_ 1 1 л2
I + 22 + 32 + 42 4" • • • — 6 >
1 1 1
где под суммой бесконечного ряда 1 4" Т2" + "з2” 4* Ч2" + • • • -
69
понимается предел, к которому стремится величина 1+^+.••
...4- -L при
и2
I
- - - 22
я -> оо (ср. также раздел «Четыре формулы для чис-
ла л» книги [6], в котором дается существенное развитие этого
результата).
333. а) На окружности, описанной около правильно-
го п-угольпика Л,Л2...ЛП, взята точка М. Доказать, что
сумма квадратов расстояний от этой точки до всех вер-
шин //.-угольника не зависит от положения точки на ок-
ружности и равна 2nR2, где R есть радиус окружности.
б) Доказать, что сумма квадратов расстояний от про-
извольной точки М, взятой в плоскости правильного
«-угольника ЛИг. -. .Л„, до всех вершин «-угольника зави-
сит только от расстояния / точки М от центра О много-
угольника и равна n(R2jrl2), где R есть радиус окружно-
сти, описанной около «-угольника. *
в) Доказать, что утверждение предыдущей задачи
остается в силе и в том случае, когда точка А1 не лежит
в плоскости «-угольника Л(Л2 ... Л„.
334. На дуге Л1Л„ окружности, описанной около пра-
вильного «-угольника AjA2 ... Л„, взята точка М. Дока-
зать, что:
а) если п четно, то сумма квадратов расстояний от
точки М до вершин «-угольника с четными номерами
равна сумме квадратов расстояний от этой же точки до
нечетных вершин;
б) если « нечетно, то сумма расстояний от точки М
до вершин «-угольника с четными номерами равна сум-
ме расстояний от этой же точки до нечетных
вершин.
Примечание. Геометрическое доказательство теоремы зада-
чи 334 б) см. в решении задачи 137 книги [8].
335. Радиус окружности, описанной около правильно-
го «-угольника Л[Л2 ... А„, равен R. Доказать, что:
а) сумма квадратов всех сторон и всех диагоналей
«-угбльника равна n2R2;
б) сумма всех сторон и всех диагоналей «-угольника
равна«ctg-^- R;
в) произведение всех сторон и всех диагоналей
п п(п—1)
«-угольника равно п~2 ,
70
336*. Найти сумму 50-х степеней всех сторон и всех
диагоналей правильного 100-угольника, вписанного в ок-
ружность радиуса R.
337. Известно, что |г-+ — | = а; какое наибольшее и
какое наименьшее значения может иметь модуль |г|
комплексного числа г?
338. Пусть сумма п комплексных чисел равна нулю,
доказать, что среди них найдутся два числа, аргументы
которых разнятся не менее чем на 120°.
Можно ли заменить здесь величину 120° меньшей?
339. Пусть Ci, с2, ..., сп, г —такие комплексные чис-
ла, что
--------1---------1- ... н---------
г — С! г — с2 ' г — сп
= 0.
Доказать, что если числа С\, с2, .. ., сп представляются
на комплексной плоскости вершинами выпуклого
«-угольника, то число z представляется точкой, лежащей
внутри этого «-угольника.
11. НЕСКОЛЬКО ЗАДАЧ ИЗ ТЕОРИИ ЧИСЕЛ
3'40. Теорема Ферма. Доказать, что если р есть
простое число, то разность ар—а при любом целом а де-
лится на р.
Примечание. Частными случаями этой теоремы являются
предложения задач 46 а)—д).
3'41. Теор ема Эйлера. Пусть N есть какое-то
целое число и г — число чисел ряда 1, 2, 3, ..., N— 1,
взаимно простых с N. Доказать, что если а есть произ-
вольное целое число, взаимно простое с N, то разность
ar— 1 делится на N.
Примечание. Если число N — простое, то все выписанные
числа взаимно просты с N, т. е. r = N— 1, и теорема Эйлера сводит-
ся к следующей: разность ал’-1—1, где N — простое, делится на /V.
Отсюда видно, что теорему Ферма (см. задачу 340) можно рас-
сматривать как частный случай теоремы Эйлера.
Если N—pn, где р — простое, то из N—1=рп — 1 чисел 1, 2,
3,..., N—1 не будут взаимно простыми с N=pn только числа р,
%Р, Зр,..., N — р= (рп~1—1)р. Таким образом, в этом случае
г = (рп — 1) — (p"-i — 1) _ рП — рп~1, и теорема Эйлера сводится
71
к следующей: разность av 1 — 1,где р — простое, а а не делится
на р, обязательно делится на рп.
Если W = р“‘р“2 • • • Pkk< где Ръ •••> Рй —различные между
собой простые числа, то число г простых чисел, меньших W и взаим-
но простых с IV, дается формулой
(см., например, [64] — [68]). Если N = pn — степень простого числа
р, то эта формула дает
т. е. результат, полученный выше.
342*. Согласно теореме Эйлера разность 2к— 1, где
k—5n—5'1-1, делится на 5" (см. задачу 341, в частности,
примечание к этой задаче). Доказать, что ни при каком
k, меньшем чем 5n—5"-1, разность 2й—1 не делится на5п.
3!43. Выпишем подряд последовательные степени чис-
ла 2:
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096,...
Легко заметить, что в этом ряду чисел последние цифры
периодически повторяются с периодом 4:
2, 4, 8, 6, 2, 4, 8, 6, 2, 4, 8, 6, ...
Доказать, что и последние 10 цифр в этом ряду чисел,
начиная с некоторого числа, также будут периодически
повторяться. Найти длину периода и номер числа в ря-
ду, начиная с которого наблюдается периодичность.
344/. Доказать, что существует такая степень числа 2,
последние 1000 цифр которой все будут единицами и
двойками.
345. Пара (различных) натуральных чисел т и га на-
зывается «хорошей», если эти числа состоят из одинако-
вых простых делителей, взятых, однако, в (вообще гово-
ря) несовпадающих степенях (пример: 90 = 2-32-5 и
150 = 2-3-52), и «очень хорошей», если «хорошими»явля-
ются и пара т, п и пара гаг+1, га/-1 (пример: 6=2-3 и
48=24-3 — ведь 6-f-l = 7, a 48-J-1 = 49=72). Конечно или
бесконечно число «очень хороших» пар натуральных
чисел?
72
346. Пусть а, «+</, a-\-2d, a-\-3d, ...-—произвольная
(бесконечная) арифметическая прогрессия, начальный
член а и разность d которой являются натуральными
числами. Доказать, что прогрессия содержит бесконечно
много членов, разложение которых на простые множите-
ли содержит одни и те же множители (но взятые, разу-
меется, в разных степенях).
347. Тео рема Вильсона1). Доказать, что если
целое число р — простое, то число (р—1)1 + 1 делится на
р; если же р — составное, то (р—1)1 + 1 не делится на р.
348. Доказать, что
а) для каждого простого числа р можно найти такие
целые числа хну, что х2+у2+1 делится на р;
б)* если простое число р дает при делении на 4 оста-
ток 1 (и для нечетных простых чисел — только в этом
случае), существует такое целое число х, что х2+1 де-
лится на р.
Задача 348 связана с проблематикой, касающейся представления
натуральных чисел в виде сумм степеней (с показателями степени
п>1) других натуральных чисел (эта проблематика отражена в
большинстве книг и статей, отнесенных в списке литературы к этому
циклу задач). Так, из результата задачи 3486) можно вывести, что
натуральное число N в том и только в том случае может быть пред-
ставлено в виде суммы квадратов двух натуральных чисел, когда в
разложение N на простые множители все простые множители вида
4«+3 (множители, дающие при делении на 4 остаток 3) входят в
четных степенях. Из результата задачи 348а) можно вывести кра-
сивую теорему о том, что все без исключения натуральные числа мо-
гут быть представлены в виде суммы квадратов четырех (или мень-
шего количества) натуральных чисел', последний результат, в свою
очередь, позволяет установить, что все натуральные числа могут
также быть представлены в виде суммы ограниченного числа четвер-
тых степеней натуральных чисел,— скажем, в виде суммы 53 (или
меньшего количества) полных четвертых степеней натуральных чисел.
(Более тонкие средства позволяют заменить здесь оценку 53 на 21,
однако и этот результат, видимо, не является окончательным: скорее
всего каждое натуральное число может быть представлено в виде
суммы не более чем 19 полных четвертых степеней целых чисел.)
Доказано также, что всякое целое число представимо в виде суммы
кубов не более чем девяти целых чисел (вот здесь число 9 не может
быть заменено меньшим!).
Все эти предложения охватываются следующей замечательной
теоремой: для любого целого положительного числа k существует
такое целое число N (разумеется, зависящее от k), что каждое це-
лое положительное число представимо в виде суммы не более чем
N слагаемых, являющихся k-ми степенями целых чисел. Эта послед-
1) Александр Вильсон (1714«—1786)—шотландский астроном
и математик-любитель, профессор астрономии в Глазго.
73
няя теорема имеет несколько различных доказательств, но до самого
последнего времени были известны лишь такие ее доказательства, ко-
торые используют очень сложный математический аппарат (отно-
сящийся к высшей математике). Лишь в 1942 г. ленинградский
математик Ю. В. Линник дал чисто арифметическое ее доказа-
тельство (см. [72]), которое, однако, является исключительно
сложным. Установлено также, например, что каждое рациональное
число может быть представлено в виде суммы не более чем трех
кубов рациональных чисел, хотя, например, число 1 не может быть
представлено в виде суммы кубов двух рациональных чисел (дока-
зательство этого последнего факта имеется, например, Ё книгах
[53] и [54]).
349. Доказать, что существует бесконечно много про-
стых чисел.
350. а) Доказать, что среди членов арифметических
прогрессий 3, 7, 11, 15, 19, 23, ... и 5, 11, 17, 23, 29, 35,...
имеется бесконечно много простых чисел.
б) * Доказать, что среди членов арифметической про-
грессии
11, 21, 31, 41, 51, 61, ...
имеется бесконечно много простых чисел.
Аналогично решению задач 350а)—б), но несколько сложнее,
можно также доказать, что и среди членов арифметической прогрес-
сии 5, 9, 13, 17, 21, 25,... имеется бесконечно много простых чисел.
Имеет место и общее предложение о существовании бесконечного
числа простых чисел в каждой арифметической прогрессии, пер-
вый член которой взаимно прост с ее разностью, однако доказатель-
ство этого предложения является чрезвычайно сложным (интересно
отметить, что не использующее высшей математики, хотя и очень
сложное, доказательство этой классической теоремы теории чисел
было найдено впервые лишь в 1950 г. датским математиком
А. Сельбергом; до этого были известны лишь доказательства,
относящиеся к высшей математике).
РЕШЕНИЯ
1. Пусть А— первый из двух выбранных учеников, а В — вто-
рой. Если А и В стоят п одном поперечном ряду, то В выше А, ибо
А — самый низкий ученик в своем поперечном ряду; если А и В сто-
ят в одном продольном ряду, то В также выше А, ибо В самый вы-
сокий ученик в своем продольном ряду; наконец, если А нВ стоят
в разных поперечных и разных продольных рядах и С стоит в том же
поперечном ряду, что и А, и в том же продольном ряду, что и В, то
В выше А, так как В выше С, а А ниже С.
2. Составим общую сумму чисел всех рукопожатий, сделанных
когда-либо каждым из людей. Эта сумма обязательно четна, потому
что каждое рукопожатие, которым обменялись два лица А и В, уве-
личивает па 1 число рукопожатий, сделанных А, и на 1 число руко-
пожатий, сделанных В, и, следовательно, дает слагаемое 2 в общей
сумме. Но, с другой стороны, эта сумма составляется из чисел руко-
пожатий, сделанных каждым отдельным человеком. Из четности
суммы вытекает, что число нечетных слагаемых в ней четно, что
и требовалось доказать.
3. Пусть А—одно из данных лиц; ясно, что либо Г А имеет
среди присутствующих трех знакомых Bi, В2 и В3; либо 2° имеются
трое лиц Ci, С2 и С3, пи с одним из которых А не знаком (среди 5
отличных от А лиц у него есть либо трое знакомых, либо трое не-
знакомых). В случае 1° если В1г В2 и В3 попарно незнакомы, то они
образуют требуемую тройку; если же, например, В} и В2 знакомы, то
имеем тройку попарно знакомых лиц A, Bt и В2. Аналогично, если
в случае 2° С;, С2 и Сз попарно знакомы, то-они образуют нужную
нам тройку; если же, скажем, С], не знаком с С2, то мы приходим
к тройке A, Ci и С2.
4. а) Каждое из N присутствующих лиц может иметь 0, 1, 2,...
..., N—1 знакомых. Здесь мы имеем N возможных значений числа
знакомых; однако если некто имеет 0 знакомых, то никто не имеет
N — 1 знакомых (и наоборот — если некто имеет N—1 знакомого,
то никто не имеет 0 знакомых). Отсюда уже следует, что двое лиц с
одним и тем же числом знакомых обязательно существуют (ср. со
сказанным о принципе Дирихле на стр. 10).
б) Занумеруем присутствующих на заседании N лиц номерами
1, 2,..., N и рассмотрим такое «распределение знакомств»: пусть
N
для всех значений i=0, 1, 2,где /< -g-, лицо с номером N — i
знакомо со всеми лицами, кроме первых i лиц (т. е. А-е лицо знакомо
со всеми без исключения; (N — 1)-е — со всеми, кроме 1-го лица;
(Л/ — 2)-е— со всеми, кроме 1-го и 2-го;...); все же лица с номерами
Л'-1-1
I, где Is^isS—2—между собой незнакомы. В таком случае, при
75
N=3, очевидно, 1-е и 2-е лица знакомы лишь с 3-м, а 3-е лицо имеет
двух знакомых; аналогично, при Л'=4 1-е лицо знакомо лишь с 4-м;
2-е — с 4-м и с 3-м; 3-е — с 4-м и со 2-м; 4-е имеет трех знакомых.
Точно так же можно убедиться, что при //=26+1 нечетном чис-
ла п, знакомых у 1-го лица имеют значения: = 1, «2 = 2, ...
..., nh = k, пк+1 = k, пк+г — k + 1...nN = Л — 1, а при N =
= 26 4-2 четном = 1, n2 = 2........nk+i — k + 1, nA+2 = & + 1>
па+3 = £-|-2, ..., nN = N—1. Таким образом, здесь во всех слу-
чаях никакие трое лиц не имеют одинакового числа знакомых.
5. Если все присутствующие знакомы друг с другом, то возмож-
ность рассадить таким образом 4-х человек сомнения не вызывает.
Пусть теперь А и В незнакомы между собой. Каждый из них имеет
среди остальных 2п— 2 присутствующих не менее п знакомых; так
как п-\-п = 2п— (2п— 2)4-2, то у А и В имеется, минимум, два об-
щих знакомых Ci и Сг— и мы можем посадить А и В напротив друг
друга, а между ними посадить Cf и С2.
6. Рассмотрим ученого А, имеющего среди присутствующих наи-
большее число п знакомых (или одного из таких ученых, если их не-
сколько); при этом п>0, поскольку мы предположили, что некото-
рые из участников конгресса знакомы друг с другом. Все знакомые
А имеют разное число знакомых (ибо любые два из них имеют
общего знакомого Л); при этом ни один из них не имеет больше чем
п знакомых. Поэтому один из знакомых А (некто В) обязательно
имеет одного знакомого, второй—-двух, третий—трех....наконец,
последний (п й) знакомый А, так же как и А, имеет п знакомых.
Существование лица'В и доказывает утверждение задачи.
7. Выберем каких-то трех делегатов конгресса; среди них най-
дутся двое, знающие один язык — их-то мы и поместим в одном
номере гостиницы. Из оставшихся 998 делегатов снова отберем троих,
среди которых снова найдутся двое, которых можно будет разме-
стить в одном номере —„и т. д.„ пока у нас не останутся всего 4 де-
легата А, В, С и D. Если каждые два из них могут говорить между
собой, то с размещением этих делегатов не будет никаких трудностей;
если же А и В между собой не говорят, то и С, и О могут служить
для них переводчиками (что и делает возможным общение в трой-
ках А, В, С и А, В, D делегатов); это позволяет поместить, скажем
С в один номер с A, a D — в один номер с В.
8. Пусть А— какой-то один из присутствующих на конференции
ученых; с каждым из 16 остальных он говорит на одном из трех
(или на меньшем числе, если он не владеет, всеми тремя) языков.
Нетрудно' видеть, что имеется такой язык (назовем его «тарабар-
ским»), па котором А разговаривает не менее чем с 6 учеными: в са-
мом деле, в противном случае собеседников у А будет не больше чем
5-3 = 15, а по условию задачи любые два ученых могут говорить
между собой. Если двое из этих 6 ученых говорят между собой на
тарабарском языке, то утверждение задачи доказано; если же это не
так, то между собой 6 ученых говорят лишь на двух языках.
Пусть теперь В — произвольный из выделенных 6 ученых. Ясно,
что найдутся такие 3 из 5 остальных ученых, с которыми он говорит
па одном н том же («таратарабарском») языке: ведь если бы это
было не так, то среди 5 ученых В мог бы иметь не более чем 2-2=4
собеседников. Если хоть какие-то два — скажем С и D — из этих
трех участников конференции говорят между собой на таратарабар-
ском языке, то мы уже получаем тройку ученых В, С и D, разговари-
вающих между собой на одном языке; если же эти трое ученых
76
между собой говорят на третьем («таратаратарабарском») языке, jo
они и составляют искомую тройку.
9. а) Выберем одного из собравшихся А; всех знакомых с ним
лиц мы обозначим через At, А2,..., А/,. Ясно, что никакие два из
этих двух лиц не знакомы друг с другом и каждые два лица — ска-
жем, At и А< — имеют двух общих знакомых: А и некоторое лицо
„ k(k-l)
A{j; здесь t, / = 1, 2, ..., k и i ф j. При этом никакие два из-g-
лиц Л,2, очевидно, не совпадают, ибо в противном случае это лицо
имело бы с Л не менее трех общих знакомых. С другой стороны, так
как каждое не знакомое с А лицо имеет с А двух общих знакомых
(очевидно, из числа лиц Ль Л2, .. ., Лл), то Ai2, Л13, ..., Лд_ьл —
это в с е не знакомые с Л лица, и, значит, общее число п присутству-
ющих на собрании людей равно
(1 —это Л; k — это лица Л г,--j---—эт0 лица Л()).
Заметим теперь, что в силу равенства (*), которое можно пере-
писать еще и так:
lA+k — (2п — 2)=0, (**)
имеем
1 । 1 /8/г — 7 — 1
k “ — -%- + у — + (2п - 2) =-----------2-----
(второй корень квадратного уравнения (**) й'=—у— у у+2п—2
не подходит, ибо он отрицателен). Таким образом, число k знакомых
с некоторым лицом Л лиц однозначно определяется по общему числу
п присутствующих на собрании лиц, т. е. оно является одним
и тем же для всех лиц Л.
б) В силу (*) имеем
т. е. п должно быть на единицу больше так называемого треуголь-
#(&+1)
ного числа') —т,— При этом для записываемого по формуле (***)
числа п количество знакомых у каждого из присутствующих лиц
равно k; здесь k = 1, 2, 3,... — произвольное натуральное число.
10. Пусть Л, В и С — какие-то три жителя города. Ясно, что
возможен случай, когда все они дружат между собой-, возмож-
но также, что один из них (скажем, А) не дружит ни с В, ни с С,
а В и С дружат между собой: тогда для того, чтобы Л, В н С все
подружились, достаточно, чтобы Л «начал новую жизнь». Нетрудно
•) По этому поводу см., например, [64], стр. 122—123.
77
также видеть, что два других случая: когда все три жителя А, В й
С между собой враждуют и когда один житель,— например, тот же
А,— дружит с В и с С, а те враждуют между собой, уже невоз-
можны-. в этих случаях среди трех пар А, В; А, С и В, С жителей
Многообразия имеется нечетное (3 или 1) число в пар врагов и чет-
ное (0 или 2) число д пар друзей; при любых изменениях отноше-
ний в этой тройке лиц (во всех случаях, когда А, В или С «начина-
ют новую жизнь») четность чисел в и д не меняется (нечетное число
в может замениться лишь нечетным же числом в', а четное число
д — четным же числом д'), в силу чего все лица А, В и С никогда
не смогут подружиться между собой (число в не сможет стать
равным 0).
Описанное строение «отношения дружбы» между любыми тремя
лицами А, В и С доказывает, что в пределах всего города это от-
ношение можно описать весьма просто: в городе имеются две группы
жителей (две партии Ж и Л9), такие, что все жители принадлежат
либо к одной, либо к другой партии (но никогда — к обеим сразу),
причем каждые два члена одной партии между собой дружат, а жи-
тели, принадлежащие к разным партиям, обязательно враждуют.
В самом деле, присоединим к нашим трем жителям А, В и С города
Многообразие еще одного жителя D; в таком случае, если А и В
дружат между собой и D дружит хоть с одним из них, то он дружит
и со вторым — и, значит, принадлежит к партии, в которую входят
и А, и В; если же А и В между собой враждуют, то D дружит
лишь с одним из них (но с одним дружит непременно!). Это рассуж-
дение обеспечивает возможность разбиения четверки жителей А, В,
С и D на две партии Ж и АС (впрочем, одна из этих партий может
быть и «пустой»: так будет, если все жители А, В, С и D дружат
между собой). Поступая так же и дальше, т. е. последовательно
присоединяя к уже рассмотренным жителям города по одному чело-
веку, мы докажем возможность разбиения на две партии всех
10 000 жителей города.
Теперь доказательство утверждения задачи не представляет уже
никакого труда. Если все жители города дружат между собой, то
нам и доказывать нечего; если же ни одна из партий Ж и АС не
«пуста», то мы предложим каждый день одному из участников пар-
тии Ж «начинать новую жизнь», т. е,, попросту, переходить в партию
АС. Если в партии Ж имеется k человек, то все жители города смо-
гут подружиться за k дней; отсюда ясно, что 5000 дней («14 лет)
заведомо будет достаточно для того, чтобы все жители города
смогли подружиться (ибо хоть одна из партий Ж и АС содержит не
более 5000 членов).
11. Естественно называть «дорогой» отрезок пути между двумя
замками; все замки страны Оз связаны каким-то конечным числом
п дорог. Если рыцарь странствует по стране достаточно долго, то он
проедет достаточно много дорог; если это число Дэ 4«+1, то хоть по
одной дороге АВ (где А и В —замки) он проедет не менее 5 раз.
При этом не менее 3 раз он проедет по этой дороге в одном и том
же направлении (скажем, от Л кВ); поэтому, если из замка В, кро-
ме ВА, ведут еще две дороги ВС и BD, то рыцарь минимум дваж-
ды,— скажем, после i-ro и после /-го посещения замка В, где />й—
сворачивал, выезжая из В (куда он оба раза приезжал из /4) в одну
и ту же сторону, скажем, в сторону замка С. Но из условий зада-
чи тогда следует, что не только в i-e и в /-е посещение
В рыцарь приехал в В из одного замка —из замка А,— но и в Л он
78
оба раза приезжал из одного и того же замка (из замка Р в обозна-
чениях рис. 4: ведь если рыцарь после В свернул на дорогу ВС,
т. е. налево, то в А он должен был свернуть направо, т. е. приехать
в А он должен был из Р). Аналогично этому устанавливается, что
полностью совпадают пути рыцаря, предшествующие двум рассматри-
ваемым посещениям замка В-, так, в замок Р он оба раза попал из
одного и того же замка (из замка U рис. 4), и т. д. Но тогда, если
рыцарь до t-го посещения В миновал, начиная с выезда из своего
замка X, какое-то число k замков, то и за k замков до /-го посещения
В он снова был в X, что и доказывает утверждение задачи.
12. Условимся называть «друзьями» любых двух рыцарей, не яв-
ляющихся врагами; далее, начнем с того, что рассадим всех ры-
царей за круглым столом произвольно. Пусть где-то за столом
сидят рядом рыцарь А и его враг В; для определенности будем счи-
тать, что В сидит справа от А. Мы утверждаем, что за столом най-
дется такое место, где рядом сидят рыцари А' — друг А и В' — друг
В, причем В' сидит справа от А' (см. рис. 5, а). В самом деле, ры-
царь А имеет не менее п друзей; мест справа от них также имеется
и, а врагов у В не более п— 1 —значит, хоть одно из мест справа
79
от друга А' рыцаря А занимает друг В' рыцаря В. Пересадим теперь
в обратном порядке всех рыцарей, сидящих справа от А, начиная
с рыцаря В и вплоть до рыцаря А' (рис. 5, б). Ясно, что при этом
изменятся лишь пары А, В и А', В' соседей — они заменятся на пары
друзей А, А' и В, В'. Таким образом, число пар сидящих рядом вра-
гов уменьшится минимум на 1 (оно уменьшится даже на 2, если ры-
цари А'‘и В' — враги). Продолжая пересаживать рыцарей таким же
образом и далее, Мерлин может окончательно разъединить за сто-
лом все пары сидящих рядом врагов.
13. а) Разделим наши монеты на три группы: две группы по 27
монет и одну в 26 монет. При первом взвешивании поместим на
чашки весов группы по 27 монет. Если весы не уравновесятся, то
фальшивая монета находится на более «легкой» чашке. Если же ве-
сы окажутся в равновесии, то фальшивая монета содержится в груп-
пе из 26 монет. Таким образом, нам достаточно научиться решать
задачу: тремя взвешиваниями выделить фальшивую монету из группы
в 27 монет (задача выделить фальшивую монету из группы в 26 мо-
нет может быть сведена к этой задаче, например, добавлением к
группе из 26 монет еще одной произвольной монеты из числа ос-
тальных 54).
При втором взвешивании разделим группу в 27 монет на три
группы по 9 монет в каждой. Поместив на обе-чашки весов по груп-
пе из 9 монет, найдем группу из 9 монет, в которой содержится
фальшивая монета.
Разделив группу из 9 монет, одна из которых фальшивая, на
три группы по 3 монеты, мы третьим взвешиванием выделим тройку
монет, в которой содержится фальшивая.
Наконец, тем же путем при четвертом взвешивании найдем фаль-
шивую монету.
б) Пусть k—натуральное число, удовлетворяющее неравенствам
3й-1 < nig 3й. Покажем, что это число k удовлетворяет условиям
задачи.
Прежде всего покажем, что при помощи k взвешиваний всегда
можно определить фальшивую монету. Разделим наши монеты на
три группы так, чтобы в двух равных группах было по 3й"1 (или
меньше) монет, а число монет в третьей группе было бы не больше
3й-1 (это возможно, ибо n=g34). Положив на чашки весов две группы
из равного числа монет, мы определим, в какой из трех групп содер-
жится фальшивая монета (ср. с решением задачи а)). Таким образом,
после первого взвешивания мы выделим группу из 3й-1 монет, среди
которых содержится фальшивая- (если окажется, что фальшивая
монета находится в группе, содержащей меньше 3й-1 монет, то мы
можем дополнить эту группу монет произвольными монетами до
3й-1). При каждом последующем взвешивании будем делить наши
монеты на три равные группы и определять, в какой из них находится
монета. ТакихМ образом, после k взвешиваний мы придем к группе из
одной монеты, т. е. выделим фальшивую монету.
Теперь остается показать, что k есть минимальное число
взвешиваний, с помощью которых всегда можно выделить фальши-
вую монету, т. е. что при любых способах взвешивания результаты
взвешиваний могут сложиться таким неблагоприятным для нас обра-
зом, что после k — 1 взвешиваний фальшивая монета не будет вы-
делена.
При каждом взвешивании монеты распадаются на три группы:
монеты, попавшие на одну чашку, попавшие на другую чашку и не
80
попавшие ни на одну из чашек. Если на чашки весов было положено
одинаковое число монет и весы уравновесились, то фальшивая моне-
та заведомо находится в группе монет, не попавших при взвешивании
ни на одну чашку. Если одна из чашек перетянет (при равном числе
монет на чашках), то фальшивая монета находится на второй чашке.
Наконец, если на чашки весов было положено разное число монет,
то в случае, когда перетянула чашка, где монет больше, фальшивая
монета может оказаться в любой из трех групп и такое взвешивание
вообще не даст нам никаких сведений о местонахождении фальши-
вой монеты. Пусть теперь при произвольно производимых взвешива-
ниях результат взвешивания каждый раз оказывается наиболее не-
благоприятным, т. е. фальшивая монета каждый раз оказывается
в той из трех групп, которая содержит наибольшее число монет.
Тогда при каждом взвешивании число монет группы, содержащей
фальшивую монету, убывает не более чем в 3 раза (ибо при делении
некоторого числа монет на три группы всегда по крайней мере одна
из трех групп содержит не менее чем треть от общего числа монет);
поэтому после k — 1 взвешиваний число монет группы, содержащей
п
фальшивую монету, остается не меньшим чем и так как п->
>3Й~1, то после k—1 взвешиваний фальшивая монета не будет
выделена.
Примечание. Можно коротко записать ответ задачи в такой
форме: минимальное число взвешиваний, необходимое для выделения
Г I 11
фальшивой монеты из группы в п монет, есть log3l п —— . + 1, где
прямые скобки обозначают целую часть числа (см. стр. 37).
14. Положим на чашки весов по одному кубику (первое взве-
шивание). При этом могут иметь место два различных случая.
1°. При первом взвешивании одна чашка весов
перетянула. В таком случае из двух взвешиваемых кубиков
один обязательно является алюминиевым, а второй — дюралевым.
Далее кладем эти два кубика на одну чашку весов, а на вторую —
последовательно по паре оставшихся кубиков (разбиение 18 остав-
шихся кубиков на 9 пар производим произвольно). Если какая-ни-
будь пара кубиков перетягивает нашу пару, то это значит, что оба
кубика во второй паре дюралевые; если перетягивает первая пара,
то оба кубика второй пары — алюминиевые; если обе пары имеют
один вес, то, значит, вторая пара тоже содержит один алюминиевый
и один дюралевый кубики. Таким образом, в случае 1° мы можем
определить число дюралевых кубиков при помощи 10 взвешиваний
(одно взвешивание и еще 9).
2°. При первом взвешивании чашки весов оста-
лись в равновесии. В таком случае кубики первой пары
или оба алюминиевые, или оба дюралевые. Кладем, далее, эти два
кубика на одну чашку весов, а на вторую — последовательно кладем
по паре кубиков из числа оставшихся 18. Пусть первые k из этих
пар оказываются одного веса с первоначальной, а (й-Н)-я пара —
Другого веса. (Если А*=9, то все кубики оказываются одного веса
и, следовательно, дюралевых кубиков нет вовсе; случай /г=0 ничем
Не отличается от общего случая). Предположим для определенности,
что (£-)-1)-я пара оказалась более тяжелой, чем первоначальная
Д. О. Шклярский и др, В1
(рассуждение мало изменилось бы, если (&+1)-я пара оказалась
бы более легкой). В таком случае первые два кубика, а следователь-
но, и кубики тех k пар, которые оказались с ними одного веса, обя-
зательно алюминиевые. Итак, мы произвели пока 1 + (&+1) =&+2
взвешиваний и выделили при этом /г+1 пар алюминиевых кубиков.
Теперь положим на чашки весов по кубику из последней взвешен-
ной пары ((&+3)-е взвешивание). Если оба кубика окажутся оди-
накового веса, то оба они должны быть дюралевыми; в противном
случае — один из них алюминиевый, а второй дюралевый. В обоих
случаях мы можем после k+З взвешиваний указать пару из двух
кубиков, один из которых алюминиевый, а второй дюралевый. С по-
мощью этой пары мы 8 — k взвешиваниями определим число дюра-
левых кубиков среди оставшихся 2'0—2 (/г+2)= 16—2k кубиков
аналогично тому, как мы поступали в случае Г. Общее число взве-
шиваний в случае 2° будет равно k + 3 + (8 — k) = 11.
15. Разделим наши монеты на три группы по четыре монеты
в каждой. При первом взвешивании поместим на каждую чашку
весов по группе из четырех монет. Возможны два варианта:
1°. Чашки весов уравновесились.
2°. Одна из чашек перевесила.
Рассмотрим оба варианта в отдельности.
1°. При первом взвешивании чашки весов урав-
новесились. Следовательно, фальшивая монета находится в
оставшейся группе, а 8 монет на весах — настоящие. Перенумеруем
монеты из оставшейся группы: 1, 2, 3, 4. Положим при втором взве-
шивании монеты 1, 2 и 3 на одну чашку, а на другую — три монеты
из числа восьми заведомо настоящих. Возможны два случая:
А) Чашки весов уравновесились. Тогда монета 4 — фальшивая.
Сравнивая третьим взвешиванием ее с настоящей, мы находим,
легче она или тяжелее, чем настоящая.
Б) Одна из чашек перетянула. В этом случая фальшивой явля-
ется одна из монет 1, 2 или 3. При этом, если перетянула чашка
с настоящими монетами, то фальшивая монета легче настоящих;
одним взвешиванием мы без труда выделяем более легкую из трех
монет: 1, 2 и 3 (ср. с решением задачи 13а)). Если же перетянула
чашка с монетами 1(, 2, 3, то фальшивая монета тяжелее настоящих;
и в этом случае ее легко определить одним взвешиванием.
2°. При первом взвешивании одна из чашек ве-
сов перетянула. Тогда все монеты в оставшейся группе —
настоящие. Обозначим монеты, лежавшие на перетянувшей чашке,
через 1, 2-, 3, 4 (если одна из этих монет фальшивая, то она тяже-
лее настоящих), а монеты на другой чашке — через 1', 2', 3', 4' (если
одна из этих монет фальшивая, то она легче настоящих). При
втором взвешивании поместим на одну чашку монеты 1, 2 и 1', .а на
другую — монеты 3, 4 и 2'. Возможны опять-таки различные случаи:
А) Чашки уравновесились. Тогда фальшивая одна из монет 3'
или 4' (и при этом она легче настоящих). При третьем взвешивании
поместим на одну чашку весов монету 3', а на вторую — монету 4';
та из этих монет, которая окажется легче другой, и будет фаль-
шивой.
Б) Перетянула чашка с монетами 1, 2, 1'. В этом случае монеты
3, 4 и 1' — настоящие; в самом деле, если бы одна из монет 3, 4
была бы тяжелее остальных или монета 1' была бы легче остальных,
то при втором взвешивании чашка, на которой лежат монеты 3, 4
и 2', должна была бы перетянуть, чего на самом деле не случилось,
82
Итак, фальшивой является одна из монет 1, 2 (в этом случае фаль-
шивая монета тяжелее настоящих) или 2' (в этом случае фальшивая
монета легче настоящих). Положим при третьем взвешивании на
одну чашку монету 1, а па другую — монету 2. Если чашки уравно-
весились, то фальшивая монета 2', а если одна из чашек перетянула,
то на перетянувшей чашке лежит фальшивая монета.
В) Перетянула чашка с монетами 3. 4, 2'. Рассуждая аналогич-
но предыдущему, мы заключаем, что монеты 1, 2 и 2' — настоящие
и что либо одна из монет 3, 4 фальшивая и тяжелее настоящих, либо
монета 1' фальшивая и легче настоящих. При третьем взвешивании
положим на одну чашку монету 3, а на другую — монету 4. Если
весы уравновесились, то фальшивая монета 1'. Если же одна из ча-
шек перетянула, то па ней и находится фальшивая монета.
16. а) Достаточно распилить одно третье звено; при этом цепоч-
ка распадется на две части, содержащие соответственно 2 и 4 зве-
на, и на одно отдельное (распиленное) звено. В первый день постоя-
лец отдаст это звено; по второй — заберет его обратно и отдаст
взамен часть цепочки, состоящую из двух звеньев; в третий — добавит
снова распиленное звено; в четвертый — заберет все, что дал раньше,
и передаст часть цепочки из четырех звеньев; в пятый—добавит еще
раз распиленное звено; в шестой — возьмет обратно это звено
и даст взамен часть цепочки из двух звеньев; в седьмой — отдаст
последнее звено.
б) Удобно сначала разобрать следующую задачу: при каком
наибольшем п достаточно распилить k звеньев п-звенной цепи для
того, чтобы любое число звеньев от 1 до п можно было получить,
взяв некоторые из образовавшихся частей цепи? Для решения этой
задачи рассмотрим, каково наиболее выгодное расположение k рас-
пиленных звеньев. Так как после перепиливания k звеньев у нас бу-
дет k отдельных (распиленных) звеньев, то любое число звеньев от
1 до k мы сможем набрать уже только из них. Но &+1 звеньев мы
уже не сможем получить, если у пас не будет части, состоящей из
«+1 или менее звеньев. Ясно, что наиболее выгодно будет иметь
часть точно из /г-|-1 звеньев; тогда из этой части и k отдельных
звеньев мы сможем набрать любое число от 1 до 2/г-р1. Для того
чтобы можно было получить также 2й-|-2 = 2 (k-\-1) звеньев, нам
надо будет иметь еще часть, содержащую 2 (/г-f-l) или менее звень-
ев; наиболее выгодно для пас будет, если эта часть будет содер-
жать ровно 2(й-)-1) звеньев. Теперь мы можем уже составить все
числа от 1 до 2/?4-1 + 2(£-pl) =4/e-j-3; следующая по величине часть,
которая нам необходима,— это часть, содержащая 4(£-}-1) звеньев.
Продолжая рассуждать таким же образом, убедимся, что наиболее
выгодным будет, если й-pl частей, получающихся после того, как мы
распилили k звеньев (отдельные k звеньев, получающихся при этом, мы
здесь не засчитываем в число частей), будут иметь соответственно сле-
дующие числа звеньев:
k+l, 2(^+1), 4(/г+ 1), 8(6+ 1),..., 2ft(A+ 1).
В этом случае любое число звеньев от 1 и до
n = k+ {£+1+2(й+1)+4(А+1)+...4-2^+1)} = .
= A+(2A + 1 — 1) (Н-1) = 26 + I (k+1) — 1
можно будет составить из частей цепи.
6* 83
Итак, если 2kk^n^2k+i(k + l) — I, то можно обойтись k раз-
рывами цепи, но нельзя обойтись k—1 разрывами. В частности,
при- 2^пС7 Л=1, при 160<пС383 й=5,
при 8^п<23 й=2, при 384^895 k—&,
при 24=С«^63 k — З, при 896^n^2047 k — 7.
при 64^п^ 159 й = 4,
Итак, мы видим, что при «=2000 наименьшее число распиленных
звеньев равно 7. Условия задачи будут выполнены, если выбрать
эти звенья так, чтобы получающиеся 8 частей цепи (7 отдельных
звеньев мы здесь не считаем) имели соответственно 8, 16, 32, 64, 128,
256, 512 и 977 звеньев.
17. Пусть S — какая-то станция метро, Т — самая далекая от S
станция, т. е. такая, что кратчайший путь из S в Т ведет через
большее (или, по крайней мере, не меньшее) число станций, чем
кратчайший путь от S до любой другой станции. Закроем теперь стан-
цию Т. При этом из S мы по-прежнему сможем проехать в любую
другую (не закрытую) станцию U, ибо кратчайший путь из S
в U никак не может вести через Т — ведь иначе станция U была бы
расположена дальше от S, чем станция Т. Поэтому, если U и V —
две какие угодно отличные от Т станции метро, то из одной из них мы
заведомо сможем проехать в другую, минуя Т: для этого достаточно,
например, если U и V отличны от S, проехать из U в 5, а отту-
да — в V,
18. Будем доказывать утверждение задачи методом мате-
матической индукции по числу городских перекрестков (из
которых исходят более двух дорог). Если в Зурбагане имеются
всего два перекрестка А и В, то утверждение задачи очевидно: из
А в В ведут не менее двух дорог (если бы такая дорога была одна,
то при введении по ней одностороннего движения — скажем, в на-
правлении от А кВ — мы не смогли бы проехать из В в 4); поэтому
установив по одной из этих дорог движение от А к В, а по вто-
рой — от В кА, мы сможем проехать от любого перекрестка до
любого, отличного от него. Это простое рассуждение неожиданно
«работает» и в общей ситуации. Предположим, что для всех городов,
число перекрестков в которых не превосходит п, утверждение зада-
ча уже доказано-, рассмотрим теперь новый город (пусть это и бу-
дет Зурбаган), имеющий п-f-l перекресток. Рассмотрим два сосед-
них из этих-перекрестков — перекрестки А и В, соединенные улицей
АВ. Ясно, что поскольку после введения на улице АВ (при ее ре-
монте) одностороннего движения — скажем, от Л кВ — проехать
от В к Л было возможно, то из перекрестка В в перекресток Л ве-
дет некоторая не включающая улицы АВ «цепочка» улиц. (Разуме-
ется, эту «цепочку» можно считать не имеющей самопересечений —
ведь если -бы опа дважды проходила через один и тот же перекре-
сток С, то «цикл» между первым вхождением в С и последующим
вхождением в ту же точку мы могли бы просто отбросить.) Таким
образом, мы приходим к существованию в Зурбагане «кольца»
s — замкнутой сети улиц, ведущей из Л в В, а затем (через ряд
«промежуточных» перекрестков)—снова в Л. Рассмотрим теперь
условный город, план которого получается из плана Зурбагана
«склеиванием» всех перекрестков нашего кольца s в один перекре-
сток S, из которого исходят все улицы, реально «упирающиеся» в
84
кольцо з1). Число перекрестков такого условного города меньше
n+ 1; поэтому, по предположению индукции, в нем можно ввести по
всем улицам одностороннее движение с соблюдением требований
задачи. Если мы затем оставим движение по всем не входящим в
кольцо а улицам таким же, каким оно было в этом условном «го-
роде», а по кольцу s пустим движение в одном (безразлично каком!)
направлении, то на всех улицах Зурбагана будет установлено одно-
стороннее движение — и притом с любого перекрестка можно будет
проехать в любой другой.
19. Ясно, что если в стране имеются 2 города, соединенные
одним шоссе с односторонним движением по нему, то из одного
города вообще не удастся попасть во второй. Если городов 4, то
мы можем считать их вершинами четырехугольника при
этом либо движение по контуру четырехугольника является «цик-
лическим» (рис. .6, а), либо хоть одна из вершин — например, вер-
шина At — такова, что две проходящие через нее стороны четырех-
угольника изображают ведущие из города шоссе (рис. 6, б). Но в
Рис. 6.
первом случае вершины четырехугольника равноправны и любой
выбор направлений по диагоналям четырехугольника по существу
не отличается от любого другого, а меж тем, на рис. б, а мы не
можем с заездом в один лишь город проехать из Л3 в Д2. Если же
шоссе AtA2 и AiAt ведут из Ai, то для того, чтобы мы могли с
соблюдением требований задачи проехать из Л2 и из в Ль на-
правления движения на шоссе Л2Л3, Л4Л3 и Л3Л[ надо выбрать
такими, как указано стрелками на рис. 6, б; но при этом мы снова
приходим к «симметричной» ситуации, позволяющей ограничиться
рассмотрением варианта, отвечающего какому-то (какому угодно!)
) «План» города здесь можно понимать просто как таблицу,
в которой перечислены все улицы города и все перекрестки, причем
указано, какие улицы упираются в какие перекрестки — реально мо-
жет случиться, что полученный описанным 'образом план «условно-
го'города» нарисовать на листе бумаги будет нельзя (а только лишь
на глобусе или более сложной поверхности — нам это совершенно
неважно).
85
выбору направления движения по шоссе А2А4,— а в случае рис. б, б
из А4 в 42 нельзя проехать с заездом в один лишь город. При п =>
= 3 или 6 выбор направлений движения с соблюдением всех, по-
ставленных требований возможен (см. рис. 7, а и б; на рис. 7, б' мы
даже ограничились изображением не всех шоссе).
а]
Далее воспользуемся методом математической ин-
дукции. А именно, пусть для некоторого числа п городов утвер-
ждение задачи уже доказано; покажем, что тогда оно будет спра-
ведливо и для на 2 большего
числа городов п + 2. Для этого
направления движения на всех
шоссе, соединяющих любые
два из первых п городов
-41, А2... А„, мы устано-
вим такими, чтобы из любого
из этих городов в любой дру-
гой можно было проехать с
заездом не более чем в один
«промежуточный» город (это
возможно в силу предположе-
ния индукции). Далее, повеем
шоссе, ведущим из («+1)-го
города Дп + i в один из го-
родов Аь Аг, ..., А„, направим
движение в сторону городов
AIt А2.... Ап, а из каждо-
го из этих городов направим
движение в сторону (ц + 2)-го
города А„+2 (рис. 8); тогда из
Ап + 1 в каждый из городов
Ai, А2....Ап и из каждого из
этих городов в Ап+2 можно
будет попасть без заездов
в какой-либо другой город. Наконец, направим движение по сое-
диняющему А„+1 и А„+2 шоссе от А„+2 к Ап+1 — тогда из А»+2 в
Ап+1 мы попадем «за один шаг», а из Ап4-2 в любой из городов Ai,
86
Из.....Ап и из любого из этих городов в Л„ + 1 — за два «шага»
(с заездом, соответственно, в Л„+1 или в Дп+з).
Так как утверждение задачи справедливо для п = 3 и для
п = 6, то из' доказанного следует, что оно также справедливо для
всех нечетных п 3 и для всех чётных п ^б.
20. Вот более «математическая» формулировка той же задачи.
На плоскости (на карте Швамбрании) имеется 100 точек (городов);
каждые две точки соединены либо сплошной линией (это означает,
что между соответствующими городами имеется прямая телефон-
ная связь), либо пунктирной линией (означающей наличие авиа-
рейсов из одного города в другой); при этом известно, что из лю-
бой из заданных точек (из любого города) в любую другую мож-
но пройти как по цепочке сплошных линий, соединяющих наши
точки, так и по цепочке пунктирных линий. Нам требуется дока-
зать, что в таком случае среди имеющихся 100 точек можно вы-
брать такие 4, что здесь тоже из каждой точки можно пройти в
любую из трех других как по цепочке сплошных, так и по цепоч-
ке пунктирных линий, используя при этом лишь линии, соединяю-
щие наши 4 точки.
Доказывать это утверждение мы будем от противного:
предположим, что такой четверки не существует, и, пользуясь этим,
выделим из наших 100 точек-городов бесконечную их последова-
тельность, что, разумеется, невозможно.
Мы начнем с некоторых (каких угодно!) точек Aj и Д2, соеди-
ненных сплошной линией. По условию Ai и А2 можно также со-
единить цепочкой пунктирных линий; пусть AiA3A3A3 ... А2— крат-
чайшая из таких цепочек, т. е. цепочка, проходящая через наи-
меньшее число промежуточных точек (городов). В таком случае
любые две не соседние точки этой цепочки соединены сплошной
линией — ведь иначе мы могли бы сократить нашу цепочку, просто
Рис. 9.
отбросив все города, промежуточные между этими двумя. Но от-
сюда следует, что если бы наша цепочка содержала более одного
промежуточного города — скажем, содержала, бы города А3, А3
и Д3 (где А3 может и совпадать с А2),— то города Дь Д3, А3 и А3
(см. рис. 9, а) уже образовывали бы требуемую четверку городов
(по нашему предположению отсутствующую!), поэтому Aj и А2 со-
единены «пунктирным двусторонними» Д;ДзД2.
87
_ Рассмотрим теперь (соединенные пунктирной линией!)' города
Ла и Л3; в точности, как и ранее, устанавливается, что существует
состоящий всего из двух звеньев сплошной путь Л2Л4Л3 из Л2 в
Л3. Докажем, что точка Л4 соединена с At сплошной линией. В са-
мом деле, если бы Л4 и At были соединены пунктирной линией, то
Ль Л2, Л3 и Л4 образовывали бы запрещенную по нашему предпо-
ложению четверку городов с требуемыми свойствами (ср. рис. 9,6).
Итак, мы нашли такие 4 точки Ль Л2, Л3 и Л4, что Л2 соедине-
на с.Л, сплошной линией; Л3 соединена с Л1 и с Л2 пунктирными
линиями; Л4 соединена с Ль Л2 и Л3 сплошными линиями. Далее
воспользуемся методом математической индукции.
Предположим, что мы уже нашли такие точки Ль Л2, Л3,..., Л,,
что каждая из точек Л3, Д5,... (точек с нечетными номера-
ми) соединена со всеми предшествующими точками пунктирными
линиями, а каждая из точек Л2, Л4,... (точек с четными номе-
рами) соединена с каждой из предшествующих ей точек сплошны-
ми линиями, и покажем, что этот ряд точек можно продолжить.
Пусть, для определенности, линия Л^-И,- является сплошной-, рас-
смотрим кратчайшую пунктирную ломаную соединяю-
щую Л/-1 и Л,-. Ясно, что точка A,-+i не совпадает ни с одной из
точек Ль Л2.....Лг_2 (и, конечно, Aj)—ведь все предшест-
вующие Л,-] точки соединены с одной из точек Л4_|, Л, сплошной
линией, а со второй — пунктирной, в то время как А,+1 соединена
пунктирными линиями с ними обеими. С другой стороны, со всеми
точками Ль Л2,..., Лг_2 (а также и с Л;_:, Л<) точка Л1+1 соеди-
нена пунктирными линиями, ибо если линия AjAi+,- (где/Ci—1) —
сплошная, то точки Лд Л4_[, Л,-, Л,+1 образуют «запрещен-
ную» по нашему предположению четверку точек (рис. 9, б).
Тем самым мы «продолжили на один шаг» конструируемую
цепочку Ль Л2,..., Л4_1, At, Л(+1,... точек-городов, которую, та-
ким образом, можно сделать сколь угодно длинной.
21, Для того чтобы обойти все 64 клетки шахматной доски,
побывав на каждом поле один раз, конь должен сделать 63 хода.
Так как при каждом ходе конь переходит с белого поля на черное
или с черного на белое, то после ходов с четными номерами конь
будет попадать на поля того же цвета, что и исходное, а после
ходов с нечетными номерами — на поля другого цвета. Поэтому
конь не может 63-м ходом попасть на поле, находящееся на одной
диагонали с исходным, так как эти поля окрашены в один цвет.
22. Король может избрать следующую «самоубийственную» (но
ведь самоубийство и является его целью!) стратегию: сначала он
перейдет в нижний левый угол доски, а оттуда двинется по диаго-
нали слева вверх направо. После того, как король сделает 1-й ход
по диагонали, он окажется на помеченном звездочкой на рис. 10, а
поле; при этом если хоть одна ладья (после ответа черных на пос-
ледний ход короля) окажется вне заштрихованного на этом рисун-
ке квадрата размера 997X997, то король сможет стать под удар
следующим своим хбдом. Аналогично устанавливается, что после
998 ходов по диагонали, когда король окажется на поле, помечен-
ном звездочкой на рис. 10, б, все черные ладьи должны будут на-
ходиться в заштрихованном на этом рисунке квадрате. При этом
если в процессе движения короля хоть одна ладья осталась на той
же горизонтальной строке или на том же вертикальном столбце
шахматной доски, где она стояла ранее, то король'в процессе своего
движения пересечет эту строку или этот столбец — и тем самым
88
окажется под боем. Поэтому, если «черные» стремятся не брать
короля, то за время движения короля от положения рис. 10, а до
положения рис. 10, б (король за это время сделал 997 ходов)
каждая из 499 ладей должна сделать минимум 2 хода (ибо каждым
ходом она меняет либо строку, на которой стоит, либо столбец, но
Рис. 10.
ходов у ладей не хватит времени (королю ведь достаточно сделать
лишь 997 ходов!).
23. Изменим порядок расположения полей по кругу, а именно,
расположим их в порядке, при котором можно было бы перехо-
дить с одного поля на соседнее. Иными словами, после поля 1 по-
местим 6 (ибо по условию задачи с поля 1 можно перейти на 6),
после б поместим поле 11 (с поля б можно перейти на 11), затем
4 (ибо с поля 11 можно перейти на 4), и т. д. При этом мы полу-
чим порядок полей, изображенный на следующей схеме:
к с ж
; 6 -------->-;; ------->- k -*------------------>• 2
.. .»
s -в------>- 3 -с-----10 -й------->• 5 -*------12 -*-------7
3
Мы можем считать, что имеем 12 нолей, расположенных имен-
но таким образом (ведь фактически занимаемое полем место зна-
чения не имеет) и занумерованных так, как это указано на нашей
схеме. При этом фишки первоначально стояли так, как это обозна-
чено на схеме буквами сверху и снизу полей (буква К обозначает
красную фишку, буква Ж желтую; буква 3 — зеленую и буква
С — синюю). Правило движения фишек при этом новом располо-
жении полей оказывается чрезвычайно простым — каждая фишка
89 •
может сдвинуться на одно поле влево или вправо, если только это
соседнее поле не занято.
Теперь совершенно ясно, что единственный способ, каким фиш-
ки могут поменяться местами, — это двигаться по кругу в одном
или другом направлении: ведь ни одна фишка не может «пере-
гнать» другую, ибо другая преграждает ей путь. Таким образом,
если фишка К займет поле 4, то фишка С должна будет занять
поле 2, фишка Ж —поле 5 и фишка 3— поле 1. Если фишка К
займет поле 2, то фишка С должна будет занять поле 5, фишка
Ж — поле 1, фишка 3 — поле 4. Если фишка К займет поле 5, то
фишка С должна будет занять поле 1, фишка Ж — поле 4 и фиш-
ка 3 — поле 2.
Никакие другие новые расположения фишек невозможны.
24. Докажем, прежде всего, что если в некотором коллективе
студентов каждый из трех языков —а (английский), ф (француз-
ский) и н (немецкий) знают ровно п человек, где плл2, то можно
составить такую группу студентов, в которой каждый язык будут
знать ровно 2 человека. Ясно, что из сформулированного предло-
жения утверждение задачи уже вытекает: выбрав (и исключив из
рассмотрения) указанную группу студентов, мы придем к совокуп-
ности студентов, в которой каждый из трех языков знают ровно
50 — 2 = 48 студентов; из этой совокупности студентов мы снова
можем выбрать группу, в которой каждый язык знают ровно 2 сту-
дента, после чего у нас останется коллектив, в котором каждый
язык знают ровно 48 — 2 = 46 студентов, и т. д. Объединив затем
пять отобранных таким образом небольших групп, в которых каж-
дый язык знают по 2 человека, мы получим первую из интересую-
щих нас групп, в которой каждый язык знают ровно 10 человек;
далее так же (т. е. исходя из «маленьких» групп, в которых каж-
дый язык знают ровно 2 студента) мы станем составлять вторую и
третью группы студентов (каждая из них будет состоять из 5 «ма-
леньких» групп).
Для доказательства напечатанного выше курсивом утвержде-
ния можно использовать метод математической индук-
ции. В самом деле, ясно, что если п = 2, то наше утверждение
выполняется (рассматриваемая группа здесь — это совокупность
всех студентов); предположим теперь, что оно верно для всех
значений п, меньших некоторого, и докажем, что в таком случае
оно справедливо и для этого значения п. Условимся обозначать
число студентов, знающих только английский язык, через Na; знаю-
щих английский и французский языки, но не немецкий, через Nafi,
и т. д.; соответственно символ а (или а', или а") будет обозна-
чать студента, знающего только английский язык; символ аф (или
(аф)')—студента, знающего языки а и ф, но не н, и Т. д. Если
при этом Na ¥= 0, =/= 0, Nп =£ 0, то мы просто исключим из наше-
го коллектива трех студентов а, ф и н и придем к новой совокупно-
сти студентов, для которой наше утверждение выполняется в силу
предположения индукции; аналогично этому, если ?/а^н¥=0, то мы
откинем студента афн и снова придем к новому коллективу, для
которого наше утверждение верно. Далее, если Л^^О, 7Уан=/=и и
Ntfn^O, то сформулированное предложение выполняется тривиаль-
но — требуемую группу составляют три студента аф, ан и фн.
Наконец, если два из чисел Wass, Nап и Л^« отличны от нуля,
а третье,— скажем, последнее из них — равно нулю, то отличны от
нуля числа N# и NH (ибо в объединении всех студентов аф, (аф)',
9Э
и т. д. и всех студентов ан, (ан)', и т. д. больше студентов знают
язык а, чем язык ф и чем язык н); поэтому мы можем исключить
из числа студентов двух студентов аф и н и снова прийти к кол-
лективу студентов, в котором каждый язык знают п — 1 человек и
в котором, по предположению индукции, требуемую «малую» группу
студентов составить можно. Аналогично, если скажем, лишь
=И= 0, a Nan — N$n = 0, то, очевидно, Nn 0 — и мы можем сно-
ва использовать предположение индукции, удалив студентов аф и
н. [Заметим, что равенства N аф = Nan = N $п = 0 (и Na$n = 0)
противоречат предположению, что хоть одно из чисел Na, N& и
Д'и равно нулю.]
Примечание. Ясно, что числа 50 и 10 в условии этой за-
дачи являются случайными; в точности так же можно доказать, что
если в нашем коллективе студентов каждый из трех языков (где,
впрочем, и число 3 можно пытаться заменять другими) знают ровно
п студентов, то из описанных «малых» групп можно конструировать
группы, в которых каждый из языков знают, любое не большее п
заданное четное число m студентов; однако предположение о четно-
сти m здесь является существенным (попытайтесь доказать это!)
25. а) Ясно, что наименьшее значение «среднего места»
равно 1—это значение достигается, если все судьи приписали 1-е
место одному и тому же спортсмену. С другой стороны, 5 или бо-
лее спортсменов получить (у разных судей) первое место не могут:
в самом деле, эти п > 5 спортсменов получили бы тогда в совокуп-
ности у девяти судей 9 первых мест и 9/г — 9^9-5— 9 = 36 иных
мест (ибо всего 9 судей приписывают им 9/г мест); по условию за-
дачи ни одно из этих мест не может быть ниже 4-го, что невозмож-
но, так как мест с 3-го по 4е судьи указывают лишь 3-9 = 27.
Таким образом, остается лишь рассмотреть случаи, когда 1-е место
(у разных судей) получили 2, 3 или 4 спортсмена.
10 Если 1-е место судьями приписано лишь двум спортсменам,
то один из них назван 1-м не менее чем пятью судьями — и так
как остальными судьями он поставлен не ниже чем на 4-е место,
1
то «среднее место» этого спортсмена не ниже -д- (5-1+4-4) =
2° Если 1-е место приписано трем спортсменам, то в совокуп-
ности эти спортсмены получили 9 первых мест и еще 3-9 — 9= 18
иных мест, ни одно из которых не может быть ниже четвертого; но
так как 9 судей могут указать лишь 9 четвертых мест, то в «худ-
шем» случае наши спортсмены получили 9 четвертых и 9 третьих
мест. Таким образом, общая сумма приписанных этим трем спорт-
сменам мест не больше 9-11-}- 9-4 + 9-3 — 72, в силу чего хоть
72
один из них имеет не большую -jj- = 24 сумму мест и «среднее ме-
24 / 2 \
сто», не худшее -д~ = I-
3° Наконец, если 1-е место приписано четырем спортсменам, то
эти 4 лица получили в совокупности 9 первых мест и еще 4-9 —
— 9 = 27 иных мест, не низших 4-го; из них 9 могут быть 4-ми
91
местами, 9 — 3-ми и последние 9 — 2-ми. Таким образом, общая
сумма мест четырех спортсменов здесь равна 9-1 <4-9-2 4-9-3 4-
4-9-4 = 90 (<4-23); а значит, лучший из этих четырех спортсме-
нов имеет сумму мест, не большую 22, и «среднее место», не худ-
22 / 4 2 \
шее — (^=2—
Итак, «среднее место» лучшего спортсмена никак не может
быть ниже 2—^-', при этом равняться 2— оно может лишь в том слу-
чае, когда каждый из трех лучших спортсменов получил у трех
судей 1-е место, у трех других — 3-е и у. трех последних — 4-е (так
что в этом случае победителями соревнований явятся сразу три
спортсмена).
Примечание. Разумеется, те же рассуждения, где лишь
вместо А-го места фигурирует (21—А)-е, показывает что «среднее
место» последнего спортсмена никак не может быть выше ^-^"(но
1 .
может равняться 18-д-).
б) Ясно, что после каждого тура соревнований номер сильней-
шего из оставшихся участников соревнований не уменьшается; при
этом увеличиться он может не более чем на 2 (если сильнейшего
теннисиста случайно победил теннисист, номер которого на две
единицы выше, чем у него). Так как 1024 = 210 и после каждого
тура число участников соревнований уменьшается вдвое, то всего
мы будем иметь 10 туров соревнования, после которых останется
лишь 2° = 1 теннисист — победитель соревнования. Поскольку пос-
ле каждого тура номер лучшего из оставшихся теннисистов может
возрасти на 2, то отсюда, как будто, вытекает, что победителем
соревнований может оказаться 21-й по списку теннисист.
На самом деле, однако, и 21-й теннисист не имеет шансов ока-
заться победителем. В самом деле, для этого необходимо, чтобы
на каждом этапе соревнований выбывали два сильнейших игрока;
другими словами, надо, чтобы в первом туре выбыли 1-й и 2-й иг-
роки, проигравшие, соответственно, 3-му и 4-му; во втором туре
выбыли 3-й и 4-й игроки, проигравшие, соответственно, 5-му и 6-му,
и т. д. Но в таком случае в полуфинальных соревнованиях должны
были выбыть. 17-й и 18-й игроки, проигравшие 19-му и 26-му; по-
этому 19-й и 20-й игроки выходят в финал — и победителем
соревнований становится один из них, а не игрок с номером 21.
Покажем, наконец, что 20-й игрок победителем соревнований
оказаться может. В самом деле, при наличии всего 21 — 2 игроков,
разумеется, победителем может оказаться игрок с номером 2 = 2-1;
если же теннисистов 22 = 4, то победителем может стать теннисист
с номером 2-2 = 4: в паре первых двух игроков может победить
2-й, в паре двух других — 4-й, а 4-й, в принципе, может и выиграть
финал у 2-го. Аналогично, если игроков 23 = 8, то победителем
может оказаться 6-й теннисист: в самом деле, если четверо сильней-
ших игроков попадут в одну подгруппу, то в ней сильнейшим
может оказаться 4-й; во второй подгруппе 6-й теннисист может и
выиграть у 5-го; при этом в финале он встретится с 4-м, кото-
рого может и победить. Точно так же с помощью метода м а-
92
тематической индукции легко доказать, что победителем
в соревнованиях 2" теннисистов может оказаться (2п)-й по силе
теннисист: для этого лишь надо, чтобы первые 2п — 2 игрока попа-
ли в одну подгруппу из 2"-1 игроков, где (в силу предположения
индукции) победителем может стать (2п — 2)-й теннисист; во вто-
рой же подгруппе победителем вполне может стать (2п)-й игрок,
которому после этого надо лишь в финале выиграть у (2и — 2)-го
игрока,— может быть, и трудная, по возможная задача.
26. Обозначим число комцлектрв медалей, оставшихся не вру-
ченными к началу 1-го дня соревнования, через Л';, где i= 1,2,...
..., п; можно, впрочем, считать, что величина Л\- имеет смысл и
при i > п, обращаясь в этих случаях в 0. Из условий задачи
(и нашего соглашения) вытекает, что Nn = п,
кроме того, значения и Nj+i связаны соотношением:
1 6
= -V j - f - -у (Л' J -i)^~ - I),
или Nt = -£-JVw+ i. (*)
Из (*) последовательно находим
/7 \
~ п “Г Nn+1 + rtJi
Nn^.i = "Г л + (n — i)j
/ 7 \2 7
Nn^-2 ~ (1Г/ «+—(«- 1) + (П - 2)1
/ 7 \8 I 7 \2 7
tfn_3 = ПГ rt + “ (ra “ В + "Г (« - 2) + (« - 3)1
/ 7 \n—*—1 / 7 \n—1—2
л+1‘б) («— 1) + (‘б) (л-2)4-...+ <
(общая формула, разумеется, без всякого труда доказывается ме-
тодом математической индукции).
Таким образом, мы получаем:
/ 7 \п— 1 / 7 \п^»2 / 7 \п—-8
л+ — И-1)+т (л-2)+...
К 7 \п—1 [ 7 \п—2 / 7 \п—3 1
+ (jr) +И/ +--- + 1]-
г/ 7 \п—2 / 7 \П—з 7 1
(“Г] -^2(’Г) + • • • "Ь (л — 2) -g Н(л—1) =51-л 5г,
где через Si и Ss обозначены две заключенные в квадратные
скобки суммы. Но по формуле суммы членов геометрической
93
прогрессии, очевидно,
С другой стороны, как легко видеть,
/ 7 \ / 7 \п—1 / 7 \n—2* / 7 \
[~]-S2 — S'2 = (irj + • •• + («—1) =
так что
S2 = 36
— 6л,
и, следовательно,
г/ 7 \n 1 Г/7 \п 1 / 7\п
JV = 6 НН -1 п-36 к — 1 4- 6л =6 (л — 6) НН 4-36.
(**)
7«(л—6)
Так как N — целое число, то и число '~б'п~—>а значит и
л — 6
дп—1 должны быть целыми; поэтому л кратно 6. С другой
стороны, очевидно, что при всех k 2 имеет место неравенство
6/г — 6 < 66й-1, или k—1 < 66*1-2 (почему?)—и, значит, дробь
л — 6
п_р при л > 6 не может быть целым числом. Таким образом, мы
6
приходим к единственному возможному решению задачи: л = 6 и,
значит (в силу (**)) N = 36.
27. Первое решение. Пусть л — число орехов, которое
досталось утром каждому из приятелей; в таком случае 5л + 1
есть число орехов, которое было утром в мешке. Последний из
, 5л -|- 1
проснувшихся ночью, очевидно, взял себе—-—, а до этого в меш-
25л 4- 9
—4-----орехов.
Предпоследний проснувшийся
_ 1 25л 4- 9
мешке было ----4*
„ 1 125л 4- 61
себе-4-•---J6---, а до этого
1 125л 4-61 625л 4-369
в мешке было 5-^-------pg---4" * —------54-----орехов; второй взял
1 625л 4- 369 ’ 1 625л 4- 369 ,
себе -------64----> а д0 этого в мешке было ----------64---+ 1 а
ке было 5 —jp—+1 =
1 25л 4- 9
взял себе , а
125л + 61
+ 1 =----jg---орехов;
до этого в
третий взял
94
3125л+ 2101 „ 1 3125л+ 2101
= --256----1 оРехов; наконец, первый взял себе ---256----
а первоначально в мешке было
1 3125л+ 2101 , 15625л+Н529
^== 5.-4'---256----+ 1 - "
1024
265л + 265
15Л+П+-П0&—
орехов. Так как это число должно быть целым, то 265 (л + 1) долж-
но делиться ыа 1024. Наименьшее значение л, удовлетворяющее
этому условию, равно, очевидно, 1023 и в этом случае
IV = 15 - 1023 + 11 + 265 = 15 621.
Второе решение. Эту задачу можно решить значительно
быстрее и почти без всяких подсчетов, если внимательно рассмот-
реть те условия, которые накладывает ее содержание на общее
число N орехов. Первое условие задачи заключается в том, что при
первом разделе на пять частей в остатке остается один орех. Это
условие означает, что N при делении на 5 должно дать в остатке
1, т. е. N = 5/ + 1; числа, удовлетворяющие этому условию, встре-
чаются в натуральном ряду чисел с интервалом в пять чисел, и,
зная одно такое число, мы можем найти неограниченно много дру-
гих, прибавляя к нему (или вычитая из него) числа , кратные 5.
4
Второе условие задачи утверждает, что k (N—1)==4/дает
при делении на 5 остаток 1, т. е. k — 5li+ 1. Это требование равно-
сильно тому, что I дает при делении на 5 остаток 4 или что N =
= 5/ + 1 дает при делении на 25 остаток 21; числа, удовлетворяю-
щие этому условию, встречаются в числовом ряду с интервалом в
25 чисел, и, зная одно такое число, мы можем получить сколько
угодно других, прибавляя кЙгему (или вычитая из него) числа, крат-
ные 25. Точно так же третье условие задачи утверждает, что =
4
= -5- (k — 1) = 4G дает при делении на 5 остаток 1; это условие
определяет остаток от деления числа /1 на 5 или остатки от деления
чисел k и I на 25, или остаток от деления N на 125. Все условия
задачи определяют остаток от деления числа N на 5S= 15 625;
числа, удовлетворяющие этим условиям, встречаются в натуральном
ряду чисел с интервалом в 15 625.
Мы могли бы подсчитать остаток, который дает при делении на
5е число N, но в этом нет нужды. Дело в том, что одно число, удов-
летворяющее всем условиям задачи, является очевидным. Этим чис-
лом является —4. Действительно, при делении на 5 число —4 дает
в частном —1 и в остатке +1; поэтому, если вычесть из —4 число
4
1 и взять -g- от полученной разности, уже делящейся на 5, то мы
получим то же число —4. Также и при всех последующих делениях
на 5 мы будем иметь тот же остаток + 1. Правда, число —4 не
может служить ответом нашей задачи, так как, по условию, число N
должно быть положительным; но, зная одно число, удовлетворяющее
условиям задачи, мы можем получить сколько угодно других, при-
бавляя к нашему числу кратные 5°, Наименьшее положительное
95
число, удовлетворяющее условиям, есть, очевидно, — 4 + 5* =«'
= 15625 — 4 =15621.
28. Обозначим число овец в стаде через л; в таком случае
братья взяли за каждую овцу п рублей и, следовательно, всего
выручили N — п • п = п? рублей. Пусть d есть число целых десят-
ков числа п, а е — число единиц; тогда п = 10d + е и
N = (lOd + е)2 = 100d2 + 20de + е2.
Из условий дележа следует, что старшему брату досталось од-
ной десяткой больше, чем младшему, т. е. что общая сумма N со-
держит нечетное число десятков (и какой-то остаток). Но
100d2 + 20de = 20d(5d + е) делится на 20 (содержит четное число
десятков); следовательно, число е2 должно содержать нечетное число
десятков. Так как е меньше 10 (е есть остаток от деления числа-п
на 10), то е2 может иметь только одно из следующих значений:
1, 4, 9, 16, 25, 36, 49, 64, 81.
Но из этих чисел только 16 и 36 содержат нечетное число десят-
ков; следовательно, е2 равно 16 или 36. Оба эти числа оканчиваются
на 6; значит, тот остаток, который получил младший брат взамен
нехвативших ему 10 рублей, равен 6 рублям, и старший получил на
4 рубля больше младшего. Поэтому, для того чтобы раздел был
справедливым, старший должен еще доплатить младшему 2 рубля.
Следовательно, перочинный нож был оценен в 2 рубля.
29. а) Наш календарь устроен следующим образом. Каждый год
имеет 365 дней. Исключением являются годы, номера которых де-
лятся на 4: эти годы (високосные годы) имеют лишний 366-й день
(29 февраля). Однако и это правило имеет исключения: годы, номе-
ра которых делятся на 100, по не делятся на 400, имеют не 366 дней,
а 365, т. е. не являются високосными; так, 1900 и 1800 гг. не были
високосными, не будет високосным и 2100 г., в то время как 2000 г.
будет високосным (2000 делится на 400). Задача заключается ,в том,
чтобы выяснить, каким днем чаще бывает по нашему календарю
1 января: субботой или воскресеньем.
Промежутки, через которые следуют друг за другом числа 1 ян-
варя, не всегда постоянны, но эти промежутки изменяются периоди-
чески, с периодом в 400 лет. При этом 400 лет содержат целое число
недель: действительно, невисокосный год содержит 52 недели и еще
1 день, а високосный — 52 недели и 2 дня; в течение четырех лег
(из которых- один високосный) набегает, таким образом, сверх
4 • 52 недель еще 5 дней; в течение 400 лет должно было бы набе-
жать еще 500 дней, но так как три года, делящиеся на 100, но не
делящиеся на 400, не являются високосными, то за 400 лет сверх
40'0 52 недель набегает всего 500 — 3 — 497 дней, т. е. ровно 71 не-
деля. Поэтому нам достаточно выяснить, каким днем чаще бывает
1 января за какие-либо 400 лет; этим днем будет чаще 1 января и
за любые другие 400 лет.
Рассмотрим теперь промежуток в 400 лет с 1901 по 2301 г.
Отметим, что если в течение 28 лет каждый четвертый год является
високосным (т. е. эти 28 лет не содержат года, номер которого де-
лится на 100, но не делится на 400), то эти 28 лет содержат целое
число недель: в течение каждых четырех лет набегает сверх целого
числа недель еще 5 дней, а за 28 лет набегает 5 • 7 = 35 дней, т. е.
5 недель. Теперь отметим, что 1 января 1952 г. было вторником. Так
96
как каждый невисокосный год содержит целое число недель и один
день-, а високосный — целое число недель и 2 дня, то 1 января
1953 г.— четверг (1952 г.— високосный), 1 января 1954 г.— пятница,
1 января 1955 г,—суббота, и т. д.; точно так ж.е 1 января 1951 г.
было понедельником, 1 января 1950 г. было воскресеньем, и т. д.
Таким образом, подсчитываем, что за 28 лет с 1929 по 1956 г. 1 ян-
варя является каждым из семи дней недели ровно по 4 раза. Точно
такое же распределение дней, с которых начинается новый.. год,
было и в течение 28 лет с 1901 по 1928 г. (напоминаем, что 28 лет,
среди которых каждый четвертый является високосным, содержит
целое число недель, и, следовательно, через каждые 28 лет будет
повторяться точно такое же распределение первых дней года, как
и в предыдущие 28 лет); такое же распределение первых дней года
будет и в периоды 1957—1984, 1985—2012 (2000 г., как делящийся
на 400, будет високосным), 2013—2040, 2041—2068 и 2069—2096 гг.
Итак, в промежутке 1901—2096 гг. 1 января будет одинаковое число
раз каждым днем недели.
Далее, 1 января 2097 г. будет тем же самым днем, что 1 января
1901 г. или 1 января 1929 г., т. е. вторником, 1 января 2098 г. будет
средой, 1 января 2099 г.— четвергом, 1 января 21'00 г.— пятнице !,
1 января 2101 г.— субботой (2100 год не будет високосным). После-
дующие 28 лет будут отличаться от промежутка 1901—1928 гг. тем,
что они начались не со вторника, а с субботы; это вызовет соответ-
ствующую перестановку дней, которыми будут являться 1 января;
однако, так как в течение 28 лет с 1901 по 1928 г. 1 января ’было
ровно по 4 раза каждым днем недели, то и в промежутке с 2101 по
2128 г. 1 января будет каждым днем недели по 4 раза. Это сообра-
жение относится и к промежуткам 2129—2156 гг. и 2157—2184 гг.;
2185 г. начнется с того же самого дня, что и 2101, т. е. с субботы.
Это позволяет определить, с каких дней будут начинаться годы
с 2185 по 2201. Простой подсчет показывает, что в промежутке
между 2185 и 2200 гг. 1 января будет по 2 раза понедельником, сре-
дой, четвергом, пятницей и субботой и по 3 раза — воскресеньем
и вторником. 1 января 2201 г. будет четвергом. В течение 3 • 28 =
= 84 лет с 2201 по 2284 г. 1 января будет каждым днем недели
одинаковое число раз. 1 января 2285 г. будет тем же днем, что и
1 января 2201 г., т. е. четвергом. Это позволяет определить распре-
деление дней, с которых начинается год в интервале с 2285 по
2300 г.; оказывается, в течение этого интервала 1 января будет по
2 раза понедельником, вторником, средой, четвергом и субботой и по
3 раза — воскресеньем и пятницей. Таким образом, сверх тех перио-
дов, в течение которых 1 января бывает одинаковое число раз каж-
дым днем недели, мы получили еще 2 + 2 = 4 понедельника, 1 +
+3 + 2=6 вторников, 1 + 2 + 2 = 5 сред, 1 + 2 + 2 = 5 четвер-
гов, 1 +2 + 3 = 6 пятниц, 2-f-2 = 4 субботы и 3 + 3 = 6 воскре-
сений. Отсюда следует, что 1 января чаще бывает воскресеньем,
чем субботой.
б) Аналогично решению задачи 29а) можно показать, что в ин-
тервале 400 лет 30-е число бывает воскресеньем 687 раз, понедель-
ником 685 раз, вторником 685 раз, средой 687 раз, четвергом 684 ра-
за, пятницей 688 раз, субботой 684 раза. Итак, Чаще всего 30-е число
приходится на пятницу.
30. Легко видеть, что при зачеркивании последней цифры це-
лое число уменьшается не меньше чем в 10 раз. Ровно в 10 раз
уменьшаются при зачеркивании последней цифры числа, оканчива-
7 Д. О. Шклярский и др.
97
ющиеся нулем; следовательно, все эти числа удовлетворяют условию
задачи.
Допустим теперь, что целое число х при зачеркивании последней
цифры уменьшается в целое число раз, большее чем 10, а именно
в ЮН-а раз (а 25s 1); пусть у — число целых десятков числа х (не
цифра, а число!); z— цифра единиц': X— Юу + г. После отбрасыва-
ния последней цифры число х переходит в число у; поэтому наши
условия дают
х = (10 + а) • у,
или
10y + z= (1.0 +а) • у,
откуда
z = ау.
Так как г < 10, то и у < 10, а <_ 10; следовательно, числа, обла-
дающие нужным свойством, двузначны и при отбрасывании послед-
ней цифры могут уменьшиться не более чем в 19 раз. Теперь легко
видеть, что при зачеркивании последней цифры в 11 раз уменьшают-
ся только числа II, 22, 33, 44, 55, 66, 77, 88 и 99; в самом деле, если
10 + а — 11, то а = 1; следовательно, z = ау — у, х — 10у -j- z =
= 11*/, где у = 1, 2, 3,..., 9. Аналогично найдем, что в 12 раз
уменьшаются лишь числа 12, 24, 36, 48; в 13 раз—13, 26, 39; в 14
раз—14, 28; в 15, 16, 17, 18 и 19 раз — только соответственно числа
15, 16, 17, 18 и 19.
31. а) Пусть искомое число имеет £ + 1 цифр; в таком случае
оно имеет вид 6 10* +у, где у есть ^-значное число (которое мо-
жет начинаться с одного или нескольких нулей). По условию зада-
чи имеем;
6 • 10* + у = 25 • у,
откуда
6-10*
у ~ 24 •
Отсюда вытекает, что k не может быть меньше 2 (иначе 6 • 10*
не делилось бы на 24). При /<” + 2 число у оказывается равным
25- 10*-2, т. е. имеет вид 250 ... 0. Поэтому все искомые числа имеют
(й—2)нулей
вид 6250 ... 0 (п = 0, 1, 2,...).
пнулей
б) Решая задачу: найти число, начинающееся с данной цифры
а и уменьшающееся при зачеркивании этой цифры в 35 раз, анало-
гично задаче а), мы придем к следующему равенству:
п-10*
у~ 34 ’
где у — целое число (см. решение задачи а)). Но это равенство,
очевидно, не можег иметь места ни при каких целых а 9 и k.
Примечание. Совершенно аналогично решениям задач 31а)
и б) можно показать, что число, начинающееся с известной цифры а,
может уменьшаться при зачеркивании этой цифры в целое число Ь
раз только в том случае, если Ь—1 есть большее а число,
такое, что все простые делители 6 — 1, отличные от
2 и 5, входят (и притомв не меньшей степени) также
а
и в состав числа п (т. е. что есть правильная дробь,
98
которую можно превратить в конечную десятичную дробь). Так, на-
пример, никакое число не может при зачеркивании первой цифры
уменьшаться в 85 раз (85—1 == 84 делится на 3 • 7, а никакая цифра
не может одновременно делиться на 3 и на 7), а число, уменьшающееся
при зачеркивании первой цифры в 15 раз, должно начинаться с
цифры 7 (15—1 = 14 делится на 7). Общий вид чисел, которые при
зачеркивании известной первой цифры а уменьшаются в данное
число b раз, легко найги.
32. а) Покажем прежде всего, что никакое число N не может
уменьшиться в 9 раз при зачеркивании цифры, стоящей дальше чем
на втором месте. Действительно, если это'не так, то обозначая
цифры числа N через По, ап, т. е. полагая
а0 • 10" + • 10"-’ + ... + а„ = N,
Л7
мы заключим, что число -у имеет п цифр, первые две из которых
аа и йь т. е.
ao.10"-1 + ai-10n-2+....= V*
Умножая последнее равенство на 10 и вычитая первое, получим:
V<!0n-1.
что невозможно, так как
уу = ао-1Оп—1 + ... > IO""1.
С другой стороны, из признака делимости на 9 вытекает, что
если число N делится на 9 одновременно с числом, получаемым из
N вычеркиванием одной цифры, то эта цифра есть 0 или 9. Таким
образом, в нашем случае возможно только, что первая или вторая
цифра числа N равна 0 или 9 и вычеркивание этой цифры равно-
сильно делению N на 9. Но первая цифра W не может равняться 0,
N
а если бы она была равна 9, то число -у имело бы столько же
цифр, сколько N, и не могло получаться из N вычеркиванием одной
цифры. Далее, если вторая цифра N равна 9 и число, получаемое
N
из W зачеркиванием этой цифры, равно -у, то мы имеем:
Л7 = й0 • 10“ + 9 • 10"-1 + а2 • 10"-! + ... + «„,
-у =ao-10’l-1 + «3-10n-2+... + an,
откуда опять, умножая второе равенство на 10 и вычитая из него
первое, получим: _
4 <«“-
(ибо й2^9) . Таким образом, мы убеждаемся, ч то для того, чтобы
7* 99
уменьшить число W в 9 раз, в нем надо зачеркнуть
цифру 0, стоящую на втором месте.
Теперь мы имеем:
JV = а0 10" + аг • 10"-2 + ... + я„,
у = а0.1Оп-1+а2.Юп-2+ ... +пп.
Отсюда следует
= Л'-о0-10п + ао-1&п-1 = N— ао-10п-1-9
и, наконец,
9 9 ~ 9 а° и
N
последнее означает, что, для того чтобы разделить число у на 9,
в нем достаточно зачеркнуть первую цифру.
б) Имеем (см. решение задачи а)):
N „ <
откуда сразу следует
а,,. 10й-1-81
N ~ 8
Теперь, считая а0 равным соответственно 1, 2, 3, и т. д„
получим, что N может быть равно одному из чисел 10 125,
2025, 30 375, 405, 50 625, 6975, 70 875 или отличаться от одного из
этих чисел каким-то количеством нулей в конце (а0 не может быть
равно 8 или 9, так как в этом случае вторая цифра N уже не бу-
дет нулем).
33. а) Аналогично решению задачи 32 а) в предположении, что
целое число N уменьшается в т раз при зачеркивании третьей циф-
ры, имеем:
N = a0- 10"+ai- 10"-1+а2- 10"—2-f- ... -|-й„,
10-у ао-1Оп + п1-1Оп~14-а3-1Оп-2+ ... + ап-10.
1 и — ffl п__3
При /п<10 получаем———N < 10 что невозможно, так как
—у- > у a jg А = д0-Ю"—14-... > 10п~*. При т> 11 получаем
1П \ что невозможно по аналогичной причине
т— 10
----- -А<
т
т— 10 1 . ,
“—~—> То I.Наконец, если т=11, то должно быть—дг < Ю”-1 ,
N N
т. е. у = ~ имеет на Д®е Цифры меньше, чем N, что тоже невоз-
можно.
100
Таким образом, единственным возможным случаем является
т=10; следовательно, условию задачи удовлетворяют числа, все
цифры которых кроме первых двух — нули, и только эти числа.
Примечание. Совершенно аналогично можно показать, что
единственные целые числа, уменьшающиеся в целое число раз при
вычеркивании /г-й цифры, где k > 3, суть числа, все цифры которых
кроме первых k — 1 — нули.
б) Аналогично решению задачи 32 имеем, принимая, что целое
число N уменьшается при вычеркивании второй цифры в т раз:
N — a0-Ю’Ч-йг 10п-|+а2-10"“»+... +йп,
— — о0-Юп—1 4- о2-10п—2+
Отсюда следует
яли после несложных преобразований
(Эао+^НО"-^
— м । . к ,
Последнее выражение можно еще представить в следующем
виде:
N = at-10n + av 10п—1 - а0 •! 0п—1 +.
Но, с другой стороны, мы знаем, что А есть (л4-1)-значное число,
начинающееся с цифр а0 и OU
АГ = а0. Ю" + а, • 10""1 + а2 • 10""2 4- • • • 4- о».
где можно считать, что не все цифры а2, .... ап равны нулю (про-
тивоположный случай сводится к рассмотрению двузначных чи-
сел Л'; см. решение задачи 30). Таким образом, должно иметь место
неравенство
о<-fl0.10n-tч-<ю-1,
или, что равносильно,
9ай 4- я,
“о < "ТГ-Г < ао + 1 • (**)
Итак, окончательно мы имеем следующие результаты. Искомые
числа N выражаются формулой (*), где О^По^Э, 0^ai^9; так
как N целое, а т и т — 1 взаимно просты, то отсюда следует, что
, 9п0 + Ct „
простую Дробь । можно обратить в десятичную. При этом воз-
можные значения а0, ai и т должны удовлетворять неравенству (**)
(кроме того, отдельно следует присоединить к возможным значе-
ниям N двузначные числа, полученные в решении задачи 30).
101
Теперь остается только последовательно рассмотреть все возможные
значения а0.
1°. а0 = 1. В этом случае неравенство (**) дает
1 <
18
т — 1’
т— 1 <18;
т — 1 > 4;
придавая т—1 последовательно значения 5, 6, 7,,.., 17 и выби-
рая каждый раз подходящие значения а,, мы получаем следующие
значения N:
#=108; 105; 10 125, 1125, 12 375, 135, 14 625, 1575,
16 875; 121, 132, ' 143, 154, 165, 176, 187, 198; 1625,
195; 192, 180 625, 19 125,
к каждому из которых еще можно приписать в конце' произвольное
число нулей.
Аналогично далее получаем;
2°. й0=2:
А=2025, 21 375, 225, 23 625, 2475, 25 875; 231, 242,
253, 264, 275, 286, 297; 2925.
3°. а0=3;
#=30 725, 315, 32 625, 3375, 34 875; 341, 352, 363,
4°. «о = 4: 374, 385, 396.
# = 405, 41 625, 4275, 43 875; 451, 462, 473, 484, 495.
5°. й0 = 5:
# = 50 625 5175, 52 875; 561, 572, 583, 594.
6°. йо = 6: #= 7° йп = 7; 6075 ; 61 875; # = 781, 671, 682, 792. 693.
8°. й0 = 8:
#=891.
Значению аа—9 не отвечает ни одно значение N.
Всего, включая результаты задачи 30, мы получаем для числа N
104 значения, к каждому из которых еще можно приписать в кон-
це произвольное количество нулей.
34. а) Первое решение. Обозначим (m-значное) число,
которое получается, если отбросить у искомого числа первую циф-
ру 1, через X. В таком случае мы по условию задачи имеем;
(l-10m-h¥) .3=10X4-1,
откуда
3-10™—1
Х= 7
Из последнего равенства уже нетрудно определить число X. Для
этого надо число 3-10”‘ = 30 000... делить на 7, пока в остатке не
102
получйтся 1. В результате имеем:
3000...0 I7
9Я I-----------
— 42 857
20
14
60
56
40
35
50
49
1
Таким образом, наименьшее возможное значение числа X равно
42 857, а наименьшее значение искомого числа 142 857.
В процессе деления можно было бы не останавливаться на пер-
вой единице, а продолжать деление до следующей, и т. д.; при этом
мы получили бы числа
142 857 U2857 ... 142 857,
k раз
тоже удовлетворяющие условию задачи.
Второе решение. Обозначим вторую цифру искомого чис-
ла через х, третью — через у, и т. д., т. е. предположим, что иско-
мое число имеет вид lxy...zt (черта наверху означает, что здесь
мы имеем не произведение 1 -х-у ... z-t, а число, составленное из
цифр 1, х, у, z, I). В таком случае по условию задачи имеем:
1ху ... zt-3 = xy ... z/1.
Отсюда следует, что / = 7 (ни в каком ином случае произведение
слева не оканчивалось бы на 1). Следовательно, цифра десятков
числа, которое стоит справа, равна 7. Но это возможно только, ес-
ли произведение г 3 оканчивается на 7—2 = 5 (два десятка справа
получаются за счет произведения последней цифры искомого числа 7
на 3), т. е. 2=5. Теперь мы знаем уже цифру сотен числа справа:
5; поэтому цифра сотен искомого числа должна давать при умно-
жении на 3 число, оканчивающееся на 5—1=4 (1 есть цифра де-
сятков произведения 5-3). Вычисления закончатся ,тогда, когда мы
придем к первой цифре 1. Их удобно расположить следующим об-
разом:
1 4 2 8 57 42857
х з — 1
4—1=3, 2—0=2, 8—2=6, 5—1=4, 7—2=5 '
(вычисления проводятся справа налево). Таким образом, наи-
меньшим числом, удовлетворяющим условиям задачи, будет
142 857.
Если в наших вычислениях не останавливаться на первой полу-
ченной единице, а продолжать дальше, то мы получим другие числа,
103
удовлетворяющие условию задачи:
142 857 142 857 ... 142 857.
А раз
б) Так как при увеличении такого числа втрое количество
цифр его не увеличилось, то первая цифра числа может быть равна
только 1, 2 или 3.
Как мы видели в решении задачи а), она может быть равна 1.
Покажем теперь, что она не может быть равна 3.
Действительно, если первая цифра искомого числа равна 3, то
вторая цифра, равная первой цифре утроенного данного числа, рав-
на 9. Но результат умножения на 3 числа, начинающегося с цифр 39,
имеет больше цифр, чем само исходное число; поэтому оно не мо-
жет получаться из первоначального числа перенесением первой циф-
ры в конец.
Предоставляем читателям самостоятельно доказать, что искомые
числа могут начинаться с цифры 2. Наименьшее подобное число
есть 285 714; все такие числа, начинающиеся с цифры 2, имеют вид
285 714 285 714 ... 285 714
k раз
(доказательство аналогично решению задачи а)).
35. Первое решение. Пусть число X удовлетворяет условиям
задачи: z
Х = а,а2 ... an_[6 и 4Х = $а1аз ... ап-ь
где at, а2, ..., а„_|, 6 — цифры числа X. Так как последняя цифра X
есть 6, то последняя цифра on-i числа 4Х есть 4; таким образом,
X = а,а2 ... ап_2 46, что позволяет найти предпоследнюю цифру
ап-2 — 8 числа 4Х. Записав теперь X в виде ... 846, мы сможем
найти, что ап-з = 3, и т. д. Этот процесс мы будем продолжать до
тех пор, пока не получим в числе 4Х цифры 6, которую можно счи-
тать перенесенной из конца числа X. Так мы находим, что наи-
меньшее возможное число, удовлетворяющее условию задачи,
есть Л'=153 846; при этом 4А'=615 384.
Второе решение. Так как искомое число X оканчивается
цифрой 6, то его можно записать в виде Х=10х+6, где х— чис-
ло, получающееся из X зачеркиванием последней цифры 6. Если
число х является n-значным, то из условия задачи вытекает, что
4-(10х+6)=6-10"+х,
т. е.
2(юп____4)
39х = 6-(10п — 4), или х =------pg----. (*)
1 о
Число 10” —4, очевидно, равно 6, или 96, или 996, или 9996, ...
Наименьшее из таких чисел, кратное 13,— это число 99 996=13-7692;
ему отвечает значение п = 5. Но в таком случае равенство (*) дает
х=15 384, и, значит, Х=153 846.
36. Если при увеличении числа в 5 раз количество его цифр
не меняется, то искомое число должно, начинаться с цифры 1. При
104
перенесении этой цифры в конец мы получим число, оканчивающее-
ся цифрой 1. Но такое число не может делиться на 5.
Так же доказывается, что не существует чисел, увеличивающих-
ся в 6'или 8 раз от перестановки начальной цифры в конец.
37. Первое решение. Так как произведение искомого чис-
ла на 2 имеет то же самое число цифр, то первая цифра числа не
может быть больше 4. Так как при перенесении первой цифры в
конец мы должны получить четное число (удвоенное исходное чис-
ло), то первая цифра должна быть четной. Поэтому она может быть
равна только 2 или 4.
Теперь, предполагая, что первая цифра искомого числа равна 2
или 4, и обозначая число, получаемое из искомого отбрасыванием
первой цифры, через X, мы получим аналогично первому решению
задачи 34а):
ю у 1 о у 4-10”1-2 210m- 1
(2-10 Х)-2 — 10-Х 4- 2, откуда X ==--g----==-----...——19
или
(4-10т4-Х)-2 = 10 X4-4, откуда X = ~4 = —,
ОХ
Но обе полученные формулы для числа X невозможны (целое
число не может быть равно дроби, числитель которой нечетен, а
знаменатель четен).
Второе решение. Как и в первом решении, убеждаемся,
что первая цифра числа может быть равна только 2 или 4. Далее
получаем в принятых ранее обозначениях (см. второе решение за-
дачи 34а)):
2ху ... zt • 2 — ху ... zt2 или 4ху ... zt • 2 — ху ... zti.
В первом случае t может быть равно только 1 или 6 (в про-
тивном случае произведение слева не может оканчиваться цифрой
2). Но если 1=1, толы получаем слева число, не делящееся на 4,
а справа — число, делящееся на 4 (оканчивающееся на 12). Если
/ = 6, то, наоборот, слева будет стоять число, делящееся на 4,
а справа —не делящееся на 4 (оканчивающееся па 62).
Во втором случае t может быть равно 2 или 7. Но если 1 = 2,
то аналогично второму решению задачи 34а) находим, что z = 1
или 6; при z = 1 произведение слева делится на 8 (произведение
на 2 числа, оканчивающегося на 12), а число справа — не делится
на 8 (оканчивается на 124); при z = 6 число справа делится на 8,
а произведение слева — только на 4. Аналогично показывается,
что t не может равняться 7.
38. а) Первое решение. Число, увеличивающееся при пе-
ренесении первой цифры в “конец в 7 раз, должно начинаться
с цифры 1 (иначе число, большее первоначального в 7 раз, будет
иметь больше цифр, чем первоначальное). Обозначая далее
т-з н а ч н о е число, полученное из исходного отбрасыванием пер-
вой цифры, через X, мы будем иметь (ср. с решением задачи 34а))
(1 • 10т 4- X) - .7 •= 10 • Х+ 1,
откуда получаем:
7-10тп—1
х= 3
105
Но очевидно, что подобное число X ни при каком т не будет
/7-10т-1 _
т-значным I------g---->• 10 I-
Аналогично можно доказать, что не существует чисел, увели-
чивающихся в 9 раз от перестановки . начальной цифры в конец.
Второе решение. Как в первом решении, показываем,
что искомое число может начинаться только с цифры 1. Далее,
имеем в принятых обозначениях:
\ху ... zt 7 = ху ... zt\.
Отсюда следует, что произведение t • 7 оканчивается цифрой 1.
Следовательно, t = 3. Подставим это значение t: имеем
1ху ... z3 • 7 = ху_... г31. Ввиду того что 3-7 = 21, а произве-
дение числа z3 на 7 оканчивается на 31, произве-
дение z • 7 должно оканчиваться на 1. Следовательно, z также
равно 3. Таким же образом доказывается, что каждая следующая
(если рассматривать с конца) цифра нашего числа равна 3.
Но начальная цифра должна быть 1. Этого мы никогда достичь
не можем. Поэтому чисел, увеличивающихся в 7 раз от переста-
новки начальной цифры в конец, не существует.
Аналогично можно доказать, что не существует чисел, увели-
чивающихся от перестановки начальной цифры в конец в 9 раз.
б) Первое решение. Так как произведение искомого чис-
ла на 4 имеет не больше цифр, чем само число, то первая цифра
числа должна быть не больше 2. Так как при перенесении первой
цифры в конец мы получаем четное число, то первая цифра должна
быть равна 2. Далее, обозначая через X m-значное число, которое
получается из искомого при отбрасывании первой цифры, имеем:
о ф 1 лтп _ п
(2- 10m -ф Х)-4 = 10Х + 2, откуда Х =-------g----,
8-10™ —2 1пП1
что невозможно, так как------g----> 10 (ср. с .первым решением
задачи а)).
Второе решение. Как в первом решении, получаем, что
первая цифра искомого числа может быть только 2. Далее имеем:
2ху ... zt‘4=xy ... zt2,
откуда следует, что t — З или 8 (7-4 оканчивается на 2).
Если бы t равнялось 8, то число справа оканчивалось бы на
82 и не могло бы делиться на 4. Если же t = 3, то
2ху ... гЗ-4—ху ... z32,
откуда _______
2ху .. .zO-4—ху...
и _______ ___________
2ху ... г-4*=ху ...z2.
Таким образом, мы видим, что число 2ху. ..г обладает тем же
свойством, что и 2ху ...zt. Поэтому, применив те же рассуждения,
100
получим г = 3. Продолжая дальше эти вычисления и двигаясь по-
следовательно справа налево, мы получим, что в десятичной записи
нашего числа стоят только цифры 3. В то же время оно начинается
с 2. Значит, такого числа не существует.
39. Первое решение. Обозначим неизвестные пока циф-
ры искомого числа через х, у, ..., z, t. В таком случае в обозначе-
ниях второго решения задачи 34 а) имеем:
---------------------------- 1 ------------
. ixy ... zt--у = ху ... zt7,
или
ху... ztl-3 — 7xy . ..zt.
Теперь сразу ясно, что /=1; после этого мы можем опреде-
лить цифру г (17-3 оканчивается на 51; значит, z=5) и так после-
довательно с конца находить новые и новые цифры искомого чис-
ла. Вычисление следует прекратить тогда, когда мы придем к циф-
ре 7. Его удобно расположить следующим образом:
241379310344827586206896551 7241379310344827586206896551
......................... 7-3= ............................;
(вычисления проводятся справа налево). Таким образом,'наи-
меньшим числом, удовлетворяющим условиям задачи, будет
7 241 379 310 344 827 586 206 896 551.
Если в наших вычислениях не останавливаться на первой се-
мерке, а продолжать дальше, то мы получим другие числа, удов-
летворяющие условию задачи. Все такие числа будут иметь вид
72413793103448275862С6896551 ... 7241379310344827586206896551.
k раз
Второе решение. Пусть 7xyz .. .t — искомое число. Тог-
да при делении его на 3 получится число xyz... /7. Запишем это в
виде
7xyz ... t | 3
xyz ... t7
Отсюда ясно, что х = 2. Если мы запишем в делимом и част-
ном это значение, то можно будет найти вторую цифру частного;
воспользовавшись ею, можно будет найти третью цифру делимого;
отсюда можно найти третью цифру частного, и т. д. Процесс за-
кончится тогда, когда последняя полученная цифра частного бу-
дет 7, а выписанное делимое разделится на 3 без остатка.
Легко видеть, что это число является искомым, так как если
мы в нем переставим 7 из начала в конец, то получится число,
записанное нами в качестве частного, т. е. втрое меньшее.
Так как до этого места мы по написанным уже цифрам с необ-
ходимостью получали следующую, то указанное число будет наи-
меньшим, обладающим требуемым свойством. Вычисления можно
расположить так: в верхней строке будем выписывать цифры де-
лимого, во второй • строке — число, при делении которого иа 3
107
получается очередная цифра частного, а в нижней — эту цифру}
72413793103448275862
7 12 4 11 23 27 9 3 1 10 13 14 24 8 22 17 25 18 6 2
24137931034482758620
0 6 8 9 6 5 5 1
20 26 28 19 16 15 5 21
6 8 9 6 5 5 17
Итак, наименьшее число, обладающее требуемым свойством:
7 241 379 310 344 827 586 206 896 551.
Третье решение. Аналогично первому решению задачи
34 а), используя похожие обозначения, будем иметь:
(7- 10th-J- Х)-4- = 10Х + 7,
О
откуда
v 710™ —2!
Л - 29
Таким образом, задача сводится к определению такого числа
вида 70 000..., которое при делении на 29 дает в остатке 21. Пре-
доставляем читателю самому проверить, что при этом мы прихо-
дим к тому же результату, что и в первых двух решениях.
Примечание. Аналогично можно решить следующую за-
дачу:
Найти наименьшее число, начинающееся с известной цифры,
которое уменьшается в 3 раза от перестановки первой цифры в ко-
нец. Для того чтобы можно было искать и решения, начинающиеся
с цифр 1 и 2, будем считать, что 0 может стоять в начале числа.
Если в начале числа стоит цифра 0, то легко убедиться, что
требуемым свойством обладает лишь число 0. Выпишем остальные
числа, обладающие этим свойством:
1 034 482 758 620 689 655 172 413 793
2 068 965 517 241 379 310 344 827 586
3 103 448 275 862 068 965 517 241 379
4 137 931 034 482 758 620 689 655 172
5 172-413 793 103 448 275 862 068 965
6 206 896 551 724 137 931 034 482 758
8 275 862 068 965 517 241 379 310 344
9 310 344 827 586 206 896 551 724 137
Таким же способом можно решить задачу:
Найти наименьшее целое число, начинающееся заданной циф-
рой а и уменьшающееся от перестановки этой цифры в конец
в I раз. Найти все такие числа.
40. а) По условию задачи имеем:
ху... zt а = tz... ух,
где а есть одно из чисел 2, 3, 5, 6, 7 или 8.
Если а = 5, то х должно равняться 1, так как иначе число
ху ... zt 5 будет иметь больше цифр, чем ху .,, zt (случай х = О
108
исключаем, так как в этом случае у.. .zt = 2 • tz.. .у, т. е. мы
приходим к той же задаче с а=*2). Но число tz...y\ не может
делиться на 5. Аналогично доказываем, что а не может быть рав-
но 6 или 8.
Если а = 7, то х тоже должно равняться 1. Но в таком слу-
чае t должно равняться трем,— иначе ly...zt'7 не будет оканчи-
ваться цифрой 1. А равенство \у ... z3 • 7 =3z . ..</!,• очевидно, яв-
ляется абсурдным (левая часть равенства явно больше правой).
Если а = 2, то х не может быть больше 4. А так как число
tz...yx в этом случае четно, то х должно быть равно 2 или 4.
Но при х = 4 цифра t (первая цифра числа 4у ... zt 2) может
быть равна только 8 или 9, а ни 4у ... z8 2, ни 4у ... z9 • 2 не
могут оканчиваться на 4. Если х = 2, то t (первая цифра числа
2у ... zt 2) может быть равна только 4 или 5; но ни 2у ... z4 2,
ни 2у ... z5 • 2 не могут оканчиваться на 2.
Наконец, если а — 3, то х не может быть больше 3. Если х =
= 1, то t должно быть равно 7 (t-З оканчивается на 1); если х =
= 2, то t должно быть равно 4; если х = 3, то t должно быть рав-
но 1. Но в первом случае tz... ух больше, чем xy...zt-З, а во
втором и в третьем — меньше.
б) Пусть ху .. .zt — такое число| тогда
ху ... zt • 4 = tz ... ух.
Так, как xy...zt-4 имеет то же число цифр, что и xy...zt, то х
может быть равен лишь 0, 1 или 2; так как tz... ух делится на 4,
то х должен быть четным. Следовательно, х может быть равен О
или 2.
Пусть х = 0. Очевидно, что число 0 обладает требуемым свой-
ством. Будем допускать десятичные записи, в начале которых мо-
жет стоять один или несколько нулей. Тогда мы имеем y...zt-4 =
= tz ... у0, откуда t = 0 (нбо t < 4) н у ... z-4 = z... у. если
число обладает требуемым свойством и начинается нулем, то оно
оканчивается также нулем, и число, которое получится, если мы за-
черкнем первый и последний нули, также будет обладать требуе-
мым свойством.
Поэтому достаточно рассмотреть случай х = 2. Тогда имеем
2у ... zt-4 = tz ... у2. Ввиду того что 2-4 = 8, t может быть рав-
но лишь 8 или 9. Но произведение t-4 оканчивается на 2; следова-
тельно, /= 8, т. е. можно написать 2у ... z8-4 = 8z ... у2. Так как
23 • 4 > 90, у может быть равно лишь 0, 1 или 2; но при любом г
в произведении z8-4 цифра десятков нечетная. Следовательно, у —
= 1, Так как нам известны две последние цифры произведения
2у... z8 • 4, то для предпоследней цифры z этого числа остаются
лишь две возможности: z может быть равно лишь 2 или 7. Но 21Х
X 4 > 82, значит, z = 7. ______
Итак, наше число, имеет вид 21 ... 78. Если оно четырехзначно,
то мы получаем число 2178, удовлетворяющее условию задачи. Рас-
смотрим теперь случай, когда число цифр рассматриваемого числа
109
больше 4? В этом случае имеем:
21uv ... rs78'-4 = 87sr... vu!2,
или после очевидных преобразований
84 • 10к+2 + 312 + uv... rsOO 4 = 87 • 10ft+; + 12 + sr ... vuOO,
uv ... rs • 4 + 3 = 3sr ... vu.
Так как число uv...rs при умножении на 4 дает число, имею-
щее больше цифр, чем оно само, и при этом начинающееся с циф-
ры 3 (или, в крайнем случае, с комбинации цифр 29), то и может
быть равно только 9, 8 или 7. Так как Ззг... vu нечетно, то и мо-
жет быть равно только .9 или 7. Рассмотрим эти случаи последова-
тельно.
1°. и — 9. В таком случае, очевидно, получаем:
9у ... rs • 4 + 3 = 3sr ... у9,
'откуда следует, что з = 9 (s • 4 оканчивается на 6; если s — 4, то
34г ... v9 меньше, чем 9у...г4-4 + 3) и
9о ... г9-4 + 3 = 39г ... у9, v ... г-4 + 3 — Зг ... v,
т. е. число, получаемое из uv...rs отбрасыванием цифры 9 в нача-
ле и в конце, обладает тем же свойством, что и само число uv... rs.
В частности, u.v...rs может равняться 9, 99, 999, и т. д.; при этом
мы получаем числа
21 978,219 978,2 199 978,...,
удовлетворяющие условию задачи.
2°. и = 7. В этом случае имеем:
7у ... rs-4 3 = 3sr ... vl,
откуда аналогично тому, как мы рассуждали в начале решения зада-
чи, легко получить, что s = 1; v = 8; г »=» 2, т. е. что число uv ... rs
имеет вид 78 ... 21 и что число, которое получается из uv ... rs отбра-
сыванием 78 в начале и 21 в конце, в 4 раза меньше своего обра-
щенного.
Отсюда видно, что если число, в 4 раза меньшее своего обра-
щенного, отлично от чисел ряда
0,2178, 21 978, 219 978....2199... 978, 2199... 9978....... (*)
k цифр (Л+1) цифр
то в начале и в конце его стоит одна и та же последовательность
цифр, составляющих одно из чисел этого ряда, и если зачеркнуть
эти цифры (и в начале и в конце), то получится также число, в
4 раза меньшее своего, обращенного, или, как в случае числа
21 782 178, при этом будут зачеркнуты все цифры нашего числа.
Поэтому десятичная запись любого числа, в 4 раза меньшего
своего обращенного, имеет вид
РЛ,.. Рп—[РпРп—I • • • Р%Р i
ПО
или же
P[P2 . . . Pn-iPnPnPn-l ... P2Pi,
где Pt, Р2, ..., Рп — последовательности цифр, составляющие какие-
либо числа из написанного выше ряда (*)-.Таковы, например, числа:
2 197 821 978, 2 199 782 178 219 978,
21 978 021 997 800 219 978 021 978, 02 199 999 780
(последнее число следует считать решением задачи, если условиться,
что можно в начале десятичной записи числа ставить 0).
. Аналогично доказывается, что все числа, в 9 раз меньшие свое-
го обращенного, получаются из чисел ряда
0, 1089, 10989, 109989......1099...989, 1099 ... 9989, ...
k раз (&+1) раз
таким же образом, как и числа, в 4 раза меньшие своего обращен-
ного, получаются из чисел ряда (*).
41. а) Обозначим число, составленное первыми тремя цифрами
искомого числа N, через р, а число, образуемое тремя последними
цифрами числа N, — через q. В таком случае условие задачи даст
1000? + р = 6(1000р+?) ( = 6А),
откуда
(1000? + р) — (ЮООр + ?) = 999(? —р) — 5Л1.
т. е. N делится на 999.
Далее, р + ? — (ЮООр + ?)—999р = N — 999р, откуда следу-
ет, что р + ? тоже делится на 999. Но р и ?— трехзначные числа,
которые, очевидно, не могут оба равняться 999; следовательно,
р + ? = 999.
Теперь без труда находим:
(1000? +р) + (1000р + ?) = 1001 (р + ?) = 7А
и, значит,
7/7 = 999 999, 77= 142 857.
б) Совершенно аналогично решению задачи а), обозначая че-
рез р число, образуемое первыми четырьмя цифрами искомого чис-
ла N, а через ? — число, образуемое последними четырьмя цифрами,
находим:
7N — 10 001 (р + ?) = 99 999 999,
что невозможно при целом N (ибо 99 999 999 не делится на 7).
42. Пусть х — число, удовлетворяющее этому условию. Так ка-к
6х, так же как их, — шестизначное число, то первая цифра деся-
тичной записи числа х равна 1. Поэтому:
1) первые цифры десятичной записи чисел х, 2х, Зх, 4х, 5х и 6х
все различны, следовательно, составляют полный набор цифр, участ-
вующих в десятичной записи числа х;.
2) все цифры в десятичной записи числа х различны между
собой.
111
Среди етих цифр нет 0, поэтому последняя цифра числа х не-
четна (иначе 5х оканчивается нулем) и отлична от 5 (иначе 2х
оканчивается нулем). Вследствие этого последние цифры десятич-
ной записи чисел х, 2х, Зх, 4х, 5х и 6х все различны, а значит, так-
же составляют полный набор цифр, участвующих в десятичной за-
писи числа х. Поэтому среди них есть 1. Оканчиваться на 1 мо-
жет лишь число Зх, так как 2х, 4х и 6х оканчиваются на четные
цифры, 5х оканчивается на 5, а в десятичной записи х уже есть 1
(первая цифра). Следовательно, х оканчивается цифрой 7, 2х —
цифрой 4, Зх — цифрой 1, 4х — цифрой 8, 5х — цифрой 5 и 6х — циф-
рой 2. Так как первые цифры этих чисел — цифры того же набора,
расположенные в возрастающем порядке, то можно написать:
х-1 = 1 * * * * 7,
ф 2 se 2 * * * * 4
х-З = 4 * * * * 1,
х-4 = 5****8,
х-5 = 7*** *5,
х-6 = 8** * * 2
(звездочки стоят на месте неизвестных нам пока цифр).
Отметим теперь, что в выписанной таблице не только в каж-
дой строке стоят в каком-то порядке шесть разных цифр 1, 2, 4, 5,
7 и 8, но и в каждом столбце стоят в каком-то порядке те же са-
мые шесть разных цифр. Действительно, предположим, например,
что в числах х-2 и х-5 на третьем месте стоит одна и та же циф-
ра а (а может иметь одно из двух значений, не занятых первыми и
последними цифрами рассматриваемых двух чисел). В таком случае
разность х-5—х-2 = х-З будет представлять собой шестизначное
число, в десятичной записи которого на третьем месте стоит циф-
ра 0 илн.цифра 9 (это следует из прабила вычитания многознач-
ных чисел «столбиком»). Но это невозможно, так как мы знаем,
что число х-З записывается цифрами 1, 2, 4, 5, 7 и 8.
Сложим теперь числа
х. 1 = 1 * * * * 7,
х-2 = 2 * * * * 4,
х-З = 4 * * * * 1,
х-4 =5**”8,
х-5 = 7 * * * * 5,
х-6 = 8 * * * * 2
«столбиком», учитывая, что сумма цифр каждого столбца равна 1 +
+ 2-)-4 + 5-|-7 + 8 = 27. Мы получим:
х-21 = 2 999 997,
или х = 142 857. Это и есть искомое число; действительно,
х = 142857,
2Х = 285714,
Зх = 428571,
4х = 571428,
5х = 714285,
6х = 857142.
112
43. Пусть А = xyz = 100х + 10г/ + z — искомое число, х, у,
г — цифры числа. Перестановками цифр из А получаются числа
Л\ = yxz = 1001/ + 10х + z, ..Л'5 = zyx — 1OOz-J-1 Оу + х. Сумма
N + Nt + ... +jV5 всех этих чисел должна равняться ушестеренному
числу А, откуда без труда получаем:
(2-100+ 2-10+ 2) (x + y + z) = 6(100x+10i/ + z)
(ибо в шестерке чисел N, N3, N3, Л+ iV5 каждая из цифр, на-
пример, х, 2 раза встречается на первом месте, 2 раза — на втором
и 2 раза — на третьем), или
37 (х 4- у 4" г) = ЮОх 4- 101/ 4~ z,
т. е.
63х = 27 г/ 4- 36z.
Сокращая обе части на 9, находим:
7х = Зу 4- 4z, или 7(х — у) = 4(г — у).
Но разности х — у и z — у по абсолютной величине не превос-
ходят 9, откуда вытекает, что последнее равенство возможна
лишь, если
х — у = 0, г— у = 0, или х — у = 4, г — у—1, или
х — у = — 4, г — у = — 7.
При этом если г — у — 7, то z = 9, 8 или 7; если z — у = — 7, то
у — 9, 8 или 7; поэтому (отбрасывая сомнительное «решение» N =»
= ООО) получаем 15 возможных значений числа А:
А = 111, 222, 333, 444, 555, 666, 777, 888, 999, 407,
518, 629, 370, 481 или 592.
44. Ясно, что числа А и А' должны быть 10-значными; пусть
А = й1Са9й8... й[ и А' = й10йдй8... а1 (йю, at, а8, • •., а> — последова-
тельные цифры числаА, а й10, й9......а(—цифры числа А'). Пред-
ставим себе процесс сложения «столбиком» чисел А и А’. Ясно,
что в сумме может получиться число Ю10 — 10 000 000 000 лишь в
том случае, если существует такой номер i (где 0 i 9), что
«1 4~ а\ = 0, й2 4- а2 = 0...ц. 4- в' = О,
fli+l + вЖ ~ 10, ai+2 + fli+2 = 9......«Ю + «Ю = 9 (*)
(если 1 = 9, то равных девяти сумм й;.|_2 4- а^2, я/уз + огуЗ’ •••
просто нет, а если i = 0, то отсутствуют равные нулю суммы
а14-я1', ..., ai 4~ й,-). Сложим теперь все суммы (*); мы получим
(а1 4~ fli) 4- (°г4- аг) + ••• + (аю + flio) = Ю + 9(9— Г).
А так как й i, а2, .. ., йю и а{; й2.а10 — это одниите же циф-
ры (только взятые в разном порядке), то в правой части последнего
8 Д. О. Шклярский и др,
113
равенства стоит четное число 2(ai + «2 + • • • + «ю); поэтому, чис-
ло 10 + 9(9 — I) тоже четно. Отсюда следует, что число / — обяза-
тельно нечетно, т. е. i не может быть нулем (i = 1, или 3, или
5, ...); поэтому aj + Я] = 0, т. е. at = af = 0. Но это и означает,
что числа Л и Д' делятся на 10.
45. Представим себе выписанные друг под другом числа М и
N и процесс сложения «столбиком» этих чисел; при этом пусть все
цифры полученной суммы Л1 + А — нечетные. Отсюда следует, что
сумма цифр последнего столбика нечетна; а тогда и сумма цифр
первого столбика, отличающегося от последнего столбца лишь по-
рядком цифр, также нечетна. Но это возможно лишь в том случае,
если при сложении цифр 2-го столбца из этого столбца в первый не
переносится единица, т. е. если сумма цифр 2-го (а значит — и пред-
последнего) столбца меньше 10. Поэтому из предпоследнего столбца
также не переносится в 3-й от конца столбец единица: ведь случай,
когда сумма цифр предпоследнего столбца равна 9 (т. е. < 10), но
единица из этого столбца в следующий все же переносится за счет
заимствованной из последнего столбца единицы, явно невозможен,
ибо в этом случае предпоследняя цифра суммы Л1 + N будет рав-
на 0, т. е. окажется четной. Таким образом, два последних (и
два первых) столбца пашей суммы никак не влияют на остальные
цифры суммы М + N\ поэтому мы можем отбросить в числах Л1
и W по две первые и две последние цифры — и продолжать наши
рассмотрения, исходя уже из «усеченных» (13-значных) чисел
и А;.
Составим теперь сумму М; + А[ чисел и Л+ при этом,
как и выше, можно показать, что если все цифры числа ЛЕ + N\
нечетные, то при сложении столбиком 13-значных чисел ЛЕ и Nt
два последних и два первых столбца не влияют на «средние» циф-
ры суммы Afi -+ A<i (на все цифры, кроме двух первых и двух
последних). Поэтому мы можем «усечь» также и числа ЛЕ и N\,
отбросив в каждом из них по две последние и по две первые
цифры и перейдя, таким образом, к 9-значным числам ЛЕ и N2.
С числами Л12 и N2 мы затем производим ту же операцию, пере-
ходя к 5-значным числам Л1з и А3; наконец, мы таким же образом
«усекаем» числа ЛЕ и Аз, переходя к (однозначным!) числам
и А4, записываемым одной («средней») цифрой чисел М и N. Но ясно,
что цифры (точнее — цифра!) числа Mt + А4 = 2ЛЕ не могут быть
нечетными (ибо число 2Л14 четно!); этим и устанавливается, что
также и все цифры суммы М + N не могут быть нечетными.
Примечание. Ясно, что проведенное рассуждение имеет
общий характер, сохраняя силу для любых двух «перевернутых»
чисел М и N, число цифр в каждом из которых имеет вид- 4п + 1,
т. е. дает при делении на 4 остаток 1. Если же число цифр числа
Л1 (и «перевернутого» числа N) не имеет вида 4и+1, то сумма
М + N может записываться одними лишь нечетными цифрами
(докажите это!).
46. а) п3— п ~ (п—1)п(п + 1), а из трех последовательных
целых чисел одно обязательно делится на 3.
б) л5 — п = п(п—1) (л + 1) (лг + 1). Если целое число окан-
чивается одной из цифр 0, 1, 4, 5, 6 или 9, то один из первых
трех множителей делится на 5. Если п оканчивается одной из
114
цифр 2, 3, 7 или 8, то п2 оканчивается на 4 или 9 и п2 -|- I делится
на 5.
в) п7 — п — п(п-\)(п+— п + \)(п2+п+ 1). Если п
делится на 7 или дает при делении на 7 остаток 1 или 6, то один из
первых трех множителей делится на 7. Если п дает при делении на 7
остаток 2 (л = 76 4-2), то п2 дает при делении на 7 остаток 4
(л2 = 49А2 4- 286 4- 4) и, следовательно, п2 4- п 4- 1 делится иа 7.
Точно так же показывается, что если п дает при делении на 7
остаток 4, то п2 4- п 4- 1 делится на 7, а если п дает при делении
на 7 остаток 3 или 5, то и2 — и 4- 1 делится на 7.
г) л11 — п = п(п—1) (л 4- 1) (л8 4- ns 4- п* 4- п2 4- !)• Если п
делится на 11 или дает при делении на 11 остаток 1 или 10,
то один из первых трех множителей делится на 11. Если п дает
при делении на 11 остаток 2 или9(л = 1 \k ± 2), то п2 дает при де-
лении на 11 остаток 4 (п2 = 121 А2 ± 44А 4- 4, л4 — остаток
5=16 — 11, л6 — остаток 9 = 20 — 11 (л6 = л4 • л2 = (1 l#i 4- 5) X
X (11 ^2 4- 4) = 121^1^2 4~ 11(4^1 4~ 4~ 20) и л8 •— остаток 3 =
= 25 — 22; отсюда следует, что л8 4-л6 4-л4 4-«2 4-1 делится на 11.
Точно так же показывается, что л8 4- л6 4- л4 4- л2 4- 1 делится
.на 11, если л дает при делении на 11 остаток ±3, ±4 или ±5.
д) Л13 — Л = Л (л — 1) (л 4- 1) (л2 4- 1) (л4 — Л2 4- 1) (л4 4- Л2 4- 1).
Аналогично решению предыдущих задач замечаем, что если л де-
лится на 13 или дает при делении на 13 остаток ±1, то один
из первых трех-множителей делится на 13; если л дает при делении
на 13 остаток ±5, то л2 4- 1 делится на 13; если л дает при деле-
нии на 13 остаток ±2 пли ±6, то л4 — л2 4- 1 делится на 13; если
л дает при делении на 13 остаток ±3 или ±4, то л4 4-л2 4- 1
делится на 13.
47. а) Разность одинаковых четных степеней делится на сумму
оснований; поэтому 36п — 26п = 272п — 82п делится на 27 4" 8 = 35.
б) Нетрудно проверить, что
л5 — 5л? 4- 4л = л(л2 — 1) (л2 — 4) = (л — 2) (л — 1)л(л 4- 1) (л 4- 2).
Но из пяти последовательных целых чисел одно наверное делится
на 5, по крайней мере одно на 3 и по крайней мере два на 2,
причем из этих двух последних чисел одно наверное делится на 4.
Таким образом, произведение пяти последовательных целых чисел
всегда делится на 5 • 3 • 2 • 4 = 120 (ср. с решением задачи 46а)).
в) Воспользуемся тождеством
л2 4- 'Зл 4- 5 = (л 4- 7) (л - 4) 4- 33.
Для того чтобы это выражение делилось на 11, необходимо,
чтобы (л 4-7) (л — 4) делилось на 11. Но так как (л 4-7) — (л—
— 4) = 11, то оба сомножителя делятся или не делятся на 11 одно-
временно. Поэтому если (л 4-7) (л — 4) делится на 11, то оно делит-
ся и на 121 и, следовательно, (л 4-7) (л —4) 4- 33 не может делить-
ся на 121.
48. а) Нетрудно проверить, что
56 786 730 = 2 3 • 5 • 7 11 • 13 • 31 61;
таким образом, остается доказать, что наше выражение делится
на каждый из этих простых делителей. Если т и п оба нечетны,
то лг60— л’° — четно; следовательно, тп(те0 — л60) обязательно
четно (делится на 2). Далее из результата задачи 46 следует, что
8*
115
если k равно 3, 5, 7, 11 или 13 и п ие делится на k, то разность
ль1 — 1 обязательно будет делиться на k. Отсюда, в частности,
вытекает, что если т и п не делятся на 3, то тб°— 1 = (,п30)2— 1
и пв0— 1 = (га30)2—1 делятся на 3, т. е. иг60 и л60 дают при деле-
нии иа 3 один и тот же остаток 1; следовательно, если тп не де-
лится на 3, то т№ — л60 .делится на 3 и, значит, произведение
mn(mso— л60) делится на 3 во всех- случаях. Точно так же дока-
зывается, что разность
те0 — пв0 = (/л13)4—(л13)4 = (т10)6—(л10)3 =
= (;л6)10—(л3)10 = (т5)12—(л5)12
делится на 5, если ни т, ни п не делятся на 5; делится иа 7,
если ни т, ни п не делятся на 7; делится на 11, если ни т, ни п
не делятся на 11; делится на 13, если ни т, ни п не делятся на 13.
Таким образом, мы доказали, что mn(mw — пм) всегда делится
на 2 3 - 5 • 7 • 11 • 13.
Аналогично показывается, что выражение тп(т'я— л60) де-
лится на 31 и на 61 (так как л31 — л при всяком целом л делится
на 31 и л61 — л при всяком целом л делится на 61; см. ниже зада-
чу 340).
б) Представим данное выражение в виде
(лг — 2л) (т — п) (т + л) (т + 2л) (т ф- Зл).
При л Ф 0 все пять сомножителей этого произведения попарно
различны. Между тем число 33 нельзя разложить более чем на че-
тыре различных целых множителя (разложение на четыре множи-
теля возможно несколькими способами, например, 33= (—11) X
ХЗ • 1 • (— 1) или 33 = 11 • (—3) • 1 (— 1)).
При л = 0 наше выражение есть /л5 и не равно 33 ни при
каком целом т.
49. Заметим, прежде всего, что 323 = 17 19; таким образом,
нам надо выяснить, когда выписанное в условии задачи число N
делится и на 17, и на 19. Пусть сначала число п = 2k — четное.
Ясно, что 20" — 3" при всех л делится на 20—3= 17; с другой
стороны, 16" — 1" = 162й— 1“’делится на 162—12=(16—1)Х
X (16 + 1) = 15 • 17, а значит, при четном л также и число 16" — 1
делится на 17, т. е. в этом случае N = (20"—3") + (16"— 1)
делится на 17. С другой стороны, число 20" — 1 при всех л делит-
ся на 20—1 — 19, а число 16"—3'* = 162"—3“ делится на 162 —
— З2 = (16 — 3) (16 + 3) = 19- 13, т. е. также делится на 19; поэ-
тому и число N = (20" — 1) + (16"—3”) делится на 19. Таким
образом, при всех четных п число N на 323 делится. С другой
стороны, если А = 2^ + 1 нечетно, то число 20"—3" по-преж-
нему делится на 17; поскольку же 16“— 1 делится на .17, то 162й
при делении на 17 дает остаток 1, а значит, число 16“ +1 =
= 16“ • 16 при делении на 17 дает остаток 1 16 = 16; поэтому
число 16" — 1 = 16“ + 1 — 1 на 17 не делится (оно дает при
делении на 17 остаток 15). Таким образом, при л нечетном число
N ие делится уже на. 17—и тем более оно не делится на 323.
Итак, число jV делится на 323 в том и только в том случае,
когда л — четное.
50. Если число л оканчивается, соотвественно, цифрой 0, 1, 2,
3, 4, 5, 6, 7, 8, 9, то л2 оканчивается цифрой 0, 1, 4, 9, 6, 5, 6, 9, 4,
116
1 и, значит, п3 + п оканчивается на 0, 2, 6, 2, О, О, 2, 6, 2, 0, а чис-
ло п3 + п + 1 оканчивается цифрой 1, 3, 7, 3, 1, 1, 3, 7, 3, 1. Таким
образом, число п3 + п + 1 никогда не кончается цифрой 0 или 5,
г. е. никогда ие делится на 5 (а значит,' не делится и на 1955).
51. Всякое целое число или делится на 5 или может быть пред-
ставлено в одном из следующих четырех видов 5k + 1, 5k + 2, 5* — 2
или 5k — 1. Если число делится на 5, то его сотая степень, очевид-
но, делится на 53 = 125. Далее, по формуле бинома Ньютона по-
лучим:
(5k ± 1)юо = (5*)100± ... + -в°29;- (5*)2 ± 100-5*+1,
где все невыписанные члены содержат множитель 5k в степени,
не меньшей 3, и, следовательно, делятся на 125. Аналогично
100-99
(5k + 2)100 = (5*),00± ... + ь2 (5*)2-298 + 100-5*-2" + 2100.
100-99
Но । д (5*)2 = 125-990*2 и 100 5k = 125-4* делятся на 125. Что
касается числа 2100, то его можно представить в виде
50-49
(5— 1)»о = 550 — ... Н-уу-б-50-5 + 1,
откуда видно, что оно дает при делении на 125 остаток 1.
Итак, сотая степень числа, делящегося на 5, делится на 125; со-
тая степень числа, не делящегося на 5, дает при делении на 125
остаток 1.
52. Нам надо доказать, что если N взаимно просто с 10, то
А101—N = N(Nm—1) делится на 1000, т. е. что А100—1 делится
на 1С00. Прежде всего совершенно ясно, что если А нечетно, то
А100—1 = (А50 + 1) (А25 + 1) (А25 — 1) делится на 8. Далее, из ре-
зультата предыдущей задачи следует, что если А не делится на 5, то
А100—1 делится на 125. Таким образом, мы видим, что действитель-
но А100—1 при А, взаимно простом с 10, делится на 8-125 = 1000.
53. Пусть А — искомое число; тогда, в частности, А2 — А окан-
чивается тремя нулями, т. е. делится на 1000. Так как № — А =
= А(А— 1), а А и А—1 —взаимно простые числа, то это возмож-
но лишь в том случае, когда одно из этих чисел делится на 8, а вто-
рое— на 125 (на 1000 ни одно из этих чисел само делиться не мо-
жет, так как А трехзначно).
Если А есть трехзначное число, делящееся на 125, то А—1, как
легко проверить, будет делиться на 8, лишь если А = 625, А — 1 =
= 624. Так х<е легко проверяется, что если А—1 есть трехзначное
число, делящееся на 125, то А будет делиться на 8 лишь при А —
— 1 = 375, А = 376.
Заметим теперь, что так как А’1-1 — 1 при любом целом * ^ 2
делится без остатка на А — 1, то АЛ — А = A(Aft_| — 1) при любом
целом * будет делиться без остатка на А (А— 1) = А2 — А; поэтому
если А2 — А оканчивается тремя нулями, то и АА—А при любом
целом * ^ 2 будет оканчиваться тремя нулями, т. е. А* будет окан-
чиваться теми же тремя цифрами, что и А. Отсюда вытекает,
что числа 625 и 376 (и только они) удовлетворяют условиям
задачи.
117
54. Найдем две последние цифры числа №°. Число №’ делится
на 4 (ибо А четно). Далее, число jV не делится на 5 (иначе оно де-
лилось бы на 10) и, значит, представимо в виде 5k ± 1 или в виде
5k ± 2 (ср. с решением задачи 51). Но число
20-19
(5Л± I)20 = (5k)20± 20(5k) 19+ ... + -^-(5k)2 ± 20’5%+ 1
дает при делении на 25 остаток 1, а число
(5&±2)20 = (5/г)20± 20 (5£),9-2 + ...
20-19
... +Ту (5A)2'218 ± 20-56-219 + 220
дает при делении на 25 тот же остаток, что и число 220 — (210)2 =
= (1024)2 = (1025—I)2, т. е. тоже остаток 1. Из того, что число
№° дает при делении на 25 остаток 1, следует, что последними дву-
мя цифрами этого числа могут быть лишь цифры 01, 26, 51 или 76.
Учитывая еще, что Л'20 должно делиться на 4, получим, что двумя
последними цифрами этого числа могут быть лишь цифры 76. Итак,
цифрой десятков числа №° будет цифра 7.
Найдем теперь три последние цифры числа №°°. Число Л,20° де-
лится на 8. Далее, так как N взаимно просто с 5, то №°° дает при
делении на 125 остаток 1 (см. решение задачи 51): №°° = 125Z? 4- 1.
Но тогда и №°° = (125k + I)2 = 1252Л2 + 2506 + 1 дает при делении
на 125 остаток 1. Следовательно, jV200 может оканчиваться цифрами
126, 251, 376, 501, 626, 751 или 876; по так как N200 делится на 8, то
оно должно оканчиваться цифрами 376. Итак, цифра сотен числа
№°° равна 3.
Примечание. Нетрудно видеть, что уже число N1B9 обяза-
тельно оканчивается тремя цифрами 376.
п (п 4* 1)
55. Сумма 1 + 2 + 3 + ... +и равна ------>' следовательно,
нам надо доказать, 'что если k нечетно, то S* = 1к + 2* + Зк + ... +
л(л+1)
+ ,п.к делится на -g---•
Отметим прежде всего, что при k нечетном ак + bk делится на
а + Ь. Рассмотрим теперь отдельно два случая:
А. ЧисЛо п четно. В таком случае сумма S* делится на n + 1,
так как каждая из сумм
. . . . . . / n / n \fe
lft + nft, 2k + (п- l)h, 3h + (n-2)\ .... (-g- \ + (-g + 1J
делится на
1 + л £= 2 -|- (л — 1) = 3-Ь(п — 2) = ... — -g- + ^~g~ + 1 j ;
п
сумма S* делится также на -g-, ибо 1*+(л—1)*, 2s + (л —2)*,
[п / п I п \k п
3* + (л — 3)\ ..., гр—1 I + I ' I . I "J" I 'nh все делятся на тр
118
Б. Число п нечетно. В этом случае сумма S* делится на —?—,
/п — 1 \А
так как Iй + пк, 2к (п — l)ft, 3й + (л — 2)й, ...» I—g— ) -]~
/л 3\^ /л -j- 1 л 1
Н~ ——) I _— i все делятся на —g—; Sft делится также на п,
/ п — 1 \А
так как 1*г (л — I)*, 2й + (и — 2)й, 3й + (п — 3)\ ..I—— j +
, /n~4~ i
+1—g—I все Делятся на п.
56. Пусть
N = ап • 10’* + an-i • 10"-' + ап-! • Ю"-2 4- ... 4- Oi • 10 —|- <То
— данное число (ап, an-i, ап-2....at, а0 — цифры числа, которые
могут принимать значения 0, 1, 2, ..9).
Вычтем из W число
Л1=До — в] -|- Os — о3 4* .., ± ап,
представляющее собой алгебраическую сумму цифр чис-
ла jV, взятых с чередующимися знаками. Группируя
подходящим образом члены, мы получим число
N — M = (104-1) 4-а2(102 — 1) 4-оз(Ю34-1) 4-
4- а4(ю4 — 1) 4- . .. 4* оп (10" ± 1),
делящееся на 11, ибо каждое его слагаемое делится на II. (Из то-
го, что при перемножении чисел остатки, даваемые ими при деле-
нии на некоторое число, перемножаются, легко вывести, что
10й =(11 - 1)й
дает при делении на 11 остаток — 1 при k нечетном и остаток 4- 1
при k четном.) Таким образом, разность N — М делится на 11, т. е.
число W делится пли не делится на 11 одновремен-
но с ч и с л о м М.
57. Число 15 дает при делении на 7 остаток 1. Отсюда следует,
что и
I52 = (7-2 4- 1)-(7-2 4- 1) = 7m 4-1
дает при делении на 7 остаток 1,
153 = 152-15 =(7т 4- 1) (7 -2 4- 1) = 7и2 '4- 1
дает при делении на 7 остаток 1, и вообще любая степень числа 15
при делении на 7 дает остаток 1. Если мы теперь вычтем из задан-
ного нам числа сумму 14-24-34~44-..-4-14 = 105, то, сгруппи-
ровав соответствующим образом члены, мы получим:
13(15— 1) 4- 12(152 — 1) 4-
4-Н(153— 1) 4- ... 4-2(151г — 1) 4-1 (15‘3 — 1),
т. е. число, делящееся на 7. Но из того; что разность заданного
числа и числа 105 = 7 • 15 -делится на 7, следует, что исходное
число тоже делится на 7.
119
58. Пусть К есть л-значное число. Среди (п + 2)-значных
чисел, начинающихся цифрами 1, 0 (т. е. среди чисел вида
lOfliQj... а„, где 1, 0, йц ..., а„—цифры числа), всегда найдется,
по крайней мере, одно, делящееся на К. Пусть это число есть
10i>i62 ... bn- Тогда, по условию, числа bib? ... bnlQnbibs ... fcn01
оба делятся на К. Их разность равна 9 и также делится на К.
Но у 9 делителями служат лишь 1, 3 и 9, откуда и следует наше
утверждение.
59. Ясно, что d = 333 ... 33 = 3 111 ... 11 — Зп', поэтому ис-
то троек 100 единиц
комое число N = 1111 ... 11 должно делиться без остатка на чис-
k единиц
ла п и 3 (п не делится на 3, ибо сумма цифр числа и, равная
100, не делится на 3). Но если число k— ЮО9 + г, где г < 100
(но г > 0), то, очевидно, N = 11 .. . 1100 .. . 00 + 11. . . 11 = М + У?,
100g единиц г нулей г единиц
где R = 11.. . 11 , а М = 11... 1100.. .00 делится на п (для
г единиц ' 100g единиц г нулей
того чтобы убедиться в этом, достаточно представить себе про-
цесс деления «углом» М на и). Таким образом, W делится на п
в том и только в том случае, когда R = 0, т. е. когда г — 0,
и, значит, k делится на 100.
Теперь, если 6=1009, то сумма цифр числа N равна 1ОО9; она
делится на 3 (а значит — и W делится на 3) в том и только в том
случае, если q делится на 3. Поэтому, наименьшее число W = 111 ... 11,
k единиц
делящееся на d, будет состоять из 300 единиц.
60. Поскольку а, очевидно, число четное, то нам надо только
доказать, что произведение аА делится на 3. Так как последняя циф-
ра числа 2Л+1 = 2^ та же, что и у числа 2а (где а — последняя
цифра Д'), то, последовательно умножая степени двойки еще на 2
(т. е. последовательно увеличивая показатель степени), мы найдем,
что последние цифры чисел ряда 2‘ — 2, 22 = 4, 23 == 8, 24 =16,
25 = 32, ... образуют следующую периодически повторяющуюся
последовательность:
2, 4, 8, 6, 2, 4, 8, 6, 2, 4, 8, 6, ...
С другой-стороны, если 2* = N дает при делении на 3 остаток 1,
то число 2/1+1 = 2/V дает при делении на 3 остаток 2, а если N =
— 31 + 2, то число 2*+’ — 2N имеет вид 3- (21) + 4 = 3- (21 + 1)+ I,
т. е. дает при делении на 3 остаток 1; поэтому та же последова-
тельность степеней двойки дает при делении на 3 следующие чере-
дующиеся остатки:
2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, ...
Таким образом, если число W кончается цифрой 2 или 8 (если
а = 2 или а = 8), то N при делении на 3 дает остаток 2, а если
а = 4, то W при делении на 3 дает остаток 1 (случай же, когда
а = 6, нам вообще не интересен, ибо здесь произведение аА = 6А
наверняка будет делиться на 6). Отсюда следует, что во всех этих
трех случаях число N — а = ЮЛ делится на 3, а значит, и А бу-
дет делиться на 3. Таким образом, произведение аА делится на 6
120
при всех однако при k = 1, 2 или 3 это заключение неинте-
ресно, ибо здесь А = 0 (и аА = 0 делится на любое число).
61. Нам надо показать, что число
N = 27 195е — 10 887s + 10 152s
делится без остатка на 26 460 = 22-33-5-72. Доказательство прово-
дится в два приема.
1 °. ^ = 27 195® — (10 8878 — 10 1 528).
Но 27 195 = 3-5-72-37; следовательно, это число делится на
5-72. С другой стороны, разность, заключенная в круглые скобки,
делится на
10 887- 10 152 = 735 = 3-5-72
(ибо разность восьмых степеней двух чисел делится на разность ос-
нований). Отсюда следует, что W делится на 5-72.
2°. W = (27 195® — 10 8878) + 10 152®.
Но 10 1 52 = 23 3’ • 47 делится на 22 • З3. С другой стороны, разность,
заключенная в круглые скобки, делится на
27 195— 10 887 = 16 308 = 22-33-151.
Таким образом, N делится на 22-33.
Так как N делится на 5-72 и 22-33, то N делится и на произве-
дение этих чисел, равное 26 460.
62. Нетрудно проверить, что
1110— I10 =
= (11 — 1) (И9 + 11® + 1Н+ пб + П’+ Н<+ нз+н2+11 + 1).
Легко видеть, что второй сомножитель в правой части делится на 10,
так как он представляет собой сумму 10 слагаемых, каждое из ко-
торых оканчивается на 1.
Итак, II10—1 есть произведение Ю на число, делящееся на 10,
и, значит, делится на 100.
63. 22225555 + 55552222 =
= (22 2 25555 + 45555) + (55552222 — 42222) — (45555 — 42222).
Из трех выражений, стоящих в круглых скобках, первое делит-
ся на 2222 + 4 = 2226 = 7-318 (сумма нечетных степеней делится
на сумму оснований) и, следовательно, делится на 7; второе тоже
делится на 7, так как оно делится на 5555 — 4 = 5551 = 7-793
(разность любых целых степеней делится на разность оснований).
Что касается третьего выражения, то его можно переписать в виде
42222(43333_________________1) 42222(641111_J),
откуда видно, что оно делится на разность 64— 1 = 63 и, следова-
тельно, делится на 7 (разность одинаковых целых степеней делится
на разность оснований).
____64. Воспользуемся методом математической индукции. Число
ааа, составленное из трех одинаковых цифр а (черта наверху постав-
лена, чтобы не путать с произведением а-а а), делится на 3 (так
121
как сумма цифр этого числа, равная За, делится на 3). Далее, пред-
положим, что наше утверждение уже доказано для каждого числа,
составленного из З'1 одинаковых цифр. Число, составленное из 3"+1
одинаковых цифр, можно представить в следующем виде:
аа ... а аа ... а аа ... а — аа ... а-100 ... 0100 ... 01.
Зп раз Зп раз Зп раз Зп раз Зп цифр Зп цифр
Но из двух сомножителей первый в силу предположения индукции
делится на 3”, а второй делится на 3 (сумма цифр этого числа рав-
на 3); следовательно, все произведение делится на Зп+)
65. Заметим прежде всего, что 106— 1 = 999 999 делится на 7
(так как 999 999 = 7-142 857). Отсюда легко следует, что 10*, где,
N — какое угодно целое число, дает при делении на 7 такой же
остаток, как и 10г, где г есть остаток от деления W на 6. Действи-
тельно, если W = 6k + г, то
до* — юг = 106,t+r — 10г = 10’(106'1 — 1) =
= 10г • (106 — 1) (10“-6 + 10Sft-12... + 10е -г 1)
делится на 7.
Но любая целая степень 10 дает при делении на 6 остаток 4;
в самом деле, 10" — 4 =999 ... 96 всегда делится па 2 3 = 6 (в си-
(п—1) раз
лу признаков делимости на 2 и на 3). Таким образом, все сложные
показатели степени у слагаемых нашей суммы дают при делении на
6 остаток 4. Следовательно, каждое из этих 10 слагаемых дает при
делении на 7 такой Же остаток, как и число 104, а вся сумма —та-
кой же остаток, как и число
104 + Ю4 + 10’ + 104 + 104 + 104 + Ю4 + 104 + 104 + 104 =
= Ю5 = 100 000 = 7-14 285 + 5.
Итак, искомый остаток равен 5.
66. а) Каждая четная степень 9 представима в виде
92п = 81п = 81-81 ... 81
п раз
и, следовательно, оканчивается цифрой !. Каждая нечетная степень
9 представима в виде 92,1+1 = 9-81” и, следовательно, оканчивается
цифрой 9 (как произведение числа, оканчивающегося единицей,
на 9). В частности, 9(9,) есть нечетная степень 9; значит, 9(ь’) окан-
чивается цифрой 9.
Заметим теперь, что любая целая степень 6 оканчивается циф-
рой 6; действительно, б1 = 6, и если 6П оканчивается на 6, то и
gn+! _ gn.g оканчивается на 6. Но 16п оканчивается па ту же циф-
ру, что и 6П; следовательно, любая целая степень 16 оканчивается
цифрой 6. Таким образом, любая степень двойки, кратная четы-
рем, оканчивается шестеркой (ибо 24« = 16п). Но З4—1 делится
на 3+1=4; значит, 2<3<~оканчивается цифрой 6, а 2(3<) =
= 2 • 2(3 —^оканчивается цифрой 2 (как произведение 2 на число,
оканчивающееся шестеркой).
122
б) Нам надо найти остаток от деления 2999 на 100 (это и есть
две последние цифры числа 2999). Покажем прежде всего, что при
делении на 25 число 21000 дает остаток 1. Действительно, 2‘° + 1 —
= 1024 + 1 — 1025 делится на 25; следовательно, и 22° — 1 = (2'° +
+ 1)(210—1) делится на 25, а 21000 — 1 = (220 ) 50 1 делится на
220— 1. Отсюда вытекает, что последние две цифры числа 21000 мо-
гут образовать число 01, или 01 + 25 = 26, или 01 + 50 = 51, или
01 + 75 = 76; но так как 21000, конечно, делится на 4, то этими циф-
рами могут быть только 76. Таким образом, 2999 равно частному от
деления числа, оканчивающегося на 76, на 2, т. е. оно может окан-
чиваться только цифрами 38 или 88 (так как 76:2 = 38, 176:2 =
= 88). Но так как это число делится на 4, то оно оканчивается
цифрами 88.
Найдем теперь остаток от деления числа З999 на 100. Напомним,
что каждая четная степень 9 оканчивается цифрой 1, а каждая не-
четная степень 9 — цифрой 9 (см. решение задачи а)). Воспользо-
вавшись этим, найдем остаток от деления числа 95 + 1 на 100:
95 + 1 =(9+ 1) • (94 — 93 -Т 92 — 9 + 1)= 10-(94 — 93 + 92 — 9 + 1),
а в алгебраической сумме, стоящей в скобках, каждое из трех по-
ложительных слагаемых оканчивается на 1 и каждое из двух от-
рицательных слагаемых — на 9; таким образом, число 94 + 92 + 1
оканчивается на 3, а число 93 + 9— на 8 и, значит, все выражение,
стоящее в скобках, оканчивается на 5. Итак, число 95+1 при делении
на ICO дает остаток 10 • 5 = 50. Отсюда вытекает, что число 9!0— 1 =
= (9Э + 1) (95 — 1) делится на 1 СО, атак как З1000 — 1 = 9500 — 1 =
_ (910)so _ 1 делится на дю — J (разность целых степеней делится на
разность оснований), то и З1000 — 1 делится на 100. Таким образом,
число З1000 оканчивается цифрами 01. Но это число делится на з’;
следовательно, его число сотен при делении на 3 должно давать
в остатке 2 (если бы при делении сотен на 3 в остатке оставалась
одна сотня или пи одной, то это число сотен плюс 01 не могло
бы делиться на 3). Итак, мы нашли, что число З999 = З1000 :3
должно оканчиваться теми же двумя цифрами, что и число
201 : 3 = 67.
в) Нам надо найти остаток от деления числа 14^14'4^ = (7-2/14*4)
на 100,— это и есть две последние цифры числа 14(14' \ Найдем в от-
дельности остаток от деления на 100 чисел 7^14' и 2(14'4>.
Число 74 — 1 = 2 401 — 1 = 2 4 00 делится на 100. Отсюда сле-
дует, что если п = 4k делится на 4, то 7" — 1 делится на 100 (ибо
74* — 1 — (74)й — (1)й делится на 74 — 1). Но 1414 = 214 • 7й делит-
ся на 4; следовательно, 7^1414^— 1 делится.на 100 и, значит, число 7^14*4
оканчивается цифрами 01.
Далее, в решении задачи б) было показано, что 220 — 1 делится
на 25; следовательно, если п — 20k делится на 20, то 2П — 1 делит-
ся на 25. Найдем теперь остаток от деления числа 14й на 20. Оче-
видно, 14!4 = 2|4-714. Но 214 = 4-212; так как 212—1 = (24)3—1 де-
лится на 24—1 = 16—1 = 15, то 4(212—1) делится на 20, а сле-
довательно, 214 = 4-212 дает при делении на 20 остаток 4. Далее,
714 = 49-712; так как 712 дает при делении на 20 остаток 1 (так как
12 делится на 4, то 712— 1 делится на 10Э), то 49-712 дает при де-
лении на 20 такой же остаток, как и число 49, т.,е. 9. Таким обра-
зом, 1414 = 214-714 дает при делении на 20 такой же остаток, как
123
и произведение 4 • 9 — 36, т. е. остаток 16: 1414 = 20К + 16. А отсю-
да следует, что 2<14'4) =216 • 220к дает при делении на 25 такой же
остаток, как и число 21в = 65 536, т. е. 2^14' может оканчиваться
только цифрами 11, 36, 61 или 86. Но так как делится на 4,
то 2<14'4) оканчивается цифрами 36.
Итак, число 7<14'4> оканчивается цифрами 01, а число 2(!414)—циф-
рами 36. Следовательно, их произведение 7*14'4> . 2<14‘' = 14<14“)
оканчивается цифрами 36.
qg9
67. а) Ясно, что оба числа 9' и 9J оканчиваются цифрой 9
(ср. с решением задачи 66а))—таким образом, последние цифры
у них совпадают. Далее, по формуле бинома Ньютона,
А = 9э9 = (10 — 1)99 =
•= 10а—c^io0-1 + С^- 10а—2 — ... 4- С1а .10— 1
И
В = 9э99= (10— I)999 =
= 10b—C4-10b_i + cg-10b-2 —... +CJ-10—1,
где а = 99 и b = Э99; таким образом, две последние цифры рассмат-:
риваемых чисел совпадают с двумя последними цифрами чисел
С4-10 — 1 = 10а —1 и С'-Ю — 1 = 10b— 1.
Но (см. снова решение задачи 66а)) числа а — 9s и b = 9®9 оба
оканчиваются цифрой 9; поэтому числа 10а и 10b оканчиваются
цифрами 90—и числа А и В оканчиваются цифрами 89.
б) Аналогично решению задачи а) здесь можно найти шесть
последних цифр двух рассматриваемых чисел (причем роль лежаще-
го в основе решения задачи а) равенства 9= 10—1 здесь будет
играть соотношение 72 = 50— 1) и убедиться, что эти цифры оди-
наковы. Однако в виду некоторой громоздкости такого решения
(ведь речь здесь идет не о двух, а о шести последних цифрах!) мы
предпочтем пойти по другому пути.
Нам надо убедиться, что совпадают 6 последних цифр чисел
* т7
А = 7“ и В — 7Ь, где теперь а = 7 и b = 7 , т. е. что разность
А —В = 7" — 7Ь = 7Ь (7<-ь — 1)
(а значит, и число
D = 7“ — 1,
где d = а — Ь) делится на 1 000 000 = 2В • 5s; таким образом, за-
дача сводится к выяснению того, на какие степени двойки и пя-
терки делится число D, имеющее вид 7d — 1, где d— некоторое
натуральное число. Рассмотрим отдельно вопросы о делимости числа
D на 2“ (где нам надо доказать, что а 6) ио делимости D на 5В.
Г. Пусть = 7е—1, где с — 2vq (здесь q нечетно); мы ут-
верждаем, что при этом С = 2“₽Р, где Р нечетно, а (зависящий
лишь от р, но не от ql) показатель степени ау при р > 1 удовлет-
124
воряет («рекуррентному») соотношению:
ар = aP-i + 1. (*)
Но поскольку число 7<2')— 1 = 72— 1 — 48 делится на 24 = 16
(но не на 25) и, значит, он = 4, то из (*) с очевидностью вытекает:
а? = Р + 3 при всех р I
— если наибольшая степень двойки, на которую делится число с,
равна р 1, то наибольшая степень аР двойки, на которую делит-
ся число С = 7е — 1, равна р + 3 (при р = О имеем а» = 1, по-
скольку число 72° —1 =7 — 1 =6 делится лишь на 2).
Покажем сперва, что число аР не зависит от у, это вытекает
из следующей формулы:
7(2Р«)_ j ж (72Р)9_19гз
= [72Р - 1] { [7(2Р)<?—1] + [7(2Р)]9—2 + [7(2Р)д—з] + ... + |),
где стоящая в фигурной скобке сумма нечетного числа q нечетных
-fl , я
слагаемых, очевидно, нечетна — и, значит, число 7 — 1 делится
на ту же степень двойки, что и число 7’! —1, Поэтому далее можно
считать, что q = 1, т. е. заменить число С = 7 — 1 числом Ср =
«=72Р—1.
Теперь нам остается лишь воспользоваться формулой
CP = 72P-1 = (72P-1)2-P =
= [72Р-,-1] [72Р-1 + 1] =СР-1-С\
Поскольку 7 дает при делении на 4 остаток —1, то 7™ дает при
делении на 4 остаток —1 при m нечетном и остаток +1 при m
четном, а значит, 7~ + 1 (и даже 72п 4- 1) при любом (натураль-
ном) п дает при делении на 4, остаток 2, т. е. делится на 2, но не де-
лится уже на 22. Таким образом, в равенстве = Cp^i С
левая часть Ср делится на 2 ₽, число Ср_| делится на 2 , а С'
делится лишь на 2, откуда и вытекает формула (*).
[Ясно, что случай р = 1 является особым, ибо здесь С == 72° + 1 =
= 7+1 =8 делится не только на 21, но на 23 — отличие возникает
вследствие того, что в этом единственном случае показатель стеле-
на 2° в выражении для С' — число нечетное.]
Итак, для определения показателя степени а в формуле D =»
= 7d — 1 ~ 2“ • Q (где Q нечетно) надо лишь выяснить, на какую
степень двойки делится число d = а — Ь=7а‘—7Ь> = 7]li (7dl—1)
^7
(т. е. число 7d‘ — 1), где а, = 71‘ , bi = 77, ad, = а,— b\.
А для этого, как мы .знаем, необходимо (и достаточно) установить,
на какую степень дврйки делится показатель степени dj = at—
— bi = 7°’— 7Ь» = 7Ь*(7dl — 1). где 02= 77’, <>2 = 7 и d2=>
=as — Ь2 =~7а> — 7Ь‘ = 7Ьз (7dl — 1), где теперь Ьз =1, аз — 77
125
и d3 = а3 — b3 = 77 — 1. Но поскольку число 7 — нечетно, то d3 =
= 77—1 делится лишь на 2“° = 21 = 2. Отсюда, в свою очередь,
вытекает, что число 7da — 1 делится на 2“‘ = 24; таким образом,
число d2 = 7Ьэ ( 7d3—1) делится на 24—и, значит, число 7d*—1
делится на 2“4 = 27. Но если d1 = 7(,2(7dl—1) делится на 27,
то 7d‘— 1 делится на 2“’ — 210; поэтому и d = 7Ь* (7^* — 1)
делится на 210, и, следовательно, D = 2d — 1 делится на2“‘“ = 213.
2°. Совершенно аналогично рассматривается и вопрос о дели-
мости чисел С = 7е—1, где теперь только уместно считать с =
= 5rs, на степени пятерки; однако здесь целесообразно оговорить,
что (не делящееся на 5) число s делится, по крайней мере, на 22,
ибо случай, когда s нечетно или делится лишь на 2, но не на 4,
приводит к несколько иным выводам. При s = 4si, или с = 5Г 4si,
. где S| — целое, наибольшая степень [Jr пятерки, на которую делится
число С, как и выше, зависит лишь от показателя степени г в фор-
муле для с, т. е. число рг не зависит от sr, при этом по-прежнему
имеет место аналогичное (*) («рекуррентное») соотношение
+ = ₽г_, + 1.
А так как число 74— 1 = (72)2 — 1 = (72 + 1) (72— 1) = 50 - 48
делится' на 52 = 25, т. е. [Зо = 2, то из (**) следует, что при всех
г + О
₽г = г + 2
— если показатель степени с в выражении С = 7е — 1 делится
на 4 и наибольшая степень пятерки, на которую делится с, равна
г, то наибольшая степень рг пятерки, на которую делится С, равна
г + 2.
Для доказательства независимости от Sj достаточно вос-
пользоваться формулой:
С = 7е - 1 = 75r'4s‘- 1 = (75r'4)S1 - Is- =
' = И’4- 1] {[7br'4)]s‘-1+ [7(5r-4>]S1~2+ ... + 7<5Г-4)+ 1].
Но так как 74 = (72)2 = (50 — I)2 — 502 — 2-50 + 1 дает при де-
лении на 5 остаток 1, то и число (74) п при любом п дает при де-
лении на 5 остаток 1; поэтому в фигурной скобке в правой части
последней формулы стоит сумма s( чисел, каждое из которых дает
при делении на 5 остаток 1, откуда, поскольку S] не делится на 5,
вытекает, что эта сумма не делится на 5. Поэтому число С =*
= 7°г'4®‘ — 1 делится на ту же степень пятерки, что и число Ег =
— 75Г'4 — 1, чт0 позволяет в дальнейшем считать Si = 1, т. е. заме-
нить число С числом Ег.
Далее,
Ет = 75Г'4 — 1 = _р =,
= (75Г-1'4 - 1) 1(75Г-1-4)4 + (75Г-1-4)\+ (75Г-’-4)2 +
+ 75Г~1,4 + 1} =Ег-\-Е'.
Отсюда, прежде всего, следует, что Ег делится на Er-i, т. е. Ег
126 . '
делится на не меньшую степень пятерки, чем Ег-г, другими словами
pr > pr_i, или, так как = 2,
2 = С Р1 < й < . . .
Таким образом, ’ при всех г 1 число £7—1 = 7&Г 1'i—1 делится
на 25, а значит число ег— 1 = е — 75 ’4дает при делении на 25
остаток 1, — и любая степень ек числа е также дает при делении
на 25 остаток 1. А так как стоящее в фигурных скобках в правой
части формулы для Ет выражение Е' равно сумме е4 е3 + е2 +
+ е-|- 1, то оно дает при делении на 25 остаток 5, т. е. Е' делится
на 51, но не делится на 52. Отсюда и из формулы Ег = Ег-\ • Е'
и вытекает соотношение (**).
Обратимся теперь снова к интересующему нас числу А—В =
= 7Ь D, где D — 7d— 1. Поскольку, как мы видели выше, число
d на 4 делится (оно делится даже на 210 = 1024), то нам остается
только выяснить, на какую степень пятерки делится число d —
= 7а‘— 7Ь1 — 7Ь‘(7d‘— 1),где dt — at— bi (см. конец п. 1° реше-
ния настоящей задачи). Но так как dt также делится на 4 (и даже
на 27), то наша задача сводится к определению того, на какую
степень 5 делится число dt — 7(‘2 — 7Ьг = 71'2 (7',г— 1), где d2 —
= а2— 62 == 7а’— 7Ьэ = 7Ь’(7С,“—1) делится на 4 (даже на 24)
и d3 = 77— 1. Но, как мы знаем, число d3 делится на 2 и не де-
лится на 4, т. е. d3 = 2/, где f—нечетно; поэтому 7d‘ — 1 ₽= 49f —
— 1 = (50—1)^—1 на 5 не делится (дает при делении на 5 оста-
ток — 2, т. е. остаток 3); с другой стороны, число 7da — 1 (как и число
d2 = 7Ьз (7da — 1)) уже делится на 4. Но отсюда следует, что число
7',! — 1 делится на 5-’’ = 52 (и не делится на более высокую
степень пятерки); поэтому d{ = 7bl (Т1г— 1) делится на 52 и d =
= 7bi(7d'—1) делится на 5^2 = 54, а Ь = 7d — 1 (и рассматри-
ваемое в этой задаче число А — В — 7Ь • D) делится на 5^'4 = 5е.
Это рассуждение и завершает решение задачи.
Примечание. Ясно, что совершенно аналогично решению
этой задачи можно установить, что числа Ап+г и А„, составленные
наподобие фигурирующих в настоящей задаче чисел А и В
из (л-(-2)-х, соответственно из п семерок, имеют 2л — 2 одинако-
вые последние цифры; рекомендуем читателю самостоятельно по-
стараться оценить число одинаковых последних цифр у чисел Ап
и А,„, составленных из п, соответственно из m семерок (здесь естест-
венно начинать со случая небольших разностей п — tn).
68. а) Если перемножить два числа, одно из которых оканчи-
вается на цифру а, а второе на цифру Ь, то их произведение будет
оканчиваться па ту же цифру, что и произведение ab. Это замечание
позволяет просто решить поставленную задачу. Будем последователь-
но производить возвышения в степень, следя только за последней циф-
рой числа: 72 оканчивается цифрой 9, 73 — 72 • 7 оканчивается циф-
рой 3, 74 = 73 • 7 оканчивается цифрой 1 и 77 = 74 • 73 оканчивается
цифрой 3.
Далее, точно таким же образом найдем, что (77)7 оканчивается
снова цифрой 7 (действительно, (77)2 оканчивается цифрой 9, (77)3
оканчивается цифрой 7, (77)4 оканчивается цифрой 1 и((77)7 окан-
127
чивается цифрой 7). Отсюда следует, что число ((77)7)7 оканчива-
ется той же цифрой, что и число 77, Т. е. Цифрой 3, число (((7')7)7)7
оканчивается снова цифрой 7, и т. д. Продолжая таким же образом,
мы после нечетного числа возведений в степень 7 будем каждый
раз приходить к числу, оканчивающемуся цифрой 3, а после чет-
ного числа возведений в степень 7 — к числу, оканчивающемуся
цифрой 7. Так как 1000 есть число четное, то интересующее нас
число оканчивается цифрой 7.
Если одно число оканчивается двузначным числом А, а вто-
рое— двузначным числом В, то их произведение оканчивается
на те же самые две цифры, что и произведение А • В. Это
позволяет найти и две последние цифры интересующего нас числа.
Как прежде, проверяем, что 77 оканчивается двумя цифрами 43,
а (77)' оканчивается теми же цифрами, что и 437, а именно цифра-
ми 07. Отсюда следует, что, возводя последовательно числа 7, 77,
(77)7,... в степень 7, мы после нечетного числа возведений в степень
будем приходить к числу, оканчивающемуся цифрами 43, а после
четного числа возведений — к числу, оканчивающемуся цифрами
07. Следовательно, искомое число оканчивается цифрами 07.
б) В решении задачи а) мы видели, что 74 оканчивается циф-
рой 1. Отсюда следует, что 74ft = (74) тоже оканчивается цифрой
1 и 74ft~l~1, где / есть одно из чисел 0, 1, 2 или 3, оканчивается
той же цифрой, что и7г (74А"^г Таким образом, задача сво-
дится к тому, чтобы определить, какой остаток дает при делении
на 4 число, являющееся степенью, в которую надо возвести 7,
чтобы получить число задачи.
Степень, в которую в задаче возводится число 7, сама
представляет собой 7 в некоторой очень большой степени;
'нам надо выяснить, какой остаток дает эта степень семи при деле-
нии на 4. Но 7 = 8—1; отсюда следует, что 72 = (8—1) • (8—1)
дает при делении на 4 остаток 1, 73 = 72 • (8— 1) дает при делении
на 4 остаток — 1 (или, что то же самое, остаток 3) и вообще каж-
дая четная степень 7 дает при делении на 4 остаток 1, а нечетная — ос-
таток — 1 (т. е. +3). Но интересующая нас в настоящем случае сте-
пень 7 заведомо является числом нечетным (так как она сама есть
степень 7), а следовательно, фигурирующее в условии задачи число
имеет вид 74ft^3 и, следовательно, оканчивается той же цифрой,
что и 73, т. е. цифрой 3.
Так как 74 оканчивается цифрами 01, то 74ft+J оканчивается да-
же геми же двумя цифрами, что и 7‘. Следовательно, интересую-
щее нас число оканчивается теми же двумя цифрами, что и число 73,
т. е. цифрами 43.
69. Рассмотрим последовательно числа:
1°. 21 = 9,
2°. Za = 9Z‘ = (10— l)z* -
= 10z‘ — ClZi-10z‘~l + ... + clZi-io — 1,
где опущенные члены разложения все делятся на 100. Но Cz =9;
следовательно, две последние цифры числа Z2 будут теми же самыми,
128
что и две последние цифры числа 9 • 10 — 1 = 89.
3’. Z3 = 9Zj = (10 — l)Zs =
- ioz* — с* -ioZ2—1 + ... -ci - io2 + cl - io - i.
4^3 1 Z^2
Ho Z3 оканчивается на 89; следовательно, C^ = Z., оканчивается на
2 Z., (Z.,-1) ...89-... 88
89, a Cz2 — j—9 j—9--- (точками обозначены неиз-
вестные цифры) оканчивается цифрой 6. Следовательно, три послед-
ние цифры числа Z3 будут теми же самыми что и три последние циф-
ры числа — 600 + 890 — 1 — 289.
4’.' Z4 = 9Zj = (10 - l)z’ =
= ioZj — с£- ю2’-1 -н -H c}t-юз — c^-io2 4-Cz/io — i.
Так как Z3 оканчивается на 289, тег и Cl7 — Z3 оканчивается на 289;
2 Z3(Z3 —1) .. .289-. . .288
1-2 1-2
оканчивается на 16;
_3 Z3 (Z.< — 1) (Z3 — 2) ...289-...288-...287
~~ 1-2-3 1-2-3
оканчивается цифрой 4. Следовательно, четыре последние цифры чис-
ла Z4 будут теми же самыми, что и последние четыре цифры числа
4000 — 1600 + 2890 — 1 = 5289.
5°. Z5 = 9Z‘ - (10- l)z‘ 10z‘ —с£- 10z‘~1 + ...
... - с’^ • ю1 + с|4• 103 — С^ • 102 + C|(• 10 — 1.
Так как Z4 оканчивается па 5289, го С7 — Z4 оканчивается на 5289;
Z4 (Z}— 1) ,, .5289-...5288
'Czt.^ 1-2 “= 1-2
оканчивается на 116;
3 Z4(Z4— 1)(Z4 — 2) ...5289-.. .5288-...5287
CZl = 1-2-3 ” 1-2-3
оканчивается на 64; наконец,
,4 Z4(Z4— 1)(Z4 — 2)(Z4—3) ...5289-...5288-... 5287-...5286
Z< — 1-2-3-4 = 1-2-3-4
оканчивается цифрой 6. Следовательно, Z5 оканчивается на те же
9 Д. О. Шклярскпй и др.
129
самые пять цифр, что и число
— 60 000 + 64 000— 11 600 + 52 890 — 1 = 45 289.'
Далее из того, что последние четыре цифры числа Z5 совпадают
с последними четырьмя цифдами числа Z«, следует, что последние
пять цифр числа Ze = 9Z‘ — (10—l)Zs совпадают с последними
пятью цифрами числа Z6(=9z‘). Точно так же показывается, что
все числа ряда
Zs, Z„ = 9Z\ Z, = 9Z‘, • •, Лооо = 9Z”’. Лоо1 = 9Z1' <”
оканчиваются на о^ип и те же пять цифр, а именно на 45 289. Но
21001 это и есть число условия задачи.
70. Найдем, прежде всего, остатки от деления на 13 чисел 5"
и га* 5 для ряда первых значений п = 0, 1, 2, ... При этом удобнее
начать с чисел 5П;
0 1 2 3 1
Число 5п 1 5 25 125 625
Остаток от деления 5” на 13 1 5 —1 —5 1
[Здесь мы пишем «остаток — 1» вместо «остаток 12» и «остаток —3»
вместо «остаток 8», что позволяет очень просто находить все следую-
щие остатки: если 5П дает при делении на 13 остаток — 1, т. е. 5" =
= 13ft—1, где k—целое, то 5n+1 = 5П • 5 — (13ft — 1)5 =
= 13(5ft) —5 дает при делении на 13 остаток —5; аналогично, если
5” дает при делении на 13 остаток —5, т. е. 5"1 = 13/ — 5, то
5тЧ 1 = 5т • 5 •₽ (13Z — 5)5 = 13(57) — 25 = 13(5/ — 2) 4- 1 дает при
делении на 13 остаток 1.] Продолжать таблицу далее нам нет нужды:
поскольку 54 «= 13? + 1, то 5s = 54 • 5 = (13? + 1)5 дает при деле-
нии на 13 тот же остаток, что и число 5 (остаток 5); число 5е =
= 5‘ . 52 = (13? -р 1)52 дает при делении на 13 тот же остаток, что
и число 52 (остаток — 1), и т. д.; таким образом, в нашем «.ряду ос-
татков» последовательно чередуются числа 1, 5, —1, —5.
Аналогично можно составить и таблицу остатков от деления на
13 чисел га5, где п = 0, 1, 2, .... и т. д. Но число (13р4-г)5 =
= (13р + г) (13р + г) . ,.(13р + г) дает при делении на 13 тот же
5 множителей
остаток, что и число г5; поэтому нам достаточно ограничиться значе-
ниями п = 0, 1, 2, 3, .... 12. Далее, если число п равно (или дает
при делении на 13 остаток)^, а число п2 дает при делении на 13
остаток 7, то число га5 = п2 п2 п дает при делении на 13 тот же
остаток, что и произведение t • t 7 s это обстоятельство может
облегчить составление требуемой таблицы для значений п •= 4, 5, 6.
Наконец, заметим еще, что если число л5 дает при делении на 13
остаток и, то число (13 — га)5 =(13— га)(13— га)...(13 — га) дае('
5 множителей
при делении на 13 тот же остаток, что и число (—га)5, т. е. остаток
— и, или 13 — и. *
130
Теперь мы можем составить нашу таблицу:
п п> п2 Остаток от деления п2 на 13 Остаток от деления л5 на 13 0 0 0 1 1 1 2 32 6 3 243 —4 4 16 3 3-3-4, пли —3 5 25 —1 -1 (—1)5 — 5
п /г5 п2 Остаток от деления п2 на 13 Остаток от деления л5 на 13 6 36 —3 —3-—3-6, или 2 —2 8 -5 9 3 10 4 11 -6 12 —1
(отвечающие значениям п = 7, 8, .... 12 остатки выписываются исхо-
дя из того, что числа п5 и (13 —л)5 дают при делении на 13 «допол-
нительные» остатки и и —и). После же значения п — 12 в нашей
таблице будут «периодически» повторяться те же остатки 0, 1, 6, —4,
—3, 5, 2, —2, —5, 3, 4, —6, —1.
Так как первая таблица имеет «период» 4, а вторая — «период»
13, то значение 4- 13 = 52 является «периодом» объединения обеих
таблиц: при увеличении п на число 52 (или па любое число, крат-
ное 52) остатки от деления на 13 обоих чисел 5" и п5 не меняются.
Далее, нас могут интересовать лишь те столбцы второй таблицы, ко-
торые отвечают остаткам ± I и ±5 (ибо в первой таблице чередуются
лишь остатки 1, 5, — 1, — 5). Но в пределах от п = 0 до п = 51
остаток 1 во второй таблице отвечает значениями =1, 1 + 13 = 14,
1 + 2-13 — 27 и 1 + 3 13 = 40; из эгих четырех чисел лишь 14
имеет вид 4х -+ 2, которому в первой таблице соответствует остаток
—1; таким образом, число п = 14 удовлетворяет требуемому условию
(514 -|- 145 делится на 13). Аналогично, остаток — 1 во второй таб-
лице в тех же пределах отвечает значениям п = 12, 12 + 13 = 25,
12 + 2 • 13 = 38 и 12 + 3 • 13 = 51; из этих чисел лишь 12 имеет
вид 4г/, который в первой таблице приводит к остатку 1. Точно так
же остаток 5 во второй таблице отвечает значениям п = 5, 5 + 13 —
18, 5 + 2 • 13 = 31 и 5 + 3 • 13 = 44, а остаток — 5 — значениям
л « 8, 8 + 13 = 21, 8 + 2 • 13 = 34 и 8 + 3 • 13 — 47; но из первых
четырех чисел лишь 31 имеет вид 4г + 3. обеспечивающий остаток
— 5 от деления 531 на 13, а из последних четырех чисел только 21
имеет вид 4w + 1, обеспечивающий остаток 5 от деления 521 на 13.
Таким образом, в пределах О S7 п S7 52 требуемому условию удовлет-
воряют следующие четыре натуральных числа: п == 12, 14, 21 и 31;
•се же множество удовлетворяющих условию задачи натуральных
чисел состоит из следующих четырех «серий» чисел:
п = 52m +12, п •= 52т + 14 (т. е. п = 26(2т) + 12 и
и = 26(2m + 1) — 12);
п = 52m + 21 и n = 52m + 31 (т. е. п = 52/п ± 21);
здесь т •= 0, 1, 2, ... (и лишь в формуле п = 52m —21 надо счи-
тать т>0).
Ясно, что наименьшее п, удовлетворяющее условиям зада-
чи — это п = 12.
71. Ясно, что две последние цифры чисел п, пг, п3,..., где п —
целое неотрицательное число, зависят лишь от двух последних цифр
числа п — это следует из правила умножения многозначных
чисел «столбиком». С другой стороны, последние цифры 100 последо-
вательных целых неотрицательных чисел обязательно пробегают ряд
значений 00, 01, 02.. 99-(хотя, вообще говоря, и не в этом поряд-
ке); поэтому наша задача сводится к нахождению двух последних
цифр суммы (при а = 4 и а — 8)
Л'а = 0а + 1“ + 2а + ... + 99а.
а) Если п = IОх + у — двузначное число, то
га4 = (Юх + г/)4 = 104х4 + 4 • 103х31/ + 6 • 10W + 4 • 10хг/3 + у\
причем на две последние цифры числа /г4 влияют лишь два последних
слагаемых, ибо все остальные слагаемые оканчиваются двумя нуля-
ми. Следовательно, нам надо найти лишь две последние цифры
сумм
S2j4-10«/3 и SS*°1/4 (=1OS1/4L
кд х у \ v J
где х и у независимо друг от друга пробегают значения от 0 до 9
и положено 0° = 1 (так что У х° — 0° + 1° + ... + 9° = 10).
х
Заметим теперь, что при фиксированном у
24-Юху3 = 4-10(0+ 1 -1- 2 + 3 + 4 + 5 +6+7+8+9)-у3=1800г/3
X
оканчивается двумя нулями; поэтому и22 4-10xt/3 оканчивается
х V
двумя нулями — и не 'вносит никакого вклада в две последние циф-
ры числа Nt. Итак, нам осталось лишь найти две последние цифры
числа
10 5 р4 =10(04 + I4 + 24 + З4 + 44 + 54 + 64 + 74 + 84 + 94) = 10S4,
v
или последнюю цифру суммы S4.
Но эту задачу решить легко: в нижеследующей таблице после-
довательно выписаны последние цифры чисел у, у2 и у*:
у 0 1 234 56789
у2 0149656 9 41
/ 0 16 1 6 5 6 16 1
132
Поэтому последняя цифра суммы <$« совпадает с последней цифрой
суммы
О + 1 + 6 + 1 + ... + 1 == 4(1 4-6) 4-5 = 33,
а значит, две последние цифры суммы N< (а также и фигурирующего
в условии задачи числа)—это 30.
б) В точности аналогично решению задачи а) находим, что и
при а~8 две последние цифры суммы (а значит, и интересующе-
го нас числа) совпадают с двумя последними цифрами числа 10S8,
где Sj = О8 + Is 4-• • 4~ 98. Но из выписанной таблицы последних
цифр чисел у*, а также из равенства yik = (У*)к следует, что чис-
ло yih (где у — цифра) оканчивается той же цифрой, что и у*. Поэ-
тому и при а = 8 две последние цифры рассматриваемого числа бу-
дут теми же, что и при а = 4, т. е. это будут цифры 30.
Примечание. Нетрудно видеть, что тот же результат мы
получим и при всех кратных 4 значениях а, т.е.приа =,4,8, 12, 16,...
72. Согласно формуле для суммы членов геометрической про-
грессии
5О1ооо — 1 5О1ои — I
N~ 50—1 “ 49
1
Но обращается в чистую периодическую десятичную дробь, пе-
риод которой, состоящий из 42 знаков, нетрудно найти простым де-
лением:
1
= 0, (020408163265306122448979591836734693877551),
или сокращенно
-^ = 0,(Р),
где Р изображает выписанную выше последовательность из 42 цифр.
Ближайшее к показателю степени 1000 целое кратное числа 42
есть 1008 •= 24 • 42. Следовательно,
Ю100’ 1
— = Ю'»»8 • ~РР ...Р, Р...
24 раза
Таким образом, дробь
чз чу---------.
24 раза
есть целое число, состоящее и? 1008 цифр, которые можно разбить
на 24 группы из повторяющихся 42 цифр (фактически число М
содержит не 1008 цифр, а 1007, так как наше число Р начинается
нулем).
Составим теперь разность между интересующим нас числом N
и числом М:
N .,5^- 10»w-1 IO1008 —1 51000— 10*
" ~m 49 — 49 ~ 49 ‘ '
133
Так как разность У — М двух Целых чисел — Целое число и 101МЙ
взаимно просто с 49, то 5W00 — 108 должно делиться на 49. Следова-
51000___________________ю»
тельно, число х =----------- является целым и разность N — М =
= 1О!00° • х оканчивается на 1000 нулей. Таким образом, последние
1000 цифр числа У —те же самые, что и последние 1000 цифр чис-
ла М, а именно:
рРР ... Р
23 раза
Где р — группа из 34 цифр, являющихся последними 34 цифрами
числа Р.
73. Обозначим исходное число М — 10.4 + а, где а — последняя
цифра А4; тогда, полученное из Л1 указанным способом число N бу-
дет, очевидно, равно а Ю6"-1 4-4, где &п — число цифр числа AI.
Образуем теперь выражение
Л1 - ЗА/ = (104 +а) — (3 10®"-’а 4-34) = 74 -(3 • Ю6»-* — 1)д.
Уменьшаемое Л1 в левой части делится на 7 по условию; число 7.4,
очевидно, делится на 7; если мы докажем, что на 7 делится и число
3 • Ю6"-1— 1 (а значит, и выражение (3 • 10s"-1 — 1)а), то на 7
должно будет делиться и число ЗУ, а значит и число N.
Число 10 дает при делении на 7 остаток 3, число 102 — тот же
остаток, что и число 3 • 3 = 9, т. е. остаток 2, а значит, число 103 =
«= 102 10 — остаток 2-3 = 6; число 106 = 103 • 103 дает при деле-
нии па 7 тот же остаток, что и 6 • 6 = 36, т. е. остаток 1, и, значит,
это число имеет вид 7k 4- 1; число 105 = 103 • 102 дает при делении
на 7 тот же остаток, что и 6-2=12, т. в. остаток 5, другими сло-
вами, оно имеет вид 71 4- 5; поэтому
]0«п-1 = i06n—6 . 105 . Ю‘ =
= (7 k 4-l)(7fe + 1) - (7k -1- 1)(7/ 4- 5) = 7 У 4- 5,
ii— 1 раз
т. е. это число дает при делении на 7 остаток 5. Наконец, число
3 106и~1 при делении на 7 дает тот же остаток, что и 3-5=15,
т. е. остаток 1, а значит, число 3 • Ю6"-1 — 1 делится на 7.
Это и доказывает утверждение задачи.
74. Число пулей в конце числа показывает, сколько раз 10 встре-
чается сомножителем в этом числе. Число 10 равно произведению
2 5; в произведении всех целых чисел от 1 до 100 множитель 2 вхо-
дит в большей степени, чем множитель 5. Следовательно, произведе-
ние 1 2 • 3. ..100 делится на такую степень 10 (т. е. оканчивается
на такое число нулей), сколько это произведение содержит множите-
лей 5. Но до 100 имеется 20 чисел, кратных пяти, причем четыре из
них (25, 50, 75 и 100) кратны также 25, т. е. содержат по два мно-
жителя 5. Следовательно, всего в произведении 1 -2-3. ..100 число
5 встретится сомножителем 24 раза; поэтому и нулей в конце этого
произведения будет 24.
75. Первое решение задач а) и б). Решим сначала за-
дачу а). Пусть /4-1, /4-2, ..., / + п будут п произвольных, после-
довательных целых чисел. Подсчитаем для каждого простого числа р
наивысшую степень т, с которой оно входит в произведение п!,
134
и наивысшую степень s, с которой оно входит в произведение (/ + 1.
...(/ +я). Для этого обозначим череэ пц число чисел ряда 1, 2, ...
..п, в которые р входит по крайней мере в первой степени, через
тг — число чисел того же ряда, в которые р входит по крайней мере
во второй степени, и т. д. Тогда показатель, с которым р входит в
nl, будет равен т = mt + /и2 +...
Если теперь S[ — число чисел ряда /-}- 1, ..., t + п, делящихся
на р, si — число чисел этого же ряда, делящихся на р2, и т. д., то
показатель s, с которым р входит в произведение (/ + !)...(/ + «),
равен s = si + з2 •
Но число чисел ряда /+ 1, ..., t + я” делящихся на р, не мень-
ше чем mi. Действительно, среди чисел t + 1, • t + н находятся
также числа t + р, t + 2р, .... t + mtp, а в каждом промежутке меж-
ду t + kp и t + (k + 1)р (k = О, I, 2, .... m, — 1) есть хотя бы
одно число, делящееся на р. Таким образом, sI т<; аналогично
5s Ш2, и т. д., а потому s’> т. Но это означает, что каждый про-
стой сомножитель числа п\ входит в состав числа (/ 4- 1)...(/ + л),
причем в степени, не меньшей чем он входит в «!, т. е. число (/+!).,.
...(/ + п) делится на п\.
б) Произведение первых а сомножителей в nl совпадает с а!;
произведение следующих b сомножителей в силу задачи а) делится
иа 6!; произведение следующих с сомножителей — на с!, и т. д. Так
как а + 6 + с + ... + А^л, то отсюда следует, что п! разделится
на а'.Ь'.. . ./<!
Другое р е ш е н п е з а д а ч а) и б). Решим сначала задачу
б). Показатель т, с которым некоторое простое число р входит в
п!, как мы 'видели, равен т = т\ + ш2 + ..., где т.\ — число чисел
а, кратных р, т2 — кратных р2, и т. д. Но число чисел,
г 1 Г П а 1
Р J
«I а а
— .... —целые части дробей.. .(см. стр. 37). Таким образом,
ряда 1, 2,
кратных р,
1 я
.кратных р2— равно —- пт. д., где
L P2 1
а
_Р2
Пусть теперь р — любое простое число.
т=
L р
Тогда показатель, с которым р войдет в числитель, равен -2_ I 4-
[л 1 L Р J
I + . Показатель, с которым р войдет в знаменатель, равен
Г а 1 , Г а 1 f 1 ! I л
L р J L р2 J L р J Lp2J L р J L р2
Но так как п а + b + ... + /г, то, используя результат задачи 201,
1), мы получим отсюда, что
Т. е. р войдет в числитель в большей степени, чем в знаменатель.
Значит, наша дробь есть целое число.
135
Решим теперь задачу а). Дополним для этого произведение
(Z + !)...(/ +л) до (Z + л)!. По только что доказанному дробь
(/4-п) ... (/ + 1W-1) ... 1 (п.4-0! (/+ 0 •-?(^ + п)
n\t{t~ !)...! “ п!/1 ~ л!
есть число целое.
в) (л!)! есть произведение я! первых целых чисел. Но эти п\
чисел можно разбить на (п.— 1)! групп по п последовательных це-
лых чисел, а произведение чисел каждой из этих групп в силу ре-
зультата задачи а) делится на я!.
г) Пусть рассматриваемые числа будут а, а + d, а + 2d, ...
..., а + (п — l)d. Докажем сначала, что существует такое целое
число k, что произведение kd дает при делении на я! в остатке 1.
Действительно, рассмотрим я!— 1 чисел d, 2d, 3d, ..(я!— l)d.
Ни одно и? этих чисел не делится на я!, так как d взаимно просто
с п\. С другой стороны, никакие два произведения pd и qd, где р,
q— целые числа, меньшие я!, не могут давать при делении па я!
одинаковые остатки, так как иначе разность pd — qd = [р — g)d де-
лилась бы на я!. Таким образом, рассматриваемые п\ — 1 чисел дол-
жны при делении на я! давать п\ — 1 разных остатков, откуда вы-
текает существование числа k, такого, что произведение kd дает при
делении на п! остаток 1: kd = г • п\ + 1.
Обозначим теперь ka через А. Тогда мы имеем:
ka = А,
k(a d) = А + kd — (Д + !)+'• я!,
k(a + 2d) = А = 2kd =» (Д + 2) + 2г • я’,
*[а+ („_ l)d] = А + (n-I)kd == [Д + (/г-1)] + (я —1)г • Ш.
Отсюда следует, что произведение
k " а (а + d) (а Д- 2d)... [а + (л — 1) d]
дает при делении на я! такой же остаток, как и произведение
А (А + 1)(Д + 2)...[Д + (я— 1)]. Но последнее из этих двух произ.
ведений делится на nl в силу задачи a), a kn взаимно просто с я!,
так как, если бы k не было взаимно просто с л!, kd тоже не могло
бы быть взаимно просто с я!.
1000!
76. Число сочетаний из 1000 элементов по 500 равно
, Г10001
+ I 343 I
Так как 7 — простое число, то наивысшая степень, с которой 7 вой-
дет в 1000! (см. второе решение задачи 756), равна ^1^9]+^1229
— 142 + 20 + 2 = 164. Наивысшая степень, с которой 7 вой-
дет в 500!, равиа|299 + [|^] =71 + Ю + 1 = 82. Следо-
вательно, наивысшая степень, с которой 7 войдет в знаменатель, рав-
на 82 • 2 = 164. Таким образом, и числитель и знаменатель содержат
7 в 164-й степени. После сокращения числитель не будет уже содер-
136
, I боб!
1каТь мНоЖп4елем 7, п следоваТельНО, целое число (5Qp;y~не ДелиТ-
ся на 7.
77. а) Число (я—1)! не делится на «'только в том случае,
если п — простое число или если п — 4. Действительно, если п —
составное число, которое можно представить в виде произведения
двух неравных множителей а и Ь, то и а и b меньше п — 1 и, следо-
вательно, входят в состав (п — 1)!; значит, (я—1)! делится на
ab = я. Если п есть квадрат простого числа р, большего двух, то
я—1 = р2—1 > 2р. Поэтому и р и 2р входят в состав (я—1)!;
значит, (я— 1)! делится на р • 2р = 2р2 = 2я. Итак, условию зада-
чи удовлетворяют только числа 2, 3, 4, 5, 7, 11, 13, 17, 19, 23, 29, 31,
37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, т. е. число 4 и все
простые числа меньшие 100.
б) (я—1)! не делится на я2 только в следующих случаях: я
есть простое число, я есть удвоенное простое число, п = 8, я = 9.
Действительно, если я не является ни простым числом, ни удвоенным
простым числом, ни квадратом простого числа и не равно ин 8, ни
16, то п можно представить в виде я = ab, где а и b — различные
числа, не меньшие 3. Мы будем считать, что b > а, а 3. В таком
случае числа a, b, 2а, 2Ь, За все меньше я — 1 и при этом а, b и 2Ь
заведомо различны, а из чисел 2а и За хотя бы одно отлично ог
чисел а, b и 26. Таким образом, в (я— 1)! входят множители а, Ь,
2Ь, 2а или а, 6, 26, За (а может быть, входят и все множители а, 6,
26, 2а, За); во всех случаях (я — 1)! делится на а262 = я2.
Далее, если я = р2, где р есть простое число большее 4, то
я — 1 > 4р и (я —1)! содержит множители р, 2р, Зр, 4р и. следо-
вательно, делится на р4 = я2. Если я = 2р, то (я—1)! не делится
на р2, а, следовательно, и па я2; когда я = 8 или 9, то (п— 1)! не
делится на я2 (7! не делится на 82 и 8! не делится на 92); когда я =
= 16, то (я—1)! делится на я2 (15! содержит множители 2,4 —
= 22, 6 = 3 • 2, 8 = 23, 10 = 2 - 5, 12 = 22 • 3, 14 = 2-7 и, следо-
вательно, делится на 2[+2+i+3+i+s+i _ 211 = 162 • 23).
Таким образом, условию задачи б) удовлетворяют все числа,
удовлетворяющие условию задачи а), и, кроме того, числа 6, 8, 9,
10," 14, 22, 26, 34, 38, 46, 58, 62, 74, 82, 86, 94, т. е, все простые числа,
все удвоенные простые числа и числа 8 и 9.
78. Предположим, что число я делится на все числа яг, меньшие
пли равные У п. Составим общее наименьшее кратное К всех таких
чисел т. В него, очевидно, будут входить все простые числа, мень-
шие Д/я, причем каждое простое число р в такой степени k, что
Рк<Уп, но pfi+1> У п. Предположим, что число простых чисел,
меньших У п, равно I; эти простые числа мы обозначим через
Рь Ра> .. ., Pi- Наименьшее общее кратное К всех чисел, меньших
У~п,представляет собой произведениерj'p*2... р*<, где ki таково, что
Р,1 С угя< р*1"^1, k2 таково, что р%* < Уп < р*1^1 , и т. д.
Перемножив теперь I неравенств
/я < р*‘+‘, Уп < и...Уп < р?+1,
получим;
(Уп)1<Р^1Р^...Р^.
137
Но Р1‘+’р2а+’ ... P?'+1 = Pi'pI* •• • Pl1 • Р1Рг ••• Pl ибо
Pl'P^1 •.. Phil — К, а следовательно, P\Pi .. .pi С К. Таким образом,
имеем:
(УИ)г < №.
Но так как согласно нашему предположению п должно делиться
на К, то Л п; следовательно, (У п)1 < п2._Отсюда I < 4; так как
pi, ..., pi — все простые числа, меньшие Ул, то р< = 7> Уп (чет-
вертое простое число есть 7) и п < 49.
Перебирая все числа, меньшие 49, мы без труда убеждаемся, что
из них требуемым свойством обладают только числа 24, 12, 8, 6,
4 и 2.
79. а) Обозначим пять последовательных целых чисел через
п — 2, л—1, л, л 4-1, л + 2.
Тогда
(л — 2)2 + (л — I)2 + л2 + (л + I)2 +(л + 2)2 =
= 5л2 + 10 = 5(л2 + 2).
Если бы число 5(л2 + 2) было полным квадратом, то оно де-
лилось бы на 25, следовательно, п2 -f- 2 делилось бы на 5. Но это
возможно лишь в том случае, если последняя цифра числа л2 есть
либо 8, либо 3, а никакой квадрат целого чи<;ла ие оканчивается на
эти цифры.
б) Из трех последовательных целых чисел одно наверное де-
лится на 3, второе дает при делении на 3 остаток 1 и третье —
остаток 2 или же, что равносильно, остаток—1. При перемножении
чисел остатки от деления их на какое-либо число тоже перемножа-
ются; в самом деле,
(pk -|- г) (qk + s) «= pqk2 + pks -|- qkr -ф rs «= k(pqk + ps-^-qr) -|- rs.
Поэтому, если число при делении па 3 дает остаток 1, то любая его
степень при делении на 3 тоже дает остаток 1; если же число при
делении на 3 дает остаток—1, то любая его нечетная степень при
делении на 3 дает остаток— 1, а любая четная — остаток 1.
Таким образом, из трех четных степеней последовательных целых
чисел одна делится на 3, а две другие дают при делении на 3 оста-
ток 1. Следовательно, сумма четных степеней трех последовательных
целых чисел дает при делении на 3 остаток 2, или, что то же самое,
остаток — 1. А мы уже видели, что такой остаток не может дать
при делении на 3 четная степень никакого целого числа.
Примечание. Интересно отметить, что в приведенном дока-
зательстве.нигде не используется тот факт, что четные степени, в кото-
рые возводятся три числа, одинаковы. Таким образом, имеет место
следующее предложение — более общее, чем утверждение задачи:
сумма четных степеней (может быть различных!) трех последова-
тельных целых чисел не может быть четной степенью никакого
целого числа.
в) Как мы видели в решении задачи б), сумма четных степеней
трех последовательных целых чисел дает при делении на 3 остаток 2.
Отсюда вытекает, что сумма четных степеней девяти последователь-
138
ных чисел дает при делении на 3 остаток 2 + 2 4- 2 = 6, т. е. де-
лится на 3. Докажем теперь, что сумма одинаковых четных степеней
девяти последовательных целых чисел не делится на З2 = 9; отсюда
будет сразу следовать утверждение задачи .
И? девяти последовательных целых чисел одно обязательно де-
лится на 9, одно дает при делении на 9 остаток 1, одно — остаток 2,
и т. д. Отсюда следует, что если 2k есть общая степень в которую
возводятся девять чисел, то наша сумма дает при делении на 9 тот
же самый остаток, что и сумма
О -j- р* + '22* + Э2* + 4s* + 52'1 + б2'* + 7г" + 82Л,
или сумма
2(1*4 4*4-7*)
(так как З2 и 62 делятся на 9; I2 и 82 = 64 дают при делении на 9
остаток 1; 22 = 4 и 72 — 49 дают при делении на 9 остаток 4;
42 = 16 и 52 = 25 дают при делении на 9 остаток 7).
Отметим теперь, что I3 = 1, 43 = 64 и 73 = 343 все дают при
делении па 9 остаток 1. Отсюда следует, что если k — 31, то
1* + 4* + 7h — 1' 4- 64' 4- 343' дает при делении на 9 тот же оста-
ток, что и сумма 1' + 1' 4- 1' = 3, т. е. не делится на 9; если k —
= 31 + 1, то 1* 4- 4* + 1к — 1' • 1 4- 64' • 4 4- 343' • 7 дает при деле-
нии на 9 тот же остаток, что и сумма 1 • 1 4- 1 • 4 + 1 • 7 = 12, т, е.
не дедится на 9; если k — 31 4- 2. то 1* 4- 4* 4- 7* ~ 1' • 1 4- 64' 42 +
4- 343' • 72 дает при делении на 9 тот же остаток, что и сумма 1 • 1 +
4- 1 • 16 + 1 • 49 = 66, т. е. не делится на 9.
80. а) Сумма цифр каждого из чисел А и В равна
14-24-3 + 44-54-64-7 = 28?
отсюда следует, что оба числа дают при делении на 9 остаток 1
(каждое число дает при делении на 9 такой же остаток, как и сумма
А
его цифр). Но если бы было “д"= п, или, что то же самое, А = пВ,
где п — целое число, отличное от 1, то из того, что В = 9N 4- 1,
следовало бы, что А = пВ = 9Л1 4- п; таким образом, п должно да-
вать при делении на 9 остаток 1. Наименьшее такое число п
д
есть 10; но 10,так как оба числа А и В состоят из 7 цифр.
б) Обозначим искомые числа через N, 2ЛГ, 3N. Каждое целое
число дает при делении на 9 такой же остаток, кек и его сумма цифр;
поэтому сумма М + 2# + 31V дает при делении на 9 такой же оста-
ток, как и сумма 1 + 2 + 3 + ... + 9 =45, т. е. 6Л7 (а следователь-
но, и 3N) делится на 9.
' Так как ЗЛ' трехзначно, то первая цифра числа W не может быть
больше 3; поэтому последняя цифра N не может равняться 1 (так
как в этом случае 2N оканчивается цифрой 2, а ЗЛГ — цифрой 3
и все три цифры 1, 2, 3 оказываются занятыми). Число N не может
также оканчиваться цифрой 5 (в этом случае 2Л' оканчивалось бы
нулем). Предположим теперь, что последняя цифра N есть 2; в та-
ком случае последние цифры 2/V и 3^ равны соответственно 4 и 6.
Для двух первых цифр 3N остаются возможными значения 1, 3, 5,
7, 8 и 9; так как сумма всех цифр ЗЛ' кратна 9, то первые две цифры
3N есть 3 и 9 или 5 и 7. Проверяя все представляющиеся случац,
находим одну тройку чисел, удовлетворяющих условию задачи; 192,
139
384, 576. Аналогично исследуются случаи, когда N оканчивается на 3,
4, 6, 7, 8 или 9; при этом обнаруживаются еще три решения задачи:
273, 546, 819; 327, 654, 981 и 219, 438, 657.
81. Полный квадрат может оканчиваться только цифрами 0, 1, 4,
9, 6 и 5. Далее, квадрат каждого четного числа, очевидно, делится
на 4, а квадрат нечетного числа дает при делении на 4 остаток 1
((2k)2 = 4k2, (2k + I)2 = 4(й2 + &) + 1); поэтому квадрат никакого
числа не может оканчиваться цифрами 11, 99, 66 и 55 (числа, окан-
чивающиеся двумя цифрами 11, 99, 66 или 55, дают при делении на 4
соответственно остатки 3, 3, 2 и 3). Рассмотрим, наконец, какие
остатки может давать квадрат целого числа при делении на 16. Каж-
дое целое число можно представить в одном из следующих видов;
86, 86 4z 1, 86 4z 2, 8k 4z 3 или 8k 4- 4;
квадраты этих чисел имеют вид
16- (462), 16(462 ±6) + 1, 16(462±26) +4,
16(462±36) 4-9 или 16(4624- 46 4- 1).
Таким образом, мы видим, что квадрат целого числа или делится на
16 или дает при делении иа 16 один и? остатков 1, 4 и 9. Число же,
оканчивающееся цифрами 4444, дает при делении на 16 остаток 12 и,
следовательно, не может быть полным квадратом.
Итак, если полный квадрат оканчивается четырьмя одинаковыми
цифрами, то эти цифры — четыре нуля (например, 1002 = 10 000).
82. Обозначим стороны прямоугольника через х и у, а диаго-
наль— через г; тогда по теореме Пифагора будем иметь:
х2 + у2 = г2.
Нам надо доказать, что произведение ху делится на 12. Покажем
сначала, что это произведение делится иа 3, а затем — что оно де-
лится на 4. Так как
(3* 4-l)s == 3(3*2+ 2Л) + 1 и (36 4- 2)2 = 3(362 4- 46 + 1) 4-1.
то квадрат каждого числа, не кратного 3, дает при делении на 3
остаток 1. Поэтому, если бы ни х ни у не делились на 3, то сумма
х2 + у2 давала бы при делении на 3 остаток 2 и поэтому не могла бы
быть равна квадрату никакого целого числа. Следовательно, если
х2 + У2 равно квадрату целого числа z, то хотя бы одно из чисел
х и у делится на 3, а значит, и ху делится на 3.
Далее ясно, что оба числа х и у одновременно нечетными быть
не могут; если х — 2т + 1, у — 2п + 1, то
х2 + у2 •= 4т2 + 4т 4- 1 + 4п2 + 4п 4-1 = 4(т2 + т п2 + п) 2
не может равняться квадрату никакого целого числа (квадрат нечет-
ного числа нечетен, а квадрат четного числа делится на 4). Если
и х, и у — четные числа, то их произведение делится на 4. Предполо-
жим теперь, что х четно, а // — нечетно: х = 2т, у = 2п 4- 1- Чис-
ло z при этом будет нечетным (ибо г2 = х2 + у2 нечетно): z = 2р 4-.
+ 1. В этом случае имеем:
(2m)2 = (2р 4- I)2 - (2п 4-1)2 = 4р2 4- 4р 4- 1 - 4п2 - 4« - 1,
или 2
« ” р(р+1) — «(«+1).
140
Отсюда вытекает, что т* четно (произведения последовательных целых
чисел р(р + 1) и п(и + 1) оба четные); следовательно, т четно
и х = 2т делится на 4. Значит, и в этом случае произведение ху
делится на 4.
83. По формуле решения квадратного уравнения имеем:
_ ь + УЬ2 — 4ас ,
2а
следовательно, для того чтобы корни уравнения были рациональны,
надо, чтобы выражение Ь2 — 4ас являлось полным квадратом. Поло-
жим & = 2n + 1, а = 2р -ф- 1, с = 2q + 1; в таком случае будем
иметь:
b2~ 4ас *= (2/1 + l)s-4(2p+ 1) (2? + 1) = 4п* + 4п —
— 16pq — 8р — Sq - 3 = 8 (n(n.L^
2pq—p~q—l] + 5.
Так как это число нечетно
п (п '4- 1)
. 2
есть
целое число, ибо произве-
дение двух последовательных целых чисел
всегда четно), то оно мо-
жет быть квадратом только нечетного числа. Но каждое нечетное
число можно представить в виде 4k ± 1; квадрат этого числа равен
(4ft ± 1)» 16ft2 ± 8ft + 1 = 8(2ft2 ± ft) + 1
и, следовательно, всегда дает при делении на 8 остаток 1. Посколь-
ку число Ь2— 4ас дает при делении на 8 остаток 5, оно не может
являться полным квадратом.
84. Имеем:
1 , 1 , 1________3+ Ч-б/г + 2
п п + 1 "г п + 2 — п (п 1) {п + 2) ’
Числитель нашей дроби не делится-на 3, а знаменатель делится,
так как он является произведением трех последовательных целых
чисел. Следовательно, в знаменателе есть множители, отличные от
2 и 5, а потому в рагложении получится бесконечная перио-
дическая десятичная дробь.
Из двух целых чисел п и и + 1 одно должно быть четным. Если
четно n+ 1, то п нечетно, следовательно, нечетно Зп2, а потому и весь
числитель. Если же п четно, то и п + 2 делится па 2 и, следовательно,
внаменатель наверняка делится на 22; числитель же делится только
иа 2, так как если п = 2ft, то
Зп2 + 6п+ 2 =. 12ft2 + 12ft + 2 = 2(6fts + 6ft+ 1).
Поэтому знаменатель полученной после сокращения дроби не будет
взаимно прост с 10, и десятичная дробь будет смешанной перио-
дической.
И!
85. а), б). Приведем все слагаемые в сумме
М =*+••• + — М
2 п \
_1_
п
---Г“о + • • • + —Г—
п + 2 п + т
к общему знаменателю. Из всех дробей, входящих в нашу сумму,
рассмотрим ту, в знаменателе которой стоит самая высокая степень
двух (такая дробь может быть только одна). Тогда во все осталь-
ные дроби число 2 войдет дополнительным множителем, в то время
как в этой дроби дополнительным множителем обязательно будет
число нечетное. У всей дроби Л1 (или N) знаменатель есть, конечно,
число четное, а числитель, как мы видим, состоит из суммы некото-
рого числа четных чисел и одного нечетного. Следовательно, числи-
тель есть число нечетное, а потому вся дробь не может быть целой.
в) Рассмотрим дробь в сумме Л, в знаменателе которой стоит
самая высокая (A-я) степень числа 3. Так как у нас знаменателями
являются только нечетные числа, то дробь -—в сумме отсут.
Л ’ о
ствует. Поэтому при приведении суммы дробей к общему знаменате-
лю дополнительные множители всех дробей, кроме рассмотренной,
будет делиться на 3. а дополнительный множитель этой дроби не бу-
дет делиться на 3. Следовательно, в сумме получим дробь, знамена-
тель которой делится на 3,
а3 + 2а
86- Дробь + За2+ !
а4 4- За2 J- 1
но с дробью —аз 2а
а числитель не
сократима или
t а2 + 1
” а + а’Ч- 2а’
делится.
несократима одновремен-
или — одновременно с
дробью
°2 + 1 П Л fl2 + 1
аз 2а‘ ДР°°Ь аз 2а сокРатима или несократима одно.
а34-2а а
временно с дробью —а-j- j > или —одновременно с дробью
а „ , а
дЗ Дробь a2_|_ f сократима или несократима одновременно с
' а2 + 1 , 1 1
дробью ——• “ “ т —. или — одновременно с дробью—, которая
при целом а, очевидно, несократима.
б) Если как число ч = 5л + 6, так и число з — 8л + 7 делятся
на целое число d, то на d делится также их разность р = з — ч =
= Зп + 1 и разность pt — ч — р = 2п + 5, а также разности pj =
— Р — Pi — п — 4; рз = Pi — Рг = п + 9; pt = Рз — рз «= 13. Таким
образом, на d обязательно должно делиться (простое!) число 13, от-
куда видно, что d может иметь лишь одно только значение 13. То,
что значение d = 13 возможно, легко показать на примере; так, если
5л + 6 26
л = 4, то дробь gn у = -дд- сократима на 13.
87. Ясно, что достаточно доказать утверждение задачи в пред-
положении, что во второй раз мы начали чтение со второй циф-
ры первоначального числа: ведь, сдвигаясь подобным образом на
одну цифру, мы можем последовательно перейти от заданной
начальной цифры числа к любой другой, принимаемой в новом чтении
142-
За начальную; еблй же На каждом шаге мы будем йоДучать дёлящеё-
ся на 27 число, то оно будет делиться на этот множитель и после
любого количества подобных «шагов». Итак, пусть первая цифра
прочитанного первоначально 1953-значного числа ai » а; образуемое
остальными цифрами 1952-значиое число обозначим через В. В таком
случае наше «первое» число равно а 101952 + В, а прочитанное, на-
чиная со 2-й цифры (с начала числа В), число будет равно В • 10 + а.
Нам дано, что число а 101952 4- В делится на 27. Но число
101952 _ 1 состоит из 1952 девяток; разделив это число на 9, мы полу-
чим число из 1952 выписанных подряд единиц, дающее при делении
на 3 такой же остаток, как и сумма его цифр 1952, т. е. остаток 2;
следовательно, число 101952 — 1 дает при делении на 27 остаток
2 • 9 = 18, а число 101Э52 — остаток . 19. Поэтому, обозначив Остаток
от деления числа В иа 27 через Ь, мы получим, что а 101952 + В
дает при делении на 27 такой же остаток, как и число 19а + Z»; та-
ким образом, условие задачи утверждает, что число Л1 = 19а + b
делится на 27.
Перейдем теперь к «новому» числу В • 10 +а. Это число даёт
при делении па 27 тот же остаток, что и число N = 10& + а; таким
образом, наша задача сводится к доказательству того, что если М —
= 19а + b делится на 27, то и N — 10В + а делится на 27. Но пос-
леднее утверждение очевидно, ибо 10Л1 — Л' = 189а делится на 27
(так как 189 = 27 • 7), a N = 10Л1 — 189а.
88. Очевидно, что десятичная запись всех чисел 5", где п — на-
туральное, оканчивается цифрой 5; поэтому и запись числа а = 51000
оканчивается цифрой 5 (не нулем!). Предположим теперь, что в за-
писи числа а встречаются и нули; пусть первый из них (считая с
конца!) стоит на i-м месте. Ясно, что число 51000 • 10i-1 оканчивается
цифра ми 5000 ... 0; поэтому i—1 последних цифр десятичной запи-
i—1 нулей
си суммы О] — 51000 + 51000 • 1О'~1 не отличаются от (— 1 последних
цифр числа а (т. е. все они отличны от нуля), а i-я с конца цифра
числа а, есть 5 (т. е. тоже не нуль!). Исправив таким образом i-ю циф-
ру (для чего нам пришлось заменить число а числом аь десятичная
запись которого содержит больше цифр), мы перейдем к следующей
от конца цифре (разумеется, цифре числа aj, которая равна нулю
(если только такая цифра есть), и точно таким же путем исправим
и ее: если равна нулю /-я от конца цифра числа ai (где, конечно, j >
> t), то это число мы заменим числом a2 = at + 51000 • КЯ-1, которое
также делится на 51000 и у которого уже / последних цифр отличны
от нуля (на /-м от конца месте стоит цифра 5).
Если продолжая этот процесс, мы придем к какому-то числу ak
(где & = 0, 1, 2, ...; под а0 мы понимаем само число а = 51000), де-
сятичная запись которого не содержит нулей, то утверждение задачи
доказано; но так как число цифр чисел а0 = а, а^ а2,... все время
возрастает, то наш процесс может и никогда не кончиться. Однако
если мы дошли в наших построениях до какого-то числа а,, 1000 пос-
ледних цифр которого отличны от нуля, то далее мы можем ине про-
должать. В самом деле, число а< = 1010ад А + В, где десятичную
вались числа В составляют 1000 последних цифр числа at (и, значит,
все цифры числа В отличны от нуля), а десятичная запись числа А
состоит из всех предшествующих 1000-4 цифр числа а(. Отсюда ела-
Яует, что
в. 4,-10’“» А,
141
и, значит, число В делится на 51000 (поскольку иа 51000 делятся и Л/
и 1О1000 А = 21000 • 51000 • 4).
89. Числа нашего ряда имеют вид 1 + 104 + 108 + ... + Ю4*.
Рассмотрим наряду с этими числами числа 1 + 10* + 104 + 10е <
...+ 102*. Непосредственной проверкой нетрудно убедится в том,
что
104*+4 — 1 = (104— 1) • (1 + 104 + 108 + ,..+ 104*).
102*+2 — 1 = (102—1) • (1 + 102 + 104 + .,.+ 102*).
Кроме того, очевидно,
]04*+4 — 1 = (Ю2*+2— J) (102*+2 + 1).
Сопоставляя все эти равенства, получаем:
104ft+4 — 1 = (104 — 1) (1 + 104 + 108 + . .. + 10*) =•
= (102 — 1) (1 + 102 + 104 + ... + 102*)(102*+2 + 1),
104—1
или, так как 'jpa = 102 + 1 = 101,
(1 + 104 + 108 + ... +104ft) • 101 =
= (14- IO2 4- 104 4- ...+ 102*) (102*+2 + 1).
Так как 101 есть простое число, то или 1 + 102 + 104 4- ... + Ю2А,
или 102*+2 + 1 делится на 101; при этом, если k>\, то частное боль-
ше 1. Сократив на 101, мы получим, что число 1 + 104 + 108 4-•..
.. . + 104* при k > 1 разлагается по крайней мере на два множи-
теля, что и требовалось доказать. При k = 1 мы имеем число 104 +
4- 1 = 10001, которое тоже является составным (10 001 — ТА 137).
Примечание. Точно так же можно доказать, что и все
числа ряда
100... о 100 ... 01, 100 ... 0 100 ... 0 100 ... 01, ...
(2^4-1) раз (2&4-1) раз (2fe-J-l) раз (2fe|- 1J раз (264-1) раз
являются составными.
90. Заметим, что
- (22”—1 4" 1) (з2”-2 4- 1) (22"“2- 1) = ...
... = (22”“1 4- 1) (2-”“2 4- 1) (22"-3 + 1) ... (22 4- 1) (2 + 1)
(в силу формулы а2 — Ьг *= (аЬ) (а— Ь); последний множитель
2 — 1 = 1 можно отбросить). Таким образом, число 22"—1 =(22П4"
4-1)—2 делится на все предыдущие числа нашего ряда. Отсюда
следует, что если 22"4- 1 и 22Й4- 1, где k < п, имеют общий делитель,
то на этот общий делитель должно делиться и число 2. Но 2 не мо-
жет быть общим делителем двух чисел последовательности, так как
все эти числа нечетные; следовательно, каждые два числа последо-
вательности являются взаимно простыми.
91. 2п, разумеется, не может делиться на 3. Если 2" дает при
делении на 3 остаток 1, то 2П — 1 делится иа 3; если 2" дает при
144
делении Иа 3 остаток 2, то 2" 4- 1 делится на 3. Поэтому во всех
случаях одно из двух чисел 2" — 1 и 2п4-1 делится иа 3, и следо-
вательно, если оба эти числа больше 3, то они не могут быть одно-
временно простыми.
92. а) Если бы простое число р > 3 давало при делении на 3
остаток 2, то 8р — 1 делилось бы на 3. Поэтому число р должно да-
вать при делении на 3 остаток 1; но в этом случае 8р + 1 делится
на 3. Если же р = 3, то 8р + 1 =25 — тоже составное число.
б) Если р не делится на 3, то р2 дает при делении на 3 остаток
1 (см. решение задачи 796)) и, следовательно, 8р2 + 1 делится на 3.
Таким образом, должно быть р = 3, 8р2 + 1 = 73. Но в этом слу-
чае и число 8р2 — 1 =71 — простое число.
93. Простые числа кроме 2 и 3 дают при делении на 6 остаток
1 или 5, ибо если бы число давало при делении иа § остаток 2 или
4, то оно было бы четным, а если бы оно давало остаток 3, то де-
лилось бы на 3. Таким образом, любое простое число, большее 3,
можно записать в виде 6м + 1 или 6м + 5. Квадраты этих выраже-
ний имеют вид 36м2 + 12и + 1 и 36м2 + 60м + 25. В обоих случаях
при делении на 12 получается в остатке 1.
94. Из трех чисел, имеющих вид 6м + 1 или 6м + 5 (см. преды-
дущую задачу), по крайней мере два имеют одинаковый вид. Сле-
довательно, их разность, равная d или 2d, где d — разность прогрес-
сии, делится на 6; поэтому d делится на 3. Кроме того, d как раз-
ность двух нечетных чисел делится на 2, поэтому d делится на 6.
(См. также решение задачи 95а).)
95. а) Так как простые числа (кроме 2)—-числа нечетные, то
разность прогрессии — число четное. Далее, если бы разность прог-
рессии не делилась на 3, то три члена прогрессии at, ai + d, at + 2d
все давали бы разные остатки при делении на 3 (разность никаких
двух из них не делится на 3) и, следовательно, хотя бы одно из них
делилось бы на 3, что невозможно, так как все члены прогрессии по
условию — простые числа (если ai = 3, то о, + 3d тоже делится на
3). Точно так же, если бы d не делилось на 5, то все числа alt + d,
Ci + 2d, О] + 3d и + + 4d давали бы при делении на 5 разное остат-
ки и, следовательно, одно из них делилось бы на 5. Аналогично по-
казывается, что если все члены арифметической прогрессии — прос-
тые, то разность прогрессии должна делиться на 7. Итак, разность
d искомой прогрессии должна быть кратна 2 • 3 • 5 • 7 = 210; d =
= 2106.
По условию задачи
Ою s==i Oi 4- 9d = Д1 + 18906 <С 3000.
Но это неравенство невозможно при k 2; значит, 6=1, Отсюдй
следует, что а, < 3000—-9d = 1110.
Далее 210=11-19+1; следовательно, (т+1)-й член прог-
рессии можно представить в виде
am+1 = a,-+ (11-19 4-1) • т — 11 • 19m4- (ai + m).
Отсюда следует, что если О| дает при делении на II остаток 2, то
«io делится на 11; если а,- дает при делении на 11 остаток 3, то а9
делится на 11, и т. д. Таким образом, доказываем, что ах не может
давать при делении на 11 остаток 2, 3, 4, ... или 10. Если at отлич-
но от 11, то ai не может делиться иа 11 (ибо О] — простое); значит,
°i или равно 11, или дает при делении на 11 остаток 1. Далее,
Ю Д. О. Шклярский я др, 145
йСПоЛьзуя то, что 216 = 13 • 16 + 2 и; следоватеЛьйб,
am+i = О] + (13 • 16 + 2)т = 13 • 16m + (at + 2m),
можно показать, что а, при делении на 13 может давать только
остатки 2, 4, 6, 8, 10 или 12. Учитывая, что О| нечетно (ибо все чле-
ны прогрессии нечетны), мы заключаем, что а, или равно 11 или име-
ет один из следующих видов:
2 • 11 - 13/ + 23 = 286/ + 23, 286/ + 45, 286/ + 67,
286/+ 155, 286/+ 177 или 286/ + 199.
Поскольку at < 1 ПО, нам остается только проверить следую-
щие возможные значения щ:
И; 23, 309, 595, 881; 45, 331, 615, 903; 67, 353, 637, 925; 155, 441, 727,
1 013; 177, 463, 749, 1 035; 199, 485, 771, 1 057.
Простыми из этих чисел являются только:
11 , 23, 881, 331, 67, 353, 727, 1 013, 463 и 199.
Проверив соответствующие 10 прогрессий, мы найдем единствен-
ную прогрессию, удовлетворяющую условиям задачи:
199, 409, 619, 829, 1 039, 1 249, 1 459, 1 669, 1 879, 2 089.
б) Задача решается аналогично задаче а). Прежде всего, если
щ отлично от 11, то совершенно аналогично решению задачи а) по-
казывается, что знаменатель d прогрессии должен быть пропорцио-
нален 2 • 3 • 5 • 7 • 11 = 2 310 (d = 2 310£); отсюда вытекает, что
а ;1 = + + 23 100А > 20 000.
Остается исследовать случай щ — 11; здесь можно толь-
ко утверждать, что d = 210/?. Воспользовавшись тем, что 210 =
= 13-16 + 2, мы сможем записать следующее выражение для об-
щего члена прогрессии;
а„+1 = 11 + (13 • 16 + 2)Ап = 13(16/гп + 1) + 2(^п—1).
Но при k = 1, 2, 3, 4, 5, 7, 8, 9, 10 удается подобрать такой
номер п <_ 10, что kn — 1 делится на 13 и, следовательно, on+i
делится на 13 и не является простым; это значение п будет соответ-
ственно равно 1, 7, 9, 10, 8, 2, 5, 3, 4. Если же k = 6, d = 210 6 =,
= 1 260, то
«4 = 11 +3-1 260 = 3791
делится па 17. Таким образом, если а; = 11, то k > 10, а следова-
тельно, d 2 100 и опять в») > 20 000.
Примечание. В задачах а) и б), в соответствии с обычным
употреблением термина «простое число», мы считали все члены прог-
рессии положительными. Если же не требовать этого (т. е. называть
«простым» такое целое число п, которое не имеет делителей, отлич-
ных от ±1 и ±п), то удовлетворяющие условиям задачи б) прогрес-
сии существуют (вот пример такой прогрессии— 11, 199, 409, 619,
829, 1039, 1249, 1459, 1669, 1879, 2089).
96. а) Если два неравных числа отличаются одно от другого не
больше чем на 4, то они не могут иметь общих делителей, больших 4,
не
Таким образом, два числа из наших пяти последовательных чисел
могут иметь или общин делитель 2, или общий делитель 3, или об-
щий делитель 4, или быть взаимно простыми. Из пяти последователь-
ных чисел по крайней мере два будут нечетны; из двух последователь-
ных нечетных чисел по крайней мере одно не будет делиться на 3.
Следовательно, среди наших чисел имеется хотя бы одно нечетное
число, не делящееся иа 3; это число заведомо будет взаимно просто
с остальными четырьмя числами.
б) Решение этой задачи близко к решению задачи а), но значи-
тельно сложнее. Если два неравных числа отличаются друг от дру-
га не больше чем на 15, то они не могут иметь общих делителей
больших 15. Так как два числа заведомо взаимно просты, если они
не имеют общих простых делителей, го, для того, чтобы доказать
нашу теорему, достаточно показать, что среди 16 последовательных
целых чисел можно найти число, не имеющее с остальными 15 чис-
лами — общих делителей 2, 3, 5, 7, и 13: это число и будет взаимно
просто со всеми остальными.
Прежде всего нз 16 чисел вычеркнем как не удовлетворяющие
нашим требованиям восемь четных чисел; после этого у нас останется
восемь последовательных нечетных чисел. Из восьми последователь-
ных нечетных чисел, очевидно, на 3 делятся или 1-е, 4-е, 7-е, или 2-е,
5-е, 8-е, или 3-е, 6-е; на 5 делятся или 1-е и 6-е, или 2-е и 7-е, или
3-е и 8-е, или же только одно число; на 7 делятся или 1-е и 8-е, или
же только одно число; на 11 и 13 делится не больше одного чис-
ла. Если среди наших восьми последовательных нечетных чисел име-
ется не больше пяти чисел, делящихся па 3, или па 5, или на 7, то
среди этих восьми чисел найдется число, не делящееся ни на 3, ни
на 5, ни на 7, ни па 11, ни на 13; это число заведомо будет взаимно
просто со всеми остальными. Рассмотрим теперь все те случаи, когда
чисел, делящихся или на 3, или на 5, или на 7, будет не меньше 6.
Пусть среди наших восьми нечетных последовательных чисел на
3 делятся три числа; тогда на 5 могут делиться два из оставшихся
чисел только в том случае, если одно нз крайних чисел делится на 3,
а второе — на 5. Вычеркнув эти пять чисел, мы оставим 2-е, 5-е и
6-е числа, или же 7-е, 4-е, и 3-е числа. Рассмотрим сначала первый
случай. 2-е, 5-е и 6-е нечетные числа являются в ряду всех 16 после-
довательных чисел 4-м, 10-м и 12-м или 3-м, 9-м и 11-м числами.
Ни одно из этих чисел не может иметь ни с одним из остальных 15
чисел общий делитель 13, так как каждое из остальных чисел от-
личается от него меньше чем на 13. Следовательно, если эти три чис-
ла не делятся ни на 3, ни на 5, то одно из них (а именно, то, которое
не делится ни на 7, ни на 11) будет взаимно просто со всеми осталь-
ными числами. Точно так же проводится доказательство и в том
случае, когда после вычеркивания чисел, делящихся на 3 и на 5,
остаются 3-е, 4-е и 7-е числа.
Если из наших восьми чисел на 3 делятся три числа, то на 7 ие
могут делиться никакие два из оставшихся. Если же на 3 делттся
только два числа, 3-е и 6-е, то возможно, что из оставшихся на 7 де-
лятся два, а именно 1-е и 8-е, и на 5 делятся два: 2-е и 7-е. Вычерк-
нув эти шесть чисел, мы оставим из наших восьми нечетных чисел
4-е и 5-е, которые не будут уже делиться ни иа 3, ни на 5, ни на 7.
Оба эти числа будут взаимно простыми с каждым иэ остальных 15
чисел нашей последовательности, так как каждое из остальных чисел
отличается от них меньше чем на 11 и поэтому не может иметь с
ними общий делитель 11 или 13.
10*
147
Итак, мы полностью доказали, что из 16 последовательных
целых чисел всегда можно выбрать одно, взаимно простое с ос-
тальными.
Примечание. Аналогично, но более просто доказывается,
что из 8 или из 10, или из любого другого числа, меньшего 16,
последовательных целых чисел всегда можно выбрать одно, взаимно
простое с остальными. Для 17 чисел это предложение уже неверно:
например, среди 17 последовательных чисел от 1 184 до I 220 нет
ни одного взаимно простого со всеми остальными. По-виднмому, и
для любого другого числа k, большего 16, можно найти k последо-
вательных целых чисел, среди которых нет ни одного взаимно прос-
того со всеми остальными; однако доказательство этого общего пред-
ложения, как будто, неизвестно.
97. Искомое число будет равно произведению At • Bt, где Ai
состоит из 666 цифр 9, а В\— из 666 цифр 2. Но Ai на 1 меньше
числа 10666, выражаемого единицей с 666 нулями. Поэтому умножить
число В1 на это число — то же самое, что умножить Bt на 106и (при
этом получится число, состоящее из 666 двоек и 666 нулей) и из ре-
зультата вычесть число Bt. Нетрудно видеть, что получаемая раз-
ность будет иметь вид 22 ... 2177 ... 78.
665 раз 665 раз
98. Число 777 777 делится без остатка на 1061 и дает в частном
777. Поэтому число 777... 700000 дает при делении на 1001 в
996 раз
частном
777000777000 ... 77700000.
Грузда 7770S3повторяется 166 раз
Тах как, кроме того, число 77 777 дает при делении на 1001 в
частном 77 и в остатке 700, то частное от деления А иа 1 001 имеет
вид
777000777000 ... 77700077,
группа 777000 повторяется 166 раз
а остаток равен 700.
99. Так как число 222 222 не является полным квадратом, то
десятичная запись искомого числа имеет вид 222222а7а8 ... ап’ где
п7, а8, ..., ап — какие-то неизвестные нам цифры.
Предположим сначала, что число п цифр искомого числа четно:
п — 2k. Будем теперь извлекать корень из этого числа по обычным
правилам: _____________________
j/-22 22 22 а7а8 ... а2й_ia2k = 471 “*05
16
87 I 6 22
7)609
941 13 22
1 941
9424 3 81 а7п8
4 3 76 9 6
942805 XjXjXg а,а1аацац
5 4714026
148
'(пятая цифра результата есть 0, так как Xi, очевидно, может быть
равно только 4 или 5 и, следовательно, меньше 9; по аналогичной
причине шестая цифра, если она последняя, есть 5).
Остаток равен нулю, если ад = 4, а10 = 0, ац = 2, ац = 5;
Xi = 4, Хд = 7, х3 = 1, откуда легко выводим ад = 6 + 1 = 7, а7 =
= (7 + 9)—10 = 6. Таким образом, наименьшее число, имеющее
четное число цифр и удовлетворяющее условию задачи, есть
222 222 674 025 = 471 4052.
Аналогично рассматривается случай, когда п — 2k + 1 нечетно:
"J/"2 22 22 2a7asOg ... ао^ао&-|-1 — 149071 ...
_£
24 I 1 22
4 I 96
289 26 22
9 26 01
29807 21 2a7asas
7 20 86 4 9
298141 1 298142 xix.2x3x4aioau 2 9 8 1 4 1
Так как число, образованное цифрами хь Хд, не меньше 33 =
(= 119—86) и не больше 43 (= 129—86), то шестая цифра корня
равна 1, причем на этом процесс извлечения корня не обрывается,
а продолжается дальше. Следовательно, наименьшее число, имеющее
нечетное число цифр и удовлетворяющее условию задачи, не менее
чем тринадцатизначно, т. е. превосходит число 222 222 674 025. Итак,
искомым числом будет 222 222 674 025.
100. Из равенства т2 = п2 + 1954 вытекает, что числа т2 и
п2 — одинаковой четности (т. е. оба четные или оба нечетные); сле-
довательно, то же можно сказать и о числах m и п. Но в таком слу-
чае число 1954 = tn2 — п2 = (т + п) (т— п) обязательно должно
делиться на 4 (ибо числа т + п и т— п — оба четные), в то время
как 1954 на 4 не делится. Следовательно, требуемых чисел т и п
не существует.
101. Искомое шестизначное число, начинающееся с цифр 523 и
делящее'ся без остатка на .7 • 8 • 9 = 504, можно представить в виде
523 000 + X, где X — трехзначное число. Но непосредственное деле-
ние дает 523 000 = 504 • 1037 + 352, т. е. 523 000 дает при делении
иа 504 остаток 352. Так как сумма числа 523 000 и трехзначного чис-
ла X должна делиться на 504, то отсюда следует, что X может быть
равно либо
504 — 352 •= 152,
либо
2 • 504 — 352 = 656
(ибо число 3 • 504 — 352 уже четырехзначно). Итак, условию задачи
удовлетворяют два числа: 523 152 и 523 656.
102. Пусть N — искомое число. По условию задачи мы имеем:
АГ= 131^+ 112 = 132/+ 98,
где k н / — целые положительные числа. При этом так как N
149
четырехзначно, то, очевидно,
Л'— 98_. 10 000 —98
1 ~ 132 132 *= 75>
Далее, имеем:
131/г + 112 = 132Z +98; 131 (6— /)=/—14.
Отсюда видно, что если k — I отлично от нуля, то I — 14 по абсолют-
ной величине превосходит 130, что невозможно, если I 75. Таким
образом, должно быть k — I = 0, k = I, откуда сразу получаем:
/ — 14 = 0, k = I = 14,
N = 131 • 11 + 112 = (132 • 14 +98) = 1946.
103. а) Выписанное в условии задачи 2п-?начное число можно про-
образовать так:
4-102”*-1 + 9-Ю2”-2 + 4-102”-3 + 9 (102”~4 + 102п—5 + ...
... + 10") + 510”-1 + 5.10п—2 = 4- 102”~1 + 9102"-2 +
lf)n—з__1
+ 4-10-'1”3 г 9- 10”----g-----ь 5-Ю”-1 + 5-10'1-2 =»
= 4-102”-1 + 9-102п~2 +5-102,!-3 — 10” + 5-10п—1 +
+ 5-10п~2 =-£-(8-102,1-1 + 18 102п-2+ 10- 102ге—3 —
— 2-10” + 10”+ Ю”-1) = -у (9-Ю2”-1 + 9-102п~2 — 9'10п~1) =
{(10” — 1)+ 10n-’]-9-10n-1
“---------------2------------•
Но этому же равна н сумма арифметической прогрессии е раз-
ностью 1, первым членом 10"“* и последним членом 10“ — 1 (число
членов прогрессии равно 10п — 10“-1 = 9 • 10п~1)—сумма всех
л-значных чисел.
б) Число тех из рассматриваемых чисел, у которых па первом
месте стоит данная цифра а (а может быть равно 1, 2, 3, 4 или 5),
есть 6 • 6 • 3 = 108 (ибо на втором и третьем месте может стоять
любая из шести цифр 0, 1, 2, 3, 4, 5, а иа третьем месте — любая
из трех цифр 0, 2, 4, так как рассматриваются только четные чис-
ла). Отсюда общая сумма всех целых тысяч, содержащихся во всех
наших числах, равна (1+ 2 + 3 + 4 +5)- 108- 1000 => 1 620 000.
Аналогично, число чисел, у которых на втором месте стоит дан-
ная цифра, равно 5 • 6 • 3 = 90, так как на первом месте может
стоять одна из пяти цифр 1, 2, 3, 4 или 5. Отсюда общая сумма
всех целых сотен (после вычета всех целых тысяч), содержащихся
во всех наших числах, равна (1 + 2 + 3 + 4 +5)- 90- 100 = 135 000.
Таким же образом получаем, что общая сумма всех целых де-
сятков равна (1 + 2 + 3 + 4 + б)-9О - 10 = 13500 и, наконец, сум-
ма единиц равна (2 + 4) • 5 • 6 • 6 • 1 = 1080.
Искомая сумма равна
1 620 000 + 135 000 + 13 500 + 1080 = 1 769 580.
150
. * 164, Рассмотрим сначала йсе Целые числа от д до 99 999990; при
этом те из этих чисел, которые имеют меньше восьми цифр, допол-
ним слева нудями так, чтобы они стали восьмизначными. Мы будем
иметь 100 000 000 восьмизначных чисел, для записи которых нам по-
требуется, очевидно, 800 000 000 цифр. При этом здесь каждая из
10 цифр будет использована равное число раз, поскольку все они
совершенно равноправны (нуль может стоять на первом месте точно
так же, как и всякая другая цифра). Следовательно, каждая цифра
будет у нас использована 80 000 000 раз.
Теперь подсчитаем, сколько здесь будет лишних пулей (т. е. ну-
лей, приписанных спереди чисел, имеющих меньше восьми цифр).
Однозначных чисел (не считая нуля) имеется всего' девять, двузнач-
ных чисел 99—9 = 90, трехзначных чисел 999—99 = 900, и т. д.
Так как к однозначной цифре мы приписали слева семь нулей, к
двузначной — шесть, и т. д., то общее число лишних нулей (не счи-
тая цифр первого числа, которое у нас записывалось так: 00 000 000)
будет равно
7-9 + 6-90 + 5-900 + 4'9000 + 3-90000 + 2-900000 +
+ 1 9000 000 = 11 111 103,
Припишем теперь 1 слева первого числа 00 000 000; при этом мы
получим все целые числа от 1 до 100 000 000. Мы видим, что для
записи этих чисел требуется 80 000 000 двоек, троек, и т. д. до девя-
ток, 80 000 001 единица (одну лишнюю единицу мы приписали слева
числа 00 000 000) и 80 000 000 — 11 111 103 = 68 888 897 нулей.
105. Однозначных чисел всего имеется девять, двузначных всего
имеется 99 — 9 — 90, трехзначных 999 — 99 = 900 и вообще п-знач-
ных 9 • 10”-1.
Однозначные числа займут в выписанном нами ряду девять мест,
двузначные 90 • 2 = 180 мест, трехзначных 900 • 3 = 2700 мест,
четырехзначные 9000-4 = 36 000 мест, пятизначные 90 000 - 5 =
i= 450 000 мест. Отсюда видно, что интересующая нас цифра будет
принадлежать пяти-'начному числу.
• Цифры, принадлежащие не более чем четырехзначным числам,
будут иметь номера от 1 и до 9 + 180 + 2700 + 36 000 = 38 889. Для
того чтобы узнать, сколько пятизначных чисел уложится в промежут-
ке от 38 889-го места до - 206 788-го, надо разделить разность
206 788 — 38 889 = 167 899 на 5 (деление с остатком):
206 788 — 38 889 = 5 • 33 579 + 4.
Таким образом, искомая цифра будет принадлежать 33 580-му
пятизначному числу, т. е. числу 43 579 (так как первое пятизначное
число есть 10000). В этом числе интересующая нас цифра стоит па
4-м месте. Следовательно, искомая цифра есть 7.
106. Допустим, что дробь 0,1234... — периодическая, п — число
цифр периода, k — число цифр до периода. Рассмотрим число jV =
«= 10'“, где т — какое-нибудь целое число, не меньшее чем п + k;
это есть единица с т нулями на конце. При составлении нашей дро-
би мы выписываем подряд все целые числа; следовательно, где-то
будет расположено и число N. Но из того, что в ряду цифр нашей
бесконечной десятичной дроби где-то стоят подряд т п -|- k нулей,
следует, что период дроби состоит из одних нулей. Так как это,
очевидно, невозможно, то дробь 0,1234 ... — непериодическая.
151
107. Хорошо известно, что каждое Целое положительной чйслб
N дает при делении на 9 тот же остаток, что и сумма его цифр. (Это
следует из того, что стоящая на (k + 1)-м от конца месте цифра ah
десятичной записи N символизирует слагаемое • 10* в разложении
N по степеням десяти; но а* • 10* = а* • (99... 9 + 1) = 99... 9а* +
+ а* дает при делении на 9 тот же остаток, что и а*.) Отсюда выте-
кает, что если число N дает при делении на 9 остаток г+0, то при
многократной замене Числа суммой его цифр мы в конце концов
придем к однозначному числу г, а если N делится на 9 —к числу 9.
Таким образом, единицы-среди нашего миллиарда однозначных чисел
будут соответствовать числам 1, 10, 19. 28, .... 1000 000 000, даю-
щим при делении на 9 остаток 1, а двойки—числам 2, 11, 20,
29, ..., 999 999 992, дающим при делении на 9 остаток 2. Но первых
чисел, очевидно, на одно больше, чем вторых; поэтому единиц мы
получим на одну больше, чем двоек.
108. а) Не может. Если десятичная запись числа N — п2 оканчи-
вается нулем, то она обязательно оканчивается четным числом нулей
и число Nt, получаемое из JV вычеркиванием этих нулей в конце, так-
же является полным квадратом; поэтому достаточно доказать, что
не может являться полным квадратом число, записываемое лишь
цифрами 6 и 0 п кончающееся цифрой 6. Но такое число кончается
либо цифрами 06, либо цифрами 66, т. е. оно делится на 2 и не делит-
ся на 4; а значит, и е может быть полным квадратом.
б) Не может. Если десятичная запись числа N = п2 оканчивает-
ся цифрой 5, то и п должно оканчиваться той же цифрой, т. е. п =
= 10П| + 5,п2 = (10«1 + 5)2 = lOOnf+ 100/?+ 25 = ЮОяДп, + 1) +
+25; таким образом, число JV — 1 OO.Vi + 25 оканчивается цифрами 25
и <Vi = ri\(щ -j- 1). Но ясно, что последняя цифра произведения
И1('Г1 + 1) совпадает с последней цифрой произведения последних
цифр чисел П\ и П1 + 1, которая может представлять собой лишь циф-
ру 0, 2 или 6, ибо произведения 0-1, 4-5, 5-6 и 9 - 0 кончаются
цифрой 0, произведения 1-2, 3-4, 6-7 и 8 • 9 — цифрой 2 и произ-
ведения 2-3 и 7 • 8 — цифрой 6. Таким образом, последней цифрой
числа 7Vt — и третьей от конца цифрой числа N — обязательно являет-
ся цифра 6, ибо ни комбинацией цифр 025, ни цифрами 225 число N
кончаться не может (запись JV вообще ие содержит цифры 0, а циф-
ру 2 содержит лишь один раз). Но если W = 1000^2 + 625, то N
дёлится на 53 — 125 (ибо и 1000,V2, и 625 делятся на 125); а тогда,
поскольку N есть полный квадрат, N делится даже на 54 = 625.
Но если N делится на 54, то и число 1000Л'2 = N — 625 делится
на 54, а значит, .V2 делится на 5. Если же Ns делится на 5, то оканчи-
ваться запись этого числа может лишь цифрами 0 или 5; а это зна-
чит, что запись числа N оканчивается четырьмя цифрами 0625 или
5625, что, однако, невозможно (ибо запись (V содержит лишь одну
цифру 5 и вовсе не содержит цифры 0).
109. Для того, чтобы доказать требуемое утверждение, достаточ-
но проверить, что 444 445-значное число А, полученное выписыванием
друг за другом 88 889 пятизначных чисел щ, а2, а3,.... assess, делит-
ся на какое-либо отличное от 2 число. Но А делится на 11 111. В са-
мом деле, наше число А = а1а2а3...а88а887а8в 888а88 889, очевидно, равно
А = <z88 ess + assess * 105 +а se se? * Ю10 + •.. + a? • Ю44 44® =
= (ai + a2 + ... + Osh ess + a8s ess) + ass ssb (105 — 1) +
+a86)887(1010 -l)+... + a1 (1044 44°-1). (*)
152
А гак как яь а2, .... aaS8S9—это все целые числа от 11 111 до
99 999, то их сумма равна
11 111 + 11 112+ 11 113 + ... + 99 999 =
11 111 + 99 999
=--------_--------88889 = 11 111-5-88 889
т. е. она делится на 11111. Все остальные слагаемые правой части
формулы (*) тоже делятся на 11111 (ибо при всех натуральных й
разность 105А — 1 = (Ю5)4— 1* делится па разность оснований
105 — 1 = 99 999 = 9 • 11 111, а значит и на 11111); поэтому А де-
лится на 11111. __________
110. Пусть искомое число X — a0aia2 . . .ад (где а0, а.. а9 —
цифры числа); при этом а0 есть количество нулей среди цифр X, а1 —
количество единиц, а2— количество двоек, и т. д. Поэтому сумма
всех цифр X равна
Яо + 01 + о2 + ... + а9 — я0 0 + ai • 1 + а2 • 2 + ... + ад • 9,
откуда получаем
д0 = а2 -f- 2я3 + Зя< + 4я3 + 5og -f- 6я7 + 7я3 + 8яэ. (*)
Равенство ай = 0 исключается условиями задачи (иначе число
X не было бы 10-значным; впрочем, условие я0 =й= О сразу следует
и из (*)); равенство а<, = 1 приводит к невозможным значениям
а0 — а2 — 1, ai = 8 (ибо всего мы должны иметь 10 цифр), все ос-
тальные цифры — нули; равенство а0 = 2 совместимо лишь с (также
невозможными!) значениями а0 = а2 = 2, = 6, все остальные циф-
ры — нули, или я3 = 2, а3 — 1, я, = 7, остальные цифры —нули.
Пусть теперь аа = т>2; равенство (*) мы перепишем так:
1 — ^2 + -р . . , + (1 — 1)й{ + , . . + 8Яд (**)
(если i — 3, то слагаемые 2я3 и (Z— 1)а» совпадают; если т. — 9, то
совпадают (i— 1)я( и 8«s). При этом я,- —число равных i цифр чис-
ла X —отлично от нуля (ибо а0 — т); с другой стороны, (**) невоз-
можно при я( > 1, так что at = 1. Поэтому (**) можно переписать
так:
1 = «2 + 2яз+ .•+(< —2)а,_1 + io,-+1+ ... +8о9, (*”’)
откуда сразу следует, что а2 — 1, а все отличные от а0, яь а2 и я,-
цифры числа X равны нулю. Но если я2 — 1, то среди цифр числа X
есть двойка, которой, очевидно, может быть лишь цифра яь Таким
образом, в десятичной записи X отличны от нуля лишь цифры
я0 ( = 1), Я] = 2, а2 = 1 и я,- = 1, т. е. среди цифр X есть i нулей,
2 единицы, 1 двойка и 1 цифра I, откуда (поскольку X 10-тначно) I =
= 10-2 - 1 — 1 = 6.
Итак, X = 6 210 001 000 (легко проверить, что это число действи-
тельно удовлетворяет всем условиям задачи).
111. Так как А = 999 999 999 = 1 000 000 000 — 1,то произведение
АХ = 109Х — X = х>х2. .. х>,000 000 000 — х{х2 .. ,хк, где Х =
== xtx2 .. .хк — произвольное натуральное число (записываемое циф-
рами xltx2....хк). Нам требуется, чтобы число АХ записывалось
153
одними единицами, т. е. чтобы было
х,х2 ... xftOOO ООО 000 — л-л ... х* = 11 ... 1111,
или ..
Х1Л-2 ... Х/,000 ООО 000 — 11 ... 1111 = Xj-vs ... х*.
А так как все цифры вычитаемого нам известны, то мы можем про-
изводить вычитание «столбиком», последовательно определяя все
цифры числа X, начиная с последней:
8 цифр
(7) (8)... (8) (8) (9)
ООО 000
ООО
... 1 1 ... 1 1 1111111111,
...6 7 ... 7 7 7 888 888 889*
9 цифр
где сверху в скобках выписываются последовательно определяемые
цифры числа X. Этот процесс придется продолжать до тех пор, пока
мы не придем к группе единиц, которые при образовании разности
сократятся: ведь только за счет того, что полученное в разности чис-
ло X будет в нашей записи начинаться с группы (разумеется, не
учитываемых) нулей, можно будет добиться совпадения записей X
в уменьшаемом и в разности!
Окончательно мы приходим к следующему значению числа Л'
= Л'о:
Хо 11 ... 1 22 ... 2 33 ... 3 ... 77 ... 7 88 ... 8 9;
9 цифр 9 цифр 9 цифр 9 цифр 8 цифр
запись этого числа состоит из 9 + 9 + ... 9 +8+1= 72 цифр.
7 слагаемых
Полученное число Хо является, очевидно, н а и м е н ь ш и м из
всех обладающих требуемым свойством, но оно не является единст-
венным таким числом. У нас процесс вычитания завершился, когда
в начале образующего разность числа X появились 9 цифр 0, кото-
рые мы просто отбросили, считая, что их можно не засчитывать,
ибо ими запись X начинается. Можно, однако, счесть все эти циф-
ры 0 «существенными», выписать их вслед за цифрами 1 в уменьшае-
мом и продолжать вычитание. Ясно, что после этих девяти нулей
у нас снова начнут появляться цифры числа Хо— и запись X
приобретет вид:
Х1 = Хо 00 ... 0 Хо,
9 цифр
где Хо— десятичная запись числа Хо. Вообще, как следует из нашего
рассуждения, все удовлетворяющие условию задачи числа X имеют
вид:
X - Хп = Хо 00 ... 0 Хо 00 ... О Хо 00 .... О Хо ... Хо 00 ... О А'о,
9 цифр 9 цифр 9 цифр 9 цифр
где число п наборов из девяти последовательных нулей может быть
любым: п — 0, 1, 2, ...; число Х„ состоит из 72(n + 1) + 9п = 8In +
+ 72 цифр.
154
112. Пусть число А = anan_t... а2а, н-значно. Мы можем, разу-
меется, считать, что Qit^O, ибо нули в конце записи А можно просто
отбросить — это не^изменит суммы цифр числа AN для любого N.
Рассмотрим теперь число N = 10™ — 1 = 999... 9, где т Са п. Оче-
т девяток
видно, что число
AN — 10тА — Аж anan__t ... at ООО ... 0 — .. а{ —
— «nan-i (ui—1) 999 ... 9(9 —ап) (9—.(9—a.,) (10—Oj)
m—n девяток
имеет ту же сумму 9т цифр, что и число N.
113. Заметим, прежде всего, что утверждение задачи можно счи-
тать верным и при т «= 0 (в таком случае оговорка п^2 становится
необязательной—мы можем допускать и п «= 1), если только поло-
жить 0° = 1 (поскольку а-' — 1 для всех а). Пусть, например, п = 1;
обозначая все четные цифры (включая и цифру 0) через аь аа, • •
а нечетные цифры — через (Ji, р2, .... получим:
а.° 4 аЯ 4 ...= 0° 4 2° 4 4° 4 6° 4- 8° = 1 4- 1 4 1 4 1 4 1 = 5
II
4- + . .. ^ 1° + 3° + 5° 4- 7° + 9° == 1 + 1 4- 1 + 1 + 1 =- 5.
Перейдем теперь к следующему значению п: пусть п — 2; через
di, а2, ... и Pi, р2, мы по-прежнему обозначим все четные и все
нечетные цифры, а через Д|, А2,.. и Si, В2 ... — все не более чем
двузначные числа с четной, соответственно с нечетной суммами цифр.
Так как, очевидно, каждое число А, имеет либо вид a*ai( = 10a* 4-
+ ai), либо вид Юр* + а числа Sj, напротив, имеют вид
— 1 Осе* + 4 и р*а; — Юр* + а/, то, обозначая через 24,- и через
28; сумму всевозможных не более чем двузначных неотрицательных
чисел с четной, соответственно с нечетной суммами цифр, а через 2a*
и 2р( —сумму всех четных и всех нечетных цифр, получим:
2 Д. = 2 (10ah - 2 (10₽к + ₽/) =
->о(2% + 2Ш(2«г + 2Ю
и, аналогично,
2 в.~ 2 (1 °% + ₽г) + 2 (1«0 -
^10(2ай + 2Pj4(2iV2O;
эти два равенства и доказывают, что 2Д,- = 2В;.
В точности то же рассуждение лежит в основе общего доказа-
тельства требуемого утверждения методом математиче-
ской индукции. Пусть мы уже установили справедливость
его для некоторого п (и всех /п<л); рассмотрим следую-
щее натуральное число л + 1 (и какую-то степень т < л 4- 1). Усло-
вимся обозначать все не более чем л-значные неотрицательные числа
155
с четной, соответственно с нечетной суммами цифр, через at, а2,..,
и через bi, b2, ..., далее, как и раньше, все не более чем (« + 1)-
значные числа с четной, соответственно с нечетной суммами цифр обо-
значим через Л2, ... и через Bi, В2, ...; наконец, сохраним обо-
значения ai, а2,.,. и 0Ь р2,... для четных и для нечетных цифр. По
предположению индукции имеем
2qa*=26£ (=snp) для всех р<«; (*)
к к
кроме того, условимся обозначать через
V=2“K2«: <**)
к к
сумму р-х степеней всех не более чем n-значных чисел. _
Заметим далее, что каждое число At имеет либо вид akai =
= 10аА + либо вид — 10&а + 0ц аналогично, числа В} могут
иметь форму а*0( = 10д* + 0/ или bkai — 10&л + at. Используя ана-
логичные употребленным выше обозначения, найдем
2 < = 2 04 + “0™+204 + ₽г)т; адесь «<« + !•
Но, по формуле бинома Ньютона, например,
(10ай + а;)т = Ют-а^ + С^-10т~*а£~ ‘а, +
+ (%- 10т—2а™—2а2 + ... + С™~1
Поэтому, используя обозначения ('♦), получим:
У(ю«Лн-а/)™ = ют2«Г + фют-12«Г“12а/ +
ч- с2т ют~22 «Г-2 2 aF + • •• + cm-1 •10 2 ак 2 «Г-1 +
+2 аГ=Ют2 <+ Ф «г +
+cl- 10ra-2Sn.n.-22 «?+•..+CS"1 • 10^.12 аГ-1 + 2 аГ
М, аналогично,
2 04 + ₽/)m =10<h 2 ьк + ю"1-12 ьк 2 Р< +
+ с2т 1 о”1-2 ь^-2 20?+...+ с™-1 • ю 2 ьк 2 +
+ 2 ₽“ “lom2 cim- 1ом~4,т_12 Р’ +
+ с2т • ю™-2 Чт_2 2 ₽2+ • • •+. юЧ12 Р?-1 + 2 РГ-
Таким образом, .....
2лГ“2(1Ч + «г)та + 2(14 + ₽дга-
“ + С2т. 10т-2Чт_25112 + ...
... + c;rMosMsl<m,1 + sMB.
156
Используя те же обозначения (*) и (**), формулу бинома Нью-
тона и производя аналогичные преобразования, мы придем к точно
такому же выражению для суммы
3 В? = 3 (1<Ч + + 2 m + агЛ
что и доказывает требуемое утверждение.
Несправедливость выписанного в условии задачи тождества для
степеней т^п следует уже из того, что при п = т — 1 имеем:
2а‘ =0+2-!-4 + 6+8 =20, а
2 ₽‘ = 2 ₽; = 1 + 3 + 5 + 7 + 9 = 25.
114. Выпишем в каждой строке, начиная с третьей, четыре пер-
вых числа и поставим на месте четного числа букву ч, а на месте,
нечетного числа — букву и. Получится полоса:
н ч н ч
н н ч н
« ч ч ч
н н н ч
н ч н ч
Мы .видим, что пятая строка полосы совпала с первой.
С другой’ стороны, четность или нечетность первых четырех чисел
каждой строки нашего числового треугольника зависит только от
четности или нечетности первых четырех чисел предыдущей строки;
следовательно, в нашей полосе строки будут периодически повто-
ряться через каждые четыре строки. Так как в каждой из четырех
первых строк полосы имеется четное число, то отсюда вытекает,
что оно будет и во всех последующих строках.
115. Докажем, что сумма чисел каждой строки нашей таблицы
делится на 1958:2 = 979, причем сумма чисел каждой строки, начи-
ная со 2-й, делится даже на 1958; отсюда уже следует утверждение
задачи, поскольку в последней (нижней) строке имеется единственное
число и «сумма чисел» этой строки совпадает с этим числом. Ясно,
что сумма Si чисел верхней строки (сумма первых 1958 чисел нату-
рального ряда, образующих арифметическую прогрессию) равна
’/2(1958 • 1959), т. е. Si делится на 1958: 2. Далее сумма S2 чисел 2-й
строки, очевидно, равна: S2 = (0 + 1) + (1 + 2) + (2 + 3) + ...
...+(1956+ 1957)+ (1957 + 1958)= 2S, — (0 + 1958), поскольку
почти все слагаемые суммы Si входят в выписанное выражение S2
дважды — исключение составляют лишь «крайние» члены 0 и 1958,
которые входят в S2 по одному разу. Но поскольку и 2Sj и 0 +
+ 1958 = 1958 делятся на 1958, то и сумма S2 па 1958 делится.
Перейдем теперь к 3-й строке нашей таблицы. Ясно, что сумма
S3 всех чисел этой строки равна
S3 = (1 + 3) + (3 + 5)+ ...+(3913 + 3915) = 2S2- (1 +3915);
в самом деле, в выражении для S3 фигурируют дважды все числа
из 2-й строки, кроме одних лишь «крайних» чисел 1 н 3915, которые
157
входят в сумму $з по одному разу. Но числа второго ряда 1 и 3915
имеют следующее происхождение: 1 = 0+1 и 3915 = 1957 + 1958;
поэтому
1 + 3915 = (0 + 1) +(1957+ 1958) =
= (0 + 1958) + (1 + 1957) = 2 1958
делится на 1958, откуда н вытекает, что также и сумма S3 делится
на 1958.
Эю рассуждение может быть продолжено. Так, сумма S4 всех
чисел 4-й строки равна
$4 = 253—• (4 +7828),
где 4 (= 1 + 3) и 7828 (= 3913 + 3915) — «крайние» числа 3-й стро-
ки. Ио из правила образования нашей таблицы сразу следует, что
4 + 7828 = (1 + 3) + (3913 + 3915) =
= (0+ !) + (! +2)+ (1956 + 1957)+ (1957 + 1958) =
= (0 + 1958) + (1 + 1957) + (1 + 1957) + (2 + 1956) = 4-1958
делится на 1958, откуда и вытекает делимость на 1958 суммы Точ-
но так же устанавливается делимость на 1958 суммы чисел всех
последующих строк (формальное доказательство можно провести
методом математической индукции), что и завершает доказательство
требуемого утверждения. ___ -
116. Ясно, что если на столбе указаны числа xyz|xj(/|Z,- (где х,
у, ... — цифры), то Xsy^i = 999 — xyz и, значит, z, = 9— z, tj\ =
= 9 — у, Xi = 9 — х. (Если х = 9 или х — у = 9, то цифры xt =
= 0, или Xi — у\ = 0 па столбе не проставляются.) Отсюда сразу
следует, что если х = у = г (и, значит, х} = у, = zt = 9 — х), то
наши условия будут выполнены; это дает 10 удовлетворяющих усло-
вию вадачи столбов (отвечающих расстояниям 0 = 000, 111,
222, ..., 999 км от пункта Л). Если же число xyz записывается двумя
разными цифрами, то эти цифры должны быть таковы, что каждая
из них дополняет вторую до числа 9 — в этом случае и число
XiyiZi = 9 — х, 9 — у. 9 —z будет записываться теми же цифрами.
Подобных пар цифр существует, очевидно, пять; (0, 9), (1, 8), (2,7),
(3, 6) и (-1, 5); а грехзначных чисел, записывающихся двумя данны-
ми цифрами а и Ь, имеется всего шесть: три и? них записываются
двумя цифрами а и одной цифрой b (которая может занимать любо*
из 3-х имеющихся мест) и, аналогично, три числа записываются од-
ной цифрой а и двумя цифрами Ь. Таким образом, мы получаем еще
б • 6 = 30 удовлетворяющих условию задачи расстояний искомого
столба от пункта А; поэтому общее число удовлетворяющих сформу-
лированным требованиям столбов: 10+30 = 40
117. Первое решение. Семь сеансов (считая от начала сеан-
са до начала следующего) заняли меньше 13 часов (1-й сеанс на-
чался не раньше 12 час, а 7-й кончился до 1 часа ночи), а 5 сеансов
заняли больше 9 часов (2-й сеанс начался до 14 час., а 6-й кон-
чился не раньше 23 час.). Следовательно, длительность сеанса мень-
ше чем 1 час. 52 мин. и больше чем 1 час 48 мин Отсюда длитель-
ность сеанса равна 1 час. 50 мин , ибо она выражается всегда числом
мииут, кратным 5.
158
Так как первый сеанс кончится до 14 час., то он мог начаться
либо в 12 час. 00 мин., либо в 12 час. 05 мин.; соответственно этому
второй сеанс начинается в 13 час. 50 мин. нли в 13 час. 55 мин.,
и т. д.
Если не требовать, чтобы длительность сеанса была кратной пяти
минутам, то мы получим не два, а большее число возможных реше-
ний задачи.
Второе решение. Пусть 12 + у — начало l-ro сеанса, ах —
продолжительность сеанса (х и у выражаются в часах). Тогда сеан-
сы начинаются в следующие часы:
отсюда
1-й в 12 -j- у (от 12 час. до 13 час.);
2-й в 12 + у + х (от 13 час. до 14 час.);
7-й в 12 + у + 6х (от 23 час. до 24 час.);
8-й в 12 + у + 7х (от 24 час. до 1 час.);
12 12 + //<13, или 0 < у < 1,
12 + х + у < 14,
12 + 6% + у < 24,
12 + !х -|- у < 25,
13 +
23 +
24 +
или 1 < х + у < 2,
или 11 < 6х + у < 12,
или 12 < 7х + у < 13.
Отбрасывая неравенства, вытекающие из других, получим сис-
тему:
О у < 1; 1 < х + у < 2; 11 < 6х + у, 7х + у < 13,
которую нетрудно решить графически (рис. 11). Решение (х, у) дает-
любая точка из заштрихованного четырехугольника PQQiPi.
118. Будем считать, что каждый час шлагбаум закрыт от 0 мин. до
5 мин. и от 38 мин. до 43 мин. Если указанные 5-минутные интервалы
начинаются, скажем, за 1 мии. до подхода поезда к шлагбауму,
то мы просто «переведем часы назад на 1 мин.» (а после решения
задачи, чтобы исправить составленное с использованием неверных
159
часов расписание движения автобусов, снова переведем на 1 мии.
стрелки часов). Отметим иа циферблате часов все положения минут-
ной стрелки, отвечающие моментам, когда автобус проходит шлаг-
баум — для этого пометим черточкой время (о мин. прохождения пер-
вого (с начала суток) автобуса, а затем, двигаясь в направлении вра-
щения часовой стрелки, станем отмечать последующие моменты
/о + Т, /о + 2Г, и т. д., откладывая каждый раз по циферблату дугу,
отвечающему интервалу в Т мии. Нам надо так выбрать 10 и То,
Рис. 12.
чтобы нн одна из полученных отметок не попала в «запрещенные»
(заштрихованные на рис. 12) интервалы времени от 0 до 5 мии. и от
38 до 43 мин.
Заметим, прежде всего, что среди полученных таким образом от-
меток на циферблате могут иметься на более 12 различных1). В са-
мом деле, пусть R и Rt — две ближайшие друг к другу отметки иа
циферблате, которым отвечает угол RORi = а° (где О — центр
циферблата), соответствующий временному интервалу в т мин.; от-
метки R и Ri указывают моменты времени t0 + IT и /о + где i
’) Ясно, что общее число отметок на циферблате, в принципе,
может быть даже бесконечно большим. [Можно доказать,
что бесконечно большим это число отметок будет в том случае, если
интервал Т несоизмерим с интервалом в 1 час., отвечающим «полно-
му» повороту минутной стрелки (повороту на угол в 360°), причем
если это последнее обстоятельство имеет место, то отметки на цифер-
блате будут расположены «плотно», т. е. среди них найдутся отмет-
ки, удаленные от произвольно выбранной точки М циферблата на
. (дуговое) расстояние, меньшее любого наперед заданного (сколь
угодно малого!) числа е.]
160
и i — какие-то целые числа. В таком случае два автобуса — i-й и /-й
(где мы считаем / > г) —следуют один за другим через целое число
k часов ±т минут; для определенности условимся считать, что вре-
менной интервал между автобусами равен 'k час. + т мйн., так что
<jRRi имеет на циферблате направление вращения часовой стрелки
(рис. 12; в рассуждениях почти ничего не изменилось бы, если бы
\yRRi имела обратное направление). В таком случае [/ + (/ — ()]-й
(т. е. (2/— <)-й) автобус будет следовать за j-м через k час. т мин.,
и моменту его проезда через железнодорожный путь отвечает на ци-
ферблате отметка R2 такая, что '^RiRz = <->RRi = <z°; [(2j— 1) + 1
+ (/— /)]-му (т. e.’ (3/ — 2г)-му) автобусу отвечает такая отметка
R3, что = а°, и т. д. С другой стороны, [i— (/— /)]-й (т. е.
(2/— /)-й) автобус следует за k час. и т мин. до ото, т. е. ему отве-
чает отметка R~i такая, что R_\ и Ri расположены по разные сто-
роны от R и \jR-\R= ^jRRi — ct°, и т. д. Таким путем мы получим
на циферблате «сетку» отметок, расположенных друг от .друга на
«дуговом» растоянии в а°, или на «временном» расстоянии в т мин.;
ясно, что если т < 5 (или а < 30°, поскольку 5 мин. на циферблате
отвечает центральный угол в 30°), то хоть одна из этих отметок по-
падет в «запрещенный» интервал времени и соответствующему авто-
бусу путь через переезд будет закрыт. Но если на циферблате име-
ется система отметок, причем наименьшее из (дуговых) расстояний
360°
между отметками 5s 30°, то общее число отметок < уу = 12.
Итак, расписание движения автобусов указывается на цифер-
блате k «5 12 отметками R, Ri, R3,...; из сказанного выше вытека-
ет, что v/ RRi = су RtRi = о R2R3 = .. т. е. что RRiR3.. . Rh-i
( = Mk) —это вписанный в окружность циферблата правильны й
А-угольник. Нам надо найти все k, отвечающие правильным мно-
гоугольникам Мь, которые можно так повернуть вокруг центра
О циферблата, чтобы ни одна вершина Mk не попала на зашт-
рихованные на рис. 12 дуги АВ и CD. Ясно, что при k = 1 (один
автобус в час) или k — 2 (два автобуса; здесь надо указать на
циферблате две диаметрально противоположные отмет-
ки R и Ri, не попадающие па дуги АВ и CD) это возможно; условие
Г < 30 мин. требует указать решения задачи, отвечающие значени-
ям k > 2. С другой стороны, очевидно, что значение k = 12 (т. е.
а° = 30° и т = 5 мин.) нам не подходит: свободной от отметок дуга
АВ может быть лишь в том случае, если ее концы А и В совпадают
с какими-то отметками R и Ri; но в таком случае 9-я отметка отве-
чает моменту времени 0 + 8-5 мин. = 40 мин.— и она попадает на
Дугу CD. Аналогично, не подходят нам также значения k = 10, 9 и
/ 60 60 2 60 4 \
71 т. е. значеният = Jo"—6 мин., -у = бумин. и —=8умзн. ;
так, если т = 6 мин., то ближайшая за А отметка R, если только
она не попадает на дугу АВ, должна разместиться где-то внутри
(временного) интервала [5 мин., 6 мин.]; но тогда 7-му автобусу
ответит отметка, приходящаяся на временной интервал [5 + 6-6 =
= 41 мин., 6+6-6 = 42 мин.], целиком принадлежащий «запре-
щенной» Дуге CD. (Проверьте сами, что если отметка R попадает
Г 2 ] Г 4 1
на интервал 5 мин. , бу мин. , соответственно 5 мин. , 8у мни. ,
го 6-й, соответственно 5-й автобус неизбежно попадут в интервал
I4 Д. Q. Шк.тирский и др.
161
CD.) Напротив, значения k— 11, 8, 6, 5, 4 и 3, отвечающие значе-
60 5 60 60 60
ниям т = -ц- = 5-ц-мин., -у = 12 мин., у = 15 мин. и-у=20мин.,
являются допустимыми: так, например, если £= 11, то автобусы
могут проезжать шлагбаум, скажем, в моменты времени 5 мин.,
5 10 4 9 3 8
Юу мин. , 15 у мин. , 21 у мин. , 26у мин. , 32уумин., 37у
2 7 16
мин., 43у мин., 48у мин., 54ц- мин. и 59ц мин., а если k = 5, то воз-
можно следующее расписание движения, автобусов: автобусы про-
ходят шлагбаум в 8 мин., 8 + 12 = 20 мин., 32 мин., 44 мин. и 56 мин.
Таким образом, при 7 < 30 мин. требуемым образом движение
автобуса можно организовать при Т — 20 мин., 15 мин., 12 мин.,
1 5
7 -у мин. и 5 ц мин. — и только при этих значениях 1.
119. Пусть N = abc, где а, Ь, с — цифры числа; ясно, что для «круг-
N
лых» чисел N = 100, 200... 900 имеем ур зр с = 100. Далее, если
число N — не «круглое», то b + с > 0 и a-f-b-t-c^a-j-l, а так
как старшая цифра N равна а, то N < (а + 1) 100 и
(А+ЛИОО = 100.
Д! + /> + С Ц -ф- 1
Таким образом, наибольшее значение рассматриваемого отноше<
ния равно 100; достигается это значение лишь для «круглых» чисел.
Примечание. Точно так же доказывается, что наибольшее
значение отношения +значного числа N = akak-i.. .аг к сумме ah +
+ а/,.. 4- а, его цифр равно Ю*-1; достигается оио лишь для
«круглых» чисел, k — 1 последних цифр которых — нули.
120. В данном числе 19-2 цифры; в числе, полученном из него вычер-
киванием 1С0 цифр — 92 цифры.
а) Первые цифры интересующего нас числа должны быть воз-
можно большими. Мы можем сделать так, чтобы это число начи-
налось с 5 девяток, заимствовав эти девятки из чисел 9, 19, 29, 39
и 49; при этом нам придется вычеркнуть 8 + 19 + 19 + 19 + 19 = 84
цифры. После этого следующая цифра уже не может быть сделана
девяткой, так как для этого нам пришлось бы вычеркнуть еще 19
цифр (чтобы «добраться» до ближайшей девятки — цифры числа 59);
при этом вычеркнуто будет 84 + 19 = 103 цифры., т. е. больше чем
нужно.
Ближайшая к оставшимся цифрам восьм:рка относится к числу
58; для того чтобы она следовала непосредственно за девятками,
пришлось бы вычеркнуть еще 17 цифр, что тоже невозможно (ибо
84 + 17.= 101 > 100). Поэтому лучшее, что мы можем сделать,—
это вычеркнуть еще 15 цифр, предшествующих семерке в числе 57.
Итак, всего мы вычеркнули пока 84+ 15 = 99 цифр; нам позволено
вычеркнуть еще одну цифру. Ясно, что целесообразно вычеркнуть
пятерку в числе 58; итак, требуемое число:
9999978096061.. .100.
162
б) Мы можем побиться, чтобы оставшееся число начиналось с
5 нулей (эти нули фигурируют в записи чисел 10, 20, 30, 40 и 50); при
этом вычеркнуты будут 10 + 19 + 19 + 19 + 19 = 86 цифр. До сле-
дующего нуля (в числе 60) мы добраться не можем; однако, вычерк-
нув всего одну пятерку, мы сделаем так, чтобы за 5 нулями в полу-
ченном числе следовала единица. Следующую за этим цифру мы не
можем сделать также единицей; однако, вычеркнув еще одну пя-
терку, мы сделаем следующую цифру двойкой. Это рассуждение
можно продолжить; так мы убедимся, что, вычеркнув всего 86 +
+ 1 + 1 + 1 + 1 = 90 цифр, мы придем к числу, начинающемуся с
комбинации цифр: 000001234, вслед за которыми следуют цифры
55565758596061... Ясно, что цифра, следующая за выписанными вы-
ше первыми девятью цифрами искомого числа, может быть пятеркой,
но не может быть меньше 5; для того же, чтобы она оказалась пя-
теркой, нам вообще не потребуется никаких вычеркиваний цифр. Пос-
ле этого мы,— наконец-то!— получаем возможность добраться до
нуля вычеркнув 10 предшествующих ему цифр (что еще допустимо);
поэтому интересующее нас число таково:
00000123450616263. . .100
(это число начинается с пяти нулей, так что реально оно содер-
жит 87 значащих цифр).
121. а) Первые цифры трех искомых чисеч должны быть наимень-
шими; следовательно, эти числа в десятичной записи имеют вид:
[Аа, 2ВЬ, ЗСс,
где символ xyz обозначает число, записываемое цифрами х, у, г
Докажем, что: 1) А < В <С; 2) а <Ь < с; 3) каждая и?
цифр а, Ь, с больше каждой из цифр А, В, С.
Действительно: __ _
1) Если бы, например, было А > В, то мы имели бы Аа > ВЬ
и ТАа-^ВЬ — 2Ло_Тйй_ = (100 + До) • (200 + ВЬ) — (200_+ Аа)Х
X(100 + Дй) = 100(До— ВЬ) > 0 и, следовательно, [ВЬ • 2Аа X
X ЗСс < [Аа • 2ВЬ • ЗСс.
2) Если бы, например, было а > Ь, то мы имели бы
1До • 2ВЬ — Ш - 2Ва = (10 • ЙГ+ а) (10 • 2В~+Ь) —
— (10 • 1Д+ Ь) (10 • 2В~+а) = (10 -2В — 10 • 1Д) (а — Ь) > 0
и, следовательно, !АЬ 2Ва • ЗСс < [Аа 2ВЬ ЗСс.
3) Если бы было С > а, С = а + %, где х > 0 (в силу 1) и
2) С — самая большая из цифр А, В, С, а о — самая маленькая из
цифр о, Ь, с), то мы имяди бы ।
1Аа ЗСс — [Ас Зас = [Аа (Зое + 10х) — ([Аа + х) (Зое) =
= х (10 • [Аа — Зас) >0
и, следовательно, [АС 2ВЬ Зас < [Аа 2ВЬ ЗСс.
Из 1), 2) и 3) следует
Д<В<С<о<&<с,
!!♦
163
и искомое произведение имеет вид
147 • 258 • 369.
б) Искомое произведение должно иметь вид
9Аа' 8ВЛ ТСс.
Аналогично решению задачи а) можно доказать, что 1) А <
< В < С, 2) а < b < с, 3) каждая из цифр а, Ь, с меньше каждой
из цифр А, В, С.
Из 1), 2) и 3) следует, что
a<i<c<A<S<C
и, следовательно, искомое произведение имеет вид
941 • 852 • 763.
122. Нам дано, что т -ф (m + 1) -ф .,. + (т -ф k) = 1000. По
формуле суммы членов арифметической прогрессии имеем:
2т -ф k
. ,(А-ф 1) д Ю00,
или
(2т-ф А)(А-ф 1) 2000.
Так как
(2m + А) — (i+l)=2m- 1
нечетно, то из двух последних множителей один четен, а второй
нечетен. Кроме того, очевидно, 2т-фА>А-ф1. Отсюда вытекает,
что наша задача имеет следующие решения:
2т + А = 2000, А + 1 = 1, т = 1000, А = 0;
2m ~ф А = 400, А -ф 1 = 5, т = 198, А = 4;
2m -ф А »» 80, А + 1 = 25, т = 28, А = 24;
2т + А = 125, А+ 1 = 16, т == 55, А = 15.
123. а) Пусть наше число N отлично от любой степени 2. Тогда
имеет место равенство
^ = 2'(2/+l),
где 2* — наибольшая' степень 2, на которую делится N (А может
быть равно нулю), а 2/ -ф 1— наибольший нечетный делитель числа
N. Далее, имеем:
(2ft -Z) + (2*—1+ 1)+ ... +(2?! — I + 2/— 1)-ф (2ft — /-ф 2/) -
- (2<+,)(2»-е-Н2«-1 + 2й| _ 2, (и + 1( _
При этом, если несколько первых из этих 21 + 1 последователь-
ных целых чисел будут отрицательными (т. е. I >• 2й), то их можно
будет сократить с первыми положительными числами и Л' опять
представится в виде суммы некоторого числа (меньшего 21 + 1)
п о л о ж к т е л ь и ы х целых чисел.
1М
Предположим теперь, что какое-нибудь число вида 2к можно
представить в виде суммы т последовательных целых положитель-
ных чисел я, я + 1,..., п + т — 2, п + т — 1. Тогда
2А+1 = 2 [я + (я + 1) + ... +(я + т— 2) + (я + т — 1)J =
= т(п п т — 1) — т(2п + т — 1).
Но разность (2я + т—1)—т = 2я—1 нечетна, следовательно,
одно из чисел, т или 2и ф- т—1, нечетно (причем оба они отличны
от 1, ибо т> 1 ия>0). Значит, последнее равенство невозможно
(ибо 2'1 + 1 не имеет нечетных делителей, отличных от 1).
б) Имеем:
(2и + 1) + (2я + 3) + (2/г + 5) + ... + (2,-я - 1) =
(2/г Н- 1) + (2т - 1)
—-----------и---------• (т — я) = (т + п) (т — я).
Поэтому если число представимо в виде суммы последовательных
нечетных чисел, то оно составное (разлагается па множители т + п
и т — п). С другой стороны, каждое нечетное составное число /V
можно представить в виде произведения двух нечетных множи-
телей а и b (а Ь) и, следовательно, N = ab — (т + я) (т— п),
а-!-Ь а — Ь
где т = —g—> п = —’ ссть сУмма нечетных чисел от а — о + I
до а + b — 1.
Далее, в формуле N — (т п) (т — п) множители т + я и
т— я оба четны или оба нечетны; если N четно, то эти множители,
очевидно, должны быть четными. Но в таком случае N делится на 4
(и яг + я и яг — я делятся па 2); следовательно, если четное число
N не делится на 4, то его нельзя представить в виде суммы после-
довательных нечетных чисел. Если же N — 4я делится на 4, то /V
можно представить в виде суммы двух последовательных нечетных
чисел 27г — 1 п 2я + 1.
в) Легко видеть, что
(все слагаемые этой суммы нечетны, ибо я6"1 и я одновременно
четны или нечетны).
124. Обозначим эти числа через я, я + 1, я ф- 2, я ф-3. Сумма
их произведения и единицы имеет вид
п(п + 1) (,! + 2) (я ф- 3) ф- 1 = [я (я ф- 3) ] [(я ф- I.) (я + 2)] -|- 1 =
= (я2 + Зя) (я2 + Зя + 2) + 1 =
= (я2ф-3я)2 + 2(я2ф-3я) ф- 1 = (я2 ф-Зя + I)2;
следовательно, эта сумма является квадратом целого числа (я2 ф-
+ 3я+ 1).
125. Докажем, что эти числа принимают не более четырех раз-
личных значений. Допустим, что это неверно и среди наших 4я
165
Чисел существует пять чисел at, а2, Оз, сц, аз, попарно различных меж-
ду собой. Будем считать, что ai < а2 < аз < а4 < аз-
Рассмотрим числа а2, аз и а4. Согласно нашему условию из
них можно составить геометрическую пропорцию; следовательно,
произведение двух из этих чисел (крайних членов пропорции) рав-
но произведению двух других. Но это возможно только, если
а,а4 = агаз
(равенство ai<l3 — а2а4 невозможно, так как а, <а2, а3 < а4; еще
очевиднее, что не может иметь места равенство а[О2 = «зйз)-
Рассмотрим теперь числа а4, а2, а3, а$. Таким же образом, как
и выше, можно доказать, что afls = а2а4- Следовательно, =
= в|Я3, а4 — а5, что противоречит нашему предположению.
Итак, мы доказали, что каждое из 4я чисел принимает одно из
не более чем четырех различных значений. Поэтому какое-нибудь,
из этих значений принимается не менее "чем п числами.
126. Разложим сначала девять гирь, веса которых равны соот-
ветственно п2, (п+1)2, (« + 2)2,..., (п + 8)2, па три группы сле-
дующим образом:
I группа п3, (я-)-5)5, (fti-J-7)2:
п! + (« + 5)2+(п + 7)2 = 3+ + 24/г + 74;
II группа (n-Ь I)2, (« -f- З)2, (л + 8)2:
(я + 1)2+(« + 3)2+(» + 8)2 = Зя2 + 24» + 74;
III группа («4-2)2, (/: + 4)2, (п + 6)2:
(»+2)2+(n+4)2+(«+6)2 = Зп2+24л+56.
Таким образом, мы видим, что вес первой и второй групп-один
и тот же, а третья — легче их на 18. Затем следующие за ними де-
вять гирь разложим аналогично, однако так, чтобы первая и третья
группы имели одинаковый вес, а вторая была легче их па 18; нако-
нец, последующие девять гирь разложим так, чтобы вторая и третья
группы имели одинаковый вес, а первая была легче их па 18. Сгруп-
пировав затем все первые, все вторые и все третьи группы этих
трех разбиений, мы получим разложение любых 27 последователь-
ных гирь на три группы равного веса.
127. Из условия задачи, прежде всего, следует, что все гари
одновременно имеют или четный, или нечетный вес. Действи-
тельно, из того, что каждые 12 гирь можно разбить на две группы
равного веса, следует, что общий вес каждых 12 гирь четен. При
этом общий вес 12 гирь останется четным и в том случае, если про-
извольную из них заменить отложенной 13-й гирей. А это возможно
только в том случае, если вес каждой из 12 гирь четен или нечртен
одновременно с весом отложенной 13-й гири, что и приводит к на-
шему заключению.
Вычтем теперь из весов всех гирь вес самой легкой гири (или
самых легких, если их несколько). При этом мы, очевидно, получим
новую систему гирь, которая тоже удовлетворяет условиям задачи;
следовательно, веса всех новых гирь тоже имеют одинаковую чет-
ность. А так как среди новых гирь имеются «гири» нулевого веса,
го вес всех новых гирь должен быть четным. Разделим, веса всех
гирь на два; при этом мы получим новую систему гирь, тоже удов-
летворяющую условиям задачи,
*63
Предположим теперь, что не все исходные гири имеют одинако-
вый вес. В таком случае не все гири второй системы, веса которых
получаются-мз весов первоначальных гирь вычитанием веса иаилег-
чайших гирь, будут «нулевыми». В этом случае путем последова-
тельного деления весов всех гирь на два мы в конце концов придем
к системе гирь, часть из которых имеет четный вес (например, вес
«нуль»), а часть — нечетный вес. Но мы уже показали, что такая
система гирь не может существовать. Полученное противоречие и
доказывает утверждение задачи.
Примечание. В условии задачи требовалось, чтобы веса
всех гирь были целыми числами,- Однако нетрудно видеть, что если
считать веса гирь числами рациональными, а не целыми, результа г
задачи не изменится. Действительно, в этом случае, умножив веса
всех гирь па некоторый множитель (приведя все веса к общему зна-
менателю и отбросив знаменатель), можно свести задачу к случаю
целых весов. Более того, если позволить весам гирь быть произволь-
ными иррациональными числами, мы все равно сможем утверждать,
что все они равны между собой: это следует из того, что можно
найти рациональные числа, сколь угодно близкие к данным иррацио-
нальным числам (рекомендуем читателю попытаться самостоятельно
провести полное доказательство; следует, впрочем, предупредить,
что сделать это аккуратно не так уж просто).
128. Заметим, прежде всего, что если для каких-то натуральных
k и l^k полученные описанным образом четверки а>., Ьь, ctl, dh и
a,, bt, Ci, dt одинаковы, то либо все числа ah = alt = Ь;, с>, =
= ci, dk = di равны нулю, либо все они положительны. В самом
деле, если хоть одно из чисел a, b, с, d, равно нулю, то не позже
чем на четвертом «шагу» мы приходим к строчке из одних лишь ну-
лей, которая затем неограниченно повторяется; при этом ранее
никакие две из выписанных четверок чисел не совпадают. Действи-
тельно, если равно нулю ровно одно из наших чисел, скажем а =
= 0, то первые 4 четверки выглядят так:
О, Ь, с, d; 0, be, cd, 0; 0, bc2d, 0, 0; 0, 0, 0, 0
— здесь никакие две из первых трех четверок не могут совпасть,
поскольку нули в них стоят на разных местах. Ясно также, что ес-
ли более чем одно из чисел a, b, с, d равно нулю, то к чет-
верке нулей мы также придем не позже чем на 4-м шагу, причем и
здесь легко проверить, что не состоящие из одних нулей четверки
обязательно будут все различны.
Сказанным исчерпывается разбор случая, когда abed = 0;
пусть теперь abed #= 0. Ясно, что здесь все числа всех четверок бу-
дут отличны от нуля. Далее, если среди чисел a, b, с, d отрицатель-
ным является только одно — скажем, первое, — то обозначая по-
ложительное число символом «+», а отрицательное — символом
«—», мы придем к следующему чередованию знаков в первых пяти
последовательностях:
—F + +; —НН—> -----F;----------> + + + +;
таким образом, здесь 5-я четверка состоит из одних лишь положи-
тельных чисел, причем ранее никакие две четверки не могут сов-
пасть, ибо чередование знаков в них различно. Из выписанной схе-
мы видно также, что если среди чисел a, b, с, d имеются два со-
седних отрицательных (как во 2-й из выписанных четверок: ведь
167
упорядочение чисел в четверках здесь надо считать «циклическим»,
так что 1-е и 4-е числа являются «соседними»), или два не сосед-
них отрицательных (как в 3-й четверке), или четыре отрицательных
(как в 4-й четверке), то также не позже чем на 4-м шагу мы при-
дем к одним лишь положительным числам (и ранее этого четверки
будут различными). Аналогично рассматривается случай'четверки из
трех отрицательных и одного положительного числа, на первом же ша-
гу переходящей во 2-ю из выписанных выше четверок:
+--------; - + -J- - + - +;------------; + + + + .
Итак, далее мы можем считать все числа a, b, с, d положитель-
ными; положим еще abed — р. При этом, очевидно,
= (ab) (be) (cd) {da) = {abcd)\ = р2;
аналогично, с2Ь2с2^2 = (ai1b1cldl)2 = р4; a3b3c3d3 = р8 и вообще
akbhckdk = (р)2 (где k = 0, 1, 2,...; под а3, ba, с9, d0 мы понима-
ем исходные числа a, b, с, d). Поэтому, если четверки ак, Ьк, ск, dk
и а;, bi, Ci, di (где I > k) совпадут, то
Л , i , , 2^ __,
р = akbkchdh = alblcldl = p^ и, значит, p~ 4 = 1, т. e. p = l.
Пусть теперь abed = 1 (ясно, что нам надо разобрать лишь
этот случай). В таком случае, поскольку cd = то из двух чисел
аЬ и cd одно 1, а второе ^1; для определенности положим, что
ab = а 1, a cd = — < 1. Аналогично, из пар чисел Ьс и
1
da = одно не меньше, а второе не больше единицы; для опре-
1
деленности будем считать, что Ьс «= р 1, a da — < 1 и что
<х ед; р (все иные варианты, по существу, не отличаются от рассматри-
ваемого). В таком случае мы последовательно получаем следующие
четверки чисел:
11 В 1 а 11
а. Ь, с. d; а, Р, —, -р оф, —, р Р, р, а-.
При этом во 2-й четверке наибольшее число равно а; в 3-й оно
равно сф р== а; в 4-й четверке оно равно а2 ар, и т. д. (заметим,
что 4-я четверка отличается от 2-й только тем, что роль а и р в
ней играют числа а2 и р2).
Итак, мы видим, что наибольшее из чисел четверки все время
не убывает. Если а > 1, р > 1, то наибольшее число даже все вре-
мя растет; поэтому здесь никакие две четверки, каждая из кото-
рых отлична от 1-й, не могут совпадать между собой. Более того,
если отлично от 1 хоть одно из двух чисел а и {3, то и тогда ника-
кие две четверки чисел, отличные от 1-й четверки, никогда не сов-
падут. В самом деле, еели а > 1, а Р == 1, то 2-я и следующие за
пен четверки имеют вид:
1 1 Г 1
а- ' v-а- v-а; 11 '• а2‘
таким образом, здеСь через Два шага наибольшее число Чет-
верки увеличивается (что не позволяет четверке совпасть с какой-
либо из предшествующих), а в двух первых четверках числа тоже
различны. Поэтому, если совпадают между собой k-я и l-я четвер-
ки, где / > 1, то а = f = 1; но в таком случае все четверки
чисел, начиная со 2-й, совпадают между собой (это — четверки из
одних единиц).
__Мы до сих пор игнорировали в наших рассуждениях 1-ю чет-
верку а, Ь, с, d\ следовало бы еще выяснить, не может ли она
совпасть с одной из последующих. Но это исключено из-за того,
что, как мы видели, во всех четверках чисел, начиная со 2-й, име-
ются две пары чисел, произведение которых равно 1; поэтому, если
четверка a, b, с, d совпадает с одной из последующих и,’ скажем,
Ьс — fJ > 1 и ab = а fJ > 1, то (поскольку cd = — 1 и
1 ' -
da = "jpC 0 придется считать, что ас = bd = 1. Это предположе-
ние приводит к следующим значениям чисел 1-й четверки:
/ / А -4-
F р ’ ' г «
(почему?), что снова позволяет воспользоваться сравнением наи-
больших чисел а и "/оф 1-й и 2-й четверок, совпадающих лишь
при [3 — а, т. е. тогда, когда наша 1-я четверка совпадает со 2-й
четверкой, отвечающей случаю fJ = 1, и «эволюционирует» далее,
как эта 2-я четверка. Аналогично рассматривается и случай Р = 1.
Это рассуждение и завершает доказательство теоремы.
Примечание. Решение задачи позволяет также оценить
количество «шагов», необходимых для того, чтобы все получаемые
четверки чисел стали совпадать друг с другом (в том случае, когда
эти четверки не все различны): для случая abed = 0, как мы ви-
дели, совйадают все четверки, начиная с 4-й; для случая положи-
.тельпых чисел a, b, с, d, таких, что ab = be = cd = da = 1, сов-
падают все четверки, начиная со 2-й (а если эти равенства не вы-
полняются, то никакие две четверки не совпадают между собой);
для случая не обязательно положительных чисел могут понадо-
биться еще 4 шага для того, чтобы сделать все числа положитель-
ными.
129. Поскольку квадрат каждого из чисел а,- (где i = 1, 2,
..., N = 2й) равен единице, то первые три последовательности чи-
сел имеют следующий вид:
Cl ,v -1,
«1,
а,а2,
о
<?2,
Д2Л3, ... <2 у —
2
...»
2
dNCl{\
2
таким образом, в 3-й последовательности все числа получаются ум-
ножением каждого из чисел последовательности на следующее за
ним через одно (последовательность мы считаем «циклической», т. е.
169
Полагаем, что за числом aN следует at, затем а2, и т. д.). Анало-
гично, еще через два шага мы будем иметь набор, получающийся
из 3-го в точности так же, как 3-й получается из 1-го, т. е. набор
(а1“з) («з«з) “ (^4) (а4Щ) = а2а6,..,, (а«а2) (а2а4) = а«а4,
числа которого получаются из первого (циклического) набора пе-
ремножением чисел, Следующих один за другим через 3. Еще че-
рез £ шага мы получим набор, получающийся из 5-го в точности
так же, 5-й набор получается из 1-го, т. е, набор
(а5а9) = ага2, (а2а6) (о6а10) = а2а10,.... (яЛ-а4) (а4а8) = aNas,
числа которого получаются из первоначального набора перемноже-
нием чисел, следующих один за другим через 7.
Вообще через 2? шагов мы придем к набору
2Т +1 2Р+2 N 2Р
получаемому из первоначального перемножением чисел, следующих
один за другим через 2? — 1 чисел. Но отсюда следует, что через
2к шагов мы придем к последовательности, получающейся из нашей
(циклической!) последовательности перемножением чисел, следую-
щих друг за другом через 2к— 1 = N—1 номеров, т. е. к последо-
вательности
== и । = 1 , а2в2 == 1 , . • , HjyHjy ~ Щу 1 ,
состоящей из одних единиц.
130. Покажем, прежде всего, что при переходе от исходного
набора чисел а1г а2...., ап к «производному» набору а1, й2, ..., ап
наши числа «выравниваются», т. е. разность между наибольшим и
наименьшим из чисел не увеличивается. В самом деле, поскольку
полусумма (среднее арифметическое) двух чисел всегда не больше
наибольшего из них (и равна наибольшему лишь, если числа рав-
ны), то наибольшее из чисел а[, а2, ап, равное полусумме ка-
ких-то двух чисел первоначального набора, не превосходит наиболь-
шего из этих двух чисел, а тем самым — и наибольшего из всех п
чисел а,; таким образом, при переходе от набора к набору
наибольшее число может лишь уменьшиться. Более того, из этого
рассуждения видно, что наибольшее из чисел может рав-
няться наибольшему из чисел а< лишь в том случае, когда в на-
боре at наибольшее число А встречается несколько раз, причем в
этом наборе (считающемся упорядоченным циклически, т. е. так,
что за ап следует снова щ) стоят подряд два равных А числа.
Далее, легко видеть, что если в наборе чисел а( наибольшая по
длине цепочка из следующих друг за другом равных А чисел имеет
длину k (где А<я), то в наборе чисел ai будет иметься цепочка
из следующих друг за другом k — 1 равных А чисел: так, если
Ц(+1 = а<+г “ .. ..= Я(+* =• А (а а4 < А и < А), то
= “ • • • “ ai+k—1 = А (а < А и < А). Поэтому пос-
ле k—1 шагов мы придем к числам..., среди кото-
170
рых не будет двух следующих подряд равных А чисел, а на следую-
щем, k-м шагу максимальное среди рассматриваемых чисел умень-
шите я; следовательно, если не все числа at равны друг другу, мы
можем быть уверены, что при (п— \)-кратном повторении описанной
в условии задачи процедуры наибольшее из рассматриваемых чисел
уменьшится. Точно так же доказывается, что наименьшее из рас-
сматриваемых чисел никогда не уменьшается, а если пе все числа
равны друг другу, то после (п — 1)-кратного повторения нашей
процедуры оно наверняка увеличится.
Но если числа at, 02, .... ап и все последовательно получаемые
из них числа — целые, то «выравнивание» их, т. е. уменьшение раз-
ности между наибольшим и наименьшим, неизбежно приведет в
конце концов к тому, что эта разность станет равной нулю, т. е. что
все числа сравняются между собой. В самом деле, первоначально
эта разность А—а = max а, — min я, равнялась какому-то целому
г г
положительному числу р; при уменьшении А = max а, или при уве-
i
личении а = min а, эта разность уменьшается не меньше чем на
единицу — и, следовательно, пе более чем через р таких шагов опа
станет равной нулю. Поэтому, если мы покажем, что не все равные
между собой числа а,, а2,..., ап никогда не приведут нас к системе
одинаковых чисел, то утверждение задачи будет доказано.
Рассмотрим теперь, как одинаковые числа Ъ± = а ,
Ь2 = а<^, ..., 6 могут получиться из неодинаковых чисел
г __ „(т —1) г _ „(т—1) г __ „(т—1)
Ст — <?! , с2 — а2 , .. •, сп — ап
Ясно, что для этого побходимо, чтобы числа Ci, с2, с3, ... «сов-
падали через одно», т. е. чтобы выполнялись равенства
С1 = с3 = с5 = ...( = с) и с2 = с4 = с6 ==...(= С). (*)
Но так как числа ct, с2, с3, ... упорядочены циклически, т. е. число
сп + 1 надо считать совпадающим с сь то равенства (*) (где С #= с)
вовсе невозможны при п = 2/ + 1 нечетном (когда числа
n-|- 1 = 2/+ 2 и 1 имеют разную четность); поэтому остается
предположить, что п — 21 четно. Сделаем теперь еще один «шаг
назад», вернувшись от чисел ct, с2,..., сп к предшествующим им
числам di = aj"1-2), d3 — а^~2), .. ., dn = а^~2\ Мы, очевид-
но, имеем
d4+d3 d3 + d4 i+^S!
ci — 2 > C3 - g • • • > c2i_j = 2 (**)
и
но из равенств (**) и (*) следует, что d, + d2 + d-, + ... + d2i =
= 2lc, а из равенств (***) и (*) — что d, + d2 + d3 + ... +d2( =
•= 2ZC =/= 2lc. Полученное противоречие и завершает доказательство.
171
131. Выясним, прежде всего, при каких числах х, у, г возможно
совпадение троек (xn, Уп, zn) и (х, у, г). Так как все тройки чи-
сел, начиная с хь «Л, Zi, заведомо неотрицательны, то и числа х,
У, г должны быть неотрицательными. Условимся, далее, считать,
что х Дэ у z и Xi yf 53 Zi при всех i = 1, 2, 3,... Поскольку,
очевидно, Xi — xi_1 — zt_t при всех 1 (где под х0 и г0 понима-
ются числа х и г), то х Дэ лч Дэ х2 Зэ х3 Дэ ..., причем, если хоть
одно число z{ (i = 0, 1, 2,...) больше нуля, то Х;+1 < х,- < х (и
все Xj, где j > i, также меньше х); поэтому, если хп = х, то Zi = О
при t = 0, 1,..., п — 1. Таким образом, должно быть z = 0 и
г, = 0, откуда уже вытекает, что либо у — х (и г, = х — (/ = 0),
либо у = г = 0 (и = у — z = 0). Итак, мы видим, что для
совпадения тройки чисел (х, у, г) с какой-либо тройкой (х„, уп, г„)
необходимо, чтобы исходная тройка имела (при х = 1)
либо вид (1, 1, 0), либо вид (1, 0, 0). При этом второй случай
.'ложно сразу же откинуть, ибо от тройки (1, 0, 0) мы переходим к
(отличной от исходной) тройке (1, 1, 0); поэтому, если Х = 1 и
тройка (х, у, г) совпадает с (х„, уп, г„), то (х, у, г) —это тройка
чисел (1, 1, 0) (и тройки (х„, уп, zn) при всех п имеют такое же
строение)!
132. а) Отметим, что четность или нечетность разности двух
чисел зависит только от четности и нечетности уменьшаемого и вы-
читаемого. Условимся обозначать четные числа буквой ч, а нечет-
ные— буквой н. Всего возможны следующие шесть существенно
различных комбинаций начальных чисел А, В, С, D: Г ч, ч, ч, ч;
2° ч, ч, ч, и; 3° ч, ч, н, «; 4° ч, и, ч, н; 5° ч, н, и, и и 6° и, н, н, н\
все остальные комбинации могут быть получены из этих шести
циклической перестановкой чисел (перестановкой без изменения по-
рядка; при этом 1-е число считается следующим за 4-м). Прове-
рим, что во всех случаях не позднее чем через четыре шага мы
придем к четверке четных чисел. Действительно, комбинация 1°
сразу состоит из четных чисел; в случае комбинации 6° мы в один
пшг приходим к комбинации 1°; в случае комбинации 4° мы в один
шаг приходим к комбинации 6° и, следовательно, в два шага —
к комбинации Г; в случае комбинации 3° мы в один шаг приходим
к комбинации 4° и, следовательно, в три шага — к комбинации 1°;
наконец, в случае комбинаций 2° и 5° мы в один шаг приходим
к комбинации 3° (в случае комбинации 5° — к комбинации, получа-
ющейся из 3° циклической перестановкой) и, следовательно, в че-
тыре шага — к комбинации Г. Таким образом, мы во всех слу-
чаях через четыре шага придем к четверке четных чисел.
Продолжили теперь процесс образования новых четверок чисел;
так же, как выше, мы убедимся, что еще через четыре шага мы
придем к числам, делящимся па 4, еще через четыре шага — к чис-
лам, делящимся на 8, и т. д. Таким образом, продолжая процесс
достаточно долго, мы сможем прийти к четверке чисел, делящихся
па любую (сколь угодно высокую!) степень двух. Так как чис-
ла по абсолютной величина не увеличиваются, то это означает, что
мы, в конце концов, придем к четверке чисел, состоящей из одних
нулей (если все числа А, В, С, D меньше 2”, то мы заведомо при-
дем к четверке нулей через 4п шагов, но можем прийти к ней и
значительно раньше).
Примечание. Аналогично можно показать, что если взять
не 4, а 8, 16, ...или любое другое число n = 2ft целых положитель-
172
ных чисел, то, поступая аналогично вышеизложенному, мы через
конечное число шагов придем к системе п чисел, являющихся ну-
лями. Если число п не является степенью двух, то дело обстоит
по-другому; так, например, исходя из тройки чисел 1, 1, 0, мы ни-
когда не придем к тройке 0, 0, 0:
1, 1, 0,
0, 1, 1,
1, 0, 1,
1, 1, 0,
(ср. с решением задачи 131).
, , 01 Ь, с, d,
б) Ясно, что если числа А = —, В = -т—, С = —, D = —д-
й0 оо с» d0
суть рациональные дроби, то, умножая их все на определенный мно-
житель k (па общий знаменатель всех дробей, например, па a:}bac<dA,
мы придем к целым числам А' = kA, В' — kB, С = kC и D‘ = kD,
а из того, что утверждение задачи а) верно для чисел А', В', С"
и D', следует, что оно верно также и для чисел А, В, С и D.
Если числа А, В, С, D иррациональны, то утверждение задачи
а) может уже и не выполняться. Для доказательства этого до-
статочно указать хотя бы одну четверку чисел А, В, С, D, для
которых это будет так. Положим 4 = 1, В = х, С = х2, D — x3, где
х — какое-то положительное число, которое мы можем выбрать по
своему усмотрению. При этом, оче-
видно,
Д1=|х—11, В1—\х2—х|=х|х—1|,,
С, = | х3 — х21 = х21 х — 11,
Dt = |х3 — 11 = (х2 + х + 1) |х — 11,
т. е. числа 4,, Bt, Ct, Dt пропорци-
ональны 1, х, х2 и х2 + х 4- 1. Поэто-
му, если мы- сумеем подобрать х
так, чтобы выполнялось равенство
х2+х + 1 = х3, (*)
то числа At, Bi, Cit окажутся про-
порциональными А, В, С, D — и наш
процесс получения последовательных
четверок чисел никогда не кончится.
Но из рис. 13, на котором совмест-
но изображены графики функций
(1 \2 о
х + J + ~4~ (это
есть парабола) и у = х3 (кубическая
парабола), видно, что соответствую-
щие линии пересекаются в некото-
рой точке М(хо, Уо), так что х =
= х0 —это есть (положительный) корень уравнения (*). Тем са-
мым мы установили существование таких (очевидно — иррациональ-
ных!) чисел А — 1, В = Хо, С = Xq и D = Хц (= Xq + х0 -|-1), для
которых утверждение задачи а) неверно.
173
133. а) Нетрудно видеть, что следующее расположение 100 пер-'
вых целых чисел удовлетворяет условию задачи:
10 9 8 7 6 5 4 3 2 1 20 19 18 17 16 15 14 13 12 11
30 29 28 27 26.25 24 23 22 21 40 39 38 37 36 35 34 33 32 31
50 49 48 47 46 45 44 43 42 41 60 59 58 57 56 55 54 53 52 51
70 69 68 67 66 65 64 63 62 61 80 79 78 77 76 75 74 73 72 71
90 89 88 87 86 85 84 83 82 81 100 99 98 97 96 95 94 93 92 91.
б) Пусть есть первое (самое левое) из выписанных чисел;
0*2^—первое из оставшихся, большее чем а^; (И)1*— первое из сле-
дующих за а?,1’, большее чем а^\ и т. д. Таким образом мы соста-
вим последовательность возрастающих чисел
Если в этой последовательности имеется больше 10 чисел
(т. е. если i’i > 10), то задача уже решена Если же Ц 10,
то мы вычеркнем все эти числа и из оставшихся 101 — и чисел
составим точно таким же образом новую последователь-
ность а^, а-^1, а32\..., возрастающих чисел. Продолжая этот
процесс, мы выделим из наших 101 чисел ряд возрастающих
последовательностей. Если хотя бы одна из этих последовательно-
стей содержит больше 10 чисел, то наша задача уже решена; таким
образом, нам остается только рассмотреть случай, когда в каждой
из выделенных последовательностей имеется не больше 10 чисел.
Так как у нас имеется всего 101 число, то в рассматриваемом
случае общее число k выделенных последовательностей возраста-
ющих чисел не может быть меньше 11. В таком случае мы утвержда-
ем, что в ряду из 1-01 числа можно выбрать 11 чисел, следующих
один за другим в убывающем порядке. Эти числа мы будем
выбирать с конца следующим образом. Последним из них будет
последнее число последней из наших возрастающих последо-
вательностей. Затем выберем число из предпоследней последова-
тельности, расположенное слева от ближе всего к нему. Это
число больше ибо в противном случае в процессе построения
предпоследней последовательности мы бы выписали вслед за ним
число a(.k>, в то время как на самом деле число попало в
другую последовательность. Точно так же вслед за этим выписы-
ваем число из третьей от конца последовательности, расположенное
слева от выбранного числа предпоследней последовательности, бли-
же всего к нему, и т. д. Таким образом мы построим последова-
тельность чисел, которые идут возрастая, если их рассматривать
в порядке справа налево, т. е. убывающую последовательность;
число членов этой последовательности равно числу k выбранных
возрастающих последовательностей, т. е. не меньше 11.
Примечание. Совершенно аналогично можно доказать, что
(п—1)= целых положительных чисел можно расположить так, что
никакие п из них не будут следовать одно за другим в порядке
возрастания или убывания, но при любом расположении k > (п — I)2
целых положительных чисел какие-то п из этих чисел обя-
174
аательно будут Следовать одно за другим в порядке возрастания
или убывания.
134. а) Первое решение. Рассмотрим наибольшие нечет-
ные делители выбранных 101 чисел, т. е. числа, которые получают-
ся, если разделить каждое число на наибольшую степень двойки,
которую оно содержит множителем. Так как различных нечетных
чисел, не превосходящих 20'0, имеется всего 100, то среди этих
наибольших нечетных делителей чисел будут два одинаковых. Но
это означает, что среди наших 101 чисел имеются два, отличаю-
щихся одно от другого только тем, что множитель 2 входит в эти
числа в разных степенях. Очевидно, что большее из этих чисел бу-
дет делиться на второе.
Второе решение. Можно также доказать это предложе-
ние методом математической индукции. Проверим, что
если из четырех чисел 1, 2, 3 и 4 выбраны три числа, то одно из них
делится на другое (еще легче видеть, что если из чисел 1,2 выбраны
два числа, то одно из них делится на второе). Докажем теперь, что
если из 2п чисел от 1 до 2п нельзя выбрать п + 1 чисел так, чтобы
никакое из них не делилось на другое, то из первых 2(п + 1) целых
положительных чисел нельзя будет выбрать п + 2 чисел так, чтобы
ни одно из них не делилось па другое.
Действительно, рассмотрим какие-либо п + 2 чисел, выбранных
из первых 2 (я + 1) целых положительных чисел. Если среди них
нет чисел 2п + 1 и 2п + 2 или есть только одно из этих чисел, то
среди них есть « + 1 чисел, не превосходящих 2п, и по сделанному
предположению одно из этих чисел обязательно делится на другое.
Если среди них есть оба числа 2п + 1 и 2п + 2 и есть также число
п+1, то мы уже имеем пару чисел, делящихся одно на другое,
а именно, п + 1 и 2п + 2. Наконец, если среди наших чисел есть
числа 2п + 1 и 2п + 2, но нет числа п + 1, то исключим из рассмот-
рения числа 2п + 1 и 2п + 2 и добавим «+1. Мы получим «+1
чисел, не превосходящих 2п; по сделанному предположению одно
из этих чисел делится на другое. Если это число не есть п + 1,
то мы уже получаем пару чисел из выбранных нами Л+ 2 чисел,
одно из которых делится на другое. Если же число, ’делящееся на
другое, есть п + 1, то и 2п + 2 делится на одно из выбранных
чисел.
б) Выберем наши числа следующим образом: нечетные числа
от 101 до 199 ( 50 чисел), нечетные числа от 51 до 99, умноженные
каждое на 2' (25 чисел), нечетные числа от 27 до 49, умноженные
каждое на 4 (12 чисел), нечетные числа от 13 до 25, умноженные
каждое на 8 (7 чисел), нечетные числа от 7 до 11, умноженные
каждое на 16 (3 числа), числа 3-32, 5-32, 1-64.
в) Предположим, что мы выбрали 100 целых чисел, не пре-
восходящих 200, ни одно из которых не делится на другое; дока-
жем, что среди этих чисел не может быть ни одного из чисел 1—15.
Как в первом решении задачи а), рассмотрим все наибольшие
нечетные делители выбранных чисел; очевидно, это будут все не-
четные числа, не превосходящие 200 (см. решение задачи а)).
В частности, среди этих нечетных делителей есть числа 1, 3, 9, 27
и 81. Так как никакие два из чисел, отвечающих этим нечетным
делителям, не делятся одно на другое, то число, содержащее не-
четный делитель 27, должно делиться на 2 в степени не ниже
первой; число, содержащее нечетный делитель 9,— на 2 в степени
175
не ниже второй; число, содержащее делитель 3,— на 2 в степени,
не ниже третьей и число, содержащее делитель 1,— на 2 в степени
не ниже четвертой. Но это значит, что числа 1, 2* = 1-2, 3, 4 = 1 • 22,
6 = 3 • 2, 8 = 1 • 23, 9 и 12 = 3 • 22 не входят в число 200 чисел.
Точно так же, рассматривая числа, имеющие наибольшими не-
четными делителями 5, 15' и 45, убеждаемся, что среди наших чи-
сел нет чисел 5, 10 = 5-2, 15; рассматривая числа, имеющие
наибольшими нечетными делителями 7 и 21, убеждаемся, что среди
200 чисел нет числа 7; рассматривая числа, имеющие наибольшими
нечетными делителями 11 и 33, убеждаемся, что среди наших чисел
нет 11, и, рассматривая числа, имеющие наибольшими нечетными
делителями 13 и 39, убеждаемся, что среди них нет числа 13.
Примечание. Аналогично решениям задач а)—в) можно
показать, что из 2я (или меньше) первых целых положительных
чисел нельзя выбрать «4-1 чисел так, чтобы никакие два не дели-
лись одно па другое, но можно выбрать п (или меньше) таких
чисел. При этом, если 3й < 2п < Зй+1, то из 2п первых целых чи-
сел нельзя выбрать п чисел, хотя бы одно из которых
меньше 2й и таких, что никакое из этих чисел не делится на
другое, по можно выбрать п таких чисел, наименьшее из которых
равно 2й (так, из 200 чисел можно выбрать 100, наименьшее
из которых равно 16 и ни одно из которых не делится на другое).
135. а) Рассмотрим наименьшие по абсолютной величине остат-
ки, которые дают наши числа при делении на 100 (т. е. если какое-
либо число а дает при делении па 100 остаток, больший 50, то мы
будем производить деление с избытком и рассмотрим отрицатель-
ный остаток —г; а = 100 q — г, где 0<г<50). Так, как поло-
жительных чисел, не превосходящих 50, существует всего 51 (а
именно, 0, 1, 2,..., 50), а остатков мы имеем 52, то два из этих
остатков равны по абсолютной величине. Если эти остатки равны
и по знаку, то разность соответствующих чисел делится на 100;
если они противоположны, то сумма чисел делится на 100.
б) Пусть о,, а2, а3 ..., «юо— данные числа (расположенные
в произвольном порядке). Рассмотрим суммы
S1 — Hi, S2 ~ СТ 4“ а2, 5з — яр 4“ 4" а3, • • •
. • • , S100 = 01 4“ й2 + й3 4- • • • + О100-
Так как этих сумм имеется 100, то в том случае, когда ни одна из
них не делится па 100, по крайней мере две из сумм дают при
делении на 100 одинаковые остатки (ибо различных не равных ну-
лю остатков от деления на 100 существует только 99). Вычтя из
большей из двух сумм, дающих одинаковые остатки, меньшую,
мы получим некоторую сумму вида а* + 1 4- пк+2 + ...+ а,п, кото-
рая будет делиться на 100.
Примечание. Разумеется, в точности аналогично решению
этой задачи можно показать, что из любых п целых чисел (где
п — произвольное натуральное число) всегда можно отобрать не-
сколько, сумма которых делится на п.
в) Если все рассматриваемые числа равны между собой (и,
значит равны 2), то утверждение задачи очевидно: сумма любых 50
чисел равна 100. Если, скажем, а.., =^а2, то рассмотрим следующие
17G
суммы (ср. с решением задачи б)):
S1 = О], Sj = Й2> S3 = 01 + И2,
$4 = Q] 02 + Oj, • • •, stOO = Ol Н- а2 + . • • + ^9Э-
Как и выше, заключаем, что либо одна из этих сумм делится на
100, либо две из них дают при делении на 100 одинаковые остат-
ки, а тогда разность st—sj этих двух сумм определяет набор на-
ших чисел, сумма которых делится на 100. (Заметим, что посколь-
ку щ #= а2 и at, а2 100, «суммы» s, =at и s2 = а2 не могут да-
вать при делении на 100 одинаковые остатки.) Но если сумма
некоторых из наших чисел (не всех — в нее наверное не входит
число йюо) делится на 100, то, поскольку эта сумма положительна
и меньше 200, она обязательно равна 100.
г) Заметим, прежде всего, что из любых четырех целых чисел
можно выбрать два, сумма которых делится на 2, и что из любых
десяти целых чисел можно выбрать пять, сумма которых делится
на 5; эти утверждения, родственные тому, которое нам требуется
доказать, разумеется, проще него (и, кроме того, используются в
его доказательстве). Впрочем, все перечисленные оценки (включая
и результат настоящей задачи) можно еще и.несколько улучшить:
два числа, сумма которых делится на 2, можно отобрать из любой
совокупности трех чисел; точно так же пять чисел, сумма кото-
рых делится на 5, можно отобрать из любой совокупности девя-
ти чисел, а 100 чисег, сумма которых делится на 100, можно
отобрать из любой совокупности 199 чисел (см. Примечание в кон-
це решения задачи).
Итак, мы последовательно будем доказывать три факта.
1°. Пусть даны 3 числа at, а2 и а3; из них можно выбрать
2 числа так, чтобы сумма этих чисел делилась на 2. Это предло-
жение является совершенно очевидным: достаточно выбрать два
числа - одинаковой четности (оба четные или оба нечет-
ные), а такие числа среди наших трех конечно есть.
Ясно, что основным в этом простом рассуждении является воз-
можность замены самих чисел at, а2 и аз их остатками гь г2 и г3
от деления на 2: ведь если сумма остатков делится на 2, то и сум-
ма самих чисел делится на 2. Но числа г}, г2 и г3 могут иметь
лишь значения 0 или 1 — и здесь совсем легко "видеть, что среди
них всегда есть 2, сумма которых делится на 2.
2°. Рассмотрим теперь 9 чисел at, а2, ..., а9; мы утверждаем,
что из них можно выбрать 5 чисел так, чтобы сумма этих чисег
делилась на 5. Заменим опять сами числа at (где »= 1, 2,..., 9)
их остатками г, от деления на 5. Все числа г, имеют одно из пяти
значений 0, 1, 2, 3 или 4; с этими маленькими числами удобнее ра-
ботать, чем с самими числами at. Но, кроме того, ко всем 9 числам
rt можно прибавить одно и то же (или отнять от них одно и то
же) произвольно выбранное число с — ведь при этом остаток от
деления Суммы произвольных 5 наших чисел на 5 не изменится.
[Разумеется, после этой операции «сдвига» остатков мы снова за-
меним полученные числа ц ±с их остатками от деления па 5;
эти новые остатки мы по-прежнему будем обозначать через г,.]
Это замечание позволяет считать, что среди 9 чисел г, (каждое из
которых равно 0, 1, 2, 3 или 4) число 0 встречается реже, чем
остальные остатки: ведь если бы среди наших чисел было больше
всего чисел k > 0, то мы просто отняли бы от всех чисел по k.
12 Д. о. Шклярский и др. 177
При этом ясно, что число f нулей может заключаться 6 пределах
2 t --<9 ,(/ > 1, так как среди 9 чисел хоть один остаток повто-
ряется дважды!); при этом, если /^5, то доказывать нечего: в
этом случае мы имеем 5 делящихся на 5 чисел, сумма которых то-
же, конечно, делится на 5.
Дальнейшие рассуждения несложны, но несколько кропотливы.
Если t = 2, то в нашей совокупности девяти остатков г, ни одно
число не повторяется более чем 2 раза; другими словами, 4 остат-
ка повторяются в этой совокупности дважды, и лишь один встреча-
ется однократно. Но тогда с помощью того же приема «сдвига»
всех остатков на одно и то же число с мы можем добиться равен-
ства этого «непарного» остатка числу 4. Но если совокупность чи-
сел представляет собой набор чисел 0, 0, 1, 1, 2, 2, 3, 3, 4 (мы счи-
таем, что здесь последовательно выписаны числа rI: г2, гз.... гя),
то, например, сумма О + г2 + + г«4-г7 делится на 5 (равна 5).
Если же t = 3 или 4, то условимся считать, что и = г2 = г3 = О
и что все числа г$, г^,..., г9 отличны от нуля; при этом число rs
может равняться 0 или быть, больше 0—это нам безразлично.
Далее, из совокупности 5 (отличных от 0) чисел rs, re, r7, rs и rs
всегда можно отобрать несколько (больше одного!) чисел так, что-
бы их сумма делилась на 5 — доказать это можно аналогично ре-
шению задачи б) (ср. с Примечанием в конце решения задачи б)).
Дополнив же затем полученную совокупность чисел нужным чис-
лом нулей из числа чисел rlt га и гг до пяти чисел (возможно, впро-
чем, что нам не придется эти числа дополнять), мы и придем к со-
вокупности пяти чисел, сумма которых делится на 5.
3°. Теперь мы можем установить, что из совокупности произ-
вольных 199 чисел alt а2..., а199 всегда можно выбрать 1ОЭ чисел,
сумма которых делится на 100. Ясно, что из этих 199 чисел можно
выбрать 99 пар чисел одинаковой четности: будем выде-
лять такие пары последовательно; после того как мы отберем 98
пар, у нас останутся 3 числа, из которых, в силу п. 1°, последние
2 требуемых числа выбрать можно. Перенумеруем наши числа, счи-
тая, что и а2, а3 и а4,..а197 и ат — числа одинаковой четно-
сти; затем заменим каждые два числа в2<-1 и й2< (где 1 = 1, 2,,.
99) их полусуммой bt = . Ясно, что если среди 99 (це-
лых) чисел bt мы сможем выбрать 50, сумма которых делится на 50, то
(в два раза большая) сумма всех чисел а(, отвечающих 50 ото-
бранным числам bt, будет делиться на 100. Таким образом, нам
достаточно установить, что из каждых 99 целых чисел можно вы-
брать 50, сумма которых делится на 50. Далее, в точности, как и
выше, отберем из 99 чисел bt 49 пар чисел одинаковой чет-
ности. Считая, что Ь| и Ь2, &з и &4,..., Ь97 и Ь98 — числа одинако-
вой четности, заменим каждые два числа 62ft-i и
2....49) одним числом — их полусуммой cft= ——1
bv, (где. k = 1,
4-
-------; при этом,
если сумма каких-то 25 чисел са будет делиться на 25, го сумма 50
отвечающих им чисел bt будет делиться на 50. Однако далее этот
прием уже отказывается работать, так как 25 — число нечетное;
поэтому теперь нам придется объединять числа с* не в пары, а в
пятерки чисел.
Из каждых 9 чисел, как мы знаем, можно выбрать 5 чисел,
сумма которых делится на 5; тем более из числа наших 49 чисел
178
ck можно выбрать 5 таких чисел — назовем их сь с2, с3, с4, с3.
После этого у нас останется 49 — 5 = 44 числа, из которых можно
выбрать еще 5 чисел, сумма которых делится на 5,— и затем продол-
жать этот процесс далее. Выделив таким образом 8 пятерок чисел,
таких, что сумма чисел в каждой пятерке делится на 5, мы придем
к оставшейся совокупности 49 — 8-5 = 9 чисел, из которых, в силу
п. 2°, нам удастся выбрать последнюю, девятую пятерку. Теперь
заменим каждую пятерку чисел с5г_4, с5г_3, cgi-s, c3i_,L, сы их сред-
ним арифметическим dl = )i~4 3 --------id. Ясно, что если
мы найдем 5 чисел d:, сумма которых делится на 5, то (в 5 раз боль-
шая этой суммы!) сумма отвечающих им чисел ch будет делиться
на 25, — а возможность выбора таких чисел c!t нам как раз и тре-
буется доказать. Но (здесь мы снова апеллируем к п. 2°!) из 9
чисел di, d2, d3, d4, rf5, d6, d7, ds и ds, пять чисел, сумма которых
делится на 5, выбрать можно, чем и завершается доказательство.
Примечание. В обобщение пп. 1°, 2° и 3° решения и задачи г)
можно также установить, что из каждых 2п — 1 целых чисел (где
п — произвольное натуральное число) можно выбрать п чисел так,
чтобы сумма их делилась на и; однако доказательство этого обще-
го факта значительно сложнее вывода его частных случаев, отве-
чающих значениям п — 2, п = 5 или даже п = 100.
136. Так как сумма всех наших чисел равна 1, а наибольшее
1
из них равно то общее количество чисел не меньше 2k. Будем
доказывать наше утверждение от противного, т. е. предполо-
жим, что в любой группе из k чисел нашей последовательности
наименьшее не превосходит половины наибольшего, и пока-
жем, что это предположение приводит к противоречию. При сде-
ланном предположении для группы из k чисел <Xi, а2,..., ак (где
01~~2k—наибольшее число, a ак—наименьшее) будем иметь
1
ак < ~2~ ох; аналогично, из рассмотрения группы о4, а*+1,..., a2k-i
1 1
чисел получаем <т2а—i ^~2~ak < ~22 ai> из рассмотрения чисел a2t-i,
a2h.... аЗЛ_2 (эта группа чисел существует лишь при 3k — 2 п)
1 1
имеем a3k_2 < 1 ~2з ai< и т- А- Суммируя все получен-
ные неравенства, заключаем, что
S = а3 + ah + a2A_1 + a3h_2 -ф- ... <
11 / 1 1 \
+ 2 ai + 22 ai + • • < I 1 2 22 ' ‘~ 20] (*)
(первые две суммы слева содержат лишь конечное число членов, а
, 1 1
1 + + ~22 + • • • понимается бесконечная геометрическая
прогрессия). А так как наша последовательность at, а2, а3, ...
12* 179
'является невозрастающей, то
а2 4" ah + l 4" 4" fl3A-1 + . , » S < 2tZb
fl3 4" ak f-2 4“ °2А + ! 4" ^3A 4- • • • 5 < 2^1,
Яй-1 4" a2k-2 + a3k-3 4- • • 5 < 2fl].
Сложив, наконец, неравенство (*) и все неравенства (**), по-
лучим:
ai + а2. 4” аз 4~ • • • + ап 'С 4~ 2^1 т 4 2gt — 2kaY =
k слагаемых
= 2k • = 1,
в то время .как по условию задачи а, + а2 + • • + = 1. Полу-
ченное противоречие и доказывает требуемое утверждение.
137. Будем обходить наш круг, например, по часовой стрелке,
начиная с нулика, пока снова не придем к этому же нулику. При
этом всех переходов от нулика (к нулику или крестику) будет
столько, сколько нуликов, т. е. q. В числе этих переходов будут
переходы к нулику — их столько, сколько пар рядом стоящих нули-
ков, т. е. Ь. Тогда переходов от нулика к крестику будет q — b.
Аналогично, при таком же обходе можно подсчитать число пе-
реходов от крестика к нулику — их будет р — а.
Но число переходов от нулика к крестику равно числу перехо-
дов от крестика к нулику, так как по завершении обхода мы долж-
ны остановиться опять на исходном нулике. Значит, q — b = р — а,
откуда
а — b — р — q.
138. Ясно, что если какое-либо число = k, то рассматривае-
мое произведение равно нулю (четно), а если мы переставим в ряду
чисел 1, 2, 3, 4,..., 2m — 1, 2m каждые два соседних числа, придя
к последовательности it = 2, i2 = 1, 1з = 4, it — 3,..., izm-t = 2m,
i2m ~ 2m — 1, то произведение
(1 — it) (2 — i2) .. . (2m — i2m) —
= (—1) • 1 • (—1) • 1 • ... • (—1) • 1 = (—1)“ • 1“ = (—l)m
будет нечетным.-, поэтому нам остается лишь показать, что при п —
= 2m +1 нечетном рассматриваемое произведение будет чет-
ным всегда.
Первое доказательство. Среди чисел 1, 2............... п =
2т; -L- 1 \
—~—Учетных (это будут числа
2, 4,..., 2m); поэтому среди чисел it, 12. in четных чисел с не-
четными номерами будет не больше чем m (ибо мы имеем всего m
четных чисел) и нечетных чисел с четными номерами будет тоже
не больше пг (ибо всего-то мы имеем m четных номеров). Таким
образом, объединение всех номеров первого и второго классов не
может охватывать все п = 2m + 1 номеров; поэтому найдется такой
номер I, что либо и ii и I четны, либо и ii и I нечетны. Но в обоих
случаях разность. it — I будет четной; поэтому произведение всех
множителей k — ik, где k = 1, 2,..., 2m + 1, заведомо будет
четным.
I fl
«= 2m + 1 будет всего m I <_ —
180
Второе доказательство. Так как сумма вс<** ппссмат-
рнваемых множителей
(1-11) + (2-у + (3-У +...+ (л-1„) -
= (1+2 + 3+ ... + п)-(1+2 + 3+ ...-гл) -0.
то при п нечетном все эти множители не могут быть нечетными
(ибо сумма нечетного числа нечетных чисел нечетна). Поэтому сре-
ди этих множителей имеется хоть один четный — а значит, их
произведение четно.
139. Ясно, что поскольку каждое из произведений XiX2, x2xt,..,
xnxt равно +1 или —1, то сумма всех этих произведений может
равняться пулю лишь в том случае, если число слагаемых в ней
ге = 2ш— четно и m из этих слагаемых равны +1, a m других
равны —1. Но если —1 равны ровно m произведений из числа xtx2,
х2х3,_ х3х4,..., х хпхь то в цепочке хь х2, х3,..., x„~i, х„, Xi
происходит m перемен знаков. Отсюда уже следует, что число m
должно быть четным (in — 2k), а значит, п делится на 4 (п = 46),
ибо первое и последнее числа этой цепочки совпадают, и, значит,
число перемен знаков между ними не может быть нечетным.
140. Отнесем к одной группе все те числа, десятичная запись
которых содержит четное число единиц; все же числа, в записи ко-
торых фигурирует нечетное число единиц, составят вторую группу.
Пусть А и В — два различных десятизначных числа из одной груп-
пы. Если записи А и В содержат одно и то же число п единиц
(где 1 п гф 9, ведь если я = 0 или п = 10, то числа А и В не
могут быть различными), то, предположив, что на каком-то опре-
деленном (i-м) месте в записи А стоит цифра 1, а в записи В —
цифра 2, мы вынуждены будем считать, что на другом (/-м) месте,
напротив, в записи А стоит 2, а в записи В—цифра 1: ведь записи
обоих чисел содержат поровну единиц. Но в таком случае в записи
суммы А + В и на i-м и на /-м местах будет стоять цифра 3, т. е.
эта запись будет содержать не меньше двух троек. Если же запись
числа А включает п единиц, а запись В содержит пг п единиц,
где, скажем, п > т, то поскольку числа п и т — одинаковой
четности (т. е. оба четные или оба нечетные: ведь А и В — чис-
ла из одной группы), то п — т Дэ 2, и, значит, найдутся, по край-
ней мере, два такие места, скажем k-e и /-е, что в записи А на этих
местах стоит цифра 1, а в записи В — цифра 2. Отсюда следует, что
в записи суммы А + В и на fe-м, и на /-м местах (снова — не менее
чем на двух местах) будет стоять цифра 3.
141. Выпишем наши пять 100-значных чисел одно под другим;
в каждом разряде (т. е. в каждом столбце) рассмотрим всевозмож-
ные пары цифр. Из 5 цифр можно, очевидно, составить 10 пар
цифр; поэтому всего мы будем иметь 10-100 — 1000 пар цифр. При
этом в каждом столбе будут встречаться обе разные цифры 1 и
2; если среди них имеется одна цифра 1 и четыре цифры 2 (или
наоборот), то пар одинаковых цифр будет 6, а если в столбце имеют-
ся две цифры 1 и три цифры 2 (или наоборот), то число пар
одинаковых цифр будет равно 4. Таким образом, общее число пар
одинаковых цифр (по всем 100 разрядам) может - колебаться в
пределах от 4-100 = 400 до 6-100 — 600._ ________________
С другой стороны, если А = а,а2 ... a1(w и В = btb2... btm —
Два из наших чисел, то, как мы знаем, среди пар цифр а4 и
с2 и Ь2, .... а100 и Ьюо будет равно г пар одинаковых чисел. А так
181
как из 5 чисел можно образовать 10 пар чисел, то таким путем мы
насчитаем Юг пар одинаковых чисел. Так мы приходим к двойно-
му неравенству
400 < Юг С 600,
откуда и следует, что 40 sC г 60.
Примечание. Разумеется, то же рассуждение показывает,
что если считать наши пять чисел я-значными, то определенное та-
2 3
ким же путем число г должно заключаться в пределах: уя<г^ уя;
рекомендуем читателю самостоятельно рассмотреть вопрос об ана-
логичных оценках числа г при замене количества 5 наших чисел
другим их количеством.
142. Ясно, что достаточно убедиться в возможности с помощью
наших «шагов» изменить любой знак 1-го набора, не меняя ни од-
ного из других знаков-, ведь тогда, меняя последовательно все те
знаки 1-го набора, которые отличны от стоящих па тех же местах
знаков 2-го набора, мы переведем 1-й набор во 2-й. Но изменить
одновременно два произвольных знака — скажем, Рй знак о, и j-il
знак О;—1-го набора мы, очевидно, можем: для этого достаточно
дополнить паши два знака еще какими-то 10 (разумеется, одними
И теми же!) знаками аЙ2,..., 1-го набора до двух групп а;,
аА , ak,„ 11 °/i1’ аА2....cta10 из И знаков, а затем по-
следовательно изменить сначала знаки о <,<4, , а/;2,.. .а затем—
анаки a-, Теперь пусть ор— произвольно выбран-
ный знак 1-го набора; дополним его еще 10 знаками a a9z,..., о
до группы оп, ........а из 11 знаков, а затем сначала поменяем
все эти знаки, а потом — с помощью описанного выше приема —
знаки а„ и о„, затем — знакио„ , о„ .... наконец,— знании и о_ .
41 Щ 4.1 4i> ’ ’ 4» 4in'
При этом мы сохраним прежними все знаки 1-го набора, кроме од-
ного лишь знака оР,—-откуда и следует утверждение задачи.
143. Предположим, что за какой-то понедельник шахматист
сыграл Qi партий, за понедельник и вторник — а2 партий, за три
дня — а3 партий, и т. д., наконец, за 77 дней — а77 партий. Рассмот-
рим теперь следующую совокупность чисел: ац а2, а3.....а77; at + 20,
а21-]- 2'0, а3 4- 20,..., о77 4- 20.
Всего мы имеем здесь 2-77 = 154 числа, каждое из которых не
больше чем 132 4- 20 = 152 (число а77 не больше чем 11-12= 132,
так как 77 дней — это ровно 11 недель); следовательно, по крайней
мере, два из этих 154 чисел равны между собой (ср. со сказанным
на стр. 10). Но никакие два числа из ряда ai, а2, а3,..., а77 не могут
быть равны между собой (ибо шахматист каждый день играет не
меньше одной партии); точно так же не могут быть равны между
собой никакие два числа из ряда Qi 4~ 20, а2Ч-20, а320............
а77 4- 20. Таким образом, для каких-то k и / должно иметь место
равенство
аь = аг 4- 20;
это равенство означает, что —at = 20, т. е. что за k—I дней,
с (/4-1)-го по k-й включительно, шахматист сыграл ровно 20
партий.
182
144. Первое р е ш е н и е. Рассмотрим остатки от Деления чисел
1,11,111...1111 ... 1
N единиц
ва N. Так как этих чисел N, а различных не равных нулю остат-
ков при делении на N может получиться только N— 1, то если ни
одно из этих чисел не делится на N (противное доказывало бы
предложение задачи), то какие-то два из них, например
К = 11 ... 1 и L = 1111 ... 1 (/>*),
k единиц I единиц
дают при делении на N один и тот же остаток. В таком слу-
чае разность
L — К= Н ... 100 ... О
I—и единиц h нулей
делится на N.
Если W взаимно просто с 10, то из делимости числа L — К, =
= 11 ... 1 • 10* на N следует, что число 11 ... 1 делится на N.
I — k единиц I—k единиц
1
Второе решение. Рассмотрим разложение числа в пе-
риодическую десятичную дробь:
1 ------------------------- , ------------- .
—=0, ЬГЬ2 ... Ьк (а^аг ... а;) (где aYa2 ... с^ — период ).
По правилу обращения периодических десятичных дробей в обыкно-
венные, мы будем иметь:
1 ЬгЬ2 ... bka^a2 . .. at — btb2 ... bk
999 ... 9 00 ... 0
I девяток k нулей
Отсюда вытекает, что число А — 999 ... 900 ... 0 делится на N. Но
I девяток k нулей
А = 9Л1, где А1 = 11 ... 100 ... 0. Рассмотрим теперь число
I единиц k нулей
В = 11 ... 100 ... 011 ... 100 . .. О ... 11 ... 100 .. .0,
I цифр k цифр I цифр k цифр I цифр k цифр
получающееся, если число А] выписать 9 раз подряд. Очевидно, что
В равно произведению числа Ai на число
100 ... 0 100 ... 0 ... 100 ... 01,
(I+ft) цифр(1-Ьk)цИфр (Щ-й)цифр
8 раз
делящееся на 9 (по признаку делимости на 9). Следовательно, чис-
ло В, состоящее из одних единиц и нулей, делится на 9Л1 = А, а
значит, и на АГ.
Если jV взаимно просто с 10, то при обращении в десятич-
ную дробь дает дробь чисто периодическую, так что В в
этом случае будет состоять из одних единиц.
183
Примечание. Ясно, что еСлй запись числа А состоит Из р
единиц, а запись В — из pq единиц, то В делится на А; поэтому
(в предположении, что N взаимно просто с 10; впрочем, это верно
и в общем случае) существует даже бесконечно много чисел,
удовлетворяющих условию задачи.
145. Пусть a.v и aJv+1 = aN + d — два последователь-
ных члена нашей прогрессии; тогда расстояние между соответст-
вующими точками Av и Л.у.ц числовой оси равно разности d прог-
рессии., Пусть d > 0; если число d — нецелое, то обозначим через
«={</}=</— [</] > 0 дробную часть числа d (ср. стр. 3"), а ес-
ли d—-целое, то примем а равным 1 (во всех случаях а равно
разности между d и наибольшим из меньших d целых чисел). Мы
хотим так-расположить наши отрезки длины 1, чтобы можно было
утверждать, что хоть одна из точек A ,v попадет на один из отрез-
ков системы, иными словами, чтобы можно было исключить случай,
когда все точки Л» попадают в промежутки между отрезками.
Но если имеет место именно этот последний случай, то каждый из
отрезков Л уЛ .у + i длины d будет состоять из целого числа отрезков
системы (общая длина которых, разумеется, выражается целым
числом) и некоторого числа промежутков между отрезками (вклю-
чая сюда и два нецелых промежутка); ясно, что общая длина всех
этих промежутков (и двух частей промежутков) никак не может
быть меньше а. Поэтому, если нам удастся указать систему отрез-
ков, в которой для достаточно больших номеров N число а нельзя
«набрать» из длин (и частей длин) промежутков между отрезками,
то для этой системы и будет выполняться стоящее в условии задачи
требование.
Сказанное делает ясной следующую конструкцию. Расположим
на положительной полуоси единичные отрезки, начиная с отрезка
(1, 2), так, чтобы промежутки между соседними отрезками образо-
вывали, скажем, геометрическую прогрессию со знаменателем
т. е вслед за (1, 2) расположим отрезок (3, 4), затем — отрезок
(1 1 л / з з \ ( 7 7 \
4 —2, 5 — I, затем — отрезок 15 —, 6 — 1, затем — отрезок 16 _,7 — 1,
и т. д. (см. рис. 14); при этом каждый следующий промежуток будет
f—।—3—Е-----3----о----Е----3—Е—1—3-Н----Е-&--
-J -2 -/ 0 12 5 0 5 6
Рис. 14.
вдвое меньше предыдущего). Тогда сумма длин всех промежутков
1 + "2’ + '^'+д' + .- - = 2, а сумма длин всех промежутков, начи-
111 1
ная с (I + 1) -го, -g- + +...«= будет при достаточ-
но большом i сколь угодно мала. Поэтому, каково бы ни было
(отвечающее выбранной нами арифметической прогрессии с положи-'
тельной разностью d) число а = {d} (или а = 1), всегда найдется
184
такой номер i0, что к > , т. е. а > Я,- . Следовательно, если
21° х <0
N настолько велико, что все промежутки вплоть до i'o-го располо-
жены слева от точки Av (а этого всегда можно достигнуть, ибо
при d > 0 последовательность At, Аг, А3, .. ., Ап, ... уходит неогра-
ниченно далеко вправо), то на отрезок ЛЛ'Дп+1 длины d могут
попасть лишь начинающиеся с О’о + 1)-го промежутки длин
1,1 „
2io+2 > •• Но так как сумма Ri0 длин всех этих проме-
жутков меньше а, то обе точки А л и Av-ц не могуг одновременно
принадлежать этим промежуткам — и хоть одна из них непремен-
но попадет на отрезок нашей системы.
Мы до сих пор считали, что d > 0; для того чтобы доказать
утверждение задачи и для арифметических прогрессий с отрица-
тельной разностью d, достаточно продолжить нашу систему от-
резков на отрицательную полуось числовой оси, скажем, отразив ее
симметрично от нулевой точки О.
146. Прежде всего очевидно, что ии одна
из рассматриваемых
дробей не 'равна целому числу: действительно, если бы, например,
т — 1)
какая-то дробь ----—----- (k— одно из чисел 1, 2, 3, ..
была целым числом, то т + п должно было бы иметь общие делите-
ли с числом т (ибо k < т и не может делиться на т); но тогда
и число п == (т и) — т не было бы взаимно просто с т. Далее ни-
какие две из этих
(k — одно из
то мы имели
чисел
бы
дробей не равны друг другу: если бы было
k (т n) I (т 4- п)
т ~~ п
1, 2, ..., т — 1; I — одно из чисел 1, 2.п — 1),
k
т = — п,
п не
были
П),
и срова т и
может делиться на
Рассмотрим теперь
меньшее т + л. Дроби
бы взаимно простыми (так как I < п и не
некоторое целое положительное число А,
k
т
I
п ’
2 (in п)
k (т -|- п)
т
т
т
Ат
остаются меньшими А, пока < Ат, или число
[Ат 1
------ числа ~ ” 7~~~ .
т + nJ т т л
Точно так же дроби
т 4- л 2 (т 4- л)
п ’ п '
Ап
остаются меньшими А, пока I <_ —-р-у
/ (т 4- п)
п
число таких дробей равно
Относительно обозначений см. стр. 37.
целой части |1 числа —dlL_. Числа —и &п оба
-* [т + nJ т + п т J- п т-)-п
не целые, ибо т, п и т + п попарно взаимно просты; сумма этих
двух чисел равна А:
Ат , Ап
--------------— л
т + п 1 т + п
Но если сумма двух чисел а и [3, не являющихся целыми, равна
целому числу А, то
[а] + И = А — 1;
доказательство этого предложения сразу следует из рис. 15. Таким
образом,
]_т + nJ Lm + nJ
откуда следует, что в интервале (О, Л) числовой оси имеется ровно
А — 1 наших дробей.
Рис. 15.
Из доказанного сразу вытекает утверждение задачи. Действи-
тельно, положим сначала Л = 1; мы получим, что в интервале (0, 1)
вовсе нет наших дробей. Далее, пусть Л = 2; из того, что в интер-
вале (0, 2) имеется одна дробь, вытекает, что одна дробь есть в
интервале (1, 2). Затем положим А == 3; из того, что в интервале
(О, 3) содержатся две дроби, т. е. на одну больше, чем в интервале
(О, 2), вытекает, что в интервале (2, 3) имеется одна из наших дро-
бей. Продолжая рассуждать таким же образом, мы полностью до-
кажем требуемое предложение.
147. Первое решение. Если число а заключено р интерва-
1000 1000
ле —— а'_> ——;—г, то всего имеется, очевидно, т целых чисел,
tTl til -j*" 1
не превосходящих ЮС0, кратных а (а именно а, 2а, За, ..., та).
Поэтому если мы обозначим через k\ число тех из наших чисел,
1000
которые заключены между 1000 и' ~ g ; через А’з— число
чисел, за-
10С0 1000
ключенных между —и —у-; через — число чисел, заключеп-
1000 1000
ных между и —, и т. д., то мы будем иметь всего
k\ -f- 20. 3k$ + ...
чисел, не превосходящих ГООО и кратных хотя бы одному из наших
186
чисел. Но по условию задачи все эти кратные различны; следова-
тельно,
&1+2Й2 + 3/г3 + . . .< 1000.
Теперь остается заметить, что сумма обратных величин всех
наших чисел меньше чем
, 1 , , ' , , 1 . _ 2fet 4~ З^г 4~ + • • •
юоо 1 юоо юоо + ~ 1000
2 3 ~~V~
1000
(здесь мы заменили k\ наибольших из наших чисел на —; сле-
. 1000 ЮОО
дующие k2 чисел— на —g—; следующие «3 чисел — на ——,
и т. д.). Но
2/г, +3^ + 4А3 + ... =
•= (&i + 2/г2 ЗЛ'3—р- ...) + (k[ + k2 + й3 + ...) =
= (ki + 2/г2 + 3/г3 1+ ...) + n < 1000 + п < 2000;
следовательно, сумма обратных величин всех наших чисел меньше 2‘.
Второе решение. Приведем здесь еще один изящный ва-
риант того же рассуждения. Число членов ряда 1, 2, ..., 1000, деля-
Г 10001
щихся на целое число Яд, очевидно, равно целой части —— дроби
L ak J
юоо
----. Так как наименьшее общее кратное любых двух из чисел Яь
ak
а2, ..., ап больше 1000, то среди чисел 1, 2, 3... 1000 не найдется
пи одного, делящегося одновременно на два из чисел Я1, я2, .... ап.
Отсюда вытекает, что число членов ряда 1, 2, 3... 1000, делящих-
ся хотя бы на одно из чисел alt а2, а3,.ап, равно сумме
г Так как в ряду 1, 2, 3,..., ЮОО всего имеется 1000 чисел, то
должно быть
10001 Г10001 Г10001 Г10001
---- + ------- + ------- + • • + ------ <
Я1 J ' L fl2 J 1 [ а3 ] ‘ ' L ап J
1000.
Но целая часть дроби отличается от самой дроби меньше чем на
единицу, т. е.
10001
Я1 ]
1000
Я1
1000
я2
1,
Г10001
1000
Следовательно,
1000
Я1
/ 1000
к ап ~
< 1000,
187
т. е.
1000 1000 1000
— + — + —
at 1 аг 1 а3
4- ... +---< 1000 + л <2000,
а„
и, таким образом,
1 J_L 1
01 + а2 + '' * Н" а.
Примечание. Оценку настоящей задачи можно значительно
уточнить. Рассмотрим все кратные наших чисел, не превосходящие
500. Очевидно, /ц из наших чисел будут сами больше 500; k2 + kt
500
чисел будут не большем 500, но больше -jj-; А4 + А3 чисел будут
500 500
не больше , но больше —, и т. д. Отсюда, в точности как
в первом решении задачи, заключаем, что общее число чисел, не
превосходящих 500 и кратных хотя бы одному из заданных п чисел,
равно
(k2 + k3) + 2(А’4 + ks) + 3(/г6 + k7) + ... ;
следовательно,
(А2 + А3) + 2(А4 4- k$) + 3(Ag + k7) 4- . • • <-500.
Отметим теперь, что разность 500—[(А2 4* Аз) Ч-2(А4 4-Ад) 4-
+ 3 (Аз-рА?) + ...] выражает число чисел, не превосходящих 500 и
не кратных ни одному из наших чисел, а разность 1000 —
— (Л” 1 + 2&а 1-^-ЗЛз—число чисел, не превосходящих 1000 н
не кратных ни одному из наших чисел. Следовательно,
500— [(Аг 4" k2) +2 (k 4+ А5) Ч~3(Аб + Ат) +...] <
< 1000— (Л-j + 2А2+'ЗАз + ...),
откуда получаем:
(At + А2) + 2 (А3 4- A4) + 3(А5 + Ag) + ... <500.
Теперь остается только заметить, что
2А| + ЗА2 + 4Аз + 5А4 4* 6Ад 7А6 4~ • • • <
< (Ai + 2Aj + ЗА3 + 4А4 4- 5Ад + 6А6 4~ • ) 4~
4~ [(Ai 4~ А2) 4~ 2 (Аз 4_ А4) 4- 3(Aj + А6) 4* • • • ] <
< 1000 4- 500 = 1500
и, следовательно, сумма обратных величин всех наших чисел, мень-
2АГ + ЗА2 4~ 4А3 4- ... 1
шая ----------1000--------’ наверняка меньше
Аналогично, рассматривая кратные наших чисел, не превосходя-
щие 333, можно доказать, что сумма обратных величин всех наших
чисел даже меньше l~rj~-
Отметим еще, что число 1000 в условии этой задачи можно за-
менить любым другим целым числом,
188
148. Рассмотрим, как образуется разложение простой дроби
в периодическую десятичную дробь
— = А, . ahaia.2 ... айахаг ...
(здесь А—целое число, a at, а2, .... ак — цифры периода дроби).
Очевидно, что А есть частное от деления q на р:
q = Ар + ?t,
где остаток q-. меньший р. Далее Аа, есть частное от деления 10?
на р (Aat составлено из цифр числа А и цифры «1):
10? = Aat-р + ?2, где q2 < р.
Точно так же
t 102 q — Аа^з • р + ...... 10* q = Аа{а2 ... ак • р + ?й + ь ...
Период дроби начнется снова в тот момент, когда при делении
какого-либо числа 10й? на р мы получим тот же остаток ?ft+i — ?,,
что и при делении числа q на р. Таким образом, число k цифр в
периоде дроби определится как наименьшая степень 10, такая, что
10й? дает при делении на р тот же самый остаток, что и ?. Послед-
нее означает, что разность 10*?— ? = (10* — 1)? делится на р
или что разность 10* — 1 делится на р (ибо q, разумеется, вза-
имно просто С р).
Предположим теперь, что k четно: k = 2Z; из того, что разность
1021 — 1 == (102— 1) (10г + 1) делится на р, следует, что либо 10'—1
делится на р, либо 10'+ 1 делится па р. Но 102—1 не может де-
литься на р, так как в противном случае 10г давало бы при делении
?
на р тот же самый остаток, что и ?, и период дроби —равнялся
бы I, а не k = 21. Таким образом, мы заключаем, что 10' + 1 де-
лится на р.
г г 101 ? , ?
Из последнего результата следует, что сумма -f- -2- есть
целое число. Но
- *= AaiOi .. .Gj, ... Я; ... -4-
+ А, ata2 ... alal+l ... аг1 .. -i
таким образом, сумма дробей
О, <J/+ia'+2 • • |22/й|вз ... в;... 4" 0, аха2... ад+1... a2i...
есть целое число. Так как каждая из этих дробей меньше 1 и боль-
ше нуля, то эта сумма должна равняться 1 = 0,999..., что возмож-
но только в том случае, если
Д] -ф- == 9, G2 4" ^1+2 = 9, . . . , Cli 4- (ty = 9.
Из последних соотношений сразу следует, что
Qi 4* Os 4- • • • 4~ 02i _ 9
2/ V
189
Если же k нечетно, то равенство
di 4" ai + • • • +
2
2
k
очевидно, невозможно, так как знаменатель дроби, стоящей в левой
части этого равенства, не делится на 2.
149. Число цифр в периодах дробей — и ( равно наи-
меньшим целым положительным числам k и I, таким, что 10* — 1
делится на рп, соответственно 10'—1 делится на р" + 1 (см. решение
предыдущей задачи). Составим теперь разность
(КУ — 1) — (10* — 1) = 10* (10'-* — 1).
Из того, что эта разность делится на рп, следует, что 10,_* — 1 де-
лится на рп. Покажем теперь, что из того, что 10'-*—1 делится
на рп и 10*—1 делится на рп, следует, что и 10'*— 1, где d есть
общий наибольший делитель чисел I — k и k, делится иа рп.
Действительно, пусть I—k = qk-^-r. В таком случае имеем:
10'-* —1 = 109*+r—1 = 10г(109*—.1) + (10r—1).
Но Ю9*— 1 = (10*)9 — I9 делится на 10* — 1, т. е. делится на р";
следовательно, и 10г—1 делится на рп. Точно так же показывается,
что и 10г‘— 1, где rt есть остаток от деления k на г, делится на
р"; что 10г*—1, где гг есть остаток от деления г на /у,’делится
на'р”; что ЮГз— 1, где г3 есть остаток от деления п на zy, делится
на рп, и т. д. ’). Но нетрудно показать, что ряд чисел г, rit г2,...
должен закончиться числом d. Действительно, так как I — k и k
делятся на d, то и г= (/ — k)—qk делится на d; так как k и г
делятся на d, то и rt делится на d; так как г и г\ делятся на d,
то и г2 делится на d, и т. д.; следовательно, все числа нашего ряда
делятся на d. С другой стороны, если последнее число в этом ряду
есть rh (т. е. rh^i делится на rk, так что следующий за гк остаток
уже равен нулю),, то гй-1 делится на гк, гк_2 делится на гк (ибо
гк~1 и rh делятся на г*); гк-з делится на гк (ибо гА_2 и г*-, делятся
на г*), и т. д; наконец, k и I — k делятся на гк. Но в таком случае
неравенство г к > d противоречило бы тому, что d есть общий
наибольший делитель I — k и k.
По условию k есть наименьшее целое число, такое, что
10* — 1 делится на рп. Поэтому из того, что 10d — 1 тоже делится
на рп, следует что d = k, I — k кратно k и, значит, I кратно k:
I = km.
Разложим теперь 10'—1 на множители:
10' — 1 = 10*™ — 1 =
= (10* — 1) (10<™-"* + 10<™-2'* + ... + 10*1-4-1).
Так как 10* — 1 делится на р", то 10* дает при делении на р"
остаток 1, откуда следует, что и 102* = 10*-10* дает при делении
на рп остаток 1 и 103* = 102*-10* дает при делении на рп остаток
1, и т. д. Следовательно, каждый член суммы, стоящей в скобках,
дает при делении на р" остаток 1 и, таким образом, вся сумма дает
остаток т. Отсюда следует, что если 10* — 1 не делилось на р"+1,
') Этот процесс получения ряда последовательных остатков rlt
rs, ... носит название алгоритма Евклида.
190
то наименьшее значение I, такое, что 101—1 делится на pn+1, равно
pk\ при этом1 10’*— 1 делится на pn+1, но не делится на рп~г (ибо
выражение в скобках не делится на р2).
Отсюда и вытекает утверждение задачи.
150. а) Пусть а — первая, а b — последняя цифра искомого
числа N. Тогда это число равно 1000 а + 100 а + 10 6 + 6 = 1100 а +
+ 116 = 11 (100 а + 6). Так как число N является точным квадра-
том, то из того, что оно делится на 11, вытекает, что оно делится и
N
на 121, т. е. уу- = 100а + Ь делится на 11. Но
100а + b = 99а + {а + b) = 11 9а + (а + Ь).
Следовательно, а + b делится на 11. Так как и а, и Ь не больше
9 и а не равно 0, то 1 + а + b + 18, а потому а + b = И.
Отсюда
100а+ 6 = 11-9а + 11 = 11 (9а + 1),
N 100а+ 6
121 = 11 = 9а + '•
Так как N — точный квадрат, то ууу — также точный квадрат. Но
из чисел вида 9а + 1, где а меняется от 1 до 9, только 9-7 + 1 =
= 64 является точным квадратом. Следовательно, N = 121-64 =
= 7744 = 882.
б) Пусть а — цифра десятков этого числа, а & — цифра единиц.
Тогда число равно 10а + Ь, а число, записанное этими же цифрами
в обратном порядке, равно 106 + а. В силу условия задачи, 10а +
+ 6 + 106 + а = 11 (а + 6) = 62.
Отсюда Следует, что /г2 делится на 11, поэтому а + 6 также де-
лится на 11. Так как а + & + 18, то это возможно лишь в случае,
если а + 6 — 11, k2 = 121. Таким образом, искомыми числами яв-
ляются
29, 38, 47, 56, 65, 74, 83, 92.
151. Обозначим двузначное число, образованное первыми двумя
цифрами искомого числа N, через а, а число, образованное его дву-
мя последними цифрами, — через 6. В таком случае N = 100а + 6,
так что условие задачи дает
100а + 6 = (а + 6)2,
или
99а = (а + 6)2 — (а + 6) = (а + 6) (а + 6 — 1). (*)
Итак, произведение (а + 6) (а + 6—1) должно делиться на 99.
Рассмотрим теперь отдельные возможные случаи.
а
1°. а + 6 = 996, а+6 — 1 — Так как а и 6 — двузначные
числа, то k + 2, причем случай 6 = 2 сразу приводит к не удовлет-
воряющим основному равенству (*) значениям а = 99, 6 = 99.
Таким образом, приходится считать, что
6=1, а + 6 = 99, а = а + 6 — 1=98, W-= 9801 = (98 + I)2.
2°. а + 6 = 11m, а + 6 — 1 = 9а, тп = а. В этом случае имеем
9n = 11m—1. Из того, что Пт — 1 делится иа 9, следует, что чис-
191
ло т дает при делении на 9 остаток 5 (непосредственной проверкой
убеждаемся, что если бы т давало при делении на 9 какой-либо
другой остаток, то Пт — 1 не делилось бы на 9). Итак, m = 9/Ц- 5,
откуда следует, что 9м = 99/ + 54, п — 11/ + 6. Теперь имеем:
d = mn= (9/ + 5) (И/ + 6) = 9912 + 109/+ 30.
Так как а число двузначное, то отсюда сразу вытекает, что
t — 0. Следовательно, а = 30, а + b = 11m = 55, b =25, N =
= 3025 = (30 + 25)2.
3°. а + b = 9т, а + b — 1 = 11 п, тп = а. Исследование, анало-
гичное тому, которое мы провели в случае 2°, дает единственный
ответ Л' = 2025 = (20 + 25)2.
4°. а + b = 33m, а + b — 1 = Зл или а + b = 3m, а + Ъ — 1 =
= 33л, что невозможно, так как a-j- b и а + & — 1 — чи+а взаимно
простые.
5°. а + Ъ — 1 = 99k, а + b = -у-. В этом случае имеем
, (а + b) (а + b — 1)
а + b — 1 =99, а b = 100, а =-----------gg-------= 100, что не-
возможно. Итак, условию задачи удовлетвопяют лишь числа 9801,
3025 и 2025.
152. а) Четырехзначное число, записываемое четырьмя четными
цифрами, может начинаться с цифр 2, 4, 6 или 8; другими Словами,
оно заключено между 1999 и 3000, или между 3999 и 5000, или меж-
ду 5999 и 7000, или между 7999 и 9000. Поэтому корень квадратный
из этого числа заключается между 44 и 55, или между 63 и 71, или
между 77 и 84, нли между 89 и 95. Заметим еще, что так как
(10х + у)2 = 100х2 + 20ху + у2, то при 0 У^9 цифра десятков
числа (10х + у)2 четна или нечетна одновременно с цифрой десятков
числа у2. Поэтому корень квадратный из искомого числа не может
оканчиваться цифрами 4 и 6.
Так как корень квадратный из искомого числа четен, то он мо-
жет равняться лишь одному из следующих 10 чисел:
48, 50, 52, 68, 70, 78, 80, 82, 90 и 92.
Непосредственная проверка показывает, что условию задачи удов-
летворяют числа:
682 = 4624 ; 782 = 6084; 802 = 6400; 922 = 8464.
б) Рассуждения, аналогичные тем, которые привели нас к ре-
шению задачи а), показывают, что вовсе не существует четырех-
значных чисел, являющихся полными квадратами и записывающихся
четырьмя недетны-ми цифрами.
153. а) Обозначим цифры сотен, десятков и единиц искомого
числа N соответственно через х, у, и г, так что N = КЮх + IQy + z.
В таком случае условие задачи дает
100х + 10у + г = х! + у\ + zl.
Отметим, что 71 = 5040 есть число четырехзначное; поэтому ни
одна цифра числа N не может превосходить 6. Следовательно, само
число N не превосходит 700, откуда вытекает, что ни одна его циф-
ра не может превосходить 5 (ибо 6! = 720 > 700). Хотя бы одна
цифра числа N равна 5, так как даже 3-4! — 72 < 100, а А/ трех-
192
значно. При этом х не может быть равно 5, так как даже 3-5! =
«== 360 < 500. Отсюда следует также, что х не превосходит 3. Да-
лее можно утверждать, что х не превосходит 2, так как даже 3! 4-
+ 2 • 5! = 246 < 300. Но число 255 не удовлетворяет условию зада-
чи, а если лишь одна цифра искомого числа равна 5, то х не может
быть больше 1, ибо даже 2! + 5! 4- 4! = 146 < 200. Более того, так
как 1! + 5! + 4! =» 145 < 150, то мы заключаем, что у не может
превосходить 4; следовательно, г = 5, так как ходя бы одна цифра
числа N должна равняться 5. Таким образом, мы имеем х = 1,
4 у 7? 0 и z «= 5; это позволяет легко обнаружить единственное
решение задачи: N <= 145.
б) Искомое число N не может иметь больше чем три цифры,
так как даже 4-Э2 = 324 — число трехзначное. Поэтому мы можем
написать N = 1СЭ.т.-|- Юг/ + z, где х, у, z— цифры числа; при этом
х или даже хну одновременно могут быть равны нулю.
Из условия задачи имеем ЮОх + Ют/ + z ™ х2 4- у2 + г2, откуда
(100 —х)х + (10-#)# = z(z- 1). (*)
Из последнего равенства прежде всего следует, что х = 0 —
в противном случае число, стоящее в левой части равенства, не
меньше чем 90(х 1, 100—х 90, (10 — у)у 0), а число, стоя-
щее справа, не больше чем 9-8 = 72 (ибо z =67 9). Следовательно,
уравнение (*) имеет вид (10 — у)у = z(z — 1). Легко проверить,
что это последнее равенство не удовлетворяется ни при каких целых
положительных х и у, не превосходящих 9, если только у 0.
Если у = 0, то мы имеем единственное очевидное решение г = 1.
Таким образом, условию задачи удовлетворяет единственное
число N — I.
154. а) Очевидно, что искомое число N не может иметь более
четырех цифр, так как сумма цифр пятизначного числа не превос-
ходит 5-9 = 45, а 452 = 2025— число четырехзначное. Далее, так
как 4-9 = 36, а 362 = 1296, то при N четырехзначном первая цифра
Л’ не превосходит 1. Но 1 + 3 9 = 28, а 282 = 784 трехзначно; зна-
чит, N вообще не может быть четырехзначным числом. Итак, мы
можем предположить, что W = 100x4- Юг/+ z, где х, у, г — цифры
искомого числа; при этом возможно, что х = 0 или даже х = у = 0.
Теперь условие задачи можно записать в виде
ЮОх + 10# + z = (х + у + г)2,
или
99х + 9# = (х + у + г)2 — (х + у + z) = (х + у + z) (x+#-f-z— 1).
Таким образом, мы видим, что либо х 4- г/+ г, либо х 4- у +
+ г-1 делится на 9 (каждое из этих двух чисел делиться на 3 не
может, так как они взаимно простые). Но 1 sg х + у 4- z 27.
Рассмотрим теперь отдельно все представляющиеся случаи.
Г. х 4- г/ 4- z — 1 =0; 99х + 9г/ = 0, х >== # = 0, z = 1; N = 1.
2°. х + У 4- г = 9; 99х 4- 9# = 9 8 = 72, х = 0, 9# = 72, # = 8,
г = 1; N = 81 ( = (84- I)2)-
3°. х 4- у 4- г — 1 = 9; 99х 4- 9# = 9 10 = 90, х = 0, 9# = 90,
что невозможно.
4°. х 4- у 4- г = 18; 99х + 9# = 18 • 17 == 306, х = 3, у — 1, г =
= 18 — (3 4- 1) — 14, что невозможно.
13 Д. О. Шклярский и др. ЮЗ
5°. х + у + г — 1 .= 18; 99х + 9у = 19 • 18 = 342, х = 3, у = 5,
г = 19 — (3 + 5) = 11, что невозможно.
6°. х + у + г = 27; 99х + 9у = 27 • 26 = 702, х = 7, у = 1,
г = 27 — (7 + 1) = 19, что невозможно.
Итак, условию задачи удовлетворяют только числа 1 и 81.
б) Куб трехзначного числа может содержать не более девяти
цифр; поэтому сумма цифр куба этого числа не превосходит 9-9 =
= 81 < 1ОЭ. Отсюда следует, что искомое число не может быть
трехзначным; аналогично показывается, что оно не может содержать
и больше трех цифр. Итак, искомое число обязательно будет одно-
значным или двузначным.
Куб двузначного числа не может иметь более шести цифр; по-
этому сумма цифр куба не превосходит 6-9 = 54. Итак, искомое
число не может превосходить 54. Но если куб числа, не превосходя-
щего 54, даже'и имеет шесть цифр, то первая цифра его равна 1;
поэтому сумма цифр куба не превосходит 5-9+ 1 = 46. Итак, иско-
мое число не превосходит 46.
Если число не превосходит 46, то куб его содержит не более
пяти цифр, и так как он меньше 99 999, то сумма цифр куба не
превосходит 4-9 + 8 = 44; так как куб числа 44 есть пятизначное
число, оканчивающееся на 4, то и 44 больше суммы цифр своего
куба. Итак, искомое число не превосходит 43.
Далее, так как сумма цифр каждого числа дает при делении
на 9 такой же остаток, как и само число, то искомое число и его
куб должны давать при делении на 9 одинаковые остатки. Но это
возможно только в том случае, если искомое число дает при деле-
нии на 9 остаток —1, 0 или 1.
Итак, искомое число не превосходит 43 и дает при делении на
9 остаток —1, 0 или 1. Этим условиям удовлетворяют лишь следую-
щие 13 чисел:
1, 8, 9, 10, 17, 18,-19, 26, 27, 28, 35, 36, 37.
Проверка показывает, что условию задачи удовлетворяют числа:
1 (р = 1), 8(83 = 512), 17(17® = 4193),
18(183 = 5832), 26(263 = 17 576), 27(273 = 19683).
155. а) Непосредственной проверкой убеждаемся, что при х < 5
единственными решениями нашего уравнения будут числа х = 1,
у = ± 1 и х — 3, у = ±3. Докажем теперь, что при х 5 реше-
ний нет. Для этого заметим, что 1! + 2! + 3! + 4! = 33 оканчива-
ется цифрой 3, а 51, 6!, 7!,... все оканчиваются нулем. Таким обра-
зом, при х 5 сумма 1! + 2! + ... + х\ оканчивается цифрой 3, а
поэтому не может равняться квадрату целого числа у (никакой
квадрат целого числа не оканчивается на 3).
б) Рассмотрим два случая:
1°. z = 2п — четное число. Этот случай легко сводится к пре-
дыдущей задаче, ибо у2п = (уп)2. Таким образом, при четном г
решения таковы:
х = 1; у = ± 1; г — любое четное;
х = 3; у = ± 3; г = 2.
2°. г — нечетное число. При г = 1 годится любое значение х,
причем у = 1! + 2! + ... + х!. • Пусть г 3. Заметим, что 1! + 2! +
194
4-3!+4! 4-5!+6!+714-8! = 46 233. Число 46 233 делится на 9,
но не делится на 27, а при п 9 число nl делится на 27. Сумма
9! + 10! + ... +х! делится на 27; поскольку, однако, 1! + 2! + ... +
+ 8! делится на 9, но не делится на 27, вся сумма 1! + 2! +... +
+ х! при х > 8 делится на 9, но не делится на 27. Для того чтобы
уг делилось на 9, необходимо, чтобы у делилось на 3. Но тогда
у! делится на 27 (ибо z 3) и, следовательно, при х 8, z 3
решений в целых числах нет. Остается рассмотреть случай х < 8.
Имеем 1! = 1 = 1г, где z — любое натуральное число; 11 + 2! = 3,
т. е. не равно никакой целой, отличной от 1 степени никакого нату-
рального числа; 1! + 2! + 3! = З2, и далее:
1! + 2! + 3! + 4! = 33,
1! + 2! + ... + 5! = 153,
1! + 2! + ... + 6! = 873,
1! 4- 2! + .. . + 7! = 5913.
Ни одно из чисел 33, 153, 873 и 5913 не является целой, отлич-
ной от единицы степенью никакого натурального числа. Таким обра-
зом, при нечетном z окончательно имеем лишь следующие решения:
х = 1, у = 1, z = любое нечетное;
х — любое натуральное, у — 1! + 2! + ... + х!, г = 1.
156. Пусть
а‘ + Ьг + с2 + d2 = 2П.
Обозначим наибольшую степень двойки, на которую делятся все
четыре числа а, Ь, с и d, через р. Сократив обе части нашего равен-
ства на 22?, мы получим:
й2 + Ь2 + с2 + d2 = 2n-2p ,
где из четырех чисел alt bt, ct, dt, хотя бы одно является нечетным.
Если из четырех чисел Пь &b Ci, d1 только одно или три явля-
ются нечетными, то о2 + + dj нечетно и наше равенство не-
возможно. Если из чисел ait bi, cb di два, например at = 26 + I и
6i = 21+ 1, являются нечетными, а остальные два, ct = 2m и d> =
= 2п, четны, то мы имеем:
+ b\ + cf + d? = 462 + 4k + 1 + 4Р + 41 + 1 + 4m2 + 4л2 =
= 2[2(62 + 6 + I2 + 1 + m2 + n2) + 1],
что противоречит тому, что а2 + + d2 = 2П—2р не имеет нечет-
ных делителей (выражение в квадратных скобках не может рав-
няться единице, так как в противном случае мы имели бы k — I =
,= т = п =0, С] = di = 0 и с = d = 0). Если же все четыре чис-
ла й! = 2k + 1, 6, = 21 +1, = 2m + 1, di = 2n + 1 нечетны, то
мы имеем:
e?+6i+ci+rfl = 462 + 46 + 1 + 4/2 + 41+ 1 + 4m2 + 4пг =
+ 4m + 1 + 4/г2 + 4п + 1 =
= 4[6(6 + 1) + 1(1 + 1) + m(m + 1) + п(л + 1) +1].
Но произведение двух последовательных целых чисел всегда
четно (один из сомножителей обязательно четен). Следовательно,
13* 195
выражение в квадратных скобках нечетно, и, значит, оно равно 1.
Таким образом, п — 2р — 2, п = 2р + 2 и k = l = m = n. = 0,
a, - — Ct = d, — 1, a = b = c = d = 2?.
Итак, если n есть число нечетное, то 2" вовсе не разлагается
на Сумму четырех квадратов; если п = 2р четно, то 2" допускает
единственное разложение
22? «= (г*-1)2 -}- (2?-1)2 + (2₽-')2+ (2р-')2.
157. а) Первое решение. Уравнение
х2 + У2+ = 2xyz
удовлетворяется значениями х = О, у = 0, z = 0. При этом если
одно из чисел х, у, z равно 0, то и остальные должны быть равны
0, ибо сумма их квадратов в этом случае равна 0.
Пусть теперь все числа х, у, г, удовлетворяющие нашему урав-
нению, отличны от 0. Каждое из них можно представить в виде
х = 2ах, у = 2Spi, г = 2TZ|,
где %], yt, Zi нечетны (если какое-нибудь из чисел х, у или г нечет-
но, то соответствующий показатель степени 2 равен 0).
Так как х, у, г входят в наше уравнение симметрично, то мож-
но считать, что х делится на наименьшую степень 2, а 2 — на наи-
большую, т. е что
а С Р 7-
Выясним, на какую степень 2 делится левая часть нашего ра-
венства.
1°. Если а < р гС ч или же а = р = 7, то после вынесения за
скобки 22“ в скобках будет стоять сумма нечетного и двух четных
чисел или же сумма трех нечетных чисел, т. е. нечетное число.
2°. Если же a =.р < 7, то можно написать:
х = 2“(2£ 4-1), у = 2'42/4- 1), ' г = 2“ 2т.
В этом случае
х2+ г/2 + г2 = 22“[(2^ 4- I)2 + (2/4- 1)2442.н)2] =
= 22“ (41г2 4- 4А + 1 4- 4/2 4- 4/ 4- I + 4/п2) =
= 22“+1 [2 (1г2 4- k 4- /24- /4- т2) 4- 1],
т. е. после вынесения за скобки 22“Т 1 в скобках остается нечетное
число.
С другой стороны, правая часть равенства делится на
2«+s+v+i. но правая часть равенства должна делиться на такую же
степень 2, что и левая.
В случае 1° отсюда следует, что 2а = а4-Р4~74-1- Так как
а Р =£ 7, то из этого равенства следует абсурдное неравенство
2а За 4- 1.
В случае 2° отсюда следует, что 2а 4* 1 — а + Р + 7 + 1 Так
как а = р < ч, то отсюда следует неравенство 2а 4* 1 > За 4- 1,
которое также не может иметь места.
Следовательно, не существует -решений в целых числах уравне-
ния х2 4~ У2 + 22 = 2хуг, отличных от решения х = 0, у = 0, г «= 0.
186
Второе решение. Так как сумма квадратов чисел X, у й
z четна, то либо все эти числа четны, либо одно из них четно, а два
нечетны. Но в последнем случае сумма х2 + у2 + г2 делилась бы
только на 2, а произведение 2хуг — на 4 (сравните с первым реше-
нием задачи). Итак, мы можем считать, что х, у и г четны: х = 2хь
у = 2у!,'г = £zb Подставляя эти значения в наше исходное урав-
нение и сокращая на 4, получаем:
х2! + у\ + 2i = 4x1ylz1.
Отсюда, в точности как выше, выводим, что числа xb yi, zt —
все четные. Но в таком случае, обозначив X] = 2х2, yi — 2уг, г, ==
„ А х у г
“ 2г2, мы для чисел х2= у = —, 1/г = —, z2 *= ~ получим урав-
нение
х2 “Ь У2 4* г2 = 3x2t/2z.2,
откуда, как прежде, выводится, что эти числа тоже четные.
Продолжая тот же процесс, мы заключаем, что все числа
х у г х у г
х. У, г; у , 1/1 = у, Zi =» у; х, = —, уг = —, г2 = —;
х у г
= т ’Уа = ”Г ’гз = ~8; • •
у
’ * * ’ % к 2^ * 2^ ' *"
— четные (числа Хь, yk, zk должны удовлетворять уравнению х^ +
+ У* + гй = 2*+Ч Vh)' Но это возможно только в том случае,
если х — у = г = 0.
б) Так же, как и выше, доказывается, что единственным реше-
нием уравнения х2 + у2 4- z2 + v2 = 2xyzv в целых числах является
решение х — 0, у = 0, z = 0, и = 0.
Здесь специального рассмотрения заслуживает случай, когда
наивысшие степени 2, на которые делятся х, у, z и v, одинаковы,
т. е. когда
х = 2a(2k + 1), у = 2а(2/+ 1),
z = 2а(2т +0, v = 2а(2л + 1),
где а — целое неотрицательное число, a k, I, т и п — целые числа.
Тогда
х2 + у2 + z2 + V2 = 22'х [ (4/г2 + 4k + 1) + (4/2 + 4/ + 1) +
4- (4т2 -|- 4т + 1) + (4л2 4~ 4п + 1) 1 =
== 22a+2(k2 + k + I2 + I + т2 + т + n2 + «+ 1) =
= 22“+2[^(*+ 1) +1(1+ О +т(т+ 1) +«(«+ 1) + 1].
Но выражение в квадратных скобках обязательно нечетно
(см. выше, стр. 195). Поэтому наивысшая степень 2, на кото-
рую делится левая часть равенства, равна 2а + 2. Правая же часть
делится на 24“+1. Поэтому должно выполняться равенство 2а+2 —
== 4а 1, что невозможно при целых а.
197
Второе решение задачи б) аналогично второму решению
задачи а) и предоставляется читателю.
158. а) Пусть х, у, г— какие-то три целых положительных чис-
ла, удовлетворяющих уравнению
х2 + у2 + z2 = kxyz. (♦)
Покажем прежде всего, что всегда можно считать справедли-
выми неравенства
(т. е., другими словами, что ни одно из слагаемых, стоящих в левой
части уравнения (*), не превосходит половины правой части).
kxy
Действительно, если бы было, например, г> —2~,то мы рассмотрели
бы не числа х, у, г, а м'еньшие числа х, у и Zi = kxy — г, которые,
как нетрудно видеть, тоже удовлетворяют уравнению (*):
х2 + у2 + {kxy — z)2 = kxy {kxy — г).
Если из этих новых чисел какое-нибудь опять будет больше произ-
k
ведения двух других, умноженного Ha~g-,TO мы проведем снова
аналогичную замену и так будем поступать до тех пор, пока не
станут выполняться условия (**) (после этого наш процесс уже
не приведет к уменьшению чисел х, у, г).
Будем считать, что х у г. Прежде всего из того, что
kxy
У z С ~ , следует
kx
1 > -g-; kx > 2.
Уравнение (*), очевидно, можно переписать в виде
Так каке гС -у, , то при замене в левой части последнего равенства
числа г на у z эта левая часть возрастает (или — в случае у = z
— не меняется); следовательно,
х2 + г/2 + ^-уу>^.
Отсюда, раскрывая скобки, получаем:
х2 + 2у2 kxy2.
Так как по условию х у, то тем более
№+2у2 > kxy2,
т. е.
kx 3.
198
Таким образом, мы имеем 2 < kx 3, т. е. kx равно 2 или 3.
Но если kx = 2, то уравнение (*) принимает вид
х2 + у1 + гг = 2рг, или х2 + (у — г)2 = О,
откуда х = 0 и kx =* 0, а не 2. Следовательно, kx = 3 и, значит,
k может равняться только 1 или 3. Нетрудно убедиться на простых
примерах, что эти значения k являются возможными (см. решение
задачи б)).
б) Продолжим рассуждения, которые привели к решению задачи
а). Выше мы имели х2 + 2у2 kxy2\ так как kx = 3, то это нера-
венство можно переписать в виде
х2 + 2у2 Зу2, или х2 5= у2.
Но мы предполагали, что х ^.у; следовательно, х = у. Пола-
гая теперь в основном уравнении (*) х = у, kx = 3, мы получим:
2х2 + г2 = Зхг, или (г — х) (г — 2х) — 0.
kxy Зу Зх
Таким образом, г — х или z = 2х. Но так какг<~у = -у = у >
то г не может равняться 2х; следовательно, г = х.
Итак, мы видим, что если только выполняются условия (**), то
должно быть х = у = z. Но так как kx = 3, то х может быть pas'-
но только 1 или 3. Соответственно этому получаем два решения
уравнения (*):
х = г/ = z = 1 (k = 3)
и
х = у = г = 3 (k = 1).
В решении задачи а) мы видели, что всякую тройку чисел х,
у, z, удовлетворяющих уравнению (*), можно последовательными
подстановками вида zt = kxy — г привести к тройке чисел, удов-
летворяющих неравенствам (**). Но если zt = kxy — г, то г =
= kxy — г,; поэтому каждое решение уравнения (*) можно полу-
чить из выписанных выше наименьших решений последовательными
подстановками вида Z\ = kxy — г. В частности, таким образом, по-
лучаем следующие решения уравнения (*), не превосходящие 1000:
1°. Случай k = 3.
х = 1 1 1 1 1 1 1 12 2 2 5 5
у = 1 1 2 5 13 34 89 233 5 29 169 13 29
г = 1 2 5 13 34 89 233 610 29 169 985 194 433
2°. Случай k — 1.
х = 3 3 3 3 3 3 36 6 15
у = 3 3 6 15 39 102 267 15’ 87 39
г = 3 6 15 39 102 267 699 87 507 582
(то, что решения, отвечающие значению k = 1, получаются из ре-
шений, отвечающие значению k = 3, простым умножением чисел х,
У и г на 3, сразу следует из того, что так связаны между собой
наименьшие решения уравнений х2 + у2 + г2 = xyz и х2 + у2 +
+ г2 = Зхуг).
199
। 139. Из равенства ? » 2(i/’+ 2^) (где х, у, г — целые) сле-
дует, что х = 2.Г[ — четное, что позволяет переписать наше уравне-
ние так:
8*3— 2у3 — 4z3 = 0, или 4х3 —у3 — 2z3 =0.
Дак как у3 = 2 (2х3— г3), то у = 2yi— четное; поэтому имеем
4х3 — 8у3 — 2г3 = 0, или 2xf — 4yf — г3=0._
Наконец, поскольку z3 = 2 (х3 — 2yf), то и г ~ 2zi — четное, и мы
получаем
2х] — 4у® — 8г3 =0, или х3 — 2yf — 4zf » 0.
Таким образом, если х, у, z — решение исходного уравнения, то
х у
все эти три числа — четные, причем их половины Xj = yi — ~,
Zj — ~2 удовлетворяют точно такому же уравнению;
х3 — 2у3 — 4г, = 0.
Отсюда следует, что и числа хг = 2х2, yi = 2у2, Zi — 2г2 — четные,
причем и числа х2, у2, z2 удовлетворяют исходному уравнению, т. е.
и они являются четными, и т. д. Окончательно мы заключаем, что
целые числа х, у, г делятся на любую степень двойки, что, разу-
меется, возможно лишь в том случае, когда все они равны нулю.
Итак, единственное решение исходного уравнения в целых числах
имеет вид
х = у = z = 0.
160. Дополним левую часть уравнения до полного квадрата,
для чего достаточно умножить обе части уравнения на 4 и приба-
вить к ним по 1:
(2х + I)2 = 4yi + 4у3 + 4у2 + 4у + 1.
Но
4у4 + 4у3 + 4у2 + 4у + 1 = (4у4 + 4у3 + у2) + (Зу2 + 4у + 1) =
= (2у2 + у)2 + (Зу2 + 4у+ 1) ( = (Р(У))2 + <2(У));
а так как квадратный трехчлен Q(y) = Зу2 -ф 4у + 1 имеет (вещест-
венные) корни yi = —1 и у2 = — — , то при всех целых у, отличных
от у = —1, этот трехчлен положителен (см. график функции t =
=Зу24-4у+1 на рис. 16, а), и, значит, (2х + I)2 > (Д(у))2 =
= (2У2 + У)2.
, С другой стороны, мы имеем
4у< + 4у3 + 4у2 + 4у + 1 =
«= (2у2 + у + 1)2 + (2у — у2) ( «= (Pi (у))2 + Qi (у)).
Но график функции Qi(y)=2y —у2 имеет изображенный на
рис. 16, б вид (корни квадратного двучлена Qi(y) равны 0 и 2), и,
200
значит, при всех целых у, отличных от 0, 1 и 2, имеем Qi(f/) С О,
откуда (2х+1)»< (Рх(у))2 = (2у2 + у + I)2.
Таким образом, при всех целых у —1, 0, 1 и 2 имеет место
двойное неравенство
(2у2 + у+ 1)2> (2х+1)2> (2у2 + у)2,
т. е. при таких у величина (2х + I)2 заключена между квадратами
Рис. 16.
двух последовательных целых чисел Q(y) и Qi(i/), и поэтому число
2х + 1 не может быть целым.
Итак, если у — целое число, то х может быть целым лишь при
у = —1, 0, 1 и 2, т. е. когда правая часть исходного уравнения рав-
на 0, 0, 4 и 30. Нам осталось только решить 3 квадратных уравнения
хг + х = с, где с = 0, 4 или 30. (*)
Целые корни этих уравнений таковы:
х = 0 или — 1 (при с == 0); х = 5 или — 6 (при с = 30;
при с = 4 уравнение (*) целых корней не имеет).
Таким образом, окончательно получаем следующий набор решений
заданного уравнения в целых числах (здесь запись (а, Ь) означает,
что х = а, у — Ь):
(0, -1), (-1, -1); (0, 0), (-1, 0); (5, 2), (-6, 2)
(всего 6 решений).
161. При у — 1 мы приходим к квадратному уравнению
х2 + (х + I)2 = (х + 2)2 или х2 — 2х — 3 = 0,
имеющему единственный целый положительный корень х = 3 (вто-
рой корень уравнения х = —1 отрицателен). Пусть теперь у>1.
Заметим, что поскольку x2v и (х + 2)2и — числа одинаковой четно-
сти, то число (x-f- I)2» [ = (х -j- 2)2>' — х2*] будет четным; поэтому
201
и число «4-1 =2xi — четное. Далее мы имеем
(2xI)sv = (х+ I)2» = (х + 2)^ — х2» =
= (2х(+ I)2*'— (2х!-1)Ч (*)
Раскрыв скобки в стоящих справа выражениях с помощью формулы
бинома Ньютона, получаем:
(2х1)2!' = 2 [с|у (2x^-1 4- C^x^v-3 4- ... 4- (2ху)],
что, уединяя в левую часть последний член правой части равенства,
можно переписать еще и так:
2 • 2у • 2xt =
= (2Х1)2и -2-2у (2xx)2^—1 - 2 • С|у (2xi)2!/-3 - ,.. - 2-С3у (2х^
(заметьте, что поскольку у ;> 2, то 2у 4). Но все стоящие справа
члены, очевидно, делятся на (2XJ3, откуда вытекает, что у должно
делиться на х2.
Далее, разделив обе части равенства (*) на (2х1)2ч, получим:
/ 1 \2у [ , \2у
1= 14-J- — 1— ‘ ,
\ 2X1/ \ 2Xj/
( 1 \2у ( 1 \2v
откуда следует, что I 1 4“ z— I *=1+1 — 75— < 2. Но, с другой
стороны, в силу той же формулы бинома Ньютона
(1+2r)2V=1+2y’27 + C^U)2+,- =
У
1+
1 г.
и, значит,
I/ У ,
1 4- — < 2, или — < 1, откуда у < х1(
Х1 Х1
о
что, однако, противоречит делимости у на Хр Поэтому наше урав-
нение не имеет таких решений, что у > 1 и все решения уравнения
исчерпываются одним найденным выше: у = 1, х = 3.
J62. Обозначим' х 4- J//x4--. -+Vx через Ау (х); в таком случае,
у корней
очевидно,
х4- Ду—! (х) = х4- Vх 4- • • • 4- Vх = z2, или Ау_1 (х) = г2— х
у—1 корней
Таким образом, если число Ау(х) — г — целое, то и число Av-i(x)
(= z2 — х)—целое; но тогда и число Ау_2(х) ( = (г2 — х)2— х)
— тоже целое, и 4v_3(x) — целое....и Д(х) = Ух — целое. А из
того, что. у^х — t — целое, следует, что х = t2 (где t — целое).
202
Ясно, что для любого целого t значения х = fl, у — 1, г = t
являются решениями нашего уравнения. Пусть теперь у>\. При
этом числа
Ai(x) ~Vx = t и А2 (х) = + У х = У fl + t = У t (/ + 1)
должны быть целыми; но числа t и / + 1 — взаимно простые, отку-
да следует, что произведение может быть полным квад-
ратом, лишь если и t, и <4-1—полные квадраты, т. е. если
t = 0. А если t — 0, то, очевидно, х = 0 и Аа(х) =0 при л ю-
б о м х.
Таким образом, все решения рассматриваемого уравнения та-
ковы: х = /2, у = 1 н г — t (где t — любое целое число; если корни
понимаются в арифметическом смысле, то t следует считать нату-
ральным числом), и х = 0, y — t— произвольное натуральное
число, z = 0.
163. Воспользуемся методом доказательства от противно-
г о: предположим, что выписанное в условии задачи уравнение име-
ет решения в целых х и у лишь для конечного числа простых
значений р и что наибольшим из них является n-е простое число
Рп. Составим теперь число 2-3-5-7-11 • 13-...-р„ — х и рассмотрим
выражение Х = х24-х+1. Так как число X—1=х24-х =
= х(х 4- 1) делится на все простые числа 2, 3, 5,..., рп, то число X
не может делиться ни на одно из них; поэтому число X имеет боль-
ший рп простой делитель Р, т. е. X = Ру, где у — некоторое нату-
ральное число. (Здесь не исключен, разумеется, случай Р = X,
у = 1.) Таким образом, для р = Р наше уравнение имеет решение
х, у в целых числах, что противоречит предположению о том, что
рп — наибольшее простое значение коэффициента р, при кото-
ром такое решение существует. Полученное предположение и дока-
зывает утверждение задачи.
Примечание. Очевидна близость этого рассуждения к из-
вестному доказательству теоремы о существовании бесконечного
числа простых чисел (см. решение задачи 349).
164. Задача состоит в том, чтобы решить в целых положитель-
ных числах следующую систему уравнений (х, у, г и и — искомые
числа):
хг + у + г + и= (х 4- о)2,
y2 + x + z + u= (у + а>)2,
z2 + х + у + и = (z + /)2
u2 + x + y + z= (и + s)2,
или
у + г + и — 2vx + о2,
х + г'+ и = 2wy 4- w2,
х + У + и = 21г + fl,
х 4- у ф- г = 2su 4- s2-
203
Сложив все уравнения (*), получим:
(2о — 3)х+ (2w — 3)y + (2/ —3)z+ (2s —3)« ++
+ w2 + t2 + s2 = 0. (••)
Отметим прежде всего, что из равенства (**) следует, что хотя
бы одно из чисел 2v — 3, 2w — 3, 2/ — 3, 2s — 3 отрицательно, —
иначе мы имели бы в левой части этого равенства сумму положи-
тельных чисел. Предположим, например, что 2v— 3 < 0. Это воз-
можно только в том случае, если v -= 0 или и = 1. В первом слу-
чае первое уравнение системы (*) сразу дает у + z + и '=» 0, что
невозможно, если у, z, и положительны. Поэтому надо считать, что
все числа v, tv, t, s положительны и v = 1. В таком случае равен-
ство (**) перепишется в виде
х— (2w — 3)у+ (2t — 3)z+ (2s —3)и + w2 + t2 + s2 + 1. (***)
Рассмотрим теперь разные возможные случаи.
1°. Числа х, у, г, и все попарно различны. В этом
случае и числа у, w, t, s все попарно различны; действительно, счи-
тая, например, что v == w, мы получим, вычитая друг из друга пер-
вые два равенства (*), у — х = 2v(x — у), что невозможно при v
положительном и х ф у. Далее, первое из равенств (*) в предполо-
жении v •= 1 дает 2х = у + z + и — 1, х = У + -2-г + ~и — ~2">
что несовместимо с равенством (***), где коэффициенты при у, г и
и в правой части — целые положительные (ибо w, t, s не могут быть
равны 1, так как они не равны v, а о = 1). Итак, этот случай яв-
ляется невозможным.
2°. Д’В а из чисел х, у, г, и равны между собой;
остальные различны. Здесь надо отдельно рассмотреть два
подслучая.
A) z = и. В этом случае t = s. Равенство (***) и первое урав-
нение (*) здесь принимают вид
(2а> — 3)г/+ 2(2/— 3)z + to2 + 2/2 + 1;
2х — у + 2z — 1;
эти равенства по-прежнему несовместимы.
Б) х — у. Здесь w = v = 1. Равенство (**) и первое из ра-
венств (*) в этом случае соответственно имеют вид
2х = (2t — 3)z + (2s — 3)u + t2 + s2 + 2
и
X " z + и — 1.
Подставляя второе из этих равенств в первое, получим:
(2/ —5)z+ (2s — 5)u +/2 + s2 + 4 = 0, (*♦*)
откуда следует, что хотя бы одно из двух чисел 2t — 5, 2s — 5
должно быть отрицательным. Пусть 2t — 5 < 0; так как / > 0 и
t ф 1 (ибо 0=1; / ¥= о, так как z Ф х), то, следовательно, t = 2.
204
Теперь, прибавляя к третьему уравнению (*) удвоенное первое
3
уравнение, находим 4г + 4х + 6 = 4х 4- 2г + За, т. е. г = — и — 3.
Полагая в уравнении ("*’) i — 2, г — -у- и —3, получим:
(4s — 13)и + 2s2 + 22 = 0.
Отсюда ясно, что 4s — 13 < 0. Так как s > 0, s =£ 1, s ¥= 2,
то, очевидно, s = 3. Подставляя.все эти значения в уравнения (*),
получаем систему трех уравнений первой степени с тремя неизвест-
ными:
х г и = 2х 1,
2х —и — 4г —4,
2х + г = би + 9,
из которой без труда находим х( = у) = 96, г = 57, и = 40.
3°. С р е д и чисел х, у, г, и имеются две п а р ы п о-
парно равных. Пусть, например, х = у, г = и. В таком слу-
чае первое уравнение (*) дает х = 2г— 1; подставляя этот резуль-
тат в уравнение (**):
х = (2/ -3)г + /2+ 1,
находим:
(2/— 5) г + /2 + 2 = 0.
Отсюда следует, что 2/ — 5 < 0, или гак как / > 0, / #= 1, то / = 2.
Теперь уравнения (*) принимают вид
х + 2г = 2х + 1,
2х + г = 4г + 4,
откуда х( = у) = 11, г( = и) г= 6.
4°. Т р и из чисел х, у, г, и равны между собой.
Здесь тоже приходится отдельно рассматривать два подслучая.
А) у = г — и. В этом случае уравнение (***) и первое урав-
нение ',*) принимают вид
х = 3 (2ге> — 3) у + За>2 + 1; 2х = Зу — 1
и, очевидно, являются несовместимыми.
Б) х — у — г. Первое уравнение (*) дает в рассматриваемом
случае
2х + и = 2х + 1,
откуда и = 1; последнее уравнение (*) дает
g fg I- 2)
Зх = 2su 4- s2 = 2s -J- s2; х =-я---•
О
Но х — целое число; следовательно, или s или s-f-2 должно де-
литься на 3, т. е. s = 3k, х = £(3£ + 2), или s == 3k— 2, х =
= (3k— 2)k\ здесь k — произвольное целое число.
5°.. Все числа х, у, г, и равны между собой.
В этом случае первое уравнение (*) сразу дает Зх == 2х + 1, х = 1.
«05
Итак, мы получаем следующие решения задачи:
х = у = 96, z — 57, м = 40; х = у = 11, г = и = 6;
х = у = z = k(3k ± 2), и = l;x = y = z = u = 1
(случай k = 1 и знака «—» в предшествующих формулах),
165. Обозначая искомые числа через х и у, имеем:
х + у = ху,
или
ху — X — у+ 1 = 1,
(х-1)(1/-1) = 1.
Но так как единицу можно только двумя способами разложить
в произведение целых множителей, то сразу получаем:
х— 1 = 1, у — 1 = 1; ж = 2, у = 2,
или
х — 1 = —1, у — 1 = —1; х = 0, у = 0.
166. Прежде всего устанавливаем, что хотя бы одно из трех
чисел х, у, и z, таких, что
должно быть меньше 4: если бы все эти числа были 7г 4, то сумма
111 1113
— + —была бы +~+ ~ = — Таким обра-
зом, если считать, что х sj у sg z, то для х остаются возможными
только два значения: х = 2 и х = 3 (ибо х > 1). Рассмотрим эти
две возможности в отдельности.
11 11
1) х = 2; тогда — + — = 1 — — = -g*. Приведя дроби к об-
щему знаменателю и отбросив знаменатель, получим:
уг — 2у — 2г = 0, уг — 2у — 2г -f- 4 = 4,
или
(z/-2)(z-2) = 4.
Так как у и z больше 1, то у — 2 и z — 2 не могут быть отри-
цательными и возможны только следующие случаи:
А) у — 2 = 2, z — 2 — 2; у = 4, z = 4.
Б) у — 2 = 1, г — 2 = 4; у = 3, г = 6.
11 12
2) х — 3; тогда — + — = 1 — — = или
у Z X о
2уг — Зу — Зг = 0, 4уг — бу - 6г + 9 = 9, (2у — 3) (2г — 3) = 9.
Так как у 7г х .= 3, 2у — 3^3, 2г — 3^3, то возможен только
один случай:
2у — 3 = 3, 2z — 3 = 3; у = 3, z = 3.
Таким образом, все решения задачи даются следующими равен-
ствами:
111 111 111
т + 'г+т^!; 2 + 3 + 6 =1: з + з + з
206
167. а) Из уравнения, очевидно, следует, что х, у > п; поло-
жим х = п -|- хь у = п + уь В таком случае наше уравнение пре-
образуется так:
+ ТйЬ? = 4" - или ("2 + пх^ +('12 + =
— п2 + ПХг + ПУ! + ХхУг, т. е. х^ = п2. (*)
Но ясно, что при п простом равенство (*) допускает лишь три ре-
шения в натуральных числах хь у>, а именно, (xb yi) = (п, п), или
(1, п2), или (n2, 1), что приводит к трем решениям исходного урав-
нения:
(х, у) — (2п, 2п), (n+ 1, п(п+ 1)), (га(ге-Ь 1), п + 1). (**)
Если же п = ab—составное, то возможно также, скажем, решение
(хь J/i) = (а2, &2), что дает отличные от (**) значения х и у.
1 1 1
б) Если — -j- — = ~ , то, избавляясь от знаменателя дроби,
мы получим:
пх + пу = ху,
что равносильно
(х — п)(у—п) = п2
(ср. с решением задачи а)). Последнее уравнение имеет 2v—1 ре-
шений в целых числах, где v есть число делителей числа п2 (включая
1 и само число п2): для того чтобы получить все эти решения, надо
п2
выписать 2у возможных систем вида х — п — d, у — п = —и
п2
х— п = —d, у — п ———(где d есть делитель числа п2), кроме
системы х — п.= —п, у — п = — п, которая приводит к абсурдно-
му в условиях данной задачи результату: х = 0, у — 0.
Если п = 14, то п2 = 196 и делители числа п2 = 196 имеют
вид:
1, 2, 4, 7, 14, 28, 49, 98, 196.
Соответственно этому мы получаем следующие 17 решений на-
шего уравнения:
х 15 16 18 21 28 42 63 112 210 13 12
у 210 112 63 42 28 21 18 16 15 —182 —84
х 10 7 — 14 — 35 —84 — 182
у —35 —14 7 10 12 13’
в) Заданное уравнение можно привести к виду
(х — г) (у — г) = г2 (*)
(см. решение задачи а)). Пусть теперь t есть общий наибольший
делитель трех чисел х, у и г, т. е. х = xtf, у — yd, z = zd, где xb
У1 и Zi взаимно просты. Далее обозначим через m общий наиболь-
ший делитель чисел Х[ и zt и через п — общий наибольший делитель
чисел У\ и гь т. е, положим X] «= mx2, zx = mz2; ух = пу2, zx = zn2,
207
где х2 н z2, У1 и z2 взаимно просты. Числа т и п взаимно просты,
ибо xb yt и Zj взаимно просты. Так как Zi делится и на т, и на п, то
можем положить zt — тпр.
Подставим теперь в основное уравнение (*) х = mx2t, у = ny2t,
г = mnpt. По сокращении на mnt2 будем иметь:
(х2 — пр) (у2 — тр) = тпр2. (♦♦)
Но х2 взаимно просто с р, ибо т есть общий наибольший
делитель чисел Xi = тх2 и zt = тпр; аналогично у2 взаимно про-
сто с р. По раскрытии-же скобок в уравнении (**) мы получаем,
что х2у2 = х2тр у2пр делится на р. Отсюда следует, что р == 1,
и наше уравнение принимает вид
(х2— п){у2 — т) «= тп.
х2 взаимно просто с п, ибо три числа х< «= тх2, yt = пу2 и z} =•
= тп взаимно просты. Следовательно, х2 — п взаимно просто с п,
а следовательно, у2 — т делится на п. Аналогично х2 — п делится
на т. Таким образом, х2 — п = ± т, у2 — т =» ± п; х2 = ± у2 =
— zt т + п и, следовательно,
х — т(т n)t, у = ± п(т + n)t, z = mnt,
где т, п, t — произвольные целые числа.
168. а) Из равенства х* = у* видно, что простые делители чисел
х и у — одни и те же:
х = Р?‘Р22 У= Р1’Р22 • • • Рпп>
где pi, р2...рп — простые числа. Тогда, ввиду нашего равенства,
а.\У = [hx, а.гу = 32х, ..., апу — Р„х.
Будем считать, что у > х; тогда из написанных равенств следует,
что
ai < Pi, а2 < .....ап < ₽п.
Следовательно, у делится на х, у = kx, где k — целое. Подставим
это значение у в наше равенство:
xftx = (kx)*.
Отсюда, извлекая корень х-й степени, получим:
хй = kx, или xk~l = k.
Так как у > х, то k > 1, откуда х > 1. Но легко видеть, что
22-1 = 2, а при х > 2 или k > 2 всегда х4-1 > k. Действительно,
при k >• 2, х 2
Xfc-l 2л-1 > ki
так как уже 23-1 > 3, а при k = 2, х > 2
х6"1 = х > 2 = k.
Поэтому единственным решением нашего уравнения в целых поло-
жительных числах будет х = 2, k = 2, у = kx ~ 4.
у
б) Обозначим отношение — через k, тогда у = kx. Подставляя
это выражение для у в наше уравнение, получим:
х^ =(fex)x,
208
или, Извлекая из обеих частей корень Степени х и затем деля на х,
х*-1 = k,
откуда
1 1 А
x = kk~i, у = kkk~l = kh~l.
„ 1 - р
Пусть рациональное число ___j равно несократимой дроби
1
Подставляя это выражение для в наши формулы, получим:
, , <?,.,<? P_ + q k р ±q
р r+q
л \ V f е....:. .7 j 4.
\ Р ) \ Р !
Так как р и q взаимно просты, то, для того чтобы х и у были
рациональными числами, нобходимо, очевидно, чтобы из целых чи-
сел р и р + q можно было извлечь корень степени q. Но так как
при q 2 и р = л« будет иметь место неравенство
nq <р + q < (п + I)9 = nq + qnq~1 + ^-^2—" nq~2 + ...,
то это возможно только при 9=1.
Итак, все положительные рациональные числа, удовлетворяющие
нашему уравнению, даются формулой
х = у = (L+2F1,
\ р / \ р 1
где р — произвольное целое число (кроме 0 и — 1).
169. Пусть п — число восьмиклассников, т — число очков, на-
бранных каждым из иих. В таком случае число очков, набранных
всеми участниками турнира, равно тп + 8. Это число равно числу
сыгранных партий. Так как участников турнира /1ф2и каждый
играл по одному разу с каждым из п + 1 остальных, то ими всего
(и 2) (и -ф- 1)
было сыграно ------2------партий (в произведении (п + 2)(n + 1)
каждая партия учитывается 2 раза). Таким образом, мы получаем:
(п + 2) (п + 1)
тп + 8 =-------2------->
или, после несложных преобразований,
п(п + 3— 2т) = 14.
Здесь п — целое число; число в скобках — также целое (ибо т —
либо целое, либо дробь с знаменателем 2).
Так как п — делитель 14, то п может быть равно одному из
чисел 1, 2, 7, 14. Значения п — 1 и п = 2 мы должны отбросить,
так как в этом случае общее число участников не превышает 4 и
Ава семиклассника не могли бы набрать вдвоем 8 очков.
Д. О. Шклярскнй и др. 209
Остается п = 7 и п = 14.
Если п = 7, то 7(7 + 3 — 2т) — 14; т — 4.
Если п — 14, то 14(14 + 3 — 2т) = 14; т = 8.
170. Пусть девятиклассников было п и набрали они т очков.
Тогда десятиклассников было 10п и набрали они 4,5m очков. Всех
же участников турнира было 1 In и набрали они 5,5m очков.
Общее число набранных всеми очков равно числу сыгранных
11п(11п— 1)
партий. Партий сыграно было------%------• Отсюда
11п(Пп—1)
5,5m =------2------
и, следовательно,
т = n(l In — 1).
Каждый девятиклассник сыграл 11п — 1 партий (ибо число
участников турнира равно 1 In), а потому п девятиклассников могли
набрать п(11п—1) очков только в случае, если каждый из них
выиграл все партии. Это возможно лишь при n = 1 (так как два
девятиклассника не могут одновременно выиграть друг у друга).
Итак, получаем единственное решение п = 1, т = 10.
171. По условию задачи имеем:
/р (Р — а) (Р — Ъ) (р — с) = 2р,
где а, Ь, с — целые числа и р =----с,--• Обозначим р — а == х,
р —Ь = у, р —с = z; тогда будем иметь:
/(х + р + z) xyz = 2 (х + у + г),
или, возведя обе части равенства в квадрат,
xyz = 4(х + у + г).
Здесь х, у и z — или целые положительные числа, или же полови-
ны нечетных целых чисел. Но второй случай невозможен, так как
тогда слева у нас стояло бы дробное число, а справа — целое. Итак,
х, у и z — целые.
Пусть теперь х у г. Из нашего уравнения найдем, что
_ 4У + 4z
х ~ уг — 4’
следовательно, мы будем иметь:
4у + 4г
уг — 4 > у'
Последнее неравенство можно умножить на yz — 4 (ясно, что
yz — 4 > 0, ибо иначе х было бы отрицательным) и рассматривать
как квадратное неравенство относительно у:
y2z — 8y — 4z^O,T.e.(y — yi)(y — y2)^O, (*)
где У1 и у2 — корни уравнения zy2 — 8р — 4z = 0, зависящие,
210
разумеете^, от 2:
4 + /16 + 4z2 „ 4 — V 16+ 4г2
---------------, у2-------------
Но у2 отрицательно и, значит, всегда у—г/г >0 (ибо у поло-
жительно); следовательно, для того чтобы выполнялось неравенство
(*), надо чтобы было
о, .«нжг,
г
Итак, имеем уг 4+ /16 + 4г2 откуда и подавно z2 —4^
"|/16 + 4г2 (ибо г^~у). Возведя обе части в квадрат, получим:
Z4 —8г2+ 16 + 16 + 4z2; z4 < 12z2,
что, очевидно, выполняется только при геДЗ.
Рассмотрим теперь ряд возможных случаев.
Пг = 1,у<1±1®?<9; х = Ю4г = ^±_4 будет
1 уг — 4 у — 4
целым положительным только, если у — 5 (в этом случае х = 24),
у — 6 (в этом случае х = 14), у = 8 (в этом случае х = 9).
„ <4 + /16 + 4 • 4^.. „_4(/ + 4г _4г/ + 8 _
у О, X- -
=------9 будет целым и не меньшим у только, если у =3 (в этом
У
случае х = 10) и у = 4 (в этом случае х = 6).
3’. г = 3, 4+/16 + 4-9<4- г = у = з х=4у + 4г
3 уг — 4
не будет целым.
Итак, мы получили следующие пять решений задачи:
X У 2 *+у-±г=Р а b С
24 5 1 30 6 25 29
14 6 1 21 7 15 20
9 8 1 18 9 10 17
10 3 2 15 5 12 13
6 4 2 12 6 8 10
172. Первую строку таблицы можно переписать так: 0+1,
0 + 2 0 + п; последний столбец запишем в виде: 0 + п, п + п,
2п + п,..(п— 1)п + п. Каждое число таблицы представлено те-
перь в виде суммы двух чисел, причем первое слагаемое одинаково
у всех чисел, стоящих в одной строке, а второе — у всех чисел од-
ного столбца. Так как среди выбранных чисел будет по одному
14*
211
слагаемому из каждого столбца и по одному слагаемому из каж-
дой строки, то сумма всех первых слагаемых выбранных чисел
равна
, , п2 (п — 1)
О п 4- 2л (л — 1) л = л ,
а сумма вторых слагаемых —
п (п + 1)
1 + 2 + .. + и = ~ 2Т—'•
Таким образом, общая сумма S всех отобранных чисел равна
п(п2 — п) , n(n-J-l) л(пг + 1)
2 + 2 = 2
173. Пусть п нечетно. Если наша таблица симметрична от-
носительно указанной в условии диагонали (эту диагональ мы будем
называть «главной» и обозначать буквой d), то каждому числу,
расположенному сверху от <1, будет отвечать равное ему число,
расположенное снизу от d: это число занимает место, симметричное
относительно d месту, на котором стоит первое число. Отсюда сле-
дует, что совокупность всех расположенных сверху от d чисел сов-
падает с совокупностью чисел, расположенных снизу от d; поэтому,
в совокупности всех не принадлежащих диагонали d чисел нашей
таблицы любое число k встречается четное число а* раз (воз-
можно, что ак — 0). А так как в каждой из п строк таблицы каж-
дое число k встречается точно один раз (ибо п мест этой строки
занимают п чисел 1, 2,..., п), то всего число k встречается в нашей
таблице нечетное число п раз; поэтому на диагонали d число k
встретится нечетное число п — а/, раз. Отсюда следует, что
каждое число k (где 1 sg k п) хотя бы раз встретится на диаго-
нали d (ибо нуль — число четное), а так как эта диагональ содер-
жит всего п чисел, то каждое из чисел I, 2,..., п встретится на ней
ровно один раз. [Отсюда, в частности, вытекает, что а, — а2 =
= — ап = п — I.
1 2
таблицы ।
мулированное утверждение может не выполняться-, близкие к при-
веденным выше рассуждения показывают, что при п четном оно
даже не может выполняться (ибо в этом случае каждое число k
встретится на главной диагонали d четное число п — ак раз).
174. Условимся обозначать число, стоящее на пересечении i-ii
строки и /-го столбца таблицы, через а,]; в таком случае =
= 1......п3, riiei, j=^l,..., п. Пусть теперь 1=о^ ; тогда по условию
задачи 2 •= и т. д. — вплоть до п1 = a При
этом числа Л, /2, /з,..., /«“+1 разумеется, не все различны: ведь они могут
иметь лишь п различных значений 1, 2,..., п. Заметим, что каждое
конкретное значение k встречается в ряду чисел /,, /2, /2, /3, /з, ..
!п'’ /п*+1Р0ВН0 2” Ра3, поскольку наша таблица содержит
п чисел в fe-й .строке и п чисел в k-м столбце. Л так как «внутри» це-
почки /1, /г, /2, ji, ini, in>+t (т. е. не на первом и не на послед-
нем месте) каждое число повторяется дважды, то из того, что значе-
ние h должно входить .в цепочку четное число 2п раз, следует, что
212
показывает, что при п четном сфор-
ji — наша цепочка обязательно завершается тем же числом
/ь которым она начиналась. ,
Таким образом, задача требует оценить разность между сум-
мой чисел /i-й строки таблицы и суммой чисел /i-го ее столбца —
столбца, номер которого совпадает с номером рассматриваемой
строки. Но, в силу правила образования таблицы, если aj^ ^з
(где / /пг и, следовательно, пара (/, /]) не является в нашей це-
почке последней, т. е. s п2), то s + 1 = aj j ; другими словами,
каждому отличному от п2 числу s из ц-го столбца отвечает в ji-й
строке число s + 1. При этом полученные таким путем числа s + 1 =
= aj j —это все числа /i-й строки, кроме одного лишь числа 1
(которое, очевидно, не может следовать ни за каким из чисел /,-го
столбца, поскольку является самым малым в таблице); поэтому,
если обозначить отличные от п2 числа /i-го столбца через S[, s2,...
.... Sn-i, то отличные от 1 числа /,-й строки будут равны Si + 1,
s2 + 1,..., s„-i + 1. А отсюда уже следует, что разность меж-
ду суммой чисел /-го столбца и суммой чисел /-й строки будет равна:
(si + s2 + • • + S„_| + п2) —
— [ (S1 + 0 + (s2 + 1 ) + • • • + (Sn-1 + 1 ) + 1 ] = и2 — п.
175. Ясно, что если — элемент таблицы, стоящий в ней на
пересечении i-й строки и /-го столбца (где i, / = 1, 2,... или
т, соответственно п), то во всех таблицах, получаемых из исходной
«допустимыми» преобразованиями, на этом месте стоит либо число
ац, либо число —atj (ибо наши преобразования таблиц сводятся
к переменам знаков некоторых из входящих в таблицу чисел). По-
этому общее число «допустимых» таблиц заведомо не превосходит
2"‘", т. е. конечно. (Число 2тп равно количеству всевозможных
наборов тп чисел ац, каждое из которых может иметь два значе-
ния.) Из конечности числа рассматриваемых таблиц следует, что
среди них можно указать такую, для которой сумма всех входящих
в нее чисел максимальна (или несколько таблиц с одной и
той же суммой чисел, большей суммы чисел всех других допустимых
таблиц). Но если в такой «максимальной» таблице сумма элементов
какой-либо строки или какого-либо столбца отрицательна, то, по-
меняв знаки всех чисел этой строки или этого столбца, мы придем
к новой «допустимой» таблице с большей суммой входящих в нее
чисел; поэтому в «максимальной» таблице суммы всех элементов
любой строки и любого столбца заведомо неотрицательны.
176. Обозначим сумму всех чисел таблицы буквой 5; сумму
всех чисел i-й строки (где I =1, 2,..., 103) —через sr, сумму всех
чисел /-го столбца (где / =1, 2,..., 80) —через о,; наконец, число,
стоящее в пересечении i-й строки и /-го столбца, обозначим через
flij. По условию задачи
ац = SiO), (*)
откуда
Si = Oil + ai2 + • • + Or S5 =
= Si О] + SiO2 + . . . -|- Si080 = Si (01 + 02 + • . . + 0eo) =
= SjS (i = 1,..., 100),
и, значит, либо S = 1, либо все s, = 0. Но если si = 0 при всех
213
1= 1,..., 100, то, в силу (*), все Элементы ац нашей таблицы
равны нулю. А так как, по условию задачи, «угловой» элемент
Яп > 0, то S = 1.
177. Из равенства чисел, выписанных в симметричных относи-
тельно диагонали клетках, следует, что среди наших 64 Чисел не бо-
лее 20 различных (см. рис. 17, на котором числами 1, 2,..., 20 обо-
8 7 5 4 1 7
7 74 12 11 здр 2
W Ж |7Шф^
5 72 20 /р/ш/ 4
4 77 19 2фШ2 5
% в
2 9 <7^ 77 72 74 7
1 4 8
Рис. 17.
значены какие-то числа а(, а2, ..., а2о,
не обязательно все различные между
собой); при этом числа, скажем, г-й
строки (где! == 1, 2....8) совпада-
ют с числами (9 — /)-й строки и i-ro
и (9 — !)-го столбцов. Если найдет-
ся такое /, то сумма чисел !-й стро-
ки больше 518, то то же справедливо
и для (9 —!) -й строки и для !-го и
(9 —!)-го столбцов (см. тот же рис.
17, где принято i = 3 и соответствую-
щие строки и столбцы заштрихова-
ны) ; сложив эти четыре (одинаковые)
суммы чисел, мы получим результат,
заведомо не меньший 4 518 = 2072.
При этом в соответствующей сум-
ме четыре числа, стоящие на клетках,
отмеченных на рис. 17 двойной штри-
ховкой, будут учитываться дважды,
а числа, стоящие в остальных за-
штрихованных клетках — один раз; поэтому общая сумма всех вы-
писанных в заштрихованных клетках чисел будет не меньше чем
2072 — а, где о — сумма чисел, выписанных в дважды заштрихо-
ванных клетках. А так кай, по условию задачи, а 112 (ибо 112
это сумма чисел, выписанных во всех диагональных клетках),
то сумма «заштрихованных» чисел не меньше чем 2072—112 =
= 1960 — в то время как сумма всех вообще выписанных чисел
равна 1956. Полученное противоречие и доказывает утверждение
задачи.
178. Заметим, что наше условие равносильно следующему: для
любых четырех номеров i, j, k и I, где i =/» k и i l, имеет место
равенство: a,, + ам = afei -|- aJ(, другими словами, для любого взя-
того на доске прямоугольника ABCD (рис. 18, а) сумма чисел, стоя-
щих в двух его противоположных вершинах А и С, равна сумме
чисел, стоящих в двух других вершинах В и D. В самом деле, пред-
положим, что в вершинах А И С находятся две из наших п ладей;
разумеется, эти ладьи можно будет переставить в клетки В и D
с тем, чтобы они по-прежнему держали под боем i-ю и k-ю строку и
/-й и Z-й столбцы. Таким образом, при указанной перестановке сум-
ма всех покрытых ладьями чисел не может измениться; поэтому-то
сумма стоящих в клетках А и С чисел обязательно равна сумме чи-
сел, стоящих в клетках В и D.
Далее уже все просто: обозначим числа, стоящие в нижней стро-
ке доски, через ух, у2. Уп, а числа, стоящие в ее первом столб-
це,—через у\, У\ + х2, Ух + хз,.... Ух + хп (рис. 18, б); кроме того,
положим X] = 0. Ясно, что при этом для чисел нижней (1-й) строки
и левого (1-го) столбца имеем ан = ух = Хх + ух (ибо Xi = 0);
а;1 = Xj + ух. С другой стороны, если i > 1, j > 1, то стоящее в
клетке М число ах) можно вычислить, исходя из выделенного на
214
рис. 18, б прямоугольника MPOQ: в силу доказанного ранее имеем
ац + У\ = (xt i+ yt) + у,, откуда а{) = х. + У).
Нетрудно видеть, что если существуют такие числа хь хг,..., х„;
Уи Уг,---, Уп, что atj = х, ф- yj, то в указанное в формулировке за-
дачи условие, связанное с расстановкой на доске ладей (таких «до-
пустимых» расстановок ладей будет п!—почему?), обязательно вы-
полняется.
179. Ясно, что при / = k = I связывающее xtl, xjh и xftj урав-
нение принимает вид Зх^ = 0; таким образом, хц =0 при всех
УД
п (
Z-'Ч^ № 1
№ —
1
Уз Л
Рис. 18.
i = 1, 2...п. Пусть теперь k = / =£ i; тогда то же равенство при-
нимает вид;
Xij ф- Xjj -j-Xjf — 0,
откуда, в силу того, что xj} = 0, имеем Хц = —xi}. Наконец, про-
суммируем все равенства, отвечающие номерам i, /, 1; i, /, 2; ..., i,
j, n, где i и j— какие-то фиксированные номера; мы получим:
ПХ1} ф- (X;t ф- Xj2<+ • • + х,„) — (х.1 — Xi2 — . . . —Xin) ~ 0
(здесь использована то, что xki — —хц,)- Поэтому, обозначив
-r(Xil + *i2+--- + X<n) = /i> l'=1-2.........П’
получим:
Xjj == ti '— tj.
180. Ясно, что для «доски» размером 1 X 1 (состоящей из одной
единственной клетки) утверждение задачи выполняется (здесь оно
бессодержательно: ведь наша «доска» состоит из единственной клет-
ки, в которой стоит звездочка); это делает возможным использова-
ние метода математической индукции. При п — 2,
очевидно, доска будет содержать столбец (а следовательно, и стро-
ку), в котором имеется точно одна звездочка; переставив, если это
215
понадобится, Строки и столбцы так, чтобы свободное место оказа-
лось правым верхним, мы придем к таблице, имеющей «треуголь-
ное» строение (см. рис. 19, а, где знак «+» означает, что в соответст-
вующей клетке звездочка может как стоять, так и не стоять). До-
кажем, что и при произвольном п строки и столбцы таблицы можно
переставить так, чтобы таблица приняла «треугольный» вид, т. е.
чтобы все звездочки в таблице стояли на идущей сверху вниз на-
право диагонали и, быть может, под ней, — однако все клетки над
диагональю обязательно были пустыми. В самом деле предположим,
*
+
0)
51
Рис. 19.
что это уже доказано для удовлетворяющих нашим условиям таб-
лиц размером (п — 1) X (п—1), и рассмотрим таблицу размером
п X п. Эта таблица содержит столбец, в котором имеется ровно од-
на звездочка; переставим этот столбец на последнее место, а затем
переставим строки так, чтобы звездочка в нем оказалась внизу
(рис. 19, б), и вычеркнем содержащую эту звездочку строку и по-,
следний столбец. При этом мы придем к таблице размером (п— 1) X
Х(«—1), также удовлетворяющей условиям задачи; по предполо-
жению индукции строки и столбцы этой таблицы можно переста-
вить так, чтобы она имела «треугольный» вид, после чего примет
«треугольный» вид и исходная таблица.
«Треугольное» строение рассматриваемых таблиц (его можно
считать «треугольным», ибо с точки зрения интересующих нас свойств
таблиц допустимы любые перестановки строк и столбцов) доказы-
вает равноправность строк и столбцов таблицы, а значит и справед-
ливость утверждения задачи (наглядно очевидного для «треуголь-
ных» таблиц).
181. а) На доске размером 4X4 имеются 4 столбца, 4 строки и
2-7 = 14 параллельных диагонали рядов (из которых 4 «ряда», со-
держат лишь по одной угловой клетке); нетрудно убедиться, что
каждый из этих 4 + 4+ 14 = 22 вертикальных, горизонтальных или
наклонных рядов содержит четное число (а именно — либо 0, либо 2)
заштрихованных на рис. 20, а клеток. Но первоначально лишь
одна из этих клеток содержала знак «—»; поэтому при всех наших
переменах знаков число заштрихованных клеток, помеченных знаком
«—», останется нечетным — и, значит, никогда не станет рав-
ным 0.
б) Где бы ни был расположенный на доске знак «—», мы всег-
да можем «вырезать» из нашей доски размером 8 Х8 «малую» доску
размером 4X4 так, чтобы на ней расположение знаков было таким,
216
кек в условии задачи а) (см. рис. 20, б — в, где изображены два
возможных варианта расположения знака «—» на большей доске).
А так как наши изменения знаков на большой доске порождают на
«малой» доске описанные в условии задачи а) перемены знаков, то
требуемый результат следует из результата задачи а).
182. а) Подсчитаем, прежде всего, число всевозможных квадра-
тов размером 3X3 и размером 4X4, которые можно разместить на
Рис. 20.
шахматной доске. Ясно, что левый нижний угол квадрата размером
3X3 может совпасть с любой клеткой квадрата размером 6X6, за-
штрихованного на рис. 21 горизонтальной штриховкой, а левый ниж-
ний угол квадрата размером 4X4 — с любой клеткой (меньшего)
квадрата размером 5X5, заштрихованного на том же рис. 21 вер-
тикальной штриховкой; таким образом, все-
го мы имеем на доске 6-6 4- 5-5 = 36 +
4-25 = 61 квадрат размером 3X3, или
4X4. Поэтому, исходя из доски, на всех
клетках которой стоят знаки «+», мы мо-
жем описанными операциями получить
не более 261 возможных распределений
знаков во всех клетках доски, ибо в каж-
дом из 61 рассматриваемых квадратов мы
можем, независимо от остальных квадра-
тов, изменить все знаки или не менять их.
А так как всего возможных распределений
знаков «-(-» и «—» в 64 клетках шахмат-
ной доски существует 2S4 > 261, то, исходя
из доски с одними лишь знаками «4-», лю-
бое распределение знаков на доске полу-
чить нельзя. Но если рассмотреть теперь
Рис. 21.
какое-либо распределение знаков, которое нельзя получить описан-
ным образом из распределения, содержащего только знаки «4~»>
то, и обратно, исходя из этого распределения знаков, мы никогда
не сможем прийти к одним лишь знакам «+», откуда и следует
отрицательный ответ на вопрос задачи.
б) Эта задача очень близка к задаче а). Общее число «(2X2)-
квадратов», которые можно выделить из шахматной доски, равно
7-7 = 49, а число пар соседних строк или соседних столбцов доски
217
равно 7 4-7=14; таким образом, мы имеем 1049+14 1063 способов
менять последние цифры чисел, стоящих в клетках доски. (К числу
этих 1063 способов относится и тот, когда ни одна цифра не меня-
ется). Отсюда следует, что, исходя из расположения чисел, такого,
что все числа оканчиваются на 0, мы не можем получить все вооб-
ще возможные распределения последних цифр чисел, стоящих в 64
клетках доски, ибо число таких распределений равно Ю64 > 1063;
поэтому найдутся такие распределения последних цифр, от которых
нельзя перейти к «нулевому».
Примечание. Разумеется, решение (и отрицательный ре-
зультат) задачи сохраняет силу и в том случае, если требуется.до-
биться делимости всех чисел таблицы не на 10, а на любое другое
натуральное число п, скажем на число 1976.
183. а) Сможет. Ясно, что, выбирая по одному камню из всех
кучек, мальчик может добиться того, чтобы хоть в одной кучке ос-
тался единственный камень. Затем, удваивая число камней в
той кучке (или в тех кучках), в которой имеется 1 камень, и снова
вычитая по камню из всех кучек, мальчик уменьшит на единицу
число камней в кучках, где оно отлично от 1, сохранив 1 камень в
кучках, где этот камень был единственным. Продолжая поступать
так же, мальчик может добиться того, чтобы во всех кучках оста-
лось по одному камню; после этого он может забрать их все.
б) Эта задача во всем подобна задаче а) (заметим, что фигу-
рирующие в задаче а) числа камней можно расположить в виде
«таблицы» из одной строки и трех столбцов — по одному числу в
столбце). В самом деле, если мы сначала будем рассматривать чис-
ла лишь одной,— скажем, 1-й —строки, то наши операции позволят
удвоить любое из чисел этой строки или вычесть единицу из всех
этих чисел; поэтому, в точности как в решении задачи а), можно об-
ратить все числа этой строки в 0. После этого мы точно так же об-
ратим в 0 все числа 2-й строки — и так поступим со всеми строками
таблицы.
184. Запишем число а в «двоичной системе счисления»1), т. е.
в виде
а = ап-2п 4- an-i-2n-1 4- ап-2-2п~2 + ... 4" ®i ’2 4- 1,
где все «цифры» а0, а;, .... а„-г, «n-ь ап равны 0 или 1 (стар-
шую «цифру» ап числа а, разумеется, можно считать равной 1). Яс-
но, что если число а четно, то Ио — 0 и а1=-£=ап,2п-14-
4-а„_г2п_2 4-ап_2-2п-3 4-... 4-1; если же а нечетно, то
а - 1 -V
а-, = 1—и число ai =—2—имеет точно такое же строение. Таким
образом, если а записывается в двоичной системе счисления после-
довательностью «цифр» а = gnan-i«n-2 а1юо, то Qi записывается
в той же системе счисления как а\ = а„а„1ап-2. «г, соответ-
ственно этому д2 записывается как а2 = сспап_1... а2, а3 — как аз =
= anan-i... а2, и т. д.— вплоть до числа' а„ = а„ = 1. С другой
стороны, очевидно, bi = 2b, b2 = 2bt = 22b, b3 = 23b, и т. д.—
вплоть до числа Ьп = 2"&.
’) См., например, [47].
218
' Ясно, что at = anOLn-i ал = an 2n-i + an-i • 2n-f-1 + ...
... +a1+i • 2 + a< • 1 (где i = 0, I, 2,..., li) будет нечетным, если
«цифра» а, равна 1 (напомним, что а,- может равняться лишь О
или 1). Таким образом, в этом случае bt = 2’ Ь = (а, • 2!)Ь. По-
этому интересующую нас сумму всех отвечающих нечетным
ai, можно записать так:
[ап -2” +an_i-2n-1 + ... + ai-2 + ao-l] & =
= a,nan-i... aia0 • b = ab,
где в сумме a„-2п + . + ar2 + а0- 1 (=а) реаль-
но участвуют лишь слагаемые, отвечающие равным 1 значениям
«цифр» ап, а»-:, • •а».
185. Самое короткое решение этой задачи доставляет метод
математической индукции. Условимся обозначать £-е
число Фибоначчи, где k = 1, 2, 3..через ик. Предположим, что
наше утверждение уже доказано для всех натуральных чисел п,
меньших k-ro числа Фибоначчи и*; справедливость его для всех чи-
сел, например, меньших и5 — 5, легко проверить непосредственно.
Ясно, что то же утверждение будет выполняться и для числа ик.
Далее, поскольку все числа между ик и ик+1 = ик + uft_I предста-
вимы в виде ик + т, где 0<т<«л_1, и поскольку, по предположе-
нию индукции, все меньшие ик-\ числа т могут быть представлены
в виде суммы каких-то различных чисел Фибоначчи, номера которых
меньше k — 1, то число п = ик + т также представляется в виде
суммы чисел Фибоначчи («старшее» из которых есть ик, а номера
остальных меньше k—1). Таким образом, мы установили, что наше
предположение верно и для всех натуральных чисел, меньших ил-i,
откуда и вытекает его справедливость для всех натуральных чисел.
Примечание. Из доказанного следует, что в рассматривае-
мых суммах чисел Фибоначчи (где мы, разумеется, считаем, скажем,
2 = и3, но не 2 = 1 + 1 = Ui + «2, или 4 = 3+ 1 = и4 + и2, а не 4 =|
= 2 + 1 + 1 = и3 + u2 + и,) не могут фигурировать два «соседних»
числа Фибоначчи (почему?); нетрудно показать, что всевозможные
суммы чисел Фибоначчи, удовлетворяющие последнему условию —
это и есть все натуральные числа, причем каждое число встречается
в последовательности всех таких сумм единственный раз (ср.
с решением задачи 129 из книги [6]).
186. Нас интересуют суммы sk = us+1 + иА+2 + ... + ик+& вось-
ми последовательных чисел Фибоначчи. Поскольку числа Фибоначчи,
очевидно, монотонно возрастают: щ = и2 < «з < и4 < ... < ип <
<ип+1<..„ то ясно, что утверждение задачи будет доказано,
если мы покажем, что сумма sk заключена между и*+9 и ил+ю,
т. е. что Ий+9 < s* < Wfc + io. Но ясно, что
И*+9 = Ил+8 + иЛ+7 < иЛ+8 + иЛ+7 + иЛ+6 + • . + = sh‘>
таким образом, остается лишь доказать неравенство s* < «л-но. Не-
трудно, однако, видеть, что сумма Sn = Ui + u2 + из + ... + ип
первых п чисел Фибоначчи на единицу меньше (п + 2)-го числа
ип+2; установить это можно, например методом математи-
ческой индукции. В самом деле, очевидно, S2 = 1 + 1 =
<= з — 1 = ц4 — 1; с другой стороны, если требуемое утверждение
справедливо для какого-то номера п, то, заменяя п на п + I и
219
используя предположение индукции, получим:
Sn + l = + Ui + . . . -f- Un l-f- Un + l = Sn + Un + l =
•= (un+2.— 1) + un + l = (un + l + Ип+2) ~~ 1 “ 4n+3— 1>
— что и требовалось доказать. А теперь сразу получаем:
Si = Wft+1 + Uk+2 + • • • + U*+8 — Sh + 8 — S* =
= (Ufc +10 — 1) — (иЛ + 2 — 1) = (A + |o — U/,+2 < “й+Ю,
чем и завершается решение задачи.
Примечания. 1. Ясно, что так же можно доказать,, что
сумма любых т последовательных чисел Фибоначчи, где т 3,
не может быть числом Фибоначчи.
2. Неравенство •< И/, + 10 можно также доказать, последова-
тельно преобразуя выражение для uA+0I:
Ий + 10 = мй+9 + Uk + 8 = (Uft + 8 + Uk+j) + Ий+8 =•
= Ufc+8 + «й+7 + (((Л+7 + мй+б) = Uf,+S + «Л+7 + Wfc+6 +
+ (ий+8 + ий+б) = мй+8 + »й+7 +ы*+6 + Ий+5 4* («й+5 4* Uk+t) — . . .
, . . =«й+8 + Uft+7 + • • • + wft+2 4* (мй + 2 + Wfe + 1) = Sfc 4" Ufc+2 > Sh-
187. Условимся обозначать остатки от деления чисел Фибоначчи
«1, «2, из,. •. на 5 через аь аг, а3, •.. Ясно, что из равенства и* =
» Uk-i 4* “а-2, где k •= 3, 4, 5,..., следует, что
pfc-j + a^, если aA_1 + aA_2<5;
a. = { (*)
|aft_! + aft_2 —5, если aft_j 4-aft_2 > 5.
Формулы (*) позволяют выписать сколь угодно много членов пос-
ледовательности а.,.-.
1, 1, 2, 3, 0, 3, 3, 1, 4, 0, 4, 4, 3, 2, 0, 2, 2, 4, 1, 0, 1, 1, ...
При этом для того, чтобы выписать любое число следующих далее
членов последовательности aft, нам уже нет нужды прибегать к фор-
мулам (*): ведь а2| = аь а22 = а2, и, значит, (в силу (*)), а23 =
= а3, «24 = «4, и т. д., т. е. «последовательность остатков» ab a2,
a3,... является периодической с периодом 20. А так как в пер-
вой серии из 20 остатков а* на 5-м, 10-м, 15-м и 20-м местах стоят
нули, но также и впоследствии на всех кратных 5 местах в этой пос-
ледовательности будут стоять нули.
188. Оставим в каждом члене ряда Фибоначчи, записывающем-
ся пятью и более цифрами, только последние четыре цифры. У нас
получится последовательность чисел, каждое из которых меньше
чем 104. Обозначим через йй член этой последовательности, стоящий
на k-м месте. Заметим, что если нам известно ak + i и йй, то мы мо-
жем вычислить ай-i, ибо (k—1)-й член ряда Фибоначчи равен раз-
ности (А 4- 1)-го и k-то членов, а последние четыре цифры разности
можно определить по последним четырем цифрам уменьшаемого и
вычитаемого. Отсюда следует, что если для некоторых номеров k
и п окажется, что ah = ап+к, йй-н = un+s + i, то тогда йл-i =
= ап+й_], йй-2 = «п+й-2.......«1 = «п + ь Но так как at •= 0, то это
будет означать, что a„ + i = 0, т. е. что в ряде Фибоначчи на
(«4- 1)'м месте стоит число, оканчивающееся четырьмя нулями.
220
Остается показать, что среди 108 + 1 пар
ai, ait
Оз,
а108 а10»+1>
а108+1> а108+2
найдутся хотя бы две одинаковые. Но это непременно будет так,
ибо все числа а,, а2, а3.ajo8+2 не превышают 104, а из 104 чи-
сел 0, 1, 2, 3, 4, ..., 9999 можно составить только 104-104 = 10s
различных пар (ибо первое число может принимать 104 различных
значений и второе число может принимать J04 различных значений).
Примечание. Можно даже точно указать первое из чисел
ряда Фибоначчи, оканчивающееся четырьмя нулями; номер этого
числа 7501 (см. задачу 174 книги [5] и следствия из нее).
189. Поскольку при п > 1 имеем
ап ~ (ап-1 + а 7) ~ а«—1 + 2 + Тз > ап-1 + 2>
\ ан-1 / ап^
то из а2 = 1 получаем
а|> 1 +2 = 3, al > 1 + 2-2 = 5, > 1 + 3-2 — 7, ...
.... af00> 1 + 99-2 — 199,
откуда и следует, что. йюо > У 199 > 14. Аналогично, используя
неравенство
9 / 1 V , 1 ,
an~lan-l+a ) = ап-1 + 2 + ~2 <ап-1 + 3,
\ ип—\/ an_i
также верное при всех п>1 (причем в равенство оно обращается
лишь при п = 2), получаем:
а|-= 1.3-4, af<l + 2-3—7, а\ < 1 + 3-3 = 10, ...
.... 4оо< 1 + "'3 = 29®>
откуда вытекает, что Як» < 1/298< 18.
190. Первое решение. Дополним нашу последовательность
чисел еще одним числом а„ + 1, таким, что |an + i| = |on + 11, возве-
дем в квадрат все данные в условии задачи равенства (включая
сюда и «дополнительное» равенство, связывающее числа а„ и a„+i):
= 0, eg = («1 + I)2 = + 2й1 + 1,
аз = (а2 + I)2 = а\ + 2яг+ 1, ..., а2„» а^ + 2an_t + 1,
an+l==an+2an+1'
221
и затем Сложим их:
а 1 + а2 + аз + • • • + ап + ап+1 = ° + а1 + а2 + • • •
• • • + an—1 + ап +2(а1 + а2 + а3 + • • • + ап) + П • 1 .
Из последнего равенства следует, что
2 (а1 + «2 + «з + • • • +«п) = ~ п + ап+1 > —п,
а значит,
а1 + а« + аз + • • • +ап 1
- > — -у •
Второе решение. Заметим, что при п = 1 рассматривав-
01
мое среднее арифметическое равно — = 0; при п = 2 (где, очевидно,
2 , , , ,, «1 + а2 0 + а2
а2 = I и, значит, а2 = + 1 или — I) оно равно —— = —2— =
о2 1 1 ' ,
~2~, т. е. равно % или —~2~> таким образом, в этих двух случаях требу-
емое неравенство выполняется. Воспользуемся теперь методом
математической индукции: предположим, что в случае,
когда количество рассматриваемых чисел меньше п, утверждение
задачи справедливо, и покажем, что в таком случае оно будет вы-
полняться также и для п чисел. Пусть at, а2, ..., ап — удовлетво-
ряющая условиям задачи последовательность п чисел, и пусть ат
(где т — один из номеров 1, 2, 3, ..., или п)—наименьшее из
них. В таком случае, разумеется, можно считать, что ат<0 (ибо
если все наши числа неотрицательны, то нам и доказывать нечего:
конечно, тут их среднее арифметическое больше—g-)11 что ~
= — am-i— 1 (ибо лишь в этом случае [ат| = |am-i + 1| и
От < am-i), т. е. среднее арифметическое чисел ат_, и ап
ат—1 + ат 1
2 2 '
Заметим теперь, что если исключить из нашей последовательно-
сти числа am-i и ат, то оставшиеся m — 2 числа также будут
удовлетворять требуемым условиям. В самом деле, ясно, что m #= 1
(ибо at = 0, а ат < 0)—именно поэтому мы и можем говорить о
числе am-i. Далее, если т = 2, то ат = «2 = — 1> а3 = О (ибо
|а3| = |а2 + 1 [), и мы, разумеется, можем отбросить числа fli и а2
и начинать последовательность сразу с а3( = 0); аналогично, если
т = п, то мы можем отбросить два последних числа ап_} и а„ и
оставшиеся числа по-прежнему будут удовлетворять требуемым ра-
венствам. Наконец, если 3^/и^я— 1, то
|flm-2 + 11 = |am-i | = |—ат — 1| и | о,,, +11 — 10/п + 11 =1—ат — 11,
так что |ат_г-|-1| = |am+!|—и, значит, в самом деле числа а,,
а2....ат-2, am+i, а„ будут удовлетворять требуемым в фор-
мулировке задачи условиям.
222
ат— 1 + ат — ~ 1:
ат+1 + +ап
... +й
Теперь, по предположению индукции, выполняющемуся для
п — 2 чисел,
+ • • • +«т—2 + ат+1 + ...+ап 1
——>_ 2 ,
те. ai + а2 + ... + йт_2 + «ш+1 + •• • + ап > ~ ~2* (п — 2).
С другой стороны, как мы уже знаем,
‘ О-т—1 + ат 1
-------------2----= -Т' т'е'
поэтому
«1 + й2 + • • • + От_ 2 + ат— 1 + ат +
> — “2* (п — 2) + (— 1) -2“п,т. е. ------------ > —
— что нам и требовалось доказать.
191. Нетрудно понять, что наибольшим числом нашей последо-
вательности может быть лишь одно из первых двух чисел Со и а\
(ибо каждое ак при k > 2 обязательно < max^-!, Легко
даже видеть, что в наибольшей по длине последовательности самым
большим является именно число at, ибо если последовательность
начинается с чисел at, аг, а3,..., где а, > а2, то ее можно,
не меняя, «продолжить назад», условившись начинать так:
а0 = О] — а2, ait а2 = |й[— а0|, аз,... (здесь, очевидно, at >
> а0 = й! — а2). Поэтому в дальнейшем мы ограничимся лишь рас-
смотрением последовательностей, начинающихся с наибольшего
числа й2 (нам только при этом придется в окончательном ответе уве-
личить длину последовательности на 1 за счет «нулевого» по номеру
числа йо = й1 — й2).
Ясно, что если наибольший член последовательности а, = 1, то
последовательность состоит не более чем из двух чисел (продол-
жить ее можно лишь одним числом а2 = 1); если наибольший член
последовательности й1 = 2, то количество входящих в последова-
тельность чисел sg 3 (если й2 = 2, то последовательность имеет вид:
2, 2, а если а2 = 1, то она такова: 2, 1, 1); если at = 3, то число
входящих в последовательность чисел sS 5 (полагая, что а2 = 3, 2
или 1, мы приходим к последовательностям: 3, 3; или 3, 2, 1;
или, наконец, 3, 1, 2, 1, 1). Эти примеры подсказывают заключение
о том, что «оптимальная» последовательность, по-видимому, должна
начинаться с чисел й[ = га, а2 = 1. При этом начало ее выглядит так:
п, 1, п — 1, га — 2, 1, .... (*)
откуда вытекает, что, обозначив количество чисел, составляющих
последовательность (*), через kn, мы получим:
=3 + ^-2 (**)
(ведь, начиная с 4-го члена а, = п — 2, мы приходим к подоб-
ной же последовательности, где п заменено на п — 2).
') Ср. сноску на стр. 228.
223
Из соотношения (**) находим:
k, = 2, k3 = 3, ks = 3 + 2 = 5, ki = 3 + 3 = 6,
ks <= 3 + 5 = 8, kt «= 3 + 6 = 9, ..
все эти числа kn задаются следующей формулой:
, ГЗч+11
Ь _____:— (***\
П L 2 J ’
где квадратные скобки, как всегда (ср. стр. 37); обозначают целую
часть числа. (Формулу (***), разумеется, совсем просто вывести
из (**) с помощью метода математической индукции:
для п = 1 и п = 2 она, как мы видели, справедлива; если (•*’) верно
для значения п — 2, то для значения п это соотношение тоже верно:
, , [3 (и — 2) + 11 Г Зп 1 1 \
*п^Ап-2 + 3 = [ 2 J + 3 = L 2 ]/
Итак, мы уже построили (начинающуюся с наибольшего чис-
ла!) последовательность (*), длина kn которой связана с величи-
ной п наибольшего числа соотношением (***); покажем теперь,
что если описанная в условии задачи последовательность, начина-
ется с наибольшего числа at = п, то длина ее не может
превзойти указываемого формулой (***) числа kn. Доказывать
это мы будем, естественно, по индукции: предположим, что на-
печатанное курсивом утверждение уже доказано для всех значений
п, меньших, некоторого (а справедливость его для значений п = 1, 2
и 3 мы уже проверили), и покажем, что тогда оно будет справед-
ливо и для значения п. В самом деле, пусть задана удовлетворяю-
щая условиям задачи последовательность, начинающаяся числами:
п, 'т, ...,
где т п. Далее рассмотрим ряд вариантов, отвечающих разным
значениям т.
1°. Если т — п, то последовательность обрывается на 2-м чле-
не; для нее наше утверждение, конечно, выполнено.
а
2°. Если п — четное число ит-"—, то последовательность
п п
обрывается на 3-м члене: п, -у, — , и здесь тоже, разумеется,
длина последовательности меньше kn.
п
3°. Если п > то, отбросив в нашей последовательности
первое число п, мы получим «в остатке» последовательность т,
п — т,..., тоже начинающуюся с большего числа т; по предполо-
жению индукции, этот «остаток» содержит не более ^т—
чисел. Но так как одно число мы при этом отбросили и так
как т п — 1, то вся последовательность содержит не более чем
ГЗтг + !] Г3(п—1)4-1-] Г Зч 1 ГЗ,.г4-1]
1 + [ 2 J 1 [ 2 | j 2 1'^ j 2 ] ~п
чисел.
221
(3m 4- 11
I 2 1
4°. Если, наконец, т <. -,то наша последовательность начи-
нается так: п, т, п — т, п — 2т, т, ... При этом если п — 2т т
п
(т. е. т гС g), то «остаток» последовательности, получающийся
после отбрасывания первых трех чисел (остаток, начинающийся
с числа п — 2т), таков, что наибольшим в этой последовательности
чисел является первое ее число; поэтому, по предположению индук-
ции, количество содержащихся в остатке чисел не превосходит
Г3(п —2т)4-1] Г3(п — 2)4-11 ГЗп 4-I
kn—2m — I 2 ] 2 I ~ 2
(ибо 1), и, значит, общее число чисел не превосходит
з«4-1]
2
Если же п — 2т <_ т (т. е. т
«э
), то поскольку здесь шестое число
последовательности т — (п — 2т) < т, то начинающийся с пято-
го числа т «остаток» будет таков, что в нем наибольшее число т
стоит на первом месте; поэтому число чисел «остатка» km —
[3m 4- Ч [Эл 4" 21
= —j— < —j— —и снова общее количество входящих
.........Г3«+ 2], . J3n4-1] ,
в последовательность чисел — 4* 4 < —g—= ,
Тем самым мы полностью доказали утверждение, относящееся
к последовательностям, начинающимся с наибольшего числа. А от-
3-1967 + Г
2
сюда следует, что заданная в условии задачи последовательность
не может содержать больше чем 1 4- = 1 4~
= 2952 числа; количество входящих в последовательность чисел
равно 2952 в том и только в том случае, если она начинается с чи-
сел: 1966, 1967, 1, 1966, 1965, 1, 1964, 1963, 1, ...
192. Будем доказывать наше утверждение от противного.
Предположим, что в последовательности чисел an ai«2, а|а2аз, ...
имеется лишь конечное число составных. Ясно, что в этом
случае в последовательности цифр ои, а2, а3,... имеется лишь ко-
нечное число четных цифр (ибо каждое число, десятичная
запись которого кончается че-тной цифрой, является составным),
и, значит, все цифры an, йп+i, an+2.......начиная с какой-то п-й
цифры, будут нечетными. Точно так же устанавливается, что в на-
шей последовательности a)( а,, аз, ... цифр будет лишь конечное
число пятерок (ибо каждое число, оканчивающееся на 5, де-
лится на 5); таким образом, начиная с какого-то места в последо-
вательности будут встречаться лишь единицы, тройки и семерки
(ибо девяток в ней нет по условию задачи). Но приписывание
к числу тройки в конце не меняет остатка от деления этого числа
на 3, а приписывание. единицы или семерки увеличивает остаток
от деления на 3 на единицу (ибо 7 = 2-34-1); поэтому если
число единиц и семерок в нашем ряду цифр бесконечно, то каждое
третье из оканчивающихся на 1 или на 7 чисел будут делиться на 3,
т. е. будет составным. Таким образом, если, стремиться к тому,
чтобы лишь конечное число чисел ряда аь а,а2, aia2a3,... были
; 15 Д О. Шклярский и др,
В. '
№
составными, мы должны, начиная с какого-то /V-го места в ряду
цифр аь а2, а3.....приписывать в конце ранее имеющегося числа
тройку, при этом мы приходим к последовательности чисел вида
М = . aN-l 333 ... 3 = ЮМ + ЗВ,
h раз
где А = aja2 ... 1 и В — 111 ... Г, здесь k = 1, 2, 3, ...
h раз
Пусть теперь р—простой делитель числа А (возможно, сов-
падающий с Л); можно считать р отличным от 2 и от 5, ибо если
N достаточно велико, то a,v-i = 1, 7 или 3 (значение a.v-i = 3
здесь ие исключается!). Но существует бесконечно много
таких значений k, что записываемое с помощью k единиц число В
делится на р (см. Примечание в конце решения задачи 144); всем
этим значениям k отвечают составные (делящиеся на Л) числа М =
= 10М + ЗВ, т. е. вопреки сделанному предположению среди чи-
сел М имеется бесконечно много составных. Полученное противоре-
чие и доказывает утверждение задачи.
193. а) Четность или нечетность последней цифры суммы че-
тырех цифр (другими словами — самой этой суммы) зависит лишь
от четности или нечетности рассматриваемых цифр. Если буквой н
обозначить нечетное, а буквой ч — четное число, то легко видеть,
что наша последовательность начинается так:
ннннчннннчннннч ...,
причем далее она, очевидно, продолжается периодически:
после каждых четырех нечетных чисел (н) следует одно четное чис-
ло (ч). Но отсюда уже следует, что последовательность 1234, имею-
щая характер нчнч, нигде не может встретиться в нашем ряду цифр.
б) Различных четверок цифр, каждая из которых может иметь
10 значений: 0, 1, ..., 9, существует 104; поэтому в последователь-
ности из 10 004 цифр обязательно два раза встретится' одна
и та же четверка (образованная соседними цифрами). Но если
1-я, (i’+ 1)-я, (1-|-2)-я и (1 + 3)-я цифры совпадают с j-й, (/+ 1)-й,
(/ + 2) -й и (j’ + 3)-й цифрами (где мы считаем /<i), то, в силу
самого закона образования последовательности, (i—1)-я цифра
совпадает с (/—1)-й, (1 —2)-я—с (/ —2)-й, и т. д. Поэтому
(‘ — /—1)-я, (i — /)-я (i —/+1)-я и (i —/ + 2)-я цифры нашей
последовательности обязательно совпадут с 1-й, 2-п, 3-й и 4-й циф-
рами, т. е. они образуют четверку 1975.
194. Ответ на первый воцрос задачи является совсем простым:
ясно, что среди 8-значных и еще меньших чисел мы не можем
встретить такого, сумма цифр которого равна 9 • 9 = 81, а среди
9-значных чисел таким является одно лишь число 999 999 999;
соответственно этому в ряду (**) число 81 впервые встретится
на 111111111-м месте; следующее за ним число ряда (**) будет 9
(сумма цифр числа 1 000 000 008).
Несложен и ответ на второй вопрос. Так как среди тех чисел
ряда (**), которые отвечают не более чем трехзначным числам ря-
да (*), число 27 встретится единственный раз (на 111-м месте
в этом ряду — в ряду (*) на этом месте стоит число 999), то здесь
не приходится рассчитывать на четырехкратное повторение числа
27. Среди же четырехзначных чисел ряда (*) можно отыскать
226
4 последовательных числа, сумма цифр которых равна 27 — это
будут числа 3969, 3978, 3987 и 3996; ясно, что соответствующие
числа 27, 27, 27, 27 ряда (**) предшествуют первой тройке чисел
36 в этом ряду (и даже вообще первому числу 36, отвечающему
числу 9999 ряда (*)).
Менее определенно сформулирован последний вопрос,— а между
тем именно с ним и связаны пути подбора указанной выше чет-
верки чисел 3969, ... Не останавливаясь на подробном обсуждении
этого вопроса, укажем лишь, что строение чисел ряда (**) связано
с монотонностью ряда цифр в числах, получаемых делением чисел
ряда (*) на 9; в частности, числа 441 (= 3969:9), 442, 443, 444,
отвечающие рассмотренной четверке чисел ряда (*), таковы, что их
цифры не возрастают. Выпишем, например, в таблицу все числа
от 1 до ПО, где жирным набраны двузначные числа, для которых
цифры числа (отличные от цифры 0) не возрастают, и трех-
значные числа, цифры которых (снова отличные от 0) н е у бывают.
1 2 3 4 5 6 7 8 9 10 11
12 13 14 15 16 17 18 19 20 21 22
23 24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41 42 *43 44
45 46 47 48 49 50 51 52 53 54 55
56 57 58 59 60 61 62 63 64 65 66
67 68 69 70 71 72 73 74 75 76 77
78 79 80 81 82 83 84 85 86 87 88
89 90 91 92 93 94 95 96 97 98 99
100 101 102 103 104 105 106 107 108 109 ПО
Умножив все эти числа на 9 и образовав ДЛЯ каждого из них сум-
му цифр, мы придем к такой красивой таблице:
9 9 9 9 9 9 9 9 9 9 18
9 9 9 9 9 9 9 9 9 18 18
9 9 9 9 9 9 9 9 18 18 18
9 9 9 9 9 9 9 18 18 18 18
9 9 9 9 9 9 18 18 18 18 18
9 9 9 9 9 18 18 18 18 18 18
9 9 9 9 18 18 18 18 18 18 18
9 9 9 18 18 18 18 18 18 18 18
9 9 18 18 18 18 18 18 18 18 18
9 18 18 18 18 18 18 18 18 18 18
Существуют и Другие изящные KOI нфигурацни чисел последова
тельности (**).
195. Заметим, прежде всего, что каждый из наборов Jo, Л,
J2, ... получается из предшествующего добавлением к нему некото-
рого количества новых чисел; при этом все ранее имевшиеся числа
в новом наборе сохраняются. Легко видеть, далее, что все вновь
15*
227
появляющиеся в наборе /„ числа будут больше п-, поэтому число
1973 в наборах с номерами, большими 1973, уже не возникает —
и все такие наборы содержат одно и то же количество чисел
1973. Докажем теиерь, что фиксированная пара чисел а, b (где а
стоит, скажем, слева от Ь; таким образом, а, Ь и Ь, а мы счи-
таем разными парами!) встретится в последовательности /о, Л,
/2, • , In, . наборов ровно один раз, если числа а и b взаимно
просты, и не встретится ни разу в противном случае. Это утвержде-
ние очевидно для пар чисел а, Ь, наибольшее из которых не пре-
восходит 2 (таких пар имеется всего две: 1, 2 и 2, 1 — и встречает-
ся каждая из этих пар один лишь раз, а именно, в последователь-
ности Ц-. 1, 2, 1); докажем его методом математической
индукции. Предположим, что наше утверждение уже доказано
для всех таких пар чисел а, b что max [а, Ь] <п‘), и покажем
что оно будет справедливо и для пар а, Ь, где max [а, &] = п.
В самом деле, пусть а, b — пара целых положительных чисел, где,
скажет.!, max [а, b] = Ь = п. Ясно, что пара а, b может появиться
в каком-то наборе h лишь в том случае, если в предыдущем набо-
ре lk-i мы имели пару стоящих рядом чисел а, Ь — а. Но поскольку
max [а, Ь—а] <тах[а, &](= b — п), то в силу предположения
индукции пара чисел а, b—а встречалась в наших наборах /1,...
..., h-t один раз, если а и Ь — а взаимно просты, и ни разу,
если а и Ь—а имеют общий делитель d > l.'Ho отсюда сразу сле-
дует что и пара чисел а, b встречается в наших наборах один раз,
если а и & взаимно просты, и не встречается вовсе в противном
случае: ведь числа а и b взаимно просты в том и только в том
случае, если взаимно простыми являются числа а и Ь — а.
Теперь уже ясно, что, поскольку число 1973 — простое (про-
весьте это!), в наших наборах по одному разу встретится каждая
из пар чисел 1,1972; 2,1971; 3,1970; ...; 1971,2; 1972,1 —ведь всеэто
суть пары взаимно простых чисел. А отсюда следует, что число 1973
встречается в наборах 1п с номерами п > 1973 (в частности, в на-
боре Лоооооо) ровно 1972 раза (это число равно количеству пар
1,1972; 2,1971; ...; 1972,1).
Примечание. Из решения задачи также следует, что про-
извольное натуральное число N встречается в наборах 1п (где п >
> А) ровно <р(А) раз, где <$(N) —число чисел, меньших N и вза-
имно простых с А; относительно вычисления (по числу А) величи-
ны <р(А) см. Примечание,» условию задачи 341 (стр. 71—72).
1S6. Пусть (где всеа(, 1=1, 2, 3, 4,—цифры 0 или 1)
последние четыре цифры последовательности. Ёсли бы в по-
следовательности нигде не стояли подряд цифры aia2«3a40, то ее
можно было бы продолжить, приписав в конце 0; аналогично, ес-
ли бы из последовательности цифр нельзя было бы выделить пятер-
ки цифр a1a2a3a4l, то мы могли бы приписать в конце цифру 1.
Поэтому в нашей последовательности три раза встречаются после-
довательные четверки цифр (за одной из' них следует
цифра 0; за второй — цифра 1; третья стоит в конце). Двум из этих
четверок предшествуют цифры 0 и 1, а третьей уже не может пред-
шествовать никакая цифра (Хо (ибо иначе в последовательности
дважды встретилась бы пятерка цифр «оа^азои); поэтому третий
’) Символ тах[а, 6] означает большее (точнее — не меньшее)
из чисел а, Ъ; так, max[2, 7] = 7 и шах [4, 4] = 4.
228
раз четверка цифр а^азС^ должна стоять в начале последо-
вательности.
197. Число N представляет собой произведение всех простых
чисел от 2 до 37 включительно; каждый делитель числа N пред-
ставляет собой произведение некоторых из этих чисел. Покажем,
что утверждение задачи справедливо для любого числа zVft =
“ 2-3-5-7- ... -Pk — произведения k первых простых чисел').
Докажем наше утверждение методом математической
индукции (по числу k). Ясно, что при £ = 1 мы приходим к
числу All = 2, имеющему лишь два делителя 1 и 2, под которыми бу-
дут подписаны, соответственно, числа 4-1 и — 1; здесь 4- 1 4-
4- (— 1) =0. Далее, пусть наше утверждение уже доказано для чис-
ла Nk, равного произведению k первых простых чисел; другими сло-
вами, мы считаем доказанным, что число Nk имеет четное число 2п
делителей (включая сюда числа 1 и Nh), п из которых представля-
ют собой произведение четного числа простых сомножителей (эти
делители мы условимся называть «четными»; к их числу относится,
в частности, число 1, которое имеет четное число нуль простых
множителей, поскольку 1 не причисляют ни к простым, ни к со-
ставным натуральным числам), а п остальных — произведение не-
четного числа простых множителей (их мы назовем «нечетными» де-
лителями Nk). Докажем, что утверждение задачи будет верно и
для числа Nh+i = Nk Pk+i, где Ps+i— (k 4- l)-e простое число. Яс-
но, что все делители числа Nk являются также и делителями числа
Nk+i', это дает 2п делителей Nk+i, из которых п являются «четны-
ми», а п остальных — «нечетными». Но наряду с этим число Л,й+1
имеет и делители, не являющиеся делителями числа Nk,— те, кото-
рые делятся па p*+i- Их можно получить умножением всех дели-
телей числа Nk на рк+р при этом п «четных» делителей Nk дадут п
делителей Nk+i, каждый из которых состоит из нечетного числа про-
стых множителей, а п «нечетных» делителей -V* дадут п «четных» де-
лителей Л\+1. Таким,образом, мы видим, что число N*+i имеет все-
го 4« делителей, 2и(=и-|-Ц) из которых «четны» и 2н(=и4-
4- п) — «нечетны». Поэтому для него выписанные в нижнем ря-
ду числа —это 2п чисел +1 и 2п чисел —1; в сумме они также
дадут 0.
Примечание. Приведенное рассуждение позволяет даже не-
сколько уточнить высказанное в условии утверждение: из него сле-
дует, что число Nk имеет 2й-1 «четных» и 2й-1 «нечетных» делите-
лей (в частности, фигурирующее в условии задачи число N =* Л'ы
имеет 211 = 2048 «четных» и 2048 «нечетных» делителей), и, значит,
в случае числа Nk выписанный в нижней строке ряд чисел состоит
из 2й-1 (2048 в случае числа N) чисел 4- 1 и 2й-1 чисел —1.
198. Из того, что р и q— взаимно просты, с помощью алгорит-
ма Евклида устанавливается, что любое целое число п можно
представить в виде:
п = рх 4- qy, где х и у — целые числа. (*)
В самом деле, пусть р > q\ тогда р = qd 4- г, где 0 < г < q, т. в.
г •= р • 1 4- q{— d) (— рх\ 4- qyx)
. ') Оно справедливо даже для всех «свободных от квадратов»
натуральных чисел, т. е. таких, которые разлагаются в произведение
попарно различных простых множителей.
229
(здесь d— частное, а г — остаток от деления р на q). Далее, имеем
q = rdi + И, где 0 < г1 < г (число rt — остаток от деления q на г);
объединяя эти два равенства, получаем представление гх в виде (*):
И = q — rdi = q—{pxt + qy^ ==
=p(—xtdi)+q(l — уА)=рх2 + qy2,
где x2( = —xyii = —dt) и y2( = 1 —Pidi = 1 + dd,) — целые числа.
Затем, полагая г = r\d2 + г2, где 0<г2<Гь и пользуясь предше-
ствующим равенством, мы точно так же можем представить г2 в
виде комбинации рх3 -j- qy3 чисел р и q, и т. д.— вплоть до обще-
го наибольшего делителя 1 чисел р и q. (Легко видеть,
что последний отличный от нуля остаток будет общим наибольшим
делителем чисел р и q — в рассматриваемом случае он равен 1.) Но
если единицу можно записать в виде 1 = pxk + qy^, где хк, Уь —
целые числа, то и любое число п — п-1 = n(pxk + qyk) =
= р(пхк)+ q(nyk) можно записать в виде (*).
Далее, из того, что р и q взаимно просты, вытекает, что
если п представляется в виде (*) двумя разными способами:
п = рх + qy — рх' + qy', где х, у: х', у' — целые, (**)
то х — х' кратно q и у — у' кратно р: в самом деле, из (**), напри-
у — у'
мер, следует что р(х-х') = — q(y — у'), или х — х' = — q—-— ,
и так как р и q не имеют общих простых делителей, то х — х' делит-
ся на q. Последнее утверждение можно сформулировать как утверж-
дение об «единственности» представления (*): каждое целое чис-
ло п можно — и притом единственным образом — записать в
виде (*), где 0 х < q: в самом деле, число х в формуле (*) всегда
можно представить в виде х = kq + Хо, где 0 ха < q (х0 есть
остаток от деления х на q); при этом
п = рх + qy = p(kq + Xfd+qy = рх0^+ q(pk + у) = pxa + qy0,
где 0 ^x о < q и x0, r/o — целые (***),
С другой стороны, два разных представления (***) (т. е. равен-
ство (**), где 0 х < q и 0 < х' < </) невозможны, ибо при этом
|х — х'| < q и разность х — х' не делится на q. Число га, очевидно,
будет «хорошим», если уа в формуле (**♦) неотрицательно, и «пло-
хим», если уа отрицательно: ведь если п = рх0 -ф- qy0, где 0 Хо < q
и Уа < 0, то, заменив х0 на х = х0 — /.q и уа на у = х0 + Хр,
где К — целое, мы никогда не придем к представлению (*) числа га,
в котором х и у оба неотрицательны.
Эти замечания позволяют без труда решить задачу.
а) Очевидно, наименьшим «хорошим» числом является число
О = О-р + О-р; наибольшим «плохим» числом, в силу сказанного
выше, является число вида (***), где х0 — наибольшее из «допусти-
мых» (положительных) чисел, т. е. х0 — q — 1, а уа — наименьшее
из отрицательных чисел, т. е. у3 — — 1; таким образом, наибольшее
«плохое» число Р = p(q — 1)+ q(— 1) = pq — р — q. При этом есте-
ственно считать, что эти два числа 0 и Р как раз и «дополняют»
друг друга до фигурирующего в условии задачи числа А, т. е. что
за число А следует принять Р = pq — р — q. И действительно, если
число га имеет вид (***), то число
п' = А — га = (pq — р — р) —(рх0 + рр0) =»
= p(q — 1 — X0)+ q(— 1 — уа)
230
имеет тот же вид (***), где только роль х0 играет число х 0 =
— q—1—х0, а роль уп— число г/0 =— 1—Уп. Но если О^хо^
—1, то и Q^x0^.q—1 и из чисел г/0 и у0 одно положительно,
а другое отрицательно; это и доказывает утверждение задачи.
б) Первое решение. Из результата задачи а) непосред-
ственно следует, что среди чисел п, где = pq— р — q
(Р—это наибольшее «плохое» число), ровно половина будет «пло-
хими», а остальные — «хорошими»; так как при этом мы учтем все
натуральные «плохие» числа, то интересующее нас количество t та-
ких чисел
_ Р + 1 _ ~ Р ~ + 1 _ (р— О (g— 1)
2 “ 2 ~ 2
Второе решение. «Плохими»
числа п, которые представимы в виде
и рх0 + qy-,> 0 (ибо число п положи-
тельно). На плоскости с координата-
ми х0, у0 линии х0 = q, Уа — 0, рх0 +
+ РУо — 0 выделяют заштрихован-
ный на рис. 22 треугольник; нам надо
найти число «целых точек» в этом
треугольнике. Но ясно, что это число
ровно вдвое меньше числа «целых
точек» в прямоугольнике ОАВС (на
диагонали прямоугольника «целых
точек» нет, ибо р и q взаимно про-
сты). Так как число «целых точек»
внутри прямоугольника, очевидно,
равно (р—!)-(<?— 1), то мы при-
ходим к тому же значению искомо-
го числа t, что и выше.
199. Первое решение. Нам
надо доказать, что каждое целое
неотрицательное число п единственным образом представляется
являются такие натуральные
(***), где 0 sg Хо < <7, уа < О
в виде:
(х + у)2 + Зх + у (х + у)2 4- (х + у) + 2х
п ~ 2 “ 2 ~
(х + У)2+ (X + у) , Х(Х+1) ,
=---------j-------+ х ~----2----+ х’
где X — х + у и, значит, X 0 и 0 х X (напомним, что чис-
ла х и у неотрицательны). Но ясно, что при фиксированном
и х, меняющемся в «допустимых» пределах от 0 до X, число п =
Х(Х + 1) ,
=------2---"Г х будет принимать все целые значения в пределах
Х(.* + 1) Х(Х+ 1)
от N х —-----g----(случай х = 0) и доЛх =-------g--+ Я (случай
х — Х), причем каждое из этих значений встретится по одному разу. Сле-
л, , , *(* + 1) , у , , (Х + 1)(Х + 2)
дующее целое число Лх +1 =----------- + X + 1 =---------%------
отвечает на единицу большему значению X (значению %+ 1) и ве-
личине х = 0; при изменении х от 0 до X + 1 мы точно так же
231
получим все целые числа от^^_|=------------j------ до ,VY р1==
Л'х+2—1, и т. д. Это рассуждение доказывает утверждение задачи.
Второе решение. Перенумеруем все точки плоскости с не-
отрицательными координатами (х, у) в таком порядке, как это по-
казано на рис. 23. Мы утверждаем, что при этом точка с кОордина-
(х "+ У)г + Зх + у
тами х, у получит номер п=-----------5--------—отсюда и будет
следовать утверждение задачи,
Рис. 23.
ибо в такой бесконечной цепочке
точек х, у точка с (целым неотри-
цательным) номером п встретится
ровно один раз.
Доказательство можно провес-
ти индукцией по п. Ясно, что
номер п = 0 будет иметь точка
с координатами (0,0) а номер 1 —
точка с координатами (0,1); при
этом
„ (0+ О)2 + 3-0 + 0
0 =---------к-------- и
(0+ 1)2 + 30 + 1
2
Предположим теперь, что для всех
точек нашей цепочки, вплоть до
точки с номером п, требуемое ут-
верждение уже доказано; при этом
««-я» точка пусть имеет координаты х, у. Если здесь у¥=0, то
«(п+1)-я» точка будет иметь координаты х + 1, у—1— и дей-
ствительно
[(х+1) + (у — I)]2 + 3 (х + 1) + (у — 1) (х + у)2 + 3х4-*/ , ,
; _ 2 т-1
«= п + 1;
если же у 0, то «(я + 1)-я» точка имеет координаты (0, х + 1)—
и также
(0 + х + !)• + 3-0 + (х + 1) (х + 0)2 + Зх + 0 ,, ,
*» - --------—----------g-----------4 1 «=* п -г 1.
р
200. Каждой несократимой дроби—, где
0 < р < 100, О < q sS 100, (*)
сопоставим точку М с координатами р, q; при этом неравенства (*)
указывают, что точка Л1 расположена внутри заштрихованного на
рйс. 24 квадрата X = ОАСВ, ограниченного осями координат и
прямыми х «я 100 и у «= 100 (или, в крайнем случае, М принадле-
жит стороне АС или стороне ВС квадрата X), а несократимость
дроби £ означает, что на отрезке ОМ нет никаких отличных от М
«целых» точек (точек с целыми координатами: в самом деле, равен-
232
ства р — kplt q — kqi, указывающие, что дробь ~ можно сокра-
тить на k, означают, что отрезку ОМ принадлежит также целая точ-
ка. Mi(pi «/J. При этом если высекаемый квадратом Ж на прохо-
дящей через О прямой I отрезок ОР содержит п целых точек (р0, q0),
(2ро, 2<уо), (Зро, 3<7Л), .... (про, nqa) (где Afo(po, самая близкая
к О из этих точек), то (поскольку пр0 С 100, nq0 С 100) име9мр0«*^-
/ 100 100 1004 100/ 100 iqq . Ю0\
, Ро /100\
и, значит несократимая дробь — учитывается в слагаемых d — Ь
Рис. 24,
/100\ /1004
<4 2 I.......<4 п / суммы S, т. е. всего участвует в этой сумме
2р0 Зр0 пр0
п раз (а сократимые дроби тр-~, я—, разумеется, вообще
не учитываются в сумме S). Таким образом, вклад дроби ~в сум-
чо
му S равен п, т. е. равен числу целых точек на отрезке ОР.
Из доказанного следует, что общее число учитываемых в сум-
ме S дробей — т. е. численное значение суммы S — равно полному
числу всех целых точек в квадрате Ж, т. е. S = 100-100 = 10 000.
201. 1) Пусть х— любое действительное число. Тогда его мож-
но представить в виде суммы х=[х]4-а, где а — неотрицательное
число меньшее единицы. Представим теперь у в виде у — [«/] +
+ р (0 СР < О- Тогда х + у = [х] + [{/]+ а + р. Так как а +
+ 3 5s 0, то из этого равенства видно, что [х] + [у] есть целое чис-
ло, не превосходящее х + у. А так как [х + у] есть наибольшее
из таких целых чисел, то [х -f- у] [х] + [р].
2) Первое решение. Представим х в виде [х] +а, где
0С«<1. Пусть целое число [х] при делении на п дает в част-
ном q и в остатке г, т. е. [х] = t/п т г |0 < г < — 1). В таком
случае имеем:
п 1 п ’
х = qn + г + а == qn -f- гг,
233
X
п
где Г) =
п.
х 1 Г[х]1
— = <? = I — , что и требовалось
доказать. -
Второе решение. Рассмотрим все целые числа, делящие-
[х 1
— .Рассмотрим
также все целые числа, делящиеся на п и не большие [х]. Их число
Г[х]1
равно — . Но так как это — одни и те же числа, то их количества
равны; следовательно, —
X
п
3) Если (х) = [х] (т. е. х— [х] <
, то
[2х] = 2[х]
и [2х] - [х] = 2[х] — [х] = [х] = х + g-j; если
же (х) = [х] + 1 т. е. х— [х] то|х + yj = [х] + 1, [2х] =
= 2[х] + 1 — и опять [2х] — [х] = 2[х] + 1 — [х] = [х] + 1 =
= [х+4].
4) Первое решение. Представим х в виде х = [х] а.
Так как 0 а < 1, то а содержится между некоторыми двумя
соседними из дробей -, —,
k k + 1 k
~ и —-—, т. е. пусть —
п п п
п — k — 1
х +-----п---
п — 1 п
—-—, —.Пусть эти дроби будут
, 1,
а < ——. тогда имеем:
п — k — 1
п <
п — k
n — k
п — k — 1
+ —-п-= И + 1,
k п — k
п -W + - + —=[х]+1
и
п — 1 п — 1 k 4- 1 п — 1
Х ~7Г =W + « + — <М + — + — =
п 4- k
= W + + 2.
Отсюда следует, что
234
т. с.
Г п — Г
р + -^— ] = И+ !•
Так как первых чисел п— k, а вторых k, то
[х] + [х + п 1 + ... + [х 4
п — Г
п
= (п — k) [х] + * ([я] + 1) = п Iх] +
Но тому же равна и целая часть числа их. Действительно,
так как k sg na < k + 1, то na = k + p, где 0 (3 < 1. Следова-
тельно,
[их] = [n[x] + na] — [n[x] + k + p] — n[x] + k.
Таким образом, доказано, что
[х] + fx + п ] + ... 4- [х
п — И
= [пх].
Второе решение. Рассмотрим левую часть равенства.
1 1 и — 1
Если 0 х <“, то все числа х, х + —, ..., х 4- —~— меньше 1,
а целая часть от них равна 0; [их] тоже равно 0. Поэтому для
таких х равенство верно.
„ 1
Пусть теперь х — произвольное. Если увеличить х на-^ , то все
слагаемые в левой части сдвинутся на одно место вправо, а послед-
Г п —11
нее слагаемое х + ——перейдет в [х + 1], которое на 1 больше,
1
чем [х]. Значит, с увеличением х на —левая часть увеличивается
1
на 1. Правая часть с увеличением х на —тоже увеличивается на 1.
Для любого х можно найти такое число а, заключенное между 0
1 / 1 \ т
и — 0 4 а <С ~ I, что х отличается от а на —, где т — целое
число. Отсюда следует, что равенство сохраняется при любом х.
202. Первое решение. В силу результата задачи 201 3)
интересующая нас сумма (которая, очевидно, содержит лишь ко-
нечное число отличных от нуля членов) равна
' п 11 Г п 11 Г п 11
Т + т + т + т + "8' + т+ --- =
235
Второе решение. При п=1 рассматриваемая сумма,
очевидно, равна 1. Далее, при замене п на п -f- 1 каждый член
суммы либо не меняется, либо возрастает на 1; при этом реально
возрастает на 1 единственный член этой суммы — отвечаю-
щий такому значению k, что 2й есть наивысшая степень двойки,
на которую делится л-f- 1. В самом деле, если п + 1 = 2h(2/zz + 1),
то
n + 1 + 2ft
2*+1
в то время как при i Ф k имеем
и + 1 + 2{
2'+*
п + 2'
2i+l
Отсюда, в силу принципа математической пн
(почему?),
д у к и и и,
вытекает, что интересующая нас сумма при всех п равна п.
203. Отметим все точки плоскости с обеими целыми координа-
тами («целые» точки), для которых 1 х q — 1, 1 у р — 1
(х и у — координаты точек). Эти точки лежат внутри прямоуголь-
ника ОАВС, длины сторон которого равны ОА — q и ОС — р
(рис. 25); число всех точек равно (q—1)(р—1). Проведем диаго-
наль ОВ прямоугольника. Ясно, что на этой диагонали не будет
расположена ни одна «целая» точка (координаты х и у всех точек
х ОА q
диагонали ОВ связаны соотношением — = ; но так как q
и р—взаимно простые, то не существует целых положительных
х У \
чисел х < р и у <Z q, таких, что — = — I. Заметим теперь, что чис-
ло «целых» точек, имеющих абсциссу, равную k (k — какое-то целое
236
положительное число, меньшее <?)', и расположенных под диаго-
налью ОВ, равно целой части длины отрезка MN, изображен-
ОМ kp
ного на рис. 25. Так как MN = • АВ = —, то это число рав-
г*р] л-
но — . Следовательно, сумма
I и
Р 1 , Г2Р] . Г3р1 , .[(<?- 1)р
?JT[?J + br ‘ + L ~
равна общему числу всех «целых» точек, расположенных под диа-
гональю ОВ. Но всего внутри прямоугольника имеется (q—1) X
X (р—1) «целых» точек; из симметрии расположения этих точек
относительно центра прямоугольника ОАВС следует, что ровно
половина из них расположена под диагональю ОВ (здесь сущест-
венно, что на самой диагонали не лежит ни одна из точек). Таким
образом,
Р 1 Г2Р1
Ч J + [ Я ]
+ М+’”+1 ? J
(р—1)(р—1)
2
Точно так же доказывается, что
[_£.] > i । Г (p — 1) (p — n ~ i)
[ p ~’~[pj 1 LT’]-' '""l p ~ 2
204. Первое решение. При n = 1 мы в левой и правой
частях равенств имеем по одному члену, равному 1; следовательно,
в этом случае равенства справедливы. Докажем теперь, что если
наше равенство справедливо для какого-то значения п, то оно
будет справедливо и для значения n.-f- I; в силу принципа мате-
матической индукции, отсюда будет следовать, что равен-
ство справедливо при всех значениях п.
Отметим, что если п + 1 не делится на ki
Ц 4“ 1 ==* qk г,
где остаток г заключен между 1 и k— 1, то п = qk + г', где г' =
г—1, т. е. О г' si k — 2; отсюда следует, что в этом случае
Гл 4- П Г п 1 х р
величины —£— и -j- совпадают (обе они равны q). Если же
Ги + 1 ] Г и
п + 1 делится на k-. « + 1 — qk, то, очевидно, —£— = q, l~g
+ 1. Таким образом,
[«4-11 Г п '
-р-1, т. е. Т
-£ , если k не есть делитель числа п + 1;
п
1, если k есть делитель числа п + 1.
237
А отсюда вытекает, что:
, + 1 ] , [п + 1] , , [п 4-1]
а L 1 j+i2-v' l'i+d^
т. е. если
то
то
/2 —J— 11 Гм 4- 1 "1
.4-]+2 НН
Гп + 11
+ ... + (« + i)HnJ =
= СТ1 + <4 + • • • + бп + <Тп+1.
Второе решение. Число чисел ряда 1, 2, 3..........п, деля-
Г п 1 [
щихся на какое-то выбранное число k, рацно Iэто будут числа
Г п "I \
k, 2k, 3k, •••> сумма делителей k всех таких чисел равна
[п 1
. Отсюда следует, что:
[п] Г n 1 Г га 1 Г п 1
_р + -2” +--- + |^' + • • + "га” Равиа числу
чисел ряда 1, 2, 3, ..., п, делящихся на 1, плюс число чисел это-
го ряда, делящихся на 2, .. ., плюс число чисел этого ряда,
делящихся на п. Но этому же равна сумма Ч + т2 + т3 + ... т„.
г п ] г п 1 Г п 1 Г « ]
б) Сумма 1 — +2 -j- + ... + k Н- 4- • • • + равна
сумме делителей 1 всех- чисел ряда 1, 2, 3, . .., п, плюс сумма дели-
телей 2 всех чисел этого ряда, плюс сумма делителей 3 всех чисел
этого ряда, ..., плюс сумма делителей п всех чисел этого ряда. Но
этому же равна и сумма Oi 4- 4- Оз + • • • 4“ °п-
238
Третье решение. Приведем еще йзящНбе ГеОМеТрйческбё
решение задачи, близкое ко второму решению. Рассмотрим равно-
стороннюю гиперболу (график обратной пропорциональности) у =>
k
= ~ , или, что то же самое, ху = k (точнее, ветвь этой гиперболы,
расположенную в первом координатном углу; см. рис. 26, а))-
Отметим, кроме того, в первом координатном углу все точки
с целыми координатами. Тогда, если х есть делитель ч’исла k, то на
равносторонней гиперболе ху = k есть целочисленная точка с абс-
циссой х. Обратно, если гипербола ху — k проходит через целочис-
ленную точку с абсциссой х, то х есть делитель числа k. Таким об-
разом, число п, делителей числа k равно числу целочисленных
точек, лежащих на гиперболе ху — k; сумма делителей сц этого
числа равна сумме абсцисс целочисленных точек, лежащих на ги-
перболе ху = k. Далее, воспользуемся еще тем, что все гиперболы
ху = 1, ху = 2, ху = 3, ..., ху = п — 1 расположены ниже гипер-
болы ху = п. Отсюда можно сделать следующие выводы.
а) Сумма Ti + т2 + т3+ ...'+тн равна числу всех целочислен-
ных точек, лежащих под гиперболой ху — п (и па самой гипербо-
ле). Но, с другой стороны, ни одна из этих точек не имеет абсцис-
сы, большей п\ число же целочисленных точек с абсциссой k,
расположенных под гиперболой, равно целой части длины отрез-
Г п ] п
ка MN, изображенного на рис. 26, а), т. е. -£• , так как MN—
(сравните с решением задачи 203). Таким образом, имеем:
Гн] г « 1 Г 1 Гп1
Tt + т2 + т3 + ... + тп = — + 2_ + у + --- + Н' •
б) Припишем каждой целочисленной точке номер, равный ее
абсциссе (рис. 26, б)); в таком случае сумма Oi + о2 + о3 + ... + ап
равна сумме номеров всех целочисленных точек, расположенных.
239
n 1 Г п Г п 1 Г п ]
т] + 2[т| + 3[т|+••• + " hr]-
ючно боль-
под гиперболой ху = п. С другой стороны, сумма номеров всех
Г п 1
таких точек, имеющих абсциссу k, равна k 1-^- .Таким образом,
имеем:
° 14* + бз + • • 4' °п =
205. Очевидно, что (2 + "l/2)n + (2—]/2)п есть целое число;
действительно, если (2 -j-У 2)п = ап 4" Ьп У2, где ап и Ьп — целые
числа, то (2 — "|/2)п = ап — Ьп "|/2(это вытекает из формулы бинома
Ньютона, а также может быть доказано методом математической
индукции). Так как (2— }/2)п< 1, то отсюда следует, что
[(2 + У2У] «= (2 + /2)п + (2 — У2)п — I
и, следовательно,
(2 + У2)п — [(2 + /2)п] = 1 — (2 — У2)п.
Но так как (2-/2)< 1, то, взяв степень м доста
шой, можно сделать выражение (2 — УЪ)п сколь угодно малым.
А если (2 — У 2)п < 0,000001, то
(2 + У2)п - [(2 + У2)п] = 1 - (2 — У2)п > 0,999999.
206. а) Первое решение. Так как (2 /з)п -ф- (2 — /з)п
есть целое число и (2 — /з)п <; 1, то
[(2 + /з)п] = (2 + /з)п + (2 - Уз)п - 1
(сравните с решением задачи 205). Но, раскрыв скобки по формуле
бинома Ньютона, получим, что
(2 + /3)п 4- (2 - /§)п = 2 (2П + С22п~2-3 4- '* З2 4~ • •)
делится на 2 и, следовательно, [(2 4- /3)п] =(2 4- /3)” 4-
4-(2 — /3)" —* 1 нечетно.
Второе решение. Число (2 4-/з)" можно представить
в виде ап + ^п/3, где ап и Ьп — целые числа. Докажем, что
^-3&2 = 1.
Доказательство проведем методом математической индукции.
Прежде всего для п = 1 имеем at = 2, i>i = 1 и 22 — 3 • 1 = 1.
Далее предположим, что для некоторого п
(2 + /ЗУ = ап 4- Ьп УЗ,
240
л л
где а,г~ If в таком случае имеем:
(2 + /З)п+1 = (а„ + Ьп /5) (2 + /3) =
= (2fln + 36n) + (fln + 26n)^-
Отсюда йп -|-j —— 2ап ЗЬц j bn + i —— а-п “t* 26^, Следовательно,
4+1 - 3&*+1 = (2«n + 3&J2 - 3 (ап + 26J2 = «2 - 3&2 = 1.
Тем самым доказано, что а2 — 362 = 1 при любом п.
Отсюда следует, что
[«п + \ уз] = ап + [&п /3] = ап + [/^2] =.
= ап + |Van - *] = ап + (ап ~ >) = 2ап - 1
т. е. [(2 + /3)"] = [ап + &п У^З1] нечетно.
б) Заметим, что
[(1 + |<з)п] = К1 + ^3)п + (1 — /З)п- 1 при га четном,
|( 1 + /з)п -J- (1 — ]/3)n при га нечетном.
Действительно, стоящая в нашей формуле справа сумма является
целым числом (см. первое решение задачи а)). При га четном 0 <
< (1 — У 3) п < 1, а при га нечетном — 1 < (1 — у 3)71 <0.
Рассмотрим теперь отдельно случаи четного и нечетного, га.
1) га четно, п — 2т; тогда
[(1 + /З)2т] = (1 + /з)2т + (1 - ]<3)2т - 1 =
= !(1 + /З)2!т + {(1 - /З)2}т - 1 «
= (4 + 2 /з)т + (4 - 2 /З)т — 1 =
= 2т !(2-Ь/з)т + (2 — /з)т} — 1.
Но стоящее в фигурных скобках число является, очевидно, целым,
и следовательно, число [(1 + У 3)т] = 2mN — 1 всегда нечетно. Та-
ким образом, при четном га наивысшая степень 2, на которую делится
1(1 +/3)л] , равна нулю.
2) п нечетно, п = 2т + 1; тогда
[(1 + yl)2m+1] = (1 + j/3)2m+1 + (i - Гз)2т+1 =
= (4 + 2 /З)т (1 + /з) + (4 — 2 у"з)т (1 — /з) =
= 2т {(2 + /3)”! (1 + /з) + (2— /з)т(1 -/3)) =
-= 2т {((2 + /З)т + (2 - /ЗГ) +
+ /3 ((2 + /З)т - (2 - /3)т)}.
16 д. о. Щклярскнй и др, - 241
Пусть (2 + /з)т = ат + Ьт 1^3, где ат и Ьт — целые числа; тогда
(2 — /з)"‘ = ат — Ьт 1^3. Подставив эти значения, получим;
[(1 + /3)2«+Ч = 2т [ат + Ьт /3 + ат - Ьт /3 +
+ /Ч^ + ^з-^+ьтГз)} =
= 2™(2am+66m) = 2’”+1 (ат + ЗЬт).
Но ат + 36m нечетно. Действительно,
(“т + 3fcm) («т - 3U = 4 - 94 = (4 - 34) - 64 =1 - 64
(см. второе решение задачи а)). Так как 1 —662п нечетно, то оба
множителя (ат + 36га) и (ат — ЗЬт) нечетны. Следовательно, наи-
высшая степень 2, на которую делится [(1 + У З)7'] при нечетном
п = 2т + 1, равна
207. Из того, что (2 + ]^5)р + (2 — ]^5)р — целое число и — I <
<(2 —]^5)р < 0 (ибо р нечетно), следует, что
[(2 + /5)р] = (2 + /5)р + (2 - V5)р
(сравните с решениями задач 205 и 206). По формуле бинома Нью-
тона имеем:
(2 + /б)р + (2 - /5)р =
( Р—Ц
= 2 (2Р + С22р~25 + С42р~452 + ... +Ср~12-5 2 ),
так что
[(2 + /5)р] - 2р+‘ =
[ р~* 'l
= 2 (/?22р~25 + С42р~452 +-----\-Ср~]2-5 2 /.
Но все биномиальные коэффициенты
2 _ р(р- 1) 4 _ р(р-1) (р — 2) (Р-3) j __
t-p— Ь2 • ср- 1-2-3-4 -р
делятся на простое число р (ибо числитель выражения для Ср де-
лится на р, а знаменатель не делится). Значит, и разность
[(2 + /5)р] - 2р+1 делится на р, что и требовалось доказать.
_ п (п — 1) (п — 2) ... (п — р + Н
208. Ср =----------Из р последователь-
ных целых чисел п, п — 1, п — 2, п — р + 1 одно и только одно чис-
ло делится на р; обозначим это число буквой В таком случае
242
Гп I N
I —1 = —и разность, стоящая в условии задачи, принимает вид
п(я — 1) ... (#4- 1)ЛГ(ЛГ — 1) ... (n —р4- 1) N
pl ~ Р '
Заметим теперь, что числа я, ,п— 1........ N + 1, N—1. ...
..., п — р + 1 дают при делении на р всевозможные остатки 1, 2, 3,...
..., р — 1 (р последовательных целых чисел от п — р + 1 до п да-
ют при делении на р все остатки 0, 1, 2, .... р—1, причем каждый
из них по одному разу). Отсюда следует, что разность
я(я-1) ... (ЛГ+ I) (Af — 1) ... (п-р+ 1)_(р-1)!
делится на р (для доказательства достаточно перемножить почленно
все равенства п — k,p 4- аь п — 1 = k2p 4- а2, ..., N 4- 1 = k,p +
4~ Qi, N — 1 = А1+1р 4- а,+1, ..., п — р 4" 1 = kp—\p 4- йр-ь где А,,
k2,..., — целые числа, a at, а2,..., равны числам 1,
2, .... р—1, взятым в каком-то неизвестном нам порядке). Умно-
N
жая эту разность на целое число —, получим:
я (и — 1) ... (и — р 4~ 1) АГ (р — 1)!
Р ~ р ’
новая разность, разумеется, будет по-прежнему делиться на р. Раз-
делив, наконец, оба члена последней разности на (р—1)!, мы при-
дем к требуемому результату (частное от деления на (р—1)! также
будет делиться на р, ибо (р— 1)! взаимно просто с р).
209. Пусть а > 0. Ясно, что значение а = 1 удовлетворяет усло-
вию задачи; если же а > 1 и, соответственно,— = р < 1, то [а],
[2а], [За], ..., [Л'а] все различны между собой — и нам лишь надо,
чтобы были все различны числа Гр], [2{5], [Зр], ..., [Аф]. Но по-
скольку [Аф] Л'р < .V, то [Аф] N—1—и единственная воз-
можность для N неотрицательных чисел [р], [2р], ..., [Аф] прини-
мать N различных значений доставляется равенствами
[М =0, [2Н = 1, [Зр] =2,..., [Аф] = ЛГ-1. (*)
А так как равенство [Ар] = А—1 равносильно неравенствам
k — 1 ^4 Ар < А, т. е.
₽<1 (* = 1,2......А), (**)
то система равенств (*) равносильна неравенствам (**), т. е. двой-
ному неравенству
Итак, если а > 1, то —— «S ₽ = ^"<1, и, значит, 1 < а
N А— 1
< уу__।, а если а < 1,то — «S а < 1 (мы это, по существу, уже
16* 243
выше доказали). Присоединяя сюда значение а = 1, заключаем, что
N— 1 N
при а > 0 должно быть—ду— гс сс гс аналогично этому уста-
N— 1 N
навливается, что при а < 0 должно быть — —> а > — __________j.
Г 1 ]
210. Первое решение. Очевидно, что (а) = а 4* р та-
ким образом, равенство, которое нам требуется доказать, принимает вид
/V
г N 11 , Г ‘V >1 ГN 1 1
N 2 + 2 +h + 2 И 8 + 2 р
Пусть теперь
= ап 2” ап-1 211 ~' + ... -]-оi 2 + a-j
(ап, an~i, .... ai, а0 равны 0 или 1)—разложение числа N по степе-
ням двойки (запись N в двоичной системе счисления). В таком слу-
чае, очевидно:
[ 2 + 2 ] = [ап'2П 1 +• ап—1’2" 2+ •• • + «г + ° 2
“ЯП'2П 1 + о„_ j-2n 2 + ... 4- ai + а0,
Г—Д-—1 L 9'1-2 1 п on—3 , , Qi + I ,
[4 + 2] [V2 +----Г 2 “И
=ап-2"-2 + ап_1-2п-3+ ... +ai,
и
= О
(напоминаем, что а„,..., ай равны 0 или 1). Таким образом, имеем:
«= <2n (2n—1-|-2П—2 4-... 4-1 + 04-
+ о„_( (2П-2 4- 2’1-3 + ... + 1 + 1) 4- ... + О! (1 + 1) + а0 =
= an2n 4~ 4+ • • • + Oj'2 4- а» — N,
что и требовалось доказать.
244
Второе решение. Очевидно, что число нечетных чисел,
а , /V+1 Г Д'], ,
не превосходящих N, равно-g, если N четно, и равно—g—=|2" 1 ’
(N\
если N нечетно, т. е. равно I -% • Точно так же число не превосходя-
щих N четных чисел, не делящихся на 4, равно |_”4Д ’ если делится
ГАП
на 4 или дает при делении на 4 остаток 1, и равно l-j- + 1, если N да-
ет при делении на 4 остаток 2 или 3; другими словами, это число всег-
/ N \
да равно! Точно гак же число не превосходящих N чисел, деля-
ГАП
щихся на 4, но не делящихся на 8, равно -g- , если N делится на 8
или дает при делании на 8 остатки 1, 2 или 3, и равно -g-j -j- 1 в против-
(N\
ном случае, т. е. это число всегда равно -g- . Аналогично доказывает-
ся, что равно числу не превосходящих N чисел, делящихся на
/А\
8 и не делящихся на 16; j gg I равно числу не превосходящих N чи-
сел, делящихся на 16, но не делящихся на 32, и т. д. Таким образом
мы переберем все целые числа от 1 до А'; следовательно,
что и требовалось доказать.
211. Легко проверить, что 210 = 1024; таким образом, 2100 =
= Ю2410. Так как ЮОО10 — 1030 представляет собой число, состав-
ленное из единицы с 30 нулями, а 102410 > ЮОО10, то число 2100 =
= 102410 не может иметь меньше 31 цифры. С другой стороны,
1024'° _ /1025\10 /41Ч1»
ЮОО10 < (jOOoj ~^4бу =
11 11 11 11 11 11 11 41 41 41
40 40 40 40'40 40 40 40 40’40 <
41403938373635343332 41
40 39 38 37 36’35 34’33 32 ЗТ = 31 <10’
так как
41 40 39
40 <39 <38 ИТ‘ Д'
[ 41 1 40 . 1
(^ибо 40 -- 1 + 40; 39- 1 + 39 , и т. д.
245
Таким образом,
2100 = 1O2410 < 10-100010,
откуда следует, что 2,0° содержит меньше 32 цифр. Итак, число 2100
состоит из 31 цифры.
Примечание. Эту задачу очень легко решить, если пользо-
ваться логарифмами: так как log 2 = 0,30103, то log 2100 =
= 100 log 2 = 30,103 и, следовательно, число 2100 имеет 31 цифру.
Смысл задачи состоит в том, чтобы получить этот результат, ие
пользуясь логарифмами.
212. а) Первое решение. Обозначим произведение
1 3 5 99
’ "б" • • Too через А и рассмотрим еще произведение
246 98 т
5 = 3 ' 5 ’ 7 ••• 99' Так как
2 1 4 3 6 5 98 ^ 97 99
3 > 2 ’ 5 > 4 ’ 7 > 6.......99 > 93’ 1 > 100’
то В > А. Но
98 99 __ _1_
А'В ~ 2 ' 3 ' 4 ' 5 ' 6 ' 7 99'100 " 100’
Отсюда следует, что
A2<AjB=jQQ, а значит, A<Jq.
Далее, В < 2Д = —ТОО’ иб°
_2_ 3_ А 5 6 7 98 99
3 < 4 ’ 5 < 6 ’ 7 < 8 ’ ’ ’ ‘ ’ 99 < 100'
Следовательно,
А-2А > АВ = тхх и, значит, А> —г-?=.
ЮО ’ 103/2
Второе решение. Обозначим, как выше,
11А "
2'4'6 •” 100 “ А-
Тогда
I2 З2 52 992
А “ 22 42 62 • ЮО2 ’
откуда
12 З2 — 1 52 — 1
22' 42 ' 62
992 — 1
ЮО2
I2 З2 52 992
< 22 — 1 '42 — Гб2 - 1 ' ЮО2 - Г
24G
Разлагая теперь числители дробей слева й знаменатели дробей спра-
ва по формуле разности квадр'атов, получим:
1 2-4 4-6 98100 1 3-3 5-5 99-99
2-2'4.4 6-6’" 100-100 < А < 1 -3'3-5’5-7 99-101’
или после сокращения
200 <101’ ЮУ2< ^УТоТ^Ю’
что и требовалось доказать.
Примечание. Совершенно так же можно доказать и более
общее соотношение
1 1 3 5 2п —- 1 1
2Д/п< 2 ' 4 ' 6 2п <у^’
б) Докажем, что при л>1
1 3 5 2п ~ 1 1
24’6'” 2п < /Зп -j- 1 ’
Доказательство проще всего провести методом математической
индукции. При п = 1 имеем:
J_______1
2 “ УЗ-1 + Г
Предположим теперь, что для какого-то значения п
1 3 5 2п— 1 1
2'1’6”’ 2п С /Зп+ 1 '
2/1 4~ 1
Умножим обе части последнего неравенства на 2п^~2'
1 3 5 2п~ 1 2п -J- 1 2п -J- 1
2 ' 4 ' 6 ''' 2/i '2/i + 2 |2п 2) /Зп 4- 1 ‘
Но
/ 2п + 1 У________________(2п4- О2
\(2п 4- 2) /Зп + 1/ 12пз 4-28п2 4- 20п 4-4
(2п-Н_)2_________________(2"+1)2 „ 1
(12л3 4~ 28л2 4- 19л + 4) 4- л ~ (2п 4- I)2 (Зл 4- 4) л <3л 4- 4’
откуда следует, что
2л 4- 1 1
(2л 4- 2) /Зп4- 1 </Зп4-4‘
Таким образом, получаем:
1 3 5 2л — 1 2л 4- 1
2 ' 4 ' 6 ’' • 2л ’2л 4- 2 < /з
247
Отсюда, в силу принципа индукции, Заключаем, что при всяком П
1 3 5 2л — 1 1
2 ' 4 'Т ••• 2п < /Зп + 1’
причем равенство достигается только при п = 1.
Подставим теперь в последнее неравенство п = 50. Мы получим:
1 3 5 99 1__________1__________1
2'4'6 “• 100 < /3.504- 1 *” /151 ~ 12,288...’
что даже сильнее того, что нам требовалось доказать.
213. Решение задачи вытекает из следующих двух очевидных не-
равенств:
31“ < 32“ -= (25) 11 = 25'1!= 255
и
1714>1614=(24)14=24-14=256 (>255),
откуда 31“ < 1714. (Заметим, что десятичная запись чисел 31“ и
17й содержит несколько десятков цифр; вычислить эти числа точ-
но— нелегкая задача.)
214. а) Так как 2 22 = 24 = 16 < 27 = З3, то, очевидно, при лю-
бом п > 1 (и, в частности, при п = 1000)
_222 ,233 зЗ3
22' (п 4- 1 число) <22' (л чисел) < 3®' (л чисел).
(При п = 2 последнее неравенство обращается в равенство, но пер-
вое неравенство остается строгим; в единственном случае п = 1 на-
ше неравенство вообще меняет знак: ясно, что 4 = 22 > 3.)
б) Докажем, что при любом п > 1 (в частности, и при п =
= 1000) имеет место неравенство
.•4 .-'3 ,-3
444 (л—1 цифр) < 223 (л цифр)<3®3 (л цифр);
здесь последнее неравенство очевидно, так что доказать надо лишь
первое неравенство. Но его можно установить с помощью метода
математичввкой индукции. Ясно, что при л = 2, л —
— 2 = 0 слева и справа стоит одно и то же число 4 = 22; предполо-
жим, что соответствующее неравенство уже доказано для некоторого
значения л, и рассмотрим «следующее» значение л 4~ 1 > 3. Мы
имеем:
..4 ..4 .'3
— 4i4 (п четверок) = (22)44 (л—1 четверка) < (2")2-
(п — 2 тройки; здесь используется предположение индукции) =
.-а ( ,-з \
оЗ' I ?3 ’ -L 1 I
= 22,2 (л — 2 тройки) =22Х 1 (л — 2 тройки) <
, " ,'3
О.З3
< 2' (л — 1 тройка),
,.з
ибо, очевидно, 3® (л—1 тройка) > 23' 4-1 (в последней
«сверхстепени» участвуют л— 1 цифр).
248
Это рассуждение и завершает доказательство требуемого нера-
венства.
215. Пусть запись числа 1974" содержит k цифр; это означает, что
10*-1 1974" < 10*. (Так как 1974" > 1000" = 103", то ясно, что
k Зп.) Если запись числа 1974" + 2" содержит больше чем k цифр,
то 1974" + 2" 10*. Но поскольку 1974" = 2"-987", а 1974" +
+ 2" — 2" (987" + 1), то мы имеем, сокращая соответствущие нера-
венства на 2",
987" < 2*~"-5*. а 987" + 1 > 2*~"-5*,
что возможно только, если 987" + 1 — 2*~п • 5* (а 987" =
= 2*~" • 5* — 1).
Так как k — п Зп— п = 2п, то при п > 2 число 2*~" • Б"
кратно 8 (и даже 16). С другой стороны, 987 дает при делении на 8
остаток 3; поэтому 987" дает при делении на 8 тот же остаток, что
и 3". Но возводя последовательно 3 в степени 1, 2, 3, ... и заменяя
каждый раз само число остатком от его деления на 8, мы получим,
что.степени тройки дают при делении на 8 чередующийся ряд остат-
ков: 3, 1, 3, 1; 3, 1; ...; поэтому число 987" + 1 может при делении
на 8 давать лишь остатки 4 и 2— и никогда не разделится на 8
без остатка. Полученное противоречие и доказывает утверждение
задачи.
216. Так как 36т при любом натуральном т кончается циф-
рой 6, а 5" при любом натуральном п кончается цифрой 5, то при
36"* >5" разность 36“ — 5" оканчивается цифрой 1, а при 36т <
< 5" разность 5"—36"’ оканчивается цифрой 9; поэтому десятич-
ная запись числа N «= |36™— 5” | может кончаться лишь цифрами
1 и 9, и наименьшие возможные значения его — это 1, 9 и 11. Но
при т = 1, п = 2, очевидно, N => 11; покажем, что равенства Л' =» 9
и N = 1 невозможны, т. с., что значение N «= 11 и является наи-
меньшим. В самом деле, из равенства 5" — 36т => 9 вытекало
бы, что 5" «= 36’" + 9 кратно 9, что невозможно; из равенства же
36'" — б" •= 1 вытекало бы, что 5" = 36т — 1 = 62”1 — 1 —
•= (6’" + 1) (6т — 1), т. е. что 6’" — 1=5*, a 6m + 1 “ 5""*. Но
число 6'" + 1 оканчивается цифрой 7 — и никак не может быть сте-
пенью 5, что и требовалось доказать.
217. Имеем:
.1 гВо______________» 2 3... 100_________
2юо^юо- 260 (1-2-3 ... 50)-230 (1 2-3 ...50) m
1-2-3 ... 100 1-3-5.-/99
“ (2-4-6 ... 100)-(2-4-6 ... 100) “ 2-4-6 ... 100’
Далее остается только применить результат задачи 212а).
218. Требуется определить, что больше: 101"—99" или 100".
Составим отношение
101"—99я _ (100+1)"—(100—1)" 2(сп' ЮО^+Сп- Ю0п~3+-)
100" “* 100" “ 100" .
—2) , \
вс‘Ч100+ 31-ЮО3 -Г---Ь
249
Отсюда сразу ясно, что это отношение больше 1 при п 50.
Покажем, что при п = 49 оно тоже больше 1:
/49 49-48-47 \ / 4§ 18 424\
2|joo + 31-юоз + •J>2^ioo+ 100» ) >
/49 1002Х
>дюо+ юо»у- *•
Покажем теперь, что при п = 48 наше отношение будет уже
меньше 1. Действительно,
/48 48-47-46 48-47-46-45-44 \
2(j00 + 31-100» + 51-1006 +--J<
/48 483
<2 ^100 +(1-2-3)•ЮО3 +
48s , 487 , \
+ (1-2-3) (2-3) ЮО6 + (1-2-3) (2-3) (2-3) 100’+ --J =
_ / 48 J_/^8\3 1 /48\5 \
~2\joo + 6 l^iooy + б2 (jooy + •• •)<
48
ЮО________ 9600
<2 “эбн^1’
1 6 \jooj
Тем более, при п < 48 отношение будет меньше 1.
Итак, окончательно получаем: 99" 4-Ю0” больше чем 101" при
п 48 и меньше чем 101” при п > 48.
219. Докажем предварительно, что произведение п последова-
тельных целых чисел больше чем квадратный корень из произведения
крайних чисел в степени п. Обозначим эти числа через а, а + 1, ...
..., а + п—1. Тогда А-е число от начала будет a-^k— 1, А-е от
конца а + п — k. Их произведение
(а + k — 1) (а + п — k) — а2 4- ап — а 4- (k — 1) (п — k)
^а24-ап — а = а(а-\-п—1),
где равенство может достигаться только при k = 1 или k = п. Дру-
гими словами, произведение двух чисел, равноотстоящих от концов
(в случае нечетного п эти два числа могут, в частности, оба равняться
среднему числу), всегда больше чем произведение крайних. Но тог-
да произведение всех чисел
а(а+ 1) ... (а 4- п~ 1) > la (а + п — 1)] 2 = [У а (а + п — 1) ]п,
где знак равенства имеет место только при п = 1 нли п — 2.’
Докажем теперь, что 3001 > ЮО300. Имеем:
1-2 ... 25 >/25^= 525;
26... 50 > (К26Д0)25 > 352&;
250
51 ... 100 > (/51- 100)5fl > 7050;
101 ... 200 > /Ю0100-/200100 = 10200 250;
201 ... 300 > /200^-/300^ == 10200• 250• З50.
Перемножая левые и правые части неравенств, получим:
300! > 525 • 3525 • 7050 • 104Ш • 2100 • Зьо =
_ 550 . у25 . £50 . 2 450 . 1Q4C0 , 2100 . З50 = 10500 • 725 • 14s0 • З50 —
= Ю500 • 2125 • 4225 1425 > 10мо • 2025 • 4025 • 1425 =
= Ю550 • 225 • 425 1425 = 10550 1 1225 =
= 10600 • 1,1225 > 10600 = 10030“.
Примечание. Более общий результат сформулирован в ус-
ловии задачи 223.
220. Докажем, что для любого целого положительного k п
k I 1 \h k k-
1 + ~ <1+т+'Ч2'
Доказательство проведем методом индукции. Для k = 1 оно очевид-
но. Пусть теперь оно справедливо для некоторого k\ докажем его
для k + 1. Имеем:
k + 1 ~ k k + 1
заметим, что здесь мы не пользовались тем, что kSZn. Следователь,
но, это неравенство справедливо для любого целого положительно-
го k. Полагая теперь k^n, получим:
Л , 1 \h+1 Д 1 \kl, 1 \ ( k k‘\! 1 \
(1+ П ) + п ) + п}< + п + я2Д1 + т) =
_ k + 1 + 2fe + 1 k-Y 1 fe2
. ~ 1 п + п2 ~ л2 + п3 ~
. fe+ 1 , (fe+ 1)2_ л (fe+ l)-fe2
п П2 п3 <'
, .Lid л + 1)а
< 1 + п + П2
ибо n[k + 1)> k2 при n^k.
Подставив в выведенные неравенства значение к = п, получим:
п п2
‘+“7 + 7?
251
(1,000001 )1000000 =
221. В силу результата предыдущей задачи
1 \ юооооо
1 + 1 000 оооу >2’
222. Очевидно, имеем:
(Ю01 )989 ziooiy000 1 / 1 у000 1 1
(iooo)locu = uooo; 'looi “Д1 + юоо) 1001<3’iooi<'1
(см. задачу 220) и, следовательно,
ЮОО1000 > 1001м9.
223. Пусть неравенства задачи справедливы для некоторого п.
Чтобы показать справедливость их для п 4- 1, достаточно прове-
рить справедливость следующих неравенств:
п /п + 1\п+1 / п
> п 4- 1 ) :уз
После сокращения на п 4- 1 эти неравенства приводятся к неравеп-
1 / I \п 1 I 1 \п
ствам-g-! 1+~1 1 1 + ~1 «которые следуют из нера-
/ 1 \п
венств 2 1 4- — < 3.
Остается только заметить, что для п, равного 6, утверждение
?адачи справедливо, ибо
6 \в / 6 \«
— ] = 3е = 729, 61= 720, —) = 2в=64.
п + 1\п+1 / п \
—2~ ) Ч~1
224. а) По формуле бинома Ньютона имеем:
I 1 \n j I „о 1
гп—1 1 □_ 2___.
п п'1-1 ‘ пп~
I п (п—I) 1 п (п—1)(п —2) I
= 1 +«— 4- Ji 3!
, n (п — 1) ... 2 1 и (п — 1) ... 1 . 1
" • + (п— 1)! n»-l + п\
252
/ 1 \"+1
Из сравнения этих выражений сразу следует, что I 1 + I
1 + , откуда и вытекает утверждение задачи,
б) Составим отношение
1 \’1+1 / 1 \n /n-J-lV’+i / п \п
п \ ' у 1 п — 11 ~~ ( п ) ' I п — 1) ~
(п+ 1)"+1 (п - 1)п [п2 — 1\п л+ 1 / 1 \п [ 1 \
п2«+1 * п* ) ’ П “ V ~ "2 / \ + " /
Но при п^2
n(ri'--l) 1 п(п — 1)(п — 2) 1
2! Тй"— 31 п« +
п (гг — 1) (п — 2) (п —3) 1
4! п8
1 1 1 Г 1 Л JW _2 \ 1
п 2 ns п /\ п )
1 1 1 1 1
— п + 2 п2 2 п3 '
С другой стороны,
откуда и следует, утверждение задачи.
225. Доказательство проведем методом математической
индукции.
1°. Докажем, что
/ п \п
п\ > ) (*)
253
при любом целом положительном п. Действительно, при п = 1 это
неравенство очевидно выполняется: 1! = 1 Предположим те-
перь, что неравенство (*) уже доказано, и покажем, что в таком слу-
чае будет выполняться неравенство
(п+1)!
п + 1\п+1
в /
В силу результата задачи 224а)
Используя неравенство (*), получаем:
В силу принципа математической индукции, отсюда вытекает, что
неравенство (*) верно при любом целом положительном п.
2 °. Перейдем к неравенству
, _ ! п \п
«I < п Нг) • (**)
Нам надо доказать, что это неравенство выполняется для всех це-
лых п, больших 6. С помощью логарифмических таблиц (особенно
удобны здесь таблицы натуральных логарифмов) нетрудно проверить,
что при п = 7 неравенство (**) справедливо;
7\7
в /
т. е. 6! <Ц+~j , ибо In 6! = In 720 » 6,58, а
/ 7 V
In — = 7(1п7 — 1) « 6,62.
Предположим теперь, что неравенство (**) уже доказано. В си-
лу результата задачи 224 б)
/ 1 \п+1
р+—) >е- т-е-
е
п /
254
А теперь из неравенства (**) выводим:
(л + 1)! = (л + 1)/г! <(п + 1) п =
//г+1\М-1 пп+1е
= ) (/г + 1)п+1 =
, , ,, Л» + 1\п+1 е , , , ,.М+1\п+1
-(«+!)— I -----------------j-yT+T <<« т-О — ) >
т. е. будет верно аналогичное неравенство, в котором п заменено
на /г +1- Так как при п = 7 неравенство (**) верно, то отсюда, в
силу принципа математической индукции, вытекает., что оно будет
верно при любом целом п, большем 6, что и требовалось доказать.
226. Воспользуемся тем, что в сумме S — xh + xk~l -f- х*~2 + ...
... + х + 1 при х > 1 наибольшим является первый член и наи-
меньшим — последний, а при х < 1 — наоборот. Отсюда следует, что
(k + l)xfe > S > k + 1, если х>1;
(k + 1)х* < S < k +1, если x < 1.
Умножив теперь обе части полученных неравенств на х— 1, получим'
при х=£ 1
(й+ 1)хк(х~ 1) > Хк+> — 1 > (fc+ 1)(х — 1).
ГТ Р
Положим теперь в этом неравенстве х — ^^’, тогда найдем:
(*+ 1) Pk Pkvi-(P- l)ft+1 (fe+ 1) (р —1)\
(р-1)А+1> (p-l)ftH > (p-l)H-i ’
p 4- 1
аналогично, положив x. = —-—, получим:
(A+ l)(p + l)fe (p+ (ft+ l)pft
ph+1 > ph+l > pM-i •
Отсюда имеем:
(p + l)ft+1 — pk+1 > (ft + l)p* > pK+l — (P — 1) *+1,
или, положив здесь последовательно р = 1, 2, 3..п,
21.4-1 _ 1*4-1 >(^ 4- 1)Р > 1*4-1 _ О,
3*4-1_2* + 1 > (&+ 1)2Л > 2* + ‘ — 1*+>,
4*4-1 _ 3*4-1 >(*+ 1)3* > 3*4-1 _ 2*4-1,
(„+ 1)*4-1 —п*4-1 >(*+ 1)„* > „* + 1_(л— 1)*+!.
Сложив все эти неравенства, получим:
{„+ 1)*+‘ —1 >(fe+ 1) (1* + 2* + 3h + .. .!+«’) > «*+',
255
или, разделив все члены неравенства на k + 1,
ГЛ , 1 V+1 111 ьхк
п‘
Но отсюда и следует неравенство, которое требовалось доказать.
227. а) Прежде всего очевидно
1 1 1 1 1 1____L
п + 1 + п 4- 2^~ ' ’ ’ 2/г > 2/г + 2п + " ' 2п ~ 2 '
п раз
С другой стороны, имеем:
1 1 1 , _i______ir/_i_ Д_\
п 'fi+l-^fi-j-2'^'','T2n— 2 л 2л j "Г
, ( 1 , 1________\ / 1 1___________\ , , /_1_ _£\1
-г(п+1-г2н — 11 + (/г + 2 + 2/г — 2_/ г ‘ ‘~ (2/г п Д =
1 [ Зп. Зп , 3/г
~2 Ъ? + 2п2 + (и — 1) + 2/г2 + 2(/г —2)
1 ' Зп ( Зп , Зп'
2 2п2 "И 2/г2 Т • • 2/г2
(п+О раз
1 3. _ 3 , 3 3 ( 1
2 (n + ‘1 2/г ~ 4 "Г 4/г < 4 /г ’
откуда и вытекает второе утверждение задачи,
б) Отметим прежде-всего, что
1 I 1 J_______1_
З/г + Зп + 1 < 2/г 2/г п '
Теперь получаем:
1 1 , ,1 , / 1 , 1 \
/г+1+/г + 2+ "' +3/1-1+^ 3/г + Зп + 1) <
1,1, ,1 1 2/г
<~ + '7Г + ••• + ~ + “ = Т = 2-
2/г—1 раз
С другой стороны, имеем:
_L_ + _J_+ +_Ue_L|7_!_ + _L_U
/г + 1 + п + 2 + З/г + 1 2 |_(n + 1 + 3/г + 1J +
+(;rh+&) + (/г-4-з + з/г— 1) + ••• + (з/г+ 1 ^/г+ 1)] =
1 [ 4п + 2 t 4/г 4- 2 ,
“ Т[(2/г + I)2 — тг2 + (2n+ I)2—(/г - I)2 +
256
4n+2 ' 4я + 2 1
+(2/1+ 1)2—(n-2)2+ ••• + (2n+ 1)2 — «а] >
1 Г 4n + 2 ( 4n 4 2 f ( 4n + 2
> 2 |(2n+ 1)2+ ( n+ 1)2 + •• + (2n + l)a =
(2n+l) раз
1 4n _l 2
= у (2n + l)(2rt+ 1)2 = 1
228. а) Прежде всего докажем, что
2 УТГу! — 2/л<~<2/л-2 /Л=Л.
У п
Действительно,
о.- 2(]/ЙЛ-/)(/Ж4/й)
2 у n + I - 2 п=----------т=------=»
У п + 1 + У и
_____2 2_____1
Уп ~У 1 ~У Уп<~ Уп ~У Уп У п
и аналогично доказывается вторая часть неравенства.
Теперь имеем:
1 4- -L 4 X + ... + * > | + 2 [(уз — у2) +
у 2 )3 У1 ООО 000
4 (У 4 _ Уз) 4 ... 4 (/1 000 001 — У1 000 000)] =
= 1 4 2(/1 С00 001 — /2) > 2-1001 —/84 1 >
> 2000 — 3 4 1 = 1998.
Аналогично
1 4 -U 4 -U 4 ... 4—т=== < 1 4 2 [(/2 — 1)4
у 2 у 3 у/ 1 000 000
4 (/3 —/2)4 ... 4(/1 000 000 —УЛ999 999) =
= 1 42(/1 000 000 — 1) = 1 4 2-999 = 1999.
Следовательно, целая часть суммы 1
“|/'2 + У 3 + ' ‘+ V1 000 000
равна 1998.
б) Совершенно аналогично решению задачи а) получаем:
___[___ 1 1
УПГооб + -УТйооГ+ + у 1 ооо ооо>
> 2 [(УТоооТ -yioooo)4 (УТооог — yioloi) 4 ...
• • + (У 1 000 001 - У1 ооо ооо)] =
= 2(У1 000 001 — У1000б)>2 (1000 — 100) = 1800
1? Д О Шкчярский и др,
257
и
yioooo + yiotoT+ + д/i оооооо<
< 2 [(1/Тоооб — 1/9999) + (1/iOOOT — Д/ТОООб + ...
... + Д/l ОООООО —1/999 999)] =
= 2 (1/1 ОООООО — 1/9999) =
= 2000 — 1/39996 < 2000 — 199,98 = 1800,02.
1 1 , 1
Следовательно, сумма - 4-' ; -%- • 4- • • • + T7s====x=
У 1/10 000 1/10001 г 1/1 ОООООО
с точностью до 0,02 будет равна 1800.
229. Прежде всего отметим, что из сравнения двух выражений
/ 1 V 11
1 +— = 1 +2 —+
I 1 п } 1 п 1 п1
и
/ 2 1 \3 1 4-1 8 1
у+ 3 п J “ 1 + 2 п + 3 л2 + 27 п3
следует, что при каждом целом положительном п
/ 2 1 \3 / IV
( 1 + -о--> 1 + — .
( 1 3 п ) ' п )
, - 2
' 2 1 / 1 \~
Отсюда имеем: l+"g-II + ~1 . Умножая последнее нера-
2 2 2 —
венство нал 3 , получаем: л 3 +у п 3 >(«+ I)3 и окончательно
р > -у +о2—^п2]
Аналогично
_2__1_V
1 ~ 3 п ) =
1—2 —
— — — — —'>1—2—4- —
3 п2 27 п3 1 п + л'
1 1
так как х- л
3 п2 27 пя
АД.
3 п
8 1 11 1 1 Л
•у ~г — > 0 j, откуда следует
, 2
1 о -± -1
„3 „ 3 („ 1)3
/I I)
258
Теперь можем написать:
+ з - • • • ~Ь ч— ~>
/4 /5 /1 000 000
... + (у! ООО 0012 — 000 0002)] =
= -у (у"! ООО 002 000 001 — у Тб) > у. 10 000 — у 54 >
> 15 000 — 4 = 14 996.
С другой стороны,
1.1 1
у'Т ' ул5 ' уЧ ООО 000
... + (У 1 000 0002 — у/999 9992)] =
= у ('.у '1 ООО 000 000 000 — >^9),< у (10 000 — 2) = 14 997.
Таким образом, целая часть суммы +37~ + • • + 3Z —
равна 14 996.
230. а) Очевидно, имеем:
1 , 1 , 1 _ 1 1 , 1
102 + II2 + + 10002> 10-11 + 11-12+ ••• + 1000-1001 ~
7 1 1 \ / ! 1 \ /1 1 \
1,10 — llj + ^ll — 12 ]+•• + ^1000“ 1001 j ~
1 1
= -у— Tool >о,1 —0,001 = 0,099
и аналогично
1 1 1 1 1 1 _
102 + П2 + • • • + ЮОО2 <9-10 + 10-11 + ••• + 999 1000 ~
_ /_1_ J_\ /_1_ J_\ ( 1 1 \ _
— 9 ~ 10 J + (^ 10 ~ 11 )+•• + (999 — 1000j~
= -y-i<0-ll2-0,0°l =0,111.
Следовательно, сумма у» + ур + • • + iООО3 с точностью Д°
0,006 равна 0,105.
17* 259
б) Отметим прежде всего, что
1,1,1, ,1^1 1 ..................................................
10! + 11! + 12| + ••• + ЮОО! > 10! “3 628 800 ~ °.000000275-
С другой стороны,
1 1 _1_ 1
10! + 111 + 12! + + 1000! <
1 ( 9 , 10 , 11 999 1
< 9 (10!+ 11! 12! + + 1000!J ~
1 /10“ ' Н“ 1 12—1 1000—п
= 9 ( 10! + 11! + 12! +•••+ 1000! J ~
1 ( 1 1 1 1,1 1 ,1 1 'I
= 9 [9! ~ 10! + 10! — И! + 11! ~ 1-2! + •" + 999! ~ 1000!)
1 / 1 1 \ 1 1 1
= 9 I 9! “ 1000! < 9'9! = 3265 920 ~ 0,С00000305,
Таким образом, сумма Jqi + тп+ - + Т000! с точностью
до 0,000000015 равна 0,00000029.
231. Докажем, что сумму
1 1 1 1
1 + 2 + 3 + ••• +п-1 + п
можно сделать больше любого числа Af. Будем считать N целым и
возьмем п = 22Л’; тогда
1 1 1 1 1 1 , / 1 , 1 \
1 + ~ + "з" + т т- ••• + +V “ 1 “ 2 + (^3 + 4)“
/ 1 1 1 _1_\ ( 1 1
+ т + в у! + ' ’ ’ !ч22ЛГ~1 + 1 22jV“1 + 2 '
••• + 2жи'1' + 2^) >1 ++ + " + ~ ->л/+!
2?Граа
1
(каждая сумма в скобках больше —в силу результата задачи 227а)).
Примечание. Можно было бы так же доказать утверждение
задачи, исходя из результата задачи 227 б).
232. Обозначим через пк
10^ и "ЙЖ’ включая ЙЛ’
1 1
ложенное между и
число незачеркнутых слагаемых между
но не .Если слагаемое", распо-
не было зачеркнуто, то из слагаемых
1 1 1
1
10?’ 10? + 1’ 10?-4-2....10? + 8’ 10? + 9’ Расположенных между
260
1 1
10ft и 10fe+f
будет зачеркнуто только последнее; если же слагаемой
1 1 1
— было зачеркнуто, то все слагаемые 'др" f, ..
4 1
10^ g также будут зачеркнуты. Отсюда следует, что
1
10? + 8
nh = 9/г*-!.
Так как п0 — 8 рз слагаемых 1, —........-g-, -д- зачерк-
1 \
иуто ТОЛЬКО -д- I, то
П1 = 8 • 9 = 72, п2 = 8 • 92, .,nk = 8 • 9й.
11 1 '
Пусть теперь в сумме 1 -f- -у + —+ •• • + “ число п <
< 10™+’. Дополним ее до суммы 1 + -%- + ~ . + "рТЛП-----".
вычеркнем члены, знаменатели которых содержат девятку, и сгруп-
пируем оставшиеся члены:
! 1 1 1 \
(j + 2 + 3 + •••+ 8 ) +
/J_ 1 1 1 1 J_\
+ 10 + И + 12 + ••• + 18 + 20 + ”• + 88 +
<1-/г0+ |Q -Mi + | QQ" n'i ! •••+ |Q7n—1 'nm — 1 +
(m+l) раз
так как вместо каждой скобки поставлено произведение наибольше-
го слагаемого этой скобки на число членов в скобке. Продолжим эту
оценку дальше;
11 1 1
1 • «0 + То П! + 100 • «2 + • • + • Пт^1 + • пт =
/ 9 02 9m —1 9m \
= 8 I * + 10 + 10'- + • • + Ю’п—1 10т ) =
gm+l
1 ~ 10m+1 1
== 8- --§— < 8----g- =810 = 80.
1 “ТО 1 — То
Таким образом, утверждение задачи доказано.
261
233. а) Предположим, что в сумме 1 + f + "д + • . • +
I 1
число п меньше чем 2/‘+1. Рассмотрим сумму 1-|-Дрг + "дТ +
1
;•• + (2"+1 -1)2
и аналогично решению задачи 231 сгруппируем
члены следующим образом:
что и требовалось доказать.
Примечание. Совершенно так же
число а больше 1, то при любом п
можно показать, что если
1 1 1 2а-1
Таким образом, при любом а > 1 сумма
1+ 2а + 3« +---+^
остается ограниченной, сколь бы большое значение п мы ни брали
1 1 1
(из задачи 231 следует, что при а С 1 сумма 1+ —— + —— +~
- . - •- ' 2 3“ '
может быть сделана сколь угодно большой, если только выбрать
достаточно большое значение п).
б) Очевидно, имеем:
1 1 1 1 1
22 + За + 42 + 52 + • • + „2 <
I 1 п 1 , 1 , 1 , 1
>U-2^ 4 J + 2-з +3 4 + 4-5 + +(п-1)л==
/ 1 , 1 , 1 . , 1 \ 1
~ ^1-2 +2-3+з-4+ +(л—'!)«/ 4 ’
262
Но, так как j- — — при всех k = 2, 3.....п,
111 1 1
1-2 + 2-3 + 3-4+••• +(?-1)“ = 1~Т<1
и, следовательно,
что и требовалось доказать.
234. Докажем, прежде всего, что
1,11 1 1
1+2 + з + 4Т'--, + п-1+п<
/11 I \ / 1 1 1 \
<[Ч- 2 + 4 + ,,--+2fc)v+ 3. +—+••• +Т") X---
где k— такое целое число, что 2й я < 2ll+1, a pt— наибольшее
простое число, не превосходящее п. Действительно, раскроем скобки
в правой части неравенства. Так как каждое целое число т от
1 до п представимо в виде произведения степеней простых чисел
1, 3, 5, .... рс.
т=2а' 3“2 5“s ... pfi.
где все показатели аи а2, а3...«г — целые неотрицательные числа,
не превосходящие, разумеется, k, то в этой сумме встретится член,
равный — , который получится, если взять из первой скобки
2а>’
1 1
из второй—, из третьей— , п т. д. Поэтому в правой части неравен-
О и
ства после раскрытия скобок будут стоять в с е слагаемые!,
— ------ —и еще какие-то другие положительные слагаемые.
4 .....п — I ’ п
Значит, правая часть нашего неравенства в самом деле больше левой.
Логарифмируя это неравенство, мы получим;
/111 1 1 \
’’Ц1 + 2 + 3 + 4 + ?- • + я - 1 + п}<
, Г/ 1 1 I \/ 1 1 , 1 \
<lg + 2 + 4 + •" + 2й 3 + 9 + ••• + 3Й
/ 1 1 1
• -•х(1 + Pl+ р1+- + р*]\
1263
/11 1 \
4- !g 3 + g 4-4- 3h)+ •••
- + lg(1 + ^+7F+-"+H)-
Но для всякого целого k и целого р 2
g I 1 + ~ + 72"+ рЗ +••.• +
1 V21g3
Ph)< Р
Действительно, имеем:
1___
1 1 1 * ~Pft+1 . 1 р
р + р2 + • • • 4- pk - 1 < _ 1 — р — 1
1 р р
= 1 4
Но из результата задачи 220 следует
и, очевидно,
<3, 1 4-^i<P ^3,
1g з
Р-р
4'+^
2 1g 3 1g 3
р р— Г
Таким образом, мы заключаем, что
( 1 1 \
1g 4- 2 +
„21ё3 21g3
< 2 + 3 +
2 1g 3
5 +
2 lg 3
1 . Pl
, /111 1 \
-2 lg3( 2 + 3 + 5 + ‘,, + pJ’
Если бы существовало такое число N, что для всякого целого поло-
111 1
жительного I сумма 1 4~ “jT 4" "IF ~5~ 4~ •• • 4~ ~р~ была бы мень-
ше N, то для всякого целого положительного числа п выполнялось
бы неравенство
/111 1 1 \
lg + 2 + 3 + 4 п]<
< 2 ig з (4- 4- 4- + 4 + • • • + т;) <2 (iV~3;
234
Отсюда послё потенцирования следовало бы, что
1 + 1“ + “ + т + ••• ~ <32<N-i) = Л?1’
где не зависит от п. Но в задаче 231 было доказано, что такого
числа Л4 не существует; следовательно, не существует и такого чис-
ла N, что для всякого целого положительного /
111 1
1 + 2 + 3+5 +,,,+ рг <N>
где pi — l-е простое число в ряду натуральных чисел.
235. Нетрудно видеть, что (а 4- b -(- с)3 — а3 — Ь1 — с3 —
= 3(а -)- Ь) (Ь с) (с -f- а) (проверьте это!); поэтому достаточно до-
казать, что
Р(а, Ь, с) = (а 4- b 4- с)зм — а333 — Ь333 — с333
делится на а 4- Ь, на b с и 'на а 4- с. Но, очевидно, многочлен (с
буквенными коэффициентами) Р(х, Ь, с) — (% 4" + с) 333 — *333—
— (,ззз_сззз от переменной х при подстановке в него вместо х зна-
чения —b обращается в нуль; поэтому Р(х, Ь, с) делится на х —
— (—Ь) = х 4- Ь, а значит, Р(а, Ь, с) делится на а 4- Ь. Аналогич-
но доказывается и то, что Р(а, Ь, с) делится на bс и на с-j-а
(это также следует из того, что буквы а, Ь, с входят в выражение
для Р(а, Ь, с) симметрично).
__ (а3)5 — 1___________________(а3—1 )(п12 + а9 4-а3 4-а3 + 1)
— (а — 1) (а4 4~ «3 + а2 + а -г 1) ~ (« — 1)(а4 + я8 + а2 4- а 4* 1)
__ (а2 4- а 4~ 1)(а124~ а9 4~ а6 4-а3 + 1)
— а4 4-а3 4-а2 4-а 4~ 1-
Но непосредственное деление дает
а12 + а94- 4~ а3 4- 1
а4 4“ а3 4~ а2 4- а 4~ 1
= а8 — а7 4- а6 — а* 4* а3 — а 4- 1
и, следовательно,
а10 4- а5 4- 1 = (а2 4- а 4- 1) (а8 — а7 + а5 — а4 4- а3 — а 4- 1).
237. Первое решение. Обозначим наши многочлены соот-
ветственно через В и А. В таком случае имеем:
В— А = (х99М — х9) 4- (х8888 — х8) 4- (х7777 — х7) 4- (хвввв — хв) 4-
4- (х5555 — х5) 4- (х4444 — х4) 4- (х3333 — х3) 4~
4- (х2222— X2 ) 4- (х1111—х) ==
= х9[(х10)999 — 1] 4- Х8[(Х10)888 — 1] + X7[(X1U)"'— 1J 4-
4- х6 [ (х'°)665 — 1 ] 4- х~' [ (я10) 555 — 1 ] 4- х4 [ (х10) 444 — 1 ] 4~
4- х3[(х10)333 — 1] 4- х2[(х10)222 — 1 ] 4-х[(х!0)и1 — 1].
Но каждое выражение в скобках делится на х10—1, а следова-
х10 — 1
тельно, и на А = х______j . Таким образом, мы видим, что В—А де-
лится на А, а значит, и В делится на А.
265
Второе решение.
хе + х8 + х1 + х6 4- х5 4- х4 + х3 + х2 4- х 4- 1 = •
х10 — 1 (х — 1) (х — «1) (х — а2) (х — а3) ... (х — а9)
= х— 1 “ х — 1 =
= (х — ai) (х — а2) ... (х — а9),
2£п
где а* = cos -jg- 4- «' sin -Jq- (k = 1, 2, ..9), ибо корни уравнения
х10—1 = 0 — корни, десятой степени из единицы — имеют именно
такой вид. Следовательно, для того чтобы доказать наше утвержде-
ние, достаточно проверить, что
X9999 д-SSSS + д-7777 д-555 х4444 д.3333 д-2222 д.1111 [
делится на каждый из множителей (х—aj, (х — а2), ..., (х — а9).
Но последнее равносильно тому, что уравнение
д-9999 дЗЗЗЗ Х7Ш дММ д.5555 д-1444
4-Х3333 4-Х2222 4-х"11 4- 1 = о (*)
имеет корни ось а2, “з.....а9- Проверим, что эти значения дейст-
вительно удовлетворяют уравнению (*): так как а^° = 1
(k = 1, 2, 3, ..., 9), то
„9999 _ „9990+9 _ <„104999 „9 _ „9.
аА ~ ak — J aA — ak'
a8888 = „8880+8 = („10)888 „8 = „ т_ д>
И
„9999 + „8888 + „7777 + „6660 + „5555 + „4447 + „3333 +
+ а2й222 4-^1И + 1 =
= aA + aA + aA + aA + «А + aA + + aA + aA + 1 = 0
(k = 1, 2....9).
238. а) Первое решение. Имеем:
a3 4- b3 4- c3 — 3abc =
= a3 4- 3ab (a 4- b) -+ b3 4- c3 — 3abc — 3ab (a 4- b) =
= a3 4~ 3a2b 4- 3ab2 4- b3 -+ c3 — 3ab (c 4- a 4- b) =
= (a 4- b)3 4- c3 — 3ab (a 4- b 4- c) =
= [(a 4- b) 4- c] [(a 4- b)2— (a 4- b)c 4- c2J — 3ab(a 4- b + c) ==
= (a 4- b 4- c) [(a-4- b)2— (a 4- b)c 4- c'2— Зой] =
— (a + b 4- c) (a2 -+ 2ab + b2 — ac — be c2 — 3ab) =
= (a 4- b 4- c) (a21+ b2 4- c2 — ab — ac — be).
Второе решение. Заменим в обозначениях задачи букву а
на х и положим х 4- b 4- с = 0; преобразовав (х4-Ь4-с)3,
266
получим, что х3 + b3 + с3 — ЗхЬс = 0, если х -|- b + с = 0. Поэтому
уравнение х3—ЗЬсх + Ь3 + с3 = 0 имеет корень х — — b—с, и
многочлен х3 — ЗЬсх + Ь3 4- с3 делится на х — (— b — с) .= х + Ь +
Ч- с, а значит а3 + Ь3 + с3—ЗаЬс делится на а + b + с. Выполнив
непосредственно деление (для чего удобно рассматривать многочле;
ны а3 — 3abc + b3-f-c3 и а + Ь с расположенными по степеням
буквы а), мы придем к прежнему результату:
а? + Ь3 + с3 — ЗаЬс = (а + Ь + с) (а2 + Ь2 + с2 — ab — ас—Ьс).
б) Подберем такие два числа а и Ь, чтобы иметь равенство
х3 -|- рх + q = х3 + а3 + Ь3 — ЗаЬх.
р
Для этого достаточно, чтобы было а3 + b3 = q, ab ——-g-;
из этой системы двух уравнений с двумя неизвестными нетрудно оп-
п3
ределить а и Ь. Имеем а3 + b3 = q, а3Ь3 = —отсюда следует, что
р3
а3 и Ь3 — корни квадратного уравнения z2 — qz — =0 и, следова-
тельно ’),
“-1/#-|/Ч-~/4+£- о
Теперь, в силу результата задачи а), имеем’
х3 + рх + q — х3 + а3 + Ь3 — ЗаЬх =
= (а + b + х) (а2 + Ь2 + х2 — ab — ах — Ьх).
Следовательно, решение нашего кубического уравнения сводится
к решению уравнения первой степени:
а + b х = 0,
откуда имеем:
X] — — а — Ь,
или
|/ 2 + У 4 + 27 |/ 2 У 4 27’
и квадратного уравнения
х2 — (а + Ь) х + а2 + Ь2 — ab = 0;
) Числа а и Ь, определяемые по формулам (*). являются дей-
q2 р3 q2 р3
ствительными, если-j" +-jjy > 0- Если то под
знаком корпя третьей степени в формулах (*) будут комплексные
числа. В этом случае числа а и b тоже являются комплексными; их мож-
но отыскать, например, с помощью формулы для корня n-й степе-
ни из комплексного числа. При этом за а можно с равным основа-
нием принять любое из трех значений корня кубического из комплекс-
1 /~ -I пЗ
ного числа -л- + I/ — 1 ; тогда b определим из соотноше-
z г 4 27
Р
ния ab = — ~й“.
267
отсюда следует
_ а 4- Ь , (а — &) У 3 _ a + b _ (a — b) УЗ .
X о —। “т- и, -If Л о —— • 1 " • »
2 • 2 2 2
где а и Ь определяются формулами (*). ______
239. П е р в о е решение. Обозначим ~\/а + х через у, получим
систему из двух уравнений.
Уа 4- х = у, У а — у = х.
Возведем эти уравнения в квадрат;
а 4- х = у2, а — у = х2.
Вычтем из первого второе:
х + у = у2~х2,
или
X2 — У2 4- X + У = У + У) У — У + 1) = °-
Отсюда имеются две возможности:
1) х 4- У — 0; у = —х и х2 — х — а = 0, откуда
42=4 ± Va+ -г
2) х — у + 1 — 0; тогда у ~ % + 1 и х2 + % + 1 — а = 0,
откуда
*3,4 = - 4 1 V"a~~T'
Можно убедиться проверкой, что при соответствующем выборе
знака у каждого из радикалов, встречающихся в исходном уравне-
нии, корни Х|, Л'2, Х3 И Х4 удовлетворяют этому уравнению1).
Второе решение. Освободимся от радикалов в нашем урав-
нении:
а — Vа 4- х = х2,
(а — х2)2 = а 4- х,
х4 — '2ах2 — х 4- а2 — а = 0.
Таким образом, мы приходим к уравнению четвертой степени.
Однако это последнее уравнение является квадратным по отношению
к а. Решим это уравнение относительно а, т. е. примем на время,
') Если же, как это иногда делается, считать все корни положи-
тельными, то уравнение будет иметь единственный корень х3 =
4+/«—г-
если а 1, и вовсе не будет иметь корней, если
а< 1.
268
что х нам известно, а наоборот, а требуется определить:
а2 — (2х2.+ 1)а + х4 — х = О,
а _ 2х2 4-1+1^4х4 + 4х2 + 1 — 4х4 + 4х _
_ 2х2 + 1 + /4х2 + 4х + 1 _ 2х2 + 1 + (2х 4- 1)
2 = 2
Я|=х2 + х+1, а2 = х2—х.
Таким образом, мы видим, что уравнение
а2 — (2х2 + !) л + х4 — х = О
имеет корни
. щ = х2 + х + 1, а2 = х2 — х,
откуда согласно общим свойствам квадратных уравнений
а2 — (2х2 + 1) а + х4 — х — (а — <Zj) (а — а2) =
= (а — х2 — х — 1) (а — х2 + х).
Таким обрагом, наше уравнение принимает вид
(х2 — х — а) (х2 + х — а + I) =0
и без труда решается:
ч2=4-± /а+4’
х, , = — + 1/-L + а — 1 = -2_4-1/"а-Х.
3,4 2 ~ Г 4 2 ~ Г 4
240. Первое решение. Обозначим
х2 + 2ах + -L = у, — а + 1/ а2 + х — -L = yv
16 ' 16
В таком случае наше уравнение принимает вид
У = У\-
Выразим теперь х через yi. Простое вычисление дает
9 1
х ~~ + %аУ1 + [g •
Таким образом, мы видим, что х выражается через у\ точно та-
ким же образом, как у через х. Отсюда следует, что если мы начер-
тим графики функций
1
У — х2 + 2ах IQ
и
ух = — а + 1/д2 + х — _L,
Г 16
269
то эти графики (параболы) будут симметричны относительно бис-
сектрисы первого координатного угла (рис. 27; каждой точке х =
= х0, у = у0 первого графика отвечает симметричная относительне
биссектрисы координатного угла точка х = (/«, У = х0 второго гра-
фика). Точки пересечения этих
двух графиков отвечают таким
значениям х, что у = уь т. е.
корням нашего уравнения; эти
точки обязательно лежат на оси
симметрии обеих кривых, т. е.
удовлетворяют условию
У — X = Vi.
т. е.
Решая уравнение у — х,
1
х2 + 2ах + -jg- = х,
мы получаем:
х - 1 - 2“
*1.2 ~
16 ’
Можно убедиться проверкой, что при 0 <а < оба эти корня
являются действительными и удовлетворяют исходному уравнению.
Второе решение. Эту задачу можно решить и более обыч-
ным путем. Избавляясь от радикала в уравнении, получим:
(х2 + 2ах + а + -1') = а2 + х — -1,
\ 16 / 16
или после раскрытия скобок и приведения подобных членов
х4 + 4ax'J + [4а2 + 2а 4
4
. а
8
0.
Левую часть получившегося уравнения можно разложить на множи-
тели:
х4 4~ (2а*—— 1) X3 4--1 х2 4-
10 J
4- [(2а + 1) х3 4- (4а2 - 1) х2 4- (-±- 4- х] 4-
L \ 8 16 / J
4- и 2а 4- 21) х2 4- [4а2 + — —
|Д 16 ) \ 8
16
= |х2 + (2а-1)х + -±-
х2+(2а+ 1)* + (2а+41)|.
\ 16 / I
270
Отсюда сразу получаем решений!
-г2 + (2а - 1) х + = О,
х2 (2а + 1) х + 2а + щ = О,
х =_1+2п , •.А/1+2ау_2 17
хз,4 -Т-±р \—2~] а Тб”
1
При О < а < первые два. корня являются действительными и
удовлетворяют исходному уравнению; последние два корня — комп-
лексные.
241. Для того чтобы при действительном х левая часть уравнения
была действительна, необходимо, чтобы все подкоренные выражения
были положительны. Обозначая эти положительные подкоренные вы-
ражения, начиная с последнего (т. е. с Зх) и до первого, через
Уз....Уп_р Уп, будем иметь:
Зх = х + 2х = Ур
х 4- 2У1 — Уг<
х + 2уг = у},
X + 2уп_2 = у2_р
* + 2yn_j = у2,
где все числа уи у%,, уп действительны и положительны. Само
исходное уравнение в новых обозначениях примет вид
У п == X.
Докажем теперь, что у\ = х. Действительно, предположим, на-
пример, что х > у\. В таком случае из сравнения первого и второго
из наших равенств будет следовать, что у\ > у^. Точно так же из
сравнения второго и третьего равенств находим, что у? > уз; далее,
аналогично получаем, что
Уз > у4 > • • > Уп-1 > Уп.
Таким образом, при х > У\ будем иметь х > уп, что противоречит
уравнению. Аналогично доказывается, что и при х < yt не может
быть уп — х (в этом случае обязательно х < у„).
Так как у\ — Зх, то, следовательно, должно быть
Зх = х2,
откуда сразу получаем два единственно возможных значения х:
х, = 3, х2 = 0.
271
Проверка показывает, что оба эти значения удовлетворяют наше-
му уравнению.
Примечание. Наметим здесь еще Один метод решения урав-
нения
V<x+ 21/r% + 2]/x+ ... +2 /х + 2х = х. (*)
п радикалов
Подставим в левую часть этого уравнения вместо последнего чис-
ла х его выражение, даваемое равенством (*); получим:
х = * * * * * х + 2 + 2 Кх + + 2 Ух + 2х .
2п радикалов
Далее, снова заменяя последнее х подобным же образом, будем
иметь:
х — l' х + 2 "К х 2|Zx 4- ... +2 /х + 2х =
Зп радикалов
= X + 2 / х 4- 2 Ух + ... + 2 У'х 4- 2х = ...
4п радикалов
На основании этого мы можем записать:
х = V х+ гКх +2 Yx + •••=
= Пт )^х - 2 I х 2 Г х 2 Ух--2х .(**)
N-+ оо •11 — ———————-
Лт радикалов
Отсюда получаем:
х = V x-]-2'Zx+2/x+ ... =
= "V х + 2 [l^x + 2 Ух + 2Д/х + ...] = /х + 2х, (***)
откуда имеем х= уг.3х,х2 = 3х и, следовательно, Xi = 0, х2 = 3.
В частности, это решение срату показывает, что корни уравнения (*)
не зависят от п (ибо уравнение (**) не зависит от «).
Приведенное рассуждение в таком виде нельзя, разумеется, счи-
тать решением задачи, поскольку не доказано существование предела
(**) й не обоснованы преобразования (***). Однако это рассуждение
можно сделать совсем строгим.
272
242. Будем последовательно упрощать дробь, стоящую слева:
х
. ] ! !_______1 ! х +1 _3* +2.
2х + 1 ~ 1 + 2х + 1 ~ 2х + 1 ’ • •
х+ 1
Окончательно мы получим какое-то уравнение вида
ах + b
---i—j = х,
сх + а
где а, Ь, с и d — неизвестные нам целые числа. Это уравнение равно-
сильно квадратному уравнению х(сх + d) = ах -)- Ь; отсю-
да следует, что наше исходное уравнение может иметь не больше
двух различных корней (тождеством это уравнение быть не может,
так как иначе ему удовлетворяли бы любые значения х, а х = О,
очевидно, уравнению не удовлетворяет).
Но дв.а корня нашего уравнения нетрудно найти. Действительно,
предположим, что х таково, что
1
1 4- -- = X.
1 X
В таком случае, последовательно упрощая нашу дробь «с конца» мы
будем получать
1 1 1
1+ —= 1+ х = х; 1+ х -х;...
и окончательно придем к тождеству
х = х.
1
Таким образом, мы видим, что корни уравнения 1 + —- = х,
пли х2 — х — 1 = 0, т. е.
удовлетворяют заданному уравнению. Никаких других корней это
уравнение иметь не может.
Примечание. Наметим здесь еще один метод решения рас-
сматриваемого уравнения (сравните с примечанием к решению за-
дачи 241). Подставим в левую часть уравнения вместо х его выраже-
ние в виде многоэтажной дроби, даваемое самим уравнением. При
этом мы получим точно такое же уравнение, где, однако, в много-
этажной дроби слева знак дроби будет повторяться 2п раз. Продол-
жая далее тот же процесс, мы будем приходить к таким же уравне-
ниям, где слева будет стоять дробь, имеющая все больше и больше.
18 д, о. Шклярский и др.
273
«ЭТажей». На этом- оснований Мы можем напйсаТЬ:
х —
= 1-f-Iim--j—
W-*»1+-----j.
1+Т+7 ’ (*)
1
. +1 + —
Знак дроби повторяется N раз
где слева стоит бесконечное выражение. Отсюда получаем:
т. е. то же квадратное уравнение для х, которое фигурировало и в
приведенном выше решении задачи. Такое решение исходного урав-
нения сразу показывает, что корни его не могут зависеть от п.
Приведенное рассуждение в таком виде нельзя считать решением
задачи, так как не доказано существование предела (*) и равенство
х этому пределу и не обоснованы преобразования (**). Однако, это
рассуждение можно сделать вполне строгим.
243. Имеем:
х+3—4/х— 1 = х — 1 — 4/Г=1 + 4 =
= (/ЛЛ)2 — 4 У~х^1 + 4 = (/Г=Л — 2)2
и аналогично
х+ 8 — б/Г=Л = х— 1 -б/ГЛ + 9 = (/ЛИ — з)2.
Таким образом, наше уравнение можно записать в виде
]/()/ГЛ-2)Г + (лЛ-зГ = 1
или, так как мы считаем все корни положительными,
1/5ЛЛ — 2| + — з| = 1,
где |у| обозначает абсолютную величину числа у.
Рассмотрим теперь несколько случаев.
1°. Если Ух—1—2 > О, Ух—1—3 > О, т. е. если
/ЛЛ >3, х — 1 > 9, х > 10, то . | /ЛЛ — 2 | =
— Ух — 1—2, | j/x — 1 — 3 | = Ух — 1 — 3 и уравнение
274
принимает вид
/х_1_2 + /х—1—3=1,
откуда
2Ух—1=6, х—1=9, х = 10.
2°. Если Vх ~ 1 —2 + 0, х — 1—3^0, т. е. если
Ух— 1 > 2, х > 5, но Ух— 1 < 3, х < 10, то
Ifx— 1 — 2| = _ 2, |/7=Т — 3| =— + 3
и уравнение превращается в тождество
2 — Ух^П + 3 = 1.
Таким образом, нашему уравнению удовлетворяют все значе-
ния х между х = 5 и х = 10.
3°. Если Ух — 1 — 2 < 0, Ух — 1 — 3 < 0, т. е. если
~]/х — 1^2, х+5, то П/х — 1 —2| = -Ух —1+2, \~У х — 1 — 3| =
=—Ух — 1 + 3 и уравнение принимает вид
— Ух—1 + 2 — УТ=1 + 3 = 1,
откуда
2/х — 1=4, х— 1 = 4, х = 5.
4°. Случай Ух — 1 — 2 + 0, ~\/ х — 1 — 3 + 0, очевидно, не-
возможен.
Таким образом, решением этого уравнения служат все значе-
ния х между х = 5 и х = 10, т. е. 5 'С *+ 10.
244. Для того чтобы решить это уравнение, мы будем искать
сначала его корни, лежащие на отрезке от 2 до <х>, затем на отрез-
ках от 1 до 2, от 0 до 1, от — 1 до 0 и от — оо до — 1.
1°. Пусть х + 2. Тогда х + 1 > 0, х > 0, х — 1 > 0, х — 2 + 0;
поэтому | х + 1 | — х + 1, ] х | = х, | х — 11 = х — 1; | х — 2 | =
= х — 2, и мы получаем уравнение
х+1— х + 3(х— 1)— 2(х — 2) = х + 2,
которое удовлетворяется тождественно.
Таким образом, любое число, большее либо равное 2, является
корнем нашего уравнения.
2°. Пусть 1 х < 2. Тогда х + 1 > 0, х > 0, х — 1>0 и
х — 2 С 0 и, значит, |х+ 11 = х+ 1, |х| = х, |х— 1|=х— 1,
|х — 2| = — (х — 2).
Таким образом, мы получаем уравнение
х+1—х + 3(х—1)+2(х — 2) = х + 2.
Отсюда 4х = 8, х = 2, т. е. лежит вне отрезка 1 + х < 2. Сле-
довательно, наше уравнение не имеет корней, больших либо равных 1,
ио меньших 2,
18*
275
3°. Пусть, далее, 0 х < 1. Тогда имеем:
|х+1| =х+ 1, |х| = х,
| х — 1| = — (х — 1), \х — 21 = — (х — 2).
Значит,
х + 1—х — 3 (х — 1) + 2 (х — 2) == х + 2, х — — 1,
т. е. лежит вне отрезка 0 х < 1.
Получаем, что корней, больших либо равных 0, но меньших 1,
нет.
4°. Пусть теперь — 1 х < 0. Тогда |х + 11 = х + 1,
|х| = — х, |х — 11 = — (х — 1) и |х — 21 = — (х — 2);
х + 1 + х — 3(х— 1) + 2 (х — 2) = х + 2,
что невозможно, т. е. на этом участке также нег корней.
5°. Наконец, пусть х < — 1. При этом | х + 1 | = — (х + 1),
|х| = — х, | х — 1 | = — (х — 1) и |х — 2 | = — (х — 2);
— (х-4- 1) 4- х —3(х— 1) +2(х —2) = х + 2, х = — 2.
Получаем еще один корень х = — 2.
Окончательно уравнению удовлетворяют: число — 2 и любое чис-
ло, большее либо равное 2.
Рис. 28.
Примечание. Результаты настоящей задачи становятся со-
вершенно ясными, если изобразить график функции
у ~ | х + 11 — ]х| -f- 31х — 11 — 21х — 21 — (х + 2).
На рис. 28 изображены тонкими линиями графики функций
У1 = |* + 11, У2 = — |х|, уз = 3]х — 11, г/4 = — 2|х — 2| и у, =
276
= — (х 4- 2) и жирной линией—график функции У — У1+У2Ф-
+ Уз + У4 + Уз («сложение графиков»). Из этого чертежа сразу вид-
но, что у обращается в нуль на луче х> 2 и еще в одной точке
х = — 2.
245. Обозначим правую часть рассматриваемого уравнения п-й
степени через fn(x). Легко видеть, что уравнение ft(x) = 0, т. е.
1—х = 0, имеет корень х, = 1; уравнение fs(x) =0, т. е.
х(х — 1) — 2х + 2 = 0, или х2 — Зх + 2 = 0, имеет корни х, = 1 и
х2 = 2. Докажем теперь, что уравнение fn (х) = 0 имеет следующие
корни:
X] = 1, Х2 = 2, Х3 = 3, . . ., Хп—] = п— 1, хп = п. (*)
Воспользуемся методом математической индукции,
т. е. предположим, что наше утверждение уже доказано для уравне-
ния fn (х) = 0, и проверим, что в таком случае уравнение f„ + i (х) =0
имеет корни (*) и дополнительный корень х„ + 1 — п + 1. Прежде все-
го, ясно, что поскольку
fn+t W
. , . ; , ,,„3-1 х (х — 1) (х —2) ... (х —»+ 1) (х —п)
„+) + (-!) (п+1)!
то если уравнение fn (х) =0 имеет корни (*), то те же корни имеет
и уравнение f„+j(x). Наконец, равенство fn + t (п + 1) =0, т. е.
п + 1 (п + 1) п (п + 1) п(п — 1) (
1 1+1-2 1-2-3 “г--'
можно, очевидно, записать так:
1 - с‘+1 + C2n+i - с3п+1 + ... + (- 1Г+ = о, (-)
ъ (n + 1) П (п------ 1)...(п - ^+2;
где «= -----------------------------------— так называемые
биномиальные коэффициенты; но по формуле бинома Ньютона пра-
вая часть (**) равна (1 —1)" + 1 = 0, откуда и следует, что число
хп + 1 = п+1 также является корнем уравнение + -н(х) =0.
246. Обозначим через {х)=х—[х] так называемую дробную
часть числа х (см. стр. 37); ясно, что 0 еД {х} < 1 и что [х] —
= х—{х}. Таким образом, наше уравнение можно переписать так:
х3 — (х — {х}) = 3, или х3 — х = 3— {х},
откуда следует, что 2 < ха — х еД 3. Но, очевидно, при хТ»2 мы
имеем х3 — х = х (х2— 1) 2 (4 — 1) = 6 > 3; при х < — 1 имеем
х2 — 1 >0 и х3 — х = х(х2 — 1) < 0 < 2; при х = — 1 имеем х3 —
—. х = 0 < 2; при — 1 < х 0 имеем х3 — х sg — х < 1; при 0 <
< х еД 1 имеем х3 — х < х3 еД 1. Поэтому должно быть 1 < х < 2
и, значит, [х] = 1. А тогда исходное уравнение принимает вид;
’ 3 г *
х3 — 1 =3, откуда х3 = 4 и х = у 4
— это и есть (единственное) решение задачи.
277
247. Из первого уравнения системы немедленно получаем:
у2 = х2, у = ± х.
Подставляя это значение у2 во второе уравнение, находим:
(х —а)2 + х2=1 (*)
— квадратное уравнение, которое, вообще говоря, дает два значе-
ния х. Так как каждому значению х отвечают два значения у, то всего
система имеет четыре решения.
Число решений системы уменьшается до трех, если одно из зна-
чений х равно нулю; нулевому значению х (и только нулевому зна-
чению) соответствует единственное значение у = 0, а не два разных
значения у = ± х. Подставляя х = 0 в уравнение (*), получаем:
а2 = 1, а = ± 1;
только при этих значениях а система имеет три решения.
Число решений системы уменьшается до двух, если уравнение
для х имеет одно-единственное значение. Для того чтобы квадратное
уравнение (х — а)2-)-х2=1, или 2х2— 2ах + а2—1 = 0, имело
единственный корень (два совпадающих значения корня), надо,
чтобы было _
а2 _ 2 (Я2 _ 1) = о, а2 = 2, а = ± /2 ;
при этих значениях а система имеет два решения.
248. а) Решая систему, получаем:
а3 — 1 — а2 + а
х = а2—!’ У = а2 — 1 ’
Отсюда видно, что если а -|- 1 0 и а — 1 ¥= 0, то система имеет
а2 + а + 1 — а
единственное решение х — —а _ ।, У — а ьсли а = — 1
или а = + 1, то наши формулы теряют смысл; в первом случае
мы приходим к системе
Г— х + у — 11
[ X— у = 1,
которая противоречива (не имеет решений), во втором случае —
к системе
(х Ч- У — 1>
(х + у = 1,
которая имеет бесконечно много решений (х произвольно, у = 1 — х).
б) Решая систему, получаем:
а4 — 1 — а3 а
х = а2 — 1’ у = а2 — 1 '
Таким образом, и здесь, если а2 — 1 0, го система имеет единст
венное решение х = а2 + 1, у — — а. В. случаях же а = — 1 и а =
= 1 мы приходим к системам
(— х У ~ — 1, (х у ~ 1,
1 , и (
l X— у = 1 (х + у = 1,
которые имеют бесконечно много решений.
278 ' • ,
й) Из первого и второго уравнений получаем:
у z = \—ах и ay + z = а — х;
рассматривая эти два равенства как систему двух уравнений с двумя
неизвестными у и г, имеем:
а—х—1 + ах (а—1)(1 -|~х)
У = а— 1 = а—1
а (1 — ах) — a 4- х — х (а2 — 1)
г — а — 1 ~ а — 1
Таким образом, если а 1, то у — 1 + х, г = —(1 4-а)х; подстав-
ляя эти значения у и z в третье уравнение, находим:
х +(1 + х) — <г(1 + а)х = а2, х(2 — а — а2) = а2 — 1,
— х(а + 2) (а — 1) = а2 — 1.
Поэтому при а — 1 =4= 0, а + 2 0 система имеет единственное
решение
а2 - 1 а + 1 1
х~ («Н-2)(а-1)~ а^2’ у~1+х~а + 2’
В случаях а = 1 и а = —2 мы приходим соответственно к системам
хЧ-(/ + ? = 1,
х+ z/-j- г = 1,
х + у + z = 1
— 2х + у + г = 1,
и х— 2у + г = — 2,
х + у — 2г = 4,
первая из которых имеет бесконечно много решений, а вторая не
имеет ни одного решения (складывая первые два уравнения второй
системы, мы получаем —х — у -\-2г = — 1, что противоречит треть-
ему уравнению).
249. Вычитая второе уравнение из первого и шестое из пятого
и приравнивая два полученных выражения для х2—х3, получим:
а,(а2— а3) = а4(а2— а3), или (ai — а4) (а2— а3) = 0.
Точно так же, составляя по два различных выражения для раз-
ностей X]—х2 и Х|—х3, получим еще два соотношения:
(си — a2) (a3 — a4) = 0, (— a8) (a2 — a4) = 0.
И? первого из полученных трех соотношений следует, что =
= а4 или а2 = а3. Предположим для определенности, что а2 ='
= а3 = а. Из второго соотношения следует, что щ = а или а4 = а.
Каждое из этих равенств обращает третье соотношение в тождество.
Таким образом, для того чтобы наша система была сов-
местной, необходимо, чтобы три из четырех вели-
чин ai, а2, а3, а4 б ы л и равны м е ж д у с о б о й.
Предположим теперь, что щ = а2 = а3 = а, а4 = fi. Вспоминая
те выражения для разностей Х| — х2. xt — х3, х2 — х3, при помощи
279
которых мы получили Соотношения между otj, а2, й3 и а4, Немедлен-
но получаем:
X] = х2 — х3.
Обозначим теперь xt = х2 — х3 просто через х, a xt — через у.
В таком случае наши шесть уравнений с четырьмя неизвестными
перейдут в два уравнения с двумя неизвестными:
2х = а2, х + у = ар,
откуда
а2 [ • а \
х — g » У ~ & I Р 2 / *
Примечание. Аналогичными рассуждениями можно пока-
зать, что более общая система
Xj+x.,+ + ^m_1+xm = a1a2 ... am_iam,
*1 + х2 + ... -f- xm_j +xm+1 = a4a2 ... ат_(ат+1,
A/i-J-m—iT^n+m—2~Ь ' ‘ i~T~Xn an-\-m—m—2" ' 'an—lan’
состоящая из С™ уравнений с n неизвестными (л>и + 1), будет
разрешима только в следующих двух случаях:
1° ai = а2 = . .. = a„-i = а; а„ = [3
I ап n—i[R п—1 \\
I в этом случае %i = х2 = ...= xn_I— хп=а Ip—all,
2° п— т + 1 или больше из величин аь а2.......ап равны нулю
(в этом случае xi = х2 = ...= х„ =0).
250. Из первого уравнения получаем х = 2 —у; подставляем во
второе:
2г/ — у1 — = 1,
или
z1 + у2 — 2у 4- 1 = 0, т. е. z2 + (у — 1)2 = 0.
Каждое из слагаемых последнего равенства неотрицательно и,
следовательно, равно нулю. Отсюда
z = 0,. у = 1
и, значит,
х = 1.»
Таким образом, система имеет единственное действительное ре-
шение
251. Если х4 + у4 = 1, то либо х4 =1, у4 = 0, либо х4 = О,
у4 = 1, либо, наконец, 0 < х4, у4 < I (ибо числа х4 и у4 неотрица-
тельны). Но при х4 < 1, у4 < 1 мы имеем также |х| < 1 и |г/| <1,
а в таком случае
х4 = |х41 = |х3| • |х| < ]хэ|, у4 < |г/3|
и Iх3| + |г/3| > х4 +у4 = 1,
откуда следует, что два числа х, у одного знака, такие, что |х| < 1,
|г/| < 1 не могут служить решением нашей системы. Еще яснее, что
280
и два числа х, у разных знаков, где |х| < 1, [у| < 1, тоже не мо-
гут служить решением, ибо в этом случае
х3 + у3 < |х3>+ £/3| < тах(|х3|, |р3|) <1.
Таким образом, решения системы приходится искать среди таких
значений х, у, что х4 =1, у4 = 0, или наоборот, т. е. среди пар
х = ±1, у = О и х = 0, г/ = ±1; ясно, что из этих четырех пар чи-
сел решениями являются только две-, х = 1, у = 0 и х = 0, у = 1.
252. Одно решение (точнее система решений) очевидно: xt —
= х2~= х3 = х4 = xs = 0, х — произвольно; поэтому далее мы бу-
дем считать, что хоть одно из х, (i = 1, 2, 3, 4, 5) отлично от ну-
ля. Далее, из первого и последнего уравнений системы имеем
Л'з = хх2— Xi и х3 = xxj— х2; (*)
аналогично, второе и предпоследнее ее уравнения дают
Х4 = ХХ3 — Х2 И Х4 = XXS — X]. (**)
Подставив в (**) х3 и х$ из (*), находим
х4 = (х2 — 1)х2 — XX | и х4 = (х2 — 1)Х1 — хх2. .(***)
Приравняем теперь правые части (***):
(х2 — 1) х2 — XX1 = (х2 — l)xj — хх2,
или
(X2 + X — 1) Х1 = (х2 + X — 1) х2.
Далее естественно различать два случая. Если х2 + х — 1 =т^= О,
то, очевидно, Xi — х2. Но все неизвестные хь х2, х3, х4, х5 входят
в наши уравнения симметрично (одинаково); поэтому точно так же
можно установить, что в этом случае х2 = х3, х3 = х^ х4 = х5.
Таким образом, здесь мы имеем х, = х2 = х3 = х4 = х5; подставив
эти значения в исходные уравнения, находим, что х = 2. Наконец, ес-
ли х2 -J- х — 1 = о( т. е. х2 — 1 = — х и х = —L —| то
\ 2 /
(***) —это одно уравнение
х4 = — х(х2 + х,). ’ (****)
Непосредственной подстановкой легко убедиться, что в этом случае
значения х3 = хх2— хь х4 = —х(Х[4-х2) и х5 = xxt—х2 удовлет-
воряют нашей системе при произвольных X: и х2.
Ответ: xt — х2 = х3 = х4 = х5 = 0, х произвольно; xt =
= Х2 = Х3 = Х4 = Х5 произвольны, X = 2; Х1 и х2 произвольны,
, . ч — 1 ± Ys
Х3 = ХХ2 — XI, Х4 = — X (X! + х2) , Xs = ХХ4 — Х2, X =*= ----.
253. Пусть х, у, z, t — искомые числа и xyzt = А; заметим, что
А =И= 0, поскольку если, например, х = 0, то условия задачи приводят
к противоречивым равенствам р = и = / = 2и yzt — 2. Далее, урав-
нение х + yzt — 2 можно переписать так;
А
х Д- -j- = 2, или х2 — 2х + А = 0.
Аналогично получаем
у2 - 2у + А = 0, z2 — 2z + А = 0, И — 2t + А = 0.
28J
Но уравнение х2— 2х + А =0 может иметь (при данном 4) лишь
два разных корня; поэтому среди чисел х, у, г, t имеется не более
двух различных. Далее мы рассмотрим отдельно несколько возмож-
ных случаев.
1°. Если х = у = z = t, то наши уравнения дают
х 4- х3 = 2, или х3 + х — 2 = 0,
или, наконец, (х — 1) (х2ф- х + 2) = 0,
— 1 ± У~
откуда х\ = 1, х2, s = ------g---- Таким образом, здесь мы
имеем единственное решение системы в вещественных числах:
х — y = z = t— 1.
2". Если х — у = z, a t может быть и иным, то условия задачи
дают
х + хЧ = 2 и t + х3 = 2. (*)
Вычитая равенства (*) одно из другого, получаем:
х3 — хЧ — х + t = 0, или (х — I) (х2 — 1) =0;
поэтому либо х = t (этот случай мы уже разобрали выше), либо
х = ±1. Но при х = 1 первое из уравнений (*) сразу дает t =
= 1 — и мы снова приходим к полученному выше решению; если же
х — — 1, то то же уравнение дает t = 3.
3°. Если х = у и z — t, то система сводится- к следующей:
х + xz2 = 2, z + x2z — 2. (**)
Вычитая почленно эти уравнения, получаем:
х — z xz2 — x2z = 0, или (х — z)(l—хг) = 0.
Но равенство х = z сразу приводит нас к случаю 1°, а если xz = 1
и (в силу первого из уравнений (**)) х + г = 2, то мы снова нахо-
дим уже известное решение х = z = 1.
Ответ: либо все 4 числа равны 1, либо три и? них равны — 1
и одно равно 3.
254. Для того чтобы подчеркнуть полную симметрию уравнении
нашей системы относительно входящих в систему неизвестных и коэф-
фициентов при этих неизвестных, обозначим х = хь у = х2, г — х3
и t = х4; а — <гь b = а2, с — а3, d = о4; при этом наши уравнения
можно будет записать так:
4
= I (i = 1,2, 3,4). (*)
j=l
Далее, пусть, например, at > а2 > а3 > а4\ тогда имеем
(О] — а2)х2 4- (ai — а3)х3 4- (а1 — a4)xt = 1,
(а,— а2)х1 4-(«2 —а3)х34- (а2 —а4)х4 = 1, (**)
(Д1 — Пз)х1 4- (а2 — а3)х2 4~ (а3 — а4)х4 = 1,
(ар — a4)xi 4- (a2 — a4)x2 -ф (п4 — а3)х3 = 1.
Вычтем из первого уравнения системы (**) второе, из второго —
282
третье и из третьего — четвертое; мы получим:
(Л] — а2) (— X] -|- х2 Н- х3 + х4) = О,
'' (Я2 — Оз) (— Х1 — х2 + х3 + х4) = О,
(а3 — а4) (— X] — х2 — х3 + х4) — 0.
Так как числа аь а2, а3, а4 попарно различны, то
X, = Х2 + Х3 + Х4, X] + Х2 = Х3 + Х4, X] + х2 + х3 = х4,
откуда следует, что
х2 = х3 = 0, х, = х4,
а тогда (например, из последнего из уравнений (**)) находим:
1
х, =-------•
01 —а4
Проверка показывает, что значения х2 = х3 == 0, Xi = х4 =
1
= ------— действительно удовлетворяют всем уравнениям системы.
“1 «4
Ответ: если а> b > с > cL то х ~ t =-----------3. w = z = 0.
а — а?
255. Обозначим х2— Х[ — Хь л3 — х2 = Х2, ..хп—xn_i —
“ Хп_1, Xi —хп = Хп> Тогда Ai 4- Х2 +• • .4" Хп_i 4- Хп =0, а
заданную систему уравнений можно переписать так:
UX% 4- (Ь — 1) 4- С = X1, — 1) Х-2 4” = ^2» •••
.... ах2 + (&—1)хп + с = Хп. (*)
Но ясно, что если дискриминант Л = (Ь — I)2 — 4ас стоящих в левой
части (*) квадратных двучленов отрицателен, то все эти двучлены
сохраняют знак (а именно, их знак совпадает со знаком а); поэто-
му все неизвестные Хь Х2, ..., Хп должны иметь тот же знак, что и
коэффициент а уравнений — и сумма их не может равняться нулю,
т. е. наша система не имеет вещественных решений. Если Д = О,
1 — Ь
то правые части уравнений (*) лишь при Х] — —(соответствен-
1—6\
но при х2 = х3 = ... •= х„ — I принимают значение 0 (а при
других значениях хь х2, ..., хп они имеют тот же знак, что и чис-
ло а); поэтому равенство Л’1 + Х2 + ...-|-Л’п=0 возможно лишь
1 — b
при Х\ = Х2 = ... = Хп — 0 и X: — х2 — ... — хп = • Нако-
нец при Д > 0 наша система имеет, по крайней мере, два разных
решения
Х1 = Х2 = . . . = Хп = X* И Xj = х2 = . .. — хп = xj,
. 1 — b + /(1 — 6)2 —4ас
где х1,2 =------------2а----------•
256. Рассмотрим отдельно два случая.
1°. п четно. Перемножив «нечетные» (т. е. 1-е, 3-е, ...
..., (п— 1)-е) и «четные» уравнения нашей системы, получим:
Х1Х2Хз... хп а^а^а^... оп_[ и XjX2x3... хп = o2o40g... ап,
283
откуда ясно, что при ata3a5... an-j Ф а2а4ае.. ,ап система вовсе йе
имеет решений. Если же a^as... an_t = а2а4а6... ап, то, приняв
значение xt каким угодно (конечно, отличным от 0), мы затем
из 1-го, 2-го, . ., (п — 1)-го уравнений системы последовательно на-
ходим:
Подстановка всех этих значений в последнее уравнение показывает,
что оно тоже удовлетворяется.
2°. п нечетно. - Разделив произведение «нечетных» (1-го,
3-го, ..., /г-го) уравнений на произведение «четных» уравнений, по-
лучим:
... а Л а
х^~а-----------а----’ откУДа *i = ± 1/ ——----------------- (*)
U2U4 • • • U п—j |/ — j
(напомним, что все at положительны). Далее из 1-го, 2-го, ...
..., (п— 1)-го уравнений последовательно находим:
«п—1
*1 8 *2 п Xn_t
Проверка показывает, что при этом в силу (*) удовлетворяется так-
же и последнее уравнение системы.
Ответ: 0, если п четно и а^з... a„_, а2а4... а„; бесконечно
много, если п четно и ata3... ап_, = a2af... а„; 2, если п нечетно,
257. а) Заметим, прежде всего, что если х0 является корнем
уравнения, то — х0 есть также корень. Следовательно, отрицатель-
ных корней столько же, сколько и положительных. Далее, число О
есть корень уравнения. Таким образом, нам достаточно найти число
х
положительных корней. Отметим теперь, что если >=sinx,
то
|х| = ЮО]sin х| < 100 • 1 = 100.
Мы получаем, что корень уравнения по абсолютной величине
больше 100 быть не может.
Разделим участок оси Ох от х = 0 до х — 100 на отрезки
длиной 2л (последний отрезок может иметь меньшую длину) и под-
считаем число корней нашего уравнения на каждом из этих отрез-
ков. Обратимся к рис. 29.
На первом отрезке’ (от 0 до 2л) имеется один положительный
корень (и один корень нуль), на каждом следующем, исключая
последний, — по два корня. Для того чтобы определить число кор-
100
ней на последнем отрезке, оценим его размеры: заключается,
/100 „ 100 \
очевидно, между 15 и 16 l-jy ™ 6,66 .... > 2л; -jg- = 6,25 < 2л ;
следовательно, всего мы имеем 15 отрезков длиной по 2л и одни
неполный отрезок. Длина этого последнего отрезка равна 100 —
— 15 • 2л > 5 > л; следовательно, на этом отрезке целиком поме-
284
щается положительная полуволна синусоиды и, значит, на нем
тоже имеются два корня.
Итак, всего мы имеем 1 + 14 2 + 2 = 31 положительный ко-
рень нашего уравнения. Столько же имеется отрицательных корней,
и еще один корень равен нулю.
Окончательно общее число корней равно 31 -2-4-1 =63.
Рис. 29.
б) Решение этой задачи аналогично решению задачи а).
Прежде всего очевидно, что если sin х = 1g х, то х <: 10 (в про-
тивном случае левая часть нашего равенства не больше 1, а пра-
вая— больше). Так как 2 • 2л > 10, то на участке оси Ох от х =
= 0 до х = 10 помещаются одна полная волна синусоиды у =
= sin х и часть следующей волны (рис. 30). График г/ = 1g х,
очевидно, пересекает первую волну синусоиды в одной точке. Далее,
л 5л
так как 2л гДД < 10, то в точке х = -%- имеем sin х = 1 > 1g х
и, значит, график у = 1g х пересекает первую половину второй по-
ложительной полуволны: так как lg х = 1 > sin х в точке х= 10,
то он должен пересечь и вторую половину этой полуволны. Таким
образом, мы заключаем, что уравнение sin х — 1g х имеет всего
три корня.
258. Сложив левые части всех, наших неравенств, мы получим
сумму чисел ai, а2, ..., ам, а100, каждое из которых берется с коэф-
фициентом 1 4-(—4) 4-3 = 0, т. е. число 0. Но если сумма 100
неотрицательных чисел равна нулю, то все эти числа равны нулю;
таким образом, наша система неравенств реально обращается
в систему равенств:
ai — 4а2 + Заз = 0, а2 — 1а3 4- За4 = Д.. Оюо — 4а, 4- За2 = 0,
285.
которую можно также переписать следующим образом:
а, — а2 = 3(а2 —а3), а2 — а3 = З(а3 —а4), а3 —а4 ==
= 3(а4— а3), ..Одд — Oioo = 3(aioo — 01), Оюо — 01 = 3(0] — а2).
Теперь последовательно получаем:
01 — о2 = 3(а2 — о3) = З2(а3 — о4) == 33(а4 — а5) = ...
... = 3" (оюо-О]) = 3IUU(0] — а2).
Но из равенства oi — о2 = 3100(Я1— а2) следует, что щ—а2 = 0;
1 1
поэтому и а2 — а3 =-д-(0] — а2)= 0, и а3 — а4 =—(а2— о3) =
1
= 0, . . ., И 0,00 — О] = 2 (о29 — Оюо) = 0.
Таким образом, все наши числа ait а2, ..., адд, аюо равны между
собой; поэтому, если о, = 1, то и а2 = о3 = ... = а1Оо — 1.
259. Первое решение. Перепишем наши неравенства сле-
дующим образом:
/4 = — о — b с ~ф d О,
В = ab — ас — ad — be — bd -ф cd > 0, (*)
С — abc 4- abd — acd — bed > 0,
и рассмотрим уравнение
P(x) = (x —a)(x—6)(х-фс)(х-фй() =
= x4 + Ax3 -ф Bx2 -ф Cx -ф abed = 0.
Поскольку все коэффициенты этого уравнения в силу неравенств (*)
и положительности чисел я, b, с, d положительны, то оно не имеет
положительных корней (при х > О и Р(х) — х* -ф Ах3 -ф Вх2 -ф
-ф Сх -ф abed >0); но, с другой стороны, уравнение Р(х) =0 име-
ет даже два положительных корня х = а и х = Ь. Полученное про-
тиворечие и доказывает требуемое утверждение.
Второе решение. Из первых двух неравенств задачи сле-
дует, что
(a -ф b)2(c + d) < (с -ф d) {ab -ф cd), или (а + b)2< ab + cd (**)
(ведь <?4-d>0); аналогично, из двух последних неравенств полу-
чаем:
{а -ф b)2(c -ф d)cd < (ab -ф cd) (с -ф d)ab, или
(а + bycd < (ab -ф cd)ab. (***)
Но так как (а -ф b)2—4ab = (а— Ь)2^ 0 и, значит, (а + b)2^ 4аЬ,
то из неравенств (**) и (***) следует:
4ab < ab -ф cd a 4abcd < (ab -ф cd)ab,
т. е. cd > 3ab a 4cd < ab -ф cd, или ab > 3cd,
1
— но невозможно, чтобы одновременно было cd > ЗаЬ и cd <-g ab.
286
260. Так как, очевидно,
(г-Уг+У^ + У2+ ... +/2) X
п радикалов
Х(2+ У 2+ 1/2 + К2+... + Г2) = 22 —
п радикалов
-(2+]/Л2 + У2+ ... +V2) =2 — ]/Л2 + У2+... + )/2 ,
х п—1 радикалов п—1 радикалов
то фигурирующая в условии задача дробь равна числу, обратному
выражению
Rn = 2 + К2 + У2 + -~ - + V2;
п—1 радикалов
таким образом, остается лишь показать, что Rn < 4. Докажем это
методом математической индукции. Ясно, что Ri =
= 2 < 4 и что
если Дп_| <4, то и Rn = 2 У Rn—1 < 2 + У^ = 4 •
Примечание. Нетрудно видеть, что lim Rn = 4; в самом
П-+ОО
деле последовательность Rn имеет предел, так как она ограничена
(Rn < 4 при всех л) и монотонно возрастает (Rn+i > Rn, ибо Rn+t
получается из Rn, если под знаком последнего радикала заменить 2
большим числом 2 + У2)\ положив Игл/?„ = /? = г2 и устремляя
п в соотношении /?„+, = 2+УRn к бесконечности, получим в преде-
ле: г2 = 2 + г, или (2 — г) (1 + г) = 0, т. е. г = 2 (ведь г > 0) и
R — 4. Отсюда следует, что при п -> оо предел выписанной в условии
1
задачи дроби равенпоэтому улучшить данную в условии задачи
оценку нельзя.
261. Пусть а, Ь, с — данные числа; так как abc = 1, то с —
Второе условие задачи утверждает, что
«+ b + с > — + — + “. или а + b + ^>— + — + ab; (*)
но неравенство (*) можно преобразовать так:
1 1 I , ,
ab-a — b+ 1 <ab— а — ь 4-1.
ИЛИ
( = ±(а- !)(&- 1)].
287
Таким образом, неравенство (*) равносильно следующему:
*) (Ь—*)>(а—>)(*—>)> или (а— 1) (& — 1) — 1)> 0..
Поэтому из трех чисел а— 1; b— 1 и-L — 1( = с— 1) имеется чет,
ное число отрицательных; другими словами, две из этих разностей
отрицательны, а третья положительна, что нам и требовалось дока-
зать.[Ясно, что все три разности положительными быть не могут,
L 1
ибо если e> 1 и b > I, то заведомо с = <1 и, значит, разность
262. Ясно, что числа 1959 и 1090 в формулировке этой задачи
являются случайными — факт, который нам требуется доказать,
состоит в том, что если все ai > 0 и = вт + а2 + • • • + йп ~ 1>
п
то сумма Sn4= У аиа1г а - всевозм°жных произведений
’ h.ij..............гд=1 ‘ г"' г<
по k из п наших чисел (где 1О/г<д) всегда ^1, причем, если
k > 1, то эта сумма строго < 1. Доказать это можно, например, м е-
тодом математической индукции по числам п и k. Ясно,
что при п = 1 и при п = 2 утверждение задачи справедливо; далее
предположим его уже доказанным для всех п, меньших данного,
а для этого п— справедливым для всех k, меньших фиксирован-
ного /г>2 (при любом п п k = 1 утверждение задачи тривиально).
71
Рассмотрим теперь сумму $пЛ = 2 ai.ai,...aib
Выделяя в этой сумме все произведения, содержащие множитель ап,
получим:
п—1
п—1
+ { i " % = Sn—l,k-l'an + Sn—i,ft>
где Sn_i, и Sn_[, s — суммы всевозможных произведений по
k — 1 и k сомножителей из чисел а,, а2,..., Но сумма этих
последних п— 1 чисел равна
Й1 + й2 + • • • + On-i = (ai + «г + . •. + ап-1 + ап) —ап = 1 — ап.
Заменим теперь числа at, а2, ., ап^1 числами а’, =г—— а! =
1 1 “ ап 1
а2 , ап—1
= 1 _ „ > •••. ап—\ ~ ГТ1а-> сУмыа которых уже равна 1; суммы
un ип
же всевозможных произведений по k—1 и по k из этих новых
п— 1 чисел мы обозначим через S j и S'n_tk По предполо-
жению индукции, 1 и S„_j <1; с другой стороны,
28?
в силу пропорциональности чисел а'{ и а, (где i= 1..... п—1),
очевидно, имеем:
5n-i,fe-i an)k 1 < (1 an)ft 1
и sn—t.k =5»— i.fe’O — an)ft<(1 ~an)k-
Теперь окончательно получаем:
Sr,,h. = Sn~i,k-i'an + Sn-l,fe < (* ~an)k~1-an + (' ~anf =
= (1 - lan + (1 - = (1 - «J*-1 < 1 -
— что и требовалось доказать.
263. При N = 2 мы имеем лишь одну пару удовлетворяющих
условию задачи чисел т и п, а именно, т = 1, п = 2; здесь «сумма»
$2 рассматриваемых дробей-j—2 ~~2~- При N — 3 таких пар чисел бу-
дет уже две (пары т = 1, п = 3 и т — 2, п — 3); сумма s3 рас-
1 1 1
сматриваемых дробей здесь«3 ~ + 2~3="2"- Докажем теперь, что
для любого натурального N > 1 интересующая нас сумма рае-
на2
Так как для Л^ = 2 и Л^ = 3 сформулированное утверждение
верно, то мы можем воспользоваться методом математиче-
ской индукции. Предположим, что некоторая суммаsw_t=-g-;
1
докажем, что тогда и зЛ = -g-. Ясно, что суммы s2y-i и s1V связаны
^следующим образом: для получения из суммы Sjv-i суммы s.v надо,
с одной стороны, исключить все слагаемые суммы s,v-i, имеющие
1 1 М
вид —, где m + п = N, т. е. имеющие вид -рты--7? (здесь 1< i < ~к~
тп 1 v* l> z
и числа i п N—i взаимно просты). С другой стороны, к сумме
s.v-i надо прибавить всевозможные дроби вида где 1 j < N
и числа j и N взаимно просты. Но так как для каждого i
1 1 1
I (Л' — г) iN + (iV — i) N
и числа i, W — i взаимно просты тогда и только тогда, когда взаимно
просты i и N, а значит и N — I и N, то сумма Sv получается из сум-
мы sN-1 исключением ряда дробей вида и добавлением
вместо каждой такой дроби «компенсирующей» ее суммы дробей
1 1 I 1 \
iN + (дг —,) до поэтому sjV — 2 J.
264. Мы утверждаем, что все наши 1973 числа одинаковы. В са-
мом деле, пусть, это не так и, скажем, ai = а? = аз =.. , = ai=£ai+i.
Для простоты перенумеруем наши числа циклически, присвоив номер
1 числу а>, номер 2 — числу a;+i, и т. д.— вплоть до числа a»—i
19 Д. О. Шклярский и др.
289
которое теперь получит номер 1973. Итак, далее мы будем считать,
что наши числа не все равны, причем О| =/= а2, например at > а2
(случай а1 <а2 рассматривается аналогично).
Ясно, что из выписанных в условии задачи равенств следует,
что либо все рассматриваемые числа больше 1, либо все Они меньше
1, либо, наконец, все эти числа равны 1. Но в последнем случае все
числа ак (где k= 1, 2,..., 1973) равны между собой, поэтому нам
остается рассмотреть два других случая.
1°. Все числа ак больше 1. В таком случае
из а“2 = о“3 и ai > аг
из а',1’ = а“4 и а2 < а3
из а^4 = а"’ и о3>о4
следует, что а2 < аЙ.
следует, что а3 > at;
следует, что о4<^а5;
Таким образом, мы имеем:
> а2 < а3 > о4 < а3. .. > а1272 < 01973 > ai < а2-
Полученное противоречие at > а2 и aj <. а2 и
чае 1° обязательно а, = а2 = а3 = ... =01973.
2°. Все числа а меньше 1. В этом случае
доказывает, что в слу-
из о"2 = а“2
и й! > а2 следует, что а2 > а3;
из а“3 = °з' и о2>а3 следует, что а3>а4;
Таким образом, здесь мы имеем:
О| > О2 О3 > О4 > . . . > 01973 > 0[.
Полученное противоречие at > а, показывает, что и в этом случае
все ак обязательно равны между собой.
265. Предложение задачи является справедливым при и = 1 и
м = 2, ибо
xj + х® = 1 + 1 = 2, х4 + ха = 6,
X, + х| = (Xi + х2)2 — 2х4х2 = (6)2 — 2-1 =34.
Далее мы имеем:
х” + *2 = (Х1-1 + х2-1) ~ + х2~2) =
= 6(хГ1 + хГ*)-1-(*Г2 + *Г2).
ИЛИ
4 + 4 =
= 5 (х"-1 + х^-1) + [(хГ' + 4-1) - + 4“2)]. (’)
290
Из этой формулы прежде всего следует, что если х” 2 + х 2 2
и х"-1 + х"—1— целые числа, то и х” -f- х2 — целое число, откуда, в
силу принципа математической индукции, вытекает
первое утверждение задачи.
Пусть теперь п есть первое натуральное число, такое,
что х^ + х^делится на 5. Из формулы (*) следует, что в этом слу-
чае разность (х?-1 + Х2~1) — (х”~2 + х2~2)также должна делить-
ся на 5. Но, заменив в формуле (*) пна п— 1, мы получим:
xj1-1 + х^-1 =
= 5 (х?-2 + х2~2) + (хр-2 + х£~2) - (х"~3 + х£-3),
откуда следует, что
vn—з । з __
Х1 т х2 ~
= 5fx"~2 + x?-2
хГ2
*1+4
тоже должно делиться на 5, что противоречит предположению о том,
что для всех чисел т, меньших п, х™ + х™ не делится на 5. От-
сюда следует, что такого целого положительного п, для которого
х” + х2 Делится на 5, вовсе не может существовать. Легко видеть,
что утверждение задачи верно и для целых отрицательных п: если
*1+4 = У
1 х^п + х-п
_2_____1______£_ _ у—п । — п
х^~п (X!X2)—п 1 2
— целое число, не делящееся на 5, так как — п > 0.
266. Предположим, что сумма а, + а2 + • • • + Оюоо содержит п
положительных и 1000 — п отрицательных членов. В таком случае
все попарные произведения п положительных членов (их, очевидно,
п (п — 1) \
будет ---2----- и все попарные произведения 1000 — п отрицатель-
/ (1000 — л) (1000 — п
ных членов J их число равно -------------------
2
лржительными, а произведения положительных членов на
тельные (их будет л(1000— и))—отрицательны. Условие
требует, ,чтобы было
п(п- 1) (1000 —л) (1000 —п—1)
---2----+------------5------------= л (1000 — л),
будут по-
отрица-
задачи
2
или
П2- п + (1000 - л)2- (1000 - л)
•---------------------------------= 1000 л—л3,
2
„ . 999 000
2п2 — 2000л + —2—
1000 ± /1 000 000 — 999 000
п =--------------_--------------
= 0,
1000 ± V1000
2
а это, очевидно, невозможно.
19*
291
В случае второго выражения мы, рассуждая аналогично, при-
дем к условию
10 000 + /10 000 10 000 + 100
п = . 2 = 2
Отсюда следует, что это выражение может содержать равное число
положительных и отрицательных удвоенных произведений; для этого
10 000+ 100
достаточно, чтобы исходный многочлен содержал-----2------= 5050
10 000 —100
положительных членов и ------------- = 4950 отрицательных (или
5050 отрицательных членов и 4950 положительных).
267. Прежде всего имеем:
(Г 2 — 1)1 = У 2- /I;
(/2 — 1)2 = 3 — 2 /2 = /9-/8.
Докажем теперь, что если только
(У 2 — l)2/;1 = В У 2 — А = /2Д2 —/Д2
можно представить в виде/Л' —|+v — 1, т. е. если 2В2 — А2 — 1,
то и число
(/2— l)2ft+1 = В' /2 — А’
можно представить в гаком виде, т. е. 2В'2— /Г2 = 1. Для этого
достаточно заметить, что
(/2-1)2^+! =(/2-l)2ft-1(/2-l)2 =
(В /2 — А) (3 — 2 /2) = (ЗВ + 2А) /2 — (4В + ЗД);
следовательно,
В' = ЗВ + 2А, А' = 4В + ЗА
и
'В'2 —А'2 = 2(ЗВ + 2А)2 — (4В + ЗА)2 =
18 В2 + 24 АВ + 8 А2 — 16 В2 — 24 АВ — 9 А2 =
= 2В2 —А2 = 1,
что и требовалось доказать.
Точно так же показывается, что если число(/2 — l)2ft= С — D } 2
можно представить в виде/М— /W—1, то и число()/'2—l)2Zt+2=
= С — D' У2 можно представить в таком виде.
Отсюда, в силу принципа математической индукции, вытекает
утверждение задачи.
268. Если (А + В /з)2 =0+0 /Т, то С = А2_+ ЗВ2, D = 2АВ
и (А — В ]/3)2 = А2 + ЗВ2 — 2АВ Д/3 = С — D Д/3. Следовательно,
если бы было (А + В Д/3 )2 = 99 999 + 111 111 Д/3, то было ’бы так-
же (А— В Д/з)2 = 99 999 — 111 111 Д/з, что невозможно, так как
99 999 — 111 111Д/3 меньше нуля, а квадрат каждого действительного
числа больше нуля.
292
3 ””
269. Предположим, что у^2 = р q~\/r, и возведем обе части
этого равенства в куб. В таком случае получим:
или
2 = р3 -]- Зр2? ~[/r + 3pq2r 4- q3r Уг,
2 = Р (р2 + Зр2г) + q (Зр2 + р2г) }/г .
Покажем теперь, что если у"2 = р + <7 Уг, то |/2 е«гь рацио-
на л ьное число. Действительно, если q = 0, то у2 — р есть
рациональное число. Если q У= 0 и Зр2 + q2r =И= 0, то из последнего
равенства следует
_ 2-р(^ + ЗгД/-)
Vr ~ q (Зр2 + q2r) ’
откуда
в,-;; _ 2 — р (р2 + Зд2г)
2-P + q q (3р2 q2r} ,
т. е. опять рационально. Если же Зр2 + q2r = 0, то
q2r = — Зр2, 2 = р[р2 + 3( -Зр2)] = — 8р3,
3 --
и опять у 2 = — 2р есть число рациональное.
Таким образом, нам остается только показать, что у' 2 не явля-
ется рациональным числом. Это доказательство хорошо известно.
3 — т т3
В самохм деле, если у 2 равен несократимой дроби — , то 2 = ^-,
т3 = 2п3. Таким образом, число т3 (а также и т) есть четное число,
т3
следовательно, оно делится на 8. В таком случае п3~ —тоже должно
быть четным, а следовательно, и п четно, что противоречит предпо-
т
ложению о несократимости дроби —. Итак, предположение, что
з___ z_
у 2 = р q у г, привело нас к абсурду.
п + У/i2 — 4
270. Обозначим-----%---= х; в таком случае
1 2 2 (п—~\/п2— 4) п— Уп2 — 4
х п -{- У п2 — 4 4 2
1
так что х удовлетворяет квадратному уравнению х + — = п. Но
1 1
если число х + — —целое (= п), то число х"» + —тоже це-
лое, что легко доказывается методом математической ин-
дукции: если считать уже известным, что все числа а, =
=хг +—р- при всех i sg N —целые, то и число a.v + i =
V1 х
293
1
XN+1
тоже целое,
как это
вытекает из следующей
выкладки:
Ln+i д_ ....'.-Л -х/л-1 4- - —=
Iх хЛ'‘/
“ °ЛТ-Н + aN—1*
откуда
a.v + i = o.vfli — o.v-i.
Таким образом, обозначив хт = у, мы имеем у + — = k,
У
rnek(=am)—натуральное число; решая это квадратное уравнение
/? + "|/ 1г- — 4
относительно у, получаем у =----------. по так как число х =
п + 1/п2 — 4
=-------2-----> 1, то и хт — у > 1, откуда и следует, что у =
, /г + 1Д^4 / 1 k — \
_ х™ — А— 2 I а хт — 2 </'
271. Заметим, прежде всего, что вещественное число а не может
двумя разными способами быть представлено в виде суммы а =
х 4- у 1/2, где х и у рациональны, ибо если а = а 4-й'|/2=а]+
+5,1/2 (где а, Ь, а,, Ь\ рациональны), то "|/2 = у — Ь’ чт0 (в силУ
рациональности разностей а — ai и Ь,— b и иррациональности чис-
ла ~\/2) возможно лишь при а — а, и Ь — Ь\. Таким образом, из вы-
писанного в условии задачи равенства, которое можно «развернуть»
по формулам бинома Ньютона:
(X + Y Д/2) + (Z + Т V2) =5 + 4 1/2,
где
X = х2п + С$пх2п~2 • 2у2 + ...;
У = С’пх2п-1у+С^,1х2"-3-2уЗ+
и т. д., вытекает
Х + 2 = 5иУ+7’ = 4.
(*)
Вычтя теперь почленно из первого из равенств (*) второе равен-
ство, умноженное на }2, получим:
(X - У Д/2) + (2 — Т 1/2) =5-4 1/2,
или (х — у 1/2)2" + (z — t l/2)2n = 5 - 4 1/2, (*»)
которое, таким образом, обязательно должно выполняться, если
только имеет место выписанное в условии задачи равенство. Однако
294
из второй формы равенства (**) сразу следует его невозможность,
ибо здесь левая часть равенства положительна, а его правая часть —
отрицательна. Отсюда и вытекает, что и выписанное в условии за-
дачи равенство не может иметь-места.
272. Нельзя. В самом деле, пусть мы kt раз переливали воду
из 1-й бочки во 2-ю первым ковшом и k2 раз переливали тем же
ковшом воду из 2-й бочки в 1-ю; окончательно мы при этом перели-
ли из i-й бочки во 2-ю (ki—k2)~]/2 = k Д/2 литров воды, где целое
число k = k, — k2 может быть и неположительным. Аналогично, пе-
реливая воду li раз из 1-й бочки во 2-ю вторым ковшом и 12 раз
тем же ковшом переливая воду из 2-й бочки в 1-ю, мы всего пе-
рельем из 1-й бочки во 2-ю (/j — /2) (2-”|/2) =/-(2— Д/2) литров
воды, где число / — целое; поэтому условие задачи требует выполне-
ния равенства А"|/2 -ф-1 (2 — "|/2)= 1, или (/ — k) "|/2 — 21 — 1, т. е.
_ 21____1 -
V2-—Г ^о так как число Д/2—’иррациональное, то последнее
равенство может иметь место (при целых k и /), лишь если I — k —
= 0 (т. е. I = k) и 2/ — 1 = 0, откуда / =-у , что, однако, невоз-
можно, ибо Z — целое число.
273. Первое решение. В задаче требуется найти все ра-
циональные решения (х, у) (где у 0) уравнения Зх2 — 5х + 9 =
= у2 с двумя неизвестными х и у (ср. с циклом задач 5). Очевидно,
что одно решение имеет вид х = 0, у = 3. Положим х = хь у =
= yi + 3; тогда получим:
3%£ — у^ — 5х, — 6ух = 0.
m
Для всякого решения (хь yi), отличного от (0, 0), — = —, где
Л1 1<
m и п—взаимно простые целые числа, у\ = хг (m/п); следователь-
но, имеем:
9 т2 9 т
Зх, — *1 — 5%1 — 6 — Xj = 0,
5/:2 + бтп 5п2 -4- 6/шг
или, поскольку х 0, Xj = ___т2 Формула х = дд2 _ т2
и дает полный ответ на вопрос задачи (ответ х = 0 получается
при /1 = 0).
Второе решение. Если (х, у)—рациональная точка кри-
вой второго порядка (гиперболы) у2 = 3х2—ахф-Э, то отношение
у — 3
k ='——р ационально (может быть, бесконечно). С другой сто
роны, если k рационально, то прямая у — kx + 3 пересекает кривую
„ /6^ + 5 3/г2 + 5£ + 9\
в двух рациональных точках: (0, 3) и 1g_^2-, —g___— . Отсю-
да следует, что все рациональные точки кривой отвечают таким х,
6/г - |- 5
чтох = д—
274. Пусть х2 + рх-|-9=0 и у2 + ру + q\ = 0 — исходное и
«округленное» уравнения, где |</i — = |е| «0,01.. Вычитая
295
второе уравнение из первого, найдем; (х2— у2) + р(х— у) = q\ —
— у = г, или (х— у) (х + </ + р) =е, откуда, обозначив через Xi
и у<, близкие друг другу корни двух наших уравнений, а через х2—
второй корень первого из этих уравнений, так что — (%! + х2) = р,
получим:
. ,_______I е | _________| е |___________I е | _ | е |
1 У' Х11 ~ I И + Уг + Р I ~ I 2Xi — (Xj + х2) | | Xi — х, | Д’
— что нам и требовалось доказать.
275. Ясно, что если среди наших чисел имеется несколько целых,
то их можно просто отбросить — ведь разность между суммой округ-
лений любого количества чисел и суммой самих этих чисел не изме-
нится от дополнения множества чисел еще какими-то целыми числа-
ми, а сумма чисел при этом увеличится; поэтому если утверждение
задачи верно для любых нецелых чисел, то оно верно и для
любых чисел. Обозначим теперь сами числа через а,, а2, ..., их
целые части — через [а,], [а2],..., [ап]; их дробные части {а;} =
= й; — [а,] (где 1 = 1, 2,..., п) — через аь а2,.... ап (ср. выше,
стр. 37); при этом условимся располагать числа так, чтобы их дроб-
ные части не убывали:
О < ai а2 eg ... sg ап < 1.
Округлим теперь k первых чисел аг (здесь 1 sg i Eg k\ выбор числа
k, где 0 fig k п, мы еще уточним в дальнейшем) до (меньших их)
чисел [а,]; оставшиеся же п — k чисел а, (где k < j eg) п) округ-
лим до больших чисел [<z,] + 1. Ясно, что ошибка при замене сум-
мы чисел суммой их округлений будет наибольшей для сумм
а1 + а2 + • • +о/< и a/J + 1 + о)<+2 + • • -f-On—в первом случае она
будет равна
ос: + а2 + ... +а* kcch,
а во втором —
(1 — aft+i) + (I — ай+2) +...+(! — а„) Eg (п — k) (1 — aA+i).
Таким образом, условие задачи будет выполнено, если k тако-
во, что
п + 1 п + 1
— и (п - k) (1 - aft+1) < —
Пусть теперь k — наибольшее из таких целых чисел, что^а^^
п 1 п 1
<——, или ah О (это k может равняться и 0); оговорка о
том, что число k— наибольшее возможное, ознаачет, что,
п + 1
заменив номер k на &+ 1, мы уже получаем ц • Но
из последнего неравенства следует, что
, / я + 1 \
(n k) (1 «ft-p]) < (я — &) — 4 _р_ 1
/ п 1 \ п -р 1
Проверим, что (и — 6)11 — 4 I "С —4— • Действительно, это
29G
неравенство равносильно неравенству
(га -/г) (4* — п + 3) С (п+ !)(£+ 1);
последнее же равносильно очевидному, справедливому при всех п и
k, неравенству
[п — (2k + I)]2 > 0.
Примечание. Из решения задачи нетрудно усмотреть, что
при п = 21 + 1 нечетном улучшить оценку задачи нельзя (соответст-
вующий пример мы получим, положив Щ = аз = • • • ап ГДС,
очевидно, оптимальным будет вариант, когда мы I чисел заменим
нулями, a Z1 остальных — единицами или наоборот); если же
п — 21 четно, то величину (и-{-1)/4 в условии задачи можно умень-
шить (почему- на сколько?).
276. Ясно, что при а < 0,001 округление а0 числа а равно 0,
йо
а значит, и частное — (и любое округление этого частного) равно
0; поэтому далее мы будем считать, что а 0,001. Но при этом,
разумеется, и а0 0= 0,001, в то время как «погрешность приближе-
ния» а = а — а0 < 0,001; поэтому интересующая нас дробь
d = "" = я ~ ю = 1 _ ю
а а а
заключена между 0 и 1: ясно, что 0 < </sj) 1. Далее из того, что
а < 0,001, а а0 > 0,001, следует, что а < а, и, значит, а + а = 2а <
а 1
< а0 + а = а, откуда — <?-2- и ПОЭТОМУ
d = l-^ >1 (и 1) (*)
и 2
— вот эта оценка дроби d является уже окончательной, ибо отпошс-
а
ние о = — может принимать любое значение в пределах 0 о <С
1 1
< "2"(а значит, d— любое значение в пределах < d 1). В са-
мом деле, приняв равным 0,001, мы получим, что дробь б ~
= ^^=-б7оо“+ а“- ОткУДа
6
а = 0,001 (**)
такое а при любом 6 ^где 0 < 6 < удовлетворяет неравенству
0 =4 а < 0,001, а соответствующее а = 0,001 + а отвечает значению
d = 1—6. Ясно, что если 6 пробегает все значения между 0 и -Ь,
то d принимает все значения от g", до 1, т. е. d может иметь любое
из следующих значений 0; 0,5; 0,501; 0,502; 0,999; 1.
277. Рассмотрим 1001 число
0 • а = 0, а, 2а, За, ..., 1000а
297
й Возьмем дробную часть каждого йз этих чисел (разность между
данным числом и наибольшим целым числом, не превосходящим
данного). Эти дробные части будут представлять собой 1001 число,
не превосходящее 1. Разделим теперь отрезок числовой оси от 0 до 1
на 1000 равных отрезков длины Jqqq (к каждому отрезку мы бу-
дем причислять его левый конец, но не причислять правый) и рас-
смотрим распределение точек, изображающих наши дробные части,
по этим отрезкам. Так как число отрезков равно 1000, а число то-
чек 1001, то, по крайней мере, в одном отрезке будут находиться
две точки. Но это означает, что существуют два таких неравных
числа р и q (оба не превосходящих 1000), что разность дробных до-
лей чисел ра и qa меньше Тббб ’
Пусть, например, р> q. Рассмотрим число (р — q)а = ра— qa.
Так как ра — Р dt, qa = Q + d?, где P и Q — целые числа, d, и
di — дробные доли ра и qa, то (р.— q)a — (Р—Q) + — d2 отли-
1
чается от целого числа Р — Q меньше чем’ на Тббб’ Но это означа-
Р — Q 1
ет, что дробь р _q отличается от а меньше чем на 0,001-
278. а) Если число а меньше 1, то и ~\/аменьше 1. Предполо-
жим теперь, что десятичная дробь, равная 1/а, начинается с мень-
/- I 1 V00
шего числа девяток, чел 100; это означает, что"|/а<1—IТо/
Возводя обе части последнего неравенства в квадрат, получим:
Но
/ 1 \100 / 1 \200
“<1—2(Тоу + (io) •
п, значит, десятичная дробь, равная а, не может начинаться со 100
девяток.
б) Заметим, прежде всего чтоО, 1111... 111 =-g-0,9999.. .999=-gX
100 единиц 100 девяток
/ / 1 \100\ 1 -I / /1 \ 100
Xll—I То) Втаким образом, нам требуется оценить—|/ 1—( Тб) '
Далее мы ограничимся рассмотрением одной лишь задачи 4), из
результата которой вытекают и результаты остальных задач.
Известно, что при любом 1 имеет место неравенство Д/1—а<
<1 — Т а, поскольку 11------aj = 1 — а + а2 > 1 —а; поэтому
1/ / 1 \1°0
<
, 1 f 1 У°°/
1 — т (То / = °’.9999 ... 9995^.
\ 100 девяток J
298
Уточним эту оценку — найдем два таких положительных числа Ci
и с2, что
1 / 1 хюо / 1 \200
1— T^ioj — C1[io) >
-i / I 1 \ too 1 / 1 \100 / 1 \200
> V 1 — (Jo/ > 1 ~~2 [10/ “ c* 110/ •
Возведя в квадрат все члены двойного неравенства
1 /------------------- 1
1 — а — Сха2 > у 1 — а > 1 — ~2~ а — с:а' >
получим:
1 + а2 + суа4 — а — 2с1а2 + с,а3 > 1 — а />
> 1 + -j- а2 4- с|а4 — а — 2с,а2 + с2а3,
или, вычитая из всех частей неравенства 1 — а и сокращая затем
на а2:
/ 1 \ ? , / 1 \ ,
-4- — 2ct + cYa + ср- > 0 > 1 -5- — 2сг I + с2а + с'2а2.
/ 1 \100
Нас интересует случай а=1уд ; покажем, что здесь можно,
1 1 Л ( 1 V02 1 .
например, принять су =-g- + удр а ~ 0,125 +1ц)1 и с3 =~д-~7
1 /1\101
ууЯ = -0,125+ (То) • Действительно, при любом а>0
1 I 1 । 1 \ II. 1 \ 1 V
4 8 + 100 й/ Ц 8 ' 100 а)а ' [в + 100aJ °2 =
[ 1 1 \
“4 8 ~ 50/ а + • • • > 0;
/ 1 \100
с другой стороны, при а = I pg I
1 / 1 1 / 1 1 \ / 1 1 V
~4 2 У + 10 й/ 8 10 “J ° + \ 8 + 10 =
! 1 1 \ Г 1 ! 1 1 VI
- “ 5 — 8 J а + [10 + У + 10 а) J й2 < 0 ’
/ 1 1 \ 3/1 уоо
поскольку I "g* — "g" I а = 4Q I IQ I явно больше последнего члена
/I I \ 37 37 /1 \200
неравенства, близкого к I ]q + 54 I а2 “ 320 fl2 "’326 (То)
299
Таким образом, мы имеем
Последнее двойное неравенство можно переписать так:
0,9999 ... 99949999 ... 9998749999...999 > |/ 1 — >
100 девяток 99 девяток 99 девяток
> 0,9999 ... 99949999 .. . 9998749999 ... 999,
100 девяток 99 девяток 98 девяток
откуда, деля на 3, получаем, что с точностью до 301 знака после
запятой
0,1111 ... 111 %0,3333... 33316666 . 66624999... 999.
100 единиц 100 троек 100 шестерок 98 девяток
279. а) Обозначим 1,00000000004 через а, а 1,00000000002 —
через р. В таком случае фигурирующие в условии задачи выражения
1 + а 1 + 3
примут вид к + 11 [-<.- + • Так как а > 3. то, очевидно,
1+ к 1 1 1 1 1 + 3
а2 “ а2 + а < (З2 [4 — [З2 ’
и, наконец,
1 + а /1 + а + а2\ _ /1 + (3 + (З2 \ 1 + ₽
1 + а + а2 “ 1 ’ 1 + а / 1 ‘ \ 1 + ₽ j = 1 + ₽ + |32
Таким образом, второе из двух выражений больше первого.
б) Обозначим фигурирующие в условии задачи выражения со-
ответственно через А и В. Тогда, очевидно, имеем:
1 1 + а + а2 + .. . + ап 1 ' П 1 , 1 , _L 1
ап1 1 ' ’ ’ 1 а
300
Отсюда сразу следует, что ~ 11 > следовательно, В > А.
280. Будем исходить из формулы
(X —а)2 — (х —а)2 = X2 —х2—2а(Х —х).
Следовательно,
[(X — й])2 4- (X — а2)2 4-... + (X — а,,)2] -
‘ — [(* —Д1)2+ (х — а2)2 4- • • • 4-(* —а„)2] =
= п(Х2 — х2) — 2(а, 4- а2 4- ... 4-а„) (X — х).
ai + + • • • + ап
Если положить в последнем выражении х — --------------------------,
то оно будет положительным; действительно, мы будем иметь:
[(Х-Я1)24- (X - а2)2 4- • • • 4- (X - й(1)2] -
— [(х —ai)24- (х —а2)24-. ,.4-(х —а„)2] =
= п (X2 — х2) — 2пх (X — х) = п (X2 — х2 — 2Хх + 2х2) =
= п(Х — х)2 0.
Отсюда вытекает, что искомым значением х является
п
281, а) Мы имеем всего три существенно различных располо-
жения:
1°. at, а2, а-„ а4.
Ф) = (й) — а2у2 4- (а2 — й3)2 4- (а3 — а4)2 4- («г —
2°. ai, а3, а2, а4:
ф2 = (й1 — а3)2 4- (а3 — а2)2 + (а2 — а4)2 4- (а4 — flj2,
3°. аь а2, а4, а3:
Фз = («1 — а2)2+ (а2— а4)2 4- (а4 — а3)24- (а3 — at)2.
Но легко видеть, что
Фз — Ф, = — 2а2а4 — 2й1Я3 + 2а2а3 4- ^а^ =
= 2(fl2 — ai) (Оз —а4) < 0;
Ф3 — Ф2 — — 2П|а2 — 2а3а4 4“ 2й2й3 4~ 2й1й4 =
= 2(й3 — flj (а2 — а4) < 0.
Следовательно, требуемое расположение имеет вид: at, а2, а4, а3.
б) Первое решение. Рассмотрим выражение
Ф = (% - %)2 + (ai2 - %)2+ • • • + {ain-1 “ “in)2 +
+ (ai
\ г/1 11)
где , ai2..., а. — наши п чисел, расположенные в требуемом
301
порядке. Пусть а^, аг , (а < Р) — какие-то два из этих чисел. Мы
утверждаем, что если aia больше (или наоборот меньше)
а., то а, больше (соответственно меньше) а,.,,1).
’а—1 гР+1
Действительно, если бы это было не так, т. е. если бы было
* — aip+l) < т0 пеРестановка> изменяющая поря-
док чисел а{&, ага^..........ai$ на обратный, уменьшила бы
величину суммы Ф, так как разность новой суммы Ф' и первоначаль-
ной суммы Ф будет, очевидно, равна
ф' - ф = - ~ 2aia%+i + 2aia^aia + 2%aifi + l =
Это замечание позволяет получить полное решение задачи.
Прежде всего, так как циклическая перестановка всех чисел (т. е.
перестановка, при которой сохраняется порядок чисел, выписанных
одно за другим по кругу) не меняет величины суммы Ф, то мы
можем считать, что а; есть наименьшее из наших чисел а,, т. е. и = 1.
Отсюда можно вывести, что a t и а:песть два следующих по величине
числа. Действительно, если бы было, например ai$ ¥= п), то
мы имели бы {а, —а.Д/а. —а}„ ,) <0, а если бы было а, <
а,- (Р 2), то мы имели быГа.- —а- Д(а, —а,-о)<0 . Так как
‘п I. н ‘р—п гр/
можно изменить порядок следования в цепочке а-^, , ...,
aii на обратный без того, чтобы изменить сумму Ф, то мы можем
считать, что а, < а, , i2 = 2, *„ = 3.
12 1п П
Далее мы утверждаем, что числа а;3, следуют по величи-
не за уже использованными числамиа. , а, , а, :действительно, если бы
J ‘1 ‘2
было, например, а, а, (р =/= 1, 2; п — 1, п), то мы имели бы
3 1р
(ai3 aip) (аг2 а’₽+1)<0. А так как, кроме того, должно быть
Точно так же показывается, что числа и а. —следующие
по величине за уже использованными и а, < а, „(т. е. А = 6,
ч ‘п—2
in-2 •= 7), что числа ais и —следующие по величине заранее
использованными и -а^ <.Oi =8,fo—з = 9), и т. д. Окончатель-
но приходим к следующему расположению чисел:
^а2 —а4 —о6 —...-«„_2Ч
при п = 2k четном Да
Ха3 — а5 — аап_( п
а2 а4 ав ... оп_ ।
при п = 2k + 1 нечетном аД
— -а-,—
•~ап
’) Здесь мы условно считаем, а.° = а,{
302
(черточки указывают порядок Следования чисел; так, например,
для п четного имеем расположение а>, а2, at, ае .. , я„_2, а„, an-i, ...
. ., О;, Os, из).
Второе решение. Если каким-либо образом догадаться,
что искомое расположение имеет такой вид, как указано в конце
первого решения, то доказательство этого факта можно получить
при помощи метода математической индукции. Действительно, при
п — 4 доказательство получается весьма просто (см. решение зада-
чи а)). Предположим теперь, что для какого-то четного п мы уже
доказали, что сумма Фп, соответствующая выписанному в конце
первого решения расположению чисел я, < я2 < я3 < ... < ип,
меньше суммы Ф'п, соответствующей любому другому расположе-
нию. Покажем теперь, что сумма Фя+1, соответствующая выписан-
ному выше расположению п + 1 чисел at <Z а2 < Яз < • • < ап <
< я„ + |, меньше суммы Ф'п+1, соответствующей какому-либо друго-
му расположению п + 1 чисел. Имеем:
Ф„ + 1 — Фп = (Я„ — Яп+1)2 + (Я„ + 1 — Яп-О2— (Я„ — Яп-1)2 =
== 2я2п + 1 2я,(яг(.|.। 2яп —[Яи.^| ~|~ 2ап-1Я„ г=
=г= 2(яп+1 я„)(яп+1 яп_]).
С другой стороны, если в расположении, отвечающем сумме
Ф„4-1, число я„+! стояло между какими-то числами яа и яр и Фп
отвечает расположению п чисел, которое получается из расположе-
ния п + 1 чисел, приводящего к сумме Фп , вычеркиванием числа
вп+l, то
Фп+1 “ Фп == (Qa~ a»+l)2 + (°n+J - ай)2 - (°-х ~ af,T =
~ 2an4-l 2яаяп_|_( 2а&ап^ + 2яаЯр —
= 2 (“n+l - M (fln+l - Qp) > Фл-Н “ %-
Таким образом, мы видим, что
Ф,. + 1 - 4+1 = К - <] + [(Фп+1 - фп) - (<+1 - Фп)] < О
(первая скобка неположительна в силу предположения индукции,
вторая — по доказанному). При этом, если сумма , отличается
от Ф„ + 1, то либо Фп — Фп < 0 (и, следовательно, Фп+1—Фп_[4<
< 0), либо (Фп+1 — Фп)— (Фп+1~фп)<® (и, следовательно,
опять Фп+1 < Ф„+1).Аналогично осуществляется переход от п к
п + 1, если п нечетно.
Третье решение. Задача имеет также несложное геомет-
рическое решение. Изобразим числа < я2 < я3 < ... <я„ точка-
ми А2, Аз,..., А„ на числовой оси; отрезки А|А2, А2А3, ...
. .. А„-1Ап обозначим соответственно через dj, d2, d3.dn-i- В таком
случае сумма Ф = (%-%)2+(Ч-Ч)2+ ... + (я,.^ — +
+ (“in- ai>)2 =/1<1Л12+ AiaAi3 + • •• + Ain_iAin^ Ai„A'i, Равна
сумме квадратов длин звеньев «ломаной» А^А^А^ ... Aj _lAinAj,
(все звенья которой лежат на одной прямой; рис. 31, я)).
303
Так как наша замкнутая ломаная покрывает весь отрезок AiAn,
то каждый из отрезков AkAk+i = dk минимум два раза входит в
нашу ломаную (один раз в направлении от Ак к второй раз —
в обратном направлении). Поэтому, в каком бы порядке мы ни рас-
полагали точки, сумма Ф, если выразить ее через отрезки di, d> . ..
..dn-i и раскрыть скобки, обязательно содержит член2с^, а следо-
вательно, и все члены 2dp 2d|....2dA___Далее, пусть Ak-iAk —
= dk-\ и АьА/,+1 = dk — два соседних из рассматриваемых отрезков.
A Az А
А.
Ai As
А/ А% А}
Aj А$\
S)
Рис. 31.
Очевидно, что если звено ломаной, покрывающее отрезок А^Аь-н в на-
правлении от Ак к Ak+i, начинается в точке Ак, то звено, покрывающее
этот отрезок в обратном направлении, не может кончаться в точке
А/,; поэтому во всех случаях должно существовать звено, которое
покрывает одновременно отрезки As-iAs и AfcAft+i. А отсюда выте-
кает, что сумма Ф во всех случаях должна содержать член 2dk-idh,
а следовательно, и все члены 2did2, 2d2d3....2d„-2d„-1.
Теперь остается только заметить, что в случае, если расположе-
ние точек таково, как указано в конце первого решения задачи, то
Ф = 2rf| + 2d| + •. • + + 2d1d2 A 2d2d3 -j- ... -j- 2dn_2d1!_1
(рис. 31, б)). Отсюда и из сказанного выше вытекает, чТо в этом
случае сумма Ф будет наименьшей.
282. а) Отметим, прежде всего, что мы с самого начала можем
считать все щ, а2,..., a,t; &i, b2,.. Ьп положительными; в против-
ном случае мы изменили бы знаки отрицательных чисел на противо-
положные: левая часть неравенства при этом не изменится, а правая
может только увеличиться. Рассмотрим теперь ломаную A0AiA2...
...Ап, такую, что проекции отрезков АОАЬ АА, • на ось
Ох равны соответственно а1( а2.. ап, а проекции этих же отрез-
ков на ось Оу — bi, b2,..., Ьп; при этом пусть каждая вершина ло-
маной расположена правее и выше предшествующей (рис. 32). В та-
ком случае из теоремы Пифагора следует, что
АА=У<“1 + £,1> А1А.,-^Уа| + />|,..., =-|/а2 +
А0Ап = + аг+ + %)2 + (А А А + - - - А Ьп)\
откуда и получается неравенство задачи.
Ломаная A0AiA2...A„ будет равна отрезку А0А„ только в
том случае, если все звенья этой ломаной являются продолжениями
одно другого (ломаная является отрезком прямой). Нетрудно ви-
деть, что это обстоятельство будет иметь место в том случае, если
ЗС4
di аг an
= ... ; лишь в этом случае имеет место равенство
]/а1 + + ]Ла| + bl + ... + У а2п + b2 =
= У (<Ч + «2 + • • • + %)2 + (6j + &2 + • • • + bn)i.
б). Обозначим через h высоту пирамиды, через at, 02,..., ап —
стороны основания (at + а2 + ... + ал = Р) и через &ь й2... Ьп —
Рис. 32.
длины перпендикуляров, опущенных из основания высоты на сторо-
/ 1 1 1 \
ны основания "у аА + у й262 + • • • + у ап^п = S) • В таком слу-
чае боковая поверхность S пирамиды будет равна
ai а2 "|Уb2 + h2 + ... + у ап |/ Л2.
Но согласно неравенству задачи а)
2 2 = У У У2 + (aji)2 + У(а2&2)2 + (aJi)2 + . . .
•••+/(“,?„ У2+ (%Л)2>
> V(а^ + а2й2 + ... + anbn)2 + (aih 4- a.,h + ... + я„Л)2 =
= 1/4S2 +А2?2,
причем равенство достигается только, если aibi : tub?: ... : anbn =
= aih : a2h anh, t. e. &i = й2 = • • • = bn.
Отсюда и вытекает утверждение задачи.
283. Рассмотрим отдельно случаи п четного и п нечетного.
Г. Число п четно. Построим ступенчатую ломаную
'А1А2А3 •.. <4„Лп + 1Л„+2 так, чтобы длины всех отрезков А:А2, A2AS,
A3At, ..., A„+IAn+3 равнялись единице и отрезки AiA2, А3А4,
А$Ав Ап—iAn, An4.iAn+i были бы параллельны между собой и
20 Д, О. Шклярский и др.
305
перпендикулярны к отрезкам А2А3, Д4Д5.....Д„Лп+! (рис. 33; на
нем п — 4). На каждом из отрезков Д,Д1+| (4=1, 2, ..., п+1)
или на его продолжении возьмем точку Bt так, чтобы длина отрезка
В;Д,+1 равнялась a,(an+i мы полагаем здесь равным оь т. е. Вп-м
выберем так, чтобы было Вп „+2 = 0!); при этом точку В,
мы будем располагать левее или ниже точки А >+1, если о,- > 0, и
правее или выше точки Д<+1, если ог < 0 (на рис. 33 0 < а < 1,
О < а, < 1; Оз > Г, 04 < 0). Проведем теперь ломаную BiB2 ... B„+i.
По теореме Пифагора
BiBi+i — + Bi+i Л1+1 •
Но BtAi+i = ai и, как легко видеть, = |1 — а1+1|; следо-
вательно,
Мж = /о2 + (1-ож)+
Таким образом, интересующая нас сумма
of 4~ (1 — о2)2 + о| + (1 — о3)2 + ...
... +'|/о/2!_1 +(1 -а„)2+ q2+(1 - и,/
равна длине ломаной В^Вз... Вп+1.
Очевидно, что длина ломаной BiB2B3... В„+1 всегда не меньше,
чем длина отрезка BiB„+i. Вычислим теперь длину этого отрезка.
С этой целью построим прямоугольный треугольник BiCB„+1
306
(рис. 33). Тогда
ВХС = Л2Л3 + Я4Л5 + ... + ЛпДп+1 = у
и
п
CBn+l = AtA2 + + ... + ^п—Ип = ~2~
(ибо Л1В| = 4„+IBn+i = 11 — aj). Отсюда
,---------------- Г t п \2 / п \2 п У 2
BiBn+i = V (BlCy- + (СВп+1)2 = 1/ [ 2j = —.
что и доказывает требуемое неравенство.
Теперь уже легко выяснить, в каком случае в этом неравенстве
знак можно заменить знаком равенства. Для этого необходимо,
чтобы все точки В2, В3,-..., Вп лежали на прямой В1Вп+1 (т. е. В(
должно совпадать с точкой пересечения прямых BtBn + i и Ai?l, + i).
Так как прямая BtBn+l образует угол 45° с прямой ДС (ибо ВС =
= CBn+i), то это будет при
В1Л2 = А2В2 = В3А4 = А^В^ = ...'= Bn-iA п == А„Вп,
т.е. при а, «= (1 —а2) = а3 = (1 —а4) = ... = а„_! = (1 —ап).
Итак, при п четном равенство достигается при
а,. = аз = ... = ап_[ = а, . а2 = а4 =... = ап — 1 — а,
где а может быть любым.
2°. Число п нечетно1). Положим а„+| = at, ап+2 =
= а2,..., а2п — ап и рассмотрим сумму
j/'af-У (1—ai)2 + — яз)2+-->
•• • + а2п~ 1 + (* ~ а2п)2 + а2п + U “ а1)2 •
которая, очевидно, будет равна удвоенной сумме;
—н2)’+ с5 + (1—«3)2+...
• ••+]/On-i + (> ~a-lt)2 + (1 — агу
(каждое слагаемое этой последней суммы в первой сумме встреча-
2n )/2
ется дважды). Но по уже доказанному первая сумма<—1
отсюда вытекает, что
j/^+ (1 — а2)2 + 02 А- (1 — а3)2 + ...
••• + «П—I + (* — an)2 + а п + (1 —
т. е. мы получили требуемое неравенство.
*) Мы предоставляем читателю выяснить па примере п. = 3,
почему доказательство, проведенное для четного п, не проходит для
п нечетного.
20* 307
Знак равенства в последнем неравенстве имеет место только,
если
= ^3 == . • • = = 1 — а2 ~ ==...= 1 — ^2п
(см. выше случай Г). Но так как у нас ai = ап+1 и п нечетно, то
последнее равенство возможно только, если
1
ai = «2 = • •• = ап = 2-
284. Первое решение. Обе части равенства положительны,
поэтому, возводя их в квадрат, получим:
1 — xf + 1 - х| + 2 ]/(l - xf) (1 — 4) < 4 — (4 + 2хЛ + 4)’
т. е. ______________
2]/(1 — 4)(1 — х?) <2 — 2xtx2,
]/(1—4)(1—4) <1—
Возведем опять обе части в квадрат:
1 — 4 — 4 + *1*2 1 — 2х1х2 + Х1Х2’
перенося все члены направо, получим:
Последнее неравенство очевидно; равенство здесь имеет место
лишь при Хг = х2. Отсюда вытекает, что исходное неравенство
всегда имеет место и обра-
щается в равенство лишь при
Д’] == %2.
Второе решение. Эта
задача имеет и геометрическое
решение; аналогичные решения
можно найти и для многих зна-
чительно более сложных задач.
Введем на плоскости прямо-
угольную декартову систему
координат и рассмотрим окруж-
ность с центром в начале коор-
динат и радиусом, равным еди-
нице (рис. 34'). Координаты х,
у точек этой окружности будут
связаны соотношением
х® + У2 = 1.
Рис. 34. Отме1им теперь на оси Ох
две точки Mi и М2, имеющие
абсциссы Xi и х2, так как |xj 1 и |х2| 1, то обе точки будут
расположены внутри (или на границе) единичной окружности. Вос-
ставим в этих точках перпендикуляры к оси абсцисс до пересечения
их с верхней полуокружностью в точках N; и N2; тогда, очевидно,
308
MiNi = у 1 —x; и Af2./V2 = y 1 —Xg. Заметим теперь, что абсциссу
Xi + X,
'—2—" будет иметь середина М отрезка ЛфЛЬ1). Отсюда вытекает,
что величина 1/ 1—(2— / будет равна длине отрезка MN,
где W есть точка пересечения с окружностью перпендикуляра к оси
абсцисс, восставленного в точке Л1. Но сумма ЛЬЛЬ +442A/2 равна
удвоенной длине средней линии N'M трапеции М^^2М2, т. е. мень-
ше, чем удвоенная длина отрезка MN. Тем самым нужное нам нера-
венство доказано; из доказательства видно, что это неравенство
обращается в равенство, лишь если точки ЛЬ и Л12 совпадают, т. е.
если Xi = х2.
Примечание. Прием, примененный во втором решении за-
дачи 284, позволяет вывести много интересных неравенств. Так, на-
пример, рассмотрим сферу с центром в начале координат и радиу-
сом 1 (рис. 35); и пусть Mt и М2 — две произвольные точки плоско-
сти Оху, расположенные внутри или па границе сферы, Nt и Ад—
') Эю утверждение очевидно, если х,- и х2 положительны; легко
проверить, что оно остается справедливым и при любых знаках
х, и х2. (Заметим, впрочем, что приведенное в условии задачи нера-
венство достаточно доказать для положительных х, и х2: действи-
тельно, если Xi и х2 неположительны, то, заменив эти числа их
абсолютными значениями, мы не изменим левой части неравенства,
а правую уменьшим.)
309
Точки пересечения со сферой перпендикуляров к плоскости Оху, вос-
ставленных в точках Л41 и М2, N и N'—точки пересечения перпен-
дикуляра, восставленного к плоскости Оху в середине М отрезка
AfiAf2, со сферой и с отрезком NtN2. Если (xt, z/i) и (х2, У2) —коор-
динаты точек М, и М2, то -
Л41Л\ = ]/1 — х, — у\ , M2N2 = ]/"1 — х% — yj ,
/ 1х, +х.,\2 /Уг + Уг\2 , 1
ми = 1/ 1 - - MN' = у (ад, +ад2),.
и из того, что MU' MN, вытекает, что
(*)
если только все подкоренные выражения положительны; равенство
здесь имеет место только в том случае, когда лт = х2, ух — у2, т. е.
когда точки М1 и М2 совпадают.
Точно так же, восставив к плоскости Оху перпендикуляры, в
трех точках Mi, М2 и М3 и в точке М пересечения медиан треуголь-
ника MiM2M3 (рис. 36), придем к неравенству
310
выражающему, что отрезок ММ' не превосходит отрезка ММ. Нера
венство (**) тоже имеет место во всех случаях, когда все подкорен-
ные выражения положительны; равенство здесь имеет место, лишь
когда xt = х2 = х3 и У\ = у2 = уз, т. е. когда точки Afb М2 и Af3
все совпадают между собой.
Заменяя сферу конусом, вершина которого совпадает с началом
координат, осью служит ось Ог и угол при вершине равен 90°
(рис. 37), получим неравенство
V х\ + У1 + + у\ + ]/х| + у\ >
j2 .1 + +
справедливое при любых хь х2, х3; У1, У2, Уз’, равенство здесь будет
х2 х3
иметь место только в том случае, когда ~—,т. е. когда
У\ У-2 Уз
точки W], N2 и Мз лежат на одной образующей конуса. Ал-
гебраическое доказательство неравенств (*), (**) и (***) пред-
ставляет очень большие трудности.
(л \
-у + eos х , то
COS Sin X— Sin COS X = COS Sin X + COS I + cos X I =
Я I I • Я r
~2“ + COS X 4- Sin X “2“ + cos X — sin X
— 2 cos---------5---------- cos--------5----------
Ho
cos x + sin x I = У cos2 x -f- 2 cos x sin x -f- sin2x =
= /1 + sin 2x < /2.
(|cos x + sin x| =| 2 , только если sin 2x — 1) и точно так же
| cos x — sin x I — Уcos2 x — 2 cos x sin x -f- sin2 x =
== У1 — sin 2x < У 2
(|cosx— sin x| = У2 , только если sin 2x — —1). А так как
л 3,14
-у я ~2~ = 1,57 больше чем у 2 ss 1,41, то отсюда следует, что
л ,
-у + cos х + sm х
-у > g • >0 и
—g- + cos х -j- sin х
значит, как cos----------5---------
я ,
-у + cos X — sin X
так и cos----------п-------
311
Всегда положительны. Таким образом, разность cos sin х — sin cos х
всегда положительна, т. е. cos sin х при любом х больше чем
sin cos х.
286. а) Обозначим log^ эт = a, log5it = &. Из равенства
2“ = л, 56 — л получаем л1'/о = 2, л1/ь = 5, л1/а-л1/ь = 2-5 = 10,
я1/а+1/ь _ pg, ц0 п2 ~ 3J42 < ю, откуда следует справедливость
1 1
неравенства + -у > 2, что и требовалось доказать.
б) Обозначим log2n = a, log„ 2 = Ь. В таком случае имеем
2° = л, ль = 2; из второго равенства вытекает 21/ь = л, или b =
1
= Теперь наше неравенство принимает вид
1 1
ПГ+ТГ>2,
«2+1
а ’
а2 + 1 > 2а,
(ибо для каждого отличного от
Последнее неравенство является
очевидным.
287. Первое решение.
Требуется доказать, что если р >
> а, то
a) sin р — sin а < р — а.
Но, очевидно,
sin р — sin а =
. ₽ —а Р + а
— 2 sin —g— cos —g— <
Р — а
<2——-1 = Р - а
(ибо для каждого отличного от
нуля угла х первой четверти
sin .Г < X, COS X < I1)).
б) tg р — tg а > р — а.
Но, очевидно,
Р —а < tg(P —а)=*
tg р — tg а
= 14T?W^<tg3-tga
нуля угла х первой четверти
tgx > х >)).
Второе решение. Рассмотрим здесь только задачу а), так
как решение задачи б) совершенно аналогично.
Проведем единичную окружность с центром в точке О, и пусть
дуга АЕ равна а и дуга AF равна р. Если ЕМ и FP — перпендику-
’) См., например, ниже стр. 345.
312
ляры, опущенные из точек Е и F на радиус ОА (рис. 38), то
I
‘-’ДОЕА = g S'n Я’
5Д0ЕА = ” Sin р
и
'-’сект ОБА 2 а’ '-’сект ОБА р Р>
где буква S, как обычно, означает, площадь.
Отсюда следует, что
ОС — Sin ОС = 25сеГмАтЕ
и, следовательно,
(3 — Sin (3 = 25сегмАЕБ
а — sin а < 0 — sin р.
288. Пусть АЕ и AF — дуги единичной окружности с центром
в точке О, равные соответственно а и (3, В и С — точки пересечения
перпендикуляра, восставленного в точке А к диаметру ОА, с пря-
мыми ОЕ и OF, М и N — точки пересечения перпендикуляра, опу-
щенного из точки Е на диаметр ОА с прямыми ОА и OF (см.
рис. 38). Тогда имеем:
1 __________________1_
SAOAB = 2 Я’ SAOAC = 2
"^сект ОАЕ 2 а’ ®сект OAF 2 Р
и, следовательно,
tg а _ SAOAB tg [3 __ SAQA С
а ‘-’сект ОАЕ Р ^сект OAF
Но, как нетрудно видеть,
Действительно,
SAOAB SAOBC
'-’сект ОАЕ ^сект OEF
SAOAB
‘-’сект ОАЕ
SAOAB
$АОЕМ
SAOBC > SAOBC
‘-’сект OEF SaOEN
SAOAB SAOBC
$АОЕМ SAOEN
$АОВС $АОАВ
Из того, что т---------------, следует, что
° сект OEF ^сектОАЕ
$ДОАВ ~Ь S&OBC > $АОАВ
•^сект ОАЕ 4“ ^сектОКЕ ^сектОАК
т. е.
ЧТО
что
SAOAC
сектОА.К
и требовалось доказать,
5 ДРАВ
^сектОАЕ
313
289. Пусть
arcsin cos arsin x = a.
Угол a заключен в пределах O^a^-j-.ибо 0 cos arcsjn х 1
^так как — < arcsin х Далее, sin а = cos arcsin х; следо-
вательно,
arcsinх = + I — — а) и х = sin 4- | — — а ) = + cos а.
- \ 2 / L~ \ 2 )\
л
Точно так же, если arccos sin arccos х — jj, то 0 р (ибо
О sin arccos х 1, так как О arccos х =С л) и cos р = sin arccos х;
следовательно,
arccos х = -2L + Р и х = cos = ± sin р.
Из того, что cos а = sin р ( = ± х), заключаем:
л
а + р = arcsin cos arcsin х + arccos sin arccos x = -g-.
290. Предположим, что сумма
cos 32x + a3i cos 31x + a30 cos 30x + a2S cos 29x +...
... + a2 cos 2x + a, cos x (*)
при всех значениях x принимает только положительные значения.
Заменим в этой сумме х на хД- л; мы придем к выражению
cos 32 (х + л) + а31 cos 31 (х + л) + a30 cos 30 (х 4- л) 4-
4- а2д cos 29(х -|- л) + ... +а2 cos 2(х + л) + at cos(x 4- л) =
= cos 32х — а31 cos 31х 4- a30cos ЗОх — a29cos 29х + ...
... + a2cos2x — at cos х, (**)
которое тоже должно принимать при всех значениях х положитель-
ные значения. А в таком случае и полусумма выражений (*) и (**),
равная
cos 32х + а30 cos ЗОх 4-... + Щ cos 4х + а2 cos 2х,
тоже будет принимать при всех х только положительные значения.
л
Теперь заменим в последнем выражении х на х +~2~> получим:
cos32|x+ ] -j- a,,, cos 30 (х + -£-) +
cos 28 ^х + ~Ь • • • "Ь П4 cos 4 ^х -f- -Д-
азп cos ЗОх +
., -j- а4 cos 4х — а2 cos 2х,
4-
«2 cos 2 ^х + -Д-j = cos 32х —
cos 28х — .
314
Составив полусумму двух последних выражений, найдем, что сумма
cos 32х + «28 cos 28х + а24 cos 24х + ,.. + as cos 8х + а4 cos 4х
тоже должна принимать при всех х только положительные зна-
чения.
„ л
Заменяя в последнем выражении х нах-|--уи составляя полу-
сумму полученного выражения и первоначального, мы придем к
сумме
cos 32 х + e24 cos 24х + cos 16х -J- «8 cos 8х;
заменяя в ней х Hax + "g~ и складывая полученное выражение с
первоначальным, мы придем к сумме
Cos 32х + «16 cos 16х;
наконец, точно так же убеждаемся, что выражение
cos 32х
тоже должно принимать при всех значениях х только положитель-
л
ные значения. Но при x=-gg- последнее выражение равно —1.
Полученное противоречие и доказывает утверждение задачи.
291. Будем исходить из формулы для синуса половинного
угла:
2 sin ~2~ ~ ±1^2 — 2 cos а,
где знак корня берется в соответствии с известным правилом знаков
для синуса. Пользуясь этой формулой, мы будем последовательно
определять синусы углов
«1 45°; 45°; / а4 + • 45°; ...
। । ... 4-
\ 2
а‘а‘Л ~ . 45-
2П—1 /
Предположим, что мы уже определили синус угла
। а1аг . ।
«1 -Г -g- -Н —j— И
45°,
где ah а2, а3.. принимают какие-то значения, равные 1 или
315
— 1. Так как
2 / а + а'а- + ... + a'a,J ••• ah+a^ ••• akak+f ] . 45о
\ 2 4 —I 2k '
= + 90° + (а2 + 4- • • • + -гй—--^^+‘^1 • 45°
~ \ 2 2ft—1 /
где знак плюс соответствует а, = 4- ], а знак минус fl| = — 1, и
cos + 90° + f g3 + £*£? 4- ... + -? — 'j 45° =
— “ \ 2 2 ’"1 )
= - sin L + + ... • 45°,
\ 2 2' /
то мы можем после этого определить синус следующего угла:
а,а2 .. • Ojj । UiOi ... '
+ 2*-1 2^ :
ч / / duct's (1лСУ> • . • ^ь_1_{ \
= ± ]/ 2 4- 2 sin U + -у1 4- ... 4- -fe^f + ) • 45 •
При этом следует иметь в виду, что так как все рассматривае-
мые углы по абсолютной величине меньше90° (ибо даже 4"
1 1 \ 1
4--J- 4* ••• 4* I- 45° = 90° — меньше 90°), а знак этих уг-
лов определяется знаком aIt то корень квадратный в последних фор-
мулах следует брать со знаком плюс или минус в зависимости от
знака Я|. Другими словами, можно написать:
2sin^ai + £^4- ... 4-а1й'^2Л + й- У 45°
= Й1 j/2+2sin уа-4^-г...4-^^^Му 45-.
Теперь, прежде всего, очевидно, что
2 sin аг 45° = at У 2.
Отсюда последовательно получаем:
2 sin У 4- 45° = 2 4- а2 У 2,
2 sin L + ^2 4- 45° = at 2 + а2 |/ 2 + а3 И Г,
316
2sin(ai 4- £1^ 4-
\ 2, 4
, OiOgOgOj
8
45° =
= flj V 2 + a2 V's + a3 /2 + a4 /2,
что и требовалось доказать.
292. Предположим, что разложение заданного выражения по
степеням х имеет вид
(1 — 3x-r3x2')‘41ti + Зх — Зх2)744 = Л + Л.х + А2х2 + ... + Апх'г,
где До, Alt А2... Ап — неизвестные нам коэффициенты, сумму ко-
торых требуется определить, ап — степень этого выражения (кото-
рая, как легко видеть, равна 743-2 + 744'2 = 2974). Положим в
этом равенстве х = 1; тогда получим:
1743.1741 = До + Л1+/12 + ...+Д11.
Таким образом, искомая сумма равна единице.
293. Раскрыв скобки и сделав приведение подобных членов в
двух рассматриваемых выражениях, мы получим два многочлена
относительно х. Заменим теперь в наших выражениях х на —х. При
этом нам придется заменить х на —х также и в полученных мно-
гочленах, т. е. в каждом из них оставить прежние коэффициенты
при х в четных степенях и заменить знаки коэффициентов па обрат-
ные при х в нечетных степенях. В частности, коэффициенты при х20
при этой операции не изменяется. Таким образом, мы видим, что
наши два многочлена имеют те же коэффициенты при х20, что и
многочлены, получаемые при раскрытии скобок и приведении подоб-
ных членов в выражениях (1 + х2 -ф х3) 1000 и (1—х2— х3) 1000.
Но ясно, что первый из этих новых многочленов имеет больший
коэффициент при х20. Действительно, при раскрытии скобок в пер-
вом выражении мы по 1учим исключительно положительные коэф-
фициенты при различных степенях х, и при приведении подобных
членов все эти коэффициенты будут складываться. Во втором вы-
ражении при раскрытии скобок мы получим при различных степенях
х коэффициенты, имеющие те же абсолютные величины, что и коэф-
фициенты первого многочлена, но знаки их могут быть различны —
и при приведении подобных членов у нас произойдет умень-
шение коэффициентов.
Итак, после раскрытия скобок и приведения подобных членов
в выражениях (1+х2— х3)1000 и (1 —х2 ф х3)1000 мы получим в
первом из них больший коэффициент при х20, чем во втором.
317
294. Утверждение задачи непосредственно 'вытекает из следую-
щих преобразований:
1 — х + хг — х3 + ... — х" + х100) (1 + х + х2 + х3 + ..,
.. .1+ х” + х100) = [(1 + х2 + х4 + ... 4-х100) —
— х(1 + х2 4- х4 + ... + х98)] [(1 Н- х2 + х4 + ... + х100) 4-
. 4-х(1 4-х2 4-х4 4-... 4- х98)] =
= (14-х2 4-х4 4-...4-х100)2 — х2(1 4-х2 4-х4 4-... 4-х98)2.
295. а) Согласно формуле суммы геометрической прогрессии и
формуле бинома Ньютона имеем:
(14-х) 1000 + х(1 4- х)999 4-х2(1 4- х)998,4-.. . 4- х1000 =
4. х — (1 + х)1000 х1001 — (1 4- х)1001
—~х------------------=-------х_ ] _х--------- = (1 + х)1001 - х1001 =
1 i 1
= 1 + 1001X 4- с*т X2 4- cf001 X3 4-... 4- 1001х1000.
5П 1001!
Таким образом, искомый коэффициент равен Cjooi ~ 501 951! ‘
б) Обозначим наше выражение через Р(х). Тогда имеем:
(1 +х)Р(х) — Р(х) = [(1 +х)2 4- 2(1 4-х)9 4-...
...4-999(1 4-х)1000 4- 1000(1 4-х)1001] — [(1 4-х)4-2(1 4-х)2-)-
4-3(114-х)34-...4- 1000(1 4-х) 1000] = 1000(1 4-х)1001-
— [ (1 +х) 4- (14-х)24- (14-х) 34-.. .4-(14-х) 1000] = 1000 (14-х)1001—
_ (| 4-^)10°1-(1+ х)_ = о1 _ (1 4-х)1001 — (1 4-х)
1 4- х — 1 ' 1 ' х
Отсюда
, 1000(1 4-х)1001 (1 4-Х)1001 —(1 4-Х)
Z5 (X) = х — Х2 -
- 1000 [1001 4-С1001« + С1001х2+ + 1001X999 4-х1000] —
- [с 1001 + с 1 о01* + СШ1*2 + • • • + Ю01Х"8 4- X"9 ].
Таким образом, искомый коэффициент равен
51 Г52 1 000-1001! 1001!
1ооос1001 — с1001 51! 950! — 52! 949! =>
1001! „ ............ 51050-1001!
“ 52! • 950! I52 ’ 1000 9501 52! • 950! ‘
296. Найдем, прежде всего, свободный член, который получится,
если в выражении
(... ((х —2)2 — 2)2 — ... —2)2
к раз
318
раскрыть скобки и привести подобные члены. Он равен значению
этого выражения при х — 0, т. е.
(((— 2)2 — 2)2— 2)2 — ... — 2)2 =
Л раз
= (... ((4 — 2)2 — 2)2 — ... — 2)2 =
k—1 раз
= (. ((4 — 2)2 — 2)2 — ... — 2)2 = ...
А—2 раза
.... = ((4 — 2)2 — 2)2 = (4 — 2)2 = 4.
Обозначим теперь через А к — коэффициент при х, через ВА—
коэффициент при х3 и через Рьх3 — сумму членов, которые содержат
х в более высоких степенях. Тогда имеем:
( ...((х-2)2-2)2-...-2)2 = Pkx* + Bkx3 + Akx + 4.
k раз
С другой стороны,
( (((х —2)2 —2)2 —2)2 — ... — 2)2 =
А раз
= (( ((х—2)2—2)2---2)2— 2)2 =
= [(i*3 + Bk_tx3 + Ah_iX + 4) - 2]2 =
= (P^x3 + Bfe_1x2 + Ak_tx + 2)2 =
= PLi*’ + + {2Pk_iAh_i + Bt-iP +
+ (4Pft_1 + x3 + (4Bfe_! + Al_,)x3 +
+ 44ft_tx + 4 = [p2_ixs + W^B^x* +
+ (2Pft_)4ft-i + Ski) x + (4Р*_! + 2BA_f x2 +
+ (4Sa—1 + Ak—i) x2 + 44ft_(X + 4.
Отсюда
Ak = 4Л—1< въ= Ai—i + 4Sa—i-
Так как (x — 2)2 = x3 — 4x4-4, to 4, =—4. Следовательно,
Ai = — 4- 4 = —42, A3 — —43,..., и вообще Ah = —4*.
Вычислим теперь В„:
Вк = + 4Bft_t = 4ft2_( + 4 (42_2 + 45ft_2) =
= А2,-, + 442_2 + 42 (Я2_3 + 4Bft_3) =
^A'i-l+ 4^_2 + 42^-з + 43 (Л 1_4 + 4Bft_4) = ...
• • = + 44^_2 + 424fe_3 + .. .
,.. + 4ft—3 Al + 4fe-2 a2 + 4*-l fli.
319
Подставляя сюда
Bi = 1, Д! = — 4, Д2 = — 42,
А3 = — 43_____= -4й-1,
получим:
Bk — 42й—2 4. 4 . 4 2/4—4 4. 42 . 42ft—6 4А—2 . 42 .j. 4^—1 . 1 _
_ 42А—2 42/г—з _j_ 42^—4 4*14-1 4?! _l 46—1 =
= 4Й—1 (1 + 4 + 42+ 43 + ... + 4й-2 + 4й-1) =
_ 4й — 1 _ 42k~1 — 4й-1
4 — 1 3
297. a>' П e p в 0 e p e ш e н и e. Так как при любом целом поло-
жительном k двучлен xk — 1 делится на х— 1, то
х 4- х3 х9 4- х27 4- х81 + х243 = (х — 1) + (х3 — 1) 14
+ (х9— 1) + (х27— 1) 4- (х81— 1) + (х243 — 1 ) 4-6
дает при делении на х — 1 остаток 6.
Второе решение. Обозначим частное от деления х + х3 +
4 х9 4- х27 4- х81 -к243 на х—1 через q(x) и остаток через г. Тогда
х -j- х3 -j- х9 + л27 4- х81 4" х243 = <?(х) (х — 1) 4 г.
Полагая в этом равенстве х = 1, получим 6 = г.
б) Аналогично второму решению предыдущей задачи предпо-
ложим, что q(x) есть частное от деления нашего многочлена на
х2—1, а г{х -|- г2 есть искомый остаток (остаток от деления много-
члена на квадратный трехчлен является двучленом первой степени):
х 4- х3 4- х9 4- х27 4- х81 4- *243 = q(x) (х2-1)4- г{х 4 г2.
Полагая в последнем равенстве х = 1 и х = — 1, мы получаем:
6 = Г] 4" г2 — 6 = — г, 4- г2, откуда г1 = 6, г2 = 0.
Таким образом, искомый остаток равен 6х.
298. Пусть р(х) есть наш неизвестный многочлен, q(x)—част-
ное от деления этого многочлена на (х — 1) (х — 2),'г(х) = ах b —
искомый остаток:
р(х) = (х—1)(х —2)</(х) 4-<гх4-&. (*)
По условию задачи имеем:
р(х) = (х— 1)7)(х) 14-2, откуда р(1) = 2;
р(х) = (х — 2)qi(x) 4 1, откуда р(2) = 1.
Подставляя теперь в равенство (*) х = 1 и х = 2, получаем:
2 = р(1) = а-\-Ь,
1 = р(2) = 2а 4- Ь,
откуда
а = — 1, 6 = 3.
Таким образом, искомый остаток есть —х 4- 3.
320
299. Многочлен х4 + х8 + 2х2 + х + 1 можно разложить на мно-
жители; он равен (х2 4-1) (х2 + х + 1). Отсюда легко усмотреть,
что этот многочлен является делителем многочлена
х12—1 = (х«— 1)(х6+ 1) = (х3 — 1)(х3+ 1)(х2 + 1)(х4-х2 + 1),
а именно:
х12—1
х4 + х3 + 2х2 + х + 1 = (х—1)(х’ + 1)(х‘-х2+1) =
_________________х12 — I _____________
~ Xs — х’ — х6 + 2х5 — 2х8 + х2 + х — 1 ’
Разделить х1951 — 1 на х4 + х3 + 2х2 + х + 1 — это то же самое,
что разделить х1951— 1 на х12—1, а затем результат помножить на
Xs — х7 — х6 + 2х5 — 2х3 + х2 -|- х—1. Но легко видеть, что
•У.’951 ~ 1 = д.1939 + Х1927 _|_ *191» + Х1903 + . . . 4- X29 + X7 + ТТЗ " Г
(в этом легко убедиться, если произвести деление «углом» по пра-
вилам деления расположенных многочленов или если заметить, что
xi95i — [ _ х7[(х12)262— I] х7— I и воспользоваться известной
формулой деления разности четных степеней двух одночленов на
разность оснований). Отсюда следует, что искомый коэффициент
совпадает с коэффициентом при х14 в произведении
X (х8 — х7 — хя -|- 2х5 — 2х3 + х2 + х — 1)
который равен —1.
300. Из выписанного в условии задачи тождества следует,
что искомый многочлен Р(х) = Р„(х) (где п — степень многочле-
на) делится на х, т. е. Р„(х) =хР„_1(х), где P„-i(x)—какой-то
новый многочлен степени п — 1. Поэтому
Р(х— 1) = (х— l)Pn-i(x — 1),
и, значит,
х(х—1)Р„_1(х—1) =хР(х—1) == (х —26)Р(х),
в силу чего Р(х) делится и на х— 1, т. е. Рп(х) = х(х— 1)/’„_2(х)
(на х—1 делится многочлен Р„_|(х) — (х—1)Р„_2(х)). Новта-
ком случае Р(х—1) = (х — 1) (х — 2)Рп_3(х — 1), и мы получаем:
х(х — 1) (х — 2)Р„_2(х — 1) —
= (х — 26) Р„(х) = (х — 26)х(х — 1)Рп_2(х),
— откуда следует, что Р„(х) делится и на х —2 (т.е. Рп_2(х) де-
лится на х —2), и, значит, Рп(х) = х(х—1) (х — 2)Р„_3(х). Под-
ставляя это значение Р(х) в исходное соотношение, мы аналогично
убеждаемся в том, что Р(х) делится и на х—3, т. е. Рп(х) —
= х(х — 1) (х — 2) (х — 3)Р„_4(х), и т. д.
21 Д. О. Шклярский и др.
321
Продолжая поступать таким же образом, мы в конце концов
приходим к следующей форме многочлена Р(х):
Р(х) = Рп(х) = х(х- 1)(х—2)(х — 3) ... (х — 25)Р„_26(х).
Подставляя в заданное тождество это выражение многочлена
Р(х), мы получим:
х(х—1)(х —2) ... (х — 26)Рп-2в(х— 1) =
= (х — 26)х(х — 1) ... (х — 25)/’„-2б(х),
откуда вытекает, что для многочлена Рп_26(х) Q(x) степени
п — 26
Q(x-l)sQ(x). (*)
Ясно, что если Q(x) = Q0(x) = с — многочлен нулевой степени
(число!), то соотношение (*) имеет место; покажем, что оно
имеет место только в этом случае. В самом деле, если Q(x) =
= Q* (х) = aoxk + а1х'1-1 + ... + ak_,x -j- ak, где k > 1 и a0 =/= 0,
то, приравнивая с обеих сторон тождества (*)
o0(x — 1)k + aI (x — 1)й-1 + ... — aaxk + o1xft“I 4- ...
коэффициенты при x*-1, в силу формулы бинома Ньютона, полу-
чаем:
kaa 4-0! = О], или а0 = О,
что, однако, противоречит предположению а0 =/= 0. Таким образом,
k = О, Q (х) = с и
Р(х) = сх(х — 1) (х — 2) ... (х — 25)
— многочлен 26-й степени.
301. а) Если все коэффициенты Р(х) неотрицательны, то все
числа s(1), s(2), s(3), ... имеют смысл. Рассмотрим такую
степень десяти N = 10й, что W больше всех коэффициентов
о0, ai, о2, ... многочлена Р(х). Тогда число P((V) = P(10ft), оче-
видно, начинается с тех цифр, которыми записывается коэффициент
о.) многочлена; затем (после, быть может, некоторого числа нулей)
идут цифры числа Оь затем (возможно, опять после нулей) —
цифры числа о2, и т. д. —вплоть до цифр числа оп; поэтому число
s(10'i)=S равно сумме всех цифр всех чисел а0, о,, ..., ап. Но
этому же самому числу S равны и величины s(10fe+1), s (10ll+2),...
откуда и следует, что в последовательности s(1), s(2), ... число
S встречается бесконечно много раз.
б) Ясно,- что если старший коэффициент о0 многочлена Р(х)
отрицателен, то среди чисел s (1), s (2), s (3), ... будет вообще
лишь конечное число имеющих смысл (ибо при всех достаточно
больших х многочлен Р(х) имеет тот же знак, что и его старший
, Р (х)
коэффициент о0 — это следует, например, из того, что lim -- = 1).
Х->оо а0Х
Таким "образом, остается лишь рассмотреть случай аа > 0. Но
в этом случае, как мы покажем, существует таков число М > О,
что у «сдвинутого» многочлена Р(х) = P(x-j-M) все коэффициен-
ты положительны. Отсюда будет следовать, что последовательность
s(l), s(2), s(3), ... сумм цифр чисел Р(1), Р(2), Р(3), ... содержит
322
бесконечно много одинаковых чисел, а так. как, очевидно, s(l) =
= s(Af'+1), _s(2)= s(Af + 2), s(3) = s(M+ 3), ..., то и последо-
вательность s(l), s(2), s(3), ... также содержит бесконечно много
одинаковых чисел.
Итак, нам остается лишь доказать напечатанное выше курсивом
утверждение. Но если
Р(х) = Р(х + М) =
= а0(х + М) "+ at(x + М) + а2(х + М) п~2 + ...
... + a„_i(x+M)+a„ = aoX"+aiXn~1+a2*"~2+ .. Ч-Яп-ьН-Яп,
то, в силу формулы бинома Ньютона,
= ао С^Мп ’ + я, • С^п_1Мп 1 ... +
где 1 = 0, 1, 2, ..., п. Таким образом, а, имеет вид многочлена
(степени п — i) от М со старшим коэффициентом а0-Сгп>0', поэтому
все at (где i — 1, 2, ...; заметим, что а0 = а0 > 0) при достаточно
большом М будут положительны, что и требовалось доказать.
302. Пусть многочлены f(x) и g(y) имеют свободные члены аа
(т. е. [(х) = а0 + atx + ... + апхп) и Ьо. Положим в равенстве
х2ооу2оо j _ f(x)g(y) переменное х равным 0; тогда получим
, 1 1
aog(y) = 1, т. е.g\y)=~', таким образом, g(y) равно— при всех у,
Оо
1
е. это есть постоянная — (многочлен
а» '
т.
нулевой степени). Анало-
гично доказывается, что f(x)=-^—, т. е. f (х) g (у) = а"у~
=/= х200р200 + 1. Полученное противоречие и доказывает утвержде-
ние задачи.
303. Так как- (квадратное) уравнение р(х) = ах1 + Ьх 4- с — х
не имеет вещественных корней, то квадратный трехчлен р(х)—х =
= йх2+(Ь — 1)х + с при всех х принимает значения одного знака,
скажем, р(х)—х>0 при всех х Но в таком случае для любого
х = х0 имеем р(р(х0)) — р(х0) > 0, т. е. р(р(х0))> р(хо), и так как,
по предположению, р(х0)—х0 > 0, т. е. р(х0)> х0, то р(р(х0))>х0
и, значит, хоне может служить корнем уравнения (4-й степени)
р(р(х)) = х.
304. Будем считать, что а 0—в противном случае мы заме-
ним многочлен р(х) на (удовлетворяющий тем же условиям) много-
член— р(х) =—ах2—Ьх — с. Аналогично будем считать и что
Ь 5г 0—в противном случае мы заменим р(х) на р(—х) = ах2 —
— Ьх + с. Подставив теперь значения х = 1, х = 0 и х = — 1 в не-
равенство |р(х) | = |ax2 + &x + c| 1, получим
| а -|- Ь + с | 1, | с | 1 и | a — & + с|^1, т. е. | с | 1
и |а + Ь | ^2, | a — Ь | 2
Далее, если с>0и, значит, (при |х|^1) 0 сх2 с, а
— Ь СТ Ьх СТ Ь, имеем
Pix = cx2 + &x + a^c+& + asg: 1
и pi (х) = сх2 + Ьх + а > 0 + (— Ь) + а = а — Ь 2г — 2,
21*
323
откуда следует, что |р,(х)|<2. Аналогично, при с С О, когда
с сх2 0 (и по-прежнему — Ь Ьх Ь),
р\ (х) = сх2 + Ьх 4- а 0 4- Ь 4- а = а 4- Ь 2
и Pi (х) — сх2 4- Ьх 4- а > с 4- (—Ь) 4-а = а — Ь + с — 1,
откуда вытекает, что и здесь |р,(х) | sg: 2.
305. Исключим из рассмотрения мало интересный случай а = О,
когда три уравнения (1), (2) и (3) являются уравнениями 1-й степе-
ни, т. е. имеют единственный корень каждое, и все совпадают меж-
ду собой (здесь Xi = X2 = х3), а также случай, когда, скажем,
с — 0 и наши три уравнения имеют корни^——, 0^, О^и^——, oj
— здесь корень х3 = 0 уравнения (3) заключен между любым корнем
уравнения (1) и любым из корней уравнения (2)).
Далее, если ах^ -f- bxt 4- с = 0, то
q г п \ й п а п
2 Xi 4~ Ьхх 4- с — 4~ Ьхх 4- с) 2 xi = 2 х1'’
аналогично, если — ах| ~ Ьхг 4- с = 0, то
а 2 2 3 2^2
-у 4- Ьх2 4- с = — ах% + Z>x2 4- с 4- -у ах% = — ах?.
Следовательно, величины х% 4- Ьх\ 4- с =— _1_ ax^j и х|-р
(3 -Л
= —-ах~, имеют разные знаки. Но это означает, что
а
точки (Х|, /(х,)) и (х2, /(хг)) параболы у = /(х) =-ух2 4- Ьх Ц- с
лежат по разные стороны от оси х, откуда и следует, что существу-
ет промежуточная между этими точками точка (х3, 0) параболы,
в которой эта кривая пересекает ось х; х3 и есть искомый корень
уравнения (3).
306. Если а и р— корни уравнения
то
Следовательно,
х2 4- рх 4- q = О,
(х — а) (х — Р) = х2 4- рх 4- <?.
(а-7)(р-7) (а-б)(р-б) =
= [(7 — а)(7 — Р)][(6 — а)(6 — Р)] = (f4-л 4-<?)(с24-р6 4-<?).
Но
74-6 = — Р, 76 = Q
(а — 7) (Р — 7) (а — 6) (Р — 6) = (72 4- РТ 4- <?) (62 4- рб + <?) =
= 72б2 4- Р72б + Р72 4- Р762 4- р27б 4- Р<?7 4-рб2 4- pq& 4- q2 =
= (7б)24-Р7б(т4-6)4- р[(74-6)2—2у6]4-р27б4-рр(74-6)4-?2 =
= Q2 - pFQ 4- q(P2 -2Q)4- P-Q - pyP 4- q2 =
= Q2 + q^-pP{Q + q)+qP^ + p2Q-2qQ.
324
307. Первое решение. Вычислим из второго уравнения
коэффициент а и подставим его в первое уравнение. Тогда получим:
а = — (х2 4- х),
х2 — (х2 + х)х + 1 =0,
х3— 1 = 0,
(х—1)(х24-х+ 1)=0.
Отсюда имеем:
и, следовательно, так как а = —(х2 + х), то а, — —2, а2, з = 1.
Второе решение. Используя результат задачи 306, мы мо-
жем утверждать, что, для того чтобы наши уравнения имели хотя
бы один общий корень, необходимо и достаточно, чтобы обращалось
в нуль выражение
а2+ 1 — а • 1 (а + 1) + 1 + а3 — 2а = а3 — За + 2 =
= (а — 1) (а2 + а — 2) = (а - 1)2(а + 2).
Отсюда получаем:
ai = —2, а2, з = 1.
308. а) Пусть (х — а) (х—10)+ 1 — (х + Ь) (х + с). Полагая
в обеих частях равенства х = — Ь, получим:
' (_ ь - а) (-& - 10) + 1 = (- b + b) (— b + с) = 0.
Отсюда
(& + а)(&+ 10)= — 1.
Так как а и Ь — целые, то Ьа и & + 10 — также целые. Но
— 1 может быть представлена в виде произведения двух целых чи-
сел только одним способом: — 1 = 1 (— 1). Поэтому имеются
только две возможности:
1) & + 10 = 1, & = — 9; тогда b а — — 9 + а = — 1,
т. е. а = 8:
(х — 8)(х— 10)+ 1 = (х —9)2.
2) & + 10 = — 1, Ь — — 11; тогда &+а =—11 +а = 1,
т. е. а = 12:
(х— 12) (х— 10)+1 =(х—II)2.
б) Так как многочлен четвертой степени можно разложить или
в произведение многочлена первой степени и многочлена третьей
степени или в произведение двух многочленов второй степени, то
нам следует рассмотреть отдельна два случая:
А) х(х — а) (х — Ь) (х — с) + 1 = (х + р) (х3 + <?х2 + rx + s) (*)
(коэффициенты в правой части равенства при х в первом множите-
ле и при х3 во втором множителе оба равны 1 или оба равны — 1,
325
так как в произведении этих множителей коэффициент при х4 должен
быть равен коэффициенту при х4 в выражении х(х— а) (х — 6)Х
Х(х — с)+1, т. е. 1; равенство же х(х— а) (х — Ь) (х — с) + 1 =
= (—х+р])(—х3 + <?ix2 + fix + Si) можно привести к виду (*),
умножив оба сомножителя правой части' на — 1).
Положив в равенстве (*) последовательно х = О, х = а, х = b
и х =' с и учитывая, что 1 разлагается на множители только двумя
способами 1 = 1-1 = (—1)-(— 1), мы получим, что четыре раз-
личных числа 0 + р = р, а>± р, Ь + р и с + р (напоминаем, что
числа 0, а, Ь„ с все различны) могут иметь только два значения + 1
и — 1, что невозможно.
Б) х(х — а) (х — 6)(х— с)+1 = (,х2 + рх + <?) (х2 + гх + s).
Отсюда, как и выше, получаем, что при х = 0, х = а, х = 6и
х = с оба многочлена, как х2 + рх+р, так и x2+rx.-|- s, принимают
значения I или —1. Но квадратный трехчлен х2 + рх + q не может
принимать одно и то же значение а при трех различных значениях
х (в противном случае квадратное уравнение х2 + рх + q — а = П
имело бы три различных корня), откуда следует, что при двух из
четырех значений х — 0, х = а, х = Ь, х =с этот трехчлен прини-
мает значение 1, а при двух других — значение —1. Предположим,
что О2 + р- 0-|-р = р= 1, и пусть х = а есть то из значений х — а,
х = b и х = с, при котором этот трехчлен принимает то же самое
значение 1; в таком случае при х = b и х = с он принимает значе-
ние — 1. Итак, мы имеем:
а2 + pa + 1 = 1, Ь2 + рЬ + 1= — 1, с2 + pc + 1 = — 1.
Из а2 + ра = а (а р) = 0 следует, что а + р = О, р = — а
(ибо, по предположению, а=/=0). Таким образом, два последних ра-
венства принимают вид
Ь2 — ab = b(b — а) =—2, с2 — ас = с(с — а) =—2.
Вычитая из первого равенства второе, получим:
Ь2 — ab — с2 + ас = (Ь — с) (6 + с) — а (Ь — с) —
= (Ь — с) (Ь + с — а) = О,
откуда, так как b =#= с, имеем: & + с— а — 0, а — b + с, b — а =
= — с, с — а =; — Ь. Теперь из равенства
6(6 — а) — —Ьс = — 2
получаем следующие значения для Ь, с и а:
6=1, с = 2, а = 6 + с = 3,
х(х — а) (х — 6) (х — с) + 1 = х(х — 3) (х — 1) (х — 2)+ 1 =
«= (х2 — Зх + 1)2
и
6 = — 1, с — — 2, а = Ь + с — — 3,
х(х — а) (х — 6) (х — с) + 1 = х(х + 3) (х + 1) (х + 2)+ 1 =
„ = (х2 + Зх + 1)5
326
Аналогично, если х2 4- рх + q принимает при х = 0, и х = а
значение — 1, при х — Ь и х = с значение + 1, то мы имеем:
<? = — !, а2 + ра — 1 = — 1, b2 + pb — Г= 1, с2 + рс — 1 = 1,
откуда
р = — а, Ъ{Ь — а) = с (с — а) = 2, Ь2 — ab — с2 + ас = О,
(Ь — с)(Ь-\-с — а) = О, а = b + с, b — а = —с, —Ьс — 2.
Мы получаем, таким образом, еще две возможные системы значений
для а, b и с:
b = 2, с = — 1, а = b + с =
х(х — а) (х — Ь) (х — с) = х(х — 1) (х — 2) (х +1) + 1 =
= (х2 — х — I)2;
.6 = 1, с——2, а = Ьс = — 1,
х(х — а) (х — 6) (х — с) = х(х + 1) (х — 1) (х + 2) + 1 =
= (х2 + х — I)2.
Примечание. Другое решение этой задачи приведено в заклю-
чительной части решения задачи 309 б).
309. а) Предположим, что
(х —а,)(х —а2) (х — а3)...(х — а„) — 1 = р(х)р(х),
где р(х) и q(x) —многочлены с целыми коэффициентами, сумма сте-
пеней которых равна л; можно считать, что в обоих этих многочле-
нах старший коэффициент равен 1 (сравните с решением предыду-
щей задачи). Подставляя в это равенство значения х = аь х = а2,
х = а3,_ • • •, х = а„ и учитывая, что — 1 разлагается на два целых
множителя единственным образом: — 1 — !•(— I), мы получим, что
р(х) = 1, р(х) = — 1, или наоборот, при каждом из рассматривае-
мых значений х. Таким образом, мы видим, что сумма р(х) + <?(х)
равна нулю при х = аь а2, аз, ап. Итак, уравнение р(х) +
4-^(х)=0 имеет своими корнями Xi = aIt х2 = а2, ..., хп = ап\
отсюда следует, что многочлен р(х) + q(x) делится- на х — аь
х—а2, .. ., х — ал, а следовательно, и на произведение
(х — ai) (х — а2) ... (х — ап). Но степень уравнения р(х) + р(х) = 0,
равная наибольшей степени многочленов р(х), р(х), меньше п (п есть
степень выражения (х — а,)(х— а2)...(х— а„)—1). Отсюда сле-
дует, что р(х)+р(х) не может делиться на произведение
(х — nJ (х — о2)...(х— оп), а следовательно, разложение, существо-
вание которого мы предположили, невозможно.
б) Предположим, что
(х —oi)(x —о2)(х —а3)...(х —о„)+ 1 = р(х)р(х),
где р(х) и q(х) — многочлены с целыми коэффициентами, старшие
коэффициенты которых равны 1. Подставив в это равенство значе-
ния х = аь х = а2, х = а3, ..., х = ап, мы получим, что при каж-
дом из рассматриваемых значений х
р(х) = 1, <?(х)=1 или р(х) = — 1, р(х)= — 1.
Таким образом, р(х)—р(х) обращается в нуль при п различных
значениях х, и, следовательно, во-первых, р(х)—p(x)=0, p(x)s
327
*&q(x) (сравните с решением задачи а)) и, во-вторых, число п чет-
но: п = 2 k, где k есть степень каждого из многочленов р(х) = q(x).
Перепишем теперь наше равенство в виде
или (% — ai)(* — а2)(х-а3)...(х — a2k) =[р(х)]2 - 1,
(,x — ai)(x — a2)(x — a3)...(x — a2k) = [p(x)+ 1][р(х) — 1].
Итак, произведение двух многочленов р(х) + 1 и р(х')—1 об-
ращается в нуль при х — ai, х — а2, х = а3....х = a2k. Следова-
тельно, при каждом из этих значений х обращается в нуль хотя бы
один из сомножителей, а это значит, что или р(х) + 1, или р(х) — 1
делится на х — аь или р(х) + 1, или р(х) — 1 делится на х — а2, и
т. д. Так как многочлен степени k не может делиться на произведе-
ние больше чем k различных выражений вида х— о, и так как из
того, что многочлен степени k со старшим коэффициентом 1 делится
на произведение k выражений вида х — т, следует, что он равен
этому произведению, то мы можем утверждать, что р(х) + 1 равно
произведению k из 2k сомножителей левой части последнего равен-
ства, а р(х)— 1 равно произведению остальных k сомножителей.
Предположим, например, что
р(х) + 1 = (х — Oi)(x — а3)...(х — a2k_1),
р(х)—1 = (х — а2) (х — а4).. .(х — a2ft).
Вычитая из первого равенства второе, получим:
2 = (х — а,) (х — а3) ... (х — а2л-1) — (х — а2) (х — а4) .. (х — а2к).
Подставив сюда, например, х = а2, мы получим разложение
числа 2 в произведение k целых множителей:
2= (а2 —ai)(a2 —«з). ..(«2 —«24-1).
Так как число 2 нельзя разложить в произведение больше чем
трех различных множителей, то отсюда сразу следует, что k s: 3.
Но случай k = 3 тоже является невозможным по следующей при-
чине. Число 2 может быть разложено в произведение трех различных
сомножителей только одним единственным способом: 2 = 1 (— 1)Х
Х(—2). Предположим, что k = 3, а4 < а3 < а5. Тогда 2=(а2 —
— й]) (а2 — а3) (а2 — я5), где а2 — а, > а2 — а3 > а2 — а5, и, следова-
тельно, а2 — ai = l, о2— о3 —— 1, а2 — а5 =—2. Подставив в
формулу
2 = (х — (х — о3) (х — о5) — (х — а2) (х — а4) (х — as)
х — а4, мы придем к другому разложению 2 на три различных мно-
жителя: 2 = (о4— 01) (а4 — а3) (а4 — о5), где тоже a4 — at>a4 —
— а3>а4 — а5. Отсюда следует, что а4-~а1 = 1, а4 — а3 = — 1,
а4 — а5 = —2 и, значит, а4 = а2, что противоречит условию задачи.
Итак, возможными являются только два случая: k = 2 и k = 1.
1°. Если k х= 1, то мы имеем:
2= (% — О]) —(ха2),
откуда а2 = а, + 2, 'и, обозначая ai просто через а, получим:
(х — oj (х — а2).+ 1 = (х —- а) (х — а — 2) + 1 = (х — а — 1)*
(сравните с решением задачи 308 а)).
328
2°. Если k — 2, то имеем:
2 — (х — ах)(х — а3) — (х — а2) (х — а4),
где будем считать ах < а3, а2 < а4. Подставляя в последнее равен-
ство х = а2 и х = <г4, получим:
2 = (а2— ai) (а2— а3), а2 — ар> а2 — а3,
2 = (а4 — ах)(а4 — а3), а4 — ах > а4 — а3.
Но 2 можно разложить на два множителя, следующих в убы-
вающем порядке, только двумя способами: 2 = 2 • 1- и 2 = (— 1)Х
Х(—2). Так как, кроме того, а2— ах < а4 — ах, то мы имеем:
<22—<21= — 1, П2 — <23 = —2,
<г4 — <2| = 2, а4 — а3 — 1,
откуда, обозначая ах через а, получим:
<22 = <2 — 1, «з = <2 1, <24 — <2 4“ 2
И
(х — ах)(х — а2)(х — <г3) (х — а4) 4- 1 =
= (х — а) (х — а 4- 1) (х — а — 1) (х — а — 2) 4-1 =
= [х2 — (2а — 1)х -|- а2 4- а — I]2
(ср. с решением задачи 3086)).
310. Аналогично решению предыдущей задачи из предполагае-
мого равенства
(х — <Х])2(х—— а2)2(х— а3)2... (х — а„)24- 1 = р(х)<?(х), (*)
где р(х), q(x)—какие-то многочлены с целыми коэффициентами
(и с коэффициентами при старших членах, равными 1), следует,
что либо р(х) = 1, р(х) = 1, либо р(х) = — 1, р(х) = — 1
при каждом из значений х = <2Ь х = а2, х = а3, ..., х = ап. По-
кажем, что многочлен р(х) (и, разумеется, также и <?(х)) мо-
жет быть либо при всех значениях х = <zb х = а2, ..., х — ап
равен 1, либо при всех этих значениях х равен — 1.
В самом деле, если бы, например, многочлен р(х) при х = а,-
принимал значение 1, а при х = <а,— значение — 1, то при некото-
ром промежуточном значении х, заключенном между а,- и <2j, он
обращался бы в нуль (если график функции у — р(х) при х = а,
находится сверху от оси Ох, а при х = а,- оказывается снизу
от этой оси, то непрерывная кривая у = р(х) где-то между х = ах
и х = а,- пересекает ось Ох), что невозможно, ибо левая часть
равенства (*) всегда 1 и потому в нуль обратиться не может.
Предположим, что как р(х), так и q(x) при x=<2i, х=а2, ..., х =
= ап принимают значения 1. В таком случае как р(х)— 1, так и
q(x) — 1 обращаются в нуль при х = ах, х = а2....х = ап и, сле-
довательно р(х) — 1 и р(х) — 1 делятся на произведение (х — щ) X
Х(х — а2)...(х — а„). Так как сумма степеней многочленов р(х)
и р(х) равна степени (х — а,)2(х — а2)2... (х — а„)2 4- 1, т. е. 2п,
ТО р(х) — 1 = (X — <21) . . . (X — ап) И р(х) — 1 = (X — 221)...
(х — а„) (ср. с.решением предыдущей задачи),
329
Таким образом, мы преходим к равенству
(х — я,)2(х — я2)2... (х — а„)2+ 1 = P(x)q(x) =
.= [(х — а,) ... (х —я„) + 1][(х —я,) ... (х — я„) + 1] =
= (х —я1)2(х —я2)2... (х —я„)2 +
+ 2(х — Я;) (х — я2) ... (х —а„) + 1,
откуда
(х — Я]) (х — я2) ... (х — я„) ss О,
что неверно. Точно так же доказывается, что р(х) и q(x) не могут
принимать в точках х = аь х — я2.......х = ап значения — 1
(в этом случае мы получили бы р(х) = <?(х) = (х — aJX
Х(х —а2) ••• (х — ап) — 1).
Итак, мы видим, что разложение выражения
(х — Я|)2(х — я2)2... (х — ап)2+ 1
в произведение двух многочленов с целыми коэффициентами
невозможно.
311. Пусть многочлен Р(х) равен 7 при х = я, х = Ь, х = с
и х = d. В таком случае уравнение Р(х) —7 = 0 имеет четыре
целых корня а, Ь, с и d. Это значит, что многочлен Р{х) — 7 делит-
ся на х — а, х — Ь, х — с, х — d '), т. е.
Р(х) — 7 = (х — я) (х— &) (х — с) (х — d)p(x),
где р(х) может равняться 1.
Предположим теперь, что многочлен Р(х) принимает при целом
значении х = Л значение 14. Подставив х = А в последнее равен-
ство, мы получим:
7 = (Л-я) (Л — Ь)(А — с) (A— d)p(A),
что невозможно, так как целые числа А — а, А — Ь, А -— с и Л — d
все различны, а 7 нельзя разложить в произведение пяти множи-
телей, из которых по крайней мере четыре отличны друг от друга.'
312. Если многочлен седьмой степени Р(х). разлагается в про-
изведение двух многочленов р(х) и <?(х) с целыми коэффициента-
ми, то степень хотя бы одного из сомножителей не больше 3;
будем считать, что этим сомножителем является р(х). Если Р(х)
при семи целых значениях х принимает значение ± 1, то р(х) при
тех же значениях х тоже принимает значения ± 1 (так как
р(х)р(х) = Р(х)). Среди семи целых значений х, при которых j>(x)
принимает значения ± 1, найдутся четыре таких, при которых
р(х) принимает значение 1, или четыре таких, при которых р(х) прини-
мает значение — 1. В первом случае уравнение третьей степени
р(х) — 1=0 имеет четыре корня, во втором случае уравнение
р(х) 4-1=0 имеет четыре корня. Ни то, ни другое не может
иметь места, так как, например, в первом случае р(х) — 1 должно
«
‘) Пусть Р(х)—7 дает при делении на х — я остаток г.
Р(х)—7 = (х-я)<2(х)+г.
• Подставляя в это равенство х = а, получаем 7 — 7 = 0 + г, т. е,
г = 0, и, значит, Р(х) — 7 = (х — a)Q(x) делится на х — я.
330
было бы делиться на многочлен четвертой степени (сравните с ре-
шением задачи ЗО9а)).
313. Пусть р и q— два целых числа, одновременно четных
или нечетных. Тогда разность Р(р)—P(q) четна. Действительно,
выражение
Р(Р) — P(q) = a0(pn—qn) J-аДрп-i —9«-i) + ...
... + а„_2(р2 — q2) +an-i(p — q)
делится на четное число р — q.
В частности, при р четном разность Р(р)—Р(0) четна. Но
по условию Р(0) нечетно: следовательно, Р(р) также нечетно, а по-
тому Р(р) 0. Аналогично при р нечетном разность Р(р)—Р(1)
четна; так как по условию Р(1) нечетно, то отсюда, как и выше,
следует, что Р(р) =/= 0.
Следовательно, Р(х) не может обращаться в нуль ни при
каком целом значении х (как четном, так и нечетном), т. е. много-
член Р(х) не имеет целых корней.
314. Предположим, что уравнение Р(х) = 0 имеет рациональ-
k I k \
ный корень х= т.е. PI—-1=0. Разложим многочлен Р(х)
по степеням х — р, т. е. запишем его в виде
Р(х) = с0(х —р)" +с,(х —р)"-1 +
+ с2(х — р)’»-2+...+ сп-1(Х— р) +с„,
где со, су, с2, ..., с„— некоторые целые числа, которые нетрудно
найти, если известны аР, alt ..., ап (с0 равно старшему коэффици-
енту аэ многочлена Р(х), с, — старшему коэффициенту многочлена
Р(х)—с0(х — р)п степени п—1, с2 — старшему коэффициенту
многочлена Р(х) — с0(х— р)п — с1(х — р)п-1 степени п — 2, и т. д.).
Подставив х = р в последнее выражение для Р(х), мы получим
сп = Р(р) = ± I.
k
Подставив в это же выражение х = — и умножив результат
на 1п, мы получим:
lnP (jLj = с0 (k - pl)n + СХ1 (Й - pl)n-^ +
+ с2/2 (k— pl)n 2 + ... +’cn_1/n * (k— pZ)сп?” = 0,
/ k \
откуда следует, что если Р (-j-I — 0, то
Ст>1 — ± 1П ^—CoCk — plyi—l —
k—pl k — pl
- cxl (k — pl)n~2— ... —cn_2ln~2(k — pl)— сп_х1п~1
есть целое число. Но так как pl делится , на I, a k взаимно-просто
с I ^йначе дробь можно было бы сократ.ить\то k — pl взаимно
331
просто с I, а следовательно, k — pl взаимно просто и с 1п. Отсюда,
+ 1п
следует, что —- может быть целым числом только, если
k — pl
k — pl = ± i.
Точно так же докажем, что и k — ql = ± 1- >
Вычтя теперь равенство k — pl = ± 1 из равенства k — ql —
= ± 1, мы получим:
(р — q) I = 0, или ( р — q'jl = ±2.
Но (р — q)l > 0, так как p>q и 1> 0, а следовательно,
(р — р)/ — 2, k — pl = — 1, k — ql = 1.
Итак, если р — q > 2, то уравнение Р(х) =0 вовсе не может
иметь рациональных корней. Если же р — <7 = 2 или р — q = 1,
k
то рациональный корень -у- может существовать. При этом, скла-
дывая равенства
k — pl = — 1, k — ql = 1,
мы получаем:
k Р 4- q
2k-(p + q)l-^0, —
что и требовалось доказать.
315. а) Предположим, что наш многочлен можно разложить
на множители с целыми коэффициентами:
%2222 2л.222О 4х2218 _|_ . _ . 2220х2 + 2222 =
= (апхп + ап-ххп-' + ап_2хп~2 + ... + а0) X
X (Ьтх™ + + Ьт_2хт~2 + ... + 60),
где т + п = 2222. В таком случае а0Ь0 = 2222 и, следовательно,
из двух целых чисел а0, &о одно является четным, а другое — не-
четным. Предположим, что а0 есть четное число, а Ьо — нечетное.
Мы утверждаем, что в таком случае все коэффициенты многочлена
а„хп .+ an-iXn-' + . .. + а0 должны быть четными. Действитель-
но, предположим, что есть первый с конца нечетный коэффици-
ент этого многочлена. Коэффициент при xk в произведении
(апхп + а„-1хп-' + ... + а0) (Ьтхт + + ... + 60)
будет равен
йнЬо + Яй—1 + Qk-ibi + ... + ciobk (*)
(в случае, если k > т, эта сумма окончится членом ak-mbm). Этот
коэффициент равен соответствующему коэффициенту при xk в ис-
ходном многочлене, т. е. равен нулю, если k нечетно, и представля-
ет собой четное число, если k четно (ибо все коэффициенты много-
члена, заданного в условии задачи, кроме первого, четны, a k
гС п < 2222). Но так как, по предположению, все числа Лк-г,
а.ь-з...а0 четны, то в сумме (*) все члены, кроме первого, четны
и, следовательно, четным должно быть и произведение ал&о, что
невозможно, так как ак и Ьо нечетны.
Таким образом, мы видим, что все коэффициенты многочлена
a„xn + an-ixn-1 + ... + По должны быть четны, что противоречит
332
тому, что апЬт должно равняться единице. Следовательно, неверно
и наше предположение о возможности разложения данного много-
члена в произведение двух многочленов с целыми коэффициентами.
б) Положим х — у+1- В таком случае мы получим:
х260 д-249 д.248 +___|_ х [ =
= (!/+1)2И + (!/+ 1)249 +...+ (</+!) + ! =
= у™ 4- 251 г/2« + Cz251y™ + c32ily™ + ... + С^у + 251.
Дальше, используя то, что все, кроме первого, коэффициен-
ты полученного многочлена делятся на простое число 251
251 • 250 • 249 .. . (251 — k + 1)\ ,
ибо С,-, =----------------------------!—' и что свободный член
\ 1 2 3 ... k ]
многочлена, равный 251, не делится на 2512, мы можем почти дослов-
но повторить рассуждения решения задачи а), заменив лишь чет-
ность и нечетность коэффициентов делимостью на 251. Таким обра-
зом, мы докажем, что если бы наш многочлен разлагался в произ-
ведение двух множителей, то все коэффициенты одного из сомно-
жителей должны были бы делиться на 251, что невозможно, ибо
первый коэффициент нашего многочлена равен 1.
316. Запишем многочлены в виде
А = а0 + atx + а2х'2 4-... 4- апхп
и
* В = b0 + btx + b2x2 + ... + Ьтхт.
Так как по условию в произведении не все коэффициенты делятся
на 4, _то у обоих многочленов все коэффициенты не могут быть
четными. Следовательно, у одного из них, например у многочлена
В, не все коэффициенты четные. Допустим, что в многочлене А тоже
есть нечетные коэффициенты. Рассмотрим первый из них (имеющий
наименьший номер); пусть это будет коэффициент а,. Пусть, далее,
первый нечетный коэффициент многочлена В будет &л. Рассмотрим
коэффициент при в произведении многочленов А и В. Степень
xk+s в произведении могла получиться только из таких степеней х,
сумма показателей которых равна k 4- s; следовательно, этот коэф-
фициент равен
dobk + s + + + . . . 4" as-ibh +1 4- Osbk +
+ а«+1Ьл-1 + ... + а,+кЬ0.
В этой сумме все произведения, стоящие до члена а,Ьк, четны,
так как четны все числа а0, а,....а,_ь Также четны все произве-
дения, стоящие после сцЬь, так как &л-1, &*-2, .... Ь<<— четные
числа. Произведение же а,Ьк — число нечетное, так как и а,, и —
числа нечетные. Следовательно, и наша сумма нечетна, что противо-
речит тому, что в произведении все коэффициенты четны. Таким об-
разом, предположение, что у многочлена А есть нечетные коэффи-
циенты, неверно, и, следовательно, все коэффициенты А — четные
числа. А это и требовалось доказать.
317. Докажем, что при любом рациональном, но не целом зна-
чении х многочлен Р(х) не может быть целым числом, а значит,
не равен нулю, ибо нуль — целое число.
333
Пусть х—-—где р и q взаимно просты. Тогда
Р (х) = хп + ai*” 1 + a-zXn 2 4- ... + + ап =
Р" + Д1РП~*<? + ЛгРп~2д 2~г 4- ап-1РдП~{ + апдп _
дп
рп + д (atPn~l + ОгРп~2<7 + + an tppn~2 + апдп~')
Число рп, как и р, взаимно просто с q-, следовательно, рп 4-
'+ q(a}pn~l + ... + anqn~x) также взаимно просто с q, а значит,
и с qn. Поэтому у нас получилась несократимая дробь, которая
не может быть равна целому числу.
318. Пусть N — некоторое целое число и P{N) = М. При лю-
бом целом k
P(N + kM) — P(N) = a0[(N + kM)" — Nn] +
+ ai[(W + PAf)n-1-Af«-1] + ... + a„_1[(W + PAl) - JV]
делится на kM (ибо (N + kM)1— Nl делится на (N-^-kM)—N =
= kM), а значит, и на Af; поэтому P(N + kM) делится на М при
любом целом k.
Таким образом, если доказать, что среди значений P(N-\-kM)
(k = 0, 1, 2, ...) встречаются числа, отличные от ± М, то тем
самым будет доказано, что не все они являются простыми. Но мно-
гочлен Р(х) п-й степени принимает любое значение А, самое боль-
шее для п различных значений х (ибо иначе уравнение n-й степени
Р(х)—А =0 имело бы больше п корней). Таким образом, среди
первых 2п+1 значений P(N 4- kM) (k = 0, 1, 2, ..., 2/г) имеется
по крайней мере одно, отличное от 4- М и — М.
319. Заметим прежде всего, что каждый многочлен /i-й степени
Р(х) можно представить в виде суммы многочленов
1 - 2 3 ... /г
Л>(х) = 1, Р1(х)=х,
X (х — 1) X (х
Pi W = - ! . 2~-.....Рп U) =------
взятых с некоторыми коэффициентами:
Р(х) = ЬпРп (х) 4- &п-Л-1 (х) 4-... 4_Ь1/31 (х) 4-Ь0^о(х)-
b
если — равно старшему
/г!
и ЬпРп(х) имеют одинако-
bn-t
того,-----— равно старше-
(«—!)!
Для доказательства этого заметим, что
коэффициенту многочлена Р(х), то Р(х)
вые коэффициенты при х"; если, кроме
му коэффициенту Р(х) — ЬпРп (х), то Р(х) и ЬпР„ (х) 4- bn-iPn-i{x)
имеют одинаковые коэффициенты при хп и хп~'‘, если, кроме того,
334
-—^равно старшему коэффициенту многочлена Р(х)—ЬпРп(х)—
— bn-lPn-l(x), ТО Р(х) И Ь„Рп(Х) + &п_|Р„_1(х) + Ьп-2Рп~2(х)
имеют одинаковые коэффициенты при хп, х'1-1 и хп~2, и т. д.; таким
образом, можно определить b„, b„-i bi, b0 так, чтобы много-
члены Р(х) и Ь„Р„(х) + -I- ... + &1Л(х) + Ь0Ра(х) пол-
ностью совпадали.
Пусть теперь многочлен п-й степени Р(х) таков, что Р(0),
Р(1), .... Р(п)—целые числа. Как и всякий многочлен, его можно
представить в виде
Р(х) — Ь0Ра(х) -|- biP^(x) -|- Ь2Р 2 (х) + ... + Ь „Р „ (х).
Заметим, что
Р,(0)=Р2(0)=... = Ри(0) =
==Р2(1)= ^(1)= ... =РП(1)== Рз(2)= ... = Р„(2)= ... -
... = Pn-i(n — 2) = Рп(п — 2) = Рп(п~ 1) = О,
Ро(О) = Pi(l) = Р2(2) = ... = Pn-i(n- 1) = Р„(п) = 1.
Поэтому
Р(0) = &0Р0(0), откуда &о = /’(О);
Р(1) = Ь0Р0( 1) + feiPtfl), откуда &, = Р(1) — й0Л>(1);
Р(2)=6оР0(2)+Ь1Р,(2)+&2Р2(2),
откуда
Ь2 = Р(2) -&оРо(2) -6^42);
Р(п) = Ь0Р„(п) + biP^n) + ... + &„-iPn_i(n) + ЪпРп(п),
откуда Ь„ = Р(п)— b0P0(n)— b^fn)— ... — &n_tP„_i(n).
Таким образом, все коэффициенты b0, bt, b2.... Ьп являются
целыми числами.
320. а) Из решения задачи 319 следует, что подобный многочлен
можно представить в виде суммы многочленов Pt>(x), Pt(x),_ ...
..., Рп (х) с ц е л ы м и коэффициентами Отсюда и из того, что много-
члены Р0(х), РДх), ..., Рп (х) принимают целые значения при каж-
дом целом х (см. задачу.75а)), следует утверждение задачи.
б) Если многочлен Р(х) = а„хп -f- an_iXn_I + ап~2Хп~'2 + ...
... + atx + а0 принимает целые значения при х = k, k + 1, k +2, ...
..., k+n, то многочлен Q(x) = Л(х + k) = ап (х -j- k) n+ a„_1(x +
+ k)n-1 + • • • + «i(x + й) + a0 принимает целые значения при х = 0,
1, 2, 3, .... п. В силу задачи а) отсюда следует, что Q(x) принимает
целые значения при всех целых х. А отсюда мы заключаем, что и
многочлен Р(х) — Q(x — k) принимает целые значения при всех це-
лых х.
в) Пусть многочлен Р(х) = апхп + an_txn-1 + ... + а^х а0
принимает целые значения при х = 0, 1, 4, 9, .... п2. Тогда много-
член Q(x) = Р(х2) = а„(х2)" + а„-,(х2)’1-1 + ...+aixz 4-а0 сте-
пени 2п принимает целые значения при 2п + 1 последовательных зна-
чениях х = —п, —(л—1), —(п — 2), ,,— 1, 0, 1, .>, л—1, л.
835
В самом деле, очевидно, Q(0)=P(0), Q(l) = Q(— 1) = P(l)',
Q(2)=Q(-2)=P(4), Q(3)=Q(-3)=P(9), .... Q(n)=Q(-n)==
-= P(n2), а все эти числа по условию являются целыми. Следова-
тельно, В' силу задачи б) многочлен Q(x) принимает целые значения
при каждом целом значении х. А это и означает, что P(k2) = Q(k)
при любом целом k есть число целое.
_ х(х— 1)
Примером может служить многочлен Р(х) =——для которого
х2(х2 — 1) х2(х — 1)(х+0
Q (х) = Р (х2) = -----L - ------- - --
12 ~ 12
(х+ 2) (х+ 1) х (х — 1) (х-j- 1)х(х—1)
— 2 1 О О И 1-2-3
1 2 • 3 • 4
321. а) Используя формулу Муавра и формулу бинома Ньюто-
на, будем иметь:
cos 5а + i sin 5а = (cos а + i sin а)5 =
= cos5 а + 5 cos4 а i sin а + 10cos3 a(i sin a)2 +
4- 10 cos2 a(i sin a)3 + 5 cos a(i sin a)4 4- (i sin a)5 =
= (cos5 a — 10 cos3 a sin2 a + 5 cos a sin4 a) 4-
+ i(5 cos4a sin a — 10 cos2 a sin3 a -j- sin5 a).
Приравнивая действительные и мнимые части слева и справа, полу-
чаем требуемые формулы.
б) Аналогично решению задачи а) имеем:
cos па + i sin па = (cos а + i sin a)n —
— cos" a + cos"-1 ai sin a 4- C2 cos"-2 a (i sin a)2 4-
+ C3 cos"-3 a (i sin a)3 + cos"-4 a (i sin a)4
— (cos" a — C2 cos"-2 a sin2 a + C4 cosn—4 a sin4 a — ...) 4-
+ i a sin a — C3 cos"-3 a sin3 a 4- ...).
Отсюда и вытекают нужные формулы.
322. Согласно формулам задачи 321 б) имеем:
' sin 6a 6cos6asina — 20 cos3 a sin3 a 4-6 cos a sin5a
® a — cos 6a — cos6 a — 15 cos4 a sin2 a 4- 15 cos2 a sin4 a — sin6 a’
Разделив числитель и знаменатель последней дроби на cos3 a,
получаем искомую формулу:
„ 6 tg a — 20 tg3 a 4- 6 tg5 a
ig 6a - j _ 15 tg2 a + is tg4 a — tg6 a ‘
1
323. Уравнение x4-~ = 2 cos a перепишем в виде
x2 4- 1 = 2x cos a, или x2 — 2x cos a 4- 1 = 0.
Значит, __________
x = cos a ± pcos2 a — 1 = cos a ±' sin a.
336
Отсюда вытекает, что
хп = cos п а ± i sin п а;
1 1 _ . .
—— =----------г-т-:——- == cos па + I sin па.
хп cos па + i sin па т
После сложения получим:
хп 4—- =2cos п а.
х'1
S24. Рассмотрим сумму
[cos ф + i sin <р] + [cos (<р + а) + i sin (q> + а) ] +
+ [cos (ср + 2а)-И sin(<p + 2а) ]+ ... + [cos (ср + па) 4-i sin (ср 4- па)].
Наша задача сводится к вычислению коэффициентов при мнимой и
действительной частях этой суммы. Обозначая cos ф + i sin ф через
а и cos а + i sin а через х и применяя формулу для произведения
комплексных чисел и формулу Муавра, найдем, что рассматриваемая
сумма равна
а + ах + ах2 4- • • • 4- ахп =
_ ахп+* — a cos (и + 1) а + i sin (n + 1) а — 1
- = (cos ф + i sin ф)-------cos а 4-i sin а — 1-------=
[(cos (n + 1) a — 1) + i sin (n + 1) a]
= (cos Ф + i sinФ)---------[(c-3s a— I) H-f siHa]-------=
— 2 sin2 —2— a + 2i sin —2— a cos —2— a
= (cos ф + i sin ф)--------------------------------------=
— 2 sin2 -y 4- 2i sin у cos -y
n 4- • Г n 4- 1 , «4-1 ]
2i sin —2— a cos —2— a "r * sln —2— a
= (cos Ф 4" ‘ sin <₽) -----------—;---------------4----- =
а Г a al
2i sin -y cos у 4- । sin у
. «4-1
sin —g— a
—----------— (cos ф 4- ‘ sin ф) X
siny
a \
2 J
( n + 1 , . . n 4~ 1 \ I ®
I cos —— a 4- i sin —2— a 11 cos — — i sin
X ------------------------------------------------
cos2 — 4- sin2 -y
sin-y-af / nx / n у
-------— cos I ф 4- -у I a 4- ( sin I ф -f- -у a I
siny L \ J \ /
22 Д. О, Шклярский и др, 337
(здесь снова используется формула умножения комплексных чисел,
а а / а \ [ а \Х
а также то, что cos —— i sin— = cost----------I 4- i sin I — II.
Отсюда сразу следуют требуемые формулы.
1 + cos 2х
325. Воспользуемся тем, что cos2x = ------7,---• Отсюда, исполь-
зуя результат предыдущей задачи, получим:
cos2 а + cos2 2а + • • + cos2 па =
1
= -у [cos 2а + cos 4а + ... + cos 2па + ”1 =
1 Esin (n + 1) а cos па J п sin (п + 1) а cos па и — 1
~ 2 [ sin а + 2 ~ 2 sin а + 2 ‘
А так как sin2x = 1 — cos2x, то
sin2a + sin2 2a + ... + sin2 na =
sin (n 4- 1) a cos na n — 1 n 4- 1 sin (n + 1) a cos na
~n 2 sin a ~~ 2 — 2 2 sin a
326. Требуется вычислить действительную часть и коэффициент
при мнимой части суммы
(cos a 4- ‘ sin a) 4- С„ (cos 2a + i sin 2a) 4-
4- (cos 3a + i sin 3a) 4- ... 4" (cos (n + 1) a 4-1 sin (n 4- 1) a).
Обозначая cos a 4-i sin a через x и используя формулу Муавра
и формулу бинома Ньютона, преобразуем эту сумму следующим
образом:
х + С,1/2 + С& 4- • • • 4- Хп+1 = х (х + 1 )п =
= (cos a 4- ‘ sin a) (cos a + 1 + i sin a)” =
/ a a a
= (cos a + i sin a) 12 cos2 4- 2/ cos-y sin ~
_ _ a ! na , na \
= 2 cos — (cos a 4- i sin a) I cos —% 4- i sin —
n a I n 4- 2 n 4- 2 \
= 2 cos -y cos —g— a 4-' sin —— a .
Отсюда следует," что
cos a 4~ cos 2a + On cos 3a + cos (n + 1) a =
„„ „ a n 4- 2
= 2 cos -y cos —2~ a,
sin «4CJ, sin 2a 4- C2n sin 3a ф- ... 4- sin (n-J- 1)« =
„„ „a n 4- 2
= 2 cos -y sin —g— a.
333
327. Воспользуемся формулой
sin A sin В = -у- [cos (4 — В) — соз (4 + В)].
Отсюда следует, что нашу сумму можно представить в виде
1 Г (т — п) п 2(т— п) л 3(т— п) л
— cos ------р----+ cos--------р---+ cos---------р------+ • ••
(р—l)(zn— л) л! 1 Г (zn + п) л
... + cos---------------j - — |_cos----------+
2 (т + п) л 3 (т + п) л (р—1) (т + zt) л'
+ cos-----------4- cos----------4- ... + cos---------------
Но сумма
kn 2/гл 3+ (р — I ) /гл
cos — + cos — + соз — + ... + COS------------
равна р— 1, если k делится на 2р (в этом случае каждое слагаемое
суммы равно 1); в случае же, когда k не делится на 2р, эта сумма,
в силу результата задачи 324, равна
pkn (р — 1) kn
sin cos
kn
sin2?
I л /гл\
\k 2 ~ 2р)
- 1 = sin ------------ 1
если k нечетно,
если k четно.
Отметим еще, что оба числа т + п и т—п будут четны или нечетны
одновременно; в частности, если т 4- п или т — п делится на 2р,
то и т 4 п, и т — п — четные числа. Отсюда вытекает равенство,
требуемое условием задачи.
328. Рассмотрим уравнение x2n+I— 1 — 0, корни которого:
2л 2л 4л 4л
!- cos 27+7 + Zsln 2Г=Н’ COS2T+1 + l’sin27+7’ •••
4пп , . 4пп
C0S2^Ti+1'Sln гГП-
Так как коэффициент при х2п в уравнении равен нулю, то сумма
всех этих корней равна нулю: .
[2л 4л , 4лп 1 ,
1 + cos 2^Tl + cos 27+7 + • • • + cos 27+7] +
[2л 4л 4пл I
sln27+7 + sin 2п+~1 + • • • + si"27+7] = °-
Следовательно, выражение в каждой скобке равно нулю, откуда,
в частности,
2л , 4л 4пл
cos 27+7 +cosТТЛ ' ••• +С05 27+7 = “к
22*
339
Но
и т.
2л 4/гл
cos 2ЙТТ = cos 2/г + 1’
д., значит,
о Г _2л, . 4л
2ICOS 2/г+ 1 +cos2n+ 1
4л (4п — 2) п
Cos 2п + 1 = cos 2/i + 1 ’
, 2пл
+ --.+СО3 2МП
т. е.
2л 4л 2пл 1
Cos 2/г + 1 + cos 2/г + 1 + • • • + Cos 2/г + 1 = ~
sin (- 2ИТ1)
Примечание. Можно также решить эту задачу, исходя из
формул задачи 324.
329. а) В силу результата задачи 3216) имеем:
sin (2п + 1) а = Cij/i+l U — sin2 а)” s'n а —
— Cfn+1 (1 — sin2 а)"-1 sin3 а+ ..•+(— l)n sin2n+’ а.
л 2л . пл
Отсюда вытекает, что числа 0, sin^ р sin р • • •> sln 2/г + 1 ’
л . { 2л \ . 2л
2п + 1 ’ SIn Н 2п + 1 — sin 2п+1 ’ ’ ’'
, ( пл \ , Пл
... , sin ( — 2/г + J j = — sm 2^-qrr
являются корнями такого уравнения (2п + I) -й степени:
С2п+1 (1 - *2)П * - С32„+1 (1 - х2)"-1 х3 +...+(- 1)" х2^ = 0.
л 2л
Следовательно, числа sin2^ _р-|, sin2 + р
являются корнями уравнения /г-степени:
sin2
«л
2/1+ 1
C‘n+1 (1 - х)" - C32n+1 (1 - х)"-1 х +...+(- 1)" х" = 0.
б) Заменим в формуле задачи 3216) п на 2/г + I и запишем
ее в следующем виде:
sin (2/г + 1) а = sin2n+1 а (c£n+1 ctg2n а — С?„+1 ctg2n~2 а +
+ C52n+ie‘g2n-4«-.- )•
_ л 2л Зл пл
Отсюда следует, что при а =2^+j> 2Г+1 ’ 2Й++’”-’ 2^++
имеет место равенство
C2n+1 ctg2" « - C2n+1 Ctg2”—2 а + c|„+1 ctg2n-4 а - ... = 0,
т. е. что числа ctg2^+j ctS 2п+1 являют<:я корнями
340
следующего уравнения n-й степени:
С1 Гп — С3 Гп~ 1 4-Г5 Гп—2 _ —Л
и2п+1х с2п+1х 4-<-2п+1х
330. а) Сумма корней уравнения n-й степени
/>3 /^5
„ 2п+1 n—1 . 2n+i п—2
х — Г1 х -т Г1 х
с2п+1 °2п+1
= 0
(см. решение задачи 229 6)) равна коэффициенту при хп~1, взятому
с обратным знаком, т. е.
ctg2 2п + 1 + ctg2 2М~1 + ctg22T="i + • • • + cfg2 2Г+“1 =
/^3
_ ^2п+1 ft(2n— 1)
C2n+1 3
6) Так как cosec2 a = ctg2 a + 1, то из формулы задачи а)
следует
„ л „ 2л ,3л
cosec- + СО5ес22ГП + cosec 2^Н + ' ’ '
пл п (2п—1) 2п(п-|-1)
• • • + cosec 2МП =-----3----+ п =-------3----•
п 2л
331. а) Первое решение. Числа sin2 sin22^-_j_ р •••
пл
•••’ s‘n22n + 1 являются корнями уравнения л-й степени, полу-
ченного в решении задачи 329а). Коэффициент при старшем члене
хп этого уравнения равен (—1)п[С12п+1 4- С|п+1 . + C^+i1 + *]
Но сумма в квадратных скобках составляет половину от общей сум-
мы биномиальных коэффициентов 14-С|п_(.1+С2П_|_14-.. •+С'|”_|_1 + 1,
равной, как известно, (1 + l)2n+1 = 22n+1; следовательно, коэффи-
циент при хп в нашем уравнении равен (—1)п22п. Далее, свобод-
ный член этого уравнения есть = 2п + 1. Но произведение
корней уравнения п-й степени равно свободному члену приведенно-
го уравнения (уравнения с коэффициентом при старшем члене,
равным единице), умноженному на (—1)п, т. е. равно свободному
члену, умноженному на (—1)" и деленному на коэффициент при
старшем члене. Отсюда имеем:
, . „ я . „ 2л , лп „ 2п + 1
(—1) stf2/] + j sin 2rt 1 s,n 2n + l=H) 22n
и, следовательно,
л . 2л . пл Д/2/i + 1
®1П 2/г + 1 Sln 2п + I • ’ Sln 2п + 1 = "
341
Аналогично можно доказать, что
л . 2л . (п — 1) л Уп
s,n 2Н- sm 27 • • • SIn —2п~~ = 7=1-
Второе решение. Корни уравнения х2п — 1 = О равны
л , л 2л 2л
h -1, COS —+<sin—, cos—+(Sin—,
Зл Зл (2n—1)л (2п—1)л
cos V + i sin —, .... cos--------4- i sin -— -.
f L r t t L • 4
Поэтому имеем:
x2n — 1 = (x — 1) (x 4- 1) [x. — cos — / sin j X
( 2л 2л \ I (n —1)л (n—1)л\
X x — cos — — i sin — ... x — cos -------— i sin------ X
\ '• **' 1 \ '* I
X x — cos
(2n — 1) л_
n ~
. . (2n —l)n’
l sin--------
n
(2n — k) л kn (2n — k) n kn
Ho cos----------= cos —, sm -------------= — sin —; отсюда сле-
дует, что
/ л л \ / (2п—1)л (2/г — 1)л\
х — cos — — i sm — х — cos--------------- — i sin--------- =
I n n I I II И I
= x2 — 2x cos + 1,
/ 2л 2л \ I (2n — 2) л (2n — 2) л\
x — cos — — / sin x — cos--------------- — i sin--------- —-
I n n I i n n I
„ „ 2л
— x2 — 2x cos — + 1,
' ( n — 1) Л (// —
x — cos--------------— i sin---------
n n
х — cos----------
ii
. . (n + 1) Л\ (n— l)n
i sin-7----I = x2 — 2x cos ------
и
Поэтому разложение многочлена x2n — 1 на множители можно
переписать так:
х2п — 1 = (х2 — 1) [ х2 — 2х cos
x2 — 2x cos
(n — 1)л
x2 — 2x cos —-----
n
342
Отсюда
г2" — I
= X2"-2 + X2”-4 + ... + х2 + 1 =
— (х'2 ~ 2х cos — + 1 j (х2 — 2х cos п + 1 j X ...
/ „ (п — 1) л \
... X I х2 — 2х cos ---+ 1 I.
Положив здесь х = 1 и воспользовавшись тем, что 2 — 2 cos а =
„ а
= 4 sin2—, получим:
п-i л „ 2л . (л — 1) л
п = 4 sin2 2^ sin2 ...sin2——,
откуда вытекает, что
л 2л (л — 1) л фп
sin 27 sin 27 sin 2л = ^=T-
Аналогично можно доказать, что
л 2л . пл yr2n + 1
sin •••sln2T+'l = _.2»
б) Требуемый результат может быть получен совершенно ана-
логично первому или второму решению задачи а); однако мы здесь
не будем повторять этих решений, а сразу выведем нужные форму-
лы из формул задачи а).
Так как
л . 2лл . Зл . (2п—2)л
sln 2n + 1 = s,n 2л + 1 ’ s,n 2л + 1 = sin 2n + 1 ’
5л . (2л — 4) л
s,n2n+7 = s,n "2п+Г: •••>
ТО
2.1 . 4л . 6л . 2мл
sln 2л 4- 1 Sln 2п + 1 sln 2л + 1 • • • sln 2л + 1 =
. л . 2л . Зл пл 1^2/1 + 1
Sln 27+7 Sln 27+7 Sln 27+7 • • • Sln 2/г + 1 = 2”
(см. а)). Разделив эту формулу почленно на З’п277-73'п 27+7
пл У2п + i
... sin । — и воспользовавшись тем, что
2л л л . 4л
Sln 27+7 = 2 Sln 2л + 1 cos 2n + 1 ’ Sln 2/г + I =
, 2л 2л 2лл „ , пл пл
= 2 s,n 2л + 1 cos 2л + Р • ••* sin 2л + 1 = 2 ®1п 2л + 1 cos 2л + 1’
343
получаем:
л 2л Зл лл 1
cos 2и + 1 cos 2л-f-1 cos 2и1 cos2«+ 1 = 2" ’
Аналогично имеем:
I л 2л (л — 1)л\/. л 2л (п—1)л\
(cos 27cos 2л"‘*'СО5'—~ Д81п 2?s,n 2? '2n J °
1 . л . 2л . (л — 1) л
= —sm—sin —...sin--------------.
„ л . (n — 1)л . 2л (n — 2) л л
Ho sin—- = sin-------, sin—= sin——-------, .... sm~9* = l;
П П /I Г1 £
поэтому
. л . 2л (л — 1) л
при n — 2k + 1 нечетном sin— sm— ... sin------=
I . л . 2л kn \2 f У 2k + 1 \s n
= ^m 2* + 1 sln 2k + 1 ' * • sln 2k + 1) = l J ~2^’’
n, . л . 2л . (л — l)n
при n = 2k четном sin*— sin — ... sin------=
r n n n
I . Я . 2л . (А— 1)л\2 I Vk V n
-- (шп 2k sin 2A ... sin 2k j — [ 2a-i I -
(см. задачу а)). Отсюда получаем:
n
л 2л (л — 1)л 1 2“ 1 У п
2п cos 2п "• cos 2п = 2ft—1 Уп ~ "JF-i'
2n—1
Примечание. Разделив формулы задач 331а) и б) одну на
другую, получим:
. л , 2л лл --
tg2n+ 1 tg 2л+ 1 ••• tg 2л + 1 “ У2п+ 1;
л 2л (л — 1) л
tg 2^ tgF7 IF" ='
Впрочем, второе из этих равенств совершенно очевидно, так как
kn (п — k) п kn kn
tg2?tg----2^--= tg F Ctg F = 1 п₽и k==i- 2- "-1 и
tg T"= 1. Из этого равенства и второй формулы задачи 331а) мож-
, , , л 2л (л — 1) л
но было бы просто вывести формулу cos-^ cos 2^- ... cos---=
Уп
2 «—1
Можно также получить эти формулы аналогично' первому ре-
шению задачи 331а).
344
332. Покажем, что для любого положительного угла, меньшего
л
~2'
sin а < а < tg а.
Имеем (рис. 39):
о -J2 •
‘-’ДАОВ ~ 2 slna>
____1_
•^сект АОВ~~ 2 а’
1
$ААОС ~ 2
(радиус круга принимаем равным еди-
нице, углы измеряются в радианах).
Но так как S&aob Scbetaob
<Saaoc, to sina<a<tga.
Из того, что sin a < a < tg a,
следует, что ctg a < — < cosec a. Поэтому из формул задач 330а)
и б) вытекает:
п(2п — 1)
3
= ctg2 2TTI + 2ТТГ +ctg2 2ТТ1 + • • • + ct§2 Йп <
/2гг + IV /2лЦ- I у /2п+ 1\2 , рЦ-г 1\2
л 2л
< cosec2 2—у + cosec2 +
Зп пл 2п (п + 1)
+cosec2 2ГП + • • +cosec 2ГП = 3 •
Разделив все члены последнего двойного неравенства на
(2л + I)2
—^5-----, будем иметь:
2п 2п — 1 л2
2м -j^ 1 2м 1 6
2п 2п + 2 л2 / 1 \/ 1 '1 л2
<2л+ Г2/? + 1' 6 ==(1“2л + 1Д1+2п +
что и требовалось доказать.
333. а) Предположим, что точка Л! взята на дуге Д|ДП окруж-
ности (рис. 40). Обозначим дугу МА{ через а; в таком случае дуги
348
МАг, Л1Д3.....Л1ЛП соответственно равны
, 2л
a+V
4л
п
, 2(п— 1) л
а 4-------,
Но длина хорды АВ окружности радиуса /? равна 2Psin~2-
(это можно легко усмотреть из равнобедренного треугольника АОВ~,
Рис. 42.
где О — центр окружности). Отсюда видно, что интересующая нас
сумма равна
Г а /а л \ [.а 2л \
4Р2 sin2 sin21-j- + — I + sin21 -у + ”)+••
346
1 — cos 2х
известной формулой sin2x=--------<5----, получим, что это выражение
равно
S = — cos а + cos [а
4л
п
/ 2(п —
... + cos I а +-------
Но по формуле задачи 324 имеем:
/ 2л \ [ 2 (л — 1) л'
cos а + cos а 4- — 4- ... 4- cos а 4------------
\ 1 п ‘ ‘ \ 1 п
{ (п — I) л'
sin л cos I а +-------~-----
= 0,
sin---
п
следовательно, S = -j-. Отсюда и вытекает утверждение задачи.
Примечание. При п = 2т четном (рис. 41) утверждение за-
дачи является очевидным, так как, в силу теоремы Пифагора,
МА2 + MA2m+i = МА2 + MAl+2 = ... = МА2т + МА2т = 4W.
'б) Пусть /41В|, А2В2, ..А „ Вп — перпендикуляры, опущенные
из точек Д|, Д2, ..., Ап на прямую ОМ (рис. 42, а). В таком случае
по известной теореме имеем:
МAl = ЛЮ2 + 0A-h—2M0- OBh Р у- /?2 — 2/ OBh
(k = 1, 2....и), где отрезки ОВк берутся со знаками 4* или —
в зависимости от того, расположена ли точка Вк на луче ОМ или
вне его. Следовательно,
МА2 4* МА2 4- • • + МА' =
= л(/2 4- R2) - 2l(OBt + ОВ2 4- ... 4- ОВп).
Но если zL М О А} = а, то
. I 2л \
ОВХ = ОА j cos Z. AjOM = % cos а, ОВг = /? cos I а, +
а+”п~ ’ •••• 05п = Я cos I а 4----й---~1.
А так как в решении задачи а) было показано, что
/ 2л \ / 2 (п — 1) л\
cos а 4- cos I а 4“ + • • • 4“ cos I а 4----I = 0,
то OBi 4* ОВ2 4- ... 4- ОВп = 0; отсюда и вытекает утверждение
задачи.
347
Примечание, При п = 2m четном (рис. 42, б), утверждение
задачи доказывается геометрически: в этом случае 0В-, + 0Bm+i —
= ОВ^ ОВт^.2— 0Вт oBjm = 0.
в) Пусть Л!, — проекция точки М на плоскость п-угольника
(рис. 43). В таком случае имеем/И,4^ = MtA^ -|- ММ? (fe=l, 2, ...
..п) и, следовательно,
МА? + МА1^г ... + МА2 =
= MtA% + MtAj + ... + MiA2 + п-ММ*.
Но MjA2 + MtA% + ... + Л41-Д2 = п (/<2 + ОМ2) (см. задачу б)) и
/2 = ОМ2 =0M^~MLM2. Отсюда и вытекает утверждение задачи.
334. а) Утверждение задачи сразу следует из теоремы задачи
333а), если учесть, что при п четном четные (и нечетные) вершины
n-угольника сами служат вершинами вписанных в окружность пра-
п
вильных -^--угольников.
б) Пусть n = 2m + l. Из решения задачи 333а) выводим, что
достаточно доказать равенство между собой следующих сумм:
а (а 2л \ /а 4л \
S1 = sm-j-+ sin 2 + ^Г+\| + 81П (V + ^T+Tj+--
. ( a. 2mn \
... -Hin + 2^+7|
348
о . ( а , л \ , . ( а Зл \
Sa -зпЦ 2 +2m + jj + sin + 2^+1]+ •••
. . ( а
... + sin I ~2
Но, согласно задаче 324, имеем:
. (т + I) л . / а тя \
Sln-2^+7" sin "Г + 2^+1
Si = -------------д------------
sin 2m + 1
(2m — 1 j n\
2m 4- 1 j'
тл . I a , л , (m — 1) n\
. sin 2m + 1 Sln I 2 + 2m + I ~ 2m + 1 /
S2 = ’ „ = Sj
sin 2m + 1
что и доказывает теорему.
335. а) В силу задачи 333 а) сумма квадратов расстояний от
точки окружности, описанной около правильного n-угольника, до
всех его вершин равна 2л/?2. Предполагая, что М совпадает с A h
получаем, что сумма всех сторон и диагоналей л-угольника, выходя-
щих из одной вершины, равна 2л/?2. Если умножить эту сумму на п
(число вершин л-угольника), то мы получим удвоенную сумму всех
сторон и диагоналей л-угольника (так как каждая сторона или диа-
гональ имеет два конца, то она будет фигурировать в такой сумме
дважды). Отсюда искомая сумма равна -^-2nR.2 =
б) Сумма всех сторон и диагоналей правильного многоугольни-
ка, выходящих из одной вершины At, равна
л 4л
2/? sin — + sin — 4- ... + sin
. л (п — 1) л
sm т sin —Тп------ я
=
sin27
(ср. задачу 3346)). Умножая эту сумму на л и деля пополам, полу-
л
чаем требуемый результат: wctgg^.
в) Произведение всех сторон и всех диагоналей «-угольника,
выходящих из одной вершины, очевидно, равно
2n~ ipn—1 sin — sin — Sjn —--------_ 2ti—1 —2—
n n n 2n—-1
(см. задачу 331a)). Возводя это произведение в п-ю степень и из-
влекая затем квадратный корень, получаем требуемый результат.
336,. Вычислим сумму 50-х степеней всех сторон и всех диагона-
лей 100-угольника, выходящих из одной вершины А[. Задача сводится
349
к нахождению суммы
! л \60 7 2л \50 I 99л\Б0
2 = f 27? sin-j-QQ 1 + I 2R sin-jpg I + ... + I 2R sm j^q j
(сравните с решением задачи 333a)). Таким образом, нам надо сум-
мировать 50-е степени синусов некоторых углов. Но
„ /(cos а + i sin а)— (cos а — isina)\60
sinboa=^------------------------------------j =
\ X ) 1 I 1 \50
— __оьо = — 2й v — x I ’
где обозначено cos a + I sin a = x; в таком случае cos a — i sin a =
1
= —. Следовательно,
— 2C1O cos 48a + 2C?0 cos 46a — 2C2q.cos 2a + C|q)
[здесь использовано то, что xk =(cos ka + i sin Aa) + (cos ka —
— i sin ka) = 2 cos £u].
Итак, сумма 2 может быть переписана следующим образом;
2 = — R60
/ л 2л 99л\
2 (cos 50 jjjjj + cos 50 jjjjj + ... + cos50jjjq j —
л । / л 2л 99л \
— 2C50 ^eos 48 Too + cos 48LOO + • • • + cos 48foo ] +
+ 2C5o (cos 46Too +cos 46 [to + • • • + cOS 46To5") ~
+ 2^50 ^c0s 2 ] 00 + cos 100 + • • • + cos 2 100 j 99C50j ~
= _ R50 [2S1 - 2C'OS2 + 2C520s3 - ... + 2C2qS25 - 99C25],
35e
где через sb s2, .... s25 обозначены суммы, стоящие в круглых скоб-
ках, Но из формулы задачи 324 сразу следует, что si = S) = ... =
= s25 — —1. Следовательно, имеем:
S = 7?60 (2 - 2С‘3 + 2с|0 - ... + 2С5?04 + 99Cjq) =
= ^°(1-С1о + С50-С5о+---+С50-С5о + С52в-...
• • • + С50 - С.50 + 1 + ЮОС 25) =
= RM [(I — I)500 + loocfl] = lOOC^/?50.
Отсюда сразу получаем, что сумма 50-х степеней всех сторон
и всех диагоналей 100-угольника равна
100S „ = „ 5000-501
2 — бОООС5о/?5 = (251)2
-г-Т
г
337. Так как |г| = |г| = |— г| = |— г| и г + у-,| = г +
1
— г—-=- , то достаточно рассмотреть лишь
г
чисел г, г,— г и —г, которое лежит в первой четверти. Если |г|
гает наибольшего возможного значения, то
Поэтому достаточно найти те г, модуль
большим возможным; при этом
|г|> Пусть аргумент <р чис-
Л т
ла г нам задан; 0 + ф + jj". i°r"
да из рис. 44 имеем (напомним,
то из
дости-
Y7j-~ наименьшег°-
которых является наи-
что | г + — J = а; ниже обозна-
чено |z | = г):
+ = г2 + 2 cos 2<р =
1 Рис. 44.
= л2 + 72 —2 + 4 cos2 ф =
1 V
г — — I +4 cos2 ф.
1
Так как, согласно нашему предположению, ~ , то с ростом г
1 / 1 \2
растет и разность г—и наоборот. Но I г — — 1 = а2 — 4соэ2ф =+
п I 1 \« 1
=+а2; при ф=~2" имеем г—— 1 = а2. При этом г——~а, г =
=у(а+ Уа2 + 4)-
351
Соответственно этому наибольшее значение |г| =^,а-А- 4)
а наименьшее
достигается при г — %
= -у- (рЛа2 + 4 — а) — при г = — — ()Ла2 + 4 — а)-
338. Ясно, что три комплексных числа 1 (= l + i-0==cos0 +
, Zsin0) -1 + V3i ,ono , . ..
ч“ i sin u), 2 '
— 120°) + tsin(—
них
cos 120° + i sin 120°) и --------g----
таковы, что аргументы каждых
на 120°, а сумма всех чисел равна
нулю — поэтому заменить в усло-
вии задачи величину 120° боль-
шей заведомо невозможно. Пусть
теперь |0( — 0,| < 120°, где I,
! = 1, 2....... п и i ¥= j (здесь
0i, 02... 0n — аргументы наших
комплексных чисел; ясно, что если
одно из этих чисел равно нулю
и, следовательно, не имеет одно-
значно определенного аргумента,
то это число можно просто отки-
нуть); докажем, что в этом случае
равенство Zi+z2+.. .-f-z„=O иметь
места не может. В самом де-
ле, из сделанного предположения
вытекает, что отвечающие комп-
лексным ЧИСЛаМ Z], z2, ..., z„ точ-
ки Ль А2, ..., Ап комплексной пло-
скости с полярными координатами
(Г|, 0t), (г2, 02).... (г„, 0„)
принадлежат некоторому меньшему
120° углу POQ, ограниченному
лучами 0 == (J* и 0 = 0/, где Аь
и Ai — «крайние» из наших точек,
с «крайними» значениями аргумен-
120°))
разнятся в точности
(= COS (
двух из
т. е. отвечающие числам zft и z;
тов (рис. 45). Пусть луч OR, отвечающий значению 0 = 0о поляр-
ного угла,— это биссектриса <zPOQ, ,а, z0 = cos 0n4-i sin 0О—
комплексное число единичного модуля, изображаемое точкой Ао это-
, г1
го луча. Так как числа г. — —— [r[cos(0 — 00) + isin(0 — 0o)J,
zo
, .... z„—— имеют те же модули rlt гг, ..гп, что и числа
2 *о п го
Z|, z2, .. ., z„ , но аргументы 0, — 0О, 02 — 0о, •t‘0n —0о вместо
аргументов 0j, 02.. 0п чисел zb z2 .. .„ zn. то отвечающие числам
г’, г'2, ..., гп точки А'2, .... ^„комплексной плоскости полу-
чаются из точек At, Л2....А„ поворотом вокруг О на угол 0О по
часовой стрелке. Но отсюда следует, что все эти точки принад-
лежат полученному из POQ указанным поворотом углу P'OQ' <
< 120°, биссектриса OR' которого совпадает с осью Ох веществен-
ных чисел. А отсюда, в свою очередь, вытекает, что вещественные
части а,, а2.......ап чисел г1 = al -|- ib^, г2 = а2 + ib^, •••
352
, zn — an ~ribn асе положительны; поэтому сумма
z'j + 4 + • • • + z'n ~(a\-v ib\) + («2 + ib2~) + • • + «г + i&n) «=
“(«; + «2+-+<) + ‘'(i'tT»2-r ••• +&n)
никак не может равняться нулю (ибо ai + Н' • • • 4~ ап^> 0)* Но из
того, что
' , ' , , ' г1 , г= , , гп
г! 1 г2'Г ••• гг’1 г0 ' г0 ‘ ••• ' г0
. (г1-г гг + • -г гп).” 0,
следует, что также и Zi + z2 + ... + zn #= 0.
339. Предположим, что отвечающая комплексному числу z точка
А комплексной плоскости не принадлежит выпуклому, многоугольни-
ку С\С2 ... С„, вершины которого отвечают числам cb с2, сп
Рис. 43.
(рис. 46). В этом случае все лучи ACh АС2....АС„ снаправлены
в одну сторону» в том смысле, что все эти лучи лежат по одну
сторону от некоторой прямой I, проходящей через А. Заметим теперь,
23 д. о. Шклярский и др. 383
что, $ силу правила вычитания комплексных чисел, числам «1 =
в z — С], г2 — z — с2, ..., zn — г — сп отвечают на комплексной
плоскости такие точки At, А2, .... А„, что векторы OAt, ОА2, ...
..., ОАп равны векторам CiA, С2А, .... СпА; поэтому все лучи OA't,
0А2, .,ОАа лежат по одну сторону от проходящей через О пря-
мой ll\\l. С другой стороны, если ш'=-^-,то при to = r(cos0 4-
4- i sin 6) имеем w' =.—[cos (— 0) 4- i sin (— 0) ], т. e, числа ы и co'
изображаются такими точками В и В' комплексной плоскости, что
лучи ОВ и OB' симметричны относительно оси Ох вещественных чи-
,1 1 , I ,1
сел. Отсюда следует, что числам г)==—= Z2~ 7"....гп “7
отвечают такие точкиЛр А2,..., Ап, что лучи OAt, ОАо.ОАп сим-
метричны лучам О А,, ОА2............................. ОАп относительно оси Ох,
откуда следует, что все эти лучи лежат по одну сторону от пря-
мой I", симметричной /'• относительно оси Ох (см. тот же рис. 46).
Дальнейшая часть доказательства близка к решению задачи
338. Если г0 = cos 0о 4-1 sin Оо — комплексное число модуля 1, изоб-
- - и/ " » гп
ражаемое точкой прямой Г, то HH-cnaZj , г2 = -у...... гп
изображаются точками 4(’, А2, .... Ап, получаемыми из точек А।
Аг..... А п поворотом вокруг О на угол Оо; поэтому все оии
лежат по одну сторону от оси Ох, получаемой тем же поворотом из пря-
мой I". Но отсюда следует, что коэффициенты b2.......Ьп при
мнимых частях чисел zj = 4- г., ~ а“2 4- ‘&2> • -, z'n — ап + ‘Ai
все одного знака — и, значит,
г1 + г2 + • • • + гп = (“1 + а2 + • • • ~г ап) 4-
4- z 4- *2 + • • • + ьп) * °-
ибо 4- b2 4- • • • 4" Ъп 0. А из того, что
„ » „ г1 г2 гп
г14-г2+-..+гп=—4- —4-..,4- —=
= (zi 4- z2 4- - - - 4- zn) — + °<
вытекает, что также и
4-г2 4-+ гп = 4-JT73; Н-• • • + 777^ 0-
340. Первое решение. Пусть а не делится на р. В таком
случае числа а, 2а, За, ..., (р — 1)а тоя<е не будут делиться на р
и все будут давать при делении на р разные остатки: действительно,
если бы ka и 1а (где р— \ k > I) давали бы при делении на р
одинаковые остатки, то разность ka — la—(k — 1)а делилась бы на
р, что невозможно, так как р простое, а не делится на р и k — I
меньше р. Но все возможные остатки при делении на р исчерпы-
354
Даются р— 1 числами 1, 2, 3, р — 1. Таким образом, должно
быть:
а = qtp + ah 2а = q3p + а2, За = q3p + а3, (р — 1)а =
= q-p-iP + Op-i,
где Оь аг, .... ар-\ — числа 1, 2.р—1, взятые в каком-то по-
рядке. Перемножая все эти равенства, получим:
. [1-2- ... -{р— l)]a?-‘ = Np + OjOj... ap_b
или
[1-2- ... -(p— l)](ar-' — 1)= Np.
Отсюда следует, что а?-1 — 1 делится на р, а значит, и п? — а де-
лится на р.
Если а делится на р, то утверждение теоремы Ферма является
очевидным.
Второе решение. Теорема является очевидной при а — 7,
так как в этом случае о? — а = 1 — 1 =0 делится на любое число
Будем теперь доказывать ее методом математической ин-
дукции, т. е. предположим, что нам уже известно, что а? — а
делится на р, и докажем, что в этом случае (а + 1)?— (а-|- 1) де-
лится на р.
По формуле бинбма Ньютона
(«+ 1)₽-(а+ 1) =
•» ар + pap~i 4- С2ар~2 4- С3рар~3 4- ... 4- РаА- 1 — а— 1 «
•= (ар — а) 4- рар—1 4* С2ар~2 4- ... 4- Cp~~2as + ра.
Но все биномиальные коэффициенты
rk Р(р—1)(р —2) ... (р —1)
cp=I 1-2-З...А
делятся на простое число р, так как числитель выписанного выраже-
ния содержит множитель р, а знаменатель не содержит этого мно-
жителя. А так как, по предположению, и а?—а делится на р, то
(а + 1) ? —(а + 1) делится на р.
Примечание. Приведем еще один .изящный вариант того
же самого доказательства. В силу того, что все биноминальные коэф-
фициенты Ср делятся на р, разность
(4 + В)р — Ар — Вр =
*=рАр-1В + С2Ар-2В*+ ... +Ср-2А2Вр~2 +РАВр~2,
где А, В — какие угодно целые числа, всегда делится на р. Последо-
вательным применением этого результата получаем, что
(А А- В А- С)р — Ар — Вр — Ср =
= {[(А +В)+Ср— (А А- В)р -Ср}А-(АА- Вр — АР — ВР
всегда делится на р,
(А + В + С + D)p—Ap— Bp—Cp—Dp ={[(AA-BA-C)A-D]p —
— (А А- в а С) Р— Dp} А-(А А- В А- С) Р—ар — Bp — Ср
23*
355
всегда делится на р и вообще
(4 + В + С + ... + К) ? - — Вг — Cp—... — К»
всегда делится на р.
Положив теперь в последнем соотношении А = В ~ С = ...
... — К •=*= 1 и взяв число этих чисел равным а, мы придем к теоре-
ме Ферма: — а делится на р.
341. Доказательство теоремы Эйлера совершенно' аналогично
первому доказательству теоремы Ферма; г чисел, меньших N и взаим-
но простых с N, мы обозначим через kt, k2, ks, . , kr. Рассмотрим
г чисел k\a, k2a...kra. Все они взаимно просты с N (ибо а вза-
имно просто с Л1 по условию задачи), и все они дают при делении
на N различные остатки (это доказывается в точности так же, как
в решении задачи 340). Отсюда следует, что
h,a = qxN + ab k2a = q2N + a2, . . ., k,.a = qrN -f- ar,
где ai, a2, ..ar — это те же числа kt, k2, ..kr, только располо-
женные в другом порядке. Перемножав все наши равенства, по-
лучим:
kik2 ... krar = MN + aia2... ar, kik2 ... kr(ar — 1) — MN,
откуда и следует, что число аг — 1 делится на N.
342. Доказательство проведем методом математической индук-
ции. Прежде всего очевидно, что при п — 1 предложение задачи
справедливо: 21 — 1 = 1, 22— 1=3 и 23— 1=7 не делятся иа 5.
Докажем еще это предложение для п = 2. Пусть 2й есть наимень-
шая степень числа 2, дающая при делении на 5“ = 25 остаток 1
(т. е. такая, что 2й— 1 делится на 25); предположим, что k < 52 —
— 5 = 25 — 5 = 20. Если 20 пе делится па /?, так что 20 = qk +
4- г, где г < k, то мы будем иметь:
22°— 1 = 2чк+г— 1 = 2Г(29Й — 1) + (2г _ 1).
Но 220 — 1 делится на 25, в силу теоремы Эйлера, a 2«й—1 =
= (2й)’ — 1« делится на 2h — 1, т. е., в силу нашего предположения,
тоже делится на 25; следовательно, и 2Г— 1, делится на 25, что про-
тиворечит тому, Что k есть наименьшее число, для которого
2й — 1 делится на 25. Итак, k должно быть делителем числа 20, т. е.
может равняться только 2, 4, 5 или 10. Но 22— 1 = 3, 25— 1 = 31
и 210— 1 = 1023 не делятся даже на 5, а 24— 1 = 15 делится на 5,
но не делится на 25. Значит, действительно и для п = 2 предложе-
ние задачи справедливо.
Предположим теперь, что для какого-то п предложение задачи
справедливо, а для значения п+1 оно неверно: наименьшее k, та-
кое, что 2й — 1 делится на 5п+1, меньше чем 5я+1—5" = 4-5’1.
В точности, как выше (для п = 2), доказывается, что k должно яв-
ляться делителем числа 4-5". С другой стороны, аналогично доказы-
вается, что число 5" — 5"-1 = 4-5"-1 должно являться делителем
числа k: если бы было k = <7-4-5п-1 + г, где г < 4-5:1~'1, то чис-
ло 5Г — 1 делилось бы на 5", что противоречит предположению о
справедливости утверждения задачи для числа п. Таким образом,-
для k остается единственное возможное значение, а именно: k ~
=4-5"-1.
Так как число 2'°п~*—5П~~2—1=24-5п—'2—1 делится на 5"-1
(в силу теоремы Эйлера) и не делится на 5П (иначе предложение
356
задачи не было бы справедливо для числа л), то 2*-5п ? -5П
4- 1, где q не делится на 5. Воспользовавшись теперь формулой
(а + ft)5 = а5 + 5a4ft -ф 10a3ft2 + 10о263 + 5aft’ + ft3,
получим:
= (г4'5"-2)s — 1 =(9.5и-1+1)5-1 ==
= 5”+1 (<75 • 54”-6 + <74 • 53,,~4 + 2q° 52"-3 ф- 2qt 5"-2) +
откуда видно,что 2*'зП 1 — 1 не делится на 5’1+1. Итак, действитель-
но, из справедливости предложения задачи для какого-то я следует
справедливость его и для «4-1.
343. По теореме Эйлера (см. задачу 341) число 23'°~3’—1 =
— 24-5’ — 1 = 27 812 500 — 1 делится на 510; следовательно, при
^10 разность 27 812 500+п—2" = 2п (27 8,2 500 — 1) делится на 1010,
т. е. последние 10 цифр чисел 27 8|2 500+’1 и 2" совпадают. Это озна-
чает, что последние 10 цифр чисел ряда 21, 22, 23, .... 2", ... повто-
ряются через каждые 7 812 500 чисел, причем эта периодичность на-
чинается с десятого числа этого ряда —с числа 210.
То, что период на самом деле не меньше чем 7 812 500, сле-
дует из результата задачи 342.
Примечание. Аналогично доказывается, что последние п
цифр чисел рассматриваемого ряда повторяются через каждые
4-5”_| чисел, начиная с л-го числа этого ряда (так, например,
последние две цифры повторяются, начиная со второго числа,
через каждые 20 чисел).
344. Докажем даже более общее предложение, а именно, что
каково бы ни было целое число N, всегда найдется такая степень
числа 2, последние N цифр которой все будут единицами и двойками.
Так как 25 = 32 и 29 = 512, то при N = 1 п N = 2 это утверждение
справедливо. Далее доказательство мы проведем при помощи
метода математической индукции. Предположим, что
последние N цифр числа 2" являются единицами и двойками, и до-
кажем, что в таком случае найдется степень числа 2, последние
N + 1 цифр которой являются единицами и двойками. Согласно
сделанному предположению 2" •= 10Л7а + ft, где ft есть М-значное
число, записываемое с помощью двух цифр: 1 и 2. Обозначим чис-
ло 5JV — 5;V-1 = 4 • 5Л'_'‘ буквой г; тогда согласно теореме Эйлера
(задача 341) разность 2Г—1 будет делиться на 5'v. Отсюда выте-
кает, что если целое число k делится на 2JV+1, то разность 2rk — k =
=/г(2г—1) будет делиться на 2- 10-v, т. е. N последних цифр
чисел 2rk и k будут совпадать, а (Л7 + 1)-е с конца цифры этих чи-
сел будут одинаковой четности.
Рассмотрим теперь следующие пять степеней числа 2:
2?,"ЬГ = 2Г ♦ 2л Qii+2r — 2Г ♦ 2л+г 2п+'Лг -— 2Г • с2п^г
%п+4г __ 2г . 2П +Зг
Согласно доказанному последние М цифр всех этих чисел совпа-
дают между собой (т. е. все они оканчиваются тем же числом Ь,
составленным из двоек и единиц, что и число 2"), а (М+П-е
с конца цифры у всех у них одновременно четны или нечетны.
Докажем теперь, что ни у каких двух из этих пяти чисел (N + 1)-е
с конца цифры не могут быть одинаковыми Действительно, разность
357
любых двух из наших чисел представима в виде 2п+т1Г (2т‘т—1)
где mt = 0, 1,2 или 3, а т2 = 1, 2, 3 или 4. Если бы эта разность
делилась на 10^', то число 2тгГ —1 должно было бы делиться
на 5-v+1; но так как
т2г = т2 • (5Л’ — 5Л'_|) < 5 • (5Л' — 5Л'-') = 5*+> — 5Л’,
то это противоречит результату задачи 342.
Итак, (7V-+- 1)-е с конца цифры выписанных пяти чисел — это
или 1, 3, 5, 7 и 9 (в каком-то неизвестном нам порядке) или же
О, 2, 4, 6 и 8. В обоих случаях хотя бы для одного из этих чисел
(N + 1)-я с конца цифра равна 1 или 2. Значит, во всех случаях
существует степень числа 2, последние N 4- 1 цифр которой все
являются единицами и двойками; в силу принципа математической
индукции отсюда следует требуемое предложение.
345. Ясно, что пара натуральных чисел п и п2 является «хо-
рошей» при любом п > 1. С другой стороны, пара чисел п—1
и пг—1 = (п—1) (п 4- 1) наверное будет «хорошей», если число
п -f- 1 представляет собой целую степень двойки, т. е. п 4- 1 = 2*,
где k 1 — целое число: в самом деле, в таком случае числа
п — 1 и п2 — 1 = 2к (п — 1)
отличаются лишь тем, что во второе из них простой делитель 2
входит в степени, на k большей, чем в первое (число п—1 содер-
жит простой делитель 2, ибо при /14-1= 2к, т. е. при п = 2к — 1,
также и число п—1 = 2к — 2 является четным). Отсюда уже вы-
текает бесконечность числа «очень хороших» пар: ведь такими яв-
ляются, например, все пары'чисел
п— 1 = 2»—2 и л2 - 1 = (п — 1)(п 4- 1) = 2s (2к —2),
где k = 1, 2, 3, ...
346. Ясно, что начальный член а и разность d прогрессии мож-
но считать числами взаимно простыми: ведь если бы и а, и d де-
лились на какое-то число k > 1, то мы просто сократили бы все
члены -прогрессии на k. Если же а и d взаимно просты, то в силу
теоремы Эйлера (задача 341) найдется такое целое число г, что
ат—I, а следовательно, и а'+1— а делятся на d. Но в таком слу-
чае аг+1—а = Nd, т. е. ar+1 = а 4- Nd, где N—натуральное чис-.
ло, т. е. число ar+1 принадлежит нашей арифметической прогрес-
сии. Более того, в таком случае также и все числа arR+1, где k =
= 1, 2, 3, ..., принадлежат прогрессии, поскольку агк—1 =
— (аг—1) (аг(*-1> 4-аги-2) 4^ • • + 1) делится на аг—1, т. е. де-
лится на d; следовательно, и ark+i — а = Md делится на d
и = а 4- Md есть (М 4- 1)-й член прогрессии. Ясно, что числа
a, ar+1, a2r+1, a3r+1, ... разлагаются на одинаковые простые мно-
жители (в разных степенях), что и завершает доказательство
утверждения задачи.
347. Пусть а — какое-нибудь из чисел ряда 2, 3, ..., р — 2.
Рассмотрим числа
а, 2а, ..., (р — 1)а. i
Никакие два из этих чисел не могут давать одинаковых остатков
при делении на р; следовательно, эти числа дают при делении
на р остатки 1, 2, ..., р — 1 и притом каждый из этих остатков по-
лучается только один раз (ср. с решением задачи 340). В частности,
458
найдется такое целое число b из ряда 1, 2, .... р — 1, что ba при
делении на р дает остаток 1. При этом ft =/= 1 и ft =/= р— 1, ибо 2
s? a sg р — 2; следовательно, при ft= 1 число Ьа = а при деле-
нии на р дает остаток а^=Л, а при Ь = р—1 число Ьа =
= (р—1)а = ра— а при делении на р дает остаток р — а ф 1.
Кроме того, ft =/= а, так как если бы а2 при делении на р давало
остаток 1, то а2—1 — (а-|-1)(а—1) делилось бы на р, что воз-
можно только при а = 1 и а = р— 1. Следовательно, 2 sC ft sj
sg р — 2 и ft =/= а, т. е. все числа 2, 3....... р — 2 распада-
ются на пары чисел, произведение которых при делении на р дает
остаток 1.
Р —3
Произведение 2-3-...- (р — 2), содержащее —<5— таких пар
чйсел, тоже дает при делении на р остаток 1. Число р—1 при де-
лении на р дает остаток —1. Следовательно, (р—1)! =
= 1 • 2 3 • • (р —2)-(р — 1) = [2 • 3 - ... • (р — 2)] • (р — 1) при
делении на р дает остаток —1, т. е. (р—l)! = ftp—1; (р — 1)! +
+ 1 = kp. Таким образом, (р — 1)! + 1 делится на р.
Если р — непростое, то оно имеет простой делитель q < р.
Тогда (р—1)! делится на q\ поэтому (р—1)! -f- 1 не делится на q
и, значит, не может делиться также и на р.
348. а) Если р = 2, то р = I2 + О2 + 1. Пусть теперь простое
число р нечетно; покажем, что можно найти два числа х и у,
, Р
ооа меньших чем -g-, удовлетворяющих условию задачи.
Рассмотрим — чисел 0, 1, 2, ..., . Квадраты любых
двух из этих чисел будут давать при делении на р различные
остатки; действительно, если было бы
х] = ktp -j-r и 4 = k.1P 4- г,
то имело бы место равенство
X] — X?} = (%х — x2)(xt + хг) = (ftj — k2) р,
т. е ( у,—л-2) (л-[ + ,г2) делилось бы на р, что невозможно, так как
л-2 <-|-и-V1 + %2 < Р, l-Vi —Л'2|<р (напоминаем, что
р -j- 1
р — простое). Итак, —чисел
02,12,22,...,(Р-^)2
Р + 1
при делении на р дают —%— различных остатков. Отсюда вытека-
р 1
ет, что и следующие —g— (отрицательных!) чисел: —1, —I2—1,
02 1 (Р~ Л2 1 Р+1
— 22 — 1, ...» — I — — 1 также при делении на р дают —н—
\ 2. j
различных остатков (если бы — xj—1 и —Xg—1давали одинако-
359
вне остатки, то и х\ и х? давали бы одинаковые остатки) *). Но
так как при делении на р могут встречаться лишь р различных
остатков (а именно, 0, 1, 2, ..р—1), то ясно, что из р +1 чи-
сел О2, I2, 22, — 1, — I2—I, — 22 — 1,..., — /g
\ 2 Г \ 2 )
по крайней мере два дают при делении на р одинаковые остат-
ки. В силу доказанного выше из такой пары чисел одно обязатель-
но должно быть вида х2, а второе — вида—у2—1. Но если
х2 «= kp + г и — у2 — 1 =» 1р + г, то
х2 + у2 = (k — 1)р — 1 -= тр — 1,
т. е. х2 + у2 + 1 = тр делится на р.
Примечание. В условии задачи можно требовать даже, •-
, Р ,
чтобы оба искомых числа х и у не превосходили т. е. чтооы
сумма х2 + у2 + 1 была меньше р2, и, значит, частное т от деления
суммы х2 + у2 + 1 иа р было меньше р.
б) Пусть р = 4п + 1 — простое число. В силу теоремы Виль-
сона (задача 347) число
(р— 1)! + 1 = 1 • 2 • 3 • ... • (4n) + 1
делится на р. Заменим теперь в последнем выражении все множп-
Р — '
тели большие —<5—= 2п, через разности числа р и чисел меньших
Р~1
2 •
(р- 1)! + 1 = 1 . 2-3 • .... 2/1(р-2,ч)(р-2п + 1) • ...X
Х(Р — 1) + 1 = (1 • 2 • 3 • ... • 2/1) [Ар + (— l)2-'2n X
X (2/» — 1) • ... • 1] + 1 /1,р+ (1 • 2 • 3 • ... • 2п)2 +1.
Так как это число делится на р, то и сумма ((2и)!)2 + 1 делит-
ся на р. Итак, условию задачи удовлетворяет число х = (2п)!
-=(р—V
\ 2 /
Примечание. Заметим, что если число х дает при делении
на р остаток хь то из того, что х2 + 1 — (kp + xj 2+ 1 = (Р2р +
+ 2kxi)p +*+ 1 делится на р, следует, что и х|+1 делится на р.
Поэтому в условии задачи можно всегда считать, что число х
меньше р, х2 + 1 меньше рл и частное т от деления х2 +1 на р
меньше р.
*) Частное k и остаток г от деления целого числа а на число р
определяются формулой а = kp + г, где 0 =+ г < р (если а отри-
цательно, то и частное k отрицательно).
360
349. Существование бесконечного числа простых чисел следует
из результата задачи 234 (из этой задачи вытекает даже, что прос-
тые числа встречаются в ряду всех целых чисел достаточно «часто»,
например, «чаще», чем квадраты; см. примечание к этой задаче). Из
результата задачи 90 также можно усмотреть, что простых чисел
существует .бесконечно много: если бы всего существовало только п
простых чисел, то пе могло бы быть больше чем п взаимно простых
друг с другом чисел. Но наиболее простым доказательством теоре-
мы о бесконечности числа простых чисел является следующее до-
казательство, принадлежавшее Евклиду.
Предположим, что имеется всего п простых чисел 2, 3, 5, 7,
11,..., рп- Образуем число N — 2 • 3 5 • 7 • 11 • ... • рп + 1. Число .V
больше всех простых чисел 2, 3, 5, .... рп и поэтому должно быть
составным. Но так как N—1 делится на 2, 3, 5, 7, ..., рп, то N
взаимно просто со всеми простыми числами. Полученное противоре-
чие и доказывает теорему.
350. а) Доказательство этой теоремы очень близко к доказа-
тельству Евклида бесконечное:и числа простых чисел. Предположим,
что среди чисел вида 4/г — 1 имеется только конечное число прос-
тых чисел, а именно 3, 7, 11, 19, 23, ..., рп- Составим число N =
= 4(3-7-11 • 19-23-.. .-рп)—1- Оно больше всех принадлежащих
прогрессии простых 'чисел и, следовательно, должно быть составным.
Разложим число N па простые множители. Среди них не может быть
чисел вида 4k—1, так как число N -j- 1 — 4(3-7-11 • 19-23... рп) де-
лится на все простые числа вида 4k— 1, а следовательно, N взаим-
но просто со всеми этими числами. Так как N нечетно, то оно долж-
но представлять собой произведение нескольких простых чисел вида
4k + 1. Но это невозможно, так как произведение двух чисел вида
4k + 1 имеет тог же вид-:
(4/г; + 1) (4/г2 + 1) = I6M2 + 4/е, + 4Л2 + 1 =
-=4(4^2 + И, + *2)+1 =. 4/?3 + 1,
а следовательно, и произведение нескольких чисел вида 4k + 1 имеет
тот же вид, в то время как число N имеет вид 4k— 1. Полученное
противоречие и доказывает теорему.
Аналогично доказывается, что существует бесконечно много
простых чисел, принадлежащих прогрессии 5, 11, 17, 23, ... (простых
чисел вида 6/г — 1).
б) Доказательство настоящей теоремы несколько сложнее дока-
зательств теорем задачи а), хотя построено на той же идее.
Предположим, что в ряду чисел И, 21, 31, 41, 51, 61, ... имеет-
ся только конечное число простых: 11, 31, 41, 61, ..., рп. Составим
число М ==> (11 -31 -41 -61.. -Рп)5 — 1. Оно взаимно просто со всеми
простыми числами 11, 31, 41, .... рп, так как число N + 1 делится
на все эти числа. Обозначим произведение 11 -31 -41...р„ через
а, тогда N — а5 — 1 = (а — )) (а4 4- а3 t? -f- a -f- 1).
Рассмотрим, какие простые делители может иметь второй мно-
житель а4 + а3 + а2 + а + 1 последнего произведения. Очевидно, что
а4 + а3 + а2 + а 4- 1 не делится на 2 (сумма пяти нечетных чисел
нечетна). Далее, а4 4- а3 + а2 4- а 4- 1 делится на 5, поскольку а
оканчивается на 1 (как произведение ряда чисел, каждое из которых
оканчивается на 1), а2, а3 и а4 все оканчиваются на 1 и, следователь-
но, сумма а4 + а3 + a2 -f- а 4- 1 оканчивается на 5. Пусть теперь р
361
есть простой деЛитель числа а4 + а3 4- а1 4- а + I, отличный от 5.
В таком случае а — 1 не может делиться, на р, так как иначе а
имело бы вид kp 4- 1, следовательно, а2, а3 и а4 (равные соответст-
венно (kp + I)2, (kp-\- I)3 и (kp + I)4) имели бы такой же вид и
число
а44-а34-а24-а4-1 = (kp+1) 4+ (kp+1) 3+ (kp+V)2+(kp + 1)4-1
давало бы при делении на р остаток 5. Отсюда следует, что р — 1
должно делиться на 5. Действительно, предположим, например, что
р—1 дает при делении на 5 остаток 4: р—1 = 5k 4- 4. Отметим,
что в силу теоремы Ферма (задача 240) а?-1 — 1 делится на р. Но
в этом случае
ПР-1 — 1 = fl5k+4 _ [ _ (в5Л — 1) _|_ — 1),
а так как а5к— 1 = (а5)*— Is делится на а5— 1, а значит и на р,
то и а4—1 делится на р. Но а5—1 — а(а4—1) 4- (а—1); следо-
вательно, если а5—1 и а4—1 делятся на р, то и а—1 .должно
было бы делиться на р, что, как мы уже показали выше, невозмож-
но. Аналогично показывается, что число р—Г не может давать при
делении на 5 остатки 1, 2 или 3.
Итак, р— 1 делится на 5 и четно (р— 1 четно, ибо р нечетно);
следовательно, р—1 делится на 10 и, значит, р имеет вид Юйф- 1,
т. е. принадлежит наше!1! прогрессии. Итак, нами установлено, что
простыми делителями числа а4 4* а3 4- а2 4- а -)- 1 могут быть только
число 5 и простые числа вида 10/г4* 1.
Но число а4 4-а3 4-а2 4~ а 4~ 1, очевидно, больше 5 и не делится
на 52 = 25. Действительно, число а оканчивается на 1 и, следова-
тельно, имеет вид 5k 4- 1. ’ Далее, по формуле бинома Ньютона
а4 4-а3 4-а2 4-а 4- 1 = (5k 4- I)4 4- (5k 4- 1)э4- (5k 4- 1)24-
4-5А 4- 1 4-1 = 625^4-4-125^4-6-25^4-4-5^4-
4- 1 4- 125*3 4-3-25^4-3-5* 4- 1 4-25£2 4-2• 5£ 4- 1 4-
14- 5k 4- 1 + 1 = 625*4 4- 5- 125А3 + 10-25*2 4- 10-5fe 4- 5 =
=5-[5(25/г4 4- 25й3 4* 10/г2-4-2^)4-1]-
Отсюда следует, что это число, а значит, и число N — а5—1
должно иметь хотя бы один простой делитель вида 10& 4- 1. Но,
по нашему предположению, N взаимно просто со всеми просты-
ми числами вида 106 4-1. Полученное противоречие и доказывает
теорему.
Примечание. Отметим, что проведенное доказательство поч-
ти без всяких изменений позволяет доказать, что во всякой арифме-
тической прогрессии, составленной из чисел вида 2рй-4-1, где р —
какое-то нечетное простое число, имеется бесконечно много простых
чисел.
ОТВЕТЫ И УКАЗАНИЯ
1. Самый высокий из самых низких.
2. Составьте сумму всех сделанных каждым из людей рукопо-
жатий.
3. Пусть А — произвольное лицо; оно имеет либо трех знако-
мых, либо существуют трое лиц, с которыми А незнаком.
4. а) Не может, б) Постройте пример удовлетворяющего ус-
ловиям задачи «распределения знакомств».
5. Докажите, что если А и В незнакомы, то они имеют двух
общих знакомых.
6. Рассмотрите ученого, имеющего среди присутствующих
наибольшее число знакомых.
7. Последовательно исключайте из числа делегатов пары гово-
рящих на одном языке.
8. Пусть А — произвольный участник конференции; найдется
такой язык, на котором он может говорить не менее чем с 6 дру-
гими участниками.
k (А+-1)
9. п =-----g-----+ ।, гДе k — целое.
10. 5000 дней (в городе существуют две такие 'партии, что два
жителя дружат в том и только в том случае, когда они принадле-
жат к одной партии).
11. Если странствия рыцаря длятся достаточно долго, то най-
дется такой участок АВ пути (где А и В-—замки), по которому
(в направлении от А к В) рыцарь проедет не менее трех раз.
,12 . Пусть А и В — два рядом сидящих врага; докажите, что
Мерлин может пересадить часть рыцарей так, чтобы пара сидящих
рядом врагов заменилась парой А, А' сидящих рядом друзей, а пи
одна пара соседей-друзей не заменилась парой врагов.
13. а) При первом взвешивании поместите на каждую чашку
по 27 монет, б) Число k определяется неравенствами 3ft~' < п.
3*.
14. Сначала положите на чашку весов по одному кубику;
затем, положив на одну чашку оба эти кубика, на вторую кладите
поочередно по паре из оставшихся кубиков.
15. При первом взвешивании поместите на каждую чашку ве-
сов по четыре монеты.
16. а) Одно звено, б) 7 звеньев.
17. Пусть S — какая-то станция метро; рассмотрите самую да-
лекую от нее станцию Т.
18—19. Воспользуйтесь методом математической индукции.
20. Воспользуйтесь методом доказательства от противного:
предположите, что утверждение задачи неверно, и, пользуясь этим,
постройте бесконечную цепочку городов Швамбрании (при кон-
363
струировании этой цепочки удобно воспользоваться методом мате-1
матической индукции).
21. Нельзя.
22. Королю достаточно пройти в один из углов доски и далее
идти по диагонали доски.
23. Измените порядок следования полей так, чтобы с каждого
поля можно было перейти на соседнее.
24. Докажите (скажем, методом математической индукции),
что если в некотором коллективе студентов каждый из трех языков
знает ровно п человек (где п ^2), то можно составить такую
группу студентов, в которой каждый язык знают ровно 2 человека.
2
25. а) 2-3-. б) 20.
26. 6 дней; 36 комплектов медалей.
27. 15 621.
28. Два рубля.
29. а) Закон чередования дней в году по нашему календарю
таков: через каждые четыре года один год, номер которого делит-
ся на 4, является високосным; исключение составляют годы, номера
которых делятся па 100, но не делятся на 400. Отсюда легко ус-
мотреть, что 400 лет содержат целое число недель; следовательно,
остается проверить, начинается ли в течение каких-либо 400 лет
новый год чаще с субботы или с воскресенья. Ответ: с воскре-
сенья. б) На пятницу.
30. Все числа, оканчивающиеся на 0, и двузначные числа:
11, 23, 33, 44, 55, 66, 77, 88, 99; 12, 24, 36, 48; 13, 26, 39; 14,
28; 15; 16; 17; 18; 19.
31. а) 6250... 0, п — 0, 1, 2, ... б) Попытайтесь решить sa-
il раз
дачу: найти целое число, начинающееся с известной цифры а и при
зачеркивании этой цифры уменьшающееся в 35 раз.
32. а) Докажите предварительно, что число уменьшается в 9 раз
при зачеркивании цифры 0, стоящей на втором месте, б) 10 125 2025,
30 375, 405, 50 625, 6075, 70 875 (к каждому из этих чисел можно
еще приписать в конце произвольное число нулей).
33. а) Числа, у которых все цифры, кроме первых двух, нули,
б) Рассмотрите отдельно случаи, когда первая цифра искомого
числа есть 1, 2, 3, .... 9. Всего имеется 104 различных числа, удов-
летворяющих условию задачи, к каждому из которых можно в кон-
це приписать произвольное число нулей.
34. а) Наименьшее возможное число 142 857. б) Цифрами 1 пли
2. Наименьшее число, начинающееся цифрой 2, есть 285 714.
35. 153 846.
36. Используйте то, что числа, которые делятся на 5, должны
оканчиваться цифрами 0 или 5; числа, которые делятся на 6 или
на 8, оканчиваются четной цифрой.
37. Попытайтесь решить задачу: найти число, увеличивающееся
вдвое от перенесения начальной цифры в конец.
38. Решается аналогично предыдущей задаче.
39. Наименьшее число, удовлетворяющее условию задачи,
7 241 379 310 344 827 586 206 896 551.
40. а) Число, меньшее своего обращенного в 5, 6, 8 или 7 раз,
должно начинаться с цифры 1; число, меньшее своего обращенного
в 2 и 3 раза, может начинаться с цифр 1, 2, 3, 4, соответственно
364
1, 2, 3. б) Числа, в 4 раза меньшие своего обращенного,—это числа
О, 2 178, 21 978, 219 978, 2 199 978............. (*)
и числа, десятичная запись которых PiP?.. .Pn-iPnPn-i- • -РгР\, где
Pi, Рг, „Рп — какие-то числа ряда (*).
41. а) 142 857. б) Попытайтесь найти восьмизначное число, уве-
личивающееся в 6 раз при перестановке четырех последних цифр на
первые четыре места с сохранением их порядка.
42. 142 857.
43. 111, 222, 333, ..., 999, 407, 518, 629, 370, 481, 592.
44—45. Рассмотрите процесс сложения «столбиком» рассмат-
риваемых чисел.
46. Разложите на множители многочлены, выписанные в усло-
вии задачи; рассмотрите, какие остатки может давать число п при
делении на 3 (соответственно на 5, на 7, и т. д.).
47. а) Воспользуйтесь тем, что разность одинаковых четных сте-
пеней делится на сумму оснований, б) См. указание к задаче 46.
48. а) 56 786 730 =» 2 3 • 5 • 7 11 • 13 • 31 61. Далее восполь-
зуйтесь предложениями задач 46 а) — д) и аналогичными предло-
жениями, вытекающими из теоремы Ферма (см. задачу 340). б) Раз-
ложите заданное выражение на множители и сравните число мно-
жителей с числом множителей числа 33.
в) Воспользуйтесь тем, что п2 Д- Зга Д- 5 = (п Д- 7) (га — 4) Д- 33.
49. При четных и.
50. Не существует.
51. Воспользуйтесь тем, что всякое целое число, не делящееся
на 5, можно представить в виде 5k ± 1 пли о/г ± 2. Ответ; 0 или 1.
52. Воспользуйтесь результатом предыдущей задачи.
53. 625 и 376.
54. Найдите две последние цифры числа N2Q, три последние
цифры числа №°°. Ответ: 7; 3.
га (га -г 1)
5а. 1 Д-2 Д- 3 ... Д- п —----g---• Группируя отдельные члены
суммы 1* Д- 2k Д- З1* Д-... Д- п\ докажите, что эта сумма делится
п п Д-1
на ~2~ и на (га Д- 1), или на га и на ——.
56. Разность суммы цифр числа, стоящих на четных местах,
и суммы цифр, стоящих на нечетных местах, должна делиться
на 11.
57. Число делится на 7.
58. Всегда можно найти число, начинающееся с цифр 1, 0
и делящееся на К. Переставляя подходящим образом цифры этого
числа и вычитая одно из другого два делящихся на числа, можно
доказать, что 9 делится на К.
59. Искомое число состоит из 300 единиц.
60. Рассмотрите последние цифры чисел Л1 = 2А (где k — 1,
2, 3, ...), а также остатки от деления чисел N иа 3. •
61. 26 460 = 22 • З3 • 5 • I2. Докажите в отдельности, что задан-
ное выражение делится на 5 • 72 и что оно делится на 22 З3.
62. Воспользуйтесь тождеством
Ipo— ро=
(Ц _ 1) (Ц9 Д- 118Д- П7 Д- И6 Д- Н5 Д- 11< Д- И3 Д- П2 Д- 11 Д- 1).
365
63. Запишите данное число в виде
(2222s555 + 45555) + (55552222 — 42222) — (45SS5 — 2222).
64. Воспользуйтесь методом математической индукции.
65. Воспользуйтесь тем, что 10е—1 =999 999 делится на 7
и что любая степень десяти дает при делении на 6 остаток 4. От-
вет: 5.
66. а) 9; 2. б) 88; 67. в) Найдите, какими двумя цифрами окан-
чиваются числа 2 И*14). Ответ: 36.
67. а) Оба числа оканчиваются цифрами 89. б) Докажите, что
разность рассматриваемых чисел делится на 1 000 000 = 2е • 56.
68. а) 7; 07. б) 3; 43.
69. Рассмотрите числа
Z, = 9, Z2 = 9Z‘, Z3 = 9Z‘....Z]ool = 9Z‘”“" = N
и определите последовательно одну последнюю цифру числа Zt,
две последние цифры числа Z2, три последние цифры числа Z3, че-
тыре последние цифры числа Z4, пять последних цифр числа Zs,
пять последних цифр чисел Z6, Z7, ..., Z100i — N. Ответ: 45 289.
70. Составьте таблицы остатков от деления на 13 чисел 5" и
п5. Наименьшее п, удовлетворяющее условию задачи,— это п = 12.
71. При всех а, кратных 4, последние цифры рассматриваемого
числа — это 30.
72. Искомые 1000 цифр будут рРР ... Р, где
23 раза
Р = 020408163265306122448979591836734693877551
1
— период чистой периодической дроби, в которую обращается -jg-,
ар — группа последних 34 цифр числа Р. Для доказательства вос-
пользуйтесь тем, что
50iooo_i soieoo — j
N~ 50— 1 ~ 49
73. Рассмотрите разность М — 3N.
74. 24.
75. а) Сравните степени, в которых входит какое-нибудь прос-
тое число р в произведение а! и в произведение (Г'+ 1) (t + 2)...
...(^4-а). б), в) Воспользуйтесь результатом задачи а), г) Дока-
жите сначала существование такого числа k, что kd, где d— раз-
ность прогрессии, дает при делении на п! остаток 1.
76. Не делится.
77. а) (п— 1)! не делится иа п, если п простое число или п =’
= 4. б) (п—1)! не делится на п2, если п есть простое число,
удвоенное простое число, или если п = 8, п = 9.
78. Докажите, что все такие числа меньше 72 = 49. Ответ:
24, 12, 8, 6, 4 и 2.
79. а) Докажите, что сумма квадратов пяти последовательных
целых чисел делится на 5, ио не делится на 25.
б) Определите остаток, который дает сумма четных степеней
трех последовательных целых чисел при делении на 3.
в) Определите остаток, который дает сумма одинаковых четных
степеней девяти последовательных целых чисел при делении на 9.
366
80. а). Найдите остатки деления чисел А и В на 9. б) 192, 384,
576, или 273, 546, 819, или 327, 654, 981 или 219, 438, 657.
81. Четырьмя нулями.
82. Воспользуйтесь теоремой Пифагора.
83. Рассмотрите остаток от деления Ь2— 4ас иа 8.
84. Докажите, что при сложении дробей и возможном сокраще-
нии суммы получится дробь, знаменатель которой делйтся на 3 и на 2.
85. Для доказательства того, что числа Л4 и jV не являются це-
лыми, надо показать, что после сложения мы получим дробь, знаме-
натель которой делится на более высокую степень 2, чем числитель.
Доказывая, что число К не является целым, надо в предше-
ствующих рассуждениях заменить степень двойки степенью тройки.
86. а) Воспользуйтесь тем, что дробь plq сократима или несок-
ратима одновременно с дробью q/p. б) На 13.
87. Пусть N = а 10'952 + А — одно из читаемых указанным в ус-
ловии задачи образом чисел (где а — первая цифра N); докажите,
что если JV делится на 27, то и число ЛЧ = 10А + а делится на 27?
88. Докажите, что если в записи числа а = 51000 есть нули, то
можно указать делящееся на а число, первый нуль в записи которого
(если он имеется) расположен дальше от конца числа, чем у а.
89. Докажите сначала тождество
(1 4- 104 + 108 + ... + 104*) • 101 = (Н-102 + . .. + IO2*) (102h + 24-l).
90. Покажите, что (22" +0 — 2 делится на все предшествующие
числа заданной последовательности; отсюда будет следовать, что
23” + 1не может иметь с предыдущим числом последовательности
общий делитель, отличный от 2.
91. Рассмотрите, какие остатки могут давать числа 2" — 1 и
2n + 1 при делении на 3.
92. а) Рассмотрите, какие остатки могут давать числа р, 8р — 1
и 8р+1 при делении на 3. б) Рассмотрите, какие остатки могут да-
вать числа р, вр2 + 1 и Яр2 — 1 при делении на 3.
93. Рассмотрите, какие остатки может давать простое число при
делении на 6.
94. См. указание к предыдущей задаче.
95. а) Докажите, что разность прогрессии должна делиться на
2 • 3 • 5 7 = 210. Ответ: 199, 409, 619, ..., 2089. б) Докажите,
что если первый член прогрессии отличен от 11, то разность должна
делиться на 2 • 3 • 5 • 7 • 11 = 2310; если первый член равен 11, то
разность должна делиться на 210. [При решении задач а) и б) удоб-
но пользоваться таблицами простых чисел.]
96. а) Таким будет нечетное число, не делящееся на 3.
б) Достаточно найти число, ие имеющее с остальными 15 из
рассматриваемых 16 чисел общих множителей 2, 3, 5, 7, 11 и 13.
22... 2177... 78.
97. Произведение равно --— ——-—
r г 665 раз 665раз
98. Частное равно777 000 777 000 . .. 777 000 77,
-----------------------------.--- ... — - остаток 700.
группа 777000 повторяется 106 раз
99. 222 222 674 025 = 471 4052.
100. Не существуют.
101. 523 152 и 523 656.
102. 1946.
367
103. а) Преобразуйте выписанное число и сравните его с выра-
жением для суммы членов арифметической прогрессии с разностью 1,
первым членом 10" ~ 1 и последним членом 10" ' 1- б) 1 769 580.
104. Рассмотрите сначала все целые числа от 0 до 99 999 999,
приписав к тем из них, которые имеют меньше восьми, цифр, нули
слева так, чтобы эти числа стали восьмизначными.
105. 7.
106. Нет.
107. Единиц будет на одну больше, чем двоек.
108. Не может.
109. Это число делится на 11 111.
ПО. 6 210 001 000.
111. Так как заданное число А = 109 — 1, то для любого числа
Л' = xtx2 ... xh имеем АХ =.v1x2... лд000000000 — х^х2 ... xh = Л! —
— N; рассмотрите процесс вычитания «столбиком» Л' из М.
112. Условию задачи удовлетворяют все такие N А, что N =
= 10"’ — 1.
113. Воспользуйтесь методом математической индукции (по чис-
лу п); при т Js п утверждение задачи неверно.
114. Уже на одном из первых четырех мест каждой строки
встретится четное число.
115. Докажите, что сумма всех чисел каждой строки таблицы
(начиная со 2-й) делится на 1958.
116. 40.
117. Если начало 1-го сеанса 12 + х, а продолжительность сеан-
са у, то х и у удовлетворяют системе линейных неравенств.
1 5
118. Возможны значения Т = 20, 15, 12, 7-у и 5 уг мин.
119. 100.
120. Искомое число должно начинаться с наибольшего возмож-
ного количества девяток, соотвественно нулей.
121. а) 147, 258, 369; б) 941, 852, 763.'
122—123. Воспользуйтесь формулой для суммы членов арифме-
тической прогрессии.
124. Представьте выражение п(п + 1) (л Ч- 2) (л + 3) + 1 в виде
квадрата многочлена.
125. Докажите, что среди рассматриваемых чисел не может быть
больше четырех попарно различных.
126. Разбейте 9 гирь последовательно возрастающих весов на
три группы, две из которых имеют одинаковый вес, а третья легче их.
127. Докажите, что веса всех гирь четны или все они нечетны.
128. Достаточно рассмотреть случай, когда все рассматриваемые
числа положительны, а их произведение равно 1.
129. К такому набору мы наверняка придем через 2й шагов.
130. Докажите, что в процессе описанного преобразования си-
стем чисел эти числа постепенно выравниваются.
131. (х, у, z) = (l, 1, 0).
132. а) Докажите, прежде всего, что каковы бы ни были перво-
начальные числа, мы вскере получим четверку чётных чисел, б) Для
рациональных чисел утверждение задачи а) сохраняет силу, а для
иррациональных — нет (здесь можно подобрать числа так, чтобы
все четверки были пропорциональны исходной).
133. б) Постройте возрастающую последовательность, начиная
с первого из выписанных 101 числа. Если в этой последовательности
368 . '
будет- меньше 11 чисел, to вычеркните эти числа и построить, новую
возрастающую последовательность, начинающуюся с первого остав-
. шегося числа; если и в этой последовательности будет меньше 11 чи-
сел, то вычеркните и ее и постройте новую возрастающую последо-
вательность, и т. д. Если все построенные последовательности со-
держат меньше 11 чисел, то у нас будет не меньше 11 последова-
тельностей; используя это обстоятельство, можно построить убываю-
щую последовательность из 11 чисел.
134. Рассмотрите наибольшие нечетные делители этих чисел.
135. а) Рассмотрите наименьшие ио абсолютной величине остат-
ки, которые дают числа при делении на 100.
б) Пусть ai, аг, .... аюо — данные числа. Рассмотрите остатки
от деления на 109 чисел щ, щ + а2, а1 -ф а2 4- п3, ...
в) Если сумма нескольких чисел <200 и делится па 120, то опа
равна 100.
г) Докажите последовательно, что из любых 3 целых чисел мож-
но отобрать 2, сумма которых делится на 2; из любых 9 целых чи-
сел можно отобрать 5, сумма которых делится на 5; из. любых 199
целых чисел можно отобрать 100, сумма которых делится на 100
(в доказательстве 3-го факта используются первые два).
136. Воспользуйтесь методом доказательства от противного.
137. Рассмотрите число переходов (при движении по кругу в
одном направлении) от крестика к нулику и от нулика к крестику.
138. Рассмотрите сумму всех множителей этого произведения.
139. Половина слагаемых рассматриваемой суммы должна рав-
няться + 1, а вторая половина — равняться —1.
140. Отнесите к 1-й группе все числа, запись которых содержит
четное число единиц.
141. Выпишите 5 чисел одно под другим; тогда в каждом стол-
бике число пар одинаковых цифр лежит в пределах от 400 до 600,
Ц2. Докажите, что за несколько «шагов» можно изменить лю-
бой знак, сохраняя все остальные.
143. Используйте-принцип Дирихле (см. стр. 10).
144. Разложите число в (периодическую) десятичную дробь.
145. Пусть d — разность прогрессии и а = {d} (см. стр. 37) при
нецелом d и а = 1 при целом d; достаточно расположить отрезки
так, чтобы отрезок длины а нельзя был® «набрать» из (расположен-
ных «далеко» от точки, отвечающей начальному члену прогрессии)
промежутков между рассматриваемыми отрезками (и их частей).
146. Докажите, что в интервале (0, 4) числовой оси (где А <
< m 4- п) содержится ровно А — I из наших дробей.
147. Обозначьте через ki(i— 1, 2, 3, ...) число тех из наших
1000 1000
чисел, которые заключаются между —— и , и подсчитайте
число меньших 1000 чисел, кратных хотя бы одному из чисел щ,
с2, . .ап.
р
148. Длина k периода — может быть определена как наимень-
шая степень k, для которой 10* — 1 делится на q. Если k 21, то
отсюда следует, что 10' 4- 1 делится на <?, т. е. есть це-
<7
лое число. Из- последнего можно вывести, что в периоде
24 д. о. Шклярский и др.
369
aia2 .. . aidi+lai+2 ... ak дроби —
ai + Я/+1 = Ч2 4" 01+2 = ... = Oi 4- o2 — 9.
149. Воспользуйтесь тем, что число цифр в периодах дробей
ап ап+1
“п"11 "п’+Т равно наименьшим положительным числам k и I таким, что
10*— 1 делится на рп, соответственно 10'—1 делится на рп + 1.
150. а) 7744. б) 29, 38, 47, 56, 65, 74, 83 и 92.
151. Если а — число, образованное первыми двумя цифрами ис-
комого числа, а b — число, образованное двумя последними цифрами,
то 99а = (а + Ь)2— (а + Ь) = (а + b) (а + b — 1). Ответ: 9801,
3025, 2025.
152. а) 4624, 6084, 6400, 8464. б) Таких чисел вовсе нет.
153. а) 145. б) Только число 1.
154. а) 1, 81. б) 1, 8, 17, 18, 26, 27.
155. а) х не может быть больше 4. О т в е т: х = 1, у == ± 1;
х = 3, у = ± 3. б) х = 1, у — ± 1, z — любое четное; х = 3,
у = ± 3, z — 2;х=1,у = 1, z— любое нечетное; х— любое поло-
жительно, у = 11 + 2! + ... 4- х!, z = 1.
156. Рассмотрите, на какую степень двойки могут делиться ис-
комые четыре числа. Ответ: при п нечетном разложение невоз-
можно, при п четном существует единственное разложение:
/ п Л 2 I п ,\2 I п \2 in ,\2
-Т-‘I — т_|1 1
2П=\2 / 4-\2“ ) 4-\2 /4-\2 /.
157. См. указание к задаче 156. В задаче б) аналогично задаче
а) единственный ответ: х = у = г = и = 0.
158. а) Можно показать, что если х, у и z удовлетворяют вы-
kxy
писанному равенству, и, например, z > -g-, то эти числа можно
уменьшить, с тем чтобы они продолжали удовлетворять тому же
kyz kxz kxy
равенству. Если жех^-у, г —% и х у z, то долж-
но быть 2 kx 3. Ответ: k = 1 и k = 3. б) Каждую такую
тройку целых чисел можно получить при помощи последовательных
подстановок вида х, = х, у, = у, z( = kxy — z из одной из троек 1,
1, 1 и 3, 3, 3. Всего в пределах первой тысячи 23 тройки целых чисел,
удовлетворяющих условиям задачи.
159. Докажите, что х, у, z — четные. Ответ: х ~ у = z —
160. (х, у) = (0. - 1), (- 1, - 1), (0, 0), (- 1, 0), (5, 2), (-6,2).
161. х = 3, у = 1.
162. х ~ п2, у — 1, z — п или х = 0, у = т, z — 0.
163. Предположите, что утверждение задачи неверно, и рассмот-
рите наибольшее простое число, для которого имеется решения.
164. Последовательно рассмотрите случаи, когда все четыре чис-
ла различны; два числа равны, остальные различны; две пары чи-
сел попарно равны, и т. д. Ответы: 96, 96, 57, 40; 11, II, 6, 6;
А(3/г±2), k(3k±2), k(3k±2) 1 (k — произвольное целое число,
такое, что k(3k ± 2) положительно); 1, 1, 1, 1.
165. 2, 2 и 0, 0.
JL,_L J____________L 1 J__________L 1 . ]
166. 1— 2 I 4 + 4 - 2 + з 4- 6 - З^З^З-
Ч7П
167. а) Положите x « Xi 4- n, у = </i + n. б) Ср. с указанием
к задаче а), в) x = m(m + n)t, у = n(m 4- n)t, z = mnt, где m, n,
t — произвольные целые числа.
168. а) Пусть у > х; покажите, что в этом случае у делится нах.
[п-l i\p /д4-1\р+1
Ответ: х »= 2, у = 4. б) х = 1 > р ') ’ где —
произвольное целое число, отличное от 0 и — 1.
169. 7 или 14.
170. Из соотношения количества очков, набранных девятиклас-
сниками, и числа сыгранных ими партий можно получить, что все
девятиклассники выиграли все сыгранные ими партии. Отсюда сле-
дует, что в турнире участвовал единственный девятиклассник.'
171. Обозначьте р— а = х, р — b = у, р — с = г, где а, Ь,
с—стороны треугольника, а р — его полупериметр. В таком случае
задача сведется к решению в целых числах уравнения хуг 4(х -j-
4у + 4г
+ у + г), или х = __4'. Условие х у можно рассматривать как
квадратное неравенство относительно у (с коэффициентами, зави-
сящими от г); отсюда можно найти границы, в которых должны
заключаться г и у (всего задача имеет 5 решений). -
п (п* 4- 1)
172. 5,—
173. Докажите, что каждое число встретится на диагонали не-
четное число раз. При п четном утверждение задачи неверно.
174. На tv— п.
175. Рассмотрите ту из таблиц, получаемых описанным образом,
у которой сумма всех чисел таблицы максимальна.
176. 1.
177. Воспользуйтесь тем, что в i-й строке, (9 — ()-й строке,
i-м столбце и (9 — 1)-м столбце выписаны одни и те же числа.
178. Воспользуйтесь тем, что aij + aki = akj + а» для любых
i, /, k, I.
179. Воспользуйтесь тем, что при всех I и j имеем ан = 0,
ал = — at}.
180. Воспользуйтесь методом математической индукции.
181. а) Рассмотрите, как меняются знаки, стоящие в 8 клетках,
примыкающих к краям доски, но не угловых, б) Сведите задачу к
задаче а).
182. а) Не всегда (докажите, что не любое распределение знаков
можно получить описанным образом из доски, на всех клетках ко-
торой стоят знаки «+»). б) Не всегда (ср. с указанием к задаче а)).
183. а) Сможет, б) Можно последовательно обратить в 0 все
числа 1-й, затем 2-й, и т. д. строк.
184. Запишите число а в двоичной системе счисления.
!| 185. Воспользуйтесь методом математической индукции.
186. Пусть ип+1ип+2 + ... + и„+8 =» sn (где uk—k-e число
Фибоначчи); докажите, что ип+я <sn < un+io.
187. Рассмотрите последовательность остатков от деления чи-
сел Фибоначчи на 5.
188. Последние четыре цифры разности вполне определяются
последними четырьмя цифрами уменьшаемого и вычитаемого. Дока-
жите, что существуют п и k такие, что последние четыре цифры
(n + k)-ro и (п k 4- 1)-го чисел Фибоначчи соответственно рав-
ны последним цифрам k-ro и (fe + 1)-го чисел; в таком случае пос-
24*
371
ледние четыре цифры (n-\-k— 1)-го числа будут равны последним
четырем цифрам (k — 1)-го числа Фибоначчи, и т. д. Так можно
найти число Фибоначчи, последние четыре цифры которого совпа-
дают с последними четырьмя цифрами первого числа, равного нулю.
189. Воспользуйтесь тем, что 1 + 2<«n<^an—1 + 3>
190. Первое решение. Дополните последовательность чис-
лом «п+ь Второе решение. Воспользуйтесь методом матема-
тической индукции.
191, 2952 (докажите, что наибольшее число чисел в удовлетво-
ряющей условиям задачи последовательности, начинающейся с наи-
большего числа ар « п, равно
192. Воспользуйтесь методом доказательства от противного; рас-
смотрите, какими могут быть цифры а„, а„+1..... при приписыва-
нии которых ранее имеющееся число все время остается простым.
193. а) не встретятся; б) встретятся.
194. Число 81 впервые встретится на 111111 111-м месте; 4 раза
подряд 27 встретится раньше, чем впервые встретится число 36.
195. 1972 раза (воспользуйтесь тем, что если числа а и b взаим-
но просты, то пара а, b единственный раз встретится в нашем ряду
/о, Л, ... наборов, а если а и & не взаимно просты — не встретятся
ни разу).
196. Пусть а4, а3, а2, at — 4 последние цифры последовательно-
сти; выясните, сколько раз встречается в нашей последовательности
группа цифр адхг^-за,.
197. Пусть Л\ — произведение k первых простых чисел; докажите
(методом математической индукции), что наше утверждение верно
для чисел Nk при любом k.
198. Докажите, что любое натуральное число п можно един-
ственным образом представить в виде п = рх + qy, где х и у —
целые и О С х < ?.
199. Представьте фигурирующее в условии задачи число в виде
X(z¥+1)
----2----+ х’ где Х>0,
200. Рассмотрите все точки с целочисленными координатами
(х, у), расположенные внутри квадрата, ограниченного осями коор-
динат и прямыми х* = 100 и у = 100.
201. Представьте х в виде х == [х] + а, где а •« {х}.
202. Восполыуйтесь результатом задачи 201 3).
203. Рассмотрите все точки с целочисленными координатами
у р
х, у, где 0 < х < <7, 0 < у < р к~<~-
204. Воспользуйтесь методом математической индукции. (Можно
также решить задачу, исходя из геометрических соображений; для
этого надо рассмотреть все точки с целыми координатами, располо-
женные в первом координатном углу под гиперболой ху •= п.)
205—207. В решении задачи 205 следует использовать то, что
[(2 4-уТ)”1 = (2 + уТ)" + (2-/2")'1— 1.
Аналогично решаются и задачи 206а), б), 207.
208. Из р последовательных чисел п, п—1, п — 2, ..., п — р 4- 1
одно (и только одно) делится на р; если это число равно N, то
372
iv r> I П I
— ~y- Таким образом, разность С"—I—I можно записать так:
n(n—1) ... (У + !)#(#—1) ... (n — p-i 1) ,у
р! Р ‘
N—1
209. Если а>0, то ——
( N \
210. Докажите, что равно числу не превосходящих Л це-
лых чисел, делящихся на 2й-1, но не делящихся на 2й.
211. 31.
N— Г
2 4
212. а) Сравните данное произведение со следующим: -g- • •
6 98
• ~7~ ' '' ~99 и'™ возве'1ите доказываемое неравенство в квадрат.
б) Докажите, пользуясь методом математической индукции, что
I 3 5 2/г — 1 1
2 ’ 4 ' 6 2/г ** у Зп ’
213. Второе.
214. а) Первое из чисел меньше., б) Первое из чисел больше
(воспользуйтесь методом математической индукции).
215. Докажите, что если 10й-1 1974" < 10й, то невозможно
неравенство 1974" + 2" 10й.
216. ±11.
217. Воспользуйтесь неравенством задачи 212а).
218. 99" + 100" больше, чем 101" при п еД 48, и меньше, чем
101" при и > 48.
219. 300!
220. Докажите предварительно, что для любого целого положи-
тельного k п
221 —222. Воспользуйтесь результатом задачи 220.
223. Воспользуйтесь методом математической индукции.
224. Используйте формулу бинома Ньютона.
225. Воспользуйтесь методом математической индукции,
226. Воспользуйтесь неравенством
(k + 1)х»(х — 1) > хй+> — 1 > (Z>+ 1)(х — 1),
из которого можно получить, что для каждого целого положи-
тельного р
(р + О'*4-1 —рй+1 > (k + 1)рй > ps+1— (р— 1)*+’.
227. Эти неравенства можно получить, заменив члены сумм
большими (соответственно меньшими) числами, может быть, предва-
рительно сгруппировав подходящим образом эти члены (т. е. преоб-
разовав суммы в новые, состоящие из меньшего числа членов).
228. Докажите предварительно, что 2~]/п + 1 — 2”|/n < —j= <
_____ V п
<2/п —2/п—1. Ответы: а) 1998.6.) 1800.
373
229. Докажите предварительно, что
“I- R'(л + 1 )2 — < з~ДГ < ~2~ R7^2 ~ + *)3 ] •
у п
Ответ: 14 996.
230. а) 0,105. б) Воспользуйтесь тем, что
1 1 1 ( 1__'1(9 Ю , И , , 999 ]
10! + 11! + 121+’ *• + 1000! [[of + Н! + 121 •“ + 10001]'
Ответ: 0,00000029.
231. Воспользуйтесь результатом задачи 227.
232. Найдите предварительно число незачеркнутых слагаемых
между i и ’
233. а) Решается аналогично задаче 231. б) Воспользуйтесь, тем,
11 , 1 . 1
чт0 1 • 2 + 2 • 3 +'"-+ (п - 1) п “ 1 — п '
234. Докажите, что для всякого целого k и целого р 2
। Л , 1 , 1 , 1 , , 1 21g3
Ч " р + рз + рз+----грЧ< р
Воспользовавшись этим, выведите, что
ig(i-+-r+4-+4‘+"'+-4+—)<
\ 2 3 * п — In)
, /11 I 1 \
<21g3[2 -г з + — + ••• +Т[]’
где pi — наибольшее простое число среди чисел от 1 до п.
235. Воспользуйтесь тождеством (а + Ь + с)3 — а3 — Ь3—с3—
= 3(а + Ь) (Ь + с) (с + а).
(и0)3 — 1
236. Воспользуйтесь тем, что а10 + а5 4- 1 = 5_. , а а15 —
— Г= (а3)5—1.
237. Докажите, что разность (х9999 4- х8888 4- ... 4- хш1 + 1) —
— (х9 4- Xs + .,. + х + 1) делится на х9 4- х8 4~ • • 4~х 4- 1.
238. а) а3 4- 53 + с3.— ЗаЬс делится на а + Ь 4- с. б) хх =— а—Ь,
где а, Ь^Г-^±У+
239. Избавьтесь от радикалов и решите полученное уравнение
относительно а.
1
240. Воспользуйтесь тем, что если х2 4- 2ах 4- "jg" — У, то х =
= — а 4-1/ а2 4- у — —L; рассмотрите графики функций у = х2 4-
г 16
+ 2ах +-L и ух «= — а 4- 1/а2 + х — -L.
16 г 10
.474
241. Докажите, что должно быть Зх = х*.
242. а) Докажите, что должно быть । q—= х.
243. Корни уравнения — все числа, заключенные между 5 и 10.
244. Корни уравнения: число — 2 и любое число не меньшее 2.
245. .ri = 1, х2 =.2, ..., х„ = п.
246. х = |<4.
247. При а = ± 1 система имеет три решения; прн а = + У 2
система имеет два решения.
248. а) При а = —1 система не имеет решений, при а — 1
система имеет бесконечно много решений, б) При а = ± 1 система
имеет бесконечно много решений, в) При а = 1 система имеет
бесконечно много решений, при а = — 2 — не имеет ни одного ре-
шения.
249. Для того чтобы система имела решения, необходимо, что-
бы три из четырех чисел ai, as, a3, a4 были равны между собой.
Если
a4 = а2 = «з = а, а4 = ₽. то *1=х2 =-’ х3 = х4 = — -у-)-
250. Единственное вещественное решение х = 1, у = 1, г — 0.
251. х= 1, (/=0 и с=О, у=1.
252. х1=х2=х3 = х4 = х5=О, х произвольно; xt = x2=x3=x4 = x5
произвольны, х=2; х= ~ , X; и х2 произвольны, х3=хх2 — ХЬ
Х4 =—X(Xi+Xs), Х5 = ХХ| — х2.
253. Все числа равны 1, или три из них равны —1, а последнее
равно 3.
254. При а > b > с > d имеем х ~ t — а_____у = г = 0.
255. Заметьте, что в зависимости от знака Д= (Ь—I)2 — 4ас
квадратный двучлен ai,2 + (Ь—l)g + c либо сохраняет знак при
всех g, либо обращается в 0 при единственном значении либо
имеет два разных корня £ = и g = g2.
256. 0, если п четно и а,аз... an-i =/= а2аА... в„; бесконечно мно-
го, если п четно и atas... a„-i = a2a4... an; 2, если n нечетно.
' 257. а) Число действительных корней уравнения равно числу
точек пересечения прямой у ='[oq х и синусоиды г/= sin х. б) Чис-
ло корней равно числу точек пересечения синусоиды у = sin х и ло-
гарифмической кривой у = log х.
258. Все числа аь а2,..., а100 равны между собой.
259. Рассмотрите коэффициенты уравнения Р(х) = (х — а) X
X (х — Ь) (х + с) (х + d) = 0.
260. Рассмотрите число, обратное фигурирующей в условии за-
дачи дроби; избавьтесь от радикалов в знаменателе полученной
дроби.
261. Если а, b и — данные числа, то условие задачи утвер-
ждает, что а Ь + > — + — + ab.
375
2б2. Докажите (методом математической индукции), что для лю-
бых (натуральных) п и k из равенства 1 суммы п положительных
чисел вытекает, что сумма всевозможных произведений по k (где
1 < k п) из наших чисел меньше 1.
263. Ц--
264. Все числа at (где i — 1, 2,..., 1973) равны между собой
(рассмотрите отдельно случаи щ > 1 и щ < 1).
265. Воспользуйтесь методом математической индукции.
266. Не может (дтя второго многочлена ответ положителен).
267. Воспользуйтесь методом математической индукции.
268. Если 99 999 + 11Г111 Уз ----- (А + В /з)3, то 99 999 —
-111111)3== (А —В Уз)3.
269. Докажите, что если ') 2 = р + q то ) 2 есть рациональ-
ное число.
1
270. Пусть А = хт; тогда хф- — — п.
271. Не существуют,
272. Нельзя.
б/г -L 5
273. При х—где/г — рационально.
274. Оцените разность — %! близких корней уравнений
х2 + рх + q = о и <4 + РУ + qi = 0, где \q, — q] ® 0,01.
275. Обозначим через 0 < а, < Яг < ... < а.п дробные части
наших чисел «1, а2,..., ап\ округлите числа аь а2, ... ah по недо-
статку, а числа Яа-н, йл+г,-, —по избытку; подберите k.
276. 0; 0,5; 0,501; 0,502;...; 0,999; 1.
277. Рассмотрите дробные части чисел 0, а, 2а, За,..., 1030а;
воспользуйтесь принципом Дирихле (стр. 10).
278. а) Докажите, что если а< 1— (0,1)1ии,тои У а < 1—(0,1)]0|).
б) Воспользуйтесь тем, что рассматриваемое число х равно
1 1/ / 1 \|,ш
-у у 1 — ('jo’) -Ответ: с точностью до 300 цифр полте
запятой;
х = 0,3333 ... 333 166 666 ... 6666 250000 ... 000
100 троек .100 шестерок 07 пулей
279. Второе из двух выражений больше первого.
at + а., 4-...+ а„
280. х =_------------.—И.
п
281. a) at, а2, а4, а3. б) Докажите, что если и — какие-
то два из заданных чисел (а <8 ) и а. ,, а, — числа, стоящие
1а—1 ‘₽+1
в искомом расположении перед и после ajfi то
(%-%) (%-1~%м)>0-
376
282. а) Рассмотрите ломаную ДоДj.42 ... Л такую, что проекции
отрезков Д0Д1, Д1Д2....ДП_|ДП на ось Ох равны соответственно
Яг, аг...ап, а на ось Оу — bit b2, ..Ьп. Равенство имеет место,
ах °2 °п п
если -у ™ -г- = ... = -г— . б) Воспользуйтесь неравенством за-
12 ип
дачи а).
283. При п четном задача может быть "решена геометрически
аналогично решению задачи 282а); случай нечетного п может быть
сведен к случаю четного п. Равенство имеет место при п четном,
если а> *= 1 — а2 - а3 = 1 — at = ... = n„_j — а„, а при п нечет-
1
ном — только если а: = а2 = ... = ап = -у.
284. Возведите обе части неравенства в квадрат.
285. cos sin х больше, чем sin cos х при любом х.
286. а) Если Jog2n = a, log?, л = Ь, то ь ~ 10. б) Если
1
log 2л = о, 1одл2 = b, то b ~
287. а) Воспользуйтесь тем, что для каждого угла х первой
четверти sin х < х. б) Воспользуйтесь тем, что для каждого угла х
первой четверти tg х > х.
288. Воспользуйтесь геометрическим определением тангенсов как
длин отрезков в тригонометрическом круге или как удвоенных пло-
щадей некоторых треугольников.
л
289. aresin cos arcsin х -f- arccos sin arccos x = —.
290. Замените в сумме cos 32x + c31 cos 31x + ...й! cos x
угол x на x + л и сложите полученное выражение с первона-
чальным.
а Г-----------------
291. Исходя из формулы 2 sin у= + У 2 — 2 cos а, вы-
числите
последовательно при п = 1, 2, ...
292. 1.
293. Воспользуйтесь тем, что данные многочлены имеют те же
самые коэффициенты при с20, что и (1 + х2 + х3) 1000, соответственно
(1 _X2_X3jlOOO
294. Воспользуйтесь формулой (й4-&)7й— Ь) — а2— Ь2.
1001! ' ,, 51050.1001!
295. а) С1001*=50! -951!’ 1000 Сloot ~ 52! • 950! ‘
296. Обозначим данное выражение через Пл; в таком случае
Пл = (Пл-i — 2)2. Ответ: (42'1-1 — 4ft-‘) : 3.
297. а) 6. б) 6х.
298. —х + 3.
299. Воспользуйтесь тем, что многочлен х4 + х3 + 2х2 + х + 1
есть делитель двучлена х12—1. Ответ: —1.
300. Р(х) = сх(х — 1) (х — 2) ... (х — 26), где с — постоянное.
301. а) Рассмотрите числа P(10;'f), где N достаточно велико,
б) Воспользуйтесь результатом задачи а).
377
302. Положите в равенстве х200у200 L = f(x)g(y) сначала
у = 0, а затем х = 0.
303. Воспользуйтесь тем, что квадратный трехчлен -р(х)—х
сохраняет знак при всех х.
304. Воспользуйтесь неравенствами |р(1) | 1, |р(0) | sgll и
305. Рассмотрите два числа p(xt) и р(х2), где р(х) — многочлен,
стоящий в левой части уравнения (3).
306. Q2 + q2 - pP(Q + q)+ qP2 + Qp2 - 2Qq.
307. a — 1 и a = —2.
308. a) a = 8 и a = 12. 6) b = 1, c = 2, a = 3; b = — 1,
c = — 2, a = — 3; b = 2, c = — 1, a = 1 и b = 1, c = — 2, a = —1.
309. а) Никогда, б). Только если n = 2, a2 = ai + 2 и n = 4;
a2 = aI — 1, a3 = «! + 1, a4 = a! -J- 2.
310. Воспользуйтесь тем, что если
(х — О1)2(х — а2)2... (х —a„)2+ 1 = р(х)р(х),
то р(х) и q(x), так же как и (х — ai)2(x — аи)2 • (•*— «п)2+ 1, ни
при каком х не обращаются в нуль и поэтому не могут менять знака.
В остальном решение аналогично решению задачи 309а).
311. Используйте то, что 14—7 — 7 нельзя разложить в произ-
ведение нескольких целых множителей, из который четыре являются
различными.
312. Воспользуйтесь тем, что если многочлен разлагается па
множители с целыми коэффициентами, то при тех х, при которых
многочлен равен ±1, сомножители его тоже равны ±1, а также тем,
что многочлен третьей степени не может принимать одно и то же
значение более трех раз.
313. Воспользуйтесь тем, что если р и q — два целых числа, то
Р(р) —P(q) делится на p — q.
314. Докажите, что если Р
— ql = ± 1-
315. а) Приравняйте коэффициенты при одинаковых степенях х
в обеих частях равенства
(а0 + срх + а2х2 + ... +a„xn) (Ьй + Ь}х + Ь2х2 +&„хп) =
= Со + 4- С2Х2 -р , . . -f- C,, + mX'i + 'n
и, воспользовавшись полученной формулой, покажите, что если бы
рассматриваемый многочлен разлагался на два множителя, то все
коэффициенты одного из сомножителей должны были бы быть чет-
ными (что невозможно, так как в исходном многочлене старший
коэффициент равен 1).
б) Положите в рассматриваемом многочлене х — у -р 1 и затем
аналогично решению задачи а) покажите, что если бы полученный
многочлен разлагался на два множителя, то все коэффициенты од-
ного из сомножителей делились бы на простое число 251.
316. Воспользуйтесь той же формулой, что и при решении зада-
чи 315а) (см. указание к этой задаче).
317. Докажите, что где -2——несократимая дробь, не
может быть целым числом.
318. Пусть P(N) = Л4; докажите, что P(N -р kM)—P(N) при
всяком k делится па .1'1.
— 0, то k — pl = ± 1 и k
319. Представьте многочлен Р(х), принимающий при целых х
целые значения, в виде суммы Р(х]i = b0P0(x) +ftiPi(x) +...
... У ЬпРп(х) с неопределенными коэффициентами Ьо, Ь,-, ..Ьп,
где (при целом х k) Pk (x) = С*, и определите эти коэффициенты,
подставляя в последнее равенство последовательно х =
= 0, 1, 2, 3, ..п.
320. а) См. указание к предыдущей задаче, б) Сделайте в мно-
гочлене замену переменных: у = х + к. в) Рассмотрите многочлен
Q(x) = Р(х2).
321. Воспользуйтесь формулой Муавра.
322. Воспользуйтесь результатом задачи 3216).
323. Если х 4- ~ = 2 cos а, то х = cos а ± i sin а.
324. Воспользуйтесь формулой Муавра.
325. Воспользуйтесь результатом предыдущей задачи. Ответ:
п — 1 sin (п + 1) a cos па
cos2 а. + cos2 2а + ... + cos2 п а = "» - +----5-7Д ------.
326. Воспользуйтесь формулами Муавра и бинома Ньютона.
327. Воспользуйтесь формулой
sin A sin В = ~2~ [cos (А — В) — cos (4 4- В)]
и результатами задачи 324.
328. Рассмотрите корни уравнения х2и+1 — 1=0.
329. Воспользуйтесь формулами задачи 3216).
330. Воспользуйтесь результатом задачи 3296).
и (2п— 1) 2п(л+1)
Ответ: а)---j---. 6)---3--.
331. Воспользуйтесь результатом задачи 329а).
У 2п У 1 У п 1 "|/й
Ответ: а)----------- и -^j. б) — и
332. Воспользуйтесь тем, что если а есть угол первой четверти,
то sin а < а < tg а.
333. а), б). Воспользуйтесь формулой задачи 324. в) Воспользуй-
тесь результатом задачи б).
334. а) Воспользуйтесь предложением задачи 333а). б) Вос-
пользуйтесь формулой задачи 324.
335. а) Воспользуйтесь предложением задачи 333а). б) См.
указание к задаче 3346). в) Воспользуйтесь результатом задачи 331а).
336. Воспользовавшись формулой Муавра, представьте sin50 а в
виде суммы косинусов углов, кратных а, взятых с некоторыми ко-
эффициентами. Ответ: 5000 = (5000 50! /?50) : (25!)2
337. Наибольшее значение: |г| (а У У а2 у 4); наименьшее
I г| == 4" (Уа2 + 4 — а).
338. Докажите, что если наибольшая из разностей аргументов
наших чисел меньше 120°, то их можно умножить на число единич-
ного модуля так, чтобы вещественная часть суммы полученных про-
изведений была положительна. Заменить в условии задачи величину
120° большей нельзя.
379
339. Воспользуйтесь тем, что если изображающая г точка А ком-
плексной плоскости лежит вне отвечающего числам сь с2,..., с„
многоугольника М — CiC2... С„, то опа лежит «по одну сторону» от
М в том смысле, что все векторы AM, где МеМ, направлены в одну
сторону от некоторой проходящей через А прямой /.
340. Воспользуйтесь тем, что если а не делится на р, то числа
а, 2а, За,.... (р—1)а дают при делении на р различные остатки.
341. Воспользуйтесь тем, что если Ai, k2,..., kr — все целые
числа меньшие N и взаимно простые с N, то числа kta, k2a, ,.., kra
дают при делении на W разные остатки.
342. Воспользуйтесь методом математической индукции.
343. Воспользуйтесь теоремой Эйлера (задача 341).
344. Докажите, пользуясь методом математической индукции,
что, каково бы пи было целое число N, всегда найдется такая сте-
пень числа 2, N последних цифр которой все будут единицами и
двойками; при доказательстве воспользуйтесь теоремой Эйлера (за-
дача 341) и предложением задачи 342.
345. Ясно, что пара чисел п и п2 является «хорошей»; сравните
разложения на множители чисел п— 1 и п2— 1.
346. Пусть and взаимно просты; с помощью теоремы Эйлера
(задача 341) докажите, что прогрессия содержит бесконечно много
натуральных степеней числа а.
347. См. указание к задаче 340.
348. а) Докажите, что для каждого нечетного простого числа
р существуют ' два таких целых положительных числа х, у (где
тр-ь что 11 У2 ~ 1 Дак>т при делении на р одинаковые остат-
ки. б) Воспользуйтесь теоремой Вильсона (задача 347).
349. Пусть Pi, р2,..., рп—п простых чисел. Найдите число,
которое не делится ни на одно из этих чисел и больше каждого
из них.
350. а) Пусть р,, р2,,.., рп — п простых чисел вида Мг — 1
(или 6/е—1). Найдите число вида 4 Л'— 1 (или 6Л’—1), которое не
делится ни на одно из чисел pi, р2,..., рп и больше каждого из них.
б) Идея решения близка к использованной в решении задачи а).
ЛИТЕРАТУРА
А. Сборники «Олимпиадских» задач
На русском языке имеется много книг, из которых можно черпать допол-
нительные задачи повышенной трудности (задачи «олимпиадного» типа).
Из их числа, в первую очередь, хочется указать следующие:
1. А. А. Л е м а н (сост.), Сборник задач московских математических
олимпиад, М., «Просвещение», 1965.
2. Н. Б. Васильев, А. А. Егоров, Сборник подготовительных
задач к Всероссийской олимпиаде юных математиков, М., Учпед-
гиз, 19'63.
3. Е. А. М о р о з о в а, И. С. П е т р а к о в, Международные матема-
тические олимпиады, М., «Просвещение», 1971.
4. И. Л. Бабинская, Задачи математических олимпиад, М., «На-
ука», 1975.
Книги серии «Библиотека математического кружка»
5. Е. Б. Д ы н к и и, В. А. Успенски й, Математические беседы,
М.— Л., Гостехиздаг, 1952.
6, А. М. Я гл ом, И. М. Я г л о м, Неэлементарные задачи в эле-
ментарном изложении, М., Гостехиздат, 1954.
7. И. М. Я г л о м, В. Г. Б о л т я н с к и и, Выпуклые фигуры, М.— Л.,
Гостехиздат, 1951.
8. Д. О. Ш к л я р с к и й, Н. Н. 4 е н ц о в, И. М. Я г л о м, Избран-
ные задачи и теоремы планиметрии, М., «Наука», 1967.
9. Д. О. Ш к л я р с к и й, Н. Н. Ч е н ц о в, И. М. Я г л о м. Избран-
ные задачи и теоремы элементарной математики; геометрия (сте-
реометрия), М., Гостехиздат, 1954.
10. Д. О. Ш к л. я р с к и й, Н. Н. Ч е н ц о в, И. М. Я г л о м, Геомет-
рические неравенства и задачи на максимум и минимум, М.,
«Наука», 1970.
11. Д. О. Шклярский, Н. Н. Ченцов, И. М. Яглом, Гео-
метрические оценки и задачи из комбинаторной геометрии, М.,
«Наука», 1974.
Книги серии «Библиотечка физико-математической школы»
12. Е. Б. Дынкин, С. А. Молчанов, А. Л. Розенталь,
А. К. Толпы го, Математические задачи, М., «Наука», 1971,
13. Е. Б. Д ы н к и н, С. А. М о л ч а н о в, А. Л. Р о з е п т а л ь, Ма-
тематические соревнования (арифметика и алгебра), М., «На-
ука», 1970.
14. Н. Б. В а с и л ь е в, С. А. Молчанов, А. Л. Розенталь,
А. П. Савин, Математические соревнования (геометрия), М.,
«Наука», 1974, .
381
15. С. И. Гельфанд, М. Л. Гер вер, А. А. Кириллов,
Н. Н. Коистаитииов, А. Г. Кушнеренко, Задачи по
элементарной математике (последовательности, комбинаторика,
пределы), М., «Наука», 1965 (см. также А. А. Кириллов, Пре-
делы, М., «Наука», 1973),
а также другие книги той же серии, хоть и не имеющие характера задачни-
ков, но содержащие много удачных задач н упражнений:
16. Н. Б. Васильев, В. Л. Г у т е н м а х е р, Прямые и кривые,
М., «Наука», 1970.
17. М. И. Башмаков Уравнения и неравенства, М., «Наука», 1971.
18. И. М. Гельфанд, Е. Г. Глаголева, А» А. Кириллов,
Метод координат, М., «Наука», 1973.
19. И. М. Г е л ь ф а н д, Е. Г. Г л а г о л е в а, Э. Э. Ш н о л ь, Функ-
ции и графики (основные приемы), М., «Наука», 1973.
Наконец, следует еще назвать книги:
20. Г. Штейн га уз, Сто задач, М., «Наука», 1976.
21. В. А. К р е ч м а р, Задачник по алгебре, М., «Наука», 1972.
22, Б. Н. Делоне, О. К- Житомирский, Задачник по геомет-
рии, М., Физматгиз, 1959.
Журналы и непериодические сборники
23. Журнал «Квант».
24. Журнал «Математика в школе».
25. Сборники «Математическое просвещение» (новая серия; 1957—
1961).
Здесь имеются в виду раздел «Задачник ,,Кванта”» (и примыкающие
к этому разделу заметки и статьи, также содержащие, как правило, много
задач); раздел задач сборников «Математическое просвещение»; регулярно
помещаемые в журнале «Математика в школе», отчеты о московских, всесо-
юзных и международных олимпиадах, содержащие перечень всех предложен*
ных задач, и тщательно составленный обзор нх решений.
Б. Общая литература о том, как решать задачи
26. Д. П о й а, Математическое открытие, М., «Наука», 1976.
27. Д. П о й а, Математика и правдоподобные рассуждения, М.,
«Наука», 1975.
28. Д. П о й а, Как решать задачу, М., Учпедгиз, 1959.
В книгах 126]—[28] обсуждается сам процесс решения задачи и даются
прямые рекомендации решающим; особый интерес представляют первые две из
них, в которых общие положения автора иллюстрируются многочисленными
примерами и задачами для самостоятельного решения.
В. Литература к отдельным циклам задач
1. Вводные задачи
«Логические» задачи типа многих, собранных в этом цикле задач, широ-
ко представлены в книгах о «математических развлечениях», рассчитанных
на учащихся средних классов школы:
29. Б. А. К о р д е м с к и й, Математическая смекалка, М., «Наука»,
1965.
30. А. П. Д о м (Тр я д, Математические игры и развлечения, М.. Физ-
матгиз, 1961.
382
31. М. Гарднер, Математические чудеса и тайны, М., «Наука»
1964.
32. В. Литцман, Веселое и занимательное о числах и фигурах,
АГ, Фнзматгиз, 1963.
33. Еленьский, По следам Пифагора, М., Детгиз, 1961.
См. также рассчитанные на несколько более опытного читателя книги се-
рии переводных сочинений иа ту же тему, выпускаемые издательством «Мир»;
34. М. Гарднер, Математические головоломки и развлечения, М.,
«Мир», 1971.
35. М. Г а р д н е р, Математические досуги, М., «Мир», 1972.
36. М. Гарднер, Математические новеллы, М., «Мир», 1974.
37. Л. Кэррол, История с узелками, М., «Мир», 1973.
38. Г. Ш т е й и г а у з, Мысли и размышления. М., «/Чир», 1974.
39. Г. Э. Дьюдени, 520 головоломок, М., «Мир», 1975.
40. С. Г о лом б, Полимино, М., «Мир», 1975.
41. Д. Б и з а м, Я. Г е р ц е г, Игры и логика, М., «Мир», 1975.
Допо тигельная литература к циклу 1
42. И. С. С о м и н с к и й, Л. И. Г о л о в и н а, И. М. Я г л о м, О ма-
тематической индукции, М., «Наука», 1967 (см. также И. С. С о-
минский, Метод математической индукции, М., «Наука», 1975;
Л. И. Головина, И. М. Я г лом, Индукция в геометрии, М.,
Фнзматгиз, 1961).
43. О. О р е, Графы и их приложения, М., «Мир», 1965.
44. А. М. Я г л о м, И. М. Я г л о м, Вероятность и информация, М.,
«Наука», 1973.
3. Задачи на делимость чисел
45. В. Г. Бо л т я н с к и й, Г. Г. Л е в и т а с, Делимость чисел и про-
стые числа, сборник «Дополнительные главы во курсу матема-
тики в 7—8 кл. для факультативных занятий» (сост. К. П. Сикор-
ский), М., «Просвещение», 1974, стр. 5—69.
46. Н. Н. Воробьев, Признаки делимости, М., «Наука», 1974.
47. С. В. Ф о м и н, Системы счисления, М., «Наука», 1975.
4. Разные задачи по арифметике
Из числа сборников арифметических задач, в когоры,х можно найти допол-
нительные задачи, в первую очередь, хочется упомянуть (весьма, впрочем,
непростую) книгу
48. В. С ер пине кий, 100 простых, но одновременно и трудных
вопросов арифметики, М., Учпедгиз, 1961
(ср. [52]—[53] и [70]—[71]), а также гораздо более доступные для начинающих
сборники:
49. А. И. О с т р о в с к и й, 75 задач по элементарной математике —
простых, но..., М., «Просвещение», 1966.
50. А. И. О с т р о в с к и й, Б. А. Кор дем с кий, Геометрия помо-
гает арифметике, М., Фнзматгиз, 1960.
5. Решение уравнёйий в целых числах
51. А. О. Гельфонд, Решение уравнений в целых числах, М.— Л.,
Гостехиздат, 1952.
52. В. С е р п и н с к и й, О решении уравнений в целых числах, М.,
Физматгиз, 1961,
-383
53. В. Серпинский, Пифагоровы треугольники, М., Учпедгиз,
1959.
54. А. Я. Хипчин, Великая теорема Ферма, М.— Л., ОНТИ, 1934.
6. Матрицы, последовательности, функции
55. А. К о ф м а н, Р. Ф о р, Займемся исследованием операций, М.,
«Мир», 1966.
56. Дж. Кеме п и, Дж. Спел л, Дж. Томпсон, Введение в ко-
нечную математику, гл. V—VII, М., «Мир», 1964.
57. Н. Н. Воробьев, Числа Фибоначчи, М., «Наука», 1969.
58. А. И. Маркушевич, Возвратные последовательности, М,,
«Наука», 1975.
8—10. Д о п о л и и т е л ь н а я литература по алгебре
59. Д. К. Фаддеев, И. С. С о м и и с к и й, Алгебра, М., «Наука»,
1966.
60. И. С. С о м и п с к и й, Элементарная алгебра, М., Физматгиз,
1963.
61. В. Г. Болтянский, Ю. В. Сидоров, М. И. Шабунин,
Лекции и задачи по элементарной математике, AV, «Наука», 1974.
62. А. И. М а р к у ш е в и ч, Деление с остатком в арифметике и в
алгебре, М.— Л., Изд. Акад. пед. наук РСФСР, 1949.
63. Р. О. Кузьмин, Д. К- Фаддеев, Алгебра и арифметика
комплексных чисел, Л., Учпедгиз, 1939.
11. Несколько задач из теории чисел
64. И. В. Арнольд, Теория чисел, М., Учпедгиз, 1939.
65. А. А. Б у х ш т а б, Теория чисел, М., «Просвещение», 1966.
66. И. М. Виноградов, Основы теории чисел. М., «Наука», 1972.
67. Г. Д э в е п п о р т, Высшая арифметика, М., «Наука», 1965.
68. А. Я- X и и ч и н, Элементы теории чисел, Энциклопедия элемен-
тарной математики, кн. 1 (математика), М.— Л., Гостехиздат,
1951, стр. 251—353.
69. Л. Г. Шнирельмзн, Простые числа, М.— Л., Гостехиздат,
1940.'
70. В. Серп и и с к и п, 250 задач по элементарной теории чисел, М.,
«Просвещение», 1968.
71. В. Серпинский, Что мы знаем и чего не знаем о простых
числах, М.— Л., Физматгиз, 1963.
72. А. Я- Хипчин, Три жемчужины теории чисел, М.— Л., Гостех-
издат, 1948.