й
Л < х - 5
1964
ЗБРАННЫЕ





ЭЛЕМЕНТАРНОЙ
АТЕМАТИКИ
МИНСК



В. ПЛАТОНОВ, к. АРЛЮК, В. ЗАРЕЦКИЙ, Н. МЕТЕЛЬСКИЙ, Л. ТУТАЕВ
ИЗБРАННЫЕ ЗАДАЧИ ЭЛЕМЕНТАРНОЙ
МАТЕМАТИКИ
Под общей редакцией доцента Л. ТУТАЕВА
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА» МИНСК 1964
Настоящий сборник составлен с целью предложить учителям И' учащимся задачи для внеклассной работы. Сборник поможет учащимся техникумов и профтехучилищ в лучшем усвоении предмета математики, его могут использовать студенты педагогических институтов при проведении педагогической практики в школе. Авторы расширили и дополнили ранее изданные «Избранные задачи элементарной математики» (Минск, 1961) с тем, чтобы сборником мог пользоваться каждый школьник, интересующийся задачами повышенной трудности, методами и способами их решения. Включенные в сборник задачи соответствуют программам указанного класса, ко всем задачам даны указания или решения.
Разделение задач по классам следует признать условным. Некоторые задачи, отнесенные к VII классу, полезно решать учащимся старших классов. Другие задачи отнесены к IX или X классу только по степени трудности их решения.
Просьба критические высказывания и пожелания направлять по адресу: Минск, Белорусский государственный университет им. В. И. Ленина, математический факультет, кафедра геометрии,, доценту Тутаеву Л. К.
ЗАДАЧИ
VII КЛА СС
дробь
2.
число
Найти все целые и положительные и, при которых
Зп2—Зп+20
—— принимает целые значения.
Доказать, что при любых целых и положительных п
целое и положительное.
3.	Доказать, что п5 — 5и34“4л при целом п делится на 120.
4.	Доказать, что если п — натуральное число, то и(и2	5) делится на 6.
5.	Найти цифры хну пятизначного числа, которое в десятичной системе записывается так: 42х4у, если известно, что это число делится на 72.
6.	Написать цифры вместо букв: абвгде жзи
мнпр к8л стд
уфч
шяэе
шяэе
7.	Для нумерации страниц учебника потребовалось 411 цифр. Сколько страниц в учебнике?
8.	Сколькими нулями оканчивается число, полученное от умножения всех чисел от 1 до 100?
9.	Доказать, что сумма квадратов пяти последовательных целых положительных чисел никогда не является квадратом целого числа.
1*
3
10.	Доказать, что у числа, являющегося точным квадратом, произведение двух последних цифр четно.
11.	Доказать, что если между цифрами числа 1331 написать по равному количеству нулей, то получится точный куб.
12.	Доказать, что нет целых чисел, которые от перестановки начальной и конечной цифры увеличивались бьп в 5, в 6 или в 8 раз.
13.	Найти такое трехзначное число, удвоив которое мы получим число, выражающее количество цифр, необходимое для написания всех последовательных целых чисел от 1 до этого трехзначного числа.
14.	Найти наименьшее число, записываемое одними! единицами, которое делилось бы на число 33... 3 (сто троек).
15.	Доказать, что если разность, полученная от вычитания числа, выраженного тремя последними цифрами данного числа, из числа, выраженного всеми остальными цифрами (или наоборот), равна 0 или делится на 7, на 11, на 13, то все данное число делится соответственно на 7, или на 11, или на 13. (Признак делимости на 7, 11, 13.)
16.	Найти признак делимости на 7 числа, записанного в восьмеричной системе.
17.	Найти признак делимости на 9 числа, записанного в восьмеричной системе.
18.	Найти все простые числа р такие, что р24*8— простое число.
19.	Доказать, что квадрат любого простого числа,, кроме двух и трех, при делении на 24 дает в остатке L
20.	Доказать, что всякое простое число при делении на 30 дает в остатке снова простое число.
21.	2Р—1 и 2?—1 взаимно просты. Доказать, что р и q—так же взаимно просты. Обратно, если р и q— взаимно просты, то 2Р — 1 и — 1 взаимно просты.
он п	1	3	5	99	. 1
22,	Доказать, что: ---*---g- • • • -jog- < -[o’-
23.	Определить несократимую дробь, которая не изменяет своей величины от прибавления к числителю 21, а к знаменателю 28,
24.	Два одинаковых катера, имеющие одинаковую скорость в стоячей воде, проходят по двум рекам одинаковое расстояние по течению и возвращаются обратно. В какой реке на эту поездку потребуется больше времени:
4
в реке с быстрым течением или в реке с медленным течением?
25.	Решить систему п уравнений с п неизвестными:
*1 _ *2
аг а2 9
х2 __ х3
а2 ~ а3*
хп-\ _ х„
ап-\ а" ’
. -ч*24~“Н •••
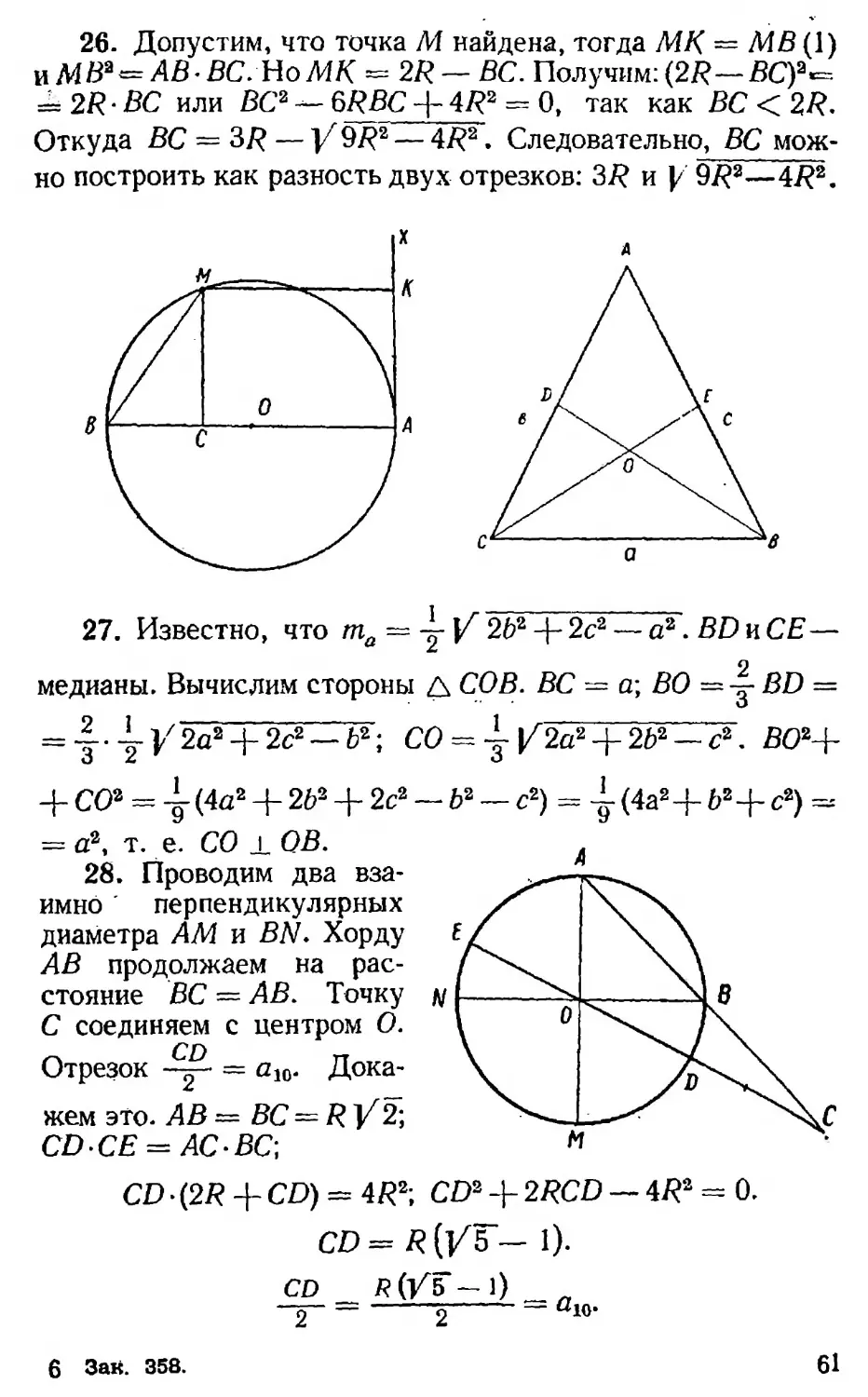
26.	Узнать, через сколько минут после того, как часы показывали 9 часов, минутная стрелка догонит часовую.
27.	В каком году родились люди, которым в 1958 году исполнилось столько лет, какова сумма цифр года их рождения?
28.	В треугольнике АВС высота ha составляет поло-вину биссектрисы внешнего угла этого треугольника при вершине А. Найти разность углов В и С.
29.	Тысяча точек являются вершинами выпуклого ты-сячеугольника, внутри которого расположено 500 точек так, что никакие три из них не лежат на одной прямой. Многоугольник разрезается на треугольники, вершинами которых являются только данные 1500 точек. Сколько получится треугольников?
30.	Точки, симметричные точке пересечения высот треугольника относительно трех его сторон, лежат на окружности, описанной около этого треугольника.
31.	На плоскости проведена замкнутая ломаная линия, все звенья которой имеют длину / и любые два соседних звена взаимно перпендикулярны. Доказать, что число звеньев кратно 4.
32.	Доказать, что прямые, соединяющие последовательные центры квадратов, построенных на сторонах параллелограмма и примыкающих к ним извне, образуют квадрат.
33.	Построить треугольник по вершине, точке пересечения высот и середине противоположной стороны.
34.	Около правильного треугольника описать квадрат, имеющий с ним общую вершину.
5
35.	В данную окружность вписать трапецию, если известна ее боковая сторона и расстояние от центра до точки пересечения диагоналей. .
36.	По высоте, опущенной из вершины прямого угла, и разности острых углов построить прямоугольный треугольник.
VIII КЛА С С
1. Доказать, что
ab (а 4" Ъ — 2с) Ьс (Ь -|- с — 2а) ас (а 4- с — 26) > О при а > О, b > 0, с > 0.
2. Доказать, что из равенства
а ' b ] с а-]-Ь-{-с
вытекает равенство
ерли п нечетное.
3. Доказать, что выражение
делится на и, если п — число нечетное.
4.	Натуральные числа а и Ь взаимно просты. Доказать, что наименьший общий делитель чисел а-\-Ь и а24~62 равен 1 или 2.
5.	Доказать, что многочлены:
а5 + 4а3 + За и а* 4- За2 Ц- 1
не имеют общих делителей ни при каком целом а.
6.	Доказать, что уравнение
2х2 — 5у2 = 7
не имеет решений в целых числах.
7.	Решить уравнение
х3 2 /з № + Зх Н- |/"З — 1 = 0.
8.	Определить а так, чтобы сумма квадратов корней уравнения х2 -|- (2 — а)х~ а — 3 = 0 была наименьшей.
6
9.	Найти действительные решения системы уравнений: ( х* + у* = 17
I х + у = 3.
10.	Доказать тождество:
1	1	। ±_1	!	।__?______1	_	1	|
2'3	4 т ‘' т2<! - 1 2k k + 1 г
, 1 . ,1
' k + 2 "• • • ' ' 2k'
11.	Если п — произвольное число, то существует число, кратное п, записанное с помощью двоек и нулей. Доказать.
12.	Вычеркнуть 100 цифр из числа:
123456789101112 ...... 9899100 так, чтобы полученное
число было наибольшим.
13.	Решить уравнение:
|хЦ-1| — |х|4-3|х — 1 [ — 21 х — 21 = | х 4~ 21.
14.	Если многочлен с целыми коэффициентами
f(x) = а0 х3 4- ах х2 4- а2 х -ф- а3
при х — 0 и х = 1 принимает нечетное значение, то он не имеет целых корней. Доказать.
15.	Найти положительное четырехзначное число, кратное 7 и представляющее собой сумму куба и квадрата некоторого целого числа.
Ь2 + с2 — а2
16. Дано:
а2+д2 —с2
2Ьс
2ас
2аЬ
= 1.
Доказать, что две из этих дробей равны -|- 1, а одна из них — 1.
17.	Построить такой равнобедренный треугольник, чтобы периметр всякого вписанного прямоугольника был бы величиной постоянной.
18.	Стороны одного треугольника равны медианам второго треугольника. Найти отношение площадей этих треугольников.
19.	Если все квадраты, вписанные в треугольник так, что две вершины расположены на стороне треугольника, а две другие вершины на двух других сторонах треугольника, равны между собой, то треугольник равносторонний. Доказать.
20.	Если произведение диагоналей четырехугольника равно сумме произведений противоположных сторон, то около него можно описать окружность. Доказать.
7
21.	На одной стороне треугольника дана точка А. Требуется провести через нее прямую так, чтобы она разделила площадь треугольника на две равные части.
22.	Из точки О внутри треугольника АВС на его стороны опущены перпендикуляры ta, tb, tc. Доказать, что Т~ + £ + -Г = 1 • h»hc- высоты Д АВС.) •iQ,	'lC
23.	В равнобедренном треугольнике радиус описанной окружности /?, а радиус вписанной — г.
Найти стороны треугольника.
24.	Найти на стороне данного треугольника точку так, чтобы перпендикуляр, опущенный из нее на другую сторону, делил площадь данного треугольника пополам.
25.	В разностороннем треугольнике стороны пропорциональны медианам. Найти коэффициент пропорциональности.
26.	а, Ь и с — стороны треугольника ЛВС; R — радиус описанного круга; Z, т и п — расстояния центра тяжести от сторон треугольника. Доказать, что R =
27.	Через точку внутри квадрата провести прямую, отсекающую от него фигуру с наименьшей площадью.
28.	Доказать, что нет* равнобедренного треугольника, у которого вписанная окружность делила бы медиану на три равные части.
29.	Построить прямоугольную трапецию так, чтобы разность между удвоенным квадратом большей диагонали и квадратом меньшей диагонали равнялась а2 (а— данный отрезок).
30.	Построить треугольник, зная, что длины сторон его составляют арифметическую прогрессию, биссектриса, проведенная к средней стороне, равна I и угол, лежащий против биссектрисы, равен а.
31.	В данный прямоугольник вписать ромб со стороной а (вершины ромба принадлежат разным сторонам прямоугольника).
32.	Из пяти данных окружностей любые четыре проходят через одну точку. Доказать, что найдется точка, через которую проходят все пять окружностей.
33.	Если трапеция описана около окружности, то прямая, соединяющая точки касания оснований, и прямая, соединяющая точки касания боковых сторон, проходят через точку пересечения диагоналей.
8
34.	В шахматном турнире участвовало 8 человек, сыгравших по одной партии с каждым из остальных участников. Все они набрали различное количество очков. Шахматист, занявший второе место, набрал столько же очков, сколько четыре последних вместе. Как сыграли между собой шахматисты, занявшие третье и седьмое место?
35.	Дан произвольный выпуклый четырехугольник: 1) вписать в него квадрат и 2) описать около него квадрат.
36.	Доказать, что площадь прямоугольника, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей прямоугольников, подобных этому прямоугольнику; гипотенуза и катеты — сходственные стороны прямоугольников.
37.	Если сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полу периметру, то четырехугольник — параллелограмм. Доказать.
38.	Через точку внутри угла провести прямую, отсекающую от этого угла треугольник с наименьшей площадью.
39.	Найти точку, из которой видны под равными углами три последовательных отрезка АВ, BCt CD одной прямой.
40.	Построить трапецию, зная углы при основании и диагонали.
41.	Круг радиуса R катится внутри круга радиуса 2R (без скольжения). Какие линии описывают точки катящегося круга?
42.	При помощи одной линейки провести прямую, параллельную основаниям данной трапеции так, чтобы ее отрезок, заключенный внутри трапеции, делился диагоналями на три равные части.
43.	Стороны любого треугольника есть стороны правильных треугольников, примыкающих к данному извне. Доказать, что точки пересечения высот этих треугольников — вершины правильного треугольника.
44.	Дана прямая и точка на ней. Восстановить из этой точки перпендикуляр к прямой с помощью одной двухсторонней линейки (линейка с параллельными краями).
45.	Пусть at b, с, d — величины последовательных сторон четырехугольника, около которого можно описать окружность; I и f — величины диагоналей. Доказать, что If = ас + bd.
9
46.	На окружности, описанной около равностороннего треугольника АВС, взята точка М. Доказать, что наибольший из отрезков МА, МВ и МС равен сумме двух остальных.
47.	Доказать, что среди всех прямоугольных треугольников с общей гипотенузой равнобедренный треугольник имеет наибольший радиус вписанной окружности.
48.	Если внутренние касательные двух окружностей взаимноперпендикулярны, то отрезок, отсекаемый внутренними касательными на внешней касательной, равен сумме радиусов этих окружностей. Доказать.
49.	Найти площадь треугольника, образованного двумя внутренними и одной внешней касательной двух окружностей, если внутренние касательные взаимно перпендикулярны.
50.	Отрезок длиной а разделить на 2, 3, ..., п частей, используя циркуль постоянного размера а и линейку.
51.	Дана окружность, центр которой не указан, и точка М вне ее. Опустить из этой точки перпендикуляр на заданный диаметр с помощью одной линейки.
IX КЛАСС
1.	Найти последние две цифры числа 799 .
2.	Доказать, что число вида (1О'г10п~1	... +
-|- 1)-(10л + 1 —|— 5) —1 есть точный квадрат.
3.	Найти трехзначное число, являющееся точным квадратом N2, и такое, чтобы произведение его цифр было равно N—1.
4.	Доказать, что если п — четное число, то число 13" 4- 6 делится на 7.
5.	Доказать, что при любом натуральном п имеет место неравенство
22" +."зГ + 4Г + • • • +	1 •
6.	Даны п различных положительных чисел аъ а2, ..., ап. Из них составляют всевозможные суммы с любым числом слагаемых (от 1 до /г). Доказать, что из этих сумм найдется по крайней мере —Цу—~ попарно неравных.
7.	Найти двузначное число, равное неполному квадрату суммы его цифр.
10
8.	Число 531441 надо разбить на такие числа, чтобы первое из них было 1, второе — в k раз больше, третье — в k раз больше суммы первых двух, четвертое — в k раз больше суммы первых трех и т. д. Последнее число — в k раз больше суммы всех предыдущих. Найти множитель k и число слагаемых, если известно, что оно не менее четырех.
9.	Доказать, что при всяком целом п > 1
10.	Определить целую часть числа
1 -|- -L Н--L + . . . 4- у :L- .
1 У 2 У 3	' у 1000000
11.	Доказать, что
при условии, что все числа xlt х2, .... хп одного знака и больше, чем — 1.
12.	Найти сумму
5 _	1______।_____!_____и ।_____________1________
п v 1 + г 3 ' р 3 + у 5 — * ’ * V 2п — 1 + У 2п + 1 *
13.	При каком условии радикал Ут 4~ К а + V Ь~уУ с можно представить в виде суммы трех радикалов У х ~у + У У~\~ V z, где х, у, z — положительные рациональные числа?
14.	Показать, что если а > Ь > 0, то разность между средним арифметическим и средним геометрическим этих
(а — Ь? (а — Ь)2 чисе^и находится между - -g-—— и - - - •.
15г Уничтожить иррациональность в знаменателе дроби ______________________59_______
1 + 3 ~2 — 2 у' Т
|6. Доказать, что выражение
2	2У х__1
равно -=---- при 1 4 х < 2 и —— при х > 2.
17.	Показать, что для того, чтобы дробь	‘L
QjX	£?jX ~p c
11
имела значение, не зависящее от х, необходимо и достаточно соблюдение условия
а __ ь ___ с
~ bi “ "с?*
18,	Найти наибольшее и наименьшее значения функции
__2х2 4- 6х + 6
У х2 + 4х + 5 ’
19.	Доказать, что трехчлен: х24~ 5хЦ- 16 ни при каком цеф^ значении х не делится на 169.
20	Решить систему уравнений:
( х2 4- у J/ ху = 336
| у2 4-х V ху = 112.
21.	Решить уравнение:
У + ^89 + х = 5.
22j Решить уравнение:
ь	_
Vа — У	х ~ х-
2$. Решить уравнение
Р/-ТП— Р'— Рг—ГТ
У Ь -f- X F X .у X Ь____Л
х а * b
241 Решить уравнение
(в2 — а)2 (х2 — х +1)3 = (а2 — а + 1)®(х2 — х)2.
2Э. Найти все действительные решения уравнения:
17= + T7==f = 28 - 4 УТ^. -	.
ух —2 Vy~\
26.	Дана окружность, диаметр которой АВ, и касательная АХ, Требуется найти на окружности такую точку М, чтобы расстояние от этой точки до касательной равнялось бы расстоянию от этой же точки до другого конца диаметра В,
27.	Доказать, что если стороны А АВС связаны соотношением 62 + & = 5а2, то две медианы, выходящие из вершин В и С, взаимно перпендикулярны.
28.	Не прибегая к делению радиуса в среднем и крайнем отношении, найти построением сторону а10 правильного десятиугольника, вписанного в круг радиуса /?.
12
29.	Дана четверть круга АОВ (центр в О) радиуса R и полуокружность с центром в Olf. построенная на АО как на диаметре (внутри данной четверти круга). Радиус этой полуокружности, перпендикулярный к ОД, встречает окружности О и Ог в точках М и N. Найти периметр и площадь криволинейной трапеции MNOB.
30.	На сколько частей делят плоскость I прямых общего положения (прямые находятся в общем положении, если среди них нет параллельных и никакие три из этих прямых не пересекаются в одной точке)?
31.	Доказать, что если плоский многоугольник имеет' несколько осей симметрии, то они пересекаются в одной точке.
32.	На прямой дано р отрезков. Доказать, что если каждые два из них имеют общую точку, то существует по крайней мере одна точка, принадлежащая всем отрезкам.
33.	Доказать, что если фигура имеет два центра симметрии, то она имеет бесчисленное количество центров симметрии.
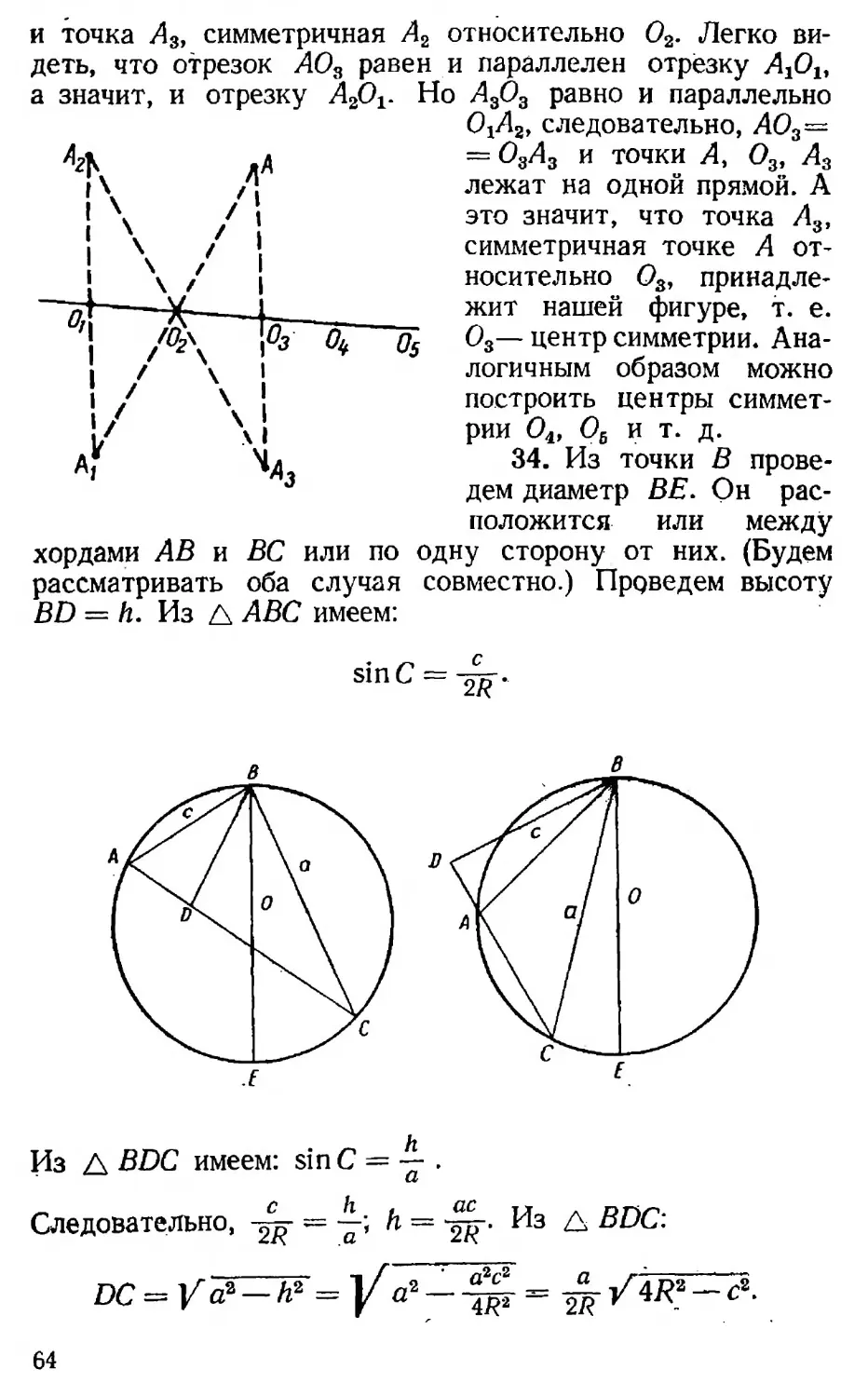
34.	В окружности радиуса R проведены хорды АВ — с и ВС = а. Определить длину хорды АС.
35.	На катетах и гипотенузе прямоугольного треугольника, как на диаметрах, построены полуокружности: две первые — вне треугольника, третья по ту сторону от гипотенузы, где лежит треугольник. Доказать, что сумма площадей двух луночек, заключенных между каждой из меньших окружностей, и большей окружностью, равна площади данного треугольника.
36.	Окружность радиуса, равного высоте правильного треугольника, катится по одной из сторон этого треугольника так, что остальные стороны высекают из окружности некоторую дугу. Доказать, что дуга при любом положении окружности равна 60^.
37.	Построить циркулем и линейкой выражение
X КЛАСС
1. Доказать, что если п — целое число, большее 2, то
13
2. Если х и у — целые, взаимно простые числа, то на ибольший общий делитель чисел х — у и
хп ~1хп ~2 ухп у2...	хуп~24-Уп“1
есть делитель числа п. Доказать.
’ 3» Найти основание всех таких систем счисления, в которых любая нечетная степень всякого натурального числа оканчивается той же цифрой, что и само это число.
4.	Найти такие вещественные числа а, b и р, qt чтобы равенство (2х — I)20 — (ах 4~ &)20 (*2 4" Рх + 9)10 выполнялось при любых х.
5.	Если р и q — простые числа «близнецы» (р — 1 = = (/4'1)» то Рр-\~Яд кратно р4"7* Доказать.
6.	Доказать, что при любых натуральных числах k и п выражение kn + 2 4- (& 4_ 1)2л + 1 делится на k2 + k 4- 1.
7.	Доказать неравенство:
k (1 4- a2k) — ak	a2ti ~1 4~ a2k ~2 4~ • • • + а2	а,
если а>0 и k — целое положительное число.
8.	Замечено, что среднее арифметическое k первых цифр числа к стремится при возрастании* числа k к 4,5.
Доказать, что при этом число 10 минус т: также обладает этим свойством.
9.	Доказать, что в любом тридцатизначном числе, в записи которого участвуют только цифры 1, 2 и 3, можно найти две тройки из подряд стоящих цифр такие, что образованные ими трехзначные числа равны.
10.	Сколько цифр имеет число
10Ч104—1) . 10*(10*——2) 1-2.	>"	1-2-3.
[всего (1044-1) членов]?
11.	Доказать, что выражение 4ПЦ- 15п— 1» гДе п—на-туральное число, делится на 9.
12.	Доказать, что сумма I3 4- 23 4- З3 4~ - * • 4~ п3 ПРИ лю" бом целом п есть квадрат целого числа.
13.	Дано бп-значное число, делящееся на 7. Доказать, что число, полученное из него перестановкой последней цифры на место начальной, также делится на 7.
14.	Доказать, что
п.
15.	Доказать невозможность такого треугольника, в котором одновременно и, стороны и углы составляли бы арифметическую прогрессию.
14- ю4 4-
4- ... +1
14
16.	Вычислить сумму:
__L_ +___________1___+ ... +_______!____+______1____
cos х- cos у 1 COS у COS 2	1 COS t-COSU ’ COS И-COSO ’
если дано, что x, у, z ... , /, и, v образуют арифметическую прогрессию, разность которой равна г.
17.	Доказать, что если квадраты сторон треугольника составляют арифметическую прогрессию, то треугольник, сторонами которого служат медианы данного, подобен данному.
18.	Стороны треугольника составляют геометрическую прогрессию. Доказать, что такой треугольник подобен треугольнику, сторонами которого служат высоты данного.
19.	Даны десять чисел s2... <isI0, которые являются попарно взятыми суммами пяти чисел <^*2^ •	Выразить числа х через числа s.
*	/ п	\2	п	п
I Х7	1	X? 2 X? 2
20.	Доказать, что | Jz j	|	7	7
\Z==:1	/	/=1	/ = 1
где bt — любые действительные числа.
21.	Дана возрастающая последовательность целых чисел а0, аъ а2, ...» ап, для которой а0 = 0, а1 — 1, а каждое aL (i = 2, 3» 4, ..., п) является наименьшим числом, не образующим арифметической прогрессии ни с какими двумя предыдущими числами последовательности. Доказать, что общий член ak последовательности есть число, которое получается из номера fe, если, его записать в двоичной, но прочесть в троичной системах исчисления.
22.	Дана арифметическая прогрессия, члены которой — целые положительные числа. Известно, что ватой прогрессии есть член, являющийся полным квадратом. Доказать, что прогрессия, содержит множество таких членов.
23.	Доказать, что I/ 2, \/ 3,	5 не могут быть чле-
нами одной арифметической прогрессии.
24.	Канал имеет прямоугольный поворот. Какой максимальной площади прямоугольный плот может пройти по этому каналу, если ширина канала й?
25.	Основания четырех логарифмов одного и того же числа образуют геометрическую прогрессию со знаменателем, равным- этому числу. Найти эти логарифмы, если известно, что сумма первых двух из них равна сумме остальных.
15
26.	Доказать тождество:
logo W • logd W 4- log* W • log, N + log, N  loga N logo N  log» Л' • logc N
logo»c Л'
27.	Решить неравенство:
4Л — 2-52v < 10 ».
28.	Решить уравнение:
logcos х sin X 4- logsin л COS X — 2.
29.	Найти предел выражения:
V 3 /5 /з /gyf...
30.	Решить систему:
ху — у\ ах = b-v, где а > 0, b > 0, а Ф 1, Ь =£ 1.
31.	Доказать, что У 5 у _i_ 7 _ р' 5 у~2 — 7—рацио-нальное число.
32.	Решить уравнение
(Р 2 4- р У)Л 4- (/2-|/з)» - 8.
33.	Доказать, что если
x(y + z — x) _ y(x-^z — y) = z(x + y — z) !g X	lg у	1g 2
TO
ХУух Zvyz — XzZx.
34.	Решить уравнение:
%2 — 10x + 15 __ 3x
x2 — 6x + 15 x2 — 8x + 15*
35.	Доказать, что |x+y|2-H*—У I2 ~2(|x |24- |f/|2), где x, у — комплексные числа.
36.	На сторонах треугольника АВС вне его построены квадраты, имеющие центры соответственно в точках Аг, Въ Сх. Доказать, что, сдвигая параллельно отрезки ААЪ ВВЪ ССЪ можно получить треугольник со сторонами — этими отрезками.
37.	На плоскости дано п точек. Известно, что среда любых трех из них имеются две, расстояние между которыми не больше 1. Доказать, что на плоскость можно положить два круга радиуса 1, которые закроют все эти точки.
16
38.	На плоскости даны п точек, расположенных так, ^<то на каждой прямой, соединяющей две из этих точек, Улежит по крайней мере еще одна из них. Доказать, что все л точек лежат на одной прямой.
39.	Каково наибольшее число точек пересечения диагоналей выпуклого n-угольника, лежащих внутри него?
40.	Треугольник разбит на меньшие треугольники так, что последние примыкают друг к другу либо по целой стороне, либо в вершинах. Вершины основного треугольника занумерованы цифрами 1, 2, 3. Вершины меньших треугольников занумерованы так, что вершинам, лежащим на сторонах исходного треугольника, приписан номер любой из вершин, примыкающих к данной стороне. Нумерация ’внутренних вершин произвольна. Доказать, что среди <малых треугольников найдется по крайней мере один, 'занумерованный всеми тремя цифрами.
41.	На плоскости даны и точек, не все из которых ’лежат на одной прямой. Доказать, что среди прямых, соединяющих всевозможные пары этих точек, обязательно будет не менее и различных.
42.	Чему равно общее число членов в разложении (a + b + rf)rt?
г 43. Показать, что средний член разложения (а х)2п 'равен
I-3-5...(2/1 — 1)-2W
1-2-3. .. п.
(1 V*
1 н—) < з.
шахматном турнире принимали участие учащиеся двух классов, причем учащихся одного класса было в 10 раз ‘боляще, чем учащихся другого класса. Каждый участник турнира встречался с любым другим только один раз.
При подведении итогов турнира оказалось, что учащиеся класса с большим числом участников набрали вместе в 4,5 раза больше очков, чем все учащиеся другого класса.
\ Сколько очков набрали учащиеся класса с меньшим числом участников?
46.	Доказать, что
1—зс4я + згс42п - ззс4л ч-... - з4" -1 с\п -1- з4" =
= 1 — bc'in + 52С22Л —59 Cln 4- ... — 52п -1	+ 52".
££ Зак. 358.
47.	Доказать, что если в треугольнике стороны удовлетворяют соотношению
1	,	1	_	3
я 6 4“ £ а + +жс’ то один из углов его равен 60°.
48.	Решить уравнение:
26 sin2 х2 + 12 cos 2х 4- 5 sin 2х = 13.
49.	Решить неравенство:
sin 2х — cos 2х 4- 1 q
sin 2х -(- cos 2х — 1
50.	В треугольнике его углы а и р связаны соотношением:
з
cos а 4~ cos р — cos (а 4- 3) = -ъ~.
Доказать, что треугольник правильный.
51.	Углы треугольника связаны соотношением: sin а = 2 sin р* cos 7.
Доказать, что треугольник равнобедренный.
52.	Доказать, что asina4~^cosa не зависит от а, . а а
если tg -у- =	.
53.	Доказать, что если число а иррационально, то функция cos ах 4- cos х не является периодической.
54.	Доказать, что в четырехугольнике, вписанном в окружность, имеет место равенство:
sin Д: sin В = (ad 4~ be): (ab 4~ cd), где А и В — два соседних угла, стороны а и b примыкают к углу А; с и d — к углу С.
55.	Доказать, что в тупоугольном треугольнике сумма квадратов синусов внутренних углов меньше двух.
56.	Сколько корней имеет уравнение:
Sin X =
57.	Найти действительные решения уравнения
sin” х 4--“ cos” х 4—,
1 cos”1 X	1 sin'" X
в котором тип обозначают положительные нечетные числа.
18
58.	Доказать неравенство cos а 4-a*sin а > 1, где
а
О
.	59. По полю проходит прямолинейная дорога. Чело-
век, стоящий на дороге в точке А, может двигаться по полю со скоростью не более 3 км/час и по дороге со скоростью не более 6 км/час.
Найти геометрическое место точек, в которые он может попасть за 1 час.
60.	Доказать, что наименьший объем имеет описанный около шара конус, высота которого вдвое больше диаметра шара.
61.	Доказать, что объем правильной пирамиды всегда меньше куба ее бокового ребра.
62.	Доказать, что не существует многогранника с нечетным числом граней, все грани которого являются многоугольниками с нечетным числом сторон.
63.	Доказать, что радиус шара, вписанного в много-гранник, равен где V — объем многогранника, aS — о
его поверхность.
64.	В данный треугольник вписать параллелограмм наибольшей площади с данным острым углом так, чтобы две вершины параллелограмма лежали на основании, а две другие — на боковых сторонах.
65.	Около конуса, радиус основания которого равен /?, а угол между образующей и основанием равен а, расположены п равных шаров, каждый из которых касается двух соседних, боковой поверхности конуса извне и плоскости его основания.
Найти радиус шара.
66.	Какому условию должны удовлетворять ребра тетраэдра, чтобы существовал шар, касающийся всех его ребер.
67.	Доказать, что сечение параллелепипеда плоскостью не может быть правильным пятиугольником.
68.	При каком условии можно получить тетраэдр сгибанием по прямым листа, имеющего форму треугольника?
Доказать, что из 12 углов граней такого тетраэдра различных может быть только три и сумма трех таких различных углов равна двум прямым.
2*
19
69.	Дана треугольная пирамида. Доказать, что
где 7? — радиус шара, вписанного в пирамиду, hlt h2, h3,	—
длины перпендикуляров, опущенных из вершин пирамиды на противоположные грани.
70.	Вычислить плоский угол при вершине правильной четырехугольной пирамиды, если известно, что центр вписанного и описанного шаров совпадают.
71.	Три шара радиуса R касаются одной и той. же плоскости и каждый из них касается двух других.
Найти радиус шара, касающегося плоскости и трех данных шаров.
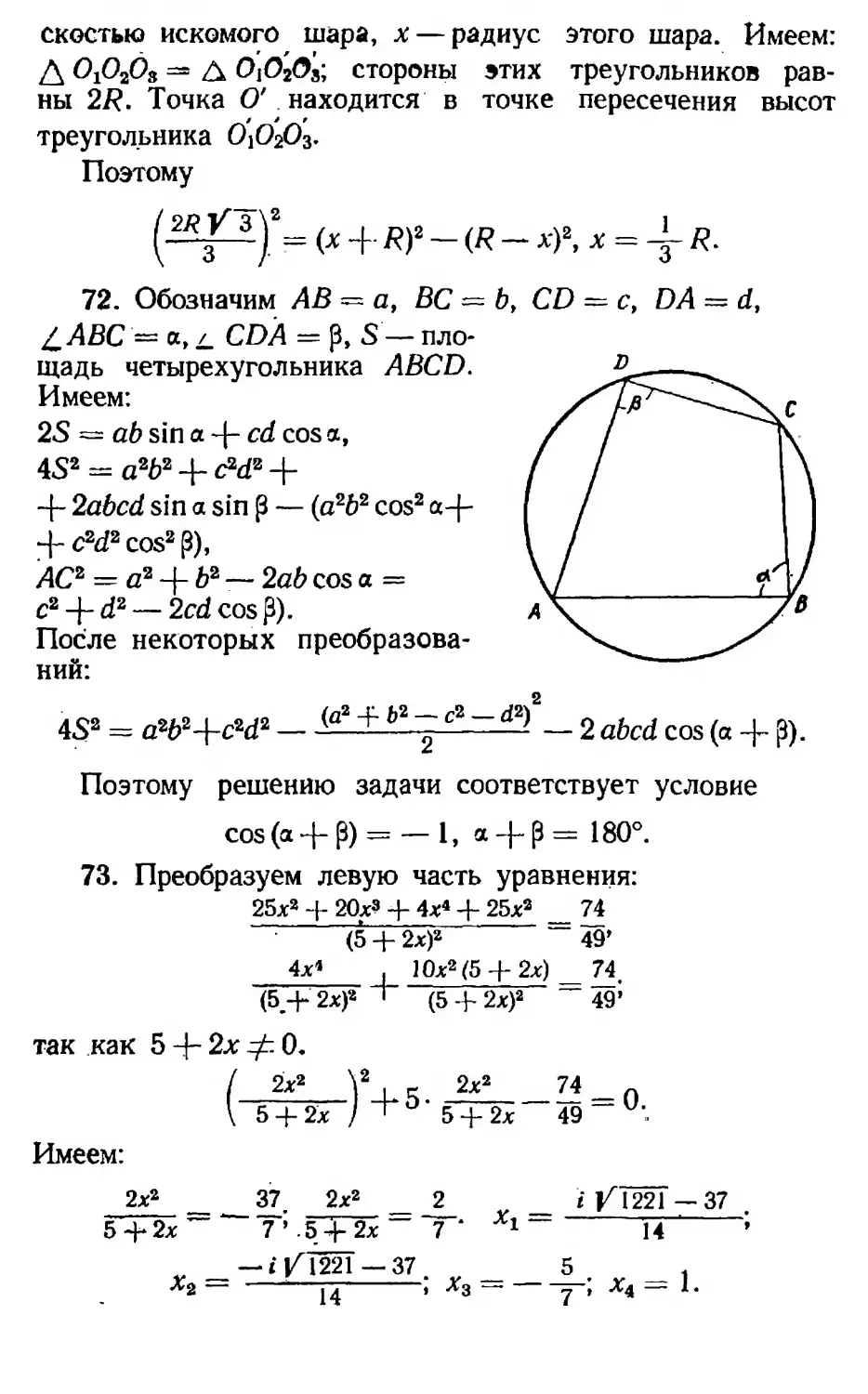
72.	Из всех четырехугольников с одними и теми же сторонами четырехугольник, около которого можно описать окружность, имеет наибольшую площадь. Доказать.
73.	Решить уравнение:
25х2	_ 74
(5 + 2х)2 ~ 19 ‘
ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
V11 КЛАСС
. Зп®—3«4-20 Зп(п—1)4-20 _ Q .	20
] . -------:--- = --------1---- -- Oft + •———г.
...	п — 1	п — 1	1 п — 1
4 Следовательно, дробь будет целым числом тогда, когда 520
— целое число.
I; п = 2,3, 5, 6, 11,21.
;? о л4 । л3 . Ил2 . п ______п (п + 1)(п + 2) (л + 3) .
”24 1	’ Т ""	24	'
О 3. пб — 5ft3 4ft — п (п2 — 1) (и2 — 4)—(п — 2) (ft — 1)Х Mn(ft+l)(n + 2).
4' Из пяти последовательных чисел одно наверное делится
5, по крайней мере одно делится на 3 и по крайней Йёре два — на 2, причем одно из этих двух последних чисел делится на 4. Следовательно, произведение пяти последовательных целых чисел делится на 5’3*4-2 = 120. ; 4. Чтобы данное число делилось на 6, необходимо недостаточно, чтобы оно делилось на 2 и на 3.
J При четном п данное число делится на 2. Если же п ёфчетно, то и2 4" 5 делится на 2. В самом деле:
п = 2т — 1, {2т — 1 )2 4* 5 = 4m2 — 4т 4~ 6.
Шли п делится на 3, то и данное число делится на 3. Ерли же п не делится на 3, то в остатке может полу-Ч^Ться 1 или 2. Тогда имеем во втором сомножителе:
a)	(3fe-M)24-5 = 9A’24-6/fe4-6;
б)	(Зй 4- 2)2 4- 5 = 9й2 4- 12й 4- 9,
21
т. е. второй сомножитель обязательно будет делиться, если п не кратно трем.
5. Первая цифра частного 5, так как 42x4// 72
72 • 6 = 432 > 42х.	~~360  58
т,	,	on	6x4
Вторая цифра частного 8 или 9.	57g
(х + 2) 8у
1) Если вторая цифра частного 8, то полученное в остатке трехзначное число (х 4-2) 8 у должно делиться на 72. Из таких чисел только 288 имеет цифру десятков 8.
х|-2-2; х = 0; у = 8.
2) Если вторая цифра частного 9, то имеем:
42x4// 72
360	“59“
6x4
648
(х — 5) бу кратно 72; по цифре 6 находим, что это число 360.
х — 5 = 3; х = 8; у = 0.
(х — 5) бу
6.	жзи X 8 = уфч, отсюда ж = 1; стд — уфч = шяэ, значит, з = 0 или 1. Но жзи X к = мнпр, откуда я = 9 и аналогично л — 9. Тогда з = 1, а и = 2.
110768:112 = 989.
7.	Для нумерации страниц учебника употребили: 9 однозначных чисел — 9 цифр; все двузначные числа — 90 чисел— 180 цифр. Всеми однозначными и двузначными числами занумеровано 99 страниц, и на это ушло 189 цифр. Осталось 411 —189 = 222 цифры, которые ушли на написание 222:3 = 74 трехзначных чисел. В учебнике 173 страницы.
8.	Заметим, что 2-5 = 10. Так как четных чисел в этом произведении больше, чем чисел, кратных 5, то надо подсчитывать количество сомножителей, кратных 5. Нетрудно видеть, что их будет 20. Но среди этих множителей есть числа 25, 75, 50 и 100 — кратные 25. Поэтому всего произведений 2-5 будет 24. Следовательно, это произведение оканчивается 24 нулями.
9.	Обозначим пять последовательных целых чисел следующим образом: (и — 2), (п — 1), и, (л 4" 1), (пЦ-2), тогда (п — 2)2 4-(п — I)2 + л2 + (n + I)2 4- (л + 2)2 = 5 (и2 + 2). Для того, чтобы 5 (л2-|-2) было квадратом, необходимо, чтобы л2 4- 2 делилось на 5, т. е. л2 должно оканчиваться на 3 или 8, что невозможно. Следовательно, л2 4- 2 не делится на 5.
22
10.	Пусть число В является точным квадратом числа
А = ап10п-\- ... —10 —]—й 0.
Две последние цифры числа В получаются при умножении Прела nj 10 4-а0 на себя. Если aQ — четное число, то утверждение справедливо. Пусть теперь а0— нечетно, /тогда легко проверить, что у а- вторая цифра всегда четная. Вторая же цифра числа В получается, если ко второй цифре числа 2ata010 добавить вторую цифру числа а* и, быть может, полученную сумму уменьшить на число, Кратное 10, следовательно, если а0 — нечетно, то вторая цифра числа В будет четным числом.
11.	Вставим между цифрами числа 1331 по п нулей. Получим число N = 1000...03000...03000...01. Это число имеет Зп-|-4 цифры и может быть записано так:
N = ю^ + з_рю2п-г2.з^10^ + 1 .3^1 =
<= (Юл + 1 4-I)3.
12.	Пусть а^2.. -ak — данное число, aka2 ... ak _ i ar— число, полученное из него перестановкой первой и последней цифры. Для выполнения требований задачи необходимо, чтобы аг = 1, так как при аг > 2, aka2 ... i а2 не сможет быть больше в 5, тем более в 6 или в 8 раз. Таким образом, ar = 1.
Но никакое целое число при умножении на 5, 6 или 8 не может оканчиваться на 1.
13.	Обозначив искомое число через х, составим урав-
нение:
9 + 90-2 + (х — 99). 3 = 2х
Ответ: 108.
14.	Если число А = 111 .... 1 делится на 33 .... 3, т	“6Г
то А делится на 3 и делится на В — 11 ... 1 , Но если 10б" '
А делится на В, то т = 1-100. С другой стороны, так как А делится на 3, то т должно делиться на 3, т. е. т = — Зл-100. Наименьшее число с таким свойством будет при tn = 300.
Ответ: число состоит из 300 единиц.
15.	Пусть дано число А. Обозначив число, выраженное тремя последними цифрами числа А, через а число,
23
выраженное всеми остальными цифрами, через Л4, будем иметь:
А = М • 1000 4* N. Число 1000 4~ 1 делится и на 7, и на 11, и на 13. Заметив это, преобразуем полученную сумму: А = М (1000 +0 — которую можно записать:
А= /И-1001 — (Л1— N), если M>N и Д = ЛЫ001+(М —М), если М < N.
Так как М • 1001 всегда делится и на 7, и на 11, и на 13, то, для того чтобы число А делилось на 7, или на 11, или на 13, необходимо и достаточно, чтобы разности (Л4 — 7V) или (У — /И) делились соответственно на 7, или на И, или на 13.
16.	Пусть А = ап 8п ~1 + ап _ 18п ~2 + ... +
8* при делении на 7 дает в остатке 1, значит А при делении на 7 дает в остатке число
г — ап 1 + ••• ~har
Отсюда вытекает такой признак делимости: число А тогда и только тогда делится на 7, если сумма всех его цифр делится на' 7.
17.	Пусть Д = ап8п~1	18Л~24~ ••• +^i-
8* при делении на 9 дает в остатке либо 1, либо—I в зависимости от того, четно или нечетно число k. Тогда число А при делении на 9 дает остаток с точностью до знака, равный
г = ап — ап _ 1 4- ап _ 2 — • • • + аг.
Таким образом, число А тогда и только тогда делится на 9, если знакочередующаяся сумма всех его цифр делится на 9.
18.	Всякое простое число р>3 имеет один из следующих двух видов:
1) р = ЗА> + 1,
2) р = ЗА4-2.
Пусть р = ЗА 4“ 1, тогда (ЗА 4" О2 + 8 “ 9А2 + 6А 4- 9. Это число делится на 3 и, значит, не является простым. Пусть теперь р — ЗА2, тогда (ЗА + 2)2 4- 8 — 9А2 4" 12А 4“ 12 делится на 3, т. е. опять не простое число.
Наконец рассмотрим два оставшихся простых числа:
р —2 и 3. Если р = 2, то р24-8=12 — число не простое. При р — 3 имеем р24~8 — 17— число простое.
Ответ: р — 3.
24
fL Пусть p — любое простое число, причем р > 3. ^-1)4-1- Покажем, что р2 — 1 делится на 24, д и будет следовать утверждение задачи, р2 — 1 = — 1)(р+ О' Так как р — простое число и р > 3, то ечетное число, заведомо не делящееся на 3. Тогда из чисел р— 1 или р+1 обязательно делится на 3. ое из них делится на два, а так как среди двух довательных четных чисел одно всегда делится на 4, т, р2 — 1 делится на 8.
L Пусть p = 30n + m, где р — простое число, - остаток, /и < 30 и т — нечетное число. Тогда т т делиться лишь на числа, отличные от 3 и 5. Если же где mi>7, то т2 — 1 или т2^>7. Второй й, очевидно, отпадает, значит, tn — простое число.
Пусть р и q имеют общий делитель d, тогда jfc pjd, q = qtd.
‘2p — 1 = (2rf)P* — 1 = (2rf — l)(2rfCP« — »_}_
4- 2* (pi - « + ... -|- Г);
2< — 1 = (2rf)*« — 1 = (2rf — 1) (2d	- '> 4-
_j_ 24 (41 - 2) 4-
+ 0-
4 Следовательно, если 2p—1 и 24 * * 7—1 взаимно просты, ТО р и q также взаимно просты, т. е. d = 1.
? Пусть теперь р и q взаимно просты и р > q. Если d+ общий делитель чисел 2р — 1 и 2* — 1, то d — дели-т^ль также числа 2р— 2q = 2^(2р~~^— 1). Так как 2k— 1
2 не делится (k >0), то 2р - — 1 делится на d. Если ше р — q> q, то, рассуждая аналогично, получим, что — 1 делится на d, где р — lq <q. Обозначим р — lq^= и, повторяя рассуждения, найдем 4 такое, что 2Й*Aft — 1 делится на d, где q — ltqi < qr Таким образом Дойдем до qt = 1, т. е. 2— 1 = 1 делится на d, откуда d зев 1 .
1 1 22. Наряду с заданным произведением, которое обозна-.	2	4	98
чйм через а, рассмотрим произведение b — -g- . -g- ... gg-.
ггагко видеть, что а-Ь = т^.
.^ркак как а < Ь, то а < -tq-.
25
23. Обозначим эту дробь —, тогда m ~ тп-^ п	п 4* п
-I- 21п гпп -Г- 28/л; 21н	28/д; —-
1	1	’ п 4
24.	Пусть х км/час— собственная скорость катера, у км/час и z км/час — скорости течений рек, у > г; расстояние, пройденное каждым катером в одном направлении, s км\ время движения, затраченное на весь путь, в реке с быстрым течением часов, с медленным течением /2 часов.
Из сравнения полученных дробей приходим к выводу:
f ^2*
25.	Так как правая часть первого уравнения такая же, как и левая часть второго, а правая часть второго такая же, как и левая часть третьего уравнения, то:
/1 _ /2 _ *з =	= хп — 1 _ хп.
а1	а3	ап — 1 аП 9
на основании свойства равных отношений имеем:
откуда:
хг	А	сьА
— = —;-------i-----:—> xi = —i-----n-----i—•
al aL + a2 4" * ‘ ’ + an	al + a2 + • • • Г аП
Аналогично получаем значения других неизвестных.
26.	Минутной стрелке, чтобы догнать часовую, надо пройти на 45 минутных делений больше часовой стрелки. Так как часовая стрелка проходит одно деление за 12 минут, то она за каждую минуту проходит деления и, следовательно, минутная стрелка нагоняет ее за каждую минуту на делений. На 45 делений потребуется
,г 11	45-12	540 ,n 1
45:12 = “ТГ = ТГ = 49 7Г МИНУТ-
26
27.	Выразив цифры года рождения этих людей буквами а, Ь, с и d, будем иметь abed = 1000 а -ф-100 b -}- Ю с 4-Ц-d; 1958 — (1000 а 4- 100 Ь-\- 10 c-f-d) = «4 Ь + сЦ-d; %;= 1; b = 9 (b — 8 быть не может, так как это не удовлетворит смыслу задачи).
Следовательно, 1958 — (1000 -|~ 900 -1-10 с -1- d) = 1 4-4- 9 4- с -f- d, откуда d — ?8~-	. Так как d — число
целое, то 11с есть число четное, тогда с = 2, 4, 6, 8. Делаем испытание:
1)	если с = 2, то d = 13.— не удовлетворяет;
2)	если с = 4, то d — 2;
3)	если с = 6, то d — — 2 — не удовлетворяет;
Итак, d = 2; с = 4.
Люди родились в 1942 году, что соответствует требованию задачи: 1	9 -f- 4 4* 2 — 16; 1958— 1942 = 16.
28. Обозначим высоту ha — AAlt данную биссектрису — — AD. Имеем /,Л1ЛР = 60°, Z. BAD = DAE = д 1, /_ВАЕ = 180° —Л.
£ 1 = 90° —A LABD 4- z 1 4 30° = 180°.
i_ABD = 60° 4- А = 180° — В, А 4- 2В = 240°,
В—с = (л 4- 2В) —(л 4- в 4 с) = 60°.
\ .29. Подсчитаем сумму углов всех полученных треугольников. Легко видеть, что она равна сумме всех вну-'ф&них углов тысячеугольника и 4d-500, т. е. равна 2>8 + 2d ’1000 1998’2d-
ЯУтсюда число полученных треугольников равно:
1998-2d 2d
~ 1998.
|Й). Точки Д, В и С лежат на окружности, описан-нШ около треугольника АВС. Докажем, что точки Olt О2> ^(симметричные с точкой О пересечения высот дДВС
27
относительно всех его сторон) лежат на той же окружности,.
Рассмотрим четырехугольник АОгВС и установим, что он вписан в окружность, проходящую через точки А, В. С. Имеем:
о
D
Z. OtBA = Z ABD - 90° — Z BAD;
/_0}АВ = /_ВАМ = 90° — /_АВМ;
^о±вс+ ао.ас^ l(\ba+ ^АВС+ Z оив + + £ ВАС = 90°— /ВДР+ /АВМ+ 90°— АВМА-^BAD= 180°.
Отсюда следует, что четырехугольник А(\ВС вписав в окружность, проходящую через точки А, В, С. Следователь^ но, точка Oj лежит на рассмот^ ренной окружности. Аналогична устанавливается, что точки 0$ и О2 лежат на той же окруж* \ ности.
31.	Проведем две взаимнб
г
перпендикулярные прямые, па* раллельные соответственно звеньям ломаной линии. Оче* видно, что звеньев ломаной линии, параллельных перй вой прямой, будет столько же, сколько звеньев, параллельны! второй прямой. В то же время число звеньев, параллелью ных каждой из прямых, будет четным. Следовательно, число всех звеньев будет равно сумме равных четных чисел, т. е. будет делиться на 4.
32.	Достаточно доказать, что все заштрихованные треугольники равны. Покажем, например, что /\ОхС02 ~ £\fi2DO3. В остальных случаях рассуждения совершенно аналогичны. Действительно, (\C~OgD, О2С— =O2D как половины диагоналей
равных квадратов.
ZO1CO2 = 90е -I- £BCD = 90° 4- ZDiDD2 = /0JX)3. Следовательно, указанные треугольники равны, ибо у них равны две стороны и угол между ними.
28
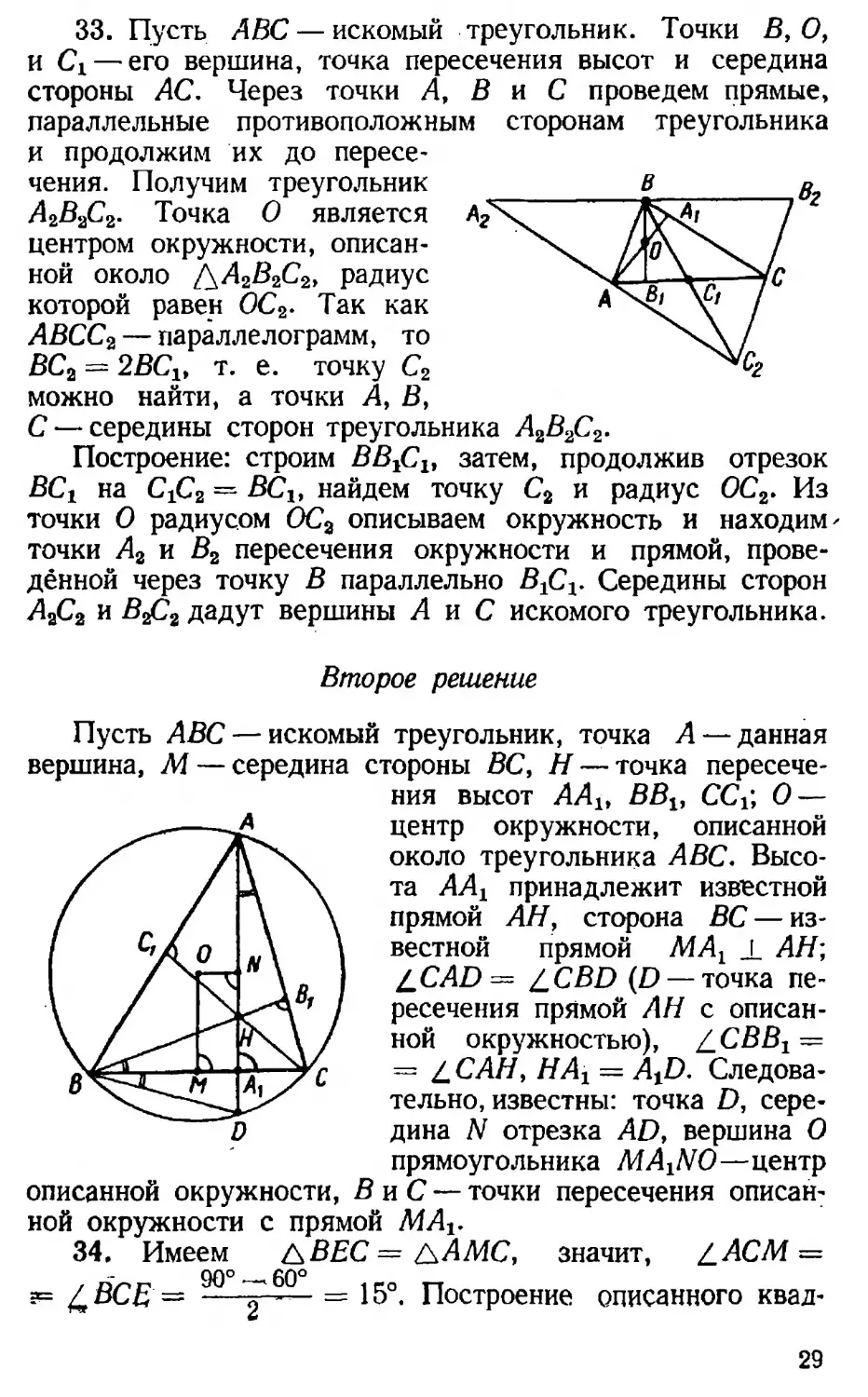
33.	Пусть ABC — искомый треугольник. Точки В, О, и Сх— его вершина, точка пересечения высот и середина стороны АС. Через точки А, В и С проведем прямые, параллельные противоположным сторонам треугольника и продолжим их до пересе’ чения. Получим треугольник _______________в__________о?
А2В2С2. Точка О является	ЛхА 7
центром окружности, описан-	/
ной около /\А2В2С2> радиус	\л
которой равен 0С2. Так как	V/ /
АВСС2 — параллелограмм, то	^х\/
ВС2 = 2BClt т. е. точку С2 можно найти, а точки Л, В,
С — середины сторон треугольника А2В2С2.
Построение: строим ВВ^С19 затем, продолжив отрезок ВСг на СХС2 = ВСЪ найдем точку С2 и радиус 0С2. Из точки О радиусом ОС2 описываем окружность и находим, точки А2 и В2 пересечения окружности и прямой, проведённой через точку В параллельно В^С^ Середины сторон А2С2 и В£2 дадут вершины А и С искомого треугольника.
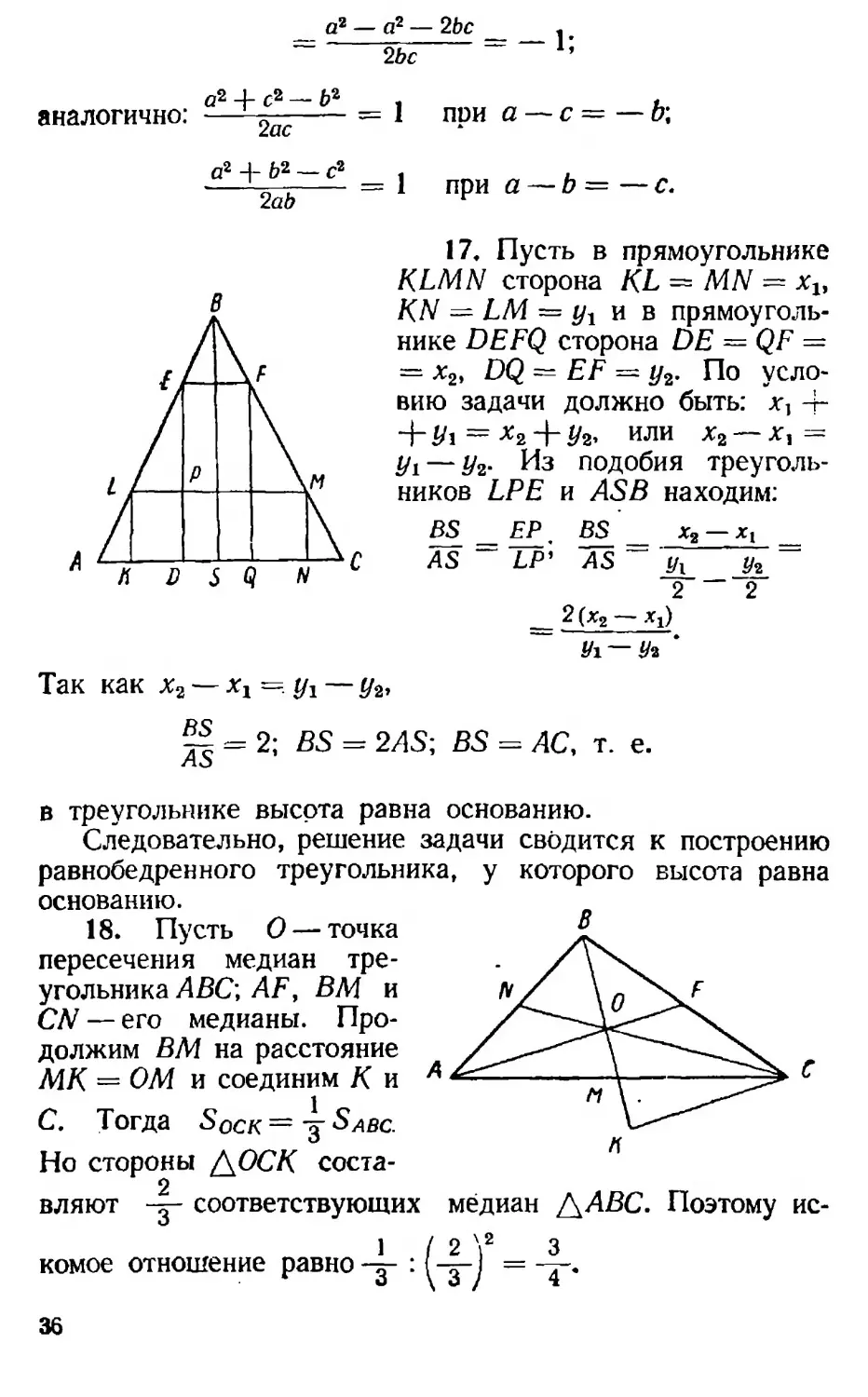
Второе решение
Пусть АВС — искомый треугольник, точка А — данная вершина, М — середина стороны ВС, Н — точка пересечения высот AAlt BBlr CCi, О — центр окружности, описанной около треугольника АВС. Высота АА} принадлежит известной прямой АН, сторона ВС — известной прямой MAr j_ АН; £CAD== /_CBD (D — точка пересечения прямой АН с описанной окружностью), £СВВг — = ^САН, НАг = AtD. Следовательно, известны: точка D, середина N отрезка AD, вершина О прямоугольника МА±НО—центр
описанной окружности, В и С — точки пересечения описанной окружности с прямой МАг.
34.	Имеем дВВС=дЛЛ4С, значит, /_АСМ = ?= 4 ВСЕ = 90	= 15°. Построение описанного квад-
29
рата, вершина которого совпадает с вершиной С, проводится следующим образом. Строим углы ВСЕ и АСМ. из точек А и В опускаем перпендикуляры на соответствующие стороны углов и про--	£ должаем их до пересечения в точ-
D	\ \	Квадрат EDMC — искомый.
\	/ \\	35. Пусть ABCD — искомая
\	/	\ \	трапеция. CD — ее боковая сторо-
\ /	на, 00г — расстояние от центра
\/_________Ч Р окружности до точки пересечения
А Г	L диагоналей трапеции. Очевидно,
что о АВ = СД. следовательно, м	lCBD=£BCA. Тогда zCOxD=
=2- s-CBD. Так как отрезок СО известен, то угол CBD. а значит, и угол COrD можно найти.
Таким образом, точка 0х является пересечением двух геометрических мест: с одной стороны 0х лежит на окружности радиуса ООг с центром в точке О, а с другой — на дуге окружности, из точек которой отрезок CD виден под данным углом СОхО. Отсюда вытекает построение. Находим угол COrD. строим точку (Д (их может быть, очевидно, две) и находим точки А и В.
36. Высота, указанная в условии, разделяет искомый треугольник на два так, что катеты иско
мого треугольника служат гипотенузами полученных двух. Пользуясь условиями задачи, можно построить один из этих треугольников с меньшей гипотенузой и потом — искомый треугольник.
VIII КЛАСС
1.	Известно, что	Применим это соотно-
шение для решения задачи. Имеем:
ab (а 4' b — 2с) 4~ Ьс (6 с — 2а) 4~ ас (а 4- с — 2Ь) =
=abc( — + —— 2+— +— — 2 + т + т~2) =
\ б? 1 с 1 а ч	1 b 1 о /
30
так как а > О, b > О, с>0 и каждое из чисел, стоящих в круглых скобках, не меньше нуля.
2.	Преобразуем данное равенство:
(яб -р ас -|- be) (а + b 4~ с) = abc\
(а 4- b) Ьс 4- (fl 4" ас + (fl + ty ab + (а 4~ Ь) с2 — 0;
(а + Ь)[(а + с) (Ь + с) = 0.
Отсюда следует, что имеет место по крайней мере один из трех возможных случаев:
I)	а4"^ = 0 и а = — Z?;
2)	a -j- с = 0 и а = — с;
3)	b 4“с ~ 0 и b — — с.
Значит, данное неравенство верно, если хотя бы два из трех чисел а, b и с равны по абсолютной величине и противоположны по знаку. Но в этом случае то же будет иметь место и для чисел ап, Ьп и сп, где п — нечетное число, поэтому замена а, Ь и с соответственно ап. Ьп и сп не нарушит данного равенства. Полученное при этой замене равенство и есть то, которое требовалось доказать»-
(п-2)(п-1)+ ...];
отсюда видно, что данное выражение делится на п.
Замечание: следует отметить, что п3, так как при п = 2 предложение неверно.
4.	Достаточно доказать, что не существует числа d, большего 2, на которое делились бы числа а-\-Ь и а24~ 4"62 (при условии, что а и b взаимно просты).
Если а2 + Ь2 и а 4- b делятся на d, то и числа 2а2 = = (а2 4- Ь2) 4- (а — Ь) (а + Ь) и 2Ь2 = (а2 + Ь2) + (Ь — а) (а + -\-Ь) делятся на d. Но поскольку числа а и b взаимно просты, то числа а2 и Ь2 также взаимно просты; следовательно, 2а2 и 2Ь2 не могут делиться на число d, большее 2,
31
поэтому и числа а 4- b • и а2 4~ Ь2 не могут делиться на число d. Но на 2 они делятся, так как на 2 делятся 2а2 и 2Ь2.
5.	а5 4а3 4* За = а (а2 4~ 1)(а2 + 3) и а4 4- За2 4- 1 = — а2(а2 4- 3) 4* 1 • Пусть а0 — некоторое целое число. Тогда делители числа а„ 4~ 4а’ 4~ За0 являются делителями по крайней мере одного из чисел а0, а-й 4- 1 и а2 4* 3. Пусть число d—делитель числа а0 или числа а2 4-3. Очевидно, что это число не может быть делителем числа а* 4~ За2 4" !• Пусть d — делитель числа а2 4-1. Так как a*4-3a£4" + l=a* + 3a24-2-l=(o24-l)(a24-2)-l, то очевидно, что d не может быть делителем числа aj 4~ 4-За2 4-1-
6.	Из уравнения видно, что у должен быть нечетным числом. Положив г/ = 2z 4_ 1 • получим
2хг — 20г2 — 20z — 5 = 7
или
х2 — Юг2 — Юг = 6,
откуда следует, что х есть чётное число. Положим х = 2и. Тогда 2и2 — 5г (г —|— 1) = 3, что невозможно, так как г (г 4" 1) есть четное число.
7.	При У 3 = а данное уравнение принимает вид: х8 -j- 2ax2 а?х а — 1 = 0
или
xa2 + (2x2+l)a-H,v3 — 1) = 0.
Решая это уравнение относительно а (здесь х Ф 0), имеем;
а = ~(2х2+ 1) ±(2^+D 2х
Итак, получаем:
1)	а = 1 — х, т. е. х = 1 — а или ху — 1 — }/~3;
2)	а = —х + или x2 + (a+ 1)х4~ 1 =0, откуда А,	*
_	4
-(^34-1) х /12
находим, что х2, з = — --—-— -
8.	х2 4- = (л'14- *2)г — 2xjX2 = (a — 2)2 4- 2 (a 4~ 3) = = a2 — 2a 4-10. Исследуем трехчлен a2 — 2a 4* Ю.
D = — 36 < 0.
a2 —2a 4-10 = (a—I)2 4-9.
32
Наименьшее значение этого трехчлена 9 при а == 1.
9.	х4 У* = (*s + У2)2 — 2х2у2 ~ [(х 4~ у)2 — 2ху]2 — — 2х2у2 = (9 — 2ху)2 — 2х2у2\ х2у2 — 18ху —32 = 0.
х У = 3	( х 4- У = 3 ху = 2; ху = 16,
<
ху = 2 I ху = 16
(1; 2); (2; 1).
10.	Прибавим и вычтем из левой части сумму I _J_ г I J_ I JL 2 * 4 ‘ 6 + 8	10 ”•	2k*
Сделав группировку, получим:
11.	При делении любого целого числа на п остаток либо равен нулю, либо меньше п.
Если среди га различных чисел, написанных только* двойками: 2,22, 222, ... , 222 .... 2, найдется число, крат-
га
ное га, тогда остается приписать справа один и л к несколько нулей и положение доказано. Если же среди этих чисел не будет числа, кратного га, то по крайней мере два числа при делении на га дадут одинаковые остатки, ибо остатки будут 1,2, ... , га— 1, а чисел га. Разность этих двух чисел кратно га и состоит из двоек и нулей.
12.	При вычеркивании цифр надо учитывать, что цифры нельзя переставлять и что наибольшее число будет получаться, если в старшем разряде будет 9 единиц.
Вычеркиваем первые 8 цифр, затем от 10 до 18 и единицу у числа 19, т. е. еще 19 цифр и т. д. до 4 у числа 49. Итого вычеркнуто цифр: 8+ 19 4- 19 4~ 19 4~ 4- 19 = 84. Вычеркиваем далее 50, 51, 52, 53, 54, 55, 56» и цифры 5 у 57 и 58.
Остается число: 9999978596061 .... 9899100.
3 Зак. 358.
33
13.	|х 1| — И + 3 |х — 1| — 2 ]х — 2| — |х 4- 2|. Для решения уравнения надо абсолютные значения заменить выражениями, заведомо не отрицательными. Рассмотрим это уравнение на следующих промежутках:
надо решить шесть уравнений.
1)	При х < — 2
— (х-|-1) —(—х)4-3(1 — х) —2(2 —х) = —х —2; 0-х = 0;х< —2.
2)	При —2<х<— 1
— (*4-1)4-* + 3(1 — х) —2(2 —х) = х-|-2. х — — 2.
3)	При — 1 < х <0
х 1 4~ % 4~ 3(1 — х) — 2 (2 — х) = х 4- 2. 0-х = —2. Решения нет.
4)0<х<1;
х4-1—х4-3(1—х) —2(2 —х) = х4-2;
— 2х — 2; х — — 1. Решения нет.
5) 1 <х<2;
-*+1— *4-3(х— 1) — 2(2 — х) = х + 2;
4х = 8; х — 2. Решения нет.
6) х > 2;
х 4~ 1 — х 4~ Зх — 3 — 2х 4“ 4 = х 4" 2;
0-х = 0; х> 2.
Ответ: х < — 2; х > 2.
14. Рассмотрим два целых числа р и q. Покажем, что р не может быть корнем этой функции. Заметим, что корнем функций называется такое значение аргумента, при котором функция равна нулю.
Если (р— q)— четное число, тогда
f(P) — f (?) = а0 (Р3 — <7®) 4- ai (Р* — <72) 4- «2 (Р — <7) — четное число.
Если q = 1, тогда р — нечетное число, f (р) равно сумме четного и нечетного чисел, есть число нечетное и, следовательно, не равно нулю.
J4
Пусть q = 0, тогда р — четное число, f (р) аналогично предыдущему не равно нулю.
15. Из условия, что х — у2у3 и х является четырехзначным числом, следует, что
1000 < у2 + у3 < 10000, 1000 <р2(1 +{/) < 10000.
При у ~ 9
У = Ю
х = 810.
х = 1100.
С увеличением у в 2 раза х увеличивается примерно в 8 раз. Рассмотрим:
У = 20;
У — 21;
»/ = 22;
х = 8400;
х = 9702;
х= 11132.
Поэтому 9 <_у <22.
Так как х = у2(у-{-1) и это число должно быть кратно 7, то хоть один из двух множителей у2 и (у 1) должен быть кратен 7.
Из значений у, удовлетворяющих этому условию» остаются 13, 14, 20 и 21.
Ответ: 132(134~ 1)= 2366.
142(14 4- 1) = 2940.
202-21	—8400.
2Р-22	=9702,
(^2 1 ^2__	\
—--------------IJ +
(а — Ь 4- с) (а — с 4- Ь) (Ь + с — а).
2abc	’
(а — 4~ с) (а — с + Ь) (Ь с — а) 2abc
так как мы к левой части данного выражения прибавим — 1 — 1 + 1 = — 1; эта дробь равна нулю в том случае, если либо: а — Ь-\-с — 0; а — с-\Ь = 0\ Ь-\-с.— а = 0. Отсюда имеем а — Ь = — с\ а — с = — b\ b + с = а. Если
. ,	д24-^ — а2 (Ь 4-£)2 — 2Ьс — а*
Ь-\-с~а, то 2Ьс — 2Ьс
4 Зак. 358.
35
a2 — a2 — 2bc 2bc
аналогично:
Q2 +	— b2
2ac
при a — c — — b\
1 при a — b = — c.
2ab
17. Пусть в прямоугольнике KLMN сторона KL ~ MN = xlt KN = LM = и в прямоугольнике DEFQ сторона DE = QF = — x2i DQ = EF = y2. По условию задачи должно быть: Xj -r + ^1 = ^2 + ^ или Х2 — X' = У! — у2. Из подобия треугольников LPE и ASB находим:
BS _	ЕР,	BS	_	х2 — xi
4S	LP1	AS	~	ух у2
2	2
__ 2 (х2 — *х)
У1 — У2 ‘
Так как х2 — хх = ух — у2,
= 2; BS = 2AS; BS = АС, т. е.
в треугольнике высота равна основанию.
Следовательно, решение задачи сводится к построению равнобедренного треугольника, у которого высота равна
основанию.
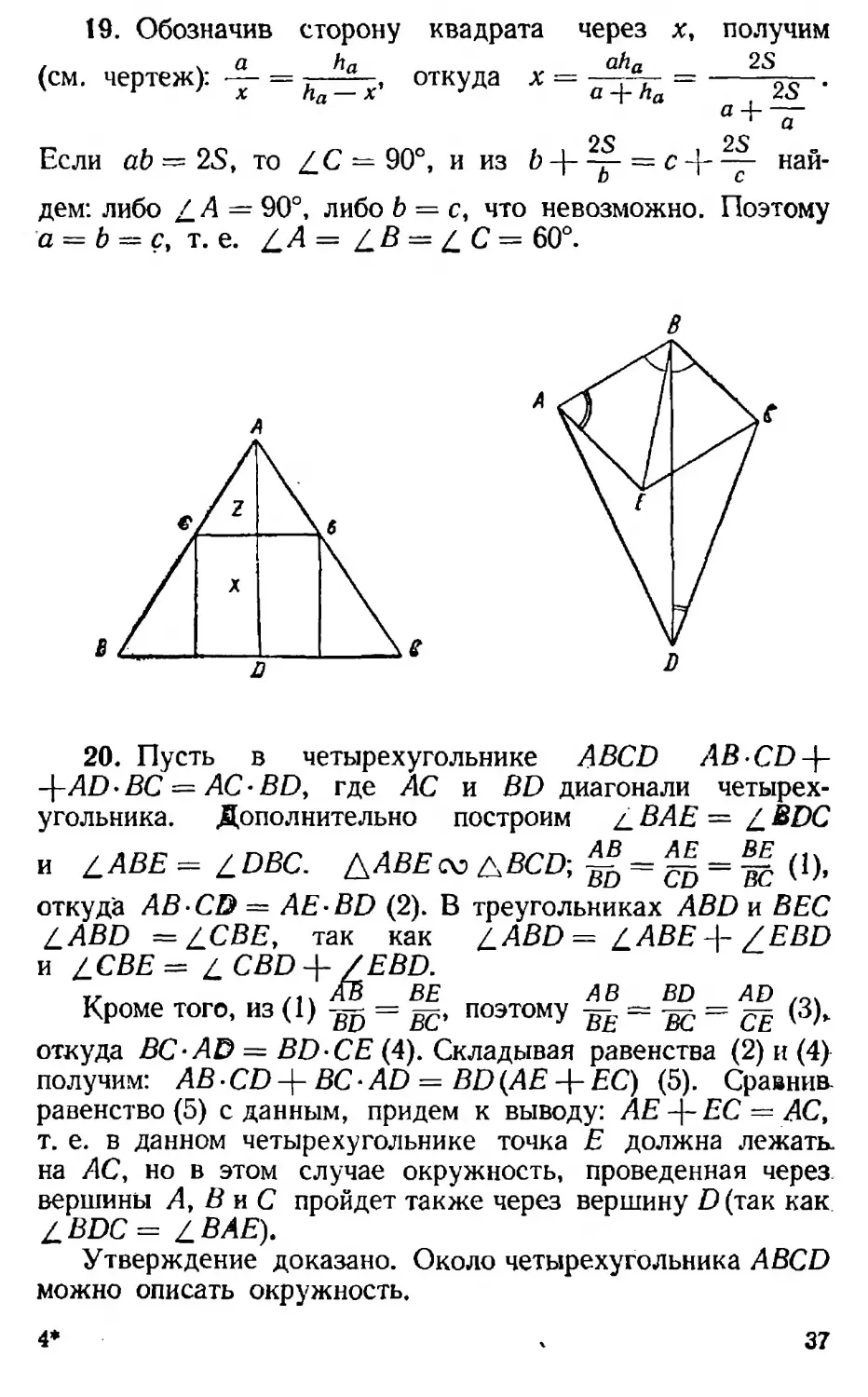
18. Пусть О — точка пересечения медиан треугольника ABC; AF, ВМ и CN — его медианы. Продолжим ВМ на расстояние МК = ОМ и соединим К и С, Тогда Sock =Sавс. Но стороны А\ОСК соста-
2
вляют соответствующих
к
медиан ДЛВС. Поэтому ис
1
комое отношение равно -g- :
36
19.	Обозначив сторону квадрата через х, получим
(см. чертеж):
а = ha
х ha — х'
Если ab == 2S, то /С — 90°, и из
откуда
дем: либо /. А — 90°, либо b = с, что невозможно. Поэтому а = b — с, т. е. = /_В — £_С = 60°.
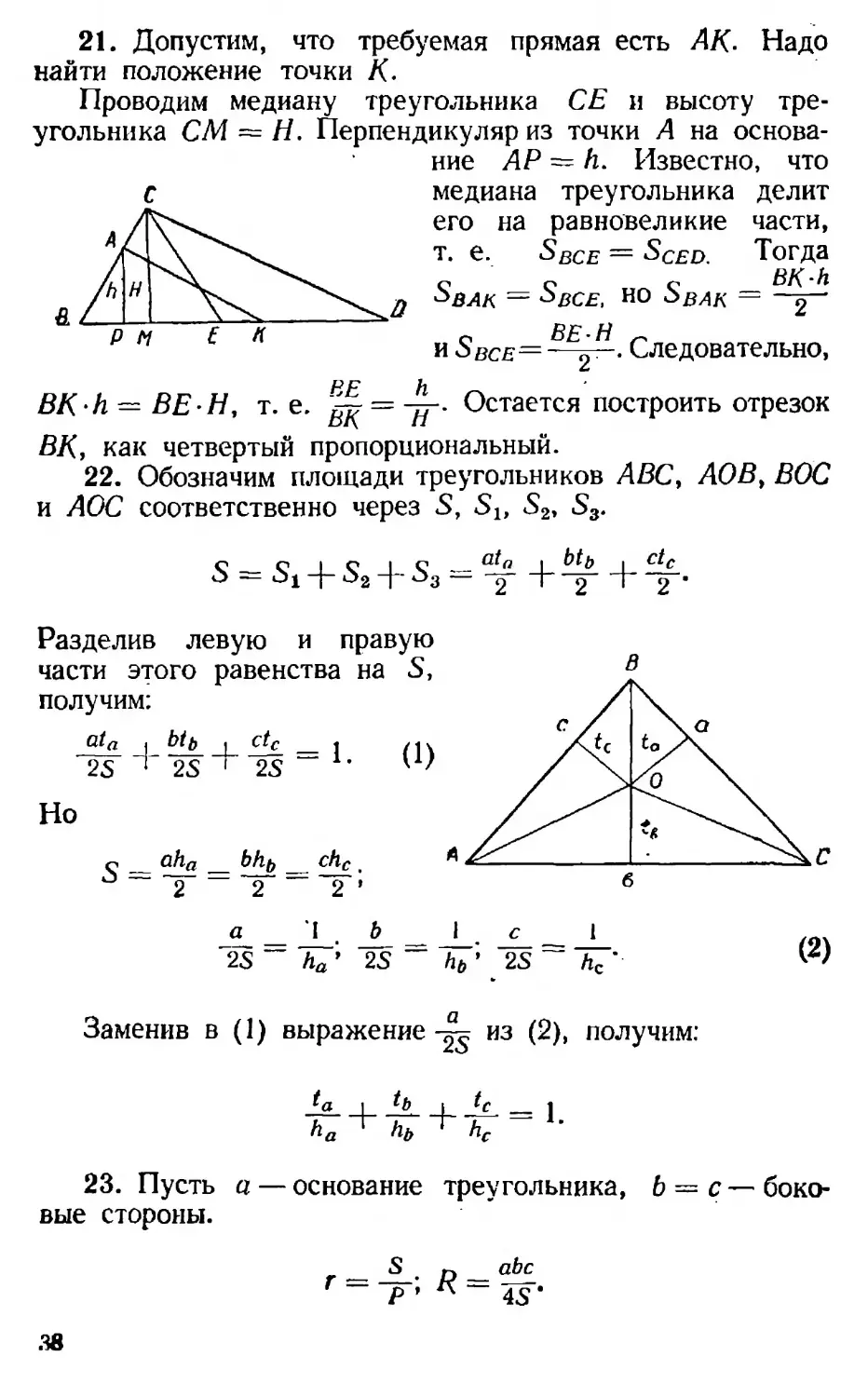
20.	Пусть в четырехугольнике ABCD AB-CD-\--\-AD-BC = AC-BD, где АС и ВО диагонали четырехугольника. Дополнительно построим д BAE = £ BDC и L АВЕ = z DBC. £\АВЕоо ДBCD, = = (О, откуда АВ  CD = АЕ • BD (2). В треугольниках ABD и ВЕС LABD = LCBE, так как /_ABD = £ЛВЕ-|- /EBD и /_СВЕ = £ CBD 4- /EBD.
т/	/1ч АВ BE	АВ BD AD /оч
Кроме того, из (1) -gg = ^, поэтому	(3),
откуда ВС-AD = BD-CE (4). Складывая равенства (2) и (4) получим: АВ • CD + ВС - AD = BD (АЕ + ЕС) (5). Сравнив, равенство (5) с данным, придем к выводу: АЕ -\-ЕС = АС, т. е. в данном четырехугольнике точка Е должна лежать на АС, но в этом случае окружность, проведенная через вершины А, В и С пройдет также через вершину О (так как Д BDC = Z ВАЕ).
Утверждение доказано. Около четырехугольника ABCD можно описать окружность.
37
21.	Допустим, что требуемая прямая есть Л/С Надо найти положение точки К.
Проводим медиану треугольника СЕ и высоту треугольника СМ = И. Перпендикуляр из точки А на основание АР = й. Известно, что
медиана треугольника делит его на равновеликие	части,
т. е. Sbce = Sced.	Тогда
о	о	с	МЛ
^ВАК = ^ВСЕ, НО О ВАК — ~ 2~~
с	ВЕ-Н „
и Звсе=—9—• Следовательно,
РЕ h
BK h — ВЕ Н. т. е. = тр Остается построить отрезок ВК, как четвертый пропорциональный.
22.	Обозначим площади треугольников АВС. ЛОВ. ВОС и АОС соответственно через S, Sb S2, S3.
s = st+s2+s3 = ^
Разделив левую и правую части этого равенства на S, получим:
I btfr j etc __ «
28 ‘ 28 ' 28	’
Но
aha _ bhb _ chc, ~ 2 ~ 2 ” 2 ’
btb 2
ctc
2 ’
а ___ I b_______I с 1
28	"28 ~ ИГ’ "28 ~ ~h^'
Заменив в (1) выражение-^ из (2), получим:
23.	Пусть а — основание треугольника, Ь = с—боковые стороны.
Перемножив их левые и правые части, будем иметь
Г% = 4Р ИЛИ
- 2^2ЬУ	(О
Вычислим высоту Н треугольника двумя способами:
//=jA2-4--	(2)
/? =	4S/? = пб2; 2aHR = ab2; Н =	(3)
а2 64
Из (2) и (3) имеем: Ь2-у- = отсюда
а =	| 47?2 —I2.	(4)
Подставив это значение а в (1), получим уравнение относительно b
2/?/-(-1- V47?2 —д2 + 2б) \ К	J
Ъ3 К4Я2 —ь2. R
откуда, сделав соответствующие преобразования, получим: (27?r —fe2) |/4Я2 — d2 = — 4Rr.
Возведя обе части в квадрат и преобразовав, получим: Ь* — 4/? (7? + г) b2 + 4R*r (4R + г) = 0. «
Из этого находим Ь, а из ( 24. К — искомая точка.
BD j_ АС; КМ ± АС и делит площадь треугольника АВС пополам; имеем:
2КМ  МС = АС  BD, (1)
из подобия л BDC и &КМС:
находим а.
Пусть в треугольнике АВС
BD _ DC. КМ ~~ МС'
KM-DC = BD-MC.
(2)
Разделив (1) на (2) получим:
MC=}/-±-AC-DC,
т. е. МС — средняя пропорциональная между	АС и DC.
5 Зак. 358.
39
Построив МС и восстановив из точки М перпендикуляр до пересечения с ВС, получим точку К.
25.	По условию имеем:	= х (так как
против большей стороны лежит меньшая медиана). Отсюда: та — сх\ mb — bx\ тс = ах.	(1)
По известной формуле:
4ml = 2b2 + 2с2 —а2;
4ml = 2а2 4- 2с2 — Ь2;
4ml = 2а2 4* 262 — с2.
После сложения получим:
4 (ml 4- mt + ml) = 3 (а2 + 62 + с2).
Заменив та, ть и те из (1), найдем:
4х2 (а2 + Ь2 4- с2) = 3 (а2 + 62 4~ с2);
,	3 /Т
х== Т’ х = -г.
26.	Центр тяжести О треугольника находится в точке пересечения медиан, поэтому площадь каждого из треугольников АОВ, ВОС и АОС равна -4- площади S данного &АВС, т. е. имеем
al Ьт сп. S ,	,	2S
-s- =	= -о- = -а* или al = от = сп —
Z Z Z и	о
Делим все члены этого равенства на abc:
I ___ т ___ п ___ 2S
be са ab ЗаЬс*
По свойству равных отношений:
2S
ЗаЬс *
1 . 2S	1
= 4R’ ЗаЬс	6/?'	СДелав
40
подстановку, получим:
I + т + п 1
. 1— = -fd и отсюда ab + Ьс + ас 67?
ab + Ьс + яс
6 (/ + т + п)'
27.	Если данная точка совпадает с центром квадрата, то любая прямая, проходящая через эту точку, делит
квадрат на две равновеликие части. Если точка Р расположена внутри квадрата ABCD, притом ближе к диагонали АС, чем к диагонали BD и внутри треугольника АОВ (О — точка пересечения диа
fl
А
гоналей), то искомой фигурой будет треугольник с точкой Dj на стороне AD, точкой В± на стороне АВ и с точкой Р — в середине гипотенузы B^D^
28.	Пусть в равнобедренном треугольнике АВС с основанием АВ и медианами ААЪ СС± вписанная окружность К пересекает медиану ААг в точках Р и Q так, что АР = PQ — = QAt. Тогда дАА]В должен быть равнобедренным с основанием ЛЛХ и точка Q — принадлежать медиане ССХ. Окружность К должна содержать Съ Р, Q, и _ CXPQ — 90°; отрезок РСг служит высотой и медианой дЛ(?С1 с прямым углом при вершине Сх. Поэтому д CjAAi— £ АА1В=45°, /_АВАг —	= что невозможно.
29.	Если х и у — длины диагоналей искомой трапеции, то, в соответствии с условием задачи,	-
%2	_|_ у2
41
Этому соотношению удовлетворяют стороны четырехугольника ABCD, вписанного в окружность с произвольным диаметром АС > а: АВ = а, ВС — у, CD ~ х, DA = х.
Если через концы произвольного отрезка LM У [про-вести параллельные одинаково направленные лучи LL' и ММ', на луче LL' построить точку Р при условии МР — у, а на луче ММ' — точку N при условии LN = х, то трапеция LMNP будет одной из искомых.
Задача имеет бесконечное множество решений.
30. Имеем: с — --Т-
CCV = 1, Z ВАС а;
АС^С^В = Ь:а, АС1^С1В = с;
ACt = kfe,
СгВ — \а, Л(& + а) = с, \2с == с,
Пользуясь этими условиями, можно построить треугольник, подобный дАВС, а потом — и сам дАВС.
31.	Пусть в прямоугольник ABCD вписан ромб A2B2C2D2; их общий центр О; Ви С19 Dt — середины сторон АВ, ВС, CD, DA\ АВ = 2с, AD=2b.
ocl + OD22 = a2; ?
ЛЛ2 __	а2№
— Z2 i 72 '

д ODJ)2, OD2 = kOC2,
32.	Обозначим через klf k2, k3, k4, k5 данные окружности. На окружности kr, произвольно взятой из данных окружностей, в соответствии с условием задачи, должны быть точки ее пересечения с тройками окружностей; (1%, 1%, &<)• (^з» ^4, М» (^2»	^5)- Если эти точки разные, то ок-
ружности ki и k4 должны совпадать между собой, что противоречит условию задачи. Следовательно, две из этих точек должны совпадать одна с другой. Но через такую точку будут проходить все данные окружности.
42
33.	Пусть ABCD—данная трапеция, О — центр впи-санной окружности, L, М, N, Р — точки прикосновения окружности соответственно к сторонам АВ, ВС, CD, DA и АВ || DC. Треугольники AOD и ВОС — прямоугольные с гипотенузами AD и ВС, так как суммы их острых углов равны прямому углу. Обозначим отрезки AL = АР = а, BL^BM = b, СМ = = CN = c, DN = DP = — d. Поэтому ad — be=
= ОЯ = ОМ2;
a:c — b:d.	(I)
Точки L, О, N принадлежат одной прямо’, перпендикулярной к основаниям трапеции. Если Q— точка пересечения прямых АС и £/V, то AQ:QC = а: с — LQ:QN.
Пусть Q1 — точка пересечения прямых BD и LN. Тогда
BQ';Q4)~b:d.
В силу условия (I) точки Q и Q* совпадают между собой, то есть прямая, соединяющая точки касания оснований, проходит через пересечения диагоналей. Будем теперь считать точку Q только пересечением прямых АС и МР. Через точку С проведем прямую, параллельную прямой AD. Обозначим через R и S точки пересечения этой прямой с окружностью и Т—с прямой РМ. Имеем: ^SP = ^PR-Углы MPD и РМС измеряются ~-^PNM, Следовательно,
МТС измеряется половиною той же дуги: ДЛ4ТС—равнобедренный. Из подобия треугольников APQ и CTQ и из-равенства СМ = СТ следует: AQ: QC = а: с. А это значит, что точка Q находится в пересечении диагоналей трапеции.
34.	Шахматист, занявший второе место, не мог набрать оольше 6 очков, так как не меньше 6 очков набрали четыре шахматиста, занявшие последние места и игравшие только между собой.
Наибольшее число очков, которое мог набрать участник этого турнира, равно 7. Если шахматист, занявший первое
43
место, набрал 7 очков, то занявший второе место не мог иметь более шести очков из-за проигрыша первому. В соответствии с условием задачи он должен набрать 6 очков. Если участник, занявший первое место, набрал 6,5 или менее очков, то занявший второе место не мог опять иметь более и менее б очков.
35.	Пусть вершины данного четырехугольника ABCD принадлежат соответственно сторонам искомого квадрата DiABjCp Тогда вершина Dr принадлежит окружности К с диаметром AD, а вершина В± — окружности Кг с диаметром ВС; диагональ B1D1 пересекает эти окружности К и Кг в точках Въ Р, Q, где Р — середина полуокружности, не содержащей точку D± на окружности К, a Q —середина полуокружности, не содержащей точку Вг на окружности

АР окружности К, не содержащая точку А', DxQ окружности Ki, не содержащая
; Если ASiCiDi—произвольный квадрат,	А^'В окруж-
ности К вмещает угол а, CiC'D окружности Кг вмещает угол р, вмещает угол а1? о .
точку С', вмещает угол рь то четырехугольник подобен данному.
36.	Обозначим стороны прямоугольников a, at; b, b^ с, cv Имеем а = har, b = hbx, с = hc^ Следовательно, треугольник со сторонами аъ Ъг, сг подобен данному треугольнику. Пользу; ясь этим условием, получим доказательство предложенного утверждения.
37. Пусть у выпуклого четырехугольникаТДВСЛ точки /И, Р, N, Q середины сторон АВ, ВС, CD, DA, точка Е—
44
середина диагонали АС, точка О — в пересечении отрезков PQ и MN.
При данном условии для решения задачи достаточно доказать совпадение точек О и Е. Если бы эти точки не совпадали, то
ME 4- EN > MN, PE + EQ>PQ, BP + QD + BM + ND >MN + PQ.
А в соответствии с условием задачи, BP + QD + ВМ -]-ND = MN + PQ
противоречит последнему неравенству.
38.	Через точку Р, данную внутри угла АВС, проведем прямую, параллельную стороне ВС, до пересечения со стороной АВ в точке Q; отложим отрезок = BQ; через точку А± проведем прямую AtP до пересечения со сто-чроной ВС в точке С\. Треугольник AtBCi— искомый. Если прямая, проходящая через точку Р, отсекает треугольник А2ВС2, то на стороне А2С2 есть точка D, такая, что C-J3 || ВА, Л AtA2P = А СгОР, пл. Д А2ВС2 > пл. А
39.	Пусть АВ, ВС, CD — данные отрезки, О — искомая точка, т. е. АОВ = £ ВОС = COD.
АОС ОВ является биссектрисой, зна-
В треугольнике
АО АВ , чит ОС ~~ ВС ~ 1'
Точно также из
треугольника BOD вытекает, что
ов _ вс _ / 0D ~ CD “ /2’
45
Таким образом, точка О лежит на пересечении двух окружностей, одна из которых есть геометрическое место точек, отношение расстояний от которых до данных точек А и С равно а другая — геометрическое место точек, отношение расстояний от которых до точек В и D рав-но /2.
Построив указанные окружности, найдем точку О.
40.	Если ABCD— искомая трапеция, АВ || DC, О — точ-04 АС ,,
ка пересечения диагоналей, то	Можно постро-
ить	Л'В'С' сс Л АВС, где S — точка
л	пересечения прямых AD и ВС с угла-
/ \	ми L B'A'D' = а и Z А'В'С' = р,
/ I \	точка О' в пересечении диагоналей
р/ / \л	и точка 7И' — в пересечении прямых
/\ЪА	Л'В' с S'O'. Здесь А'М' - М'В'. Точ-
/	\	ку О' можно найти в пересечении
/ s' /	\	прямой S'O' с окружностью Аполло-
ния — геометрическим местом точек
Д	Р'А' АС
М	Р’1 ~Р7В7 во’ Получим трапецию
A'B'C'D' cv трапеции ABCD. После этого легко построить и искомую фигуру.
41.	Пусть в начальный момент точка Ах катящегося
круга находится в, точке соприкосновения этого круга с данным неподвижным. Диа-
метрально противоположная точке Ai катящегося круга находится в центре О данного неподвижного круга. Если А2 — точка соприкосновения катящегося круга с данным неподвижным в другой момент, О2—центр этого круга, а точка Ах заняла положение В и радиальные меры углов а = /_ АгОА2, с? = = £ ВОА2, то длина о АХА2 =
= a2R, длина ВА2 = yR, ОО2 = О2В — R. Это значит, что точка В находится на диаметре ОАХ неподвижного
круга.
Ответ: каждая точка катящегося круга описывает диаметр данного неподвижного круга.
42.	В трапеции ABCD сторона АВ || CD, точка О — в
46
пересечении диагоналей. Если S— точка пересечения прямых AD и ВС, то прямая OS пересекает основания АВ
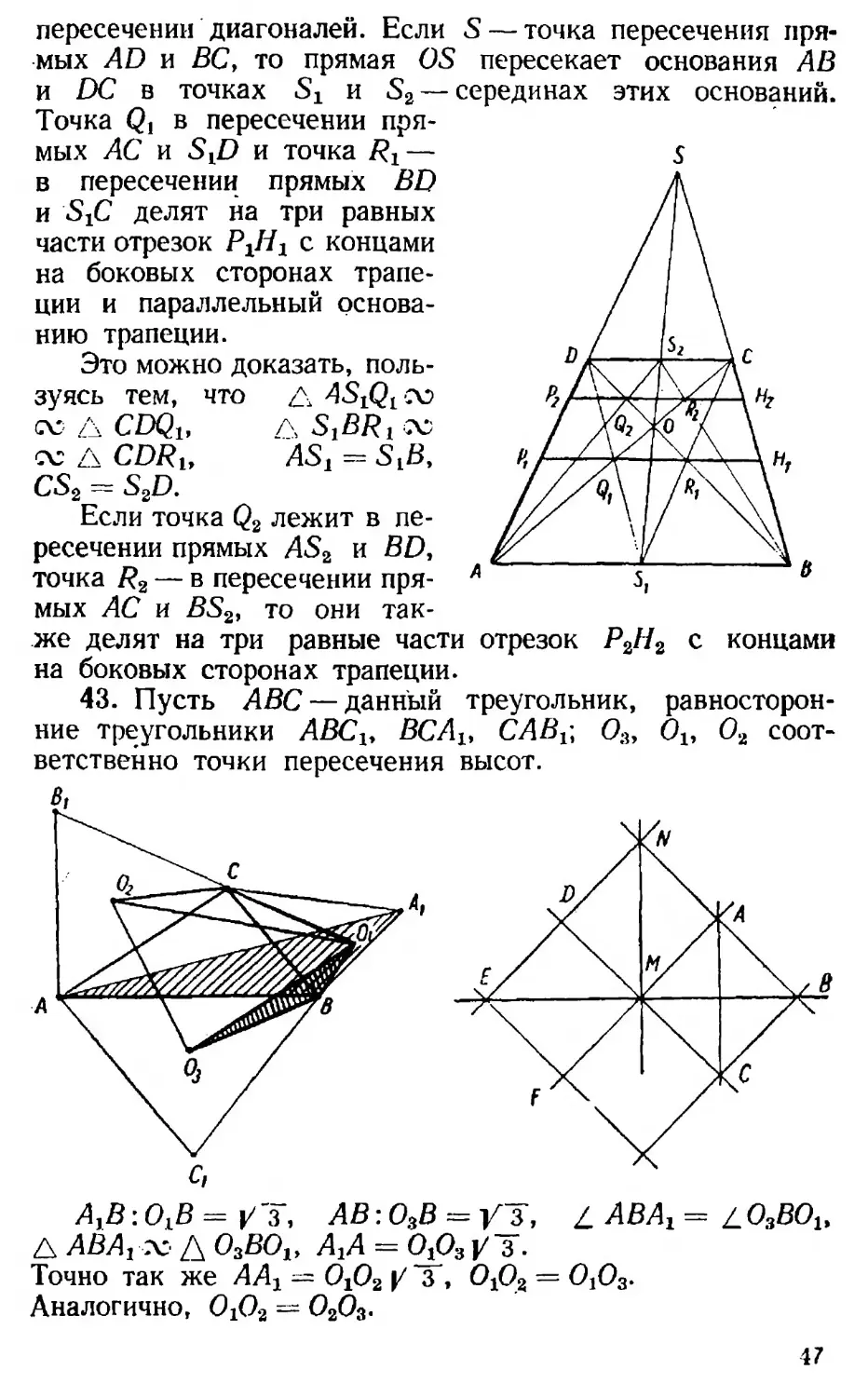
и DC в точках Sx и S2 — Точка Q] в пересечении прямых АС и S,D и точка — в пересечении прямых BD и S/? делят на три равных части отрезок РХН, с концами на боковых сторонах трапеции и параллельный основанию трапеции.
Это можно доказать, пользуясь тем, что д ^S^gv GV A CDQi, Д S^GV gv Л CDR„ AS, = Stfi, CS2 - S2O.
Если точка Q2 лежит в пересечении прямых AS2 и BD, точка /?2 — в пересечении пря
серединах этих оснований.
мых АС и BS2, то они так-
же делят на три равные части отрезок Р2Н2 с концами на боковых сторонах трапеции.
43.	Пусть АВС — данный треугольник, равносторонние треугольники АВС,, ВСА„ САВ,\ О3, 0„ 02 соот-
ветственно точки пересечения высот. Bi
А,В\О,В = |/з, АВ:О3В — Уз, £ АВА, =/_03В0и А АВА, gv Д О3ВО„ А,А = 0,03 у з .
Точно так же АА, — 0,02 У X, О,О2 = О,О3.
Аналогично, О,О2 — О2О3.
17
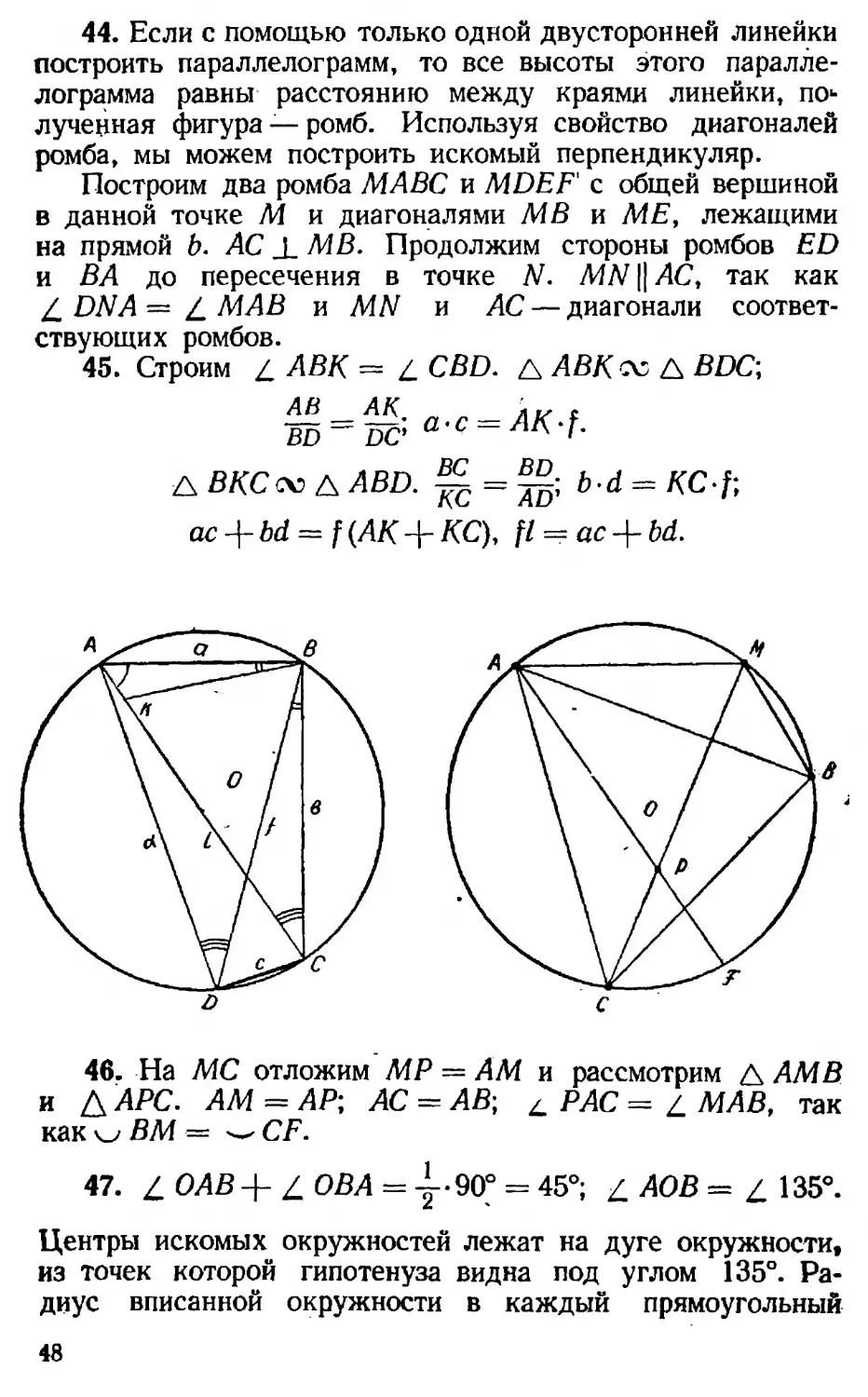
44.	Если с помощью только одной двусторонней линейки построить параллелограмм, то все высоты этого параллелограмма равны расстоянию между краями линейки, по*-лученная фигура — ромб. Используя свойство диагоналей ромба, мы можем построить искомый перпендикуляр.
Построим два ромба МАВС и MDEF с общей вершиной в данной точке М и диагоналями МВ и ME, лежащими на прямой b. AC I МВ. Продолжим стороны ромбов ED и BA rq пересечения в точке ЛЛ MN || АС, так как £ DNA — Z МАВ и MN и АС — диагонали соответствующих ромбов.
45.	Строим £ АВК ~ £ CBD. Л ЛВД cv Л BDC;
АВ АК	о
BD ~ DC' а'с~
А ВКСюк ABD. = bd = KC-f;
ас + bd = f(АК+ КС), fl = ac-\-bd.
46.	На МС отложим MP = AM и рассмотрим Л АМВ и Д АРС. AM = АР; АС = АВ; L РАС = £ МАВ, так как о ВМ — CF.
47.	А ОАВ + Z ОВА = —90° = 45°; £ АОВ = £ 135°. » 4
Центры искомых окружностей лежат на дуге окружности, из точек которой гипотенуза видна под углом 135°. Радиус вписанной окружности в каждый прямоугольный
48
треугольник — расстояние соответствующей точки ГМТ центров до гипотенузы. Ясно, что середина этой дуги находится от гипотенузы на наибольшем расстоянии.
Остается показать, что окружность этого радиуса вписывается в равнобедренный треугольник с данной гипотенузой.
Действительно, так как центр этой окружности лежит на перпендикуляре .ОР, восстановленном из середины гипотенузы, то отрезки АК = ВМ = АР.
Кроме этого, СК = СМ. Поэтому АС = СВ.
48.
AM - АМъ
AM = AK + KM = AK + (R + r);
АМ± = АВ + ВМъ АВ-^ВМХ — AK-^(R-\-r)\ AB — (R + r) = AK — BM^ BN = BN^ BNX = AB + ANt
49
BN = BP 4- PN = BP + {R-\- r);
AB-[-ANt—BP-L-(R-\~r);
AB — (R^rr) = BP — N1A.
Так как BP = BMt и AR == ANr, то AR — BMV — ВМг — — AR, t. e. AR = BMt.
Из этого следует, что
ЛВ = # + г.
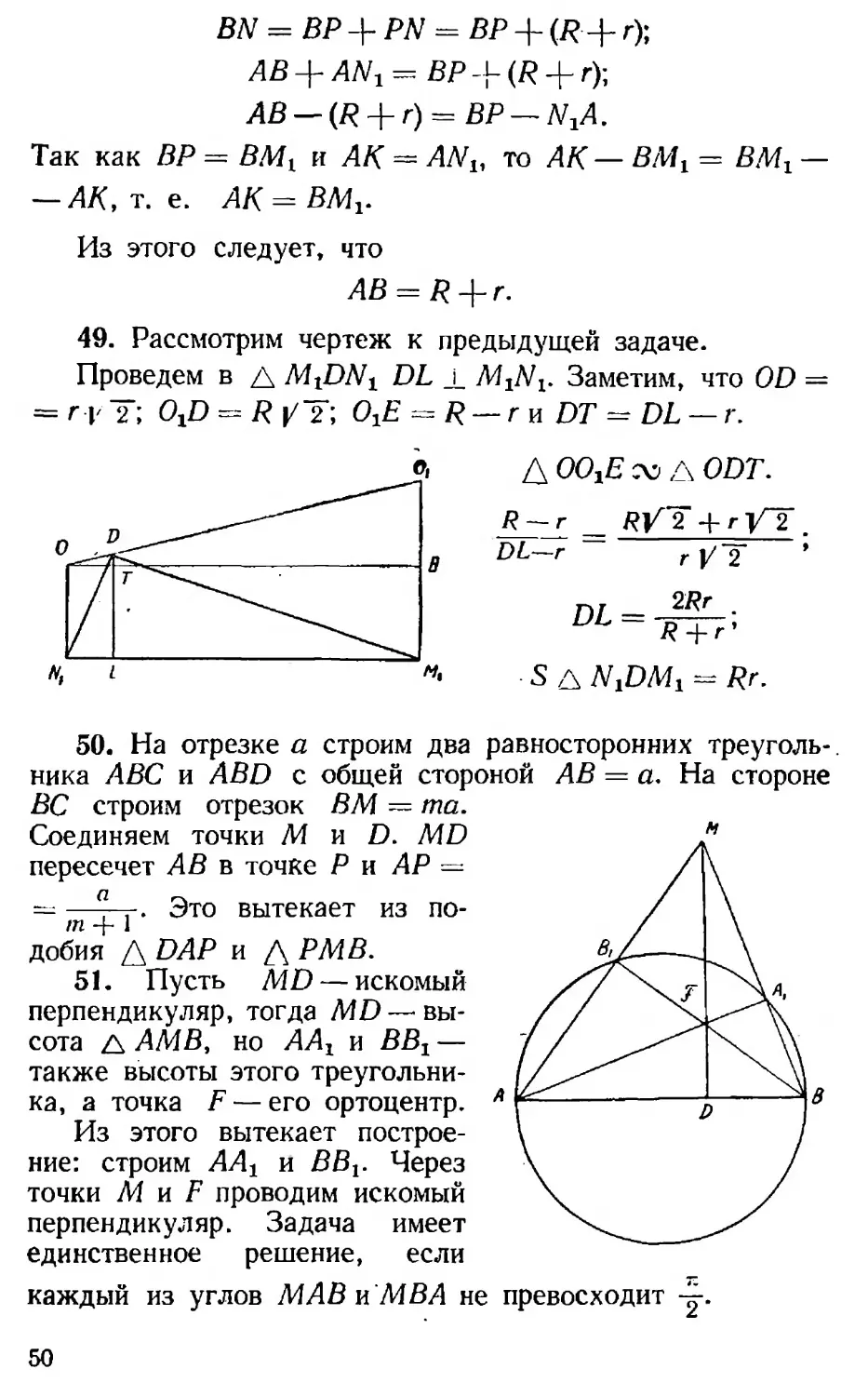
49.	Рассмотрим чертеж к предыдущей задаче.
Проведем в Л /Их-ОЛ^ DL i M-jN^. Заметим, что 0D = = г г~2\ CRD = R у~2; ОгЕ = R — r и DT — DL — г.
Д ООгЕ сч A ODT.
R~_r _	2 + г УТ.
DL—r ~ г у~2	’
S Д NiDMt = Rr.
50.	На отрезке а строим два равносторонних треугольника АВС и ABD с общей стороной АВ = а. На стороне ВС строим отрезок ВМ — та. Соединяем точки М и D. MD пересечет АВ в точке Р и АР = — —т-г. Это вытекает из по-добия Д DAP и Д РМВ.
51.	Пусть MD — искомый перпендикуляр, тогда MD— высота л АМВ, но ААТ и ВВг — также высоты этого треугольника, а точка F— его ортоцентр. А Из этого вытекает построение: строим AAt и ВВг. Через точки М и F проводим искомый перпендикуляр. Задача имеет единственное решение, если
каждый из углов МАВ п MBA не превосходит —. А»
50
IX КЛАСС
1	gse = (8 l)fl9 = 8m 4~ 1, где m — целое число.
Отсюда:
79®8 = 7*т и = (74)2т-7 = 24012"* - 7 = (24004- I)2”1-7 = = (100«4- 1)-7 = 100-7п4-7, где п — целое число.
Из этого видно, что две последние цифры данного числа образуют совокупность 07.
2.	Выражение в первой скобке есть геометрическая прогрессия с первым членом 1 и* знаменателем 10.
(10" + 10«~1 + ... + 1).(10«+1 + 5) + 1 -
1Г/И-1 — 1	]п2(п+1) I д inn + I I д
= —х--------(10"+’ 4- 5) 4- 1 = —------—tL =
if	if
3.	По условию задачи 100^№< 1000, следовательно, 10<ЛГ<31.
Пусть N2 = 100х -р 10у4-2	(1)
xyz = N — 1;	(2)
zi£0, так как произведение xyz в этом случае равно нулю, z — нечетное число, так как в противном случае четно N [из (1)], a N— 1, равное xyz, нечетно, что невозможно. Итак, г — нечетно, следовательно, N — нечетно, AZ — 1 — четно. Кроме того, z может быть равным только 1, 5 или 9. Пользуясь таблицей квадратов, выбираем трехзначные числа, оканчивающиеся на 1, 5 или 9, произведение цифр которых меньше 31: 121, 225, 361, 441.
Второму условию удовлетворяет только 361.
4.	Докажем способом математической индукции. Пусть п — 2k, где k = 1, тогда утверждение справедливо:
132= 169 = 7-24 4-1.
Допустим, что для некоторого k выполняется равенство: 132* = 7m 4“ 1; (m — число натуральное).
Переходим ст k к k-]- 1.
В таком случае:
132(л+1) = !32Л. ;32	(7/п_[_ 1).(7.24 4- 1) =
= 7 (169m 4-24) 4-1;
51
Следовательно, предположение справедливо.
5.	Обозначим через Sn сумму
о - А. Ад_А +	4- А
22 т 32 Т 42 Т Т п2 ♦
Так как
1 1 = 1________________1_
п2 < п (п — 1) п — 1 п *
то
о 1
Складывая эти неравенства, получим: s„ < 1--------------i-; отсюда Sn < 1.
6.	Можно считать, что числа расположены в порядке возрастания:
< ^2 < &3 < Я4 ...»
Рассмотрим числа а1г , ... , ап.
ап + аъ ап-\-а2, ап + а3, ап+а^ ... , ап-^аг.-ъ | ап—1 | ^1» &п | —1 ”4” *“ > "I —1 ( —2*
Продолжая составление сумм подобным способом,* получим:
А an—k а19 ^лА^п—1А ••• А
A an—k А	•• • >	А ап—! А- ••• А ап—k А ап—k—1
и т. д. Наконец:
#л А ап~ 1А ап—2 А • • • А ^1*
Очевидно, что числа возрастают и, следовательно, различны. Количество этих чисел /г 4” (л—1)А(П— 2) А А А1 = п^П~^ 1" соответствует требованиям задачи.
Замечание: Первые п натуральных чисел составляют пример п положительных различных чисел, из которых нельзя соста-(л+1)
вить более чем —различных сумм, мг
52
7. Согласно условию,
10х у = х2 Ц- ху + у2 или 10x-|-r/-j-xt/ = (x4-z/)2.
Так как
х 9 и у < 9, то	10х 4- У 4" ху <: 180, (х 4- у)г <1180,
а тогда
х + ^< 13.
Но при х-\-у = 13 наибольшее значение выражение 10х -\-у 4- ху получит, очевидно, при х — 9, у = 4:
10х 4" У + ху < 130;
следовательно, (х 4- у)2 < 130 и х ~\-у	11.
При х 4- У — 11
10х-|- у-\-ху < ПО,
откуда	х 4~ У < Ю.
При х 4 У = Ю значения х = 9, у = 1 удовлетворяют условию задачи.
При х 4- у = 9 условию задачи удовлетворяют х = 6, У = 3.
При х-\-у —&,х-\-у = 1, х + у = 6, х-^у = 5, как нетрудно в этом убедиться, решений нет.
При х у — 4 имеем решение х — 1, у — 3.
Ответ: 91; 63; 13.
8. Согласно условию задачи сумма слагаемых представляется так: 1 +^ + (1	+	+ U +^)3^ +
+ ... 4-(1	+	= 531441	где
число слагаемых.
Так как последнее слагаемое равно (1 -]-k)n~2-k, то сумма всех ему предыдущих (l+^)rt~2; тогда З12 = (1 —|— + й)«-2 4-(1 4-fe)n-2.fe===(l 4-£)П-2(1 4-fe) = (l +/г)л-1,ИЛИ п—1/  12 14-* = 1/з12 = зп“1.
Но число слагаемых должно быть не меньше четырех, тт	12
Делаем испытание, зная, что есть число целое и что делители 12 есть 2, 3, 4, 6, 12:
1) если п — 1 = 3, то Их = 4; тогда 1 -j- k — З4; кг = 80; 2) если п — 1 ~ 4, то п2 — 5; тогда 1 —= З3; k2 = 26;
53
3) если п — 1 = 6, то п3 — 7; тогда 1 Ц- & = З2; k3 = 8;
4) если п — 1 = 12, то п4 = 13; тогда 1 й —^3; й4 = 2.
Итак, получаем четыре значения для множителя k (80, 26, 8 и 2) и соответственно им возможное число слагаемых (4, 5, 7, 13).
2п раз
С другой стороны
10, Покажем, что 2 И п +1 — 2у п <	< 2	—
т Л
— 2 у л — 1. • В самом деле, 2 j/ п + 1 — 2 У~п = _ 2(.|Z»+ i — l/'n~)(K« + 1 +/й~)
У п+1 +У п
у п -у i -у у п у п ~у у п у п
Точно также, 2 ^п — 2у п — 1 =
2(У п —У п — 1 )(/П +/п—1) =	2
F п + V п — 1	р п — 1 >
2	1
> У п + V п У п '
54
Теперь имеем:
1 + j/y + уу + ••• + у ] ООО 000" »>. 1 + 2 [(/ 3	У~2) +
+(/Т — р'"3) + ... + (/1000001 —у 1000000)] =
= 1 +2 (УI oooooi — Уг~) > 1 + 2 • 1000 — У~8 > 2000 — — 3 + 1 = 1998.
В то же время 1 +	+ j/-§- + ••• + у юооооо^
+2](/'2—1)+(/3" —/Т)+ ... +(/ 1 000 000-/999 999)] = — 1+2 (/1 000 обо — 1) = 1 + 2 • 999 = 1999.
Таким образом, целая часть указанной суммы равна 1998-
11. Доказательство проводится методом индукции. Пусть неравенство верно для k множителей. Тогда
(1 + Xi) (1 + хг) ••• (1 + xk) О +**+1)	(1 +*! + х2 +
+ -.. + xft)(l +%*+|) = (1 +*1 +-*в+ '••• +xfe + Xft+i) + + (*> + ... +xft)xft+I> 1 +%j +х2+ ... +x*+i, так как (х1+^а+ ••• +х*.)х*+1 ^>0, ввиду того, что все х( имеют один и тот же знак.
19	_______?........ У п + 2 —У~п
У п + У п +2 ~	2
Л = 4-1(Гз -/Т) + (/Т-/Т) + ...
— /2^=Л)] = у (/2/Г+Т — 1).
13.	Положим У т + ]/ ~а + У~Ь '+ ]/ ~с = /Т -|- У~у + j/T. Возведем обе части равенства в квадрат. Получим х -р Н- 2 = /и, 2у ху = У а , 2 У хг — У Ь , 2Ууг =
=*= УТ-
Решим данную систему относительно х, у, г:
____ У abc ____V abc ______V abc Х ~ 2с ’ У ~ 2Ь ” 2 ~~ 2а ’
т. е. abc должно быть точным квадратом:
ab + ас -Ь Ьс
14.	Рассмотрим неравенство:
а-\-Ь	,—
—2-----V аЬ
(а — 6)а, Sb ’
55
— у ab;
(1)
Рассмотрим неравенство:
(д — Ь? 8а
(а — Ь)2 4а
(УТ - У Т)2;
(2)
Неравенства (1) и (2) справедливы, так как а > b > 0.
15.	Умножив знаменатель на а	(а, Ь
и с — неопределенные коэффициенты): (14—3 J/T — — 2J/T)(a	и сделав приведение подоб-
ных, получим (а — 4Ь -|- 6с) -|- (За 4" b — 4с) у ~2— (2а — — ЗЬ — с) 3/Т.
За 4-6 — 4с = О
2а — 36 — с = О
1) Исключив 6, получим: 11а = 13с; jy = ур•
Исключив из системы (1) с, получим: =	=
—	Приняв коэффициент пропорциональности рав-
ным единице, получим: а — 13; 6 = 5; с = II.
Следовательно, умножив числитель и знаменатель данной дроби на 134-5	11 У~4 и, сделав преобразова-
ния, получим:
13 + 5J/T4- НУТ.
16.	Возведем обе части этого равенства в квадрат;
56
1)	Если 1<^х<2, то |х— 2| =—(х— 2) и поэтому
2 2х	2	_ 2х 2 (х — 2) _____	4
У “ (х — 2)2 “ х —2 ~ (X — 2)2 (х — 2)~ “ (7— 2)2 ’
а так как г/>0, то у есть арифметическое значение корня квадратного из этого выражения. Следовательно,
__ I Г 4	_	2	_	2	__	2
У~ Г (х— 2)2 — |х — 2| — —(х —2) ~ 2 —х'
2)	Если х > 2, то х — 2 > 0, значит ] х — 21 = х — 2, а поэтому if =	+ 7^2 =	+
. 2(х — 2) _ 4(х — 1) “ГкХ_2)2 - (Х-2)2
и, следовательно,
При х — 2 данное выражение не имеет смысла.
17.	Пусть данная дробь имеет одно и то же постоян* ное численное значение при любых численных значениях х, которое обозначим через т, т. е.
ах2 + Ьх + с aLx2 + biX +
откуда
(а — ахт) х2 ~\-(Ь — ^т) х + (с — с^т) = 0.	(1)
Равенство (1) тождественно равно нулю по условию при любом значении х\ это возможно только тогда, когда коэффициенты при х2, х и свободный член одновременно равны нулю, т. е.
а — Ci т — 0, Ь — Ь^т = 0, с —	— 0,
откуда
а   b	с
ai	Ьх
(2)
57
Но если соотношение (2) выполнено, то данная дробь не зависит от х, следовательно, соотношение (2) является условием не только необходимым, но и достаточным.
18.	Из данного равенства находим:
(у — 2)х24-(4у — 6)х4-5«/ — 6 = 0.
Установим, при каких значениях у к — действительное число. Если уф 2, то
3-2у ± Vе (3-2g)a-(y-2)(5j/-6) У~ 2
_ 3 —2у ± lz—(^ — 4^ 4- 3)
Для того, чтобы х было действительным числом, необходимо и достаточно, чтобы — (у2 — 4 у 4~ 3) 0, или — (у — 3)(у — 1)^0. Это неравенство удовлетворяется при 1 < у < 3; так как при х = — 3 у = 3, а при х — — 1 у = 1, то 1 и 3 — соответственно наименьшее и наибольшее значения функции.
19.	Представим данный трехчлен в таком виде:
х2 + 5х + 16 = х2 + 5х — 36 + 36 + 16 = (х + 9) (х — 4) +
ч	4-52.	(1)
Если при некотором целом значении х данный многочлен делится на 169, то при этом . же значении х он делится на 13. Следовательно, при этом значении х выражение (х-|--9)(х — 4) должно делиться на 13, ибо 52 делится на 13. Значит, по крайней мере один из сомножителей произведения (х + 9)(х — 4) делится на 13. Но (х-[-9) — — (х — 4) = 13. Поэтому и другой сомножитель делится на 13, а следовательно, и произведение делится на 169. Но так как 52 на 169 не делится, то двучлен (!) на 169 ни при каком целом х не может делиться.
20.	Пусть x — ty. Получим у 7 y2(t |<7 4~ 1) = 336, i/2(Z/7+l)= 112.
х ~ 18; у = 2.
21.	Полагая 8 — х — а4 и 89 4- * = 64»
получим СИ
стему
а фЬ — 5 а4 4- д4 = 97.
58
Пользуясь тем, что а4 -\-Ь4 = (а2 -|- 62)2 — 2а2Ь2 = [(а + 6)2 — — 2аЬ]2— 2а2Ь2, и тем, что а+6 — 5, получим уравнение (25 — 2аЬ)2 — 2а2Ь2 = 97, или 2а2Ь2 — lOOab Ц- 528 — 0, или a2fc2_5062b_p264 = 0.
Отсюда: 1) ab=6 и 2) ab = 44.
Теперь остается решить две системы:
1)
а -\-Ь = 5
ab = 6
2) / а-г 6 = 5 ( ab = 44.
Первая система дает а = 2, Ь = 3 и а = 3, 6 = 2.
Вторая система действительных решений не имеет.
Пользуясь, например, уравнением 8 — х = а4 и полученными значениями неизвестного а, найдем действительные корни данного иррационального уравнения:
1) Xi = — 8 и 2) ха = — 73.
22.	Возведя обе части уравнения в квадрат, получим:
х4 — 2ах2 — х -|- а2 — а — 0.
Решим это уравнение относительно а:
а2 — а (2х2 4-1) + х4 — х — 0.
Разложив квадратный трехчлен на линейные множители, получим: (х2 + х — а 1) {х2 — х — а) — 0.
Находим: Xi, 2 =
— 1 ± V 4а — з.
2
*3, 4“
23.	Так как р есть любое натуральное число, большее 1,
то должно быть b + х > 0 и х>0. Имеем: fy~b~-\-x
59
Так как
О, то и > 0. Отсюда х ==
Ъ а
\ a J
Для х > 0 должно быть Ь > а\ если а < 0 и b < 0, то |а| > |&|.
Для существования решения нужно, чтобы а и b были одного знака и чтобы Ь > а.
24.	При а = 0 и а = 1 уравнение имеет два двукратных корня: Xj,2 ~ — 0, Хз, 4=1. Если афО и а 1, то ни 0 ни 1 не являются корнями данного уравнения. Непосредственной проверкой легко убедиться, что если xt—корень данного уравнения, то —, 1 — хг тоже являются его
корнями. Отсюда вытекает, что и
и
степени, из них,
также являются корнями данного уравнения.
Так как уравнение при аф 0 и аф 1 — шестой то оно имеет шесть корней, причем, зная один легко получить остальные корни. Но, очевидно, что а — корень данного уравнения. Поэтому имеем:' Xi = а, х2 == —, х3 — 1 а, х4 — л _ а, х5 — 1 а, х6 — а _ j.
1 — допустимые значения неизвестных.
36	4/----7?	6
25. х > 2, у Преобразуем: 4 Ух — 2 +
4 ,
Получим уравнение:
Из этого следует, что 2 j/x — 2 —- - — = 0 и УУ— 1 —
Получим решение: х = 11, у = 5.
60
26.	Допустим, что точка М найдена, тогда МК — МВ (1) и МВ2 = АВ- ВС. НоМК = 2R — BC. Получим: (27?—ВС)а«= == 2R- ВС или ВС2 — SRBC + 47?8 = 0, так как ВС < 27?. Откуда ВС — 3R — ]/ 97?2 — 47?2. Следовательно, ВС можно построить как разность двух отрезков: 37? и у 9R2—4R2.
27.	Известно, что то —	V 2b2 -j- 2с2 — а2. BD и СЕ —
2
медианы. Вычислим стороны Л СОВ. ВС — а; ВО —BD = о
= 2.^.р/2а8 + 2с2 —Ь2; СО = У |Л2а2 + 262 — с2. ВО24-
+ СО2 = у (4а2 + 2Ь2 + 2с2 = а2, т. е. СО _L ОВ.
28.	Проводим два взаимно перпендикулярных диаметра AM и BN. Хорду АВ продолжаем на расстояние ВС = АВ. Точку С соединяем с центром О.
CD
Отрезок -у- = а 10. Докажем это. АВ = ВС — R ]/2; CDCE = АС-ВС;
CD - (2R 4- CD) = 4R2;
CD= I
CD _ R (1 2 ~
61
6 Зак. 358.
29.	Периметр трапеции Р—^BM~\-MN~\-^jNO-\-OB. (1) В Л МОуО гипотенуза ОМ — /?, а катет 001 = -j-; следовательно, ОМОХ — 30е. Но тогда и ВОМ — 30е, т. е.
ВМ равна окружности О.
^ВМ= =	(2)
*
Из Л МОГО находим МО± . Тогда MN = MOi—-_A,01_^£_4„«<q=j).	о.
Далее	находим: NO ~ 2л ~	(4)
X	fcr	1
OB = R.	(5)
Подставляя (2), (3), (4) и (5) в (1), получим:
Площадь S трапеции найдем как
S = «$сект. ВОЛ! '"И ЛЮО> <5сект. OOXN*
Находим последовательно:
о	1	D2. с	Я2 Из
^сект. ВОМ = “jy W МООХ ~--g--•
Q	__ к7?2
»-> сект NOOX — 1бГ~*
s=«'(t+w)-
30.	Покажем, что после проведения fe-й прямой на плоскости число частей увеличивается на k.
Пусть на плоскости уже проведены k прямых общего положения. Проведем (£—|— 1)-ю прямую. (А-|- 1)-я прямая пересекается с уже имеющимися k прямыми, в k точках, которые делят ее на k 1 частей. Следовательно, (k 4- 1)-я прямая рассечет ровно k 1 частей из всех имевшихся ранее частей плоскости. Так как каждая из этих частей разбивается на две части, то после проведения прямой общее число частей увеличивается на (k-41). Отсюда вытекает, что I прямых общего положения разбивают плоскости на
62
31.	Можно доказать, что любые две оси симметрии пересекаются внутри многоугольника. Покажем, что третья ось симметрии пройдет через точку пересечения двух данных. Для доказательства предположим противное. Тогда три оси симметрии образуют некоторый треугольник АВС.
Выберем внутри треугольника АВС произ-вольную точку О/Любая точка М плоскости лежит, очевидно, по ту же сторону, что и О, по крайней мере от одной из осей симметрии. Соединим точку О с наиболее удаленной от нее
точкой М многоугольника. Пусть О и М лежат по одну сторону от оси АВ. Точка Mlt симметричная М относительно АВ, также принадлежит многоугольнику. Пусть О(\— перпендикуляр, опущенный из точки О на MMi. Ввиду симметрии точек М и Л4Ъ M^N — NM. В то же время > MOlt значит, ОМг > ОД1, что противоречит тому, что М — самая далекая от О точка многоугольника.
Полученное противоречие доказывает утверждение.
32.	Пусть Аь ..Ар— левые, а Въ В2, ..., Вр— правые концы данных отрезков. Тогда любая точка At (I — 1, 2, ...» р) лежит левее любой точки By (j = 1, ..., р) или совпадает с ней. Действительно, если бы точка А{ лежала правее точки By, то отрезки AjBj и AiBi не имели бы общих точек. Выберем теперь среди точек At самую правую точку Aki а среди By—самую левую точку Bz. Тогда отрезок AkBl принадлежит всем данным отрезкам AiBi (i = 1, 2, ..., р). В самом деле, точки Ak и Bz принад
лежат каждому из данных отрезков, следовательно, это же верно и для отрезка AaBz. Нетрудно убедиться в том, что точки Ak и Bt могут совпадать, тогда отрезок AkBl превращается в точку.
33.	Пусть фигура имеет два центра симметрии Ох и Отразим точку 0х симметрично относительно О2 и покажем, что полученная точка О3 также будет центром симметрии. Пусть А — произвольная точка фигуры. Тогда точка Alt симметричная А относительно О2, также принадлежит фигуре, ибо 02 — центр симметрии. По той же причине принадлежат фигуре точка А2, симметричная Д относительно Ог,
6*
63
и точка А3, симметричная Л2 деть, что отрезок Л03 равен а значит, и отрезку Л2О1- Ь
хордами АВ и ВС или по рассматривать оба случая BD = ft. Из Д АВС имеем:
sin(
относительно 02. Легко ви-и параллелен отрезку Л^, э Л3О3 равно и параллельно ОхЛ2, следовательно, АО3~ = О3Л3 и точки Л, О3, Л3 лежат на одной прямой. А это значит, что точка Л3, симметричная точке Л от-носительно О3, принадлежит нашей фигуре, т. е. 03— центр симметрии. Аналогичным образом можно построить центры симметрии 04, О5 и т. д.
34. Из точки В проведем диаметр BE. Он расположится или между одну сторону от них. (Будем совместно.) Проведем высоту
Из BDC:
Из A BDC имеем: sin С = — .
_	с h , ас
Следовательно,	п —
i sir - *
64
Из /\.ADB:
AD = V<?-h* = y=^-Г4/?2-а2.
Для 1-го и 2-го случаев соответственно имеем: АС = DC:J~
- AD. Отсюда: АС =
Примечание: На чертежах с < а. В случае с а а и с поменяются в конечном выражении местами.
35.	Пусть катеты треугольника равны а и £?. Находим сумму площадей треугольника и двух полукругов, построенных на катетах.
4аЬ + т. (а2 + Ь2)
8
Находим сумму площадей искомых лунок, как разность между найденной площадью фигуры и площадью полукруга, построенного на гипотенузе, как на диаметре.
с	n(a2-]-b2) __ ab
о	g	— -у-.
36.	Через точку О проводим диаметр, параллельный стороне АВ и строим Д ОА'В', симметричный треугольнику АВО относительно этой оси.
z. M0N измеряется
Так как 00 — ось . симметрии пересекающихся окружностей, то о MN — о М'П' и так как /. M0N = 60°, следовательно MN == 60°.
37.	Представим заданное
выражение в виде х =
=V / а4 4-

. Под квадратным корнем находится многочлен
4-го измерения. Нужно оставить под знаком корня выра-
жение 2-го измерения, чтобы корень оказался однородным
выражением 1-го измерения:
65
Л /	/ Ь2 'i2
Строим теперь отрезок у = !/ а2	, а затем отрезок
х = У'ау.
X КЛАСС
1.	Показатель степени есть сумма натуральных чисел от 1 до и—1, значит,
2 2	+ 2 + з +.+ (п— 1)	2.22.2® •	• 2
Так как п > 2, то 2Л > n-|- L и, следовательно, 2«22*23- ... -2n~l > 1-2-3-4 ... n = nl Значит:
2.	Обозначим частное от деления многочлена хп~1-[-хп~2у +	У)
на разность х — у через Q(x. у). По теореме Безу имеем:
F(х, у) = (х — у) • Q (х,	.
Обозначим наибольший общий делитель для F(x, у) и х — у через D.
Тогда: F(xt у) — kD и х — у = lDt где k и I — целые. Отсюда следует, что D• k = D • I• Q (х, у) + пуп^1, или п — 1 fe = /-Q(x,y)+-L_.
Так как D не является делителем у (ибо в противйом случае у и х — у имели бы общий делитель, а следова-л к	х п • У1”1
тельно, х и у также имели бы общий делитель), а ----<
целое, то D является делителем п.
3.	Обозначим основание системы счисления через и, а последнюю цифру некоторого числа, записанного в этой системе, через а. Очевидно, что а < n, а n> 1.
Натуральное число, оканчивающееся цифрой а, можно записать так: Кп-\-а. Имеем: (Kn-\-a)2k^1 = Ln-j-a2^1, где /Си L — натуральные числа- Согласно условию: a2k +1 = = Мп + а (Л4 — натуральное число).
66
Тогда: a2k н — а = Мп и a(ak 1) (ak — 1) = Мп.
Умножим обе части этого равенства на ak^x.
Получим: ak (ак 1) (ak — 1) = Nn (N — натуральное число).
При любых натуральных значениях k и а < 10 левая часть, как произведение трех последовательных натуральных чисел, делится на 2, 3 и 6 и только на них. Следовательно, п может быть равно одному из этих трех чисел.
4.	Перепишем тождество, данное в условии, в таком виде:
(2х — I)20 = (ах 4" ^)20 + U2 + Рх + <7)10-
При х == 4* левая часть обращается в нуль. В правой части оба слагаемых всегда больше или равны 0 (все рас-сматриваемые числа действительны), поэтому при к = оба слагаемых должны обратиться в 0. Итак,	= 0,
откуда а ==—2Ь. Теперь тождество принимает вид: (2х — 1 )20 = (— 2Ьх + ЬУ° 4- (х2 + рх + «у)10, или (2х — — 1)20-(1 — 620) = (х24-рх4-9)10- Сравнивая коэффициенты при старшей степени в обеих частях, получим:
1	_|_29/920	1
220(1 -62°) = 1; 620 - 1 —i-; Ь =	.
Теперь тождество принимает вид:
/	1 \2°	*
(х~ 2J = (х2 + РХ ~Н)10-
Отсюда имеем:
Проверка того, что оба результата удовлетворяют требованиям задачи, не составляет труда.
5.	Пусть р> q\ р и q — нечетные.
По формуле
ат — Ьт = (а—ь)(ат^1 +аш-26 4-а"г^3Ь2Ц- ... -j-fr"*-1)
67
имеем:
Рр - 1 - (р - 1)(рР-! 4- р^2 + рр-з +	+ 1) з=
= (р— 1) (2^+1), так как рР-1 4~ Рр~2 4“ •  • 4~ 1 — число нечетное.
По формуле (для нечетного т):
am-]-bm = (a -J- b) (ат -1 — ат ~2Ь 4- ат ~3Ь2 —	-±-Ьт~1)
имеем:
974-1 ==(674_1)(^-1^^4-^-~з_	+1) =
= (9+1)(2п+1).
Здесь и и — целые числа. Значит, рР+97 = (рр _ 1) 4- (qi + 1) = (р _ 1) (2k + 1) + + (<7+ 1)(2/г4~ 1) = 2(р— 1)(£4-п-|-1) =
-(р-1+?+1)(* + «+1)-(Р + ^)(^ + п4-1).
Из этого следует, что рр 4~ 97 делится на р 4~ 7-Замечание: Сформулированное в задаче предложение имеет место и для любых нечетных натуральных р и 9, таких, что р ~ 9 4“ 2.
6.	Докажем с помощью математической индукции. При n = 1 fert+24-(fe4- I)2n+i = fe34-.(fe4-l)3 = 2634-3/г24-3fe+ 4~ 1 = 2k (k2 4- k 4- 1) 4- + & 4“ 1 делится на fe2 4~ k 4- 1. Пусть теперь выражение kn [ 24~(^4“ 1)2ги 1 делится на
& 4~ 1 ПРИ п —
т.
Докажем, что делимость имеет место при п — т 4- 1.
Итак,
fcm+2	p2zn + J
^+^4-1
-целое число.
Тогда:
A(w+I)+2 + (^+ i)2'*43 km+2^k + (k 4- 1)2ш+1.<л+ 1)2
+ k 4-1 •	—	k2 4- k + 1
Aim + 2-^+^4-l)2/n+1-^2 + 2^ + 1)
—	k2 4- k + 1
= k rn t 2 -k + k2(k+ l)2m+1 + 2A(Zj+ l)2zrt + l +(k 4- l)2m + l
~	k2 + k + 1
A?[fem+24-(^+ i)2m + 1] 4-(&4- 1)2т+14Л24-^4- 1)
k!n 2
2m + 1
по предположению — целое число. Утверждение доказано.
68
7.	Поделив данное неравенство на ak и учитывая, что ak 0, получим следующее неравенство
+	>ak-1+ak~i+	(О
эквивалентное данному. Группируя окаймляющие члены в правой части полученного неравенства, приведем эту часть к виду
Перенесем единицу из левой части неравенства (1) в правую часть и заметим, что 1 ~ а° = Для доказательства исходного неравенства достаточно доказать следующее неравенство
справедливое при О С i k.
Действительно, рассмотрим разность:
ak 4’ Ц- —	-----г—г ~ ak~' — О + 1
‘ ak	ak~l	v
__(a1 — 1 )(a2A	— 1)
ak
Очевидно, обе круглые скобки в числителе правой части имеют один и тот же знак, как при а > 1, так и при а < 1, следовательно, (2) доказано. -
8.	Заметим, что числа 10 и тс могут быть представлены бесконечными десятичными дробями 10 — 9,999 ... 9 ..., тс = а0, ах а2 а3 ... ап, где aQ = 3, #1=1, а2 = 4, ... Убедимся, что бесконечная десятичная дробь (9 -т-а0), (9 — #i) (9 — а2) представляет собой число 10 — тс. В самом деле, сумма указанной- дроби и дроби, представляющей число тс, очевидно, равна дроби 9,999...9..., равной 10. Так как по условию lim ~ i ~~» то
Нт (9 — gp) + (9 — Q1) + • - ♦ + (9 — ап) = 9 — П 4- оо	л ]
_ ]im g° + Q.ib •_+_£* = 4i5.
П-^оо	П + 1
69
9.	В тридцатизначном числе троек из подряд стоящих цифр 28. Из цифр 1, 2 и 3 можно составить не более 27 различных трехзначных чисел. Таким образом, из 28 трехзначных чисел, по крайней мере, два равны.
10.	Данный ряд чисел представляет собой разложение бинома Ньютона, если положить х — а — \\ п= 104, т. е.
(1	= 21®4 = 210000.
Характеристика логарифма этого числа — ЗОЮ, следовательно, число 21000 имеет ЗОН цифр.
11.	При п>2 мы имеем (пользуясь формулой бинома): 4" + 15п— 1 =(34-1)"+15п— 1 = 3"4-З^С;... +
+ з2сГ2 4- ЗСГ14-1 + 15п—1 =
= 9(З"-24-3"-3ci4- ... 4-сГ2)4-18п,
и q6a слагаемых, очевидно, делятся на 9.
12.	Докажем методом математической индукции I8 = I2 134-23 = 14-8 =(14-2)2
13 + 284-33 = 36 = 62 - (1 4-2 4-3)2...........
184-23 + зз+ ... 4-п3 = (14-24-34-	+и)2 =
13.	Пусть аъ а2, ... а^п — данное число, ••• Абл—1 — число, полученное перестановкой последней цифры на первое место.
Заметим, что 106я — 1 делится на 7. Действительно, 1034-1 = 1001 делится на 7, а 106п—1 всегда делится при п>0 на 1034~ 1.
Рассмотрим число абЛ(Ю6л—1), которое делится на 7. Тогда
Дб/г (106" — 1) 4-... а^п	... Ябп-Ю
также делится на 7. Отсюда, очевидно, следует, что . а^п-1 делится на 7.
70
14.	Пусть k п, тогда k(n —	> п.
Действительно, kn — &24~ k — п~ п(п — 1) — k (k — 1) = = (п — k)(k—-1)0. Если п — четное, то (/г!)2 разбивается на п сомножителей, каждый из которых не меньше, чем п, значит, (п!)2^пл. Если же п— нечетно, то (я!)2 опять разбивается на п сомножителей, п — 1 из которых будут такого же типа, как и в четном случае, а /2-й сомножитель
I п + 1 \2 , I п — 1	. л
—^—) — л = 1—2—I >0, значит,
[—и утверждение верно и в этом случае.
15.	Имеем стороны: а\ а-\-г; а 4- 2г и углы соответственно: а; а <р; а4-2<р.
По теореме синусов:
а ___ а + г _____ а ф 2г
sin a sin (а + <р) sin (а ф 2<р) ’ отсюда
а + (а + 2г)	= а + r	2 (а + г) _
sina + sin (а Ф 2ср) sin (а + 9)	2 sin (а + <р) COS<p
а-\-г sin (а + ср) * Отсюда cos ср = 1; <р = 0, т. е. треугольник равноугольный, а значит равносторонний.
16.	Напишем ряд тождеств:
tgl/ — tgx =
sin (у — х) _ sin г
COS X»COS у	COS X’COSу'
sin (z — у) - sin r cos i/-cos z cos y-cos г ’
tgu — tg/ =
sinfu — 0
cos t * cos и
sin r _ • cost-cos и ’
» sin (v — u) sinr
V — tg и = -------------- = -------------.
° cos cost; COSU‘ cos V
Сложив левые и правые части, получим:
tg v — tg х = sin г |-!------1-----J----
°	°	\ cos X • cos у 1 cos у • COS z
4------!----1
’ cos и • cos V /
Отсюда:
1
cos x-cos у
I-—1— 1 cos у • cos z tg у — tg X _ sinr
1
COS COS У
sin (y — x) cos у-cos x-sinr ’
71
17.	По условию задачи 262 == а2 -|- с2.
„	, 2Ьг + 2с2 — в2 3 ,	,	2а2 4- 2с2 — Ь*
Поэтому ГПа = ----L-^------ = -т- С, ПЦ = --—т------- =
3.2	,	2я2 + 262 — с2 3 2
= т ; тс =---------Hj------= т а2.
Отсюда tn,: mh: тГ = с: b : а. И	U	С-
18.	Пусть а < Ь < с, тогда hc<_hb< ha.
2S 2S 2S
Нужно доказать, что а: b: с ~ hc: hb : ha = —: -у : — Ill	а	I	с	111
= — : -г: или что : -г :	: -/: —.
с b a	b2 b Ь2	с b а
Но по условию t»2 — ас. Значит, действительно, a t 1 . с _____________ а . 1 , с _ 111
b2 ’ b ‘ 62 ас ’ b ’ ас с ' b ’ а‘
19.	Очевидно, что S2	х2» •S2=x1-|-x3. S9 = x3-|-
+ *5, S10 = x4.+ x5. Каждое	(/ = 1, 2, ..., 5) входит
точно в четыре суммы Sy, следовательно, S = Sx -|- S2 + -|- • • • + Slo = 4 (хх + х2 4- • •+ *ь)’ Из выражений для S1( S.2, Зю, S легко находим Хл — S2 + Sw-------7-. Ана-
• s
логично из выражений для S2, S10, S находим х2 = у —
*Sa Slo.
Точно также находятся
20.	Рассмотрим выражение	^)2> являющееся
€=1 л квадратным трехчленом Ах2 + 2Вх С, где А = 2 Г=1 п	п
С=^Ь При всех действительных значе-1=1	1
ниях х этот трехчлен принимает неотрицательное значение, следовательно, его дискриминант В2 — АС <. 0, т. е.
(2«а)‘
п п
1=1 1=1
72
21.	Покажем сначала, что никакие три числа Ь < с < d, записанные в троичной системе цифрами 0 и 1, не образуют арифметической прогрессии. Действительно, число b-\~d имеет в записи цифру 1, а число 2с записывается лишь цифрами 0 и 2, так что равенство b -J- d = 2с невозможно. Далее, если аъ .ak — члены данной последовательности, первые k изч которых записываются цифрами 0 и 1, то любое число, записываемое нулями и единицами и не превосходящее afci является членом последовательности (это есть следствие условия минимальности). Покажем, наконец, что все члены последовательности выражаются числами, записываемыми в троичной системе цифрами 0 и 1. В самом деле, утверждение справедливо для а0 и аг. Пусть оно справедливо для а0, аъ а2 . -. ak. Если в троичную запись числа ak входит цифра 2, то число Ь, получающееся из ak после замены всех цифр 2 цифрой 0, в силу сказанного выше, совпадает с одним из*
0» 1» 2, ... G/j—i).
Число ai-\-ak записывается лишь нулями и двойками, и, следовательно, 4~ ak = 2с, где г —число, записываемое нулями и единицами. Так как at < ak, то с < ak и поэтому с = aj(j < k). Равенство ai -|- ак = 2аj показывает, что числа at, aj и ak образуют арифметическую прогрессию. Полученное противоречие доказывает справедливость утверждения задачи.
22.	Пусть разность прогрессии равна d и один из ее членов — а = т2, где т — натуральное число. Тогда число {т + d)2 = m2 + 2md -f- d2 — a 4~ d (2m 4" d) является членом прогрессии (так как оно имеет вид a-\-nd, (п— целое) и вообще число (m + kd)2 = т2 -|- 2kmd 4- k2d2 = а 4~ 4- d {2km 4- k2) является членом прогрессии при любом k. Мы указали тем самым бесконечное количество членов прогрессии, являющихся точными квадратами.
23.	Допустим противное: пусть J/2, )/гЗ, являются членами некоторой арифметической прогрессии, тогда
/3 — /2 = md, V5—/2 = nd
(d — разность прогрессии, m и п — целые числа), откуда: т (J/5 — /2) = п (|/3 — / 2);
m У 5 — п у 3 — (т — п) У 2.
73
возводим обе части равенства в квадрат
5m2 + Зя2 — 2тп |/15 = 2 (т — и)2, и, следовательно,. ,	5т2 -I- Зп2 — 2 (т — п)2
и 15 =---------ё----1, а это невозможно, так как
г	2тп
У 15 есть число иррациональное.
24.	Для того чтобы плот мог находиться в канале, по крайней мере одна из его сторон не должна превосходить Л, Если и другая его сторона не превосходит й, то в этом случае максимальная площадь й2 будет у квадратного плота со стороной й. Такой плот, очевидно, "может пройти по каналу. Если вторая сторона плота больше й, то, проходя поворот, плот сам может повернуться и в некоторый момент его стороны должны образовать угол в 45° с берегами канала. При этом плот должен находиться внутри равнобедренного, прямоугольного треугольника АВС. Если плот имеет максимальную площадь, то две его вершины должны находиться на катетах, а одна из сторон на гипотенузе. В противном случае мы сможем увеличить его площадь за счет удлинения его сторон. Обозначим одну из его сторон через а, а другую, лежащую на гипотенузе, через Ь. Тогда S = ab. Заметим, что АС = 2й J/2 = 2а + Тогда о	Лй2 М2 ,^/Ki
h \2
. Отсюда S максимально при а ~
При этом & = 2й ]^2—2а = й |Л2. S = h2. Этот плот v & можно повернуть внутри канала вокруг точки О — вершины угла канала, так как он находится внутри окружности радиуса h с центром в точке О.
25.	Пусть logvx = z. Имеем: logrvx = - J-fe—- =
J	6 У	ЬЛ> 10gy(jQ/)
logyX	z	z	z
По условию задачи z + “j"4 или после упрощения
г
z
откуда
з
г =
74
26.	Воспользуемся формулой logs А —	.
log JV • logjJV + logbV • logcW + logcA/ • logaW = . . 1	1 , 1 1	, 1 1	_
logwa ’	logw6 T logw6	’ )ogNc	' logjyt	’ logwa
 l°Sy c + l°8wa +	&	logw (obc)
logw a-logN *-logA, c ~ logA,a-logjVb-logA,c “ ___________1 __________ _______________________logqrfcA'__ \ogaN AagbN AogrN
1	.	1	.	1	Jogafl<W
logaW \ogbN	\ogcN
27.	Разделим все члены неравенства на 10х. Получим
(4-r-2(iy<L
(2	2
—j = у> 0, получим неравенство у------1,
или у2 — у — 2 < 0. Отсюда: (у-(-1) (£/ — 2) < 0, а так как (y-f- 1) > 0, то разделив на у-\-1, найдем
У — 2 < 0, у < 2,	2. х > logo.4 2.
28.	Воспользовавшись формулой logz,a = '^y*, приведем данное уравнение к такому:
logcos к sin х 4-= 2 или log?os х sin X— JObCOS х 5111 х
— 2 logcos X sin X + 1 =0.
Отсюда:
(logcos x sin X — 1J2 = 0, logcos X sin X = 1. sin X =
= cos x. tg x = 1, x = 2Ы
Здесь нельзя написать x = kit +пр так как ПРИ “ 2п-}-1 будет sin х < 0 и cos х < 0, а этого не должно быть, потому что cos# и sinx являются основаниями логарифмов и не могут быть отрицательными.
75
2	1
Отсюда: 3 3 • 5 3 = уЗ2 • 3 = у 45.
30.	х > 0; у > 0 (так как хну —основания показательных функций) *
( #lgx = xlgy(l) v 1gя
Ulga = t/lg6(2) У ’б6
Уравнение (3) имеет положительные решения х > 0, у > О при условии > 0.
Следовательно, данная система не имеет решений, если одно из чисел а и Ь больше, а другое меньше 1. Будем считать, что эти числа либо оба больше 1, либо оба
меньше 1, тогда > 0. Подставив у из (3) в (1) и 1g о
сократив на х (х>0), получим — l)lgx=lg-~p (4) Если 1g а ф lg b, т. е. если афЪ, то из уравнения (4) находим х, а затем из уравнения (3) — у. Если а = Ь, то (4) удовлетворяется тождественно, а исходная система примет вид: х? — ух, ах = аУ, откуда х = у.
f\gb\ -lg±, /IqdV—___________
Ответ: x = {-т^—) ig6-iga, w = /—) ig ь-igесли a \ 1g a /	’ u klqa/
и b (оба) больше, либо меньше 1 и а =/= Ь\ у = х, где х любое положительное число, если а = Ь. Система противоречива, если одно из чисел а и b больше, а другое меньше 1.
31.	Обозначим у/~ 5 /2^-7 —5/2 — 7 = *• Тогда х3 = 14 — Зх. Отсюда: х3 4* Зх — 14 = 0.
(х3 —8) + (Зх —6) = (х —2)(х24-2х + 4)4-3(х — 2) = = (х — 2) (х2 + 2х + 7) = 0. Xi = 2, х2, з — комплексные числа. Значит, х = 2.
Ответ: у 5/Т-(-7 —	5/"2 — 7 =2.
76
32.	Легко видеть, что(1/ 9_1/ з )*=
____(/2+/Т)
Обозначим (]/"2Ц~1/ У)* == JA тогда получим уравнение у2 — 8у-|- 1 = 0, из которого находам у = 4 ±г ]/15. log 4 zt У 15
Ответ: х = —*	= •
log У 2 +ГЗ
33.	Из пропорций: 1g у =	1g х,
Ice- г(*+у"гЬсх 162 xfe + z-x) lgx’
Прологарифмировав хУух zyyz = xzzx, получаем
у 1g х + х 1g у = у 1g г + z 1g у = z 1g х 4- х 1g г.
Подставим в последнее значения 1g у и 1g z.
+<^4-4	**+
	;2xyz — —т~х~--i%хУг — —7	2xyz.
x(y-j- г — х) J х(уг —х) J x(y-j- г — х) 3
34.	Данное уравнение равносильно следующей смешанной системе:
(х2 — 10х + 15) (х2 — 8х 4-15) = Зх(х2 — 6x4- 15Х х2 — 6х 4" 15^0; х2 — 8х -|- 15 4 0-
После преобразований уравнения этой системы получим:
х* — 21х3 4- 128х2 — 315х 4 225 = 0;
х< — 7х3 — 14х3 4- 15х2 4- 98х2 4- 15х2 — 210х — 105х 4
4- 225=0; х2 (х2 — 7х 4-15) — 14х (х2 — 7х 4-15) 4-15 (х2 — — 7x4-15) = 0;
(х2 — 7х 4-15) (х2 — 14х 4-15) = 0.
Ответ: хг = ~	-1—; х3 — 7 4-]/34;
х2 = -7 ~ ^Ц--; х4 = 7 -1 34.
7 Зак. 358
• 77
35.	Пусть х~а-\-Ы\ y = c-\-di. Тогда |*-b£/|2 + 44*-H2H(«+0H*4-W4-|(«-*)4-+ (6 - d) i |2 = (а + с)2 + (6-Н)8 + («- с)в +
4- (Ь — d)2 = 2 [(а2 4- Ь2) 4- (с2 + d2)] = 2 (| х |2 4-1 у |2).
36.	Обозначим отрезки а — ВС, b — СА, с = АВ и А3, В2, С2— соответственно середины сторон ВС, С А, АВ. Имеем векторы Л/Ц = с 4—s- а 4"	= а 4“ b 4"
4- b%Bi, cCi = ь 4—9~ с 4~ 020ij cl 4~ 4~ с = о и ^42^4^ 4-4—»
4-#2^1 + C2C1 = 0, так как отрезки Л2ЛЬ В2В19 С2СГ могут быть сторонами треугольника, полученного из треугольника А2В2С после поворота его на 90°.
Следовательно,
что и требовалось доказать.
37.	Возьмем две точки Л и В из данных п точек, расстояние между которыми — наибольшее, и положим на^ плоскость два круга радиуса 1 с центром в точках А и В .соответственно. Тогда любая из данных п точек попа
дет, по крайней мере, в один из двух кругов. Действительно, если С — одна из данных п точек, то и ЛС и ВС
не превосходят длины отрезка АВ, значит, либо ЛС, либо ВС имеет длину, не превосходящую 1.
38.	Предположим противное, т. е., что существуют три точки Л, В и С из числа данных и точек, не лежа-
щие на одной прямой. Проведем через точку Л прямую ALV, не содержащую, кроме Л, других точек из числа данных и не параллельную прямой ВС. Проведем все прямые, соединяющие
м
попарно заданные п точек. Эти прямые пересекут прямую MN в ряде точек, среди которых выберем точку Р, расположенную ближе всего к точке Л. Пусть, далее MrN — та из прямых, которая пересекает прямую MN в точке Р. По условию задачи на прямой MjW должны быть расположены по крайней мере три из
78
Наших точек. Обозначим эти точки через Я» S. Воспользуемся теперь тем, что на прямой AR, кроме точек А и R, обязательно должна быть расположена еще хотя бы одна точка О из наших п точек. Рассмотрим прямые OP, OQ, OR, OS, которые пересекут прямую MN в четырех точках Р, Qi, А и Но точка расположена ближе к точке А, следовательно, мы пришли к противоречию, ибо предположили, что Р есть та из точек пересечения прямых с MN, которая расположена ближе всего к А. Полученное противоречие показывает, что все п точек лежат на одной прямой.
39.	Каждая точка пересечения диагоналей определяется заданием двух диагоналей, которые в ней пересекаются и которые в свою очередь определяются четырьмя вершинами многоугольника. Следовательно, искомое число не превосходит Ch, совпадая с ним, например, в случае выпуклого четырехугольника.
40.	Докажем, что число малых треугольников вида (1, 2, 3) будет нечетным, следовательно, будет существовать по крайней мере один такой треугольник. Каждый треугольник разбиения, вершины которого занумерованы цифрами 1, 2, 3 (число таких треугольников мы обозначим через X), имеет единственную сторону, концы которой занумерованы цифрами 1, 2; каждый треугольник, вершины которого занумерованы цифрами 1, 2, 2 или цифрами 1, 1, 2 (число таких треугольников мы обозначим буквой У), имеет две стороны, концы которых имеют номера 1 и 2. Остальные треугольники разбиения не имеют сторон, занумерованных цифрами 1, 2. Отсюда следует, что общее число сторон треугольников, занумерованных цифрами 1, 2, равно Х4-2У, где каждый отрезок, занумерованный цифрами 1, 2, расположенный внутри основного треугольника, считается дважды, ибо он входит в качестве стороны в два треугольника, расположенных по разные стороны от этого отрезка. Каждый же из отрезков 1, 2, расположенных на сторонах основного треугольника, является стороной лишь одного из треугольников разбиения и, следовательно, учитывается один раз. Таким образом, если обозначим число отрезков 1, 2, расположенных внутри большого треугольника, через А, а число таких отрезков, расположенных на стороне 1, 2 основного треугольника, через В, то будем иметь X 2У— = 2A-j~£.
79
Отсюда вытекает, что число X является четным или нечетным одновременно с числом В, и достаточно доказать, что В — всегда нечетно. Двигаясь вдоль стороны 1, 2 основного треугольника от вершины 1 к вершине 2, после нечетного числа отрезков 1, 2 будем встречать вершины разбиения, занумерованные цифрой 2, а после четного числа таких отрезков — вершины, занумерованные цифрой 1. Но так как последняя вершина “разбиения, расположенная на рассматриваемой стороне, есть вершина 2, то общее число отрезков 1, 2, находящихся на стороне 1, 2 основного.треугольника, должно быть нечетным. Значит, число В, а вместе с ним и X, также нечетные числа.
41.	Число п должно быть не меньше трех (ибо не все п точек лежат на одной прямой). Если п = 3, то утверждение очевидно: три точки, не лежащие на одной прямой, соединяются попарно точно тремя прямыми. При*-меним теперь метод математической’ индукции: предположим, что для п точек теорема уже доказана, и покажем, что-в таком случае она справедлива и для п-|-1 точек. Рассмотрим все прямые, соединяющие попарно п 1 точек. Согласно результату задачи 38, хотя бы на одной из этих прямых должны быть расположены только две точки Ап и Ап + 1 из нашей совокупности. Если точки А19 Д2,..., Ап расположены на одной прямой, то общее число прямых, очевидно, будет точно равно л 4-1: это будут п прямых, соединяющих точку Ап + i с точками Аь А2, ..., Ап, и прямая, на которой расположены эти последние п точек. Если же п точек Alf А2, ..., Ап не лежат на одной прямой, то по предположению индукции среди прямых, соединяющих попарно точки А19 А2, ..., Ап, будет не менее п различных. Добавим теперь сюда все прямые, соединяющие Ап + i с точками Аь ..., Ап. Так как на прямой АпАп +1 не расположена ни одна из точек
А2, ..., то эта прямая не содержится' среди прямых, соединяющих попарно точки Ах, А2, ..Ап. Тем самым мы докажем, что число прямых стало не меньше п +1. В силу принципа индукции отсюда вытекает, что утверждение справедливо для любого числа точек.
42.	(a+&+d)"=[(6z4-	=(a4-d)n+ С\ (a-\-b)n - >d
+ C^(a + fe)"-2d2+	+ С"“1 (а4-6)d"-Ч- dn.
В разложении по формуле бинома Ньютона каждого из’
80
полученных членов будем иметь следующее число чле нов:
в члене (а-\-Ь)п будет (н-j-l) членов разложения
» » (а Ь)п “1 »п »	»
» »	(а 4~ Ь)п ~2 » (п — 1) »	»
• •	•••• • • • • •	••
» »	(а 4- Ь)2	»	3	»	»
» »	(а 4“ Ь)1	»	2	»	»
» »	(а 4~ b)°	»	1	»	»
Всего членов получим:
(п + 1) + п4-(п-1)4- ... 4-34-24-1.
Суммируя, как арифметическую прогрессию, найдем
43.	Всего членов в разложении будет (2п4~ 0- Средня * лр	п „ 2п (2п — 1) (2л — 2)-(п+1) апхп
НИИ член Тп + 1 = С2папхп =---— п -------------------‘
Умножив члены дроби на п!, получим Тп +1 = _	1-2-3 ... 2„а”хп
1-2-3 ... n-1-2-3 ... п ’
Числитель содержит и четных сомножителей и п нечетных. Большее четное число равно 2п, нечетное — (2/1— 1).
т 1-3-5 ... (2п — 1)-2-4-6 ... 2па,'хп _ 1-2-3...n-l-2-З...п	“
_ 1 -3-5... (2n— l)-2rt (1-2-3... ti}anxn =
1-2-З...П-1-2-З...Л	“
_ 1-3-5...(2п — 1)-2лалхл
1-2-3- ... п
45.	Пусть в турнире участвовало х шахматистов одного класса и 10х шахматистов другого класса, всего 11 х чел. Число сыгранных партий, а также и количество .	11х(11х—1)
всех очков, набранных всеми участниками, равно —
81
Так как эти очки поделены между классами в отношении 1:4,5, то класс с меньшим числом участников набрал
11Х<121^1Г~1) 2 = * U1* — J)
очков, а другой---------——— очков. Учащиеся класса с
меньшим числом участников сыграли партий между собой ———— и 10х2 с, шахматистами другого класса. Получим неравенство:
х(11х — 1) < Юх2 +	?- или х2 < х.
' £
Поскольку X > О, ТО X < 1.
Так как х — целое число и больше нуля, то х = 1, значит класс с меньшим числом участников набрал очков: 1.(11—1)= 10.
46.	Данное равенство по формуле бинома Ньютона заменяется следующим:
(1 — З)4" = (1 — 5)2л;
(— 2)4" = (— 4)2я;
[(- 2)4]л = [(- 4)2]";
16я = 16".
47.	Приведем данное соотношение к целому виду:
1	।	1	3 д-Ьс4-а + &	_	3
a4-fr_*_b + c	a + b-f'c* ab -f- ас b2 -j- be a -f- b -j-c’
(fl -f- 2b + c) (a + b	c) = 3 (ab 4- ac 4- fe2 + be).
Перемножив и приведя подобные члены, получим:
Ь2 = а2-)-с2— ас.	(1)
С другой стороны имеем:
Ь2 = а2 4- с2 — 2ac cos В.	(2)
Из сравнения (1) и (2) находим:
2cos5=1; cos В =	£_В = 60°.
48.	Делим все члены уравнения на 13:
2sin2x2 4* || cos 2х 4- Ц sin 2х = 1.
Вводим вспомогательный угол <р равенством о 12 cos 2<р = Т5,
82
тогда sin 2<р = 4 а уравнение преобразуется так:
2 sin® х® cos 2ф cos 2х 4~ sin 2<jp sin 2x = 1.
2 sin2x® 4- cos (2x — 2<p) = 1.
1 — cos 2x2 4~ cos (2x — 2<p) = 1. cos 2x2 — cos (2x — 2<p) = 0.
2 sin (x2 4~ x — <?) sin (x — q> — x2) = 0.
Получаем два уравнения:
1) sin (x2 4- x — tp) = 0.
X2 4- X — <f = kit.
x2 4- x—(<p 4* kit) = o.
_ ~ 1 ± П + 4? +
2) sin (x — <p — x2) = 0. X — <p — x2 — kit.
x2 — x 4" <? + kit — 0.
I zt k 1 — 4<p— 4kn 2
sin2x — cqs2x + I__2 sin x-cosx + 2 sin2x _ cosx+sin x
sin 2x + cos2x — l~2 sin x-cosx — 2 sin2x ~~cosx~sin x
49.
Поэтому неравенство равносильно такому * _Ltgx или (I 4" tg х) (I — tg х) > 0, исключая х = kit, при котором левая часть данного неравенства теряет смысл, но является решением преобразованного.
Таким образом, получаем:
1—tg2x>0, tg2x< 1, | tg х | < 1, — l<tgx< 1, kit—Z_<x<Cfot, kit<Zx < kit4~-j-; k = 0; ~±sl; _ 2,...
50.	cos a 4" cos ? — 2cos  • cos —cos (я 4- P) = = 2cos2-^4-^ — 1.
; Следовательно, заданное равенство можно преобразовать так:
п я -4- 3	я — В о оя + 8	1 п
2cos - 2 • cos —~ — 2 cos2  - ~ — g- = 0,
83
/ e + 3	1 а — 3\3 I 1	-2й — ₽ А
(cos—----rC0S~2J +-j-sm2	= 0.
Но сумма квадратов вещественных чисел тогда и только тогда равна нулю, когда каждое из этих чисел равно нулю. Отсюда sin» у- — Q и cos -а у ------~cos^y^ = 0.
Из первого, учитывая, что а и р — углы треугольника, получим а = р. Тогда, подставив а — р во второе, найдем: cos а —	= 0, cos а — а — 60°.
Итак, а = р = 60°. Тогда и третий угол равен 60°, т. е. треугольник правильный.
51.	sin а — 2 sin р • cos 7 = sin (р 4- 7) 4~ sin (р — у), но так как а, р и 7 углы треугольника, то sin (р 4“ 7) = sin а. Поэтому sin а — sin а 4- sin (Р — 7).
Отсюда'sin (Р — 7) = 0, и так как р и 7 углы треугольника, то 7 = Р’, и, следовательно, b = с.
52.	Воспользовавшись формулами, выражающими тригонометрические функции sin а и cos а через тангенс половинного аргумента, получим:
53.	Предположим противное, т. е. пусть существует такое число Т 0, что cos а (х 4' Т) 4~ cos (х 4- T)=cos ох 4-4“ cos х.
Положим в этом равенстве х = 0, тогда cos аТ 4- cosT= = 14-1; отсюда 1 — cosaT4-1 — cosТ = 0.
Из последнего равенства имеем: sin-^-=0, sin-^-=0, следовательно, Т =	= 262тс.
Из этих равенств получаем a-2fej~ — 2fe2ir, т. е. а = Л2 = что противоречит иррациональности а.
Значит, Т ~= 0.
84
54.	Sabcd ~ Sabc S^cd = Sabd Sbcd-	(1)
Sabc = 4- fee • sin B.
Sacd — 4- ad sin D = ~ ad sin (it — B) =	ad sin B.
Sabd = 4- ab si n A;	SBcd =
— cd sin С == Д- cd sin A.
Из (1) следует, что
-i- (fee -{- ad) sin В —
— 4- ab sin A	-L- cd sin A,
а отсюда:
sin A: sin B—(ad -f- be): (ab + cd).
55.	Пусть a, p— острые, а 7 — тупой углы треугольника. Так как sin27< 1, то для выполнения указанного в задаче неравенства достаточно показать, что sin2a4-+ sin2p < 1.
а + р < 90°, значит, р < 90° — а.
sin2 а + sin2p < sin2 а + sin2 (90° — а) = sin2 a -f~ *c°s2а = 1 •
56.	Число корней равно числу точек пересечения графиков функций sin % и Эти точки могут лежать в промежутке: — 100 < х<С 100. На половине этого промежутка 100 вложится периодов
Ответ: 63 корня.
57.	Легко проверить, что данное уравнение удовлетворяется при sin х —cos х, т. е. при х~ -|-йк. Докажем,
что других-решений данное уравнение не имеет.
Во-первых, заметим, что sin х ф 0, cos х ф 0. Во-вторых, sinx и cosx имеют одинаковые .знаки. В самом деле, переписав данное уравнение в эквивалентной форме
—=------cos"x ~
cosmx	smmx
— sinn х,
заметим, что при cos х < 0 < sin х правая часть уравнения положительна, левая — отрицательна; при cos х > 0 > sinx — наоборот. Следовательно, sinx-cosx>0.
85
Если sinx<cosx<0 или 0 <2 sin х < cosx, тс sinrt х cos" х и —< •. (иб© тип нечетные числа! cosmx sin"1 X 4	'
и почленным сложением получаем:
sinn х -|-
1 cosmx
cos'1 X +
1
sinmx ’
Если sin х > cos x > 0 или 0 > sin х > cos х, то аналогично имеем
. „ . 1 „ . 1
SinnX 4----cos"x -к . от .
1 cosmx	1 sinmx
Таким образом, из данного уравнения следует лишь sin х = cos х и поэтому х =	4- Ьк.
58.	Так как	то а > sin а, или
а sin а > sin2 а.
Также имеем, что cosa>cos2a.
Сложив два этих неравенства, получим, что
cos a 4- a -.sin a > 1.
59,	Если человек из точки А будет идти только по полю, то он, очевидно, сможет попасть за один час в любую точку внутри круга радиуса Зое центром в точке Л и не сможет попасть ни в одну точку вне это-го круга. Обозначим через и А2 точки на дороге, отстоящие от точки А на расстоянии 6 км* Проведем из этих точек касательные к кругу, рассмотренному выше. Докажем, что фигура, содержащаяся внутри контура, образованного отрезками касательных от точек АТ и А2 до точек касания с кругом и дугами окружностей, заключенными между точками касания ВВг и ССЪ является искомым геометрическим местом. Для этого достаточно доказать, что человек, идя сначала только по дороге, а затем по полю, или только по полю сможет попасть в любую точку этой фигуры за один час и не сможет за это время попасть ни в какую точку вне указанной фигуры. Действительно, если человек, стоящий на дороге, через некоторое время сходит с нее, а затем снова возвращается на дорогу, то при этом он тратит времени больше, чем идя только по дороге. Пусть человек идет t часов по дороге со скоростью 6 км в час (/•<; 1) до некоторой точки М на отрезке АА19 а оставшееся время идет по полю прямо-
86
линейно со скоростью 3 км J час, тогда через один час он окажется на окружности радиуса 3(1—t) км с центром в точке М. Покажем, что эта окружность касается прямых ЛХВХ и Л2Сг. Восстановим из точки М перпендикуляр к прямой /IjBt до пересечения с этой прямой в точке N. Очевидно, что достаточно показать, что MN = = 3(1 — t) км. Прямоугольные треугольники АВ^ и MNAX подобны, отсюда	• > но AAj_ = 6 км, МАг =
=6 (1—t) км, АВ1 ~ 3 км, следовательно, МУ=3(1 — t) км. Таким образом, наша окружность касается прямых Л^ и ЛхВ! фигуры Л1В1В2Л2С2С1, что и доказывает наше утверждение.
60.	Проведем радиус в точку касания N образующей ВС. ON = г. Обозначим ВМ = х, из подобных треугольников BDC и ON В находим:
BD _ BN . nr_ BD-0N _(2г + х)г DC — ON ’ ~~ BN ~ BN ’
По свойству касательной и секущих имеем:
BN2 = BD-BM = (2г~\ х)X, BN = /(2r-f-x)x.
Подставив в (1), получим:
JJQ _ X*' ~	'
KOK=4^DC2'BD=
(1)
(2)
(3)
Зх
Зх
Итак, конус будет иметь наименьший объем меньшем значении дроби
при
(4)
наи-
(5)
Отсюда имеем:
(У —	± Уу(У — 8г)
Для того чтобы х был действительным, необходимо,, чтобы у был не мен ьше 8г, у > 8г.
Отсюда наименьшим значением для у является 8 г. При у — 4г	8г — 4г Л
этом значении у х = п„— = 2г, а 2	2
BD = х + 2г = 4г.
61.	Обозначим ребро правильной п-угольной .пирамиды через /, угол между этим ребром и плоскостью основания — через а. Объем пирамиды меньше объема V2 опи
санного около нее конуса.
/3	/3
Для конуса имеем:	----------------
”/2 cos а  I • sin а
----------н—> но так как cos z • sin 1, то
COS a-sin 21
6
к cos а - sin 2а
Следовательно, тем более
/3
62.	Пусть многогранник имеет Z ребер и т граней, причем число сторон в гранях п19 п2, ... пт. Так как каждое ребро является общей стороной двух смежных граней, то ребер у многогранника в два раза меньше числа всех сторон всех его граней, т. е. Пх -|- п2 +... 4-+	= 2Z.
Но это равенство невозможно, если все. числа пъ п2, ... пт, букут нечетными и число их нечетно, так как тогда сумма таких чисел дает нечетное число, в то время как 2/ — четное.
63.	Соединив центр вписанного шара со всеми вершинами многогранника, мы разобъем многогранник на пирамиды, основаниями которых служат грани данного многогранника, все они имеют общую вершину в центре шара и высотами их являются радиусы вписанного в данный многогранник шара. Объем многогранника равён сумме объемов получившихся пирамид:
88
64. Пусть в треугольник АВС вписан произвольный параллелограмм PMNQ с данным острым углом и параллелограмм B^CxDE, где ВГСГ — средняя линия треуголь-
ника, равная Площадь параллелограмма B^DE ah
равна-4—, где а — сторона BCt a h — высота треугольника, опущенная на сторону ВС. Площадь параллелограмма PMNQ равна
Из
и АВуСг имеем:
А
подобия треугольников АРМ
Значит, Spmnq < BBxcxde- Таким образом, параллелограмм BjCiDE является искомым.
65. Пусть д ABS представляет сечение конуса пло-
скостью, проходящей через
его вершину 5, высоту OS и центр 01 одного из указанных и шаров, Нг — проекция центра 01 на плоскость основания конуса, х — искомый радиус. Имеем:
Если О2 — центр соседнего шара и Н2— его проекция на плоскость основания конусаг то
OHi~OH2 = R + xtg^-;
1
медиана	ОМ = ОНХ sin -—
• *	-	/т
89
Следовательно, после простых вычислений
Я
180°	4 а *
C0S.T~ “ tg-F
66.	Равны суммы всех его противоположных ребер.
67.	Если бы плоскость пересекла все боковые ребра параллелепипеда и одно основание, то две стороны обра-. зовавшегося пятиугольника были бы параллельными между собой, чего нет в правильном пятиугольнике.
68.	Прямые, по которым надо сгибать лист, £	должны проходить через
середины сторон треуголь-/	\	ника, образованного лис-
д/2-------том. Эти прямые разбива-
ют лист на 4 равных /	\	/	\ треугольника. Треугольник
Z 2\/f X должен быть остроуголь-д	:ным.
Cf	Доказать существова-
ние равенства.
69.	Пусть Яг— площадь Д ABC. S2 — площадь Д ЯЛ fi, Я3 — площадь Л SBC. Я4 — площадь ДЯЛС, V — объем шара. Имеем:
Sxhr = S2h2 = S3h3 Я4й4 = 3V.
Пользуясь этими равенствами, можем получить требуемое соотношение.
70.	Расстояния от. вершин основания до точек соприкосновения вписанного шара с боковыми гранями равны между собою и половине диагонали основания. Поэтому треугольник, вершины которого совпадают с концами сторон основания и с точкой прикосновения боковой грани, содержащей эту сторону, равен треугольнику с вершинами в тех же концах стороны основания и в центре основания. Вершины указанной боковой грани находятся на описанном шаре. Поэтому можно доказать, что плоский угол при вершине равен половине прямого угла.
71.	Пусть точки 0lt02,03— центры данный шаров, а ОьО2,О'з — точки соприкосновения этих шаров с плоскостью, точки О и О' — центр и точка соприкосновения с пло
90
скостью искомого шара, х— радиус этого шара. Имеем: Л ОхО2б3 — Л О^ОгО'ъ, стороны этих треугольников равны 2R. Точка О' находится в точке пересечения высот треугольника O1O2O3.
Поэтому
(2RV	, I /п	\2	1 П
(—f— I. = (X 4- Я)2 — (R — Л-)2, х = -J- R.
72.	Обозначим АВ — а, ВС = £АВС — а, /_ CD А — р, S — площадь четырехугольника ABCD. Имеем:
2S = ab sin a-[-cd cos а,
4S2 = а262 + А/3 +
+ 2abcd sin а sin р — (а262 cos2 a-J-
4~ c2d2 cos2 Р),
AC2 = а2 4" b2 — 2ab cos a =
c2 d2 — 2cd cos P).
После некоторых преобразований:
bt CD = c, DA = d,
4S2 = a2&24-c2d2 —L_E--------------12 — 2 abed cos (a + p).
Поэтому решению задачи соответствует условие
cos(a4-£) = — 1, a-|-p= 180°.
73.	Преобразуем левую часть уравнения:
25х2 -|- 20х2 + 4х« + 25х2 _ 74
(5 + 2х)2	49’
4х*	. 10х2(5 + 2х) _ 74.
(5.+ 2х)2 “•	(5 + 2х)2	~ 49’
так как 5 4- 2х ф 0.
( 2*2	2х2	74 _ Q
\ 5 + 2х / '	54-2х	49
Имеем:
2х2 _	37.	2х2 _ 2	_ i К1221 — 37
5-Ь2х~	7’.54-2х— 7' Х1	14	’
_-i/1221 -37.	5	.
Л2 —	[4	, Л3 —	у-, х4 — 1.
В. Платонов, К. Арлюк, В. Зарецкий, Н. Метельский, JJ. Тутаев
Избранные задачи элементарной математики
Редактор Шердюкова С. И.
Худож. редактор Валентович В. И. Техредактор Жук В. Н.
Корректор Кришталь В. К.
АТ 04468. Сдано в набор 13/VII 1964 г. Подп. к печати 22/Х 1964 г.
Тираж 36000 экз. Бумага 84х108/а2 Печ. л. 2,875 (4,83).
Уч.-изд. л. 6,34. Изд. Кя 994. Заказ 358. Цена 19 коп.
Издательство «Высшая школа» Государственного комитета Совета’ Министров БССР по печати Минск, Кирова, 24.
Типография изд-ва «Звязда». Минск, Ленинский проспект, 79.
БЕСПЛАТНЫЕ УЧЕБНИКИ! ВРЕМЕН СССР
БОЛЬШАЯ БИБЛИОТЕКА НА САЙТЕ «СОВЕТСКОЕ ВРЕМЯ»
sovietime.ru
СКАЧАТЬ